Упругие волны в твердых телах. Применение для обработки сигналов - Дьелесан Э., Руайе Д.

Автор: Дьелесан Э. Руайе Д.

Теги: строение материи обработка сигналов радиоволны физика твердого тела радиосигналы

Год: 1982

Похожие

Акустические кристаллы

Электреты

Неразрушающий контроль. Справочник. Том 4. Акустическая тензометрия. Магнитопорошковый метод контроля. Капиллярный контроль

Схемотехника и применение мощных импульсных устройств

Текст

УПРУГИЕ
ВОЛНЫ
В ТВЕРДЫХ
ТЕЛАХ
ПРИМЕНЕНИЕ
ДЛЯ ОБРАБОТКИ
СИГНАЛОВ
Перевод с французского
под редакцией В. В. ЛЕМАНОВА
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1982
22.37
Д92
УДК 539 2
ONDES ELASTIQUES
DANS LES SOLIDES
APPLICATION
AU TRAITEMENT DU SIGNAL
Par
E. DIEULESAINT ET D. ROYER
Masson et Cle
1974
ДЬЕЛЕСАН Э., РУАЙЕ Д. Упругие волны в твердых телах. Применение
для обработки сигналов. Пер. с франц./Под ред. В. В. Леманова.— М.: Нау- !
ка. Главная редакция физико-математической литературы, 1982,-424 с.
Книга известных французских ученых Э. Дьелесана и Д. Руайе посвй- «
щена рассмотрению принципов и устройств акустической обработки инфор- I
мации. В ней излагаются основные вопросы физической акустики твердого '
тела и вопросы разнообразных технических применений, основанных на не-
пользовании объемных и поверхностных упругих волн в твердых телах.
Для научных работников, инженеров, студентов старших курсов и ас-
пирантов, интересующихся вопросами применения упругих волн в твердых !
телах для обработки радиосигналов, может быть полезна специалистам, ;
занимающимся фундаментальными исследованиями в области акустики
твердого тела.
Рис. 272, библ. 383 назв. j

1704030000 — 039
Д~053(02)-82 99-81
©Masson et Cle, 1974
©Издательство «Наука».
Главная редакция
физико-математической f
литературы. 11
Перевод на русский язык, 1982 ,'
ИГ ДАВЛЕНИЕ
. ’ж? редактора перевода.................... ........................
\ .'Предисловие к русскому изданию . . . . ..................
^А^едеийе............................................................
Глава 1. Общие сведения. Волны. Сигналы. Линейные системы
^.'^54.1. Общие свойства волн........................................
4?' 1.1.1. Плоская бегущая волна (14). 1.1.2. Отражение плоской бегущей
ЖЪ’а. войны (17). 1.1.3. Групповая скорость (24),
А 1.2. Распространение упругих волн..............................
2/'®» 4А1. Сплошная среда. Макроскопическое рассмотрение (27). 1.2.2. Це-
Ж И’;.', йочка атомов. Микроскопическое рассмотрение (29).
«'•'Зь'Д'А Сигналы. Линейные стационарные системы....................
ЭК'Лф Сигналы реальные и фиктивные. Дельта-функция Дирака (34).
ф 1-3.2. Спектр сигнала. Преобразование Фурье (36). 1.3.3. Частотный от-
клик линейной стационарной системы (44). 1.3.4. Импульсный отклик
Ж5..1 (45). 1.3.5. Отклик на сигнал произвольного вида (47). 1.3.6. Связь меж-
ДУ спектром сигнала и диаграммой направленности излучателя (48).
««Упражнения.........................................................
Жж,л;а в Д 2- Элементы кристаллографии
Определение кристаллического состояния...............................
tai 2-2. Кристаллическая структура...................................
’ 2.2.1. Периодичность кристаллической среды. Решетка. Ряды. Плоские
W-® • сетки. Ячейки (59). 2.2.2. Атомная структура. Базис (63),
£ ®‘2.3. Симметрия направлений кристаллов............................
waSf 2.3.1. Операции точечной симметрии. Определения (66). 2.3.2. Точечная
симметрия решеток (70). 2.3.3. Классы точечной симметрии кристал-
Ягщ лов (78).
1 Яе.*А Пространственная симметрия.................................
Й»И» 2.4.1. Винтовые оси (82). 2.4.2. Плоскость скользящего отражения (82).
ЖЙй-л 2.4.3. Пространственные группы (83).
ЖЖ2.5. Примеры кристаллических структур..............................
ЖДУ' 2.5.1. Плотнейшие упаковки (83). 2.5.2. Структура некоторых часто
ЧавМ,. - используемых веществ (84).
, JK?. йражнения....................... .............................
ЯВ^ава 3. Тензорное представление физических свойств кристаллов
ЖД1. Связь между внешним воздействием и реакцией кристалла
'1Ж3.2. Преобразование ортогональной системы координат ....
’АйИкД Определение тензоров..........................................
ЛЕЖА Ограничения, налагаемые симметрией кристаллов на число не-
Ш зависимых компонент тензоров......................................
3.4.1. Матрицы операций точечной симметрии кристаллов (99). 3.4.2.
Роль центра симметрии (100). 3.4.3. Сокращение числа независимых
компонент тензора диэлектрической проницаемости (101).
'^^Р.5. Собственные векторы и собственные значения тензора второго
ранга................................................................
Тензорное представление элементов поверхности j . . .
жнения.....................................................
13
13
26
33
103
107
108
ОГЛАВЛЕНИЕ
Глава 4. Статическая теория упругости ... .... 11®
§ 41. Деформации...................................................114
§ 42. Напряжения.....................<............................114'
4.2.1. Определение тензора напряжений (115). 4.2.2. Условия равнове- ’
сия (116). я
§ 4.3. Связь напряжений с деформациями. Модули упругости . . . 119
§ 4.4. Энергия упругой деформации. Соотношения Максвелла . . 121
§ 45. Ограничения, налагаемые на число независимых модулей уп-
ругости симметрией кристаллов................................124
4.5.1. Изотропное твердое тело (125). 4.5.2. Кристаллы (126). '
Упражнения....................................................... 133
Глава 5. Динамическая теория упругости.............................138
§ 5.1. Упругие волны в неограниченном кристалле....................142
5.1.1. Уравнение движения (142). 5.1.2. Общие свойства плоских упру-
гих волн (144). 5.1.3. Распространение вдоль направлений, связанных
с элементами симметрии (146). 5.1.4. Упругие волны в изотропной сре-
де (148). 5.1.5. Поток упругой энергии (150). 5.1.6. Характеристические
поверхности (156).
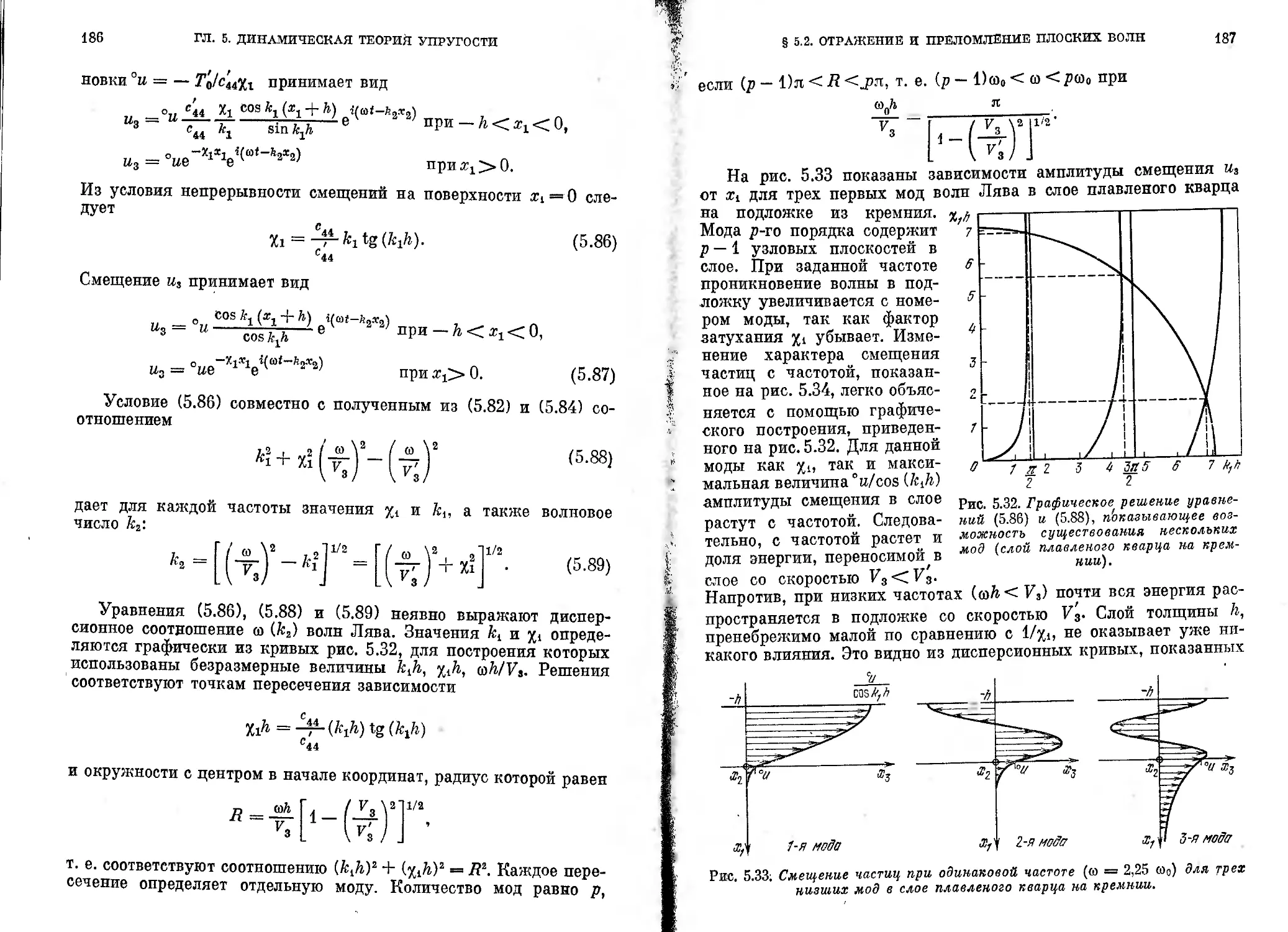
8 5.2. Отражение и преломление плоских упругих волн .... 175
5.2.1. Уравнение непрерывности (175). 5.2.2. Падение волны с попереч-
ной горизонтальной поляризацией (178). 5.2.3. Отражение на свобод-
ной поверхности (181). 5.2.4. Волны Лява (183). J
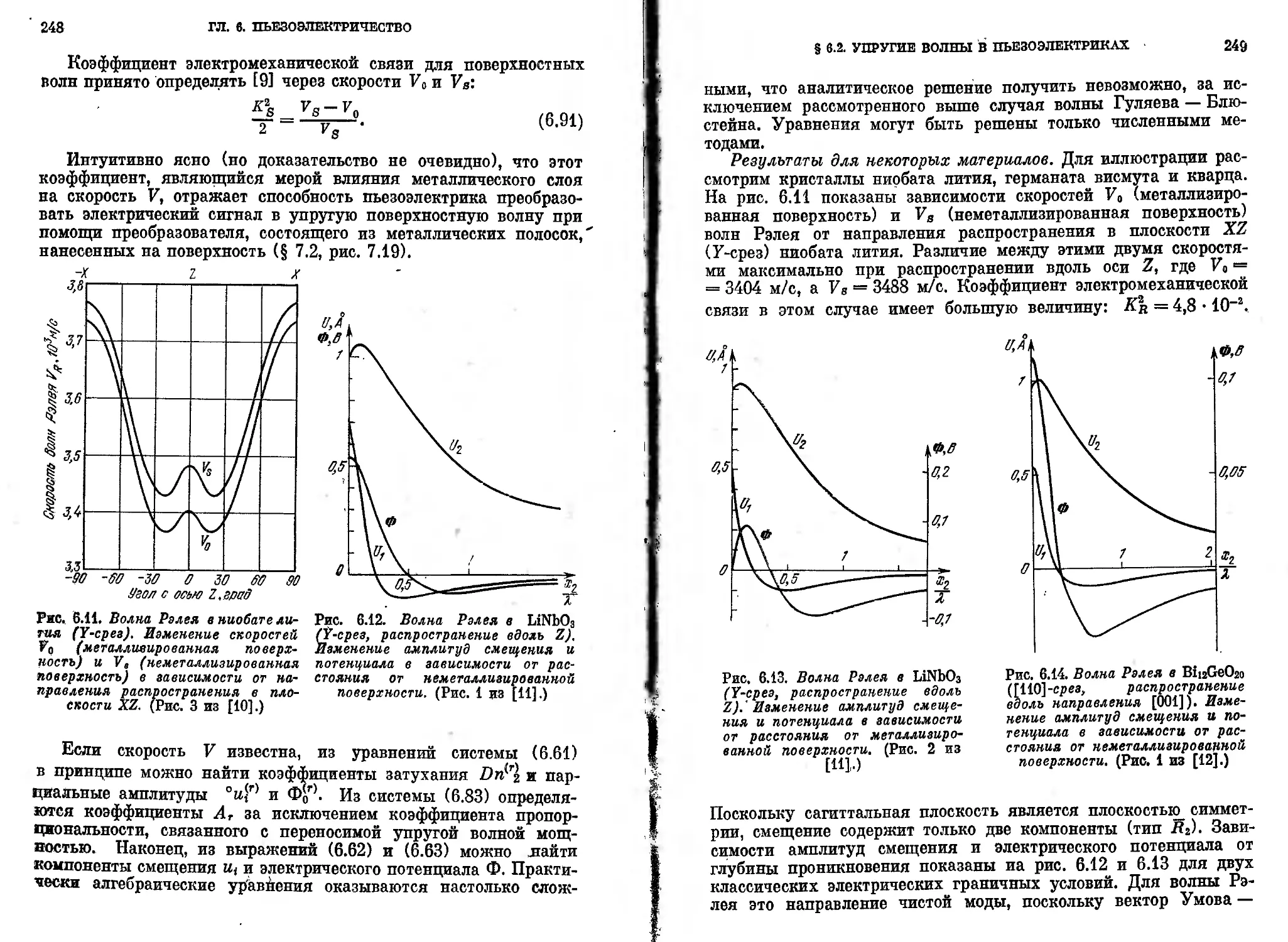
8 5.3. Поверхностные упругие волны. Волны Рэлея ... .189
5.3.1. Изотропная среда (191). 5.3.2. Анизотропная среда (196).
Упражнения.........................................................204
Глйва 6. Пьезоэлектричество.................. . .208
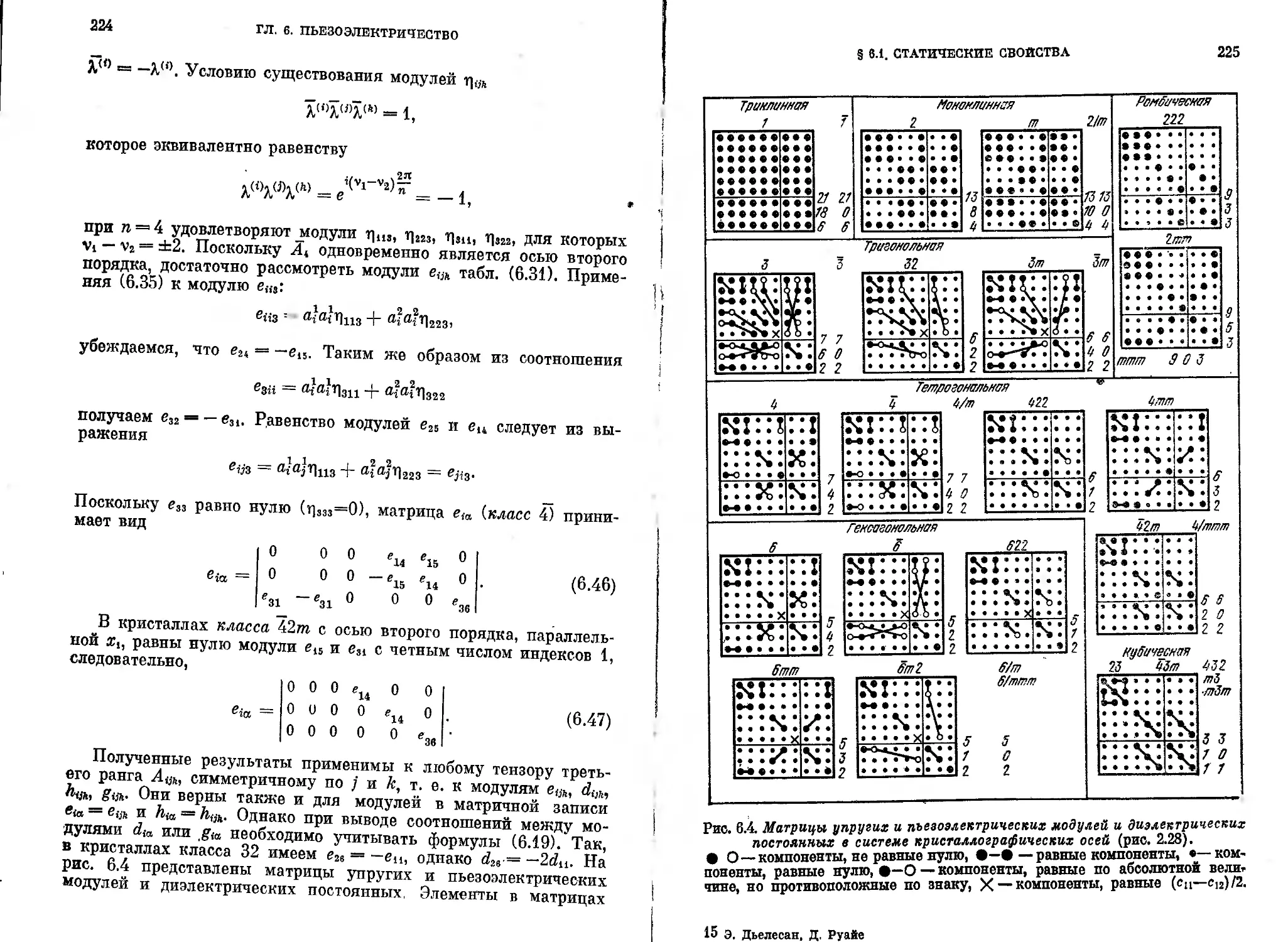
§ 6.1. Статические свойства.....................................208
6.1.1. Принципы симметрии Кюри. Применение к пьезоэлектричеству
(208). 6.1.2. Физический механизм. Одномерная Модель (210). 6.1.3. Тен-
зорные выражения пьезоэлектрического эффекта (214). 6.1.4. Ограниче-
ния, налагаемые симметрией кристаллов на число независимых пьезо-
электрических модулей (218), , i
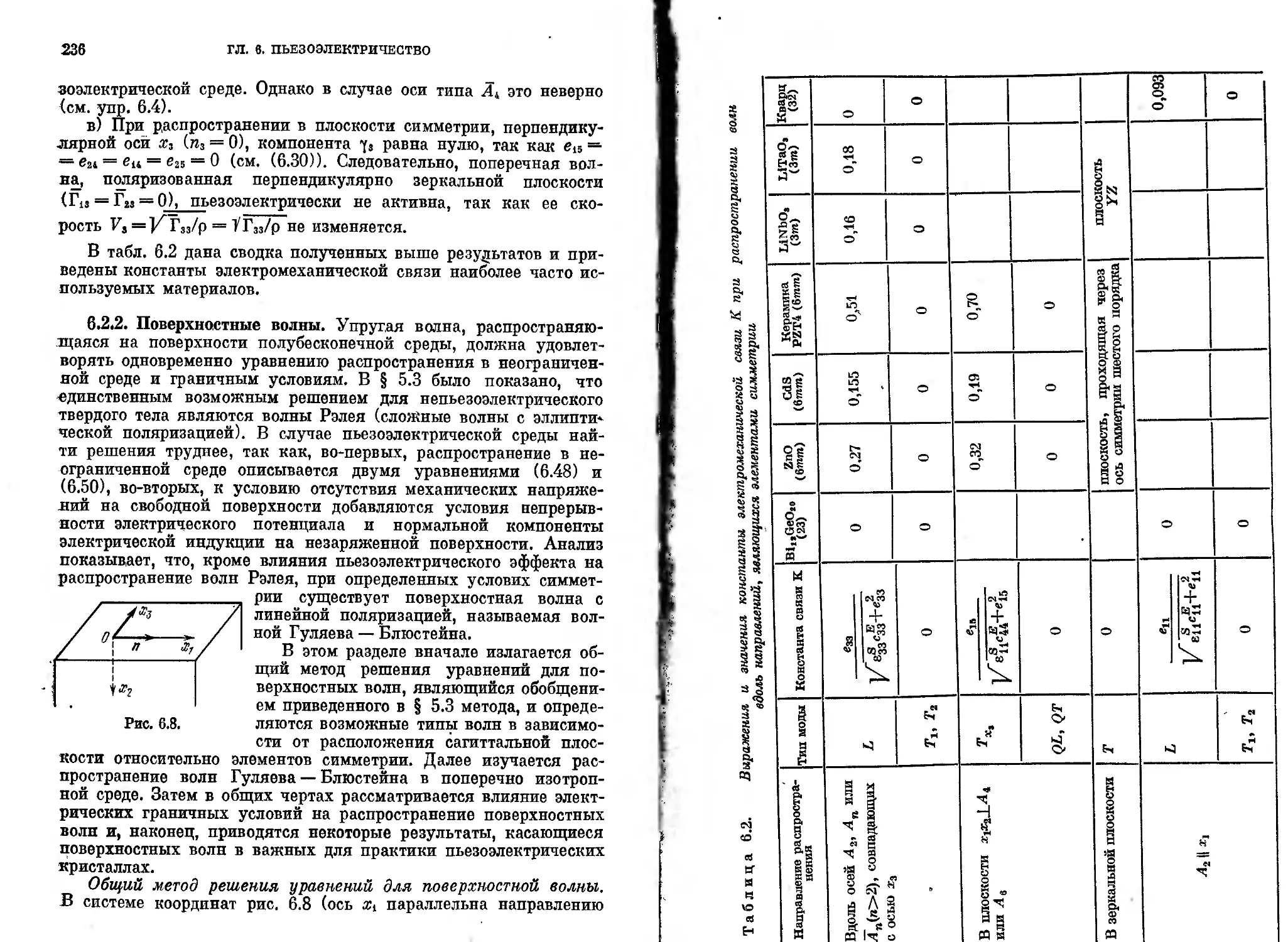
8 6.2? Упругие волны в пьезоэлектрических кристаллах .... 227
6.2.1. Неограниченная среда. Объемные волны (228). 6.2.2. Поверхност-
ные волны (236). .
Упражнения............... . . - 25^
Глава 7. Возбуждение и регистрация упругих волн ..... 255
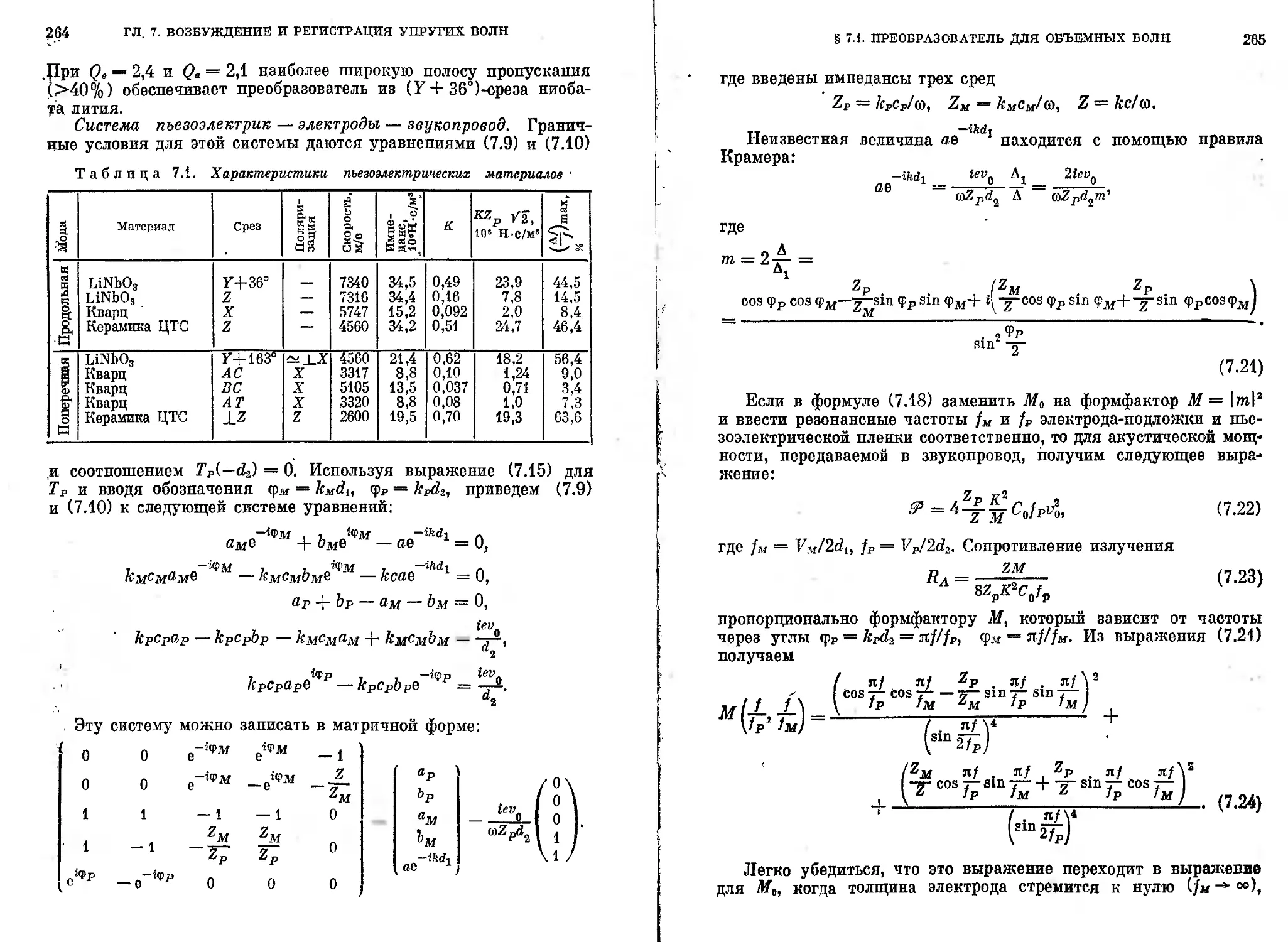
§ 7.1. Пьезоэлектрический преобразователь для объемных волн . . 255
7.1.1. Прямой расчет мощности упругих волн (256). 7.1.2. Эквивалент-
ная схема (272). 7.1.3. Коэффициент электромеханической связи (277).
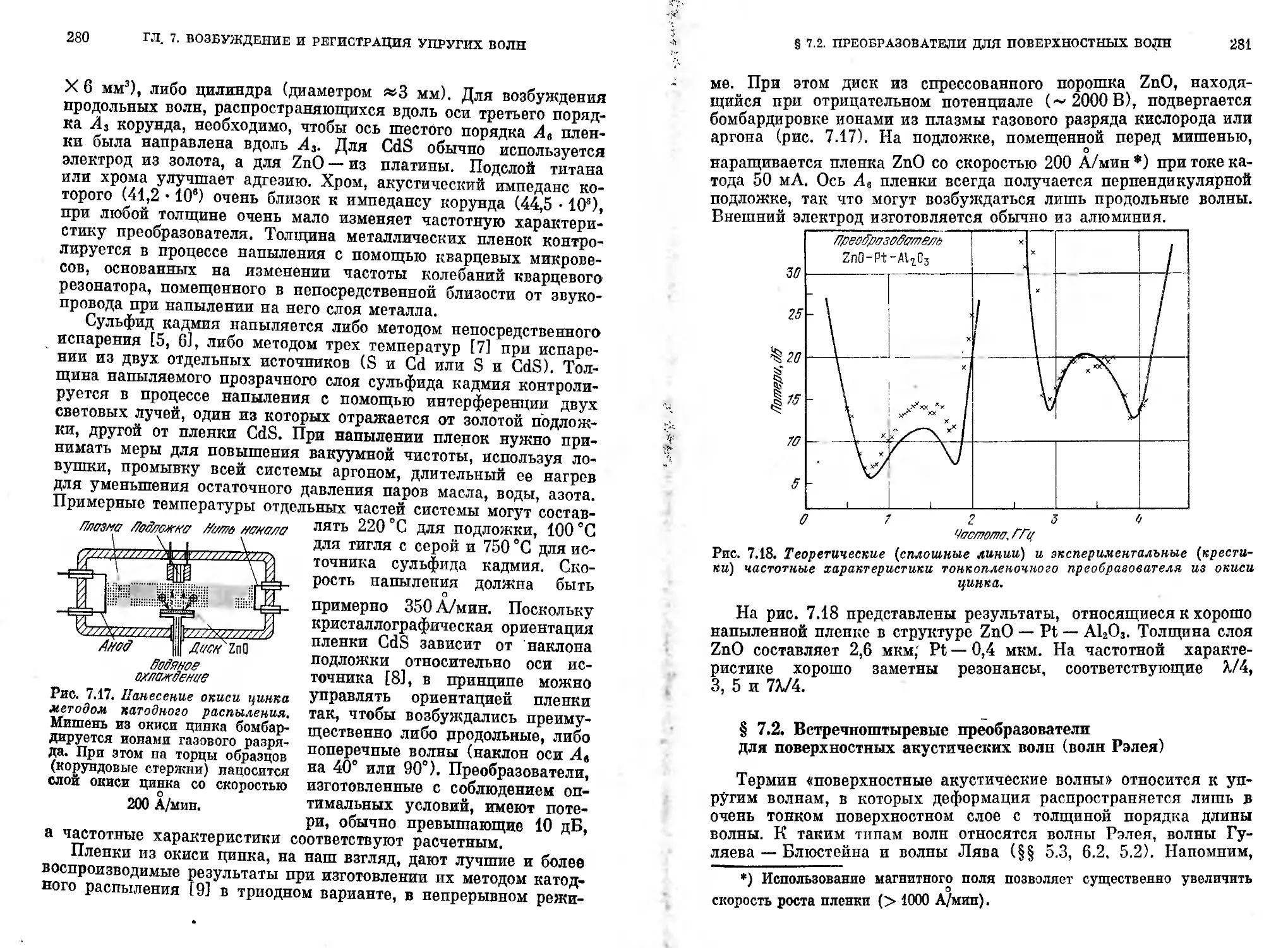
7.1.4. Вопросы технологии (279).
§ 7.2. Встречноштыревые преобразователи для поверхностных аку-
стических волн (воли Рэлея) .......................................281
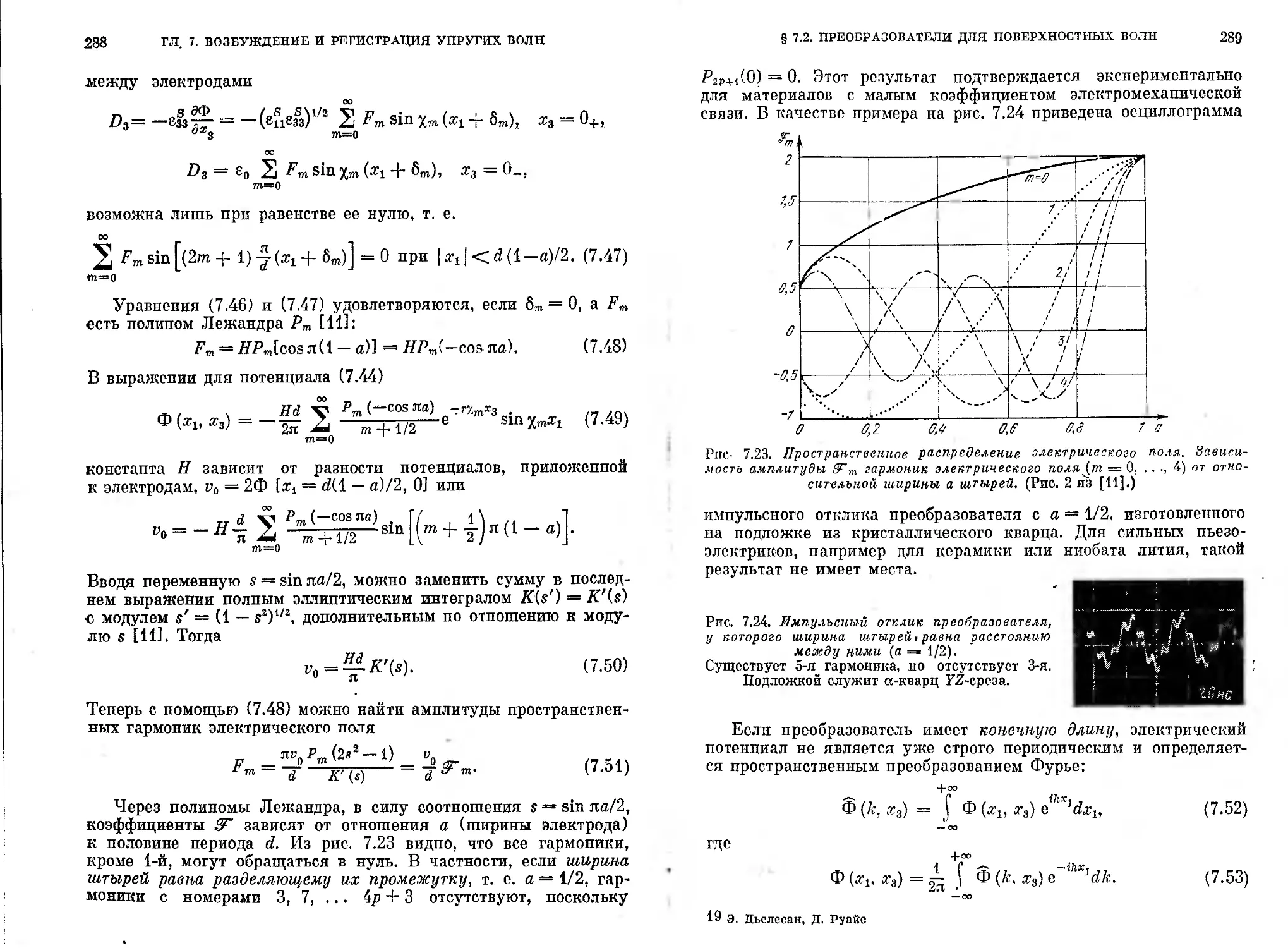
7.2.1. Принцип действия (282). 7.2.2. Распределение электрического по-
ля (286). 7.2.3. Возбуждение упругих волн (290). 7.2.4. Метод дискрет-
ных источников (298). 7.2.5. Электрическая эквивалентная схема (305).
7.2.6. Вопросы технологии (307).
Упражнения......................... .... . 30»
Г л а в а 8. Взаимодействие упругих волп со светом . 313
§ 8.Г. Основные виды дифракции света на звуке . . . . 314
8 8.2. Распространение света в кристаллах..........................315
8.2Л. Оптическая индикатриса (316). 8.2.2. Поверхность показателей
преломления (318).
§ 8.3. Фбтоупругий тензор.........................................319
8.3.1. Теория Поккельса (320). 8.3.2. Теория Нельсона и Лэкса (324).
8.3.3. Пьезоэлектрические кристаллы. Электрооптический эффект (326).
§ 8.4. Дифракция света на акустическом пучке......................327
8.4.1. Нормальное падение (328). 8.4.2. Брэгговская геометрия (332). _
§ 8.5. Взаимодействие света с поверхностными акустическими волнами 343
Упражнения................................................... » 346
ОГЛАВЛЕНИЕ
в а 9. Применение упругих волн для обработки сигналов .
Общая структура акустической линии.........................
9.1.1. Преобразование электрического сигнала в упругую волну (350).
9.1.2. Распространение упругих волн (351). 9.1.3. Взаимодействие упру-
гой волны с внешней волной (351). 9.1.4- Преобразование обработан-
ной волны в электрический сигнал (352). •
Задержка сигналов..........................................
9.2.1. Линия задержки на объемных волнах (353). 9.2.2. Линии задерж-
ки на волнах Рэлея (356). 9.2.3. Акустооптическая линия с регулиру-
емой задержкой (358).
9.3. Сжатие импульсов..........................................
9.3.1. Согласованный фильтр (360). 9.3.2. Сигналы с линейной модуля-
цией частоты (361). 9.3.3. Дисперсионные линии на объемных упругих
волнах (369). 9.3.4. Дисперсионные линии на волнах Лява (372). 9.3.5.
Согласованные фильтры па волнах Рэлея (373). 9.3.6. Акустооптическис
согласованные фильтры (385).
Полосовые фильтры..........................................
Память . ...............................................
на решетке поверхностных волн . ... .
для спектрального анализа (для преобразования
ОТ РЕДАКТОРА ПЕРЕВОДА
Вниманию советского читателя предлагается перевод книги
«Упругие волны в твердых телах. Применение для обработки
сигналов», которую написали известные французские специали-
сты в области акустики твердого тела Э. Дьелесан и Д. Руайе.
Акустика твердого тела, как хорошо известно, представляет
собой один из бурно развивающихся в последние годы разделов
физики твердого тела. Значительный вклад в развитие этой об-
ласти исследований внесли советские ученые. Еще в 30-е годы
появились теоретические работы А. И. Ахиезера [1] и Л. Д. Лан-
дау и Ю. Б. Румера [2], в которых рассматривались механизмы
решеточного затухания высокочастотных акустических волн в
кристаллах. (Интересно отметить, что лишь четверть века спустя
эти механизмы затухания были подтверждены экспериментально
и послужили основой для многих последующих эксперименталь-
ных и теоретических исследований.) В работах К. С. Александ-
рова [3] и Ф. И. Федорова [4] были рассмотрены основные осо-
бенности распространения акустических волн в анизотропных
средах. Для развития экспериментальных методов акустики твер-
дого тела определяющими явились работы С. Я. Соколова [51 и
К. Н. Баранского [61, которым впервые удалось возбудить и ис-
следовать в кристаллах распространение акустических волн с ча-
стотами около 10е Гц. В современной акустике твердого тела
хорошо освоены, частоты до 10*° Гц и имеются отдельные работы,
в которых изучается возбуждение и распространение в кристал-
лах акустических волн с частотами около 10“ Гц.
Использование высокочастотныхг акустических волн позволяет
экспериментально исследовать многие фундаментальные явления
и процессы в физике твердого тела, которые протекают с уча-
стием акустических фононов [7]. Акустооптическое взаимодей-
ствие [8—10], взаимодействие со свободными носителями в полу-
проводниках [11, 12], с электронами проводимости в металлах
[13], акустический парамагнитный резонанс [14, 15], взаимодей-
ствия с мягкой модой при фазовых переходах [16] и со спино-
выми волнами в-магнитных кристаллах [17], нелинейные эффек-
ты при распространении акустических волн [18] — вот краткий
ОТ РЕДАКТОРА ПЕРЕВОДА
Л
\ Перечень тех вопросов, которые изучаются в современной аку-
Ж-'стике твердого тела. Мцргие из перечисленных вопросов уже на-
ж&тли свое отражение в монографиях [19—211.
ОДнако интерес к этой области физики связан не только с
К^фундамвитальными исследованиями, но и с большими возмож-
|Овостями технических применений. Использование акустических
роли в кристаллах позволяет создавать линии задержки и фильт-
I *ры [22], устройства управления лазерным излучением [23, 24],
* < акустооптические устройства обработки сигналов [25] и т. д.
’ возможности технических применений акустических методов зна-
чительно расширились, когда наряду с объемными стали исполь-
И^яоваться поверхностные акустические волны [26]. Ряд выгодных
^бобенностей, связанных с возбуждением и распространением этих
н в кристаллах, дает возможность создавать на их основе
ичные высокоэффективные устройства обработки сигналов
27, 281, включая и акустооптические (291.
?•. Авторы книги «Упругие волны в твердых телах. Применение
лдля обработки сигналов» не ставят перед собой цель рассмотреть
цсе направления акустики твердого тела, как это сделано, напри-
1 Step, в монографии [201. Основная задача книги — рассмотрение
лишь тех аспектов физической акустики, которые являются су-
; ществепными для технических приложений. Книга включает в
х-себя изложение общих вопросов распространения волн и теории
сигналов, описание физических свойств кристаллов с помощью
/тензоров, рассмотрение особенностей распространения акустиче-
ских волн в кристаллах. Многие из этих общих вопросов подроб-
но изложены сейчас в, ряде учебников и монографий, однако
Сиключение их в данную книгу оправдано стремлением авторов по
«возможности облегчить читателю знакомство с акустикой твердо-
л^о тела и с ее техническими приложениями, которым посвящена
//Заключительная часть книги. В ней рассматриваются линии за-
‘\;(И&ржки на объемных и поверхностных акустических волнах,
^согласованные фильтры, устройства свертки сигналов, дефлекто-
’.. ры и модуляторы лазерного излучения.
/ К сожалению, авторы исключили из рассмотрения устройства
поверхностных акустических волнах, в которых используется
£i" Цкустоэлектропное взаимодействие со свободными носителями в
«.^полупроводниках. В книге рассматривается только особый случай
&$йкустоэлектронного взаимодействия, а именно взаимодействие
^Поверхностной акустической волны в пьезоэлектрике со вторич-
ii.’tatTMrr электронами, созданными над его поверхностью. (Следует
метить, что начало этому направлению исследований было
ложено работами С. Я. Соколова [30].) Хотя такое взаимодей-
ие и является очень перспективным для технического исполь-
вания, как это показали последующие работы [31, 32], выпол-
ённые в нашей стране, тем не менее значительный интерес
8\ ОТ РЕДАКТОРА ПЕРЕВОДА
представляют и устройства, основанные на взаимодействии по-
верхностных акустических волн со свободными носителями в по-
лупроводниках. Впервые эти вопросы были рассмотрены
Ю. В. Гуляевым и В. И. Пустовойтом f331 и в настоящее Ъремя
как в нашей (см., например, [341), так и в зарубежной литера-
туре опубликовано большое количество экспериментальных и
теоретических работ, посвященных исследованию акустоэлектрон-
ного взаимодействия для поверхностных акустических волн и
разработке технических устройств. Со многими из таких уст-
ройств читатель может ознакомиться по материалам переведен-
ного на русский язык тематического выпуска журнала [35]
с предисловием Ю. В. Гуляева, в котором дается краткий очерк
развития и анализ перспектив акустоэлектроники.
Для общего ознакомления с целым рядом вопросов теории
и техники ультразвука может оказаться полезным энциклопеди-
ческий справочник [361.
Оценивая книгу в целом, можно сказать, что авторам удалось
написать полезную монографию, в которой ясно и четко изложе-
ны основные вопросы акустики твердого тела, рассмотрены раз-
личные типы акустических волн в кристаллах и на основе конк-
ретных примеров показаны большие возможности практических
применений акустических методов. Книга, несомненно, будет
служить полезным пособием для студентов, аспирантов, научных
работников и инженеров, желающих ознакомиться с основами
акустики твердого тела и с ее техническими приложениями.
При переводе книги учтены некоторые дополнения и исправ-
ления авторов по сравнению с французским изданием. Несколько
расширена также библиография общего характера, главным об-
разом, за счет работ советских авторов.
Перевод книги выполнили: А. М. Дьяконов (гл. 1, 7, 8),
Е. В. Парная (предисловие, гл. 2—4), Д. Чиплис (гл. 5, 6, 9).
В. В. Леманов
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Эта книга была написана в 1973 году, а издана на француз-
м языке в 1974 году. И хотя с тех пор исследования в области
[Ики упругих волн и их применений получили дальнейшее
житие, фундаментальные. сведения, содержащиеся в книге, со-
и свою силу и в 1980 году. В связи с этим при подготовке
Некого издания мы не внесли особо существенных изменений,
отдельных местах добавлены необходимые замечания, а в две
едние главы включены сведения, отражающие совремепное
^стояние вопроса.
Так, например, к главе 7 (Возбуждение и регистрация упру-
йфолн) добавлен раздел о полосе пропускания преобразовате-
I на объемных волнах. Добавлены также одна фраза и две
, касающиеся интересной возможности управления ско-
ю роста пленки из окиси цинка с помощью магнитного поля.
В главе 8 (Взаимодействие упругих волн со светом) введен
Явочный раздел 8.3.2, где излагается теория Нельсона и Лэк-
i учитывающая роль локального вращения оптической инди-
рисы при распространении поперечных волн. Изложение воп-
о взаимодействии света с поверхностными упругими волнами
Иолько расширено и дополнено двумя новыми рисунками.
Некоторые новые технические достижения, расширяющие об-
сть применения упругих волн в электронике, отражены в до-
клениях, сделанных к главе 9 (Применение упругих волн для
1работки сигналов). Сюда относятся: применение отражателей
рхностных волн для фильтров на стоячих волнах, использо-
*"е полупроводников для реализации устройств памяти и
тки, осуществление устройств сжатия луча или многоканаль-
| фильтров с помощью решетчатых ответвителей, соединение
^версионных линий для выполнения преобразования Фурье и
10
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
для спектрального анализа сигналов. К этой главе добавлено пять
новых рисунков и два упражнения.
Мы надеемся, что редактор русского перевода, профессор
В. В. Леманов из института им. Иоффе в Ленинграде, сможет
внести необходимые дополнения, отражающие последние дости-
жения советских исследователей. Заранее выражаем ему свою
признательность и приносим также нашу благодарность всем
сотрудникам, принимавшим участие в переводе, а также работ-
никам издательства «Наука».
Любые критические замечания и предложения советских чи-
тателей будут встречены нами с вниманием и благодарностью.
Париж, 1.12.1980 Э Дъелесан, Д. Руайе
ВВЕДЕНИЕ
Настоящая книга рассчитана на студентов, владеющих основа-
^».^-ми физики, инженеров и преподавателей, интересующихся дости-
ЗяЖЙкениями современной техники. Несколько предварительных за-
>мечаний о структуре этой книги.
: Для изучения процессов распространения упругих волн в ани-
зотропных твердых телах требуется знание симметрии кристал-
j лов и свойств тензоров, посредством которых выражается реак-
I >Ция кристаллов на внешние воздействия; кроме того, при описании
; /устройств, применяемых для обработки сигналов, часто исполь-
; зуется преобразование Фурье. Обмен мнениями со студентами и
L инженерами, имеющими различную подготовку, показал, что было
, бы полезно напомнить читателям этот материал. Такими сообра-
жениями объясняется содержание первых трех глав.
I Глава 4 содержит определение деформаций и напряжений,
! >асчет энергии' упругой деформации и перечисление компонент
; Тензоров модулей упругости в кристаллах. При первом чтении не
[следует углубляться в доказательства, относящиеся к упрощению
[' ’’ вида тензоров.
г ... Глава 5, в которой обсуждается распространение упругих
«Волн, является фундаментальной. Анализ бесконечных сред за-
канчивается рассмотрением поверхностей обратных скоростей для
,.^аких кристаллов, как кремний, рутил, корунд... Другие кристал-
ла» читатель сможет исследовать но аналогии с этими примерами.
"^Что касается сред конечных размеров, то здесь обсуждаются
^Вопросы распространения волн на поверхности твердого тела (вол-
Рэлея) и в элементарной слоистой среде, состоящей из тон-
'цого слоя на твердом полупространстве (волны Лява). В соответ-
?ствии с этим задача об отражении и преломлении упругих волн
решается только для простых случаев, встречающихся преимуще-
ственно при изучении упомянутых двух типов волн. Волноводы
>гы исключили из рассмотрения. По нашему мнению, сказанного
С первой главе вполне достаточно, чтобы читатель мог разобрать-
в уже не новых применениях волн, распространяющихся в
Бердых пластинах (волн Лэмба), которые кратко обсуждаются
t последней главе.
12
ВВЕДЕНИЕ
В пьезоэлектрических кристаллах характер распространения
волн изменяется, и при определенных условиях, накладываемых
симметрией, в них могут существовать особые поверхностные
волны (волны Гуляева — Блюстейна). Эти вопросы обсуждаются
в главе 6, после тензорного описания пьезоэлектрического эффек-
та; При чтении можно опустить ряд доказательств, в частности,
доказательства, касающиеся ограничений, накладываемых сим-
метрией кристаллов на пьезоэлектрические модули, однако важно
понимать результаты, обобщенные в таблицах.
Глава 7 посвящена методам генерации упругих волн. Рассмат-
риваются два основных типа пьезоэлектрических преобразовате-
лей: нагруженный резонатор для объемных волн и встречношты-
ревой преобразователь для поверхностных волн. Вывод уравне-
ния, описывающего работу второго преобразователя, довольно сло-
жен, и, несмотря на ряд упрощающих предположений, некоторые
вычисления оказываются длинными. Нетерпеливые читатели мо-
гут, поняв принцип генерации волн Рэлея, перейти прямо к ме-
тоду дискретных источников.
Как известно, упругие волны могут взаимодействовать со
светом. Это явление в связи с широким распространением лазе*-
ров используется не только для сканирования и модуляции све-
товых пучков, но и для изучения свойств самих упругих волн.
В главе 8 уточняются условия такого взаимодействия.
В последней главе рассматриваются применения упругих волн
для обработки сигналов: задержка и сжатие импульсов, фильтра-
ция и т. п. Диапазон используемых частот лежит в пределах от
нескольких мегагерц до нескольких гигагерц. Эта область физики
настолько быстро развивается, что мы поставили себе целью
изложить только принципиальные вопросы, а не описывать пос-
ледние достижения. По этой причине нами выбраны для иллюст-
рации текста фотографии линий, работающих на довольно низких
частотах, чтобы лучше были видны детали преобразователей.
Несмотря на то что описанные в книге применения упругих
войн относятся только к электронике, книга должна заинтересо-
вать и специалистов в других областях техники: в металлургии
(определение' дефектности образцов), в медицине (обнаружение
инородных тел или опухолей).
С большим сожалением мы оставили в стороне такие вопро-
сы, как взаимодействие упругих волн с электронами, однако
эффект усиления, обусловленный таким взаимодействием, к на-
стоящему времени не прошел еще стадию лабораторных иссле-
дований. Дополняют изложение упражнения с подробными реше-
ниями, предлагаемые в конце каждой главы.
Э. Дъелесан, Д. Руайе
ГЛАВА 1
ОБЩИЕ СВЕДЕНИЯ. ВОЛНЫ. СИГНАЛЫ.
ЛИНЕЙНЫЕ СИСТЕМЫ
Настоящая глава состоит из трех основных частей. В первой
содержатся сведения о характеристиках бегущих и стоячих плос-
ких волн, о волнах в волноводах, а также приводится определе-
ние групповой скорости волн.
Во второй части рассматривается распространение упругих
волн и приводятся уравнения распространения для сплошной
Среды (жидкость) и для среды дискретной (твердое тело с учетом
атомной структуры). Цель этой части — ознакомить читателя с
тем подходом, который принят в настоящей книге. Среда, в ко-
торой распространяются упругие волны, является твердой и чаще
всего анизотропной (кристалл), но она рассматривается как
СцЛошная среда без дисперсии, поскольку область изучаемых ча-
стот не превышает 10 ГГц и расположена далеко от предельной
частоты кристаллической решетки.
Третья часть посвящена спектрам сигналов и выяснению свя-
зи между частотными и импульсными характеристиками линей-
ной стационарной системы. Решение этих вопросов основывается
иа преобразовании Фурье, а их знание необходимо для понима-
ния гл. 9, в которой рассматриваются практические устройства.
Изложение свойств дельта-функции Дирака и преобразования
Фурье не является математически строгим. Углубление в теорию
распределений и изложение условий сходимости отвлекло бы чи-
тателя от основного содержания, т. е. от выяснения соотношения
между временным и спектральным подходами в анализе систем,
в то время как реальные физические сигналы удовлетворяют ус-
ловиям существования интегралов, с которыми мы будем иметь
дело.
§ 1.1. Общие свойства волн
Любое локальное нарушение равновесия среды, вообще гово-
ря, создает распространяющееся в ней возмущение, т. е. бегущую
Волну. Для описания волны вводятся следующие параметры: ско-
рость, частота и волновой вектор, причем их определения не за-
' 14
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
§ 1.1. ОБЩИЕ СВОЙСТВА ВОЛН
висят от природы возмущения. В случае ограниченной среды
бегущая волна отражается на границах. Таким образом возника-
ют либо стоячая волна, либо волна в волноводе. Уточним эти
понятия.
а)
S)
Рис. 1.1. Распространение возму-
щения.
Существовавшее в момент времени
to в точке с координатой ®о воз-
мущение и распространяется со
скоростью V и достигает в мо-
мент времени t точки с координа-
той х, причем х = ®о + V(t — to).
а) Момент времени to, б) мо-
мент времени t.
от величины t — x/V. так как
1.1.1. Плоская бегущая волна. Для наблюдения за распростра-
нением какого-либо возмущения необходимо в некоторой фикси-
рованной точке пространства реги-
стрировать изменения во времени
соответствующей характерной ве-
личины. Для наблюдателя, нахо-
дящегося в точке с координатой
я?0, эта величина в момент време-
ни t0 принимает значение и
(рис. 1.1). Допустим, что возмуще-
ние не изменяется в процессе
распространения, например не за-
тухает, а лишь перемещается с
постоянной скоростью, V, тогда
величина и имеет одинаковые зна-
чения в точках х в моменты вре-
мени t, удовлетворяющие соотно-
шению X = Хо + V(t — to), или
t — x/V — to — Xo/V.
Функция u(x, t), описывающая
данное явление, зависит лишь
она принимает одни и те же зна-
чения для любых х и tnpn постоянной величине t — x/V, т. е.
u(x,t) = F[t-^. (1.1)
Эта функция F(t — x/V) описывает волну, бегущую в положитель-
ном направлении оси х. Если же распространение происходит
в отрицательном направлении, то
и(т, t) = F^t + -у).
При одновременном распространении в одной среде волн, бе-
гущих в противоположных направлениях, получается результи-
рующее возмущение
и(х, 0 = +
. Среди всех возможных видов возмущений особенно большое
значение имеют синусоидальные колебания около некоторого
среднего положения, поскольку возмущения других видов можно
рассматривать как суперпозицию синусоидальных колебаний.
*» Рассмотрим акустическую волну, излучаемую плоской мемб-
фаной, совершающей синусоидальные колебания:
и = A cos cot.
«На расстоянии х от начала координат эта волна будет иметь- вид
£ и =Acosco(t —
где величина и обозначает смещение некоторой плоскости среды,
’«но она может также представлять изменение давления или плот-
| ности в некотором сечении, параллельном плоскости мембраны.
₽ Если через Т обозначить период колебаний, то f=i/T— ча-
Встота, которая следующим образом связана с круговой частотой:
I Ш = ^=2п/,
t и предыдущее уравнение можно записать в виде
и = A cos 2л (у - у-),
t где X = VT — длина волны, т. е. расстояние, на которое распрост-
раняется возмущение за один период. Поскольку через иромежу-
. ток времени Т состояние исследуемой системы повторяется, то
в каждый данный момент времени длине волны X соответствует
расстояние, разделяющее одинаковые состояния среды, например
два последовательных максимума величины и.
Выражение для волны удобно также записывать в виде
и = A cos (cot —= A cos (cot — кх),
где к = <в/Е = 2л/Х называется волновым числом. Величина кх
В каждый момент времени характеризует сдвиг фаз в точке х
относительно начала координат, в нашем случае это сдвиг фаз
между колебаниями в точке х среды и колебаниями мембраны.
Введем обобщенную фазу волны ср:
Ф = cot — кх.
Волновое число к связано с изменением фазы <р в зависимости
от расстояния х в данный момент времени как
*“-(&),• <‘-2)
а круговая частота со выражается через изменение фазы ф во вре-
мени в данной точке в виде
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Таким образом, существует определенное пространственно-вре-
менное соответствие:
Время Пространство
Период Т ] _ 2л Круговая частота соТ Длина волны 1 ) 2л Волновое число к %
Рис. 1.2. Плоская волна.
В произвольной точке Р, оп-
ределяемой вектором х = ОР,
колебание, создаваемое волной,
распространяющейся вдоль
единичного вектора п, имеет
вид н(х, t) = F(t — nx/P).
Скорость распространения возмущения V — а/к носит назва-
ние фазовой скорости. Это скорость, с которой должен переме-
щаться наблюдатель для того, чтобы в каждый мойент времени
видеть колебание в одной и той же фазе, т. е. ®(t — x/V) = const.
Волна при этом представляется неподвижной.
В предыдущем примере частицы, расположенные в плоскости,
параллельной плоскости мембраны, колеблются в фазе, и движе-
ние в каждой точке этой плоскости
волнового фронта определено, по-
скольку дано расстояние х от нача-
ла координат. Для описания коле-
бательного состояния в некоторой
точке Р, определенной вектором
х = ОР, соединяющим начало коор-
динат с этой точкой, нужно ввести
единичный вектор п, перпендику-
лярный к волновым
(рис. 1.2). Абсцисса х точки Р пред-
ставляет собой проекцию вектора
х на направление п, т. е.
х = пх.
Подставляя это выражение в (1.1),
получаем
(1.4)
(1.4) в прямоугольной системе коор-
Для записи выражения ____ _ ___________ __________
динат нужно ввести координаты точки (х3, х2, х3 — составляющие
вектора х) и направляющие косинусы (п„ п2, ге4 — составляющие
вектора п), тогда
и
В случае плоской синусоидальной волны имеем
--у) = A cos (at — kx),
где введен волновой вектор к = an/V = 2лп/% = кп.
*! § 1.1. ОБЩИЕ СВОЙСТВА ВОЛН 17
В: Очевидно, что если распространение волны сопровождается
Поглощением или усилением, ее амплитуда зависит от располо-
Bl ния точки наблюдения Р, т. о. от х, и тогда
В и — Л(х) cos (at — kx).
К Представление синусоидальных функций в комплексной форме. Наряду
В действительными числами, величины, встречающиеся в физике, часто
Выражаются комплексными числами. Использование комплексных чисел
представления синусоидальных величин основывается на том факте,
Ь- о все линейные соотношения с действительными коэффициентами между
индексными числами справедливы по отдельности для их действительных
Ь мнимых частей. Физические уравнения очень часто являются линейными
В'- действительными коэффициентами. Синусоидальную величину и =
A cos (cot + Ф) удобно представлять в комплексной форме
№ ие = Ле1(в<+®’, и = Re ие,
[уде символ Re ис обозначает действительную часть ис, что связано со сле-
r-дующими свойствами экспоненциальной функции.
I у Для суммы колебаний одной и той же частоты зависимость от времени
рможет быть выражена одним коэффициентом перед знаком суммы
L 2ие = еШ2Ле*Ф-
, Производная по времени сводится к умножению на г«:
I ч ,
1Г = i<SMc-
г Квадрат амплитуды колебания дается выражением
А2 = иеи*,
а*—комплексно сопряженная функция. Плоская синусоидальная
одна в комплексной форме выражается в виде
Цс = Ае«’<“‘-кх).
1.1.2. Отражение плоской бегущей врлны. Если среда распрост-
ранения не является безграничной и однородной и, в особенно-
сти, если свойства среды резко меняются на расстоянии порядка
длины волны, то волна может частично или полностью отражать-
ся. Отражение происходит и на границе между двумя средами
с различными свойствами. Граничные условия на поверхности
раздела зависят от природы волн и оказываются, вообще говоря,
более простыми, если возмущение не может распространяться в
одной из сред и величина, характеризующая колебание, равна
нулю по одну сторону границы и должна принимать нулевое
значейие на самой границе в силу условия непрерывности.
Нормальное падение. Стоячая волна. Если волна
uj(x, t)=Fi(t—y]
падает перпендикулярно поверхности раздела Двух сред, то в
2 Э. Дьелесан, Д. Руайе
' »; <ичтовыйпщи;(Г»4147р
18
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
противоположном
волна
направлении распространяется отраженная
uR{x, t)=FR[t +у).
Предположим, что на границе раздела (абсолютно отражаю-
щей) *) в любой момент времени амплитуда колебаний равна
нулю. Помещая начало оси абсцисс на поверхности раздела,
Рис. 1.3. Полное отражение бегу- Рис. 1.4. Стоячая волна.
щей волны. Полное отражение бегущей си-
Отраженное возмущение снимет- нусоидальной волны создает сис-
рично относительно начала коор- тему стоячих волн.
динат О, помещенного на отра-
женной стенке.
t -Т/8 t-T/h
получаем (при любом i1) u/0, i) + uB(0, t) = 0, или FB(t) = — F^t).
Отсюда следует, что отраженная волна
Ur = — Fi {t + -prj
в каждый момент времени симметрична падающей относительно
начала координат (рис. 1.3). В результате такого полного отра-
жения возникает волна
и = UI + Ur = Fl [t — -у) — Fi(t + -y-j-
В случае синусоидальных волн
и = A j^cosco —у) — cosffl^ -f- -y-^j =24 sin oi sin
♦) Конкретизировать природу волны или границы раздела нет необ-
ходимости при условии, что существует некоторая характерная величина,
которая на границе приобретает нулевое значение. Например, в случае уп-
ругой волны смещение частиц равно нулю на жестко закрепленной стенке,
а изменение давления равно нулю на свободной поверхности. Другие при-
меры. На конце разомкнутой линии сила тока равна нулю, а при коротком
замыкании нулю равна разность потенциалов. На идеально проводящей
стенке тангенциальная составляющая электрического поля электромагнит-
ной волны равна нулю. Неявно предполагается также, что рассматриваемая
величина сохраняет свое значение при отражении. Сложная задача отраже-
ния упругих волн на границе двух твердых тел рассматривается в § 5.2.
§ 1.1. ОБЩИЕ СВОЙСТВА ВОЛН 19
колебание является произведением двух функций, одна из кото-
рых зависит от времени, другая — от расстояния. Все признаки
распространяющихся волн исчезают, и формируется стоячая вол-
, на, характеризующаяся тем, что все точки среды колеблются
в фазе, но с разными амплитудами, как это показано на рис. 1.4,
где представлено несколько последовательных стадий колебания.
Точки, координаты которых соответствуют соотношению сож/Р =
•’ = —пл, п = 0, 1, 2, 3, ..., и в которых амплитуда колебаний всег-
да равна нулю, называются узлами. На половине расстояний
между узлами находятся пучности, в которых амплитуда макси-
мальна. Расстояние между двумя смежными узлами либо пучпо-
« стями равно половине длины волны.
Если отражение не является полным, то амплитуда отраженной волны
Ar оказывается меньше, чем амплитуда падающей волны Аг, поскольку
часть этой волны проходит в другую среду. Результирующая волна
и = Aj cos й [t — JL j — Ar cos й =
ir e (Л, _ Ля) cose(f+ Ля [cos® + -£-)]
; является суммой бегущей и стоячей волн:
| и = (Л; — Лл) cos й [i — -р-j + 2Лл sin at sin -у--
Принято определять коэффициент стоячей волны (КСВ) как отношение
максимальных и минимальных амплитуд колебания:
^1 “Ь Л я
г КСВ=^7=^7’ (1>5)
КСВ принимает бесконечное значение в случае чисто стоячих волн и равен
единице для бегущих волн. КСВ непосредственно связан с коэффициентом
отражения г = Лд/Л/:
ксв =
%
| Рассмотрим теперь волну, распространяющуюся между двумя
параллельными идеально отражающими плоскостями, располо-
Й. женными в точках х = 0 и х = —Д. Для того чтобы стоячая волна
Ц и 2А sin sin -у-
B имела нулевую амплитуду и на границе х = — Д, необходимо
к выполнение соотношения ®Д/Р = пл, п — целое, или соотношения
Существовать могут только такие стоячие волны, для которых
^Частота кратна отношению V/2L,. Несколько первых собственных
|2*
20
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
мод колебаний такого резонатора показаны на рис. 1.5. Четные
моды антисимметричны, а нечетные — симметричны относительно
плоскости, делящей резонатор пополам.
Косое падение. Волны в волноводе. Предположим теперь, что
волновой вектор падающей волны не перпендикулярен к плоско-
Рис. 1.5. Резонатор.
Низшие моды резонатора, образо-
ванного двумя полностью отражаю-
щими стенками.
Рис. 1.6. Отражение при косом
падении.
Волна перемещается в направ-
лении жа, благодаря последо-
вательным отражениям от
двух параллельных стенок.
сти раздела. В выбранной системе координат (рис. 1.6) падаю-
щая водна имеет вид
ut = A cos (соt — k2xt — k2x2).
Пусть k' — волновой вектор волны, полностью отраженной плос-
костью Xi = 0, тогда
Ur = — 4 COS (cot — k'jXx — k2x2).
Для того чтобы результирующее колебание
h + k* + k* \
и = 2А sin I cot--2 xt----------- 2 - х21 X
X sm I у— xt + 2 х21
обращалось в нуль во всех точках плоскости Xi = 0, необходимо
выполнение равенства к2 = к2, а из сохранения волнового числа
(к = к' = co/F) — ki = ± кг. К значению, не равному тождествен-
но нулю, приводит только решение кг = — кх, и, следовательно,
получим
и = 2А sin (<nt — к2х2) sin к^.
Волновые векторы падающей и отраженной волн оказываются
симметричными относительно отражающей поверхности.
§ 1.1. ОБЩИЕ СВОЙСТВА ВОЛН
21
Для того чтобы колебание и обращалось в нуль также и на
L второй границе (при xt “ —Lt), должно выполняться условие
= пЧГ' n = 1, 2, 3, ...
" Выражение
и = 2А sin (<of — к2х2) sin ~
соответствует волне, распространяющейся вдоль направления хг
в пространстве между стенками
УЗЛОВЫМИ ПЛОСКОСТЯМИ. ЭТО — Bi
отражающими стенками. Ее фа-
зовая скорость Vo = а/к2 боль-
ше фазовой скорости волны
в свободном пространстве, V =
= a/к. Действительно, из-за
косого распространения волн
скорость перемещения волно-
вых фронтов вдоль оси волно-
вода оказывается больше.
Каждому значению целого чис-
Xt = I) И Xi = — Lt, являющимися
>лна в волноводе, образованном
Рис. 1.7. Распространение волны в
волноводе.
Волна в волноводе имеет узлы на
стенках волновода, а также внут-
ри него, если номер моды п > 1.
Здесь п = 2 (1-я антисимметричная
мода).
разом связан с волновым векто-
ла п соответствует определен-
ная мода, причем п-я мода со-
держит п — 1 узловых плоско-
стей, расположенных на рав-
ных расстояниях и параллель-
ных друг другу (рис. 1.7).
Волновой вектор волны в
волноводе, к0 = Ь3, следующим с
ром волны в свободном пространстве:
kl = к2 - kl = к2 - ^2-
Наименьшее возможное значение к (kc = x/Lt) соответствует
максимальной длине волны = 2Д, называемой длиной волны
отсечки. В волноводе могут распространяться лишь волны с ча-
стотой, превышающей частоту отсечки fe = V/2Lt. Действительно,
для / <fe волновой вектор оказывается мнимой величиной, и
волна поглощается при входе в волновод.
Волновод является примером структуры с дисперсией, в кото-
рой скорость распространения волны зависит от ее частоты.
Дисперсия связана с геометрией волновода*). Частота оказыва-
♦) В тонких пластинках, однако, существует недисперсионная мода
упругих волн, так называемая мода нулевого порядка (раздел 9.3.3), кото-
рая не имеет аналогов для электромагнитных волн.
22
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
ется не пропорциональной волновому числу к0. Соотношение меж-
ду этими величинами, называемое дисперсионным соотно-
шением *),
(о -7Л = у[^+(^)2]1/2’ (1’6)
представлено на рис. 1.8 в приведенных координатах для несколь-
ких первых мод. Вблизи
Рис 1.8. Дисперсионные зависимости
для волновода.
При значении круговой частоты <й —
= Vk а приведенная фазовая скорость
VG/V 1-й моды равна наклону прямой,
соединяющей начало координат с изоб-
ражающей точкой на кривой, соответ-
ствующей данной моде.
частоты отсечки и кратных
ей частот волновод облада-
ет сильной дисперсией.
Если поместить две до-
полнительные отражающие
плоскости х2 = 0 И Х2 =
= —L2, то установившиеся
колебания можно рассмат-
ривать как результат нало-
жения падающей волны
Uj =24 sin (at — к2х2) X
• f ni"
X sin I I
и волны, отраженной от пло-
скости х2 = О,
uR = — 24 sin {at + к2х2) X
X sm j
Стоячая волна
/ п.п \
и = uj 4- uR = — 44 sin к2х2 sin I xt I cos at
должна иметь узел при х2 = —L2, для чего необходимо выполне-
ние соотношения
к2 — n2 = 1, 2, 3,.
Для такого колебания
(пл \ / пл \
sin I Xr I coscoi
*) Если в среде распространяется большое число волн с разными ско-
ростями и если при отражении от стенок происходит преобразование одной
волны в другую, то дисперсионное соотношение оказывается более слож-
ным. Это является общим случаем для упругих волн.
§ 1.1. ОБЩИЕ СВОЙСТВА ВОЛН
23
разрешенные частоты даются выражением = к2 = к* + к3 или
В рассматриваемом двумерном резонаторе могут существовать
лишь такие моды колебаний, частота которых является одной из
собственных частот, определяемых уравнением (1.7). Для пере-
хода к трехмерному случаю достаточно представить, что волна
может распространяться вдоль направления х3, перпендикуляр-
ного плоскости XiOxz. Эта волноводная мода с волновым вектором
к, выражается следующим образом:
= 44 sin sin cos — к3х3).
Если в точке ж3 = 0 закрыть волновод отражающей стенкой,
то интерференция между падающей волной ut и отраженной
волной
UR = — 44 sin sin ^2 j COS (®* +
приведет к образованию волны с определенной частотой:
(пл X / пл \
-£—Xij sin smk3x3cosat.
Резонатор в форме параллелепипеда с еще одной стенкой при
х3 = —Ls допускает лишь моды колебаний
_ . . / П,л \ / п л \ / п л \
и = 84 sm I-g—I sin I х31 sin I х3 I sin at
с частотами

Замечание. Следует подчеркнуть, что простые формулы
для волноводов и резонаторов получены в предположении отсут-
ствия трансформации волн при отражении. Эти формулы верны
для упругой волны в жидкости, заключенной между отражаю-
щими стенками, но, как следует из § 5.2, полученные выражения
не справедливы, вообще говоря, в случае распространения упру-
гих волн в твердом теле, поскольку при отражении от границы
волна преобразуется в этом случае в целый набор волн с раз-
личными поляризациями и скоростями. Однако имеется исклю-
чение, относящееся к случаю, когда волна создает смещение ча-
24
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
стиц среды, параллельное волновым фронтам и перпендикуляр-
ное волновому вектору. Формулы (1.6), (1.7) и зависимости на
рис. 1.8 применимы для этой волны, так как она не изменяется
при отражении. Мы еще встретимся с таким случаем в разделе
9.3.3 при рассмотрении поперечных волн в ленточных дисперси-
онных волноводах.
1.1.3. Групповая скорость. До сих пор мы рассматривали лишь
монохроматические волны, т. е. синусоидальные колебания, за-
данные на бесконечном временном интервале и имеющие по-
стоянные амплитуду и частоту. Взятые в таком чистом, идеаль-
ном виде, эти волны представляют мало интереса для практики.
В самом деле, наблюдатель, который следит за распространени-
ем монохроматической волны, получает не больше сведений от
этого процесса, чем от наблюдения за стабильным течением од-
нородного потока жидкости. Передача информации связана
с введением некоторой аномалии, некоторого изменения определен-
ных характеристических параметров. Поток жидкости может
нести сообщение либо когда по пему, например, плывет щепка,
либо если он становится менее или более полноводным. Точно так
же для передачи информации с помощью волны необходимо из-
менять хотя бы один из двух ее параметров: амплитуду или
фазу. Такая несущая информацию сложная волна не является
уже монохроматической, так как либо ее амплитуда, либо ча-
стота оказываются промодулированными передаваемым сигналом,
но ее можно представить в виде суммы бесконечного числа мо-
нохроматических волн с различными амплитудами и частотами
(группа волн или волновой пакет).
Выбирая в качестве переменной волновое число к, получаем
волновой пакет
и (я, t) = f А (к) е^-кх^к, (1.8)
где А (к) — спектральная плотность амплитуды волнового пакета.
В зависимости от того, обладает среда дисперсией или нет,
нужно различать два случая. Если в среде отсутствует диспер-
сия, т. е. скорость распространения волнового пакета V не зави-
сит от частоты, то на расстоянии хл каждая из составляющих
пакета запаздывает на одну и ту же величину ta = xJV. Через
промежуток времени в точке на расстоянии хл появляется весь
волновой пакет без изменений. В среде без дисперсии волна
сложной формы распространяется без искажения. Это свойство
можно выразить по-разному:
— скорость распространения волнового пакета не зависит от
частоты;
§ 1.1. ОБЩИЕ СВОЙСТВА ВОЛН
25
— набег фаз при прохождении расстояния ха, Ф = —соЖо/И,
пропорционален частоте;
— время запаздывания волнового пакета, определяемое как
= —йФ/й(в = ж0/У, не зависит от частоты.
Рассмотрим теперь распространение группы волн в среде,
обладающей дисперсией. Обычно частота /0 несущей волны ве-
лика по сравнению с частотой модулирующего сигнала, а спект-
ральная плотность амплитуды волнового пакета А(к) имеет су-
щественную величину лишь в малой области около значения
ка = й(,/У((в0). В этих условиях можно ограничиться 1-м поряд-
ком разложения дисперсионного соотношения вблизи к0:
а(к)^<а(к0) + ^^к~к0).
Величина =
ражения (1.8) следует
имеет размерность скорости. Тогда
из вы-
и (х, t) = feov*.'lf J А (к)
что можно записать в виде
и(Ж,#)-еЧ>(ж-7г0» (1-9)
положив и(х, 0) = F{x) и £20 = co(fco) — Под-
выражение (1.9) показывает, что за время t группа волн
смещается на расстояние х = Vgt. Таким образом, в среде, обла-
дающей дисперсией, волновой пакет с центральным значением
волнового числа ка распространяется со скоростью
ММ.’
называемой групповой скоростью.
В случае, когда среда обладает дисперсией, волновой пакет
искажается по мере распространения. Этот результат не следует
непосредственно из полученных выше формул, так как при их
выводе мы ограничились лишь первым порядком в разложении
дисперсионного соотношения. Искажения могут быть связаны,
например, с тем, что высокочастотные составляющие, формирую-
щие фронт сигнала, будут распространяться медленнее низкоча-
стотных составляющих, относящихся к слабоизменяющейся части
сигнала (вершине импульса, например). В таком случае вершина
импульса как бы перегоняет фронт сигнала. Максимум такой
группы волн находится в некоторый момент времени t в точке
с координатой х, характерной тем, что здесь, интерферируя,
26
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
складываются волны наибольшей амплитуды. Для такого сложе-
ния необходимо, чтобы составляющие с волновыми числами вбли-
зи к0 оказались в фазе, т. е. при к — ка
или
<р(7с) = (otklt— кх — const,
Как видно, и этот метод, называемый методом стационарной
фазы, снова показывает, что волновой пакет перемещается с груп-
повой скоростью, определяемой формулой (1.10). В отсутствие
затухания эта скорость представ-
ляет собой и скорость переноса
энергии волнового пакета.
В качестве примера обратимся
снова к волноводу, рассмотренно-
му в разделе 1.1.2. С помощью
соотношения (1.6) получим зна-
чение групповой скорости волн
в волноводе
Рис. 1.9. В волноводе фазовая
скорость Vo больше, а групповая
скорость Ve меньше скорости V
распространения волны в свобод-
ном пространстве.
Так как фазовая скорость
V “ v (ъ* _ц n2"2 Y/2
то произведение
VgVo = Р,
т. е. постоянно и равно квадрату скорости распространения вол-
ны в свободном пространстве. Зависимости Ve и Vo от частоты
представлены на рис. 1.9.
§ 1.2. Распространение упругих волн
Предыдущее рассмотрение имело общий характер, независимо
от природы волн и механизма их распространения. Упругие вол-
ны неразрывно связаны с материальной средой, они обусловлены
смещениями частиц вещества и могут существовать лишь в га-
зообразных, жидких или твердых средах в отличие от электро-
магнитных волн, которые могут распространяться и в вакууме.
Распространение упругих волн подчиняется законам механики
Ньютона. Рассмотрим сначала на основе этих законов жидкость,
частицы в которой можно считать свободными, а затем — твердое
§ 1.2. РАСПРОСТРАНЕНИЕ УПРУГИХ ВОЛН
27
тело, атомы которого связаны. Первый случай исследуется в мак-
роскопическом масштабе, второй — в микроскопическом (атом-
ном).
Колеблющаяся
~~ мембрана
! кх^и) h
° Iх 1 \в м\м‘
(бХ +6u)
и*би\
1.2.1. Сплошная среда. Макроскопическое рассмотрение. Рас-
смотрим снова случай плоской волны, которая возбуждается в
жидкости (воздухе) с помощью плоской колеблющейся мембраны.
Когда мембрана покоится, давление, оказываемое на жидкость,
однородно и равно р0. Смещаясь, например, в сторону положи-
тельных ж, мембрана сжимает прилегающий к ней слой жидко-
сти ОА (рис. 1.10). Это по-
ложение неустойчиво, так
как жидкость расширяет-
ся, сжимая в свою очередь
соседний слой АВ. Так и
происходит постепенное
распространение волны,
причем сжатия сменяются
разрежениями, а давление
оказывается зависящим от
координаты х и от време-
ни. Силы, действующие на
некоторый слой MN, огра-
ниченный координатами х
и x + dx, не уравновешиваются, благодаря чему этот слой сдви-
гается и принимает новое положение M'N’.
Пусть и(ж, t) — смещение в некоторый момент времени t пло-
скости М, соответствующей координате х, тогда смещение пло-
скости N будет u + du, где du= (du/dx)dx. Если s —площадь
рассматриваемого сечения, то сила, действующая на жидкость,
расположенную слева от фронта волны, проходящей через М',
равна
х х<-и х*ищ/х+би X
х+бх
Рис. 1.10. Колебания мембраны в жидко-
сти создают продольную волну, которая,
распространяясь, вызывает последователь-
ные сжатия и разрежения слоев ОА,
АВ, ..., MN жидкости.
FM> =sp(x + и, t),
а сила, действующая на жидкость справа от N' равна
Fn, = —sp (x + u + dx + du,t) = — (ж+ и, t) + %£(dx + du)j.
Результирующая сил давления, действующая на слой жидкости
M'N',
dF = FM' + FNl -s^-{dx+du)=-s^-(l + ^dx,
связывает ускорение 7 = 52n/5i2 с массой dm = p^sdx слоя MN
(р0 — плотность жидкости в состоянии покоя, т. е. при давлении
28
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
р0). Используя основное уравнение динамики dF = ^dm, получаем
д2и , др [. . ди \ ,
или
д2И _ _ _1_ д(Др)
at2 р0 дх \ ' дх /
(1.11)
где давление на слой M'N' представлено в виде р(х + и, t) = р0 +
+ 'Ар.
Отклонение давления Др от его значения в состоянии покоя
р0 связано с изменением объема Др слоя MN через коэффициент
сжимаемости %:
Этот всегда положительный коэффициент полностью характери-
зует упругие свойства невязкой жидкости. Рассматриваемый
объем изменяется от значения dv0 = sdx при давлении р0 (поло-
жение MN) до значения dv = s(l + du/dx)dx при давлении р0 +
+ Др (положение M'N'). Относительное изменение объема
At> _ dv — dv0 _ ди
v — dv0 ~ дх
Подставляя изменение давления Др —^--^-в получаем
д2и_______1 д2и / . . ди \
dt2 “ Р0Х дх2 \ + 9х)’
(1.12)
Соотношение между изменением давления и относительным
изменением объема является линейным только при выполнении
неравенства
При выполнении этого неравенства, подставляя в уравнение
(1.12) выражение 1/(рож) = V2, получим волновое уравнение для
непрерывной (сплошной) среды
= (1.13)
dt2 дх2
Аналогичному дифференциальному уравнению удовлетворяют
избыточное давление и плотность. Уравнение (1.13) в частных
производных описывает изменение во времени и пространстве
смещения частиц в жидкости. Оно получается в результате рас-
смотрения последовательного воздействия некоторого слоя жидко-
§ 1.2. РАСПРОСТРАНЕНИЕ УПРУГИХ ВОЛН
29
сти на соседние слои. Любые функции и(х, t) вида
u(x,t)=p(t±-^
удовлетворяют уравнению (1.13). Таким образом, возмущение
распространяется со скоростью V.
Волновое уравнение (1.13) имеет весьма общий характер и
применимо к возмущениям разной природы (механической, элект-
рической).
Замечания.
1. Поляризация. В простом примере с жидкостью колебание
и частиц перпендикулярно к волновым плоскостям (фронтам),
т. е. параллельно волновому вектору. В таких случаях говорят о
продольной поляризации волны. В твердом теле колебания частиц
могут быть перпендикулярны волновому вектору, и волна будет
иметь в этом случае поперечную поляризацию (гл. 5). Для этого
необходимо, чтобы среда допускала распространение сдвиговых
колебаний. В жидкостях, не обладающих вязкостью, могут рас-
пространяться лишь продольные волны.
2. Частотный предел. Существует ли частотный предел для
волн, которые могут распространяться в газе, где молекулы нахо-
дятся в постоянном движении? Колебания мембраны создают
последовательность максимумов и минимумов давления (или плот-
ности). Волна может распространяться лишь в том случае, когда
расстояние между последовательными максимумом и минимумом
велико по сравнению с длиной свободного пробега частиц lm
(среднее расстояние, которое проходит частица между двумя
столкновениями). В противном случае молекулы за один пробег
заполняют область с пониженной плотностью, и связанное с вол-
ной возмущение рассасывается. Указанное условие требует, что-
бы длина волны превышала длину свободного пробега молекул
А » Zm, т. е. / < F/Zm.
Численные оценки. Для кислорода, например, V = 315 м/с при
О °C, lm = 4,9 см при 10-3 мм рт. ст., отсюда предельная частота
составляет 6400 Гц.
1.2.2. Цепочка атомов. Микроскопическое рассмотрение. В твер-
дом теле равновесные положения атомов фиксированы. Для очень
малых длин волн, когда длина волны оказывается сравнимой с
межатомным расстоянием, среду уже нельзя рассматривать как
непрерывную, и это накладывает предел на частоту упругих волн.
В настоящем разделе мы установим этот предел для случая твер-
дого тела, состоящего из атомов одного сорта. Атомы расположе-
ны в узлах правильной трехмерной решетки (раздел 2.2.1), т. е.
в точках пересечения трех семейств параллельных прямых, каж-
30
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Рис. 1.11. Кристаллическая решет-
ка, деформированная при про-
хождении плоской продольной
волны, распространяющейся вдоль
рядов атомов в направлении век-
тора а.
Достаточно рассматривать сме-
шение атомов одной цепочки.
дое из которых параллельно одному из трех главных взаимно
перпендикулярных направлений векторов а, Ь, с (рис. 1.11). Уп-
ругая плоская продольная волна, распространяющаяся вдоль од-
ного из этих направлений (например, вдоль а), заставляет одно-
временно колебаться все ато-
мы, расположенные в пло-
скостях, перпендикулярных
волновому вектору. Посколь-
ку' все ряды атомов, парал-
лельные вектору а, колеблют-
ся одинаково, достаточно
рассмотреть лишь одну це-
почку одинаковых и равноот-
стоящих атомов (рис. 1.12).
Если в такой цепочке
один из атомов смещается,
то, благодаря существующим
силам связи, приходят в
движение и два ближайших
соседних атома и т. д. Це-
почка деформируется по ме-
ре того, как по ней распространяется возмущение. Будем счи-
тать, что взаимодействие ограничивается лишь ближайшими
соседями и деформации достаточно малы, так что возвра-
щающие силы Ft и F2, действующие на каждый атом, ока-
зываются пропорциональными
изменению расстояний между
рассматриваемым атомом и его
ближайшими соседями относи-
тельно равновесного значе-
ния а.
Обозначая через ип смеще-
ние атома п с координатой хп
в состоянии равновесия, мож-
но следующим образом выра-
зить силы, действующие на
и-ю частицу со стороны ато-
мов с номерами п — 1 и п+ 1:
F, = KCun-t - ип),
F2 = £(un+1 — un).
Рис. 1.12. Распространение про-
дольного возмущения в цепочке
• атомов.
Пружинки изображают силы свя-
зи между атомами, а —межатом-
ное расстояние.
Уравнение движения для частицы с номером п и массой М имеет
ВИД
д2и
M-^ = K(un+l + un-l-2un). (1.14)
§ 1.2. РАСПРОСТРАНЕНИЕ УПРУГИХ ВОЛН
31
Пусть одна из частиц, расположенная в начале координат,
совершает синусоидальные колебания
щ = Ле’”'.
В непрерывном режиме и в отсутствие затухания колебания каж-
дого атома будут идентичны колебаниям исходного атома (с точ-
ностью до разности фаз)
un=4e^+®4
Подставляя в уравнение (1.14) ип и аналогичные выражения для
un_i и и„+1, получаем
(—Ма>2 + 2К) Хе(“<+Фп) = Я4е’’и< (™n+1 + е'®”-1),
или
-Мю2 + 2К = К [е*(Фп+1-Фп) + . (1.15)
Для того чтобы правая часть этого уравнения была бы действи-
тельной (как и левая), разность фаз колебаний двух соседних
частиц, АФ, должна быть постоянна вдоль цепочки:
Фя - Фп_, = Фп+1 - Ф„ = АФ.
Поскольку в равновесии атомы расположены на равных расстоя-
ниях, фаза Фп пропорциональна координате жп:
Ф„ = — кхп, т. е. АФ = -ка,
где к есть, по определению, волновое число (см. (1.2)). Смеще-
ние ип = Ае соответствует продольной волне, распростра-
няющейся с фазовой скоростью V = а/к.
Подставляя АФ = —ка в уравнение (1.15), получаем диспер-
сионное соотношение
М и2 = 2К (1 - cos к а) = 4£ sin2
или
° = 2/ 5Нпт|-
Эта периодическая дисперсионная кривая представлена на
рис. 1.13 в интервале [—л/а, +л/а], называемом первой зоной
Бриллюэна. Для малых волновых чисел (ка < 1) дисперсионная
зависимость представляет собой прямую линию
w « 1/ri ка,
г М
наклон которой Vo = а^К/М определяет скорость распространения
упругих волн низких частот. Когда длина волны оказывается
32
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
33
одного порядка с межатомным расстоянием а (ка»л), в среде
возникает дисперсия. Так как Isin ка/2\ < 1, частота упругих
волн, которые могут распространяться в кристалле, оказывается
ограниченной частотой отсечки
f = 1]/A = L>
‘с л V М ла’
При этом значении частоты групповая скорость Vg — da/dk
обращается в нуль, так как касательная к дисперсионной кривой
Рис. 1.13. Одноатомная цепочка.
Дисперсионные зависимости <в (fc)
для продольной моды.
Для каждой частоты, меньшей
частоты отсечки <вс, могут рас-
пространяться две волны в про-
тивоположных направлениях с
разными по знаку волновыми
числами.
оказывается горизонтальной. Отношение ип+1/ип = е~'ка прини-
мает тогда значение —1. Это означает, что два соседних атома
совершают колебания в противофазе.
Численные оценки. Скорость распространения 70 упругих волн
низких частот в твердых телах заключена между значениями 1000
и 10000 м/с. Межатомные расстояния составляют несколько А.
Если принять Vo — 5000 м/с и а = 5 А = 5 • 10~40 м, то частота
отсечки оказывается равной
/0 = 3,2 • 1042 Гц = 3200 ГГц.
Это значение много выше тех частот, которые рассматриваются
в данной книге (от нескольких МГц до нескольких ГГц) и кото-
рые расположены в начале дисперсионной кривой, в той области,
где частота пропорциональна волновому числу. Длина волны
А = V0/f для этих частот меняется от миллиметров до микромет-
ров и является весьма большой величиной по сравнению с меж-
атомными расстояниями, так что среда может считаться
сплошной.
Замечания.
1. Поперечные моды. Смещения частиц могут быть попереч-
ными, направленными, например, вдоль базисных векторов b и с
атомной цепочки (рис. 1.11). В каждом случае возвращающие,
силы будут различными, так что для направления распростране-
ния а существуют три различные дисперсионные кривые
(рис. 1.14). Одна .из них —для продольной волны L (поляриза-
ция вдоль а), другая —для поперечной волны (поляризация
Рис. 1.14. Одноатомная
цепочка. Дисперсионные
зависимости (к > 0) для
трех мод.
вдоль Ь), третья — для поперечной волны Г2 (поляризация
вдоль с).
Для другого направления эти кривые будут иными, поскольку
фазовая скорость зависит от направления волнового вектора.
В области частот, низких по сравнению с частотой отсечки,
дисперсия упругих волн в кристалле от-
сутствует, но он остается анизотропным.
2. Оптические ветви. Если цепочка
состоит из двух сортов атомов (Упр. 1.6),
все предыдущие результаты остаются
в силе по отношению к центру массы мо-
лекулы, но к кривой, аналогичной той,
которая изображена на рис. 1.13 (и назы-
вается акустической ветвью), добавляет-
ся еще одна кривая (так называемая оп-
тическая ветвь), находящаяся при любых
волновых числах всегда в области высо-
ких частот (рис. 1.25). Две эти ветви осо-
бенно- сильно различаются при больших
длинах волн Оса« 1); на низких часто-
тах молекула колеблется как целое (аку-
стическая ветвь), движение же атомов около неподвижного цент-
ра масс происходит на высокой частоте (оптическая ветвь), рав-
ной собственной частоте продольных колебаний молекулы. Если
принять во внимание все поперечные моды, то дисперсионная
кривая будет состоять из 6 ветвей. Этот результат можно обоб-
щить: если ячейка содержит р атомов, то в дисперсионной кри-
вой будет Зр ветвей, из которых Зр — 3 являются оптическими.
3. Тепловые волны. Рассматриваемые здесь упругие волны яв-
ляются когерентными, связанными с движением ансамбля частиц,
но во всех веществах существуют тепловые упругие волны, вы-
зываемые беспорядочными колебаниями атомов. Наличие этих
волн объясняет тепловые свойства веществ (изменение теплоем-
кости с температурой).
§ 1.3. Сигналы. Линейные стационарные системы
Устройства, рассматриваемые в последней главе, с помощью
упругих волн обрабатывают сигналы, т. е. преобразовывают сиг-
нал s,(f), поданный на вход, в сигнал s2(i) на выходе. Какова
бы ни была природа устройства, будь то электрический, либо ме-
ханический фильтр или же какой-то иной четырехполюсник,
всегда можно установить общие соотношения между $,(£) и s2(f)
при одном условии — что система линейна и стационарна.
Система считается линейной, если при входных сигналах s[ (I)
и si(i) получаются отклики соответственно s2(f) и s2 (0, а при
3 Э. Дьелесан, Д. Руайе
34
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
сигнале на входе (f) + (О откликом является ks2(t) + Ц$2(О
при любых скалярных X и ц. Стационарность означает, что от-
кликом на сигнал s/i + x) является s2(f+x), каковы бы ни бы-
ли т и st(i).
1.3.1. Сигналы реальные и фиктивные. Дельта-функция Ди-
рака. Функция s(t), представляющая изменение во времени не-
которой физической величины, является действительной, непре-
рывной и ограниченной во времени. Удобно ввести некоторые
математические функции, обладающие очень полезными свой-
ствами. Среди этих функций самыми важными являются следу-
ющие. Гармоническая комплексная функция е<2я/* с частотой / =
= со/2л, изменяющейся от — °° до +°°. Дельта-функция Дирака
6(f), имеющая бесконечно малую длительность и бесконечно
большую амплитуду при t = 0 и единичную площадь. Ступенча-
тая функция Хэвисайда У«), представляющая единичный скачок
сигнала при t = 0.
Изучая отклик на сигналы, представленные двумя первыми
из этих функций, мы введем две характеристики системы и уста-
новим связь между ними.
Для корректного определения функции Дирака нужно обра-
титься к теории распределений. Распределение Т является ли-
нейным непрерывным функционалом на пространстве беско-
нечно дифференцируемых функций с ограниченной областью оп-
ределения. Этот функционал каждой функции ф, принадлежащей
ЗУ, приводит в соответствие некоторый скаляр, обозначаемый
Т(ф).
Таким образом, локально суммируемая функция g может слу-
жить для определения распределения Tg с помощью соотношения
Tg (Ф) = f S (®) (*) (1.16)
Существуют и другие способы задания распределений. Рас-
пределение Дирака 6х0 в точке ха приводит в соответствие лю-
бой функции ф(ж), непрерывной в точке ха, ее значение в этой
точке:
6»0(Ф) = Ф(*о).
Вместо распределения 6Яо физики предпочитают пользоваться
функцией Дирака 6(ж —ж0), причем определяется выражени-
ем, аналогичным (1.16) (при любой ф(ж)):
+«>
J 5(ж~ Xo)^(x)dx = ф(ж). (1.17)
§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
35
Из этого уравнения видно, что функция Дирака 6U — хй) должна
равняться нулю для всех х^=хь т. е. 6(ж) = 0 (при лг^О). Из
соотношения (1.17) следует, что
ф(ж0) J 6 (ж — x0)dx = ^{x0),
J f>(x)dx = \, т. е. 6(0) = +оо.
' П(Ёг+хг)
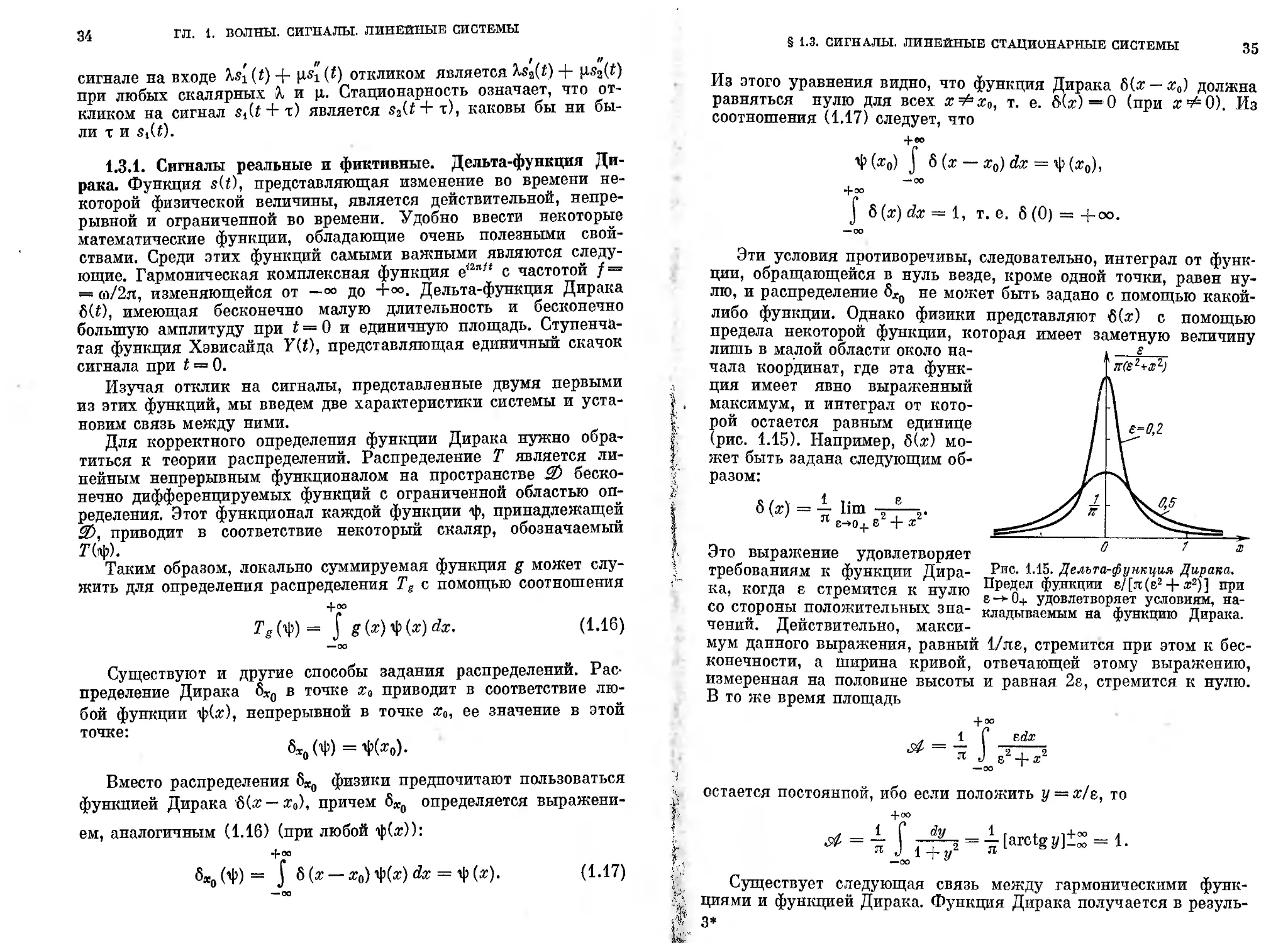
Рис. 1.15. Дельта-функция Дирака.
Предел функции в/ [л (е2 + ж2) ] при
е->0+ удовлетворяет условиям, на-
кладываемым на функцию Дирака.
Эти условия противоречивы, следовательно, интеграл от функ-
ции, обращающейся в нуль везде, кроме одной точки, равен ну-
лю, и распределение бХ() не может быть задано с помощью какой-
либо функции. Однако физики представляют б(ог) с помощью
предела некоторой функции, которая имеет заметную величину
лишь в малой области около на-
чала координат, где эта функ-
ция имеет явно выраженный
максимум, и интеграл от кото-
рой остается равным единице
(рис. 1.15). Например, 6(ж) мо-
жет быть задана следующим об-
разом:
6 («) — Нм » 8
' яе-»о+8г + х2
Это выражение удовлетворяет
требованиям к функции Дира-
ка, когда е стремится к нулю
со стороны положительных зна-
чений. Действительно, макси-
мум данного выражения, равный 1/ле, стремится при этом к бес-
конечности, а ширина кривой, отвечающей этому выражению,
измеренная на половине высоты и равная 2е, стремится к нулю.
В то же время площадь
остается постоянной, ибо если положить у = х/ъ, то
+00
= V f riS = -H-[arctgy]--= 1-
71 J 1 + у 71
Существует следующая связь между гармоническими функ-
циями и функцией Дирака. Функция Дирака получается в резуль-
3*
36
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
тате сложения бесконечного числа гармонических сигналов еди-
ничной амплитуды:
6 (t) = J eiin,tdf.
(1.18)
Это равенство нужно понимать в терминах распределений, т. е.
интегрирование (см. (1.16)) произведения функции ф(я) на левую
или правую часть данного равенства должно приводить к одному
и тому же результату. Покажем справедливость соотношения
(1.18), для чего преобразуем его правую часть:
s(f) = f ei2n,t# = lim f =
-oo e->0+ -oo
[° +00 1 \
J + f = ta 1(^+ Г=в)
и, наконец, получим

Использование входного сигнала в виде функции Дирака эк-
вивалентно подаче одновременно целого ансамбля гармонических
функций с частотами от — «> до +<».
Физически функция Дирака представляет собой короткий
импульс, длительность которого значительно меньше постоянной
времени системы. Эта функция позволяет получить такую же
информацию о системе, какую дает ее снятая по точкам частот-
ная характеристика.
1.3.2. Спектр сигнала. Преобразование Фурьё. Гармонические
функции обладают фундаментальным свойством: они образуют
полный базис в пространстве функций, суммируемых по модулю,
и любой физический сигнал s(t) можно разложить в бесконечный
ряд гармонических колебаний
S(f)- f S (f)eiinftdf.
(1.19)
Функция S(f) составляет его спектр. Для определения S(f)
вычислим интеграл
J(V)= J e~i2nvts(t)dt.
s 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ 37
Подставляя вместо s(f) его выражение (1.19), получаем
Z(v)= J ,$(/)£ J ei2n('-v)<d/| d/.
Из формулы (1.18)
+J = 8(/-v)
следует, что
Z(v)= j* S(/)8(/-v)d/ = S(v).
Переходя к переменной /, получаем окончательно
+«>
S(f) = J e~i2n,ts(t)dt. (1.20)
Из этого соотношения видно, что спектр сигнала есть его преоб-
разование Фурье. Действительно, результат преобразования
Фурье некоторой суммируемой по модулю функции g(x) есть
+ оо
G(s) = f g(x)e~iinacdx.
Запишем это соотношение символически в виде
gGr) => G(s),
или
G(s) <= giU).
Символ <= обозначает обратное преобразование Фурье, введенное
ранее (см. (1.19)):
g(x)= j G (s) J2nexds.
Для некоторого физического сигнала s(i), являющегося дей-
ствительной функцией времени, справедливо следующее соотно-
шение:
+ 00
$(-/) = J eiinfls(t)dt =
Действительная часть спектра является четной функцией:
Re £(-/) = Re 5(f),
38
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
39
Рис. 1.16. Спектр действитель-
а мнимая — нечетной (рис. 1.16):
Im $(-/) =-Im $(/).
Таким образом, для восстановле-
ния действительного сигнала доста-
точно знать только половину спектра
(область положительных частот)
s (t) = 2Re ] S(f)ei2n/tdf.
о
ного сигнала.
Действительная часть спект- Если мы теперь будем считать,
ра —четная, мнимая — нечет- чт0 сигнал §(/) состоит из четной
пая- $+О) и нечетной $_(£) Частей s(f) =
= s+(f)+«_(£), то его спектр можно записать следующим образом:
S (/) = +J s+ (t) e~iwftdt + J s_ (i) e~i2nftdt,
Дифференцирование. Если 5(/) является спектром сигнала
з(£), то спектр сигнала ds/dt имеет вид i2nfS(j). Доказательство
состоит в следующем:
f g e~^dt = f Hm SJt + M) -s(t)
JooA^° Д
используя предыдущую теорему, получаем
Дифференцирование подчеркивает в спектре высокие частоты,
ослабляет низкие частоты и полностью подавляет нулевую ча-
стоту.
Амплитудная модуляция. Найдем спектр синусоидального
сигнала s(t) — e(t) cos 2n/0f частоты /0, модулированного по амп-
литуде огибающей e(t), имеющей спектр £(/), Для преобразова-
ния Фурье этого сигнала имеем
ИЛИ
oo <»
5 (/) = 2 j s+ (0 cos 2n/i dt - 21 J s_ (£) sin 2nft dt.
О о
Спектр является действительным и четным, если сигнал чет-
ный ($+(£) = 0), и мнимым и нечетным, если сигнал нечетный
(«_(*) = 0).
Рассмотрим, как скажутся на спектре некоторые изменения,
вносимые в сигнал.
Преобразование подобия. Если S(f) является спектром s(t),
то спектр сигнала s(at) имеет вид Действительно,
J s (at) e~l2nfdt = ^ J s(at)e a d(at)
Сжатие сигнала во времени приводит к соответствующему
расширению его спектра и наоборот.
Сдвиг во времени. Спектр сигнала s(/ + x) есть е’2я/т5(/).
Действительно,
Y s(t + т) e~l2nftdt = +f 5 (i + Т) e-^^e^d (t + r) -
=.eiwftS(f).
Сдвиг сигнала во времени, например постоянная задержка,
вызывает фазовый сдвиг спектра, пропорциональный частоте.
4-00
S (/) = J е-йя//е (t) cos 2nfot dt =
= у Е (J — /0) y Е (f + /0).
Спектр,, сигнала получается путем сдвига исходного спектра
огибающей, уменьшенного по амплитуде в два раза, влево и впра-
во на величину, равную частоте несущей (рис. 1.17).
Частотная модуляция. В этом случае можно обобщить преды-
дущий результат. Пусть сигнал s(t) — e(t) cos cp(i) модулирован
по частоте, иными словами, его фаза <p(f) является нелинейной
функцией времени:
<р(£) = <M + if>(£).
Д Разлагая косинус и используя обозначение со = 2л/, запишем
* спектр этого сигнала в виде *)
'К +%>
S (а) = у J е (t) exp i [(<в0 — со) t + t|> (£)] dt +
ж +«>
I +7 J e (t) exp — i [(co0 + co) t +
Ж *) Использование обозначения co облегчает запись. Строго говоря, сле-
ж довало бы воспользоваться иными обозначениями для S и Е.
40 ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Обозначая через £(©) спектр eit) exp h|)(0, имеем
£(©) = f e(t)expi[^(t) — wt]dt. (1.21)
Для 1$(<в) получаем
S (<в) = у Е (© — ®0) + у Е* ® —
Если огибающая является четной функцией, е(—t) = е(0, и
если модуляция частоты
Рис. 1.17. Спектр синусоидального сигнала, модулированного по амплитуде.
Спектр получается, если разделить пополам амплитуду спектра огибающей
и сместить его в обе стороны по оси частот на величину, равную несущей
частоте.
симметрично относительно центральной частоты ®0, ф(—£) =
= 1|)(0, то Е(—со) = E(w) и
5(ю) = 1^(®-®0) + 4^*(® + ®0). (1.22)
Спектр состоит из двух частей, одинаковых по амплитуде, но
противоположных по фазе и расположенных около частот ®0
и — со0.
Этот спектр можно с хорошим приближением получить с по-
мощью метода стационарной фазы. Изменение фазы ait) —
= i])(£) — (at во времени вызывает очень быстрые осцилляции
expiotf. Таким образом, для данной частоты ®Р основной вклад
в интеграл (1.21) дает некоторый интервал вблизи значения tp,
где фаза ap(t) = i|>(j) — стационарна. Тогда tp и ®р оказыва-

§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ 41
ются связанными соотношением
(d«p/dt)fp = 0, т. е. ip' (tp) = ©р = © (tp) - ©0. (1.23)
«J Вблизи значений tp получаем
§ ар (t) « ap (ip) 4- — сср (tp) (t — tp)2.
j Подставляя это разложение в интеграл (1.21), имеем
+«>
£ (®р)« etap(<p) J е (t) exp [2 а!р (tp) (t - tp)2] dt.
Если огибающая e(t) изменяется медленнее, чем экспонента, то
можно записать •
4-00
Е (Юр)« е (tp) е “р(*р) J exp ар (tp) (t - tp^ dt.
Заменяя переменные
aP (tp) (t — Л>)2 = 2лу2, dt = i /”:-ji - j dy,
t । p ( p) *
t имеем
в “ Vr^hie <'’> e'“’<'’) T
r lap(/p)| -JOO
v Учитывая, что
J e™yidy = e’”'4,
| получаем
£(©p)« |/g^e(tp)expi[-J + ap(tp)], (1.24)
в или, возвращаясь к фазе ipCt),
£(©р)« е (tp) exp t [f + ip (tp) - ©ptpj. (1.25)
Ц. Правая часть, являющаяся неявной функцией частоты ор (благо-
К’ даря зависимости от tp и в силу соотношения (1.23)), вообще мо-
Ц жет служить хорошей аппроксимацией спектра £(©). Примене-
№ вие этой формулы к сигналу, линейно модулированному по ча-
к- стоте, рассматривается в упр. 1.7. Что касается модуля спектра,
Рис. 1.18. Таблица преобразований Фурье.
Поскольку сигналы и спектры па практике всегда ограничены, эту таблицу
нужно рассматривать с точки зрения физика: например, функция (sin х)/х
имеет свой фурье-образ, который тем ближе к прямоугольному импульсу,
чем большее число боковых лепестков мы принимаем во внимание. С ма-
тематической точки зрения 3-я строчка таблицы, если ее читать справа
налево, приводит к ошибочному результату. Поскольку функция (sin х)1х
не является суммируемой по модулю, она не имеет преобразования Фурье.
§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ 43
то он выражается следующим простым образом:
1Ж/-/0)12« lf(/)le2[i(/)], (1.26)
поскольку из соотношения (1.23) следует
fp = f(tp)-f0, fW ^2nf'(tp) = 7^7^
где f'(/) — производная от времени по мгновенному значению ча-
стоты сигнала.
Для того чтобы приведенные сведения были более конкрет-
ными, на рис. 1.18 дано несколько примеров прямого и обратного
Рис. 1.19. Спектр прямоугольного радиоимпульса (импульса с несущей).
преобразования Фурье для некоторых функций сопряженных,
безразмерных переменных х и $.
Из рис. 1.18 можно сразу получить спектры часто встреча-
ющихся сигналов. Например, в случае импульса длительностью 0
с амплитудой Лис частотой заполнения (несущей) /0 (рис. 1.19)
достаточно взять преобразование Фурье для прямоугольного ви-
деоимпульса единичной длительности и амплитуды (третий ряд
на рис. 1.18), т. е.
гг, .___sin ns
П
Интересующий нас сигнал записывается в виде
а (0 = АП cos 2nfot.
В силу теоремы подобия для спектра огибающей имеем
Е(/) = еЛ^<
Если теперь воспользоваться теоремой модуляции, то получаем
спектр сигнала
S(f) —A .Sin^(/+7O)0] я1П[л(/-/0)е?
Расстояние между двумя нулями спектральной функции, бли-
жайшими к центральной частоте /о, составляет 2/0. Ширина
44
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
спектра на уровне —3 дБ, по отношению к максимуму, равна
0,885/0.
Из первого ряда рис. 1.18 видно, что фурье-образ гауссовой
функции — тоже гауссова функция. Второй ряд получается из
первого в результате применения теоремы о дифференцировании.
(Напомним, что спектр дельта-функции Дирака равен 1 для всех
частот, удовлетворяющих соотношению (1.18).) Два последних
ряда рис. 1.18 показывают, что спектр синусоидального сигнала
частоты /о состоит из двух линий, расположенных при значениях
+/о и -/о.
В качестве упражнения читателю предоставляется возмож-
ность убедиться в справедливости тех соотношений, которые не
были здесь доказаны.
Рассмотрим теперь отклик линейной стационарной системы.
1.3.3. Частотный отклик линейной стационарной системы.
Если откликом на гармонический сигнал $,(£) = е’м| с круговой
частотой со является sz(t), то откликом на сигнал со сдвигом, во
времени, sAz + r) — e^sSt), будет, в силу стационарности и ли-
нейности системы,
sz(t + т) = e<fflts2(i).
Полагая t + т = /0, получаем
Поскольку это соотношение выполняется вне зависимости от то-
го, какие значения принимают t0 и t, произведение sz(t)e~,at =
— не зависит от времени, а его значение Ж®) является
функцией частоты и представляет собой частотный отклик систе-
мы. Величина Ж®) называется также передаточной функцией
системы.
Итак, отклик на гармонический сигнал Si(^) = e’“' представ-
ляет собой гармоническую .функцию той же частоты
52(Й=Ж®)е{“‘. (1.28)
Действие системы сводится к линейному преобразованию, причем
каждая величина elai является собственной функцией с собствен-
ным значением Ж®).
Приложим ко входу системы действительный гармонический
сигнал
(t) = COS (fit = -i----.
Для того чтобы сигнал на выходе
^(0 = |к(®)е<йг + Н(-ш)е-^]
§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
45
был тоже действительным, необходимо выполнение условия
[Ж®) e<atl* = Я(-<о) е-*'
или
Я*(®) = Ж-®).
Вводя модуль и аргумент Ф(ю) для Ж®) = 1Жи)1е<ф(в>, по-
лучаем
oi(wt+Ф) t о-г(<й/+Ф)
s2 = (и) | --------= | Н(®) | cos (®f + Ф).
Отклик на гармонический сигнал единичной амплитуды пред-
ставляет собой также гармоническую функцию (той же частоты),
амплитуда и фаза которой равны соответственно модулю и аргу-
менту передаточной функции системы.
1.3.4. Импульсный отклик. Импульсный отклик hit), называе-
мый также переходной характеристикой системы, является откли-
ком на сигнал в виде дельта-функции Дирака 6(2).
На основе соотношения (1.17), входной сигнал можно пред-
ставить в виде
si(0 — J Si(t)6(# — т)йт.
В силу линейности и стационарности системы сигнал на выходе
имеет вид
s2(i) = J sl(r)h(t —x)dx. (1.29)
Такая операция по отношению к s,(f) и hit) называется сверт-
кой. По определению, свертка двух функций fix) и gix) есть
функция вида
+«>
С(ж)= J / (у) g (х - у) dy (1.30)
или, в сокращенном обозначении,
Cix) = fix) * gix).
Вычисление свертки распадается на три следующие операции,
как это показано на рис. 1.20.
1. Инверсия и трансляция функции gix), которая при этом
переходит в gix — у).
2. Вычисление произведения функций gix - у) и fiy).
3. Вычисление интеграла (площади) от этого произведения (см.
(1.30)).
46
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Рис. 1.20. Свертка двух функций.
а) Функции /(«) и 6) инверсия и
смещение функции g(x)-, в) перемно-
жение f(y) и g(x— у); г) величина
С (®)= f f(y)g(z— y)dy.
Свертка обладает свойством коммутативности (а также —
ассоциативности), поскольку при замене переменной и = х — у в
интеграле получаем
+“
f*g = J f(x — u)g(u)du =
= g*f-
Интересно сравнить функ-
цию свертки с функцией кор-
реляции, определенной сле-
дующим образом:
Г(ж)= J f(y)g*(y-x)dy.
(1.31)
Для действительной функ-
ции g вычисление Г (ж) вклю-
чает те же этапы, что и вы-
числение С(х), с той лишь
разницей, что не требуется
инверсии функции g. Если g
тождественна /, то Г(ж) пред-
ставляет собой автокорреля-
цию функции /.
Согласно соотношению (1.29), отклик на входной гармониче-
ский сигнал Si(^) = е’"’1 имеет вид
sa(0 = J eitt>xh(t — х) dx
или (при подстановке и = t — т)
s^t) = P^ e~itt>uh(u)du.
Коэффициент пропорциональности между выходным и вход-
ным гармоническими сигналами есть просто передаточная функ-
ция (см. (1.28)), следовательно,
+<»
Н(а>) = J (Tiath(t)dt. (1.32)
Таким образом, передаточная функция и переходная импульс-
ная характеристика связаны преобразованием Фурье. Отсюда еле-
§ 1,3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ 47
дует, чтр передаточная функция линейной стационарной системы
является спектром ее импульсного отклика, и если обратить соот«
ношение (1.32), то видно, что переходная характеристика являет-
ся обратным преобразованием Фурье от частотной характеристи-
ки, т. е.
4-оо
h (0 = ‘J d™ftH(f)df. (1.33)
1.3.5. Отклик па сигнал произвольного вида. Теперь у нас
имеется два метода нахождения отклика линейной стационарной
системы на произвольное воздействие.
1. Временной анализ процессов, дающий значение s2(i) как
свержу импульсного отклика с входным сигналом:
s2U) = fe(i)*sl(0. (1.34)
2. Гармонический анализ, основанный на представлении вход-
ного сигнала в виде суммы гармонических функций:
«1(0 = J Si(/)ei2^/,
что в силу линейности системы приводит к выражению
Спектр выходного сигнала является произведением спектра
входного сигнала на передаточную функцию системы:
51(/)=Я(/)51(/). (1.35)
Это следует из соотношения (1.34), поскольку фурье-образ
свертки двух функций равен произведению фурье-образов каждой
из этих функций.
Прохождение сигнала через линейную стационарную систему
сопровождается сдвигом фаз Ф(со), равным аргументу передаточ-
ной функции. Так как этот сдвиг не пропорционален частоте,
система обладает дисперсией. Запаздывание группы составляю-
щих сигнала с частотами вблизи ®0 определяется, как в разделе
1.1.3, т. е.
Все эти результаты сведены в табл, 1.1, где пары функций,
связанных преобразованием Фурье, соединены стрелками.
48
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Таблица 1.1. Отклик линейной стационарной системы
„ „ . ЛИНЕЙНАЯ СТАЦИОНАРНАЯ Вход * СИСТЕМА >-Выход
Гармонический сигнал 12 л/4 е н(п Гармонический сигнал Я(/)е^
Синусоидальный сигнал cos 2nft H(f)= eW" Синусоидальный сигнал, сдвинутый по фазе, |Я(/)|/соз (2л/4+Ф)
Импульсная функция Дирака 6(4) Импульсный отклик h(t)
Сигнал Sj.(4) его спектр Si(J) Свертка с h(f) умножение на H(f) Сигнал s2(t)=h(t)*s1(t) ~ его спектр
Рис. 1.21. Колебания одномерного
вибратора.
Колебания из точки Р приходят
в точку М с запаздыванием по
X
фазе на величину 2л ysin а отно-
сительно колебаний, исходящих
из центра излучателя О.
1.3.6. Связь между спектром сигнала и диаграммой направ-
ленности излучателя. Преобразование Фурье используется во
многих областях физики. Оно выявляет различные пары сопря-
женных переменных, например, частоту / и время t в теории
сигнала, импульс р и координату г в квантовой механике, направ-
ление sin а и апертуру х/К излу-
чателя. Последнее будет показано
ниже.
В самом деле, вопрос об излу-
чении включает две следующие
задачи.
1. Излучение антенны самой
по себе, как источника энергии
(активный элемент).
2. Дифракция параллельного
пучка на апертуре, переизлучаю-
щей энергию падающего на нее
пучка (пассивный элемент).
Рассмотрим- одномерный излу-
чатель, распределенный вдоль
оси х (рис. 1.21), и пусть и(х) =
= А(.х) cos [<о£ + Ф(ж)] есть коле-
бания в точке Р с координатой х.
Запишем эти колебания в виде
и(х) = Re [go(®)e<ffl,l,
где через g0(x) = Л(ж)е£ф(1) обозначено распределение комплекс-
ных амплитуд по излучателю. На расстоянии г амплитуда коле-
§ 1.3. СИГНАЛЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
49-
баний, создаваемых элементом излучателя, заключенным между х
и х+ dx, равна
g0(x)(T™£dx.
Показатель 2л(гА) отражает отставание по фазе для волны, про-
шедшей расстояние г. Полное колебание в точке М, заданной
вектором R = ОМ, определяется суммой
Go(R)= J g0(x)e~^dx. (1.37>
Вдали от излучателя, т. е. на расстоянии R = ОМ, большом
по сравнению с длиной антенны, г(ж) > х для любого х, спра-
ведливо следующее приближение: г = R + х sin а. Тогда выраже-
ние (1.37) будет иметь вид
-l2^sina
Go (R) = е % J g0 (*)е dx,
—оо
.2 JTR
т. е. оно распадается на множитель е , учитывающий отста-
вание по фазе на среднем расстоянии R, и на множитель, отра-
жающий угловые зависимости:
-г2л—sina
G0(sina) = J g0(^)e x dx.
На большом расстоянии угловое распределение излучения,.
G0(sina), связано с распределением амплитуды по излучателю,
gt(x), через преобразование Фурье. Чтобы записать это в привыч-
ном виде, положим s = sin а и вместо х введем безразмерную
координату жА, тогда
где g(x/K) = gM.
Функция G(s), пропорциональная G0(s), называется диаграм-
мкой направленности излучения или угловым спектром излучате-
ля. С помощью обратного преобразования Фурье получаем
4 Э. Дьелесан, Д. Руайе
-50
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Поскольку s = sina, пределы интегрирования в действитель-
ности ограничены интервалом —1, +1. Для того чтобы результат
интегрирования мало отличался от g(x/)j, необходимо обращение
•в нуль G(s) для |s| > 1, иными словами, излучатель должен быть
достаточно направленным.
Рис. 1.22. Диаграммы направленности одиночных излучателей: протяженно-
го (а), узкого (б) и синхронных излучателей: протяженных (в), узких (г).
Следующие соотношения подчеркивают аналогию излучателей
с сигналами и их спектрами.
Сигналы Излучатели
Время t Приведенная координата xfk
Частота / Направление s = sin се
Сигнал s(i) Распределение амплитуды по
излучателю g(;r/A)
Спектр S(/) Диаграмма направленности
G(s)
Приведенные ниже примеры легко проанализировать с по-
мощью преобразования Фурье (рис. 1.18).
УПРАЖНЕНИЯ
5t
Диаграмма направленности антенны, имеющей длину аХ, да-
ется выражением
sin nsa
ns
Апертуре с размерами, меньшими X, соответствует плоский
(равномерный) угловой спектр.
Диаграмма направленности двух антенн, имеющих каждая
длину а и расположенных на расстоянии 2&Л друг от друга,,
имеет вид
0 sin nsa__
2-------cos Zitos.
ns
Диаграмма направленности двух излучателей с апертурами,
меньшими длины волны А (ср. с опытом Юнга по интерференции,
света от двух малых отверстий), описывается выражением
cos 2nbs.
Все эти примеры проиллюстрированы рис. 1.22. Они показывают^
что чем больше размеры антенны по сравнению с длиной волнык
тем более направленной является такая антенна.
Мы предполагали до сих пор, что колебания описываются
скалярными величинами. Полученные результаты остаются в си-,
ле и для колебаний векторного характера, поскольку в соответ-
ствии со сделанными предположениями излучение наблюдается
вдали от источника, а среда считается изотропной.
Упражнения
1.1. Докажите соотношение
(Re ^-Re = у Re [ w1w*].
Символ <> означает среднее во времени и uk = Ake^at + Фй\ к = 1, 2.
Решение.
(Re lyRe »2) = AjA^ (cOs (cot + Фг) cos (со/ + Ф2)> =
= (cos (Фх + Ф2 + 2(04) + cos (Ф2 —
Так как среднее значение косинуса равно нулю, то
A A i
(Re itj-Re = -y^-cos (Ф2 — Ф2) = — Re
1.2. Предполагая, что сжатие происходит адиабатически (рр’ = const),
получить выражение для скорости звука в идеальном газе с молярной мае-'
Сой М при температуре О. В качестве примера взять воздух при О °C (М
; •= 29 г/моль, у = 1,4).
52
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Решение. Коэффициент адиабатической сжимаемости получается из
1 1 / Зр \
уравнения адиабаты pvv = const: ха = — = — ~ Используя
формулу V — 1/УроХ для идеального газа, получаем V •= Т/^М/М. Для воз-
духа V = 330 м/с.
1.3. Показать, что отношение Др/u приращения давления Др к колеба-
тельной скорости и = du/dt частиц есть величина постоянная для бегущей
волны в жидкости.
Решение. Так как u—F(t — x/V), Ар — —и “ =
то Др/и = 1/%Р-= роР. Постоянная Z — р0Р является импедансом еди-
ницы поверхности среды (в механике импеданс определяется как отноше-
ние силы к скорости).
1.4. Используя условие непрерывности смещения и и приращения дав-
1 1 I V 1 “ 1 Z Gpouteftuon Gonna t
.Отраженная Gonna 1) X
Рис. 1.23. Отражение и прохождение
волны на границе двух сред с раз-
ными упругими импедансами.
ления Др на границе двух сред с раз-
личными упругими импедансами
(упр. 1.3) Z и Z', определить коэффи-
циенты отражения Ar/Ai и пропус-
кания Ат/Аг (рис. 1.23).
Решение. Из условия непре-
рывности смещения на границе х —
= 0 следует, что + Ав =» Ат.
Учитывая результаты предыдущего
упражнения, получаем (Др) / = Zui,
(Ар)в = —ZuB, (Ар)т —Z'ut, а из
непрерывности приращения давле-
ния следует, что (Др)г + (Др)в «=
= (Др)т- Таким образом, Z(Ai —
-Ав) = Z'AT.
Коэффициенты отражения и пропускания
Ад Z — Z' 2Z
aJ=z + zh лу= z + z'
зависят только от отношения упругих импедансов. Предельные случаи:
1) Z/Z’ = оо; Ar/Ai = — 1, At/Ai =0. Отражение является полным и сме-
щение равно нулю на абсолютно жесткой поверхности. 2) Z'/Z — 0: Ав/Ai =
=1. Отражение является полным и приращение давления Др обращается
в нуль на свободной поверхности. При х > 0 уже нет материальной сре-
ды (Z' = 0, т. е. р' = 0), а следовательно, нет и смещения.
1.5. Показать, что уравнение движения частицы (1.14) при % > а сво-
дится к уравнению распространения для непрерывной среды (1.13).
Решение. Если X » а, разность nn+i — »п заменяется бесконечно ма-
лой величиной du, т. е.
цп+х — ип f ип ~ ип-1 _= ( djA
а ~ Win-и' а = \дх)хп'
Уравнение (1.14) принимает вид
УПРАЖНЕНИЯ
53
Аналогичные рассуждения приводят к уравнению (1.13):
д2и Ка2 д2и д2и
dt2 ~ м дх2 ~ Г° дх2'
при этом учтено, что Fo= аТ/К/M есть скорость низкочастотных упругих
волн.
1.6, Дана цепочка равноотстоящих атомов, причем атомы с четным но-
мером имеют массу Mt, а атомы с нечетным номером — массу Af2 > Mi
(рис. 1.24). Написать уравнения движе-
ния атомов с номерами 2л и 2п + 1- Йо-
лагая и2п — Hie^®*-5"40) и u2n+i = —©-----------О-----®------О----"©—
= 42е<Гт(_<2п+1)'1О1, пайти дисперсион- ' п ~ 2п 2пЧ
пое соотношение со (к) и построить дис- --------
персионные кривые. Рассмотреть слу- Рис. 1.24. Цепочка из атомов двух
чаи ka С 1 и ка = л/2. сортов.
Решение. Уравнения движе-
ния атомов с номерами 2л и 2л +1 аналогичны уравнению (1.14):'
М1 = К (“2П+1 + «2П-1 - 2«ап)(
М2 = К (“2П+2 + И2п ~ 2«2п+1)'
Используя выражения для смещения частиц, получаем
(гЯ-ЛМЛ!— (2^ cos ка)Аг = О,
- (2К cos ka) A , + (2К — М^)А2 = 0.
Условие совместности этих двух однородных уравнений:
2К — Мх<о2 — 2К cos ka I
- 2К cos ka 2K — М2<л2 | =°
дает дисперсионное соотношение
«а)2=А:(^ + ^)т^[(^+^) “43^] •
Дисперсионная зависимость со ДА) имеет такой же вид, как и в случае
цепочки из одного сорта атомов (рис. 1.25). Если ka < 1, решения юi «
№ у2£(1/Л/1 + 1/М2) ак и 4) ^=Л2 соответствуют распространению упругой
волны со скоростью Уо = a^2KI(Mi +Л/2), поэтому эта ветвь и называется
«акустической». При ка < 1 получаются и другие решения: со2 =
= У2К (1/Л/1 + 1/Л/2) и MjAi + М2А2 = 0. Два соседних атома колеблются
в противофазе с амплитудами 41 и 42, так что центр массы молекулы оста-
ется неподвижным. Если каждая из этих двух частиц несет противополож-
ный заряд (ионы), оказывается возможным возбудить указанное колебание
с помощью электрического поля с частотой со2(0)/2л (»1012-4-1013 Гц),
лежащей в инфракрасной области спектра. С последним обстоятельством
и связано название «оптическая» ветвь, данное кривой <о2(к).
54
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
В случае ка = л/2 для частот <0i и ю2 получаем
щj = ^2К1Мч и А1 = 0 более легкие атомы неподвижны,
со2 = V2K7^i и As = 0 тяжелые атомы неподвижны.
1.7. С помощью метода стационарной фазы определить спектр радиоим-
пульса длительности 0, несущая которого линейно промодулирована по
частоте в полосе В (рис. 9.12):
Рис. 1.25. Дисперсионные зависи-
мости для цепочки из атомов
двух сортов {продольные моды).
з (4) = П cos <p (4), причем
/ = _1_Ё2= f + — t
' 2л dt ' ° 0 ‘
Решение. Для данного сигнала
В
ф(4) = л-д-4 и из формулы (1.23) по-
лучаем
В 0
“р - 2я © fp - в fp-
Обращаясь к выражению (1.25), нахо-
дим, что
Спектр £(/) = у Е ( / — /0) + у Е* ( / /0) состоит из двух прямоуголь-
ников, имеющих ширину В и центральные частоты /0 и —/о- Фаза изменяет-
ся с частотой по параболическому закону. Полный расчет, приведенный в
разделе 9.3.2, показывает, что приближение стационарной фазы тем справед-
ливее, чем сильнее неравенство В® > 1.
1.8. Вычислить преобразование Фурье от е-яж2 при условии, что
+ оо
J е-та2&=1.
Решение.
G {s) = [ e-™\-^xdx = e-ns2 f е-^+,'^2йт.
Поскольку комплексная функция е гое2 не имеет полюса, интеграл
по контуру Г на рис. 1.26 равен нулю:
*dx + i § e~"(a+iv)2dy +
УПРАЖНЕНИЯ
55
При а -> оо существует только интеграл
[ е-«(х+ад2йа;= J е-лх2йа. = 1
для любых s, откуда G (s) — е я®2.
1.9. Показать, что Л (ж) = П(я) *П(ж), Отсюда с помощью теоремы
о преобразовании Фурье от свертки получить, что Л (х) (sin ns/да)2.
Решение. Интеграл свертки П(у)П(®—у)ду численно равен
общей площади двух прямоугольников, середипа одного из которых нахо-
дится в точке у=х, а другого —в точке у = 0 (зависимость Л (я)
Рис. 1.26. Контур интегрирования.
Рис. 1.27. Свертка двух прямо-
угольных импульсов.
на рис. 1.27). Так как преобразование Фурье от свертки равно
произведению преобразований Фурье, получаем Л (я) = П(я) « П(я) =>
(sin да/ns)2.
1.10. Доказать соотношение
2 е_’2лтх = 6(z-n).
т=-м п=—оо
4-оо
Решение. Введем функцию Т (х) = 2 е~г2Ятж, при этом
Ч-оо
е-’2яхТ(ж)= 2 е-*2Я<т+1>* = Т (х), т. е. (e"i2ra - 1) Т (ж) = 0.
Ш=-00
Последнее уравнение показывает, что Т(х) равно нулю для всех нецелых
х. Рассмотрим интеграл от произведения Т(х) на некоторую функцию g(x)i
V +«
/= J T(x)g(x)dx = 2 Zn’
In= J T(x)g(x)dx. n — целое.
56
ГЛ. 1. ВОЛНЫ. СИГНАЛЫ. ЛИНЕЙНЫЕ СИСТЕМЫ
Так как в интервале pi—
за исключением точки х = п, то
-^функция Т(х) равна нулю везде»
Постоянная С не зависит от целого числа п, так как Т(х +1) = Т(х). На-
конец, получаем соотношение
+“ +00 +» _ +«
Т (х) g (х) dx = 2 е г2ятхе («) dx = С 2 £(”)• t1-38)
-оо т=—оо П=-00
С помощью фурье-образа G(s) от g(x) перепишем предыдущее выра-
жение в виде
2 G(m) = C 2 (1.39)
т=—оо п=—оо
Для нахождения постоянной С достаточно конкретизировать вид g(®). На-
пример, если
g(x) = П(я), G(s) = sinns/ns,
то С = 1, так как g(0) = G(0) = 1 и g(n) = G(n) = 0, когда п 0.
Из (1.39) получаем формулу Пуассона: 2 G(m)= 2 а из
т=-оо п=~оо
соотношения (1.38) при любой g(x) следует искомая формула:
т(х)= 2 6 (*-«)= S e-i2Itmx- (1Л0>
00 щ=—00
1.11. Записать в явном виде выражение 6(g(®)].
+ 00
Решение. Вычислим интеграл I = J /(т) 3 [g (ж)] dx путем замены
переменной у = g(z):
dy = | g' (x) | dx,
г V t r -1, и _ /(*o)
_jJ(2/)k'[r1(y)H |£'(*o)l’
где яо — один из нулей функции g(x), т. е. ®о = ?”’(0). Если g(x) обраща-
ется в нуль для множества значений хп [g'(xn) Ф 0], то

ГЛАВА 2
ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Упругие волны могут распространяться в любой материаль-
ной среде, но их амплитуда убывает по мере распространения,
поскольку взаимодействие между атомами не является чисто уп-
ругим. Поглощение волн тем слабее, чем упорядоченнее среда.
Таким образом, в жидкости потери больше, чем в твердом теле,
а в аморфном или поликристаллическом веществе больше, чем в
монокристалле. С другой стороны, эти потери очень быстро рас-
тут с частотой, так что жидкости невозможно использовать на
частотах выше 50 МГц, а на частотах порядка гигагерца приме-
няются только монокристаллы. В силу анизотропии кристаллов
определенные направления являются более благоприятными для
распространения какого-либо типа волн; например, волновой век-
тор и вектор потока энергии коллинеарны только вдоль особых
направлений. Кроме того, для возбуждения упругих волн высо-
кой частоты необходимы пьезоэлектрические кристаллы. Для по-
нимания явлений распространения и генерации упругих волн
требуется четкое знание свойств кристаллов и, в особенности, их
симметрии.
В этой главе кристаллическая структура анализируется на
основе представлений о решетке и базисе. Кристаллы делятся
на классы в соответствии с симметрией направлений, играющей
очень важную роль, поскольку она обусловливает симметрию
макроскопических свойств кристалла. Пространственная симмет-
рия обсуждается только в связи с микроскопическим строением
кристалла. Описывается структура некоторых кристаллов, исполь-
зуемых на практике.
§ 2.1. Определение кристаллического состояния
Среди твердых тел следует различать аморфные и кристалли-
ческие. Первые, не имеющие характерных геометрических форм,
являются всего лишь вязкими жидкостями*). При нагревании
*) Между двумя крайними разновидностями, жидкостью и монокри-
сталлом, находятся жидкие кристаллы, характеризуемые упорядоченностью
вдоль одного или двух направлений, и поликристаллические твердые тела,
состоящие из большого числа микроскопических монокристаллов, поведе-
ние которых в макроскопическом смысле изотропно,
58
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
они постепенно плавятся, и их текучесть непрерывно растет с
температурой (случай смол, стекол), а при охлаждении происхо-
дит увеличение вязкости. При этом на кривой уменьшения тем-
пературы, как функции времени, нет горизонтального участка.
Напротив, в случае кристаллического твердого тела в процес-
се охлаждения расплава температура стабилизируется, как только
появляются зародыши твердой фазы в форме многогранников,
т. е. кристаллы. Все эти многогранники выпуклы и подобны друг
другу, т. е. двугранные углы между естественными гранями
•кристаллов одного вида являются внешними и постоянными не-
зависимо от формы образца.
Многогранники кварца, например, представляют собой гекса-
гональные призмы с пирамидами на концах. Две грани призмы
образуют между собой угол ровно в 120°,
угол между гранью призмы и прилегаю-
щей гранью пирамиды равен 14Г47',
а угол между двумя смежными гранями
пирамиды равен 133°44' (рис. 2.1).
Рис. 2.2. Сечение призмы реально-
го кристалла кварца.
Многоугольник в сечении отлича-
ется от правильного шестиуголь-
ника, но углы между гранями
равны 120е.
Рис. 2.1. Кристалл кварца с иде-
ально развитыми гранями.
Кроме граней призмы и пира-
мид, существуют три пары ма-
леньких граней s и х, которые
понижают симметрию оси приз-
мы до третьего порядка.
Несмотря на то что грани кристалла могут развиваться раз-
личным образом, как это видно из сечения, перпендикулярного
оси призмы (рис. 2.2), ориентация граней остается постоянной:
семейство нормалей к граням кристалла, восстановленных из
любой точки пространства, образует одну и ту же геометрическую
фигуру. Это свойство, называемое законом постоянства углов,
было сформулировано Ромэ Де Лилем в XVIII в.
Изучение кристаллов показывает, что кристаллическая среда
анизотропна и однородна.
Анизотропия проявляется прежде всего в строго определенной
ориентации граней, а также в фигурах удара (например, фигуры
в виде звезды на слюде, образованные острым предметом), в раз-
§ 2.2. КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
59
личной форме фигур травления в зависимости от обрабатываемых
граней (например, сернистый кадмий), в свойстве кристаллов
колоться вдоль выделенных плоскостей (слюда, кальцит). Наблю-
дение таких эффектов легло в основу гипотезы об упорядоченно-
сти, периодичности структуры материи на атомном уровне, сфор-
мулированной Р. Ж. Аюи в XVIII в. Эта гипотеза была подтверж-
дена в 1912 г. экспериментами по дифракции рентгеновских
лучей на кристаллах, поставленными Фридрихом по инициативе
Лауэ. Следует отметить, что из-за анизотропии кристаллов мно-
гие их механические свойства, в “том числе скорость распростра-
нения упругих волн, зависят от направления. Для большей части
физических свойств кристаллов характерно плавное изменение
с направлением, однако ряд свойств, таких как дифракция рент-
геновских лучей или спайность, меняется скачком.
Однородность кристаллической среды следует из того факта,
что вырезанные из кристалла макроскопические образцы, имею-
щие одинаковые размеры и ориентацию, не отличаются друг от
друга по своим характеристикам. На атомном уровне, на котором
кристаллическая среда дискретна, однородность сохраняется в
смысле Бравэ: вдоль трех различных направлений в кристалле
существует бесконечная последовательность точек, гомологичных
какой-либо одной точке, иначе говоря, обладающих одинаковым
атомным окружением.
§ 2.2. Кристаллическая структура
Внешний вид и макроскопические свойства кристаллов наво-
дят на мысль, что их можно классифицировать в соответствии
с симметрией нормалей к естественным граням, о которой гово-
рят, как о симметрии направлений. Перечисление классов сим-
метрии направлений требует знания атомной структуры, обуслов-
ливающей макроскопические свойства кристаллов, поэтому начнем
с описания структуры кристаллической среды.
2.2.1. Периодичность кристаллической среды. Решетка. Ряды.
Плоские сетки. Ячейки. Кристаллическая среда характеризуется
наличием бесконечного числа точек, геометрически эквивалент-
ных некоторой точке О кристалла. Все эти гомологичные точки
имеют одинаковое атомное окружение и получаются друг из
друга последовательностью элементарных трансляций на три век-
тора а, Ь, с. Положение некоторой точки М, гомологичной на-
чальной точке О, задается вектором
ОМ = ma + nb + ре,
где т, п и р — целые числа.
60
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Набор таких гомологичных точек, называемых узлами, обра-
зует трехмерную решетку, которая отражает периодичность кри-
сталла во всех направлениях (рис. 2.3).
Решетка может быть разложена на простые компоненты: од-
номерные ряды, двумерные плоские сетки и трехмерные ячейки.
Ряды. Узлы решетки расположены на пересечении трех се-
мейств параллельных прямых. На рис. 2.4 показано разделение-
Рис. 2.4. Ряды.
Узлы плоской решетки располо-
жены на пересечении двух лю-
бых семейств прямых Dt, D* D3..~
Для семейства прямых D3 вектор
R — 2а — Ь.
Рис. 2.3. Кристаллическая решетка.
Все узлы решетки эквивалентны, т. е.
имеют такое же атомное окружение, что
и исходная точка О. Положение узлов
определяется вектором ОМ — ma +
4* иЬ +ре.
на два семейства параллельных прямых для более наглядного
случая плоской решетки. На каждой из этих прямых, называе-
мых рядами, узлы решетки находятся на равном расстоянии друг
от друга. Три целых взаимно простых числа и, и, w определяют
ряд [u, v, id посредством вектора
RuA« = ua + vb + we,
соединяющего узел с его ближайшим соседом. Так, на рис. 2.4
(ю = 0) ряды _семейства прямых D3 обозначаются символом [2,.
1, 01, причем 1 соответствует значению —1.
Из этого рисунка видно, что линейная плотность узлов зави-
сит от направления, она максимальна для рядов с малыми ин-
дексами, таких как Dt [1, 0, 0] или D2 [0, 1, .0), и уменьшается
для рядов с большими индексами, таких как D3 [2, 1, 0]. Для
данного кристалла с фиксированным числом узлов в единиц©
объема направлению с наибольшей плотностью узлов соответству-
ет максимальное расстояние между соседними рядами. Так как
атомы расположены плотнее вдоль рядов с малыми индексами,
то и силы сцепления для них больше. В некоторых кристаллах
силы связи атомов внутри ряда и между соседними рядами раз-
личаются настолько, что материал расщепляется на нити (слу-
чай асбеста).
§ 2.2. КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
61
Плоские сетки. Все узлы решетки можно разместить в одном-
семействе параллельных эквидистантных плоскостей, называемых
плоскими сетками, которые получаются друг из друга элементар-
ной трансляцией вдоль некоторого ряда, не принадлежащего
плоскостям этого семейства (рис. 2.5).
Для обозначения семейств плоских сеток Миллер ввел спе-
циальные индексы. Поскольку один узел находится в начале ко-
ординат и по одному узлу на концах векторов а, Ь, с, то через:
каждую из этих четырех точек проходит одна плоская сетка
рассматриваемого семейства. В о'бщем случае, часть остальных
плоскостей располагается между ними так, что каждый вектор
основных трансляций делится на равные отрезки. Если расстоя-
ние между двумя соседними
плоскостями равно a/h вдоль
вектора a, b/k вдоль Ь, сП
Рис. 2.6. Индексы Миллера,
Расстояние между соседними пло-
скостями равно а/2 вдоль а, 6/3 —
вдоль Ь, с/2 — вдоль с. Числа 2, 3, 2
являются индексами Миллера этого
семейства плоских сеток.
Рис. 2.5. Семейство плоских
сеток.
вдоль с, то целые числа h, k, I и есть, по определению, индек-
сы Миллера данного семейства плоских сеток. Обозначение khkl)
определяет совокупность плоскостей, а не какую-либо отдельную
плоскость (рис. 2.6). Отрицательный индекс отмечается чертой
сверху, т. е. к. Один из индексов равен нулю, если плоскости па-
раллельны соответствующей оси.
При фиксированном количестве узлов в единице объема плос-
кие сетки с малыми индексами Миллера (100), (010), (001), наи-
более удаленные друг от друга, обладают максимальным числом
узлов на единицу площади, или максимальной ретикулярной
плотностью. Такие плоскости играют важную роль: они сильнее
отражают рентгеновское излучение и, кроме того, являются плос-
костями спайности, так как атомы внутри плоскостей сильно
взаимодействуют между собой, а межплоскостные связи относи-
тельно слабы.
<52
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Ячейки. Решетку можно также представить в виде совокуп-
ности одинаковых параллелепипедов, построенных на трех векто-
рах основных трансляций а, Ь, с (рис. 2.7). Узлы располагаются
а вершинах этих параллелепипедов, или ячеек.
Для данного кристалла решетка определена однозначно, но,
тем не менее, ее можно построить с помощью других векторов
трансляций at, bi, ct и ввести другие ячейки, как показано на
рис. 2.8 для случая плоской решетки.
Рис. 2.7. Ячейки.
Решетку можно представить в
виде совокупности одинаковых
параллелепипедов, или ячеек.
Рис. 2.8. Решетку можно постро-
ить с помощью различных век-
торов основных трансляций, и,
следовательно, рассматривать раз-
личные ячейки.
Ячейки, построенные на трех векторах основных трансляций,
называются примитивными, так как не содержат других узлов,
кроме находящихся в восьми вершинах. Каждый из этих узлов
принадлежит, наряду с рассматриваемой, еще семи другим ячей-
кам, так что на долю данной ячейки приходится только 1/8 узла,
а в целом на примитивную ячейку приходится только один узел.
Сложная ячейка содержит больше чем один узел. Допустим, что
ячейка построена па векторах
а' = ща + r.b + и>.с, b' = w2a + r2b + w2e, с' = w3a + r3b + w3c,
тогда ее объем V равен абсолютной величине смешанного про-
изведения [а'Ь'с']. Поскольку
|“i У1 wi
U2 Р2 W2
“з рз W3
то V' =pV, где V = laEbc] | — объем примитивной ячейки и р —
абсолютная величина определителя. Объем рассматриваемой слож-
ной ячейки в р раз больше объема V, занимаемого одним узлом.
Решетку часто описывают с помощью сложной ячейки, более
симметричной, чем примитивная. Такое описание удобно, напри-
мер, в случае гранецентрированной кубической решетки (г. ц. к.),
а[Ьс],
§ 2.2. КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
63:
в которой узлы располагаются в вершинах и в центре всех
шести граней примитивной кубической решетки (рис. 2.9, а). Мы
оставляем читателю проверку того, что речь идет именно о ре-
шетке, т. е. окружение каждого узла одно и то же, находится ли-
грани куба. Сложная кубическая
л 6)
Рис. 2.9. Гранецентрированная кубиче-
ская решетка (г.ц.к.').
Гранецентрированная кубическая ре-
шетка (б) получается добавлением од-
ного узла в центр каждой грани ячей-
ки примитивной кубической решетки
(а). Объем элементарной ячейки-
(г.ц.к.) в четыре раза больше объема
примитивной ячейки, представляющей
собой ромбоэдр, построенный на векто-
рах а, Ь, с.
он в вершине или в центре
ячейка содержит четыре уз-
ла, так как каждый из шести
узлов на гранях принадле-
жит двум ячейкам (4 = 8-
• 1/8 + 6 • 1/2). Примитивная
ячейка, построенная на век-
торах, которые связывают ка-
кую-либо вершину с центра-
ми трех граней, сходящихся
в этой вершине, представля-
ет собой ромбоэдр (рис. 2.9, б).
Ячейка, обладающая той
же симметрией, что и решет-
ка, называется элементарной.
Элементарная ячейка может
быть и примитивной, и слож-
ной, как для гранецентриро-
ванной кубической решетки.
Другие примеры элементарных ячеек будут рассмотрены в разде-
ле 2.3.2, посвященном классификации решеток.
2.2.2. Атомная структура. Базис. Атомная структура кристалла;
однозначно определяется, если известна решетка и базис, т. е.
совокупность атомов, расположенных в узлах решетки (рис. 2.10).
• • • • <
• • • •
• • • • "С
• • • • ’С ’С
Решетка + базис = Кристалл
Рис. 2.10. Атомная структура кристалла.
Кристалл образуется при присоединении группы атомов (базиса) к каждо-
му узлу решетки.
В простейшем случае базис состоит из одного атома, при присое-
динении которого к каждому узлу решетки образуется кристалл.
Примером могут служить многочисленные металлы с кубической
гранецентрированной решеткой: медь (3,61), серебро (4.071), зо-
лотЬ (4,070), алюминий (4,041), никель, платина... (Число
*64
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
65
в скобках указывает размер ребра кубической ячейки в ангстре-
мах.) Элементарная ячейка этих металлов содержит четыре атома,
например, атомы с координатами: 0, 0, 0; 1/2, 1/2, 0; 1/2, 0, 1/2;
Ю, 1/2, 1/2 (ребро куба принято за единицу), остальные ’при-
надлежат соседним ячейкам. На рис. 2.11, а показан вид сверху
Рис. 2.11. Примеры кубических структур:
а) гранецентрированная, б) объемноцентрированная, в) гранецентрирован-
'«^;™„С-КОТ°РОИ С0СТ0!1Т из„даУх атомов (структура типа алмаза); объем
кубической элементарной ячейки в четыре раза больше, чем объем ромбо-
эдрической примитивной ячейки.
па такую структуру. Число штрихов в кружках указывает поло-
жение атомов по вертикали, причем каждый штрих соответствует
расстоянию, равному четверти ребра. Другие металлы (литий,
натрии, калии, хром) имеют объемноцентрированную кубическую
решетку с одним атомом в каждом узле, элементарная ячейка
которой содержит два атома с приведенными координатами 0, 0,
V и 1/2, 1/2, 1/2 (рис. 2.11, б).
Такие моноатомные кристаллы, как кремний и германий,
имеют более сложную структуру типа алмаза. Их решетка хотя и
является гранецентрированной кубической, но элементарная ячей-
па, объем которой равен четырем объемам примитивной ячейки
содержит восемь атомов в положениях 0, 0, 0; 1/2. 1/2 0- 1/2 о’
V? ?/Л2,1/2; л1/4,1/4,1/4; 3/41 3/4’ 1/4; 3/4> 1/4> 3’/4; 1/4>’
d/4, б/4 (рис. 2.11, в, слева). Четыре последних положения по-
лучаются из четырех первых при трансляции на четверть диаго-
нали. Два атома, образующие базис, имеют, таким образом, ко-
ординаты 0, 0, 0 и 1/4, 1/4, 1/4. К такому же выводу приводит
рассмотрение ромбоэдрической примитивной ячейки, содержащей
два атома (рис. 2.11, в, справа).
Если базис состоит из двух различных атомов, то структура
кристалла совпадает со структурой цинковой обманки (ZnS) или
арсенида галлия (GaAs).
В качестве другого примера двухатомного соединения укажем
хлористый цезий, кристаллизующийся в простой кубической ре-
шетке, базис которой включает один ион С!-1 в вершине куба
(0, 0, 0) и ион Cs+ в центре (1/2, 1/2, 1/2).
§ 2.3. Симметрия направлений кристаллов
Периодичность кристаллической среды можно выявить только
измерениями в масштабе параметров ячейки (нескольких ангст-
рем), например, с помощью дифракции рентгеновских лучей.
С макроскопической точки зрения элементарные трансляции ре-
шетки бесконечно малы, так что ее периодичность непосредствен-
но не влияет на физические свойства кристалла, вследствие чего
кристалл можно рассматривать как непрерывную, но вместе с
тем анизотропную среду. Анизотропия кристаллов не является
полной, поскольку для произвольного направления могут суще-
ствовать эквивалентные направления, вдоль которых макроскопи-
ческие свойства кристалла одинаковы. Совокупность операций
симметрии, которые переводят кристалл в положение, макроско-
пически неотличимое от первоначального, составляет симметрию
направлений кристалла, или точечную симметрию. Термин «то-
чечная» связан с тем, что, если не учитывать трансляции, пре-
образования симметрии сохраняют неподвижной, по крайней мере,
одну точку.
Точечная симметрия кристалла может быть определена через
симметрию совокупности нормалей к естественным граням, ори-
ентация которых связана с физическими свойствами кристалла и,
в том числе, с его формой. Основываясь на том, что набор этих
полубесконечиых нормалей остается неизменным для данного
типа кристаллов, можно установить все возможные классы сим-
метрии направлений для различных кристаллических состояний.
Однако мы будем следовать другим путем, пользуясь получен-
ными выше результатами по кристаллической структуре, а имен-
но; определив предварительно элементы точечной симметрии и
установив ряд полезных соотношений, мы рассмотрим’ в первую
очередь точечную симметрию решетки, а затем симметрию кри-
сталла. Периодичность решетки сокращает число возможных эле-
ментов симметрии и приводит к некоторым соотношениям между
ними, так что для решеток существует только семь групп сим-
метрии, каждая из которых определяет одну кристаллическую
систему. Так как симметрия различных решеток может совпадать,
то Бравэ вывел четырнадцать способов размещения точек в
пространстве. Симметрия кристалла (решетка + базис), не превы-
шающая симметрии решетки, получается, если исключить некото-
рые ..элементы класса симметрии решетки. Найденные 32 класса
симметрии направлений кристаллов естественным образом укла-
дываются в семь кристаллических систем.
5 Э. Дьелесан, Д. Руайе
66
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
2.3.1. Операции точечной симметрии. Определения. Существу-
ют два типа элементов симметрии.
1. Элементы прямой симметрии, которые сводятся к осям сим-
метрии. (Используются также термины «поворотные оси» и «оси
вращения».) Кристалл обладает осью симметрии Ап порядка п
(п —целое число), если поворот вокруг этой оси на угол 2л/п
переводит его в положение, неотличимое от исходного.
2. Элементы инверсионной симметрии, которые делятся на
центр симметрии и инверсионные (зеркально-поворотные) оси.
Центр симметрии С соответствует инверсии, или преобразованию
симметрии относительно точки, тогда как наличие инверсионной
оси Ап порядка п означает, что поворот кристалла вокруг этой
оси на угол 2л/п с последующей инверсией относительно некото-
рой точки оси переводит кристалл в положение, неотличимое от
исходного. Последовательность этих двух операций, обозначаемая
точкой, коммутативна: Ап = Ап С = С • Ап.
Симметрия относительно плоскости — это частный случай ин-
версионной оси. Из рис. 2.12 следует, что инверсионная ось вто-
рого порядка эквивалентна плоскости симметрии, или зеркальной
Рис. 2.12. Инверсионная
ось второго порядка (Л2)
еквивалентна перпендику-
лярной плоскости симмет-
рии М.
Тис. 2.13. Стереографическая проекция.
а) Треугольники SOp и SPN подобны:
Sp/2R = R/SP. Стереографическая проек-
ция представляет собой инверсию относи-
тельно сферы радиуса V2fl, так как Sp X
X SP = 2Й5. б) Прямая D изображается
проекциями точек, dt и d2, ее пересечений
со сферой. Плоскость М изображается дву-
мя дугами окружностей, и гп^.
плоскости М, перпендикулярной оси в точке инверсии, т. е.
Аг = М.
Аналогично, центр симметрии эквивалентен инверсионной оси
первого порядка, т. е. X — С.
Стереографическая проекция. Для установления более слож-
ных соотношений между элементами точечной симметрии удобно
пользоваться кристаллографическими проекциями на плоскость,
например, стереографической проекцией (рис. 2.13, а), которая
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
67
отображает точки сферы радиуса R на экваториальную плоскость
Е при помощи инверсии относительно сферы радиуса R12 с
центрами в южном полюсе S для точек северной полусферы и
в северном полюсе N для точек южной полусферы. Благодаря
замене центров инверсии все точки проектируются внутри эква-
ториального круга. Как всякая инверсия, стереографическая
проекция сохраняет углы, т. е. проекции двух кривых, проведен-
ных на сфере и пересекающихся в некоторой точке С под углом а,
пересекаются в проекции точки С под тем же углом а. Проек-
ции точек северной полусферы и Ькватора обозначаются крести-
ком (X), проекции точек южной полусферы — точкой с кружком
(®). Прямая изображается проекциями точек, в которых она пе-
ресекается со сферой; плоскость, проходящая через центр, про-
ектируется в виде двух дуг окружности, симметричных относи-
тельно линии пересечения этой плоскости с экваториальным
кругом (рис. 2.13, б). На стереограмме, отображающей свойства
точечной симметрии, ось север — юг, как правило, совмещается
с осью симметрии наивысшего порядка и центр сферы помеща-
ется в центр симметрии; все построения делаются пунктиром,
сплошными линиями изображаются только проекции.
Соотношения эквивалентности. Начнем с соотношений, вклю-
чающих один элемент инверсионной симметрии.
а) Инверсионная ось порядка п (п — нечетное') эквивалентна
оси симметрии порядка п и центру симметрии.
Действительно, последовательность п операций инверсионной
симметрии
(J„)n = (Л„ • С) • (4П С)... (4Я • С) - (4П)П Сп
также является операцией симметрии кристалла. Кроме того,
(4„)я =7 (Z — тождественная операция) и, следовательно,
(Дп)п = Сп. Эта операция сводится к одной инверсии, если п —
нечетно (n = 2p +1):
Сп = Cip • С = С {С2р = 1).
Соотношение (Л’2₽+1)2р+* = С устанавливает наличие центра сим-
метрии. С другой стороны, совокупность операций
J„.C = 4n.Ci = 4n
тождественна оси симметрии. Таким образом, инверсионная ось
нечетного порядка эквивалентна сочетанию оси симметрии и
центра симметрии, т. е. 42p+i ^Д2Р+1С.
Стереограмма 2.14, а иллюстрирует это свойство для случая
п = 3.
Замечание. В записи Д2Р+1С оба элемента предполагаются
независимыми, тогда как в записи А„ == Ап • С точка обозначает
последовательность двух операций.
5*
68
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
б) Инверсионная ось порядка п (и -— четкое) порождает кол-
линеарную ось симметрии порядка п/2.
Действительно,
(Я»)2 = (4„.С) .(4n-C)==(4„)\
Если п — 2р, (Лп)2 соответствует повороту на угол 2 • 2л/2р =
= 2л/р, откуда следует, что (Л2Р)г = Лв. На рис. 2.14, б показан
случай п = 4.
Рис. 2.14. Свойства инверсионных осей.
Положения точек рг, рз, являющихся отображениями исходной точки р;,
показывают справедливость следующих утверждений: а) инверсионная ось
третьего порядка эквивалентна оси симметрии третьего порядка и центру
симметрии, б) инверсионная ось четвертого порядка содержит ось симмет-
рии второго порядка, в) инверсионная ось шестого порядка эквивалентна
оси симметрии третьего порядка и перпендикулярной ей плоскости сим-
метрии.
в) Если, кроме того, р = п/2 — нечетное число, то существует
плоскость симметрии, перпендикулярная оси.
Поскольку р нечетно, Ср = С и операция
(Л2в)’ = (Л2в?-С” = Л2-С = Лг
тождественна отражению в перпендикулярной плоскости М.
Так как предыдущее свойство б) остается в силе, то при
нечетном р А2р ня
Черта в правой части тождества указывает на то, что плос-
кость симметрии перпендикулярна оси. Свойство в) иллюстриру-
ется стереограммой 2.14, в для случая п = 6.
На рисунках оси принято обозначать следующими символами:
а) оси симметрии:
Порядок | 2 J 4 6
Символ |о Д □ О
б) инверсионные оси:
Пг.ровок I / зев
Символ IО А 0 О
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
69
В символах инверсионных осей отражены полученные выше ре-
зультаты. Если добавить инверсионную ось второго порядка,
эквивалентную перпендикулярной плоскости симметрии, символы
осей становятся символами элементов симметрии кристаллов
(§ 2.3, раздел 2.3.2).
Наличие в кристалле нескольких элементов симметрии в об-
щем случае приводит к появлению других элементов. Рассмотрим
некоторые из наиболее часто встречающихся примеров.
г) Ось симметрии порядка п (п-— четное) и центр симметрии
порождают плоскость симметрии, перпендикулярную оси.
Это свойство сразу следует из преобразования
(А2,)>-С = А2'С = А2^М
и кратко записывается в виде 42РС -> С.
д) Ось симметрии порядка п и перпендикулярная ей ось вто-
рого порядка порождают п перпендикулярных осей второго по-
рядка, образующих между собой угол п/п.
Пусть точки р2 и рз являются отображениями исходной точки
Pi соответственно при повороте вокруг оси второго порядка А2
и при повороте на угол 2л/п (рис. 2.15). Точка р3 получается из
р2 при повороте вокруг оси второго порядка А2, образующей
угол л/n с осью А2. При повторном применении операции Ап по-
лучается п осей второго порядка.
Рис. 2.15. Сочетание оси второго порядка и оси симметрии порядка п порож-
дает п осей второго порядка.
а) Если п нечетно, все оси второго порядка эквивалентны, б) если п четно,
оси эквивалентны через одну.
Если ось Ап имеет нечетный порядок (п = 2р + 1), то две пос-
ледовательные оси второго порядка переходят одна в другую при
повороте (4П)Р на угол р • 2л/п — л — Л/п. Все эти эквивалент-
ные оси обозначаются одним символом: Аг. Таким образом,
42р+142 -> Л.2р+1 (2р + 1) 42.
Напротив, если п — четное (п=2р), угол л — 2л/л=(р — 1)2л/п
кратен 2л/п, так что оси второго порядка эквивалентны только
70
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
через одну. Они объединяются в две группы по р элементов каж-
дая и, следовательно,
А2 -> 42рр42р42.
На рис. 2.15, а, б показано отмеченное различие осей второго
порядка для случаев п = 3 и п = 4.
е) Ось симметрии порядка п и плоскость симметрии, проходя-
Рис. 2.16. Ось симметрии, по-
рядка п и плоскость сим-
метрии, проходящая через
згу ось, порождают п плос-
костей симметрии.
щая через эту ось, порождают п пло-
скостей симметрии, образующих меж-
ду собой угол л/п.
Доказательство аналогично доказа-
тельству предыдущего свойства
(рис. 2.16). Таким же образом можно
показать, что для нечетного п все пло-
скости симметрии эквивалентны и, сле-
довательно, 42P+iJf' -*• 42Р+1(2р + 1W'.
Для четного п существуют плоскости
симметрии двух типов, М" и М", так
что АгрМ' -> АгррМ'рМ".
ж) Инверсионная ось порядка п
(п — нечетное') и ось второго порядка порождают п эквивалент-
ных осей второго порядка и п плоскостей симметрии, перпен-
дикулярных этим осям.
Это утверждение следует из
свойств а), д) и г):
42p+i42 si 42р+1С42
(2р-Ц)<
->л2р+1 (2р + 1)ЛГ с.
2.3.2. Точечная симметрия
решеток. Вследствие периодич-
ности решетки могут существо-
Рис. 2.17. Всякая прямая, проходя-
щая через узел и параллельная а)
оси симметрии или б) инверсионной
оси порядка п,- является соответст-
венно осью симметрии или инверси-
онной осью.
4?
6)
вать только оси симметрии оп-
ределенного порядка. Это по-
зволяет легко найти все классы
симметрии решеток.
Элементы симметрии ре-
шетки. Периодичность решет-
ки влечет за собой определенные свойства симметрии.
а) Всякая прямая, параллельная оси симметрии порядка п и
проведенная через узел, является осью симметрии тозо же
порядка.
Действительно, при повороте на угол 2л/п вокруг оси симмет-
рии 4П узел Р переходит в N (рис. 2.17, а). Ось Ап в которую
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИИ КРИСТАЛЛОВ
переходит ось Ап при трансляции на вектор NP, может быть также
получена поворотом оси Ап на угол 2л/п вокруг узла Р. Таким
образом, через произвольный узел Р проходит ось симметрии по-
рядка п.
Это свойство справедливо и для инверсионных осей
(рис. 2.17, б). В частности, всякая плоскость, параллельная плос-
кости симметрии решетки и проведенная через узел, является
плоскостью симметрии.
Рис. 2.18. Ось симметрии,
проходящая через узел, сов-
падает с рядом решетки.
Рис. 2.19. Ось симметрии по-
рядка п > 2 порождает п
перпендикулярных осей
второго порядка.
б) Всякая ось симметрии, проходящая через узел, совпадает с
рядом решетки. Обозначим через Nt, N2, ..., N„ узлы решетки,
гомологичные узлу при повороте на угол 2л/п вокруг оси Ап
(рис. 2.18). Вектор решетки
R = 2 PNi или R = пРО + £ А
i=l i=l
параллелен оси Ап, так как У ON—0. Таким образом, Ап явля-
ется рядом решетки.
в) Всякий узел решетки является центром симметрии.
г) Ось симметрии порядка п>2 порождает п перпендикуляр-
ных осей второго порядка.
Пусть вектор ОР, соединяет два узла решетки (рис. 2.19);
поворот на угол 2л/и вокруг оси Ап, проходящей через узел О,
переводит узел Р, в Р2. Преобразование симметрии относительно
точки О переводит узел Р, в Р, и Рг в Р4. Узлы Pt, Р2 и Р*, Ps
переходят друг в друга при повороте на угол л вокруг ряда ОС,
параллельного PJPt. Если А и В — узлы, ближайшие к узлу О
72
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
на оси, то элементарная ячейка, образованная узлами О, В, Р3
и Р4, получается из ячейки, построенной на векторах О A, OPi и
ОР2, при повороте на угол л вокруг ОС. Таким образом, направ-
ление ОС совпадает с осью второго порядка решетки.
д) Решетка может обладать осями симметрии только первого,
второго, третьего, четвертого и шестого порядков.
Рассмотрим вновь рис. 2.18, предполагая теперь, что исходный
узел Ni расположен на расстоянии a = NaN3 от оси, равном пе-
риоду ряда N2Na, Поскольку векторы А^АГ* и N2N3 параллельны,
то длина отрезка кратна периоду N2Na ряда, имеющего то
же направление, т. е. NiNa = pN2Na, где р — целое число. Это
соотношение записывается также в виде
+ ВД + ММ = pAW
или, после скалярного умножения на N2Na,
aa(2cos^4-l) = pa2,
так как (2V27V3, — .(А^А^, ^з^з) = a2cos^.
Значения n должны удовлетворять уравнению
2cos^ + 1 = р, р — целое число.
Поскольку' значения косинуса находятся в промежутке между
—1 и +1, целое число р может принимать только пять значений:
—1, 0, 1, 2, 3, которым соответствуют значения п, равные 1, 2,
3, 4, 6. Полученный результат применим, очевидно, к инверсион-
ным осям. Действительно, благодаря тому, что каждый узел яв-
ляется центром симметрии, порядок расположения узлов М,
N2, ..., Nn на окружности сохраняется и для случая инверсион-
ной оси.
Семь кристаллических систем. Рассмотрим группы точечной
симметрии, совместимые с периодичностью решетки.
Самая простая из них содержит только центр симметрии С.
Присоединение к центру симметрии оси симметрии второго
порядка приводит к появлению плоскости симметрии М, перпен-
дикулярной этой оси, и симметрия решетки записывается в. виде
' МС'
Решетка может обладать тремя ^взаимно перпендикулярными
осями второго порядка Ла, А2 и А2 и центром симметрии. Со-
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
73
летание этих элементов симметрии порождает три плоскости сим-
метрии Л/, М' и М", перпендикулярные осям:
Другие комбинации осей второго порядка невозможны.
Решетка, обладающая осью А,, при наличии центра симмет-
рии с необходимостью содержит три оси Л2 и три плоскости
симметрии М', так что ее симметрия записывается в виде
Если решетка обладает осью Л4, то оси второго порядка по-
парно эквивалентны:
М 2М'2М"Ъ’
Наличие оси 4в приводит к появлению осей второго порядка,
объединенных по три:
£в 34^34;
М ЗМ' ЗМ" °*
Шестью перечисленными сочетаниями элементов точечной
симметрии исчерпываются все возможные типы симметрии ре-
шеток, обладающих не более чем одной
осью высшего порядка (п>2). Можно
показать, что для решеток, обладающих
несколькими осями высшего порядка,
существует только одна комбинация
элементов, симметрии, соответствующая
полной симметрии куба (рис. 2,20)
и содержащая четыре оси Л3, направ-
ленные вдоль диагоналей куба, три
оси Л4, перпендикулярные граням,
шесть осей А 2, соединяющих середины
противоположных ребер, и центр сим-
метрии, порождающий плоскости сим-
метрии, перпендикулярные осям Л4 и
А2. Таким образом, симметрия кубиче-
ской решетки записывается в виде
ЗЛ4
ЗМ
4Лз ЗМ'
С.
Исходя из представления о точечной симметрии решетки
кристалла, можно определить семь кристаллических систем, по-
лагая, что решетки всех кристаллов, принадлежащих к одной
74
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
кристаллической системе, имеют одинаковую точечную сим-
метрию, соответствующую одной из семи рассмотренных выше
групп.
Кристаллическая система характеризуется геометрической
формой ячейки, которая порождает все решетки с одной и той
же симметрией. Форма ячеек изменяется от параллелепипеда
самого общего вида (триклинная система) до куба (кубическая
система). В промежуточных случаях ячейка представляет собой
прямую призму с произвольным основанием (моноклинная систе-
ма), прямоугольный параллелепипед (ромбическая система),
ромбоэдр с гранями в виде шести одинаковых ромбов (тригональ-
ная система), прямую призму с квадратом в основании (тетра-
гональная система) и прямую призму с основанием в виде ромба,
имеющего угол у = 120” (гексагональная система). На рис. 2.21
приводятся данные, относящиеся к семи кристаллическим систе-
мам: точечная симметрия решетки, форма ячейки, углы а, 0, 7
между ребрами ячейки, длины а, Ь, с этих ребер.
Решетки Бравэ. В общем случае несколько типов решеток
имеют одинаковую точечную симметрию, так что к одной
кристаллической системе могут относиться кристаллы с различ-
ными решетками. Кроме семи решеток, называемых примитив-
ными (В), которые имеют в качестве ячейки параллелепипед из
числа изображенных на рис. 2.21, существуют другие типы ре-
шеток, полученные добавлением узлов в ячейку. Поскольку все
узлы решетки должны находиться в одинаковом окружении, до-
полнительные узлы можно помещать только в центр ячейки или
граней. В самом деле, для того чтобы составлять решетку, распре-
деление точек в вершинах (4) ячейки и внутри нее (В) должно
быть инвариантным относительно трансляции на вектор, соеди-
няющий два произвольных узла. Для трансляций вида АА или
ВВ это всегда так, независимо от положения узла В в ячейке.
Кроме того, точка Bt, полученная из Во при трансляции на век-
тор А0Ва, соединяющий вершину 40 с внутренним узлом Во,
должна совпасть с одной из вершин ячейки (рис. 2.22).
Если Bt при трансляции совмещается с А1г узел Во находится
в центре ячейки, в результате получается объемноцентрированная
решетка (Z). Для того чтобы узел В, совпал с одной из вершин
А2, А4, Аг, узел Во должен находиться в центре" одной из граней
ячейки. Такое расположение узлов приводит к базоцентрирован-
ной решетке (С), с узлами в центрах двух противоположных
граней примитивной ячейки. Размещение точек в пространстве,
при котором узел Во находится в середине ребра (точка В, при
трансляции совмещается с одной из точек 4S, Ав, 4?), не пред-
ставляет интереса, так как приводит к примитивной решетке,
длина ребра которой в два раза меньше длины ребра исходной
решетки.
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
75
Система Симметрия Ячейка Углы Ребра
триклинная с lS a+6*c
моноклинная ~МС .0 a=y-90° fl>90° 0*6 *c
ромбическая Ч г М М’ М" «-/3-y-90° o*b*c
тригональная (ромбоэдрическая) ЗА, ala/ai/ a=fi~p*90° o-6^c
тетрагональная (кбабратнаяч Аь 2А2 2А2 М 2М' 2М" i a-=fi^-9C° wb*c
гексаганальная 4 ЗА23£ м зм' зм" 6 a^SO” ^720° u=b*c
кубическая ^Аь.. 6А'г г ЗМ 6М' 6 a^b*c
Рис. 2.21. Сель кристаллических систем.
76
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Размещение точек, полученное при центрировании всех граней
примитивной ячейки, можно рассматривать как две решетки С,
узлы которых на рис. 2.23 обозначены по-разному (черные и бе-
лые кружки). Поскольку эти две решетки совмещаются при
трансляции на вектор АВ, равный половине диагонали одной из
граней, то возникающая при их наложении гранецентрированная
Рис. 2.23. Гранецентрированная
решетка (F).
Решетку, полученную при цент-
рировании всех граней прими-
тивной ячейки, можно предста-
вить в виде двух решеток типа С,
узлы которых, обозначенные чер-
ными и белыми кружками, пере-
ходят друг в друга при трансля-
ции на вектор АВ.
Рис. 2.22. Построение новой ре-
шетки на основе примитивной.
Дополнительный узел Ва должен
располагаться в центре ячейки
или какой-либо грани для того,
чтобы структура была инвариант-
ной относительно трансляции на
вектор ЛоДо-
решетка (F) так же, как и предыдущие, является производной от
примитивной решетки.
На рис. 2.24 изображены 14 решеток Бравэ. Три решетки,
получаемые из примитивной, I, С и F, содержатся не во всех
кристаллических системах, так как некоторые из них можно све-
сти к решеткам другого типа. Так, например, решетки I, С и F
триклинной системы сводятся к примитивным решеткам с мень-
шей по размеру триклинной ячейкой.
В моноклинной системе различают только примитивную ре-
шетку (Р) и решетку с двумя центрированными прямоугольными
гранями (С), так как решетка с центрированными косоугольными
гранями сводится к моноклинной решетке Р 'с меньшим углом
р (рис. 2.25, а), а решетки I и F фактически представляют собой
решетку С (рис. 2.25, бив).
В то же время все ромбические решетки Р, I, С и F различны
между собой. В тригональной системе имеется только одна при-
митивная решетка Бравэ, ее часто обозначают R (ромбоэдриче-
ская). Действительно, с одной стороны, решетка I является ре-
шеткой R с меньшей ячейкой (рис. 2.26, а), с другой стороны, не
существует решетки С, так как вследствие эквивалентности
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
77
шести граней ромбоэдра необходимо центрировать их все, а это
снова приводит к решетке R с меньшей ячейкой (рис. 2.26,6).
У кристаллов тетрагональной симметрии есть только два воз-
можных типа решеток, Р и I. В самом деле, решетку С можно
получить только при центрировании квадратов в основании, так
триннинная 1 ноненлинная - : Э
/ лиан ttr с 44- ,U- F -
тригональная Р или ''Р те > ’трогоиалбно/ > Л 7 /
генсагональная li ирбиивсиан 1
Рис. 2.24. Четырнадцать решеток Бравэ.
как четыре остальные прямоугольные грани эквивалентны между
собой. Однако из рис. 2.27, а видно, что в этом случае решетка
сводится к тетрагональной решетке Р с меньшей ячейкой. Ана-
логично решетка F сводится к тетрагональной решетке I
(рис. 2.27, б). Единственная гексагональная решетка принадлежит
к типу Р, так как решетки I, С и F не обладают осью симметрии
шестого порядка.
78
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Кубическая система включает три решетки Р, I и F. Решетка
С не может существовать, поскольку, чтобы сохранить симметрию
системы, надо центрировать все шесть граней куба.
л б'' б)
Рис. 2.25. Моноклинная система.
а) Решетка с центрированными косоугольными гранями сводится к моно-
клинной решетке Р с ячейкой ABCDEFGH-, б) решетка I представляет со-
бой моноклинную решетку С с ячейкой ABCDIJKL-, в) решетка F сводится
к моноклинной решетке С с ячейкой ABCDEFGH.
Четырнадцать решеток Бравэ представляют всё способы раз-
мещения в пространстве бесконечного множества гомологичных
точек.
2.3.3. Классы точечной симметрии кристаллов. При присоеди-
нении группы атомов (базиса) к каждому узлу решетки симмет-
рия кристаллической структуры может только уменьшиться,
вследствие чего симметрия кристалла не превышает симметрию
решетки. Таким образом, в отличие от решеток, кристалл не
обладает с необходимостью ни центром симметрии, ни п осями
Рис. 2.27. Тетрагональная система.
а) Решетка С сводится к решетке Р с
меньшей ячейкой; б) решетка F экви-
валентна решетке I.
Рис. 2.26. Тригональная система.
В тригональной системе сущест-
вует только одна примитивная
решетка.
второго порядка, появляющимися из-за наличия оси вращения
порядка га >2. Классы симметрии направлений кристаллов ка-
кой-либо системы выводятся из соответствующего класса решетки
при последовательном исключении этих элементов. Классы сим-
метрии кристаллов всех систем приведены на рис. 2.28, где пере-
§ 2.3. СИММЕТРИЯ НАПРАВЛЕНИЙ КРИСТАЛЛОВ
79
Рис. 2.28. 32 класса точечной симметрии кристаллов.
80 ГЛ. 2, ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
числены элементы симметрии (вверху), указаны их стереографи-
ческая проекция и обозначения по Герману — Могену (внизу).
Первая колонка объединяет семь классов решеток, определенных
в разделе 2.3.2. Кристаллы, обладающие той же точечной сим-
метрией, что и их решетка, называются голоэдрическими. Клас-
сы, обладающие вдвое и вчетверо меиыпим числом преобразова-
ний симметрии, называются соответственно геми- и. тетардоэдри-
ческими.
Класс без элементов симметрии, полученный исключением
центра симметрии из триклинного голоэдрического класса (1),
обозначается 1.
При исключении центра симметрии из класса моноклинных
решеток 2/т (симметрия ^2С) сохраняется либо ось второго
порядка — класс 2, либо плоскость симметрии — класс т.
Тем же способом из ромбического голоэдрического класса
^2 ^2
ттт с симметрией д/дрдр’С’ получается класс 222, в кото-
ром сохранены три оси второго порядка А2, А^, А[, или класс
2тт, в котором имеются ось 42 и две плоскости симметрии М'
и М", проходящие через эту ось.
Из тригонального класса с симметрией решетки
с одной стороны, при исключении центра симметрии можно вы-
вести класс 32 с симметрией Л3ЗЛ2 и класс Зиг с симметрией
ЛзЗАГ, с другой стороны, при исключении трех осей второго
порядка, а следовательно, и трех плоскостей симметрии М', мож-
но получить класс 3 (симметрия 48С' = 4Гз), а при исключении
С — класс 3 с симметрией 43.
Исключение центра симметрии из классов тетрагональных
А 24' 24" „ А 24' 24"
решеток с симметрией С или ~ С при-
водит
к трем новым классам, в которых, кроме оси высшего поряд-
ка, сохраняются следующие элементы симметрии:
а) все оси второго порядка — класс 422 с симметрией
А42А^2А^
б) все плоскости симметрии — класс 4игтп с симметрией
АК2М'2М"\
в) поочередно ось второго порядка и плоскость симметрии —
класс 42 m с симметрией At2A[2M",
а также к двум классам 4 и 4 с симметрией Л4 и X, в кото-
рых исключены все перечисленные выше элементы. Единствен-
§ 2.4. ПРОСТРАНСТВЕННАЯ СИММЕТРИЯ
81
ный тетрагональный класс, обладающий центром симметрии,
обозначается 4/т и имеет симметрию С.
Семь классов гексагональной симметрии получаются аналогич-
ным образом.
Симметрия куба 4Л3 С или ~ 443 С при ис-
ключении центра симметрии_приводит к двум классам: 432 (сим-
метрия 3444Л3642) и 43m (ЗЛ4 4A,6M'). Минимальная симметрия,
совместимая с четырьмя осями третьего порядка, характер-
ными для кубической системы, имеет' вид ЗЛг4Л3 (класс 23).
Добавление центра симметрии С ведет к появлению плоскостей
симметрии М, перпендикулярных осям второго порядка. Соответ-
ствующий класс с симметрией ЬА3С обозначается m3.
Каждая кристаллическая система характеризуется наличием
определенных элементов симметрии:
триклинная
моноклинная
ромбическая
тригональная
тетрагональная
гексагональная
кубическая
одна ось симметрии первого порядка
одна ось симметрии второго порядка
три оси симметрии второго порядка
одна ось симметрии третьего порядка
одна ось симметрии четвертого порядка
одна ось симметрии шестого порядка
три оси симметрии второго порядка и
четыре оси симметрии третьего порядка.
В тех случаях, когда характер оси не уточняется, она может
быть как осью симметрии, так и инверсионной осью.
Рассмотренные 32 класса (рис. 2.28) охватывают все много-
образие кристаллов, причем среди естественных и искусственных
кристаллов можно найти представителей каждого класса.
Поскольку кристаллы анизотропны по отношению к большей
части физических свойств, определение физических констант
имеет смысл, только если задано положение координатных осей
относительно элементов симметрии. Мы пользуемся для всех
классов системой трех ортогональных осей, показанных вверху
справа на рис. 2.28, при этом принятое в кристаллографии обо-
значение осей X, Y, Z заменяется на ж1? ж2. xt, более удобное
для тензорного описания.
§ 2.4. Пространственная симметрия
Рассмотренные 32 класса точечной симметрии относятся ис-
ключительно к симметрии макроскопических свойств кристалла.
Полное описание симметрии кристаллической среды требует вве-
6 Э. Дьелесан. Д. Руайе
82
ГЛ, 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
дения неточечных операций симметрии, совмещающих кристал-
лическую структуру саму с собой. Элементами этой пространст-
венной симметрии кристаллической структуры являются винто-
вые оси 4n.t, соответствующие вращению на угол 2л/п, сопро-
вождающемуся трансляцией, т. е. переносом на вектор t вдоль
оси и плоскости скользящего отражения Mt, соответствующие
операции симметрии относительно плоскости М с последующей
трансляцией на вектор t в этой плоскости.
Сочетание инверсионных осей с трансляциями не приводит к
новым типам элементов симметрии.
2.4.1. Винтовые оси. Порядок п винтовой оси может прини-
мать значения 2, 3, 4 и 6, поскольку винтовая ось не отличается
от простой оси симметрии в точечной симметрии. Результат
действия п операций Ап, t дает трансляцию на вектор nt, парал-
лельный оси. Для того чтобы кристаллическая структура совпала
сама с собой, вектор nt должен быть кратным периоду Ru»w ряда
[w, v, ш], параллельного оси, и, следовательно,
t — пъ — целое.
Можно выбрать t < RUVw, т. е. т< п, при этом векторы транс-
ляций равны
t0 = 0, tj = — RUw, t2 = — Rurw, ..., t n= —-— Rurw.
Символы винтовых осей пространственной симметрии кристал-
лов даны ниже, рядом с сокращенным обозначением nm:
2 0 2Д
ЗА 3,Д з2Д
«□ ^з-tr
ff5^
Так, например, 4t обозначает поворот на угол 2л/4, сопровож-
дающийся трансляцией на вектор R/4 вдоль оси (рис. 2.29).
На рис. 2.30 изображена структура типа алмаза (германий, крем-
ний), в которой есть винтовые оси четвертого порядка.
2.4.2. Плоскость скользящего отражения. Трансляция на век-
тор 2t является результатом двух операций Mt и должна при-
водить к трансляции плоской сетки параллельно плоскости М,
таким образом, что
2t = гвд + т2а2,
где а, и а2 —векторы основных трансляций в этой плоской сетке
§ 2.5. ПРИМЕРЫ КРИСТАЛЛИЧЕСКИХ СТРУКТУР
83
и mt, тпг — целые числа. Поскольку трансляция бесконечной
кристаллической структуры на вектор щ или а2 не приводит ни
Рис. 2.29. Четыре винтовые оси четвер- Рис. 2.30. Винтовые оси
того порядка. структуры алмаза.
значения 0 и 1, и, следовательно, возможны трансляции на
векторы
t 0, t = -jj-ai, t = уа2, t = (aj 4- а2).
На рис. 2.31 показан пример плоскости скользящего отражения.
Рис. 2.31. Плоскость скользя-
щего отражения.
Вектор трансляции t равен по-
ловине периода а.
!
2.4.3. Пространственные группы. Рассмотрев возможные ва-
рианты сочетаний кристаллических решеток всех систем с вин-
товыми осями различных порядков и плоскостями скользящего
отражения, ПТенфлис и Федоров показали, что кристаллические
структуры можно разделить на 230 пространственных групп.
§ 2.5. Примеры кристаллических структур
При описании структуры материалов, используемых на прак-
тике, часто встречается понятие плотнейшей упаковки, поэтому
нам представляется полезным рассмотреть два способа укладки
плотных слоев, состоящих из одинаковых шаров.
2.5. 1. Плотнейшие упаковки. Первый слой соприкасающихся
шаров с центрами в точках А укладывается так, как показано
на рис. 2.32, а центры шаров второго слоя располагаются над
промежутками В первого слоя. Для третьего слоя имеются две
6*
84
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
возможности в зависимости от того, помещаются ли промежутки
этого слоя над точками С или точками А. В первом случае слои
— чередуются с периодом АВС.
\ Такая структура, называемая
L ) плотнейшей кубической, приво-
Дит к кубической гранецентри-
Г д’у' ‘г-Гб'кие рованнной ячейке (рис. 2.33, б),
) _/ „ ось третьего порядка которой
перпендикулярна плоскости
рис. 2.33, а. Второй случай —
правильная последовательность
Рис. 2.32. Плотнейшая упаковка оди- ^ВАВ.. • приводит к плот-
нейшей гексагональной струк-
туре из двойных гексагональ-
наковых шаров.
ных ячеек (рис. 2.34). Отношение длин ребер равно с/а = 2У2/3 «
« 1,633 (упр. 2.11).
Читатель может сам попробовать уложить шарики (или тен-
нисные мячики) этими двумя способами. Самое трудное — это
помешать шарикам раскатиться.
Рис. 2.33. Плотнейшая кубическая структура.
а) Упаковка АВС и сечение кубической ячейки, перпендикулярное диаго-
нали куба; б) ячейка г. ц. к. решетки, полученная при такой упаковке.
‘В центре куба и в серединах ребер имеются октаэдрические полости,
а на расстояниях от вершин, равных 1/4 диагонали куба, имеются тетраэд-
рические полости.
При плотнейшей упаковке между слоями остается два рода
полостей. Тетраэдрическая полость образуется, если на три сопри-
касающихся шара положить четвертый шар. Октаэдрическая по-
лость, расположенная в центре октаэдра, образуется тремя смеж-
ными шарами одного слоя и тремя ближайшими шарами следую-
щего слоя. В некоторых кристаллах атомы одного сорта плотно
упакованы, тогда как атомы другого сорта заполняют полости.
2.5. 2. Структура некоторых часто используемых веществ.
Перед тем как описывать свойства материалов, используемых
§ 2.5. ПРИМЕРЫ КРИСТАЛЛИЧЕСКИХ СТРУКТУР
85
в акустике, напомним, что в общем случае вещество может су-
ществовать в нескольких кристаллических модификациях в за-
висимости от температуры и условий кристаллизации. Эти моди-
фикации называются аллотропными. Физические свойства твер-
дого тела могут изменяться в широких пределах при неизменной
химической формуле. Например, в зависимости от того, ниже или
выше его температура некоторой критической величины, такой
Рис. 2.34. Плотнейшая гексагональная структура.
а) Упаковка АВАВ... шаров и гексагональная ячейка; б) двойная гекса-
гональная ячейка. Отношение с/а = 2|2/3 = 1,633.
материал является или не является пьезоэлектриком. Укажем,
что из 32 кристаллических классов пьезоэффект разрешен толь-
ко в 20. (Подробное рассмотрение пьезоэлектричества, т. е. воз-
никновения поляризации при деформации, проводится в гл. 6.)
Среди этих 20 классов, для которых общим является отсутствие
центра-симметрии, в 10 классах возможны пироэлектрические
явления (упр. 3.4). Кристаллы этих 10 классов полярны, т. е.
могут обладать спонтанной электрической поляризацией. В обыч-
ных условиях спонтанная поляризация не наблюдается, так как
она компенсируется перераспределением свободных зарядов
внутри и на поверхности кристалла, но при изменении темпера-
туры эта компенсация нарушается, поскольку величина диполь-
ного момента зависит от температуры. В этом случае поляриза-
ция пироэлектриков приводит к возникновению тока во внешней
цепи. Если направление поляризации зависит (например, может
измениться на противоположное) от внешнего электрического
поля, то пироэлектрический кристалл называется сегнетоэлектри-
ком. Для зависимости поляризации сегнетоэлектриков от элект-
рического поля характерна петля гистерезиса. При температуре,
превышающей определенную величину (температуру Кюри),
спонтанная поляризация исчезает. В таком параэлектрическом
состоянии поляризация кристаллов линейно зависит от электри-
ческого. поля. Диэлектрическая проницаемость этих веществ,
часто имеющая большую величину, очень чувствительна, особен-
но в окрестности точки Кюри, к любому внешнему воздействию
86
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
(термическому, механическому). Различие в поведении таких ве-
ществ объясняется изменением кристаллической структуры в
точке Кюри. Структура параэлектрической фазы более симметрич-
на, чем структура сегнетоэлектрической фазы. Укажем в качест-
ве примера, что титанат бария (BaTiOs), один из наиболее изу-
ченных сегнетоэлектрических материалов, кристаллизуется в ку-
бической структуре (тпЗтп) при температуре Т > 120 °C. При
уменьшении температуры ячейка деформируется, переходя по-
следовательно в тетрагональную (10tfC< Т< 120 “О, ромбичес-
кую (—70вС< Т< 10 °C) и затем в ромбоэдрическую (Г <—70 °C).
Сегнетоэлектрические материалы можно разделить на две
группы в соответствии с их химическим строением [1]. В первой
группе сегнетоэлектричество обусловлено водородной связью
(сегнетова соль, или двойная натриево-калиевая соль винной
кислоты, дигидрофосфаты калия (КН2РО4) и других щелочных
металлов). Во второй группе сегнетоэлектрические свойства
связаны с искажением основной структуры кислородных октаэд-
ров. К этой группе принадлежат BaTiO, (титанат бария),
LiNbOs (ниобат лития), LiTaOs (танталат лития). Пьезоэлектри-
ческие свойства ниобата лития широко используются в акустике,
поэтому мы детально рассмотрим его структуру. Однако предва-
рительно мы приведем данные о строении сульфида кадмия
(CdS), пьезополупроводника, который применяется для изуче-
ния взаимодействия электронов с упругими волнами, окиси
цинка (ZnO), используемой для пленочных преобразователей,
корунда (А12О3), который благодаря небольшому коэффициенту
затухания ультразвука и невысокой стоимости применяется в
качестве высокочастотных звукопроводов (/>1000 МГц), и квар-
ца, широкое использование которого связано, главным образом,
с тем, что его свойства слабо меняются с температурой.
Сульфид кадмия (CdS). Окись цинка (ZnO). Сульфид кадмия
и окись цинка кристаллизуются в гексагональной системе с сим-
метрией 6mm. Параметры гексагональной ячейки
CdS: а = 4,13 А, с = 6,69 А, с/а = 1,62;
ZnO: а = 3,24 А, с = 5,19 А, с/а = 1,60
В обоих случаях величина отношения с/а очень близка к со-
ответствующей величине для идеальной плотно упакованной
гексагональной структуры (1,61). Анионы (сера, кислород) обра-
зуют плотнейшую упаковку, половина тетраэдрических полостей
которой занята катионами (кадмий, цинк), имеющими прибли-
зительно в два раза меньший диаметр. Такая структура типа
вюрцита изображена на рис. 2.35. Винтовая ось шестого порядка
является полярной.
§ 2.5. ПРИМЕРЫ КРИСТАЛЛИЧЕСКИХ СТРУКТУР
87
Корунд (А120з). Корунд, или окись алюминия, кристаллизу-
ется в тригональной системе с точечной симметрией Зтп. Атомы
кислорода образуют плотнейшую упаковку типа АВАВ... Атомы
алюминия занимают две из трех октаэдрических полостей,
Рис. 2.35. Структура типа вюрци-
та (CdS, ZnO).
Рис. 2.36. Структура корунда.
Атомы алюминия (•) распола-
гаются между слоями кислорода
АВАВ...
расположенных между слоями А и В в соответствии с формулой
А12О3 (рис. 2.36). Направление, перпендикулярное плоскостям,
образованным ионами кислорода, является осью третьего поряд-
ка, и ромбоэдрическая ячейка имеет следующие параметры: а =
= 3,51 А, а = 85'46'.
Кварц (SiO2). Двуокись кремния существует как в кристал-
лическом виде (кварц, тридимит, кристобалит), так и в аморфном
виде (кварцевое стекло). Кроме того, каждая кристаллическая
Рис. 2.37. Структура а-кварца.
Связанные вершинами тетраэдры
SiO4 располагаются вдоль вин-(+)
товой оси третьего порядка (30,
перпендикулярной плоскости ри-
сунка. Индексы в кружках ука-
зывают положение атомов по
вертикали вдоль ребра с, длина
которого принята за единицу.
Атомы кремния находятся в по-
ложениях 0, 1/3, 2/3, атомы кисло-
рода — в положениях и, и' =
= »+1/3, и? = в+ 2/3 и v, о', (7)
v". Из рентгенографических дан-vi/
ных следует, что и = 0,11 и v =
= 0,22 [2].
Кислород
Кремний
форма обладает двумя аллотропными модификациями аир.
Тригональный а-кварц стабилен при температуре ниже 573 °C,
тогда как гексагональный p-кварц стабилен в диапазоне темпе-
ратур от 573’С до 870'С. Наибольший интерес представляет
а-кварц, так как он является пьезоэлектриком. Точечная сим-
метрия кристаллов а-кварца, принадлежащих к классу 32, не
88
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
содержит плоскости симметрии, поэтому а-кварц встречается в
двух энантиоморфных формах: правовращающей (правый а-кварц)
и левовращающей (левый а-кварц). Оптическая ось а-кварца
совпадает с осью третьего порядка (Z), три оси второго порядка
(X), перпендикулярные ребрам прямой гексагональной призмы,
являются полярными (электрические оси). Представление о
структуре а-кварца дает рис. 2.37, изображающий проекцию
атомов Si и О на плоскость, пер-
пендикулярную винтовой оси Z
(t = c/3).
Ниобат лития (LiNbOs). Танта-
лит лития (LiTaO3). Титанат ба-
рия (BaTiOs). Ниобат лития при-
надлежит к классу 3m. Ромбоэд-
рическая ячейка (а = 5,492 А, а =
= 55°53') содержит две молекулы
LiNbOs. Как уже отмечалось, нио-
бат лития является сегнетоэлект-
риком, и основу его структуры
составляют кислородные октаэд-
ры. Как и в корунде, ионы кисло-
рода образуют плотную гексаго-
нальную упаковку [3] и две из
трех октаэдрических полостей за-
няты ионами металлов (Li и Nb).
Если знаком 0 обозначить не-
занятую полость, то последовательность заполнения пустот вдоль
оси третьего порядка имеет вид: Nb, Li, 0, Nb, Li, 0, Nb, ...
(рис. 2.38). Поскольку ионы ниобия и лития имеют существенно
различные диаметры, остов октаэдров деформируется и катионы
смещаются из центров полостей.
Рис. 2.39. Структура перовски-
та АВО3.
Ион В находится в центре ок-
таэдра, образованного шестью
ионами кислорода. Каждый
октаэдр связан с другими все-
ми своими вершинами. Ионы
А занимают вершины куба,
содержащего октаэдр.
Другой подход к рассмотрению структуры LiNbOs состоит
в том, что за основу принимается структура перовскита, соответ-
ствующая параэлектрическому состоянию (Г > 1200 °C), в кото-
УПРАЖНЕНИЯ
89
рой ионы кислорода образуют остов из октаэдров. Представление
о строении кислородных октаэдров можно получить из рис. 2.33, б,
если не принимать во внимание ионы, расположенные в верши-
нах куба (рис. 2.39). Большие по размеру ионы металлов (А)
соединения ABOS занимают вершины куба, находящиеся между
двумя октаэдрами, а меньшие по размеру ионы (В) помещаются
в центре октаэдров. Точечная симметрия соответствует симмет-
рии куба игЗтп. Структура сегнетоэлектрического состояния при
комнатной температуре получается при искажении параэлектри-
ческой структуры. В случае ниобата литий ионы металлов (А =
= Li, В = Nb) смещаются, создавая поляризацию вдоль выделен-
ного направления и понижая симметрию до Зт. Подобное рас-
смотрение применимо также к BaTiOs и KNbO3, но для BaTiO3 *),
имеющего при комнатной температуре симметрию 4тт, искаже-
ние структуры перовскита происходит вдоль оси А4, а для KNbO3,
имеющего симметрию 2тт,— вдоль оси Л2.
Кристаллы танталата лития (LiTaO3) имеют такую же струк-
туру, как и кристаллы LiNbO3, только ионы Nb заменяются иона-
ми Та. Параметры ромбоэдрической ячейки равны: а = 5,47 А и
а = 56°10'.
Упражнения
2.1. Чему равны индексы Миллера, определяющие плоскости ACGE,
BDHF, EBD и_ряды AC, AG кубической решетки на рис. 2.40?
Ответ. (НО), (110), (111), [НО], [ill].
2.2. Показать, что объем кубической ячейки
гранецентрированной решетки в четыре раза
больше, чем объем примитивной ромбоэдриче-
ской ячейки.
Решение. Если принять ребро куба за
единицу и воспользоваться обозначениями на
рис. 2.9, б, то векторы основных трансляций, об-
разующие ромбоэдр, имеют следующие составля-
ющие:
Рис. 2.40.
а(1/2, 1/2, 0), Ь(1/2, 0, 1/2), с(0, 1/2, 1/2)
и, следовательно, V = |а[Ъс] | = 1/4.
2.3. Найти плотность алюминия А127, кристал-
лизующегося в гранецентрированной решетке
с ребром а = 4,04 А. Число Авогадро N =
=6,023-Ю23 моль-1.
Решение. Поскольку в ячейке с объемом а3 содержится 4 атома, то
р = 4Ж/,Уа3 = 2,72 103 кг/м3.
2.4. Ионы Са2+ в кристаллах флюорита (Ca40Fj9) образуют гранецент?
рировапную решетку с ребром а = 5,45 А. Найти плотность флюорита.
*) Титанат бария изготавливается чаще всего в виде керамики, так как
рост монокристаллов очень сложен.
90
ГЛ. 2. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Решение. Учитывая, что кубическая ячейка содержит четыре моле-
кулы, получаем р = 3,20 • 10® кг/м®.
2.5. Найти расстояние между плоскостями (100), (110), (111) для трех
кубических решеток. Какая плоскость в каждом случае имеет наибольшую
плотность узлов?
Решение. Для примитивной кубической решетки
<lioo = о, <1но = oV2/2, du1! = «УЗ/З.
Для объемноцентрированной кубической решетки
<?юо = °/2, <11 ю — аУ2/2, <1щ = аУЗ/6.
Для гранецентрированной кубической решетки
<lioo в а/2, <1цо = «V2/4, <1ш = ауЗ/З.
Наибольшую плотность узлов имеют плоскости, находящиеся на максималь-
ном расстоянии друг от друга. Индексы этих плоскостей подчеркнуты.
2.6. Найти угол а ромбоэдрической ячейки гранецентрированиой ре-
шетки.
Решение. Из скалярного произведения а • b получаем а = 60°.
2.7. Какой вид имеет уравнение семейства плоскостей (hkl) в системе
координат xyz, оси которой совпадают с векторами основных трансляций
а, Ь, с?
Решение. Координатные оси пересекаются n-й плоскостью семейства
в точках А (жп = na/h, 0, 0), В (0, уп = nb/k, 0), С (0, 0, zn = пс/1), считая
от начала координат. Следовательно, уравнение этой плоскости имеет вид
2.8. Чему равно расстояние между двумя соседними плоскостями се-
мейства (hkl) в кубической решетке?
Решение. В соответствии с результатом предыдущего упражнения
уравнение первой плоскости имеет вид
hx + ку + lz = а.
Следовательно, ее расстояние от начала координат равно
2.9. Найти объем V ячейки как функцию параметров а, Ь, с и углов а =
= (Ь,“7), р = (аТс), ч = (afb). Использовать выражение
Iaa ab ас I
ba bb be I
са cb сс 1
для представления V в виде V = abcF(a, Р, "f). Определить F(a, ₽, у) для
каждой кристаллической системы,
Решение.
Ie2 ab cos у ас cos 01 | 1 cos у cos Р|
ab cos у 62 be cos а == а*&2с® cos у 1 cos cd
ас cos р be cos а с2 I | cos р cos а 1 |
УПРАЖНЕНИЯ
91
Отсюда получаем
V = obey 1 + 2 cos <х cos р cos 7 — cos2 а — cos2 fl — cos2 4 = abcF(a, p, 7).
Триклинная система: F = yi + 2 cos a cos P cos у — cos2 a — cos2p — cos2y.
Моноклинная система: F = sin p.
Ромбическая, тетрагональная, кубическая системы: F = 1.
Тригональная система; F — У1 + 2 cos3 a — 3 cos2 a.
Гексагональная система: F = У 3/2.
2.10. К какому классу точечной симметрии относится пряпильный
тетраэдр?
Решение. На рис. 2.41 показаны четыре беи третьего порядка, пер-
пендикулярные граням, три инверсионные оси четвертого порядка, перпен-
дикулярные противоположным ребрам, и шесть плоскостей симметрии.
Таким образом, точечная симметрия правиль-
ного_ тетраэдра соответствует симметрии клас-
са 43m кубической системы.
2.11. Найти отношение с/а гексагональной
ячейки с упаковкой АВАВ (рис. 2.34, б).
Решение. Три шара А и один шар В
образуют тетраэдр с ребром а = 2г высотой
2гУ2/3 = с/2, откуда с/а = 2У2/3 = 1,633.
2.12. Чему равен фактор заполнения fr (от-
ношение объема, занятого шарами, к общему
объему) двух структур с плотнейшей упаковкой?
Решение. Для упаковки АВС (рис. 2.33)
между длиной ребра а кубической решетки_ и
радиусом г шаров существует соотношение а}'2 =
=4г. Так как ячейка содержит четыре шара, то
Рис. 2.41. Элементы сим-
метрии правильного тет-
раэдра.
/ = _J-------= _£L_ = 0,74.
(21/2"г)® 31/2
В случае упаковки АВАВ гексагональная ячейка, объем которой V =
= са2УЗ/2 = 8У2 г3, содержит два шара. Тогда
f =_____-__ =--------= и,/Ч.
8V2 г3 31/2
Нет ничего удивительного в том, что факторы заполнения одинаковы,
поскольку обе структуры построены из соприкасающихся шаров.
2.13. Чему равно число тетраэдрических и октаэдрических полостей, при-
ходящихся на одну кубическую ячейку с плотнейшей упаковкой ABCt
Решение. На рис. 2.33, б видны 8 тетраэдрических полостей (по од-
ной у каждой вершины) и 4 октаэдрические полости (одна в центре куба
и 12 в серединах ребер, общих для четырех кубиков).
ГЛАВА 3
ТЕНЗОРНОЕ ПРЕДСТАВЛЕНИЕ
ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
В предыдущей главе кристаллическая структура рассматри-
валась как результат пространственных трансляций, заданных
тремя элементарными векторами, совокупности атомов, или ба-
зиса. Такая трехмерная периодическая структура обладает опре-
деленными элементами макроскопической симметрии, в соответ-
ствии с которыми все кристаллы можно разделить на 32 класса.
Из общих соображений ясно, что физические и химические свой-
ства кристаллов зависят как от вида атомов, так и от их взаим-
ного расположения, т. е. от симметрии. Кристаллы, принадлежа-
щие к одному классу точечной симметрии, одинаково ведут себя
по отношению к одинаково направленным внешним воздействи-
ям, независимо от природы атомов, составляющих базис. Эта
особенность кристаллов лучше всего раскрывается при тензор-
ном подходе к описанию физических свойств кристаллических
веществ. Напомним, что понятие тензора было введено в конце
XIX в. У. Фойгтом при определении механических напряжений
в твердом теле (слово «тензор» происходит от «tension» — на-
пряжение). В тензорном анализе физические величины класси-
фицируются согласно законам преобразования их компонент
при изменении системы координат. В тех случаях, когда преоб-
разование системы координат Соответствует операции симметрии
кристалла, из тождественности макроскопических свойств крис-
талла в обеих системах следуют соотношения между компонен-
тами тензоров, характеризующих эти физические свойства, и в
связи с этим происходит уменьшение числа независимых ком-
понент. В качестве примера мы воспользуемся ниже тензором
диэлектрической проницаемости второго ранга. Более сложные
случаи тензоров третьего и четвертого рангов обсуждаются в
гл. 6 и 4, посвященных пьезоэлектричеству и статической упру-
гости. Поскольку в дальнейшем нам придется находить собствен-
ные значения и собственные векторы тензоров второго ранга,
напомним некоторые основные положения тензорного анализа.
§ 3.1. ВНЕШНЕЕ ВОЗДЕЙСТВИЕ И РЕАКЦИЯ КРИСТАЛЛА
93
§ 3.1. Связь между внешним воздействием
и реакцией кристалла
Рис. 3.1. Связь между
внешним воздействием
и реакцией кристалла.
В анизотропной среде
векторы воздействия 3?
и реакции <S (3?) на него
кристалла в общем слу-
чае не параллельны. Ог-
раничиваясь первыми
членами в разложении
& (S) (линейное при-
ближение), можно полу-
чить между 8 и 3? сле-
дующие соотношения:
S1 = ЛнЗ*! + Л12^Л
й’г =
Понятие тензора возникает при установлении линейных
соотношений между внешним воздействием и реакцией на него
в анизотропных средах. В общем случае некоторое воздействие,
приложенное к кристаллу вдоль одного направления, вызывает
ответную реакцию в другом направлении (рис. 3.1). Например,
в диэлектрической среде электрическое а
поле создает поляризацию в направлении, ' г
не совпадающем с направлением поля.
Если причина S’ и следствие S явля-
ются векторными величинами, то наибо-
лее общее линейное соотношение между
компонентами <£г, <S3 следствия и ком-
понентами 3?2, S?3 причины в одной
и той же системе координат приводит
к появлению коэффициентов Ац:
Я^А^ + А^ + А^,
&2=А213\ +А 22^2 + А 33S3,
S,3 = A3iSl + A33S3 + A33S3
или в сокращенной записи
= I, 7 = 1, 2,3.
По повторяющемуся (немому) индексу j
подразумевается суммирование от 1 до 3
(правило Эйнштейна). Девять компонент
AiS образуют тензор второго ранга. Для
единообразия вектор, например или
St, принято называть тензором первого ранга, а скаляр, напри-
мер температуру,— тензором нулевого ранга.
Тензоры S’t или и тензор A(j имеют различную природу.
Тензоры S, или обозначают физические величины, тогда как
тензор AiS характеризует вещество, поскольку он описывает
векторную реакцию кристалла на векторное воздействие St.
Скалярная величина (температура, энергия) представляется тен-
зором нулевого ранга, векторная величина (напряженность
электрического поля, сила) — тензором первого ранга, более слож-
ные величины (деформации, напряжения) — тензорами второго
ранга. Физические свойства кристаллов описываются тензорами
разного ранга: нулевого (теплоемкость), первого (пироэлектри-
чество), второго (диэлектрическая проницаемость, электропро-
водность, тепловое расширение), третьего (пьезоэлектричество),
четвертого (упругость)... Например, связь между индукцией й
94
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
напряженностью электрического поля
Di = &цЕ}
(3.1)
определяет тензор диэлектрической проницаемости ей.
Однако для характеристики данного физического свойства
недостаточно ввести девять компонент Aif, необходимо дополни-
тельно задать систему координат, относительно которой опреде-
ляются компоненты тензора, так как в другой системе эти ком-
поненты принимают новые значения Ау. Поскольку оба набора
этих значений характеризуют одно физическое свойство, не за-
висящее от выбора системы отсчета, то, следовательно, между
ними существует соотношение, связанное с преобразованием
координатных осей. В § 3.3 дается определение тензоров через
законы преобразования их компонент, но предварительно в
§ 3.2 рассматривается матричное представление преобразования
координат.
§ 3.2. Преобразование ортогональной системы координат
Преобразование системы координат полностью определяется
девятью коэффициентами а,, которые входят в соотношения,
выражающие новые базисные векторы е1? е2, е3 через старые
векторы е4, е2, es:
е< = a<eft (3.2)
(подразумевается суммирование по немому индексу к).
Коэффициенты а* образуют матрицу а, в которой строка с
номером I составлена из компонент а?, определяющих вектор е
в базисе е»:
(а1 4 ai\
4 <4 “И-
«в а| а|/
Обратное соотношение позволяет с помощью элементов Р1
матрицы р записать базисные векторы е» через векторы е,-:
е& = (3.3)
Связь между коэффициентами pi и а? получается при под-
становке е* в уравнение (3.2): = a^Piej. Использование сим-
вола Кронекера (6Ч = О, если i¥=j, и 6« = 1, если ( = /) при-
§ 3.2. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ КООРДИНАТ
95
водит к выражению е, = буе^, откуда
(а?₽Г-бу) ej = 0. (3.4)
Векторы линейно независимы, так как они образуют базис,
следовательно, все коэффициенты в уравнении (3.4) должны рав-
няться нулю и
= бу. (3.5)
Из правил перемножения матриц следует, что матрица р яв-
ляется обратной по отношению к матрице преобразования коор-
динат а. Решение системы (3.5) приводит к следующему виду
компонент
где Afj —минор определителя 1а| матрицы а, полученный вы-
черкиванием /-Й строки и А-го столбца.
В дальнейшем будут использоваться только системы коорди-
нат с ортонормированным базисом, т. е. е,е; — бу и efte; = б/,/.
В этом случае обратная матрица р просто связана с матрицей
а. Действительно, первое скалярное произведение записывается
с помощью соотношений о' = и ej = ajei в виде а|а)(е^ег) =
=б{/ или, так как efee; = бы, = бу. Сравнение этого соот-
ношения с формулой (3.5) показывает, что Рь = а|-
Таким образом, матрица £, обратная по отношению к матри-
це а преобразования системы координат с ортонормированным
базисом, получается, если поменять местами строки и столбцы
матрицы а (транспонированная матрица а‘). Матрица а, для
которой обратная матрица совпадает с транспонированной, на-
зывается ортогональной.
Пусть хк — координаты точки М, т. к. компоненты вектора
х = ОМ, в базисе ек и xi — координаты той же точки в базисе
е,, тогда х = — х^. Заменяя еЛ выражением (3.3), получаем
х = оъ&е,- = Xie'i.
Поскольку разложение вектора по базисным векторам одно-
значно, то новые координаты х{ выражаются через старые с
помощью соотношения хг = Рл, сходного в случае ортогональ-
ных систем координат (₽£ = а<) с соотношением (3.2):
х{ = aUk- (3.6)
96 ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
§ 3.3. Определение тензоров
Физические величины различаются в зависимости от того,
как они меняются при преобразовании системы координат. Мы
ограничимся только системами отсчета с ортоиормироваиным
базисом, для которых законы преобразования координат точки
(3.6) и базисных векторов (3.2) одинаковы. Введем следующие
определения.
а) Скаляр — это величина, не зависящая от выбора системы
отсчета, инвариант, или тензор нулевого ранга. Инвариантность
скалярной функции координат /(ж,, ж2, ж2) выражается ра-
венством
/(ж17ж2, х3) = /(ж^, Ж2, Жд).
Примеры инвариантов: температура, энергия, электростати-
ческий потенциал.
б) Любая совокупность трех величин А<, преобразующихся
при изменении системы координат как базисные векторы е{, яв-
ляется тензором первого ранга, или вектором: А} = aiAk.
Примеры векторов: компоненты любого вектора, заданного
в пространстве трех базисных векторов е;, составляют тензор
первого ранга (ср. с (3.6)). Три производные dj/dx, составляют
вектор, называемый градиентом скалярной функции /(ж{). Дейст-
вительно, составляющие градиента в новой системе координат
df = df
dx^ ^xk дх[
выражаются через компоненты df/dxh в старой системе с по-
мощью коэффициентов dxh/dx-t. Обращая соотношение (3.6), по-
лучаем xh = РйЖ1 = а<x'i, так что компоненты градиента преобра-
зуются по закону
в) Набор девяти величин А.(], преобразующихся как произве-
дение составляющих двух векторов, образует тензор второго
ранга: = а*а}Аы.
Эти девять компонент записываются в виде таблицы, заклю-
ченной в квадратные скобки, чтобы можно было отличать ее от
матрицы преобразования а:
[Л11 Л12 Л13 "I
Л21 Л22 Л23 I.
Л31 Л32 Л3з]
Несмотря на внешнее сходство, матрицы и тензоры абсолютно
различны по смыслу, так как компоненты устанавливают
§ 3.3. ОПРЕДЕЛЕНИЕ ТЕНЗОРОВ
97
связь между двумя системами координат, в то время как тензор
И,у представляет собой физическую (или математическую) вели-
чину, задаваемую в одной системе координат девятью числами.
Пример тензора второго ранга: производные дА^дхк состав-
ляющих вектора (доказательство аналогично доказательству,
примененному к градиенту).
На основе тензора А.{} можно составить инвариант, суммируя
его диагональные компоненты. Получающуюся при этом вели-
чину 4и + 422 + 432 называют следом тензора и кратко записы-
вают в виде А.«, подразумевая суммирование по повторяющемуся
индексу. При преобразовании ортогональйой системы координат
след тензора не меняется, т. е.А'ц — а<а{4йг = Ац, так как
а?а’ = Sfei.B частном случае тензора вида = его след, т. е.
инвариант А{ВЛ, равен скалярному произведению векторов At и
Bj. Свертка тензора А;А{ = C4i)2 + (42)2 + С43)2 = А2 дает квад-
рат длины вектора А{.
г) Определение легко обобщить. Тензором ранга г называется
совокупность Зг составляющих, имеющих г индексов, которые
при изменении координат преобразуются по следующему закону:
А...ць... = • • • а’а™а™ ... A..jmn.... (3.7)
Операция составления следа тензора второго ранга является
частным случаем свертки по индексам, поскольку величины
4..„да... (по повторяющемуся индексу j проводится суммирова-
ние), полученные из компонент тензора 4...w... ранга г, обра-
зуют тензор ранга г — 2. Действительно, при изменении коорди-
нат компоненты преобразуются по закону:
Х.уя... = • a?a”afa? ... 4...mnpg....
или, так как a”af = 8пР,
A,..iiii... — •, • di ...
Следующее правило часто бывает полезным для установле-
ния тензорного характера величин: линейное соотношение между
тензором А.„о... ранга пг и тензором В..м... ранга п определяет
тензор ранга тп + п
А.~ С..я1м..В..м... (3.8)
Доказательство. При преобразовании системы координат
A...pq... = • • • OipfXq . . . (3.9)
В..м...= (3.10)
поскольку при переходе от новых координат к старым исполь-
зуется обратная матрица р. Подставляя (3.10) в (3.8) и (3.8)
7 Э. Дьелесан, Д. Руайе
93
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
в (3.9) и используя соотношение К = а*, получаем
А'..Рд... = (... аХа?“з • • С...цы..,) В'...т
Множитель в скобках —это не что иное, как С...Р5Г8..., следо-
вательно, величины C...w... преобразуются как компоненты тен-
зора ранга m + п, т. е.
С...pqrs... — • • apag«ras ... С ...цм...'
Дополнение. Символ Кронекера бу представляет собой тензор
второго ранга, так как At = ЬцА}.
Модули упругости сам, связывающие тензор напряжений Ту
с тензором деформаций Sht, образуют тензор четвертого ранга:
Ту = Сум^ы.
§ 3.4. Ограничения, налагаемые симметрией кристаллов
на число независимых компонент тензоров
Пусть Л.„ул...— компоненты тензора, выражающего некоторое
физическое свойство кристалла, в системе координат xlt х2, ха и
A...ijk... — компоненты этого тензора в той же системе координат
для новой ориентации кристалла, полученной после применения
операции (F. Чтобы выразить через A...Pqr..., отметим, что
ту же ориентацию кристалла относительно координатных осей
можно получить, применяя обратную операцию &~1 к системе ко-
ординат, оставляя при этом кристалл неподвижным (рис. 3.2).
Рис. 3.2. Эквивалентность поворота кристалла и преобравования координат,
а) начальное положение кристалла и осей координат; б) поворот кристал-
ла на угол ф вокруг оси ®з; в) поворот системы координат на угол —ф.
Следовательно, вводя матрицу а преобразования координат,
соответствующую операции (F-1, согласно (3.7) имеем:
Если 'З представляет собой одну из операций класса точечной
симметрии кристалла, то новая ориентация кристалла относитель-
§ 3.4. ОГРАНИЧЕНИЯ, НАЛАГАЕМЫЕ СИММЕТРИЕЙ
99
но системы отсчета х,, х2, х3 в макроскопическом смысле неот-
личима от исходной ориентации, что выражается равенством
Таким образом, инвариантность физических свойств по отно-
шению к определенным операциям симметрии ведет к соотно-
шениям
= • • • afa3?a£ ... A...pgr..., (3.11)
уменьшающим число независимых компонент тензоров. Посколь-
ку операция, обратная операции симм'етрии кристалла (& = Ап
или Ап), также является операцией симметрии ((F-1 = ^п-1), то
матрица а преобразования координат соответствует одной из
операций класса симметрии направлений кристалла.
3.4.1. Матрицы операций точечной симметрии кристаллов.
Элементами симметрии кристаллов могут быть оси симметрии,
инверсионные оси, плоскости симметрии и центр симметрии
(раздел 2.3.1). При повороте на угол <р вокруг оси х3 (рис. 3.3, а)
б>
Рис. 3.3. Поворот системы координат а) вокруг оси х3 и б) вокруг направ-
ления [111].
новые базисные векторые, выражаются через старые:
= (cos ф) ех -}- (sin ф) е2,
е2 = — (sin ф) er + (cos ф) е2,
ез = е3.
Матрица преобразования координат при повороте на угол ф
вокруг Яз, таким образом, имеет вид
cos ф sin ф
sin ф cos ф
(3.12)
7*
100
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
Матрица, соответствующая симметрии относительно точки,
принятой за начало координат, есть
41' 7 £)
Матрица преобразования координат при повороте на угол
2л/п с последующей инверсией получается из соотношения Ап =
Ох3,2Л/п = а^лп/п-ас.
Для плоскости симметрии, перпендикулярной оси х3, имеем
матрицу преобразования
/1 0 0 \
=u J-J
Поворот на угол 2л/3 (ось третьего порядка) вокруг диаго-
нали куба (направление [111]), построенного на трех базисных
векторах (рис. 3.3,6), приводит к циклической перестановке ко-
ординатных осей: ег е2, е2 = е3, е3 = е17 которая выражается
матрицей
/0 1 о \
“[1111.2Л/3 0 0 1 )•
\ 1 0 0 J
3.4.2. Роль центра симметрии. В случае операции инверсии
матрица а диагональна (а^ = — 6^), поэтому общее условие ин-
вариантности (3.11) сводится к виду:
~ - • • aittjOCft . - . ^4...ijft...,
или для тензора ранга п:
= (-l)M...(rt.„. (3.13)
Если п — нечетно, то (—1)” = —1, и из полученного соотноше-
ния следует равенство нулю всех компонент . тензора. Таким
образом, кристаллы, принадлежащие к одному из одиннадцати
центросимметричных классов, не могут обладать физическими
свойствами, которые выражаются тензорами нечетного ранга.
Сказанное, в частности, относится к пьезоэлектрическому эф-
фекту (п = 3).
Если ранг п — четный, то соотношение (3.13) не вносит ни-
чего нового. Наличие центра симметрии не оказывает никакого
влияния на физические свойства, выражаемые тензорами четного
ранга. Следовательно, исходя из этих свойств, невозможно опре-
§ 3.4. ОГРАНИЧЕНИЯ, НАЛАГАЕМЫЕ СИММЕТРИЕЙ
101
делить характер осей, т. е. невозможно определить, являются
они осями симметрии или инверсионными осями. Поэтому огра-
ничения, накладываемые на число независимых компонент тен-
зоров, минимальны в кристаллах, принадлежащих тем классам
кристаллической системы, в которых имеется одна или несколько
осей симметрии или инверсионных осей (раздел 2.3.3). Эти заме-
чания иллюстрируются на примере тензора диэлектрической
проницаемости.
3.4.3. Сокращение числа независимых компонент тензора
диэлектрической проницаемости. Из термодинамических сообра-
жений (аналогичных развитым в § 4.4 для тензора упругих мо-
дулей) следует, что тензор диэлектрической проницаемости, оп-
ределенный соотношением (3.1), симметричен, т. е. ,еу = еА. Ус-
ловие инвариантности (3.11) записывается в виде
Hij =aiajehi. (3.14)
Ранг тензора четный, поэтому для кристаллов триклинной
системы, обладающих, самое большее, центром симметрии, все
шесть компонент тензора остаются независимыми:
[еи е12 е1з1
®12 е22 е23 I.
613 ®23 e33j
Если принять, что ось х3 ортогональной системы координат
параллельна оси симметрии второго порядка или инверсионной
оси (эквивалентной плоскости симметрии) кристаллов моноклин
ной системы, то матрица преобразования системы координат при
повороте вокруг этих осей окажется диагональной:
/-1 0 0 \ / 1 0 О \
аА2цЖз= 0 -10 или ам±ж Jo 1 0 .
\ 0 0 1/ \ О О -1 /
Из условия (3.14) еу = следует, что компоненты тензора
с одним индексом 3 (a|af = — 1,если г=/=3) равны нулю, это сво-
дит число независимых компонент тензора моноклинной системы
к четырем:
Р11 е12 °1
1«у] = ®12 Е22 0 •
L0 0 м
Кристаллы ромбической системы имеют три перпендикуляр-
ные оси симметрии или инверсионные оси второго порядка, ко-
торые выбираются в качестве осей координат. Достаточно при-
менить проведенное выше рассуждение к каждой из осей, т. е.
102
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
к каждому индексу, чтобы заметить, что все недиагональные
элементы равны нулю:
Для кристаллов тригональной, тетрагональной и гексагональ-
ной систем ось Ап или Ап (п > 2) принимается за ось х3. Матри-
ца преобразования осей координат в этом случае дается выраже-
нием (3.12) с ф = 2л/тг<л. Применяя соотношение (3.14) к elS
и 823, получаем
е18 ~ ala^tl3 = «1813 + aie23, так как «1 = 0,
823 = — а^з + а|е23, так как а| = 0,
или
els( 1 — cos ф) — 823 sin ф = 0,
е13 sin ф + е23(1 — cos ф) = 0.
Поскольку ф не равно нулю, из этих выражений следует е13 =
в 823 = 0.
Для еи получаем
Bii =* «i«i£hj = «i«i (е12 -|- е21) -J- oticc|e11 aiafe22,
8lt sin2 ф — (е12 4- 82t) cos ф sin ф + е22 sin2 ф.
Разделив последнее равенство на зт2ф, имеем
8ц — 822 = (sl24-e2i) ctg ф. (3.15)
Аналогичные вычисления для 8t2 приводят к соотношению
8и — 822 = — (812 + е21) tg ф. (3.16)
Поскольку ф отличается от л, из (3.15) и (3.16) следует, что
8t2 + 82i = 0, 822 = 8ц и ,812 = — 82i = 0, так как тензор сим-
метричен.
Кристаллы тригональной, тетрагональной и гексагональной
систем обладают только двумя независимыми диэлектрическими
ПОСТОЯННЫМИ 8ц и 833:
Для кристаллов кубической системы, имеющих, по меньшей
мере, элементы симметрии 4А3 и ЗА2 (оси второго порядка при-
нимаются за оси координат), отличны от нуля только диагональ-
§ 3.5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ
103
ные элементы, как и для кристаллов ромбической системы.
Кроме того, поворот вокруг оси третьего порядка [111] приводит
к циклической перестановке индексов (1, 2, 3) (2, 3, 1), откуда
следует ен = е22 = е33 = ®, т. е. в кубической системе
[е 0 01
0 в 0 I
0 0 8 J
Кристалл кубической симметрии является изотропным ди-
электриком, для которого векторы индукции и напряженности
электрического поля коллинеарны, т. е. Df = eZ?«.
§ 3.5. Собственные векторы и собственные значения
тензора второго ранга
В линейном приближении решение большого числа физических
задач приводит к системе трех (или п) однородных линейных
уравнений (i = 1, 2, 3) с тремя (или п) неизвестными ut, и^, щ:
= (3.17)
где коэффициенты принимают вполне определенные зна-
чения. Для того чтобы эта система имела решение, отличное от
и, = иг = из = 0, необходимо, чтобы определитель, составленный
из коэффициентов Ci}, был равен нулю:
I С11 ^13 |
| Су | = ^21 С22 С28 _. о.
| Сз1 С32 Cgg j
Это равенство является условием совместности трех уравне-
ний (3.17). Примером однородной линейной системы могут слу-
жить уравнения для нахождения компонент и, собственных век-
торов и собственных значений X тензора Лд:
AtjUj = Xu$. (3.18)
Поскольку Ut = система преобразуется к виду, аналогичному
(3.17):
(Л.у-Х6«)и, = 0. (3.19)
Собственные значения X определяются из условия совмест-
ности
I ли х л12 л13 I
|Лу-Х6„|= Л21 Л3 = 0, (3.20)
I А31 А32 <433 ~|
которое приводит к уравнению 3-й степени относительно X так
104
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
называемому секулярному уравнению:
(Ли — Х)(Л2г — Х)С4зз X) Л-Л21Лз2Л18 + Л 12Л23Лз1 —
— (Л22 — Х)Л31Л is — (Л„ — Х)Л2зЛ32 — (Л33 — Х)Л1гЛ21 = 0.
В общем случае оно имеет три различных корня Х(,), Х(2) и
А(3>, которые называются собственными или главными значени-
ями тензора A(j. Каждому собственному значению Кт *) соответ-
ствуют компоненты i4ft) собственного вектора, которые удовлетво-
ряют трем связанным уравнениям:
Аци^ = X(ft)i4fe). (3.21)
В действительности величины полученные умножением
компонент собственного вектора на произвольный скаляр ц,
также являются компонентами собственного вектора с собствен-
ным значением кт, так что правильнее было бы говорить о соб-
ственных, или главных направлениях тензора.
Для составляющих А^ тензора в системе координат, базис
которой образован собственными векторами (преполагается, что
они нормированы, т. е. i4ft) = бу,), соотношение (3.21) принимает
вид Л#бл = X№)6,fi, или Аы = Таким образом, тензор в
представлении собственных векторов оказывается диагональным:
[Х<» 0 0 1
0 х<2> о I
о О х<8)
Нетрудно видеть, что след тензора, т. е. инвариант Л.«, равен
сумме собственных значений:
Л« = 2.(,> + 1(2»+1(*>. (3.22)
Если два собственных значения, например, Х'2> и Х(3) равны
между собой, то любая линейная комбинация компонент и|2) и
и<3> собственных векторов (щ = + Нзмг8)) также является
компонентой собственного вектора. Действительно, Аци, =
= |12Луи|2)+ р8Луи)3) или AijUj = Х(2) (|A2i42) + |T8i48)) = Х(2)щ.
Дважды вырожденному собственному значению соответствует
уже не одно направление, а главная плоскость, проходящая через
векторы п(2) и п(3).
*) Индекс к в взят в скобки, чтобы отличать его от индекса, обо-
значающего составляющие. Правило суммирования Эйнштейна не распро-
страняется на индексы в скобках.
§ 3.5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ 105
Симметричные тензоры. Докажем два фундаментальных свой-
ства симметричных тензоров с вещественными компонентами
(Л« = ЛД
1. Собственные значения тензоров вещественны.
2. Главные направления, соответствующие разным собствен-
ным значениям, ортогональны.
Первое свойство можно установить, рассматривая свертку
произведения обеих частей равенства (3.18) на компоненты век-
тора Ui:
u*AijUj = ки* щ* (3.23)
После перестановки немых индексов i и / это соотношение запи-
шется в виде Щ = Kui щ. Учитывая симметричность тензора
(Ац = Ац), получаем Uj Лущ = Zu, Поскольку компоненты тен-
зора вещественны, то комплексно сопряженное соотношение имеет
вид щАцщ = . Из сравнения полученного соотношения с
выражением (3.23) следует вещественность собственных значений
(Х = Х*).
Для доказательства второго свойства запишем уравнения для
компонент собственных векторов и и^:
Аци^ -- Х(1) Ui1’,
Лъ.ыр) = 1(2) и|2)
и составим в обоих случаях произведение i4ni42):
Луи^иГ
А^и^ - Л?>и?\
Почленно вычитая второе равенство из первого
А^>^ - - k(2)] ufW
и переставляя немые индексы i и / в первом члене
(Лд - Лу) и^и^> - [Х(1) -1(2)] и<№\
получаем, что скалярное произведение равно нулю, если
тензор симметричен (Л# = Лц) и собственные значения различны
(Х(,,-%(2>^=0).
Двум одинаковым собственным значениям соответствует глав-
ная плоскость, перпендикулярная третьему собственному векто-
ру. В этой плоскости всегда можно выбрать два ортогональных
вектора, так что во всех случаях главные направления симмет-
ричного тензора образуют ортогональный триэдр.
Отыскание собственных значений и собственных векторов
особенно просто в тех случаях, когда по крайней мере две из
106
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
трех недиагональных составляющих тензора, скажем, А13 и Л23,
равны нулю. Разложение определителя (3.20) по элементам
третьей строки или третьего столбца
— X)[(Ai — Х)(Лг2 — X) — (А 12)2] — 0
сразу позволяет найти корень Х<3) = Л33. Два других собствен-
ных значения X(i) и Л(2) являются решениями уравнения второй
степени
*№) = А1 + А2 _ /(422-A^+4(412)2, (3.24)
где к —1,2. Из системы (3.21)
[Ах - X(ft)] и™ + A12u2k) = 0,
4rf) + K-^)]>44 = 0,
[Л53-^>1^ = 0.
следует, что главное направление для собственного значения
X(S) — As совпадает с осью ж3, так чтои[3) = и23) = 0 и и(38) — про-
извольно. Для 4ВУХ других собственных значений из условия
¥* А33 (к == 1, 2) следует i4ft) = 0 и
UW ^)_ли
и<» ~ А2
Главные направления, лежащие в плоскости х,х2, задаются
углами и р2 — Pi + л/2, которые они образуют с осью х,:
и№> _________________
tg₽ft = j^ = «-(-1)" /а2+1,
где а=> (As —AJ/2A2. Для двойного угла справедливо выра-
жение
tg2|V
2[«-(-l)fe /а2+1]_
1 _ [а2 + а2 + 1— 2а(— 1)'! V а2 + 1]
Подставляя в него выражение для а, получаем соотношение
tg2₽ft =
(3.25)
которое позволяет определить оба главных направления, если
учесть два решения для угла 2$к, отличающиеся на л.
§ 3.6. ЭЛЕМЕНТЫ ПОВЕРХНОСТИ
107
§ 3.6. Тензорное представление элементов поверхности
В дальнейшем нам понадобится вычислять интегралы от
тензорных величин вдоль кривой на поверхности и в объеме.
В первом случае элементом интегрирования является вектор
dxs, и интеграл от тензора записывается как [ A..^.dx^
с
При интегрировании по поверхности роль бесконечно малого
элемента играет параллелограмм, построенный на векторах
dx(1) и dx<2). Площадь проекции этого«параллелограмма на ко-
ординатную плоскость xsxh равна
dsjk = dx^dx'h* — dx^dxj^.
Величины dsjt. образуют антисимметричный тензор второго ранга
1° dsi2 Чз1
- dsis 0 Чз ,
— <Чз -ds23 0 J
для обозначения трех независимых компонент которого вводится
индекс I, т. е. ds^ds^. Последовательность индексов i, /, к
должна получаться из чисел 1,2,3 четным числом парных пере-
становок:
ds1 = ds23 = г?«21)г?Жз2) — dx^dx™,
ds2 = ds31 dx^dx^ — dx^dx^,
ds3 = ds12 = dx^’dx^ — dx^dx^.
Правило преобразования тензоров (3.6) применимо к компо-
нентам dsn только при таких изменениях системы координат,
при которых сохраняется относительная ориентация координат-
ных осей, т. е. при поворотах. Если происходит инверсия осей
координат (при операциях симметрии относительно точки или
плоскости), в соотношении (3.6) следует поменять знак (упр. 3.5).
Псевдовектор, или аксиальный вектор ds представляет собой не
что иное, как векторное произведение двух векторов dx(1) и dx<2).
Согласно свойствам векторного произведения вектор ds => dx(i) X
Xdx<2> перпендикулярен плоскости, проходящей через dx(1) и
dx(2), и длина его равна площади параллелограмма ds. Следова-
тельно, вместо антисимметричного тензора dsih в качестве элемен-
та интегрирования берется псевдовектор ds. Вводя посредством
равенства ds = Ids единичный вектор I, нормальный к поверхно-
сти, для интеграла от тензора Л....... по поверхности $ получаем
f A^Jtds.
108
ГЛ. 3. ТЕНЗОРЫ ФИЗИЧЕСКИХ СВОЙСТВ КРИСТАЛЛОВ
Если поверхность s замкнута, этот интеграл с помощью тео-
ремы Грина преобразуется в интеграл по объему. Векторная
запись этой теоремы
J Ads = J (div A)dv
s V
в тензорных обозначениях приобретает вид
J Ajdsi = J Aikds = У dv,
где v — объем, ограниченный замкнутой поверхностью s. Для
тензора 4. произвольного ранга имеем:
У 4...г...lids = У—dv. (3.26)
Напомним, что
дА...г... дА.дА...2... дА...3...
fai ~~ fa~ । дх^ дх^ ’
Упражнения ®
3.1. Показать, что определитель ортогональной матрицы а равен ± 1.
Решение. Определитель обратной матрицы 0 — а* равен 1/|а|, от-
куда ]а|2= 1.
3.4 Записать матрицы поворота на угол ф вокруг осей хх и х2.
Решение.
3.3. Вектор v и единичный вектор и связаны соотношением v, = Ацщ,
причем = Какую поверхность описывает конец вектора v при вра-
щении вектора и?
Решение. Собственные значения симметричного тензора Ац дейст-
вительны, а главные направления ортогональны. Таким образом, используя
условие^ = 1, получаем
vi vl гз
i^r+K<iT + iW=1’
Конец вектра v описывает эллипсоид.
3.4. Вещество является пироэлектриком, если изменение температуры
ДИ вызывает электрическую поляризацию Р, = ргАО. В каких классах то-
чечной симметрии возможен пироэлектрический эффект?
Решение. Тензор пироэлектрических коэффициентов равен нулю
для_одиннадцати классов, обладающих центром симметрии: 1, 2/т, ттт,
3, 3m, 4/m, 4/ттт, 6/m, б/ттт, m3, тЗт. Для класса 1
Pi = [Pi Р2 Рз] -
УПРАЖНЕНИЯ
Наличие оси симметрии любого порядка, параллельной оси х3, приводит
к равенству pt = р2 — 0, а наличие плоскости симметрии, перпендикуляр-
ной оси х3, приводит к равенству нулю компоненты р3. Учитывая это, по-
лучаем
Pt = [р1 р2 0] для класса т,
pt = [0 0 р3] для классов 2, 3, 4, 6, 2тт, Зт, imm, 6mm
и pi = 0 для всех остальных классов.
Таким образом, пироэлектрический эффект может существовать только в де-
сяти классах, имеющих самое большее одну ось симметрии без перпенди-
кулярной плоскости симметрии.
3.5. Показать, что три независимые компоненты At = А23, А2 = Л31 и
Л3 — Л12 антисимметричного тензора Ац преобразуются как компоненты
вектора, если сохраняется взаимная ориентация осей о^Аюгональной сис-
темы координат.
Реше ние. Соотношение (3.7) Л^/г = a^arkAgr , перегруппировывая
члены Aqr и Лгд = — Адг, можно преобразовать к виду
АЛ = 5 (ajak-aiak)Agr-
q<r
Предположим, что j < к и q < г, тогда выражение М? — — а^а£
является минором определителя |а| матрицы a к-, р Ф q, г). Так
как, по определению, Л- =Л^, , то, если перестановка индексов г, ], к пред-
ставляет собой четную перестановку чисел 1. 2. 3.
А\ = (— П‘+1Л-,,, когда / < к,
Ар = (— 1)р+1Лдг, когда q < г.
Отсюда следует А[ = 2 (~ 1)г+рМ%Ар. Для ортогонального преобразова-
р
ния компоненты обратной матрицы имеют вид
. (- l)i+pMf
Рр—......|~а| =<•
Следовательно, Лг-= | а | (afЛ, фичем определитель |а| = ±1 в зависи-
мости от того, меняется или не меняется при изменении системы отсчета
взаимная ориентация координатных осей.
ГЛАВА 4
СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
В настоящей главе рассматриваются деформации и напряже-
ния в твердых телах и вводятся коэффициенты, характеризую-
щие их упругие свойства. Эти коэффициенты являются компо-
нентами тензора четвертого ранга, однако из-за симметрии тен-
зоров деформации и напряжения и ограничений, накладывае-
мых законами термодинамики, число компонент этого тензора
в любой среде не может превышать 21. Для описания упругих
свойств кристаллов триклинной системы необходимо максималь-
ное число коэффициентов (21); в других системах число этих
коэффициентов значительно сокращается благодаря симметрии
кристаллов, например, для кристаллов кубической системы су-
ществует всего три независимых коэффициента.
§ 4.1. Деформации
Начнем с простого случая растяжения стержня, а затем пе-
рейдем к общему случаю деформации твердых тел.
Рассмотрим упругий прямой стержень длиной L, конец О
которого жестко закреплен (рис. 4.1). Под действием растяги-
Рис. 4.1. Деформация стержня.
Под действием силы F стержень
удлиняется, при этом точки М и N,
отстоящие друг от друга на рассто-
янии Дж, смещаются на и (ж) и
и(ж-{-Дж) и переходят в положения
М' и N'. Деформация S в точке М-.
ы (ж + Дж) — ц (ж) du
й — .Ит Аж — dr.
вающей силы F, приложенной к свободному концу, стержень
удлиняется. Деформация сохраняется, пока действует сила рас-
тяжения. Относительное удлинение равно (Z/ — L)/L, где L’ —
§ 4.1. ДЕФОРМАЦИИ
111
длина стержня в деформированном состоянии*). Поскольку
в общем случае отдельные участки стержня деформируются по-
разному, то необходимо определять деформацию малого элемен-
та стержня, а затем, в пределе, деформацию вблизи какой-либо
точки.
Возьмем в качестве малого элемента участок MN стержня,
концы которого в недеформированном состоянии имеют коорди-
наты х и х + Дж. Под действием силы F точки М и N переходят
в положение М' и N' с координатами соответственно х + и(х) и
ж + Дж + и(ж + Дж). Относительное удлинение элемента MN при
этом равно
M'N' — MN u(x + &x) — u(x}
По определению, деформация S стержня в окрестности точ-
ки М с координатой ж равна пределу этого отношения при
стремлении Дж к нулю, иначе говоря, производной и по ж:
S = ^(£...±.^)-^). = (4.1)
Дх-*О Дг dx
Следует отметить, что деформация представляет собой без-
размерную величину, поэтому введение системы отсчета необхо-
димо только для того, чтобы задать положение точки, в которой
эта деформация рассматривается.
В примере со стержнем под действием силы точки могут
смещаться на разные расстояния, но только вдоль одного на-
правления, так что деформация сводится к удлинению, если не
принимать во внимание уменьшение диаметра. В общем случае
твердого тела произвольной формы нет никаких оснований для
того, чтобы две его точки, как бы близки они ни были, под дей-
ствием внешних сил смещались в одном направлении. Таким
образом, отдельные участки деформированного тела отклоняют-
ся от положений равновесия не только на разную величину, но
и под разными углами к направлению приложенной силы.
Рассмотрим произвольную точку среды, положение которой
определяется координатами ж,, ж2, ж3, т. е. проекциями радиус-
вектора х, проведенного из начала координат О в данную точку.
Под действием внешних сил все точки тела смещаются. В де-
формированном состоянии положение рассматриваемой точки
задается вектором х' с компонентами ж<, причем х' = х + и.
•) В действительности деформация не сводится только к удлинению
стержня, так как при растяжении уменьшается его диаметр. Относительное
изменение диаметра пропорционально относительному удлинению (упр.
112
ГП. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
то наряду с уменьшением
Рис. 4.2. Деформация твер-
дого тела.
Две близкие точки М и N
смещаются на разные рас-
стояния и в различных на-
правлениях.
Смещение и является непрерывной функцией координат xh.
Поскольку две бесконечно близкие точки М и N, разность ра-
диус-векторов которых первоначально равнялась вектору dx =
= хк — хм с компонентами dxt, смещаются на различные векто-
ры Ни И Ujv,
un = uM + du, du = dxi (4.2)
(по немому индексу i подразумевается суммирование от 1 до 3),
или увеличением расстояния между
точками происходит поворот отрезка
MN (рис. 4.2).
В деформированном состоянии
разность радиус-векторов точек М и
N равна dx' = x'N — хм = dx -1 du ,
и квадрат расстояния между этими
точками записывается в виде
(dx')2 = (dx)2 + 2(dx)(du) + (du)2.
Преобразуя скалярные произведе-
ния (dx')2 — (dx)2 = 2dXfdUi + duhduk
и заменяя компоненты du,-, duh их
выражениями из (4.2), получаем
(dx')2 - (dx)2 .=
_ du, ouk duh
= 2 -^7 dx'dxi + -^7 ~d^ dx'dxi-
(4.3)
Поскольку перестановка немых индексов i и j не изменяет сум-
мы, т. е.
dw, dUj
~dxidxj = —dxjdxi, (4.4)
то соотношение (4.3) записывается в симметризованной форме *)
(ди, ди, диь ди. \
-4 + -d^ + -4~4)dx^
или (dx')2— (dx)2 — 2S(jdxtdxj, где введено обозначение
♦) Из соотношения (4.4) следует, что антисимметричный тензор
Rii=[(duildXj) — (dUjldxi)]/2 не входит в выражение для изменения дли-
ны. Этот тензор определяет поворот тела, который не приводит к деформа-
ции, так что представление деформации симметричным тензором является
оправданным. Однако, в ряде случаев, например при рассмотрении фотоуп-
ругости, антисимметричный тензор следует учитывать (см. 8.3.2).
§ 4.1. ДЕФОРМАЦИИ
113
Девять величин S-ц образуют тензор второго ранга, так как
сумма 28^х$х}, равная разности квадратов длин отрезка MN
после и до деформации, представляет собой инвариант. Этот тен-
зор называется тензором деформаций.
Почти во всех рассматриваемых случаях деформации малы,
иначе говоря, мало относительное изменение расстояний в твер-
дом теле: dut/dxj С1. При этом условии в выражении (4.5)
можно пренебречь величиной второго порядка малости
{dujdx^i.dujdxi) по сравнению с членом первого порядка dujdx^
Тогда компоненты тензора деформаций принимают вид
=
1 7 (>u-r dUj \
~2 \~Sx7 + )•
(4.6)
Тензор Sa симметричен (Sy = Si(), поэтому из девяти его ком-
понент различны только шесть. Значение компонент зависит от
координат рассматриваемой точки М. Таким образом, состояние
деформированной среды описывается полем симметричных тен-
зоров второго ранга.
В каждой точке тензор Sy можно привести к главным осям
или собственным направлениям. Ориентация главных осей ме-
няется от точки к точке, но, поскольку тензор Stj симметричен,
то они остаются ортогональными между собой (§ 3.5).
В системе главных осей |2, Вз отличны от нуля только
диагональные составляющие тензора, равные собственным зна-
чениям S(1), S(2>, 8(а>. Тогда величина деформации определяется
выражениями
т. е. деформация сводится к трем независимым растяжениям
вдоль главных осей: d^-^ = (1 -f- S<4>) rZgy i = 1, 2, 3. По-
скольку главные оси взаимно ортогональны, элемент объема
dV = d^d^di,, после деформации становится равным
dV = d^d&Rs = (1 + S<D) (1 + S&) (1 + S®) dV
или в линейном приближении
dV' = (1 + S<‘> + S(2> + Sw)dV.
Таким образом, относительное увеличение объема А=
= (dV' — dV)/dV равно сумме собственных значений тензора
деформаций. Согласно (3.22) эта сумма равна следу Se =
= S„ + S22 + SS3 тензора в рассматриваемой точке:
А = 5-<*> + S<2’ + Sт. * * * * * (s). (4.7)
8 Э. Дьелесан, Д. Руайе
114
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Рис. 4.3. Физический смысл сдвиго-
вой компоненты Si2.
Угол между двумя взаимно перпен-
дикулярными элементарными отрез-
ками MNi и MN2 при деформации
уменьшается на 2Si2.
Компоненты Si} (i¥=j), не
равные нулю в случаях, когда
имеются смещения duj, пер-
пендикулярные элементу dxt,
соответствуют сдвигу. Предпо-
ложим в качестве примера, что
единственной недиагональной
компонентой является S12. Два
бесконечно малых элемента MNt
и MN2, первоначально направ-
ленные вдоль осей Xi и х2, в
процессе деформации не ос-
таются перпендикулярными
(рис. 4.3), так как точка М сме-
щается на вектор п, точка Nt —
на вектор u + du<l> и точка N2 —
на u + du(2>, причем компонен-.
ты du(1> равны (.dut/dx^dxi,
{dujdxjdxi, 0, а компоненты du(2) равны (dut/dx2)dx2, (ди2/дх2) X
X dx2, 0, поскольку (dus/dxi) = (dus/dx2) = 0 (Sls = S2s = 0 по пред-
положению). После деформации угол у12 между двумя отрезками
равен
7<г = л/2 - ifi - 72,
где
дхг axi дх{
tg )’1 М'Р. ~ дй. ~ дйГ
1 1 1 1 ох
Поскольку деформации предполагаются малыми (ди{/дх5 < 1), то
tg 71 « 7, « duJdXi и 7z » дщ/дх2. Следовательно,
vu=-r-(-^+-^)=l-2S»- «•»>
Изменение угла между двумя взаимно перпендикулярными
отрезками dxt и dXj за счет деформации сдвига S(j равно — 2S{j.
§ 4.2. Напряжения
Деформации в твердом теле возникают под действием внеш-
них сил. Эти силы могут быть поверхностными или объемными.
Для описания действия сил на вещество вводится либо объем-
ная плотность силы (поле тяготения), либо момент силы, прило-
женной к единице объема (электрическое поле для кристалла
с полярными молекулами). В деформированном теле возникают
§ 4.2. НАПРЯЖЕНИЯ
115
упругие напряжения, которые стремятся вернуть его в первона-
чальное состояние и обеспечивают равновесие среды. Напряже-
ния передаются от точки к точке за счет взаимодействия между
атомами, эффективный радиус которого (несколько межатомных
расстояний) весьма мал с макроскопической точки зрения. От-
сюда следует, что среда, окружающая некоторый объем, дей-
ствует на него только через поверхность раздела*). Мы опреде-
лим в первую очередь напряжения на поверхности, перпендику-
лярной одной из осей координат, затем на произвольно ориен-
тированной поверхности и, наконец, выведем условия равнове-
сия твердого тела в деформированном состоянии.
4.2.1. Определение тензора напряжений. Обозначим через
ДЛ проекцию на ось ортогональной системы координат силы
AF, с которой на элемент поверхности Дяк, перпендикулярный
оси хк, действует среда, находящаяся со стороны возрастающих
значений хк (рис. 4.4). Напряжение Tik определяется как предел
Рис. 4.4. Элемент поверхности,
перпендикулярный оси координат.
К элементу поверхности Дх2, нор-
маль к которому параллельна оси
®2, приложены напряжения 7i2,
Т-п и Г32, причем, например, Ti2
определяется как
Рис. 45. Произвольно ориентиро-
ванный элемент поверхности.
Сила Т зависит от направления
нормали 1 к элементу поверхно-
сти ds:
Л(1) = Ttklk.
отношения AFi/Ask при Asfc, стремящемся к нулю:
2“ <ы>
♦) В некоторых веществах (например, пьезоэлектриках) при деформа-
ции возникают поля с большим радиусом действия. В таком случае про-
водимое ниже рассмотрение уже не является строгим. Тем не менее, выво-
ды, следующие из него, на наш взгляд, полностью применимы и к этим
веществам.
8*
116
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Таким образом, Tih представляет собой i-ю компоненту силы,
действующей на единицу поверхности, перпендикулярной оси xh.
Согласно принципу равенства действия и противодействия,
среда, расположенная со стороны убывающих значений xh, дей-
ствует на элемент поверхности Asft с силой AF' = — AF.
Чтобы получить в явном виде выражение для силы Т(1),
с которой на элемент ds произвольной ориентации действует сре-
да, находящаяся со стороны единичной нормали 1 (Zlt 12, 13) к
этому элементу, надо спроектировать этот элемент поверхности
на три координатные плоскости. К построенному таким способом
тетраэдру (рис. 4.5) приложены как силы со стороны окружаю-
щего его вещества, так и внешние силы, плотность которых
равна feit. Результирующая этих сил записывается в виде
dF' = T(l)ds + dF'<*> + dF'<2> + dF'<s> + ГЧг, (4.10)
где dF'<h) — сила, действующая па треугольник площадью dsh,
перпендикулярный оси xh.
Проектируя силы на j-ю ось и принимая во внимание опре-
деление компоненты Tik, получаем =—dF<ii}=— TikdS(ky.
Скобки показывают, что по индексу к не проводится суммиро-
вание. Следовательно, уравнение (4.10) можно представить
в виде:
dF’i - Ti (1) ds — (TudSi + T^ds^ + Tisdss) -f- f^dv.
Поскольку dsk — lhds, то результирующая сила, действующая на
тетраэдр, равна
dF-^lTd^-TMds+^dv,
откуда следует, что объемная плотность силы dFjdv остается
конечной только при выполнении соотношения
7\(1) = ад, (4.11)
так как dv — бесконечно малая величина более высокого поряд-
ка, чем ds. Выражение (4.11) позволяет найти силу Т(1), дей-
ствующую на произвольную поверхность, ориентация которой
задается вектором нормали 1 (в (4.11) подразумевается суммиро-
вание по немому индексу к). Девять величин Tih, определяющих
упругие силы в деформированной среде, образуют тензор второго
ранга, называемый тензором напряжений, поскольку 7,(1) и lh
являются компонентами двух векторов Т(1) и 1.
4.2.2. Условия равновесия. Если тело находится в состоянии
равновесия, то результирующая сила и момент сил, действую-
щие на произвольный объем внутри тела, равны нулю. Допу-
стим, что напряжения в среде вызываются силами, приложенны-
§ 4.2. НАПРЯЖЕНИЯ
117
ми к поверхности тела. Благодаря принципу равенства действия
и противодействия результирующая сил взаимодействия между
различными частями некоторого объема v внутри тела равна ну-
лю. Таким образом, сила F, действующая на этот объем, равна
сумме сил со стороны окружающей среды. Поскольку эти силы
приложены к поверхности раздела s, то результирующая сила F
равна интегралу от Т(1) по поверхности s:
F = fT(l)ds.
Подставляя в это равенство выражение 7\(1) через соглас-
но (4.11), получаем для составляющих F, следующее соотно-
шение:
Поверхностный интеграл преобразуется в интеграл по объе-
му с помощью обобщенной теоремы Грина (3.26):
Подынтегральное выражение представляет собой силу ft, дей-
ствующую на единицу объема деформированного тела:
f{ = dTih/dxh. (4.12)
Если на тело действуют только поверхностные силы, то из
условия равновесия F{ = 0 следует, что /. = О или
dTik/dxk = 0. (4.13)
В присутствии объемных сил, возникающих, например, в по-
ле тяготения g, уравнение равновесия принимает вид
dTvJdXb + pgi = 0. (4.14)
где р — плотность вещества.
Поскольку момент силы Т относительно начала координат
можпо представить как векторное произведение хХТ, то он
является антисимметричным тензором второго ранга с компо-
нентами TjXi — T{xs. В соответствии с принципом равенства дей-
ствия и противодействия компоненты момента сил, действующих
на объем v, можно найти, беря интеграл по поверхности s этого
объема:
Мц = f (TjXi — Тгх}) ds.
Поверхностный интеграл
Мц = J* Ti^Xj) lhds,
118
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
полученный при замене Tf на Tihlk и Tj на TjKlki преобразуется
в объемный интеграл
Л/у = J (Tj^Xi TikXj) dv.
Раскрывая скобки, это выражение можно привести к виду
ПдТхъ m дх. 1
~d^Xi~~d^xi+T}h ~d^~Tik'd^\dv-
Выражение, стоящее под знаком интеграла, упрощается, если
принять во внимание условие равновесия (4.13) и независимость
координат хг.
М» = j (ЗДь - ТМ dv = f (Тя - Ту) dv. (4.15)
V V
Поскольку объем v был выбран произвольным образом, то из ра-
венства нулю компонент момента следует соотношение
Тц = Т„, (4.16)
выполняющееся при любых значениях i и /.
Благодаря симметрии тензора напряжений число его незави-
симых компонент сводится к шести:
Тп, Т22, Tss — напряжения, нормальные к поверхности,
Т1г, Т23, Т„ — тангенциальные напряжения.
Если на единичный объем среды действует вращающий мо-
мент G, то момент, приложенный к объему v, равен
Мц 4- J Ghdv, причем индекс к выбирается так, чтобы последо-
вательность i, j, к получалась четной перестановкой чисел 1, 2, 3.
Из условия равновесия следует
В этом случае тензор напряжений уже не симметричен. Та-*
кая ситуация реализуется, если кристалл с полярными молеку-
лами поместить в электрическое поле (например между двумя
электродами, как в случае пьезопреобразователя). Тем не менее,
мы будем считать, что симметрия тензора Ti} сохраняется, пока
вращающий момент мал по величине.
Внешние силы, приложенные к поверхности твердого тела,
вызывают механические напряжения в каждой точке поверхно-
сти. Сумма сил р, действующих на единицу поверхности тела,
равна упругой силе Т(1), где 1 — внешняя нормаль (напомним,
§ 4.3. СВЯЗЬ НАПРЯЖЕНИЙ С ДЕФОРМАЦИЯМИ
119
что Т(1) была определена как сила, с которой действует на еди-
ницу поверхности среда, находящаяся со стороны нормали). Гра-
ничное условие, которое должно удовлетворяться в любой точке
поверхности деформированного тела, имеет вид
р< = 7’.-(1) = 7’Л (4.17)
§ 4.3. Связь напряжений с деформациями.
Модули упругости
Среда называется упругой, если ее первоначальная конфигу-
рация восстанавливается, когда перестают действовать внешние
силы. Возврат в исходное состояние происходит за счет работы
внутренних сил, при этом напряжения и деформации одновре-
менно становятся равными нулю. В упругой (не пьезоэлектриче-
ской) среде между напряжениями и деформациями существует
взаимно однозначное соответствие. Опыт показывает, что упру-
гие свойства большей части веществ при условии малости де-
формаций описываются членом первого порядка разложения в
ряд Тейлора функции Тц(5ы):
Ту (Ski) —
“To(0)+(S’k,^ 5м+4(й^;).„, w~+ •••
®тпп~°
или, так как Га(0) = 0, то
Гij = CijuSu, (4.18)
где введено обозначение
<4Л9>
Коэффициенты cw, выражающие в самом общем виде линей-
ное соотношение между тензорами второго ранга и Ту, обра-
зуют тензор четвертого ранга, называемый тензором модулей
упругости. Пропорциональность напряжений и деформаций была
впервые установлена в XVII веке Гуком для простого случая
растяжения стержня.
Тензор четвертого ранга обладает 3‘=81 компонентами. По-
скольку тензоры Ti} и Su симметричны, то модули упругости,
введенные посредством соотношения (4.19), не меняются при
перестановке двух первых или двух последних индексов:
Ciikl — СЛЫ И Сум = Сщм
(4.29)
120
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Выражая деформации через смещения, можно записать закон
Гука (4.18) в виде
т 1 z. ди* <_ 1 л
— Ciiki -g^- + — сам •
Поскольку сда = eijlk, обе суммы равны между собой и
ди,
Tij = gx^ • (4.21)
Соотношения симметрии (4.20) сводят число независимых
модулей упругости с 81 до 36. Действительно, поскольку в паре
индексов (if) порядок не играет роли, то существует только
шесть различных парных комбинаций, пронумерованных от 1
до 6 следующим образом:
(1D-1, (22)-^2 (33) ->3,
(4.22)
(23) = (32)-> 4, (31) = (13)-5, (12) = (21)-*• 6.
Если принять, что ca₽ = ciftz, где (ij)-*a и (W-* £ в соот-
ветствии с (4.22), то из независимых модулей упругости, отме-
ченных двумя индексами а и j}, принимающими значения от 1
до 6, можно составить квадратную таблицу 6X6 с 36 компонен-
тами. Примеры обозначений:
Си — C112S = Си32, Съв = C1S12 = С1321 = Сз,21 = СзИ2.
Такое матричное обозначение можно распространить на де-
формации и напряжения, тогда закон Гука запишется в виде
7’a = cafi8e, а, 0 = 1, 2, .... 6. (4.23)
Однако, если принять для напряжений условное обозначение
Ta = TiS (4.24)
в соответствии с (4.22), то следует положить
«5ц, Si = 822, $3 — S33,
(4.25)
84 = 2823, 85 = 28,з, 8в = 2812
для того, чтобы соотношение (4.23) действительно выражало бы
закон Гука. Например, выражение для по формуле (4.18)
= cllw8w = CuuSu + СиггЗгг +
"Ь 6,133833 + 2с,,2з82з "I" 2сц,з8,з + 2с,1128,2
тождественно равно выражению для Г, согласно (4.23)
Tt—CuSt + ci2Sz + C13S3 + 0,484 + c158s + cle8e,
только если удовлетворяются соотношения (4.25).
§ 4.4. ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ 121
Для того чтобы выразить деформации как функции напряже-
ний, можно обратить закон Гука:
S<j = si}MTu. (4.26)
Коэффициенты податливости образуют тензор четвертого
ранга, обладающий теми же свойствами симметрии, что и тензор
c<jM, т. е. SfjU = Элы и вам = Sjjik.
Аналогичным образом решение системы уравнений (4.23)
относительно Sa приводит к соотношению
Sa~sa9T9, (4.27)
в котором матрица saf> представляет собой матрицу, обратную
матрице cafi: зор = (саВ)"‘ или sapCBT = 6ат, где 6ат — символ Кро-
некера.
Связь коэффициентов зац и stjki можно получить, например,
сравнивая выражение (4.26) для 513:
>$13 = 8ццТц + 81322^22 ®13мГ„ "Ь ЗЗшзГгЗ "I" 23131з2\з + 2313127’12
с разложением (4.27) для S5 = 2<$13 при учете обозначений (4.24):
Sst—2S1311, -Ss2 = 2S1322> ^53 = 2S1333,
S54“4Sjs23, $SS ~ 4S1S13, Sse — 4S1312.
Эту связь можно представить в общем виде
SaB = 2РЗвд, (4.28)
где р — число индексов, превышающих 3, в паре (оф).
Дальнейшее сокращение числа независимых модулей упруго-
сти проводится на основе законов термодинамики.
§ 4.4. Энергия упругой деформации.
Соотношения Максвелла
Работа, совершаемая внешними силами в процессе деформа-
ции, накапливается в теле в виде потенциальной энергии. Как
только внешние силы перестают действовать, энергия упругой
деформации преобразуется в работу упругих сил, за счет чего
тело принимает первоначальную форму. Работа внешних сил при
деформации тела, затрачиваемая на изменение du смещения и,
складывается из работы объемных и поверхностных сил:
6 И7 = J pgdudv 4- f pduds,
где g — сила, действующая на единицу массы, и р — сила, дей-
ствующая на единицу поверхности. Выражение для 8W можно
122
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
записать также в виде
6Ж = j pgiduidv + f Piduids.
Предположим, что в каждый момент устанавливается равно-
весное состояние, соответствующее величине приложенных сил;
тогда изменение состояния является термодинамически обрати-
мым процессом и, следовательно, выполняются условия равнове-
сия (4.14) и (4.17). Заменяя р( на Тл1к, получаем
6Ж = f pgiduidv + f Tihduilhds.
Второе слагаемое преобразуется к интегралу по объему:
6Ж = J pgiduidv + J JL-(Tihdui) dv.
Беря производную под знаком интеграла и перегруппировывая
слагаемые, можно в правой части равенства выделить под инте-
гралом величину pg{ + dTik/dxh, которая в любой момент времени
равна нулю в силу условия равновесия (4.14):
6Ж = J (pgl + duidv + J Tihd dv. (4.29)
Таким образом, выражение для работы внешних сил, затрачивае-
мой на элементарное изменение состояния, принимает вид
или, поскольку Т{к — Ты,
аж - 4- у тяа (-§ + -£;)*’ = ]’ т,Аа».
Работа 6Ж внешних сил, совершаемая при деформации dSik
единицы объема, равна
6Г = ТА
- В дальнейшем термодинамические величины, относящиеся к
единице объема тела, мы будем обозначать прописными буквами.
Тогда изменение внутренней энергии единицы объема W) запи-
шется в виде
<2<2/ = 6Г + 6£, (4.30)
где б<? — количество тепла, полученное единицей объема тела.
§ 4.4. ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ
123
Согласно первому началу термодинамики <2/ является функцией
состояния тела и dfU представляет собой полный дифференциал,
тогда как по отдельности 6Ж и не составляют полных диф-
ференциалов. Из второго начала термодинамики для обратимого
процесса следует соотношение — Ма, где — абсолютная тем-
пература и о — энтропия, отнесенная к единице объема.
Выражение (4.30) можно переписать в виде
dm = Ma + TikdSik. (4.31)
Таким образом, внутренняя энергия деформированного тела яв-
ляется функцией энтропии и деформации, т. е. t2/=’f2/(o, 5«), и,
следовательно, TfK= wU/dS^, где индекс о означает, что част-
ная производная берется при постоянной энтропии.
Подставляя это выражение в соотношение (4.19), определяю-
щее модули упругости c{jhi = (dTtj/dS„) и скт = (дТм/д8ц), по-
лучаем
Перестановка двух первых индексов с двумя последними не
меняет величины изоэнтропийных (о = const) модулей упругости.
Именно эти модули определяют скорость распространения упру-
гих волн, для которых за период колебаний не успевает устано-
виться теплообмен с окружающей средой, поскольку из условия
б£? = 0 для обратимого процесса вытекает условие da = 0. Соот-
ношение симметрии (4.32), так называемое соотношение Макс-
велла, справедливо и при других термодинамических условиях.
Для его вывода достаточно рассмотреть подходящую функцию со-
стояния, например, для изотермических процессов (й = const) —
свободную энергию, определяемую как — йо. В самом де-
ле, принимая во внимание (4.31), получаем
L _0йй + TikdSth. (4.33)
Свободная энергия зависит от температуры й и деформаций 5Й,
т. е. 3^=»^’(й, Sft). Отсюда следует, что Т{к = (dP/dS^t, и для
изотермических модулей упругости выполняется соотношение
(0) I д2&~ М)
В пределах справедливости закона Гука изменение внутрен-
ней энергии, даваемое выражением (4.31), записывается в виде
dm = $da 4- ShidSij
или при перестановке пар немых индексов (у) и (W)
dm = fida 4- -у {^liShidSij 4- c^iaSijdS^^
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Это выражение можно преобразовать, принимая во внимание со-
отношение Максвелла (4.32):
d<U = ftda 4- -у- (SijShi).
Интегрируя полученное равенство, выражаем внутреннюю энер-
гию деформированного тела в виде
<2/ (о, Sih) = % (о) + 4 c^SijSM,
где fytQ(a) — внутренняя энергия недеформированного тела,
%0(а) = сЫ(в, 5Л = 0). Свободную энергию единицы объема мож-
но получить тем же способом, но исходя из соотношения (4.33),
(Ф, Stk) — &~0 (ft) + c^iSijShl.
Таким образом, внутренняя энергия или свободная энергия
механического происхождения, которую мы называем, не уточ-
няя термодинамических условий, потенциальной упругой энер-
гией (в расчете на единицу объема), представляется квадратич-
ной формой от деформаций
Ф =4 cHkiSijSki. (4.34.)
В зависимости от того, является процесс деформации адиаба-
тическим или изотермическим, эта величина равна увеличению
внутренней энергии или свободной энергии единицы объема тела.
§ 4.5. Ограничения, налагаемые на число
независимых модулей упругости симметрией кристаллов
Соотношение Максвелла (4.32), которое следует из термоди-
намических соображений, справедливо в любой среде. В матрич-
ных обозначениях оно записывается как caS = сра. Таблица 6X6
коэффициентов са₽ (триклинная система) симметрична относи-
тельно главной диагонали:
С11 С12 С13 С14 с15 с16
с12 С22 с23 С24 с25 С26
(сар) = Cls Сэз "35 'зв : (4.35)
с14 С24 с34 С44 с45 С46
С15 С25 С35 С45 С55 С56
С1в С2в С3в С46 С56 СМ
За счет этого свойства симметрии число независимых компо-
нент уменьшается до 21 (6 + 5 + 3+ 2 + 1). Поскольку наличие
центра симметрии в кристаллах не приводит к дополнительным
ограничениям, то кристаллы триклинной системы характеризу-
ются максимальным числом независимых модулей упругости
§ 4.5. ЧИСЛО НЕЗАВИСИМЫХ МОДУЛЕЙ УПРУГОСТИ
125
(21). Симметрия остальных кристаллических систем приводит к
значительному сокращению числа независимых модулей упру-
гости. Переходя к другому крайнему случаю, покажем вначале,
что механические свойства изотропного твердого тела, обладаю-
щего наивысшей симметрией, полностью описываются двумя
постоянными.
4.5.1. Изотропное твердое тело. Физические константы изо-
тропного материала, по определению, не зависят от выбора си-
стемы координат. В частности, тензор модулей упругости сда
инвариантен относительно любых преобразований ортогональных
систем координат (вращения, инверсии относительно точки, от-
ражения в плоскости). Однако таким свойством обладает только
скаляр или единичный тензор бу, следовательно, каждую ком-
поненту Сцы можно выразить через составляющие единичного
тензора. В силу симметрии Ьц — бц существуют только три раз-
личные комбинации компонент бу, содержащие четыре индекса
ijkl: бубы, 6Л, б<('бй. Таким образом, тензор cfjM можно предста-
вить в виде суы = Хбубдг + |Л1бжб,7 + щбнбд, где X, |х„ ц2 — кон-
станты. Кроме того, из условия суы = ciiM следует, что ц, = ц2 = ц.
Остальные соотношения симметрии автоматически выполняются,
так что
Сум = Хб«б« + ц(б«б« + б«бл). (4.36)
Таким образом, механические свойства изотропной среды
описываются двумя независимыми константами, например, коэф-
фициентами Ламэ Аир.
Нумеруя пары индексов U/) и (kl) числами от 1 до 6, по-
лучаем
Си = с22 = с33 = X + 2ц,
с,2 = с22 = Сц = А, (4.37)
С44 = с55 =.С6в = Ц = (Си - С,г)/2,
двенадцать других модулей cyw равны нулю, так как в них со-
держится нечетное число разных индексов ijkl (например, с25 =
= с2213). Если выразить все компоненты через clt и с12, то матри-
ца caf, для изотропной среды примет следующий вид:
126
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
В изотропной среде закон Гука сводится к следующим двум
уравнениям Ламэ.
Для нормальных напряжений (Ги, Тгг, Тм)
Tti — Сци8ы “ (Лбы + 2цбйкбл)|5ы = К(8ц 4* S22 4“ 833) 4- (4.39)
для тангенциальных напряжений (Ту, i ¥= /)
Ту e CjflaSu — |л(6ибя 4- б.«6д)5м = 2ц5у. (4.40)
Уравнения (4.39) и (4.40) легко объединить в одно:
Ту = М6у+2И&л (4.41)
в котором А = Su + S22 + Sss — относительное изменение объема
Ap/v.
Соотношение (4.40) показывает, что ц = Ту/2£у является
коэффициентом пропорциональности между сдвиговым напряже-
нием Ti} и изменением угла между двумя первоначально перпен-
дикулярными осями Xi и Xj (рис. 4.3).
4.5.2. Кристаллы. В ортогональных системах координат общее
условие инвариантности (3.11) для тензора модулей упругости
записывается в виде
сцм = а?аМа?Срд„. (4.42)
Как уже отмечалось, кристаллы триклинной системы харак-
теризуются 21 модулем упругости, которые приведены в (4.35).
В кристаллах моноклинной системы матрицу преобразования
координат а можно свести к диагональной форме, если направить
ось Хз параллельно оси симметрии второго порядка или инвер-
сионной оси (эквивалентной плоскости симметрии),
/-1 0 0\
а = ± 0-10.
\ 0 0 1/
В этом случае соотношение (4.42) преобразуется к виду
сам = a|ajafeajcyfel,
и из него вытекает равенство нулю модулей упругости, имеющих
нечетное число индексов 3, для которых = — 1. Матри-
ца (4.43) содержит 13 независимых компонент, у которых ин-
декс 3 либо отсутствует, либо повторяется два или четыре раза:
С11 С12 С13 0 0 С1в
С12 С22 С23 0 0 С2в
(Сар) = С13 С23 С33 0 0 С3в 0 0 0 С44 С45 0 (4.43)
0 0 0 С48 0
С1в С2в С3в 0 0 Свв
§ 4.5. ЧИСЛО НЕЗАВИСИМЫХ МОДУЛЕЙ УПРУГОСТИ
Для кристаллов ромбической системы в качестве осей коор-
динат выбираются три ортогональные оси симметрии или инвер-
сионные оси второго порядка. Применяя проведенное выше рас-
суждение к каждой оси, т. е. к каждому индексу, можно пока-
зать, что тензор модулей упругости содержит только 9 незави-
симых компонент, в которых любой индекс повторяется четное
число раз:
(4.44)
Симметрия кристаллов кубической системы в качестве обяза-
тельных элементов включает четыре оси А, и три оси симметрии
второго порядка, которые принимаются за оси координат. В мат-
рице модулей упругости отличны от нуля те же компоненты, что
и для кристаллов ромбической системы. При повороте на угол
2я/3 вокруг оси третьего порядка, направленной вдоль [111], ось
х, преобразуется в хг, хг в xs и х3 в xit следовательно, модули
упругости cw должны быть инвариантными относительно цикли-
ческой перестановки индексов (123) -> (231) -> (312). Это требо-
вание влечет за собой соотношения
С11И и ^2222, ^2222 = С3333, <4122— С22ЗЗ = С33Ц, CJ212 — С2323— Сз131»
благодаря которым число независимых модулей упругости в кри-
сталлах кубической системы сводится к трем (сп, с12, с*4). Мат-
рица (4.44) для кубической системы принимает вид
Кристаллы, имеющие одну ось высшего порядка Ап (п>2).
Кристаллы тригональной, тетрагональной и гексагональной си-
стем содержат одну ось симметрии или инверсионную ось поряд-
ка выше 2, которая принимается за ось х3. Матрица а поворота
вокруг главной оси в дапном случае не диагональна:
(созф sin <р 0\
— sin ф cos ф О I, ф = ±5. ф л. (4.46)
0 0 1/ п
128
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
§ 4.5. ЧИСЛО НЕЗАВИСИМЫХ МОДУЛЁЙ УПРУГОСТИ
При этом трудно пользоваться соотношением инвариантности
(4.42), поскольку оно связывает друг с другом слишком много
компонент. Для того чтобы получить диагональную матрицу
преобразования координат, достаточно перейти к базису, образо-
ванному собственными векторами §(1), ?(2\ £(3) матрицы поворо-
та. Для этого надо решить систему уравнений, аналогичную
(3.19),
(4 - X6ift) Ik = 0. (4.47)
Собственные значения X определяются из условия совместно-
сти, аналогичного (3.20):
Icos <р — X sin ф О I
— sin ф cos ф — X 0 0.
0 0 1 - XI
Вычисляя определитель, получаем [(-X — cos ф)2 + sin2 <р] (1 — Х)=0,
откуда
X(,’ = ef’, х(2’ = е-”, Х(’> = 1. (4.48)
Каждому собственному значению соответствует собственный
вектор %(<), компоненты которого находятся из решения системы
(4.47):
для Х(,)
| Bi (— t sin <р) +|2 sin <р = 0,
1(1-е’Ф)?8= 0,
= |» = 0;
для Х(2) Ь = 0,
для Х(” = |2 = 0, £3 — произвольно.
Поскольку компоненты векторов являются комплексными чис-
лами, то для нормировки этих векторов надо составить произве-
дение &£*. Окончательный результат запишется в виде
НЙ’Й’0)' ПтГтМ1 <4Л9)
Обозначим символом уад модули упругости в ортонормиро-
ванием базисе ^(1), ?(2), ?(3). Тогда соотношение инвариантности
(4.42) сводится к уад = Х(,)Х0)Х(А)Х',,Хад, поскольку в этом базисе
матрица преобразования координат диагональна. Пусть Vi и v2 —
число индексов 1 и 2 в наборе ijkl. Принимая во внимание соот-
ношения (4.48), получаем
' XWX W> = exp [i (vx - v2) ^].
Следовательно, модули у<й< не равны нулю, если число v, — v2
кратно порядку оси п, так как при этом X(<)X(J)X(i,X(n — 1. Это
условие всегда выполняется для пяти модулей упругости у1122,
Кии» Тми, fsssa, для которых v1 = v2. В случае кристаллов
гексагональной системы (п = 6) других вариантов не может быть,
поэтому эти кристаллы обладают только пятью независимыми
модулями упругости. В то же время в кристаллах тригональной
системы имеется семь независимых модулей, поскольку отличны
от нуля Уше и умы (vt-v2 = ±3). Столько же модулей упругости
насчитывается в кристаллах тетрагональной системы (п = 4),
в которых не равны нулю fun и I2222 (vi —v2 = ±4).
Обратный переход к модулям Сад осуществляется с помощью
соотношения
сцм = a?afyrkaiypqTS, (4.50)
где а — матрица перехода от системы координат ж,, х2, х, (модули
сад) к системе с базисом £(1), 1(2), V’’ (модули у.ад), i-ю строку
которой образуют компоненты (4.49) собственного вектора V’
в системе отсчета ®i, ж2, х3:
/1/У2 i/y? о\
а = tf-^2 1/V2 0 . (4.51)
\ 0 0 1/
Соотношение (4.50) упрощается вследствие сокращения числа
модулей iMr«. Кроме того, поскольку компонента af = 1 явля-
ется единственным отличным от нуля множителем с индексом 3,
то в разложении (4.50) фигурируют только те модули уР4Г„ у ко-
торых положение индекса 3 совпадает с его положением в моду-
ле Cjfhi.
Детальное рассмотрение начнем с тригональной системы,
в которой отличны от нуля модули 7зззз, Тзз12, faeis, Tins, 'Тгггз,
f1122, 11212.
В порядке убывания числф индексов 3 получаем:
сзззз = 7зззз, следовательно, с33 #= 0;
С33и и с3323 равны нулю, лак как y33i3 = у3323 = 0, т. е. с35 = с34 = 0;
модули упругости с двумя индексами 3 (с{/33 и с<3»3) выражаются через
11233 = 12133 И 11323 = 12313*
Ч-33 = Ж + Ф))?1233-
Поскольку + a|a|, то Ci'133 =» с2233, или с13 = са, и
поскольку = 0. то сщз = 0, или с33 = 0. Аналогичным обра-
зом, из разложения
" С13йЗ = (вН+вМ)Ъ2з
следует emu = с2323, или С55 = си, и сМ13 = 0, или =г 0;
9 Э. Дьелесан, Д. Руайе
130
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
для модулей с одним индексом 3 соотношение (4.50) записывается в
виде
сШз = 44Фшз + 4аИ?2223’
откуда
1 г , X 2___________
С22Й“ 2 ЯЛ113 *" 2 ЯЛг23 — С11М’
1 1 . 1 2
ci223 = ~ ~2 аг?1113 + ~2 Я^2223 = “ СШЗ’
пли в матричных обозначениях при к = 2 сц = —с14, при к = 1 с%, — —с15,
при i в 1 с« = —cis и при i = 2 сц=* —с$ь, следовательно, сц — —с24 =
= С56 И CS5 =' —С15 = с4в;
модули спи, сии, сш5, с2221, Сцм> ^1212, не содержащие индекса 3, вы-
ражаются через fuss и 71212:
с w - (4444 + 4444) vU28 +
+ (44+44) (4я? + 44)?1212’ <4-52)
откуда
сии = 2 (44)2(^И22 + fysn) = — ~2 (^1122 + 2Ъп) ’
си = с22 = — У (’'’ыгг + ^шг)- (4,53)
Рассмотрим модуль сщг:
С1И2 + 4я! (Я1Я2 + 44) (ТШ2 + 2V1212) = °’
так как + <г|а| = 0. Таким же способом можно показать, что Cg^i =
в 0, следовательно, сю = с^ = 0.
Между спи, сц22 и с121з должна существовать связь, поскольку число
независимых модулей без индекса 3 равно двум. Действительно, из разло-
жения (4.52) следует, что сц22 = (7112г —271212)/2 = ci2 и c!2i2 = —7пи/2 =
= сее. Принимая во внимание соотношение (4.53), получаем с66 = (сц —
— С12)/2.
Полученные результаты (.тригональная система) отражены
в приведенной ниже матрице:
си С12 С13 С14 С25 0
С12 е11 С13 ~ с14 С25 0
С13 С13 сзз 0 0 0
(Са₽)= С14 — С14 0 С44 0 С25 (4.54)
~С25 С25 0 0 С44 С14
0 0 0 С25 С14 С11 ~ С12 2
В классах 32, 3m, 3m наличие осей второго порядка, перпен-
дикулярных главной оси, накладывает дополнительные условия,
§ 4.5. ЧИСЛО НЕЗАВИСИМЫХ МОДУЛЕЙ УПРУГОСТИ
131
которые приводят к равенству нулю модулей упругости сда, со-
держащих нечетное число индексов 1, если принять, что коорди-
натная ось Xi направлена вдоль одной из этих осей (сравните со
случаем моноклинной системы). В этих классах число незави-
симых модулей упругости сводится к шести, поскольку с15 =
= сшз = 0.
В кристаллах тетрагональной системы соотношения между
модулями с четырьмя, тремя и двумя индексами 3 те же, что п
в тригональной системе, поскольку в обоих случаях ненулевые
компоненты одинаковы. В то же время модули упругости, со-
держащие один индекс 3, равны нулю, так как у1113 = ^2г23 = 0, и,
следовательно, с14 = с24 = с15 = с25 — с4в = с5в = 0.
Модули, не имеющие индекса 3, выражаются через у11И, 42222,
41122 И У1212:
cijkl — ®i®j®fe®lYllll + ®i®j®fc®/Y2222 ~b
где под с% понимается разложение (4.52) для соответствую-
щего модуля в случае п = 3. Учитывая соотношение (4.53), по-
лучаем
еда— 4 (Yim + Y2222) 2 (Y1122 + 2Y1212),
ИЛИ Сц = С22. Поскольку Сш2 и С$21 равны нулю, ТО С1112 =
— i(fint — Т222г)/4 = — С2221, ИЛИ с2в = —С1в.
Четыре независимых модуля упругости си, с12, с16, с66, не
имеющих индекса 3, и модули с13, с33, с44 составляют следующую
матрицу {тетрагональная система):
0
0
0
(са₽) —
С12
С13
0
о
с16
си
С13
0
0
“с1в
13
С13
сзз
0
0
0
44
0
0
0
0
0
0
те
— С16
о
о
о
с66
(4.55)
Для классов 422, 4mm, 42m, 4/mmm модуль еш! = Сц = 0, так
как в нем содержится нечетное число индексов 1 (ось парал-
лельна одной из осей второго порядка, перпендикулярных глав-
ной оси).
В теории упругости главную ось кристаллов гексагональной
системы (ось шестого порядка) можно рассматривать как комби-
нацию осей второго и третьего порядков. Таким образом, матри-
ца Cat получается наложением матриц (4.43) и (4.54) моноклин-
9*
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
ной и тригональной систем: сп ci2 с1з 0 0 0 С12 с11 С13 0 0 0 С13 С13 сзз 0 0 0 (м)= 0 0 0 с44 0 0 0 0 0 0 0 0 0 0 0 0 С112 — (4.56)
Тензор с такими компонентами инвариантен относительно по-
ворота на любой угол вокруг оси шестого порядка. Это свойство,
доказываемое в упр. 4.4, формулируется по-разному:
плоскости, перпендикулярные главной оси, изотропны с точки
Рис. 4.6. Вид тензоров модулей упругости са&-
• О — компоненты, не равные нулю, —равные компоненты, «—ком-
поненты, равные нулю, ®—О-компоненты, равные по абсолютной величи-
не, но противоположные по знаку, X — компоненты, равные (сц — с12)/2.
УПРАЖНЕНИЯ
133
все плоскости, проходящие через главную ось, и все направ-
ления, составляющие с этой осью одинаковые углы, эквивалент-
ны между собой.
Вид тензоров модулей упругости для кристаллов всех систем
приведен на рис. 4.6. Симметрия относительно главной диагонали
не отражена. Число независимых компонент указано внизу, спра-
ва от каждой матрицы.
Матрицы, приведенные на этом рисунке, применимы также
к коэффициентам податливости Однако, чтобы найти соот-
ношения между этими коэффициентами, необходимо принять во
внимание выражение (4.28) sa9 = 2pstjM, где р — число индексов,
превышающих 3, в паре (а, [}). Например, в кристаллах триго-
нальной и гексагональной систем и в изотропной среде Сщ2 =
= (сип — с1122)/2 или с6в = (сн — с12)/2. Аналогичное соотношение
существует для коэффициентов
S1212 — (Sim — 5ц22)/2,
но, поскольку se6 = 4s12t2, = и s12==Sn22, Tosee==2(sn — Si2).
В табл. 4.1 приведены модули упругости и плотность некото-
рых кристаллов, объединенных в группы по их принадлежности
к одной кристаллической системе. Для пьезоэлектрических кри-
сталлов, отмеченных звездочкой, даны модули cfp, опреде-
ленные в разделе 6.1.3. Модули упругости по порядку величины
равны 10“ Па.
Упражнения
4.1. Стержень, имеющий осевую симметрию, подвешен вертикально
(рис. 4.7). Как должна меняться площадь сечения з(г), чтобы среднее на-
пряжение Г, обусловленное весом стержня, оставалось ।
постоянным (не зависящим от ^). У/ZZZZZZZa zzzzzzz<yzz
Решение. \ so /
pgj s(x)dx
Т = “7(3----------- const = Л
Дифференцируя, получаем — pgs(x) = T^ds/dx), от-
куда
s = s0 exp (—pgar/To).
4.2. Найти коэффициент сжимаемости х =—А/p р , 7
(А — относительное увеличение объема) кристалла с‘
под действием гидростатического давления.
Решение. Так как Тм = —р6м, то закон Гука принимает вид =
= SijkiTki = —psi-hh- Используя формулу (4.7) для Д = Ди/у, получаем вы-
ражение А = Sn = —psnkk и
X = Шьь = «и + s22 + S33 + 2(®is + S23 + s3i)-
Таблица 4.1. Модули упругости и плотность
Вещество Класс Модули упругости, 1О10 Па Плотность, 103 кг/м3 Ссылки
Кубическая система и изотропные среды Сц С12 с.и р
Алюминий (А1) ’Арсенид галия (GaAs) Алюмоиттриевый гранат (A1SY3O12) Железоиттриевый гранат (Fe5Y3O12) *Германат висмута (Bi12GeO2o) Золото (Au) Платина (Pt) Плавленый кварц (SiO2) Кремний (Si) Вольфрам (W) тЗт 43т тЗт тЗт тЗт изотропный лгЗт 10,73 11,88 33,2 20,9 12,8 19,25 34,7 7,85 16,56 52,24 6,08 5,38 11,07 10,77 3,05 16,30 25,1 1,61 6,39 20,44 2,83 5,94 11,50 7,64 4 ,24 7,65 3,12 7,95 16,06 2,702 5,307 4,55 5,17 9,23 19,3 21,4 2,203 2,329 19,26 [1] 2] 3 3 4 [6 [7] 18 J
Гексагональная система С11 С12 <5з с33 Си
Бериллий (Be) ’Керамика ЦТС-4 (поперечно-изотроп- ная) ♦Окись цинка (ZnO) ’Сульфид кадмия (CdS) Титан (Ti) 6/ттт Зтт &тт 6/ттт 29,23 13,9 20,97 8,565 16,24 2,67 7,8 12,11 5,32 9,20 1,4 7,4 10,51 4,62 6,90 33,64 11,5 21,09 9,36 18,07 16,25 2,56 4,25 1,49 4,67 1,848 7,5 5,676 4.824 4,506 [9] [25] ИО] ГН] [12]

Тетрагональная система С13 с33 с44 свв с1в
Индий Молибдат свинца (РЬМоО4) Молибдат кальция (СаМоО4) ’Парателлурит (ТеО2) Рутил (ТЮ2) ’Титанат бария (BaTiO3) 4/ттт 41т 4/т 422 4/ттт 4тт 4,53 10,92 14,5 5,6 27,3 27,5 4,00 6,83 6,6 5,1 17,6 17,9 4,15 5,28 4,46 2,2 14,9 15,2 4,51 9,17 12,65 10,6 48,4 16,5 0,651 2,67 3,69 2,65 12,5 5,43 1,21 3,37 4,5 6,6 19,4 11.3 0 1,36 1,3 0 0 0 7,28 6,95 4,255 6,00 4,25 6.02 [13] [14] [15]; [16] [17] [18]
Тригональная система С11 С12 с13 Сзз Си см
Корунд (А12О3) ’Ниобат лития (LiNbO3) ’Танталат лития (LiTaO3) *а-кварц (SiO2) ’Теллур (Те) Зт Зт Зт 32 32 49,7 20,3 23,3 8,67 3.27 16,3 5,3 4,7 0,70 0,86 11,1 7,5 8,0 1,19 2,49 49,8 24,5 27,5 10,72 7.22 14,7 6,0 9,4 5,79 3,12 -2,35 0,9 —1,1 -1,79 1.24 3,986 4,7 7,45 2,648 6,25 [19] [20] [20] [21] [22]
Ромбическая система си Си С13 с22 С 23 Сзз С44 С55 свв Р
•Йодноватая кислота (ШО3) •Ниобат бария и натрия (Ba2NaNb5O15) 222 3,01 23,9 1,61 10,4 1,11 5,0 5,80 24,7 0,80 5,2 4,29 13,5 1,69 6,5 2,06 6,6 i 1,58 7,6 4,64 5,30 [23] [24]
136
ГЛ. 4. СТАТИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
4.3. Выразить через модули упругости модуль Юнга Е и коэффициент
Пуассона v изотропного тела, определяемые выражениями
М 1 F Ad М v F
I ~~ Е s ’ d ~~ v I ~ Е s ’
где AZ/Z и Ad/d — относительные удлинение и изменение диаметра цилиндра
сечением s под действием однородного напряжения F/s, приложенного вдоль
оси «1.
Решение. Деформации тела равны <$ц = (11Е)Тц, 8ц = 8к =
= — (у/Е)Тц. Для изотропного тела Т22 = с12(<$ц + S33) + сц8ц — 0, отку-
да
v = с12/(сц + с12),
и Тц — сп8ц + с12(522 + 533), следовательно,
Сц —2c12v = cu —2с22/(си +с12).
4.4. Показать, что модули упругости кристаллов гексагональной систе-
мы инвариантны относительно поворота на любой угол вокруг оси шестого
порядка.
Решение. Рассмотрим, как меняются пять независимых модулей
«зз, «is, «44, «is, «н при преобразовании координат, описываемом матрицей
(3.12):
саы =
Таким образом, «3333 = аза3а3а|«3333’ откуда следует «33 = «33. В соотно-
шении «11зз = aiaia3a3cP533 отличны от нуля только слагаемые с р = д =
= 1 или 2, следовательно, «43 = с13 cos2 <р + «23 sin2 <р = с13, так как с23 =
= «is. Из соотношения с'323 = a£a]Jep3r3 следует «44= «44 cos2cp + «55 siп2<р=
= «44, так как с5з = «44. Соотношение «4122 =>iaia2a2cpqr5, если учесть, что
р, q,r,S^ 3, сводится к виду «п=(сц+с22— 4cee) cos2 'Р sin2 *Р + С21 sin4(p+
+ с12соз4ф. Подставляя вместо с66 выражение («и— ci2)/2, получаем
е’2 = (2 соз2 <р sin2 <р + sin4 ср + cos4 <р) «12 = (cos2 ср + sin2 ср)2 с12 = с12. Ана-
логично с1х = Си1
.’ 4.5. Выразить коэффициенты податливости sa₽ через модули упругости
кац для кристаллов тетрагональной (классы 4/mmm, 422, 4mm, 42тп),’..гекса-
гональной и кубической систем.
i Решение. Обращая матрицу ««з, получаем «м = 1/с« и з№ = 1/с66.
j Остальные, соотношения можно вывести следующим образом. Три пер-
вых уравнений системы (4.23)
• Т1 = «и^! + cI2S,2 + c]3S3,
! Т2 = c12St + Сц|$2 + «i3S3,
। Тз = С1з5( + c13S2 + c33S3,
Ьри йычитйнии второго уравнения из первого преобразуются к виду
Т1 — ^2=(сц—сц) (Si — S2),
: F2 = Ca(Si — S2) + (сц + cn)Si -|- cu53,
Тз = «is (Si — Si) + 2ci3S2 + c33S3.
УПРАЖНЕНИЯ
137
Осуществляя аналогичное преобразование с уравнениями (4.27) и вводя
переменные — Т2, хг = Т2, т3 = Т3, щ — St — S2, <т2 = S2, os = S3,
нетрудно видеть, что матрица
Лц-®12 °г °\
I S12 Sll+-S12 ®13 I
\ S13 2*13 ®33/
является обратной по отношению к матрице
All — С12 0 0 \
I С12 С11 + С12 С13 I,
\ С13 2с1з езз/
откуда следуют соотношения
«11 — «12 = 1/(Сц — С12), «п + «12 = Сзз/с2, «13 = —с1з/«21
«33 = («II + «12)/«2,
где с2 = (сп + «12) с33 — 2с^3-
ГЛАВА 5
ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
В этой главе будет проведен подробный анализ распростра-
нения упругих волн в твердых телах. Известно, что в зависи-
мости от условий распространения существует много различных
типов упругих волн: волны Рэлея, Гуляева — Блюстейна, Лэмба,
Лява, Стоунли... Однако следует отметить, что по существу
имеются только два основных типа волн:
1) Продольные волны, или волны сжатия (рис. 5.1. а), ко-
торым свойственно смещение частиц, параллельное направлению
распространения, т. е, поляризация этих волн параллельна вол-
новому вектору. Распространение плоской продольной волны
сопровождается изменением расстояния между параллельными
плоскостями, содержащими частицы, при этом изменяется объ-
Рис. 5.1. Упругие волны в неограниченной изотропной среде.
а) Продольная волна: волновой вектор и поляризация волны параллельны.
Частицы А, В, С колеблются вдоль одной прямой. В заданный момент време-
ни волна представляет собой последовательность областей сжатия и разре-
жения. б) Поперечная волна: поляризация и волновой вектор перпендику-
лярны. Частицы А, В, С отклоняются в обе стороны от прямой, на которой
они находятся в отсутствие волны. Плоскости, перпендикулярные волновому
вектору, скользят одна относительно другой, причем расстояния между ни-
ми не меняются.
2) Поперечные или сдвиговые волны (рис. 5.1, б), смещение
частиц в которых перпендикулярно волновому вектору. Сколь-
жение параллельных плоскостей не приводит к изменению
объема.
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
139
Эти волны распространяются в неограниченных изотропных
твердых средах (раздел 5.1.4). Термин «неограниченная» прак-
тически означает, что размеры среды велики по сравнению с
размерами волнового пучка и краевыми эффектами можно
пренебречь.
Если среда, по-прежнему неограниченная, является анизо-
тропной, т. е. кристаллической, то в любом направлении, как
будет показано в разделах 5.1.1 и 5.1.2, могут распространяться
три волны и, в наиболее сложном случае, ни одна из них не яв-
ляется ни чисто продольной, йи чисто поперечной. В таком слу-
чае имеются следующие три волны.
Квазипродолъная волна, называемая так потому, что части-
цы совершают колебания вдоль направления, образующего с вол-
новым вектором угол, отличный от нуля,
быстрая квазипоперечная волна,
медленная квазипоперечная волна.
Поляризации этих трех волн, распространяющихся с разны-
ми скоростями, всегда взаимно перпендикулярны. Векторы по-
тока энергии, определяющие направление переноса энергии для
каждой из волн, образуют разные углы с волновыми векторами.
Очевидно, что такие волны не представляют интереса для прак-
тических применений,' когда предпочтительнее выбирать особые
направления, такие как оси симметрии, вдоль которых распрост-
раняются чистые моды. Для них вектор потока энергии и волно-
вой вектор параллельны, как в изотропном твердом теле (раз-
делы 5.1.3 и 5.1.5).
Для ограниченной среды должны выполняться граничные ус-
ловия для механических и электрических (для пьезоэлектриче-
ской среды) величин (например, отсутствие механических напря-
жений на свободной поверхности, непрерывность нормальных
составляющих электрической индукции в отсутствие зарядов),
и волны, которые могут распространяться вблизи границ среды, не
являются более (за некоторыми исключениями) простыми волна-
ми, поскольку они содержат продольную и одну или две попе-
речные компоненты.
Рассмотрим кратко свойства таких волн.
На поверхности полубесконечной среды может распростра-
няться сложная волна — волна Рэлея (названная по имени уче-
ного, открывшего эти волны в 1885 г.). В простом случае изо-
тропного твердого тела эта волна содержит продольную и попе-
речную компоненты, сдвинутые по фазе на л/2 и лежащие в
сагиттальной плоскости, определяемой волновым вектором и нор-
малью к поверхности (рис. 5.2, а и б). Каждая из компонент
убывает с глубиной’ по-разному. Поскольку продольная компонен-
та меняет знак, проходя через нуль на глубине, примерно равной
0,2Х, поляризация волны становится чисто поперечной, а затем
140
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
среде смещение частиц происхо-
дит в сагиттальной плоскости и
содержит продольную и попереч-
ную компоненты, сдвинутые по
фазе,на л/2, амплитуды которых
убывают по разным законам. Ко-
нец вектора поляризации описы-
вает на поверхности эллипс об-
ратного знака (а). Смещение рав-
но нулю на глубине 2Л. Волна
вызывает искривление поверхно-
сти (б) (рис. 1 из [8]). в) Волна,
Гуляева — Блюстейна. Чисто по-
перечная поляризация параллель-
на поверхности пьезоэлектриче-
ского материала. Амплитуда сме-
щения частиц убывает экспонен-
циально с глубиной. Поверхность
остается плоской. -
опять эллиптической с противоположным направлением враще-
ния. Смещение частиц становится равным нулю, начиная с глу-
бины порядка 2Х (см. рис. 5.39).
. На поверхности полубесконечной пьезоэлектрической среды
возможно распространение поперечной поверхностней волны, по-
ляризованной параллельно поверхности (рис. 5.2, в), и с глуби-
Рис. 5.3. Волны Лэмба.
а) Симметричные волны. По обе стороны средней плоскости продольные
компоненты равны между собой, а поперечные компоненты имеют противо-
положные направления, б) Антисимметричные волны. По обе стороны сред-
ней плоскости продольные компоненты имеют противоположные направле-
ния, а поперечные — одинаковые.
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
141
ной проникновения тем меньшей, чем сильнее пьезоэлектриче-
ские свойства среды (раздел 6.2.2). Толщина слоя вещества, на-
ходящегося в движении под действием этих волн, называемых
волнами Гуляева — Блюстейна, больше, чем в случае волн Рэлея,
и может составлять, например, 100%.
Рис. 5.4. Упругие волны на границе двух твердых тел.
а) Для определенных сочетаний твердых тел, когда выполняются условия
непрерывности, волна Рэлея распространяется по обе стороны границы.
Такая волна на границе называется волной Стоунли. Справа показан при-
мер зависимости продольной и поперечной составляющих от ж3 для систе-
мы алюминий — вольфрам [1]. б) Волна Лява. Это поперечная волна, ко-
торая обладает дисперсией и распространяется в среде, состоящей из слоя
и подложки, при определенных условиях симметрии и определенных зна-
чениях скоростей (V' > К) в материалах.
Если среда ограничена двумя параллельными плоскостями,
волны Рэлея распространяются на каждой из плоскостей, пока
расстояние между ними велико по сравнению с длиной. волны.
Если это расстояние порядка %, возникают волны Лэмба, сим-
метричные или антисимметричные (рис. 5.3).
142
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Все сказанное выше относится к однородной среде. Для неод-
нородной среды, состоящей, например, из двух материалов с раз-
личными упругими свойствами, можно выделить два основных
случая в зависимости от относительных поперечных размеров
прилегающих тел. Первый случай показан на рис. 5.4, а. Вдоль
плоскости раздела двух изотропных полубесконечных твердых тел
распространяется волна, называемая волной Стоунли. Смещение
происходит в сагиттальной плоскости и убывает по обе стороны
от плоскости раздела. Второй случай (тонкий слой на полубеско-
нечной подложке) представлен на рис. 5.4, б. Такие поверхност-
ные волны с поперечной поляризацией называются волнами
Лява. Волны Стоунли и Лява существуют только при выполнении
определенных условий, например, скорость поперечной волны в
тонком слое должна быть меньше скорости в подложке (раз-
дел 5.2.4).
В заключение отметим, что Рзлей, Ляв и Стоунли открыли
волны, носящие их имена, при изучении распространения коле-
баний, вызванных землетрясениями.
§ 5.1. Упругие волны в неограниченном кристалле
В предыдущей главе предполагалось, что после деформации
тела все его точки остаются в стационарном состоянии. Смещение
щ каждой точки зависит только от ее начальных координат xh.
Теперь же 'будем считать, что в среде, через которую проходит
некоторое возмущение, все точки находятся в локальном движе-
нии. Смещение каждой материальной точки изменяется во вре-
мени по закону us = t).
5.1.1. Уравнение движения. Уравнение движения следует из
основного закона динамики Т? = т*(. В разделе 4.2.2 было пока-
зано, что сила, действующая на единичный объем тела, испыты-
вающий внутренние напряжения равна Д = дТц/дх^.
Без учета силы тяжести ускорение дгщ!д1? ъррлъ оси i, сооб-
щаемое этой силой массе р единичного объема, равно
При использовании закона Гука в форме (4.21) Тц = cw dui/dxk
уравнение движения принимает вид
д2и- d2Ui
= (5‘2^
Эта система трех дифференциальных уравнений второго по-
рядка является обобщением для трехмерной анизотропной среды
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
143
уравнения движения (1.13) для жидкости:
По аналогии с общим решением этого уравнения u = F(t — ж/V),
где V2 = 1/р%, будем искать решение в виде плоской волны, рас-
пространяющейся в направлении, определяемом единичным век-
тором п(п1? п2, н3), перпендикулярным фронту волны, согласно
уравнению nx = const:

(5.3)
Для определения фазовой скорости V и поляризации, т. е.
направления смещения частиц °ц( волны, подставим выражение
(5.3) в уравнение распространения (5.2). Обозначая через F"
вторую производную функции F, получаем
П-2 F' d'Ul
дх- lV ’ дх}дхк
Таким образом,
рощР" = CijMnjnh°ui р,
р720н.{ = Cijkinpiifui. (5.4)
Вводя тензор второго ранга
Г« = СцмЩПъ,, (5.5)
запишем предыдущее уравнение, называемое уравнением Кри-
стоффеля, в виде
Г«°иг = pV2°ud. (5.6)
Это уравнение показывает, что поляризация °щ является соб-
ственным вектором тензора Г« с собственным значением у =
= рУ2 (здесь и дальше используются результаты § 3.5).
Таким образом, для определения скорости и поляризации
плоских волн, распространяющихся вдоль направления п в кри-
сталле с модулем упругости cijkl, нужно найти собственные зна-
чения и собственные векторы тензора Г« = СцыП,пк. В общем слу-
чае для данного направления существуют три скорости распрост-
144
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
ранения, являющиеся корнями секулярного уравнения
1Г«-рР6«|=0, (5.7)
выражающего условие совместности системы трех однородных
уравнений (5.6). Каждой скорости соответствует собственный
вектор, определяющий направление смещения в среде (поляризаг
цию волны).
5.1.2, Общие свойства плоских упругих волн. Вследствие
свойств симметрии упругих модулей ((4.20) и (4.32)) тензор Га
является симметричным:
Гц = = СмцП]П)1 = = Гл;
и, следовательно, его собственные значения являются действи-
тельными величинами, а его собственные векторы ортогональны
(§ 3.5). Более того, собственные значения *f = pV2 положительны
(условие действительности скорости распространения У). Для
доказательства этого свойства вернемся к уравнению (5.6), кото-
рое после умножения на дает
в^Г4/°мг
Y= •«« *
Знак 7 определяется знаком числителя
euiVi°ul = °uinjCij)llnhaul.
Плотность же упругой энергии (4.34) Ф = l/iCijuSiiSM явля-
ется положительной независимо от деформации, т. е. для любого
симметричного тензора второго ранга Sis. В случае произвольного
тензора Ai}, который может быть разложен на симметричную
Л$ = (Лу + Ля)/2 и антисимметричную Лу = (Лу — Л#)/2 части,
произведение вида
Р = ЛусуйгЛйг = (Лу + Лу) Cijhi (Л^ + Aki)
сводится к величине
Р = ^CijkiA^i,
поскольку из перестановки индексов г, /, по которым производит-
ся суммирование, следует, что
= ATicjikl ~ —АЦсЦЫ = 0,
и поэтому Р = АцСшАи является положительной величиной для
любого тензора Л<,. В частности, для AiS = получаем
Р = °пщ^ми1Пк = °UiTttUi> 0, т. е. у > 0.
Поскольку собственные значения действительны и положи-
тельны, в общем случае существуют три плоские волны, рас-
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
пространяющиеся в одном направлении с разными скоростями и
ортогональными поляризациями (рис. 5.5).
Вектор смещения и, вообще говоря, не является параллель-
ным или перпендикулярным направлению распространения п.
Волна, поляризация которой наиболее близка к направлению п,
называется квазипродолыюй, две другие носят названия квази-
поперечных. Последние обычно всегда распространяются медлен-
нее, чем квазипродольная. Лишь при распространении вдоль осо-
бых направлений волны являются чисто продольными или попе-
речными [2, 3].
Рис. 5.5. Анизотропная среда. Общий случай.
В кристалле вдоль направления п могут рас-
пространяться три плоские волны, каждая со
своей скоростью. Волна, смещение в которой
°и<’> наиболее близко к вектору п, называет-
ся квазипродольной волной. Ее скорость обыч-
но больше скоростей двух других волн, име-
ющих поляризации °и<2> и °и<3> и называемых
квазипоперечными. Три вектора “и'1», °и'2>,
°и<3> взаимно перпендикулярны.
Прежде чем приступить к изучению распространения волн
вдоль направлений, связанных с элементами симметрии, получим
выражение для компонент тензора Г.(( = СцмП}пк. Суммируя по
индексам ; и к, имеем
Гц = Cin/nf + Ci22/ni + Ci33(«3 + (cil21 + c1211) И1И2 +
4~ (cil31 4~ ri311) «1^3 + (ci23l + ci321) ^2n3-
Отсюда получаем шесть компонент тензора Г«:
Гц = + с66и| + с88и| + 2с16п1п2 + 2c18nxn3 + 2с5вп2п3,
Г12 -- cienl + c2Sn% + с45п| + (с12 + с66) +
4~ (С14 + С5б) П1П3 + (С4в + С2б) ге2П3>
Г13 = + Cien% 4- С38и| + (с14 + с8в) nxn2 4-
+ (<43 4- С5В) П1П3 + (сзв 4- с48) п2п3,
Г23 — севп1 4" с22^2 4" с44ге8 4” 2С26^1^2 4~ 2с4вЦ1ге3 4" 2с24^2^3»
Г83 = С56^1 + С24^2 + С34И3 + (С46 + Сад) ПХП2 4-
+ (с3в + с4б) га1га3 + (С23 + С44) П2ПЗУ
Г33 — c55ni + с44га1 + сззпз + 2с48п1п2 4~ 4~ 2с34п2п8,
Гп —Г12> Г31 = Г13, Г32 = Гад. (5.8)
Ю Э. Дьелесан, Д. Руайе
146 ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
5.1.3. Распространение вдоль направлений, связанных с эле-
ментами симметрии.
а) Тензор Г,« при распространении вдоль оси xz (и( = п2 = О,
п3 = 1) имеет вид Г.« = ci23i или в явной форме
ГС55 С45 С35~|
1»3 = Р« ‘44 С34 ’
LC35 С34 C3sJ
Если ось х3 совпадает с осью второго порядка кристалла моно-
клинной системы (см. (4.43)), то с35 = с34 = 0. Тогда
ГС55 с45 ° 1
Г*ЗИ2 = %5 С44 ° Ь
L о о %3J
Для этого случая получаем продольную волну со скоростью Vt =
= Ус33/р и две поперечные волны с разными скоростями (§ 3.5).
Если ось х3 является одной из осей второго порядка кристал-
ла ромбической системы, с45 также равно нулю. Поперечная вол-
на со скоростью V2 = Vc44/p поляризована вдоль х2, а другая по-
перечная волна со скоростью V3 = Vc55/p поляризована вдоль «1.
При распространении вдоль оси симметрии порядка р>2 си =
= с55, и обе поперечные волны имеют одинаковую скорость, поля-
ризация же может иметь любое направление в плоскости, перпен-
дикулярной оси, так как оба собственных значения одинаковы.
Поперечные волны в этом случае являются вырожденными. Такое
направление, вдоль которого может распространяться поперечная
волна с произвольной поляризацией, называется акустической
осью. Условия равенства скоростей двух поперечных волн могут
выполняться не только для осей симметрии, но также и для дру-
гих направлений.
Эти результаты можно получить и из соображений симметрии.
Если п совпадает с осью симметрии Ар, симметрия системы кри-
сталл — направление распространения определяется этой осью.
Следовательно, поляризации волн должны быть инвариантными
по отношению к повороту вокруг п на угол 2л/р, но это возможно
лишь для чисто продольных или поперечных волн. Более того,
если р > 2, вектор смещения поперечной волны °и и полученный
в результате поворота вектор °и' не коллинеарны (рис. 5.6). Так
как им соответствует одна и та же скорость, т. е. то же самое
собственное значение тензора Гй, каждый вектор, перпендикуляр-
ный АР, может быть разложен на составляющие вдоль °и и °п' и,
следовательно, является собственным вектором тензора Г« с тем
же собственным значением. Тогда поперечные волны с произволь-
ной поляризацией распространяются с одинаковой скоростью.
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
б) Рассмотрим распространение волны в плоскости симметрии
или в плоскости, перпендикулярной оси симметрии АР четного
порядка. В обоих случаях существует ось второго порядка; по-
скольку упругие свойства и направление распространения инва-
риантны по отношению к инверсии (раздел 3.4.2) и имеет место
Рис. 5.6. Распространение волны
вдоль оси симметрии Ар (р > 2)
Любой вектор, перпендикулярный
Ар, может быть разложен на ком-
поненты вдоль векторов °и и °и',
связанных друг с другом .преоб-
разованием поворота на угол 2п/р,
и является собственным векто-
ром тензора Г, с тем же самым
собственным значением, как у
векторов °и и °и'.
Ар(р-г,4,б)
Рис. 5.7. В любом направлении п,
перпендикулярном оси симметрии
четного порядка Ар (простой или
инверсионной), существует попе-
речная волна, поляризованная
вдоль Ар.
равенство АгС — Аг = М, система кристалл — волна симметрична
по отношению к плоскости, перпендикулярной оси АР. Поляриза-
ции волн могут быть лишь параллельными Ар (поперечная волна Т)
или лежать в плоскости, перпендикулярной АР (квазипродйльная
волна QL и квазипоперечная волна фТ) (рис. 5.7). Такое рассмот-
рение показывает, что компоненты тензора Г13 и Г23 в плоскости
^1^2, которая перпендикулярна оси Ар, совпадающей с осью х3,
равны нулю:
В случае оси четвертого или шестого порядка выражение для
Г3з, полученное из (5.8) при п3 = О,
Г33 = С55Й1 + с44^2 + 2с^П1П2,
упрощается, так как с45 = 0 и с55 = с44 (см. (4.55) и (4.56)):
Гзз — С44 (И1 + — С44-
10*
148
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Скорость поперечной волны У3 = УГзз/р = Vc44/p не зависит от
направления распространения в плоскости, перпендикулярной оси
симметрии четвертого или шестого порядков.
5.1.4. Упругие волны в изотропной среде. В изотропной среде
упругие модули выражаются через константы Ламе X и р. с по-
мощью соотношения (4.36):
Сам ==Х6у6ы + р(6й6,-г + Мд),
и компоненты тензора Г« записываются в виде
+ fj.(SiAnjnk + дид^п^)
или
Г« = (X + р)ад +
С помощью выражений (4.37) X + ц = (сн + с1а)/2, р =
= (сц — с12)/2 получаем
Гн = С1Ц--1а щщ + nhnkbu. (5.9)
Поскольку nknk — п2 = 1, то
Гн
и уравнение для собственных векторов (5.6) запишется в виде
С11^С^ПгП1°щ + Г11-2 С]2 °щ = pV2°uj.
Выражая его в векторной форме
£11+_Нг (п Оц) п ^ру2

получаем два решения:
1) п°п = 0, которое соответствует вырожденной поперечной
волне, распространяющейся со скоростью VT = У(си — с12)/2р;
2) Мп (если п°п ¥= 0), которое соответствует продольной вол-
не, распространяющейся со скоростью VL = VcH/p, так как
(n0u)n = n20u = °u.
Таким образом, в изотропном твердом теле плоские волны яв-
ляются продольными или поперечными, и их скорости не зави-
сят от направления распространения. Более того, так как компо-
нента с12 положительна, то
vT < vLm (5.Ю)
в любом изотропном твердом теле.
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ 14g
Такое разложение на две волны, распространяющиеся с раз-
ными скоростями VL и VT, применимо также для любой формы
волны (не плоской). Вернемся к уравнению распространения (5.2)
и запишем его в виде
52и.
= (5.11)
Оператор дифференцирования Д« = d^/kdxjdx^) получается из
тензора Г« заменой п}пк оператором дг/{дх$х^.
Произведем эту подстановку в соотношение (5.9):
с11+с12 б2 , Си —с12® *
д« = —— — + —-— 6ПА,
где А = d2/dxk — оператор Лапласа. Уравнение (5.11) принимает
вид:
или в векторной форме, после подстановки dujdxi = div и и =
= (Au)f,
р р ~--*2 grad div u + Au.
Выразим си и с 1г через скорости плоских волн VL = Уси/р и
VT = У (си — с12)/2р. Тогда
§ = Tj-Au + (71 - 71) grad divu. (5.12)'
Вектор и всегда можно разложить на вихревую ит и потенци-
альную Uz, части: u = uT + uL, где divuT = 0 и rotub = 0. Уравне-
ние (5.12) записывается в виде:
= ^тд«т -г72гАиь + (71 - 71) grad div uL.
Используя соотношение grad div uL = Диь + rot rot uL = Диь, по-
лучаем
Оба выражения в скобках равны нулю, поскольку их дивергенция
150
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
и ротор равны нулю:
- °, - пдих - о. •
Эти два уравнения описывают распространение двух незави-
симых смещений uL и иг, соответственно со скоростями VL и VT.
В общем случае одновременно распространяются волна сжатия
(с относительным изменением объема, равным divuj со ско-
ростью VL и сдвиговая волна (divur — 0) со скоростью VT.
5.1.5. Поток упругой энергии. Распространение упругой волны
сопровождается переносом энергии. В этом параграфе будет по-
казано, что этот перенос может быть выражен через поток векто-
ра Умова — Пойнтинга, равный количеству энергии, переносимой
волной за единицу времени через единицу площади, и для случая
плоской волны будут вычислены компоненты вектора скорости
переноса энергии, равного отношению вектора Умова — Пойнтин-
га к плотности энергии.
Вектор Умова — Пойнтинга. Кинетическая энергия движения
вещества входит в выражение (4.29) для работы, совершаемой
внешними силами над твердым телом объема v0:
&W = J (pgi + duidv 4- J Tihd dv.
”o ®0
Действительно, сила, действующая на единицу объема, р£< +
+ dTtlJdxK, не равна нулю
Преобразуя второй член таким же образом, как в § 4.4, получаем
6ТГ = J р du^dv J TikdSikdv.
’о ®о
Поскольку dui представляет собой смещение за время dt (dut =
= {dUi/dt'jdt'), то первый член записывается в виде:
где для плотности кинетической энергии введено обозначение
=Тр(а?) • <5ЛЗ>
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
151
Работа сил, действующих на объем у0, оказывается равной
б И7 = f dffcdv + J d®dv = f d + Ф) dv,
где d<3) == TihdSi& — изменение потенциальной энергии единицы
объема, т. е. внутренней энергии (,d<%) при постоянной энтропии
или свободной энергии (с^Т") при изотермических условиях. Рабо-
та внешних сил (6W) увеличивает полную упругую энергию Е^ =
= j (<?с + ф) dv на величину dE<> = б T V.
”о
Энергия Е, содержащаяся в объеме v внутри тела, меняется
с течением времени. Ее увеличение dE равно работе механических
напряжений 7\(1), действующих на каждую точку поверхности
раздела s со стороны окружающей среды:
dE = j T’i(l) duids,
или, после подстановки вместо ТД1),
dE = J Tikhduids.
Изменение энергии, содержащейся в объеме v, за единицу вре-
мени
принимает вид
=0.
(5.14)
Здесь введен вектор Р с компонентами
ди-
Pk
(5.15)
Из уравнения (5.14) видно, что изменение энергии, содержа-
щейся в объеме v, обусловлено потоком вектора Р через поверх-
ность s, ограничивающую объем v. Вектор Р называется вектором
Умова — Пойнтинга, его направление является направлением рас-
пространения энергии, а его длина равна количеству энергии, пе-
реносимому через единицу поверхности, перпендикулярной к на-
правлению распространения энергии, за единицу времени (плот-
ность потока мощности). Обозначим через Vе скорость переноса
энергии, а через <£ — полную энергию единицы объема. Тогда
152
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Р = &Ve. Вектор скорости переноса энергии, параллельный Р,
выражается в виде
V* = ₽/<?. (5.16)
Скорость переноса энергии плоской упругой волны. В случае
плоской упругой волны смещение щ удовлетворяет соотношению
(5.3). Подставляя
ди-
1T-V .(5-17)
в (5.13), получаем для плотности кинетической энергии
#e = lp°u?F'2. (5.18)
Плотность потенциальной энергии (4.34)
гт 1 о 1 ди1
ф = у CiwSijSht = у ciM
после подстановки
5и{ . р' ди, р>
— -^-nkUly (5.19)
принимает вид
1 F'2
ф = у сцмп}пк °Ui °ut
Наконец, уравнение Кристоффеля (5.4) после умножения на
BUi дает
cnhinjnk °щ = pF2 °и?. (5.20)
Потенциальная энергия тогда выражается в виде:
ф = Хр°и?Г'2. (5.21)
Из сравнения (5.18) и (5.21) видно, что потенциальная и кине-
тическая энергии плоской волны равны. Плотность полной энер-
гии
g> = pou|F2. (5.22)
Значение вектора Умова — Пойнтинга
с учетом соотношений (5.17) и (5.19) можно записать в виде
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
153
Скорость переноса энергии получаем, разделив значение
на плотность полной энергии &:
(5.23)
р°и?7
Вводя единичный вектор смещения, можно записать
W = М = 1. (5.24)
Скорость Vе дает направление переноса энергии, т. е. направ-
ление акустического луча. Если этот луч перпендикулярен пло-
скому фронту волны, т. е. параллелен п, то говорят о распростра-
нении «.чистой» моды*). Направления распространения чистых
мод имеют важное значение. Кристаллы, используемые в практи-
ческих устройствах, таких как, например, линии задержки, имеют
форму длинных цилиндров или параллелепипедов, на торцах ко-
торых находятся преобразователи (рис. 9.2). Чтобы акустический
пучок, излученный одним преобразователем, был принят вторым,
вектор Умова — Пойнтинга должен быть параллельным оси стерж-
ня, т. е. волновой вектор должен быть перпендикулярным торце-
вым плоскостям кристалла. Систематическое исследование направ-
лений распространения чистых мод было проведено для кристал-
лов кубической, гексагональной и тетрагональной систем L4J.
Образуем скалярное произведение
г.-у,%,
и заменим числитель выражением (5.20). Тогда
Ven = V. (5.25)
Из этого уравнения видно, что проекция скорости переноса
энергии на направление распространения равна фазовой скорости
Рис. 5.8. Проекция скорости
переноса энергии Vе на на-
правление распространения
п равна фазовой скорости V
плоской волны.
плоской волны (рис. 5.8). Следовательно, Vе всегда больше (или
равно) V.
*) Термин «чистая» мода часто употребляется в литературе и для обо-
значения волн со строго продольной йлй поперечной поляризацией [3]. Эти
два определения совпадают только для продольных волн (упр. 5.2 и при-
мер в конце этого раздела).
154
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Интересно сравнить скорость переноса энергии с групповой
скоростью Vg, определенной в разделе 1.1.3 соотношением (1.10)
Ve = дса/дк. В трехмерном пространстве компоненты групповой
скорости равны
Ff = dtiddkj, kj = knj.
Решение секулярного уравнения (5.7)
\cwnfnh ~ рИ26«| = 0 (5.26)
дает зависимость фазовой скорости V от направления распростра-
нения п;, т. е.
У = /(»,).
Умножение (5.26) на к6, т. е. умножение каждой строки определи-
теля на к2-.
\ciWknjknk — pk2V2f>u\ = 0,
приводит к такому же соотношению между ® = kV п к, = knh
т. е. ® = f(k}) и, следовательно,
= dMj = 9V/dn}. (5.27)
Отсюда
Вычислим dV/dn}, взяв производную от V2 из выражения (5.20):
27^1
dni
_ dV _ »k°ui°ul
1 дп, Vkl p°u?V ’
(5.28)
Групповая скорость V* оказывается равной скорости переноса
энергии Vе, определяемой выражением (5.23).
Заметим, что соотношение Ven = V следует из теоремы Эйлера
для однородных функций: если f является однородной функцией
порядка р, то
df
niWi=Pf>
Из соотношения и = Vk = 1(кп() видно, что V = /(п<) является
однородной функцией от первого порядка:
щ =V, отсюда пVе = V.
Из этой теоремы, примененной к однородной функции от nt
нулевого порядка 7* = д¥!дщ, следует
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ 155
Пример. Для конкретизации понятия скорости переноса
энергии найдем направление акустического луча при_распростра-
нении вдоль оси третьего порядка в корунде (класс Зт). Матри-
ца са₽ приведена на рис. 4.6. Поскольку пк = бм, из (5.24) для
скорости переноса энергии получаем
(5 29)
Для продольной волны, распространяющейся со скоростью
Р1 = Ус33/р (раздел 5.1.3), смещение °а< = б(3, и отсюда следует,
что вектор Vе имеет компоненты *
Свз/ру, = 0, c«/pV1 = 0, cJpV^V,.
Эта продольная мода является чистой.
Для вырожденной поперечной волны, распространяющейся со
скоростью V2 = Vc44/p, смещение имеет произвольное направление
Рис. 5.9. Распространение волны вдоль оси третьего
порядка.
Направление скорости переноса энергии Vе вырож-
денной поперечной волны с поляризацией °и сос-
тавляет постоянный угол 0е с направлением распро-
странения п, совпадающим с осью третьего поряд-
ка. Для корунда 0е = 9°.
в плоскости (рис. 5.9):
щ = cos <р, иг = sin ф, а3 = 0.
Развертывая выражение (5.29)
p727i = с1131 cos2 ф 4- (с{ш 4- ci2S1) cos ф sin ф 4- cj2S2 sin2 ф ,
получаем для скорости переноса энергии:
= с15 cos2 ф 4- («14 + с5в)cos ф sin ф 4- ₽4в sin2 ф,
pF2V$ = с8в «оз2 ф 4- (с4в 4- с25) cos ф sin ф 4- си sin2 ф,
pF27$ = с5Б cos2 ф 4- («54 + «4б) cos Ф sin ф + с44 sin2 ф.
Имея в виду равенство нулю модулей ci5, с4е, «25, с45 и соотно-
156
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
шения с53 = с14 = —с24 и cS5 = ctt, получаем:
pV2V{ = cu sin 2ф, p7s7£ = с14 cos 2<р, рУ2У| = с44.
Таким образом, вектор Vе имеет следующие компоненты:
г, = ^«»2ф, П = $».
Угол 0е между Vе и осью третьего порядка не зависит от <р,
tgOe= |cul/cH, (5.30)
следовательно, при вращении поляризации поперечной волны в
плоскости xtx2 вектор скорости переноса энергии описывает конус
с углом при вершине 0е. В случае кристаллов корунда
с,* = -2,35 • 1010 Па, си = 14,74 • 1010 Па, 0е = 9е.
Ось третьего порядка — это единственная ось симметрии, не
являющаяся направлением распространения чистых мод. Действи-
тельно, для п = 2, 4 и 6 модуль си равен нулю, поэтому 0е — 0.
5.1.6. Характеристические поверхности. Подобно тому, как в
оптике кристаллов используются поверхности показателей прелом-
ления- и волновые поверхности, для описания распространения
упругих волн в кристаллах оказываются полезными различные
характеристические поверхности.
Определения и свойства. Проведем из начала координат пер-
пендикулярно фронту волны вектор, длина которого равна фазо-
вой скорости V. Геометрическое место концов векторов Т = Fn,
соответствующих разным направлениям распространения, называ-
ется поверхностью скоростей. В общем случае эта поверхность со-
стоит из трех полостей. Одна соответствует квазипродольной вол-
не (поверхность Vt) и две — квазипоперечным волнам (поверхно-
сти V2 и 73). Поскольку в любом направлении скорость квазипро-
дольных волн обычно больше *) скорости квазипоперечных волн,
поверхность V\ находится вне поверхностей V2 и V3, не соприка-
саясь с ними. Наоборот, поверхности V2 и V3 имеют общие точки
в направлениях акустических осей, например, вдоль оси симмет-
рии порядка р > 2. В случае изотропной среды' поверхности ско-
ростей представляют собой две сферы с радиусами VL и VT.
Поверхностью обратных скоростей* **) (L) называется геомет-
рическое место концов векторов L = п/7, проведенных из задан-
ной точки О. Поскольку векторы L и Т коллинеарны, и LV — 1,
♦) Существуют исключения, например в ТеО2 (табл. 5.2).
**) Употребляются также термины: поверхность рефракции, поверх-
ность медленпостей. {Прим, ред.)
§ 5,1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
157
поверхности скоростей и обратных скоростей связаны друг с дру-
гом операцией инверсии относительно единичной сферы с центром
инверсии в начале координат О. Поверхность обратных скоростей,
аналогичная поверхности показателей преломления в оптике, иг-
рает важную роль при рассмотрении
отражения и преломления упругих
волн (§ 5.2). Кроме того, эта поверх-
ность интересна тем, что, наряду с
фазовой скоростью, позволяет опреде-
лить направление переноса энергии.
Действительно, если L и L + dL —
радиус-векторы в бесконечно близких
направлениях п и n + dn, то вектор
направлен по касательной к поверх-
ности обратных скоростей (рис. 5.10).
Свертка выражения
_ д (»j/F) = dV
dnk dnk v Vidnh
Рис. 5.10. Поверхность обрат-
ных скоростей и скорость пе-
реноса энергии.
Скорость переноса энергии в
каждой точке перпендикуляр-
на поверхности обратных ско-
ростей: VedL = 0.
с компонентами У* скорости переноса энергии дает:
Принимая во внимание соотношения (5.25) V"m = V и (5.28)
V‘h = Vl = dV/dnh, получаем
йд. , dL,
V‘ z— = 0; V dL = dnk = 0 для всех dL.
dnk dnk
Применяя это условие ортогональности для всех векторов dL,
лежащих в плоскости, касательной к поверхности обратных ско-
ростей, получаем, что скорость переноса энергии в каждой точке
нормальна к поверхности обратных скоростей. Как и в предыду-
щем случае, существуют три поверхности обратных скоростей, од-
нако поверхность, соответствующая квазипродольной волне, на-
ходится внутри поверхностей для квазипоперечных волн.
Третья поверхность, которая называется волновой поверх-
ностью *), представляет собой геометрическое место точек, зани-
маемых концом вектора скорости переноса энергии Vе, проведен-
ного из точки О, при изменении направления распространения.
♦) Употребляются также термины: поверхность лучевых скоростей, лу-
чевая поверхность. (Прим, ред.)
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Длина радиус-вектора, соединяющего начала координат О с точ-
кой на поверхности R, равна расстоянию, которое упругая энер-
гия проходит за единицу времени. Следовательно, волновая по-
верхность представляет собой геометрическое место точек, до ко-
торых за единицу времени дойдут колебания, возбужденные в
начальный момент точечным источником, находящимся в точке О.
Эта поверхность является также поверхностью равных фаз, так
как все ее точки начинают колебаться в один и тот же момент
времени. Волновая поверхность обладает и другим замечательным
свойством: направление распространения плоской волны, скорость
Рис. 5.11. Волновая поверх-
ность и направление распро-
странения.
Плоскость волны Р проходит
через конец вектора скорости
переноса энергии V* касатель-
но к волновой поверхности.
Рис. 5.12. Поверхность скоростей и
волновая поверхность.
Поверхность скоростей есть геомет-
рическое место ортогональных про-
екций центра О на плоскости, каса-
тельные к волновой поверхности
(подера). Наоборот, волновая по-
верхность является огибающей се-
мейства плоскостей, проходящих че-
рез концы проведенных из центра
О векторов Т и препендикулярных
этим векторам.

переноса энергии которой равна Vе, оказывается перпендикуляр-
ным к волновой поверхности в соответствующей точке. Действи-
тельно, из соотношений
VeL=l и VedL = 0 .
следует
LdV = О
или nrfV' = 0, так как L = n/V.
Следовательно, вектор п перпендикулярен любому вектору dVe,
лежащему в плоскости, касательной к волновой поверхности
(рис. 5.11).
Легко перейти от волновой поверхности к поверхности скоро-
стей и наоборот (рис. 5.12). Проведем через точку А плоскость Р,
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
951
касательную к волновой поверхности R. Из соотношения V'n = V
видно, что фазовая скорость V является проекцией радиус-вектора
ОА = V' на нормаль п к волновой поверхности п. Следовательно,
конец В вектора У’ является основанием перпендикуляра, опущен-
ного из точки О на плоскость Р. Таким образом, поверхность ско-
ростей есть подера волновой поверхности, т. е. геометрическое ме-
сто ортогональных проекций точки О на плоскости, касательные
к волновой поверхности. С другой стороны, волновая поверхность
является огибающей семейства плоскостей, проведенных через ко-
нец вектора У, исходящего из точки О, перпендикулярно этому
вектору.
Примеры поверхностей обратных скоростей. Ниже приводятся
примеры поверхностей обратных скоро-
стей для некоторых кристаллов. На пло-
скости можно изобразить только сечение /
этих поверхностей. Если плоскость сече- у
ния является плоскостью симметрии для /
упругих свойств (зеркальная плоскость /
или плоскость, перпендикулярная оси сим-
метрии четного порядка), поверхность
симметрична по отношению к этой пло-
скости. Следовательно, нормаль к поверх-
ности лежит в плоскости сечения. На- „
правление распространения задается дву- ^спространенияТз^
мя углами 0 и ф, как показано на ется углами 0 и <р.
рис. 5.13,
Из = cos 0. (5.31)
Секулярное уравнение аналитически может быть решено толь-
ко для особых направлений или плоскостей, для которых по край-
ней мере две из трех недиагональных компонент тензора Г« равны
нулю. В этом случае определитель может быть выражен в виде
произведения полиномов первого или второго порядка по V2
(§ 3.5).
а) Кубическая система. Выражение (5.8) для компонент тен-
зора Г« упрощается, если принять во внимание матрицу са$ (4.45)
для кристаллов кубической системы:
nxn8,
160
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Кроме того, если волна распространяется р плоскости грани куба,
например (001), то fti = cos<p, n2 = sin<p, n, = 0, следовательно,
Ги = Г23 = 0и тензор Г« имеет следующий вид:
ГГц г12 0 1
Гн = I Г12 Г22 0 ,
L0 0 м
где
Гц = Сц cos2 <р + с44 sin2 <р,
Г22 Сц sin2 ф + с44 cos2 ф, rss = ct4.
Г42 = (с12 + с44) cos ф sin ф,
Для любого направления распространения в плоскости (001)
всегда существует поперечная волна, поляризованная вдоль оси
скорость 73 = Ус44/р которой не зависит от угла ф. Две другие
скорости получаются из решения уравнения для собственных зна-
чений 7 = рУ2 согласно формуле (3.24):
Ti.2 = ± 4 /(Гц-Г22)2+4(Г1а)2. (5.33)
Зависимость скоростей У, и У2 от угла ф дается выражениями
2рУ? = си + с44 + / (cu — с44)2 cos 2ф + (с12 + с44)2 sin2 2ф, (5.34)
2рУ| = сц + с44 — V(сп — с44)2 cos 2ф + (с12 4- с44)2 sin2 2ф. (5.35)
В общем случае поляризация этих волн не является ни чисто
продольной, ни чисто поперечной. При ф = 0 или л/2 одна ско-
рость У1 = Усц/р соответствует продольной волне, а другая У2 =
= Гс44/р — поперечной волне. Для других направлений выраже-
ния (5.34) и (5.35) дают скорости У4 и У2 соответственно квази-
продольной и квазипоперечной мод.
Сечения поверхности обратных скоростей для кремния пост-
роены на рис. 5.14 при использовании модулей упругости из
табл. 4.1. Полученные сечения отражают наивысшую симметрию
кубической системы, так как тензор модулей упругости, который
одинаков для пяти классов этой системы, инвариантен по отно-
шению к операциям голоэдрического класса. Скорость квазипо-
перечной волны экстремальна в направлениях [100] и [НО] и
выражается формулами
УД 1001 = У2[110] = Г(си-с)/2р.
Отношение этих скоростей
г2И001
V2[110]- V 'и-с12
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ 161
характеризует анизотропию кристалла с точки зрения механиче-
ских свойств. Вид сечений поверхности обратных скоростей для
кремния соответствует наиболее распространенному случаю, когда
фактор анизотропии
А = 2с44/(си - с12) (5.36)
больше единицы (для Si А = 1,565). При А < 1 знак кривизны
сечений изменяется как, например, в пьезоэлектрическом мате-
риале, германате висмута (Bi12GeO20) (рис. 6.5). Отметим, что для
изотропного тела А = 1.
Направления поляризаций также изменяются с направлением
распространения. Углы и (J2, которые образуют с осью век-
торы смещения квазипродольпой и квазипоперечной волн, даются
формулой (3.25) tg20 = 2Г12/(Ги—Г22), и в плоскости (001) кри-
сталла кубической системы
tg2p = ^i£«tg2(p. (5.37)
С11 44
На рис. 5.15 показано отклонение (Pi —<р) вектора смещения
квазипродольпой волны от направления распространения в пло-
скости (001) кремния. Отклонение максимально при угле фм==
И Э. Дьелесан, Д. Руайе
162
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
= 18°52', удовлетворяющем условию
Максимальная величина отклонения (7° 16') равна
Pi — Фм = т— 2<рм.
Рассмотрим теперь распространение в плоскости (НО). Удобно
пользоваться системой координата?!, x'z, х3, полученной поворо-
том кристаллографической системы координат xt, х2, х3 на угол
л/4 вокруг оси Хз (рис. 5.16). Матрица модулей упругости сар
Рис. 545. Кубическая система. Отклоне-
ние (Pi —<р) вектора смещения квази-
продольной волны от направления рас-
пространения в плоскости (001) крем-
ния.
Рис. 5.16. Кубическая система.
Повернутая сцстема коорди-
нат Тр ж2, ®д, используемая
для вычисления скоростей в
плоскости (110).
имеет такой же вид, как для кристаллов тетрагональной системы
с с1в = 0, так как ось совпадает с осью симметрии второго поряд-
ка. Выражение (5.8) для компонент тензора Г« с учетом (4.55)
и значений тщ = sin 0, га2 = 0, п3 = cos 0 сводится к выражению
г Гн о г;31
г,о г;2 о I
1г13 ° ГззА
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
163
где
Гн = сц sin® 0 + cti cos2 0, Г13 = sin 20,
Г22 = с'бв sin2 0 + Си cos2 0, Г33 = С44 sin2 0 + с33 cos2 0.
Таким образом, в этом случае имеется поперечная волна, по-
ляризованная вдоль х2, т. е. вдоль направления [НО], со ско-
ростью _ _______________________
У8 = У^Е2® = c8»sin!ie + cMCO32e ,
п две волны, квазипродольная и квазипоперечная. со скоростями
соответственно Vt и V2-_____________________
2рГ212 = Гц + Г33 ± ]/” (Гп — Г33)® -|- 4 (Г13)® =
= С44 + Сц sin2 0 + с33 cos 0 ±
± К[(сц - С44) sin2 0 + (С44 — С33) cos2 о]2 + (cw + С44)2 sin2 20.
Поскольку модули упругости всегда задаются в кристаллогра-
фической системе координат, следует выразить постоянные сар
через са₽ с помощью матрицы преобразования координат
/ 1/1/2 1/1/2 0\
с4= -1/У2 1/У2 0 .
\ 0 0 1/
Из соотношения еда = aia]arhaicpqT3 получаем
СЗЗЗЗ = С33з3, С33 = С33 = Сц, I
Саиз = а^а|с1313 + а1а%с3333 = (а2а2 + aja|) с44, см = с44,
СцЗЗ = alalC1133 + а1а1С2233 — (а1а1 + а1а1) С13, с13 = с13 = С12,
1 ’ _ си ~ с!2
С1212 — "4 С11 + "4 С22 ~~2 с12’ — 2 ’
Спи = -yCn-l- уС22 + с6в + -|-С12, Сц = + С44.
Отсюда для скоростей поперечной (И3), квазипродольпой (Т7,) и
квазипоперечной (У2) волн имеем:
Гз " У^4 C°S2 6 + Cjl2p-3 Sin2 9’ (5,38)
2рГц2 = с4< + (с44 + -пу—) sin2 0 + cu cos2 0 ±
± l/[g-^—?sin20 + (С44 -Сц)cos20] + (с12 + С44)2sin220.
(5.39)
И*
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Сечения плоскостью (110) поверхности обратных скоростей i/Vt,
1/V2, 1/Va для кремния показаны на рис. 5.17.
В табл. 5.1 указаны направления поляризаций и приведены
выражения для скоростей вдоль особых направлений распростра-
нения, а также численные значения скорости в некоторых кри-
сталлах кубической системы (кремний, арсенид галлия (GaAs),
алюминий, золото, платина).
Рис. 5.17. Кубическая система. Сечения поверхности обратных скоростей
кремния плоскостью (110).
б) Тетрагональная система. Тензор Кристоффеля для кристал-
лов тетрагональной системы с учетом (5.8) и (4.55) имеет вид
Гц = СцП1 + cMnl 4- С44Я3 + 2с1вп1па,
Г12 = С1в (га1 — ni) + (С12 4* С6в)
Г13 = (С13 + С44) ИД, (5
Г22 = свап1 4" с11п2 + с44п3 — 2с1вП1П2,
Г2З = (с13 + С44) П2и3,
Г33 = с44 (и1 + П1) + С33И3-
Если волна распространяется в плоскости, перпендикулярной
оси четвертого порядка (n^coscp, n2 = siH(p, п3 = 0), тензор Г«
имеет вид
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
165
где
Гц — Гц cos2 <р + cee sin2 ф + с1в sin 2ф,
Г12 = С16 cos 2ф (с12 +св9) '2 ф,
Г22 = с66 COS2 ф + сХ1 sin2 ф — с16 sin 2ф,
Гзз ~ с44-
Секулярное уравнение идентично секулярному уравнению ку-
бической системы, и, следовательно, в этом случае имеется по-
Таблица 5.1. Кубическая система
Ml Поляриза- ция •*) Скорость Числовые значения V, м/с
S1 GaAs ») Al AU Pt
[100] [100] (L) 8433 4735 6300 3158 4025
плоскость (100) (Г) 5843 3347 3236 1482 1891
[НО] ИЮ] (L) "|/ сп+с1г+2с44 V 2р 9134 5242 6450 3376 4189
[ЙО] (Г) 4673 2478 2935 874 1498
[001] (Г) Vr-t 5843 3347 3236 1482 1891
[111] [HU W |/ Cii+2ci2+4c44 9360 5401 6496 3447 4242
плоскость [111] (D . / с11~с12~Нс44 v зр 5085 2798 3039 1114 1639
*) В GaAs скорость рассчитала в пренебрежении пьезоэлектрическими свойствами.
**) (L) — продольная волна, (Т) — поперечная волна.
перечная волна, поляризованная вдоль я2, со скоростью V3 =
= Ус44/р и две волны, поляризованные в плоскости (001), со ско-
ростями ______________________
2pVb = Ги + Г22 ± /(Гп- Г22)2 + 4 (Г12)2.
Выражая Гц, Г22, Г12 через модули упругости, получаем
2рГ1,а = с'и + с68 ±_____________________________________________
± V [(сп— свв) cos 2ф4-2с16 sin 2ф]2 + [(с12+ c6e) sin 2ф+2с1в cos 2ф]2,
166
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
ИЛИ
2pFi2,2 = сп + С66 ±
±К(Сц—Сев)2 cos2 2cp+(c12+c6e)2sin2 2ф4-2с1в(сп4-с12) sin 4ф+4с?в.
(5.41)
Скорость Vi (знак +) соответствует квазипродольной волне,
V2 (знак —) — квазипоперечной волне.
Для кристаллов, принадлежащих к классам 422, 4mm, 42m,
4/mmm, модуль с1в равен нулю, и формулы сводятся к виду
2рЦ8 = сн + свв ± (си — cee)2 cos2 2<р + (ci2 + св6)2 sin2 2<р. (5.42)
На рис. 5.18 показаны сечения поверхности обратных скоро-
стей плоскостью (001) для рутила (ТЮ2, класс 4/mmm), построен-
ные при использовании модулей упругости из табл. 4.1. Для
этих сечений характерна высокая степень анизотропии вследствие
большой величины отношения
А — 2сы/(сц — Ciz) = 4.
Скорость квазипоперечной волны в направлении [100] в два
раза больше, чем в направлении [110].
В табл. 5.2 приведены скорости упругих волн в некоторых
кристаллах, принадлежащих к классам, для которых в кристалло-
графической системе координат с16 = 0 (рутил TiO2, парателлурит
ТеО2, индий In).
Таблица 5.2. Тетрагональная система,
классы 422, 4тт, 42т, 4/ттт
Is № Поляризация Скорость Число вые значения V, м/с
TiO2 Те02 *) ЛП
[100] [100] (L) У<щ/р 8014 3050 2495
[010] (Т) V<WP 6756 3317 1290
[001] (Г) Уо?р 5424 2100 946
[НО] [1W] (Ь) V (сц+с12+2с6б)/2р 9923 4663 2740
[110] (Г) V (сп—с1з)/2р 3378 616 603
[001] (Г) Ус«/р 5424 2100 946
[001] [001] (L) У^/р 10671 4200 2490
плоскость (001) (7’) Ус«/р 5424 2100 946
*) Отметим, что в парателлурите (ТеО2) в направлении [1001 поперечная волна (Г)
имеет ббльшую скорость, чем продольная (£).
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
167
Рис. 5.19. Тетрагональная система, классы 4, 4, 4/и. Сечения поверхности
обратных скоростей молибдата свинца (4/те) плоскостью (001).
168
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Для классов точечной симметрии 4, 4, 4/т модуль с1в не ра-
вен нулю. На рис. 5.19 показаны сечения поверхности обратных
скоростей плоскостью (001) для молибдата свинца РЬМО4 (класс
4/?п, модули упругости из табл. 4.1). Полученные сечения подобны
сечениям для рутила, повернутым в плоскости (001) на угол ф0.
Это подобие не является случайным, а вытекает из возможности
такого преобразования координат, при котором модуль исче-
зает. Действительно (упр. 5.5), с{6 = 0 в системе координат, по-
вернутой на угол фо, определяемый соотношением
124фо = 4с1в/(с11-с12-2с6в). (5.43)
В направлениях хг и х2, а также под 45° к этим направлениям
волны, поляризованные в плоскости (001), являются продольными
или поперечными. В двух случаях это чистые моды. Для молибда-
та свинца фо = —16° и направления чистых мод составляют углы
—16° и +29” (= —16° + 45°) с кристаллографической осью [100].
Таким образом, скорости в кристаллах этого типа могут быть
вычислены двумя способами.
1. С помощью полных формул (5.41) при использовании моду-
лей cat, заданных в кристаллографической системе координат.
2. С помощью упрощенных формул (5.42) с использованием
новых модулей сар в системе координат, повернутой вокруг оси
на угол ф', в которой с1в 0.
Второй "способ имееет то преимущество, что позволяет найти
направления чистых мод и получить простые выражения для ско-
рости в этих важных для практики направлениях, например, вдоль
оси х{ имеем Vt = и?2=|/4в/р (для молибдата свинца
F, = 3780 м/с, V2 = 2460 м/с).
в) Гексагональная система. В кристаллах гексагональной систе-
мы все плоскости, проходящие через ось симметрии шестого по-
рядка, эквивалентны с точки зрения упругих свойств (упр. 4.4).
Характеристические поверхности являются поверхностями враще-
ния вокруг этой оси. По той же причине скорости упругих волн
не зависят от направления распространения в плоскости (001),
перпендикулярной оси шестого порядка. Для расчета скоростей
выпишем тензор Г« кристаллов гексагональной системы:
Г- _2 , „ „2 , „ Я
11 — С11га1 + сввИ2 + С44П3?
Г12 = (C12+ %) П2П2,
Г13 = (С13 + С41) га1га31
п 2 , 2 । 2 (5.44)
^22 = СввП1 + СПП2 + С44П3>
Г23 = (Ci8 + с44) ra2ra3,
Г33 — сы (га1 + гаг) + сззгез,
г
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ 16»
где с66 = (си — с12)/2. В простом случае направления [100] тензор
Г становится диагональным:
Ри 0 0 1
Г = 0 евв 0 I
L ° 0 с44]
Таким образом, в плоскости (001) могут распространяться про-
дольная волна со скоростью V,.=• Усп/р, поперечная волна, поля-
ризованная в плоскости (001), со скоростью V2 = Vcee/p и попереч-
ная волна, поляризованная параллельно оси Ав, со скоростью
V3 = Ус41/р.
Сечения поверхности обратных скоростей плоскостью (001)
представляют собой окружности с радиусами
Ур/сн, Vp/eM, Vp/cw.
В плоскости, проходящей через ось Л6, скорости зависят от
угла между осью 4e(a:s) и направлением распространения п. Для
плоскости т2т3
nt = 0, n2 = sin 0, п3 = cos 0, т. е. Г12 = Г13 ™ 0,
и тензор Г« записывается в виде
[Гц 0 о!
0 Г22 Г23 L
0 Г23 ГЗзЗ
где -
I\ i = см sin2 0 + с44 cos2 0, Г22 — Сц sin2 0 + си cos2 0,
(5.45)
Г23 = (Cis + Си) sin 0 COS 0, Г33 ’= Сц sin2 0 + Сзз cos2 0.
Поперечная волна, поляризация которой перпендикулярна пло-
скости, проходящей через ось Ав, распространяется со скоростью
Г, = 1/5=-/^8 + ^’С. (S.46)
где се6 = (сц — Си)/2.
Скорости двух других мод, которые поляризованы в плоско-
сти, проходящей через Л8, даются соотношением
2рУ112 = Г22 + Г33 ± /(Г22 - Г,з)2 + 4Г|з.
Подстановка выражений (5.45) для Г22, Г23, Г33 как функций от 0
170
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
в случае квазипродольной волны дает
2рУ2 = cit + Сц sin2 0 + с33 cos2 0 +
+ V 1(^11 — с«) sin2 9 + (С44 — Сзз) cos2 0]2 + (с13 + с44)2 sin2 20,
(5.47)
а в случае квазипоперечной —
2р73 == с44 + cu sin2 0 + с33 cos2 0 —
— V[(Сц — С44) sin2 0 + (с44 — с33) cos2 0]2 + (с13 + с44)2 sin2 20.
(5.48)
Сечения поверхности обратных скоростей плоскостью, прохо-
дящей через ось Ав, на рис. 5.20 для бериллия получены при ис-
пользовании величин cih и р из табл. 4.1. В табл. 5.3 даны числен-
ные значения скоростей для бериллия (Be) и титана (Ti).

- кбизтоперетт
Рис. 5.20. Гексагональная система. Сечения поверхности обратных, скоро-
стей бериллия плоскостью, проходящей через ось шестого порядка.
г) Тригональная система. Если модуль с25 ¥» 0, расчет оказыва-
ется весьма сложным. Кристаллы этой системы, используемые
в практических устройствах (корунд, кварц, ниобат лития), при-
надлежат к классам Зтп, 32, 3 m, для которых с25 = 0. Матрица
модулей упругости приведена на рис. 4.6, а тензор Г имеет
§ 5.1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
171
следующие компоненты:
Гц - Сцп1 + с6вп2 + с44п3 + 2ci4«2n3»
Гц = (<*12 + Сев) и1га2 + 2с,14721П3,
Гхз - 2с14п1п2 + (с13 -j- С44) П-1.П3,
Г22 — сввп1 + С11п2 + С44л| — 2с14П27г3,
Ггз — С14 («1 — пТ) + (с13 + с44) п2п3,
Г33 - с44 (И1 4~ Пз) 4" С33п|.
где св6 = (си — с12)/2.
В любом направлении, перпендикулярном оси третьего поряд-
ка = cos <р, n2 = sin<p, га3 = 0), ни одна из компонент Г« не
Таблица 5.3. Гексагональная система
Направление рас- пространения Поляризация Скорость Числовые значения V, м/с
Be Ti
Вдоль оси Z Z (£) Плоскость X Z (Т) т/сззф Ус44/р 13 490 9 380 6330 3220
Перпендикулярно оси Z Продольная Поперечная 1 Z Поперечная || Z У (сп—cia)/2p Ус«/р 12 580 8 480 9 380 6000 2795 3220
равна нулю, так что уравнение для собственных значений может
быть решено только численными методами, за исключением на-
правлений xt и х2.
Вдоль направления (щ = 1, га2 = п3 = 0) тензор
Г -
рн 0 0 1
0 С6в С14
L 0 С14 C41J
дает продольную волну со скоростью V = Усп/р и две поперечные
волны со скоростями V2 и V3-
2pTZ2 = Сев + С44 + (С6в — С44)2 + 4С14, (5.50)
2pTzg — свв + с44 — (свв — с4<)г + 4с|4. (5.51)
172
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Вдоль направления хг (п2 = 1, п1 = п3 = 0) имеем
Гсвв 0 °1
1=0 си — с14 I
L ° ~ с14 С44 J
и для этого направления существует поперечная волна, поляризо-
ванная вдоль оси со скоростью Vs = Vcee/p, квазипродольная
волна со скоростью Vt, определяемой соотношением
2pV? = сп + с44 + (си — с44)2 + 4с24, (5.52)
и квазипоперечная волна со скоростью
2pV| = сп + с44 — ]/"(с1Х — с44)2 -|- 4сХ4 . (5.53)
Сечения поверхности обратных скоростей плоскостью XY для
корунда показаны на рис. 5.21 (значения cto и р взяты из
табл. 4.1).
При распространении в плоскости a^s (плоскость симметрии
YZ) п,. —0, п2 — sin 0, n3 = cos 0, и тензор Г принимает вид
Гги о о!
г= о г22 г231
1° Г23 Г3з]
где
гн = с66 sin2 0 + с44 cos2 0 + с14 sin 20,
Г22 = cusin2 0 + с44 cos2 0 — с14 sin 20,
(с +е ч (5.54)
Г23 = - с14 sin2 0 + ( 13 а sin 20,
Г33 = с44 sin2 0 + с8з cos2 0.
Таким образом, в плоскости YZ существует поперечная волна,
поляризованная вдоль со скоростью
V,. + (5.55)
квазипродольная и квазипоперечная волны соответственно со ско-
ростями Vt и V2: __________________
2рУ1,з = Г22-Ь Г33 ± (Г22 — Г33)2 + 4Г2з =
= с44 -j- Сц sin2 0 с33 cos2 0 — с14 sin 20 ±
± {(сц sin2 0 —с33 cos2 0 -J- с44 cos 20 — с14 sin 20)2 +
Н- [(с» + с44) sin 20 - 2с14 sin2 0]2}V*. (5.56)
§ 5,1. УПРУГИЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ КРИСТАЛЛЕ
173
Рис. 5.21. Тригональная система, классы Зт, 32, Зт. Сечения поверхности
обратных скоростей корунда (Зт) плоскостью XY.
Поскольку плоскость XY не является зеркальной плоскостью, она не со-
держит нормали к поверхности обратных скоростей. Следовательно, ось У
не является направлением распространения чистой моды. Из рис. 5.22 вид-
но, что скорость переноса энергии направлена под углом к плоскости се-
чения XY.
Рис. 5.22. Тригональная система, классы Зт, 32, Зт. Сечения поверхности
обратных скоростей корунда (Зт) плоскостью YZ,
ГЛ. о. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Из рис. 5.22 видно, что ось третьего порядка йе является
направлением чистой моды для поперечных волн (см. примеры в
разделе 5.1.5). Действительно, ось х3 не перпендикулярна поверх-
ностям обратных скоростей. Однако в плоскости YZ имеются
направления чистых мод для поперечной волны, поляризованпой
вдоль X. Чтобы их найти, вычислим компоненты скорости перено-
са энергии с помощью формулы (5.24) или в зависимости от угла
В (nt = 0, п2 = sin 0, п3 — cos6):
V" = поскольку °щ = 6ц.
Эти компоненты оказываются равными
Vе П Vе - Sin 0 + "1* C0S 9 Vе c14Sin0 + C44COS0
Их-и, , Из- -
Вектор скорости переноса энергии (акустический луч) образу-
ет с осью Z угол 0е, удовлетворяющий соотношению
У2 _ cg6 sin 0 + сц cos 0
tg° ' r*~c14sin0 + c44cos0-
На рис. 5.23 показано отклонение (0 — 0е) акустического луча
от направления распространения в плоскости YZ. Поперечная
поперечной волны от направления распространения^ в плоскости УХ ко-
рунда.
волна является чистой, если 0' = 0, т. е. при углах 0t и 02, удов-
летворяющих соотношению
tg20 = 2c14/(c44-c.e). (5.58)
Для корунда 01 = 33°28' и = —56°32'. Эти интересные на-
правления чистых поперечных мод обозначены на рис. 5.22 пря-
мыми АС и ВС.
5.2. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН 175
§ 5.2. Отражение и преломление плоских упругих волн
При прохождении монохроматической плоской упругой волны
с определенной поляризацией через границу раздела двух кристал-
лических сред в общем случае возникают три волны по каждую
сторону от границы. Падающая квазипродольная волна может
порождать в кристалле, в котором опа распространяется, квази-
продольную и квазипоперечные (медленную и быструю) отражен-
ные волны, а во втором кристалле — также квазипродольную и
квазипоперечные (медленную и быструю) прошедшие (или пре-
ломленные) волны. Наиболее простым является случай двух изо-
тропных сред, поскольку в этом случае волна порождает не более
двух волн в каждой из сред, а их поляризации являются чисто
продольными или чисто поперечными
5.2.1. Уравнение непрерывности. Задача об отражении и пре-
ломлении волн ставится следующим образом. При известных на-
правлении распространения, поляризации, амплитуде падающей
волны и заданных упругих свойствах обеих сред требуется найти
направления распространения, поляризации и амплитуды отра-
женных и преломленных волн, а также скорости переноса энер-
гии для каждой волны. Решение получается с помощью уравнений
распространения для каждой среды и граничных условий на по-
верхности раздела, причем аналитические решения возможны
лишь для некоторых частных случаев.
Если обе среды жестко связаны между собой по поверхности
раздела, граничные условия сводятся к непрерывности смещений
ut и механических напряжений Т{ в каждой точке границы. Урав-
нение плоскости раздела с единичным нормальным вектором
l(Zi, l2, Z3) и с началом координат на границе раздела имеет вид
1х = 0.
Граничные условия требуют, чтобы в каждой точке поверхности
раздела в любой момент времени выполнялись соотношения
uf + 2 и? - 5 Ui, (5.59)
R Т
Т1 + ^Т^ = ^ (5.60)
R Т
Здесь индексами I, R, Т обозначены соответственно падающие,
отраженные и прошедшие волны. Для синусоидальных плоских
волн из условия непрерывности смещений
+ 2 £ омтег(йтг_ктх) (5 61)
R Т
176
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
следует, что в любой момент времени
СО* = сог = СО7
и в любой точке плоскости 1х = О,
ksx = kTx = k7x.
(5.62)
(5.63)
При отражении и преломлении волн их частота не меняется.
Кроме того, из сравнения с уравнением 1х = 0 выражения
(5.63), записанного в виде
(k* — к7)х = 0, (кг - к7)х = О,
видно, что векторы (к* — к7) и (кт — к7) перпендикулярны к пло-
скости раздела двух сред. Следовательно, все волновые векторы
Рис. 5.24. Закон преломле-
ния.
Проекции на границу раз-
дела волновых векторов ks
и kT отраженной и прелом-
ленной волны равны проек-
ции волнового вектора к*
падающей волны.
Рис. 5.25. Геометрическое построение вол-
новых векторов для волн отраженной и
преломленной на границе кремний — плав-
леный кварц.
Падающая квазипродольная волна порож-
дает отраженные квазипродольную и ква-
зипоперечную волны и преломленные про-
дольную и поперечную волны.
лежат в плоскости падения, определяемой нормалью I и волновым
вектором к7, а проекции всех волновых векторов на плоскость
раздела равны (рис. 5.24). Последнее условие записывается в виде
kR sin 0s = kT sin 0r = k’ sin 07. (5.64)
Здесь 07, 0s, 0Г есть соответственно углы падения, отражения и
преломления. Так как частоты всех волн равны между собой, их
направления распространения определяются из соотношения
sineWO*) = sin 077(80 = sin 07/7(07), (5.65)
либо геометрическим построением поверхностей обратных скоро-
§ Sj.2. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН 177
стей для обеих сред. На рис. 5.25 показано такое построение для
случая кубического кристалла (кремния), граничащего в пло-
скости (010) с изотропной средой (плавленый кварц). Квазипро-
дольная волна, распространяющаяся в плоскости (001) кристалла,
порождает квазипродольную и квазипоперечную отраженные вол-
ны, а также продольную и поперечную волны в изотропной среде.
Отраженная волна с поляризацией, перпендикулярной плоскости
падения, не возбуждается, так как смещение падающей волны
не содержит компоненты вдоль этого направления.
Построение поверхностей обратных скоростей позволяет также
определить скорости переноса энергии для каждой из волн. С уче-
том сказанного о поверхностях обратных скоростей можно пред-
ставить следующие возможные случаи.
1. Перпендикуляр на границу раздела, проходящий через кон-
цы векторов обратной скорости, не пересекает одну из поверхно-
стей обратных скоростей. Амплитуда соответствующей волны
быстро убывает. Аналитически это выражается мнимым решени-
ем дисперсионного уравнения для прошедшей волны
ет-й’+кмй’-
При равенстве на поверхности раздела проекций волновых век-
торов преломленной и падающей волн и к\ нормальная ком-
понента/^ является мнимой, если к\ > ®/F\ т. е. поскольку&в =
— со sin 0Т/У, то
sin2eJ - (р-)2. (5.66)
Амплитуда волны во второй среде убывает экспоненциально.
Критический угол падения 0с, при котором к± = 0 и 0Т = л/2, оп-
ределяется из соотношения
sin 0с =
2. Волновой вектор и вектор потока энергии одной и той же
волны могут быть направлены в разные стороны от поверхности
раздела. В этом случае энергия волны отражается обратно, не-
смотря на преломление волнового вектора.
Перед тем, как рассматривать конкретный пример, запишем
упрощенные граничные условия, исключив члены, одинаковые для
каждой точки раздела. Условие непрерывности смещений получа-
ется из (5.59) в виде
°и\ + S V = IM- (5.67)
R Т
V
12 э. Дьелесан, Д. Руайе
178
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
§ 512. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН
179
С учетом закона Гука
Tij — — icnkiki°uke <ш< кх)
условие непрерывности механических напряжений можно запи-
сать в виде
cwii [к!ои[ + Ж ) = cwl} 2 к? °и%, (5.68)
где сум— модули упругости второй среды.
5.2.2. Падение волны с поперечной горизонтальной поляриза-
цией. В разделе 5.1.36 было показано, что плоскость, перпендику-
лярная оси симметрии четвертого или шестого порядков, изотроп-
на для поперечной волны, поляризованной вдоль этой оси, т. е.
скорость волны V3 = Vc44/p не зависит от направления распростра-
нения. Следовательно, наиболее простым случаем преломления
волн на границе двух кристаллических сред является случай, по-
казанный на рис. 5.26. Будем считать при этом, что каждая из
Рис. 5.26. Отражение и преломление
поперечной волны с горизонтальной
поляризацией (ГН) на границе двух
кристаллов, имеющих оси Л4 или Лв,
перпендикулярные плоскости паде-
ния (или на границе двух изотроп-
ных сред).
сред имеет ось симметрии четвертого или шестого порядков, на-
правленную вдоль х3 параллельно поверхности раздела, и что на
границу падает поперечная волна, поляризованная вдоль ж3 и с
волновым вектором в плоскости х3х2, которую мы будем называть
горизонтальной поперечной волной.
В обеих средах векторы смещения волн могут быть только
параллельны или перпендикулярны оси симметрии гс3 и, следова-
тельно, на границе возникают только две волны, отраженная и
преломленная, с той же поляризацией, как и у падающей волны.
Эти условия выполняются в случае двух изотропных твердых тел.
Поскольку для каждой волны = Он6<3, из условия непрерывно-
сти смещений следует, что
V + 0HH = °ur. (5.69)
Соотношение (5.68) с учетом Ц = и °щ=°м6м можно за-
писать в виде
ansi (к{ “и1 + fc? °ыл) = c'usiki °ит,
или
Й131 (&i °м7-|-А:л °ил)-|-£1132(^2 °и -|- Ал °wH) = Ci131ki °иТ-1-сцз2к3 °иГ.
В кристаллах с осями симметрии Ai или Лв не равны нулю
лишь модули с индексом 1 = 3, т. е. с3131 = с55 = с44 и Сз18! с'м
(см. (4.55) и (4.56)). Следовательно,
cti (к{ °и! + к? °uR) = c'utf °ит. (5.70)
Решение уравнений (5.69) и (5.70) непосредственно дает коэф-
фициент отражения
и коэффициент прохождения
Ar-W-d. + l.
Из (5.65) следует, что 0Л = Q1 и
sin 0T/sin О7 = 73/Р3. (5.72)
Производя замены kR = — к? = A7cos07 и к{ = —Arcos0T, коэф-
фициент Ап можно выразить через углы падения и отражения
при помощи соотношения
cos 07 — с’мкт cos 0Г
я с^к' cos 07 + cos 0Т
Введем акустические импедансы Z3 = pF3, Z3 = рТ3 для попе-
речных волн в каждом кристалле. Тогда
кгси = с44 = = кт с ы = (DZ3.
Подставляя эти соотношения в предыдущее выражение, получаем
Z3 COS07 — Z3cosOr ,
Н~ Z3 cos 0' + z; cos0T ’ (5<73)
2Z„ cos 01
Ат = Ад -j- 1 = - 11 . , (5.74)
Z3 cos 01 + Z3 cos 0T
Связь 0T с 01 дается выражением (5.72).
Характер изменения коэффициентов отражения и прохожде-
ния волн при изменении угла падения 07 зависит от отношений
12*
180
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
акустических импедансов Z3/Z3 и скоростей V3/V3. Если
г;/г3<1, то 0Г < 0', и для преломленной волны критический угол
не существует. Кроме того, если Z3IZ3 < 1, то при угле 0Г, удов-
летворяющем соотношению cos 01/cos 0Г = 2з/23, коэффициент от-
ражения Ая становится равным нулю, и волна полностью прохо-
дит во вторую среду. На рис. 5.27 показан коэффициент отраже-
ния для случая, когда волна из кремния (У, = 5843 м/с, Zs =
= 13,6 • 10* Н • с/м3) проходит в SiO2 (V3 = 3763 м/с, Z3 — 8,29х
X 10е II• с/м3). При V3 > V3 амплитуда волны во второй среде
быстро убывает, если угол падения 01 превышает критический
угол 0е, определяемый соотношением sin 0С — F3/V3. В этом слу-
чае нормальная к поверхности раздела компонента к% волнового
вектора становится мнимой, к3 = i%T, и, согласно (5.71), ко-
эффициент отражения Ай является комплексной величиной:
<<с°з9;+‘у'.
сMkl costf - Icихт
Так как модуль Ай равен единице, при угле падения, превы-
шающем критический, наступает полное отражение волны. Соот-
Рис. 5.27. Коэффициент отраже-
ния от границы Si — SiOj попе-
речной волны с горизонтальной
поляризацией как функция угла
падения.
Рис. 5.28. Коэффициент отражения от
границы SiOj — Si поперечной волны с
горизонтальной поляризацией как функ-
ция угла падения.
При углах, больших критического угла
0С = 40°, отражение является полным,
Ил|=1.
ношение амплитуд прошедшей и падающей волн уже не имеет
смысла коэффициента прохождения, так как амплитуда прошед-
шей волны не постоянна, а убывает экспоненциально в глубь вто-
§ 5.2. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН
181
г рой среды. Этот случай изображен на рис. 5.28 для той же пары
материалов, но при падении волны в SiO2.
5.2.3. Отражение на свободной поверхности. В случае свобод-
ной поверхности твердого тела (граница с воздухом или другим
газом, находящимся при низком давлении) проходящие волны
не существуют, и единственным граничным условием является
отсутствие механических напряжений в каждой точке свободной
граничной поверхности, — или
(5.75)
Это условие можно получить из (5.68), приравнивая нулю мо-
дули упругости второй среды: cyftI=O. Тогда в рассмотренном вы*
ше примере при Z3 = 0 получаем Ая => 1, т. е. поперечная волна,
поляризованная параллельно свободной поверхности, полностью
отражается.
Бмуум
Рис. 5.29. Отражение продольной плос- кой волны от свободной поверхности хг
изотропного твердого тела или гексаго- нального кристалла, ось 4$ которого перпендикулярна плоскости падения. В1-в^ 'а7
Продольная волна, падающая на свободную поверхность изо-
тропного тела или гексагонального кристалла, ось Ав которого пер-
пендикулярна плоскости падения, порождает две отраженные вол-
ны — продольную и поперечную, обозначаемые соответственно ин-
' дексами*) L и Т (рис. 5.29). Поскольку в плоскости падения
среда изотропна, то
kL = к1 = ю/Гь, к'/к1 = VJVt,
Из (5.64) следует, что
Оь = 0', sin 07sin 0Г = VT/VL. (5.76)
В граничном условии (5.75), требующем отсутствия механи-
ческих напряжений в плоскости ж2а:3,
ам (*/ °4 + к[ °и£ + к? °и0 = 0 (5.77)
индексы I и к принимают лишь значения 1 или 2, так как все
векторы к и "и лежат в плоскости х{х2, и при этом их компоненты
*) Отраженные продольную и поперечные волны следовало бы обозна-
• чить индексами RL и RT. Опущенные буквы не должны приводить к не-
( доразумениям, поскольку в данном случае прошедшие волны не сущест-
? вуют.
182
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
равны:
(—ZcIcos0z. frLp1 cos01. , г |fcTCOS0Г.
UIsin0I ’ |/czsin01’ lfcTsin0T’
ouH—°UICOS0II ОцГ, I°ULCOS0\ 0 t(—oursin0r
l°uTsin0z ’ U |ouLsin01’ ° l°urcos0r
При i = 1 выражение (5.77), содержащее лишь модули с11И = си
и Сц22 = с12, приобретает вид
сп [к1 (°и' + V) cos2 0J - sin 20г] +
+ С12 [к1 (°ит + V) sin2 01 + sin 20т] = 0.
При i = 2 не равны модули сшг = с2121 = с6в:
°и1 + °uL) sin 20г + °иткт cos 20irJ = 0.
При г = 3 все члены выражения (5.77) равны нулю. Две неизве-
стные величины Al = °uL/°uI и Ат — °игГи1 удовлетворяют урав-
нениям
(1 + Аь) к1 (си cos2 0J + с12 sin2 01) — Аткт (-*-2~la) sin 20г = 0,
(5.78)
(Al - 1) к1 sin 201 + Аткт cos 20г = 0.
Преобразуем выражение
F = cu cos2 07 + cl2 sin2 0J = си + (c12 — си) sin2 0J,
подставляя скорости продольной волны 7z, = Vctl/p и поперечной
волны VT = У(сц — с12)/р:
Г^рП-грУ^т2©1.
Отсюда с учетом соотношения (5.76) получаем
F = рУ1(1 - 2 sin20r) = рП cos 20г.
Подставляя это выражение в (5.78) и заменяя кт/кт отношени-
ем VJVt, находим, что
Al (jr;) cos 20г — Ат sin 2бг = — cos 20rf
Al sin 20z 4- AT cos 20T = sin 201.
§ 5.2. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН
183
Решение системы дает коэффициент отражения продольной
волны
А °UL sin 20J sin 20г - {Vl/VtY cos 20r
I’“‘V sin 202 sin20r + (VL/Vr)2 cos 20r
и коэффициент преобразования в поперечную волну
. °ит 2(7j/PT)cos20rsin 201 V, _ч _оГ
V sin20/sin20r+(PL/Pr) cos220r
(5.80)
(5.79)
где 0T и 07 связаны соотношением (5.76). Так как VT/VL < 1/V2,
угол 0F < л/4 и коэффициент Ат положителен при любом значении
угла падения. Напротив, как видно из рис. 5.30, коэффициент AL
Рис. 5.30. Коэффициент отраже-
ния продольной волны от свобод-
ной поверхности изотропного
твердого тела как функция угла
падения при разных значениях
VTIVL.
Для плавленого кварца
VTIVL = 0,63 (рис. 3 из [5]).
превращается в нуль при двух значениях угла падения, если
Vt/Vl > 0,565. В этом случае падающая продольная волна порож-
дает только поперечную отраженную волну. Это свойство исполь-
зуется для преобразования продольной волны в поперечную.
5.2.4. Волны Лява. Волнами Лява (рис. 5.31) называются по-
верхностные волны с поперечной поляризацией, распространяю-
щиеся в полубесконечной среде, на которую нанесен тонкий слой
с другими упругими свойствами. Этот слой, жестко связанный с
подложкой, играет роль одномерного волновода с неодинаковыми
стенками. Наличием подложки обусловлено отсутствие частоты от-
сечки, свойственной волноводу, состоящему только из одного тон-
кого слоя (раздел 1.1.2). Можно ожидать, что величина скорости
184
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
распространения волны, лежащая в интервале значений скоростей
в слое и в подложке, изменяется с частотой. Интерес к волнам
Лява обусловлен прежде всего именно их дисперсионными свой-
ствами.
Обратимся к ‘рис. 5.31. Пусть кристалл имеет ось симметрии
четвертого или шестого порядка, направленную вдоль is. В этом
случае плоскость XtX2 изотропна для поперечной волны со сме-
Вакуум
А^илиАд Плет11
0 © СщУз
или As
г ч>
Подложка
Рис. 5.31. Волны Лява.
Поперечная волна с горизонтальной по-
ляризацией распространяется вдоль оси
хз, последовательно отражаясь от сво-
бодной поверхности и от границы с
подложкой.
щением w3 и волновым век-
тором k(fct, k2, 0). Волна, от-
раженная на свободной по-
верхности Xt = —h, имеет та-
кую же поляризацию, как и
падающая волна, и ее вол-
новой вектор равен k'(—kt,
к2, 0). Возникающая в ре-
зультате волна, которая рас-
пространяется вдоль хг, созда-
ет лишь напряжения сдвига
ди9
= С44^ У32 = С44^_

Условию отсутствия механических напряжений Tt = T(jlj —
e — Tn на свободной поверхности х{ = — h должна удовлетворять
только компонента Tsl, выражение для которой, как и в разделе
1.1.2, получается из суперпозиции падающей и отраженной волн:
Т i = _ ^е<(<0«+й1(к1+Л)-?12х2]
или, после подстановки Та = —ИА,
Тп = То sin /cj (xl 4- при — h < хг < 0. (5.81)
Скорость поперечной волны в материале, из которого изготовлен
слой, есть Vs = Tc44/p, и компоненты волнового вектора
k(kt, k2, кг — 0) удовлетворяют соотношению
F = kl 4- kl = (®/V3)2. (5.82)
Поскольку kt — действительная величина, то
k2<®/V3. (5.83)
Волна Лява является поверхностной волной *), поэтому напряже-
*) Отметим, что граничное условие 7si = 0 также удовлетворяется, если
«з не зависит от агх. Это решение соответствует поперечной волне с гори-
зонтальной поляризацией и постоянной амплитудой, распространяющейся
в слое или в подложке (скорость У3 или Кд).
§ 5.2. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН
185
I НИЯ Та, созданные в подложке,
i T31 = T0e4 11 22/пригх>0
-• обязательно должны убывать с rt. Для этого необходимо, чтобы
к{ = —«Х1 ПРИ Xi>°-
i'j. Кроме того, из условия непрерывности механических напря-
' жений в каждой точке поверхности раздела Хз =* 0 следует, что
X — к2.Напряжение Tsl тогда записывается в виде
f Г31 = при а?!> О,
a Xi' и к2 удовлетворяют соотношению
к[2 + к? = (<в/У3)2 = kl - х?, (5.84)
, где V3 =]/с44/р', — скорость поперечной волны в подложке. Что-
бы величина Xi была действительной, необходимо выполнение не-
равенства
fc2>®/73. (5.85)
Неравенства (5.83) и (5.85) выполняются одновременно толь-
ко в том сучае, еслиИ3>К3.
Обязательным условием существования волны Лява является
: требование, чтобы скорость поперечных волн в подложке была
больше скорости волны с той же поляризацией в слое. Значение
•; фазовой скорости волны Лява = <п/к2 находится тогда в ин-
I тервале между двумя значениями
Vs (слой) < 7Ф < Vs (подложка).
£ Из условия непрерывности механических напряжений на по-
£ верхности Хз = 0 следует, что То sin kji = TQ.
Напряжение сдвига равно
, sin к, (х, + h\ i(<at-k2x2)
T>i=T« Sln>,> 6 прч-4<»1<0,
T„ - прих9>0.
i Смещение иа получается интегрированием уравнения Гука в
m ди m > дич
; слое: г31 = с44-^- и в подложке: г81 = с44-^-, и после подста-
186
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЙ УПРУГОСТИ
новки °и = — To/cM^i принимает вид
„ - о,,в-ХЛЛм<-М2) nnnr'sf)
W-g — U-“ “ ПрИД/^>^>и.
Из условия непрерывности смещений на поверхности а:1=0 сле-
дует
%i = -^Mg(M). (5.86)
С44
Смещение и2 принимает вид
cos кг (х. + h) , п
и*=и......cos^ е } при - h < Ж1< О,
и3 = °we-xirie1(“<_ft2-ra) При Х1> о. (5.87)
Условие (5.86) совместно с полученным из (5.82) и (5.84) со-
отношением
** +*5 (-%)’" (t)’ ,5'88)
дает для каждой частоты значения и к2, а также волновое
число к2:
Уравнения (5.86), (5.88) и (5.89) неявно выражают диспер-
сионное соотношение ® (к2) волн Лява. Значения к1 и %i опреде-
ляются графически из кривых рис. 5.32, для построения которых
использованы безразмерные величины kji, fah, ah/Vt. Решения
соответствуют точкам пересечения зависимости
= ^(k1h)lg(klh)
С44
и окружности с центром в начале координат, радиус которой равен
т. е. соответствуют соотношению (к^г)2 + (^/i)2 = R2. Каждое пере-
сечение определяет отдельную моду. Количество мод равно р,
§ 5.2. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ВОЛН
187
если (р — l)n<R <jm, т. е. (р — 1)ю0 < со < рсоо при
<о0Л л
На рис. 5.33 показаны зависимости амплитуды смещения м5
от Xi для трех первых мод волн Лява в слое плавленого кварца
на подложке из кремния.
Мода р-го порядка содержит
р — 1 узловых плоскостей в
слое. При заданной частоте
проникновение волны в под-
ложку увеличивается с номе-
ром моды, так как фактор
затухания убывает. Изме-
нение характера смещения
частиц с частотой, показан-
ное на рис. 5.34, легко объяс-
няется с помощью графиче-
ского построения, приведен-
ного на рис. 5.32. Для данной
моды как так и макси-
мальная величина °u/cos (&Л)
Рис. 5.32. Графическое решение уравне-
ний (5.86) и (5.88), показывающее воз-
можность существования нескольких
мод (слой плавленого кварца на крем-
нии).
амплитуды смещения в слое
растут с частотой. Следова-
тельно, с частотой растет и
доля энергии, переносимой в
слое со скоростью Г3<73.
Напротив, при низких частотах (ah < Fs) почти вся энергия рас-
пространяется в подложке со скоростью V3. Слой толщины h,
пренебрежимо малой по сравнению с l/%i, не оказывает уже ни-
какого влияния. Это видно из дисперсионных кривых, показанных
1-я мода
Рис. 5.33; Смещение частиц при одинаковой частоте (со = 2,25 а>о) для трех
низших мод в слое плавленого кварца на кремнии.
188
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Рис. 5.35, Волны Лява. Дисперси-
онные кривые со (Лг2) в приведен-
ных координатах для низших мод
в слое плавленого кварца на
кремнии.
Рис. 5.36. Волны Лява (слой плав-
леного кварца на кремнии). Частот-
ная зависимость фазовой и группо-
вой скоростей.
Пунктирной кривой изображена за-
висимость времени задержки xg =
= l/Vt, где в качестве единицы вы-
брано время задержки т = l/Vt для
поперечной волны с горизонтальной
поляризацией в материале слоя.
Ж § 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ 189
Ж на рис. 5.35 в приведенных координатах ah/V2 и k2h. Ветви раз-
ж пых мод начинаются в точках, эквидистантно расположенных на
ж прямой с наклоном V'3/V3, отвечающей соотношению © = K8fc2.
Действительно, для частот отсечки сор= р®0 при %i = 0 для соот-
[ ветствующей моды имеет место равенство а>р =V#fc2. С ростом ча-
стоты кривые асимптотически приближаются к прямой й = Г5/г2.
Можно убедиться (упр. 5.7), что фазовая скорость F, = <л/кг и
; групповая скорость Ve~ d(a/dk2 зависят от нормированной частоты
th/V2 так, как это показано на рис. 5.36.
§ 5.3. Поверхностные упругие волны. Волны Рэлея
В предыдущем параграфе было показано, что волна с попе-
речной горизонтальной поляризацией может распространяться ли-
бо в слое, либо в его окрестности. Эта волна, называемая волной
Лява, является поверхностной в системе слой — подложка, неод-
нородность которой обусловливает дисперсионные свойства. Пред-
ставляет интерес выяснить, может ли волна распространяться на
поверхности совершенно однородной среды, в отсутствие какого-
либо слоя и, следовательно, дисперсии. Действительно, такая по-
верхностная волна существует, при-
чем, как показал Рэлей в 1885 г.
[6], она не является линейно поля-
ризованной. Смещение этой сложной
волны содержит как продольную,
так и поперечную составляющие,
которые удолетворяют условию от- Рис Система К00рдинат
сутствия механических напряжении для волн рЭЛея.
на свободной поверхности.
Упругая волна, распространяющаяся в ограниченной среде,
должна удовлетворять как уравнению распространения (5.2)
dzui
РУТ = c^kl ’
dt dxjdxk
так й граничному условию (4.17) на поверхности
Pi = Ttjlj.
Для среды, занимающей полупространство х3 > 0 и неограни-
ченной вдоль направлений х{ и х2 (рис. 5.37), условие отсутствия
внешних сил на поверхности х3 = 0 записывается в виде pt = О,
ИЛИ, ПОСКОЛЬКУ
Т’у =ei3»;^--0 при ;г3 — 0. (5.90)
Среди решений, удовлетворяющих этим граничным условиям,
будем искать решения, соответствующие поверхностным волнам,
190
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
амплитуда которых затухает в глубь среды (вдоль оси х3). Рас-
смотрим смещение в форме
°uke е , где Re х > 0.
Направление распространения этой волны лежит на свободной
поверхности и определяется направляющими косинусами щ и п2,
а амплитуда смещения экспоненциально затухает с расстоянием
от поверхности. Чтобы получить выражение типа использовавше-
гося ранее, введем обозначение % = I — п3, где ns является не
третьей компонентой вектора п, а неизвестной величиной, кото-
рую требуется определить [7]. Подстановка
в уравнение распространения приводит, как и в разделе 5.1.1,
к уравнению Кристоффеля
р V2 °и( = °Ui.
Приравнивая нулю определитель
I Cijkinjnk — pV26jj | = О,
(5.91)
получаем уравнение шестой степени по п3, в которое скорость V
входит как параметр. Если коэффициенты при степенях п» дей-
ствительны, уравнение имеет три пары комплексно сопряженных
корней., Физический смысл имеют только три корня с отрицатель-
ной мнимой частью (пз \ \ пз3))» поскольку другие корни с
Re % < 0 соответствуют волнам с экспоненциально нарастающей
вдоль х3 амплитудой. Каждому значению соответствует
собственный вектор °ик\ и следовательно, смещение имеет вид
,.(г) _ о (r)„iw [ f п\
«к = uh e If-------------у— I.
(5.92)
Общее решение является линейной комбинацией этих трех
компонент смещения, распространяющихся с одинаковой ско-
ростью V,
ик = 1 Ат4\ (5.93)
Г=1
Коэффициенты А, и скорость V находятся подстановкой
выражения (5.93) в граничное условие (5.90) на свободной
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ ,
191
поверхности = 0:
= 0.
*3=0
Из выражения
й v v '
следует граничное условие
2 ci3kmP °U?AT = 0, I = 1,2,3.
(5.94)
Скорость волн Рэлея является решением секулярного уравне-
ния, выражающего совместимость системы этих трех однород-
ных уравнений. Хотя общий путь решения довольно прост, при-
менительно к анизотропным средам он быстро приводит к выра-
жениям, которые могут быть решены только численными метода-
ми. В связи с этим рассмотрим сначала случай изотропной среды.
5.3.1. Изотропная среда. Вводя обозначения скоростей плоских
волн в неограниченной изотропной среде Уь = Уси/р и VT =
= У(сц — С1з)/2р, выражение (5.9)
можно записать в виде
г« = р [(П - П) тщ + УММ-
Уравнение Кристоффеля (5.6)
Г« Ч = рУ2 Ч
принимает вид
(F1 - П) («: °ut) Щ = (У2 - УЫ) °Ui. (5.95)
Рассмотрим два случая:
1. n°Ui^0; из уравнения (5.95) следует, что пропорцио-
нально п{, т. е. °щ — Вп{ и
(пг °ui) nt — пгВщ = nl °щ.
Приравнивая коэффициенты при °и( в обеих частях уравнения
(5.95), получаем (Vl — Ут) га® = У2 — УуПл или
У2 = Vl nf. (5.96)
192
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
2. n°ut = 0; отсюда
V2 = ге|. (5.97)
Поскольку среда изотропная, всегда можно выбрать направ-
ление распространения вдоль координатных осей, например
вдоль Ж1, при этом m = 1, п2 = 0.
Решений (5,96) и (5.97) уравнения для собственных значений
определяют п3 как функцию скорости распространения V.
Из первого решения И2 = V& (1 + из) следует, что V < VL,
так как коэффициент п3 должен быть мнимым:
Из второго решения V2 = Ру (1 + ”з) следует
т . / V2 \1/2
В обоих случаях решение со знаком плюс отбрасывается, по-
скольку при % = i -jr < 0 °но приводит к волне с экспоненци-
ально нарастающей вдоль х3 амплитудой, что не имеет физическо-
го смысла. В качестве собственных выберем следующие векторы.
1. Для = — г(1 — Г2/И1)1/2 вектор °u(n с компонента-
ми °Ц1) = 1, °«21) — 0, °и(з1) = Пз \ которые удовлетворяют соот-
ношению °U{1) = Вщ при В = 1.
2. Для и32) = п33) = — I (1 — 7S/Vy)1/S два независимых
вектора °п(2) и °и(3) с компонентами соответственно °ui2) = 0,.
°u(22) = 1, °и{з} = 0 и Oi43’ = — т?43>, °43) = 0, °м(33) = 1, которые
удовлетворяют соотношению n°ut = 0 или + п3°и3 = 0.
Развернем по индексу i граничное условие (5.94)
Г=1
учитывая матрицу (4.38) модулей упругости изотропного твердо-
го тела:
i = 1 сшз S (nir) Ч’ + »зг) °^г)) Аг = 0,
i = 2 с2ззз S (4Г> + 4Г) °«(2Г)) Ат = 0,
i == 3 (сззпп1Г) °wir) + Сзз22геа^ + с33з3ПзГ) °и3г)) Аг = 0.
Эти уравнения можно упростить, поскольку = 1 и п3г) = 0’
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ
193
при любом значении г. Подстановка Пзг) = q приводит их к виду
3(°4r) + groulr))A,. = 0,
Sgr°i4r4 = O, (5.98)
S (с12 °Wj.r) + cll?r °u8F>) Ar = 0.
Используя заданные значения компонент °и^ собственных век-
торов и суммируя по индексу г, получаем
+ 0 • А2 4- (1 — ql) Л3 = 0,
0-Лх 4- q2A2 0»Л3 = 0, (5.99)
(с12 + сы?1) Л1 + 0 • Л2 + (— с12 + си) 9з^з = 0.
Из второго уравнения этой однородной системы следует, что
Л2 — 0. Два других уравнения являются совместными, если опре-
делитель из коэффициентов при At и Л» равен нулю:
2?1?з (си — с1г) —’ (1 ~ 7з) (ci2 + си?1) = О-
Учитывая, что
cu-Ci2 = 2pF2T, 1-9| = 2-72/7$,
си 4- си?! = Р (П - 2V2r) - рП (1 - 74'71) = - р7у (2 - 7«/7j),
получаем
/ р-2\1/2/ у2\1/2 / у2\2
(*-%) -(2Ч)- (S-,00)
Производя алгебраические выкладки, можно показать, что это
Й>авнение является уравнением третьей степени относительно Т2.
одставляя z = (7/Уг)2, получаем
или
z3_8(z-1)^z_2^1-^] =0. (5.101)
Неизвестную величину z можно найти графически по точкам
пересечения кубической зависимости г/i = z’/8 с параболой уг =
“ (z— l)[z — 2(1 — (7r/7z,)2)]. Из зависимостей на рис. 5.38, по-
строенных при экстремальных значениях 7т/7ь = 0 и 7Т/7Ь =
13 Э. Дьелесаи, Д. Руайе
194
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
= 1/72, видно, что существует только один положительный корень
zR, заключенный в интервале между 0,912 и 0,764. Это решение
выражает скорость волн Рэлея через соотношение Pb/Ft = Vzb,
величина которого изменяется
в пределах от 0,955 до 0,874 при
изменении отношения Vt/Vl от
0 до 1/72. Формула Викторова
[8] дает полезное приближен-
ное выражение для
Рис. 5.38. Графическое решение
уравнения (5.101), определяющее
скорость VB волн Рэлея в двух пре-
дельных случаях: VrlVi. — 0 и
VT/VL = 1/72.
7Д 0,718-(7Г/7Ь)2
VT 0,75 - (Fr/Fb)2 '
Тот факт, что Ря всегда
меньше VT, можно объяснить
отсутствием среды над свобод-
ной поверхностью, что приво-
дит как бы к уменьшению мо-
дулей упругости.
При V = Vn’ 1-е и 3-е урав-
нения системы (5.99) оказыва-
пропорционально 4^
ются одинаковыми и, следовательно, 4.
. 2gl А
Компоненты смещения uk = 3 Аг
_ Л /„(1) 2gl ,.(8)\
U2 = Qt
п - A
М3 — Л1 Iй» J _ ?2 и3 j
с учетом соотношения (5.92) и значений компонент °Wftr> можно
записать в виде
= Аг
2gig3
u2 = О,
(5.102)
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ
195
Введем обозначения
(5.103)
а = _ _2ад_ = Ц*-гур1)1/а(1-*1/г2т)1/а
1-4 2-FV4
Здесь Хп —длина волны Рэлея. Учитывая (5.100), имеем
шение
соотно-
(5.104)
Для компонент смещения окончательно получаем:
(5.105)
Поскольку п2 = 0, вектор смещения лежит в плоскости, про-
веденной через направление распространения х3 и нормаль к сво-
бодной поверхности х3. Эта плоскость называется сагиттальной.
Множитель i означает, что компонента п3 сдвинута по фазе на
п/2 по отношению к iij. Величины смещения находятся иэ дей-
ствительных частей этих компонент:
Re = L\ (х3) cos ® Н — уМ,
/ (5.106)
Re и3 = U 3 (х3) sin о) 11 — I.
\ V*/
Таким образом, при распространении волны Рэлея частицы
среды движутся по эллиптической траектории на любой глубине
xs. Поскольку законы изменения амплитуды с глубиной Ul(x3') и
Us(x3) оказываются разными:
£7,(х.) = (е"’Л-
то эллипс деформируется, и поляризация вдали от поверхности
13*
196
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
может стать линейной. Зависимости на рис. 5.39 показывают из-
менение амплитуд продольной (ЕЛ) и поперечной (Е73) компонент
смещения в плавленом кварце (Fn = 3410 м/с). Этот пример ти-
пичен для многих изотропных материалов: на поверхности попе-
речная компонента примерно в полтора раза больше продольной,
причем последняя на глубине порядка 0,2Хп меняет знак.
Рис. 5.39. Волны Рэлея в изо-
тропном твердом теле (плав-
леный кварц).
Изменение с глубиной ампли-
туд продольной (Ui) и попе-
речной (U3) компонент сме-
щения.
Рис. 5.40. Волны Рэлея на поверхно-
сти кристалла кубической системы
(GaAs) в направлении [100] в пло-
скости (001).
Амплитуды продольной (171) и по-
перечной (С7а) компонент смещения
убывают с осцилляциями (см.
(5425)).
5.3.2. Анизотропная среда. Для кристаллической среды урав-
нения могут быть решены только численными методами. Ре-
зультаты вычисления приводят к следующим отличиям от случая
изотропного тела.
1. Скорость поверхностных волн зависит от направления рас-
пространения в плоскости свободной поверхности, за исключе-
нием случая поверхности, перпендикулярной оси симметрии
шестого порядка (CdS, ZnO).
2. Если сагиттальная плоскость не является плоскостью сим-
метрии упругих свойств, вместо двух появляются три ортого-
нальные компоненты вектора смещения. Вершина вектора описы-
вает эллипс в плоскости, лежащей под углом к сагиттальной пло-
скости.
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ
197
3. Корни п^ секулярного уравнения (5.91) уже не чисто
мнимые, а комплексные. Следовательно, амплитуды компонент
вектора смещения стремятся к нулю, осциллируя при этом, как
показано на рис. 5.40.
4. В общем случае направление потока энергии не совпа-
дает с направлением распространения. Чистыми модами волны
Рэлея являются лишь при распространении в определенных пло-
скостях и вдоль особых направлений, имеющих важное практи-
ческое значение.
5. Вдоль особых направлений в определенных плоскостях су-
ществует решение типа волны Рэлея, фазовая скорость которой
превышает фазовую скорость медленной поперечной волны в этом
же направлении. Вблизи этих особых направлений волна не яв-
ляется в строгом смысле поверхностной. Возникает составляющая,
которая приводит к излучению энергии в глубь материала. Это
решение, для которого амплитуды смещения при бесконечном уда-
лении от поверхности не равны нулю, соответствует так называе-
мой псевдоповерхностной волне [9] (по-английски «pseudo» или
«leaky surface wave»).
Пример, выбранный для иллюстрации общего метода, изложен-
ного в начале § 5.3, показывает сложность вычисленной даже в
самом простом случае анизотропной среды.
Распространение волны Рэлея вдоль направления [100] пло-
скости (001) кубического кристалла. Поскольку nt = 1 и п2 = 0,
выражения (5.3) для компонент тензора Г« в кубическом кри-
сталле после подстановки п3 = q принимают вид
Гц = с)г + с44?2, Г12 = 0, Г13= (с12 + с44)д,
Г22 = с44(1 + <72), Г23 = 0, Г33 = с44 4* ctiq2.
Поскольку Г12 = Г33 = 0, секулярное уравнение приводится к диа-
гональному виду
(Г22 - рП [(Гп - рУ2) (Г33 - рУ2) - Г|3] = 0.
Корень ?2 = п(32) определяется из уравнения с44 (1 + ql) =рУ®
или q3 = У2/Уу — 1 после подстановки скорости вырожден-
ной поперечной волны VT=Yclt/p. Величина q2 будет мни-
мой при условии, что V>VT, где К —скорость волны Рэлея.
Тогда
q2 .-i(l-7W2r)1/2.
Два других корня ?i = ra3J) и q3 п33> являются решениями
биквадратного уравнения
(сп - рУ2 + с44д2)(с44 - рУ2 + ctlg2) - (с12 + с44) V = 0,
198
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
которое можно переписать в виде
СцС44(?2)2 + ?21 (Си — РР)СИ + (с44 ~ pVa)c44 — (Си + СцР] +
+ (си-рР)(с44-рР) = 0. (5.108)
Компоненты собственных векторов °utl) и °ut5) вдоль оси хг
равны нулю. Другие две компоненты °ul и °и3 удовлетворяют со-
отношению (Ги — pF2)0»! + Г13°п3 = 0. Принимая °ul = 1, получаем
°и3 = - (Гн - рУ2)/Г13,
или для каждого из собственных векторов °и(1) и °и(3)
п — °»(1) Pl — и3 / <5ло9>
Рз = °из ) _ _ С11 ~Ь С44?3 (С12 + С44) Чз
С учетом этих результатов °u(2)(0, 1, 0), °и<3’(1, 0, р3: имеет тот же вид, как и как отличными от нуля ок ?(< для собственных векторов °u(l)(l,0,pi), > получаем, что граничное условие (5.94) в случае изотропной среды (5.98), так азываются те же компоненты °и£\ с^: ’«Г + ?г °4Г)) Ат = 0, 2дг°4’’)Л = 0,
2 (С12 °и\ 1 > + Сц?г °4 )) Аг = 0.
С учетом выражений для компонент получаем
(pi + <71М1 + 0 • 42 + (р3 + д3)43 = О,
О A, + q2A2 + 0 А3 = 0, (5.110)
(cl2 + cllg1pl)21l.+ 0 -Л2 + (с12 + Сцд3р3)А3 = 0.
Из второго уравнения следует, что А2 = 0. Условием совмест-
ности двух других уравнений является равенство нулю определи-
теля, составленного из коэффициентов при Л{ й А3:
(Д1 + ?1)(с12 + СнРзУз) - (р3 + g3)(c12 + CuPiffi) = 0. (5.111)
Из выражений (5.109), подставляя с = Сц — р!72, получаем
РтЧт--^ + С^\, Г-1,3, (5.112),
\ 12 Т Ч*)
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ
199
После подстановки последних соотношений в (5.111) и сокраще-
ния на общий множитель имеем
(с — с12д|) [с12 (с1в + с44) — ссп — cuc14g?] qt —
(С <42<?1) [<42 (С12 + C4d) — СС11 — С11С44?з] ?3 ~ О"
Группируя члены, получаем уравнение
<42<41С44?1 03 (9х - <?з) - СС11С44 (<71 - ?з) + <42 [<42 (<42 + Сц)~
— ccu] qiq3(q! — q3) + с [с12 (с12 + с44) ссп] (q-t q3) — 04
которое, после деления на (<?* — g3) и переноса членов, содержа-
щих q^, в правую часть, можно записать в виде
<:12<!11С44?к23 - «41<44 + ?з) + <- [<42 (<42 + ~ <*111 =
= («12 + <44) (<*и - 4) ?1?з- (5.114)
Произведение q\q3 и сумма ?2 + ql корней уравнения вто-
рой степени по д2 = п3 (5.108) определяются соотношениями
CxiWfrl = с (с44 - р72),.
<41С44 (?1 + 9з) = ССХХ + С44 (С44 Р^2) (<42 +
Левая часть уравнения (5.114) (которую обозначим символом М)
после подстановки этих выражений принимает вид
М = с12с(с44 — рР) + с[ссц + с44(с44 — р V2) — (с12 + с44)2 +
+ С12(с12 + с44) — ССц1 = с[(с44 — рР)(С12 + с44) — С44(С12 + с44)],
или, после упрощений,
М=— pV2c(ci2 + c44).
Возведем в квадрат правую часть (которую обозначим симво-
лохМ N) уравнения (5.114):
№ = (С12 + <44)2 (^11 ~ 4)2 CC(44~PF2) •
11 44
Равенство Л/2 = N2 приводит к соотношению
(pF2)2 сси (ссц - Си)2 (1 - р72/с44).
После подстановки
200
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
(здесь Vt есть скорость продольной волны в направлении [100])
уравнение 3-й степени по R, из которого определяется скорость
волн Рэлея VR = VLRl,\ записывается с учетом того, что с — си —
— pV2 = Сц(1 — R), в виде
ЯЧ1 -Я) = [1 - - л]2 (1-^R )• (5.116)
Впервые это уравнение получил Стоунли [10].
Смещение определяется выражениями (5.92) и (5.93):
п(г) I Х1 \
Отсюда для каждой компоненты, учитывая, что Лг = 0 и °«i1) =
= °u<3) = 1, имеем
u3 = A e R

Как и в изотропной среде, частицы движутся в сагиттальной
плоскости (плоскость симметрии (010)). Предположим, что ре-
шения д2 уравнения 2-й степени (5.108) являются комплексно со-
пряженными:
g2 = (?e±(29) где q>q и О<0<л/2.
Физически приемлемыми являются только корни с отрицательной
мнимой частью и д3:
qi = -Уёе.<в = -g - ih, д3 = iQe-i9 = g - ih = -?1*, (5.118)
где ^ = V(?cos0, h = l/QshiQ. Из выражений (5.109) видно, что
р3 ——Pi. Подстановка р1=ге_<’’, из которой следует, что
ce~ie + с „ Qei9
Р.--ге'',дае, ™
Г2 = (‘: + ^cos28+(c-c44C)asin29
(С12 + С44)2<?
tg П = Сс +-^ tg е. (5.120)
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ
Отношение A3/At находится из системы (5.110), которая при
V = Vn сводится к первому уравнению
или, с учетом соотношения (5.113),
А3
Л
Заменяя qt и q3 их значениями и учитывая, что модуль отноше-
ния Aa/Ai равен единице, получаем

с e~ie — с12<? eie
с eie - е12(? е-’0
= е~йа,
(5.121)
где а определяется соотношением
(5.122)
Из формул (5.120) и (5.122) видно, что между углами ц и а
существует связь. Можно убедиться, что г] = 2сс — л/2 (см. При-
ложение), и следовательно,
Pi = ire~iia, р3 = ireaa. (5.123)
Продольная (iii) и поперечная (и3) компоненты смещения на-
ходятся путем подстановки выражений для gf, q3 (см. (5.118)),
Pt, Рз (см. 5.123)) и Аз/Ai (см. (5.121)) в соотношение (5.117):
н1 = Л1е R \е R + e-i2“e /е Vr),
u^iAje KR[e-^e lR +e *RJe \ VrJ
ИЛИ
—2 лЛу-- / д, \ Г / /р \ 1
Ui = 241е R cos ^2jrg-^+oJ exp Qco “"7/ —
u3 — i2Ajr e %R cos ^2ng~--------aj exp i ^co — a]
Действительные компоненты смещений
Re — Ul (x3) cos co I t —) — a
г / Rx \ ] (5,124)
Re u3 = U3 (x3) sin о h — A ) — al
202
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Рис. 5.41. Волны Рэлея в кристалле
кремния в направлении [100] в пло-
скости (001).
Изменение с глубиной амплитуд
продольной (Z7i) и поперечной (С73)
компонент смещения.
сдвинуты по фазе па л/2. Следовательно, частицы среды при дви-
жении описывают эллипс, оси которого направлены параллель-
но и перпендикулярно поверхности распространения. Амплитуды
продольной (СЛ) и поперечной (t/s) компонент смещения
_2яЛг~ / х \
U1(x3)=2A1e л cos ( + а)
х й ' (5.125)
U3 (*з) = — 2^ir е л cos I 2ngy2----а
экспоненциально убывают вдоль оси х3 со скоростью, определяе-
мой мнимой частью корней qi и q3) при этом убывание имеет ос-
циллирующий характер с пространственным периодом кв/g, рав-
ным отношению длины волны к действительной части корней
и q3.
Изменение амплитуд UJA^ и —U3IA^ в зависимости от норми-
рованной глубины для арсенида галлия показано на
рис. 5.40*). При значениях'
упругих модулей, приведенных
в табл. 4.1, уравнению Стоунли
удовлетворяет величина R =
= 0,3305, следовательно, Уя =
— 2720 м/с. Корни ?! и q3 явля-
ются комплексными, причем
g — 0,5613, /i = 0,4017. Тогда из
выражений (5.119) и (5.122) сле-
дует, что г = 1,185 и а = 54°23'.
Осциллирующий характер
изменений амплитуды смеще-
ния с глубиной объясняется тем,
что, в отличие от случая изо-
тропной среды, корни n3w явля-
ются не чисто мнимыми, а ком-
плексными. Для кристаллов ку-
бической симметрии это имеет
место, если" фактор анизотро-
пии А — 2с44/(си — с12) больше
единицы. Для GaAs А = 1,83.
Для кремния, фактор анизотро-
пии у которого тоже больше единицы (4 = 1,565), получаем:
Уд = 4917 м/с, £ = 0,4808, h = 0,4556, г = 1,226, а = 58°0Г. Ком-
поненты смещения волн Рэлея в кремнии показаны на рис. 5.41.
♦) Пьезоэлектрические свойства этого материала не влияют на распро-
странение волн Рэлея в направлении [100] в плоскости (001).
§ 5.3. ПОВЕРХНОСТНЫЕ УПРУГИЕ ВОЛНЫ. ВОЛНЫ РЭЛЕЯ 203
Волны Рэлея возбуждаются непосредственно на поверхности
кристалла под действием электрического поля (§ 7.2). Следова-
тельно, для этого необходимы пьезоэлектрические материалы.
Условия распространения волн Рэлея в наиболее часто использу-
емых на практике пьезоэлектрических кристаллах (кварц, ниобат
лития) рассматриваются в разделе 6.2.2 следующей главы.
Приложение. Соотношение между углами t] и а. Пусть
2ЬсцС44 = c2u (1 — R) + с44 -— (С1а "I” С44^»
(п.1)
Комплексные корни уравнения (5.108) выражаются в виде
gJ = -6±i(d-d2)‘/2 = Ce±f2e
или •
р’=<г = (1-л)[1—
1^ = -^-- М
Соотношение ц = 2а — л/2, справедливость которого нужно
доказать, можно записать в виде tga(tga —2tgr|) — 1 = 0, или,
с учетом выражений (5.120), (5.122) и (п. 2),
(^t4-24t7v) <С + 6>—7тН"(1?_г’)=0-
\ С С + с44^ / с 12^
Числитель равен 2QN, где
2V = — с3 -|- (2с12 + с44) c*Q -J- (2с44 + с12) сс12@2 —
— С12С4лС3 + (СС44 + С12@)'
Подставляя Q2 = (1 — /?)(! — Rcll/cu') и учитывая, что согласно
уравнению Стоунли
(? = Л(17Л) . где 4 = 1------ф- - R,
получаем N = (1 — RYM, причем
М = Сц — ССц + 2&СцС44 + c12 (2С44+ С12) 1----— j j +
+ (2^12 + С41) — С12 С44 -4* Я&СцСц^..
204
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Из (п. 1) следует
2&СцС44 = ссп — с12 (2с44 + с12) — сис44Я = с2пА — с44 (2с124-сп/?),
ЛГ = — СнЯ [е44 4- 2с12 + £C44C11 [1 — Я----i4~)
+ 2с41с12 (1 — R) -j- cuCi2/? 4-^-^-А — с42 (2с12 4- enZ?)l,
С44 J
таким образом,
М = 4Л.Я Г - 2 - 41 + + -Я - Лф-1 = 0,
I С44 А С44 J
и соотношение д = 2а — л/2 доказано.
Упражнения
5.1. В случае плоской синусоидальной чистой моды с амплитудой а
найти среднюю мощность Ф, переносимую пучком с помощью сечения А.
Решение. Для чистой моды
& (Р)А = 7<^>Л.
Для синусоидальной волны F(J) = cos cot Из (5.22) имеем
<<?> = paV <sin2co«> = -|-ра2сог
или, подставляя введенный в упр. 1.3 импеданс единицы площади Z — pF,
получаем
S' = -^-Zm2a2A.
5.2. Показать, что продольная волна всегда является чистой модой.
Решение. Поскольку °uj = rij, скорость переноса энергии согласно
(5.24) равна
С учетом уравнения Кристоффеля Г«вщ = pF2°uf получаем
" Ff = F X = Vnit
т. е. скорость переноса энергии параллельна направлению распространения.
5.3. Доказать, что если в направлении п распространяется чистая мода
с поляризацией °и и со скоростью F, то вдоль направления °и с той же ско-
ростью распространяется чистая мода, поляризованная вдоль п. Приложе-
ние: показать, что в плоскости YZ тригонального кристалла существует
только два направления чистых мод для поперечной волны, поляризован-
ной вдоль X (прямые АС и ВС на рис. 5.22).
УПРАЖНЕНИЯ
205
Решение. С учетом (5.24) условие существования чистой моды У* =
= Vnt имеет вид
сцми°щпк = 7 = рУ2,
или после перестановки индексов, поскольку = с<дг,
Ciik°u°Ukni = ^гц.
Из сравнения с уравнением Кристоффеля (5.4) видно, что п является
вектором поляризации волны, распространяющейся со скоростью V в на-
правлении °н. Эта мода является чистой, так как согласно (5.4)
Cijkinsni°uk = 7°и(.
Для чистой моды направления распространения и поляризации взаимо-
заменяемы. Таким образом, в кристалле с симметрией 3m, 3m, 32 попереч-
ная волна, поляризованная вдоль X, является чистой модой при распрост-
ранении вдоль двух взаимно перпендикулярных направлений в плоскости
YZ, совпадающих с направлениями поляризации невырожденных чистых
поперечных мод, которые могут распространяться вдоль осей второго по-
рядка А2 или Аг, направленных вдоль X.
5.4. Выразить через полярный угол 0е направление скорости переноса
энергии поперечной волны, поляризованной перпендикулярно плоскости,
проходящей через ось шестого порядка гексагонального кристалла. При
каком значении угла 0 отклонение (0 — 0г) имеет максимальную величину?
Решение. При указанном в разделе 5.1.6 выборе осей и( = 6ц, пх =
= О, П2 = sin 0, п3 = cos 0 из (5.24) следует
Vе — и ,
или
тге „ Sin 0 cos 0 .
0> V2~CM рУ ’ F3~ С44 рУ
tg0e = —7 = ~^tg0 = *tg0, где
П С44 С44
Отклонение (0 — 0е) максимально при d0e/d0 = 1 или, согласно получен-
ному выше выражению, при выполнении условия
cos 6м _ д/Г
COS 0ц
Подстановка выражения
/ ds?-1 - /
в равенство tg 0ц = к tg 0М дает
5.5. Найти угол <р0, на который нужно повернуть систему координат ®i,
хг, хз вокруг оси хз, чтобы модуль с1в кристалла с симметрией 4, 4 или 4/т
обратился в нуль.
206
ГЛ. 5. ДИНАМИЧЕСКАЯ ТЕОРИЯ УПРУГОСТИ
Решение. С учетом выражения (3.12) для матрицы поворота а{ на
угол <р вокруг оси х3 в новый модуль
С16 = СИ12 в а1а1а1а2СЦМ
входят только модули ctjki матрицы 4.55, которые не содержат индекса 3,
а именно:
«ЦП = «2222 = Сц, СЦ22 = С|2, Сцц = С66,
СЦ12 = Cte, Сии « —С16.
Коэффициенты при сц, сц, сев и cie равны соответственно
аи = ajajajaj 4- a2a®a®a| = — cos3<p sin ф + з1п3ф cos ф =
'in 2ф 1
= —g— (— cos 2Ф) — —4~ sin ^ф.
ai2 = aiaiaia2 + aiaiaia2 = с°83ф sin ф — sin3<p cos ф = — sin 4ф,
= (а1а1 + а1аг) (а1а2 + а1аг)= sin 2Ф cos 2ф = -у sin 4Ф>
flie = а1а1 (а!а2 + а1аг) + а1а2 (®1а1 + а1а1) “
— aftf (а|а2 + a2aj) — aja2 (aja2 + а2а|) =
= соз2ф cos 2ф — J*n^2^ _ «jn2(p cos 2ф — 2ф _ соя22ф — з!п22ф =
= cos 4ф.
Из выражения
ci'e = -у “ —--2 ~2 ) sin 4Ф + с1вcos 4Ф
видно, что с1в становится равным нулю при угле фо, удовлетворяющем ус-
ловию
5.6. На какой угол нужно повернуть координатную систему ®i, Х2, хз
вокруг оси я?з, чтобы обратился в нуль модуль сзз кристалла с симметрией 3
и 3?
Решение. Поскольку = 63f) новый модуль с*Б в развернутом
виде
С2В = С2213 = а2а2а1СШЗ
содержит лишь модули cijM ci,j,k^3 или, согласно 4.54,
Сщз = — С35, с221з = сзз, стз = Сзиз = сц, сцзз = сц,
С2223 = — Сц, С1233 = С2123 = «25.
УПРАЖНЕНИЯ
Отсюда получаем
с25 ~ с25 (cosS|P — 3 sin2<p cos ф) + с14 (sin3T — 3 соз2ф sin ф) .
Новый модуль с26 = c2s cos Зф — с14 sin Зф обращается в нуль при угле ф0,
удовлетворяющем условию
1?Зф0 = Си/См.
5.7. Найти выражения для фазовой = co/i2 и групповой Vg =* da/dkf
скоростей волн Лява.
Решение. Согласно (5.82)
Рф 1
Дифференцируя соотношение (5.86), (5.82) и (5.84), получаем
ГЛАВА 6
ПЬЕЗОЭЛЕКТРИЧЕСТВО
При изучении упругих волн необходимо учитывать пьезо-
электрическую связь между упругими и электрическими свойст-
вами, которая существует в определенных материалах. Большин-
ство устройств, преобразующих механическую энергию в электри-
ческую и наоборот, действуют на основе прямого или обратного
пьезоэлектрического эффекта*) (два основных типа преобразова-
телей, используемых для возбуждения объемных и поверхност-
ных волн, описаны в следующей главе). Кроме того, пьезоэлект-
рический эффект позволяет использовать замечательные механи-
ческие свойства некоторых кристаллов, такие как высокая доб-
ротность для фильтрации сигналов в электронике. Электромеха-
нические резонаторы, изготовленные, например, из кварца,
включаются непосредственно в электрическую цепь, где их коле-
бания поддерживаются электрическим полем. Настоящая глава
состоит из двух частей. В первой рассматриваются статические
свойства кристаллов, вторая посвящена распространению упругих
волн в пьезоэлектрических средах.
§ 6.1. Статические свойства
В этом параграфе будут рассмотрены принципы Кюри, по-
служившие основой для открытия пьезоэлектричества; будет дано
элементарное объяснение электромеханической связи и рассмот-
рены различные тензорные соотношения между электрическими
и механическими величинами, а также число компонент пьезо-
электрических тензоров.
6.1.1. Принципы симметрии Кюри. Применение к пьезоэлект-
ричеству. Пьезоэлектрический эффект состоит в том, что в неко-
торых кристаллах под действием механических напряжений возни-
•) Применяются также магнитострикционные преобразователи, однако
они работают только на низких частотах.
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
209
Рис. 6.1. Характеристическая
симметрия сжатия или растя-
жения, возникающего в ре-
зультате действия двух проти-
воположных сил:
кает электрическая поляризация (прямой эффект), а приложенное
к кристаллу электрическое поле приводит к его деформации (об-
ратный эффект). Открытие прямого пьезоэлектрического эффекта
Пьером и Жаком Кюри в 1880 г. следовало непосредственно из
принципов, связывающих симметрию и асимметрию причин и
следствий. Выясняя условия, налагаемые симметрией, которые до
этого использовались более или ме-
нее интуитивно, Пьер Кюри сформу-
лировал два принципа.
1) Явление обладает всеми эле-
ментами симметрии, которыми обла-
дают причины его порождающие
(следствия могут обладать более вы-
сокой симметрией, чем причины).
2) Асимметрия явления предопре-
делена асимметрией причин, его по-
рождающих. Каждое явление харак-
теризуется совокупностью возмож-
ных элементов симметрии. Так, эле-
ментами симметрии скалярной вели-
чины, например температуры, явля-
ются бесконечное число изотропных
осей симметрии А „ и перпендикуляр-
ных им зеркальных плоскостей М,
а ^также центр симметрии, т. е.
• С. Полярному вектору (электрическое поле, например)
соответствуют одна изотропная ось А„ и бесконечное число зер-
кальных плоскостей М, проходящих через эту ось, т. е. А„ °° М.
Сжатие (или растяжение), являющееся результатом двух про-
тивоположных сил (рис. 6.1), характеризуется симметрией
г
М ооМ'ь‘
Оба принципа Кюри объединяются в следующей формулиров-
ке; явление может существовать только в системе, являющейся
подгруппой характеристической симметрии явления.
Применительно к прямому пьезоэлектрическому эффекту, опи-
сывающему возникновение электрической поляризации при сжа-
тии кристалла, необходимо, чтобы система кристалл — сжатие бы-
ла подгруппой характеристической симметрии электрической по-
ляризации В частности, система должна быть лишена
центра симметрии; поскольку сжатие обладает центром симмет-
рии, его не должно быть в кристалле. Следовательно, кристаллы
с центром симметрии не могут быть пьезоэлектриками. Этот
вывод Кюри был подтвержден на опыте: пьезоэлектрические
свойства были обнаружены у кристаллов, принадлежащих 21 клас-
14 Э. Дьелесав. Д. Руайе
210
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
су без центра симметрии, за исключением класса 432 кубиче-
ской системы.
Принципы симметрии позволяют также указать направление,
в котором следует прикладывать механическое напряжение для вы-
явления пьезоэлектрических свойств. Так, в а-кварце, принадле-
жащем к классу 32, сжатие (или растяжение) вдоль оси симмет-
рии третьего порядка (рис. 6.2) не создает поляризации, посколь-
ку общая симметрия кристалла и сжатия (Л3ЗЛ2) не является
подгруппой симметрии явления Напротив, симметрия си-
стемы кристалл — сжатие вдоль оси второго порядка оказывается
совместимой с появлением поляризации Р вдоль этой оси
(рис. 6.2,6). Сжатие, перпендикулярное оси второго порядка А2
а) 5) б>
Рис. 6.2. Применение принципов Кюри в случае кварца.
Для существования пьезоэлектрического эффекта система кристалл — сжа-
тие должна являться подгруппой симметрии поляризации: Ах <х>М. а) Сжа-
тие вдоль оси третьего порядка не создает пьезоэффекта, так как симмет-
рия системы (Л3ЗЛ2) не является подгруппой симметрии поляризации,
б) Сжатие вдоль оси второго порядка создает поляризацию вдоль этой же
оси. в) Сжатйе перпендикулярно осям Л3, А2 создает поляризацию вдоль Л2.
и оси третьего порядка (рис. 6.2, в), создает поляризацию вдоль
оси А2, которая является единственным общим элементом симмет-
рии кристалла и сжатия.
6.1.2. Физический механизм. Одномерная модель. В 2.5.2 отме-
чалось, что кристалл сульфида кадмия состоит из чередующихся
слоев ионов серы и кадмия. В направлении, перпендикулярном
слоям, т. е. вдоль симметрии шестого порядка, ионы образуют
одинаковые цепочки, связанные друг с другом винтовой осью 63
(рис. 2.35). Одна такая цепочка показана на рис. 6.3, а.
В случае внешних воздействий (механическое напряжение,
электрическое поле), направленных вдоль оси шестого порядка,
достаточно рассматривать только одну цепочку, так как все ионы
слоя смещаются на одинаковую величину. Вообразим, что ионы
серы и кадмия с эффективными зарядами соответственно — q и
+7 связаны между собой пружинками. Поскольку по отношению
к каждому иону два его ближайших соседа расположены несим-
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
211
метрично, пружинки по обе стороны иона имеют разные жестко-
сти Kt и К2. Цепочка ионов может быть разделена на звенья дли-
ной а, содержащие два диполя с моментами -у-(я — Ь) и--
(рис. 6.3, а). Следовательно, дипольный момент молекулы
Ро = -у (« - 26).
Если b не равно а/2, то поляризация единичного объема Рв
не равна нулю в равновесном состоянии. Следовательно, среда яв-
ляется полярной, при этом
Р0 = ^(а-2Ь),
где п — число молекул CdS в единице объема.
g) q£ -qE ~Егль
ЕуЛ(а-Ь)
Рис. 6.3. Пьезоэлектрический эффект в кристалле сульфида кадмия.
а) Размещение ионов серы и кадмия в ряд параллельно оси шестого по-
рядка (з). б) Деформация цепочки под действием электрического поля Е.
Ионы Cd и S смещаются в противоположных направлениях. Длина элемен-
тарного звена изменяется на величину Да.
Такая одномерная модель наглядно показывает взаимосвязь
механических и электрических свойств пьезоэлектрического кри-
сталла.
1. Под действием механического напряжения цепочка дефор-
мируется. Изменение расстояний а и b приводит к изменению
поляризации
Р=ДР0 = ^-(Да-2Д&). (6.1)
Это прямой пьезоэлектрический эффект.
2. Электрическое поле смещает в противоположных направле-
ниях положительные и отрицательные ионы, и расстояние (а —Ь)
увеличивается, а расстояние Ъ уменьшается. При неодинаковых
жесткостях пружинок возникает деформация. Это обратный пье-
зоэлектрический эффект.
14*
212
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
Будем искать соотношения между величинами механически-
ми — напряжением Т и деформацией S, и электрическими — по-
лем Е и наведенной поляризацией Р или индукцией D — е^Е +
+ Р. Из условия статического равновесия каждого иона следует
(рис. 6.3,6):
—qE + Kl&(.a — b')—K2kb = O. (6.2)
Чтобы найти выражение для тензора механических напряже-
ний Т, рассмотрим сечение, перпендикулярное оси Ав. Расстоя-
ние между двумя соседними цепочками ионов вдоль винтовой
оси 6S равно полупериоду решетки я/2 (рис. 2.35). Следовательно,
плоскость, перпендикулярная оси Ав, поочередно пересекает пру-
жинки с жесткостью Kt и К2. В первом случае сила, с которой
правая часть цепочки действует на левую, равна А = KtMa— Ь),
а во втором случае F = К2\Ъ. Обозначая буквой N число цепочек,
пересекающих единичную площадку, перпендикулярную к As,
получаем выражение для упругого напряжения, т. е. силы на
единицу площади,
Т А/сгД («-&)+ ^-К2\Ъ,
поскольку имеется одинаковое количество пружинок каждого ти-
па. Так как N — па, то
Т =-у[К1Дя+(^2-ЛГ1)ДЫ. (6.3)
Наведенная поляризация находится путем подстановки выра-
жения
(М)
полученного из уравнения (6.2), в соотношение (6.1):
Это выражение содержит два члена. Первый, пропорциональный
электрическому полю, определяет ионную поляризуемость крис-
талла, Хюн = nrfKKt + К2). Второй член, пропорциональный де-
формации S = ka/a, выражает прямой пьезоэлектрический эф-
фект; тогда
р = Xton# + eS,
где е — пьезоэлектрический модуль, равный
е=(х+*9 я‘ (б,б)
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
213
Полная поляризация с учетом электронной восприимчивости %в1
/?=(%lon + Xel)^+e5,
поэтому электрическая индукция D может быть записана в виде
D = ъЕ + eS, (6.7)
где диэлектрическая проницаемость е = во + Хюп + Хеь
Механическое напряжение находится подстановкой выраже-
ния (6.4) для ЛЬ в (6.3):
Это выражение можно записать в виде
T = cS-eE, (6.8)
где с = па2К1К2/(.К2 +— модуль упругости и е — введенный
выше пьезоэлектрический модуль. Из выражения (6.6) видно, что
в одномерной модели существование пьезоэлектрического эффек-
та обусловлено асимметрией сил реакции, т. е. жесткостей пру-
жинок (е = 0, если К2 = КС). Уравнение (6.8) можно интерпрети-
ровать разными способами.
1) В отсутствие деформаций (случай цепочки с закрепленны-
ми концами) электрическое поле создает механическое напряже-
ние Т = —еЕ.
2) В отсутствие механических напряжений электрическое по-
ле вызывает деформацию S = еЕ/с. Следует иметь в виду, что в
действительности модуль е является одной из компонент тензора
третьего ранга, так как электрическая индукция Dx — тензор пер-
вого ранга (вектор), а деформация — тензор второго ранга. В ко-
ординатной системе, ось х2 которой направлена вдоль оси шестого
порядка, уравнение (6.7) можно записать в виде
= 833^3 + вззз^зз.
Вышеизложенная модель качественно объясняет природу
пьезоэлектричества в асимметричных ионных кристаллах. В дей-
ствительности механизм является более сложным, поскольку пье-
зоэлектрическим эффектом обладают и такие кристаллы, как тел-
лур Те [1] или селен Se [21, содержащие один тип атомов. В этом
случае электрическую поляризацию, созданную деформацией,
следует объяснить изменением распределения электронов. Что же
касается поликристаллических материалов, таких как керамика,
то они приобретают пьезоэлектрические свойства только после
специальной обработки. Например, в керамике типа ЦТС, пред-
ставляющей собой соединение циркония, титана и свинца, обра-
зуются сегнетоэлектрические домены (§ 2.5), которые при изго-
товлении керамики ориентируются произвольным образом. При-
214
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
ложение сильного электрического поля (около 20 000 В/см) при
нагреве до примерно 100°С приводит к упорядочению доменов.
Это состояние частично 'сохраняется при комнатной температуре
и в отсутствие электрического поля. Остаточная поляризация и,
следовательно, пьезоэлектрический эффект исчезают выше тем-
пературы Кюри, которая лежит обычно между 200 и 400 °C.
С точки зрения симметрии направление поляризации представ-
ляет собой изотропную ось. Все проходящие через эту ось плос-
кости эквивалентны, следовательно, среда является поперечно
изотропной.
6.1.3. Тензорные выражения пьезоэлектрического эффекта. Об-
общение для трехмерного случая выражения (6.7) дает определе-
ние тензора третьего ранга ецк
Dt = ztiEj + eijkSjh. (6.9)
Пьезоэлектрические модули связывают изменение элект-
рической индукции Dt с деформацией Sjk при постоянном элект-
рическом поле:
/ dD. \
= (ел0)
Поскольку Sjk = SU, тензор eilk симметричен по двум послед-
ним индексам / и к, т. е. ejft = eikj.
Следовательно, число пьезоэлектрических модулей уменьшает-
ся с 27 (число независимых компонент любого тензора третьего
ранга) до 18. Действительно, пара двух последних индексов / и
к принимает только шесть различных значений, обозначаемых
числом а согласно правилу (4.22) § 4.3:
в{а = e<jh, t = 1, 2, 3, а = (/, к} = 1, 2, ..., 6.
Пьезоэлектрические модули могут быть записаны в виде таб-
лицы, содержащей три строки <Л — 1, 2, 3) и шесть столбцов (а =
-1, ..., 6):
ец е12 е13 е14 е15 е16
eia ~ е21 622 е23 е24 6 25 626 • . (6.11)
I е31 е32 е33 е34 е35 е3в I
Используя матричную запись и для деформации согласно соотно-
шениям (4.25), можно записать уравнение (6.9) в виде
Di = EiSEj + BfaSa.
Коэффициент обратного пьезоэлектрического эффекта, связы-
вающий механическое напряжение Tjh и электрическое поле Е{
в обобщенном уравнении (6.8), получается из модуля с по-
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
215
мощью термодинамических соотношений. Внешние силы, дейст-
вующие на пьезоэлектрическую среду, имеют одновременно ме-
ханическую и электрическую природу. Следовательно, работа,
совершаемая при изменении состояния кристалла, кроме механи-
ческой части, приведенной в § 4.4,
6ГМ = ТЛ,
содержит электрическую часть
Для обратимого процесса изменение внутренней энергии единицы
объема
dPll = fide + TjhdS}h + EtdDi,
где О — абсолютная температура, а о — энтропия единицы объ-
шения (6.9) и (6.13) составляют первую систему уравнений со-
ции и электрической индукции. Введем далее термодинамический
потенциал
S=<U-EiDi.
Изменение этой функции состояния есть полный дифференциал
dS = Odo + TjhdSjk ~ DfdEi,
где
Поскольку вторые производные не зависят от порядка дифферен-
цирования, то
(=
k^i/a.S WJa.E [dEidS}k)0-
Из этого соотношения следует, что если при постоянном
электрическом поле деформация создает электрическую индук-
цию, т. е. (dDt/dSjkK.E = eiJk, то приложение электрического поля
приводит к появлению механических напряжений в зажатом
кристалле (деформация постоянна), т. е.
ЙЕ(М2>
при этом коэффициенты пропорциональности для обоих эффек-
тов имеют противоположные знаки. Таким образом, обратный
пьезоэлектрический эффект является термодинамическим след-
ствием прямого эффекта, В линейной области коэффициенты е(}*
предполагаются постоянными, и интегрирование соотношения
216
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
(6.12) при постоянных а и S дает
Если в кристалле возникают также деформации Sim, то механи-
ческое напряжение
T’jft = — BijkEi C^im Sim. (6.13)
Индекс E указывает, что модуль упругости в законе Гука
*"= (6Л4)
связывает механические напряжения и деформации при посто-
янном электрическом поле. Такое уточнение необходимо, по-
скольку в пьезоэлектрическом материале величины механических
коэффициентов зависят от электрических условий. Аналогично
входящий в (6.9) коэффициент еч представляет собой диэлектри-
ческую проницаемость при постоянной деформации еу. Соотно-
шения (6.9) и (6.13) составляют первую систему уравнений со-
стояния, которая в матричной записи имеет вид
Га = с®р5р-в{аЕй =1,2,3, (6.15 а)
Di = e^E} + eiaSa, а,р = !,..., 6. (6.15 6)
Эти уравнения определяют механическое напряжение и элект-
рическую индукцию как функции независимых переменных —
электрического поля и деформации.
При других сочетаниях независимых переменных (Z) и S, D
и Т или Е и Т) уравнения состояния пьезоэлектрической среды
принимают другие формы. Изменение термодинамического потен-
циала
ST = £ - TlkSih ~<U- EiDt - TShSjk
равно
d&~ = Od<r — SlhdTjh — DidEt.
Отсюда видно, что является функцией переменных Tjk и Et,
т. е. 5^(0, Tft, Ei), и следовательно,
Равенство вторых производных
вместе с соотношениями, определяющими коэффициент податли-
вости sfhim при постоянном электрическом поле и диэлектриче-
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
217
скую проницаемость еу при постоянном напряжении,
S^’n = (w^)E’ е«=(-^7-)т’ <6Л7>
приводит после интегрирования ко второй системе уравнений
состояния, в которой независимыми переменными являются
электрическое поле и механическое напряжение:
Sfa = dijkEi + SfalmTim,
Di — eyEj + dijkTjk.
Эти уравнения можно записать в матричной форме:
Sa = $арТр 4* diaE{, (6.18 а)
Di = efjEj J- d{aTa, (6.18 6)
при этом из соотношений (4.24) для Та и (4.25) для Sa следует
dta = diSk при а С 3, dia — 2dijh при а > 3. (6.19)
Пьезоэлектрические (е(а, й<а) и механические (cfp, s„p) коэф-
фициенты не являются независимыми. Подставляя выражение
Sp = di^Ei -|- sfvTv в уравнение (6.15а), получаем
Та — (— eia 4~ Capdip) Ei + C^pSpyTy = бдуТу
при любых независимых переменных Е( и 7\ и, следовательно,
capsp? = Sav, (6.20)
Cia = dipcpa- (6.21)
Из первого соотношения вытекает, что матрица ь’«р является
обратной по отношению к матрице с«р (как и в непьезоэлектри-
ческом материале). Второе соотношение позволяет найти модули
eia из модулей dta или наоборот с помощью формулы
dip ~ eiasaP- (6.22)
Чтобы связать еу с е®, подставим выражение для механиче-
ского напряжения Та = — e^Ej + cap5p в уравнение (6.186):
Di (еу — diae,-a) Ej + diaC«p5 р.
Учитывая выражение (6.156), получаем
8У — 8О — diaCja, = diac„pdjp. (6.23)
Диэлектрическую проницаемость еу зажатого кристалла изме-
рить очень трудно. Выражение (6.23) позволяет вычислить ее
218
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
из пьезоэлектрических модулей и диэлектрической проницаемо-
сти 8у свободного кристалла, обычно измеряемой на опыте. Раз-
личие между еу и еу существенно для сильных пьезоэлектриков.
Например, в ниобате лития (LiNbOs)
е[х = 74,3.10-11 Ф/м, efi = 38,9-10"п Ф/м.
Системы уравнений (6.15) и (6.18) наиболее часто использу-
ются на практике. Две другие системы уравнений состояния, в
которых электрической независимой переменной является индук-
ция D(, получаются при рассмотрении внутренней энергии ^(о,
S}h, £)<) и энтальпии <3$?(ст, Т!к, Di) = eU — TjkSjk. Для независимых
переменных D и 8 имеем
— hijhSjk, „
т _ Т) a , п (6.24)
где Cjhm есть тензор модулей упругости при постоянной элект-
рической индукции, а Ру — тензор, обратный тензору еу. Пьезо-
электрический модуль hilk, определяемый как
= - (74L=" (w)s = ~ (6,25)
записывается в матричной форме: hi}k — hia. Для независимых
переменных D и Т уравнения состояний имеют вид
Ei = ?>iiDj — gijkTjk,
n (b.Zo)
Sjk = SikimTim + gijkDi.
Пьезоэлектрический модуль gtjk равен взятой co знаком минус
второй производной энтальпии по независимым переменным
Di и Т}к, т. е.
<6-27>
В матричной записи gia = gtjh при а=1, 2, 3 и gia = 2g(jk при
а > 3.
6.1.4. Ограничения, налагаемые симметрией кристаллов на
число независимых пьезоэлектрических модулей. Условие инвари-
антности компонент пьезоэлектрического тензора по отношению
к операции симметрии, соответствующей матрице преобразования
базиса а, согласно (3.11) имеет вид
eijh = (6.28)
Рассмотрим результаты операций точечной симметрии кристалла.
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
219
а) Центр симметрии. Поскольку а* = — 6*, соотношение
(6.28) принимает вид = (— 1)%*, следовательно,
е<л = 0 при любых I, ], к.
Пьезоэлектрический тензор равен нулю с одиннадцати центро-
симметричных классах:
1, 2/т, ттт, 3, Зт, 4/т, 4/ттт, 6/т, 6/ттт, m3, тЗт.
Мы пришли к результату, уже полученному из принципов сим-
метрии Кюри (раздел 6.1.1).
б) Плоскость симметрии. Матрица преобразования координат
диагональна. При выборе оси х3 перпендикулярно зеркальной
плоскости матрица
/1 0 0\
а О' 1 0 .
ко 0 -1/
Из условия (6.28)
eijh — (6.29)
следует, что компоненты с нечетным числом индексов 3 равны
нулю. Число модулей eiee для кристаллов класса т (.М±-х3)
уменьшается до десяти:
1*11 *12 *13 0 0 *13 |
«1а= *21 *22 *23 0 0 *23 I* 1 0 0 0 *34 *35 0 1 (6.30)
поворота на угол л вокруг
в) Ось второго порядка. Матрица
оси х3 имеет вид
/—1 О
а = 0 — 1
\ О О
Из уравнения (6.29) следует, что компоненты с четным чис
лом индексов 3 равны нулю. Таблица eia для кристаллов класса
2 (Л211жз) является дополнительной к таблице класса т:
10 0 0 е15 0 I
eia = О 0 0 е24 е25 0 . (6.31)
I *31 *32 *33 ® *33 I
г) Несколько осей второго порядка. Не равные нулю модули
в кристаллах класса 222 имеют нечетное число каждого из индек-
сов, т. е. только е123, е213, е312 =И= 0:
1° 0 0 еи 0 0 1
ега — ® 0 0 о <?25 0 . (6.32)
1° 0 0 0 0 *зв 1
220
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
В кристаллах класса 2тт наличие зеркальных плоскостей,,
перпендикулярных осям xt и х2, приводит к равенству нулю мо-
дулей с нечетным числом индексов 1 и 2 таблицы (6.31), т. е.
= е123, е22 = е213, е33 — вц2:
10 0 0 о е15 01
eia= о 0 0, е24 0 0 . (6.33)
Кристаллы классов 23 и 43т кубической системы обладают
тремя осями симметрии второго порядка, совпадающими с осями
координат xh хг, х3. Поскольку поворот на угол 2л/3 вокруг оси
третьего порядка, направленной вдоль направления [1111, ведет
к взаимной перестановке осей xh х2, х3, 222 — е123, е312, е231 — равны между собой: три модуля для класса
10 0 0 еи 0 0 1
^=0 0 0 0 ем 0 . (6.34)
|0 0 0 0 0 '’14 1
д) Ось симметрии порядка п>2. Чтобы определить форму
матрицы пьезоэлектрических модулей для кристаллов с главной
осью симметрип третьего, четвертого или шестого порядков, сле-
дует использовать метод, примененный в разделе 4.5.2 при умень-
шении числа независимых модулей упругости. При тех же обоз-
начениях условие инвариантности новых модулей записыва-
ется в базисе собственных векторов |(t), |<2), |(3> матрицы пово-
рота (4.46) в виде
При заданных собственных значениях, равных
Х(,)= ei2"/n, 1(2) — е_2я/п, Х(3) = 1,
модуль r|ift не равен нулю, если разность (vi — v2) чисел индек-
сов 1 и 2 кратна п, так как в этом случае произведение
=е<(*1~',2)2Я/правно единице. Этому условию всегда удовлетворяют
модули т]12з, т121з, Цз12 и т)33з, для которых v, = v2. При п = 4 или
п = 6 все остальные модули равны нулю, а при п = 3 кроме вы-
шеуказанных не равны нулю модули и ц222, для которых Vj —
- v2 = ± 3.
Возврат к модулям eijK производится с помощью соотношения
€ijh — a2aj (IfeY]Zmn>
(6.35)
где (а) — матрица перехода от системы координат «1( х2, х3
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
221
(модули e(rt) к базису собственных векторов §(1), §(3’:
/1/3/2" i/]/2 о\
а = I 1/3/2 1/1/2 0 .
\ 0 0 1/
Рассмотрим сначала кристаллы классов 4 и 6, пьезоэлектри-
ческие тензоры е,й которых одинаковы, поскольку в обоих слу-
чаях не равны нулю те же компоненты ц,й. Поскольку ось А,
или Ав является одновременно и осью второго порядка, достаточ-
но рассмотреть отличные от нуля компоненты таблицы (6.31)
для кристаллов класса 2. Модули с одним индексом 3 тица езД,
где j, к^=3, выражаются через ц312 == ц321 в виде
e3jk = (ajak 4" Л 312, (6.36)
в частности,
^ЗН = 2fflj6jT]3i2 = ^Лз12> ОТСЮДа ₽31 = ₽32!
ез12 = (ffli4 + «1«г) Л 312 = °, отсюда е39 = 0.
Для модулей e{js с одним индексом 3 при i, j 3 имеем
еЦЗ = ®1а1Л123 + ®1®}л2135
^3 = аЗа} (Л123 + Л213) = ~2 (Л123 Л213)
или е15 = e2i. Из выражений для е123 и е213, полученных из (6.35)»
е123 = у (Л123 Л21з)>
а213 ' - "2" (— Л123 + Л213),
видно, что эти два модуля равны по абсолютной величине, но
имеют разные знаки, т. е. ен = — е25. При е333 = Лззз, отличном
от нуля, матрица eia (классы 4 и 6) имеет вид
10 0 0 01
^= 0 0 0 е15 -еи 0. (6.37)
Гз1 *31 *зз 0 0 °1
Для кристаллов классов 422 и 622, имеющих три взаимно
перпендикулярные оси второго порядка (рис. 2.28), достаточно
совместить таблицы (6.32) и (6.37):
10 0 0 0 01
В1а О 0 0 0 -ем 0 . (6.38)
|о о о о о о|
Аналогичным образом с учетом таблицы (6.33) класса 2mm.
222
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
получается матрица для кристаллов классов 4mm и 6mm:
10 0 0 0 е15 °1
eia = 0 0 0 *24 0 ° (6.39)
1 *31 *зг *зз 0 0 о|
В упр. 6.3 требуется доказать, что пьезоэлектрический тензор
для классов 4тт и бтт инвариантен по отношению к повороту
на любой угол вокруг оси х3. Учитывая замечание по поводу уп-
ругих свойств кристаллов гексагональной системы (раздел 4.5.2
и упр. 4.4), можно показать, что электромеханические свойства
кристаллов симметрии бтт инвариантны по отношению к пово-
роту на любой угол вокруг оси шестого порядка. Поскольку пьезо-
электрическая керамика обладает такой же поперечной изотро-
пией в плоскости, перпендикулярной направлению поляризации,
то ее упругие, электрические и пьезоэлектрические свойства опи-
сываются с помощью тензоров класса бтт.
Класс 432 кубической системы, обладающий всеми элемента-
ми симметрии класса 422, может иметь, таким образом, не более
одного пьезоэлектрического модуля е14 = — е25. Однако ось треть-
его порядка, направленная вдоль [111], позволяет осуществить
перестановку индексов 1, 2, 3, поэтому еш = е221 и eu = e2S =
= —е25 = 0, т. е. все компоненты е(а равны нулю. Таким образом,
кристаллы класса 432 не обладают пьезоэлектрическими свой-
ствами, несмотря на отсутствие в них центра симметрии:
eia = 0.
Установленные выше соотношения между модулями с одним
и тремя индексами 3 классов 4 и 6 применимы и для кристаллов,
имеющих ось третьего порядка. Однако здесь модули без индек-
са 3 не равны нулю. Они выражаются через т]ш и т]222 следую-
щим образом:
tijk = ФХпш + (6.40)
В частности,
е<22 = ~2 (— + ^Лгзг) = — е.Иъ
и, следовательно, при г = 1, 2 получаем
е12 = — ен, е22 = — e2j.
Таким же образом из выражения (6.40) следует
еИ2 = 2 (*Пш Лггг) — — е222,
е212 ~ 2 ( Лш + ^Лггг) —
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
223
Матрица е,-о {класс 3) принимает вид
I *11 ~ *11 0 *14
-*32 *22 0 *15
I *31 *31 *33 °
*24 *22
~ *14 -*11
О О
(6.41}
При наличии оси второго
«нулю модули матрицы (6.41),
1 (раздел 6.1.4в), а именно
порядка, параллельной Xi, равны
имеющие четное число индексов
eia — еа4,
615 5=3 — в22, 621-------в225 6з1 = е32, е33«
Кристаллы класса 32 имеют только два независимых пьезо-
электрических модуля etl и etl, следовательно,
I *11 “ *11 0 *14 0 0 I
eia= О ООО —M-d. (6.42}
| О ООО о о I
При наличии плоскости симметрии, перпендикулярной к оси
xh равны нулю модули с одним и тремя индексами 1 матрицы
(6.41): еи = е11 = О. Матрица eia кристаллов класса Зт имеет вид
I О О О О *Х5 -еи|
eia = | — *22 *22 0 *15 0 0 • (6.43}
I *31 *31 *33 0 0 0 I
е) Инверсионная главная ось. Поскольку инверсионная ось-
шестого порядка эквивалентна симметрии 3/т (раздел 2.3.1),
матрица для кристаллов класса 6 непосредственно следует
из (6.30) и (6.41)
I *и -*и 0 0 0 -*22|
С1а= -*22 *22 0 0 0 -*ц . (6.44}
I 0 0 0 0 0 0 I
При наличии оси второго порядка, параллельной ж,, в кри-
сталлах класса 6т2 из предыдущей таблицы исчезает модуль-
е22, не имеющий индекса 1 (раздел 6.1.4в), следовательно,
|*и -*н 0 0 0 0 I
eia = 0 0 0 0 0 -еп I (6.45)
I 0 0 0 0 0 0 I
Для инверсионной оси четвертого порядка будем использо-
вать общий метод. Матрица поворота — инверсии а равна — а,
и векторы §(<) являются также собственными векторами для а,
при этом собственные значения удовлетворяют равенству
224
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
A(i> “ —1(<). Условию существования модулей -q£jfe
= 1, i
которое эквивалентно равенству
= e’(V1"V2)^ = _ 1,
при П = 4 удовлетворяют модули Циз, Т]223, Лаи, T1S22, ДЛЯ которых
Vi — v2 = ±2. Поскольку At одновременно является осью второго '
порядка, достаточно рассмотреть модули табл. (6.31). Приме-
няя (6.35) к модулю eii3:
еНЗ ‘ 4" ®г®гЛ223> j
убеждаемся, что е24 = —е15. Таким же образом из соотношения ।
езн = йг^Лзи + ei®iHs22
получаем е32 = — е31. Равенство модулей е25 и еи следует из вы-
ражения
еО'з — а1в;Лпз + ^г^зЛггз — ез1з-
Поскольку е33 равно нулю (ц3зз=0), матрица eta (класс 4) прини-
мает вид
I 0 0 0 ‘14 ‘15 0 I
6fa= 0 0 0 -е15 ем О I (6.46)
|‘з1 ~‘з1 0 0 0 ‘J
В кристаллах класса ^2т с осью второго
ной Xi, равны нулю модули
следовательно,
10 О О
eia = Р U 0
|о о о
ец и
порядка, параллель-
е31 с четным числом индексов 1,
‘14 0 0 I
о е„ 0 I (6.47)
0 0 ‘звГ
Полученные результаты применимы к любому тензору треть-
его ранга Лед, симметричному по j и к, т. е. к модулям бед,
Лед, £ед. Они верны также и для модулей в матричной записи
е<а = вед и hia = Лед. Однако при выводе соотношений между мо-
дулями dia или ,gja необходимо учитывать формулы (6.19). Так,
в кристаллах класса 32 имеем e2e = — elb однако d26 = —2dn. На
рис. 6.4 представлены матрицы упругих и пьезоэлектрических
модулей и диэлектрических постоянных. Элементы в матрицах
§ 6.1. СТАТИЧЕСКИЕ СВОЙСТВА
225
Рис. 6.4. Матрацы упругих и пьезоэлектрических модулей и диэлектрических
постоянных в системе кристаллографических осей (рис. 2.28).
• О—компоненты, не равные нулю, равные компоненты, •— ком-
поненты, равные нулю, •—О — компоненты, равные по абсолютной вели-
чине, но противоположные по знаку, X — компоненты, равные (сп—с12)/2.
15 э. Дьелесан, Д. Руайе
Таблица 6.1. Пьезоэлектрические модули
и диэлектрические проницаемости
Вещество Класс Пьезоэлектрический мо- дуль, Кл/м1 Диэлектри- ческая про- ницаемость, 10-11Ф/м к
Кубическая система «14 8S
Арсенид галлия (GaAs) Германат висмута (Bi12GeOM) 43m 23 -0,16 0,99 9,73 34,2 [3] [4], гл. 4
Гексагональная сис- тема «15 «31 «S3 „8 eil е33
Керамика ЦТС-4 (по- перечно-изотропная) Окись цинка (ZnO) Сульфид кадмия &тт 12,7 -0,59 -0,21 -5,2 -0,61 -0,24 15,1 1,14 0,44 650 7,38 7,99 560 7,83 8,44 [25], гл. 4
Тетрагональная сис- тема «14 «15 «31 «33 611 fS е33
Парателлурит (ТеО2) Титанат бария (BaTiOs) 422 4mm 0,22 0 0 21,3 0 -2,65 0 3,64 20 1744 20 97 [16], гл. 4 [18], гл .4
Тригональная система «н «14 '15 «22 «31 «33 efi 4
Ниобат лития (LiNbOs) Танталат лития (LiTaO.j а-кварц (SiO2) 3m 3m 32 0 0 0,171 0 0 -0,04 3,7 2,6 0 2,5 1,6 0 0,2 0 0 1,3 1,9 О’ 38,9 36,3 3,92 25,7 38,1 4,1 [20], гл. 4 [21], гл, 4
Ромбическая система «15 е24 «31 «32 «33 •ft е22 „8 Бзз
Ниобат бария и нат- рия (Ba2NaNb5O15) 2mm 2,8 3,4 -о, 4-0,3 4,3 196 201 28 [24], гл, 4
§ 8.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
227
расположены следующим образом:
cii «и • • Си «22 • • • • СЕ (1) tii e2i eai «U • eta faia)
«И в! «21 eia e3i (hta) • e,f • <)
Симметрия относительно главной диагонали не принимается во
внимание. Справа внизу от каждой матрицы указано число ком-
понент тензоров, описывающих упругие, электрические и пьезо-
электрические свойства кристаллов, принадлежащих к разным
классам точечной симметрии.
В табл. 6.1. приведены пьезоэлектрические модули е,а и диэ-
лектрические проницаемости 8у некоторых материалов, имею-
щих практическое значение.
§ 6.2. Упругие волны в пьезоэлектрических кристаллах
В пьезоэлектрической среде связь между электрическими и
механическими величинами, выражаемая в статическом случае
с помощью уравнений состояния типа (6.15), приводит к взаимо-
действию упругих и электромагнитных волн. Действительно, из-
за соотношения (6.13) в уравнении динамики появляется член,
содержащий электрическое поле, а вследствие соотношения (6.9)
в уравнениях Максвелла возникают члены, содержащие механи-
ческую деформацию. При анализе распространения волн в пьезо-
электрике в принципе нужно решать одновременно уравнение
Ньютона и уравнения Максвелла. Решения представляют собой
смешанные упруго-электромагнитные волны, т. е. упругие волны
со скоростью распространения V, сопровождаемые электрическим
полем, и электромагнитные волны со скоростью распространения
v «105 V, сопровождаемые механической деформацией. Для пер-
вого типа волн можно пренебречь магнитным полем, которое соз-
дается электрическим, перемещающимся со скоростью V, малой
по сравнению со скоростью v электромагнитных волн. Тогда со-
гласно уравнению Максвелла
rot Е = — « О,
и электрическое поле Е выражается, как в электростатике, через
скалярный потенциал Ф, т. е. Е = —grad Ф.
15*
228
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
Электромагнитная энергия пренебрежимо мала по сравнению
с упругой энергией. Напротив, для второго типа волн упругая
энергия оказывается пренебрежимо малой по сравнению с элект-
ромагнитной.
Таким образом, даже в сильных пьезоэлектриках взаимодей-
ствие между тремя упругими и двумя электромагнитными вол-
нами оказывается весьма слабым из-за большой разницы соот-
ветствующих скоростей (v/V = 10‘ -г 10s). Следовательно, распро-
странение волн можно рассматривать независимо. Ниже упругие
волны рассматриваются без учета электромагнитных эффектов
в предположении, что поле является электростатическим, т. е.
в квазистатическом приближении. Сначала проводится анализ
распространения объемных волн (в неограниченной среде), а за-
тем — поверхностных волн (в полубесконечной среде).
6.2.1. Неограниченная среда. Объемные волны. Для случая
плоских волн выведем вначале уравнение для собственных зна-
чений тензора Гя, подобное уравнению Кристоффеля в § 5.1, а
затем с помощью поверхностей обратных скоростей проиллюстри-
руем влияние электромеханической связи на примере некоторых
пьезоэлектрических материалов.
Уравнения распространения. Тензор Кристоффеля. Выраже-
ние (6.13) для механического напряжения
Тц = CijMS)a — ehijEk
„ „ _ 1 fduh ди, \
после подстановки выражении для деформации Ski =yl I
гт дФ
и квазистатического электрического поля Ek = — gj- принима-
ет вид
т ди1_,а 8Ф
Ti^c^d7h + e^dTk-
Тогда основное уравнение динамики (5.1)
02м{ 9Ti} Е д\ ЭгФ
P7F = ^7 = CiiM + ем}д^Гк (6>48)
С другой стороны, электрическая индукция
Dj=ejkiSM + &fhEk = ejM (6.49)
должна удовлетворять уравнению Пуассона для непроводящей
среды dDi/dx} = 0. Следовательно,
„ д\ „S д2Ф п
}kl^k ^dx^h-°-
(6.50)
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
229
Уравнение распространения для смещения а{ получаем, ис-
ключая электрический потенциал Ф из уравнений (6.48) и (6.50).
В случае плоской волны, распространяющейся в направлении njt
величины а( и Ф имеют вид
Щ = Ф = Ф(/(*-^), (6.51)
а электрическое поле является продольным:
_ (?Ф Tli _
где F' есть производная функции F. Подставляя в (6.48) и (6.50)
выражения
а2ф ™
dt2 ’ ’ dxjteh у2 1 ’ dXjdxh у2 0
и вводя обозначения
Гн = Cijkinjnk, yi = емргргь, е = еДп3-пь, (6.52)
получаем систему уравнений
pV2 °Ui = T,ieui 4- ^Фо,
(6.53)
eui - еФ0 = 0.
Исключая электрический потенциал Фо имеем
рГ2°М1=(гп+^)°М1. (6.54)
Поляризации 0«,- упругих волн определяются, как и в случае
непьезоэлектрической среды, собственными векторами тензора
второго ранга
Г« = ГП + ^, (6.55)
собственные значения которого у = pV2 дают фазовые скорости
в выбранном направлении. Поляризации трех плоских волн всег-
да взаимно перпендикулярны, поскольку тензор Г« симметричен.
Чтобы показать, как зависит от направления распространения
добавочный член, обусловленный пьезоэффектом, добавим в вы-
ражения (5.8) разложение по компонентам у»:
У1 = ец;П1 4-С22!П2 + ^331п3 +
+ (e12J 4 е21(/ п1п2 + (е13( 4“ e31l')nln3 4“ (е23/ 4- е32/)П2П3>-
230
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
где для каждого значения индекса I находим
71 = е11И1 + е26П2 + е35ге3 + (е1в + е21)ге1П2 +
+ (е15 + е31) П1П3 + (е25 + е3в) П2П3>
Та = е16П1 + е22П2 + е34ге3 + (е12 + е2в) П1П2 + (g gg)
+ (е14 + езв) ге1пз + (е2» + езг) ге2газ>
Тз = е15П1 + е24И2 + е33п3 + (е14 + е2&) П1П2 +
+ (613 + е3б) Л1П3 + (623 + е34)пап3.
Влияние пьезоэлектрического эффекта на скорость распрост-
ранения может быть описано как изменение упругости среды.
Действительно, тензор Кристоффеля можно записать, как и для
непьезоэлектрической среды, в виде
Г« = СциП;Пк,
где
= 4, + (6.57)
Wk
Величины с(?ы, называемые «ужесточенными» модулями, не яв-
ляются настоящими модулями упругости, поскольку они опре-
делены только для плоских упругих волн и зависят от направле-
ния распространения. Поэтому при рассмотрении следующих при-
меров предпочтительно использовать выражения (6.55) и (6.56).
Примеры поверхностей обратных скоростей в пьезоэлектриче-
ских кристаллах.
а) Распространение волн в плоскости (001) пьезоэлектриче-
ского кубического кристалла (Bii2GeO20).
Матрица (6.34) модулей одинакова для двух классов кубиче-
ской системы 43m и 23, симметрия которых разрешает существо-
вание пьезоэлектрического эффекта. Поскольку не равны нулю
только модули eu = е25 = е33, выражение (6.56) сводится к
71 = 2е14пгп3, ^2 = 2e147i17i3, Чз = 2вцП1П2.
В плоскости (001), где Wj = cos ф, п2 = sin ф, п3 = 0,
7i = Y» = 0, 73 = е148ш2ф. .
Компоненты ri3 и Г23 равны нулю, как и в случае непьезоэлект-
рического_кубического кристалла (раздел 5.1.6). Кроме того,
Ги = Гц, Г22 = Г22, Г12 = Г|2. Изменяется только Г33:
Г33 = Г33 —|- = cf4 —1г sin2 2ф.
6 и 8н
Выражение (5.33) для скоростей и V2 квазипродольной и
квазипоперечной волн, поляризованных в плоскости (001), со-
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
231
держащее только компоненты Гц, Г22, Г12, остается неизменным,
следовательно, Vt и V2 и в этом случае определяются формулами
(5.34) и (5.35), в которые подставляются модули упругости сцн
при постоянном электрическом поле. Пьезоэлектрический эффект
не оказывает влияния на эти моды, так как сопровождающие их
деформации Sti, S22, S12 не создают продольного электрического
Рис. 6.5. Сечения поверхности обратных скоростей германата висмута
(класс 23) плоскостью (001).
Пьезоактивна лишь поперечная волна, как это видно из расхождения с ок-
ружностью, полученной без учета пьезоэффекта и обозначенной пунктиром.
поля (для этого необходимо существование модулей eijh без ин-
декса 3). Эти волны не взаимодействуют с электрическими поля-
ми. Напротив, скорость Ps поперечной волны с поляризацией
[ООН изменяется, при этом она теперь зависит от направления
распространения:
ГТ ( е2 \1/2
Величина этого изменения непосредственно связана с вели-
чиной константы электромеханической связи, определяемой соот-
ношением
X = еи
]^е1Л + еи ’
232
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
следовательно,
В кристалле германата висмута (Bi12GeO20, класс 23, модули
в табл. 4.1 и 6.1), для которого сечение поверхности обратных
скоростей плоскостью (001) показано на рис. 6.5, константа элект-
ромеханической связи К = 0,32 и максимальное относительнее
изменение скорости V3 (в направлении [110]) равно
б) Распространение волн в плоскости 7Z ниобата лития.
Ниобат лития — пьезоэлектрический кристалл (раздел 2.5.2)
класса Зт тригональной системы. С учетом пьезоэлектрического
Рис. 6.6. Селения поверхности обратных скоростей ниобата лития (класс 3m)
плоскостью YZ.
Пунктирные кривые получены без учета пьезоэффекта. Поперечная мода
пьезоэлектрически не активна.
тензора (6.43) и выражения (6.56) для направления распростра-
нения, лежащего в плоскости симметрии KZ = 0, пг = sin й-
Пз = cos 6), получаем:
Ъ-0,
7г = е22 sin2 9 + (е15 + е31) sin 0 cos 0,
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ 233
7з = Cis sin2 0 4- е3з cos2 0,
6 = 611 sin2 0 + 6М cos2 0.
В разделе 5.1.6 было установлено, что для этого сечения по-
верхности обратных скоростей Г12 = Ги = 0, а остальные компо-
ненты тензора Г« определяются выражениями (5.54). Следова-
тельно, не равны нулю лишь следующие компоненты «ужест-
ченного» тензора Кристоффеля:
Гц = Гп, Г22 = Г22 -|- -р Г23 = Г23 + Г33 =Г33 + -р
Таким образом, имеется поперечная волна, поляризованная
перпендикулярно плоскости YZ, на скорость которой Vs —}'Ги/р
пьезоэлектрический эффект влияния не оказывает. Напротив, это
влияние существенно для квазипродольной и квазипоперечной
волн, поляризованных в плоскости YZ, скорости которых, соот-
ветственно Vi и V2, определяются соотношением
2р( Ki,2)2 = Г22 + Г33 ± V (Г22-Гзз)2 + 4(Т„)2. (6.58)-
Насколько существенно влияние пьезоэлектрического эффек-
та в этом кристалле, видно из рис. 6.6, где сплошные кривые по-
лучены с использованием модулей иэ табл. 4.1 и 6.1, а пунктир-
ные даны без учета пьезоэлектрического эффекта.
в) Распространение в плоскости YZ окиси цинка. Окись цин-
ка принадлежит к классу Ътт. Согласно матрице (6.39) и выра-
жениям (6.56) имеем
Y1 = (615 + 631) «1«3,
?2 = (615 + 631) ra2R3, /с -п.
Z 2 , 2\ . 2 (6.59;.
Уз ~ е15 \П1 + + е33п3,
е = еХ1 (п? + + е33п|.
В плоскости YZ (ль = 0, п2 = sin 0, п3 = cos 0) это дает
Ух = °, У г = 631 sin 20, у3 = б18 sin2 0 -f- е33 cos 0,
е = eu sin2 0 + е33 cos2 0.
С учетом результатов раздела 5.1.6 получаем
Гц = Г1Х, Г12 = Г12 = О, Г13 = 1\3 = О,
Г22 — Г22 + Г23 = Г93Гзз = Г33
234
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
Таким образом, в этом случае имеем три волны: поперечную, по-
ляризованную перпендикулярно плоскости У7, скорость которой
определяется выражением (5.46), и две пьезоэлектрически актив-
ные волны — квазипродольную и квазипоперечную — со скоро-
стями соответственно V\ и V2 (см. (6.58)). Эти результаты пред-
ставлены на рис. 6.7.
Рис. 6.7. Сечения поверхности обратных скоростей окиси цинка (класс
6 mm) плоскостью, проходящей через ось симметрии шестого порядка.
Пунктирные кривые получены без учета пьезоэффекта. Поперечная мода
пьезоэлектрически пассивна.
Распространение вдоль направлений, связанных с элементами
'Симметрии. С целью определения констант электромеханической
связи для наиболее важных направлений ниже рассмотрено рас-
пространение волн вдоль оси симметрии, в плоскости, перпенди-
кулярной оси четвертого или шестого порядка, и в плоскости
симметрии.
а) При распространении вдоль оси симметрии, совпадающей
с осью ж3 (raj = 0, п2 = 0, п3 = 1), выражения (6.56) упрощаются:
Ъ = «35, = е34, Уз = взз.
Из матриц eia видно, что в кристаллах, имеющих направлен-
ную вдоль ж, простую ось любого порядка п или инверсионную
ось порядка п ¥> 2, модули е34 и е35 равны_нулю. С учетом резуль-
татов раздела 5.1.3 получаем, что Г13 и Г23 равны нулю, и един-
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ 235
ственной компонентой тензора Г, изменяющейся из-за пьезо-
электрического эффекта, является
Гзз = сзз + 633/е33-
Следовательно, обе поперечные моды, распространяющиеся
вдоль оси симметрии (кроме Л2), пьезоэлектрически не активны,
а константа электромеханической связи продольной волны
g — езз
]^6ззсзз + езз
Эта константа также может быть равна нулю, если е33 = 0 из-за
наличия других элементов симметрии. Такой случай имеет место
в кварце (класс 32).
б) При распространении в плоскости, перпендикулярной про-
стой оси симметрии четвертого или шестого порядков, направлен-
ной вдоль оси ж3, ns = 0 и из (6.56) следует
Ti = епп[ + е2вп1 + (ем + е21) пгп2,
?2 ~ е1вП1 + е22П1 + (е12 + е2б) И1П2>
Уз = 6i5ni + e24«i + (614 + егз) На-
значения у, и fa равны нулю, так как согласно матрице (6.37)
еи = е2в = е1в = е21 = е22 = 0. С учетом результатов раздела 5.1.36
(Г)3 = Г2) = 0) видно, что в любом направлении в плоскости мо-
жет распространяться поперечная волна, поляризованная вдоль
оси х3. Кроме того, поскольку е25 = — е14 и е24 = е15, компонента
7з имеет постоянную величину:
?3 = 615 (”1 + «1) = 615.
Следовательно, квазипродольные и квазипоперечные волны,
поляризованные в плоскости распространения Ж1Ж2, перпендику-
лярной оси четвертого или шестого порядка, пьезоэлектрически
не активны. Скорость Va поперечной волны (Т), поляризованной
вдоль оси симметрии, не зависит от направления распростране-
ния в плоскости XtX2:
при этом константа электромеханической связи для этой волны
К = —=====
К811С44 + ^16
Плоскость ж4ж2 изотропна для поперечной волны, как и в непье-
236
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
зоэлектрической среде. Однако в случае оси типа Л4 это неверно
(см. упр. 6.4).
в) При распространении в плоскости симметрии, перпендику-
лярной оси ж3 (п3 = 0), компонента у, равна нулю, так как е15 =
= вц = е14 = е25 = 0 (см. (6.30)). Следовательно, поперечная вол-
на, поляризованная перпендикулярно зеркальной плоскости
(Г13 = Гг5 = 0), пьезоэлектрически не активна, так как ее ско-
рость Vs =КТзз/р = ТТзз/р не изменяется.
В табл. 6.2 дана сводка полученных выше результатов и при-
ведены константы электромеханической связи наиболее часто ис-
пользуемых материалов.
6.2.2. Поверхностные волны. Упругая волна, распространяю-
щаяся на поверхности полубесконечной среды, должна удовлет-
ворять одновременно уравнению распространения в неограничен-
ной среде и граничным условиям. В § 5.3 было показано, что
единственным возможным решением для непьезоэлектрического
твердого тела являются волны Рэлея (сложные волны с эллипти-
ческой поляризацией). В случае пьезоэлектрической среды най-
ти решения труднее, так как, во-первых, распространение в не-
ограниченной среде описывается двумя уравнениями (6.48) и
(6.50), во-вторых, к условию отсутствия механических напряже-
ний на свободной поверхности добавляются условия непрерыв-
ности электрического потенциала и нормальной компоненты
электрической индукции на незаряженной поверхности. Анализ
показывает, что, кроме влияния пьезоэлектрического эффекта на
распространение волн Рэлея, при определенных услових симмет-
_____________ рии существует поверхностная волна с
/ /\ линейной поляризацией, называемая вол-
/ п/ ; / ной Гуляева — Блюстейна.
/ ! / В этом РазДепе вначале излагается об-
Г । | щий метод решения уравнений для по-
I верхностных волн, являющийся обобщени-
' . I ем приведенного в § 5.3 метода, и опреде-
Рис. 6.8. ляются возможные типы волн в зависимо-
сти от расположения сагиттальной плос-
кости относительно элементов симметрии. Далее изучается рас-
пространение волн Гуляева — Блюстейна в поперечно изотроп-
ной среде. Затем в общих чертах рассматривается влияние элект-
рических граничных условий на распространение поверхностных
волн и, наконец, приводятся некоторые результаты, касающиеся
поверхностных волн в важных для практики пьезоэлектрических
кристаллах.
Общий метод решения уравнений для поверхностной волны.
В системе координат рис. 6.8 (ось ж4 параллельна направлению

238
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
распространения, ось х2 перпендикулярна свободной поверхности,
определяемой уравнением ж2 = 0) будем искать решение, в кото-
ром смещение
-хх» {<0(4~чг)
= °ufte ze v \ где Re % > О,
и связанный с ним электрический потенциал
экспоненциально убывают в глубь материала. Подставляя, как и в
§ 5.3 (только здесь роль п, играет компонента п2),
«1 = 11 «з = О, X = уге2г гДе Im «2 < 0.,
получаем компоненты смещения и потенциала в форме, анало-
гичной выражению (6.51):
/ njxA
ик = °ике^ v < Ф = Ф0еЦ‘-4-). (6.60)
Полагая V параметром, который нужно определить из усло-
вия совместности этих четырех однородных уравнений, получа-
ем уравнение с действительными коэффициентами восьмого по-
рядка по п2=д, из корней которого приемлемы только четыре с от-
отрицательной мнимой частью. Для каждого из значений п^= qT
(здесь г = 1,2.3,4) из системы (6.61) находятся соответствующие
смещение и потенциал Ф(ог). Общее решение является ли-
нейной комбинацией этих четырех простых волн, распространяю-
щихся с одинаковой скоростью 7:
щ = 1 Аг °и?>А" 1 v ') = (1 Аг 'и? 4(6.62)
Ф = S АгФ<г)е^‘“ г ' = ( S ЯгФ(0г)е“М2) Н* v\ (6.63)
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
239
где Xr= Скорость V и коэффициенты Аг определяются с по-
мощью механических и электрических граничных условий на
свободной поверхности «2 = 0 (раздел 6.2.2). Следующее отсюда
уравнение относительно V2 имеет, в общем случае, один физиче-
ски приемлемый корень, которому соответствуют коэффициенты
затухания %, с положительной действительной частью.
Волна, смещение которой имеет три компоненты, сопровож-
дается электрическим полем в сагиттальной плоскости:
Это решение представляет собой сложную пироэлектрически ак-
тивную волну Рэлея, которую мы обозначим R3. Для определен-
ных сагиттальных плоскостей возможно существование двух
скоростей. Одна из них (7Л) соответствует поляризованной в са-
гиттальной плоскости простой пьезоэлектрически не,активной
волне Рэлея, обозначим ее Т?2, вторая (Рв) соответствует поляри-
зованной перпендикулярно сагиттальной плоскости волне, кото-
рая сопровождается электрическим полем и называется волной
Гуляева — Блюстейна (В). Эти две волны распространяются не-
зависимо с различными скоростями. Кроме упомянутых двух пре-
дельных случаев, возможно распространение пьезоэлектрически
активной волны Рэлея, имеющей две компоненты (Л2). Следует
напомнить, что в непьезоэлектрической среде возможны два типа
волн Рэлея: с тремя (2?s) и с двумя (Т?2) компонентами.
В пьезоэлектрическом кристалле мода R3 не может существо-
вать, так как три компоненты смещения создают все возможные
деформации и, следовательно, хотя бы одна из них создает
электрическое поле. По этой же причине и волна Гуляева — Блю-
стейна всегда сосуществует с модой Rt, поскольку третья компо-
нента смещения, перпендикулярная сагиттальной плоскости,
должна сопровождаться электрическим полем, если это не имеет
места для двух других компонент.
Перечисленным пяти случаям соответствуют различные част-
ные формы системы уравнений (6.61), в которых по соображени-
ям симметрии определенные компоненты Г« и *({ равны нулю.
Учет симметрии. Необходимыми и достаточными условиями
существования решения системы (6.61), соответствующего сме-
щению, перпендикулярному сагиттальной плоскости (ki = b2 =
= 0, Uj^O), являются
Г15 = Г2, = 0, 7i = f2 = 0 (6.64)
пли
Г13 = Г22 = 0, 7з = 0, т. е. Фо = О. (6.65)
240
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
Согласно выражению (при = 1, п2 = q, п> = 0)
Гц = с^к1П,пк = сии + Cuuq2 + (сц2г + с^и) q
(6.66)
условие Ги = Г23 = 0 выполняется, если все модули упругости с
одним индексом 3 равны нулю. Для этого достаточно (как видно
из уменьшения числа независимых модулей для кристалла моно-
клинной системы (см. (4.43)), чтобы сагиттальная плоскость пред-
ставляла собой плоскость упругой симметрии — зеркальную либо
перпендикулярную простой или инверсионной оси Л2Р. В случае
= ешп}пк = ем + е2<2д2 + (ец2 + е2«)д (6.67)
для выполнения условия = у2 = 0 нужно, чтобы все пьезоэлект-
рические модули без индекса 3 были равны нулю. Это требова-
ние выполняется, если сагиттальная плоскость х&г перпенди-
кулярна простой оси симметрии второго порядка (раздел 6.1.4в).
Таким образом, соотношение (6.64) удовлетворяется одновре-
менно, если сагиттальная плоскость перпендикулярна оси сим-
метрии четного порядка (содержащей ось второго порядка.)
В этом случае система (6.61) разделяется на две независимые си-
стемы. Первая иэ них,
/Ги-рГ Гц ’
( ги г„-рг’1
отвечает пьезоэлектрически неактивной простой
(Т?2), а вторая,
(6.68)
0,
волне Рэлея
'гзз-рг2 ?з
°.
(6.69)
соответствует пьезоэлектрически активной горизонтально-попе-
речной (поляризация °ws) волне Гуляева — Блюстейна (В).
При выполнении условий (6.65) система (6.61) сводится к
(Г33 - pF2) °и3 = 0,
/Гн-рг* г12
Г12 г22-ру* Ь 4=0. (6.70)
\ -е/ \фо/ .
Здесь существуют решение типа /?2 наряду с непьезоактивной
горизонтально-поперечной волной. Из условия у»==0 согласно
(6.67) следует
в15 = е24 = 0 и е14 + е25 = 0. (6.71)
Кроме того, поскольку модули упругости с одним индексом 3 рав-
ны нулю (условие Ги = Г22 = 0), деформации 5ц, 512, 522 волны
Рэлея не создают напряжения Ti2. Следовательно, из граничного
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
условия Т22в0, которое можно записать в виде Т32 = — епзЕ( = 0,
получаем, что е14 = е25 0, поскольку Е3 = 0 и согласно (6.71)
е223 = е24 = 0. Из матрицы (6.30) видно, что модули е14, е15, е24, е25
равны нулю, только если плоскость XtX2 является зеркальной
плоскостью. Следовательно, пьезоэлектрически активная волна
Рис. 6.9. Сагиттальные плоскости, в которых существуют волны Гуляева —
Блюстейна, волны Рэлея с двумя компонентами или Бг, в зависимости
от того, обладает кристалл пьезоэффектом или нет.
Пьезоэлектрические классы отмечены звездочкой, а и 0 — углы, на которые
нужно повернуть оси координат для обращения в нуль соответственно
модулей. с25 и cie (упр. 5.6 и 5.5). Аналогичная таблица для волн Лява да-
на в [5].
Рэлея с двумя компонентами смещения существует только в том
случае, если сагиттальная плоскость является плоскостью сим-
метрии.
Полученные результаты можно обобщить следующим образом:
1) Сагиттальная плоскость -U42 — моды В + /?2,
16 э, Дьеяесан, Д. Руайе
242
ГЛ 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
2) Сагиттальная плоскость W — мода В2.
На рис. 6.9 показаны результаты применения этих двух тео-
рем для каждого класса точечной симметрии.
Волна Гуляева — Блюстейна. Волна Гуляева — Блюстейна
[6, 71 может существовать и в случае оси Лв, перпендикулярной
сагиттальной плоскости, поскольку ось Ав содержит и ось Аг.
Для пьезоэлектрического кристалла или керамики с симметрией
6mm оси и х2 могут быть расположены произвольно в плос-
кости, перпендикулярной оси шестого порядка. При п, = 1, п2 =
= q, п3 = 0 из выражений (5.44) и (6.59) получаем
Гзз = С^1(1 + д2), Тз = ^15 (1 + д2),; е=Ец(1 + ?г).
Условие совместности системы (6.69):
(1 + 52)
= 0
*15 (1 + 92) - 811
выполняется для двух значений и q2: с отрицательной мнимой
частью qt = — i и q2, определяемого соотношением
М.(1 + Й)-Р^+ &(! + $ = °
611
или, поскольку с?4 = cf4 4- ef5/sn (упр. 6.2),
—1-
*44
Если скорость волны Гуляева — Блюстейна меньше скорости по-
перечной объемной волны с той же поляризацией Гт = V CuJpn
то q2 является мнимым: ______
= = (6.72)
При q = qt из первого уравнения системы (6.69) следует, что
= 0,; при q = q2 из второго уравнения получаем Ф® =
= (^15^п) °из2>. Общее решение типа (6.62) и (6.63) после под-
становки °г42) ~ В *) может быть записано в виде
u3 = 5e у 2е ' у< (6.73а)
ф = (ф^е-7*2 4- Де-ВуХ2'1 е{“(<-уА (6.736)
_________________ \ 6 н /
♦) Коэффициенты Л1 и Л2 здесь не нужны, поскольку они содержатся
в Ф(« и °и<2) = В.
§ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
243
Потенциал Фо1 и скорость V определяются уравнениями непре-
рывности на свободной поверхности х2 = 0. Ниже нам понадобит-
ся выражение для нормальной компоненты электрической ин-
дукции
D, = -Ъ £ = £ e„®iuЛ(».М)
В граничное условие для механических величин Т’12 = 0 вхо-
дит только компонента поскольку согласно (6.39) в волне Гу-
ляева — Блюстейна деформации S32, S3i и электрическое поле с
компонентами Eh Е2 создают только напряжения TSi, Г22:
т _ ^диз,д «Ф
Подстановка выражений (6.73) в равенство Т32 = 0 при х2 = О
Дает
Р (С44 + "j5) В + ^Фо15 = о,
\ 6ц /
Ф^1) = -₽^В = -1^51 (6.75)
15 К еП
где
К = ——===== = —- *1Б
/еИС?4 /^ + ^6
есть константа электромеханической связи для поперечной вол-
ны. Волна Гуляева — Блюстейна, удовлетворяющая механиче-
ским граничным условиям на свободной поверхности, описыва-
ется выражениями
и3=Ве г е ' ',
(6.76 а)
*15 п! ~₽?*2 ₽ Ч*-?)
е v —-^е у е v VI.
и \ л /
(6.766)
Коэффициент затухания ₽ = И 1 — Г2/?т и, следовательно, ско-
рость распространения V определяются электрическими гранич-
ными условиями. Рассмотрим два типичных случая.
а) Поверхность покрыта металлическим слоем, толщина ко-
торого мала по сравнению с длиной волны, имеющим нулевой
потенциал (поверхность по-прежнему остается механически сво-
244
ГЛ. в. ПЬЕЗОЭЛЕКТРИЧЕСТВО
бодной). Из равенства нулю электрического потенциала при х2 =
= 0 следует
Р = (6.77)
Скорость волны Гуляева — Блюстейна
(6.78)
оказывается весьма близкой к скорости поперечной волны VT.
Затухание амплитуд смещения (6.76а) и потенциала (6.766) рас-
тет с увеличением константы элект-
ромеханической связи согласно выра-
жениям
Г71=Вс-Г'=”!/’Л
_ “и в
На рис. 6.10 приведены зависи-
мости амплитуд смещения и потен-
циала от глубины для сульфида кад-
мия, у которого К = 0,19, т. е. В =
= 0,036, VB = 0,9994, VT = 1788 м/с.
б) Для неметаллизированной по-
верхности потенциал Ф и нормаль-
ная компонента электрической ин-
дукции должны быть непрерывны-
ми. Условие непрерывности потен-
циала в любой момент времени и в
приводит к тому, что электрический
Рис. 6.10. Волна Гуляева —
Блюстейна в сульфиде кадмия.
Амплитуды смещения (попе-
речного) и электрического по-
тенциала в случае металлизи-
рованной поверхности.
любой точке поверхности _г___„____ .___„ „„ „_____________
потенциал в вакууме Ф', описываемый уравнением Лапласа
э2Ф' а2Ф' 0
дх* + дх* '
должен зависеть от t и х таким же образом, как и Ф. Решение,
обращающееся в нуль при х2 = — °°,
Ф'= Ф^е '
равно Ф (см. (6.766)) при ха = 0, если
ф; = !1&5/1_
(6.79)
(6.80)
Условие непрерывности нормальной компоненты индукции,
которое с учетом (6.74) можно записать в виде
ецФо1) = —eo®c>
$ 6.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
245
после замены Фо1) и Фо их выражениями (6.75) и (6.80) приводит
к соотношению

Коэффициент затухания
2 + еи/е0
(6.81)
уменьшается в отношении, близком к величине относительной ди-
электрической проницаемости. В случае неметаллизированной по-
верхности волна Гуляева — Блюстейна глубже проникает в ма-
териал. Для CdS имеем
Ви/во = 9; отсюда ₽ = 0,0036.
Изменяется также и скорость, остающаяся, однако, при этом
весьма близкой к скорости поперечной объемной волны:
<6-82>
В обоих случаях глубина проникновения волны Гуляева —
Блюстейна много больше длины волны (от 10 до 100Х), чем и
объясняется малое отличие ее скорости от скорости поперечной
объемной волны.
Влияние электрических граничных условий. Вернемся к об-
щему случаю для рассмотрения влияния электрических гранич-
ных условий на распространение поверхностных волн, в частно-
сти, на их скорость. Условие равенства нулю механических на-
пряжений на свободной поверхности х2 = 0 кристалла записыва-
ется в виде
7’12 = С1Ш + ®Агг i = 1, 2, 3.
Подстановка сюда выражений (6.62) и (6.63) для смещения
и потенциала поверхностной волны
Т„ - 2Л„[w4’> (-£ пГ>) + 4’)] е
приводит к системе трех уравнений (i = 1, 2, 3) с четырьмя неиз-
вестными Аг (г=1,4)
3 Л71$,-= 0, (6.83)
246
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
где
= cw°u^r) + e№W. (6.84)
Из электрических граничных условий следует непрерывность
электрического потенциала Ф и нормальной компоненты элект-
рической индукции
п . dUh с дф
На поверхности х2 — 0 имеем
D, -
да(0;- SapS’H' Л
r=l
(6.85)
где Z?ar) = Выражение для электриче-
ского потенциала на поверхности следует непосредственно из
(6.63):
Ф (0) = 2 ЛФ(оГ)ев’^”?1 (6.86)
Система трех уравнений (6.83) позволяет найти три неизвест-
ных коэффициента Аг как функцию четвертого коэффициента.
Потенциал Ф и компонента индукции D2, которые на свободной
поверхности выражаются линейной комбинацией коэффициентов
Ат, пропорциональны в действительности только одному из этих
коэффициентов. Соотношение этих величин, не зависящее от Аг,
определяет поверхностный импеданс Zb 181:
Ф(0) # Я7.
PJ0) = 1 TZs‘ (6-87)
С учетом (6.85) и (6.86) это соотношение можно записать в виде
24ф“г>-^2адП=о-
Это уравнение вместе с тремя уравнениями (6.83) образует cue-
§ 8.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
247
тему однородных уравнений. Они совместны, если равен нулю
определитель
у(1) 112 т(3) 1 12
т(1) 1 22 т(2) 1 22 т(3) 7 22 ^2
4V т(») 7 32 *1?
Ф^-i^Z^) Ф^-^ZgD^ ®W-!gZsD^(«-^ZsD<«
который может быть представлен как сумма двух определи-
телей
Д1(Г) + У2вД1(У) = 0,
где и Дг являются функциями скорости распространения V.
Окружающая среда также характеризуется некоторым импедан-
сом Zo. Из условия непрерывности Ф и Dt на поверхности следу-
ет, что ZS = ZO, и скорость поверхностных волн определяется
уравнением
(6.88)
Д1(У) + Г2оД2(У) = О.
Как и для волн Гуляева — Блюстейна, следует рассмотреть
два основных случая.
а) Поверхность покрыта очень тонким металлическим слоем,
имеющим нулевой потенциал. Тогда импеданс равен нулю, и
скорость Vo определяется соотношением
Д,(Ио) = О.
(6.89)
б) Пьезоэлектрик граничит с вакуумом. Потенциал Ф', кото-
рый должен удовлетворять уравнению Лапласа, обращаться в
нуль при хг = — оо и быть непрерывным на плоскости яг3 = О,
определится выражением (6.79). Отсюда имеем
и для импеданса = (<»/№) (Ф' (0)/Р2(0)) получаем Zo -> i/(e0F).
При таких граничных условиях скорость поверхностной волны
является решением уравнения
Д1(Г8) + 1Да(78) = 0.
(6.90)
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
Коэффициент электромеханической связи для поверхностных
волн принято определять [9] через скорости Vo и Vs:
(6.91)
Интуитивно ясно (но доказательство не очевидно), что этот
коэффициент, являющийся мерой влияния металлического слоя
на скорость V, отражает способность пьезоэлектрика преобразо-
вать электрический сигнал в упругую поверхностную волну при
помощи преобразователя, состоящего из металлических полосок,
нанесенных на поверхность (§ 7.2, рис. 7.19).
Рис. 6.11. Волна Рэлея в ниобате ли-
тия (Y-срез). Изменение скоростей
Vo (металлизированная поверх-
ность) и V, (неметаллизированная
поверхность) в зависимости от на-
правления распространения в пло-
скости XZ. (Рис. 3 из [10].)
Рис. 6.12. Волна Рэлея в LiNbO3
(Y-срез, распространение вдоль Z).
Изменение амплитуд смещения и
потенциала в зависимости от рас-
стояния от неметаллизированной
поверхности. (Рис. 1 из [И].)
Если скорость V известна, из уравнений системы (6.61)
в принципе можно найти коэффициенты затухания и пар-
циальные амплитуды и Фу>. Из системы (6.83) определя-
ются коэффициенты Ат за исключением коэффициента пропор-
циональности, связанного с переносимой упругой волной мощ-
ностью. Наконец, из выражений (6.62) и (6.63) можно лайти
компоненты смещения щ и электрического потенциала Ф. Практи-
чески алгебраические уравнения оказываются настолько слож-
§ В.2. УПРУГИЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИКАХ
249
ными, что аналитическое решение получить невозможно, за ис-
ключением рассмотренного выше случая волны Гуляева — Блю-
стейна. Уравнения могут быть решены только численными ме-
тодами.
Результаты для некоторых материалов. Для иллюстрации рас-
смотрим кристаллы ниобата лития, германата висмута и кварца.
На рис. 6.11 показаны зависимости скоростей То (металлизиро-
ванная поверхность) и V8 (неметаллизированная поверхность)
волн Рэлея от направления распространения в плоскости XZ
(У-срез) ниобата лития. Различие между этими двумя скоростя-
ми максимально при распространении вдоль оси Z, где =
= 3404 м/с, a V8 = 3488 м/с. Коэффициент электромеханической
связи в этом случае имеет большую величину: Яд = 4,8 • 10-2.
Рис. 6.13. Волна Рэлея в LiNbOj
(Y-среэ, распространение вдоль
Z).' Изменение амплитуд смеще-
ния и потенциала в зависимости
от расстояния от металлизиро-
ванной поверхности. (Рис. 2 из
Поскольку сагиттальная плоскость является плоскостью_ симмет-
рии, смещение содержит только две компоненты (тип /?2). Зави-
симости амплитуд смещения и электрического потенциала от
глубины проникновения показаны иа рис. 6.12 и 6.13 для двух
классических электрических граничных условий. Для волны Рэ-
лея это направление чистой моды, поскольку вектор Умова —
250
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
Пойнтинга, который параллелен поверхности, должен лежать
в сагиттальной плоскости (плоскость симметрии YZ).
Зависимости на рис. 6.14 относятся к германату висмута
(BiuGeOso, класс 23) при распространении вдоль направления
[ООН в плоскости (110). Сагиттальная плоскость (110) не явля-
ется зеркальной, тем не менее распространяется волна типа /?2
(рис. 6.9), так как эта плоскость является плоскостью симметрии
упругих и пьезоэлектрических свойств. Действительно, тензоры
Сцм и eiih класса 23 имеют те же _ненулевые компоненты, как
и соответствующие тензоры класса 43m, в котором плоскость (110)
является зеркальной. Сравнение электрического потенциала Ф на
рис. 6.12 и 6.14 показывает, что германат висмута является бо-
лее слабым пьезоэлектриком, чем ниобат лития.
Кварц (класс 32) не обладает зеркальной плоскостью симмет-
рии и, как_ видно из рис. 6.9, для него не существует волна Рэ-
лея типа Л2. Однако имеются направления чистых мод типа 7?s,
например ось второго порядка X в плоскости XZ (У-срез). Конец
вектора смещения описывает эллипс, лежащий в плоскости, по-
вернутой относительно сагиттальной на 43° вокруг оси X. Ско-
рость равна 3154 м/с. На рис. 6.15 показана скорость волн Рэлея,
Рис. 6.15. Скорость волн Рзлея, распространяющихся вдоль оси X, как функ-
ция угла среза р кристалла кварца. (Рис. 3 из [13].)
распространяющихся в направлении X на поверхности, нормаль
к которой лежит в плоскости YZ и составляет угол § с осью У.
57-срез, соответствующий ₽ = 42,5°, замечателен тем, что темпе-
ратурный коэффициент (при 25 °C) равен нулю [14]. Несмотря
на более слабый пьезоэлектрический эффект, кварц часто исполь-
зуется в устройствах на поверхностных волнах, так как он может
быть изготовлен в виде монокристаллов большого размера при
разумной цене, легко полируется и отличается высокой темпе-
ратурной стабильностью. Для УХ-среза (нормаль к поверхности
Таблица 6.3. Наиболее интересное срезы и направления
распространения чистых поверхностных мод
в некоторых пьезоэлектрических материалах
Срез и направление распространения волны 1 <o e & 5 I°7 g| 2 ай м hi & I I S’ s i I il IF-. Kg S 1 1
Кубическая система Bi12GeO20 GaAg
(100) [010] (100) [011] (110) [001] (110) [110] (110) [110] (111) [110] я? 1« 1ы «ч «ч 1624 1683 1625 1755 2160 1708 0 1,4 0,8 1,0 0 1,7 [15] 2720 2865 2820 3354 2400 0 0,07 0,02 0,02 0 [9]
Класс Ътт ZnO CdS
Z — любое XY XY XZ в' R3 «2 2702 2838 2623 2680 0,88 0,35 0 1,1 [9] 1731 1800 1730 1718 0,47 0,12 0 0,52 [9]
Класс Зт LiNbO3 LiTaOs
YZ ZY [У+131,5°]Х Rt R3 R3 R3 3488 3903 4000 3503 4,8 2,2 5,54 5,36 [10] [10] [16] [17] 3230 3329 [18] [18]
-у х#
Класс 32 а-кварц Se
YX 5Т(У-42,5°)Х R3 R3 3154 3160 0,22 0,16 [13] [13] 810 1,7 [19]
252
ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
вдоль У, направление распространения вдоль X) коэффициент
электромеханической связи Kr= 0,22.10-2.
В табл. 6.3 приведены некоторые характеристики для ряда
материалов, представляющих практический интерес.
Упражнения
6.1. Используя принцип Кюри, найти кристаллографические классы,
для которых под действием гидростатического сжатия возникает электри-
ческая поляризация.
Решение. Поскольку гидростатическое сжатие, действующее во
всех направлениях с равной силой, имеет сферическую симметрию, симмет-
рия кристалла должна представлять собой подгруппу характерной симмет-
рии поляризации А^ооМ, Это условие выполняется для одиннадцати по-
лярных классов: 1, 2, т, 2тт, 3, 3m, 4, 4, 4mm, 6, 6mm, в которых проявля-
ется и пироэлектричество.
6.2. Выразить модули «®р через с^р и е{а.
Решение. Умножение уравнения (6.156) на ₽®г приводит к
- ₽&A = £h+ Pfei'ip^p
или
Ei — $ikDh. ~ Pffeefep^p.
Подстановка в (6.15а) дает
Та ~ (саР + ^сЛтАр^р — eioftikDk’
откуда следует
сар — сар + eiaPffeeftp-
6.3. Показать, что пьезоэлектрический тензор для классов 4mm и 6mm
инвариантен по отношению к любому повороту вокруг оси х3.
Решение. Новые компоненты находятся с помощью матрицы
поворота а, определяемой выражением (3,12):
еИк ~ a?alakepqr-
Поскольку не равны нулю (см. (6.39)) только коэффициенты вцз = е223 =
= «15, вззз = «33 И ези = «322 = «31, a а£ = 6ftg, имеем
«Уй = (“Н + аН) W15 + МзвЬЗвЗЗ + Ж + Ф1) 8<ЗеЗГ
Воспользуемся этим выражением для нахождения новых пьезомодулей клас-
сов 4 и 6, беря соответствующие е« из (6.37):
<23 = Ж + aial) eis в °’
откуда е^4== 0,
откуда ^ = 1.^,
откуда «;8 = «33,
откуда е31=сзг
'333 ~ еззз'
!зп=Ж+аМ)
Таким образом, новый тензор оказывается идентичен исходному.
УПРАЖНЕНИЯ
253
6.4. Найти скорость F3 поперечной волны, поляризованной вдоль оси Л4.
Решение. С учетом выражения (6.46) из (6.56) получаем (при ni =
= cos ф, n2 = sin ф, из = 0):
Vi = 12 = о, Чз = ©15 cos 2ф + «14 sin 2ф.
Согласно результатам раздела 5.1.36 имеем
„„«-Г -Г 1 .» I
?V3 ~ 1 33 — Г33 + 8 44 + »s
е11
6.5. Из рис. 6.9 следует, что для класса 622 волна Гуляева — Блюстейна
существует в любой сагиттальной плоскости, проходящей через ось At, даже
если она не перпендикулярна одной из шести бинарных осей. Доказать это
утверждение.
Решение. Достаточно показать, что тензор е4д инвариантен по от-
ношению к любому повороту вокруг оси х3||Я3. Для данного класса (матрица
(6.38)) только модули «123 = е14 и ejis = — «и не равны нулю, следовательно,
= (а|а?а’ — а?а]а®) еи. При этом в (6.37):
е'31 = 0, так как к =f= 3;
еш = <5 = ° и гззз = еи = 0’ таккак i =/,й = 3;
< = <23 = ( cos2 ф + sb2 ф)«14, откуда < = еи.
e1S~"e15 ' &А6
Рис. 6.16.
6.6. Два идентичных пьезоэлектрических кристалла симметрии 6 mm же-
стко связаны, при этом их оси Ав направлены в противоположные стороны
(рис. 6.16). Показать, что в плоскости раздела
(х2 = 0) распространяется поверхностная
волна, поляризованная параллельно осям
(Согласно [20].)
Решение. В обоих кристаллах уравне-
ния распространения одинаковы и идентичны
уравнениям раздела 6.2.2. Поэтому можно вос-
пользоваться результатами раздела 6.2.2, ес-
ли для хг < 0 принять «44=^4 и е'15= —е15,
так как оси Ав рассматриваемых кристаллов
направлены в противоположные стороны. Смещение и3 и потенциал Ф при
z2>0 даются выражениями (6.73а, б). Для ж2 < 0 следует измелить зна-
ки модуля ffis и показателей экспоненты, чтобы амплитуда волны убывала
при г2->-— оо:
Коэффициент В не изменяется вследствие условия непрерывности сме-
щения при Х2 = 0, а согласно выражению (6.72) имеем р = ]/Ч — V2 / Ур.
Запишем условия непрерывности при z2=0. Было показано, что в условие
254 ГЛ. 6. ПЬЕЗОЭЛЕКТРИЧЕСТВО
непрерывности тензора механических напряжений входит только компонен-
та Г32:
-₽^-е15ф(1)=^-е15ф;а)«
откуда
ф^)-ф«=^И-Л.
в15
Из условия непрерывности потенциала следует
2г
ф;(1)-ф^=^5-
Два последних уравнения являются совместными, если ₽“вн/(в11см)=
= К2, что приводит к значению скорости распространения V = Гт|1 — К*,
равному скорости волны Гуляева — Блюстейна на металлизированной по-
верхности одного из кристаллов. Это объясняется непрерывностью нор-
мальных компонент электрической индукции: D%= у 8ЦФ^ согласно
выражению (6.74) и D* и-уецФ^ вследствие смены знака показате-
лей экспоненты при х2 < 0. Поскольку
ф;<и —
потенциалы Ф и Ф' на плоскости раздела обращаются в нуль:
ГЛАВА 7
ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
В гл. 5, посвященной динамической теории упругости (а так-
же в § 6.2), изучалось распространение основных типов упругих
волн в кристаллах без анализа способов их возбуждения. Перей-
дем теперь к описанию методов возбуждения и регистрации объ-
емных (продольных и сдвиговых) и поверхностных волн (волн
Рэлея), используя сведения о пьезоэлектрическом эффекте из
гл. 6. Преобразователь для объемных волн можно исследовать
на основе классической модели, одинаково пригодной как для
монокристаллической пластинки, жестко закрепленной на звуко-
проводе, так и для пьезоэлектрической пленки, нанесенной на
торец звукопровода (пленки используются для достаточно высо-
ких, />1000 МГц, частот). В случае поверхностных волн мы
ограничимся рассмотрением встречноштыревых преобразователей,
имеющих наиболее широкое применение. Каждому типу преоб-
разователей посвящен отдельный параграф.
§ 7.1. Пьезоэлектрический преобразователь
для объемных волн
Как видно из рис. 7.1, преобразователь состоит из пьезоэлек-
трического материала, на который нанесены два металлических
электрода. Электрическое поле сигнала, приложенное к электро-
Рис. 7.1. Структура преобразователя
для объемных волн.
Пьезоэлектрик возбуждается электЦ
рическим полем сигнала, приложен-
ным к двум электродам.
Пьезоэлектрик Збуколровод
Электроды \ уд-----------—\------
Сигнал
" 7
дам, вызывает колебания пьезоэлектрика с амплитудой, состав-
ляющей малую долю длины упругой волны. Звуковой пучок, се-
чение которого определяется внешним электродом, проходит че-
рез внутренний электрод, нанесенный на торец звукопровода.
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
257
256
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Ориентация пьезоэлектрика выбирается таким образом, чтобы
преимущественно возбуждалась желаемая упругая мода. Напри-
мер, в случае окиси цинка для возбуждения продольных волн ось
шестого порядка должна быть параллельна направлению элек-
трического поля. Преобразователь устанавливается таким обра-
зом, чтобы в звукопроводе распространялась чистая мода и что-
бы поток энергии был направлен вдоль оси звукопровода.
Анализ работы такого преобразователя может быть проведен
двумя способами. Первый состоит в непосредственном расчете
мощности упругих волн с использованием уравнений распростра-
нения волн в каждой среде с учетом соответствующих гранич-
ных условий. Второй способ основан на
том, что преобразователь и звукопро-
вод представляются с помощью эквива-
лентных электрических схем, а затем
к ним применяются законы Кирх-
гофа.
Вакуум
Рис. 7.2. Схематическое изо-
бражение преобразователя.
7.1.1. Прямой расчет мощности уп-
ругих волн. Рассмотрим практически
важный случай, когда в среде возбуж-
дается и распространяется единствен-
ная (продольная или сдвиговая) волна.
Это условие накладывает известные ог-
раничения на упругие и пьезоэлектри-
ческие постоянные.
Условия применимости одномерной модели. На рис. 7.2 указа-
но расположение осей координату, у, у (обозначения у, у, у
используются для кристаллографических осей). Толщина d2
пьезоэлектрика, в котором происходит возбуждение упругих волн,
мала по сравнению с другими размерами, и можно считать, что
электрическое поле параллельно у, а плоскости х3 = const яв-
ляются плоскостями равной фазы. Направление распространения,
параллельное х3> сохраняется на каждой из границ: = па = О,
п3 = 1.
Продольная волна может распространяться вдоль оси х3, если
последняя является главной осью тензора Кристоффеля, т. е.
Г^3 = Г33 = 0. При условии, что = п2 = 0, а п3 = 1, из (5.8)
следует
с34 — с35 = 0- (7.1)
Для пьезоэлектрической пленки Г» = Гг'г 4-у$уг/е (раздел 6.2.1),
кроме того, у = у2 = 0 и согласно (6.56)
= езь = 0- (7-2)
Отличие от нуля пьезомодуля е33 позволяет возбуждать продоль-
ную волну с помощью электрического поля, параллельного у.
Аналогичным способом можно получить следующие условия воз-
буждения и распространения сдвиговой волны, поляризованной
вдоль х^.
С« = С35 = О, Уз = 41 = 0 и е35=/=0. (7.3)
Если эти условия выполняются, уравнение (6.15а), опуская
индексы, можно записать в следующем виде:
Т = сЕ^-еЕ, (7.4)
где х = у, Е = Е3, а другие обозначения зависят от того, про-
дольные или сдвиговые волны рассматриваются. Для продольных
волн нужно брать
Т = Т33, и = и3, сЕ = с33, е = е33,
а для сдвиговых —
Т = Т31, и = /у, сЕ = Уз, е = уз-
Смещение и напряжение в каждой из частей преобразовате-
ля даются выражениями
us = ase~lks* + bseksX, (7.5)
Ts = - ikscl [ase~iksx - bsehsX) - eE8SP, (7.6)
где в качестве S нужно подставлять М для электрода-подложки,
Р — для пьезоэлектрика, Е — для внешнего электрода (рис. 7.2).
Символ Кронекера б показывает, что член еЕ существует только
в пьезоэлектрике. В уравнениях (7.5) и (7.6) опущен множитель
е<иг, поскольку все соотношения линейны. В звукопроводе волна
является бегущей, т. е.
и = ae~iht, (7.7)
Т = - ikcae~tkx. (7.8)
Семь неизвестных а, ам, Ьм, аР, ЬР, аЕ, ЬЕ определяются из се-
ми уравнений с граничными условиями, учитывающими непре-
рывность смещений и напряжений на границе между подложкой
»м(й1) = »(di), (7.9а)
ТМ = TW, (7.96)
между пьезоэлектриком и подложкой,
Нр(0) = нм(0), (7.10а)
УДО) = Тм(0) (7.106)
17 э. Дьелесан, Д. Руайе
258
ГЛ 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
и между внешним электродом и пьезоэлектриком:
uE(—d2) = иР(—di), (7.fla)
TE(-d2) = TP(-di). (7.116)
На свободной поверхности внешнего электрода выполняется со-
отношение
ГЕ(-й2) = 0. (7.12)
Решение этой системы дает значения амплитуд а, а, и Ъ,
в виде функций от электрического поля на границах 0 и —d2
пьезоэлектрика. Практически измеряемой величиной является
разность потенциалов v = voeiat, приложенная к электродам,
причем
-d2
v0 = J — Edx.
о
С другой стороны, в силу одномерности задачи, уравнение
Пуассона для диэлектрика, dDi / дх\ = 0, сводится в рассматривае-
мом случае к dD3 / дх3 = 0. Составляющая вектора электрической
индукции D3 = D является величиной постоянной и выражает-
ся формулой (6.15):
D^E-e^, е« = 4. (7.13)
Интегрирование от 0 до — d2 дает
—Dd2 = —Esvo + e(up(—d2) — uP(O)). (7.14)
Исключая Е из соотношений (7.4) и (7.13), получаем явное вы-
ражение модуля упругости пьезоэлектрика при постоянном D,
с® = сЕ + е2/е®, откуда
T„ = c^-^D. (7.14а)
Подставляя в (7.14) выражение для и из (7.5), получаем
отсюда для напряжения ТР находим
где к. с. обозначает комплексно сопряженную величину.
§ 7.1 ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
259
Множитель е2/ (eSc°/cPcZ2) содержит квадрат константы
электромеханической связи № = e2/(escf + е2) = е2/esc° (раз-
дел 6.2.1). Толщина пьезоэлектрической пластинки d2 примерно
равна половине длины волны {kPd2 « л), поэтому отношение
е2 К2 К2
мало по сравнению с 1 для типичного пьезоэлектрика {К < 0,3,
т. е. К2 <0,1), и напряжение ТР выражается в виде функции от
разности потенциалов v0:
ТР= — ikPc° (aPe~ikpx - bPeikpX) - е (7.15)
Выражая амплитуду через v0, можно вычислить полезную аку-
стическую мощность (упр. 5.1):
=4-7<о21а|2Д (7.16)
Рис. 7.3. Упрощенная
схема преобразовате-
ля при толщине
электродов много
меньшей длины вол-
ны.

где Z — акустический импеданс в расчете на единицу поверхно-
сти звукопровода, А — сечение пучка. В общем случае решение
может быть получено только численным пу-
тем с использованием ЭВМ (и особенно при
наличии дополнительных слоев в структуре
преобразователя), поскольку алгебраические
выражения быстро усложняются по мере
роста числа параметров, и интерпретация
результатов становится трудной.
Применим поэтому изложенный выше ме-
тод к двум наиболее простым структурам.
В первой из них, изображенной на рис. 7.3,
толщина электродов много меньше длины
волны, так что их влиянием на распростра-
нение упругих волн можно полностью пре-
небречь. Результаты, получающиеся в этом
случае,— частотная характеристика преобра-
зователя как функция отношения импедан-
сов пьезоэлектрика и звукопровода — приме-
нимы в случае низкочастотных преобразователей (на частотах,
меньших 100 МГц). Вторая структура соответствует высоко-
частотному преобразователю, состоящему из тонкого слоя пьезо-
электрика, нанесенного на звукопровод. В этом случае необходи-
мо учитывать влияние электрода-подложки. Для заданной пары
материалов пьезоэлектрик — звукопровод мы проанализируем
влияние материала и толщины электрода-подложки на частотную
характеристику преобразователя.
17*
260 гл. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Система пьезоэлектрик — звукопровод. Используя обозначения
рис. 7.3, запишем граничные условия
иР(0) — и(0) = 0,
Тр(0) - 740) = О,
Тр(-й) = 0.
Отсюда, используя выражение для ТР из (7.15) и вводя обозна-
чение <р — kpd, получаем систему уравнений
ар -f- bp — а — О,
крСрйр — крСрЬр — кса = i-^-,
крСрар^ — kpCpbpS :<р = i
где Ср — модуль упругости пьезоэлектрика при постоянной ин-
дукции D. Вводя акустические импедансы двух рассматриваемых
сред, ZP = kpCp/at, Z = кс/а, преобразуем эту систему к виду
ар -f- Ьр = а,
^(аР-ЬР) = а+
Z р Z р evn
(аР — bp) cos q> + i (aP + bP) sin ф = i
Последнее уравнение
/ ev \ Zp ev
Г + ^;cos<p+
позволяет найти неизвестную амплитуду а:
- ; еР0 1 — COS ф _ 9
а~ wdZ , Zp . ~^<i)dZm'
cos ф + г -g- sin ф 0
где m0 = ^cos ф i sin ф) sin2-|-. Согласно формуле (7.16)
мощность упругих волн
&8dZ | mQ |2 d
пропорциональна квадрату коэффициента электромеханической
связи К2 = е2/(евСр) и емкости Со = &BA/d жестко закрепленного
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
261
преобразователя, т. е.
_ 2КаС0ср ,
& ~ dZM. У01
где формфактор Л/о определяется выражением
Л/в = К12 =
(7.17)
Введем резонансную частоту пьезопреобразователя, для кото-
рой толщина преобразователя d равна половине длины волны,
fp = VP/2d. Поскольку сР = ZPVP, средняя мощность упругих волн
может быть выражена как
^ = 4Х2С0/РД^. (7.18)
В последнем выражении от частоты зависит лишь формфактор
Мо (в силу частотной зависимости угла <р: <р = kPd = л///₽). Как
следует из (7.17),
(7.19)
При постоянной амплитуде электрического напряжения v0
формфактор определяет частотную характеристику преобразова-
теля. Сопротивление излучения Ла, которое определяется соотно-
шением 0 = 2^-, оказывается пропорциональным
Зависимость частотных характеристик преобразователя от со*
отношения акустических импедансов ZP/Z показана на рис. 7.4,
где представлено изменение величины >
101g (Мо = 101g (8Х2С0/РЛл)
как функции приведенной частоты для различных значений
ZplZ. Ход этих зависимостей объясняется следующим образом.
Если импеданс звукопровода мал по сравнению с импедансом
пьезоэлектрика, то поверхности преобразователя можно считать
практически свободными, и преобразователь резонирует на поло-
вине длины волны (например, для ZP/Z = 2). Поэтому при / = fP
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
сопротивление излучения имеет минимум, который соответствует
максимуму мощности возбуждаемых упругих волн. Если же, на-
оборот,. Z велико по сравнению с ZP (например, ZP/Z = 0,5 или
0,25), преобразователь, у которого одна поверхность свободна,

Рис. 7.4. Система преобразователь — звукопровод.
Если акустический импеданс звукопровода Z меньше, чем импеданс пьезо-
преобразователя ZP, то преобразователь резонирует на частоте, соответству-
ющей Хр/2 (например, для ZP/Z = 2). В противном случае резонанс имеет
место на частотах, соответствующих ХР/4 и ЗЛР/4 (ZF/Z — 0,25).
а другая оказывается достаточно закрепленной, резонирует на
частотах, соответствующих ХР/4 и ЗХР/4. Сопротивление излуче-
ния оказывается минимальным вблизи значений / = 0,5/Р и / —
— 1,5/Р. Значение Zp/Z = 1/V2 является критическим. При мень-
ших значениях отношения ZP/Z кривые на рис. 7.4 имеют уже
два минимума. Вблизи критического значения ZP!Z форма частот-
ной характеристики преобразователя приближается к прямоуголь-
ной с достаточно широкой плоской частью по обе стороны от ре-
зонансной частоты /Р.
Полоса пропускания. До сих пор при анализе частотной ха-
рактеристики учитывалось только отношение акустических импе-
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН 263
дансов, в действительности же, если принимать во внимание и
электрический импеданс преобразователя, частотная характери-
стика должна зависеть и от коэффициента электромеханической
связи.
Если f = (Л70 = 1), электрическая добротность выражается
следующим образом:
п— nZ
ЬКггр’
Если ZP>Z, то излучаемая акустическая мощность Р достига-
ет максимума. Используя разложение величины Л/о вблизи /₽,
можно установить, что относительная полоса пропускания, ^опре-
деляемая акустическими импедансами, дается выражением —
откуда находим акустическую добротность
- 2 Z ’
Полная полоса пропускания преобразователя максимальна, если
Qe = Qa, т. е. если Z — K12ZP, и тогда
(v) =4-= ^«0,9^.
\ t /max Q л
Поскольку в общем случае К< 1/V2, условие ZP>Z удовлетво-
ряется.
На практике как материал звукопровода, так и тип волны яв-
ляются вполне определенными, заданными величинами, следова-
тельно, заданным можно считать и акустический импеданс Z =
= р7. При этом наиболее широкую полосу пропускания имеет
такой преобразователь, для которого произведение KZP1/2 оказы-
вается наиболее близким к Z. Таким образом, если KZPl/2 > Z,
т. е. Qa > Qt, полоса пропускания ограничивается возможностью
механического согласования, если же KZPl/2 < Z, т. е. Qe > Qtt,
то полоса пропускания ограничивается возможностью электриче-
ского согласования.
В табл. 7.1 даются характеристики наиболее важных материа-
лов, используемых для пьезоэлектрических преобразователей.
Пример. Акустооптический модулятор (см. табл. 8.2).
В данном устройстве необходимо возбуждать продольные акусти-
ческие волны вдоль направления (001) в кристаллах молибдата
свинца (7 = 3630 м/с, р = 6950 кг/м’, Z = 25,2 • 10е Н • с/м3).
J64 ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
При Qe = 2,4 и Qa = 2,1 наиболее широкую полосу пропускания
(>40%) обеспечивает преобразователь из (У + 36°)-среза ниоба-
?а лития.
Система пьезоэлектрик — электроды — звукопровод. Гранич-
ные условия для этой системы даются уравнениями (7.9) и (7.10)
Таблица 7,1. Характеристики пьезоэлектрических материалов-
I вИоДт 1 Материал Срез h Is ( h । V Й5, К KZp V2. 10» H-c/m’ S
к 2 1 LiNbO3 У+36° 7340 34,5 0,49 23,9 44,5
LiNbO3 Z —- 7316 34,4 0,16 7,8 14,5
Кварц X —— 5747 15,2 0,092 2,0 8,4
Керамика ЦТС Z — 4560 34,2 0,51 24,7 46,4
LiNbO3 у-н 63° 4560 21,4 0,62 18,2 56,4
i Кварц АС X 3317 8,8 0,10 1,24 9,0
g Кварц ВС X 5105 13,5 0,037 0,71 3,4
§* Кварц АТ X 3320 8,8 0,08 1,0 7 3
1 Керамика ЦТС 12 z 2600 19,5 0,70 19,3 63^6
,и соотношением ГР(—d2) = 0. Используя выражение (7.15) для
ТР и вводя обозначения фм = kMdi, фР = kPd2, приведем (7.9)
и (7.10) к следующей системе уравнений:
Амсдгаме — кмСмЪм® Фм — ксае 1 = 0,
ар 4- Ьр — ам — Ьм = 0,
крСрйр — kpCpbp — кмСм^м + кщСмЬм — -3г2,
крсрареч’р — крСрЪрО~гЧ1р =
. Эту систему можно записать в матричной форме:
§7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
265
где введены импедансы трех сред
Zp = крСр/<в, Zm = кмСм/®, Z — кс/(л.
тт ~ik<h
Неизвестная величина ае находится с помощью правила
Крамера:
-ikd], _ ievQ £, _ 2г^0
ае a>Zpd2 "Д ~ toZpdjn’
где
т = 2^- =
zp . . ,(zm . zp . \
COS Фр COS <PM—Z^sln фрЗШ Фм+ ^•^“COS фр sin фЛ{Г-}- —Sin фрСОЗфм|
(7.21)
Если в формуле (7.18) заменить Л/о на формфактор М = |тп|2
и ввести резонансные частоты /м и /Р электрода-подложки и пье-
зоэлектрической пленки соответственно, то для акустической мощ-
ности, передаваемой в звукопровод, получим следующее выра-
жение:
= (7.22)
где /м = VM/2di, fP = Vp/2d2. Сопротивление излучения
ZM
Wp&Cofp
(7.23)
пропорционально формфактору М, который зависит от частоты
через углы <рР = kPd2 = л///Р, <рм = Из выражения (7.21)
получаем
/ л/ л/ ZP , af . л/\2
.. COST-COST--у—sin Т-sin 7—
мН 1\ \ fP ZM fp Jm) ,
(ZM af . л/ ZP . л/ л/\2
-7- cos t— sin t— + -7- Sln 7“ cos 7—
, И fp fM z fp /м) (724)
(-ЙУ
Легко убедиться, что это выражение переходит в выражение
для когда толщина электрода стремится к нулю (/м -*«»),
266
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
т. е.

Из симметрии функции двух переменных f/fM) сле-
дует, что в принципе достаточно знать ее в интервале изменения
f/fe и ///м от нуля до единицы. На рис. 7.5 и 7.7 представлены
/ 7 \в \ \ Г
\\ । \ \ WawT I /*° 1 1 Я
Рис. 7.5. Кривые постоянного формфактора М системы CdS — Al — AI2O3 для
продольной моды.
Преобразователю, для которого 1рЦм « 0,25, соответствует вертикальная
плоскость, пересекающая плоскость рисунка по ОС.
частотные зависимости величины lOlgAf в виде сечений плоско-
стями М = const соответствующих поверхностей. Эти кривые по-
строены [1] для двух случаев, типичных с точки зрения акусти-
ческих импедансов. В одном случае электрод между пленкой из
сульфида кадмия и звукопроводом из корунда изготовлен из алю-
миния, в другом — из золота. Ось шестого порядка сульфида кад-
мия параллельна электрическому полю, так что возбуждается
только продольная волна, которая распространяется в корунде
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
267
вдоль реи третьего порядка. В связи с этим здесь применима од?
номер.иая модель.
Характеристика такого преобразователя описывается сечением
поверхности Mtf/jP, f/fM) вертикальной плоскостью, проходящей
///м fp
через начало координат, так как отношение -щ— = — имеет по-
стоянное значение, определяемое толщиной пленок и скоростью
распространения. Прямые А, В, С, D на рис. 7.5 и 7.7 являются
Рис. 7.6. Система CdS—Al—A12Oj {продольная мода).
В зависимости от толщины алюминиевого электрода на частотных характе-
ристиках имеются один или два минимума.
следами таких плоскостей. На рис. 7.6 представлена частотная
характеристика для системы CdS—А1—А12О3, а на рис. 7.8 — для
системы CdS—Аи—А12О3. Вид этих кривых с физической точки
зрения можно объяснить следующим образом. Акустический им-
педанс сульфида кадмия (ZP = 21,5 • 10е Н • с/м3) много меньше,
268
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
чем импеданс корунда (Z — 44,5 • 106 Н • с/м3), поэтому при ну-
левой толщине металлического электрода (кривая Л) преобразо-
ватель, одна из поверхностей которого в данном случае свободна,
а другая является почти закрепленной, резонирует на частотах,
соответствующих Х/4 (///> = 0,5) и 3V4 (///₽ = 1,5). Около этих
Рис. 7.7. Кривые постоянного формфактора М системы CdS—Au—А12О3 для
продольной моды.
Преобразователю с заданной величиной fP/fM соответствует вертикальная
плоскость, пересекающая плоскость рисунка, например, по ОВ.
резонансных точек формфактор имеет два минимума, соответству-
ющих максимумам мощности упругих волн. Добавление пленки
из золота с импедансом *) ZM = 64 • 10е Н • с/м3 может, независи-
мо. от ее толщины, лишь углубить эти минимумы (кривые А и В
на рис. 7.8). Если же между сульфидом кадмия и корундом по-
•' •) Металлическая пленка, нанесенная на кристалл корунда, не явля-
ется монокристаллической, хотя ось третьего порядка корунда способствует
#осту пленки вдоль направления [111]. Акустический импеданс пленки
.Получается как среднее между значениями, характерными для направле-
йии [100] и [111].
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН 269
мостить алюминиевую пленку с импедансом ZM = 17,5 X
X 10е ИЦ-с/м3, то она при толщине, равной Х/4, будет играть роль
трансформатора импедансов. В результате импеданс на внутрен-
ней поверхности преобразователя (х = 0) принимает значение
Zt = Zm/Z = 6,9.10е И-с/м8,
так что эту поверхность можно считать практически свободной.
Преобразователь резонирует при толщине, равной Z/2 (/ = /₽),
Рис. 7.8. Система CdS—Au—А12О3 {продольная мода).
Частотная характеристика всегда имеет два минимума.
и его частотная характеристика имеет лишь один минимум (кри-
вые В и С на рис. 7.6). За изменением формфактора при перехо-
де от двух минимумов к одному легко проследить, поворачивая
вокруг начала- координат след характеристической плоскости.
Формфактор для системы ZnO—Pt—А12Оа, изображенный на
рис. 7.9, похож на формфактор для системы CdS — Au — A12OS,
поскольку последовательности импедансов в обоих случаях ана-
логичны:
Zzno = 35 10е Н - с/м»; ZPt = 87 • 10е; ZAl2os = 44,5.10е.
До сих пор мы не учитывали влияния внешнего электрода,
который обычно изготавливается из алюминиевой или серебря-
270 ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
ной пленки. Пока толщина этой пленки мала по сравнений с тол-
щиной самого пьезопреобразователя (менее 10%), ее наличие
приводит лишь к небольшому сдвигу частотных зависимостей
формфактора в сторону низких частот.
Рис. 7.9. Кривые постоянного формфактора М системы ZnO—Pt—А12О3 для
продольной моды при изменении f/fP и f/fM от 0 до 1.
Следует отметить сходство с рис. 7.7.
Численные оценки. Для последней из рассмотренных систем
ZnO—Pt—А120з на частоте /р = 1 ГГц толщина пленки окиси
цинка (Рр = 6330 м/с) составляет
d2 = = 3,2 мкм,
а статическая емкость преобразователя с площадью поперечного
сечения А = 1 мм2 равна
Со = =26 пФ.
При заданном коэффициенте электромеханической связи для
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
271
продольных ВОЛН,
А'2 =
= 0,073,
сопротивление излучения составляет (в омах)
Ra =----« 84 М
8ZpK2Cofp
Электрический сигнал с амплитудой напряжения у0 = 1 В и с
такой частотой, что М = 1, создает акустическую мощность
Р= ^«6 мВт.
Электрическое согласование. Потери преобразования. Если ма-
териал пьезопреобразователя является идеальным изолятором, то
электрический ток есть только ток смещения, плотность которого
на единицу поверхности составляет
/ = dDldt = iaD.
Воспользовавшись (7.14), для амплитуды электрического напря-
жения получим
a D е
v0 = [ир (0) - иР (- d2)],
а для электрического импеданса преобразователя найдем выра-
жение, содержащее два члена:
г> = “ ЙП - 1“р (0) - “р (_ d,))-
Первый из них представляет собой импеданс, соответствующий
Рис. 7.10. Эквивалентная схема преобра-
зователя.
Со — статическая емкость, Л а—сопротив-
ление излучения, зависящее от частоты.
С помощью сопротивления R учитывают-
ся электрические и упругие потери в
пленках.
статической емкости Се = e,sA/d2. Второй член в случае матери-
ала со средними пьезоэлектрическими свойствами (№ < л) сво-
дится к сопротивлению излучения ПА, которое характеризует пре-
образование электрической энергии в механическую.
В реальных случаях в эквивалентную схему преобразователя
необходимо добавить сопротивление R, связанное с другими ис-
точниками электрических потерь (рис. 7.10). Эти потери имеют
большое значение в случае высокочастотных преобразователей,
что обусловлено следующими обстоятельствами:
ГЛ, 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
1) такие пьезоэлектрические материалы, как CdS, ZnO, явля-
ются полупроводниками, а не изоляторами, )
2) на частотах, превышающих 1 ГГц, сильно возрастают ди-
электрические потери,
3) сопротивление металлических пленок отлично от нуля,
4) немонокристаллические пленки поглощают упругие волны.
Эксперимент показывает, что эквивалентное сопротивление по-
терь R оказывается меньше, чем сопротивление излучения RA.
Электрическая мощность, передаваемая в преобразователь
генератора с э. д. с. е0 и внутренним сопротивлением 7?0, оказы-
вается максимальной лишь при согласовании импедансов. Потери
на преобразование ZT определяются как отношение этой макси-
мальной мощности = ^/3R0 — v%/2R0 к мощности упругих
волн, возбуждаемых в кристалле, Ф — V$/2RA-.
Т = 53d/53 =Ra/R0.
При согласовании импедансов
7?
ЯА
~iT'
Это определение потерь преобразования имеет смысл только
в случае, когда согласование осуществляется во всей полосе час-
тот преобразователя. Поскольку RA изменяется с частотой, ука-
занное выше условие эквивалентно требованию малости R по
сравнению с ЙА. Если влияние емкости Сл скомпенсировано на
центральной частоте /Р с помощью индуктивности L (рис. 7.10),
то необходимо, чтобы величина, обратная электрической доброт-
ности Q преобразователя,
т-я^А‘+^)’ ,7-25>
во всей полосе пропускания преобразователя была больше, чем
формфактор М, который имеет величину порядка 0,5 (рис. 7.4,
7.6 и 7.8). Поскольку член
(7.26)
меньше 1, вышеприведенное условие выполняется при R<RA.
Генератор в таком случае оказывается согласованным с сопротив-
лением R, а потери преобразования, имеющие значительную ве-
личину, пропорциональны формфактору М:
<’-27>
7.1,2. Эквивалентная схема. . Систему, изображенную на
рис. 7.2, можно исследовать с помощью эквивалентной электро-
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН 273
механической схемы [2]. Такая схема составляется из отдельных
цепей, соответствующих каждому элементу системы, причем ме-
ханические силы и скорости заменяются электрическими напря-
жениями и токами.
а) Звукопровод бесконечной длины, имеющий сечение А,
в котором распространяется бегущая волна, может быть охарак-
теризован своим механическим импедансом 26 = — А, равным от-
ношению силы F = —AT к колебательной скорости й^ди/dt,
так что
=^L£!L = ^u.
дх со dt
б) Эквивалентную схему для пластинки толщины d, имеющей
сечение А и ограниченной плоскостями х = xt и х = хг, можно
построить, используя соотношения между силами Л и А и ско-
ростями di и й2 на поверхностях пластинки:
и, = ice (ae-ift*i + &eift*i),
ii2 = ia (ae-ifce2 + &elfi*2).
Вычисляя из этой системы коэффициенты а и Ъ,
и е ihxi — u.e~ih*2
iab=- та—-
и подставляя их в выражение для силы, аналогичное (7.6),
F — ickA(ae~ikx — ЬеЛх') = ^(zcoae-1** — г<оЬе"“),
получаем
тг£я)
F‘~Z{T^kT—щтт) №ят-г,.
тт 1 1 . kd
Используя равенство -tgjgf = ]ld — tg —i имеем
Fi = ттта (M1 “ Т") “ь
Fa = 7ЖЭ (“* “ -т) ua-
(7.28а)
(7.286)
Применяя к этим соотношениям законы Кирхгофа, получаем схе-
18 э. Дьелесан, Д. Руайе
274 ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Рис. 7.11. Механическая экви-
валентная схема пластинки из
непьезоэлектрического мате-
риала толщины d с механиче-
ским импедансом
му, изображенную на рис. 7.11. Это и есть эквивалентная схема
для рассматриваемой пластинки.
в) В случае пьезоэлектрика напряжение Т дается формулой
(7.14а), которая, после подстановки в нее h = е/е3, принимает
вид
Все предыдущие результаты бу-
дут иметь силу и в этом случае
при замене Т на Т + hD. Посколь-
ку нормальная составляющая элек-
трической индукции D является по-
стоянной, для нахождения сил
Fit 2 = — АТ^ 2 достаточно прибавить
член hDA к правой части выраже-
ний (7.28).
Ток смещения I = ta>DA, проходящий через пластинку с сече-
нием А, можно рассчитать из электрического напряжения, при-
ложенного к металлизированным поверхностям (рис. 7.12):
v = J Edx = — h(u2 — Ui).
х, 8
(7.29)
Вводя скорости и, и й2, получаем
или
I = i&CoV — hC^iii — йг). (7.30)
Напомним, что Со = г3А/А представляет собой емкость жестко
закрепленного преобразователя. Дополнительный член hDA =»
Рис. 742. Электромеханический трансформатор, моделирующий пьезоэлект-
рический эффект.
= hit io можно реализовать с помощью некоторого электромеха-
нического трансформатора, в первичной цепи которого протека-
ет ток йС0(М1 — й2) = i®Coy — I, а во вторичной имеет место ме-
ханическое перемещение со скоростью (Hi — й2), так что коэф-
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
275
Рис. 7.13. Электромеханическая
эквивалентная схема пластин-
ки из пьезоэлектрика толщи-
ны d с механическим импе-
дансом Z.
Схема имеет один электриче-
ский вход и два механических
выхода.
фициент трансформации N = hCa (рис. 7.12). Таким образом, бла-
годаря емкости —Со, включенной последовательно с первичной
цепью трансформатора, сила, возникающая на выводах С и D его
вторичной цепи, оказывается равной
F . hC0 (vA - vB) = ДС0 [ v - hC° (.^---г) ]
или, при учете (7.30), F = hl/ia>.
Эквивалентная схема, имеющая один электрический вход и
два механических выхода, изображена на рис. 7.13.
Эквивалентная схема преобразо-
вателя, представленная на рис. 7.14,
получается путем соединения от-
дельных схем, соответствующих
каждому из элементов преобразова-
теля. Выводы эквивалентной схемы,
соответствующие свободной поверх-
ности внешнего электрода, оказыва-
ются замкнутыми накоротко из-за
очень малого акустического импе-
данса воздуха. Возбуждаемую аку-
стическую мощность можно вычис-
лить, зная амплитуду Ft силы, при-
ложенной к границе между преобра-
зователем и звукопроводом:
г) Рассмотрим в качестве приме-
ра резонатор, состоящий из тонкой
пьезоэлектрической пластинки, ме-
тализированной с двух сторон. Считая, что толщина электродов
мала, эквивалентную схему резонатора получим, закорачивая два
механических выхода схемы, изображенной на рис. 7.13. Вторич-
ная цепь трансформатора нагружена на механический импеданс

kd 2 \_______________IZ
2 sin&d/- „ kd'
2tg-2
При трансформации в первичную цепь этот импеданс делится на
№ = Л2Со. Электрический импеданс резонатора
(«.г 1 \
№ *сою I
Г
№ )
18*
216
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
ИЛИ
Ze~ tg7/-
Поскольку Z = cA/VCt — e8A/d, h = е/ъв, то
£5 = L X =
aZ Rsc<od л cod'
Рис. 7.14. Полная эквивалентная схема для преобразователя, изображенного
на рис. 7.1.
Слева схема замкнута, что соответствует свободной поверхности преобра-
зователя, граничащей с воздухом, справа схема нагружена на механиче-
ский импеданс Z звукопровода.
нической связи, получаем
(7.31)
На рис. 7.15 представлена частотная зависимость модуля ад-
митанса Y = 1/Ze резонатора. Эта величина обращается в нуль
Рис. 7.15. Частотная зависимость
модуля адмитанса пьезоэлектри-
ческого резонатора.
Прямая) У| = С»® изображает ад-
митанс статической емкости Со.
В действительности на резонанс-
ных частотах адмитанс остается
конечным из-за потерь при рас-
пространении и отражении волн.
»- Это же относится к импедансу
f„5fa f вблизи частот антирезонанса.
§ 7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН
277
при всех частотах, соответствующих нечетным гармоникам час-
тоты антирезонанса
<7-32>
и терпит разрыв (Ze = 0) на частотах резонанса /г”\ т. е. на та-
ких частотах, для которых
Вводя частоту fa, получаем
Измерение частоты антирезонанса'-/о и первой резонансной
частоты fT = /г(1) позволяет определить скорость распространения,
V = 2fad, и коэффициент электромеханической связи для возбуж-
даемой моды,
(7.34)
За исключением материалов с сильной связью (К > 0,3), от-
ношение (/а — /г)//а оказывается очень малым, и поэтому
(7.35)
4 Та
В случае кварца ЛТ-среза (сдвиговые волны) коэффициент
связи равен 0,07, и относительная разность частот резонанса и ан-
тирезонанса составляет всего лишь 0,2%. Эта разность уменьша-
ется как 1/п2 для мод колебаний с номером п, большим 1
(упр. 7.3). Вблизи резонанса эквивалентную схему можно уп-
ростить (упр. 7.4).
7.1.3. Коэффициент электромеханической связи. При изучении
распространения упругих волн в пьезоэлектрических материалах
(§ 6.2) была введена величина К — е^/ИеДсра-|- e2v, названная
коэффициентом электромеханической связи. Относительный вклад
пьезоэффекта в скорость звука имеет порядок величины КУ 2.
В этой главе мы вновь встречаемся с коэффициентом К. Мощ-
ность упругих волн, возбуждаемых преобразователем (см. (7.22)),
а также относительная разность частот резонанса и антирезонан-
са пропорциональны квадрату коэффициента электромеханиче-
ской связи при К С 1. Коэффициент электромеханической связи
выражает степень связи между электрическими и механически-
278 ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
ми свойствами пьезоэлектрика и характеризует способность того
или иного материала превращать электрическую энергию в меха-
ническую и наоборот. Выражение для К имеет простой вид толь-
ко для направлений, связанных с элементами симметрии
(табл. 6.2). Формула (7.34) может служить для определения
коэффициента электромеханической связи в направлениях, пер-
пендикулярных плоскопараллельным граням резонатора. Для
этих случаев К определяется путем измерения частот резонанса
и антирезонанса возбуждаемых мод колебаний.
Изменение коэффициента К в плоскости симметрии YZ кри-
сталла LiNbOa изображено на рис. 7.16. Две кривые относятся
z
Угол с осью У,гроУ
Рис. 7.16. Зависимость коэффициентов электромеханической связи KL и Кт
от направления в плоскости YZ кристаллов LiNbOa. (Рис. 13 из [3].)
к квазипродольной и квазипоперечной модам, поляризованным в
плоскости YZ, при этом третья мода не возбуждается. Направле-
ния, в которых один из коэффициентов связи обращается в нуль,
представляют особый интерес, так как в этих направлениях воз-
можно возбуждение в чистом виде лишь одной моды. Особенно
важными являются направления +36° и +163° по отношению
к оси У. В первом из них квазипоперечная волна -не возбужда-
ется, а коэффициент связи для квазипродольной волны оказыва-
ется очень высоким (KL = 0,49). Во втором случае отсутствует
квазипродольная волна, а квазипоперечная волна имеет еще боль-
ший коэффициент связи (Кт = 0,62). Пластинки соответствующих
срезов используются для изготовления преобразователей на час-
тоты до нескольких сотен мегагерц. Следует отметить, что боль-
шая величина коэффициента электромеханической связи в случае
преобразователей с малыми потерями CR > /?л) облегчает согла-
сование в широком диапазоне частот, так как электрическая доб-
ротность согласно (7.25) и (7.26) по порядку величины равна
1/К1. (1
По определению (см. (7.32)), /<>= V/2d, и если Л? < 1, то
А « V0/2d, где Г» — скорость без учета пьезоэффекта. Отсюда яс-
§7.1. ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ОБЪЕМНЫХ ВОЛН 279
но, что ход кривых на рис. 7.16 является следствием зависимо-
стей, приведенных на рис. 6.7.
7.1.4. Вопросы технологии. В зависимости от длины волны
при изготовлении преобразователей применяется различная тех-
нология. Если М2 превышает 0,1 мм (/ = 25 МГц при V =
= 5000 м/с), металлизированный преобразователь из пьезоэлект-
рического монокристалла или из пьезокерамики закрепляется
непосредственно на звукопроводе с помощью относительно тол-
стой склейки, например, эпоксидной смолы. Если значение М2
заключено между 10 и 100 мкм, пластинка из пьезокристалла
с относительно большой толщиной 00,1 мм) закрепляется на
звукопроводе методом диффузии индия [4], а затем с помощью
шлифовки и полировки ее толщина доводится до необходимого
значения. В лабораторных условиях удается достичь толщины
в несколько микрон при окончательной доводке с помощью ион-
ной бомбардировки. Процедура диффузионной сварки преобра-
зователя с помощью индия начинается с вакуумного напыления
на каждую из поверхностей тонкой пленки хрома (от 150 до
300 А), необходимой для увеличения сцепления с поверхностью,
затем пленки золота (1500 А) и, наконец,—индия (2500 А). Пос-
ле напыления индия звукопровод и преобразователь без нару-
шения вакуума (во избежание окисления) прижимаются
друг к другу, и к ним с помощью гидравлического пресса при-
кладывается давление около 2 • 107 Па в течение примерно
20 минут.
При значениях М2 порядка 1 мкм пьезоэлектрическая плен-
ка наносится в вакууме на звукопровод, на который предвари-
тельно напыляется тонкая металлическая пленка, служащая элек-
тродом-подложкой. Полезная площадь преобразователя (диаметр
около 1 мм) определяется размерами внешнего электрода, также
напыляемого в вакууме. Следует отметить трудность получения
пьезоэлектрической пленки определенной ориентации. Это связа-
но с тем, что пленка получается немонокристаллической и усло-
вия ее роста сильно зависят от металлического подслоя, свойства
которого сами в большой степени определяются кристаллографи-
ческой ориентацией звукопровода. В этом состоит один из недо-
статков данной технологии по сравнению с технологией преоб-
разователей в виде монокристаллических пластин, для которых
ориентация пластин выбирается независимо от ориентации под-
ложки, что позволяет возбуждать нужную моду колебаний
(см. 7.1.3).
Особенно хорошо изучены тонкие пленки из CdS и ZnO, на-
пыляемые на звукопроводы из корунда. Эти звукопроводы обыч-
но имеют форму либо параллелепипеда (например, 20 X 6 X
280
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
X 6 мм3), либо цилиндра (диаметром «3 мм). Для возбуждения
продольных волн, распространяющихся вдоль оси третьего поряд-
ка Ал корунда, необходимо, чтобы ось шестого порядка As плен-
ки была направлена вдоль А3. Для CdS обычно используется
электрод из золота, а для ZnO — из платины. Подслой титана
или хрома улучшает адгезию. Хром, акустический импеданс ко-
торого (41,2 • 10е) очень близок к импедансу корунда (44,5 • 10°),
при любой толщине очень мало изменяет частотную характери-
стику преобразователя. Толщина металлических пленок контро-
лируется в процессе напыления с помощью кварцевых микрове-
сов, основанных на изменении частоты колебаний кварцевого
резонатора, помещенного в непосредственной близости от звуко-
провода при напылении на него слоя металла.
Сульфид кадмия напыляется либо методом непосредственного
испарения [5, 6], либо методом трех температур (7] при испаре-
нии из двух отдельных источников (S и Cd или S и CdS). Тол-
щина напыляемого прозрачного слоя сульфида кадмия контроли-
руется в процессе напыления с помощью интерференции двух
световых лучей, один из которых отражается от золотой подлож-
ки, другой от пленки CdS. При напылении пленок нужно при-
нимать меры для повышения вакуумной чистоты, используя ло-
вушки, промывку всей системы аргоном, длительный ее нагрев
для уменьшения остаточного давления паров масла, воды, азота.
Примерные температуры отдельных частей системы могут состав-
лять 220 °C для подложки, 100 °C
для тигля с серой и 750 °C для ис-
точника сульфида кадмия. Ско-
рость напыления должна быть
примерно 350 А/мин. Поскольку
кристаллографическая ориентация
пленки CdS зависит от наклона
подложки относительно оси ис-
точника [8], в принципе можно
управлять ориентацией пленки
так, чтобы возбуждались преиму-
щественно либо
поперечные волн
на 40° или 90°).
изготовленные с соблюдением оп-
тимальных условий, имеют поте-
ри, обычно превышающие 10 дБ,
а частотные характеристики соответствуют расчетным.
Пленки из окиси цинка, на наш взгляд, дают лучшие и более
воспроизводимые результаты при изготовлении их методом катод-
ного распыления [9] в триодном варианте, в непрерывном режи-
Плазма Лодложиа Мит иаиоло
Водяное
охлаждение
Рис. 7.17. Нанесение окиси цинка
методом катодного распыления.
Мишень из окиси цинка бомбар-
дируется ионами газового разря-
да. При этом на торцы образцов
(корундовые стержни) наносится
слой окиси цинка со скоростью
200 А/мин.
продольные, либо
ы (наклон оси At
Преобразователи,
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОДИ 281
ме. При этом диск из спрессованного порошка ZnO, находя-
щийся при отрицательном потенциале (~ 2000 В), подвергается
бомбардировке ионами из плазмы газового разряда кислорода или
аргона (рис. 7.17). На подложке, помещенной перед мишенью,
наращивается пленка ZnO со скоростью 200 А/мин*) при токе ка-
тода 50 мА. Ось 48 пленки всегда получается перпендикулярной
подложке, так что могут возбуждаться лишь продольные волны.
Внешний электрод изготовляется обычно из алюминия.
Рис. 7.18. Теоретические (сплошные линии) и экспериментальные (крести-
ки) частотные характеристики тонкопленочного преобразователя из окиси
цинка.
На рис. 7.18 представлены результаты, относящиеся к хорошо
напыленной пленке в структуре ZnO — Pt — А12О3. Толщина слоя
ZnO составляет 2,6 мкм; Pt — 0,4 мкм. На частотной характе-
ристике хорошо заметны резонансы, соответствующие V4,
3, 5 и 7V4.
§ 7.2. Встречноштыревые преобразователи
для поверхностных акустических волн (волн Рэлея)
Термин «поверхностные акустические волны» относится к уп-
ругим волнам, в которых деформация распространяется лишь в
очень тонком поверхностном слое с толщиной порядка длины
волны. К таким типам волн относятся волны Рэлея, волны Гу-
ляева — Блюстейна и волны Лява (§§ 5.3, 6.2. 5.2). Напомним,
*) Использование магнитного поля позволяет существенно увеличить
скорость роста пленки (> 1000 А/мин).
282 ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
что два последних типа волн представляют собой поперечные
волны, причем в случае волн Гуляева — Блюстейиа они распро-
страняются вблизи поверхности из-за пьезоэффекта, а в случае
волн Лява — в силу неоднородности среды (пленка на подлож-
ке). Волны Рэлея, которые мы здесь будем рассматривать, пред-
ставляют собой волны смешанного типа. Они могут распростра-
няться по поверхности любой среды. Смещение в этой волне со-
стоит в простейшем случае из продольной и поперечной состав-
ляющих, сдвинутых по фазе на л/2, причем смещение стремится
к нулю на глубине порядка двух длин волн. Несмотря на то что
деформация в волне Рэлея имеет довольно сложный характер,
у этих волн есть свои существенные преимущества. Волны Рэлея
могут возбуждаться и приниматься с помощью встречиоштыре-
вых преобразователей, нанесенных на пьезоэлектрик. Эти преоб-
разователи достаточно просты в изготовлении и, кроме того, от-
крывают ряд дополнительных возможностей при обработке сиг-
налов помимо простого электромеханического преобразования *).
Прежде чем перейти к описанию свойств встречноштыревого пре-
образователя и применений волн Рэлея в электронике, отметим,
что эти волны могут более или менее успешно возбуждаться пу-
тем преобразования объемных волн при их скользящем отраже-
нии, либо при дифракции на решетке из неоднородностей (на-
пример, металлических штрихов), регулярно распределенных в
пространстве. В работе [10] содержится подробное описание раз-
личных методов возбуждения поверхностных акустических волн.
7.2.1. Принцип действия. Встречноштыревой преобразователь
состоит, как это видно на рис. 7.19, из двух гребенчатых электро-
дов, нанесенных на пьезоэлектрическую подложку. Электрическое
напряжение, приложенное к этим двум электродам, создает поле,
которое в свою очередь вызывает сжатия и растяжения среды
вблизи ее поверхности, что приводит к возникновению разных
типов упругих волн (раздел 7.2.3). В отношении волн Рэлея, из-
лучаемых перпендикулярно штырям преобразователя, сам преоб-
разователь можно рассматривать как систему излучателей уль-
тразвука. Если приложенное к преобразователю напряжение яв-
ляется синусоидальным, колебания этих отдельных излучателей
складываются при условии, что расстояние d между двумя сосед-
ними штырями равно половине длины упругой волны.
*) Эти же преобразователи могут использоваться для возбуждения
волн Гуляева — Блюстейна и волн Лява, но указанные волны находят го-
раздо меньшее применение. В случае волн Гуляева — Блюстейна это объяс-
няется довольно жесткими требованиями к симметрии среды, а примене-
ние волн Лява затрудняется требованиями высокой степени однородности
и равномерности толщины пленки, необходимой для их возбуждения и
распространения.
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 283
Рис. 7.19. Встречноштыревой преобразо-
ватель.
Электрическое напряжение, приложен-
ное между штыревыми электродами,
создает деформацию поверхности мате-
риала.
этого значения,
возбуждаемые
рами штырей, j
Действительно, возмущение, создаваемое в момент времени t
парой штырей при приложении к этой паре напряжения задан-
ной полярности, распространяется со скоростью волн Рэлея Уя
на расстояние 1/2 за время Т/2. В момент времени t + Т/2 это
возмущение достигает соседней пары штырей, к которым приложе-
но напряжение другого зна-
ка, так что возмущение, соз-
даваемое этой парой шты-
рей, складывается в фазе с
возмущением от первой па-
ры. Частота /0 = 7в/2й, со-
ответствующая такому эф-
фекту накопления, называ-
ется частотой синхронизма
или резонансной частотой.
Если частота отклоняется от
то сигналы,
разными па-
гже не скла-
дываются в фазе, и результирующий сигнал уменьшается. В свя-
зи с этим полоса пропускания преобразователя уменьшается при
увеличении числа пар штырей. Переходную характеристику пре-
образователя, состоящего из N штырей, можно найти с помощью
его отклика -на импульсный сигнал. Импульс, длительность ко-
торого мала по сравнению с временем распространения упругой
волны между парой штырей, будучи приложен к электродам пре-
образователя, возбуждает одновременно N — 1 источник ультра-
звука. Так как электрическое поле изменяет знак на каждой
смежной паре штырей, возбуждаемый сигнал Деформации оказы-
вается периодическим. Его пространственный период равен уд-
военному расстоянию d между осями соседних штырей (рис. 7.19).
Длительность сигнала 0 равна активной длине преобразователя
L — (.N—i)d, деленной на скорость волн Рэлея:
rR Ч
(7.36)
Если интуитивно отождествить импульсный отклик преобразова-
теля с некоторой синусоидой, имеющей частоту /0 = VR/2d и про-
должительность 0, то частотная характеристика, которая пред-
ставляет собой преобразование Фурье от импульсного отклика,
будет иметь вид функции (.sinx'i/x (см. (1.27)), причем
ж = Я0(/_/о) = (У-1)|^.
Таким образом, полоса пропускания на уровне 3 дБ (х =
= ±0,885л/2) оказывается обратно пропорциональной числу
284
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
интервалов между штырями:
(7.37)
На практике для нахождения импульсного отклика преобра-
зователя необходимо получить электрический сигнал с помощью
приемного преобразователя, например, встречноштыревого типа.
Электрическое поле, сопровождающее упругую волну, во время
прохождения волной электродов преобразователя создает на них
изменяющуюся во времени разность потенциалов. Форма этого
сигнала зависит от числа штырей приемного преобразователя.
Рассмотрим два типичных случая.
а) Приемный преобразователь, состоящий из одной пары шты-
рей (рис. 7.20, а). Поскольку процесс преобразования происходит
Входной
сигнал
Рис. 7.20. Импульсный отклик линии задержки с двумя встречноштыревыми,
преобразователями.
а) Приемный преобразователь содержит одну пару электродов; б) прием-
ный преобразователь идентичен возбуждающему.
в узкой полоске, параллельной волновым фронтам, электрический
сигнал точно воспроизводит соответствующий сигнал упругой
деформации по мере того, как упругая волна проходит под при-
емным преобразователем.
б) Приемный преобразователь, идентичный возбуждающему
(рис. 7.20, б). Амплитуда электрического напряжения на преобра-
зователе нарастает, начиная с момента времени т = l/VR, когда
передний фронт пакета упругих волн доходит до первой пары
штырей, достигает максимума в момент времени т + 0, когда од-
новременно возбуждаются все штыри-приемники ультразвука, и
затем уменьшается. Импульсный отклик, имеющий треугольную
огибающую и длительность 20, является автокорреляционной
функцией импульсного отклика преобразователя. Таким образом,
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН
285
переходная характеристика линии задержки с двумя одинаковы-
ми преобразователями представляет собой функцию [(sin ж)/ж]2
с полосой пропускания по уровню 3 дБ:
/0 ЛГ-Г
(7.38)
На рис. 7.21 приведен импульсный отклик линии задержки на
кварце (У-срез, X — направление распространения) с двумя оди-
наковыми преобразователями, состоящими из 60 штырей, и с
центральной частотой /„ = 17 МГц. Треугольная форма огибаю-
щей и ее длительность 20 = 3,5 мкс свидетельствуют о том, что
Рис. 7.21. Импульсный отклик линии задержки
с двумя одинаковыми преобразователями из
60 штырей с центральной частотой 17 МГц.
переходная характеристика каждого преобразователя имеет вид
(sin х)/х (0 = L/Vr = (N- 1)/2/0 = 1,74 мкс).
Такой интуитивный подход является не вполне точным, по-
скольку, если сигнал, излучаемый при воздействии короткого им-
пульса, имеет периодичность и длительность, определяемые пере-
дающим преобразователем, то он не обязательно будет сину-
соидальным. В таком случае переходная характеристика будет
определяться функциями (sin х)/х с центральными частотами ,/0,
3/0, 5/0... Кроме того, мы предполагали, что преобразователь из-
лучает волны Рэлея т. е. считали, что деформации, характерные
для рэлеевских волн, связаны с составляющими электрического
поля через пьезоэлектрические константы вещества. Более глу-
бокий анализ возбуждения упругих волн с помощью встречно-
штыревого преобразователя требует в первую очередь знания
распределения электрического поля, и для такого анализа необ-
ходимы довольно длительные вычисления. Если же допустить, что
встречноштыревой преобразователь возбуждает только волны Рэ-
лея, то можно, опустив промежуточные разделы, перейти непо-
средственно к разделу 7.2.4.
286
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
7.2.2. Распределение электрического поля. На рис. 7.22 пока-
зана геометрия преобразователя и положение осей координат.
Штыри считаются достаточно длинными, так что ни одна из ве-
личин не зависит от координаты ж2. Толщина металлической
пленки много меньше расстояния А
между штырями. Для простоты бу-
дем также считать, что среда изо-
тропна в плоскости свободной по-
верхности (это имеет место для
кристаллов класса Gmm или пьезо-
электрической керамики с осью сим-
метрии, направленной вдоль х3 внутрь
вещества). К электродам приложено
синусоидальное напряжение v = voe{at. В рамках квазистатиче-
ского приближения (§ 6.2) электрическое поле определяется по-
тенциалом
л,
j ad ;
рз
Рис. 7.22. Элементарная ячей-
ка преобразователя.
Ф(я„ t) = Ф(^)е(“'.
Электрическая индукция удовлетворяет уравнению Пуассо-
на для диэлектрика: dDJdXi^0. Так как коэффициент электро-
механической связи кристалла мал, можно пренебречь вкладом в
электрическую индукцию от возбужденных упругих волн. Урав-
нение (6.156) будет иметь вид
п о®та г.^
Di = EijEj = — 8у^-,
а потенциал Ф удовлетворяет уравнению Лапласа
Поскольку материал изотропен в поперечном направлении
и д!дх3 = 0, последнее уравнение сведется к уравнению
еи + ®зз = 0. (7.39)
Для бесконечного преобразователя из-за чередования электродов
при любых ®1, х3 должны выполняться условия симметрии
Ф(а:1 + 2й, аг3)=Ф(я:1, ««).
(7.40)
Ф(я:1 + 2d, Хз~) =* ФСгц ж3).
Будем искать решения в виде
. Ф(^, х3) = f(xl')g{xs).
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 287
Уравнение (7.39) запишется при этом следующим образом:
/'// = e^/efig = -х8,
где константа % — действительная величина, поскольку / должна
быть периодической функцией от xt. Решения имеют следую-
щий вид:
7 = FsinxGr1 + 6), (7.41)
g = Ge-rXX* (7.42)
при % > О, г — (еи/е®з)1/2, так как потенциал должен уменьшать-
ся внутри вещества. Условия симметрии (7.40), которые можно
записать как
f(xt + d) + /(xt) = 0 или 2F sin [^(а?* + б) + %d/2] cos %d/2 <= 0,
определяют допустимые значения х:
Xm = (2?n + l)|, щ = 0,1,2... (7.43)
Общее решение представляет собой линейную комбинацию
нечетных гармоник с пространственным периодом 2d:
0(^X3) = -2^е_гХт13sinxm(®i + M, *з>0, (7-44)
7П=0 ^7)1
где -1/Xm = Gm..
Электрический потенциал в вакууме (я:3 < 0), где 8ц = 833 =»
= 8о, обращается в нуль при ж3 = — °°. Этот потенциал выражает-
ся в форме, аналогичной (7.44) при г = — 1, с теми же коэффици-
ентами Fm и бт, в силу непрерывности Ф на границе х3 = 0. Ко-
эффициенты Fm и бт определяются электрическими граничными
условиями на свободной поверхности. Тангенциальная составля-
ющая электрического поля
Е1 = = J Fme~TV3 cos + 6m) (7.45)
0Х1 m=0
должна обращаться в нуль на границах с металлическими элек-
тродами, т. е.
2 Fmcos[(2m+ 1)-^(л + М] = 0 ПРИ d(l -а))2<|Ж1|<й|2.
(7-46)
Поскольку коэффициенты Fm и бя для кристалла и для ва-
куума равны, непрерывность нормальной составляющей индукции
288 ГЛ 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 289
между электродами
D3=—езз^ ——(епезз)1/2 S Fm sin Xm (#i + 5m), ж3 = 0+,
ох3 т=о
D3 = е0 2 Гт sin Хтп (яч + 6т), х3 = 0_,
тп=о
возможна лишь прп равенстве ее нулю, т, е.
2 Fm sin [(2m + 1) -J (xt + 6т)] = 0 при | х, | < d (1—а)/2. (7.47)
Уравнения (7.46) и (7.47) удовлетворяются, если 6™ = О, a Fm
есть полином Лежандра Рт [Ш:
Fm = HPmlcos л(1 — а)1 = НРп{—cos ла). (7.48)
В выражении для потенциала (7.44)
* —^2 (7.®)
7П=0 '
константа Н зависит от разности потенциалов, приложенной
к электродам, = 2Ф (zt = d(l — а)/2, 0] или
Вводя переменную s =* sin ла/2, можно заменить сумму в послед-
нем выражении полным эллиптическим интегралом Kls') = К'($)
с модулем $' = (! — $2)1/2, дополнительным по отношению к моду-
лю s [1U. Тогда
v0 = ^K'(s). (7.50)
Теперь с помощью (7.48) можно найти амплитуды пространствен-
ных гармоник электрического поля
Через полиномы Лежандра, в силу соотношения $ = sin ла/2,
коэффициенты 3~ зависят от отношения а (ширины электрода)
к половине периода d. Из рис. 7.23 видно, что все гармоники,
кроме 1-й, могут обращаться в нуль. В частности, если ширина
штырей равна разделяющему их промежутку, т. е. а = 1/2, гар-
моники с номерами 3, 7, ... 4р + 3 отсутствуют, поскольку
Р2р+1(0) = 0. Этот результат подтверждается экспериментально
для материалов с малым коэффициентом электромеханической
связи. В качестве примера на рис. 7.24 приведена осциллограмма
Рис- 7.23. Пространственное распределение электрического поля. Зависи-
мость амплитуды гармоник электрического поля (т = 0.........4) от отно-
сительной ширины а штырей. (Рис. 2 из [И].)
импульсного отклика преобразователя с а = 1/2, изготовленного
па подложке из кристаллического кварца. Для сильных пьезо-
электриков, например для керамики или ниобата лития, такой
результат не имеет места.
Рис. 7.24. Импульсный отклик преобразователя,
у которого ширина штырейгравна расстоянию
между ними (а — 1/2).
Существует 5-я гармоника, но отсутствует 3-я.
Подложкой служит ct-кварц У2-среза.
Если преобразователь имеет конечную длину, электрический
потенциал не является уже строго периодическим и определяет-
ся пространственным преобразованием Фурье:
4-00
ф(£, а;3) = [ Ф(а-х, х3) ekXldxx, (7.52)
где
+«
Ф (о-p х3) = 1 f Ф (k, Х3) e"hx,dk. (7.53)
19 э. Льелесан, Д. Руайе
290
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Уравнение Лапласа (7.39) для Ф принимает вид
-г&Ф + cfs = 0д
Ф (к, х3) = Ф (к) е гкХз, причем г/с>0. (7.54)
Для вычисления Ф0(А;) = Ф(к, 0) предположим, что электриче-
ское поле равно нулю вне преобразователя (IrrJ > L/2), а при
\хД < L/2 равно полю, создаваемому бесконечным преобразова-
телем той же геометрии. Делая такое предположение, мы вновь
пренебрегаем электрическим полем, сопровождающим упругую
волну, а также считаем, что преобразователь содержит большое
число штырей. Согласно теореме дифференцирования (раз-
дел 1.3.2) фурье-образ составляющей электрического поля =
в ЗФ/5ЯГ1 имеет вид
£1 (Агд ®3) = J [хи х3) е***1^ = 1кФ (к, х3).
Используя выражение (7.45) для электрического поля при бт = 0,
Ei (®i, 0) = Fm cos (xma-i),
получаем
W = - 4 2 Рт f COS (x^i) e’^dji =•
К m=O —L/2
I V г f «ln(‘-Xm)£/2 , sin (* + >:„) 1/2 ]
—T", ”1 *=£ +--------1 <7'55)
7.2.3. Возбуждение упругих волн. Прежде чем решать уравне-
ния движения, покажем с помощью качественных рассужде-
ний, что встречноштыревой преобразователь пригоден для воз-
буждения волн Рэлея [12]. Воспользовавшись матрицей пьезо-
электрических коэффициентов для поперечно изотропного тела,
можно найти механические напряжения, создаваемые тангенци-
альной Ei и нормальной Е3 составляющими электрического поля:
( 0 0 0 0 е15 0\
0 0 0 0 0 .
езз *31 езз ООО/
Напряжения Тц = е31Е3 и Tl3 — el3Ei могут порождать соот-
ветственно продольную и поперечную волны, распространяющие-
ся вдоль направления xt. Так как гармоники одного и того же
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 291
порядка от составляющих электрического поля и Е3 сдвину-
ты по фазе на п/2 вдоль оси xt, то возникающие механические
смещения щ и и3 можно рассматривать как продольную и попе-
речную составляющие волны Рэлея, излучаемой в направлении
Напряжения Т23 = е31Е3 и Т33 = е33Е3 вызывают паразитные
явления.
Решение уравнения распространения. Для нахождения излу-
ченных волн необходимо решить уравнение распространения
(6.48), с учетом распределения потенциала, определяемого гео-
метрией преобразователя:
Р ^2 “ iihl dxjSxh dxjdxk
Для поперечно изотропной среды и при д!дх2 = 0 это уравне-
ние имеет вид
(C11£j+ + р(°2) И1 + (С13 + См) = -('15 + бз1) 4^3*
(c«e£| + + р“2) “2 = 0’ (7.56а, б,в)
/ а2 5а \ 52ф а2ф
(С13 + с44) + ^44 — + с33 — + р® J и3 = - е15 - е33 —.
Поскольку и2 не связано ни с электрическим полем, ни с дру-
гими составляющими щ и и3, смещение частиц происходит только
в сагиттальной плоскости XtX3. Для исключения переменной из
двух других связанных дифференциальных уравнений воспользу-
емся фурье-образом щ(А, х3) для смещений [13], определяемым
выражением
(*1,^3) = § и3(к,х3)е ikXldk, (7.57)
а также фурье-образом для потенциала (соотношение (7.53)). Вво-
дя фазовую скорость V = а/к и имея в виду, что c№/dx3 = — гкФ,
вместо (7.56а) и (7.56в) получаем:
[ (pF2 - cu) А2 + с44 Д pi — (с13 + с44) - - irk2 (е15 + е31) Ф,
1 3 3 (7.58а,б)
- ik (си + с44) Д- + (pF2—с44) А2+с33 Дj и3 = к2 (е15 - г2е33) Ф.
19*
292
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Решение этой системы дифференциальных уравнений выража-
ется в виде суммы общего решения системы без правой части и
частного решения полных уравнений. Будем искать частное ре-
шение в виде
(7.59)
где bi и Ь3 определяются соотношениями
(рV2 - с„ + i*cu)bi + ir(cu + с44)Ь3 = -гг(е18 + е31), (7.60а)
ir(cI3 + cu)bi + (рР — с44 + т*Сзз)Ь3 = (б15 — 1*е3з), (7.606)
которые получаются из рассматриваемой системы при подстанов-
ке (7.59).
Общее решение системы уравнений без правой части имеет
вид
где q определяется из условия совместности двух линейных одно-
родных уравнений, получающихся после подстановки (7.61) в си-
стему (7.58) без правой части:
(си - рР + cuq2')°u1 + q(cl3 + c44)°u3 = 0, (7.62а)
?(ct3 + СцГщ + (с44 — рР + c33g2)°u3 — 0 (7.626)
или
' С33с44д4 + 52[с33(сп - рР) + С44(с44 - рР) -
- (с13 + с«)2] + (си - рР)(с44 - рР) = 0. (7.63)
Отметим сходство между (7.63) и уравнением (5.108), опреде-
ляющим показатель затухания волн Рэлея. Разница связана лишь
с тем, что в настоящем случае рассматривается гексагональный
кристалл, а не кубический. Поэтому, если положить °u) = 1, то
амплитуда р = °и3 будет определяться выражением, аналогичным
(5.109):
Р = °и3 -
(С13 + С44) д
(7.64)
Запишем (7.63) как уравнение относительно произведения qk,
для чего умножим (7.63) на к1:
c33cti (qk)* + (qk)* [с38сц (к* - kl) + cU (к* - к*т) -
- (С13 + с44)2Н + сис44 (к* - к!)(к* - к*т) = 0. (7.65)
Здесь kL = a>/VL а кт = (a/VT — волновые числа продольной и по-
перечной волн, имеющих соответственно скорости Р’ь’=" Усц/р и
Рт = Ус44/р в направлении xt. Поскольку смещение щ должно
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН
293
быть конечным, годятся только два корня, qtk и q3k, имеющих
отрицательные мнимые части. Этим корням соответствуют два
значения амплитуды, °и(31) — ргиОи(33)=р3. Принимая во внимание
(7.59), получаем общее решение:
£=л1в-”>“«+ (7.вва>
S, (7.666)
Коэффициенты At и А3 определяются граничными условиями на
свободной поверхности х3 = 0 при любых ж(:
Л3 = ci3hi + еМз = 0. (7.67)
Поскольку д/дх2 = 0 и и2 = 0, для Т23 указанное условие выпол-
няется автоматически:
/5и3 ди2 \ 5Ф
?23 = С2323 + е223 •
Остальные два равенства (для 1=1 и 1 = 3),
С1313 ( +1^) + 6113 = °’ (7,68а)
сзззз-^г + сззп|^ + еззз = 0» (7.686)
можно переписать, используя фурье-образы щ, и3 и Ф:
с« (5; “ г’^3) = ikev&
du ~ d$
сзз ~dz^ ~ ^кс1зи1 — езз •
Используя выражения для и3, и3 и Ф, получим для х3 = 0:
c44(gi + р,)А, + c44(?j + рз)Л3 = —(eis + саЬ3 - ircubi)^,
(7.69а, б)
(си + c33piqi)Ai + (cis + c33p3q3)A3 = ('ire33+ irc33b3 — СщЬ^Фо.
Неизвестные At и А3 пропорциональны Фо:
(7.70)
где
А = (pi + ?i)(cis + c33p3q3) - (р3 + ?з)(cis + СззР191). (7.71)
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАПИЯ УПРУГИХ ВОЛН
Отметим, что, заменяя pt и q{ их выражениями через V, полу-
чаем уравнение Д(У) =0, аналогичное (5.116). Корни этого урав-
нения дают значения скорости волн Рэлея VR. Величина А (А) об-
ращается в нуль при к = кц=*(д/Уя. Для нахождения смещений
Хз) воспользуемся преобразованием Фурье (7.57):
«з(яц*з) = (7.72а, б)
- i Т(* Т *
Полюсы подынтегрального выражения, к = ±кв, обращающие
в нуль определитель Д, находятся на контуре интегрирования,
в силу того, что мы пренебрегли затуханием. Полюс, имеющий по-
ложительную действительную часть и соответствующий распро-
странению в направлении Xi > 0, должен обладать отрицательной
мнимой частью (/с к — kR-^ (ц, где т]>0), так как произведение
~ihRxl -т>х1
е е должно стремиться к нулю при Xi -> +°°. Аналогично,
затухание в направлении Xi < 0 связано с другим полюсом kR =
= — kR + гт]. Затухание можно не учитывать, если выбрать кон-
тур интегрирования таким образом, чтобы он обходил полюс — ка
снизу, а полюс —сверху (рис. 7.25).
Рис. 7.25. Контур интегри-
рования для среды без по-
терь.
Рис. 7.26. Вдали от преобразователя
объемные волны излучаются преиму-
щественно в тех направлениях, где
в результате интерференции проис-
ходит их сложение.
Объемные волны. Для того чтобы определить различие между
объемными и поверхностными волнами, вычислим интегралы
вдали от преобразователя (Я -* °°) в данном направлении 9
(рис.7.26). Поскольку ж, = У? sin 0, а Хз =*Rcos6, два первых чле-
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 295
на в формулах для смещений (7.72а, б) выражаются через инте-
гралы типа:
I = J e(fc) exp [— iRk (q cos 0 + sin 0)] dk, (7.73)
где
'»=stF- <’•”)
Вклад от последнего члена при R °° стремится к нулю, по-
скольку е гкХз — е-гййсо®0-► 0 (напомним, что тк > 0).
Полагая
ф(А) = MgOc) cos 0 +sin 0], (7.75)
получим для интеграла I следующее выражение:
Z(0)= §.e(k)e~iiwdk. (7.76)
При больших R экспонента будет быстро осциллировать в тех
областях!, где ф(/с) сильно меняется при изменении к. Предельное
значение интеграла на больших расстояниях можно вычислить
методом стационарной фазы (раздел 1.3.2). Здесь вместо времени
будет фигурировать переменная к, вместо частоты со — величина
0, а вместо а — ее значение а = —7?ф. Тогда на основе формулы
(1.24) имеем
7<в)=/ (7-77)
где ко — такое значение переменной к, при котором фаза ста-
ционарна, т. е.
(V- <7-78’
Интеграл 7(0) уменьшается с расстоянием как 7?_1/г, что свя-
зано с выполнением закона сохранения энергии для упругих
волн. Вдали от преобразователя волны являются практически
плоскими, а их скорость совпадает со скоростью либо квазипро-
дольных (Ю, либо квазипоперечных (И2) волн. Величина скоро-
сти зависит от направления распространения: Vli2 — fin,., п2, ns).
Зависимость от направления можно выразить через угол 0. Тогда
п, = sin 0, пг = 0, п} = cos 0 и
Vi.2(0) /(sin 0, 0, cos 0).
В явном виде указанные зависимости приведены в § 5.1 (см.
(5.47) и (5.48)). Введенный ранее параметр V — &/к равен V(g) =
296 ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
=•/(1, 0, д), так как для плоской волны
ni = T^ = 1’ П2==тй-2 = ()’
Поскольку f является однородной функцией 1-й степени
(§ 5.1), /(sin 0, 0, q sin 9) = 7(g) sin 0, левая часть этого равен-
ства дает значение 7i.i(0) для q =* g0 = ctg 0, или
— 7t.2(0)-7(g,)sin0.
Равенство фаз интеграла I и плоской волны, имеющей ско-
рость Vl или V2,
<p(W - ©/Vi, 2(0) - ©/7(q„) sin 0, (7.79)
можно, учитывая (7.75), выразить следующим образом:
ktlqUco) cos 0 + sin 01 = Zf(g0)/sin 0.
Равенство (7.79) выполняется при условии, что q(k0) =*qo~
= cos 0/ sin 0 или ka — k(qo') =* co/7(g0), т. e. при двух значениях kQ:
^01 ~ кДб)" S^n = V2 (0) S^n O'
Зависимость амплитуды этих двух волн от угла 0,
(7-80>
дает диаграмму направленности излучения преобразователя. Если
преобразователь содержит большое число штырей (L»d), функ-
ция Ф0(Аг), определяемая выражением (7.55), имеет заметную ве-
личину лишь для к, близких к ±%т. Объемные волны излучаются
в направлениях, соответствующих 0т и определяемых соотноше-
нием ©sin0m/71.2(0m) = ±(2m +l)n/d, отражающим условие сло-
жения волн при их интерференции (рис. 7.26):
2d sin 0m = ±(2m + 1)Х1( 2(0m).
Это условие выполняется для частот, превышающих 7(n/2)/2d,
где 7(п/2) — скорость продольной или поперечной волны в на-
правлении Xi.
Волны Рэлея. В этом случае в интеграле 7’следует дополни-
тельно учесть вклад от полюсов — kR и +kR функции eU). Ука-
занный вклад можно вычислить методом вычетов
IR = 2ni Res [е (k)]hRe~'R*kR\ (7.81)
Из выражения (7.75) для <f(k) видно, что с увеличением R мно-
житель е = е " v е " стремится к нулю, по-
скольку корни qk уравнения (7.65) имеют отрицательные мни-
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН
297
мые части. Рассматриваемый вклад от полюсов, обращающийся
в нуль при всех 0, кроме 0 = л/2, соответствует волне Рэлея,
распространяющейся вдоль свободной поверхности. Смещения ил
п и, можно вычислить методом вычетов с контуром интегри-
рования в виде полуокружности бесконечного радиуса, располо-
женной в нижней полуплоскости при > 0 и в верхней полу-
плоскости при xt < 0 так, чтобы множитель е обращался в
нуль на данной полуплоскости (рис. 7.25). Полюс соответ-
ствует волне, распространяющейся в положительном направле-
нии xt, а полюс —кд — волне, распространяющейся в отрица-
тельном направлении ягь Так как Ь, и Ъ3 являются аналитиче-
скими функциями к, третий член подынтегральных выражений
(7.72а, б) обращается в нуль. Два оставшихся интеграла можно
вычислить с помощью выражения для 7Л, если в качестве выче-
та взять
печ re 1 gfa> %(Ад) _ _ Д_ fa) к ф }
Ы*н VR[dv)vR
Составляющие смещений частиц выражаются следующим об-
разом: .
ui (a-i, *з,
ikR<&0(kR) (D ^-igfiB-Гз , р vr)
-------^д"1" '"Iе “г "3е J е »
(7.82 а, б)
из fa, ^з, О
VR dV
Индекс R показывает, что все величины в правой части вычисля-
ются при V = VB или к = кд = со/Уя. Так как смещения оказыва-
ются функциями от V2 или от к2, волны Рэлея, излучаемые в про-
тивоположных направлениях, имеют одинаковую амплитуду. За-
висимость амплитуды от частоты выражается через величину
Н = 1кДФй(кД}, которая, с учетом (7.55), имеет вид
Используя выражение (7.43) для %т, получим
298
ГЛ 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Поскольку Fm -- &~т, имеем
ун sin^[/-(2m + l)/0]
Н (/) = vo — 2л[/-(2тп + 1)/0] +
sin^ [/+ (2m + 1)/0]
+ ^т 2«|7 + (2т+1)/0] • (7<83>
Частотная характеристика преобразователя определяется функ-
циями вида (зшж)/ж с центральными частотами, соответствующи-
ми нечетным гармоникам частоты синхронизма f0, с постоянной
полосой пропускания и с амплитудой, пропорциональной коэф-
фициентам STm. Согласно соотношению (1.27), импульсный отклик
характеризуется длительностью 0 = Л/7Н и амплитудой А =
= Vnvjd-.
h (t) = П (§-) V grm cos (2m + 1) fot. (7.84)
Отметим, что для данного электрического напряжения v0 им-
пульсный отклик обратно пропорционален расстоянию между
штырями d, т. е. пропорционален резонансной частоте /0 (так как
электрическое поле Е пропорционально vB/d).
Амплитуда излучаемых волн Рэлея зависит от относительной
ширины а штырей преобразователя. При прочих равных услови-
ях, как показано в [14, 15], амплитуда максимальна при а = 1/2,
т. е. когда ширина штырей равна расстоянию между ними (%0/4).'
7.2.4. Метод дискретных источников. В двух предыдущих раз-
делах разобраны лишь наиболее простые случаи. Считалось, что
вещество поперечно изотропно и обладает слабыми пьезоэлектри-
ческими свойствами. Кроме того, рассматривались преобразовате-
ли со штырями одинаковой длины, расположенными на равных
расстояниях. Как видно из проведенного рассмотрения, даже в
таком простом случае анализ встречноштырев'ого преобразовате-
ля достаточно сложен. Вместе с тем следует заметить, что вид
частотной характеристики не зависит от материала, из которого
изготовлен преобразователь. В связи со сказанным представляется
полезным рассмотреть некоторый общий метод, с помощью кото-
рого можно было бы вычислять частотную характеристику встреч-
ноштыревого преобразователя со штырями разной длины, распо-
ложенными на различных расстояниях друг от друга. В методе
дискретных источников, или в «дельта-методе» [16, 17], каждая
пара штырей заменяется генератором или приемником ультра-
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН
299
звука бесконечно малой протяженности, расположенным, напри-
мер, на средней линии между двумя штырями, как это изобра-
жено на рис. 7.27. Каждому источнику приписывается амплитуда
А, пропорциональная длине 10 области перекрытия штырей, со
Рис. 7.27. Схема применения метода дискретных источников.
Преобразователь представляется в виде последовательности дискретных
излучателей, размещенных между штырями на средней линии. Амплитуды
колебаний излучателей пропорциональны длине перекрытия штырей.
знаком + или — в зависимости от направления электрическо-
го поля.
При сделанных предположениях импульсную характеристику
преобразователя можно представить в виде суммы функций Ди-
рака
h(t) = ^snAnd(t-tn). (7.85)
। Здесь sn = (—1)" учитывает смену знака электрического поля на
каждом промежутке между штырями. Частотная характеристика
. Н (/) = f h (t) e~i2nftdt
определяется выражением
Я(/) = ЗМпе"^я. (7.86)
п
Для того чтобы убедиться в применимости метода дискретных
источников, используем его для анализа преобразователя с N ре-
гулярно расположенными штырями одинаковой длины. В этом
случае sn= (-!)", Лп = А = const, tn = to + nd!VR =»to + n/2f0.
300
ГЛ 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Частотная характеристика выражается следующим образом:
N—1
Н (/) = Л0е-’2л/,° 2 (- 4)П ехР inn f}
П=О \ 'о/
или,, поскольку (—1)" = е<пп,
Н (/) - 40е~’2Я/,° 2 exp — inn .
Суммирование приводит к выражению:
С учетом расфазировки, связанной со средним запаздыванием,
равным т —10 + (N — 2)/4/0 = to + (2V — 2)d/2VB, выражение для
частотной характеристики будет иметь вид
i sin(Ar —1) л—л-т—
//(/) =40---------7-у" '• (7-87)
sinn-^
Вблизи частот fm = (2т + 1)/0 (где т — целое), удовлетворяющих
соотношению (/— /0)/2/0 = (/ — /т)/2/0 + т и обращающих в нуль
числитель и знаменатель выражения (7.87), #(/) принимает вид
L
sinnjr (/-/то)
Нт (f) — 4
sin (TV — 1) л
A -S-
ло а
.(7.88)
Единственное отличие полученного выражения от формулы
(7.83) заключается в том, что теперь вклады от нечетных гармо-
ник имеют одинаковые амплитуды, а не пропорциональны ^7"т,
как это было раньше.
Метод дискретных источников позволяет решать важную для
практики задачу синтеза преобразователя с заданной импульсной
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН
301
характеристикой (или передаточной функцией). Пусть, напри-
мер, импульсный отклик
A(i) = e(f) cos (pit) (7.89)
соответствует требуемой импульсной характеристике. Здесь поло-
жительная огибающая определяет амплитудную модуляцию, а ча-
стотная модуляция учитывается б помощью фазы, зависящей от
времени, (pit) (рис. 7.28):
/ - (7.90)
Для определения положения хп = VRtn дискретных источников
всегда можно ввести функцию git), удовлетворяющую равенству
gitn) = п, где п — целое.
Приписывая каждому из источников амплитуду,-равную hitn),
мы производим выборки из импульсной характеристики, так что
сама характеристика может быть представлена в виде суммы
heit)-- ^hiWgftj-nl-. h(t)^8[git) - п\ (7.91)
n n
или, учитывая решение упр. 1.11,
heit) = СОЗФ^)6(#-М. (7-92)
Такое распределение источников, с амплитудами, имеющими
в принципе произвольные знаки, довольно трудно реализовать с
помощью встречноштыревого преобразователя. Предпочтительнее
выбрать моменты времени tn так, чтобы они удовлетворяли соот-
ношению
tp(fn)= пп или cos (pitn) — i—l)n (7.93)
с тем, чтобы знаки источников чередовались (рис. 7.28). Если по-
ложить git) = (pit)/n, то выражение (7.92) примет вид
heit)- 2(-1)n^JS^-^)- (7-94)
Па самом' деле подобная сумма дельта-функций содержит в
себе нечто большее, чем функцию hit) = eit) cos cp(i), что видно
из рис. 7.29. Применяя формулу (1.40) (полученную в упр. 1.10)
S s ix — п) = У е~’2ятх _ 1 2 2 cos i2nmx)
к соотношению (7.91) при x — g = <p/n, получим
heit) * h(t)-\-2e(t) 2 cos<рcos(2тп<р)
302
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
или, преобразовав произведение косинусов под знаком суммы,
ht (0 = 2А (i) -f- 2е (i) У cos (2т + 1) ф.
Дискретизованная импульсная характеристика
= h (t) + е (t) 2 cos (2т + 1) Ф
(7.95)
помимо заданной характеристики h(t) = e(t) соэф(г) содержит еще
функции с той же огибающей,
Рис. 7.28. Синтез импульсного от-
клика.
Отклик представляется серией
равноотстоящих по фазе выборок.
Амплитуды этих выборок пропор-
циональны мгновенным значени-
ям частоты.
но с мгновенными частотами,
Рис. 7.29. Сумме дельта-функций
соответствует не только сину-
соида с основной частотой /о,
но и все гармоники с частотами
(2?п + 1)/0.
соответствующими нечетным гармоникам основной характеристи-
ки h(t).
Длина перекрытия штырей 1п пропорциональна амплитуде Ап
источников. Величину Ап можно найти из выражения (7.94):
то(*п)
2Ф' (tn)'
(7.96)
Если выбрать промежуток между штырями и их ширину оди-
наковыми и равными четверти мгновенного значения длины вол-
ны, то расстояние между осями двух штырей, составляющих ис-
точник n-порядка, можно найти из соотношения
л VR nVR
П~ 2 “2/(tn)~<P'(*n)*
(7.97)
Заданную импульсную характеристику можно получить, если
с помощью соответствующего фильтра исключить гармоники. Та-
кой полосовой фильтр практически может быть реализован в ви-
де встречноштыревого приемного преобразователя и согласую-
щих цепей.
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН
В случае дисперсионных линий, описание которых дается в
разделе 9.3.5, число штырей в преобразователе должно быть очень
большим. Например, для получения импульса длительностью
0 = 10 мкс с центральной частотой f0 = 60 МГц требуется пример-
но 2/о0 = 1200 штырей. Уменьшение числа штырей облегчает
изготовление маски (фотошаблона) и ослабляет паразитные взаи-
модействия, связанные с прохождением через все штыри волн,
Рис. 7.30. Уменьшение числа элект-
родов преобразователя путем дис-
кретизации.
Требуемый импульсный отклик (б)
можно получить двумя способами.
При расположении излучателей в
каждой точке tn, отвечающей усло-
вию <p(tn) = пл. получается преоб-
разователь (а). Если разместить из-
лучатели в точках tn, отвечающих
условию = (в данном
случае Q = 5), то преобразователь
будет иметь вид в).

возбуждаемых на краях преобразователя. Такое уменьшение мо-
жет быть достигнуто способом, показанным на рис. 7.30. Рассто-
яние между осями штырей, составляющих источники, всегда
соответствующее моментам времени tn, равно Mtn)/2Q. Гармоника
с номером Q = 2m + 1 выбирается с помощью фильтра, имеющего
центральную частоту Qfa. Импульсная характеристика hq(t) =
= e(t) cos [(>ф(£)], соответствующая частоте, в Q раз превышаю-
щей основную, реализуется в таком случае с тем же числом шты-
рей. Аналогичным образом сигнал на основной частоте можно
получить, если взять в Q раз меньше выборок в моменты времени
tn, определяемые соотношением
<p(£n) = Qntrt, (7.98)
а, следовательно, число штырей тоже уменьшается в Q раз.
Замечание. Искажение фронта волны. До сих пор нами
рассматривалась одномерная задача и предполагалось, что волна,
излучаемая преобразователем, является плоской, а ее фронт па-
раллелен штырям. Исследование поперечного сечения акустиче-
304
ГЛ 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
ского пучка показывает, что при изменении длины штырей вол-
новой фронт деформируется, что особенно сильно проявляется в
случае, когда материал подложки имеет большую величину ко-
S)
Рис. 7.31. Искажение волнового фронта (а) и коррекция с помощью холос-
тых штырей (б). Подложка из LiNbOs.
Частота возбуждения 57 МГц является резонансной для излучателей с
наиболее длинными электродами. Фаза волны измерялась на расстоянии
0,89 см от центра преобразователя. (Рис. 2 из [18].)
эффициента электромеханической связи (например, LiNbOs). Эта
деформация волнового фронта вызвана неоднородностью преобра-
зователя, поскольку скорость волн Рэлея на поверхности пьезо-
электрика изменяется из-за присутствия металлической пленки*)
*) Если материал и не является пьезоэлектриком, скорость волн Рэ-
лея все равно зависит от нанесенной на поверхность подложки металлиле-
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 305
(раздел 6.2.2). Если длина штырей различна, волны, излучаемые
отдельными частями линейного источника, проходят разный путь
ио металлизированной поверхности и приобретают различный
набег фаз (эффект линзы). Пример подобного поведения воли
[18] приведен на рис. 7.31, а. Измерение здесь проводилось мето-
дом емкостного зонда, когда вольфрамовое острие находится в
контакте с поверхностью [19]. Разность фаз между волнами, рас-
пространяющимися в центральной части преобразователя (где
длина акустического пути максимальна) и на периферии, дости-
гает 120°. Искажение фронта волн, распространяющихся в про-
тивоположном направлении, оказывается иным, так как преобра-
зователь не симметричен. Такие набеги фаз и связанные с ними
искажения волнового фронта приводят к нежелательной интер-
ференции в приемном преобразователе (состоящем из штырей
прямоугольной формы). Эти набеги фаз можно существенно
уменьшить, если ввести в преобразователь холостые штыри
(рис. 7.31, б). Такие штыри не являются активными, поскольку
имеют тот же потенциал, что и соседние, но опи делают
более равномерным распределение металла по поверхности под-
ложки*).
7.2.5. Электрическая эквивалентная схема. Преобразователь,
состоящий из двух электродов гребенчатой формы, вблизи резо?
нансной частоты может быть представлен комбинацией емкости
и сопротивления. Сопротивление включает как омическое сопро-
тивление электродов, так и сопротивление излучения. Емкость
зависит от числа штырей, расстояния между ними и от диэлект-
рической проницаемости материала подложки [И, 20].
ской пленки. Этот эффект, имеющий характер простой механической на-
грузки, в случае металлических пленок из таких легких металлов, как алю-
миний, пренебрежимо мал.
*) Здесь нужно упомянуть о другом эффекте, приводящем к аналогич-
ным интерференционным искажениям, Изменение механического и элект-
рического импеданса поверхности из-за нанесенных на нее металлических
гребенчатых электродов приводит к отражению падающей на преобразова-
тель упругой волны. Анализ происходящих здесь процессов не прост. Они
имеют наибольшее значение в случае подложек с сильной электромехани-
ческой связью и зависят не только от частоты упругих волн, но и от на-
грузки преобразователя. Было предложено несколько конструкций преобра-
зователей, приводящих к ослаблению этих нежелательных эффектов. На-
пример, предложено рассекать каждый штырь преобразователя вдоль на
две части. В обычном преобразователе штыри имеют ширину Х/4 и разде-
лены промежутками также Х/4, поэтому волны, отражающиеся от двух
смежных штырей, складываются, так как разность фаз между отраженными
волнами в этом случае составляет 2л. Если же каждый из штырей.рассечь
вдоль пополам, то в принципе отраженные волны должны гасить друг дру-
га. поскольку теперь имеются неоднородности шириной Х/8, разделенные
промежутками, имеющими ширину также л/8, что приводит к разности фаз
между отраженными волнами, равной л (см. [30], [31]).
20 Э. Дьелссаи, Д. Руайе
306 гл. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Для того чтобы определить импеданс встречноштыревого пре-
образователя, можно разделить его на секции [21] длиной 2d и
для каждой из секций построить эквивалентную схему так, как
это делал Мэзон в случае преобразователя объемных волн (раз-
дел 7.1.2). Разделение преобразователя на секции облегчается,
если можно считать одну из составляющих электрического поля
преобладающей. Если преобладает тангенциальная составляющая
(приближение «продольного поля»), за основу можно принять
схему, приведенную на рис. 7.13. Если же наиболее существенной
оказывается нормальная составляющая поля (приближение «попе-
речного поля»), эквивалентную схему можно получить из преды-
дущей, если в ней замкнуть емкость —Со (упр. 7.2). Поскольку
на каждой из секций электрическое поле меняет знак, для опи-
сания всей структуры следует соединить эквивалентные схемы
последовательно по их механическим выходам и параллельно по
электрическим входам. В обычном выражении для проводимости
излучения появляется численный множитель, что можно пояснить
с помощью следующего простого рассуждения. Мощность волн
Рэлея, излучаемых источником, пропорциональна частоте /0 и
средней электрической энергии, запасенной в подложке между
двумя соседними штырями,
= ^Csvlfo,
где ц — коэффициент пропорциональности, а Св — емкость, при-
ходящаяся на один межэлектродный промежуток преобразовате-
ля. На резонансной частоте ja=:Vn/2d N— 1 источник излучает
в фазе, и общая мощность 5*, излучаемая преобразователем, равна
(2У-1)2^в, т. е.
=(^-1)2П^о/о-
Проводимость излучения выражается следующим образом:
G0 = ^ = 2(Ar-l)®T]Cs/0. (7.99)
Когда частота отличается от резонансной, отдельные источники
уже больше не находятся в фазе и проводимость G равна вели-
чине Go, умноженной на квадрат выражения (7.'87):
G = Go х = (N - 1) £ (7.100)
\ ж / z ;0
Формулы (7.99) и (7.100) переходят в соответствующие выра-
жения из работы [21] при замене ц •• 2Kr:
G0 = 4(AT-l)^Gtot/o, (7.Ю1)
где Cm = QV-l)Gs — полная емкость преобразователя. В действи-
Рис. 7.32. Эквивалентная
злектрическая схема встреч-
ноштыревого преобразова-
теля.
§ 7.2. ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПОВЕРХНОСТНЫХ ВОЛН 307
тельности, поскольку преобразователь излучает еще и объемные
волны (раздел 7.2.3), эквивалентная электрическая схема
(рис. 7.32) содержит дополнительные проводимости. Для согласо-
вания с генератором емкость Ctot нейтрализуется с помощью ин-
дуктивности так, чтобы получился резонанс на частоте /о. Таким
образом, полоса пропускания имеет максимум при определенном
числе электродов, которое зависит от коэффициента электромеха-
нической связи (см. упр. 7.8).
7.2.6. Вопросы технологии. Ширина каждого штыря обычно
равна Х0/4. Для частот, меньших 300 МГц, длины упругих волн в
большинстве материалов превышают 10 мкм, и для изготовления
преобразователей можно пользоваться
хорошо известным в микроэлектронике
методом фотолитографии. Для более
высоких частот ширина штырей стано-
вится порядка длины волн света (при
/о = 1000 МГц % « 3 мкм), и явления
дифракции кладут предел применимо-
сти метода фотолитографии. В этом
случае можно использовать электрон-
ную литографию, поскольку длина вол-
ны, соответствующая электрбнам, оказывается чрезвычайно ма-
лой: % < 1 А для электронов с энергией 10 КэВ.
Насколько нам известно, устройства на поверхностных волнах,
используемые в настоящее время (гл. 9), изготовляются с по-
мощью обычной технологии, разработанной для интегральных
схем [22]. Эта технология имеет ряд вариантов [23] и состоит в
том, что на плоскую полированную подложку (изготовленную из
кристаллического кварца, ниобата лития и подобных материалов
и имеющую форму тонких пластин длиной в несколько сантимет-
ров, шириной порядка сантиметра и толщиной около двух мил-
лиметров) методом напыления в вакууме наносится однородная
металлическая пленка, например, алюминиевая, толщиной 6000 А.
Затем в специальной центрифуге пленка металла покрывается
фоторезистом. На покрытую фоторезистом металлическую пленку
накладывается фотошаблон с изображением преобразователя, фо-
торезист засвечивается через шаблон и при этом полимеризуется.
При последующем химическом травлении фоторезист, а затем и
металл в незасвеченных местах удаляются. Фотошаблон изготов-
ляется в крупном масштабе (например, 1X1 м2) с помощью ко-
ординатографа. По возможности оба преобразователя, входящих
в устройство, изготовляются одновременно.
Метод электронной литографии еще не вышел из стен лабора-
тории [24]. Для него требуется оборудование, аналогичное скани-
20*
308 ГЛ 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
рующему электронному микроскопу. Метод состоит в том, что
покрытая резистом металлизированная подложка «засвечивается»
с помощью пучка электронов (сечение пучка меньше 500 А). По-
рядок операций может быть следующим [25]. Нанесение на изоли-
рующую подложку тонкой алюминиевой пленки (200 А), необхо-
димой для ликвидации статического электрического заряда по-
верхности, нанесение тонкого слоя резиста (пленка толщиной
-* ,4000 А из полиметилметакрилата), облучение пучком электронов
(20 КэВ) по программе, автоматически воспроизводящей изобра-
жение преобразователя [261, селективное химическое травление
засвеченного резиста, повторное нанесение алюминиевой пленки
(~1500 А) на протравленный металл и на остатки резиста, раство-
рение резиста, покрытого алюминием (при этом остаются лишь
те участки напыленного металла, которые соответствуют штырям
преобразователя), ионная бомбардировка всей системы для удале-
ния остатков тонкой металлической пленки алюминия между
штырями, в процессе которой толщина штырей уменьшается.
При использовании этой технологии удалось создать преобра-
зователи, работающие на частотах до 3500 МГц [27]. В таких
преобразователях ширина штыря составляет примерно 0,15 мкм.
Целесообразность использования устройств с подобными преобра-
зователями остается под вопросом из-за больших потерь на высо-
ких частотах (>10- дБ/мкс для LiNbO3). По-видимому, трудно
практически использовать частоты выше 1500 МГц. Отметим еще
другой тип преобразователя, так называемый решетчатый [28].
Он состоит из последовательности электрически изолированных
параллельных металлических штрихов, причем первый и послед-
ний штрихи служат электродами. Для некоторой заданной шири-
ны штриха такой преобразователь имеет резонансную частоту,
в два раза превышающую частоту аналогичного по размерам
встречноштыревого преобразователя. Таким образом, решетчатый
преобразователь проще по конструкции, но он имеет большие
потери.
В случае преобразователей, изготовленных методом литогра-
фии, все устройство, независимо от рабочей частоты, помещается
в корпус с осушителем для предохранения от пыли и влаги.
Упражнения
7.1. Каков акустический импеданс в точке х == 0 у пластинки толщиной
х = d (рис. 7.2)? Рассмотреть случаи di = Хм/2, dt =
Решение. Для 0 < х < dt смещение п напряжение равны соответ-
ственно
• u = 4e«“'-te) + B^at+hx\ Т = сы^
УПРАЖНЕНИЯ
акустический импеданс
-т Ac~ihx ~~B(>ikx
т ~ и ~~ м Ае~гкх + Ве’Лх
равен Z для х — dh а коэффициент
В
Тогда для х — 0 акустический импеданс
Z + iZM tg
ZT = zm ZM+ iZ tg dx ’
откуда получаем:
для dx = XM/2 (/cdx = л): Zr(0) = Z,
для d1 = XM/4 (kd1 = л/2): ZT (0) = 2?M/Z.
7.2. Пусть имеется бесконечно длинный пьезоэлектрический брусок
ширины L и толщины I < L. На него нанесены электроды так, что воз-
буждается продольная волна, распространяющаяся вдоль оси х3 (рис. 7.33).
Какова скорость этой волны? Воспользоваться методом, изложенным в
разделе 7.1.2в, и построить эквивалентную схему для пластинки с дли-
ной d.
Решение. Механическое напряжение и электрическую индукцию
можно выразить через компоненты деформации 5зз = диз/дхз и электри-
ческого поля ECSi. 0. О'):
следует, что скорость волны V = (с^/р)1/2, поскольку Ei не зависит от х3
(плоскости «1 = 0 и xt — I являются эквипотенциальными). Введем упро-
щенные обозначения: я3 — х, и3 = и, Еу = Е, Dt = D, с^3 = с, е^= г, е13=
= е = he, TS3 = Т = —FHL. Из уравнения (7.102) следует, что для опре-
деления сил, действующих на плоскостях х == 0 и х == d, к выражениям
(7.28) нужно добавить постоянный член
eElL = hmCov, (7.104)
где m = 1/d, Со = eLdll, v El.
310
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
Ток можно выразить как 1 = dQldt = UaQ, где Q — заряд на электроде,
расположенном при xi = О,
Q = J Dds = L J Ddx = LdzE — Le {ui —
Если ввести скорости на каждой из поверхностей: Si = ccoui (при
х — 0) и Й2 = icowa (при х = d), то выражение для тока примет вид
1 = iaCov — hmC0(Hi — й2),
(7.105)
и эквивалентная схема, вытекающая из формул (7.104) и (7.105), не со-
держит уже емкости — Со, а коэффициент трансформации W = hmC0.
7.3. Как с изменением номера п = 2р +1 изменяется относительная раз-
ность 8Я= (/”’ - между частотами резонанса и антирезонанса?
Решение. Поскольку /(ап) =/ап и Дп) = nfa (1 — еп), левая часть
выражения (7.33) принимает вид
- АП) г2
*2 г т; = ~та—i ~ я— (так как еп < !)•
lnsn
Отсюда
4Z£2
7.4. Показать, что эквивалентная схема резонатора, имеющего форму
бруска (упр. 7.2), вблизи резонанса сводится к схеме, изображенной на
ПТ.» 7 OZ Т — П
рис. 7.34. Вычислить w Ci.
Решение. Импеданс во вторичной цепи транс-
са a>r = nV/d равен
„ _ iZ inZ
2tg[я(1 + e)/2) ~ 4 8’
где 8= (co — ©r)/cor. Это выражение аналогично выра-
жению для импеданса контура вблизи частоты резо-
где Z = я278со, и '§’ = 8/л^сог.
При пересчете в первичную цепь трансформатора.с коэффициентом
трансформации N = /гтаСо = eL получим
с ^d 8с2 e.sLd 8 К2 _1К2ГТ
-n^vziL'nW г 'n2i-x2Co"n’- со’
где =(eT/es) CQ— емкость при постоянном (нулевом) механическом
напряжении, а
Z____plLd масса
<^7 уьпа маииа
1 = Jv2= 87V5’= 8№
УПРАЖНЕНИЯ
311
встречноштыревого преобразователя,
Рис. 7.35.
Численные оценки; I = 0,5 мм, L = 4 мм, d = 10 мм, ет = 4 • 10 11 Ф/м,
е = 0,1 Кл/м2, р = 3 • 103 кг/м3, X2 = 10"3, т. е. Со — 3,2 пФ, Ct ==
= 2,6 • 10-3 пФ, Li = 47 Гн.
7.5. Считая, что волны Рэлея возбуждаются однородно и в строго огра-
ниченной области под электродами -------------------
изобразить импульсный отклик:
1) преобразователя с тремя электро-
дами, 2) линии, состоящей из воз-
буждающего преобразователя из трех
электродов и приемного преобразо-
вателя из четырех электродов.
Решение. 1) рис. 7.35, а,
2) корреляция сигналов рис. 7.35, а ________
и б, т. е. рис. 7.35, в.
7.6. Два одинаковых преобразователя Т\ и Тг, разделенные расстояни-
ем Z, излучают вдоль одной прямой в обоих направлениях волны частоты /0.'
Как выбрать I и разность фаз напряжений, питающих преобразователи
и Ti, чтобы система из двух указанных преобразователей излучала волны
только в одном направлении?
Решение. В одном из направлений электрическая (ф) и простран-
ственная (ф) разности фаз складываются, в другом — вычитаются. Преобра-
зователь будет однонаправленным, если
ф + ф == л и ф —= 0, т. е. ф = ф = л/2 или I = W4 — V/4 fo-
7.7. Линия задержки состоит из возбуждающего преобразователя, состо-
ящего из W наклонных электродов -----------------------------'
(N > 1), и из прямого приемного преоб-
разователя (рис. 7.36). Какова частот-
ная характеристика этой линии, если
степень наклона 0П преобразователя
изменяется линейно с координатой
хп = пХо/2 в пределах от —0о до +0О
(0о мало)? См. [29].
Решение. Разлагая каждый из
источников на элементы dy, для сигна-
ла, соответствующего n-му источнику,
получаем
волны, излученной прямым преобразователем с длиной Ъ:
— амплитуда
Если велико, то распределение источников является квазинепрерыв-
ным и частотный отклик Н (со) (~ 1)п Ап = 2 Ап cos (—Т-2) можно
312
ГЛ. 7. ВОЗБУЖДЕНИЕ И РЕГИСТРАЦИЯ УПРУГИХ ВОЛН
выразить с помощью интеграла
II (со) = j А (.г) cos j -j-,
где
. /&0(ж)со\
2^)
А № - V &В(Ж)Ю
2V
(здесь опущено среднее время запаздывания т = 1/V). В случае линейного
изменения угла наклона 0 = 2 Qqx/L получим
В силу того, что N > 1, область интегрирования можно расширить до
± оо, а частоту в множителях вида (sin а)/а, входящих в подынтегральное
выражение, допустимо считать постоянной и равной со — ио (так как поло-
са пропускания узкая); частотный отклик рассматриваемой системы выра-
жается с помощью фурье-образа функции (sina)/a с несущей:
Я(<6)=у- | cos 2nfotei2!lftdt,
где t — xlV r В = 2bQ0faIL. Таким образом, частотная характеристика
/7 (со) является прямоугольной с центральной частотой ± f0 (раздел 1.3.2):
и с -относительной полосой £//e = 2b0o/Z- = 4&0о/[ (А7 — 1)Хо].
7.8. Каково число No электродов, обеспечивающее максимальную отно-
сительную полосу пропускания в случае простого преобразователя, согла-
сованного с помощью индуктивности? В качестве примеров рассмотреть
LiNbO3 (FZ-срез) и SiOs (FX-срез), а численные данные взять из матри-
цы (6.18).
Р е ш е н и е. Согласно выражению (7.37) эффективная акустическая до-
бротность Qa = (N— 1)/1,77. Электрическая добротность, обеспечиваемая
согласованием, выражается следующим образом (см. (7.101)):
= £tot%= л
Go 2(N-1)K2R‘
Если N велико, то Д///о = UQa, если N мало, то А///о = 1/(?е. Относительная
полоса Д///о максимальна при Qa = Qe. Отсюда
Для LiNbO3: No = 9, (Д///о)тах — 0,23; для SiO3: -Vo = 37, (Д///о)тах
0,05.
ГЛАВА 8
ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
Процесс взаимодействуя упругих волн со светом был изучен
теоретически Л. Бриллюэном еще в 1922 г. [11 *). Первые экспе-
рименты выполнили в 1932 г. Р. Люка и П. Бикар [2] во Фран-
ции и Ф. Сирс [3] в США.
Дифракция света на ультразвуке, обнаруженная в этих экспе-
риментах, использовалась в дальнейшем главным образом для
измерения скорости распространения упругих волн в различных
материалах. Верхний предел частоты ультразвука был при этом
порядка 30. МГц.
С появлением таких новых элементов, как лазер и акустиче-
ский СВЧ преобразователь (§ 7.1), для акустооптического взаимо-
действия открылась новая область применения, связанная с воз-
можностью быстрого и значительного изменения интенсивности,
направления и даже частоты светового луча. С другой стороны,
дифракция света на ультразвуке по-прежнему остается важным
методом измерения количественных характеристик (однородности,
затухания, пространственного распределения) потоков упругих
волн, распространяющихся в твердых телах. Световой луч в этом
случае играет роль зонда, проникающего внутрь твердого тела.
Настоящая глава начинается с краткого обзора особенностей
распространения света в кристаллах, затем вводится и определя-
ется фотоупругий тензор и излагаются основные результаты тео-
рии взаимодействия света с упругими волнами. Однако прежде,
чем переходить к общим вопросам акустооптического взаимодей-
ствия, представляется полезным уточнить, при каких условиях
реализуются различные виды дифракции света на звуке. Эти виды
дифракции обычно известны как эффекты Бриллюэна, Дебая —
Сирса, Люка и Бикара, Рамана — Ната и Брэгга.
*) Независимо этот вопрос исследовался Л. И. Мандельштамом: Ман-
дельштам Л. И.— Жури. Русск. физ.-хим. об-ва, 1926. т. 58, с. 381. (Прим,
ред.)
314
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
§8.1. Основные виды дифракции света на звуке
Следует различать три основных случая дифракции.
Первый из них изображен на рис. 8.1. Диаметр светового пуч-
ка меньше длины волны звука, и плавное изменение показателя
преломления приводит лишь к изгибу световых лучей (эффект
миража).
Второй вид дифракции представлен на рис. 8.2. В этом случае
ширина светового пучка велика по сравнению с длиной звуковой
волны. Периодическое изменение показателя преломления при-
Рис. 8.1. Отклонение свето-
вых лучей, вызванное уп-
ругой волной.
Световой пучок А, прохо-
дящий через участок с уве-
личенным значением пока-
зателя преломления, схо-
дится, а пучок В, проходя-
щий через участок с умень-
шенным значением показа-
теля преломления, расхо-
дится.
Рис. 8.2. Эффект дифракционной решетки.
Когда ширина светового пучка велика по
сравнению с длиной волны звука, из-за от-
клонения световых лучей образуется несколь-
ко источников а, Ъ, ... [2]. Интерференция
волн от этих источников приводит к тому,
что дифрагированное излучение наблюдает-
ся только в определенных направлениях. Та-
кую картину можно также объяснить, если
рассматривать фазовые сдвиги света, вызван-
ные бегущей волной изменения показателя
преломления.
водит к появлению световых лучей, имеющих различные направ-
ления и интенсивности. Это явление можно объяснить, если пред-
положить, что из-за искривления световых лучей образуется
несколько фокусов, которые начинают действовать как источни-
ки [2]. Интерференция волн, излучаемых различными источника-
ми, приводит к формированию отдельных световых лучей. Это
явление можно объяснить также, если рассмотреть фазовые сдви-
ги, приобретаемые световой волной в среде, где распространяется
волна изменения показателя преломления [4]. Именно такой точ-
§ 8.2. РАСПРОСТРАНЕНИЕ СВЕТА В КРИСТАЛЛАХ
315
Рис. 8.3. Режим Брэгга,
При вполне определенном угле
падения и при условии, что све-
товые лучи пересекают несколько
идентичных волновых фронтов,
наблюдается единственный ди-
фрагированный световой луч,
а все остальные гасятся из-за ин-
терференции.
ки зрения мы и будем придерживаться. Читателя, интересующе-
гося более общим теоретическим рассмотрением данного вопроса,
основанным на непосредственном решении уравнений Максвелла,
мы отсылаем к работам, указан-
ным в списке литературы к этой
главе.
В третьем случае (рис. 8.3)
угол между световым лучом и на-
правлением звукового потока, а
также ширина звукового пучка
выбраны так,, что после диф-
ракции выходит только один луч
света, а все остальные гасятся
из-за интерференции.
Термин «эффект Бриллюэна»
относится вообще к любому слу-
чаю взаимодействия электромаг-
нитных и упругих (когерентных
пли некогерентных) волн. Эффек-
ты Дебая — Сирса, Люка — Бика-
ра, Рамана — Пата представляют
собой второй из рассмотренных
видов дифракции (в разных стра-
нах используются разные назва-
ния). Третий вид часто называется эффектом Брэгга из-за сход-
ства с дифракцией рентгеновских лучей на кристаллической ре-
шетке.
§ 8.2. Распространение света в кристаллах
При прохождении света через кристаллы наблюдается двупре-
ломление, связанное с естественной анизотропией кристаллов. Так,
например, пластина кальцита (СаСО3) расщепляет падающий луч
света на два луча с взаимно перпендикулярными поляризациями.
Анизотропия, вызывающая двупреломление, может быть усилена
или даже создана в изотропных средах или в кристаллах кубиче-
ской системы с помощью некоторых внешних «сил», таких, на-
пример, как электрическое поле (электрооптический эффект) или
же механическое напряжение (фотоупругий или акустооптиче-
ский эффект, который нас и интересует).
При изучении распространения света в кристаллах удобно
пользоваться так называемой оптической индикатрисой или по-
верхностью показателей преломления, которые получаются из
уравнений Максвелла (уравнений распространения электромаг-
нитных волн). Изложим кратко основные необходимые сведения
из этой области.
316 гл. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
8.2.1. Оптическая индикатриса. В изотропной среде свет, неза-
висимо от направления, распространяется со скоростью
Р = _1= = _Д==_1= = _2Х= = А,
/80[х„ /егрг /егрг п
где е0 и Цо — диэлектрическая и магнитная проницаемости ва-
куума, в, ц, Ег — е/е0, цг = ц/цо — абсолютные и относительные
проницаемости вещества соответственно, а п = Уегцг — показатель
преломления вещества. Для немагнитных материалов ц, = 1 и
п — 1/ег. В настоящей главе мы будем пользоваться лишь относи-
тельной диэлектрической проницаемостью. Для упрощения записи
будем опускать индекс г. Оптическая индикатриса для изотропной
среды
4 + 4 + 4 Х1 1
е п2
или Вх 1= 1, где В = 1/е представляет собой сферу.
Диэлектрические свойства анизотропной среды описываются
симметричным тензором е« или же обратным тензором Вц, назы-
ваемым тензором непроницаемости
= (8.1)
В этом случае оптическая индикатриса определяется уравнением
BijXtXi = 1. (8.2)
Используя соотношение — еоецЕ; и решая уравнения Мак-
свелла, получим, что в данном направлении могут распространять-
ся две плоские волны, поляризованные во взаимно перпендику-
лярных направлениях и имеющие различные скорости. Направле-
ния поляризации и скорости этих волн можно найти из оптиче-
ской индикатрисы.
Направления векторов электрического смещения указанных
двух волн, D(1) и D(2), совпадают с осями эллипса, который полу-
чается при сечении оптической индикатрисы экваториальной пло-
скостью* Р, перпендикулярной волновому вектору К (рис. 8.4).
Показатели преломления, соответствующие двум скоростям волн,
равны длинам полуосей этого же эллипса.
Оптическая индикатриса обладает, очевидно, симметрией рас-
сматриваемого кристалла, и все кристаллы по их оптическим
свойствам можно разбить на три группы. К этому же выводу
можно прийти, рассматривая симметричный тензор Вц и число
его ненулевых компонент с учетом симметрии кристалла (раз-
дел 3.4.3).
Двуосные кристаллы. У таких кристаллов отсутствуют оси сим-
метрии выше второго порядка, и они относятся к триклинной, мо-
§ 8.2. РАСПРОСТРАНЕНИЕ СВЕТА В КРИСТАЛЛАХ
317
иоклинной и ромбической системам. Поскольку три главные оси
эллипсоида являются осями симметрии второго порядка, то если
у кристалла имеется одна или три такие оси, они должны совпа-
дать с одной или тремя осями эллипсоида. В триклинных кристал-
лах в общем случае ориентация оптической индикатрисы не свя-
зана с симметрией кристалла. В систе-
ме главных осей уравнение оптической
индикатрисы имеет вид
Рис. 8.4. Оптическая инди-
катриса.
Вдоль направления К мо-
гут распространяться две
волны с взаимно перпенди-
кулярными поляризациями
и D<2> и со скоростями
Р] = Ро/тД1) и v2 = Ро/га<^
соответственно.
где nt, п2, п3 *) — главные значения по-
казателя преломления, численно равные
длинам полуосей эллипсоида. Обычный
эллипсоид имеет два круговых эквато-.
риальных сечения, симметричных от-
носительно двух главных осей и содер-
жащих третью ось. Нормали к этим
сечениям являются оптическими ося-
ми. Для волн, распространяющихся
вдоль оптических осей, существует
только один показатель преломления
(соответствующий радиусу круга сечения), направление поля-
ризации может быть любым, а скорость всех волн одинакова,
т. е. для этих направлений отсутствует двупреломление. При рас-
пространении света вдоль оптических осей кристаллы ведут се-
бя как изотропные тела.
Одноосные кристаллы. У этой группы кристаллов (тригональ-
ной, тетрагональной и гексагональной систем) имеется ось сим-
метрии Ап порядка выше второго (я > 2). Одна из главных осей
эллипсоида совпадает с Ап и является его осью вращения. Если
волна распространяется вдоль Ап, то ее волновой фронт пересека-
ет оптическую индикатрису по кругу, поэтому направление поля-
ризации произвольно, показатель преломления имеет единствен-
ное значение (равное радиусу получающегося в сечении круга),
и кристалл ведет себя как изотропное тело, т. е. ось Ап является
оптической осью. Таким образом, оптическая индикатриса одно-
осных кристаллов определяется двумя числами п0 и пе, где п0 —
показатель преломления для обыкновенного луча, равный ради-
усу кругового сечения, а пе — показатель преломления для не-
обыкновенного луча, равный длине полуоси эллипсоида в направ-
*) В предыдущих главах индексами К, тц, п2, п3 обозначались соответ-
ственно коэффициент связи и компоненты направления распространения.
Поскольку в данной главе указанные величины не используются, это не
должно привести к недоразумениям.
318 ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
лении Ап. Уравнение оптической индикатрисы для одноосного
кристалла имеет вид
Если пе > По, эллипсоид вытянут вдоль оптической оси, и со-
ответствующие кристаллы (например, кварц) называются поло-
жительными одноосными, если же пе < п0, эллипсоид сжат вдоль
оптической оси, и кристаллы называются отрицательными одно-
осными. В упр. 8.1 показывается, что в случае распространения в
одноосном кристалле двух волн, поляризованных во взаимно пер-
пендикулярных направлениях, показатель преломления для одной
из них не зависит от направления распространения и всегда ра-
вен По, в то время как для другой волны он изменяется от
По ДО Пе.
Оптически изотропные кристаллы. Кристаллы этой группы
имеют несколько осей симметрии выше второго порядка и при-
надлежат, следовательно, к кубической системе (44s). Оптиче-
ская индикатриса в этом случае имеет несколько осей вращения,
т. е. она вырождается в сферу, определяемую единственным пока-
зателем преломления. В этих кристаллах, как в стекле или жид-
кости, световая волна, независимо от направления, распространя-
ется с одной и той же скоростью и сохраняет заданную поля-
ризацию.
Следует сделать два замечания. В отличие от того, что для на-
глядности обычно изображается на рисунках, разность между зна-
чениями пе и По всегда мала, а следовательно, оптическая инди-
катриса весьма близка к сфере. Для кварца, например, п0 = 1,5442,
а пе = 1,5533. Диэлектрические проницаемости зависят от частоты.
Каждому диапазону частот соответствует своя оптическая индика-
триса. В пьезоэлектрическом материале значения диэлектрических
констант, определяющих оптическую индикатрису, отличаются от
значений, которые используются при вычислении скорости звука.
8.2.2. Поверхность показателей преломления. Как следует из
предыдущего изложения, длина радиус-вектора для оптической
индикатрисы пропорциональна показателю преломления волны,
поляризованной в данном направлении. Этим объясняется широ-
кое применение оптической индикатрисы при анализе оптических
явлений. Другой полезной поверхностью является поверхность по-
казателей преломления (поверхность волнового вектора), для по-
строения которой вдоль волнового вектора откладываются отрезки,
пропорциональные показателям преломления. Поскольку показа-
тель преломления обратно пропорционален скорости, поверхность
показателей преломления имеет такой же смысл, как поверхность
§ 8.3. ФОТОУПРУГИЙ ТЕНЗОР
319
медленности в теории упругости. Поверхность показателей пре-
ломления является двуполостной, так как в каждом направлении
могут распространяться две волны с взаимно перпендикулярными
поляризациями (и разными скоростя-
ми). На рис. 8.5 приведена поверх-
ность показателей преломления для по-
ложительного одноосного кристалла.
Двуполостная поверхность показате-
лей преломления распадается на сфе-
ру и эллипсоид. Сфера соответствует
обыкновенной волне, которая, вне за-
висимости от направления, всегда рас-
пространяется со скоростью у0 = v0/no.
Сфера и эллипсоид касаются друг дру-
га в двух точках, лежащих на опти-
ческой оси, а длина второй полуоси эл-
Оптичесяая ось
Рис. 8.5. Поверхность пока-
зателей преломления поло-
жительного одноосного
липсоида равна пе. Направление рас-
пространения энергии перпендикуляр-
но поверхности показателей преломле-
ния и в случае эллипсоида составляет
некоторый угол а с волновым векто-
ром, Очевидно, что а зависит от нап-
равления распространения волны и об-
ращается в нуль только в направлении
главных осей. Особенно удобно поль-
кристалла (пе > п0).
Эта поверхность получает-
ся, если вдоль данного на-
правления К откладывать
отрезки, равные =
= no = const и nW. Не-
обыкновенный луч составля-
ет с направлением К угол
а, который обращается в
нуль только при 0 = 0 и
зоваться поверхностью показателей
преломления для построения хода преломленной волны по извест-
ной падающей (диаграммы волновых векторов в разделе 8.4.2).
§ 8.3. Фотоупругий тензор
Оптические свойства невозмущенного кристалла описываются
оптической индикатрисой, соответствующей уравнению
BijXtXj = 1.
Деформация кристалла приводит к изменению оптической ин-
дикатрисы и, следовательно, к изменению ДВ« тензора Bi}, при
этом следует различать два основных случая. В первом случае
деформация кристалла не приводит к повороту отдельных элемен-
тов его объема, а может иметь место лишь поворот всего кристал-
ла как целого. Во втором случае при деформации может проис-
ходить поворот отдельных элементов объема кристалла, при этом
происходит и локальный поворот оптической индикатрисы, раз-
личный для разных элементов объема. Для пьезоэлектрических
кристаллов, кроме того, в фотоупругом эффекте появляется допол-
320 ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
нительный вклад, обусловленный электрооптическим взаимо-
действием.
8.3.1. Теория Поккельса. Эта теория справедлива для оптиче-
ски изотропных непьезоэлектрических кристаллов (кубические
классы тЗт, m3, 432) или в случае однородной статической де-
формации и деформации, создаваемой продольной упругой волной.
Тогда величину Д5« можно выразить через деформацию Su:
^Btj = piihlSht. (8.5)
Безразмерные коэффициенты pi}ki являются компонентами фото-
упругого тензора четвертого ранга.
Величину Д5У можно выразить и через компоненты тензора
механического напряжения Ты:
\Btj = ЯдаТы. (8.6)
Тензор Яда называется пьезооптическим. С помощью закона Гука
Гу ==
можно получить соотношение:
Pijmn — ftijhlChlmn- (8.7)
Поскольку тензоры 5У и Skt симметричные, можно, как и в
§ 4.3, воспользоваться сокращенной записью:
В ц = Ва,
s =(Ski при0<3,
Р \2Ski при (3 > 3 .
В матричной форме уравнение (8.5) принимает вид
Д5а = РаЛ, • (8.8)
где Ран = Рим при а, ₽ = 1, 2, ..., 6.
Следует, однако, заметить, что в общем случае р^ не равно
ps<x в отличие от модулей упругости, для которых из термодинами-
ческого потенциала вытекает симметрия по перестановке индексов
а и р (§ 4.4). Таким образом, фотоупругий тензор для триклин-
ной системы содержит 36 независимых компонент. Симметрия
кристалла приводит к уменьшению числа компонент тензора, что
можно показать, используя метод, изложенный в § 4.5. Матрицы
компонент тензора фотоупругости представлены на рис. 8.6, они
имеют такой же вид и для пьезооптического тензора Яда. Справа
внизу около каждой матрицы дано число независимых компо-
нент тензора. Для установления связи с компонентами nOfj, опре-
деляемыми из соотношения Д5а = яарГр, необходимо иметь
§ 8.3. ФОТОУПРУГИЙ ТЕНЗОР
321
Рис. 8.6. Таблица фотоупругих коэффициентов раъ (теория Поккельса).
• О —компоненты, не равные нулю, равные компоненты, • —
компоненты, равные нулю, •—О—компоненты, равные по абсолютной ве-
личине, но противоположные по знаку, X — компоненты, равные
(Рп—Р12)Д
21 Э. Дьелесан, Д. Руайе
322
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
в виду, что
Лап = луы при р 3, Ла₽ = 2л«м при 0 > 3. (8.9)
Фотоупругие коэффициенты для большинства практически ис-
пользуемых веществ довольно мало различаются между собой й
находятся в пределах 0,2—0,3, как это видно из табл. 8.1. Таким
Таблица 8.1. Фотоупругие коэффициенты для некоторых веществ,
измеренные по дифракции света с Ло= 0,6328 мкм
(в случае кварца Ао~~О,589 мкм)
Вещество Ри Р12 Рг, p!2 P13 p,t Pas Pss Pss Pu
Кварц плав- леный а-НЮ3 0,121 0,406 0,270 0,277 Р12 0,279 Pu 0,343 P12 0,304 Pit 0,503 Pu 0,334 Pu 0,305 P12 0,310 0 0
РЬМоО* (4/т) TiO2 0,24 0,24 Р12 Pn 0,255 0,175 0,300 P1S Psi 0
0,011 0,172 Pit Pn 0,168 0,096 0.058 Pis Psi 0
(i/mmm) ТеО2 (422) LiNbOg 0,007 0,187 Pit Pn 0,340 0,090 0,240 Pis Psi 0
0,036 0,072 Pit Pu 0,092 0,178 0,088 P13 Psi 0,07 ♦)
TJTaOs 0,080 0,080 Pit Pn 0,094 0,086 0,150 Pis Psi 0,031
(3m) а-кварц (32) 0,138 0,250 Pit Pu 0,259 0,258 0,098 i »13 Psi -0.029
Вещество Ри Pit Pu Pu Psi P«< Литерату- ра
Кварц плав- леный a-HIOs 0 0 [- -0,075] 0 0 Pu 0 0 0 0 Pu 0,092 [5] [6]
PbMoO4 (4/m) TiO2 (4/ттт) ТеО2 (422) LiNbO3 0 0,067 -0,01 Pu 0,017 0,013 0,05 [14], гл .4
0 0 -0,17 0 0 Pu Pu 0 0 0 0 -0,046 [7] [8]
0,155 — 0 Pu 0 0 [-0,018] [7]
ЫТаО3 0,024 0,022 0 Pu 0 0 [0,00] [7]
(3m) а-кварц (32) —0,042 -0,068 0 Pu 0 0 [- •0,056] [9]
*) Значение определено в работе [32]. Значения фотоупругих коэффициентов в квадратных скобках равны <Pit-Pis)/2.
§ 8.3. ФОТОУПРУГИЙ ТЕНЗОР
323
образом, для типичной деформации S —10“’ величины A5(j ока-
зываются весьма малыми, порядка 10_в.
Для дальнейшего полезно установить связь между величинами
\Вц и Ае». Поскольку рассматриваемые изменения AS,* и Ае«
тензоров Bih и еи малы, их можно получить дифференцирова-
нием уравнения (8.1), определяющего тензор Bjk\
Ае,Д* + ЕуАВЛ = 0.
Умножая это уравнение на ew и учитывая, что 5дЕ*( = б,7, полу-
чаем Дей = — ЕуАбдЕы или, используя (8.5),
Аё,7 = —^iiPikmn^klSmn- (8.10)
В качестве примера вычислим величины Ав« и Ап в случае
деформации Stt в кубическом кристалле класса тЗт. Диэлектри-
ческий тензор кубического кристалла можно представить в фор-
ме E<j == вбу, так что
Авй “ &2pilmnSmn
или, конкретно для деформации 51 и
Ае« = -s2p((115u.
Как следует из рис. 8.6, для кристаллов класса тЗт отличны от
нуля только фотоупругие коэффициенты р1Ш = ри, р22и = Pit и
Рззи = Pit- Соответствующие изменения диэлектрической прони-
цаемости выражаются следующим образом:
Авц = —Е2рц5ц, Ае22 = Аезз = — &2Р1г8ц,
причем Ае« = 0, если
Поскольку тензор в« остается диагональным, осями координат
являются главные оси оптической индикатрисы деформированного
кристалла. Главными значениями показателя преломления будут
И^Уе + АЕи, п2 = Из = Ve + Aez2.
Изменения Аей малы, а п = Уе, так что
Ki № П^1 -)-= И “Ь
где Ап( = Дей/2и, или
Ап1=--уРи^и. <8Л1>
Дп2 = Дп3=-4-р125и. (8.12)
Кристалл становится одноосным с оптической осью вдоль оси
Xi. Световая волна с произвольной поляризацией, распространяю-
щаяся вдоль направлений х2 и х2, испытывает двупреломление.
21*
324 ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
Однако если падающая волна поляризована вдоль главной оси,
то при прохождении кристалла поляризация не изменяется. Вол-
на испытывает только отставание (опережение) по фазе, если
показатель преломления вдоль данной оси возрастает (убывает).
При последующем изложении (§ 8.4) мы будем иметь в виду
только этот случай.
8.3.2. Теория Нельсона и Лэкса. Если при деформации возни-
кают локальные повороты, как это происходит в случае распро-
странения сдвиговых волн, то требуется более общее рассмотре-
ние фотоупругого тензора [10]. В уравнении (8.5) шестикомпо-
нентный симметричный тензор 8Ы следует заменить девятикомпо-
нентным градиентом смещения dujdxi
= рцы (8.13)
Полученный таким образом новый фотоупругий тензор pw уже
не является симметричным по двум последним индексам к и I.
Пусть рщЫ) — симметричная часть этого тензора, a pism — его ан-
тисимметричная часть. Так как
Зи.
— SM + Rki, (8.14)
где с помощью антисимметричного тензора
n 1 (duk dui ) „
учитывается локальный поворот, то получаем, что Д5у — (рщы» +
+ Ру[М])('$’ы+Яы), или
АВц == Pij(M)Ski "I" PijtkijRkh (8.15)
поскольку произведение симметричного тензора на антисиммет-
ричный обращается в нуль.
Сравнение уравнений (8.5) и (8.15) показывает, что симмет-
ричная часть pijW тождественна тензору рцы- Антисимметричная
часть рти], которая относится исключительно к локальному пово-
роту оптической индикатрисы, может быть выражена через ком-
поненты тензора Вц. Действительно, когда бесконечно малый эле-
мент объема испытывает локальный поворот, его координаты х(
принимают значения х{, а компоненты Вц превращаются в В'^.
определяемые равенством *)
, дх. дх',
В” = -8^-^ Bhl’
*) Такое преобразование компонент является обобщением преобразова-
ния, описанного в § 3.2, на случай, когда новые координаты не являются
линейными функциями исходных координат.
§ 8.3, ФОТОУПРУГИИ ТЕНЗОР 325
Смещение и4 определяется из соотношения Xi = Xi + щ, следова-
тельно, dx'i/dxi — 64j + dui/dxj. Полагая в уравнении (8.14) Stj —
*= 0, получаем
dx'i/dxj = 6j3- + Rij,
Таким образом, величину Д5^ = Вц — Вц можно представить в ви-
де \Btj= + Rih)(8ji + RjJBu — B(j, Или, если пренебречь члена-
ми второго порядка малости, АВ{) = RikBttj +RsBu и, наконец,
A5i3- = (5«6jk — 5w6«)7?w
Если сравнить полученное выражение с (8.15), в котором поло-
жить Su = 0, то можно видеть, что — это антисимметричная
часть тензора, заключенного в круглые скобки, т. е.
PiHki] — у (BiiSjk + — Bih6ji — Bkfiil). (8.16)
Для всех систем, за исключением триклинной и моноклинной,
главные оси совпадают с кристаллографическими осями, и в этой
системе координат получаем
В и = -у 6ib
ni
где п( = п,, п2, п3 — главные значения показателя преломления.
Уравнение (8.16) принимает вид
Pij[feZ] = 4"(т?' — — (8-17)
и единственными ненулевыми компонентами являются
Р12[Т2] = — Р12[21] =-r(zr~T2')‘
Ргз[23] = — Ргз[32] —-~ (8.18)
Р13[131 = -Р13[31] = — ТгУ
По сравнению с фотоупругим тензором Поккельса измененными
оказываются лишь три последних элемента (pu, pSs, Рее) главной
диагонали матриц на рис. 8.6. В случае изотропной среды и ку-
бических кристаллов изменения вообще отсутствуют (р«ы = рщк)
поскольку П1 — п2 = п3. Для одноосных кристаллов (гексагональ-
ной, тетрагональной, тригональной систем) p12[i'aj = 0, раз[2з] =
— Parisi, поскольку п, = п2. Существующее в теории Поккельса
22 э, Дьелесан, Д. Руайе
326
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
равенство р^-ры, т. е. />2з(2з> — Рщиу (рис. 8.6), распадается па
Два: _ _
Рзззз — Ргз(23) "Г Раз[2з] — Р1313,
(8.19)
Ргз2з= Ргз(2з> — />гз[2з] ~ Р1ззь
В случае ромбических кристаллов существуют все три антисим-
метричных компоненты: p12[i2j, Рззгаз], Pisrisi- В каждой из матриц
вместо этих дополнительных компонент принято ставить кружок.
Например, кристаллам класса 422 будет соответствовать такая
матрица:
Линии, соединяющие точки или кружки, изображают связи меж-
ду компонентами, вытекающие из уравнений (8.19). Фотоупругие
тензоры моноклинного и триклинного классов содержат по 7 и 13
дополнительных компонент соответственно.
Выводы изложенной выше теории были недавно подтвержде-
ны в экспериментах, выполненных Нельсоном с сотрудниками на
рутиле (класс 4/ттт) и кальците (класс Зтп). непьезоэлектри-
ках, обладающих сильным двупреломлением.
Для рутила получены значения [11]:
Р2323 — />1313 = 9 • IO"4, />2332 = />1331 = —255 • 10—4J
для кальцита [12]:
/>2332 ~ />1313 = —И 10“3, />2332 = />1331 = —105 • 10-3.
Уравнение (8.10) для изменения диэлектрической проницаемо-
сти можно легко обобщить:
AeiZ = - 2^Pjkmn ehl. (8.20)
охп
8.3.3. Пьезоэлектрические кристаллы. Электрооптический эф-
фект. Изменения оптической индикатрисы могут быть вызваны и
приложенным к кристаллу электрическим полем. Этот эффект,
называемый электрооптическим, описывается уравнением
Д5« = ГцгЕр.
§ 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ 327
Как и пьезоэлектрический тензор, электрооптический тензор
третьего ранга rilp обращается в нуль в случае центросимметрич-
ных кристаллов.
В пьезоэлектрическом кристалле распространение упругих
волн сопровождается в общем случае возникновением продольно-
го электрического поля. Для направления, параллельного единич-
ному вектору п, это поле может быть определено из уравнения
(6.49)
Е =-п n^kl dUl
Р Р epqnpnqdxk'
Благодаря электрооптическому эффекту возникающее при пьезо-
эффекте электрическое поле в свою очередь вызывает изменения
диэлектрической проницаемости. Поэтому в дополнение к рас-
смотренному выше прямому фотоупругому эффекту в пьезоэлек-
триках возможен еще косвенный (наведенный) фотоупругий эф-
фект, описываемый уравнением
I epqnpnq I dxk
Величина косвенного фотоупругого эффекта определяется мно-
жителем, заключенным в круглые скобки, который зависит от
направления распространения:
spqnpnq
В некоторых случаях вклад от косвенного эффекта может быть
существенным, или даже преобладающим. Например, волна, рас-
пространяющаяся в направлении [111] в кристаллах а-ШО3
(класс 222), вызывает косвенный фотоупругий эффект, причем
Рйп =0,013, в то время как прямой фотоупругий эффект при дан-
ной геометрии отсутствует [13].
§ 8.4. Дифракция света на акустическом пучке
Поскольку тензоры диэлектрической проницаемости и показа-
телей преломления зависят от деформации среды, то упругую
волну в среде сопровождает распространяющаяся с той же ско-
ростью волна изменения показателя преломления. Для того чтобы
выяснить, как это влияет на световые волны, рассмотрим про-
стейший случай, т. е. случай оптически изотропной среды, когда
поляризация света не изменяется. Пусть в изотропной среде рас-
пространяется продольная синусоидальная упругая волна, пучок
монохроматического света направлен перпендикулярно или под
углом Брэгга по отношению к волновому вектору упругой волны,
22*
328
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
а поляризация света параллельна или перпендикулярна этому
вектору.
8.4.1. Нормальное падение. Продольная волна, распространя-
ющаяся в направлении xit вызывает последовательные периоди-
ческие сжатия и разрежения среды, что приводит к увеличению
или к уменьшению показателя преломления по сравнению с его
первоначальным значением п0:
n = n0 + Arasinco^t — (8.22)
где «о — частота, а У — скорость упругой волны.
Световые волны в среде распространяются быстрее (медлен-
нее) там, где показатель преломления меньше (больше). Для све-
товой волны, распространяющейся в направлении х2, справедливо
следующее выражение:
а — A cos kit — пхХ (8.23)
Начало отсчета фазового угла выбрано на передней границе аку-
стического пучка (х2 = 0, рис. 8.7); До —длина волны света в ва-
Вакуум
ботовые
фронты
светового
пучка
вещество Вакуум
Рис. 8.7. Из-за изменения показателя
преломления Ап между точками Pi
и Р2, разделенными расстоянием в
длину волны X, возникает сдвиг фаз
2л. Этот сдвиг фаз определяет угол
наклона 01 волновых фронтов света,
дифрагированного в 1-й порядок и
имеющего частоту £2 + со. Угол 0]
определяется из соотношения
sin 0! = Л/%.
При выходе света из кристалла в
вакуум угол дифракции становится
равен 0°, причем sin 0° = Ло/Х.
кууме. Если пренебречь затуханием, то выражение для световой
волны, прошедшей акустический пучок толщины е, будет иметь
вид
а = A cos + Фо +ДФ sin со (г—^j, (8.24)
где Фо = —(2лпо/Ло)е = —(2л/Л)е —сдвиг фазы волны, определяе-
мый средним значением п0 показателя преломления, а ДФ =
= —(2ле/Ло)Дп —модуляция фазы волны, вызванная переменной
частью Дп показателя преломления.
§ 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ
329
В любой точке на границе акустического пучка (х2 = е, xt =
= const) световая волна оказывается промодулированной по фазе,
и эта модуляция зависит только от времени. Выясним, каков
спектр такой волны. Обозначая t — xJV через т, получим
4 = cos (ДФ sin oat) cos (Qi + Фо) — sin (ДФ sin cot) sin (Qt + Фо).
(8.25)
Выражения cos (ДФ sin <вт) и sin (ДФ sin сот) можно разложить
по функциям Бесселя:
cos (ДФ sin <вт) = Jо (ДФ) + 2 2 ^чр (ДФ)cos 2рсотл
p=i
sin (ДФ sin <вт) = 2 2 ар-i (ДФ) sin (2р — 1) сот.
p=i
Подставляя эти соотношения в (8.25), получаем
4 Jo (ДФ) cos (Qi + Фо) + 2 (дф)2 cos (Qi+ фо) cos’2p®T -
p=i
— 2 4p-i (Дф) 2 sin фо) sin (2Р ~ !)WT-
Замена произведений тригонометрических функций их суммами
приводит к следующему выражению:
4- = J0(A®)cos(Qi+®0) +
+• 2 J^p (Аф) tcos №+2(°<пт+ф«)+cos (Qt ~ 2-р<йт+фо)1 +
Р=1
+ 2 Лр-1 (Дф) [cos (Qt + (2р — 1) ®т + Фо) —
— cos(Qt —(2р —1)сот4-Фо)1
или, в более краткой форме:
-4 = 4 (ДФ) cos (Qt + Фо) +
+ 2 4v(A<I>)[cos(Qi + MoT+ Ф0)-Н-1)*соз^-#©т+Ф0)].
N=1 (8.26)
330
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
Таким образом, спектр световой волны имеет максимум на
частоте Q (несущая) и симметрично расположенные боковые ле-
пестки на частотах Q ±Na, поскольку т = t — xJV, где N — целое
число. Зависимость амплитуд колебаний несущей и боковых ча-
стот от набега фаз ДФ дается функциями Бесселя 70, Jlt h
(рис. 8.8).
В данный момент времени фазовый угол несущей Фо = —2ле/Д
не зависит от Xi, иными словами, волновые фронты параллельны
Рис. 8.8. Функции Бесселя Ja, Jh
J2, ..., характеризующие зависи-
мость амплитуд прямой волны и бо~
новых составляющих более высоких
порядков от набега фаз Дф.
волновым фронтам падающей волны. Это не справедливо для
волн, соответствующих боковым частотам. Например, в случае
волны
Г Лео®, 1
JN (АФ) cos'l(Q + N<b) t + Фо----p-lj
фаза Фу зависит от xiy т. е. от места, где световой луч пересекает
границу акустического пучка. Действительно,
Л ... „ Л®,
Ф№ Фо-------j? = Фо - 2л
где А, — длина волны звука. Интерференция волн одного порядка,
излучаемых на границе акустического пучка (х2 = е), приводит
к их сложению только в случае, если они распространяются под
углом 0К (рис. 8.7). Для волн, исходящих из точек А и Р2 и рас-
пространяющихся под углом 0х, отставание по фазе — (2л/Л)Р1М
из-за разности хода PJM компенсируется первоначальным опере-
жением АФу — (2nN/K)P2Pi, т. е.
- РгМ + 2л-~ Р2РХ = 0
или, поскольку PtM = РзР, sin 0W,
sin0w = JvA (8.27)
Спектральная составляющая порядка N с частотой Q + Mn от-
клоняется на угол 0у (определяемый выражением (8.27)). Что
касается составляющих с частотами Q — Na, то они испытывают
симметричные отклонения (рис. 8.9).
§ 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ
331
Таким образом, синусоидальное изменение показателя прелом-
ления (вызванное упругой волной) оказывает на световую волну
такое же влияние, как фазовая дифракционная решетка. Входя-
щий в кристалл луч света, параллельный волновым фронтам
Рис. 8.9.’ Дифракция света на акустиче-
ском пучке. Нормальное падение.
Падающий луч расщепляется на не-
сколько дифрагированных лучей, сим-
метричных относительно направления
падения.
.Дифрогиробтные
Упругая Полна
упругой волны, распадается на ряд лучей, расходящихся под уг-
лами 0К, симметрично относительно направления падения света.
При этом
sin бдг = ± N -у-.
Для продольных волн частоты 200 МГц в плавленом кварце
и для гелий-неонового лазера (Ло == 0,63 мкм) имеем:
VL = 5,96 • 10s м/с, % = 30 мкм,
Ло = 0,633 мкм, п — 1,46, Л = 0,433 мкм,
sin 0j « 0j = 1,45 • 10-2 рад = 0°50'.
Критическая ширина. Предыдущие рассуждения справедливы,
только если ширина акустического пучка е не превосходит неко-
торого критического значения ес. Действительно, волны с боковы-
ми частотами возбуждаются на всем пути падающей волны, а не
только на границах. Разделим мысленно акустический пучок на
отдельные слои, параллельные направлению распространения Xi,
а затем повторим все предыдущие рассуждения для каждого та-
кого слоя. Тогда для слоев с координатами и х2 +1 боковые
частоты Q + Mb и углы 0к будут одинаковыми (рис. 8.10). Для
каждого порядка просуммируем вклады от этих слоев. Фронт
волны, излученной в точке с координатой х2 под углом 0к в мо-
мент t — l/v, достигает точки (?, в момент времени t, а волновой
фронт волны, излученной в точке с координатой х2 + 1, достигает
в это же время точки Q2. Разность фаз между двумя указанными
волнами составляет
П = -^-(1 —cos0jy)
332
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
или, поскольку мало,

Если расстояние между слоями ZW = V/(A№), то разность фаз
между волнами, исходящими от смежных слоев, равна л (т) = л)
и волны гасят друг друга. Если ширина акустического пучка пре-
вышает 1К, то излучение одного из слоев гасится излучением дру-
Рис. 8.10. Нормальное падение.
Критическая ширина.
Фронт световой волны Л-порядка,
излученной в момент времени
t — l/v в точке с координатой хъ
распространяется под углом 0w
и достигает точки Qi в момент
времени t. Фронт волны ЛГ-поряд-
->• ка, излученной в точке с коорди-
натой хг +I, в тот же момент
времени t приходит в точку Q3.
Сдвиг фаз между двумя этими
волнами
т) = 2nZ( —cos0w)/A »
того слоя, расположенного на расстоянии от первого. В идеале
ширина акустического пучка не должна превышать критической
величины для 1-го порядка, которая равна
e.-^WA.
(8.28)
Чем выше частота, тем труднее выполнить это условие. Напри-
мер, в случае плавленого кварца (Ло= 0,633 мкм) при 100 МГц
ее = 8,4 мм, а при 300 МГц ее = 0,93 мм.
8.4.2. Брэгговская геометрия. С практической точки зрения
случай брэгговской геометрии оказывается наиболее важным, так
как при этом получается единственный дифрагированный луч све-
та. Брэгговская геометрия получается при таком выборе угла па-
дения а, чтобы в результате интерференции складывались только
Рис. 8.11. Наклонное падение.
Для того чтобы волны, возник-
шие от дифракции 1-го порядка
падающих лучей IiPi и /2Р2, при
интерференции складывались, не-
обходимо выполнить условие:
sin а + sin (6 — а) = Л/Л. Сло-
жение волн, возникающих на всем
пути каждого из лучей, происхо-
дит при условии
1 — cos 9 = (Л/Л) sin а, или
а =. 0/2.
§ 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ
333
световые волны с частотой, соответствующие 1-му порядку ди-
фракции (рис. 8.11).
Угол падения. Выясним сначала, какой угол дифракции 6 со-
ответствует выбранному углу падения а. Угол 0 можно найти из
условия, что для световых волн, исходящих из точек Л и Pt
(рис. 8.11), отставание по фазе из-за разности хода должно ком-
пенсироваться опережением, вызываемыми модуляцией показателя
преломления звуковой волной:
Р Р
—д~ (/’А)11А11/<г)+2л * 8 = О
или
sin а + sin (0 — а) = ЛА. (8.29)
Потребуем, кроме того, чтобы волны, исходящие из точек Р2
и Р3, независимо от величины I, всегда были в фазе. Выражение
для разности фаз между волновыми фронтами Q2 и Qz в данный
момент времени t включает член, учитывающий распространение
световой волны под углом, (2л//Л)(1 — cos0), и член, связанный
с упругой волной, (—2л7А) sin а:
0_7/1 —cosO sin ст
П-2лЦ—-------------— )•
Эта разность фаз обращается в нуль при любых I при условии,
что
1 — cos 0 = у sin а.
С учетом (8.29) предыдущее уравнение переходит в
Л п . е /0 \
— =2 sin у cosi-g— а),
если
.9 /О V
sin у = cos I "2— а I sin а.
Это уравнение удовлетворяется при а == 0/2, тогда
зп1а = Л/2Х = Л//2У. (8.30)
Волновые фронты упругих волн служат как бы зеркалами, от ко-
торых отражается падающий пучок света (рис. 8.12). Условие
(8.30), совпадающее с соотношением при дифракции рентгенов-
ских лучей на кристаллической решетке, называется условием
Брэгга. Если угол падения удовлетворяет условию Брэгга, то
дифракция происходит только в 1-й порядок. Конечно, падающая
волна с несущей частотой на всем своем пути возбуждает волны
всевозможных порядков, но только для 1-го порядка при интер-
ференции происходит сложение волн, для всех остальных поряд-
ков волны гасятся. Эффект сложения интерферирующих волн бу-
дет тем сильнее, нем большее числЬ волновых фронтов звука
334 гл. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
пересекает световой луч. В случае малых а указанное обстоя-
тельство приводит к условию
еа > К или е > 2Х7Л = 2ее.
Рис. 8.12. Режим Брзгга.
Световой луч должен пере-
секать несколько волновых
фронтов упругих волн.
Следует отметить, что если луч света падает в направлении,
симметричном показанному на рис. 8.12, то дифрагированный в
1-й порядок свет будет иметь частоту Q — со.
Интенсивность дифрагированного
луча. Коэффициент акустооптической
добротности. Для сравнения акустооп-
тических свойств различных материа-
лов удобно ввести коэффициент аку-
стооптической добротности, показыва-
ющий, какая часть света, падающего
под углом Брэгга, отклоняется в про-
цессе дифракции. Пусть Ао и А(х2) —
амплитуды падающей световой волны
при ее входе в звуковой пучок и по
прохождении в нем расстояния х2 соот-
ветственно. С помощью приближенно-
го выражения
при ж<1,
сохраняя только члены 1-го порядка малости, можно привести
уравнение (8.26) для световой волны в точке с координатой х2 +
+ dx2 к следующему упрощенному виду:
а (х2 + dx2, t) = А (х2) cos (Qt 4- 6Ф0) 4-
+ йФ [cos (Qt 4- <вт 4~ 6Ф0) — cos (Qt — сот 4- 6Ф0)], (8.31)
где йФ = —v Дпй®2 = — dx2, 6Ф0 = —4“ dx2; — фазовый
Л0 е л
сдвиг, связанный с прохождением волной слоя dx2. Для компо-
ненты, удовлетворяющей условию Брэгга (и имеющей, например,
частоту Q4- <b), амплитуды всех волн, излучаемых последова-
тельными слоями акустического пучка, складываются. При этом
приращение dB амплитуды В(х2) компоненты Q 4- св, возбуждае-
мой в слое толщины х2г можно в соответствии с (8.31) выразить
следующим образом:
dB = у ЙФ = А dx2. (8.32)
Одновременно происходит уменьшение амплитуды падающей вол-
ны света. Из закона сохранения энергии А2 4- В2 = А% следует
§ 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ
335
AdA + BdB = Q, откуда, используя (8.32), получаем
_ л ДФ ЛА___________________________р ДФ
йж2 ~ 2е ’ Лх*~ а 2е'
Амплитуды А и В удовлетворяют одному и тому же дифференци-
альному уравнению
решения которого должны подчиняться граничным условиям
5 = 0, А =А„ при яг2 “ 0. Кроме того, должен соблюдаться закон
сохранения энергии. Решениями дифференциального уравнения
являются
В = 408шЦ^ж2, А = Ао cos х2.
Относительная интенсивность дифрагированного луча при вы-
ходе из акустического пучка (я2 = е) равна
Выразим теперь изменение показателя преломления Ап, вхо-
дящее в уравнение 1ДФ1 = (2ле/Ло)|Дп|, через среднюю плот-
ность акустической мощности
Р = (| с52) V = 1 pV’S2. (8.34)
Изменение показателя преломления связано с деформацией соот-
ношением (8.11):

Если через М обозначить коэффициент акустооптической доброт-
ности [14]:
(8.35)
, . , 2яе 1 / МР
то I ДФ I = д- |/ —.
Относительная интенсивность дифрагированного луча,
(8.36)
может, в принципе, достигать единицы (полное отклонение па-
дающего света). Плотность мощности упругих волн, необходимая
336
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
для отклонения определенной части падающего света, оказыва-
ется обратно пропорциональной коэффициенту акустооптической
добротности М вещества. Как уже отмечалось, фотоупругие коэф-
фициенты для самых эффективных срезов кристаллов находятся
в пределах 0,2—0,3. Другие параметры вещества, от которых за-
висит коэффициент М,— показатель преломления п и скорость
звука V. Параметры эти в общем случае не являются независимы-
ми [15]. Показатель преломления п входит в выражение для М
в 6-й степени, а скорость V — в 3-й степени. Для веществ, про-
зрачных в видимой части спектра, показатель преломления обыч-
но не превышает 2,5. Скорость продольных звуковых волн нахо-
дится в пределах от 1000 до 10000 м/с. Обычно вещества с ма-
лыми скоростями звука характеризуются повышенным поглощени-
ем упругих волн. В связи с этим следует отметить, что жидкости,
несмотря на их значительные коэффициенты акустооптической
добротности, не могут использоваться на частотах выше
50 МГц. На этих частотах поглощение звука в воде превышает
5 дБ/см и растет с частотой по квадратичному закону. В табл. 8.2
приведены значения коэффициентов поглощения звука на часто-
те 500 МГц для ряда материалов. Там же даны значения коэф-
фициентов акустооптической добротности относительно акусто-
оптической добротности плавленого кварца, равной
Мо = 1,51 • 10-‘s кг“* • с3.
(n = 1,46, р = 0,27, р = 2,2 • 103 кг/м3, V = 5,960 м/с).
Из табл. 8.2, например, видно, что кристаллы а-НЮ3 облада-
ют высокой акустооптической добротностью (55). Недостатком
этого материала является его сильная гигроскопичность. Чрезвы-
чайно высокая акустооптическая добротность (515) парателлури-
та (ТеО2) связана с очень малой скоростью сдвиговых волн вдоль
направления [110]. К сожалению, сильное поглощение этих волн
(6 дБ/см на частоте 100 МГц) препятствует использованию пара-
теллурита на более высоких частотах. В настоящее время наибо-
лее интересным материалом представляется молибдат свинца
(РЬМоО4). Рутил (TiO2) и ниобат лития (LiNbOj) могут быть ис-
пользованы в области высоких частот, где эти материалы имеют
достаточно малое поглощение звука. Оценим среднюю мощность
упругих волн 53 = Р • е2, необходимую для 50% отклонения света
гелий-неонового лазера (Ао = 0,6328 мкм) при квадратном сече-
нии преобразователя со стороной е. Из уравнения (8.36) получаем
откуда следует, что необходимая мощность составляет 33 Вт для
плавленого кварца и только-1,4 Вт для молибдата свинца.

338 ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
Ширина полосы частот при брэгговской дифракции. Хотя ус-
ловие Брэгга, связывающее угол падения а0 и частоту упругой
волны /о, и является достаточно строгим, благодаря естественной
расходимости акустического пучка можно получить конечную по-
лосу частот акустооптического взаимодействия. В разделе 1.3.6
уже указывалось, что диаграмма направленности преобразовате-
ля, имеющего ширину е — аК, определяется на большом расстоя-
нии от преобразователя выражением
Л(Ла) = Д,2Ц^-1>.
где s = sin Да » Да, а Да — угловое отклонение от среднего на-
правления акустического пучка (т. е. от оси образца, звукопрово-
да). Поскольку угол падения остается постоянным, взаимодействие
Рис. 8.13, Ширина полосы взаи-
модействия с учетом расходимо-
сти акустического пучка.
На частоте /, отличной от /о, вза-
имодействие происходит с теми
упругими волнами, для которых
направление распространения
ОМ удовлетворяет условию Брэг-
га а0 + Да = A//2F. Интенсив-
ность отклоненного светового
пучка, пропорциональная Л2, при
этом уменьшается.
с упругими волнами, распространяющимися под некоторым углом
Да к оси акустического пучка, происходит на частоте /, отличной
от /о (рис. 8.13). Как следует из (8.30),
В предположении, что взаимодействие является слабым, ин-
тенсивность отклоненного луча пропорциональна мощности упру-
гих волн и имеет место соотношение
31п<теА/(/~/о)1
*(/) _ [~Л(Да)~|о _ ‘ L 272 J
Фо) I Л J ГяеАФ-А>)12 ’
L гр2 г
Ширина полосы частот на уровне половинной интенсивности
(3 дБ) равна
= <8-37)
причем предполагается, что эта полоса достаточно узка, т. е.
f « А. При V = 4000 м/с, Ав = 0,63 мкм, п — 2 и /0 — 600 МГц
ширина полосы Д/= 100 МГц.
g 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ 339
Если же частоту сигнала поддерживать постоянной, а образец
поворачивать, что изменения интенсивности отклоненного луча
будут соответствовать диаграмме направленности преобразователя
(с изменением углов из-за соотношения Д0 = 2Да), т. е.
. ЛеА>А9
4 (0О + Л0) __ sin2 “27“
i (0О) '
Число разрешимых положений. Угол отклонения 0 светового
луча при его взаимодействии с акустическим пучком частоты /
равен двойному углу Брэгга:
0 = 2а«А = АЛ
Изменение частоты Д/ приводит к изменению угла Д0:
де = 4д/.
Если угловая расходимость Д£$ светового луча с изменением
его диаметра D определяется дифракционной расходимостью, т. е.
Д^ = Л/Л, то число разрешимых положений луча дается выра-
жением
Лгв-^-5д/=ГгД/,
где Тв — время прохождения упругих волн через апертуру свето-
вого луча. Для того чтобы получить NB = 300, необходимо, напри-
мер, обеспечить Д/ = 100 МГц и7в = 3 мкс. При скорости звука
4000 м/с (или 4 мм/мкс) диаметр светового луча должен состав-
лять 12 мм. Обычно приходится специально расширять лазерный
луч. Как ясно из предыдущего, частота ультразвука определяется
необходимой полосой частот. Затухание упругих волн на этой
частоте и на рабочей длине TBV не должно быть слишком боль-
шим. В молибдате свинца, например, затухание на частоте
300 МГц составляет 1 дБ/см.
Таким образом, брэгговской дифракции присущи следующие
особенности. Интенсивность единственного отклоненного луча про-
порциональна интенсивности акустического пучка. Угол отклоне-
ния пропорционален частоте упругих волн. Частота отклоненной
световой волны отличается от частоты падающего света на вели-
чину, равную частоте упругих волн.
Первая из особенностей брэгговской дифракции используется
в модуляторах света (§ 9.8), вторая —в дефлекторах (§ 9.8 и
раздел 8.3.6), а третья — в устройствах для плавной и переменной,
задержки электрических сигналов (см. 9.2.3).
340 ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
Рассмотрим теперь несколько случаев взаимодействия волн
с изменением состояния поляризации света. Особо остановимся на
коллинеарном случае, когда отсутствует отклонение светового луча.
Векторная диаграмма. Изменение состояния поляризации.
Уравнение (8.30), определяющее угол Брэгга а = 0/2, можно за-
писать в виде
4sin4 = ^‘
Рис. 8.14. Диаграмма
волновых векторов.
В оптически изотропном
материале векторный
треугольник является
почти равнобедренным.
Этому уравнению соответствует треугольник, изображенный на
рис. 8.14. Он связывает волновые векторы падающей (Кг) и ди-
фрагированной (Ко) световых волн и вол-
новой вектор упругой волны (к). Соотно-
шение между указанными векторами,
Ко = Кг ± к, (8.38)
отражает закон сохранения импульса, в то
время как соотношение между частотами,
Qo = Q ± со, (8.39)
соответствует закону сохранения энергии.
При тех условиях, которые были при-
няты нами ранее (оптически изотропный
материал, продольные звуковые волны,
одинаковая поляризация у падающего и
дифрагированного лучей), рассматривае-
мый треугольник является почти равно-
бедренным (/«Ей KD » Кг). В анизотропных средах (кристал-
лах) Ко и Kf не обязательно должны иметь одинаковую длину.
В том случае, когда поляризации падающего и дифрагированного
света различны, скорости света для падающего и дифрагирован-
ного лучей не равны и треугольник волновых векторов уже не
является равнобедренным, а угол падения ai не равен углу диф-
ракции Ио [16].
Рассмотрим в качестве примера тригональный кристалл, при-
надлежащий к одному из трех классов: Зт, 32 или 3m. Фото-
упругий тензор таких кристаллов дается на рис. 8.6. Как следует
иь уравнения (8.20), сдвиговая упругая волна,' распространяю-
щаяся вдоль оси Xi (кристаллографическая ось X) и поляризован-
ная вдоль х3, вызывает изменение диэлектрической проницаемости
Де« следующего вида:
= — 2e«EnP«siS13.
Единственными отличными от нуля компонентами типа рц31 явля-
ются р1231 и р1331 (рис. 8.6). Вклад в фотоупругость из-за наведен-
ного электрооптического эффекта мЪжно вычислить с помощью
уравнения (8.21). В данном случае нужно положить п4 = 1, п2 =
§ 8.4. ДИФРАКЦИЯ СВЕТА НА АКУСТИЧЕСКОМ ПУЧКЕ
341
п3 = 0, тогда получаем
Для кристаллов классов 32 и Зт этот вклад отсутствует, так как
е15 = 0. В кристаллах класса Зт существуют только компоненты
Р1231 = — гв1е15/е}
Тензор Де« имеет вид
где Де12 = е22 (гс1е15 — епр1231) —, Де13 = е33(г51е15 — еир1331)
Световая волна, поляризованная вдоль х3 (рис. 8.15), сопро-
вождается электрическим полем, имеющим компоненты (0, 0,
£'3 = £'cosQZ). Это поле вызывает электрическое смещение
Поскольку нас интересует только поляризация дифрагированной
волны, в выражении для Dt мы положили е0 = 1. Так как Де<3 =
= (Aei3)o sin at, возникновение дифрагированной волны с частотой
Рис. 8.15. Диаграмма волновых векторов. Од-
клонения светового луча.
Q + со связано с членом, содержащим произведение синуса и ко-
синуса. Эта дифрагированная волна поляризована вдоль х3, по-
скольку отлична от нуля только компонента Де^. Таким образом,
при акустооптическом взаимодействии происходит изменение по-
ляризации световой волны. При построении векторной диаграммы
теперь нужно пользоваться обеими полостями поверхности пока-
зателя преломления—сферой и эллипсоидом. При сечении этих
поверхностей плоскостью х3х2 получаются две окружности с ра-
диусами пе и п0, поскольку оптическая ось является осью враще-
ния поверхности показателя преломления. Конец волнового век-
23 э. Дьелесан, Д. Руайе
342
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
тора К7 падающего света лежит на окружности радиуса п, (что
соответствует поляризации вдоль Жз), в то время как конец вол-
нового вектора KD дифрагированного света (поляризованного в
плоскости XiX2) лежит на окружности радиуса п„ (рис. 8.15).
Нужно отметить, что в случае, когда падающий луч имеет не-
обыкновенную поляризацию, имеются, вообще говоря, два дифра-
гированных луча, соответствующих различным частотам звука.
Рассмотрим теперь продольную упругую волну, распространя-
ющуюся вдоль оси х1 в кристаллах тех же классов (32, 3m и 3m).
Эта волна вызывает деформацию 5И. Как такая деформация
влияет на распространение световой волны, поляризованной вдоль
оси х3 и падающей в направлении х{ (коллинеарное взаимодей-
ствие)? Согласно теории Поккельса, справедливой в данном слу-
чае, изменение диэлектрической проницаемости
Де« = —ей8ирни5ц
с помощью таблицы коэффициентов рац можно привести к следу-
ющему виду:
[Деи 0 0 1
0 Д®22 Ае23 Ь
0 Д®23 Дв3з]
где
Двц = —(8ii)!piiiSi, Двгг = •~(en)2pi2‘S't,
Де22 = -8n8S3p4lSi, Д833 = -(ЕззУрцЗь
Электрооптический эффект, имеющий место только в кристаллах
класса 32 (р*ш = — гщец/гц), вносит вклад в компоненты ра,
Р12 и Ри.
Направление поляризации волны с частотой и + Q определя-
ется величиной ДД:
ДД = ДейД,
или
ДД = О, ДД = Де2зД, ДД = Де3зД.
В случае коллинеарного взаимодействия условию Брэгга мож-
’но удовлетворить, только если поляризация света при дифракции
изменяется (иначе KD = Кг и к = 0). Таким образом, для приня-
той нами поляризации падающего света дифрагированный луч
должен быть поляризован как обыкновенный, т. е. вдоль оси xt
(0, Де23Д, 0). Соответствующая векторная диаграмма приведена
на рис. 8.16 для случая положительного одноосного кристалла
(пе > п0). Из этой диаграммы следует условие
| к| = Kz - KD = ^(Пе - п0) = (8.40)
\ § 8.5. АКУСТООПТИКА ПОВЕРХНОСТНЫХ ВОЛН
343
т. е. частота волн должна быть равна
/ = ^("е — ”<>)•
(8.41)
Если же частота упругой волны задана, то дифрагировать мо-
гут только такие световые волны, которые удовлетворяют усло-
вию (8.40). Этот факт используется для создания оптических
фильтров, настраиваемых изменением частоты звуковой волны
Рис. 8.16, Коллинеарное взаимодействие. i \ \
Для того чтобы из необыкновенного луча Т7^ I Л- |
(волновой вектор К/) с длиной волны Xi Л ' g > < у
получить обыкновенный луч (волновой К,1/
вектор KD), частота упругой волны долж- / /
вектор Кв), частота упругой волны долж-
на быть / = V(пе — п0)/Ао. Знаками f и
® указана поляризация.
Ч №
(стоячей или бегущей) [17, 18]. Так, например, в случае сдвиго-
вых упругих волн в молибдате кальция (СаМоО4) при изменении
частоты этих волн от 40 до 68 МГц можно перестраивать про-
пускание света в диапазоне от 6700 до 5100 А с полосой про-
пускания 8 А.
§ 8.5. Взаимодействие света
с поверхностными акустическими волнами
До сих пор мы рассматривали взаимодействие света с про-
дольными или сдвиговыми объемными акустическими волнами.
Световые волны могут испытывать дифракцию и на поверхност-
ных волнах, особенно на волнах Рэлея. Поскольку эти волны
имеют как продольную, так и сдвиговую компоненты, можно ожи-
дать одновременного проявления описанных выше эффектов. На-
пример, только часть дифрагированного излучения будет иметь
повернутую поляризацию [19]. Кроме того, волны Рэлея приводят
к деформации поверхности, что вызывает дифракцию отражен-
ного света [20]. Рассмотрим два наиболее важных случая взаи-
модействия света с поверхностными волнами.
В первом случае (рис. 8.17) от поверхности кристалла отра-
жается луч света, диаметр которого меньше акустической длины
волны [21]. В этих условиях не нужно учитывать модуляцию
показателя преломления. При распространении волны поверхность
становится как бы гофрированной и происходит изменение угла
отражения тонкого зондирующего светового луча с частотой зву-
ковой волны. Для того чтобы интенсивность света, принимаемого
детектором, изменялась также с частотой звука, на пути свето-
вого луча ставится клин. Электрический сигнал, снимаемый с фо-
23*
344 гл. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОЙ
тодетектора, сдвинут по фазе относительно сигнала, приложен-
ного к преобразователю. Этот сдвиг фаз зависит от места на по-
верхности, куда падает пробный луч света. Двум точкам, отстоя-
щим друг от друга на полволны, соответствуют сигналы, отлича-
ющиеся по фазе на л. Двигая луч по поверхности, можно иссле-
довать ее свойства. Дефекты и иные особенности на поверхности
можно наблюдать на экране осциллографа, если движение свето-
Рис. 8.17. Схема эксперимента
по исследованию поверхности
методом отклонения светового
луча.
Отраженный тонкий луч света
колеблется с частотой звука.
Рис. 8.18. Изображение на экране инди-
катора при использовании метода от-
клонения светового луча.
Рэлеевские волны с частотой 8 МГц
распространялись по поверхности сталь-
ной пластинки. Две черные линии, иду-
щие поперек волновых фронтов звуко-
вой волны, соответствуют двум царапи-
нам на поверхности пластинки (по дан-
ным опыта длина царапин 15 мм).
(Рис. На из [21].)
вого луча по исследуемой поверхности синхронизовать с переме-
щением электронного луча по экрану, причем яркость на экране
осциллографа должна быть пропорциональна фазовому сдвигу
светового луча в данной точке поверхности.
На рис. 8.18 приведены результаты исследования поверхности
стальной пластинки, на которой сделаны две Царапины, парал-
лельные направлению распространения волны Рэлея (/ = 8 МГц).
Место расположения царапин легко обнаруживается по излому
волновых фронтов звуковой поверхностной волны.
Ориентация клина оказывается весьма существенной. В зави-
симости от того, перпендикулярен или параллелен его край вол-
новым фронтам звука, количество света, достигающего фотодетек-
тора при осцилляции отраженного луча, изменяется от нуля до
максимального значения. Таким образом, с помощью соответству-
ющей ориентации клина можно визуализировать упругие волны,
§ 8.5. АКУСТООПТИКА ПОВЕРХНОСТНЫХ ВОЛН
345
Дифрагированный
световой пучон
Пленочный
световой •.
Потречношто/реВой преобразователь
Рис. 8.19. Акустооптическая дифрак-
ция на волнах Рэлея в случае тонко-
пленочного световода.
идущие в различных направлениях. Указанным способом можно
регистрировать упругие волны, которым соответствует плотность
мощности порядка единиц ватт на сантиметр или амплитуда,
меньшая 0,1 А.
Для второго случая взаимодействия света с поверхностными
волнами оказывается существенной модуляция показателя пре-
ломления. Этот эффект имеет место, лишь когда световой и аку-
стический пучки лежат в одной
плоскости [22]. При этом энер-
гия светового луча должна быть
сосредоточена преимущественно
вблизи поверхности. Хорошим
решением, удовлетворяющим
этому условию, является созда-
ние на поверхности кри-
сталла тонкопленочного свето-
вода (рис. 8.19). Световод на-
носится на пьезоэлектрическую
подложку, которая одновремен-
но служит средой для возбуж-
дения и распространения по-
верхностной акустической вол-
ны [23]. Световод может быть
изготовлен из стекла с показателем преломления большим, чем
у подложки. Световые волны вводятся в световод и выводятся
из него с помощью двух решеток [24]. Толщина световода
(*1 мкм) меньше акустической длины волны (32 мкм в кварце
при 100 МГц). В другом варианте и световод и звукопровод из-
готовляются из одного и того же материала, например ниобата
или танталита лития. В этих материалах тонкий световод может
быть создан экзодиффузией лития при нагреве кристалла [25,
26], но лучших результатов можно достичь с помощью диффу-
зии в подложку таких металлов, как Ni, Ап или Ag [27]. Ос-
новные особенности акустооптического взаимодействия с объ-
емными волнами в известной степени имеют место и здесь.
При угле падения, соответствующем условию Брэгга, существует
только один дифрагированный луч. В случае дифракции в состав-
ной структуре (со световодом в виде слоя из материала, отлич-
ного от подложки) для отклонения практически 100% падающего
света требуется ~1 Вт электрической мощности [28, 29]. Более
эффективной оказывается структура с диффузионным световодом.
В этом случае для 10Q% отклонения падающего света требуется
только 0,1 Вт электрической мощности [30]. Однако полоса ча-
стот этих дефлекторов ограничена несколькими десятками мега-
герц. Для расширения полосы частот необходимо применять пре-
образователи более сложной конструкции [31].
346
ГЛ. 8. ВЗАИМОДЕЙСТВИЕ УПРУГИХ ВОЛН СО СВЕТОМ
Упражнения
8.1. Как ч одноосном кристалле показатели преломления зависят от на-
правления распространения, определенного с помощью полярного угла 0
(рис. 8.20)?
Решение. Для волны с поляризацией D<>) показатель преломления
»<*) = По при любых 0.
Для волны с поляризацией D<2) показатель преломления удовлетворяет
уравнению
причем 11 = 0, is = — п cos 0, xs = п sin 0. Отсюда
„(2) =___________.
(n2 cos2 0 + re2 sin2 0)1/2 "
8.2. Монохроматическая световая волна распространяется вдоль оси х2
кристалла, в котором во всех направлениях плоскости х\х3 распространяют-
ся упругие волны одной и той же частоты. Что бу-
№ дет видно на экране, параллельном плоскости х\хз
Ои расположенном на расстоянии D? Что изменится
в случае изотропной среды?
Решение. Отклоненный луч, соответствую-
щий 1-му порядку дифракции, распространяется под
утлом 0 « АД в vflFV (см. (8.27)). В направлении
распространения п активной упругой волны он даст
% светлое пятно на расстоянии d = DvjIFV, обратно
пропорциональном скорости распространения уп-
ругой волны в направлении п. Поскольку по Ус-
ловию упругая волна распространяется в любом
направлении в плоскости ат^з, на экране будут вид-
ны три сечения поверхности обратных скоростей
Рис. 8.20. плоскостью х{х2 (раздел 5.1.6). В случае изотроп-
ного тела это будут две окружности. Изложенные
здесь явления лежат в основе метода, предложенного Шеффером и
Бергманом для определения скорости упругих волн.
8.3. Каковы будут при условиях, приведенных в табл. 8.2, фотоупругие
коэффициенты и значения показателя преломления, входящие в выражение
акустооптической добротности для парателлурита (ТеОа) ?
Решение. 1. Упругая волна, поляризованная вдоль направления
[110] и распространяющаяся вдоль [110], вызывает деформацию
поскольку d/Pzt = д/дх2 и °а2 = —°и1. Плотность мощности упругой вол-
ны Р = <г,>У, где
<^> = ~2 ctjhlSijSkl = ~2 1С11 + с22 — 2с1г1511 = (с11 “ с1г) 511’
может быть представлена в форме (8.34). где S = 2Slt:
р = грг’з2! = у pf3s2.
УПРАЖНЕНИЯ
347
В соответствии с уравнением (8.20)
[ди1
(?iZll — PiZ22) + (Pil21 “ PiZ12) -
— —eiisll (Pilll ~ Pilin'
так как для одноосного кристалла p«2i = Pmz. Отсюда
Дв11 = ~в11 (₽11 - Р12) 511 = ~ДВ22’
Дб12 = Дё13 = ДВ23 = °’
Двзз = “ взз (Р31 “ Р32) 5п = 0 ПРИ Р™ = Ры-
При заданной поляризации (Eh Е3, 0) световой волны, падающей вдоль
оси Z (ее показатель преломления »0), дифрагированная волна, связанная
с = ЛвцЕ1 + A8iS£2 (при этом ADt = Aen^i, AZ)2 = — Дец£2, AD3 = 0),
имеет амплитуду, пропорциональную Лец. Величина Двп связана с деформа-
цией S = 2 5И:
Дзп = —Р11 2 ?12 8 = —z*pS
с помощью фотоупругого коэффициента р = (рц — рц)/2.
2. В случае продольной упругой волны, распространяющейся вдоль на-
правления [001], S = S33 и Де» = — Вцецризз833, или
ДВ11 = -В11Р135 = ДВ22’ ДВ33 = -ВЗЗР335’
Asy = 0 при i #= /.
Благодаря тому, что в данном случае эффективным является коэффи-
циент р = р13, световая волна с поляризацией (Еи 0, 0) и показателем
преломления п0 при дифракции приобретает иную поляризацию (ДО1 =
= Дец-Ei, 0, 0).
8.4. Убедиться, что значения коэффициента акустооптической доброт-
ности РЬМоО4 для обоих случаев, приведенных в табл. 8.2 (поляризация све-
та либо параллельна, либо перпендикулярна плоскости, в которой лежит
волновой вектор упругой волны), очень близки друг к другу по величине.
Решение. Деформация 53з вызывает изменения показателя прелом-
ления
Дв22 = Дв11 = ~ В11^13533’ Дв33 = —ВЗЗРз3533'
а) Поляризация, параллельная указанной плоскости (0, 0, Е3). При
этом показатель преломления равен пе, а AZ>3 = Авзз^зз и р = рзз, откуда
Л/ = пМз/рИ = 23,9М0-
б) Поляризация, перпендикулярная той же плоскости {Е\, 0, 0). В этом
случае показатель преломления равен п0) а AZ>i = ЛвцВц р = р\3 и тогда
М=пМз/ррЗ = 23,5М0.
8.5. Показать, что ширина полосы при акустооптической взаимодейст-
вии в режиме Брэгга обратно пропорциональна времени, необходимому для
того, чтобы акустический волновой фронт пересек световой пучок под углом
Брэгга.
Решение.
At = ea0!V = еЛ/o/V5 или Д/ = 1,77/At (см. (8.37)).
ГЛАВА 9
ПРИМЕНЕНИЕ УПРУГИХ ВОЛН
ДЛЯ ОБРАБОТКИ СИГНАЛОВ
Упругие волны используются в электронике со времени раз-
работки ламповых усилителей в годы первой мировой войны.
До этого упругие волны в основном использовались для изучения
землетрясений. Регистрируя время прихода возмущения в раз-
ные точки, геофизики пытались определить эпицентр сейсмиче-
ских толчков.
В 1916 г. Шиловски и Ланжевен выдвинули идею о приме-
нении упругих волн для обнаружения подводных объектов с по-
мощью приема эхо-сигналов. Используя результаты исследований
Жака и Пьера Кюри, которые после своего открытия пьезоэлект-
ричества в 1880 г. создали кварцевые весы, Поль Ланжевен раз-
работал пьезоэлектрические преобразователи (составленные из
кварца и стали) для излучения в воду упругих волн и приема
этих волн, отраженных различными препятствиями, при частоте
примерно 150 кГц. Это устройство, впоследствии названное «со-
наром» *), получило значительное развитие как в гражданской,
так и в военной областях применения. Известно, что, позволяя
обнаружить вражеские подводные лодки, сонары сыграли важную
роль в уменьшении потерь морского флота союзников, который,
в частности, осуществлял навигацию между США и Великобри-
танией, во время второй мировой войны. Сонар повсеместно при-
меняется для обнаружения скоплений рыбы, -съемки рельефа
морского дна, в морских научно-исследовательских работах. Хотя
настоящая книга посвящена распространению упругих волн в
твердых телах, мы сочли уместным привести эти примеры при-
менения, поскольку они представляют важный исторический и
практический интерес [11.
В 1920 г. Кэди использовал высокую добротность пьезоэлект-
рических кварцевых резонаторов, включив их в электрические
цепи для фильтрации сигналов или стабилизации частоты гене-
*) Слово «сонар» произошло от сокращенных английских слов: SOund
NAvigation and Ranging.
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
раторов. Резонатор, как было показано в разделе 7.1.2, представ-
ляет собой особый случай преобразователя. Кварцевые фильтры,
состоящие из многих резонаторов, стали классическими элемен-
тами цепей, причем они продолжают совершенствоваться (моно-
литные фильтры). Основные характеристики таких фильтров
приводятся здесь (§ 9.4) лишь с целью сравнения их с фильтра-
ми на волнах Рэлея.
Запоминание информации в форме упругих волн стало при-
меняться с развитием радиолокации и электронно-вычислитель-
ных машин (период 1940—1945 гг.). Первые жидкостные линии
задержки (на воде, ртути) исследовались в Англии и США. Пер-
вые твердотельные (стекло, плавленый кварц) линии задержки
были созданы в Германии (см. исторический обзор [2]). Эти ли-
нии с кварцевыми преобразователями работали на частотах до
10 Мгц при полосе пропускания в несколько МГц и обеспечива-
ли задержку порядка 100 мкс. Время задержки впоследствии
было увеличено на порядок, благодаря созданию линий задерж-
ки особой формы (многоугольные линии задержки с многократ-
ными отражениями [2D.
В 1960 г. сотрудники лаборатории Бэлл в США обратили
внимание [3] *) на интересные возможности, возникающие при
сжатии радиоимпульсов в радиолокационных системах, и начали
исследования дисперсионных устройств на упругих волнах, позво-
ляющих осуществлять такое сжатие, после этого были разрабо-
таны различные принципы создания дисперсионных линий за-
держки: изменение групповой скорости определенных мод в вол-
новодах (волны Лэмба), интерференция объемных и, позднее,
поверхностных волн (волны Рэлея) при различных структурах
преобразователей, совмещение сред с различными скоростями
распространения (волны Лява).
Предметом настоящей главы является описание сравнительно
недавних разработок, иллюстрирующих применение различных
принципов. При этом здесь не ставится задача приводить рабочие
характеристики устройств, хотя часто даются оценки порядка
величины различных параметров. Устройства классифицируются
согласно функциям, которые они выполняют: задержка, сжатие
импульсов, фильтрация, память, свертка. По мере возможности
уточняется состояние разработки устройств; некоторые из них
пока находятся в стадии лабораторных исследований, другие
”)До выхода в свет указанной работы в разных странах, в том числе
и в США, проводились исследования в этой области, результаты которых не
были опубликованы. Например, во Франции технический директор фирмы
«Томсон CSF» Карпантье осуществил в 1959 г. эксперименты по сжатию
импульсов (М. Карпантье, А. Адамсбом «Устройство для сжатия импуль-
сов», французский патент Р. V. 800423, 17 июля 1959 г., патент США 3213452,
19 октября 1965 г.).
350
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
изготовляются промышленностью. Глава заканчивается описа-
нием ответвителя на поверхностных волнах, акустооптического
модулятора и дефлектора. Представляется целесообразным рас-
смотреть сначала общую структуру устройства на упругих вол-
нах (акустической линии).
§ 9.1. Общая структура акустической линии
Акустические линии, рассматриваемые в настоящей главе,
служат для обработки электрических сигналов, т. е. для задан-
ного изменения их параметров. Независимо от того, какой об-
работке подвергается сигнал, линию можно представить в наи-
более полном ее варианте, показанном на рис. 9.1.
1 Внешняя
Волна
„ \\ПреоВразо-\ \Раслроот-\ _ \взаипоВеВ-\ . \РреоВразо-\ .
воте ГПу| fe
\двраВотаи-
Лно/и сигнал
Рис. 9.1. Общая структура линий задержки на упругих волнах.
9.1.1, Преобразование электрического сигнала в упругую
волну. Обрабатываемый электрический сигнал, модулированный
по фазе или амплитуде, на входе линии преобразуется в упру-
гую волну.
Это преобразование энергии, основанное на возбуждении
электрическим полем сигнала механических колебаний в пьезо-
электрическом материале, может быть осуществлено таким об-
разом, что преобразователь представляет собой один локализо-
ванный источник (§ 7.1) или же совокупность источников, рас-
пределенных, например, на поверхности (§ 7.2). В последнем
случае можно использовать интерференцию волн, излучаемых
распределенными источниками, и элемент 1 блок-схемы на
рис. 9.1 будет уже играть роль не только преобразователя. Опре-
деленное расположение распределенных ультразвуковых источ-
ников может задавать определенную обработку сигнала.
В преобразователе, сигнал на который поступает через согла-
сующую цепь, возникают потери, зависящие, во-первых, от цент-
ральной частоты и ширины спектра преобразуемого сигнала и,
во-вторых, от природы возбуждаемых упругих волн. Эти потери
составляют от единиц до десятков децибел. Частота упругих
волн, используемых в устройствах, в настоящее время лежит в
пределах от нескольких МГц до нескольких ГГц.
§ 9.1.0БЩАЯ СТРУКТУРА АКУСТИЧЕСКОЙ ЛИНИИ
351
9.1.2. Распространение упругих волн. Возбужденные в среде
упругие волны распространяются, в зависимости от их типа,
либо в объеме, либо по поверхности, но их скорость всегда при-
мерно в 10s раз меньше скорости электромагнитных волн. Имен-
но это свойство упругих волн проходить за микросекунду всего
лишь несколько миллиметров используется для задержки сигнала
в блоке 2 на рис. 9.1.
Среда распространения, или звукопровод (здесь рассматри-
ваются только твердотельные линии) может быть однородной и
изотропной (например, стержень из плавленого кварца), анизо-
тропной (например, монокристалл А12О3) или слоистой (напри-
мер, тонкий слой на подложке). В случае кристалла его срез
должен быть выбран таким образом, чтобы распространялась
требуемая мода. Скорость волны при этом не зависит от частоты,
поскольку длина волны много больше межатомных расстояний
(см. 1.2.2). В случае слоистой среды скорость волны изменяется
с частотой в пределах от значения скорости в слое rfo ее значе-
ния в подложке. Время задержки сигнала зависит при этом от
частоты. Дисперсия имеет место также в однородном материале
при распространении в волноводе (см. 1.1.2).
Возможны различные варианты звукопроводов: стержень,
многогранник (волна внутри многогранника совершает путь по
ломаной линии, многократно отражаясь от разных граней и обес-
печивая большое время задержки — до 1000 мкс), длинная лента
(дисперсионная линия). При необходимости осуществляется
преобразование мод при отражении (см. 5.2.3).
Коэффициент поглощения упругих волн (рис. 9.3) зависит от
материала и от поляризации волны и увеличивается при этом с
частотой. Дефекты среды весьма существенны, если они имеют
размеры порядка длины волны. При прочих равных условиях
потери в поликристаллических материалах всегда больше, чем в
монокристаллических,
9.1.3, Взаимодействие упругой волны с внешней волной. Эле-
мент 3 блок-схемы на рис. 9.1 соответствует взаимодействию
упругой волны и какой-либо другой, введенной извне, волны.
Это может быть световая волна или волна объемного заряда, свя-
занная с движением электронов.
Результатом взаимодействия упругой волны со световой вол-
ной является дифрагированная световая волна, которая содер-
жит информацию о характеристиках как упругой (частота, ин-
тенсивность), так и падающей световой (пространственная и вре-
менная модуляции) волн. Дифракция возникает из-за периоди-
ческого во времени и в пространстве изменения показателя пре-
ломления, которое всегда сопровождает упругую волну (§ 8.4).
Элементом 5 блок-схемы обозначено устройство модуляции, влия-
352
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
ющей обычно на форму сигнала. Например, это может быть мас-
ка, задающая пространственное отражение кода сигнала.
В результате взаимодействия упругой волны с электронами,
движущимися в направлении распространения волны, возникает
поглощение или усиление упругой волны в зависимости от того,
меньше или больше скорости звука скорость движения носите-
лей. Для существования взаимодействия необходимо, чтобы среда
обладала пьезоэлектрическими (упругая волна сопровождается
электрическим полем) и полупроводниковыми (движение носи-
телей заряда) свойствами [4]. Обоими свойствами может обладать
один и тот же кристалл, например, сульфид кадмия, окись цин-
ка, и в этом случае взаимодействие происходит в объеме ма-
териала. Однако более широкие возможности открываются, если
каждым свойством обладают разные материалы, причем взаимо-
действие упругой волны с носителями заряда обеспечивается
близким расположением таких материалов. Для этого случая
очень подходят поверхностные волны, особенно если полупровод-
ник нанесен на пьезоэлектрическую подложку в виде тонкого
слоя. Таким образом, можно получить усиление упругих волн
на несколько десятков децибел [5]. Однако эффекты усиления
здесь рассматриваться не будут, так как, насколько мы можем
судить, эти исследования не вышли пока за пределы лаборатор-
ных разработок.
9.1.4. Преобразование обработанной волны в электрический
сигнал. Для получения на выходе линии обработанного сигнала
необходимо преобразовать в электрический сигнал волну, полу-
ченную в результате взаимодействия. Это преобразование в за-
висимости от типа волны осуществляется с помощью локализо-
ванного или распределенного на поверхности преобразователя,
аналогичного преобразователю на входе линии, или же преобра-
зователя другого типа, например, фотоумножителя или фотодио-
да, если носителем информации после взаимодействия является
световая волна. Характеристику преобразователя и согласующих
цепей следует выбирать таким образом, чтобы не вносить иска-
жений в обработанный сигнал.
§ 9.2. Задержка сигналов
В настоящем параграфе мы ограничимся рассмотрением сра-
внительно новых разработок: линий задержки на объемных вол-
нах с тонкопленочными преобразователями с рабочей частотой
свыше 1 ГГц, линий задержки на волнах Рэлея и акустоопти-
ческих линий с плавно регулируемой задержкой. Мы не будем
рассматривать линии задержки на объемных волнах, изготовлен-
ные по более классической технологии с использованием индие-
вых связок и монокристаллических преобразователей с после-
§ 9.2. ЗАДЕРЖКА СИГНАЛОВ
355
дующим уменьшением их толщины*) (/< 1000 • МГц), а также
линии задержки с керамическими преобразователями (/ < 50 МГц).
Различные типы существующих низкочастотных линий задерж-
ки описаны в [6].
9.2.1. Линии задержки на объемных волнах. До разработки
акустических линий задержки не существовало устройств, позво-
ляющих задерживать сигналы с частотой порядка одного гига-
герца на время порядка микросекунд. Хотя задержку можно
получить и с помощью коаксиального кабеля, однако для задерж-
ки на 2 мкс требуется около 400 м кабеля, и наряду с большими
размерами такое устройство характеризуется высокими потерями
распространения (больше 100 дБ при частоте 1 ГГц). Практиче-
ски использование кабеля ограничивается временами задержки
до 0,1 мкс и частотами меньше 1 ГГц. Акустические линии за-
держки, занимающие объем в несколько кубических сантиметров,
позволяют получить время задержки более 10 мкс с разумными
потерями до частот около 5 ГГц.
Акустическая линия задержки (рис. 9.2) содержит преобразо-
ватель продольных волн, изготовленный, например, из окиси
которого определяет время
задержки, и выходной пре-
образователь, также из оки-
си цинка. Входной и выход-
ЗОдюп/ювод
ной преобразователи анало- Рис. 92. Устройство линии задержки
гичны, однако, их; ТОЛЩИНЫ Иг объемных волн [70].
следовательно, резонансные
частоты обычно берутся разными с целью увеличения ширины
полосы пропускания. В качестве звукопровода выбран корунд, по-
скольку этот материал может быть получен в виде длинных стерж-
ней (до 30 см) при разумной пене, а коэффициент поглощения в
корунде сравнительно мал (1 дБ/мкс при 2 ГГц), как это следует
из рис. 9.3, где показаны потери распространения упругих волн
в некоторых материалах. Эти потери растут пропорционально
квадрату частоты.
Между кабелем, по которому подается сигнал, и каждым пре-
образователем включена полосковая керамическая линия для
♦) Эта техника в настоящее время значительно усовершенствована.
Так, использование ионной бомбардировки позволяет получить толщину
преобразователей из ниобата лития ~1 мкм ГГц). Возможно, что
линии задержки, изготовленные таким способом, окажутся конкурентоспо-
собными с линиями, описанными в настоящей главе, так как монокристал-
лические преобразователи имеют более низкие потери, чем тонкопленочные
преобразователи, и обеспечивают более широкий выбор материалов звуко-
провода (см. 7.1.4).
354
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
согласования источника сигнала с преобразователем (рис. 9.4).
Контакт между преобразователем и полосковой линией обеспе-
чивается золотой проволокой (диаметр 50 мкм), прикрепленной
методом термокомпрессии к внешнему (алюминиевому) электро-
ду. Диаметр этого электрода, не превышающий одного миллимет-
ра, определяет емкость преобразователя и его пьезоэлектрически
активную площадь.
Рис. 9.3. Поглощение упругих волн в зависимости от частоты в некоторых
твердых телах. (Рис. 4 из [70].)
Примеры характеристик. Поскольку согласование на концах
звукопровода длиной I никогда не является идеальным, время
задержки, с относительной точностью до 10—*, можно определить
по измерениям резонансных частот / = nV/21, где п — целое чис-
ло, для которых при наложении прямой и отраженных волн на-
пряжение на выходе получается максимальным. Время задержки
вычисляется по количеству максимумов n2 — П1, содержащихся
в интервале между частотами ft и /4:
На рис. 9.5 представлены основные характеристики линии
задержки [7] на 2 мкс с центральной частотой 1,5 ГГц. При
полосе пропускания 700 МГц потери составляют 33 дБ. Коэф-
фициент стоячей волны (КСВ) (см. 1.1.2) на входе и на выходе
§ 9.2. ЗАДЕРЖКА СИГНАЛОВ
355
меньше 2. Уровень паразитного сигнала, являющегося 1-м эхо-
сигналом, на 20 дБ ниже уровня сигнала первого прохождения.
Незадержанный сигнал прямой наводки на 30 дБ слабее по-
лезного.
Рис. 9.4. Линия задержки объемных волн.
а) Монокристалл А12О3 диаметром 3 мм с тонкопленочными преобразовате-
лями из окиси цинка на торцах; б) линия в коаксиальном исполнении.
Ниже дана сводка параметров, характеризующих рабочую
область линий задержки этого типа. Не следует, однако, считать
приведенные цифры предельными.
Центральная частота /0 от 0,5 до 10 ГГц
Относительная полоса пропускания 50%
Время задержки т от 0,5 до 10 мкс
Температурная нестабильность времени задержки
Д А12О3) (от -50 °C до 120 °C) 25 • 10"» °C"1
356
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Коэффициент стоячей волны
Уровень прямой наводки на выходе
Уровень 1-го эхо-сигнала
Вносимые потери
-зВдБ
от —15 до —30 дБ
от 20 до 80 дБ
Вносимые потери включают потери нескольких типов:
1) потери на преобразование, которые растут с увеличением
ширины полосы пропускания;
2) потери при распространении, которые пропорциональны
времени задержки и квадрату частоты;
3) дифракционные потери (обусловленные расходимостью
акустического пучка), которые зависят от размеров преобразова-
телей, частоты и времени задержки (см. 1.3.6).
Особым видом является линия задержки, работающая в ре-
жиме «на отражение», которая имеет преобразователь только на
одном конце звукопровода, а от противоположного свободного
торца происходит отражение упругой волны. На сверхвысоких
частотах под действием одного радиоимпульса легко можно по-
лучить до десятка эхо-импульсов, следующих один за другим
через двойное время прохождения. Специальная (выпуклая) фор-
ма торцевых поверхностей, обеспечивающая фокусировку акусти-
ческого пучка при каждом отражении и подавление паразитных
эхо-сигналов, позволяет получить очень больший времена задерж-
ки, но за счет ширины полосы пропускания. Например, задержку,
равную 100 мкс, можно получить при полосе пропускания по-
рядка 5%.
9.2.2. Линии задержки на волнах Рэлея. Свойство волн Рэ-
лея распространяться на поверхности твердого тела используется
для создания многоотводных линий с фиксированной задержкой,
хотя рабочие частоты таких линий в настоящее время (/<
<400 МГц) ниже, чем для линий на объемных волнах. Вместе
с тем уже имеются лабораторные макеты линий задержки на
поверхностных волнах с рабочей частотой выше одного гигагер-
ца [8, 9].
В качестве подложки-звукопровода используются пьезоэлект-
рические монокристаллы кварца (У- или ЗТ-срез, направление
распространения X) или ниобата лития (У-с’рез, направление
распространения Z). Задержка на одну микросекунду получается
при прохождении волной расстояния 3,15 мм в кварце и 3,49 мм
в LiNbOa. На рис. 9.6 изображена кварцевая линия задержки с
десятью выходными преобразователями. Ширина полосы про-
пускания линии превышает 6 МГц при средней частоте 31 МГц.
Каждый преобразователь состоит из четырех пар штырей шири-
ной 26 мкм. Величина потерь составляет около 35 дБ, изменяясь
при этом от выхода к выходу не более чем на несколько децибел.
§ 9.2. ЗАДЕРЖКА СИГНАЛОВ
357
На основе преобразователей, структура которых показана на
рис. 9.7, были созданы широкополосные (50%) линии задержки
с одним выходом. Преобразователи имеют переменный шаг, и при
этом выходной преобразователь соответствует входному при сме-
щении всех его элементов на расстояние I, которое определяет
время задержки, одинаковое для всех частот.
Рис. 9.6. Линия задержки волн Рэлея.
Каждый преобразователь состоит из 8 штырей шириной 26 мкм.
Волны Рэлея распространяются с умеренными потерями на
искривленных поверхностях, радиус кривизны которых много
больше длины волны [10, 11]. Это свойство используется в цикли-
ческих (рис. 9.8) и спиральных линиях задержки [12. 13].
При использовании материалов с малой скоростью звука в
принципе можно получить весьма большие времена задержки (до
1 мс). Так, траектория длиной 10 см на кристалле BiI2GeO20
((Ш)-срез, направление распространения [110], 7= 1708 м/с)
выходное входной
преобразователь преобразователь
\ воглототель /
Рис. 9.8. Циклическая линия за-
держки.
Радиус кривизны много больше
длины волны.
соответствует задержке 58,5 мс. Во избежание расхождения
акустического пучка и обусловленных этим потерь можно создать
волноводное распространение с помощью полоскового волновода,
нанесенного на поверхность [14]. Для компенсации затухания в
358
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
циклических линиях задержки (несколько децибел на один цикл
с числом циклов до нескольких десятков при 100 МГц) можно
использовать акустоэлектронное усиление дрейфом-. носителей
[15; 161, о принципах которого упоминалось в разделе 9.1.3.
Многоотводные линии задержки являются основным элемен-
том дискретных фильтров. Выборки сигнала, снятые с различных
преобразователей, взвешиваются и затем суммируются (см. раз-
дел 9.3.5).
Линии задержки на волнах Рэлея используются также в ге-
нераторах [16]. Такие генераторы могут работать на частотах
более высоких, чем те, что достигаются в соответствующих
устройствах с линиями задержки на объемных волнах (§ 9.4).
Акустооптичсская линия.....^регулируемой задержкой.
В гл/ й было показано, что дифракция света на^у’пругйх волнах"
при угле Брэгга приводит к единственному отклоненному пучку
света с частотой F~jk где F и / — частоты падающей световой
и упругой волн соответственно. Смешивая отклоненный пучок
с исходным световым пучком частоты F, можно получить сигнал
частоты /, задержанный по отношению к электрическому сиг-
налу, возбуждающему акустический преобразователь, на время
т = 1/V, где I — расстояние между преобразователем и областью
акустооптического взаимодействия, а V — скорость распростра-
нения упругих волн. Изменение расстояния I приводит к изме-
нению^ времени задержки т [17]. Были созданы линии с регули-
руемой задержкой, устройство которых показано на рис. 9.9 [18].
| Лазерном к |----'ьЗермло
Рис. 9.9. Сигнал, поданный на вход, задерживается на время т =l/V,
При неподвижном пучке лазера время задержки плавно изменяется благо-
даря перемещению кристалла.
Свет от лазера разделяется па два пучка, при этом дифраги-
рованная часть одного из них совмещается с прямоцрошедшим
светом другого пучка и попадает в фотодиод. Ток в фотодиоде,
пропорциональный квадрату амплитуды световой волны, имеет
составляющую той же частоты, что и сигнал, поданный на вход-
ной преобразователь.
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
359
Приведем типичные характеристики линии задержки такого
типа, используемой для градуировки радиолокационных высото-
меров:
— изменение времени задержки плавным перемещением
кристалла поперек луча лазера в пределах от 50 нс до 6 мкс;
— центральная частота 800 МГц;
— полоса пропускания 200 МГц;
— потери 80 дБ;
— материал — кварц (Х-срез), Г = 5720 м/с;
— тонкопленочный преобразователь продольных волн из
окиси цинка.
Более низкие потери, но меньшие времена задержки получа-
ются при использовании других материалов, таких как рутил
(Гь = 10670 м/с вдоль направления [001]).
§ 9.3. Сжатие импульсов
В современных радиолокаторах и акустических локаторах
(сонарах) широко используется сжатие импульсов. Это позволяет
увеличить дальность действия локатора при неизменных средней
мощности и разрешающей способности, или же увеличить раз-
решение при той же дальности действия. Классические локаторы
излучают импульсы с одной несущей частотой, длительность
которых определяется требуемой точностью обнаружения. По-
скольку амплитуда импульсов ограничена техническими причи-
нами (нельзя превысить допустимую максимальную мощность
ламп передатчика), выбор длительности импульса определяет и
дальность действия. Эти противоречия между требованиями уве-
личения дальности и точности, однако, являются только кажу-
щимися, поскольку если дальность действия' есть функция
длительности импульса, то разрешающая способность зависит
только от ширины спектра, а эти две величины — длительность
и ширина спектра — могут быть выбраны отдельно.
В работе [19] показано, что лучшему разрешению соответст-
вует наибольшая ширина спектра При заданной длительности
импульса ширину спектра можно увеличить, например модуля-
цией частоты несущей. Однако на эхо-сигнал, отраженный целью,
как в современном, так и в классическом локаторе накладыва-
ется шум, подавить который полосовым фильтром легче, когда
сигнал имеет узкий спектр (классический радар). В современном
локаторе для выделения из шумов сигнала с широким спектром
требуется более сложная система детектирования, которая долж-
на быть согласованной с сигналом, причем с учетом природы
шума. В случае белого гауссова шума выделение информации
наилучшим образом осуществляется при использовании фильтра,
который вырабатывает автокорреляцию сигнала [20, 21]. Сжатие
360
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
361
во времени, которое получается в результате этого, позволяет
точно определить время прихода эхо-сигнала и улучшает разре-
шающую способность.
9.3.1. Согласованный фильтр. Если импульсный отклик h(t)
фильтра, согласованного с реальным сигналом s^t), имеет вид
W = S1(-1), (9.2)
то сигнал на выходе фильтра s2(l), определяемый соотношением
(1.29), является автокорреляцией сигнала s^t) (см. (1.31)):
4-00
S2(l) = J (т)(т — 0 (9.3)
Соотношение (9.2) выражает тот факт, что импульсный отклик
согласованного фильтра представляет собой обращенный во вре-
мени сигнал (рис. 9.10). Такой фильтр физически не может
Рис. 9.10. Импульсный отклик h(t) фильтра, согласованною с реальным сиг-
налом Si(t), представляет собой обращенный во времени и задержанный на
постоянную величину t0 сигнал s^t).
быть реализован. Действительно, в этом случае следствие (им-
пульсный отклик) предшествовало бы причине (импульс 6(1)).
Любой реальный фильтр вносит задержку 10. Соотношение между
сигналом и импульсным откликом реального фильтра имеет вид
Л(1) = CsAlo — 1), С = const. » (9.4)
Реальный согласованный фильтр содержит линию задержки.
Преобразование Фурье выражения (9.4) дает
Я (со) — CS* (со) (59.
Таким образом, с точностью до сдвига фазы, связанного с вре-
менем задержки 10, частотным откликом Жсо) согласованного
фильтра является функция, комплексно сопряженная спектру
5(со) сигнала sit). В последующих выкладках мы будем опускать
физически неизбежную константу tQ, вводя ее лишь в конечный
результат.
Рис. 9.11. Кодированные сигналы
с частотной (а), амплитудной (б)
и фазовой (в) модуляцией.
На практике сигнал sSt) может иметь разную форму. Как
уже отмечалось, спектр сигнала можно расширить модуляцией
частоты или другими способами кодирования. Изменение во вре-
мени одного из .трех параметров волны — амплитуды, фазы или
частоты — может быть непрерывным (аналоговый код) или диск-
ретным (цифровой код).
На рис. 9.11 представлены примеры трех типов сигнала:
прямоугольный радиоимпульс длительностью 0 с модулирован-
ной несущей частотой, последова-
тельность импульсов с полной
длительностью 0, разделенная на
Nинтервалов (цифр двоичного ко-
да) и состоящая из определенной
последовательности элементарных
импульсов длительностью 6 =
=0/А, и радиоимпульс длитель-
ностью 0 с инверсией фазы несу-
щей частоты. Акустические ли-
нии, предназначенные для обра-
ботки сигналов этих трех типов,
описаны в последующих разде-
лах. Наиболее подробно рассмат-
риваются дисперсионные линии,
согласованные с линейно модули-
рованным по частоте сигналом.
Целью упр. 9.1 является графиче-
ское определение импульсного от-
клика фильтра, согласованного с сигналом, изображенным на
рис. 9.11, б.
9.3.2. Сигналы с линейной модуляцией частоты. В случае
сигнала, линейно модулированного по частоте (рис. 9.12), вре-
менная зависимость мгновенной угловой частоты сигнала имеет
вид
d<Pi , ♦ © 1 9
® = ~dt ®о+ПРИ ~
(9.6)
Сигнал с прямоугольной огибающей можно записать как
«х(0 = пШ costpJO,
(9.7)
где
<Pi (О = + зt2-
(9.8)
24 Э. Дьелесан, Д. Руайе
362
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Импульсный отклик фильтра, согласованного с этим сигналом,
с учетом (9.2) имеет вид
h(t) = Cn(§-)cos(®0t —Цу).’
Сжатый импульс. Отклик s2(f) на сигнал s,(i), поданный на
согласованный фильтр, является автокорреляцией функции s^t)
к Mt)
Рис. 9.12. Линейная частотная модуля-
ция.
а) Зависимость мгновенной частоты от
4 Йф-
времени, / = -±-_£.6) Сигнал s(f)s
Л л иЛ
= П(«/0) cos q>i(i)- e) Импульсный от-
клик &(t) = s(— t) фильтра, согласо-
ванного-с этим сигналом.
(см. (9.3)). Из рис. 9.13 — автокорреляции импульса, линейно
модулированного по частоте, следует, что
а2(0 = 0 при |t|>02
МО = С j cos(®0r4- н у)cos[®0(т — t) + н(-^-у-^]drt
где
тг = t — 0/2, т2 = 0/2 при 0 < t < 0;
Тх = — 0/2, т2 = t -j- 0/2 при — 0 < t < 0.
(9.10)
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
Преобразуя произведение косинусов в сумму
S2(O = у J cos|®0*4- + 7 У COS ^®0 (2т —0 +
+ ^[т2 + (т-0г]рт
и опуская второй интеграл, который приводит к сигналу с часто-
той 2<в0 и в устройстве не регистрируется, получаем
cf sin[«0t + p#(T-t/2)] р _
s2= Т [-------------Ft “
= sin|y (тг — Ti)j COS [(Во* + у (т2 + Т1 — о]*
Согласно соотношениям (9.10) т2 + т4 ='f, т2 — п — 0 — lf| и s2(f)
при —0 < t < 0 записывается в виде
sin (9 — |t|) siny(0 — |t|)(Q_f(|)
®2 (0 = C —5—------- cos (00* = C ~-f--------cos <o0l.
(9.11)
Сигнал на выходе, представляющий собой сжатый импульс,
в интервале своего существования [—0, 0] имеет огибающую,
Рис. 9.13. Автокорреляция импульса, sf(r-fy p/n s,(r-tf)
линейно модулированного по часто- [------'
В зависимости от знака t пределы ! *г<?¥/$// \0 j
“,егрпкнж+йв/2'в'21 * И «-? {—*
изменяющуюся как произведение функции (sin®)/® на линейные
зависимости 0— lil, которые образуют треугольник автокорреля-
ционной функции от прямоугольной огибающей входного сигна-
ла. Радиоимпульс на выходе имеет постоянную несущую частоту,
равную центральной частоте входного сигнала /0 = <в0/2л.
Обозначим девиацию частоты входного сигнала В = у.0/2л.
Огибающая e2(i) сжатого импульса зависит только от произведе-
ния BQ = R. В зависимости от приведенной переменной £/0 имеем
е2 Ь 2 t
nR ©
(9.12)
24*
364
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
На рис. 9.14 показан сигнал на выходе фильтра с BQ = 10.
В области максимумов огибающая сжатого импульса приближен-
ие sin(nRw)
но может быть описана функцией е2 (t)» —------------. При этом
nJ? -Q
длительность центрального пика на уровне 3 дБ равна
At = 2^.0 = 2^. (9.13)
Таким образом, сигнал с длительностью 0 сжат во времени в
1,137? раз.
Предполагая отсутствие потерь в пассивном фильтре, из за-
кона сохранения энергии можно получить, что амплитуда им-
пульса составляет примерно V7?0 ==С0/2, где С » У2ц/л.
По сравнению с основным пиком уровень боковых лепестков
1-го порядка ниже на 13,3 дБ, а 2-го порядка — на 18 дБ.
Спектр сигнала. Частотный отклик согласованного фильтра.
Спектр сигнала с линейной частотной модуляцией, являющийся
комплексно сопряженной функцией по отношению к частотному
отклику согласованного фильтра, находится из выражения (1.22):
(®) -= 1 Ех (ш - ®0) + у Е* (то + ©0). (9.14)
При et(t) = n(t/0) и TCt)»^2^ из соотношения (1.21) следует
+9/2
^(ш) J exp - 2^)1 dt.
-й/2 L
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
365
Прибавляя и вычитая ю2/ц2 в показателе экспоненты, получаем
ш2 +0/2
^(со) =е"^ f exp[f(f -
—0/2
Подстановка I'pX/— ы/р.) = Уля, dt= Ул/цйя приводит интеграл
к виду
^(®) f (9.15)
-*i
где
При больших R пределы интегрирования равны — оо и +«>,
если |со! < лВ. Поскольку
+ °о ДХ2 ,л_
J е 2 dx- /2е 4,
то hm Ег (со) У2л/рехр [i (л/4 — со2/2р)] ПРИ — лВ < со < лВ. На-
В-»оо
против, если Icol > лВ, интеграл равен нулю, так как пределы
интегрирования очень близки. Приходим к результату, получен-
ному в упр. 1.7 методом стационарной фазы: огибающая спектра
линейно модулированного по частоте сигнала представляет собой
прямоугольник, ширина которого равна девиации частоты В,
а центр соответствует центральной частоте /о.
Если произведение 50 имеет конечную величину, спектр
(9.15) выражается через интегралы Френеля
х х
С (X) - J cos — dx, S (х) = f sin ~ dx (9.17)
о 0
соотношением
_____<2a
5г (®) = J/ e [С (Хг) + C (X2) + IS (Хг) + IS (X2)]. (9.18)
Из зависимостей на рис. 9.15 видно, что форма спектра с
ростом В приближается к прямоугольной. Эти кривые напоми-
нают получаемую в оптике [22] дифракционную картину при
прохождении света через узкую щель с прямолинейными парал-
лельными краями (рис. 9.16). Освещенность экрана, помещен-
366
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
ного на расстоянии b от щели ширины d, освещенной источни-
ком, находящимся на расстоянии а, зависит от соотношения R =
= d4a + ЬМУ-аЬ, которое играет роль произведения S0, только
вместо частоты здесь входит расстояние z, а вместо девиации
частоты В — ширина Д геометрического изображения щели на
Рис. 9.15. Амплитуда спектра сигнала с линейной частотной модуляцией
приближается к прямоугольнику с ростом произведения ВО = R. (Рис. 6.6
из [21].)
экране. Таким образом, можно провести аналогию между согла-
сованным фильтром, который производит сжатие во времени
частотно модулированного импульса, и линзой, фокусирующей, в
пространстве пучок параллельных световых лучей [23]. Если
все точки щели колеблются в фазе (а = °°), кривые рис. 9.15
Рис. 9.16. На конечном расстоянии
от щели распределение освещен-
ности экрана напоминает спект-
ральную характеристику сигнала
с линейной частотной модуля-
цией.
изображают (при R = df/hb и замене В на d) диаграмму направ-
ленности прямолинейного преобразователя с шириной d, измерен-
ную на конечном расстоянии Ъ, много большем d.
Частотный отклик согласованного фильтра, согласно (9.5) и
(9.14) и с учетом С = У2р./л, есть
Я(ш) = j/^5*((o)e =
= У[Е* (со - соо) + Е1 (® + ®о)]е“ш‘°.
Полагая (что неявно делалось выше), что обе части спектра с
центральными частотами ±со0 очень слабо перекрываются, полу-
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
367
чаем из (9.18) частотный отклик для со > 0:
(9Л9)
где введены обозначения
Р = С(А’1) + С(Х2), <? = 5(А1) + 5(А2). (9.20)
Значения X, и Х2 находятся из выражения (9.16) подстановкой
(со — (о0) вместо ®. Фаза частотного отклика Ж со) представляет
собой сумму двух членов:
Ф(со) = ФДсо) + Ф2(со). (9.21)
Наиболее важный член
фг(®) = ^Г^-^о (9.22)
дает линейную зависимость времени групповой задержки от
частоты
Фильтр, согласованный с частотно модулированным сигналом,
неизбежно является дисперсионным; причем зависимость вре-
мени задержки от частоты имеет наклон, противоположный на-
клону зависимости мгновенной частоты от времени (рис. 9.17).
Рис. 9.17. Зависимость времени групповой задержки от частоты.
Частота сигнала растет во времени, и, следовательно, низкочастотные со-
ставляющие имеют бблыпую задержку.
Такой дисперсией и объясняется процесс сжатия импульса:
низкочастотные составляющие в начале сигнала задерживаются
фильтром на большее время, чем высокочастотные составляющие,
приходящие в конце сигнала.
Второй член в выражении для фазы,
Ф2 (со) = — arctg 2-, (9.24)
368
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
приводит к флуктуациям времени групповой задержки
Ат - d^_PQ'-QP'
е da р- Q2
43 учетом выражений (9.20) и (9.17) получаем
Р ~ da + *о ~ лВ V 2 ^C0S 2 A1 C0S
Заменяя разность тригонометрических функций их произведением,
запишем относительные флуктуации времени групповой задерж-
ки в виде

р«»^(4+Ч)+<?в!»^(Ч+Ч)
Р2 + (Я •
(9.25)
В полосе пропускания Р » Q « 1 относительная амплитуда
.флуктуаций, имеющая величину порядка l/nV7?, убывает с ро
стом Я. Величина Атв равна нулю на частотах, удовлетворяющих
условию XI — Х% = 4р, р — целое число, или, согласно (9.16),
= (9.26)
т. е. период флуктуаций с ростом R уменьшается. Этот вывод
подтверждает рис. 9.18.
Предыдущий анализ показывает, что произведение BQ явля-
ется важным параметром как для временных, так и спектраль-
ных характеристик. Между тем, одно и то же значение R можно
получить при большой величине В и малой величине 0, напри-
мер, В = 20 МГц, 0 = 5 мкс, или же при малой В и большой 0,
например, В — 100 КГц, 0 = 1 мс. Сигналы первого класса (ис-
пользуемые в радиолокации) могут быть обработаны только в
высокочастотных линиях, второй класс сигналов (используемых
в звуколокации) требует линии большой длины (в несколько
метров). Большинство приводимых нами примеров относится к
линиям, предназначенным для обработки сигналов сравнительно
малой длительности* Исключение составляют самые старые уст-
ройства — дисперсионные линии задержки на объемных волпах,
о которых пойдет речь в следующем разделе. Три других типа
линий задержки (на волнах Лява, на волнах Рэлея и акусто-
оптические), которые рассматриваются далее, способны обраба-
тывать различные сигналы и используются наиболее широко,
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
9.3.3. Дисперсионные линии на объемных упругих волнах.
Принцип согласованной фильтрации реализуется в различных
формах. Первые фильтры представляли собой чисто электриче-
ские цепи на основе ячеек Т-типа. Их недостатком является
большое количество элементов и, следовательно, значительные
размеры. Менее громоздкими являются устройства на упругих
Рис. 9.18. Относительные флуктуации времени групповой задержки ATg/в*
при Вв = 25. (Рис. 14 из [24].)
волнах, которые в их рабочем диапазоне частот успешно заменя-
ют электрические фильтры. В однородной среде упругие волны
распространяются без дисперсии, по крайней мере пока длина
волны намного превышает межатомные расстояния (см. 1.2.2).
Напомним, что Л = 10 А при частотах порядка 3000 ГГц, а такие
частоты уже не относятся к области радиоэлектроники. Таким
образом, дисперсионные свойства линий задержки на объемных
волнах следует создавать за счет геометрии звукопровода [25].
В изотропном твердом теле при распространении в направле-
нии Xi поперечной волны, поляризованной вдоль хг, возникает*
только напряжение TiZ = cBBSiZ, и, следовательно, на всей свобод-
370
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
ной поверхности, перпендикулярной х3, выполняется граничное
условие Та — 0. Таким образом, в тонкой пластинке или широкой
ленте существует недисперсионная мода со скоростью VT (мода
нулевого порядка). Однако эта горизонтальная поперечная волна
Tff, которая сохраняется при отражении от свободных поверх-
ностей волновода, порождает моды более высокого порядка,
дисперсионные кривые которых напоминают приведенную на
рис. 1.8 зависимость. Изменение времени групповой задержки,
следующее из этой зависимости, используется для создания ли-
ний, согласованных с модулированным (нелинейно) по частоте
сигналом [261, работающих в диапазоне между частотами отсечки
двух первых мод. На частотах в несколько МГц можно получить
коэффициент сжатия порядка 100 при длительности импульса
свыше 500 мкс. Одним из недостатков такого типа линий явля-
ется наличие паразитных сигналов от моды нулевогб порядка,
которые трудно подавить.
С этой точки зрения к лучшим результатам приводит исполь-
зование волн Лэмба [27]. Дисперсионный эффект возникает здесь
благодаря изменению с частотой соотношения продольных (D
и поперечных (TV) составляющих этих волн, которые имеют раз-
ные скорости. Зависимость времени групповой задержки от ча-
стоты, приведенная на рис. 9.19 для первой моды сжатия, имеет
Рис. 9.19. Волны Лэмба. Изменение
времени групповой задержки с ча-
стотой / для 1-й симметричной моды в
изотропной ленте длины I и толщины
h при VTIVL = 0,5.
На низких частотах доля продольных
волн более значительна, чем попереч-
ных, на высоких частотах — наоборот.
При очень высоких частотах (X h)
скорость стремится к значению скоро-
сти волн Рэлея Рд.
линейную область вблизи точки перегиба *). Линии задержки
такого типа были созданы из алюминиевого сплава для частот
ниже 5 МГц и из стали, более пригодной для изготовления тон-
ких лент, для частот до 30 МГц. Отклонения, от линейности
ограничивают относительную девиацию частоты величиной 10%.
Коэффициент сжатия достигает 100, длительность импульса со-
ставляет от 50 мкс до нескольких миллисекунд (одной миллисе-
кунде соответствует алюминиевая лента длиной примерно 4 м).
*) Эта зависимость получается из классических дисперсионных урав-
нении [27], называемых уравнениями Рэлея —Лэмба. Они не приводились
в настоящей книге (как и уравнения Пошамера — Шрэя для цилиндров),
так как общее изучение волноводного распространения волн в лентах или
трубах выходит за рамки рассматриваемых вопросов.
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
371
Потери обычно составляют менее 40 дБ, а уровень боковых ле-
пестков ниже 30 дБ. Для увеличения линейности использовались
ленты с участками разной толщины (рис. 9.20) или с плавно
изменяющейся толщиной [28]. Такие линии при прочих равных
параметрах (линейность, коэффициент сжатия) обладают большей
относительной шириной полосы пропу-
скания (40%) и меньшей длиной, i________________।-----1 ।
а следовательно, и меньшими потерями. | '
Изгибные волны и волны сжатия, ' I_______
подобные волнам Лэмба, могут распро- рис. 920 дисперсионная
страняться в проволоках или трубах. линия задержки с учаетка-
Разработаны линии задержки со сред- ми разной толщины.
ней частотой в несколько сот кило-
герц и длительностью импульса до нескольких миллисекунд.
Кроме волноводного, в устройствах используются и другие
принципы осуществления дисперсии, как, например, принцип
дифракционной решетки [29, 30]. На рис. 9.21 показана линия за-
держки с двумя перпендикулярными решетками. Решетка Е, состоя-
щая из элементарных источников, возбуждаемых синфазно, излуча-
Поглотителв
ет бездисперсионные поперечные вол-
ны. Решетка R, состоящая из элемен-
тов, соединенных параллельно, игра-
ет роль приемного преобразователя.
Дисперсия обусловлена различием
расстояний, которые проходят вол-
ны разных частот,- Поскольку в ка-
Рис. 9.22. Уголковая дисперсион-
ная линия задержки.
Резонансные частоты выходных
преобразователей различаются
между собой.
Рис. 9.21. Дисперсионная линия
задержки с перпендикулярными
дифракционными решетками.
Преобразователи расположены
таким образом, что путь зависит
от частоты.
честве звукопровода выбран диэлектрик (плавленый кварц), сред-
няя частота и, следовательно, полоса пропускания здесь больше,
например, соответственно 45 МГц и 20 МГц [6]. Сообщалось о
величине коэффициента сжатия, равной 400.
По геометрии к этой линии задержки близка уголковая ли-
ния [31, 32], хотя ее работа основана на другом принципе
(рис. 9.22). Элементы, составляющие приемный преобразователь,
работают как резонаторы. Они расположены таким образом, что
372
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
расстояние между цельным излучающим преобразователем и
двумя соседними приемными преобразователями различаются на
длину волны для их резонансной частоты. Требуемый закон
дисперсии получается выбором расстояний между резонаторами.
Наклон зависимости времени групповой задержки от частоты
может быть положительным или отрицательным, в зависимости
от того, дальше или ближе от излучающего преобразователя
находятся высокочастотные резонаторы.
9.3.4. Дисперсионные линии на волнах Лява. Скорость упру-
гих волн, распространяющихся в среде, состоящей из тонкого
слоя на полубесконечной подложке, изменяется с частотой. Вол-
ны Лява рассмотрены в 'разделе 5.2.4. На низких частотах их
фазовая скорость равна скорости в подложке (F'), а на высоких
частотах она равна скорости в слое (F<F'). Такую дисперсию
можно использовать для создания фильтров, согласованных с
линейно модулированным по частоте сигналом, поскольку зави-
симость времени групповой задержки от частоты (рис. 5.39)
имеет точку перегиба,
в области которого ее можно
рассматривать как линей-
ную.
Исследовались различные
сочетания материалов [34]:
медь на бериллии, вольфрам
на бериллии, стекло на плав-
леном кварце, двуокись
кремния (SiO2) на кремнии.
Последнее сочетание облада-
ет технологическим преиму-
ществом — слой получается
термическим окислением мо-
нокристаллической подлож-
___ Поликристалличность металлических слоев ограничивает
применение структур первых двух типов частотами до 50 МГц.
В противоположность этому, линии с аморфными слоями (дву-
окись кремния) работают до более высоких частот. Толщина слоя,
Лрео^разова/лель
Электроды
Ллеино
Лодтмжа
Рис. 9.23. Линия задержки на волнах
Лява с двумя преобразователями, при-
крепленными к поверхности и имею-
щими активную ширину %о/2 и очень
широкую диаграмму направленности.
Возбужденные 777-волны отражаются
от границы и проходят в слой.
(Рис. 5 из [34].)
слой.
ки.
зависящая от частоты и материала, составляет десятки микрон
при 10 МГц. Получение однородного и равномерного слоя на
всей длине подложки является серьезной проблемой, которая
затрудняет воспроизводимость параметров линии.
На рис. 9.23 показан образец линии задержки с двумя при-
крепленными к поверхности преобразователями. Они представ-
ляют собой резонансные пластинки из керамики или ниобата
лития (в зависимости от частоты), возбуждающие горизонталь-
ные поперечные волны (TH). Ширина электрода выбирается
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
373
п^мерно равной половине длины волны на центральной частоте
с Целью получения очень широкой диаграммы направленности.
При этом часть энергии отражается от границы. слой — подложка
и проходит в слой.
Вис. 9.24 соответствует линии задержки вольфрам — бериллий
с центральной частотой 32,5 МГц (толщина h = 4 мкм) и длиной
7,5 см. Хорошая линейность сохраняется в полосе частот, при-
мерно равной 100%, однако из-за значительного изменения по-
терь (14 дБ) девиация частоты практически не превышает
10 МГц. Зависимость времени групповой задержки от частоты
Рис. 9.24 Дисперсионная линия за- Рис. 9.25. Дисперсионная линия за-
держки на волнах Лява (W—Be). держки SiOa—Si.
Зависимость времени групповой за- Изменение времени групповой за-
держки и потерь от частоты держки с частотой для волн Лява
(Рис. 12 и 13 из [34].) и волн Рэлея. (Рис. 15 из [34].)
0 = 0,8 мкс, В = 80 МГц при центральной частоте 130 МГц (h —
= 5 мкм). Собственные потери в линии составляют 50 дБ при
неравномерности до 5 дБ в полосе пропускания. Был создан
лабораторный макет устройства с величиной сжатия, близкой
к 1000 (/о = 300 МГц, В — 215 МГц, 0 = 4,85 мкс), однако не-
равномерность потерь в этом устройстве превышала 10 дБ [35].
В слоистой структуре возможно также возбуждение и распро-
странение дисперсионных волн Рэлея (рис. 9.25). В этом случае
преобразователь ориентирован так, чтобы возбуждалась волна,
поляризованная в сагиттальной плоскости.
9.3.5. Согласованные фильтры на волнах Рэлея. Сложность
волн Рэлея компенсируется их важным достоинством: они воз-
буждаются (и принимаются) встречноштыревыми преобразовате-
лями, изготовляемыми при помощи простой технологии. Такие
374
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
/
преобразователи эквивалентны дискретному распределению
ультразвуковых источников (приемников), фаза и относительная
интенсивность излучения которых определяются независимо по-
ложением и активной длиной штыревых электродов (см. 7.2.4).
Следовательно, выбором соответствующей геометрии преобразо-
вателей можно осуществить большое разнообразие импульсных
откликов фильтров.
Дисперсионные линии задержки для частотно модулирован-
ного сигнала. Схема действия фильтра, согласованного с частотно
модулированным сигналом, показана на рис. 9.26. Дисперсия
Рис. 9.26. Дисперсионная линия задержки на волнах Рэлея, согласованная
с частотно модулированным сигналом.
а) Импульсный отклик. Следует сравнить с сигналом, по отношению к ко-
торому отклик должен быть обращен во времени. 6) Сжатый импульс. Вы-
сокочастотные составляющие в конце сигнала возбуждают край В преобра-
зователя в момент прихода туда волн Рэлея, излученных на входе А пре-
образователя низкочастотными составляющими в начале сигнала.
возникает из-за изменения расстояния между электродами вдоль
преобразователя. Низкочастотные составляющие излучаются в
основном областями с большими межэлектродными расстояния-
ми, высокочастотные — областями с малыми межэлектродными
расстояниями. Источник волн Рэлея как бы движется при изме-
нении частоты. Поскольку приемный преобразователь с большой
полосой пропускания четко локализован, путь, проходимый уп-
ругими волнами, изменяется с частотой. Из сравнения формы
сигнала и структуры преобразователя или его импульсного от-
клика (рис. 9.26, а) следует выполнение условия h(t) =s(te — t).
Согласно (9.9) фаза импульсного отклика фильтра, согласован-
ного с линейно модулированным по частоте сигналом, имеет вид
2л - № 02’ 2 2-
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
375
Ё соответствии с методом дискретных источников, изложен-
ным\в разделе 7.2.4, источники должны находиться в точках
Хп = ¥л£п, где моменты времени t„ определяются условием
cp(in) =*= пл:
q-— 2/о^п + п = 0, =-^ р — у/"! — ]. (9.27)
Целое число п определяется длительностью 0 импульсного от-
клика:
Так, при /о = 50 МГц, 0 = 6 мкс преобразователь содержит
N = 2/о0 = 600 электродов. Длина перекрытия соседних электро-
дов находится из выражения (7.96) с учетом того, что огибающая
имеет прямоугольную форму:
= Wo »
V (W
(9.28)
В рассматриваемом здесь случае, когда согласование с сиг-
налом обеспечивается только входным преобразователем, роль
выходного преобразователя сводится лишь к созданию электри-
ческого сигнала. Полоса пропускания Д/ этого преобразователя
должна быть больше девиации частоты, поэтому он имеет малое
число электродов, так как согласно выражению (7.37) N— 1 =
= 1,77 /0/Д/.
Предыдущие расчеты проведены для идеальных условий без
учета изменения скорости волн Рэлея под металлическими элект-
родами, которые закорачивают тангенциальную компоненту элект-
?ического поля волны, и без учета влияния массы электродов
для алюминия этот эффект выражен слабее, чем для золота)
и взаимодействия между источниками благодаря обратному
пьезоэлектрическому эффекту. Тем не менее опыт хорошо под-
тверждает теорию, если кристалл является слабым пьезоэлектри-
ком, таким как кварц. С другой стороны, в случае необходимости
можно слегка изменить структуру преобразователя с целью по-
лучения требуемого импульсного отклика. На этом принципе
создано большое число дисперсионных линий задержки со сле-
дующими типичными параметрами:
Центральная частота
Относительная девиация частоты
1лительность сигнала
Троизведение BB—R
10 МГц < /о < 400 МГц
^<50%
1 мкс < 0 < 50 мкс
10 < R < 1000
376 ГЛ. 9. ОБРАБОТКА СИГНАЛОВ /
Потери (а-кварц) от 30 до 50 дБ ,
Температурный коэффициент — (а-кварц, I У-срез —2,4 • 107® °C-*
Т (JU J I
направление распространения X) [36] [ ST-срез 0 j
Ниобат лития, несмотря на меньшие потери, используется
реже из-за значительного температурного коэффициента (8,5410~s)
и паразитных эффектов, обусловленных большой величиной коэф-
фициента электромеханической связи.
На рис. 9.27 показана одна из первых линий задержки про-
мышленного изготовления. Она изготовлена из кварца (У-срез,
направление распространения X), центральная рабочая частота
Рис. 9.27. Кварцевая дисперсионная линия задержки на волнах Рэлея,
to = 14 МГц, В = 5,5 МГц, 0 = 4 мкс. Средняя ширина штыревых электро-
дов равна 56 мкм.
равна 14 МГц (В — 5,5 МГц, 0 = 4 мкс) при коэффициенте сжа-
тия, равном 24. В действительности длина входного преобразо-
вателя больше, чем используемая его часть, и равна 14,7 мм, что
соответствует изменению частоты от 10,8 МГц до 17,1 МГц.
Кроме того, длина всех штыревых электродов сделана одинаковой.
Для формирования импульсного отклика предусмотрено исполь-
зование частотного и амплитудного ограничителей, соответствен-
но для подавления сигнала свертки' в приемном, преобразователе
и получения постоянной амплитуды выходного сигнала. Входной
импеданс эквивалентен параллельно соединенным емкости по-
рядка 20 пФ и сопротивлению 70 кОм. Приемный преобразова-
тель имеет всего лишь шесть штыревых электродов шириной
56 мкм. Уровень боковых лепестков сжатого импульса (рис. 9.28)
на 16 дБ ниже центрального пика. На рис. 9.29 показан частот-
ный отклик такой линии. С ростом произведения В0 форма оги-
бающей частотного отклика приближается к прямоугольной в
соответствии с предсказаниями раздела 9.3.2, в чем можпо убе-
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
377
\
диться из рис. 9.29 б, на котором показан импульсный отклик
дисперсионной линии при В® = 90.
В радиолокации различие между центральным пиком и боко-
выми лепестками должно превышать 13,3 дБ, что обеспечивает
согласованную фильтрацию линейно модулированного по частоте
сигнала при В® > 1. Еще большее подавление боковых лепестков
можно получить, используя два способа.
Первый заключается в изменении по определенному закону
длины перекрытия штыревых электродов входного преобразова-
теля при неизменном их положении [37]. Для изображенного
на рис. 9.30 преобразователя с весовой функцией Дольфа — Че-
бышева [38] расчет (в предположении бесконечной «гребенки»)
дает подавление в 40 дБ, а экспериментальные данные — 27 дБ.
Такое расхождение, обусловленное конечными размерами «гре-
бенки», является существенным, поскольку коэффициент сжатия
небольшой. Вместе с тем выигрыш в подавлении уровня боковых
лепестков достигается за счет увеличения ширины сжатого им-
пульса (рис. 9.31) и роста потерь. Кроме того, фильтр уже не
является согласованным с сигналом, поскольку измененный им-
пульсный отклик больше не соответствует соотношению (9.2).
Второй способ, дающий такое же, но без вышеуказанного не-
достатка, подавление уровня боковых лепестков, более предпочти-
телен, однако в этом случае сигнал должен быть модулирован по
частоте нелинейно [39]. Мгновенная частота со временем может,
например, изменяться по S-образному закону, который получа-
ется наложением одного периода синусоиды на прямую (рис. 9.32).
Уровень боковых лепестков зависит от относительной амплитуды
синусоиды [40]. На рис. 9.33 показан сжатый импульс на выходе
линии задержки с центральной частотой /0 = 14 МГц (5 =
= 5,5 МГц, 0 = 4 мкс)', для которой расчетная и эксперименталь-
ная величины режекции равны соответственно —27,5 дБ и
—25 дБ. Сигнал автокорреляции уже не описывается зависи-
мостью (sinrr)/a:, его длительность &t на уровне 3 дБ превышает
величину 1/5, поэтому соотношение длительностей сигнала и
сжатого импульса (18) меньше произведения 50 = 22. Линия
задержки, работающая на более высоких частотах (/0 = 22 МГп,
5 = 5 МГц, 0 = 5,6 мкс), показана на рис. 9.34. Фронты импуль-
сного отклика (рис. 9,35, а) не являются крутыми в результате
свертки сигнала, излученного входным преобразователем, с прямо-
угольным импульсным откликом приемного преобразователя
(с длительностью 0,17 мкс). Сжатый импульс (рис. 9.35, б, в)
имеет ширину на уровне 3 дБ, равную 0,3 мкс, а уровень боко-
вых лепестков составляет —25 дБ. Согласно теории (упр. 9.2)
уровень 1-го бокового лепестка ниже остальных.
При работе с длинными импульсами (0 > 15 мкс) можно, как
это показано в разделе 7.2.4, использовать дискретизацию пре-
25 э. Дьелесан, Д. Руайе
378
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Рис. 9.28. Сжатый импульс на выходе линии задержки, показанной на
рис. 9.27.
Ширина на уровне 3 дВ составляет 0,17 мкс. Уровень боковых лепестков
f —16 дБ.
^-Ча^отныи отклик, а) Линия задержки, показанная на рис. 9.27.
1-°“ = 22). 6) Линия задержки с произведением Вв = 90 (/о = 26 МГн.
в = 9 МГц, 0 = 10 мкс). Ср. с рис. 9.15.
Рис. 9.30. Дисперсионная линия задержки с амплитудным взвешиванием,
ta = 14 МГц, В — 5,5 МГц, 0 = 4 мкс.
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
379
Рис. 9.31. Сравнение сжатых импульсов
на выходе линий задержки, показанных
на рис. 9.27 и 9.30.
Взвешивание подавляет боковые ле-
пестки, но увеличивает ширину импуль-
са.
Рис. 9.32. Зависимость мгно-
венной частоты от времени
для сигнала с нелинейной ча-
стотной модуляцией.
Рис. 9.33. Сжатый импульс на выходе линии с
S-образной характеристикой задержки: fB =
— 14 МГц, В = 5,5 МГц, 0 = 4 мкс, боковые ле-
пестки — 25 дВ.
Рис. 9.34. Дисперсионная линия с S-образной характеристикой задержки:
fa = 22 МГц, В = 5 МГц, 0 = 5,6 мкс.
25*
380
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Рис. 9.35. Отклик линии задержки, по-
казанной на рис. 9.34, на короткий им-
пульс (а) и на сигнал (би в).
<’ <А’"
Рис. 9.36. Дискретизированная линия задержки с S-образной характеристи-
кой задержки: Q = 15, /9 = 40 МГц, В = 2 МГц, 0 = 20 мкс.
а) Часть входного преобразователя, б) Сжатый импульс.
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
381
образователей для уменьшения количества штыревых электродов.
На рис. 9.36 показана линия такого типа с фактором дискрети-
зации Q = 15 и длительностью импульса 0 = 20 мкс. Источники,
образованные парой электродов шириной Х/4 = 20 мкм с цент-
ральной частотой /о = 40 МГц, расположены согласно S-образному
закону частотно-временной зависимости. Расстояния между
дискретами равны 15 V2. Приемный преобразователь имеет боль-
шое число штырей (2V = 40), поскольку относительная девиация
частоты составляет только 1/20 (5 = 2 МГц). Коэффициент сжа-
тия сигнала равен 30 при уровне боковых лепестков —24 дБ
(рис. 9.36, б).
Примечание.
Линии с отражающими решетками. Как и все волны, упругие
волны могут отражаться от неоднородностей, поэтому последова-
тельность неоднородностей, расположенных по определенному
закону на ленте, в которой распространяются объемные ТЯ-вол-
ны, или на поверхности, вдоль
которой распространяются вол
ны Рэлея, позволяет осуще-
ствить контролируемую дис-
персию [41J. Такими неодно-
родностями могут быть штрихи
на поверхности или канавки.
В последнее время были про-
ведены специальные исследова-
ния отражения от канавок. От-
ражение изучалось в низкоча-
стотных линиях задержки из
металлической ленты [42] ив
линиях задержки на волнах Рэ-
лея [43]. Принцип действия
таких линий с использованием
Приемник
Рис. 9.37. Линия задержки с диспер-
сионной отражающей решеткой.
Волны Рэлея отражаются под пря-
мым углом в области, где шаг ре-
шетки равен длине волны.
волн Рэлея, разработанный в ла-
боратории Линкольна (Массачусетский технологический институт,
США), показан на рис. 9.37. Линия содержит два бездисперсион-
ных встречноштыревых преобразователя и две решетки наклон-
ных канавок с переменным шагом. Волны, излученные передаю-
щим преобразователем, отражаются под прямым углом от первой
наклонной решетки в той ее области, где шаг решетки равен
длине волны. Так как период решетки растет с удалением от
входа, высокочастотные волны проходят меньшее расстояние, чем
низкочастотные. Вторая наклонная решетка, выполняющая та-
кую же роль, как и первая, направляет волны к входному пре-
образователю.
Коэффициент отражения г является функцией глубины ка-
навки [44], и при h/K < 10-21 г| ® V3X, а скорость волн, распрост-
раняющихся под решеткой, практически не меняется. Таким
382
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
образом, изменяя глубину канавки (и, если требуется, их длину),
можно реализовать амплитудное взвешивание и подавить боко-
вые лепестки сжатого импульса.
Такой метод положил начало новому поколению дисперсион-
ных линий с высоким коэффициентом сжатия, например, 1500
[45] (/о — 200 МГц, В = 50 МГц, 0 = 30 мкс, потери ~40 дБ, бо-
ковые лепестки —15 дБ без взвешивания, подложка LiNbO9).
Была достигнута даже величина, превышающая 5000 [46] (Д =
= 1000 МГц, В = 512 МГц, 0 = 10 мкс, потери ~ 60 дБ, боковые
лепестки —20 дБ с внутренним взвешиванием, подложка
LiNbO3). Большое количество отражающих канавок (12 000 во
втором случае) создавалось методом ионной бомбардировки [47].
Так как неоднородность импеданса, приводящая к отражению,
имеет чисто механическую природу, можно использовать и не-
пьезоэлектрические вещества, однако в этом случае возникает
проблема возбуждения волн Рэлея. Она, в принципе, может быть
решена с помощью преобразователей, прикрепленных на концах
линии, как это делается в низкочастотных ленточных линиях
задержки на ГЯ-волнах [42]. Отметим, что в этом случае также
получен коэффициент сжатия, превышающий 1000, однако при
большей длительности импульса (/»= 10 МГц, 5 = 5 МГц, 0 =
= 250 мкс, потери 30 дБ).
Трансверсальные фильтры. Как уже отмечалось, частотная
модуляция не является единственным примером кодирования.
В телекоммуникации используются дискретные коды. Наиболее
простым является двоичный код, т. е. последовательность знаков
1, 0 или 1, —1, следующих один за другим через регулярные
промежутки времени. Двоичное кодирование и декодирование
можно весьма просто осуществить с помощью волн Рэлея, ампли-
туда или фаза которых может нести нужную информацию. Оба
случая показаны на рис. 9.38 и 9.39. Короткий импульс, подан-
ный на входной преобразователь кодирующего устройства, воз-
буждает кодированный акустический сигнал. Этот сигнал прини-
мается декодирующим устройством, выходной преобразователь
которого (трансверсальный, согласованный фильтр) вырабатывает
функцию автокорреляции. В качестве примера на рис. 9.40, а
показана автокорреляция сигнала с фазовой модуляцией (фаза
принимает только два значения 0 или л), кодированного в виде
последовательности 111011001010000. Несущая частота равна
60 МГц. Если вместо сигнала sit) используется сигнал, обращен-
ный во времени, s(—i), идентичный импульсному отклику деко-
дирующего устройства, согласования уже нет, и выходной сигнал
имеет вид, показанный на рис. 9.40, б.
Двоичный код Баркера с фазовой модуляцией, содержащий N
битов,. дает автокорреляционный сигнал с отношением уровней
центрального пика и боковых лепестков, равным N. Следователь-
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
383
но, в любой момент времени, кратный длительности бита, кор-
реляционный сигнал принимает значения N и 0, ±1. Это условие
ограничивает длительность кода тринадцатью битами при нечет-
ном N. При четном N используется не более 4 битов. На рис. 9.39
показан пятибитовой код Баркера.
Декодер
Рис. 9.38. Двоичный амплитудный код.
а) Получение сигнала при подаче короткого импульса на вход линии за-
держки на волнах Рэлея, б) Прием с помощью фильтра, согласованного с
сигналом декодирующего устройства.
Рис. 9.39. Двоичный фазовый код.
а) Получение сигнала. Обращение фазы достигается обратным включением
штырей приемника волн Рэлея, б) Прием с помощью фильтра, согласован-
ного с сигналом декодирующего устройства.
384
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Расположение элементов преобразователя в одну линию мож-
но с успехом заменить наклонным их расположением, особенно
если нужно избежать паразитных сигналов, возникающих при
Рис. 9.40. Фильтр, согласованный с сигналом s(t), закодированным инвер-
сией фазы согласно последовательности (111011001010000) при несущей ча-
стоте 60 МГц. а) Автокорреляция сигнала s(«). б) Отклик на сигнал «(£),
обращенный во времени и не согласованный с фильтром.
отражениях в сильном пьезоэлектрике. На рис. 9.41 показано
различие в откликах в этих двух случаях для тринадцатибито-
вого кода Баркера при использовании подложки из пиобата
лития.
Рис. 9.41. Расположение в ряд (а) и под углом (б)преобразователей на
подложке из ниобата лития.'Сравнение автокорреляционных сигналов для
тринадцатибитового кода Баркера, полученного с помощью волн Рэлея.
Элементы выходного преобразователя декодирующего устрой-
ства можно расположить так, что они образуют многофазный
код, т. е. фаза изменяется па величину 2л/п. а пе только на л.
§ 9.3. СЖАТИЕ ИМПУЛЬСОВ
385
Кроме того, изменением активной длины элементов преобразова-
теля можно добиться уменьшения боковых лепестков. На одной
подложке может находиться несколько независимых линий с
дополнительными кодами (например, с кодом Голея), при этом
сумма автокорреляционных сигналов от каждой из линий пред-
ставляет собой сигнал без боковых лепестков (упр. 9.3).
пучон
Опорт/6
транспарант
Рис. 9.42. Распознавание образов.
Прохождение искомого объекта ми-
мо эталона приводит к появлению
максимума освещения в фокусе Р
линзы L.

9.3.6. Акустооптические согласованные фильтры. Проблема
распознавания образов в оптике также приводит к принципу
согласованного фильтра. Эталон располагается на пути светового
луча, сфокусированного с помощью линзы. Различные исследуе-
мые объекты последовательно совмещаются, подобно кадрам
кинофильма, с эталоном (рис. 9.42). Для искомого объекта в
фокусе линзы получается мак-
симум освещения. Необходи-
мость записи информации па
какой-либо носитель приводит
к задержке результатов обра-
ботки. Используя дифракцию
света на упругих волнах, элек-
трические сигналы можно об-
рабатывать в реальном мас-
штабе времени согласно схеме
рис. 9.43. Пусть имеется коди-
рованный по амплитуде сиг-
пал с фиксированной несущей
частотой. Этот сигнал подается
на преобразователь, который
немедленно преобразует его в
пакет упругих волн, например продольных. Свет, дифрагирован-
ный под углом Брэгга, соответствующим несущей частоте, соби-
рается в точке, лежащей в фокальной плоскости. Падающий све-
товой пучок модулируется с помощью амплитудной маски, явля-
ющейся пространственным отображением кода. Регистрируемая
интенсивность света, пропорциональная квадрату автокорреляци-
онной функции сигнала, достигает максимума, если все элемен-
ты волнового пакета совпадают с отверстиями эталона-маски.
В случае сигнала, кодированного по фазе, амплитудная маска
заменяется фазовой пластинкой.
В эксперименте Торкэ и Боза использовался модулированный
по фазе сигнал, распространяющийся в виде продольных волн
в кристалле молибдата свинца. Для дифракции применялся ла-
зер с длиной волны 6328 А. Основные условия эксперимента со-
стояли в следующем:
1) код — двоичный, 255 битов, с длительностью 20 нс,
2) несущая частота 175 МГц,
386
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
3) преобразователь — пластинка ниобата лития на индиевой
связке с полосой пропускания 70 МГц,
4) звукопровод — РЬМоО4, направление распространения [001]
(VL = 3630 м/с), активная длина 19,125 мм,
5) относительная интенсивность отклоненного света 60% при
электрической мощности 1 Вт,:
Рис. 9.43. Акустооптический согласованный фильтр.
Свет, дифрагированный на сигнале, преобразованном в упругую волну, и
собранный в точке фокальной плоскости линзы, имеет максимальную ин-
тенсивность, если элементы волнового пакета находятся напротив отвер-
стий маски (отображения кода).
. 6) фазовая пластинка из кремния, изменение фазы на л
создается различием в толщине на 0,69 мкм.
Результат эксперимента показан на рис. 9.44. Длительность
корреляционного пика 20 нс находится в согласии с теоретиче-
ским коэффициентом сжатия, равным 255.
Следует отметить, что кодирован-
Рис. 9.44. Акустооптический со-
гласованный фильтр.
Сжатый импульс.
ный сигнал создается с помощью
короткого импульса, подаваемого на
вход линии, подобной описанной
выше, но с амплитудной маской, ко-
торая использовалась для изготов-
ления фазовой пластинки методом
ионного травления. Распространение
импульса упругих волн вдоль маски
приводит к появлению кодированно-
го сигнала на выходе фотоумножи-
теля, регистрирующего дифрагиро-
ванный свет. Модулированный по
фазе сигнал получается при подаче
сигнала от фотоумножителя и несущей частоты на кольцевой
модулятор, где и происходит инверсия фазы согласно коду.
Оптическое устройство упрощается в случае сигнала, линей-
но модулированного по частоте (ЛЧМ-сигнал), поскольку здесь
S 9.4. ПОЛОСОВЫЕ ФИЛЬТРЫ
387
не требуется маска с отображением кода. В разделе 8.4.2 было
показано, что угол отклонения 0 светового луча пропорционален
частоте упругих волн, Следовательно, этот угол 0 » Ао/% =
= А>//7 изменяется вдоль длины линии по закону 0 = (Ао/о/7) +
+ [A0B(i — Ж1/7)]/70, в котором учитывается модуляция часто-
ты (см. (9.6)) и распространение сигнала в направлении xt.
ты (см. (9.6)) и распространение
Дифрагированный луч сходится
в направлении среднего отклоне-
ния (0 = Afl/o/V) на расстоянии
D, определяемом соотношением
(рис. 9.45)
MD = -dQ/dxt = AoB/V20.
(9.29)
При В — 50 МГц, 0 = 5 мкс,
Ао = 0,6328 мкм, 7 = 3630 м/с
(РЬМоО*) получаем D = 2,1 м. Это
расстояние может быть уменьше-
но с помощью обычной оптики.
Если приемник расположен в
точке, где сходится пучок, изме-
нение интенсивности света во вре-
мени пропорционально квадрату l________
сигнала, линейно модулированного по частоте. Эксперименталь-
но были получены значения коэффициента сжатия до несколь-
ких сотен [48, 49]
ЛЧМ’ CUDНОЛ
Рис. 9.45. Сжатие импульса с по-
мощью дифракции Брегга.
При изменении угла отклонения
0 с частотой дифрагированный
луч сходится на расстоянии D =
= 6Р/ВЛо.
автокорреляционной функции
§ 9.4. Полосовые фильтры
Здесь не ставится задача подробного описания фильтров на
объемных упругих волнах. Характеристики пьезоэлектрического
резонатора, основного элемента таких фильтров, упоминалось в
разделе 7.1.2. Классические кварцевые фильтры, изготовленные в
настоящее время в сотнях миллионов экземпляров, используются
в области частот от 50 кГц до 150 МГц (выше 30 МГц кварцевые
пластинки работают обычно на гармониках, поскольку их толщи-
ну трудно сделать меньше 50 мкм). Начиная с работ Ланжевена
и создания Кэди в 1918 г. первого генератора с кварцевой стаби-
лизацией [50], эти фильтры описываются во многих публикаци-
ях. Их широкое применение объясняется свойствами кварца, ма-
териала твердого, слабо подверженного влиянию окружающей
среды, и тем, что в кварцевом резонаторе сочетаются высокая
добротность (>104) и прекрасные температурная (нестабильность
меньше 10"“ ’С-1) и временная стабильности. Полоса пропуска-
ния этих фильтров ограничивается различием между частотами
388
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
резонанса и антирезонанса, т. е. коэффициентом электромехани-
ческой связи (А/// < К2/2~). Кварцевые фильтры (А2« 10"2) отли-
чаются, следовательно, высокой селективностью. Пьезоэлектриче-
ская керамика обладает более высоким значением коэффициента
К2 (К2« 10-1, следовательно, А///<5%), однако посредственная
температурная стабильность и более высокие потери ограничива-
ют ее применение низкочастотной областью (/ < 30 МГц). Новые
материалы, такие как танталат лития (LiTaO3), находятся в на-
стоящее время в стадии исследований.
К кварцевым фильтрам, состоящим из дискретных элементов,
в настоящее время приблизились монолитные фильтры. В инте-
гральной структуре таких фильтров резонаторы, расположенные
на одной и той же пластинке, связаны механическими колеба-
ниями, исчезающими вне металлизированных областей [51].
В фильтрах на объемных волнах используются стоячие волны.
Передаточная функция, как правило, имеет форму прямоуголь-
ника с центральной резонансной частотой, определяемой толщи-
ной пластинки. Полоса пропускания зависит от материала, а вно-
симые потери очень малы при использовании монокристаллов с
высокой механической добротностью (меньше нескольких дБ).
В фильтрах на волнах Рэлея, описываемых ниже, использу-
ются бегущие упругие волны (за исключением фильтров, состоя-
щих из резонаторов на поверхностных волнах, подобных тем,
о которых говорится в 3-м замечании на стр. 393). Передаточная
функция здесь определяется структурой преобразователя с ши-
риной штырей, задаваемой частотой, которая может достигать не-
скольких сотен мегагерц. Из-за трудностей согласования потери
здесь более значительны (> 20 дБ), коэффициент электромехани-
ческой связи материала мал, а относительная полоса пропуска-
ния велика. На высоких частотах к потерям преобразования при-
бавляются потери распространения. Это и является в настоящее
время препятствием, мешающим промышленному освоению та-
ких полосовых фильтров.
Передаточная функция линии задержки на волнах Рэлея,
один из преобразователей которой имеет электроды постоянной
длины, превышающей ширину акустического пучка, излучаемого
другим преобразователем, равна произведению передаточных
функций обоих преобразователей*). Если приемный преобразо-
ватель имеет малое число электродов, а следовательно, широкую
полосу пропускания, передаточная функция и импульсный отк-
лик определяются структурой излучателя. Изменение длины
электродов «гребенки» по закону I (sin обеспечивает прямо-
*) Это неверно, если длина электродов каждого из преобразователей из-
меняется. Анализ в этом случае оказывается более сложным, а расчет
фильтра — весьма трудным [52].
§ 9.4. ПОЛОСОВЫЕ ФИЛЬТРЫ
389
угольную передаточную функцию. Действительно, частотному от-
клику в форме прямоугольника шириной В с центральной часто-
той /о
#(/) • П при / > 0 (9.30)
соответствует импульсный отклик (рис. 1.18)
A(0-22?^^cos2n/0*. (9.31)
Согласно методу, изложенному в разделе 7.2.4, дискретные
источники должны соответствовать моментам времени t„, удов-
летворяющим условию <р(£п) = 2л/о^п=гал, т. е. tn = и/2/0, или быть
расположены в эквидистантных точках с координатами хп =
— nVR/2f0, а их амплитуда должна быть пропорциональна ве-
личине
На рис. 9.46, а показан фильтр, выполненный на подложке из
кварца (У.Х-срез) с электродами из алюминия [5.3]. Инверсия
фазы в точках, соответствующих нулю функции (sin х)/х, осу-
ществляется разнесением на длину полуволны двух соседних
штырей того же электрода. Огибающая импульсного отклика хо-
рошо повторяет рисунок преобразователя. На рис. 9.46, б при-
веден импульсный отклик этого фильтра, а на рис. 9.46, в — его
теоретическая и экспериментальная частотные характеристики.
Обе зависимости отличаются от прямоугольных, поскольку преоб-
разователь имеет конечные размеры, и функция (sin ж)Лг опреде-
ляется только ограниченным числом лепестков. Центральная ча-
стота равна 25 МГц, полоса пропускания — 2 МГц, режекция —
21 дБ. Потери с согласованным правым (на рис. 9.46, а) преобра-
зователем составляют около 30 дБ.
Для получения треугольной передаточной функции требуется
преобразователь с активной длиной штырей, изменяющейся по
закону ((sin ж)/ж)2 (рис. 1.18). Два фильтра такого типа были
объединены с целью создания частотного дискриминатора [54].
Отклик каждого из фильтров равен нулю на центральной частоте
другого фильтра (28 и 32 МГц). После вычитания постоянных
напряжений, создаваемых детекторными диодами, присоединен-
ными к выходу каждого фильтра, получается линейная характе-
ристика в полосе 0,7 МГц при средней частоте 30 МГц (рис. 9.47).
Однако потери в кварцевой подложке оказались высокими
(45 дБ).
390
ГЛ. 9. ОБРАБОТКА сигналов
Для получения узкой относительной полосы пропускания не-
обходимо, чтобы один или оба преобразователя имели большое
число штырей. Например, для получения полосы пропускания
Рис. 9.46. Полосовой фильтр.
а) «Гребенка» в форме (sin х)/х. б) Импульсный отклик, в) Теоретический
(I) и экспериментальный (2) частотные отклики.
100 кГц при центральной частоте 100 МГц необходима линия с
двумя идентичными преобразователями, имеющими по 1270 шты-
рей каждый (выражение (7.38)). Средством уменьшения этого
Рис. 9.47. Отклик частотно-
го дискриминатора на вол-
нах Рэлея.
чрезмерно большого количества штырей является дискретизация
обоих преобразователей [55] с шагом, n-кратпым (с разными
коэффициентами п, и п2 для каждого преобразователя) периоду
решетки 2d=VR/fa. Частотный отклик каждого преобразова-
§ 9.4. ПОЛОСОВЫЕ ФИЛЬТРЫ
391
теля представляет собой последовательность пиков на частотах
/о + ptJn. Разность частот двух соседних пиков равна обратному
времени распространения п//0 между двумя дискретами (упр. 9.4).
Передаточная функция фильтра имеет максимум на частоте
/о + 6/, при которой пики обоих преобразователей совпадают:
т. е. на центральной частоте /0 и частотах, отличающихся от нее
на величину, кратную f0/q, где q есть наибольший общий дели-
тель чисел П\ и пг. На рис. 9.48 показан кварцевый фильтр
Рис. 9.48. Два идентичных узкополосных фильтра на одном монокристалле
кварца (/о = 102,5 МГц, Д/ = 32 кГц).
Расстояние между дискретами входного (выходного) преобразователя, сос-
тоящими из двух штырей, равно 55 (45 Хо).
(п4 = 55, п2 = 45) с центральной частотой 102,5 МГц и полосой
пропускания 32 кГц. Потери при согласовании составляют около
20 дБ.
Для получения передаточной функции, обращающейся в нуль
на определенных частотах, следует соединить параллельно две
идентичные линии с близкими временами задержки, отличающи-
мися на величину т. Импульсному отклику такого устройства
hit) + h(t — т) соответствует, согласно разделу 1.3.2, частотный
отклик
<Э0(/) = H(f) + Я(/)е-Вя/т = 2Я(/)е-’я/т cos л/т,
равный нулю па частотах /п = (« + 4)
На рис. 9.49 приведен пример отклика фильтра с централь-
ной частотой 100 МГц и расстоянием между нулями 3,3 МГц.
В заключение отметим, что можно синтезировать любую пе-
редаточную функцию соответствущим выбором формы преобразо-
вателя, которая находится из требуемого импульсного отклика
392
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
с помощью метода дискретных источников. Этот принцип в на-
стоящее время используется для создания телевизионных фильт-
ров на промежуточных частотах (от 26 до 40 МГц) [56, 57].
Основными проблемами являются уровень потерь, материал под-
ложки и, следовательно, себестоимость.
Примечание.
1. Фильтры с отражающими решетками. Техника отражаю-
щих решеток, описанная в примечании к разделу 9.3.5, приме-
нялась [581 для создания полосовых фильтров на волнах Рэлея
Рис. 9.49. Режекторнъгй фильтр.
Частотный отклик фильтра,
состоящего из двух различных
линий задержки. Расстояние
между соседними нулями
3,3 МГц.
(примерные параметры: центральная частота 200 МГц, относи-
тельная полоса пропускания 3%, потери в отражателе 10 дБ).
Фильтрация обеспечивается отражающей решеткой с определен-
ным шагом и размерами канавок. Эта техника представляется
особенно пригодной для узкополосных фильтров (с полосой менее
0,5 МГц при центральной частоте 200 МГц).
2. Фильтры с преобразователями, имеющими штыри постоян-
ной длины. С учетом выражения
s (0 = е (0 cos «о* = cos ф (t) cos <oot =
= у cos [co0? + ф (*)] + 1 cos [«0Z - ф (*)], (9.32)
где eU) = cos ф(£), т. e. ф(£) = arccos e(£), модулированный no
амплитуде сигнал можно рассматривать как сумму двух сигналов
постоянной амплитуды, модулированных по фазе. Если е(£) яв-
ляется четной функцией, то ф(—£)=ф(£). Обозначая символом
g(O первый член в правой части (&.32), функцию s{t) можно за-
писать в виде
s(0 =g(t) + g(-t).
Идея синтеза s(f) из функции g(t) и обращенной во времени
функции g(—f) использована в фильтрах на волнах Рэлея [59],
в частности, для получения импульсного отклика (9.31). Такой
фильтр содержит центральный преобразователь Тя, соответству-
ющий функции g, и по обе стороны от него два широкополосных
преобразователя Т, и Т2. Короткий импульс, поданный на Та,
возбуждает две волны, распространяющиеся в противоположных
§ 9.5. ПАМЯТЬ
393
Рис. 9.50. Схема резонатора на поверх-
ностных волнах.
Волны, излучаемые преобразователем,
отражаются от решеток, состоящих из
металлизированных полосок или кана-
вок.
направлениях. Одна из них, соответствующая g(t), возбуждает
преобразователь Tt, вторая, g(—t), возбуждает Т2. Сложение сиг-
налов, полученных на преобразователях Ti и Тг, дает s(t). Так
как штыри преобразователей имеют постоянную длину, этот тип
фильтра обладает тем преимуществом, что не приводит к иска-
жению фронта волны (примечание к разделу 7.2.4).
3. Фильтры на стоячих волнах. Выше было показано, что в
линиях задержки и полосовых фильтрах на бегущих волнах мо-
гут использоваться отражения волн от решеток, состоящих из
последовательности металлизированных полосок или канавок. По-
добные решетки можно применять и для создания резонаторов
[60], [611, конструкция которых изображена на рис. 9.50. Волны,
излучаемые преобразовате-
лем, отражаются от решеток,
играющих роль зеркал. На
определенной частоте, зави-
сящей от периода решеток
и от расстояния между ни-
ми, устанавливается режим
стоячих волн. При использо-
вании решеток, содержащих
до нескольких сотен элемен-
тов, удается достичь доброт-
ности резонатора порядка
20 000 [62]. Несмотря на то,
что такая добротность мень-
ше, чем у резонаторов на
объемных волнах, резонанс-
ные устройства па поверх-
ностных волнах удобнее тем, что могут работать на частотах
в несколько сотен мегагерц, причем механическое крепление
кристалла не влияет существенно на их работу. Плоская кон-
струкция рассматриваемых резонаторов допускает их легкое объ-
единение в требуемую систему. Можно осуществить каскадное
соединение резонаторов [63], либо связать их с помощью ре-
шетчатого ответвителя (§ 9.7), либо, изменяя длину элементов
решеток, осуществить взвешивание. В настоящее время исследу-
ются отражатели, созданные методами ионной имплантации [64]
и плазменного травления [62].
§ 9.5. Память
Величина скорости упругих волн (1 < V < 13 мм/мкс), и дли-
на используемых на опыте твердотельных звукопроводов с при-
емлемыми потерями позволяют накапливать в линии задержки
большое количество информации. Поскольку информация не мо-
26 э. Дьелесан, Д. Руайе
394
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
жет быть зафиксирована, по крайней мере простыми способами,
в линии поддерживается ее циркуляция с помощью обратной
связи, которая обеспечивает, благодаря усилителю, компенсацию
потерь. Характеристики этих устройств циркуляционной памяти
определяются свойствами линий задержки, которые являются ос-
новной частью таких устройств: частота повторения /л составляет
долю несущей частоты, время выборки тА тем больше, чем длин-
нее линия и, следовательно, больше информационная емкость.
Линия на объемных волнах, работающая на частоте повторения
100 МГц, может, например, сохранять в памяти fRxA = 1000 битов
при тА = 10 мкс.
Линии на поверхностных волнах имеют два преимущества,
а именно: информацию можно кодировать и считывать при по-
мощи промежуточных отводов (сокращение времени выборки).
Усилитель
1 Момент
2 / бремени
Л ’•
л -ЦП!
Н+2 NMN_____________'ll
Л fillin’Л lllllllp^
8)
Рис. 9.51. Устройство DELTIC.
а) Временные выборки сигнала с очень большой длительностью, требую-
щей согласованного нереализуемого фильтра, сдвигаются во времени с по-
мощью циркуляционной линии задержки, б) Временное перераспределение
выборок,
Циркуляционная память используется в устройстве сжатия
DELTIC *) [65] для сигнала, предварительно подвергнутого диск-
ретизации. На выходе линии с временем задержки т выборки
сигнала с длительностью б = r/N, следующие одна за другой че-
рез время (т + 6), группируются в пакеты по N, как показано
на рис. '9.51, а.
") DELTIC: DElay Line for Time Compression.
§ 9.5. ПАМЯТЬ
395
Принцип действия устройства заключается в следующем. Ког-
да выборка 1, задержанная на время первого прохождения линии,
вновь поступает на вход, вслед за ней подается следующая вы-
борка 2. К этим двум выборкам, после прохождения ими линии
задержки, присоединяется выборка 3, а затем аналогичным об-
разом и последующие выборки (рис. 9.51, б). Когда линия за-
полнена, содержащиеся в ней N выборок (т = М5) выводятся в
одном пакете. Таким образом, выборки, разделенные до их по-
ступления на вход линии временными интервалами т + б = (.N +
+ 1)6, на выходе следуют одна за другой через время 6, т. е.
мгновенная частота сигнала увеличивается в N +1 раз. Таким
образом, может быть обработан очень длинный сигнал (0 « 1 с,
В«100 Гц), например, сигнал звуколокатора, согласованный
фильтр для которого физически невозможно реализовать. Сигнал,
разделенный на N выборок (2V«1OQO) с длительностью 0 = N(N +
+1)6 = (N + 1)т, сжимается в импульс с длительностью т
(«1 мс) и измененной частотой (/V + 1)В («100 кГц), который
уже можно обработать (после изменения частоты) с помощью
ленточной дисперсионной линии (см. 9.3.3).
Следует указать на принцип статической памяти, находящий-
ся в стадии лабораторных исследований [66]. В его основе лежит
Первичный пучок электронов
Пьезоэлектрический 'Потенциал Преойразоватепь
кристалл
Рис. 9.52. Запись сигналов (и обращение их во времени).
Вторичные электроны распределяются в соответствии с электрическим по-
тенциалом, сопровождающим волну Рэлея, и создают электростатическое
изображение сигнала. Электронное распределение сохраняется на изолиру-
ющей подложке, создавая механические напряжения. Новый поток электро-
нов снимает напряжения и создает две волны, распространяющиеся в про-
тивоположных направлениях. (Рис. 1 из [66].)
запись информации на поверхности кристалла с помощью элект-
ронного луча. Принцип ясен из рис. 9.52. Сигнал, преобразован-
ный в упругие волны Рэлея, при своем распространении сопро-
вождается волной электрического поля, поскольку подложка об-
ладает пьезоэлектрическими свойствами. Одновременно поверх-
26*
396
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
ность подвергается бомбардировке первичными электронами с
энергией в несколько сот электронвольт в течение времени, мно-
го мрньшего периода упругой волны. Первичные электроны вы-
бивают из изолирующего материала подложки вторичные элект-
роны, которые из-за своей малой энергии в несколько электрон-
вольт «чувствуют» потенциал порядка одного вольта, созданный
упругой волной. Те из электронов, которые возвращаются на по-
верхность, собираются преимущественно в областях положитель-
ного потенциала. Поскольку подложка изолирующая, электроны
остаются там при дальнейшем распространении волны. Поверх-
ностное распределение этих зарядов поддерживает кристалл в ме-
ханически напряженном состоянии и создает электростатическое
изображение сигнала, причем эта картина может сохраняться в
течение весьма большого времени (несколько минут), если по-
верхность имеет хорошие изолирующие свойства и не возникают
паразитные заряды. Считывание информации производится по-
вторным облучением подложки электронным пучком, в результа-
те чего должен исчезнуть или уменьшиться электрический потен-
циал, а следовательно, и механические напряжения, создаваемые
скопившимися зарядами. Резкое уменьшение напряжений порож-
дает две волны, которые распространяются в противоположных
направлениях. При этом волна, распространяющаяся к выходно-
му преобразователю, идентична записанному сигналу, а вторая
волна, распространяющаяся к входному преобразователю, явля-
ется обращением этого сигнала во времени.
Рис. 9.53. Сигналы в устройстве, изображенном на рис. 9.52. Сигналы на вы-
ходном преобразователе без запоминания (я) и после запоминания в тече-
ние 160 мс .(б). Сигнал, принятый входным преобразователем после запо-
минания в течение 160 мс (в). (Рис. 2 из [66].)
Опыты проводились на кварце при частоте 30 МГц. Пример
нолучеппых результатов представлен на рис. 9.53. Здесь показа-
ны сигнал, принятый выходным преобразователем после прохож-
дения линии (а), сигнал, принятый этим же преобразователем
после записи и считывания через 160 мс (б), и сигнал, обращен-
ный во времени, принятый входным преобразователем через та-
§ 9.6. СВЕРТКА
397
кое же время хранения. Потери запоминания, измеренные как
отношение мощности сигналов (рис. 9.53, а и б), составляют око-
ло 60 дБ. Поскольку электромеханическое преобразование проис-
ходит два раза, эти потери пропорциональны К*. Плотность тока
в электронном пучке, необходимая для записи и считывания, со-
ставляет около 100 мА/см2.
Использовать электроны, движущиеся в вакууме, оказывается
достаточно неудобно. В настоящее время исследуются возможно-
сти создания устройств, в которых бы применялись полупровод-
ники. В одном из предложенных устройств полупроводниковая
пластина с нанесенной на ней матрицей диодов помещается в
непосредственной близости от подложки-звукопровод.а из пьезо-
электрика, в котором распространяются волны Рэлея [67]. Элект-
рическое поле звуковой волны изменяет состояние полупроводни-
ковых диодов. Это изменение состояния может быть «замороже-
но», если на полупроводник во время прохождения звуковой вол-
ной области, занятой диодами, подать импульс электрического
напряжения, имеющий длительность много меньшую, чем период
звуковой волны.
§ 9.6. Свертка
Выше везде неявно подразумевалось, что амплитуды деформа-
ции, т. е. относительное изменение расстояний в твердом теле,
много меньше пороговых значений (5 < 10-4), при которых пере-
стают быть справедливыми упрощенные выражения тензора де-
формации (§ 4.1) и закона Гука (§ 4.3). При отсутствии линей-
ной зависимости между механическими напряжениями и дефор-
мациями теория, изложенная в предыдущих разделах, уже неточ-
на. Анализ нелинейных явлений требует введения дополнитель-
ных упругих постоянных. В первом приближении в выражения,
используемые в линейной теории, добавляются члены более вы-
сокого порядка. Квадратичное выражение для потенциальной
упругой энергии (4.34) дополняется членами третьего порядка
типа CijkipqSijSMSpq. Связь между механическими напряжениями и
деформацией теперь записывается в виде
Т ij = CtfalSbl + CjjhlpqShlSpq.
Отсюда можно получить уравнение распространения упругих
волн, содержащее упругие постоянные 3-го порядка [68]. Это
сложное уравнение, тем не менее, может быть решено в явном
виде для простых случаев (папример, продольных волн, распрост-
раняющихся в неограниченной среде). Без проведения расчетов
можно качественно предсказать следующие результаты. Монохро-
матическая волна при распространении порождает волны на ча-
стотах гармоник [69J; две волны с частотами и /2, взаимодей-
398
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
ствуя в твердом теле, создают волны с суммарной (/, + /2) и раз-
ностной (Д —/2) частотами. Учет граничных условий делает изу-
чение нелинейных явлений для поверхностных волн крайне труд-
ной задачей [70]. Углубление в математические проблемы нели-
нейности выхбдит за рамки настоящей книги. Здесь наш интерес
направлен на возможность использования этих явлений для по-
лучения произведения функций.
Пусть имеются два модулированных по амплитуде сигнала
sAt) =А1(Л') cos (f)it, s2W = 42(£) cos co2f, возбуждающих волны, ко-
торые распространяются в противоположных направлениях со
скоростью V:
ux(£. = -di — pj cos — кхх),
Н2 (^> ^) = ^2 “Т" pFCOS (®2< Ч” ^'2^') •
Их взаимодействие приводит к появлению двух новых волн
и3 (t, х) = ВАХ [t — у) А2 (t + у.) cos [(©J + ®2) t - (кх — к2) х],
щ (t, х) = ВАХ - у) А2 [t + cos [(©, - ®2) t - (kx + k2) ar],
где В — коэффициент нелинейности. На выходе преобразователя
длиной L, регистрирующего, например, волну с волновым векто-
ром (kt — k2), возникает электрическое напряжение с частотой
(®i + <в2) и амплитудой
+ Ь/2
л(о=₽ f <9-33>
-L/2 k К 7
Если оба сигнала представляют собой импульсы с длитель-
ностью, малой по сравнению с временем распространения L/V
под преобразователем, последний можно считать бесконечным, и
подстановка t — x/V=x позволяет выразить амплитуду A^t) как
функцию свертки огибающих двух сигналов:
+ 00
43 (t) = pV j Ах (т) А2 (2t - т) dr. (9.34)
Однако по сравнению с выражением для свертки (1.30), сиг-
нал 43(i) сжат во времени с коэффициентом 2. Действительно,
в отличие от рассмотренных выше случаев, где одну из функций
представляла неподвижная «гребенка», здесь оба множителя соз-
даются волнами, которые распространяются в противоположных
направлениях с относительной скоростью, равной 2V.
§ 9.6. СВЕРТКА
399
Такой тип устройства был осуществлен на объемных [71] и
поверхностных [72, 731 волнах. Простота работы с волнами Рэлея
на пьезоэлектрическом материале*) и высокая плотность их
энергии облегчают эксперимент. Сигнал свертки регистрируется
встречиоштыревым преобразователем, расстояние между электро-
дами которого d3 = X3/2 определяется длиной волны A3 = 2n/|kt —
— k2l. Если оба сигнала имеют одинаковую частоту, то d3 равно
бесконечности, и в качестве преобразователя используется сплош-
ной электрод. Пространственно-однородное электрическое поле с
частотой 2ю регистрируется между этим электродом и заземлен-
ным электродом (рис. 9.54). На рис. 9.55 показан выходной сиг-
нал, полученный на линии задержки из монокристаллического
LiNbO3 при подаче на оба входа импульсов с длительностью
6 мкс, мощностью 1 Вт и несущей частотой 150 МГц. Выходной
сигнал с частотой 300 МГц и мощностью менее 1 мкВт действи-
тельно имеет треугольную форму.
Рис. 9.54. Принципиальная схема
эксперимента по осуществлению
сверГки двух сигналов одинако-
вой частоты е использованием не-
линейности волн Рэлея.
Рис. 9.55. Свертка (а) прямоуголь-
ного импульса (о).
Несущая частота 150 МГц. Отметим,
что основание треугольника равно
ширине прямоугольника, а не ее
удвоенному значению.
Если один из сигналов, который назовем опорным, получен
инверсией во времени другого сигнала, то выходной сигнал пред-
ставляет собой автокорреляционную функцию. Одно из преиму-
ществ такого устройства по сравнению с согласованными фильт-
рами, описанными в разделе 9.3.5, состоит в том, что опорный
сигнал можно изменять с помощью электронных устройств, а сле-
довательно, можно быстро осуществлять автокорреляцию разли-
чающихся между собой, т. е. по-разному кодированных, сигналов.
Для повышения эффективности нелинейного взаимодействия
следует увеличивать плотность мощности. Поскольку глубину про-
никновения волн Рэлея (порядка длины волны) уменьшить уже
нельзя, нужно сокращать поперечный размер пучка. Этого можно
достичь с помощью устройства сжатия [74]. Устройство сжатия,
*) В этом случае нужно учитывать нелинейность пьезоэффекта, кото-
рая может привести к столь же значительному взаимодействию, как и уп-
ругая нелинейность.
400
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
способное уменьшить ширину пучка более чем в 10 раз, представ-
ляет собой ответвитель с асимметричными решетками (см. § 9.7).
Если пучки, подлежащие сжатию, достаточно узки, то в устрой-
стве, изображенном на рис. 9.54, нижний заземленный электрод
можно заменить двумя узкими полосками, расположенными по
обе стороны от центрального электрода, нанесенного поверх обла-
сти взаимодействия. Этот центральный электрод служит также
волноводом, благодаря разности скоростей упругих волн в под-
ложке и металлической пленке. Такая конструкция удобна тем,
что она плоская.
Один из конвольверов подобного типа, разработанный фирмой
«Томсон — ЦСФ», характеризуется примерно следующими пара-
метрами: фактор билинейности 70 дБ-м-1 (F=101g (P/PiA),
где Р3 — выходная мощность, PiP2 — произведение мощностей на
входе), центральная частота / = 150 МГц, ширина полосы входных
сигналов 5 = 40 МГц, время обработки 0 = 12 мкс, динамический
диапазон >70 дБ, максимальная входная мощность 1 Вт.
Лучшими техническими данными (/ = 300 МГц, 50 = 1000) об-
ладает гораздо более сложное устройство, основанное на электрон-
ной нелинейности [751. Такая нелинейность возникает в пластине
из полупроводящего кремния, с наложенным на нее звукопроводом
из монокристалла пьезоэлектрика — ниобата лития, в котором во
встречных направлениях распространяются две поверхностные
волны [76]. Нелинейность при этом связана с тем, что электриче-
ское поле, возникающее в поверхностном обедненном слое SiO2—
—Si, пропорционально квадрату электрического поля, возбуждае-
мого при взаимодействии двух указанных волн. Реализация тако-
го составного конвольвера сталкивается со значительными трудно-
стями, поскольку зазор между кристаллами кремния и ниобата
лития должен быть меньше десятой части длины волны. Зазор
такого размера можно осуществить с помощью специальных очень
тонких выступов, играющих роль ограничителей. Указанные вы-
ступы наносятся на кристалл ниобата лития методами фотограви-
ровки и. ионной бомбардировки [77]. Важной особенностью полу-
проводникового материала является свойство памяти. При считы-
вании сигнал может быть получен в той же форме, что и при за-
писи, но можно считывать и сигнал, обращенный во времени,
а также получить свертку записанного сигнала с любым другим,
распространяющимся в звукопроводе.
§ 9.7. Ответвитель на решетке поверхностных волн
Как известно, два электромагнитных волновода могут быть
связаны таким образом, что распространяющаяся в одном вол-
новоде энергия может частично или полностью передаваться в
другой [78]. Метод стыковки волповодов и использования отвер-
§ 9.7. ОТВЕТВИТЕЛЬ НА РЕШЕТКЕ ПОВЕРХНОСТНЫХ ВОЛН 401
Симметричная мода „ _
\ Антм'- <метричная моей
стий в общих стенках переносится в область упругих волн. Два
волновода для поверхностных волн, образованные, например,
металлическими полосками, нанесенными на подложку, могут
быть расположены достаточно близко, чтобы между ними воз-
никло взаимодействие через подложку. Однако существует дру-
гое, оригинальное и весьма изобретательное решение [79, 801.
Взаимодействие между двумя дорожками обеспечивается с по-
мощью металлических штырей,
нанесенных на пьезоэлектри-
ческую подложку, как это по-
казано на рис. 9.56. Волна
Рэлея, возбужденная вдоль до-
рожки А, создает электрическое
напряжение между штрихами.
Это напряжение возбуждает
волну Рэлея на дорожке В.
Полная передача энергии вол-
ны из одной дорожки в дру-
гую достигается при длине от-
ветвителя Lt, которая легко
находится с помощью класси-
ческого описания мод 181J.
Волна состоит из симметрич-
ной и антисимметричной мод (рис. 9.56). На скорость Fs симмет-
ричной моды металлические штыри не влияют, так как ток не
может течь в направлении распространения. Напротив, скорость
Vл антисимметричной моды равна скорости Vo волн Рэлея, если
поверхность покрыта металлическим слоем (раздел 6.2.2), по-
скольку электрический потенциал, связанный с этой модой, об-
ращается в нуль из-за движения зарядов вдоль металлических
штырей. Согласно формуле (6.91) имеем

Устройстдо
сСязи
Рис. 9.56. Ответвитель на решетке
поверхностных волн.
Две моды распространяются под от-
ветвителем с различными скоростя-
ми, длина ответвителя соответству-
ет сдвигу фаз на л на выходе.
V4 (М5>
Фазы обеих мод отличаются на л при длине Lt ответвителя:
Длина Lt выражается через коэффициент связи К и длину вол-
ны Рэлея Л соотношением Lt = L/K\ Обозначая шаг решетки
через d, получаем, что число штырей
(9.36)
Таким образом, моды разделяются на дорожке А и восстанавли-
ваются на дорожке В, и волна, поступающая по дорожке А под
ответвитель длины Lt, выходит из него по дорожке В. В действи-
402
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
тельности простое выражение (9.35) получено в предположении,
что металлический слой ответвителя является идеальным изоля-
тором в направлении распространения и идеальным проводником
в перпендикулярном направлении. Такая анизотропия на прак-
тике осуществляется с помощью металлических полосок, и пе-
риодичность реального ответвителя приводит к провалам в ча-
стотной зависимости (первый провал соответствует резонансной
частоте /0 = V/2d) и снижает эффективность взаимодействия.
В предположении, что наличие полосок эквивалентно дискрети-
зации синусоидального сигнала на дорожке А и его восстанов-
лению с помощью периодической структуры на дорожке В, ос-
лабление взаимодействия [821 можно выразить множителем
’ где =° ^nad/X, a ad — активная длина металлической
полоски. Выражение (9.36) принимает тогда вид
<9-37>
Кс“Ц й/2 /
Чтобы полученные в эксперименте результаты совпали с рас-
четными, необходима подгонка параметров а и К2. Коэффициент
а точно не совпадает с относительной долей а металлизирован-
ной поверхности ответвителя (а = га), а для К2 следует учесть
поправочный множитель F:
Nt = 1 — cos (лга///0) ’ где 1° = 2d’
Как и для встречноштыревого преобразователя, максималь-
ная эффективность ответвителя (максимальная величина FK2')
достигается при а = 1/2. Для ниобата лития YZ-среза при а = 1/2,
г =1,7 и FK2 = 0,043 практическая формула имеет вид [83]
195///0
1 — cos (153///0) ’
(9.39)
где аргумент косинуса выражен в градусах.
На рис. 9.57 представлена зависимость числа Nt штрихов, не-
обходимого для 100%-ного ответвления из одного канала в дру-
гой, от приведенной частоты ///0. Вблизи минимума (///» = 0,873,
Nt = 101) число штрихов изменяется медленно. Здесь кривая на-
несена пунктиром. Это связано с тем, что использованная тео-
рия не учитывает влияния многократных отражений, имеющих
место в этой области. В случае, если значение частоты / задано,
длину ответвителя можно уменьшить при условии, что сократит-
ся пространственный период, а соответствующая частота /0 =
= V/2d увеличится. Это обстоятельство также проиллюстрирова-
§ 9.7. ОТВЕТВИТЕЛЬ НА РЕШЕТКЕ ПОВЕРХНОСТНЫХ ВОЛН 403
Рис. 9.57. Характеристики решеточного от-
ветвителя. Зависимости числа штрихов Nt,
необходимого для 100%-ного ответвления
энергии ив канала в канал (сплошная кри-
вая), и произведения длины ответвителя
на частоту (пунктирная кривая) от приве-
денного значения частоты f/fo.
но на рис. 9.57, где приведена пунктирная кривая, изображаю-
щая зависимость произведения длины ответвителя на частоту от
приведенной частоты. Видно, что в случае /о = 2/ длина ответви-
теля уменьшается на 30%. Такое уменьшение может оказаться
существенным и если раз-
меры устройства играют
определяющую роль.
О превосходной работе
этого исключительно про-
стого ответвителя свиде-
тельствуют осциллограм-
мы, приведенные на
рис. 9.58, для ответвителя
с 140 штырями на LiNbO3.
Потери при передаче энер-
гии с одной дорожки на
другую составляют 0,5 дБ
при 45 МГц, развязка
между двумя дорожками
на выходе превышает
30 дБ. Среди многочис-
ленных применений, осу-
ществленных (LiNbO3, YZ-
срез) или предложенных
авторами этого устройст-
ва [83], отметим сле-
дующие: режектор объемных волн (ответвитель не пропускает
объемные волны, возбужденные входным преобразователем), от-
ветвитель между различными подложками, делитель акустиче-
ского пучка (ответвитель на 3 дБ, L = Lt/2), двойной тройник,
устройство сжатия пучка. (См. также упр. 9.6 и 9.7.)
Схема устройства для сжатия пучка приведена на рис. 9.59.
Это устройство представляет собой асимметричный ответвитель.
В этом случае представление входного сигнала в виде симмет-
ричной и антисимметричной мод с разными скоростями не столь
очевидно. Анализ, проведенный в [84], показывает, что разность
фаз сигналов в двух каналах, связанная с различием скоростей
волн, прошедших через две системы металлических штрихов раз-
личной длины, может быть скомпенсирована небольшим измене-
нием периода одного из каналов. Число штрихов, необходимое
для полной передачи энергии из канала в канал с _коэффициен-
том сжатия г, получается в этом случае в (Уг + 1/Уг)/2 раз боль-
шим, чем для симметричного ответвителя.
Как симметричный, так и асимметричный ответвители явля-
ются фильтрами. Простейшее устройство (рис. 9.56) обладает
частотой отсечки /0, соответствующей расстоянию между метал-
404
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
лическими штрихами, равному V2. Фильтрующие свойства от-
ветвителя, состоящего из двух решеток, могут использоваться в
различных устройствах, один из примеров которых приведен на
рис. 9.60. Шаг решеток изменяется в поперечном направлении.
Рис. 9.58. Пропускание и отражение в решеточном ответвителе.
При длине Lt ответвителя сигнал, поступающий на вход 7, почти полностью
выходит из выхода 3. (Рис. 6 из [83].)
Если входной сигнал имеет широкий спектр, то на выходе будут
иметь место лишь такие сигналы, для которых dA + dB = 1. По-
скольку период dB непрерывно изменяется, отдельные спектраль-
ные составляющие входного сигнала можно выделять с помощью
Рис. 9.60. Многоканальный фильтр.
Падающая волна «дифрагирует» (благода-
ря пьезоэффекту) на каждой из металли-
ческих полосок. Выходной сигнал, пред-
ставляющий собой сумму всех дифраги-
рованных пучков, излучается только об-
ластью решетки, расположенной в канале
В, где dA + dB = X.
Рис. 9.59. Устройство сжатия
пучка.
Ширина канала А больше, чем
канала В. Плотность мощно-
сти в выходном пучке больше,
чем во входном.
избирательно настроенных приемных преобразователей. С по-
мощью подобной структуры осуществлен фильтр, позволяющий
разделить 5 каналов (145</<150 МГц) [85].
§ 9.8. УСТРОЙСТВА ДЛЯ СПЕКТРАЛЬНОГО АНАЛИЗА 405
§ 9.8. Устройства для спектрального анализа
(для преобразования Фурье)
Преобразованием Фурье S(f) некоторого сигнала s(f) назы-
вается выражение (см. 1.3.2):
4-50
S(f)- J $ (т) е_{2я,тйт. (9.40)
Для осуществления этой операции с помощью дисперсионных
линий [86, 871, имеющих импульсные отклики вида D±(t) =
_ e±w<2 (см 9.3.2), сделаем замену переменных и проведем
преобразование
—2ti = — f — т2 + (t — т)2.
Тогда из (9.40) следует
S (pi) - [s (т) е-'я^2]
или, в символической форме,
S = Z>_-[(s-Z>_)*Z>+]. (9.41)
Множитель в квадратных скобках представляет собой сигнал на
выходе фильтра, имеющего импульсный отклик D+(t) при подаче
сигнала s(t) -D-(t) на его вход (§ 1.3). Исходя пз соотношения
+ “>
J e~iac~dx = 1, можно написать выражение
/jre”^+j e^wt-T)2dr = l.
Умножим обе его части на 5(pf) и получим
S (pt) /йе“^е13ЧА<а5 (nt) "j ein^e~iin,ltxdi.
Интеграл представляет собой фурье-образ функции D+(t) при
/ = nt. Поскольку произведение фурье-образов от s(t) и D+(t)
равно фурье-образу свертки s * D+, получим
5(нО = /Йе~,Ге^2 J [s(T)*P+(T)]e-i2WtTdr =
= /ре"^ +J [з (т) * D+ (т)] dr.
406
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Так как интеграл представляет собой свертку, S(p,i) можно сим-
волически представить в виде
S (lit) = /йе"‘Г В+ * [Р_ • (б * Л+)].
Рис. 9.61. Преобразование Фурье,
а) Устройство типа УСУ (умно-
жение — свертка — умножение),
содержащее две дисперсионные
линии с импульсным откликом
D_ = е—1яр4 и одну — с импульс-
ным откликом В+= е,яр,‘2. б) Ус-
тройство типа СУС (свертка —
умножение — свертка), содержа-
щее две дисперсионные линии
D+ и одну Р_.
Заметим, что это выражение с точностью до множителя мож-
но получить из (9.41) путем перестановки функций свертки и
умножения, а также — сигналов D+ и D_. На рис. 9.61 представ-
лены две схемы, реализующие указанные соотношения. На прак-
тике сигналы D+ и Р_ являются импульсными откликами дис-
персионных линий на.волнах Рэ-
лея (рис. 9.26). Осуществить эти
схемы, а иными словами,— спект-
ральный анализ в реальном
масштабе времени можно благо-
даря наличию линий с отражаю-
щими решетками, обладающих
большой величиной произведения
BQ (несколько тысяч) и обеспечи-
вающих получение сигналов с хо-
рошо определенными амплитудой
и фазой. Характеристики этих ли-
ний, играющих ту же роль, что
линзы в оптике, определяют па-
раметры соответствующих анали-
заторов спектра.
В схеме рис. 9.61 конечная дли-
тельность 0_ импульсного откли-
ка 1-й линии опредс
шение по времени
20 мкс) анализатора,
ли на вход подать синусоидаль-
ную волну с частотой /, на выхо-
де получим не бесконечно узкую
линию на частоте /, а сигнал с
огибающей (sin ж)/#, ширина ко-
торой определяет разрешающую
способность и оказывается обрат-
но пропорциональной 0_. Уровень нежелательных боковых ле-
пестков (—13 дБ) можно снизить с помощью соответствующего
взвешивания, но, как следует из раздела 9.3.5 и упр. 9.2, это вле-
чет за собой ухудшение разрешения из-за расширения цент-
рального лепестка. Учитывая перемножение сигналов s(t) й
D-(t), соответствующее свертке их спектров, получим, что полоса
пропускания В+ —110+ фильтра D+ должна быть по крайней
мере равна сумме ширин спектров В8 сигнала и В- = ц©_
зляет разре-
(например
Поэтому, ес-
§ 9.9. ДЕФЛЕКТОР И МОДУЛЯТОР СВЕТА
407
дисперсионной линии:
ц0+ —Вв + Ц0-.
Длительность 0S выборки сигнала в лучшем случае равна 0_, и
величина BSQB для рассматриваемой системы составляет
BSQB = р(0+ — 0-)0—
Это произведение максимально и равно Ц0+/4 = 5+0+/4 в слу-
чае 0_ = 0+/2. Отсюда следует, что рабочая спектральная об-
ласть и разрешение оказываются равны соответственно ц0+/2 и
1/0- = 2/0+. Учитывая, что центральная частота линии харак-
теризуется величиной порядка сотен мегагерц, а длина ее может
превышать 10 см, получим для рабочей спектральной области
величину в несколько десятков мегагерц при разрешении в де-
сятки килогерц.
Устройства, осуществляющие преобразование Фурье, могут
использоваться не только для спектрального анализа [881, на их
основе можно, например, создать линии с плавной переменной
задержкой сигналов или же реализовать корреляционную функ-
цию путем вычисления простого произведения. Поскольку при
анализе отдельные спектральные составляющие возникают по-
следовательно во времени, их можно изменять или отфильтровы-
вать по желанию с помощью соответствующим образом управ-
ляемых схем. Один из конкретных примеров использования по-
добных устройств в системах спутниковой связи приведен в [891.
В этих системах фурье-преобразователи применяются для демо-
дуляции частотно-кодированных сигналов.
§ 9.9. Дефлектор и модулятор света на упругих волнах
В конце раздела 8.4.2 отмечалось, что коллинеарное взаимо-
действие между световцми и упругими волнами было использо-
вано для создания оптического перестраиваемого фильтра, а в
разделах 9.2.3 и 9.3.6 описывались два устройства, в которых
использовано это взаимодействие: линия переменной задержки
и согласованный фильтр. Представляется целесообразным оста-
новиться здесь на таком важном устройстве, как дефлектор или
модулятор света на упругих волнах. Световой пучок является
прекрасным носителем информации, а упругие волны дают воз-
можность осуществлять его пространственную или временную
модуляцию.
На рис. 9.62 показан дефлектор, работающий в режиме Брэг-
га на центральной частоте около 300 МГц. В качестве звукопро-
вода используется молибдат свинца. На одном из торцов на
индиевой связке укреплен преобразователь из ниобата лития. На
противоположном торце находится поглотитель упругих волн.
408
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Электрическое согласование преобразователя с генератором сиг-
налов осуществляется с помощью полосковой линии. По обе сто-
роны кристалла расположены призмы. Их роль [90] состоит в
расширении падающего светового луча вдоль звукопровода с
целью увеличения перекрытия с упругими волнами (см. 8.4.2) и
в уменьшении сечения дифрагированного пучка на выходе для
Рис. 9.62. Акустооптический дефлектор.
Упругие волны распространяются в кристалле молибдата свинца, имеющем
форму параллелепипеда. Призмы на входе предназначены для расширения
светового пучка с целью увеличения количества разрешимых положений.
Призмы на выходе восстанавливают прежние размеры пучка.
того, чтобы отклоненный пучок дефлектора был идентичным па-
дающему. Призмы предпочтительнее линз, поскольку они сохра-
няют плоский фронт волн, а также увеличивают угол отклоне-
ния. При электрической мощности на преобразователе Вт
отклоняется примерно 50% падающего света, а число разреши-
мых положений составляет около 500 [91]. Акустооптический
модулятор имеет такой же вид, как и дефлектор, с той лишь
разницей, что оп не содержит призм, расширяющих луч, а кри-
сталл имеет меньшую длину. Типичный модулятор дает 70%|
отклоненного света при управляющей мощности 1 Вт и времени
нарастания импульсов 30 нс.
Использование в телевидении. Для демонстрации возможно-
стей акустооптического дефлектора и модулятора были проведе-
ны многочисленные лабораторные эксперименты по их исполь-
§ 9.9. ДЕФЛЕКТОР И МОДУЛЯТОР СВЕТА
40»
зованию в телевидении [92]. Остановимся на схеме эксперимента
(рис. 9.63), проведенного в нашей лаборатории Р. Торкэ. Сигнал
видеочастоты подается на модулятор, который непосредственна
Рис. 9.63. Схема, эксперимента по использованию дефлектора и модулятора
в телевидении.
Световой луч модулируется по интенсивности (и отклоняется по горизон-
тали) упругими волнами переменной интенсивности (и частоты).

действует на световой пучок от аргонового лазера. Модулирован-
ный световой пучок отклоняется по горизонтали дефлектором,
управляемым генератором строчной развертки. Поскольку изоб-
ражение длительностью 20 мс со-
стоит из 625 строк, на прохожде-
ние каждой строки затрачивается
32 мкс. Более медленное отклоне-
ние луча по вертикали обеспечи-
вается зеркалом гальванометра,
который питается пилообразным
напряжением с частотой 50 Гц.
При использовании лазера с мощ-
ностью 2 Вт изображение может
быть спроектировано на экран с
площадью, которая превышает
один квадратный метр [93] (см.
рис. 9.64).
Л
Рис. 9.64. Снимок изображения,
спроектированного на экран с ли*
нейными размерами 50 см.
27 Э. Дьелесан, Д. Руайе
410
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
Очевидно, что при необходимости можно осуществить быст-
рое отклонение в двух направлениях, если объединить два деф-
лектора. Таким образом, устройство объемом в несколько куби-
ческих сантиметров, состоящее из кристалла с преобразователем,
который преобразует управляющий электрический сигнал в уп-
ругие волны, позволяет осуществить почти 100%-ную модуляцию
светового сигнала и его отклонение в несколько сотен разреши-
мых положений за исключительно короткое время (10 мкс). Та-
кие устройства, в настоящее время выходящие из стадии лабора-
торных исследований, должны найти применение в различных
областях телевидения.
Упражнения
9.1. Определить отклик фильтра, согласованного с сигналом, изобра-
женным на рис. 9.11 б.
Решение. Функция автокорреляции сигнала, осуществленная, на-
пример, графически согласно указаниям раздела 1.3.4, показана на рис. 9.65,
9.2. Найти с помощью ме-
тода стационарной фазы, из- / I . . . .
ложенного в разделе 1.3.2, ежа- \ / I ---------
тый импульс $2 (f) на выхо- \ / 1 71 ,„',г
Рис. 9.65. Рис, 9.66. Огибающая сжатого импуль-
са на выходе дисперсионной линии с
S-образной характеристикой задержки
при а = 1/2 (сплошная кривая).
с сигналом Si(t) = П(//6) cos [2n/o<+который модулирован по
частоте по S-образному закону:

а — const,
При -0/2 < t < 0/2 или /о — В/2 < f < /о + В/2.
Решение. Сигнал $2(t) находится из его спектра 82(f) =
H(f)St(f) = |Si(/) |2 с помощью соотношения s2(t) = | Sr(f) |2 eiin^df.
УПРАЖНЕНИЯ
411
Соотношение (1.26) при ei [<(/)] = П((/ — fo)/B) дает
Их (/ - /о) г«п (Ч^) I [* +> c°s (2л Ч^)]-
Согласно (1.22) выражение | 5, (/) |2 = у | (/ - /0) |’- + |1 (/ + /0) |\
и огибающая сигнала на выходе s2(<) e2(i) cos (2л/о«) имеет вид
. . 0 Г . 2л/\ 0 sin W Г. (ДО8 1
е^ = 2В J (l + «coS-^je^/ = yj-J^rПц.в_к_2_ •
-В/2 L J
Из рис. 9.66 видно, что в результате умножения члена sin (nffQ/jtSt на
функцию в скобках, которая равна нулю при Bt = 1/У1 — а, центральный
пик расширяется, а 1-й боковой лепесток уменьшается больше, чем ос-
тальные лепестки, амплитуда кото-
рых умножается на (1 —а).
9.3. Показать, что сумма автокор-
реляционных сигналов каждой па-
ры импульсов, показанных на
рис. 9.67, не имеет боковых лепестков.
Ответ, Рис. 9.67, б.
9.4. Какой частотный отклик
имеет преобразователь, состоящий из
бесконечной последовательности ди-
скретов, разделенных промежутками
длины ге%о и образованных пятью
штырями?
Решение. Импульсный от-
клик представляет собой последова-
тельность импульсов шириной 2//о,
следующих друг' за другом через
время т = n/fa
л(0 =
Рис. 9.67. Дополнительные коды Го~
лея.
а) Сигналы, б) их автокорреляция
и сумма.
Согласно результатам раздела 1.3.2 спектр_огибающей имеет вид
. 2л/
sin ~7~ +00
—хг 2 е~Мх
или с учетом (1.40)
. 2л/
sin-7- +оо
Частотный отклик Н у Е (f —• /0) + у Е (J + /0) представляет собой
27*
412
ГЛ. 9. ОБРАБОТКА СИГНАЛОВ
последовательность пиков на частотах f == ±/0 + pfo/n с высотой, модули-
рованной по закону (sin х) /х.
9.5. Каким должен быть период выборки Т на входе устройства
DELTIC, чтобы получить обращение сигнала во времени?
Ответ, Т = (N — 1)6.
9.6. Пусть as и ал — амплитуды, в данном случае различные, соответ-
ственно симметричной и антисимметричной мод (см. рис. 9.56):
as = (Ао + Во)/2 и ал = (4о—Bq)I2,
тде Ав и Во — амплитуды входных волн для каналов А и В соответственно.
Выразить зависимость амплитуд этих волн от величин Ло и Во после про-
хождения расстояния х в ответвителе. Рассмотреть случаи Во = 0, х = Lt
и х — Lt/2,
Решение.
4(x) = ase-iwx/Vs + aXiWX/VA’ 5 (х) = «Se~iwx/Vs -^е’^Ч
или
А (х) = e~ia (а8е-‘ф + аАе{ф), В (х) = e~ia (“s6"1® - аАе1ф),
го / 1 , 1 \ <о/1 1 \ п х п
причем а=2~1р----гр-Ф = -гЦ (7^ Iх ~ ~2 ~L^' Опуская мно-
житель е_<о, выражающий среднее время задержки, получим:
(Л(х)\ / созФ —/з1пФ\М0'
(x)j = Ч f sin Ф соэФ И#о
Если сигнал есть только в канале А, т. е. Во = 0, то
А (х) = 40 cos Ф, В (х) = — iA0 sin Ф.
В случае Ф = л/2, т. е. х = Lt, A (Lt) = 0, B(Lt) — — Мо.
Волна Рэлея, входящая в канал А, выходит из .канала В.
Если Ф = л/4, х = Л,/2 и A(Lt/2) = Ао№, а B(Lt/2) =
= — lAoli/2. В этом случае пучок, входящий в канал А,
создает сигналы в каналах А и В, одинаковые по интен-
сивности, но со сдвигом фаз л/2.
9.7. Штрихи в канале А ответвителя, имеющего дли-
ну Ltl2, сдвинуты на небольшую величину относительно
Рис. 9.68. штрихов в канале В (рис. 9.68). Показать, что если ча-
стота пучка с амплитудой захватывающего оба кана-
ла, увеличивается, то выходной сигнал возникает попеременно на выхо-
дах А и В.
Решение. Сигнал па входе До — ^e~ifi , BQ = si, где 6 = tod/Vs»
л на выходе:
А = ^(е-’6 ~ т. е. | 4| = V1 + sin 6,
В = (1 — ie~ls), т.е. | В | = si У1 — sin 6;
А = .si VX В = 0 при 6 = (4fc + 1) п/2, т. е. / = (4fc + 1) Vs/4d;
А = О, В = si УГ при 6 = (4А -1) п/2, т.е./ = (4k — 1) Vs/4d,
ЛИТЕРАТУРА
К предисловию редактора перевода
1. Ахиезер А. И.— ЖЭТФ, 1938, т. 8, с. 1318.
2. Ландау Л. Д. Сборник трудов,— М.: Наука, 1969, т. 1, с. 227.
3. Александров К. С,—Кристаллография, 1956, т. 1. с. 718; 1958, т. 3, с. 620;
1962, т. 7, с. 735.
4. Федоров Ф. И. Теория упругих волн в кристаллах.—М.: Наука, 1965.
5, Соколов С. Я.-ЖТФ, 1949, т. 19, с. 274.
6. Баранский К. II.- ДАН СССР, 1957, т. 114, с. 517.
7. Леманов В. В., Смоленский Г А.— УФН, 1972, т. 108, с. 465.
8. Фабелинский II. Л. Молекулярное рассеяние света,—М.: Наука, 1965.
9. Рытое С. М.- ЖЭТФ, 1935, т. 5, с. 843; Изв. АН СССР, Сер. физ., 1937,
т. 2 с. 223.
10. Гуляев Ю. В., Проклов В. В., Шкердин Г. Я,—УФН, 1978, т. 124, С. 61.
11. Гуревич В. Л.— ФТП, 1969, т. 2, с. 1557.
12. Пустовойт В. Я,-УФН, 1969, т. 97, с. 257.
13. Гальперин Ю. М., Гуревич В. Л., Козу б В. Я-УФН, 1979, т. 128, с. 107.
14. Альтшулер С. А., Кочелаев Б. И., Леушин А. М,— УФН, 1961, т. 75, с. 459.
15. Шутилов В. А,— Акуст. журн., 1962, т. 8, с. 383.
16. Блинц Р., Жекш Б. Сегнетоэлектрики и антисегнетоэлектрики.— М.:
Мир, 1975.
17. Ахиезер А. И., Барьяхтар В. Г., Пелетнинский С. В. Спиновые волны.—
М.: Наука, 1967.
18. Зарембо Л. К., Красильников В. А.— УФН, 1970, т. 102, с. 549.
19. Груэлл Р., Эльбаум Ч., Чик Б. Ультразвуковые методы в физике твер-
дого тела.— М.: Мир, 1972.
20. Такер Д., Рэмптон В. Гиперзвук в физике твердого тела.— М.: Мир, 1975.
21. Гуревич В. Л. Кинетика фононных систем.—М.: Наука, 1980.
22. Физическая акустика/Под ред. У. Мэзона.—М.: Мир, 1966, т. 1, ч. А.
23. Мустель Е. Р., Парыгин В. Н. Методы модуляции и сканирования све-
та,—М.: Наука, 1970. .
24. Магдич Л. Н., Молчанов В. Я. Акустооптические устройства и их при-
менение.— М.: Сов. радио, 1978.
25. Кулаков С. В. Акустооптические устройства спектрального и корреля-
ционного анализа сигналов,— Л.: Наука, 1978.
26. Викторов И. А. Физические основы применения ультразвуковых волн
Рэлея и Лэмба в технике.— М.: Наука, 1966.
27. Каринский С. С. Устройства обработки сигналов на ультразвуковых по-
верхностных волнах.— М.: Сов. радио, 1975
28. Речицкий В. И. Акустоэлектронные радиокомпоненты.— М.: Сов. радио,
1980.
29. Яковкин И. Б., Петров Д. В. Дифракция света на акустических поверх-
ностных волнах.— Новосибирск: Наука, 1979.
30. Соколов С. Я,- ЖТФ, 1941, т. И, с. 160; 1949, т. 19, с. 271.
414
ЛИТЕРАТУРА
31. Шерман А. Б., Добровольский А. А., Балашова Е. В. и др,— Письма в
ЖТФ, 1975, т. 1, с. 1108.
32. Шерман А. Б., Добровольский А. А., Леманов В. В. и др,— Письма в
ЖТФ, 1979, т. 5, с. 1124.
33. Гуляев Ю. В., Пустовойт В. И.— ЖЭТФ, 1964, т. 47, с. 2251.
34. Упругие поверхностные волны/Под ред. С. В. Богданова.— Новосибирск?
Наука, 1974.
35. ТИИЭР, 1976, т. 64, вып. 5.
36. Ультразвук. Маленькая энциклопедия/Под ред. И. П. Голяминой.— М.5
Сов. энциклопедия, 1979.
Глава 1
Литература общего характера
Bok J., Morel Р. Cours de physique. Mecanique-Ondes — Р.: Hermann, 1968.
Elmore W. C., Heald M. A. The physics of waves.— N. Y.: McGraw-Hill, 1969.
Горелик Г. С. Колебания и волны,—2-е изд.—М.: Физматгиз, 1959.
Крауфорд Ф. Волны: Пер. с англ,—М.: Наука, 1974.—Берклеевский курс
физики, т. 3, Механика.
Grivet Р. Physique de lignes de haute frequence et d’ultra haute frequence.—
P.: Masson et C1®, 1969, t. 1, ch. 5, p. 195.
Ефимов И. E. Радиочастотные линии передачи.— М.: Сов. радио, 1964.
Brillouin L. Wave propagation in periodic structures.—N. Y.: Dover, 1953.
Бриллюэн Л., Народи M. Распространение волн в периодических структу-
рах: Пер. с фр./Под ред. П. А. Рязина,— М.: ИЛ, 1959.
Schwartz L. Methodes mathematiques pour les sciences physiques.—P.: Her-
mann, 1965.
Гельфанд И. M., Шилов Г. Е. Обобщенные функции и действия над ними.—
2-е изд.— М.: Физматгиз, 1959.
Roubine Е. Introduction a la theorie de la communication.— P.: Masson et C1®,
Bracewell R. The Fourier transform and its applications.—N. Y: McGraw-Hill,
1965.
Харкевич А. А. Спектры и анализ.—3-е изд., перераб.—М.: Гостехиздат,
1957.
Глава 2
Цитируемая литература
1. Eyraud L. Dielectriques solides anisotropes et ferroelectricite.—P-: Gauthier-
Villars, 1967, ch. 6.
2. Schubert K. Kristallstrukturen zweikomponentiger phasen.—Berlin: Sprin-
ger Verlag, 1964, p. 200, fig. 6.
3. Me paw H. D. Ferroelectricity in cristals.— L.: Methuen' and Co, 1957, ch. 5,
i. Di Domenico M. (Jr.), Wemple S. H — Oxygen-octahedra ferroelectrics.—
J. Appl. Phys., 1969, v. 40, p. 720.
Литература общего характера
Kahan Th.—In: Les groupes en cristallographie/Par Curien H.—P.: Dunod,
1971, t. 2, p. 49—144.
Weigel D. Algebre et geometrie cristalline et moleculaire.— P.: Masson et C1®,
1972.
Ландау Л. Д., Лифшиц E. M. Квантовая механика.— M.: Наука, 1974, гл. XII.
ЛИТЕРАТУРА 415
Локс Р., Голд А. Симметрия в твердом теле.— М.: Наука, 1970.
Хамермеш М. Теория групп и ее применение к физическим проблемам.—»
М.: Мир, 1966.
Летрашень М. И., Трифонов Е. Д. Применение теории групп в квантовой ме-
ханике.— М.: Наука, 1967.
Флинт Е. Е. Начала кристаллографии,— М.: Высшая школа, 1961.
Глава 3
Литература общего характера
Brillouin L. Les tenseurs en mecanique et en elasticite.—P.: Masson et Cle,
в 1949.
F Bauer E. Champs de vecteurs et de tenseurs.— P.: Masson et Cle, 1955.
Nye J. F. Proprietes physique des cristaux.—P.: Dunod, 1961, ch. 1 et 2. Пе-
ь ревод: Най Дж. Физические свойства кристаллов,— М.: ИЛ. 1960,
гл. 1 и 2.
и Сиротин Ю. И., М. П. Шасколъская. Основы кристаллофизики.— М.: Наука,
f 1979.
[Глава 4
Цитируемая литература
1. Vallin J. et al.— J. Appl. Phys., 1964, v. 35, p. 1825.
| 2. Bateman T. B., McSklmin H. J.. Whelan J. M.— J. Appl. Phys., 1959, v. 30,
* p. 544.
t 3. Spencer E. G. et al.- J. Appl. Phys., 1963, v. 34, p. 3059.
4. Slobodntk A. J. (Jr), Sethares J. C.— J. Appl. Phys., 1972, v. 43, p. 247,
5. Chang Y. A., Himmel L.— J. Appl. Phys., 1966, v. 37, p. 3567.
6. Macjarlane R. E., Raine J. A., Jones С. К,— Phys. Letters, 1965, v. 18, p. 91.
| 7. Hall J. J.— Phys. Rev., 1967, v. 161, p. 765.
Г 8. Lawrie R., Gonas A. M.— J. Appl. Phys., 1967, v. 38, p. 4505.
9. Smith J. F., Arbogast C. L.— J. Appl. Phys., 1960, v. 31, p. 99.
10. Bateman T. B.— J. Appl. Phys., 1962, v. 33, p. 3309.
« 11. Corll J. A.— Phys. Rev., 1967, v. 157, p. 653.
i 12. Fischer F. S., Renken C. J.— Phys. Rev., 1964, v. 135A, p. 482.
? 13. Chandrasekhar B. S., Rayne J. A.— Phys. Rev., 1962, v. 124, p. 1011.
’’ 14. Coquin G. A., Pinnow D. A., Warner A. W.— J. Appl. Phys., 1971, v. 42,
p. 2164.
15. Alton W. J., Barlow A. J — J. Appl. Phys., 1967, v. 38, p. 3817.
16. Omacht Y., Uchida N.— J. Appl. Phys., 1970, v. 41, p. 2307.
17. Verma R. K.— J. Geophys. Rev., 1960, v. 65, p. 757.
18. Berllcourt D., Jaffe H.— Phys. Rev., 1958, v. Ill, p. 143.
19. Wachtman J. B. et al.— J. Res. Natl. Bur. Std., 1960, v. 64A, p. 213.
20. Warner A. W., Опое M., Coquin G. A.—J. Acoust. Soc. Am., 1967, v. 42,
p. 1223.
21. Bechman R.— Phys. Rev., 1958, v. 110, p. 1060.
22. Malgrange J. L., Quentin G., Thuilller J. M.— Phys. Stat. Sol., 1964, v. 4,
p. 139.
23. Haussuhl S.— Acta Cryst., 1968, v. 24A, p. 697.
24. Warner A. W., Coquin G. A., Fink J. £.— J. Appl. Phys., 1969, v. 40,
p. 4353.
25. Jaffe H., Berlincourt D. A.— Proc. IEEE, 1965, v. 53, p. 1372.
416
ЛИТЕРАТУРА
Литература общего характера
Nye J. F. Proprietes physiques des cristaux.—P.: Dunod, 1961, ch. V, VI,
VIII. Перевод: Най Дж Физические свойства кристаллов.—М.: ИЛ,
1960, гл. V, VI, VIII.
Федоров Ф. И. Теория упругих воли в кристаллах,— М.: Мир, 1965.
Bhagavantam S. Crystal symmetry and Physical properties.—L. and N. Y.:
Academic Press, 1966, ch. 11.
Ландау Л. Д., Лифшиц E. M. Теория упругости.— M.: Мир, 1967.
Bruhal G., Kastler A. Cours de physique generale. Thermodynamique.—
P.: Masson et Cle, 1962, ch. IX.
Сиротин Ю. И., M. П. Шаскольская. Основы кристаллофизики,— М.: Наука,
1979.
Шутилов В. А. Основы физики ультразвука,—Л.: Изд-во ЛГУ, 1980.
Глава 5
Цитируемая литература
1. Farnell G. W., Adler Е. L.— In: Physical Acoustics/Ed. W. P. Mason and
R. N. Thurston.— N. Y.: Academic Press, 1972, v. 9, p. 35—127.
2. Borgnis F. E.— Phys. Rev., 1955, v. 98, p. 1000—1005.
3. Brugger K.— J. Appl. Phys., 1965, v. 36, p. 759—768.
4. Levelut A.— Acta Cryst., 1969, v. A25, p. 553—563.
5. Arenberg D. L.— J. Acoust. Soc. Am., 1948, v. 20, p. 1—25.
6. Lord Rayleigh — Proc. London Math. Soc.. 1885, v. 17, p. 4—11.
7. Farnell G. PF.—In: Physical Acoustics/Ed. W. P. Mason and R. N. Thur-
ston.—N. Y.: Academic Press, 1970, v. 6, p. 109—166. Перевод: Физиче-
ская акустика/Под ред. У.-Мэзона и Р. Терстона.—М.: Мир, 1973, т. 6,
с. 139-202.
8. Викторов И. А. Физические основы применения волн Рэлея и Лэмба в
технике.— М.: Наука, 1966.
9. Lim Т. С., Farnell G. W.— J. Acoust. Soc. Am., 1969, v. 45, p. 845—851.
10. Stoneley R — Proc. Roy. Soc., 1955, v. A232, p. 447—458.
Литература общего характера
Федоров Ф. И. Теория упругих волн в кристаллах.— М.: Наука, 1965.
Auld В. A. Acoustic fields and waves in solids.— N. Y.: Wiley-Interscience,
1973.
Ландау Л. Д., Лифшиц E. M. Теория упругости.— M: Наука, 1965.
Redwood М. R. Mechanical wave guides.— L.: Pergamon Press, 1960.
Musgrave M. J. P. The propagation of elastic waves in crystals and other ani-
sotropic media.— Reports Prog, in Phys., 1959, v. 22, ,p. 74—96.
Farnell G. W.— Can. J. Phys., 1961, v. 39, p. 65—80.
Tournois P., Lardat C.— IEEE Trans. Sonics Ultrason., 1969, v. SU-16,
p. 107-117.
Kajtmura K., Inaba R., Mikoshiba N— Appl. Phys. Lett., 1971, v. 19,
p. 182.
Lawrence M. IV., Davies L. IF.— Appl. Phys. Lett., 1972, v. 20, p. 328.
Шутилов В. А. Основы физики ультразвука.—Л.: Изд-во ЛГУ, 1980.
Меркулов Л. Г., Яковлев Л. А. Особенности распространения и отражения
ультразвуковых лучей в кристаллах,—Акуст. журн., 1962, т. 8, с. 99.
Домаркас А., Чиплис Д. Трансформация мод при отражении акустической
волны от границы двух кристаллов,— Труды вузов. Лит. ССР, Ульт-
развук, 1978, № 10, с. 10—15.
ЛИТЕРАТУРА
417
Глава 6
Цитируемая литература
1. Quentin G., Thuilller J. М,— Solid State Commun., 1964, v. 2, p. 115.
2. Bouat J., Thuillier J. M.— Phys. Lett., 1971, v. 37A.
3. Arlt G., Quadflieg A-Phys. Status Solidi, 1968, v. 25, p. 323.
4. Farnell G. W.— In: Physical Acoustics/Ed. W. P. Mason and R. N. Thur-
ston.—N. Y.: Academic Press, 1970, v. 6, ch. 3, paragr. VI. Перевод: Фи-
зическая акустика/Под ред. У. Мэзона и Р. Терстона.— М.: Мир, 1973,
т. 6, с. 139-202.
5. Maerfeld С., Lardat С.— С. R. Acad. Sc. Paris, 1970, v. 270, p. 1187.
6. Bleustein J. L — Appl. Phys. Lett., 1968, v. 13, p. 412.
7. Гуляев Ю. 5,—Письма в ЖЭТФ, 1969, т. 9, вып. 1, с. 63.
8. Ingebrigtsen К. A.— J. Appl. Phys., 1969, v. 40, р. 2681.
9. Campbell J. J., Jones W. R.— J. Appl. Phys., 1970, v. 41, p. 2796.
10. Campbell J. J., Jones W. I?.—IEEE Trans. Son. Ultrason., 1968,. v. SU-15,
p. 209.
11. Moriamez M. et al.— Revue Phys. Appl., 1971, v. 6, p. 333.
12. Bridoux E. et al.— Appl. Phys. Lett., 1971, v. 19, p. 523.
13. Coquin G. A., Tiersten H. F.— J. Acoust. Soc. Am., 1967, v. 41, p. 921.
14. Schulz M. B., Matsinger B. J., Holland M. G.— J. Appl. Phys., 1970,
v. 41, p. 2755.
15. Pratt R. G., Simpson G., Crossley Ж A.—Electron. Lett., 1972, v. 8,
16 Slobodnik A. J. (Jr.). Conway E. D.— Electron. Lett., 1970, v. 6, p. 171.
17. Slobodnik A. J. (Jr.), Szabo T. L.— Electron. Lett., 1971, v. 7, p. 257.
18. Slobodnik A. J. (Jr.), Conway E. D.— Microwave acoustics handbook,
AFCRL Report No. 70-0164,—Bedford, Mass., U. S. A., 1970, v. 1.
19. Dieulesaint E. et al.— IEEE Ultrasonics Symposium Proc., 1973, p. 383.
20. Maerfeld C., Tournois P — Appl. Phys. Lett., 1971, v. 19. p. 117.
Литература общего характера
Ogawa Т,— Japan. J. Appl. Phys., 1971, v. 10, p. 72.
Nye J. F. Propri&es physiques des cristaux.—P: Dunod, 1961, ch. 7.
Перевод: Най Д. Физические свойства кристаллов.—М.: Мир, 1967.
Bhagavantam S. Crystal symmetry and physical properties.—L. and N. Y.:
Academic Press, 1966.
Berlincourt D. A., Curran D. R., J affe H.— In. Physical Acoustics/Ed.
W. P. Mason and R. N. Thurston.— N. Y.: Acadefic Press, 1964, v. 1A, ch. 3.
Перевод: Физическая акустика/Под ред. У. Мэзона и Р. Терстона.—
М.: Мир, 1966, т. 1, ч. А.
Куате J. J.— J. Acoust. Soc. Am., 1949, v. 21, p. 159.
Auld B. A. Acoustic fields and waves in solids.—N. Y.: Wiley-Interscience,
1973, v. 1, ch. 8.
Tseng С. C. White R. M.— J. Appl. Phys., 1967. v. 38, p. 4274.
Tseng С. C.— J. Appl. Phys., 1970, v. 41, p. 2270.
Greebe C. A. A. J. et al.— Physics Reports, 1971, v. 1C, p. 235.
Глава 7
Цитируемая литература
1. Trotel J., Dieulesaint E., Autin B.— Electron. Lett., 1968, v. 4, p. 156.
2. Mason W. P. Electromechanical transducers and wave filters.—Princeton,
N. J.: Van Nostrand. 1948, p. 201-399^
418 ЛИТЕРАТУРА
3. Warner A. W., Опое М., Coquin G. А.— J. Acoust. Soc. Am., 1967, v. 42,.
p. 1223.
4. Sittig E. K., Warner A. W., Cook H. D.— Ultrasonics, 1969, v. 7, p. 108.
5. Foster N. F.— IEEE Trans. Son Ultrason, 1964, v. SU-11, p. 63.
6. De Klerk J., Kelly E. F — Appl. Phys. Lett, 1964, v. 5, p. 2.
7. Foster N. F. et al.— IEEE Trans. Son. Ultrason., 1968, v. SU-15, p. 28.
8. Foster N. F — Proc. IEEE, 1965, v. 53, p. 1400.
9. Rozgonyi G. A., Polito W. A—Appl. Phys. Lett., 1966, v. 8, p. 220.
10. White R. M — Proc. IEEE., 1970, v. 58, p. 1238.
11. Engan H.— IEEE Trans. Electron. Devices, 1969, v. ED-16, p. 1014.
12. De Klerk J.— Ultrasonics, 1971, v. 9, p. 35.
13. Joshi S. G., White R. M.— J. Acoust Soc. Am., 1969, v. 46, p. 17.
14. Coquin G. A., Tiersten H. F.— J. Acoust. Soc. Am., 1967, v. 41, p. 921.
15. Redwood M., Milsom R. F.— Electron. Lett, 1970, v. 6, p. 437.
16. Tancrell R. H., Holland M. G.— Proc. IEEE., 1971, v. 59, p. 393.
17. Atzeni C., Masotti L. Acoustic surface waves and acousto-optic devices./
Ed. T. Kallard.— N. Y.: Optosonic Press, 1971, v. 4, p. 69—80.
18. Tancrell.R. H., Williamson R. С,— Appl. Phys. Lett., 1971, V. 19, p. 456.
19. Richardson B. A., Kino G. S.— Appl. Phys. Lett., 1970, v. 16, p. 82.
20. Parnell G. W. et al.— IEEE Trans. Son. Ultrason., 1970, v. SU-17, p. 188.
21. Smith W. R. et al.— IEEE Trans. Microwave Theory Tech., 1969, v. MTT-17,
p. 856.
22. Lyon-Caen R. Circuits logiques integers.— P.: Masson et Cle, 1968, ch. 2.
23. Smith H. I., Bachner F. J., Efremov N.— l. Electrochemical society, 1971,
v. 118, p. 821.
24. Broers A. N., Lean E. G., Hatzakis M.— Appl. Phys. Lett., 1969, v. 15,
p. 98.
25. Hartemann P., Arnodo C., Gaudry R.— J. Physique, 1972, v. C6, 33, p. 266.
26. Cahen O., Sigelle R., Trotel J.— 14st National Meeting The Electrochemi-
cal Society, Houston, U, S. A., 1972.
27. Lean E. G., Broers A. N.— The Microwave Journal, 1970, v. 13, p. 97.
28. Bahr A. J., Lee R. E„ Podell A. F — Proc. IEEE, 1972, v. 60, p. 443.
29. Van den Heuvel A. P — Appl. Phys. Lett., 1972, v. 21, p. 280.
30. De Vries A. J., Miller R. L., Wojcik T. J.— IEEE Ultras, Sympos. Proc,
1972, p. 353.
31. Bristol T. W. et al.— IEEE Ultras. Symos. Proc., 1972, p. 43.
Литература общего характера
Brockelsby C. F., Palfreeman J. S., Gibson R. IE. Ultrasonic delay lines.—L.:
Iliffe L. T. D, 1963, ch. 3.
Kikuchi Y. Ultrasonic transducers.—Tokyo: Corona Pub. Co, 1969.
Перевод: Ультразвуковые преобразователи/Под ред. Е. Кикучи,— М.:
Meeker Т. R.— Ultrasonics, 1972, v. 10, р. 26.
Sitting Е. К.— ImPhysical Acoustics/Ed. W. Р. Mason and R. N. Thurston.—
N. Y.: Academic Press, 1972, v. 9, p. 221—275.
Ree der T. M., Winslow D. К,— IEEE Trans. Microwave Theory Tech., 1969.
v. MTT-17, p. 927.
Tiersten H F. Linear piezoelectric plate vibrations.— N. Y.: Plenum Press,
Mason IP. Р,— In: Physical Acoustics/Ed. W. P. Mason and R. N. Thurston.—
N. Y.: Academic Press, 1964. Перевод: Физическая акустика/Под ред.
У. Мэзона и Р. Терстона,— М.: Мир, 1966, т. 1, ч. А.
Miller G. F., Purvey Н,— Proc. Roy. Soc., 1954, v. A223, p. 521.
White R. M., Voltmer F. W.— Appl. Phys. Lett., 1965, v. 7, p. 314.
ЛИТЕРАТУРА
419
Tseng С. С — IEEE Trans. Electron. Devices, 1968, v. ED-15, p. 586.
Collins J. H. et al.— Proc. IEEE, 1969, v. 57, p. 833.
Redwood M., Milsom R. F.— Electron. Lett., 1970, v. 6, p. 437.
De Clerk.— Ultrasonics, 1971, v. 9, p. 35.
Milsom R. F., Redwood M.— Proc. IEEE, 1971, v. 118, p. 831.
Krairoiananan T., Redwood M.— Proc. IEEE, 1971, v. 118, p. 305.
Schmidt R. V,— J. Appl. Phys., 1972, v. 43, p. 2498.
Smith W. R., Gerard H. M., Jones W. R.— IEEE Trans. Microwave Theory
Tech., 1972, v. MTT-20, p. 458.
Hickernell F. S., Brewer J. W.— Appl. Phys. Lett., 1972, v. 21. p. 389.
Kino G. S., Wagers R. S — J. Appl. Phys., 1973, v. 44, p. 1480.
Ganguly A. K., Vassell M. 0.- J. Appl. Phys. 1973, v. 44, p. 1072.
Arzt R. M., Salzmann E., Dransjeld A.—Appl. Phys. Lett., 1967, v. 10, p. 165.
Humphry es R. F., Ash E. A — Electron. Lett., 1969, v. 5, p. 175.
Dakss M. L., Lean E. G.— Appl. Phys. Lett., 1971, v. 18, p. 137.
Claiborne L. T., Staples E. J., Harris J. L.— Appl. Phys. Lett.. 1971, v. 19, p. 58.
Bruun M., Ludvik S., Quote C. F.— Appl. Phys. Lett., 1971, v. 18, p. 118.
Greeneich E. W., Muller R. S— Appl. Phys. Lett., 1972, v. 20, p. 156.
Морозов А. И., Проклов В. В., Станковский Б. А. и др; Пьезополупроводни-
ковые преобразователи и их применение.— М.: Энергия, 1973.
Кенигсберг Н. Л., Чернец А Н., Космачева Т. С. и др. Тонкопленочные
гиперзвуковые преобразователи на основе сульфида кадмия.— ФТТ,
1970, т. 12, с. 1861.
Викторов И. А., Талашев А. А. Преобразователи для возбуждения и приема
высокочастотных поверхностных волн,—Акуст. журнал, 1971, т. 17,
с. 309.
Марахонов В. М., Новик Г. А., Пикарников В. П. Исследование роста полу-
проводниковых пленок CdS, полученных совместным испарением суль-
фида кадмия и серы.—Электронная техника, 1971, т. 8, вып. 3, с. 19.
Домаркас В. И., Кажис Р.— И. Ю. Контрольно-измерительные пьезоэлект-
рические преобразователи.— Вильнюс: Минтис, 1974.
Глобин Г. М., Кенигсберг Н. Л., Тараканов В. В. и др. Тонкопленочные пре-
образователи из окиси цинка для возбуждения продольных и попереч-
ных гиперзвуковых волн.— Акуст. журнал, 1974, т. 20, с. 317.
Королюк А. П., Мацаков Л. Я., Васильченко В. В. Определение упругих
и пьезокристаллических постоянных монокристаллов ниобата лития.—
Кристаллография, 1970, т. 15, вып. 5, с. 1028—1032.
Глава 8
Цитируемая литература
1. Brillouin L.— Ann. de Phys., 1922, v. 17, p. 88.
2. Lucas R., Biquard P.— J. Physique, 1932, v. 10, p. 464.
3. Debye P., Sears F. PF.—Proc. Nat. Acad. Sc., 1932, v. 18, p. 409.
4. Adler R.— IEEE Spectrum. 1967, v. 4, p. 42.
5. Primak W., Post D.— J. Appl. Phys., 1959, v. 30, p. 779.
6. Pinnow D. A., Dixon R. W.— Appl. Phys. Lett., 1968, v. 13, p. 156.
7. Dixon R. W.- J. AppL Phys., 1967, v. 38, p. 5149.
8. Uehida N., Ohmachi Y.— J. Appl. Phys., 1969, v. 40, p. 4692.
9. Pockels F.—Ann. Physik. Chem., 1889, v. 37, p. 269—372.
10. Nelson D. F., Lax M.— Phys. Rev. Lett., 1970, v. 24, p. 379.
11. Nelson D. F., Lazay P. D.— Phys. Rev. Lett., 1970, v. 25, p. 1187.
12. Nelson D. F.. Lazay P. D., Lax M.— Phys. Rev., 1972, v. В 6, p. 3109.
13. Nelson D. F., Lax M- Phys. Rev., 1971, v. В 3, p. 2778.
14. Smith T. M., Korpel A.— IEEE J. Quantum Electron., 1965, v. QE-1, p. 283.
15. Pinnow D. A — IEEE J. Quantum Electron., 1970, v. QE-6, p. 223.
16. Dixon R. W.— IEEE J. Quantum Electron., 1967, v. QE-3, p. 85.
420
ЛИТЕРАТУРА
17. Harris S. E., Nleh S. T. K., Winslow D. K.— Appl. Pbys. Lett., 1969, v. 15,
p. 325.
18. Harris S. E., Nleh S. T. K., Feigelson H. S.— Appl. Phys. Lett., 1970, v. 17,
p. 223.
19. Montgomery R. M., Young E. H. (Jr.).— J. Appl. Phys., 1971, v. 42, p. 2585.
20. Korpel A., Laub L. J., Sievering H. C.— Appl. Phys. Lett., 1967, v. 10,
p. 295^
21. Adler R., Korpel A., Desmares P.— IEEE Trans. Son. Ultrason., 1968,
v. SU-15, p. 157.
22. Salzmann E., Weismann D.— J. Appl. Phys., 1969, v. 40, p. 3408.
23. Tien P. K., Ulrich R., Martin R. J.— Appl. Phys. Lett.,' 1969, v. 14, p. 291.
24. Dakss M. L. et al.- Appl. Phys. Lett., 1970, v. 17, p. 265.
25. Kaminov I. P., Carruthers J. R.— Appl. Phys. Lett., 1973, v. 22, p. 326.
26. Schmidt R. V., Kaminow I. P., Carruthers J. R.— Appl. Phys. Lett., 1973,
v. 23, p. 417.
27. Schmidt R. V., Kaminow I. P.— Appl. Phys. Lett., 1974, v. 25, p. 458.
28. Kuhn L. et al — Appl. Phys. Lett, 1970, v. 17, p. 265.
29. Hartemann P. et al.— J. Physique, 1972, v. C6, p. 216.
30. Schmidt R. V., Kaminow I. Р,— IEEE J. Quantum Electron., 1975,
v. QE-II, p. 57.
31. Tsai C. S. et al.— Appl. Phys. Lett., 1975, v. 26, p. 140.
32. Reintjes J., Schulz M. B.— J. Appl. Phys., 1968, v. 39, p. 5254.
Литература общего характера
Bruhat G., Kastler A. Cours de physique g^nerale — Optique.— P. Masson,
1965, ch. 20.
Nye J. F. Physical properties of crystals.—Oxford: Clarendon Press, 1960,
ch. 13. Перевод: пай Д. Физические свойства кристаллов,—М.: Мир,
Bhagavantam S. Crystal symmetry and Physical properties.—L. and N. Y.:
Academic Press, 1966, ch. 16.
Сиротин Ю. И., Шаскольская M. П. Основы кристаллофизики,— М.: Наука,
1975.
Raman С. V., Nath N. S. N — Proc. Indian Acad. Sci., 1935, v. 2, p. 406, 413,
ibid, 1936, v. 3, p. 75, 119, 459, v. 4. p. 222.
Bhatia A. B., Noble W. S.— Proc. Roy. Soo., 1953, v. 220A, p. 356.
Slater J. C.- Rev. Mod. Phys., 1958, v. 30, p. 197.
Quate C. F., Wilkinson C. D., Winslow D. K.— Proc. IEEE, 1965, v. 53, p. 1604.
Cohen M. G., Gordon E. I.— Bell Syst. Tech. J., 1965, v. 44, p. 693.
Gordon E. I.— Proc. IEEE., 1966, v. 54. p. 1391.
Klein W. R., Cook B. D.— IEEE Trans. Son. Ultrason., 1967, v. SU-14, p. 123.
Spencer E. G., Lenzo P. V., Ballman A.— Proc. IEEE., 1967, v. 55, p. 2074.
Dixon R. W.— IEEE Trans. Electron. Devices, 1970, v. ED-17, p. 229.
Damon R. W., Maloney W. T., McMahon D. H.— In: Physical Acoustics/Ed.
W. P. Mason and R N. Thurston.— N. Y.: Academic Press, 1970, v. 7, ch. 5.
Перевод: Физическая акустика/Под ред, У. Мэзоиа и Р. Терстона,—
М: Мир, 1974, т. 7.
Bauza J. М., Carles С., Torguet R.— Acoustica, 1974, v. 30, № 4.
Sapriel J. L’Acousto-optique.— P.: Masson, 1976.
Рытое С. M. Дифракция света на ультразвуковых волнах,— Изв. АН СССР,
сер. физ., 1937, т. 2, с. 222.
Фабелинский И. Л. Взаимодействие света н звука— Изв. АН СССР, сер.
физ., 1971, т. 35, с. 874.
Гуляев Ю. В., Проклов В. В., Шкердин Г. Н. Дифракция света на звуке в
твердых телах.— УФН, 1978, т. 124, с. 61,
ЛИТЕРАТУРА
421
Леманов В. В., Шакин О. В. Рассеяние света на упругих волнах в одноос-
ных кристаллах.— ФТТ, 1972, т. 14, с. 229.
Мустелъ Е. Р., Парыгин В. Н. Методы модуляции и сканирования света.—
М.: Наука, 1970.
Писаревский Ю. В., Сильвестрова И. М. Рассеяние света на упругих волнах
в оптически двуосных кристаллах.— Кристаллография, 1973, т. 18, с. 1003.
Slobodnik A. J. (Jr.)— Appl. Phys. Lett., 1969, v. 14, p. 94.
Lean E. G., Powell C. G.— Proc. IEEE, 1970, v. 58, p. 1939.
Kuhn L., Heidrich P. F., Lean E. G.— Appl. Phys. Lett., 1971, v. 19, p. 428.
Lean E. G.— In: Progress in optics/Ed. E. Wolf.— Amsterdam: North-Holland,
1973, v. 11, ch. 3.
Sasaki H., Kushibiki J., Chubachi A.—Appl. Phys. Lett., 1974, v. 25, p. 476.
Bridoux E. et al.— J. Appl. Phys., 1974, v. 45, p. 5156.
Глава 9
Цитируемая литература
1. Hunt F. V. Electroacoustics. The analysis of transduction, and its histo-
rical background.— N. Y.: John Wiley and Sons, 1954, ch. 1.
2. Arenberg D. L.— J, Acoust Soc. Am., 1948, v. 20, p. 1—25.
3. Klauder J. B. et al.— Bell Syst. Tech. 1, 1960, v. 39, p. 745.
4. McFee J. H — In: Physical Acoustics/Ed. W. P. Mason and R. N. Thurston.—
N. Y.: Academic Press, 1966, v. 4A, ch. 1. Перевод: Физическая акустика./
Под ред. У. Мазона и Р. Терстона.— М.: Мир, 1969, т. 4, ч. А.
5. Collins J. Н., Lakin К. М., Hagon Р. J.— Proc. IEEE, 1969, v. 57, р. 740.
6. Eveleth J. И,— Proc. IEEE, 1965, v. 53, p. 1406.
7. Defranould Ph.— European microwave conference. Stockholm, 1971.
8. Hartemann P., Arnodo C., Gaudry B.— J. Physique, 1972, v. C6. 33, p, 266,
9. Hartemann P., Arnodo C.— Electron. Lett., 1972, v. 8, p. 265.
10. Rulf B.— J. Acoust. Soc. Am., 1969, v. 45, p. 493.
11. Викторов И. А. Физические основы применения ультразвуковых волк
Рэлея и Лэмба в технике,— М.: Наука, 1966, с. 29—42.
12. Bond W. L., Reeder Т., Shaw Н. J.— Electron. Lett., 1971, v. 7, p. 79.
13. Lewis M. F., Patterson E.— Appl. Phys. Lett., 1971, v. 18, p. 143.
14. Adkins L. R., Hughes A. J.—J. Appl. Phys., 1971, v. 42, p. 1819.
15. Kino G., Reeder T. M.— IEEE Trans. Electron. Devices. 1971, v. ED-18,
p. 909.
16. Coldren L. A.— IEEE Trans. Son. Ultrason., 1973, v. SU-20, p. 17.
16a. Lewis M. F — Ultrasonics, 1974, v. 12, p. 115.
17. Brienza M. J., Demaria A. J.— Appl. Phys. Lett., 1966, v. 9, p. 312.
18. Cahen O., Dieulesaint E., Torguet R.— C. R. Acad. Sc. Paris, 1968, v. 266,
p. 1009.
19. Woodward P. M. Probability and information theory with applications to
radar.— Oxford: Pergamon Press, 1953.
20. Carpentier M. Radars. Concepts nouveaux.— P.: Dunod_, 1966, ch. 2.
21. Cook С. E., Bernfeld M. Radar signals: an introduction to theory and
application.— N. Y.: Academic Press, 1967, ch. 2.
22. Bruhat G., Kastler A. Cours de physique generate. Optique.— P.: Masson
et Cle, 1965.
23. Tournois P.— Ann. de Radutelectricite, 1964, v. 78, p. 267.
24. Hartemann P. Filtres dispersifs a ondes elastiques do Rayleigh. These,
universite de Paris-Sud (Orsay), 1973.
25. Meeker T. R., Meitzler A. H.— In: Physical Acoustics/Ed. W. P. Mason
and R. N. Thurston.— N. Y.: Academic Press, 1964, v. 1A, p. 111—167.
Перевод: Физическая акустика/Под ред. У. Мэзона и Р. Терстона,—М.:
Мир, 1966, т. 1, ч. А. «
422
ЛИТЕРАТУРА
26. May J. E. (Jr.).—In: Physical Acoustics/Ed. W. P. Mason and R. N. Thur-
ston.— N. Y.: Academic Press, 1964, v. 1A, p. 417—483. Перевод: Физическая
акустика/Под ред. У. Мэзона и Р. Терстона.—М.: Мир, 1966, т. 1, ч. А.
27. Викторов И. А. Физические основы применения ультразвуковых волн
Рэлея и Лэмба в технике.— М.: Наука, 1966.
28. Fitch А. Н.— J. Acoust. Soc. Am., 1963, v. 35, p. 709.
29. Duncan R. S., Parker M. R. (Jr.).— Proc. IEEE, 1965, v. 53, p. 413.
30. Coquin G. A., Tsu R.— Proc. IEEE, 1965, v. 53, p. 581.
31. Miller D. E., Parker M. R.— Proc. IEEE, 1966, v. 54, p. 891.
32. Mortley W. S.- Marconi Rev., 1965, v. 28, p. 273.
,33. Tournois P., Lardat C — IEEE Trans. Son. Ultrason., 1969, v. SU-16, p. 107.
34. Lardat C., Maerfeld C., Tournois P.— Proc. IEEE, 1971, v. 59, p. 355.
35. Lardat C., Tournois P.— IEEE Ultrason. Symposium Proc., 1972,
p. 280.
36. Schulz M. B., Matsinger B. J., Holland M. G — J. Appl. Phys., 1970, v. 41.
p. 2755.
37. Hartemann P., Dieulesaint Т,— Electron. Lett., 1969, v. 5, p. 219.
38. Cook С. E., Bernfeld M. Radar signals: an introduction to theory and
application.— N. Y.: Academic Press, 1967, p. 178.
39. Key E. L., Fowle E. N., Haggarty R. D.— Lincoln Lab. M. I. T., Le-
xington, Massachusetts, Tech. Rept. 207, sept. 1969,
40. Hartemann P., Dieulesaint E.— Onde electrique, 1971, v. 51, p. 523.
41. Sitting E. K., Coquin G. A.— IEEE Trans. Son. Ultrason., 1968, v. SU-15,
p. 111.
42. Martin T. A.— IEEE Trans. Microwave Theory Tech., 1973, v. MTT-21,
p. 186.
43. Williamson R. C., Smith H. /.— Electron. Lett., 1972, v. 8, p. 401.
44. Williamson R. C., Smith H. I.— IEEE Trans. Microwave Theory Tech-,
1973, v. MTT-21, p. 195.
45. Li R. С. M.— IEEE Ultrasonics Symposium Proc., 1972, p. 263.
46. Smith H. I., Williamson R. C., Brogan W. T.— IEEE Ultrasonics Sympo-
sium Proc., 1972, p. 198.
47. Williamson R. C., Dolat V. S., Smith H. I.— IEEE Ultrasonics Sympo-
sium. Proc., 1973, p. 490.
48. Schulz’ M. B., Holland M. G., Davis L. (Jr.) — Appl. Phys. Lett., 1967,
v. 11, p. 237. ,
49. Collins J. H., Lean E. G. H., Shaw H. 7.—Appl. Phys. Lett., 1967, v. 11,
p. 240.
50. См. [1] c. 53-57.
51. Spencer W. J.— In: Physical Acoustics/Ed. W. P. Mason and R. N. Thur-
ston.— N. Y.: Academic Press, 1972, v. 9, p. 167—220.
52. Tancrell R. H., Holland M. G.— Proc. IEEE, 1971, v. 59, p. 393.
53. Hartemann P., Dieulesaint E.— Electron. Lett., 1969, v. 5, p. 657.
54. Hartemann P., Menager O.—Electron. Lett., 1972, v. 8, p. 214.
55. Hartemann P.— Electron. Lett., 1971, v. 7, p. 674.
56. De Vries A. J. et-al.— IEEE Ultrasonics Symposium, St-Louis, U, S. A.,
1969, paper G-5.
57. Chauvin D., Coussot G., Dieulesaint E.— Electron. Lett., 1971, v. 17, p. 491.
58. Melngailis J., Smith J. M., Cafarella J. Н,— IEEE Ultrasonics Symposium
Proc., 1972, p. 221.
59. Atzeni C., Manes G., Masotti L.— IEEE Ultrasonics Symposium Proc., 1973,
p. 414.
60. Staples E. J., Schoenwald J. S„ Rosenfeld R. C. et al.— IEEE Ultrasonics
Symposium Proc., 1974, p. 245.
€1. Li R. С. M., Williamson R. C., Flanders D. C. et al.— IEEE Ultrasonics
Symposium Proc., 1974, p. 257.
ЛИТЕРАТУРА
423
62. Miller S. P., Stlgall R. E., Shreve W. R.— IEEE Ultrasonics Symposium
Proc., 1975, p. 474.
63. Cross P. S., Smith R. S„ Haydl W. Н,— Electron. Lett., 1975, v. 11, p. 244.
64. Hartemann P.— IEEE Ultrasonics Symposium Proc., 1975, p. 303.
65. Anderson V. C— Harvard Acoust. Lab., Cambridge, Massachusetts, Tech.
Mem. № 37,1956.
66. Bert A. G., Epsztein B., Kantorowicz G.— Appl. Phys. Lett., 1972, v. 21,
p. 50.
67. Ingebrigsten K. A., Cohen R. A., Mountain R. W.— Appl. Phys. Lett., 1975,
v. 26, p. 596.
68. Thurston R. N.— In: Physical Acoustics/Ed. W. P. Mason and R. N. Thur-
ston.— N. Y.: Academic Press, 1964, v. 1A, p. 91—109.
Перевод: Физическая акустика/Под ред. У. Мэзона.—М: Мир, 1'966, т. 1,
69. Adler Е. et al.— IEEE Trans. Son. Ultrason., 1973, v. SU-20, p. 13.
70. Liamov V. E„ Hsu T. H., White R. M.— J. Appl. Phys., 1972, v. 43, p. 800.
71. Quote C. F., Thompson R. B— Appl. Phys. Lett., 1970, v. 16, p. 494.
72. Svaasand L. O— Appl. Phys. Lett., 1969, v. 15, p. 300.
73. Luukkala M„ Kino G. S— Appl. Phys. Lett., 1971, v. 18, p. 393.
74. Dejranould P., Maerfeld C.— Proc. IEEE, 1976, v. 64, p. 748.
75. Das P., Araghi M. N., Wang W. C— Appl. Phys. Lett., 1972, v. 21, p. 152.
76. Kino G. S.,— Proc. IEEE, 1976, v. 64. p. 724.
77. Smith J. M., Stern E., Bers A., Cafarella J— IEEE Ultrasonics Sympo-
sium Proc^ 1973, p. 142.
78. Grivet P. Physique des lignes HF et UHF.—P.: Masson et C1®, 1974, t. 3,
ch. 10.
79. Marshall F. G., Paige E. G. S— Electron. Lett., 1971, v. 7, p. 460.
80. Marshall F. G.. Newton С. O., Paige E. G. S — IEEE Trans. Microwave
Theory Tech., 1973, v. MTT-21, p. 206.
81. Louisell W. H. Coupled mode and parametric electronics.—N. Y.: Wiley,
1960. Перевод: Луиселл У. Связанные и параметрические колебания в
электронике.—М.: ИЛ, 1963.
82. Мах J. MEthodes et techniques de traitement du signal et applications
aux mesures physiques.— P.: Masson et C1®, 1972, t. 1. ch. 7.
83. Marshall F. G., Newton С. O., Paige E. G. S.— IEEE Trans. Microwave
Theory Tech., 1973, v. MTT-21, p. 216.
84. Maerfeld C., Dejranould P., Farnell G. W.— IEEE Ultrasonics Sympo-
sium Proc., 1973, p. 155.
85. Feldmann M., Henajf J.— Proc. European Microwave Conf., 1976, p. 239.
86. Grant P. M., Jack M. A., Collins J. H.— Electron. Lett.. 1975. v. 11, p. 468.
p. 468.
87. Jack M. A., Manes G. F., Grant P. M. et al.— IEEE Ultrasonics Sympo-
sium Proc., 1976, p. 376.
88. Jack M. A., Grant P. M., Collins J. H.— Proc. IEEE, 1980, v. 68, p. 450.
89. Williamson R. C., Dolat V. S., Rhodes R. R. et al.— IEEE Ultrasonics Sym-
posium Proc., 1979, p. 741.
90. Gires F.— Revue Phys. AppliquEe, 1969, v. 4, p. 505.
91. Torguet R., Dieulesaint E. Electron. Lett., 1969, v. 5, p. 632.
92. Korpel A. et al— Appl. Opt, 1966, v. 5, p. 1667.
93. Torguet Д. Etude theorique et experimentale de 1’interaction de la lumie-
re avec des ondes acoustiques de forte puissance. These, iniversitE de Pa-
ris 6, 1973.
Литература общего характера
White R. M.— Proc. IEEE, 1970, v. 58, p. 1238.
Dieulesaint E.— L’onde Electrique, 1970, v. 50, p. 899.
424
ЛИТЕРАТУРА
Burnsweig J., Gregory E. H.. Wagner R. J.— IEEE J. Solid state circuits, 1970,
v. SC-5, p. 310.
Sabine IL, Cole P. IL— Ultrasonics, 1971, v. 9, p. 103.
Kino G. S., Matthews H.— IEEE Spectrum, 1971, v. 18, p. 22.
Gandolfo G. A., Grasse C. L., Schmitt E. J.— Microwaves, 1971, V. 10, p. 44.
Glowinski A.— L’onde olectrique, 1972, v. 52, p. 54.
IDieulesalnt E — J. Physique, 1972, v. 33, p. C6-176.
De Klerk J.— J. Physique, 1972, v. 33, p. C6-182.
.Dieulesaint E., Hartemann P.— Ultrasonics, 1973, v. 11, p. 24.
Kino G. S., Shaw J.— Scientific American, 1972, oct., p. 51.
Tancrell R. H. et <zl.—Proc. IEEE, 1969, v. 57, p. 1211.
Atzeni C.— IEEE Trans. Son. Ultrason., 1971, v. SU-18, p. 193.
Pedinoff M. E., Gerard IL M., Judd G. W.— IEEE Trans. Son. Ultrason., 1972,
v. SU-19, p. 395.
Squire W. D., Whitehouse H. J., Alsup J. M.— IEEE Trans. Microwave Theory
Tech., 1969, v. MTT-17, p. 1020.
Jones W. C., Hartmann C. S., Claiborne L. T — IEEE Trans. Son Ultrason.,
1971, v. SU-18, p. 21.
'Tseng С. C — IEEE Trans. Son. Ultrason., 1971, v. SU-18, p. 103.
Atzeni C., Masotti L.— Alta Frequenza, 1973, v. 52, p. 84.
Каринский С. С. Устройства обработки сигналов на ультразвуковых по-
верхностных волнах.— М.: Сов. радио, 1975.
Эжен Дьелесан, Даниэль Руайе
УПРУГИЕ ВОЛНЫ В ТВЕРДЫХ ТЕЛАХ.
Применение для обработки сигналов
Редактор Н. А. Михалина
Техн, редактор Л, В. Лихачева. Корректор А. Л. Ипатова
ИВ 11679
Сдано в набор 05.06.81. Подписано к печати 26.02.82. Формат 60х90‘/,«, бумага
тип. X 2. Обыкновенная гарнитура. Высокая печать. Условн. печ. л. 26,5. Уч.-изд.
л. 26.11. Тираж 3600 акз. Заказ № 610. Цена 4 руб. 20 к.
Издательство «Наука»
Главная редакция физико-математической литературы
1170'1, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука»
630077, Новосибирск, 77, Станиславского, 25