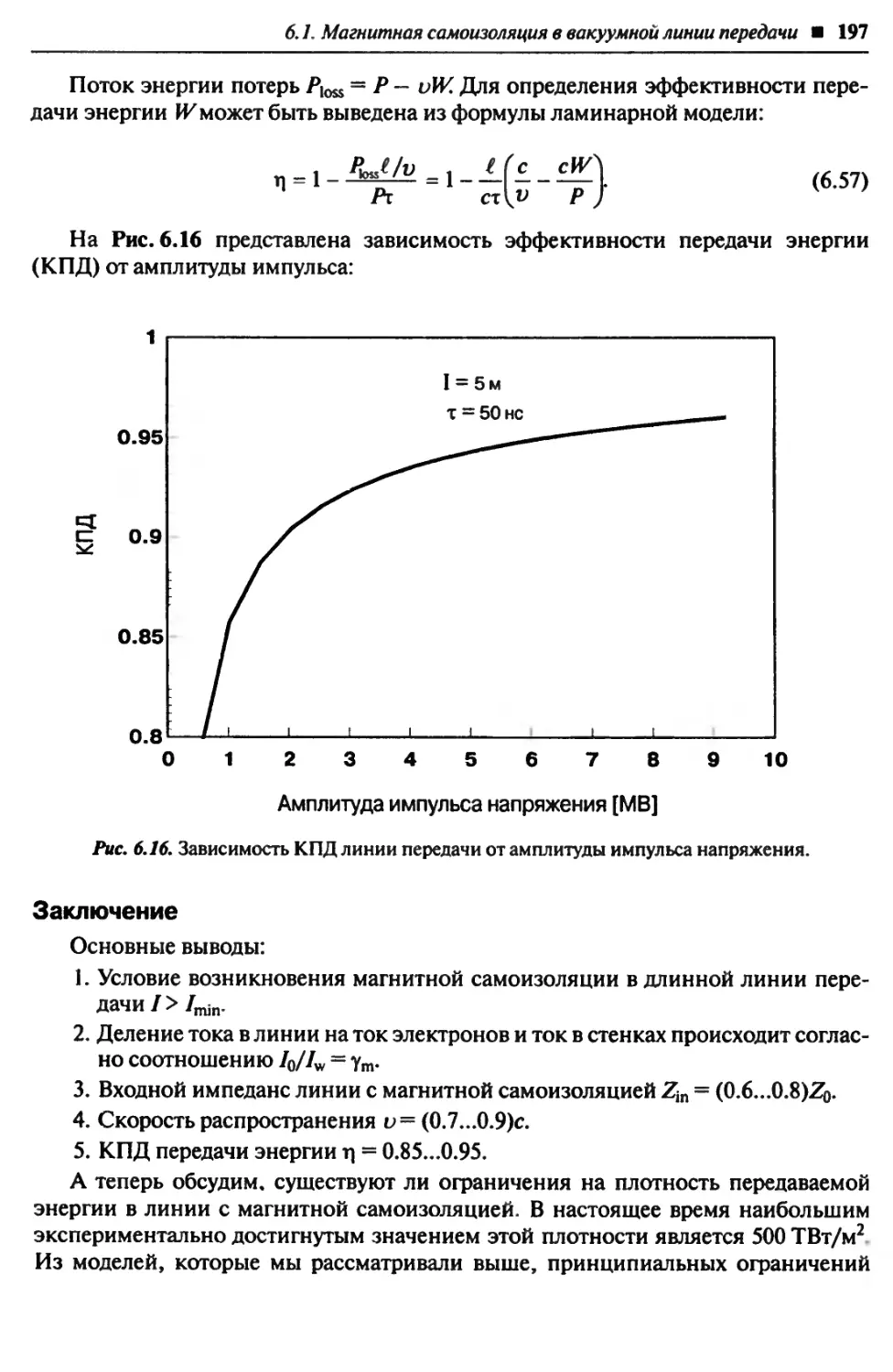
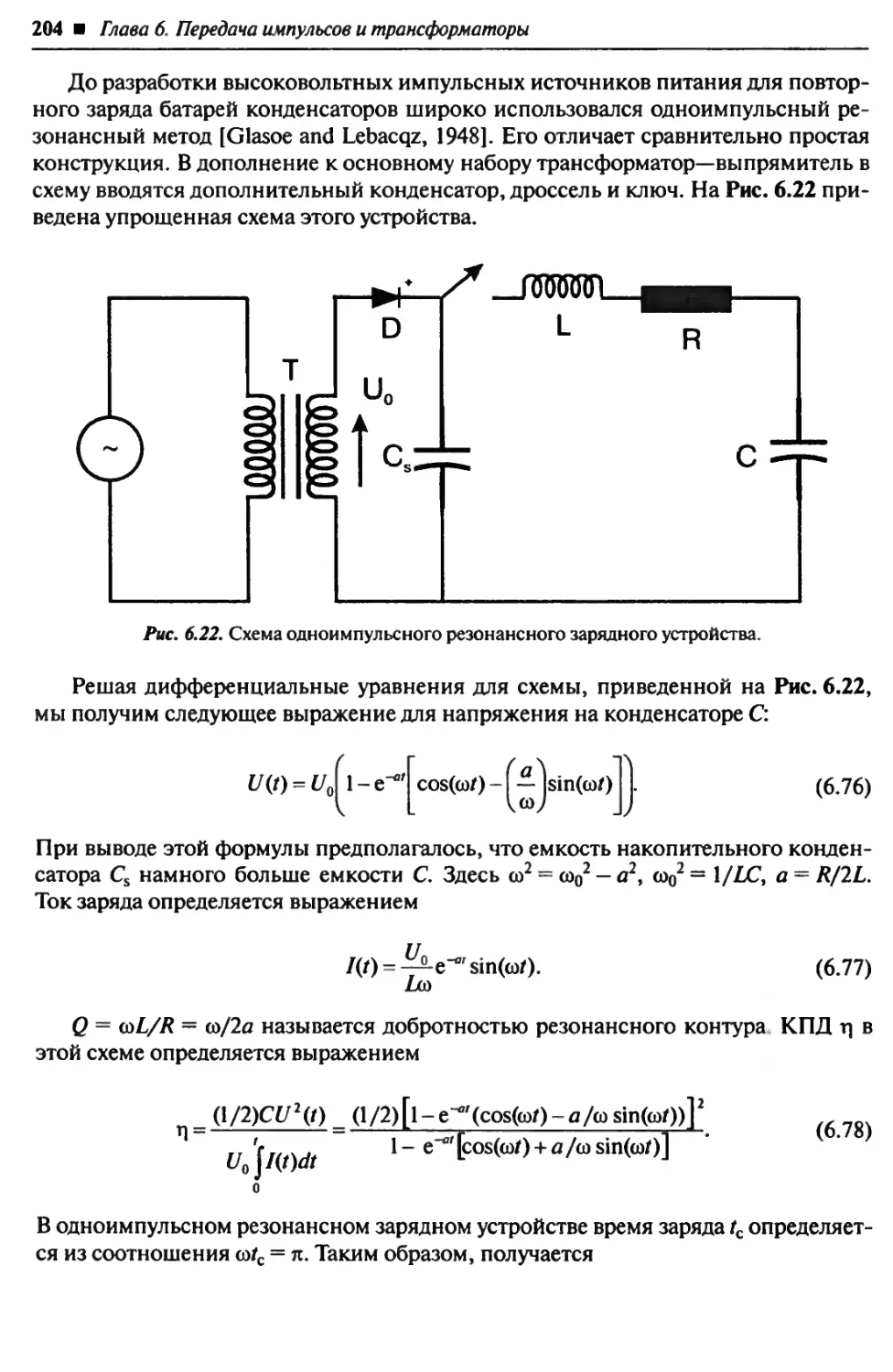
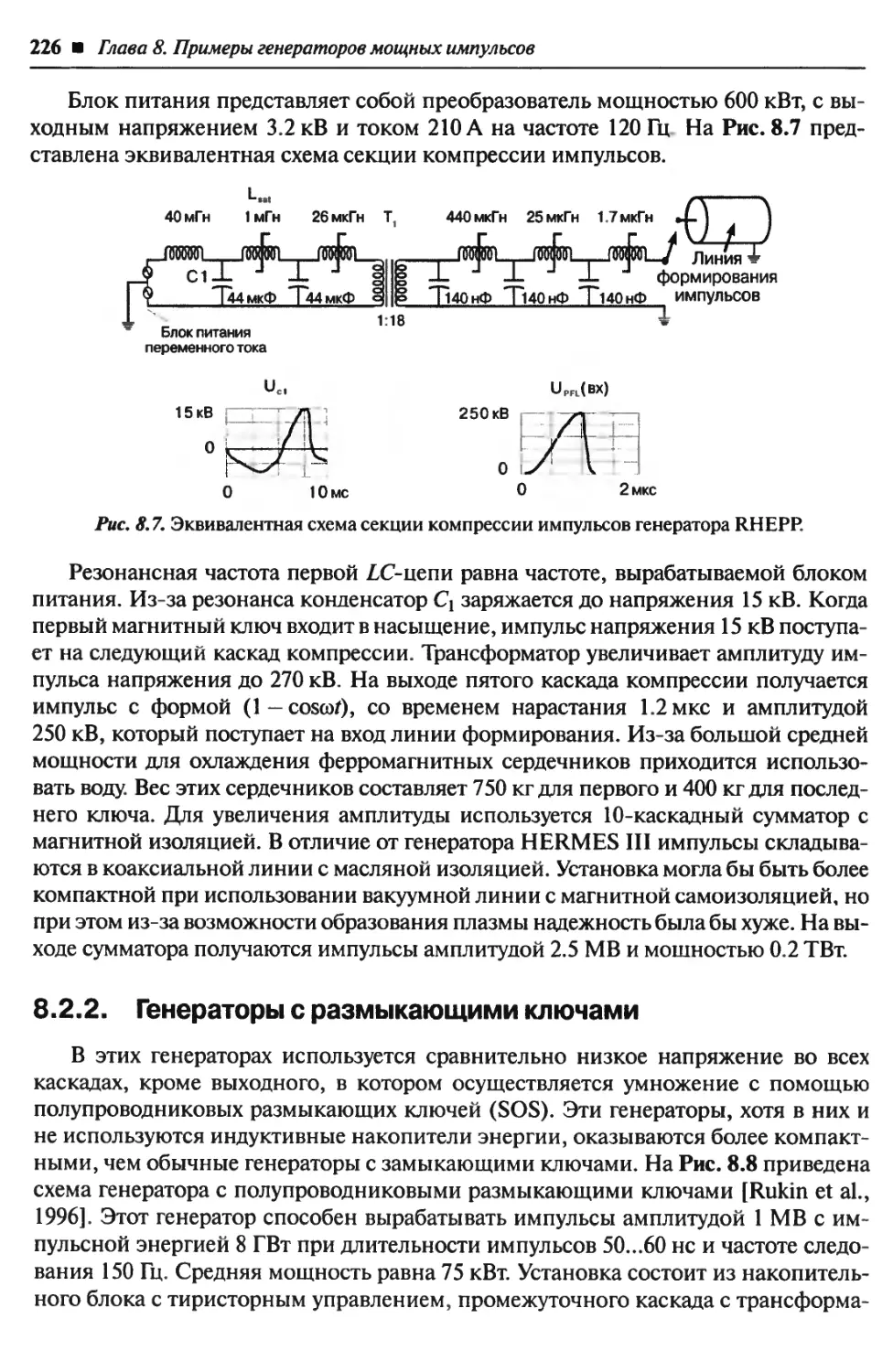
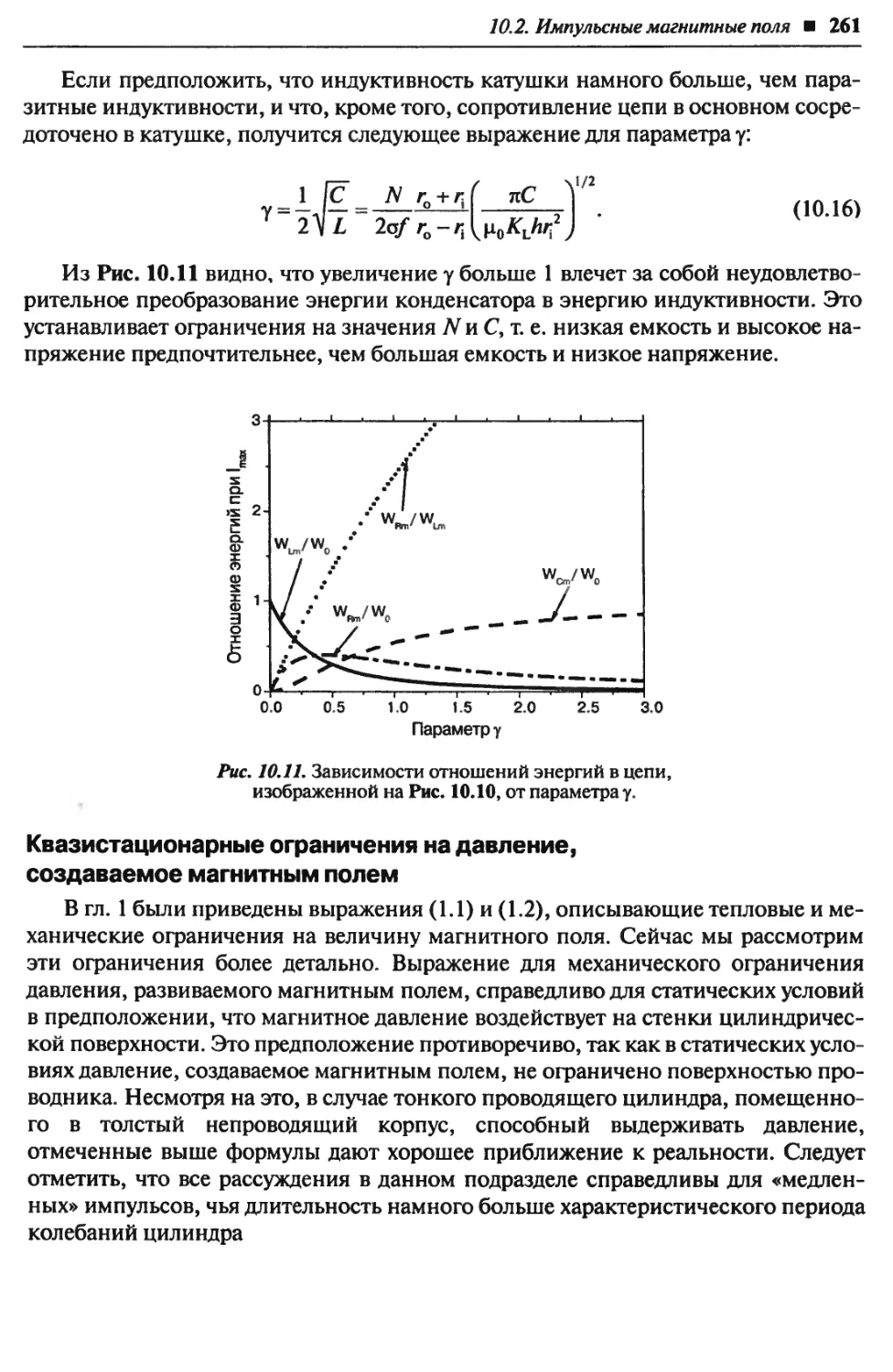
Автор: Блум Х.
Теги: электротехника радиоаппаратура (радиоэлектронная аппаратура) импульсные устройства физика электроника
ISBN: 978-5-94120-191-4
Год: 2008
Текст
СЕРИЯ
Силовая электроника
Хансиоахим Блум
СХЕМОТЕХНИКА
И ПРИМЕНЕНИЕ
МОЩНЫХ ИМПУЛЬСНЫХ
УСТРОЙСТВ
Перевод с английского
канд. техн. наук.
А. М. Рабодзея
ОДЭКА
Москва
Издательский дом «Додэка-ХХ1»
2008
УДК 621.374
ББК 32.844+32.847
Б70
Блум, Хансиоахим.
Б70 Схемотехника и применение мощных импульсных устройств / Хансиоахим
Блум ; пер. с англ. Рабодзея А. М. — М.: Додэка-ХХ1, 2008. — 352 с.: ил.
(Серия «Силовая электроника»?).
ISBN 978-5-94120-191-4
В книге изложены физические и технические основы создания и применения
импульсов высокого напряжения с очень большой мощностью и энергией. В первой
части описаны компоненты, материалы и методы измерений, используемые в тех-
нике получения мощных импульсов. Во второй части — некоторые из наиболее пер-
спективных применений этой техники в биоэлектрике, поверхностной обработке
металлов, медицине, селективном размельчении различных материалов и т.д., а
именно: генераторы мощных импульсов электрического и магнитного поля, источ-
ники интенсивного импульсного излучения и импульсных электрических разрядов.
Книга представляет собой, по сути, путеводитель по огромному количеству пуб-
ликаций поданной тематике, как классических, так и современных.
Книга предназначена широкому кругу читателей, которые хотят ближе ознако-
миться с основными идеями и методами, используемыми в сфере мощных импуль-
сных устройств, а особо будет полезна студентам, преподавателям вузов, инженерам
и ученым.
УДК 621.374
ББК 32.844+32.847
ISBN 978-5-94120-191-4 (рус)
ISBN 3-540-26137-0 (англ.)
© Springer-Xferlag Berlin Heidelberg 2006
©Додэка-XXI, 2008
® Серия «Силовая электроника»
ОГЛАВЛЕНИЕ
Предисловие переводчика .............................................7
Символы и аббревиатуры...............................................8
Предисловие .......................................................12
Глава 1. ВВЕДЕНИЕ..................................................15
1.1. Схемотехника мощных импульсных устройств......................15
1.2. Преимущества..................................................19
Глава 2. СТАТИЧЕСКАЯ И ИМПУЛЬСНАЯ ЭЛЕКТРИЧЕСКАЯ ПРОЧНОСТЬ
ДИЭЛЕКТРИКОВ......................................................21
2.1. Введение.......................................................21
2.2. Газы....................................................... 23
2.3. Жидкости.........................-........................... 42
2.4. Твердые тела...................................................58
2.5. Статистическая интерпретация измерений электрической прочности.66
Глава 3. НАКОПЛЕНИЕ ЭНЕРГИИ.........................................71
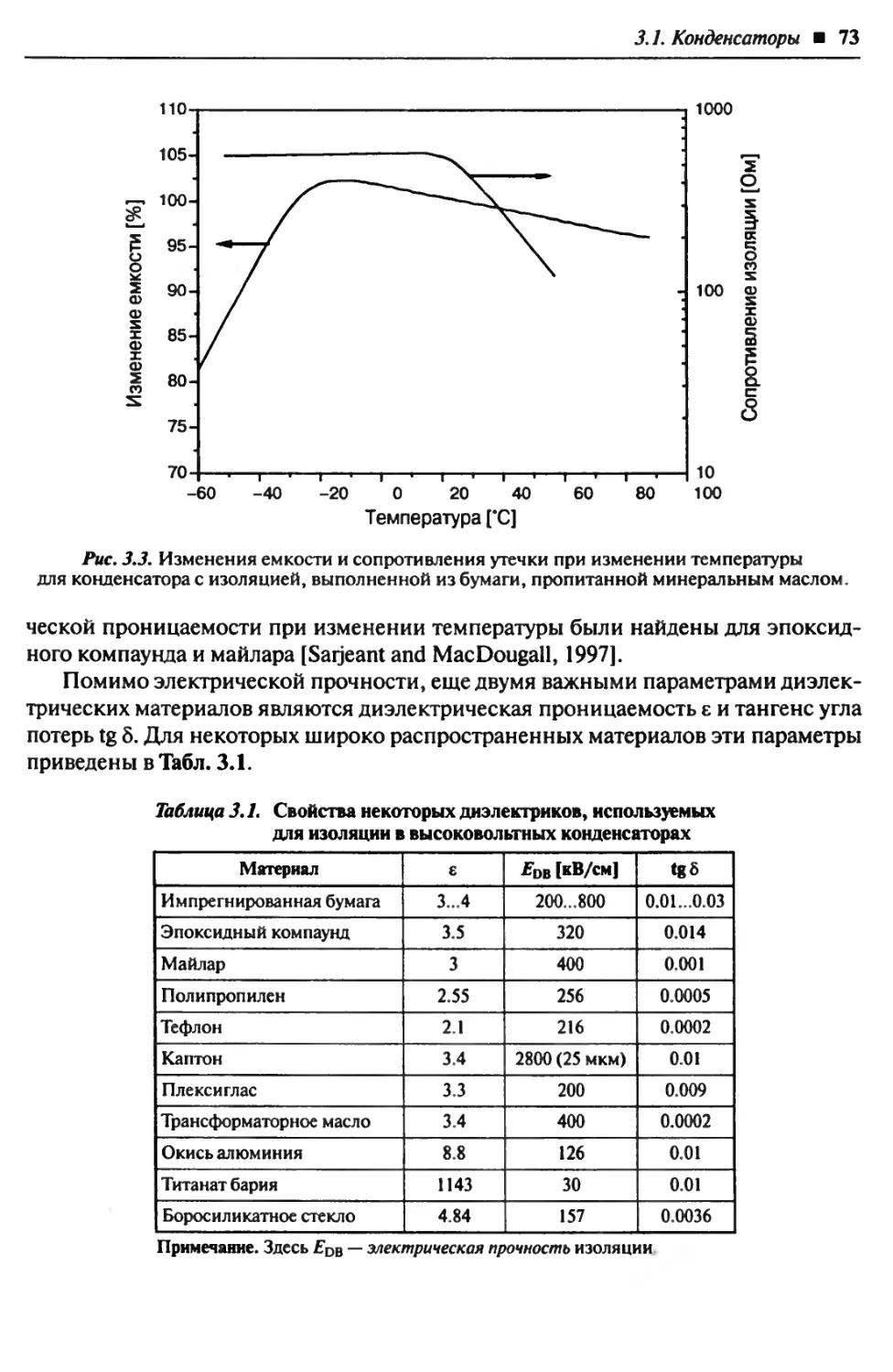
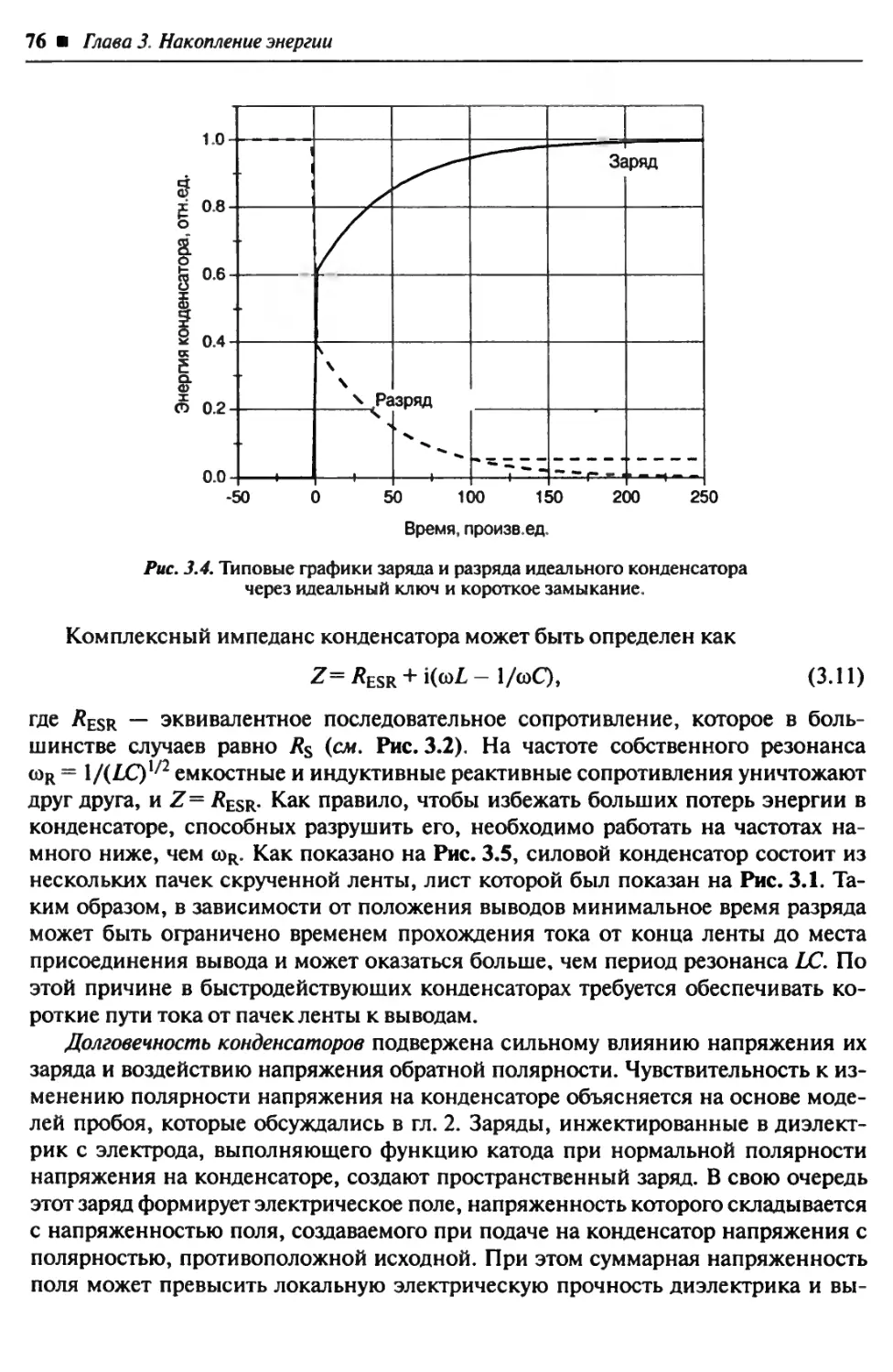
3.1. Конденсаторы................................................ 71
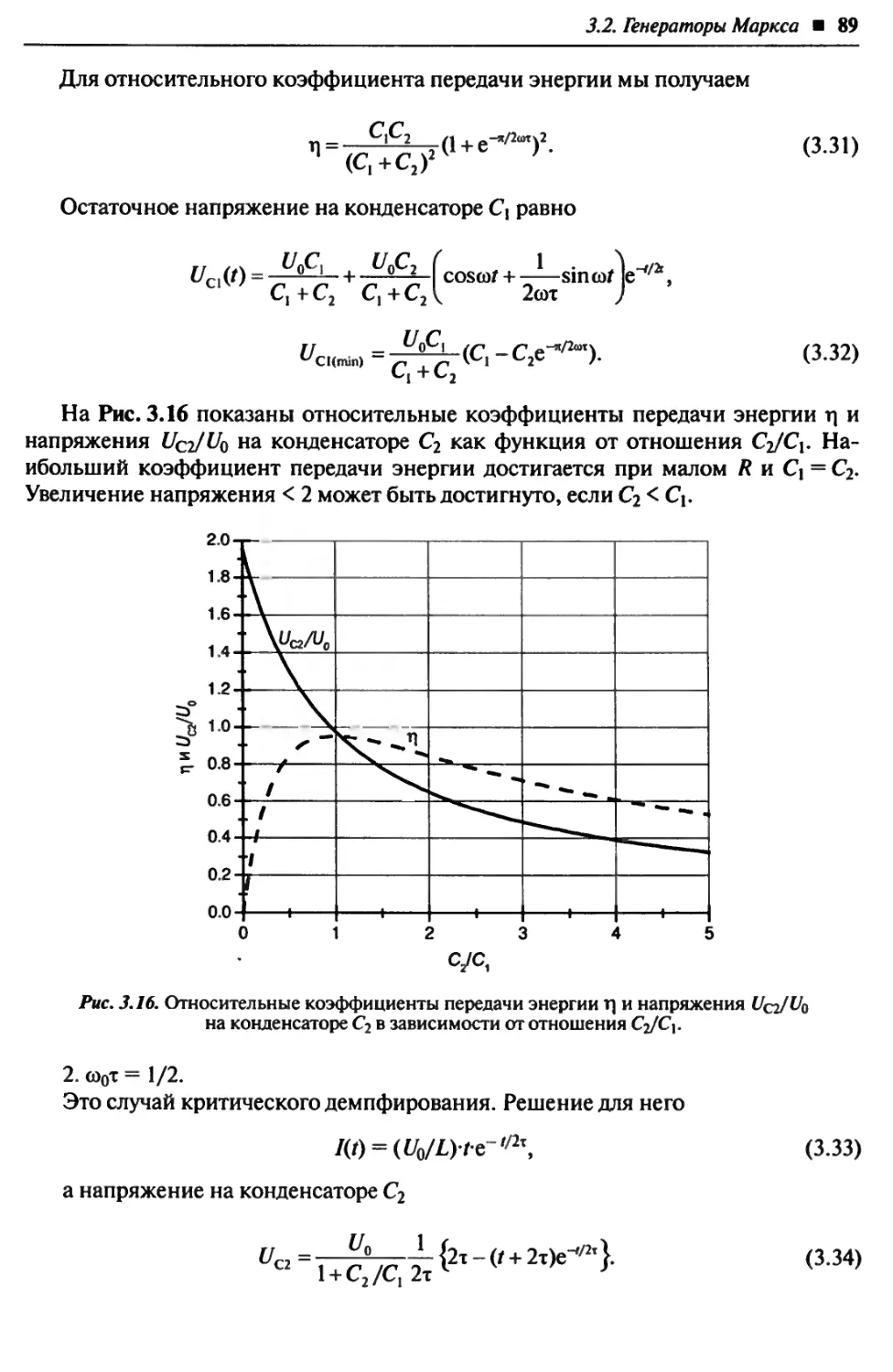
3.2. Генераторы Маркса............................................. 79
3.3. Индуктивные накопители энергии.... 90
3.4. Умножение мощности и напряжения................................91
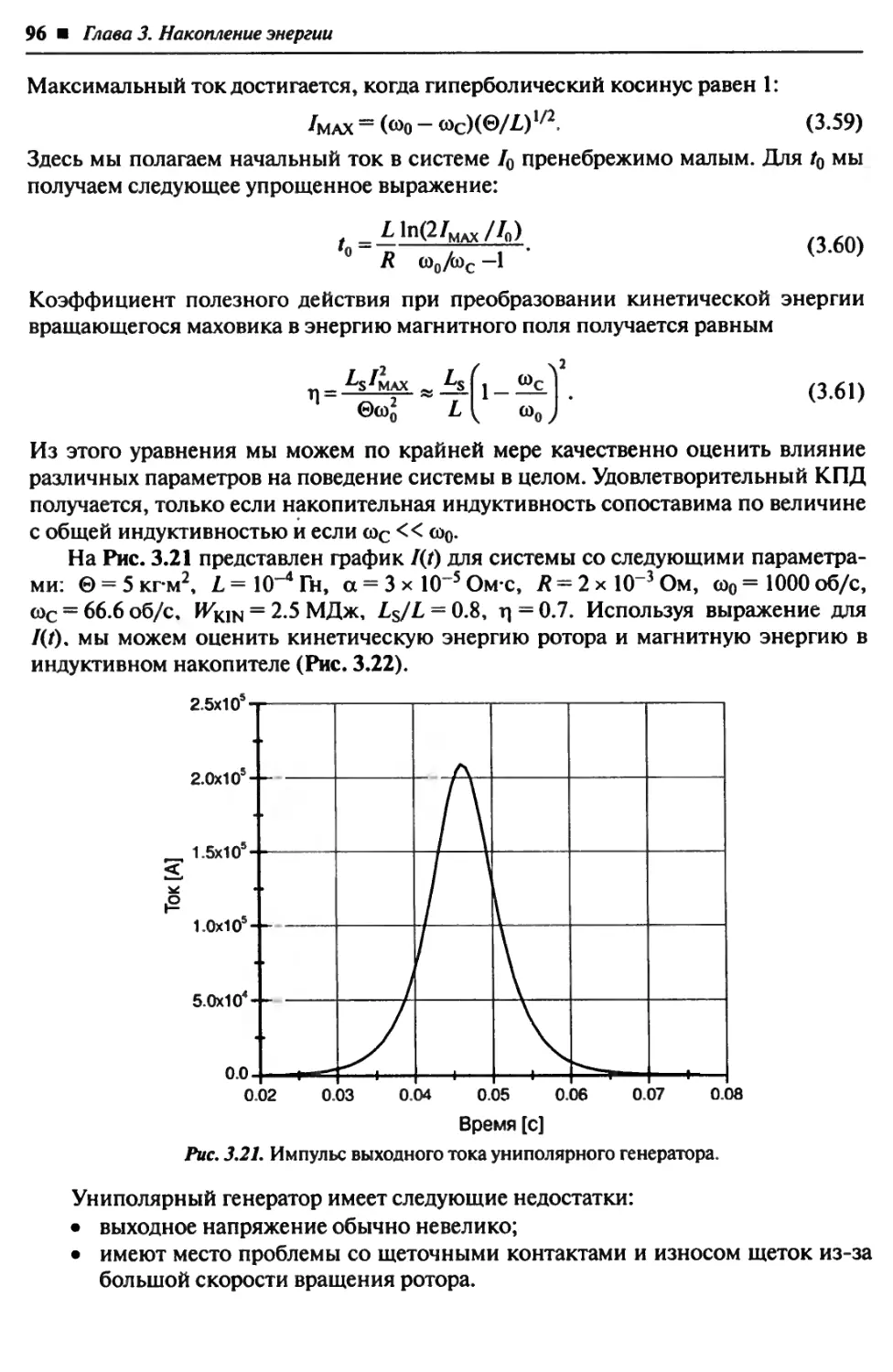
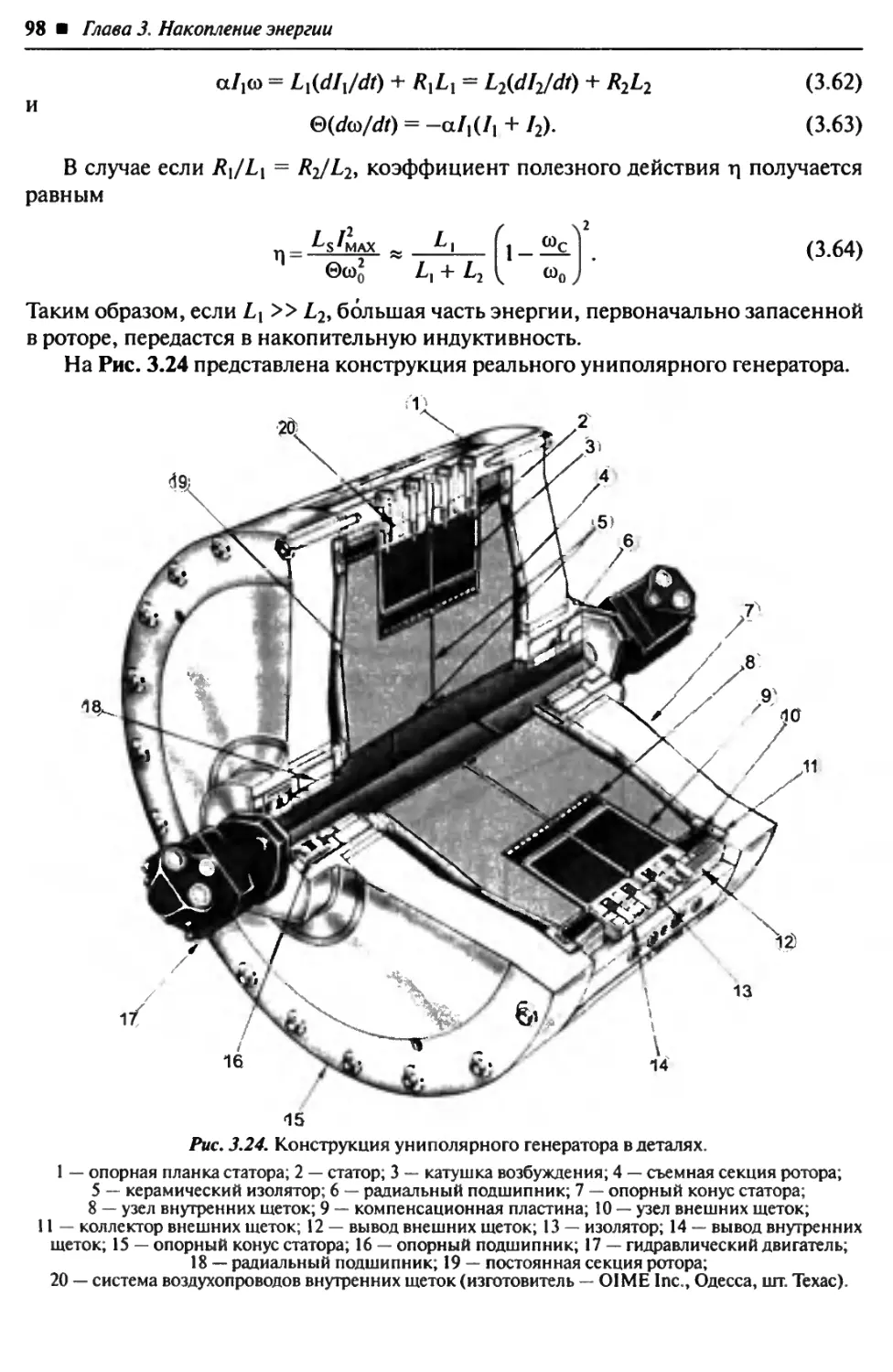
3.5. Роторные и униполярные генераторы. 93
Глава 4. КЛЮЧИ....... 99
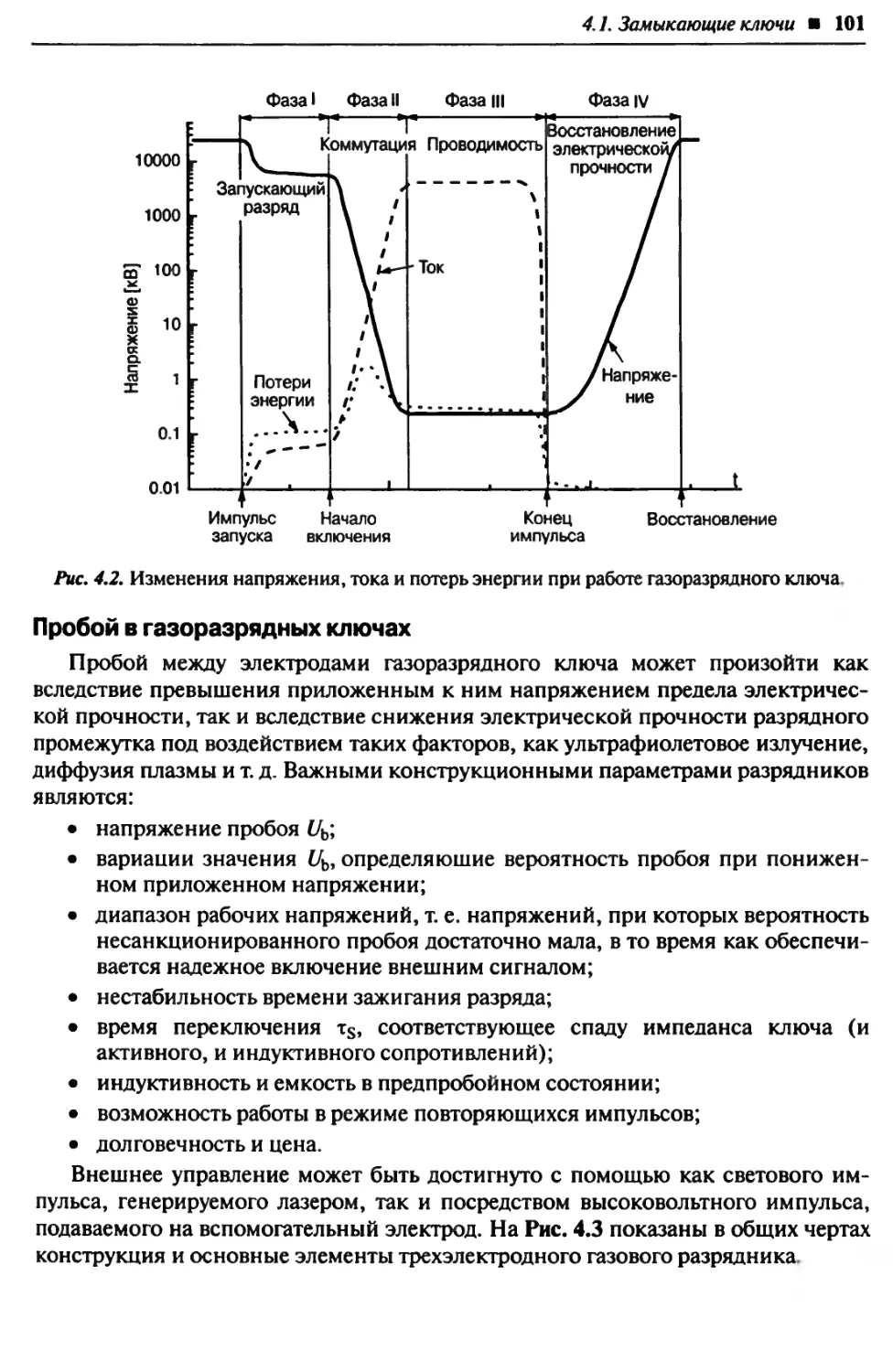
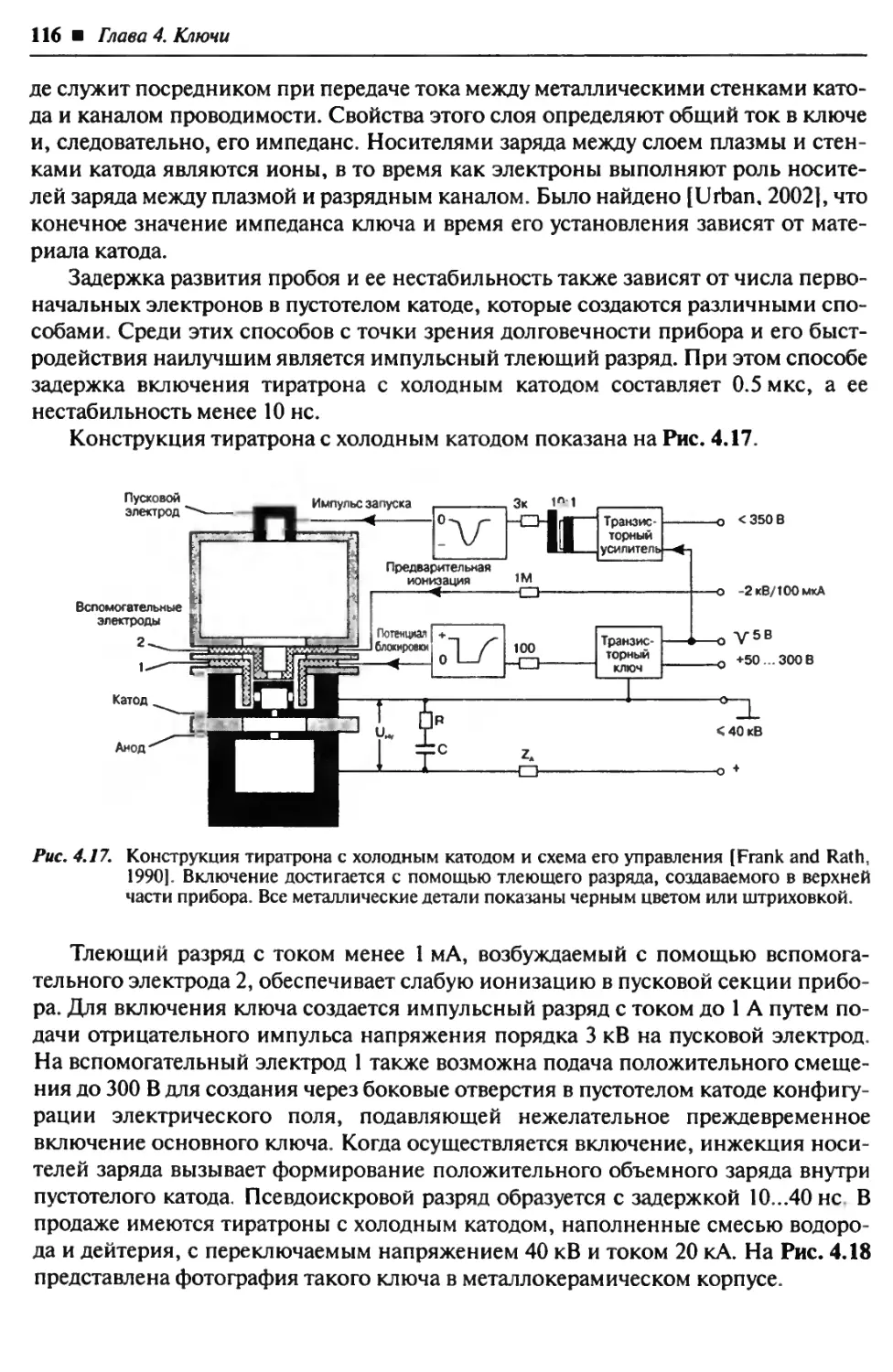
4.1. Замыкающие ключи............................................. 99
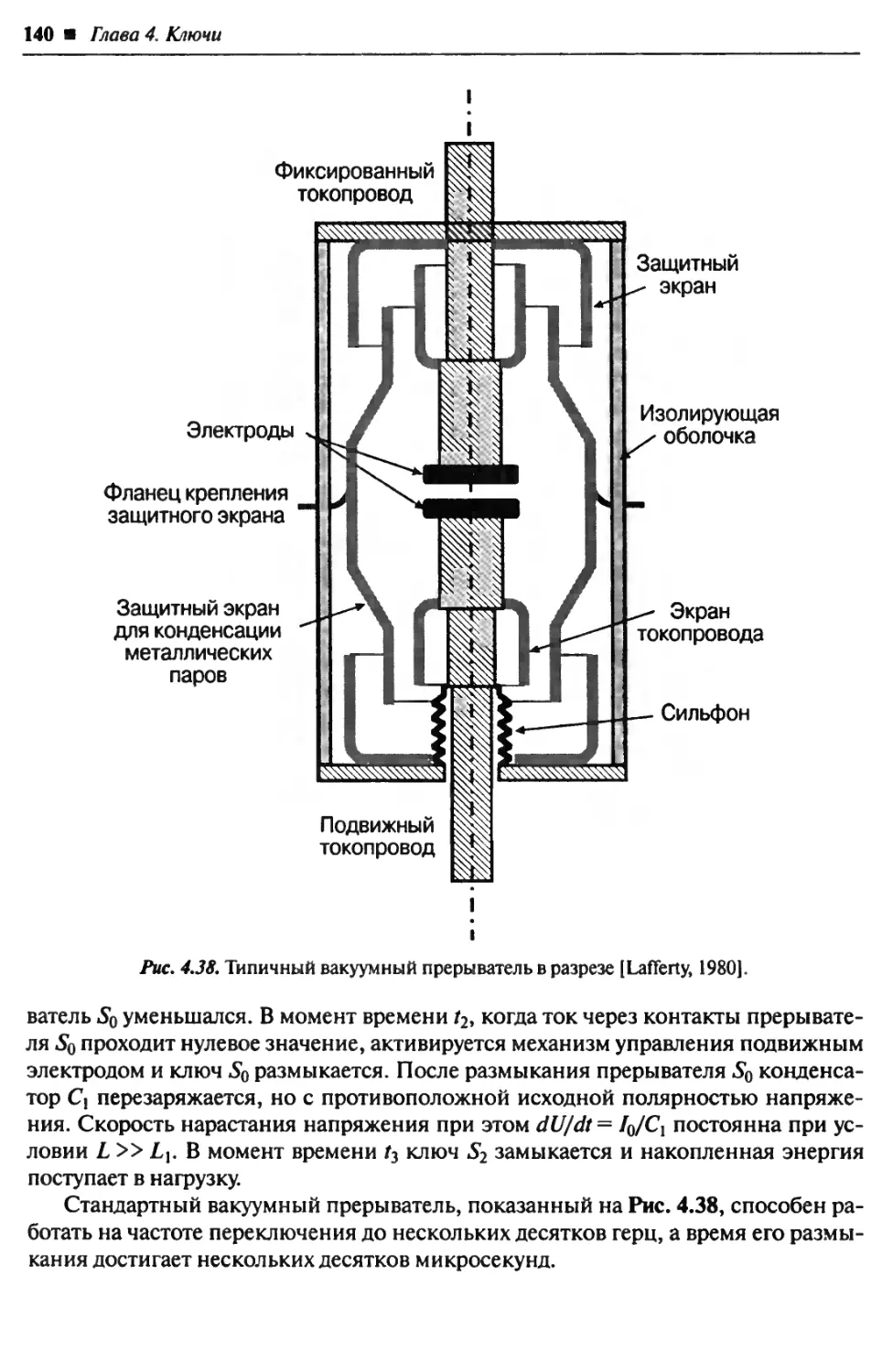
4.2. Размыкающие ключи........................................... 137
Глава 5. ЦЕПИ ФОРМИРОВАНИЯ ИМПУЛЬСОВ ............................ 153
5.1. Длинные линии............................................... 153
5.2. Я£С-цепи......................................................163
5.3. Моделирование цепей с помощью программы LEITER.. 170
Глава 6. ПЕРЕДАЧА ИМПУЛЬСОВ И ТРАНСФОРМАТОРЫ......... 175
6.1. Магнитная самоизоляция в вакуумной линии передачи.............175
6 Оглавление
6.2. Импульсные трансформаторы................................. .... 198
6.3. Высоковольтные источники питания............................ 203
6.4. Трансформаторные линии........................................209
Глава 7. СЛОЖЕНИЕ МОЩНОСТЕЙ И НАПРЯЖЕНИЙ .... .....................211
7.1. Сложение мощностей.......................................... 211
7.2. Сложение напряжений......................................... 212
Глава 8. ПРИМЕРЫ ГЕНЕРАТОРОВ МОЩНЫХ ИМПУЛЬСОВ . 220
8.1. Генераторы одиночных импульсов.............................. 220
8.2. Генераторы повторяющихся импульсов.......................... 225
Глава 9. СРЕДСТВА ИЗМЕРЕНИЙ ..................................... 229
9.1. Датчики электромагнитного поля .... 229
9.2. Измерение тока с помощью резисторов......................... 236
9.3. Измерение тока с использованием эффекта Фарадея...............238
9.4. Электрооптические способы измерения напряженности электрических полей... 240
9.5. Магнитный анализатор энергии ионов.......................... 242
9.6. Монитор напряжения............................................243
Глава 10. ПРИМЕНЕНИЕ ИМПУЛЬСНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ..................245
10.1. Импульсные электрические поля................................245
10.2. Импульсные магнитные поля....................................257
Глава 11. ИСТОЧНИКИ МОЩНОГО ИЗЛУЧЕНИЯ..............................276
11.1. Генераторы мощных электронных пучков.........................276
11.2. Ионные пучки большой мощности................................291
Глава 12. ИМПУЛЬСНЫЕ РАЗРЯДЫ В ТВЕРДЫХ ТЕЛАХ И ЖИДКОСТЯХ................300
12.1. Экстракорпоральная ударная литотрипсия.......................300
12.2. Разрушение твердых диэлектриков с помощью электрических импульсов.302
12.3. Применение в промышленности..................................313
Список литературы................................................ 327
Предметный указатель...............................................343
О программе LEITER.................................................347
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
В своей книге автор — известный германский ученый-физик Хансиоахим
Блум — представил обширнейший обзор по методам и средствам генерации
сверхмощных импульсов электрической энергии. Отдельная часть книги описы-
вает их практическое применение в различных областях, таких как медицина,
промышленность и т. д. Выражаю надежду, что эта книга найдет своих читателей,
которые оценят грандиозность описанного оборудования и найдут полезное и
для своей работы.
Благодарю за помощь в научном редактировании перевода С. С. Гапонова,
канд. физ.-мат. наук М. И. Калинина и канд. техн, наук В. К. Попова.
А. Н. Рабодзей, канд. техн, наук
СИМВОЛЫ И АББРЕВИАТУРЫ
Символы
А А В С векторный потенциал; векторный элемент площади площадь магнитная индукция емкость; постоянная Эйлера (0.577)
с скорость света
Су ь d Е удельная теплоемкость смещение расстояние напряженность электрического поля
е F F(Ej) Г(И0 G G(p) Gn, Gp g H,H H Я(0 h I /о Ia 4r 4 заряд электрона сила вероятность отказа за время т при напряженности поля Е Ферми—Дирака функция энергии W проводимость; модуль сдвига передаточная функция скорости генерации электронов и дырок геометрический коэффициент напряженность магнитного поля функция Гамильтона функция Хевисайда постоянная Планка; толщина ток общий ток в вакуумной линии передачи ток Альфвена критический ток ток стенок
Символы и аббревиатуры 9
i мнимая единица
i(p) ток, преобразованный по Фурье или Лапласу
/(О малосигнальный ток
J интеграл плотности тока
J плотность тока
К постоянная Керра
к постоянная Больцмана; подвижность
к+ постоянные
L индуктивность
Id диффузионная длина
f длина
М макроскопическая масса
т масса частицы
гп0 масса частицы в состоянии покоя
N общее число частиц
п число атомов в единице объема
Р канонический момент
Ра1 энергия в согласованной нагрузке
РаЬ вероятность перехода из состояния а в состояние b
р давление газа
Q тепловая энергия; удельная плотность энергии; заряд электронов на еди-
ницу длины вакуумной линии передачи
q плотность поверхностного заряда
R сопротивление
Rn, Rp скорости рекомбинации электронов и дырок соответственно
г радиус
S вектор Пойнтинга
5 длина канала; путь
Т период; температура; время задержки; коэффициент передачи
t время
U напряжение
и скорость
и(р) напряжение, преобразованное по Лапласу
«(/) малосигнальное напряжение
(и) средняя скорость ансамбля частиц
V объем; постоянная Верде
И+, W_ уровни энергии
И<цйП кинетическая энергия
плотность кинетической энергии
10 Символы и аббревиатуры
X Y Z Z(JD а пространственная координата модуль Юнга импеданс число разрешенных состояний на единичную энергию в интервале W коэффициент ионизации
С1п» ар Р коэффициенты ионизации для электронов и дырок в полупроводнике и/с, скорость частиц по отношению к скорости света; коэффициент уве- личения поля
Г гамма-функция
У 5 5ф tgS е w/c, релятивистский фактор коэффициент рекомбинации глубина проникновения магнитного поля тангенс угла относительная диэлектрическая проницаемость
е0 п 0 Лаь X диэлектрическая проницаемость вакуума поверхностная энергия КПД; коэффициент присоединения электронов момент инерции энергия реконфигурации среднее расстояние между столкновениями; теплопроводность
И Цо Рп»Мр V относительная магнитная проницаемость; подвижность магнитная проницаемость вакуума подвижности электронов и дырок в полупроводниках частота
Vei $(5) п частота столкновений электронов и ионов относительная ожидаемая интенсивность отказов под воздействием 5 функция Пашена
Q М "О коэффициент отражения макроскопическое поперечное сечение предел текучести микроскопическое поперечное сечение; проводимость; дисперсия
Ста Т Ф стандартное отклонение постоянная времени; время между столкновениями магнитный поток
Ф X у(5) со потенциал; работа выхода эффективное отношение удельных теплоемкостей вероятность того, что один образец выдержит воздействие S угловая частота; коэффициент вторичной эмиссии электронов
Символы и аббревиатуры 11
Аббревиатуры
ADP DIN (Ammonium Dihydrogen Phosphate) — дигидрофосфат аммония (Deutsche Industrienorm) — Германский промышленный стандарт
FRANKA (Fragmentierungsanlage Karlsruhe) — установка для размельчения
FWHM (г. Карлсруэ) (Full Width at Half Maximum) — длительность импульса (длительность по уровню половины от его максимальной амплитуды)
GESA (Gepulste Elektronenstrahlenanlage) — генератор импульсных пучков электронов
GTO HELIA (Gate turn-off thyristor) — запираемый тиристор (High-Eneigy Linear Induction Accelerator) — линейный ускоритель вы- сокой энергии для легких ионов (г. Карлсруэ)
IGBT (Insulated-Gate Bipolar Transistor) — биполярные транзисторы с изоли- рованным затвором (БТИЗ)
KALIF (Karlsruhe Light-Ion Facility) — линейный ускоритель для легких ионов (г. Карлсруэ)
KDP КЕА (Kalium Dideuterium Phosphate) — дидейтерийфосфат калия (Karlsruher Elektroporations Anlage) — установка для обработки растительных клеток импульсами электрического поля (г. Карлсруэ)
PBFA (Particle Beam Fusin Accelerator) — ускоритель частиц для ядерного синтеза
RHEPP (Repetitive High-Energy Pulsed Power) — повторяющиеся импульсы вы- сокой мощности
SOS (Semiconductor Opening Switch) — полупроводниковый размыкающий ключ
ТЕ ТМ (Transverse Electric) — поперечная электрическая волна (Transverse Magnetic) — поперечная магнитная волна
ПРЕДИСЛОВИЕ
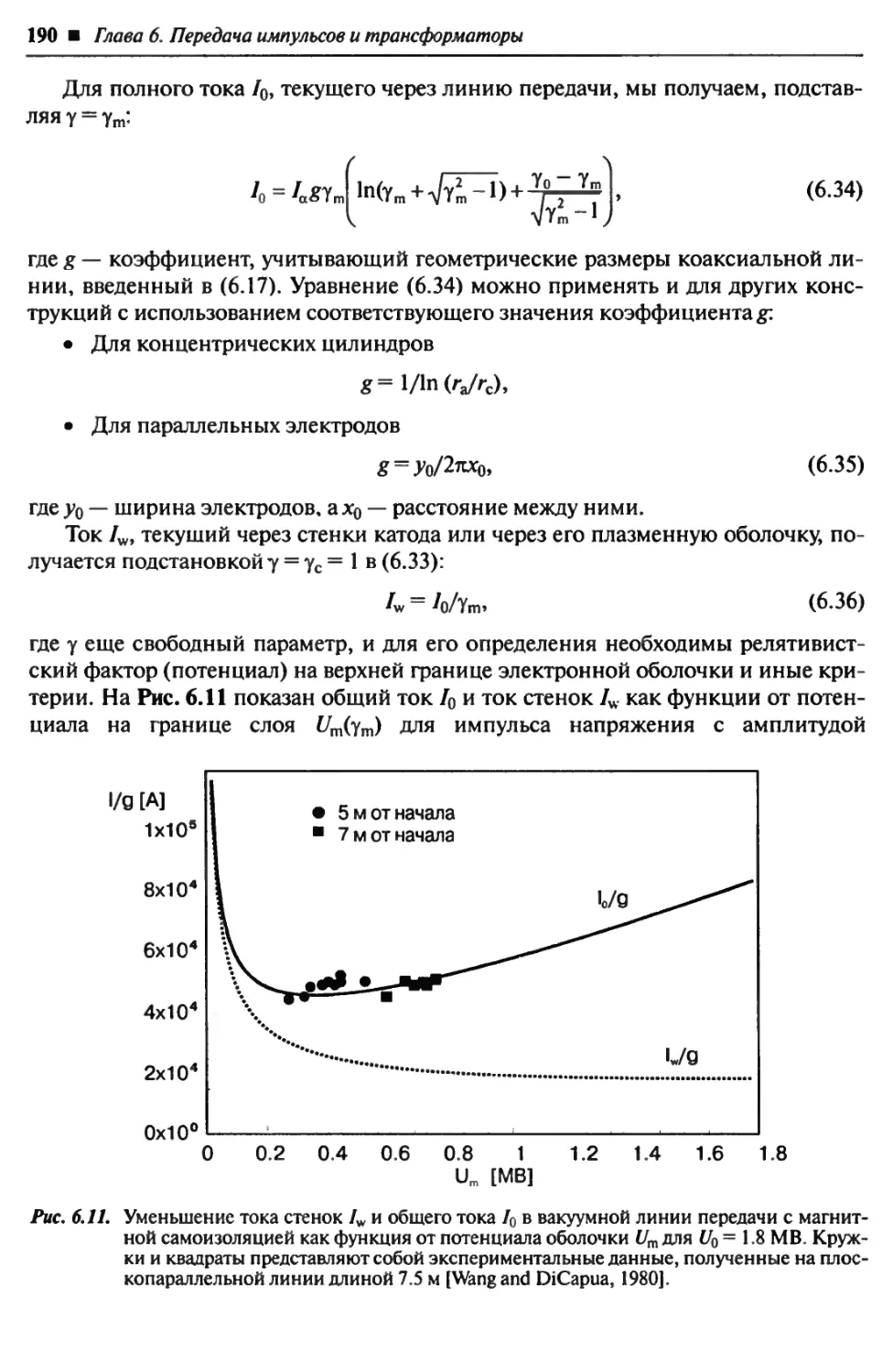
Эта книга о мощных импульсных устройствах обобщает курс лекций, кото-
рый я читал в течение десяти лет в техническом университете города Карлсруэ
(Германия). Первоначально планировавшийся только для германских студентов
курс стал в 1998 г. частью курсов, предлагаемых иностранным студентам со всего
мира Международным департаментом университета. Цель настоящей книги —
дать студентам начальные знания в этой области, с тем чтобы они имели необхо-
димую основу для изучения более сложной литературы. Кроме того, она должна
помочь инженерам и ученым из других областей ближе познакомиться с основ-
ными идеями и методами, используемыми в сфере мощных импульсных уст-
ройств. и достичь понимания их возможностей для решения различных проблем.
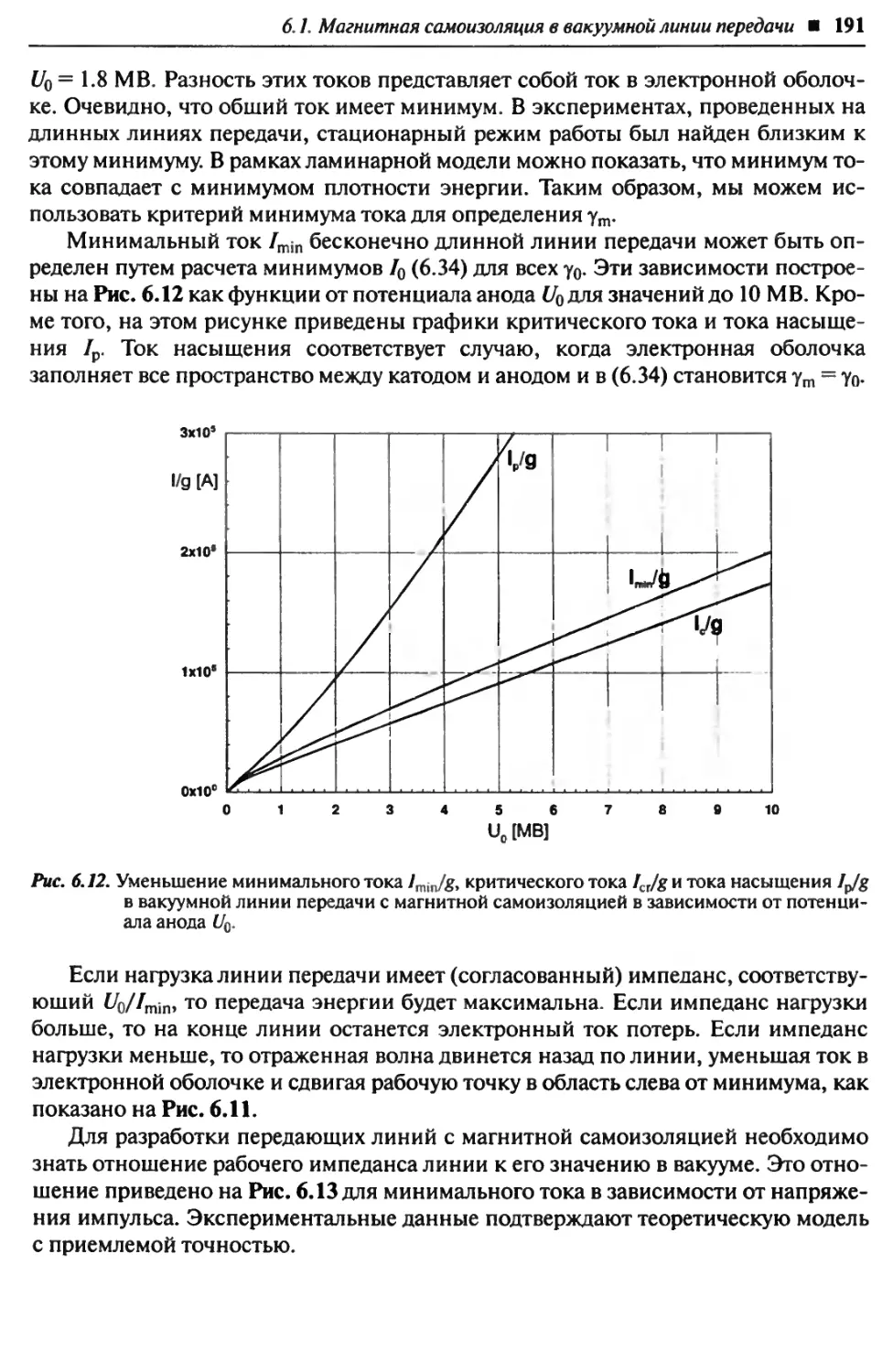
Главная особенность мощных импульсных устройств — очень высокое отноше-
ние их импульсной мощности к ее среднему значению. При этом начинают про-
являться пороговые и нелинейные эффекты. Другой набор достоинств является
следствием короткой длительности импульсов, что позволяет использовать их
для временного разрешения (например, в радарах и импульсной рентгеногра-
фии), а также избежать нежелательных явлений (например, электрического про-
боя или потерь на нагрев). Методы и техника создания и применения мощных
импульсов оказали благотворное действие в таких областях науки, как электро-
техника, экспериментальная физика, биотехнология, технология пищевых про-
дуктов и материаловедение.
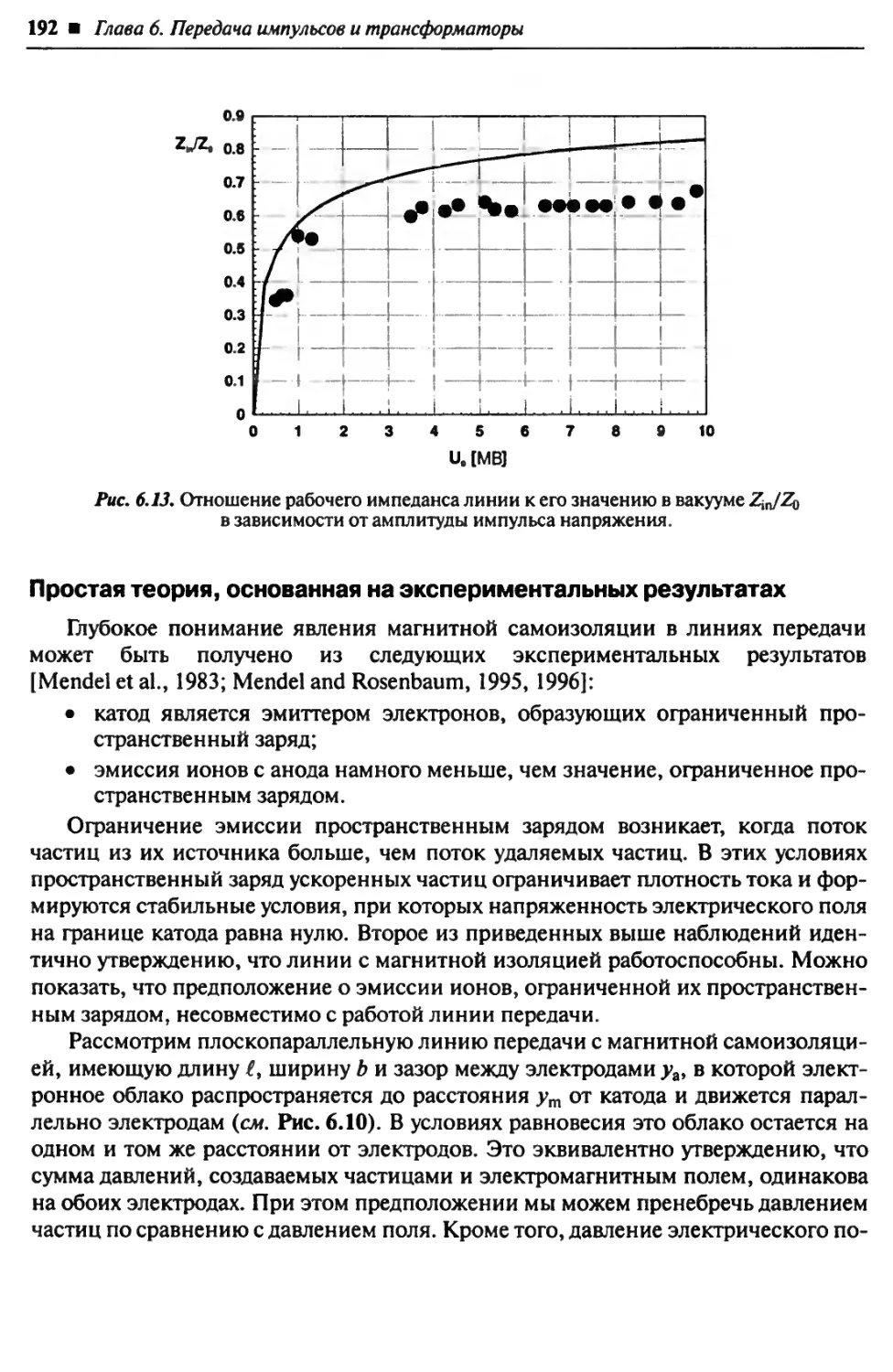
В 1995 г., когда я начал читать этот курс, я обнаружил отсутствие учебников,
в которых бы давалось введение в эту область. Хотя ряд неопубликованных ма-
териалов, основанных на работах Дж. С. Мартина (J. С. Martin) из Олдермасто-
на (Aldermaston), написанных в 1960—1970 гг., по интенсивным наносекунд-
ным источникам рентгеновских лучей, и был в широком пользовании во мно-
гих лабораториях, занимавшихся мощными импульсными устройствами, он не
является адекватной заменой учебнику. Эта ситуация не изменилась и в 1996 г.,
когда Т. Мартин (Т. Martin), А Гуентер (A. Guenther) и М. Кристиансен (М.
Kristiansen) опубликовали труды Дж. С. Мартина в книге, озаглавленной «Дж. С.
Мартин, Об Импульсной Энергии» (J. С. Martin, On Pulsed Power). Однако мно-
жество эмпирических формул, полученных Дж. С. Мартином, остаются еще
Предисловие 13
очень полезными для конструирования мощных импульсных устройств и вос-
произведены в данной книге, обычно с сохранением первоначальных единиц
измерений.
Даже идеальный учебник никогда не бывает завершенным. Постоянно появ-
ляются новые и захватывающие разработки, и для получения последней инфор-
мации я рекомендую читателям обращаться к материалам Международных кон-
ференций по мощным импульсам, проводимых каждые два года Институтом ин-
женеров по электротехнике и радиоэлектронике (IEEE International Pulsed Power
Conference), к запискам Симпозиумов по мощным модуляторам (Power Modulator
Symposia) и трудам Международных конференций по пучкам частиц высокой
мощности (International Conference on High-Power Particle Beam).
В течение многих лет большинство новых разработок в области мощных им-
пульсов появлялось в США, и Международные конференции по мощным им-
пульсам, с 1976 г. проводимые исключительно в США, подтверждают это положе-
ние. Я сделал первые шаги в этой области в 1980 г., в Корнеллском университете,
штат Нью-Йорк, где в это время велись исследования по формированию импуль-
сных ионных пучков. После падения железного занавеса стало известно, что
большие успехи были достигнуты в области мощных импульсов и в Советском
Союзе. Хотя многие задачи и были чисто военными, для гражданского примене-
ния также был сделан ряд инноваций, ставших основой для нескольких науч-
но-исследовательских программ в Японии, Европе и США. В последнее время
новая научная дисциплина — биоэлектрика, чьим объектом исследований являет-
ся взаимодействие сильных импульсных электрических полей с биологическими
клетками, — быстро развивается в США (Университет Олд Доминион, Норфолк,
штат Вирджиния), Японии (Университет Кумамото, о. Кюсю), Германии (Науч-
но-исследовательский центр в г. Карлсруэ) и других странах. Будет справедливо
сказать, что содержание глав этой книги в основном отражает мои собственные
интересы и результаты работ моей исследовательской группы в Институте мощ-
ных импульсов и микроволновой техники при Научно-исследовательском центре
в г. Карлсруэ.
Хотя большая часть этой книги создавалась по вечерам и в выходные дни, мое
шестимесячное пребывание в качестве приглашенного профессора в Университе-
те Кумамото в 2003 г. ускорило эту работу. Таким образом, я очень признателен
г-ну Акияме (Н. Akiyama) за это приглашение. Исследования в области импуль-
сов большой мощности не были бы возможны без инициативы Г. Кесслера
(G. Kessler) в 1979 г. по запуску программы по использованию пучков легких ио-
нов для получения энергии из термоядерного синтеза в Институте физики ней-
тронов и технологии реакторов (г. Карлсруэ). После его отставки в 1999 г. эту про-
грамму в Карлсруэ решено было остановить. Как это часто случается в научных
исследованиях, кризис открыл возможности для реализации новых подходов, и я
благодарен М. Тамму (М. Thumm) за его постоянную поддержку наших начина-
ний по промышленному применению мощных импульсов во вновь образованном
Институте мощных импульсов и микроволновой техники. В книге описывается
программа для расчета линий передач LEITER, написанная моим бывшим колле-
гой Д. Рушем (D. Rusch), и я ему благодарен за разрешение на использование
14 Предисловие
этой программы0. Мне хотелось бы также поблагодарить коллег: В. Дна (W. Ап),
К. Баумунга (К. Baumung), В. Фрея (W. Frey), X. Гизе (Н. Giese), П. Хоппе (Р.
Норрё), Г. Мюллера (G. Muller), М. Сака (М. Sack), С. Шлутхайса (С. Schultheip)
и А. Вайзенбургера (A. Weisenburger), чей профессиональный опыт был использо-
ван в этой книге.
Я благодарен моей жене Урсуле за терпение; она, конечно, много страдала,
пока я работал над книгой, ведь это мешало нам проводить совместные уикэнды.
Теперь все позади.
X. Блум
*’ Программу для расчета линий передач LEITER скачать с сайта издательства «Додэка-XXI» по
адресу http://www.dodeca.su/files/leiter.rar. — Примеч. изд.
ГЛАВА
ВВЕДЕНИЕ
1.1. Схемотехника мощных импульсных устройств
Импульсные устройства — это схемы, в которых запасенная электрическая
энергия выделяется на нагрузке в форме коротких одиночных импульсов или в
форме последовательности коротких импульсов с управляемой частотой повторе-
ния. Цель этой книги — описать физические и технические основы производства
и применения высоковольтных импульсов с очень большой мощностью и энер-
гией. Такие импульсы требуются для ряда нагрузок, либо способных работать
только в импульсном режиме, либо обеспечивающих улучшение характеристик
при работе в импульсных режимах.
Мы будем говорить об электрических импульсах с мощностями порядка гига-
ватта (109 Вт) при энергии в импульсе порядка килоджоуля и более. В настоящее
время для одиночных импульсов наивысшие достигнутые энергия и мощность
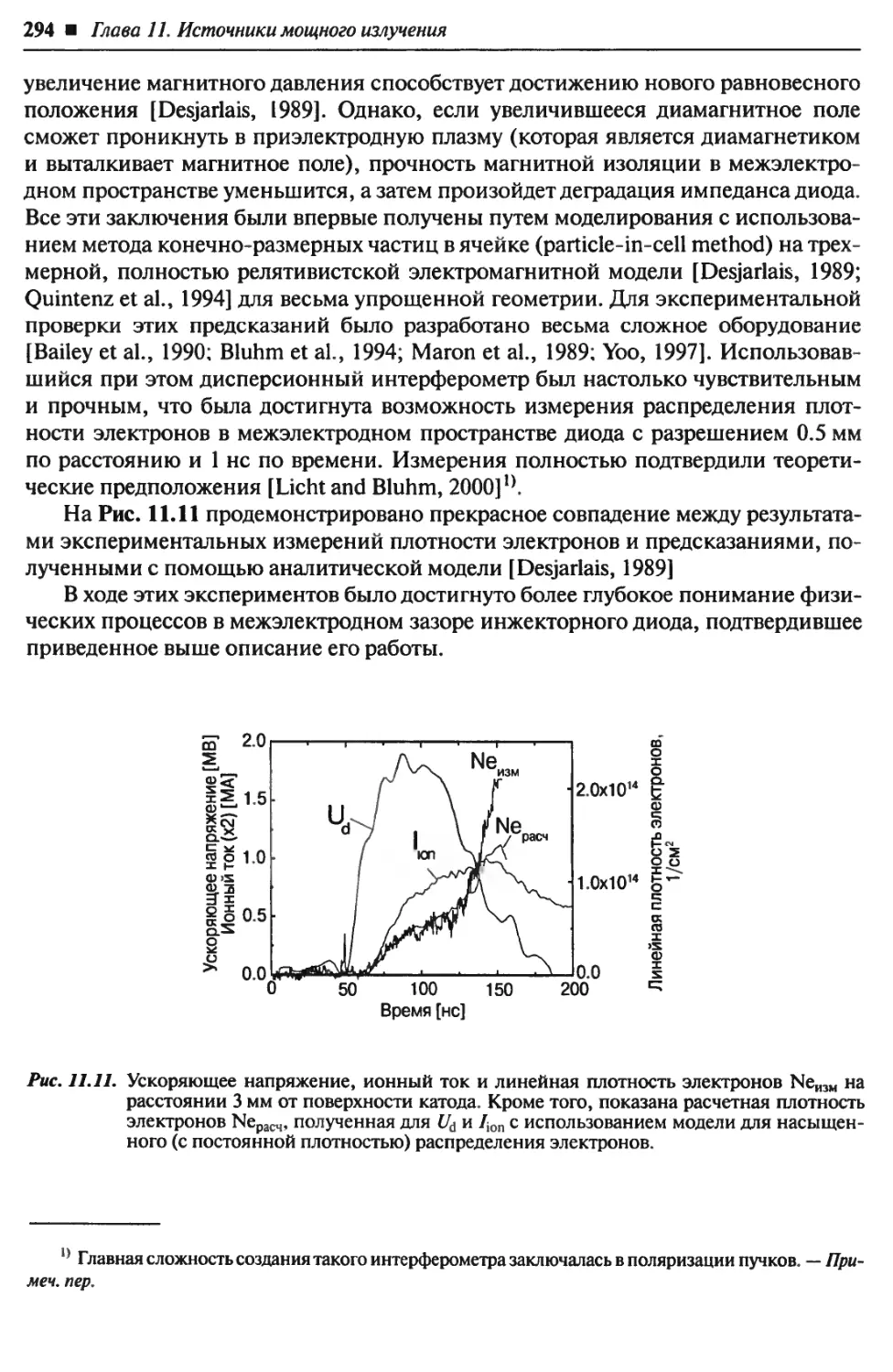
имеют порядок 100 МДж и несколько сот тераватт соответственно. При этом на-
пряжение составляет от 10 кВ до 50 МВ, а ток — от 1 кА до 10 МА.
В дополнение к мощности и энергии импульсы характеризуются формой, т. е.
временем нарастания и спада, а также длительностью плоской вершины и ее не-
равномерностью. Типовые значения полной длительности импульсов, которые
мы будем рассматривать, находятся в диапазоне от нескольких наносекунд до не-
скольких микросекунд. Основные временные параметры импульсов показаны на
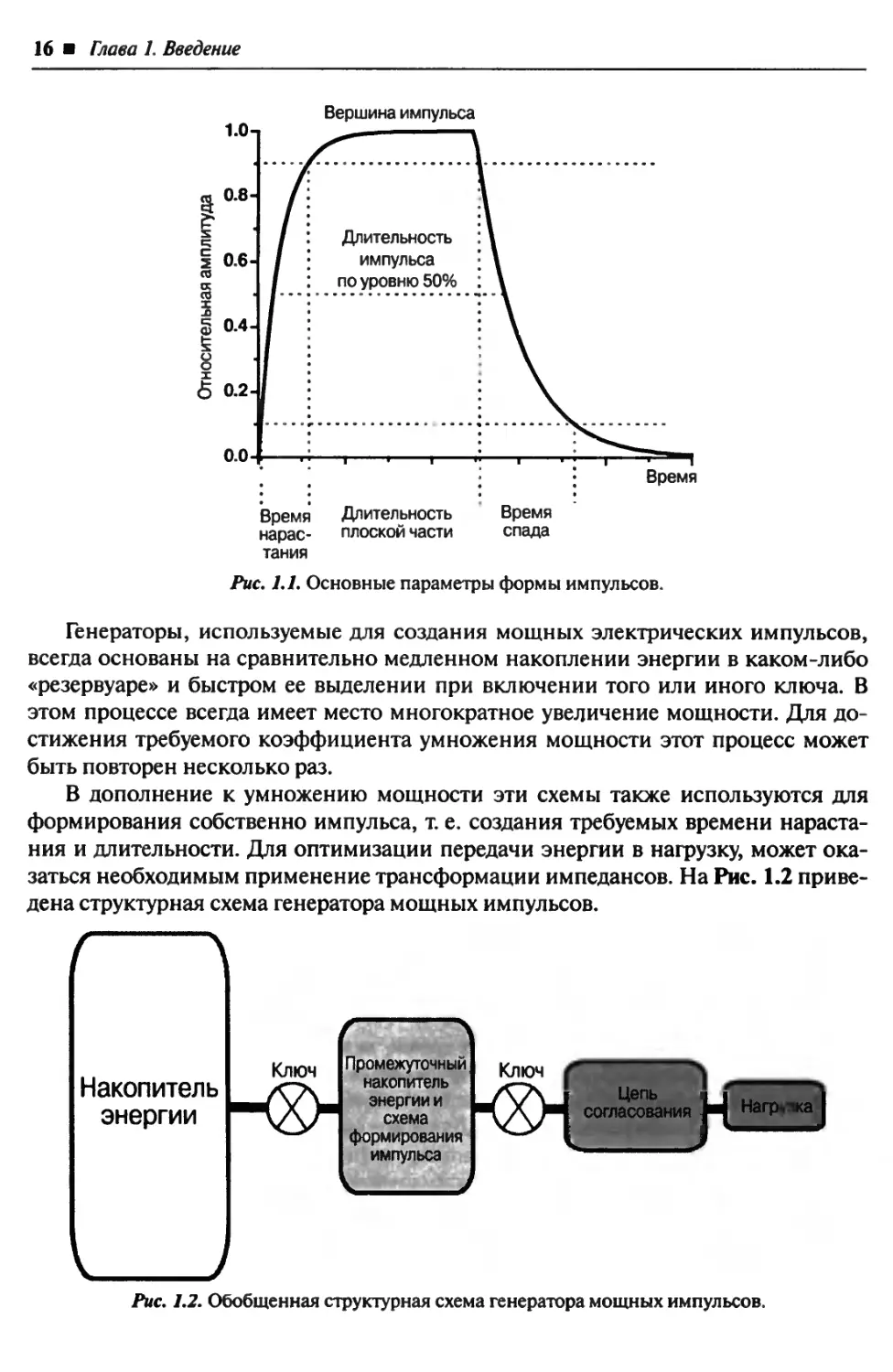
Рис. 1.1.
Время нарастания определяется как время, за которое напряжение нарастает
от 10 до 90% амплитуды. Аналогично определяется и время спада. И время нарас-
тания, и время спада импульсов зависят от импеданса нагрузки, который в боль-
шинстве случаев меняется во времени. Для длительности импульса нет однознач-
ного определения. Иногда под длительностью импульса понимается его длитель-
ность по уровню половины от его максимальной амплитуды (FWHM). Однако
для некоторых приложений лучше определять длительность по уровню 90% от
максимальной амплитуды. Плоскостность (неравномерность) вершины импульса
является важным требованием при управлении некоторыми нагрузками, напри-
мер элементами Поккельса.
16 Глава 1. Введение
Рис. 1.1. Основные параметры формы импульсов.
Генераторы, используемые для создания мощных электрических импульсов,
всегда основаны на сравнительно медленном накоплении энергии в каком-либо
«резервуаре» и быстром ее выделении при включении того или иного ключа. В
этом процессе всегда имеет место многократное увеличение мощности. Для до-
стижения требуемого коэффициента умножения мощности этот процесс может
быть повторен несколько раз.
В дополнение к умножению мощности эти схемы также используются для
формирования собственно импульса, т. е. создания требуемых времени нараста-
ния и длительности. Для оптимизации передачи энергии в нагрузку, может ока-
заться необходимым применение трансформации импедансов. На Рис. 1.2 приве-
дена структурная схема генератора мощных импульсов.
Рис. 1.2. Обобщенная структурная схема генератора мощных импульсов.
1.1. Схемотехника мощных импульсных устройств 17
Энергия может быть накоплена в химической, механической или электричес-
кой формах. В некоторых приборах химические взрывчатые вещества использу-
ются для сжатия предварительно созданного магнитного поля и тем самым увели-
чения энергии, которая может быть из него получена. Химические накопители
энергии мы обсудим в гл. 10 этой книги.
Механическая энергия может быть накоплена и сохранена в форме кинети-
ческой энергии вращения ротора. В этом случае энергия равна = (1/2) ©со2,
где 0 — момент инерции, а <о — угловая скорость вращения. Для массивного ци-
линдра 0 = (1/2)Л/г2, где Мн г — масса и радиус цилиндра соответственно. Таким
образом, плотность запасаемой во вращающемся роторе энергии равна
wkin = (1/4)г2со2. Предел плотности энергии ограничен в этом случае механичес-
кой прочностью материала, использованного в конструкции ротора. Взаимосвязь
между пределом текучести Е и максимальной скоростью вращения соМАХ описы-
вается формулой Е = рсо2МАХг2/2. Для цилиндра из нержавеющей стали радиусом
1 м получается сомах = 400/с. При этом достигается плотность запасаемой энер-
гии wKIN = 4 х Ю4 Дж/кг = 3.1 х Ю8 Дж/м3, что намного больше, чем у накопите-
лей электрической энергии. Проблемой для механических накопителей является
высвобождение этой энергии за достаточно короткое время. Таким образом, в об-
щем случае, чтобы получить от механического накопителя энергии требуемый
уровень мощности в импульсе, требуется еще несколько каскадов электрического
преобразования энергии.
Электрическая энергия может быть накоплена либо с помощью конденсатора
в форме электрического поля, либо с помощью индуктивности в форме магнит-
ного поля. В первом случае мы имеем wE = ее0£2/2, что, при использовании про-
питанной маслом бумаги в качестве изолятора с е = 6 и электрической прочнос-
тью £ = 0.78 х Ю8 В/м, обеспечивает максимальную плотность запасаемой энер-
гии и>Е = 161 кДж/м3. С учетом ограничений, накладываемых, например,
необходимостью корпусирования конденсатора, реально достижимая плотность
энергии в этом случае оказывается вдвое меньше, т. е. 80 кДж/м3.
Для накопленной в магнитном поле энергии — wB = £2/2ццо. Факторами, ог-
раничивающими плотность запасаемой энергии, в этом случае являются расплав-
ление поверхности проводников либо механические силы, воздействующие на
элементы конструкции катушки индуктивности. Нагрев поверхности проводни-
ков происходит под воздействием вихревых токов, возбуждаемых магнитным по-
лем. Для проводящего полупространства температура поверхности в общем виде
определяется уравнением [Knoepfel, 1970]
c,p7’(0,Z) = -l-S2(0,/)8(r), (1.1)
2go
где cv и р — удельная теплоемкость и плотность материала проводника,
Т(0, /) — температура поверхности,
В(0, 0 — магнитная индукция на поверхности проводника,
0(0 — коэффициент, зависящий от формы импульсов поля.
18 Глава 1. Введение
Для меди максимальное значение магнитной индукции находится в пределах
50... 100 Тл (в зависимости от формы импульсов). Для определения ограничений,
возникающих из-за механических сил, мы используем критерий статического
воздействия на защитную оболочку, справедливый для времени нарастания тока
(и, следовательно, продолжительности импульса механического давления), боль-
шего, чем период собственных колебании в защитной оболочке [Knoepfel, 1970]:
го ~г»2
2Мо Ч2*'/
(1.2)
где Еу — предел текучести материала защитной оболочки,
го и и — внешний и внутренний радиусы защитной оболочки соответственно.
Для толстого цилиндра (го = 2^) из медно-бериллиевого сплава
(Еу — Ю00 н/мм2) получается В < 38 Тл. В этом случае средняя плотность энергии
внутри защитной оболочки (т. е. радиуса го) равна wB = 39000 кДж/м3. Отсюда
следует, что, даже принимая во внимание необходимость введения в конструк-
цию магнитных накопителей энергии узлов крепления, изоляции и т.д., плот-
ность накапливаемой энергии в магнитном поле превышает на два порядка мак-
симально возможную плотность энергии в электрическом поле.
На Рис. 1.3 приведена структурная схема генератора с емкостным накопите-
лем энергии. В этом генераторе используется один или несколько замыкающих
ключей, которые остаются разомкнутыми в процессе заряда накопителя и сохра-
нения его заряженного состояния. Когда ключ замыкается, вследствие того что
ток разряда намного превосходит ток заряда конденсатора, происходит умноже-
ние мощности
Плотность энергии: we = ее0 F/2 (Ю...80 кДж/м3)
10 кВт, 20 с
JC—————————1
100 ГВт, 1 мкс
Рис. 1.3. Структурная схема генератора с емкостным накопителем энергии и замыкающим клю-
чом. Приведенные значения мощностей и времени характерны для генераторов мощ-
ных одиночных импульсов. До нагрузки доходит около 50% накопленной энергии.
1.2. Преимущества 19
Генератор с индуктивным накопителем энергии (Рис. 1.4) требует использова-
ния размыкающего ключа, который должен быть замкнут и пропускать большой
ток во время накопления энергии. После завершения процесса «зарядки» ключ
должен мгновенно разомкнуться и при этом противостоять воздействию импуль-
са высокого напряжения. В генераторе с индуктивным накопителем энергии ум-
ножение мощности достигается увеличением напряжения. Для уменьшения по-
терь в процессе «зарядки» для генератора с индуктивным накопителем энергии
требуется источник питания с большим выходным током. Из-за того, что размы-
кающие ключи с подходящими параметрами намного сложнее сделать, чем замы-
кающие ключи, в большинстве генераторов импульсов большой мощности при-
меняются емкостные накопители энергии, хотя они и имеют намного меньшую
удельную плотность энергии, чем индуктивные.
Плотность энергии = В2/(2 цц0) (1...50 МДж/м3)
1ТВт, 100 нс
18 ГВт, 10 мкс
200 кВт, 1 с
ГТТ------L
Зарядное Индуктивный Размыкающий Линия Замыкающий Нагрузка
устройство накопитель ключ передачи ключ
Каскад сжатия времени
2. Каскад сжатия времени
Рис. 1.4. Структурная схема генератора с индуктивным накопителем энергии и размыкающим
ключом Только первый каскад сжатия времени имеет индуктивный накопитель.
Второй каскад имеет емкостный накопитель и замыкающий ключ. Как и ранее, поте-
ри составляют около 50%.
1.2. Преимущества
Так в чем же уникальные преимущества импульсов большой мощности? Ос-
новной их характеристикой является большое отношение импульсной мощности
к ее среднему значению. При этом могут быть использованы явления, обладаю-
щие некими порогами возникновения, а также нелинейные эффекты. Например,
импульс сильного электрического поля может вскрыть мембраны биологических
клеток или привести к взрывному возникновению автоэмиссии электронов из
металлических поверхностей. Кроме того, большое отношение импульсной мощ-
ности к ее среднему значению способствует подавлению зачастую нежелательных
тепловых процессов и позволяет избежать возникновения таких явлений, как
электрический пробой. Использование коротких импульсов обеспечивает высо-
кое разрешение, например, в радиолокации или рентгеновской радиографии.
20 Глава 1. Введение
Начиная со Второй мировой войны, развитие импульсной техники в основ-
ном следовало требованиям военной техники как в части оружия, использующего
импульсы большой мощности, так и в части инструментов для моделирования и
диагностики. Значительные усилия были приложены к разработке таких систем,
как электромагнитные пушки и лучевое оружие. Несмотря на эти усилия, за ис-
ключением импульсных радиолокаторов, ни одно из военных применений техни-
ки высокой мощности не получило развития. Однако для военных научных и ис-
следовательских программ было разработано много систем, использовавших им-
пульсы большой мощности. К ним, например, относятся установки для изучения
воздействия ядерного оружия, для определения свойств материалов под воздейс-
твием высоких ударных нагрузок и генерации мощных импульсов жесткого рент-
геновского излучения для получения изображений быстропротекающих
процессов.
Недавний прогресс в разработке надежных и доступных компонентов для
построения систем генерации импульсов большой мощности (таких, как высоко-
вольтные конденсаторы с большим сроком службы и новые типы высоковоль-
тных полупроводниковых ключей) возбудили новую волну интереса к использо-
ванию импульсов большой мощности для коммерческих и индустриальных це-
лей. В отличие от военных применений в этом случае на первый план выступают
экономические соображения.
Основные области применения импульсов большой мощности
(1 ГВт...100ТВт, 1 кДж... 100 МДж, 10 кВ...5О МВ) это:
• создание импульсных электрических и магнитных полей;
• источники интенсивных излучений (электронов, ионов, рентгеновских лу-
чей, сверхвысокочастотных радиоволн);
• создание электрических разрядов (плазмы).
(Области применения будут детально рассмотрены в гл. 10... 12.) Мощные им-
пульсы успешно применяются, например, в медицине для дефибрилляции и ли-
тотрипсии, в пищевой промышленности для стерилизации продуктов рентгенов-
ским излучением. Принцип действия дефибрилляторов и литотрипсеров основан
на воздействии электрического поля и импульсов давления, создаваемых элект-
рическими разрядами.
Очевидно, что использование импульсов большой мощности может принести
успех только в тех областях применения, где они оказываются эффективнее су-
ществующих приемов, или для выполнения задач, которые иначе не разрешимы.
Книгу можно условно разделить на две части. В первой части (гл. 2...9) пред-
ставлены физические и электрические основы техники получения мощных им-
пульсов. Во второй части (гл. 10... 12) описаны некоторые из наиболее перспек-
тивных, находящихся на стадии становления областей применения этой техники
ГЛАВА
СТАТИЧЕСКАЯ И ИМПУЛЬСНАЯ
ЭЛЕКТРИЧЕСКАЯ ПРОЧНОСТЬ
ДИЭЛЕКТРИКОВ
2.1. Введение
Газы, жидкости и твердые диэлектрические вещества используются как изо-
ляторы в таких устройствах, как конденсаторы, высоковольтные линии передачи
энергии и трансформаторы, а также в качестве рабочей среды в ключах. Предель-
ные характеристики этих устройств определяются электрической прочностью ис-
пользуемого диэлектрика и его диэлектрической проницаемостью.
Электрическая прочность изолятора может быть качественно определена как
максимальная напряженность электрического поля, которую данный материал
может выдержать в течение определенного времени. А вот при количественном
рассмотрении приходится сталкиваться с большим числом разнообразных явле-
ний. Факторы, которые влияют на электрическую прочность, могут быть выраже-
ны в виде интегрального воздействия напряженности поля и времени, связанного
с вероятностью отказа (пробоя) следующим выражением:
ln[l-F(E,O] = -aJ'£VW.
Здесь Е(Е, Z) представляет собой вероятность пробоя за время t под воздействием
напряженности поля Е, которое, в свою очередь, может быть функцией t; а, b и a
являются постоянными, которые должны быть определены экспериментально.
Другими факторами, влияющими на электрическую прочность, являются геомет-
рия образца, давление, температура и материал, из которого изготовлены элект-
роды.
Пробой диэлектриков представляет собой явление, подчиняющееся законам
статистики. Невозможно предсказать с определенностью время наступления про-
боя, можно лишь рассчитать вероятность пробоя при заданной напряженности
поля, определяемой напряжением и геометрией электродов. На микроскопичес-
ком уровне для пробоя требуется наличие заряженных частиц, которые получают
достаточно энергии от приложенного электрического поля, чтобы ионизировать
вещество и породить новые заряженные частицы. В большинстве случаев в про-
22 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
цессах пробоя доминируют электроны ввиду их намного большей подвижности
по сравнению с ионами
Для того чтобы электроны получили достаточную энергию из поля между
столкновениями, их средний свободный пробег в данном веществе должен быть
довольно большим. Если пренебречь тем, что в разных веществах энергии иони-
зации отличаются, и допустить, что средний свободный пробег зависит исключи-
тельно от плотности данного вещества, электрическая прочность должна быть
одинаковой для веществ с равной плотностью. На Рис. 2.1 показан график зави-
симости электрической прочности различных веществ от их плотности. Из этого
графика следует, что электрическая прочность слабо зависит от состояния вещес-
тва и сильно — от его плотности.
Рис. 2.1. Статическая электрическая прочность различных газов и жидкостей
в зависимости от плотности (Cooke, 1998].
Если газы и жидкости самовосстанавливаются после пробоя, т. е. их электри-
ческая прочность возвращается к исходному значению1), то твердые диэлектрики
разрушаются необратимо. С другой стороны, твердые диэлектрики всегда необ-
ходимы, если требуется противостоять механическим силам. Жидкие диэлектри-
ки предпочтительны при необходимости обеспечения отвода большого количест-
ва тепла.
Несмотря на ряд общих черт в явлении электрического пробоя в разных сре-
дах, существует и много различий, особенно в возникновении и развитии разря-
да. Таким образом, приходится рассматривать газы, жидкости и твердые тела раз-
дельно. В следующих разделах мы рассмотрим электрическую прочность этих ма-
териалов феноменологически, с выделением практических аспектов и формул,
полезных при конструировании импульсных устройств большой мощности.
° Если не происходит химических реакций. — Примеч. пер.
2.2. Газы 23
2.2. Газы
2.2.1. Статический пробой
Электрическая прочность газов определяется величиной их эффективного
поперечного атомного и молекулярного сечения, зависящего от скорости взаи-
модействия с электронами. Особый интерес представляют сечения ионизации и
рекомбинации°.
Понятие сечение реакции (эффективное поперечное сечение частиц газа ) ос-
новано на предположении, что взаимодействие между «атомным снарядом» и
атомом или молекулой может возникнуть, только если «снаряд» пролетает через
определенную площадь вокруг центра этих атома или молекулы. Сечение реак-
ции, таким образом, можно рассматривать как площадь мишени, в которую необ-
ходимо попасть, чтобы получить ту или иную реакцию (ионизации, возбуждения,
рекомбинации и т. д.). Следовательно, если мы имеем п атомов в единице объема
газового слоя толщиной dx и сечением о, то получится nAdx мишеней на площади
А, которые маскируют площадь nAdxa. Вероятность того, что частица вызовет
взаимодействие в этом слое, таким образом, равна cndx = Ldx. Следовательно, ес-
ли N частиц войдут в этот слой, число прошедших слой частиц, не претерпевших
столкновений, уменьшится на величину dN=—Y.Ndx. После прохождения слоя
толщиной х только N(x) = NqCxp(-'Lx) частиц не подвергнутся взаимодействию.
Средний свободный пробег частиц X, таким образом, равен
х = р—(2 °
О '*0
А теперь рассмотрим движение электронов в электрическом поле с напряжен-
ностью Е. В среднем, за время между двумя столкновениями, их кинетическая
энергия увеличится на еЕХ. = (т/2)1?. Их скорость возрастет на и = (2eEX/m)i/2.
Если и намного больше, чем тепловая скорость, устанавливается распределение
скоростей, отличное от распределения Максвелла. Форма кривой этого распреде-
ления g(v)duопределяется воздействием электрического поля Ей плотностью га-
за п, которые определяют значение А.. Однако, вследствие того что сечение а за-
висит от энергии, X также зависит от энергии. Определение самосогласованного
(взаимосвязанного) распределения g(u)du, таким образом, оказывается сложной
проблемой, которую мы не будем рассматривать здесь (например, см.
[Llewellyn-Jones, 1957]).
Предположим, что нам известна равновесная функция распределения скоро-
стей g(v)du потока электронов, движущихся в газе под воздействием однородного
электрического поля. Найдем число столкновений в секунду, вызывающих увели-
чение числа электронов, т, = X Ju является средним временем между ионизацион-
ными столкновениями электронов со скоростью и. Следовательно, скорость ио-
0 А также время рекомбинации. — Примеч. пер.
24 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
низации будет 1/т, = и/\ = EjU Тогда число электронов вследствие ионизации
увеличится на
—NAY,vg(v)dv.
nt J
(2.2)
Если мы сейчас заменим dN/dt на 8N/8t + tSN/Sx, и предположим, что поток
электронов не увеличивается, т. е. 57V/5r = О, и введем среднюю скорость потока
< и>, то можно записать dNe = Neadx, где
$Y,(v)vg(v)dv
а = ------------
< v>
(2.3)
Здесь а — коэффициент ионизации. С этими определениями можно рассчитать
рост электронов в лавине под воздействием электрического поля:
Nc(x) = TVoexp(ax). (2.4)
Важно понимать, что а/p является исключительно функцией Е/р, где р явля-
ется давлением газа при нормальных условиях. Это может быть выведено, если
разложить g( и) в ряд Тейлора относительно <и> и принять во внимание тот факт,
что <и> должна быть пропорциональна квадратному корню напряженности
электрического поля, умноженного на средний свободный пробег X, который об-
ратно пропорционален давлению р. Следовательно,
v./p = F(E/p}. (2.5)
Из этих рассуждений следует, что можно вывести отношение а/p или эквива-
лентное ему a/n из доступных данных относительно сечений взаимодействия. На
Рис. 2.2 приведены для сравнения экспериментальные результаты определения
а/п для азота и расчетные значения этого отношения.
Вторичные электроны могут высвобождаться из катода под воздействием ио-
нов, дрейфующих к нему. При этом также могут возникать кванты света из-за
процессов рекомбинации и перехода атомов или молекул газа из возбужденного в
невозбужденное состояние. Таким образом, существует связь между первичной
лавиной электронов и вторичными лавинами. Если предположить, что любой
электрон, который движется в слое лавины dx, высвобождает a>dx электронов из
катода, то можно найти условия баланса следующим путем. (Здесь со — коэффи-
циент вторичной эмиссии электронов.)
Пусть N(x) — число электронов в потоке на его сечении х. Тогда, после про-
хождения пути dx, их число увеличится вследствие ионизационных столкновений
на величину dN= N(x)adx. Если катод покидает N(Q) электронов, то анода до-
стигнут N(d) = 7V(0)exp(ad), где d — расстояние между анодом и катодом В стаци-
2.2. Газы 25
онарном состоянии каждый электрон, проходя путь dx, высвобождает (&dx вто-
ричных электронов. Таким образом, общее число электронов, покинувших катод,
равно
d
N(G) = N0+(^N(x)dx,
о
МО) = М + - M0)(eerf -1).
а
(2.6а)
(2.66)
Решая относительно МО) и подставляя результат в уравнение для N(d), полу-
чаем
М<0=
№
1-((о/а)(е“"-1)’
(2.7)
где Nq — число электронов, покинувших катод под влиянием внешнего воздейс-
твия. Как следует из этого выражения, при условии y(eaJ — 1) = 1 лавинообразный
рост числа электронов не имеет ограничения (здесь у = <о/а). Это условие извест-
но как условие Таунсенда для зажигания самостоятельного разряда. В этом случае
изоляционный слой в промежутке катод—анод пробивается и развивается само-
поддерживающийся разряд.
Вследствие того что a/р является исключительно функцией Е/р, и в предпо-
ложении, что со/Р также является функцией Е/р (что было подтверждено экспе-
риментально), условие Таунсенда представляет функциональную связь расстоя-
Е/П [Тд]
Рис. 2.2. Экспериментальные и расчетные значения a/л для азота [Meek and Craggs, 1978].
Значение Е/п указано в старых единицах измерения — Таунсендах (Тд) причем
1Тд= IO"17 Всм2.
26 Глава 2 Статическая и импульсная электрическая прочность диэлектриков
ния между электродами d и напряжением, при котором возникает пробой.
В обозначениях а/p =f(E/p) и со/р = Е(Е/р), условие Таунсенда можно переписать в
следующей форме:
ЛЕ/рУ ' ’
Так как Е= U/d, выражение (2.8), после решения относительно U, может быть
записано в форме
иъ = n(pd), (2.9)
которая означает, что напряжение пробоя иъ в зазоре с однородным электричес-
ким полем является функцией П произведения давления на расстояние между
электродами для данного газа и материала электродов. Это соотношение извест-
но как закон Пашена [Paschen, 1889].
В некоторых условиях функциональная связь между а/p и Е/р может быть ап-
проксимирована выражением
а/р = Ле"^/£, (2.10)
где А и В являются постоянными для данного газа. Вводя это соотношение в (2.8)
и используя экспериментально установленный факт, что у слабо зависит от Е/р в
широком диапазоне, и после решения относительно иъ, выражение (2.9) можно
преобразовать к виду
Bpd
1п[Лр<//1п(1+1/у)]’
(2.П)
Из этого уравнения следует, что при больших и малых значениях pd напряже-
ние пробоя иъ возрастает. Следовательно, кривая зависимости {/в отpd имеет ми-
нимум, известный как минимум Пашена. Расчет значения этого минимального
напряжения пробоя из уравнения (2.11) дает следующий результат:
^впип=е1п
В
А
(2.12)
Аналогично минимальное значение pd равно
Р^Втп
InQ + l/r)
А
(2.13)
При напряжениях ниже, чем £/Вт|П, невозможно вызвать пробой в зазоре меж-
ду электродами с однородным электрическим полем, и при этом не имеет значе-
ния, каковы давление или расстояние между электродами. На Рис. 2.3 приведены
полученные экспериментально напряжения пробоя при различных значениях pd
для атмосферного воздуха и кривая Пашена, рассчитанная теоретически с ис-
пользованием параметров, указанных в Табл. 2.1.
2.2. Газы 27
pd[6ap«MM]
Рис. 2.3. Экспериментальные и расчетные кривые Пашена для атмосферного воздуха.
Таблица 2.1. Экспериментально определенные значения постоянных Л и В для различных газов
Газ А [1/(мм-бар)] В [кВ/(мм*бар>] Диапазон применимости Е/р [кВ/мм*бар]
Воздух ИЗО 27.4 11...45
n2 977 25.5 8...45
Н2 376 9.8 11...30
Не 210 2.6 2...11
Аг 1020 13.5 8...45
СО2 1500 34.9 37...75
Теоретически при некоторых (достаточно малых) значениях pd напряжение
пробоя обращается в бесконечность из-за того, что становится невозможно со-
здать лавину электронов. На практике этого не происходит, потому что при очень
больших напряженностях электрического поля возникает так называемая холод-
ная эмиссия электронов из электродов
Наиболее широко используемым газом с высокой электрической прочностью
является гексафторид серы SF6. Он входит в группу так называемых электронега-
тивных газов, обладающих способностью присоединять к своим молекулам элек-
троны, которые при этом превращаются в отрицательные ионы. Для описания по-
ведения данных газов при пробое следует ввести коэффициент присоединения т).
Которую теория Таунсенда не учитывает, равно как термоэлектронную. — Примеч. пер.
28 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Этот коэффициент определяет вероятность присоединения электрона на единич-
ную величину его пробега. Аналогично а/p, rj/p является функцией Е/р. Кроме
SFg, некоторые другие газы, содержащие галогены (Cl, F, I и т. д.), а также О2 явля-
ются электронегативными. Эффективный коэффициент ионизации ае определя-
ется как разность между а и гр
ае = а - т| = pf(E/p). (2.14)
Формирование лавины электронов становится возможным, только если ае боль-
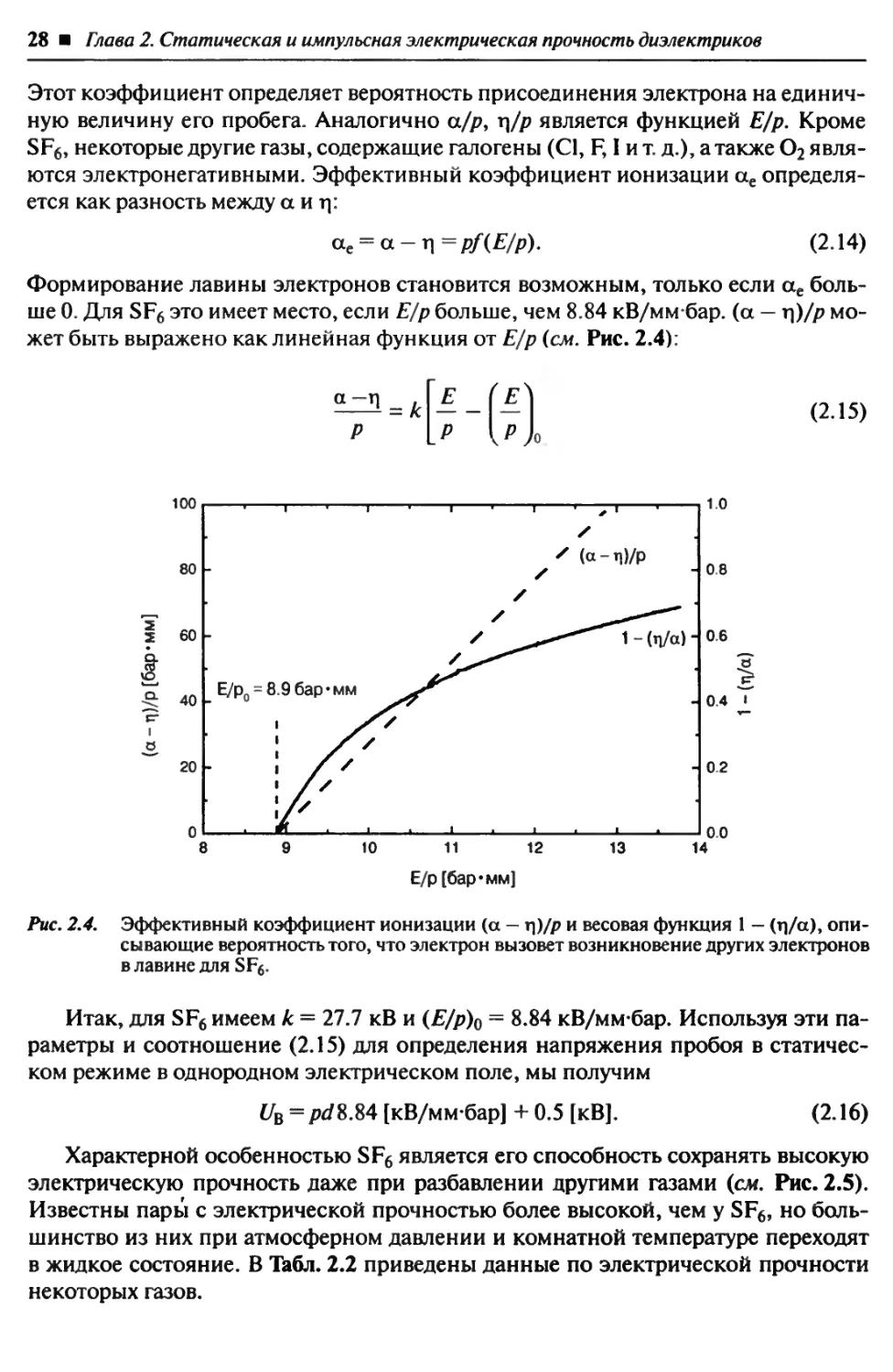
ше 0. Для SF6 это имеет место, если Е/р больше, чем 8.84 кВ/мм-бар. (а — т])/р мо-
жет быть выражено как линейная функция от Е/р (см. Рис. 2.4):
a—n , Е (Е
----1 = к----—
р \.р--------W
(2.15)
Рис. 2.4. Эффективный коэффициент ионизации (а — г|)/Р и весовая функция 1 — (n/а), опи-
сывающие вероятность того, что электрон вызовет возникновение других электронов
в лавине для SF6.
Итак, для SF6 имеем к = 27.7 кВ и (Е/р)$ = 8.84 кВ/мм-бар. Используя эти па-
раметры и соотношение (2.15) для определения напряжения пробоя в статичес-
ком режиме в однородном электрическом поле, мы получим
UB = рг/8.84 [кВ/ммбар] + 0.5 [кВ]. (2.16)
Характерной особенностью SF6 является его способность сохранять высокую
электрическую прочность даже при разбавлении другими газами (см. Рис. 2.5).
Известны пары с электрической прочностью более высокой, чем у SF6, но боль-
шинство из них при атмосферном давлении и комнатной температуре переходят
в жидкое состояние. В Табл. 2.2 приведены данные по электрической прочности
некоторых газов.
2.2. Газы 29
Содержание SF6 [%]
Рис. 2.5. Зависимость напряжения пробоя от содержания SF6 в смесях с азотом и воздухом
Таблица 2.2. Относительная электрическая прочность
различных газов
Газ Относительная электрическая прочность
Воздух 1
n2 1
SF6 2.5
CsFg 5.5
Н2 0.5
Другое полезное приближенное соотношение для напряжения пробоя можно
вывести, если применить квадратичную подстановку для относительного коэф-
фициента ионизации. Это соотношение особенно хорошо подходит для газов, не
являющихся электронегативными или проявляющих это свойство лишь в малой
степени:
Р Р
(2.17)
Используя это соотношение и решая относительно t/B, мы получим
U^fE/p^pd + cipd)''2.
(2.18)
Уравнение (2.18) справедливо только для больших значений pd. В Табл. 2.3 приве-
дены значения постоянных, используемых в (2.18) для различных газов.
30 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Таблица 2.3. Постоянные, используемые в (2.18) для различных
газов
Газ (£/р)о [кВДммбар)] с [кВ/(мм-бар)|/2]
СО2 3.21 5.88
Воздух 2.44 2.12
n2 2.44 4.85
Н2 1.01 2.42
Средняя электрическая прочность газов может существенно изменяться, если
электроды имеют сферическую или цилиндрическую форму. Это особенно замет-
но, если расстояние между электродами существенно больше, чем их радиусы,
т. е. d > R. Это явление может быть учтено путем введения в формулу (2.18) коэф-
фициента увеличения поля б, равного отношению максимальной и средней на-
пряженностей полей в зазоре:
^(E/p\pd+ c(pd)^
S’
В Табл. 2.4 приведены формулы для расчета б для различных конфигураций
электродов.
Таблица 2.4. Коэффициенты увеличения поля для различных конфигураций электродов
Конфигурация б ~ ^MAx/^MEAN
Концентрические цилиндры 6 = (Д/г—1)/1п(Д/г)
Равные сферы 8 = Х/2галяХ/г» 1;X= d—2r
Равные параллельные цилиндры 8 = X/(2r 1п(А/г)) для Х/г » 1; X = d - 2г
Примечание. R,r— радиусы, d — расстояния между центрами.
Выражение (2.18) может быть использовано и для очень неоднородных кон-
фигураций электрических полей, но в этом случае взамен d следует применять
эффективное расстояние между электродами ^eff- В таких полях лавина движет-
ся в направлении более низкой напряженности поля. Из поведения эффективно-
го коэффициента ионизации следует, что, если напряженность поля падает при-
мерно до 80% от его значения вблизи электрода на дистанции, соответствующей
20 актам ионизации, лавина не может существовать (см. обсуждение стримерного
пробоя ниже). Таким образом, JEFF определяется как расстояние, на котором на-
пряженность поля падает до 80% от ее максимального значения. Для сферичес-
ких и цилиндрических электродов JEFF = 0.115г и 0.23г соответственно, где г —
радиус кривизны их поверхности.
До сих пор мы пренебрегали пространственным зарядом, который создается в
электронной лавине. Это неверно, если при атмосферном давлении число частиц
в лавине увеличивается до 1О6...1О8. Сравнительно малоподвижные ионы остают-
ся в хвосте лавины, в то время как более подвижные электроны образуют ее голо-
вную часть сферической формы. Можно легко найти напряженность электричес-
2.2. Газы 31
кого поля, создаваемого в лавине, содержащей N заряженных частиц. Так как
плотность заряда растет с коэффициентом е на расстоянии 1/а, можно записать
Esc =-^-^- = 1.5х10"7В/см.
sc 4ле0(1/а)* 2 (1/а)2 '
(2.20)
Для N = 107 и а-1 = 10-2 см, получается Esc = 15 кВ/см, что может составлять
большую часть от приложенного внешнего поля.
На Рис. 2.6 качественно изображены поля, формирующиеся вблизи лавины.
Пространственным зарядом лавины поле позади и впереди нее увеличивается
(по сравнению с приложенным внешним полем Eq) и уменьшается в промежутке
между облаками электронов и ионов. В соответствии с результатами исследова-
ний, выполненных Ретером [Raether, 1964], ультрафиолетовое излучение, возни-
кающее из-за рекомбинации и перехода атомов или молекул газа из возбужден-
ного в невозбужденное состояние, порождает ионизацию и возникновение элек-
тронов как впереди, так и позади лавины, инициализируя следующие лавины,
которые в конце концов и образуют проводящий мост между анодом и катодом.
Из-за того что вблизи хвоста лавины поле наиболее высокое, ионизация и воз-
никновение электронов здесь происходят более эффективно^. Этот вид разви-
Рис. 2.6. Влияние пространственного заряда, создаваемого лавиной, на электрическое поле в
зазоре. Ионы менее подвижны, чем электроны, и образуют с ними диполь. Создавае-
мое пространственным зарядом поле увеличивает напряженность поля рядом с голо-
вой и хвостом лавины2).
” Это характерно для искрового типа разряда, в основе которого лежит стримерный механизм:
рост сильно ионизованной области от анода к катоду, после того как головка лавины-родоначальницы
достигла анода. — Примеч. пер.
2) Происходит так называемое кажущееся приближение анода к катоду. — Примеч. пер.
32 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
тия разряда называется стримерный механизм. Стримеры не обязательно возника-
ют на катоде. Если критическая плотность зарядов достигнута в объеме разрядно-
го промежутка, стримеры начинают расти и в сторону катода, и в сторону анода.
Возникновение фотоэлектронов на больших расстояниях от главного стримера
может привести к быстрому формированию канала проводимости При атмос-
ферном давлении наблюдались скорости распространения разряда в
100... 1000 см/мкс. Ретер (Raether) определил критические стадии лавинного пробоя
путем экспериментальных наблюдений, выполнявшихся в диффузионной каме-
ре0. Он обнаружил, что стримеры развиваются при axCR ~ 20, где xCR — среднее
положение ионизованного облака, когда оно становится критическим. Исполь-
зуя эти данные, можно рассчитать критическое число электронов в лавине при
атмосферном давлении:
NCR = eaXcK = 108. (2.21)
Эта цифра была подтверждена моделированием с использованием метода
Монте-Карло [Kunhardt and Tzeng, 1988]. Соответствующая плотность зарядов
найдена равной приблизительно 1014 см-3. Не удивительно, что при этих плот-
ностях в стримерных каналах возникает экранирование пространственным заря-
дом (по Дебаю).
2.2.2. Импульсный пробой
До сих пор мы обсуждали только электрический пробой при статических ус-
ловиях, т. е. предполагалось, что напряжение на разрядном промежутке возраста-
ет так медленно, что задержки в формировании каналов проводимости не сущес-
твенны.
Однако если на разрядный промежуток подать импульс с высокой скоростью
нарастания напряжения, то следует учитывать, что для возникновения пробоя
требуется некоторое время. Как показано на Рис. 2.7, можно выделить несколько
интервалов времени, создающих задержку формирования каналов проводимости:
• /0 — время от начала импульса до достижения напряжением значения L/B
(пробивного напряжения в статическом режиме),
• ts~ задержка времени, определяемая вероятностью формирования
лавины,
• ГА — время формирования лавины до достижения критической плотности
зарядов,
• *arc — время установления низкоомной дуги в разрядном промежутке.
Задержка времени ts зависит от вероятности появления свободных электро-
нов в разрядном промежутке. Возникновение этих электронов может быть вызва-
но освещением разрядного промежутка или поверхности катода электромагнит-
ным излучением. В частности, ультрафиолетовое излучение, рентгеновские лучи
и
Камера Ретера — модифицированная камера Вильсона, наполненная парами спирта. — Примеч. пер.
2.2. Газы 33
Рис. 2.7. Характерные задержки формирования импульсного пробоя в газовой среде.
и гамма-излучение от источников радиации очень эффективно вызывают иони-
зацию газовых атомов и молекул и создают фотоэмиссию.
В зависимости от географического положения и местных условий естествен-
ная радиоактивность и космическое излучение каждую секунду при атмосферном
давлении производят 0.1...10 свободных электронов в кубическом сантиметре га-
за. Эти электроны могут присоединиться к молекулам газа и создать стационар-
ную концентрацию до нескольких тысяч отрицательно заряженных ионов в куби-
ческом сантиметре электронегативного газа за несколько минут. В SF6 концент-
рация 2500 ионов SF7 на кубический сантиметр была достигнута за 5 мин
[Kindersberger, 1986]. Когда такой газ подвергается воздействию электрического
поля, из-за столкновений молекул часть электронов может отделиться от отрица-
тельных ионов и внести свой вклад в образование свободных электронов. Ско-
рость отделения электронов на единицу объема л8 зависит от плотности отрица-
тельных ионов ип в объеме газа, скорости дрейфа ионов ц, и коэффициента удар-
ного отрыва электронов 5:
л8(0 = 5лпц
Ц»= Pmix^-
(2.22)
Подвижность мм ex зависит от вида ионов и состава газа. В Табл. 2.5 приведены
значения подвижности ионов SF6 для различных смесей аргона и SF6. Зависи-
мость 5/л для ионов SF6 представлена на Рис. 2.8
Таблица 2.5. Подвижность ионов SF6 для различных смесей аргона и SF6
Подвижность в зависимости от давления 2% SF6 5% SF6 10% SF6
ММ1х(1 бар)см2В_|с * 2.2 2.0 1.71
Pmix(2 бар) см2В_|с"’ 1.2 1.08 0.92
34 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Е/п[Тд]
Рис. 2.8. Зависимость 8/л для ионов SF6 [Hilmert and Schmidt, 1991].
При напряженности электрического поля в несколько сот тысяч вольт на санти-
метр, вследствие туннельного эффекта, увеличивается число электронов, вырывае-
мых из металлической поверхности электродов. Плотность тока этих электронов
может быть описана уравнением Фоулера—Нордхейма [Fowler and Nordheim, 1928]:
1.54х1О~*0*Е* [ 6.83х10У/2е(у)]
1 ч> ехр1 ₽£ г
0(у) = 0.956 - 1.Обу2, (2.23)
у = 3.8х
Ф
Здесь плотность тока j выражена в А/см2, напряженность электрического по-
ля Е— в В/см, работа <р — в эВ. 0 является коэффициентом, учитывающим нали-
чие особых условий эмиссии из локальных областей на металлической поверх-
ности. Наиболее важными центрами эмиссии являются диэлектрические вклю-
чения, металлические микровыступы и абсорбированные газы [Korolev and
Mesyats, 1999]. Для диэлектрических включений и микровыступов зависимость
эмиссии от напряженности поля может быть описана уравнением Фоулера—
Нордхейма (2.23). Важность увеличения поля вблизи центров эмиссии становит-
ся очевидной, если рассчитать число электронов в секунду по формуле (2.23).
Чтобы обеспечить поток электронов 106 в секунду с площади 1 см2, требуется на-
пряженность электрического поля 1.2 х 107 В/см. А если локальные центры эмис-
сии обеспечивают значение 0= 100, то же число электронов будет получено с
площади 10-12 см2 при напряженности поля 2.4 х Ю5 В/см.
2.2. Газы 35
Таким образом, общее число электронов в разрядном промежутке является
суммой электронов, попадающих туда из трех источников:
MO=7V0n + 7VF(O+M(O. (2 24)
Здесь только первое слагаемое, представляющее число естественно существую-
щих свободных электронов, не зависит от времени. N^t), которое выражает число
электронов, возникающих вследствие полевой эмиссии, получается интегрирова-
нием j/e (2.23) по площади поверхности катода. N^(t), скорость отрыва электро-
нов, получается интегрированием (2.22) по объему разрядного промежутка.
Не каждый свободный электрон в разрядном промежутке способен иниции-
ровать лавину, даже если приложенное напряжение выше статического пробив-
ного напряжения. Это особенно характерно для электронегативных газов. Лави-
ны могут расти только в тех областях разрядного промежутка, где локальная на-
пряженность электрического поля превышает некоторое критическое значение.
Для электронегативных газов критическая напряженность поля является такой
напряженностью, при которой коэффициент ионизации а становится больше,
чем коэффициент захвата электронов т| (см. Рис. 2.4).
Вероятность того, что один электрон вызовет лавину, определяется локальным
значением 1 — л/а [Legler, 1961]; g(E/p) = 1 — т]/а может быть использована как
весовая функция для каждого свободного электрона в разрядном промежутке.
Чтобы определить «производительность» электронов по части возможности
вызвать лавину, следует умножить каждый элемент поверхности или объема, где
могут появиться свободные электроны, на функцию g(E(t, х, у, z)/p).
dNa = r( E(r,x,y,z)1 j(E(t,x,y,z)) dA +
dt F I P / e (2.25)
+ J [8 (£(z> Xf y> z)) /inv n(E (z, x, y, z)) + л0] dV,
v V P )
где л0 — число естественно существующих свободных электронов на единицу объ-
ема. На Рис. 2.9 показаны эквивалентные поверхности, соответствующие контурам
весовой функции g(E(t, х, у, z)/p) для двух различных конфигураций электродов.
Мы можем найти dNa с вероятностью p(Z) dt, что пробой произойдет в интер-
вал времени г. t + dt, предполагая, что он не произошел до момента г. Используя
эти определения, мы получим из теории условной вероятности [Papoulis, 1965]:
-fdN./лл (2.26)
F(Z) = 1—е° . v
Здесь F(f) — вероятность того, что пробой произойдет до истечения времени t.
Соответствующая плотность вероятности ДО будет равна
f(t) =—- е 0 . (2.27)
dt
36 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
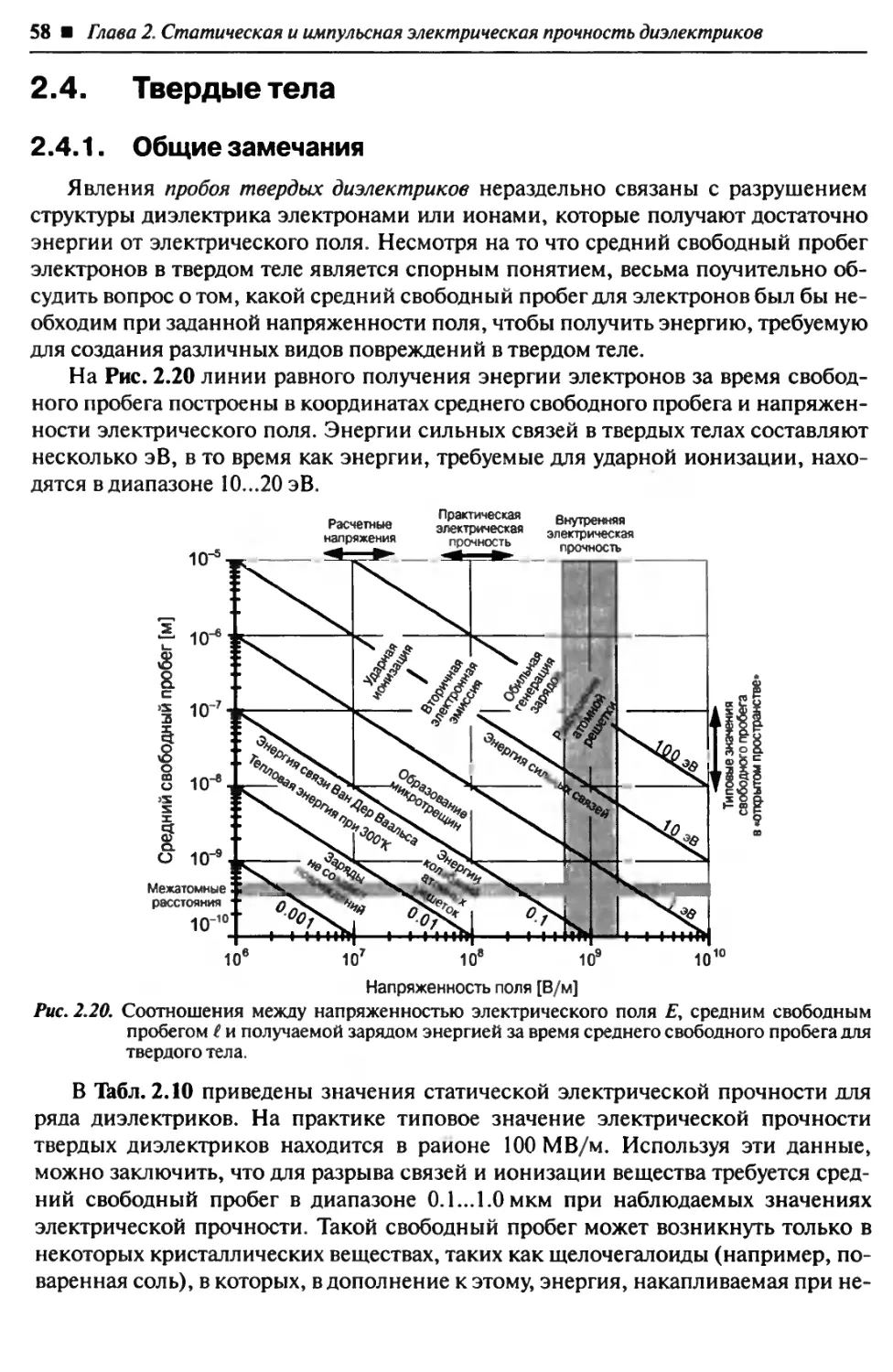
Рис. 2.9. Распределение эквипотенциальных поверхностей между двумя электродами различ-
ной конфигурации. Разными оттенками серого цвета помечены 10%-ные изменения
напряженности поля.
В качестве примера рассмотрим временное распределение возникновения са-
мостоятельного пробоя в зазоре 1 см, заполненного сухим азотом при давлении
1 бар и находящегося под воздействием однородного электрического поля. Ис-
пользуя (2.17), мы получаем напряжение статического пробоя 31 кВ. Примем
скорость нарастания напряжения равной 6 МВ/с. Предположим также, что катод
покрыт 100 эмиссионно-активными участками площадью 1О~,осм2, каждый с
Р= 100. Найдем вероятность F(t) и плотность вероятности ДО пробоя как функ-
цию времени, предполагая, что в возникновении электронов в зазоре участвует
только полевая эмиссия. Из уравнений (2.23) и (2.25)...(2.27) мы получим резуль-
таты, показанные на Рис. 2.10. Требуется только 5.2 мс для достижения напряже-
ния статического пробоя, а среднее время возникновения лавины составляет
25.4 мс. В этот момент напряженность поля в зазоре достигает 152 кВ/см.
После того как сформируется первая лавина электронов, пробой может раз-
виваться в двух различных направлениях. В течение пробоя Таунсенда могут воз-
никать несколько последовательных лавин, пока не возникнет квазистабильный
тлеющий разряд или не произойдет переход из тлеющего разряда в дуговой. При
стримерном механизме пробоя одна лавина оказывается достаточно мощной,
чтобы создать критическое число электронов еще до достижения лавиной анода.
Электроны, находящиеся в головной части лавины, создают искажение поля, ко-
торое в конечном счете управляет самораспространением лавины. В этих двух
случаях интервалы времени достижения критической плотности зарядов гА между
собой очень существенно различаются.
Для пробоя Таунсенда мы определяли время формирования как время, проте-
кающее до того, как будет достигнуто критическое число лавин в разрядном про-
межутке. Так как механизм Таунсенда предполагает, что вторичные электроны
высвобождаются на катоде из-за взаимодействия между фотонами и ионами,
можно ожидать, что появление последующих лавин будет происходить из иных
мест на поверхности катода и тем самым создавать разряд в большем объеме.
Предполагая, что электрическое поле в разрядном промежутке не искажается
2.2. Газы 37
Рис. 2.10. Вероятность лавинного пробоя и соответствующая ей плотность вероятности
для зазора в 1 см в сухом азоте. Скорость увеличения напряжения 6 МВ/с, поле однородное.
объемным зарядом и что вероятность ионизации зависит только от локальной на-
пряженности электрического поля, Леглер рассчитал время формирования для
этого случая [Legler, 1955]. Он получил следующее выражение для времени фор-
мирования лавины, начинающейся с одного электрона, вылетевшего из катода:
fA = к— = 1п(еСлск1т(м -0)х _d_ (2.28)
ре£ 1пр нЛ
Здесь поле в зазоре d между электродами предполагается однородным, к — среднее
число лавин до достижения 2VCRIT, С — постоянная Эйлера (0.577), ц = - 1) —
коэффициент обратной связи, описывающий число электронов, покинувших ка-
тод, на одну лавину, це — подвижность электронов и Е — напряженность элект-
рического поля.
Из-за формирования положительно заряженными ионами пространственно-
го заряда вблизи анода происходит увеличение напряженности поля вне области
пространственного заряда, и волна ионизации распространяется вперед, к катоду,
и назад, от катода к аноду, до тех пор, пока не установится стабильный тлеющий
разряд [Doran, 1968].
Для стримерного пробоя перенапряжение должно быть достаточно большим,
чтобы критическое число электронов WCrit в разрядном промежутке было до-
стигнуто за одну лавину. Это имеет место при напряжении, на 15...20% большем,
чем напряжение статического пробоя. Ранее отмечалось, что около 108 электро-
нов должно быть создано в лавине в газе при атмосферном давлении, прежде чем
будет достигнуто условие образования стримеров, т. е. axCR~ 18. Если известна
38 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
средняя скорость дрейфа электронов мы можем найти /А из соотношения
ГА = xcr/^drift = 18/(at>DRiFT)- Однако, так как скорость дрейфа электронов зави-
сит от напряженности электрического поля, ее довольно трудно оценить, особен-
но в случае неоднородных полей.
Для технологических целей иногда используется соотношение площадь—время.
При этом для определения /А требуются только геометрические параметры и фор-
ма импульса напряжения. Однако этот метод применим, только если время ста-
тистической задержки rs намного меньше времени /А. Не существует строгого
обоснования этого метода, но существуют некоторые правдоподобные рассужде-
ния [Kind, 1958]. Скорость роста лавины v(x, f) зависит от геометрии разрядного
промежутка и превышения напряжением на нем напряжения статического про-
боя, т. е. разности U(t) — Uq. Предположим, что эти зависимости могут быть опи-
саны разделением переменных:
и{х, t) = ад [U(t) - t/0] =dx/dt.
Здесь К(х) определяется только геометрией разрядного промежутка. После интег-
рирования получается:
d 'о+/>+'«
fer F-
(2.29)
Физический смысл этого выражения состоит в том, что для данной геометрии
разрядного промежутка только интеграл по времени от напряжения, превышаю-
щего значение t/0, определяет время формирования лавины, т. е. если значение F
в (2.29) определено для одной формы импульса, то оно может быть использовано
и для любых других форм для расчета значения /А. Иллюстрации к этому методу
приведены на Рис. 2.11.
Рис. 2.11. Взаимосвязь времени формирования лавины с формой импульсов напряжения,
определяемая условием F\ = F2 = fj.
2.2. Газы 39
2.2.3. Формирование искрового разряда
После того как стример замкнет разрядный промежуток, между анодом и ка-
тодом появляется проводящий канал. Ток в этом канале, зависящий от импеданса
источника высокого напряжения, начинает греть и ионизировать газ до тех пор,
пока не установится низкоомное состояние канала. Для описания перехода от ка-
нала стримера к низковольтному электродуговому каналу в литературе было
предложено несколько моделей. Наиболее широко применяется закон, эмпири-
чески полученный Тендером [Toepier, 1924, 1927]. Физическое обоснование было
дано Пфейфером [Pheifier, 1971]. Следуя его аргументам, предположим, что имеет
место слабо проводящий столб газа, но его проводимость увеличивается за счет
ионизации при столкновениях.
dnt = ntadx. (2.30)
Заменяя dx на uedt и полагая ие = |деЕ, мы получим
dne = nc<x\xtEdt. (2.31)
Принимая во внимание, что средняя плотность тока может быть записана как
j=nc \xteE и интегрируя по времени формирования канала t, мы получим следую-
щее выражение для средней плотности электронов ле(Г):
о
«.(') = “ fjdt, (232)
е
где ие — средняя скорость дрейфа электронов,
це— подвижность электронов,
Е— средняя напряженность поля в проводящем канале
Предполагая распределение плотности тока в проводящем канале однород-
ным, можно выразить его сопротивление как
R = — —— s
f I л (Г)ц e£nrf2 г ’ (2.33)
аце|/от
о
где 5 — длина канала,
rf— его радиус.
Закон Тендера гласит, что сопротивление обратно пропорционально заряду,
который протекает через канал. Ввиду нагрева протекающим током канал расши-
ряется. Этот эффект не обсуждается в рамках закона Теплера. Таким образом,
этот закон справедлив только для ограниченного времени после образования ка-
нала, обычно 10 нс при атмосферном давлении.
Закон Вейцеля и Ромпа [Rompe and Wfeizel, 1944] основан на аналогичных пред-
положениях. В частности, эти авторы тоже пренебрегали расширением канала.
Соответственно они пришли к похожему выражению:
40 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Rf(t) =
(2.34)
Здесь а является постоянной, ар — давлением газа.
Другой подход был выполнен Брагинским [Braginskii, 1958]. Он учитывал воз-
можность теплового расширения плазмы в канале, но предполагал, что удельная
проводимость плазмы не зависит от времени. Результирующее выражение закона
Брагинского
Л(0 =------7-----
nab1 J I2,idt
о
(2.35)
Здесь b — постоянная, зависящая от плотности, проводимости и термодинами-
ческих свойств плазмы, а о — средняя проводимость плазмы в канале. В Табл. 2.6
приведены значения постоянных для некоторых газов, используемых в разных
законах.
Таблица 2.6. Постоянные для некоторых газов, используемых в разных законах [Pfeiffer, 1971]
Пз kT = 1/аре (10-4 В’с/см) а (атм см2/В2 с) ofc2 (104 А,/3см/В-с)
Воздух 0.5...0.6 — —
n2 0.4 1.1 3.5
СО2 0.5 1.0 3
Аргон 0.085 25 10
Используя соотношение Теплера, можно получить уравнения для тока в раз-
ряде и характерных временных параметров, определяющих его увеличение, и
уменьшение падения напряжения на разрядном промежутке. Для этих целей мы
используем эквивалентную схему, приведенную на Рис. 2.12,
Рис. 2.12. Эквивалентная схема разрядной цепи
2.2. Газы 41
В этой модели мы пренебрегаем индуктивностью разряда и емкостью разряд-
ного промежутка. Uq — напряжение зажигания разряда, a Zo — импеданс цепи пи-
тания. Максимальный ток, протекающий по этой цепи, равен
/мах = M)/(Z0 + R{) * Uq/Zq. (2.36)
Возможность исключения R{ из рассмотрения обусловлена тем, что обычно
Zq » Rf. Вводя у = ///мах и используя соотношение Теплера, мы получаем следу-
ющие уравнения для цепи, изображенной на Рис. 2.12:
Д, jd - у)
dt=—\
Ео\
(2.37)
Постоянная С, определенная из предположения, что в начале разряда
у = I//мах = 10-3, в нашем случае равна 5.906. На Рис. 2.13 приведен график изме-
нения ///мах в зависимости от времени для разряда в азоте, возникающего при
£0=Ю5В/с.
Рис. 2.13. Относительный ток разряда как функция времени для цепи, показанной на Рис. 2.12.
Используя (2.37), мы можем найти время роста тока от 0.1 до 0.9 максималь-
ного значения равным 13.2 к/Eq и постоянную времени тг = 6.84 к/Eq.
В литературе встречаются и другие выражения для определения тг. Широко
используется формула, эмпирически выведенная Дж. С. Мартином [Martin et al.,
1996] на основе множества экспериментальных данных и расчетов:
42 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
88 17
4/3^/3УРо
нс,
(2.38)
где Zo — импеданс цепи питания, Ом, Ео — напряженность поля в начале зажига-
ния разряда, кВ/см, р — плотность газа, причем р0 — плотность при нормальных
условиях.
В этом подразделе мы показали, что электрический пробой газа зависит от из-
менения напряжения на разрядном промежутке во времени после превышения
им напряжения статического пробоя. Если импульс напряжения достаточно ко-
роткий, пробой может и не произойти, даже если приложенное напряжение пре-
восходит напряжение статического пробоя данного разрядного промежутка. Это
происходит, когда время формирования стримера и образования проводящего ка-
нала между электродами больше, чем длительность импульса напряжения.
Дж. С. Мартин [Martin et al., 1996] исследовал пробой для конфигурации электро-
дов «точка—плоскость» с использованием генератора импульсов напряжения
треугольной формы и вывел следующее экспериментальное соотношение:
1^0
(2.39)
где знаки + и — относятся к полярности электрода «точка», d — зазор между элек-
тродами в сантиметрах, Кип — постоянные, приведенные в ТЬбл. 2.7, /efr— экви-
валентное время в микросекундах для импульса прямоугольной формы с длитель-
ностью и p/pq— отношение давления газа в разрядном промежутке к
атмосферному давлению, £ьт измеряется в кВ/см. Диапазон применимости этой
формулы 105 < р < 5 х 105 Па.
Таблица 2.7. Эмпирические параметры для конфигурации
электродов «точка—плоскость»
Параметр Воздух Фреон Гексафторид серы
к* 22 36 44
/С 22 60 72
п 0.6 0.4 0.4
2.3. Жидкости
2.3.1. Основные электрические процессы
Даже в настоящее время нет всеобъемлющей теории электрического пробоя в
жидкостях. Однако основные процессы начала пробоя могут быть разделены на
две категории: процессы, связанные с объемом жидкости, и процессы, происхо-
дящие на электродах. В обсуждении этих вопросов мы в основном будем следо-
вать результатам фундаментальных работ Льюиса [Lewis, 1985, 1987, 1993, 1994а,
Ь, с, 1996,1998].
2.3. Жидкости 43
Процессы в объеме
Заряды в объеме жидкости могут возникать вследствие диссоциации молекул
или из-за их инжекции с электродов. Диссоциация не приводит к созданию заря-
да в жидкости. Напротив, электроны, проходящие через электроды, могут при-
вести к появлению избыточного или недостаточного заряда в объеме жидкости.
Передача заряда происходит через изменение электронных состояний молекул
или кластеров, на короткое время возникающих в жидкости.
Электронное состояние жидкостей определяется электронным состоянием
отдельных молекул. Молекулы газа могут иметь два характерных электронных
состояния: положительного иона, когда молекула потеряла электрон, и отрица-
тельного иона, когда электрон присоединился к молекуле. Электронное состоя-
ние положительных ионов имеет энергию И^ДО), соответствующую потенциалу
ионизации, а отрицательных ионов имеет энергию ИС(0), соответствующую по-
тенциалу отрыва. В жидкостях эти ионизированные состояния преобразуются
поляризационным откликом окружающих ионы молекул, и уровни энергии, со-
ответствующие полностью поляризованному состоянию, сдвигаются до И+(оо)
до ИС_(оо) соответственно (Рис. 2.14).
Энергия, связанная с этим диапазоном, И^О) — И^оо), состоит из двух частей:
первая связана с поляризуемостью молекулярных орбит, а вторая представляет
собой коллективный диэлектрический отклик более удаленных молекул. Когда
состояние ионов изменяется из-за увеличения или уменьшения электронов, ре-
организация молекул происходит намного медленнее, чем это требуется для пе-
Состояния отрицательных ионов Состояния положительных ионов
P(W)
Рис. 2.14. Энергетические состояния положительных и отрицательных ионов в жидкости.
И+(оо) и ИС(оо) соответствуют полностью локализованным состояниям вследствие
полной коллективной поляризации. Уровни энергии расширены в соответствии
с распределением Гаусса Р(И0 из-за теплового возбуждения. Электроны с энергиями
более Ио могут рассматриваться квазисвободными.
44 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
ремещения электронов. Вследствие теплового возбуждения каждый электронный
уровень будет заменен распределением Гаусса. Это также справедливо и для всех
состояний между И^О) и ИХ со) в соответствии с различными степенями поляриза-
ции. Таким образом, мы получаем две расширенные полосы гауссовой формы
распределения, связанные с двумя видами ионов, и движение электронов и ды-
рок в объеме жидкости может быть описано зонной моделью, похожей на модель
для аморфных твердых тел. Примеси, подобные кислороду, могут улавливать
электроны в состояниях с энергией много ниже Ж_(оо).
Избыточные заряды могут оставаться в локализованном, квазилокализованном
и квазисвободном состоянии в зоне проводимости. Квазисвободное состояние мо-
жет существовать при энергиях выше И<_(0) для электронов и ниже ЖДО) для ды-
рок. Носители можно рассматривать как свободные, если они движутся через пос-
ледовательность состояний в зоне, не задерживаясь настолько долго, чтобы индуци-
ровать полную электронную поляризацию. Энергетическое состояние свободных
избыточных электронов зависит от суперпозиции сил притяжения и отталкивания
окружающих молекул. В квазисвободном состоянии эти силы компенсируют друг
друга. В общем энергия электронов Ко, при которой это происходит, находится вы-
ше уровня вакуума. Для н-гексана эта энергия составляет около 0.1 эВ.
Квазилокализованные состояния находятся вокруг И^Доо) и И<_(оо)
в зоне между ИС(0) и И^О). Эти состояния соответствуют различной подвижнос-
ти носителей заряда. Электроны и дырки, которые становятся полностью поля-
ризованными, дрейфуют как ионы с их сопутствующими поляризационными
экранами (поляронами), с подвижностями менее чем 10-5 м2В-1с_|. Из-за воз-
действия тепловых флуктуаций, падающего излучения или сильного электричес-
кого поля электроны или дырки могут освободиться из поляризационной ловуш-
ки и стать квазисвободными. В этом состоянии подвижность становится больше
10“3 м2В“1с“|. В промежуточном районе электроны можно рассматривать находя-
щимися в квазилокализованном состоянии, которое характеризуется сильными
вариациями локальных потенциалов в невозмущенной жидкости.
В молекулярных кластерах, существующих в жидкостях, электроны движутся в
поле с периодически изменяющимся потенциалом. Под воздействием электри-
ческого поля потенциальные ямы уменьшаются как по глубине, так и по ширине.
Первоначально квазилокализованные электроны движутся благодаря резонансно-
му туннелированию, как это показано на Рис. 2.15. Так как они должны достичь
свободного уровня равной энергии, они после туннелирования будут иметь чрез-
мерную энергию над уровнем основного состояния. Эта энергия преимуществен-
но рассеивается в виде энергии фононов, что приводит к нагреву молекул вдоль
пути движения электронов. При очень высоких электрических полях некоторые
электроны смогут перепрыгнуть через потенциальные ямы (см. Рис. 2.15). Во вре-
мя этих «подскоков» разность энергии между начальным и конечным состояния-
ми опять рассеивается или в тепло, или через эмиссию фотонов. При переходе из
кластера в кластер потенциальные ямы становятся глубже и шире и тем самым
препятствуют движению электронов.
В квазисвободном состоянии подвижность электронов и дырок определяется
рассеивающими столкновениями с молекулами жидкости, в которых они возбуж-
2.3. Жидкости 45
V(x)
---►
X
Рис. 2.15. Передвижение избыточных электронов между молекулярными состояниями механиз-
мом резонансного туннелирования под воздействием электрического поля.
дают колебания различных видов и происходит потеря энергии, приобретенной
из электрического поля. Вероятность свободных электронов попасть в ловушку
зависит среди прочих факторов, от их кинетической энергии, приобретаемой во
время дрейфа в электрическом поле.
Во время прохождения через жидкость электроны могут существовать ка-
кое-то время в квазисвободном состоянии и какое-то время в состоянии локали-
зации, и можно описать их движение через эффективную подвижность, завися-
щую от времени, проводимом в свободном и захваченном ловушками состояниях
tf и tt соответственно:
Ре = (Рг if + Pt Л)/(Уг + А)- (2.40)
Здесь и представляют собой подвижность электронов в свободном и захва-
ченном ловушками состояниях соответственно. Время нахождения электрона в
ловушке определяется энергией тепловой активации Et, необходимой для его ос-
вобождения:
rt = Го exp(Et Д7),
(2.41)
46 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
где г0 — величина, обратная частоте повторных попыток освобождения. Для угле-
водородов значение Et было найдено равным 0.24 эВ [Fueki et al., 1972].
При высокой напряженности электрического поля rt значительно уменьшает-
ся, так как потенциальный барьер, локализующий электроны, становится ниже
со стороны анода, как показано на Рис. 2.15. Для большинства этих интервалов
времени электрон, освободившись из ловушки, движется далее в зоне проводи-
мости, где его скорость дрейфа ограничивается процессами столкновений, опи-
санными выше. При очень высокой напряженности поля скорость дрейфа может
превысить тепловую скорость и скорость потребления энергии из поля может
стать очень большой. В углеводородах при 108 В/м эта скорость достигает
1014 эВ/с. Эта энергия при рассеянии возбуждает различные моды колебаний мо-
лекул с типовыми значениями энергии hv порядка нескольких десятков эВ. Если
энергия электронов становится больше, чем Av, сечение неупругих соударений
быстро падает и электроны могут получить достаточно энергии для возбуждения
следующих мод в терминах энергии, вплоть до молекулярной диссоциации и ио-
низации. Ионизация очень важна в образовании пробоя, так как она генерирует
вторичные электроны и положительные ионы, или дырки, что создает возмож-
ность образования лавины в жидкости. Однако в связи с тем, что только около
0.1 эВ на молекулу требуется для нагрева жидкости от нормальной температуры
до температуры кипения, в нормальных условиях, задолго до того, как произой-
дет лавинный пробой, в жидкости могут образоваться участки пониженной плот-
ности. В этих участках электронные лавины могут появляться при намного более
низких напряженностях электрического поля, формируются увеличивающиеся в
размерах газовые каналы, что становится стартовой точкой возникновения стри-
меров, подобно тому, как это имеет место в газах (см. ниже). Вблизи головы стри-
мера электрическое поле значительно увеличивается, что способствует распро-
странению канала. Этот механизм объясняет экспериментально установленную
независимость скорости распространения стримера в некоторых пределах.
Положительные ионы в диэлектрических жидкостях имеют подвижность, близкую
к подвижности ионов в электролитах, составляющую порядка 10-7... 10-8 м2В_,с_|. Од-
нако положительные ионы в жидкостях можно рассматривать и как молекулярные
дырки, а движение дырок в зоне валентности может быть намного легче, чем ионов.
Но на самом деле условия движения дырок более сложные, чем электронов, и найден-
ные подвижности дырок в жидкостях примерно в 10 раз меньше, чем электронов в оди-
наковых полях. Движение дырок требует квантового механизма резонансного тунне-
лирования электронов между занятым и свободным уровнями состояний с равной
энергией. Вероятность туннелирования через потенциальный барьер И(х) при энергии
Wзависит от следующего фактора:
ехр
—4л
~h~
*1
^2m(V(x)-W)dx
xi
(2.42)
где т — эффективная масса электрона, axj и%2 — пространственные пределы V(x)
при энергии W Если приложено электрическое поле, ширина потенциального
барьера уменьшается и скорость туннелирования увеличивается В поле напря-
2.3. Жидкости 47
женностью 108 В/м электрон получает энергию 0.075 эВ на каждом шагу перехо-
да. Эта энергия должна быть рассеяна, что приводит к нагреву молекул вдоль пу-
ти дырки.
Процессы на электродах
Процессы на электродах играют доминирующую роль при возникновении
пробоя в жидкостях. В большинстве случаев, и особенно в импульсных режимах,
пробой развивается именно от электродов. Избыточные электроны или дырки,
являющиеся основной причиной развития пробоя, могут инжектироваться из ме-
таллических электродов в жидкость. Этот процесс в большой степени определя-
ется детальной структурой границы раздела электрод—жидкость. На Рис. 2.16
изображена граница металл—диэлектрик в состоянии равновесия (при прило-
женном извне напряжении, равном нулю) [Lewis, 1994b]. Облако электронов,
движущихся вокруг положительных ионов в металле, частично распространяется
и в жидкость.
Рис. 2.16. Граница раздела металл—жидкость:
А — положительные ионы в металле; В — внешнее электронное облако;
С — внутренний слой Гельмгольца; D — внешний слой Гельмгольца;
Е — слой объемного заряда Гуи—Чэпмена.
К этому отрицательно заряженному поверхностному слою химически или
физически присоединяется монослой ионов или молекул, которые образуют
внутренний слой Гельмгольца (ВСГ). Этот слой может быть сильно структурирован,
особенно если молекулы в нем полярны. Таким образом, электрические свойства
жидкости в непосредственной близости от электрода сильно отличаются от тако-
вых в остальном объеме жидкости.
За внутренним слоем Гельмгольца следует переходной слой — внешний слой
Гельмгольца, — где поляризация ионов приближается к равновесному состоя-
нию. А за внешним слоем Гельмгольца следует диффузионная область, слой объ-
емного заряда Гуи—Чэпмена, где присутствуют избыточные ионы одного знака.
Это возникает вследствие того, что ионов, притянутых в слои Гельмгольца, недо-
статочно, чтобы скомпенсировать весь заряд на электроде, и остаточное электри-
48 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
ческое поле создает этот дополнительный заряженный слой. В жидкостях с малой
концентрацией ионов этот слой простирается далеко от электрода
Внутренний слой Гельмгольца может стать двойным, особенно если ионы,
движущиеся к поверхности электрода, нейтрализуются не очень быстро. Этому
может способствовать диэлектрическая (оксидная или углеводородная) пленка,
покрывающая металлическую поверхность электрода. При этих условиях напря-
женность электрического поля может достигать 109 В/см. Разность потенциаль-
ной энергии по обе стороны двойного слоя изменяет эффективную работу выхода
электронов [Dekker, 1964], а также облегчает прохождение электронов через ок-
сидный слой.
Модель, описывающая прохождение электронов из металла через диэлектрик
в вакуум, была создана Латамом [Latham, 1981]. С небольшими изменениями она
пригодна и для описания проникновения электронов в жидкость. В соответствии
с этой моделью электроны пересекают диэлектрический слой под воздействием
электрического поля с ускорением, так что попадают в жидкость как горячие
электроны. Модель Латама предсказывает вольт-амперные характеристики, по-
добные описываемым уравнением Фоулера—Нордхейма, но с существенно ины-
ми значениями параметров.
Льюис [Lewis, 1987] предположил, что подобные слои, существующие и на
аноде, увеличивают инжекцию дырок в жидкость.
Если между электродами приложена разность потенциалов, отрицательные ио-
ны и электроны будут отталкиваться от катода, а положительные ионы и дырки —
притягиваться. Противоположные процессы происходят на аноде. Если перенос
зарядов через границу металла затруднен, ионы не могут быть нейтрализованы на
электродах и электроды становятся чрезмерно поляризованными. Это приводит к
существенному увеличению сопротивления всей системы. Заряды, скопившиеся
на поверхности металла, могут значительно изменить распределение потенциаль-
ной энергии по сравнению с картиной классического распределения.
Внешнее приложенное напряжение будет увеличивать максимум распределе-
ния потенциалов, передвигая его ближе к электроду при увеличении напряжения.
При напряженности поля свыше 107 В/м этот максимум приближается к электро-
ду на дистанцию, сопоставимую с размерами атомов. В этом случае влияние внут-
реннего слоя Гельмгольца ослабевает. Если в жидкости (как в воде) присутствуют
полярные молекулы, то они могут присоединиться к электроду с высокой степе-
нью организованности, что радикально изменяет потенциальный барьер. Пере-
нос заряда через границу металл—жидкость возможен только между состояниями
с равной энергией. Перенос электронов с катода на состояние W_ имеет низкую
вероятность, так как уровень Ферми в металле лежит ниже гауссовою распреде-
ления состояний ИС (см. Рис. 2.17). С другой стороны, перенос к состоянию ИС
становится легче, так как зона этих состояний находится существенно ниже
энергии Ферми. Аналогичные рассуждения относятся и к дыркам на аноде, где
перенос электронов из состояния ИС достижим легче. Скорость переноса зарядов
будет зависеть от плотности занятых состояний в эмитирующем материале, кото-
рые перекрываются с плотностью свободных состояний в зоне приема зарядов, и,
конечно, от вероятности туннелирования.
2.3. Жидкости 49
То?2эВ
W(0)
6.5 эВ
W.(0)
Уровень вакуума
—►
P(W)
Рис. 2.17. Условия на границе раздела между металлическим катодом и диэлектрической жид-
костью до (вверху) и после (внизу) контакта. Перенос электронов к отрицательно за-
ряженным ионам с состояниями И<_ энергетически труден, а перенос к положитель-
но заряженным ионам с состояниями W+ легок. Однако скорость переноса зависит от
числа свободных состояний в приграничном слое жидкости. Перекрытие между со-
стояниями, занятыми свободными электронами в металле, и свободными состояния-
ми И<_ в жидкости может возникнуть при высокой напряженности поля.
2.3.2. Стримерный пробой
В зависимости от их направления стримеры называются положительными и
отрицательными. Положительные стримеры распространяются к катоду, а
отрицательные — к аноду. Кроме того, стримеры обеих полярностей классифици-
руются как первичные, вторичные и третичные в зависимости от их структуры,
напряженности поля при их возникновении и скорости распространения. В
Табл. 2.8 приведены встречающиеся виды стримеров.
50 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Таблица 2.8. Типы стримеров в трансформаторном масле [Badent, 1996]
Тйп Структура Скорость [км/с] Напряженность поля при возникновении стримера [МВ/м] Диаметр главной ветви [мкм] Свечение
Положительная полярность
Первичные Нить или зонтик 2...3 400...600 10...50 Нет
Вторичные Ветвь ели 11...32 1200... 1600 80...90 Нет
Третичные Тонкий канал с ма- ленькими ответвлени- ями > 100 >2000 80...90 Да
Отрицательная полярность
Первичные Голова, как дерево без листьев 1...16 300...400 30...70 Нет
Вторичные Голова, как дерево без листьев; малое развет- вление 3...55 300...400 30...70 Нет
Третичные Тонкий канал с ма- лым разветвлением >65 400...2000 30...70 Да
Медленные стримеры имеют кустообразную форму, в то время как быстрые —
нитеобразную. Фотографирование теневым методом показало, что стримеры со-
стоят из газообразной фазы. Таким образом, электрическая прочность жидкостей
должна возрастать с увеличением давления. И действительно, было установлено
ее повышение в 3...4 раза при увеличении давления до 40 бар (для трансформа-
торного масла). С другой стороны, температура имеет второстепенное значение.
В ходе распространения между электродами скорость стримеров проходит через
минимум. Если длительность импульса напряжения недостаточна, то канал стри-
мера распадается на цепочку пузырьков.
Катодная инициация
Основным процессом при возникновении отрицательных стримеров является
инжекция горячих электронов в жидкость, как было описано выше, или из точек
эмиссии в диэлектрике (оксиде), или с металлических микровыступов. Такие
точки эмиссии не обязательно расположены на поверхности электрода, но могут
быть связаны и с частицами примесей в жидкости. Как бы там ни было, в боль-
шинстве случаев эмиссия начинается от электродов, особенно под воздействием
импульсных электрических полей. Если инжектируемая плотность тока электро-
нов в жидкость достаточно велика, на поверхности электрода могут сформиро-
ваться газовые пузырьки с критическим размером и плотностью. Джонс и Кун-
хардт проанализировали этот процесс и получили в результате, что необходимым
условием для формирования стабильного центра парообразования является со-
здаваемая адиабатически удельная плотность энергии в 109Дж/м3 (для воды)
[Jones and Kunhardt, 1995а, Ь]. Этот критерий сохраняется для широкого диапазо-
на плотности энергии и внешнего давления. Значительно меньше энергии требу-
ется для расширения центра парообразования до критического размера при до-
2.3. Жидкости 51
статочно низкой плотности (л < лс), когда имеет место ударная электронная ио-
низация и стример может расти в газе до критического значения агс = 18. Здесь
а — коэффициент иойизации, а гс — радиус пузырька; агс = 18 является необхо-
димым условием возникновения стримера в газе (см. разд. 2.2). Для воды гс и лс
составляют около 10~6 м и 1.4 х 1026 м-3 соответственно.
Еще не вполне понятно, с помощью какого механизма столь большие плот-
ности электронного тока, приводящие к требуемому для образования пузырьков
перегреву, могут быть созданы в жидкости. Кажется, что для создания требуемого
туннельного тока необходимы невообразимо большие локальные значения на-
пряженности поля. Однако значение туннельного тока ограничено числом до-
ступных состояний в приграничном слое жидкости, и поэтому представляется
неправдоподобным, что в него может быть эмитировано достаточно свободных
электронов. Электроны, попавшие в состояния РИ+, становятся локализованны-
ми, а эмиссия в состояния ИС — энергетически трудна. Вследствие этого недавно
было предположено, что важную роль в инжекции электронов в жидкость может
играть электрокапиллярность [Lewis, 1998]. Электрокапиллярность создает рас-
тягивающую механическую силу, направленную перпендикулярно приложенно-
му электрическому полю, и может создавать пустоты в жидкости и маленькие
трещины в приграничном слое жидкости. Другим сценарием образования участ-
ков с пониженной плотностью является стимуляция высвобождения газов, рас-
творенных в жидкости. Это преимущественно может происходить при неровных
поверхностях электродов.
Полевая эмиссия в свободные зоны облегчена и может таким образом обеспе-
чить инжекцию достаточного числа электронов для возникновения стримеров в
жидкости. Но вскоре после начала эта эмиссия останавливается из-за образова-
ния отрицательного пространственного заряда в жидкости, который ослабляет
поле вблизи центров эмиссии и усиливает его в жидкости, в передней части про-
странственного заряда. В зависимости от силы электрического поля могут сущес-
твовать различные механизмы переноса электронов в жидкости, как было отме-
чено в разд. 2.2. Разница в подвижности электронов, связанная с этими процесса-
ми, приводит к различию скоростей нагрева вдоль пути электронов и создает
участки с пониженной плотностью, а в итоге образуются газовые каналы. Элект-
роны в этих каналах могут ускоряться по направлению к острию стримера и попа-
дать в жидкость, где они формируют новое облако пространственного заряда, и
начинается новый цикл нагрева и испарения. В этом циклическом процессе важ-
но отметить, что участок между облаком пространственного заряда в жидкости
впереди канала и границей газового канала становится нагрет достаточно для
формирования области с малой плотностью до того, как пространственный заряд
начнет отталкивать дополнительные электроны (Рис. 2.18). В противном случае
распространение стримера прекращается, и он распадается. Другим условием яв-
ляется достаточная проводимость хвостовой части разрядного канала, обеспечи-
вающая потенциал его передней части близким к потенциалу электрода.
Когда стример приближается к аноду, поле вблизи его острия увеличивается и
другие, более эффективные механизмы переноса электронов могут стать возмож-
ными, что приводит к ускорению нагрева и тем самым увеличению скорости рас-
52 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
пространения стримера, вызывая при этом возникновение вторичных, а если на-
пряженность поля очень высокая, то и третичных стримеров [Badent, 1996].
Наблюдалось, что если дистанция захвата электронов в головной части стри-
мера уменьшена путем добавления в жидкость веществ-поглотителей, то ско-
рость распространения стримера увеличивается [Devins et al., 1981]. Это явление
может быть объяснено с помощью модели, рассмотренной выше, если учесть тот
факт, что когда энергия электронов высвобождается в меньшем объеме, то требу-
ется меньшее время для формирования области с малой плотностью. Вместе с тем
примеси, уменьшающие ионизационный потенциал, не оказывают заметного
влияния на скорость распространения стримеров.
Положительный стример
Рис. 2.18. Возможные сценарии продвижения отрицательных и положительных стримеров в
жидкости. Инжекция горячих электронов из центров эмиссии на катоде приводит к
локальному нагреву жидкости и, если напряженность электрического поля достаточ-
но велика, а избыточные электроны можно рассматривать как квазисвободные вы-
зывает расширение газового канала стримера. Электроны со стороны анода, высво-
божденные из ловушек и молекул с низким потенциалом ионизации, притягиваются
в область увеличенного поля и снова могут передать достаточно энергии жидкости,
если локальное поле достаточно сильное для формирования области с малой плот-
ностью. Положительный пространственный заряд, остающийся сзади, способствует
увеличению локального поля.
2.3. Жидкости 53
Анодная инициация
Постижение процессов, происходящих при анодной инициации, еще труд-
нее. В соответствии с [Lewis, 1987] положительный стример может возникнуть
вследствие инжекции дырок из микрочастиц оксида на поверхности анода. Ин-
жекция дырок может существовать не только на границе раздела металл—жид-
кость, но и на границе жидкость—плазма в стримере. Однако распространение
дырок в жидкости может происходить только через механизм электронного резо-
нансного туннелирования, которое имеет весьма низкую вероятность при наблю-
даемых напряженностях поля, вызывающих пробой.
Другим механизмом анодной инициации стримеров, рассмотренным Баде-
нтом [Badent, 1996], было освобождение электронов из ловушек, квазилокальных
состояний, или из молекул с низким потенциалом ионизации электрическим по-
лем вблизи микровыступов на аноде. Эти электроны ускоряются в направлении
центров увеличенного ноля на металле анода (Рис. 2.18). Затем пространствен-
ный заряд, связанный с облаком электронов, увеличивает поле вблизи микровы-
ступов, что вызывает пробой между облаком электронов и вершиной микровы-
ступа, причем выделяющаяся энергия оказывается достаточной для образования
области пониженной плотности. Ионы, оставшиеся позади, в жидкости, создают
свое облако пространственного заряда, которое уменьшает поле между этим об-
лаком и передней частью разрядного канала и увеличивает поле в направлении к
катоду. Для продвижения газового канала стримера область пониженной плот-
ности должна возникнуть до того, как положительный объемный заряд ионизи-
рованных молекул уменьшит поле перед головной частью стримера ниже крити-
ческого значения. И снова увеличение поля вблизи головы стримера может со-
храняться, только если проводимость канала остается достаточно большой.
Это описание возбуждения положительных стримеров и их продвижения не
противоречит экспериментам, в которых поглотители электронов (например, SF6
или СС14) не оказывали какого-либо действия, а примеси, снижающие потенциал
ионизации, приводили к увеличению скорости стримеров [Beroual, 1993].
Вода
Вода — один из наиболее важных жидких диэлектриков, применяемых в сис-
темах с импульсами большой мощности. Она имеет сравнительно высокую элек-
трическую прочность (до 3 х 107 В/м) при длительности импульсов до микросе-
кунды и благодаря высокой диэлектрической проницаемости0 способна накап-
ливать достаточно много энергии за короткое время. Большинство рассуждений,
приведенных выше относительно электрических характеристик органических
диэлектриков, справедливы и применительно к воде. Однако следует упомянуть и
некоторые отличия. По сравнению с молекулами органических жидкостей моле-
кулы воды имеют простую структуру, и внутримолекулярный перенос электронов
становится незначительным. Молекулы воды имеют большой дипольный момент
и свойства воды в слое вблизи границы с металлом сильно отличаются от таковых
*’ Около 81 до частот 1 ГГц или длительности фронта 1 нс. — Примеч. пер.
54 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
в толще. Ориентация молекул воды вблизи металлической поверхности зависит
от полярности. Методом рассеяния рентгеновских лучей было найдено, что вбли-
зи катода ориентация молекул оказывается «кислородом кверху», в то время как
вблизи анода — «кислородом вниз». При этом в первом слое воды создается на-
много большая плотность, чем в ее объеме [Toney et al., 1994]. Предполагается,
что эта структура создает сильное препятствие переносу электронов и формиро-
ванию зазоров в пограничном слое из-за электрокапиллярности.
Небольшая часть (10“7) молекул воды всегда диссоциирована на ионы Н+ и
ОН". Эти ионы создают остаточную удельную проводимость 4 х 10-6 См/м даже у
очень чистой воды. Таким образом, д ля постоянного напряжения вода является не
подходящим изолятором. Ионы в воде движутся к электродам и влияют на струк-
туру пограничного слоя, а следовательно, и на перенос электронов. Несмотря на
это, ионный ток не влияет на развитие пробоя при длительностях импульсов на-
пряжения менее микросекунды. Это было продемонстрировано даже с одномо-
лярным раствором соли (58.454 г соли на 1 л воды) [Jones and Kunhardt, 1994]. Вода
также растворяет большое количество газов (N2,02, СО2), что может приводить к
образованию газовых пузырей и тем самым способствовать появлению стримеров.
Было найдено, что динамическая электрическая прочность воды возрастает при
увеличении давления и что время задержки пробоя в дважды дистиллированной
воде без газов становится больше на 50% [Jones and Kunhardt, 1994].
2.3.3. Практические соображения
Как и газы, жидкости имеют большое положительное качество самовосста-
новления, т. е. после пробоя их электрическая прочность возвращается к перво-
начальному значению. Вода, широко применяемая в качестве изолятора в техни-
ке коротких импульсов, имеет высокое значение диэлектрической проницаемос-
ти (е « 81), что позволяет накапливать энергию с высокой плотностью.
В жидкостях с высокой степенью очистки электрическая прочность изоляции
составляет около 100 МВ/м. К сожалению, жидкости легко загрязняются, а многие
виды загрязнений представляют собой твердые частицы и растворенные газы. Если
напряжение приложено постоянно, твердые частицы выстраиваются параллельно
силовым линиям поля и искажают его, так что пробой может возникнуть при отно-
сительно более низком напряжении. Такое выстраивание примесей является срав-
нительно медленным процессом, и маловероятно, что это воздействует на электри-
ческую прочность при импульсах напряжения короче 1 мс. В общем влияние при-
месей не велико при импульсах длительностью не более нескольких микросекунд.
В дополнение к твердым частицам растворенные газы оказывают влияние на
электрическую прочность жидкостей. Под воздействием электрического поля
растворенные газы могут выйти из раствора, образуя пузыри. Так как напряжен-
ность поля в пузырях увеличивается, в них могут возникать ионизация и образо-
вываться лавины, что приводит к снижению электрической прочности пузырей
по сравнению с таковой у жидкости. Разряды в пузырях воздействуют на жид-
кость таким образом, что возникает больше газа и пузыри растут в размерах.
Минеральное масло также является одним из наиболее важных жидких диэ-
лектриков. Оно используется как изоляционная и теплоотводящая среда в транс-
2.3. Жидкости 55
форматорах, проходных изоляторах и конденсаторах. Минеральное масло спо-
собно абсорбировать влагу, что уменьшает его электрическую прочность [Kiichler,
1996]. Способность масла растворять воду возрастает с увеличением температуры.
Таким образом, изоляционные свойства масла следует держать под контролем,
особенно в негерметизированных системах. Частичные разряды разлагают масло
Выделяющиеся при этом Н2, СН4, С2Н4 и другие газы могут скапливаться в том
или ином месте, что влечет за собой катастрофическую аварию высоковольтной
системы. Состав газов, растворенных в масле, может быть использован для диа-
гностики и идентификации вида неисправности, т. е. коронного разряда, искре-
ния или образования электрической дуги.
Вследствие склонности к загрязнению жидкости не следует использовать для
изоляции при постоянной напряженности поля выше, чем 10 МВ/м. Очень часто
жидкости применяют совместно с твердыми диэлектриками, где они обеспечива-
ют заполнение пустот и выдавливают газовые включения. Пропитанная маслом
бумага широко используется как изолятор в высоковольтных конденсаторах.
Из рассуждений, представленных в предыдущем разделе, с очевидностью сле-
дует, что электрическая прочность жидкостей должна зависеть от времени. В им-
пульсных системах изолирующая жидкость очень часто подвергается воздейс-
твию коротких импульсов. Дж. С. Мартин и его сотрудники в Олдермастоне из-
мерили электрическую прочность трансформаторного масла и воды в
микросекундном диапазоне длительностей воздействия и получили различные
эмпирические формулы, которые очень полезны для конструирования импуль-
сных генераторов [Martin et al., 1996]. Эти формулы представлены далее. Однако
следует обратить внимание на диапазон их применимости и тот факт, что они яв-
ляются приближенными. Также важно отметить, что напряжение пробоя, полу-
чаемое из этих формул, соответствует вероятности пробоя 50%. Для определения
полей с более высокими запасами по безопасности следует использовать элемен-
ты статистики Вейбулла (см. ниже).
Однородное распределение поля
Так как в жидкостях импульсный пробой начинается с электродов, напряжен-
ность поля при пробое должна зависеть от их площади. Для однородного поля и
импульсов длительностью 10мкс>г>0.1 мкс напряженность поля при пробое
приблизительно определяется из выражения
£г1/зЛ1/ю = ^±> (2.43)
где Е— напряженность электрического поля, превышающая порог для статичес-
кого пробоя в МВ/м, t— эффективная длительность импульса в мкс, А — пло-
щадь электрода в см2. Эффективная длительность импульса определяется как его
длительность, при которой напряжение превышает значение 0.63VMAX. Констан-
ты к равны:
• для трансформаторного масла к± = 0.5;
• для воды к+ — 0.3, к_ = 0.6.
Для полей со слабой дивергенцией в выражении (2.43) должно применяться
максимальное поле в приэлектродной области с учетом эффекта поляризации, а в
56 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
качестве значения А принимается площадь электрода, подверженная воздействию
поля с напряженностью более 90% от максимального значения. Для более корот-
ких интервалов времени, 7 нс < t < 30 нс, и напряжений в диапазоне О.4.. 1.1 МВ
для воды было получено несколько иное выражение [WnDevender, 1976]:
£/0.39^0.06 = 0 304 х j0.65 (2.44)
Для обеспечения лучшего совпадения с результатами экспериментов Ван Де-
вендер счел необходимым ввести в формулу расстояние между электродами d. Все
размерности в этой формуле такие же, как и в (2.43); d выражено в см.
При воздействии коротких импульсов напряжения электрическая про-
чность воды становится сопоставимой с прочностью других жидких изолято-
ров. При 1 мкс она достигает 40 МВ/м. Если вода используется в качестве диэ-
лектрика в системах импульсного накопления энергии, то она должна быть деи-
онизована не столько из-за влияния примесей на импульсную электрическую
прочность, сколько для ограничения потерь, связанных с проводимостью. Как
было отмечено выше, благодаря диссоциации молекул даже полностью деиони-
зованная вода имеет остаточную проводимость о = 4 х 10-6 См/м. Постоянная
времени саморазряда для воды равна т = еео/о =180 мкс. При контакте с возду-
хом, из-за растворения и диссоциации СО2, проводимость воды увеличивается
до о = 10"4 См/м, что приводит к т = 7.3 мкс. Таким образом, энергия в систе-
мах с водяной изоляцией может храниться только в течение весьма короткого
времени, определяемого меньшим из значений, связанных с пробоем (2.43) или
саморазрядом.
Сильно неоднородное распределение поля
Средняя скорость стримеров была измерена с конфигурациями электродов
«точка—плоскость» и «ребро—плоскость» для ряда жидкостей при напряжении
0.1...5.0 МВ. Полученные эмпирические формулы особенно полезны при конс-
труировании ключей с жидким диэлектриком.
В диапазоне 0.1...1.0 МВ для минерального масла и других органических жид-
костей применимо выражение
v=d/t = kUn, (2.45)
где и— средняя скорость стримеров, см/мкс,
U— приложенное напряжение, МВ.
Отметим, что и зависит от U и не зависит от напряженности поля Е. Это отра-
жает тот факт, что напряженность поля Е в головной части стримера определяется
только приложенным напряжением и радиусом канала стримера. Параметры, ис-
пользуемые в выражении (2.45), приведены в Ткбл. 2.9.
Таблица 2.9. Параметры, используемые в формуле (2.45)
Жидкость А+ л+ л_
Масло 90 1.75 31 1.28
Глицерин 41 0.55 51 1.25
СС14 168 1.63 166 1.71
2.3. Жидкости 57
В диапазоне 1...5 МВ разница между положительными и отрицательными
стримерами в масле исчезает, для обеих полярностей становится справедливым
выражение
и/1/4 = 6.35 х IO"5 UL6. (2.46)
Для воды соответствующие соотношения различаются сильнее. В диапазоне
0.1...1.0 МВ и длительности импульса более 100 нс получается:
• U,/2 = 2.21 х 10-2 UQ 6 — для положительной точки,
• ь//3 = 4.02 х 10-41/11 — для отрицательной точки, (2.47)
где и — в м/с, U— в В, t — в с. Из (2.47), введя и = d/t и EBR = U/d, мы можем по-
лучить выражение для электрической прочности:
• EBR = 5.47 х 102d1,3/t0 833 — для положительной точки,
• Ebr = 1.22 х 103/(d0.0909^0.606^ _ ддн отрицательной точки. (2.48)
На Рис. 2.19 приведены графики зависимости импульсной электрической
прочности воды от длительности импульсов напряжения, построенные на основе
зависимостей (2.48). Обращает на себя внимание быстрое увеличение электри-
Длительность импульса [с]
Рис. 2.19. Средняя импульсная электрическая прочность воды для конфигураций «точка—плос-
кость» или «ребро—плоскость». Графики построены для зазора 4 см и амплитуды им-
пульсов 0.1.„1.0 МВ.
ческой прочности при уменьшении длительности импульсов. Эта особенность
является основой некоторых применений воды в импульсных системах большой
мощности, которые мы рассмотрим в гл. 11.
58 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
2.4. Твердые тела
2.4.1. Общие замечания
Явления пробоя твердых диэлектриков нераздельно связаны с разрушением
структуры диэлектрика электронами или ионами, которые получают достаточно
энергии от электрического поля. Несмотря на то что средний свободный пробег
электронов в твердом теле является спорным понятием, весьма поучительно об-
судить вопрос о том, какой средний свободный пробег для электронов был бы не-
обходим при заданной напряженности поля, чтобы получить энергию, требуемую
для создания различных видов повреждений в твердом теле.
На Рис. 2.20 линии равного получения энергии электронов за время свобод-
ного пробега построены в координатах среднего свободного пробега и напряжен-
ности электрического поля. Энергии сильных связей в твердых телах составляют
несколько эВ, в то время как энергии, требуемые для ударной ионизации, нахо-
дятся в диапазоне 10...20 эВ.
Рис. 2.20. Соотношения между напряженностью электрического поля Е, средним свободным
пробегом I и получаемой зарядом энергией за время среднего свободного пробега для
твердого тела.
В Табл. 2.10 приведены значения статической электрической прочности для
ряда диэлектриков. На практике типовое значение электрической прочности
твердых диэлектриков находится в районе 100 МВ/м. Используя эти данные,
можно заключить, что для разрыва связей и ионизации вещества требуется сред-
ний свободный пробег в диапазоне 0.1...1.0мкм при наблюдаемых значениях
электрической прочности. Такой свободный пробег может возникнуть только в
некоторых кристаллических веществах, таких как щелочегалоиды (например, по-
варенная соль), в которых, в дополнение к этому, энергия, накапливаемая при не-
2.4. Твердые тела 59
скольких поочередных столкновениях, создает хвост распределения энергии
электронов. Однако шансы вызвать лавину электронов в решетках типа 1-D или
2-D, характерных для полимеров, очень малы. Таким образом, можно заключить,
что электрическое разрушение может произойти, только если порог разрушения
снижен или если электроны получили возможность иметь достаточно большой
свободный пробег. Весьма возможно, что в твердых телах имеет место комбина-
ция этих явлений.
Таблица 2.10. Диэлектрическая проницаемость и электрическая прочность некоторых
изоляционных материалов
Диэлектрик Диэлектрическая проницаемость, с Электрическая прочность [МВ/м]
Воздух 1.0 3.0
Оксид алюминия 7.0 11.8
Композиция титанат бария + + наполнитель 500...6000 2.0
Каптон 3.6 275
Бумага, пропитанная маслом 6 78
Люсит 3.3 20
Майлар 2.5 200
Полиэтилен 2.2 177
Полипропилен 2.5 378
Полисульфон 3.1 315
Стекло пирекс 4...6 20
SF6 1.0 8 (при атм. давл.)
Тефлон 2.0 59
Трансформаторное масло 2.2 10...40
Вода 80 20 (для t < 10 мкс)
Прежде чем обсуждать возможные механизмы, которые могут создавать необ-
ходимые условия для пробоя, просуммируем некоторые общие черты пробоев в
твердых диэлектриках, наблюдаемые экспериментально.
Величина напряженности поля, вызывающего пробой, зависит от множества
факторов, таких как временная зависимость электрического поля, конфигурация
образцов и материал электродов. В общем было найдено прогрессирующее
уменьшение электрической прочности с увеличением толщины образца, в то вре-
мя как временная зависимость описывается статистикой Вейбулла (см. ниже).
На Рис. 2.21 схематически отображена зависимость электрической прочности от
времени экспозиции и толщины образца. Самая высокая электрическая прочность
достигается за короткое время и у тонких образцов. Область вокруг начала кривых на
Рис. 2.21 называется «внутренней» электрической прочностью. Это та прочность, ко-
торую данное вещество имело бы в отсутствие дефектов и внешних воздействий, на-
пример инжекции зарядов из металлических электродов. «Внутренняя» электричес-
кая прочность на два-три порядка больше, чем расчетные значения, используемые
на практике. Наиболее высокие зафиксированные значения электрической про-
чности для ряда различных веществ находятся в пределах 100... 1000 МВ/м, хотя для
щелочегалоидов электрическая прочность ниже 100 МВ/м.
60 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Рис. 2.21. Схематическое изображение зависимости электрической прочности Ев
от времени экспозиции t и толщины образца d.
У большинства изоляционных материалов электрическая прочность не зави-
сит от температуры (начиная от криогенной и вплоть до критически высокой),
когда она падает очень сильно
Общие экспериментально установленные черты пробоев в твердых диэлект-
риках можно просуммировать так [Jonscher and Lacoste. 1984]:
• Пробой имеет вероятностный характер. Он подчиняется распределению
Вейбулла (см. ниже), которое включает интеграл по времени и напряжен-
ности поля, отражающий эффект памяти в веществе.
• «Внутренняя» электрическая прочность лежит в очень узком диапазоне для
физически и химически различных веществ.
• Конечным результатом пробоя всегда является формирование узкого плаз-
менного канала. Другие видимые явления предшествуют и сопровождают
пробой, но канал при этом не образуется.
• Инжекция электронов с электродов ускоряет возникновение пробоя.
Наличие макроскопических дефектов в материале изолятора (т. е. пустот или
проводящих включений) сокращает время пробоя. Скорость снижения электри-
ческой прочности со временем (старение) материалов подвержена сильному вли-
янию инжекции носителей заряда и захвату их ловушками. Другими факторами
являются возбуждаемые электрическим полем механические нагрузки, которые
приводят к формированию микропор и диффузии загрязнений.
2.4. Твердые тела 61
2.4.2. Перенос зарядов, инжекция и пробой
На основе общих результатов экспериментальных исследований, описанных
в предыдущем подразделе, Джоншером и Лакостом была разработана феномено-
логическая модель пробоя [Jonscher and Lacoste, 1984]. В этой модели предполага-
ется, что материал подвергается повреждению до того, как произойдет его окон-
чательный пробой. Однако ничего не сказано о молекулярном механизме этих
повреждений. Тем не менее улучшение электрической прочности твердых диэ-
лектриков, которого от нас требует будущее, диктует необходимость детального
изучения фундаментальных электрических свойств этих материалов. Электри-
ческий пробой должен, как минимум, начинаться с молекулярного уровня. Таким
образом, в этом подразделе мы будем рассматривать перенос зарядов, инжекцию
зарядов и пробой сначала на молекулярном уровне, следуя при этом описаниям
этих процессов, приведенным в [Lewis, 1984, 1989, 1990; Lewis and Bowen, 1984;
leda, 1984; Zeller et al., 1984].
Перенос зарядов
На сегодняшний день наиболее важными твердыми изоляционными матери-
алами в технике мощных импульсов являются органические полимерные диэлек-
трики, такие как полиэтилен или литая эпоксидная смола. Эти диэлектрики со-
стоят из длинноцепочечных молекул с сильными ковалентными связями в цепи и
слабыми вандерваальсовыми силами между цепями. Они могут образовывать как
регулярные кристаллические, так и аморфные области. На Рис. 2.22 приведено
схематическое изображение структуры полукристаллического полимера. Крис-
таллические чешуйки (около 1 мкм в длину и 10 нм в толщину) состоят из линей-
ных, параллельных цепей, образующих стабильную орторомбическую сетку, пре-
Рис. 2.22. Схематическое изображение чешуйчатой структуры полукристаллического полиме-
ра. Связанные молекулы соединяют два кристаллических участка. Окончания цепей
молекул, их скрутки, петли и складки существуют в аморфном участке, а параллель-
ные цепи формируют кристаллическую чешуйку.
62 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
рываемую аморфными участками толщиной 1...10 нм. Кристаллические участки
могут быть связаны цепями молекул, пересекающими аморфные участки. В зави-
симости от метода производства до 80% объема полиэтилена может быть в крис-
таллической форме. Примеси, включающие газы и воду, сравнительно легко мо-
гут быть встроены в аморфные участки.
Сложная структура полимеров весьма усложняет моделирование их электро-
проводности. Внутри периодического распределения потенциалов вдоль молеку-
лярной цепи пространственно расширенные состояния электронов порождают
формирование структуры с раздельными энергетическими зонами, соответству-
ющими зонам проводимости и валентности в полупроводниках (Рис. 2.23).
Рис. 2.23. Зонная структура участка протяженной цепи молекул полимера, совпадающего по
направлению с полем. При очень сильных полях избыточные электроны, освободив-
шиеся из ловушек, могут двигаться в квазисвободном состоянии в зоне проводимос-
ти вдоль цепи. В конце цепи, чтобы достичь следующей цепи, они должны совершить
туннельный переход.
Вследствие слабой связи между цепями молекул справедливо предположить,
что электронные состояния в твердых полимерах подобны таковым в изолиро-
ванных молекулярных цепях. Вследствие того что электронное сродство у моле-
кулярных цепей полиэтилена отрицательно (зона проводимости находится при-
мерно на 1 эВ выше уровня для вакуума), по путям между цепями перенос сво-
бодных электронов происходит быстрее, чем по путям внутри цепей [Lewis, 2002].
Электроны будут двигаться в периодическом потенциале вдоль поверхности це-
пи. Дырки, напротив, могут существовать только в валентной зоне. Таким обра-
зом, их перенос должен осуществляться внутри молекул. Оба механизма переноса
зарядов осуществляются легче вдоль звеньев, лежащих в направлении приложен-
ного электрического поля. Окончания цепей молекул, их скрутки, складки и раз-
ветвления нарушают периодичность и приводят к локализации зарядов. Дальней-
шее их движение может происходить только за счет перепрыгивания или тунне-
лирования между изолированными состояниями. Подобный механизм был
описан в разд. 2.3 для переноса электронов между зонами на малых расстояниях в
жидкости. Скорость переноса электронов очень чувствительна к природе потен-
2.4. Твердые тела 63
циального барьера. Для ее оценки Реди и Хопфилдом [Redi and Hopfield, 1980]
было получено упрощенное выражение, видоизмененное Льюисом [Lewis, 1990]:
Аь = vabexp(—2 aab/?)exp(- W&b/kT), (2.49)
где vab— частота повторных попыток освобождения, равная 1О12...1О13 с-1;
ааЬ— коэффициент перекрытия волновых функций состояний на участках а
и Ь, находящихся на расстоянии А;
И^ь— разность энергий между состояниями а и Ь, включая энергии преобра-
зования Аа и Аь (см. ниже).
Наряду с возможностью захвата ловушками в основных молекулярных зве-
ньях электроны и дырки могут быть захвачены ловушками, создаваемыми при-
месями. В полиэтилене были найдены примеси (Na+, К+, СГ и О2) с плотнос-
тями порядка 1023/м3. Акцепторы и доноры этих видов приводят к преобразова-
нию окружающих полимерных матриц в зависимости от их заряда. Связанная с
этим энергия преобразования А действует так же, как мы уже обсуждали в
разд. 2.3 применительно к жидкостям. Когда заряд переносится в такой участок
или из него, поляризация будет изменяться в соответствии с новым состоянием
заряда. Поэтому А становится зависящей от продолжительности времени, в те-
чение которого состояние заряда не изменяется. Такие же рассуждения спра-
ведливы и применительно к зарядам, захваченным ловушками в полимерных
молекулах.
Продолжительность пребывания (время прилипания) /tr в любом локализо-
ванном состоянии, которая обратно пропорциональна РаЬ, сильно зависит от раз-
ности энергий между состояниями И^ь. Для характерных значений vab и ааЬЯ это
время составляет 6 ч при И^ь = 1 эВ и 10-9 с при И^ь = 0.2 эВ.
Контакт металл—диэлектрик
Большая ширина запрещенной зоны в полимерах-изоляторах (> 8 эВ) делает
маловероятной тепловую генерацию подвижных носителей заряда. Создание
подвижных носителей зарядов происходит только путем введения подходящих
примесей или инжекцией электронов или дырок из металлических электродов.
Металлический электрод, находящийся в контакте с твердым диэлектриком,
будет переносить заряд в диэлектрик. Измерения показали, что примерно 1 из 103
состояний на поверхности полимера становятся либо окисленными, либо восста-
новленными вследствие этого переноса заряда [Bouattou and Lowell, 1988]. Меха-
низмом этого переноса опять служат резонансное туннелирование, включающее
свободные и занятые электронные состояния в металле вблизи уровня Ферми, и
донорные и акцепторные состояния на поверхности полимера. Здесь картина по-
добна той, которая имеет место для контакта между металлом и жидким диэлект-
риком (Рис. 2.17). Так как и донорные, и акцепторные состояния могут совмест-
но существовать на поверхности полимера, то и электроны, и дырки могут пере-
мещаться между металлом и поверхностью полимера, хотя и с разными
скоростями. Под воздействием сильного электрического поля знак инжектируе-
мых зарядов может локально изменяться, так как энергетические зоны в диэлект-
рике сдвигаются относительно уровня Ферми. Если заряд остается на поверхнос-
64 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
тных состояниях, дальнейшее туннелирование останавливается и перенос заря-
дов на поверхность диэлектрика блокируется.
В сильных электрических полях из-за того, что становятся доступными состо-
яния с более высокой энергией, из металла в диэлектрик будет переходить боль-
ше носителей заряда. В то же время заряды могут с поверхности проникнуть
внутрь полимера, уменьшая блокирующее действие поверхностного заряда. Про-
никновение зарядов внутрь полимера происходит вдоль молекулярных цепочек в
направлении силовых линий электрического поля. При еще более высоком элек-
трическом поле электроны могут достичь возбужденных состояний. Выход из
возбужденного состояния сопровождается высвобождением энергии, которая от
электронов передается молекулам и нагревает их. В конечном счете при самой
высокой напряженности поля электроны могут достичь зоны с расширенными
состояниями проводимости (см. Рис. 2.23). Здесь единственным механизмом рас-
сеяния энергии становится возбуждение колебаний в кристаллической решетке,
и может быть достигнута кинетическая энергия, достаточная для ионизации. Од-
нако эта зона проводимости будет еще ограничена степенью совпадения направ-
ления молекулярной цепи с направлением поля. Эффективная подвижность но-
сителей заряда может быть определена в соответствии с (2.48), при этом следует
учитывать различие интервалов времени, которые носители проводят в зоне про-
водимости и в ловушках.
Пробой
Электроны и дырки, инжектированные из металла электродов или высвобож-
денные из мелких ловушек и впоследствии накопленные в молекулярных состоя-
ниях, могут сконцентрировать значительную плотность энергии. Скотхеймом
[Skotheim, 1986] было предположено, что аналогично процессам в проводящих
полимерах восстановленные или окисленные добавки играют важную роль в со-
здании квазисвободных электронов и дырок в объеме вещества. Таким образом,
не только инжекция зарядов из металлической поверхности может привести к ло-
кальной концентрации зарядов. Под воздействием сильного электрического поля
эти заряды могут быть высвобождены за короткое время механизмом каскадного
туннельного перехода. При этом создается путь, по которому проходят следую-
щие заряды. Предполагается, что высвобождаемая энергия в этом процессе спо-
собна вызвать новые и увеличить существующие дефекты.
Эта фаза может быть названа проводящей фазой [Jonscher and Lacoste, 1984].
В таких полимерах, как полиэтилен, электрические и механические свойства
близко взаимосвязаны. Сильные электрические поля способны изменить морфо-
логию изолятора и создать микропустоты. Если плотность дефектов становится
достаточно большой, они могут сливаться вместе и образовывать кластер дефек-
тов. Кластер обеспечивает более свободное движение носителей зарядов, попада-
ющих в него. Таким образом, эти носители достигают возможности получить
больше энергии и расширить кластер, который начинает расти вдоль силовых ли-
ний поля. Электроны могут при этом получить энергию, соответствующую их
среднему свободному пробегу, который составляет много межатомных расстоя-
ний. На этой стадии в материале могут быть видны «елочные ветви».
2.4. Твердые тела 65
При небольших скоростях формирования дефектов тепловой механизм их за-
живления может скомпенсировать дефектообразование, что объясняет существо-
вание пороговых напряженностей полей, ниже которых не происходит пробоев,
сколь долго ни продолжалось бы воздействие поля.
Важной особенностью роста кластеров является самофокусировка. Она воз-
никает после того, как внутри кластера образуется плазма. Так как электроны на-
много подвижнее ионов, они (под воздействием электрического поля) покидают
кластер, и кластер приобретает положительный заряд, который в свою очередь
притягивает новые электроны. Этот процесс сравним с возникновением стриме-
ров в жидкостях.
С увеличением числа случайно распределенных удлиненных кластеров созда-
ется их взаимное выстраивание, создающее благоприятные условия для протека-
ния тока через удобно расположенные дефекты. В этих-то условиях и возникает
канал теплового пробоя. Схематическая иллюстрация к этой кумулятивной моде-
ли пробоя представлена на Рис. 2.24 [Jonscher and Lacoste, 1984].
Напряженность поля Напряженность поля Изменение
меньше пороговой больше пороговой шкалы
4
Увеличение времени экспозиции
ТУ 1 и
О ОО
со
до °
OOQO
о ОО О
<д °
3 О
Равновесие между Новые дефекты
возникновением формируются
и залечиванием быстрее, чем
дефектов залечиваются
"С—ЗТЗ
° о со о
°'
ooqoo 1
о О
Ос о°
О'
06
о<6 оО
Q>° cPcflo
oQx>° X5
Ц} оэ °
QQ Q
Совместное
воздействие
поля и времени
приводит
кобразованию
кластеров
Кластеры Расширившиеся
расширяются дефекты
в направлении выстраиваются
поля и формируют
Фокусирование канал ПР°®ОЯ
вследствие
формирования
заряда
Рис. 2.24. Схематическое изображение развития во времени дефектов под воздействием
электрического поля, приводящего к окончательному пробою диэлектрика.
Из предыдущего обсуждения становится вероятным, что для толстых образ-
цов электрическая прочность зависит от объема материала, находящегося под воз-
действием поля. Пренебрегая зависимостью от времени, что допустимо при дли-
тельности импульсов более 100 нс, Дж. С. Мартин эмпирически определил следу-
ющее выражение для напряженности поля, соответствующего пробою
диэлектриков:
£И1/,0 = Л.
(2 50)
66 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Значения постоянных к для некоторых пластмасс приведены в Табл. 2.11. Для
неоднородных полей используется максимальное значение напряженности поля и
объем, в котором напряженность поля превышает 90% от максимального значения.
Таблица 2.11. Значения постоянных к для некоторых пластмасс
Диэлектрик к
Полиэтилен 2.5
Перспекс 3.3
Майлар 3.6
Также понятно, что электрическая прочность твердых диэлектриков умень-
шается с числом импульсов напряжения. Это уменьшение очень сильно зависит
от отношения рабочего значения напряженности поля F0P к его пробивному зна-
чению Ев:
Mjfe^b/W1. (2.51)
Здесь A\jfe — ожидаемое число импульсов, которое изолятор должен пережить, а
п — коэффициент, зависящий от материала изолятора (для полиэтилена п = 8,
для майлара л = 16).
С точки зрения технологии важно, что при очень коротких импульсах элект-
рическая прочность некоторых жидкостей (особенно воды) выше, чем у множес-
тва твердых диэлектриков. Это наблюдение особенно справедливо для многоком-
понентных и составных материалов, содержащих много дефектов, пор и границ
раздела разных веществ. Этот факт является основой технологии электроимпуль-
сного размельчения, описанной в гл. 12.
2.5. Статистическая интерпретация измерений
электрической прочности
Эмпирические формулы, приведенные выше, основаны на интерпретации эк-
спериментальных результатов с использованием теории надежности. В теории на-
дежности (см., например, [Barlow and Proscan, 1975]) дано определение относитель-
ной ожидаемой интенсивности отказов ^(5)^5для воздействий Sчерез выражение
dn(S) = - n(S) Q(S)dS, (2.52)
где dn(S) — число образцов, вышедших из строя, если воздействие было увеличе-
но от S до 5 + dS в предположении, что n(S) образцов выдержали воздействие 5.
Интегрируя (2.52), получим
ln^ = -fc(S')J5',
«о о
^2 = v(3) = e 0
«о
(2.53)
2.5. Статистическая интерпретация измерений электрической прочности 67
Если предположить, что все образцы подчиняются одинаковым статистичес-
ким распределениям, мы можем также сказать, что y(S) представляет вероят-
ность того, что один образец выдержит воздействие 5. Тогда F(S) = 1 — у(5) — ве-
роятность отказа этого образца, аД5) — соответствующая функция распределе-
ния плотности вероятности:
Для определения интенсивности отказов для определенных технических систем
необходимо найти выражение для относительной ожидаемой интенсивности от-
казов Q. Например, в случае распада радиоактивных ядер относительная интен-
сивность распада £(/) является постоянной (£(/) = а), т. е. не зависит от предыду-
щей «истории», и мы получаем хорошо известный экспоненциальный закон
радиоактивного распада:
л(О/ло = е"аг.
(2.55)
Для технических систем, однако, очень часто интенсивность отказов экспо-
ненциально увеличивается с увеличением воздействия:
US) = aSa.
В этом случае мы получаем вейбулловское распределение отказов:
F(5) = l-e^’'/a+1
(2.56)
(2.57)
Если определить <S> как величину S, при которой вероятность отказа равна
1 — 1/е = 63%, мы можем переписать это выражение следующим образом'
Г(5) = 1-е"у/<5>)
(2.58)
где В= a + 1. Уравнение (2.58) является простейшей формой двухпараметричес-
кого вейбулловского распределения. Как было отмечено ранее, имеется порог So,
при воздействии ниже которого в системе отказы не возникают, вне зависимости
от продолжительности воздействия. Это может быть представлено в виде трехпа-
раметрического распределения Вейбулла, которое применимо при S > Sq:
F(S) = l-e-,(S-5o)/<5>1
(2.59)
Построение графика ln[ 1/( 1 — /)] в двойном логарифмическом масштабе дает
прямую линию, из параметров которой могут быть получены параметры распре-
деления {см. Рис. 2.25).
Измерения напряженности поля, приводящей к пробою, обычно выполняют-
ся с использованием маленьких образцов. Вследствие этого становится необхо-
димым экстраполировать их результаты на большие образцы. Обсудим, как мож-
но выполнить эту экстраполяцию. Для этих целей предположим, что большой
68 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Рис. 2.25. График распределения Вебулла (2.58). Справа по оси ординат указана интегральная
вероятность отказа, соответствующая каждому значению In[1/(1 — Л] Точке F= 63%
соответствует значение <5> на оси абсцисс. Наклон графика в двойном логарифми-
ческом масштабе соответствует значению В = а + 1.
изолятор может быть разделен на N маленьких секций, чьи распределения веро-
ятностей «выживания» y(S/<S>) одинаковы и известны. Затем, в соответствии с
теорией статистики, мы получаем следующее выражение для вероятности
того, что большой изолятор выдержит воздействие 5:
V(S/<5n>) = M$/<S>)]N.
(2.60)
Далее мы предполагаем, что вероятности «выживания» для маленького и большо-
го изоляторов подчиняются одинаковым распределениям (2.58), но с различны-
ми электрическими прочностями <S> и <-5’n>. Используя (2.58), мы можем опре-
делить коэффициент масштабирования для <SN> в зависимости от размера
(площади или объема) изолятора:
_ „-(5/<5>)"jV _ .-(SN1'1 /<$>)*
— V —• V
_ a-(S/<SN>)a
— V
f s
< SN >
(2.61)
= v
/
Таким образом, получается <5N> = <S>/W1/B. Здесь TV пропорционально либо
отношению площадей, т. е. N= An/^j (для жидкостей при импульсных воздейс-
твиях, тонких листов диэлектрика и т. д.), либо отношению объемов, т. е.
/V = (для толстых твердых диэлектриков). При статистической оценке экс-
периментальных результатов еще полезна дисперсия:
2.5. Статистическая интерпретация измерений электрической прочности 69
(о/<5>)2 = Г(1 + 2/В) - Г2(1 + 1/5),
о/<5>=10% =>5=10,
(2.62)
где Г — известная гамма-функция. В некоторых случаях простой расчет диспер-
сии позволяет определить коэффициент масштабирования.
Ранее было отмечено, что величина, которая определяет воздействие на изо-
лятор, пропорциональна j^(E—Eoytvdt, и для импульсного скачка вероятность
отказа 5для Е> Eq получается:
5(5,0 = 1-е^'(£‘д’)‘.
(2.63)
Чтобы определить параметры этого распределения экспериментально, на ис-
пытуемый образец подают импульсный скачок напряжения, создающего фикси-
рованное значение напряженности поля Е= Еа, и измеряют время до пробоя.
Временное распределение событий пробоя получается из F(E, t) путем дифферен-
цирования:
ЛЕа, t) = cat'-'(E. - Е0)‘ехр[-с/«(£а - £b)‘L (2.64)
Это распределение имеет максимум при
>„ = [—(E.-E*)-” I , (265)
I са I
а среднее время до пробоя равно
<4 >=г[— - Q'*",
I a I
(2.66)
где Г — гамма-функция.
Построение графика распределения Вейбулла (2.63) в двойном логарифми-
ческом масштабе позволяет определить значение а и зависимость среднего вре-
мени до пробоя от напряженности поля, а график функции (2.66) позволяет опре-
делить Eq и b/а, когда значения <гь> измерены при нескольких ЕЛ. Из соотноше-
ния F[cf(Ea — 50)ь = 1] =0.632 легко определить с. Таким образом, можно
получить все параметры распределения вероятности пробоя из серии измерений
с различными значениями £а.
В заключение отметим еще раз, что эмпирические формулы, представленные
в предыдущем разделе, справедливы для вероятности пробоя 50%. Если требуется
более высокая степень надежности, следует вернуться к соответствующему рас-
пределению Вейбулла, чтобы рассчитать допустимое воздействие. Рассмотрим
следующий пример.
70 Глава 2. Статическая и импульсная электрическая прочность диэлектриков
Пример
В случае, когда более высокий потенциал приложен к положительному элект-
роду и имеет место однородное распределение поля, электрическая прочность во-
ды определяется выражением (2.43), которое связывает превышение напряжен-
ностью поля порогового значения Е, время t и площадь Л соотношением
Е/,/зу41/,о = Л+ = О.3,
где Е — в MB, t — в мкс, А — в см2. Предположим, что Г = 0.05 мкс и
А = 10 м2 = 105см2. Найдем электрическую прочность при вероятности пробоя
10%. Введем переменную S=Etx,i. Для вероятности пробоя 50% значение Зо.5
равно k+/AXfXQ, из чего прямо выводим, что В = 10.
Таким образом, S подчиняется следующему вейбулловскому распределению
(Рис. 2.25):
——— 1= 1 - е457*5**’*
<S> )
Соотношение между ЗЬ.5и <^> определяется формулой
<r V > = ^° 5 =
(1п2),/л (А 1п2)|/|0
(2.67)
(2.68)
Для нашего примера получается <5> = 9.84 х 10-2. Далее мы должны опреде-
лить So i для Г=0.1, т. е. 1п(1п( 1/0.9)) = 101п(501/<5>), и, таким образом,
So 1 = <5>е~0-225. Следовательно, 50л = 7.85 х 10-2 и Еол = 0.213 МВ/см.
ГЛАВА
НАКОПЛЕНИЕ ЭНЕРГИИ
Любой прибор для накопления энергии, подходящий для применения в сис-
темах генерации мощных импульсов, должен отвечать следующим требованиям:
• высокая плотность энергии;
• высокая электрическая прочность;
• способность обеспечивать большой ток разряда;
• длительное время хранения энергии (малая скорость утечки энергии);
• высокий КПД при заряде и разряде;
• большой коэффициент умножения мощности (отношение мощности при
разряде к мощности при заряде);
• способность к работе с повторяющимися импульсами и долговечность;
• низкая цена.
Очевидно, что некоторые из этих требований противоречат друг другу, и в зави-
симости от области конкретного применения и ограничений, накладываемых, на-
пример, условиями эксплуатации, приходится искать те или иные компромиссы.
3.1. Конденсаторы
Несмотря на низкую плотность запасаемой энергии, высоковольтные кон-
денсаторы являются основой большинства систем генерации мощных импульсов.
Основными причинами этого являются надежность конденсаторов, способность
работы с повторяющимися импульсами и тот факт, что быстродействующие за-
мыкающие ключи намного легче сделать по сравнению с размыкающими ключа-
ми, требующимися при использовании индуктивных накопителей энергии. Кро-
ме того, время хранения энергии у конденсаторов намного больше, чем у индук-
тивных накопителей энергии, что удобнее во многих применениях.
Для конденсатора емкостью С накопленная энергия 1¥с = (\/2)CU2, где U—
напряжение на конденсаторе. Емкость С пропорциональна площади его пластин
А и диэлектрической проницаемости е и обратно пропорциональна толщине диэ-
лектрика d: C=EEoA/d. На Рис. 3.1 представлены основные элементы конструк-
ции конденсаторов. В большинстве конденсаторов электрическое соединение
72 Глава 3. Накопление энергии
Рис. 3.1. Элементы конструкции плоского конденсатора.
между электродами и выводами выполняется либо пайкой, либо прессованием.
Изолирующая полоса вокруг электродов предотвращает поверхностный пробой
между электродами.
Эквивалентная схема конденсатора приведена на Рис. 3.2. Последовательное
сопротивление складывающееся из сопротивлений выводов и электродов,
обычно имеет порядок 0.1 Ом. Параллельное сопротивление R представляет со-
бой сопротивление утечки тока через диэлектрик и материал корпуса. Индуктив-
ность L связана с конструкцией конденсатора и является фактором, ограничива-
ющим пиковый ток разряда: /Р = t/(C/£)1/2. Емкость и сопротивление утечки за-
висят от температуры, напряжения, влажности и времени хранения
конденсатора. Изменения емкости и сопротивления утечки при изменении тем-
пературы для конденсатора с изоляцией, выполненной из бумаги, пропитанной
минеральным маслом, показаны на Рис. 3.3. Еще большее изменение диэлектри-
Последовательное
сопротивление
я
Сопротивление
диэлектрика
и корпуса
L
Индуктивность
электродов и выводов
О
Рис. 3.2. Эквивалентная схема конденсатора
3.1. Конденсаторы 73
Рис. 3.3. Изменения емкости и сопротивления утечки при изменении температуры
для конденсатора с изоляцией, выполненной из бумаги, пропитанной минеральным маслом.
ческой проницаемости при изменении температуры были найдены для эпоксид-
ного компаунда и майлара [Saijeant and MacDougall, 1997].
Помимо электрической прочности, еще двумя важными параметрами диэлек-
трических материалов являются диэлектрическая проницаемость е и тангенс угла
потерь tg 5. Для некоторых широко распространенных материалов эти параметры
приведены в Табл. 3.1.
Таблица 3.1. Свойства некоторых диэлектриков, используемых
для изоляции в высоковольтных конденсаторах
Материал е ЕЬв [кВ/см] tg5
Импрегнированная бумага 3...4 200...800 0.01...0.03
Эпоксидный компаунд 3.5 320 0.014
Майлар 3 400 0.001
Полипропилен 2.55 256 0.0005
Тефлон 2.1 216 0.0002
Кантон 3.4 2800 (25 мкм) 0.01
Плексиглас 3.3 200 0.009
Трансформаторное масло 3.4 400 0.0002
Окись алюминия 8.8 126 0.01
Титанат бария 1143 30 0.01
Боросиликатное стекло 4.84 157 0.0036
Примечание. Здесь EDB — электрическая прочность изоляции
74 Глава 3. Накопление энергии
Высоковольтность конденсаторов определяется не только электрической
прочностью изоляции, но и формой, площадью и видом металла, используемого
для выводов, а также их соединением с изоляцией, заполняющей корпус. Иногда
эти факторы являются определяющими. Кроме того, на высоковольтность оказы-
вают влияние условия эксплуатации. Температура, давление, влажность и изме-
нение полярности приложенного напряжения могут воздействовать на напряже-
ние пробоя.
Когда конденсатор заряжается или разряжается достаточно быстро, его
мгновенная емкость отличается от значения в стационарном режиме. Это явле-
ние обусловлено конечным временем релаксации поляризации, которое также
связано с потерями в конденсаторе. Для рассмотрения этого эффекта предполо-
жим, что к конденсатору приложено переменное напряжение, возбуждающее в
диэлектрике переменное электрическое поле. В общем случае и поляризация Р,
и смещение (индукция) D будут по фазе отставать от приложенного электричес-
кого поля.
Если рассматривать напряженность электрического поля Е на частоте со как
E=E0c°S(o/, (3.1)
мы получим
D = Z>ocos (tot — 5) = D\ cos со/ + £>2 sin «о/, (3.2)
где б — фазовый угол, D\ = Z)0cos 5 и D2 = Z>osin 5.
Для большинства диэлектриков Dq пропорционально Ео, но отношение Dq/Eq
обычно зависит от частоты. Для описания этой зависимости вводят две диэлект-
рические постоянные, зависящие от частоты:
е'(со) = DJEq = (Z)0/E0)cos б,
(3.3)
£"(со) = DJEq = (Dq/Eq) sin 5.
В соответствии с (3.3) мы получаем соотношение
tg 8 = е"(со)/е'(со). (3.4)
Так как е'(со) и е"(со) зависят от частоты, фазовый угол 8 тоже оказывается
частотно-зависимым. Мы сейчас покажем, что энергия, рассеиваемая в диэлект-
рике в форме тепла, пропорциональна е"(со). Плотность тока в конденсаторе
равна
j = dq/dt = dD/dt = со(—D\ sin со/ + D2 cos co/), (3.5)
где использовано выражение (3.2). Здесь q — поверхностная плотность зарядов на
электродах конденсатора. Таким образом, плотность энергии, рассеиваемой в ди-
электрике на единицу объема за единицу времени, равна
2я<»
w = \jEdt. (3.6)
0
3.1. Конденсаторы 75
Подставляя j и Е, легко найти
(3.7)
Корректно было бы коэффициентом потерь называть sin 5; однако часто за ко-
эффициент потерь принимают tg 5. Это допустимо только при малых значениях 5.
В общем диэлектрическая поляризация может рассматриваться как сумма двух
компонент:
P=PS + PD, (3.8)
где индексы S и D указывают на спонтанную и дипольную поляризацию соот-
ветственно. Р$ существует благодаря поляризации электронов и атомов, которая
возникает очень быстро, в то время как PD существует в веществах, состоящих из
молекул с постоянным электрическим дипольным моментом Если поле мгно-
венно включить, PD достигнет конечного, стационарного состояния с постоян-
ной времени т. Таким образом, в этом случае можно записать
(3.9)
Стационарное значение = Ps + PDST. Вследствие того что плотность энер-
гии w в конденсаторе определяется как
w = ie0a)E2+|p£, (3.10)
мы получаем быструю компоненту, чьей зависимостью от времени можно пре-
небречь при обычных скоростях переключения (не менее наносекунд) в генера-
торах мощных импульсов, и релаксационную компоненту, которая влияет на про-
цессы заряда и разряда конденсаторов.
Как показано на Рис. 3.4, требуется некоторое время, прежде чем конденсатор
получит полный заряд. На этих графиках мы предполагаем, что имеем дело с иде-
альным конденсатором, без сопротивлений и индуктивностей, а источник напря-
жения имеет нулевой импеданс. При разряде через короткое замыкание предпо-
лагается, что используется идеальный ключ. На практике при снижении напря-
жения в процессе разряда конденсатора до некоторого критического значения
может случиться, что разряд в газонаполненном ключе погаснет раньше, чем
конденсатор полностью разрядится. В этом случае поляризация может продол-
жать уменьшаться до стационарного значения, которое будет меньше предшест-
вовавшего значения, а напряжение на конденсаторе может вновь возрасти, что
влечет за собой опасность для обслуживающего персонала и диктует необходи-
мость постоянного заземления конденсатора в нерабочем состоянии. Этот случай
отражен на Рис. 3.4 горизонтальной пунктирной линией. Постоянное заземление
необходимо еще и потому, что электроны, которые в заряженном конденсаторе
проникают в диэлектрик, могут диффундировать обратно и вновь зарядить кон-
денсатор.
76 Глава 3. Накопление энергии
Рис. 3.4. Типовые графики заряда и разряда идеального конденсатора
через идеальный ключ и короткое замыкание.
Комплексный импеданс конденсатора может быть определен как
Z= 7?esr + — 1/соС), (3.11)
где AESR — эквивалентное последовательное сопротивление, которое в боль-
шинстве случаев равно R$ (см. Рис. 3.2). На частоте собственного резонанса
coR = 1/(£С)1/2 емкостные и индуктивные реактивные сопротивления уничтожают
друг друга, и Z= /?esr- Как правило, чтобы избежать больших потерь энергии в
конденсаторе, способных разрушить его, необходимо работать на частотах на-
много ниже, чем coR. Как показано на Рис. 3.5, силовой конденсатор состоит из
нескольких пачек скрученной ленты, лист которой был показан на Рис. 3.1. Та-
ким образом, в зависимости от положения выводов минимальное время разряда
может быть ограничено временем прохождения тока от конца ленты до места
присоединения вывода и может оказаться больше, чем период резонанса LC. По
этой причине в быстродействующих конденсаторах требуется обеспечивать ко-
роткие пути тока от пачек ленты к выводам.
Долговечность конденсаторов подвержена сильному влиянию напряжения их
заряда и воздействию напряжения обратной полярности. Чувствительность к из-
менению полярности напряжения на конденсаторе объясняется на основе моде-
лей пробоя, которые обсуждались в гл. 2. Заряды, инжектированные в диэлект-
рик с электрода, выполняющего функцию катода при нормальной полярности
напряжения на конденсаторе, создают пространственный заряд. В свою очередь
этот заряд формирует электрическое поле, напряженность которого складывается
с напряженностью поля, создаваемого при подаче на конденсатор напряжения с
полярностью, противоположной исходной. При этом суммарная напряженность
поля может превысить локальную электрическую прочность диэлектрика и вы-
3.1. Конденсаторы 77
Рис. 3.5. Силовой конденсатор на 60 кВ, 0.2 мкФ, состоящий из шести пачек скрученной лен-
ты. Корпус демонтирован. Выводы вставлены в пластиковый держатель, показанный
слева.
звать его повреждение. На Рис. 3.6 и 3.7 показаны графики ожидаемой долговеч-
ности конденсаторов с высокой плотностью энергии как функции от процентно-
го значения рабочего напряжения относительно максимально допустимого, а
также как функции от обратного напряжения. Для промышленных применений
мощных импульсов часто требуется долговечность, при которой конденсатор
должен выдержать более 108 циклов заряд—разряд. Это может быть достигнуто
либо путем использования конденсаторов при напряжениях, намного меньших,
чем их максимально допустимые напряжения, либо путем использования в кон-
денсаторах очень консервативной изоляции, т. е. ценой увеличения размеров и
снижения плотности запасаемой энергии.
Отказы конденсаторов в основном происходят по следующим причинам: по-
верхностный пробой на краю полосы изоляции конденсаторной секции, пробой
в области пустот и примесей в диэлектрике, образование электрической дуги в
зоне присоединения выводов методом прессования. Электрическая дуга превра-
щает в газ изоляционный материал, что приводит к увеличению давления в кор-
пусе конденсатора. Этого можно избежать, если все контакты соединены пайкой
или сваркой. Поверхностный пробой может быть предотвращен путем создания
более плавного распределения поля вблизи краев конденсатора с помощью ре-
зистивного слоя. Для этого, например, изоляционную бумагу пропитывают раз-
бавленным раствором сульфата меди в воде. Однако этот прием приводит к силь-
78 Глава 3. Накопление энергии
Рис. 3.6. Ожидаемая долговечность конденсатора в зависимости от рабочего напряжения.
Обратное напряжение в % от максимально допустимого
Рис. 3.7. Ожидаемая долговечность конденсатора в зависимости
от напряжения обратной полярности.
ному увеличению токов утечки и уменьшению времени хранения энергии в кон-
денсаторах с такой изоляцией. Пробой диэлектрика в конденсаторах с
металлопленочными электродами, имеющими ограниченную плотность тока, не
обязательно сопровождается выходом конденсатора из строя. Если пробой воз-
никает в маленьком пятне, ток, протекающий в этом месте, испаряет металлиза-
цию вокруг зоны пробоя, и, за исключением незначительного уменьшения ем-
3.2. Генераторы Маркса 79
кости, конденсатор сохраняет способность к функционированию [Slenes et al.,
2001]. Процесс «самозалечивания» металлопленочных конденсаторов проиллюс-
трирован на Рис. 3.8.
Рис. 3.8. Металлопленочный конденсатор с «самозалеченным» местом пробоя.
3.2. Генераторы Маркса
3.2.1. Классические генераторы Маркса
Как правило, высоковольтные импульсные конденсаторы изготавливаются на
напряжения до 100 кВ. Основная причина этого — непозволительно большие
размеры трансформаторов на напряжение свыше 100 кВ, используемые в источ-
никах заряда конденсаторов. Для получения импульсов с большей амплитудой
может быть применена схема генератора Маркса. Основная схема была запатен-
тована Эрвином Марксом (Ervin Marx) в 1923 г. [Marx, 1923, 1924]. Принцип ее
действия основан на заряде нескольких конденсаторов, включенных параллель-
но, и затем переключении их в схему последовательного включения для разряда.
Таким образом, выходное напряжение оказывается равно напряжению, до кото-
рого заряжен конденсатор, умноженному на число конденсаторов в системе. На
Рис. 3.9 приведена простейшая схема генератора Маркса с однополярным заря-
дом конденсаторов и в отсутствие паразитных емкостей. Конденсаторы в ней за-
ряжаются через резисторы RL при разомкнутых ключах.
Когда происходит замыкание первого ключа, напряжение в точке С становит-
ся равным напряжению источника питания Uo. Таким образом, в точке D напря-
жение подскакивает до 2{/0. При этом напряжение на втором ключе (в качестве
которого обычно используется разрядник) становится тоже равным 2t/0, и, если
80 Глава 3. Накопление энергии
в) ।__|| nU° Л____________ К нагрузке
т С/п
Рис. 3.9. Схема генератора Маркса с однополярным зарядом конденсаторов через резисторы
Rl (а). Конфигурация схемы после замыкания ключей (б). Эквивалентная схема гене-
ратора Маркса после замыкания ключей (в).
он выбран правильно, данный разрядник пробивается. Этот процесс продолжает-
ся до тех пор. пока все разрядники последовательно не пробьются. Продолжи-
тельность такого состояния составляет обычно несколько микросекунд.
На Рис. 3.10а приведена схема генератора Маркса, в которой используется
двухполярный заряд конденсаторов. В этой конструкции требуется только поло-
вина от числа ключей, необходимых для простейшей схемы. В начале напряже-
ние на каждом ключе равно 2£/0. После замыкания ключей схема генератора при-
обретает вид, показанный на Рис. 3.106. Эквивалентная схема после замыкания
ключей показана на Рис. З.Юв. Здесь L — суммарная индуктивность конденсато-
ра, проводников, соединяющих его с ключами, и самих ключей. Общая емкость
конденсатора См в состоянии формирования импульса напряжения на нагрузке
равна С/In, а общая индуктивность £м = л£§ + 2л£с, где п — число каскадов, a £s
и £с — индуктивности ключей и конденсаторов соответственно. Конечно, на-
копленная энергия = 2л(1/2)С{/02. Импеданс генератора Маркса равен
ZM = (£М/СМ)1/2 = л[2(2£с + £S)/CO],/2. Этими соотношениями определяется
энергия, которую генератор может отдать в нагрузку.
Чем меньше импеданс, тем больше величина доступной энергии. Вследствие
того что импеданс увеличивается с увеличением числа каскадов л, становится всё
труднее и труднее увеличить мощность генераторов Маркса до уровня тераватт и
более. Таким образом, основной функцией генераторов Маркса в генераторах
сверхмощных импульсов является осуществление заряда конденсатора промежу-
точного каскада. В этом конденсаторе в качестве диэлектрика обычно использу-
3.2. Генераторы Маркса 81
К нагрузке
Рис. 3.10. Схема генератора Маркса с двухполярным зарядом конденсаторов {а). Конфигурация
схемы после замыкания ключей (6). Эквивалентная схема после замыкания ключей (в)
Паразитные емкости не показаны.
ется масло или вода. Из-за того, что электрическая прочность воды зависит от про-
должительности воздействия электрического поля, для получения высокой плот-
ности энергии заряд этого конденсатора должен осуществляться как можно
быстрее. Для получения полной передачи энергии емкость конденсатора в про-
межуточном каскаде должна равняться эквивалентной емкости генератора Марк-
са при замкнутых ключах. Следовательно, время заряда пропорционально перио-
ду колебаний т в генераторе Маркса.
При выражении См и LM через накопленную энергию и выходное напряже-
ние генератора Маркса следует, что при фиксированной амплитуде импульса на-
пряжения время заряда пропорционально квадратному корню из запасенной
энергии
т ~ -ЛмОи» См ~ И'м/б/м2, £м ~ UM,
(3.12)
82 Глава 3. Накопление энергии
Таким образом, для достижения высокой плотности энергии и получения ко-
ротких мощных импульсов может оказаться более выгодно синхронизовать рабо-
ту нескольких генераторов Маркса, заряжающих уменьшенной энергией один
конденсатор промежуточного каскада с водяной изоляцией.
Вернемся к схеме простейшего генератора Маркса, приведенной на Рис. 3.9.
После того как все ключи, за исключением последнего, замкнутся, каждый из
конденсаторов начнет разряжаться через два резистора, соединенных параллель-
но. Постоянная времени этого разряда
т=|4С0. (3.13)
Если нагрузка подключена к выходу генератора Маркса, то постоянная вре-
мени его разряда зависит от импеданса нагрузки. Для того чтобы передать в на-
грузку больше энергии, эта постоянная времени должна быть меньше т из выра-
жения (3.13). Рассеяние энергии на токоограничительных резисторах как при за-
ряде, так и при разряде конденсаторов в генераторе Маркса нежелательно из-за
снижения КПД. Иногда взамен резисторов в зарядных цепях применяют дроссе-
ли. В этом случае постоянная времени саморазряда после замыкания ключей ста-
новится
(1 Y/2
т = 2л1 1£lC0I (3.14)
И в этом случае т нужно делать в несколько раз больше, чем длительность вы-
ходного импульса.
Современные источники питания способны заряжать конденсаторы постоян-
ным током (см. разд. 6.3). Однако, вследствие того что резисторы в генераторе
Маркса при заряде конденсаторов соединены последовательно, конденсаторы за-
ряжаются с разной скоростью. Приближенно время заряда /i-го конденсатора
можно найти из формулы
Tn = ALQ»2. (3.15)
В этом случае разность ДГ/0 в напряжениях между первым и последним кон-
денсаторами после заряда их в течение времени t равна
Д(/о/(/о = (ЛкСо»2)//. (3.16)
Допустимое значение AU0/UG определяет минимальное время заряда t. Для ра-
боты с последовательностью импульсов это отношение определяет максималь-
ную частоту их следования.
Запуск генератора Маркса вызывает начало процесса формирования выход-
ного импульса напряжения в выбранный момент времени. При конструировании
генератора Маркса важными целями являются достижение малой вероятности
включения его ключей до подачи сигнала запуска, большой диапазон интервалов
между выходными импульсами и малое «дрожание» выходных импульсов напря-
жения. Под «дрожанием» здесь понимается статистическое стандартное отклоне-
3.2. Генераторы Маркса 83
ние времени включения. В большинстве генераторов Маркса в качестве ключа в
первом каскаде используются трехэлектродный разрядник, а в последующих
каскадах — двухэлектродные разрядники. Включение достигается подачей им-
пульса зажигания на управляющий электрод трехэлектродного разрядника
(см. разд. 4.1).
Ранее при обсуждении работы генераторов Маркса мы пренебрегали паразит-
ными емкостями. Паразитные емкости между накопительными конденсаторами
и землей обозначаются Cs. Паразитные емкости могут также возникать между
землей и точками А, В, F и т. д. CG является суммой емкости между электродами
ключей и емкости между корпусами конденсаторов. Паразитные емкости играют
большую роль в работе генератора Маркса. Для обсуждения их влияния мы ис-
пользуем более реальную схему генератора Маркса, представленную на Рис. 3.11.
На ней распределенные емкости Cs обозначены эквивалентными дискретными
емкостями для каждой секции генератора.
Рис. 3.11. Схема генератора Маркса, где паразитные емкости между накопительными конден-
саторами и землей обозначены Cs, а между электродами ключей — Сс. Исключены
паразитные емкости между землей и точками А, В, F и т. д.
Предположим, что все конденсаторы заряжены до напряжения Uq. После за-
мыкания ключа паразитная емкость в точке D стремится удержать потенциал
этой точки равным потенциалу земли. Однако, вследствие того что емкость Со
обычно намного больше емкости Cs, потенциал точки D быстро возрастает до зна-
чения, близкого к Uq. Затем потенциал точки В подпрыгивает до напряжения 2 Со.
Следующий ключ (разрядник) S2 замкнется (пробьется), только если напряжение
на нем будет превышать напряжение пробоя в течение достаточно длительного
времени. Паразитные емкости CG ключа S2 и Cs в точке Н образуют емкостный де-
литель напряжения, так что напряжение на ключе S2 получается равным
AC=2C0/(1+Cg/Cs). (3.17)
При конструировании генераторов Маркса необходимо принимать меры к
тому, чтобы сделать отношение CG/CS достаточно малым. Этого можно достичь,
например, размещением заземленной пластины вблизи корпуса конденсатора Со-
Однако даже при этом перенапряжение на ключе S2 не может сохраняться
очень долго Когда точка D заряжена до напряжения Со, точка Н стремится при-
84 Глава 3. Накопление энергии
обрести этот же потенциал, так как они соединены через резистор Параллель-
но с этим процессом точка F стремится зарядиться до напряжения 2t/0 вследствие
того, что она имеет соединение с точкой В, имеющей этот потенциал. Если ем-
кость Со достаточно велика по сравнению с Cs, ее можно рассматривать как ис-
точник напряжения величиной —£/0, и потенциал точки Н будет также стремиться
к значению £/0 вследствие этого процесса. Из-за того, что оба процесса действуют
одновременно, постоянная времени заряда Cs в точке Н будет равна l/2/?LCs.
Следствием этого является уменьшение напряжения на ключе S2, происходящее с
этой постоянной времени, которое в конце концов стремится к значению С/о. От-
сюда следует, что ключ должен быть сконструирован так, чтобы он пробился при
перенапряжении Д(/ за время, намного меньшее, чем 1/2RLC$. Это обсуждение
можно распространить и на следующие ключи. Однако, в связи с тем что в них
перенапряжения становятся все больше и больше, становится все легче и легче
обеспечить их пробой.
Чтобы предотвратить преждевременный запуск генератора Маркса, каждый
ключ должен иметь достаточные запасы по напряжению пробоя. Можно опреде-
лить этот коэффициент запаса как отношение т между пробивным напряжением
ключа иъ и рабочим напряжением Uq. Тогда, чтобы произошел пробой, напряже-
ние на ключе должно достичь большего значения, чем т Uq. Из принципа работы
генератора Маркса следует, что т не может быть больше 2. Более того, для надеж-
ного включения т должно быть много меньше 2.
Вместо включения одного ключа можно организовать пробой в к первых раз-
рядниках. Хотя это и увеличивает перенапряжение на разряднике номер (к + 1)
до значения
&U = kUQ
2
1 +
(3.18)
к сильному увеличению коэффициента запаса т это не приводит вследствие того,
что, как мы увидим далее (разд. 4.1), надежное поджигание трехэлектродных раз-
рядников возможно только при т < 1.5.
В схеме генератора Маркса, приведенной на Рис. 3.9, волна возбуждения пе-
редается от одной к следующему ключу через емкостную связь. Такие генераторы
называют имеющими п = 1. На Рис. 3.12 приведена схема генератора Маркса, в
котором связь осуществляется через каждые два ключа (п = 2) [Nation, 1979]. Для
этого в схему введены конденсаторы Сс, имеющие сравнительно большую ем-
кость. Для того чтобы разобраться в принципе работы схемы, предположим, что
первые (р — 1) ключей уже замкнуты, так что потенциал в точке А равен pUq. Как
и в предыдущем случае, емкости между накопительными конденсаторами и зем-
лей Cs и между электродами ключей Cg с конденсатором Сс образуют делитель
напряжения, и потенциал в точке В оказывается равен
2.U С
UB = (p-2)U0+ с .
(3.19)
3.2. Генераторы Маркса 85
Рис. 3.12. Схема генератора Маркса с емкостной связью через каждые два ключа (п = 2).
Таким образом, разность потенциалов между точками А и В получается
A[/=2t/0/(l+CG/Cs). (3.20)
Во время разряда конденсатора Сс через резистор Л эта разность потенциалов
стремится к значению 21/0 (вместо £/0 у генераторов Маркса с п = 1). Это является
особенностью генераторов Маркса с п = 2, в которых емкость конденсатора Сс
велика, а резисторы в цепях заряда и заземления соединяют ключи через один. В
конфигурации генератора Маркса с п = 3 соединяют ключи через два, и достига-
ется перенапряжение на ключах, равное 3£/0. Однако в этом случае необходимо
принудительно включать по крайней мере два ключа. Преимущество генераторов
86 Глава 3. Накопление энергии
Маркса с высокими значениями п состоит в их сравнительно высокой устойчи-
вости к самопроизвольному включению. Вместе с тем их включение обычно про-
исходит более медленно. Надежность последовательного включения разрядников
может быть улучшена с помощью линии оптической связи в ультрафиолетовом
диапазоне между смежными разрядниками. При этом после пробоя в первом раз-
ряднике достигается предварительная ионизация газа в последующих разрядни-
ках и уменьшается время задержки развития пробоя.
Если генератор Маркса размещен в металлическом корпусе, паразитные ем-
кости могут быть определены в соответствии со следующим правилом: конструк-
ция генератора Маркса предполагается одним металлическим проводником, а
паразитные емкости каждой секции предполагаются равными общей паразитной
емкости, деленной на число секций.
Вследствие колебательных процессов, возможных в генераторах Маркса, на-
пряжение на конденсаторах может изменять полярность. Как мы уже знаем, это
уменьшает срок службы конденсаторов, и желательно не допускать подобных яв-
лений. Мощный электронный ключ, соединенный параллельно выходу генерато-
ра и включаемый в начале изменения полярности напряжения, может решить эту
задачу. Как правило, из-за низкого напряжения в начале процесса изменения по-
лярности требуется принудительное включение этого ключа.
Время нарастания выходного напряжения генератора Маркса может быть со-
кращено при использовании дополнительных конденсатора СР и ключа 5Р
(Рис. 3.13). На этом рисунке генератор Маркса представлен в виде последователь-
но включенных конденсатора См и индуктивности £м- Конденсатор СР заряжает-
ся до напряжения Up = UM2 СМ/(СМ + Ср)
Рис. 3.13. Схема улучшения переднего фронта импульса.
3.2.2. LC-генераторы Маркса
На Рис. 3.14 приведена схема генератора Маркса, в котором используются
£С-цепи. Впервые она была предложена Фитчем из Лабораторий Максвелла
(Maxwell Labs) [Fitch, 1964]. С тех пор эта схема известна как генератор Фитча.
Как показано на Рис. 3.14, последовательно включенные конденсаторы заря-
жаются с противоположной полярностью напряжения. Таким образом, в началь-
3.2. Генераторы Маркса 87
ный момент сумма их напряжений (выходное напряжение) равна нулю. Когда
ключи замыкаются, возникает колебательный процесс, приводящий к измене-
нию полярности каждого второго конденсатора, и через половину периода этих
колебаний выходное напряжение станет равным nU0, где п — число конденсато-
ров. Преимуществом этой схемы является малое значение ее выходной индуктив-
ности, так как индуктивности ключей находятся вне цепи разряда конденсаторов.
Трудность состоит в необходимости одновременного включения ключей, со
сколь это возможно малым дрожанием, ибо в противном случае в некоторых сек-
циях возможно возникновение перенапряжений. Выходное напряжение в зави-
симости от времени описывается выражением U(t) = (1/2)л(/0[1 — e“,/2Tcos(co/)];
здесь со2 = 1/£С, т = L/R, где R — сумма сопротивлений ключа, конденсатора и
соединительных проводов.
3.2.3. Базовый каскад передачи энергии мощных импульсов
Выше уже было отмечено, что генераторы Маркса очень часто используются
для быстрой зарядки промежуточных накопительных конденсаторов. Таким об-
разом, мы получаем ситуацию, показанную на Рис. 3.15, когда первоначально за-
ряженный конденсатор разряжается в первоначально незаряженный конденса-
Ключ L
R
Рис. 3.15. Базовая схема для определения передачи энергии из С| в С2.
88 Глава 3. Накопление энергии
тор. Вследствие важности для техники передачи импульсов большой мощности
этот процесс мы рассмотрим в деталях.
Уравнения энергетического баланса можно записать следующим образом:
Ли2 + \RI2dt^C2U22 = (3.21)
—+C.U. + LI— + Rt2 + C2U2 = 0, (3.22)
dt 1 1 dt dt 2 2 dt v
Ux + L^ + RI+ U2 = 0, (3.23)
—+L—+ Л/+^- = 0, (3 24)
C, dt C2 1 f
d rd2I Ddl TC+C2
— + L—r+ R—+1— -
dt dt2 dt CXC2
= 0,
где Hq является энергией, первоначально накопленной в конденсаторе С{.
Используя обозначения
т = L/R,C=CiC2/(Cl + С2), со02 = 1/ЬС, (о2 = |1/£С- 1/(2т)2|,
мы можем записать выражение (3.25) как
d2I/dt2 + X/vdl/dt + со02/ = 0. (3.26)
Решение дифференциального уравнения (3.26) получается с подстановкой
/=Лек‘, с начальными условиями /(0) = 0 и d!/dt{$) = Uq/L Для характеристичес-
ких корней 2 получается
^1.2“ э ±Ла 2 Ю0-
2т V 4т
Далее мы рассмотрим три различных случая:
1. coqt > 1/2.
Для нас это самый важный случай, а решение для него:
/= {UQ/(&L)-eT,,2x sin со/,
т и*
МАХ {L/C)42 + 0.87?
В этом случае выходное напряжение получается равным
И')*' UC [ ( 1
и^^~сГ
и _ Г1 . е-’/г®’!
vC2(max)- £ +£ lI + C
(3.27)
(3.28)
(3.29)
(3.30)
3.2. Генераторы Маркса 89
Для относительного коэффициента передачи энергии мы получаем
!) = 12 , (1 + е^/2мт)2.
(С.+С,)2'
(3.31)
Остаточное напряжение на конденсаторе С| равно
^с.(0 =
С] +• С2
t/0C2 ( 1 . Л
+ —cos cor +---sin at e ' ,
C, + C2 \ 2cot )
U C
II — 0 1 {С _c
UCI(min) “ г U2C /•
+ c2
(3.32)
На Рис. 3.16 показаны относительные коэффициенты передачи энергии т] и
напряжения Uo/Uq на конденсаторе С2 как функция от отношения Сг/Ср На-
ибольший коэффициент передачи энергии достигается при малом R и С| = С2.
Увеличение напряжения < 2 может быть достигнуто, если С2 < Ср
Рис. 3.16. Относительные коэффициенты передачи энергии т) и напряжения UqJUq
на конденсаторе С2 в зависимости от отношения Cj/Cp
2. со0т = 1 /2.
Это случай критического демпфирования. Решение для него
= (3.33)
а напряжение на конденсаторе С2
=TTfV Т <2т -('+2т)е"Й'Ь <3-34)
l + Cj/Cj ZT
90 Глава 3. Накопление энергии
Очевидно, что относительный коэффициент передачи энергии падает до зна-
чений меньше 1/4.
3. соот < 1/2.
Для завершения картины представим результаты и для этого случая:
/(/) = (М)/<о£)е" '/2tsh со/, (3.35)
Uq 2теч/2т(2е'/2т- 2<от choir-sh air)
Ua = c^L-------------------------------- (336)
3.3. Индуктивные накопители энергии
Генераторы, в которых используются емкостные накопители энергии, можно
рассматривать как усилители тока, а генераторы с индуктивными накопителями
энергии являются усилителями напряжения. Как было отмечено в гл. 1, в индук-
тивных накопителях энергия запасается в магнитном поле. При этом плотность
энергии в системах с индуктивными накопителями превышает таковую у систем
с емкостными накопителями на два порядка, даже если принять во внимание
объем, занимаемый изоляцией. На Рис. 3.17 приведена базовая схема генератора
с индуктивным накопителем энергии.
Рис. 3.17. Базовая схема генератора импульсов с индуктивным накопителем энергии.
Индуктивность L заряжается от генератора тока с выходным импедансом RG,
когда размыкающий ключ замкнут, а замыкающий ключ разомкнут. Ток через ин-
дуктивность растет до своего максимального значения IqRq/(Rq + R) по закону
7(0=4
Яд
Л+ Rq
е-|(я+Лс/Ок
(3 37)
3.4. Умножение мощности и напряжения 91
Постоянная времени нарастания тока в индуктивности rL ~ + ^g)- Если
ток нагрузки /0 велик, то зарядка индуктивности должна осуществляться быстро,
а время хранения энергии должно быть коротким. В противном случае из-за по-
терь энергии на сопротивлениях обмотки индуктивности и ключа станут непри-
емлемо большими, что приведет к снижению КПД системы. Для обеспечения
быстрого заряда индуктивного накопителя его источник питания должен иметь
высокое выходное сопротивление и большую мощность.
3.4. Умножение мощности и напряжения
Предположим, что накопительная индуктивность заряжена в момент времени
t = 0 и ток в ней при этом равен /1(0). Пренебрегая величиной R, введем паразит-
ную индуктивность L2 и заменим источник тока на импульсный источник напря-
жения Uq = IqRq, который способен обеспечить импульс тока амплитудой /0 и
длительностью тР, как это показано на Рис. 3.18. Если требуется, чтобы /1(0) был
близок к /0, значение LX/RG должно быть мало по сравнению с тР. В момент t = 0
размыкающий ключ размыкается и его сопротивление мгновенно изменяется от
нуля до конечного значения R$. Часть тока /1(0) начинает течь вместо этого ключа
через паразитную индуктивность £2 в нагрузку RL. Для тока индуктивности Ix(t) и
тока нагрузки /2(Г) мы имеем следующие уравнения:
0 = /?G/i + Lx dlx/dt + As(/i - /2), (3.38)
0 = RJ2 + Lidl^dt + /?s(/2 - Л). (3.39)
Эта система дифференциальных уравнений имеет два характеристических корня:
2L2 2£,
1± L 4£.£2[(/?L4-/?s)(/?G4-/?s)-^]
У [£1(/?L+/?s)+£2(/?G+/?s)]2
(3-40)
Puc. 3.18. Упрощенная схема для анализа процессов умножения мощности и напряжения
в генераторе с индуктивным накопителем энергии
92 Глава 3. Накопление энергии
Уравнение (3.40) может быть упрощено для R$ » RL, Lx » L2. При этих усло-
виях мы получаем
t+ = L2/Rs,
т_ = LX/(RG + AL),
(3.41)
т+ « т.
И наконец, используя начальные условия /j(0) = /(0) и /2(0) = 0, мы получим
£/(0) е-*-+Ае-'Л-
Л + ^2
bj+ £2
4(0 = /1-/2=/(0)е^-.
(3.42а)
(3.426)
(3.42в)
В этом случае время т$, в течение которого спадает ток через размыкаемый
ключ, равно xs = т+. Так как т+ « т_, ток нагрузки /2(0 определяется значением
т_. На Рис. 3.19 приведены графики тока через накопительную индуктивность Lx
до и после размыкания ключа Ix(t), тока ключа /s(0 после начала его размыкания
и тока нагрузки /2(0-
Рис. 3.19. Токи индуктивности, нагрузки и ключа в генераторе с индуктивным накопителем
энергии. (Lj = 1 мкГн, L2 = 0.1 мкГн, RG = 1 Ом, R = 0.1 Ом, R$ = 10 Ом, RL = 5 Ом.)
3.5. Роторные и униполярные генераторы 93
Мощность, выделяющаяся в нагрузке Р = /2(/)/?ь» имеет максимальное значе-
ние
, ,_RlL2,I(O)2
м (Л + А)2
l_i(lnx+l)
(3.43)
» 1
^г(^О + Л.)
Для расчета коэффициента умножения мощности М мы можем сравнить зна-
чение Рм с максимальной мощностью, которую источник питания подает в на-
грузку в отсутствие индуктивности. Конечно, при этом должно быть выполнено
условие согласования, т. е. RL = Rc:
(3.44)
Таким образом, получается, что
Ъ Rq (Д+Л2)2
(1-е-^'/А)2(1--(1пх + 1)
V х
(3.45)
М увеличивается пропорционально отношению RiJRq. Также видно, что же-
лательно обеспечивать паразитную индуктивность £2, насколько это возможно,
малой. Коэффициент умножения напряжения также растет пропорционально от-
ношению R\JRq.
А /(0)
^G ^1 + ^2 А)
(3.46)
3.5. Роторные и униполярные генераторы
Индуктивные системы накопления энергии, не использующие явления
сверхпроводимости, рассеивают энергию с постоянной времени L/R. Для повы-
шения КПД необходимо заряжать индуктивный накопитель за более короткое
время, чем L/R. Для установок с накапливаемой энергией порядка десятков мега-
джоулей, таким образом, требуются источники импульсов тока очень большой
мощности. Для этой цели приходится использовать промежуточный накопитель
энергии, например маховик. Кинетическая энергия маховика IFkjn Равна
(3-47)
где 0 — момент инерции маховика, а со — его угловая скорость вращения. Отно-
сительная плотность запасаемой энергии может достигать 300 МДж/м3 (см. гл. 1),
94 Глава 3. Накопление энергии
а сама энергия — более 100 МДж. Маховик в большинстве случаев способен от-
дать запасенную энергию за время не менее 10 мс. Подходящим для работы с ма-
ховиком генератором импульса тока является униполярный генератор, конструк-
ция которого показана на Рис. 3.20.
Центральная
щетка
Рис. 3.20. Конструкция униполярного генератора с самовозбуждением.
В униполярном генераторе маховик используется как ротор. Этот генератор
можно рассматривать как механический накопитель энергии, аналогичный кон-
денсатору с очень большой и изменяемой емкостью. Принцип действия унипо-
лярного генератора основан на законе Фарадея. Для петли напряжения мы полу-
чаем
U = —\B dA = -—j(Bxii)ds. (3.48)
Это соотношение мы вывели для электрического поля в случае неподвижного
контура, включающего маховик. Для движущегося контура мы получаем
Ё'=Ё+й*В. <3-49)
Таким образом, напряжение между двумя точками ротора на Рис. 3.20 получается
U = f (Ё+й х B)ds = jrotЁ-df + |(w х B)ds = ~\^df ~j(Bxu)ds. (3.50)
Если скорость изменения магнитной индукции мала (что характерно для унипо-
лярного генератора), то первым членом в правой части этого выражения можно
пренебречь. Второй член в правой части (3.50) создает разность потенциалов
вдоль радиуса ротора.
3.5. Роторные и униполярные генераторы 95
В генераторах с самовозбуждением магнитная индукция В создается выход-
ным током ротора [Driga et al., 2001]. Таким образом, индуцируемое напряжение
пропорционально току I и угловой скорости со:
t/=a/co, (3.51)
где a — параметр установки.
Из рассмотрения электрической цепи мы получаем
L(dl/df) + IR = alto, (3.52)
где L — индуктивность цепи генератора, в большинстве случаев равная накопи-
тельной индуктивности, а R — суммарное сопротивление ротора, катушки и кон-
тактных щеток. Из закона сохранения энергии следует, что
1 j ' 1
-&to2+-LI2+ h2Rdt = -&to2
2 2} 2 0
(3.53)
где со0 — начальная угловая скорость ротора. Дифференцируя это выражение по
времени и используя соотношение
dl/dt = (aco - R)I/L = a(co - toC)I/L, (3.54)
выведенное из (3.52), мы получаем
®dto/dt = -al2. (3.55)
Ток может расти, только если начальная угловая скорость а>о выше, чем некоторое
критическое значение сос = R/a. Путем исключения времени t из выражений (3.54)
и (3.55) мы можем получить дифференциальные уравнения относительно / и со:
L di _toc — to
0~dto~ 7 ’
/2 + ®(со-й)с)2 =у(со-сос)2 + /02 = А,
(3.56)
где А является постоянной. Используя эти уравнения для того, чтобы выразить
со — сос в (3.54) через 1, мы получим дифференциальное уравнение для /(г):
L(dl/dt) = a/l(<oo - о>с)2 + £(/02 - /2)/©]1/2. (3.57)
Интегрируя (3.57), мы получим следующее решение:
ch(a(Z- Го)7л/0£)’
, 1
Го=-^-Г1п
а у А
(3.58)
96 Глава 3. Накопление энергии
Максимальный ток достигается, когда гиперболический косинус равен 1:
/млх = («0-«с)(в/Ч1/2- (3.59)
Здесь мы полагаем начальный ток в системе /0 пренебрежимо малым. Для /0 мы
получаем следующее упрощенное выражение:
L 1п(2/мах /7о) z_
/0=-— MAx/.-Q-A. (3.60)
(О0/(йс 1
Коэффициент полезного действия при преобразовании кинетической энергии
вращающегося маховика в энергию магнитного поля получается равным
п = Ь^х (3.61)
©(Од L соо,
Из этого уравнения мы можем по крайней мере качественно оценить влияние
различных параметров на поведение системы в целом. Удовлетворительный КПД
получается, только если накопительная индуктивность сопоставима по величине
с общей индуктивностью и если а>с « о»о-
На Рис. 3.21 представлен график /(/) для системы со следующими параметра-
ми: ® = 5кг-м2, £=10“4Гн, а = 3 х 10-5 Ом-с, /? = 2 х 10-3 Ом, соо = 1000 об/с,
сос = 66.6 об/с. WkIN = 2.5 МДж, L$/L = 0.8, г] = 0.7. Используя выражение для
/(/). мы можем оценить кинетическую энергию ротора и магнитную энергию в
индуктивном накопителе (Рис. 3.22).
Время [с]
Рис. 3.21. Импульс выходного тока униполярного генератора.
Униполярный генератор имеет следующие недостатки:
• выходное напряжение обычно невелико;
• имеют место проблемы со щеточными контактами и износом щеток из-за
большой скорости вращения ротора.
3.5. Роторные и униполярные генераторы 97
Время [с]
Рис. 3.22. Графики изменения кинетической и электромагнитной (HmAG) энергии
в униполярном генераторе, нагруженном на катушку индуктивности.
Для получения более высокого выходного напряжения было предложено ис-
пользование раздельных катушек для возбуждения магнитного поля и накопле-
ния энергии [Lupton et al., 1981]. Эта конструкция показана на Рис. 3.23. Следует
отметить, что в ней упрощается решение проблемы изоляции накопительной ин-
дуктивности.
Рис. 3.23. Конструкция униполярного генератора
с раздельными катушками возбуждения и накопления энергии
Для конструкции, показанной на Рис. 3.23, справедливы следующие диффе-
ренциальные уравнения:
98 Глава 3. Накопление энергии
a/jto = L^dljdf) + RXLX = L2(dl2/dt) + R2L2
©(Jco/Л) = -а/, (7, + Z2).
(3.62)
(3.63)
В случае если R\/L\ = R2/L2, коэффициент полезного действия т] получается
равным
_ ^S^MAX ^1 Г| _
0(Oq Lx + L)\ о)0 у
(3.64)
Таким образом, если » L2i большая часть энергии, первоначально запасенной
в роторе, передастся в накопительную индуктивность.
На Рис. 3.24 представлена конструкция реального униполярного генератора.
15
Рис. 3.24. Конструкция униполярного генератора в деталях.
I — опорная планка статора; 2 — статор; 3 — катушка возбуждения; 4 — съемная секция ротора;
5 — керамический изолятор; 6 — радиальный подшипник; 7 — опорный конус статора;
8 — узел внутренних щеток; 9 — компенсационная пластина; Ю — узел внешних щеток;
11 — коллектор внешних щеток; 12 — вывод внешних щеток; 13 — изолятор; 14 — вывод внутренних
щеток; 15 — опорный конус статора; 16 — опорный подшипник; 17 — гидравлический двигатель;
18 — радиальный подшипник; 19 — постоянная секция ротора;
20 — система воздухопроводов внутренних щеток (изготовитель — OIME Inc., Одесса, шт. Техас).
ГЛАВА
КЛЮЧИ
После накопителей энергии ключи являются наиболее важными элементами
в генераторах импульсов большой мощности. Они выполняют функцию соедине-
ния устройств накопления энергии с нагрузкой. Время нарастания, форма и амп-
литуда импульсов на выходе генератора в значительной степени зависят от
свойств ключей, применяемых в системе формирования импульсов. В генерато-
рах с емкостным накоплением энергии требуются замыкающие ключи, а в гене-
раторах с индуктивным накоплением энергии — размыкающие ключи. Рассмот-
рим для начала несколько типов замыкающих ключей.
4.1. Замыкающие ключи
В этих ключах процесс замыкания связан с электрическим пробоем первона-
чально изолирующего элемента. Пробой может быть как вызван перенапряжени-
ем в цепи ключа, так и инициирован подачей специального импульса управле-
ния.
4.1.1. Газоразрядные ключи
В генераторах импульсов большой мощности наиболее широко применяются
именно газоразрядные ключи. Они просты в использовании, способны выдержи-
вать большие токи и заряды, и ими можно управлять с достаточно высокой точ-
ностью. Существует множество типов газоразрядных ключей, работающих с раз-
личными режимами по давлению газа. На Рис. 4.1 показан диапазон давлений и
рабочих напряжений для некоторых наиболее важных типов газоразрядных клю-
чей [Frank et al., 1991].
Свойства ключей, упомянутых на Рис. 4.1, мы и обсудим ниже. Во многих
применениях требуется точно управляемое начало пробоя. Используемый метод
управления оказывает большое влияние на задержку включения и ее нестабиль-
ность.
Для ключей всех систем работа может быть разделена на четыре фазы, схема-
тически показанные на Рис. 4.2:
100 Глава 4. Ключи
1. Фаза запуска включения (установление пускового разряда).
2. Переходная фаза (переход от высокого к низкому значению импеданса
ключа, также иногда называется «коммутация»).
3. Стационарная фаза (характеризуется постоянной проводимостью ключа).
4. Фаза восстановления (возвращение к исходной электрической прочности)
Давление [Па]
Рис. 4.1. Диапазоны давлений газа и рабочих напряжений различных типов газоразрядных
ключей. Кривая Пашена показана для воздуха с зазором между электродами 3 мм.
Выше этой кривой работа ключей невозможна из-за превышения напряжением элек-
трической прочности диэлектрика.
Существенные потери энергии имеют место только во время фазы коммута-
ции, когда падение напряжения на ключе еще только уменьшается, а ток растет.
Потери энергии во время этой фазы Иу можно оценить, предполагая синхрон-
ность и линейность спада напряжения и роста тока:
и; = Ъ(0/(ПЛ = ии1ы 111 - — Л = « 0.2t/M /мтк, (4.1)
о о \ Ts 7 Ts 6
где и /м — максимальные значения напряжения и тока импульса
соответственно,
ts — время переключения,
xR — время нарастания импульса (xR « 0.8 xs).
В системах с повторяющимися импульсами эту энергию требуется рассеивать
с использованием охлаждения.
4.1. Замыкающие ключи 101
Рис. 4.2. Изменения напряжения, тока и потерь энергии при работе газоразрядного ключа
Пробой в газоразрядных ключах
Пробой между электродами газоразрядного ключа может произойти как
вследствие превышения приложенным к ним напряжением предела электричес-
кой прочности, так и вследствие снижения электрической прочности разрядного
промежутка под воздействием таких факторов, как ультрафиолетовое излучение,
диффузия плазмы и т. д. Важными конструкционными параметрами разрядников
являются:
• напряжение пробоя £/ь;
• вариации значения £/ь, определяющие вероятность пробоя при понижен-
ном приложенном напряжении;
• диапазон рабочих напряжений, т. е. напряжений, при которых вероятность
несанкционированного пробоя достаточно мала, в то время как обеспечи-
вается надежное включение внешним сигналом;
• нестабильность времени зажигания разряда;
• время переключения ts, соответствующее спаду импеданса ключа (и
активного, и индуктивного сопротивлений);
• индуктивность и емкость в предпробойном состоянии;
• возможность работы в режиме повторяющихся импульсов;
• долговечность и цена.
Внешнее управление может быть достигнуто с помощью как светового им-
пульса, генерируемого лазером, так и посредством высоковольтного импульса,
подаваемого на вспомогательный электрод. На Рис. 4.3 показаны в общих чертах
конструкция и основные элементы трехэлектродного газового разрядника.
102 Глава 4. Ключи
Анод
Катод
Рис. 4.3. Основные элементы трехэлектродного газового разрядника.
На Рис. 4.4 приведена схема включения трехэлектродного разрядника.
Принято говорить о включении при перенапряжении, если сумма амплитуды
импульса управляющего напряжения с приложенным рабочим напряжением до-
статочна для пробоя зазора между управляющим электродом и анодом. Зажига-
ние разряда во втором разрядном промежутке происходит, если его напряжение
пробоя меньше, чем рабочее напряжение, приложенное к разряднику. Если для
разделения источника импульсов управления и разрядника используется конден-
сатор Сс, то из-за того, что межэлектродные емкости намного меньше значения
емкости Сс, потенциал управляющего электрода оказывается близок к потенциа-
лу земли. В этом случае необходимые условия включения разрядника могут быть
Рис. 4.4. Схема включения трехэлектродного разрядника.
Uc — выходное напряжение генератора, Ut — управляющее напряжение, Ub — напряжение пробоя
разрядника, Ubi, Ubi — напряжения пробоя отдельных разрядных промежутков разрядника
Я, — импеданс генератора, — импеданс нагрузки, Сс — разделительный конденсатор.
4.1. Замыкающие ключи 103
сформулированы следующим образом: UG + Ut > f/bb UG > t/b2, Ut < 6/b2. Отсюда
можно заключить, что t/c(MiN)= М>2> и, так как Ц(мах> = М>2, мы получаем
^G(MIN) + ^Т(МАХ) = 2t/b2 > f/bl, т. е. в пределе мы получаем Ub2 = (1/2)t/bl. Для кон-
фигурации с симметричными разрядными промежутками это означает, что уп-
равляющий электрод должен располагаться на расстоянии 2/3 дистанции от ано-
да до катода. Конечно, если управляющий электрод «плавающий», необходимо
еще обеспечить выполнение условия UG < Ubi. Таким образом, рабочий диапазон
напряжений для такого трехэлектродного разрядника получается равным
Ub2<UG < 2t/b2, или, выражая Ub2 через t7b, (1/3) Ub < UG< (2/3)£/ь. Еще лучшее ис-
пользование электрической прочности Ub полного разрядного промежутка и
больший диапазон рабочих напряжений может быть получен, если подать на уп-
равляющий электрод с помощью резистивного делителя напряжение, равное 1/3
от UG, как это показано на Рис. 4.9. В этом случае рабочий диапазон получится
(l/3)C/b<t/G<tfb.
Рис. 4.5. Временные диаграммы напряжений на управляющем электроде
и аноде трехэлектродного разрядника при его включении при перенапряжении.
гА — момент начала импульса запуска, tD — задержка включения,
tc — время коммутации, ts — время включения.
На Рис. 4.5 схематически показаны напряжения на управляющем электроде и
аноде трехэлектродного разрядника с плавающим управляющим электродом (Up)
при его включении. Распределение потенциалов в разрядных промежутках трех-
электродного ключа с управляющим электродом, имеющим исходное напряже-
ние (1/3) UG, в разных фазах его включения показано на Рис. 4.6. Включение раз-
ряда вследствие перенапряжения характеризуется тем, что оба разрядных проме-
жутка пробиваются перенапряжением. Несмотря на то что первую искру создают
перенапряжение и ультрафиолетовое излучение, пробой происходит очень быст-
104 Глава 4. Ключи
ро. Это приводит к тому, что и время включения, и время задержки включения
очень малы и имеют малые вариации (дрожание).
Управляющий электрод
Рис. 4.6. Распределение потенциалов в разрядных промежутках трехэлектродного ключа с уп-
равляющим электродом, имеющим исходное напряжение (1/3)Uq, перед включени-
ем (вверху), после приложения импульса управляющего напряжения (в середине) и
после пробоя первого межэлектродного промежутка (внизу).
Если рабочее напряжение трехэлектродного разрядника меньше, чем элект-
рическая прочность второго межэлектродного промежутка, то развивается другой
механизм пробоя. Он проиллюстрирован на Рис. 4.7. Этот вид включения ключа
называется плазменным включением. В этом случае разряд во втором межэлект-
родном промежутке возникает, только если его электрическая прочность умень-
шена под воздействием ультрафиолетового излучения, излучаемого плазменным
каналом в первом межэлектродном промежутке. В этом случае и время задержки,
и время включения намного больше, чем в предыдущем случае.
Включение разрядников, диаграммы напряжений на электродах которых
приведены на Рис. 4.5 и 4.7, происходит только при противоположных полярное-
4.1. Замыкающие ключи 105
Рис. 4.7. Временные диаграммы напряжений на управляющем электроде
и аноде трехэлектродного разрядника при его включении механизмом плазменного включения.
fA — момент начала импульса запуска, rD — задержка включения,
/с — время коммутации, — время включения.
тях рабочего и управляющего напряжений. На Рис. 4.8 изображена конструкция
газоразрядного ключа (тригатрона), для которого этого ограничения не сущест-
вует. Однако и в этой конструкции рабочие характеристики оказываются лучше,
если рабочий и управляющий импульсы напряжения противоположны по поляр-
ности. Тригатроны нормально работают в диапазоне рабочих напряжений
80...99% от напряжения пробоя t/b. Возможно включение и при рабочем напряже-
нии менее 50% от t/b, но время задержки включения и его нестабильность при та-
ких низких напряжениях обычно слишком велики. Включение тригатронов со-
провождается следующими процессами. Как только появляется импульс управ-
ления, вблизи верхушки управляющего электрода появляются стримеры,
которые затем распространяются на зону главного разрядного промежутка. Когда
Рис. 4.8. Упрощенный чертеж тригатрона и схема его включения
106 Глава 4. Клюни
стримеры достигнут противоположного электрода, приложенное поле вызывает
увеличение ионизации в канале между управляющим и прилежащим электродом.
Одновременно в этом канале развивается процесс пробоя. Конечным результа-
том этого обычно становится формирование двух дуговых разрядов, соединяю-
щих управляющий электрод с катодом и анодом. Иногда также возможно, что за-
зор между управляющим и прилежащим электродами пробьется первым. Особен-
но это характерно для случая, когда полярность управляющего импульса и
рабочего напряжения одинакова. В этом случае основной зазор в разряднике
пробивается вследствие воздействия ультрафиолетового излучения, создаваемого
первой дугой.
Анализ схемы с трехэлектродным ключом
Динамика изменения напряжения на ключе, а следовательно, и задержка
включения определяются как цепями генератора, так и особенностями схемы
включения собственно ключа. На Рис. 4.9 представлена эквивалентная схема ге-
нератора импульсов с емкостным накопителем и трехэлектродным газовым раз-
рядником с постоянным смещением на управляющем электроде.
Рис. 4.9. Схема генератора импульсов с емкостным накопителем и трехэлектродным
газовым разрядником с постоянным смещением на управляющем электроде.
В начальный момент времени предполагается, что накопительный конденса-
тор С заряжен до напряжения C/G, а на управляющем электроде с помощью высо-
коомного делителя установлено напряжение, равное 1/3 от этого значения. В до-
полнение к индуктивности Lc цепь содержит демпфирующий резистор Rc- Им-
пульс напряжения через импульсный трансформатор и разделительный
конденсатор поступает на управляющий электрод разрядника. На Рис. 4.10 пред-
ставлены временные диаграммы напряжений на управляющем электроде и аноде
трехэлектродного разрядника
Для определения влияния различных параметров схемы на время нарастания
импульса зажигания рассмотрим схему, приведенную на Рис. 4.9. Введем пара-
зитные емкости разрядных промежутков: управляющий электрод — анод С1 и уп-
равляющий электрод — катод С2. До подачи импульса управления конденсаторы
4.1. Замыкающие ключи 107
Рис. 4.10. Временные диаграммы напряжений на управляющем электроде
и аноде трехэлектродного разрядника при его включении.
С2 и Сс заряжены до напряжения (l/3)i/G. В момент времени г = 0 импульсный
трансформатор формирует треугольный импульс напряжения Ut = St. Предпола-
гая, что Ci = С2« Сс < С, мы получим следующее напряжение на управляющем
электроде:
Uc „
-S t -
3
sin(ar)
а
12С2 + Сс I 1
У 2C2CcL ~ у 2C2L
(4.2)
В конце действия импульса управления /А (Рис. 4.10) разрядный промежуток
между управляющим электродом и анодом пробивается и потенциал управляю-
щего электрода изменяется от его текущего значения до напряжения UG. Одно-
временно наблюдается уменьшение напряжения t/s (Рис. 4.9), которое, однако,
через короткое время меняет направление своего изменения и даже превышает
приложенное напряжение UG (см. Рис. 4.10).
На Рис. 4.11 приведена эквивалентная схема для расчета изменений напряже-
ния на управляющем электроде. Здесь /?$ — сопротивление разрядника, которое
предполагается зависящим от времени. В момент t = 0 конденсатор С2 заряжен до
напряжения Цо- При малом демпфировании и С » С2, а также с применением
сокращений = Rq + Rs и
_S_
(4 3)
'С
1
108 Глава 4. Ключи
мы получим следующие выражения, описывающие зависимости напряжений от
времени:
l/sOT = -l/w +(t/ + t/,o)
р __р
cos coz + —-——sin со/
2u)lc
R Y
t/t (Z) = — UtQ + (U + Ut0) 1 — e-*'/2Lc' cos ot + ——sin cor
2co£r J.
(4.4)
Пренебрегая омическим сопротивлением, мы получаем колебательный про-
цесс с амплитудой 2U + Ul0. Таким образом, в зависимости от степени демпфиро-
вания потенциал управляющего электрода при включении разрядника может
значительно превысить рабочее напряжение U.
Рис. 4.11. Эквивалентная схема для расчета изменений напряжения на управляющем электроде.
Многосекционные газоразрядные ключи с лазерным управлением
Простое увеличение размеров трехэлектродных разрядников с целью дости-
жения возможности их работы с напряжениями порядка нескольких мегавольт
требует увеличения разрядных промежутков, что в свою очередь приводит к не-
приемлемому увеличению нестабильности времени включения и индуктивности.
Вместе с тем многомодульные генераторы импульсов большой мощности требу-
ют использования ключей, обеспечивающих очень точную синхронизацию рабо-
ты отдельных генераторных модулей мегавольтных импульсов. Для решения этой
проблемы в Национальной лаборатории Сандиа (Sandia National Laboratory) бы-
ли разработаны многосекционные газоразрядные ключи с лазерным управлением
[Humphreys et al., 1985]. На Рис. 4.12 показаны схематичная конструкция такого
ключа и его эквивалентная схема.
Этот ключ был рассчитан на работу при напряжении до 6 МВ и токе 0.5 МА.
Он состоит из 15 одинаковых разрядных промежутков и секции запуска. В центре
размещены изолирующие диски, поддерживающие 15 тороидальных электродов.
4.1. Замыкающие ключи 109
Вода
Рис. 4.12. Конструкция многосекционного газоразрядного ключа с лазерным управлением
для работы при напряжении 6 МВ и токе 0.5 МА и его эквивалентная схема.
Пластмассовые стержни снаружи корпуса удерживают набор изоляторов и элект-
родов внутри, а пружина на пластине основания обеспечивает требуемую силу
сжатия набора. Рабочее напряжение составляет обычно около 90% от напряже-
ния самопробоя. При этом вероятность несанкционированного пробоя достигну-
та равной 0.1%. Из-за тороидальной формы электродов паразитные емкости раз-
рядных промежутков довольно малы Их значение относительно емкости пуско-
вой секции Ст выбрано так, что 20% от рабочего напряжения оказывается
приложенным к пусковой секции. Весь прибор имеет длину 68 см и диаметр
61 см.
110 Глава 4. Ключи
Для формирования пробоя в разрядном промежутке пусковой секции (дли-
ной 5.7 см) требуется импульс лазера KrF с энергией 25 мДж. Импульс излучения
лазера фокусируется с помощью длиннофокусной линзы в центр пусковой сек-
ции. Под воздействием импульса излучения лазера возникает искра в форме иглы
длиной около сантиметра. Эта искра увеличивает напряженность электрического
поля в пусковой секции и ускоряет распространение стримеров. Приблизительно
через 1 нс после подачи импульса лазерного излучения в пусковой секции насту-
пает пробой. Через него происходит быстрый разряд емкости Ст, и все рабочее
напряжение оказывается приложенным к остальным разрядным промежуткам.
Первой это увеличение напряжения чувствует секция 15. Затем волна зажигания
разряда последовательно распространяется на остальные секции. Между краями
смежных дисковых электродов возникает по нескольку каналов проводимости,
так что производная dU/dt становится очень большой (см. ниже). При этом ин-
дуктивность канала разряда уменьшается от 400 до 100 нГн, а время включения
уменьшается до 20 нс с нестабильностью менее 0.4 нс.
Эквивалентная схема ключа, показанная в нижней части Рис. 4.12, включает
промежуточный накопительный конденсатор Со, который заряжается от генера-
тора Маркса через индуктивность Lo до напряжения 6 МВ.
Вариант многосекционного газоразрядного ключа на напряжение 4 МВ пока-
зан на Рис. 4.13.
Рис. 4.13. Вариант многосекционного газоразрядного ключа на напряжение 4 МВ
4.1. Замыкающие ключи 111
Время нарастания импульса
Время нарастания импульса, которое, естественно, соответствует времени
спада напряжения на ключе, является суммой резистивной и индуктивной со-
ставляющих:
т = (т2+т2)1/2
lTOT llL+lRJ >
U
Ттот {dU/dt)^'
(4.5)
Спад напряжения на индуктивности L, соединенной последовательно с гене-
ратором через импеданс Z, определяется постоянной времени tl ~ Ь/£ В общем
случае точный расчет зависящей от времени индуктивности L газового разряда
невозможен. Однако в большинстве практических случаев она может быть ап-
проксимирована индуктивностью тонкой цилиндрической проволоки, располо-
женной по оси металлической трубки. Если радиус проволоки принять равным q.
длину £, а внутренний радиус трубки гА, мы получим
L = (.(\л^2п)\п(г^г\) = 2Лп(гд/г|) ~ 14£ нГн (4.6)
для £ в см. Для резистивной фазы дугового канала в жидкости или газе может
быть использовано следующее выражение [Martin et al., 1996]:
R
88 fpf
HC,
(4.7)
где E— напряженность электрического поля, выраженная в МВ/м,
Ро~ плотность в нормальных условиях.
Для твердых тел с плотностью 1 г/см3, т. е. для большинства органических
изоляторов, следует, что
2320 z. о.
т» = ,,, нс. (4 8)
Здесь значение Еснова выражено в МВ/м.
Многоканальные газовые разрядники
Многоканальные разрядники позволяют получить уменьшение индуктивнос-
ти ключа и длительности резистивной фазы разряда. Таким образом, при их ис-
пользовании могут быть получены импульсы с более короткими интервалами
времени нарастания. Кроме того, износ электродов в многоканальных ключах
уменьшается вследствие выделения энергии на большей их поверхности.
Рассмотрим, при каких условиях несколько каналов проводимости могут су-
ществовать в газовых разрядниках с большими электродами. После возникнове-
ния первого канала проводимости и начала прохождения через него большей час-
ти из максимально возможного тока напряжение на разрядном промежутке
112 Глава 4. Ключи
уменьшается, что препятствует формированию других каналов проводимости
Даже небольшое уменьшение напряжения оказывает большое влияние на воз-
можность возникновения каналов проводимости из-за того, что коэффициент
умножения а сильно зависит от напряженности электрического поля. Интервал
времени, в течение которого могут возникнуть новые каналы, таким образом, яв-
ляется только частью времени спада напряжения ттот:
Д/=/ттот- (4.9)
(Если мы посчитаем все каналы, в которых ток достигает более 50% от его макси-
мального значения в канале,/ =0.1.)
Следует к Д/добавить и переходное время, т. е. время, в течение которого ин-
формация о том, что один канал пробит, доходит до других каналов. Если длина
электродов в ключе а число каналов л, получается
TTRANS — t-lПС. (4.10)
Так как каналы не могут быть распределены однородно, мы должны взять
только часть от переходного времени/2, причем/2 = 0.8. Таким образом, получает-
ся следующее выражение для интервала времени, в течение которого могут обра-
зоваться следующие каналы:
ДГ = 0. Ittot + 0-8ttrans- (4.11)
Д/ зависит от числа каналов: индуктивная компонента ттот~ 1/л, резистивная
компонента ~ 1/л1/3, переходное время ~ 1/л.
Разброс напряжений пробоя в газовых разрядниках может быть охарактеризо-
ван стандартным отклонением оа((/)- Этот разброс напряжений пробоя приводит
к разбросу длительностей нарастания выходного напряжения Гг Соотношение
между стандартными отклонениями напряжений и времен нарастания может
быть выведено из Рис. 4.14.
Индексом «а» отмечено то, что мы имеем дело с абсолютными значениями
разбросов. Легко увидеть, что нестабильность времени возникновения каналов
оа(0 равна <s&{U)/(dU/dt). Таким образом, число каналов может быть рассчитано
из условия
2сга(/) < Д/ = 0 • 1 ттот + 0-8ttrans- (4-12)
Из этого следует, что, чтобы достичь максимально возможного числа каналов
в разряднике, следует по возможности уменьшать оа((/) и увеличивать (dU/dt).
Тиратроны
Тиратроны, в особенности водородные тиратроны, появились на свет благо-
даря усилиям, направленным на разработку эффективных радиолокационных
систем военного назначения во время Второй мировой войны. После войны они
стали настоящей рабочей лошадью во многих системах, где требовалось быстрое
включение больших напряжений. Как и газовые разрядники, тиратроны
относятся к газонаполненным ключевым приборам Однако рабочее давление
газа в тиратронах значительно ниже, чем в газовых разрядниках, и в них
4.1. Замыкающие ключи ИЗ
Рис. 4.14. Соотношение между стандартным отклонением напряжений пробоя ста( £/>
и разбросом интервалов времени нарастания выходного напряжения.
используется триодная конфигурация (см. Рис. 4.15). В большинстве тиратронов
используется водород при давлении 30...80 Па. В отличие от электровакуумных
приборов при работе в тиратронах образуется плазма, что позволяет пропускать
большие токи без существенного износа электродов.
Рабочая область тиратронов лежит слева от минимума кривой Пашена (см.
Рис. 4.1). Их максимальное напряжение ограничено полевой эмиссией, которая
возникает при полях с напряженностью более 105 В/см. Обычно расстояние меж-
ду управляющей сеткой и анодом составляет 2...3 мм, что обеспечивает макси-
мальнодопустимое напряжение на уровне 40 кВ. Некоторое увеличение этого на-
пряжения может быть достигнуто подачей на сетку напряжения смещения. Рас-
стояние между сеткой и катодом соответствует минимуму кривой Пашена £/min
для водорода. Если на сетку подать импульс запуска с напряжением U> UMWi
между катодом и сеткой возникает тлеющий разряд. Электроны из этого тлеюще-
го разряда могут проникать через отверстия в сетке в область главного разрядного
промежутка между сеткой и анодом. Вследствие ионизации газа происходит уве-
личение числа свободных носителей заряда, и между анодом, сеткой и катодом
возникает проводящий мост из плазмы.
Диапазон рабочих напряжений тиратронов составляет обычно несколько де-
сятков кВ. После зажигания разряда падение напряжения на тиратроне составля-
ет около 100 В. Таким образом, на тиратроне происходит выделение заметной
мощности, что вынуждает принимать меры к его охлаждению. Тиратроны обес-
114 Глава 4. Ключи
Рис. 4.15. Конструкция тиратрона с термокатодом (слева). Сетка окружает анод так, что значе-
ние pd исключает возможность возникновения разряда. Справа приведены падения
напряжений на нагретом катоде (жирная линия) и катоде без нагрева.
U [В]
Холодный катод
Анодное падение
напряжения
d [см]
печивают задержку включения порядка 200 нс и ее нестабильность порядка не-
скольких наносекунд. Для восстановления исходного (непроводящего) состоя-
ния необходимо сделать напряжение на аноде слегка отрицательным на
25...75 мкс, что требуется для распада плазмы в разряде.
Существенной особенностью тиратронов является применение в них источ-
ников термоэлектронной эмиссии. Важное преимущество подогревного катода
состоит в отсутствии заметного катодного падения напряжения (Рис. 4.15, спра-
ва). При холодном катоде, чтобы разогнать ионы на пути к катоду так, чтобы они
обеспечили требуемое число вторичных электронов, необходимо довольно боль-
шое напряжение. Кроме того, ионы с большой энергией, бомбардируя поверх-
ность катода, вызывают его износ, что сокращает долговечность прибора. Для ис-
ключения в фазе тлеющего разряда попадания быстрых электронов из катода
прямо в анод и повреждения его, во всех тиратронах используется экран. Отверс-
тия в экране и сетке сдвинуты относительно друг друга так, чтобы прямое про-
никновение электронов из катода в анод было исключено.
Первоначально тиратроны изготавливались в стеклянных оболочках, и их
долговечность была ограничена только 500 ч Керамические корпуса сделали их
более прочными и устойчивыми к ударам и вибрации, а также позволили обеспе-
чить эффективный отвод тепла от анода. Это, а также введение генератора водо-
рода (титана, в котором растворен водород), обеспечивающего постоянство рабо-
чего давления водорода, существенно увеличило долговечность. У современных
тиратронов достигнута долговечность в 105 ч при рабочей частоте в несколько ки-
логерц и средней рабочей мощности на уровне мегаватт.
4.1. Замыкающие ключи 115
Тиратроны с холодным катодом
Подобно обычным тиратронам, тиратроны с холодным катодом (Pseudospark
switch) работают в режиме низкого давления и при высоких значениях Е/р. В этом
режиме средний свободный пробег электронов и ионов сопоставим с межэлект-
родными расстояниями. Таким образом, большая часть электронов достигает
анода без ионизационных столкновений в газе.
Введение пустотелого катода в конструкцию, показанную на Рис. 4.16, изме-
нило конфигурацию поля и увеличило пути возможных разрядов. Диаметр отверс-
тия определяет степень проникновения поля внутрь полого катода. С помошью не-
большого количества электронов, создаваемого, например, с помощью запускаю-
щего разряда внутри пустотелого катода, инициируется псевдоискровой разряд. В
начале большинство электронов являются убегающими электронами, так как они
ускоряются до энергий, определяемых разностью потенциалов между катодом и
анодом. (Благодаря этому механизму каналы псевдоискрового разряда могут быть
использованы для создания электронных потоков большой плотности.)
Анод
Катод
Рис. 4.16. Конфигурация электрического поля
в двухэлектродной системе тиратрона с холодным катодом.
Однако механизм замыкания цепи с помощью тиратрона с холодным катодом
основан на создании высокоионизированной плазмы [Christiansen and Hartmann,
1990; Frank and Rath, 1990]. Образование плазмы сначала происходит внутри пус-
тотелого катода благодаря относительно низкому значению Е/р в этом районе.
Электроны из катода создают ионизацию в основном в области оси симметрии
системы. Положительные ионы дрейфуют назад, к катоду, образуя положитель-
ный объемный заряд (виртуальный анод), изменяющий статическое электричес-
кое поле внутри пустотелого катода. Это делает скорость генерации электронов
выше, чем скорость их потерь как внутри пустотелого катода, так и в зазоре
анод—катод. Таким образом, создается низкоомная плазма и возникает пробой
между катодом и анодом. Плотный слой плазмы вблизи стенок отверстия в като-
116 Глава 4. Ключи
де служит посредником при передаче тока между металлическими стенками като-
да и каналом проводимости. Свойства этого слоя определяют общий ток в ключе
и, следовательно, его импеданс. Носителями заряда между слоем плазмы и стен-
ками катода являются ионы, в то время как электроны выполняют роль носите-
лей заряда между плазмой и разрядным каналом. Было найдено [Urban, 2002], что
конечное значение импеданса ключа и время его установления зависят от мате-
риала катода.
Задержка развития пробоя и ее нестабильность также зависят от числа перво-
начальных электронов в пустотелом катоде, которые создаются различными спо-
собами. Среди этих способов с точки зрения долговечности прибора и его быст-
родействия наилучшим является импульсный тлеющий разряд. При этом способе
задержка включения тиратрона с холодным катодом составляет 0.5 мкс, а ее
нестабильность менее 10 нс.
Конструкция тиратрона с холодным катодом показана на Рис. 4.17.
Рис. 4.17. Конструкция тиратрона с холодным катодом и схема его управления [Frank and Rath,
1990]. Включение достигается с помощью тлеющего разряда, создаваемого в верхней
части прибора. Все металлические детали показаны черным цветом или штриховкой.
Тлеющий разряд с током менее 1 мА, возбуждаемый с помощью вспомога-
тельного электрода 2, обеспечивает слабую ионизацию в пусковой секции прибо-
ра. Для включения ключа создается импульсный разряд с током до 1 А путем по-
дачи отрицательного импульса напряжения порядка 3 кВ на пусковой электрод.
На вспомогательный электрод 1 также возможна подача положительного смеще-
ния до 300 В для создания через боковые отверстия в пустотелом катоде конфигу-
рации электрического поля, подавляющей нежелательное преждевременное
включение основного ключа. Когда осуществляется включение, инжекция носи-
телей заряда вызывает формирование положительного объемного заряда внутри
пустотелого катода. Псевдоискровой разряд образуется с задержкой 10...40 нс В
продаже имеются тиратроны с холодным катодом, наполненные смесью водоро-
да и дейтерия, с переключаемым напряжением 40 кВ и током 20 кА. На Рис. 4.18
представлена фотография такого ключа в металлокерамическом корпусе.
4.1. Замыкающие ключи 117
Рис. 4.18. Общий вид тиратрона с холодным катодом.
Игнитроны
Игнитроны являются ключами, предназначенными для коммутации очень
больших токов и напряжений. В них в качестве катода используется резервуар с
жидкой ртутью, в которую погружен поджигающий электрод. Вся конструкция
размещается в корпусе из нержавеющей стали с вакуумно-плотными стеклянны-
ми изоляторами выводов анода и поджигающего электрода. При нормальных ус-
ловиях внутреннее давление ртути составляет около 5 Па. Игнитрон способен
пропускать в импульсе заряд до 2000 К. При тяжелых условиях эксплуатации иг-
нитронов используется воздушное или водяное охлаждение.
На Рис. 4.19 показана типовая конструкция игнитрона. Чтобы избежать им-
пульсного нагрева за время нахождения в проводящем состоянии, анод игнитро-
118 Глава 4. Ключи
на обычно делают весьма массивным. Охлаждение анода осуществляется через
его основание и стенки. В случаях, когда не исключены переполюсовка тока и
пробои при обратной полярности напряжения анод—катод, в качестве материала
для анода применяют молибден Катод представляет собой ванну с ртутью, рас-
положенную на дне цилиндрического корпуса, изготовленного из нержавеющей
стали. В качестве материала для изготовления поджигающего электрода исполь-
зуют жаропрочные полупроводники, такие как карбид кремния или карбид бора,
которые не смачиваются ртутью. Таким образом, на границе ртуть—поджигаю-
щий электрод формируется отрицательный мениск ртути с относительно высо-
ким сопротивлением. Электрическая энергия в цепи поджигающего электрода
при этом в основном выделяется в маленьком объеме вблизи границы раздела
ртуть—электрод. В результате воздействия высокой плотности энергии создается
интенсивный источник ртутных паров и свободных электронов. Горячее пятно
распространяется на всю поверхность катода за 50... 100 нс. Давление паров ртути
растет очень быстро в пространстве анод—катод, и значение pd в какой-то мо-
мент достигает минимума Пашена. Так как при этом еще и присутствуют свобод-
ные электроны, развивается ионизационная лавина и прибор переходит в прово-
дящее состояние. У игнитронов время нарастания тока составляет 300...500 нс.
Проводящее состояние на участке катод—анод сохраняется до тех пор, пока
ток не уменьшится до критического значения, при котором уже не производится
достаточного количества ртутных паров, и пока не истечет время, необходимое
для рекомбинации ионов ртути и ее конденсации. Ртуть, сконденсировавшись на
Рис. 4.19. Высоковольтный игнитрон с брызгозащитным экраном (слева). Справа, в увеличен-
ном виде, изображена зона контакта поджигающего электрода с ртутью
4.1. Замыкающие ключи 119
стеклянных изоляторах, может привести к снижению пробивного напряжения и,
в худшем случае, к пробою и разрушению изоляторов. Частота повторных вклю-
чений у игнитронов не превышает 1 Гц.
Основным процессом, ограничивающим долговечность игнитронов, является
смачивание ртутью поджигающего электрода. Результатом этого становится про-
грессивное уменьшение сопротивления в зоне их контакта, что приводит к отказу
игнитрона. Смачивание вызывается электрохимическими реакциями, при кото-
рых примеси из объема поджигающего электрода диффундируют к его поверх-
ности.
В последнее время игнитроны постепенно уходят из применения из-за не-
решенных вопросов захоронения содержащего ртуть мусора.
Крайтрон
Крайтрон (Krytron) — это газоразрядный прибор с низким давлением газа, с
холодным катодом и тетрадной конфигурацией, загерметизированный в стеклян-
ном корпусе. Он работает при давлении 1.3 Па гелия. Генератор водорода отсутс-
твует. Специальная конструкция области анод—сетка совместно с используемым
низким давлением газа обеспечивают сравнительно большие рабочие напряже-
ния. Время задержки включения около 30 нс, и быстрая коммутация достигаются
за счет тлеющего разряда, поддерживаемого между специальным вспомогатель-
ным электродом и катодом.
На Рис. 4.20 представлена схема включения крайтрона с импульсным транс-
форматором, входящим в состав конструкции. Время нарастания тока у крайтро-
на составляет менее 1 нс, а максимальные значения тока и напряжения составля-
ют 3 кА и 8 кВ соответственно. Может работать с длительностью импульсов до
10 мкс и частотой повторения 1 кГц. Включение осуществляется импульсом по-
ложительной полярности, подаваемым на управляющую сетку, которая, за ис-
Рис. 4.20. Схема включения крайтрона с импульсным трансформатором,
входящим в состав конструкции.
120 Глава 4. Ключи
ключением маленького отверстия, окружает анод. При включении плазма рас-
пространяется в пространстве между управляющей сеткой и катодом. В стеклян-
ном корпусе смонтирован также эмиттер электронов (Р-частиц), содержащий
небольшое количество изотопа 63А7. Этот эмиттер обеспечивает создание неболь-
шой постоянной ионизации газа, так что надежное включение этого ключа га-
рантируется даже после длительного хранения, а также делает крайтрон в значи-
тельной степени устойчивым к разнообразным воздействиям окружающей среды.
Недостатком крайтрона является ограниченное число его включений (106), обус-
ловленное потерей газа и эрозией электродов.
Крайтроны широко применяются в быстродействующих генераторах импуль-
сов и в драйверах элементов Поккельса, а кроме того, они идеально подходят для
схем детонаторов бомб.
Управляемые вакуумные разрядники
Управляемые вакуумные разрядники являются трехэлектродными приборами и
работают при давлении внутри корпуса 0.001 Па (Рис. 4.21). Их включение осу-
ществляется путем инжекции облака плазмы. Максимальное рабочее напряже-
ние зависит только от материала поверхностей электродов. При напряжении до
100 кВ они могут пропускать ток до 10 кА. При надлежащем охлаждении они спо-
собны работать на частоте до нескольких килогерц.
Смесь газа и плазмы создается с помощью вспомогательной дуги, зажигаемой
между двумя электродами внутри полости в одном из основных электродов. В
большинстве случаев вспомогательные электроды изготавливают из титана, про-
питанного водородом. Водород выделяется из гидрида титана в основании дуги.
управления
МН Металл □ | Керамика
Рис. 4.21. Управляемый вакуумный разрядник в разрезе
В нижней части размещается коаксиальная плазменная пушка
4.1. Замыкающие ключи 121
Время включения этих ключей составляет около 100 нс, а его
нестабильность — 30 нс. Важным достоинством управляемых вакуумных разряд-
ников является положительный наклон их вольт-амперных характеристик, что
позволяет соединять несколько таких ключей параллельно. Кроме того, они име-
ют маленькие размеры, большой динамический диапазон и не требуют подогре-
ваемого катода. Однако их долговечность невелика из-за износа системы включе-
ния и эрозии электродов.
4.1.2. Полупроводниковые ключи
Ограничения на параметры полупроводниковых приборов как ключей в пер-
вую очередь связаны со сравнительно низкой подвижностью носителей зарядов в
полупроводниках и низкими рабочими температурами. Таким образом, для про-
пускания большого тока требуется большой объем полупроводникового материа-
ла. Сравнительно небольшой свободный пробег носителей заряда в полупровод-
никах не позволяет увеличивать межэлектродное расстояние для повышения ра-
бочего напряжения. Поэтому для увеличения коммутируемой мощности
приходится увеличивать плошадь полупроводниковой структуры. Это характерно
для всех типов полупроводниковых ключей.
Тиристоры
Тиристоры (или кремниевые управляемые выпрямители — КУВ) являются че-
тырехслойными полупроводниковыми приборами со структурой р+п~рп+. Эта
структура содержит три р-л-перехода и, как показано на Рис. 4.22, может быть
представлена как комбинация из п-р-п- и р-л-р-транзисторов с общим коллек-
торным переходом. Каждый из транзисторов в этой комбинации управляется то-
ком базы, поступающим из коллектора другого транзистора. Вывод управления
обычно подключен к базе л-р-л-транзистора. Профиль распределения примесей
в тиристоре показан на Рис. 4.23 [АВВ, 2001].
Вследствие высокой концентрации примесей во внешних слоях тиристорной
структуры их называют эмиттерами, а два внутренних слоя, с низкой концентра-
цией примесей, рассматриваются как базы. Сам полупроводниковый кристалл
является тонким кремниевым диском с площадью до 70 см2. Тепло, выделяемое
при работе, отводится через металлизированные контактные площадки, располо-
женные на обеих сторонах кристалла. Для улучшения эффективности теплоотво-
да к электродам прижимают медные пластины, в свою очередь охлаждаемые во-
дой.
Тиристоры могут работать в следующих трех режимах:
• при напряжении, приложенном к цепи катод—анод в обратном направле-
нии;
• при напряжении, приложенном к цепи катод—анод в прямом направле-
нии;
• в режиме проводимости, или включенном состоянии.
Если к тиристору приложено обратное напряжение, т. е. потенциал анода от-
рицательнее потенциала катода, электроны начинают двигаться к катоду, а
122 Глава 4. Ключи
Металлический
Управляющий
электрод
п-р-п
Рис. 4.22. Структура тиристора и эквивалентная схема с двумя транзисторами.
Концентрация
1200мкм
Рис. 4.23. Распределение примесей в тиристорной структуре.
4.1. Замыкающие ключи 123
дырки — к катоду. Эти потоки зарядов увеличивают пространственные заряды у
переходов J\ и J3 и уменьшают у перехода J2- Приложенное обратное напряжение
делится между переходами и Л, так что получается f/REV = Ux + t/3. Так как кон-
центрация примесей в базах существенно различна (см. Рис. 4.23). большая часть
обратного напряжения оказывается приложена к переходу Причиной этого яв-
ляется более низкое напряжение лавинного пробоя перехода J3 и возможность
протекания при этом намного больших токов, чем ток утечки перехода Таким
образом, параметры тиристора при обратном напряжении в основном определя-
ются характеристиками р-л-р-транзистора, входящего в структуру тиристора.
Когда к аноду приложен положительный потенциал, электрическое поле ус-
коряет движение электронов к аноду, а дырок — к катоду. Это увеличивает про-
странственный заряд и напряженность поля в области перехода J2. Этот переход
оказывается под обратным смещением, что препятствует протеканию тока через
него, несмотря на то, что оба других перехода смещены в прямом направлении. В
этом состоянии тиристор находится в выключенном состоянии при прямом сме-
щении. Оно может продолжаться сколь угодно долго, если приложенное напря-
жение не превышает напряжение пробоя перехода J2.
Рассмотрим процесс включения тиристора, находящегося пол воздействием
напряжения, приложенного к цепи катод—анод в прямом направлении. Если на
затвор подать достаточно большой положительный потенциал, то дырки начнут
двигаться в p-базе в направлении к катоду и начнется эмиссия электронов из ка-
тода через переход J3 для их нейтрализации. При этом вблизи границы х5 создает-
ся большая плотность зарядов в базе, а градиент их концентрации сдвигает элект-
ронно-дырочную плазму в направлении перехода J2, заполняя всю область базы
(Рис. 4.24).
Вблизи перехода J2 электроны ускоряются электрическим полем по направ-
лению к л-базе, в то время как дырки отталкиваются назад. Электроны в л-базе
вызывают инжекцию дырок через переход создавая градиент концентрации
электронно-дырочной плазмы в л-базе аналогично тому, как это происходит в
р-базе.
Когда электронно-дырочная плазма достигнет перехода J2, электроны оттал-
киваются назад, в то время как дырки ускоряются полем и, попадая в p-базу, пе-
реводят переход J3 в еще более проводящее состояние. Теперь в p-базе создается
критическая плотность зарядов и устанавливается регенеративная обратная связь
по току с коэффициентом усиления более 1. Когда ток через тиристор увеличива-
ется, часть приложенного к нему напряжения начинает падать на внешней на-
грузке и потенциал на переходе J2 уменьшается. Емкость этого перехода разряжа-
ется с помощью носителей заряда, проникающих к нему из переходов и J3. В
конце концов падение на сопротивлении нагрузки становится столь велико, что
переход J2 переключается из выключенного в полностью проводящее состояние.
При этом все три перехода тиристора оказываются под воздействием прямого
смещения, а сам тиристор включен.
Точка переключения чувствительна к амплитуде тока управляющего электро-
да, так что можно построить семейство вольт-амперных характеристик тиристора
с током управляющего перехода /g в качестве параметра (Рис. 4.25).
124 Глава 4. Ключи
Рис. 4.24. Временная последовательность распределения плотности носителей заряда
при включении тиристора [Gerlach, 1979].
-4000 В
Режим
проводимости
4000 В
Режим
обратного
смещения
Режим
прямого
смещения
Напряжение UAC
пробоя
при прямом
смещении
Лавинный пробой
при обратном
смещении
Рис. 4.25. Семейство вольт-амперных характеристик тиристоров.
4.1. Замыкающие ключи 125
Без внешнего воздействия тиристор не может вернуться назад из проводящего
состояния в выключенное. Для восстановления начального выключенного состо-
яния избыточную плотность зарядов необходимо снизить ниже критического
уровня. Для этого обычно используются два способа:
• переключение полярности протекающего через тиристор тока;
• выключение протекающего тока с одновременным выключением тока в
цепи управляющего электрода.
Обратный ток через тиристор может беспрепятственно протекать только до
тех пор, пока не будет удален избыточный заряд из эмиттерных областей перехо-
дов Jj и Jy и пока не восстановится их непроводящее состояние. Когда это про-
изойдет, область пространственного заряда расширится в базы, способствуя даль-
нейшему удалению носителей зарядов из тиристорной структуры Как бы там ни
было, обратный ток начинает быстро уменьшаться. В начале он падает с постоян-
ной скоростью dl/dt = —UREy/L, где L— индуктивность цепи (Рис. 4.26). В это
время рекомбинация зарядов еще пренебрежимо мала.
Даже после изменения полярности протекающего тока в момент времени /1
ток продолжает изменяться во времени с той же скоростью. После того как избы-
точные носители будут удалены из p-базы, прилегающей к переходу J3, в момент
времени t2 начинает восстанавливаться блокирующая способность тиристора и
напряжение на нем U(t) становится отрицательным. В это же самое время ско-
рость изменения тока уменьшается. Однако это уменьшение незначительно, так
как переход J3 не способен погасить на себе большого напряжения. Из-за высо-
кой концентрации примесей в p-базе его пробивное напряжение f/BR3 не превы-
шает 10...20 В. В момент времени г4 избыточный заряд удаляется из р-эмиттера и
переход J\ начинает запираться. При расширении барьерного слоя в переходе J\
скорость изменения тока уменьшается и становится равной нулю, когда текущее
напряжение на тиристоре приобретет значение t/REV. Так как в этот момент плот-
ность зарядов в области перехода падает очень быстро, достигнутый к тому вре-
мени уровень обратного тока /RRM не может больше сохраняться. Ток через ти-
ристор уменьшается до нуля, а напряжение возрастает, превышая приложенное
обратное напряжение:
U{t) = -{U^LdI/dt\
Большое значение dlfdt может привести к пробою и выходу из строя тиристора.
После того как ток тиристора упадет до нуля, остаточные носители зарядов ре-
комбинируют за 10... 100 мкс.
Включение тиристора можно осуществить не только электрическим током,
но и импульсом света. Фотоны с энергией, превышающей энергию запрещенной
зоны, способны создавать пары электрон—дырка как в области пространствен ко-
го заряда перехода J2, так и в базах. Эти носители зарядов ведут себя аналогично
носителям, инжектированным из управляющего электрода. Ввиду малого време-
ни жизни носителей, созданных светом в высоколегированных областях эмитте-
ров, их вклад в процессы отпирания тиристора несуществен. Для запуска процес-
са включения тиристора фототок должен превысить значение анодного тока, со-
ответствующее коэффициенту усиления 1 в цепи обратной связи.
126 Глава 4. Ключи
Рис. 4.26. Напряжение и ток в тиристоре во время коммутации [Gerlach, 1979]. Большой выброс
напряжения при спаде тока в цепи с индуктивностью может вывести тиристор из
строя. Для предупреждения этого параллельно тиристору можно подключить
АС-цепь, ограничивающую бросок напряжения.
В запираемых тиристорах (GTO — Gate Turnoff Thyristor) площадь контакта
управляющего электрода с p-базой больше, чем площадь перехода между р-базой
и л-эмиттером (Рис. 4.27). Процесс включения в этих тиристорах происходит так
же, как и в обычных, а выключение достигается путем подачи на управляющий
электрод отрицательного смещения по отношению к катоду. При этом дырки вы-
сасываются из л-эмиттера. Электроны при этом, ввиду условия нейтральности
суммарного заряда, также выталкиваются из этой области в узкий канал в центре
эмиттера. Когда радиус этого канала становится меньше диффузионной длины,
плотность зарядов уменьшается и электронная инжекция из эмиттера прекраща-
ется.
Для обеспечения возможности коммутации тиристорам больших токов при-
ходится использовать специальную геометрию управляющего электрода. Дело в
том, что при включении тиристора вначале образуется только узкий канал прово-
4.1. Замыкающие ключи 127
Рис. 4.27. Структура запираемого тиристора.
дящего состояния вблизи зоны протекания тока управляющего электрода. Для
включения в проводящее состояние всей площади тиристора требуется некоторое
время rd. Проводящее состояние распространяется в поперечном направлении в
тиристорной структуре со скоростью 0.05...0.1 мм/мкс, откуда следует, что для
полного включения тиристоров с большой площадью структуры требуется не-
сколько сот микросекунд. Чтобы исключить возможность повреждения тиристо-
ра из-за локального перегрева его структуры при включении, необходимо огра-
ничивать скорость нарастания тока при включении на уровне ниже критического
значения dlcvjdt. Для получения возможности более быстрого включения тирис-
тора управляющий электрод выполняют в форме полос или спиралей, как это по-
казано на Рис. 4.28. Если на управляющий электрод в таком тиристоре подан им-
пульс тока достаточной амплитуды, его переход J2 начинает проводить ток одно-
временно по всей площади. Для получения достаточно большого тока
управления, необходимого для обеспечения однородности токораспределения в
структуре мощного тиристора, иногда применяется вспомогательный тиристор,
интегрированный в том же кристалле.
Полоски эмиттера
Металлизация управляющего
электрода
Центральный вывод
управляющего электрода
б)
Рис. 4.28. Спиралеобразная конструкция управляющего электрода у тиристоров,
предназначенных для коммутации больших токов [Gerlach, 1979].
128 Глава 4. Ключи
Тиристоры для применения в импульсных устройствах, в отличие от обычных
тиристоров, должны выдерживать очень большую скорость нарастания тока. В
настоящее время для тиристоров со структурой, подобной структуре запираемых
тиристоров и мощных драйверов, в цепи управления достигнуты значения
30 кА/мкс.
Для обеспечения возможности пропускания тока в обратном направлении,
что необходимо в схемах с колебательными процессами, в структуру этого тирис-
тора введен диод, включенный встречно-параллельно тиристору. Низкая индук-
тивность конструкции достигается размещением схемы запуска на той же плате,
что и тиристора. При этом тиристор и схема запуска образуют единый блок. Для
достижения возможности работы при высоких напряжениях несколько тиристо-
ров могут быть соединены последовательно, как это показано на Рис. 4.29.
Рис. 4.29. Набор из четырех тиристоров, соединенных последовательно со встроенными
встречно-параллельными диодами и схемами запуска. Максимальное рабочее напря-
жение 10 кВ, пиковый ток 30 кА, максимальная скорость нарастания тока 20 кА/мкс,
рабочая частота 10...50 ГЦ. Между тиристорами видны элементы конструкции водя-
ного охлаждения. Одиночный тиристор со схемой запуска, но без элементов охлаж-
дения показан внизу.
В 1кбл. 4.1 приведены для сравнения параметры обычного тиристора, предна-
значенного для фазового управления, и тиристора, предназначенного для приме-
нения в качестве сильноточного ключа. В этой таблице t/FRM и ^rrm — макси-
мально допустимые значения амплитуды повторяющихся полуволновых импуль-
сов напряжения прямой и обратной полярности соответственно, /Tsm —
максимальное значение не повторяющегося импульса тока с длительностью гР,
/trmsm — максимально допустимый непрерывный ток.
4.]. Замыкающие ключи 129
Таблица 4.1. Параметры тиристора, предназначенного для фазового управления, и тиристора,
предназначенного для применения в качестве сильноточного ключа
EupecT1501N (тиристор для фазового управления) ABB 5SPY36L4502 (тиристор для коммутации больших токов)
t^FRM ~ 7—8 кВ ^FRM = 4.5 кВ
^FRM = I/rrm (симметричны) (Zrrm — 18 В (не симметричен)
7jsm = 45 кА при tP = 10 мс 7tsm = 140 кА при /Р = 50 мкс
7trmsm = 4000 А —
dlcpjdt - 300 А/мкс dl/dt > 10 кА/мкс
Как можно увидеть на Рис. 4.29, основными недостатками этой конструкции
являются ее сложность и большие размеры, а также, как следствие, высокая цена.
Сложность конструкции еще больше увеличивается при введении в схему узлов
защиты, предотвращающих разрушение ее элементов при неправильном функ-
ционировании. Все это вместе и является причинами, ограничивающими приме-
нение тиристоров в импульсных устройствах в настоящее время.
IGBT
IGBT (Insulated-Gate Bipolar Transistor) — биполярные транзисторы с изолиро-
ванным затвором (БТИЗ), которые соединяют в себе достоинства биполярных и
полевых транзисторов (малое сопротивление во включенном состоянии и низ-
кие потери в цепи управления соответственно). Один IGBT имеет меньшую на-
грузочную способность по току, чем тиристор в диапазоне 1000... 1800 В, но
IGBT можно легко соединять параллельно, их можно выключать, а время их
включения составляет несколько десятков наносекунд. IGBT отличается от
мощного полевого транзистора наличием дополнительной /Л-зоны, которая об-
разует коллектор (Рис. 4.30). Прибор состоит из множества маленьких элемен-
тов (10-3мм2), соединенных параллельно, и общего коллектора большой пло-
щади (несколько см2). Положительный температурный коэффициент сопротив-
ления гарантирует равенство и стабильность токов во всех элементах структуры
IGBT.
Как и в биполярном транзисторе, при включении дырки инжектируются в
л-базу и напряжение коллектор—эмиттер снижается до напряжения насыщения.
IGBT имеют ограниченную возможность работы при обратной полярности на-
пряжения коллектор—эмиттер. По этой причине, как правило, параллельно
транзистору включают дополнительный диод.
IGBT большой мощности в настоящее время имеют максимальное напряже-
ние коллектор—эмиттер до 4 кВ и ток во включенном состоянии 3 кА. IGBT ши-
роко применяются в высоковольтных установках. Однако те же причины, что и
для тиристоров — сложность конструкции и цена, в настоящее время препятству-
ют их широкому применению в качестве высоковольтных ключей в импульсных
генераторах большой мощности.
130 Глава 4. Ключи
Рис. 4.30. Структура IGBT и его эквивалентная схема
со встречно-параллельным диодом.
Полупроводниковые ключи с оптическим управлением
Принцип действия полупроводниковых ключей с оптическим управлением осно-
ван на генерации носителей зарядов в полупроводнике с помощью высокоинтен-
сивного источника света (лазера). Ток в полупроводнике подчиняется уравнению
непрерывности
V/n = е(Ап - (7П) + e(dn/dt),
(4.13)
V/p = -е(Яр - Gp) - e(dp/dt).
где Ап, Ар — скорости рекомбинации, (7П, (7Р — скорости генерации электронов
(индекс «п») и дырок (индекс «р»). Генерация электронов и дырок вызывается ли-
бо оптическим возбуждением, либо лавинной ионизацией при достаточно высо-
кой напряженности электрического поля:
^Tav ^nlAil + ар|Уп1’ (4-14)
На Рис. 4.31 представлены зависимости коэффициентов ионизации ап для
электронов и ар для дырок от инвертированного значения напряженности поля Е.
Одним из наиболее подходящих полупроводниковых материалов для лазер-
ной активации проводимости является арсенид галлия [Loubriel et al., 1995, 1997].
На Рис. 4.32 показана глубина оптической абсорбции в GaAs как функция длины
волны света. Очевидно, что для получения достаточно широкого проводящего
канала в полупроводнике следует выбирать длину волны больше 0.9 мкм. Таким
источником света является инфракрасный лазер на иттрий-алюминиевом грана-
те с неодимом, у которого фундаментальная длина волны равна 1.06 мкм.
На Рис. 4.33 показана конструкция низкоимпедансного полоскового генера-
тора импульсов с применением многоэлементного ключа на GaAs. В связи с тем
что ток утечки GaAs-ключей не позволяет использовать постоянное напряжение
для зарядки емкостей полосковой линии, используется импульсная зарядка от
другой конденсаторной цепи, показанной в верхней части Рис. 4.33. С помощью
волоконно-оптической системы излучение лазера расщепляется на ряд лучей для
4.1. Замыкающие ключи 131
Рис. 4.32. Глубина оптической абсорбции в GaAs как функция длины волны света
управления каждым из GaAs-ключей. Лазер вырабатывает импульс света в мо-
мент, когда напряжение на емкостях полосковой линии максимально.
Ключ на GaAs со световым управлением может работать в двух режимах. В ли-
нейном режиме фотопроводимость определяется числом создаваемых в полупро-
воднике носителей заряда, которое в свою очередь пропорционально интенсив-
ности света. В этом режиме плотность тока в ключе и время нахождения его в
проводящем состоянии весьма ограничены. Как можно видеть на Рис. 4.34, ток
132 Глава 4. Ключи
Рис. 4.33. Низкоимпедансный полосковый генератор импульсов с применением многоэлемент-
ного ключа на GaAs. Емкость полосковой линии должна заряжаться от генератора
импульсов тока заряда за время, меньшее, чем постоянная времени разряда полоско-
вой линии [Katschinski, 1994].
Рис. 4.34. Результаты экспериментов, выполненных на установке, представленной на Рис. 4.33. Ем-
кость полосковой линии заряжалась до 2.4 кВ (слева) и 6.4 кВ (в центре и справа). Левый
столбец графиков отражает типичное поведение GaAs-ключа в линейном режиме рабо-
ты, в то время как правый столбец относится к нелинейному режиму (с лавинным про-
боем). В центре показаны графики, соответствующие переходному случаю между этими
двумя режимами. В нижних графиках показаны напряжения на ключе и на нагрузке
[katschinski, 1994].
4.1. Замыкающие ключи 133
через ключ следует изменению мощности лазера (столбец графиков слева). Ток
прекращает течь после того, как иссякнут носители зарядов, созданные фотоио-
низацией.
В нелинейном режиме число носителей заряда увеличивается за счет иониза-
ции при их столкновениях с атомами полупроводника, и, как в газоразрядном
ключе, их размножение происходит по экспоненциальному закону. Однако импе-
данс GaAs-ключа не падает так же сильно, как у газоразрядных ключей. Падение
напряжения остается на уровне около 5 кВ/см вдоль ключа, и, таким образом, по-
тери в GaAs-ключе оказываются довольно большими (столбец графиков справа
на Рис. 4.34).
В центре на Рис. 4.34 представлен переходной случай между линейным и не-
линейным режимами работы GaAs-ключа.
Таким образом, применение полупроводниковых ключей с оптическим уп-
равлением ограничено ситуациями, где требуется очень большое быстродействие
при относительно низкой коммутируемой мощности. Большим их недостатком
является также невозможность использования в системах с зарядом постоянным
напряжением.
4.1.3. Ключи с магнитным управлением
Работа ключей с магнитным управлением основана на насыщении ферромаг-
нитного сердечника. Они работают с относительно малыми потерями, а то и без
них. На Рис. 4.35 изображена базовая схема применения магнитного ключа.
Рис. 4.35. Базовая схема с емкостным накоплением энергии и магнитным ключом {слева). Идеа-
лизированная петля гистерезиса {справа) При работе ключ переходит из состояния
остаточной магнитной индукции —в состояние насыщения В$.
Когда конденсатор заряжен, катушка с ферромагнитным сердечником внача-
ле имеет большую индуктивность. Когда под воздействием тока утечки, протека-
ющего через катушку, будет достигнуто состояние насыщения сердечника, ин-
дуктивность катушки резко уменьшится и ключ замкнется. Коэффициент умень-
шения индуктивности равен ц — относительной проницаемости материала
сердечника. В отличие от трансформатора, в котором при работе используется
134 Глава 4. Ключи
только малая часть петли гистерезиса, в магнитном ключе всегда используется
весь диапазон петли гистерезиса — от состояния остаточной магнитной индук-
ции до состояния насыщения. Для обеспечения быстрого и четкого переключе-
ния петля гистерезиса должна иметь максимально прямоугольную форму, с рез-
ким изменением магнитной проницаемости на несколько порядков при достиже-
нии состояния насыщения (Рис. 4.35).
Время, в течение которого ключ можно считать разомкнутым, зависит от се-
чения сердечника и суммы его остаточной магнитной индукции и индукции в со-
стоянии насыщения:
U(t) = d<D/dt=FdB/dt.
(4.15)
$U(t)dt = Uot = F(BR + Bs).
Здесь Uq — среднее напряжение импульса, ат— его длительность, F— площадь
сечения сердечника, a BR и В$ — остаточная магнитная индукция и индукция в
состоянии насыщения соответственно Подходящий ферромагнитный материал
должен иметь высокое значение индукции насыщения, очень крутые боковые
стороны петли гистерезиса и малую коэрцитивную силу Hq. Широко используе-
мыми ферромагнитными материалами являются ферриты и аморфные ферромаг-
нитные материалы, такие как метгласе (Metglass) и его аналог витровак
(Vitrovac)0. Метгласе и витровак являются металлическими аморфными материа-
лами, изготавливаемыми в виде очень тонких лент методом быстрого охлаждения
тонкого расплавленного слоя. Метгласе и витровак имеют более высокую индук-
цию насыщения, чем ферриты, но электропроводны. Поданной причине поверх-
ность сердечников из этих материалов должна быть покрыта слоем изолятора.
Кроме того, проводимость метгласса и витровака приводит к появлению разли-
чий между статической и динамической петлями гистерезиса.
В магнитных ключах потери можно разделить на потери намагничивания
(или гистерезиса) и потери из-за вихревых токов. Потери намагничивания опре-
деляются площадью петли гистерезиса:
W^V^HdB, (4.16)
где Vпредставляет собой объем сердечника, а интеграл берется по всей петле. По-
тери, связанные с вихревыми токами, возникают в проводящих материалах под
воздействием изменяющейся во времени магнитной индукции. Эти потери про-
порциональны квадрату индуцируемого напряжения U:
Рес~и2/р, (4.17)
где р — удельное сопротивление проводника. При очень большой скорости изме-
нения магнитного поля потери из-за вихревых токов становятся доминирующими,
n Metglass — торговая марка, принадлежащая Элайед Корпорейшн, США (Allied Corporation,
USA). Vitrovac — торговая марка, принадлежащая Вакуум Шмельце Ханау, Германия (Vacuum
Schmelze Hanau, Germany). — Примеч. авт.
4.1. Замыкающие ключи 135
а петля гистерезиса становится шире с менее крутыми боковыми сторонами, т. е.
ключ начинает отклоняться от идеального. Даже в сердечниках, изготовленных из
аморфных материалов с толщиной 20 мкм, это явление обнаруживается на очень
высоких частотах. Для листов, чья толщина d намного меньше по сравнению с ши-
риной 6, и для синусоидального граничного условия H(±d /2, = хехр(кпг)
комплексное значение магнитной индукции определяется выражением [Kupfmiiller
and Kohn, 2000]
ch(p(l + i)x)
ch(p(l+i)J/2)
(4.18)
Здесь Hq является эффективным значением магнитного поля на границе, а абсо-
лютное значение В представляет эффективное значение магнитной индукции:
В(х) = рр0Я0
ch2(Px) —sin2(Px)
ch2(p^/2> —sin2(P^/2)
(4.19)
Здесь p — величина, обратная толщине скин-слоя; р = (nvoppo)1^, где v — часто-
та, и — проводимость, р. — относительная магнитная проницаемость и ц0 — маг-
нитная проницаемость вакуума, а х изменяется от — d/2 до d/2. График функции
(4.19) представлен в левой части Рис. 4.36 для pj/2 = 2.5.
Рис. 4.36. Распределение относительного магнитного потока для тонкого листа с толщиной
Р<//2 = 2.5 (слева). Среднее значение магнитной индукции в зависимости от Р<7 (справа)
136 Глава 4. Ключи
Формулу (4.19) можно использовать и для расчета среднего эффективного
значения магнитной индукции как функции от отношения между толщиной лис-
та и глубиной скин-слоя pd. Это достигается интегрированием выражения (4.19)
по толщине листа и делением результата на bd, где b — ширина листа. Результат
представлен в выражении (4.20), где Во = рроМь а соответствующий график — в
правой части Рис. 4.36.
Bv =
/о НРоЯо
PJ
ch(pJ) —cos(pif)
ch(pj) + cos(pj)
(4.20)
Зависимость магнитной индукции от времени для синусоидального закона
может быть получена умножением (4.18) на exp(icor). Используя действительную
часть результирующего выражения, получаем
= V22?(x)sin{(of — ф(х)}.
(4.21)
Здесь В(х) определяется из (4.19), а ф(х) является пространственно зависящим
фазовым коэффициентом, получаемым из формулы
t /sh (Р(^/2 -х))sin(р(J/2 + х))+ sh (Р(J/2 + х))sin(p(d/2 -х))
ch (р( d /2 4- x))cos(p(J /2 4- х))4- ch(p( d /2 — x))cos(p( J /2 — x))
Уравнения (4.21) и (4.22) являются также хорошей аппроксимацией для полу-
синусоидальных импульсов, получаемых, например, от генератора Маркса, в ко-
тором конденсатор разряжается на линию передачи, соединенную с нагрузкой
через магнитный ключ.
Чтобы определить характеристики ключа для специфической формы импуль-
сов, требуется выполнить преобразование Фурье и рассчитать эффективную ин-
дуктивность для каждой частотной компоненты разложения Фурье. Однако для
грубой оценки часто достаточно применить выражение (4.20) для первой гармо-
ники. Конечно, следует принимать во внимание «коэффициент упаковки», т. е.
отношение площади сечения ферромагнитного сердечника к общей площади се-
чения сердечника и электроизолирующего слоя на его поверхности.
Итак, к достоинствам магнитных ключей следует отнести высокую степень
повторяемости их параметров, отсутствие износа и малое время восстановления.
К недостаткам следует отнести невозможность получения идеального прямо-
угольного импульса напряжения на выходе. В частности, ток утечки через ключ
может вызвать появление весьма продолжительной «подставки» напряжения,
предшествующей основному импульсу. Другими недостатками являются возмож-
ность работы только в одной рабочей точке и относительно большой объем уст-
ройства.
4.2. Размыкающие ключи 137
4.1.4. Заключение
В Ткбл. 4.2 приведены некоторые основные характеристики замыкающих
ключей, рассмотренных выше, и указаны диапазоны их применимости.
Таблица 4.2. Основные характеристики замыкающих ключей
Тип Максимально допустимое напряжение [кВ] Максимально допустимый импульсный ток[кА] Суммарный пропускае- мый заряд [Ас] Рабочая частота [ГЦ] (время ком- мутации [нс]) Долговечность (число выдер- живаемых импульсов) Примечания
Газовые разряд- ники 1...6000 юЧ.лооо 0.1...50 1...10 (1...1000) 1О3...1О7 Долговечность определяется эро- зией электродов
Тиратроны 5...50 0.1...10 10"3 1000 (5... 100) Ю’.-ЛО8 Применяются для накачки лазеров и в ускорителях
Игнитроны > 10 > 100 2000 1 (1000) 105... 106 Применяются для накачки лазеров и в ускорителях
Управляемые вакуумные раз- рядники 0.5...50 1...10 40 1 (10...100) > 104
Тиратроны с холодным ка- тодом 1...50 1...20 1 1...1000 (> Ю) Ю^.ЛО8 Подобны обычным тиратронам
Крайтроны 8 3 0.01...0.1 < 1000 (1...10) 107 Очень маленькая задержка и время коммутации
Магнитные ключи 1000 100... 1000 10 (5... 10000) 1О8...1О9 Невозможно уп- равление; только одна рабочая точка
Тиристоры <5 <5 10"2 10 (> 1000) 108 Можно соединять последовательно; дороги и сложны
IGBT <4 3 100 108 Можно выключать
Полупроводни- ковые ключи с оптическим уп- равлением <20 1...10 < кг4 < 10 (1...10) 1О2...1О3 Требуется источ- ник интенсивного света
4.2. Размыкающие ключи
Размыкающие переключатели характеризуются резким ростом их импеданса
при выключении [Schoenbach et. al., 1984; Guenther, 1987]. Это может быть следс-
твием как внешнего воздействия, так и некоторых внутренних процессов, кото-
рые могут зависеть от заряда, прошедшего через ключ. Механизм размыкания
может быть резистивным, индуктивным или емкостным. Примером резистивно-
го размыкающего ключа является обычный предохранитель. В индуктивных раз-
мыкающих ключах может быть реализовано сжатие магнитного потока, так что
138 Глава 4. Ключи
L(t) > L(0). В емкостных размыкающих ключах размыкание получается, если
С(Г) < С(0).
Независимо от механизма хороший размыкающий ключ должен обладать:
• возможностью находиться длительное время в проводящем состоянии;
• большим рабочим током и малыми потерями в проводящем состоянии;
• быстрым ростом импеданса при размыкании;
• высоким импедансом после размыкания и высоким напряжением во время
прерывания протекания тока;
• малым временем восстановления (т. е. высокой рабочей частотой);
• большой долговечностью (малый износ).
4.2.1. Предохранители
Возможно, наиболее широко известными размыкающими ключами являются
плавкие предохранители. В их конструкцию входит тонкая проволока или фоль-
га, помещенные в газообразную, жидкую или состоящую из твердых гранул среду.
Для этих ключей возможно очень быстрое срабатывание (< 50 нс), а время сохра-
нения проводящего состояния зависит от типа материала, применяемого для из-
готовления проводника, и от его формы и размера. На Рис. 4.37 представлена за-
висимость сопротивления алюминиевой проволоки от адиабатически поглощен-
ной удельной энергии.
Сопротивление большинства металлов растет с увеличением температуры как
в твердом, так и в жидком состоянии. Сопротивление медной проволоки, напри-
мер, увеличивается при нагреве вплоть до расплавления почти на два порядка.
Высокое механическое давление, развиваемое магнитными силами при протека-
Рис. 4.37. Сопротивление предохранителя как функция поглощенной удельной энергии
[Reinovskyetal., 1982].
4.2. Размыкающие ключи 139
нии тока через предохранитель, способно поддержать высокую плотность про-
водника даже при температуре выше критической. Только после достижения воз-
можности расширения металлический проводник разрушается. Для меди это
происходит при плотностях около 0.5... 1 г/см3. Если плотность металлических
паров достаточно мала, процесс лавинного размножения электронов может при-
вести к возникновению электрической дуги в этих парах. Целью использования
той или иной специальной среды вокруг проводника в предохранителе является
гашение этой дуги или создание условий, препятствующих ее образованию. Маг-
нитогидродинамические нестабильности и неоднородности в материале предох-
ранителя могут приводить к его преждевременному обрыву, что создает не пре-
дусмотренные воздействия на его твердые, жидкие и газообразные части. При
этом могут сформироваться поочередные дуговые разряды вдоль всей длины пре-
дохранителя. Эти явления демонстрируют важность окружающей среды для обес-
печения требуемых параметров предохранителя, применяемого в качестве размы-
кающего ключа. Если предохранитель помещен в газообразную среду или вакуум,
то по крайней мере в принципе он может работать повторно, конечно, при усло-
вии замены перегорающей проволоки в нем. Главным достоинством предохрани-
телей, используемых в качестве размыкающих ключей, является их простота и
возможность получения требуемых параметров путем варьирования сечения,
длины и числа элементов.
4.2.2. Механические прерыватели
Типичный вакуумный прерыватель состоит из двух плоских или дисковых
электродов, закрепленных один жестко, а другой подвижно внутри корпуса с но-
минальным давлением газа 0.1 Па или меньше. Такие ключи используются, на-
пример, в цепях переменного тока линий электропередачи. На Рис. 4.38 показан
типичный вакуумный прерыватель.
Подвижный электрод соединен с внешним механизмом управления через
сильфон, обеспечивающий сохранение вакуума внутри корпуса прерывателя. В
замкнутом состоянии плотное контактирование электродов обеспечивает пере-
ходное сопротивление на уровне 10...50 мкОм. При размыкании ключа, выполня-
емом с помощью механизма управления подвижным электродом, возможно воз-
никновение электрической дуги в парах материала электродов. В системах с од-
нополярным напряжением для подавления дуги используется подача на ключ
импульса тока противоположной полярности. После прекращения протекания
тока через прерыватель скорость нарастания напряжения на нем может достигать
24 кВ/мкс.
На Рис. 4.39 представлена принципиальная схема устройства, формирующего
импульс тока для подавления дуги при размыкании контактов вакуумного преры-
вателя. До момента времени через замкнутый прерыватель 50 протекает полный
ток нагрузки. Ключи и S2 при этом разомкнуты. В момент ключ 51 замыкает-
ся и конденсатор Сь предварительно заряженный до напряжения [7Ь разряжается
через дроссель Ц и ключи и 50. Полярность напряжения Ц, а следовательно, и
тока через цепь Сь £ь и 50 выбирается так, чтобы суммарный ток через преры-
140 Глава 4. Ключи
Фиксированный
токопровод
Экран
токопровода
Электроды
Фланец крепления
защитного экрана
Защитный экран
для конденсации
металлических
паров
Подвижный
токопровод
Рис. 4.38. Типичный вакуумный прерыватель в разрезе [Lafferty, 1980].
— Сильфон
Защитный
экран
Изолирующая
оболочка
ватель 5о уменьшался. В момент времени /2, когда ток через контакты прерывате-
ля So проходит нулевое значение, активируется механизм управления подвижным
электродом и ключ So размыкается. После размыкания прерывателя So конденса-
тор Q перезаряжается, но с противоположной исходной полярностью напряже-
ния. Скорость нарастания напряжения при этом dU/dt = Iq/Cx постоянна при ус-
ловии L » £|. В момент времени ключ S2 замыкается и накопленная энергия
поступает в нагрузку.
Стандартный вакуумный прерыватель, показанный на Рис. 4.38, способен ра-
ботать на частоте переключения до нескольких десятков герц, а время его размы-
кания достигает нескольких десятков микросекунд.
4.2. Размыкающие ключи 141
Рис. 4.39. Принципиальная схема устройства, формирующего импульс тока для подавления ду-
ги при размыкании контактов вакуумного прерывателя, и графики токов и напряже-
ний в ней.
4.2.3. Сверхпроводящие размыкающие ключи
В этих ключах используется переход некоторых материалов из сверхпроводя-
щего состояния в состояние с нормальной проводимостью. Сверхпроводящие
ключи обычно применяются в сочетании со сверхпроводящими устройствами на-
копления энергии. Главной проблемой сверхпроводящих ключей является отвод
тепла, выделяющегося при их работе.
Для размыкания в этих ключах могут быть использованы три способа:
• с помощью самого протекающего через ключ тока,
• подачей импульса внешнего магнитного поля,
• импульсным нагревом.
Рабочая частота зависит от скорости восстановления сверхпроводящего со-
стояния. На Рис. 4.40 схематически изображено устройство генератора импуль-
сов напряжения со сверхпроводящим ключом, управляемым с помощью внешне-
го импульсного магнитного поля, чья напряженность превышает критическое
значение для используемого сверхпроводника.
4.2.4. Плазменные размыкающие ключи
Плазменные размыкающие ключи применимы для коммутации больших токов
и имеют высокое быстродействие. В них используется плазменная перемычка с
низкой плотностью (10,3...1015 см-3), создаваемая между контактами до того, как
начнется заряд энергии в индуктивном накопителе (Рис. 4.41). Для создания
плазменной перемычки применяются генераторы различных типов.
На Рис. 4.42 представлена коаксиальная конструкция генератора импульсов с
плазменным ключом. Перед началом накопления энергии в индуктивном нако-
пителе в рабочее пространство ключа инжектируется некоторое количество газа.
142 Глава 4. Ключи
S
Рис. 4.40. Магнитное поле, создаваемое катушкой управления £А, при превышении критическо-
го значения разрушает сверхпроводимость участка цепи, по которой проходит ток
сверхпроводящего накопителя энергии L$. При этом энергия из сверхпроводящего
накопителя энергии £s поступает в нагрузку AL. Для обеспечения эффективности пе-
редачи энергии в нагрузку ее сопротивление должно быть намного меньше, чем со-
противление участка цепи с разрушенной сверхпроводимостью.
Рис. 4.41. Принцип устройства индуктивного накопителя энергии с плазменным ключом
Рис. 4.42. Коаксиальная конструкция плазменного ключа Перед началом накопления энергии в
индуктивном накопителе в рабочее пространство ключа инжектируется некоторое
количество газа. С помощью вспомогательного электрического импульса газ преоб-
разуется в проводящую плазменную перемычку.
4.2. Размыкающие ключи 143
С помощью вспомогательного электрического импульса газ преобразуется в про-
водящую плазму, замыкающую цепь индуктивного накопителя энергии. В зави-
симости от плотности плазмы после прохождения через нее некоторого заряда
плазменная проводящая перемычка разрушается и ключ переходит из проводя-
щего в непроводящее состояние.
Процессы в плазменных ключах весьма сложны и зависят не только от плот-
ности плазмы, но и от скорости инжекции газа, масс ионов, градиента плотности
и условий на электродах, а также импеданса нагрузки, в которую переключается
ток. Обычно различают три фазы работы плазменных ключей (Рис. 4.43).
плазменной
Начало фазы
проводимости
перемычки
Окончание фазы
проводимости
Фаза изоляции
Рис. 4.43. Фазы работы плазменных ключей. Контурные линии на двух верхних рисунках пока-
зывают область протекания тока. Применимость плазменного ключа определяется
качеством его изоляционных свойств после размыкания [Shpitalnik et al.. 1998: Arad et
al., 2003].
В фазе проводимости в плазму проникают и электрический ток, и магнитное
поле. Изменения во времени магнитного поля в высокоионизированной элект-
ропроводящей плазме определяются из уравнений, получаемых из закона Фара-
дея, обобщенного закона Ома без учета инерции электронов и закона Ампера без
учета тока смещения. Обобщенный закон Ома можно получить из уравнений
двухжидкостной гидродинамической модели квазинейтральной плазмы с едина-
144 Глава 4. Ключи
ковым числом электронов и однократно ионизированных атомов (ne = «j = «)
[Artsimowitsch and Sagdejew, 1983]:
nm} —L = —Ур, + епЁ+еп (ц x В) —me (ц—ve )vein,
dt
nmt = —Vpe —епЁ—еп(ре x В) + те(Ц — ve)vein.
dt
(4.23)
Здесь ц» и ц — скорости электронной и ионной компонент,
те и тх — массы электронов и ионов,
ре и pt — электронное и ионное давления соответственно,
Е — напряженность электрического поля,
В — магнитная индукция,
е — заряд электрона,
vei — частота столкновений между электронами и ионами.
Последние слагаемые в правых частях уравнений (4.23), таким образом, пред-
ставляют собой плотность силы торможения. Умножая первое из этих уравнений
на те, а второе на т„ а затем вычитая их друг из друга, пренебрегая слагаемыми
порядка mjmi и полагая, что плотность тока меняется существенно только при
t» l/vei, т. е. пренебрегая инерциальными членами в левой части, мы получим
£=CxB+2_2i?_vp!
о еп еп
(4.24)
Здесь мы ввели проводимость о = (ne2/me)/vcl. Подставляя (4.24) в закон Фарадея,
мы получим наиболее общее уравнение, описывающее проникновение магнит-
ного поля в проводящую жидкость:
дв
+---.
^ = V(dx^)-V
J*B
<еп >
(4.25)
Здесь первое слагаемое в правой части отвечает за конвекцию. Формально это то
же самое, что и вихри в невязкой жидкости [Sommerfeld, 1950]. Если это слагае-
мое является доминирующим, т. е. проводимость велика, то из этого уравнения
можно заметить, что магнитные силовые линии движутся вместе с жидкостью,
т. е. поле «вморожено» в плазму. В этом случае магнитный поток через любой
контур, сопутствующий движению вещества, остается постоянным во времени, и
доминирующим эффектом будет сжатие плазмы силой 2?хj. Если плотность
плазмы велика, такое сжатие может привести к возникновению звуковой волны в
плазме. Второе слагаемое в (4.25) есть холловский член. Он, вероятно, доминиру-
ет при масштабах £ = [(\/n)dn/dx]~], меньших, чем длина инерции ионов, т. е.
£ « c/copj, где (opi — плазменная частота ионов, а с — скорость света. Если холлов-
ское поле доминирует, магнитное поле может проникать в плазму со скоростью
ь>н = В/(2ццеп£). В этом случае скорость проникновения магнитного поля ь>н ста-
4.2. Размыкающие ключи 145
новится больше, чем скорость ионной компоненты ц. Последнее слагаемое в
(4.25) описывает обшие процессы диффузии в проводнике.
Для того чтобы проводить ток в несколько сот килоампер или даже мегаампер
в течение микросекунд, плотность плазмы должна быть порядка 1015... 1016 на см3.
При столь высокой плотности электронов сжатие плазмы магнитным полем, оп-
ределяемое первым слагаемым в (4.25), представляется адекватной моделью для
описания фазы проводимости. Струйный плазменный ключ, который мы рас-
смотрим ниже, является примером использования этого эффекта.
Для пропускания тока в течение времени менее 100 нс с последующим размы-
канием за время менее 10 нс необходима плотность плазмы около 1013 на см3. В
этих условиях проникновение магнитного поля в плазму описывается вторым
слагаемым в (4.25). Полная теория, разработанная для описания этого случая, на-
зывается электромагнитогидродинамической [Kingsepet al., 1990].
Для промежуточных плотностей оба слагаемых в (4.25) становятся равноправ-
ными. Промежуточные плотности могут возникать во время фазы проводимости
в ключах с высокой плотностью плазмы. Плазменные ключи с несколькими раз-
личными видами ионов ведут себя еще сложнее: может возникать разделение ио-
нов, и более легкие ионы могут выталкиваться в сторону нагрузки [Maron et al.,
2002].
Размыкание плазменного ключа наступает, если плазма оказывается вытолк-
нута из разрядного промежутка или саморазрушается. Импеданс ключа в разо-
мкнутом состоянии сильно зависит от магнитной самоизоляции в зазоре, перво-
начально заполненном плазмой, проводившей ток нагрузки (Рис. 4.43). Таким
образом, очевидно, что потери в ключе растут с увеличением импеданса нагрузки
и что плазменные размыкающие ключи применимы в основном с низкоимпедан-
сными нагрузками. Это также ограничивает допустимую мощность и умножение
напряжения (см. разд. 3.3).
4.2.5. Струйный плазменный ключ
Струйный плазменный ключ работает при намного большей плотности плазмы
(1015см-3), чем у быстродействующих плазменных размыкающих ключей. По
этой причине они больше подходят для времени проводимости порядка микросе-
кунд. Принцип их работы основан на магнитогидродинамическом ускорении
плазменных перемычек в зазоре между двумя электродами, как было рассмотрено
выше. Резкое увеличение ширины зазора вызывает разрыв токопроводящей пере-
мычки и переход ключа в разомкнутое состояние (Рис. 4.44).
4.2.6. Полупроводниковые размыкающие ключи
Прекращение протекания тока в полупроводниковых размыкающих ключах
(Semiconductor Opening Switches, SOS) происходит либо при выключении вне-
шнего источника ионизирующего воздействия на полупроводник (светового или
электронного потока), вызывавшего образование свободных носителей зарядов,
либо прекращением инжекции зарядов в базу р+лл+-структуры с последующим
146 Глава 4. Ключи
Рис. 4.44. Принцип работы струйного плазменного ключа:
фаза проводимости {вверху) и начало фазы размыкания (внизу).
рассасыванием накопленных носителей током обратного смещения. Как мы ви-
дели ранее, в разделе, описывающем полупроводниковые ключи с оптическим
управлением, первый метод управления не может быть использован для ключей
большой мощности.
Для того чтобы разобраться в физике работы полупроводниковых ключей, в
которых используется второй способ управления, рассмотрим сначала процессы
восстановления сопротивления в мощных кремниевых выпрямителях [Benda and
Spenke, 1967]. Структура мощного выпрямительного диода подобна структуре
p^in+- (или pin-) диода. Структура идеального р/л-диода состоит из полупровод-
никового слоя с собственной проводимостью, расположенного между сильно ле-
гированными слоями р+- и л+-типов. На практике такую структуру получить
очень сложно, и по этой причине используются структуры psn, где индекс 5 обоз-
начает слабо легированный средний слой в диоде, который может бытьр- и л-ти-
пов. Типовое распределение примесей в структуре данного диода показано на
Рис. 4.45.
4.2. Размыкающие ключи 147
Рис. 4.45. Распределение примесей в структуре мощного выпрямителя
или диода с накоплением заряда.
Диоды с накоплением заряда (ДНЗ), широко используемые для умножения
частоты, имеют такое же распределение примесей, как и мощные выпрямитель-
ные диоды. Хотя они и далеки от совершенства, оба этих типа диодов проявляют
черты размыкающего ключа. При прямом смещении центральная часть структу-
ры, показанной на Рис. 4.45, «забита» дырками, поступающими слева, и электро-
нами, поступающими справа. Это приводит к сильному увеличению концентра-
ции носителей в этой части структуры, причем, из условия нейтральности, —
л(х, /) = р(х, /), где л(х, /) намного больше концентрации примесей. Из-за этого
нарушается баланс между генерацией и рекомбинацией носителей заряда. Когда
рекомбинация преобладает, ток дырок, поступающих слева, превышает ток элек-
тронов, движущихся навстречу дыркам справа. Это имеет место не только в цент-
ральной части структуры, но и в ее высоколегированных областях. Для диодов с
резкими р-п-переходам и (р/л-диодов) это приводит к следующему распределе-
нию носителей зарядов в центральной части структуры:
л(х) =
Vf (chx/Zp _в shx/Zp'
leL^shd/Ln chd/L^
(4.26)
Здесь т — время жизни носителей заряда в центральной части структуры,^ —
плотность прямого тока, е — заряд электрона, LD — диффузионная длина, 2d —
ширина центральной части структуры, В = (цп - цр)/(рп + цД и цп и Цр — подвиж-
ности электронов и дырок соответственно.
Уравнение (4.26) в приближении справедливо и для /юл-диодов.
Средняя концентрация зарядов равна
n=jVT/2de. (4.27)
Таким образом, на плотность прямого тока оказывает влияние тот факт, что в
пределах времени жизни т накопленный заряд в единице объема 2den разрушает-
ся только рекомбинацией.
148 Глава 4. Ключи
Предположим, что в момент времени г = 0 полярность тока через выпрями-
тель изменилась и плотность тока вместо стала равнаj'r. Этот момент времени,
однако, не является моментом переключения, которое мы обсуждаем, а только
моментом начала удаления накопленного заряда из центральной части полупро-
водниковой структуры. Если обратный ток большой, то градиент концентрации
на правой и левой границах центральной области структуры меняет знак и рас-
пределение зарядов приобретает вид, показанный на Рис. 4.46. Как только на гра-
ницах центральной области концентрация носителей достигнет нуля, в ней обра-
зуется область пространственного заряда, который в полупроводнике с собствен-
ной проводимостью формируется в основном зарядом подвижных носителей, а
не фиксированными зарядами доноров или акцепторов. На левой границе цент-
ральной части структуры на Рис. 4.46 дырки поступают из накопленного заряда в
Рис. 4.46. Рассасывание зарядов из зоны их накопления
при большом обратном токе JR = 10/F (pn = Зцр, LD = d).
центре, а электроны не могут поступать из сильно легированной р-области. Та-
ким образом, электроны начинают исчезать из приграничной области, и образу-
ется нескомпенсированный заряд дырок. Аналогичный процесс протекает и в
правой части центральной области, где формируется нескомпенсированный за-
ряд из электронов. Однако вследствие различных подвижностей дырок и элект-
ронов пространственный заряд и связанное с ним падение напряжения на левой
границе возникают раньше, чем на правой. Распределение носителей заряда в
р/л-структуре в процессе их рассасывания схематически показано на Рис. 4.47.
Дырки, уходяшие влево, и электроны, уходяшие вправо, поставляются из накоп-
ленного в центральной части структуры заряда. Со временем этот заряд уменьша-
ется и в конце концов исчезает.
Границы области, которую занимают еще не рассосавшиеся заряды х = — a\(t)
и х = ат(1), движутся навстречу друг другу со скоростью, которую можно найти
следующим образом. В середине области обогащения, где градиент концентра-
4.2. Размыкающие ключи 149
р
Пространст-
венный _________
заряд и
р=п
Еще
не рассосавшиеся
носители
Центральная -------
область
г ранст-
** вен-
ный
заряд
Рис. 4.47. Распределение носителей заряда вр/л-структуре в процессе их рассасывания.
ции исчезает, токи носителей определяются только приложенным к ним полем и
соотносятся друг с другом так же, как и их подвижности:
_.Лр_;
Нп + Нр
Л-
Нп + Мр
(4.28)
В зоне пространственных зарядов, с другой стороны, весь обратный ток протека-
ет за счет носителей одного типа. Таким образом, при х = — ax(t) токи резко изме-
няются в соответствии с
4/р = -4/п = Л
__Ер__/ =___Ел__j .
Нп+НрЛ Нп + Нр
(4.29)
р •
п
N
' а |пр°^' +d
Следовательно, в течение интервала времени 5/ при х = —а, разность зарядов Д/р8/
изменяется на единицу объема согласно
А/ 8/ = ———Jr8/ = ел8а,.
Мп+Мр
(4.30)
Отсюда скорость движения левой границы зоны, которую занимают еще не рас-
сосавшиеся заряды, получается равной
dQ\ Нп Л
~dt\ рп + црел‘
(4.31)
150 Глава 4. Ключи
Соответственно для правой границы
dat Мр А
~dt\ цп + ррей'
(4.32)
Как только начинается формирование зон пространственных зарядов, напря-
жение на диоде возрастает, а ток, находящийся в зависимости от импеданса цепи,
уменьшается, как это показано на Рис. 4.48. Быстрое выключение (короткий ин-
тервал времени /r) применительно к мощным выпрямительным диодам обычно
нежелательно, так как оно может вызвать большие броски напряжения на индук-
тивностях в схеме. Кроме того, в силовых выпрямителях нежелательно большое
полное время восстановления сопротивления, так как в этот период велики потери
энергии. По этой причине силовые выпрямители оптимизируют так, чтобы умень-
шить /r + zs, но при этом увеличить zR. Что касается диодов с накоплением заряда,
то при их конструировании стремятся достигнуть быстрого переключения, но их
s’-слой довольно тонок, и они могут не выдержать большие обратные напряжения.
Рис. 4.48. Идеализированные процессы восстановления в мощных выпрямительных диодах.
Существенно лучше ведут себя дрейфовые диоды с резким восстановлением
(drift step recovery diode), впервые разработанные в Физико-техническом институ-
те имени Иоффе, в г. Санкт-Петербурге [Grekhov and Mesyats, 1999] В этих дио-
дах короткий импульс прямого тока накачки используется для создания сильно
неоднородного распределения электронно-дырочной плазмы, сконцентрирован-
ной в основном вблизи р+л-перехода. Благодаря этому профилю скорость про-
цесса «выметания» носителей заряда увеличивается на два порядка. Типовое зна-
чение времени размыкания достигает 0.5... 1.5 нс при плотности тока около
100...200 А/см2. Максимально допустимое напряжение составляет около
1...1.5 кВ. Эти диоды можно соединять последовательно без использования вы-
равнивающих делителей напряжения для достижения амплитуды импульсов на-
пряжения до 50 кВ.
Однако наилучшие характеристики в настоящее время достигнуты с ключа-
ми, названными SOS-диодами (Semiconductor Opening Switch) [Lyubutin et al.,
4.2. Размыкающие ключи 151
1996], в которых ток с плотностью до 60 кА/см2 прерывается за время менее 10 нс.
Рабочее напряжение такого одиночного ключа составляет около 1.5 кВ. Эти дио-
ды также можно соединять последовательно без делителей напряжения, и уже со-
зданы конструкции на 1 МВ. В SOS-диодах используется структура р+-р-п-п*.
Как и в мощных выпрямительных диодах, электроны и дырки поступают в об-
ласть их накопления из сильно легированных областей во время накачки прямым
током. Носителям зарядов требуются десятки наносекунд для пересечения участ-
ка структуры с сильным полем. При попадании в участок с высокой концентра-
цией носителей и слабым полем они замедляются и накапливаются в этом участ-
ке. Таким образом, большая часть накопленных носителей заряда находится в
форме квазинейтральной электронно-дырочной плазмы с границами, располо-
женными в сильно легированных областях структуры. При протекании обратного
тока два фронта скачков концентрации носителей заряда движутся в структуре
навстречу друг другу, как это было описано выше. Прерывание тока начинается в
момент достижения минимальной концентрации носителей заряда в плазме
(Рис. 4.49). Когда фронты скачков концентрации носителей приближаются к се-
редине обогащенной области, ионизированные атомы доноров и акцепторов ос-
таются нескомпенсированными. и вблизи границ сильно легированных областей
формируются пространственные заряды. На ранней стадии процесса размыкания
ключа, когда электрическое поле в этих местах велико, имеет место лавинное ум-
ножение числа носителей заряда [Engelko and Bluhm, 2004]. Важно отметить, что
размыкание ключа происходит без полного удаления плазмы из низколегирован-
ных областей его структуры.
Рис. 4.49. Схематическая иллюстрация движения фронта плазмы и образования пространствен-
ного заряда в полупроводниковом размыкающем ключе при работе с обратным сме-
щением.
152 Глава 4. Ключи
На Рис. 4.50 показан набор полупроводниковых размыкающих ключей, кото-
рый при помещении в масло имеет рабочее напряжение 100 кВ
Рис. 4.50. Набор полупроводниковых размыкающих ключей на 100 кВ
ГЛАВА
ЦЕПИ ФОРМИРОВАНИЯ ИМПУЛЬСОВ
Как правило, требуется, чтобы вершина мощных импульсов имела плоскую
форму. Чтобы создать такие импульсы, используются различные цепи с элемен-
тами £ и С. Эти цепи называются цепями формирования импульсов.
5.1. Длинные линии
Длинные линии (линии с распределенными параметрами) являются непрерыв-
ным граничным случаем цепи, состоящей из дискретных £С-элементов. Для на-
чала обсудим критерии, при которых элементы £ и С следует рассматривать как
сосредоточенные или распределенные. Ответ зависит от времени, в течение кото-
рого энергия забирается из того или иного элемента или поставляется в него. Ес-
ли это время намного больше времени, требуемого для электромагнитной волны,
чтобы пройти от одного вывода элемента до другого, то элемент можно считать
сосредоточенным элементом схемы. В противном случае его следует рассматри-
вать как длинную линию. Иногда возникают запутанные ситуации, когда энергия
поставляется в элемент медленно, и он подходит под категорию сосредоточенных
элементов, а при быстром отборе энергии из этого же элемента его следует рас-
сматривать уже как элемент с распределенными параметрами.
В Табл. 5.1 перечислены различные геометрии длинных линий и соответству-
ющие им распределенные параметры. Значения L' и С здесь обозначают индук-
тивность и емкость на единицу длины.
Для начала рассмотрим бесконечно малый участок однородной коаксиальной
линии, показанный на Рис. 5.1. Удельная индуктивность обоих проводников
(внутреннего и внешнего) может быть просуммирована и обозначена L'. Далее
объединим сопротивления на единицу длины внутреннего и внешнего проводни-
ков Л/ и Ri в один элемент R'. Обозначим проводимость на единицу длины G. С
этими упрощениями мы получаем цепь с сосредоточенными параметрами, пред-
ставленную на Рис. 5.1 внизу справа, к которой могут быть применены законы
Кирхгофа для получения дифференциальных уравнений, описывающих поведе-
ние линии. В общем случае все величины являются частотно-зависимыми как
из-за скин-эффекта, так и из-за частотной зависимости диэлектрической прони-
цаемости. В дальнейших рассуждениях, однако, мы будем предполагать, что эти
154 Глава 5. Цепи формирования импульсов
Таблица 5.1. Геометрии длинных линий и соответствующие им распределенные параметры
п/п Уравнения для расчетов Графическое изображение
1 Коаксиальная линия: С = 2nzl\n(rjrd, L' = (р/2я)1п(го/л)> 2’0=[(ц/£),/2/2п]1п(го/п) = = 60(МДг),/21п(г^) хг 1 1 'l 1
2 Двухпроводная линия С = n£/arch(Z)/J), L' = (ji/n)arch(D/d), Zb = [(p/E),/2/n]arch(D/d) о d ^0^ t
3 Линия из параллельных проводников С = zD/d, L' = nd/D, Z^^^d/D)
4 Полосковая линия С = 2eD/J, L' = nd/2D, Z^ivdt^daD) н— ° —и V А
В.(г)
dx
Рис. 5.1. Дифференциальный элемент в однородной передающей линии. Внизу справа приве-
дена эквивалентная схема с сосредоточенными параметрами, которую можно ис-
пользовать для получения дифференциальных уравнений, описывающих поведение
длинных линий.
5.1. Длинные линии 155
величины не зависят от положения х, а также от напряжения и тока. В этом слу-
чае могут быть получены, с использованием преобразования Лапласа, следующие
дифференциальные уравнения:
= (С + pC')(R + р£')к(р),
ах
2. (51)
= (G' + рС}(К + pL'Wpl
ах
В случае линии без потерь (R' = 0, (7 = 0) получается
. _ = Р с Lu(p),
dx (5.2)
, 2~ =P c blip).
dx
Решая эти дифференциальные уравнения относительно*, мы получаем
и(х,р) = их(р) = |“о(р)е (5.3)
Принимая во внимание закон обратного преобразования Лапласа,
L{ux(t - Т)} = и0(р)е~рТ, (5.4)
что приводит к следующим результатам:
w(x,/) = wx(r) =
м0(/ -xjLC7)
й0(/ + х->] L'C'\
Общее решение является линейной комбинацией обоих решений:
«х(0 = “Л* -х/с) + й0(1 + х/с).
(5.5)
(5.6)
Во всех этих уравнениях стрелка над буквенным обозначением указывает на
направление распространения волны. В выражении (5.6) L'C заменено на 1/с2,
где с — фазовая скорость распространения волны. Первое слагаемое здесь пока-
зывает, что амплитуда волны в точке х в момент времени t = t\ + х/с является та-
кой же, как и в точке х = 0 в момент t = /ь т. е. мы имеем дело с распространением
волны в направлении положительных значений х со скоростью с. Если с не зави-
сит от частоты, то распространение волны происходит без дисперсии, т. е. сохра-
няется форма волны. Второе слагаемое в выражении (5.6) описывает движение
волны с той же скоростью, но в противоположном направлении. Аналогичные
уравнения справедливы и для импульсов тока.
156 Глава 5. Цепи формирования импульсов
Подставляя решения (5.3) в уравнение цепи, получаем
d2ux(p)
dx
-pEix(p),
(5.7)
-рЛ!Сйх(р) = -pL ix(p).
Отсюда мы получаем импеданс линии:
йх(Р) = []L=7 = _“Ap1
*Ар) NC 0 ix(p)
(5.8)
Для линии без потерь, которую мы здесь рассматривали, Zo не зависит от час-
тоты. Таким образом, так же получается
Z» =
u^t-x/c)^ uQ(t + x/c)
70(t-x/c) 70(t + x/c)
(5.9)
5.1.1. Оконечные нагрузки линий и неоднородности
Сначала рассмотрим длинную линию без потерь, соединенную с произволь-
ной нагрузкой с частотно-зависимым импедансом Zip) (Рис. 5.2). В соответствии
с законом Ома для нагрузки справедливо следующее соотношение:
= + (5.10)
Если сейчас заменить токи на напряжения падающей и отраженной волн, используя
it (р) = ЗД- (Р), h (Р) = -ЗД(Р)> (5. п)
то мы получим следующий коэффициент отражения р:
Рассмотрим несколько важных частных случаев. Если Z= Z(0), то это случай со-
гласованной нагрузки. Он эквивалентен бесконечно длинной линии, так как при
этом от места присоединения нагрузки нет никакого отражения волны. Случай,
когда Z= 0, называется коротким замыканием. При этом волна полностью отра-
жается с переворотом ее фазы. Z= оо представляет собой случай обрыва цепи, и
отраженная волна складывается по амплитуде с падающей волной.
5.1. Длинные линии 157
Рис. 5.2. Линия с импедансом Zo, соединенная с нагрузкой с импедансом Z(p).
Рис. 5.3. Соединение двух линий
Аналогичные рассуждения справедливы и для соединения двух линий с импе-
дансами Z01 и Z02 (Рис. 5.3):
p=«L = Z02-Z01 (5.13)
И1 Z02 + Z01
В точке соединения двух линий мы получаем
«1+“1 = «2- (5.14)
Используя это соотношение, можно получить коэффициент передачи для им-
пульса напряжения:
Ь. = 1 + ^ = 1 + р. (5.15)
к, и,
При Z01 = ZQ2 коэффициент отражения р равен 0, и, следовательно, коэффи-
циент передачи равен 1. Однако для соединения двух линий без отражения усло-
вие Zqi = Zq2 необходимо, но недостаточно. Если геометрия линий резко меняет-
ся, то становится невозможным обеспечивать удовлетворение уравнениям Макс-
велла для суперпозиции основных волн. В этом случае начинают играть роль
волны более высокого порядка. На Рис. 5.4 показаны в разрезе места соединения
двух передающих кабелей с одинаковыми импедансами, но различными механи-
ческими размерами.
Только при плавном переходе, таком как показан на Рис. 5.4 (справа), могут
быть достигнуты условия, при которых поле не очень сильно искажается и не воз-
158 Глава 5. Цепи формирования импульсов
Рис. 5.4. Места соединения двух кабелей с одинаковыми импедансами,
но различными механическими размерами [Lewis and Vrfells, 1959].
никает отраженной волны на высоких частотах. Для высших типов волн, которые
могут возникнуть на переходе, векторы электрического и магнитного полей пере-
стают быть перпендикулярны друг другу и их фазовая скорость становится часто-
тно-зависимой. В дополнение к этому для каждого типа волн возникает частота
среза, ниже которой передача энергии невозможна. Самую низкую частоту огра-
ничения имеет тип волны, обозначаемый Яц (или ТЕи). Распределение силовых
линий электрического и магнитного полей для типа волны Яп в коаксиальной
цилиндрической линии приведено на Рис. 5.5.
Соответствующая критическая длина волны определяется из следующего
приближенного соотношения: Хсо = л(га + rfi, где гя и являются радиусами вне-
шнего и внутреннего проводников соответственно!).
Рис. 5.5. Распределение силовых линий электрического и магнитного полей для типа волны
Ян в коаксиальной цилиндрической передающей линии. Пунктирными линиями
показаны силовые линии электрического поля, а сплошными — магнитного поля.
Примечание, //-тип волны (или ТЕ — поперечный электрический) имеет
составляющую в направлении оси линии передачи, а электрическая
компонента— Ez = 0. Е-тип волны (или ТМ— поперечный магнитный) имеет
° Нижняя критическая частота существует для волноводных линий передачи. Для коаксиальных и
полосковых линий речь должна идти о верхней критической частоте. Обычный тип колебаний, кото-
рый реализуют в коаксиальном кабеле для распространения сигнала — это поперечная электромагнит-
ная волна (ТЕМ). Возможны и другие типы волн, но они нежелательны. Максимальная частота
Cutoff» при которой распространение ТЕМ-волны становится проблематичным, определяется
выражением ./cutoff = 1/(3.76(Z) + d)e1/2), где D и d—диаметры внешнего и внутреннего проводников
соответственно, а е— диэлектрическая проницаемость изолятора (см., например, Дэвис Дж.,
Карр Дж., Карманный справочник радиоинженера/ Пер. с англ. М.: Издательский дом «Додэка-ХХ1»,
2002. С. 67). — Примеч. пер.
5.1. Длинные линии 159
составляющую Ez в направлении оси, а магнитная компонента — Hz = 0. Индексы
л, т отражают число максимумов волны в различных направлениях системы
координат.
5.1.2. Длинные линии с потерями
Потери энергии при распространении электромагнитных волн вызываются
следующими причинами:
• конечное сопротивление проводников;
• ненулевая проводимость и высокочастотные свойства диэлектрической среды;
• излучение радиоволн в случае открытой линии передачи.
Соотношение для преобразованных по Лапласу напряжению и току, приве-
денное в (5.3), остается справедливым, если мы заменим L' на L'{\ + R'/pL') и С
на (7(1 + G/pC). Для достаточно высоких частот всегда R' « со£' и G « <оС.
Принимая это во внимание, для случая с малыми потерями мы получаем
R/R-G/C
2р
R/L' + G'/C
2р
(5.16)
Здесь обе величины частотно-зависимы. Вводя (5.16) в (5.3), мы получаем следу-
ющие выражения для волны с затуханием:
йх(р) = й0(р)е °'*е
(5.17)
Слагаемым ciq' на частотах ниже 109 Гц можно пренебречь. Благодаря скин-эф-
фекту R пропорционально со1/2:
R =
2
W±Rt+
2 а N 2
(5.18)
Таким образом, мы можем записать а' = £со1/2. В этом случае амплитуда импульса,
передаваемого через кабель длиной (, ослабляется в соответствии с (5.19):
({ kf
(5.19)
<р(5) = Д- (e~*2dq,
Jit }
где <p(s) — интеграл ошибки Гаусса.
160 Глава 5. Цепи формирования импульсов
На Рис. 5.6 выражение (5.19) было использовано для построения графиков за-
висимости относительной амплитуды импульсов в форме скачка напряжения,
проходящих через отрезки кабельной линии разной длины (10 и 30 м), от времени.
импульсом конца кабеля [с]
импульсом конца кабеля [с]
Рис. 5.6. Графики зависимости от времени относительной амплитуды импульсов в форме
скачка напряжения, проходящих через отрезки кабельной линии разной длины
(слева — 10 м, справа — 30 м). Тип кабеля RG58A/U (Zq = 50 Ом, к = 1.14 х 10-6 (при
1 ГГц), с/с0 = 0.659).
5.1.3. Отрезок линии как элемент схемы
Наиболее важными параметрами линии при использовании ее в качестве эле-
мента схемы являются:
• задержка времени, которая воздействует на проходящий сигнал;
• ее характеристический импеданс;
• характеристики отражения сигнала.
Для медленных сигналов или коротких кабелей входной импеданс кабеля с
несогласованным соединением не равен Zo, т. е. он не омический, а комплекс-
ный. Можно рассчитать входной импеданс короткого кабеля с характеристичес-
ким импедансом Zo и длиной £ из следующих соображений (Рис. 5.7). Напряже-
ние генератора uG(p) делится между падениями напряжения на выходном импе-
дансе генератора и входном импедансе кабеля:
ui(p) = Zi/(RG + Zl)uc. (5.20)
С другой стороны, входное напряжение должно быть равно суперпозиции
прямой и отраженной волн:
и1(р) = й,(/>) + «,(р) = й1(^ 1+^1
\ ui\P>)
“|(Р) _ п p-2pVTC7
~ Z ч “ HZC »
и((р)
pz = (Z-Z0)/(Z4-Z0).
(5.21)
5.1. Длинные линии 161
В общем случае выходной импеданс генератора Rq не согласован с входным
импедансом кабеля. Таким образом, следует учитывать и отражение возвращаю-
щейся волны от входа кабеля:
(5.22)
Далее мы получаем
иАР)-ис(Р) 7 * +tt,Cp)pRGPze А + Аз (5.23)
откуда следует »,О>) - *O(j>) ° \А + AJO PrgPz6 / (5.24)
и, наконец, “(р)=И0(₽)(г.4)(1-ко₽^-)- (5.25)
Сравнивая последнее уравнение с (5.20), мы получаем следующее выражение
для входного импеданса:
-,1+Pze-»^
Для случая с разомкнутым выходом линии получается
1 + е-’^' _ ch(.p4rCl)
(5.26)
(5.27)
162 Глава 5. Цепи формирования импульсов
Для случая co(L'C)1/2^ « 1 (который эквивалентен случаю £ « X) путем раз-
ложения экспоненциальных функций в ряд и ограничиваясь слагаемыми первого
порядка, мы получаем
% ~ % 1 + p^J UC'£Z0 —Z/Zo
1 \-p4l'C'£Zq-z/z0'
Отсюда для Z«Zq (Zo = (L'C)l/2):
Z] « Z+pL'£.
(5.28)
(5.29)
т. e. входной импеданс отрезка линии эквивалентен последовательно соединен-
ным индуктивности L'£ и импедансу нагрузки.
В противоположном случае, когда Z» Zq, получается
\/Z+pC'£‘
(5.30)
Здесь входной импеданс состоит из параллельно соединенных емкости кабеля С£
и импеданса нагрузки Z.
5.1.4. Формирование импульсов с помощью линии без потерь
На Рис. 5.8 приведена принципиальная схема линии, используемой для фор-
мирования импульсов.
Рис. 5.8. Принципиальная схема линии передачи,
используемой для формирования импульсов.
В исходном состоянии емкость этой линии заряжена до напряжения Uq. Если
посмотреть на эту линию со стороны нагрузки, то в предположении, что она заря-
жалась через резистор с очень большим сопротивлением, ее вход можно рассмат-
ривать как разомкнутый, а импеданс будет определяться выражением (5.27). Если
5.2. RLC-цепи 163
ввести время прохождения волной этой линии в одну сторону Т= (Ь'С')^2£, мож-
но записать следующее преобразование Лапласа для тока на нагрузке линии:
Up _ Uo___________________l-e-w
p(RL+ Z^cth(pT)) p(RL+ Zp) 1 + Zo - Rl/Z0 + /?Le’2'r
Uo——-----
°p(/?L+A)
I Zq Rl e~2^r
Zo + rl
Zq I e~4*T
Zo +
(5.31)
Применяя обратное преобразование Лапласа, мы получим следующее выра-
жение для тока в этом временном отрезке:
/(О = 1 - H(t - 27) - H(t - 2Т) - H(t - 47)] +
*4. "* A) "к А
(5.32)
^L+ Zpy
где H(t) — функция Хевисайда (Я(0 = 1 для t> 0 и H(t) = 0 для t < 0). На Рис. 5.9
построена функция I(t) для R\JZq = 1, R\JZq > 1 и R\JZ§ < 1.
Время
Время
Время
Рис. 5.9. Формы импульсов, получаемые при различных соотношениях RL и Zq.
5.2. RLC-цепи
Линии с распределенными параметрами не удобны для создания прямоуголь-
ных импульсов с длительностью более 500 нс. Для формирования таких импуль-
сов используются цепи с дискретными /fZC-элементами.
Прежде чем рассматривать отдельные многозвенные £С-цепи, обсудим более
общий случай. На Рис. 5.10 приведена секция многозвенной цепи с комплексными
импедансами Zx и Z^.
Используя второй закон Кирхгофа для r-й ячейки в цепи, мы получим следу-
ющее выражение в форме преобразования Лапласа для тока:
4(P)[Z1(P) + 2Z2(p)] - ir_!(p)Z2(p) - /r+i(p)Z2(p) = 0. (5.33)
Передаточная функция между двумя звеньями определяется выражением
<'г+1(р) = ад/г(Р). (5.34)
164 Глава 5. Цепи формирования импульсов
Рис. 5.10. Секция обобщенной многозвенной цепи
с комплексными импедансами Z\ и Z2.
После замены р на ico удобно выразить амплитудную составляющую также в
экспоненциальной форме:
G( ico) = g(co)ei<₽(w) = eo(w)+i<₽(w). (5.35)
Тогда выражение (5.33) превращается в
ir(ico)[Z1(ico) + 2Z2(ico) - Z2(ico)e-lfl(to)+i<₽(<o)1 - Z2(ico)efl(to)+1,p(to)] = 0 (5.36)
и, следовательно,
Z. (ico) + 2Z, (ico) _ . - / ч • / xi
1 1 2 * * * * * В = 2ch[a(co) + кр(со)]. (5.37)
Z2(ico)
Применяя правило сложения для функции гиперболического косинуса (ch),
мы получаем
1 + =ch(a(co))cos(cp(co)) + i sh (a(co))sin(cp(co)). (5.38)
2Z2(ico)
Теперь можно выделить два граничных случая:
l.g(co) = 1, т. е. а(со) = 0.
В этом случае не происходит уменьшения амплитуды, но форма импульса ос-
тается неизменной, только если также обеспечивается соотношение ср(со) = кем В
этом случае единственное, что происходит с сигналом, — это задержка его во вре-
мени. Таким образом, мы получаем звено временной задержки.
2. g(co) = 0, а я(со) = const < 0.
В этом случае получается независимое от частоты ослабление амплитуды им-
пульса, т. е. ячейка работает как идеальный аттенюатор. В дальнейшем этот слу-
чай мы рассматривать не будем.
Для звена временной задержки выражение (5.38) упрощается до
cos (<р(со)) = 1 + ZJIZ-!. (5.39)
5.2. RLC-цепи 165
Диапазон возможных значений для ZJZi ограничен, таким образом, значениями
(5.40)
т. е. задержка времени возможна, только если отношение двух комплексных со-
противлений Z] и Z2 является действительным и отрицательным числом. Таким
образом, только комбинация емкостей и индуктивностей подходит для реализа-
ции звена задержки времени. Этот результат мы получили для длинной линии.
Однако он может быть в некотором приближении использован и для ее аналога —
набора LC-звенъев, показанного на Рис. 5.11.
Рис. 5.11. Набор LC-звеньев, используемый для формирования прямоугольных импульсов.
Вводя в выражение (5.40) обозначения Z\ = ico£ и Z2 = 1/icoC, мы получим
<-соЧС<
(5.41)
Это выражение определяет диапазон частот, внутри которого распростране-
ние волны не зависит от ослабления: верхняя частота этого диапазона равна
<ои = 2/(£С)1/2. Соответственно (5.33) становится
J , 2
Lp*—^
ir-Sp)
рС рС
(5.42)
В соответствии с (5.34) и (5.35) мы ищем решение этой системы дифференци-
альных уравнений в форме
iT(p)=Ad* + ВеЛ (5.43)
Здесь мы используем аббревиатуру 6 = iq>(co) и в соответствии с (5.37) получаем
соотношение ch(0) = 1 + (LC/2)p2.
А и В являются постоянными, которые должны быть определены из гранич-
ных условий для первого и последнего звеньев. Если последний элемент п являет-
ся звеном, соединенным вместо импеданса^, показанного на Рис. 5.11, с источ-
ником напряжения и0(р), мы получим следующее выражение для преобразования
Лапласа входного тока в цепи:
»п(р) = Си0
sh(w0)
sh((n+ 1)0) — sh(«0)
(5.44)
166 Глава 5. Цепи формирования импульсов
Входной импеданс цепи определяется из выражения
„) = !fo(£)=J_ sh((n + l)6) t
in(p) PCL sh(w0)
(5.45)
Для л—> oo этот импеданс сходится, как этого и следовало ожидать, с импедансом
линии конечной длины с разомкнутым выходом (5.27):
limZQ,, л) = J^cth (рл/ЛА ) •
(5.46)
где £N = nL и CN = пС.
Zq = (L/C)^1 можно рассматривать как волновое сопротивление (импеданс)
дискретной цепи. Если сейчас предположить, что конденсаторы во всех звеньях
заряжены до напряжения t/0, а затем к цепи с помощью идеального ключа
(Рис. 5.11) подсоединяется нагрузка с импедансом Zq, то преобразованный по
Лапласу ток в согласованной нагрузке получится равным
£ (р) = I -------------.
" 4L/C+ \/pC[sh((n + l)O)/sh(«O) -1]
(5.47)
Вводя р = 2/(ZC)1/2sh(0/2), мы получим
sh(w6)
iAp) = Clh
п 0 sh ((л + 1)0) + [ 2sh(0/2)—1 ]sh(«0)
(5.48)
В общем случае обратно преобразовать это выражение невозможно.
Чтобы определить время прохождения импульса через цепь и тем самым най-
ти длительность импульса, мы поступим следующим образом. Токи на обоих кон-
цах цепи связаны следующим образом:
/Й(1ю) = 11(1со)ейи«<<о), (5.49)
и из (5.39) мы получаем следующее выражение для сдвига фазы <р(со):
<р(ю) = arccos (1 — (co2LO/2) = arccos (1 — 2(co/cou)2). (5.50)
Раскладывая правую часть в ряд, мы получим
1 ( „ 2
<p((o)=u>VZc 1+1 +
(5.51)
Для частот, намного меньших, чем сои, мы получим приближенное выражение к
(5.49) в виде
ifl(ico)«iI(i(o)ew<,>VIf.
(5.52)
5.2. RLC-цепи 167
Таким образом, осуществив обратное преобразование, мы получим, что время
прохождения импульса в одну сторону по цепи составляет около л(£С)1/2 Если
конденсаторы в звеньях цепи были заряжены до напряжения С/о, средняя ампли-
туда импульса напряжения на согласованной нагрузке получится равной £/0/2.
Длительность импульса при этом получится 2л(£С),/2. На Рис. 5.12 приведена
форма импульса напряжения, получаемого с помощью пяти £С-звеньев.
Рис. 5.12. Форма импульса напряжения, получаемого с помощью цепи,
состоящей из пяти £С-звеньев на согласованной нагрузке.
Хотя в общем форма импульса и близка к ожидаемой, имеет место существен-
ный выброс напряжения в его начале и отрицательный бросок с колебательным
процессом в конце. В некоторых применениях эти отклонения от идеальной фор-
мы недопустимы.
Анализ Фурье позволяет раскрыть причины формирования этой плохой фор-
мы импульса с помощью схемы, приведенной на Рис. 5.11. Эта цепь аппроксими-
рует прямоугольный импульс с резкими фронтами пятью слагаемыми. Однако
разложение по Фурье прямоугольного импульса дает последовательность слагае-
мых, уменьшающихся по амплитуде обратно пропорционально их номеру, т. е.
коэффициенты Фурье ап пропорциональны 1/л. Таким образом, для получения
хорошей аппроксимации к прямоугольному импульсу требуется достаточно боль-
шое число слагаемых в ряду Фурье.
Гиллемин (Guillemin) был первым, кто открыл, что намного лучшая форма
импульса может быть получена с меньшим числом элементов в схеме, если
допустимо увеличение времени нарастания импульса [Guillemin, 1944; Glasoe and
Lebacqz, 1948]. При этом может быть получена и намного более плоская вершина
импульса. Слагаемые в ряду Фурье, например, для трапецеидальной формы им-
пульса уменьшаются пропорционально 1/л2, а для импульсов с параболической
формой фронтов — пропорционально 1/л3. Однако не очевидно, что метод Фу-
168 Глава 5. Цепи формирования импульсов
рье, обычно используемый для анализа последовательности импульсов, является
эффективным инструментом для синтеза применительно к проблеме одиночных
импульсов.
В качестве примера рассмотрим цепь Гиллемина для получения импульса с тра-
пецеидальными фронтами. Начнем с рассмотрения прямоугольных и трапецеи-
дальных импульсов, как это показано на Рис. 5.13.
Идеальная линия с коротким замыканием выхода при разряде создает перио-
дические прямоугольные импульсы с амплитудой тока 2/0. Разряд на согласован-
ную нагрузку приводит к формированию одиночного прямоугольного импульса.
Периодические двухполярные импульсы можно проанализировать с помощью
В) Г)
Рис. 5.13. Концепция конструирования цепей Гкллемина:
а) выходной ток идеальной линии передачи при коротком замыкании выхода;
б) выходной ток той же линии при работе на согласованную нагрузку;
в) трапецеидальный импульс в цепи Гиллемина при коротком замыкании выхода;
г) идеальный разряд цепи Гиллемина при работе на согласованную нагрузку
5.2. RLC-цепи 169
рядов Фурье. Теперь предположим, что цепь, способная вырабатывать последова-
тельность двухполярных трапецеидальных импульсов при коротком замыкании
выхода, также создаст одиночный трапецеидальный импульс при согласованной
нагрузке. Если это правильно, то нам требуется найти цепь, которая была бы спо-
собна аппроксимировать последовательность импульсов, показанную на
Рис. 5.13в. Ряд Фурье для этой последовательности следующий:
rax _ о т V 4 sin((2fc + 1)ля) (2А + 1)лг/
°^(2Л + 1)л (2Л + 1)тш ГР
(5.53)
Здесь Гр — длительность основания трапецеидального импульса, а яГР — длитель-
ность фронта импульса (Рис. 5.13в).
Каждый член ряда Фурье представляет собой синусоидальную компоненту
тока амплитудой 21^Ьк и частотой (2Л + 1)/2гР, где
. = 2/ 4 sin((2£ + l)7ta)
* °(2£ + 1)л (2Л + 1)тш
(5.54)
Эти токи могут быть созданы с помощью схемы, показанной на Рис. 5.14. Собс-
твенные колебания тока в этой цепи описываются выражением
Рис. 5.14. ЛС-контур, используемый для отображения компонентов ряда Фурье
(5.55)
Lk и Ск в этой схеме можно найти из параметров ряда Фурье:
(2Л + 1)тгЛ/
(5.56)
Л Zu.
_________* р
к (2k + \)nZ0
Здесь Zq = Uq/2Iq — характеристический импеданс цепи. Следовательно, полная
цепь, предназначенная для создания импульсов трапецеидальной формы, должна
170 Глава 5. Цепи формирования импульсов
состоять из набора включенных параллельно АС-контуров, значения Lk и Ск в ко-
торых определяются из выражения (5.56). Эта цепь, называемая основной цепью
Гиллемина, изображена на Рис. 5.15.
Рис. 5.15. Основная цепь Гкллемина.
На Рис. 5.16 приведены импульсы напряжения, получаемые при разряде на
согласованную нагрузку цепи Гиллемина, включающей три и пять звеньев Ясно
видно, что форма импульсов значительно улучшена по сравнению с приведенной
на Рис. 5.12.
Время [мкс]
Рис. 5.16. Импульсы напряжения, получаемые при разряде на согласованную нагрузку цепи
Гиллемина, включающей три (слева) и пять (справа) звеньев.
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4
Время [мкс]
Основным недостатком цепи Гиллемина является необходимость использова-
ния конденсаторов с различной емкостью. Обычно весьма сложно и дорого найти
высоковольтные импульсные конденсаторы с необходимым значением емкости.
5.3. Моделирование цепей с помощью программы
LEITER
LEITER — это простая программа, позволяющая моделировать сложные схе-
мы передающих линий. Она особенно полезна для расчета систем с передающи-
ми линиями без потерь, характеризуемых их импедансом Z( и электрической дли-
ной (временем задержки) т,. Однако потери могут быть учтены введением диск-
ретных резисторов в нужные участки цепи. Кроме того, программа LEITER
используется и для моделирования цепей с дискретными элементами. Например,
дискретная индуктивность можно представить короткой линией передачи с
5.3. Моделирование цепей с помощью программы LEITER 171
очень большим импедансом, а дискретный конденсатор — короткой линией пе-
редачи с очень маленьким импедансом:
£/ = Z/Т/, Cj = Xi/Zi. (5.57)
Раньше мы уже видели, что амплитуду напряжения в линии можно рассмат-
ривать как суперпозицию волн, движущихся в прямом и обратном направлении
по оси х:
и = и+и.
Соответственно для токов в передающей линии получается:
и+и
z
(5.58)
(5.59)
Программа LEITER отслеживает мгновенные значения амплитуд напряжения
волн, движущихся в обоих направлениях с учетом коэффициентов передачи и от-
ражения на концах линии:
Z2-Z,
р = —---L,
Z2 + Z,’
(5.60)
2Z,
Z2 + Z]
Если к выходу элемента схемы подключено несколько линий передачи или
комбинация из линий и резисторов, Z2 в (5.60) следует заменить на суммарный
импеданс всех подключенных элементов. Передаваемая энергия в этом случае де-
лится между всеми элементами, подключенными к узлу, включая потери на вве-
денных резисторах.
На Рис. 5.17 представлены различные типы узлов, с которыми способна рабо-
тать программа LEITER. Узлы типов 6, 7 и 8 являются идеальными ключами, ко-
торые могут быть замкнуты или разомкнуты в определенный момент времени,
или замкнуты при достижении напряжением определенного значения. Узел типа
9 описывает электронный диод (пинч-диод), имеющий нелинейный импеданс. С
помощью узла типа 10 возможно моделировать источник напряжения, величина
которого изменяется во времени. Узел типа 12 позволяет рассчитать спад сопро-
тивления разрядника в соответствии с выбранной моделью разряда (Теплера,
Ромпе—Вейцеля или экспоненциальной). Индуктивность разрядника представ-
ляется коротким отрезком линии передачи. Узел типа 14 описывает плазменный
прерыватель. Узел типа 17 моделирует сопротивление разрядника, соединенного
с концом линии, и может быть использован в качестве бокового ответвителя в уз-
ле типа 5. Время задержки и импеданс линии определяются емкостью и индук-
тивностью разрядника. Возможности программы LEITER не позволяют исполь-
зовать ее для линий с повторным соединением.
На Рис. 5.18 приведен пример схемы, собранной из передающих линий. Эта
схема состоит из четырех элементов, каждый с импедансом 5 Ом. Первый эле-
172 Глава 5. Цепи формирования импульсов
Тип No
Тип No
Генератор импульсов,
параметры задаются дополнительно,
Ro=выходной импеданс
Следует соблюдать
последовательность
а, Ь.с
Делитель,
номиналы резисторов
задаются дополнительно
Разрядник
без последовательной емкости.
3 модели, параметры задаются
дополнительно
Три идеальных ключа,
размыкающихся в момент ts,
замыкающихся в момент Ц и
замыкающихся при напряжении V,
Пинч-диод,
параметры
задаются
дополнительно
Разрядник
с последовательной емкостью
14: Числовая модель PEOS,
а — сторона источника,
b—сторона нагрузки.
15: Полиномиальная модель.
Параметры в моделях 14 и 15
задаются дополнительно
Инверсия внутреннего и
внешнего проводников
Рис. 5.17. Различные типы узлов, с которыми способна работать программа LEITER.
Рис. 5.18. Собранная из передающих линий схема
для моделирования с помощью программы LEITER.
мент заряжен до напряжения 1 МВ В начале моделирования замыкается ключ,
стоящий на выходе этой линии. Элемент III и узел типа 17 на его конце описыва-
ют ключ с паразитной емкостью C = x/Z. Ключ на выходе этого звена замыкается,
когда напряжение на нем превысит 100 кВ. Последнее звено этого устройства со-
единено с согласованной нагрузкой 5 Ом. В Табл. 5.2...5.5 даны входные парамет-
ры для моделирования с помощью программы LEITER для схемы, приведенной
на Рис. 5.18. Результат моделирования показан на Рис. 5.19.
5.3. Моделирование цепей с помощью программы LEITER 173
Рис. 5.19. Изменения напряжения в точках 2, 6 и 8 (см схему на Рис. 5.18). Вследствие равенства
импедансов линий 11 и I напряжение в точке 2 после замыкания ключа становится равно
половине напряжения, до которого была заряжена линия I Основному импульсу напря-
жения на нагрузке (точка 8) предшествует бросок, обусловленный влиянием паразитной
емкости ключа, соединяющего линии II и IV. Эта емкость моделируется линией III.
Таблица 5.2. Параметры для линии передачи
Общее время Шаг по времеян Начальный момент Число шагов для усреднения
100 1.0000Е-01 0 10
Таблица 5.3. Параметры элементов, входящих в цепь
Элемент Время задержки сигнала [нс] Импеданс [Ом] М»] 4 [А]
№ 1 20.00 5.0000 1.0Е+06 0.0000
№2 10.00 5.0000 0.0000 0.0000
№3 1.00 5.0000 0.0000 0.0000
№4 20.00 5.0000 0.0000 0.0000
Таблица 5.4. Параметры узлов
Узел Тйп Смежные точки Предел A(i) Описание A(i)
№ 1 1 1 0 0 0 5.0Е+06 Сопротивление [Ом]
№2 12‘) 2 3 2 0 1.0Е+01 Напряжение пробоя [В]
№3 5 4 7 5 0 0
№4 172) 6 б 0 0 1.0Е+5 Напряжение пробоя [В]
№5 1 8 0 0 0 5.00 Сопротивление [Ом]
° Файл Typel2A.DAT — модель разрядника в соответствии с теорией Теплера 2) Файл Typel7B.DAT — модель разрядника с последовательной емкостью.
174 Глава 5. Цепи формирования импульсов
Таблица 5.5. Параметры графиков
Контролируемое напряжение в точке Код графика Шкала Цвет
8 1 1.00Е+06 1
6 1 1.00Е+06 2
2 1 1.00Е+06 3
ГЛАВА
ПЕРЕДАЧА ИМПУЛЬСОВ
И ТРАНСФОРМАТОРЫ
6.1. Магнитная самоизоляция в вакуумной линии
передачи
Для решения некоторых задач в науке и технике требуются импульсные ис-
точники излучении с плотностью мощности свыше 100 ТВт/см2 и энергией в им-
пульсе более 1 МДж. Для питания таких источников излучения высоковольтные
импульсы с мощностью более 100 ТВт необходимо сжимать до плотности свыше
ЮОТВт/м2, а еще обеспечивать их эффективную передачу к приборам, которые
генерируют требуемое излучение.
Большинство приборов, пригодных для решения этой задачи, должны рабо-
тать в вакууме. Таким образом, высоковольтные импульсы должны поступать
внутрь вакуумной камеры через изолирующую перегородку, отделяющую жидкий
диэлектрик от вакуумной секции. На Рис. 6.1 приведена конструкция такой пере-
городки с ее характерными особенностями.
Вакуум
Изолятор —
(люсит, эпоксидная
композиция и т. д.)
Металлические кольца
- — для выравнивания
распределения потенциала
Рис. 6.1. Изолирующая перегородка в линии передачи импульсов высокого напряжения
разделяющая секции и водяным, и вакуумным диэлектриками
176 Глава 6. Передача импульсов и трансформаторы
Перегородка состоит из изолирующих колец, разделенных между собой ме-
таллическими кольцами, служащими для выравнивания распределения потенци-
ала. Все эти кольца герметизированы для сохранения высокого вакуума либо с
помощью кольцевых уплотнений, либо прямо сваркой металла с диэлектриком.
Чередование проводников и диэлектриков на поверхности перегородки опреде-
ляет ее электрическую прочность. На металлических поверхностях электроны
могут производиться полевой эмиссией (см. ниже). Эти электроны могут уско-
ряться электрическим полем и сталкиваться с поверхностью изолятора. Если ко-
эффициент вторичной эмиссии материала изолятора больше единицы, то на по-
верхности изолятора накапливается положительный заряд, к которому притяги-
ваются дополнительные электроны. Кроме того, под воздействием электронной
бомбардировки могут высвобождаться абсорбированные вещества, и над поверх-
ностью изолятора может образоваться газовый слой. Если будет достигнуто кри-
тическое значение произведения плотности газа на толщину, в газовом слое фор-
мируется электронная лавина, вызывающая поверхностный пробой. Конечно,
для этого требуется наличие компоненты электрического поля, направленной по
касательной к поверхности, которая может быть создана объемным зарядом, об-
разованным в диэлектрике.
Для предотвращения накапливания заряда в диэлектрике изолирующие сек-
ции делают с наклонной поверхностью, чтобы все ускоряющиеся электроны на
своем пути удалялись от поверхности диэлектрика и собирались на металличес-
ком кольце. Измерения электрической прочности диэлектрических конусов в за-
висимости от угла наклона образующей конуса показали максимум при угле 45°
[Milton, 1972]. На Рис. 6.2 приведены графики зависимости импульсной электри-
ческой прочности различных материалов от угла наклона образующей конуса.
Рис. 6.2. Зависимости импульсной электрической прочности различных материалов
от угла наклона образующей конуса.
6.1. Магнитная самоизоляция в вакуумной линии передачи 177
Во многих случаях именно перегородка между диэлектриком и вакуумом яв-
ляется самым слабым звеном в линиях передачи высоковольтных импульсов.
Максимальная напряженность поля, которую может выдержать конструкция пе-
регородки для импульсных систем, показанная на Рис. 6.1, была эмпирически
определена [Martin et al., 1996] равной
с 7х105 D/ 1Ч
Edb _ i/e^i/io В/м, (6.1)
где t — продолжительность времени, в течение которого напряженность электри-
ческого поля превышает 87% от его максимального значения в секундах, а А —
площадь перегородки в м2. Для импульсов длительностью несколько десятков на-
носекунд электрическая прочность оказывается ниже 20 МВ/м, и, следовательно,
плотность мощности, которую можно передать через такую перегородку, оказы-
вается ниже 1 ТВт/м2. В общем случае плотность потока энергии плоской волны
дается абсолютным значением вектора Пойнтинга:
S= (6.2)
У Wo
В Ткбл. 6.1 приведены электрические прочности и плотность передаваемой
энергии для различных диэлектриков при передаче энергии через вакуумную пе-
регородку при длительностях импульсов 10... 100 нс.
Таблица 6.1. Электрическая прочность и плотность передаваемой энергии
Диэлектрик Электрическая прочность Е [МВ/м] Плотность передаваемой энергии [ТВт/м2]
Трансформаторное масло 60 15
Вода 50 60
Вакуумная перегородка 20 1
6.1.1. Пробой в вакууме между металлическими
поверхностями
При макроскопической напряженности электрического поля свыше 20 МВ/м
с поверхности металла в вакууме возникает взрывная электронная эмиссия, сопро-
вождающаяся образованием плазмы. Плазма представляет собой практически
неограниченный источник электронов с нулевой работой выхода.
Физические процессы, приводящие к полевой (автоэлектронной) эмиссии
электронов, основаны на туннельном эффекте. Сильные электрические поля
уменьшают ширину потенциального барьера, существующего между внутренней
частью металла и окружающей средой. Для объяснения этого явления рассмот-
рим металл при абсолютном нуле и предположим, что потенциальный барьер
представляет собой ступенчатую функцию (Рис. 6.3).
178 Глава 6. Передача импульсов и трансформаторы
Рис. 6.3. Механизм электронной эмиссии за счет туннельного эффекта при высокой
напряженности поля. Ось ординат представляет собой также границу раздела металл—вакуум
Потенциальная энергия электронов снаружи металла равна — еЕх. Если шири-
на потенциального барьера d станет 100 нм или меньше, электроны в окрестнос-
тях уровня Ферми становятся способными проникать через барьер за счет тунне-
лирования. Число разрешенных состояний Z(W)dWв энергетическом диапазоне
между IF и W+ dW для газа свободных электронов пропорционально И^2. Рас-
пределение электронов между этими состояниями дается функцией Ферми—Ди-
рака ДИ7), где
iW-Wf)/kT ।
V । 1
(6.3)
Таким образом, N(W)dW= Z(W)F(W)dWсостояний заняты в энергетическом
интервале Ж 1F+ dW. Когда напряженность поля становится больше, все больше
и больше электронов, находящихся ниже уровня Ферми, делают свой вклад в ток
эмиссии. В соответствии с уравнением, впервые выведенным Фоулером и Норд-
хеймом [Fowler and Nordheim, 1928], ток эмиссии как функция от напряженности
поля Едля треугольного барьера может быть записана в виде
1.54х10~6р2Е2 Г 6.83х107<р3/2е(у)]
Ф еХР[ рЕ J’
0(у)« 0.956-1.Обу2,
(6.4)
у = 3.8x10^—.
Ф
6.1. Магнитная самоизоляция в вакуумной линии передачи 179
Плотность токаJ получается в А/см2, если напряженность поля Е выражена в
В/см, а работа выхода ip — в эВ. Здесь мы также ввели коэффициент усиления по-
ля р.
Если в выражение (6.4) подставить напряженность поля 25 МВ/м, то получит-
ся плотность тока 10 нА/см2. Это намного меньше, чем наблюдается эксперимен-
тально в этих условиях. Построение графика экспериментальных значений функ-
ции 1п(//Е2) в зависимости от 1/£дает прямую линию с наклоном, который согла-
суется с выражением (6.4) при напряженности поля в 100 раз больше, чем на
самом деле.
В настоящее время существует несколько моделей, объясняющих это расхож-
дение теории и эксперимента. Самая старая и наиболее популярная модель была
предложена Месяцем [Mesyats, 1998]. В ней ответственность за локальное увели-
чение напряженности поля возлагается на микровыступы на поверхности метал-
ла, как это показано на Рис. 6.4.
Рис. 6.4. Распределение поля на вершине микровыступа и упрощенная модель
для расчета коэффициента р
Из анализа упрощенной модели, приведенной на Рис. 6.4, следует, что коэф-
фициент р достигает значения 100 при примерно таком же отношении высоты
микровыступа h к его радиусу г. Однако такие «иголки» наблюдаются весьма
редко.
Тщательные исследования, выполненные с использованием электронного
туннельного микроскопа, открыли, что очень часто диэлектрические включения
являются центрами эмиссии [Latham, 1981]. В этом случае туннельный ток из ме-
талла в диэлектрик играет доминирующую роль, а ток эмиссии подчиняется той
же зависимости от напряженности поля, что и в законе Фоулера—Нордхейма.
В более поздних моделях ток, протекающий через точки эмиссии (как микро-
выступы. так и диэлектрические включения), создает их сильный нагрев, приво-
дящий к испарению вешества. Пар затем ионизуется электронами. Однако оцен-
ка возможной степени нагрева приводит к гипотезе, что стимулированная элект-
ронами десорбция включений также играет важную роль при образовании пара и
плазмы [Halbritter, 1985, 1986].
180 Глава 6. Передача импульсов и трансформаторы
6.1.2. Качественное описание магнитной самоизоляции
Подводя итог вышеизложенному, мы констатируем, что при напряженности
электрического поля свыше 20 МВ/м вблизи металлической поверхности в вакуу-
ме за несколько наносекунд образуется слой плазмы. Таким образом, без магнит-
ной изоляции электронный ток потерь может протекать между проводниками,
что препятствует эффективной передачи энергии в вакуумную линию передачи.
На Рис. 6.5 показано, как ток в линии передачи изменяется после образования
электронной эмиссии.
До пробоя (Рис. 6.5а) в линии передачи течет только ток смещения. Магнит-
ное поле, создаваемое этим током, слишком мало, чтобы изменить траектории
электронов, если бы они и появились.
U/IZ0=F(U)
Рис. 6.5. Различные стадии развития магнитной самоизоляции в линии передачи
6.1. Магнитная самоизоляция в вакуумной линии передачи 181
После возникновения и увеличения электронного тока утечек электроны от-
клоняются магнитным полем линии передачи в направлении передачи энергии
(Рис. 6.56, в).
Когда ток превышает критическое значение, орбиты электронов перестают
достигать анода (Рис. 6.5г). Все большая и большая часть линии передачи стано-
вится изолированной магнитным полем. Электронная оболочка образует отрица-
тельно заряженный проводник, а импеданс линии передачи становится отлич-
ным от того, который был в вакууме.
Когда зона потерь распространяется по линии, большая часть ее становится
изолированной магнитным полем. Скорость распространения фронта потерь
меньше скорости света. Условия подобны тем, которые имеют место при форми-
ровании ударного фронта в динамике жидкостей. Поэтому такой вид распростра-
нения волны иногда называют ударной электромагнитной волной. Еще одна ил-
люстрация этого явления приведена на Рис. 6.6. Здесь предполагается, что на ли-
нию передачи подается импульс напряжения, возрастающий до 2 МВ. До тех пор
пока напряжение остается ниже напряжения пробоя, волна распространяется со
скоростью света. Эта часть импульса образует первичный импульс (прекурсор),
движущийся впереди основного импульса, который перемещается с меньшей
скоростью. Расстояние между прекурсором и основным импульсом увеличивает-
ся со временем. Время нарастания основного импульса зависит от условий на
фронте потерь. Внутри фронта потерь напряжение уменьшается от 2 МВ до уров-
ня напряжения прекурсора. Обычно ширина фронта потерь в несколько раз боль-
ше, чем расстояние между проводниками.
Расстояние от фронта импульса [м]
Рис. 6.6. Траектории электронов и соответствующее изменение напряжения
при прохождении импульса через линию передачи с магнитной самоизоляцией
182 Глава 6. Передача импульсов и трансформаторы
6.1.3. Количественное описание магнитной самоизоляции
Для точного описания явления магнитной самоизоляции необходимо решить
уравнения Максвелла для электромагнитного поля совместно с уравнениями Га-
мильтона для движения. Кроме того, необходимо создать модель образования
плазмы в прикатодном слое и увязать ее с системой этих уравнений. Короче, не-
обходимо решить систему дифференциальных уравнений (6.5)...(6.7).
В общем случае все это может быть выполнено только численным методом.
Метод для решения этой задачи называется метод конечно-размерных частиц в
ячейке (particle-in-cell method) [Birdsall and Langdon, 1991]. На Рис. 6.7 показана
последовательность операций при использовании метода конечно-размерных
частиц в ячейке. Вначале должно быть найдено распределение поля для заданной
геометрии. Затем при выполнении условий эмиссии на катоде начинают генери-
роваться электроны. В большинстве случаев это условие — просто пороговое зна-
чение напряженности электрического поля. В течение следующего этапа элект-
роны движутся в известном поле, и вычисляется объемный заряд и плотность то-
ка, после чего снова производится расчет поля. Электроны, образовавшиеся в
результате новой эмиссии, движутся в измененном поле вместе с оставшимися в
системе на предыдущем этапе. Эта последовательность шагов повторяется до тех
пор, пока не будет достигнута сходимость. На Рис. 6.8 показан результат приме-
нения этих расчетов для плотности электронов в вакуумной коаксиальной линии
передачи, соединенной с электронным диодом [Illy et al., 1994]. В этом случае
электрическое поле проникает в линию передачи через кольцевой зазор.
Дифференциальные уравнения, которые необходимо решать при использова-
нии метода конечно-размерных частиц в ячейке, представлены в наиболее обших
формах в выражениях (6.5)...(6.7):
*2 е2Л
or
д2Ф р
дф = Н(А)^2— -
or
(6.5)
ео
Уравнения (6.5) представляют собой максвелловские уравнения, в которых
А — магнитный векторный потенциал, определяемый через В = УхЛ, а Ф —
скалярный потенциал. Следующие уравнения:
Н = ^{т^с2)2 + с2 (Р - еА)2 + еФ,
ь дН дН
' Sq, Ч> дР(
(6.6)
Уравнения (6.6) являются релятивистскими уравнениями Гамильтона, описы-
вающими движение заряженной частицы в электромагнитном поле. Здесь и
6.1. Магнитная самоизоляция в вакуумной линии передачи 183
Рис. 6.7. Последовательность операций
при использовании метода конечно-размерных частиц в ячейке.
Р, — координаты и компоненты канонического импульса соответственно; /л0 —
масса частицы в состоянии покоя и с — скорость света в вакууме.
Последнее уравнение описывает формирование плазмы вблизи металлической
поверхности при превышении напряженностью поля критического значения Ес:
nc(r,t) = f(Ec,r,t).
(6.7)
Аналитическая модель
Аналитическая модель позволяет лучше понять параметрические зависимос-
ти магнитной самоизоляции [Baranchikov et al., 1978; Creedon, 1975; Mendel et al.,
1983; DiCapua, 1983]. Далее мы обсудим такую модель для стационарных условий
на больших расстояниях от фронта потерь. В этом случае мы имеем только чис-
тый поток тока jz в направлении оси z. При этом коаксиальная линия предполага-
ется однородной (Рис. 6.9).
184 Глава 6. Передача импульсов и трансформаторы
Рис. 6.8. Изменения электронного потока в линии передачи с магнитной самоизоляцией,
соединенной с электронным диодом.
Рис. 6.9. Компоненты тока в линии передачи с магнитной самоизоляцией.
6.1. Магнитная самоизоляция в вакуумной линии передачи 185
Набор связанных уравнений (6.5) в этих условиях упрощается. Уравнения по-
тенциалов приобретают вид
1А
г дг
дА<
дг
= -МоЛ»
1 д( дФ
----г—
г dry дг
(6.8)
Р
ео
Закон сохранения импульсов движения можно записать в форме
Рг =ymQz-eAl =0. (6 9)
Закон сохранения энергии становится
у/лос2 — еФ = /Яде2, (6.10)
Р = и/с.
Здесь р — скорость частицы относительно скорости света, а у — релятивистский
фактор, определенный в выражении
В конструкции цилиндрической формы магнитное поле связано с векторным
потенциалом и током выражением
BQ = -(dAjdr) = ixel(r)/2nr. (6.12)
Условия на аноде:
(6.13)
Последнее выражение в (6.13) получено из (6.9). Если электроны касаются
анода тангенциально, то получается ^ = РЖ. (Обычно ра >^, так как это также
может быть радиальной компонентой скорости частицы.) Электроны не достига-
ют анода при выполнении следующих условий:
(6.14)
Общий ток в линии (/о) делится на ток электронной оболочки и ток в стенке
катода, протекающий на глубине, обусловленной скин-эффектом, или ток плаз-
менной оболочки у катода. Однако априори не известно распределение этих то-
186 Глава 6. Передача импульсов и трансформаторы
ков и их сравнительный вклад в общий ток. Таким образом, нет точной взаимо-
связи между общим током в линии (/0) и условиями возникновения самоизоля-
ции, т. е. возникновение самоизоляции возможно при бесконечном множестве
распределений токов.
Если в линии ток протекает только через стенки катода, т. е. электрическое
поле на катоде остается ниже порога начала эмиссии электронов, то условие воз-
никновения самоизоляции может быть найдено для пробных электронов, запус-
каемых с катода интегрированием (6.14):
£ч,1п^=^£₽,7.- (6.15)
2л гс е
Решая это уравнение относительно /сг, мы получим
4г=/««₽аГа- (6.16)
Здесь введены следующие обозначения:
/а=Ж12^_ = 8500 А,
6 (6.17)
1
S=~x---7“’
lnra /гс
где g — коэффициент, учитывающий геометрические размеры коаксиальной ли-
нии.
/сг является критическим током. Это тот ток, при котором электроны, даже
оторвавшись от катода, не могут достичь анода. Очевидно, что этот критический
ток не является эквивалентным току образования изоляции в случае взрывной
эмиссии электронов из катода. Для определения условий образования самоизо-
ляции в данном случае необходимо знать распределение плотности тока в про-
странстве между внутренним и внешним проводниками. В рамках нашей модели
без дополнительных предположений относительно характеристик электронного
потока такое распределение получить невозможно. Возможные траектории элек-
тронов показаны на Рис. 6.10.
В ламинарном электронном потоке частицы движутся параллельно электро-
дам. В квазиламинарном потоке электроны движутся по циклоидным траектори-
ям с возвращением к катоду. Общей чертой этих двух типов траекторий является
сохранение канонического углового момента (6.9) и общей энергии (6.10). Таким
образом, произведение двух дельта-функций может описывать распределение
частиц в фазовом пространстве.
Для сравнения на Рис. 6.10 (внизу) изображен поток с обобщенным распреде-
лением энергии и момента. Однако числовое моделирование показывает, что ла-
минарный поток является самым лучшим приближением. Для этого вида потока
можно получить стационарное решение следующим путем [Creedon, 1975].
Во-первых, мы решим соответствующие дифференциальные уравнения для об-
ласти пространственного заряда. Затем объединим полученный результат с ре-
6.1. Магнитная самоизоляция в вакуумной линии передачи 187
Анод
ЩГа) -------
Ламинарные траектории электронов
Анод
иа--------
Катод
Квазиламинарные траектории электронов
Анод
и.---------
Катод
Траектории электронов
(с обобщенным распределением энергии и момента)
Катод
Рис. 6.10. Возможные траектории электронов
в вакуумной линии передачи с плоскими электродами.
О
зультатом для участка вакуума между краем электронного потока и анодом. При
этом мы предполагаем, что ионы не эмитируются с анода. Для электронного по-
тока, движущегося параллельно оси z, радиальный еи момент равен нулю, и полу-
чается
рг = 0 = -е
дФ
dr
+ evz
dAz
dr
(6.18)
= -eEt + evz Bo.
Уравнение (6.18) описывает баланс сил в направлении г Это уравнение можно
объединить с одномерным уравнением для потенциала:
1 д( д/О
г dr у dr J
= -ИоРЦ,
1 d (
----f"---
г dry dr J
(6.19)
_P_
eo
188 Глава 6. Передача импульсов и трансформаторы
Из (6.18) мы имеем dAJdr = \/игдФ/дг, что можно ввести в первое уравнение
(6.19), и это приведет к
1 д [ 1 дФ7
----г------к
г vz дг
= -НоРуг>
1А
г дг
дФ
дг
(6.20)
Р_
ео
Сейчас мы используем второе уравнение для исключения г из первого и, кро-
ме того, выразим иг и Ф через у:
еФ
тос2
(6.21)
В конце концов мы получаем
1—
дг)
(6.22)
Уравнение (6.22) является фундаментальным дифференциальным уравнени-
ем для магнитной самоизоляции, которое решается с использованием следующих
граничных условий:
уОс) = 1> Y('-m) =угт,
(6-23)
а затем результат решения складывается с решением для участка вакуума. Для по-
лучения решения удобно упростить (6.22) заменой переменных г на s, где
ds/dr = \/г. (6.24)
Уравнение (6.22) приобретает вид
d2y _ у Г дуУ
ds2 у2 -l^cls J
(6.25)
что эквивалентно
d 1 ду
ds^Y2-l dsj
= 0.
(6.26)
У (frY
у2-K5rJ ’
Интегрируя (6 26) дважды от у = 1 на катоде (s = $с) до у при s, мы получим
In (у + п/у2-1) = С, (5 - 5С).
(6.27)
6.1. Магнитная самоизоляция в вакуумной линии передачи 189
В общем случае электронная оболочка не достигает анода (см. Рис. 6.10).
Обозначив координату края электронной оболочки как sm и соответствующий
ему потенциал какут, мы можем выразить С\ через уравнение
(6.28)
Для того чтобы соотнести ут при 5т с потенциалом анода уо при sa, мы должны
найти решение для у на участке между sm и sa, а затем объединить решение с реше-
нием уравнения (6.27) для области электронной оболочки. Так как в этом участке
отсутствует пространственный заряд, эта задача упрощается до решения уравне-
ния Лапласа
d^y/ds1 = 0.
(6.29)
Выполнив двойное интегрирование и приняв во внимание граничные усло-
вия y(sm) = ym и у($а) = у0, мы получим
^y0(5-5m)-ym(5-^)
•s.
(6.30)
Радиальное электрическое поле ЕТ пропорционально dy/ds и должно иметь од-
но и то же значение при sm, если его рассчитывать из (6.27) или из (6.30). Сделав
это, мы получаем другое выражение для Ср
С,=
То ~ Ym
(^-•5m)VYm-l
(6.31)
Приравнивая (6.31) и (6.28), мы исключаем sm и получаем
1П (тт-Ьл/^-О-ЬУо-Гт/л/Гт-!
(6.32)
Используя (6.12) и принимая во внимание связь между BQ и Ет (6.18), мы полу-
чаем следующее выражение для тока /(г), текущего внутри радиуса г:
л/у -1 дг
(6.33)
Уравнение (6.33) справедливо для гс < г < гт, где гт — радиус, до которого про-
стирается электронное облако в пространстве между катодом и анодом.
190 Глава 6. Передача импульсов и трансформаторы
Для полного тока /0, текущего через линию передачи, мы получаем, подстав-
ляя у =ут:
(6.34)
где g — коэффициент, учитывающий геометрические размеры коаксиальной ли-
нии, введенный в (6.17). Уравнение (6.34) можно применять и для других конс-
трукций с использованием соответствующего значения коэффициента g:
• Для концентрических цилиндров
g= 1/ln (Га/гс),
• Для параллельных электродов
g = y0/27tx0»
(6.35)
где у0 — ширина электродов, ах0 — расстояние между ними.
Ток /w, текущий через стенки катода или через его плазменную оболочку, по-
лучается подстановкой у = ус = 1 в (6.33):
Av = VYm, (6.36)
где у еще свободный параметр, и для его определения необходимы релятивист-
ский фактор (потенциал) на верхней границе электронной оболочки и иные кри-
терии. На Рис. 6.11 показан общий ток /0 и ток стенок /w как функции от потен-
циала на границе слоя £/m(ym) для импульса напряжения с амплитудой
Рис. 6.11. Уменьшение тока стенок /w и общего тока /0 в вакуумной линии передачи с магнит-
ной самоизоляцией как функция от потенциала оболочки Um для 6/0 = 1.8 МВ. Круж-
ки и квадраты представляют собой экспериментальные данные, полученные на плос-
копараллельной линии длиной 7.5 м [Wang and DiCapua, 1980].
6.1. Магнитная самоизоляция в вакуумной линии передачи 191
Uq = 1.8 МВ. Разность этих токов представляет собой ток в электронной оболоч-
ке. Очевидно, что обший ток имеет минимум. В экспериментах, проведенных на
длинных линиях передачи, стационарный режим работы был найден близким к
этому минимуму. В рамках ламинарной модели можно показать, что минимум то-
ка совпадает с минимумом плотности энергии. Таким образом, мы можем ис-
пользовать критерий минимума тока для определения ут.
Минимальный ток /min бесконечно длинной линии передачи может быть оп-
ределен путем расчета минимумов /0 (6.34) для всех у0. Эти зависимости построе-
ны на Рис. 6.12 как функции от потенциала анода UQ для значений до 10 МВ. Кро-
ме того, на этом рисунке приведены графики критического тока и тока насыще-
ния 1р. Ток насыщения соответствует случаю, когда электронная оболочка
заполняет все пространство между катодом и анодом и в (6.34) становится ут = у0.
Рис. 6.12. Уменьшение минимального тока /mjn/g, критического тока /cr/gH тока насыщения /p/g
в вакуумной линии передачи с магнитной самоизоляцией в зависимости от потенци-
ала анода Uq.
Если нагрузка линии передачи имеет (согласованный) импеданс, соответству-
ющий f/о/Anin, то передача энергии будет максимальна. Если импеданс нагрузки
больше, то на конце линии останется электронный ток потерь. Если импеданс
нагрузки меньше, то отраженная волна двинется назад по линии, уменьшая ток в
электронной оболочке и сдвигая рабочую точку в область слева от минимума, как
показано на Рис. 6.11.
Для разработки передающих линий с магнитной самоизоляцией необходимо
знать отношение рабочего импеданса линии к его значению в вакууме. Это отно-
шение приведено на Рис. 6.13 для минимального тока в зависимости от напряже-
ния импульса. Экспериментальные данные подтверждают теоретическую модель
с приемлемой точностью.
192 Глава 6. Передача импульсов и трансформаторы
Рис. 6.13. Отношение рабочего импеданса линии к его значению в вакууме Zin/Zo
в зависимости от амплитуды импульса напряжения.
Простая теория, основанная на экспериментальных результатах
Глубокое понимание явления магнитной самоизоляции в линиях передачи
может быть получено из следующих экспериментальных результатов
[Mendeletal., 1983; Mendeland Rosenbaum, 1995, 1996]:
• катод является эмиттером электронов, образующих ограниченный про-
странственный заряд;
• эмиссия ионов с анода намного меньше, чем значение, ограниченное про-
странственным зарядом.
Ограничение эмиссии пространственным зарядом возникает, когда поток
частиц из их источника больше, чем поток удаляемых частиц. В этих условиях
пространственный заряд ускоренных частиц ограничивает плотность тока и фор-
мируются стабильные условия, при которых напряженность электрического поля
на границе катода равна нулю. Второе из приведенных выше наблюдений иден-
тично утверждению, что линии с магнитной изоляцией работоспособны. Можно
показать, что предположение о эмиссии ионов, ограниченной их пространствен-
ным зарядом, несовместимо с работой линии передачи.
Рассмотрим плоскопараллельную линию передачи с магнитной самоизоляци-
ей, имеющую длину /, ширину b и зазор между электродами уа, в которой элект-
ронное облако распространяется до расстояния ут от катода и движется парал-
лельно электродам (сл<. Рис. 6.10). В условиях равновесия это облако остается на
одном и том же расстоянии от электродов. Это эквивалентно утверждению, что
сумма давлений, создаваемых частицами и электромагнитным полем, одинакова
на обоих электродах. При этом предположении мы можем пренебречь давлением
частиц по сравнению с давлением поля. Кроме того, давление электрического по-
6.1. Магнитная самоизоляция в вакуумной линии передачи 193
ля на поверхности катода должно быть равно нулю. Таким образом, мы получаем
следующее уравнение для баланса давлений:
А2 Epff = В2
2р0 2 2ц0 ’
(6.37)
где В& и Еа — магнитная индукция и напряженность электрического поля вблизи
анода соответственно, а Вс — магнитная индукция поля вблизи катода. Выражая
магнитные поля через соответствующие токи /а и /с (Ba — wJJb, Вс = Цо 4/^)> мы
получаем для Еа.
Е. =^4^-
(6.38)
Вводя вакуумный импеданс линии Zq = (Ро/ео)1^2Уа/^> мы можем записать это в
форме
4л=4а/42-42- <6-39>
Это соотношение позволяет нам определить импеданс потока Zfi
. (6М)
где U — напряжение на линии передачи. Приведенное нами определение Zf не
связано с каким-либо особенным распределением пространственного заряда в
линии. Если распределение пространственного заряда в движущемся потоке од-
нородно, то мы получаем следующее выражение для Zf:
Z =Z mc2 ‘Ji* ~(6.41)
f 0 2e I2 '
Решая (6.40) и (6.41) для /а, мы можем определить Zf как функцию от 7С для раз-
личных значений U:
z = Zo + (Zl-2mc2U/eI2r2 (6 42)
f 2
Когда Zf определен, /а можно рассчитать из выражения (6.40).
Нестационарное распространение импульса
Как уже было отмечено ранее, электронные потери имеют место в начале им
пульса большой амплитуды, поступающего на вакуумную линию передачи, что
влияет на распространение этого импульса. А сейчас для фронта импульса и для
области далеко позади фронта мы поищем количественные соотношения между
скоростью распространения, током потерь и эффективностью передачи энергии
194 Глава 6. Передача импульсов и трансформаторы
(следуя [Baranchikov et al., 1978; Wang and DuCapua, 1980]). Для этой цели мы сде-
лаем следующие упрощающие задачу допущения:
1. Импульс напряжения имеет прямоугольную форму.
2. Пиковые значения тока и напряжения не изменяются во время прохожде-
ния импульса.
3. Фронт импульса распространяется без искажения его формы со скоростью и.
4. Впереди и позади фронта импульса производные всех величин по коорди-
нате z равны нулю.
5. Прекурсором импульса можно пренебречь.
Таким образом, все величины являются функциями только г] = z — vt и г. Не-
смотря на это, импульс несколько размывается при передаче. Мы имеем следую-
щие уравнения:
Дг, г, 0 = Дг, z - vt). (6.43)
Из закона Фарадея:
foxEdA = -—[BdA,
J dt J (6.44)
> = VxA
Преобразуя интеграл по поверхности в линейный интеграл, мы получаем
fEds=—^$Ads (6.45)
и, интегрируя (6.45) по межэлектродному пространству линии передачи {см.
Рис. 6.14, слева), имеем {Ег = 0, АТ = 0, Az{rc) = 0)
j£r (z + Az)dr - jEr (z)dr = ~ JX (ra )dz,
rc rc °' г+дг
(6.46)
U{z + Дг) - U{z) = ~ A (ra )&z.
ot
Az
Puc. 6.14. Путь интегрирования для уравнений (6.46)...(6.49).
6.1. Магнитная самоизоляция в вакуумной линии передачи 195
Далее мы получаем
dU/dz = -dAJdt. (6.47)
Используя уравнение непрерывности (6.48)
(6.51)
(6.52)
мы получим следующие уравнения аналогичным путем, т. е интегрируя по объему
элементы сечения межэлектролного пространства, умноженные на маленькое
значение z в аксиальном направлении (Рис. 6.14, справа):
dljdz = dQ/dt + dljdz, (6.49)
где Q — заряд электронов на единицу длины линии. С помощью уравнений
Az = £/г, dljdz = GU,Q = CU (6.50)
легко вывести дифференциальное телеграфное уравнение. Однако мы этим путем
не пойдем. Для получения выражения для о лучше мы используем наше предпо-
ложение о том, что все величины являются функциями только г| = z — w. Интег-
рированием по фронту импульса мы получим из (6.47)
dU/dz = dAJdt = trdAJdz.
Далее, используя стационарное решение, мы получаем
„Л
и=(Го-1)л/7т-1
С YoYm-1
Здесь мы использовали (6.13) и (6.33), имея в виду, что интегрирование между rm и
га выполнялось при постоянном /т. Аналогичным способом мы получаем выра-
жение для тока потерь /г путем интегрирования (6.49) по фронту импульса:
/о=«Л2 + М
А= Ya-Ym+Ym"1 ^53)
4 Ym(YaYm-l)
Здесь Q может быть получено из выражения (6.19) для р. Графики, приведенные
на Рис. 6.15, показывают зависимость скорости распространения и тока потерь от
амплитуды импульса напряжения. При увеличении амплитуды скорость распро-
странения приближается к скорости света. Одновременно с этим ток потерь
уменьшается. Экспериментальные данные подтверждают теоретические
выкладки.
196 Глава 6. Передача импульсов и трансформаторы
Рис. 6.15. Скорость распространения фронта и ток потерь в вакуумной линии передачи с маг-
нитной самоизоляцией в зависимости от амплитуды импульса (квадраты отражают
экспериментальные результаты [Baranchikov et al., 1978]; кружки — результат модели-
рования [Pokey and Bergeron, 1978J)
Эффективность передачи энергии
Сохранение энергии в системе, содержащей поля и частицы, описывается
следующим уравнением [Landau and Lifschitz, 1981]:
d 1 rri 1 p2 (у — l)mc2pVfZ г, (v — l)mc2 ...
— — + — e0E + —---------- \dV = - <> E*H + —-------j dA. (6.54)
5/J 2 2 e J J e ?
В его левой части показаны изменения во времени энергии поля и частиц в
рассматриваемом объеме. Правая часть описывает поток энергии через границы
этого объема. Интегрирование этого уравнения энергетического баланса по сече-
нию линии передачи приводит к получению дифференциального уравнения, свя-
зывающего полную энергию на единицу длины линии Wи энергию потока через
ее сечение Р.
8W + dP 2лг.(7-1)тсг (6.55)
dt dz е ' ' ’
Как и ранее, мы проинтегрируем (6.55) по фронту импульса, предполагая
опять, что все величины зависят от z — ut:
-vFK+P+^b_zll^£i/r = o. (6.56)
е
6. J. Магнитная самоизоляция в вакуумной линии передачи 197
Поток энергии потерь Ploss = Р — vW. Для определения эффективности пере-
дачи энергии Wможет быть выведена из формулы ламинарной модели:
Pt Р )
(6.57)
На Рис. 6.16 представлена зависимость эффективности передачи энергии
(КПД) от амплитуды импульса:
Амплитуда импульса напряжения [МВ]
Рис. 6.16. Зависимость КПД линии передачи от амплитуды импульса напряжения.
Заключение
Основные выводы:
1. Условие возникновения магнитной самоизоляции в длинной линии пере-
дачи/>7^.
2. Деление тока в линии на ток электронов и ток в стенках происходит соглас-
но соотношению /0//w = ym.
3. Входной импеданс линии с магнитной самоизоляцией Zin = (0.6...0.8)Zi).
4. Скорость распространения и= (0.7...0.9)с.
5. КПД передачи энергии г] = 0.85...0.95.
А теперь обсудим, существуют ли ограничения на плотность передаваемой
энергии в линии с магнитной самоизоляцией. В настоящее время наибольшим
экспериментально достигнутым значением этой плотности является 500 ТВт/м2
Из моделей, которые мы рассматривали выше, принципиальных ограничений
198 Глава 6. Передача импульсов и трансформаторы
получить не представляется возможным. Однако электронный ток потерь на
фронте импульса может создать очень горячую плазму на поверхности анода, что
способно привести к появлению ионного тока потерь и при расширении плазмы
на все межэлектродное пространство — к короткому замыканию линии.
6.2. Импульсные трансформаторы
Высоковольтные трансформаторы играют важную роль в технике импульсов
большой мощности. Они применяются как в узлах зарядки накопителей энергии,
так и в качестве импульсных трансформаторов. Они используются для преобра-
зования напряжений, токов и импедансов, для инвертирования полярности им-
пульсов и для разделения цепей с различными потенциалами.
Принцип работы трансформаторов основан на магнитной связи между двумя
проводящими цепями. При этом энергия на выходе всегда несколько меньше
чем на входе. Только в идеальном трансформаторе возможно преобразование
энергии без накопления или потерь. В идеальном трансформаторе нет омических
потерь, не возникают вихревые токи и нет ни гистерезиса, ни рассеяния магнит-
ного поля, т. е. весь магнитный поток проходит и через первичную, и через вто-
ричную обмотки. Направления токов и полярности напряжений в трансформато-
ре указаны на Рис. 6.17.
Рис. 6.17. Напряжения, токи и магнитное поле в трансформаторе.
Если к выводам первичной обмотки приложить напряжение (/ь индуциро-
ванное в индуктивности этой обмотки равное напряжение противоположной по-
лярности скомпенсирует его. В соответствии с законом Фарадея это напряжение
равно скорости изменения магнитного потока во всех Л\ витках обмотки:
Ui = N\d<b/dt. (6.58)
То же самое изменение потока индуцирует напряжение
U2 = -N2d<b/dt. (6.59)
6.2. Импульсные трансформаторы 199
Таким образом, отношение напряжений равно отношению числа витков в обмот-
ках:
U1/U\ = -N2/N\. (6.60).
Знак «минус» возникает из-за определения полярностей напряжений на Рис. 6.17
как параллельных токам. Соотношение (6.60) не зависит от нагрузки, т. е. тока,
потребляемого от вторичной обмотки. Оно остается справедливым и для комп-
лексных напряжений
Если вторичная обмотка разомкнута, ток по ней не течет, и весь магнитный
поток в трансформаторе создается только током в первичной обмотке. Этот ток
холостого хода /10 не связан с потреблением энергии и равен i10 = «|/(ico£). Если к
вторичной обмотке подключить нагрузку с комплексным импедансом Z, напря-
жение «2= —(Л^/М)и1 создаст ток i2 = u-JZ через нагрузку, который внесет свой
вклад в магнитный поток трансформатора. Несмотря на это, поток должен оста-
ваться постоянным, т. к. он должен быть достаточен для компенсации iq. Таким
образом, должен появиться дополнительный ток //в первичной обмотке, так,
чтобы было — —N2i2. Тогда ток в первичной обмотке станет
'ю
. • N2U2
*ю h 1,0 NXZ
(6.61)
Puc. 6.18. Диаграммы на комплексной плоскости, показывающие связь между токами
и напряжениями в первичной и вторичной обмотках идеального трансформатора.
Как показано на диаграмме Рис. 6.18, абсолютное значение тока i\ становится
больше, чем i10. Когда реактивный ток i 10 вычитается из тока первичной обмотки,
энергии в первичной и вторичной обмотках становятся равны между собой, как
это и ожидалось:
/• • X N2U2
01-'ю)«1=—Т7ТГ«.=»2«2-
/V,Z
(6.62)
200 Глава 6. Передача импульсов и трансформаторы
Если /ю « N2I2/N\i то мы получаем идеальный трансформатор, для которого
Ix = -N2h/Nb
(6 63)
Если к выводам вторичной обмотки подключен резистор, то ток и напряже-
ние в первичной обмотке связаны соотношением
= (6.64)
где п = Ni/N\. Это легко выводится из закона сохранения энергии, т. е. /j2/^' ~
= /г2/?2- Аналогично получается
£2= L^n2. (6.65)
И из (\/l)C2U2 = (1/2)С2^2мы получаем
С2= п2С2.
(6.66)
Так, используя правила трансформации (6.64)...(6.66), мы можем соотнести
все элементы схемы, находящиеся в цепи вторичной обмотки трансформатора, с
его первичной цепью. Если теперь принять во внимание сопротивления обмоток,
вихревые токи, потери на гистерезис и, в дополнение, учесть емкость между об-
мотками, мы получим эквивалентную схему реального трансформатора, приве-
денную на Рис. 6.19.
Рис. 6.19. Эквивалентная схема реального трансформатора.
Ток делится между током нагрузки и током утечки. Таким образом, всегда
1\ > 12п. (6.67)
В общем случае токи утечки нежелательны, так как они влекут за собой поте-
ри энергии.
В мощных импульсных системах трансформаторы часто используются для пе-
редачи и преобразования (увеличения) амплитуды прямоугольных импульсов.
Для расчета времени нарастания импульса на выходе в таком применении обыч-
но можно пренебречь индуктивностью L в эквивалентной схеме. Индуктивность
рассеяния, напротив, играет важную роль в определении выбросов на фронтах
импульса Для скачка напряжения на входе схемы, приведенной на Рис. 6.19, мы
получаем на выходе
6.2. Импульсные трансформаторы 201
U2(t) = nU0
( ______О -вг/*’-1»
[ijk2 -1 2J
(6.68)
V*2
Здесь Л и со даются выражениями
1 2 R+R2/n2
со =—-—=---.
(RJn^Lfi
. 1Г я 1
fa =__ __5. -|-----------
2[L, (/?2/n2)Cjco’
(6.69)
Уравнение (6.68) справедливо для к > 1.
Для случая цепи с критическим демпфированием, когда к = 1, мы получаем
иЛ,) = nU° " ° + М')е^
(6.70)
И наконец, для докритичного случая, когда к < 1,
t/2(r) = ni/0
—. l-e_bv * sin(Vl-A:2co/) + cos(\/l-£2coZ) ►.
я2/л+м LA-*2 J.
(6.71)
На Рис. 6.20 приведены формы импульсов выходного напряжения при раз-
личных степенях демпфирования.
Рис. 6.20. Отклик импульсного трансформатора на скачок напряжения на входе при различных
степенях демпфирования (А = (Jh/rifytR. + Ri/n2), п =
к = + 1/(/?2/л2О]774л, Т= 2л(£,(С1),/2)).
202 Глава 6. Передача импульсов и трансформаторы
В схеме с критическим демпфированием время нарастания выходного им-
пульса (0.1...0.9£/2тах) можно получить из (6.70):
0.537=3.35
ДС(У*2)
2Л,/2
& 72)
Здесь 7= 2л/ах Для получения меньшего времени нарастания значения L\ и Сна-
до делать как можно меньше. Следовательно, сердечник трансформатора должен
состоять из материала с высокой проницаемостью на высоких частотах, обеспе-
чивающей хорошую связь между обмотками. Емкость С представляет собой сум-
му паразитных емкостей первичной и вторичной обмоток. При этом последняя
имеет множитель п2 (С = С{ + л2С2). Таким образом, время нарастания увеличива-
ется пропорционально п. Отсюда следует, что слишком больших коэффициентов
трансформации следует по возможности избегать.
На спад напряжения вершины импульса значения Zq и С не оказывают значи-
тельного влияния. В основном постоянная времени спада вершины определяется
величиной L:
Л^ + ^/л2)
(6.73)
Понятно, что индуктивность L должна быть достаточно большой, чтобы fa была
больше длительности пропускаемого импульса.
Потери энергии возникают в реальном трансформаторе вследствие вихревых
токов и гистерезиса в ферромагнитном сердечнике, как это уже обсуждалось в
разд. 4.1.3 для магнитных ключей. Еще одной проблемой является неидеальная
связь обмоток. На практике всегда находятся участки, в которых магнитные поля
первичной и вторичной обмоток не полностью компенсируют друг друга, что
приводит к появлению индуктивности рассеяния Lx в эквивалентной схеме
трансформатора.
Кроме этого, существуют и другие ограничения на возможность передачи
формы импульса напряжения через трансформатор с ферромагнитным сердечни-
ком без искажения. Из соотношения N\d<b/dt = Uследует, что
4р Л(ДВ(О)
' dt * dt
[Я(0- Z?(0)]M = fr(t)dt < 25Л.4-
(6.74)
Это ограничение мы уже знаем из обсуждения свойств магнитных ключей
(разд. 4.1.3). Как правило, рабочий режим трансформаторов находится намно-
го ниже этого порога, что обеспечивает достаточно малые потери на гистере-
зис.
6.3. Высоковольтные источники питания 203
6.3. Высоковольтные источники питания
6.3.1. Методы заряда конденсаторов
Существует три основных метода заряда конденсаторов’.
• заряд линейным током,
• одноимпульсный заряд,
• заряд высокочастотными импульсами тока.
Упрощенная схема заряда линейным током показана на Рис. 6.21. Она состо-
ит из набора трансформатор—выпрямитель и элементов ограничения бросков то-
ка в цепи накопительного конденсатора. Ограничение бросков тока может быть
достигнуто введением фазового управления в цепи переменного тока или добав-
лением последовательных импедансов во входные или выходные цепи. Эти импе-
дансы представляют собой обычно резистор или дроссель (или и то и другое
вместе), включаемые между выходом выпрямителя и накопительным конденса-
тором. При емкостной нагрузке конденсатор фильтра обычно не применяется
Рис. 6.21. Схема зарядного устройства с резистивным ограничителем тока.
D — выпрямительный диод, Cs — сглаживающий конденсатор.
Этот тип зарядных устройств приемлем только для применений с очень низ-
кой средней мощностью, когда простота схемы является доминирующим факто-
ром при разработке, а размеры устройства, возможность регулировки и КПД не
являются критическими требованиями. Зарядное устройство, выполненное по
схеме Рис. 6.21, имеет КПД т] меньше 50% (здесь КПД — это отношение энергии,
запасенной в конденсаторе, к энергии, поступившей из источника питания):
дг !1С 1-е^/дс<
О
(6.75)
204 Глава 6. Передача импульсов и трансформаторы
До разработки высоковольтных импульсных источников питания для повтор-
ного заряда батарей конденсаторов широко использовался одноимпульсный ре-
зонансный метод [Glasoe and Lebacqz, 1948]. Его отличает сравнительно простая
конструкция. В дополнение к основному набору трансформатор—выпрямитель в
схему вводятся дополнительный конденсатор, дроссель и ключ. На Рис. 6.22 при-
ведена упрощенная схема этого устройства.
Рис. 6.22. Схема одноимпульсного резонансного зарядного устройства.
Решая дифференциальные уравнения для схемы, приведенной на Рис. 6.22,
мы получим следующее выражение для напряжения на конденсаторе С:
L7(r) = t/0 1-е
cos(wZ) - — sin(co/) .
(6.76)
При выводе этой формулы предполагалось, что емкость накопительного конден-
сатора Cs намного больше емкости С. Здесь со2 = со02 — а2, со02 = 1/^С, а ~ Rft-L.
Ток заряда определяется выражением
/(O = -^-e-ersin((oO.
Zxo
(6.77)
Q = (&L/R = со/2а называется добротностью резонансного контура КПД т| в
этой схеме определяется выражением
(1/2)СС/2(р = (1 /2) [1 - е~*' (cos(co/) - о /со sin(coQ)]2
7 1 - е-*' [с os (со/) + а /со siп(со/)]
(6.78)
В одноимпульсном резонансном зарядном устройстве время заряда tc определяет-
ся из соотношения со/с = п. Таким образом, получается
6.3. Высоковольтные источники питания 205
1 + е^/ш
l + e~*/2g
2
(6.79)
Следовательно, если параметры элементов схемы выбраны правильно, КПД
резонансного зарядного устройства может приближаться к 1. Недостатками этого
устройства являются большой вес и размеры.
Для систем средней и большой мощности, для которых минимальный зани-
маемый объем, КПД и возможность регулировки являются основными требова-
ниями, наиболее пригоден метод высокочастотной зарядки накопительного кон-
денсатора квазипостоянным током. В этих устройствах входное напряжение про-
мышленной частоты выпрямляется и поступает на генератор высокой (« 50 кГц)
частоты. Генератор высокой частоты обычно строится по схеме мостового резо-
нансного преобразователя, выходное напряжение которого после повышения его
амплитуды с помощью трансформатора вновь выпрямляется с использованием
диодов с малым временем восстановления. В мостовых преобразователях на-
ибольшие плотность мощности, надежность и, наконец, дешевизна достигаются
при использовании в качестве ключей биполярных транзисторов с изолирован-
ными затворами (IGBT). Высокая рабочая частота позволяет для получения вы-
сокого напряжения применять маленькие и легкие трансформаторы. На Рис. 6.23
приведена упрощенная схема такого зарядного устройства.
Qi
Q:
Выпрямленное
напряжение
питающей сети
Высокочастотный
преобразователь
Постоянное
выходное
напряжение
С L
JLnr
Высоко-
вольтный
трансформатор
Высоковольтный
выпрямитель
Схема
управления
Цепь
обратной связи
Местное/
Дистанционное
управление
Рис. 6.23. Упрощенная схема генератора высокочастотной зарядки
накопительного конденсатора квазипостоянным током.
206 Глава 6. Передача импульсов и трансформаторы
В схеме, приведенной на Рис. 6.23, ток через ключи и первичную обмотку
трансформатора из-за влияния последовательного резонансного контура LC име-
ет синусоидальную форму. При этом ключи включаются и выключаются при ну-
левом значении тока через них, что исключает потери при переключении. Потери
энергии на ключах в фазе проводимости малы из-за малого сопротивления клю-
чей во включенном состоянии. Тщательный анализ схемы с последовательной ре-
зонансной цепью показывает, что ток в ней представляет собой чистую синусоиду
только при нулевом выходном напряжении, т. е. при замкнутой накоротко на-
грузке. Когда накопительный конденсатор начинает заряжаться, ток моста в пря-
мом направлении увеличивается, в то время как ток в обратном направлении
уменьшается. Это происходит из-за того, что увеличивающееся напряжение на
нагрузочном конденсаторе увеличивается и отражается в первичную цепь.
Приятной особенностью преобразователя с последовательным резонансом
является то, что он ведет себя как генератор постоянного выходного тока. На
Рис. 6.24 показаны импульсы тока, заряжающие нагрузочный конденсатор Cload,
и изменение напряжения на нем в процессе зарядки. Из этих графиков следует,
что схема ведет себя как генератор постоянного тока. При изготовлении таких ус-
тановок с выходным напряжением больше 10 кВ высоковольтный трансформатор
и всю выходную секцию помещают в изолированный корпус, заполненный мас-
лом, с герметичными выводами входных и выходных цепей.
Рис. 6.24. Импульсы тока, заряжающие нагрузочный конденсатор Cload (внизу), и изменение на-
пряжения на нем в процессе зарядки (вверху) для схемы, приведенной на Рис. 6.23
(входное постоянное напряжение преобразователя 100 В, частота 25 кГц, коэффици-
ент трансформации 10).
6.3. Высоковольтные источники питания 207
В заключение определим КПД этого зарядного устройства. Напряжение на
нагрузочном конденсаторе возрастает по линейному закону U= Itf/C. Для КПД г)
мы имеем
(1/2)С(/0Г/С)2 _ t
(1 /2)С(/0/ /С)2 + Rl^t t+2RC ‘
(6.80)
Таким образом, г| приближается к 1 для t» RC, и при заряде конденсатора до на-
пряжений Uq мы получаем
(6.81)
6.3.2. Умножители напряжения
При напряжении свыше 100 кВ трансформаторы становятся не удобны в экс-
плуатации из-за чрезмерного увеличения их размеров и повышения требований к
изоляции. С умножителями напряжения, одна из схем которого показана на
Рис. 6.25, может быть достигнуто напряжение питания в мегавольтном диапазо-
не. Зарядка в этой схеме происходит по шагам. Рассмотрим изменения во време-
ни напряжений в точках 1, 2, 3 на схеме Рис. 6.25. Предположим, что энергии ис-
точника переменного напряжения достаточно для зарядки конденсатора С! за
время, равное одной четверти периода до амплитудного значения входного на-
пряжения. Тогда все точки 1...3 приобретут потенциал Uo, но, кроме Сь ни один
другой конденсатор пока не заряжен.
Когда напряжение источника питания начинает падать, заряд, накопленный
в Сь начинает перетекать в конденсатор Сг- Перенос заряда заканчивается при
минимальном напряжении источника питания. Относительно земли точки 1 и 2
(а также все остальные точки, кроме точки 0) теперь находятся при нулевом
потенциале (при Ci = С2). Когда напряжение источника питания начинает расти
от своего максимального отрицательного значения, потенциал точки 2 также рас-
тет и ток начинает течь из конденсатора С2 в С3 и Сь Когда напряжение источни-
ка в точке 0 превысит потенциал в точке 1 в течение следующей четверти периода,
С! заряжается вновь до амплитудного напряжения источника питания, и после
того, как будет пройдено пиковое значение напряжения питания, опять начина-
ется перенос заряда из Cj в С2, приводящий к увеличению потенциала в точке 2
над потенциалом в точке 1. В то же время заряд перетекает из С3 в С4. Начиная с
последней четверти второго периода, часть заряда возвращается назад из С2 в С3 и
Ci и из С4 в С5.
Эти соображения могут распространяться и на последующие периоды напря-
жения питания и другие точки схемы. Порции заряда поставляются в цепь только
через С! в течение первой четверти каждого периода. В течение времени, когда
напряжение источника питания падает (вторая и третья четверти периода), заряд
передается из нижней цепи элементов в верхнюю, а в течение четвертой четверти
и части первой четверти следующего периода часть заряда возвращается назад в
208 Глава 6. Передача импульсов и трансформаторы
Рис. 6.25. Схема умножителя напряжения (вверху) и формы напряжения на конденсаторах этой
схемы. Амплитудное напряжение источника питания 100 В, частота 10 кГц. Выходное
напряжение равно сумме напряжений на конденсаторах в нижней цепи.
звенья нижней цепи и сглаживается конденсаторами в ней (Рис. 6.25). Таким об-
разом, среднее напряжение на каждом конденсаторе увеличивается на каждом
периоде напряжения питания. В стационарном режиме напряжение на конденса-
торе С] достигает значения U$, а напряжения на остальных конденсаторах при-
ближаются к 2Uq. Более быстрое достижение состояния равновесия достигается,
если емкость конденсатора Uq выбрана намного больше, чем емкость других кон-
денсаторов. Главными достоинствами умножителя напряжения являются просто-
та изоляции и возможность использования маленьких трансформаторов.
6.4. Трансформаторные линии 209
6.4. Трансформаторные линии
Вместо импульсного трансформатора для согласования импедансов генерато-
ра и нагрузки может быть использована трансформаторная линия.
Одним из специальных типов трансформаторной линии является так называ-
емая экспоненциальная линия. Как и трансформатор, экспоненциальная линия
является передающей системой с сохранением энергии. В экспоненциальной ли-
нии индуктивность, емкость, сопротивление и проводимость на единицу длины
зависят от координаты х экспоненциально:
L'(x) = Lq х е^,
С'(х) = Со' х е~Вх,
(6.82)
7?'(х) = Rq х е^*,
С'(х) = С0'хе-в<
Коэффициент В может иметь как положительное, так и отрицательное значение.
Схематический чертеж экспоненциальной линии приведен на Рис. 6.26.
Рис. 6.26. Схематический чертеж экспоненциальной линии
с генератором импульсов и нагрузкой.
Рассмотрим линию без потерь, т. е. Rq = Gq = 0. Преобразования Лапласа для
дифференциальных уравнений, описывающих эту линию
d2u 1 dE du 2
—5-----------pLCu = 0.
dx L dx dx
d2i 1 dC di 2 n
p ECi = 0.
dx C dx dx
(6.83)
Удобно ввести зависимые от положения импеданс и задержку на единицу дли-
ны:
210 Глава 6. Передача импульсов и трансформаторы
z'=$’
(6 84)
Используя пространственную зависимость и L' и С из (6 82) мы получим
d Н р„2Т2и — п
^ + B~p2T2i = 0,
ах ах
(6.85)
гдеГ0 = (Л'0С0)1Л.
Решениями характеристического полинома для дифференциального уравне-
ния (6.85) являются
г„ г2 = -| ± ^В2+4ргТ2. (6.86)
Таким образом, общим решением является
V = UQer'x + UQ&\ (6.87)
Если В2 «4р2Т02, мы получаем
и = UGeB/lxe,~pT°x + и^в,1хет°х (6.88)
и убеждаемся, что в этом случае энергия при передаче сохраняется. Сделанное
выше допущение идентично требованию, чтобы относительное изменение импе-
данса X/Z^dZJdx = В было мало по сравнению с 4лД, где X — длина волны пере-
даваемого сигнала. Это соотношение можно вывести, если заменитьр на ico, при-
нимая во внимание, что <о = 2лД То. Конечно, в качестве X следует брать самую
длинную волну в передаваемом сигнале.
ГЛАВА
СЛОЖЕНИЕ МОЩНОСТЕЙ И НАПРЯЖЕНИЙ
7.1. Сложение мощностей
Повышение мощности и напряжения импульсов требует увеличения расстоя-
ний между электродами в линии их формирования для достижения необходимой
электрической прочности. Например, коаксиальная линия передачи с водяной
изоляцией для создания импульса с напряжением 15 МВ, мощностью 100 ТВт и
длительностью 50 нс, заряжаемая предварительно от промежуточного накопите-
ля энергии за 300 нс до напряжения 30 МВ, должна иметь диаметр 16 м. Очевид-
но, что эта линия была бы непригодна для формирования подобных коротких
прямоугольных импульсов, так как балансировка зарядов по окружности столь
большого по плошали проводника не может быть достигнута за приемлемое вре-
мя. Предел по мощности для одиночной линии передачи достигается тогда, когда
время прохождения электромагнитной волны вдоль окружности проводника ста-
новится сравнимым с временем разряда этой линии. На практике это ограничи-
вает мощность, которую можно получить от одиночной линии, на уровне около
15 ТВт.
Для уровней импульсной мощности свыше этого значения генератор прихо-
дится делить на несколько отдельных частей, которые могут быть значительно
более компактными, за счет чего доступный объем используется более эффектив-
но. Эти отдельные генераторы, естественно, управляются синхронно (Рис. 7.1).
Синхронизация независимых линий требует специальной техники, например
ключей с лазерным управлением, имеющих очень малую нестабильность задерж-
ки включения. Для согласования генераторов с нагрузкой следует иметь в виду,
что выходной импеданс генераторов должен быть связан с импедансом нагрузки
соотношением R^ = R^/n, где п — число параллельно включенных генераторов.
212 Глава 7. Сложение мощностей и напряжений
Рис. 7.1. Схематическое изображение сложения энергии от нескольких параллельно включен-
ных генераторов импульсов, работающих на общую нагрузку (Ль = Rf/n, п — число
параллельно включенных генераторов).
7.2. Сложение напряжений
7.2.1. Сложение напряжений с использованием временной
изоляции
В некоторых приложениях требуется ускоряющее напряжение в диапазоне
между 5 и 60 МВ. Столь высоковольтные импульсы невозможно создать при ис-
пользовании одиночной линии, так как одновременно требуется и большая их
мощность. Намного удобнее получать эти импульсы путем суперпозиции им-
пульсов, вырабатываемых отдельными генераторами, используя их последова-
тельное соединение. Одним из примеров такого соединения является схема
Блюмляйна (см. ниже).
Подобно последовательному соединению нескольких батарей, мы можем
собрать отдельные линии передачи в схему сложения напряжения, соединив по-
ложительный электрод одной линии передачи с отрицательным электродом дру-
гой (Рис. 7.2). Это особенно легко выполняется с полосковыми линиями. Чтобы
предотвратить короткое замыкание в цепи, точки соединений должны быть изо-
лированы, по крайней мере, на время прохождения импульса. Это может быть
достигнуто, если линии имеют достаточно большую длину.
7.2. Сложение напряжений 213
Рис. 7.2. Сложение напряжений с использованием временной изоляции.
7.2.2. Сложение напряжений с использованием индуктивной
изоляции
Более компактный генератор ускоряющего напряжения можно построить,
используя для сложения напряжений импульсов взамен временной изоляции ин-
дуктивную (магнитную) изоляцию1) [Ramirez et al., 1985]. Для объяснения при-
нципа работы этого сумматора напряжений мы рассмотрим шестикаскадную схе-
му генератора KALIF-HELIA (Karlsruhe Light Ion Facility — High Energy Linear
Induction Accelerator — линейный ускоритель высокой энергии для легких ионов
в Карлсруэ), приведенную на Рис. 7.3 и предназначенную для питания импуль-
сного источника ионных пучков.
Каждая из цилиндрических полостей, показанных на Рис. 7.3, соединена ра-
диально с двумя обычными схемами формирования импульсов с жидкостной
изоляцией. Для повышения однородности создаваемой волны точки соединения
на окружности расположены на расстоянии 180° друг от друга. Кроме того, сим-
метрия улучшена путем азимутального распределения цепей в полости. Каждая
полость может поставить в согласованную линию передачи с магнитной самоизо-
ляцией импульс напряжением 1 МВ, током 400 кА и длительностью 50 нс. Сло-
жение напряжений достигается соединением положительной стороны одной по-
лости с отрицательной стороной следующей полости. При этом неизбежно высо-
ковольтный проводник оказывается соединен с заземленным проводником. Для
того чтобы обеспечить достаточно высокий импеданс этого соединения, часть
полости вблизи ее стенки, соединенной с соседней стенкой, заполняется плас-
0 В отечественной литературе более распространен термин «магнитная изоляция», который, впро-
чем, автор тоже применяет. — Примеч. пер.
214 Глава 7. Сложение мощностей и напряжений
Входы
Рис. 7.3. Шестикаскадная схема сложения напряжения с индуктивной изоляцией.
тинчатым сердечником из ферромагнитного материала, имеющего высокую маг-
нитную проницаемость. До тех пор пока магнитная индукция не достигает насы-
щения, ток утечки через это соединение остается небольшим. Критически важ-
ным для степени магнитной изоляции является изменение во времени состояния
ферромагнитных сердечников. Ввиду того что ток утечки остается небольшим,
только пока не наступит их насыщение, продолжительность сохранения состоя-
ния изоляции ограничена, в соответствии с законом Фарадея, интегралом напря-
жение-время. Эти же самые закономерности справедливы и для магнитных
ключей, которые мы рассматривали в гл. 4.
В схеме, показанной на Рис. 7.3, сложение напряжений происходит в коакси-
альных линиях передачи с магнитной самоизоляцией. Для предотвращения отра-
жения импульсов от узлов соединения отдельных полостей импеданс линии дол-
жен возрастать скачками, т. е. увеличиваться с увеличением числа секций.
Каждую секцию в коаксиальной линии, показанной на Рис. 7.4, можно рас-
сматривать как генератор с импедансом nZ$. Этот генератор включен последова-
тельно с генератором номер (п + 1) и возбуждает вместе с ним секцию линии но-
мер (п + 1), которая, таким образом, для согласования должна иметь импеданс
(п + 1)ZO. В этом случае распространение волны вправо будет всегда встречать со-
гласованную нагрузку, а волны, распространяющиеся влево, будут полностью
поглощаться.
Для моделирования схемы с помощью такой программы, как LEITER, мы мо-
жем использовать эквивалентную схему, приведенную на Рис. 7.5. Здесь линии,
управляющие полостями, рассматриваются как источники напряжения с внут-
ренним импедансом R&. Между этими источниками напряжения и точками со-
единения добавлены линии задержки, назначение которых состоит в компенса-
ции времени распространения импульса по отрезкам вакуумной линии передачи.
Максимум передачи энергии достигается при Z1 = R&.
7.2. Сложение напряжений 215
Рис. 7.4. Эквивалентная схема последовательного сумматора импульсов напряжения
на линиях с магнитной самоизоляцией.
Рис. 7.5. Схема для моделирования с помощью программы LEITER сумматора напряжения,
приведенного на Рис. 7.3.
7.2.3. Генераторы Блюмляйна
Недостатком обычных линий формирования импульсов является то, что на
согласованной нагрузке выделяется импульс амплитудой, равной лишь половине
напряжения, до которого была заряжена линия. Кроме того, выходной ключ рас-
положен перед нагрузкой и, следовательно, при быстром заряде линии способен
пропускать часть напряжения на нагрузку до момента его включения. Эти недо-
статки преодолены в линии Блюмляйна, показанной на Рис. 7.6 [Blumlein, 1941].
В классической форме линия Блюмляйна состоит из двух линий, которые
после замыкания ключа становятся соединены последовательно. Чтобы понять
принцип ее работы, представим статическое напряжение на обоих линиях как ре-
зультат воздействия двух волн, распространяющихся в противоположных направ-
лениях. Перед зажиганием газоразрядного ключа векторы напряженности поля
волн, распространяющихся в этих линиях, имеют противоположные полярности
на концах линий и компенсируют друг друга. Следовательно, ток в нагрузке не
течет.
После замыкания ключа полярность прямой волны во внутренней линии из-
меняется. На конце линии, присоединенном к нагрузке, эта волна приобретает ту
же полярность, что и прямо распространяющаяся волна во внешней линии. Та-
ким образом, на нагрузке возникает напряжение и через нее начинает течь ток.
При согласованной нагрузке это напряжение равно Uq. Если импеданс отдельных
линий равен Z/2, то общий импеданс линии Блюмляйна равен Z.
216 Глава 7. Сложение мощностей и напряжений
На Рис. 7.7 приведена обобщенная схема генератора Блюмляйна. В ней по-
лосковые электроды заряжены так, что у соседних электродов напряжение имеет
противоположный знак. Ключи замыкаются синхронно На выходе генератора
векторы напряжений инвертируются и развивается амплитуда импульса, равная
2п Uq, где п — число ключей. Выходной импеданс этой схемы равен 2nZ
Ключи
включения включения
ключей ключей
Рис. 7.7. Схема обобщенной линии Блюмляйна.
7.2.4. Кумулятивные линии формирования импульсов
На Рис. 7.8 приведена интересная схема для умножения напряжения, извест-
ная как кумулятивная линия формирования импульсов [Smith, 1980]. Подобно
обобщенной линии Блюмляйна, она способна умножать начальное напряжение
заряда. В отличие от линии Блюмляйна в этой схеме требуется только один
7.2. Сложение напряжений 217
ключ1*. Кумулятивная линия формирования импульсов состоит из п соединенных
между собой секций линий передачи с равным временем задержки распростране-
ния. По отношению к первой секции импеданс каждой из следующих выбирается
больше во столько раз, сколько составляет для нее сумма натуральных чисел. Так,
для второй секции импеданс выбирается больше в 1 + 2 = 3 раза, для третьей — в
1 + 2 + 3 = 6 раз, для четвертой —в 1 + 2 + 3 + 4 = 10 раз и т. д. Последняя (л-я)
секция имеет импеданс, равный Zn = п(п + 1^/2, где Z\ — импеданс первой сек-
ции. После замыкания ключа 5* 2) волна разрядного тока распространяется по ли-
нии к нагрузке. При разомкнутом выходе на нем развивается импульс напряже-
ния с амплитудой —nUQ. Если импеданс нагрузки равен Zn, то на ней образуется
импульс напряжения амплитудой — hUq/2 и длительностью 2т, где т— время за-
держки распространения волны в одной секции линии. При этом накопленная в
линии энергия полностью поглощается нагрузкой.
S'
*1
Z, 3Z, 6Z, 10Z,
Рис. 7.8. Схема кумулятивной линии формирования импульсов
с возрастающим импедансом секций.
Так почему же энергия не отражается от точек скачка импеданса в этой ли-
нии? Кажется, что раньше мы уже выучили, что импульс отражается от несогла-
сованного импеданса, и только при его согласовании отражение отсутствует.
Дело в том, что в рассматриваемом случае все секции линии первоначально заря-
жены. До того как ключ замкнется, мы опять, как и с линией Блюмляйна, можем
рассматривать стационарное напряжение Uq как суперпозицию волн с амплиту-
дой Uq/2, распространяющихся в противоположных направлениях. После замы-
кания ключа в секции 1 возбуждается волна отрицательного напряжения ампли-
тудой —Uq/2, движущаяся к секции 2. Через узел соединения секций 1 и 2 эта вол-
на передается с амплитудой (—f/0/2)[2Z2/(Zi + Z2)J. При подсоединенной нагрузке
амплитуда прямо распространяющейся волны увеличивается на каждом узле со-
единения секций линии с множителем
2Z„+1/( Zn+l+Zn) - (л + 2)/(и + 1).
(7.1)
Таким образом, амплитуда волны, поступающей в секцию номер п, равна
" На самом деле, как показано на Рис. 7.8, требуется два ключа. — Примеч. пер.
2) И ключа S'. — Примеч. пер.
218 Глава 7. Сложение мощностей и напряжений
1/0 3 4 5 п п + 1 _ Uo п + 1
~Т234‘"п-1 п ~ 2 2 ( ’
Эта волна достигает нагрузки вместе с прямо распространяющейся волной амп-
литуды Ug/2 в секции номер п:
rj _ Uo п + 1 [ Uo 2ZL _ nU0 2ZL
L L 2 2 2 JZL + Z„ 2 ZL + Z/ v ’ 7
Таким образом, на согласованной нагрузке ZL + Z„ мы получаем
i/L = -«t/0/2. (7.4)
Этот импульс имеет длительность 2т, так как именно за это время отраженная вол-
на достигает нагрузки. Таким образом, энергия И^, передаваемая в нагрузку, равна
H'L = (»l/0/2)2x2-C/Z„. (7.5)
Или, так как Z„ = [и(л + l)/2]Zb
L I 2
|2 4 т
I n(n +1) Z|
(7.6)
С другой стороны, время задержки распространения волны в одной секции
линии т = ^(£'С')1/2, Z= (£'/С')1/2. Здесь (. — длина одной секции. Тогда
z; ТЩТё, 1 ’
(7.7)
где Ci — емкость первой секции. Сравнивая это выражение с энергией, запасен-
ной первоначально во всех секциях линии
^=^0 +...+%i/02
L L L L
С, Zt 2
сх 4 /(/+1)’
1V=-U22CXY—^—
2 0 ’Г*0 + 1)
1
Z + 1J
, ( 1
= и2Сх 1----—
Т л + 1
(7 8)
=-Цс,
п + 1
мы получаем, что ИЛ= WL, т. е. вся запасенная энергия передается в нагрузку. Это
также доказывает, что импульс напряжения достигает нагрузки без отражения
Впрочем, для реальной линии это не совсем так вследствие того, как мы узнали
7.2. Сложение напряжений 219
раньше, что на узлах соединения отрезков линий с разными импедансами воз-
буждаются высшие типы волн.
Недостатком схемы, приведенной на Рис. 7.8, является необходимость синх-
ронизации работы ключей S и S' В схеме, приведенной на Рис. 7.9, представляю-
щей собой комбинацию предыдущей схемы и генератора Блюмляйна, выходной
ключ S' исключен, что снимает проблему синхронизации. В этой схеме последняя
секция кумулятивной линии имеет общий высоковольтный электрод с еще одной
линией передачи такой же длины. Заземленные электроды обеих линий соедине-
ны с нагрузкой. Импеданс дополнительной линии выбран так, чтобы она постав-
ляла в согласованную нагрузку такой же ток, как и кумулятивная линия, т. е.
Uo _nUQ 1 _nUQ 1 _ 1 L/o
2Z 2 Zn 2 \n(n + \)/2}Zx и + l Z, ’
и тогда
Z = -^±J-Z1. (7.10)
Импеданс нагрузки при этом должен быть равен сумме Zn и Z':
zL = n{n^zx + ^-zx = ^+1)2z;. (7.11)
Рис. 7.9. Комбинация схемы кумулятивной линии формирования импульсов
с генератором Блюмляйна.
ГЛАВА
ПРИМЕРЫ ГЕНЕРАТОРОВ МОЩНЫХ
ИМПУЛЬСОВ
8.1. Генераторы одиночных импульсов
Для решения некоторых научных задач не требуется подачи на нагрузку пос-
ледовательности импульсов. Это относится, например, к случаям, когда после
каждого импульса необходимо довольно большое время для определения измене-
ний в исследуемом объекте или когда часть экспериментальной установки разру-
шается под воздействием импульса и должна быть заменена перед повтором. В
этих условиях устройство генератора мощных импульсов существенно упрощает-
ся. Однако некоторые эксперименты требуют для их проведения чрезвычайно
высоких мощностей.
8.1.1. КАЛИФ
КАЛИФ (KALIF — Karlsruhe Light Ion Facility) представляет собой импуль-
сный источник ионных пучков [Bluhm et al., 1985]. Используемый в нем генера-
тор импульсов — типичный представитель генераторов одиночных импульсов те-
раваттного диапазона мощностей (Рис. 8.1). Первичным накопителем энергии в
нем является двухполярный генератор Маркса, состоящий из 25 каскадов. В каж-
дом каскаде используется по два конденсатора, заряжаемые до ±100 кВ. При мак-
симальном заряде запасаемая энергия равна 250 кДж. С выхода генератора Марк-
са энергия поступает в форме импульса длительностью 1 мкс на коаксиальный
промежуточный накопительный конденсатор (линию) с водяной изоляцией и
емкостью, равной емкости последовательно соединенных конденсаторов в гене-
раторе Маркса. Импеданс этой линии равен 5 Ом, а внешний диаметр 2.5 м. Бла-
годаря достаточно большому расстоянию между внешним и внутренним электро-
дами в этой линии пробоя во время ее заряда не происходит. Между выходом это-
го промежуточного накопителя энергии и входом линии формирования
импульсов помещен водяной ключ, напряжение самопробоя которого подстроено
так, чтобы он замыкался при достижении максимального напряжения. После за-
мыкания водяного ключа накопленная в промежуточном накопителе энергия
преобразуется в электромагнитную волну с двойным временем задержки прохож-
дения, равным 300 н. Импеданс линии формирования импульсов равен 2.25 Ом, а
8.1. Генераторы одиночных импульсов 221
ее емкость и диаметр внешнего электрода такие же, как у промежуточного нако-
пителя энергии Электрическая длина линии формирования равна 25 нс. Вследс-
твие меньшего импеданса расстояние между внутренним и внешним электрода-
ми значительно меньше, чем в промежуточном накопителе, что допустимо из-за
намного меньшего времени ее заряда.
Промежуточный Линия Линия
накопитель
Генератор Маркса
/Изолятор
Промежуточный ключ5.
Масляная
изоляция
25 газовых
оазгш-
ников
Ключ
подавления
^помехи
, формирования. передачи
импульсов
5 Выходной /
I ключ
Диод
Вод яная изоляция
Вакуумная
перегородка
Вакуумные
насосы
ПИонный
пучок
Рис. 8.1. Схематическое изображение генератора импульсов мощностью 1.5 ТВт ускорителя
KALIF. Параметры импульса на границе вакуумной перегородки: мощность 1.5 ТВт,
напряжение 1.7 МВ, длительность импульса 50 нс, энергия 75 кДж, КПД 30%.
50 конденсаторов
Вакуумная
секция
На выходе линии формирования импульсов установлен набор из 14 водяных
ключей с самопробоем, которые распределены по внешней поверхности внутрен-
него электрода. Связь через ультрафиолетовое излучение между этими ключами
обеспечивает синхронность их включения. Вследствие большого числа отде-
льных ключей общие индуктивность и сопротивление оказываются довольно ма-
лы, что позволяет передавать на следующую за ключами линию передачи импульс
с крутым фронтом. Далее импульс проходит через диэлектрическую перегородку,
делящую линию передачи на две части. В перегородку встроено 11 газовых раз-
рядников. Давление газа в них выбрано так, чтобы они не пробивались при на-
пряжении импульса, предшествующего основному и обусловленного своим по-
явлением емкостной связью между линией формирования импульсов и линией
передачи. Тем самым нагрузка остается изолированной до прихода основного им-
пульса, амплитуда которого достаточна для пробоя этих разрядников. После это-
го импульс распространяется через вторую половину линии передачи и поступает
через вакуумную перегородку в нагрузку.
8.1.2. Ускоритель частиц PBFA 2 и Z-машина
В настоящее время крупнейшим в мире генератором одиночных импульсов
является Z-машина [Spielman et al., 1997], расположенная в национальной лабора-
тории «Сандия» (Sandia National Laboratories in Albuquerque) в Альбукерке, США.
Эта установка первоначально была сконструирована как ускоритель частиц
222 Глава 8. Примеры генераторов мощных импульсов
PBFA2 (Рис. 8.2) для экспериментов в области ядерного синтеза [Turman et al.,
1985]. PBFA 2 состоит из 36 генераторных модулей, каждый с мощностью, вдвое
большей, чем у генератора KALIF. Генераторные модули соединены по 9 штук па-
раллельно, а получившиеся 4 сборки соединены последовательно. Каждый из 36
двухполярных генераторов Маркса содержит 60 конденсаторов емкостью
1.35 мкФ, которые могут быть заряжены до ±100 кВ. В целом запасаемая в генера-
торах Маркса энергия составляет 14.4 МДж. С выхода генераторов Маркса энер-
гия передается в промежуточные накопители энергии, представляющие собой
конденсаторы с водяным диэлектриком. Эти конденсаторы соединены с линиями
формирования импульсов через управляемые лазером газовые разрядники.
Вследствие того что нестабильность времени включения при таком управлении
составляет менее 1 нс, стало возможным достичь высокой точности управления
всеми генераторными модулями. После зажигания разряда импульс сжимается во
времени с помощью трех линий формирования импульсов (Рис. 8.3). Линия пере-
дачи содержит переход от коаксиальной к планарной геометрии. При этом коак-
сиальная линия с импедансом 2.15 Ом расщепляется на две линии с импедансом
4.3 Ома, и в одной из этих линий положительный и отрицательный проводники
меняются местами с помощью их скручивания. Линии передачи выполнены с воз-
растающим импедансом, так что коэффициент трансформации напряжения со-
ставляет 2.8. И наконец, девять модулей соединялись в параллель, а четыре эти
сборки соединялись последовательно. Таким образом, на выходе генератора полу-
чается импульс амплитудой 14 МВ, мощностью 100 ТВт и длительностью 30 нс.
Этот импульс использовался для создания мощного потока ионов.
Около 1995 г. установка PBFA 2 была реконструирована в драйвер зет-пинча1^
(Z pinch driver). Как и в PBFA 2, в Z-машине (Рис. 8.4) в 36 генераторах Маркса
Рис. 8.2. Многомодульный генератор PBFA 2
° Зет-пинч — сжатый магнитным полем плазменный шнур, образующийся при пропускании
импульса тока в керамической трубе с разряженным газом. — Примеч. пер.
8.1. Генераторы одиночных импульсов 223
Вакуумная
перегородка
Линия Линия Линия
Промежуточный формирования формирования формирования
накопитель импульсов 1 импульсов 2 импульсов 3
Область скрутки
К нагрузке
Т рансформаторная
линия передачи
Газоразрядный
ключ
Рис. 8.3. Цепи формирования импульса в одном модуле установки PBFA 2.
Рис. 8.4. Z-машина (ускоритель элементарных частиц).
накапливается 12 МДж электрической энергии. Затем эта энергия за 1 мкс посту-
пает в коаксиальный промежуточный накопитель с водяной изоляцией. Напря-
жение в промежуточном накопителе достигает 5 МВ. Газовый разрядник с лазер-
ным управлением используется для передачи энергии во второй промежуточный
накопитель за 200 нс. Водяной ключ с самопробоем используется для передачи
энергии в двухпроводную линию с водяным диэлектриком, имеющую постоян-
ный импеданс 4.32 Ом. Амплитуда напряжения в этой точке равна 2.5 МВ, а дли-
тельность импульса напряжения на уровне половины его амплитуды составляла
105 нс. Общая энергия импульса в этой точке ускорителя равна 60 ТВт. Затем
энергия поступает в вакуумную секцию ускорителя. Здесь она проходит через че-
тыре конически сужающихся линии передачи с магнитной самоизоляцией к на-
грузке. Для сложения токов из всех четырех источников используются двойные
скрутки, показанные на Рис. 8.5.
Нагрузка для Z-машины представляет собой цилиндрические проволочные
клетки диаметром и высотой 20 мм. Каждая клетка содержит несколько сот про-
волок диаметром 5...10мкм. При протекании через них импульса тока в 20 МА
они превращаются в плазму, которая под воздействием азимутального магнитно-
224 Глава 8. Примеры генераторов мощных импульсов
круткЬ
Рис. 8.5. Двойные скрутки на выходе Z-машины.
Проволочная
клетка
го поля ускоряется в радиальном направлении. При торможении в области цент-
ральной оси кинетическая энергия плазмы преобразуется в сильный импульс
мягкого рентгеновского излучения. При этом достигается энергия излучения до
2 МДж, а мощность — несколько сот тераватт. В связи с тем что энергия рентге-
новского излучения увеличивается пропорционально квадрату тока, планируется
увеличение выходного тока Z-машины до 27 МА. Рентгеновское излучение пос-
тупает далее в полость со стенками с радиационным равновесием для получения
его равномерного распределения, требуемого для ядерного синтеза с инерцион-
ным удержанием плазмы (см. гл. 11).
8.1.3. ГЕРМЕС III
ГЕРМЕС III (HERMES III) (Рис. 8.6) является генератором импульсов ампли-
тудой 20 МВ, мощностью 16 ТВт и длительностью 40 нс [Ramirez et al., 1988]. В
нем применяется метод суммирования напряжения с магнитной изоляцией, опи-
санный в гл. 7. Каждый из десяти генераторов Маркса используется для заряда
двух коаксиальных конденсаторов в промежуточных накопителях энергии, каж-
дый из которых, в свою очередь, питает четыре линии формирования импульсов
Каждая из полостей, заполненная ферромагнитным сердечником (из материала
«метглас»), соединена с четырьмя линиями формирования импульсов амплиту-
дой 1 МВ. Полости соединены последовательно для сложения амплитуд импуль-
сов. Суммарный импульс распространяется через вакуумную линию с магнитной
самоизоляцией. Основное назначение этого генератора — создание импульсов
мощного рентгеновского излучения для моделирования воздействия оружия
8.2. Генераторы повторяющихся импульсов 225
Рис. 8.6. Генератор импульсов напряжением 20 МВ ГЕРМЕС III
8.2. Генераторы повторяющихся импульсов
В большинстве промышленных применений требуются генераторы импуль-
сов с частотой следования порядка единиц герц, чья конструкция обеспечивает
долговечность для выработки 108...109 импульсов. Для выполнения этих требова-
ний надо либо строго ограничивать мощность переключаемой энергии, либо от-
казываться от газоразрядных ключей в пользу неизнашиваемых полупроводнико-
вых или магнитных коммутационных приборов. Кроме того, накопительные кон-
денсаторы в генераторах повторяющихся импульсов приходится использовать в
режимах, намного облегченных по сравнению с максимально допустимыми, и
следить за отсутствием переполюсовки напряжения на них.
8.2.1. Генератор повторяющихся импульсов большой
мощности RHEPP
В своей последней версии генератор повторяющихся импульсов большой
мощности RHEPP (Repetitive High Energy Pulsed Power) может работать co сред-
ней мощностью 350 кВт при амплитуде импульсов на выходе 2.5 МВ, длительнос-
тью импульсов 60 нс и энергии одиночного импульса 3 кДж при частоте следова-
ния 120 Гц [Harjes et al., 1991]. В этой установке применены только магнитные за-
мыкающие ключи. Работа первых секций генератора основана на принципе
магнитной компрессии импульсов, а затем используется сложение амплитуд с по-
мощью магнитных полостей.
226 Глава 8. Примеры генераторов мощных импульсов
Блок питания представляет собой преобразователь мощностью 600 кВт, с вы-
ходным напряжением 3.2 кВ и током 210 А на частоте 120 Гц На Рис. 8.7 пред-
ставлена эквивалентная схема секции компрессии импульсов.
Рис. 8.7. Эквивалентная схема секции компрессии импульсов генератора RHEPP.
Резонансная частота первой £С-цепи равна частоте, вырабатываемой блоком
питания. Из-за резонанса конденсатор Q заряжается до напряжения 15 кВ. Когда
первый магнитный ключ входит в насыщение, импульс напряжения 15 кВ поступа-
ет на следующий каскад компрессии. Трансформатор увеличивает амплитуду им-
пульса напряжения до 270 кВ. На выходе пятого каскада компрессии получается
импульс с формой (1—coscot), со временем нарастания 1.2 мкс и амплитудой
250 кВ, который поступает на вход линии формирования. Из-за большой средней
мощности для охлаждения ферромагнитных сердечников приходится использо-
вать воду. Вес этих сердечников составляет 750 кг для первого и 400 кг для послед-
него ключа. Для увеличения амплитуды используется 10-каскадный сумматор с
магнитной изоляцией. В отличие от генератора HERMES III импульсы складыва-
ются в коаксиальной линии с масляной изоляцией. Установка могла бы быть более
компактной при использовании вакуумной линии с магнитной самоизоляцией, но
при этом из-за возможности образования плазмы надежность была бы хуже. На вы-
ходе сумматора получаются импульсы амплитудой 2.5 МВ и мощностью 0.2 ТВт.
8.2.2. Генераторы с размыкающими ключами
В этих генераторах используется сравнительно низкое напряжение во всех
каскадах, кроме выходного, в котором осуществляется умножение с помощью
полупроводниковых размыкающих ключей (SOS). Эти генераторы, хотя в них и
не используются индуктивные накопители энергии, оказываются более компакт-
ными, чем обычные генераторы с замыкающими ключами. На Рис. 8.8 приведена
схема генератора с полупроводниковыми размыкающими ключами [Rukin et al.,
1996]. Этот генератор способен вырабатывать импульсы амплитудой 1 МВ с им-
пульсной энергией 8 ГВт при длительности импульсов 50...60 нс и частоте следо-
вания 150 Гц. Средняя мощность равна 75 кВт. Установка состоит из накопитель-
ного блока с тиристорным управлением, промежуточного каскада с трансформа-
8.2. Генераторы повторяющихся импульсов 227
8 нФ
Промежуточный
каскад
Воздух
Накопительный
блок
С1
Масло
С3
8 нФ
С3
мк_
Высоковольтный
выходной каскад
Полупроводниковый
Рис. 8.8. Упрощенная схема генератора повторяющихся импульсов
с выходным напряжением 1 МВ, где МК — магнитный ключ.
тором и компрессором длительности импульсов и высоковольтного выходного
каскада с трансформатором и компрессором длительности импульсов.
Первый конденсатор С1 заряжается до 900 В за время 5 мс от источника пита-
ния. После включения тиристорного ключа энергия из конденсатора С\ передает-
ся за 100 мкс через трансформатор Т\ в конденсатор С2. При этом конденсатор С2
заряжается до 16 кВ. Ток разряда верхнего конденсатора С2 инвертирует намагни-
ченность сердечников магнитного ключа МК\ и трансформатора 7\.
После насыщения МКХ полярность напряжения на нижнем конденсаторе С2
инвертируется. Это приводит к росту напряжения на ключе МК\ до 30 кВ за
25 мкс. Затем ключ МКХ замыкается и энергия за 8 мкс передается из конденсато-
ра С2 в конденсатор С3. При этом трансформатор Т2 увеличивает напряжение до
240 кВ.
228 Глава 8. Примеры генераторов мощных импульсов
Ток разряда правого конденсатора С3 протекает через обмотку ключей МК+ и
МК_, инвертируя намагниченность их сердечников. После насыщения сердечни-
ка трансформатора Г2 полярность напряжения на левом конденсаторе С3 также
инвертируется, а напряжение на магнитном ключе МК+ возрастает за 2.5 мкс до
430 кВ. После замыкания ключа МК+ начинает течь ток через полупроводнико-
вые ключи и заряжается конденсатор С4. Амплитуда тока заряда достигает 3 кА за
0.7 мкс. Когда ключ МК_ открывается, направление протекания тока меняется на
противоположное, прекращается протекание тока через полупроводниковые
ключи, а на нагрузке R\ развивается импульс выходного напряжения1 \
° По-видимому, автор забыл упомянуть о роли индуктивности Lp, на которой-то и выделяется
импульс напряжения при размыкании полупроводниковых ключей. — Примеч. пер.
ГЛАВА
СРЕДСТВА ИЗМЕРЕНИЙ
Измерение параметров быстро изменяющихся электромагнитных полей важ-
но как для систем генерации импульсов большой мощности, так и для испытаний
высоковольтного оборудования. Основными физическими величинами при этом
всегда являются напряженность электрического поля Е и индукция магнитного
поля В, из которых могут быть выведены напряжение и ток.
Датчики, подходящие для этих измерений, не должны искажать измеряемое
поле. Это требование в основном выполняется при использовании емкостных и
индуктивных датчиков. Кроме того, этому требованию могут отвечать электрооп-
тические методы. Применение обычных резистивных делителей напряжения, ко-
торые часто создают «слабое звено» в высоковольтной изоляции, является дис-
куссионным вопросом.
9.1. Датчики электромагнитного поля
Быстрые изменения электромагнитных полей наводят токи и напряжения в
проводниках датчика. Здесь мы будем обсуждать только электрически короткие
датчики, чьи размеры малы по сравнению с расстояниями, на которых меняется
поле. Для импульса с временем нарастания тг и скоростью распространения с это
означает, что d « стг, где d — протяженность датчика в направлении распростра-
нения волны. Различают два основных типа датчиков: электрический и магнит-
ный диполь (Рис. 9.1).
Быстрое изменение электрического поля создает ток смещения с плотностью
]d = dD/dt в дополнение к току проводимости с плотностью jc — aE. Полный
ток, протекающий через площадь А, определяется как интеграл плотности этих
токов по этой площади:
1(0= jl(t)dA + f^-dA.
J J nt
A A
(9.1)
230 Глава 9. Средства измерений
Квазистационарное поле1)
Рис. 9.1. Основные типы датчиков: электрический и магнитный диполь
B(t)
00000000
00000000
В случае идеального проводящего датчика площадью А, расположенного на
изолирующем основании, выражение (9.1) может быть упрощено:
i(0 = [/c(')+i>(0]4
1(О = [а£'(О+ее0Е(»)]л.
(9.2)
Таким образом, ток, протекающий через цепь датчика, определяется электри-
ческим полем E(t), площадью датчика А, проводимостью объема, находящегося
над датчиком с, и диэлектрической проницаемостью этого объема е. Приведен-
ные выше уравнения описывают не только связь между напряженностью измеря-
емого поля и током в датчике, но и нежелательную связь между посторонними
полями и проводниками в кабеле датчика при недостаточном его экранировании.
Переменное магнитное поле, обычно связанное с электромагнитной волной,
индуцирует ток в проводящей петле. Для петли площадью А, помещенной в поле
с индукцией В, получается напряжение (9.3):
u(t) = ji(t)dA.
(9.3)
Если распределение поля однородно, то в случае, когда поле перпендикулярно
петле, это выражение упрощается:
u(t)=B(t)A.
(9.4)
Как и для датчика электрического поля, это выражение описывает не только
связь между индукцией измеряемого поля и напряжением в датчике, но и неже-
лательную связь между посторонними полями и паразитными петлями в измери-
тельной схеме. Существуют конструкции датчиков, в которых полезный сигнал
отделяется от помех.
Квазистационарное поле в данном контексте — поле изменяющееся во времени со скоростью,
удовлетворяющей условию d « схТ. — Примеч. пер.
9.1. Датчики электромагнитного поля 231
9.1.1. Емкостные датчики
Для квазистационарных полей датчик напряженности (еще называемый ем-
костным датчиком) может быть описан с помощью эквивалентной схемы, вклю-
чающей источник тока или напряжения и импеданс нагрузки. В большинстве
случаев импеданс нагрузки емкостного датчика включает емкостную компоненту
(паразитная емкость между активной частью датчика и опорной поверхностью, а
также емкость сигнального кабеля) и омическую компоненту (сопротивление
сигнального кабеля, входное сопротивление измерительного устройства и т. д.),
как это показано на Рис. 9.2.
Рис. 9.2. Эквивалентная схема нагруженного емкостного датчика.
Большинство линий формирования импульсов заполнено диэлектриком, и
можно предположить, что ст = 0. В этом случае дифференциальное уравнение и
его решение для эквивалентной схемы будут
«(О+= еео 4
i\L с
w(0 = e4/RC |^^£(Г )е'/ЛС dt',
о
(9.5)
«(/) =
ее0Л
~С~
-t-t'/вс dt'
RC
=^[E(0-«k(0],
(9.6)
где wk(0 — корректирующий член, который становится пренебрежимо мал при
RC »t, а Ет— максимальная импульсная напряженность поля. Если мы хотим
вывести значение напряжения по результатам измерения напряженности поля в
локальной области, то необходимо знать связь между E(t) и U(t). Например, для
232 Глава 9. Средства измерений
коаксиальной цилиндрической линии с наружным радиусом га и внутренним в
случае чистой волны типа ТЕМ00 мы имеем
£(/) =
U(t)
''alnra/<
(9 7)
И наконец, мы получаем
ц(0 =
• U(t).
Сга1пгаД
(9.8)
Такой же результат получается, если мы рассмотрим емкостный датчик встро-
енным в линию так, что получается емкостный делитель (Рис. 9.3):
ицу.
(9.9)
w(0 =
Сн
сн+сЕ
Рис. 9.3. Схема включения емкостного и магнитного датчиков в линию передачи.
В выражении (9.9) Сн — емкость между активной зоной датчика и противопо-
ложным (высоковольтным) электродом, а СЕ — емкость между датчиком и зем-
лей. Для цилиндрической геометрии
н ralnra/r
(9.Ю)
Кроме того, предполагается, что Сн « СЕ.
9.1. Датчики электромагнитного поля 233
9.1.2. Индуктивные датчики
В магнитном поле в соответствии с законом Фарадея на петлю из проводника
наводится напряжение
и(0= =
(9.11)
Чтобы определить индукцию, необходимо токовую петлю дополнить интег-
рирующим звеном. Эквивалентная схема этой цепи приведена на Рис. 9.4. В ней
используется простейший АС-интегратор.
Рис. 9.4. Эквивалентная схема индуктивного датчика с RC-интегратором.
На Рис. 9.4 L — индуктивность петли, a R и С — сопротивление и емкость эле-
ментов интегратора соответственно. Выходной сигнал определяется выражением
«(/) =
dt
= L— + Ri+— 17 dt*.
dt Cl
(9.12)
При R » La, где co — наибольшая из значимых частот в спектре импульса, кото-
рый требуется измерить, мы получаем
м(0 = — = RI+— 17 dt'.
dt Cl
(9.13)
Ограничивая время измерения значениями t« RC, мы получаем конечное выра-
жение для измеряемого сигнала ws(Z):
«(0 = А/(/),
ws(O = -p^ = -
о б
^&Чсф(‘НсВ(,)Л (914)
234 Глава 9. Средства измерений
Как и в случае измерения напряженности электрического поля, результат из-
мерения магнитной индукции может быть соотнесен с импульсным током, если
известна геометрия системы и присутствует только волна типа ТЕМ00. В этом
случае
(?(t) = KNI(t), (9.15)
где N — число витков в обмотке индуктивной петли. В общем случае рассчитать
коэффициент пропорциональности К с приемлемой точностью можно, только
если известны распределение тока и взаимное расположение направления маг-
нитного поля и плоскости петли. По этой причине необходимо всегда проводить
калибровку индуктивного датчика в месте его расположения.
Если распределение плотности тока в линии не известно, или если невозмож-
но провести калибровку индуктивного датчика в месте его расположения, взамен
простой токовой петли можно применить катушку Роговского. Катушка Роговс-
кого [Rogowski and Steinhaus, 1912] состоит из множества витков провода, намо-*
тайных на тороидальную образующую, через центр которой проходит проводник
с измеряемым током (Рис. 9.5). В соответствии с законом Ампера между током в
катушке Роговского и магнитной индукцией вдоль оси тора имеет место следую-
щее соотношение:
= — LB(t)ds =— £д(0*,со8(л„ Д), (9.16)
Но Mo /=1
где 5/ — среднее расстояние между двумя обмотками, a cos (iu, Bi) — косинус угла
между перпендикуляром к плоскости обмотки и направлением силовых линий
поля.
Рис. 9.5. Катушка Роговского.
9.1. Датчики электромагнитного поля 235
С другой стороны, пренебрегая пространственной зависимостью магнитной ин-
дукции через площадь А, одиночного витка тороидальной катушки, мы получим следу-
ющее выражение для напряжения, индуцируемого на выводах катушки Роговского:
u(f)= JB(0<M = £A(04cos(H/, Д). (9.17)
1=1
Предполагая, во-первых, что площадь всех витков катушки Роговского оди-
наковая, т. е. А, = А, а во-вторых, что число витков в ней на единицу длины посто-
янно, т. е. Sj = s, мы можем получить соотношение между индуцируемым напря-
жением м(0 и током /(/), протекающим через центральный проводник:
и(Г) = -И„/(О-
5
(9.18)
Как и с простой петлей, для получения напряжения, пропорционального то-
ку, можно использовать интегрирующую АС-цепь (Рис. 9.4). В этом случае необ-
ходимо также соблюдать условие R » La>, которое из-за большего значения £,
сложнее обеспечить на высоких частотах. По этой причине иногда стараются вы-
полнить противоположное условие для катушки Роговского. Если сумма внут-
реннего г и внешнего R сопротивлений мала по сравнению с и если
R « 1/соС, из (9.12) мы получаем для цепи датчика:
dy/dt & L di/dt,
/=Ф = РоЛМ/Л =_/_
L \lqN2A/s N'
us(t) = IR = RI/N.
(9.19)
(9.20)
(9.21)
Таким образом, при выполнении упомянутых условий выходной сигнал ка-
тушки Роговского пропорционален току в измеряемой цепи, т. е. ее можно рас-
сматривать как трансформатор. Очевидно, что нижняя из измеряемых частот
должна удовлетворять условию г + R « Lai Верхняя частотная граница определя-
ется резонансной частотой самой катушки Роговского (ее L и С). Длина волны
нижней частотной границы соответствует длине проволоки, которой обмотана
катушка. Расширение частотного диапазона в область более низких частот может
быть достигнуто путем введения внутрь тора ферромагнитного материала. Конеч-
но, эта мера влияет и на верхнюю частотную границу. Следует отметить, что всег-
да существует риск насыщения ферромагнитного сердечника.
Для исключения влияния витка, создаваемого самой катушкой, ее конец воз-
вращают к началу, прокладывая вдоль окружности тороида (Рис. 9.6). В связи с
тем что выходное напряжение обычно мало, как правило, катушку экранируют от
электрических помех. Экран при этом не должен образовывать короткозамкнуто-
го витка. Выводы катушки должны быть также экранированы, причем один из
выводов должен быть соединен с экраном и заземлен. Однако под воздействием
мощных, быстро изменяющихся электромагнитных полей на зазорах экрана и да-
же его поверхности может возникать искрение, приводящее к появлению ложных
сигналов.
236 Глава 9. Средства измерений
Рис. 9.6. Катушка Роговского с компенсационным витком.
При скорости нарастания импульса тока, меньшей, чем время отклика датчика,
модель катушки Роговского как цепи с сосредоточенными параметрами следует за-
менить на модель длинной линии [Kiichler and Schwab, 1987]. В этом случае напряже-
ние, индуцируемое в разных участках обмотки, достигает измерительного звена с
разными задержками времени, что искажает форму импульса. Хотя еще остается воз-
можным воспроизвести короткое время нарастания тока, если нагрузить катушку
Роговского на импеданс Z» Zo, где Zq = (L/C),/2 — импеданс катушки Роговского,
но измерять импульсы с длительностью меньше времени распространения сигнала
через катушку уже нельзя. Однако главным ограничением на применимость самоин-
тегрирующей катушки Роговского является неоднородное возбуждение отдельных
витков в катушке. Это приводит к возникновению сильных осцилляций, наложен-
ных на выходной сигнал. Так что утверждение, что выходной сигнал катушки Рогов-
ского не зависит от распределения плотности тока внутри тора, не совсем верно.
9.2. Измерение тока с помощью резисторов
Проблемы, возникающие при использовании датчиков электрического и маг-
нитного полей, могут быть преодолены при использовании резисторов (шунтов).
Использование шунтов основано на измерении падения напряжения на встроен-
ном в цепь резисторе с известным сопротивлением. Как правило, путь прохожде-
ния измеряемого тока и измерительная схема связаны не только омически, но и
через магнитное поле. При этом падение напряжения на шунте уже не пропорци-
онально измеряемому току. Для устранения или по крайней мере существенного
уменьшения магнитной связи применяется цилиндрическая симметричная конс-
трукция шунта, показанная на Рис. 9.7 [Schwab, 1981].
9.2. Измерение тока с помощью резисторов 237
Рис. 9.7. Цилиндрическая симметричная конструкция шунта,
обеспечивающая отсутствие поля в зоне размещения измерительных контактов.
Прохождение магнитного поля через материалы является главным ограниче-
нием на частотный диапазон шунтов. Аналитическое выражение для описания
проникновения магнитного поля в полый цилиндр очень громоздко [Knoepfel,
1970]. Однако в предположении, что толщина стенки цилиндра d мала по сравне-
нию с его внешним радиусом га, отклик на скачок тока амплитудой /0 может быть
аппроксимирован выражением [Malewski, 1968]
(9.22)
где U(f) — падение напряжения, измеряемое между измерительными контактами,
U* — максимальное падение напряжения:
= (9.23)
2nraJ
где f. — расстояние между контактами,
р — удельное сопротивление материала.
Характеристическое время Г* связано с временем нарастания напряжения т от
10 до 90% соотношением т = 0.25f* и дается выражением
Р
(9.24)
На Рис. 9.8 представлена конструкция шунта, позволяющего измерять ток в
коаксиальной линии передачи. Она особенно подходит для применения с ваку-
умными линиями, где электронная эмиссия и образование проводящей плазмы
являются обычным делом, а сигналы с выхода катушки Роговского сильно иска-
жаются. Шунт состоит из глубокой выемки в стенке внешнего проводника ли-
нии, которая заполняется диэлектриком (эпоксидной композицией) и покрыва-
238 Глава 9. Средства измерений
ется тонким слоем металлической фольги, которую сваривают с внутренней по-
верхностью внешнего проводника. Два контакта для измерения падения
напряжения плотно прижимаются к обратной стороне фольги.
Конструкция шунта, показанная на Рис. 9.8, может рассматриваться как па-
раллельно соединенные резистор Rf (фольга) и индуктивность £g, чье значение
определяется глубиной выемки. Сигнал, пропорциональный току, получается
только для интервалов времени короче, чем xd = L^/Rf, и длиннее, чем т = 0.25/*.
Значение xd легко достигает нескольких микросекунд, так как сопротивление
фольги составляет обычно около 10-3 Ом, а индуктивность, при подходящей глу-
бине выемки, — более 10-9 Гн. Еще одним источником погрешностей является
воздействие магнитного поля на области между измерительными контактами и
фольгой. По этой причине их необходимо делать как можно меньше размерами.
Нагрев фольги приводит к изменению ее сопротивления, что в свою очередь при-
водит к погрешностям измерений.
Рис. 9.8. Конструкция шунта для измерения тока
во внешнем проводнике коаксиальной линии передачи
9.3. Измерение тока с использованием эффекта
Фарадея
Эффект Фарадея — поворот плоскости поляризации линейно-поляризован-
ного света, проходящего через вещество при наличии магнитного поля, парал-
лельного направлению распространения света. Световые волны с правой и левой
круговой поляризацией получают различные коэффициенты преломления под
воздействием магнитного поля. По этой причине плоскость поляризации пово-
рачивается на угол, пропорциональный интегралу магнитного поля И вдоль све-
тового пути £. Конечно, это обстоятельство приводит к тому, что результат зави-
сит от распределения тока, создающего магнитное поле, относительно положе-
ния светового луча. Дилемма подобна той, что и у магнитного датчика тока.
9.3. Измерение тока с использованием эффекта Фарадея 239
Поэтому и разрешить ее можно тем же способом, используя схему, эквивалент-
ную катушке Роговского, т. е. путем создания кругового пути прохождения света,
что делает угол поворота плоскости поляризации независимым от распределения
тока. Для замкнутого светового пути можно записать
Q = V^Hdl. (9.25)
Используя закон Ампера, мы можем заменить контурный интеграл на I, где
I— полный ток внутри контура интегрирования. К здесь является коэффициен-
том пропорциональности, известным как постоянная Верде. Для каждого вещест-
ва постоянная Верде зависит от длины волны света и температуры. Для плавлено-
го кварца, при длине световой волны 633 нм, эта постоянная равна 4.1 рад/МА.
Таким образом, угол поворота плоскости поляризации 0 получается равным
0=И/. (9.26)
Проще всего сделать датчик тока на эффекте Фарадея с помощью оптическо-
го волокна. Так как состояние плоскости поляризации в отсутствие магнитного
поля должно сохраняться, для этой цели подходит только одномодовое волокно,
поддерживающее плоскость поляризации постоянной. Для увеличения чувстви-
тельности датчика волокно может быть обернуто вокруг токонесущего проводни-
ка несколько раз. Наиболее подходящим источником света является лазер с ли-
нейной поляризацией луча.
Главные проблемы появляются из-за двойного лучепреломления в оптово-
локне. Особенно неприятно, когда двойное лучепреломление возникает во вре-
мя прохождения измеряемого импульса тока, а оптоволокно испытывает меха-
нические нагрузки в чувствительной зоне датчика. Линейное двойное лучепре-
ломление возникает также при изгибе волокна. Эффект в этом случае
пропорционален (r/R)2, где г — радиус волокна, a R— радиус его изгиба. Скру-
чивание волокна в зоне чувствительности датчика в направлении вращения по-
ляризации Фарадея было использовано некоторыми экспериментаторами и да-
ло существенное уменьшение эффекта линейного двойного лучепреломления
[Stokes et а!., 1995].
Структурная схема системы измерения тока на эффекте Фарадея приведена
на Рис. 9.9. В этой системе используется лазерный диод с длиной волны излуче-
ния 830 нм и выходной мощностью 12 мВт. Он соединен с одномодовым оптово-
локном, поддерживающим постоянную плоскость поляризации света. Оптово-
локно скручено в зоне чувствительности датчика примерно на 40 оборотов на
метр в направлении вращения поляризации Фарадея. Это значительно уменьша-
ет эффект двойного лучепреломления из-за изгиба волокна в петле. Анализатор
состоит из линзы, полуволновой пластины, неполяризующей светоделительной
призмы стеклянных поляризаторов и выходных линз. Поляризаторы установле-
ны ортогонально друг другу, с тем чтобы получить квадратурные сигналы на обо-
их выходах. Оптоволокно помещено в пластиковую оболочку, защищающую его
от сдавливания и ударов.
240 Глава 9. Средства измерений
Токочувствительные
петли
Рис. 9.9. Структурная схема системы измерения тока на эффекте Фарадея.
В зависимости от того, является ли значение 0 при пиковых токах много боль-
ше или много меньше п, могут быть использованы два различных метода обра-
ботки сигналов с выходов анализатора. Если значение ©мах мало, мы используем
сумму и разность сигналов с обоих выходов:
Sj = So COS2 (6 — л/4),
S2 ~ So cos2 (0 + л/4),
5 = (Si - S2)/(S! + S2) = sin (20),
или, для 0 « л, используя (9.26),
5 =kl,
(9.27)
(9.28)
где к — коэффициент пропорциональности. Конечно, точность этих расчетов за-
висит от отношения сигнал—шум в системе и от максимального значения 0.
Если значение ©мах велико по сравнению с л, достаточно обработать один из
сигналов. Если анализатор установлен перпендикулярно первоначальному на-
правлению поляризации, сигнал получается равным
(9.29)
Чтобы получить значение /(Z), сигнал следует инвертировать цифровым спо-
собом.
Основным достоинством датчика тока на эффекте Фарадея является его ус-
тойчивость к электрическим помехам.
9.4. Электрооптические способы измерения
напряженности электрических полей
Измерения напряженности электрического поля могут быть основаны на эф-
фекте двойного лучепреломления в кристаллах или жидкостях или на изменении
коэффициентов преломления в кристаллах, когда двойное лучепреломление уже
существует при нулевом электрическом поле. Сдвиг фаз между обыкновенным и
9.4. Электрооптические способы измерения напряженности электрических полей 241
необыкновенным лучами, проходящими через датчик электрического поля, оп-
ределяется выражением
е = ^(ло(Е)-Иео(£)). (9.30)
Л
Здесь предполагается, что однородное электрическое поле приложено на всей
длине датчика Как было рассмотрено в разд. 9.3, эти фазовые сдвиги приводят
к повороту плоскости поляризации света, и может быть использована такая же
обработка сигнала [Duvillaret et al., 2002; Santos et al., 2000].
Д n = nQ — neo может зависеть от напряженности электрического поля как по
линейному, так и по квадратичному закону. Первый случай известен как эффект
Поккелъса (линейный электрооптический эффект), а второй — как эффект Керра,
или квадратичный электрооптический эффект.
Эффект Поккельса проявляется только в кристаллах, не имеющих центров
симметрии. Среди них наиболее часто используются дигидрофосфат аммония
(ADP) и дидейтерийфосфат калия (KD*P). Датчик элемента Поккельса обычно
состоит из соответствующего кристалла, оптическая ось которого расположена
параллельно лучу света и направлению электрического поля (Рис. 9.10). Поляри-
зованный луч лазера проходит сквозь кристалл и попадает на анализатор, чья
плоскость поляризации совпадает с плоскостью поляризации света в отсутствие
электрического поля1).
Рис. 9.10. Электрооптический датчик для измерения напряженности электрического поля.
11 По-видимому, опечатка. Должно быть «чья плоскость поляризации перпендикулярна плоскости
поляризации света в отсутствие электрического поля». — Примеч. пер.
242 Глава 9. Средства измерений
Характерная величина — это напряжение половины волны = -Сх/гЛ соот-
ветствующее фазовому сдвигу л; / — длина кристалла. С этими определениями
фазовый сдвиг 0 может быть записан как
Ef
Q = (9 31)
Типичные значения ИХ/2 при для Л = 546.1 нм равны 9.2 кВ для ADP и 3.4 кВ
для KD’P.
Время отклика кристалла весьма мало, что позволяет осуществлять измере-
ния с наносекундным разрешением.
В то время как эффект Поккельса существует только в твердых кристаллах,
эффект Керра может проявляться и в жидкостях, и в кристаллах. В жидкостях это
явление связано с частичным выравниванием анизотропных молекул в электри-
ческом поле. Таким образом, оказывается возможным устанавливать датчик в вы-
соковольтной системе, используя жидкость в качестве диэлектрической изолиру-
ющей среды без внесения сильных искажений в распределение электрического
поля. Это особенно полезно в импульсных системах большой мощности, в кото-
рых в качестве диэлектрика применяется вода. Недостатком, однако, является то,
что угол поворота плоскости поляризации вследствие эффекта Керра пропорцио-
нален квадрату напряженности электрического поля:
9 = 2пК£Е2, (9.32)
где К— постоянная Керра, которая, например, для воды составляет 5.1 х 10-14м/В2
при X — 589 нм. Вследствие квадратичной зависимости 0 от Е особенно выгодно
использовать при малых сигналах разностный сигнал так, как это описано в
разд. 9.3 и ясно представлено в формулах (9.27). При использовании такой схемы
обработки сигналов выходной сигнал оказывается пропорционален Е2.
9.5. Магнитный анализатор энергии ионов
Измерения напряжения в вакууме также могут быть выполнены путем опре-
деления энергии заряженных частиц, которые ускорились под воздействием раз-
ности потенциалов. Принцип действия магнитного анализатора энергии частиц
показан на Рис. 9.11. Анализатор состоит из коллиматора, круглого постоянного
магнита и набора детекторов частиц. Заряженные частицы поступают в область
магнитного поля в форме хорошо коллимированного луча и отклоняются от пря-
молинейного движения этим полем. После того как они покинут область магнит-
ного поля, они летят прямолинейно к набору детекторов. Разрешающая способ-
ность устройства по энергиям определяется степенью коллимации, размером
магнита и его силой, геометрическим расположением детекторов относительно
магнита и площадью их чувствительных окон. Подходящий набор детекторов для
этих целей может состоять из матрицы p-z-л-диодов с маленькой площадью, так
что каждый детектор соответствует маленькому интервалу энергии. Для одиноч-
9.6. Монитор напряжения 243
ных частиц угол отклонения 0 связан с их кинетической энергией и, таким об-
разом, с ускоряющим напряжением, следующим уравнением:
n n . R . ZeRB
Р = 2arctg— = 2arctg-j—
(9.33)
где р — радиус кривизны пути частиц, имеющих заряд Ze и массу т в магнитном
поле с индукцией B’,R — радиус магнита.
Если достаточно большое число ионов достигает детекторов, становится воз-
можно определить форму импульса напряжения с приемлемой точностью.
Рис. 9.11. Схема установки для измерения импульсных напряжений
с использованием анализатора энергии частиц по их отклонению магнитным полем
9.6. Монитор напряжения
Еще одним инструментом для измерения высоковольтного импульсного на-
пряжения в вакууме является специальный резистивный делитель. Так как при
очень высоком напряжении в системе всегда будут присутствовать свободные
электроны, конструкция делителя напряжения должна гарантировать, что на его
поверхности не разовьется лавинный пробой. Пример такой конструкции пока-
зан на Рис. 9.12. Она была разработана для измерений импульсов напряжения ам-
плитудой до 2.5 МВ со временем нарастания менее 2.5 нс. Общая длина составля-
ет 54 см, а внешний диаметр 15 см. Делитель имеет две секции. Первичная секция
включает в себя колонну, заполненную раствором тиосульфата натрия, имеющего
сопротивление 200 Ом. Коэффициент деления в первичной секции, равный 88:1.
достигнут помещением алюминиевого кольца, служащего выходом делителя, на
расстоянии нескольких миллиметров от электрода заземления. Резистор во вто-
ричной секции, подключенный к выходу делителя первичной секции, имеет но-
минал 5000 Ом. Когда к выходу делителя подключен осциллограф с входным со-
противлением 50 Ом, получается коэффициент деления второй секции, равный
100:1. Общий коэффициент деления получается 8800:1.
244 Глава 9. Средства измерений
Основание
Вывод делителя
напряжения
первой секции
Изолятор
для положительного
измеряемого
напряжения
Кольца
для выравнивания
градиента
Высоковольтный
электрод
Вывод делителя
напряжения
второй секции
Колонна
с раствором
тиосульфата натрия
Изолятор
для отрицательного
измеряемого
напряжения
Электрод
делителя напряжения
первой секции
Рис. 9.12. Конструкция делителя напряжения мегавольтного уровня,
предназначенного для использования в вакууме
Для исключения искрения на поверхности делителя его корпус снаружи за-
крыт набором изоляционных конусов, разделенных алюминиевыми кольцами,
уравнивающими градиент напряженности поля вдоль корпуса делителя. В качес-
тве изоляционного материала используется акрил. При положительной поляр-
ности измеряемого напряжения изоляционные конуса устанавливаются широ-
ким основанием к земле, а при отрицательной полярности — наоборот, узким ос-
нованием к земле.
ГЛАВА
ПРИМЕНЕНИЕ ИМПУЛЬСНЫХ
ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
В этой главе будут представлены примеры применения электрических и маг-
нитных полей. Конечно, все применения мощных импульсов сопровождаются
возникновением электромагнитных полей, но во многих случаях эти поля явля-
ются всего лишь инструментом для преобразования электрической энергии в
другую форму, например энергию ускоренных частиц или излучение
10.1. Импульсные электрические поля
Сильные электрические поля использовались в атомной физике для изучения
эффекта Штарка, в структурно-химическом анализе для выстраивания в ряды
молекул путем формирования их дипольного взаимодействия, в физике твердого
тела, где индуцированные фазовые переходы приводили к изменению, например,
электрического сопротивления вещества. Однако эти применения, как правило,
были весьма специфическими. Мы ограничимся обсуждением применения им-
пульсных электрических полей для биологических систем — области, к которой в
последнее время все больше растет интерес и намечаются привлекательные перс-
пективы широкомасштабного промышленного использования.
10.1.1. Введение
Электрические поля играют важную роль в биологических системах. Они уп-
равляют процессами переноса веществ через клеточные мембраны и передачи
информации нейронами. Биологические клетки представляют собой замкнутые
системы, чья внутренняя структура (клеточное ядро, органеллы и цитоплазма)
отделены от наружного пространства диэлектрическими мембранами [Campbell,
2000]. Однако эти мембраны обладают утечками через протеиновые каналы и по-
ры, которые могут быть активированы для обеспечения метаболизма клетки. Ос-
нова мембраны состоит из тонкого (5 нм) двойного изолирующего слоя фосфо-
липидов, обладающего весьма большой электрической прочностью. Электричес-
кий пробой (т. е. ее необратимое разрушение) такой мембраны происходит при
напряжении на ней свыше 1 В, что соответствует напряженности поля
246 Глава 10. Применение импульсных электромагнитных полей
2 х 106 В/см. Когда напряжение на мембране превышает пороговое значение око-
ло 0.2 В, проницаемость мембраны увеличивается. В отличие от клеточных мемб-
ран цитоплазма является электролитом (проводником). Если электрическое поле
приложено к клетке, окруженной электролитической суспензией, ионы движутся
к мембране и она становится поляризованной. Вследствие этой поляризации внут-
ри клетки через небольшое время происходит разделение зарядов, и разность по-
тенциалов, первоначально приложенная ко всей клетке, сосредотачивается на ее
мембране. Таким образом, напряженность поля на мембране возрастает по срав-
нению с внешней приложенной напряженностью во столько раз, во сколько раз-
меры клетки в направлении приложенного поля (несколько мкм) больше толщи-
ны мембраны (5 нм). На Рис. 10.1 представлена эта картина для сферической
клетки. Коэффициент умножения напряженности поля ev может достигать до-
вольно больших значений (100... 1000), что делает возможным пробой мембраны
при напряженности внешнего поля ниже динамической электрической прочнос-
ти воды, которая обычно является основным компонентом суспензии.
Рис. 10.1. Сферическая клетка в электрическом поле с напряженностью Е.
Очевидно, что степень увеличения напряженности поля на мембране зависит
от формы клетки. Для сферической клетки, показанной на Рис. 10.1, она также
зависит от азимута:
EV = Дпет/^ext = 1-5 a COS (а)/Л, (10.1)
где Етет— напряженность поля в мембране,
Еех{— напряженность внешнего поля,
а— радиус клетки,
а — азимутальный угол,
h — толщина мембраны.
Время релаксации, требуемое для полной поляризации, зависит от размеров
клетки, удельной емкости мембраны и проводимостей цитоплазмы и суспензии:
Д^тет = l-5«4<t COS(a)
[1-е-],
т = аС
Ре
2
1 + 2/
1-/
(Ю.2)
10.1. Импульсные электрические поля 247
В выражении (10.2) A£/mem — падение напряжения на мембране, т — постоян-
ная времени релаксации, р, — сопротивление цитоплазмы, ре — сопротивление
суспензии,/— объем клетки. Для клеток бактерий в городской воде с проводи-
мостью 0.1 См/м время поляризации лежит в пределах от 80 до 500 нс для малень-
ких {Listeria monocytogenes) и больших (Saccharomyces cerevisiae) клеток соответс-
твенно. Для описания процесса с произвольной формой импульсов полезна эк-
вивалентная схема, представленная на Рис. 10.2.
Рис. 10.2. Эквивалентная схема биологической клетки
Rm — сопротивление мембраны, Ст — емкость мембраны, Rs — сопротивление суспензии,
Cs — емкость суспензии, Rs — выходной импеданс генератора,
U(t) — изменяющееся во времени напряжение импульса.
Если падение напряжения на мембране A(/mem превышает критическое значе-
ние около 0.5 В, начинают расти отверстия в ней, создаваемые тепловыми флук-
туациями. Хотя точный механизм формирования пор еще не совсем ясен, боль-
шинство исследователей в этой области придерживаются двухстадийной теории
[Weaver, 1994; Weaverand Chizmadzhev, 1996; Neu and Krassowska, 1999; Teissie and
Rols, 1994]. В начале поры появляются в гидрофобной форме со скоростью, кото-
рая зависит от температуры и локальной напряженности поля. Когда радиус пор
превышает некоторое значение, они преобразуются в гидрофильную форму, под-
ходящую для обмена водорастворимых субстанций между внутренностями клет-
ки и окружающей ее средой. Сила, увеличивающая радиус поры, связана с энер-
гией формирования поры. Для гидрофобной и гидрофильной форм эти энергии
различны. Для гидрофобной формы справедливо выражение
F(r, t) = 2лАгд(оо) _ naJJ2r2, (10.3)
/оО'/'о)
а для гидрофильной — выражение
F(r ,t) = 2л£г-ngr2 +-^г—па JJ2r2.
г
(10.4)
В этих уравнениях /0 и / являются модифицированными функциями Бесселя
нулевого и первого порядка, а г0 представляет собой характерную длину слоя Гель-
248 Глава 10. Применение импульсных электромагнитных полей
мгольца, на которой происходит переход от граничных к объемным свойствам воды
(см. подразд. 2.3.1); типовое значение r0 = 1 нм; £(оо) является поверхностной энер-
гией, равной 0.05 Дж/м2; U(t) является зависимым от времени потенциалом мембра-
ны, который может быть рассчитан с помощью эквивалентной схемы, представлен-
ной на Рис. 10.2; с — постоянная; ар = (ew — ем)/2А, где h — толщина мембраны, а
г— радиус поры; ewh ем — диэлектрические проницаемости воды и мембраны со-
ответственно; £, — энергия на единицу длины периметра поры. Последние вычитае-
мые члены в (10.3) и (10.4) отображают энергию, запасаемую в емкости при наличии
и отсутствии мембраны как диэлектрика. Этой энергией обусловлена квадратичная
зависимость свободной энергии в электрическом поле. Первый член в (10.4) описы-
вает периферийные воздействия в поре, второй представляет собой поверхностную
энергию, третий — пространственное отталкивание между полярными липидами в
поре. Таблица с численными значениями постоянных из уравнений (10.3), (10.4)
можно найти в работе [Joshi and Schoenbach, 2000].
На Рис. 10.3 приведен график зависимости свободной энергии /’формирова-
ния пор от их радиуса для потенциалов 0 и 0.2 В. Под воздействием внешнего по-
ля горб на графике сильно уменьшается. При еще большем потенциале он вооб-
ще исчезает и поры начинают расти. Если во время воздействия импульсного по-
ля радиус поры превысит значение, соответствующее максимуму при нулевом
Г идрофобные поры
Г идрофильные поры
Рис. 10.3. Зависимости свободной энергии формирования пор от их радиуса
для потенциалов 0 и 0.2. Для гидрофильных пор приведены графики при потенциалах 0 и 0.2 В.
10.1. Импульсные электрические поля 249
потенциале, рост поры становится необратим, цитоплазма вытекает наружу и
клетка погибает. Если критический радиус не достигнут во время воздействия им-
пульса, пора может «залечиться» и клетка вернется к первоначальному состоя-
нию. Изменения во времени распределения радиусов пор в их ансамбле могут
быть описаны уравнением диффузии, впервые использованным Смолучовским
(Smoluchowsky) и Эйнштейном (Einstein) для описания броуновского движения
молекул [Joshi and Schoenbach, 2000]. Из модели, описанной выше, очевидно, что
амплитуда импульса электрического поля, его форма и его длительность играют
важную роль в формировании пор.
Для вскрытия клетки необходимо, чтобы длительность электрического им-
пульса была больше, чем сумма интервалов времени образования поляризован-
ного слоя на мембране и достижения критического радиуса поры. Если требуется
осуществить воздействие только на органеллы, структуру или молекулы внутри
клетки без разрушения ее мембраны, то длительность импульса должна быть ко-
роче, чем время формирования полной поляризации, т. е. обычно меньше 100 нс.
Йоси и Шоенбах [Joshi and Schoenbach, 2000] выполнили численное решение
уравнения диффузии и определили функцию плотности распределения пор для
различных внутрисхемных постоянных времени RcCm (см. Рис. 10.2) и получили
зависимости напряжения и энергии необратимого пробоя как функции мини-
мальной длительности импульса. Эти графики приведены на Рис. 10.4.
Рис. 10.4. Зависимости напряжения и энергии необратимого пробоя
как функции минимальной длительности импульса для двух постоянных времени АсСт.
Обратимая поляризация электрическим полем уже много лет используется в
фундаментальных биологических исследованиях для введения внутрь клеток ге-
нетического материала, различных препаратов и молекул. Необратимая поляри-
зация, которая может быть использована для экстрагирования материала плазмы
из клеток или для уничтожения микроорганизмов, также описана в литературе с
конца 1960-х гг. Однако промышленное применение этих приемов ограничено
250 Глава 10. Применение импульсных электромагнитных полей
только несколькими специфическими областями. Основной причиной этого яв-
ляется отсутствие подходящих генераторов импульсов напряжения для создания
полей с напряженностью до 10 МВ/м в достаточно большом объеме и обладаю-
щих приемлемой надежностью.
По сравнению с обычными методами экстрагирования материала плазмы из
клеток и стерилизации, поляризация электрическим полем имеет большие перс-
пективы применения.
10.1.2. Генераторы импульсов
Генераторы импульсов, подходящие для промышленного применения, долж-
ны обеспечивать электрические поля с напряженностью поля 0.1...10 МВ/м при
длительности импульсов 0.01...10 мкс в объемах, определяемых требуемой произ-
водительностью установки. Кроме того, чтобы получить желаемый результат,
каждая клетка должна быть подвергнута воздействию определенного числа им-
пульсов. Скорость поступления обрабатываемого вещества и протяженность зо-
ны распространения действия поля определяют требуемую частоту повторения
импульсов. По экономическим соображениям многие применения требуют до-
вольно большой производительности (>100 м3/ч), и поэтому приходится приме-
нять крупные электроды (> 1000 см2) с большим межэлектродным пространс-
твом. Типовое значение проводимости суспензии клеток составляет около
0.1 См/м. Для электрических полей с напряженностью 1 МВ/м генератор при
этом должен обеспечивать выходной ток свыше 10 кА. Это означает, что для этой
цели подходят только генераторы с низким выходным импедансом. В зависимос-
ти от межэлектродного расстояния может потребоваться амплитуда импульсов до
1 МВ. Таким образом, подходящими генераторами являются генераторы Маркса,
генераторы на £С-цепях и длинных линиях, или комбинации этих типов генера-
торов (см. разд. 3.2 и гл. 5).
10.1.3. Обработка клеток растительного происхождения
Для экстракции пищевых продуктов, таких как сахар, крахмал или масло рас-
тительного происхождения, необходимо вскрыть клеточные мембраны, а в ряде
случаев также и мембраны органелл. Это может быть выполнено с использовани-
ем тепловых, механических, химических воздействий, с помощью ферментов, а
также методом электрополяризации. Клетки растительного происхождения име-
ют большие по сравнению с бактериальными клетками размеры и требуют более
низких полей для разрушения мембран. Далее мы обсудим преимущества элект-
рополяризации по сравнению с обычными методами на примере извлечения са-
хара из сахарной свеклы, — возможно, первого крупного промышленного приме-
нения электрополяризации [Schultheiss et al., 2002; Bluhm et al., 2004].
Стандартная процедура производства сахара из сахарной свеклы включает на-
резание овощей в стружку с последующей экстракцией сока из нее при повышен-
ной температуре и при добавлении незначительного количества воды [Schiveck
and Clarke, 2001]. Сахар, растворенный в клеточном соке, может покинуть све-
10.1. Импульсные электрические поля 251
кольную стружку, только если будут разрушены мембраны клеток и вакуолей На
современных сахарных заводах это достигается путем тепловой денатурации при
температуре свыше 70°С. Перенос сахара и других водорастворимых субстанций
из свекольной стружки в воду происходит за счет диффузии. Так как коэффици-
ент диффузии зависит от температуры, температура экстракции должна быть как
можно выше. Однако при чрезмерно высокой температуре заметная часть ве-
ществ, из которых состоят стенки клеток, также денатурируется и становится во-
дорастворимой. При этом получается загрязненный свекольный сок, который в
дальнейшем требует очищения. По этой причине используется компромиссная
температурно-временная программа: сначала при температуре 7О...78°С в течение
короткого времени осуществляется денатурация, а затем при температуре
69...73°С осуществляется экстракпия.
Температурная программа также влияет и на выживание микроорганизмов,
заносимых в продукцию вместе с грязью на свекле. Процессы обмена веществ в
этих бактериях ведут к потере сахара. Некоторые микробы не погибают при на-
греве, и поэтому обычно в воду, используемую для экстракции сахара, добавляют
дезинфицирующие вещества (перекись водорода и формалин).
Менее дорогой процесс получения сахара с существенной экономией энергии
мог бы получиться, если экстракция сока выполнялась бы при пониженной тем-
пературе. Использование импульсных электрических полей как нетепловой ме-
тод разрушения клеточных мембран в овощах впервые было описано Довеншпе-
ком в 1962 г. [Doevenspeck, 1962]. Позже этот метод был также «привлечен» к не-
тепловому уничтожению микроорганизмов. Недавно Бузрара и Воробьев
[Bouzrara and Vorobiev, 2000, 2001] предложили использование комбинации давле-
ния и воздействия импульсного электрического поля для экстракции сока из са-
харной свеклы. Хотя переход на этот процесс существенно экономит энергию, он
представляет собой совершенно новую технологию и требует полного переобору-
дования сахарных заводов.
Потенциальные преимущества электрополяризации для экстракции сока из
сахарной свеклы были впервые продемонстрированы на мобильной испытатель-
ной установке, названной КЕА (Karlsruher Elektroporations Anlage — Карлсруйс-
кая электрополяризационная установка). Общий вид этой установки показан на
Рис. 10.5. Камера обработки, показанная в правой части Рис. 10.5, была изготов-
лена из полипропиленовой трубы диаметром 18 см. Было применено четыре па-
ры электродов из нержавеющей стали. Каждая пара состояла из дисковых элект-
родов диаметром 4 см и была смещена относительно другой пары на 16 см в акси-
альном направлении и на 90° в азимутальном направлении. Эта конструкция
обеспечивала воздействие достаточно высокой напряженности поля на каждую
клетку проходящей через трубу сахарной свеклы. При номинальной амплитуде
импульсов напряжения напряженность поля достигала 12 кВ/см. Обрабатывае-
мая свекла передвигалась в трубе реактора за счет действия винтового конвейера
в трубе подачи, видного в левой части Рис. 10.5. Максимальная производитель-
ность, которая достигалась в этой установке, составляла 300 кг/час.
Высоковольтные импульсы с амплитудой до 300 кВ создавались с помощью
6-каскадного генератора Маркса с низким выходным импедансом. При разряде
252 Глава 10. Применение импульсных электромагнитных полей
Рис. 10.5. Общий вид мобильной испытательной установки КЕА. Левая фотография: экран Фа-
радея, закрывающий генератор Маркса и камеру обработки (справа)', источник пита-
ния и винтовой конвейер (в середине)', бак для сбора обработанной свеклы (слева).
Правая фотография: камера обработки, состоящая из полипропиленовой трубы с че-
тырьмя парами распределенных электродов
генератора Маркса длительность импульса напряжения на уровне половины его
амплитуды составляла около 1 мкс. Каждый импульс имел энергию 0.75 Дж. Час-
тота повторения импульсов достигала 10 Гц. Для устранения излучения электро-
магнитных помех генератор Маркса и камера обработки были закрыты экраном
Фарадея. Высоковольтная часть установки питалась от стандартного источника
питания мощностью 10 кВт.
Обработанные корнеплоды свеклы резались на куски и подвергались либо хо-
лодному прессованию, либо экстрагированию сока с помощью воды при различ-
ных температурных режимах. На Рис. 10.6 показаны корнеплоды свеклы до и
Рис. 10.6. Левая фотография: корнеплоды свеклы до (справа) и после (слева) обработки импуль-
сным электрическим полем. Правая фотография: соответствующее количество сока,
полученное холодным прессованием при 32 бар.
10.1. Импульсные электрические поля 253
после обработки, а также соответствующее количество сока, полученного холод-
ным прессованием при давлении 32 бар в течение 15 мин. Капли сока, появляю-
щиеся на поверхности среза обработанных корнеплодов, являются индикаторами
того, что клеточные мембраны разрушены импульсным электрическим полем. На
Рис. 10.7 приведены графики зависимости относительного выхода продукции от
числа импульсов воздействия, или эквивалентной относительной энергии воз-
действия. Для сравнения приведен выход продукции при тепловом денатурирова-
нии при 72°С. В этом случае необходимая относительная энергия, требуемая для
нагрева свеклы от 20 до 72°С, равна 174 Дж/кг.
2.2
2.0
5 1.8
га
*
о 1.8
I
з м
со
1Д
1.0
О 2 4 8 8 10 170 172 174 176 178 180
Относительное потребление энергии, Дж/кг
Рис. 10.7. Выход сока в зависимости от потребляемой энергии при тепловой денатурации и воз-
действии импульсным электрическим полем (АО — необработанная свекла, А — об-
работанная).
Очевидно, что обработка импульсным электрическим полем имеет большой
потенциал для экономии энергии. При введении в технологический процесс про-
изводства сахара операции электрополяризационной обработки сырья экономия
энергии проистекает из двух обстоятельств: во-первых, экстракция может выпол-
няться при низких температурах, а во-вторых, при этом сок содержит меньше за-
грязнений, в том числе воды. Представляется вполне выполнимым ввести опера-
цию электрополяризации в производственные линии сахарных заводов без су-
щественного изменения остального оборудования.
Для демонстрации того, что эта технология является экономически выгодной
и обладает высокой производительностью, группой из Карлсруе была создана ус-
тановка KEA-ZAR. В ней реакторная камера представляет собой большой бара-
бан со спицами для транспортировки свеклы (Рис. 10.8). Электроды из нержаве-
ющей стали встроены в дно реакторной камеры и соединены с двумя генератора-
ми Маркса. Противоположные электроды представляют собой ленты из
нержавеющей стали, обмотанные вокруг корпуса барабана. Производительность
установки — 800 тонн в день. Генераторы Маркса вырабатывают импульсы на-
пряжения амплитудой до 350 кВ с частотой до 20 Гц.
254 Глава 10. Применение импульсных электромагнитных полей
Рис. 10.8. Схематическое изображение реакторной камеры установки KEA-ZAR (слева) Транс-
портный барабан перед установкой в реакторную камеру и корнеплоды свеклы после
обработки (справа).
10.1.4. Устранение бактериальных загрязнений
Уничтожение таких бактерий, как Escherichia coli, Bacillus се re us,
Staphylococcus aureus, с помощью сильных импульсных электрических полей бы-
ло описано в литературе еще с середины 1960-х гг. В своей пионерской работе
Сэйл и Гамильтон заключили, что наблюдавшееся экспериментально уничтоже-
ние бактерий происходило вследствие разрушения их клеточных мембран, что
приводило к распаду клеток [Sale and Hamilton, 1967]. При напряженности элек-
трического поля свыше 10 кВ/см в течение 20 мкс было найдено, что скорость
уничтожения бактерий сильно зависит от их вида. Грамположительные бакте-
рии проявили более высокую устойчивость к электрическому полю, чем грамот-
рицательные [Hiilsheger et al., 1983]. Кроме того, было обнаружено, что споры
бактерий не чувствительны к импульсным электрическим полям. Несмотря на
ранние успехи, стерилизация с помощью импульсных электрических полей ни-
когда не покидала стен исследовательских лабораторий. И снова в большой сте-
пени это было обусловлено отсутствием импульсных генераторов, пригодных
для промышленного применения. Множество опубликованных результатов про-
тиворечило друг другу. Кроме того, было найдено, что доля уничтожаемых мик-
роорганизмов достигает насыщения при увеличении числа импульсов воздейс-
твия. Таким образом, импульсное электрическое поле способно лишь умень-
шить число микробов на примерно четыре логарифмических шага. Причина
этого ограничения еще не полностью понята, но множество исследователей
склоняются к тому, что это есть следствие индивидуальных особенностей, кото-
рые делают некоторые бактерии одного и того же вида более устойчивыми к воз-
действию импульсного электрического поля, чем остальные. Возникает вопрос:
а не способны ли бактерии развивать «электропрочность»? Однако у бактерий,
подвергавшихся воздействию импульсных электрических полей на протяжении
более чем 12 их поколений, повышения «электропрочности» обнаружено не бы-
ло [Bluhm et al., 2004].
10.1. Импульсные электрические поля 255
Как бы там ни было, представляется невозможным использовать для стерили-
зации обработку только импульсным электрическим полем. Следовательно, даль-
нейшие разработки по использованию воздействия импульсным электрическим
полем в промышленности должны быть направлены на:
1. Уменьшение числа микробов для увеличения продолжительности хране-
ния продуктов питания.
2. Уменьшение бактериальных загрязнений в канализационных отходах на
очистных станциях.
3. Совмещение обработки импульсным электрическим полем с другими био-
логическими, химическими и физическими воздействиями для получения
более эффективных, экологичных и экономически привлекательных
систем.
Увеличение срока хранения продуктов питания с помошью импульсных
электрических полей очень привлекательно из-за того, что в продукты не попа-
дают токсичные вещества и не разрушаются витамины и ароматические и вкусо-
вые вещества. Даже очищенная вода, поступающая с очистных станций в при-
родные водоемы, содержит большую концентрацию бактерий, в особенности
видов, обладающих устойчивостью к антибиотикам, что может повлечь непред-
сказуемые последствия для экосистем. Уменьшение числа этих бактерий ка-
ким-либо безвредным способом могло бы принести большую пользу окружаю-
щей среде.
Существенное уменьшение бактериального загрязнения происходит под воз-
действием импульсных электрических полей, возбуждающих коронный разряд в
воде. Коронный разряд представляет собой электрический разряд с малым током.
Он возникает на металлических остриях, как это было описано в разд. 2.3.2.
Вблизи острия при этом создается очень высокая напряженность электрического
поля. Кроме того, при коронном разряде образуются сильные окислители (окси-
данты), такие как радикал ОН, озон и Н2О2, а также ультрафиолетовое излучение.
Образование оксидантов может быть увеличено путем введения в воду пузырьков
воздуха. Ожидается, что комбинация всех этих воздействий приведет к более эф-
фективному разрушению микроорганизмов в воде и, возможно, к истреблению
их спор. В больших объемах коронные разряды создавались с помощью тонких
проволочных анодов [Akiyama, 2000; Akiyama et al., 2001] и на поверхности метал-
лических цилиндров, покрытых тонким слоем пористой керамики [Sunka et al.,
1999; Sunka, 2001]. Последний вариант представляется наиболее подходящим для
промышленного применения с учетом требований по рабочему объему установки
и ее долговечности.
Недавно было найдено, что очень короткие импульсы (< 10 нс) с амплиту-
дой напряженности поля свыше 10 МВ/м могут вызывать апоптоз (гибель кле-
ток) и фрагментирование ДНК в клетках грудных желез без разрушения их мем-
бран [Schoenbach et al., 2001; Beebe et al., 2002; Buescher and Schoenbach, 2003].
Применение таких импульсов, наряду со средством воздействия на раковые
клетки и инструментом для фундаментальных биологических исследований, со-
здает предпосылки к созданию новых методов борьбы с бактериальным загряз-
нением.
256 Глава 10. Применение импульсных электромагнитных полей
10.1.5. Другие применения импульсных электрических полей
Задачей, близкой к описанной в предыдущем разделе, является борьба с био-
обрастаниями, существующими в промышленных и других системах, использую-
щих воду в больших объемах. Под термином «биообрастания» мы подразумеваем
разрастание различных биологических объектов на изначально чистой поверх-
ности. К этим объектам относятся бактерии, простейшие, грибы, моллюски и во-
доросли, которые могут быть занесены в необработанную воду из окружающей
среды и которые создают биопленки на внутренних поверхностях труб, теплооб-
менников, градирен и т. д. [Walkeret al., 1998]. Возникновение биообрастаний мо-
жет стать раздражающей проблемой во многих производственных процессах и в
окрестностях заводов и фабрик, а ее решение оказывается, как правило, весьма
дорогостоящим
Обрастание ракушками днищ морских судов и других морских сооружений
влечет за собой миллиардные затраты на борьбу с ним. Некоторые анаэробные
бактерии используют углерод, растворенный в стали, для своего обмена веществ
и тем самым ускоряют коррозию стальных конструкций в воде. Предотвращение
роста биопленок с помощью ядохимикатов часто трудноосуществимо или не при-
емлемо в связи с их воздействием на окружающую среду или несовместимостью с
производственными процессами.
По этим причинам воздействие импульсным электрическим полем представ-
ляется весьма привлекательным для устранения биообрастаний. Этот метод уже
был успешно применен для предотвращения размножения ракушек в трубах сис-
темы охлаждения морской водой на электростанции [Schoenbach et al., 1997] и
для борьбы с ростом водорослей в резервуарах для питьевой воды [Akiyama, 2000].
Другой неразработанной областью применения электрополяризации является
производство важных веществ из микроорганизмов, таких, например, как микро-
водоросли и бактерии. Микроводоросли вызывают растущий интерес как постав-
щики исходных материалов для пищевой индустрии, а также для фармацевтичес-
кой и косметической промышленности. Биополиэстер, получаемый из бактери-
альных клеток Ralstonia eutropia, например, привлекает большой интерес как
биологически совместимый материал. Его механические и химические свойства
подобны свойствам полиэтилена, и по этой причине он стал важнейшим матери-
алом для медицинских протезов. В настоящее время его получают из бактерий в
ферментационных резервуарах с помощью химически-ферментационного про-
цесса [Schumann and Muller, 2001]. Сочетание этого процесса с электрополяриза-
цией могло бы привести к более эффективному использованию химикатов и фер-
ментов для растворения клеточных мембран бактерий. В результате образования
необратимых пор диффузия веществ, растворяющих стенки клетки, могла бы про-
исходить быстрее, так же как и высвобождение гранул полимера из бактерий.
И наконец, электрополяризация имеет большой потенциал для применения в
терапии: представляется возможной быстрая и массированная доставка лекарс-
твенных веществ внутрь клеток через обратимые поры в их мембранах; таким об-
разом, может быть достигнут сильный эффект в химиотерапии раковых клеток
при одновременном уменьшении вреда для пациента [Dev and Hoffmann, 1994;
Rabussay et al., 2003].
10.2. Импульсные магнитные поля 257
10.2. Импульсные магнитные поля
10.2.1. Введение
Импульсные магнитные поля с индукцией в диапазоне до нескольких сот тесл
представляют большой интерес как для фундаментальной, так и для прикладной
науки. Ожидается открытие новых физических явлений, особенно в области по-
лей более 100 Тл. В этих полях лоренцевы силы становятся сравнимыми с куло-
новскими, которые удерживают электроны на их атомных орбитах. Например, в
атоме водорода эти две силы становятся равны между собой при значении В, по-
лучаемом из следующего выражения:
5= (13.3/л)3 х 100 Тл, (10.5)
где п — главное квантовое число.
В твердых телах энергия магнитного поля при этих значениях индукции ста-
новится сравнимой с энергией фундаментального взаимодействия, орбиты элек-
тронов сжимаются до молекулярных размеров, а расстояние между уровнями
Ландау (й/2л)сос становится больше кТ при комнатной температуре. Из этих про-
стых рассуждений очевидно, что электронные свойства твердых тел и кинетика
как физических, так и химических процессов значительно изменятся в полях
свыше 100 Тл. Многие эффекты в таких полях становятся нелинейными, и для
подтверждения теоретических расчетов следует проводить строгие эксперимен-
тальные исследования. По этим причинам в последнее десятилетие было создано
несколько лабораторий, специализирующихся в области высоких магнитных по-
лей, в Европе, США и Японии (в Берлине, Талахассе и Токио соответственно). На
сегодняшний день сильные магнитные поля играют огромную роль в материало-
ведении. Исследования изменений электрического сопротивления под воздейс-
твием магнитного поля, которые привели к открытию квантового и дробного
квантового эффекта Холла, были отмечены двумя Нобелевскими премиями. Дру-
гими областями современных исследований на основе использования сильных
магнитных полей являются высокотемпературная сверхпроводимость, магнит-
ные эффекты в твердом теле, тяжелые фермионы, переходы типа порядок—бес-
порядок в монослоях. Для получения большей информации можно рекомендо-
вать сборник трудов последней конференции по физическим явлениям в силь-
ных магнитных полях [Boebinger et al., 2002].
В физике твердого тела импульсные магнитные поля могут применяться для
создания сильных ударных волн в проводниках для определения их термодина-
мических, электрических и оптических свойств при высокой плотности энергии.
Кроме того, магнитные поля используются для удержания плазмы и изучения ее
гидродинамических нестабильностей. Импульсные магнитные поля могут при-
меняться для ускорения атомных частиц и создания интенсивных электромаг-
нитных импульсов. Всего несколько исследований было выполнено в области оп-
ределения влияния сильных магнитных полей на живые организмы. Ожидается,
что биохимические и биофизические процессы будут изменяться в присутствии
сильных магнитных полей [Maret and Dransfeld, 1985].
258 Глава 10. Применение импульсных электромагнитных полей
Вследствие ограничений, накладываемых механической прочностью матери-
алов, магнитные поля с индукцией порядка 100 Тл могут создаваться либо в виде
коротких импульсов, либо через суперпозицию постоянного и импульсного по-
лей. Достижимая индукция в стационарных полях ограничена на уровне ниже
50 Тл. Крупнейшая в мире установка, в настоящее время расположенная в Тала-
хассе, штат Флорида, США, может обеспечить поле в 45 Тл в цилиндрическом
объеме диаметром 32 мм. Самые сильные импульсные поля, которые можно со-
здать с помощью неразрушаюшейся катушки, имеют индукцию около 70 Тл, в то
время как с разрушаюшейся катушкой создавались поля до 300 Тл. Разработана
концепция генерации полей с индукцией около 500 Тл, но на очень короткое вре-
мя (~ 3 мкс) и только в маленьком объеме (диаметром 9 мм).
Для достижения более сильных полей надо использовать метод сжатия маг-
нитного потока. При этом проводники, создающие предварительное поля, сжи-
маются механически, и происходит преобразование механической энергии в
энергию магнитного поля. Далее мы сначала обсудим существующие ограниче-
ния на достижимую магнитную индукцию в системе с катушкой без сжатия поля,
а затем рассмотрим метод сжатия более детально.
10.2.2. Ограничения на магнитное поле при использовании
катушек без разрушения
Параметры катушки и цепи
Перед началом обсуждения ограничений на магнитное поле при использова-
нии многовиткового неразрушающегося соленоида рассмотрим некоторые ос-
новные соотношения между параметрами разрядной цепи и свойствами поля в
катушке. Рассматриваемая катушка изображена на Рис. 10.9.
Предположим, что в катушке А витков, а коэффициент заполнения (отноше-
ние суммы сечения всех витков к общей площади сечения катушки) есть f.
NA
h(ro-ry
(10.6)
где А — площадь сечения одного витка. Связь между напряженностью магнитно-
го поля на оси катушки в точке с координатой z описывается [Knoepfel, 1970] в
выражении
hz = -* J 21z£in +
2 [ro-ri Г.+^+СЛ-г)2 Го~Г> r.+^/f+Z2
(Ю.7)
Здесь Hq = Nl/h. и это выражение справедливо, если диаметр провода намного
меньше, чем толщина скин-слоя. Естественно, индуктивность у такой катушки
весьма велика, и, если через нее разряжается батарея конденсаторов, время раз-
10.2. Импульсные магнитные поля 259
ряда оказывается большим. Еще при этом важную роль в цепи играет сопротив-
ление катушки. Индуктивность и сопротивление определяются выражениями
П О jh r0-i\
(10.8)
где Кс — коэффициент, учитывающий краевые эффекты у катушки ограниченных
размеров [Knoepfel, 1970].
Рис. 10.9. Многовитковый соленоид.
Рис. 10.10. Эквивалентная схема разряда конденсатора
через многовитковый соленоид.
Для разрядной цепи, показанной на Рис. 10.10, выражения зависимости тока
от времени в случаях докритического и сверхкритического демпфирования полу-
чаются следующими:
, Uo f R Л . . .
/ = —-expl-------1 sin(coO>
со£ I 2L J
Uo
(Я* L
exp
Я >eM*'-e^*'
2LJ 2
(Ю.9)
(10 10)
где co = co0(l — y2)1/2, co* = co0(y2 — 1)1/2 и
260 Глава 10. Применение импульсных электромагнитных полей
“0=7Ес
(10.11)
(10.12)
Параметр цепи у определяет максимальный ток /т, протекающий через ка-
тушку, и время zm, за которое он достигается. L — сумма индуктивности катушки
Lc и паразитной индуктивности цепи £s. Из выражений, приведенных выше, для
0 < у < 1 получается
— = ехр - —j- X - arcsin^/l — у2 -,
Л л/1 ~у
—— = —,.......arcsinJl - у2.
Г/4 к XV N
Для 1 < у < оо получается
21п(у + 7у2 -1)
Т/4 п ^-1
(10.13)
(10.14)
Здесь Т- 2л/со0, a Iq = (2Wq/L)^2 — максимальный ток, достигаемый в цепи без
сопротивления.
В момент времени /т, когда ток достигает максимального значения, энергия
Ио, первоначально накопленная в конденсаторе, делится на три части. Первая
часть, И^, представляет собой энергию, рассеянную в элементах цепи. Вторая
часть представляет собой энергию магнитного поля И^. И третья часть, Ист, —
это энергия, оставшаяся в конденсаторе. Эти величины зависят от параметра у
следующим образом:
(10.15)
На Рис. 10.11 эти зависимости приведены в графической форме
10.2. Импульсные магнитные поля 261
Если предположить, что индуктивность катушки намного больше, чем пара-
зитные индуктивности, и что, кроме того, сопротивление цепи в основном сосре-
доточено в катушке, получится следующее выражение для параметра у:
= 1 = N ro + zif пС У2
Y 2\L 2qf г0-гХиок^2 J
(10.16)
Из Рис. 10.11 видно, что увеличение у больше 1 влечет за собой неудовлетво-
рительное преобразование энергии конденсатора в энергию индуктивности. Это
устанавливает ограничения на значения N и С, т. е. низкая емкость и высокое на-
пряжение предпочтительнее, чем большая емкость и низкое напряжение.
Рис. 10.11. Зависимости отношений энергий в цепи,
изображенной на Рис. 10.10, от параметра у.
Квазистационарные ограничения на давление,
создаваемое магнитным полем
В гл. 1 были приведены выражения (1.1) и (1.2), описывающие тепловые и ме-
ханические ограничения на величину магнитного поля. Сейчас мы рассмотрим
эти ограничения более детально. Выражение для механического ограничения
давления, развиваемого магнитным полем, справедливо для статических условий
в предположении, что магнитное давление воздействует на стенки цилиндричес-
кой поверхности. Это предположение противоречиво, так как в статических усло-
виях давление, создаваемое магнитным полем, не ограничено поверхностью про-
водника. Несмотря на это, в случае тонкого проводящего цилиндра, помещенно-
го в толстый непроводящий корпус, способный выдерживать давление,
отмеченные выше формулы дают хорошее приближение к реальности. Следует
отметить, что все рассуждения в данном подразделе справедливы для «медлен-
ных» импульсов, чья длительность намного больше характеристического периода
колебаний цилиндра
262 Глава 10. Применение импульсных электромагнитных полей
где г0 — радиус цилиндра,
р — плотность материала,
Y— модуль Юнга.
Давление магнитного поля может быть описано тензором напряжений Макс-
велла, который в простейшем одномерном случае дается выражением
p(r, t) = \hBzdr = -\^Bzdr =
ri и
=|н,Я?(г1Д)-|ц|,Я12(г,О.
(10.17)
В этом случае давление на поверхности получается р = ц0Н2/2. (Везде в этом под-
разделе подразумевается, что проницаемость материалов равна 1.) Для цилинд-
рической стенки с внутренним и внешним радиусами г, и го максимальная тан-
генциальная сила возникает на внутренней поверхности, где достигает значения
[Ebert, 1976]
(10.18)
Таким образом, приблизительный критерий ограничения статического магнит-
ного поля получается
1 „2 Го2-Л2
2Р“ <Ъ,г^Гу
(10.19)
где SY ~ максимальный предел текучести рассматриваемого материала.
Аналогичный критерий был выведен для длинной многослойной катушки в
предположении постоянной плотности тока и отсутствии передачи радиальных
сил от витка к витку. Здесь соотношение между магнитной индукцией в центре
катушки и максимальным давлением, возникающим на окружности радиуса
г = г0/2 (для Г) < г0/2), определено [Herlach and Ortenberg, 1996, Herlach et al.,
1996] как
2 \ ro)
(10.20)
В многовитковой, многослойной катушке с радиальной передачей давления
для г< 1.8л*1 радиальная сила может растянуть витки. Часть катушки, в которой
это происходит, дальше ведет себя как катушка с незакрепленными витками.
Из-за большого многообразия механизмов отказов катушек, предназначен-
ных для создания сильных магнитных полей, детальное моделирование часто не
10.2. Импульсные магнитные поля 263
эффективно, а приемлемая оценка максимально достижимого поля с неразруша-
емыми катушками может быть получена с использованием первого сомножителя
в выражении (10.20). В 1кбл. 10.1 приведены пределы текучести ряда материалов
и соответствующие им максимально достижимые магнитные индукции.
Таблица 10.1. Пределы текучести ряда материалов и соответствующие им максимально
достижимые магнитные индукции
Материал Отожженная медь Наторгованная медь Сплав медь-бериллий Мартенситная сталь
Предел текучести [ГПа] 0.2 0.45 1 2
Вмах [Тл] 22 33 50 70
Динамические ограничения на давление,
создаваемое магнитным полем
В условиях динамической (импульсной) нагрузки необходимо принимать во
внимание механическую инерцию. Сначала рассмотрим тонкий сверхпроводя-
щий цилиндр с толщиной стенок d, радиусом г0 и высотой А. Если длительность
импульса давления p(t) мала по сравнению с периодом собственных колебаний
То = 2лго(р/У)1/2, то импульс, передаваемый на стенки, определяется выражением
Р=2лгоЛ|р(ОЛ. (10.21)
о
Результирующее напряжение может быть получено приравниванием кинети-
ческой энергии, передаваемой цилиндру, к энергии его деформации:
р2 2яДг
— fZdAdx, Y = Y^~. (10.22)
2Л/ J 2лг0
Здесь X — давление, а М — масса цилиндра, равная 2nrqdhp. Наконец, после при-
равнивания давления в выражении (10.21) к полученному из выражения (10.22),
критерий динамического ограничения становится следующим:
<^Evd, (10.23)
где XY — снова максимальный предел текучести материала корпуса. Для прямо-
угольного импульса длительностью Т, таким образом, получается
(10.24)
2 Т 2лг0
Сравнение (10.24) с (1.2) показывает, что динамическое ограничение увеличи-
вается по сравнению со статическим на величину отношения Tq/T, которое пред-
264 Глава 10. Применение импульсных электромагнитных полей
полагается достаточно большим. Этот результат может быть преобразован и при-
менительно к многовитковому соленоиду.
Для однослойного соленоида тол шиной d и в предположении, что поле снару-
жи обмотки пренебрежимо мало, можно использовать выражение (10.22). Однако
следует учесть, что давление действует только на витки обмотки, т. е. давление
увеличивается обратно пропорционально коэффициенту заполнения:
p-lhoZS.. (Ю.25)
Тогда выражение (10.23) приобретает вид
XYdf. (Ю.26)
При выводе этого соотношения предполагалось, что цилиндр выполняет функ-
цию как инертной массы, так и эластичной оболочки. На самом деле эти функ-
ции разделены.
Тепловые ограничения
Хотя механические эффекты вызывают наиболее серьезные проблемы, нельзя
пренебрегать и тепловыми ограничениями. Баланс энергии в объеме элемента
проволоки описывается следующим уравнением:
= + (10.27)
dt о
где cv — удельная теплоемкость материала,
Хиа — тепловая и электрическая проводимости соответственно
Из-за того что проволока в катушке обычно покрыта слоем электрической
изоляции, которая также является и тепловой изоляцией, во многих случаях пос-
ледним слагаемым в правой части уравнения (10.27) можно пренебречь. Это так-
же справедливо и для диффузии магнитного поля в толстый проводник, когда
глубина проникновения тепла всегда меньше толщины скин-слоя. В нашем слу-
чае, однако, глубина проникновения магнитного поля намного больше, чем диа-
метр проволоки. Так как в общем случае пренебрегать температурной зависимос-
тью электрической проводимости нельзя, удобно сформулировать критерий для
максимальной плотности тока, при которой проволока начинает плавиться:
t Or
S=fj2dt=j<,dQ, (10.28)
о Qo
где Qo и Q{ — начальная и конечная удельные плотности энергий, cv70 и cv7}соот-
ветственно. Уравнение (10.28) показывает, что интеграл тока / зависит только от
Qo и Q{. Очевидно, что J должен оставаться ниже значения, соответствующего
10.2. Импульсные магнитные поля 265
точке плавления металла. Это значение зависит от первоначальной температуры
катушки. Для меди и алюминия, нагреваемых от комнатной температуры до темпе-
ратуры плавления, значения J составляют 0.89 х 1017 А2с-м~4 и 0.32 х 1017 А2с-м“4
соответственно. J можно увеличить с помощью предварительного охлаждения
проводника. Применяя эти результаты к случаю многовиткового соленоида,
можно получить следующее условие:
jPdt < Jsm. (10.29)
Если известна зависимость Нот 1(см., например, выражение (10.7)), то выра-
жение (10.29) можно использовать для формулировки критерия максимально до-
ступного магнитного поля до того, как катушка расплавится. Однако если катуш-
ка должна остаться «в живых» после серии импульсов, то интеграл, взятый по
всей длительности импульса, должен оставаться ниже Jsm. Для ограничения токо-
вого интеграла в катушке общепринято использовать мощный ключ, выключаю-
щий ток в цепи после достижения максимального значения поля.
10.2.3. Ограничения на поле при работе с разрушаемой
катушкой: одновитковый соленоид
Магнитные поля с индукцией более 100 Тл можно создать только в разрушае-
мых системах. В конечном счете разрушение есть последствие воздействия высо-
кой плотности энергии. Индукция в 500 Тл соответствует плотности энергии
100 кДж/см3 и может развить давление в 100 гигапаскалей. Эта плотность энергии
выше, чем в любой другой накопительной системе, включая взрывчатые вещест-
ва, и требуются специальные способы концентрации энергии, например исполь-
зование сходящихся линий передачи с низкой индуктивностью.
Для создания магнитных полей с индукцией свыше 100 Тл наиболее широко
используется одновитковая катушка (Рис. 10.12). Это простая, недорогая и меха-
нически прочная система, обеспечивающая достаточно короткое время, требуе-
мое на замену разрушающегося витка между экспериментами. Достоинством
этой системы по сравнению с системами компрессии поля (см. следующий под-
раздел) является то, что катушка при разрушении разлетается наружу от рабочей
области. При этом даже самые «нежные» образцы остаются «в живых» при экспе-
риментах и могут быть использованы повторно.
Естественно, одновитковая катушка, чьи радиальные и аксиальные размеры
составляют несколько сантиметров, имеет низкую индуктивность и короткое
время существования поля (порядка нескольких микросекунд). При этом требу-
ется применять батарею конденсаторов с низкими индуктивностью и сопротив-
лением, очень большой ток и запасенную энергию. Для создания индукции в
100 Тл требуется ток 0.8 МА на 1см аксиальной длины катушки. Из-за
ограничений на ток и энергию, которые можно получить из батареи
быстродействующих конденсаторов, приходится использовать катушки малых
размеров. В университете Гумбольдта, в Берлине, 300 Тл создавались в катушке с
внутренним диаметром 5 мм, аксиальной длиной 5 мм, толщиной стенок 2 мм
266 Глава 10. Применение импульсных электромагнитных полей
Рис. 10.12. Одновитковая катушка со сходящейся
полосковой линией передачи.
при использовании конденсаторной батареи на 60 кВ с энергией 225 кДж
[Herlachand Ortenberg, 1996].
Соотношение между напряженностью поля в центре одновитковой катушки
Яг(0) и током при длине катушки Л, внутреннем радиусе и внешнем радиусе го
определяется следующим выражением:
Яг(0) = (//А)Ан> (Ю.30)
где Кн — коэффициент, определяемый геометрией катушки. На Рис. 10.13 приве-
дены графики зависимости Ан от А/2п и г0/г\.
Рис. 10.13. Зависимость Ан от А/2г, при го/г\ = 1 [Bardotti et al., 1964] и ro/i\ = оо.
10.2. Импульсные магнитные поля 267
Из этих графиков можно заключить, что напряженность поля в достаточно
широком витке определяется только величиной тока. Однако при расширении
катушки (со скоростью около 2 км/с) после достижения точки начала разруше-
ния металла начинает увеличиваться индуктивность катушки, что влечет за собой
увеличение эффективного сопротивления и всей системы, что ограничивает мак-
симальный ток. В очень маленьких катушках (r,» 1 мм, h « 2 мм, толщина стенок
» 2 мм) наблюдалось замедленное расширение [Miura and Herlach, 1985]. Возмож-
ное объяснение этого состоит в тенденции к сжатию внутренних стенок к центру
катушки.
При очень высоких полях импульс магнитного давления вызывает ударную
волну в металле. Эта волна создает радиальное поверхностное расширение. Из
соотношения Гюгонио (Hugonoit) можно получить связь между давлением и ско-
ростями волны и частиц металла:
p = p0L>sL>, (10.31)
где ро — плотность. Для большинства металлов линейная связь между ц и и оста-
ется линейной в широком диапазоне скоростей, если только давление не очень
большое:
ц = Со + Sv. (10.32)
Используя это соотношение, можно установить связь между давлением, создавае-
мым магнитным полем, и скоростью частиц:
Д2/2цо = °(со + ЗДро» (10.33)
Это соотношение считается фундаментальным ограничением на создание очень
больших магнитных полей. Оно действует даже в отсутствие других механизмов
расширения радиуса катушки. Например, для меди, у которой с0 = 3.94 км/с,
S= 1.49, ро = 8930 кг/м3. Тогда для В = 300 Тл мы получаем и = 784 м/с, т. е. для
катушки с первоначальным внутренним диаметром 2 мм объем, заполненный по-
лем, будет увеличиваться в 2 раза каждую микросекунду. Отсюда также следует,
что тяжелые металлы, такие как тантал, в которых скорость частиц невелика,
предпочтительно применять для рассматриваемых целей. Кроме того, тантал
имеет сравнительно большое удельное сопротивление, что обеспечивает боль-
шую толшину скин-слоя для коротких импульсов, используемых в одновитковых
катушках.
10.2.4. Сжатие магнитного потока
Принципы сжатия магнитного потока
Магнитные поля с индукцией больше 500 Тл могут быть созданы только мето-
дом сжатия магнитного потока. В системах с сжатием потока замкнутый провод-
ник, окружающий «выращиваемое» поле, сжимается внешними силами, и при
этом происходит переход энергии из механической формы в магнитную. Эффек-
тивность этого преобразования может быть довольно высокой. Чтобы разобрать-
268 Глава 10. Применение импульсных электромагнитных полей
ся в процессах, сопровождающих сжатие магнитного потока, рассмотрим модель,
изображенную на Рис. 10.14. В ней толстый поршень с конечной проводимостью
движется со скоростью и внутрь ящика со сверхпроводящими стенками.
Рис. 10.14. Сверхпроводящий ящик,
в котором магнитный поток сжимается плоским поршнем с конечной проводимостью.
Предполагается, что внутри ящика было предварительно создано магнитное
поле, образующее поток Ф. Благодаря конечному сопротивлению металлического
поршня магнитный поток проникает в него, что приводит к его уменьшению
внутри ящика. Отталкиваясь от закона сохранения энергии в системе, можно вы-
вести следующее фундаментальное соотношение:
—)--------1 )--1 = -АГи (Ю.34)
dt dt
Здесь /— ток, индуцируемый в металлическом поршне, а К— сила, которую не-
обходимо преодолевать, чтобы вдвигать поршень в магнитное поле со скоростью
v. R здесь сопротивление скин-слоя, в который ток проникает в глубь поршня.
Все величины считаются изменяющимися во времени. Таким образом, первое
слагаемое в левой части уравнения (10.34) представляет собой изменение магнит-
ной энергии в системе, включающей ящик и поршень. Второе слагаемое — это
потери, а правая часть уравнения является работой, выполняемой против магнит-
ной силы в единицу времени. Механическую энергию можно выразить и в элект-
рических величинах:
K=\]*BdV.
v
(10.35)
10.2. Импульсные магнитные поля 269
Для одномерного случая, представленного на Рис. 10.14, это выражение упроща-
ется до
= (10.36)
о Но 2р0
где 2?о2/2цо — магнитное давление на поверхность поршня. Этот результат мог бы
быть получен в более общей форме при использовании тензора напряжений
Максвелла (см., например, [Becker and Sauter, 1964]). Магнитная сила, действую-
щая на несжимаемое тело, может быть выражена в терминах поверхностного по-
ля. Умножая (10.36) на — dx, можно получить изменение магнитной энергии при
этом перемещении. Следует отметить, что правая часть уравнения (10.34) равна
изменению индуктивности системы dL, умноженному на 1/2/2. Тогда (10.34) пре-
вращается в
d[(U2)LI2]
dt
+ RI2= --I2-
2 а
(10.37)
Эффективность преобразования механической энергии в магнитную зависит
от сопротивления материала поршня. Уравнение (10.37) можно преобразовать,
перенеся правую его часть влево и разделив на I
ЛФ Л
— +—Ф-0,
dt L
где введен поток Ф = L1. После интегрирования (10.38) получается
Г 'г R
Ф(Г) = Ф(0)ехр<- J—dt-.
I о
(10.38)
(10.39)
Как уже было отмечено, и R, и L зависят от времени и связаны с глубиной про-
никновения поля в толщу поршня. Часто для описания ограничений на возмож-
ность сжатия поля используется скорость диффузии потока uf. Она определяется
как отношение напряженности индуцируемого электрического поля к магнитной
индукции в поршне:
1*=Е/В. (10.40)
Значение ц- становится ясным, если рассмотреть ситуацию, когда магнитное
поле в ящике остается постоянным. В этом случае весь магнитный поток, сталки-
ваясь с движущимся поршнем, должен проникать в него, т. е. скорость проникно-
вения магнитного потока в поршень и скорость движения поршня должны быть
равны между собой. Тогда получается
E=U = d<b/dt _ Bbdtjdt
В Bb Bb ~ Bb
(10.41)
270 Глава 10. Применение импульсных электромагнитных полей
При замене Е в (10.41) на ру получается
vf = = --Р-——. (10.42)
В ц0 В дх
Теперь, чтобы найти скорость диффузии потока, следует найти В и его пространс-
твенную производную, т. е. решить уравнение магнитной диффузии:
дд_Н»^ = 0. (10.43)
р dt
Здесь предполагается, что сопротивление не зависит от пространственного располо-
жения. Кроме того, ток смещения пренебрежимо мал, что характерно для проводни-
ков, в которых основную роль играет ток проводимости. Предполагается также, что
относительная проницаемость равна 1. В одномерном случае (10.43) упрощается до
= (10.44)
dt ц0 dx2
Для решения этого уравнения часто предполагается, что магнитное поле в
ящике растет экспоненциально:
В(0,0 = BQel/x. (10.45)
Это имеет место, если « и. Таким образом, распределение поля в очень толс-
том поршне описывается выражением
t
J Jpt/Uo
/) = Воехр«
(10.46)
Для дальнейшего рассмотрения процессов, сопровождающих сжатие магнит-
ного потока, удобно ввести глубину проникновения магнитного потока 5ф так,
чтобы общий диффузионный поток мог быть выражен через индукцию на повер-
хности, умноженную на 5ф:
Б(0, /)8Ф = Ф(П = р(х, /) dx.
о
(10.47)
После интегрирования (10.46) получается
(10.48)
При тех же условиях скорость диффузии потока равна
(10 49)
10.2. Импульсные магнитные поля 271
Цилиндрическая конструкция
Цилиндрическая конструкция, сжимаемая по направлению ее оси, является
одной из самых эффективных систем сжатия магнитного потока. После сжатия
цилиндра с начальным радиусом ri0 и начальным магнитным потоком Ф = (ri0)2
до радиуса и без учета потерь индукция определяется выражением
ВД-ЫШ)2- <10.50)
Плотность магнитной энергии при этом возрастает пропорционально четвер-
той степени коэффициента сжатия. При использовании для сжатия взрыва про-
цесс сжатия прекращается, когда вся кинетическая энергия стенок цилиндра
преобразуется в энергию магнитного поля.
При работе с реальными металлами приходится считаться с их сжимаемостью
и конечной проводимостью. Как было отмечено выше, конечная проводимость
приводит к диффузии магнитного потока в цилиндрические стенки, которая мо-
жет быть описана скоростью диффузии и(. Сжатие стенок происходит под воз-
действием ударной волны, и при этом внутренние части стенок цилиндра сбли-
жаются со скоростью, соответствующей скорости частиц ир. Для большинства ви-
дов взрывов стенки цилиндра можно рассматривать как свободно движущиеся.
Только в конце процесса сжатия, когда магнитное поле растет очень быстро, ско-
рость уменьшения внутренней поверхности замедляется. В этом случае макси-
мальное поле достигается, когда сумма ц- и ир оказывается равна скорости сбли-
жения внутренних стенок i>lt:
цг=ц-+ц,. (10.51)
Уравнение (10.51) иногда называют условием «возвращения» (turnaround) [Miura
and Herlach, 1985]. Однако такое название вводит в заблуждение, т. к. внутренние
стенки цилиндра могут продолжать движение к его оси со скоростью, соответс-
твующей Of, и могут повредить испытуемый образец.
Решение задачи сжатия магнитного потока в цилиндрической конструкции
может быть выполнено только численно. При этом необходимо совместно ре-
шать магнитогидродинамические уравнения с соответствующими уравнениями
состояния, а также уравнение магнитной диффузии с учетом зависимости прово-
димости от температуры и величины магнитного поля. Кроме того, граница раз-
дела металл—поле может быть нестабильной, а для изучения природы этих неста-
бильностей следует рассматривать трехмерную геометрию.
На практике сжатие цилиндра может быть выполнено либо с использованием
взрывчатых веществ, либо электромагнитным способом. Максимальные значе-
ния индукции зависят от скорости движения внутренних стенок цилиндра, на-
чального магнитного потока и возникновения нестабильностей.
Пример установки для сжатия магнитного потока с использованием взрывча-
того вещества показан на Рис. 10.15 [Herlach and Kennedy, 1973]. В ней начальный
магнитный поток создавался с помощью катушки. На Рис. 10.16 показан график
изменения магнитной индукции в рабочей зоне этой установки. Бросается в гла-
за, что на начальном этапе сжатия магнитная индукция изменяется во времени
почти линейно, а в конце растет по экспоненциальному закону.
272 Глава 10. Применение импульсных электромагнитных полей
Рис. 10.15. Установка для сжатия магнитного потока цилиндрической конструкции.
Обычно начальный внутренний диаметр рабочей камеры составляет 8 см.
Время [мкс]
Рис. 10.16. График изменения магнитной индукции в рабочей зоне установки,
показанной на Рис. 10.15.
Сжатие магнитного потока электромагнитным способом
Сжатие рабочей зоны также можно создать с помощью мощного импульса то-
ка, протекающего через ее поверхность (Рис. 10.17). СилаухБ, связанная с этим
током, сжимает цилиндрические стенки с высокой скоростью. Кинетическая
энергия при этом отбирается от сравнительно большой исходной поверхности и
10.2. Импульсные магнитные поля 273
доставляется в маленький объем за короткое время. Эффективность преобразова-
ния электрической энергии в кинетическую в этой конструкции составляет около
10%. По этой причине для получения сильных магнитных полей требуется очень
большая энергия. Хотя установка ATLAS [Keinigs et al., 2001] была предназначена
в основном для исследований свойств материалов, она может быть использована
для создания мощных магнитных полей по рассматриваемой схеме. Составной
частью этой установки является батарея конденсаторов, способных накопить
23 МДж энергии, использованных в 12 отдельных генераторах Маркса. Батарея
конденсаторов, входящая в эту установку, может накопить энергию 23 МДж. Вы-
ходной импульс тока достигает амплитуды 32 МА с длительностью одной четвер-
ти импульса около 5 мкс. Передаваемая в относительно массивный алюминие-
вый цилиндр (J=5cm, Л = 4см, Дг= 1.6мм) кинетическая энергия составляет
1.5...2.0 МДж, при этом скорость сближения его стенок достигает 14 км/с, что на-
много больше, чем при использовании взрывчатых веществ.
Рис. 10.17. Принцип устройства установки
для сжатия магнитного потока мощным импульсом тока.
Получение импульсов энергии от устройств с компрессией
магнитного потока
Устройства с компрессией магнитного потока могут быть использованы и в
качестве генераторов мощных электромагнитных импульсов очень компактных
размеров. Благодаря большому значению dB/dt такие приборы могут быть ис-
пользованы как для сжатия энергии в маленькие объемы, так и для генерации
мощных импульсов микроволнового излучения. Магнитовзрывные генераторы
обсуждаются с 1970-х гг.
Кроме конструкции со сжимаемыми стенками цилиндра, была исследована
другая цилиндрическая конструкция, показанная на Рис. 10.18. В ней мощное
взрывчатое вещество, расположенное во внутреннем цилиндре, взрывается с од-
ного конца, так что волна сжатия движется вдоль оси к нагрузке. Расширяющаяся
внутренняя труба достигает внешней катушки, которая создавала первоначаль-
ное магнитное поле.
Для получения импульсов с энергией в много мегаджоулей генератор перво-
начального магнитного поля должен обеспечивать значительную энергию. Если
274 Глава 10. Применение импульсных электромагнитных полей
Статор Бетонная
внутренней трубы
в процессе взрыва
Рис. 10.18. Принцип устройства установки для получения импульсов мощного
микроволнового излучения путем сжатия магнитного потока продольным взрывом.
для этой цели использовать батарею конденсаторов, то ее размеры будут опреде-
ляющими для размеров всей установки. По этой причине для мобильных компак-
тных систем может оказаться предпочтительным каскадирование генераторов с
взрывным сжатием потока, т. е. использование одного генератора для создания
первоначального поля в другом генераторе. Такая конструкция показана на
Рис. 10.19 [Reinovsky et al., 1985]. В ней для согласования индуктивности второго
каскада со сравнительно низкой индуктивностью первого используется транс-
форматорная связь между каскадами. Одновитковая катушка первого каскада ок-
ружает катушку второго каскада. Первоначальный магнитный поток в первом
каскаде создается с помощью разряда сравнительно маленькой конденсаторной
батареи.
Недавно созданные генераторы импульсов энергии диапазона многих десят-
ков мегаджоулей, такие как ATLAS, Z и Shiva Star (см. труды, представленные на
Нагрузка
Рис. 10.19. Принцип устройства двухкаскадной установки
с индуктивной связью между каскадами.
10.2. Импульсные магнитные поля 275
Рис. 10.20. Принцип действия усилителя тока с использованием компрессии магнитного пото-
ка в цилиндрической конструкции. Первичный ток приводит в движение стенки ра-
бочей камеры в направлении к статору, а вторичный ток усиливается при уменьше-
нии объема, окружающего петлю статор—нагрузка [L’Eplattenier et al., 2001].
международных конференциях IEEE по мощным импульсам в 1997—2001 гг.),
сделали возможным создание систем компрессии магнитного потока с мощными
источниками тока. В такой системе ток делится на две части (Рис. 10.20). Одна
часть создает первоначальный магнитный поток, а вторая осуществляет его сжа-
тие. Умножение мощности достигается путем аккумуляции энергии в форме ки-
нетической энергии движения стенок рабочей камеры в течение сравнительно
большого времени и передачи ее в нагрузку через статор в течение намного мень-
шего времени. Как и во всех схемах компрессии магнитного потока, потери энер-
гии возникают вследствие проникновения магнитного поля в стенки рабочей ка-
меры на глубину скин-слоя и вследствие преобразования кинетической энергии в
тепло при соударении стенок рабочей камеры со статором.
ГЛАВА
ИСТОЧНИКИ МОЩНОГО ИЗЛУЧЕНИЯ
11.1. Генераторы мощных электронных пучков
В середине 1970-х гг., когда мощные пучки элементарных частиц стали пред-
метом исследования многих ученых, начались поиски эффективных, мощных ис-
точников излучения, при фокусировке которого достигались бы плотности мощ-
ности свыше 100 ТВт/см2 [Beams, 1975, 1977; Yonas, 1978]. Такие плотности мощ-
ности требовались для проведения экспериментов в области ядерного синтеза с
инерциальным удержанием плазмы. При этом для извлечения энергии ядерного
синтеза маленькую «пилюлю» из твердой смеси дейтерия и трития сжимают в 1000
раз с помощью воздействия на ее внешние стенки интенсивным потоком излуче-
ния. Затем сжатое ядерное топливо «поджигается» в какой-то точке, и волна ядер-
ного взрыва захватывает весь объем топлива. Время сжатия и время «горения» оп-
ределяются инерцией стенок и содержимого «пилюли». Чем сильнее сжато содер-
жимое «пилюли», тем большая доля его вступит в реакцию термоядерного синтеза.
Довольно скоро стало ясно, что интенсивный импульсный пучок электронов
является плохим выбором для этой цели как из-за их длинного пробега в вещест-
ве, так и из-за тормозного1* излучения, создававшегося в процессе взаимодейс-
твия электронов с материалом мишени, вызывавшего нагрев топлива внутри «пи-
люли» и тем самым препятствовавшего его сжатию до высокой плотности.
Хотя ускорители электронных пучков для ядерного синтеза не стали развивать-
ся, исследования в этой области способствовали применению их в других областях.
В настоящее время мощные импульсные электронные пучки применяются:
• для поверхностной обработки различных материалов [Muller et al., 2002],
• для накачки лазеров на эксимерах [Sethian et al., 2001 ],
• как источники мощного излучения в импульсной рентгеновской радиогра-
фии [Cooperstein, 2002],
• для создания мощного импульсного СВЧ-излучения [Granatstein and
Alexeff, 1987].
В этом разделе представлен краткий обзор первых трех областей применения
мощных импульсных пучков электронов.
° Сейчас более распространен термин «переходное излучение». — Примеч. пер.
11.1. Генераторы мощных электронных пучков 277
11.1.1. Силы, создающие пучки электронов и транспортные
ограничения
В мощных пучках траектории частиц сильно зависят от создаваемых самими
частицами электрического и магнитного полей. Эти поля следует рассчитывать
как самосогласованные с учетом распределения зарядов и плотности тока в пуч-
ке и в комбинации с внешним воздействующим полем. В общем случае систему
связанных дифференциальных уравнений можно решить только численно. Ме-
тод решения таких задач (метод конечно-размерных частиц в ячейке) был опи-
сан в подразд. 6.1.3.
Аналитическое решение для задачи движения коллектива заряженных частиц
возможно только для простых геометрий, являющихся приближением к реаль-
ным пучкам. В частности, поперечная составляющая скорости частиц должна
быть меньше, чем продольная. Для азимутально-симметричного цилиндрическо-
го пучка, чья длина много больше диаметра, имеет место следующее соотноше-
ние электрических (Гу(еп) и магнитных сил (Fy(mag)):
F^ у,г(1-Л) P2d-/m) nl n
F-M c2(l-Z) l-Л ’
Здесь/— доля нейтрализации заряда,
fm — доля уменьшения тока,
Р — отношение аксиальной составляющей скорости частиц vz к скорости
света с.
Это означает, что в не нейтрализованном пучке (fi=fm = O) направленные
внутрь магнитные силы всегда меньше, чем направленные наружу электростати-
ческие силы отталкивания частиц.
Когда пучок частиц инжектируется в вакуумную зону, пространственный за-
ряд пучка может сильно ограничить его распространение. Рассмотрение этой
проблемы в полностью трехмерном случае может оказаться весьма сложным.
Аналитическое решение может быть получено для цилиндрического пучка с ра-
диусом /о, инжектируемого в металлическую трубу радиуса R с анодным напряже-
нием, дополненным магнитным полем, направленным вдоль оси и удовлетворя-
ющим условию Б02/8л » петс2у, где пе — плотность электронов в пучке, Во — ин-
дукция магнитного поля и у = (1 — {?/с2)~1/2 — релятивистский фактор.
Определим начальную кинетическую энергию электронов как Rr, а их ко-
нечную энергию как И^. С учетом требования, чтобы относительное уменьшение
энергии частиц £ = — WoVW'r было мало, для максимального тока пучка по-
лучается следующее выражение:
г 4л/ис„о/ 1
/=------(11-2)
ц0 е 1 + 21п/?/г0
В предположении, что энергия электронов пучке равна 100 кэВ (у = 1.195,
р = 0.547), £ < 0.1, R/rQ = 2, получается ток пучка < 77 А. Энергия пучка, таким об-
278 Глава 11. Источники мощного излучения
разом, оказывается менее 7.7 МВт. Намного большая энергия электронного пуч-
ка может быть достигнута, если его инжектировать в нейтрализующую среду, та-
кую, например, как плазма.
О других ограничениях на ток из-за воздействия магнитных сил и нестабиль-
ностях в плазме можно узнать из литературы [Bogdankevich and Rukhadze, 1971;
Bogdankevichetal., 1970].
11.1.2. Источники электронов с большими токами
Большие потоки электронов могут быть получены от источников либо боль-
шой площади, либо с высокой плотностью тока. При этом речь идет о плотностях
тока порядка 104 А/м2 и площадях в несколько сот квадратных сантиметров. Су-
ществует два основных типа источников электродов: термокатод и катод, покры-
тый плазмой. Термокатод обеспечивает эмиссию с большой плотностью тока,
только если он нагрет до высокой температуры (см. разд. 4.1).
Намного легче получить источник электронов с большой плотностью и боль-
шой площадью при использовании плазмы. Плазма при этом может быть получе-
на при холодной полевой (автоэлектронной) эмиссии электронов с помощью
множества волокон, равномерно покрывающих поверхность катода. Для этих це-
лей лучше всего подходит графит. Если напряженность электрического поля на
вершинах углеродных волокон превышает несколько сот киловольт на сантиметр,
то ток автоэлектронной эмиссии нагревает волокна, испаряет материал катода^ и
вызывает десорбцию газов* 2). В конце концов возникает пробой этого газового
слоя и плазма начинает распространяться в аксиальном и радиальном направле-
ниях. Детальные исследования показали, что основным источником плазмы яв-
ляется искрение вдоль поверхности волокон [Krasik et al., 2001]. Хотя расширение
слоя плазмы и является необходимым для формирования источника электронов
большой площади, это может создать проблему, если приведет к замыканию
плазмой ускорительного промежутка.
Одна из простых и эффективных конструкций катода имеет в своей основе
большую площадку из связок углеродных волокон [Vasilevskii et al., 1980, 1981,
1986, 1988]. Соединение каждой связки волокон с высоковольтным генератором
через резистор не только обеспечивает включение всех связок в наборе, но так-
же подавляет флуктуации электронного тока и улучшает стабильность работы
катода. Кроме того, этот источник обеспечивает малую скорость генерации
плазмы, что позволяет при его работе в течение нескольких десятков микросе-
кунд избежать плазменного замыкания. Одновременное включение всех эмис-
сионных ячеек достигается при скорости нарастания импульса напряжения свы-
ше 1012 В/с.
1 Испарение острия резко снижает напряженность поля, что приводит к прекращению эмиссии с
этого участка. — Примеч. пер.
2) Возможна и сорбция газов. Поэтому никому не удалось добиться стабильных характеристик
подобных устройств. — Примеч. пер.
11.1. Генераторы мощных электронных пучков 279
Кроме волоконного катода, в качестве источников электронов применялись
ферроэлектрические катоды [Krasik et al., 2001]. В этом случае также электронная
эмиссия возникает благодаря поверхностному искрению, инициированному в
точках, где находятся тройные границы раздела металл—диэлектрик—вакуум.
11.1.3. Импульсные электронные диоды
По аналогии с вакуумными электронными трубками можно назвать прибор
для ускорения заряженных частиц, состоящий из двух электродов в вакууме,
электронным диодом. В электронном диоде катод включает в себя источник
электронов. Когда большое электрическое поле приложено между катодом и ано-
дом, электроны «высасываются» (туннелируют) из катода и ускоряются на пути к
аноду.
Если анод прозрачен для электронов, пучок может проникнуть через него и
распространяться по направлению к мишени. В большинстве диодов с большим
током электроны ускоряются в режиме с ограничением пространственным заря-
дом, когда электрическое поле обращается в нуль на поверхности катода. При ре-
лятивистских энергиях электронов для плотности тока, ограниченной пространс-
твенным зарядом, справедливо выражение [Humphries, 1990]:
Eoffloc3 [<j(Yo)]2
ed2 2
Yo = 1 + et/0//n0c2.
(П.З)
При нерелятивистских энергиях это выражение соответствует хорошо извест-
ному закону Чайлда—Ленгмюра.
4е0 [2Г
9 \т0 d2
(Н4)
где Uq — ускоряющее напряжение, приложенное к диоду,
d— расстояние анод—катод,
Уе— максимальная плотность тока, которая может быть достигнута в диоде
с расстоянием анод—катод d при напряжении Uq.
При больших токах может проявляться пинч-эффект, т. е. сжатие пучка элект-
ронов в маленькое пятно на аноде. Это сжатие происходит под воздействием
сильного азимутального магнитного поля, создаваемого самим электронным по-
током. При напряжении ускорения свыше 1 МВ и токе более 100 кА благодаря
пинч-эффекту плотность тока может превысить 1 МА/см2.
Хотя этот эффект сжатия пучков и представляет интерес для формирования
точечных источников тормозного импульсного рентгеновского излучения, необ-
ходимых для радиографии быстроперемещающихся объектов, для создания пуч-
ков с однородной плотностью тока на большой площади он является помехой.
Применение именно таких пучков электронов будет рассмотрено ниже.
280 Глава 11. Источники мощного излучения
11.1.4. Поверхностная обработка материалов
Электроны с высокой энергией при бомбардировке твердых тел отдают свою
кинетическую энергию поверхностному слою вещества в форме тепла. При этом
поверхностный слой толщиной до 100 мкм нагревается до температуры выше
точки плавления (Рис. 11.1). Глубина расплавления, конечно, зависит от вида ве-
щества, энергии электронов, плотности энергии и длительности импульсов воз-
действия. Обычно достаточно плотности энергии в 3... 15 кДж/см3 для нагрева
различных веществ от комнатной температуры до температуры плавления. Таким
образом, при достижимой плотности энергии в электронном пучке порядка не-
скольких МВт/см2 и глубине проникновения электронов с энергией 100...400 кэВ
порядка 20... 100 мкм для расплавления достаточно импульса длительностью не-
сколько десятков микросекунд. При этой длительности еще можно пренебречь
потерями тепла из расплавляемой области. При использовании пучков электро-
нов с большим током может быть получена скорость нагревало 109оС/с при пло-
щади расплавления в несколько сот квадратных сантиметров и глубине в десятки
микрометров. После окончания импульсного нагрева, вследствие отвода тепла в
объем материала, происходит закалка поверхностного слоя. При этом скорость
охлаждения достигает 107оС/с, а поверхностный слой приобретает аморфную или
нанокристаллическую (для металлов) структуру, что повышает его устойчивость к
коррозии и износу, а также увеличивает твердость. Кроме того, таким способом
можно создавать сплавы из тонких слоев поверхностного покрытия с материалом
основы.
На Рис. 11.2 приведена схема установки GESA (Научно-исследовательский
центр в Карлсруэ), представляющей собой генератор импульсных пучков элекг-
Поверхностный нагрев:
Скорость < 109сС/с
Длительность < 40 мкс
Расплавленный слой: Реструктурированный
Глубина < 100 мкм поверхностный слой
Скорость охлаждения < 107оС/с
Рис. 11.1. Схематическая иллюстрация метода поверхностной обработки металлов электронным
пучком. Благодаря быстрому охлаждению расплавленного поверхностного слоя в нем
происходят структурные и фазовые изменения, увеличиваюшие твердость и устойчи-
вость к износу, коррозии и окислению.
ронов. Для создания прямоугольных импульсов напряжения используются четы-
ре каскада АС-звеньев, заряжаемых параллельно и разряжаемых последователь-
но, как в генераторе Маркса. Каждый каскад, в свою очередь, состоит из восьми
АС-цепей и одной АС-цеп и Источником электронов является катод состоящий
11.1. Генераторы мощных электронных пучков 281
1 С 1
Высокое п
напряжение Разрядник
Блок
управления
f*
Рабочая
камера
I длительностью
| импульсов
||| «— Клапан
Магнитная
катушка
Электронные
пучок
Мишень
L8
Рис. 11.2. Схематическое изображение установки для получения импульсных электронных пуч-
ков GESA (энергия электронов 50... 150 кэВ, ток <700 А, энергетический поток на
мишени < 50 Дж/см2).
из 700 связок графитовых волокон, как было описано выше, причем каждая связ-
ка соединена с высоковольтным генератором через свой резистор [Engelko et al.,
2001а, 2001b]. Эмиссионная площадь катода 700 см2.
Первоначально приходящий импульс напряжения целиком прикладывается
на пространство катод—сетка. Это гарантирует однородное и быстрое включение
всех участков поверхности катода. После начала эмиссии напряжение делится
между пространствами катод—сетка и сетка—анод.
Магнитная фокусирующая система состоит из шести катушек, направляющих
электронный поток через передающую секцию установки длиной 50 см к мишени
и позволяющих изменять диаметр пучка в пределах 6... 10 см.
Энергию электронов можно изменять в пределах 50...150 кэВ. Ток в пучке
электронов может достигать 700 А. Схема управления длительностью импульсов
позволяет регулировать длительность в пределах 5...40 мкс. На мишени может до-
стигаться плотность тока 1...20 А/см2 при плотности энергии до 50 Дж/см2. Этого
вполне достаточно для адиабатического расплавления любых металлов.
Обработка импульсным электронным пучком очень успешно используется
для создания покрытий из сплава MCrAlY, которые широко применяются для за-
щиты от окисления лопаток газовых турбин, работающих в агрессивной атмосфе-
ре при температуре свыше 900°С.,) Без защитного покрытия металл, из которого
° MCrAlY — сплав, где М — кобальт и/или никель, a Y — иттрий и/или, по меньшей мере, один
эквивалентный металл из группы, содержащей скандий и редкоземельные элементы. — Примеч пер.
282 Глава 11. Источники мощного излучения
делают лопатки турбин, в этих условиях быстро прогора< Толщина покрытия со-
ставляет около 200 мкм, что примерно в 10 раз больше, чем глубина проникнове-
ния электронов при обработке. По этой причине металлическая основа лопаток
воздействию импульсной тепловой обработки не подвергается.
После воздействия импульса длительностью 30 мкс с энергией 120 кэВ макси-
мальная скорость охлаждения достигает 2.5 х 106оС/с, что приводит к образова-
нию стекловидного поверхностного слоя толщиной 20 мкм. Как показано на
Рис. 11.3, в расплавленной зоне первоначальная двухфазная структура меняется
на однофазную. (Для этого использовалось обычное выявление фазовой структу-
ры травлением.) При этом шероховатость поверхности значительно уменьшает-
ся, а ее твердость увеличивается с 440 до 1200 HV [Strausset et al., 2001].
Рис. 11.3. Защитный слой MCrAlY после обработки импульсным электронным пучком В верх-
ней части микрофотографии показан реструктурированный поверхностный слой. В
нижней части — исходная двухфазная структура.
Когда слой MCrAlY подвергается на воздухе нагреву до 1000°С, алюминий
мигрирует к поверхности, где начинает расти окисная пленка из А12О3, которая
защищает находящийся ниже материал от дальнейшего окисления. Стабильность
слоя MCrAlY непосредственно определяет долговечность защитного оксидного
слоя.
Увеличение эффективности использования энергии очень важно для повы-
шения устойчивости энергосистем. Газовые турбины имеют наибольшую термо-
динамическую эффективность среди других машин. Еще большее повышение
эффективности могло бы быть достигнуто при больших значениях температуры
газа в турбине. В свою очередь для этого требуется термически изолировать по-
верхность лопаток турбин, чтобы удерживать на допустимом уровне температуру
основы лопаток и защитного оксидного слоя.
Пленка из термически выращенного оксида не только защищает подложку от
дальнейшего окисления, но и служит границей слоя, являющегося тепловым ба-
рьером, состоящего из окисей иттрия и циркония Долговечность такой системы
11.1. Генераторы мощных электронных пучков 283
ограничивается повреждением наружного оксидного слоя, что влечет за собой
разрушение и теплозащитного слоя. Этот вид отказа зависит от структуры пленки
из термически выращенного оксида. В связи с тем что нанесенный методом плаз-
менного распыления слой MCrAlY обычно очень шероховатый, его подвергают
механической полировке. Поверхностная обработка импульсным пучком элект-
ронов также сглаживает поверхность, но еще, как отмечалось выше, создает слой
с аморфной или нанокристаллической структурой. Как показано на Рис. 11.4, эти
два способа поверхностной обработки приводят к различным результатам. После
механической обработки растут чешуйки 0-А12О3, а после обработки поверхности
импульсным электронным пучком образуется чистый а-А12О3. В последнем слу-
чае выращенные кристаллы из окисей иттрия и циркония имеют минимальные
поперечные напряжения. Поэтому и их долговечность ожидается большей.
Рис. 11.4. Структура оксидной пленки на поверхности защитного слоя NiCrAlY после 200 часов
при 950°С: после обычной полировки нанесенного плазменным распылением пок-
рытия (слева), после обработки импульсным электронным пучком на установке
GESA (справа).
Другим, очень привлекательным, применением обработки импульсным
электронным пучком является создание сплавов на поверхностях различных
металлов. Например, создание сплава AlFe на поверхности стали проиллюстри-
ровано на Рис. 11.5. Для этого алюминиевую фольгу толщиной 18 мкм помеща-
ют на стальную поверхность. В нижней части Рис. 11.5 показано, как меняется
концентрация алюминия по глубине поверхностного слоя при использовании
1...3 импульсов и одного или двух слоев фольги. Наиболее однородное распре-
деление до глубины 20 мкм получается при использовании последовательности
из трех импульсов, которые сплавляли последовательно два слоя фольги
[Muller et al., 2005].
Создание поверхностного защитного слоя (у термически толстых образцов)
также использовалось для уменьшения коррозии стали в системах охлаждения
быстрых реакторных установок с использованием в качестве теплоносителя
свинца и сплава свинец-висмут [Muller et al., 2000, 2003]. Эти установки разраба-
тывались для преобразования долгоживущих продуктов ядерных реакций, таких
как плутоний и актиниды, получающихся в силовых ядерных реакторах, в эле-
менты с более коротким периодом полураспада или менее радиоактивные. При
температуре свыше 600°С никель легко растворяется в жидком свинце или сплаве
свинец-висмут. Защитный оксидный слой может формироваться на поверхности
284 Глава 11. Источники мощного излучения
слоя AI со стальной основой слоем А1
Рис. 11.5. Формирование сплава AlFe на поверхности стали. Фольга и поверхностный слой
сплавляются и перемешиваются под воздействием импульсного электронного пучка.
стали, если в жидких тяжелых металлах содержание кислорода поддерживается
близким к 10-5 атомных процентов. Однако этот слой, состоящий из ферромаг-
нитной и феррохромной шпинелей, растет весьма быстро, что приводит к интен-
сивному окислению стали и долговременной нестабильности. Этого можно избе-
жать, наплавив на поверхность стали слой алюминия с помощью импульсного
электронного пучка на установке GESA. Для этой цели тонкая алюминиевая
фольга помещается на поверхность стали и сплавляется с ней. образуя слой тол-
щиной несколько десятков микрометров. При этом алюминий перемешивается
со сталью вследствие конвекции, а затем, вследствие быстрого охлаждения, «вмо-
раживается» в сталь. Растворенный в жидком свинцово-висмутовом теплоноси-
теле кислород взаимодействует с алюминием, в результате чего образуется про-
чная защитная пленка из окиси алюминия, защищающая стальную подложку от
11.1. Генераторы мощных электронных пучков Z85
коррозионного воздействия. Эксперименты, проведенные в Физико-энергети-
ческом институте в г. Обнинске, и «Прометее»!), С.-Петербург, показали, что при
скорости потока 1 м/с только сталь с поверхностным содержанием алюминия
10% выдерживает 4000 ч без разрушения.
Некоторые применения — особенно обработка деталей машин и
механизмов — требуют высокой пространственной и временной однородности и
стабильности пучка электронов. Хорошо известно [Pareira, 1983; Engelko et al.,
2000,2001], что взаимодействие между электронами и мишенью приводит к отра-
жению части электронов и созданию ионов, которые изменяют профиль плот-
ности тока в пучке с прямоугольного на гауссовский. Более того, было открыто,
что имеют место осцилляции в пучке на частоте несколько мегагерц, причем их
пространственная структура и амплитуда зависят от отношения магнитных полей
вблизи мишени и вблизи анода. Исследования этих нестабильностей и путей уп-
равления ими были выполнены в работе [Muller et al., 2002а, 2002b].
11.1.5. Высокоинтенсивные KrF-лазеры
Вследствие своего высокого КПД, короткой длины волны (248 нм) и высокой
однородности луча KrF-лазеры в настоящее время рассматриваются как наиболее
привлекательные инструменты для получения энергии из ядерного синтеза
[Bodner et al., 2000]. Для исследования возможности получения мощности излу-
чения в несколько сот тераватт с энергией в несколько мегаджоулей, КПД свыше
5% и при этом с доступной стоимостью была запушена программа разработки ос-
новных технологий в этом направлении, объединившая усилия нескольких лабо-
раторий [Sethian et al., 2001].
Для накачки KrF-лазеров требуются пучки электронов с большой площадью
и током. Принята концепция разработки модульной конструкции, позволяющая
увеличивать мощность системы путем простого увеличения числа модулей в ней.
Основными задачами при разработке таких систем являются достижение их дол-
говечности, КПД и ценовой эффективности. При этом требуется создать долго-
вечный эмиттер электронов, прозрачную изоляционную структуру, отделяющую
лазерный узел от генератора электронов, систему охлаждения и подавления тур-
булентностей в газе лазера и, наконец, долговечную оптическую систему.
Обычно один модуль генератора пучка электронов обеспечивает получение
тока 100 кА при энергии электронов около 500 кэВ и длительности импульсов в
несколько сот наносекунд. На Рис. 11.6 показана конструкция системы
ELECTRA, созданной в Морской исследовательской лаборатории (Naval
Research Laboratory) в Вашингтоне (США) [Hegeler et al., 2002].
В этой системе используется первичная цепь с конденсаторным накопителем
энергии и повышающим трансформатором. Для формирования импульсов с
плоской вершиной применены две длинные линии с водяной изоляцией. На
электронный диод (генератор электронов) энергия поступает через разрядник,
>) ФГУП ЦНИИ конструкционных материалов «Прометей». — Примеч. пер.
286 Глава 11. Источники мощного излучения
Т рансформатор 1:12
Ключ
первичной цепи
(с воздушной -
изоляцией)
Линия
формирования
импульсов
!П\
Выходной ключ
(изоляция SF6,
лазерное управление)
Катод
Генератор
электронов
Конденсатор-
ная —
батарея
Магнит \
/ 0.5....1.5кГс Лазер
: Прозрачная
для электронов
изоляционная
структура
Рис. 11.6. Система ELECTRA: 500 кВ, 100 кА, 100 нс, частота следования импульсов 5 Гц.
управляемый лазером. Для исключения сжатия пучка электронов, поступающих
в газовую камеру KrF-лазера, используется сильное аксиальное магнитное поле.
На Рис. 11.7 показана конструкция KrF-лазера. Главными элементами, опре-
деляющими долговечность этого устройства, являются катод и прозрачная для
электронов структура (фольга), обеспечивающая изоляцию между вакуумом и га-
зом в рабочей камере лазера. В качестве источника электронов наиболее долго-
вечными представляются катоды из графитовых волокон или со структурой ме-
талл-диэлектрик. Для обеспечения высокой эффективности катодная эмиссия
должна быть ограничена областями между ребрами жесткости, поддерживающи-
ми изоляционную фольгу. Кроме того, для компенсации вращения электронного
пучка, вызываемого воздействием магнитного поля, катод необходимо с помо-
щью его крепления вращать в противоположную сторону.
Эксперименты показали, что пучки электронов с большой площадью подвер-
жены нестабильностям, ведущим к рассеянию энергии, а также к большой расхо-
димости электронов [Friedman et al., 2000]. Для подавления высокочастотных ко-
лебаний был построен катод с замедляющей структурой, в которой отдельные
сегменты катода соединялись между собой через резистивные элементы.
Большая долговечность изоляционной фольги, отделяющей вакуум от газа в
рабочей камере лазера (свыше 108 импульсов), возможна только при условии ее
эффективного охлаждения. Используемый для этого рециркулятор не только ох-
лаждает фольгу, но и устраняет турбулентности в газе до прихода следующего им-
пульса. Для решения этой проблемы в Морской исследовательской лаборатории
была разработана система, в основе которой использовались своеобразные жалю-
зи [Hegeler, 2003]. Эта система между импульсами направляла газ прямо к фольге,
а во время подачи импульса быстро преобразовывала турбулентный поток в ла-
минарный путем открытия жалюзи.
11.1. Генераторы мощных электронных пучков 287
Вход
Рециркулятор
лазерного
газа
Выходное
окно
лазера
Катод
Рис. 11.7. Конструкция KrF-лазера с накачкой электронным пучком.
Направление
магнитного
поля
К генератору
импульсов
напряжения
Пучок Ребра
электронов жесткости
лазера
11.1.6. Импульсная рентгенография
Импульсная рентгенография при гидродинамических экспериментах, осу-
ществляемых с использованием взрывчатых веществ, остается одним из главных
побудительных мотивов для исследований интенсивных электронных пучков и
связанных с ними разработок в области импульсов большой мощности. В част-
ности, в таких экспериментах проводится изучение на моделях ядерного оружия
преобразования актинидов в неделящиеся металлы при взрыве, направленном
вовнутрь. В отличие от промышленных рентгенографических установок, в кото-
рых для уменьшения повреждения анода и увеличения его долговечности элект-
роны распределяют по его площади (чтобы ограничить плотность тока), источни-
ки рентгеновского излучения высокой интенсивности для гидродинамических
экспериментов являются приборами одноразового действия.
В таких источниках главными требованиями являются высокое пространс-
твенное разрешение, достаточная для проникновения через исследуемые объек-
ты энергия и интенсивность излучения в зоне расположения детекторов. Кроме
288 Глава 11. Источники мощного излучения
того, для отслеживания временных изменений в объекте во время взрыва жела-
тельна возможность получения нескольких импульсов излучения подряд.
На Рис. 11.8 изображена конструкция рентгенографической установки с то-
чечным источником излучения, наиболее широко применяемой для получения
изображений в динамических экспериментах Точечный импульсный источник
фотонов с высокой энергией, создаваемых тормозным излучением, проецирует
изучаемый объект на фотопленку большого размера или другую систему записи
изображений.
Рис. 11.8. Конструкция рентгенографической установки с точечным источником излучения,
применяемая для исследования быстропротекающих процессов
Разрешение в такой установке в основном определяется размерами источника
излучения, которые зависят от его конструкции. Целью является уменьшение его
размеров до долей миллиметра. В настоящее время исследованы четыре различ-
ные диодные структуры (Рис. 11.9) [Maenchen et al., 2002]. Источник рентгеновс-
кого излучения с самосжатым пучком электронов работает при токе свыше крити-
ческого значения
U = 8.5^ - кА, (11.5)
где Rc — радиус катода,
d— аксиальный зазор в вакууме.
Этот ток создает сильное азимутальное магнитное поле, которое сжимает пу-
чок электронов на их пути к плоскости анода. Этот эффект усиливается под воз-
действием движущихся в противоположном направлении положительных ионов,
выбитых электронами из анода. Таким образом, формируется маленькое фокус-
ное пятно электронного пучка на аноде. Недостатком этого источника рентге-
новского излучения является образование плазмы в прианодной области, кото-
рая может распространиться на все пространство катод—анод и замкнуть его.
Кроме того, «помахивание» электронного пучка в процессе его сжатия создает га-
ло на рентгеновских снимках. Типовое значение размера излучающей поверхнос-
ти в этих диодах составляют 2 мм, а плотность энергии электронного пучка со-
ставляет около 1 ТВт/см2.
] 1.1. Генераторы мощных электронных пучков 289
Самосжимаемые
Рис. 11.9. Конструкции диодов для создания интенсивного рентгеновского излучения:
а) источник рентгеновского излучения с самосжатым пучком электронов;
б) параксиальный диод, справа показаны траектории электронов;
в) диод со стержневым анодом;
г) диод с магнитной иммерсией.
Более стабильный импеданс и стабильные размеры излучающего пятна до-
стигаются в параксиальном диоде, показанном на Рис. 11.96. В этих диодах созда-
ется широкий электронный пучок, который поступает в газонаполненную каме-
ру. В ней за несколько наносекунд электроны ионизируют газ. При этом про-
странственный заряд электронов компенсируется плазмой, а магнитное поле
фокусирует пучок электронов в маленькое пятно на поверхности мишени. Из-за
того, что в этих диодах зазор катод—анод довольно большой, а плотность элект-
ронного тока мала, расширение плазмы из камеры незначительно, что и обеспе-
чивает высокую стабильность импеданса. В общем параксиальные диоды были
настоящей «рабочей лошадью» в установках для импульсной рентгенографии в
течение многих десятилетий.
Совсем недавно привлекли к себе внимание в качестве источников рентгенов-
ского излучения диоды со стержневым анодом (rod pinch) [Cooperstein et al., 2001].
Такая конструкция показана на Рис. 11.9в. В ней анод заканчивается стержнем ма-
лого диаметра, проходящим через выемку в катоде. Электроны с катода самосжи-
маются на анодном стержне. Размер излучающего пятна определяется исключи-
тельно диаметром стержня, который, впрочем, из-за расширения плазмы вокруг
его поверхности увеличивается при работе. В этой конструкции диаметр излучаю-
щего пятна был достигнут менее 1 мм. Большинство электронов попадают на
анодный стержень в радиальном направлении, что уменьшает интенсивность
290 Глава 11. Источники мощного излучения
излучения в желаемом фронтальном направлении. Несмотря на это, диоды со
стержневым анодом стали надежными источниками высокоинтенсивного
излучения для радиографии при ускоряющем напряжении до 6 МВ.
В отличие от диодов со стержневым анодом диоды с магнитной иммерсией
(magnetically immersed diode) работают при отрицательной полярности
питающего напряжения (Рис. 11.9г) [Maenchen et al., 2002]. Эмиттер (катод) в них
представляет собой очень маленькую иглу, расположенную в сильном магнитном
поле, создаваемом соленоидом. Это поле удерживает орбиты электронов в преде-
лах узкого цилиндра. Диаметр этого цилиндра определяет размер излучающего
пятна на аноде. Однако очень высокая плотность тока на поверхности анода со-
здает горячую плазму, ионы которой взаимодействуют с электронами, что порож-
дает нестабильность пучка электронов. Кроме того, вращение пучка электронов
также увеличивает эффективный диаметр излучающего пятна.
Применительно к источникам тормозного рентгеновского излучения из ме-
таллов с большим атомным числом доза излучения на расстоянии 1 м на 1 кулон
заряда равна
12.9С/2 8 ехр|- .(^ + О-5)РД (11.6)
[ 0.67л J
где U — ускоряющее напряжение в МВ,
Р±— релятивистская компонента скорости электронного пучка, поперечная
к радиографической оси.
Таким образом, чтобы достичь высоких доз излучения, предпочтительно ис-
пользовать большое ускоряющее напряжение. Рассеяние излучения объектом
вызывает образование шумового фона на рентгеновском изображении. При этом
рассеивание увеличивается с увеличением свободного пробега излучения через
объект. Для объектов, изготовленных из металлов с высоким атомным числом,
коэффициент ослабления рентгеновского излучения имеет минимум при
3...4 МэВ и увеличивается при более высоких энергиях. Очевидно, что минимум
коэффициента ослабления соответствует максимуму среднего свободного пробе-
га. Таким образом, имеется верхний предел энергии ускорителей для создания
рентгеновского излучения, и ее увеличение выше него уже не дает соответствую-
щего увеличения дозы излучения. Более того, полезная для формирования рент-
геновского изображения доза является сложной функцией от спектра тормозного
излучения, коэффициентов поглощения материалов, применяемых в исследуе-
мом объекте, и спектральной чувствительности детектора изображения. Таким
образом, при планировании экспериментов с рентгенографией быстропротекаю-
щих процессов приходится проводить детальный аналитический, численный и
экспериментальный анализ [Ekdahl, 2001].
Разрешение на получаемых изображениях, кроме упомянутых выше причин,
сильно зависит от движения объекта. Ударное давление при гидродинамических эк-
спериментах с использованием высокомощных взрывчатых веществ достигает мно-
гих мегабар, а соответствующая такому давлению скорость — 1 см/мкс. Для обеспе-
чения разрешения в 1 мм, таким образом, необходимо подавать на источник рентге-
новских лучей импульсы ускоряющего напряжения длительностью 100 нс и менее.
11.2. Ионные пучки большой мощности 291
11.2. Ионные пучки большой мощности
Интенсивные пучки легких ионов являются перспективным инструментом в
исследованиях свойств материалов [Kanel et al., 1998], получения энергии при
термоядерном синтезе [VanDevender and Bluhm. 1999] и бор-нейтронозахватной
терапии (boron neutron capture) [Bluhm and Hoppe, 1999]. Эти пучки ионов обес-
печивают технически простой и дешевый путь доставки высокой плотности мощ-
ности (до нескольких десятков ТВт/г) в конденсированные среды. Ключевым
элементом установок для создания ионных пучков является ускоритель, состоя-
щий из двух каскадов: инжекторного диода и ускорительного диода, причем оба
они работают при плотности энергии в несколько десятков ГВт/см2 и напряжен-
ности электрического поля в несколько МВ/см. И плотность мощности, и напря-
женность поля в этих установках на два порядка больше, чем в обычных ускори-
телях. Питание установок для создания ионных пучков осуществляется от генера-
тора повторяющихся импульсов длительностью 100 нс, мощностью до 5...7 ТВт и
напряжением до 10 МВ. Наиболее привлекательным подходом для создания та-
ких генераторов считается [Moses et al., 1989] ускоритель с линейной индукцией
HELIA [Ramirez et al., 1985] (см. гл. 7).
Наиболее высокие требования предъявляются к ускорителям для получения
энергии из термоядерного синтеза. В конечном счете каждый модуль ионного ус-
корителя должен быть способен поставить пучок ионов с атомными массами
больше 4, энергией частиц свыше 30 МэВ, энергией импульса более 500 кДж при
уровне мощности больше чем 10 ТВт. Если плотность энергии в ускорительном
зазоре ограничена уровнем менее 10 ГВт/см2, то из ускорителя должен был исхо-
дить пучок ионов с площадью его сечения 1000 см2. Для фокусировки этого пучка
с целью получения плотности мощности свыше ЮТВт/см2 требуется его про-
странственное сжатие более чем в 1000 раз. К тому же в ряде случаев допустимо
лишь очень незначительное расхождение пучка0.
Далее будут рассмотрены последние достижения в разработке подходящих ис-
точников ионов, систем передачи пучка ионов и физике работы ускорителей.
11.2.1. Физика ускорителей
В некоторой степени представляется возможным разделить разработку уско-
рителей легких ионов на три части: разработка источника ионов, инжекторного
диода и ускорительного диода. Хотя и существует взаимосвязь между физикой
источников электронов и ионов, рассматриваемые физические процессы в зна-
чительной мере определяются высокой плотностью энергии в ускорителе.
Инжекторный диод
В этой области было проведено много работ, и ниже будут обобщены их ре-
зультаты [Bailey et al., 1995; Mehlhorn et al., 1994; Hanson et al., 1992; Greenly et al.,
1994,1996; Bluhm et al., 1992; Licht et al., 1998].
*’ Теоретически ограниченное «соотношением неопределенностей», а практически — длиной
волны де Бройля. — Примеч. пер.
292 Глава 11. Источники мощного излучения
Инжекторный диод (Рис. 11.10) состоит из массивного анода и полого катода,
разделенных расстоянием в несколько миллиметров. Импульс напряжения амп-
литудой в несколько мегавольт и длительностью несколько десятков наносекунд
прикладывается к межэлектродному пространству. Перед подачей этого импульса
напряжения на поверхности анода следует создать источник ионов. В большинс-
тве конструкций, однако, источником ионов служит слой плазмы, создаваемый
одновременно с подачей импульса ускоряющего напряжения. Вследствие воз-
действия большой напряженности электрического поля в межэлектродном про-
странстве мгновенно1* начинается автоэлектронная (полевая) эмиссия электро-
нов из катода, приводящая к созданию плазмы.
Прианодный
слой плазмы
Электронная оболочка
(виртуальный катод)
Анод
О
Ионы
Край катода
Прикатодная
плазма
Дрейф ионов
в направлении
ЕхВ
Рис. 11.10. Схематическое изображение инжекторного диода с полым катодом. Сильное элект-
рическое поле вызывает взрывную эмиссию электронов с поверхности катода, со-
провождающуюся образованием плазмы вблизи его краев. Магнитное поле исполь-
зуется для создания препятствия на пути электронов к аноду. Электроны дрейфуют
под действием сил Лоренца в направлении векторного произведения электрическо-
го и магнитного поля и образуют электронную оболочку (виртуальный катод).
В общем случае в диоде текут и электронный, и ионный токи. При ограниче-
нии этих токов пространственным зарядом отношение плотности ионного тока к
плотности электронного тока определяется соотношением
Л V
(И.7)
Это соотношение может быть интерпретировано и другим способом:
j'Jje
(П.8)
° «Мгновенно» — это образное выражение автора. Есть понятие «время выхода электрона», кото-
рое не позволяет получить импульс с нулевой задержкой образования плазмы. — Примеч. пер.
11.2. Ионные пучки большой мощности 293
т. е. плотности токов обратно пропорциональны времени пребывания электронов
и ионов в межэлектродном пространстве. Здесь жизни те и т, определяются выра-
жениями
\dx
T*=k’
О е
(11.9)
Таким образом, доля ионного тока может быть увеличена путем удлинения траек-
торий электронов в межэлектродном пространстве диода. Отклонение электро-
нов может быть достигнуто с помощью магнитного поля, направление которого
перпендикулярно направлению электрического поля. При этом магнитное поле
может быть создано либо самими токами в диоде, либо внешним воздействием. В
первом случае эффективность выхода ионов может достичь 50% [Goldstein and
Lee, 1975; Humphries, 1980], а во втором — 90% [Johnson et al., 1979].
Множество физических явлений в межэлектродном пространстве можно изу-
чать независимо от природы источника ионов, если только этот источник одно-
роден и не расширяется слишком быстро поперек силовых магнитных линий.
Однако в большинстве случаев доминирующим является электронный поток в
диоде вдоль силовых магнитных линий, формирующий электронную оболочку и
виртуальный катод. Первоначально эта электронная оболочка очень тонкая и
дрейфует в направлении вектора, определяемого произведением Е*В
(Рис. 11.10). Его нестабильности, известные как диокотронные (diocotron)
[Buneman, 1966], способствуют распространению электронов поперек межэлект-
родного пространства за несколько наносекунд^. Если электронная оболочка
придвинется близко к аноду, то высокочастотные диокотронные нестабильности,
чье влияние на расхождение пучка ионов незначительно, сменяются низкочас-
тотными нестабильностями, чей период примерно равен времени пролета ионов
через межэлектродное пространство [Lemke and Slutz, 1995]. В этом случае рас-
хождение пучка ионов может оказаться очень сильным.
Возникновение нестабильностей и распространение электронной оболочки
на все межэлектродное пространство оказывают сильное воздействие на работу
диода. Так как в мошных диолах плотность тока обычно ограничивается про-
странственным зарядом, компенсация заряда, которая происходит при расшире-
нии электронной оболочки, приводит к увеличению ионного тока до намного
больших значений, чем определяемые из закона Чайлда—Ленгмюра (11.4). Это, в
свою очередь, приводит к сдвигу виртуального катода ближе к аноду. При этом
11 Явление хорошо известно в двухэлектродных СВЧ приборах со скрещенными полями с 1955 г. и
используется в диокотронных усилителях. Диокотронный эффект заключается в том, что
инжектированный электронный пучок не обладает устойчивостью и при отсутствии замедляющей
системы. В этих условиях возбуждаются волны пространственного заряда с нарастающей амплитудой.
Применяется в магнетронных усилителях для повышения коэффициента усиления. — Примеч. пер.
294 Глава 11. Источники мощного излучения
увеличение магнитного давления способствует достижению нового равновесного
положения [Desjarlais, 1989]. Однако, если увеличившееся диамагнитное поле
сможет проникнуть в приэлектродную плазму (которая является диамагнетиком
и выталкивает магнитное поле), прочность магнитной изоляции в межэлектро-
дном пространстве уменьшится, а затем произойдет деградация импеданса диода.
Все эти заключения были впервые получены путем моделирования с использова-
нием метода конечно-размерных частиц в ячейке (particle-in-cell method) на трех-
мерной, полностью релятивистской электромагнитной модели [Desjarlais, 1989;
Quintenz et al., 1994] для весьма упрощенной геометрии. Для экспериментальной
проверки этих предсказаний было разработано весьма сложное оборудование
[Bailey et al., 1990; Bluhm et al., 1994; Maron et al., 1989; Yoo, 1997]. Использовав-
шийся при этом дисперсионный интерферометр был настолько чувствительным
и прочным, что была достигнута возможность измерения распределения плот-
ности электронов в межэлектродном пространстве диода с разрешением 0.5 мм
по расстоянию и 1 нс по времени. Измерения полностью подтвердили теорети-
ческие предположения [Licht and Bluhm, 2000]n.
На Рис. 11.11 продемонстрировано прекрасное совпадение между результата-
ми экспериментальных измерений плотности электронов и предсказаниями, по-
лученными с помощью аналитической модели [Desjarlais, 1989]
В ходе этих экспериментов было достигнуто более глубокое понимание физи-
ческих процессов в межэлектродном зазоре инжекторного диода, подтвердившее
приведенное выше описание его работы.
Рис. 11.11. Ускоряющее напряжение, ионный ток и линейная плотность электронов NeH3M на
расстоянии 3 мм от поверхности катода. Кроме того, показана расчетная плотность
электронов Nepac4. полученная для t/d и /ion с использованием модели для насыщен-
ного (с постоянной плотностью) распределения электронов.
° Главная сложность создания такого интерферометра заключалась в поляризации пучков. — При-
меч. пер.
11.2. Ионные пучки большой мощности 295
Ускорительный диод
Существующий опыт работы с однокаскадными инжекторными диодами с
магнитной изоляцией показывает, что рабочая стабильность и низкое расхожде-
ние ионного пучка достижимы только при использовании многокаскадных уско-
рителей. Однако в связи с быстрым увеличением сложности системы при введе-
нии в нее дополнительных каскадов, представляется неправдоподобным, что в
ней может быть больше двух каскадов (Рис. 11.12). Ввиду наличия сильных
собственных полей в пучке ионов, между каскадами необходимо вводить
нейтрализацию пространственного заряда. Для этой цели межкаскадная секция
ускорителя должна быть наполнена газом или плазмой и отделена от зоны
высокого вакуума, который требуется в ускорителе.
Инжектор Ускорительный каскад
Магнитные катушки
Рис. 11.12. Схематическое изображение двухкаскадного инжекторного диода. Изолирующее
магнитное поле в ускорительных зазорах устанавливается с помощью шести кату-
шек, питаемых от батареи конденсаторов. Дальнейшее движение ионов происходит
в газонаполненной пролетной трубе.
Ожидания уменьшения расхождения пучка основаны на различии времени
пролета ионами разных ускоряющих промежутков. Таким образом, влияния
нестабильностей не складываются когерентно от каскада к каскаду, а расхожде-
ние ионов должно уменьшиться. Моделирование с использованием метода ко-
нечно-размерных частиц в ячейке (программа «Квиксильвер») [Quintenz et al.,
1994] подтвердило, что при достаточно низких плотностях пучка расхождение ио-
нов может быть значительно уменьшено с помощью дополнительного ускорения
(post-acceleration) [Slutzetal., 1994].
С двухкаскадными ускорительными диодами было проведено лишь несколь-
ко предварительных экспериментов [Lockner et al., 1993; Miyamoto et al., 1992;
Lockner et al., 1994], причем большинство из них при очень низких напряжениях
и мощностях. Несмотря на это, такие эксперименты показали сильное уменьше-
ние расхождения пучка.
Некоторые из этих результатов получены для конструкции, в которой корпус
инжекционного диода был несколько расширен в сторону ускорительного диода.
Так как напряженности электрических полей должны быть одинаковыми по амп-
литуде, виртуальный катод также должен образоваться, и весьма вероятно, что
296 Глава 11. Источники мощного излучения
межэлектродное пространство ускорительного диода будет также заполнено пол-
ностью объемным зарядом электронов. Однако имеется определенное различие
между дополнительным ускорителем и инжектором, которое требует дополни-
тельного обсуждения. Было найдено [Slutz and Desjarlais, 1990], что, как и в одно-
каскадном случае, существует верхний предел ускоряющего напряжения (/2*, за-
висящий от энергии ионов W и прочности магнитной изоляции В, при превыше-
нии которого ток с неограниченной плотностью может возникнуть в каскаде без
образования виртуального анода. Также известно, что при превышении плотнос-
тью однополярного тока в ускорительном промежутке некоторого предела j(U2)
возникают нестабильности, которые препятствуют передаче тока через этот про-
межуток [Birdsall and Bridges, 1961].
Такие же ограничения имеют место и в случае двухполярного тока. Однако они
возникают при напряжениях ниже второго предельного значения не имею-
щего аналогов в теории многокаскадных ускорителей и зависящего от IF и В. Если
электронная оболочка заполнит весь ускоряющий промежуток дополнительного
ускорителя, U2~ = 0. Как можно увидеть на Рис. 11.13, если требуется подавление
нежелательных ионов со стороны инжектора, насыщение ограничивает конечную
энергию электронов на уровне лишь слегка выше, чем критическое напряжение
изоляции Uc, определяемое прочностью магнитной изоляции. С другой стороны,
если виртуальный анод не может создаться, следует допустить возникновение не-
которого количества нежелательных ионов, экстрагируемых со стороны анода до-
полнительного ускорителя. К счастью, расчеты ионного тока, экстрагируемого со
стороны инжектора во второй каскад, показывают, что даже их небольшое коли-
чество влечет за собой значительное увеличение t/2* [Slutz, 1993].
W/Uc
Рис. 11.13. Критические напряжения С/2. и Fz** в ускорительном промежутке дополнительного
ускорителя как функции от энергии ионов нормализованной к критическому на-
пряжению (/сдля магнитной изоляции [Slutz and Desjalais, 1990].
Из обсуждения особенностей дополнительного ускорительного каскада ста-
новится очевидно, что необходимы дополнительные экспериментальные иссле-
дования в этой области. В частности, требуется провести измерения электричес-
ких и магнитных полей с высоким временным и пространственным разрешением
11.2. Ионные пучки большой мощности 297
для идентификации режимов работы и определения существования виртуального
анода. Конечно, наибольший интерес представляют степень уменьшения рас-
хождения пучка ионов и стабильность работы дополнительного ускорительного
каскада. Результаты этих исследований пока что ожидаются.
Источники ионов
В течение последнего десятилетия основным препятствием в разработке уско-
рителей легких ионов было отсутствие подходящих источников ионов. Хотя
предварительно подготовленный источник протонов [Laqua et al., 1995] и был ис-
пользован в экспериментах на установке KALIF для исследования физических
явлений в ускорителях, он не подходит для ускоряющих напряжений порядка
30 МВ. Проблемы при разработке источников ионов связаны со следующими об-
стоятельствами:
• Источник ионов должен излучать однородный поток ионов с плотностью
тока порядка 1 кА/см2 в течение 50 нс, т. е. поставлять » 1015 ионов с каждо-
го квадратного сантиметра на площади в несколько сот квадратных санти-
метров анодной поверхности; 1015 ионов/см2 эквивалентно нескольким
атомным монослоям.
• Форма источника должна соответствовать форме анода. Если источником
ионов является плазма, то может понадобиться проводящая поверхность.
• Источник ионов не должен расширяться в ускорительный промежуток
больше чем на незначительную часть его динамической величины
(5...10 мм).
• Он должен быть готов к эмиссии, когда на диод подается импульс напря-
жения.
• Он должен излучать только один вид ионов.
• Он должен обеспечивать частоту повторения импульсов эмиссии в несколь-
ко герц и долговечность 108 импульсов. Для целей разработки ускорителей
(исследования свойств диодов и систем передачи пучков) достаточно источ-
ников однократных импульсов, но отвечающих всем другим требованиям.
Поверхности всех электродов, включая активную поверхность источников
ионов, всегда покрыты несколькими монослоями загрязнений (см. [Cuneo et al.,
1997; Cuneo, 1999] и ссылки в этих источниках). Основными адсорбатами явля-
ются Н2, Н2О, СО, СО2 и различные виды соединений CnHm, чья энергия связи с
соответствующей поверхностью электрода находится в пределах 0.4... 1.8 эВ
[Cuneo, 1999]. Кроме того, на поверхности могут присутствовать оксиды с боль-
шей энергией связи (1.7...3.5 эВ). Различные приемы очистки (нагрев и высоко-
частотный тлеющий разряд) были применены для устранения загрязнений. Од-
нако при типовых значениях давления в 10“3... 10“2 Па в больших ускорительных
установках скорость восстановления поверхностного загрязнения может дости-
гать нескольких монослоев в секунду. Таким образом, очистка может быть успеш-
ной, только если давление в вакуумной камере ниже, чем 10-3 Па.
Если адсорбенты присутствуют на поверхности электродов вблизи мощного
диода, они будут, конечно, высвобождены либо из-за электронной диффузии к
аноду, либо под воздействием бомбардировки поверхности катода рассеянными
298 Глава 11. Источники мощного излучения
ионами [Vesey et al., 1999]. Было отмечено [Cuneo et al., 1999], что вблизи мощного
диода тепловая десорбция имеет намного более важное значение, чем стимулиро-
ванная.
С этой точки зрения следует различать два типа источников ионов: источники
с полевой эмиссией и источники с эмиссией, ограниченной пространственным
зарядом. Источники с полевой эмиссией, такие как LiF, исследования которых
проводились в Сандии [Cuneo et al., 1997], больше поддаются высвобождению га-
зообразных адсорбатов с их поверхности. Если в плазме образуется слой газа из
адсорбатов, то эмиттер с нулевой работой выхода начинает конкурировать с поле-
вым эмиттером и быстро начинает доминировать в формировании состава пучка
ионов. Это явление было обнаружено на установках PBFAII и SABRE и названо
«проблемой паразитной нагрузки» (parasitic load problem). Если первоначально в
импульсном пучке основную долю составляют ионы лития, то позже в нем прева-
лируют ионы углерода, кислорода и водорода.
В случае активных (плазменных) источников с эмиссией, ограниченной про-
странственным зарядом, таких как TiH, используемых на установке KALIF
[Laqua et al., 1995], поверхностные загрязнения смешиваются с плазмой при ее
возникновении. Так как водород имеет самую большую подвижность, его ионы
доминируют на границе плазмы. По этой причине в выходящем ионном пучке
было обнаружено очень мало ионов углерода, кислорода, титана и т. д. Возмож-
ный путь преодоления влияния загрязнений на состав ионов в пучке открывается
с использованием криогенных источников ионов [Kasuya et al., 1991]. В этих ис-
точниках непосредственно перед подачей импульса напряжения газ впрыскива-
ется на поверхность предварительно охлажденного анода и замерзает в виде тон-
кого слоя, так что повторное загрязнение не успевает образоваться.
11.2.2. Системы передачи ионных пучков
Для получения энергии из реакции ядерного синтеза необходимо обеспечить
эффективную передачу мощного пучка ионов (как легких, так и тяжелых)
(Рис. 11.14). Ранее уже отмечалось, что наиболее предпочтительным способом
транспортировки в этом случае является транспортировка с самостягиванием
пучка. В этом случае объемный заряд пучка становится скомпенсированным, в то
время как магнитное поле, создаваемое самим пучком, достаточно для удержания
частиц, составляющих пучок. Для реализации этого режима требуемый ток пучка
определяется выражением
4е. > (11.10)
где ц, и — общая скорость частиц в пучке и их скорость в направлении, пер-
пендикулярном направлению передачи пучка,
1а — ток Альфвена, который определяется выражением
/„ = 31 X (11.11)
где А — атомный номер ионов,
Z— зарядовое состояние.
11.2. Ионные пучки большой мощности 299
Рис. 11.14. Схематическое изображение передачи пучка ионов с самостягиванием.
На больших временных отрезках передача пучка ионов с самостягиванием
считается невозможной вследствие быстрой ионизации газа пучком ионов, кото-
рая препятствует сохранению достаточно большого тока. Однако проведенные
числовое моделирование [Welch et al., 1996; Welch and Olson, 1996; Rose et al., 1999]
и эксперименты, выполненные в Морской исследовательской лаборатории
[Ottinger et al., 2000], позволяют предположить, что самостягивание может ока-
заться возможным в некотором диапазоне давлений газа. Теория предсказывает,
что существует «окно» давлений для самостягивания вблизи wg ~ Zwb, где ng и пъ —
плотности газа и ионов в пучке соответственно.
ГЛАВА
ИМПУЛЬСНЫЕ РАЗРЯДЫ
В ТВЕРДЫХ ТЕЛАХ И ЖИДКОСТЯХ
12.1. Экстракорпоральная ударная литотрипсия
Наряду с импульсными лазерами литотрипсия была одним из первых успеш-
ных гражданских применений техники импульсов большой мощности. Начиная с
1980 г., экстракорпоральная ударная литотрипсия1* стала наиболее эффективным
методом борьбы с болезнями, вызванными образованием камней в мочевых и
желчных системах [Coleman and Saunders, 1993]. В основе этого метода лежит фо-
кусирование ударных волн, создаваемых вне человеческого тела, на камни, рас-
положенные внутри него. Хотя детальный механизм разрушения камней еше не
полностью ясен, кажется наиболее вероятным, что в нем участвуют прямое и не-
прямое воздействие ударной волны на камни. Прямое воздействие связано с воз-
буждением растягивающих сил вследствие отражения ударных волн внутри кам-
ней, преимущественно вблизи поверхности камней и трещин в них. Непрямое
воздействие обусловлено явлениями в жидкой среде, окружающей камни, вклю-
чающими кавитацию и питтинг [Lokhandwalla and Sturtevant, 2000]. В настоящее
время несколько миллионов пациентов в мире были вылечены этим методом при
весьма незначительных побочных эффектах.
В первых установках для дистанционной литотрипсии для создания ударной
волны использовался электрический разряд в воде, причем разрядник распола-
гался в фокусе эллипсоидального рефлектора. При этом разрушаемый объект
размещался во втором фокусе эллипсоида. Как отмечалось в гл. 2, импеданс раз-
ряда в основном имеет резистивный характер, с небольшой последовательной
индуктивностью. В процессе электрического разряда его канал быстро нагревает-
ся и расширяется, создавая ударную волну в окружающей жидкости В настоящее
время применяются три типа генераторов ударных волн (Рис. 12.1):
• электрогидравлические,
• электромагнитные,
• пьезоэлектрические.
° В русскоязычной литературе чаще используется термин «дистанционная литотрипсия» (ДЛТ) —
Примеч. пер.
12.1. Экстракорпоральная ударная литотрипсия 301
В них используется разряд высоковольтных конденсаторов для создания под-
водной ударной волны. В электромагнитном генераторе применяется плоская ка-
тушка с металлической мембраной, как в подводном громкоговорителе. Импуль-
сный разряд через обмотку катушки индуцирует в мембране вихревые токи, а ме-
ханическое перемещение мембраны при этом создает плоский импульс давления
Акустическая линза используется для фокусирования волны этого давления на
объект. В пьезоэлектрических генераторах используется свойство некоторых ани-
зотропных кристаллов расширяться под воздействием электрического поля. Фо-
кусировка достигается размещением нескольких тысяч отдельных кристаллов на
сферической поверхности.
Электромагнитный
генератор
Пьезоэлектрический
генератор
Электрогидравлический
генератор
Рис. 12.1. Различные конструкции генераторов ударных волн для литотрипсии.
Типичные значения параметров разрядных цепей для различных конструкций
генераторов для литотрипсии приведены в Табл. 12.1 [Coleman and Saunders,
1993]. Электроакустическая эффективность, т. е. отношение акустической энер-
гии к электрической для всех типов преобразователей, составляет 0.1%. Форма
импульса давления, возникающего при электрогидравлическом разряде во вне-
шнем фокусе отражателя, состоит из быстро нарастающего импульса сжатия амп-
литудой до 50 МПа и следующего за ним импульса разряжения амплитудой до
10 МПа (Рис. 12.2). Импульс сжатия длится около 1 мкс, а импульс разряжения —
3...5 мкс. Для разрушения камня на фрагменты с размерами менее 1 мм, которые
могут быть выведены из организма естественными путями, требуется от несколь-
ких сот до нескольких тысяч импульсов. Было найдено, что множество неболь-
ших импульсов более эффективно, чем несколько сильных.
Таблица 12.1. Ъшичные значения параметров разрядных цепей для различных конструкций
генераторов для литотрипсии
Тип генератора Тип нагрузки Напря- жение V [кВ] Емкость С [нФ] Индук- тивность £[нГй] Сопротив- ление R [Ом] Ток/0 [кА] Энер- гия Ео [Дж] КПД [%1
Электрогидравлический Резистивная 10...30 40...200 50...200 « 1 10...30 15 0.5
Пьезоэлектрический Емкостная 2...6 300...800 1000 < 1 1...3 5 0.05
Электромагнитный Индуктивная 5...20 1000...1500 > 1000 < 1 4... 10 50 0.03
302 Глава 12. Импульсные разряды в твердых телах и жидкостях
Не так давно была обнаружена эффективность ударных волн для терапии в
ортопедии и травматологии [Haupt, 1997].
Время [мкс]
Рис. 12.2. Форма импульса давления, возникающего
при электрогидравлическом разряде во внешнем фокусе отражателя.
12.2. Разрушение твердых диэлектриков с помощью
электрических импульсов
«Скрытый» импульсный электрический разряд в твердом диэлектрике с энер-
гией 10... 100 Дж/см3 длительностью несколько микросекунд нагревает разрядные
каналы до температуры свыше 104оС. что вызывает рост давления до 109... Ю10 Па.
Разрядные каналы, первоначально шириной только в несколько десятков микро-
метров, расширяются и запускают волну давления в окружающее вещество, что
приводит к его измельчению. Уравнение баланса энергии для разрядного канала
может быть записано в виде
pdV+ dW= dQ, (12.1)
где р—давление в разрядном канале;
W— сумма внутренней энергии ушедшей на создание канала и потерь
энергии связанных с утечками давления на концах канала, излу-
чением и теплопроводностью;
Q— здесь энергия разряда.
Чтобы определить расширение канала и поле давления вокруг разряда, следу-
ет добавить уравнение движения и уравнение сохранения массы с учетом двух фаз
состояния вещества — газообразного в канале и твердого вокруг него Полное
числовое моделирование является очень сложным, а для гетерогенных материа-
12.2. Разрушение твердых диэлектриков с помощью электрических импульсов 303
лов сложного состава, возможно, и не выполнимым. Однако намного более про-
стая гидродинамическая модель с использованием в качестве граничного условия
радиуса расширяющегося канала, полученного из экспериментов, была исполь-
зована в [Burkin et al., 1975]. В работе [Zinov’ev and Semkin, 1978] потери в канале
не учитывались, а уравнение состояния использовалось в форме
^nt=P*7(X-1), (12.2)
где % — эффективное отношение удельных теплоемкостей.
Результаты этого анализа для разрядных каналов в плексигласе показаны на
Рис. 12.3 [Burkin et al., 1975; Zinov’ev and Semkin, 1978]. При распространении им-
пульса давления в твердом теле его амплитуда уменьшается, а форма приближает-
ся к треугольной, что важно для разрушения композитных материалов.
Расстояние от разрядного канала [мм]
Рис. 12.3. Расчетные профили волны давления,
возникающего в разрядном канале в плексигласе [Zinov’ev and Semkin, 1978].
Для создания разряда используется оборудование, схематически изображен-
ное на Рис. 12.4. С конденсаторного накопителя энергии быстро нарастающий
импульс напряжения амплитудой несколько сот киловольт подается на стержне-
вой электрод, касающийся обрабатываемого образца, который покоится на плос-
ком заземленном электроде. Разряд через образец возникает, если его напряже-
ние пробоя меньше, чем приложенное напряжение, а другие пути разряда снару-
жи образца имеют пробивное напряжение больше приложенного. Необходимым
условием этого является локальное превышение напряженностью поля внутри
образца пробивного значения, в то время как снаружи образца этого не происхо-
дит. Это всегда можно выполнить, если поместить образец в диэлектрическую
жидкость с более высокой электрической прочностью. Далее можно сконцентри-
ровать электрическое поле в образце и уменьшить его снаружи. Для этого требу-
ется, чтобы жидкость имела намного большую диэлектрическую проницаемость,
чем материал образца. И наконец, длина пути возможного разряда между элект-
родами через жидкость должна быть намного больше, чем путь разряда через об-
304 Глава 12. Импульсные разряды в твердых телах и жидкостях
разец. Например, при использовании образна сферической формы кратчайший
путь разряда снаружи его в л/2 раза больше, чем внутри.
Зарядное
устройство
Рис. 12.4. Установка для создания электрических разрядов
в твердых диэлектрических материалах.
Подходящей диэлектрической жидкостью является вода, чья электрическая
прочность сильно возрастает при уменьшении длительности импульса напряже-
ния. На Рис. 12.5 приведены графики зависимости динамической электрической
прочности различных вешеств в зависимости от скорости нарастания приклады-
ваемых импульсов напряжения треугольной формы. Из этих графиков видно, что
при коротких фронтах импульсов напряжения электрическая прочность воды ста-
новится выше, чем у твердых материалов (см. также разд. 2.3). Это явление было
открыто в конце 1950-х гг. в Томском политехническом университете [Sjomkin et
al., 1995] и параллельно в Олдермастоне (где оно применялось при конструирова-
нии линий для формирования мощных импульсов с низким импедансом, а в ка-
честве диэлектрика использовалась вода [Martin et al., 1996]).
Рис. 12.5. Графики зависимости динамической электрической прочности различных веществ
от скорости нарастания прикладываемых импульсов напряжения треугольной формы.
12.2. Разрушение твердых диэлектриков с помощью электрических импульсов 305
Явление увеличения динамической электрической прочности объясняется
стримерным механизмом электрического пробоя в жидкостях, где скорость стри-
мера слабо зависит от макроскопической напряженности электрического поля.
Скорее она определяется напряженностью поля вблизи верхушек газообразных
включений (см. разд. 2.3.2). Тем не менее трудно понять, почему электрическая
прочность жидкостей может стать выше, чем твердых веществ, особенно с учетом
того, что «собственная» электрическая прочность (для тонких образцов и коротко-
го времени воздействия) твердых диэлектриков выше. Не так давно было высказа-
но предположение, и были получены экспериментальные подтверждения, что на
электрическую прочность твердых веществ большое влияние могут оказывать про-
бои в газонаполненных порах внутри твердых веществ [Lisitsyn et al., 1999].
Хотя трансформаторное масло и имеет более высокую электрическую про-
чность, чем вода, оно, очевидно, не подходит для применения во многих техноло-
гических процессах, особенно в связи с проблемой повторного использования.
Вода не только имеет хорошие изоляционные свойства при коротком времени
воздействия электрическим полем, но и обладает высокой диэлектрической про-
ницаемостью и тем самым «заталкивает» силовые линии электрического поля
внутрь твердых материалов, которые обычно имеют намного меньшие значения
диэлектрической проницаемости. Конечно, данный эффект существует, только
если вода и твердый материал образуют между электродами слоистую структуру.
Однако это наиболее частая ситуация в рабочих камерах установок, наполняемых
измельчаемым материалом.
Вода также позволяет реализовать конфигурацию установки, когда оба элект-
рода контактируют с твердым телом с одной стороны (Рис. 12.6). В этом случае
разряд может, проходя через твердое тело, нанести ему удар со стороны его повер-
хности. При сканировании парой электродов поверхности образца представляет-
ся возможным удалить слой материала с большой площади.
Рис. 12.6. Расположение электродов для достижения возможности отскабливания поверхнос-
ти. При этом требуется, чтобы электрическая прочность среды между электродами
снаружи обрабатываемого образца была выше, чем внутри.
Для оценки эффективности разрушения материалов с помощью импульсных
электрических разрядов надо выполнить следующие шаги. Заряд конденсаторной
батареи обычно осуществляется с КПД г)! > 95%. В большинстве промышленных
306 Глава 12. Импульсные разряды в твердых телах и жидкостях
применений в качестве диэлектрической жидкости используется вода с проводи-
мостью около 0.6 мСм/см. Как правило, проводимость растет в ходе работы уста-
новки вследствие высвобождения солей из измельчаемых материалов. Таким об-
разом, имеют место потери на токи в электролите перед пробоем. Для минимиза-
ции этих потерь в большинстве случаев поверхность электродных стержней
покрывают слоем изоляции. Если концы электродов не контактируют с обраба-
тываемым материалом, разряд может задержаться, и потери в электролите за вре-
мя до пробоя могут существенно увеличиться, что, впрочем, зависит от качества
воды и коэффициента заполнения обрабатываемым материалом межэлектродно-
го пространства. На полупромышленной установке-прототипе FRANKA-Stein
(см. ниже) при положительной полярности импульсов напряжения коэффициент
связи т|2 был найден равным 20...40%. При отрицательной полярности этот коэф-
фициент упал ниже 10%. Однако при контроле качества воды и большом запол-
нении обрабатываемым веществом межэлектродного пространства потери могут
быть снижены до 10%, а т|2 увеличен соответственно до 90%. Было найдено, что
допустимое значение проводимости воды составляет до 2 мСм/см.
Так как электрический пробой является стохастическим явлением, не каждый
импульс напряжения приводит к разряду в твердом теле. Вероятность его может
меняться в широких пределах в зависимости от формы, рамера, диэлектрических
свойств материала, электропроводности воды и т. д. Однако при оптимальной
конфигурации вероятность пробоя т)3 достигает 0.8...0.9. Но только часть элект-
рической энергии т)4 попадает в разрядный канал. Остаток рассеивается в генера-
торе в форме омических и диэлектрических потерь. Было экспериментально оп-
ределено, что может быть достигнуто значение т|4 = 0.65...0.7. Так как электроды
не всегда касаются поверхности обрабатываемого материала, часть канала разря-
да приходится на близлежащую жидкость, что также снижает эффективность.
Следовательно, необходимо ввести еще один коэффициент, т]5, чтобы учесть это
обстоятельство (г]5 » 0.9).
Произведение всех этих коэффициентов позволяет оценить полезную часть
запасенной энергии, которая высвобождается в канале разряда как т]« 0.4. Эта
энергия Q делится в следующем соотношении:
Q=^mech+H<nt+^loss, (12.3)
где W^ech= fpdV представляет собой механическую работу по расширению раз-
рядного канала в окружающем его веществе,
потери на ионизацию и диссоциацию,
H-foss— прочие потери.
Если ввиду быстрого протекания процессов пренебречь прочими потерями,
то можно определить термодинамическую эффективность процесса
Пб = Wmech/C = 1 — H'lnt/C- Значение Q можно определить путем измерения напря-
жения и тока при разряде. Используя выражение (12.2) для % = 1.1...1.2 и выводя
значение Vиз экспериментальных наблюдений радиуса канала и давления в нем с
помощью гидродинамического моделирования, упомянутого выше [Sjomkin et
al., 1995; Burkin et al., 1975], можно установить значение т|6 = 0.1...0.2. Это относи-
тельно небольшое значение получается из-за того, что много энергии тратится на
12.2. Разрушение твердых диэлектриков с помощью электрических импульсов 307
диссоциацию и ионизацию. Прочие потери становятся важными, когда отноше-
ние радиуса канала к его длине превышает 0.1. Принимая во внимание все потери
энергии в процессе разрушения материалов импульсами высокого напряжения,
можно заключить, что только 4...8% электрической энергии оказывается доступ-
ной для воздействия на материал.
Часть этой энергии тратится на деформацию материала. Если считать главной
задачей размельчение материала, то можно заключить, что только часть доступ-
ной энергии тратится на создание новых поверхностей обрабатываемого матери-
ала. В этом случае эффективность становится равной
оА
nfrag=T^—(12.4)
"mech
где ст — удельная энергия свободной поверхности,
А — плошадь новых свободных поверхностей.
Используя предположение, что большая часть энергии тратится на
пластическую деформацию материала, представляемую как и используя при-
близительное соотношение [Sjomkin et al., 1995]
= 9стЛ1п(б/л£у), (12.5)
где SY—предел текучести (3...300x 106 Н/м2) и G — модуль сдвига
(1...4 х Ю10 Н/м2); получается стЛ »(0.013...0.47)Bzmech, т. е. rjfrag « 0.04...0.32%.
Это значение сопоставимо с КПД устройств для механического размельчения
твердых тел, который составляет 0.002... 1 %, в зависимости от степени измельче-
ния. Можно заключить, что размельчение электрическими импульсами энерге-
тически не имеет преимуществ перед механическими методами. Следовательно,
применять электроимпульсное размельчение имеет смысл там, где очевидны его
технологические преимущества. К ним относится, например, узкое распределе-
ние по размеру получаемых зерен, относительно малое загрязнение продуктов
размельчения и небольшой нагрев продуктов размельчения. Однако основным
достоинством этого метода является возможность селективного разрушения ма-
териала. Таким образом, электродинамическое размельчение может быть исполь-
зовано для разрушения или поверхностного отскабливания материалов, для их
размалывания до заданных размеров зерен и для разделения композитных мате-
риалов по их границам соединения, с оставлением в целости некоторых компо-
нентов.
12.2.2. Селективное разрушение
Повторное использование композитных материалов (таких как бетон или стек-
лопластик) или изделий, содержащих разнородные материалы (например, элект-
рическое оборудование и печатные платы), а также извлечение полезных минера-
лов из горных пород требует разделения обрабатываемых объектов на компонен-
ты. Электроимпульсное разрушение может осуществлять сепарацию материалов
вследствие следующих эффектов:
308 Глава 12. Импульсные разряды в твердых телах и жидкостях
1. На включениях, чьи диэлектрические свойства сильно отличаются от тако-
вых у основного материала, напряженность электрического поля может
сильно возрасти и притянуть траекторию разряда к этим включениям. При
этом разряд может происходить по границе включения. Этот случай схема-
тически показан на Рис. 12.7а, где проводящая сфера помещена в изолиру-
ющую основу. В этом случае сепарация включений вызывается прямо са-
мим разрядным каналом.
8)
Рис. 12.7. Механизмы сепарации компонентов композитных материалов:
а) металлические включения или включения с высокой диэлектрической проницае-
мостью могут притягивать к себе путь разряда;
б) распространение трещин от разрядного канала и их разветвление вблизи включений,
если механические свойства включений отличаются от таковых у основного материала;
в) волна давления может преобразоваться в волны растяжения и сдвига за счет отра-
жения и рефракции на включениях и отделить включения от основного материала.
2. Второй, более важный эффект связан с образованием трещин вблизи кана-
ла. Как следует из графиков, приведенных на Рис. 12.3, давление, создавае-
мое расширяющимся каналом, почти всегда превышает предел прочности
материалов, что приводит к образованию трещин. Если образующиеся тре-
щины контактируют с разрядным каналом, то продукты разряда могут про-
никать в них, что создает дополнительные силы, воздействующие на стен-
ки трещин. Особенности, динамика и интенсивность образования трещин
определяются скоростью поступления энергии в канал и свойствами мате-
риала. В ломком материале вокруг разрядного канала образуется множест-
во радиальных трещин длиной до нескольких миллиметров. Степень рас-
ширения трещин и их плотность коррелируют со скоростью
высвобождения энергии при разрядах [Sjomkin et al., 1995]. Однако число
трещин, достигших поверхности обрабатываемого образца, больше зависит
от общей энергии разряда. Следовательно, можно заключить, что для из-
мельчения требуется высокая энергия импульсов, в то время как для отка-
лывания больших фрагментов более эффективно подавать импульсы боль-
шой энергии с большей длительностью. Для обеспечения селективности
фрагментации важно понимать, что неоднородности материала вообще и
акустические неоднородности в особенности влияют на распространение
трещин в композитном материале. Причиной этого является существова-
ние повышенных механических напряжений на границах включений. Вол-
12.2. Разрушение твердых диэлектриков с помощью электрических импульсов 309
ны механических напряжений, отраженные от неоднородностей и включе-
ний, могут взаимодействовать с растущими трещинами до того, как они
достигнут включений [Gus, 1974; Sher, 1974; Martynyuk and Sher, 1974;
Volodarskaya et al., 1975]. Когда трещины достигают включений, они могут
ветвиться, как это схематически показано на Рис. 12.76, и выделять вклю-
чения из основного материала.
3. Третий эффект, приводящий к сепарации включений от основного матери-
ала, связан с падением на границы раздела включений и основного матери-
ала волны давления, создаваемой в разрядном канале [Achenbach et al.,
1970; Baron and Matthews, 1961; Pao and Mow, 1963; Kanel et al., 1996]. Схе-
матически этот эффект изображен на Рис. 12.7в. Первоначально в среде,
окружающей разрядный канал, волна давления имеет ударный характер.
Позже она преобразуется в волну давления. Было показано [Achenbach et
al., 1970], что волна сжатия из-за рефракции и отражения внутри включе-
ний преобразуется в волну растяжения. При более высоком акустическом
импедансе включений, чем основного материала, и малых амплитудах волн
давления отделение включения от основного материала возникает в облас-
ти акустической тени. А полное отделение включения от основного мате-
риала, по всей поверхности включения, наблюдалось при достаточно боль-
ших волнах давления.
Важный вопрос: возможно ли выделить включения из основного материала
без их повреждения? Хорошо известно, что ударные волны, поступающие на сво-
бодную поверхность или границу раздела материалов с сильным скачком акусти-
ческого импеданса способны привести к отслаиванию [Kanel et al., 1996]. Боль-
шим преимуществом электроимпульсного разрушения является то, что энергети-
ческие параметры генератора импульсов можно варьировать в широких пределах
и подбирать применительно к физико-механическим и акустическим свойствам
композитных материалов. Вследствие сложности и многообразия композитных
материалов параметры импульсов следует подбирать экспериментально для каж-
дого материала.
12.2.3. Оборудование для электроимпульсного разрушения
Так как пузырьки воздуха, возникающие во время высоковольтного разряда в
воде, должны исчезнуть до прихода следующего импульса напряжения, частота
следования импульсов не должна превышать 10 Гц. Таким образом, для получе-
ния производительности одной электроимпульсной установки в несколько сот
килограммов в час, что требуется в большинстве промышленных процессов из
экономических соображений, расстояние между электродами должно быть по-
рядка нескольких сантиметров. Для пробоя разрядного промежутка такого разме-
ра требуется напряжение в несколько сот киловольт. Импульсы с большой скоро-
стью нарастания и такой амплитудой можно получить с помощью генератора
Маркса [Marx, 1924] {см. разд. 3.2). Генератор Маркса при этом должен обеспечи-
вать возможность получения импульсов с энергией в несколько килоджоулей и
доставлять большую часть этой энергии в разрядный канал. Для этого необходи-
310 Глава 12. Импульсные разряды в твердых телах и жидкостях
мо низкое внутреннее сопротивление генератора Маркса, что также требуется для
получения большой скорости нарастания напряжения. Если требуется высокая
степень измельчения, то мощность импульсов должна составлять несколько гига-
ватт. Таким образом, и генератор Маркса, и цепи его соединения с рабочей каме-
рой должны иметь низкую индуктивность. Однако, когда допустимы большие
куски обработанного материала или главной целью является сепарация компо-
нентов без их разрушения, может оказаться необходимым увеличить эту индук-
тивность.
Базовая конструкция генератора Маркса для электроимпульсного разруше-
ния приведена на Рис. 12.8. Этот генератор был построен для выделения металлов
из шлака и размола некоторых специальных стекол. В его состав входило семь
каскадов по два конденсатора емкостью 72 мкФ каждый. Общая индуктивность
всей высоковольтной цепи, включая электроды, была найдена равной 7.7 мкГн.
Выходное сопротивление генератора Маркса в большой степени определяется
сопротивлением разрядников, используемых в качестве замыкающих ключей,
которое в данной конструкции составляло около 0.5 Ом. При таком малом сопро-
тивлении в рабочую камеру попадало около 80% запасенной в генераторе Маркса
энергии. Каждый конденсатор заряжался до 60 кВ. Выходные импульсы энергией
1.8 кДж получались в форме последовательных осцилляций амплитудой более
400 кВ и периодом 2.5 мкс. Несмотря на большое напряжение обратной поляр-
ности и высокую частоту осцилляций, поставщик конденсаторов (фирма Atesys)
гарантировал их способность выдержать более 108 импульсов. Электроды разряд-
ников были изготовлены из сплава медь-вольфрам в форме сфер с профилем
Рис. 12.8. Фотография генератора Маркса на 400 кВ, 1.8 кДж,
способного работать на частоте до 10 Гц с долговечностью компонентов 108 импульсов
12.2. Разрушение твердых диэлектриков с помощью электрических импульсов 311
Борда [Borda, 1766] для обеспечения их равномерного износа. Для изготовления
корпусов разрядников был использован полиэтилен.
Позади генератора Маркса на Рис. 12.8 виден его корпус, представляющий
собой толстостенную герметичную конструкцию. В рабочем состоянии корпус
заполнен трансформаторным маслом, служащим как для электрической изоля-
ции, так и для отвода тепла. Импульсы с выхода генератора передавались в рабо-
чую камеру через гибкую металлическую трубу большого диаметра.
Самыми важными аспектами при работе промышленного оборудования яв-
ляются его электробезопасность, электромагнитная совместимость и защита от
шума. Электробезопасность, даже при использовании высокого напряжения,
обеспечивается соблюдением стандартных правил и здесь не обсуждается. А вот
для обеспечения работы электронных приборов вблизи от генератора Маркса
требуется тщательная экранировка. При использовании неферромагнитных ма-
териалов трудно обеспечить экранировку магнитных полей рассеивания. С дру-
гой стороны, мю-металл может оказаться слишком дорог для некоторых приме-
нений. Однако значительно уменьшить излучение магнитного поля можно с по-
мощью экрана, выполненного в форме незамкнутой обмотки, так что
возбуждаемые в ней магнитным полем токи компенсируют друг друга. Другим
источником электромагнитного излучения и шума является разряд в рабочей ка-
мере. Таким образом, необходимо рабочую камеру конструировать так, чтобы она
являлась экраном Фарадея, или устанавливать ее в корпус-экран, служащий так-
же и для звукоизоляции.
В большинстве случаев рабочую камеру, за исключением дна, изготавливают
из полиэтилена, что способствует снижению электролитических потерь энергии.
Так как проводимость воды в процессе работы увеличивается, высоковольтный
электрод должен иметь изоляцию по всей его длине, за исключением самой вер-
хушки. В этом случае допустимо использовать металлическую рабочую камеру,
которая сама и является электромагнитным экраном. С целью уменьшения элек-
трических перегрузок в точке соединения изолятор—металл—вода верхушку
электрода делают грибообразной формы. В зависимости от назначения нижнюю
часть рабочей камеры выполняют в виде сита, сети или полусферы.
На Рис. 12.9 представлены графики напряжения и тока, а также сопротивле-
ния разрядного канала, имеющие место при различных условиях в рабочей каме-
ре. Для этой серии экспериментов межэлектродное расстояние было выбрано
равным 30 мм. Сигнал напряжения, показанный на Рис. 12.9, который измерялся
с помощью быстродействующего делителя напряжения, включает падение на-
пряжения на индуктивностях электродов и разрядного канала. Для расчета со-
противления канала Rs следует использовать выражение
----7(0—’ (126)
где £/(/) и/(0 — измеренные значения напряжения и тока соответственно,
L— индуктивность разрядной цепи между входом делителя напряже-
ния и землей.
312 Глава 12. Импульсные разряды в твердых телах и жидкостях
Рис. 12.9. Графики напряжения и тока, а также сопротивления разрядного канала, имеющие
место при различных условиях в рабочей камере. Для этой серии экспериментов
межэлектродное расстояние было выбрано равным 30 мм. Приведенные графики на-
пряжения не откорректированы с учетом индуктивности цепи.
Материал (бетон) заполнял весь межэлектродный зазор, и пробой происходил
уже на начальной стадии роста напряжения, а среднее значение сопротивления
разряда оставалось более 2 Ом. Было обнаружено, что сопротивление разряда пе-
риодически возрастало в моменты перехода тока через ноль. Это явление было
увязано с охлаждением разрядного канала через его стенки и доминированием
потерь тепла над его поступлением в эти моменты, что приводило к охлаждению
плазмы в канале. Если большая часть разряда проходила через воду, то возникала
задержка возникновения разряда, а напряжение уменьшалось из-за электролити-
ческих потерь. Соответственно максимальный ток разряда и его энергия также
уменьшались.
Для управления работой установки (определения наполненности рабочей ка-
меры и межэлектродного расстояния) можно использовать результаты измерения
сопротивления разряда, времени задержки разряда и энергетическую эффектив-
ность.
12.3. Применение в промышленности 313
12.3. Применение в промышленности
12.3.1. Повторное использование строительных материалов
Около одного кубометра бетона в год на каждого жителя Германии использу-
ется для строительства. Аналогичные количества потребляются и в других индус-
триально развитых странах. Сырье в виде гравия, песка и цемента для этого заби-
рается из природных месторождений. С другой стороны, каждый год в Германии
возникает 30 миллионов тонн отходов из бетона, раствора для кирпичной кладки
и кирпичей. Скорость утилизации этих строительных материалов очень низкая, а
применяются они лишь для второстепенных целей, например в качестве засыпки
и при строительстве противошумовых барьеров. Утилизация без деградации
свойств требует разделения отходов на песок, гравий и цемент. Разрушение стро-
ительных отходов с помощью многокаскадных зубчатых дробилок или ударных
мельниц не позволяет разделить отходы на их составляющие и производит боль-
шое количество пыли и мелких фракций.
Бетон представляет собой композитный неоднородный материал и по этой
причине хорошо подходит для разделения на составляющие компоненты с помо-
щью электродинамического размельчения. Микротрещины между наполнителем
(гранулами гравия и песка) всегда существуют даже в бетоне, не подвергавшемся
какому-либо воздействию. Под воздействием быстро изменяющейся нагрузки
происходит отделение включений от материала основы — цемента. Тйк как у
включений акустические неоднородности особенно велики, для разделения на
фракции лучше всего подходят волны давления. Таким образом, импульс давле-
ния из разрядного канала создает в основном силы сжатия и растяжения, т. е. ус-
ловия, при которых прочность бетона мала, и в нем возникают и расширяются
трещины.
На Рис. 12.10 показано, во что превращается кусок бетона после полного раз-
деления его на компоненты. Кривая гранулометрического состава полученных
компонентов очень близка к таковой у натуральных компонентов бетона данного
типа (в соответствии со стандартом DIN) [Schultheiss et al., 1998]. Самое замеча-
тельное то, что в кривой гранулометрического состава разделенных компонентов
отсутствуют крупные компоненты. Почти все частицы при этом являются одно-
минеральными. Как видно под микроскопом, частицы гравия (> 2 мм) совершен-
но свободны от загрязнений и примесей. В песке доминируют сферические час-
тицы с размерами 0.5...2 мм с редкими следами прилипшего к ним цемента. Об-
щая доля цемента в гравии и песке составляет около 1%.
Полученные составляющие бетона не имеют механических повреждений и
отвечают требованиям стандарта DIN 52104 на устойчивость к замораживанию и
воздействию росы. Бетон, изготовленный из этих компонентов, имел ту же про-
чность, что и изготовленный из природных составляющих.
Рентгенография мельчайшей фракции (< 0.063 мм) показала отсутствие в ней
кварца. Она состоит из гидросиликата кальция, эттрингита, кальцита и гидрокар-
боната кальция и алюминия.
314 Глава 12. Импульсные разряды в твердых телах и жидкостях
Рис. 12.10. Кусок бетона до обработки {справа) и после нее {слева и в центре). Обработка выпол-
нялась на разрядной установке FRANKA-0. Песок и гравий восстановлены без дегра-
дации их свойств. Цементная фракция (рядом с кусками стальной арматуры) может
быть отправлена для производства цементного клинкера.
С химической точки зрения фракция цемента очень похожа на вновь изготов-
ленный цемент. В лабораторных условиях цементный клинкер был изготовлен
обжигом при высокой температуре. Повторное использование цементной фрак-
ции имеет следующие достоинства:
1. Оно экономит природные материалы (глину и известь).
2. Исчезает необходимость размола природных материалов.
3. Не требуется декарбонизации размолотого природного материала (процесс
обжига потребляет 80% энергии при обычном производстве цемента).
4. Уменьшается выброс углекислого газа в атмосферу (в мире 7% антропоген-
ного СОг высвобождается из-за производства цемента).
5. Исчезает нужда в хранилищах цементных отходов.
Конечно, для дегидратации цементной фракции требуется энергия Но
если заменить 50% природного материала в производстве цемента на повторно
используемую цементную фракцию, то можно ожидать экономии 10%
энергии.
В Табл. 12.2 приведены некоторые характеристики процесса электроимпуль-
сного размельчения бетона, полученные с использованием лабораторной уста-
новки FRANKA-0. Генератор в ней вырабатывал импульсы напряжения амплиту-
дой 250 кВ, временем нарастания 200 нс и энергией 750 Дж. При рабочей частоте
4...5 Гц потребление энергии составляло 3...4 кВт. В ходе экспериментов кусок бе-
тона весом 2 кг разрушался за 45 с.
12.3. Применение в промышленности 315
Таблица 12.2. Некоторые характеристики процесса размельчения
бетона, полученные с использованием установки
FRANKA-0
Производительность [кг/час] 160
Средняя потребляемая мощность [кВт] 3
Удельная потребляемая энергия [кВт-час/т] 19
Для демонстрации большей производительности, вплоть до 1 т/ч, была созда-
на полупромышленная установка FRANКА-2, известная также под названием
FRANKA-Stein, общий вид которой показан на Рис. 12.11. Куски бетона в ней
транспортируются в рабочую камеру с помощью вибрационного конвейера. Об-
работанный материал экстрагируется из рабочей камеры через цилиндрический
люк в дне рабочей камеры. Время обработки управляется путем регулировки ско-
рости вращения диска, выносящего продукты обработки из люка рабочей каме-
ры. Генератор Маркса состоит из шести каскадов, питаемых от зарядного уст-
ройства мощностью 10 кВт. При напряжении заряда 60 кВ выходное напряжение
генератора достигает 350 кВ по амплитуде за 0.2...0.4 мкс, в зависимости от качес-
тва воды. Хотя и была продемонстрирована производительность этой установки,
близкая к 1 т/ч. был найден компромисс между производительностью и качест-
вом продукции на выходе. Получается так, что при быстром введении большой
Рис. 12.11. Фотография полупромышленной установки FRANKA-Stein, производящей повтор-
ное использование компонентов бетона с их полным разделением по фракциям и
производительностью 1 т/ч. Генератор Маркса размещен в цилиндрическом корпусе
сверху.
316 Глава 12. Импульсные разряды в твердых телах и жидкостях
энергии в разрядный канал (т. е. при большой мощности импульсов) возникает
большое импульсное давление в канале, что приводит к образованию множества
маленьких трещин и большой степени разрушения материала вблизи канала.
При более медленном введении энергии в канал трещин образуется меньше, но
они оказываются длиннее и откалывают от куска бетона фрагменты большего
размера.
В процессе размельчения бетона в используемую воду постоянно поступают
соли, что увеличивает ее проводимость. Для сохранения эффективности электро-
импульсного размельчения проводимость воды должна оставаться достаточно
низкой. Таким образом, или постоянно необходимо добавлять свежую пресную
воду, или, прежде всего в замкнутой системе, воду необходимо подвергать очист-
ке. По экологическим соображениям, допустим только последний вариант. К
счастью, большинство солей могут быть нейтрализованы продувкой через воду уг-
лекислого газа.
12.3.2. Обработка отходов мусоросжигания
Тепловая обработка городских твердых отходов является эффективным спо-
собом их переработки для хранения, и важность ее постоянно возрастает. Она не
только уменьшает объемы свалок, но и является источником энергии и постав-
щиком металлов и минеральных строительных материалов. Утилизация отходов с
целью получения сырья для производства бетона требует выделения металлов и
связывания тяжелых металлов. Тяжелые металлы могут быть вымыты из свежих
отходов при их контакте с водой. Неизбежное содержание в отходах негашеной
извести приводит к достижению в них щелочности (pH) более 12 единиц. При
этом растворимость ионов свинца в воде, например, увеличивается в 1000 раз по
сравнению с pH-нейтральной водой. Таким образом, свежие отходы надо выдер-
живать не менее трех месяцев до утилизации в качестве строительного материала.
За это время поглощение углекислого газа из атмосферы уменьшает их щелоч-
ность.
Было найдено, что подводное электродинамическое размельчение
(Underwater Electrodynamic Fragmentation, UWEDF) для выделения металлов из
отходов также уменьшает значение pH. Это связано с возникновением в разряд-
ном канале оксидантов. Последующие измерения растворимости твердых метал-
лов показали ее сильное уменьшение, так что в принципе хранение может быть
заменено на подводное электродинамическое размельчение прямо после печки.
Для демонстрации этого процесса в промышленных условиях на одном из го-
родских мусоросжигательных заводов была построена установка FRANKA-1. На
Рис. 12.12 приведена фотография этой установки до поставки на завод. Эта уста-
новка способна обрабатывать до 2 тонн отходов в час. Частота следования им-
пульсов равна 7 Гц, средняя мощность — 10 кВт и амплитуда импульсов — 350 кВ.
На Рис. 12.13 изображены растворимости некоторых тяжелых металлов из отхо-
дов до и после обработки на установке FRAN КА-1. Для сравнения приведены по-
роговые значения растворимостей, указанные в германских правилах LAGA Z2
для утилизированных строительных материалов.
12.3. Применение в промышленности 317
Рис. 12.12. Фотография установки FRANKA-1 до поставки на мусоросжигательный завод Эта
установка предназначена для выделения из отходов металлов и связывания тяжелых
металлов.
Рис. 12.13. Растворимости некоторых тяжелых металлов из отходов до и после обработки на ус-
тановке FRANKA-1. Для сравнения приведены пороговые значения растворимос-
тей, указанные в правилах LAGA Z2.
Проблемой при этом процессе является сильное насыщение солями исполь-
зуемой воды, что приводит к увеличению электролитических потерь. Таким обра-
зом, важной частью процесса является обессоливание используемой воды.
12.3.3. Удаление поверхностных слоев и сверление
Конструкция, показанная на Рис. 12.6, может быть использована для удале-
ния поверхностных слоев, загрязненных опасными химикатами или радионукли-
дами. Соответствующие лабораторные эксперименты были проведены в Текстро-
не (Textron) [Goldfarb et al., 1997], в Томске [Sjomkin et al., 1995] и в Исследова-
тельском центре в Карлсруэ, где установка была устроена так, что электроды
318 Глава 12. Импульсные разряды в твердых телах и жидкостях
могли перемещаться в трех измерениях в бассейне размером 2x3 метра
[Schultheiss et al., 1998].
Чтобы найти оптимальный набор параметров установки для различных мате-
риалов, можно двинуться следующим путем. Сохраняя параметры генератора им-
пульсов разряда L,Cm.U постоянными, можно определить объем удаляемого ма-
териала V за один разряд как функцию длины межэлектродного расстояния s.
При некотором значении этой длины функция будет иметь максимум. Если пов-
торить эти эксперименты с другими амплитудами напряжения U, получается на-
бор функций, подобный тому, который показан на Рис. 12.14а. Взамен V можно
построить график относительной энергии И^рес = (\/2)CU2/V. Для каждого напря-
жения U найдется минимум этой энергии и соответствующий оптимум межэлект-
родного расстояния, как это показано на Рис. 12.146. Функция построен-
ная на графике Рис. 12.14в, является кривой, соединяющей минимумы графиков
на Рис. 12.146 и напряжения U(s), соответствующие каждому минимуму. Физи-
чески это означает, что можно уменьшить требуемую относительную энергию
при увеличении межэлектродного расстояния и одновременном увеличении амп-
литуды импульсов напряжения. Значения этой амплитуды, необходимой для до-
стижения минимальной относительной энергии, приведены на Рис. 12.14в.
Однако один этот набор кривых еще не достаточен как для определения всех
параметров, так и для оптимизации процесса. В частности, накопленная в гене-
Рис. 12.14. Схематически представленная процедура определения оптимальной амплитуды им-
пульсов напряжения и емкости конденсатора в генераторе как функции межэлектро-
дного расстоянияs для минимального потребления энергии И^реС [Sjomkin et al., 1995].
12.3. Применение в промышленности 319
раторе энергия Wq еще остается свободным параметром, который следует опти-
мизировать. Вместо можно использовать С = 2FF0/Z/2 как переменную незави-
симую величину. Как следует из Рис. 12.14в, каждому значению s соответствует
оптимальное значение U. Следовательно, можно определить удаляемый объем V
как функцию С(Ио) и получить семейство кривых, показанных на Рис. 12.14г для
различных значений 5. Можно предположить, что существует пороговое значение
энергии (или емкости Cth), ниже которого удаленный объем равен нулю. Та-
ким образом, можно ожидать, что графики относительной энергии И^рес будут
иметь минимумы, как это показано на Рис. 12.14д. Каждая кривая соответствует
определенным значениям s и U(s). и, таким образом, для каждого значения С,
связанного с определенным минимумом, может быть построен график зависи-
мости от 5. Эти графики представлены на Рис. 12.14е, где все параметры — С, Um
И^рес — представлены как функции от s. Очевидно, что процедура оптимизации
может оказаться весьма громоздкой и никогда не будет выполнена систематичес-
ки, в полном объеме. Необходимо также отметить, что нет необходимости обес-
печивать наиболее экономичное техническое решение. Низкое значение относи-
тельной энергии является только одним из экономических факторов; производи-
тельность и стоимость оборудования являются другими.
В то время как в Карлсруэ была испытана только одна пара электродов, в
Текстроне использовались длинные параллельные полоски [Goldfarb et al., 1997].
Ожидалось, что в этой конструкции пробои будут случайно перемещаться вдоль
межэлектродного зазора, а удаление материала из какого-либо участка приведет к
увеличению электрической прочности в этом месте и создаст условия для пробоя
на другом, более слабом участке. Из-за этой своего рода саморегулировки пред-
полагалось получение одинаковой глубины скобления по пути движения элект-
родных полосок. Система-прототип состояла из генератора Маркса на 120 кВ с
энергией импульсов 0.8...2 Дж и частотой следования 5...40 Гц. Средняя скорость
скобления составляла 5...20 см/мин и, таким образом, была в 10 раз выше, чем у
низковольтных (20...30 кВ) электрогидравлических систем для скобления, при-
нцип действия которых основан на электрическом разряде в воде, хотя последние
и потребляют в 4 раза больше энергии. Удельное потребление энергии в высоко-
вольтной системе составляло 500... 1000 Дж/см3. На испытательной площадке Де-
партамента энергетических ресурсов (США) были также проведены испытания, в
ходе которых удалялся слой загрязненного ураном бетонного пола завода. При
этом имела место попытка получения опыта удаления загрязнений с больших по-
верхностей пола. В ходе обработки радиоактивные продукты собирались в виде
бетонного щебня или в воде, в виде суспензии мелких частиц. В последнем случае
из воды загрязнения выделялись фильтрованием или выпариванием. Повторное
загрязнение вскрытой бетонной поверхности полностью избежать невозможно,
но можно удержать малым при быстром обмене воды.
Как и в случае разделения бетона на его составляющие компоненты, проводи-
мость используемой воды возрастает со временем и нуждается в проверке. Это
особенно важно для электродов из параллельных полосок, использовавшихся в
экспериментах в Текстроне. Представляется все же предпочтительным применять
стержневые электроды, поверхность которых покрыта изоляцией, за исключени-
320 Глава 12. Импульсные разряды в твердых телах и жидкостях
ем маленького участка на верхушке. При этом амплитуда импульсов должна воз-
расти до более чем 400 кВ. При 350 кВ, в экспериментах, проведенных в Карл-
сруэ, относительное потребление энергии составляло всего 70 Дж/см3. Фотогра-
фия результатов этих испытаний, при которых был удален слой бетона до
стальной арматуры, показана на Рис. 12.15. Еще меньшее значение относитель-
ной энергии удаления поверхностного слоя было найдено в работе [Sjomkin et al.,
1995]. В ней для разрушения армированного бетона, использовался мощный
(420 кВ, 19 кДж) генератор Маркса и система электродов в форме расчески. Элек-
троды были последовательно соединены с генератором. В этой системе значения
относительной энергии удаления поверхностного слоя были найдены в пределах
7...30 Дж/см3, в зависимости от числа слоев арматуры.
Рис. 12.15. Фотография армированного бетонного блока с удаленным поверхностным слоем.
В левом верхнем углу фотографии видна использовавшаяся система из двух электро-
дов.
12.3.4. Повторное использование других материалов
В дополнение к строительным материалам были подвергнуты обработке элек-
троимпульсным воздействием и множество других веществ. Их можно разделить
на две группы:
• композитные материалы, содержащие в своем составе металлические и ди-
электрические компоненты, как, например, электрооборудование, автомо-
бильные свечи зажигания и печатные платы радиоэлектронных устройств;
• ломкие, однородные материалы, такие как стекло, кремний, пигментные
красители и минералы.
Легкое разделение металлических и неметаллических компонентов может
быть легко достигнуто для маленьких электрических приборов {см. Рис. 12.16).
Большие электрические приборы требуется до электроимпульсной обработки
разрушить на более мелкие фрагменты. В отличие от обычной обработки для вто-
ричного использования после электроимпульсной обработки металлические
компоненты остаются целыми, что позволяет намного легче восстанавливать
12.3. Применение в промышленности 321
Рис. 12.16. Электробритва до (слева) и после (справа) обработки несколькими импульсами.
драгоценные металлы. Предполагается, что разряд возникает на границах раздела
разнородных материалов и тем самым отщепляет их друг от друга.
Интерес к использованию электродинамического размельчения гомогенных
материалов основан на наблюдении тех фактов, что в ходе этого процесса вносит-
ся очень незначительное количество загрязнений и в результате получаются зерна
более однородного размера, с малым содержанием других фракций. Например,
был продемонстрирован размол боросиликатного стекла для биотехнологических
применений с размерами зерен менее 100 мкм и низким загрязнением продуктов
размола посторонними веществами. Частицы стекла в форме суспензии в воде
выводились из рабочей камеры с помощью фильтра с подходящим размером пор.
Частицы железа, попадавшие в размолотую массу из-за обгорания электродов,
удалялись из нее с помощью магнита, установленного на входе в осадочный коло-
дец. По сравнению с обычным процессом размола не только уменьшалось общее
количество примесей, но и достигалось более узкое распределение частиц стекла
по размерам, что увеличивало процент выхода. Другим достоинством электроди-
намического размельчения является то, что сравнительно малая часть материала
оказывается в контакте с горячими продуктами разряда в канале и вследствие
этого оплавляется. Таким образом, пористая структура поверхности боросили-
катных зерен — важнейшее свойство для биологических применений — сохраня-
ется для большей доли частиц, чем при обычном размоле.
12.3.5. Повторное использование эластополимерных
материалов
Электродинамическое размельчение оказалось менее успешным примени-
тельно к эластичным и ударопрочным материалам. С целью поиска путей улуч-
шения характеристик этого процесса в данной области применения были прове-
дены исследования в Томском политехническом университете [Kurets et al., 1995].
В ходе этих исследований эластичные материалы (в частности, резина) для увели-
чения их твердости помещали в жидкий азот.
Однако успех этого подхода зависит не только от увеличения твердости мате-
риала, но и от диэлектрических свойств жидкого азота. Главным недостатком
жидкого азота является его сравнительно маленькая диэлектрическая проницае-
322 Глава 12. Импульсные разряды в твердых телах и жидкостях
мость е = 1.454. Таким образом, не возникает увеличения напряженности элект-
рического поля внутри материала, помещенного в эту жидкость. Даже наоборот,
из-за того, что многие твердые материалы имеют более высокую проницаемость,
происходит некоторое увеличение напряженности поля в жидком азоте.
Хотя в литературе и можно найти значительный объем информации по харак-
теристикам электрического пробоя в жидком азоте, очень малая ее часть касается
импульсных воздействияй, типичных для электродинамического размельчения.
Обобщенные результаты, полученные из экспериментов, выполненных в Томске,
показаны на Рис. 12.17 [Kurets et al., 1995]. Здесь напряжение пробоя изображено
как функция толщины слоя жидкого азота для трех различных интервалов време-
ни нарастания импульса: 0.2 мкс, 1 мкс и 5 мс — при синусоидальной форме вол-
ны, и для двух различных типов резины — для автомобильных шин и для вакуум-
ного уплотнения, находящихся при температуре жидкого азота. Время нараста-
ния здесь всегда относится к амплитуде импульсов 250 кВ и, таким образом,
может быть выражено как крутизна фронта в 1.25 МВ/мкс, 250кВ/мкс и
50 В/мкс. Было обнаружено, что поведение жидкого азота при пробое существен-
но отличается от других диэлектрических жидкостей, таких как трансформатор-
ное масло, глицерин, спирт и вода (в нормальных условиях).
Рис. 12.17. Зависимость пробивного напряжения жидкого азота от толщины его слоя при раз-
личных скоростях нарастания. Также приведены зависимости пробивного напряже-
ния от толшины образцов для двух типов резины при криогенной температуре
[Kurets et al., 1995].
Только при толщине слоя жидкого азота менее 20 мм напряжение пробоя ли-
нейно увеличивается с увеличением зазора. При большем зазоре рост напряжения
происходит существенно медленнее. Это поведение, возможно, связано с измене-
нием механизма пробоя от поверхностного к объемному. Вероятность появления
пузырьков растет при увеличении объема. Эти пузырьки вызывают формирование
стримеров внутри объема жидкости и уменьшают ее макроскопическую электри-
ческую прочность. Образование пузырьков в емкости с жидким азотом неизбеж-
12.3. Применение в промышленности 323
но, так как его температура при атмосферном давлении соответствует точке кипе-
ния. В таких жидкостях даже кратковременный нагрев, осуществляемый токами
пробоя, может привести к появлению цепочки пузырьков, вдоль которых развива-
ется пробой раньше, чем установится путь разряда в твердом теле.
Из графиков, приведенных на Рис. 12.17, можно также заключить, что вариа-
ции электрической прочности с изменением скорости нарастания напряжения у
жидкого азота намного менее выражены, чем у воды: в то время как для воды
электрическая прочность возрастает в 10 раз при уменьшении длительности
фронтов импульсов от 1 мкс до 200 нс, соответствующее увеличение для жидкого
азота едва достигает 25%. С другой стороны, исследованные образцы резины по-
казали линейное увеличение напряжения пробоя с увеличением толщины образ-
цов.
Из этих результатов Курен и др. заключили, что для создания пробоя в твер-
дых материалах, таких как резина, с большей вероятностью, чем в жидком азоте,
необходимо прикладывать импульсы со скоростью нарастания (0.2...0.5) х 10-6с
и амплитудой 200 кВ для образцов толщиной до 30 мм.
Другой причиной уменьшения электрической прочности жидкого азота мо-
жет быть накопление в нем кристаллов льда, возникающих из-за замораживания
влаги, находящейся в окружающей атмосфере, если поверхность жидкого азота
контактирует с воздухом. Конечно, эти проблемы можно было бы существенно
уменьшить увеличением давления жидкого азота и минимизацией контакта его
поверхности с атмосферным воздухом.
Устранение пузырьков из жидкого азота может также сильно ограничить до-
стижимую скорость повторения импульсов. Если, например, 125 Дж энергии вы-
деляется в разрядном канале и преобразуется в тепло, около 0.5 л азота следует
удалить из ванны до подачи следующего импульса. Хотя вязкость жидкого азота
сравнительно мала (2.1 миллипуаз при 77°К против 1 сантипуаза для воды при
20°С), что ускоряет движение пузырьков к поверхности под воздействием сил Ар-
химеда, соответствующие эксперименты [Takahashi and Ohtsuka, 1975; Takahashi,
1977] показали, что пузырьки газообразного азота в жидком азоте движутся вверх
со скоростью только 0.2 м/с. Принимая глубину ванны с жидким азотом в 20 см,
легко получить, что для полного удаления пузырьков частота следования импуль-
сов должна быть менее 1 Гц. Однако только практические эксперименты могут
показать реальные ограничения на частоту следования импульсов.
Для изучения применимости электродинамического размельчения под слоем
жидкого азота для промышленного использования в Карлсруэ была построена ус-
тановка FRANKA-3, фотография которой приведена на Рис. 12.18. Конструкция
генератора Маркса в ней подобна тем, которые использовались в других установ-
ках FRANKA, и позволяла получать импульсы амплитудой до 300 кВ со скоро-
стью нарастания 2 МВ/мкс и энергией 440 Дж. Генератор был размешен в бочко-
образном корпусе, подвешенном над рабочей камерой с жидким азотом и запол-
ненном для обеспечения изоляции гексафторидом серы (SF6). Зазор между
электродами регулировался в пределах 30...40 мм. Рабочая камера с жидким азо-
том, изготовленная из нержавеющей стали, показанная в нижней части
Рис. 12.18, располагалась на подъемной платформе под генератором Маркса.
324 Глава 12. Импульсные разряды в твердых телах и жидкостях
Рис. 12.18. FRANKA-3, установка для изучения применимости электродинамического
размельчения под слоем жидкого азота
С использованием этой установки было подвергнуто обработке множество
различных материалов:
• компоненты автотранспортных средств, содержащие резину и пластик,
• оптико-волоконные линии передачи информации,
• печатные платы,
• ламинированные пластики,
• трубы с вакуумной изоляцией и пр.
Грубое разделение композиций металл—резина и металл—пластик было до-
стигнуто легко. Однако маленькие следы резины оставались на металлических
поверхностях, и даже увеличение продолжительности обработки не давало воз-
можности их удалить. Кроме того, на металлических поверхностях печатных плат
появлялись маленькие кратеры.
В разделении компонентов, составляющих тонкие листы, такие как печатные
платы, не было достигнуто успеха. В таких конфигурациях продукты образования
разрядного канала покидают его очень быстро, что препятствует развитию сущес-
твенного давления. Кроме того, было найдено, что множество органических ма-
териалов разлагается под воздействием высокой температуры, развивающейся в
разрядном канале, а при охлаждении образуются новые субстанции неконтроли-
руемого состава. Хотя их количество невелико и может быть допустимо в некото-
рых процессах, применительно к обработке фармацевтических и пищевых про-
дуктов это неприемлемо.
12.3. Применение в промышленности 325
По этим причинам, а также из-за значительной цены жидкого азота так и не
было найдено какой-либо области промышленного применения электродинами-
ческого размельчения или размола под слоем жидкого азота.
12.3.6. Экономические аспекты повторного использования
материалов
Экономическая эффективность любого процесса получения материалов для
повторного использования определяется ценой оборудования, удельным энерго-
потреблением, стоимостью обслуживания и ремонта оборудования, числом и
квалификацией обслуживающего персонала. В большинстве промышленных
применений для обеспечения приемлемой экономической эффективности требу-
ется большой объем выхода продукции. Применительно к существующему лабо-
раторному оборудованию для электродинамического размельчения экстраполя-
ция к установкам промышленного масштаба сталкивается с большой неопреде-
ленностью в оценке расходов.
Очевидно, что количество материала, которое может быть обработано на один
разрядный канал, ограниченно и не может быть увеличено больше, чем в опти-
мизированных лабораторных установках. Частота повторения импульсов должна
оставаться ниже 15 Гц, чтобы позволить газовым пузырькам исчезнуть между им-
пульсами. Не представляется целесообразным увеличивать амплитуду импульсов
напряжения выше 500 кВ из соображений обеспечения надежности изоляции.
При этом амплитуда импульсов определяет длину разрядных каналов и тем са-
мым доступный объем обрабатываемого материала. Другими параметрами, влия-
ющими на производительность, являются мощность импульсов и их энергия. Од-
нако снижение сопротивления разрядного канала, приводящее к снижению эф-
фективности, препятствует увеличению энергии импульса. Несмотря на это,
увеличение энергии может привести к некоторому увеличению производитель-
ности, особенно если главной задачей обработки является размол. Достижимое
увеличение производительности, конечно, зависит и от вида обрабатываемого
материала. Применительно к образцам гранита были проведены систематические
исследования [Andres, 1989], в результате которых был получен оптимальный на-
бор параметров на плоскости энергия—поле. Однако термин «дезинтеграция» не
был определен, так что трудно соотнести результаты этих исследований с удель-
ной производительностью. Что касается размельчения бетона до полного разде-
ления его составляющих, ожидается, что может быть достигнуто 3...5-кратное
увеличение производительности установок FRANKA, описанных выше, при оп-
тимизации параметров разрядных каналов. Это означает, что может быть достиг-
нута возможность получения 1...3 т полностью разделенных компонентов бетона
в час на одной установке со средней мощностью 30 кВт и частотой следования
импульсов 15 Гц. Таким образом, для достижения промышленного масштаба
100 т/ч требуется до 100 одновременно работающих установок такого типа. Каж-
дая из этих установок требует определенного пространства, необходимого для ис-
ключения создания помех работе друг друга. Представляется возможной как их
параллельная, так и последовательная работа.
326 Глава 12. Импульсные разряды в твердых телах и жидкостях
Для одновременной работы 100 установок не требуется увеличивать число их
составных частей во столько же раз. Например, генератор Маркса может работать
на более высокой частоте и распределять выходные импульсы напряжения по
различным рабочим камерам. Также и блок заряда конденсаторов соответствую-
щей мощности может обслуживать несколько конденсаторных батарей. В связи с
тем что цена мощных источников энергии увеличивается непропорционально их
мощности, существует большой потенциал для экономии при увеличении масш-
табов установок.
Износ компонентов установок и их долговечность являются еще одним важ-
ным экономическим фактором. Компонентами с самой большой скоростью из-
носа являются электроды, контактирующие с обрабатываемым материалом, и
электроды ключей. Было найдено, что потери материала со стальных электродов
при размельчении бетона составляют до 10 мкг за один импульс. Следовательно,
электрод с площадью 1 см2 потеряет примерно 1 см длины за неделю при работе
по 8 ч в день. Таким образом, необходимо постоянно подстраивать длину элект-
родов и время от времени их менять. Однако этот износ достаточно мал, чтобы
учитывать его в экономических расчетах Что касается долговечности изоляции
электродов, имеющийся опыт не позволяет ее оценить применительно к про-
мышленным условиям эксплуатации. Повреждение изоляции может произойти,
например, вследствие удара по ее поверхности фрагментом разрушаемого мате-
риала. Лабораторные эксперименты показали, что самое важное — это умень-
шать электрические нагрузки в точке контакта электрод—вода—материал, на вер-
хушке электрода.
Намного больше беспокойства вызывает износ электродов ключей. Для сфе-
рических стальных электродов была установлена потеря 3 г материала за 106 им-
пульсов. Использование медно-вольфрамовых электродов с профилем Борда и
достаточно большим диаметром должно привести к приемлемому уменьшению
износа при имеющихся плотностях энергии. Кроме того, необходима стандарт-
ная процедура регулировки давления газа в ключах, а также подстройка межэлек-
тродного зазора, выполняемая в порядке обслуживания с интервалом порядка не-
скольких недель.
Долговечность конденсаторов гарантируется на уровне свыше 108 импульсов
даже в условиях возникновения на них большого напряжения обратной поляр-
ности, характерного для электрических разрядов в рассматриваемых установках,
и в настоящее время не рассматривается как экономическое ограничение.
В зависимости от процесса, из-за попадания солей в воду может увеличиться
ее электропроводимость. При проводимости выше 1.5 мСм/см эффективная ра-
бота становится невозможной и необходимо либо заменять воду либо подвергать
ее дистилляции (деионизации), что может стать важным фактором для оценки
ценовой эффективности оборудования в целом.
СПИСОК ЛИТЕРАТУРЫ
1. ABB (2001) Catalogue: Special Components for Pulsed Power Applications. ABB
Semiconductors AG, Lenzburg, Switzerland
2. Achenbach J, Hemann J, Ziegler F (1970) Separation at the interface of a circular
inclusion and the surrounding medium under an incident compression wave. Trans.
ASME, J. Appl. Meeh. E 37: 298-304
3. Akiyama H. (2000) Streamer discharges in liquids and their applications. IEEE
Trans. Dielectr. Electr. Insulat. 7(5): 646—653
4. Akiyama H, Katsuki S, Namihira T, Ishibashi K, Kiyosaki N (2001) Production of
large volume discharges in water and their industrial applications. In: Reinovsky R,
Newton M (eds.) Proc. 28th IEEE Int. Conf, on Plasma Science and 13th IEEE Int.
Pulsed Power Conf, 17—22 June 2001, Las Vegas, pp. 150—153
5. Andres U (1989) Parameters of disintegration of rock by electrical pulses. Powder
Technol. 58: 265-269
6. Arad R, Tsigutkin K, Maron Y, Fruchtman A, Huba JD (2003) Observation of
faster-than-diffusion magnetic field penetration into a plasma. Phys, of Plasmas
10(1): 112-125
7. Artsimowitsch L. A, Sagdejew R. S (1983) Plasmaphysik fur Physiker. Teubner,
Stuttgart
8. Badent R (1996) Modell der elektronendominanten Streamerentladung in Isolierdl.
PhD thesis, University of Karlsruhe
9. Bailey J, Carlson A, Morrison R (1990) Visible spectroscopy measurements in the
PBFAII ion diode. Rev. Sci. Instrum. 61(10): 3075—3080
10. Bailey J. E, Filuk A. B, Carson A. L, Johnson D. J, Lake P, McGuire E. J,
Mehlhorn T. A, Pointon T. A, Renk T. J, Stygar W. A, Maron Y (1995)
Measurements of acceleration gap dynamics in a 20-TW applied-magnetic-field
ion diode. Phys. Rev. Lett. 74: 1771—1774
11. Baranchikov E.I, Gordeev AV, Korolev VD, Smirnov VP (1978) Magnetic
self-insulation of electron beams in vacuum lines. Sov. Phys. JETP 48(6): 1058—
1068
328 Список литературы
12. Bardotti G, Bertotti В, Gianolio L (1964) Magnetic configuration of a cylinder
with infinite conductivity. J. Math. Phys. 5: 1387—1390
13. Barlow R. E, Proscan F (1975) Statistical Theory of Reliability and Life Testing.
Holt, Rinehart and Winston, New York
14. Baron M, Matthews A (1961) Diffraction of a pressure wave by a cylindrical cavity
in an elastic medium. Trans. ASME, J. Appl. Meeh. E 28: 347—354
15. Beams (1975) Proc. Int. Topical Conf, on Electron Beam Research and Technology,
Albuquerque, NM, 3-6 November 1975, SAND76-5122
16. Beams (1977) Proc. 2nd Int. Topical Conf, on High Power Electron and Ion Beam
Research and Technology, Cornell University, Ithaca, NY, 3—5 October 1977
17. Becker R, Sauter F (1964) Theorie der Elektrizjtat. Teubner, Stuttgart
18. Beebe S. J, Fox P. M, Rec L. J, Somers K, Stark R. H, Schoenbach К. H (2002)
Nanosecond pulsed electric (nsPEF) effects on cells and tissues: apoptosis
induction and tumor growth inhibition. IEEE Trans. Plasma Sci. 30: 286—292
19. Benda H, Spenke E (1967) Reverse recovery processes in silicon power rectifiers.
Proc. IEEE 55(8): 1331-1354
20. Beroual A (1993) Electronic and gaseous processes in the prebreakdown
phenomena of dielectric liquids. J. Appl. Phys. 73(9): 4528—4533
21. Birdsall С. K, Bridges W. В (1961) Space-charge instabilities in electron diodes and
plasma converters. J. Appl. Phys. 32 (12): 2611
22. Birdsall С. K, Langdon A. В (1991) Plasma Physics via Computer Simulation. Hilger,
Bristol
23. Bluhm H (2004) Aufschluss und Abtotung biologischer Zellen mit Hilfe starker
gepulster elektrischer Felder. Fruhjahrstagung der Deutschen Physikalischen
Gesellschaft, Kiel, 08—11. Marz 2004
24. Bluhm H, Hoppe P (1999) Perspectives of high power pulse generators for the
boron neutron capture therapy (BNCT) of tumors. In: Stalling C, Kirbie H (eds.)
Proc. 12th IEEE Int. Pulsed Power Conf, Monterey, C A, Vol. 1, pp. 502—505
25. Bluhm H, Bbhnel K, Buth L, Hoppe P, Karow H. U, Klumpp A, Rusch D,
Scherer T, Schiilken H, Singer J (1985) Experiments on KFK's light-ion accelerator
KALIF. In: Turchi P. J, Rose M. F (eds.) Proc. 5th IEEE Int. Pulsed Power Conf.,
Arlington. VA, pp. 114—117
26. Bluhm H, Hoppe P, Laqua H, Rusch D (1992) Production and investigation of TW
proton beams from an annular diode using strong radial magnetic insulation fields
and a preformed anode plasma source. Proc. IEEE 80: 995—1009
27. Bluhm H, Hoppe P, Bachmann H, Bauer W, Baumung K, Buth L, Laqua H.
Ludmirski A. Rusch D, Stoltz O. Yoo S (1994) Stability and operating
characteristics of the applied В proton extraction diode on KALIF. In: Rix W,
White R (eds.) 10th Int. Conf on High Power Particle Beams, San Diego. NTIS.
Springfield, VA, pp. 77—82
28. Bluhm H, Schultheiss C, Frey W, Gusbeth C, Sack M, Strassner R (2004)
Industrial scale treatment of biological cells with pulsed electric fields. In: Kirkici H
Список литературы 329
(ed.) Conf. Record of the 26th Int. Power Modulator Conf and 2004 High-Voltage
Workshop, San Francisco, pp. 8—14
29. Blumlein AD (1941) Improvements in or relating to apparatus for generating
electrical impulses. UK Patent 589127
30. Bodner S. E, Colombant D. G, Schmitt AJ, Klapisch M (2000) High gain direct
drive target design for laser fusion. Phys. Plasmas 7: 2298—2301
31. Boebinger G, Lacerda A, Fisk Z, Gor’kov L. P, Schrieffer J. R. (eds.) (2002)
Physical Phenomena at High Magnetic Fields IV. Proc. 4th Conf., 19—25 October
2002, Santa Fe, NM. World Scientific, Singapore
32. Bogdankevich L, Rukhadze A (1971) Stability of relativistic electron beams in a
plasma and the problem of critical currents. Sov. Phys. Uspekhi 14(2): 163—179
33. Bogdankevich L, Zhelyazkov I, Rukhadze A (1970) Limiting currents in relativistic
electron beams. Sov. Phys. JETP 30(1): 174—176
34. Borda JC (1766) Sur 1'ecoulement des fluids par les orifices des vases. Mem. Acad.
Roy. Sciences, Annee 1766: 579—607
35. Bouattou B, Lowell J (1988) Contact charging and small-scale charge migration in
polymers. J. Phys. D: Appl. Phys. 21:1787—1795
36. Bouzrara H, Vorobiev E (2000) Beet juice extraction by pressing and pulsed electric
fields. Int. Sugar J. 102(1216): 194-200
37. Bouzrara H, Vorobiev E (2001) Nicht-thermisches Pressen und Auswaschen von
frischen Zuckenubenschnitzeln kombiniert mit der Anwendung eines pulsierenden
elektrischen Feldes. Zuckerindustrie 126:463—466
38. Braginskii S. I (1958) Theory of the development of a spark channel. Sov. Phys.
JETP 34(7): 1068-1074
39. Buescher E. S, Schoenbach К. H (2003) Effects of submicrosecond, high intensity
pulsed electric fields on living cells - intracellular electromanipulation. IEEE Trans.
Dielectr. Electr. Insulat. 10(5): 788—794
40. Buneman O, Levy R. H, Linson L. M (1966) Stability of crossed-field electron
beams. J. Appl. Phys. 37: 3203—3222
41. Burkin V, Makarov P, Semkin B, Shubin В (1975) Pressure field around a spark in a
solid dielectric. Sov. Phys. Techn. Phys. 20(11): 1490—1492
42. Campbell N. A (2000) Biologic. Spektrum Akademischer Verlag, Heidelberg
43. Christiansen J, Hartmann W (1990) The pseudospark. In: Schaefer G, Kristiansen
M, Guenther A (eds.) Gas Discharge Closing Switches. Plenum, New York, pp.
509-520
44. Coleman A. J, Saunders J. E (1993) A review of the physical properties and
biological effects of the high amplitude acoustic fields used in extracorporeal
lithotripsy. Ultrasonics 31(2):75—89
45. Cooke С. M (1998) Personal communication
46. Cooperstein G (2002) Status of particle beam and pulsed power research in US. In:
Mehlhorn TA, Sweeney MA (eds.) Proc. 14th Int. Conf, on High-Power Particle
Beams, 23—28 June 2002, Albuquerque, NM, pp. 3—8
330 Список литературы
47. Cooperstein G, Boiler J. R, Commisso R. J, Hinshelwood D, Mosher D, Ottinger
P. F, Schumer J. W, Stephanakis S. J, Swanekamp S. B, Weber В. V, Young F (2001)
Theoretical modeling and experimental characterization of a rod-pinch diode.
Phys. Plasmas 8:4618—4636
48. Creedon J. M (1975) Relativistic Brillouin flow in the high n/g diode. J. Appl. Phys.
46(7): 2946-2955
49. Cuneo M. E (1999) The effect of electrode contamination, cleaning and
conditioning on high-energy pulsed-power device performance. IEEE Trans.
Dielectr. Electr. Insulat. 6(4): 469—485
50. Cuneo M. E, Menge P. R, Hanson D. L, Fowler W. E, Bernard M. E, Ziska G. R,
FilukA. B, Pointon T. D, Vesey R. A, Welch D. R, Bailey J. E, Desjarlais M. P,
Lockner T. R, Mehlhom T. A, Slutz S. A, Stark M. A (1997) Results of vacuum
cleaning techniques on the performance of LiF field-threshold ion sources on
extraction applied-B ion diodes at 1—10 TW. IEEE Trans. Plasma Sci. 25(2): 229—251
51. Dekker AJ (1964) Solid State Physics. Macmillan, London
52. Desjarlais M (1989) Theory of applied-B ion diodes. Phys. Fluids В 1(8): 1709—1720
53. Dev S. B, Hofmann G. A (1994) Electrochemotherapy — a novel method of cancer
treatment. Cancer Treat. Rev. 20(1): 105—115
54. Devins J. C, Rzad S. J, Schwabe R. J (1981) Breakdown and prebreakdown
phenomena in liquids. J. Appl. Phys. 52(7): 4531—4545
55. DiCapua M. S (1980) Magnetic insulation. IEEE Trans. Plasma Sci. 11(3): 205—215
56. Doevenspeck H (1962) Uber die Beeinflussung von Zellen und Zellverbanden durch
elektrostatische Impulse. Arch. Lebensmittelhygiene 13(3): 68—69
57. Doran A. A (1968) The development of a Townsend discharge in N2 up to
breakdown investigated by image converter, intensifier, and photomultiplier
techniques. Z. Phys. 208:427—440
58. Driga M. D, Pratap S. B, Walls A. W, Kitzmiller J. R (2001) The self-excitation
process in electrical rotating machines operating in pulsed power regime. IEEE
Trans. Magn. 37(1): 295-300
59. Duvillaret L, Rialland S, Coutaz J. L (2002) Electro-optic sensors for electric field
measurements. I. Theoretical comparison among different modulation techniques.
J. Opt. Soc. Am. В 19(11): 2692-2703
60. Ebert H (ed.) (1976) Physikalisches Taschenbuch. Vieweg, Braunschweig
61. Ekdahl C (2001) Modem accelerators for radiography. In: Reinovsky R, Newton M
(eds.) Proc. 28th IEEE Int. Conf, on Plasma Science and 13th IEEE Int. Pulsed Power
Conf., 17—22 June 2001, Las Vegas, pp. 29—34
62. Engelko A, Bluhm H (2004) Optimal design of semiconductor opening switches for
use in the inductive stage of high power pulse generators. J. Appl. Phys. 95(10):
5828-5836
63. Engelko V, Kusnetsov V, Viazmenova G, Muller G, Bluhm H (2000) Influence of
electrons reflected from a target on the operation of triode-type electron sources. J.
Appl. Phys. 88(7): 3879-3888
Список литературы 331
64. Engelko V, Muller G, Bluhm H (2001a) Influence of particle fluxes from target on
characteristics of intense electron beams. Vacuum 62: 97—103
65. Engelko V, Yatsenko B, MOller G, Bluhm H (2001b) Pulsed electron beam facility
(GESA) for surface treatment of materials. Vacuum 62: 211—216
66. Fitch R. A (1964) Novel principle of transient high-voltage generation. Proc. I EE
111(4): 849-854
67. Fowler R. H, Nordheim L (1928) Electron emission in intense electric fields. Proc.
Roy. Soc. (London) 119A(781): 173—181
68. Frank K, Rath W (1990) The triggered pseudospark discharge. In: Schaefer G,
Kristiansen M, Guenther A (eds.) Gas Discharge Closing Switches. Plenum, New
York, pp. 521-530
69. Frank K, Christiansen J, Hartmann W (1991) Tnggerbare Hochleistungsschalter.
Physik in unserer Zeit 22(4): 156—164
70. Friedman M, Swanekamp S, Obenschain S, Chan Y, Ludeking L, Smithe D (2000)
Stability of large area electron beam diodes. Appl. Phys. Lett. 77: 1053—1055
71. Fueki K, Feng D. F, Kevan L (1972) A semiempirical estimate of the scattering
cross-section and mobility of excess electrons in liquid hydrocarbons. Chem. Phys.
Lett. 13:616-618
72. Gerlach W (1979) Thyristoren. Springer, Berlin, Heidelberg
73. Glasoe G. N, Lebacqz J. V (1948) Pulse Generators. MIT Radiation Laboratory
Series Vol. 5, McGraw-Hill, New York
74. Goldfarb V, Budny R, Dunton A, Shneerson G, Krivosheev S, Adamian Y (1997)
Removal of surface layer of concrete by a pulse-periodical discharge. In:
Cooperstein C, Vitkovitsky I (eds.) Proc. 11th IEEE Int. Pulsed Power Conf., 29
June—2 July 1997, Baltimore, pp. 1078—1084
75. Goldstein S. A, Lee R (1975) The ion induced pinch and enhancement of ion
current by pinched electron and ion flow in relativistic diodes. Phys. Rev. Lett. 35:
1079-1082
76. Granatstein V. L, Alexeff I (1987) High Power Microwave Sources. Artech House,
Boston
77. Greenly J. B, Appartaim R. K, Olson J. C, Brisette L (1994) Extraction ion diode
studies for optimised performance: divergence, ion species and parasitic load. In:
Rix W, White R (eds.) I Oth Int. Conf, on High Power Particle Beams, San Diego.
NTIS, Springfield. VA, pp. 398-401
78. Greenly J. B, Appartaim R. K, Olson J. C (1996) Anode plasma dynamics in an
extraction applied-5 ion diode: effects on divergence, ion species and parasitic
load. In: Jungwirth K, Ullschmied J (eds.) 11th Int. Conf, on High Power Particle
Beams, Prague, Tiskama ’K' Ltd, Prague, pp. 111—114
79. Grekhov I, Mesyats G (1999). Physical basis for high power semiconductor
nanosecond opening switches. In: Stalling C, Kirbie H (eds.) 12th IEEE Int. Pulsed
Power Conf, Monterey, CA, pp. 1158—1161
80. Guenther A. H (ed.) (1987) Opening Switches. Advances in Pulsed Power Technology.
Plenum, New York
332 Список литературы
81. Guillemin Е. А (1944) A Historical Account of the Development and a Design
Procedure for Pulse Forming Networks. Radiation Laboratory Report No. 43,
Massachusetts Institute of Technology, Cambridge, USA
82. Guz I. S (1974) Interaction between stress waves and a growing crack. J. Appl.
Meeh. Tech. Phys. 15:726-730
83. Halbritter J (1985) On contamination on electrode surfaces and electric field
limitations. IEEE Trans. Electr. Insulat. 20: 671
84. Halbritter J (1986) Dynamical enhanced electron emission and discharges at
contaminated surfaces. Appl. Phys. A (Solids Surf.) 39: 49—57
85. Hanson D. L, Cuneo M. E, McKay P. F, Maenchen J. E, Coats R. S, Poukey J. W,
Rosenthal S. E, Fowler W. E, Wenger D. F, Bernard M. A, Chavez J. R, Steams W.
F (1992) Operation of a high impedance applied-/? extraction ion diode on the
SABRE positive polarity linear induction accelerator. In: Mosher D, Cooperstein
G (eds.) 9th Int. Conf on High Power Particle Beams, Washington, DC. NTIS,
Springfield, VA, pp. 781-787
86. Harjes H. C, Penn K. J, Reed K. W, McClenahan C. R, Laderach G. E, Wavrik R. W,
Adcock J, Butler M, Mann G. A, Martinez L, Morgan F. A, Wfeber G. J, Neau E. L
(1991) Status of the repetitive high energy pulsed power project. In: Prestwich K,
White R (eds.) Proc. 8th IEEE Int. Pulsed Power Conf., San Diego, pp. 543—548
87. Hegeler F (2003) Personal communication
88. Hegeler F, Myers M. C, Friedman M, Sethian J. D, Swanekamp S. B, Rose D. V,
Wfelch D. R (2002) Efficient electron beam deposition for repetitively pulsed
krypton fluoride lasers. In: Mehlhom T. A, Sweeney M. A (eds.) Proc. 14th Int.
Conf, on High-Power Particle Beams, 23—28 June 2002, Albuquerque, NM, pp.
357-360
89. Herlach F, Kennedy J. E (1973) The dynamics of imploding liners in magnetic flux
compression experiments. J. Phys. D: Appl. Phys. 6: 661—676
90. Herlach F, Ortenberg M (1996) Pulsed magnets for strong and ultrastrong fields.
IEEE Trans. Magn. 32(4): 2438-2443
91. Herlach F, Li L, Harrison N, Bockstal L (1996) Approaching 100 T with wire
wound coils. IEEE Trans. Magn. 32(4): 2507—2510
92. Hilmert H, Schmidt W. F (1991) Electron detachment from negative ions of sulfur
hexafluoride — swarm experiments. J. Phys. D: Appl. Phys. 24:915—921
93. Hulsheger H, Poter J, Niemann E (1983) Electric field effects on bacteria and yeast
cells. Radiat. Environ. Biophys. 22:149—162
94. Humphreys D, Penn K, Cap J, Adams R, Seamen J, Turman В (1985). Rimfire: a
six megavolt laser-triggered gas-filled switch for PBFAII. In: Rose M. F, Turchi P. J
(eds.) 5th IEEE Int. Pulsed Power Conf, Arlington, VA, pp. 262—265
95. Humphries S (1990) Charged Particle Beams. Wiley, New York
96. Humphries S (1980) Intense pulsed ion beams for fusion applications. Nucl. Fusion
20:1549-1612
97. leda M (1984) Electrical conduction and carrier traps in polymeric materials. I EEE
Trans. Electr. Insulat. El-19(3): 162—178
Список литературы 333
98. Illy S, Kuntz M, Westermann T (1994) Investigations on the vacuum current in the
magnetic insulated Karlsruhe light ion facility high-energy linear induction
accelerator (KALIF—HELIA). Phys. Plasmas 1(8):2748—2761
99. Johnson D, Kuswa G, Farnsworth A, Quintenz J, Leeper R, Bums E, Humphries S
(1979) Production of 0.5-TW proton pulses with a spherical focusing magnetically
insulated diode. Phys. Rev. Lett. 42(9): 610—613
100. Jones H. M, Kunhardt E. E (1994) Pulsed dielectric breakdown of pressurized
water and salt solutions. J. Appl. Phys. 77(2): 795—805
101. Jones H. M, Kunhardt E. E (1995a). Ionic sheath formation in water and aqueous
solutions and its influence on pulsed dielectric breakdown. In: Baker W,
Cooperstein G (eds.) 10th IEEE Int. Pulsed Power Conf., 3—6 July 1995,
Albuquerque, NM, pp. 580—585
102. Jones H. M, Kunhardt E. E (1995b) Pre-breakdown currents in water and aqueous
solutions and their influence on pulsed dielectric breakdown. J. Appl. Phys. 78(5):
3308-3314
103. Jonscher A. K, Lacoste R (1984) On a cumulative model of dielectric breakdown in
solids. IEEE Trans. Electr. Insulat. EI-19(6): 567—577
104. Joshi R, Schoenbach К (2000) Electroporation dynamics in biological cells
subjected to ultrafast electrical pulses: a numerial simulation study. Phys. Rev. E
62(1): 1025-1033
105. Kanel G. I, Razorenov S. V, Utkin A. V (1996) Spallation of solids under shock
wave loading. In: Davison L, Grady D. E, Shahinpoor M (eds.) High Pressure
Shock Compression of Solids II, Springer, Berlin, Heidelberg, pp. 1—24
106. Kanel G. I, Baumung K, Bluhm H, Fortov V. E (1998) Possible applications of the
ion beams technique for investigations in the field of equation of state. Nucl.
Instrum. Methods A 415: 509—516
107. Kasuya K, Kishi Y, Kamiya T, Funatsu M (1991) Low microdiveigence
medium-mass ion beam produced from a N2O cryogenic diode. Laser Part. Beams
19: 309-316
108. Katschinski U (1994) Optisch aktivierte Galliumarsemdschalterjur die Erzeugung von
Hochleistungsimpulsen. PhD thesis, University of Braunschweig, VDI, Diisseldorf
109. Keinigs R. K, Atchison W. L, Anderson W. E, Barlsch R. R, Faehl R. J,
Flower-Maudlin E. C, Hammersberg J. E, Holtkamp D. B, Jones M. E, Kyrala G,
Lindemuth J. R, Oro D. M, Parker J. V, Preston D. L, Reinovsky R. E, Rodriguez
G, Scudder D. W, Shehey P. T, Shlachter J. S, Stokes J, Taylor A. J, Tonks D. L,
Turchi P. J, Chandler E (2001) Material science experiments on the Atlas facility.
In: Reinovsky R, Newton M (eds.) Proc. 28th IEEE Int. Conf, on Plasma Science
and 13th IEEE Int. Pulsed Power Conf., 17—22 June 2001, Las \fcgas, pp. 356—360
110. Kind D (1958) Die Aufbauflache bei Stosspannungsbeanspruchung technischer
Elektrodenanordnungen in Luft. Elektrotech. Z. 79(3): 65—69
111. Kindersberger J (1986) The Statistical Time-Lag to Discharge Inception in SF6. PhD
thesis, Technical University of Munich
334 Список литературы
112. Kingsep A. S, Chukbar К. V, Yankov V. V (1990) Electron magnetohydrodynamics.
In: Kadomtsev В. В (ed.) Rev. Plasma Phys. 16: 243—288, Consultants Bureau,
New York
113. Knoepfel H (1970) Pulsed High Magnetic Fields. North-Holland, Amsterdam
114. Kolb A. C, Strickland В. E (1995) Dual use power supply development. AIP Conf.
Proc. 25(1): 91-101
115. Korolev Y D, Mesyats G. A (1998) Physics of Pulsed Breakdown in Gases.
URO-Press, Yekaterinburg
116. Krasik Y. E, Dunaevsky A, Felsteiner J (2001) Intense electron emission from
carbon fiber cathodes. Eur. Phys. J. D 15(3): 345—348
117. Kiichler A (1996) Hochspannungstechnik. VDI, Dusseldorf
118. Kiichler A, Schwab A (1987) Raumlich ausgedehnte Sensoren fur transiente elek-
tromagnetische Felder. Arch. Elektrotechnik 70: 341—347
119. Kunhardt E. E, Tzeng Y (1988) Development of an electron avalanche and its
transition into streamers. Phys. Rev. A 38:1410—1421
120. Kiipfmuller K. Kohn G (2000) Theoretische Elektrotechnik und Elektronik: Eine
Einjuhrung. Springer. Berlin, Heidelberg
121. Kurets V. 1, Tarakanovskii E. N, Filatov G. P (1995) Electric pulse resistance of
liquid nitrogen and rubber. Russ. Phys. J. 38: 455—457
122. Lafferty J. M (1980) Vacuum Arcs, Theory and Application. Wiley, New York
123. Landau L. D, Lifschitz E. M (1981) Klassische Feldtheorie. Akademie-Verlag,
Berlin
124. Laqua H, Bluhm H, Buth L, Hoppe P (1995) Properties of the non-equilibnum
plasma from a pulsed sliding discharge in a hydrogen gas layer desorbed from a
metal hydride film. J. Appl. Phys. 77(11): 5545—5552
125. Latham R. V (1981) High Voltage Vacuum Insulation: The Physical Basis. Academic
Press, London
126. Legler W (1955) Zur Statistik der Elektronenlawinen. Z. Phys. 140(1): 221—240
127. Legler W (1961) Die Statistik der Elektronenlawinen in elektronegativen Gasen bei
hohen Feldstarken und bei grosser Gasverstarkung. Z. Naturforsch. 16a: 253—261
128. Lemke R. W, Slutz S. A (1995) A full mode set electromagnetic stability analysis of
magnetically insulated ion diodes. Phys. Plasmas 2(2): 549—556
129. L'Eplattenier P, Bavay M, Lalle В (2001) On numerical modelization and
optimization of flux compression experiments. In: Reinovsky R, Newton M (eds.)
Proc. 28th IEEE Int. Conf, on Plasma Science and 13th IEEE Int. Pulsed Power
Conf., 17—22 June 2001, Las Vegas, pp. 665—668
130. Lewis T. J (1984) The role of electrodes in conduction and breakdown phenomena
in solid dielectrics. IEEE Trans. Electr. Insulat. El-19(3): 210—216
131. Lewis T. J (1985) Electronic processes in dielectric liquids under incipient
breakdown stress. IEEE Trans. Electr. Insulat. EI-20(2): 123—132
Список литературы 335
132. Lewis Т. J (1987) An overview of electronic processes leading to dielectric
breakdown of liquids. In: Kunhardt E. E, Christophoru L. G, Luessen L. H (eds.)
The Liquid State and Its Electrical Properties. Plenum, New York, pp. 431—453
133. Lewis T. J (1989) A simple general model for charge transfer in polymers. Faraday
Discuss. Chem. Soc. 88:189—201
134. Lewis T. J (1990) Charge transport, charge injection and breakdown in polymeric
insulators. J. Phys. D: Appl. Phys. 23: 1469—1478
135. Lewis T. J (1993). The basic processes of conduction in dielectric liquids. 11th Int.
Conf, on Conduction and Breakdown in Dielectric Liquids, Baden-Dattwil.
Switzerland, pp. 32—41
136. Lewis T. J (1994a) Basic electrical processes in dielectric liquids. IEEE Trans.
Dielectr. Electr. Insulat. 1(4): 630—643
137. Lewis T. J (1994b) Nanometric dielectrics. IEEE Trans. Dielectr. Electr. Insulat.
1(4): 812-825
138. Lewis T. J (1994c) Liquid motion induced by electrocapillary action at solid
metal-liquid interfaces. J. Colloid Interface Sci. 162: 381—389
139. Lewis T. J (1996). New electro-mechanical concepts of the primary mechanism of
electrical breakdown in liquids. 12th Int. Conf, on Conduction and Breakdown in
Dielectric Liquids, Rome, pp. 273—278
140. Lewis T. J (1998) A new model for the primary process of electrical breakdown in
liquids. IEEE Trans. Dielectr. Electr. Insulat. 5(3): 306—315
141. Lewis T. J (2002) Polyethylene under electrical stress. IEEE Trans. Dielectr. Electr.
Insulat. 9(5): 717-729
142. Lewis T. J, Bowen P. J (1984) Electronic processes in biopolymer systems. IEEE
Trans. Electr. Insulat. El-19(3): 254—256
143. Lewis I. A, Wells F. H (1959) Millimicrosecond Pulse Techniques. Pergamon,
London
144. Licht V, Bluhm H (2000) A sensitive dispersion interferometer with high temporal
resolution for electron density measurements. Rev. Sci. Instrum. 71: 2710—2715
145. Licht V, Bluhm H, Hoppe P. Yoo S. J (1998) Time dependent field and particle
density measurements in the acceleration gap of a high power ion diode. In:
Markovits M, Shiloh J (eds.) 12th Ini. Conf, on High Power Particle Beams. Haifa,
Israel, pp. 203—207
146. Lisitsyn I, Inoue H, Katsuki S, Akiyama H, Nishizawa I (1999) Drilling and
demolition of rocks by pulsed power. In: Stalling C, Kirbie H (eds.) Proc. 12th IEEE
Int. Pulsed Power Conf., Monterey, CA, 27—30 June 1999, pp. 169—172
147. Llewellyn-Jones F (1957) Ionisation and Breakdown in Gases. Methuen, London
148. Lockner T. R, Slutz S, Poukey J. W, Stygar W. A (1993) Theoretical and
experimental studies of the 2-stage ion diode. In: Prestwich K, Baker W (eds.) 9th
IEEE Int. Pulsed Power Conf., Albuquerque, NM, pp. 714—717
149. Lockner T, Slutz S, Johnson D. J, Desjarlais M, Poukey J (1994) Results of the first
2-stage diode experiments on PBFAII. In: Rix W, White R (eds.) 10th Int. Conf, on
High-Power Particle Beams, San Diego. NTIS, Springfield, VA, pp. 61—64
336 Список литературы
150. Lokhandwalla М, Bradford S (2000) Fracture mechanics model of stone
comminution in ESWL and implications for tissue damage. Phys. Med. Biol.
45:1923-1940
151. Loubriel G. M, Zutavem E J, Baca A. G, Hjalmarson H. P, Helgeson W. D,
O'Malley M. W (1995) Photoconductive semiconductor switches for firing sets and
electro-optic modulators. In: Baker W, Cooperstein G (eds.) Proc. 10th IEEE Int.
Pulsed Power Conf., Albuquerque, NM, pp. 354—359
152. Loubriel G. M, Zutavern F. J, Baca A. G, Hjalmarson H. P, PlutTA, Helgeson W. D,
O'Malley M. W, Ruebush M. H, Brown D. J (1997) Photoconductive
semiconductor switches. IEEE Trans. Plasma Sci. 25(2): 124—130
153. Lupton W. H, Ford R. D, Jenkins D, Vitkovitsky I. M (1981) Homopolar generator
concept for versatile pulsed output. In: Martin TH, Guenther AH (eds.) 3rd IEEE
Int. Pulsed Power Conf., Albuquerque, NM, pp. 122—125
154. Lyubutin S. K, Mesyats G. A, Rukin S. N, Slovikovskii B. G, Turov A. M (1996)
New solid state opening switches for repetitive pulsed power technology. In:
Ullschmied J, Jungwirth К (eds.) 11th Int. Conf, on High-Power Particle Beams,
Prague, pp. 135—138
155. Maenchen J. E, Hahn K, Kincy M, Kitterman D, Lucero R, Menge P. R, Molina
J, Olson C, Rovang D. C, Fulton R. D, Carlson R, Smith J, Martinson D,
Droemer D, Gignac R, Helvin T, Ormand E, Wilkins F, Welch D. R, Oliver В. V,
Rose D. V, Bailey V, Corcoran P, Johnson D. L, Smith J. D, Wiedenheimer D,
Cooperstein G, Commisso R, Mosher D, Stephanakis S, Schumer J, Swanekamp
S, Young F, Goldsack T J, Cooper G. M, Pearce A. G, Phillips M. A, Sinclair M.
A, Thomas K. J, Williamson M, Cordova S, Woodring R, Schamiloglu E (2002)
Intense electron sources for flash radiography. In: Mehlhom T. A, Sweeney M. A
(eds.) Proc. 14th Int. Conf on High—Power Particle Beams, 23—28 June 2002,
Albuquerque, NM, pp. 117—122
156. Malewski R (1968) New device for current measurement in exploding wire circuits.
Rev. Sci. Instrum. 39: 90—94
157. Maret G, Dransfeld К (1985) Biomolecules and polymers in high steady magnetic
fields. In: Herlach F, Dransfeld К (eds.) Strong and Ultrastrong Magnetic Fields and
Their Applications. Topics in Applied Physics, Vol. 57, Springer, Berlin, Heidelberg,
pp. 143-204
158. Maron Y, Sarid E, Nahshoni E, Zahavi О (1989) Time-dependent spectroscopic
observation of the magnetic field in a high-power-diode plasma. Phys. Rev. A
39(11): 5856-5862
159. Maron Y, Arad R, Weingarten A, Tsigutkin K, Ralchenko Y. V, Osin D, Chakrabarti
N, Commisso R. J, Weber В. V (2002) Interaction of rapid magnetic fields with
plasmas and implications to pulsed-power systems. In: Kirbie H, Goebel D (eds.)
25th Int. Power Modulator Symp. and 2002 High-Voltage Workshop, Hollywood, pp.
17-22
160. Martin T. H, Guenther A. H, Kristiansen M (1996) J.C. Martin, on Pulsed Power.
Plenum, New York
Список литературы 337
161. Martynyuk Р, Sher Е (1974) Elastic-wave diffraction by a finite crack under
antiplane strain conditions. J. Appl. Meeh. Techn. Phys. 13:406—410
162. Marx E (1923) Verfahren zur Schlagpriifung von Isolatoren und anderen
elektrischen Vorrichtungen. German Patent 455933
163. Marx E (1924) Versuche uber die Pruning von Isolatoren mit Spannungsstossen.
Elektrotech. Z. 25:652-654
164 Meek J. M, Craggs J. D (1978) Electrical Breakdown of Gases. Wiley, New York
165. Mehlhom T. A, Bailey J. E, Chandler G. A, Coats R. S. Cuneo M. E, Derzon M. S,
Desjarlais M. P. Dukart R. J, Filuk A. B, Haill T. A, Ives H. C, Johnson D. J,
Leeper R. J. Lockner T. R, Mendel C. W, Menge P. R, Mix L. P, Moats A. R,
Moore W. B, Pointon T. D, Poukey J. W. Quintenz J. P, Rosenthal S. E, Rovang D.
Ruiz C. L, Slutz S. A, Stygar W. A, Wenger D. F (1994) Progress in lithium beam
power, divergence, and intensity at Sandia National Laboratories. In: Rix W, White
R (eds.) 10th Int. Conf, on High-Power Particle Beams, San Diego. NTIS,
Springfield, VA. pp. 53—60
166. Mendel C. W, Rosenthal S. E (1995) Modelling magnetically insulated devices
using flow impedance. Phys. Plasmas 2: 1332—1342
167. Mendel C. W, Rosenthal S. E (1996) Dynamic modelling of magnetically insulated
transmission line systems. Phys. Plasmas 3:4207—4219
168. Mendel C. W, Seidel D. B, Rosenthal S. E (1983) A simple theory of magnetic
insulation from basic physical considerations. Laser Part. Beams 1(3): 311—320
169. Mesyats G. A (1998) Explosive Electron Emission. URO-Press, Ekaterinburg
170. Milton О (1972) Pulsed flashover of insulators in vacuum. IEEE Trans. Electr.
Insul. 7:9-15
171. Miura N, Herlach F (1985). Strong and ultrastrong magnetic fields. In: Herlach F,
Dransfeld К (eds.) Strong and Ultrastrong Magnetic Fields and Their Applications.
Topics in Applied Physics, Vol. 57, Springer, Berlin, Heidelberg, pp. 278—297
172. Miyamoto S, Yasuike K, Imasaki K, Yamanaka C, Nakai S (1992) Intense light ion
beam divergence in single and two-stage diode. In: Konig D (ed.) 15th Int. Symp. on
Discharges and Electrical Insulation in Vacuum, Darmstadt, Germany. VDE-Verlag,
Berlin, pp. 711-715
173. Moses G. A, Kulcinski G. L, Bruggink D, Engelstad R, Lovell E, McFarlane J,
Musicki Z, Petersen R, Stanislavsky I, Wittenberg L, Kessler G, Von Mollendorff U,
Stein E, Smith I, Corcoran P, Nichimoto H, Fockler J, Cook D, Olson R (1989).
Overview of the LIBRA light ion beam fusion conceptual design. Fusion Technol.
15: 756-765
174. Muller G, Schumacher G, Zimmermann F (2000) Investigation on oxygen
controlled liquid lead corrosion of surface treated steels. J. Nucl. Mater. 278:85—95
175. Muller G, Engelko V, Bluhm H. An V, Kuznetsov V. Viazmenova G (2002a)
Precision of intense electron beams transported in vacuum by applied magnetic
field. In: Mehlhom T. A, Sweeney M. A (eds.) Proc. 14th Int. Conf, on High-Power
Particle Beams, Albuquerque, NM, 23—28 June 2002, pp. 337—340
338 Список литературы
176. Miiller G, Engelko V, Bluhm H, Heinzel A, Schumacher G, Strauss D,
Weisenburger A, Zimmermann F, Shulov V, Notchovnaia N (2002b) Application of
pulsed electron beams for improvement of material surface properties. In:
Mehlhom T. A, Sweeney MA (eds.) Proc. 14th Int. Conf, on High-Power Particle
Beams, Albuquerque, NM, 23—28 June 2002, pp. 325—328
177. Muller G, Heinzel A, Schumacher G, Weisenburger A (2003) Control of oxygen
concentration in liquid lead and lead-bismuth. J. Nucl. Mater. 321: 256—262
178. Muller G, Engelko V, Weisenburger A, Heinzel A (2005) Surface alloying by pulsed
intense electron beams. Vacuum 77:469—474
179. Nation J (1979) High-power electron and ion beam generation. Part. Accel. 10: 1—
30
180. Neu J, Krassowska W (1999) Asymptotic model of electroporation. Phys. Rev. E
59(3): 3471-3482
181. Ottinger P. F, Young F. C, Stephanakis S. J, Rose D. V, Neri J. M, Weber В. V,
Myers M. C, Hinshelwood D, Mosher D, Olson C. L, Welch D. R (2000)
Self-pinched transport of an intense proton beam. Phys. Plasmas 7(1): 346—358
182. Pao Y. H, Mow C (1963) Scattering of plane compressional waves by a spherical
obstacle. J. Appl. Phys. 34(3): 493—499
183. Papoulis A (1968) Systems and Transforms with Applications in Optics.
McGraw-Hill, New York
184. Pareira N. R (1983) Electron backscatter and impedance in one-dimensional
space-charge limited diodes. J. Appl. Phys. 54(11): 6307—6310
185. Paschen F (1889) Uber die zum Funkeniibergang in Luft, Wasserstoff und
Kohlensaure bei verschiedenen Drucken erforderliche Potentialdifferenz. Ann.
Phys. Chem. 37: 69—96
186. Pfeiffer W (1971) Der Spannungszusammenbruch an Funkenstrecken in
komprimierten Gasen. Z. Angew. Phys. 32(4): 265—273
187. Poukey J. W, Bergeron K. D (1978) Space-charge effects in long coaxial vacuum
transmission lines. Phys. Lett. 32(1): 8—10
188. Quintenz J, Seidel D, Kiefer M, Pointon T, Coats R, Rosenthal S, Mehlhom T,
Desjarlais M, Krall N (1994) Simulation codes for light-ion diode modelling. Laser
Part. Beams 12(2): 283-324
189. Rabussay D, Dev N. B, Fewell J, Smith L. C, Widera G, Zhang L (2003)
Enhancement of therapeutic drug and DNA delivery into cells by electroporation.
J. Phys. D: Appl. Phys. 36: 348-363
190. Raether H (1964) Electron Avalanches and Breakdown in Gases. Butterworths,
London
191. Ramirez J. J, Hasti D. E, Corley J. P, Poukey J. W, Prestwich K. R, Genuario R. D,
Nishimoto H. N, Fockler J. J, Smith I. D, Champney P. D, Nielsen К. E, Schlitt L.
G, Spence P. W (1985) The four stage HELIA experiment. In: Rose MF, Turchi P. J
(eds.) Proc. 5th IEEE Int. Pulsed Power Conf, 10—12 June 1985, Arlington, VA, pp.
143-146
Список литературы 339
192. Ramirez J. J, Prestwich К. R, Alexander J. A, Corley J. P, Denison G. J, Huddle C.
W, Johnson D. L, Pate R. C, Weber G. J, Bugess E. L, Hamil R. A, Poukey J. W,
Sanford T. W, Seamons L. O, Zawadzkas G. A, Smith I. D, Spence P. W, Schlit L.
G (1988) Hermes III-A 16 TW short pulse gamma ray simulator. In: Bauer W,
Schmidt W (eds.) Proc. 7th Int. Conf, on High-Power Particle Beams, Karlsruhe,
Germany, 4—8 July 1988, pp. 148—157
193. Redi M, Hopfield J. J (1980) Theory of thermal and photo-assisted electron
tunnelling. J. Chem. Phys. 72(12): 6651—6660
194. Reinovsky R. E, Smith D. L, Baker W. L, Degnan J. H, Henderson R. P, Kohn R. J,
Kloc D. A, Foderick N. F (1982) Inductive store pulse compression system for
driving high speed plasma implosions. IEEE Trans. Plasma Sci. 10: 73—81
195. Reinovsky R. E, Levi P. S, Welby J. M (1985) An economical, 2 stage flux
compression generator system. In: Rose M. F, Turchi P. J (eds.) Proc. 5th IEEE Int.
Pulsed Power Conf, 10—12 June 1985, Arlington, VA, pp. 216—219
196. Rogowski W, Steinhaus W (1912) Die Messung der magnetischen Spannung.
(Messung des Linienintegrals der magnetischen Feldstarke). Arch. Elektrotechnik
1(4): 141-150
197. Rompe R, Weizel W (1944) Uber das Toeplersche Funkengesetz. Z. Phys. 122: 9—
12
198. Rose D. V, Ottinger P. F, Welch D. R, Oliver В. V, Olson C. L (1999) Numerical
simulations of self-pinched transport of intense ion beams in low-pressure gases.
Phys. Plasmas 6(10): 4094-4103
199. Rukin S. N, Kotov Y. A, Mesyats G. A, Filatov A. L, Lyubutin S. K, Alichkin Y. A,
Darznek S. A, Telnov V. A, Slovikovskii B. G, Timoshenkov S. P, Bushlyakov A. I,
Turov A. M (1996) Pulsed power accelerator technology based on solid-state
semiconductor opening switches. In: Jungwirth K, Ullschmied J (eds.) Proc. 11th
Int. Conf, on High Power Particle Beams, Prague, 10—14 June 1996, pp. 33—36
200. Rusch D (1991) Handbuch zum Programm LEITER. Numerische Simulation
pulstechnischer Netzwerke, Forschungszentrum Karlsruhe, unpublished
201. Sale A, Hamilton W (1967) Effects of high electric fields on microorganisms — I.
Killing of bacteria and yeasts. Biochem. Biophys. Acta 148:781—788
202. Santos J. C, Taplamacioglu С. M, Hidaka К (2000) Pockels high-voltage
measurement system. IEEE Trans. Power Delivery 15(1): 8—13
203. Sarjeant W. J, MacDougall F. W (1997) Capacitors for high power electronics. In:
Cooperstein G, Vitkovitsky I (eds.) Proc. 11th IEEE Int. Pulsed Power Conf.,
Baltimore, MD, pp. 603—609
204. Schiweck H, Clarke M (2001) In: Ullmann's Encyclopedia of Industrial Chemistry,
6th edn, 2001 Electronic Release. Wiley-VCH, Weinheim
205. Schoenbach K, Kristiansen M, Schaefer G (1984) A review of opening switch
technology for inductive energy storage. Proc. IEEE 72(8): 1019—1040
206. Schoenbach К. H, Peterkin F. E, Alden R. W, Beebe S. J (1997) The effect of pulsed
electric fields on biological cells: experiments and applications. IEEE Trans.
Plasma Sci. 25(2): 284-292
340 Список литературы
207. Schoenbach К. Н, Beebe S. J, Buescher Е. S (2001) Intracellular effect of
ultrashort pulses. Bioelectromagnetics 22:440—448
208. Schultheiss C, Strassner R, Bluhm H, Stemmermann P (1998) Concrete recycling
and scraping by electrodynamic fragmentation. In: Bluhm H (ed.) Physics of Intense
Light Ion Beams. Production of High Energy Density in Matter, and Pulsed Power
Applications, Annual Report 1996/97, Karlsruhe, FZKA-Report 6205
209. Schultheiss C, Bluhm H, Mayer H, Kern M, Michelberger T, Witte G (2002)
Processing of sugar beets with pulsed electric fields. IEEE Trans. Plasma Sci. 30(4):
1547-1551
210. Schumann D, Muller RA (2001) Verfahren zur Gewinnung von
Polyhydroxyalkanoaten (PHA) oder deren Copolymeren. German Patent DE 100
13514 C2
211. Schwab A. J (1981) Hochspannungsmefltechnik. Springer, Berlin, Heidelberg
212. Sethian J. D, Hegeler F, Myers M, Friedman M, Obenschain S, Lehmberg R,
Guiliani J. Kepple P, Swanekamp S, Smith I, Weidenheimer D, Morton D, Schlitt
L, Smilgys R, Searles S (2001) The Electra KrF laser program. In: Reinovsky R,
Newton M (eds.) Proc. 28th IEEE Int. Conf, on Plasma Science and 13th IEEE Int.
Pulsed Power Conf, 17—22 June 2001, Las \fegas, pp. 232—236
213. Sher E (1974) Investigation of the dynamics of the development of cracks by the
method of photoelelasticity. J. Appl. Meeh. Techn. Phys. 16(6): 858—864
214. Shpitalnik R, Weingarten A, Gomberoff K, Krasik Y, Maron Y (1998) Observations
of two-dimensional magnetic field evolution in a plasma opening switch. Phys.
Plasmas 5(3): 792-798
215. Sjomkin B. W, Ussow A. F, Kurets V. 1 (1995) The Principles of Electric Impulse
Destruction of Materials. Russian Academy of Sciences. Kola Science Centre (in
Russian)
216. Skotheim T. A (1986) Handbook of Conducting Polymers. Dekker, New York
217. Slenes К. M, Winsor P, Scholz T, Hudis M (2001) Pulse power capability of high
energy density capacitors based on a new dielectric material. IEEE Trans. Magn.
37(1): 324-327
218. Slutz S. A (1993) Ion emission from anode foils during multistage acceleration of
intense ion beams. Phys. Fluids В 5(1): 209—215
219. Slutz S. A, Desjarlais M. P (1990) Theory of multistage intense ion beam
acceleration. J. Appl. Phys. 67(11): 6705—6717
220. Slutz S. A, Poukey J. W, Pointon T. D (1994) Simulations of magnetically insulated
multistage ion diodes. Phys. Plasmas 1(6): 2072—2081
221. Smith 1. D (1980) A novel voltage multiplication scheme using transmission lines.
Report, AWRE Aldermaston, unpublished
222. Sommerfeld A (1950) Vorlesungen ubher Theoretische Physik. Akademische
Verlagsgesellschaft, Leipzig
223. Spielman R. B, Stygar W. A, Seamen J. F, Long F, Ives H, Garcia R, Wagoner T,
Struve K. W, Mostrom M, Smith I, Spence P, Corcoran P (1997) Pulsed power
Список литературы 341
performance of PBFA Z. In: Cooperstein C, Vitkovitsky I (eds.) Proc. 11th IEEE
Int. Pulsed Power Conf, 29 June — 2 July 1997, Baltimore, pp. 709—714
224. Stokes J. L, Bartsch R. R, Cochrane J.C, Chrien R. E, Forman P. J, Looney L. D,
Tabaka L. J, Veeser L. R, Marshall B. R, Broste W. B, Warthen B. J (1995) Precision
current measurements on Pegasus II using Faraday rotation. In: Baker W, Cooper-
stein G (eds.) Proc. 10th IEEE Int. Pulsed Power Conf, Albuquerque, NM, pp.
378-385
225. Strauss D, Muller G, Schuhmacher G, Engelko V, Stamm W, Clemens D,
Quadakkers W. J (2001) Oxide scale growth on MCrAIYbond coatings after pulsed
electron beam treatment. Surf. Coat. Technol. 135:196—201
226. Sunka P (2001) Pulse electrical discharges in water and their applications. Phys.
Plasmas 8(5): 2587-2594
227. Sunka P, Babicky V, Clupek M (1999) Generation of chemically active species by
electrical discharges in water. Plasma Sources Sci. Technol. 8: 258—265
228. Takahashi Y (1977) Koronaentladungen in flussigem Stickstoff. Bull. Facul. Sci.
Eng., Chuo Univ. 20: 247-255
229. Takahashi Y, Ohtsuka К (1975) Corona discharges and bubbling in liquid nitrogen.
J. Phys. D 8: 165-169
230. Teissie J, Rols M (1994) Manipulation of cell cytoskeleton affects the lifetime of
cell membrane electropermeabilization. Ann. N.Y. Acad. Sci. 720: 98—110
231. Toepier M (1924) Stossspannung, Uberschlag und Durchschlag bei Isolatoren.
Elektrotechn. Z. 45:1045-1050
232. Toepier M (1927) Zur Bestimmung der Funkenkonstante. Arch. Elektrotechn. 18:
549-562
233. Toney M. F, Howard J. N, Richer J, Borges G. L, Gordon J. G, Melroy O. R,
Wiesler D. G, Yee D, Sorensen L. В (1994) Voltage-dependent ordering of water
molecules at an electrode-electrolyte interface. Nature 368:444—446
234. Turman B. N, Martin T. H, Neau E. L, Humphreys D. R, Bloomquist D. D, Cook
D. L, Goldstein S. A, Schneider L. X, McDaniel D. H, Wilson J. M, Hamil R. A,
Barr G. W, \&nDevender J. P (1985) PBFA II, A 100 TW pulsed power driver for
the inertial confinement fusion program. In: Turchi P. J, Rose M. F (eds.) Proc. 5th
IEEE Int. Pulsed Power Conf., Arlington, VA, pp. 155—161
235. Urban J (2002) Spektroskopische und elektrische Charakterisierung des
Entladever-haltens von Pseudofunken-Schaltsystemen. PhD thesis, University of Er-
langen
236. VanDevender J. P (1976) Short pulse electrical breakdown strength of H2O. In:
Burkes TR, Kristiansen M (eds.) 1st IEEE Int. Pulsed Power Conf, Lubbock, TX,
pp. IIIE3.1-IIIE3.5
237. VanDevender J. P, Bluhm H (1993) Light ion accelerators for 1CF. In: Velarde G,
Ronen Y, Martinez-Vai J. M (eds.) Nuclear Fusion by Inertial Confinement, CRC
Press, Boca Raton, pp. 455—484
238. Vasilevskii M. A, Roife I. M, Engelko V. I (1980) Impedance of a diode with a
multispike explosive-emission cathode. Sov. Phys. Tech. Phys. 25(11): 1380—1382
342 Список литературы
239. X&silevskii М. A, Roife I. М, Engelko V. I (1981) Operating characteristics of
explosive-emission multipoint cathodes with microsecond pulse length. Sov. Phys.
Tech. Phys. 26(6): 671-678
240. Vasilevskii M. A, Roife I. M, Engelko V. I, Yankin E. G (1986) Dynamics of plasma
generated by a multitip explosive-emission cathode. Sov. Phys. Tech. Phys. 31(3):
284-287
241. Vasilevskii M. A., Engelko V. I., Yankin E. G. (1988) The influence of emitter
density and anode process on the time of operation of a diode with multitip
explosive emission cathodes. Sov. Phys. Tech. Phys. 33(9): 1060—1066
242. Vesey R. A, Pointon T. D, Cuneo M. E, Mehlhorn T. A, Bailey J. E, Johnson D J,
Stygar W. A (1999) Electron-anode interactions in particle-in-cell simulations of
applied-/? ion diodes. Phys. Plasmas 6(8): 3369—3387
243. Volodarskaya S. G, Guz' I. S, Kumkin I. A, Finkel V. M (1975) An investigation
into the interaction of a stress wave with a stationary macrocrack in elastic-plastic
and quasibrittle materials. J. Appl. Meeh. Tech. Phys. 13:432—437
244. Walker J, Surman S, Jass J (2000) Industrial Biofouling — Detection, Prevention and
Control. Wiley, Chichester
245. Wang M. Y, DiCapua M. S (1980) Operating point of long magnetically insulated
vacuum transmission lines. J. Appl. Phys. 51(11): 5610—5614
246. Weaver J (1994) Molecular basis for cell membrane electroporation. Ann. N.Y.
Acad. Sci. 720:141-152
247. Weaver J, Chizmadzhev Y (1996) Theory of electroporation: a review. Bioelectro-
chem. Bioenerget. 41: 135—160
248. Weizel W, Rompe R (1947) Theorie des elektrischen Funke ns. Ann. Physik 6(1):
285-300
249. Welch D. R, Olson C. L (1996) Self-pinched transport for ion-driven inertial
confinement fusion. Fusion Eng. Design 32—33:477—483
250. Welch D. R, Cuneo M. E, Olson C. L, Mehlhorn T. A (1996) Gas breakdown
effects in the generation and transport of light ion beams for fusion. Phys. Plasmas
3:2113-2121
251. Yoo S (1997) Spektroskopische Messungen im Anodenplasma evner fremdmagnetisch
isolierten Hochleistungs-Ionendiode. PhD thesis, University of Karlsruhe,
FZKA-Report 5976
252. Yoxas G (1978) Fusion power with particle beams. Sci. Am. 239: 50—61
253. Zeller H. R, Pfluger P, Bernasconi J (1984) High-mobility states and dielectric
breakdown in polymeric dielectrics. IEEE Trans. Electr. Insulat. El-19(3): 200—204
254. Zinov'ev N, Semkin В (1978) Energy balance for a spark in a solid dielectric. Sov.
Phys. Tech. Phys. 23(3): 369-370
предметный указатель
А ATLAS — 273 R RHEPP — 225
Е ELECTRA — 285 S SF6 — 28
F SOS — 145
FRAN КА — 314 z
G Z-машина — 221
GESA — 280 GTO — 126 A Анодная инициация — 53
Н Б
HELI А — 213, 291 HERMES III — 224 Бактериальных загрязнений устранение — 254
I Бетона электродинамическое размельчение — 313
IGBT-транзисторы — 129 Биологической клетки эквивалентная схема
К — 247
KALIF — 213, 220 KrF-лазеры — 285 Биообрастания — 256 Биополиэстер — 256 Биоэлектрика — 13
L Блюмляйна линии — 215
£С-генераторы Маркса — 86 £С-звено — 165 LEITER — 170 Блюмляйна схема — 212 Брагинского модель — 40 В
М Вейбулловское распределение — 67
MCrAlY— 281 Вейцеля и Ромпа модель — 39 Верде постоянная — 239
Р Витровак — 134
Particle-in-ceII method — 182 PBFA 2 —22/ Pseudospark switch — 115 Внутренняя электрическая прочность — 58, 59, 60 Водяной ключ — 220 Время нарастания — 16
344 Предметный указатель
Г
Газовые разрядники многоканальные — ill
Газоразрядные ключи — 99
- с лазерным управлением — 108
Гельмгольца слой — 47, 248
Генератор Маркса — 79
- с двухполярным зарядом конденсаторов —
81
Генераторы мощных электронных пучков —
276
Гиллемина цепь — 168
Глубина оптической абсорбции — 130
Гугонио соотношение — 267
Гуи—Чэпмена слой объемного заряда — 47
д
Датчики
- емкостные — 231
- индуктивные — 233
- электромагнитного поля — 229
Динамические ограничения на давление,
создаваемое магнитным полем — 263
Диод
- импульсный электронный — 279
- инжекторный — 291
- параксиальный — 289
- ускорительный — 295
Диокотронные нестабильности — 293
Диэлектрическая поляризация — 75
Диэлектрические включения — 179
Длинные линии — 153
Длинные линии с потерями — 159
Е
Емкостный датчик — 232
Емкостный делитель напряжения — 83
3
Замыкающие ключи — 99
Заряд объемный — 30
Зарядное устройство — 203
Зет-пинч — 222
И
Игнитроны — 117
Измерение тока с использованием эффекта
Фарадея — 238
Измерение тока с помощью резисторов — 236
Импульсная рентгенография — 287
Импульсные магнитные поля — 257
Импульсные электронные диоды — 279
Индуктивные накопители энергии — 90
Инжекторный диод — 291
Ионные пучки большой мощности — 291
Источники ионов — 297
Источники электронов — 278
К
Катодная инициация — 50
Катушка Роговского — 234
КЕА — 251
Керра эффект — 241
Клеточных мембран разрушение — 245
Ключи
- плазменные размыкающие — 141
- полупроводниковые к с оптическим управ-
лением — 130
- полупроводниковые размыкающие — 145
- с магнитным управлением — 133
Композитных материалов разрушение — 303
Конденсатор — 71
- долговечность — 76
Контакт металл—диэлектрик — 63
Коррозия стали в жидком сплаве свинец-
висмут — 283
Коэффициент ионизации — 24
Коэффициенты увеличения поля для
различных конфигураций электродов — 30
КПД — 203
Крайтрон — 119
Кумулятивные линии формирования
импульсов — 216
Л
Лавинный пробой — 27, 32, 46, 132
- вероятность — 37
Литотрипсия — 300
Лопатки турбин — 282
М
Магнитная самоизоляция — 175,180
Магнитный анализатор энергии ионов — 242
Метгласе — 134
Метод конечно-размерных частиц в ячейке
— 182
Методы заряда конденсаторов — 203
Механические прерыватели — 139
Многозвенная цепь — 163
Многоканальные газовые разрядники — 111
Моделирование цепей — 170
Модель Брагинского — 40
Модель Вейцеля и Ромпа — 39
Модель Теплера — 39
Монитор напряжения — 243
Предметный указатель 345
О
Оборудование для электроимпульсного
разрушения — 309
Обработка клеток растительного
происхождения — 250
Ограничения на магнитное поле при
использовании катушек без разрушения —
258
Ограничения на поле при работе с
разрушаемой катушкой — 265
Одновитковая катушка — 265
Отрезок линии как элемент схемы — 160
П
Пашена закон — 26
Пашена минимум — 26
Перенос зарядов — 61
Плазма — 278
Плазменные размыкающие ключи — 141
Поверхностная обработка материалов — 280
Повторное использование композитных
материалов — 307
Повторное использование
эластополимерных материалов — 321
Подогревный катод — 114
Поккельса эффект — 241
Полиэтилен — 59
Полупроводниковые ключи с оптическим
управлением — 130
Полупроводниковые размыкающие ключи —
145
Получение импульсов энергии от устройств с
компрессией магнитного потока — 273
Поляризация клеточных мембран — 246
Предохранители — 138
Пробой в вакууме между металлическими
поверхностями — 177
Пробой в газоразрядных ключах — 101
Пробой импульсный — 32
Пробой твердых диэлектриков — 58
Производство сахара — 250
Процессы на электродах — 47
Пустотелый катод — 115
Р
Радиационная терапия — 291
Размыкающие ключи — 137
Разрушение твердых диэлектриков
с помощью электрических импульсов — 302
Распределение примесей в тиристорной
структуре — 122
Расходимость электронов — 286
Резонансное туннелирование — 44
С
Самосжатый пучок электронов — 288, 289
Сверхпроводящие размыкающие ключи —
141
Селективное разрушение — 307
Сечение реакции — 23
Сжатие магнитного потока — 267
Сжатие магнитного потока
электромагнитным способом — 272
Сложение мощностей — 211
Сложение напряжений — 212
Сложение напряжений с использованием
временной изоляции — 212
Сложение напряжений с использованием
индуктивной изоляции — 213
Соотношение площадь—время — 38
Стримерный пробой в жидкостях — 49
Стримеры в газах — 32
Струйный плазменный ключ — 145
Т
Тангенс угла потерь tg 8 — 73
Таунсенда пробой — 36
Таунсенда условие — 25, 26
Теплера модель — 39
Тиратроны — 112
Тиратроны с холодным катодом — 115
Тиристор
- запираемый — 126
Тиристоры — 121
Ток пучка — 277, 298
Точечный источник рентгеновского
излучения — 288
Трансформаторные линии — 209
Трансформаторы импульсные — 198
Тригатрон — 105
У
Углеродные волокна — 278
Умножение мощности и напряжения — 91
Умножители напряжения — 207
Униполярные генераторы — 93
Управляемые вакуумные разрядники — 120
Ускорительный диод — 295
Ф
Формирование импульсов с помощью линии
без потерь — 162
Фоулера—Нордхейма уравнение — 34
346 Предметный указатель
Ч
Чайлда—Ленгмюра закон — 279
Э
Экономические аспекты повторного
использования материалов — 325
Электрическая прочность — 59, 65, 73, 177
- ВОДЫ — 70, 81, 304
- динамическая — 304
- жидкого азота — 323
- статистическая интерпретация — 66
- статическая — 22
Электронегативные газы — 27
Электронная эмиссия — 177
Электронное состояние жидкостей — 43
Электрооптические эффекты — 240
Эффект Керра — 241
Эффект Поккельса — 241
Эффективность передачи энергии — 196
Я
Ядерный синтез — 276
О ПРОГРАММЕ LEITER
Программу для расчета линий передач LEITER можно скачать по адресу
http://www.dodeca.su/files/leiter.rar.
Инсталлировать данную программу нужно следующим образом.
Папку \LEITER скопировать на диск С:, что легко сделать в окне Explorer’a
перетаскиванием имени папки на иконку жесткого диска. Имя папки на диске
останется \LEITER.
Подготовленные ярлыки программ находятся в папке \LE1TER1.3, их можно
перетащить на рабочий стол из Explorer’a или сразу скопировать всю папку на ра-
бочий стол и запускать оттуда.
Ярлыки программ ссылаются на папку C:\LEITER. Если необходимо пере-
именовать папку LEITER, то надо сделать соответствующие изменения в каждом
ярлыке.
Более детальную информацию можно прочитать в Help'e: см. файлы
LeiterSE.hlp или LeiterLE.hlp.
ХАНСИОАХИМ БЛУМ
Схемотехника мощных импульсных устройств
Главный редактор В. М. Халикеев
Ответственный редактор И. А. Корабельникова
Технический редактор Н. В. Тищенко
Верстальщик И. С. Каинова
Корректор Г. Б. Абудеева
Подписано в печать 13.05.2008. Формат 70x100/16. Бумага офсетная.
Гарнитура «NewtonC». Печать офсетная.
Объем 22 п. л. Усл. п. л. 24,5
Тираж 2000 экз. Код PPS. Заказ № 219
Издательский дом «Додэка-ХХ!»
ОКП 95 3000
105318 Москва, а/я 70
Тел./факс: (495) 366-24-29, 366-09-22
E-mail: books@dodeca.ru; red@dodeca.ru
Отпечатано с готовых диапозитивов в ОАО «Московская типография № 6»
115088 Москва, ул. Южнопортовая, 24
силоплм злвкюникл
£) Springer
СХЕМОТЕХНИКА
И ПРИМЕНЕНИЕ
МОЩНЫХ ИМПУЛЬСНЫХ
УСТРОЙСТВ
СХЕМОТЕХНИКА И ПРИМЕНЕНИЕ
МОЩНЫХ ИМПУЛЬСНЫХ УСТРОЙСТВ
В книге изложены физические и технические
основы создания и применения импульсов
высокого напряжения с очень большой мощ-
ностью и энергией. В первой части описаны
компоненты, материалы и методы измерений,
используемые в технике получения мощных
импульсов.
Во второй части — некоторые из наиболее перспективных приме-
нений этой техники в биоэлектрике, поверхностной обработке ме-
таллов, медицине, селективном размельчении различных материа-
лов и т. д., а именно: генераторы мощных импульсов электрического
и магнитного поля, источники интенсивного импульсного излучения
и импульсных электрических разрядов.
Книга представляет собой, по сути, путеводитель по огромному
количеству публикаций по данной тематике, как классических,
так и современных.
Книга предназначена широкому кругу читателей, которые хотят
ближе ознакомиться с основными идеями и методами, используе-
мыми в сфере мощных импульсных устройств, а также будет
полезна студентам, преподавателям вузов, инженерам и ученым.
ISBN 978-5-941-20-191-4
9
785941
201914