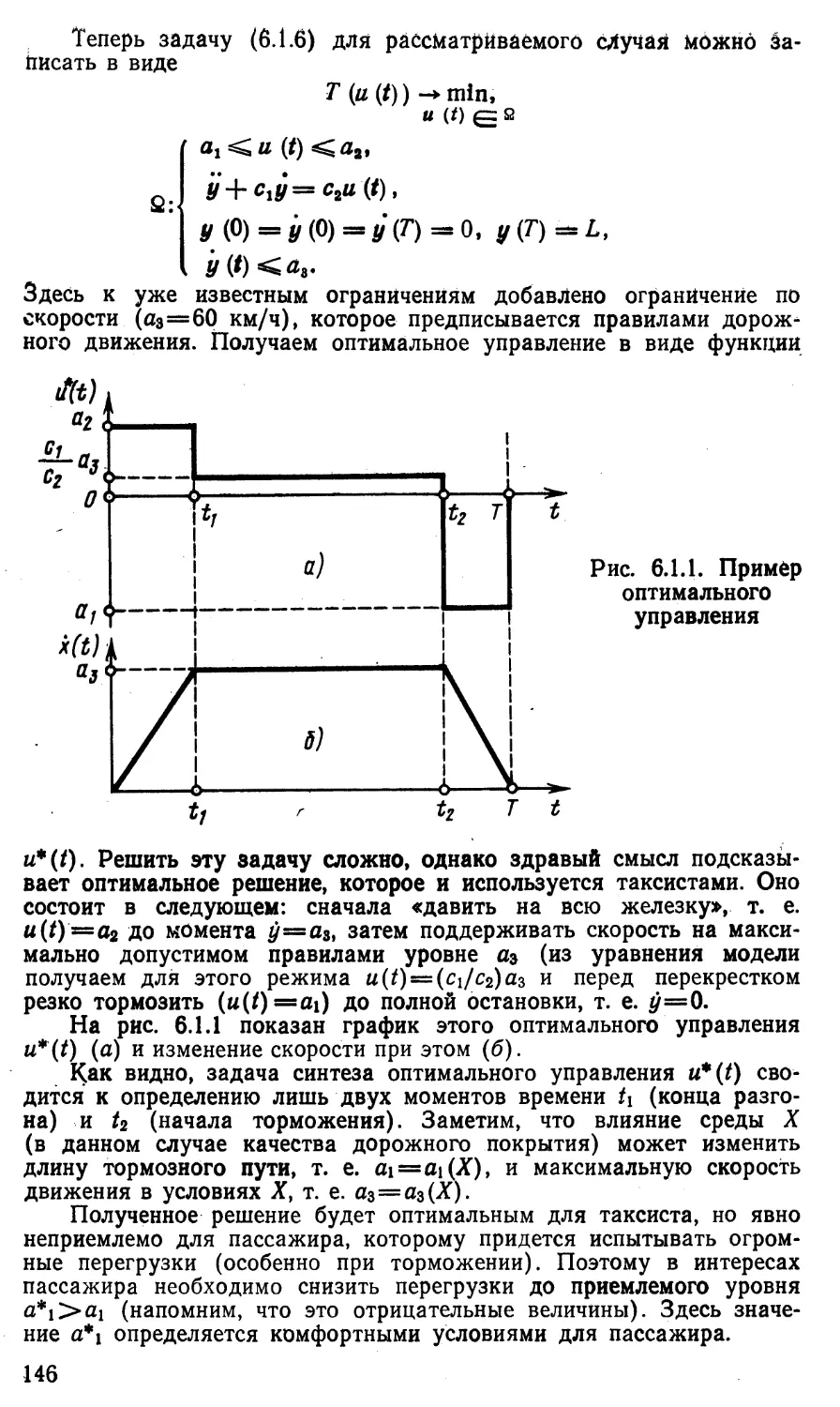
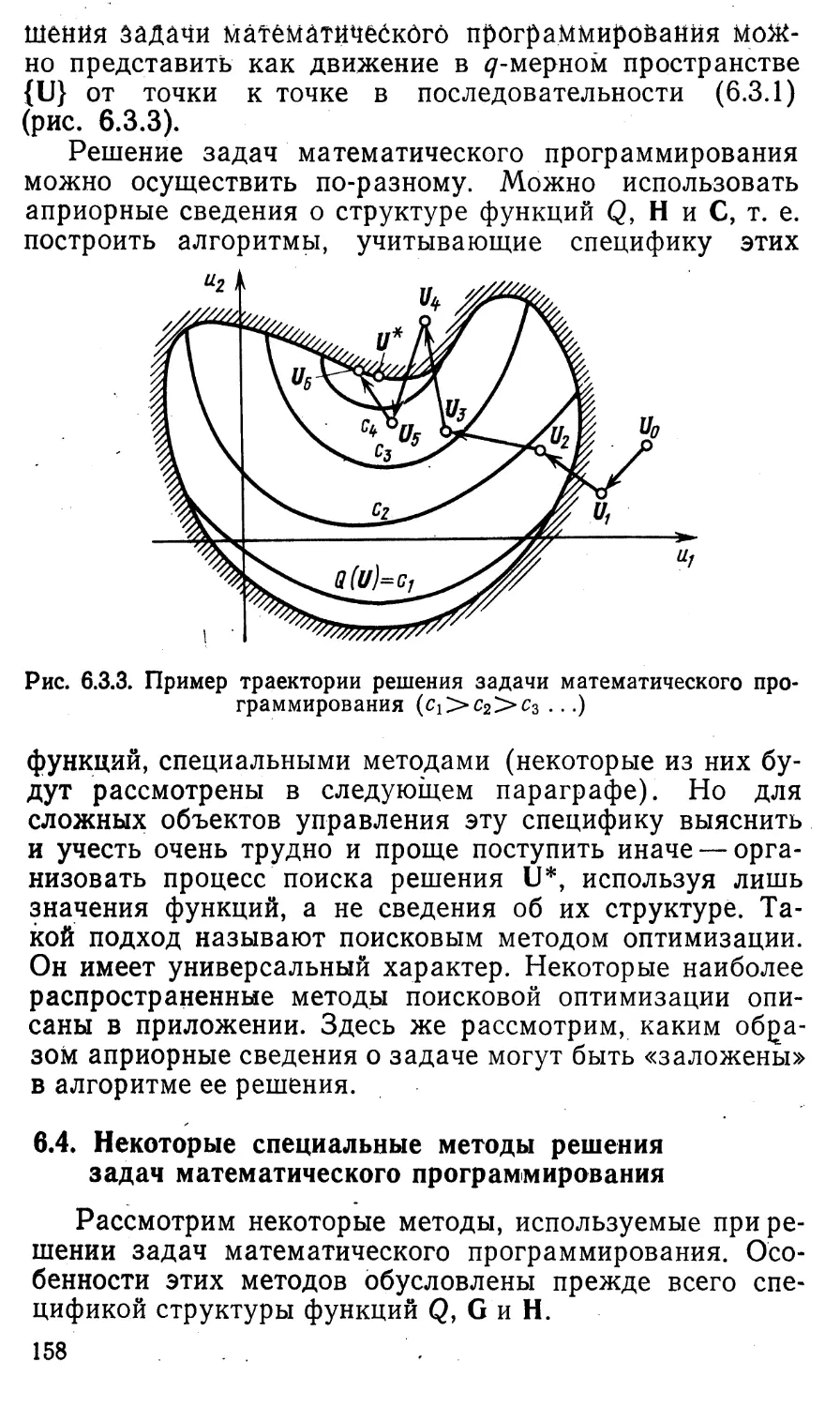
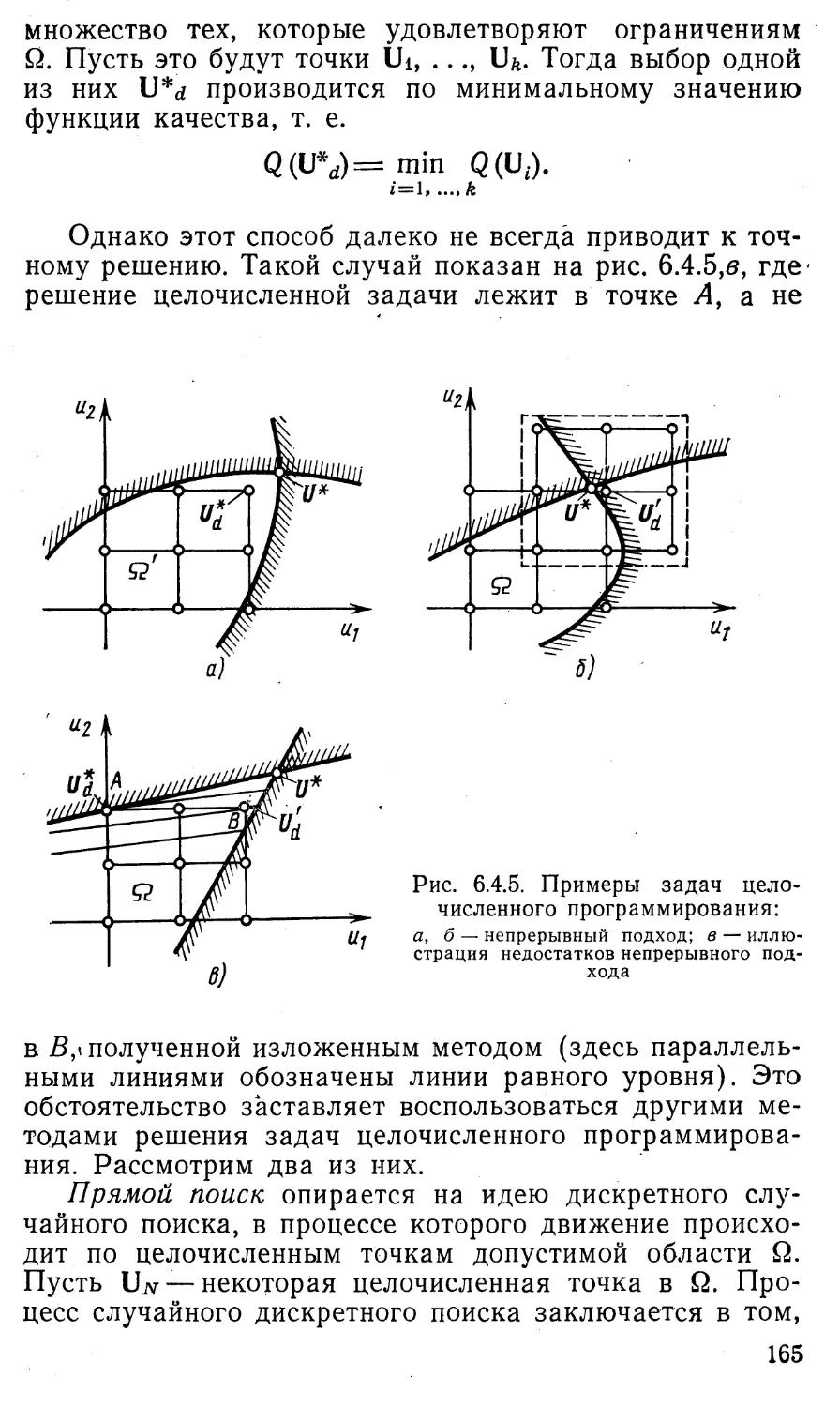
Похожие
Текст
Л. А. Растригин
СОВРЕМЕННЫЕ
ПРИНЦИПЫ
УПРАВЛЕНИЯ
СЛОЖНЫМИ
ОБЪЕКТАМИ
ББК 32.815
Р 24
УДК 681.5 — 007
Растригин J1. А.
Р 24 Современные принципы управления сложными
объектами. — М.: Сов. радио, 1980. —232 с. ил.
В пер.: 90 к.
Книга является первым в мировой литературе опытом «сквоз¬
ного» изложения современных принципов, подходов и методов управ¬
ления сложными формализуемыми объектами различной физической
природы — техническими, технологическими и т. д. Для ее чтения до¬
статочно знания основ современной математики в объеме обычного
курса вуза. Книга рассчитана на инженеров различных специально¬
стей, желающих ознакомиться с методами теории и практики управ¬
ления сложными объектами.
30502-021 ББК 32.815
Р ------------- 49-79 2704080330
046 (01)-80 687.3
Редакция кибернетической литературы
ИБ № 512
ЛЕОНАРД АНДРЕЕВИЧ РАСТРИГИН
Современные принципы управления
Сложными объектами
Научный редактор 7*. А. Колоскова
Редактор Т. М. Любимова
Художник В. Б. Кухта
Технический редактор И. В. Орлова
Корректор И. М, Давыдова
Сдано в набор 26.09.79 Подписано в печать 27.12.79 Т-21645
Формат 84ХЮ81/*» Бумага типографская № 2 Гарнитуре лятературпая
Печать высокая Объем 12, J8 уел. п. л. 12,36 уч.-нзд. л. Тираж 12 000 эка.
За к* 290 Иена 90 к.
Издательство «Советское радио», Москва, Главпочтамт, а/я 693
Московская типография № И) «Союз полиграф преете»
Государственного Комитета СССР
по делаы издательств, полиграфии н книжкой торговли.
Москва, М-114. Шлюзовая наб.. 10
© Издательство «Советское радио», 1980 г.
От автора
Знание некоторых принципов нередко
возмещает незнание некоторых фак¬
тов.
ГЕЛЬВЕЦИИ
Характерным для нашего времени является стремле¬
ние использовать формальные (математические) мето¬
ды для управления сложными объектами. На этом пути
сделано уже достаточно много. Однако при синтезе
процесса управления сложной системой неизбежно так¬
же использование неформальных (экспертных) методов.
Это обстоятельство нельзя рассматривать как «замета¬
ние мусора под коврик». Дело в том, что эксперт яв¬
ляется таким же источником информации, как любой
датчик, и, как всякий датчик, обладает своими особен¬
ностями, которые необходимо учитывать при его исполь¬
зовании. Сочетание формальных и неформальных мето¬
дов и является спецификой управления сложным объ¬
ектом, которая отражена в этой книге.
В книге рассмотрены все этапы управления сложным
объектом — от формулировки целей управления до кор¬
рекции этих целей в процессе эксплуатации созданной
системы управления.
Процесс создания управления в книге рассмотрен
с алгоритмической точки зрения, независимо от того,
с помощью каких вычислительных средств эти алгорит¬
мы будут реализованы (и будут ли реализованы вооб¬
ще). В этом плане книгу дополняют руководства по
проектированию систем управления (см., например:
В. Н. Захаров, Д. А. Поспелов и В. Е. Хазацкий. Си¬
стемы управления.— М.: Энергия, 1977), в которых рас¬
смотрены способы и средства реализации алгоритмов
управления на современной вычислительной технике.
Автор поставил цель — в доступной для инженера
форме рассмотреть все восемь этапов управления слож¬
ным объектом. Каждая глава посвящена одному из эта¬
3
пов создания системы управления. Так, гл. 1 посвяЩеМ
первому этапу всякого управления — формулировке цели
управления, гл. 2 — второму этапу — выделению объекта
управления из среды. Следующие три главы посвящены
синтезу модели выбранного управления (гл. 3 — струк¬
турному синтезу модели, а гл. 4 и 5 — параметрическому
пассивному (при идентификации) и активному (при экс¬
периментировании с объектом). Синтез управления на
базе созданной модели объекта рассмотрен в гл. 6. Гл. 7
посвящена этапу реализации управления. И, наконец,
в последней главе рассматривается этап коррекции си¬
стемы управления (модели, объекта и целей) на базе
полученной в процессе управления информации.
В книге представлен и оригинальный материал* Так,
например, первые две главы целиком отражают иссле¬
дования автором процессов целеобразования и вы¬
деления объекта из среды. В остальных главах пред¬
ложения автора «вклиниваются» в материал, известный
специалистам.
Естественно, что объять необъятную проблему
управления сложными объектами в восьми главах не¬
возможно. Поэтому автор рассмотрел лишь те алгорит¬
мы, методы и подходы теории и практики управления,
которые наилучшим образом отражают современные
принципы управления сложным объектом. При этом оче¬
видно, что какие-то аспекты проблемы управления вовсе
не рассмотрены. Так, совершенно не представлены
в книге иерархические подходы к описанию и управле¬
нию сложными объектами — так называемый систем¬
ный подход, модели АСУ и т. д. Основная, пожалуй,
тому причина — ограниченный объем книги.
Было бы ошибочным считать эту книгу справочным
руководством. Ее задача — дать читателю представле¬
ние об эффективно используемых сейчас принципах,
подходах и методах управления сложными объектами.
А рецептуру, необходимую для конкретного применения
изложенных подходов, можно найти в книгах, приведен¬
ных в литературных комментариях, сопровождающих
каждую главу.
В основу книги положен преддипломный курс, читае¬
мый автором вот уже более десяти лет на факультете
автоматики и вычислительной техники Рижского поли¬
технического института. Это обстоятельство определило
синтетический и обобщающий характер изложения, кото¬
4
рый опирается на представления, сложившиеся у стуДен^
тов за все годы обучения. Это же позволило (и застави¬
ло) рассмотреть почти все разрозненные методы совре¬
менной кибернетики с единых позиций управления слож¬
ным объектом.
Для понимания содержания книги достаточно зна¬
ния математики в объеме вузовского курса: специальные
вопросы оптимизации рассмотрены в приложении. Для
беглого ознакомления с основными идеями и принци¬
пами управления сложными объектами можно прочитать
лишь введение (для этого знание математики вовсе не
обязательно). Если читатель выйдет за рамки этого
введения, то цель автора будет достигнута.
С рукописью книги ознакомились ее рецензенты
В. А. Абчук,. И. А. Полетаев, чьи многочисленные кри¬
тические замечания заставили автора значительно пере¬
работать книгу, Ю. И. Неймарк, добрые советы которого
были учтены в окончательной редакции, А. Н. Скляревич,
тщательность которого всегда помогает автору, а также
В. П. и Ф. П. Тарасенко, советы которых позволили
уточнить важные обстоятельства управления сложными
объектами. Ценные замечания сделали по гл. 3 и 4
А. Н. Рубан, по гл. 5 —Ю. П. Адлер и А. М. Кориков,
по гл. 6 — Ф. М. Кириллова. Всем им автор приносит
глубокую благодарность.
Предисловие
...все простое — правда, а все слож¬
ное — неправда.
Г. СКОВОРОДА
Каждый из нас хоть раз в жизни выступал в роли
руководителя, и всех нас волнуют вопросы управления
и их принципы. Именно поэтому давайте сразу огово¬
римся, что здесь мы будем рассматривать управление
объектами, поведение которых удается описать фор¬
мально, т. е. используя математический аппарат и совре¬
менные электронные вычислительные машины (ЭВМ).
И не будем путать такое управление с руководством,
которое представляет собой управление пока неформа-
лизуемыми объектами (например, государством, кол¬
лективом, личностью и т. д.).
Управление — вешь сложная, тонкая и важная. Од¬
нако разговор об управлении хочется начать не со
сложности, а ... с простоты. По глубокому убеждению
автора, все научные принципы и идеи всегда и везде
(в том числе и в области управления) простоты в своей
основе. Но эта простота порой бывает обманчива.
Путь от сложного к простому прям и ясен: было
сложно, разобрались — стало просто и ясно. Но есть и
другой путь. Он связан, как правило, с применением
формального подхода, т. е. с использованием матема¬
тического аппарата. Не будем терять времени на вы¬
яснение того, зачем нужен формальный подход. Просто
без него очень часто нельзя эффективно решить постав¬
ленную задачу, особенно в области управления. В лю¬
бом случае формальный подход позволяет использовать
ЭВМ. Формализм нужен, и без него не обойтись, осо¬
бенно тогда, когда мы хотим переложить трудности
решения задачи на ЭВМ. Это остро ощущается при
решении задач управления сложными системами: все
здесь настолько запутанно и сложно, что мысль о при¬
влечении вычислительной машины для «распутывания»
6
этой сложности кажется спасительной. Но именно здесь
и начинается усложнение и без того сложной задачи,
т. е. ее формализация.
Специалисты (нематематики) не любят применять
этот подход и обращаются к нему лишь в крайнем
случае по многим причинам. Во-первых, в дебрях фор’
мализма чувствуют себя хорошо только математики,
а специалисту-нематематику здесь трудно, так как он
опирается на содержательный (физический) смысл за-
дачи, ему же вместо этого предлагают всевозможные
уравнения, алгоритм, преобразования и т. д. Но это еще
не самое страшное. Не понимая толком всех математи¬
ческих премудростей, специалист, особенно если он не
очень твердо понимает, чего же он хочет, перестает
верить себе, и, как говорят, «математика торжествует
над здравым смыслом». К сожалению, эта ситуация не
придумана автором.
Именно поэтому так важно в процессе формализации
задачи и ее решения формальными методами сохранить
в неприкосновенности тот самый спасительный злравътй
смысл, который так ценится в неформальных подходах.
А это по силам только специалисту, понимающему воз¬
можности формального подхода и трезво оценивающему
его сильные и слабые стороны.
Нет формализма «на любой случай». Нас будет ин¬
тересовать формализм, необходимый для управления.
Здесь термин «управление» применяется в самом широ¬
ком смысле: как совокупность действий, направленных
на достижение поставленных целей. Под такое опре¬
деление, как легко видеть, подпадают в принципе все
разумные действия. Однако далеко не все их удается
формализовать. Мы в этой книге будем рассматривать
лишь формальные стороны управления, позволяющие
решать задачу управления сложным объектом с по¬
мощью ЭВМ. В строке остаются социальные, психологи¬
ческие и другие гуманитарные аспекты управления, кото¬
рые оказывают влияние на некоторые коэффициенты
уравнений или приводят к появлению некоторых очевид¬
ных ограничений.
В настоящее время разработаны многочисленные
эффективные формальные методы синтеза управления,
опирающиеся как на определенные математические мо¬
дели типа идентификации, планирования экспериментов,
математического программирования, так и на нефор¬
7
мальные методы решения задач, реализуемые эксперта¬
ми. Сочетание этих двух методов формального и нефор¬
мального позволяет решать сложнейшие задачи
управления и образует основу для управления сложны¬
ми объектами. Именно это обстоятельство характеризует
процессы управления сложными объектами и представ¬
ляет собой основной аспект данной книги. Экспертный
подход проявляется в большей мере на первых этапах
управления, а формальный — на последующих.
ВВЕДЕНИЕ
В.1. Что такое управление?
Едва ли целесообразно в настоящее время вводить
строгое определение понятия управления. Дело в том,
что эта область знаний (теории и практики управления)
со времени выхода книги Н. Винера о кибернетике на¬
столько бурно развивается, что само понятие управления
претерпевает неизбежные изменения, отражающие его
новые аспекты как в теоретическом, так и прикладном
плане.
Американского математика Норберта Винера (1894—
1964) по праву считают создателем кибернетики. Он
назвал ее «наукой об управлении и связи в животном
и машине». Однако это определение уже не полно. Дей¬
ствительно, сейчас проблема связи вышла за рамки
кибернетики. Шире понимается и область применения —
она распространяется и на общество. Мало кого устроит
управление вообще: нужно в определенном смысле на¬
илучшее, оптимальное управление (ради достижения
этой оптимальности и создается наука управления).
Поэтому сейчас под кибернетикой понимают науку об
оптимальном управлении сложными динамическими си¬
стемами, подразумевая и машину, и животное, и об¬
щество, и любую другую сложную систему. Нас в этой
книге будут интересовать в основном технические объ¬
екты управления, хотя описанные принципы могут быть
применены для управления объектами более широкой
природы.
Под управлением будем понимать процесс органи¬
зации такого целенаправленного воздействия на объект,
в результате которого объект переходит в требуемое
(целевое) состояние. В этом определении, как и во вся¬
ком другом, одно понятие подменяется другими. Это,
прежде всего, понятия «объект», «цель», «воздействие»,
«состояние». Хотя указанные понятия интуитивно оче¬
видны и понимаются всеми примерно одинаково, они
все же нуждаются в пояснении.
9
Объектом управления будем называть ту часть окру¬
жающего мира, состояние которой нас интересует и на
которую мы можем воздействовать целенаправленно,
т. е. управлять ею. Обозначим буквой X воздействие
среды на объект (это вход объекта), а буквой Y — со¬
стояние объекта (это его выход). На рис. В.1.1. объект
изображен в виде прямоугольника. Не будем пока кон¬
кретизировать эти обозначения (это будет сделано в по¬
следующих главах). Важно то, что об объекте и о X и
Y мы можем говорить содержательно, т. е. описывать
их на каком-то удобном нам языке (необязательно фор¬
мальном).
Например, если объектом управления является авто¬
мобиль, то X определяет состояние его среды, т. е. до¬
рожного покрытия, атмосфе¬
ры, освещенности, а также
Шг\06ъекгпЩ,
:!
Объект
Субъект
I
Рис. В.1.1. Взаимодействие
объекта со средой
Рис. В. 1.2. Схема взаимодей¬
ствия субъекта со средой и
объектом
положение его органов управления (шофер для авто-'
мобиля тоже среда); Y — состояние автомобиля, опре¬
деляемое в основном скоростью движения, давлением
масла, температурой и оборотами двигателя и т. п.
Очевидно, что состояние объекта Y зависит от состояния
его среды X, т. е. между ними имеется какая-то связь,
характер и вид которой пока может быть и неизвестен.
Это обстоятельство на рис. В.1.1 изображено графиче¬
ски, но его же можно представить в виде формулы
Y=F°(X), (В.1.1)
где F0 обозначает связь между входом и выходом объ¬
екта. Эту связь в математике для статических объектов
называют функцией, а для динамических — оператором.
Таким образом, в самом общем случае F° является не¬
известным пока оператором, связывающим вход X и
выход У объекта. Этот оператор характеризует специ¬
фику объекта с точки зрения управления.
Говоря об управлении как о целенаправленном про¬
цессе, нельзя не обратить внимание на то, чьи цели реа¬
10
лизуются в процессе управления, т. е. кому нужно это
управление. Поэтому совершенно необходимо ввести
в рассмотрение фигуру субъекта, который является ис¬
точником целей, реализуемых управлением. Эти цели
возникают у субъекта под давлением его собственных
потребностей, связанных с жизнедеятельностью субъек¬
та и его взаимодействием с внешней средой и объектом
управления. (Заметим, что под субъектом совершенно не
обязательно подразумевать конкретную личность; это
может быть группа людей, объединенная по некоторому
признаку, и даже все человечество, если рассматри¬
вается управление глобальными объектами, такими, как
окружающая среда, космос и т. д.)
Появление при анализе управления субъекта с его
потребностями совершенно необходимо, если мы хотим
понять, как образуются цели управления.
Говоря о причинах управления, следует помнить
известное правило криминалистов при расследовании
преступления «Ищите, кому это выгодно!». Применяя
это правило к управлению, мы приходим ... к нашему
субъекту: только ему нужно и выгодно управление.
Так как фигура субъекта важна для управления,
выделим его из среды, как показано на рис. В. 1.2.
Субъект находится в той же среде, что и объект, т. е.
воспринимает состояние X среды. Одновременно, и это
самое главное, на него влияет состояние Y объекта.
Если состояние У объекта удовлетворяет потребностям
субъекта, взаимодействующим с этим объектом и ис¬
пользующим его для своих целей, то никакого управле¬
ния ему не нужно. Если же это состояние не устраивает
субъекта, то ему необходимо организовать такое воз¬
действие на объект, которое переведет его в новое со¬
стояние, удовлетворяющее субъекта. Это воздействие и
есть управление. Отсюда и следует один из «принципов»
управления: оно происходит от неудовлетворенности
субъекта ситуацией, сложившейся в объекте.
При полном благополучии субъекта, т. е. при удо¬
влетворении объектом всех потребностей субъекта,
управление не нужно. Однако удобно (хотя это и услов¬
но) считать, что субъект всегда формулирует свою
цель, реализация которой в объекте приведет, по мне¬
нию субъекта, к удовлетворению его потребностей. Эта
цель представляет собой набор требований, предъявляе¬
мых субъектом к состоянию объекта,
U
Обозначим цель субъекта Z* (звездочкой будем обо¬
значать все желаемое). Эта цель по сути дела опре¬
деляет, каким должен быть объект с точки зрения
субъекта. Проверить выполнение цели Z* в объекте
можно только по его состоянию У, но для этого состоя¬
ние У объекта следует выразить на языке целей субъек¬
та, т. е. выполнить преобразование
Z=W(Y). (В.1.2)
В частном случае может оказаться, что Z=Yy т. е.
субъект формулирует свои цели на языке состояний
объекта. Например, пусть цель Z заключается в том,
чтобы скорость автомобиля была равна 60 км/ч. Спи¬
дометр на приборном щитке показывает действительную
скорость У в тех же единицах (км/ч). В этом случае
Ч^У^гггг У, так как нет необходимости «переводить» по¬
казания спидометра на язык нашей цели: это уже сде¬
лано. Но если мы едем на иностранной машине, в кото¬
рой скорость определяется в милях/ч, то Т^^У.
Действительно, в этом случае Z=0,63 У, т. е. приходится
фиксируемое прибором состояние объекта У [миль/ч]
«переводить» на язык целей субъекта [км/ч].
Очевидно, что равенство
Z=Z* (В. 1.3)
свидетельствует о том, что состояние объекта удовле¬
творяет целям субъекта, т. е. цели субъекта выполнены.
Если же
Z=^Z*, (В.1.4)
то цели субъекта не реализованы в этом объекте. Это
последнее обстоятельство заставляет субъекта решить
дилемму: либо смириться с Z и в результате терпеть
определенный ущерб, связанный с недостижением своих
целей Z*, а следовательно, с неудовлетворением потреб¬
ностей, либо создать систему управления, которая реа¬
лизовала бы его цели Z* в объекте, но при этом затра¬
тить определенные средства на ее создание и эксплуа¬
тацию. (Здесь под системой управления понимаются
все мероприятия, связанные с выработкой и реализа¬
цией управления.)
На «смирение» идут в большинстве случаев. Этот
принцип даже подтверждается народной мудростью.
Говоря строго, терпение— тоже управление, но внутрец*
13
нее, направленной на сдерживание и ограничение по¬
требностей субъекта. Это управление потребностями.
В какой-то мере это даже разумно. Действительно, если
можно терпеть, то острой надобности в управлении нет.
К управлению обращаются как к крайней мере.
Дело в том, что за управление надо платить и часто
дорогой ценой! Это прежде всего затраты на сбор ин¬
формации об объекте, на синтез его модели, на выработ¬
ку управления и реализацию его и т. д. и т. п. Именно
поэтому к управлению обращаются в исключительных
случаях. Однако такие исключительные случаи встре¬
чаются слишком часто (виной тому растущие потребно¬
сти субъекта), что и заставляет разрабатывать общие
методы управления, рассматриваемые в этой книге.
Если цели важные (т. е. потребности, их породившие,
насущные), то субъект идет на создание системы управ¬
ления. Для этого ему прежде всего необходимо опреде¬
лить, каким образом можно воздействовать на объект,
т. е. определить каналы управления. Ими могут быть
некоторые из входов X объекта, которые поддаются
целенаправленному изменению. Но обычно этого бывает
мало, и приходится создавать новые каналы управления
объектом, которые до этого не существовали. Так, чтобы
изменять направление движения телеги, пришлось соз¬
дать руль, с помощью которого можно воздействовать
на ориентацию колес. Это и есть новый канал управле¬
ния.
Так или иначе в целом ряде случаев для реализации
управления создаются специальные каналы управления.
Обозначим буквой U это управление. Очевидно, что те¬
перь состояние объекта управления зависит от двух
факторов — состояния среды (X) и состояния управле¬
ния (U):
Y=Fo(Xy U), (В. 1.5)
где F0 — по-прежнему оператор работы объекта, но те¬
перь он учитывает еще и управление U.
Теперь уже можно говорить о создании системы
управления, под которой будем понимать все необходи¬
мые алгоритмы обработки информации и средства их
реализации, объединенные для достижения заданных
целей управления в объекте. Заметим, что система
управления далеко не всегда реализуется «в металле».
Она может быть реализована в виде системы правил,
договоров и обязательств (вообще алгоритмов), которые
реализуются в процессе управления. Так, систему управ¬
ления образует любой оператор вместе с объектом, ко¬
торым он управляет. Например, шофер за рулем авто¬
машины образует с ней систему управления. В этом
случае органы управления автомашины (руль, педаль
газа, тормоз и т. д.) являются теми каналами управле¬
ния U, с помощью которого шофер изменяет состояние
автомашины Y в желаемом ему направлении Z*. В дан¬
ном случае «управляющее устройство» (шофер) и субъ¬
ект, задающий цель Z*, совпадают.
В.2. Система управления
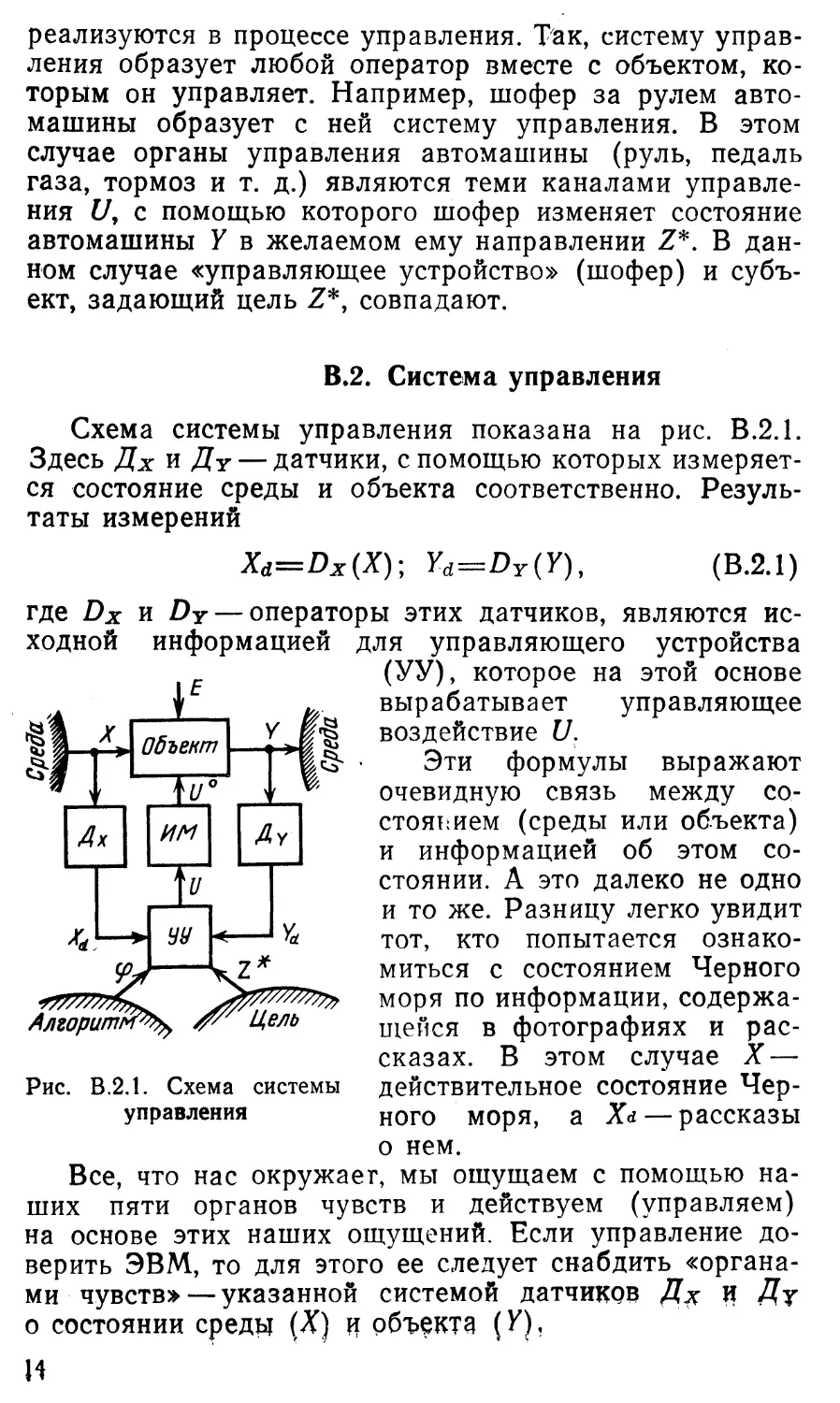
Схема системы управления показана на рис. В.2.1.
Здесь Дх и Ду — датчики, с помощью которых измеряет¬
ся состояние среды и объекта соответственно. Резуль¬
таты измерений
Xd=Dx{X)- Yd=Dr{Y),
(В.2.1)
где Dx и Dy — операторы этих датчиков, являются ис¬
ходной информацией для управляющего устройства
(УУ), которое на этой основе
вырабатывает управляющее
воздействие U.
Эти формулы выражают
очевидную связь между со¬
стоянием (среды или объекта)
и информацией об этом со¬
стоянии. А это далеко не одно
и то же. Разницу легко увидит
тот, кто попытается ознако¬
миться с состоянием Черного
моря по информации, содержа¬
щейся в фотографиях и рас¬
сказах. В этом случае X —
действительное состояние Чер¬
ного моря, a Xd — рассказы
о нем.
Все, что нас окружает, мы ощущаем с помощью на¬
ших пяти органов чувств и действуем (управляем)
на основе этих наших ощущений. Если управление до¬
верить ЭВМ, то для этого ее следует снабдить «органа¬
ми чувств»— указанной системой датчиков Д# и Ду
о состоянии среды (Я) и объекта (Y),
Рис. В.2.1. Схема системы
управления
и
Таким образом, в основе процесса управления лежит
информация о сложившейся ситуации:
/ = {Xd, Yd), (В.2.2)
хотя она всегда является неполной. Эта неполнота,
прежде всего, связана с ограниченными возможностями
всякой системы сбора информации / и необходимостью
«платы» за эту информацию. А при ограниченных ресур¬
сах, выделяемых обычно на управление, указанное об¬
стоятельство приводит к постоянному дефициту инфор¬
мации о поведении среды и объекта.
Сказанное заставляет образовать еще один вход объ¬
екта—ненаблюдаемое возмущение Е (см. рис. В.2.1),
под которым подразумеваются все ненаблюдаемые внеш¬
ние и внутренние факторы объекта, влияющие на его
состояние Y, т. е. Y=F°(X, U, Е), что уточняет (В.1.5).
Относительно входа Е могут выдвигаться лишь опреде¬
ленные предположения, но непосредственно этот кход не
измеряется. Вход Е образуют прежде всего неизмеряе-
мые параметры среды (например, температура внешней
среды при автоматическом управлении температурой
камеры холодильника) и всякого рода случайные изме¬
нения характеристик самого объекта (например, дрейф
его характеристик).
Таким образом, объект управления имеет три входа:
наблюдаемый (X), управляемый, а следовательно, и
наблюдаемый (£/°) и ненаблюдаемый (Е). Заметим, что
управляющее воздействие (команда, вырабатываемая
управляющим устройством) U представляет собой ин¬
формацию о том, в какое положение должны быть при¬
ведены управляемые входы объекта U0. «Отработка»
этой команды осуществляется исполнительными меха¬
низмами (ИМ), которые и изменяют состояние управ¬
ляемого входа U0 объекта. Будем для простоты пред¬
полагать, что исполнительные механизмы мгновенно
выполняют команду U и поэтому U°=U, т. е. можно не
различать U0 и U (случай и°ф11 исследуется теорией
автоматического управления, а точнее теорией следящих
систем, хорошо и весьма полно разработанной).
Для целенаправленного функционирования управля¬
ющего устройства ему кроме информации (В.2.2) необ¬
ходимо сообщить цель Z* управления, т. е. к чему ему
следует стремиться в процессе управления, и алгоритм
управления, т. е. указание, как добиться этой цели.
15
Итак, введены очень важные понятия: цель и алгоритм
Если понятие цели интуитивно ясно - это то, к чему мы
стремимся, то понятие алгоритма нуждается в поясне¬
нии. Под алгоритмом в данном случае мы понимаем
четкое недвусмысленное правило, инструкцию, указание,
что и как следует делать, чтобы добиться заданной цели
Z* в сложившейся ситуации I.
Например, любая инструкция по применению ле¬
карства, прилагаемая к нему, является алгоритмом, так
как она указывает, в каких случаях (/) следует, а в ка¬
ких не следует применять это лекарство. Целью (Z*)
здесь является выздоровление больного, а управление —
дозировка лекарства (нулевая дозировка тоже является
управлением). Но инструкция «иди туда, не знаю куда,
принеси то, не знаю что» не может быть названа алго¬
ритмом, хотя и имеет его структуру.
Теперь, располагая информацией о состояниях сре¬
ды, объекта и цели, можно представить управление U
как результат работы алгоритма:
£/=ф(/, Z*), (В.2.3)
где ф — алгоритм управления. Он представляет собой
оператор ф=ф (•, •), перерабатывающий информацию
о среде, объекте и цели в управление U, реализация ко¬
торого U0 должна переводить объект в требуемое со¬
стояние Z*.
Таким образом, основными факторами всякого управ¬
ления, которые присущи любой системе управления
объектом, являются:
— цель управления (Z*);
— информация о состоянии объекта и среды (/);
— воздействие на объект, т. е. собственно управление
(U);
— алгоритм управления (ф).
Заметим, что слово «управление» обычно используют
в двух смыслах. В широком смысле это процесс дости¬
жения поставленных целей (в этом смысле мы его при¬
меняли раньше), а в узком — всякое целенаправленное
воздействие на объект (нажатие кнопки, поворот руля,
выделение ресурса и т. д.).
Если исключить из перечня основных факторов
управления хотя бы один, управление станет невозмож¬
ным. Именно этим обстоятельством, например, во время
военных действий пользуются диверсионные группы, на-
16
\
правляя свои удары против системы управления вой¬
сками противника. Объектом диверсии чаще бывают
системы коммуникации, с помощью которых передается
информация / и управляющее воздействие U, а также
штабы, где реализуемся алгоритм управления q> войсками.
Таким образом, управление в широком смысле опре¬
деляется множеством целей {Z*}, которые поступают
в систему управления извне (фигурными скобками {а}
всюду мы будем обозначать множество элементов а).
Эти цели ставит субъект, являющийся потребителем бу¬
дущей системы управления объектом. Субъект выступает
в качестве заказчика на создание системы управления.
Созданием же этой системы управления занимается про¬
ектировщик.
Однако, прежде чем принять решение о создании
системы управления, необходимо рассмотреть все этапы
управления, независимо от того, с помощью каких ма¬
териальных средств будут реализованы эти этапы. Та¬
кой алгоритмический анализ управления является осно¬
вой для принятия решения о создании системы управле¬
ния и степени ее автоматизации.
При этом анализе следует учитывать фактор слож¬
ности объекта управления. Дело в том, что управление
простым объектом в настоящее время не представляет
труда. Примером управления простым объектом являет¬
ся автоматический процесс поддержания температуры
на заданном (целевом) уровне, который реализуется
в любом холодильнике. Здесь алгоритм управления тем¬
пературой крайне прост: включить охлаждение, если
температура в камере выше заданной, и выключить,
если — ниже или равна заданной. Вот и все!
Все трудности управления определяются сложностью
объекта, поэтому следует начинать именно с объекта,
а не с алгоритма управления им. Попробуем разобрать¬
ся, что называть простым, а что сложным объектом
управления без ссылки на управление. К сожалению,
кратким определением здесь ограничиться не удастся.
Поэтому придется посвятить этому вопросу целый пара¬
граф.
В.З. Что такое «сложный объект управления»?
Это понятие в настоящее время еще строго не опре¬
делено. Возможно, что такое определение никогда и не
появится, а если и появится, то тогда, когда в нем, по
2—299
17
сути дела, отпадет острая необходимость. Интуитивное
представление о сложном объекте довольно точно соот¬
ветствует тому понятию, которое /спользуется в тео¬
рии управления (оно то и применяется в этой книге).
Приведем некоторые черты (но не формальные призна¬
ки) сложной системы. Их много. Рассмотрим основные.
<Ц) Отсутствие математического описания и необходи¬
мость в нем является обязательной чертой сложного
объекта управления. Под математическим описанием
подразумевается наличие алгоритма (правил, инструк¬
ции) вычисления состояния Y объекта по наблюдениям
его входов — управляемого U и неуправляемого, но на¬
блюдаемого X. С этой точки зрения современная бал¬
листическая (или космическая) ракета не является
сложной системой, так как ее движение описывается
уравнениями классической механики (законами Ньюто¬
на), которые легко составить и решить, коль скоро из¬
вестны конструктивные параметры ракеты и свойства
среды. Поэтому поведение ракеты более определенно,
чем поведение муравья, которого по праву следует от¬
нести к сложной системе, так как его поведение пока *
даже и не пытаются описать математически.
Простые объекты управления могут тоже не иметь
математического описания. Так, для управления темпе¬
ратурой в комнате совершенно не обязательно знать,
какова математическая зависимость между температу¬
рой нагревателя и температурой в этой комнате. Од¬
нако если простыми объектами можно управлять без
их математической модели, то сложными уже нельзя.
Так, при необходимости очень точного поддержания за¬
данной температуры без математической модели уже не
обойдешься. Здесь требование точности делает простой
объект управления сложным. Этот вывод позволяет
сформулировать следующее утверждение: если хочешь
управлять сложной системой с использованием нормаль¬
ных методов, то придется создать ее математическую
модель. Это обстоятельство обычно охлаждает горячие
головы, желающие управлять «всем и вся» с помощью
вычислительной машины.
2. Стохастичность поведения сложных объектов
управления является также очень важной чертой, харак¬
теризующей трудности процессов анализа и управления
ими. Эта черта обусловлена не столько наличием ка¬
ких-то специальных источников случайных помех в объ¬
18
екте управления, сколько сложностью объекта и
связанным с этим неизбежным обилием всякого рода
второстепенных точки зрения целей управления,
разумеется) процессов. Поэтому его поведение зачастую
оказывается неожиданным для исследователя, причем
эту неожиданность удобнее рассматривать как случай¬
ный фактор и трактовать как зашумленность, чем раз¬
бираться в механизме второстепенных процессов, про¬
текающих в сложном объекте. Любой сложный объект
содержит большое число такого рода неожиданностей,
которые и являются свидетельством его сложности. Та¬
ковы биологические, социальные, технологические и мно¬
гие другие объекты исследования и управления.
Здесь проявляется любопытная тенденция — назы¬
вать случайным то, что второстепенно и несущественно
для реализации целей управления в этом объекте.
В действительности, если разобраться, эта «случай¬
ность» может оказаться вовсе и не случайной. Но в дан-
ном случае очень удобно считать случайным все то, что
непонятно. Этот подход хорошо развит в настоящее
время в виде статистической теории управления (заме¬
тим, что понятия «статистический» и «стохастический»
эквивалентны).
3. «Нетерпимость» к управлению является, пожалуй,
самой досадной чертой сложного объекта управления,
затрудняющей управление им. Дело в том, что сложный
объект существует и функционирует независимо от субъ¬
екта и его потребностей. Так, любой технологический
процесс существует для производства продукции, а не
для управления им. Управление имеет внешний харак¬
тер по отношению к объекту. Естественно, что вследст¬
вие этого всякое управление нарушает «нормальное»
функционирование объекта, т. е. изменяет его само¬
стоятельное поведение и делает зависимым от субъекта.
Особенно наглядно это обстоятельство проявляется
в активных объектах, содержащих в себе людей или
их коллективы (например, когда объектами управления
являются технологический участок, цех или завод).
Здесь трудно рассчитывать на то, что собственные цели
такого сложного объекта совпадут с целями управления.
Скорее они будут в чем-то противоречить друг другу.
Это и вызывает негативную реакцию сложного объекта
на управление, если цель управления не согласована
с его собственной цельк?.
19
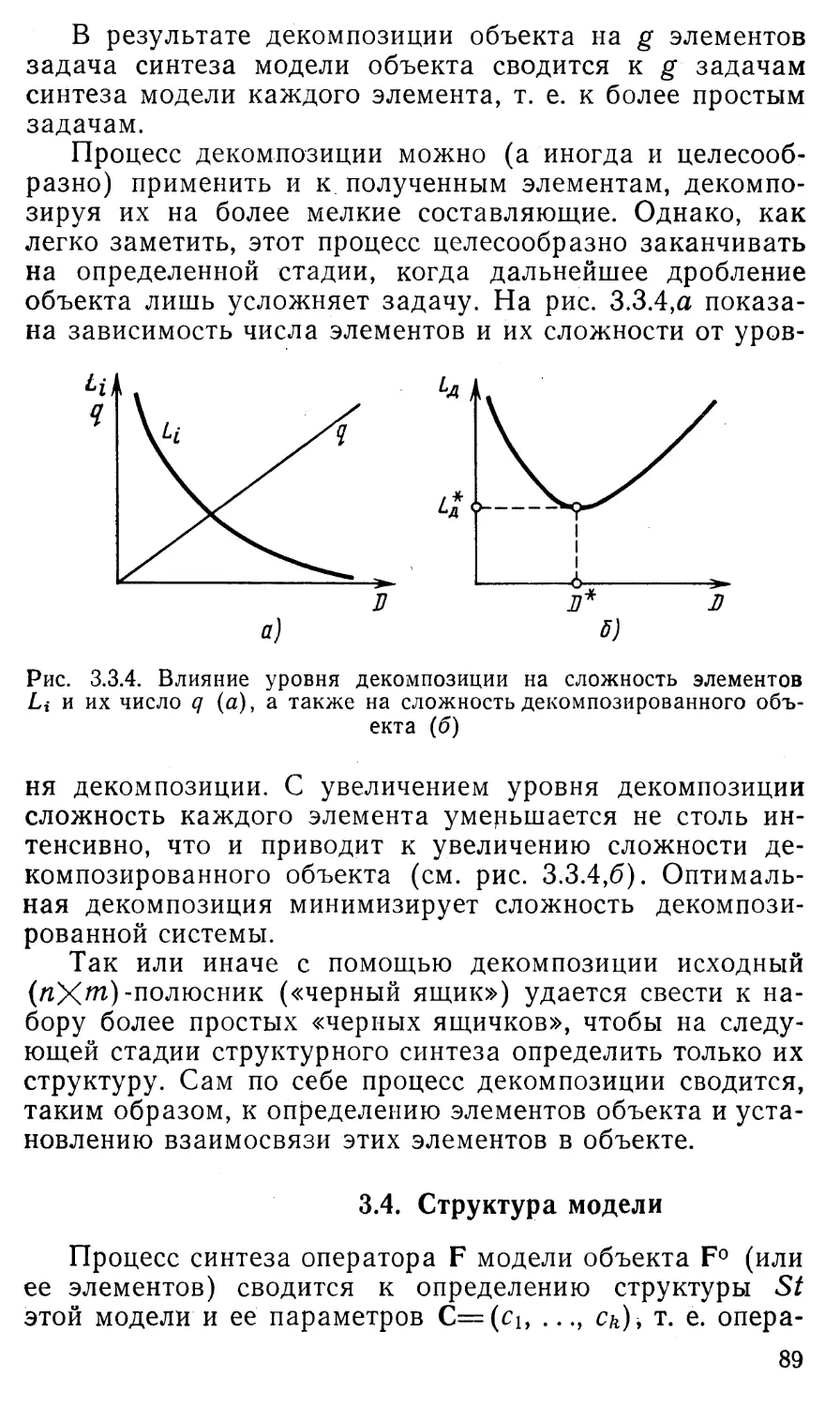
4. Нестационарность сложного объекта управления
естественно вытекает из его сложности. Эта черта про¬
является в дрейфе характеристик объекта, в «уплыва¬
нии» его параметров, т. е. в эволюции объекта во вре¬
мени. Чем сложнее объект, тем рельефнее проявляется
эта его черта, что создает серьезные трудности при
синтезе модели такого сложного объекта и управлении
им. Чем сложнее объект, тем быстрее он меняется.
В обыденной жизни с этим процессом мы сталкиваемся,
наблюдая амортизацию (старение) окружающих нас
вещей и предметов. Причем эта амортизация для слож¬
ных вещей идет, как правило, быстрее, чем для простых.
Так, телевизор или автомобиль «стареют» быстрее,
чем молоток. Следствием нестационарности является
следующая существенная черта сложного объекта.
5. Невоспроизводимость экспериментов. Проявляется
эта черта в различной реакции объекта на одну и ту же
ситуацию или управление в различные моменты вре¬
мени. Сложный объект все время как бы перестает
быть самим собой, т. е. постоянно меняется. Этого нель¬
зя не учитывать при синтезе модели объекта управле¬
ния, для чего вводится ее коррекция.
Все эти обстоятельства приводят к тому, что цель
управления таким объектом в полной мере никогда не
достигается. Действительно, для синтеза управления U
требуется время, за которое объект изменяется непред¬
виденным образом, в результате это управление уже
наверняка не приведет к желаемому результату Z*.
Эффективным способом борьбы с перечисленными
свойствами сложного объекта управления является
экстраполяция поведения системы, т. е. выяснение на¬
правления ее эволюции. В этом случае управление U
производится с упреждением, с учетом замеченного изме¬
нения объекта. Другой способ состоит в сокращении
цикла управления, чтобы за время синтеза управления
объект сильно не изменился.
Список «досадных» черт сложного объекта управле¬
ния можно было бы продолжить. Однако следует пом¬
нить, что это лишь черты, присущие сложному объекту,
но ни в коей мере не его формальные признаки. Отсут¬
ствие одной или даже нескольких из указанных черт
вовсе не обязательно делает объект простым. Эти черты
имеют неформальный характер, но тем не менее позво¬
ляют характеризовать сложный объект управление
29
В.4. Этапы управления сложным объектом
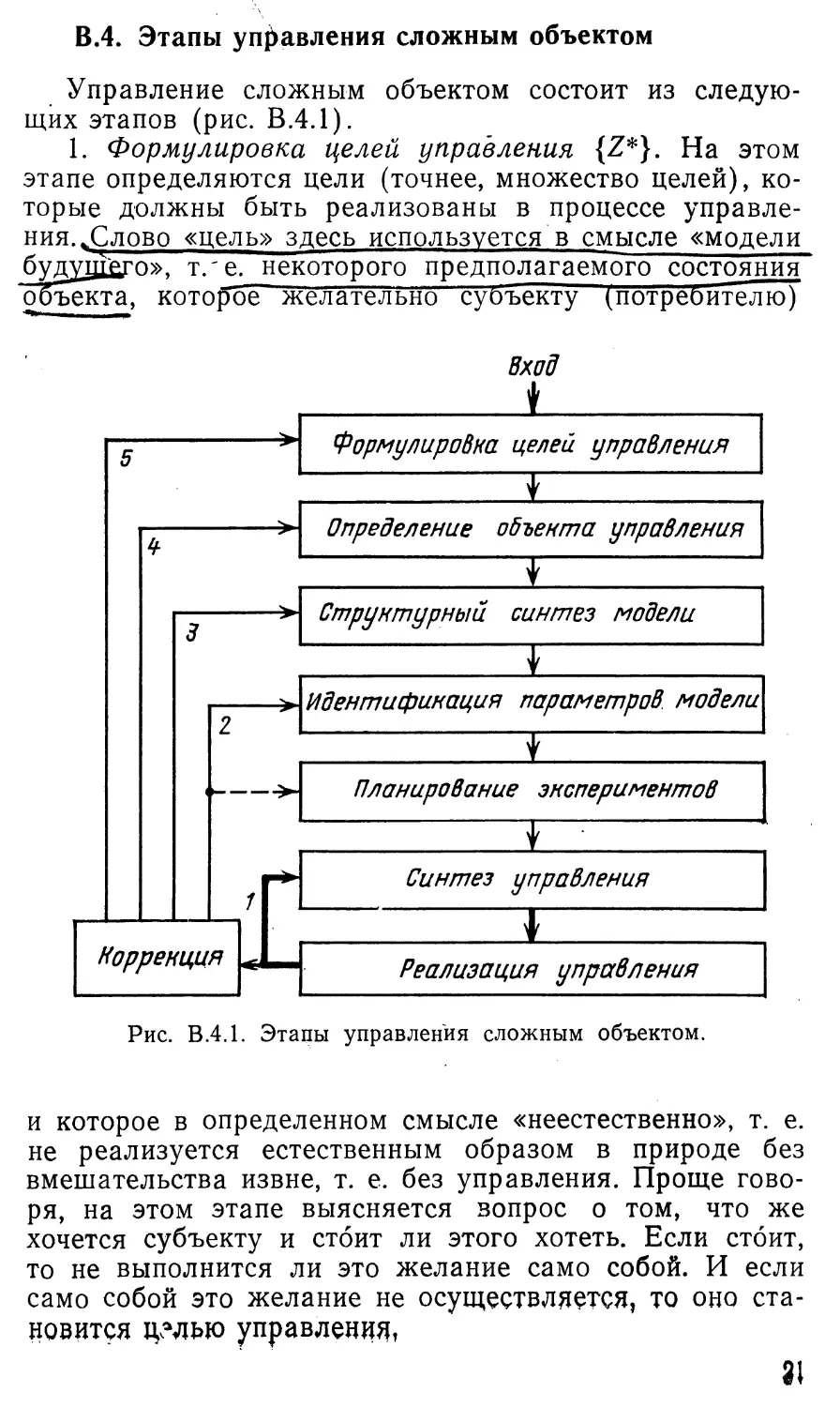
Управление сложным объектом состоит из следую¬
щих этапов (рис. В.4.1).
1. Формулировка целей управления {Z*}. На этом
этапе определяются цели (точнее, множество целей), ко¬
торые должны быть реализованы в процессе управле¬
ния. Слово "цель" здесь используется в смысле "моделибудущего", т. е. некоторого предполагаемого состояния
объекта, которое" желательно субъекту (потребителю)
Вход
Рис. В.4.1. Этапы управления сложным объектом.
и которое в определенном смысле «неестественно», т. е.
не реализуется естественным образом в природе без
вмешательства извне, т. е. без управления. Проще гово¬
ря, на этом этапе выясняется вопрос о том, что же
хочется субъекту и стоит ли этого хотеть. Если стоит,
то не выполнится ли это желание само собой. И если
само собой это желание не осуществляется, то оно ста¬
новится целью управления,
31
Так, поддерживать температуру t в помещении на
определенном необходимом уровне /* независимо от
состояния погоды можно только с помощью управления.
Это управление может быть автоматическим (с по¬
мощью кондиционера) или неавтоматическим (ручным),
но в любом случае целью такого управления является
Z*: t\=t* = const, причем константа t* может изменяться
в зависимости от обстоятельств (потребностейсубъекта).
Задание множества целей {Z*} в данном случае сво¬
дится к определению диапазона температур, внутри ко¬
торого может когда-либо при каких-то неизвестных об¬
стоятельствах располагаться целевая (т. е. необходимая
субъекту) температура ^*. Автоматическое управление
в данном случае связано с аппаратной реализацией
алгоритма: автоматически включать нагреватель при
t\<t* и выключать его при t>t*. Так работает термо¬
регулятор. Однако этот же алгоритм можно реализовать
и в ручном неавтоматическом варианте.
2. Определение объекта управления. Этот этап свя¬
зан с выделением той части среды потребителя, состоя¬
ние которой его интересует в связи с реализацией сфор¬
мулированных им целей. Это и есть объект управления.
Например, выданный диапазон целевых температур
определяет объект управления, т. е. ту часть пространст¬
ва, состояние которой необходимо контролировать (из¬
мерять температуру) и на которую следует воздейство¬
вать (подогревать или охлаждать в различных местах),
чтобы выполнить заданные цели управления {Z*}.
Часто объект управления ясен и определен с самого
начала (автомобиль, радиоприемник, завод и т. д.). Но
в ряде случаев, когда он связан со средой многочислен¬
ными и сильными связями, определить его нелегко. По¬
пробуйте определить сферу вашего управления (т. е.
объект) при поддержании чистоты в квартире. Кварти¬
ра? Но грязь на лестничной клетке заставляет жало¬
ваться коменданту. А это — управление, целью которого
является все та же чистота в вашей квартире. Вот
объект и расширился: им стала и лестница. Отсутствие
асфальтовых дорожек у дома заставит вас обратиться
в райисполком все с той же целью поддержания чистоты
в квартире, т. е. вашим объектом управления становится
двор дома, и т. д.
Последующие три этапа управления связаны с соз¬
данием модели о0ъекта управления, которая нужна для
№
синтеза управления. Только с помощью модели объекта
можно построить управление U, переводящее сложный
объект в требуемое (целевое) состояние Z*. Без модели
процесс управления можно реализовать лишь методом
проб и ошибок. что неприемлемо при управлении слож¬
ным объектом, так как требует слишком больших за¬
трат времени и заставляет «дергать» объект ошибоч¬
ными действиями (шагами).
Под моделью объекта управления будем понимать
зависимость F, связывающую состояние Y объекта с его
входами — неуправляемым X и управляемым U\
Y=F(X, U). (В.4.1)
В отличие от оператора объекта F0 в (В. 1.5), который
неизвестен, модель F представляет собой высказывание
относительно связи между входами X и U модели и ее
выходом на любом удобном языке. В общем случае мо¬
дель F определяется некоторым алгоритмом (правилом,
инструкцией), который указывает, как, располагая ин¬
формацией о входах X и U, определить выход У, не об¬
ращаясь к реальному объекту. Процесс синтеза модели
объекта обычно происходит в три этапа.
3. Структурный синтез модели. На этом этапе опре¬
деляется вид зависимости F без учета значений ее пара¬
метров. Произведем условно следующую операцию:
«расщепим» модель F на ее структуру St и параметры
Си • • •> ck, т. е. представим модель в виде пары:
F=(St, С), (В.4.2)
где С=(си ..., ch)—вектор параметров модели (век¬
торы всюду будем обозначать полужирными буквами).
На этапе структурного синтеза определяется лишь
структура St модели, а конкретными значениями пара¬
метров С не интересуются.
Под структурой в общем случае принято понимать
вид элементов, из которых состоит объект, и отношении
между элементами. Описывать структуру удобнее всего
графом, вершины которого — элементы объекта, а ду¬
ги — отношения, в которые вступают элементы объекта.
Так, завод как объект управления состоит из цехов,
отделов, служб и т. д. (это его элементы), связанных
между собой отношениями подчиненности, материальных
и информационных потоков и т. д.
Структура объекта управления может быть различ¬
ной в зависимости от целей управления. Проиллюстри-
23
руем эту мысль на следующем (не очень серьезном)
примере. Один и тот же объект — завод, имеет различ¬
ную структуру в зависимости от целей управления. Так,
с точки зрения целей министерства завод является пре¬
образователем выделяемых фондов (денежных и мате¬
риальных) в готовую продукцию. Работники завода
рассматривают его как преобразователь их труда
в зарплату (мы намеренно упростили схему). Медицин¬
ские учреждения относятся к тому же заводу как к ис¬
точнику всякого рода производственных травм и про¬
фессиональных заболеваний, а санитарная служба счи¬
тает, что завод производит отходы, загрязняющие среду.
Существует много разнообразных структур моделей
объекта управления. Линейность, статичность, детерми¬
нированность, дискретность и т. д. являются структур¬
ными категориями. Например, линейная статическая не¬
прерывная детерминированная структура объекта одно¬
значно определяет следующий вид для F:
Y=F(X, U) =c0+CiX+c2£/,
где конкретные значения параметров с0, с\, с2 пока не
важны, важен лишь вид зависимости F, т. е. линейность
структуры St.
Таким образом, на этапе структурного синтеза опре¬
деляется лишь вид и характер модели F, а ее пара¬
метры С определяются на последующих двух этапах
управления.
4. Идентификация параметров модели объекта свя¬
зана с определением численных значений параметров
С=(с1,...,ck) в режиме нормального функционирова¬
ния, т. е. без организаций" специальных управляющих
воздействий на объект. Исходной информацией для
идентификации являются структура St и наблюдения за
поведением входа X(t) и выхода Y(t) объекта при его
взаимодействии со средой. Таким образом, пара
/(*)=(*(*), m (в.4.3)
является в общем случае основным источником инфор¬
мации при идентификации.
*) Заметим, что иногда под идентификацией подразумевают про¬
цесс определения параметров модели безотносительно к тому, в ка¬
ком режиме работает объект. Поэтому различают пассивную и
активную идентификацию. В этой книге рассматривается пассивная
идентификация, а планирование эксперимента является активной
идентификацией (см. следующий пункт).
24
Искусство идентификации — это искусство пассивно-
го наблюдения. Таково было основное кредо древней
науки: уметь наблюдать не вмешиваясь. На это есть
свои основания, так как всякое вмешательство искажает
естественный ход наблюдаемого явления. Более того,
результаты эксперимента некоторым образом предопре¬
деляются его целями. Очень часто в эксперименте мы
получаем не то, что есть, а, грубо говоря, то. что хочет¬
ся, и связано это не с недобросовестностью эксперимен¬
татора, а с психологией процесса познания. Именно
поэтому пассивное наблюдение остается и сейчас эф¬
фективным инструментом познания окружающего нас
мира.
Необходимость пассивного наблюдения связана еще
и с тем, что часто сложные объекты не допускают экспе¬
риментов с ними. По-видимому, эти соображения поро¬
дили нелепое понятие «пассивного эксперимента». Экс¬
перимент не может быть пассивным — он всегда активен!
Речь идет просто о пассивном наблюдении.
Как легко заметить, информация (В.4.3) позволяет
определить зависимость состояния объекта лишь от вхо¬
да X: Y=F(X), которая отличается от искомой модели
(В.4.1). Для выяснения зависимости выхода Y объекта
от управляемых входов U необходимо преднамеренно их
изменять, т. е. «поэкспериментировать» с объектом. Од¬
нако, как сказано выше, сложный объект «не любит»
экспериментов, нарушающих режим его нормальной
функционирования. Поэтому эксперимент, которого нель¬
зя избежать, следует проводить, минимально возмущая
объект, но так, чтобы получить при этом максимальную
информацию о влиянии варьируемых параметров на
выход объекта. Этому служит следующий этап — пла¬
нирование экспериментов.
5. Планирование экспериментов. На этом этапе глав¬
ным является синтез плана эксперимента, позволяющего
с максимальной эффективностью определить параметры
модели объекта управления.
Для статического объекта этот план О представляет
собой набор состояний управляемого входа объекта:
U=(U19..., UN), (BAA)
£ для динамического — план-функцию
(5==U(t), (В.4.5)
ц
т. е. программу изменения во времени управляемого
входа объекта. Эксперимент на объекте позволяет опре¬
делить реакцию объекта на это воздействие. Для ста¬
тического объекта эта реакция образует ряд
Yu ■ ■ Yn, (В.4.6)
где Yi=F°(Ui), i=l, ..., N, — реакция объекта в i-м
эксперименте, а для динамического Y(t) = F°(U(t)).
Теперь N пар If.
*i = {Ut>Yi)> l=h...,N, (В.4.7)
для статического объекта и пара I:
I = (U(t), У(0) (В.4.8)
для динамического объекта являются исходной инфор¬
мацией для определения параметров С модели F:
Y=F(U). (В.4.9)
Как видно, после проведения эксперимента задача опре¬
деления параметров модели сведена к задаче иденти¬
фикации (см. предыдущий этап).
Для получения модели вида (В.4.1) необходимо рас¬
сматривать уже тройки наблюдений /*:
/, = <*„ Ui9 У/>, *=1,..., N, (В.4.10)
или
I=(X(t), £/(/), У(/)), 0<f<7\ (В.4.11)
т. е. в процессе планирования экспериментов с объектом
необходимо учитывать и состояние среды X.
Следует отметить, что в процессе планирования экс¬
периментов с объектом у экспериментатора могут изме¬
ниться представления о структуре модели (например,
первоначальная гипотеза о линейности модели будет за¬
менена гипотезой о нелинейности определенного вида).
Это обстоятельство заставляет снова обращаться
к структурному синтезу, точнее, вводить коррекцию
структуры модели. Сказанное несколько «размывает»
понятие планирования эксперимента, распространяя его
и на процессы выбора структуры модели и на ее кор¬
рекцию.
Понятие планирования эксперимента чрезвычайно
емкое и насыщенное. Планировать эксперименты можно
не только для выяснения параметров модели, о чем мы
§6
уже сказали, йо и для выбора одной йз предполагаемый
структур и т. д. Если, например, в качестве объекта
управления выступает человек, то можно планировать
эксперименты по выяснению некоторых его специфиче¬
ских свойств, представляющих интерес для управления
(скажем, для выяснения профессиональных склонностей
при профотборе). Такие эксперименты называются пси¬
хологическими тестами. Испытуемому пои этом предла¬
гают решить ряд задач (тестов) и по ответам судят
о его склонностях, т. е. образуют модель испытуемого.
Составление подобных тестов производится методами
планирования экспериментов, с помощью которых выяс¬
няется «принадлежность» испытуемого к той или иной
профессиональной структуре.
Таким образом, на этапе планирования эксперимен¬
тов определяются параметры модели, которые нельзя
определить на этапе идентификации, и корректируется
структура модели. Но цель обоих этапов — окончатель¬
ное создание модели F объекта управления F0. На этом
задачу синтеза модели, которой были посвящены три
последних этапа (3, 4 и 5), можно считать выполненной.
Полученная модель является исходной для процесса
синтеза управления.
6. Синтез управления. Этот этап связан с принятием
решения о том, каково должно быть управление С/,
чтобы достигнуть заданной цели Z* управления объек¬
том. Это решение опирается на имеющуюся модель F
объекта, заданную цель Z*, полученную информацию
о состоянии X среды и выделенный ресурс управления
R, который чаще всего представляет собой ограничения,
накладываемые на управление U в связи со спецификой
объекта и возможностями системы управления (времен¬
ными, энергетическими, материальными и т. д.).
Естественно синтезированное управление U считать
оптимальным, т. е. U=U*, так как оно должно удовле¬
творить поставленной цели Z* управления. В общем
случае оно представляет собой программу изменения
управляемых параметров во времени, т. е.
U* = U*(t). (В.4.12)
Эту программу предстоит реализовать на следующем
этапе. Примером программы оптимального управления,
которое каждый из нас испытал на себе, является план
медицинского лечения, прописываемого врачом: «Ну-с,
27
батенька, будем делать так ...», й далее следует п6-
дробный план U* лечебных мероприятий, который учи¬
тывает: цель Z* (побыстрее сделать больного «практи¬
чески» здоровым при минимальном ущербе, наносимом
лечением, т. е. минимальном риске осложнений и т. п.),
состояние X среды (время года, жилищные условия
больного, наличие заботливых родственников и т. д.),
ресурс R больного (возможность достать дефицитные
лекарства) и поликлиники (наличие необходимых при¬
боров и оборудования для диагностики и лечения), мо¬
дель F объекта, т. е. представление врача о больном
в данный момент с медицинской точки зрения (т. е.
диагноз, анализы, переносимость больным определенных
лекарств, дисциплинированность, психическое состояние
и т. д.).
7. Реализация управления связана с реализацией
программы оптимального управления (В.4.12), получен¬
ной на предыдущем этапе. Этот процесс не вызывает
затруднений, если сведения о состояниях среды X, объ¬
екта Y и его модели F были достоверны. Однако к мо¬
менту реализации все могло измениться. Для учета
такого рода изменений требуется соответствующая кор¬
рекция управления U в процессе его реализации. Ис¬
ходной информацией для такой коррекции является но¬
вое состояние среды к моменту реализации управления
или прогноз этого состояния. Если объект активный,
т. е. содержит людей, цели которых могут не совпадать
с целями управления, то в процессе реализации управ¬
ления следует учитывать и это обстоятельство. В этом
случае, очевидно, не удастся в полной мере достичь по¬
ставленных целей, но следует действовать так, чтобы
отклонение от них было минимальным.
Поэтому план оптимального управления U*(t) и его
реализация часто отличаются так же, как благие на¬
мерения в жизни от их осуществления. Реализовать
управление часто бывает труднее, чем синтезировать.
Например, планы всех оптимальных диет для похудания
нарушаются потому, что они требуют реализации, т. е.
каких-то ограничений в еде, что просто невыносимо
для толстяков. Здесь неучет этого обстоятельства и де¬
лает нереализуемым такое управление.
Реализовав управление и получив новое состояние
объекта, можно обнаружить, достигнута поставленная
цель или нет. Скорее всего цель управления не будет
28
достигнута (напомним* что мы управляем сложным
объектом, который благодаря своей зашумленности и
нестационарное™ не позволяет ограничиться однократ¬
ным актом управления). Поэтому приходится возвра¬
щаться к одному из предыдущих этапов. Даже в самом
лучшем случае, когда поставленная цель оказывается
достигнутой, необходимость обращения к предыдущему
этапу вызывается изменением состояния среды X или
сменой цели управления Z*. Таким образом, при самом
благоприятном стечении обстоятельств обращаются
к этапу синтеза управления для определения нового
управления, которое отражает новую ситуацию, сложив¬
шуюся в среде, и новую цель. Так функционирует стан¬
дартный контур управления (см. стрелку У на рис. В.4.1).
8. Коррекция. Этот этап обусловлен спецификой
сложного объекта управления и заключается в возвра¬
щении к одному из предыдущих этапов управления (см.
стрелки 2—5 на рис. В.4.1). Дело в том, что все реше¬
ния, принимаемые на предыдущих этапах, приближен¬
ные, опираются на старую информацию и отражают со¬
стояние объекта лишь в прошедшие моменты времени.
Коррекция может затрагивать различные этапы. Про¬
стейшая коррекция связана с подстройкой параметров С
модели (см. стрелку 2 на рис. В.4.1). Такого рода кор¬
рекцию обычно называют адаптацией модели. Иногда
может оказаться, что оптимальное управление U*(t) не
обеспечивает необходимой вариабельности (разнообра¬
зия) управляемого входа объекта для эффективной по¬
следующей коррекции параметров С модели. Тогда при¬
ходится обращаться к планированию экспериментов
с объектом в процессе управления им путем добавления
специальных тестовых сигналов к управлению (см.
штриховую стрелку на рис. В.4.1). Такое управление на¬
зывают дуальным, т. е. двойственным, так как его за¬
дачей является не только достижение целей управления,
но и коррекция параметров модели объекта.
Однако коррекции параметров С модели может ока¬
заться недостаточно, если изменилась структура объ¬
екта. Поэтому время от времени необходима коррекция
структуры модели St, т. е. приведение ее в соответствие
с изменяющейся структурой объекта (см. стрелку 3 на
рис. В.4.1).
Далее коррекция может коснуться самого объекта,
точнее, границы раздела объекта и среды. Это бывает
29
необходимо при значительном изменении (эволюции)
объекта и окружающей его среды. В этом случае кор¬
рекция «узаконит» новые взаимоотношения нового объ¬
екта со средой (см. стрелку 4 на рис. В.4.1).
И последнее. Созданная система управления по ряду
причин (значительное изменение свойств среды и объ¬
екта) может не реализовать все исходное множество
целей управления {Z*}, которые породили эту систему,
или реализовать их недостаточно эффективно. Тогда
возникает необходимость коррекции целей управления,
которая заключается в определении нового множества
целей, достигаемых с помощью этой системы управле¬
ния. В результате этой коррекции потребитель узнает,
какие же цели данная система управления действитель¬
но может реализовать в объекте (см. стрелку 5 на
рис. В.4.1).
Реализация указанных мер и образует адаптивную
систему управления, которая приспосабливается к из¬
меняющимся свойствам среды, объекта и потребностям
ее потребителя. Любопытно, что очень часто потреби¬
теля удовлетворяет созданная система управления, не¬
смотря на то, что она не реализует всех его исходных
целей. Предоставленная ему возможность достижения
каких-то новых целей (ранее ненужных ему) деформи¬
рует его потребности в осуществлении легкодостижимых
целей. Так, часто мы едим не потому, что голодны,
а потому, что так сложились обстоятельства, а «аппе¬
тит приходит во время еды». Легкость в достижении
целей питания порождает именно эти цели. Особенно
ярко этот механизм проявляется в капиталистическом
обществе, где с помощью мощной рекламы предложение
порождает спрос, т. е. потребность.
Заметим, что чем больше номер стрелки на рис. В.4.1,
тем реже срабатывает эта обратная связь. Благодаря
функционированию описанной системы коррекции систе¬
ма управления все время приводится в соответствие
с изменяющимися средой и объектом управления. В ре¬
зультате система управления как бы эволюционирует
вместе с объектом и средой, но так, чтобы все время
хорошо выполнялись цели управления. Если же эта
эволюция объекта управления заходит настолько далеко,
что исходное множество целей перестает выполняться,
то коррекция целей обеспечивает эволюцию целей управ¬
ления.
30
Очевидно, что не все описанные выше восемь этапов
управления всегда присутствуют при синтезе системы
управления. В ряде случаев некоторых может и не
быть. Например, когда объект управления уже выделен
из среды (самолет, космический корабль и т. д.) или
нет необходимости в этапе планирования эксперимента,
так как модель объекта настолько проста и «прозрачна»,
что все ее параметры можно определить без специально
организованного эксперимента. Может отсутствовать
этап формулировки целей управления: настолько они
очевидны и естественны. Природа не столь «злонамерен¬
на», и при работе реальных систем управления редко
приходится реализовать все этапы управления, как
правило, некоторые этапы просто выпадают в силу спе¬
цифики целей и объекта управления. Так, при управле¬
нии автомашиной не возникает проблемы выбора объек¬
та управления, а при лечении больного цель всегда одна
и та же — вылечить и не повредить. Но в любом случае
при управлении сложным объектом должен существо¬
вать этап коррекции модели объекта управления. Необ¬
ходимость этого этапа вызвана сложностью объекта
управления. Только для простых объектов он может
отсутствовать. Однако будем готовы к самому худшему
и рассмотрим все восемь этапов, замкнутые в железное
кольцо системы управления!
В.5. Как сделать коктейль?
(Несерьезная иллюстрация серьезных этапов
управления)
Проиллюстрируем рассмотренные в, предыдущем
параграфе этапы управления сложным объектом на шу¬
точном примере решения задачи приготовления коктейля.
Итак, вам необходимо составить рецепт коктейля,
который, с одной стороны, должен быть вкусным и до¬
статочно крепким, а с другой — не слишком дорогим.
Предстоит принять решение о том, что и в каком коли¬
честве покупать, чтобы получить то, что требуется. А. что
требуется? Какие конкретные цели должны быть дости¬
гнуты при этом?
Целевыми критериями всякого коктейля, как из¬
вестно, являются его вкусовые качества, крепость и
стоимость единицы объема. Пусть г\—вкусовые качест¬
ву коктейля, z<i — его крепость (например, в градусах),
3!
гг — стоимость одного литра смеси (например, в руб¬
лях), щ — относительное содержание i-го компонента
коктейля, где, например, t=l — фруктовый сок, /=2 —
сухое вино, /=3 — коньяк и т. д. Всего имеется п ком-
П
понентов (i=l, ..п), так что 2 ui = 1 и и^О.
/=1
Рис. В.5.1. Схема «систе¬
мы управления» для со¬
ставления коктейля
Вектор и=(нь ип) определяет состав коктейля.
От этого вектора каким-то определением, но пока не¬
известным образом зависят все три критерия:
zl=*h(V)t z2=f2(V), z3=fs(U),
где fi, U и /з — пока неизвестные целевые функции.
Сформулируем задачу приготовления коктейля как
задачу управления. Объектом управления в данном слу¬
чае является сам коктейль и гость, который его оцени¬
вает (см. рис. В.5.1), неуправляемым входом X —
исходные компоненты коктейля, а управляемым U — их
относительное содержание. Выходом этого объекта яв¬
ляются свойства коктейля, оцененные вашим гостем,
Y= (гь 22, z3), а «управляющим устройством» (УУ) —
бармен (это Вы) (рис. В.5.1).
Прежде всего сформулируем цели этого управления
(этап 1). Они, как уже сказано, зависят от потребно¬
стей субъекта, т. е. потребителей коктейля — ваших
гостей.
Если гость — лакомка, то основное внимание он уде¬
ляет вкусовым качествам коктейля, и естественно кри¬
терий Z\ (вкусовые качества коктейля) считать экстре¬
мальным критерием, который (точнее, целевую функцию
fi(U)) следует максимизировать в процессе управления.
Критерий г2 (крепость) следует ограничить снизу;
32
■Z2>02, где a2 — минимальная крепость, которая устроит
наших гостей," а критерий z3 (стоимость) нужно ограни¬
чить сверху: г3^а3, где а3— максимальная стоимость
одного литра коктейля, определяемая вашим бюджетом.
Как легко заметить, этим определяется цель лакомки:
Z* : {zi-нmax; z2>a2; z3'^a3}.
Это означает, что потребности лакомки будут удовле¬
творены, если максимизировать вкусовые качества кок¬
тейля, а его крепость и стоимость ограничить числами
(х<2 и а3.
Легко определить цель любителей крепких напитков:
Z* : {z\^a,\\ z2->max; £з<Яз},
т. е. максимизировать крепость коктейля, ограничив при
этом его минимальные вкусовые качества числом а\ и
максимальную стоимость одного литра числом а3.
Аналогично определяется цель ограниченного в сред¬
ствах хозяина, минизирующего стоимость коктейля:
Z* : {z\^a\, г2;>а2; %-Hnin}.
Как видно, для задания любой из указанных целей не¬
обходимо задать два из трех чисел: а2, а3. Таким
образом, для лакомки предстоит решить задачу вида
fж (VO —^ max ’ Q :(f2^ (В 5
/l1 USB, 1\Ш<а» ( }
т. e. следует (->-) максимизировать (max) функцию
fi(U), определяющую вкусовые качества коктейля, при
определенных ограничениях, накладываемых на функ¬
ции f2(^) и /з(Ч), определяющие зависимость крепости
и стоимости коктейля от его состава U (буквой Qi обо¬
значено множество № удовлетворяющее указанным
ограничениям по крепости и стоимости).
Здесь впервые введена символика оптимизации, ко¬
торая широко будет использоваться далее (общая по¬
становка задачи оптимизации и эффективные способы
ее решения даны в приложении).
Если субъекта больше волнует крепость коктейля, то
предстоит решить уже другую задачу:
L (U)—► max ,
u<=Qa \ f3OJ)<a3,
3-299
33
где следует (->) с помощью состава U максимизировать
(max) крепость коктейля, сохранив его вкусовые ка¬
чества и стоимость в оговоренных пределах (ai и а$).
И, наконец, для субъекта, сильно ограниченного
в средствах, естественно сформулировать задачу в та¬
ком виде:
т. е. варьируя состав U коктейля, следует (->) миними¬
зировать (min) его стоимость, выполнив при этом опре¬
деленные требования i£23 к вкусовым качествам и крепо¬
сти коктейля.
Далее в соответствии с § В.4 и схемой рис. В.4.1 сле¬
дует этап 2 —выделение объекта управления из среды.
Но для данной задачи объект был определен ранее —
это сам коктейль (гость здесь играет роль датчика).
На следующем, третьем, этапе — структурном синте¬
зе модели объекта, необходимо определить характер
управляемых и неуправляемых воздействий на объект
и структуру модели, т. е. вид зависимости свойств кок¬
тейля от выбранных спиртных напитков и соков, а также
от их относительного содержания.
Таким образом, в процессе структурного синтеза мо¬
дели объекта надо определить вид функций f3-(U) (/=
= 1, 2, 3). Прежде всего необходимо определить струк¬
туру управления, т. е. вид вектора U=(«i, ..., ип).
Иными словами, следует содержательно описать каж¬
дую переменную, т. е. какой именно сок или вино
«скрывается» под индексом i в переменной щ, и задать
размерность п вектора составом U. Далее следует опре¬
делить характер зависимости интересующих нас функ¬
ций от аргумента U.
Крепость и стоимость коктейля, как известно, строго
линейно зависят от концентрации его компонентов:
здесь с 12 — относительная крепость t-ro компонента. На¬
пример, сухому вину (i=2), имеющему крепость 10°,
приписывается относительная крепость Сг2=0,1; ciS —
стоимость одного литра t-ro компонента. Чтобы опреде¬
/3 (U) — min ,
ие23
П
п
34
лить эти параметры, достаточно взглянуть на этикетки
бутылок, где приведены крепость c*2 (в градусах) и
стоимость Cis (в рублях за объем, равный емкости бу¬
тылки).
А как быть с функцией вкусовых качеств fi(U)? Как
зависит вкус коктейля от соотношения его компонентов?
Легко заметить, что она будет для каждого субъекта
индивидуальной. А так как коктейль общий и время на
приготовление ограничено, т. е. нет времени исследовать
вкус каждого потребителя коктейля, то функцию /1 сле¬
дует задать достаточно простой. Простейшей является
линейная функция
i=1
где Сг 1 — «вкусовые» коэффициенты качества i-го компо¬
нента. Конечно, линейная функция лишь приближенно
отражает действительную зависимость вкуса от содер¬
жания компонентов. Но возможно, что удачным выбо¬
ром коэффициентов Сц (i— 1, ..., п) удастся хорошо
аппроксимировать эту функцию. На этом этапе струк¬
турный синтез модели объекта управления можно счи¬
тать законченным.
Теперь нужно определить числовые значения «вку¬
совых» коэффициентов сц (i= 1, ..., п). Прежде всего,
никаких объективных данных здесь не существует, да
и не должно быть, так как давно известно, что «на вкус
и цвет товарищей нет». Для оценки значений этих ко¬
эффициентов следует воспользоваться - этапом иденти¬
фикации, в процессе которого оцениваются коэффициен¬
ты Ciз (i= 1, ..., п) на основе информации, полученной
из наблюдений за вашим гостем в аналогичных ситуа¬
циях. Если же таких данных нет, то следует приступить
к этапу планирования эксперимента. Он может быть
произведен различным образом. Проще всего спросить
у гостя, что он больше предпочитает из того, что есть
в вашем баре. Для этого потребителю будущего коктей¬
ля следует задать ряд таких вопросов, ответы на кото¬
рые несли бы информацию, необходимую для определе¬
ния искомых коэффициентов. Такой опрос является экс¬
периментом с объектом, трудоемкость и сложность
которого определяются числом вопросов и их труд¬
ностью. Если же в вашем баре есть соки и вина, которых
3*
35
не.знает ваш гость, то эксперимент слёДуёТ расширить
до их дегустации. Проделав необходимые эксперименты
с будущими потребителями коктейля (как это делать,
мы обсудим ниже в гл. 3), можно определить искомые
значения «вкусовых» коэффициентов. На этом заканчи¬
вается синтез модели объекта.
Далее следует перейти к этапу принятия решения,
точнее, синтезу управления, т. е. определению оптималь¬
ного состава U*. Для этого необходимо решить задачу
(В.5.1), где функции fi (i= 1, 2, 3) уже известны (на¬
деемся, что вы выберете цель лакомки).
Рассмотрим к примеру случай трех компонентов
(п=3): £= 1—фруктовый сок, i=2 — сухое вино, i=
= 3 — коньяк. Получаем для них исходные данные:
/
СН
l=s 1 (сок)
/=2 (вино)
/=3
(коньяк)
Единица измерения
Источник
информа¬
ции
1
Cil
c,,=l
с21=0,75
с31=0,5
Вкус
Экспер¬
2
Ci2
с,2=0
^22:=^> 1
Относительная
крепость
тиз з
Этикетка
3
ciz
c„=l
с 2 З^З
С33= 16
Стоимость 1 л(руб.)
•
36
Для определенности дальнейших рассуждений кон¬
кретизируем цель. Пусть а2=0,1 — минимально допусти¬
мая крепость смеси, а а3=3,5— максимально допусти¬
мая стоимость 1 л (это константы цели лакомки). Те¬
перь задачу синтеза оптимального состава коктейля
можно записать так:
где в ограничения Q\ дополнительно введены очевидные
условия, налагаемые на щ\
Исключая третье условие в О, (мз=1—Щ—U2), по¬
лучаем после очевидных преобразований задачу в виде
+ + ► max ,
Mi, и2£2'!
Q,
4 их -f- 3^2 < 3,
\Ъих-\- 13г/2^ 12,5,
и2^= I,
0, и2^0.
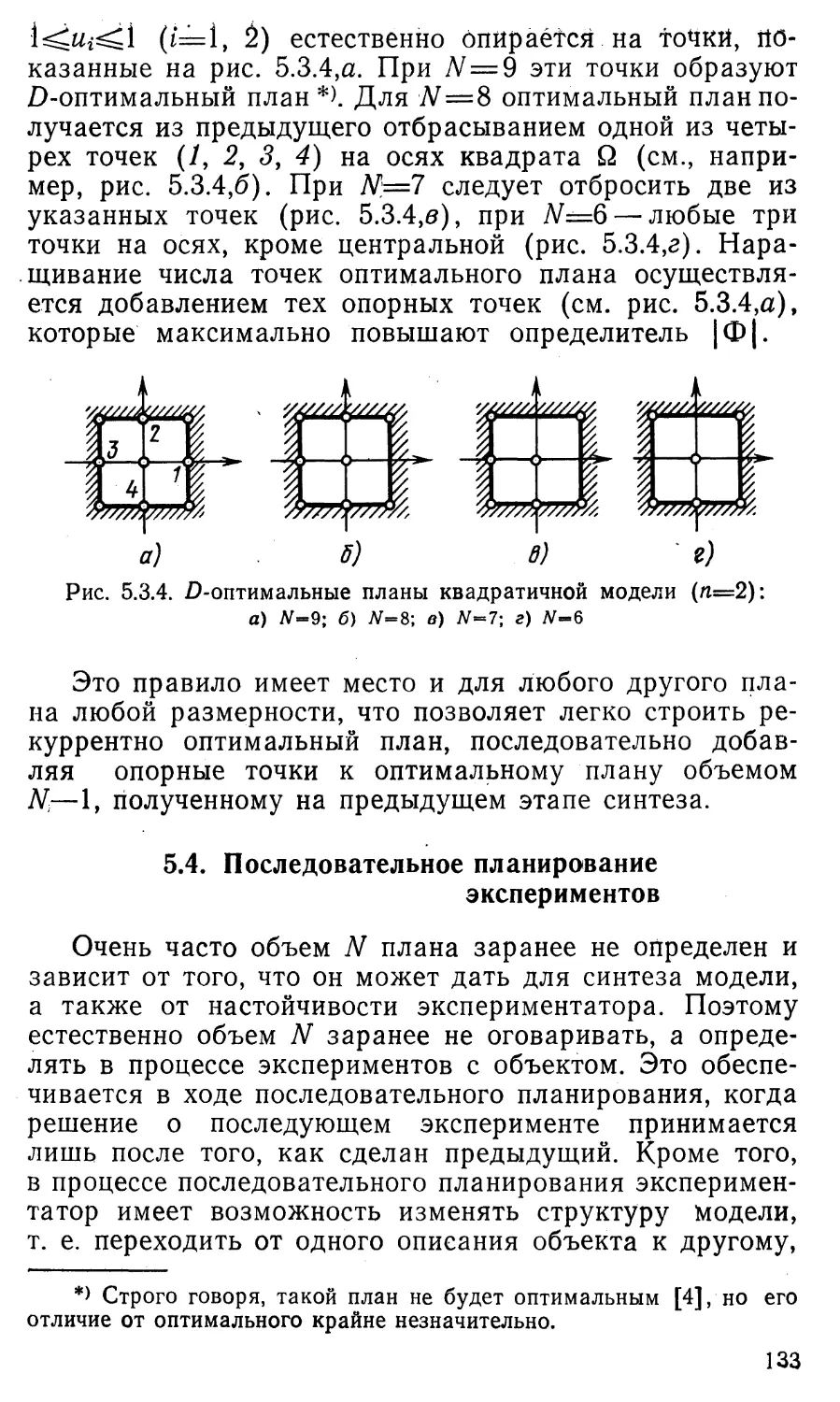
Область Q'\ показана на рис. В.5.2 (она не заштрихова¬
на). Как видно, эта зона представляет собой треуголь¬
ник ABC в левом верхнем углу. Теперь на этом тре¬
угольнике надо найти точку, максимизирующую линей¬
ную функцию
Z\ = 0,5 U\ + 0,25 и% -Ь 0,5,
пыражающую вкусовые качества коктейля. Очевидно,
что максимальное значение линейная функция прини¬
мает на границе зоны Q'b а точнее, в одной из вершин
треугольника ABC. Вычислим значения Z\ в этих вер¬
шинах:
2) (Л) =0,75;
Zl {В) = 0,5-0,21 0,25 • 0,7Д+ 0,5=0,78;
2i (С) = 0,25 • 0,9&- 0,5=0,74.
Следовательно, точка В и есть решение поставленной
задачи. Таким образом, оптимальный состав первого
коктейля таков:
и*\ = 0,21; а*2=0,72; и*г=0,07,
где иъ вычислено с помощью выражения иъ= \—Щ—и2.
Вкусовые качества такого коктейля определяются зна¬
чением 2*1 = 0,78. Полученный рецепт и следует считать
первым оптимальным решением. На этом заканчивается
этап синтеза управления.
Пропустим этап реализации этого управления —
едва ли он вызовет у Вас затруднения, хотя возможно,
что отсутствие необходимых вин в ближайшем магазине
(среде) и заставит Вас пересмотреть структуру модели,
т. е. выбрать другие компоненты коктейля. Это и будет
той самой коррекцией управления, вызванной измене¬
нием состояния среды к моменту реализации управле¬
37
ния, которая необходима для эффективного достижения
цели управления.
Перейдем к следующему этапу — коррекции. Реакция
У объекта (ваших гостей) на реализованное управление
(коктейль) определяет справедливость (адекватность)
модели. Едва ли Вы ожидали единодушного одобрения
своего рецепта. Очевидно, что разнобой в оценках дол¬
жен быть. Однако средняя оценка при правильной мо¬
дели должна совпадать с полученной в расчете, т. е.
z* 1=0,78. Если средняя экспертная оценка значительно
отличается от этой (даже в лучшую сторону), то модель
нуждается в коррекции, т. е. изменении параметров Сц
(i=l, ..., п). Например, если экспертная оценка кок-
А
Рис. В.5.2. Плоскость со¬
ставов коктейля при а2=
=0,4, аз=3,5.
0 0,21 и? 1 '
тейля оказалась равной £i = 0,6, то параметры модели
можно откорректировать, например, так:
с'ц= (0,6/0,78)Сц=0у77с{и
где c'i 1 — новые значения параметров, при которых по¬
лучим г* 1 = 0,6. Следующий коктейль, полученный с по¬
мощью откорректированной модели, должен больше
понравиться гостям.
Если подобного рода коррекция не улучшает управ¬
ление, то следует скорректировать структуру модели,
например, используя нелинейную функцию вкусовых
качеств коктейля или выбирая другие компоненты и т. д.
AL———
38
Так или иначе, но информация, полученная после
реализации управления, является исходной для коррек¬
ции модели управляемого объекта. А если этот объект,
как в нашем примере, является сложной системой с из¬
меняющимися во времени свойствами за счет дрейфа
ее характеристик, то коррекция модели неизбежна даже
и гипотетическом случае точного синтеза модели в на¬
чальный момент.
Коррекция может затронуть и объект управления,
если вы обратитесь на завод с просьбой выпускать но¬
вые сорта соков или вин. И, наконец, можно корректи¬
ровать цели, изменяя параметры аи а2 и а3 и переходя
к другому минимизируемому критерию (вплоть до кофе
пли огуречного рассола).
В заключение отметим, что описанный пример был
придуман автором только как забавная иллюстрация
этапов управления сложной системой. Если же читатель
попробует воспользоваться изложенным подходом для
приготовления настоящего коктейля, автор снимает с се¬
бя всякую ответственность за последствия.
ЛИТЕРАТУРНЫМ КОММЕНТАРИИ К ВВЕДЕНИЮ
Первые книги по кибернетике, написанные Н. Винером почти
тридцать лет назад, до сих пор не потеряли своей значимости. Бу¬
дучи классиком,/ Н. Винер умел простым языком излагать очень
тонкие и глубокие аспекты новой науки. Поэтому читателю будет
интересно прочитать отдельные главы из этих книг (см. [1, 2]).
О кибернетике написано много доступных книг. Среди них осо¬
бое место занимают книга У. Эшби 1[3], в которой простота изло¬
жения удивительно сочетается с глубиной идей, и книга Ст. Бира
[4], которому удалось, не применяя никакого математического аппа¬
рата, поставить и решить ряд интереснейших задач управления
сложными объектами типа современного промышленного пред¬
приятия.
Научно-популярные издания по кибернетике обычно обсуждают
различные аспекты этой науки [5—7]. Отметим [5] —первую книгу
по кибернетике на русском языке.
Описанные в § В. 1.4 восемь этапов управления сложным объ¬
ектом являются конкретным руководством к действию при желании
управлять таким объектом. Однако это желание может быть удов¬
летворено лишь в случае, если удастся' формализовать объект и
процесс управления. Если же такая формализация затруднительна
или невозможна, то следует обращаться к так называемому систем¬
ному подходу (или анализу), который представляет собой по сути
дела некий полуформализованный здравый смысл. По этому поводу
написано много книг и руководств. Отметим лишь основные.
Этапы системного подхода (например, изложенного В. М. Глуш-
ковым [8]) во многом совпадают с приведенными в § В.1.4 этапами
управления сложным объектом. Основные моменты подхода очень
39
ясно изложены в книге [9], где сопоставлены и различные его моди¬
фикации ![10—13]. Интересные обобщения системного подхода име¬
ются в книгах [14—16].
Следует отметить, что системный подход в управлении сложны¬
ми объектами обычно связан с руководством этими объектами, т. е.
с неформальными методами управления. Это очень хорошо показано
в работе [15]. Именно поэтому системный подход и не нашел места
в данной книге, которая посвящена формальным методам управле¬
ния, а не руководству (см. предисловие).
Таким образом, с точки зрения системного подхода (или анали¬
за) предложенную в книге восьмиэтапную процедуру управления
сложными объектами можно рассматривать как некий прикладной
системный анализ, подразумевая под этим свод формальных приемов
(сочетаемых с неформальными источниками информации — экспер¬
тами), позволяющих конструктивно решать задачу управления слож¬
ными объектами.
СПИСОК ЛИТЕРАТУРЫ
1. Винер Н. Кибернетика: Пер. с англ. — М.: Сов. радио, 1968,
с. 5—97, 182—256, 285—313.
2. Винер Н. Кибернетика и общество: Пер. с англ. — М.: ИЛ, 1958.
3. Росс Эшби У. Введение в кибернетику: Пер. с англ. — М.: ИЛ,
1959.
4. Ст. Бир. Кибернетика и управление производством: Пер.
с англ. — М.: Физматгиз, 1963.
5. Полетаев И. А. Сигнал. — М.: Сов. радио, 1958.
6. Растригин J1. А. Этот случайный, случайный, случайный мир. —
М.: Молодая гвардия, 1974.
7. Растригин J1. А., Граве П. С. Кибернетика как она есть. — М.:
Молодая гвардия, 1975, 208 с.
8. Глушков В. М. Введение в АСУ. — Киев: Техника, 1974,
с. 146—163.
9. Черняк Ю. И. Системный анализ в управлении экономикой. —
М.: Экономика, 1975, с. 41—60.
10. Оптнер С. JI. Системный анализ для решения деловых и про¬
мышленных проблем. — М.: Сов. радио, 1969.
11. Федоренко Н. П. О методах социально-экономического прогно¬
зирования.— В кн.: Методология прогнозирования экономиче¬
ского развития СССР. — М.: Экономика, 1971.
12. Янг С. Системное управление организацией: Пер. с англ. —-М.:
Сов. радио, 1972.
13. Клиланд Д., Кинг В. Системный анализ и целевое управление:
Пер. с англ. — М.: Сов. радио, 1974, с. 25—37.
14. Основы системного подхода и их приложение к разработке тер¬
риториальных автоматизированных систем управления. — Томск:
Изд-во Томского университета, 1976, с. 3—145.
15. Джонсон Р., Каст Ф., Розенцвейг Д. Системы и руководство:
Пер. с англ.— М.: Сов. радио, 1971.
16. Системное проектирование АСУ хозяйством области./ Под ред.
Ф, И. Перегудова. — М.: Статистика, 1977,
ГЛАВА 1
ФОРМУЛИРОВКА ЦЕЛЕЙ УПРАВЛЕНИЯ
В основе всякого управления лежит информация
о том, чего собственно добивается, что хочет субъект
от объекта, т. е. каковы его цели {Z*} (точнее, множест¬
во целей). Именно эта информация определяет объект
и систему управления им. Процесс формулировки целей
предшествует всей процедуре управления и поэтому
в значительной мере формирует ее.
1.1. Парадокс цели
Между целью и объектом, в котором реализуется
эта цель, вообще говоря, существует двусторонняя связь:
цель влияет на выбор объекта, а объект, в свою оче¬
редь, определяет характер цели. Эта взаимная обуслов¬
ленность цели и объекта связана с тем, что субъект не
может формулировать свою цель, не имея хотя бы
какого-то предварительного (априорного) представления
об объекте, в котором эта цель должна быть реализо¬
вана. Дело в том, что проверка выполнения (или невы¬
полнения) заданной цели осуществляется путем анализа
состояния Y объекта. Поэтому для проверки реализуе¬
мости цели просто необходимо знать, что наблюдать
(измерять) в объекте. Это означает, что в процессе
формулирования целей следует иметь довольно четкие
представления об объекте будущего управления.
Таким образом, существует своеобразный парадокс:
цель определяется объектом, а объект — целью. Этот
парадокс разрешается довольно просто. Субъект, фор¬
мулируя цель, всегда имеет какие-то представления об
объекте. Эти представления могут быть очень прибли¬
женными, но всегда отражают некоторые его свойства,
достаточные для эффективной формулировки целей
управления. Именно поэтому формулировка цели
с той или иной степенью точности почти всегда воз¬
можна.
Объект управления целиком и полностью опреде¬
ляется целью управления. Следует, однако, помнить, что
далеко не всякий объект и не всегда полностью удовле¬
творяет щелям управления, т. е.. далеко не все сформу¬
лированные цели достижимы при имеющихся ресурсах,
41
ВЫДеЛяемых на управление. Действительно, всегда МоЖ-
но сформулировать такие нереальные дели, которые при
ограниченном ресурсе ни на каком объекте не могут
быть реализованы. Это обстоятельство обычно застав¬
ляет корректировать цели управления, что, в свою оче¬
редь, неизбежно изменяет объект управления и т. д.
Именно поэтому цель не возникает отдельно от объекта.
По-видимому, субъект обдумывает различные варианты
цели и объекта одновременно, они связаны друг с дру¬
гом и активно взаимодействуют. Однако с методологи¬
ческой точки зрения, удобно разделить эти процессы,
т. е. синтез цели рассмотреть независимо от процесса
выделения объекта из среды, хотя в действительности
они идут параллельно.
Таким образом, отмеченный выше парадокс цели
удобно разрешить, исключив обратное влияние объекта
на цель. Это влияние можно учесть на следующем этапе,
после того как определен объект и изучены его возмож¬
ности с точки зрения достижения поставленной цели.
Если окажется, что не существует объекта, в необходи¬
мой мере удовлетворяющего поставленной цели, то
нужно скорректировать цель, так как она в данном слу¬
чае недостижима.
Теперь рассмотрим процесс образования целей и ис¬
следуем его специфику. Здесь уместно вспомнить, что
цели, о которых идет речь в этой главе, выдвигаются
субъектом. Поэтому естественно разобраться, что пред¬
ставляет собой субъект, чьи цели мы предполагаем реа¬
лизовать с помощью синтезируемой системы управления.
Для этого следует рассмотреть модель субъекта.
1.2. Модель субъекта
Прежде всего отметим, что субъект является актив¬
ной стороной и отражает в процессе своего взаимодей¬
ствия со средой не только, состояние этой среды, но и
свои собственные интересы и потребности, связанные
с жизнедеятельностью. Заметим, что при управлении
большими сложными объектами в качестве субъекта
может выступать не только один человек, но и большая
группа людей. Поэтому под субъектом мы, вообще го¬
воря, будем понимать активную систему, чьи интересы
должны быть отражены в системе управления (ради них
она и создается).
42
Пусть у субъекта имеется k различных потребностей,
каждую из которых мы будем характеризовать числом
т — степенью ее выраженности, насущности, актуально¬
сти. Очевидно, что потребности изменяются во времени
н зависимости от состояния субъекта и среды, в которой
он находится. Таким образом, в каждый момент вре¬
мени субъект характеризуется набором (вектором)
своих потребностей:
А=(аь ..., а,, ..., ан). (1-2.1)
Естественно считать, что
аг^0, f=l, ..., k, (1.2.2)
т. е. актуальность потребности не может принимать от¬
рицательных значений и при отсутствии i-й потребности
т—0.. Например, в простейшем случае можно рассмот¬
реть лишь три примитивные потребности: жажда, голод
и секс (k—З). Такой субъект, очевидно, будет форму¬
лировать лишь «животные» цели, что и определит соот¬
ветственно характер его поведения.
Забежим вперед и предположим, что субъект умеет
достигать поставленные цели, т. е. он располагает си¬
стемой реализации этих целей, (это и есть система
управления). Тогда его поведение будет сводиться к фор¬
мулировке цели управления и к достижению этой цели,
т. е. к осуществлению равенства
Z=Z* (1.2.3)
с помощью управления U. Напомним, что Z — состояние
объекта, описанное на языке целей {Z*}. -«Перевод»
с одного языка на другой осуществляется функцией Чг,
рассмотренной выше (В.1.2): Z=W(Y), где Чг(-)—за¬
данная функция, определенная на состояниях У объекта.
Не будем рассматривать, как субъект добивается реали¬
зации целей управления, т. е. как он определяет U. До¬
статочно знать, что он каким-то образом умеет это де¬
лать, т. е. уже располагает эффективной системой
управления, которая «отрабатывает» заданные ей це¬
ли Z*.
Взаимоотношения субъекта с этой системой управ¬
ления (СУ) показаны на рис. 1.2.1, где штриховой ли¬
нией выделена СУ, реализующая заданную ей цель Z*.
Субъект здесь выступает как датчик целей, отрабаты¬
43
ваемых СУ. При этом потребности субъекта удовлетво¬
ряются с помощью канала Y.
Задача субъекта, таким образом, сводится к тому,
чтобы эффективно сформулировать цель управления.
Для этого он прежде всего должен уметь отличать «хо¬
рошие» цели от «плохих». Говоря языком математики,
субъект должен иметь специальную функцию меры ка¬
чества цели и-(■£*)> т. е. своеобразную функцию неком-
Рис. 1.2.1. Схема взаимодействия субъекта с системой управления
фортности, которая определена на множестве всех воз¬
можных целей {Z*}. Эта функция позволяет сравнивать
две цели Z*i и Z*2 следующим образом. Если
HCZ^X^Z*,), (1.2.4)
то цель Z* 1 предпочтительнее («лучше») цели Z*2, что
выражается так:
2*.>2*2, (1.2.5)
где >» — знак предпочтения (читается «более предпо¬
чтительно, чем»). При |x(Z*i) = n(Z*2) цели эквива¬
лентны, т. е. Z*i~Z*2. Заметим, что цели могут быть
эквивалентны для субъекта, но никак не совпадать.
Таким образом, выбор оптимальной цели сводится
к минимизации функции fi(Z*), т. е. к решению задачи
(i (Z*) — min r>Z**. (1.2.6)
z*e{z*}
Это выражение обозначает: следует (->) минимизиро¬
вать (min) функцию ц(-). варьируя ее аргумент Z*
44
в пределах заданного множества целей {Z*}, которое
состоит из допустимых целей. Результатом решения этой
задачи является (это обозначается знаком =$>) Z** —
наилучшая в данных обстоятельствах цель.
Приведем примеры образования меры fi(-). Ее мож¬
но определить, например, как взвешенную сумму:
>=2 ь1**’ (L2J)
1=1
где bi>0 (/= 1, ..., k)—«веса» потребностей, характе¬
ризующие значимость соответствующей потребности для
жизнедеятельности субъекта. Эти величины определяют¬
ся с помощью экспертных оценок, т. е. путем соответст¬
вующим образом организованного опроса специалистов,
хорошо знающих потребности субъекта (см. § 2.4).
Можно предложить и другую зависимость:
шах Ьрц (1.2.8)
i=\,...,k
которая характеризуется наиболее актуальной важней¬
шей потребностью.
Как легко заметить, величина jli определяет неком-
фортность субъекта, которую он, естественно, желает
минимизировать с помощью выбора соответствующей
цели Z*, реализация которой наибольшим образом сни¬
зит эту некомфортность.
Реализация выбранной цели должна изменять по¬
требности субъекта в сторону их уменьшения (для «хо¬
роших» целей):
где Ai — исходные, а А2 — полученные в результате реа¬
лизации цели Z* потребности (1.2.1). Естественно потре¬
бовать, чтобы при этом А2 минимизировало функцию
(1.2.7) или (1.2.8) при &i = const. Но для этого необхо¬
димо установить связь (1.2.9) в виде зависимости
А2=Ф(Аь Z*, S), (1.2.10)
где 5 — ситуация, сложившаяся в окружающей среде
к моменту выбора цели Z*, в простейшем случае S=
= (X, У), т. е. это состояние среды, окружающей
субъект.
Если бы эта зависимость была известна, то, подстав¬
ляя ее в (1.2.7) или в (1.2.8), мы получили бы искомую
45
функцию |x(Z*), минимизация которой однозначно опре¬
делила бы оптимальную цель субъекта. Однако зависи¬
мость (1.2.10) пока может реализоваться лишь челове¬
ком в виде рассуждений следующего рода: «Мои по¬
требности At; Если я в ситуации S поставлю цель Z*
и достигну ее, то мои потребности станут равными А2.
Если А2 меня удовлетворяет, то я выбираю эту цель.
В противном случае я пробую другую цель и т. д.». Мы
пока можем только предполагать, каким образом субъ¬
ект определяет состояние своих потребностей А2 по ис¬
ходным состояниям ситуации 5 потребности At и цели
Z*. В этом ему помогают имеющиеся модели среды,
собственной персоны и опыт применения этих моделей.
Таким образом, описанный механизм образования
оптимальных целей управления может быть положен
в основу создания формального «датчика целей». Од¬
нако для этого мы должны располагать двумя функ¬
циями: функцией некомфортности ц(А) в виде (1.2.7)
или (1.2.8) или в каком-то другом виде и функцией из¬
менения потребностей •,) (1.2.10), которая даст
возможность определить потребности, возникающие
в результате реализации цели Z*. Пока с этой задачей
в полной мере справляется только человек. Однако это
не означает, что процедуру формулировки цели следует
пустить «на самотек». Существуют вполне определенные
способы выражения целей, и, коль скоро цель осознана,
она должна быть выражена с помощью вполне опреде¬
ленных терминов, образующих язык формулировки це¬
лей Z*. Итак, рассмотрим этот язык, т. е. определим,
каким образом можно формально задавать цель Z*.
1.3. Пространства ситуаций и целей
Субъект в процессе общения с окружающей его сре¬
дой фиксирует свое внимание прежде всего на тех ее
параметрах (свойствах) Si, ..., si, которые влияют на
его потребности, т. е. на величины щ (i= 1, ..k),
определяющие состояние некомфортности субъекта. По
значениям этих параметров субъект может судить о со¬
стоянии среды. Но, будучи активным, субъект, естест¬
венно, желает изменить эту среду так, чтобы уменьшить
свою некомфортностЬ в ней, т. е. управлять ею. Это и
заставляет его искать в среде такие параметры, изме¬
нить которые он в состоянии, причем так, чтобы это
изменение понизило его некомфортность в этой среде
46
(напомним, что объекта еще нет, его elite йредстойт вы¬
делить из среды, из той ее части, которую захочет изме¬
нять субъект). Естественно считать, что субъект, обра¬
зуя свои цели, учитывает только те параметры, с по¬
мощью которых он может улучшить свое состояние
в этой среде. Так, например, желая увеличить скорость
автомобиля, водитель обращает внимание только на два
фактора его среды: положение педали газа и показания
спидометра. Тормоз, сцепление и другие факторы в этот
момент его не волнуют.
Параметры, которые определяют потребности субъ¬
екта, но не могут быть им изменены, вообще говоря,
косвенно влияют на его поведение при целеобразовании.
Здесь вступает в «игру» механизм эмоций, образуя то
или иное настроение (например, раздражение), что не
может оказать влияния на процесс образования цели.
Так, неудовлетворенное желание обогнать при недоста¬
точной мощности двигателя не может не вызвать нервоз¬
ности водителя и в конечном счете повлияет на его по¬
ведение. Однако механизмы такого рода здесь рассмат¬
риваться не будут.
Таким образом, субъект воспринимает окружающую
среду как некую ситуацию, которая описывается ко¬
нечным или бесконечным набором параметров:
S=(su ..., */), (1.3.1)
каждый из которых «волнует» субъекта, так как влияет
на его некомфортность, и может быть им изменен, т. е.
воспринимаемая им ситуация всегда управляема:
S(U)=i[si(U), Si(U)], (1-3.2)
где и=(мь ид)—управление субъекта, т. е.
ии ..., uq — управляемые параметры среды.
Например, для водителя контролируемыми парамет¬
рами ситуации являются: Si— скорость автомашины,
s2 — положение (разворот) колес и т. д., а управляемы¬
ми: щ—положение педали газа, щ — положение руле¬
вого колеса и т. д.
Теперь введем понятие пространства ситуаций {$}.
Оно образуется указанными параметрами s* (i= 1, ...,/)
(1.3.1). Каждая точка этого пространства , определяет
какую-то конкретную ситуацию, сложившуюся вокруг
субъекта (рис. 1.3.1). В это пространство {S} отражают¬
ся окружающие субъекта среда и различные объекты.
47
Естественный дрейф ситуации, вызванный изменением
(эволюцией) среды, связанным, возможно, с действиями
других субъектов, приводит к смещению точки S вдоль
какой-то траектории (см. линию на рис. 1.3.1).
Таким образом, su ..., si — это параметры среды
субъекта, которые влияют на него, воспринимаются им
и могут быть им изменены посредством определенных
воздействий U на среду.
Однако свои цели субъект формулирует не в терми¬
нах состояния среды S. Для этого ему удобнее опери¬
ровать иными свойственными-ему понятиями, которые
представляются в виде перемен¬
ных Zi (i= 1, р) (назовем их
целевыми). Пусть эти перемен¬
ные описываются вектором
Z=(zi, ..., Zp), (1.3.3)
где каждая целевая переменная
Zi однозначно определяется ситу¬
ацией S, т. е.
Zi=%(S), i= 1, ..., р, (1.3.4)
а функции г|)г( •) определяют
связь состояния среды S и целе¬
вого параметра Z\. В каждый кон¬
кретный момент Zi является числом, характеризующим
значение этого целевого параметра (например, темпера¬
туры, длины, стоимости и т. д. или определяет наличие
(1) или отсутствие (0) определенного свойства среды
(например, наличие каких-то важных субъекту факто¬
ров). В векторной форме эта связь выражается в виде
Z='F(S), (1.3.5)
где
... Ы-У) (1*3.6)
— определенная заданная вектор-функция, связывающая
состояние среды и целевые переменные.
Преобразование 4я информации к виду Z необходи¬
мо еще и потому, что субъект обычно формулирует свои
цели в терминах и понятиях, связанных, но не тождест¬
венных измеряемым. В' частном случае может оказаться,
что Z=Y (р = 1)у но это бывает редко. Например, при
управлении температурным режимом объекта достаточ¬
но измерять температуру, т. е. z=y=t. Однако для
Рис. 1.3.1. Траектория
дрейфа (эволюции) S (t)
ситуации в пространстве
ситуаций
48
создания комфортных условий onepafopy необходймб
измерять не только температуру, но и влажность, в то
иремя как цель формулируется в виде ограничения на
их определенную комбинацию.
Рассмотрим р-мерное пространство целей {Z}, кото¬
рое образуется точками (1.3.3). Это пространство удоб¬
но субъекту тем, что по поводу каждой его координаты
он может высказать свое требование (цель), выполнение
которого, по мнению субъекта, приведет к удовлетворе¬
нию какой-то или нескольких из его потребностей А.
Свою цель субъект формулирует в виде условного
вектора цели
2*=(г*и ... 2*р), (1.3.7)
где 2*г — уже не числа, а требования к состоянию S
среды, выраженные целевой переменной Zi — ypi(S). Эти
цели-требования могут иметь различный характер, но
форма их представления должна быть унифицирована.
Их необходимо свести к одной из следующих форм:
1) 2** — приравнять: Zi=a,i\ это требование озна¬
чает, что i-я целевая переменная Zi=tyi(S) должна быть
равна заданной величине а*;
2) z*j — ограничить; Zj^bj, что выражает требова¬
ние, налагаемое на /-ю целевую переменную, она не
должна быть меньше заданного порога bj\
3) г*/— минимизировать: zi-*inin, т. е. I-я целевая
переменная должна быть минимальна.
Следовательно, для задания целей необходимо опре¬
делить прежде всего их структуру, т. е. принадлежность
к одной из этих трех форм, а затем задать числа щ и
bj (i= 1, ..., kx\ j= 1, ..., &2), где k\ и k2 — количества
целей первого и второго рода. Если какие-либо цели
субъекта не могут быть сведены к одной из этих форм,
то нельзя говорить о формальном создании системы
управления для достижения этих целей. Однако прак¬
тика показывает, что к такого рода требованиям («при¬
равнять», «ограничить» и «минимизировать») можно
свести почти все ситуации, которые встречаются субъек¬
ту и для управления которыми создается система управ¬
ления.
Заметим, что вначале цели субъекта имеют аморф¬
ный, неопределенный характер. В лучшем случае их
удается описать на языке предпочтений, т. е. указать
наиболее предпочтительные ситуации, к которым стре-
4—299
49
Штйя субъект. Аналйз этих ситуации й дйет возмож¬
ность построить целевой вектор (1.3.7).
Таким образом, процесс формулировки целей субъ¬
екта связан, во-первых, с определением вектор-функции
(1.3.6) и, во-вторых, с указанием требований, налагае¬
мых на каждую составляющую этого вектора.
-Пример. Измеряется температура в т точках печи: si, ..., sm.
Необходимо так управлять температурным режимом этой печати
(например, изменяя во времени подачу топлива), чтобы перепад тем¬
ператур в соседних точках не превышал заданного значения Д.
Рис. 1.3.2. Взаимодействие пространства целей (а) и ситуаций (б)
в примере управления температурным режимом печи
В этой задаче m-мерное пространство ситуаций образуется по¬
казаниями датчиков si, ..., sm, а целевое пространство {Z} имеет
размерность т—1 и определяется функциями:
Цель Z* в этом случае представляется неравенствами вида
(рис. 1.3.2,а)
Рассмотрим, как отражается цель Z* в пространство
ситуаций {S}. Для этого достаточно рассмотреть область
S*, определяемую системой всех целевых требований:
где kz — число экстремальных целевых требований. Це¬
левая точка или область S*, удовлетворяющая всем
требованиям одновременно, и является тем состоянием
среды, которого добивается субъект. Однако удастся ему
это или нет, зависит от его возможностей воздейство¬
вать на эту среду, т. е. от вида зависимости (4.3.2)
О A z1
\ Л)
Zi—tj)i (S) s—1 |S{+i—Si |, I—1, • • •» ttl 1.
Z*: г<<Д, /=1, ..., m—\=k2.
{ Ф/ (^) — ” 9 ^ £““" 1' * * • 9 *
S':|<MS)^J/f / = К (1*3.8)
I
<h(S)—*min, / ==* 1,..., kv
50
и от ресурсов Я управления, которыми располагает
субъект. Ресурсные ограничения приводят к тому, что
управление U субъекта ограничено
(1.3.9)
где {Щя — множество управлений, ограниченное ресур¬
сами R, который определяется энергетическими, мате¬
риальными и другими возможностями субъекта.
Рассмотрим целевую область {S*} пространства ситуаций для
рассмотренного выше примера. Она определяется неравенствами
{S*}: |sf+i—s«|«£A, t= 1, ..., т— 1.
На рис. 1.3.2.6 показано пространство ситуаций {S} с этой целевой
областью {S*}. Как видно, задание целевого требования Z* удобнее
делать в целевом пространстве {Z}. Задать целевую область {S*}
в {S}, минуя стадию Z*. в общем случае затруднительно.
Теперь рассмотрим взаимодействие целевой области
{S*} и траектории изменения
среды S(t) под действием
внешних факторов (рис. 1.3.3),
т. е. дрейф ситуации. Если эта
траектория проходит через це¬
левую область, никакого уп¬
равления субъекту не нужно.
Ему достаточно дождаться,
когда внешние обстоятельства
приведут к тому, что S(^)c=
cr{S*}. Однако рассчитывать
на подобное маловероятное со¬
впадение неразумно, хотя оно
в принципе и возможно.
Именно поэтому субъект пред¬
почитает управлять ситуацией, т. е. он целенаправленно
ноздействует на среду и изменяет ее:
Рис. 1.3.3. Взаимодействие
траекторий дрейфа S(t) и
управления S(U, t) с целе¬
вой зоной {S*}
гак, чтобы
S=S(и, о,
S(U, 0o{S*},
(1.3.10)
(1.3.11)
т. е. чтобы достигались его цели. В этих выражениях
время t обозначает влияние дрейфа на свойства среды.
Таким образом, управление U необходимо субъекту
для того, чтобы добиться достижения цели управления
II скомпенсировать дрейф ситуации, который, как пра-
Ш1ЛО, нарушает целевое условие (1.3.11).
Г 51
Именно поэтому всякое управление следует рассмат¬
ривать с двух точек зрения: как средство достижения
поставленных целей и как средство компенсации небла¬
гоприятных изменений в среде, препятствующих этому.
Заметим в заключение, что под параметрами ситуа¬
ции S, сложившейся в среде, здесь и в дальнейшем
подразумеваются измеряемые параметры собственно
среды X и объекта Y, которые могут изменяться субъ¬
ектом с помощью управления U, т. е. Y = F°(X, U). Та¬
ким образом,
S=(X, F°(X, U)). (1.3.12)
Однако такая дифференциация S возникает лишь
после выделения объекта из среды, которое рассмотрено
в следующей главе.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИИ К ГЛАВЕ 1
Примат цели в задачах управления часто оспаривается на осно¬
ве того, что в биологических системах управления, поражающих
своей сложностью, целесообразностью и надежностью, никакой цели
нет. Этот парадокс можно легко разрешить, если вспомнить, что
в биологических системах управления функцию цели выполняет со¬
стояние другой системы, стоящей выше в биологической иерархии.
Такой принцип обычно реализуется и в «рукотворных» системах
иерархического управления, где цель каждого уровня «спускается»
ему сверху. Этим, разумеется, не решается вопрос о том, как обра¬
зована цель верхним уровнем. Поэтому проблема образования цели
в иерархической постановке не решается, а переадресуется руковод¬
ству. Причем у руководства возникают специфические проблемы
координации целей, спускаемых подчиненным. Эти вопросы детально
рассмотрены в книге /[1] (пожалуй, это — первое детальное иссле¬
дование иерархических систем управления), . где, однако, вопрос
образования цели не рассматривается.
Описанная в § 1.2 модель субъекта очень схематична и не мо¬
жет помочь при формализации процессов образования «хороших»
целей. Она приведена лишь для того, чтобы дать представление
о существовании сложных механизмов целеобразования у субьекта,
о которых мы пока что мало знаем. Она впервые описана в [2].
Более подробно специфика субъекта как целеустремленной си¬
стемы рассмотрена в великолепной книге /[3], где без лишнего фор¬
мализма, доступно и в то же время глубоко проанализировано сточ¬
ки зрения управления человеческое поведение как система достиже¬
ния целей. Однако механизмы целеобразования и здесь не рассмат¬
риваются.
Процессам целеобразования в последнее время очень много вни¬
мания уделяют психологи, справедливо определяющие цель как
первооснову поведения, которое является традиционно психологиче¬
ской сферой. В работе [4] механизмы целеобразования рассмотре¬
ны именно с этих позиций, но не связаны с процессами управления,
рассматриваемыми в данной книге. Здесь же рассмотрен процесс
формализации целей, т. е. представления их в численную форму.
52
СПИСОК ЛИТЕРАТУРЫ
1. Месарович М., Мако Д., Такахара И. Теория иерархических мно¬
гоуровневых систем. — М.: Мир, 1973.
2. Граве П. С., Растригин J1* А. Об одной математической модели
синтеза поведения (подсознательный уровень). — Адаптивные
системы: — Рига: Зинатне, 1972, вып. 2, с. 5—15.
3. Акофф Р., Эмери Ф. О целеустремленных системах. Пер.
с англ. — М.: Сов. радио, 1974.
4. Психологические механизмы целеобразования. — М.: Наука, 1977
Г Л АВА 2
ОПРЕДЕЛЕНИЕ ОБЪЕКТА УПРАВЛЕНИЯ
Задача выделения объекта управления из среды воз¬
никает после формулировки и описания множества це¬
лей управления {Z*}. Процесс выделения объекта дол¬
жен заканчиваться определением границ объекта F0
(будем обозначать объект его оператором F°)y отделя¬
ющих его от среды, т. е. таким описанием этого объекта,
которое недвусмысленно определяет его границы. В ря¬
де случаев, когда границы объекта очевидны, такой
проблемы не возникает. Это бывает, когда объект до¬
статочно автономен (самолет, корабль, любой -прибор,
автомашина и т. д.). Однако в других случаях связи
объекта со средой настолько сильны и разнообразны,
что порой очень трудно понять, где кончается объект и
начинается среда. Именно такой случай рассматривает¬
ся в настоящей главе.
2.1. Анализ проблемы
Естественно возникает вопрос, а важно ли, где про¬
водить границу раздела объекта и среды, если она
нигде явно не видна? Оказывается важно и даже очень.
Проиллюстрируем сказанное простым примером.
Пусть мы собираемся создать систему управления
каким-то технологическим процессом. Ограничиваются
ли рамки объекта только этим процессом? Ответить на
этот вопрос нельзя, поскольку границы объекта управ¬
ления зависят от целей, которым должен удовлетворять
указанный процесс и его продукция. Если цели доста¬
точно четкие (например, достижение определенного
53
качества или ритмичности работы), то неизбежно при¬
ходится управлять не только самим процессом, но и его
входом, т. е. сырьем, которое перерабатывается в ходе
этого процесса. Это означает, что в объект управления
мы должны включить и поставщика сырья. А в некото¬
рых случаях управлять приходится и сырьем, поступаю¬
щим к поставщику. (Заметим, что необходимость в та¬
ком управлении явилась одной из причин создания ком¬
бинатов, объединений, фирм и т. д., которые имеют
возможность управлять производством на всех стадиях).
Но нельзя впасть и в другую крайность, т. е. пытать-
- Рис. 2.1.1. К пояснению выбора границ объекта
ся управлять «всем и всея», хотя формальные основания
для этого всегда найдутся, так как связи различных
процессов и явлений можно проследить достаточно да¬
леко. Существует, однако, определенный оптимум «раз¬
меров» объекта. Попытаемся это показать.
На рис. 2.1.1 показаны два варианта объекта управ¬
ления. Здесь у\, ут— точки съема информации, не¬
обходимой для оценки реализуемости множества целей
{Z*} в объекте, причем Y=(yt, ..., ут). Эти точки
должны быть в любом варианте объекта. В первом
варианте (рис. 2.1.1,а) устанавливается связь между
входами и выходами в виде
Y=F°1(X1, U,, Е,), ' (2.1.1)
где Xi — контролируемый, Ui—управляемый, a Ei —
неконтролируемый входы.
Это!" вариант объекта можно расширить, присоеди¬
нив к нему часть среды, показанную на рис. 2.1.1,а
штриховой линией. Если попытаться управлять этой
частью среды, т. е. считать ее частью объекта, то удастся
воздействовать на ранее не управляемый вход X], что,
очевидно, расширяет возможности управления.
54
Ёа рис. 2.[Л,6 штриховой линией показан расширен¬
ный таким образом объект, для которого
Y=F°1(F°2(X2, U2) Е2), U,, Е,). (2.1.2)
Здесь управление Ui не исключается, к нему добавляет¬
ся еще U2, которое позволяет управлять дополнительно
присоединенной частью.
Как видно, состояние Y у обоих вариантов объекта
одинаковое, различны среды, а следовательно, и влия¬
ние среды на это состояние. Какой из вариантов лучше?
Для ответа на этот вопрос нужно взвесить все «за» и
«против» для обоих вариантов. Сделаем это.
Первый вариант (рис. 2.1.1,а).
«За»:
— лишь один фактор неопределенности (неконтроли¬
руемый вход) Ei,
— проще найти математическое описание, т. е. мо¬
дель объекта F°i,
— малое число точек управления Uj (для управле¬
ния понадобится мало ресурсов R).
«Против»:
— малая управляемость, так как вход Xi неуправ¬
ляемый. Этот фактор и является решающим для введе¬
ния конкурирующего второго варианта объекта.
Второй вариант (рис. 2.1.1,6).
«За»:
— возможность, хотя бы частичная, управления вхо¬
дом X-i, который непосредственно воздействует на со¬
стояние Y. Это осуществляется с помощью дополни¬
тельного канала управления U2.
«Против»:
— расширение фактора неопределенности за счет
введения дополнительной неопределенности Е2 присоеди¬
ненной части,
— усложнение математического описания, так как
необходимо описывать дополнительно присоединенную
часть F°2,
— увеличение числа точек управления, что хотя и
расширяет возможности управления, но требует и уве¬
личения ресурсов управления R или (при его неизмен¬
ности) приводит к уменьшению диапазона изменения
U= (U,, иа), т. е. к малым возможностям управления.
На первый взгляд может показаться, что во втором
варианте «против» слишком много и нужно отдать пред¬
55
почтение первому варианту объекта. Однако то единст-
венное «за», которое имеет второй вариант, может ока¬
заться решающим. Ведь нашей конечной задачей яв¬
ляется эффективное достижение заданного множества
целей {Z*}. Второй вариант по критерию достижимости
целей может оказаться лучше, чем первый.
Следовательно, задача заключается в том, чтобы
суметь достаточно эффективно различать «хорошие» и
«плохие» варианты выделения объектов из окружающей
их среды. Как этого добиться? Если бы мы располагали
формальным (математическим) описанием среды, то
процесс выделения из нее объекта принципиально не
представлял бы трудностей. Действительно, «высекая»
различные «куски» среды и называя их различными
вариантами объекта, мы всегда могли бы формально
проверить, достигаются ли заданные цели управления
в этом варианте объекта или нет. Повторяя эту про¬
цедуру для различных версий высечения, мы останови¬
лись бы на том варианте объекта, который позволяет
получить максимальную (желательно 100%-ную) управ¬
ляемость. Вот и все1
Но формального описания среды нет, и этот подход
неприемлем. Поэтому будем искать другой подход. На¬
правление поиска довольно очевидно. Всегда, когда нет
(или пока нет) формального аппарата для решения проб¬
лемы, за решением (хотя часто и очень приближенным)
обращаются к экспертам. На стадии определения объ¬
екта это единственно возможный подход. Поэтому рас¬
смотрим процесс использования экспертов для решения
поставленной задачи.
2.2. Метод экспертных оценок
Под экспертом мы будем понимать лицо, чье мнение
по интересующему нас вопросу может быть более авто¬
ритетным, чем наше. В противном случае к указанному
лицу не имеет смысла обращаться как к эксперту. Оче¬
видно, что эксперт по вопросу определения объекта
должен:
— хорошо знать среду, из которой выделяется
объект,
— хорошо знать цели управления,
— иметь представление о возможностях и средствах
управления,
56
— иметь представление о способах сбора и обработ¬
ки информации о среде и объекте.
Эксперта не просят определять объект. Его исполь¬
зуют как источник информации, необходимой для при¬
нятия решения о том, что же следует считать объектом
управления. Это решение принимает разработчик (про¬
ектировщик) системы управления. Эксперту же задают
вопросы, ответы на которые содержат требуемую ин¬
формацию. Далеко не все вопросы целесообразно зада¬
вать даже эксперту (задавать-то можно, а вот его от¬
ветам верить следует с большой осторожностью).
Начнем с отбора экспертов и их квалификации. Бу¬
дем квалификацию каждого i-го эксперта, т. е. его ком¬
петентность в обсуждаемом /-м вопросе, оценивать так
называемым коэффициентом компетентности:
0<*V<1, i=l N3, (2.2.1)
где Nj — число экспертов, 'привлекаемых к решению
/-го вопроса. При k^ = 0 i-и эксперт признается неком¬
петентным в /-м вопросе, а при этот эксперт счи¬
тается полностью компетентным. Если эти коэффициен¬
ты компетентности известны, то сразу четко определяется
число экспертов. Действительно, экспертов, чья компе¬
тентность ниже пороговой, т. е.
kU< 6j, (2.2.2)
где — заданный порог компетентности для решения
/-го вопроса, можно не беспокоить решением этой про¬
блемы. Так выясняется число Nj экспертов, привлекае¬
мых к решению /-го вопроса (величина порога б^’ на¬
значается проектировщиком).
Рассмотрим способ определения коэффициентов ком¬
петентности (2.2.1). Эти коэффициенты определяются
также экспертно, т. е. путем взаимной оценки компетент¬
ности самих экспертов. Делается это следующим обра¬
зом. Каждый i-и эксперт при решении /-го вопроса оце¬
нивает компетентность всех экспертов (в том числе и
свою) с помощью коэффициентов
0<jyfz<l, /=il, Nj. (2.2.3)
Здесь №ц — мнение /-го эксперта о компетентности /-го
эксперта при решении /то вопроса (kUi — самооценка
компетентности i-го эксперта в этом вопросе). Теперь
нетрудно определить коэффициент компетентности /-го
57
эксперта как среднее всех оценок, включая и его собст¬
венную:
1 N!
k^i= (2.2.4)
i=i
Заметим, что матрица взаимных оценок (2.2.3) может
содержать прочерки, которые означают, что оценки нет
(один эксперт не знает, а поэтому не может оценить
другого). В этом случае в формуле (2.2.4) усреднение
ведется по значащим оценкам, т. е. исключая прочерки.
Пример такой матрицы оценки компетентности:
/
1
1
2
3
л4
1
1
0,3
0,5 .
2
0,7
0,8
0,4
—
3
0,8
0,7
0,6
4
0,7
0,7
—
0,9
kfi
0,8
0,77
0,47
0,67
Здесь все средние значения kh оцениваются по трем
значащим оценкам, т. е. N,—3.
Очевидно, что этот метод самооценки экспертов не
учитывает всякого рода сложные взаимоотношения, ко¬
торые возможны между экспертами, как людьми. Это
обстоятельство нужно иметь в виду при анализе матриц
оценок компетентности. Так, если один из экспертов по¬
лучил очень высокий балл у одних и очень низкий у дру¬
гих экспертов, то это скорее всего означает или особен¬
ности его характера, или оригинальность мышления,
которые разделяются одними, но не принимаются дру¬
гими экспертами. Выявление такого рода «человеческих»
аномалий матрицы оценок компетентности позволит из¬
бежать ошибок, когда мнение семи компанейских
«глупцов» оказывается более весомо, чем мнение одного
неуживчивого «мудреца».
Располагая значениями коэффициентов компетентно¬
сти (2.2.4), можно приступить к решению /-го вопроса.
Всякая проблема в конечном счете сводится к определе¬
нию либо некоторого числа, либо набора из q чисел,
которые называют решением этой проблемы. Рассмот¬
59
рим первый случай, так как второй сводится обычно
к ^-кратному решению первого.
Пусть проблема формулируется так. «Исходя из
условий (излагаются условия, где фигурирует неизвест¬
ный фактор решающий проблему), определите Ва¬
ше мнение о значении этого фактора одним числом
Wii= ... Спасибо за экспертизу!»
Получив от всех экспертов значения W(i= 1, ...
..., Nj) (здесь могут быть и отказы от экспертизы ввиду
признания собственной некомпетентности в этой вопро¬
се; отказавшиеся эксперты автоматически выпадают из
Nj), следует принять решение о значении этого фактора.
Это значение с учетом компетентности экспертов естест¬
венно определять как средневзвешенное с весами, рав¬
ными коэффициентам компетентности:
^'=(i |*а kit' (2.2.5)
Как видно, мнение каждого эксперта взвешивается зна¬
чением его коэффициента компетентности. Поэтому
мнение малокомпетентных экспертов автоматически учи¬
тывается в меньшей степени. Следовательно, экспертов
можно не отбирать по критерию (2.2.2). Этот критерий
позволяет лишь не беспокоить экспертов, чье мнение
несущественно для решения /-го вопроса.
Формула (2.2.5) и решает поставленную задачу. Од¬
нако здеСь следует учесть и принять во внимание следу¬
ющее важное обстоятельство. Мнения экспертов, т. е.
числа могут сильно отличаться друг от друга по
двум причинам. С одной стороны, разнобой может быть
вызван тем, что экспертам трудно отвечать на постав¬
ленный вопрос. В этом случае следует изменить его по¬
становку, чтобы облегчить экспертам их задачу. С дру¬
гой стороны это может произойти и потому, что по
поводу. фактора Wi существуют две противоречащие
друг другу точки зрения, которые следует учитывать
при решении вопроса. В этом случае проектировщику
следует выявить их и присоединиться к одной из них.
Разброс мнений проще всего определять с помощью
оценки дисперсии полученных экспертных оценок:
Малая величина этой дисперсии свидетельствует о до¬
статочном единодушии экспертов.
Как видно, метод экспертных оценок позволяет ре¬
шать формально-неразрешимые проблемы. Правда, по¬
лученное решение всегда приближенно, но его можно
уточнять, увеличивая число экспертов и учитывая их
компетентность в решении этой проблемы.
Теперь применим изложенный метод к решению по¬
ставленной задачи выделения объекта из среды.
2.3. Управляемость объекта
Процедуру выделения объекта из среды естественно
строить так, чтобы в получившемся объекте реализова¬
лись цели управления, т. е. чтобы им можно было бы
эффективно управлять в ситуациях, которые склады¬
ваются в процессе управления. Для этого введем поня¬
тие управляемости объекта, под которым будем под¬
разумевать вероятность достижения задаваемых целей
в различных ситуациях.
Прежде всего рассмотрим понятие ситуации. Под
ситуацией, сложившейся в процессе управления, в самом
общем случае следует понимать тройку
S = (X, Е, Z*), (2.3.1)
определяющую состояние неуправляемых входов объек¬
та и цель, которую следует достигнуть (легко заметить,
что это определение ситуации обобщает предложенное
ранее (1.3.12), где управление U зависит в конечном
счете лишь от X и Z*). Все ситуации, которые встре¬
чаются в процессе управления данным объектом, можно
подразделить на два подмножества ситуаций — управля¬
емых, при которых заданная цель Z* всегда достигается,
и неуправляемых, когда эта цель Z* не достигается.
Обозначим {S} множество всех возможных ситуаций
S, встречающихся в процессе управления. Пусть {J^} —
подмножество ситуаций {S}, где объект неуправляем,
т. е. не все цели из {Z*} достигаются, а — подмно¬
жество ситуаций, где объект управляем, т. е. все цели
из {Z*} достигаются. Очевидно, что
{J5}U{y = {S}. (2.3.2)
Это выражение означает очевидное: каждая ситуация S
может быть или управляемой, или неуправляемой.
60
Каждому элементу множества {$}, т. е. каждой си¬
туации S, поставим в соответствие число p=p(S), кото¬
рое определяло бы вероятность появления этой ситуа¬
ции S. Если число элементов множества {S} бесконечно,
то под p(S) следует, как обычно, понимать плотность
этой вероятности. В первом (дискретном) случае
2p(S,)=1,
1=1
где А/ — общее число встречающихся ситуаций. Во вто¬
ром (непрерывном) случае
j p(S)dS=l, (2.3.3)
{S}
где интеграл берется по всему множеству {S}. Соотно¬
шение (2.3.3) выражает то обстоятельство, что вне об¬
ласти {S} не могут встретиться реальные ситуации S.
Непрерывный случай более удобен и здесь обобщает
дискретный, поэтому будем пользоваться только им, хо¬
тя для практических целей и придется вернуться
к дискретному.
Теперь уточним понятие управляемости. Управляе¬
мостью объекта будем называть вероятность того, что
случайно выбранная ситуация S управляема. Эта веро¬
ятность равна
Р= [ р (S) dS, (2.3.4)
{J's>
где интеграл берется по подмножеству управляемых си¬
туаций {Js}.
Неуправляемость определяется аналогично как
интеграл по множеству {J_} неуправляемых ситуаций:
S
р= J р (S) dS. (2.3.5)
%>
Из (2.3.2) и (2.3.3) следует, что
Р+Р= 1. (2.3.6)
Если из двух рассматриваемых вариантов объекта один
обладает большей управляемостью, чем другой, то
61
Именно этот объект при прочих равных условиях сле¬
дует предпочитать другому. Следовательно, задача вы¬
бора объекта сводится к задаче определения его управ¬
ляемости Р.
Однако^строгое определение множеств {Jg} и {JL}, а
также функции p(S) невозможно из-за отсутствия фор¬
мального описания среды. Именно поэтому для решения
этой задачи привлекаются эксперты.
Для определения (точнее, оценки) управляемости Р
объекта необходимо декомпозировать проблему, т. е.
представить ее в виде ряда более простых задач, кото¬
рые могут быть решены экспертами.
Для этого экспертам необходимо предоставить следу¬
ющие исходные данные:
1) цели управления, т. е. достаточно полное описание
множества целей управления {Z*}, которые должны
быть реализованы в объекте,
2) сведения о располагаемых ресурсах R, которые
выделены на создание системы управления и ее экс¬
плуатацию.
Обозначим эти исходные данные двойкой:
Л = ({г*}, R). ^ (2.3.7)
Экспертам должна быть предоставлена также полная
информация о предполагаемом объекте и его связях со
средой, т. е.:
3) описание объекта F0,
4) описание множества {X} контролируемых состоя¬
ний среды, которые могут быть учтены в процессе син¬
теза управления («объем» этого множества, очевидно,
зависит от ресурсов R, выделенных для организации
системы контроля и измерения X),
5) описание {U}H— множества управлений, допусти¬
мых ресурсами R (имеющейся энергией, временем, объ¬
емом памяти управляющего устройства, скоростью и
спецификой переработки информации и т. д.),
6) описание {Е} — множества неконтролируемых
факторов среды и объекта.
Эти данные об объекте обозначим четверкой:
В=(Р, {X}, {U}*, {Е}). (2.3.8)
Эксперт, располагая указанными исходными данными
А и В, должен оценить управляемость Р объекта. Обо¬
62
значив через ср алгоритм работы эксперта, в результате
можно записать
Р=Ф(Л, В). (2.3.9)
Однако, как легко представить, в этой ситуации экс¬
перту работать очень трудно. Действительно, информа¬
ция А и В хотя и содержит необходимые сведения об
управляемости Р объекта, но оценить управляемость Р,
т. е. реализовать алгоритм ср, экспертам не удается. Эта
задача слишком для них сложна. Поэтому еще раз де¬
композируем задачу. Для этого введем различные фор¬
мы управляемости и неуправляемости объекта.
Будем называть объект абсолютно управляемым
(Р=1), если каждая ситуация из {S} управляема, т. е.
цель всегда достигается. Это означает, что для любого
контролируемого состояния среды Хе{Х}, любого не¬
контролируемого входа Ее{Е} и для любой цели
Z*e{Z*} всегда найдется такое управление U*e{U}*,
которое переведет объект в требуемое состояние, т. е.
Z==Z(X, U*, E)=^(F°(X, U*, Е))_=Z*, (2.3.10)
где ЧГ(-)—преобразование пространства состояний
объекта m в пространство целей {Z}, рассмотренное
в (1.3.6); Z — состояние объекта в пространстве целей;
Z(% •, •)—функция, характеризующая зависимость
Z от X, U и Е.
Для экономной записи этого определения удобно вос¬
пользоваться так называемыми кванторами существова¬
ния (д) и всеобщности (у)- Тогда
уХ <=?{Х}, уЕ <Е {Е}, yZ* G {Z*},
au*e{u}*:Z(x, и*, e)=z*. (2.3.11)
Это на первый взгляд сложное выражение читается
очень просто: для любого X, принадлежащего множеству
{X}, что записывается в виде уХЕ!{Х}, любого Е, при¬
надлежащего множеству {Е} (т. е. уЕ0{Е}), и любого
Z* принадлежащего {Z*} (т. е. yZ*G{Z*}), существует
такое U*, принадлежащее {U}s (т. е. {UR}), при
котором Z=Z*, т. е. цель достигается.
Абсолютная управляемость (Р= 1) редко встречает¬
ся на практике при управлении сложными объектами.
Действительно, для ее обеспечения следует или значи¬
тельно сужать множество целей, или иметь постоянную
среду (X=const), или выделять очень большие ресур¬
63
сы R на управление. Как правило, абсолютно управля¬
емы либо простые объекты (например, системы автома¬
тического регулирования), либо очень ответственные
(например, системы обеспечения жизнеспособности опе¬
раторов в экстремальных условиях). Подавляющее боль¬
шинство систем управления сложными объектами нель¬
зя отнести к этому типу.
Поэтому следует ввести понятие частичной или от¬
носительной управляемости. Будем различать причины
неуправляемости. Для этого введем типы неуправляемо¬
сти следующим образом. X — неуправляемость связана
со спецификой множества W, в котором нашлось та¬
кое X, что при любом Ее{Е} не нашлось такого
UeE{U}„, при котором Z=.Z*, т. е. любая цель не до¬
стигается. Определим Х-неуправляемость формально:
J_:(3XG{X}:YEG{E}, VZ*e{Z*},
iUG{U}^:Z(X, U, E) = Z*). (2.3.12)
Здесь J_ — Х-неуправляемость и использовано отрицание
х
квантора существования д, что означает «не существу
ет» (не найдется). Выражение (2.3.12) читается следую¬
щим образом: Х'-неуправляемость определяется как су¬
ществование такого допустимого X, при котором для
любых допустимых Е и Z* не найдется такого допусти¬
мого U, при котором цель Z* будет достигнута.
Приведем пример такой ситуации. Пусть X* — энер¬
гия, требуемая для нормального функционирования
объекта. Тогда при Х'<Х*, т. е. при недостаточной по¬
ставке энергии, объект не будет работать и не выполнит
возлагаемые на него цели Z* несмотря на все усилия U,
предпринятые в рамках выделенных ресурсов R.
Е-неуправляемость вводится аналогично, как сущест¬
вование таких неконтролируемых состояний среды, при
которых при любых допустимых X не удается достигнуть
любой допустимой цели:
J_:(gEG{E}:VXG{X},
V?*G{Z*}, gUG {U}*:Z(X, U, E) = Z*). (2.3.13)
Пример. Пусть E — амортизация оборудования, которая приво¬
дит к снижению точности приборов. Очевидно, что начиная с неко¬
торого уровня амортизации потеря точности приборов будет столь
64
велика, что не позволит с их помощью реализовать заданные цели,
например выпускать качественную продукцию даже при специаль¬
ных мероприятиях U, проводимых в рамках ресурсов R.
Z^-неуправляемость характеризуется наличием таких
допустимых целей, которые при прочих допустимых
условиях никогда не достигаются:
j_:(az*e{z*}:Yxe{x},
YEG{E}, iUG{U}*:Z(X, и, E)=Z*). (2.3.14)
Это означает, что существуют допустимые цели, ко¬
торые достижимы не при всех состояниях среды. Напри-
Рис. 2.3.1. Зоны неуправляемости объекта, вызванной факторами X
и Е (а и б) и факторами Z* и X (в).
мер, цель перевыполнения плана не реализуется при
нерегулярных поставках (X) или аварийных ситуациях
(Е), которые допускают выполнение плана.
На рис. 2.3.1 для иллюстрации показано несколько
случаев неуправляемости в пространстве состояний
{S} = {X, Е, Z*}. Жирными отрезками обозначены зоны
неуправляемости, которые порождают области неуправ¬
ляемости J_, J_ и J Как видно, эти зоны могут
X Е Z*
пересекаться (см. рис. 2.3.1,б, в). Отметим это обстоя¬
тельство— мы будем использовать его в дальнейшем.
Теперь введем понятия перекрестных неуправляемо¬
стей, т. е. таких, которые зависят сразу от двух или трех
факторов X, Е, Z*, определяющих успех управления:
ХЕ-неуправляемость определяется как одновремен¬
ное существование таких X и Е, при которых не всякая
цель достижима:
J_:(a~(X, E):yz*, iU£{U}*:Z(X, U, E) = Z*). (2.3.15)
5—299
65
Например, одновременное снижение качества сырья (X)
и амортизация оборудования (Е) ставят обычно под
угрозу выполнение плана, хотя каждый из этих факто¬
ров в отдельности может быть преодолен соответствую¬
щим управлением U.
Здесь и далее для сокращения записи предпола¬
гается, что ХбЕ{Х}, ЕбЕ{Е}, Z*e{Z*}, и<={и}д.
Хг*-неуправляемость определяется аналогично:
J_:(g(X, Z*):VE, fU:Z(X, U, E) = Z*); (2.3.16)
Рис. 2.3.2. Зоны неуправляемости объекта, вызванной парными взаи¬
модействиями факторов X, Е и Z*
2*Е-неуправляемость:
.l_:(g(Z*, Е) :yXgll:Z (X, U, E) = Z*). (2.3.17)
И, наконец, ХЕ2*-неуправляемость:
:(3(Х, Е, Z*):gU:Z(X, U, E) = Z*). (2.3.18)
XEZ*
На рис. 2.3.2 зоны неуправляемости такого вида за¬
штрихованы. Как видно, они включают и зоны,
рассмотренные на рис. 2.3.1. Однако не следует путать
области неуправляемости такого вида с пересечением
областей Х-, Е- и г*-неуправляемости, показанных на
рис. 2.3.1,б и в.
Если бы с помощью экспертов удалось оценить встре¬
чаемость (вероятность появления) всех указанных видов
неуправляемости, то процесс определения управляемости
объекта свелся бы к вычислению суммы
1
(2.3.19)
6G
где pi — вероятность появления i-го вида неуправляемо¬
сти (всего их 7). Это и был бы алгоритм ф в (2.3.9).
Располагая таким алгоритмом, можно из определенного
конечного множества объектов-претендентов выбрать
один, наиболее управляемый.
Теперь снова обратимся к экспертам, они нам нужны
для оценок величин pi (i= 1, ..7), входящих в оценку
управляемости (2.3.19).
2.4. Экспертный метод оценки
управляемости объекта
Итак, следует сформулировать вопросы отобран¬
ным N экспертам таким образом, чтобы их ответы по¬
зволили принять наиболее достоверное решение об
управляемости объекта в предложенных границах. Для
этого, прежде всего, необходимо образовать конечное
число альтернатив — вариантов объекта F°b ..., F°g,
т. е. описаний:
Y = F°V (Xv, Uv, Ev), v= 1, ... , q, (2.4.1)
где Xv, Uv и Ev — соответственно наблюдаемые, управ¬
ляемые и ненаблюдаемые входы v-ro варианта объекта.
Образование вариантов (2.4.1) производится исходя из
предварительного анализа среды и целей.
Таким образом, задача определения объекта сводит¬
ся к выбору одной из альтернатив (2.4.1). Исходная
информация для этого выбора содержится в ответах
экспертов на вопросы, с помощью которых определяется
управляемость каждого варианта объекта (2.4.1). Будем
задавать экспертам такие вопросы, чтобы по ответам
определить вероятность каждого вида неуправляемости.
Для этого выявим ситуации S, при которых цели не до¬
стигаются, т. е. объект неуправляем. Эти ситуации
естественно классифицировать по видам неуправляемо¬
стей.
Экспертиза проходит в несколько этапов. Сначала
эксперты выявляют и описывают неуправляемые ситуа¬
ции. Затем составляется полный перечень таких ситуа¬
ций, объединенных по виду неуправляемости. Этот пере¬
чень предлагают экспертам для оценки вероятности
каждой ситуации. Если эти оценки не слишком различ¬
ны, то они принимаются для вычисления управляемости
объекта. Однако при большом разнобое экспертам
5:
67
предоставляется возможность изменить свою оценку,
учитывая оценки других экспертов по спорным ситуа¬
циям. Это делается до тех пор, пока оценки перестанут
сильно отличаться. По результатам этих оценок вычис¬
ляется управляемость. Рассмотрим каждый этап в от¬
дельности.
Итак, на первом этапе каждому эксперту предла¬
гается описать все неуправляемые ситуации по каждому
виду неуправляемости:
S1,),..., J__:(S\,..., S\), (2.4.2)
где S*j — /-я неуправляемая ситуация i-го вида неуправ¬
ляемости.
Очевидно, у каждого эксперта будет свой набор та¬
ких ситуаций. Эти ситуации объединяются в общий спи¬
сок неуправляемых ситуаций. Он имеет тот же вид, что
и (2.4.2), но с другими числами 1\, ..., 17.
При составлении этого списка следует следить, чтобы
ситуации в списке не повторялись. Это необходимо, так
как, например, ситуации из J можно спутать с ситуа-
ХЕ
циями, одновременно принадлежащими J_ и Jg- (ср. пере-
х
сечение областей на рис. 2.3.1, б и в и 2.3.2, а и б).
Далее каждому эксперту предлагается полный список
всех неуправляемых ситуаций
Sb .... S» (2.4.3)
без учета принадлежности ситуации виду неуправляемо¬
сти (это нужно было лишь для выявления ситуаций
(2.4.3) экспертами). Каждый /-й эксперт каждой ситуа¬
ции Si приписывает число
О^^г, » = 1, п; j— 1, ..., N, (2.4.4)
характеризующее, по его мнению, оценку вероятности
появления такой ситуации в процессе управления этим
объектом. При этом, очевидно, должно выполняться
ограничение
п
68
Заметим, что сумма
п
N (2А.5)
является мнением /-го эксперта о неуправляемости
объекта.
Однако, прежде чем определять среднюю неуправ¬
ляемость объекта, следует проверить согласованность
экспертов. Оценить эту согласованность можно по дис¬
персиям индивидуальных оценок различных ситуаций
Если найдутся такие ситуации S;, о вероятности появле¬
ния которых мнения экспертов сильно расходятся, т. е.
где 6>0 — некоторый заданный порог, то по этим си¬
туациям экспертам предлагается пересмотреть или под¬
твердить свою оценку с учетом мнений других экспертов
(эти ситуации и мнения всех экспертов по этим ситуа¬
циям сообщаются). Процедура повторяется до тех пор,
пока не выполнится условие
£>*<■6, i= 1, п.
Теперь экспертная оценка неуправляемости объекта
принимает вид
где kj — компетентность /-го эксперта (2.2.5), a Pj —
оценка неуправляемости объекта /-м экспертом (2.4.5).
На этом заканчивается экспертная оценка неуправ¬
ляемости данного варианта объекта.
Получив подобные экспертные оценки для всех q ва¬
риантов^ (2.4.1)_объекта, найдем оценки их неуправляе¬
мости Ри •••> Pq- Очевидно, что наилучший вариант
объекта тот, который имеет минимальную управляе¬
мость. Если
то /-й вариант объекта и следует считать оптимальным,
т. е. F° = F0/.
i— 1,..., п. (2.4.6)
(2.4.7)
(2.4.8)
69
Естественно, что при этом следует учитывать диспер¬
сию оценок вероятностей Pv(v=l,..., q). Если несколь¬
ко вариантов объекта окажутся статистически неразли¬
чимы, то либо следует увеличить число экспертов, либо
сообщить им дополнительную информацию о среде, це¬
лях и ресурсах, либо ввести дополнительные критерии
оценки вариантов объекта, по которым можно осущест¬
вить однозначный выбор.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИИ К ГЛАВЕ 2
Вторичность объекта по отношению к цели связана прежде все¬
го с тем, что объект является системой, которая в соответствии
с [1, 2] представляет собой множество элементов, связанных отно¬
шением, обладающим заданным свойством. Это свойство и опреде¬
ляется множеством целей, которые должны быть реализованы в дан¬
ном объекте. Таким образом, объект управления отличается от си¬
стемы вообще тем, что он образован элементами, связанными
отношением, обладающим свойством иметь возможность объекту
находиться в состояниях из заданного целевого множества. Указан¬
ная необходимость состояниям объекта соответствовать целевому
множеству и образует зависимость объекта от целей управления.
Метод экспертных оценок, рассмотренный в § 2.2, как видно,
позволяет получать ответы на вопросы, которые не могут быть полу¬
чены формально хотя бы потому, что вопросы не поставлены фор¬
мально. Таких вопросов в наше время задается значительно боль¬
ше, чем хочется сторонникам формализма. Дело в том, что сейчас
все чаще и чаще приходится управлять объектами задолго до их
исчерпывающего изучения и зачастую переходить к управлению дру¬
гими, так и не узнав достаточно предыдущие. В такой обстановке
естественно, что только экспертный метод позволяет получить отве¬
ты на поставленные вопросы. При этом приходится часто «расплачи¬
ваться» высокой дисперсией ответов, что, однако, не должно сму¬
щать, так как в настоящее время разработаны эффективные методы
принятия решения в стохастической обстановке (см., например, впол¬
не доступные книги по теории стохастических решений [3 или 4]).
Таким образом, использование экспертных решений вовсе не
является «заметанием мусора под коврик», как это может пока¬
заться. В сочетании с методами теории статистических решений экс¬
пертный метод дает вполне приемлемые результаты.
По методу экспертных оценок имеется ряд полезных руководств.
Отметим среди них '[5, 6]. Для начального ознакомления можно ре¬
комендовать две главы из доступной и обстоятельной книги [7,
с. 143—260].
Введенное в § 2.3 понятие управляемости объекта отличается
от известного ранее понятия управляемости динамической системы
(см., например, [8]), которое подразумевает существование управ¬
ления, переводящего объект в требуемое состояние. Предложенное
понятие, как видно, обобщает известное на стохастический случай.
Поэтому, по-видимому, правильнее было бы назвать введенную ха¬
рактеристику объекта статистической (или вероятностной) управляе¬
мостью, что, однако, привело бы к слишком громоздкой термино¬
логии.
70
СПИСОК ЛИТЕРАТУРЫ
I. Уемов А. И. Вещи, свойства и отношения. — М.: Изд-во АН
СССР, 1963.
:1. Уемов А. И, Системы и системные параметры. — В кн.: Пробле¬
мы формального анализа систем. — М.: Высшая школа, 1968,
с. 15—35.
3. Чернов Г., Мозес JI. Элементарная теория статистических реше¬
ний.— М.: Сов. радио, 1962.
4. Де Гроот М. Оптимальные статистические решения: Пер.
с англ. — М.: Мир, 1974.
5. Бешелев С. Д., Гурович Ф. Г. Математико-статистические мето¬
ды экспертных оценок. — М.: Статистика, 1974.
6. Экспертные оценки в научно-техническом прогнозировании. —
Киев: Наукова думка, 1974.
7. Шляпентох В. Как сегодня изучают завтра. — М.: Сов. Россия,
1975.
8. Медич Д. Статистические оптимальные линейные оценки и
управление. — М.: Энергия, 1973.
ГЛАВА 3
СТРУКТУРНЫЙ СИНТЕЗ МОДЕЛИ
ОБЪЕКТА
Структура модели объекта управления определяет
вид и характер связи между входами (X и U) и выхо¬
дами (Y) модели объекта независимо от конкретных
значений параметров, которые определяются на после¬
дующих этапах управления — этапах идентификации
(см. гл. 4) и планирования экспериментов (см. гл. 5).
Процесс структурного синтеза модели объекта разобьем
на следующие стадии:
— определение входов и выходов;
— экспертное ранжирование входов и выходов;
— декомпозиция модели;
— выбор структурных элементов модели.
Рассмотрим каждую стадию в отдельности.
3.1. Определение входов и выходов объекта
Для определения структуры модели как многополюс¬
ника (т. е. преобразователя типа «черного ящика» со
многими входами и выходами) необходимо выяснить,
какие именно входы и выходы объекта будут включены
в его модель. Для этого прежде всего выявляют всех воз-
71
можных «претендентов» на роль входов и выходов и из
них выделяют наиболее существенные, которые и обра¬
зуют многополюсник модели.
Но здесь сразу возникает вопрос о том, какие факто¬
ры в этом случае называть существенными. Ответ одно¬
значный: так как модель объекта создается для целей
управления, то существенными являются те факторы,
которые наиболее сильно влияют на осуществление це¬
лей управления в объекте. Это связано с тем, что при
формировании структуры системы управления прежде
Рис. 3.1.1. Схема взаимодействия объекта («черного ящика») со
средой
всего необходимо знать, какие воздействия будет (и мо¬
жет) испытывать объект управления и как результаты
этих воздействий связаны с достижением целей управ¬
ления объектом.
Объект связан со средой, вообще говоря, бесконечным
числом связей (рис. 3.1.1), определяющих его состояние.
При синтезе модели должны быть выявлены наиболее
сильные, существенные связи, чтобы, отбросив слабые
связи, получить минимальное число взаимодействий
объекта со средой. Однако прежде чем осуществить та¬
кое подразделение, необходимо перечислить все связи.
Очевидно, что это только наблюдаемые связи, так как
ненаблюдаемые не включаются в модель. Будем подраз¬
делять их на три типа:
— неуправляемые, но. контролируемые связи (X),
характеризующие воздействие среды на объект (из них
образуются неуправляемые входы);
— управляемые связи (U), с помощью которых
можно целенаправленно изменять состояние объекта (из
них образуются управляемые входы);
— информирующие связи (Y), позволяющие опреде¬
лить состояние объекта (из них образуются выходы
объекта).
Среда
\Среда
72
Рассмотрим каждый тип связи отдельно.
Неуправляемые связи X должны удовлетворять сле¬
дующим требованиям.
Во-первых, они должны влиять на реализацию целей
{Z*} в объекте управления. Для оценки этого влияния
можно произвести следующий мысленный эксперимент.
Пусть объект находится в состоянии Y*, которое соот¬
ветствует заданной цели Z*, т. е. цель достигнута (не¬
важно каким образом, например с помощью какого-то
необходимого для этого случая управления U*). Пусть
далее параметр хи характеризующий состояние i-й связи
объекта со средой, изменяется, т. е. изменяется среда
(но только ее i-я связь с объектом). Если это изменение
среды может изменить состояние объекта настолько, что
цель Z* не достигается, то связь Х\ существенна для
управления объектом, так как она влияет на процесс
реализации целей в объекте. В противном случае этой
связью можно пренебречь.
Во-вторых, эти связи должны эффективно и просто
измеряться. Если параметр Х\ не измеряется, т. е. не су¬
ществует методов ее измерения или они слишком слож¬
ны или дороги, то эту связь нельзя учесть при синтезе
управления и она должна рассматриваться как случай¬
ная помеха е.
Таким образом, для отбора факторов среды, которые
должны учитываться при управлении, необходима их су¬
щественность (важность) для реализации целей управ¬
ления в объекте и эффективная измеряемость (контро¬
лируемость).
Ввиду отсутствия моделей среды и объекта процесс
отбора учитываемых факторов среды производится экс¬
пертным методом, т. е. с привлечением специалистов
(экспертов), хорошо знающих объект и среду. При этом
уровень осведомленности экспертов определяет эффек¬
тивность процесса выяснения существенных связей объ¬
екта со средой. Пусть по этому принципу отобраны п
связей:
Х\у . . ., Хп• (3.1.1)
Это значит, что содержательно определена каждая связь
(например, хх — температура среды, х2 — атмосферное
давление, лг3 — напряжение и т. д.) и установлено, что
эти связи как-то влияют на реализацию целей в объекте.
Теперь рассмотрим процесс определения управляе¬
73
мых связей U — каналов будущего управления. Здесь
важнейшими критериями отбора являются:
— воздействие связи на состояние объекта, т. е. воз¬
можность компенсировать негативные изменения этого
состояния, вызванные различными факторами как среды
X, так и самого объекта F0,
— управляемость, т. е. возможность оперативно без
существенных затрат изменять состояние U каналов воз¬
действия на объект. По этим критериям также эксперт¬
ным путем содержательно определяются связи
Щ, Uq, (3.1.2)
(например, щ — расход подаваемого топлива, и2 — ко¬
манда на включение какого-то агрегата и т. д.).
И, наконец, информирующие связи Y. Они должны
удовлетворять двум естественным требованиям:
— нести информацию о выполнении (или невыполне¬
нии) целей в объекте управления,
— надежно и оперативно контролироваться (изме¬
ряться).
Выделенные таким образом информирующие связи
У\ Ут (3.1.3)
заканчивают описание объекта как «черного ящика»,
т. е. как многополюсника с неизвестной (пока) внутрен¬
ней структурой (например, у\— температура объекта,
у2 — скорость его движения и т. д.).
Таким образом, этап определения входов и выходов
заключается в содержательном описании всех тех кон¬
тролируемых входов и выходов объекта, независимо от
его внутренней структуры, которые связаны с реализа¬
цией целей в объекте. Очевидно, что их число должно
быть больше, чем будет реализовано в модели объекта.
Такая избыточность необходима для осуществления эф¬
фективного отбора наиболее существенных факторов
(связей) на следующем этапе.
3.2. Экспертное ранжирование входов
и выходов
Выделенные в предыдущем параграфе связи еще не
являются входами и выходами модели. Это лишь «пре¬
тенденты». Входами и выходами они станут после того,
как будут выделены наиболее существенные из них и
74
отброшены несущественные. Действительно, модель во-
исе не должна отражать абсолютно все стороны объекта,
т. е. не должна (да и не может) быть во всем адекватной
объекту. Для целей управления вполне достаточно вы¬
явить ее наиболее существенные связи со средой, необ¬
ходимые для управления, т. е. она может быть прибли¬
женной. Поэтому процессу выбора наиболее существен¬
ных факторов предшествует процедура ранжирования
всех их по признаку существенности для реализации це¬
лей управления.
Рассмотрим процесс ранжирования факторов х{ (i=
= 1, ..п). Ранжирование факторов U и Y происходит
аналогично.
Прежде всего, определим понятие ранжирования. Под
ранжированием будем понимать процедуру расположе¬
ния факторов Xi в порядке их существенности: на пер¬
вом месте стоит самый существенный, следом за ним
менее существенный, но самый важный из оставшихся
и т. д. Полученный таким образом ранжированный ряд
имеет вид
где i\ — номер самого существенного фактора, 12 — номер
менее существенного и т. д. до in — номера самого несу¬
щественного фактора в этом ряду.
Однако можно, а иногда и удобнее поступать иначе.
Каждому фактору хг- поставить в соответствие некоторое
целое число — его ранг ku т. е. номер фактора в ранжи¬
рованном ряду (3.2.1):
Очевидно, что первый ранг (ki= 1) имеет вход х( 9
наиболее влияющий на реализацию цели в объекте. Вто¬
рой и следующие ранги (ki=2 и т. д.) в порядке убыва¬
ния их важности имеют входы, влияние которых не столь
существенно. Таким образом, связь ранжированного
ряда (3.2.1) и рангов (3.2.2) определяется простой и оче¬
видной формулой
(3.2.1)
(3.2.2)
ki=i> i— !••••. п,
(3.2.3)
т. е. ранг фактора с номером ij равен /.
75
Например, если ранги (3.2.2) оказались равными
X't = xt, х2
ki= 3, 1,
XSi Х^у х$
5, 4, 2,
(3.2.2а)
то ранжированный ряд имеет вид Хг, Хь, xi, х4, *з. Действительно,
из (3.2:2а) видно, что первый ранг (£г= 1) имеет второй фактор,
второй — пятый и т. д. Теперь, если придется создавать систему
управления с ограниченной информацией о среде (я=3), выбор су¬
щественных факторов из (3.2.2а) очевиден. Это хг, х$ и х\. Четвер¬
тым и третьим факторами при этом пренебрегаем, причем очевидно,
что ущерб от этого решения будет минимальным, так как отброше¬
ны самые несущественные факторы.
Задача построения ранжированного ряда (3.2.1) или
эквивалентная ей задача определения рангов (3.2.2) ре¬
шается экспертами и сводится к организации эксперт¬
ного опроса и обработки результатов этого опроса, с тем
чтобы получить искомые ранги и оценить их достовер¬
ность, т. е. согласованность экспертов.
Рассмотрим два метода экспертного ранжирования:
непосредственного ранжирования и парных сравнений.
В первом методе эксперты сразу присваивают ранги фак¬
торам, которые им представлены для ранжирования, во
втором — используется парное сравнение факторов, что
упрощает задачу эксперта, но требует дальнейшей обра¬
ботки результатов для получения ранжированного ряда.
Метод непосредственного ранжирования. Пусть N экс¬
пертов ранжируют п факторов х\, •..хп. Каждому фак¬
тору каждый эксперт присваивает ранг — целое число от
1 до п. Так, i-му фактору (Xi) /-й эксперт (9j) присваи¬
вает ранг кц. В результате получается матрица мнений
экспертов размерностью NYji
где номера строк соответствуют номерам экспертов,
а номера столбцов — номерам ранжируемых факторов,
т. е. /-я строка представляет собой мнение /-го эксперта
3j, а i-й столбец — мнение всех экспертов по поводу i-го
фактора (Xi).
При назначении рангов экспертами нужно соблюдать
следующие условия:
— во-первых, сумма рангов, назначенных всем фак¬
торам каждым экспертом, должна быть одинакова. Это
76
э,
(3.2.4)
ЭЫ klN k2N
означает, что сумма элементов любой строки матрицы
равна
,="<2^1 /=1 ДГ;
i=1 /=1
— во-вторых, если эксперт какие-то q факторов счи¬
тает эквивалентными или одинаковыми по важности, то
он присваивает им один ранг. Этот ранг равен среднему
из q целых рангов, таких, которые получились бы при
условии, что эксперту удалось их проранжировать. На¬
пример, эквивалентность четырех факторов (#=4): Хи
*2, *5, *6» стоящих чна пятом месте в ранжированном ряду,
приводит к равенству их рангов:
kl=k2=ks=h= (5+6+7+8)/4=6,5.
Как видно, в этом случае ранги могут быть дробными.
Теперь, для окончательного определения искомых
рангов следует вычислить средние ранги каждого фак¬
тора:
/=1
Эти ранги и позволяют проранжировать факторы. На
первом месте ставится фактор, имеющий минимальный
средний ранг,
kx= min {fcj,
/=1 п
т. е. фактор хи на втором — фактор, имеющий минималь¬
ный из остальных средний ранг, и т. д. Полученные ран¬
ги позволяют построить ранжированный ряд факторов,
который и будет соответствовать усредненному мнению
коллектива N экспертов.
Очевидно, что далеко не всякий результат эксперт¬
ного опроса следует считать удовлетворительным. Дей¬
ствительно, если мнения экспертов сильно расходятся
(например, одна половина экспертов фактору я* присво¬
ила первый ранг, а другая — последний), то такое ран¬
жирование не может быть положено в основу решения
о выборе существенных факторов. Поэтому для оценки
результатов всякого экспертного опроса вводится крите¬
рий, характеризующий согласованность экспертов. Чем
77
выше эта согласованность, тем в большей степени можно
«верить» результатам экспертного опроса, и наоборот.
Согласованность экспертов удобно определять как
степень рассеяния средних рангов (^=1, ..п). Дей¬
ствительно, если мнения экспертов полностью совпадают,
что средние ранги представляют собой целые, не равные
друг другу числа (случай одинаковых рангов здесь пока
не рассматривается). Графически это изображено на
рис. 3.2.1,а, где точками показано расположение средних
рангов на числовой оси. Если же мнение экспертов пол-
г -9 9 9 У
0 12 п-1 п п +7
а)
г-1—. 0t)°l 0 00 0 I I .
0 12 n/Z п-1 п п+1 к
В)
Рис. 3.2.1. Средние ранги на числовой оси: при полностью совпадаю¬
щих (а), при частично совпадающих (б) мнениях экспертов
ностью расходятся, то средние ранги примерно равны
п/2. При частично согласованных мнениях ранги сгруп¬
пируются вокруг этого среднего значения (см. рис.
3.2.1,б).
Степень рассеяния, как известно, удобно определять
с помощью дисперсии. Дисперсия средних рангов по
определению равна
п
£(*)=4-5J
где
j*, = » + L
/ = 1
— математическое ожидание среднего ранга.
Определим максимальную дисперсию (она бывает,
как легко заметить, при полностью совпадающих мнени¬
ях экспертов):
Критерий согласованности экспертов удобно предста¬
вить в виде отношения
w7_P{k)_ 12 'г п-\-1 2
• Dmах n(n2-l) ч ' 2 j •
i = 1
Как видно, O^Wsgl. При W—0 мнения экспертов полно¬
стью расходятся, а при W= 1 они высказываются едино¬
гласно. Таким образом, величина № характеризует сте¬
пень согласованности экспертов. Чем ближе W к едини¬
це, т. е. чем более единодушны эксперты, тем более до¬
стоверным можно считать результат ранжирования.
Следует отметить, что эксперты должны высказывать
свое мнение независимо друг от друга, т. е. до ранжи¬
рования они не должны знать мнения других экспертов.
В противном случае возможно появление зависимых
мнений, что повышает критерий согласованности W, но
не улучшает результатов экспертного опроса, так как
зависимым мнением можно просто пренебречь.
Для того чтобы получить представление по поводу
конкретного значения критерия согласованности, кото¬
рый никогда не бывает равным ни нулю, ни единице,
чтобы считать его малым или большим, можно предло¬
жить следующий простой метод. Предположим, что т из
N экспертов абсолютно компетентны, а остальные N — т
совершенно не компетентны, т. е. принимают свое реше¬
ние чисто случайно (хотя такого, естественно, не быва¬
ет). Тогда дисперсия средних рангов будет образована
суммой
KU+<*-'») 0]=т
Разделив результат на Dmax, получим W=m/N. Таким
образом, величина W зависит от числа абсолютно ком¬
петентных экспертов (если бы они существовали, разу¬
меется). Так, при №=0,3 можно считать, что 30% экспер¬
тов были вполне компетентны, а остальные 70% прини¬
мали свое решение случайно, что, естественно, могло
оказать (а могло и не оказать!) роковое влияние на
окончательную ранжировку.
Проиллюстрируем применение этого метода на шуточном приме¬
ре ранжирования девушек. Рассмотрим довольно обычную ситуа¬
цию — разговор трех приятелей о своих девушках. Естественно, что
каждый отдает предпочтение своей. Можно ли в данном случае
применить метод экспертных оценок для объективного ранжирова¬
79
ния этих девушек по какому-то критерию (если такое ранжирование
существует, разумеется)? Оказывается, можно, несмотря на явную
пристрастность экспертов — наших приятелей. Пусть Xi — i-я де¬
вушка (/=1, 2, 3), а Эj — /-й эксперт (/=1, 2, 3). Пусть также
априори имеет место следующий объективный ряд ранжирования:
Здесь знак предпочтения )> означает «умнее, чем» или «хозяйствен-
нее, чем» или «красивее, чем» и т. д. в зависимости от выбранного
приятелями критерия. Но с этим рядом согласен лишь Э\. Э2 счи¬
тает, что Х2^Х\Р>ХгУ а Э3 придерживается собственного мнения:
Как видно, каждый согласен с рядом объективного ранжирования
лишь в той его части, которая не касается его девушки. Эти мнения
объединяются матрицей типа (3.2.4):
Хг
х»
Хг
1
2
3
см
2
1
3
Э 3
2
3
1
Легко убедиться, что средние ранги девушек ^=5/3; £2=2; /гз=7/з
отражают объективное ранжирование, т. е. экспертный опрос дал
правильный результат.
Определим согласованность наших экспертов:
W—D (И) / Dm&x— (*МПлМ=Чъ
т. е. их мнения оказались очень плохо согласованными, что и следо¬
вало ожидать. Тем не менее окончательное ранжирование оказалось
правильным. Это произошло за счет осреднения мнений экспертов,
которое исключило их индивидуальные особенности, а вместе с ними
и их ошибки.
Этот результат показывает эффективность метода
экспертных оценок даже в том случае, когда эксперты
явно расходятся во мнениях. Важно, чтобы это расхож¬
дение касалось различных ранжируемых факторов.
Отсутствие согласованности экспертов может свиде¬
тельствовать, с одной стороны, о некомпетентности экс¬
пертов, связанной с новизной или слабой изученностью
объекта исследования, с другой — о сложности объекта,
что затрудняет вынесение решения о рангах факторов.
Эксперту проще сопоставить важность некоторых факто¬
ров попарно, т. е. указать, ранг какого из двух факто¬
ров будет выше. Именно в таких ситуациях обращаются
к методу парных сравнений, который мы и рассмотрим
ниже.
80
Метод парных сравнений. Эксперту предлагается про¬
ранжировать факторы попарно, т. е. каждой паре фак¬
торов х{ и Xi поставить в соответствие число
11, еслих^х^
О, если
— 1, если xi\^xt.
Выражение x^xi означает, что i-и фактор более пред¬
почтителен при ранжировании, чем l-й. Знак ^ является
знаком эквивалентности факторов с точки зрения ран¬
жирования (или отказа от ранжирования). Числа qm
обладают очевидным свойством qn =—qu.
*1
• • •
X л
X/
0
. . .
\ tin
•
.
•
.
.
•
•
•
•
С
• • •
0
К1
ч
XJ
*1
0
1
-/
ч
-1
0
1
хз
1
-7
0
Рис. 3.2.2. Таблица предпочте- Рис. 3.2.3. Пример противоре-
ний при методе парных ссав- чивой матрицы
нений
Таким образом, каждый /-й эксперт свое мнение пред¬
ставляет в виде матрицы
Q3'=ll<7jA I, 1=1, .... и; /=1, .... N,
где верхний индекс определяет номер эксперта (см. рис.
3.2.2).
Усредним мнения экспертов. Для этого достаточно по¬
строить усредненную матрицу размерностью п'Хп
(?=Н<Ы1,
где
N
Sil ДГ Я И
/ 1
— среднее предпочтение t-ro фактора /-му. Это и есть,
мнение данной группы экспертов.
6—299 81
Определим согласованность этих экспертов. В каче¬
стве критерия согласованности аналогично предыдущему
естественно выбрать дисперсию величин qu. В силу того,
что их среднее значение равно нулю, получаем
п
= £ &<>'•
/,/=1
где суммирование производится по всей матрице Q. Ма¬
ксимальное значение дисперсии Dmax= 1 будет иметь ме¬
сто при полной согласованности экспертов. Тогда, вводя
критерий согласованности как отношение дисперсии
средних предпочтений к максимальной дисперсии, полу¬
чаем
i, l^\
я в этом случае где, очевидно, при W= 1 мне¬
ния экспертов полностью согласованы, а при W=О они
дротиворечат друг другу.
Однако здесь и при полной согласованности эксперты
могут противоречить друг другу (пример такой матрицы
приведен на рис. 3.2.3, где противоречие имеет вид
)^х2)>хъ'р>х\, т. е. оказалось, что х\^хъ и х^х\ одно¬
временно). Выявление подобных противоречий совершен¬
но необходимо не только в усредненной матрице, но и во
мнении каждого эксперта. Это делается на основе следу¬
ющего довольно очевидного правила, которое называет¬
ся правилом транзитивности. Для предпочтений оно име¬
ет вид:
если х\^>х2 и я2]>*з, то х\^>х3;
(3.2.5)
для эквивалентности
если х\^х2 и х2—хъ, то xY—х3.
Матрицы, представляющие мнение каждого эксперта,
должны удовлетворять указанному правилу транзитив¬
ности. При обнаружении противоречий они возвращают¬
ся соответствующему эксперту для исправления заме¬
ченных противоречий.
Для определения интересующих нас рангов ранжиру¬
емых факторов следует иметь правило вычисления ран¬
гов по матрице Q. Таких правил может быть много. Рас¬
смотрим некоторые из них.
.82
Правило 1. Как легко заметить, величина qu вы¬
ражает степень предпочтения i-го фактора /-му. Опреде¬
лим среднее предпочтение каждого фактора всем осталь-
ным:
п
й = я. (3.2.6)
/=1
Естественно считать, что первый ранг имеет фактор,,
среднее предпочтение которого максимально. Так, при
q0= max {^}
/ =1, ... , П
первый ранг имеет фактор xv, т. е. kv=\. Аналогично
образуются ранги остальных факторов.
Рассмотренное правило, однако, излишне усредняет
предпочтения. Так, фактор, имеющий ряд явных (т. е.
больших) предпочтений, которые легко обнаруживают
эксперты, получит первый ранг только потому, что его
второстепенность по отношению к другим факторам была
не столь ярко выражена. Именно в этом случае часто
приходится обращаться к другому правилу.
Правило 2. Это правило опирается на идею уси¬
ления контраста. С этой целью вводится порог 6. Если
предпочтение выше этого порога, то оно имеет явный ха¬
рактер, а если ниже, то оно сомнительно, т. е. факторы
скорее равноценны. Получается следующее преобразова¬
ние матрицы средних предпочтений (5 в контрастную ма¬
трицу, элементами которой являются
фг7=ф {qil)i l==z^ 1 • • •» Му
где
( —1* если q< — 6,
<р(<7)= J 0, если | q\ < б,
( 1, если q < ' б.
Как видно, это преобразование целиком и полностью
определяется-порогом б (0<6<1). При 6=1 контрастная
матрица становится нулевой и все факторы эквивалент¬
ны. При 6=0 она полностью заполняется единицами, но
при этом неизбежно появление противоречий, т. е. нару¬
шений транзитивности предпочтений (3.2.5). Поэтому
при выборе порога 6 следует помнить, что его увеличе¬
ние приводит к отказу от ранжирования, а уменьшение—
6*
83;
?к увеличению числа явных предпочтений и к опасности
'появления противоречий. Одной из возможных рекомен¬
даций по определению оптимального порога является вы¬
бор величины 6 на «пороге противоречий», т. е. такого
значения б*, небольшое уменьшение которого приводит
к противоречиям.
Пример. Пусть матрица средних предпочтений имеет вид, при¬
веденный на рис. 3.2.4,а. При 6=0,7 контрастная матрица дает сле¬
дующий ряд ранжирования:
(*)
Нули в этой матрице означают не только эквивалентность, но и
шеярко выраженное предпочтение. Поэтому полученное ранжирова-
*7
хг
Ч
ч
X/
ч
X3
Н
X/
Ч
Xj
xJ
U
ч
xj
X*
X/
0
~0,7
-ом
-Ц52
0
-1
0
0
0
-1
0
-7
0
-1
0
-/
ч
0,7
0
-0,1k
0,5
1
0
-1
0
7
0
-7
7
1
0
-1
0
*3
ом
0,7k
0
-0,78
0
1
0
-1
0
1
0
-7
0
1
0
-7
0,52
-0,5
0,78
0
0
0
7
0
7
-1
1
0
1
0
1
0
—
) ^
л
г—
JK.
г
j ^
л
{
)
~Y у Y V"
а) В) в) г)
Фис. 3.2.4. Матрица средних предпочтений (а); контрастные матрицы
при 6=0,7 (б), 6=0,5 (в) и 6*=0,52 (г)
ние непротиворечиво. В соответствии с алгоритмом понизим порог.
При 6 = 0,5 контрастная матрица (в) уже содержит противоречие,
так как Минимальный порог, при котором не полу¬
чается противоречия, равен 6* = 0,52 (см. рис. 3.2.4,г), что приво¬
дит к ранжированному ряду (*), т. е., выбрав порог 6 = 0,52 и 0,7,
получим тот же ряд (*).
Рассмотрим применение первого правила к этому примеру. По¬
лучаем с помощью (3.2.6) из рис. 3.2.4,a gi =—1,66; go=0,46; g3=
= 0,40; £4 = 0,8. Откуда согласно первому правилу получаем ранжи¬
рованный ряд вида
*4>*2>*3>*Ь (**)
Как видно, результат отличается от (*). Это означает, что либо
либо для более точного решения необходимо получить но¬
вые данные, которые бы позволили выяснить, какой из двух" рядов
ранжирования (*) или (**) имеет место в действительности.
Ы
3.3. Декомпозиция модели
До сих пор мы рассматривали объект как некий «чер¬
ный ящик», о внутреннем содержании которого ничего
не было известно, и модель представлялась многополюс¬
ником с неизвестной структурой.
На следующей стадии структурного синтеза модели
•естественно использовать дополнительную информацию
об объекте как о системе взаимодействующих элементов.
Например, такой объект управления, как завод, пред¬
ставляет собой систему взаимодействующих цехов, тех¬
нологический процесс — систе¬
му взаимодействующих опера¬
ций, организм — систему взаи¬
модействующих органов, а кол¬
лектив — систему взаимодей¬
ствующих членов этого коллек¬
тива и т. д.
Информация о подобных
структурных особенностях объ¬
екта и является исходной для
декомпозиции модели объекта,
т. е. для «расщепления» моде¬
ли на взаимодействующие элементы, отражающие слож¬
ную многоэлементную структуру объекта. Пример такой
декомпозиции показан на рис. 3.3.1, где модель с тремя
входами и тремя выходами представлена пятью более
простыми элементами (1—5).
Смысл декомпозиции заключается в том, чтобы, вос¬
пользовавшись априорными сведениями о структуре
объекта, упростить задачу синтеза модели. Это упроще¬
ние может идти по двум направлениям. С одной сторо¬
ны, каждый элемент декомпозированной системы проще
исходной (недекомпозированной) системы, что облегча¬
ет синтез модели этого элемента и, в конечном счете, мо¬
дели всего объекта. С другой стороны, упростить задачу
синтеза можно независимо от сложности элементов,
уменьшив число входов — выходов каждого элемента по
сравнению с исходным объектом.
Поясним последнее. Введем численную меру сложно¬
сти модели как «черного ящика». В основу этой меры
естественно положить трудоемкость синтеза модели, т. е.
затраты, которые необходимы для создания модели. Бу¬
дем называть эту меру сложностью. Сложность на ста-
Рис. 3.3.1. Пример деком¬
позиции модели
85
дни анализа (стадии «черного ящика») должна учиты¬
вать лишь число входов п и выходов т модели (для про¬
стоты не будем различать управляемые и неуправляе¬
мые входы). Пусть она имеет вид
L=L(n, т). (3.3.1)
Относительно вида этой функции можно сформулировать
следующие требования. Во-первых, она должна монотон¬
но возрастать по п и т. Во-вторых, число входов /г, как
правило, сильнее влияет на сложность, чем число выхо¬
дов. И последнее: эту функцию можно считать аддитив¬
ной, т. е. если объект состоит из нескольких g подсистем,
то ее сложность равна сумме сложностей этих подси¬
стем, т. е.
i=2 Lt> (3-3-2)
t=\
где Li — сложность i-й подсистемы исходного объекта.
(Заметим, что при большом g это утверждение, строго
говоря, неверно, так как сложная система не есть сумма
своих частей. Представление (3.3.2) не учитывает труд¬
ностей, связанных с разделением объекта на его части.)
Всем этим требованиям удовлетворяет, например, сле¬
дующее выражение (хотя возможны и другие представ¬
ления) :
L = n}m, (3.3.3)
где у>1, так как число входов сильнее влияет на слож¬
ность, чем число выходов. Величину у следует опреде¬
лять в зависимости от того, во сколько раз увеличивает¬
ся трудоемкость синтеза модели при увеличении числа
ее входов на единицу. Пусть трудоемкость увеличилась
в р раз, тогда из (3.3.3) имеем
(п + \)лт=^рп}т,
откуда легко получить выражение для показателя у:
y=\gpl\g(n+l/n). (3.3.4)
Применяя эту формулу для примера декомпозиции мо¬
дели, показанного на рис. 3.3.1, получаем для исходной
системы
I = 3T-3 = 3T+I,
86
а для декомпозированной
^ = S L,.= l + l+l+y+1 = 4+3'(.
i = \
Как видно, L>Lx даже при у=1, когда L=9, a L%=7.
При неизвестном y его можно считать равным единице,
что дает явно заниженную оценку сложности L.
Теперь процессе декомпозиции модели можно рассма¬
тривать как процесс минимизации ее сложности, т. е. как
решение следующей минимизационной задачи:
L —*• min (3.3.5)
Dse{D}
где D — операция декомпозиции; {D} — множество допу¬
стимых данным объектом декомпозиций; D* — оптималь¬
ная декомпозиция, минимизирующая сложность L деком¬
позируемой системы.
Рис. 3.3.2. Декомпозиция (п Хт)-полюс-
ника без учета априорных сведений
о структуре объекта
Применим формулу (3.3.3) к декомпозиции, не опира¬
ющейся на априорные сведения о структуре объекта (она
показана на рис. 3.3.2). Получаем
т т
Ья= ^ Lt= ^ «т-1 =лт/я.
i =1 i — 1
т. е. сложность декомпозированной системы не уменьши¬
лась по сравнению с исходной L. Этого следовало ожи¬
дать, так как такая декомпозиция отражает лишь воз¬
можность представления векторной модели Y=F(X)
в скалярной форме
yi=fiW. i=l, . •т, (3.3.6)
что, естественно, не упрощает задачу. Однако, если из
априорных сведений об объекте известно, что некоторые
выходы tji в (3.3.6) не зависят от некоторых входов, то
87
учет этой информации в процессе такой декомпозиции,
как легко заметить, уменьшает сложность декомпозиро¬
ванной системы, т. е. Z^<L. Действительно в этом слу-
т
чае Ьд= 2 т- е- £д<£, где я» — число входов i-го
i-1
элемента декомпозированной модели (п^п).
Приведем пример декомпозиции объекта на два раз¬
личных элемента N различными способами (рис. 3.3.3).
Это означает, что множество {£} состоит из N вариантов,
причем для различных вариантов декомпозиции числа k
и q принимают различные значения. Очевидно, что хо¬
рошей декомпозицией следует считать ту, в которой эти
х 1
г
°1 'У
Ui J
й *1
1
у\ •
а к *• г
Ч :
Ут \
I У
h
_
Рис. 3.3.3. Пример декомпозиции на два элемента
числа минимальны. Действительно, из (3.3.2) и (3.3.3)
получаем для нашей задачи
L(k, q) — (a-\-q)4i 4- k* (m -f- q) —* min D*.
{D}
Оптимальной декомпозицией Z)* из {D} будет та, кото¬
рая минимизирует L(k, q). Пусть D{ — i-я декомпозиция,
которая определяется двумя числами:
Di = {ki, qt), i— 1 N.
Решение поставленной задачи' получаем в виде D*==Dit
если •
L(kt, <7/) = min {L{hb qt)}.
I = 1,... , N
Таким образом, цель декомпозиции модели состоит
прежде всего в том, чтобы упростить последующий син¬
тез модели объекта путем ее «расщепления» на более
простые элементы. Этот процесс * обязательно должен
производиться с учетом априорной информации о струк¬
турных особенностях объекта.
88
В результате декомпозиции объекта на g элементов
задача синтеза модели объекта сводится к g задачам
синтеза модели каждого элемента, т. е. к более простым
задачам.
Процесс декомпозиции можно (а иногда и целесооб¬
разно) применить и к полученным элементам, декомпо¬
зируя их на более мелкие составляющие. Однако, как
легко заметить, этот процесс целесообразно заканчивать
на определенной стадии, когда дальнейшее дробление
объекта лишь усложняет задачу. На рис. 3.3.4,а показа¬
на зависимость числа элементов и их сложности от уров-
Рис. 3.3.4. Влияние уровня декомпозиции на сложность элементов
Li и их число q (а), а также на сложность декомпозированного объ¬
екта (б)
ня декомпозиции. С увеличением уровня декомпозиции
сложность каждого элемента уменьшается не столь ин¬
тенсивно, что и приводит к увеличению сложности де¬
композированного объекта (см. рис. 3.3.4,б). Оптималь¬
ная декомпозиция минимизирует сложность декомпози¬
рованной системы.
Так или иначе с помощью декомпозиции исходный
(п'Хт)-полюсник («черный ящик») удается свести к на¬
бору более простых «черных ящичков», чтобы на следу¬
ющей стадии структурного синтеза определить только их
структуру. Сам по себе процесс декомпозиции сводится,
таким образом, к определению элементов объекта и уста¬
новлению взаимосвязи этих элементов в объекте.
3.4. Структура модели
Процесс синтеза оператора F модели объекта F0 (или
ее элементов) сводится к определению структуры St
этой модели и ее параметров С=(сь ..., си), т. е. опера-
89
гор модели F в соответствии с (В.4.2) представляется
в виде пары
F = (St, С), (3.4.1)
а связь входов и выходов модели в виде
Y=FS*(X, U, С), (3.4.2)
где Fst — оператор преобразования со структурой St,
параметры которого для удобства вынесены в перемен¬
ные С. (Индекс St будем в дальнейшем опускать, так
как оператор без структуры не существует.) Представ¬
ление оператора преобразования в виде (3.4.2) и явля¬
ется результатом параметризации модели, для которой
определяется структура St, а неизвестными остаются
параметры модели С.
Рассмотрим основные структурные категории: дина*
мичность, нелинейность, стохастичность и нестационар-
ность модели объекта.
Динамичность. С точки зрения динамики объекта
управления целесообразно рассмотреть статическую и
динамическую структуры объекта.
Структуру объекта будем называть статической, если
для его описания достаточно привлечь модель в виде
функции F, и динамической, если для адекватного опи¬
сания необходимо привлечь операторы с памятью (на¬
пример, дифференциальные операторы, интеграторы, за¬
паздывание и т. д.).
Примером статической структуры является структу¬
ра, образуемая разложением выхода объекта по опреде¬
ленной системе линейно-независимых функций входов:
у =2 С1?1(Х, U), (3.4.3)
i — 1
где {фг*(•, •)} — заданная система функций входов, выбор
которой и определяет выбор статической структуры объ¬
екта; с 1, ..., Cf{ — параметры объекта, определяемые на
этапе идентификации (см. гл. 5). Вспомним пример
с коктейлем (§ В.5), модель которого представляла со¬
бой статическую структуру с функциями вида ф*(Х, U) =
=щ (i=l, 2, 3).
Примером динамической структуры при п=т= 1
(X=x, Y=у) является модель, описываемая линейным
90
дифференциальным уравнением
лЛ+а £^у, * а — ' а и—
dtP' P-' dtP-' +- ■ “Г 1 dt ^ <>У
=ь,щг+---+ь>1[Г+ь*х <ЗЛ4)
или в более компактной форме
S aty^=2 bixii)’
/=1 /=1
где х}= — \ ai(i = 0, ..., р — 1) и М/= 0, ...
Л* * dtJ 9 ^ г > 1 "
.., /), = 1 — параметры непрерывной модели.
В дискретном случае уравнение (3.4.3) записывается
в рекуррентной (конечно-разностной) форме:
р J+i
У г = 2, d^r-/ + 2 */*Г-/ + .. (3-4-5)
1=1 /=1
где • • •, и е1у ..ei+i — параметры дискретной мо¬
дели, ахги уг — значения входа и выхода модели в г-й
момент времени. (Время в этом случае предполагается
дискретным, т. е. t=r= 1,2,...)
Например, модель такого простого объекта, как ма¬
ятник при малых отклонениях, имеет структуру вида
+ + — й (О-
где у—угол отклонения маятника от вертикали, a x(t) —
внешняя возмущающая сила. В дискретном случае мо¬
дель маятника записывается в виде конечно-разностного
выражения
Уг=с1\Уг-\-\-с12Уг-2-\-е\Хг-
Заметим, что конечно-разностный вид модели более рас¬
пространен для описания поведения сложных систем. Мы
его будем широко применять в дальнейшем.
Нелинейность. С точки зрения реакции на внешнее
воздействие объекты удобно подразделять на линейные
и нелинейные. Под линейным объектом будем подразу¬
мевать такой объект, реакция которого на сумму двух
91
любых внешних возмущений Xi(/) и Х2(£) равна сумме
реакций на эти возмущения, т. е.
F0 (Х,(0 +Х2 (/)) =r (X, (О) +F° (Ха (/)),
(3.4.6)
причем здесь необходимо еще соблюдение условия
F°(0)=0, т. е. объект должен быть центрирован.
Линейная статическая структура описывается обыч¬
ной линейной зависимостью
У=С\ХХ+ ... -\-спхп
и в общем виде (при линейности по X и U)
У = 2 + 2 c*+iur @ЛЛ)
i=1 /=i
Примером такой зависимости являются свойства коктей¬
ля (вкус, крепость и стоимость), которые линейно зави¬
сят от состава (см. § В.5). Легко убедиться, что динами¬
ческие модели (3.4.4) и (3.4.5) также линейные. Для
этого достаточно их подставить в (3.4.6).
Типичным примером нелинейной статической струк¬
туры являются вкусовые ощущения. Например, при до¬
бавлении соли к несоленой пище вкус ее сначала улуч¬
шается, а затем при дальнейшем добавлении резко па¬
дает (этот тот самый «пересол», который «на спине»),
(Следует отметить, что в примере о коктейле, рассмот¬
ренном в § В.5, вкусовая зависимость fi(U) для просто¬
ты выбрана линейной, что является лишь приближением,
необходимым для наглядного решения задачи до кон¬
ца. В действительности эта функция нелинейна).
Маятник при больших отклонениях является другим
примером нелинейной структуры вида
4W + 'ЧГ + sin У = Ь*х (*)•
Стохастичность. Стохастический характер структуры
объекта связан с наличием в объекте и в среде различ¬
ных неконтролируемых, но существенных факторов, ко¬
торые можно моделировать статистически:
Y=F(X, U, ECO), (3.4.8)
где Е(/)—случайный процесс, моделирующий имею¬
щуюся неопределенность объекта и среды. Эта неопре¬
деленность может быть связана как с быстрым измене¬
92
нием параметров объекта, так и с помехами, наклады¬
вающимися на измерения входа и выхода объекта.
Так или иначе, но стохастический объект ведет себя?
неоднозначно в одинаковых ситуациях, что моделируется;
случайным вектором Е(/), статистические свойства кото¬
рого должны быть заданы. В простейшем случае имеем:
Y=F(X, U)+E(f). (3.4.9)
Примером такого стохастического объекта является:
любой биологический организм, который, как известно,
в одинаковых условиях ведет себя по-разному. В этом:
случае выражение F(X, U) описывает поведение объ¬
екта, которое строго зависит от внешних условий,
а все отклонения от этого регулярного поведения образу¬
ют «случайную помеху» Е(/).
Нестационарность. Нестационарность объекта связа¬
на с детерминированным или случайным изменением во
времени оператора F0 объекта. Если это изменение про¬
исходит достаточно медленно, в виде дрейфа парамет¬
ров, то его можно не учитывать, так как процесс коррек¬
ции (адаптации) модели на каждом шаге управления,
позволяет подстраивать модель и тем самым компенси¬
ровать указанный дрейф. При быстром изменении F°
характер нестационарное™ необходимо учесть в струк¬
туре модели в виде зависимости F от времени:
Y=F*(X, U, C)=F(X, U, С, О,
где время t является параметром.
Например, при линейном изменении параметров мо¬
дели получаем
C=C0+Ci.f,
где С0, Ci — параметры модели и ее изменения, которые
должны быть определены на последующем этапе иден¬
тификации.
Примером такой нестационарности является «старе¬
ние» объекта, т. е. его амортизация во времени. Это ста¬
рение выражается в определенном изменении его харак¬
тера, что и делает объект нестационарным.
Следует отметить, что указанные структурные кате¬
гории еще не определяют структуры модели, а скорее
тип ее структуры. Сам по себе процесс выбора структу¬
ры модели объекта или его элементов сводится, по сутк
9&
дела, к выбору языка описания объекта. Это описание и
есть модель.
Примерами такого рода языков являются линейная
алгебра—для синтеза линейных статистических моделей
типа (3.4.7), линейные дифференциальные уравнения —
для синтеза непрерывных линейных динамических моде¬
лей типа (3.4.4), конечно-разностные уравнения — для
синтеза дискретных линейных динамических моделей
типа (3.4.5) и т. д. Однако эти языки классической мате¬
матики пригодны для описания сравнительно несложных
объектов. Сложные объекты управления требуют созда¬
ния новых языков с большими выразительными средст¬
вами. Сейчас существует уже много таких языков.
Рассмотрим два направления в этой области — ими¬
тационные и семиотические подходы к моделированию
сложных объектов.
3.5. Имитационные модели
Под имитационным моделированием будем понимать
пошаговое моделирование поведения объекта с помощью
ЭВМ. Это означает, что фиксируются определенные мо¬
менты времени /ь ..., tN и состояние модели определяет¬
ся (вычисляется ЭВМ) последовательно в каждый из
этих моментов времени. Для этого необходимо задать
правило (алгоритм) перехода модели из одного состоя¬
ния в f следующее, т. е. преобразование Y*—*Y*+b где
Yi — состояние модели в i-й момент времени. Пусть, как
обычно, состояние модели определяется вектором Y=
= (Уь • • •> Ут)у т. е. т числами, состояние среды Х=
= (*ь хп)—п числами, а состояние управления U=
= (ии ..., uq)—q числами. Тогда имитационная модель
определяется заданием оператора F, с помощью которо¬
го можно определить состояние модели в последующий
момент времени (Yl+i), зная состояние в предыдущий Yt-
и значения Хг+] и Uf+i:
('/. Xi+1, Ui+1)-Y,+I. (3.5.1)
Грубо говоря, такая модель позволяет определить, что
«будет завтра, если известно, что имеется сегодня. Специ¬
фика имитационного моделирования и состоит в том, что
состояние объекта определяется рекуррентно на каждом
шаге, исходя только из предыдущего шага. Преобразо¬
•94
вание (3.5.1) удобно записать в виде рекуррентной фор¬
мулы
Y,+I = F(Y„ Хж, иж), (3-5.2)
где F — оператор имитаций изменения состояния модели.
Этот оператор и определяет имитационную модель объ¬
екта управления с ее структурой St и параметрами С
в соответствии с (3.4.1).
На стадии структурного синтеза имитационной моде¬
ли F определяется ее структура St и содержательный
смысл параметров С=(сь ..., с/<), численное значение
которых выясняется на этапе идентификации (см. следу¬
ющую главу).
Как легко заметить, имитационные модели обобщают
конечно-разностную модель, рассмотренную в § 3.4. Рас¬
смотрим, например, нелинейную конечно-разностную мо¬
дель, записанную в виде
У r-—f (уг—\у . Уг-Р, Хг, Xr-s),
где f — заданная функция. Введем обозначения
Yr—1=(Уг—1, • • •> Уv—р )j Хг= (хГу ..., Xr—s)-
Тогда уравнение для у,- запишется в виде
yr=f(\r-u Хг). (3.5.3)
Как видно, это выражение представляет собой частный
случай (3.5.2). Следовательно, конечно-разностные мо¬
дели являются частным случаем имитационной модели,
так же как любая функция является частным случаем
алгоритма (ведь функция тоже является правилом вы¬
числения ее значения по аргументу, т. е. алгоритмом).
Имитационные модели обладают еще одним достоин¬
ством— они позволяют учитывать неконтролируемые
факторы Е объекта, его стохастичность (3.4.8) в виде
Yi+1=F (Yf, Xi+1, и<+1, Ei+1), f=l,...,tf, (3.5.4)
где, однако, необходимо знать, каким образом фактор Е
влияет на состояние Y объекта. Для этого следует хоро¬
шо разобраться в объекте и указать совершенно точно*
как входит неконтролируемый фактор Е в оператор объ¬
екта с тем, чтобы эти данные отразить в операторе F
модели. Для работы с такой моделью необходимо знать
конкретные значения фактора Е, который, как известно,,
ненаблюдаем.
95
Это противоречие позволяет разрешить так называе¬
мый метод Монте-Карло (или метод статистических ис¬
пытаний). Для его реализации необходимо знать неко¬
торые статистические свойства фактора Е (например,
закон его распределения, корреляционные свойства
и т. д.). Эти свойства, вообще говоря, могут зависеть от
Y, X и U. Располагая этими сведениями, можно модели¬
ровать ненаблюдаемый фактор в виде случайных рядов
Е*ь Ei2> ..., Е**, /=1, ..., ЛГ, (3.5.5)
тде нижний индекс соответствует моменту дискретного
времени, а верхний — номеру моделируемого ряда (все¬
го моделируется ЛГ таких статистически эквивалентных
рядов). Разумеется, что ни один из этих рядов не явля-
«ется точной реализацией действительности, но каждый
имеет такие же статистические свойства, что и реальный.
Именно поэтому ряды (3.5.5) позволяют исследовать
«статистические свойства модели (3.5.4). Например, по¬
дведение модели «в среднем» описйвается следующим об¬
разом:
N'
Y> — — V^Y7- i—1 N
— м Hi l ' ’
/=1
тде YU — /-я реализация поведения модели в i-й момент
фремени:
Yif=F (Yit_,, Xi( U,, ЕJ,), *=I ЛГ—
Дисперсия выхода модели вычисляется очевидным
образом:
N'
/ — 1
Аналогично можно оценить и другие статистические ха¬
рактеристики имитируемого процесса.
В этом и заключается метод Монте-Карло.— он позво¬
ляет оценить статистические свойства поведения объекта
путем вероятностного «разыгрывания» поведения моде¬
ли, причем одна реализация поведения отличается от
другой различными значениями ненаблюдаемого факто¬
ра Е.
196
3.6. Семиотические модели
Синтез всякой модели является процессом формали¬
зации описания объекта, т. е. переходом 'от естественно¬
го языка к формализованному (графу, имитационной
модели, аналитическим уравнениям и т. д.), что всегда
дредставляет трудности, особенно для сложных объек¬
тов управления. До сих пор эта операция является
в значительной мере искусством. Это связано, прежде
всего, с многозначностью и «размытостью» понятий есте¬
ственного языка. Однако при описании объектов управ¬
ления с этой трудностью можно справиться, если зара¬
нее оговорить смысл употребляемых понятий, т. е. со¬
ставить нечто вроде толкового словаря.
В этом случае описание на естественном языке мож¬
но формализовать, т. е. -прямо записать в символической
форме с помощью небольшого числа определенных зна¬
ков —■ понятий, связанных непосредственно с понятиями
языка. Назовем такую модель семиотической (семиоти¬
ка— наука о знаковых системах), так как она имеет
ярко выраженный знаковый характер и поэтому очень
близка к естественному языку. Преимущества семиоти¬
ческих моделей очевидны—с их помощью можно опи¬
сывать очень широкий класс объектов управления —
практически все объекты, которые могут быть описаны
на естественном языке.
Основой построения семиотической модели является
язык описания этих моделей. Рассмотрим один из этих
языков — язык бинарных отношений. Он достаточно
прост.
Словарем языка бинарных отношений являются:
— базовые понятия (будем обозначать их символа¬
ми аи i= 1, 2, ...), которые порождаются объектом и
вводятся на основе его описания. Грубо говоря, это эле¬
менты, из которых состоит описываемый объект, напри¬
мер а\ — «лифт», а2 — «кнопка» и т. д.
— базовые отношения (будем обозначать их симво¬
лами rj, /=1, 2, ...), которые указывают на отношения
между базовыми понятиями. Необходимость такого рода
отношений очевидна, так как для описания объекта ма¬
ло описать его элементы, нужно еще указать, в каком
отношении эти элементы находятся друг к другу. Эти
отношения универсальны; для естественного языка вы¬
делено около 200 отношений, например г\ — «находить¬
ся в», г2 — «быть одновременно» и т. д. Заметим, что
7—299
97
такого рода отношения и образуют специфику этого
-языка, который постулирует их бинарность, т. е. данное
отношение между двумя понятиями или есть или нет,
а третьего не дано;
— имена, т. е. различые названия предметов, кото¬
рые используются в естественном языке (будем их обо¬
значать буквами bh> &=1, 2, ...). Для введения имен
имеется специальное базовое отношение г0 — «иметь
имя». Имена кроме обычных имен собственных типа
«Саша>>, «Маша» могут отражать важную специфику и
конкретизацию понятий, например Ъ\ — «пассажирский»,
&2 — «грузовой», Ь3=5 (число «5» — это имя) и т. д.
Таков словарь языка бинарных отношений. Он очень
удобен и конструктивен, каждое его слово ,имеет кон¬
кретное содержание, связанное с описываемым объектом
управления. Действительно, понятия и имена в него
вводятся по мере необходимости, и каждый объект по¬
рождает свой индивидуальный словарь базовых поня¬
тий, отношений и имен. Это семантика языка бинарных
отношений.
Теперь о грамматике (точнее, синтаксисе) этого язы¬
ка. Синтаксис должен точно и недвусмысленно указы¬
вать, каким образом строятся синтаксически правиль¬
ные фразы, т. е. определять формальные признаки
синтактически правильных фраз (они могут быть оши¬
бочны, как, например, «дом является частью комнаты»,
или бессмысленны, например, «проводка одновременно
с лифтом», тем не менее они синтаксическц правильны).
Синтаксически правильные фразы (Л) имеют вид:
А=аи т. е. любое базовое понятие является синтак¬
сически правильной фразой;
А= (щг^аъ), где а{ и аь — любые базовые понятия;.
rj—любое базовое отношение, кроме г0 («иметь имя»),
т. е. два базовых понятия, объединенные базовым отно¬
шением, также являются синтаксически правильной
фразой;
А—(А^Ак)9 где А{ и Аъ.—синтаксически правиль¬
ные фразы, а г,- — любое базовое отношение, кроме г0,
т. е. две синтаксически правильные фразы, объединен¬
ные базовым отношением, являются синтаксически пра¬
вильной фразой;
A=(Ajrobk)9 где А$ — синтаксически правильная фра¬
за; Ьи — любое имя, т. е. выражение «Aj имеет имя Ьц»
всегда является синтаксически правильной фразой.
98
Других видов синтаксически правильных фраз нет.
Последнее замечание исключает возможность появления
каких-то других фраз. Для ЭВМ это очень важно, так
как она не обладает опытом человека, позволяющим
сразу отсеивать неправильные конструкции.
Пример. Пусть объектом нашего анализа будет ситуация, опи¬
санная фразой естественного языка «Саша и Маша находятся в пас¬
сажирском лифте». Эта ситуация может быть описана на языке би¬
нарных отношений следующим образом. Словарь:
Базовые понятия: {
( г0 — „иметь имя“,
Базовые отношения: < гх — „находиться в“,
I г2 — «быть одновременно",
( — „Саша",
Имена: < Ь2— „Маша",
I Ь3 — „пассажирский".
Начнем с простейших фраз, которые войдут в описание си¬
туации:
Ах = — „человек по имени Саша",
Л2=(Л1Г0Ьа) — „человек по имени Маша",
= (я2го&3) — „пассажирский лифт“,
Л4 = (А1г2А2)—„человек Саша и одновременно человэк Маша"
Теперь описываемая ситуация естественно представляется в виде:
Аъ= (Л4Г1Л3)—«человек Саша и человек Маша одновременно
находятся в пассажирском лифте».
Добавление понятия «человек» здесь не является бюрократиз¬
мом. Оно необходимо, так как имена могут иметь не только люди.
Например, прибор МАША — это какой-нибудь Модифицированный
Аннигилятор с Широкополосным Аттенюатором. Тогда та же исход¬
ная ситуация («Саша и Маша находятся в лифте») запишется ина¬
че. Для этого в словарь следует ввести новое базовое понятие аз —
«прибор». Образуем нужные фразы:
А6 = (а3г0Ь2) —„прибор с названием МАША",
Л7=(Л1г2Л6)— „человек Саша одновременно с прибором
МАША\
В результате получаем
Л8= (Л7Г1Л3)—«человек Саша и прибор МАША одновременно
находятся в пассажирском лифте».
Вводя дополнительные скобки, можно описанные ситуации запи¬
сать символами словаря:
As = (((air0bi)r2 (air0b2) ) n {a2r0fa)),
А 8= (((a\r0bi)r2 (a3r0b2)) гх (а$гфъ)).
Это осуществляется прямой подстановкой выражений для Ах и А2
в Л4, которое вместе с Лз подставляется в Л5 и т. д. Естественно,
что мало кого волнует судьба Саши и Маши в лифте — это только
наглядный пример описания некоей сложившейся ситуации.
7* 99
Описанная ситуация статическая. Она интересует нас до тех пор,
пока важен факт пребывания Саши и Маши в лифте. Если же нас
интересует процесс функционирования лифта, то необходимо ввести
динамику, т. е. изменение ситуации во времени. Для того чтобы
описать движение лифта, необходимо ввести дополнительное базовое
понятие а4 — «этаж», имена для него: 1, 2, 3, ..N и базовое‘отно¬
шение г3 — «находиться на». Тогда движение лифта вверх будет со¬
провождаться последовательностью ситуаций:
Вх = (я2г3 (а4г01)) — „лифт находится на первом этаже"
BN= (а2Гз(а^ок)) —„лифт находится на N-u этаже”.
Если имеются какие-то внешние воздействия на объект, зависящие
от времени, то необходимо ввести базовое понятие аъ.— «время» и
имена этого времени: 1, 2, 3, ... (в удобных единицах — минутах,
часах и т. д.), которые изменяются от одной ситуации к другой.
Кроме того, необходимо ввести базовое отношение /ч — «порож¬
дает», которое позволяет вводить внешние воздействия с заданными
именами gь . .., gL как «порождение» определенных моментов вре¬
мени: (a5r0i)r4(ajrogi), т. е. «в i-й момент времени а$ приобретает
имя gi».
Например, с помощью базовых понятий dj — «/-я кнопка
в лифте» (/=1, ..., N) и двух имен (L = 2): gi — «нажата», g2 — «не
нажата» можно воздействовать на программу движения лифта.
Управление связано с образованием определенных ситуаций
в объекте, оно сводится к изменению имен базовых понятий, исполь¬
зуемых для описания объекта. Синтез управления состоит в образо¬
вании фраз
(Bjuiairogh)), /=1, ..., (3.6.1)
каждая из которых указывает, какое имя (gb) приобретает понятие щ
в ситуации Bj. Например, если
Bj=(a2rz(a4r0j))—«лифт находится на /-м этаже»,
то выражения
(BNr4(dir0gi))—«на N-м этаже нажимается первая кнопка»,
(Bir^jvrogi))—«на первом этаже нажимается N-я кнопка»
означают, что наши «Саша и Маша катаются на лифте». Здесь еще
необходимо добавить условие
(Bjr4(djr0g2))—«на /-м этаже /-я кнопка выключается»,
выполнение которого возлагается на автоматику лифта.
Как видно, язык бинарных отношений позволяет опи¬
сывать символически весьма сложные ситуации в слож¬
ных системах. Однако само по-себе символическое опи¬
сание почти ничего не дает (кроме, разве, сокращения
записи, что иногда бывает немаловажным обстоятельст¬
вом). Символическое описание объекта должно обеспе¬
чивать возможность выявления каких-то свойств этого
объекта, которые неочевидно следуют из его описания.
Для этого используются разного рода формальные пре¬
образования, с помощью которых можно изменять
в нужную сторону исходное описание объекта. Причем
100
делать это может ЭВМ, так как . эти преобразования
формализованы.
Преобразования опираются на алгебраические свой¬
ства базовых отношений гг*. Так, упомянутое' выше отно¬
шение г2 («быть одновременно») обладает свойством
симметрии. Это означает, что (А{г2А2) = (A2r2Ai), т. е.,
если A j происходит одновременно с Л2, то и А2 происхо¬
дит одновременно с А\. Отношение Г\ («находится в»)
транзитивно, т. е. из (А\Г\А2) и {А2г\Аъ) следует
(А\Г\АЪ). Действительно, если Ах находится внутри Л2,
а А2 — внутри Л3, то А\ находится внутри Л3 (как
в известной сказке: игла — в яйце, яйцо —в утке, утка —
в сундуке и т. д.; следовательно, игла в сундуке —это и
есть сказочное использование алгебраического свойства
транзитивности).
В настоящее время выявлено почти 400 таких
свойств, с помощью которых можно преобразовать
исходное описание.
Другим способом преобразования такого описания
объекта является образование новых понятий. Под но¬
вым понятием здесь будем подразумевать ситуацию,
часто повторяющуюся в описании объекта и связанную
с целями управлением. Так, «такси, движущееся без пас¬
сажира»— ситуация, которая очень волнует таксистов
(именно поэтому возникло жаргонное понятие «хо¬
лостяк»). Обобщаются ситуации, которые отличаются
лишь базовыми понятиями (обобщение по базовым по¬
нятиям), базовыми отношениями (обобщение по базо¬
вым отношениям) и именами (обобщение по именам).
Например, при описании работы почты очень важно
определить постоянных получателей. Ими могут быть
отдельные люди, учреждения, заводы, магазины и т. д.
Все они являются потребителями корреспонденции.
Естественно обобщить их одним понятием «абонент».
При описании многочисленных свойств какого-то
объекта, связанных с его отношением к измерительным
приборам, естественно эти отношения объединить и обоб¬
щить, образовав понятия химических, физических, со¬
циальных свойств и т. д.
Наиболее распространенно обобщение по имени.
Важно ли с точки зрения управления лифтом, что имена
его пассажиров Саша и Маша? Скорее всего нет. Поэто¬
му описание работы лифта естественно обобщить по
именам пассажиров. Это вместо громоздкого описания
101
^человек Саша и человек Маша одновременно находят¬
ся в лифте» воспользоваться столь же информативным
«Два человека в лифте».
Описанные способы преобразования исходного гро¬
моздкого описания объекта позволяют получить его
в более компактном виде и приступить на следующем
этапе к идентификации неизвестных параметров описа¬
ния (которые обычно содержат имена) и синтезу управ¬
ления (3.6.1), т. е. к определению таких имен и момен¬
тов их введения, которые позволяют на этой модели до¬
стигнуть целей управления.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИИ К ГЛАВЕ 3
Задача использования формальных подходов при определении
структуры модели является достаточно новой. Поскольку априорная
информация о структуре объекта управления очень трудно форма¬
лизуема, здесь пока почти полностью господствуют экспертные ме¬
тоды. Систематических руководств по структурному синтезу доста¬
точно широкого класса моделей объектов управления пока нет.
Можно лишь привести одну главу книги [1].
Комментарий к методу экспертных оценок был уже сделан
в гл. 2 с указанием рекомендуемой литературы. Имитационные мо¬
дели, рассмотренные в § 3.5, являются сейчас самым распространен¬
ным классом моделей, используемых для описания поведения слож¬
ных систем управления. К числу их достоинств следует отнести со¬
четаемость с классическими (аналитическими) моделями и моделями
Монте-Карло, использующими идею статистических испытаний. В на¬
стоящее время разработаны эффективные и тонкие методы имита¬
ционного моделирования, позволяющие синтезировать модели слож¬
ных технических, технологических [3, 4] и даже социально-экономи¬
ческих [12, 13] систем. Эти модели позволяют-управлять сложными
объектами, опираясь в основном на прогноз поведения такого рода
объектов с помощью имитации.
Для первого знакомства с имитационными моделями можно по¬
рекомендовать [6—8, 15]. С основными методами Монте-Карло
можно ознакомиться по '[9] и более детально по книгам [2, 10, 14].
К книгам [2—5 и 12, 13] следует обратиться при более тщательном
изучении имитационного моделирования.
В последнее время появился новый класс моделей — семиотиче¬
ские, рассмотренные в § 3.6. Они позволяют формализовать объекты,
поведение которых описывается на языке, близком к естественному.
По своим возможностям семиотические модели уступают только
естественному языку. Это обстоятельство позволяет их считать наи¬
более перспективными моделями описания сложных объектов управ¬
ления. С основными чертами и применениями семиотических моделей
можно ознакомиться по брошюре [И], а язык бинарных отношений
изложен подробно в [16], правда для информационно-поисковых
систем.
СПИСО к л ИТ ЕР АТУ Р Ы
1. Растригин JI. А., 'Маджаров Н. Е. Введение в идентификацию
объектов управления. — М.: Энергия, 1977, с. 33—49.
102
2. Ермаков С. М. Метод Монте-Карло и смежные вопросы. —• М.:
Наука, 1971, с. 86—104.
3. Бусленко Н. П. Математическое моделирование производствен¬
ных процессов на ЦЭВМ. — М.: Наука, 1964.
4. Бусленко Н. П. Моделирование сложных систем. — М.: Наука,
1968.
5. Вагнер Г. Основы исследования операций: Пер. с англ. — М.:
Мир, 1973. —Т. 3, с. 343—392.
6. Моисеев Н. Н. Математик задает вопросы. — М.: Знание, 1974,
с. 122—146.
7. Моисеев Н. Н. Имитационные модели. — В кн.: Наука и челове¬
чество: Международный ежегодник. — М.: Знание, 1973.
8. Корявов П. П., Сушков Б. Г. Имитация динамических процес¬
сов.— М.: Знание, 1973.
9. Соболь И. М. Метод Монте-Карло. — М.: Наука, 1968.
10. Полляк Ю. Г. Вероятностное моделирование на ЭВМ. — М.:
Сов. радио, 1971.
11. Поспелов Д. А. Большие системы: Ситуационное управление.—
М.: Знание, 1975.
12. Нейлор Т. Машинные имитационные эксперименты с моделями
экономических систем: Пер. с англ. — М.: Мир, 1975.
13. Форрестер Дж. Мировая динамика: Пер. с англ. — М.: Hayjca,
1978. Мир, 1974.
14. Метод статистических испытаний. — М.: Наука, 1962.
15. Шеннон К. Имитационное моделирование: Пер. с англ.—М.:
Наука, 1979.
16. Информационно-поисковая система «БИТ». — Киев: Наукова дум¬
ка, 1968.
ГЛАВА4
ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ
МОДЕЛИ
Теперь, когда структура Si оператора F модели вы¬
яснена, необходимо определить неизвестные параметры
..., си этой модели. Как сказано выше '(во введе¬
нии), эту операцию в зависимости от вида оператора F
можно реализовать двумя путями: идентификацией и
планированием экспериментов с объектом. Первый под¬
ход (идентификация) 'позволяет определить параметры
связи входа и выхода объекта (параметры модели)
в случае, если есть возможность наблюдения за изме¬
няющимся входом объекта, т. е. в режиме его нормаль¬
ной эксплуатации. Второй (планирование эксперимента)
применяют в случае, когда управляемый вход объекта
не изменяется во времени и необходимо спланиро¬
вать специальные эксперименты для. определения пара¬
метров модели, связывающей этот вход с выходом
объекта. В этой главе мы рассмотрим идентификацию
параметров модели.
103
4.1. Постановка задачи идентификации
Итак, под идентификацией модели мы подразумеваем
процесс определения ее параметров
С=(си ch) (4.1.1)
в режиме нормальной эксплуатации объекта. Структура
модели при этом известна (она определена на стадии
структурного синтеза):
Y=F(X, U, €), (4.1.2)
т. е. оператор F предполагается заданным. Это озна¬
чает, что задан алгоритм (правило, инструкция), с по-
. мощью которого можно определить состояние Y модели,
если заданы состояния X и U ее входов, а также пара¬
метры (4.1.1). Именно эти параметры определяются на
этапе идентификации.
Очевидно, что для идентификации необходимо иметь
информацию об изменении входов и выходов объекта.
Но объект пока не управляется (мы только создаем си¬
стему управления), поэтому* влияние входа U на выход
Y не может быть исследовано на этапе идентификации.
Это несколько упрощает задачу, так как вместо модели
(4.1.2) следует брать модель вида
Y=F'(X, С), (4.1.3)
в которой не фигурирует управляемый вход U (его
влияние на выход будет исследовано на этапе планиро¬
вания эксперимента).
В процессе идентификации используются исходные
данные, которые удобно подразделить на два класса:
— априорные, которые содержатся в структуре St
модели. Это означает, что должен быть задан (или опре¬
делен на этапе структурного синтеза, рассмотренного
в гл. 3) вид оператора F'. Например, вид уравнения,
граф взаимосвязи элементов модели и т. д.;
— апостериорные, которые представляют собой на¬
блюдения состояний входа X и выхода Y объекта в про¬
цессе его нормальной эксплуатации, т. е. информацию
./=(Х„ \,), (4.1.4)
где i—номер моментов времени /*, когда фиксирова¬
лись значения X и Y, т. е. Хг-=Х(^), Y<=Y(■/<), где Х(/)
и Y(/) —функции, описывающие поведение входа и вы¬
104
хода объекта в процессе его нормального функциониро¬
вания в среде. Моменты времени U обычно равномерно
покрывают промежуток времени наблюдения [О, Г],
т. е. ti=x(i—1), где т — интервал между наблюдениями
(4.1.4), т. е. x = Tl(N— 1).
Таким образом, исходные данные, необходимые для
идентификации, образуются двойкой
(St, /), (4.1.5)
т. е. структурой модели (4.1.3) и наблюдениями (4.1.4).
Процесс идентификации параметров, модели сводится
к определению параметров (4.1.1) по исходным данным
(4.1.5), т. е.
C=q>(Sf, /), (4.1.6)
где ф — алгоритм идентификации, определяющий, каким
образом можно найти параметры С, зная St и I.
В этой главе будут рассмотрены различные алгорит¬
мы ф. Эти алгоритмы подразделяются на два больших
класса: адаптивные и неадаптивные.
Под адаптивным алгоритмом идентификации пони¬
мают алгоритм, позволяющий уточнять значения иден¬
тифицируемых параметров модели по мере получения
дополнительной информации о работе объекта. Пусть на
i-м шаге адаптивной идентификации были какие-то
определенные значения идентифицируемых параметров.
Отметим их индексом i:
Сг=(с^1, . . С1к).
Пусть, далее, получена дополнительная информация,
т. е. пара наблюдений входа и выхода объекта в (/—[-1)-й
момент времени:
Л+, = (Х/+1, Y,+l>. (4.1.7)
Очевидно, что эта информация должна каким-то обра¬
зом изменить (откорректировать) имеющиеся значения
С и дать возможность получить C*+i — более точное зна¬
чение параметров. Связь между С* и C*+i определяется
адаптивным алгоритмом идентификации:
(С„ /1+1)-сг+1
или в обычной рекуррентной форме
С/+1 = Фа(С,, I1+i). (4.1.8)
105
Здесь фа — алгоритм адаптивной идентификации, кото¬
рый позволяет определить последующее значение пара¬
метров, исходя из новой информации (Ii+i) и старых
представлений о значениях параметров С*. Адаптация,
таким образом, представляет собой споёоб получения
«нового знания» путем коррекции «старого знания» на
основе новой информации.
Алгоритм (4.1.8) удобнее записать в виде
Ci+i = Ci-f-<pa(F(^i+i, С{), Ii+i), (4.1.9)
где фа — оператор адаптивной идентификации.
Если адаптивный метод
идентификации реализуется в
реальном масштабе времени,
то его называют методом са¬
монастраивающейся модели.
Схема этого метода показана
на рис. 4.1.1. Здесь на вход мо¬
дели подается вход X объекта.
Информация о состоянии объ¬
екта Y, модели F(X, С) и сре¬
ды X сообщается блоку адап¬
тации (БА), который выраба¬
тывает сигнал коррекции АС =
=фа(F(X, С), /), изменяющий
параметры модели в соответст¬
вии с (4.1.9) с помощью испол¬
нительного механизма (ИМ).
Очевидно, что для реализации адаптивных алгорит¬
мов идентификации вовсе не обязательно использовать
реальный масштаб времени. В этом случае роль объекта
играет информация I (4.1.4), которая поступает в алго¬
ритм адаптивной идентификации из памяти порциями
В противоположность адаптивному алгоритму иден¬
тификации неадаптивный позволяет получить искомые
параметры С сразу, используя всю информацию 7
(4.1.4), а не путем их постепенного уточнения (ниже бу¬
дут рассмотрены различные варианты такого алгорит¬
ма). Если информация I задана, то задачу идентифика¬
ции можно решать как адаптивным, так и не адаптив¬
ным способом. На первый взгляд может показаться, что
неадаптивный алгоритм всегда лучше адаптивного, но
Рис. 4.1.1. Схема адаптив¬
ной идентификации
106
не следует торопиться. Каждый из них имеет свои пре¬
имущества и недостатки.
Неадаптивный алгоритм позволяет сразу определить
идентифицируемые параметры С, но он сложнее и для
его реализации требуются значительные вычислитель¬
ные мощности — как правило, для этого применяют уни¬
версальные ЭВМ.
Адаптивный алгоритм проще: его легко программи¬
ровать и отлаживать. Кроме того, он может быть эффек¬
тивно реализован в специализированных вычислительных
устройствах. Применяют его обычно для идентификации
объектов с изменяющимися свойствами с дрейфующими
параметрами в режиме самонастраивающейся модели.
Однако его можно применять и для идентификации
объекта по всей информации I. В этом случае для
эффективной идентификации параметров С, как прави¬
ло, требуется многократная «прогонка» информации /
через адаптивный алгоритм.
4.2. Идентификация статических объектов
Рассмотрим модель статического объекта (4.1.3), где
вид функции F' уже определен на стадии структурного
синтеза (см. гл. 3). Эта функция может быть задана
как аналитически, так и алгоритмически, т. е. в виде
инструкций, показывающих, как ее вычислять при всех
встречающихся значениях аргументов X и С.
Выход объекта будем считать одномерным (т= 1),
т. е. Y=у. Это дает возможность записать модель
(4.1.3) в виде
У=т, С), (4.2.1)
где / — заданная на этапе структурного синтеза скаляр¬
ная функция.
Правомерность такого подхода следует из очевидной
декомпозиции задачи (4.1.3), где
Y=(«/1, Ут), F' = (fu . . ., fm) ,
на т задач вида (4.2.1), т. е. декомпозировать модель
так, как это показано на рис. 3.3.2. Это означает, что
умение идентифицировать параметры модели (4.2.1)
с одним выходом позволяет идентифицировать и много-
выходовые модели путем m-кратного повторения иден¬
тификации модели (4.2.Ц.
107
Исходные данные (4.1.4) в этом случае принима¬
ют вид
i = (Xt,yt)9 (4.2.2)
где yi — реакция объекта в i-й момент времени на вход:
Хг=С**ь •• •> xi*)> yi=y(ti), х{э=хз(и).
Рассмотрим сначала неадаптивный алгоритм иден¬
тификации, Для определения параметров С неадаптив¬
ным методом подставим данные (4.2.2) в (4.2.1). В ре¬
зультате получим систему нз N уравнений с к неизвест¬
ными:
f (Xj, Cj, ..., с^) = у19
f ..., Cfc) yN,
которую удобно записать в виде
f(XuC)=yu (4.2.3)
Очевидно, что при этом необходимо выполнение условия
N^k, В противном случае число неизвестных окажется
меньше числа уравнений и система (4.2.3) не будет иметь
однозначного решения.
Как видно, задача неадаптивной идентификации атак¬
тического объекта сводится к решению системы уравне¬
ний (4.2.3). Эта система имеет два существенных свойст¬
ва, которые и определяют трудности, возникающие при
ее решении: несовместность и трансцендентность. Ее не¬
совместность связана со случаем N>k (уравнений
больше, чем неизвестных), а трансцендентность — с про¬
извольным видом функции f. Очевидно, что все труд¬
ности неадаптивного метода решения задачи идентифи¬
кации связаны с указанными трудностями, которые при¬
ходится преодолевать при решении несовместной транс¬
цендентной системы уравнений.
Начнем с несовместности (N>ik). Несовместную си¬
стему уравнений (4.2.3) решим так называемым мето¬
дом наименьших квадратов, т. е. минимизируя суммар¬
ную невязку правых и левых частей уравнений этой си¬
стемы. Для этого образуем функцию суммарной невязки
в виде суммы квадратов невязок каждого из урав¬
нений:
Q(Q=S 1№, С)-Ы2. (4.2.4)
*=1
108
Кад видно, эта функция неотрицательна и равна нулю
при совпадении правых и левых частей уравнений ре¬
шаемой системы. При этом чем более правые части
уравнения системы (4.2.3) близки к левым, тем меньше
значение функции невязки (4.2.4). Это и дает основание
считать решением системы (4.2.3) такие значения пара¬
метров
С*=(с*ь с*к), (4.2.5)
при которых функция невязки минимальна, т. е.
Q(C*)=minQ(C).
с
Таким образом, для решения несовместной системы
уравнений (4.2.3) достаточно минимизировать функцию
суммарной невязки (4.2.4). Эту задачу можно записать
в виде
Q (С) —►min, (4.2.6)
с
которая читается так: «минимизировать функцию Q(C)
по С».
Пусть решением этой задачи является С*, для кото¬
рого при любом С выполняется очевидное неравенство
Q(C*)<Q(C), (4.2.7)
(напомним, что С — вектор (4.1.1), т. е. последователь¬
ность k компонентов Си ..Ck).
Задача идентификации статических систем сведена
таким образом к задаче минимизации некоторой спе¬
циально построенной функции многих переменных. Как
решать такую задачу? Для этого в вычислительной ма¬
тематике разработан ряд эффективных методов, учиты¬
вающих специфические особенности минимизируемой
функции Q(С).
Нам в дальнейшем придется часто прибегать к ре¬
шению задачи минимизации (не обязательно функции
невязки), поэтому наиболее эффективные современные
способы ее решения описаны в приложении. Применяя
один из этих способов, можно решить задачу идентифи¬
кации статического объекта.
Отметим, что для идентификации сложных систем
функция суммарной невязки (4.2.4) очень сложна, и не
стоит пытаться ее минимизировать «кустарным» спосо¬
бом, т. е. вручную. Такого рода попытки обречены на
109
провал. Здесь необходимо применение современных ЭВМ
и эффективных поисковых методов, описанных в прило¬
жении.
Рассмотрим простейший случай, когда функция f
имеет вид
f(X, С)=2 с1?1(Х), (4.2.8)
/=i
где <р3(Х) (/=1, ..., k)—заданная система функций
многих переменных. Специфика такой структуры заклю¬
чается в линейности функции относительно искомых па¬
раметров Ci, ..., си. Эта линейность позволяет свести за¬
дачу минимизации (4.2.6) к решению системы линейных
алгебраических уравнений, которая, как известно, реша¬
ется достаточно просто стандартными способами.
Простой вид функции (4.2.8) позволяет решить за¬
дачу минимизации (4.2.6), приравняв нулю частные про¬
изводные функции Q(C), т. е.
^=0, /= (4.2.9)
Так как f в (4.2.8) является линейной функцией отно¬
сительно С, то Q(C) в (4.2.4) —квадратичная функция,
чем и обусловливается линейность системы уравнений
(4.2.9). Действительно, подставляя (4.2.8) в (4.2.4) и
дифференцируя, получаем вместо (4.2.9) после очевид¬
ных преобразований
k
'2С/<Ь' — ‘Ч* = 0, *=1< (4.2.10)
/=1
где
N 1=1 - (4.2.11)
1)/=2 />^=1
i=i
Как видно, (4.2.10) является системой линейных алге¬
браических уравнений относительно идентифицируемых
параметров (4.1.1), которая легко решается стандартны¬
ми способами (например, методами Гаусса, Крамера
и т. д.).
110
Но здесь не следует обольщаться. Эта простота по¬
лучена ценой довольно серьезного упрощения: предпо¬
лагалось, что поведение сложного объекта можно пред¬
ставить в виде (4.2.8), т. е. имеются функции ф»ь(Х),
с помощью которых можно достаточно точно описать
поведение нашего объекта. Такое предположение редко
выполняется для сложного объекта. Так, имитационные
и ситуационные модели не могут быть идентифициро¬
ваны этим методом, поскольку подобрать такие функции
для них обычно не удается. Однако этот подход может
служить в ряде случаев первым грубым способом полу¬
чения модели сложного объекта.
Но вернемся к системе уравнений (4.2.10), которая
ниже подробно описывается. Рассмотрим матрицу этой
системы (kXk):
Фи •
•• фIk
Ф*1 •
• • Фй*
Эту матрицу называют информационной матрицей Фи¬
шера. Она симметрична, так как Для однознач¬
ного решения необходимо, чтобы определитель этой ма¬
трицы | Ф | не был бы равен нулю, т. е.
|Ф|^0. (4.2.13)
Этот определитель равен нулю в двух случаях: при k>
>N, т. е. когда недостаточно измерений, и при недоста¬
точной вариабельности входа X, т. е. когда более чем
N—k состояний Хь ..., Xjv линейно зависимы. Реагиро¬
вать на эту ситуацию можно двояко: либо увеличивать
количество наблюдений N, либо (если это не приводит
к цели ввиду линейной зависимости) уменьшить раз-'’
.мерность контролируемого входа X объекта, т. е. умень¬
шить число k.
Рассмотрим теперь адаптивную идентификацию ста¬
тического объекта. Пусть С<— значения идентифицируе¬
мых параметров на i-м шаге адаптивной идентифика¬
ции. Пусть получена новая информация h+\=
=<Х/+1, г/г-+1). Этэ информация должна изменить С* на
Сг+ь т. е. быть источником коррекции параметров:
Cf+i=Cj+ACi+i.
Задача, таким образом, состоит в определении ДС{+1 че¬
рез /*+i. Для этого образуем локальную невязку выхо-
Ш
до в. модели и объекта в момент i +1:
<7г+1 (Ci)=/i(Xi+b Сi)—у%+\- (4.2.14)
Очевидно, что величина ACj+i должна быть такой, что¬
бы уменьшить квадрат этой невязки. Этого можно легко
добиться, если шаг ДСг+i сделать «антиградиентным»,
т. е. '
ДСг-+1=—a,4-iV92i+i(Cf). (4.2.15)
Здесь af+i — некоторый положительный коэффициент
(о нем будет сказано позже), а V — «набла», знак опе¬
ратора градиента функции (см. приложение), которая
стоит за этим знаком:
— / А
v (дс,» •••> дсп)-
(Напомним, что градиент является вектором, направлен¬
ным в сторону наибольшего увеличения функции. Имен¬
но поэтому шаг делается в противоположном антигра-
диентном направлении функции q2(С), так как ее нужно
минимизировать.) •
Определим градиент функции q2(С):
-.^)=
= 2«(С)(а-1Й- *!a)=2?(C)W(C).
Подставляя сюда (4.2.14), получаем
V?s (С) = 2q (С) vc/ (X, С).
Здесь индексом С при V обозначен градиент по пара¬
метрам С. Это нужно отметить, так как функция зави¬
сит еще и от X.
Таким образом, получаем для коррекции параметров
на (/+ 1)-м шаге следующее выражение:
AQ+i== 2ai+1^i+I (С,-) ycf (х/+1> С;)>
где
„ f/v _ M(Xt+i,C) df(Xl+l, С)\
Vcr(Ai+1> ч)—■ dCt , •••, dck ) C=ct‘
(4.2.16)
112
Это выражение легко вычисляется, если известно ана¬
литическое выражение для функции /. Например, под¬
ставляя f из (4.2.8), получаем
Vcf (Xi+p Ci) = (?i (X<+.)> -> 9к (хг+.))-
Однако для сложных систем функция f определена лишь
алгоритмически и вычисление частных производных
в (4.2.16) уже не так просто. Для этого приходится вос¬
пользоваться конечно-разностными оценками производ¬
ных (см. приложение)
-- [/(X, с + &,)- f (X, С ge,)}, (4.2.17)
[/(X, C + gre/)-/(X, С)], (4.2.18>
где g>0— база оценки, а е*— единичный вектор, на¬
правленный вдоль /-й оси. Легко заметить, что при g-*~
—>"0 эти оценки стремятся
к точному значению частной а2(п+дг)
производной. ^
Теперь о выборе параме- qi(gy
тра а. При малом его зна¬
чении коррекция будет не¬
велика. Но его нельзя делать
и слишком большим, так как
при этом невязка увеличит¬
ся. Поведение величины не¬
вязки а2 в зависимости от Рис* 4’2,1* К определению па-
^ л о 1 v раметра а
а показано на рис. 4.2.1. Хо¬
рошо видно, что при а=.а*
невязка минимальна и равна нулю. Этим обстоятельст¬
вом можно воспользоваться для определения оптималь¬
ного значения а. Для этого достаточно решить задачу
однопараметрической минимизации
q2 (С — 2aq (С) VJ (X, Cfl—min, (4.2.19)
а>0
т. е. минимизировать квадрат невязки по параметру
Но, зная, что минимальное значение невязки при отсут¬
ствии помех равно нулю, эту задачу можно решить про¬
ще, приравнивая невязку нулю:
q(C — 2a?(C)vcf(X,C)) = 0. (4.2.20)
8-299
113
Решение этого уравнения и дает оптимальное значение
<х*. Для линейного случая (4.2.8) получаем из (4.2.20)
после очевидных преобразований
где Xj—/-я координата вектора входа X. В более слож¬
ных задачах, когда модель / определяется алгоритми¬
чески (например, для имитационных моделей), опти¬
мальное значение параметра а* следует определять из
решения задачи однопараметрической минимизации
(4.2.19), различные способы решения которой приведе¬
ны в приложении.
Теперь перейдем к идентификации динамических
моделей.
4.3. Идентификация динамических моделей
Как известно, динамический объект отличается от
статического тем, что его состояние Y* определяется не
только состоянием его входов Хг-, но и собственным со¬
стоянием в предыдущий момент времени Y*-i. Это и есть
та самая «память» объекта, которая делает его инер¬
ционным (в узком механическом смысле) и динами¬
ческим (в широком). Таким образом, дискретную мо¬
дель динамического объекта на стадии идентификации
можно записать в общем виде:
где F — определенная на стадии структурного синтеза
функция, которая может быть задана как аналитически,
так и алгоритмически (последняя форма задания более
распространена для сложных объектов управления). За¬
дача идентификации состоит в том, чтобы определить
параметры С=(сь ..., си) модели (4.3.1) по наблюде¬
ниям / входа и выхода объекта (см. (4.1.4)).
Заметим, что разница в выражениях (4.3.1) и (4.1.2)
состоит в том, что в (4.1.2) F — оператор, а в (4.3.1)
F — функция (отсутствие в (4.3.1) управления U несу¬
щественно, так как оно является таким же входом, как
и X, и поэтому на стадии идентификации может быть
объединено с X, если, разумеется, изменяется в режиме
нормальной эксплуатации объекта).
Y< = F(Yi_1, Хь С)
(4.3.1)
114
' Как и в предыдущем ^параграфе, будем рассматри¬
вать модель с одним выходом [т=1), что, как извест¬
но, не снижает общности рассуждений. Пусть для про¬
стоты объект имеет один вход (п=1) (ниже будет по¬
казано, как можно снять это ограничение). Исходная:
информация (4.2.2) о функционировании объекта при¬
нимает вид
1 = (х.,у.), 1, Л^, (4.3.2)*
где Xi и щ — значения входа и выхода объекта в t-й
момент времени U, т. е. Xi=x(U), yi=y{ti).
Бели состояние Y динамического объекта определя¬
ется его выходом в данный и р предыдущих моментов
времени U, ..ti-p, то такой объект называют динами¬
ческим объектом р-го порядка. Очевидно, что состояние
этого объекта определяется значениями его выхода, т. е.
вектором
Y'i= (уи г/i—1, • •., yi-p) . (4.3.3)
Теперь модель (4.3.1) динамического объекта р-го<
порядка представляется в виде
yi=f(Y',_b Х'„ С), (4.3.4)
где f — заданная на этапе структурного синтеза скаляр¬
ная функция, вектор определен в (4.3.3), а X7* — век¬
тор возмущения объекта:
Х'г=(хи Хг-и . . . , Xi-l) , (4.3.5)
который связывает поведение объекта с предыдущими V
состояниями среды. Числа р и I характеризуют структу¬
ру объекта и должны быть определены на стадии струк¬
турного синтеза модели.
Рассмотрим сначала неадаптивный метод идентифи¬
кации. В этом случае очевидно, что параметры С долж¬
ны быть такими, чтобы суммарная невязка выходов мо¬
дели и объекта
Q(C) = 2 [/(Y'.-^X',, С)-*/,]’ (4.3.6)*
i=s
была бы минимальной, где у{, Y'«_i> определяются на¬
блюдениями (4.3.2), а
s=max (p + 2, /+1), (4.3.7)
т. е. является максимальным из двух чисел р-\-2 и /-|-Ь
8* , 115-
Суммирование невязки (4.3.6), начиная с s, а не с 1,
связано с тем, что необходимо иметь I предыдущих зна¬
чений Xi И уi.
Теперь задача индентификации параметров С сводит¬
ся к минимизации функции (4.3.6):
Q(C) —>min.
с
Решить эту задачу можно одним из поисковых методов
оптимизации, изложенных в приложении. Полученные
значения параметров, обеспечивающие минимум функ¬
ции суммарной невязки (4.3.6), и являются решением
задачи идентификации динамического объекта, описы¬
ваемого моделью (4.3.4).
Например, для линейного динамического объекта,
модель которого имеет вид (3.4.5), суммарная функция
невязки (4.3.6) имеет вид
N Г р 1+1 "2
W)=S 2 С'У1-г+ 'ZCP+iXi-i+—Уг ,
i—s Lr=l /=1
где число идентифицируемых параметров k=p-\-l-\~. 1.
Как видно, это квадратичная форма, минимизация кото¬
рой сводится к решению системы линейных алгебраиче¬
ских уравнений:
Щ^- = 0, z= 1, ..., k = p-\-l-{-1.
Обобщим теперь этот подход на объекты со многими
входами 1): Х= (xj, ..., хп). В этом случае под X',-
в выражении (4.3.4 ) следует понимать значения входа
X при всех I предыдущих моментах времени:
Х'4= (X,-, Х(_1, ..., Xi-i),
тде Хг (г=i, ..., i—I) — значение входа X объекта в г-й
момент времени tr. Исходная информация в этом случае
имеет вид (4.2.2).
Таким образом, многомерность входа объекта в прин¬
ципе не усложняет алгоритма решения задачи цденти-
фикации, а делает его лишь более громоздким. Так, при
Линейной зависимости (4.3.4) по С число идентифици¬
руемых параметров увеличивается с k=p+l+1 (при
•одномерном входе) до k—p-\-n{l-\-\) (при п-мерном
входе X).
116
Теперь рассмотрим адаптивный метод идентифика¬
ции. Он состоит в минимизации на каждом шаге квад¬
рата локальной невязки выходов модели и объекта:
дЦС^) = т\\-и Х'„ С^)-Угу. (4.3.8)
Это можно осуществить соответствующим выбором кор¬
рекции АС* параметров G так же, как это было сделано
в предыдущем параграфе, но применительно к (4.3.8):
ЛСг-=—а* V Cq2 (Сг-_!),
где V — по-прежнему оператор градиента, а параметр
щ выбирается оптимальным из соображений минимиза¬
ции локальной невязки ,(4.3.8):
<7г (С,- _, — a,-vC<72 (С,. ,))-нmin а*,.
“<>°
В линейном случае (3.4.5) и при отсутствии помех
получаем
УС<72(С(_1) =2<7(Ci_i) (у{- «л_р_ь х(, ..;
«**=7. fs ^-/+3^-.
\/=l S=1
— оптимальное значение параметра а, при котором не¬
вязка <7(Сг-1+ДСг) становится равной нулю.
Заметим в заключение этой главы, что процесс иден¬
тификации параметров си ..ск модели объекта управ¬
ления всегда связан с процедурой минимизации «несо¬
ответствия» (невязки) модели и объекта, которое вычис¬
ляется как разность реакции (выходов) модели и объекта
на одинаковый вход. Эта минимизация может про¬
изводиться различными методами поиска (некоторые из
них описаны в приложении) и заканчивается определе¬
нием параметров модели С*=(с*ь ..., с*ь), которые
наиболее соответствуют имеющейся информации (4.1.4)
о работе объекта. Однако это совсем не означает, что
модель адекватна объекту. Это лишь наилучшее прибли¬
жение при выбранной структуре модели. Вопрос об
адекватности должен решаться на стадии выбора струк¬
туры модели и по величине минимальной невязки
(4.3.6). Чем больше априорной информации использу¬
ется при определении структуры моделй, тем больше
шансов получить адекватную модель.
117
ЛИТЕРАТУРНЫЙ КОММЕНТАРИЙ К ГЛАВЕ 4
Идентификация как процесс определения параметров модели по
наблюдениям, полученным в режиме нормального функционирования
объекта, исследован довольно хорошо. Для первого ознакомления
с задачей идентификации читателю рекомендуются книги [1 и 2].
Идентификация промышленных объектов является наиболее важной
практической задачей современной техники управления, и поэтому
ей уделяется большое внимание. Методы идентификации такого рода
объектов описаны в работах [3—5]. Достаточно полное (хотя и не
простое) изложение основных методов идентификации и их неко¬
торых приложений, содержится в монографии {6].
Адаптивная идентификация, рассмотренная в § 4.2, является
в большинстве случаев наиболее эффективным подходом к решению
практических задач идентификации. Ей посвящены работы [7, 8],
а в книге [9] описано очень интересное приложение адаптивной
идентификации для решения задач управления точностью прокатки
труб, реализованное на производстве, за которое ее авторы в 1976 г.
получили Государственную премию.
СПИСОК ЛИТЕРАТУРЫ
1. Райбман Н. С. Что такое идентификация? — М.: Наука, 1970.
2. Растригин JI. А., Маджаров Н. Е. Введение в идентификацию
объектов управления. — М.: Энергия, 1977.
3. Балакирев С. В., Дудников Е. Г., Цирлин А. М. Эксперименталь¬
ное определение , динамических характеристик промышленных
объектов. — М.: Энергия, 1967.
4. Ордынцев В. М. Математическое описание объектов автоматиза¬
ции.— М.: Машиностроение, 1966.
5. Райбман Н. С., Чадеев В. М. Построение моделей производ¬
ства.— М.: Энергия, 1975.
6. Эйкхофф П. Основы идентификации систем управления: Пер.
с англ. — М.: Мир, 1975.
7. Райбман Н. С., Чадеев В. М. Адаптивные модели в системах
управления. — М.: Сов. радио, 1966.
8. Райбман Н. С., Чадеев В. М. Адаптивные системы управления
технологическими процессами: методика/ Ин-т проблем управле¬
ния. — М., 1972.
9. Адаптивное управление точностью прокатки труб/ Под ред.
Ф. А. Данилова и Н. С. Райбмана. — М.: Металлургия, 1973.
ГЛАВА 5
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
Этап планирования экспериментов с объектом преж¬
де всего связан с необходимостью определить парамет¬
ры влияния на выход Y тех входов объекта, которые не
варьируются при его нормальной работе, т. е. без управ¬
ления. Очевидно, что такими входами прежде всего
118
являются определенные на этапе структурного синтеза
управляемые входы U. На этапе структурного синтеза
получена зависимость
Y=F(X, U, С), (5.0.1)
где F — определенный оператор модели, а С=(сь ...
..., сь) — неизвестные параметры объекта, которые
должны быть определены на этапе планирования экспе¬
риментов.
Другая задача планирования экспериментов возни¬
кает при определении структуры модели объекта управ¬
ления. В этом случае необходимо построить такой экспе¬
римент, чтобы полученная информация дала бы возмож¬
ность выбрать наилучшую модель из заданного набора
конкурирующих моделей и при этом определить ее па¬
раметры. Необходимость идти на такую нежелательную
операцию, как эксперименты с объектом (напомним, что
мы строим систему управления сложным объектом, кото¬
рый «не любит» экспериментов), связана с тем, что ино¬
го пути здесь нет.
Математически неизбежность экспериментов с объек¬
том вытекает из следующего простого рассуждения. Для
определения параметров С=(сь ..., ск) модели (5.0.1)
необходимо иметь исходную информацию о состоянии
входов и выходов объекта в виде троек:
/ =(Х/? Ut-, Y/), (5.0.2)
Но на стадии синтеза системы, управления вход U не
изменяется, т. е. Ui=const, так как объект еще не управ¬
ляется. Это и исключает возможность определения па¬
раметров, характеризующих связь входа U с выходом Y
на стадии идентификации. Для того чтобы определить
эти параметры, необходимо варьировать вход U и фик¬
сировать при этом поведение объекта, т. е. эксперимен¬
тировать с ним.
Будем для простоты записи рассматривать случай
Y=F(U, С). (5.0.3)
Общий случай (5.0.1) легко получится из (5.0.3) при до¬
полнительном фиксировании (записи) состояния X ере-,
ды в процессе экспериментов.
Задача планирования экспериментов заключается
в таком минимальном изменении входа U, при котором
119
полученная информация Y давала бы возможность наи¬
лучшим образом оценить значения параметров С. Рас¬
смотрим эту задачу подробнее.
5.1. Основные понятия теории
планирования экспериментов
Теория планирования экспериментов возникла как
раздел математической статистики, и поэтому в ней'
сложилась терминология, отличная от терминологии
теории управления (это следует иметь в виду при чтении
литературы по планированию).
Под объектом планирования будем подразумевать
многополюсник с q управляемыми входами U=(uu .. -
..., uq). Вид (структура) оператора F (5.0.3) уже опре¬
делен на стадии структурного синтеза модели, рассмо¬
тренного в гл. 3: Он имеет стохастическую структуру
вида (3.4.9).
Для решения задачи планирования экспериментов
следует организовать такое изменение входов U объек¬
та, чтобы можно было эффективно определить парамет¬
ры С модели и, если нужно, скорректировать структуру
St модели F.
Схема процесса планирования экспериментов пока¬
зана на рис. 5.1.1. Она напоминает схему системы управ¬
ления, рассмотренную во введении (см. рис. В.2.1). Это
не удивительно, так как планирование эксперимента
действительно является управлением объекта, но цели
этого управления специфичны — определение парамет¬
ров модели объекта, а точнее, построение модели объек¬
та управления (врзможна и коррекция структуры моде¬
ли). Как видно из рис. 5.1.1, роль управляющего устрой¬
ства выполняет процедура планирования эксперимента,
в которой указывается, каким образом следует изменять
вход U в процессе эксперимента. Сам эксперимент одно-
/V
значно определяется планом U, представляющим собой
перечень состояний входа U, которые должны быть реа¬
лизованы в объекте. Так, для статического объекта план
U имеет вид
U = (U, U„), (5.1.1)
где U«—7-й эксперимент плана, т. е, t'-e состояние входа:
и<—(«к,... ugi),
120.
План (5.1.1) полностью определяется гак называемой
матрицей планирования
и=
-и, -
• Uqt
•
1
С ..
|
UXN .
^ "
1
(5.1.2)
Для динамического объекта планом является вектор¬
ная функция времени U=U(0, т. е. зависимость входа
U от времени.
Рис. 5.1.1. Схема
процесса планиро¬
вания эксперимен¬
тов с объектом
Цели планирования эксперимента, на основе которых
строится план эксперимента U, обычно определяются
двумя факторами: ресурсом и критерием планирования.
Ресурсы планирования R состоят из выделяемых на
эксперимент средств Р (временных, материальных,
штатных и т. д.), а также области (зоны) планирова¬
ния £2, определяющей пределы изменения входа U в про¬
цессе планирования:
UgeC2. (5.1.3)
Таким образом,
R = (P,Q). (5.1.4)
Например, P=N — объем плана, т. е. число экспери¬
ментов, которое можно произвести с объектом. При
этом Q: a^Ui^bi (i=1, ..., q)—< гиперпараллелепипед
в пространстве состояний входа U, где значения гра¬
ниц at и hi (i= 1, ..., q) должны быть заданы.
Критерий планирования определяет эффективность
плана U. Этот критерий естественно зависит от плана
U и -структуры модели F объекта:
К=К(и, F). (5.1.5)
121
В качестве такого критерия планирования обычно вы¬
бирают характеристики процесса планирования, опреде¬
ляющие точность оценки параметров С модели. Напри¬
мер, это может быть сумма или произведение дисперсий
оценок определяемых параметров или максимальная
дисперсия и т. д. Минимизация такого рода критерия
с помощью плана U является, очевидно, целесообраз¬
ной мерой при планировании экспериментов.
Иногда может возникнуть ситуация, когда необходи¬
мо минимизировать не один, а несколько (р) критериев.
Тогда следует решить многокритериальную задачу
^ /
/С*(0, F)—>min, /= 1, ..., р. (5.1.6)
GehR
Для ее решения необходимо привлекать дополнитель¬
ную информацию об объекте (способы решения такого
рода задач описаны в приложении). Основой для реше¬
ния здесь являются различного рода компромиссы меж¬
ду критериями. Поэтому планы, синтезированные при
решении многокритериальной задачи (5.1.6), ^называют
компромиссными.
Как видно, цели планирования определяются исходя
из специфики объекта управления и целей его эксплуа¬
тации и управления. Нельзя забывать, что сложный
объект, которым мы занимаемся, существует и функцио¬
нирует независимо от целей будущего управления, и
поэтому вмешательство в его работу до управления им
должно происходить с большой «оглядкой». Прежде
всего это касается выбора области планирования Q.
При выборе размеров этой области неизбежен кон¬
фликт между «хозяином» объекта, т. е. лицом, ответст¬
венным за его нормальное функционирование, и проек¬
тировщиком системы управления. Если первый стремит¬
ся минимизировать размер области Q, чтобы минималь¬
но нарушать нормальную работу объекта, то второй
заинтересован в максимизации размеров £2, так как при
этом эффективность эксперимента U бывает наиболь¬
шей. Действительно, чем больше отличаются друг от
друга состояния входа (5.1.1) при эксперименте, тем
больше будет получено информации об объекте. Ука¬
занный конфликт обычно решается с помощью разум¬
ного* компромисса между обеими сторонами и приводит
122
к выбору конкретных очертаний области планирова¬
ния Q.
Таким образом, реализация целей планирования свя¬
зана с решением следующей экстремальной задачи:
K(U, F)-
^rain^U^,
u<=tf
(5.1.7)
т. е. варьируя план U в пределах выделенных ресурсов
R, следует минимизировать заданный критерий при
определенной ранее структуре модели F. Полученный
при этом план U*K естественно назвать /(-оптимальным
Рис. 5.1.2. Зона планирова¬
ния Q в пространстве управ¬
ляемых входов {и}.
Точками обозначены экспери¬
менты, образующие план U*
планом с ресурсами R для объекта с моделью F. При
изменении указанных факторов (критерия, ресурса и
объекта) оптимальный план U*x также изменяется.
На рис. 5.1.2 показан пример оптимального плана
#*, состоящего из N=5 экспериментов для статического
объекта (F—функция) с заданной структурой. В этом
случае каждый эксперимент характеризуется точкой
в пространстве входов {U}, а 'план U*k представляет
собой набор из пяти точек, принадлежащих заданной
области (зоне) планирования Q:
U% = (U„...,U5),
причем их расположение минимизирует заданный кри¬
терий К.
Заметим, что очень часто управление U имеет ди¬
скретный характер. Например, i-я рукоятка управления
объектом может находиться только в двух положениях:
«включено» (щ= 1), «выключено» (^=0); промежуточ¬
ные положения при этом исключаются. Учет этой осо¬
бенности объекта производится соответствующим опре¬
123
делением множества й, которое в дискретном случае
состоит из конечного числа элементов. Так, если i-й па¬
раметр управления щ может принимать лишь ki зна¬
чений, то число элементов множества Q равно
я
кхкг... kg =
i=1
Для двоичного (бинарного) управления (h=2, /==1, ...
..., q) получаем 2^ элементов этого множества.
Основная проблема планирования экспериментов, та¬
ким образом, заключается в эффективном решении за¬
дачи (5.1.6), т. е. в создании оптимальных планов и*на
допустимом ресурсном множестве R.
Будем рассматривать только статические.объекты, для
моделей которых F является функцией. В этом случае
план U представляет собой набор из N точек Ui, ..., Ujv
в -пространстве варьируемых параметров {U}, причем все
точки принадлежат зоне планирования: U^Q (i— 1, ...
.... N).
* Планирование экспериментов для динамического
объекта (когда F — оператор) представляет собой
функцию U=U (<)eQ, описывающую траекторию в зоне
планирования Q, причем эта траектория минимизирует
выбранный критерий /С, который в данном случае явля¬
ется функционалом *). Подходы к решению таких задач
рассмотрены в следующей главе.
Теперь рассмотрим способы формулировки критерия
планирования /С.
5.2. Критерии планирования
Рассмотрим эксперимент, целью которого является
наиболее достоверное определеняе параметров С=
— (£ь • • •> ck)- Однако понятие «достоверности» слишком
широко и размыто. Поэтому в каждом конкретном слу¬
чае формулировка критерия определенным образом свя¬
зана с целями управления Z*, но всегда зависит от точ¬
*) Напомним, что функционалом является преобразование функ¬
ции в число, например:
ностных характеристик искомых параметров. Таким»
характеристиками являются, например, дисперсия пара¬
метров С
Du=M[(Ci—Ci)2], i=l k,
(где Ci — среднее значение параметра сг, а М — знак
математического ожидания) и коэффициенты корреля¬
ции этих параметров
(С{ Ci) (Cj Cj)],
i, /= 1, . . ., k,
Эти характеристики объединяются так называемой дис¬
персионной матрицей параметров С, которую обычно
обозначают так:
Как видно, дисперсионная матрица (5.2.1) полностью
определяет статистические свойства искомых пара¬
метров С.
Естественно задать вопрос, как определять диспер¬
сионную матрицу? В общем случае это довольно слож¬
ная задача. Однако для моделей, линейных относитель¬
но искомых параметров С, т. е. моделей вида (3.4.3),
известно, что дисперсионная матрица обратна информа¬
ционной матрице Фишера (4.2.12), т. е.
Dc = о’Ф"1. (5.2.2)
Это означает, что каждый элемент дисперсионной ма¬
трицы равен
^=а2Фя/|Ф|, i,j=1, (5.2.3)
Здесь G>ji — алгебраическое дополнение элемента ipj*
матрицы Ф, которое получается из Ф вычеркиванием /-й
строки и г-го столбца и умножением (—I)’*3'; |Ф| — опре¬
делитель матрицы Ф; о2 — дисперсия случайной помехи,
накладывающейся на выход объекта в соответствии со
структурой (3.4.9).
Таким образом, зная матрицу Ф, легко по (5.2.3) по¬
лучить дисперсионную матрицу Dc,с помощью которой
можно сформулировать любые необходимые критерии
планирования.
125-
Наиболее распространенным является так называе¬
мый D-критерий, равный определителю дисперсионной
матрицы (5.2.1), т. е. обобщенной дисперсии:
План, минимизирующий этот критерий, называют D-
оптимальным.
Вообще говоря, критерием планирования может быть
.любая функция элементов дисперсионной матрицы К =
= <р(£>с). Например, К может быть максимальной диспер¬
сией (/C = maxD/f). План, минимизирующий эту дисперсию,
*=i я
называют Е-оптимальным. Если К— сумма дисперсий иско¬
мых параметров , т. е. след дисперсионной
матрицы*), то соответствующий план называют Л-опти-
мальным, и т. д.
Особое место среди многочисленных планов экспери¬
ментов занимают ортогональные планы, для которых
информационная матрица Фишера Ф диагональна.
С помощью ортогонального плана очень упрощается
процедура вычисления параметров С:
где я|)гг и г]* определены в (4.2.11). Однако не в этом
основное преимущество ортогонального плана, а во
взаимной некоррелированности оценок искомых парамет¬
ров. Действительно, диагональность информационной
матрицы Ф приводит к диагональности дисперсионной
матрицы D, откуда следует равенство нулю всех коэффи¬
циентов корреляции:
что означает указанную взаимную некоррелированность
получаемых оценок искомых параметров С. Это обстоя¬
тельство часто бывает очень важным при синтезе мо¬
дели.
Теперь рассмотрим наиболее распространенное D-
оптимальное планирование экспериментов.
K=\DC\.
(5.2.4)
С%—'фп/Лг» ^—1> • • •> &■>
Dij — 0, —1» • • •>
*> Напомним, что следом матрицы называют сумму ее диаго¬
нальных членов.
5.3. £>-оптимальное планирование
Как сказано выше, синтез D-оптимального плана
сводится к решению задачи минимизации определителя,
дисперсионной матрицы (5.2.1) или в силу (5.2.2) к мак¬
симизации определителя информационной матрицы Ф:
| Ф(0) |—тах=фЦ*,. (5>зл)<
Полученный при этом план U*d и называют D-опти¬
мальным.
Построим D-оптимальный план для линейного одномерного*
объекта:
у = с\+с2и. (5.3.2)
Элементы информационной матрицы в этом случае можно было
бы определить по формуле (4.2.11), где cpi = l, щ=и. Однако из
соображений наглядности произведем все необходимые выкладки
для рассматриваемого простого случая (п—<7=1). Для того чтобы
воспользоваться методом наименьших квадратов при определении
параметров с\ и с2 модели (5.3.2), введем условно исходную инфор¬
мацию в виде каких-то результатов эксперимента с объектом:
/ = <«/. У1) Л). (5.3.3)
где (!=(«!,..., uN) — искомый план эксперимента.
Суммарная невязка выходов модели (5.3.2) и объекта (5.3.3)
N
Q (Cl, С2) = 2 1С1 + ctui — У1]*•
i=l
Минимизируя это выражение в соответствии с методом наименьших
квадратов по с\ и Сг, получаем систему двух уравнений
N
= 2 1£ + СгЩ ~~ У‘^ = °’
i =1
N
dQ ^
= 2 Ъ ^ + СгЩ~уйUi = °-
i=i
Эту систему удобно преобразовать к виду
- 1
Cj + с2и= -дг vji,
С,В + С2И2 = ^7)2,
127
/=1
£=1
Откуда видно, что определитель информационной матрицы имеет
вид
1Ф (U)\
1 и
а и*
--и2 — (и)2.
(5.3.4)
Теперь решим задачу синтеза D-оптимального плана, максимизируя
это выражение по элементам плана U параметром щ (/=1, ..., N).
Для этого необходимо решить минимизационную задачу
гг2-— (и)2 шах,
(/==1» -• N)>
где Q: [а, Ь], т. е. задача состоит в выборе таких N чисел и\ внутри
отрезка [а, b], т. е. a^.Ui^b, которые минимизировали бы квадра¬
тичную форму (5.3.4).
Эта задача решается сразу путем следующего простого рассуж¬
дения. Легко заметить, что выражение (5.3.4) цредставляет собой
не что иное, как дисперсию точек плана 11 = (й1э ..., uN). Макси¬
мизация дисперсии N точек на отрезке требует, чтобы они были
расположены на концах этого отрезка, причем половина на одном,
а половина на другом конце.
Следовательно, D-оптимальный план =
случае при четном N выглядит так:
# (а для i ^N/2,
U 1 ( Ь для / > АГ/2;
при нечетном N возможны два эквивалентных плана:
для i<*(N — 1)/2,
для i> (N— 1)/2
.. u*N) в этом
* /а
и1==\ъ
«ли
4*1 = |
а для (W + 1) /2,
Ъ для t> (N + 1)/2.
Заметим, что в данном' случае информационная матрица (5.3.4) не-
диагональна, план неортогонален и, следовательно, получаемые при
этом оценки параметров С\ и с2 коррелированы. Действительно, их
дисперсионная матрица равна
ОС=а2ф~о2
и2
— и
— и
1
(5.3.5)
Однако это неудобство легко преодолеть. План U* можно ортогона-
лизировать, изменив систему координат так, чтобы получить к = 0,
128
что, как видно из (5.3.5), делает матрицу Ф диагональной. Для это¬
го достаточно перейти к центрированной системе координат, т. е.
расположить начало координат в центре зоны планирования Q:
а + Ь
Ъ — а Ъ —а
и,
для которых и'— 0, (м')2= 1 и матрица получает требуемый вид
О
Ф' =
О 1
План в этом случае записывается так:
U*£) = (—1 » ..., -1, 1» ..., 1),
к
у—.
N
где
N/2
(N+ 1)/2
для четных N,
для нечетных М.
Как видно, от выбора системы координат существенно зависят
корреляционные свойства определяемых параметров.
Применяя аналогичные рассуждения для D-оптималь¬
ного плана эксперимента в случае линейной многомер¬
ной модели y=ci + c\u2+ ... cq+\Uq в области Q: —1^
(гиперкуб в пространстве {f/}), получим D-
оптимальный план 0*в с координатами ^*j=± 1 (/=
=1, ..., q)y т. е. точки и* (i= 1, ..., N) должны распо¬
лагаться в углах гиперкуба, причем так, чтобы план U
при этом был ортогональным. Условия ортогональности
N
2 «л«« = 0 при 1ф1
1=1
состоят в том, что произведения двух любых столбцов
матрицы планирования (5.1.2) равны нулю. Такая ма¬
трица называется ортогональной относительно столбцов.
На рис. 5.3.1 приведены примеры различных планов для
п=2, когда Q — квадрат. Их матрицы планирования со¬
ответственно равны
U*D=U* =
1
1
0
1
—1
1
—1
0
—1
-1J
; 0° =
0
—1
1
—1
1
0
9—?99
129
Теперь рассмотрим пример квадратичной зависимости F в про¬
стейшем одномерном случае
y=ci+c2u+cau29
где функции разложения (4.2.8): ф!(м)=1; ф2{и)*=и\ щ(и)*=и2.
U2J
Q
't
sf//////.
У/^//А
“l\
■//У///У{
{//////A
Q I
%%
в)
и2
ШЩС УШШ
S?
Щ7777,
7777Ш, $777777,
Я
“1
77777#/,
0)
г)
Рис. 5.3.1. Примеры планов:
а — 2Э-оптимальный ортогональный (N—4), б — ортогональный не D-оптималь¬
ный (N-4), в — D-оптимальный неортогональный (N=*5), г —то же, но для
3
Информационная матрица Фишера (4.2.12) в этом случае, как легко
показать, приобретает вид
Ф =
где
71
U
u* '
и
h*
a8
-fa*
a8
a4 .
N
E*.
/ =
1, 2,
[=1
(5.3.6)
Любопытно, что в этом случае (при заданных переменных) ортого¬
нального плана не существует, так как при й=й2—й*=0 определи¬
тель | Ф | становится равным нулю, что исключает возможность
определения С. Поэтому для простоты синтеза плана естественно
Потребовать:
ц = й3=0, (5.3.7)
т. е. план должен быть симметричным относительно центра зрны
планирования Q.
Пусть Й: — тогда определитель информационной матри¬
цы Фишера
1
0
и2
|ф| =
0
и2
0
=
и2
0
и4
= и2[и*'- (и2)2].
Теперь построим оптимальные планы с различным объемом N,
т. е. будем варьировать число точек плана.
Я? Q'
_Л ,
т
9 Q 'few-*- шб f I 1
О “ +7 и -1 ~а 0 а +t I
а) в)
Q ?
0+1 -7 0 +/ а
5) г)
Рис. 5.3.2. К построению D-оптимальных планов на отрезке для
квадратичной зависимости F:
а, в — неоптимальные; б, г — оптимальные планы
Пусть N=3. Симметричный план в этом случае определяется
одним параметром а и имеет вид
U = (—а, 0, а)
(рис. 5.3.2,а). Для второго и четвертого моментов получаем
и* = 2/га2-, й4 = 2/3а4
и задача синтеза оптимального плана сводится к максимизации вы¬
ражения
|ф| = 4/27а6 —> max =^> а* = 1,
— 1<а<1
решение которой очевидно. Таким образом, D-оптимальный план
в этом случае имеет вид (см. рис. 5.3.2,б) U*d=(—1, 0* + !)•
Пусть N=4. Тогда, фиксируя две очевидные точки плана на его
краях (м=±1), рассмотрим симметричный план с одним неизвест¬
ным параметром а>0: U=(—1, —а, а, 1) (см. рис. 5.3.2,в), для
которого
й2==у2(1+а2); й4 = у2(1+а4)
и определитель равен
IФ11= 4/e( 1—-ct2) (1—а4).
Его максимум очевиден при а=0, что и дает D-оптимальный план
UV=<-1, 0, 0, +1)
(см. рис. 5.3.2,г), для которого |ф|=4/8. Отметим, что этот план
получен из предыдущего (N=3) добавлением ы4=0.
9* 131
Теперь рассмотрим несимметричный план U\~—1, w2=0, Uz—
= и+= 1. Для него получаем IQI^/e, т. е. этот план
U*D = (-1, 0, +1, +1),
тоже D-оптимальный.
Анализ показывает, что для квадратичного объекта
элементы D-оптимального плана при любом объеме N
группируются в трех полученных выше точках и=—1,
О, +1. Поэтому при синтезе плана для N>4 следует
манипулировать только этими точками.
S2 Q?
_А_
_А_
О
о
-/ 0 +1 и -1 О к +1 и
а) В)
Я S?
'А
О
-9-
-7 о +/ и -1 (J . +1 и
5) г)
Рис. 5.3.3. К построению D-оптимальных планов при N=5:
а, в — неоптимальные; в, г — оптимальные планы
В общем случае, когда имеется к точек и——1, q то¬
чек и=0 и т точек и—+1 (.k + q + m=N, k>m), то й=
=й3= (k—т) /N, U2=ulk={k+m) /N, и из (5.3.6) после
некоторых преобразований получаем
\<b\=4kqm/N.
Очевидно, что для максимизации этого выражения до¬
статочно иметь k=q=m=N\3, если, разумеется, N крат¬
но трем. В противном случае &, q и т должны разли¬
чаться не более чем на единицу. Так, например, планы
а и б на рис. 5.3.3 оптимальны, виг неоптимальны.
Как видно, оптимальный план объемом AA-f-l полу¬
чается из оптимального плана объемом N добавлением
одного эксперимента таким образом, чтобы новый план
был максимально равномерным.
Это правило можно распространить и на другие пла¬
ны. Так, для п=2 D-оптимальный план на квадрате—
132
(i=U 2) естественно опирается на то^кй, rto-
казанные на рис. 5.3.4,а. При N=9 эти точки образуют
D-оптимальный план *). Для N = 8 оптимальный план по¬
лучается из предыдущего отбрасыванием одной из четы¬
рех точек (7, 2, 5, 4) на осях квадрата Q (см., напри¬
мер, рис. 5.3.4,б). При N=7 следует отбросить две из
указанных точек (рис. 5.3.4,в), при N=6 — любые три
точки на осях, кроме центральной (рис. 5.3.4,г). Нара¬
щивание числа точек оптимального плана осуществля¬
ется добавлением тех опорных точек (см. рис. 5.3.4,а),
которые максимально повышают определитель |Ф|.
Рис. 5.3.4. /^-оптимальные планы квадратичной модели (п=2):
а) ЛГ-9; б) N= 8; в) ЛГ=7; г) ЛГ-6
Это правило имеет место и для любого другого пла¬
на любой размерности, что позволяет легко строить ре-
куррентно оптимальный план, последовательно добав¬
ляя опорные точки к оптимальному плану объемом
К—1, полученному на предыдущем этапе синтеза.
5.4. Последовательное планирование
экспериментов
Очень часто объем N плана заранее не определен и
зависит от того, что он может дать для синтеза модели,
а также от настойчивости экспериментатора. Поэтому
естественно объем N заранее не оговаривать, а опреде¬
лять в процессе экспериментов с объектом. Это обеспе¬
чивается в ходе последовательного планирования, когда
решение о последующем эксперименте принимается
лишь после того, как сделан предыдущий. Кроме того,
в процессе последовательного планирования эксперимен¬
татор имеет возможность изменять структуру модели,
т. е. переходить от одного описания объекта к другому,
*) Строго говоря, такой план не будет оптимальным [4], но его
отличие от оптимального крайне незначительно.
133
изменять зону планирования и критерий оптимальности.
В основе последовательного планирования лежит
очевидное соображение о том, что полученная в одном
эксперименте информация может быть использована не
только для коррекции параметров модели (как это де¬
лалось. в процессах идентификации), но и для принятия
других решений (например, об изменении структуры
модели, прекращении экспериментов, изменении крите¬
рия или зоны планирования и т. д.).
Пусть после (г — 1)-го этапа планирования сделаны
i—Ji экспериментов в точках UI_,=(U1, ..., U^j), т. е.
реализован план Uf_i. Полученная при этом информа¬
ция г/i, ..., i/i-i дала возможность синтезировать модель
у=П-,{U, С,-_1) (5.4.1)
(например, методом наименьших квадратов или каким-
либо другим методом), где fi-i — структура модели, ко¬
торая, ро мнению экспериментатора, после (i—1)-го эта¬
па наиболее полно отражает его специфику и соответ¬
ствует целям управления; Сг_i — значения параметров
этой модели на (i—1)-м этапе планирования. Распола¬
гая этой моделью, экспериментатор должен прежде все¬
го решить, удовлетворяет его эта модель или нет. В пер¬
вом случае задача синтеза модели заканчивается, во
втором — ему следует оценить, покроет ли уточненная
модель затраты на производство £-го этапа эксперимен¬
та. При отрицательном решении эксперименты заканчи¬
ваются, при положительном — следует перейти к i-му эта¬
пу эксперимента. На этом этапе необходимо опреде¬
лить:
— новую структуру fi модели, если экспериментатор
решает ее изменить;
— новую зону йi планирования эксперимента, если
в этом имеется необходимость и возможность;
— новый критерий планирования Ки если его необ¬
ходимо сменить.
Если же изменений не происходит, то £24=
—1, Ki—Ki—1»
Как известно, численное значение критерия К зави¬
сит от структуры модели, т. е. от выбранной системы
функций (<pj(U)} (/=1, ..., k) представления модели
M(W) = 2%(U) (5.4.2)
/=1
134
и от плана эксперимента U (5.1.3). При последователь¬
ном планировании на i-м этапе планируется лишь один
i-й эксперимент, который производится в состоянии U*,
т. е. планом является
6t = (CU,U;>, (5.4.3)
где иг*_1 — уже реализованный к i-му этапу план.
Положение i-го эксперимента, т. е. U*-, определяется
в результате решения следующей очевидной оптимиза¬
ционной задачи:
б/-,. U,)^mm=>U*,-. (5.4.4)
Vt&i v '
Эту задачу ввиду ее сложности следует решать одним
из поисковых методов оптимизации, рассмотренных
в приложении.
В состоянии и*г- ставится эксперимент, определяется
выход у г объекта и т. д., т. е. на следующем (iH~1)-m
этапе планирования снова определяются (или сохраня¬
ются) структура модели, зона планирования и критерий.
Естественно, что можно планировать не один, а несколь¬
ко экспериментов, т. е. вместо U* в выражение (5.4.4)
подставить U*, ..., иг*+лейг, с помощью которых и ми¬
нимизируется критерий Ki.
Так учитываются все предыдущие эксперименты U^-i
и вводятся изменения, связанные с уточнением или сме¬
ной критериев, структур и т. д.
Последовательное планирование, таким образом,
представляет собой очень гибкий инструмент, обеспечи¬
вающий экспериментатору возможность, оперативно
меняя ход эксперимента, в конечном счете получить тре¬
буемую модель объекта.
5.5. Дискриминирующие планы
Дискриминирующими обычно называют планы, по¬
зволяющие выбрать одну из нескольких гипотез о струк¬
туре связи входа и выхода объекта, т. е. о структуре
модели. Пусть имеется р конкурирующих структур (мо¬
делей)
y=/j(U, Cj), /=1, ..р, (5.5.1)
где С,- — вектор параметров /-й модели:
135
Число параметров kj, вообще говоря, может изменяться
от одной модели к другой.
Пусть имеется какой-то план, состоящий из N экспе¬
риментов, U=(Ui, ..., Ujv), и наблюдения выхода объ¬
екта при реализации этого плана уи •.Ук- Тогда вы¬
бор лучшей структуры модели сводится к определению
результирующей невязки каждой модели
Е 1№*С/) —0|]*. Р- (5.5.2)
/=1
Выбирают ту структуру, которая обеспечивает наимень¬
шую невязку. Это означает, что лучшей структурой бу¬
дет fu если
Qi = min Q,. (5.5.3)
/=i р
/V
План U*, который позволяет осуществить эту про¬
цедуру наилучшим образом, назовем оптимальным ди¬
скриминирующим. Заметим, что решение о выборе
структуры с минимальной невязкой (5.5.3) может быть
ошибочным, так как результаты дискриминирующих
экспериментов (как и всяких реальных) имеют стоха¬
стический характер. Поэтому задача синтеза оптималь¬
ного дискриминирующего плана сводится к тому, чтобы
сделать вероятность этой ошибки минимальной, т. е.
принятое решение о выборе наилучшей структуры долж¬
но иметь наибольшую достоверность. Формализуем ска¬
занное.
Пусть р — вероятность ошибочного решения, т. е.
Р=Вер [/*¥=/; | Qmin=Qj], (5.5.4)
где /* — наилучшая структура; Qmm— наименьшая из
(5.5.2) невязка. Эта вероятность зависит от дискримини¬
рующего плана U : p=p(U). Тогда оптимальным дискри¬
минирующим планом U* естественно назвать такой
план, который минимизирует эту вероятность. Для этого
необходимо решить задачу
p(U)—min=>U*. (5.5.5)
US2
Обсудим способы решения этой задачи. Рассмотрим
случай, когда значения векторов параметров С,- (/=
=1, ..., р) каждой структуры известны заранее и поэто-
136
му могут не учитываться, т. е. Ci)=/i(tT). Тогда
отыскание дискриминирующего плана сводится к опре¬
делению положения N экспериментов U* (i— 1, ..N) и
вычислению суммарных невязок в этих точках по фор¬
муле (5.5.2).
Пусть в частном случае (р=2) имеются две модели
ft и jf2 (рис. 5.5.1). Очевидно, что оптимальным здесь
следует считать дискриминирующий план, расположен¬
ный в точке, где обе модели больше всего различаются.
Рис. 5.5.1. К дискриминации Рис. 5.5.2. К определению ве-
двух одномерных моделей роятности принятия ошибочно¬
го решения при дискримина¬
ции для двух моделей
Как легко видеть, выбор такого плана эквивалентен ре¬
шению задачи (5.5.5) (ниже эта эквивалентность будет
показана строго). Таким образом, для отыскания един¬
ственной точки оптимального дискриминирующего пла¬
на достаточно решить задачу
[A(U);-/,(U)]!—шахе и*. (5.5.6)
Решение ее — точка U* — и определяет искомый план:
все N экспериментов следует располагать в этой точке,
т. е. Ui==U* (t=l, ..., N).
Рассмотрим для определенности случай, когда одна
из конкурирующих структур имеет место в действитель¬
ности (пусть это будет fi, т. е. Выход объекта име¬
ет вид
^o(U)==;l(U)+8( (5.5.7)
где е — случайная помеха эксперимента, которую пред¬
полагаем центрированной и нормальной, т. е. с нормаль¬
ным законом распределения, нулевым ожиданием и
дисперсией а2. Поэтому результаты всех N эксперимен¬
тов г/» (i— 1, ..., N) будут группироваться вокруг зна-
137
^ёния /i(U) в соответствии с распределением помехи ё.
Определим значения невязок Qj (/==1, 2). С учетом
(5.5.7) получаем
Q,=2eV (5.5.8)
i~i
2 l/a(U)—Д (U)—*ла*
1=1
Пусть A(U) —разность выходов моделей в точке U:
A(U)=fc(U)-/i(U). (5.5.9)
Тогда после очевидных преобразований получаем
Q, = #Д* (U) — 2Д (U) 2 «г + 2 б‘«-
i=i i=i
Как легко заметить, знак разности _
8 (U) = Q, (U) - Q, (U) = ЛГД’ (Ц) - 2Д (U) 2 •,
i=i
определяет выбор одной из моделей. Действительно,
если эта разность положительна, то следует выбирать
fi, а если отрицательна, то /г (напомним, что числа Qi
неотрицательны по определению). Таким образом,
Г/, при«(и)>0,
If, при «(D)<»•
Это и есть правило решения задачи (5.5.6), а следова¬
тельно, и (5.5.5).
Определим вероятность ошибки, т. е. вероятность
принятия неправильного решения при A(U)>0:
Р=Вер|4;£*«>-гД(и)]. (5-5Л1)
т. е. вероятность того, что случайная величина
N
6лг=1Г$]е‘-
i=i
превысит 72A(U). Зная вероятностные свойства TN:
M(7n) = 0; D(7n) = o*JN,
138
легко определить искомую вероятность. Она равна за¬
штрихованной площади под кривой распределения слу¬
чайной величины &n (рис. 5.5.2). Для нормального за¬
кона распределения err
' <5-5-12>
где Ф(-)—функция Лапласа, которая является моно¬
тонно возрастающей. Это свойство функции Ф(-) и
определяет выбор искомого плана, который для' миними¬
зации вероятности ошибки должен максимизировать ве¬
личину A(U), т. е. следует решать задачу (5.5.6). Если
подставить полученную точку U* в выражение (5.5.12),
то получим вероятность ошибки при оптимальном пла¬
не. С другой стороны, вероятность ошибки при таком
решении можно уменьшить, увеличив число эксперимен¬
тов N в точке U*. Таким образом, можно планировать
эксперименты, которые обеспечивают выбор модели
с любой наперед заданной степенью достоверности.
Однако в реальных задачах параметры С j (/= 1,...
. .., р) моделей (5.5.1) неизвестны, и поэтому одновре-
менно с дискриминацией следует производить оценку
этих параметров. Сделать это можно путем последова¬
тельного планирования экспериментов следующим обра¬
зом.
Пусть для простоты р=2, т. е., как и выше, решается
задача дискриминации двух моделей fi (U, Ci) и
ЫU, С2), где векторы параметров Ci и С2 неизвестны.
На (£+1)-м этапе дискриминации имеем параметры Си
и С*, для которых решаем задачу синтеза плана дискри¬
минации
| MU, С,,.)-Mil. С,,) | ->maxr>U<+, (5.5.13)
ues
Определив в эксперименте значение выхода объекта
Уi+l=/0 ( Ui+1) ,
можно откорректировать параметры, воспользовавшись
известным приемом адаптивной идентификации (см.
§ 4.2):
С*<+1»=С,,гЫСЛш, /=1, 2, (5.5.14)
где
АС/, [2®i+j^+/(C|(<) Vgf (Uf+p £/, *)»
№
а входящие в эту формулу выражения определены вы¬
ше в (4.2.14) и (4.2.16). Полученные новые значения
параметров дают возможность аналогично определить
новую точку дискриминации U*+2 и т. д.
Решение о выборе модели принимается тогда, когда
имеется уверенность, что параметры моделей определе¬
ны правильно. В этом случае при
s [f, (U„ С1ЛГ) - у? < 2 [f, (иг, С2„ - у,1*
i=1 /=1
выбирается первая модель, а при обратном неравенстве
вторая. Вероятность ошибочного решения здесь оцени¬
вается по приближенной формуле
1—П с1—<5-5-15)
Р‘=т['-ф(57к)].
Ai=\h(Vi, ClN)-h(Uu Сш)\.
Несовпадение формул (5.5.12) и (5.5.15) при Uj=U свя¬
зано с приближенностью оценки (5.5.15)? При N=1 они
совпадают.
Задачи планирования дискриминирующих экспери¬
ментов имеет двойственный характер. Здесь надо одно¬
временно добиться двух целей — определить параметры
модели и выбрать наилучшую. Противоречивость этих
требований очевидна. Действительно, для эффективно¬
сти определения параметров следует точки плана распо¬
лагать на границе области планирования, а для дискри¬
минации— в точках наибольшего различия моделей. Не¬
обходим компромисс, один из которых и изложен выше.
Таким образом, этапы синтеза модели (это этапы
3—5 на схеме рис. В.4.1) заканчиваются созданием мо¬
дели F объекта управления, которая необходима для
синтеза управления всяким сложным объектом.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИЙ К ГЛАВЕ 5
Планирование экспериментов является разделом прикладной ма¬
тематической статистики и поэтому нелегко популяризуется.
Для начального ознакомления с основными идеями планирова¬
ния экспериментов можно порекомендовать очень интересную и мас¬
терски написанную научно-популярную книгу [1] и менее популяр¬
ную, но весьма насыщенную [2].
140
Термин «планирование экспериментов» имеет два содержания.
Во-первых, так называют способы организации эксперимента на реаль¬
ном объекте для определения его модели (в этом смысле этот тер¬
мин и был использован в данной книге). Однако есть и другой
смысл — планирование экстремальных экспериментов, т. е. экспери¬
ментальное определение оптимальных условий функционирования
объекта. По сути дела, это последнее направление в планировании
эксперимента является разделом теории управления объектами типа
«черного ящика», т. е. объектами, не имеющими математического
описания. С этим важным для практики направлением можно по*
знакомиться по очень доступной и весьма содержательной кни¬
ге [3].
Но задачу экспериментального определения неизвестных пара¬
метров объекта решают иначе, так как известна структура модели
объекта. По такого рода планированию эксперимента имеется ряд
очень содержательных, хотя и не вполне доступных книг (для их
чтения необходимо знать теорию вероятностей и линейную алгебру).
Отметим среди них наиболее полные [4—6], а также *[7, 8].
Всего было предложено и использовано более 100 различных
критериев планирования (по литературным данным). Они четко под¬
разделяются на два класса. К первому относятся критерии, опреде¬
ленные на дисперсионной матрице. Значения этих критериев можно
вычислять без экспериментов. Некоторые из них рассмотрены в этой
главе. Ко второму классу относятся критерии, связанные с величи¬
ной невязки выходов объекта и его модели, т. е. с адекватностью
модели. Для определения значений этих критериев необходимо иметь
результаты экспериментов с объектом.
СПИСОК ЛИТЕРАТУРЫ
1. Хургин Я. И. Да, нет или может быть... — М.: Наука, 1977.
2. Налимов В. В. Теория эксперимента. — М.: Наука, 1971.
3. Адлер Ю. П., Маркова Е. В., Грановский Ю. В. Планирование
эксперимента при поиске оптимальных условий. — М.: Наука,
1976.
А. Федоров В. В. Теория оптимального эксперимента: планирование
регрессионных экспериментов. — М.: Наука, 1971.
5. Круг Г. К., Сосулин Ю. А., Фатуев В. А. Планирование экспе¬
римента в задачах идентификации и экстраполяции. — М.: Нау¬
ка, 1977.
6. Денисов В. И. Математическое обеспечение системы ЭВМ —
экспериментатор: регрессионный и дисперсионный анализы. — М.:
Наука, 1977.
7. Планирование эксперимента в исследовании технологических про¬
цессов: Пер. с англ./ Под ред. Э. К. Лецкого. — М.: Мир, 1977.
8. Химмельблау Д. Анализ процессов статистическими методами:
Пер. с англ.— М.: Мир, 1973.
ГЛАВА 6
СИНТЕЗ УПРАВЛЕНИЯ (ПРИНЯТИЕ РЕШЕНИЯ)
Для реализации этого этапа необходимо иметь мо¬
дель объекта F(X, U), информацию о состоянии среды
X и цель управления Z*. Процедуру определения управ¬
ления U*, решающего поставленную задачу в сложив¬
шейся ситуации, называют алгоритмом управления.
Однако прежде, чем говорить об этом алгоритме, сфор-
мулируем задачу.
Ситуация, которая складывается в процессе управле¬
ния, характеризуется тройкой
Здесь с помощью управления можно изменять лишь со¬
стояние Y объекта, модель которого
имеется в нашем распоряжении. Достижение целей
управления Z*, как показано в гл. 1, эквивалентно вы¬
полнению условий (1.3.8), которые при учете того, что
S = (X, Y ) (см. (1.3.12)), сводятся к выполнению сле¬
дующих целевых соотношений:
где функции фг, и tyz, а также числа щ и bj должны
быть заданы на стадии формулировки целей управления
(см. гл. 1). Запишем эти целевые условия в канониче¬
ской векторной форме:
6.1. Постановка задачи
(X, Y, Z*}.
(6.1.1)
Y=F(X, U)
(6.1.2)
t; (X. \)=а{ (/= 1, ....
Ф/ (X, Y) 53 bj (/= 1, ...,*,), (6.1.3)
<MX,V)-min (/= 1—,
Г н (X, Y)^0,
Z*: G (X, Y) = 0,
,ц(ХЛ)-тЧ
(6.1.4)
где
G(X, Y) = (gi(XAY), Y));
H (X, Y) = (hi (X, Y), ..., hkt (X, Y)); (6.1.5)
Q(X, ?) = (?,(X, Y),..., qkt (X, Y));
причем
gi(X, Y)=*,(X,- Y)-au i= 1, ..ki\
hj{X, Y)=%(X, Y)—bh /=1, ..
#(X, Y)=o])!(X, Y), /=1, ..k3.
Введенные функции удобно называть следующим обра¬
зом G(.,.)—функция ограничений типа равенств,
Н (.,.)—функция ограничений типа неравенств и
Q (.,.)—функция качества.
Реализовать условия (6.1.4) можно только с по¬
мощью соответствующего изменения состояния Y объ¬
екта управления. Это означает, что их выполнение воз¬
можно только при соответствующем выборе управления
U (состояние X среды изменяется независимо от нас).
Эти очевидные соображения приводят к следующей
экстремальной задаче:
Q (X, Y)-*min, (6.1.6)
U^2 v ’
где
(H(x,Y)>;o,
Q: |G(X, Y) = 0,
I Y = F (X, U),
решение которой U* и является оптимальным управле¬
нием. Здесь использована модель F (6.1.2) и учтен ре¬
сурс, выделяемый на управление, — он выражен в виде
соответствующих неравенств и равенств в £2.
Рассмотрим задачу (6.1.6) подробнее. Она требует
минимизации Q путем подбора соответствующего управ¬
ления U, которое должно, кроме того, удовлетворить
условиям й. Создается впечатление, что мы как бы про-
ранжировали наши цели, причем основными названы
экстремальные цели Q, а неэкстремальные «загнаны»
в ограничения Q. Однако это лишь кажущееся ранжи¬
рование. В действительности основным является выпол¬
143
нение ограничений £2, а экстремальные цели Q являются
вторичными: они достигаются лишь при ^условии выпол¬
нения неэкстремальных целей, т. е. ограничений й.
Таким образом, задача синтеза управления (6.1.6)
характеризуется двойкой <Q, ,й> -/экстремальными и
неэкстремальными целями, причем Достижению первых
должно предшествовать выполнение вторых. Это естест¬
венное требование широко используется нами в обыден¬
ной жизни. Действительно, мы прежде всего заботимся
о том, чтобы не впасть в противоречие с ограничения¬
ми Й. Это, например, правила уличного движения, мо¬
ральный и уголовный кодекс, правила общежития, про¬
тивопожарной безопасности и т. д. И лишь при соблю¬
дении этих естественных ограничений мы выполняем
наши экстремальные цели Q (жизненный успех и удоволь¬
ствия, счастье, признание окружающих и т. д.). А тот,
кто слишком увлекается достижением экстремальных
целей Q в ущерб ограничениям й, рискует вступить
в противоречие с законами, как моральными, так и
юридическими. Рассматриваемую задачу (6.1.6) удобно
преобразовать и записать в виде
В зависимости от вида модели F, т. е. от того, явля¬
ется ли F функцией или оператором, получаем различ¬
ные задачи, которые следует решать разными методами.
Рассмотрим сначала статический объект управления,
для которого модель F является функцией. Задача син¬
теза управления в этом случае заключается в миними¬
зации k» функций qi(X, U) (/=1, ..., k$) путем измене¬
ния q параметров ..., ид, удовлетворяющих ограни¬
чениям £2, наложенным на U. Эти ограничения связаны
с выполнением условий неотрицательности и равенства
нулю заданных функций управления U. Состояние X
среды при этом предполагается, естественно, извест¬
ным.
Примером является задача планирования производства. В этом
случае U — план производства; X — поставки сырья; О — требования
Q (X, F (X, U)) —►rain,
(6.1.7)
где
(X, F(X, U))=0,
Н (X, F (X, U)) > 0.
144
к номенклатура произвбдймых изделий, со(злюденйю норм (эезоййс-
ности в процессе производства и т. д.; Н — требования к качеству
продукции (не хУже, чем), различного рода производственные нор¬
мативы (от... и до...) и ограничения (не более, чем...). В каче¬
стве экстремальныхЧцелей Q при планировании производства могут
быть, например, производительность труда, себестоимость продук¬
ции, объем ее выпуску, отклонение от плана (его надо минимизиро¬
вать) и т. д. Моделью4^ производства здесь являются рассуждения,
позволяющие определит*» состояние Y производства при известном
состоянии среды X и плаке производства U. Эти рассуждения обыч¬
но носят имитационный характер (см. § 3.5).
Таким образом, задача математического программи¬
рования, возникающая при управлении статическими
объектами, отличается тем, что искомое управление
представляет собой набор параметров щ, • • •, Щ, a Q,
G и Н являются векторными функциями управления U.
Теперь рассмотрим динамический объект, для кото¬
рого F—оператор. В этом случае управление U пред¬
ставляет собой векторную функцию времени U (t)t a qu
hi и gj являются функционалами, а задачу (6.1.7) на¬
зывают вариационной.
Примером является задача о таксисте, которому нужно с ми¬
нимальным временем пройти от одного нерегулируемого перекрестка
до другого (нерегулируемость требует остановки перед перекрест¬
ком). Уравнение движения такси, т. е. оператор f модели, имеет вид
dt2 ~^Cl dt — с2«(0»
где у -— пройденный путь, причем #(0) =*/(0) =0, т. е. старт берется
в нулевой момент времени с нулевой скоростью; сх и с2 — параметры
торможения и разгона автомашины, они определяются на стадии
идентификации (или планирования эксперимента); u(t)—скаляр¬
ное управление (q—l) ускорением движения, которое осуществляет¬
ся педалью (акселератором) и тормозом. Оно представляет собой
силу, воздействующую на машину ai^w(0^a2, где — макси¬
мальная сила торможения (зависит от качества тормозов и состоя¬
ния дорожного покрытия); а2>0 — максимальное усилие (зависит
от мощности двигателя, качества бензина и т. д.).
Пусть Т — время движения от одного перекреста до другого.
Эта величина является функционалом, значение которого опреде¬
ляется выбранным законом управления u(t). Для нахождения зна¬
чения этого функционала необходимо решить уравнение модели
с граничными условиями
*(0)-tf(0)-*<7)-0; y(T)=Lt
где L — расстояние между перекрестками. Полученное при этом зна¬
чение функционала T=T{u(t)) и является экстремальной (миними¬
зируемой) целью.
10—299
145
Теперь задачу (6.1.6) для рассматриваемого случай можно За¬
кисать в виде
Т (и (t)) -* min,
и (t) 2
Q:
flj ^ U (t) ^0>2%
'у + сгу=с2иЦ;),
У (0) = У (0) = У (7^) = 0, y(T)^L,
У (t) ^ •
Здесь к уже известным ограничениям добавлено ограничение по
скорости (а3=60 км/ч), которое предписывается правилами дорож¬
ного движения. Получаем оптимальное управление в виде функции
Рис. 6.1.1. Пример
оптимального
управления
u*(t). Решить эту задачу сложно, однако здравый смысл подсказы¬
вает оптимальное решение, которое и используется таксистами. Оно
состоит в следующем: сначала «давить на всю железку», т. е.
u(t)—a2 до момента у~аз, затем поддерживать скорость на макси¬
мально допустимом правилами уровне (из уравнения модели
получаем для этого режима и(^) == (ci/c2) аз и перед перекрестком
резко тормозить (u(t)=sai) до полной остановки, т. е. #=0.
На рис. 6.1.1 показан график этого оптимального управления
u*(t) (а) и изменение скорости при этом (б).
Как видно, задача синтеза оптимального управления u*(t) сво¬
дится к определению лишь двух моментов времени U (конца разго¬
на) и t2 (начала торможения). Заметим, что влияние среды X
(в данном случае качества дорожного покрытия) может изменить
длину тормозного пути, т. е. ai=a\(X), и максимальную скорость
движения в условиях Х> т. е. а3=а3(Х).
Полученное решение будет оптимальным для таксиста, но явно
неприемлемо для пассажира, которому придется испытывать огром¬
ные перегрузки (особенно при торможении). Поэтому в интересах
пассажира необходимо снизить перегрузки до приемлемого уровня
я*1 >01 (напомним, что это отрицательные величины). Здесь значе¬
ние а* 1 определяется комфортными условиями для пассажира.
146
Управление динамическим объектом, таким образом,
сводится к решению вариационной задачи (6.1.6), в ко¬
торой искомое управление представляет собой функцию
времени U=U(/)‘, a Q, G и Н являются, вообще говоря,
заданными функционалами управления U(/).
Очевидно, что эта задача значительно сложнее за¬
дачи математического программирования. Поэтому ре¬
шение вариационной задачи с произвольными функцио¬
налами обычно сводят к решению задач математиче¬
ского программирования. Для этого достаточно параме¬
тризовать функцию управления U(0-
Сделать это можно двумя способами:
1) путем разложения U(f) в ряд по заданной систе¬
ме функций {Ф{(0}:
U(/) = 2 CM),
i=\
что приводит к задаче отыскания параметров, 'с и . ..., ck.
Этот подход называют параметрическим;
2) представление функции U (t) ее дискретами Ci,...
..Сь в заданные моменты времени, где С* = и(/*) (i=
=1, ..., k)—новые искомые параметры управления;
этот подход обычно называют непараметрическим, хотя
искомые параметры здесь тоже имеются.
В обоих случаях, подставляя эти выражения в (6.1.7),
получаем после очевидных преобразований задачу ма¬
тематического программирования вида
Q(X,U)-*min,
lies
Q:|0(X,U)=0,
где U=(Ci, ..., Сь) —вектор искомых параметров, a Q,
G и Н — определенные векторные функции этих пара¬
метров.
Таким образом, в конечном счете решение любой за¬
дачи синтеза управления сводится к решению задачи
математического программирования. Рассмотрим раз¬
личные трпы задач такого рода,
W 147
6.2. Классификация задач математического
программирования
Вид и число функций Q, G и Н определяют различ¬
ные типы задач математического программирования,
а следовательно, и методы их решения (для этого и
вводится классификация). В зависимости от числа &з
минимизируемых функций qi (1= 1, ..., k3) различают
однокритериальные (при &з=1) и многокритериальные
(при к3>1) задачи. В последнем случае их иногда назы¬
вают задачами векторной оптимизации (задачами опти¬
мизации с векторным критерием). Спецификой много¬
критериальной задачи математического программирова¬
ния является необходимость введения дополнительной
информации об объекте и критериях, без чего эта зада¬
ча не имеет решения. Методы решения многокритери¬
альных задач рассмотрены в приложении.
Далее будем рассматривать лишь однокритериаль¬
ные задачи (63=1), для которых Q — скалярная функ¬
ция, т. е. Q=Q.
В зависимости от вида и характера функций Q, G и
Н различают следующие задачи математического про¬
граммирования.
1. Если Q, G и Н линейны по U, то имеем задачу
линейного программирования:
1
(2(Ц) = 5ч >-min, (6.2.1)
iZi ues
ч
' 2 aikuk=c0 i= 1, ..., K<q,
*=i '
<7
k=\
где Q:
Здесь параметры ai, аш, bjk, dj и Ci определяются фак¬
торами среды X и объекта F.
Процесс решения задачи линейного программирова¬
ния естественно ориентировать на линейность выраже¬
ний (6.2.1), что реализуется так называемым симплекс¬
ным методом, который применим только для решения
задач такого рода.
Задача об оптимальном коктейле, рассмотренная вы¬
ше (см. § В.5), являлась задачей линейного програ^мц-
>148
рования. Другим примером такого рода задач является
задача об оптимальной смеси. Рассмотрим ее.
Пример. Из q видов исходного сырья Аь Аг, ..А-д, каждый из
которых состоит из п компонентов
(здесь ciik — относительное содержание i- го компонента в k-м
сырье), необходимо составить смесь заданного состава: Ci, ..., сп>
где d — относительное содержание /-го компонента в смеси.
Смесь характеризуется вектором состава U=(wi, ..uq), где
мость сырья определяется ценами: аь ..aq, где щ — стоимость еди- .
ницы /-го сырья (/=1, ..q). Стоимость единицы смеси при этом
должна быть минимальной.
Задача, таким образом, сводится к минимизации линейной функ¬
ции стоимости смеси:
где множество Q допустимых значений состава U определяется
требованиями, налагаемыми на состав смеси:
Здесь последнее неравенство и^О выражает очевидное требование,
связанное с тем, что количество сырья в смеси не может быть отри¬
цательным. Как видно, ограничения Q здесь состоят из п равенств
(G) и q неравенств (Н), причем n<q (при n=q задача вырож¬
дается в неэкстремальную). Это типичная задача линейного про¬
граммирования.
Методы решения задач линейного программирования
рассмотрены в § 6.4.
2. Другой вид задач математического программиро¬
вания — задачи выпуклого программирования, они имеют
более общий характер и формулируются следующим
образом.
Необходимо минимизировать выпуклую вниз функ¬
цию
Uk — относительное количество k-vo сырья
Стои-
я
О.) 2 allPk= сь * = I п,
| ft=!
/5=1,..., q.
Ue
(6.2.2)
149
где область Q допустимых состояний задается системой
неравенств
Q:/ti(U)S50, i=l, кг. (6.2.3)
Здесь Ai(U) —выпуклые вниз функции, что гарантирует
выпуклость области й.
Заметим, что функция f(X) называется выпуклой
вниз, если отрезок, соединяющий две любые точки этой
функции, лежит выше ее значений (рис. 6.2.1). Формаль¬
но это определение можно записать в следующем виде.
Рис. 6.2.1. К определению выпуклой
функции
Если для любой точки X; лежащей между точками Xj и
Х2, т. е. при
Х=ЯХ!+(1—Я)Х2, 0<^1, (6.2.4)
выполняется неравенство
' f(X)^f(X1) + (l-^)f(X2), (6.2.5)
то эта функция выпукла вниз. Как легко убедиться, пра¬
вая часть неравенства (6.2.5) является линейной ап¬
проксимацией функции f(X) по двум ее значениям в точ¬
ках Xi и Х2 (см. прямую на рис. 6.2.1).
Выпуклой областью £2 принято называть множество
точек, обладающих следующим свойством. Если взять
две любые точки этого множества, то отрезок прямой,
соединяющий эти точки, тоже должен принадлежать это¬
му множеству. Формально: если Xi, Х2&й, то Хей,
где точка X определена (6.2.4) как точка между
Xj и Х2.
Выпуклые функции представляют собой довольно
широкий класс функций и сравнительно хорошо могут
описывать задачи (6.1.7) синтеза управления.
Существенной особенностью задачи выпуклого про¬
граммирования является ее локальность, т. е. наличие
одного экстремума. Это означает, что при решении за¬
дач выпуклого программирования можно довольство¬
ваться отысканием локального экстремума, Свойства
160
бУпукЛосТй Минимизируемой функции Q и области й
используются при решении задач выпуклого програм¬
мирования. Заметим, что задачи линейного программи¬
рования являются частным случаем выпуклого програм¬
мирования. В этом случае легко убедиться, так как
любая линейная функция удовлетворяет условиям вы¬
пуклости. Метод решения задач выпуклого программи¬
рования описан в § 6.4.
3. Требования выпуклости далеко не всегда выпол¬
няются в задачах синтеза управления. В общем случае,
когда Q, G, Н являются произвольными нелинейными
функциями, решается задача нелинейного программиро¬
вания.
Это весьма общий вид, математического программи¬
рования. Здесь, вообще говоря, нельзя гарантировать
совпадение локального и глобального экстремумов, что
часто создает серьезные трудности при решении такого
рода задач, которые в этом случае относятся к классу
многоэкстремальных. Однако даже при одноэкстремаль-
ности задачи специальных математических методов ре¬
шения задач нелинейного программирования не сущест¬
вует. Все применяемые для этого методы являются
поисковыми методами оптимизации (некоторые из них
рассмотрены в приложении).
Типичным примером задачи нелинейного программи¬
рования могут служить задачи оптимального проекти¬
рования. При проектировании новых схем, конструкции
и систем всегда определена экстремальная цель, напри¬
мер эффективность, надежность, быстродействие, масса
конструкции и т. д. Оптимальное проектирование пред¬
ставляет собой процесс определения параметров щ, ...
..., uq конструкции, которые экстремизируют эту цель,
но не произвольно, а при соблюдении определенных
ограничений. Вид ограничений связан со строгим выпол¬
нением ряда требований. Например, необходимо исполь¬
зовать элементы конструкции определенного вида. Это—
ограничение типа равенств. Другие ограничения имеют
характер неравенств. Например, температура и возни¬
кающие напряжения не должны превышать заданных
пределов норм и т. д. Таким образом, задачи оптималь¬
ного проектирования являются типичными задачами не¬
линейного программирования, так как ограничения и
функция качества имеют обычно ярко выраженный не¬
линейный характер.
151
4. Очень часто управление (J является дискретный,
т. е. множество допустимых управлений Q конечно и
дискретно. Например, если компоненты вектора управ¬
ления Ui (i= 1, ..., q) могут принимать только целочис¬
ленные значения, в этом случае решается задача це¬
лочисленного программирования.
Пример. Задачей целочисленного программирования может слу¬
жить задача управления системой, состоящей из взаимодействующих
агрегатов, каждый i-й агрегат может либо работать (щ = 1), либо
не работать (г/г = 0). Эффективность работы этой системы Q(U)
должна быть максимизирована при заданном энергетическом ресур¬
се R:
Q (U) шах,
U €=2
\ui = {0; 1}, / = 1, .... q%
где — затраты на функционирование i-то агрегата.
Если в простейшем случае агрегаты не взаимодействуют, то
я
Q(U) = 2 Мм
(=1
где bi — эффективность работы i-го агрегата.
В результате получаем целочисленную задачу линейного про¬
граммирования.
Решение задач такого рода иногда представляет
серьезные трудности. Они будут рассмотрены в § 6.4.
5. Если Q, G и Н являются вероятностными характе¬
ристиками, то решается задача стохастического програм¬
мирования.
Напомним, что наиболее распространенными вероят¬
ностными характеристиками являются:
вероятность
p(X)dX, (6.2.6)
математическое ожидание
М (X) = j Хр (X) dX, (6.2.7)
дисперсия
D(X) — j [Х — М (X)]* р (X)dX (6.2.8)
152
и т. д., где р(Х)—плотность распределения случайного
фактора X, а интеграл многократный: он имеет крат¬
ность, равную размерности вектора X.
Примером задачи стохастического программирования
является осреднение исходной задачи (6.1.8) по случай¬
ному состоянию X среды, т. е. когда эту задачу необ¬
ходимо решать в среднем. Тогда (6.1.8) преобразуется
к виду
0(11)—* min,
ues
qJg(U)=°,
1h(U)^0,
где
Q(U)= jQ(X, U)A(X)dX; G(U) = jG(X, U)/;(X)dX
H (U)= JH(X, U)/7(X)dX,
p(X)—известная плотность распределения состояния X
среды. Эта функция п переменных Хи ..хп — входов
объекта с естественными ограничениями вида
/>(Х)> О, J/>(X)dX=l.
Интеграл здесь и выше является я-кратным и берется
по всему пространству входов {X}.
Как видно, решение задачи стохастического програм¬
мирования сводится к определению вероятностных ха¬
рактеристик, т. е. к вычислению многократных интегра¬
лов вида
J=ff(X,U)p(X)dX, (6.2.9)
что само по себе представляет серьезную вычислитель¬
ную задачу. Однако эту трудность можно преодолеть,
если воспользоваться для / его оценкой по методу Мон¬
те-Карло:
N
7лг=-ж5]№’и>* (62Л°)
/=1
где Х{ (/=1, ..., N) —независимые случайные векторы,
генерируемые в соответствии с заданной плотностью
153
распределения /?(Х). Действительно, J является средним-
значением функции /:
J = Mxf{X, U),
где Мх— математическое ожидание по X. Но выражение
(6.2.10) является оценкой этого среднего значения на
базе N, поэтому может служить приближенным значе¬
нием (6.2.9). I
Оценка (6.2.10), полученная методом Монте-Карло,
является случайной величиной и характеризуется сле¬
дующими вероятностными свойствами. Ее среднее зна¬
чение совпадает с /: М (fN) =/, т. е. оценка TN несмещен¬
ная, и в пределе Нт/^=/^, т. е. оценка состоятельная,
N-*oo '
а ее дисперсия D(fN) =c/N, где с — постоянная. Это
означает, что оценка, полученная методом Монте-Карло,
«хорошая», т. е. в среднем при любом N совпадает с ис¬
комой.
Эти свойства дают возможность записать выражение
для связи оценки и точного значения в виде
TN=J + e(clN), (6.2.11)
где e(c/N)—случайная величина с нулевым средним
и дисперсией c/N.
Выражение (6.2.11) означает, что оценка, полученная
методом Монте-Карло, отличается от точного ее значе¬
ния на случайную величину, в среднем равную нулю,
дисперсия которой уменьшается с ростом N как 1/N.
Это позволяет интерпретировать JN как результат
вычисления J со случайной помехой, которая обуслов¬
лена способом вычисления. Поэтому задачу стохастиче¬
ского программирования можно записать в стандартной
форме (6.1.8), где, однако, на каждую из используемых
функций в процессе решения налагается случайная по¬
меха, свойства которой, вообще говоря, могут быть не¬
известны. Решение подобной задачи представляет есте¬
ственные трудности, которые могут быть преодолены при
использовании поисковых методов типа стохастической
аппроксимации (см. приложение),
154
6.3. Анализ задач матёматйчёскбго
программирования
Основным методом решения задач математического
программирования является так называемый рекуррент¬
ный метод. Он заключается в построении последователь¬
ности приближенных решений задачи
Uo, Ui, Ujv, . (6.3.1)
которая обладает следующими важными свойствами:
1) каждый последующий член этой последовательно¬
сти в определенном смысле (с точки зрения решения
задачи) предпочтительней предыдущего, т. е. UN+i^>UNf
где >>— знак предпочтения;
2) эта последовательность при больших N прибли¬
жается к значению U*; которое может рассматриваться
как решение задачи. Следует отметить, что точного реше¬
ния задачи математического программирования получать
обычно не требуется, так как исходные данные в задаче
всегда приближенны. Поэтому речь может идти о при¬
ближении к рациональному решению. И лишь в частном
случае U* может быть точным решением задачи.
Рассмотрим способы формального определения ука¬
занного предпочтения. Это можно сделать различными
способами. Приведем примеры введения очевидных
предпочтений.
1. Ujv-н Ujv, если Ujv, Ujv+i&Q и Q (Ujv+i) <Q (^n) >
т. e. из допустимых решений (тех, которые удовлет¬
воряют £2) лучше то, которое дает меньшее зна¬
чение функции качества Q(U).
2. Если же Q(Un+i)=Q(Un) и Ujy+ь UjvOQ, то
Ujv+iooUjv, т. е. решения эквивалентны (счэ—знак экви¬
валентности).
3. Ujv+i)>Ujv, если Ujv+i^Q, a т. е. более
предпочтительным всегда является допустимое решение.
Этот список можно было бы продолжить. Однако
задание предпочтений не решает полностью задачу син¬
теза алгоритма решения поставленной задачи в любой
ситуации, сложившейся в процессе управления. Описан¬
ные выше предпочтения, как легко заметить, описывают
далеко не все ситуации, которые могут возникнуть при
управлении объектом. Эту задачу выполняет алгоритм.
Таким алгоритмом решения задачи математического
155
программирования будем называть оператор ср, связы¬
вающий последующие решения:
Ujv=Ujv-i+<p (/j\r, Un-u Qn-u Hjv-i).
Здесь <p — алгоритм, предписывающий, как должно из¬
мениться управление при имеющихся значениях Ujv_i,
Qjv_i=Q (Ujy-i) , Gjv—i=G (Uiv--0, Hjv-i=H (Ujv-i) и полу¬
ченной дополнительной информации In (все это и есть
сложившаяся в процессе управления ситуация).
Рис. 6.3.1. Область допустимых управлений:
а — общий случай; б — ограничения типа равенств; в — образование Q с по¬
мощью неравенств
Рассмотрим пространство решений {U}. В этом про¬
странстве условия Й выделяют определенную область
допустимых решений Чей (рис. 6.3.1,а). Размерность
области 'Q равна q—ku так как каждое ограничение —
равенство gi(U)=0 — уменьшает размерность задачи на
единицу (рис. 6.3.1,6). Ограничения типа неравенства
hj(U)^0 очерчивают границы области допустимых ре¬
шений й (рис. 6.3,1,в).
Как видно, решаемая задача однозначно определяет¬
ся областью й и скалярной функцией качества Q(U).
Эта функция образует в й скалярное поле, которое удоб¬
но в случае q—2 характеризовать линиями равного
уровня минимизируемой функции. Уравнения этих ли¬
ний
Q(U)=c=const (6.3.2)
получаем при различных значениях параметра с. Легко
заметить, что линии равного уровня на плоскости управ¬
ляемых параметров {«i, ыг} представляют собой аналог
156
топографических линий равного уровня (например, наД
уровнем моря) на географической карте. Именно поэто¬
му топографическая терминология используется при
описании задач оптимизации. Такими топографическими
терминами, широко применяемыми в теории и практике
оптимизации, являются: «линии равного уровня» (6.3.2),
которые образуют «рельеф» функции Q(U), причем
рельеф может быть разнообразным: «яма», «котлови¬
на», «впадина» (рис. 6.3.2,а), «холм» или «вершина»
с? с3
Рис. 6.3.2. Примеры «рельефов» функции качества (ci<c2<c3 ...)
(рис. 6.3.2,б), «овраг» или «щель» (рис. 6.3.2,в), «хре¬
бет» (рис. 6.3.2,г), «перевал» или «седло» (рис. 6.3.2,д),
«плоскогорье» и т. д. Эта аналогия распространяется
и на процесс решения оптимизационной задачи. Так,
движение в направлении уменьшения функции качества
называют «спуском», в направлении увеличения —
«подъемом».
Естественно, что эту наглядную аналогию можно ис¬
пользовать и для многомерных задач оптимизации при
q>2. В этом случае при q=3 линии равного уровня
становятся поверхностями, а при q>3 — гиперповерхно¬
стями равного уровня. Теперь рекуррентный процесс ре-
157
шеиия задачи матем&тмчебкбгб программирования мож¬
но представить как движение в ^-мерном пространстве
{U} от точки к точке в последовательности (6.3.1)
(рис. 6.3.3).
Решение задач математического программирования
можно осуществить по-разному. Можно использовать
априорные сведения о структуре функций Q, Н и С, т. е.
построить алгоритмы, учитывающие специфику этих
Рис. 6.3.3. Пример траектории решения задачи математического про¬
граммирования (Cl>C2>C3 ...)
функций, специальными методами (некоторые из них бу¬
дут рассмотрены в следующем параграфе). Но для
сложных объектов управления эту специфику выяснить
и учесть очень трудно и проще поступить иначе — орга¬
низовать процесс поиска решения U*, используя лишь
значения функций, а не сведения об их структуре. Та¬
кой подход называют поисковым методом оптимизации.
Он имеет универсальный характер. Некоторые наиболее
распространенные методы поисковой оптимизации опи¬
саны в приложении. Здесь же рассмотрим, каким обра¬
зом априорные сведения о задаче могут быть «заложены»
в алгоритме ее решения.
6.4. Некоторые специальные методы решения
задач математического программирования
Рассмотрим некоторые методы, используемые при ре¬
шении задач математического программирования. Осо¬
бенности этих методов обусловлены прежде всего спе¬
цификой структуры функций Q, G и Н.
158
Симплексный метод. Этот метод решения задач ли¬
нейного программирования, для которых функции Q, G,
Н линейны по U:
Q(U) = 5i aiut~+ min’ (6.4.1)
/—1 ^ S &
где
ч ^
Q: 2 bjkuk>Cj, /= 1, ..k2.
k=\
Эта запись отличается от (6.2.1), где еще есть ограни¬
чения типа равенств. Однако ввиду линейности их легко
исключить, уменьшив тем самым число независимых пе¬
ременных. С другой стороны, от ограничений типа ра¬
венств легко избавиться формальным образом, заменив
*(Uj=0 двумя: qi(U)^О и —qt(U)5*0. Будем считать,
что одна из этих операций проделана и задача линейно¬
го программирования приобрела вид (6.4.1).
Число ограничений, образующих область допустимых
решений £2 в задачах линейного программирования,
всегда должно превышать число переменных, т. е.
k2>q, (6.4.2)
иначе задача, вообще говоря, может не иметь решения.
Заметим, что обычно q из них имеют вид
0, /= 1, ..., q, (6.4.3)
т. е. решение ищется в положительном квадранте (это
связано с физическим смыслом переменных: щ — обыч¬
но количество). Введем обозначение
Aj=Ay(U) = 2 bjkUk ^/> • • •> (6.4.4)
*=i
Тогда уравнение области Q можно записать в стандарт¬
ном виде
Q : hj=hj{V)>0, /= 1, ..., fe. (6.4.5)
Легко заметить, что область представляет собой выпук¬
лый многогранник. Действительно, каждое из условий
hj (U)^0 определяет полупространство. Пересечение
всех этих полупространств может быть только или вы¬
пуклым, или пустым (при противоречивых условиях)
159
многогранником. На рис. 6.4.1 показан пример образо¬
вания такого выпуклого многогранника для q=2.
Решение задачи линейного программирования
(6.4.1) в силу линейности Q(U) лежит на поверхности
этого многогранника. Действительно, оно не может на¬
ходиться внутри его, так как в этом случае можно бы¬
ло бы снять ограничения Q. Но тогда U*->-oo в силу
линейности Q(U), поэтому
U*GQ,
(6.4.6)
где Q — граница многогранника й. Далее легко видеть,
что решение всегда лежит на одной из вершин этого
многогранника' или на грани.
В последнем случае любая точ¬
ка этой грани, в том числе и ее
вершины, в силу линейности
функции 'Q(U) может считать¬
ся решением задачи (6.4.1).
Поэтому для решения задачи
достаточно рассмотреть только
вершины многогранника Q.
И последнее, так как каж¬
дая вершина многогранника Q
определяется в общем случае q
из ограничений (6.4.5), то
в каждой вершине q ограниче¬
ний из (6.4.5) будут равны ну¬
лю, а остальные — положитель¬
ны (точнее, неотрицательны).
Рис. 6.4.1. Пример образо¬
вания выпуклого много¬
гранника Q в задаче линей¬
ного программирования
Это позволяет все вершины кодировать вектором
(6.4.7)
составляющие которого равны значениям ограничений
(6.4.5) в этой вершине. При этом вектор (6.4.7) имеет
по крайней мере q нулевых компонент, а остальные со¬
ставляющие положительны.
Например, для случая, показанного на рис. 6,4.1, по¬
лучаем следующие коды вершин А,...,Е:
Нд—(0, 0, ft,, ft4, ht),
НВ=(А,, О, О, ft4, As),
160
Hg=(0, hv ft,, hy 0).
Симплексный метод решения задачи линейного про¬
граммирования заключается в переходе по граням мно¬
гогранника Q в соседние (смежные) вершины, где зна¬
чение функции качества Q меньше, чем в исходной вер¬
шине. Алгоритм симплексного метода сводится к сле¬
дующим операциям на каждом шаге.
1. Определить все вершины 1^г) (i*= 1, ..., kN)9 смеж¬
ные с исходной на N-ш шаге, вершиной Un (здесь kN—
число вершин, смежных с Ujv).
2. Выбрать из них ту, в которой значение функции
качества минимально:
Q(<)= min Q(U^).
/ = 1, ...» ktf
3. Перейти в эту вершину, т. е.
и =и(/)
Л/Ц-1 ♦
и затем перейти к следующему (N+1)'му шагу, т. е.
искать вершины, смежные с Un+u и т. д. (см. п. 1). Ра¬
бота алгоритма заканчивается, если среди всех вершин,
смежных с \JNy не найдется ни одной с меньшим значе¬
нием функции качества, чем в исходной. В этом случае
U* = Uiv. Основная трудность симплексного метода за¬
ключается в определении смежных вершин. Эту труд¬
ность позволяют преодолеть так называемые симплекс-
таблицы, о которых можно прочесть в любом руковод¬
стве по линейному программированию (см. коммента¬
рий к этой главе).
Метод возможных направлений. Этот метод использу¬
ется для решения задач выпуклого программирования
вида
Q(U)*->min, (6.4.8)
UeS
где
Q:MU)^o, /=1.
Q(U) и ftj(U)—выпуклые вниз функции, обладающие
свойством (6.2.5). Область Q при этом выпукла
(рис. 6.4.2), так как пересечение выпуклых областей об¬
разует выпуклую область.
Решение задачи (6.4.8), вообще говоря, может на¬
ходиться как внутри области £2, так и на ее границе.
11—299
161
Введем понятие возможного направления. Пусть
Ujv — некоторая точка, принадлежащая £2(UjveQ). Тог¬
да возможное направление определяется таким векто¬
ром Y, вдоль которого функция качества Q(U) умень¬
шается без нарушения ограничений й, т. е.
Q(Uw + aY)<Q(Uw),- (6.4.9)
где Uy + aYeQ и а>0 мало.
Решение задачи определения возможного направле¬
ния Y и составляет основную трудность реализации это-
-P47SV
h(U)
Рис. 6.4.2. Пример области,
образованной выпуклыми
вниз ограничениями
Рис. 6.4.3. Пример области, для
которой антиградиентное на¬
правление не является воз¬
можным
го метода. Если исходная точка liN находится внутри
области Q (т. е. не на ее границе), лучшим является
антиградиентное направление
Y=—VQ(U.n).
Если же Ujv лежит на границе области й, антигради¬
ентное направление—VQ(Ujv) может оказаться невоз¬
можным (рис. 6.4.3, где Vh— вектор градиента ограни¬
чений Л (0)^0 в точке Ujv). Как хорошо видно, для
возможного направления Y необходимо, чтобы углы cpt
и <рг, образуемые им с векторами—VQ(UW) и Vh(VN)
были бы меньше я/2, т. е. ф{<я/2 (г=1, 2). Этому-усло¬
вию всегда можно удовлетворить, если направления век¬
торов —VQ и Vh не противоположны.
Можно потребовать и большего. Так как возможных
направлений Y существует целый набор, то естественно
выбрать из них одно, в каком-то смысле оптимальное.
Таким направлением Y* будет то, при движении по ко¬
162
торому функция качества Q(U) уменьшается наиболее
интенсивно, т. е. угол cpi минимален, и одновременно
происходит наиболее быстрое удаление от ограничения
A(U)=0, т. е. угол ф2 тоже минимален. Э.ти противоре¬
чивые требования (так как сумма Ф1+Ф2, как видно из
рис. 6.4.3, постоянна) можно удовлетворить, решив соот¬
ветствующую задачу линейного программирования (см.
руководство по выпуклому программированию в коммен¬
тариях к этой главе).
Рис. 6.4.4. К опре¬
делению величины
коэффициента а'*
После определения оптимального возможного на¬
правления Y* следует организовать спуск вдоль этого
направления, т. е. определить такое значение а* в U=
==Ujv*f a*Y, более которого а увеличить нельзя, так как
при этом либо начинает увеличиваться функция качест¬
ва Q(U), либо нарушается одно из ограничений
hj(U)^0 ( /=1, ..., fe). Для этого следует решить за¬
дачи
Q (U„ + a\*) — min гф a'0 > 0, (6.4.10)
a>0
Ay(Uw + aY*) = 0^a'/>0,/=l k2,
и выбрать из всех a'j (/=0, ..., £2) наименьшее:
a*= min a', = a',. (6.4.11)
/=0
Необходимость такого выбора хорошо видна из при¬
мера, приведенного на рис. 6.4.4, где a'0>a'/.
На этом заканчивается ^-й этап решения задачи вы¬
пуклого программирования Uw+i=Uw+a*Y*, и следует
обратиться к следующему (7V+ 1)-му, на котором для
определения возможного направления необходимо вы¬
числять градиент 1-го ограничения (6.4.11).
П*
163
Методы решения задач целочисленного программиро¬
вания. Рассмотрим методы решения задач целочисленно¬
го программирования
Q(U)-> min =>U*d, (6.4.12)
US2„
hj (U) > 0, /= 1, ..., kt,
uf^}, i=\, ..., q,
где U — конечное число дискретных значений, которые
может принимать i-й компонент вектора управления
U=(mi, ..., щ). Как видно, множество Q допустимых
ч
значений управления U конечно и имеетД/г элементов,
i=i
что при больших k или q исключает возможность пол¬
ного перебора, т. е. решения задачи (6.4.12) «в лоб».
Поэтому рассмотрим иные методы. Пусть для опреде¬
ленности «,^{1, • • •. U}-
Простейшим методом является решение непрерывной
задачи
Q(U)-+min=>U*,
Uefi!
0:ЛДи»0, i=l, ..кг,
которая получается из (6.4.12) путем снятия ограниче¬
ния на целочисленность компонентов вектора U, и выбор
в ближайшей окрестности полученного решения U*
целочисленного вектора М'л, удовлетворяющего ограни¬
чениям Q при минимальном значении функции качест¬
ва Q. Для этого следует сначала найти ближайшую це¬
лочисленную точку, округлив до целого ее координаты
(например, 2,1-»-2; 3,8-»-4), и проверить выполнение
ограничений. Если ограничения выполняются, то эту
точку и называют решением задачи целочисленного про¬
граммирования, т. е. U'd=U*d (пример такой точки по¬
казан на рис. 6.4.5,а). Если же ближайшая целочислен¬
ная точка U'd окажется вне допустимой области Q, т. е.
U'd(£Q (этот случай показан на рис. 6.4.5,б), то следу¬
ет рассмотреть ее целочисленную окрестность (она очер¬
чена штрихами на рис. 6.4.5,б), содержащую 3«—1 то¬
чек. Из этих точек прежде всего следует выделить под¬
164
множество тех, которые удовлетворяют ограничениям
Й. Пусть это будут точки Ui, ..1Л. Тогда выбор одной
из них U*d производится по минимальному значению
функции качества, т. е.
Q(U*d)=min Q (Uj).
г = 1, .... k
Однако этот способ далеко не всегда приводит к точ¬
ному решению. Такой случай показан на рис. 6.4.5,в, где*
решение целочисленной задачи лежит в точке А, а не
Рис. 6.4.5. Примеры задач цело¬
численного программирования:
а, б — непрерывный подход; в — иллю¬
страция недостатков непрерывного под¬
хода
в В,< полученной изложенным методом (здесь параллель¬
ными линиями обозначены линии равного уровня). Это
обстоятельство заставляет воспользоваться другими ме¬
тодами решения задач целочисленного программирова¬
ния. Рассмотрим два из них.
Прямой поиск опирается на идею дискретного слу¬
чайного поиска, в процессе которого движение происхо¬
дит по целочисленным точкам допустимой области Q.
Пусть \JN — некоторая целочисленная точка в Q. Про¬
цесс случайного дискретного поиска заключается в том,
165
что случайно определяется точка целочисленного окру¬
жения Ujv
u»=u„+s,
где 2= (£ь ..lq)—случайный целочисленный вектор
с компонентами, принимающими независимо и равнове¬
роятно одно из трех значений 0; —1}. Если
значение функции качества Q в точке оказалось
меньше, чем в исходной точке Ujv, то Uiv+i=U^. В про¬
тивном случае (при неудачном шаге) определяется дру¬
гой случайный вектор 2 и снова проверяются условия
уменьшения функции качества. Таким образом, алго¬
ритм дискретного случайного поиска можно записать
в виде
"+l (U,, если Q(U„ + E)>Q(U,.).
Как видно, этим осуществляется случайный перебор
целочисленного окружения исходной точки до тех пор,
пока не будет найдена точка с меньшим значением
функции качества, чем у исходной. Заметим, что ввиду
конечности множества случайных векторов {S} при не¬
удачном шаге целесообразно исключать из дальнейшего
рассмотрения на этом этапе те вектора S, которые уже
были. При этом за счет исключения ненужных повторе¬
ний повышается эффективность поиска.
Для задач дискретного выпуклого программирова¬
ния, когда 'Q(U) и H(U) —выпуклые функции, этот ме¬
тод сходится, т. е. неизбежно приводит к решению по¬
ставленной задачи UV
Обратный поиск связан с движением из точки М'л,
ближайшей к U* из допустимых, т. е. принадлежащих
области Q. Рассмотрим дискретное окружение этой точ¬
ки, состоящее из 3?—1 точек. Определяя все допустимые
(т. е. принадлежащие Q) точки, следует из них выбрать
ту, в которой значение функции качества Q минималь¬
но. Если это наименьшее значение окажется больше,
чем в исходной точке М'а, то естественно считать U'd ре¬
шением задачи. Если же меньше, то следует рассмотреть
целочисленную окрестность этой новой точки.
Обратный поиск решает задачи дискретного выпук¬
лого программирования так же успешно, как и прямой.
166
Однако для его осуществления требуется предваритель¬
но решить непрерывную задачу. Обратный поиск от пря¬
мого отличается полным перебором окрестности каждой
точки, претендующей на оптимум. Но таких полных пе¬
реборов при обратном поиске будет значительно мень¬
ше, чем случайных переборов при прямом поиске.
В сложных случаях можно рекомендовать оба мето¬
да и выбрать то решение, которое имеет наименьшее
значение функции качества.
6.5. Некоторые специальные методы решения
вариационных задач
В § 6.1 показано, как задачу синтеза управления
динамическим объектом можно свести к задаче матема¬
тического программирования (6.1.8). Для этого доста¬
точно представить искомое управление U(^) в виде на¬
бора дискрет:
Vi=U(ti) i=l, ..., А,
определение которых можно осуществить, решив ука¬
занную задачу математического программирования от¬
носительно векторных параметров Ui, ..., U& (всего при
этом приходится определять kq значений параметров,
образующих оптимальное управление).
Однако при этом подходе получается, как правило,
очень сложная многоэкстремальная задача математиче¬
ского программирования, решение которой обычно вы¬
зывает большие трудности. Именно поэтому для реше¬
ния вариационных задач часто удобнее применять спе¬
циальные методы, два из которых мы рассмотрим ниже.
Принцип максимума. Этот метод.применяется для ди¬
намических объектов, модель которых может быть запи¬
сана в виде системы обыкновенных дифференциальных
уравнений
iji=h(Уи ■ • Ут, u(t)), 1=1, т, (6.5.1)
с заданными начальными условиями при t=О г/<(0)=гД
(/=1, ..., т) и скалярным управлением. Удобно систе¬
му (6.5.1) записать в векторной форме:
Y = F(Y, u(t)),
где Y(<t) = {у\(t),..., ym(t)) —вектор переменных задачи,
a F=(/'i, ..fm)—вектор заданных функций, которые
определяют модель объекта.
167
Необходимо решить следующую задачу: перевести
объект из состояния Y0=(yi(0), ..., Ут(0)) в заданное
состояние
(6.5.2)
причем траектория Y(^) и управление u(t) должны быть
такими, чтобы удовлетворить заданным ограничениям
и экстремальной цели — минимуму заданного функцио¬
нала
где u(t)) —заданная функция. В качестве тако¬
го функционала обычно выбирают всякого рода затраты
на процесс управления. При /0 (*) = 1 получаем Q=T —
время перехода объекта из состояния Y0 в Y*.
Примером типичной задачи такого рода является за¬
дача крановщика. Нужно переместить тяжелый груз из
одной точки в другую за минимальное время. Кранов¬
щик располагает троичным управлением и={—1; 0; 1},
т. е. кран может двигаться в одну (и=—1) или другую
(и= 1) сторону и остановиться (гг=0). Неопытный кра¬
новщик тем и отличается, что обычно раскачивает груз
и долго не может его «успокоить». Оптимальное управ¬
ление u*(ti) позволяет ему за минимальное время Т
остановить груз точно в заданной точке Y*.
Таким образом, поставленная вариационная задача
формулируется в виде
где hj(-)—заданные функции ограничений типа нера¬
венств. Заметим, что в формулировке (6.5.4) не оговоре¬
ны граничные условия (6.5.2): они появятся позже.
А пока сформулирована задача о переводе объекта в ка¬
кое-то, (пока!) не интересующее нас состояние Y(Г).
т
Q(u(t))=ff,(Y(f),u(t))dt, (6.5.3)
о
(6.5.4)
'Ay(Y(0. u(Q)> 0, 1=1, ..., kv
\y,=f,(Y(f). u(t)), i= 1 m,
Hi (°) = «/V
168
Принцип максимума позволяет задачу (6.5.4) свести
к задаче максимизации так называемой функции Га¬
мильтона:
г(и(0)=2 МШт “(0)- max (6.5.5>
iZ о «кое»'
при ограничениях
Q':h}(Y(t), u(t))>0, i= I, ..„hi, (6.5.6)
где функции ,фг(0 определяют из решения системы
2т+ 1 дифференциальных уравнений вида
dfj(Y (<), u(t))
dyi
/=о
yi=fiW{t)> “Ш i= •••> т (6.5.7)
с начальными условиями
УзФ)=У°з> /=1, . ••> т9 (6.5.8)
г1)г(0)=й, i=0, ..., т.
Эта задача интересна тем, что максимизация может про¬
изводиться в каждый момент времени t, так как Г(гг(£))
не функционал, а функция и задача максимизации одно¬
мерная по параметру управления и. При этом миними¬
зируемая функция изменяется определенным образом во
времени [см. (6.5.7)] при ограничениях (6.5.6), причем
минимизацию следует осуществлять в каждый момент
времени t.
Решение этой задачи при заданных начальных усло¬
виях (6.5.8) не представляет труда. Действительно, ре¬
шение сводится к интегрированию системы дифферен¬
циальных уравнений (6.5.7) и решению задачи одномер¬
ной оптимизации (6.5.5) на каждом шаге интегрирова¬
ния (например, методом золотого сечения, описанным
в приложении).
Теперь рассмотрим вопрос о попадании в заданную
точку Y*. Очевидно, что состояние Y(^) объекта в мо¬
мент t определяется начальными условиями С=(с0,
..., ст), заданными (6.5.8), т. е. в результате решения
задачи (6.5.5) получаем У (Т) в зависимости от значений
C:Y(7)=/(C). Теперь задача определения начальных
условий С формулируется просто: их нужно подобрать
169>
так, чтобы /(C)=Y*. Но зависимость /(С) не явна, она
лолучается алгоритмически в результате решения зада¬
чи (6.5.5). Поэтому процедуру определения С естествен¬
но свести к решению минимизационной задачи:
Q (С) = | f (С) — Y* | —>min :фС*,
с
т. е. нужно подобрать такие начальные условия С, что¬
бы функция невязки Q(С) была минимальной (в идеа¬
ле равной нулю); Эту задачу следует решать поиско¬
выми методами, рассмотренными в приложении. При
Рис. 6.5.1. Схема вычислений по принципу максимума
этом определение каждой невязки Q в новой точке С
связано с решением задачи (6.5.5). При определении С*,
такого, что Q(C*)=0, получаем решение задачи (6.5.5)
в виде оптимального управления u*(t).
Как легко заметить, эту процедуру легко распро¬
странить на случай многомерного управления U(0 =
= {u\(t) ug(t)). При этом задача минимизации
(6.5.5)'становится многопараметрической, и ее следует
.решать одним из поисковых методов (см. приложение).
- Рассмотрим схему реализации вычислений по прин¬
ципу максимума. Она показана на рис. 6.5.1. Здесь 1—
блок решения системы дифференциальных уравнений
(6.5.7), на вход которого подаются управление u(t) и
начальные условия С и Y°= (у°и ..у°т). Решение этой
системы уравнений Y(t) и Чг(0 = ('фо(|0 'фт(О) по¬
даётся на блок 2, где вычисляется значение функции
Гамильтона по формуле (6.5.5), которая все время мак¬
симизируется блоком 3 по и с учетом ограничений
(6.5.6), где H=(fti, ..., /1йг) (это контур быстрой опти¬
мизации). Имеется контур медленной оптимизации, ко¬
торый решает задачу минимизации функции невязки
170
|Y(T)—Y*| путем изменения начальных условий С. Для
этого на каждом этапе вычисляется невязка Y(Т) с це¬
левым состоянием Y* (блок 5). Один шаг минимизации
(блок 6) здесь совершается после однократного реше¬
ния системы (6.5.7). Реализация такой системы на со¬
временных ЭВМ в принципе не представляет труда.
Однако функция качества Q(С) задачи внешней
(медленной) оптимизации обычно имеет многоэкстре¬
мальный характер, что заставляет обращаться к гло¬
бальным методам поиска (изложенным в приложении),
которые обычно требуют при своей реализации значи¬
тельных затрат машинного времени. Причем эти затра¬
ты сильно зависят от размерности- m объекта. Это об¬
стоятельство не позволяет использовать метод для ре¬
шения задач синтеза управления сложными объектами,
имеющими большую размерность т.
Динамическое программирование. Метод динамиче¬
ского программирования применяют обычно для много¬
экстремальных вариационных задач, решение которых
в той или иной степени сводится к организации полно¬
го перебора. Этот метод позволяет упорядочить и тем
самым значительно сократить полный перебор всех до¬
пустимых вариантов управления. Это оказывается воз¬
можным потому, что предполагается выполненным так
называемый «принцип оптимальности». Смысл его сво¬
дится к тому, что оптимальное поведение зависит толь¬
ко от исходного состояния объекта и не зависит от то¬
го, какова была предыстория попадания в это исходное
состояние. Так, управляя каким-то процессом, следует
интересоваться его состоянием только в данный момент,
так как именно от этого зависит дальнейшее управле¬
ние, а не от его предыстории.
Естественно, что этот принцип применим для доста¬
точно простых динамических систем, которые мы и
рассматриваем здесь. «Простота» здесь в том, что уже
имеется математическая модель объекта управления,
позволяющая достаточно хорошо определять будущее
поведение объекта при том или ином управлении.
Поясним суть метода динамического программирова¬
ния на примере решения следующей вариационной зада¬
чи, которая является частным случаем (6.5.4):
t
Q(u(t))= [f,(y(t), «(*))#-»min , (6.5.9)
S u (t) ^ Й
171
где
Q:
®i (t)<u(t)<wz (t),
5—А (у. «(<))» y(Q)=y*i
(6.5.10)
Рис. 6.5.2, К иллюстра¬
ции принципа оптималь¬
ности
У(Т) = У*,
где функции ограничения o>i (V) и m(t) заданы.
Задача (6.5.9), таким образом, состоит в определе¬
нии оптимального управления u*(t) (0^Л^Т) объектом
первого порядка [см. (6.5.10)],
поведение которого y(i) миними¬
зирует заданный функционал ка¬
чества \Q (6.5.9).
На рис. 6.5.2 показано реше¬
ние этой задачи — оптимальное
управление u*(t) и оптимальное
поведение объекта у* (t) на . всем
интервале. Теперь рассмотрим ка¬
кой-то момент t\ и применим прин¬
цип оптимальности, согласно ко¬
торому оптимальное управление
с момента \t\ будет зависеть только от состояния в этот
момент, т. е. y*(t\). Это очевидно. Естественно задать во¬
прос: а совпадут ли оптимальные управления, построен¬
ные из /=0 и t—ti на интервале не изменится
ли при этом оптимальное управление, а вслед за ним и
поведение объекта так, как, например, показано штрихом
на рис. 6.5.2? Ответ на этот не столь тривиальный вопрос
следует из принципа оптимальности: нет, не изменится!
Действительно, рассмотрим две реализации одного и
того же способа решения исходной задачи, т. е. опреде¬
ления оптимального управления на интервале [0, Т].
Пусть в первом случае мы получили оптимальное реше¬
ние u*(t) Теперь- разобъем решение задачи
на два этапа: [0, U] и [t\y Т] и снова решим задачу
тем же способом. Пусть полученное при этом оптималь¬
ное управление равно u*i(t) отлично от
u*i(t) (см. штриховую линию на рис. 6.5.2). Но резуль¬
тат решения задачи не должен зависеть от способа ее
решения (если, разумеется, способы правильные). По¬
этому
u*i (0 =и* (0, (6.5.11}
т. е. любая часть [tu Т] оптимальной траектории опти¬
мальна. Это не очень очевидное следствие принципа
172
оптимальности и лежит в основе вычислительной про¬
цедуры динамического программирования. Заметим, что
из (6.5.11) вовсе не следует, что любой отрезок (7Ь 12]
оптимальной траектории оптимален с точки зрения ми¬
нимума функционала качества на этом промежутке.
Если ЬФТ, то это не так. Действительно, если бы опти¬
мальность на отрезке [U, 12<Т] соответствовала опти¬
мальности на всем интервале [О, Г], то это означало
*бы, что управление на -[fi, t2\ не влияет на будущее
поведение объекта. Это бывает лишь в очень редких
случаях, которые, как правило, неинтересны, так как
задача при этом вырождается.
Теперь обратимся к методу динамического програм¬
мирования. Прежде всего сделаем задачу (6.5.9) ди¬
скретной (это упростит алгоритм вычислений), т. е. бу¬
дем рассматривать управление лишь в дискретные мо¬
менты времени:
Q(u) = 2 ui)Ati-+min , (6.5.12)
1=о “*ea
Q:
о/i <Мг- <0)"., i = 0, ..N,
&+1=0/+М^. щ)ьti>
y* = y\ yN = y*> i = 0, ..., ЛГ—1,
причем ui=u(ti); г/*=г/(^{); (a'i=m(ti)-,
Для простоты рассмотрим случай равноотстоящих
единичных моментов времени, т. е. Af=l (i=0, ...
..., N—1). Получаем
N—l
Q(U)= 2 f»(yi> “Л-* min >
ito “iSS
(6.5.13)
Q:
yi+i=yi+fiQ/i’ ui)
Уо-
Для решения этой задачи воспользуемся принципом
оптимальности, записанным в виде (6.5.11). Будем
искать решение «с конца» (t=T). Принцип оптимально¬
сти гарантирует нам, что оптимальное решение, получен¬
ное на отрезке [tu Л» будет «куском» решения исход¬
ной задачи на [0, Т].
173
Пусть условия Q допускают управление на последнем
(N—1)-м шаге в пределах Qn-\'
(рис. 6.5.3). На этом последнем шаге решается задача
попадания в точку yN=y*f т. е. задача определения кор¬
ня уравнения
y* = yN-\-\-fl(yN-U tlN-1) ^W*tf-l(2for-l), (6.5.14)
решением которой является значение управления u*N-1
в зависимости от yN-1 и независимо от того, какое зна¬
чение примет при этом мини-
минизируемый функционал Q.
Действительно, на этом послед¬
нем шаге не до оптимизации:
нужно удовлетворить гранич¬
ному условию yN=y* любой
ценой. Эта «цена» зависит от
N-l N-1 N i yN-X и равна
<PJV—1 (yN-l) —foiyN-U WiV*-l)
(6.5.15)
Рис. 6.5.3. Область допу¬
стимых управлений
(напомним, что /о — функция затрат). Запомним это об*
стоятельство.
Теперь, двигаясь от конца (t=T) к началу (/=0),
рассмотрим следующий (N—2)-й шаг (предпоследний),
который делается из пока неизвестного состояния ум-2-
Прирост минимизируемого критерия на этом шаге равен
fo(yN-2y Un-2)• В соответствии с принципом оптимально¬
сти следует минимизировать не эту величину, а все за¬
траты до конца процесса, т. е. сумму затрат на этом и
последнем шаге. Но для последнего шага затраты из¬
вестны [см. (6.5.15)]. Следовательно, надо минимизи¬
ровать сумму
U (yN-2- uN-i) + ?лг-1 (УЯ-1) — min , (6.5.16)
UN-2 е SN-2
yN-l—yN-2-\-fl(y.\r-2, WjV—2) • (6.5.17)
где
Однако начальные условия этого этапа, т. е. величина
Ук-2, нам как раз и неизвестны. Поэтому следует «заго¬
товить впрок» оптимальное управление и*W-2 для этого
шага в зависимости от неизвестного значения уп-2- Для
этого следует решить задачу (6.5.16) с учетом (6.5.17).
174
Обозначим минимальное значение затрат на послед¬
них двух этапах функцией
?tf_2 (yN-2) = min if о (UN-2- UN-2) + &N-2 +
UN—2 G ®N—2
""Ь fi (Удг_2’ —2))} *
(6.5.18>
Поступая аналогично на k-м от конца шаге, получаем
выражение суммарных затрат для последних k этапов.
/о (yN-k, UN-k) -Hpw-(fc-l) (yN-(k-1)) •
Минимизируя это выражение по uN-k с учетом того,.
что
yN-{k-\)=yN-k-\rfl (yN-k> WiV-ft),
получаем и*n-ъ. (yN-k) и определяем в результате функ¬
цию минимальных затрат:
<tN-k (Ум-к) = mino {/. (Ум-к> uff-k) +
UN—k S N—k
"Ь (Л-1) f 1 (УN—k' UN—fc))b (®*^*
где Qjv-fe — множество допустимых управлений на
k-м от конца шаге.
Таким образом, двигаясь «с конца», мы получаем сле¬
дующие необходимые в дальнейшем функции:
<Pi(*/i)> u*i(yi), •••> u*N-i(yN-\), (6.5.20)
которые характеризуют минимальные затраты (мини¬
мальное значение функционала качества Q) при движе¬
нии из исходного состояния у0 в целевое у* и зависи¬
мость оптимального управления каждого шага от era
начальных условий.
Теперь синтез оптимального управления очень
прост — он идет «вперед» с начала. На первом шаге
оптимальное управление определяется исходя из естест¬
венного условия
f.G/o. «0) +<Р. (г/о +/i (Уо> «о))—min И* ,
и о£= Й0
У*1—Уо+Ь(Уо, и*о)
— точка оптимальной траектории на первом шаге. Да¬
лее, используя полученные функции (6.5.20), имеем
175
n*i=u*i(y*i), y*2=y*i+h(y*u m*i) и т. д. до aV-i=
—U*N-\ {y*N—l) •
Таким образом, определено оптимальное управление
и*=(ы*0, и*\, U* ц~\)
и соответствующая ему оптимальная траектория
Y*=(2/o, у*и .... y*N-u У*)-
Проиллюстрируем применение метода на одном про¬
стом примере.
Пример. Найти оптимальное управление u(t), ограниченное
и переводящее объект dy/dt=y-\-u из состояния г/(0) =0
в состояние г/(3) = 1 (Т=3) с минимальными затратами, вычисляе¬
мыми с помощью функционала
3
. Q (и (<)) = j (уг + и2) dt.
о
т. е. необходимо решить следующую вариационную задачу:
Q:
Q= Г (г/2 + a2) dt -> min,
J M0sa
IU (OKI,
dy
dt
y + u,
j/(0) = 0; £/ (3) = 1.
Запишем эту задачу в дискретной форме, предполагая, что
*0=0, fi = l, /г=2, *з==3 и yi = y(ti), i = 0, 1, 2, 3, т. е. разбивая
весь интеграл [0, Т] на три участка:
2
Q=5! (y*i +tt2;) -*• mtn=»f/* = {u*„, и*,, и*2),
( — 1 <и
I </i+l=s
=2(/i+«i (t=0, 1, 2), </o=0, уз=1.
Это означает, что в данном случае N=3, <o'i——1, (o"i=l,
МУи Ui)=y2i+U2h fi{yU Ui)=yi + Ui,
j/»=0, г/*=1.
Начнем с конца (4=2). Определим управление, переводящее
объект из состояния г/2 в г/* = 1:
у* = 1=2у2+и*2.
Далее определим оптимальное управление на последнем шаге
•(второй шаг от начала)
«МЫ = 1—2 г/г (*)
176
и минимальные затраты
ф2 (У2) = У22+1 \Ц*2 (У2) ]2== by22T~fy% + 1.
Затем образуем затраты на первом шаге
ф! (У\)я У21+w2i + ф2 (у2),
где у2=2у1+щ.
Получаем суммарные затраты (от /= 1 до /=3)
ф! {У\) =^2i+w2i+5(2(/i+«i)2—4(2«/i+tti) +1.
Минимизируя эту функцию по Mi, определяем зависимость
= (1 -ЙГ.)/3 и
и минимальные затраты
?.(».) = (13Л-4Л + 1)/3. (***)
Теперь, располагая полученными зависимостями, можно строить
оптимальное управление «вперед»:
1-й шаг. Подставляя в (***) [выражение для #i = 2#0'[-
+ и0 = и0 (так как у0 = 0) и решая задачу
«оа+ Ь (и0) min,
l«ol < 1
получаем м*0=1/8.
2-й шаг. Определяем первую точку оптимальной траектории
y*i=2у0+ и* о=и* о = 1 /8.
Подставляя это значение в (**), получаем оптимальное управление
на 2-м шаге
*/*==( 1—5/8)/3=1/8.
и течку траектории
#*2=2гЛ + ы*1 = 3/8.
3-й шаг. И, наконец, получаем из (*)
Ы*2= 1—20*2= 1/4, ^3=s2i/*2-fW,,S2=l==0*,
т. е. объект вышел в заданную точку.
Определяем, таким образом, оптимальное управление U* =
*=(1/8, 1/8, 1/4) и оптимальную траекторию Y*=(0, 1/8, 3/8, 1).
Затраты при этом равны
J*=h(yo, и*о)-N>1(0*1) = 1/4.
Следует отметить, что ввиду простоты поставленной
задачи минимизацию суммарных затрат на каждом шаге
можно было сделать аналитически и получить зависи¬
мость оптимального управления от состояния в виде фор¬
мулы (см. (**) в рассмотренном примере). В более
сложных случаях это сделать не удается и приходится
зависимость
U*{(yt) (6.5.21)
12—299 177
Представлять таблично, что, естественно, снижает вы¬
числительную эффективность метода.
Подведем итоги. Как было показано, метод динами¬
ческого программирования является весьма эффектив¬
ным средством решения не очень сложных вариацион¬
ных задач. Он позволяет достаточно просто учитывать
не только ограничения на управление Ui^Qu но и огра¬
ничения, накладываемые на оптимальную траекторию
у* (О, т. е. проводить решение даже через заданный
«коридор». Для этого достаточно на каждом шаге ре¬
шать задачу оптимизации не для всех значений коорди¬
нат, а лишь для попавших в коридор на этом шаге.
Таким образом, изложенная методика динамическо¬
го программирования позволяет решать вариационные
задачи вида
и заданы области ш (О — допустимого управления
1(0—допустимой траектории, которые могут опреде¬
ленным образом изменяться во времени, а также модель
F и граничные условия Yo и Y* задачи.
- , Одним из существенных преимуществ метода являет¬
ся гарантия того, что полученное решение представляет
собой глобальный минимум функционала Q. Дело в том,
что этот функционал обычно многоэкстремален при
вариации управления u(t). Поэтому решение поставлен¬
ной задачи без применения принципа оптимальности за¬
ставляет обращаться и к поисковым методам глобальной
оптимизации (см. приложение), которые всегда требуют
значительных затрат машинного времени. Изложенный
подход снимает проблему многоэкстремальности данной
задачи.
Следует указать и на недостатки метода динамиче¬
ского программирования. К ним относится его практиче¬
т
Q (U(/))= Г ft (Y (0, U(0)dt-* min , (6.5.22)
где
Y(0) = Y°; Y(7>=Y*,
a Y = (yt, ..., £/„); U=:(u1, ..., um)
178
ская непригодность при решении задач управления объ¬
ектами размерности более чем т=2, 3. В этом случае
таблица (6.5.21) становится многомерной, что значи¬
тельно снижает эффективность метода, так как сильно
увеличивается объем необходимой памяти (примерно на
порядок для каждой единицы размерности). Это обстоя¬
тельство исключает применение этого метода для управ¬
ления объектами большой размерности, которыми обыч¬
но бывают сложные объекты управления.
В заключение этого параграфа отметим, что решение
задачи синтеза оптимального управления динамическим
объектом сводится к решению вариационной задачи,
сложность которой зависит от размерности и сложности
модели объекта. При этом решение полученной задачи
управления сложным объектом целесообразно сводить
к решению задачи математического программирования
и в редких простых случаях к рассмотренным методам,
опирающимся на идею динамического программирова¬
ния и принципа максимума, описанных в этом парагра¬
фе. Следует помнить, что для указанных методов су¬
ществует великолепно разработанная теория, которая,
увы, не помогает решать сложных задач большой раз¬
мерности, порождаемых практикой управления сложны¬
ми системами. Поэтому при синтезе управления слож¬
ным динамическим объектом следует пользоваться
методами решения многомерных и многоэкстремальных
задач математического программирования, например
специально для этого разработанными методами случай¬
ного поиска (см. приложение). Хорошая теория при ре¬
шении такого рода задач является лишь компасом, а не
инструментом и орудием. Решать же задачи приходится,
используя аппарат поисковых методов оптимизации.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИЙ К ГЛАВЕ 6
Задача синтеза управления при заданной цели и имеющейся мо¬
дели объекта управления является задачей прикладной математики,
так как сводится к решению задачи математического программиро¬
вания (это показано в § 6.1), для решения которой разработаны
необходимые вычислительные схемы.
Предлагаемая в § 6.2 классификация задач математического
программирования, естественно, неполная, как и всякая классифика¬
ция. Ее цель ориентировать читателя относительно некоторой спе¬
цифики различных типов задач математического программирования,
используемой при решении такого рода задач. Более подробную
классификацию задач математического программирования можно
найти в книгах [I-5J-
12*
179
Существует много методов решения математического програм¬
мирования. Некоторые из них рассмотрены в § 6.4. Все они исполь¬
зуют различную специфику функций Q, Н и G. Число руководств по
математическому программированию, пожалуй, даже слишком ве¬
лико. Для первого ознакомления читателю целесообразно обратить¬
ся к [6—8].
Алгоритмы решения задач линейного программирования хорошо
описаны в руководствах [1—6, 8—19, 22—24]. Задачи выпуклого
программирования анализируются и решаются в книгах [9, 15,
20, 25]. С методами решения задач целочисленного программирова¬
ния можно подробнее ознакомиться по соответствующим главам
в книгах [1—3, 13, 21, 24—28]. Кроме того, существуют задачи гео¬
метрического программирования, с которыми можно познакомиться
по [29,30].
Существующие методы решения вариационных задач, рассмот¬
ренные в § 6.5, отличаются громоздкостью алгоритма и узостью
класса решаемых им задач. Поэтому универсальным подходом к их
решению является по-прежнему сведение к соответствующей задаче
математического программирования [31]. Однако в отдельных част¬
ных случаях изложенные здесь методы могут дать значительный
эффект. Более подробно с этими методами можно ознакомиться по
руководствам [1—5, 7, 9, 12, 26, 32].
СПИСОК ЛИТЕРАТУРЫ
1. Кузин JI. Т. Основы кибернетики. — М.: Энергия, — Т. 1. Мате¬
матические основы кибернетики, 1973. — Т. 1.
2. Раскин J1. Г. Анализ сложных систем и элементы теории управ¬
ления.— М.: Сов. радио, 1976.
3. Зайченко Ю. П. Исследование операций. — Киев: Вища школа,
1975.
4. Основы кибернетики: математические основы кибернетики/ Под
ред. К. А. Пупкова. — М.: Высшая школа, 1974.
5. Интрилигатор М. Математические методы оптимизации и эко¬
номическая теория: Пер. с англ. — М.: Прогресс, 1975.
6. Гасс С. Путешествие в страну линейного программирования: Пер.
с англ. — М.: Мир, 1973.
7. Ли,Т. Г., Даме Г. Э., Гейнз У. М. Управление процессами
с помощью ЭВМ. Моделирование и оптимизация: Пер. с англ.—
М.: Сов. радио, 1972.
8. Кофман А. Методы и модели исследования операций: Пер.
с франц. — М.: Мир, 1966.
9. Габасов Р., Кириллова Ф. М. Методы оптимизации. — Минск:
Белорусе, гос. ун-т, 1975.
10. Юдин Д. Б., Гольштейн Е. Г. Линейное программирование: Тёо*
. рия, методы и приложения. — М.: Наука, 1969.
11. Гасс С. Линейное программирование: методы и приложения:
Пер. с англ. — М.: Физматгиз, 1961.
12. Коршунов Ю. М. Математические основы кибернетики. — М.:
Энергия, 1972.
13. Линейное и нелинейное программирование/ Под ред. И. Н. Ля-
шенко. — Киев: Вища школа, 1975.
14. Вагнер Г. Основы исследования операций.-г М.: Мир, 1972.
Т. 1.
180
15. Зуховицкий С. И., Авдеева JI. И Линейное и выпуклое програм¬
мирование. “т» М.: Наука, 1967.
"16. Ромакин М,’ И. Элементы линейной алгебры и линейного про¬
граммирования.— М.: Высшая школа, 1963.
17. Карпелевич Ф. И., Садовский JI. Е. Элементы линейной алгебры
и линейного программирования. — М.: Физматгиз, 1963.
18. Карлин С. Математические методы в теории игр, программиро¬
вании и экономике: Пер. с англ. — М.: 1964.
19. Басов А. С. Линейное лрограммирование в технико-экономиче¬
ских задачах. — М.: Наука, 1964.
20. Фиакко А., Мак-Кормик Г. Нелинейное программирование: Ме¬
тоды последовательной безусловной оптимизации: Пер. с англ.—
М.: Мир, 1972.
21. Корбут А. А., Финкельштейн Ю. Ю. Дискретное программирова¬
ние.— М.: Наука, 1969.
22. Юдин Д. Б., Гольштейн Е. Г. Линейное программирование — М.:
Физматгиз, 1963.
23. Гейл Д. Теория линейных экономических моделей: Пер. с англ.—
М.: ИЛ, 1963.
24. Мукачева Э. А., Рубинштейн Г. Ш. Математическое программи¬
рование.— Новосибирск: Наука, 1977.
25. Саати Т. Целочисленные методы оптимизации и связанные
с ними экстремальные проблемы: Пер. с англ. — М.: Мир, 1973.
26. Вагнер Г. Основы исследования операций в 3-х томах. — М.,
Мир, 1973. —Т. 2.
27. Лихтенштейн В. Е. Дискретность и случайность в экономико¬
математических задачах. — М.: Наука, 1973.
28. Лихтенштейн В. Е. Модели дискретного программирования. —
М.: Наука, 1971.
29. Зенер К. Геометрическое программирование и техническое про¬
ектирование: Пер. с англ. — М.: Мир, 1973.
30. Даффин Р., Питерсон Э., Зенер К. Геометрическое программи¬
рование: Пер. с англ. — М.: Мир, 1972.
31. Табак А., Куо Б. Оптимальное управление и математическое
программирование. — М.: Наука, 1975.
32. Моисеев Н. Н. Численные методы в теории оптимальных си¬
стем.— М.: Наука, 1971.
ГЛАВ А 7
РЕАЛИЗАЦИЯ УПРАВЛЕНИЯ
После решения задачи синтеза оптимального управ¬
ления U* (t), которая обсуждалась в предыдущей главе,
можно приступать к этапу управления. Это означает,
что управляемые входы объекта U должны быть пере¬
ведены в состояние, предписанное принятым решением
•U* (t). Для простых объектов управления в автоматиче¬
ском варианте эта задача решается просто —путем «от¬
работки» команды (программы) U*(<) с помощью соот¬
13—299 .181
ветствующих сервомеханизмов, автоматизирующих
процесс изменения управляемых входов U объекта.
В «ручном» варианте управляющее устройство выступа¬
ет в роли советчика, указывающего, в какое положение
следует перевести рукоятки управления объектов, а сама
реализация осуществляется персоналом, обслуживающим
этот объект. Здесь проблем не возникает, если, разу¬
меется, нет сведений о неправильной работе управляю¬
щего устройства. Проблемы появляются лишь при управ¬
лении сложным объектом. Рассмотрим их.
7.1. Постановка задачи
Проблема реализации управления возникает в том
случае, если при синтезе реализуемого управления U*
не были учтены какие-то важные факторы, влияющие на
достижение целей Z* управления в объекте. К ним отно¬
сятся, например, состояние X среды, ненаблюдаемые
факторы Е и отклонение объекта F0 от его модели F.
Причиной неопределенности являются:
— ограниченность всякого прогноза состояния среды.
Дело в том, что управление U* синтезировалось для
прогнозируемого состояния X, которое, естественно, не¬
избежно отличается от действительного;
— влияние ненаблюдаемых факторов Е, которые из¬
меняют ситуацию, складывающуюся в процессе управ¬
ления как в объекте, так и в среде;
— несоответствие между объектом F0 и его мо¬
делью F. Это несоответствие может иметь двоякий ха¬
рактер. С одной стороны, оно может быть вызвано дрей¬
фом параметров объекта за время от наблюдения его
состояния Y до момента реализации управления, а с дру¬
гой— намеренно заложено в модель F. Ради простоты
модели часто идут на заведомое игнорирование какой-то
информации об объекте, хотя ее и можно было бы полу¬
чить и использовать при синтезе модели. Расчет здесь
прост: так как в процессе реализации управления U*4
всегда возникают всякие непредвиденные обстоятельст¬
ва, то к ним заодно можно отнести и указанное несоот¬
ветствие, чтобы сразу скорректировать управление
с учетом всех имеющихся конкретных обстоятельств.
Именно поэтому реализация управления U* неизбежна
связана с его коррекцией, учитывающей условия, кото¬
182
рые сложились к данному моменту. Новое управление
имеет вид
(U*)'=U*+6U*,
где 6U* — коррекция управления, учитывающая указан¬
ные выше непредвиденные изменения в среде и объекте.
Рассмотрим два вида непредвиденных изменений ере-
ды и объекта и способы их учета при коррекции управ¬
ления.
7.2. Учет влияния среды
, Статический объект. Пусть оптимальное управление
U* синтезировано для определенного прогнозированного
состояния среды X. В действительности реализовался не
прогноз X, а Х=^Х. Информация о X позволяет скоррек¬
тировать управление, если известно, как должен реаги¬
ровать объект на управление U. Пусть эта реакция Y*.
Тогда действительная реакция Y=F(X, U*) будет отли¬
чаться от требуемой Y* на величину
6Y*=F(X, U*)—Y*.
Здесь F—функция (так как рассматривается модель
статического объекта).
Очевидно, что коррекция управления 6U должна ми¬
нимизировать эту величину, т. е. для синтеза коррекции
6U необходимо решить минимизационную задачу:
Q(8U) = |F(X, U*+6U) — Y*l-> min , (7.2.1)
au eR'
где R'— ресурсы, выделяемые на коррекцию.
Воспользуемся малостью 6U и бХ-отклонения ре¬
ального состояния среды X от прогнозируемого X: 6Х==
=Х—X. Тогда минимизируемую функцию Q(-) можно
записать в виде линейного разложения
Q(8U) =
F(X, U*) + g-8X + ^-6U-Y*
и, предположив для примера, что n=m=q=l и ресур¬
сы R' неограничены, получить из условия Q(6U)=0
в явном виде для коррекции
13*
183
где значения производных функции/(•, •) вычисляются
при и* и х.
Динамический объект. При коррекции управления
в процессе его реализации на динамическом объекте
следует минимизировать невязку между требуемым из¬
менением выхода объекта Y* (t) в процессе управления
и тем, что получается при управлении в среде X(t)^
=£X(t), где X(t) —прогноз поведения среды. Эта задача
имеет вид
т
Г [F (X (О, U* (t) + 6U (*)) — Y* (t)]2 dt min ,
oJ
где F — оператор динамической модели. Здесь, однако,
необходимо предвидеть поведение среды X(t), что мож¬
но реализовать только путем прогнозирования, однако
более позднего, чем Х(^), с помощью которого было
определено управление U*(t), и, следовательно, более
точного.
7.3. Учет активности объекта
Если объект оказался активным (как например,
учреждение, цех, завод и т. д.) и это обстоятельство не
учитывалось на стадии синтеза управления, то при его
реализации без учета активности объекта обойтись уже
нельзя. Покажем на простом примере, какие проблемы
здесь возникают.
Дело в том, состояние Y активного объекта зависит
не только от среды X и управления U, но и от некото¬
рых его внутренних параметров W=(nyb ,wi), кото¬
рые он может изменять по своему усмотрению в соответ¬
ствии со своими собственными целями Z*0 (в этом и
состоит активность объекта). Эти цели редко совпадают
с целями Z* управления, что и создает трудности при
управлении таким активным объектом.
Таким образом, состояние активного объекта можно
представить в виде Y = F0(X, U, W), где F0 —оператор
объекта.
Пусть цели Z*0 и Z*1 экстремальные. Тогда задача,
решаемая при синтезе управления U, имеет вид
Z*:QJU, W)— min зфИ* (7.3.1)
u иеЯц ■
г184
где -Q (■•»•) — целевая функция управления; /?ц— ресурс,
выделяемый на управление; U*w — принятое решение, ко¬
торое, естественно, зависит от того, какие значения па¬
раметров W объект выберет. (Состоянием среды для
простоты записи пренебрегаем, т. е. считаем среду неиз-
меняющейся.) Объект же в силу своей активности, до¬
биваясь своих целей Z*0, решает иную задачу:
Z*o: Qw (U, W) - min=>W* (7.3.2)
w weJ?w
где Qw(•»•) —целевая функция объекта; /?w —ресурс,
которым располагает объект; W* —решение, принятое
объектом, которое зависит от решения U. (Как видно,
оба решения U*w и W*u зависят друг от друга. Эта за¬
висимость может прежде всего привести к неустойчиво¬
сти ситуации, что определяется оператором F0 объекта
и функциями цели Qи Qw*, но не это главное.)
Пусть решения W*u и U*w устойчивые. Естественно
задать вопрос: а можно ли все-таки улучшить сложившую¬
ся ситуацию, т. е. уменьшить значение целевой функции
Qu при принятых решениях U*w и W*u? Оказывается,
можно. Для этого следует рассмотреть управление как
процесс взаимодействия двух равных партнеров, т. е.
учитывать, что противоположная сторона также доби¬
вается экстремальных целей. Учет этого обстоятельства
обеими сторонами (объектом и управляющим устройст¬
вом) позволяет построить такое компромиссное управ¬
ление, которое обеим сторонам обеспечивает наиболее
благоприятные условия, чем дают U*w и W* ц, получен¬
ные при решении задач (7.3.1) и (7.3.2) без учета актив¬
ности сторон.
Проиллюстрируем сказанное на простом примере. Пусть
Qw = u*+w\ Q^= (w—1)2+ (ш—1)2.
Рельеф обеих функций показан на рис. 7.3.1,а. Это концентрические
окружности с центрами (0,0) и (1,1). Решение задач (7.3.1) и (7.3.2)
Qu — (и — 1)2 + (w — О2 “* т*п =Ф и* = 1 >
и
Qw = и2 + w2 min => w* = 0
w
185
приводит к устойчивой точке В = (1,0), которая обеспечивает парт¬
нерам единичные значения их целевых функций:
Qu (1,0) = Q w (1,0) = 1. (*)
Это все, чего можно достичь, не учитывая разумности партнеров.
Но, как легко заметить на рис. 7.3.1,а, на плоскости существует
зона, где обеим сторонам обеспечиваются меньшие значения их
целевых функций (на рисунке она заштрихована). Ввиду осевой
симметрии обеих целевых функций их поведение можно рассмотреть
лишь на прямой ОЛ, соединяющей обе цели. Этот разрез показан
на рис. 7.3.1,6. Хорошо видно, что заштрихованная зона более вы¬
годна обеим сторонам, чем точка В. Так, если они договорятся под¬
держивать состояние в компромиссной точке С=(1/2, 7г), то их
1/2
и о-
б)
Рис. 7.3.1. Пример «рельефа» целевых функций (а) и показателей ка-
* чества вдоль оси АО (б)
показатели качества будут равны Qu(72> V2) = Qw(i/2, 7г) = V2,
т. е. o’6je стороны имеют двукратный выигрыш от такого решения
по сравнению с точкой В. Полученный эффект зависит от структуры
целевых функций обеих сторон. -Что же нужно сделать, чтобы реа¬
лизовать этот эффект?
В данном конкретном случае будет достаточно, если каждая
сторона сообщит значение своей целевой функции другой стороне
и они договорятся минимизировать каждый своими средствами
сумму:
Qw(u, w) + Qu (и, w) -+ min и* = 1/2,
и
Qw (и, w) + Qu (u, w) -» min =Ф w* = */2-
w
Полученное решение, однако, неустойчиво. Действительно, достаточ¬
но одной стороне (например, объекту) нарушить уговор и снова пе¬
рейти к управлению по своей целевой функции (7.3.2), то ситуация
смещается в точку Z)=(V2, 0), где объект имеет Qm>(72, 0)=4Д,
т. е. для него эта ситуация на лучше, чем договорная. Однако
значение целевой функции управляющего устройству при этом ухуд¬
шается на 3Д: Qu (V2, 0)=5Д и оно вправе перейти к'управлению
по своему критерию Qw, что возвращает систему в устойчивую точ¬
ку В=(1, 0). Как видно, указанный договор является неустойчивым,
186
но полезным состоянием взаимодействия для обеих сторон в процес¬
се управления.
Таким образом, при реализации управления активным объектом
следует обязательно учитывать его интересы и использовать дого¬
ворные отношения для того, чтобы удовлетворять не только цели
управления, но и цели объекта, что обеспечивает эффективную реа¬
лизацию целей Z*.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИЙ К ГЛАВЕ 7
Задачу реализации управления можно подразделить на две —
оперативную коррекцию управления в связи с возникновением новой
ситуации в среде и объекте и собственно реализацию этого управ¬
ления. Вторая задача связана с изменением положения органов
управления объектом ии ... uq исполнительными механизмами в со¬
ответствии с оптимальной программой U*(0, полученной на стадии
синтеза управления. Автоматическое отслеживание этой программы
производится с использованием хорошо разработанных методов тео¬
рии автоматического управления. Есть много хороших руководств
по этому вопросу, отметим некоторые из них [1—10].
Активность объекта, рассмотренную в § 7.3, строго говоря, сле¬
дует учитывать уже на стадии синтеза его модели. Это означает,
что необходимо заранее знать цели активного объекта и его воз¬
можности по реализации этих целей. Формализация этой информа¬
ций приводит к обычной модели F(X, U), синтез которой рассмот¬
рен в гл. 3—5. Некоторые способы формализации такого рода
информации рассмотрены в [11].
Если же субъект не располагает такой информацией, то на ста¬
дии реализации управления он немедленно обнаруживает результат
активности объекта, так как последний оказывается не в том со¬
стоянии, на которое рассчитывал субъект, опираясь на свою модель
этого объекта. Именно поэтому на стадии реализации управления
субъекту приходится «входить в контакт» с объектом, т. е. догова¬
риваться о «правилах игры», в которой объекту предоставляются
определенные права. Субъект также должен ограничить себя опре¬
деленными договорными обязательствами с объектом. Теперь учет
этих обязательств образует новую цель, в рамках которой и следует
строить оптимальное управление.
Этой сложной и конфликтной ситуацией занимается теория игр,
в частности, новая ветвь, связанная с неантагонистическими играми.
С этим новым направлением можно ознакомиться по брошюре [12]
и книге [13].
Активный объект всегда включает в себя человека или коллек¬
тивы. Такой объект иногда называют эргатическим. Специфика пове¬
дения эргатических систем рассмотрена в монографии [14]. Особен¬
ности поведения человека как объекта управления исследованы
в работах [15, 16].
СПИСОК ЛИТЕРАТУРЫ
1. Теория автоматического управления/ Под ред. А. В. Нетуши-
ла. — М.: Высшая школа, 1976.
2. Теория автоматического управления/ Под ред. А. В. Нетуши-
ла. — М.: Высшая школа, 1972, Ч. II.
187
3. Воронов А. А. Основы автоматического управления. — М.: Энер¬
гия, 1965. Ч. I. Линейные системы регулирования одной вели¬
чины. .
4. Воронов А. А. Основы автоматического управления. — М.: Энер¬
гия, 1966. Ч. II. Специальные линейные и нелинейные системы
автоматического регулирования одной величины.
5. Воронов А. А. Основы автоматического управления. — Л.: Энер¬
гия, 1970. Ч. III. Оптимальные многосвязные и адаптивные си¬
стемы.
6. Основы автоматического управления/ Под ред. В. С. Пугачева.—
М.: Наука, 1968. 1
7. Сапошков Р. А. Основы технической кибернетики. — М.: Высшая
школа, 1970.
8. Егоров К. В. Основы теории автоматического регулирования.—
М.: Энергия, 1967.
9. Юревич Е. И. Теория автоматического, управления. — Л.: Энер¬
гия, 1969.
10. Бесекерский В. А., Попов Е. П. Теория систем автоматического
регулирования. — М.: Наука, 1966.
И. Бурков В. Н. Основы математической.теории активных систем.—
М.: Наука, 1977.
12. Ватель И. А., Ерешко Ф. И. Математика конфликта и сотрудни¬
чества.— М.: Знание, 1973.
13. Гермейер Ю. Б. Игры с непротивоположными интересами. — М.:
Наука, 1976.
14. Павлов В. В. Начало теории эргатических систем. — Киев: Нау-
кова думка, 1975.
15. Акофф Р., Эмери Ф. О целеустремленных системах: Пер.
с англ. — М.: Сов. радио, 1974.
16. Лефевр В. А. Конфликтующие структуры. — М.: Сов. радио,
1973.
ГЛАВА 8
КОРРЕКЦИЯ СИСТЕМЫ УПРАВЛЕНИЯ
Необходимость коррекции системы управления воз¬
никает в связи с несовпадением реакции объекта Y°=
=F°(X, U) и реакции его модели Y=F(X, U) в резуль¬
тате реализации управления U в обстановке X, т. е.
Y°=*Y. (8.0.1)
При наличии помех в процессе, измерения состояний
объекта или при стохастическом характере его поведе¬
ния в качестве Y0 фигурирует его среднее значение. При
отсутствии необходимого статистического материала для
вычисления среднего, отклонение Y0 от Y при этом
должно быть достоверно, например, выходить за преде¬
лы «трех сигм».
188
Итак, при достоверном выполнении неравенства
(8.0.1) необходима коррекция системы управления. Эта
коррекция в соответствии с рис. В.4.1 может затраги¬
вать модель, объект и цели управления. В первом слу¬
чае она может распространяться как на параметры мо¬
дели, так и на ее структуру. Очевидно, что коррекция
структуры происходит реже, чем параметров, которые
могут корректироваться на каждом шаге процесса
управления.
Если коррекция модели не приводит к ожидаемому
успеху, обращаются к коррекции объекта, т. е. к изме¬
нению границ, отделяющих его от среды.
Процесс реализации целей Z* создаваемой системы
управления не может не привести к коррекции исходного
множества целей. Дело в том, что множество целей, ко¬
торое достигается реализованной системой управления,
как правило, не совпадает с исходным множеством це¬
лей. Это связано с тем, что сложный объект эволюцио¬
нирует каким-то определенным, но неизвестным нам
образом и, естественно, не все исходные цели могут быть
в нем реализованы. С другой стороны, открываются до¬
полнительные возможности по реализации новых целей.
Это и вызывает необходимость коррекции множества це¬
лей, т. е. определения действительных возможностей
данной системы управления на данном объекте.
Рассмотрим все три упомянутых вида коррекции.
8.1. Коррекция параметров модели объекта
Пусть модель объекта имеет вид
Y = F(X, U, С), (8.1.1)
где F, как обычно, структура модели, a C=(ci, ..., Си) —
ее параметры. В процессе управления изменяются оба
входа объекта X и U, что и дает возможность информа¬
цию о работе объекта на N-м шаге управления предста¬
вить в виде тройки замеров состояний:
IN = (XN> YV> (8.1.2)
где Y°n=F°(Xn, Uw).
Для статического объекта эта тройка представляет
собой набор чисел, а для динамического — набор
функций:
Л(0=(Х*Ю, 1М0> YV0). (8.1.3)
Рассмотрим коррекцию параметров модели статиче¬
189
ского и динамического объектов для случая, когда его
структура совпадает со структурой модели, т. е.
F=F°, (8.1.4)
ъ параметры объекта каким-то неизвестным, но опреде¬
ленным образом изменяются во времени, т. е.
С°=С °(f), (8.1.5)
тде С°(^)—неизвестная вектор-функция дрейфа пара¬
метров объекта.
Задачей коррекции параметров является такое изме¬
нение параметров модели С, которое отражало бы изме¬
нение параметров объекта С°(/), т. е.
С-*С°(/). (8.1.6)
Алгоритм решения этой задачи назовем алгоритмом кор¬
рекции. Он должен учитывать информацию о работе
объекта и иметь рекуррентный характер, т. е.
Cjv4-i=Civp“bcp(Cjv-i In) , (8.1.7)
где ф — алгоритм коррекции. Заметим, что рекуррент¬
ный характер алгоритма коррекции связан с самой по¬
становкой задачи коррекции. Это обстоятельство дает
возможность при коррекции модели воспользоваться так
называемым методом самонастраивающейся модели.
Схема реализации этого метода показана на рис. 8.1.1.
'Здесь система управления (она обозначена пунктиром)
реализует задаваемые ей извне цели Z*. Информация
о поведении объекта сопоставляется с реакцией модели
F на входы X и U и разность AYn=Yn—Y° поступает на
блок коррекции, который и производит коррекцию па¬
раметров модели:
ACjv+i = <p(Cjv, Xiv, Uiv, AYjv). (8.L8)
Так как модель F при векторном выходе \=(уь ..., уш)
может быть представлена в виде т моделей F=(/i, ...
..., /т), то коррекция должна иметь место для каждой
модели
*/<=/, (X, и, С'), /=1, т,
где уг — выход i-и модели; Д- — ее структура, a Ci — ее
параметры. Как показано в § 3.3, в данном случае мож¬
но рассматривать коррекцию одной модели, подразуме¬
вая, что коррекция остальных будет производиться ана¬
логично.
■190
Поэтому ниже мы будем рассматривать коррекцию
модели вида
y=*f(X, U, С) (8.1.9)
со скалярным выходом у, где } — известный оператор
модели.
Как легко заметить, процесс коррекции параметров
модели очень похож на процесс адаптивной идентифи¬
кации, рассмотренной в гл. 4. Используем эту аналогию
для синтеза алгоритмов коррекции.
Рис. 8.1.1. Схема коррекции пара¬
метров модели методом самона¬
страивающейся модели
Рассмотрим алгоритмы <р коррекции для статическо¬
го и динамического объектов.
Статический объект. Он характеризуется статической
структурой, которая описывается заданной скалярной
функцией / [см. (8.1.9)]. Используя аналогию с адаптив¬
ной идентификацией, будем искать алгоритм коррекции
среди алгоритмов минимизации локальной невязки вы¬
ходов модели и объекта в момент N:
q2N= (уи—y°N)2• (8.1.10)
Подставляя сюда выражение для выхода модели (8.1.9),
получаем эту невязку в виде функции от параметров CN
модели
q2N(CN) = (f(XN, Ujv, CN)-y°N)\ (8.1.11)
Минимизируем эту невязку, изменяя (корректируя) па¬
раметры модели, т. е. решая задачу
^«(Сдг + ДС ff+1)— min.
^ ДСЛГ+!
Система управления
1—■ '
Объект
с ° «
ж
УУ
L-p=%-~
Модель
\ас
Y-Y0
Блок
коррекции
191
Здесь естественно воспользоваться коррекцией, которая
при минимальном изменении CN обеспечивает наиболь¬
ший эффект уменьшения невязки q2. Такой коррекцией
будет градиентная коррекция
AC„+1=— *4<fN(CM), (8.1.12)
где а — положительный параметр (о нем будет сказано
ниже); Vc?2jv— градиент по С функции невязки (8.1.11)
при C — CN, который по определению равен
Vc?\ = 2ytfVcf(X#, VN, С)|с=ся> (8.1.13)
где
.. df(XN,VN,C) df(xN,vN, cM
Vc/(AW> 4v> L)— { frT » •••» dck S'
Эти выражения легко вычисляются при аналитически
заданной структуре функции f модели. Если эта функ¬
ция очень сложна или задана алгоритмически, например
для имитационной модели, ее производные могут быть
оценены следующим образом:
дс7= 2^7^ (ХЛГ> IV ^
(8.1.14)
где gi — база оценки; е, — £-й орт.
Теперь выражение для коррекции можно записать
в виде
iC»+,=- 2* If <*„• и», с») - /„| Vcf <Х„, и„, С) |с,с„.
(8.1.15)
Рассмотрим вопрос о выборе параметра а. При от¬
сутствии помех он должен назначаться из соображений
наиболее полной минимизации невязки. А так как ее ми¬
нимальное значение не может быть меньше нуля, то вы¬
бор а связан с решением задачи, рассмотренной в гл. 4:
9*дг(СА,+ДС#+1)-тт=0=ф«* (8.1.16)
а
(см. рис. 4.2.1). Эта задача однопараметрической мини*
мизации, которая может быть решена любым из извест*
ных поисковых методов (например, методом золотого
сечения, описанным в приложении П. 2).
192
Если же, исходная информация о поведении объекта
«зашумлена», то параметр а должен быть меньше а*.
Действительно, величина коррекции ACjv+r пропорцио¬
нальна невязке yN—y°N, которая при наличии помех
значительна не за счет неточности модели, а за счет по¬
мех, накладывающихся в процессе измерения состояния
объекта. Поэтому параметр а должен уменьшать кор¬
рекцию при наличии помех и тем более, чем выше уро¬
вень помех.
Таким образом, коррекция параметров статической
модели производится по формуле (8.1.15) и связана
с вычислением или оценкой градиента функции выхода
модели по корректируемым параметрам (8.1.14).
Динамический объект. В этом случае f в (8.1.9)
является оператором определенного вида, а С — векто¬
ром его параметров. Рассмотрим дискретный динамиче¬
ский объект, оператор которого имеет конечно-разност¬
ную форму вида (4.3.4). Модель его при наличии управ¬
ления записывается в виде
yN+l=f(X'N+l, Ujv+1, YV, С),
где \'N=(yN, yN_u ..., yN-p)\ / — заданная функция че¬
тырех векторных аргументов X', U, Y' и С, определенная
на стадии структурного синтеза.
Пусть реакции модели уы и объекта у°п не совпада¬
ют, т. е. уяФу°ы- Это обстоятельство заставляет обра¬
щаться к коррекции параметров С модели путем мини¬
мизации функции невязки, решая задачу
Yff(C) = [f(XV IV YY_,. С) — г/0^]2 —*-min.
Для этого естественно воспользоваться градиентным ме¬
тодом:
= CN <*Vcq N (С) |c_civ>
где для оценки градиента вида (8.1.13) необходимо
иметь оценки производных, аналогичные (8.1.14):
+e^)-f(XV 4v- *'*_>> Ctf-e,.^)], / = 1, ..k.
При этом параметр а выбирается так же, как и для ста¬
тического объекта.
Таким образом, основная трудность коррекции пара¬
метров объекта состоит в оценке градиента функции ло¬
193
кальной невязки выходов объекта и модели по коррек¬
тируемым параметрам. Однако указанная процедура
производится только на основе информации, полученной
в результате реализованного в объекте управления, к
корректирует модель именно для такого управления.
Если на следующем этапе понадобится иное управле¬
ние, которое опирается на неизвестные ранее свойства
объекта (а так и бывает в большинстве случаев), то
модель не будет «готова» к этому. Это обстоятельство»
заставляет добавлять к оптимальному управлению
U* (О так называемую изучающую добавку SU(/), ко¬
торая, не слишком искажая оптимальное управление,,
позволяла бы более качественно корректировать модель.
По сути дела речь идет о планировании экспериментов
в процессе управления. Добавку 6U(£) следует опре¬
делять таким образом, чтобы произведенная на ее основе
коррекция параметров модели АС позволила бы создать
более точную модель.
Как видно, в этом случае суммарное управление
U* (О-HU (О преследует две цели — добиться заданной
цели управления Z* и одновременно подстроить модель
объекта F. Очевидно, что в этом- случае управление
должно быть оптимальным. Такое управление, пресле¬
дующее двойную цель, получило название дуального,,
т. е. двойственного. Его методы связаны с решением опи¬
санной задачи, они очень сложны и поэтому не будут
здесь излагаться. Суть же их заключается в минимиза¬
ции некоторой функции, определяющей суммарный
ущерб от недостижения цели управления (за счет при¬
сутствия добавки 6U(£)) и неточности модели. Миними¬
зация этих потерь и дает возможность определить опти¬
мальное дуальное управление.
8.2. Коррекция структуры модели
Коррекцию структуры модели рассмотрим как пере¬
ход с одной структуры к другой в процессе управ¬
ления.
Пусть известно, что изменение структуры объекта
происходит в пределах конечного числа заданных струк¬
тур (функций или операторов) моделей: f1, ..., fk. Это
означает, что в каждый момент времени одна из этих
моделей
и, С<), i=l,...,k (8.2.1)
194
наилучшим образом описывает изменяющуюся структу¬
ру объекта
y°t=f°t(X, U),
где Сг — вектор параметров г-й модели; f°t — структура
объекта, которая изменяется каким-то неизвестным об¬
разом во времени t.
В качестве критерия эффективности структуры есте¬
ственно выбрать каким-то образом усредненную невяз¬
ку каждой модели и объекта, вычисленную до коррекции
параметров (иначе невязки будут равны нулю или близ¬
ки к нему). Пусть для статического объекта
Q<;=[/MX, и, С^)-^Л2
— невязка i-й модели на /-м шаге управления до кор¬
рекции ее параметров С\ Однако, полученные таким об¬
разом значения невязок на ;-м шаге управления Q{j, .. .
..., Qk/мало что говорят* об эффективности каждой из к
моделей, так как на эти величины влияют всякого рода
случайные факторы. Поэтому естественно ввести пока¬
затели эффективности структур в виде взвешенных сумм
этих невязок:
Qir = 2 ’ *■=!.••</ Ь- (8.2.2)*
/=1
где 0^g<l—коэффициент «забывания», который как.
бы «обесценивает» информацию, полученную на преды¬
дущих шагах (чем дальше «в прошлое», тем _меньшую
роль играют измерения). При g=О получим QiN=QiNt
т. е. взвешенная невязка равна невязке на последнем
шаге, так как при этом предыстория вся «забыта».
Можно обобщить выражение для показателей эффек¬
тивности (8.2.2), заменив весовой коэффициент gN~i'
функцией ф (/):
*‘=г...,*.
/=i
Здесь <р (•)—монотонно убывающая функция «забыва¬
ния», обладающая следующими свойствами:
В:<р(<)>0, <р(0) = 1, lim<p(i) = 0,
|->оо
9 (0 > 9 V-+ 1) (* = 0, 1, ...). (8.2.3>
19&
Теперь довольно легко выработать решающее прави¬
ло. Очевидно, что наиболее подходит та модель, показа¬
тель эффективности которой минимален. Это означает,
что на N-м шаге решение о выборе структуры прини¬
мается следующим образом:
fN=fl, если Q‘N = min (8.2.4)
1=1 k
Таким образом, процедура адаптации структуры сво¬
дится к оценке на каждом шаге показателя эффектив¬
ности для всех конкурирующих структур и выбору той,
у которой этот показатель минимален. Как видно, для
реализации указанной процедуры необходимо иметь и
постоянно корректировать параметры k моделей, из ко¬
торых лишь наилучшая используется для синтеза управ?
ления.
При наличии помех особую роль играет выбор функ¬
ции забывания <р(*)- Чем выше уровень помех в объек¬
те, тем медленнее должна убывать эта функция (тем
самым осуществляется фильтрация). Однако, с другой
стороны, при интенсивном изменении структуры объекта
эта функция должна уменьшаться достаточно быстро,
чтобы быстрее «забыть» результаты предыдущих экспе¬
риментов, уже играющих на данный момент малую роль
ввиду быстрого изменения структуры объекта. Поэтому
для синтеза оптимального решающего правила (8.2.4)
важно правильно выбрать функцию <р(-). Как это сде¬
лать?
Для этого необходимо оценить вероятность принятия
ошибочного решения Р, т. е. решения о выборе l-й струк¬
туры, в то время как в действительности лучшей оказы¬
вается другая структура. Эта вероятность зависит от
функции <р(')- Теперь задачу оптимизации решающего
правила (8.2.4) следует представить как задачу мини¬
мизации этого функционала вероятности ошибки:
Р(<р(0)-— min =»9*(г). (8.2.5)
9(0 е3
где S — множество допустимых функций, обладающих
свойствами (8.2.3); <р* (£)—оптимальная-функция «за¬
бывания».
Для определения вероятности Р ошибки необходимо
знать интенсивность и характер дрейфа структуры объ¬
екта, т. е. его-вероятностные свойства.
*06
8.3. Коррекция объекта управления
Эволюция сложного объекта F° в процессе управле¬
ния, дрейф его параметррв и характеристик, изменение
окружающей его среды, т. е. множества состояний {X},
а также множества целей {Z*} может привести к тому,
что несмотря на адаптацию параметров и структуры мо¬
дели объекта система управления не будет обеспечивать
эффективное выполнение всех заданных целей, которые
должны быть реализованы в объекте. Это обстоятельст¬
во заставляет пересмотреть границу разделения объекта
и среды, т. е. корректировать объект управления, перво¬
начальный вариант которого был определен на этапе
выделения объекта из среды (см. гл. 2).
Для коррекции объекта в процессе управления необ¬
ходимо иметь альтернативы, т. е. варианты объекта, из
которых можно осуществлять выбор при коррекции.
Пусть число таких альтернатив ограничено и ими явля¬
ются
Р01, F02, ..., F°«. (8.3.1)
Для каждого варианта объекта из (8.3.1) необходимо
иметь его модель, которая синтезируется методами, рас¬
смотренными выше (см. гл. 3—5):
Y<=F<(X*, U*), М(8.3.2)
где F{ — оператор i-й модели объекта F0<; X* — контро¬
лируемые, a U* — управляемые входы этого объекта.
Эти входы отличаются как по числу, так и по содержа¬
нию. Выходы же всех объектов Y* имеют одинаковое со¬
держание для всех объектов, но различны по своим зна¬
чениям. Оценку эффективности объекта естественно про¬
изводить по степени достижения им поставленной цели
Z* управления. Для этого необходимо ввести меру не¬
достижения цели в виде скалярной функции двух пере¬
менных
v=v(Z*,'F(Y)), (8.3.3)
где Ч**(*)—преобразование пространства состояний {Y}
объекта в целевое пространство {Z} [см. (1.3.6)].
Для целей типа равенств эту функцию можно опре¬
делить, например, так: v=|Z*—4T(Y) |2. Несколько
сложнее это сделать для целей (ограничений) типа не¬
равенств и трудно, но возможно для экстремальных це¬
197
лей. Так или иначе, но считаем, что функция (8.3.3)
определена и имеется возможность численно оценить
степень реализации заданной цели в объекте.
Предположим далее для простоты, что цель Z* и со¬
стояние X среды неизменны во времени (это задача ста¬
билизации объекта в заданном состоянии Y*=4r-I(Z*),
где V-1 — функция, обратная Ч') и нет случайных по¬
мех. Тогда решение задачи выбора лучшего из (8.3.1)
объекта заключается в последовательном переборе и
управлении каждым из g конкурирующих объектов и
фиксировании значений
v«=*(Z*,4T(Y«)), g.
Заканчивается эта процедура выбором такого объекта,
который обеспечивает наименьшее значение величины v.
Это правило записывается в простом виде:
P=F0/, если v* = min v*. (8.3.4)
*=i g
Но подобный перебор нецелесообразен при быстром
изменении свойств объекта, так как и «плохой» и «хоро¬
ший» объекты будут включаться одинаково (точнее,
почти одинаково) часто. В этом случае целесообразно
обратиться к рандомизированному правилу. Для этого
следует определить вероятности выбора того или иного
объекта:
Рх, Р*^2з (8.3.5)
где р1 — вероятность выбора t-ro объекта. Эти вероятно¬
сти можно связать со значением показателя эффектив¬
ности:
pi=f(v<), g,
где / — обратно пропорциональная функция вида f(v) =
=a/(v-H0> причем параметр а является нормирующим
множителем для выполнения условия (8.3.5) на каждом
шаге, а параметр Ь численно должен быть равным оцен¬
ке среднего значения эффективности всех объектов:
',=tSv
i=\
и поэтому должен адаптироваться в процессе управ¬
ления.
№
Ё начальный момент v‘=0 (i=i, g). ДаЛеё, пб
мере работы того или иного варианта объекта вероят¬
ности (8.3.5) будут принимать значения
pi=alivi-\-b), (8.3.6)
где V* — эффективность последнего функционирования
t'-ro варианта объекта. Как видно, в этом случае чаще
будет включаться лучший объект, что и обеспечивает
коррекцию объекта, т. е. адаптацию его границ к изме¬
няющимся свойствам объекта.
Теперь обобщим сказанное и снимем ограничения на.
состояние X среды, цель Z* и наличие помех. Эти фак¬
торы, изменяясь непредвиденным образом, сделают каж¬
дый результат оценки v стохастическим, что заставляет
обращаться к процедурам фильтрации типа
vVh = (1— a)v/Af + «vVh’ (8*3,7)
где а — коэффициент забывания (0<а^1); v*n+i—
усредненное значение эффективности i-го варианта объ¬
екта на (//-|-1)-м шаге его использования; vV+i — оцен¬
ка эффективности этого объекта по (8.3.3) на (ЛН"1)*М
шаге его использования.
Сама процедура принятия решения о выборе объекта
при этом не изменяется. Она рандомизирована, причем
вероятности альтернатив (8.3.5) при этом равны (8.3.6),
где, однако, вместо v* необходимо подставить (8.3.7).
Как легко видеть, указанная процедура при большем
«забывании» (а=1) вырождается в процедуру, рассмот¬
ренную выше, когда вероятности pi определяются толь¬
ко последней оценкой эффективности v*.
8.4. Коррекция целей управления
Пусть Л множество целей {Z}*, которые должна реа¬
лизовать созданная система управления. Это означает,
что она создавалась так, чтобы для любой цели Z*eA
и состояния среды XeS находилось управление, перево¬
дящее объект в состояние Y, соответствующее реализа¬
ции цели Z*. Однако приближенность модели, дрейф ха¬
рактеристик объекта и ограниченные возможности си¬
стемы коррекции управления при синтезе и реализации
управления приводят к тому, что множество реализуе¬
мых целей часто весьма существенно отличается от Л.
Кроме того, эволюция объекта управления й изменение
199
Свойств среды приводит к дрейфу множества реализуе¬
мых целей. Очевидно, что границы этого множества
должны интересовать потребителя системы управления,
так как они определяют ее предельные возможности.
Рассмотрим процедуру коррекции границы множест¬
ва А в процессе эксплуатации системы управления.
Прежде всего определим, что влияет на реализуемость
цели Z*. Реализуемость ее зависит от характера самой
цели и состояния X среды, в которой находится объект
управления. Таким образом, пара
! , L = (X, Z*) (8.4.1)
определяет успех или неуспех управления. Поэтому гра¬
ницу реализуемости можно очертить с помощью решаю¬
щей функции'
Я=Я(Ь), (8.4.2)
принимающей два значения (0 и 1). Если i?(L) =0, то
это значит, что цель Z* при состоянии X среды не реа¬
лизуется данной системой управления. Если же #(£.)=
=1, то цель Z* реализуется данной системой управле¬
ния при состоянии X среды.
Таким образом, возможности системы управления
можно характеризовать функцией (8.4.2). Эволюция
объекта и среды, влияющая на реализуемость целей,
должна изменять и эту решающую функцию.
В связи с этим возникают две задачи:
— как построить такую решающую функцию для
данной системы управления;
— как корректировать эту функцию с изменением
(эволюцией) объекта и среды (а может быть, и самой
системы управления).
Начнем с решения первой задачи. Для этого необ¬
ходимо иметь исходную информацию об опыте реализа¬
ции каких-то целей управления при каких-то состояниях
среды, т. е. так называемую обучающую последователь¬
ность, образуемую парами соответствий
L r+Rt, (8.4.3)
где Lj i-я пара (8.4.1), a Ri — результат работы системы
управления с этой парой (при Ri=0 цель Z*< не до¬
стигнута, а при /?»=1 достигнута). Располагая этой ин¬
формацией, необходимо построить соответствующую ре¬
шающую функцию R (L), принимающую два значения
(0 и 1). Эту задачу называют задачей ,распознавания
200
образов и состоит она в построении такого решающего
правила (распознавающей функции) по известной обу¬
чающей последовательности (8.4.3).
Существует много методов построения решающего
правила для задач распознавания образов (см. коммен¬
тарий к § 8.4). Для решенния данной задачи наиболее
подходит так называемый метод потенциальных функ¬
ций. Рассмотрим его. Прежде всего, образуем простран¬
ство {L}, в котором каждая пара (8.3.1) представляется
в виде точки. Координатами этого пространства являют¬
ся контролируемые параметры среды X и цель Z*. Та¬
ким образом, последовательность (8.4.3) представляется
в пространстве {L} в виде точек двоякого рода. Одни из
них (R=0) отражают негативный опыт применения дан¬
ной системы управления, а другие (/?=1)—положи¬
тельный.
Задачи синтеза решающего правила R(L) заключа¬
ются в том, чтобы в пространстве {L} провести поверх¬
ность, разделяющую точки с индексами R=0 и R=1.
Пусть каждая точка Lj образует в пространстве {L} «по¬
тенциал»
где qi — «заряд» в точке L{, вызывающий этот потен¬
циал:
Vi>0 — некоторая постоянная затухания потенциала;
p(L, L.)—функция расстояния между точками L и
Lj, например,
На рис. 8.4.1 показаны потенциалы (8.3.4) при раз¬
личных знаках заряда. Суммарный потенциал
(8.4.4)
(8.4.6)
*(L)=2 ML)
(8.4.7)
определяет знак заряда в любой другой точке прост-
14—299 201
ранства и тем самым реализуемость, управления в этой
точке
|1 при ЧГ(Ь)>0,
\0 при ^(^<0
или R(L) =,/2[1—sign4f(L)], где sign функция знака:
Я(Ь) =
(8.4.8)
signz-
к
При Z 0,
при z<0.
Это и есть решающая функция, которая однозначно
определяет реализуемость целей управления по наблю¬
дениям за реализацией некоторого числа (N) конкрет¬
ных целей Z*i в конкретных ситуациях X* данной систе¬
мой управления.
Теперь рассмотрим коррекцию решающей функции
(8.4.8). Необходимость такой коррекции связана со «ста¬
рением» информации (8.4.3), ее неизбежным обесцени¬
ванием. Учет такого старения очень просто произвести,
используя функцию «забывания» q> (-), которая была
введена ранее (8.2.3). Для этого достаточно величину
потенциала щ в отличие от (8.4.5) уменьшать следую¬
щим образом:
При этом номер i должен обязательно отражать исто¬
рию поступления информации L«-►/?<, т. е. номера i (i=
=1, ..., N) соответствуют дискретным моментам време-
а "Ри Rt=
1 \—f{N — 0 ПРИ Ri—о.
(8.4.9)
т
ни k реализаций цели управления в обстановке kj,
причем U<U+1.
В этом случае суммарный потенциал (8.4.7) будет
отражать в большей степени «свежую» информацию
о работе системы управления и благодаря введению
функции (8.4.9) «забывать» старую. Интенсивность это¬
го «забывания» должна зависеть от скорости эволюции
объекта и среды и отражать последнюю. Например,
функция вида
|1 пр„0<,<ЛГ„
TW \0Хпри«,<1
позволяет учитывать лишь N\ последних членов после¬
довательности (8.4.3). Чем меньше N\, тем интенсивнее
забывание. И, наоборот, при N\=N учитывается в рав¬
ной мере вся имеющаяся информация (8.3.3) и получаем
случай (8.4.5).
ЛИТЕРАТУРНЫЙ КОММЕНТАРИИ К ГЛАВЕ 8
Коррекция системы управления является формой ее адаптации
к изменяющимся факторам среды и потребностям субъекта, т. е.
к ее новому состоянию и новым целям, реализуемым системой управ¬
ления. Адаптация эта имеет параметрический и структурный харак¬
тер. В первом случае изменяются параметры системы управления
(например, параметры модели объекта, см. § 8.1), а во втором — ее
структура (см., например, § 8.2).
Математический аппарат, используемый для параметрической
коррекции в § 8.1, является по сути дела аппаратом адаптивной
идентификации, описанный с соответствующими ссылками в гл. 4.
Структурная адаптация, рассмотренная в § 8.2, 8.3, имеет аль¬
тернативный характер, т. е. дает возможность на каждом шаге
определять одну из нескольких заранее оговоренных альтернатив
(моделей в § 8.2 и объектов в § 8.3). Здесь математическим аппа¬
ратом является фильтрация (сглаживание) случайных процессов.
С этим аппаратом можно познакомится по любому руководству
о случайных процессах, например [1—4].
Изложенный в § 8.4 способ построения решающей функции на¬
зывается методом потенциальных функций '[5]. Однако для этих
целей, вообще говоря, могут быть применены и другие методы рас¬
познавания образов. Для начального ознакомления с проблемой рас¬
познавания образов читателю рекомендуется одна из книг [6, 7].
Более подробно с различными методами распознавания можно озна¬
комиться по руководствам [5, 8—10].
СПИСОК ЛИТЕРАТУРЫ
1. Свешников А. А. Прикладные методы теории случайных функ¬
ций.—М.: Наука, 1968.
2. Пугачев В. С. Теория случайных функций.— М.: Физматгиз,
1962.
14*
203
3. Бендат Дж. Основы теории случайных шумов и ее применений:
Пер. с англ. — М.: Наука, 1965.
4. Тихонов В. И. Статистическая радиотехника. — М.: Сов. радио,
1966.
5. Айзерман М. А., Браверман Э. М., Розоноэр J1. И. Метод по¬
тенциальных функций в теории обучающихся машин.
6. Аркадьев А. . Г., Браверман Э. М. Обучение машины классифи¬
кации объектов.— М.: Наука, 1971.
7. Бонгард М. М. Проблема узнавания. — М.: Наука, 1967.
8. Вапник В. Н., Червоненкис А. Я. Теория распознавания обра¬
зов: статистические проблемы обучения. — М.: Наука, 1974.
9. Персептрон — система распознавания образов/ Под ред.
А. Г. Ивахненко. — Киев: Наукова думка, 1975.
10. Загоруйко Н. Г. Методы распознавания и их применения. — М.:
Сов. радио, 1972.
ПРИЛОЖЕНИЕ
МЕТОДЫ ПОИСКОВОЕ ОПТИМИЗАЦИИ
Задача оптимизации является, пожаЛуй, самой распространен¬
ной вычислительной задачей нашего времени. Действительно, прак¬
тически все проблемы управления сводятся к отысканию оптимума
функции или функционала и на каждом этапе управления сложным
объектом приходится решать задачу оптимизации в нескольких мо¬
дификациях. Поэтому так важно владеть методами решения задачи
оптимизации. Существует много способов ее решения. Ниже описа¬
ны наиболее эффективные из них, которые неоднократно использо¬
вались в задачах управления.
П.1. Постановка задачи
Задача оптимизации функции Q = Q(X) многих переменных Х =
= (*ь . •Хъ) формируется следующим образом:
Q (X) -яшп=>Х*, (П.1.1)
где Q — множество допустимых значений переменной X, а X* — ре¬
шение задачи оптимизации, т. е.
Q(X*) = minQ(X),
причем X*eQ. Множество £2 обычно задается системой равенств
и неравенств в виде
Q.jgi(X) = °> •••’ Р<*>
' I А/(Х)>0, /= 1,...,?,
где gi(X) и hj(X)—заданные скалярные функции. Задание этих
функций, так же как и функции Q(X), может быть не только ана¬
литическим, но и алгоритмическим, т. е. с помощью алгоритма, по¬
зволяющего вычислять значения этих функций в любой заданной
точке X.
Поисковый метод решения задачи (П. 1.1) реализуется рекур¬
рентным выражением, определяющим переход от (N—1)-го прибли¬
жения к N-му:
X n=X jv - г-|нД X jv .
Шаг AXjv -зависит от ситуации в точке Xjv_r, AXjv=cp(Xjv_i), где
Ф — алгоритм поиска, определяющий рекуррентный процесс оптими¬
зации. Этот алгоритм почти полностью определяется признаками за¬
дачи оптимизации. Рассмотрим основные из них.
1. В зависимости от числа минимизируемых функций, т. е. от
размерности аргумента функции Q(X), различают однокритериальные
205
(см. tt.2—-П.5) й мнбгокритериальные векторные задачи оптимиза¬
ции, которые рассмотрены в'П.6.
_2. В зависимости от того, лежит решение X* задачи на грани¬
це Q области £2 или нет, различают безусловные (Х^ёЙ, они пред¬
ставлены в П.2—П.4) и условные (Х*ей) задачи оптимизации (их
решение рассмотрено в П.5).
3. В зависимости от числа локальных экстремумов различают
локальные или одноэкстремальные (они обсуждаются в П.2—П.З)
и глобальные или многоэкстремальные задачи (рассмотренные
в П.4).
£/7.2 $П.З
Рис. П.1.1. Структура задач поисковой оптимизации
4. В зависимости от числа п оптимизируемых параметров разли¬
чают однопараметрические (л= 1, см. П.2) и многопараметрические
(и>1 см. П.З) задачй оптимизации.
На рис. П. 1.1 показана описанная схема классификации задач
.поисковой оптимизации с указанием номеров параграфов данного
приложения, где рассмотрены основные методы решения этих задач.
П.2. Однопараметрический локальный поиск
(л=1)
Задача однопараметрического поиска записывается в виде
<2л(я) -► min=£**. (П.2.1)
х
Если функция Q (х) дифференцируема, то для решения задачи
(П.2.1) достаточно решить другую задачу
= 0. (П.2.2)
206
Если функция не дифференцируема или ее вычисление очень сложно
(например, в случае алгоритмического задания функции), то для
определения f(x) можно воспользоваться точечной оценкой
.(* + «)'-«(*-в) I. (П.2.3)
где g>0 — достаточно малая величина (база оценки, равная 2g).
Как видно из (П.2.2), задача оптимизации сводится к задаче
определения корня уравнения f(x) = 0. Поэтому для ее решения
можно воспользоваться многочисленными рекуррентными методами,
разработанными для вычисления корней. Заметим, что ввиду одно-
экстремальности функции Q(x) число корней уравнения (П.2.2) не
превышает одного.
1. Метод касательных применяют для выпуклой функции Q(x),
что соответствует монотонности ее производной f(x). Алгоритм ме¬
тода на каждом шаге сводится к линейному представлению функ¬
ции f(x) в точке Xi и решению уравнения
f (*) (*<) + (x-Xi)f' (Xi) = О,
корень которого и является следующим приближением:
*<+1=*<—/(*<)/Г (*<)•
Как видно, для этого необходимо определить вторую производную
f'(x)=Q"(x) от минимизируемой функции. Ее точечная оценка
Р(Х)=ВТ [f +
-2Q(*)+Q(x-*)].
где база оценки равна g.
Таким образом, алгоритм касательных при решении задачи одно¬
мерной оптимизации записывается в виде
glQ (х{ -f g) ~-Q(xt—g)]
Xi+1-Xi- 2[Q(Xl+g)-2Q(xt)+Q(Xi-g)] •
Как видно, для того чтобы сделать один шаг оптимизации по ме¬
тоду касательных, необходимо определить минимизируемую функ¬
цию в трех точках: Xu *i±g. Напомним, что этот метод сходится,
т. е. lim Xi—X*t лишь для выпуклой функции Q(*).
/->00
2. Метод хорд заключается в том, что функция f(x) в окрест¬
ности корня аппроксимируется хордой, соединяющей точки, лежащие
по разные стороны от корня. Пусть — две точки в окрест¬
ности корня на i-м этапе, причем (для случая минимизации)
/(*'<)< 0,/(*",)><>, (П.2.4)
т. е. они лежат по разные стороны от корня х*. Эта хорда описы¬
вается уравнением
f (X) = -y77zr^7—Hx-X't) fx"i) - (x"i-x)J (*',.)!.
207
Приравнивая это выражение нулю, получаем х*-и — очередное при¬
ближение корня. Для очередного шага образуем 'x'i+i и x"i+i сле¬
дующим образом:
x'i+i=x'i и x"i+l = Xi+i,. если f{Xi+i)>Q,
x'i+i=Xi+l и x//i+i=x"i, если f(Xi+i) <0. (П.2.5)
Здесь и в предыдущей формуле вместо f(x) следует использовать
ее точечную оценку по (П.2.3). Мётод хорд сходится и для невы¬
пуклых функций Q(*).
3. Метод дихотомии позволяет определять оценки корня f(x)
(а следовательно, минимума Q(*)) путем деления пополам отрезка,
внутри которого находится корень. Пусть, как и при методе хорд,
концами такого отрезка являются x'i<x"i, удовлетворяющие
(П.2.4). Тогда в соответствии с этим алгоритмом
ЛГг-М = 1Д(д:'г+Л:,,г) •
Для очередного шага образуется новый отрезок [х'г+i, x"i+1] по
правилу (П.2.5) и т. д. Как видно, для этого метода нет необходи¬
мости вычислять значение производной f(x), достаточно определить
ее знак. Этот метод сходится для любой одноэкстремальной функ¬
ции Q(x).
Заметим, что при реализации рассмотренных методов для точ¬
ного определения положения экстремума необходимо базу оценки
g уменьшать с ростом i. Действительно, равенство нулю точечной
оценки производной (П.2.3) минимизируемой функции, т. е.
Q (*<■+g)—1Q (*<—g)=о,
определяет экстремум лишь при g—>-0.
Теперь рассмотрим методы однопараметрической оптимизации,
не опирающиеся на определение производной f{x).
4. Метод золотого сечения. Рассмотрим алгоритм этого метода
при его работе из исходного состояния х0. Сделаем произвольный
шаг а и определим значение минимизируемой функции в полученной
точке Q(*o+a)‘ Если Q(*o+a) <Q(*o), то следующее определение
функции производится в точке *0+а(1+т), где т=(1+К 5)/2^1,62
(рис. П.2.1а), в противном случае в точке лг0—ах (рис. П.2.1.6).
Теперь на оси х имеются три точки (обозначим их х*<х2<х3) со
значениями минимизируемой функции соответственно Qb Q2 и Q3,
т. е. Qj = QW) (/=1, 2, 3). Так, в первом случае: х1=х0. х2 =
— хо + а, х3 = хо+а(\ +т), а во втором xi=xo—ах, х2 = х0, х3=х0 + а.
Здесь возможны две ситуации:
1) минимальное значение функции качества имеет средняя из
этих трех точек, т. е.
min Qj = Q2. (П.2.6)
/=1,2/3
Очевидно, что при этом минимум функции Q (я) находится между
точками х1 и х3. Поэтому следующее значение минимизируемой
функции в этом случае нужно вычислять в точке xi=x1+x3—x2.
Из четырех точек л^(/=1, ..., 4) одна крайняя отбрасывается
так, чтобы из оставшихся в средней точке значение функции Q(.a:)
было бы минимальным. Эти три точки снова обозначим х'<;х2<х3,
208
Для них имеет место соотношение (fl.2.6). Поэтому здесь сноба
следует применить это же правило. Так уточняется положение
экстремума. Критерием останова процесса может служить, как
обычно, точность оценки положения экстремума, т. е. разность
я3—х1;
2) если же minQ/ ф Q2, т. е. минимально или Qlf или Q3, то
/=1,2,3
добавляем точку
1 — % (х2— х1), если min Q,= Q1,
/=1, 2, 3
+ т (х3 — х2), если min Qt = Q3.
/=1, 2,3
Из четырех точек х1,..., *4 выбираем три следующим образом. Если
наименьшее значение функции в одной из крайних точек, то от¬
брасываем точку с наибольшим значением (это будет другая край-
Мл I а | at
ап
х0 х х0 х
й) б) -
Рис. П.2.1. Расположение точек поиска «а начальном этапе поиска
(вертикальные отрезки соответствуют значениям функции)
няя точка), а остальные обзначаем через х1<х2<х3. Эта вторая
ситуация и поэтому далее следует обращаться к 2). В противном
случае следует отбросить одну из крайних точек так, чтобы из
трех оставшихся в средней было бы наименьшее значение функции.
Обозначая аналогично эти точки, обнаруживаем, что это первая
ситуация, и следует обратиться к 1).
Таким образом, мы приходим к такому значению х*=х2, ко¬
торое и является решением задачи оптимизации, где х2 взято из
последней тройки чисел х1Сх2Сх3. (Заметим, что в принципе
можно взять и иное значение т, но при указанном т скорость схо¬
димости .процесса оптимизации будет наибольшей).
Изложенные выше методы можно применять лишь при от¬
сутствии случайных помех, накладывающихся на функцию качества
Q(*j. При наличии таких помех следует обратиться к другим
методам поиска экстремума (их алгоритмы часто называют алго¬
ритмами адаптации, подчеркивая этим, что алгоритм поиска как
бы приспосабливается, адаптируется к неопределенности, связанной
с наличием случайных помех).
5. Метод стохастической аппроксимации используется при ми¬
нимизации функций, значение которых определяется со случайной
помехой. Записывается он в виде
= №(*/ +ft+.)-«(*/-*+,)]. (П.2.7)
209
ГДё йоложйтёльйыё числа ait g{ должны удовлетворять следук>1ШШ
условиям:
00 00
limах = Hm — О, ai = °°v J] ~j < °°- (П.2.8)
i=i i = 1
Этим условиям (их называют условиями Дворецкого) удовлетворяют,
например, последовательности щ = l/iat gi= l/fi, где на выбор
параметров аир наложены ограничения вида 0<а<1, Р>0,
а—Р>72. В этом случае процесс поиска экстремума функции
Q(x) сходится независимо от уровня случайных помех, наклады¬
вающихся на эту функцию.
6. Адаптивный метод связан с адаптивным изменением длины
шага Ля в процессе поиска. Алгоритм заключается в том, что при
уменьшении минимизируемой функции делается шаг в том же на¬
правлении, а при ее увеличении — в обратном:
AV _/ если AQ| <0,
1+1 { —если AQj^sO,
где Axi=xi—xi-1; AQ<=iQ(x<)—Q(*j-i), a Yi>U 0Су2<1 —-пара-
метры, характеризующие увеличение шага Yi при движении в удач¬
ном направлении и уменьшение Y2 при реверсе, т. е. при ^переходе»
через экстремум. Алгоритм сходится при YiY2<b'
П.З. Многопараметрический локальный поиск
(п>1)
Среди алгоритмов локального поиска большое распространение
получили так называемые спусковые алгоритмы, отличающиеся про¬
цедурой опуска вдоль выбранного направления. Рассмотрим снача¬
ла их. Представим шаг ДХ* в виде
A Xi^atVt, (П.3.1)
где Vi — единичный вектор направления на i-м шаге; а< — величи¬
на этого шага. В зависимости от способа формирования вектора
Vi образуются различные методы оптимизации.
1. Покоординатный метод (Гаусса — Зайделя) характеризуется
тем, что направления V* соответствуют направлениям координат¬
ных осей, т. е. Vf=ej (/= 1,..., &), где — /-й орт, т. е. направ¬
ление /-й координаты. Следующий шаг будет производится вдоль
(/—(—1) -й координаты и т. д. до &-й, после чего движение снова
будет производиться вдоль первой, т. е. вдоль еь и т. д. Заметим,
что здесь и ниже слово «вдоль» означает движение не только в ука¬
занном направлении, но и в обратном.
2. Градиентный метод (метод наискорейшего спуска) отличает¬
ся тем, что направление Vi соответствует антиградиентному, т. е.
V| = т—dir VXQ
где dir обозначает направление вектора: dirZ=Z/|Z|, a Vx~~rPa*
210
диент, т. е. вектор с компонентами, равными частным производным
функции, стоящей под этим знаком:
Л l^L \
dHJ-
При этом методе оптимизируемые параметры изменяются так, что
минимизируемая функция вначале уменьшается наибыстрейшим
образом. Для этого, однако, необходимо знать все частные произ¬
водные этой функции или их оценки. Точечные оценки здесь име¬
ют вид
х-ч
-^-=^-[Q(X + ffe/)-Q(X)],
(П.3.2)
2j[Q(X + gej) - Q (X -ge,)},
где g>0 — база оценки.
Как легко заметить, при g—>-0 обе оценки сходятся к точно¬
му значению производной (если она существует, разумеется). Пер¬
вая оценка в (П.3.2) смещенная, а вторая — несмещенная, но тру¬
доемкость определения последней в два раза 'больше, так как для
нее функцию Q(X) приходится определять в двух состояниях Х±
±£вг.
3. Метод локального случайного поиска примечателен тем, что
направление V* является случайным: Vi=E, где S — единичный
случайный вектор, равномерно распределенный по всем направле¬
ниям пространства параметров {X}.
Для реализации каждого из описанных методов поисковой опти¬
мизации необходимо задать величину шага ai [см. (П.3.1)]. Для
определения а{ следует воспользоваться следующим очевидным со¬
ображением. Величина Q(X*) должна быть возможно малой, т. е.
необходимо решить задачу
Q (X*) = Q (X/ _ j + atVi) - min =>*•„' (П.3.3)
ai
где a*i — оптимальная величина шага. Заметим, что, вообще говоря,
это может быть и отрицательная величина (например, при случай¬
ном поиске). Эта задача однопараметрической оптимизации может
решаться стандартными методами одномерного поиска, описанными
выше (см. П.2), и обычно вызывается спуском.
4. Метод многомерной стохастической аппроксимации. Алгоритм
этого метода записывается в виде
Х/+1 = Х/ — e<+IVxQ№>.
где Vx^(Xj) —точечная оценка градиента, компонентами которой яв¬
ляются оценки частных производных, аналогичные (П,3.2):
dQ 1 '
дх,- ~2gl+i W (Хг +ft+ie/)—Q №— gi + ,e/)],
а переменные коэффициенты аг- и gi должны удовлетворять усло¬
виям Дворецкого (П.2.8).
211
П.4. Алгоритмы глобального поиска
Если минимизируемая функция Q(X) имеет больше одного
экстремума и нужно найти наименьший из них, то ни один из
описанных выше алгоритмов локального поиска не решит постав¬
ленную задачу. Для этого используют алгоритмы глобального по¬
иска. Рассмотрим некоторые из них.
1. Метод глобального случайного поиска при правильной орга¬
низации является достаточно эффективным, средством отыскания
глобального экстремума. Состоит он в следующем. В области по¬
иска Q в соответствии с заданной, например, нормальной, плот¬
ностью распределения а2) генерируются случайные точки
Хь Х2, ... Здесь W — математическое ожидание этого распределе¬
ния, а а2 — максимальная дисперсия его компонент. Смысл алгорит:
ма состоит в том, что W располагается в точке с минимальным, най¬
денным ранее значением минимизируемой функции, т. е. Wi = X*t-,
где Q(X*i)=Q*i= ™,п Q (х/)-
Алгоритм такого поиска записывается в виде рекуррентной
формулы ДЛЯ Х*г и Q*»!
f X*t—1, Q*t=Q*t-b если Q(Xi)>Q*i-u
х*/ =
I Xi, Q*i=Q(Xi), если Q(Xi)<Q*i_b
Как легко заметить, этот алгоритм гарантирует отыскание глобаль¬
ного экстремума, если плотность распределения случайных точек
не равна нулю ни в одной точке области поиска Q, т. е.
P(X|W, о)ф0 для XeQ.
Действительно, так как вероятность случайного попадания
в окрестность глобального экстремума в этом случае конечна, то
это событие рано или поздно реализуется. Однако скорее поздно,
чем рано, так как сходимость алгоритма медленная, поэтому при
реализации этого алгоритма следует принимать меры для увеличе¬
ния скорости его . сходимости.
Для этого применяется адаптация дисперсии а2 в процессе
поиска: дисперсию уменьшают при неудачных случайных пробах и
увеличивают при удачных: (Тг=сТг--1—НАогг*, где приращение ДсГг=
=|ф (а<~j, AQi-i) определяется алгоритмом адаптации. Например,
e = / при ! > О,
в/ I Тг°г-1 ПРИ AQi-i<0.
(Здесь коэффициенты Yi<l и определяются из конкретных
соображений.) Правильный выбор этих коэффициентов в значи¬
тельной мере определяет успех глобального поиска. Если они бу¬
дут близки к единице, то эффект адаптации будет незначительным,
а поиск — длительным, но результативным, т. е. будет найден гло¬
бальный экстремум. Если же отличие от единицы коэффициентов
будет существенным, то процесс закончится быстро, но глобальный
экстремум может быть не найден. Чем меньше Yi’ тем быстрее
заканчивается поиск и тем больше мы рискуем «проскочить» гло¬
бальный экстремум. При выборе Yi и Y2 следует искать разумный
компромисс между временем поиска и его надежностью.
212
2. Метод сглаживающего глобального поиска эффективно при*
меняется в случаях, когда многоэкстремальность минимизируемой
функции образуется под влиянием некой колебательной (не обяза¬
тельно периодической) составляющей Q2W, которая накладывает¬
ся на «хорошую» одноэкстремальную функцию Qi(X):
Q (X)=Qj (X)—(—Q2 (X).
Априорно это разделение неизвестно. Задача состоит в том,
чтобы «сгладить» СЫХ) и тем самым свести многоэкстремальную
задачу к локальной задаче отыскания минимума одноэкстремаль¬
ной функции Qi(X), рассмотренной в П.2—П.З.
Процедура сглаживания исходной функции Q(X) должна
иметь характер усреднения. Это усреднение производится с учетом
весовой функции p(Y), где YeQ и представляет собой вектор от¬
клонения от X. Весовая функция ,р (•) определяет вес, с которым
происходит усреднение минимизируемой функции Q(X) в окрестно¬
сти X. Поэтому она должна обладать следующими свойствами:
— неотрицательностью, т. е. p(Y)^0 для YeQ;
—нормированностью, т. е. ^ р (Y) dY = 1;
9
—5-образностью по какому-то ее внутреннему параметру q, т. е.
limp (Y) = д (Y), где д (•) —дельта-функция.
Гауссова функция
k
p(Y)=^Pvexp{_ikS^}
/=!
и многомерный «Локон Аньези»
p(Y)=//(l+?|Y|2),
где I — нормирующий множитель, являются такими функциями.
Теперь процедуру усреднения минимизируемой функции мож¬
но представить в виде 6-кратного интегрирования с весом р:
Q (X) = J Q'AX + Y)j>;(Y) dY, (П.4.1)
S3
где £(Х) — усредненное в Q значение функции Q(X).
Точное определение этого интеграла представляет большие
трудности. Поэтому его следует оценивать методом Монте-Карло.
Весовую функцию p(Y) можно рассматривать как плотность рас¬
пределения случайного вектора Y. Тогда (П.4.1) запишется в виде
Q (X) = Му Q (X + Y),
где операция математического ожидания MY берется по случайному
вектору Y, имеющему плотность распределения р (Y). Пусть
213
Yi,.... \N — конкретные реализации этого случайного вектора.
Тогда получаем монте-карловскую оценку интеграла (П.4.1)
N
(X) = Q (X + Y,). (П.4.2)
£=1
Эта оценка обладает очевидным свойством сходимости к точному
значению интеграла
lim QN(X)=Q (X)\
N-*00
Поскольку усредненная функция <?(Х) получается одноэкстре¬
мальной (так как ^(X)^Qi(X)), то к ней можно применить лю¬
бые локальные алгоритмы поиска, причем выражение (П.4.2) дает
оценку значения этой функции в точке X. Располагая этой оцен¬
кой, можно использовать любой из рассмотренных выше алгоритмов
локального поиска, т. е. решить многоэкстремальную задачу ло¬
кальным методом. Однако следует иметь в виду, что каждая реа¬
лизация оценки сглаженной таким образом функции представляет
собой случайную величину, лишь среднее значение которой равно
£(Х). Оперирование оценками ^ в процессе поиска эквивалентно
поиску при наличии случайных помех, накладывающихся на функ¬
цию Ф(Х). При этом уровень этих помех обратно пропорционален
объему выборки N [см. (П.4.2)], что позволяет управлять помехой,
точнее уменьшать ее дисперсию путем увеличения N.
Параметр q определяет степень «размытости» весовой функции.
Чем больше q, тем сильнее усреднение и «грубее» решение задачи.
При малом q усреднение мало. Очевидно, что этот параметр сле¬
дует изменять в процессе поиска. Вначале он должен быть большим
и стремиться к нулю в конце поиска. При хорошем выборе функ¬
ции q(t) процесс поиска к глобальному экстремуму сходится до¬
статочно быстро.
П.5. Условная оптимизация
Задача условной оптимизации затруднена тем, что ее ^решение
Х# лежит на границе Q допустимой области Q, т. е. X*sQ. Пре¬
одолевают эту трудность двояко. С одной стороны, можно вос¬
пользоваться спецификой области Q, т. е. учесть вид функций, се
определяющих. Этот путь используют методы математического
программирования. Некоторые из них рассмотрены в § 6.4. Однако
возможен и в ряде случаев более целесообразен другой подход,
который заключается в сведении условной задачи оптимизации
к безусловной. При этом алгоритм поиска остается прежний (см.
П.2—П.4), а основное внимание уделяется процедуре преобразова¬
ния задачи в безусловную.
. Рассмотрим основные подходы в этом направлении.
1. Метод подстановки. Он используется при наличии ограниче¬
ний типа равенств
Q : gi(X)=0, i= 1,..., p<k. (П.5.1)
Эти ограничения представляют собой систему из р уравнений с k
неизвестными. Разрешим систему относительно р переменных через
214
ббтаЛьйые k—p и подставим этй выражения в Q(X). РазМерйость
решаемой задачи понизится на р, и она становится безусловной.
Так и поступают в случае, когда это сделать легко, например для
задач линейного программирования^ типа -(6.2.1), которые в ре¬
зультате такого преобразования приводятся к виду (6.4.1).
Очевидно, что подобное преобразование осуществимо только
при аналитической разрешимости системы уравнений (П.5.1). Если
вспомнить, что в общем случае это могут быть трансцендентные
уравнения, то очевидна ограниченность такого подхода.
Однако рекуррентный метод решения задачи оптимизации по¬
зволяет обойти эту трудность следующим образом. Разобьем век¬
тор искомых параметров X на два:
Х=(Х', X2), (П.5.2)
где
XJ= (#1,..., Xk—р); Х2= (хь,—р+ь • • •» хь.), (П.5.3)
и будем минимизировать функцию качества с помощью X1, а усло¬
виям (П.5.1) удовлетворять путем соответствующего подбора X2.
Последнее сделать просто: достаточно решить систему из р урав-
HAHITWT
*,(Х*. Х2)=0, 1=1 р (П.5.4)
относительно р неизвестных X2 при заданных значениях X1. Это
можно сделать любым численным методом (см. комментарий
к П.5). Таким образом, для любого заданного X1 всегда можно
определить такое X2, при котором условия (П.5.1) для Q будут
выполнены.
Тогда исходная задача условной оптимизации трансформи¬
руется в задачу безусловной оптимизации:
Q (X1, X2) min,
Xi
где вектор X2 определяется на каждом шаге безусловной оптими¬
зации как численное решение этой системы для заданного значе¬
ния X1.
Применим этот подход и для случая, когда имеются ограни¬
чения типа неравенств
Q:^(X)^0, /=1,..., q.
В этом случае система решаемых уравнений образуется из
уравнений нарушенных неравенств
hj (X1, X2) = 0, /= (П.5.5)
где гх,..., zx — номера невыполняющихся ограничений — неравенств
Здесь размерность определяемого вектора X2 равна т — числу
нарушенных ограничений. В процессе решения системы (П.5.5) чис¬
ло т может изменяться. Вместе с ним изменяется размерность X2.
Процесс заканчивается при т—0.
©тот подход довольно просто обобщается на случай наруше¬
ния ограничений двух типов:
2./ЫХ) = о,
•U^Xy^O, /= 1 q,
где система численно решаемых уравнений образуется из всех
нарушенных ограничений.
215
2. Метод проекций. Смысл этого метода сводится к следую¬
щему. Если в процессе решения задачи (6.1.8) получено проме¬
жуточное значение Хдг+1$=й, т. е. нарушающее ограничения Й,
го его следует спроецировать на й, т. е. удовлетворить ограниче¬
ниям, и продолжать решений задачи уже из спроецированной
точки
где знак пря означает „проекция на 2е. Процедура проецироьлния
наглядно иллюстрируется рис. П.5.1. Если й:^(Х)=0, то при-
цедура проецирования представляет собой спуск на ограничение
S.i(Х)=0 (см. рис. П.5.1,а). Если же область Й определяется не¬
равенствами (рис. П.5.1,6), то проецирование приводит к одной
из точек Х°ей этой области.
Рис. П.5.1. Иллюстрация работы метода проекций при ограничениях
типа равенства (а) и неравенств (б)
Рассмотрим сначала случай, когда Й:£г(Х)=0 (/=1, ..., р<
<k). Алгоритм проецирования из точки X на й заключается в по¬
строении процесса, который бы заканчивался в достаточно малой
е-окрестности области й, т. е. при
(см. штриховые лиции на рис. П.5.1,а), где ег— заданная точность
выполнения i-ro ограничения. Этот процесс можно организовать
любым методом локального поиска из описанных в П.2, П.З. Для
этого достаточно минимизировать функцию качества вида
при начальных условиях Х=Х#+1 (рис. П.5.1,а) с остановом по
условию (П.5.7). Можно решать и другую задачу:
(П.5.6)
ЫХ°)|<8г, 1=1, ..., р
(П.5.7)
Q* (X) = 2 181 (Х)| min
i—i х
(П.5.8)
Q° (X) = max |g* (Х)|-* min
(П,5.8а)
с тем же критерием останова.
216
Аналогично можно поступить й йрй йаруШений бгранйчений
типа неравенств (см. рис. П.5.1,6). В этом случае максимизируется
функция качества вида
где {у} — множество номеров нарушенных ограничений, для кото¬
рых hj(X) <0. • Критерий останова: Q°(X)^0. Аналогично
с тем же критерием останова. Как видно, определение проекции
Х° точки X удобно производить путем минимизации степени на¬
рушения ограничений, что может быть реализовано с помощью
поисковой оптимизации специально организованных функций. Таким
образом, при использовании метода проекций для решения услов¬
ной задачи последовательно шаг за шагом рещаются две безус¬
ловные задачи, которые можно объединить в одну:
т. е. происходит перёключение с одной минимизируемой функции
качества на другую в зависимости от выполнения условий Q.
3: Метод штрафных функций. Этот метод является прямым
развитием метода проекций, но в нем процесс проецирования со¬
вмещен с минимизацией исходной функции. Идея метода заклю¬
чается в построении такой функции качества, минимум которой
представляет собой решение поставленной задачи. Эта функция
в общем случае имеет вид
где /А (.•) и /в (•) — неотрицательные функции штрафа за нарушение
ограничений типа равенств и неравенств .соответственно, которые
построены следующим образом:
т. е. при выполнении условия Q штрафа нет, а при невыполнении
вводится положительная функция штрафа.
Конструкция функций /А и /в может быть весьма разнообразной.
Например, штраф за нарушение ограничений типа равенств может
быть записан в виде
Q0 (Х)=— 2 Mx)-*min,
/<={*} х
(П.5.9)
Qo (X) = —min hj (X) -► min
/= 1 k% X
(П.5.9a)
Q* (X) rnfri,
где
o <X) = ) Q (X) при X-S'2,
} \ Q°(X) приХ<£2,
(П.5.10)
Q (X) = Q (X) + /A (gl (X), ..., gp (X)) + /B (hx (X), ..., hq (X)),
(П.5.11)
(П.5.12)
P
/a=2 airist (*))>
(П.5.13)
i=1
15—299
217
Ш ф(-)—четная функций Со следую*цймй свойствами: <р(*)^0,
Ф(0)=0, *р(я) при *>0— монотонно возрастающая функция. Эти¬
ми свойствами обладает, к примеру, такая функция ср (х) = |Х|* ,
где v>0. Частный случай такой функции штрафа при а»= 1 и
v=l представлен выше (П.5.8).
Функция /А =■= max atf (gi (X) ^обобщает функцию (ГТ.5.8а).
Ы р
Как видно, разница между методами проекций и штрафных
функций заключается в том, что во втором методе учета огра¬
ничений минимизация штрафа и минимизация основной функ¬
ции происходят одновременно, в то время как в первом эти две
процедуры разнесены во времени и происходят независимо друг от
друга.
Коэффициенты а,- в функции штрафа (П.5.13) обычно называют
коэффициентами штрафа. При а—уоо, где а= min а/, решение бзе-
условной задачи
Q(X) + /a (X)-min=*X*A
х
совпадает с решением исходной условной задачи Q (X) -► min =£ X*,
где Q : gi(X)s=0 (t= 1, ..., р). Это, очевидно, следует из того, что
с ростом величины а минимизация прежде всего коснется функции
штрафов, т. е. выполнится условие Хей, и уж после этого будет
минимизироваться функция Q(X). Таким образом,
Ит,Х*А =-Х*.
а->оо
Теперь рассмотрим ограничения типа неравенств. Функции штра¬
фа в этом случае имеют, например, следующий вид:
я
'в(Х)“2 */+(*/(*»• (П.5.14)
/=1
где (•) — функция вида
-ф (z)=—min (0, г), . (П.5.15)
. ' . / о щри z>o,
a min (0, г) = <
\ z при z < 0.
Выражение (П.5.15) является положительной функцией штра¬
фа за нарушение ограничения г>0. Причем величина этого штра¬
фа тем больше, чем сильнее нарушается ограничение г. Коэффи¬
циенты Ъj играют роль коэффициентов штрафа.
Другой вид функции штрафа
/в (X) = max (hj (X))
/=1, ...,<?
аналогичен (П.5.9а). При bоо, где Ь = тах&/, решение безуслов-
. /=1 *
ной задачи
Q (X) + /в (X) -» min =J> Х*в
218
совпадает с решением условной, где Q:hj(X)^0 (/*=!,..., q), т. е.
Ь-*оо »
Теперь, объединяя оба вида штрафных функций, получаем
безусловную задачу вида
р щ
Q (X) =Q (X) + 2 <44- {gt (X)) + 2 буф (ft/(X))-» min. (П.5.16)
1=1 /=1
Пусть минимум этой функции расположен в точке Х*АВ. В общем
случае Х*АВ ф X*. Однако при а% Ь-+оо, где а и b определены
выше, решение безусловной задачи (П.5.16) совпадает с решением
исходной задачи, т. е.
lim Х*АВ = Х*. (П.5.17)
а, Ь-+оо
Это обстоятельство и гарантирует успех методу штрафных
функций.
Несколько слов об организации процесса решения этим мето¬
дом. Для того чтобы воспользоваться свойством (П.5.17), необ¬
ходимо начать оптимизацию при малых значениях параметров а
й b, постепенно их увеличивая в процессе поиска до максимальных
значений amSLX и Ьтах. При этом большую роль играет скорость
нарастания этих параметров. Она должна быть оптимальной, т. е.
не слишком большой, но и не маленькой.
Действительно, при малой скорости нарастания а и b переход
к «max и bmax будет слишком длительны^. Однако при очень
большой скорости нарастания а и b функция Q(X) становится
овражной (см. рис. 6.3.2,в), что затрудняет ее оптимизацию и
удлиняет поиск. Лучше всего величины а и b изменять адаптивно,
т. е. увеличивать в момент, когда имеется уверенность, что найдено
решение, достаточно близкое к Х*АВ .
П.6. Многокритериальная оптимизация
До сих' пор рассматривались методы решения задачи оптими¬
зации скалярной функцией качества Q(X). Однако на практике
при оптимизации обычно требуется решение задач, в которых кри*
терий Q(X) является не скаляром, а вектором
Q(X)=(<7i(X), ..., <7m(X))
и задача состоит в одновременной минимизации всех т критериев
<7/ (X) min, 1 (П.6Л)
где Q — множество допустимых решений, то же, что и в задаче
(П.1.1).
На первый взгляд многокритериальная задача кажется нераз¬
решимой* Действительно, оешая независимо каждую из т задач
15* 219
скалярной оптимизации (П.6.1), получаем т оптимальных локаль¬
ных решений:
X*i'.qi (X*/) = min qi (X), i = 1, т.
Как легко заметить, эти решения в общем случае не совпадают,
т. е. X*i=£X*j (1фП, и, следовательно, ни одно из локальных ре¬
шений не может служить решением исходной многокритериальной
задачи.
Введем довольно очевидные понятия предпочтения и эквива¬
лентности. Состояние Xi будем называть строго более предпочти¬
тельным, чем состояние Х2, если Q(Xi)^Q(X2), т. е. среди равенств
и неравенств qi(Xi)^qi(X2) (■*= 1, - -т) всегда найдется хотя
бы одно строгое неравенство. Будем
этот факт записывать в виде Xi)>X2,
если Q(X,XQ(X2).
Если же Q(Xi)=Q(X2), то со¬
стояния Х4 и Х2 будем считать экви¬
валентными: Хг^Х2. Заметим, что
эквивалентность, вообще говоря, не
соответствует равенству. В частном
случае, когда m=k, может оказаться,
что эквивалентность соответствует ра¬
венству Xj=X?, но в общем случае
это не так.
Знаки предпочтения ()>) и экви¬
валентности (~) имеют следующие
два очевидных свойства:
1) если Xi>X2 и Х2)>Х3, то Х^Хз — транзитивное свойство
предпочтения;
2) если Xi~X2 и Х2^Хз, то Х1~Хз — транзитивное свойство
эквивалентности.
Теперь введем понятие «пространства критериев» {Q}. Это
пространство имеет размерность т (по числу критериев) и обра¬
зуется т ортогональными осями, вдоль которых откладываются
значения qi=qi(X). Между пространством параметров {X} и про¬
странством критериев {Q} имеется тесная связь. Каждая точка про¬
странства параметров X отражается в определенную точку Q
пространства критериев (обратное не всегда имеет место).
Область Q допустимых состояний X в пространстве {X} , таким
образом, отражается в определенную область S пространства кри¬
териев {Q}. На рис. П.6.1 хорошо видно, что любая точка заштри¬
хованного множеству более предпочтительна, чем точка Q(X0)
(напомним, что рассматривается задача минимизации). Это обстоя¬
тельство позволяет выделить из всего множества 5 подмножество
S* точек Q*eS*, для которых уже не найдется более предпочти¬
тельных (см. жирную линию на рис. П.6.1). Однако это вовсе не
означает, что множество S* содержит только лучшие точки. Среди
Q &S*, вообще говоря, могут оказаться, и даже наверняка име¬
ются точки, в каком-то смысле лучшие, чем некоторые из 5*, но
зато среди *5* всегда найдутся точки более предпочтительные, чем
Qф S*.
Множество Q*e{X}, которое соответствует S*, обычно называют
множеством Парето, переговорным 'множеством' или областью
Рис. П.6.1. К определению
множества Парето
220
компромисса. Важность этого множества заключается в том, что
именно оно содержит решение многокритериальной задачи (П.6.1).
Пример. Пусть k—m=2,
^1=Х2!+Х22> fj2 — (#1 О2 “Ь (^2 Л)2» (*)
Q:—(i=l, 2).
На рис. П.6.2,а показана область Q и множество Парето Q* —
это отрезок прямой между точками минимума обоих функций (*).
Область S для этого примера показана на рис. П.6.2,б, где жирная
линия соответствует множеству S*.
Таким образом, с формальной точки зрения множество Парето
следует считать решением многокритериальной задачи (П.6.1). Од-
Рис. П.6.2. Пример
нако это «решение» по существу никого не может удовлетворить.
Прежде всего хотя бы потому, что это множество решений, а нуж¬
но лишь одно. На первый взгляд кажется, что указанное обстоя¬
тельство расширяет возможности оптимизации. Действительно,
всегда можно предложить еще один дополнительный критерий
qm+1 (X) и, решив задачу оптимизации на множестве Парето
1 (Х)->т!п,
х^й*
получить оптимум X*, удовлетворяющий уже (т-{-1) -у критерию.
Но это ошибочное заключение, так как оптимум получен ценой
значительного уклонения от оптимума исходных критериев. Это
хорошо видно на рис. П.6.1, где А—положение оптимума по пер¬
вому (и только первому) критерию. Если же ввести в рассмотрение
второй критерий q2, то оптимальная точка (пусть она расположе¬
на в С) будет значительно отличаться от оптимумов А и В, где
В — оптимум по второму критерию q2. Таким образом, «свобода»,
которую представляет множество Парето, «куплена» ценой значи¬
тельного уклонения от локальных оптимумов.
Для однозначного решения многокритериальной задачи опти¬
мизации всегда необходимо введение дополнительной информа¬
ции /. При отсутствии такой информации о решении X* ничего
221
нельзя сказать кроме того, что оно лежит на множестве Парето
S*. И только. Поэтому процесс решения задачи состоит, по сути
дела, в поиске и использовании дополнительной информации /,
с помощью которой многокритериальная задача сводится к одно¬
критериальной:
^(Х)=^(^(Х),..., qm(X),/), (П.6.2)
где q (X) — скалярная функция, минимум которой на Q* является
решением исходной многокритериальной задачи; W — свертка функ¬
ции <7* (X) (i=i,..., пг), использующая необходимую информацию
/. Простейшим способом сведения многокритериальной задачи к од¬
нокритериальной является ее представление в виде стандартной
задачи однокритериального математического программирования:
<7/ (X) -► min,
rfX^Q,
:U/(X)<£, 1ф1=1,
где информация I заключается в утверждении, что минимизировать
надо /-й критерий, а остальные т—1 ограничить сверху числами
qi (i=l,..., пг). Так обычно и решались многокритериальные за¬
дачи в недалеком прошлом. Но недостаток такого метода очеви¬
ден, так как трудно определить «главный» критерий qi(X) и числа
qi ограничений. Это и заставляет обращаться к другим методам.
Таким образом, различные методы решения многокритериаль¬
ной задачи отличаются видом и способом получения информации
/, а также алгоритмом W «сворачивания» исходных критериев
в один глобальный критерий <7(Х).
Все имеющиеся методы можно подразделить на три класса:
априорные, апостериорные и адаптивные методы решения задачи
многокритериальной оптимизации. Рассмотрим их.
Априорный метод связан с построением критерия (П.6.2) на
основе только априорных сведений об объекте. Например,
т т
q (X) = 2 hqi (X); q (X) = Д <h‘ (*)
i=\ /=1 ~
и т. д., где информация I определяет значения коэффициентов
A»i, . . ., Хт-
«Сворачивание» критериев может производиться и иначе:
^(X)=p[Q(X)—Q*],
где р(*)—некоторая весовая функция расстояния (р(0)=0, р(-)^
>0); Q* — вектор минимальных значений критериев:
Q*=(^*1}.. п q*m)i (П.6.3)
где q*i~ min qi(X) (f =- 1, т).
XG5®
Здесь решение однозначно определяется заданием весовой
функции р(-). Например,
т
<7(Х)=2 (qi(X)-q*l)K
i=l
222
МоЖйо определять решение X* многокритериальной зйдачй, исхбяй
из условия совпадения относительных «убытков» по каждому из
критериев:
И (X) - q*j
q*{ - q*. • ». у-1. .... я.
Априорный метод следует использовать в том случае, если объем
априорной информации достаточно велик, чтобы однозначно вы¬
брать способ «свертывания» верх т критериев в один (П.6.2). Если
это не удается, то обращаются к апостериорному методу.
Этот метод связан с организацией обора информации / до ре¬
шения поставленной задачи. Для этого прежде всего определим,
какими свойствами должна обладать функция свертки Щ-)
(П.6.2):
1. Функция №(•) должна быть инвариантна по отношению
к преобразованию сдвига, т. е.
qm)=W(q\-\-Ciy..., cjm-\-cm)t
где си • • •, Cm — любые числа. Действительно, от добавления к лю¬
бому из критериев постоянной составляющей решение многокри¬
териальной задачи не должно изменяться. (Это свойство называют
аддитивным.)
2. Функция W(-) должна быть инвариантна к изменению
масштаба любого критерия, т. е.
<7m) = Wr(^i^ri, . . ., dmQm)y
где di — любые положительные числа. (Это свойство называют ком¬
мутативным.)
3. Функция W(-) должна быть симметричной относительно
всех критериев, т. е. иметь одинаковую структуру по i= 1,..., m.
Всем этим требованиям удовлетворяет функция
W (X) = V] <х(- (П.6.4)
Ы Ь ~Ql
где max <7/ (X), a q*t определены выше [см. (П.6.3)]. В этом
легко убедиться при помощи простой подстановки. Каждое сла¬
гаемое в (П.6.4) представляет собой не что иное, как нормирован¬
ный критерйй, который может изменяться от 0 до 1.
Теперь рассмотрим способы определения весов аг* (£=1,..., пг).
Прежде всего естественно ограничить свободу выбора этих пара¬
метров очевидными условиями
m
2а/=1> а/>0, 1=1,..., пг. (П.6.5)
/=1
Для определения параметров а; необходимо получить информа¬
цию /, которую дает экспертный опрос, например, следующим обра¬
зом. Экспертам для оценки предпочтения предъявляются несколько
пар ситуаций Х}1* и Х|2) (/= 1, ..., р) со значениями всех крите¬
риев в этих точках, т. е. qj{X\l)) и qj (Xj2)) (/= 1, ..., m; i =
223
£=i,..., p). Эксперты этим парам ставят в соответствие оДий из
трех знаков )>, -< или Это и есть необходимая информация /,
с учетом которой имеет место одно из трех соотношений:
Г(Х/‘>) (Xf>)(/=1 Р).
В результате получаем вместе с (П.6.5) систему линейных нера¬
венств и равенств относительно неизвестных весов а *, разрешая
которую стандартными методами, нетрудно найти зону допустимых
значений a* (i=l,..., пг). Теперь осталось выбрать в этой зоне
одну точку, например соответствующую центру тяжести этой зоны,
и задача определения функции W(-) решена. Далее ее следует
минимизировать одним из методов, рассмотренных выше.
Однако в таких условиях эксперту работать не всегда легко.
При произвольных ситуациях, предъявляемых ему, он будет чаще
отказываться от решения, чем принимать его. Именно в этих слу¬
чаях следует обратиться к адаптивному методу.
Такой метод опирается на использование экспертных решений
в процессе решения многокритериальной задачи. Суть его сводится
к следующему. Эксперту предъявляется какая-то i-я ситуация
Х*еЙ* (на Парето) и указываются численные значения всех кри¬
териев в этой ситуации: ^(Xi),..., ^m(Xi). Эксперт принимает
решение, по каким из пг критериев следует сделать шаг миними¬
зации (в ущерб остальным, разумеется). Эту процедуру можно
выполнить формально, переходя в точку Xi+i^S*, обладающую
свойствами
qkj&l)<qMl&l-i). (П.6.6)
где kj (/= 1,..., &*<m)—номера критериев, указанные экспертом
на i-м шаге (их к1 штук). Это и есть информация /, поступившая
на i-м шаге. Решить задачу (П.6.6) нетрудно, тем более, что точка
Х<+1 должна быть расположена недалеко от X*. В полученной
точке Xi+i определяются все значения критериев, которые снова
предъявляются эксперту, и т. д. до тех пор, пока эксперт не оста¬
новится на решении X*, которое он признает оптимальным. Это и
есть решение многокритериальной задачи.
ЛИТЕРАТУРНЫЙ КОММЕНТАРИЙ
К ПРИЛОЖЕНИЮ
Задача оптимизации, сформулированная в П.1, является по
сути дела задачей математического программирования с той раз¬
ницей, что минимизируемая функция и функции ограничений могут
быть заданы алгоритмически, т. е. правилом вычисления их значе¬
ний, а не явно аналитически, как в математическом программиро¬
вании. Это обстоятельство не позволяет воспользоваться информа¬
цией о структуре указанных функций в процессе поиска решения,
что заставляет обращаться к достаточно универсальным алгорит¬
мам поиска.
Приведенная здесь классификация очень условна (как и все
классификации) и имеет целью лишь ориентировать читателя
в структуре приложения. Более полный обзор можно найти в кни-
ге [1].
Для первого ознакомления с методами поисковой оптимизации
читателю рекомендуется научно-популярная книга [2].
224
Одномерный поиск, рассмотренный в П.2, здесь не является са¬
мостоятельным алгоритмом, так как слишком мало задач управ¬
ления сводятся к оптимизации по одной переменной. Он входит
в качестве процедуры спуска вдоль выбранного направления при
многопараметрической оптимизации. Методов одномерной оптими¬
зации много. Наиболее полно они изложены в [3].
В П.З описаны в основном лишь спусковые алгоритмы много¬
параметрической оптимизации. Однако это лишь незначительная
часть существующих методов. Их подробное изложение можно
найти в [1—8]. Кроме того, для решения оптимизационных задач
можно воспользоваться некоторыми методами нелинейного мате¬
матического программирования, не слишком сильно связанными
с характером нелинейности (см. описок литературы к гл. 6).
Поиск глобального экстремума, рассмотренный в П.4, является,
по-видимому, самой сложной задачей оптимизации. Для ее решения
привлекаются разнообразные алгоритмы случайного поиска [1, 4,
б, 7, 9—11]. Имеются и детерминированные алгоритмы глобального
поиска [12, 13].
Идея сглаживания с использованием метода Монте-Карло дала
возможность сконструировать весьма эффективные алгоритмы гло¬
бального поиска [14, 15].
' Наиболее распространенным методом решения задач условной
оптимизации является метод штрафных функций, описанный в П.5.
Более подробно. с ним можно познакомиться по [8, 16].
Задачи многокритериальной векторной оптимизации, рассмот¬
ренные в П.6, являются достаточно новым классом задач, и ос¬
новной проблемой здесь является способ сворачивания всех кри¬
териев в один глобальный. Различные способы такой свертки рас¬
смотрены в [17—19]. Популярное изложение проблемы принятия
оптимальных решений в многокритериальной ситуации можно най¬
ти в брошюре [20]. Обзоры [21, 22] и сборник [23] позволяют по¬
лучить полное представление о существующих методах многокри¬
териальной оптимизации.
СПИСОК ЛИТЕРАТУРЫ
1. Растригин JI. А. Системы экстремального упавления. — М.: Нау¬
ка, 1974.
2. Первозванский А. А. Поиск. — М.: Наука.
3. Уайлд Д. Дж. Методы поиска экстремума: Пер. с англ.— М.:
Наука, 1967.
4. Растригин JI. А. Статистические методы поиска. — М.: Наука,
1968.
5. Пшеничный Б. Н., Данилин Ю. М. Численные методы в экстре¬
мальных задачах. — М.: Наука, 1975.
6. Гурин JI. С., Дымарский Я. С., Меркулов А Д. Задачи и ме¬
тоды оптимального распределения ресурсов. — М.: Сов. радио,
7. Алгоритмы оптимизации проектных решений/ Под ред. А. И. По-
ловинкина. — М.: Энергия.
8. Химмельблау Д. Прикладное нелинейное программирование:
Пер. с англ. — М.: Мир, 1975.
9. Моцкус И. Б. Многоэкстремальные задачи в проектировании. —
М.: Наука, 1967,
225
10. Юдин Д. Б. Математические методы управления в условиях не¬
полной информации. — М.: Сов. радио, 1974.
11. Коган Б. М., Тер-Микаэлян Т. М. Решение инженерных задач
на ЦВМ. — М.: Энергия, 1964.
12. Уланов Г. М., Носуллаев Н. Н. Многоэкстремальные системы
управления. — В кн.: Техническая кибернетика/ ВИНИТИ. — М.,
1972. —Т. 4.
13. Стронгин Р. Г. Информационный метод многоэкстремальной
оптимизации при измерениях с помехами. — Изв. АН СССР, Тех¬
ническая кибернетика, 1966, № 3.
14. Катковник В. Я. Методы алгоритмической оптимизации. — В кн.:
Методы исследования нелинейных систем автоматического
управления/ Под ред. Р. А. Нелепина. — М.: Наука, 1975.
15. Катковник В. Я. Линейные оценки и стохастические задачи
оптимизации: метод параметрических операторов усреднения.—
М.: Наука, 1976.
16. Фиакко А., Мак-Кормик Г. Нелинейное программирование: ме¬
тоды последовательной безусловной минимизации: Пер. с англ.—
М.: Мир, 1972.
17. Гермейер Ю. Б. Введение в теорию исследования операций.—
М.: Наука, 1971.
18. Салуквадзе М. Е. Задачи векторной оптимизации в теории
управления. — Тбилиси: Мецниереба, 1975.
19. Гуткин Л. С. Оптимизация радиоэлектронных устройств по со¬
вокупности показателей качества. — М.: Сов. радио, 1975.
20. Солнышков Ю. С. Количественное обоснование решений. — М.:
Знание, 1971.
21. Ларичев О. И. Человеко-машинные процедуры, принятия реше¬
ний.— Автоматика и телемеханика, 1971, № 12.
22. Емельянов С. В., Борисов В. И., Молевич А. А., ЧеркашинА. М.
Модели и методы векторной оптимизации. — В кн.: Итоги нау¬
ки и техники. Техническая кибернетика, № 5. — М.: ВИНИТИ,
1973.
28. Многокритериальные 'задачи принятия решений/ Под ред.
Д. М. Гвишиани и С. В. Емельянова. — М.: Машиностроение,
1978.
Именной указатель
Абчук В. А. 180
Авдеева Л. И. 180, 1;81
Адамс Г. Э. 180
Адлер Ю. П. 5, '143
Айзерман М. А. 1203, 204
Акофф Р. 52, 53, 187, 188
Аркадьев А. Г. 203, 204
Балакирев С. В. 118
Басов А. С. 180, 181
Бендат Дж. 203, 204
Беоекерский В. А. 187, 188
Бешелев С. Д.* 70, 71
Бир С. 39, 40
Бусленко Н. П. 102„ 103
Борисов В. И. 225, 226
Браверман Э. М. 203, 204
Бонгард М. М. 203, 204
Вашер Г. 102, 103, 180, 181
Ватник В. Н. 203, 204
Ватель И. А 187, 188
Винер Н. 9, 39, 40
Воронов А. А. 187, 188*
Габасов Р. 180
Гаос С. 180
Гвишиани Д. М. 225, 226
Гейл Д. 180, 181
Гейнз |У. М. 180
Гельвеций 3
Гермейер Ю. Б. 187, 188, 225, 226
Глушков В. М. 39, 40
Гольштейн Е Г. 180, 181
Граве П. С. *39, 40, 52, 53
Грановский Ю. В. 141
де Гроот М. 70, 71
Гуровмч Ф. Г. 70, 71
Гуткин Л. С. 225, 226
Данилин Ю. М. 224, 225
Данилов Ф. А. 118
Даффин Р. 180, 181
Дворецкий 211
Денисов В. И 141
Джонсон Р. 40
Дудников Е. Г. 118
Дымарсшй Я. С. 225
Егоров К. В. 187, 188
Емельянов С. В. 225, 226
Ерешко Ф. И. 187, 188
Ермаков С. М. 102
Загоруйко Н. Г. 203, 204
Зайченко Ю. П. 179, 180
Захаров В. Н. 3
Зенер К. 180, 181
Зуховицкий С. И. 180, 181
Интрилигатор М. 179, 180
Карлин С. 180, Ш
Карпелевич Ф. И. 180, 181
Каст Ф. 40, 39
Кинг В. 39, 40
Кириллова Ф. М. 5, 180
Клиланд Д. 39, 40
Кориков А. М. 5
Коршунов Ю. М. 180
Корявов О. П. 102, 103
Коффман А. 180
Коган В. М. 225, 226
Круг Г. К. 141
Кузин Л. Т. 179, 180
Куо Б. 480, 181
Ларичев О. И. 225, 226
Лафевр В. А. 187, 188
Лецкий Э. К. 141
Ли Т. Г. 180
Лихтенштейн В. Е. 180, 181
Ляшенко И. Н. 180
Ма,к-Кормик Г. 180, 181
Маджаров Н. Е. 102, 118
Мако Д. 52, 53
Маркова Е. В. 141
Медич Д. 70, 71
Месарович М. 52, 53
Тер-Микаэлян Т. М. 225, 226
Мозес Л, 70, 71
Молевич1 А. А. 225, 226
Моисеев Н. Н. 102, 103, 180, 181
Мукачева 3. А. 180, 181
Меркулов А. Д. 225
Моцкус Н. Б. 1226.
Налимов В. В. 140, 141
Нейлор Т. 102, 103
Неймарк Ю. 5
Нетушин. А. В. 187
Носуллаев Н. Н. 225, 226
Оптнер С. Л. 40
Ордынцев В. М. 118
Павлов В. В. 18.8
Первозванекий А. А. 225
227
Йерегудов Ф. И. 4б
Питерсон Э. 180, 181
Полляк Ю. Г. 102, 103
Полетаев И. А. 5
Попов Е. П. 187, 188
Поспелов Д. А. 102, 103
Пугачев В. С. 187, 188, 203
Пупков К. А. 179, 180
Половинки'н А. И. 225
Пшеничный Б. Н. 226
Райбман Н. С. 118
Раскин Л. Г. 179, 180
Растригин J1. А. 39, 52,. 63, 102,
1118, 225
Розенцвейг Д. 40
Розоноэр 'Л. И. 203, 204
Ромакин М. И. 180, 181
Рубан А. Н. 5
Рубинштейн Г. Ш. 180
Саати Т. 180, 181
Садовский А. Е. 180, 181
Салуквадзе М. Е. 225, 226
Сапошков Р. А. 187, 188
Свешников А. А. 181, 203
Скляревмч Л. 5
Сковорода Г. 6
Соболь И. М. 102, 103
Солнышков Ю. С. 225, 226
Сосули'Н Ю. А. 141
Строи г.ин Р. Г. '225, 226 .
Сушков Б. Г. 102, 103
Табак А. 180, 181
Тарасенко В. П. 5
Тарасенко Ф. П. 5
Тахакара И. 52, 53
Тихонов В. Й. 203, 204
Уайлд Д. Дж. 224, 225
Уемов А. И. 70, 71
Уланов Г. М. 226, 226
Фату ев В. А. 141
Федоренко Н. П. 39
Федоров В. В. 141
Фюакко А. '180, 181 .
Финкельштейн Ю. Ю. 180, 181
Форрестер Дж. 102, 103
Хазацкий В. Е. 3
Химмельблау Д. 141, 2125
Хургин Я. И. 140, 141
Цирлин А. М. 118
Чадеев В. М. 118
Червоненкис А. Я. 203, 204
Черкашин А. М. 225, 226
Чернов Г. 70, 71
Черняк Ю. И. 40
Шеннон К. 102, 103
Шляпентох В. 70, 71
Эйкхофф П. 118
Эмери Ф. 52, 53
Эшби У. 39, 40
Юдин Д. В. 180, 181, 225, 226
Юревич Е. И. 187, 188
Янг С. 40
Предметный
»
Абсолютно управляемый объект 63
Адаптация модели 29
Адаптивная идентификация в за¬
дачах управления точностью
прокатки труб 118
Адаптивный алгоритм идентифика¬
ции 106
— метод 224
Аддитивная модель стохастичности
92
Активность объекта 184, 187
Алгоритм 1115
Алгоритмы случайного поиска 212
Априорные и апостериорные дан¬
ные 104
Базовые отношения 97
— понятия 97
Взаимодействие субъекта с систе¬
мой управления 44
— целевой области и траектории
изменения среды 51
Входы и выходы объекта. 71
, экспертное ранжирование 74
Выделение объекта из среды 53
Выпуклая область 151
Границы объекта 54
Декомпозиция модели 85
228
указатель
—, влияние на сложность 89
— на два элемента 88
Динамический объект 193
Д и на м ич ес к ое пр огр а м м иров а н и е
171
Динамичность 90
Дискриминирующие планы 135
Дисперсионная матрица парамет¬
ров 125
D-критерий оптимальности 126
D-оптимальное планирование 127
Задача вариаци-онн-ая 145
— нелинейного программирования
151
— оптимизации функций многих
переменных 206
— синтеза управления 179
— стохастического программирова¬
ния 152
— целочисленного программирова¬
ния 153
Задачи линейного программирова¬
ния 148
, пример образования вы¬
пуклого многогранника 160
— математического программирова¬
ния 148, 155, 179
, методы решения 158
— оптимального проектирования 151
— синтеза решающего правила 201
— целочис л енного пр огр а мм ирова -
ния 153
, методы решения 164
Знаки предпочтения и эквивалент¬
ности 220
Зоны неуправляемости 67
— планирования в- пространстве
управляемых входов 123
Игры неантагонистические 187
Идентификация динамических моде¬
лей 114
~ параметров модели объекта 24,
103 •
— промышленных объектов 118
— сложных систем 109
— статических объектов 107
— динамических моделей 114
~ промышленнкх объектов 118
. Идея усиления контраста 83
Имена 98
Имитационное моделирование 94
Коррекция объекта управления 197
— параметров модели объекта 189,
203
~ системы управления 4, 29, 188
— целей управления 199
Коэффициент компетентности 67
Критерий планирования 121, 124
— согласованности экспертов 79
Локальность задачи выпуклого
программирования 150
Линии равного уровня 157
Математическое описание 18
— программирование 145
Матрица ортогональная относитель¬
но столбцов 1Й9
— планирования '121
— средних предпочтений 84
Метод адаптивный 210
— апостериорный 223
— априорный 222
— возможных направлений 161
глобального случайного поиска
— градиентный 210
— дихотомии 208
— золотого сечения 208
— касательных 207
— Монте-Карло (статистических
испытаний) 96, 102
локального случайного поиска
непосредственного ранжирования
76
— парных сравнений 81
— подстановки 214
— покоординатный (Гаусса—Зейде-
ля) 210
— проекций 216
2^ажива1ШГЯ глобального поиска
~ стохастической аппроксимации
Методы многомерной стохастиче¬
ской аппроксимации 211
— поисковой оптимизации 205
решения вариационных задач
167, 180
Многокритериальная оптимизаций
219
Множество Парето 220
Модели имитационные 94, 102
— семиотические 97, 102
Моделирование сложных объектов
94
Модель объекта управления 22
— субъекта 42
Невоспроизводимость эксперимен¬
тов 19
Некомфортность субъекта 45
Нелинейность 91
Неадаптивный алгоритм идентифи¬
кации 106
Ненаблюдаемое возмущение 15
Нестацион арность сложного объек¬
та 20, 93
«Нетерпимость» к управлению 19
Обратный поиск 166
Объект планирования 120
— управления 9, 21, 63
, зоны неуправляемости 65
— эргатический 187
Объекты линейные 91
— нелинейные 92
Одн опар а метрический локальный
поиск 206
Оператор 10
Оптимальное управление '146, 176
Оптимальные цели управления 46
Оптимум ^размеров» объекта 54
Парадокс цели 41
Пассивное наблюдение 25
Планирование эксперимента 25, 103,
118, 140
последовательное 133
, теория 120
Правило вычисления рангов по мат¬
рице 82
— транзитивности 82
Преобразование исходных описа¬
ний 101
Признаки задачи оптимизации 205
Принцип максимума 167
Показатели эффективности струк¬
тур 196
Пространство ситуаций 47
— целей 49
Ранжирование 75
Реализация управления 181
Рекуррентный метод 155
Рельеф функции 157
— целевых функций и показателей
качества 186
Рельефы функции качества 167
Ресурсы планирования 121
Связи объекта со средней 72
Симметрия 101
Симплексный метод 159
Синтаксически правильные фразы
98
Синтез модели управления 4, 71
параметрический 103
структурный 71
— управления 26, 14'2
Система управления 11
для составления коктейля 31
Системный подход 38
Ситуация §0
229
след матрицы 126
Сложная система 18
Сложность 85
Сложный объект управления 17
Согласованность экспертов 69, 78
Старение информации 202
Статистический объект 183, 191
Стохастичность поведения сложных
объектов 18
— структуры объекта 92
Структура 23
— задач поисковой оптимизации 206
— модели 69, 102, 119
• объекта динамическая 90
статистическая 90
Структурная ‘адаптация 203
Структурный синтез модели 23, 71,
*102
Транзитивности правило 82
Управление 6, 8
— помощью формальных методов
^ динамическим объектом \4f
— сложным объектом 20
Управления реализация 4, 28
Управляемость объекта 60
, экспертный метод оценки 67
— частичная (относительная) 64
Условия Дворецкого 210
Условная оптимизация @14
Формализм ® управлении 6
Формулировка целей управления
21, 50
Функция 10
— выпуклая вниз 150
— Гамильтона 169 " .
Целевые переменные 48
Цель управления 4, 15, 41, 20
«Черный ящик» 72, 85
Экспертная оценка неуправляемо¬
сти объекта 69
Язык бинарных отношений 97
Оглавление
От автора 3
Предисловие 6
Введение 9
В.1. Что такое управление? 9
В.2. Система управления
В.З. Что такое «сложный объект управления»? 17
В.4. Этапы управления сложным объектом .... 21
В.5. Как сделать коктейль? (Несерьезная иллюстрация
серьезных этапов управления) 31
Литературный комментарий к введению . . . . . . . 39
Список литературы 40
Глава I. Формулировка целей управления 41
1.1. Парадокс цели . 41
1.2. Модель субъекта 42
1.3. Пространства ситуаций и целей 46
Литературный комментарий к главе 1 52
Список литературы 53
Глава 2. Определение объекта управления 53
2.1. Анализ проблемы 53
2.2. Метод экспертных оценок 56
2.3. Управляемость объекта 60
2.4. Экспертный метод оценки управляемости объекта 67
Литературный комментарий к главе 2 70
Список литературы . . . . . . . . . . 71
Глава 3. Структурный синтез модели объекта .... 71
3.1. Определение входов и выходов объекта .... 71
3.2. Экспертное ранжирование входов и выходов ... 74
3.3. Декомпозиция модели 85
3.4. Структура модели 89
3.5. Имитационные модели 94
3.6. Семиотические модели . . . . . . . . . 97
Литературный комментарий к главе 3 102
Список литературы 102
Глава 4. Идентификация параметров модели .103
4.1. Постановка задачи идентификации . 104
4.2. Идентификация статических объектов 107
4.3. Идентификация динамических моделей . . . . 114
Литературный комментарий к главе 4 . . . . . . . 118
Список литературы .......... 118
Глава 5. Планирование экспериментов 118
5.1. Основные понятия теории планирования экспериментов 120
5.2. Критерии планирования 124
5.3. D-оптимальное планирование . . 127
5.4. Последовательное планирование экспериментов . . 133
5.5. Дискриминирующие планы . 135
Литературный комментарий к главе 5 140
Список литературы . . 141
Глава 6. Синтез управления (принятие решения) . . 142
6.1. Постановка задачи . . . . 142
6.2. Классификация задач математического программиро¬
вания 148
6.3. Анализ задач математического программирования . 155
6.4. Некоторые специальные методы решения задач мате¬
матического программирования 158
6.5. Некоторые специальные методы решения вариацион¬
ных задач 167
Литературный комментарий к главе 6 . 179
Список литературы 180
Глава 7. Реализация управления 181
7.1. Постановка задачи 182
7.2. Учет влияния среды 183
7.3. Учет активности объекта 184
Литературный комментарий к главе 7 187
Списоклитературы . 187
Глава 8. Коррекция системы управления . . . . . 188
8.1. Коррекция параметров модели объекта . . . . 189
8.2. Коррекция структуры модели 194
8.3. Коррекция объекта управления 197
8.4. Коррекция целей управления 199
Литературный комментарий к главе 8 203
Список литературы . . . . . . . . . . 203
Пр и л о ж е н и е. Методы поисковой оптимизации .... 205
П. 1. Постановка задачи 205
П.2. Однопараметрический локальный поиск (п=Г) . 206
П.З. Многопараметрический локальный поиск (д> 1) . . 210
П.4. Алгоритмы глобального поиска . . . ' . . . 212
П.5. Условная оптимизация 214
П.6. Многокритериальная оптимизация 219
Литературный комментарий к приложению 224
Списоклитературы . . 225
Именной указатель . 227
Предметный указатель . . . 228