Автор: Берс Л.
Теги: анализ математика математический анализ учебное пособие москва высшая школа
Год: 1975
Текст
Липман Берс
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
Lipman Bers
Calculus
HOLT, RINEHART AND WINSTON, INC.
New York Chicago San Francisco Atlanta Dallas Montreal Toronto London Sydney
Липман Берс Математический анализ
Том I
Перевод с английского Л. И. Головиной, под редакцией И. М. Яглома
МОСКВА аВЫСШАЯ ШКОЛА» 1975
517.24-517.3
Б48
УДК 5174-516(075)
Рекомендовано
Учебно-методическим управлением по высшему образованию в качестве пособия для студентов высших технических учебных заведении
Берс Л.
Б48 Математический анализ. Т. I. Перевод с англ. Л. И. Головиной. Под ред. И. М. Яглома. Учеб, пособие для втузов. М., «Высш, школа», 1975.
519 с. с ил.
Переведенная с английского языка книга Л. Берёа представляет собой учебное пособие по курсу математического анализа (с элементами аналитической геометрии) и предназначается для первоначального ознакомления с предметом.
Книгу отличает большая тщательность в подборе и расположении материала, наглядность, соединяющаяся с высоким научным уровнем, а также органическая связь «чистой» математики и ее приложений.
Первый том посвящен введению в анализ, дифференциальному и интегральному исчислению функций одной переменной.
Предназначается в качестве учебного пособия для студентов втузов; может быть также использована преподавателями высших учебных заведений.
Б 20203—409 001(01)—75
БЗ—16—17—75
517.24-517.3
Издательство «Высшая школа», 1975.
ОГЛАВЛЕНИЕ
От редактора 9
Предисловие к русскому изданию 14
1. Числа 17
§ 1. Рациональные числа. Потребность в расширении понятия числа 18
1.1. Положительные дроби (18). 1.2. Рациональные числа (19). 1.3. Несоизмеримые отрезки (20).
§ 2. Сложение и умножение 22
2.1. Переменные (22). 2.2. Аксиомы поля (22). 2.3. Следствия из аксиом поля (23). Уп-
ражнения (24). 2.4. Целые числа. Степени (24). Упражнения (25). 2.5. Геометрическая прогрессия (25). Упражнения (25).
§ 3. Неравенства 26
3.1. Обозначения (26). Упражнения (26).
3.2. Другие аксиомы (26). Упражнения (27).
3.3. Решение неравенств (27). Упражнения (29). 3.4. Аксиома Архимеда (30). Упражнения (30). 3.5. Абсолютная величина (31). Упражнения (32). 3.6. Рациональные числа, определенные с помощью аксиом (33).
§ 4. Десятичное представление рациональных чисел 33
4.1. Позиционные системы счисления (33).
4.2. Десятичные дроби (34). 4.3 Бесконеч-
ные десятичные дроби (35). 4.4. Периодические десятичные дроби (37). 4.5. Вычисления с десятичными дробями (38). Упражнения (39).
§ 5. Действительные числа 39
5.1. Определение действительного числа (39). Упражнения (40). 5.2. Вычисления с действительными числами (41). 5.3. Геометрическое истолкование действительных чисел; числовая прямая (42). 5.4. Корни (43). Упражнения (45). 5.5. Дробные степени (46). Упражнения (46). 5.6. Интервалы (46). Упражнения (47).
Приложение к главе 1 М
§ 6. Полнота системы действительных чисел. Индукция 47
6.1. Границы (47). Упражнения (48). 6.2. Принцип наименьшего целого числа (48).
6.3. Математическая индукция (48). Упраж-
* нения (50). 6.4. Принцип верхней грани (50). Упражнения (51). 6.5. Аксиомы действительных чисел (52).
§ 7. Приближенные вычисления 52
7.1. Оценка точности (52). Упражнения (54).
7.2. Округление десятичных дробей (55). Упражнения (55).
§ 8. Рациональные и иррациональные числа 56
8.1. Геометрическое построение произведения и частного (56). 8.2. Следствия из аксиом поля (57). Упражнения (58). 8.3 Периодичность рациональных десятичных дробей (58) Упражнения (60). 8,4. Плотность (61). 3.5. Сумма и произведение действительных чисел (61). 8.6. Другая точка зрения (62). Задачи (63).
2. Координаты 65
§ 1. Координаты точки, Формула расстояний 66
1.1. Декартова система координат (66). Упражнения (68). 1.2. Перенос системы корди-нат (68). Упражнения (69). 1.3. Формула расстояний (69). 1.4. Координаты в пространстве (71). Упражнения (72).
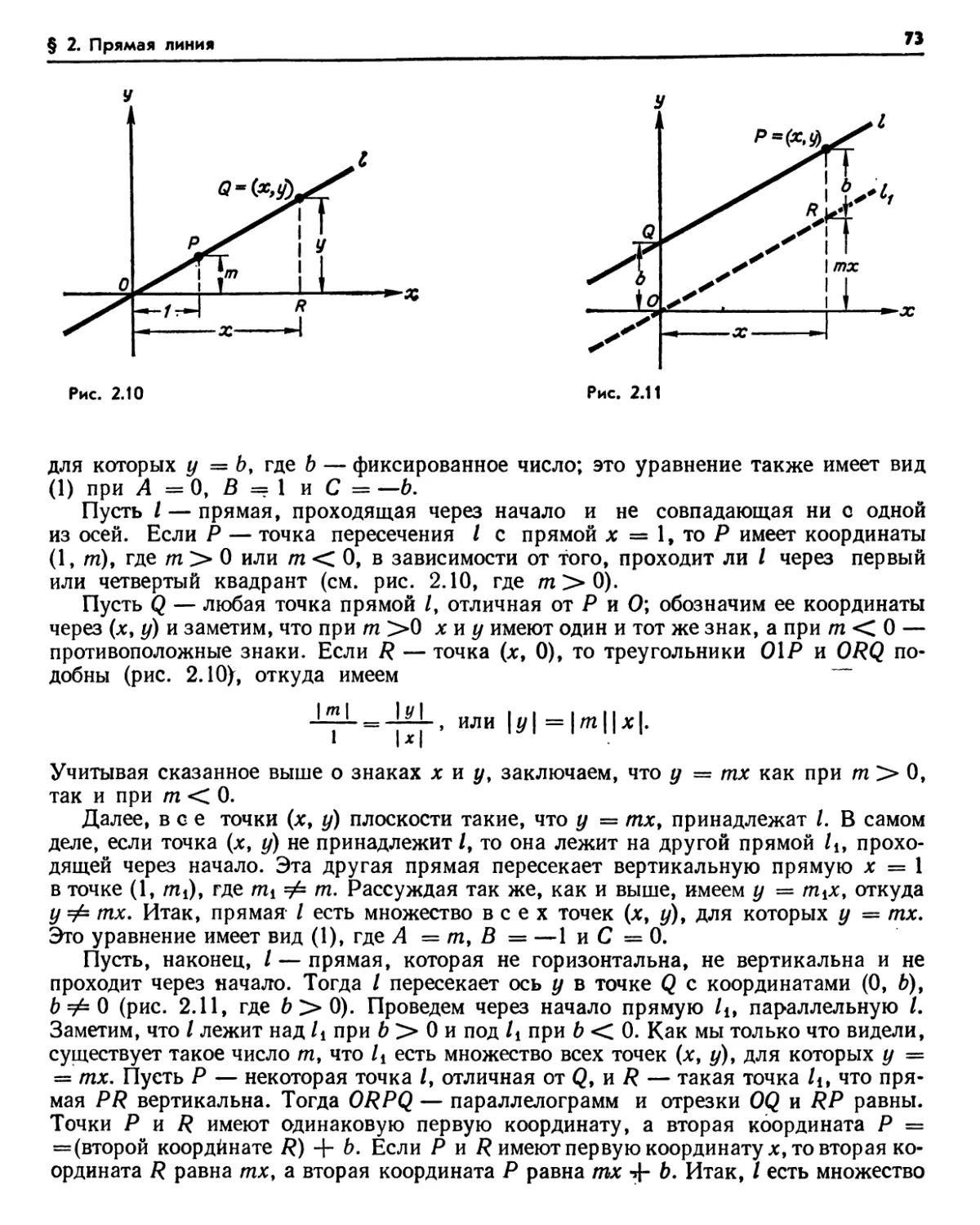
§ 2. Прямая линия 72
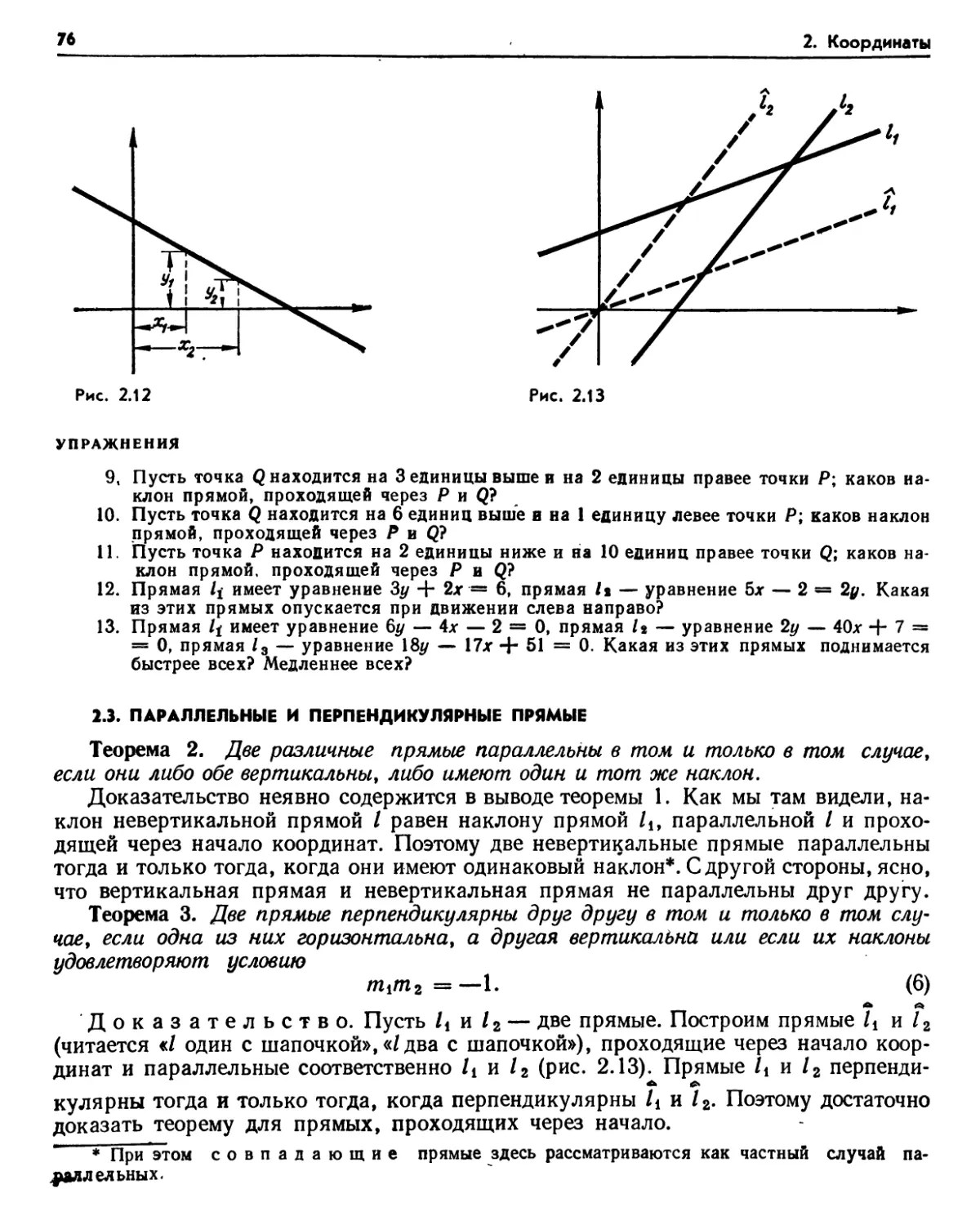
2.1. Линейные уравнения (72). Упражнения (74). 2.2. Наклон (75). Упражнения (76).
2.3. Параллельные и перпендикулярные прямые (76). Упражнения (77). 2.4. Уравнения прямых (78). Упражнения (79).
§ 3. Окружность 79
3.1. Уравнение окружности (79). Упражнения (81). 3.2. Касательная (81). Упражнения (82).
§ 4. Парабола 83
4.1. Определение параболы (83). 4.2. Свойства параболы (84). Упражнения (85). 4.3. Парабола с вертикальной осью (86). Упражнения (87). 4.4. Касательная (87). Упражнения (89).
Приложение к главе 2 89
§ 5. Квадратура параболы 89
5.1. Теорема Архимеда (89). 5.2. Доказательство Архимеда (89). 5.3. Сумма квадратов (91). Упражнения (92).
§ 6. Геометрия и числа 92
6.1. Аксиоматическая геометрия (92). 6.2. Аналитическая геометрия (93). 6.3. Алгебраический вывод аксиом (94). 6.4 Пространства более чем трех измерений (95). Упражнения (95). Задачи (95).
3. Функции 97
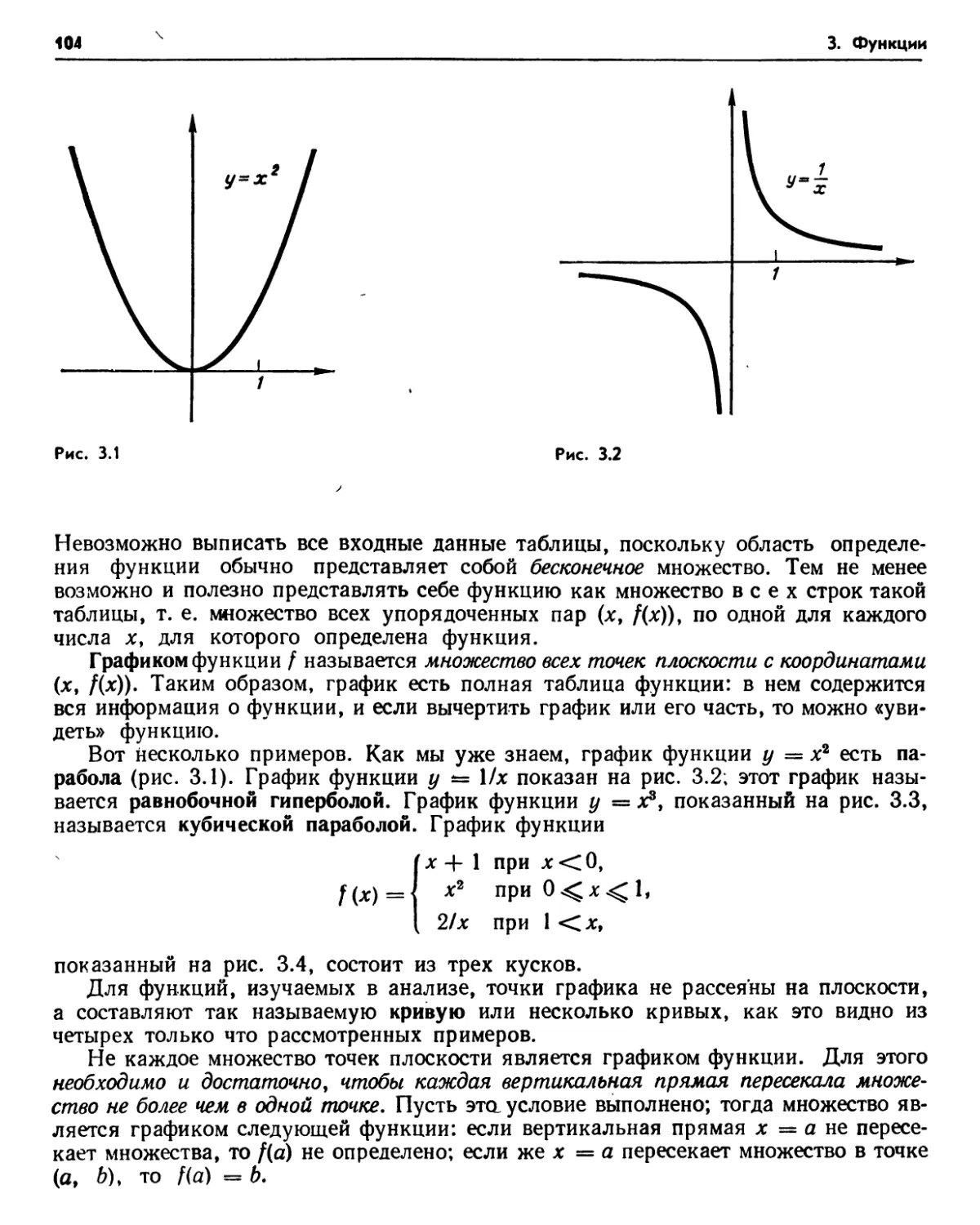
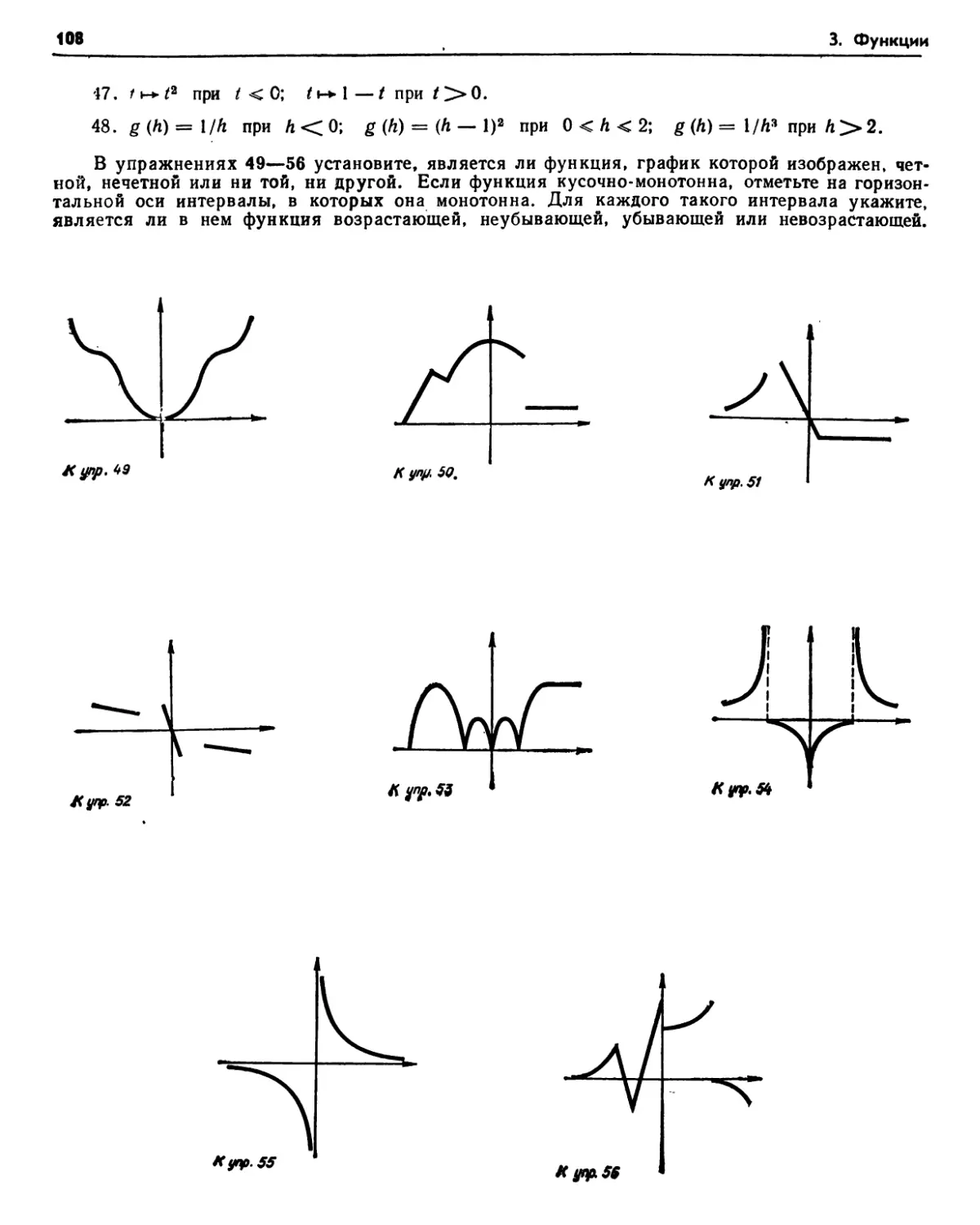
§ 1. Функции и графики 98
1.1. Функции (98). 1.2. Переменные, обозначающие функции (100). Упражнения (101).
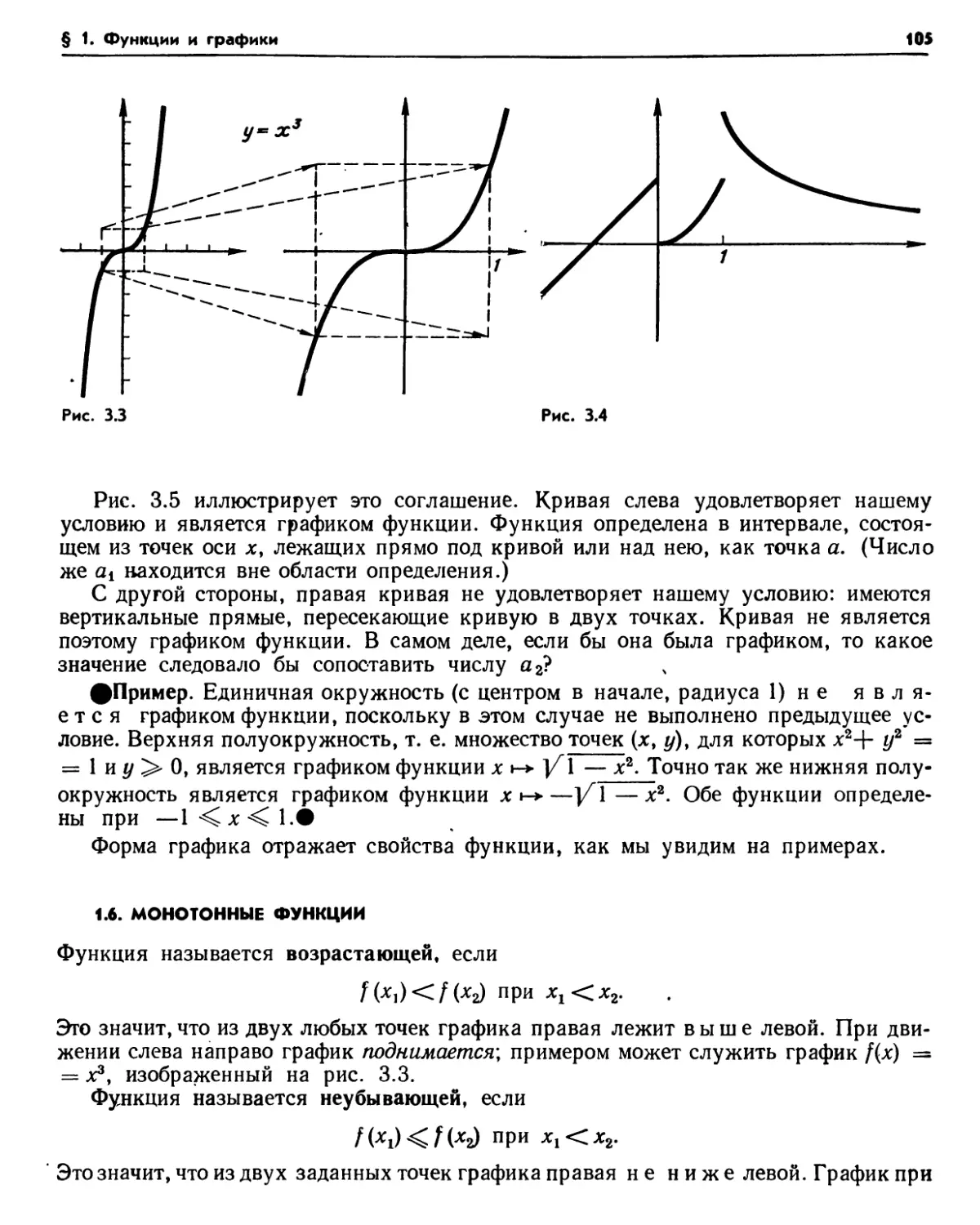
1.3. Сумма, разность, произведение и частное функций (101). 1.4. Композиция функций (102). Упражнения (102). 1.5. Графики (103). 1.6. Монотонные функции (105). 1.7. Четные и нечетные функции (106). Упражне-
6
Оглавление
ния (107). 1.8. Приложения функций (109).
Упражнения (109).
§ 2. Многочлены, рациональные и ирра-> циональные функции. Введение в теорию пределов ПО
2.1. Линейные функции (ПО). 2.2. Квадратичные функции (111) Упражнения (112).
2.3. Многочлены (112). 2.4. Деление «углом> (113). 2.5. Корни многочленов (113). Упражнения (114) 2.6. Рациональные функции
(115). Упражнения (116). 2.7. Иррациональные функции (116). Упражнения (116). 2.8. Расширение области определения рациональной функции (117). 2.9. Пределы рациональных функций (117). 2.10. Пределы других функций (118). Упражнения (120).
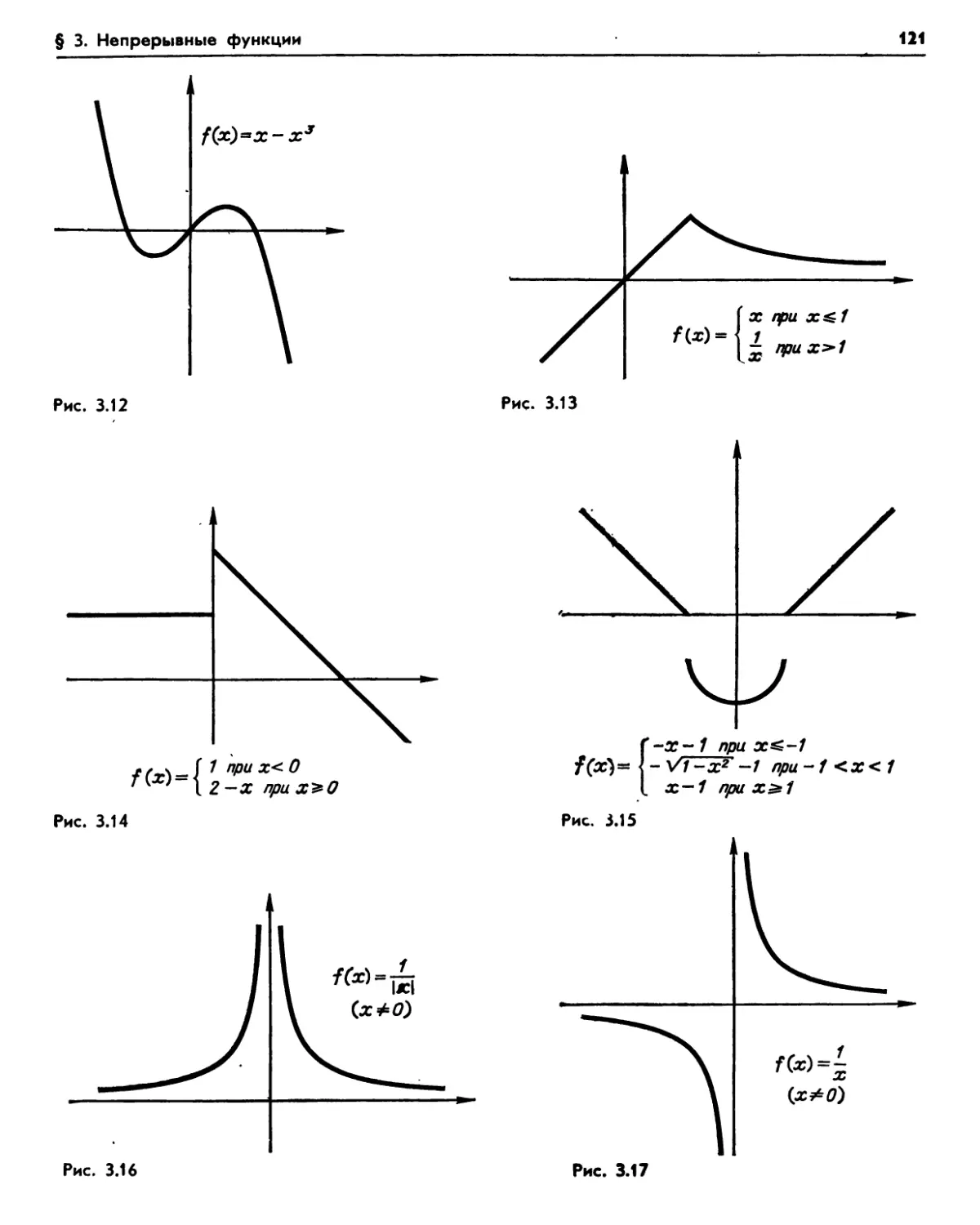
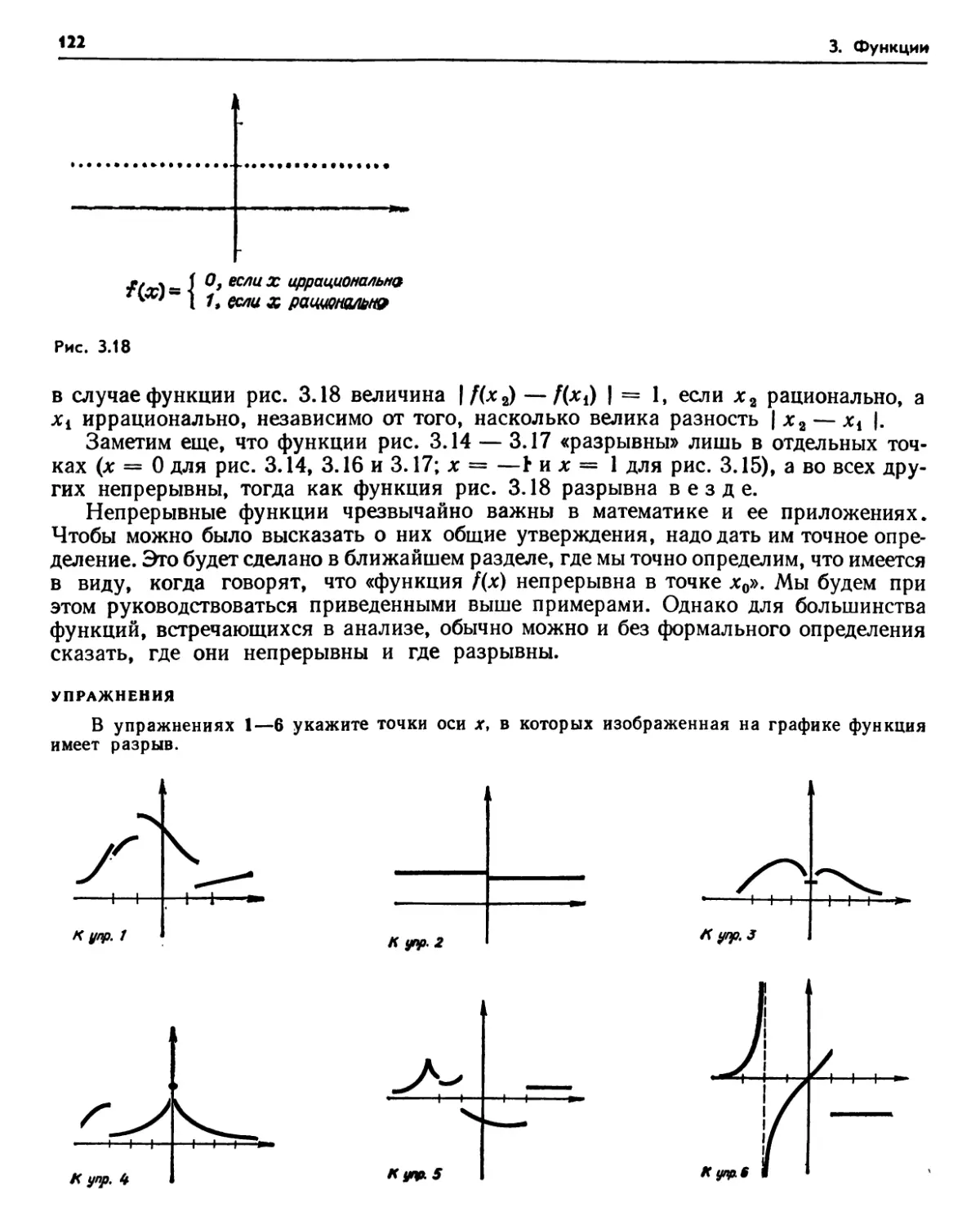
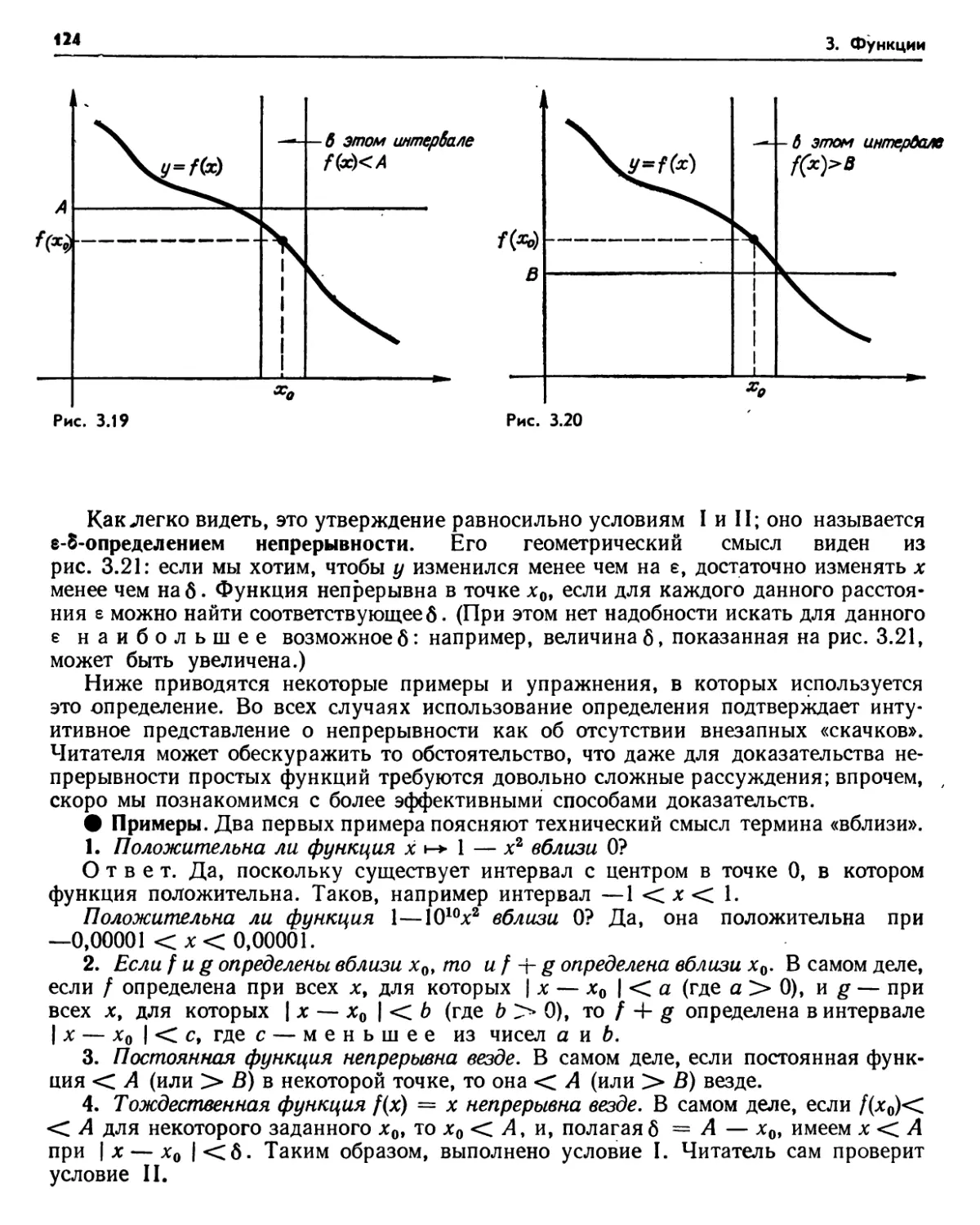
§ 3. Непрерывные функции 120
3.1. Примеры (120). Упражнения (122). 3.2. Определение непрерывности (123) Упражнения (126). 3.3. Непрерывность суммы, разности, произведения и частного (127). 3 4. Непрерывность рациональных функций (127).
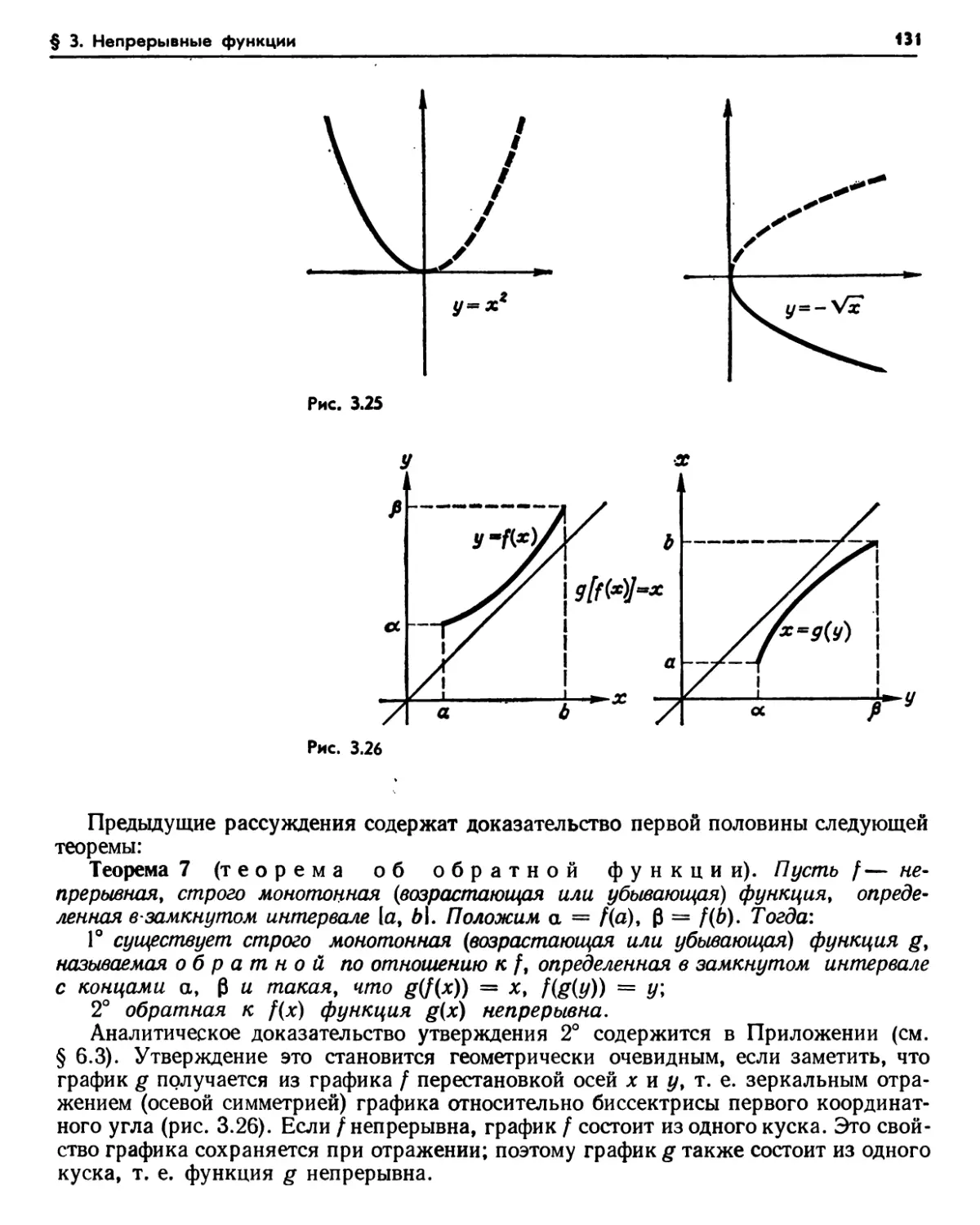
3.5. Непрерывность композиции функций (127). Упражнения (128). 3.6. Промежуточные значения (128). Упражнения (129). 3.7. Обратная функция (129). Упражнения (132).
3.8. Непрерывность иррациональных функций (132).
§ 4. Пределы
4.1. Определение предела (133). Упражнения (135). 4.2. Вычисление пределов (135). Упражнения (137). 4.3. Обобщения (137). Уп-ражнёния (139).
Приложение к главе 3 140
§ 5. Односторонние пределы, бесконечные пределы и пределы на беско нечности 140
5.1. Односторонние пределы (140). Упражнения (141). 5.2 Бесконечные пределы (141). Упражнения (142). 5.3. Пределы на бесконечности (143). Упражнения (144). 5.4. Вычисление бесконечных пределов (145). Упражнения (146).
§ 6. Доказательства . некоторых теорем о непрерывности 147
6.1. Сумма, разность, произведение и частное (147). Упражнения (148). 6.2. Композиция функций (149). Упражнение (149). 6.3. Обратная функция (149). Упражнение (149).
6.4. Вычисление бесконечных пределов (149). Упражнения (150).
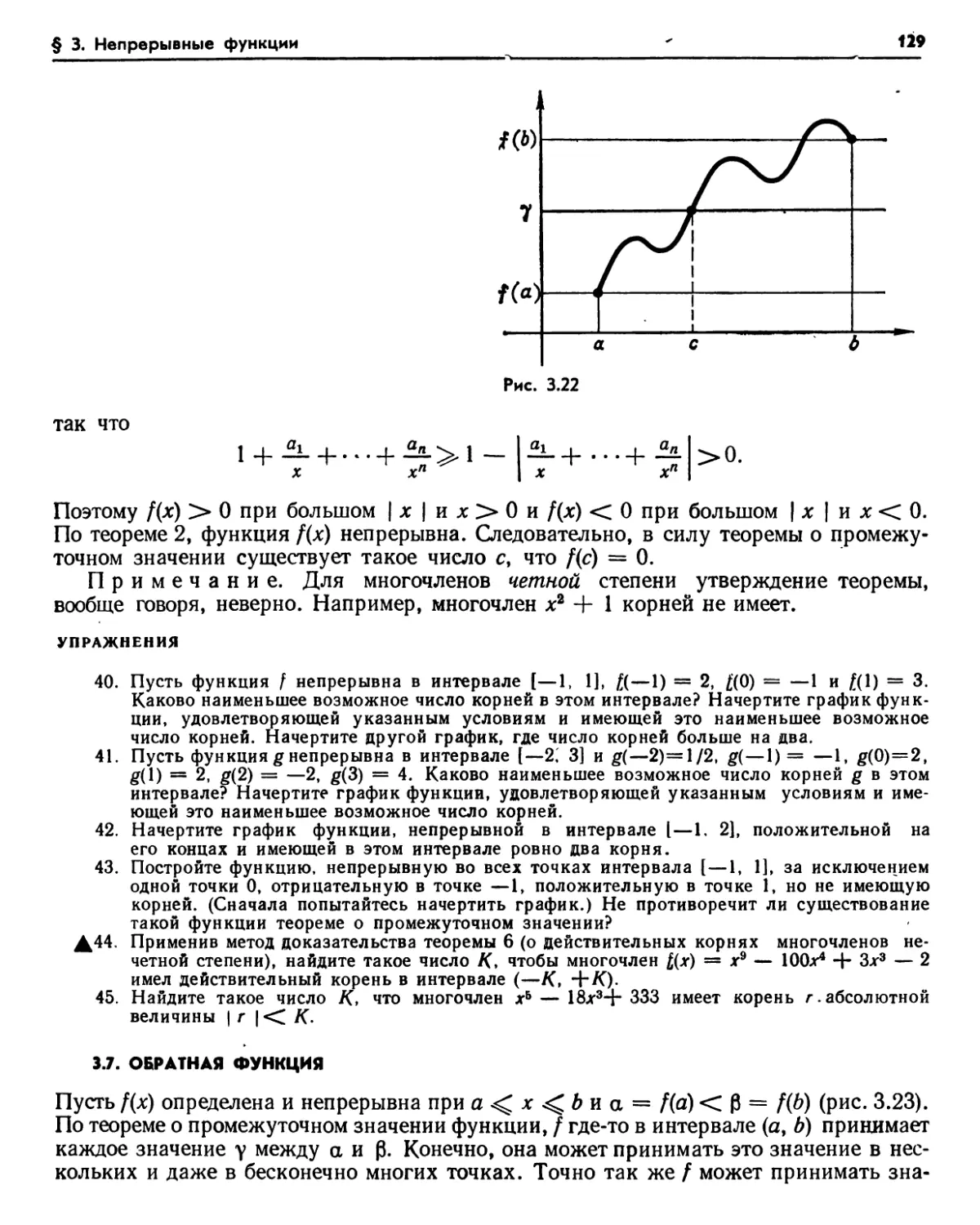
§ 7. Доказательство теоремы о промежуточном значении 150
7.1. Доказательство (150). Упражнения (151) 7.2.Необходимость доказательств (151). Задачи (151).
4. Производные 153
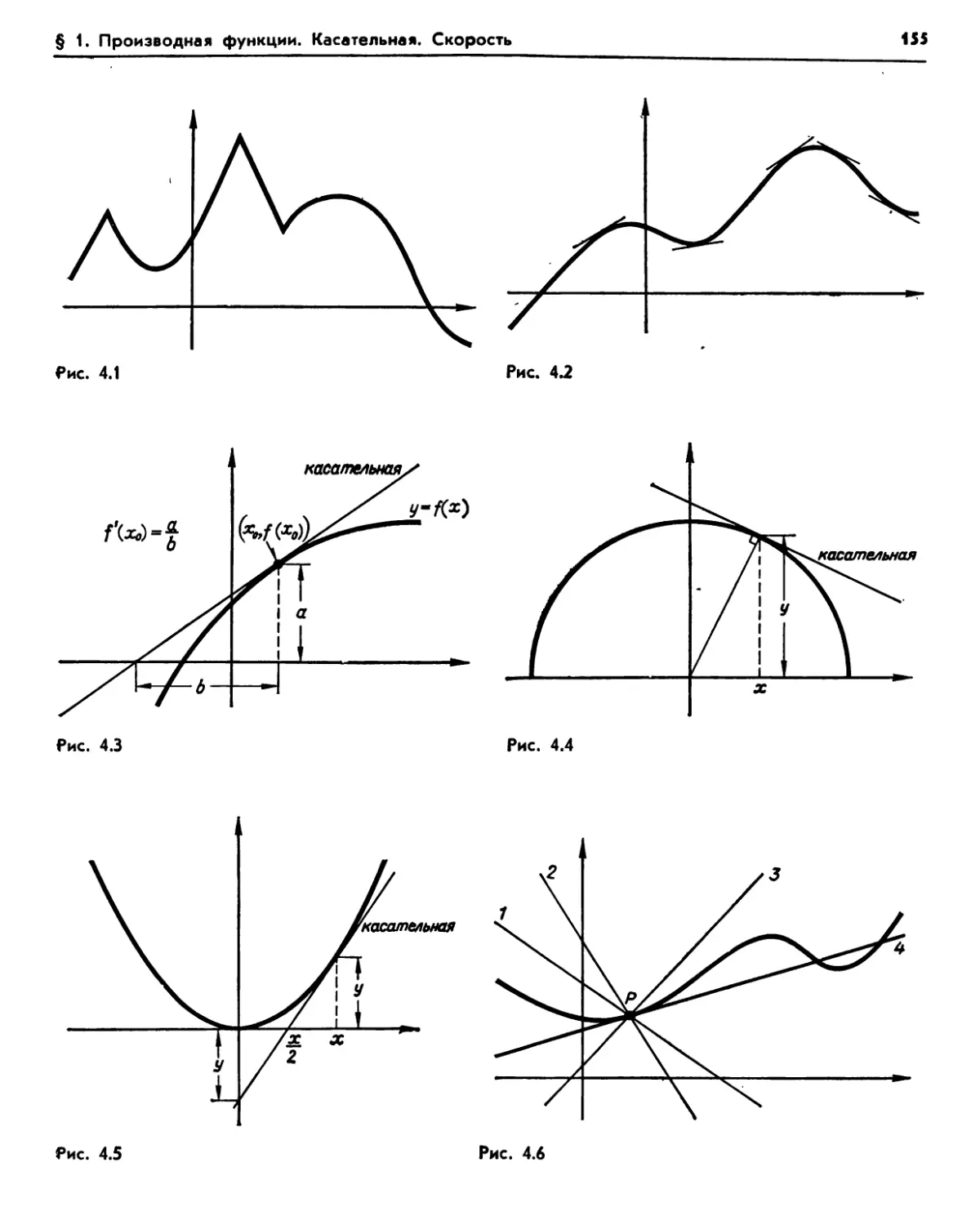
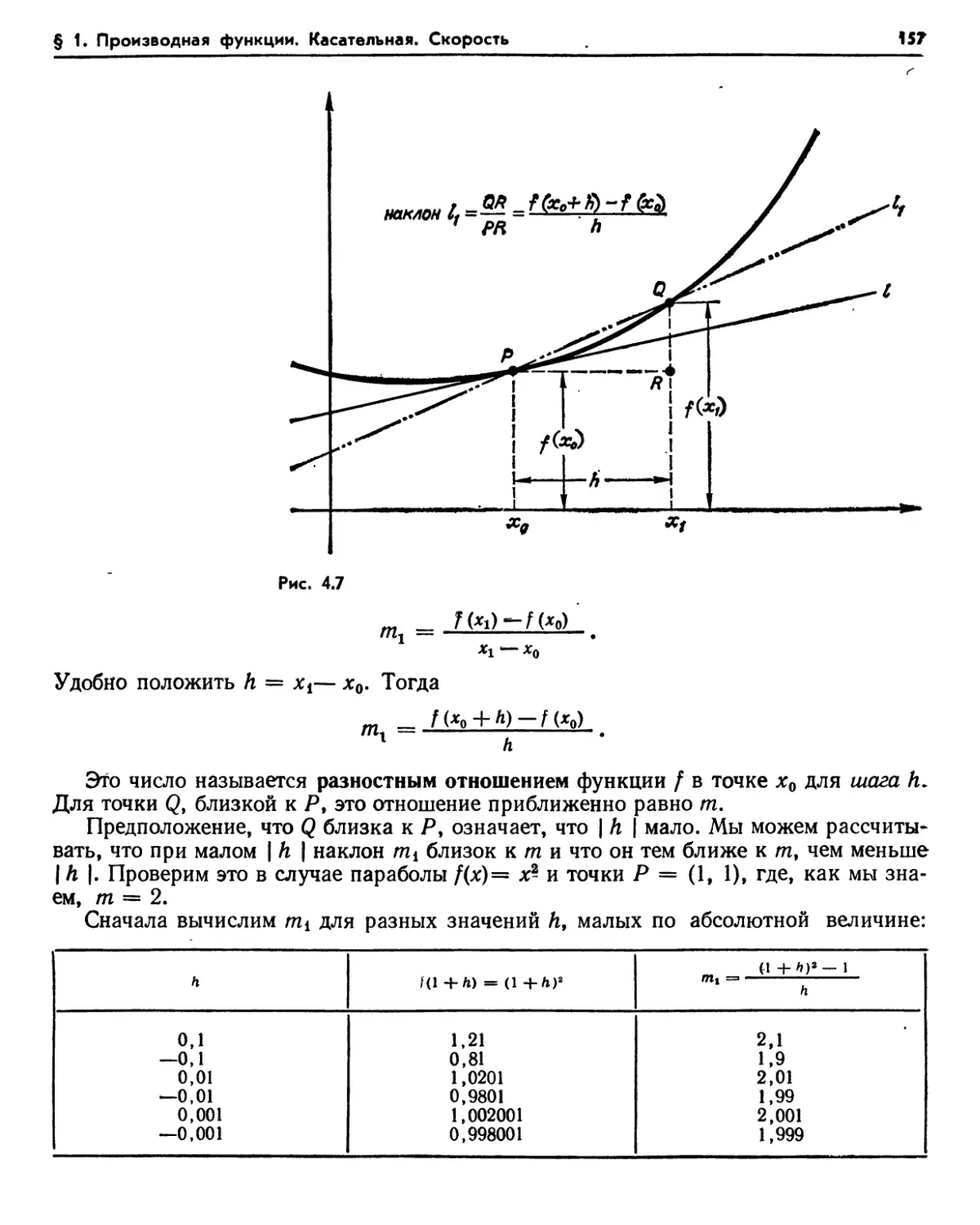
§ 1. Производная функции. Касательная. Скорость 154
1.1. Производная — наклон касательной (154). Упражнения (156). 1.2. Построение касательной (156). Упражнения (158). 1.3. Определение производной (159). 1.4. Касательная и нормаль (159). 1.5. Вычисление производной исходя из ее определения (160). Упражнения (161). 1.6. Производная — новая функция (161). Упражнения (162). 1.7. Обозначение Лейбница (163). Упражнения (164).
1.8. Теорема о линейном приближении (165). Упражнения (166). 1.9. Применение производ
ных для вычисления значений функций (166). Упражнения (167). 1.10. Непрерывность дифференцируемых функций (168). 1.11. Прямолинейное движение (168). 1.12. Равномерное движение (169) 1.13. Скорость неравномерного движения (169). Упражнения (170). 1.14. Свободное падение (170). Упражнения (172). 1.15. Быстрота изменения (172). Упражнения (173).
§ 2. Дифференцирование 173
2.1. Основные правила (173). Упражнения (175). 2.2. Набросок доказательства (175). 2.3. Дифференцирование степеней (177).
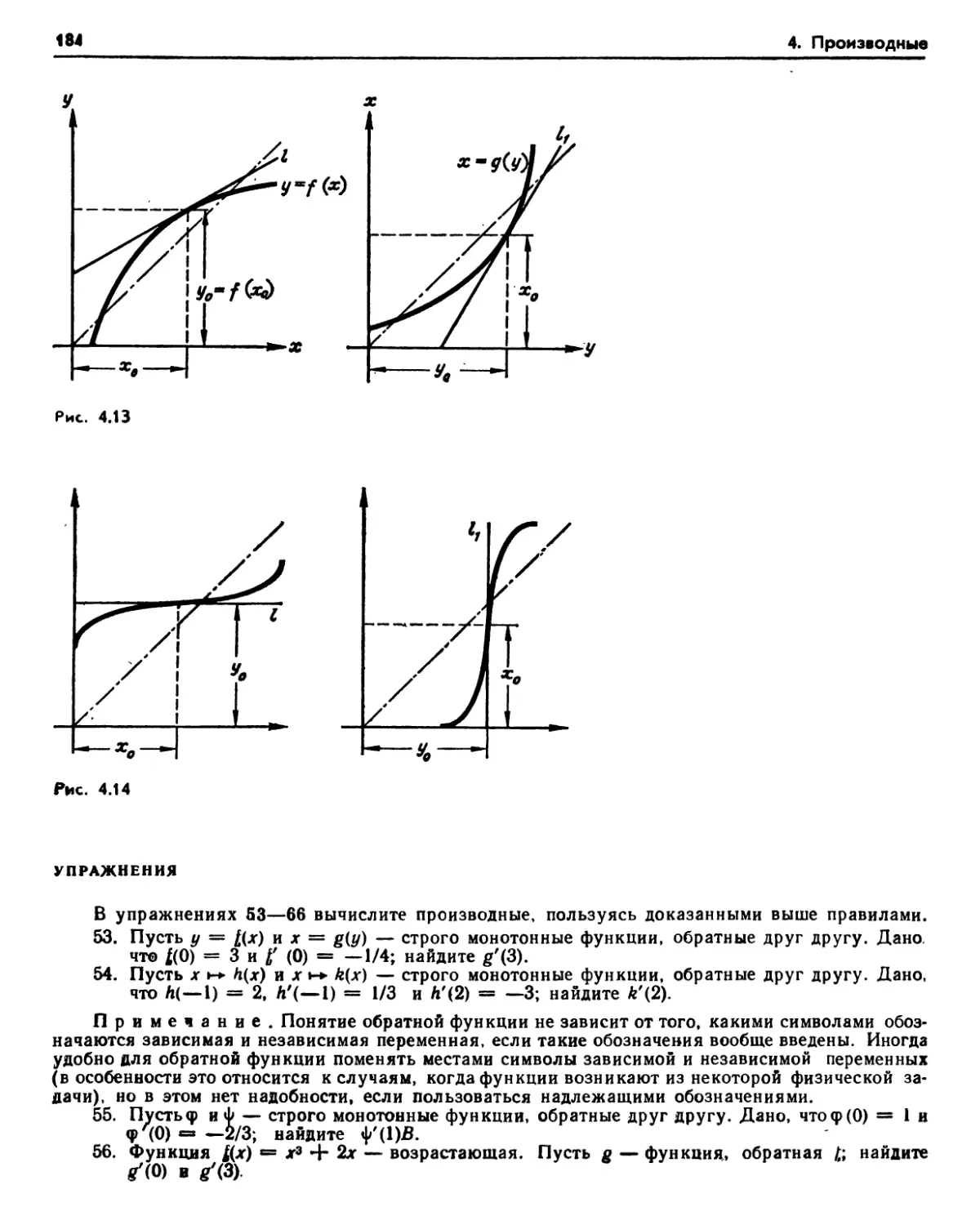
2.4. Производные многочленов и рациональных функций (179). Упражнения (179). 2.5. Цепное правило (180). Упражнения (182). 2.Ь Производные обратных функций (183).
Упражнения (184). 2.7. Дифференцирование степеней с рациональными показателями (185). 2.8. Производные иррациональных функций (186). Упражнения (187). 2.9. Недифференцируемые функции (188).
§ 3. Производные высших порядков. Ускорение 190
3.1 Производные производных (190). Упражнения (191). 3.2. Ускорение (192). 3.3. Закон Ньютона (193). Упражнения (194). 3.4. Закон Эйнштейна (195). Упражнения (196). 3.5 Предположения дифференцируемости в физике (196).
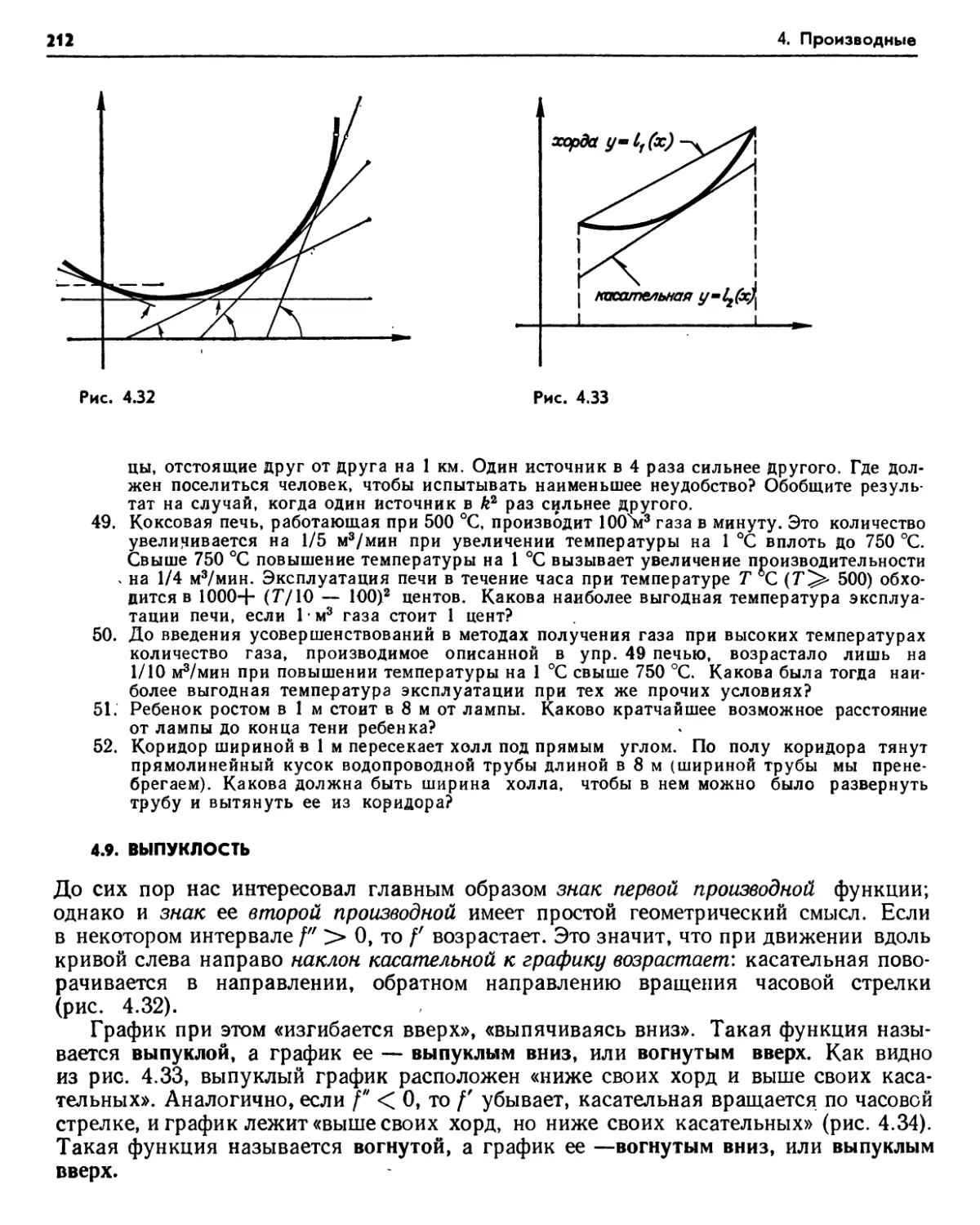
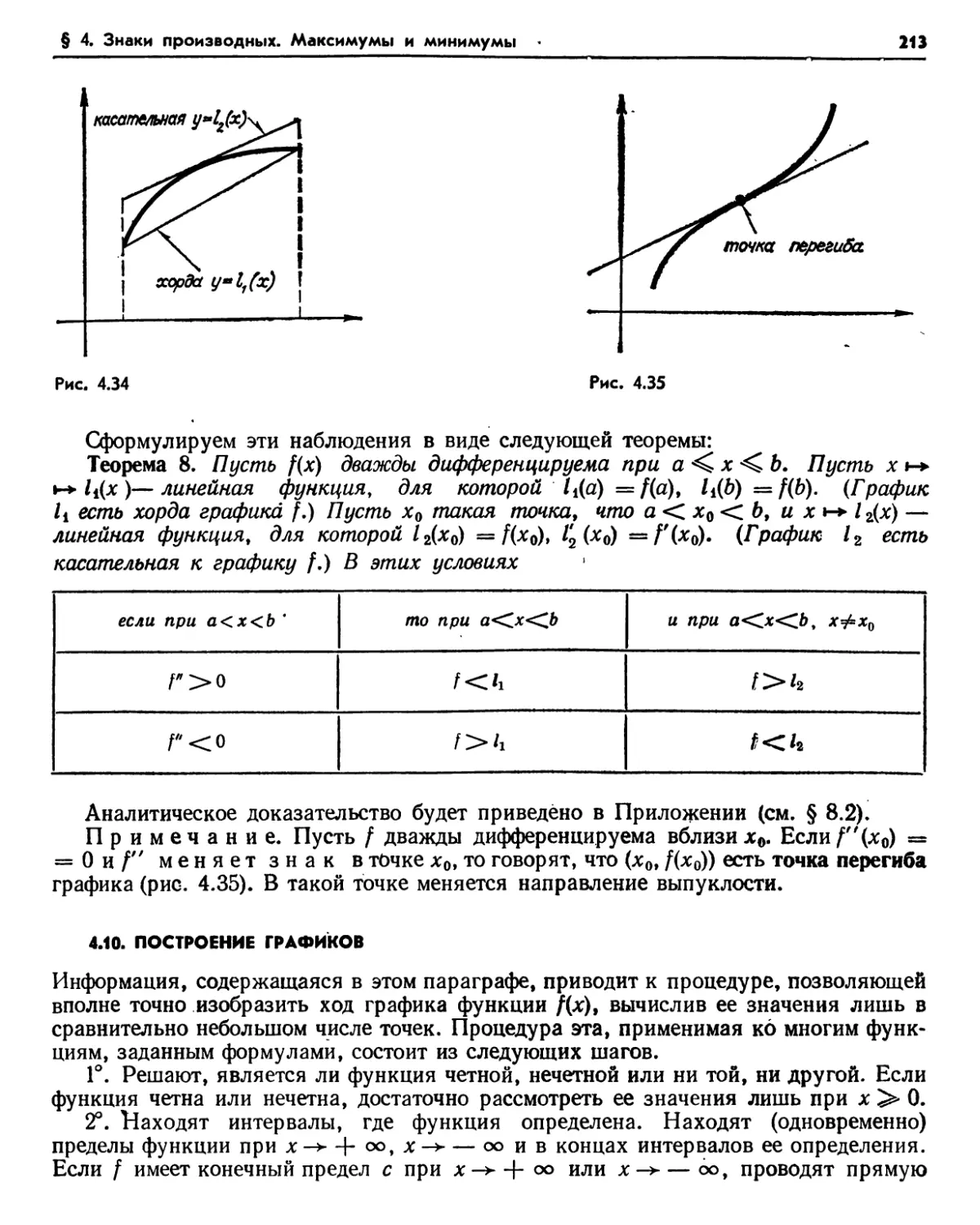
§ 4. Знаки производных. .Максимумы и минимумы ' 197
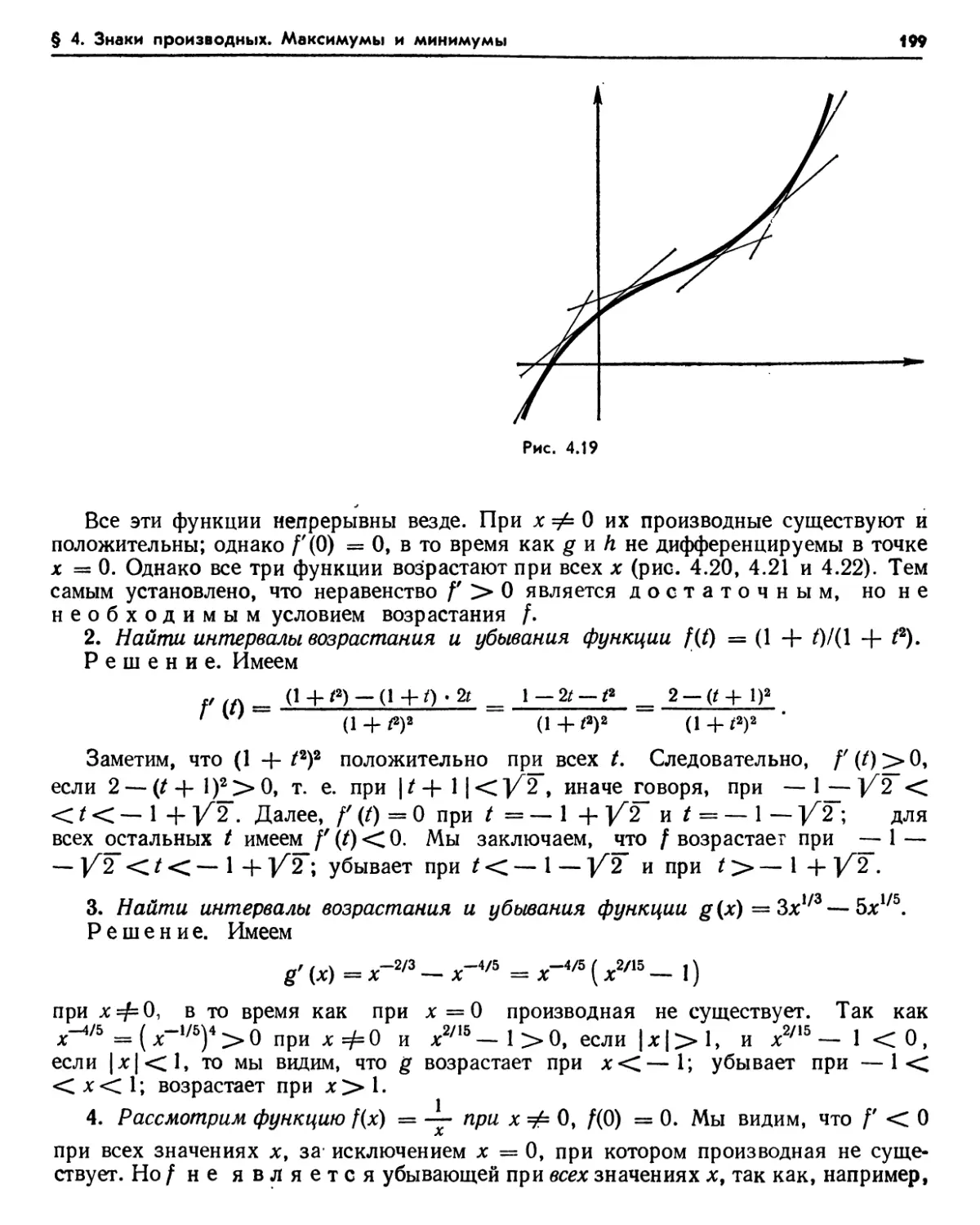
4.1 Предварительный результат (197) 4.2 Функции с производными одного знака (1.98). 4.3. Функции с неотрицательными и неположительными производными (200). Упражнения (201). 4.4. Локальные максимумы и минимумы (201). Упражнения (204). 4.5. Кусочно-монотонные функции (204). 4.6. Абсолютные максимумы и минимумы (205).
Упражнения (2051 4.7. Существование максимумов и минимумов (206), 4.8. Разыскание максимумов и минимумов (206). Упражнения (210). 4.9 Выпуклость (212). 4.10. Построение графиков (213). Упражнения (217)
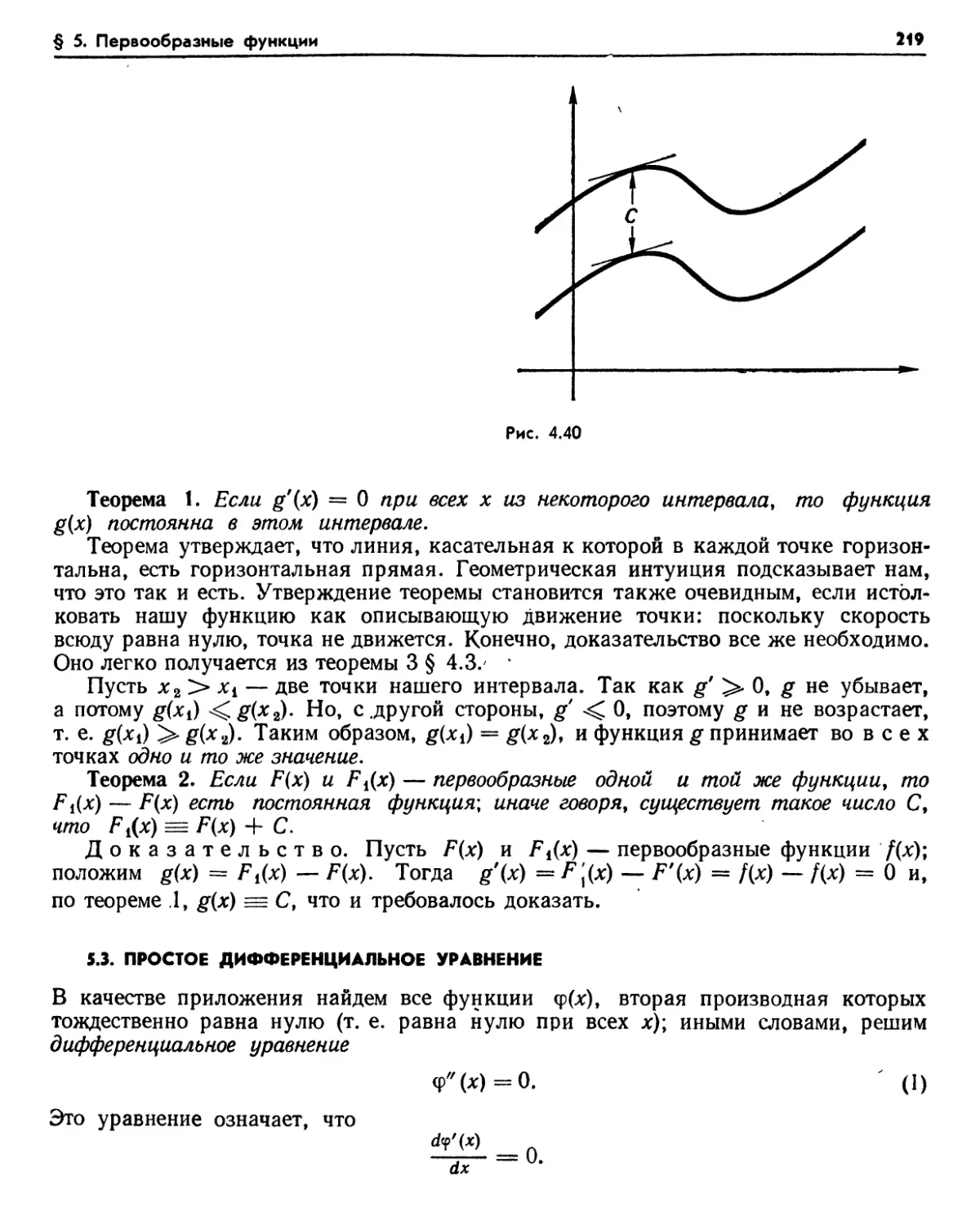
§ 5. Первообразные функции 218
5.1. Определение первообразной функции (218). 5.2. Единственность (218). 5.3. Простое дифференциальное уравнение (219). 5.4. Разыскание первообразных (220). Упражнения (221). 5.5. Инерция (222). 5.6. Вертикальное движение под действием силы тяжести (222).
Упражнения (224). 5.7. Релятивистское движение под действием постоянной силы (224). Упражнения (225). 5.8. Площадь под параболой (225). Упражнения -(227).
Приложение к главе 4 227
§ 6. Доказательство правил дифференцирования 227
6.1. Производная произведения (227). 6.2. Производная от функции, обратной данной в алгебраическом смысле (228). Упражнения (229). 6.3. Доказательство цепного правила (229). 6.4. Производная обратной функции (230).
§ 7. Односторонние производные. Бесконечные производные. Дифференцируемые и недифференцируемые функции 230
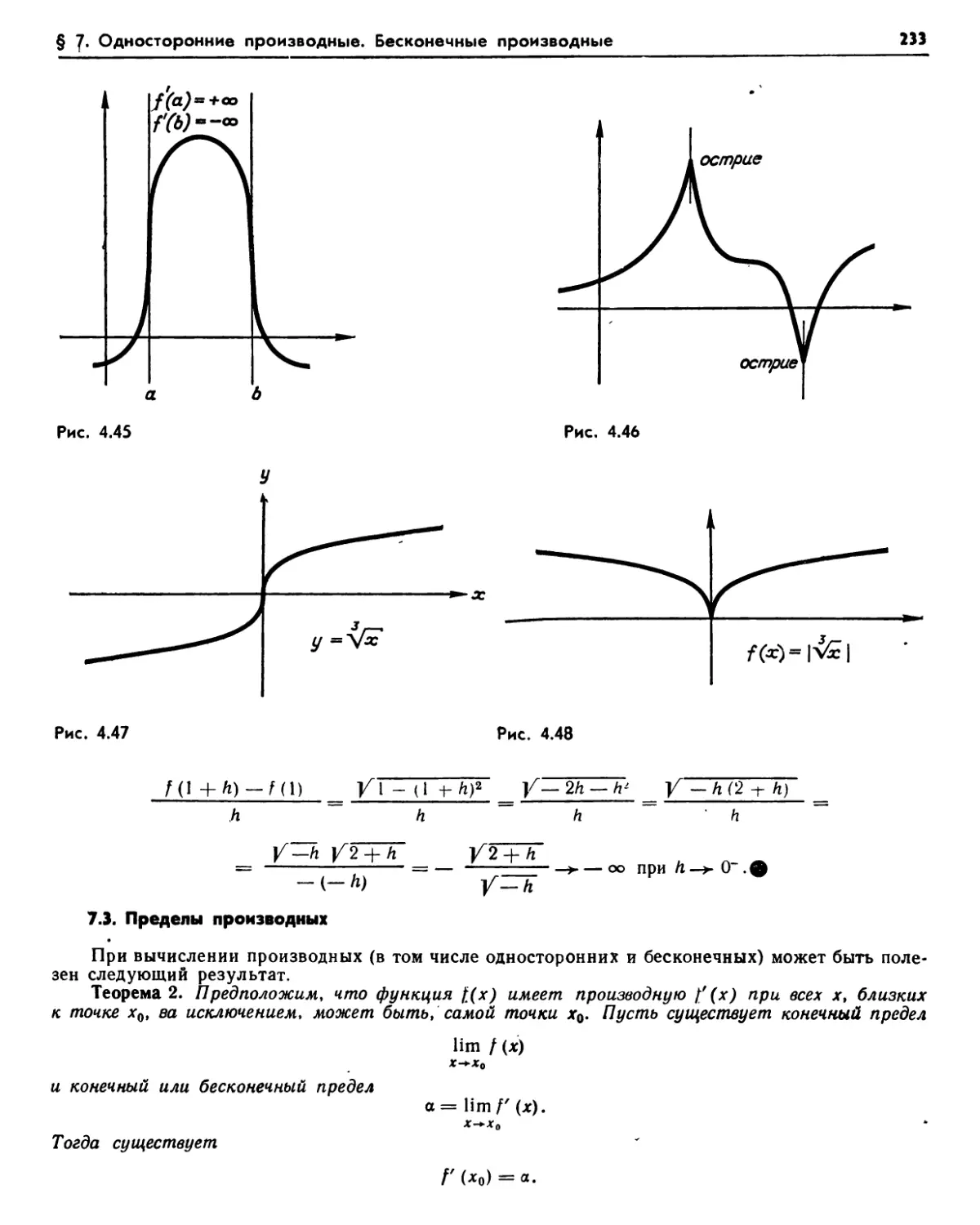
7.1. Односторонние производные (230). Упражнения (231). 7.2. Бесконечные производные (232). 7.3. Пределы производных (233). Упражнения (234).
Оглавление
7
§ 8. Доказательства * некоторых теорем о производных 234
8.1. Функции с положительной производной (234). Упражнения (235). 8.2. Функции с положительной второй производной (235). Упражнение (236). 8.3. Пределы производных (236). Упражнение (237). Задачи (237).
,5. Интегралы 239
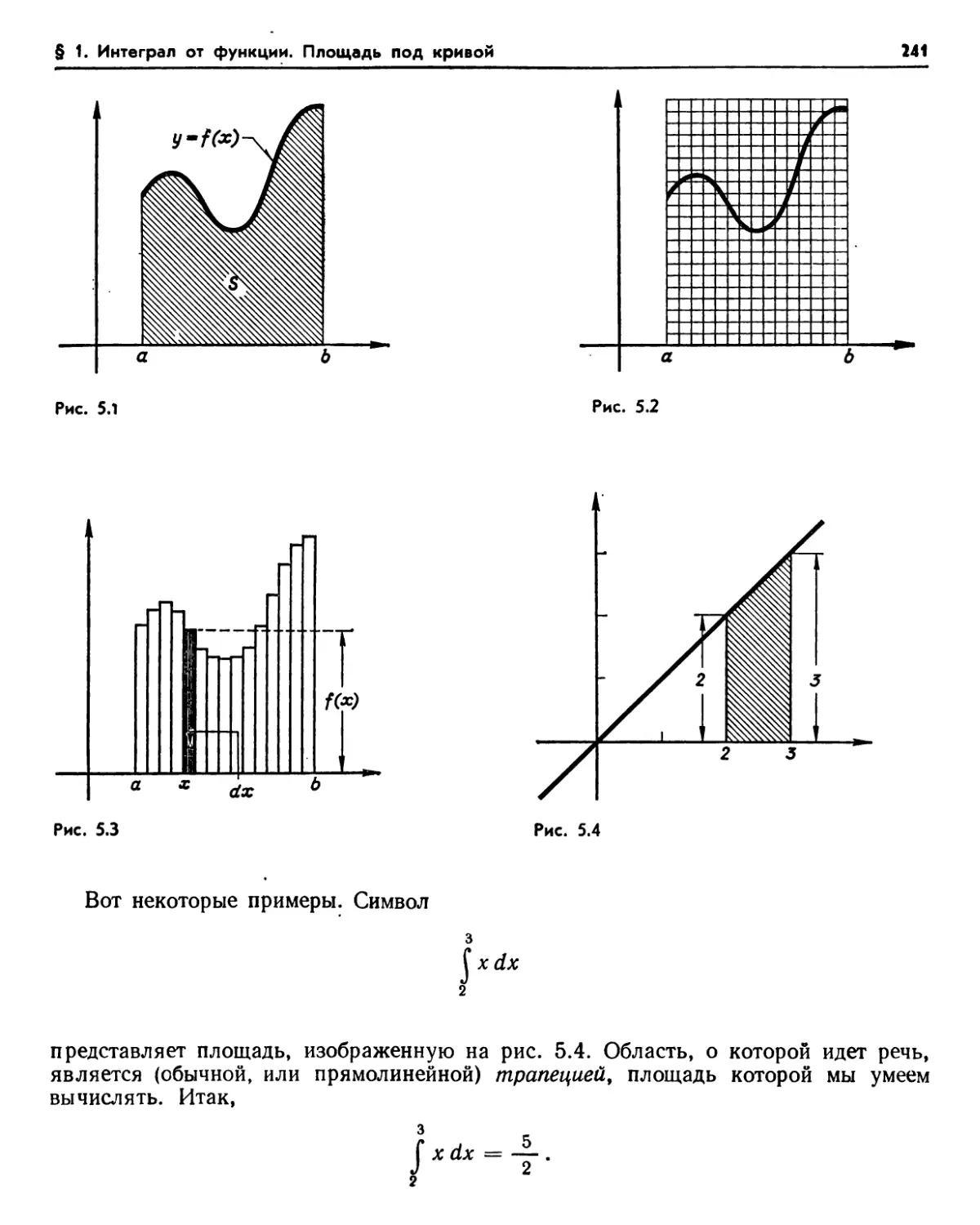
§ 1. Интеграл от функции. Площадь под кривой 240
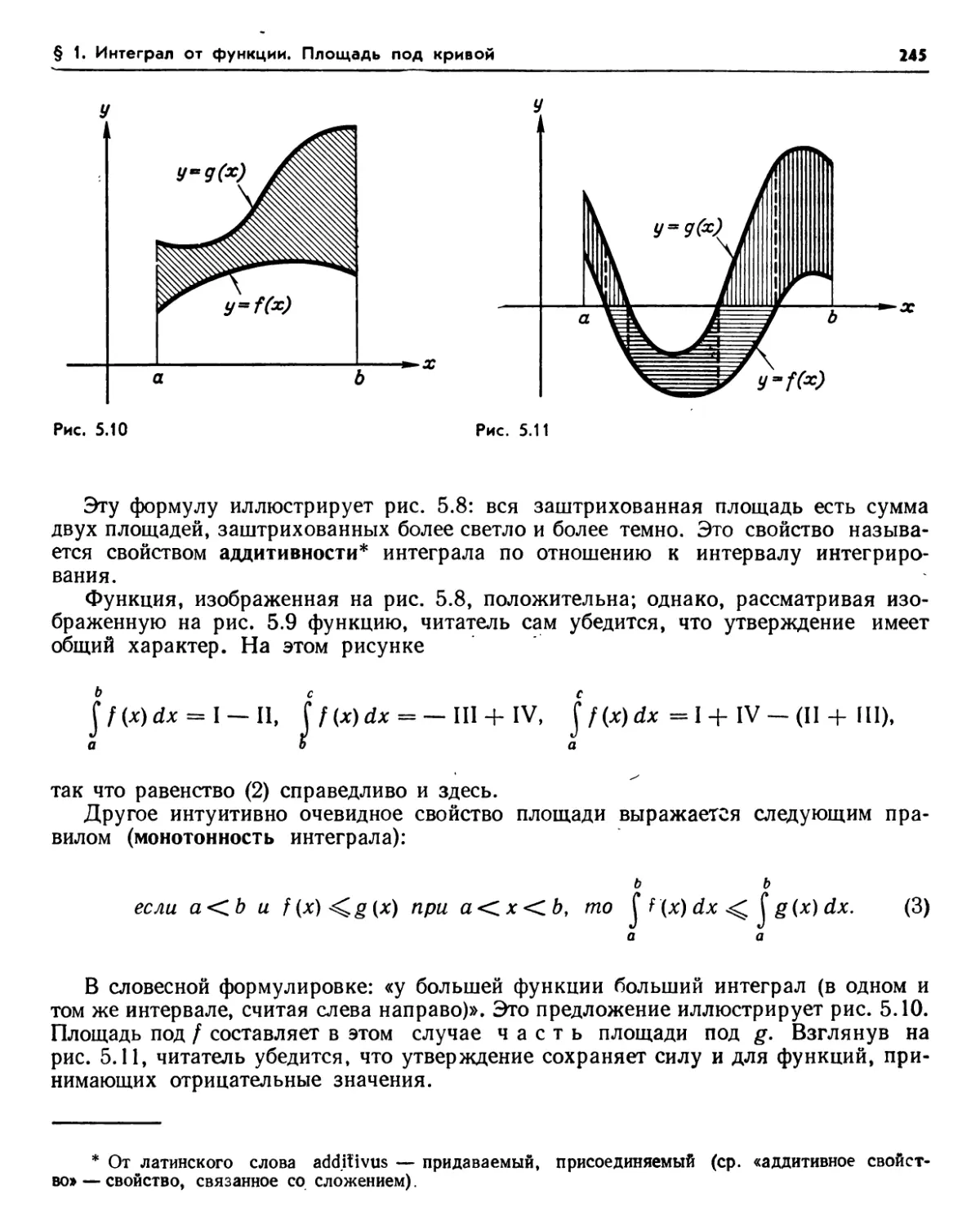
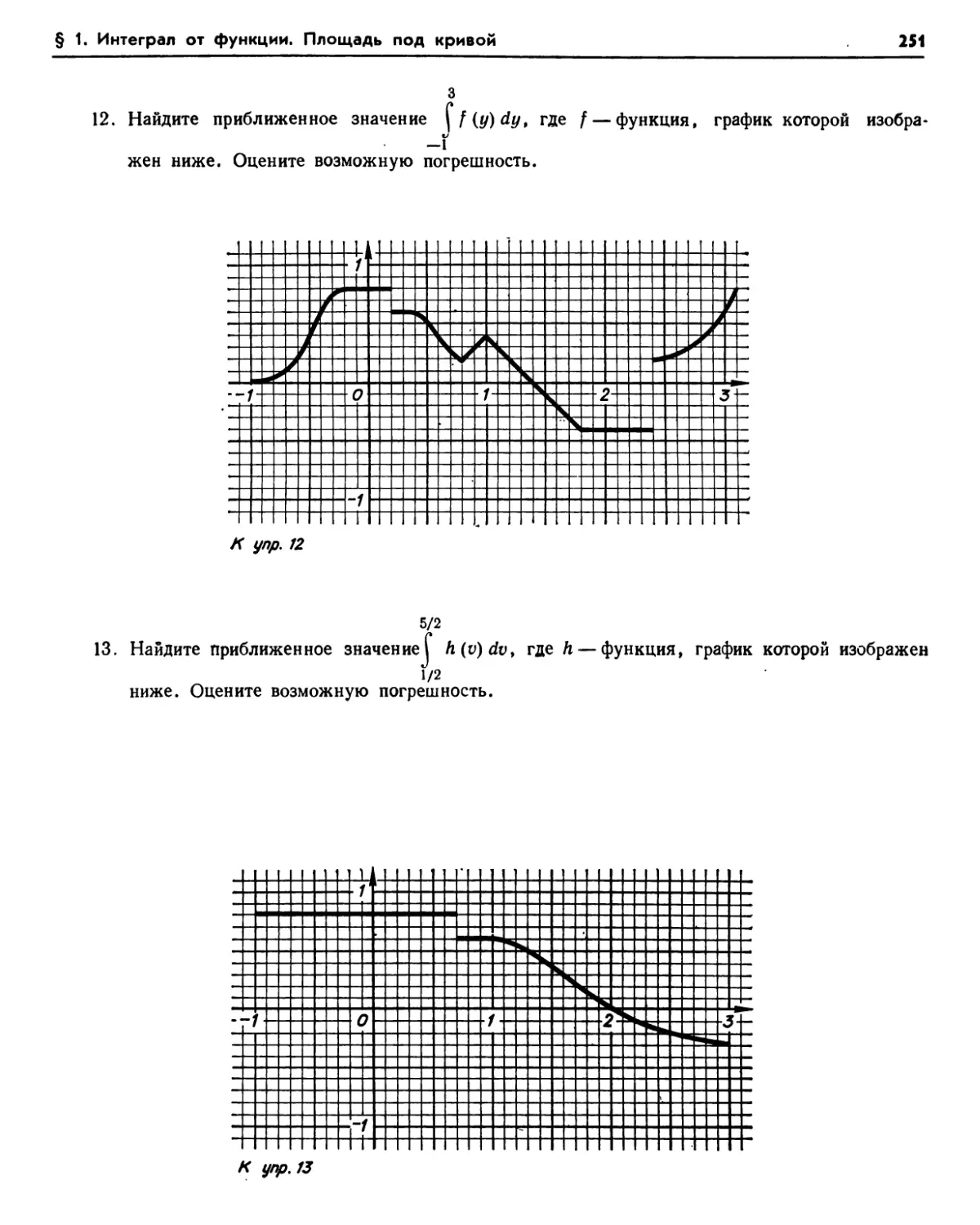
1.1. Интеграл от неотрицательной функции (240). 1.2. Интеграл от функции, принимающей отрицательные значения (242). Упражнения (243). 1.3. Три основных свойства (244). 1.4. Кусочно-непрерывные функции, ограниченные функции (246). 1.5. Ступенчатые
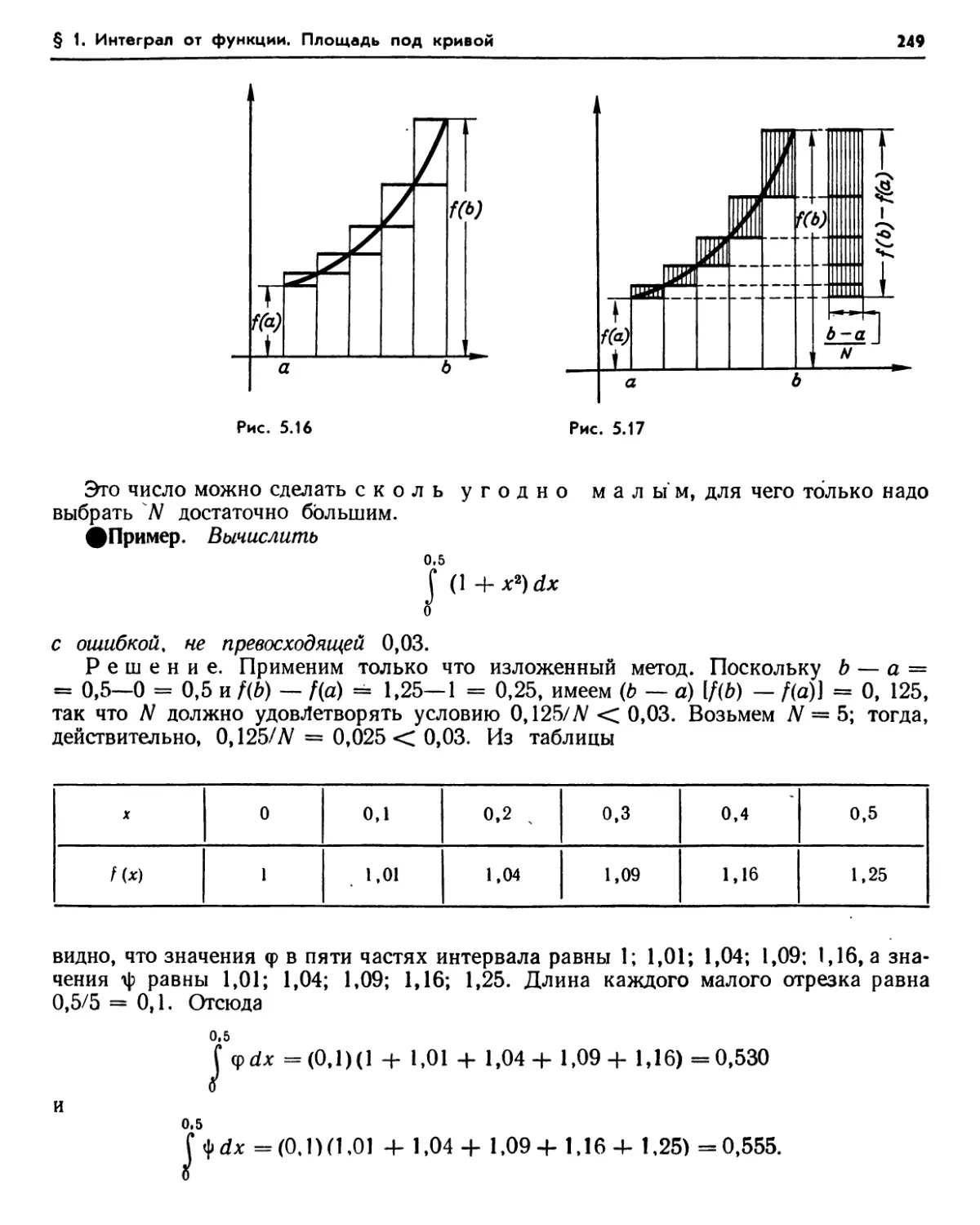
функции (247). 1.6. Вычисление интеграла (247). 1.7. Оценка погрешности для монотонной функции (248). Упражнения (250). 1.8. Аналитическое определение интеграла (253). 1.9. Расширение обозначений (254). Упражнения (255).
,§ 2. Основная теорема анализа 256
2.1. Первая часть основной теоремы (256).
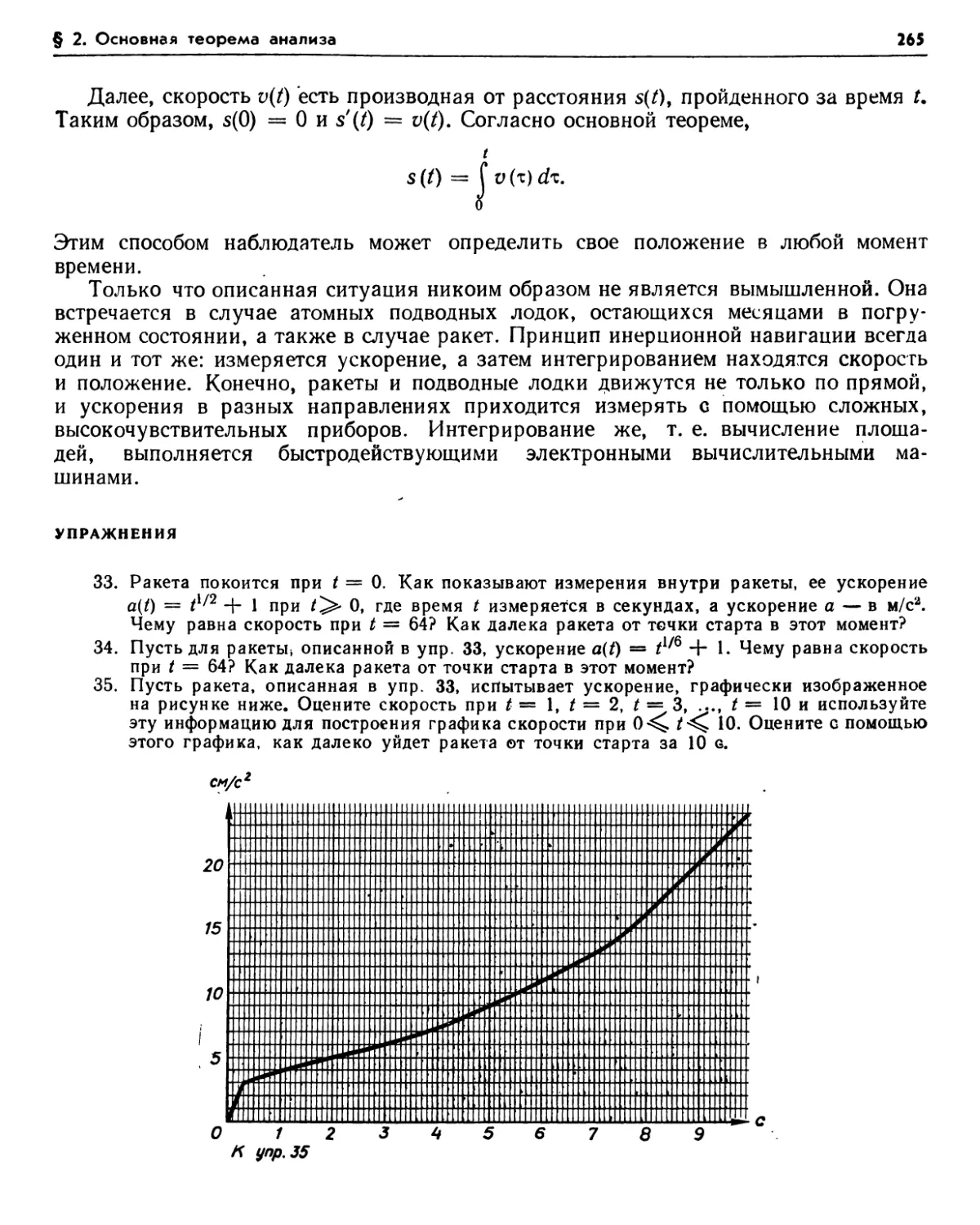
Упражнения (259). 2.2. Вторая часть основной теоремы (260). Упражнения (262). 2.3. Неопределенный интеграл (262). Упражнения (263). 2.4. Инерционная навигация (264). Упражнения (265).
§ 3. Интегрирование 266
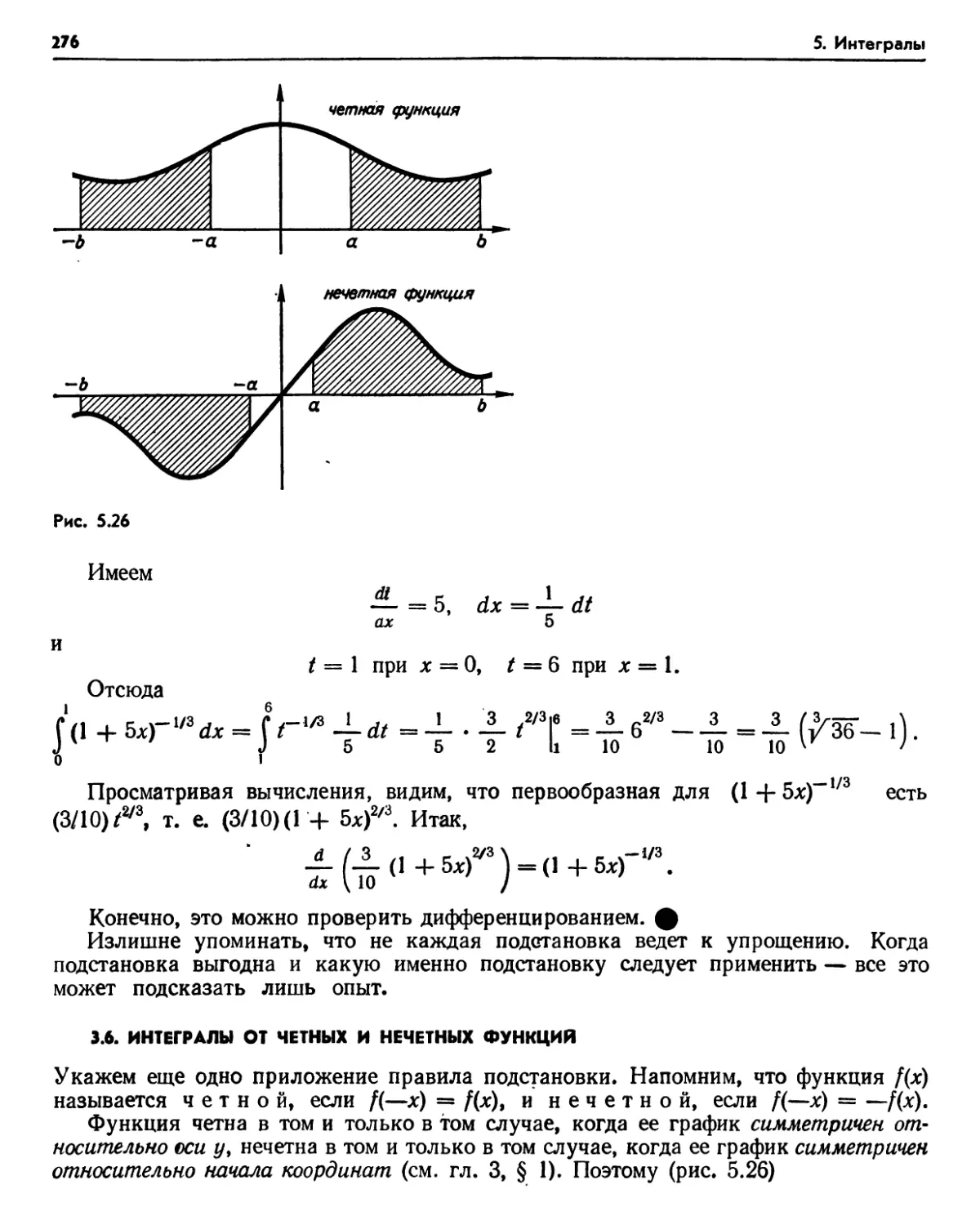
3.1. Численное и формальное интегрирование (266). 3.2. Основные правила интегрирования (266). Упражнения (268). 3.3. Интегрирование по частям (269). 3.4. Язык дифферен-, ииалов (270). Упражнения (272). 3.5. Замена переменных (273). 3.6. Интегралы от четных п нечетных функций (276). Упражнения (277). 3.7. Замечание о несобственных интегралах (278).
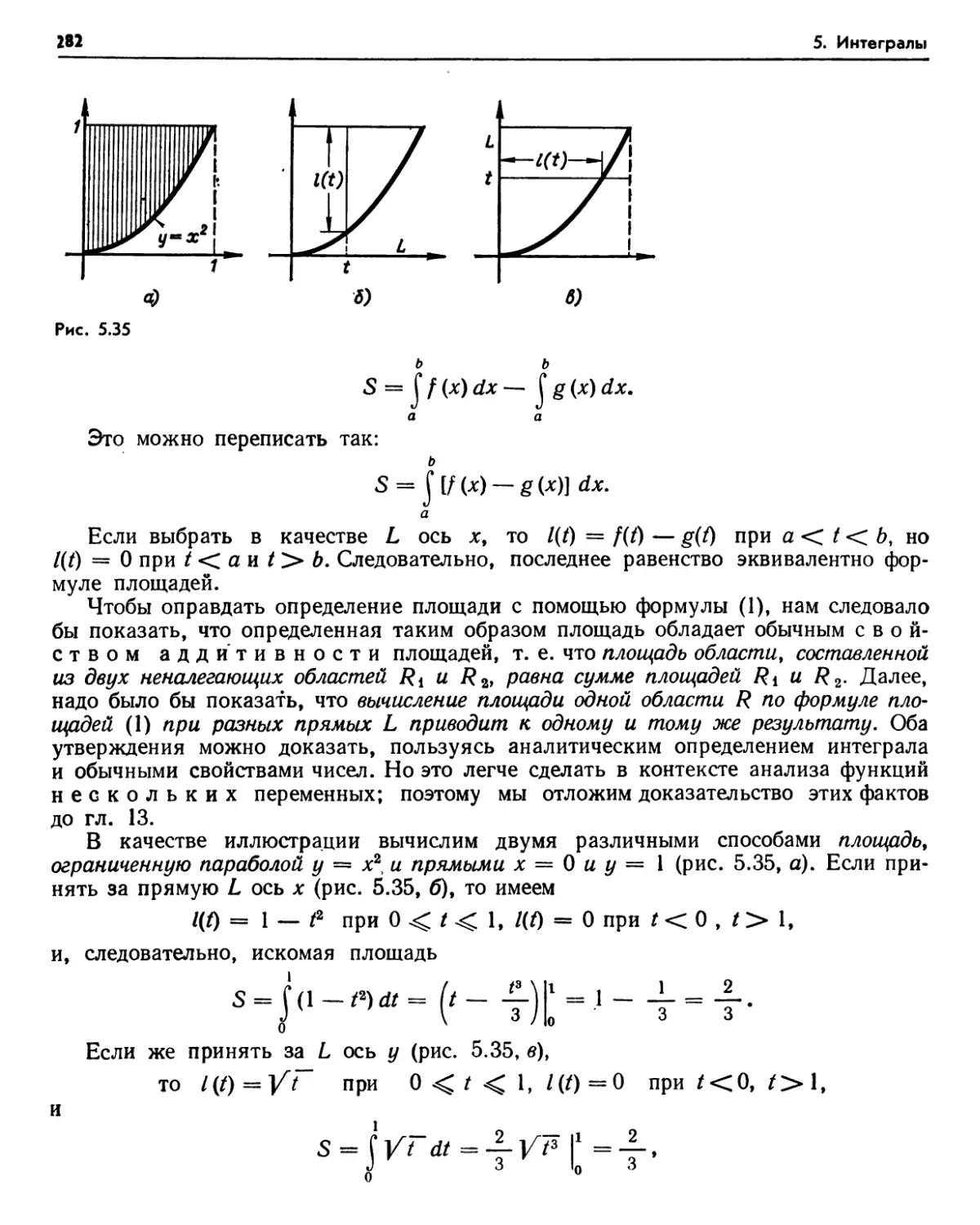
§ 4. Площадь. Объем. Длина 278
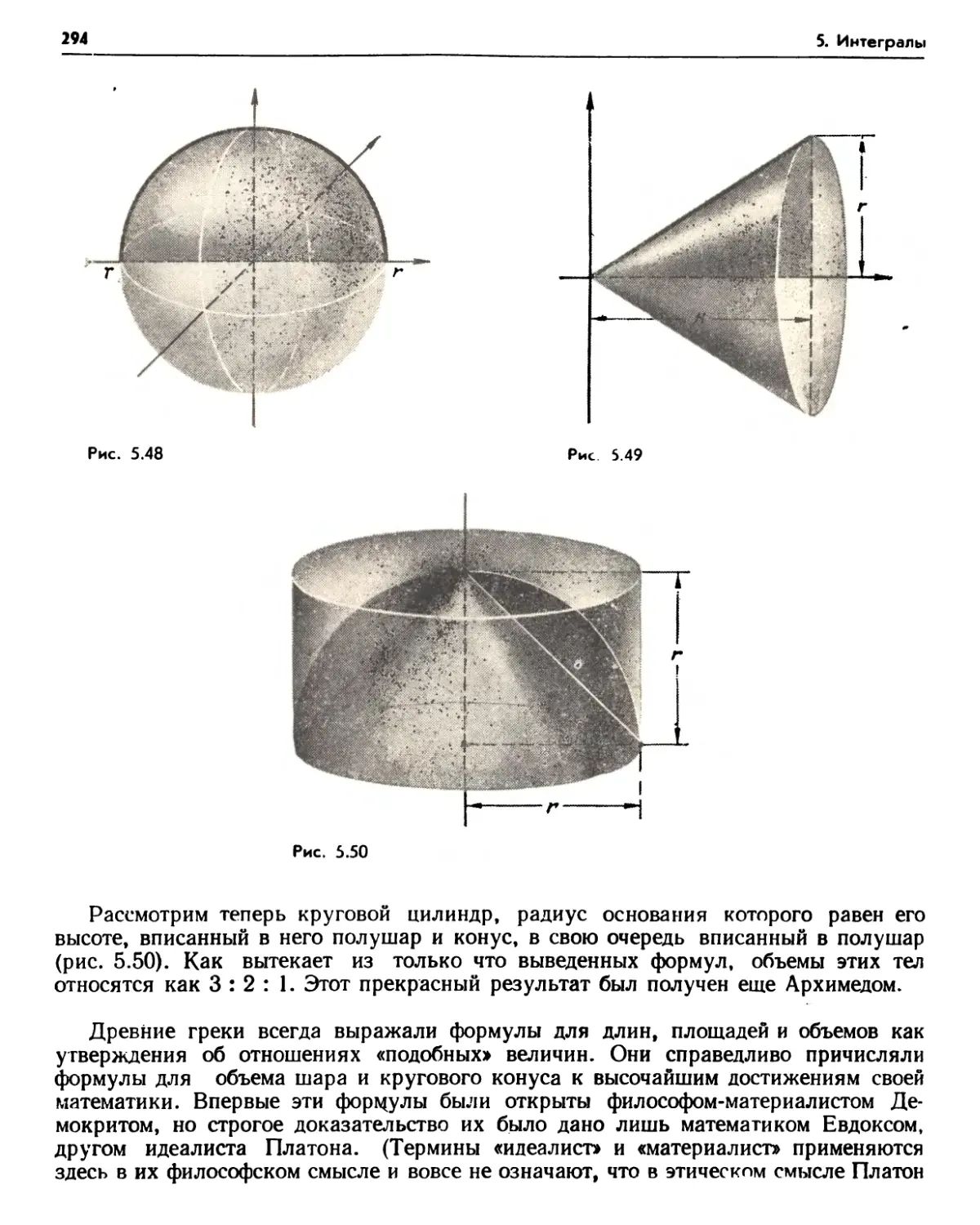
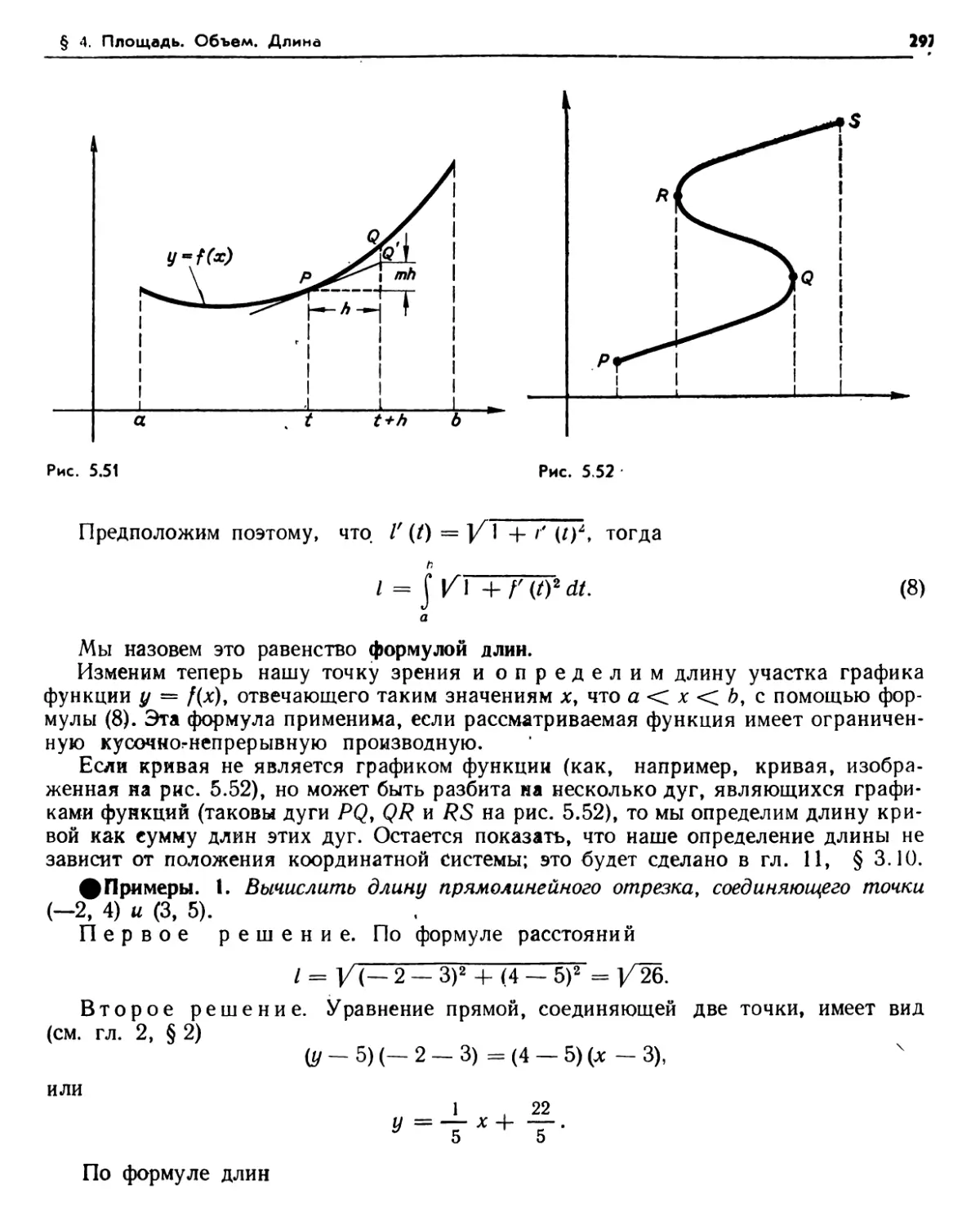
4.1. Вычисление площадей (278). 4.2. Определение площади (281). Упражнения (28-1). 4.3. Площадь круга. Число я (285). 4.4. Вычисление объемов (286). 4.5. Определение объема (290). Упражнения (290). 4.6. Тела вращения (290). 4.7. Шары и круговые конусы (293). Упражнения (295) 4.8. Длина (296). Упражнения (298). 4.9. Круговые секторы, Длина окружности (299). Упражнения (301).
Приложение к главе 5 302 §
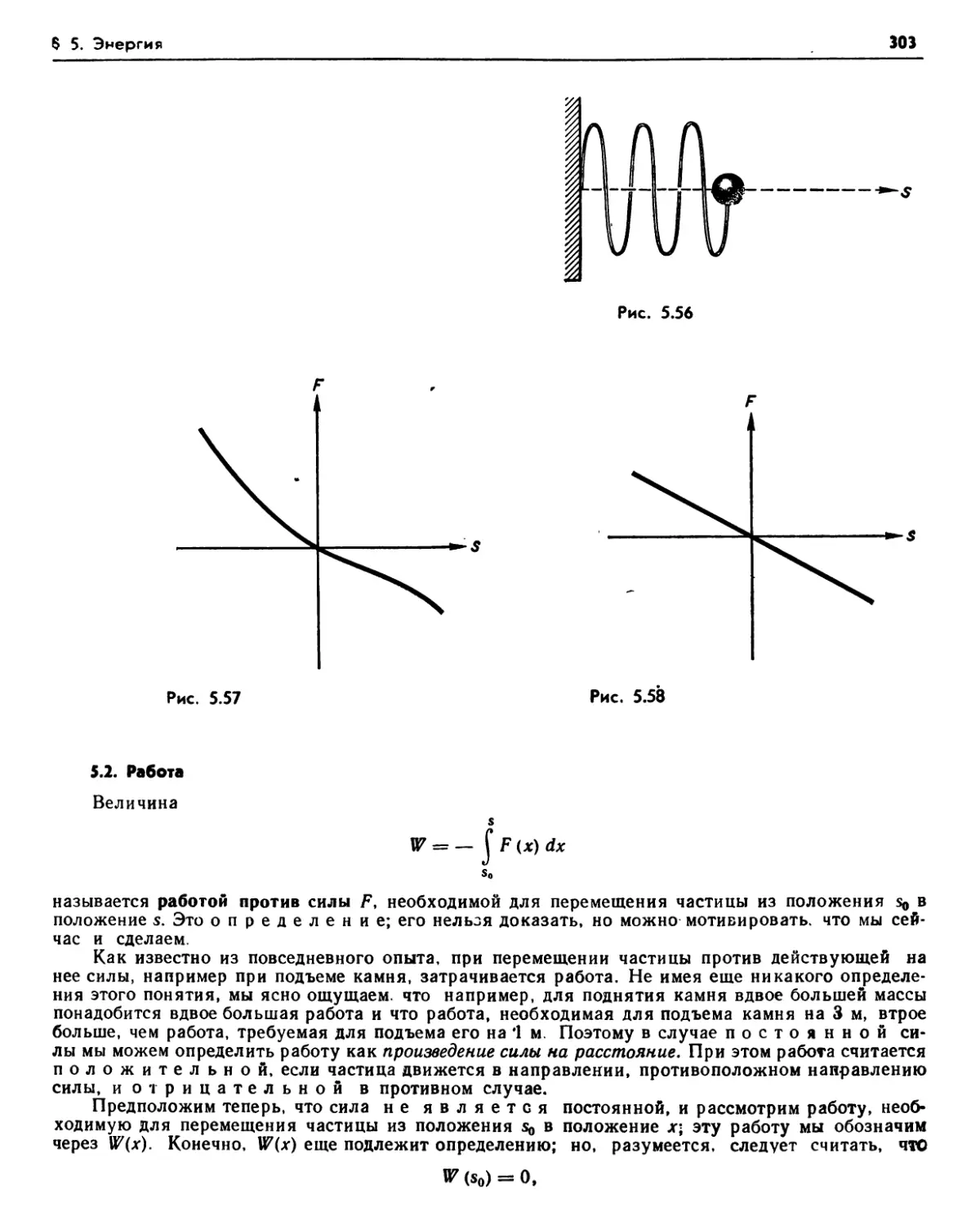
§ 5. Энергия 302
5.1. Силы, зависящие от положения (302). Упражнения (302). 5.2. Работа (303). 5.3. Потенциальная энергия (304). Упражнения (305). 0.4. Кинетическая энергия. Закон сохранения энергии (305). 55. Свободное падение (306). Упражнения (307). 5.6. Тяготение (308).
Скорость убегания (309). Упражнения (311). 5.8. Энергия и масса в теории относительности (311).
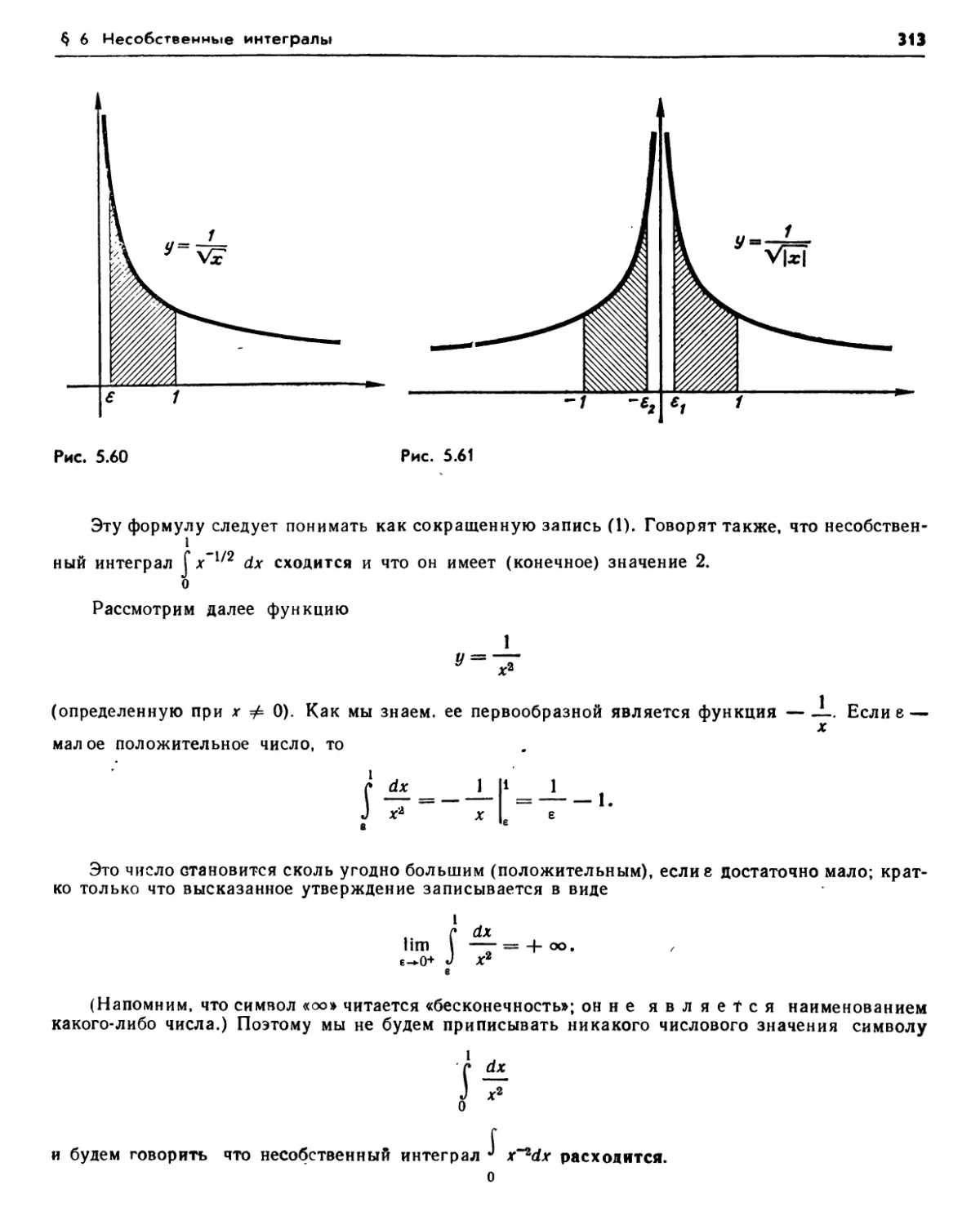
§ 6. Несобственные интегралы 312
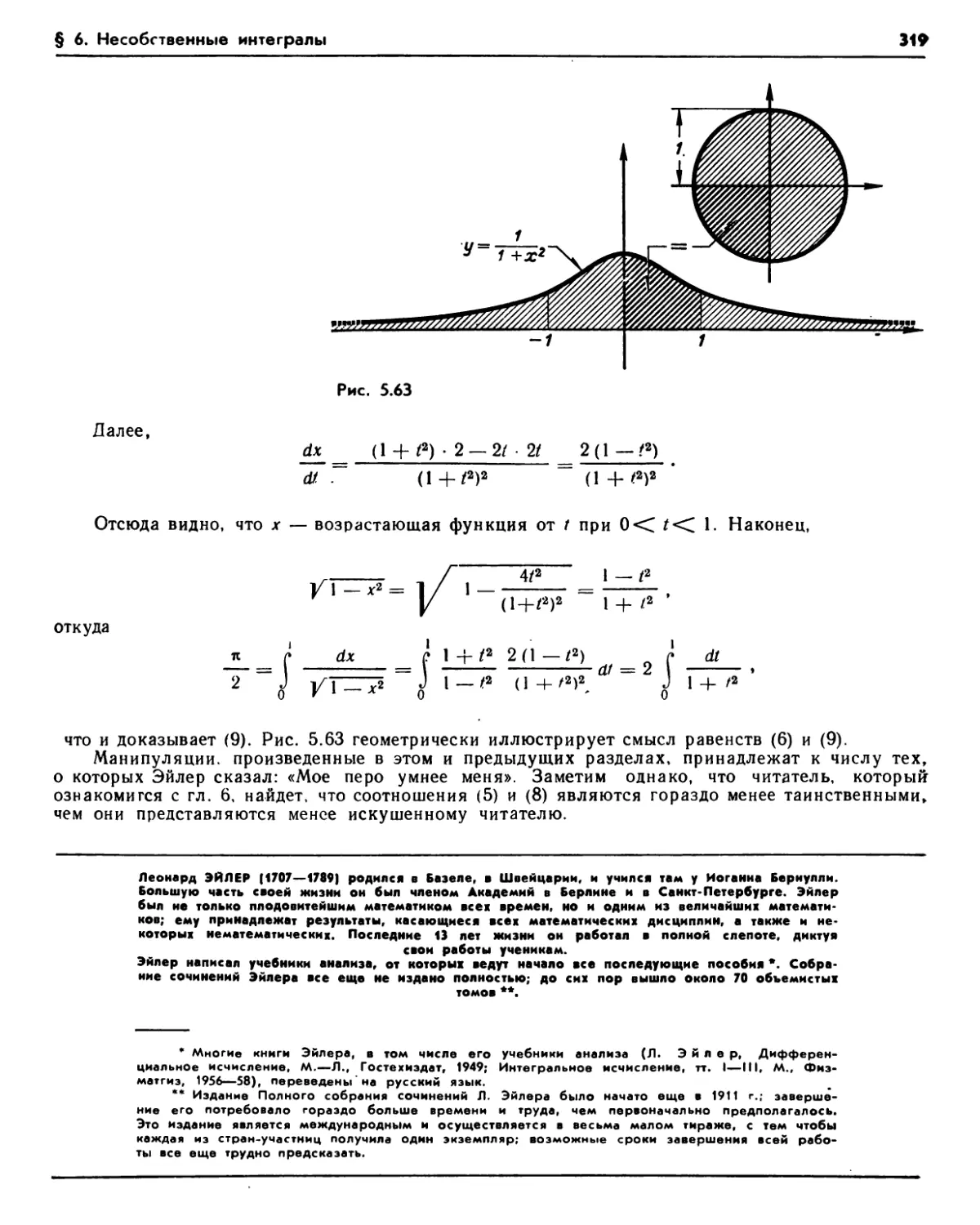
6.1. Неограниченные подынтегральные функции (312). 6.2. Бесконечные области интегрирования (314). 6.3. Другие примеры (314). Упражнения (315). 6.4. Теорема сравнения , (316). Упражнения (317). 6.5. Некоторые интегральные функции, содержащие Л (317). Упражнения (320).
§ 7. Доказательство основной теоремы 320
7.1. Доказательство непрерывности (320).
7.2. Вычисление производной (321).
§ 8. Существование интегралов 322
8.1. Интегралы от ступенчатых функций (322). 8.2. Верхние и нижние интегралы (324).
8.3. Свойства верхних и нижних интегралов (326). 8.4. Интеграл Римана (328). 8.5. Вычисление интегралов с помощью ступенчатых функций (329). 8.6. Монотонные функции (329). Упражнения (330).
§ 9. Существование несобственных интегралов 330
9.1. Пределы монотонных функций (330). 9.2 Доказательство теоремы сравнения (330). Упражнения (331). Задачи (331).
6. Трансцендентные функции 335
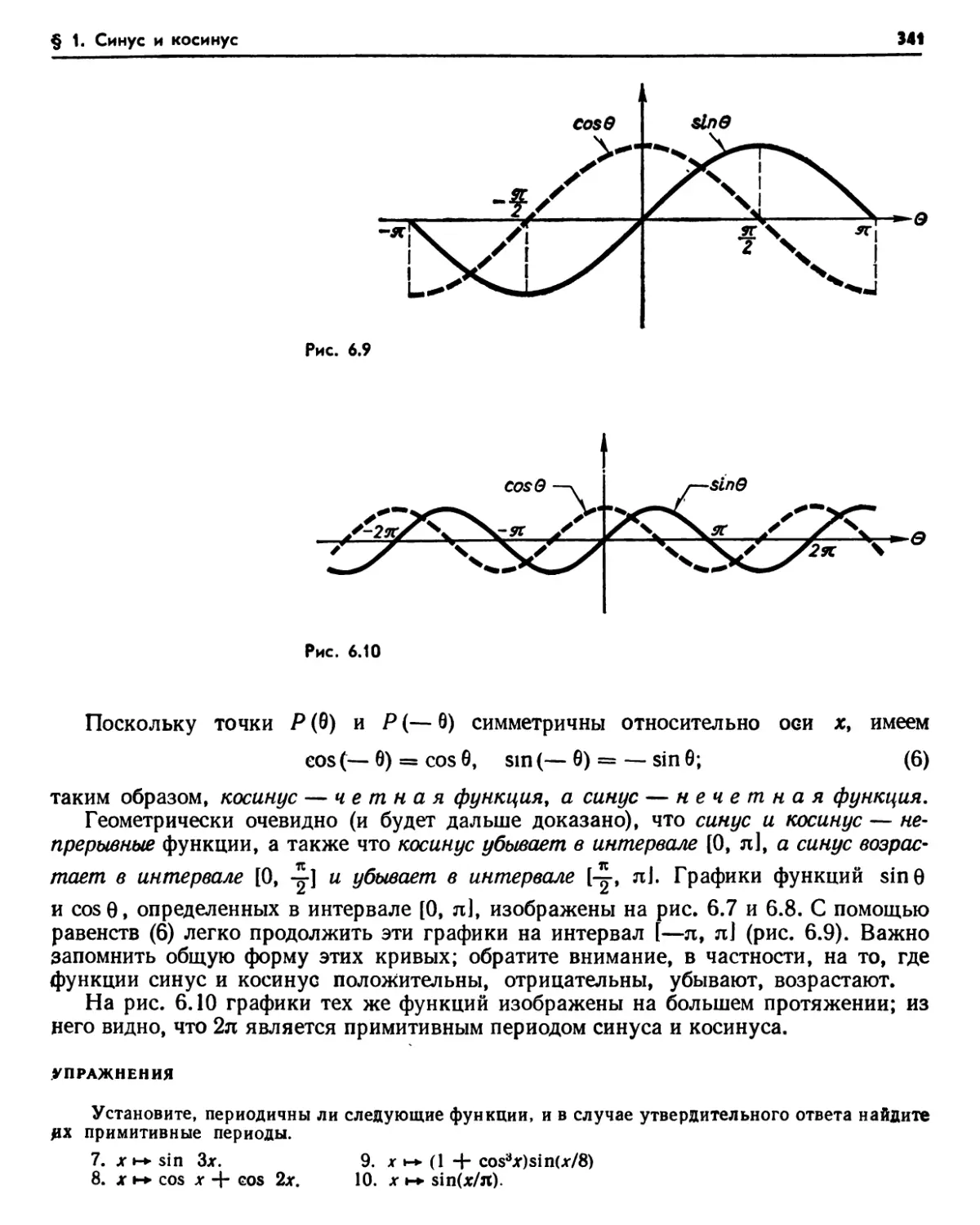
§ 1. Синус и косинус 336
1 1. Алгебраические и трансцендентные функции (336). Упражнения (337). 1.2. Периодические функции (337). 1.3. Геометрическое определение синуса и косинуса (339). Упражнения (341). 1.4. Углы (342). 1.5. Треугольники (343). 1.6. Градусы н радианы (343). Упражнения (345). 1.7. Обратные функции для синуса и косинуса (345). Упражнения (348). 1.8. Повторение (349). 1.9. Дифференцирование синуса и косинуса (350). Упражнения (351). 1.10. Дифференциальное уравнение для синуса и косинуса (352). Упражнения (354). 1.11. Теорема сложения (354). Упражнения (356). 1.12. Дифференциальное уравне-ни< второго порядка (356). 1.13. Движение упругой пружины (357). 1.14. Гармонические колебания (358). Упражнения (359).
§ 2. Тангенс и арктангенс 360
2.1. Тангенс (360) Упражнения (361). 2.2. Теорема сложения (362). 2.3. Функции sin 0 и cos 0 как рациональные функции от tg (0/2) (362). Упражнения (364). 2.4. Арктангенс
(363). Упражнения (366). 2.5. Применения арктангенса к интегрированию (367). Упражнения (367).
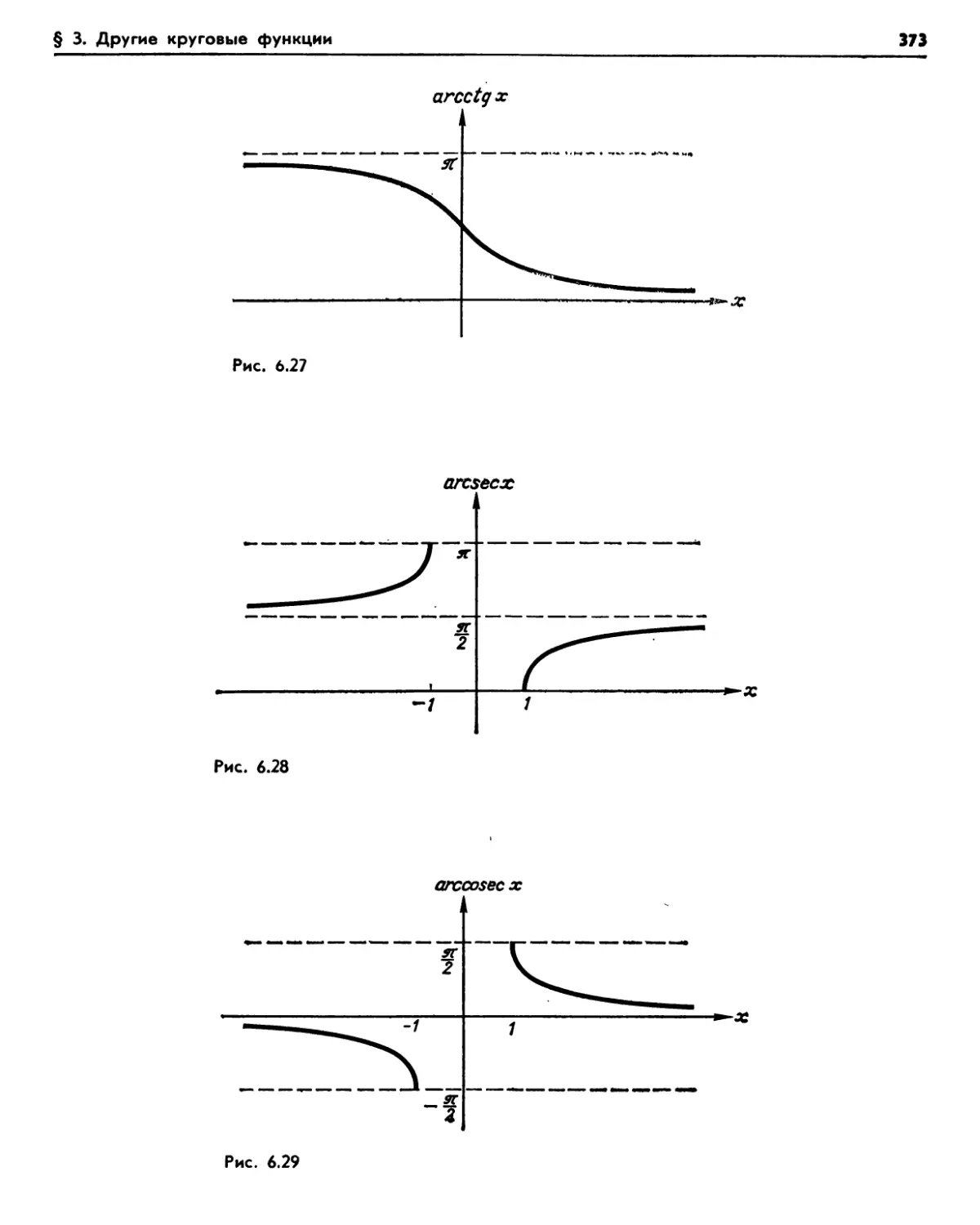
§ 3. Другие круговые функции 368
ЗЛ. Секанс, косеканс, котангенс (368). Упражнения (370). 3.2. Обратные тригонометрические функции (371). Упражнения (372).
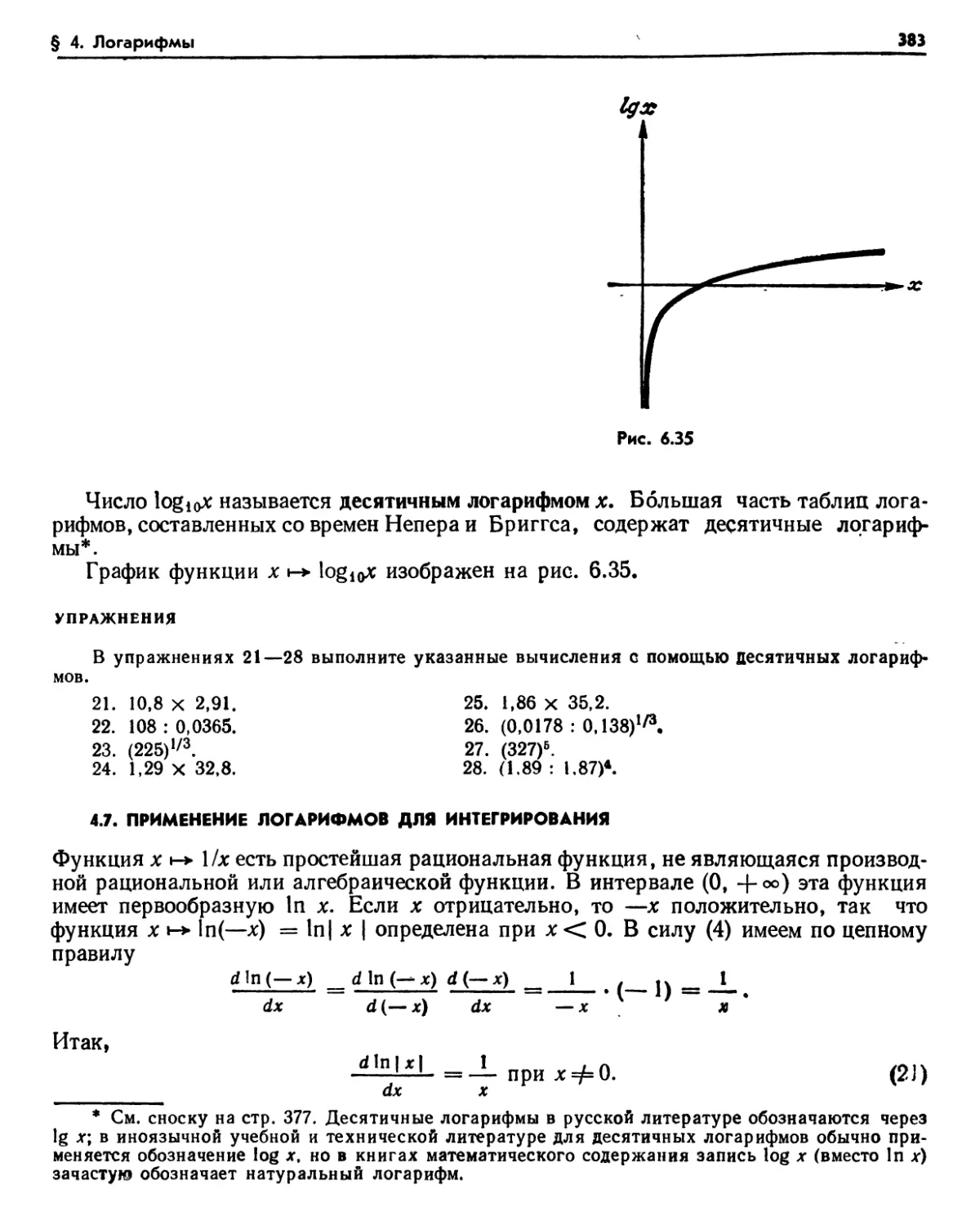
§ 4. Логарифмы , 374
4J. Потребность в логарифмах (374). Упражнения (375). 4.2 Путь к логарифмам (375).
4.3. Определение натуральных логарифмов (377). Упражнения (378). 4.4. Свойства логарифмов (379) 4.5. Число е (381). Упражнения (381). 4.6. Логарифмы по разным основаниям (382). Упражнения (383). 4.7. Применение логарифмов для интегрирования (383). Упражнения (385).
§ 5. Показательная функция 387
5.1. Иррациональные показатели (387). Уп* ражнения (389). 5.2. Свойства степеней (389).
5.3. Показательные функции (389). 5.4. Правила дифференцирования (390). Упражнения (391). 5.5. Логарифмическое дифференцирование (391). Упражнения (393). 5.6. Дифференциальное уравнение показательной функции (394). Упражнения (395). 5.7, Экспоненциальный рост (395). Упражнения (397). 5.8. Сложные проценты (397). 5.9. Показательная и логарифмическая функция как пределы (399). Упражнения (400). 5.10. Популяционный
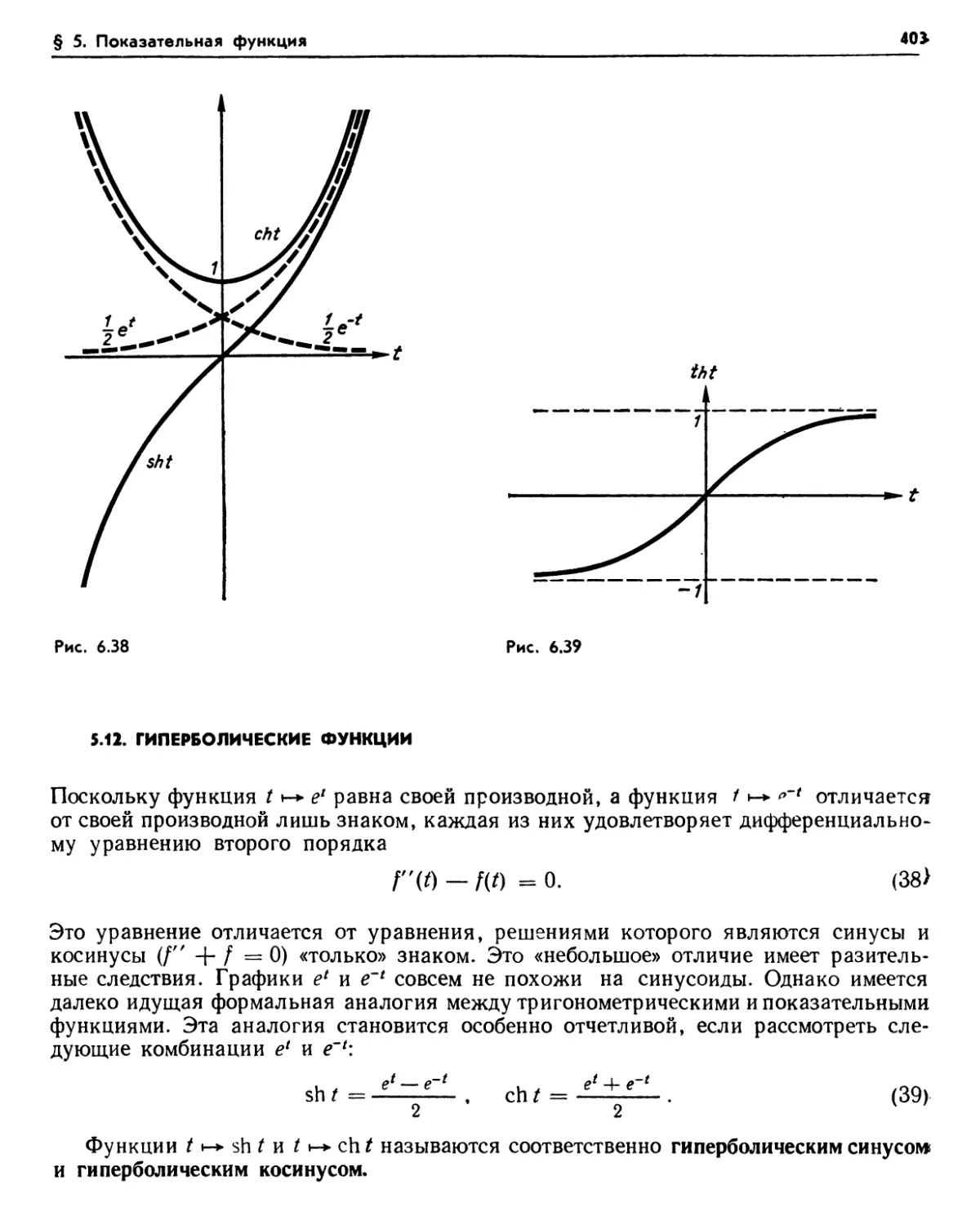
взрыв (400). Упражнение (402). 5.11. Радиоактивный распад (402). Упражнения (402). 5.12. Гиперболические функции (403). Упражнения (405).
8
Оглавление
Приложение к главе 6 406
§ 6. Другие применения показательной функции 406
6.1. Общее решение неоднородного уравнения (406). Упражнения (406). 6.2. Ядерное деление (407). 6.3. Атомные реакторы (408). 6.4. Два радиоактивных вещества (408). 6.5. Барометрическая формула (410). Упражнения (410). о
§ 7. Гиперболические функции 412
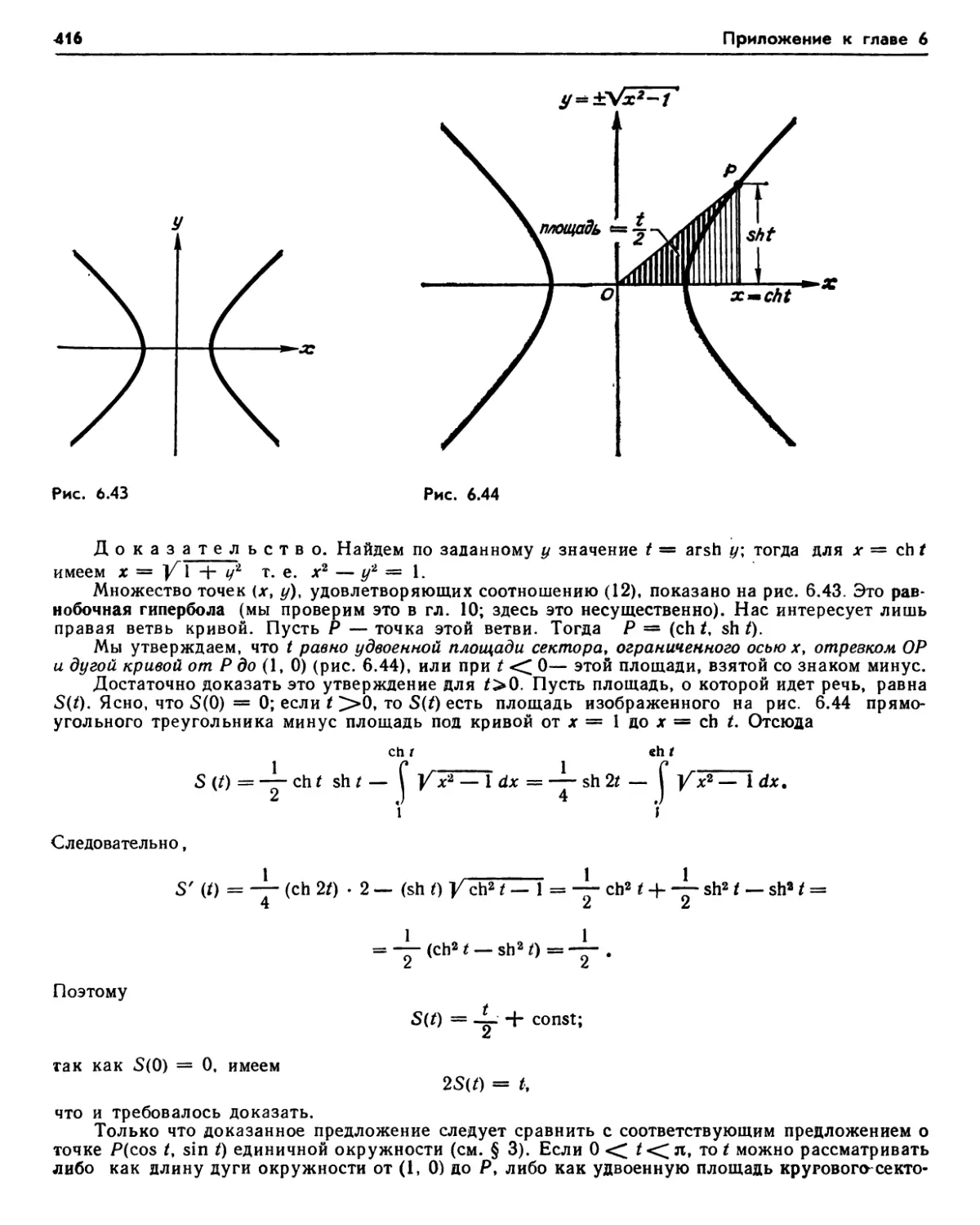
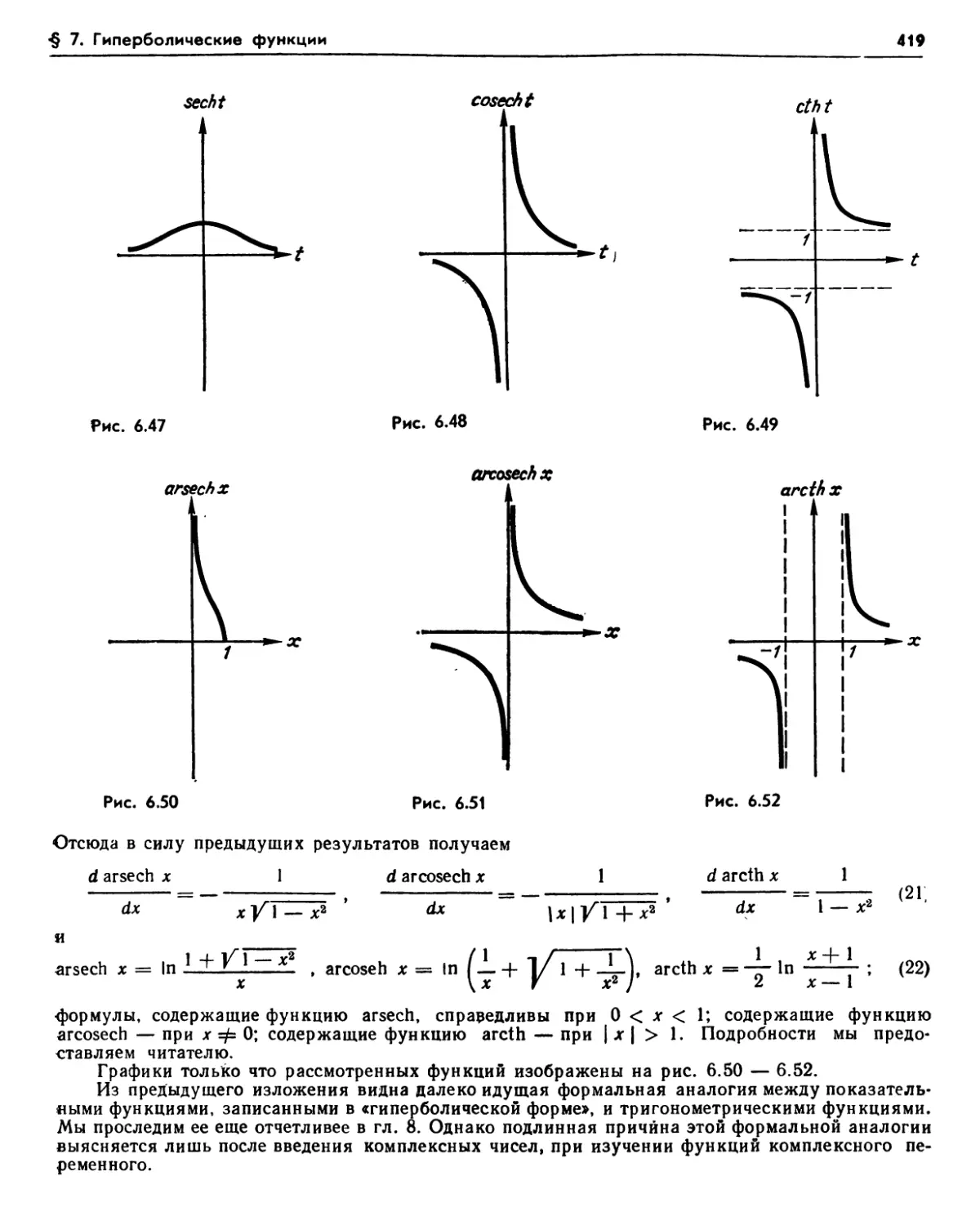
7.1. Дифференциальные уравнения (412). Упражнения (413). 7.2. Обратный гиперболический синус (413). 7.3. Обратный гиперболический косинус (414). Упражнения (415). 7.4. Геометрическое истолкование гиперболических функций (415). 7.5. Обратный, гиперболический тангенс (417). 7.6. Выражение гиперболических синуса и косинуса через гиперболический тангенс (418). 7.7. Другие гиперболические функции и им обратные (418). Упражнения (420).
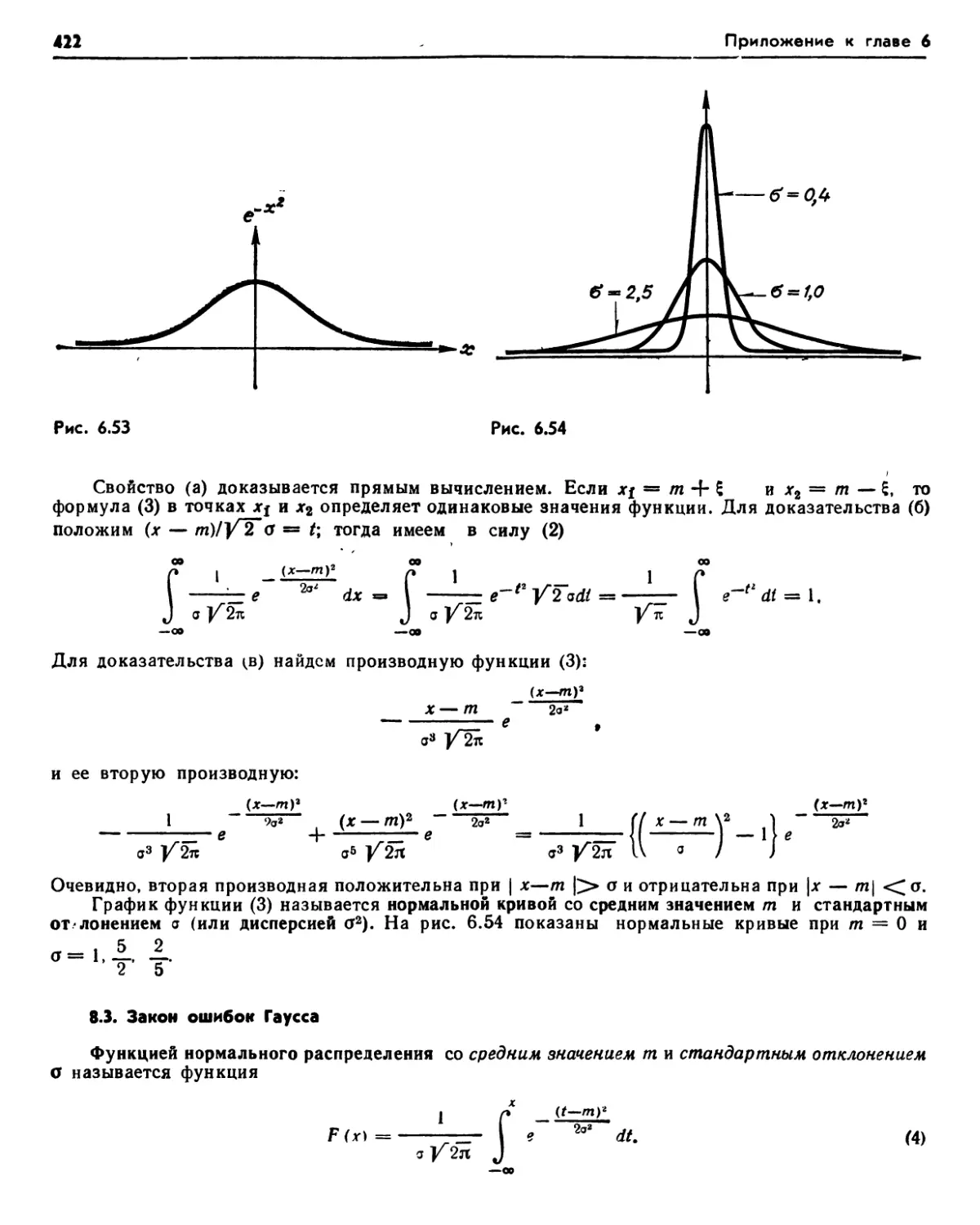
§ 8. Некоторые неэлементарные функции^и 8.1. Элементарные и неэлементарные функции (420). 8.2. Нормальная кривая (421). 8.3. Закон ошибок Гаусса (422). 8.4. Гамма-функция (424). 8.5. Функция, все производные которой в данной точке равны нулю (425). Задачи (426).
7 Техника интегрирования 429
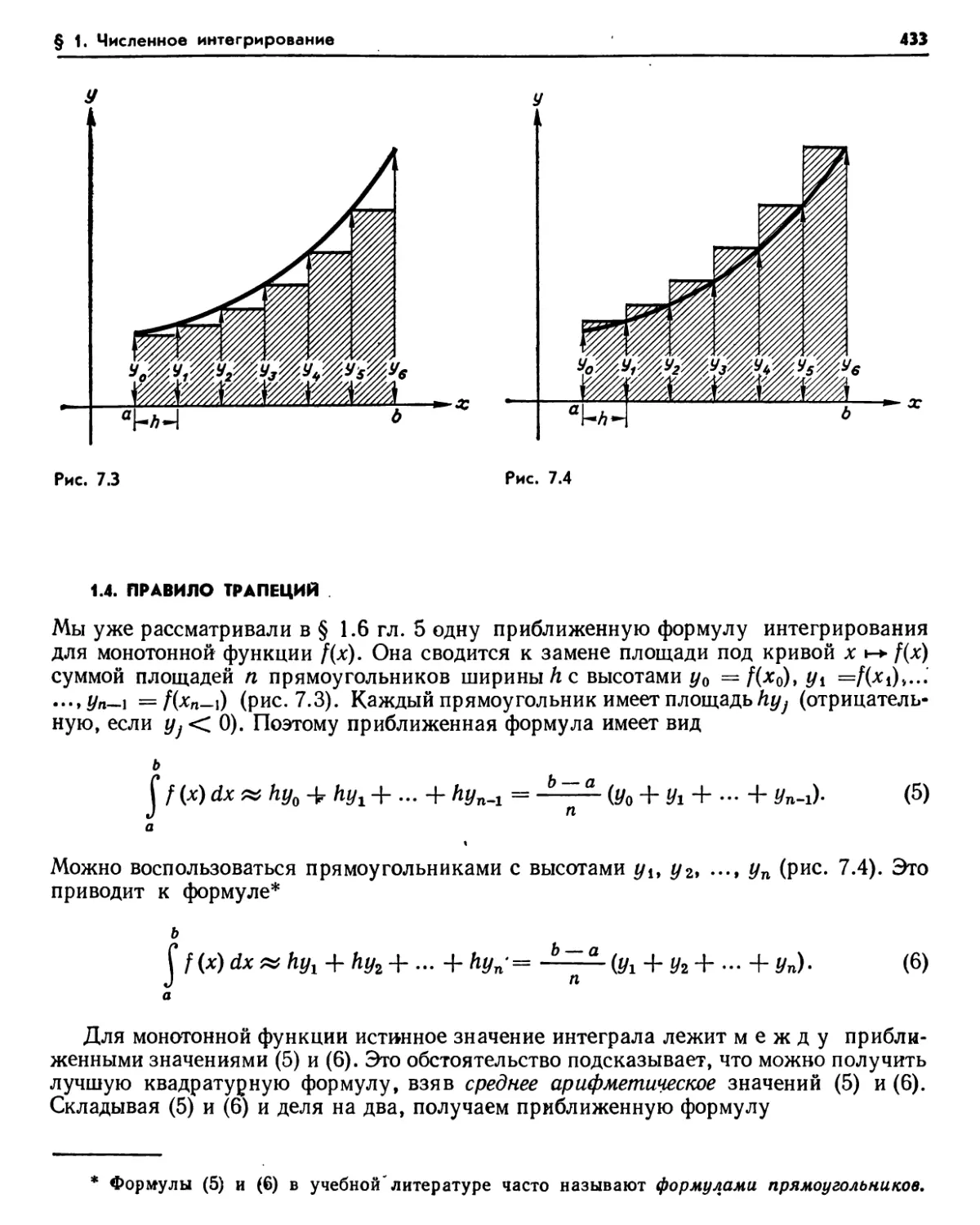
§ 1. Численное интегрирование 430
1.1. Формальное дифференцирование (430).
' 1,2. Численное дифференцирование (430).
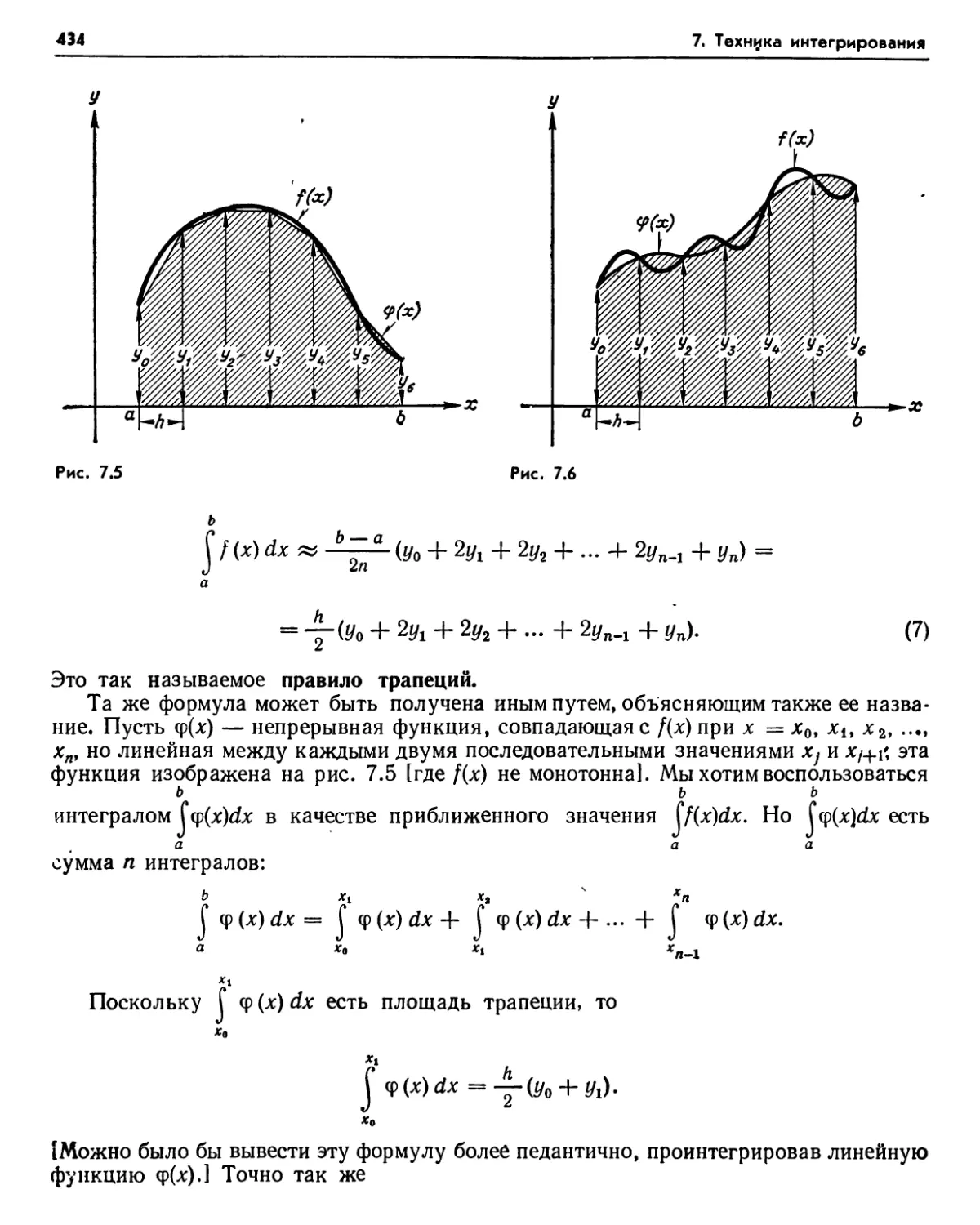
1.3. Численное интегрирование (431). 1.4. Правило трапеций (433) 1.5. Оценка погрешности для правила трапеций (435). Упражнения (436). 1.6. Правило Симпсона (436).
1.7. Оценка погрешности для правила Симпсона (438). Упражнения (441). 1.8. Погрешности метода и погрешности округления (441).
§ 2. Интегрирование рациональных функций 442
2.1. Простейшие дроби (442). 2.2. Степень линейной функции а знаменателе (442). Упражнения (444). 2.3. Степень квадратичной функции в знаменателе. Первый случай (444). Упражнения (445). 2.4. Рекуррентная формула (446). Упражнения (447). 2.5. Степень квадратичной функции в знаменателе. Второй случай (448). Упражнения (449).
2.6. Основная теорема об интегрировании ра
циональных функций (450). 2.7. Разложение на простейшие дроби (451). 2.8. Неопределенные коэффициенты (452). Упражнения (456).
§ 3. Рационализация интегралов 457 3.1. Обозначения (457). 3.2. Рациональные функции от показательной функции (458). Упражнения (459). 3.3. Корни из линейных функций (459). Упражнения (460). 3.4. Корни из дробно-линейных функций (460). Упражнения (462). 3.5. Рациональные функции от тригонометрических функций (462). Упражнения (465). 3.6. Рациональные функции от гиперболических функций (466). Упражнения (466). 3.7. Интегралы, содержащие V’l— х2 (466). Упражнения (467). 3.8. Интегралы, содержащие V X2— 1 (468). Упражнения (469) 3.9. Интегралы, содержащие V 14-х2 (469).
Упражнения (470). 3.10. Квадратные корни из квадратичных функций (470). Упражнения (471).
§ 4. Формулы приведения 472
4.1. Интегрирование функции х® еЯ (472). Упражнения (473). 4.2. Интегралы, содержащие ха (In к) п (473). Упражнения (473).
4.3. Интегралы от хп cos х и хп slnx(474). Упражнения (474). 4.4. Произведения степе-ней синус а и косинуса (475). Упражнения
!?• Произведения синусов и косинусов (478). Упражнения (479).
Приложение к главе 7 480
§ 5. Сводка формул интегрирования 480 5.1. Основные правила (480). 5.2. Степени. Рациональные функции (480). 5.3. Некоторые иррациональные функции (481). 5.4. Тригонометрические функции. Основные формулы (481). 5.5. Степени и произведения тригонометрических функций (482). 5.6. Обратные тригонометрические функции (482). 5.7. Показательная и логарифмическая функции (483). 5.8. Рационализируемые интегралы (483). Задачи (484).
Решения упражнений, помеченных знаком А 485 Алфавитный указатель 510
Указатель основных обозначений 518
От редактора
В нашей стране достаточно широко известны наиболее значительные монографии по математике, выпуском которых занимается специальное издательство «Мир». За последние годы на русском языке увидели свет также и
многие из используемых в других странах университетских учебников математики. Однако с издающимися на Западе учебниками математики для высшей технической школы наши студенты и преподаватели знакомы до сих пор еще совершенно недостаточно. Вот почему я рад представить русскому читателю «Математический анализ» видного американского математика и педагога Л. Берса, вышедший в свет первым изданием в 1969 г. и в последние годы ставший в США одним из основных пособий для математической подготовки будущих инженеров и физиков.
Профессор Липман Берс широко известен во всем мире своими исследованиями по «математическому анализу» в широком понимании этого термина, в первую очередь по теории функций комплексного переменного и дифференциальным уравнениям в частных производных; на русский язык переведен целый ряд его книг и научных статей*. Наряду с этим Л. Берс уделяет много времени и внимания научно-педагогической и научно-организационной деятельности. В течение ряда лет он возглавляет отделение математики Национальной Академии наук США; в настоящее время он занимает пост президента Американского математического общества, а также является руководителем математического отделения Колумбийского университета в Нью-Йорке и проявляет большую активность в области перестройки и модернизации системы преподавания математики в этом одном из старейших и авторитетнейших американских вузов. Проф. Л. Берс был одним из инициаторов организации известной «Исследовательской группы по школьной математике» (School Mathematics Study Group, сокращенно SMSG), объединяющей многих видных американских математиков и педагогов и руководящей всей работой в области перестройки школьного математического образования; несколько лет он возглавлял SMSG. О широком диапазоне педагогических интересов автора этой книги свидетель
* См., например, Л. Берс, Математические вопросы дозвуковой и околозвуковой газовой динамики, М., ИЛ, 1961; Л. Альфорс, Л. Берс, Пространства римановых поверхностей и квазиконформные отображения, М., ИЛ, 1961; Л. Берс, Ф. Джон, М. Шехтер, Уравнения с частными производными, М., «Мир», 1966
to.
От редактора
ствует и настоящий учебник; Л. Берс писал мне также, что в настоящее время он занят подготовкой к печати нового варианта этого учебника и одновременно работает над двумя другими книгами: составляемой им совместно с пр живающим сейчас в США видным финским математиком Ларсом Альфорсом монографией, подытоживающей исследования Альфорса и Берса в области теории функций комплексного переменного, и учебником математического анализа, рассчитанным уже не на будущих инженеров, а на медиков, биологов и экономистов. В заключение остается прибавить, что проф. Л. Берс является искренним другом нашей страны, которую он неоднократно посещал; советские математики хорошо знают Берса не только по его публикациям, но и по личным встречам и многочисленным докладам, прочитанным Берсом в Москве и в Ленинграде, в Новосибирске, Тбилиси и Ереване.
В Предисловии к русскому изданию его книги Л. Берс достаточно полно характери зует ее основные установки; нам остается сказать здесь немногое. Эта книга представляет собой начальный учебник; ее содержание далеко не покрывает принятую в наших высших технических учебных заведениях программу курса математики. Так, например, здесь отсутствует не только какое бы то ни было упоминание о теоретико-вероятностных концепциях и результатах, но исключены из нее также разделы, посвященные дифференциальным уравнениям или векторному анализу. В противоположность этому содержащийся в книге материал по аналитической геометрии полностью покрывает (или даже превосходит) потребности наших втузов, так что при использовании книги Берса во втузовском преподавании потребность в специальном учебнике аналитической геометрии отпадает.
Настоящее пособие представляет собой одновременно учебник и задачник: число сопровождающих текст упражнений, бесспорно, обеспечивает потребности преподавания. В английском оригинале книги в конце ее собраны ответы ко всем без исключения упражнениям с четными номерами; в русском переводе, однако, эти ответы исключены — в первую очередь для того, чтобы не увеличивать чрезмерно и без того очень большой объем книги. По тем же соображениям в переводе исключены и завершающие оригинал книги таблицы значений тригонометрических функций углов (заданных в градусной и радианной мерах), натуральных и десятичных логарифмов и значений показательных функций е* и е~х. Однако и в настоящем своем виде книга является настолько большой, что ее перевод оказалось целесообразным выпустить, в свет в двух томах.
От редактора
II
Некоторые основные предпосылки автора поясняют ска- . занные в Предисловии слова о двух «весьма нестандартных» книгах, оказавших на него определенное влияние: пособии видного немецкого математика О. Теплица и книге акад. Я. Б. Зельдовича*. Правда, зачастую шокирующая некоторых «чистых» математиков подчеркнуто «физическая» манера Зельдовича (особенно заметная в первых изданиях его книги) в целом осталась чужда Берсу; однако он, так же как и Зельдович, явно считает основным не наведение «математического лоска», а содержательно-прикладную сторону математического анализа. Для того чтобы продемонстрировать это, достаточно взглянуть, скажем, на содержание гл. 4 «Производная», начинающей систематическую трактовку курса анализа (в то время как первые три главы имеют характер Введения в тему книги). Уже § 1 этой главы «Производная функции. Касательная. Скорость» наряду с традиционным материалом содержит разделы, посвященные исследованиям Галилея по изучению равноускоренных движений. Темой следующего параграфа является элементарная техника дифференцирования (излагаемая, кстати сказать, без больших подробностей и нигде не становящаяся для автора самоцелью); однако уже § 3, посвященный производным высших порядков, вновь содержит экскурсы в механику: здесь подробно обсуждается как классический закон движения Ньютона, так и принадлежащее А. Эйнштейну релятивистское обобщение этого закона. Далее, § 4 гл. 4 содержит основные приложения дифференциального исчисления; в § 5 появляется понятие первообразной, которое вводится так рано (до главы об интегралах!) для того, чтобы сразу же можно было обратиться к понятию дифференциального уравнения и разобрать некоторые интегрируемые варианты как уравнения движения Ньютона, так и уравнения Эйнштейна. Подобная органическая связь «чистой» математики и ее приложений характерна и для остальных глав книги.
Следует еще отметить, что в ряде случаев Л. Берс вообще отказывается от доказательств интуитивно ясных теорем, перенося их в Приложения, адресованные не всем читателям, а только приверженцам математической строгости. Для «наглядного» стиля автора характерно свободное обращение к грубым инфинитезимальным рассмотрениям (которые он называет «математическими мифами»): рассмотрения такого рода иллюстрируют многие положения книги. Этот стиль определяет также почти полный отказ Берса от
* Я. Б. Зельдович Высшая математика для начинающих и ее приложения к физике, М., «Наука», 1970 (последнее издание)
12
От редактора
традиционной «е-о-техники», в целом остающейся ему чуждой. Так, например, обсуждение понятия непрерывности функции у = f(x) в точке х = х0 автор начинает с разбора ряда простых примеров; строгое же определение дается двумя достаточно ясными условиями геометрического характера (см. гл. 3, § 3.2). Впрочем, такая манера изложения не противоречит и достаточно высокому (особенно в Приложениях и Дополнении к книге) уровню логической требовательности, в чем-то, быть может, и излишнему для будущих инженеров (но ведь эти разделы книги читатель может и пропустить!), однако бесспорно способствующему воспитанию подлинной математической культуры. Отметим здесь и другие отступления от принятой в наших вузовских учебниках системы изложения, также направленные в сторону повышения общенаучного уровня книги: открывающее книгу аксиоматическое описание множества вещественных чисел; использование понятий /г-мерного векторного и евклидова пространств; весьма тщательно разработанную символику (например, систематическое использование редкого в нашей учебной литературе для втузов символа х •-> у для обозначения функции* или символа о для сложной функции (/ о ^)(х), т. е. композиции функций f и g) и т. д. Читатель оценит и многочисленные методические находки автора, в том числе тщательное выделение примеров, играющих в книге большую роль и иллюстрирующих основной теоретический материал: начало и конец посвященного разбору примеров текста всюду отмечены бросающимся в глаза значком •.
Определенным достоинством английской математической терминологии по сравнению с русской является ее большая краткость. В настоящем переводе мы пытались частично сохранить это преимущество, заменив некоторые из общераспространенных терминов более короткими: здесь используется слово «наклон» (английское slope) вместо обычного термина «угловой коэффициент» (заметим, что
* В настоящее время в математике укоренилось использование стрелки -> для обозначения произвольных отображений (так что за-I ись f: X -> Y, где X и Y — числовые множества, означает, что X есть область определения функции f, a Y —область ее значений)-, специфический же значок используется для поэлементных отображений, так что запись f: хн- у символизирует, что отображение, или функция, f переводит элемент х из области определения функции в число у, т. е. что y = f(x)- [Различие между записями X -► Y и хн- у можно сравнить, пожалуй, с разницей между утверждениями Хг с X и х £ Л', первое из которых означает, что (множество) Хг составляет часть X, а второе — что х есть (далее уже неделимый!) элемент множества X.]
От редактора
13
ни в одном из европейских языков это простое понятие не имеет наименования, состоящего из двух слов!), часто употребляется слово «квадрики» (английское quadrics) вместо длинного выражения «линии (или поверхности) второго порядка», слово «коники» (английское conics) вместо «конические сечения» и т. д.
Подстрочные примечания переводчика книги и редактора всюду отмечены звездочками в отличие от нумерованных сносок автора.
Профессор Берс отнесся к подготовке русского издания своего учебника с большим вниманием и интересом: он переработал и дополнил Предисловие к книге, а также прислал нам обширный (хоть и далеко не полный) список опечаток английского издания. В заключение мне приятно поблагодарить здесь автора настоящей книги за помощь и сотрудничество.
И9 М. Яглом
Предисловие к русскому изданию
Мне очень приятно, что мой учебник, составленный для американских студентов, а впоследствии переведенный на испанский язык, появится теперь и на русском языке. Мне хотелось бы выразить здесь искреннюю признательность редактору русского перевода проф. И. Яглому и переводчику доц. Л. Головиной за проделанную ими работу.
Эта книга предназначена для студентов, впервые приступающих к изучению математического анализа. Независимо от причин, побуждающих этих студентов изучать математику, их потребности, в сущности, мало различаются между собой. Первоначальный курс должен дать им представление об основных идеях анализа и развить способность свободно и сознательно использовать соответствующий язык и технику вычислений. Поэтому содержание такого курса должно быть ограничено самым существенным. Математический анализ есть искусство составлять и решать дифференциальные уравнения—таково его происхождение, и к этой цели он устремлен. Мы-исходили здесь именно из такой точки зрения, не пытаясь, конечно, предварить тот курс теории дифференциальных уравнений, который позже изучат большинство читателей этой книги.
Как и любой другой предмет, математический анализ следует изучать с надлежащим вниманием к его истории. Исходя из этого, мы снабдили книгу рядом вставок, относящихся к истории математики; исторические соображения повлияли также на выбор материала. Однако надеюсь, что это все же современный учебник анализа, написанный современным математиком, работающим в этой области. Везде, где это оказалось возможным, использованы примеры, связанные с близкими к нам по времени научными исследованиями. Что же касается языка, то я не пытался нарочито модернизировать его и почти всюду сохранял традиционные термины и обозначения.
В книге везде подчеркиваются приложения математического анализа и прежде всего — приложения к механике, сыгравшие решающую роль в его развитии. Я уверен, что эти приложения важны не только для студентов, которые вспоследствии будут применять анализ к физическим наукам или к технике, но также и для будущих математиков, биологов или специалистов по общественным наукам.
На протяжении всей книги используются и подчеркиваются интуитивные соображения—отнюдь не в качестве замены строгих рассуждений, но для подготовки и мотивировки последних.
Строгость в математике означает прежде всего добросовестность и ясность. В начальном курсе строгость нужна
Предисловие к русскому изданию
1S
для того, чтобы облегчить понимание и применение понятий. При этом нас мало заботит техническая сторона определений и доказательств. Все определения и доказательства в нашей книге правильны и точны. Однако в большинстве глав некоторые основные теоремы лишь поясняются и применяются без доказательства; доказываются они в Приложениях к главам (или, в нескольких более трудных случаях,— в Дополнении в конце книги). Эти доказательства придают книге логическую завершенность; но при построении обязательного курса они обычно могут и должны опускаться. В других разделах Приложений содержится дополнительный материал, который по желанию можно включать или не включать в начальный курс анализа.
Чтобы строгость помогала, а не препятствовала пониманию предмета, пришлось заново продумать некоторые стандартные приемы; специалист легко обнаружит такие отступления от традиции.
Наконец, я старался написать удобочитаемую книгу: я рассчитываю, что преподаватель найдет возможным оставить значительную часть материала для самостоятельной работы студентов, используя сбереженное таким образом время для пояснений, обсуждений и разбора примеров. Учащийся должен быть, однако, предупрежден, что книгу по математике следует читать медленно и по возможности — с карандашом в руках. Необходимо проверять все вычисления и восполнять рассуждения, опущенные в тексте книги. Это потребует определенных усилий, но лучшего способа научиться математике я не знаю.
Книга не предполагает какой-либо специальной подготовки, кроме умения выполнять обычные алгебраические преобразования и первоначального знакомства с геометрией. Хотя мы концентрируем основное внимание на анализе функций одной переменной, в книге излагаются также начатки аналитической геометрии и анализа функций нескольких переменных в том объеме, в каком это разумно сделать в вводном курсе анализа и в каком это возможно без пространного введения в линейную алгебру.
Для развития навыков и более основательного понимания предмета мы дополнили «теоретическую» часть учебника более чем 3000 упражнений. Читатель, ознакомившийся с соответствующей частью текста и примерами, вряд ли столкнется с какими-либо трудностями при решении упражнений, за исключением, быть может, небольшого их числа. Для помощи читателю в конце книги указаны решения нескольких сот из этих упражнений (номера таких упражнений помечены знаком А). Однако следует предупредить читателя, что задачи, собранные в конце каждой главы,
16
Предисловие к русскому изданию
Схема зависимости глав
1. Числа
2. Координаты
3. Функции
Ц. Производные
9. Векторы
Ю. Квадрика
, 5. Интегралы
6. Трансцендентные функции
о. Ряды
11. Векторные ^функции скалярного аргумента
7. Техника интегрирования
13. Кратные интегралы
12. Частные производные
часто являются довольно трудными, а в некоторых случаях они выходят за пределы содержания соответствующей главы.
Математический анализ не только полезен и богат приложениями, но и красив. Разумеется, способность к эстетической оценке математических результатов предполагает известный уровень научной культуры, достигаемый лишь в результате длительной работы; однако в конечном счете успех или неудача учебника математики измеряются в первую очередь тем, насколько способен этот учебник донести до читателя красоту своего предмета.
О содержании книги и о принятой в ней последовательности изложения можно судить по оглавлению; об основных логических Связях между главами — по приведенной выше схеме. Мы стремились к гибкости системы расположения материала, предоставляющей преподавателю (и читателю) широкие возможности варьирования порядка его изложения (или изучения). Некоторые указания на такие возможности вынесены во вводные замечания к отдельным главам.
Наконец, мне хотелось бы отметить влияние, оказанное на меня двумя весьма нестандартными книгами по математическому анализу: историческим обзором, написанным выдающимся математиком О. Теплицем, и учебником известного физика Я. Зельдовича (пока, к сожалению, мало доступным английским и американским читателям). Из книги Зельдовича заимствован ряд примеров § 6 гл. 6.
Я надеюсь, что моя книга окажется полезной и русским читателям, и был бы рад получить их отзывы и критические замечания.
Отделение математики *
Колумбийского университета, Нью*Йорк Липман Берс
1/ЧИСЛА
В качестве подготовки к изучению математического анализа мы займемся здесь рациональными и иррациональными числами и правилами действий над ними. Материал, изложенный в этой вводной главе, многим читателям покажется известным; они могут ограничиться беглым ее просмотром.
Однако поскольку параграф о неравенствах (§ 3) посвящен технике, часто используемой в дальнейшем, некоторые из упражнений в конце § 3 полезно выполнить всем читателям.
Приложение к этой главе, как и к другим главам, может быть опущено без всякого ущерба для понимания всего дальнейшего. В § 6 речь идет о математической индукции и о полноте системы действительных чисел. Эти рассуждения носят теоретический характер и будут использованы только в Приложениях к другим главам, где доказываются некоторые теоремы. Теоретическое рассмотрение понятия числа продолжается в § 8, в то время как § 7 посвящен вопросу о точности приближенных вычислений.
18
1. Числа
§ 1. РАЦИОНАЛЬНЫЕ ЧИСЛА. ПОТРЕБНОСТЬ В РАСШИРЕНИИ ПОНЯТИЯ ЧИСЛА
Создание математического анализа в XVII в. явилось поворотным пунктом в истории человеческой мысли и положило начало развитию современной математической науки. Анализ лежит в основе многих областей современной математики, а также используется во многих ее приложениях к другим наукам. Путь к созданию анализа был проложен, с одной стороны, последовательным расширением понятия числа и, с другой стороны, слиянием геометрии с алгеброй. Поэтому изложение анализа должно начинаться с обсуждения природы чисел.
1.1. ПОЛОЖИТЕЛЬНЫЕ ДРОБИ
Простейшими числами являются положительные целые (или натуральные) числа, используемые для счета: 1, 2, 3, 4, ..., а также положительные дроби, используемые для измерений: 4г ,4"» -4» ••• • Натуральные числа сами являются дробями (1 = Z □ о
1 о 2 . л
= -р, 2 =— и т. д.), а каждая положительная дробь есть отношение двух натуральных чисел. Целые положительные числа и положительные дроби вместе называются положительными рациональными числами.
- Конечно, следует различать сами числа и символы, используемые для их обозначений. Так, вместо арабских цифр 1, 2, 3, 4, ... мы могли бы пользоваться римскими цифрами I, II, III, IV, ... или какими-нибудь другими понятными символами, например *, **, ***, ****, ... .
Положительные рациональные числа и арифметические операции над ними могут быть представлены геометрически. Для этого выберем фиксированный прямолинейный отрезок в качестве единицы длины. Пусть единичный отрезок разделен на п равных отрезков (п — целое положительное число). Это можно сделать с помощью циркуля и линейки. Каждому «малому» отрезку приписываётся длинаГоворят, что отрезок имеет длину где тип — целые положительные числа, если его мож-
но разделить на т равных отрезков длины — каждый. Длина отрезка АВ обозначается через | АВ |. п
Пусть а и Ь — положительные рациональные числа, О и А — две такие точки, что | ОА | = а. Пусть, далее, В — такая точка прямой ОА, что точка А лежит между О и В и | АВ | == Ь. Тогда сумма а + Ь — положительное рациональное число, равное длине | ОВ | отрезка О В (рис. 1.1).
Коммутативный закон для сложения а + Ь — 6+ а означает, что длина отрезка ОВ будет одной и той же независимо от того, измеряется ли расстояние от О до В или от В до О. Геометрический смысл ассоциативного закона для сложения (а+ Ь) + с = а + (Ь + с) виден из рис. 1.2. Если а больше Ь, то разность х = = а— Ь, т. е. положительное рациональное число х, для которого /?+ х = а, также может быть найдена геометрически (рис. 1.3).
Произведение ab тоже является положительным рациональным числом, точно так же как частное х = т. е. число х, для которого Ьх == а, (Начиная с этого
§ 1. Рациональные числа. Потребность в расширении понятия числа
19
Рис. 1.3
места, мы часто будем писать а/b вместо—-; такой способ записи часто употребляется в печатных текстах.) Геометрическое построение отрезков длин ab и а/b изложено в Приложении (см. § 8.1).
Произведение ab можно также истолковать как площадь прямоугольника длины а и ширины Ь. Такой прямоугольник можно разрезать на куски и, собрав их в другом порядке, получить прямоугольник длины ab и ширины 1. Коммутативный закон для умножения ab = Ьа означает, что безразлично, какое из двух измерений прямоугольника называется при этом «длиной» и какое «шириной». Геометрический смысл дистрибутивного закона a(b + с) = ab-\- ас показан на рис. 1.4.
Объем прямоугольного параллелепипеда («ящика») длины а, ширины b и высоты с равен (ab)c (площади основания, умноженной на высоту). Такой ящик можно разрезать на куски и, собрав их вместе в другом порядке, получить ящик длины (ab)c. ширины 1 и высоты 1. Ассоциативный закон для умножения (ab)c = а(Ьс) следует теперь из того, что о ящике длины а, ширины Ь и высоты с можно сказать также, что •он имеет длину 6, ширину с и высоту а.
О. РАЦИОНАЛЬНЫЕ ЧИСЛА
Положительные дроби были известны уже древним цивилизациям Вавилона и Египта; как полагают, индийцы изобрели число нуль. Отрицательные рациональные з
числа —1,----g- и т. д. были введены в Италии в эпоху Возрождения. Положи-
20
1. Числа
Рис. 1.5
тельные и отрицательные целые числа и дроби вместе с нулем образуют систему рациональных чисел.
Рациональные числа могут быть представлены точками прямой линии. Для этого выберем некоторую точку на прямой (начало отсчета), обозначая эту точку через 0; выберем также и другую точку, обозначая ее через 1. Расстояние от Одо 1 принимается за единицу длины. Положительное рациональное число а изображается точкой прямой, отстоящей от 0 на расстояние а и лежащей по ту же сторону от 0, что и 1. Точка по другую сторону от 0 на том же расстоянии от нее изображает число —а.
По традиции прямая чертится горизонтально и точка 1 берется справа от 0, как показано на рис. 1.5.
Заметим, что термины «горизонтально» и «справа» не имеют математического смысла — они вводятся с помощью соображений, не имеющих отношения к математике. Мы вое же будем пользоваться выражениями «справа» и «слева», понимая под этим соответственно «в направлении от 0 к 1» и «в направлении от 1 к 0».
1Л. НЕСОИЗМЕРИМЫЕ ОТРЕЗКИ
Рациональные числа были введены для измерений, в первую очередь для измерения длины. С помощью дробей иногда удается свести процесс измерения к более элементарному процессу счета. Но это не всегда возможно. Существуют несоизмеримые отрезки—это значит, что если длину одного из таких отрезков принять за единицу, то другой не может быть выражен рациональным числом. Простейший пример представляют сторона квадрата и чего диагональ.
§ 1. Рациональные числа. Потребность в расширении понятия числа
21
Пусть сторона квадрата имеет длину 1. Если оы длина диагонали выражалась рациональным числом х, то мы имели бы х2 = 2. Это следует из теоремы Пифагора или просто из того, что площадь «большого» квадрата на рис. 1.6 вдвое больше площади «малого» квадрата. Но не существует рационального числа, квадрат которого равен 2. Напомним знаменитое доказательство этого факта.
Заметим сначала, что каждое целое число либо четно, т. е. делится на 2, либо нечетно, т. е. не делится на 2. Далее, если т — целое число и т2 четно, то т также четно.
В самом деле, если т нечетно, то т + 1 четно, откуда т + 1 = 2п, где п — целое. Следовательно, т = 2п — 1 и т2 = (2/г — 1 )(2п — 1) = 4/г2 — 4п + 1 = = 4(п2 — п) + 1 = четному числу + 1 = нечетному числу.
Пусть теперь х — рациональное число. Тогда х = plq, где р и q — целые числа. Мы можем с самого начала исключить случай, когда числа р и q — оба четные, так как в том случае множитель 2, входящий и в числитель и в знаменатель, можно сократить. Пусть теперь х2= 2. Как мы покажем, это допущение ведет к противоречию и потому неприемлемо.
Если х2 = 2, то p2lq2 = 2, или р2 = 2q2. Поэтому р2 четно. Согласно сделанному выше замечанию, р четно. Тем самым р — 2г, где г — целое положительное число, и р2 = 4г2. Но р2 = 2q2. Отсюда 4г2 = 2q2, или q2 = 2г2. Поэтому q2 четно и в силу амечания q четно. Итак, оба числа р и q четны вопреки предположению.
Существование несоизмеримых отрезков было открыто около 2500 лет назад гре^ ческими математиками. Согласно легенде, человек, объявивший об этом открытии, был наказан богами за то, что он раскрыл несовершенство мироздания. Отсюда видно, насколько греческие мыслители были потрясены открытием несоизмеримости: казалось, она разрушает не только доказательства, но и самый смысл простых геометрических теорем о длинах отрезков и отношениях их длин.
Возникшая трудность была блестяще преодолена Евдоксом, создавшим строгую теорию пропорций. В современной математике эта проблема решается иначе — введением нового вида чисел — действительных чисел; при этом оказывается, что независимо от выбора единицы длины каждый отрезок имеет длину, представимую некоторым действительным числом.
ПИФАГОР с Самоса (VI в. до н. э.) — полулегендарный основоположник- философской школы. Школа эта являлась также и религиозным братством, а затем оказалась замешанной в политические интриги.
Пифагорейцам приписывается множество математических открытий, в том числе теоремы о квадрате гипотенузы (впрочем, на самом деле известной за несколько столетий до них*), а также существования несоизмеримых отрезков. Они заметили зависимость музыкальных тонов от отношения длин струн, что, по-видимому, привело их к утверждению «все есть число». Если истолковать это в том смысле, что природа может быть описана математически, то в этой темной фразе можно усмотреть одну из самых блестящих догадок в истории мысли.
ЕВДОКС из Книда (ок. 403—355 до н. э.) жил в течение некоторого времени в Афинах, где он был связан с Академией Платона. Теория пропорций — лишь одно из его блестящих достижений. Евдоксу принадлежат также строгие доказательства различных теорем, касающихся объемов; в астрономии же он положил начало методу описания видимых движений планет путем наложения круговых движений.
* Можно предположить, что в пифагорийской школе впервые было найдено доказа* гельство знаменитой теоремы Пифагора, до этого известной как экспериментально наблюдаемый факт; в таком случае это достижение следует расценить как выдающееся.
22
1. Числе
§ 2. СЛОЖЕНИЕ И УМНОЖЕНИЕ
Потребность в расширении системы рациональных чисел была уже мотивирована в предыдущем параграфе. Первым шагом к такому расширению является более тщательное изучение свойств самих рациональных чисел.
2.1. ПЕРЕМЕННЫЕ
Имеется бесконечно много рациональных чисел, и единственный способ высказывать о них утверждения, относящиеся ко всем этим числам сразу, — употребление переменных , т. е. символов, которые могут быть замещены числами. Условимся обозначать рациональные числа буквами. Тогда, например, высказывание «а+0 = а 5' 5
для всех а» означает, что 0+ 0 = 0, 1 4- 0 = 1,-у- 4- 0 =--- и т. д. Точно так
же «а = Ь» означает, что а и b — одно и то же число, а «а#=д» означает, что а и & —разные числа.
В этом параграфе и в двух следующих мы будем часто говорить «число» вместо «рациональное число».
При строго дедуктивном изложении математики рациональные числа определяются в терминах целых положительных чисел. Сами же целые положительные числа могут быть определены аксиомами или сведены к более простым понятиям теории множеств. В нашем изложении мы, однако, принимаем понятие рационального числа за основное. Ниже перечисляются основные свойства рациональных чисел.
2.2. АКСИОМЫ ПОЛЯ
Важно отметить, что все обычные правила алгебры могут быть выведены из 12 простых аксиом.
I. Для любых а и b существует единственное число, называемое суммой а и Ь и обозначаемое через а + Ь.
2. a+6 = Z?+ а для всех aub (коммутативность сложения).
3. (а + Ь) + с = а + (Ь 4* с) для всех а, b и с (ассоциативность сложения).
4. Существует такое число, называемое нулем и обозначаемое через 0, что а 4- 0 = а для всех а.
5. Для любого а существует единственное число, называемое противоположным а и обозначаемое через — а, такое что а 4- (—а) = 0.
6. Для любых а и Ь существует единственное число, называемое произведением а и Ь и обозначаемое через ab.
7. ab = Ьа для всех а и Ь (коммутативность умножения).
8. (ab)c = а(Ьс) для всех а, Ь и с (ассоциативность умножения).
9. а(Ь + с) = ab+ ас для всех а, b и с (дистрибутивность).
10. Существует такое число, называемое единицей и обозначаемое через 1, что 1 • а = а для всех а,
11. 1 =/= 0.
12. Для любого числа а =/= 0 существует единственное число, называемое о б-ратным а и обозначаемое через а'1, такое что а (а'1) = 1.
§ 2. Сложение и умножение
23
* Аксиомы 1—5 суть аксиомы сложения; другие аксиомы относятся к умножению, аксиома же 9 связывает сложение в умножением.
Все аксиомы 1 —12 называются аксиомами поля; тот факт, что рациональные числа удовлетворяют этим аксиомам, математики кратко выражают, говоря, что рациональные числа образуют поле.
Поясним, по какой причине мы дали себе труд написать почти очевидные утверждения 1—12 и наделили их особыми именами. Дело в том, что есть много других математических систем, подчиняющихся тем же аксиомам, и полезно знать, какие правила алгебры справедливы при условии, что верны утверждения 1—12. Такова, например, система так называемых комплексных чисел (не используемая в этой книге).
2.3. СЛЕДСТВИЯ ИЗ АКСИОМ ПОЛЯ
Мы укажем теперь некоторые свойства рациональных чисел, которые могут быть выведены из аксиом 1—12 и потому выполняются в любом поле.
Условимся писать а + Ь + с вместо (а + Ь) + с и abc вместо (ab)c и аналогично для сумм и произведений более чем трех членов. Законы ассоциативности 3 и 8 гарантируют, что это не приведет к какой-либо путанице. Заметим, что ввиду законов коммутативности 2 и 7 можно писать а + с+ b вместо а+ 6+ с, Ьас вместо abc и т. д. Условимся также писать b — а вместо Ь+ (—а) и Ыа вместо Ь(а~1}. В силу законов коммутативности 2 и 7 имеем также — а + b = b + (—а) = b — а, аггЬ — ЬсГ1 == Ыа» Отметим, что
аг1 =— для а=/=0. (1)
а
Пользуясь аксиомами 1 —12 можно доказать, что
0-а = 0 для всех а. (2)
Отсюда видно, что число 0 не имеет обратного и что деление на 0 не может быть определено без нарушения наших аксиом.
Важен также следующий закон сокращения:
если ab = 0, то или а *= 0, или fe = 0. (3)
Здесь «или», как это принято в математике, принимается в смысле «неисключительного или». Утверждение «а = Оилид =0» означает, что возможны три следующих случая: (1) а = 0, 0, (2) а Ф 0, Ь = 0, (3) а = Ь = 0, тогда как случай
>(4) а#= 0, 6=#= 0 невозможен.
Из закона сокращения следует, что если произведение нескольких чисел равно 0, то п о крайней мере о д и н из множителей есть 0.
> Напомним, наконец, что
i (—а)Ь = —ab, (—а)(—6) = ab. (4)
[
; Читатели, желающие узнать, как вывести правила (2), (3), (4) и им подобные, Смогут обратиться к Приложению в конце этой главы (см. § 8.2). Начиная с этого йиеста, мы будем свободно пользоваться обычными правилами алгебры, основанными ша аксиомах 1—12.
24
1. Числа
УПРАЖНЕНИЯ
В упражнениях 1—8 выведите указанные утверждения из аксиом 1—12. На каждом шаге вашего вывода точно укажите, какой аксиомой Вы пользуетесь.
1. 2 + 300 = 300 + 2. 5. 0 + (0 + 0) = 0.
2. 0 + 2 = 2. А6. 7 + (—7) = (—6) + 6.
3. 2 + 0 = 2. 7. 1 + 1 =£ 1.
4. а + 0 = а. 8. (—76345) + 1 =/= —76345.
9. Пусть «число» означает целое положительное число вместо рационального числа.Какие из аксиом 1—12 сохранят при этом силу?
10. Пусть «число» означает ненулевое рациональное число вместо рационального числа. Какие из аксиом 1—12 сохранят при этом силу? Какие из них в этой новой системе чисел теряют смысл?
И. Пусть «число» означает целое число вместо рационального числа. Какие из аксиом 1—12 сохраняют при этом силу?
12. Пусть «число» означает положительное рациональное число вместо рационального числа. Какие из аксиом 1—12 сохраняют при этом силу?
13. Пусть «число» означает неположительное рациональное число вместо рационального числа. Какие из аксиом 1—12 сохраняют при этом силу? Какие из них в этом случае теряют смысл?
2.4 . ЦЕЛЫЕ ЧИСЛА. СТЕПЕНИ
В аксиомах поля целые числа не упоминаются. По определению, мы будем называть число целым, если оно есть 1 или получается из 1 посредством сложения и, быть может, замены числа ему противоположным. Например, 1+ 1 = 2, 2+ 1 = 3ит. д.— целые числа, так же как —1, —2, —3 и т. д.; целым является и число 0=1+ (—1).
Далее, положим, по определению,
а1 = а, а2 = а-а, а3 = а-а2 и т. д.
Для а #= 0 положим
а0 = 1.
Определив затем а”1 = будем писать
а~2 = (а'1)2 = — 1 а~3 = — и т. д. а2 а3
Выражениям 0°, О-1, О”2 и т. д. мы никакого смысла не приписываем. Из определений следуют обычные законы возведения в степень:
anbn = (аЬ)п9 ап+т = апат, (ап)т = апт.
Здесь буквы п и т означают произвольные целые числа, в то время как а, b — произвольные (рациональные) числа с одним лишь тем ограничением, что значения а = 0 и b = 0 исключаются, когда соответствующие выражения теряют смысл.
Из аксиом поля следуют также алгебраические тождества вроде (а + Ь)(а — Ь) = = а2— Ь2 или (а + b)2 = а2 + 2аЬ + Ь2.
§ 2. Сложение и умножение
25
УПРАЖНЕНИЯ
^14. Если abc = 2, то чему равно a5ft5c5?
15. Если а13 =4, то чему равно (а-7)7(а"6)"6?
16. Упростить [(а“2)4]“3.
17. Если a“1ft"V”1=2, то чему равно (abc)4?
18. Чему равно (—1)2Л при целом п?
19. Чему равно (—1)2Л+1 при целом п?
20. Верно ли, что 25 = 5v
21. Верно ли, что (23)2 = 2(32)?
22. Верно ли, что (2 +3)2=22+32?
23. Верно ли, что 2332 — 2-62?
2.5 . ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Особенно важным тождеством является формула для суммы членов геометрической прогрессии
1+<7 + ?2+ ••• (5)
'----------,------------1 — q
п членов
где 7=/= 1 и п = 1, 2, 3, 4, ...
Доказательство формулы (5) очень просто. Для любого q
(1 — q)(l + q + q2 Ч----+ qn~'} =
= (1 + q + q2 + • • • + qn~l) - q (1 + q + q2 + • • • + =
= (1 + q + q2 +------h q*-') — (q + q2 + q3 4---h qn),
откуда
(1 — q)(\ + q + q2+ ... Ч-^-1) = 1 — qn. (6)
Если 1 — <?=/= 0, то обе части последнего равенства можно разделить на 1 — q, т. е. умножить на 1/(1 — q), что и приводит к требуемой формуле.
С этим тождеством тесно связано следующее:
Ап — Вп = (А — В) (Ап~1 Ч- Лл"2В Ч- Лл“3В2 +----h В^1), (7)
справедливое для всех чисел Л, В и для п = 2, 3, 4, ... Чтобы доказать его, считая, что Л =/= 0, положим q = В/Л и умножим обе части (6) на Лл. При Л = 0 формула (7) очевидна.
УПРАЖНЕНИЯ
24. Вычислите
1 1 1
,+т+т+ + ~&"
25. Вычислите 1 4- 3 4-9 4- • • • 4-3®.
26. Покажите,
что 1 4- а2 4- а4 4- • • • 4- а18 =------
1 — а2
при всех а тА 1, а =/= — 1.
27. Найдите формулу для суммы 1 — b 4- Ь2 — Ь3 4- ••• — ft21. Верна ли эта формула для всех ft?
28. Вычислите 14-24- 41" + 4 + "9" -------2* + зГ ’
29. Чему равна разность между 1+ + •• • 4--^- й 1 +-|"+-^-+ ••• + 3^57 ?
26
1. Числа
§ 3. НЕРАВЕНСТВА Аксиомы 1—12 дают неполное описание рациональных чисел, поскольку в них нет даже речи о том, что одно число может быть меньше другого. Это понятие рассматривается в настоящем параграфе.
3.1. ОБОЗНАЧЕНИЯ
Запись «х< у» означает, что число х меньше числа у. Тот же смысл имеет запись «у > х» (читается: «у больше х»). Каждое неравенство, т. е. утверждение о том, что одно число меньше другого, может быть записано с применением либо символа <С, либо .символа >. Неравенство х имеет простой геометрический смысл: точка, представленная числом х (см. § 1.2), лежит слева от точки, представленной числом у.
Запись «х у» означает, что либо х < у, либо х = у. Так, например, верны неравенства —3 С —2 и 7 < 7, но неверно неравенство 1 1/2. Аналогично, «х > у»
означает, что либо х> у 9 либо х = у. Далее, выражения «х положительно» и «у отрицательно» имеют тот же смысл, что х> 0 и у < 0, а вместо «к е-отрицательн о» и «неположительно» пишут >0 и соответственно <^0.
УПРАЖНЕНИЯ
1. Верн® ли, что 7<< 8?
2. Верно ли, что 7 <2 8?
3. Верно ли, что 5^5?
4. Верно ли. что —7 > —5?
5. Верно ли. что ?
6. - Верно ли, что —9 > 1?
о
7. Верно ли, что — _ ?
8. Верно ли, что —5 5?
3.2. ДРУГИЕ АКСИОМЫ
Свободное обращение с неравенствами совершенно необходимо для понимания анализа. К счастью, вся техника работы с неравенствами основывается на небольшом числе простых аксиом.
13. Если а и b — два числа, то из трех следующих утверждений: ч.а = Ь», «а<й», «й < а» — одно обязательно справедливо, а остальные два ложны.
14. Если аС Ь и ЬСс, то а С с.
15. Если а<Ь, то а+ с < b + с.
16. Если аС b а с > 0, то ас С. Ьс,
Мы выражаем аксиомы 1—16 в форме утверждения о том, что рациональные числа образуют упорядоченное поле. Существуют и другие упорядоченные поля, например поле действительных чисел, которое будет введено ниже.
Рассмотрим теперь некоторые следствия из аксиом 1—16.
Если а >• 0, Ь > 0, то а + й > 0. (1)
Если а> 0, b > 0, то ab>• 0. (2)
Если а> 0, то — а < 0. (3)
Если а=/= 0, то а2> 0. (4)
Если а > 0, й < 0, то ab С 0. (5)
Если а > 0, й > 0, то > 0. (6)
4< — 3< — 2< — 1 < 0< 1 < 2< 3< 4<.... (7)
§ 3. Неравенства
27
Эти утверждения совершенно очевидны; тем не менее мы выведем их из аксиом 1—16. Пусть а> 0. Тогда в силу 15 а 4- & > 0 + b = Ь (мы используем знак > вместо С, чтобы привыкнуть к употреблению обоих символов). Если, кроме того, 6>0, тоа+6>0в силу 14. Это доказывает (1).
Если а>0и£>0, тов силу 16 ab> 0-Ь = 0. Это доказывает (2).
Если а> 0, то 0 в силу 13, поэтому либо —а> 0, либо —a <Z 0 (опять в силу 13). Если —а > 0, то вследствие (1) а + (—а) > 0, Но это значит, что 0 > 0, а это неравенство невозможно в силу 13. Таким образом, (3) справедливо.
Если а =# 0, то либо а > 0, либо а < 0. Если а > 0, то, согласно (2), а2 = аа > 0, а при а< 0 имеем в силу (3) —а> 0, откуда, согласно (2), а2 = (—а)(—0. Этим доказано (4)
Если Ь < 0, то —b > 0 в силу (3), так что если, кроме того, а > 0, то, согласно (2), а (—Ь) = —ab> 0 и в силу (3) ab = —(—ab) < 0. Этим доказано (5).
Если а> 0 и Ь> 0, то 0, потому что при -у = 0 имеем 0 = -у& = а. Неравенство -у < 0 невозможно, потому что при у<0 в силу (5) должно быть а == у-&< 0. Поэтому у>0 и (6) доказано.
Так как в силу 11 1 =/= 0 и I2 = 1, то 1 > 0 согласно (4). Таким образом, в силу 15 2=1+1>0+1 = 1. Точно так же 3 = 2 + 1 > 2, 4 = 3 + 1 > 3 и т. д. Согласно (3), имеем —1 < 0; далее, вследствие 15 —2< —1 и т. д. Этим доказано (7).
Из (7) следует, что 1 #= 2, 2 #= 3, 1 =/= 3, 1 =/= 4 и т. д. Любопытно заметить, что, используя только аксиомы поля 1—12, мы не смогли бы доказать, что 1 #= 3.
УПРАЖНЕНИЯ
9. Пусть а < b и Ь\ какое заключение можно вывести отсюда?
10. Пусть а < b и а =/= Ь; какое заключение можно вывести отсюда?
11. Пусть а < b, b < с и с < а; какое заключение можно вывести отсюда?
12. Пусть a<Z b и с\ какое заключение можно вывести отсюда?
13. Верно ли, что для всех х справедливо неравенство х + 1 >х?
14. Верно ли, что для всех х справедливо неравенство x2>x?
15. Верно ли, что для всех х справедливо неравенство х + х >х? Верно ли последнее не равенство для всех х>0?
Д16. Верно ли. что для всех х справедливо неравенство (дг2 + 1)-1< 1?
3.3 . РЕШЕНИЕ НЕРАВЕНСТВ
Из аксиомы 15 следует, что верное неравенство останется верным, если один из его членов перенести в другую часть неравенства с противоположным знаком. Иными словами, если х+ у< г, то х<г—у. В самом деле, если х+ y<Zz, то х + у + (—у) < г + (—у), или X < г — у.
Из аксиомы 16 следует, что верное неравенство останется верным* если обе части его умножить на одно и то же положительное число.
28
1. Числа
Мы покажем теперь, что верное неравенство остается верным* если умножить обе части его на одно и то же отрицательное число и изменить знак неравенства на противоположный:
если а<Ь и с < 0, то ас > Ьс.
(8)
До казательс т в о. Если c<Z 0, то —с> 0, так что в силу 16 а(—c)<Z < Ь(—с). Это значит, что —ас < —Ьс* или в силу 15 —ас+ ac<Z —Ьс+ас. Отсюда ас — Ьс> 0 и опять в силу 15 (ас — Ьс) + Ьс> 0 4- Ьс* или ас> Ьс.
Для неравенств, содержащих знак справедливы те же правила.
В качестве иллюстрации мы решим неравенство
3 — 2х < 4х — 5. (9)
«Решить» означает найти все такие числах, для которых утверждение (9) справедливо. Шаги решения аналогичны тем, с помощью которых решается уравнение 3—2х = = 4х — 5. Неравенство (9) эквивалентно неравенству —2х — 4х < —5—3, полученному переносом членов, и тем самым неравенству —6х<—8, далее, неравенству х> 8/6, полученному умножением неравенства на —1/6 и изменением знака на противоположный. Это и есть решение: неравенство (9) означает, что х> 4/3. Решение есть множество чисел: оно состоит из в с е х чисел, больших 4/3.
•Примеры. 1. Решить двойное неравенство
х — 6 < 2х — 5
х — 3.
(Ю)
Решение. Неравенство (10) означает, что х — 6 < 2х — 5и2х — 5<^х —3. Применяя к этим двум неравенствам использованный выше метод, мы видим, что (10) означает справедливость двух неравенств: —х< 1 их^2. Множество, служащее решением (10), состоит поэтому из всех таких х, что — 1 < х 2. (Это множество изображено на рис. 1.7.)
2. Решить двойное неравенство
х + 10 <Z 2х — 5 х — 3.
Решение. Это неравенство означает, что х + 10 < 2х — 5и2х — 5 < х — 3, т. е. что —х < —15 и х 2. Но это неравенство неверно ни для какогох (так что множество, служащее решением неравенства, пусто), 2х I 1
3. Для каких значений х справедливо неравенство —-£т->3? (Здесь*мы должны, x-f-1
конечно, исключить значение х = —1, поскольку деление на 0 не имеет смысла.) Решение. Это неравенство означает, что:
либо х + 1 > 0 и 2х 4- 1 > 3(х 4- 1),
либо х 4- 1 < 0 и 2х 4- 1 < 3(х 4- 1).
Но 2х + 1 > 3(х + 1) означает, что 2х 4- 1 > Зх + 3, т. е. —х> 2, или, что то же, х< —2. Но если х < —2, то х 4-1 < —1. Тем самым первый случай невозможен. С другой стороны, 2x4- 1 < 3(х + 1) означает, что х>—2. Решение, таким образом, гласит: х 4- 1 < 0 и х>—2; иными словами, —2<ix<—1 (рис. 1.8).
§ 3. Неравенства 29
•—1 ( 1 1 ' ]—1 -2-10123 1 hi Л 1 1 ч 1 -2 -1 0 1 2 5
Рис. 1.7 Рис. 1.8
I )----й—?-----J---1---
-2-10123
Рис. 1.9
4. Решить неравенство х3 <С х.
Решение. Запишем это неравенство в виде*3 — х <0, или х(х — 1)(х + 1)<0, Неравенство означает, что либо каждый из трех множителей х, х — 1 и х + 1 отрицателен, либо два из них положительны, а один отрицателен. Но для всех х мы имеем х— 1<х<х+ 1. Таким образом, решение гласит: либо х + 1 < 0, либо х — 1 < 0 и х > 0. Множество, образующее решение, состоит из всех таких х, что х < — 1, и всех таких х, что 0 < х < 1 (рис. 1.9).Ф
УПРАЖНЕНИЯ
Решите следующие неравенства.
17. х— 10>2 — 2х. 32. 6 —2х < Зх + 1 < 9 —5х.
18. х 4- 6 < 5 — Зх. 33. 1 — 6х > 2х + 5> — Зх.
19. 6х 4- 5 > х — 5. А34. 5х—2< 10х+8<2х —8.
20. 7х — 1 < 2х 4- 1. 35. 4 — Зх < 2х-|-3 < Зх — 4.
21. 2x4" И > 10 —6х. 36. 2х —3<5х + 3<2х-t-3.
22. -I12- < 2- 5 — х „ 2х— 1 37. 0< <1. х — 1
3 + Х о 23. < 3. 4 — х Зх — 1 38. 1 < <2. х—3
6 —2х *М- з+<>2' 39.2>^>_l. X х
2х 4- 4 2 х +2 40. т< ~<1. х — 2 х — 2
26/2L±a 2. X— 1 2х — 1 х х 4- 1 41. < < • х 4- 4 х 4- ч х 4- 4
27. — 5<х—4<2—х. 42. х(х — 1)<0. •
28. 0 < Зх 4- 6 < 1 — 2х. 43. х4<ха.
29. х — 2 < 2х — 3 < х 4 2. А 44. х2 4* Зх > — 2.
30. 4х 4" 2>5х 4" 3> 4х 4" 4. 31. х — 1 < 2х 4- 5 < — х — 10. 45. 2ха — 2 < х2 — х. 46. (ха— 1) (х 4-4)<0.
30
Л. Числа
34. АКСИОМА АРХИМЕДА
Хотя следующая аксиома выглядит вполне очевидной» она весьма важна.
17. Для каждого числа а существует такое целое число kt что a<Z k.
Мы назовем это предложение аксиомой Архимеда. Архимед, величайший математик древности, сформулировал равносильную аксиому в геометрических терминах; в действительности она использовалась греческими математиками задолго до Архимеда. Из аксиомы Архимеда вытекают два следствия.
Следствие 1. Если а для всех целых положительных чисел п9 пгоа^ 0.
Доказательство. Предположим, что а > 0. Тогда 1/п > 0. В силу 17 существует такое целое число s, что 1/а< $. При этом $>0, потому что иначе было бы 1/а<0. Умножив неравенство $> 1/а на положительное число a/s, получаем а> 1/s. Следовательно, неравенство а < 1/п не может соблюдаться для всех целых положительных чисел п.
Следствие 2. Если А > 1 и а А”л для всех целых положительных чисел п9 то а 0.
Доказательство. Поскольку А > 1, имеем А == 1 + b9 Ь > 0. Отсюда Ап = (1 + fe)(l + b) ..(1 + b) = 1 + nb + другие положительные числа > nb. п множителей
Таким образом, если а А~п, то я 1/пЬ и ab 1/п. Если это верно для всех целых положительных чисел п, то ab 0 в силу следствия 1. Поэтому либо ab = 0 и а = 0 по закону сокращения, либо ab <Z 0 и а < 0.
УПРАЖНЕНИЯ
47. Пусть a<Z —Для всех целых положительных чисел л; какое заключение можно едется
лать о числе а?
48. Для каких чисел х неравенство —(1010)Н < х < (1010)~^ справедливо при / = 1, 2, 3, ...?
49. Для каких чисел х неравенство 1—2' < х справедливо при / = 1, 2, 3, ...?
Д50. Для каких чисел х неравенство 1—1(П < х <. 1 + 1(Н справедливо при / = 1, 2, 3, ...?
51. Для каких чисел х неравенство 3*^ < х < 2~7 справедливо при / = 1, 2, 3, ...?
52. Для каких чисел х неравенство х < 4(п + I)-2 справедливо при всех целых положительных числах л?
АРХИМЕД из Сиракуз (287—212 до и. в.) провел ббльшую часть своей жизни в родном городе, за исключением времени пребывания в Александрии, где он учился в знаменитом Музее — центре вллинистической цивилизации. Сохранились многие из его трудов.* Архимед был глубоким математиком, а также основоположником статики: он открыл закон плавающих тел и принципы рычага.
Когда римляне осадили Сиракузы, изобветенвя Архимеда были использованы для защиты города; однако рассказы древних авторов о его военных машинах, по-видимому, содержат значительные '|реувеличения. Архимед был убит римъпим солдатом во время грабежа Сиракуз.
* Оми переведены н на русский язык: Архимед, Сочинения, М.( Фиэматгиэ, 1962.
§ 3. Неравенства
31
3.5 . АБСОЛЮТНАЯ ВЕЛИЧИНА
Абсолютной величиной рационального числа а называется число, обозначаемое через |а| и определяемое формулой1
{а при а О,
— а при а<0.
Например, | — 5| = 5, |^-| = .
Очевидно,
|а | > 0, если а =/= 0, |0| =0 и
|afe|=|a||6|, |a-‘| = |a|-‘, =
Абсолютная величина числа допускает и геометрическое истолкование. Если числа изображаются точками на прямой, то | а | есть расстояние от точки а до точки 0 (рис. 1.10). Поэтому (как видно из рис. 1.11)
| а | < а означает, что —а <а<а.
Далее., | а — Ь \ есть расстояние между точками а и Ь, как легко усмотреть из различных случаев, изображенных на рис. 1.12. Когда мы говорим, что два числа близки друг к другу, мы имеем под этим в виду, что абсолютная величина их разности мала. Так, например, —11/10 ближе к —1, чем 5 к 6, потому что | —11/10—(—1) | = 1/10, в то время как | 5—6 । = 1.
Геометрически очевидно, что расстояние между двумя точками (на прямой) не превосходит суммы их расстояний от третьей точки. Записывая это утверждение для случая, когда две точки изображают числа а и 6, а третья точка есть начало 0, мы приходим к очень простому, но очень важному свойству абсолютных величин чрсел — к так называемому неравенству треугольника: •
|a+6|<|al + I. (Н)
Мы дадим аналитическое доказательство неравенства треугольника («аналитическое» здесь означает «основанное исключительно на свойствах чисел»).
Если а = 0 или Ь = 0, то (11) очевидно. Если а и Ь положительны, то положительно также а 4- 6, и мы имеем a = | а |, 6 = |& |иа+6 = |а+&|. Если а и b отрицательны, то отрицательно и а + Ь, и мы имеем а = — | а |, b = —| b |, а + Ь = — | a + & |. В обоих случаях (11) справедливо, причем здесь имеет место равенство левой и правой частей (11). Если я>0и6<0, то a = | а |, Ь = —| Ь | и а + Ь = \ а \ — | Ь |. Таким образом, либо | а + Ь | = | а | — I & I» либо Ja+&|= — (|а|— |6|) = |6|— |а|. Поскольку |a| — j&|<|a| + + | b | и | Ь | — | а | < | а | + | & |» то и здесь (11) выполняется (со знаком < строгого неравенства). Случай а < 0, Ь > 0 рассматривается аналогично.
1 То же определение сохраняет смысл в применении к любому упорядоченному полю.
«
1. Числа
Рис. 1.10
Рис. 1.11
|-------1 а-6|---
—1--•--1--1-*--1--1--1-♦--Н
а О Ь
|-—|а-д|—-|
—1--1—I—I—♦—♦—|------1-i—♦-
О а b
Рис. 1.12
Следствиями неравенства треугольника являются неравенство
|а+6 + с|< | а | + \Ь |+ |с |
и аналогичные неравенства с большим числом членов.
•Пример. Если a^x^bua^ff^b, /по | у — — а.
Геометрическое доказательство. Представим числа точками прямой. Тогда точки х и у лежат между точками а и Ь. Поэтому расстояние между ними, | у — х |, не превосходит расстояния между конечными точками, т. е. | Ь— а|.
Аналитическое доказательство. Пусть сначала х у. Тогда Прибавим ко всем частям неравенства —х. Тогда получаем а—х^
—х^Ь — х. Поскольку —— а9 имеем: 0 z/— х Ь— а и \у — * I Ь — а. Если у х, то аналогичные рассуждения приводят к тому же результату.
Читатель, вероятно, заметил, что геометрическое рассуждение .значительно проще аналитического. Аналитическое рассуждение использовано здесь лишь для подкрепления нашей геометрической интуиции. •
УПРАЖНЕНИЯ
53. Что такое |—31?
54. Что такое |4—6—8|?^
55. Что такое |(—3)а|?
56. Что больше: |2—3| или |21 + |—3|?
57. Покажите, что |х2| = |х|^.
58. Верно ли, что |дг5| =/= |х|5, если 0?
59. Для каклх чисел х справедливо неравенство |х—1| 2“^ при / = 1, 2, 3, ...?
60. Покажите, что |а + b + с| |я| + |Ь\ + |с| .
61. Покажите, что |а—д|^>|а| — |Ь|.
А 62. Покажите, что |а—Ь\ > IH.-lMI- ..
63. Покажите, что |а—b—с| > |а| —|д| —|с|.
64. Покажите, что | а—Ь | < г тогда и только тогда, когда b — r< а < Ъ + г, где г >0.
65. К какому из чисел —22 или 3 ближе число —10?
66. К какому из чисел 0 или —7 ближе число —4?
67 Ближе ли —78 к 68, чем —14 к —100?
68. Что меньше: расстояние между —10 и 13 или между —36 и —54?
69 Найдите для каждого из множеств, описанных в левом «толбце, равное ему множество в правом столбце:
§ 4. Десятичное представление рациональных чисел
33
(I) Множество чисел, расстояние которых от 3 меньше 2.
(II) Множество чисел, расстояние которых от—1 больше 3.
(III) Множество чисел, расстояние которых от —2 меньше 4 и больше 1.
(IV) Множество чисел, расстояние которых от — 1 меньше, чем их расстояние от I.
(V) Множество чисел, расстояние которых от О больше их расстояния от —2.
(VI) Множество чисел, расстояние которых от 1 больше, чем расстояние от а до —1.
(VII) Множество чисел, расстояние которых от а меньше их расстояния от —1, но больше расстояния от а до —I.
(1) Множество таких х, что|х—1| >
> |а- 1|.
(2) Множество таких х, что |х—II < < |х + 1|.
(3) Множество таких х, что |х — 3|<^2.
(4) Множество таких х, что|х — 1| >3.
(5) Множество таких х, что |а + II < < |х — а| < |х + 1|-
(6) Множество таких х, что |х + 1| >3.
(7) Множество таких х,
(8) Множество таких > |х + 2|.
(9) Множество таких < |х + 2| < 4.
(10) Множество таких <|а|< х — 1.
что |х + 1| <
X, что |х| >
X, ЧТО 1 <
X, что х<
3.6. РАЦИОНАЛЬНЫЕ ЧИСЛА, ОПРЕДЕЛЕННЫЕ С ПОМОЩЬЮ АКСИОМ
Аксиомы 1—17 все еще недостаточны для полного описания всех свойств рациональных чисел. Если мы хотим определить рациональные числа с помощью аксиом, то мы должны добавить к аксиомам 1—17 еще одну:
для каждого рационального числа а существует такое целое число ги=/=0, что число та — целое,
В силу этой аксиомы всякое рациональное число есть отношение (ratio), а именно отношение двух целых чисел. Это обстоятельство объясняет происхождение самого термина «рациональное» число.
§ 4. ДЕСЯТИЧНОЕ ПРЕДСТАВЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
4.1. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
В искусстве счета можно указать три главных переворота, способствовавших большому прогрессу в этой области. Последний из них, связанный с возникновением электронных вычислительных машин, произошел буквально на наших глазах. Второй, а именно изобретение логарифмов, относится к XVII столетию. Первое же продвижение, без которого были бы невозможны и два последующих, состояло в развитии позиционной системы счисления.
Система чисел, которой мы пользуемся, называется десятичной (децимальной), или системой с основанием десять, поскольку в этой системе каждое целое положи
34
1. Числа
тельное число представляется в виде суммы степеней десяти (латинское decern). Так, 203 = 2-10а+ 0-101 + 3-10°. Эта система пришла в Европу из мусульманского мира, с которым христиане вплотную столкнулись в эпоху крестовых походов; отсюда возникло и название «арабские цифры». Однако арабы заимствовали позиционную систему счисления у индийцев, которые в свою очередь получили ее от эллинистической цивилизации; греческие же астрономы научились такой системе счисления от вавилонян, которые использовали ее еще до 1500 г. до н. э.
Позиционная система счисления имеет ряд преимуществ перед римской нумерацией или системами записи чисел у евреев и греков, применявших в качестве наименований чисел буквы алфавита. Используя лишь немногие знаки (в нашей системе записи — цифры 0, 1, ..., 9), можно записать и назвать любое число, а запомнив таблицы сложения и умножения для этих основных символов, можно вычислить сумму и произведение двух любых целых чисел, используя простую механизированную процедуру.
Разумеется, выбор основания произволен, популярность же числа десять объясняется лишь анатомией и случайными соображениями (наличием у человека десяти пальцев на руках). Как показывает британская монетная система, система мер и весов, используемых в странах, говорящих на английском языке*, а также французское название числа 80 — quatre-vingt, т. е. 4-20, — люди экспериментировали также с другими основаниями. Например, вавилоняне в своей системе счисления, которой пользовался также греческий астроном Птолемей, принимали за основание число 60. Эта шестидесятиричная система сохранилась до наших дней в наших общепринятых единицах измерения времени (1 час = 60 минутам, 1 минута == 60 секундам). Система с наименьшим возможным основанием, а именно 2, называется бинарной. Она широко используется в электронных вычислительных машинах, поскольку два символа, 0 и 1, легко представлять с помощью двух позиций переключателя. В принципе, однако, одно основание ничем не хуже (нои не лучше!) другого; поэтому мы здесь ограничимся обычными десятичными обозначениями.
4.2. ДЕСЯТИЧНЫЕ ДРОБИ
Некоторые дроби также могут быть представлены в десятичной системе. Надо только прибегнуть к одному добавочному символу — (разделительной) запятой. Правило состоит в следующем: если а—неотрицательное целое число и а4, а2, •••> — т десятичных знаков, каждый из которых есть одно из чисел 0, 1, 2, ...» 9, то, по определению (или соглашению),
а,аха2 ... а = а + — + + ... + —. (1)
12 т 10 102 10™
ПТОЛЕМЕЙ (около 100—187 и. >.) был математиком, астрономом и географом. Его астрономический трактат, известный под арабским названием «Альмагест», является сводом всей греческой астрономии, включая данные наблюдений, математические методы (в частности, сферическую тригонометрию), а также так называемую птолемееву систему мира с неподвижной Землей в качестве центра Вселенной.
* В настоящее время и в странах английского языка происходит повсеместный переход к метрической (десятичной) системе мер и весов.
4. Десятичное представление рациональных чисел
35
Мы называем такое выражение конечной десятичной дробью. Значение такой дроби не меняется, если дописать справа любое число нулей. Так, 2 = 2,0 = 2,00, 3/2 = = 1,5 = 1,50 и т. д.
Арифметические действия над конечными десятичными дробями столь же просты, как и соответствующие действия над целыми числами, если только соблюдать некоторые известные правила относительно положения запятой.
Какие же рациональные числа могут быть представлены конечными десятичными дробями? Если привести дроби к общему знаменателю 10я1, то, как легко видеть, a,did2 ••• ат — (целое)/КУ1 = (целое)/(произведение двоек и пятерок). Обратно, если х = plq, где р и q — целые числа и q — произведение двоек и пятерок, то мы можем умножить числитель и знаменатель на одно и то же число, представив таким образом х в виде целого числа, деленного на степень десяти, что может быть в свою очередь записано в виде конечной десятичной дроби. Например,
29==»1±=-11L=1,16. (2)
Иными словами, рациональное число может быть записано в виде конечной десятичной дроби в том и только в том случае, если оно имеет вид p/q, где р viq взаимно просты (дробь несократима) и q есть произведение двоек и пятерок.
Число 1/3 не может быть записано в виде конечной десятичной дроби. Вместо этого пишут
-i- = 0,33333... (и т. д., все последующие цифры суть тройки). (3)
Это простое, но удивительное равенство базируется на глубоких идеях, которые заслуживают более подробного обсуждения.
4.3. БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ДРОБИ
Мы свяжем с каждым положительным рациональным числом бесконечную десятичную дробь. Пусть х — рассматриваемое число и а — наибольшее целое число, меньшее х. (Существование такого целого числа очевидно и вытекает из аксиомы Архимеда.) Заметим, что
а < х -С а + 1,
15
и условимся писать а слева от запятой. (Если х = -у— , то а = 2, потому что
2 < < 3.)
Далее, рассмотрим 10 чисел:
и
I 0 ,1 ,2 ,9
п — а Н---, и -|-----, и -4- —, . . ., а -|--
10 10 10 10
найдем наибольшее из них, которое еще меньше х. Пусть это будет а + . За-
метим, что
а + —
10 или в десятичных обозначениях
a + ^_ + _L, ю ю
a,cii < х < a,a.i + КГ1,
36
1. Числа
и условимся писать сц справа от запятой. (Если х = -у, то а! =1, потому что 15
2,1 < -у<; 2,2.) Далее, найдем тем же способом знак а2, который также является одним из чисел 0, 1, ..., 9, так что
a,aia? < х сца^а 2 + Ю"2,
/о 15
и запишем а2 справа от ар (В случае х = -у имеем а2 = 4, поскольку 2,14 < 15
< -у- 2,15.) Продолжая действовать таким же способом, мы найдем беско-
нечную последовательность знаков аь а2, а3, ... таких, что
а,аха2. . . am<z х . ат + 1О’т при т = 0, 1, 2, 3, . . .
(4)
Как мы покажем, при этом не может случиться, что все а, начиная с некоторого ah, равны 0. В самом деле, в этом случае мы имели бы a,aia2... am = a,aia2... ah при m > k\ отсюда в силу (4)
a,ax . . . < х a, + 1
при tn = k + 1, k 4- 2, ... ; следовательно, для всех целых положительных tn имеем 0< х — a,ai ...(!*< 10"m и, по следствию 2 из аксиомы Архимеда (см. § 3.4), 0< х — a,ai ... aft^0. Но тогда 0 < 0, что невозможно. Итак, a,a<a2 ... в с е г -д а является бесконечной десятичной дробью.
Два различных положительных рациональных числа х и у никогда не могут привести к* од ной и той же десятичной дроби а, а !а2 ... . В самом деле, в этом случае мы имели бы неравенства (4) и те же неравенства для у, т. е.
а,04... ат<у • - • ат + 10”m, tn = 0, 1,2,...
(5)
Из (4) и (5) заключаем (см. пример в § 3.5), что | у — х | < 10“т при т = = 1,2,..., так что в силу следствия 2 из аксиомы Архимеда | у — х | =0, откуда х = У-
Итак, зная х, мы можем вычислить a,ata2... , а знание a,aia2... определяет х. Мы можем поэтому использовать a,aia2 ... в качестве наименования (или обозначения) числа х. Это значит, что мы можем писать
х — a,a^a 2a 3
Только что написанное равенство означает попросту, что справедливы все неравенства (4); a,aia2a3... называется бесконечным десятичным разложением числа х. Число —х, противоположное х, может быть тогда записано в виде —х = = —a,aia2a3... . Для числа 0 не вводится нового обозначения.
Бесконечное десятичное разложение числа представляет собой строку неравенств, описывающих это число все с большей и большей точностью; все эти неравенства, вместе взятые, полностью определяют число. В частности, равенство (3) означает, что
0<4-<1: 0,3<-L<0.4: 0,33< —<0,34; 0,333 < — <0,334 и т. д.
§ 4. Десятичное представление рациональных чисел
37
4.4. ПЕРИОДИЧЕСКИЕ ДЕСЯТИЧНЫЕ ДРОБИ
Мы покажем теперь, как можно найти бесконечное десятичное разложение любого рационального числа.
Число 29/25 можно представить в виде конечной десятичной дроби, поскольку 25 = 52. Выше мы нашли эту конечную десятичную дробь [см. формулу (2)]. Можно также, что обычно оказывается проще, получить ту же десятичную дробь посредством деления столбиком:
29,00125
1,16
40 29
25 , так что —= 1,16.
---- 25
150
150
[Вычисления здесь, разумеется, по существу те же, что и в формуле (2).] Бесконечное десятичное разложение того же числа есть
-^- = 1,15999... (все девятки), (6)
что можно записать также в виде
— = 1,159, 25
где черта означает, что 9 повторяется бесконечное число раз. Чтобы проверить (6), заметим, что
п раз п раз
1,1599?.. 9< 1,16 < 1,1599 ... 9+ 10~л‘2 при п = 1, 2,... . (7)
Эта строка неравенств означает то же, что и равенство (6).
Те же рассуждения применяются к любому положительному рациональному числу х = p/q, где р и q — целые числа, если это число может быть записано в виде конечной десятичной дроби. Конечное десятичное разложение может быть получено посредством деления столбиком. Чтобы получить бесконечное десятичное разложение, надо уменьшить последний десятичный знак на 1, а затем дописать бесконечную строку девяток. Например, 1/2 = 0,5 = 0,4999... = 0,49; 3 = 2,999... = 2,9.
Если применить деление столбиком к рациональному числу х = p/q, которое не может быть представлено конечной десятичной дробью, то процесс никогда не остановится и мы сразу получим бесконечное десятичное разложение х. Чтобы убедиться в этом, лучше всего рассмотреть конкретный пример; возьмем число 23/18. Первые три шага деления столбиком имеют вид
38
1. Числа
23,000... 118 1*L 1,27
50
36
140
126
14
Остаток равен 14-10"2 =0,14. Таким образом,
23 = (1,27) • 18 + 14 • 10-2, или = 1,27 4- • 10"2< 1,28. (8)
Поэтому 1,27 < 23/18 < 1,28, откуда видно, что 1,27 — первые три значащие цифры десятичного разложения числа 23/18. Этот же способ применим и в общем случае.
Оказывается, что бесконечное десятичное разложение рационального числа всегда периодично: в этом разложении, начиная с некоторого места, бесконечно периодически повторяется определенная группа цифр (может быть, состоящая из единственной цифры). Повторения могут начаться сразу после запятой или через несколько знаков после нее. Например,
= 0,232323... (повторяется 23) = 0,2^,
= 1,2303030... (повторяется 30) = 1,230.
Обратно, каждая периодическая десятичная дробь является десятичным разложением некоторого рационального числа. Доказательство этого любопытного факта мы отнесем в Приложение (см. § 8.3). Он, однако, не играет никакой роли в реальных вычислениях, выполняемых с десятичными дробями.
4.5. ВЫЧИСЛЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ
В вычислениях с десятичными дробями, как вручную, так и с помощью вычислительной машины, нельзя использовать бесконечное число знаков. Поэтому всегда необходимо производить округление, т. е. заменять каждую бесконечную десятичную дробь конечной. Простейший способ округления состоит в том, что выбирается неотрицательное целое число т и в каждом числе х сохраняется лишь т первых десятичных знаков после запятой. Это значит, что каждое число х заменяется конечной десятичной дробью X такой, что | X — х | < 10“т. Округление может понадобиться и в том случае, если мы используем конечное десятичное разложение числа х (здесь мы считаем, что такое разложение существует).
Как велика может быть ошибка, допускаемая при вычислении х + у9 х — у, асу и х/у9 если сохранять лишь т десятичных знаков после запятой? Можно рассчитывать, что ошибка будет малой, если т велико, и что, выбирая т достаточно большим, можно вычислить сумму, разность, произведение и частное двух рациональных
§ 5. Действительные числа
39
чисел слюбой желаемой степенью точности. Мы покажем в Приложении (см. § 7.2), что это действительно так.
Отметим, что в нашем описании правил вычислений с десятичными дробями мы ни разу не использовали того факта, что рассматриваемые десятичные дроби происходят от разложения рациональных чисел, т. е. являются периодическими. Возникает вопрос, нельзя ли рассматривать также бесконечные непериодические десятичные дроби? В действительности такие десятичные дроби существуют, и их существование подсказывает один из возможных способов определения действительных чисел — как бесконечных десятичных дробей, периодических или непериодических. Более того, именно таким способом были впервые введены действительные числа — математики работали с ними задолго до того, как это понятие было формализовано и подвергнуто анализу.
УПРАЖНЕНИЯ
Пусть х, у, г — рациональные числа, бесконечные десятичные разложения которых начинаются следующим образом: х = 1,0234107..., у == 1,0235106..., г = 1,0235106... .
Укажите, истинно или ложно каждое из приведенных ниже утверждений; ответьте также, достаточно ли данной выше информации для того, чтобы установить справедливость или ложность этих утверждений.
1. 1,02 <х < 1,03. 5. х + у< ; 2,048. 9. |/ = г.
2. *< 1,03. 6. х + у< ; 2,046. 10. уг >1,04.
3. х > 1,0234107. 7. х + У> >-2,04692. 11. х= 1,0234108.
4. X < У- 8. x<zz. 12. х= 1,0234109.
Для следующих рациональных чисел найдите первые четыре десятичные знака после запятой их бесконечного десятичного разложения.
13. 2/3. 16. 777/33. 18. 29/25.
14. 3/2. 17. 777/333. 19. 250/29.
15. 10000. 20. 1/100.
§ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
5.1. ОПРЕДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
Имеются различные равносильные определения действительных чисел. Мы воспользуемся следующим определением:
Положительное действительное число есть • бесконечная десятичная дробь
fl,a |CL 2® з» • • •
Здесь а — целое положительное число или нуль, а каждое а есть один из десятичных знаков 0, I, ..., 9, причем бесконечное число знаков а отлично от нуля. Последнее условие означает, что десятичная дробь не завершается рядом сплошных ну
40
1. Числа
лей. Может случиться, что бесконечная десятичная дробь a,dia2... представляет собой рациональное число. (Так обстоит дело, если десятичная дробь является периодической.) Мы условимся включать рациональные числа в состав множества действительных чисел. Таким образом, 1/3 оказывается другим наименованием действительного числа 0,333... = 0,3, а 1,5 — другим наименованием действительного числа 1,4999... = 1,49.
Пусть х = a,aia2a3... и у = 6,₽iP2P3...—два положительных действительных числа. Утверждение «х = у» означает попросту, что а = 6, а2 = Р2
и т. д. П о определению, «х < у» означает, что либо а < 6, либо а = b и oh < Pi, либо а = 6, (Xi = р! и а2 < р2 и т. д. Таким образом, х меньше у, если первый десятичный знак х, отличный от соответствующего десятичного знака у, меньше этого знака, например 2,30783... < 2,30899.... Только что данное определение совместимо со свойствами рациональных чисел. Например, 7/3 < < 12/5 независимо от того, мыслим ли мы 7/3 и 12/5 как ^рациональные числа или как действительные числа 2,333... = 2,3 и 2,3999 = 2,39.
Далее, в силу нашего определения для каждого положительного действительного числа х утверждение
х = a,aia2... (бесконечная десятичная дробь) равносильно строке неравенств
^>а1 • • • ат < х < а»а1 • • • ат + т = 1, 2, 3,...,
как было и в случае рациональных чисел.
Отрицательное действительное число определяется как бесконечная десятичная дробь, снабженная знаком «—» (минус). Если десятичная дробь является периодической, мы отождествляем это действительное число с соответствующим отрицательным рациональным числом. По определению, «—a,aia2... <—6,Р1Р2...» означает, что 6,PiP2«*« < a,ai<x2... . Это определение также совместимо со свойствами рациональных чисел. Наконец, мы включаем 0 в состав действительных чисел и уславливаемся, что —a,aia2... <0и 0< a,aia2... .
Положительные и отрицательные действительные числа вместе с нулем составляют множество действительных чисел. Множество действительных чисел содержит множество рациональных чисел в качестве подмножества. Действительное число, которое не является рациональным, называется иррациональным. Например, 2, 1010010001000010... есть иррациональное число, поскольку эта бесконечная десятичная дробь — непериодическая. Читатель может легко убедиться, что действительные числа удовлетворяют аксиомам порядка 13 и 14 из § 3.2 и 17 из § 3.4.
УПРАЖНЕНИЯ
1. Пусть х = 0,45637070070007 ... и у = 0,4563707; какое из этих двух чисел больше?
2. Укажите рациональное число, лежащее между 0,102030405060708090100110120... и
0,1121314151617181911011111211... . __ _
3. Расположите числа х =0.20406080100120..., у = 0.204060 и z =0.20406 в возрастающем порядке
§ 5. Действительные числа
41
4. Расположите числа х = 0,293949, у = 0,293949 и г =0,293949596979... в возрастающем порядке. _______ ______________
5. Укажите иррациональное число, лежащее между 0,00112 и 0,00112001120011. (Можно при этом предположить, что непериодические десятичные дроби представляют иррациональные числа.)
5.2. ВЫЧИСЛЕНИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
Пусть мы хотим сложить два действительных числа, например два положительных действительных числа х = a,ata2a3... и у = &,₽1020з--- • Тогда естественно «округлить» два эти числа, отбросив все знаки, например после /n-го, а затем сложить полученные рациональные числа a,aia2...am и Можно рассчитывать,
что мы получим при этом рациональное число, близкое к «истинной» сумме х и у и притом сколь угодно близкое к ней, если выбрать т достаточно большим. То же верно и для умножения: можно рассчитывать, что если т достаточно велико, то произведение чисел a,aia2...am и b,₽i02---₽m будет сколь угодно близко к «истинному» произведению х и у.
Но что представляют собой «истинная» сумма и «истинное» произведение двух действительных чисел? Можно ли их точно определить? Ответ дает следующее
Предложение А. Сумма и произведение двух любых действительных чисел могут быть определены таким образом, чтобы это определение было совместимо со свойствами рациональных чисел и чтобы остались справедливыми все аксиомы 1—17.
Доказательство предложения А в действительности не представляет трудности, но несколько длинно и содержит некоторые тонкости; мы его здесь опускаем. Мы рекомендуем читателю пока принять предложение А на веру. Поступая таким образом, читатель будет следовать превосходным примерам. Основоположники анализа и великие математики, развивавшие и применявшие анализ в течение ряда столетий, считали самоочевидным, что можно работать с действительными числами, следуя обычным правилам алгебры. Необходимость в доказательстве, как и само доказательство, возникли в середине XIX в., когда Дедекиндом и Кантором были развиты два эквивалентных варианта теории действительного числа.
Предложение А часто кратко выражают так: действительные числа образуют
упорядоченное архимедово поле.
Допустив справедливость этого предложения, мы можем свободно пользоваться всеми следствиями из аксиом поля и аксиом порядка, выведенными выше. С помощью округлений мы можем также применять изложенные выше методы для вычисления сумм и произведений (а также разностей и частных) действительных чисел с любой желательной степенью точности. Мы проверим это в Приложении (см. § 7), где будут также выведены формулы для оценки получаемых при этом погрешностей.
Рихард ДЕДЕКИНД 11831—1916) первоначально был алгебраистом; он является одним из основоположников так называемой «абстрактной» алгебры.
Георг КАНТОР (1845—1918) один создал теорию бесконечных множеств, что явилось, быть может, самым революционным открытием в истории математики после изобретения математического анализа. Этим был создан общий язык для большей части математики. Теория множеств привела также к неожиданным парадоксам и логическим трудностям, до сих пор не вполне устраненным. Развитие современной математической логики было ответом на вызов, который каиторова теория множеств бросила всей математике.
Кантор учился в Берлине, а затем преподавал в малоизвестном провинциальном университете. Жизнь его была омрачена резкими научными спорами и завершилась тяжелой душевной болезнью.
42
1. Числа
5.3. ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ; ЧИСЛОВАЯ ПРЯМАЯ
Свойства поля и другие свойства действительных чисел безоговорочно принимались рядом поколений математиков, поскольку они имеют естественное и простое геометрическое истолкование.
Рассмотрим опять прямую линию с отмеченными на ней точками 0 и 1. Представим себе, что на ней отмечены все точки, соответствующие рациональным числам (рис. 1.13).
Существует бесконечное множество таких «рациональных точек», но сверх того существует бесконечное множество и таких точек, которые не соответствуют никакому рациональному числу. Так обстоит дело для любой точки Р, служащей концом отрезка ОР, несоизмеримого с отрезком 01.
С другой стороны, как мы покажем, каждой точке Р можно сопоставить действительное число. Рассмотрим сначала случай, когда точка Р лежит справа от 0. Точка Р считается «заданной». Это значит, что если Q — какая-либо другая точка прямой, отличная от Р, то нам известно, лежит ли точка Q слева или справа от Р. Найдем наибольшее целое число а, для которого точка а лежит слева отР. Тогда а>0 и Р не лежит справа от а + 1. Пусть, далее, at — наибольшее из чисел 0, 1, ..., 9, для котогого Р лежит справа от точки a,ai = а 4-^ . Тогда Р либо лежит слева от a,aA Ч—либо совпадает с a9at 4—Далее, найдем наибольшее а2 из чисел 0, 1, ..., 9, для которого Р лежит справа от a,aia2, и т. д. Мы получаем таким образом бесконечную последовательность десятичных знаков a,aia2a3..., обладающую тем свойством, что Р расположена справа от a,ai(x2 ...am, но не справа от a,aid 2...am-f- 10“m при т = 0, 1, 2, ... . Этот процесс иллюстрируется на рис. 1.14, где a,aia2a3 ... = 1,305 ... .
Если Р являлась рациональной точкой, т. е. точкой, соответствующей некоторому рациональному чйслу х, то a,aia2a3... есть бесконечное десятичное разложение числа х. Это ясно из сравнения только что изложенного с методом, примененным в § 4.3.
Мы сформулируем далее три предложения, которые принимаются в качестве геометрическ их аксиом, так как они согласуются с нашей геометрической интуицией.
1. Десятичная дробь a,aia2... , соответствующая точке Р (находящейся справа от О), бесконечна. (Наша геометрическая интуиция подсказывает, что Р не может лежать справа от некоторой рациональной точки, например с, если она не расположена также справа от рациональной точки с -f- 10"т при некотором целом т > 0.)
Действительное число a,ai(i2... называется координатой точки Р.
2. Две различные точки Р и Q, лежащие справа от точки О, не могут иметь одинаковые координаты.
3. Каждое действительное число х > 0 является координатой некоторой точки прямой, лежащей справа от точки О.
Далее, мы приписываем точке О координату 0, каждой же точке Q слева от О — координату — х, где х— координата точки Р, лежащей справа от О и такой, что отрезки OQ и ОР равны.
§ 5. Действительные числа
43
Р
Рис. 1.13 Рис. 1.14
Таким образом, мы приписали каждой точке прямой единственное действительное число в качестве ее координаты, причем каждое действительное число оказывается координатой единственной точки прямой. Это выражают словами: мы установили взаимно однозначное соответствие между действительными числами и точками прямой. Конечно, это соответствие зависит от выбора двух точек с координатами О и 1.
Мы будем часто пользоваться следующими выражениями, не различая их: действительное число х, точка с координатой х или просто точка х.
Прямую, на которой отмечены точки 0 и 1, обычно называют числовой прямой. Она представляет собой идеализированную измерительную ленту, которой можно пользоваться для измерения любого отрезка. В самом деле, пусть АВ есть отрезок. Тогда на числовой прямой существует справа от О единственная такая точка Р, что отрезок АВ равен отрезку ОР. По определению, координата точки Р равна длине отрезка АВ. Эта длина есть рациональное или иррациональное число в зависимости от того, соизмерим ли отрезок АВ с единичным отрезком 01.
Теперь мы можем построить геометрически суммы и произведения действительных чисел, как мы это сделали в § 1 для рациональных чисел. Это убеждает нас в том, что действительные числа подчиняются обычным правилам алгебры.
5.4. КОРНИ
Пусть с — положительное действительное число. Тогда существует единственное такое положительное действительное число х, что х2 = с. Справедливость этого утверждения геометрически очевидна, поскольку существует построение с помощью циркуля и линейки (указанное на рис. 1.15), которое позволяет по заданному единичному отрезку и заданному отрезку длины с получить отрезок такой длины х, что х2 = с. Число с обозначается через Ус или У~с.
Справедливо также более сильное предложение:
Теорема 1. Для каждого положительного действительного числа с и каждого целого п > 1 существует единственное положительное действительное число х такое, что хп = с.
Это число х называется корнем д-й степени из с и обозначается через х = Ус. Мы полагаем, кроме того, У 0 = 0, а для нечетного п также У —с = — У а Б самом деле, 0л= 0, и для нечетных п имеем ( —У7]п = — с.
44
1. Числа
Рис. 1.15
Ясно, что теорема о существовании корней не может быть справедлива в поле рациональных чисел. Например, число иррационально (см. § 1.3).
Мы докажем эту теорему, предложив метод вычисления с (разумеется, мы не ищем здесь наиболее эффективный метод).
Лемма. Пусть х и у — положительные числа и п — целое положительное число; тогда
если x<Zy> то xn<Zyn (1)
и
если xn<zyn, то x<Zy- (2)
Доказательство. Если 0 < х < у, то х2 < ху и ху < у2 в силу 16 и поэтому вследствие 14 х2< у2. Далее, в силу 16 x?<Z у2х и у2 х < г/3, откуда х3 < у3. Продолжая это рассуждение, мы получаем (1). Далее, из (1) следует (2). В самом деле, если бы было неверно неравенство х < у, то было бы либо х = у и хп = уп, либо у < х и, по только что доказанному, уп< хп.
Из леммы сразу же вытекает, что для заданного п и с > 0 существует не более чем одно положительное число х, для которого хп = с. Из леммы видно также, как вычислить у с, например у 13, предполагая, что такое число существует. Нам надо найти такое неотрицательное целое число а и такие десятичные знаки dbd2, d3,... , каждый из которых есть одно из чисел 0, 1, ..., 9, чтобы было у^ с = .
Как мы знаем, это означает, что
ал^2 • • • <Z 1^с < а,ахаг • • • + Ю"* для k = 0, 1, 2, . . . . (3)
Итак, мы сначала находим а как наибольшее целое число, для которого ап< с; затем си — как наибольшее из чисел 0, 1, ..., 9, для которого (а&дп<с\ затем а2— как наибольшее из чисел 0, 1, ... , 9, для которого (a,did2)" < с, и т. д.
В нашем примере а = 2, поскольку 23 = 8 и З3 = 27; ах = 3, поскольку 2,33 = 12,167 и 2,43 = 13,824; а2 = 5, ибо 2,353 = 12,977... и 2,363 = 13,144 ... .
Таким образом, у 13 = 2,35... .
Мы получили число х= a,aid2a3... . Очевидно, имеем a,did2...dfe<x<^ < a,did2...dfe+ 10’* при k = 0, 1, 2, ... и в силу леммы
(a,ax . . . aj" < Хл (a, ax . . . ал + 10’*)", k = 0, 1, 2,... . (4)
§ 5. Действительные числа
45
Сравнивая эту формулу с (3), мы видим, что для всех k числа си хп лежат в одном и том же интервале длины
Lk — (а,«!... <хА + Ю-*)" — (а,а1... <хА)".
Поэтому (ср. с примером в § 3.5)
|х" - с| <Lft.
Чтобы вычислить L'ft, мы воспользуемся тождеством (7) из § 2.5:
А” — Вп = (Я — В) (Ап~‘ 4- А"~2В 4- А^В2 4-... 4- В”-1).
Положим А = a,<tja2... аА 4- 10-* и В = а,. .ак. Тогда А — В = 10“* и В <; < А а 4- 1. Но Lk = А" — Вп и, следовательно,
La = 10-* (Л”-’ 4- А^В 4- А^В2 4- A™ В* 4------1- В"-1) < IO‘*n(a 4- IF*1.
Мы заключаем, что
। с'— < 10_* для всех целых k.
гца 1)л 1
Отсюда в силу следствия 2 из аксиомы Архимеда (см. § 3.4) имеем | Xя— с | = = 0 и хп = с.
Мы нашли некоторое решение уравнения Xя = с. Согласно лемме, никакого другого положительного решения не существует. Тем самым теорема полностью доказана.
УПРАЖНЕНИЯ
В следующих упражнениях надо учитывать все знаки до и после запятой; напри мер число 211,35 имеет 5 знаков.
з /
6. Вычислите первые 3 знака в десятичном разложении числа у 7 .
7. Вычислите первые 3 знака в десятичном разложении числа 7,9 .
8. Вычислите первые 3 знака в десятичном разложении числа (—26)1/3.
9 Вычислите первые 2 знака в десятичном разложении числа ]/*80 .
Д10. Пусть х = 1,01001000100001вычислите первые 4 знака в десятичном разложении Зу— числа у х .
II Пусть х ® 1,11213141516.... вычислите первые 4 знака в десятичном разложении числа У — у * •
4 у__
12. Вычислите первые 4 знака в десятичном разложении числа у I I 3г
13. Вычислите первые 4 знака в десятичном разложении числа у 1003 .
46
1. Числа
5. 5. ДРОБНЫЕ СТЕПЕНИ
Мы можем теперь определить дробные степени, т. е. придать смысл выражению сг9 где с — положительное число иг — рациональное число. По определению,
*/« 4/— ( q/-\р
С =у СР = (у с J ,
где pnq — целые числа, q> 0, а дробь p/q предполагается несократимой. Если с — отрицательное число, то cf можно определить только в том случае, когда рациональная дробь г, которую мы считаем несократимой, имеет нечетный знаменатель. В этом случае можно применить указанное выше определение. Наконец, при с = 0 полагают cf = 0 для всех положительных рациональных г.
Это определение выбрано таким образом, что установленные в § 2.4 законы для степеней сохраняют силу во всех тех случаях, когда'они имеют смысл. Проверка нетрудна, и мы не будем здесь ею заниматься.
•Пример. (— 1)1/3 = у^— 1 = —у^Г" = — 1. Однако нельзя написать
(_ 1),/3 s (_ if6=^(—2 =i.e
УПРАЖНЕНИЯ
Упростите следующие выражения!
И. [1Г(7гТ]‘ 17.
1S. /(- . 18. /(х-.
16.
5. 6. ИНТЕРВАЛЫ
Теперь уместно ввести терминологию, используемую дальше на протяжении всей книги.
Пусть а и Ь— такие числа, то Ь. (Начиная с этого места слово «число» всегда означает действительное число.) Множество всех таких чисел х, что a<Zx<Zb9 называется открытым интервалом (а, Ь). Слово «открытый» здесь означает, что числа а и Ь н е включаются в наше множество: интервал (а, Ь) состоит из всех точек отрезка числовой прямой с концами а и Ь, за исключением самих концов отрезка. Множество всех таких х, что а х Ь, называется замкнутым интервалом [a, bl; оно состоит из всех точек указанного выше отрезка, включая концы. Множество всех таких х, что а х < Ь, называется полуоткрытым интервалом [а, Ь); обозначение (а, Ь] понятно само собой*. Во всех случаях b— а называется длиной, а точка (а + Ь)/2 — серединой, или центром, интервала (открытого, замкнутого или полуоткрытого).
Все рассмотренные выше интервалы называются конечными. Множество всех таких х, что х> а, называется бесконечным интервалом (а, + оо). Аналогично, [а, + оо) есть множество всех таких х, что х >> а; (—оо, Ь) есть множество всех та
• В русской учебной литературе замкнутый интервал часто называют сегментом (или просто отрезком); открытый интервал — просто интервалом, а интервалы [а, Ь) и (а, 6] — полуинтервалами.
§ 6. Полнота системы действительных чисел. Индукция
47
ких х, что х< Ь\ (— оо, &] есть множество всех таких х, что х 6. Наконец, вся числовая прямая обозначается через (—оо, оо).
Символы —{-оо, —оо читаются: «плюс бесконечность» и «минус бесконечность». Эти слова не являются наименованиями чисел.
Теорема 2. Каждый интервал любого рода содержит бесконечно много рациональных чисел и бесконечно много иррациональных чисел.
Это нисколько не удивительно. Формальное доказательство можно найти в Приложении (см. § 8.4).
УПРАЖНЕНИЯ
19. Принадлежит ли число 5 (открытому) интервалу (5, 6)?
20. Принадлежит ли число 5 (замкнутому) интервалу [5, 15]?
21. Принадлежит ли число —1 (полуоткрытому) интервалу [—2, —1)?
22. Принадлежит ли число 0 (замкнутому) интервалу [0, 2]?
23. Принадлежит ли число 4 (полуоткрытому) интервалу [—1, 5)?
24. Какая точка служит центром интервала (—3, 1)?
25. Укажите замкнутый интервал с центром 1/2 и длиной 2.
26. Найдите интервал, содержащий точки 1/10“-/ + 1 при / = —1, 0, 1, 2, 3, ...» но не содержащий точки 1.
Приложение к главе 1
$ 6. Полнота системы действительных чисел. Индукция
Рациональные числа и действительные числа, как и некоторые другие системы чисел, равным образом удовлетворяют аксиомам 1—17. В этом параграфе мы рассмотрим свойства, отличающие систему действительных чисел от других множеств чисел, также удовлетворяющих аксиомам 1—17. Мы рассмотрим этот вопрос совместно с обсуждением метода математической индукции
6.1. Границы
Пусть 8 — множество (совокупность) действительных чисел. Мы будем говорить, что «х — элемент множества 8», или «х принадлежит 8», или «х находится в 8», чтобы указать, что х есть один из предметов, составляющих множество &. (Часто это утверждение передают краткой записью «хе8».) Множество, не содержащее никаких элементов, называется пустым.
Число с называется верхней границей множества 8, если каждое число х из 8 удовлетворяет неравенству х^.с. При этом несущественно, принадлежит ли число с множеству 8 или нет.
Множество 8 называется ограниченным сверху, если оно имеет верхнюю границу; В противном случае оно называется неограниченным сверху. ‘
Число с называется нижией границей множества 8, если х для всех х из 8. Если у 8 существует нижняя граница, то 8 называется ограниченным снизу. Множество называется ограниченным, если оно ограничено и сверху, и снизу. (Пустое множество, по соглашению, считается ограниченным.)
В случае, если верхняя граница 8 является также элементом 8, она называется наибольшим элементом* 8. Нижняя граница множества 8, которая также является элементом 8, называется наименьшим элементом** 8. Очевидно, что 8 может иметь самое большее один наибольший элемент и самое большее один наименьший элемент.
* Для наибольшего элемента используется запись шах х.
** Здесь используется запись min х.
48
Приложение к главе 1
Множество чисел можно рассматривать как множество точек числовой прямой. Верхняя (нижняя) граница множества S есть такая точка, что ни один элемент множества S не лежит справа (слева) от нее.
•Примеры. Интервал (—10, +оо) ограничен снизу, но не сверху. Интервал (—100, Ю0) ограничен. Каждое конечное множество, т. е. множество с конечным числом элементов, ограничено.
Если S состоит из чисел 1, 2 и —5, то 2 есть его верхняя граница; числа 2,0001 и 1010 также являются верхними границами этого множества. Если S — множество всех отрицательных рациональных чисел, то 0 есть его верхняя граница. Верхней границей является также любое положительное число. Если S — множество всех целых чисел, то S не имеет верхних границ.
Нуль является наименьшим элементом множества всех неотрицательных рациональных чисел. Интервал (—2, 3) не имеет ни наибольшего, ни наименьшего элемента.®
УПРАЖНЕНИЯ
1. Является ли 1 верхней границей интервала (—3, 1]?
2. Является ли 12 верхней границей интервала (—1, 0)?
3. Является ли 3 нижней границей интервала (3, +оо)?
4. Является ли 2 нижней границей интервала (—оо, 2]?
5. Ограничено ли множество всех целых чисел, делящихся на 3? Ограничено ли оно сверху? Ограничено ли оно снизу?
^6. Ограничено ли множество всех целых чисел, являющихся квадратами целых чисел? Ограничено ли оно сверху? Ограничено ли оно снизу?
7. Найдите наименьший и наибольший элементы множества
[ 3 3 3 4 4 4 5 5 5 )
( 1 ’ 4 ’ 5* 1 ’ 3’ 5 * 1’ 3* 4 J ’
8. Имеет ли интервал (0, 2) наименьший элемент? Наибольший элемент? ( 1 2 3 4 )
9. Имеет ли бесконечное множество j -g-» -у > — * “Гр-” |наименьший элемент? Наибольший элемент? Ограничено ли оно?
10. Имеет ли множество рациональных чисел в интервале [0, 1) наименьший элемент? Наибольший элемент? Является ли ]^2 верхней границей этого множества?
6.2. Принцип наименьшего целого числа
Прежде чем заняться некоторым очень важным свойством действительных чисел, будет полезно ознакомиться со сходным свойством целых чисел.
I. Пусть S — непустое множество целых чисел. Если S ограничено снизу, то S содержит наименьший элемент.
Это утверждение почти очевидно. Оно принимается, быть может, в несколько иной форме в любом аксиоматическом изложении теории целых чисел. Мы назовем утверждение I принципом наименьшего целого числа. Из этого принципа немедленно вытекает следствие:
Г. Пусть S — непустое множество целых чисел. Если S ограничено сверху, то S содержит наибольший элемент.
Доказател ьство. Пусть Т — множество всех чисел, противоположных элементам S. Тогда х принадлежит Т в том и только том случае, если —х принадлежит S. Т — непустое множество целых чисел. Пусть с — верхняя граница S. Тогда у < с для всех у из S. Следовательно, —с < —у для всех у из S, откуда вытекает, что —с — нижняя граница множества Т. Согласно 1, Т имеет наименьший элемент Ь. Тогда —b — наибольший элемент S.
6.3. Математическая индукция
Принцип наименьшего целого числа лежит в основе доказательств по методу математической индукции. Мы разъясним этот метод на примере, выбрав результат, который нам будет полезен в дальнейшем.
§ 6. Полнота системы действительных чисел. Индукция
49
Мы хотим вывести формулу для суммы квадратов т первых целых положительных чисел. Формула гласит:
т3 т2 т
р + г2.-]- 3? + • • -+т2=— + — + — • □ z о
(1>
Мы утверждаем, что эта формула справедлива для всех целых положительных т. Если это утверждение ложно, то существует некоторое целое положительное число, для которого соотношение (1) неверно: множество целых положительных чисел mt для которых (1) ложно, оказывается непустым. Это множество ограничено снизу,' поскольку состоит из положительных целых чисел; поэтому в нем, согласно принципу наименьшего целого числа, имеется наименьшее число; обозначим это число через г. Тогда либо г = 1 (случай 1), либо г > 1 (случай 2). В случае 2 можно положить г = k + 1, где k >0 — целое число.
Заметим, теперь, что случай 1 невозможен. Иными словами, соотношение, подлежащее доказательству, при т = 1 справедливо. В самом деле, при т = 1 соотношение (1) имеет вид
1 =
Но случай 2 также невозможен. Действительно, в этом случае было бы
I2 + 22 + • . . + k2 + (k + I)2 ф
(fe 4- I)3 (fe+ I)2 fe4- 1
3 + 2 + 6 ’
в то время как
£3
I2 4- 22 4- . . . 4- *2 = — 4- — 4- — . □ z о
(2)
(3)
Прибавляя к обеим частям формулы (3) (А + I)2, получаем
k3 k3 k
р + 22 + • • • + k3 + (k + I)2 = — + — + — + (k + Ц, □ ZD
что после простых преобразований дает
+ * + ... + *. + + ,). _ + + Л±1.
□ z о
Но это противоречит (2).
Итак, (1) справедливо для всех целых положительных т.
Приведенный пример типичен. Если мы хотим доказать, что некоторое утверждение, относящееся ко всем целым положительным числам, справедливо, то поступаем следующим образом.
1. Первый шаг: показываем, что утверждение справедливо для целого числа 1.
2. Второй шаг: показываем, что если утверждение справедливо для некоторого целого числа k >0, то оно справедливо и для числа k 4" 1.
Строго говоря, метод математической индукции следует применять каждый раз, когда доказывается теорема обо всех целых положительных числах. Если, однако, ситуация очень проста, то обычно (и вполне законно) заменяют формальное доказательство по индукции несколько неопределенным выражением «и так далее». Так мы поступили, например, в § 5.4 при выводе предложения: если Q<Z x<Z у и /и >0 — целое число, то xm<Z Ут-
Покажем, как выглядит в этом случае формальное доказательство по индукции.
1. Первый шаг. При т = 1 утверждение гласит: если 0< дг< у, то у. Это верно.
2. Второй шаг. Предположим, что утверждение верно для некоторого фиксированного целого числа k 2>0. Тогда при 0< у имеем xk<Z yk> В силу 16 отсюда следует, что хл+1 __ xkx<^ ykx и ykx<Z yky = #*+1, а потому, согласно 14, Итак, утверждение
справедливо и для k 4" 1.
Это завершает доказательство.
so
Приложение к главе 1
УПРАЖНЕНИЯ
В упражнениях 11—20 проведите доказательства методом математической индукции. 11. Докажите, что
. Л п (п + 1)
14-24-3+.. . + л = -
для каждого целого положительного числа п.
12. Докажите, что
1— пп
1 4- Q. 4- а2 4--h qn‘r = -—~
1 — q
для каждого целого положительного числа п и любого числа q =/= 1. Заметим, что это было доказано прямым путем в § 2.
13. Докажите, что 1 4- 3 4- 5 4- • • • 4- (2м — 1) = л2 для каждого целого положительного числа п.
^14. Докажите, что
1-2 + 2.3-1-3.4 + • • • + я (я + 1) = -{”+.!)(я + 2) О
для каждого целого положительного числа п.
15. Докажите, что
1,11 1 п
4~----Ч- 1 ' 4“ * • • 4“---= "
1.2~2«3~3*4' л (л 4-1) „4-1
для каждого целого положительного числа п.
16. Докажите, что Зл2^ 2п + 1 для каждого целого положительного числа п.
17. Докажите, что Зл^> Зп для каждого целого положительного числа п.
Д18. Докажите, что 4Л л2 для каждого целого положительного числа п. 19. Докажите, что п3^> Зп + 3 для п = 3, 4, 5, ... . 20. Докажите, что л3^> л2 + 3 для л = 2, 3, 4, ... .
6.4. Принцип верхней грани
Предложения I и Г не обязательно справедливы для множеств действительных чисел. Так, множество S всех отрицательных чисел не имеет наибольшего элемента. Но множество всех верхних границ для этого множества имеет наименьший элемент, а именно 0. Эта си* туация оказывается типичной. Мы сформулируем теперь так называемый принцип верхней грани ^иногда говорят также точной верхней грани), или аксиому полноты, для действительных чисел. Эта аквиома должна быть присоединена к аксиомам 1—17.
18. Непустое множество действительных чисел, ограниченное сверху, имеет наименьшую верхнюю границу (или, как еще говорят, верхнюю грань).
Это значит, что если для рассматриваемого множества S существуют числа, большие или равные всем элементам этого множества, то вреди таких чисел имеется наименьшее. Наименьшая верхняя граница (или «верхняя грань»*) может принадлежать или не принадлежать множеству 5 Далее, если вое элементы S рациональны, наименьшая верхняя граница может оказаться иррациональным числом.
Из аксиомы 18 вытекает такое простое следствие!
18х. Непустое множество действительных чисел, ограниченное снизу, имеет наибольшую нижнюю границу (или нижнюю грань**),
* Запись: sup х, кеЗ
♦♦ Запись? inf х.
reS
§ 6. Полнота системы действительных чисел.. Индукция
51
Мы рекомендуем читателю вывести 18' из 18, взяв в качестве образца вывод Г из i.
Дадим геометрическое истолкование аксиомы 18. Пусть S — непустое множество на прямой. Пусть а — такая точка, что справа от а нет ни одной точки S. Тогда существует такая точка Ь, что: (I) справа от b нет ни одной то’Гки S и (2) если с—точка, лежащая слева от Ь, то существует точка множества S, лежащая справа от с.
Интуитивно очевидно, что действительные числа удовлетворяют аксиомам I—17; однако доказательство этого факта непросто. Что касается аксиомы 18, то смысл ее понять нелегко и она вовсе не очевидна. Доказательство ее, однако, нетрудно. Прежде чем приступать к нему, отметим, что на протяжении этой книги аксиома 18 будет использована лишь в немногих случаях, но каждый раз в решающем месте рассуждения. Точно так же как математическая индукция явно или неявно присутствует во всех теоремах, касающихся целых чисел, принцип верхней грани присутствует во всех существенных теоремах о действительных числах.
Доказательство утверждения 18. Следующее доказательство представляет собой обобщение рассуждения, примененного в § 5.4 при вычислении корней. Пусть S — непустое множество действительных чисел и с — верхняя граница этого множества. Мы вычислим наименьшую верхнюю границу множества S.
Согласно аксиоме Архимеда 17, существует такое целое число Л, что Это число k является, таким образом, верхней границей множества S. Множество всех целых чисел, служащих верхними границами S, само ограничено снизу и имеет, согласно I, наименьший элемент. Пусть таким элементом будет а + 1. Целое число а не является верхней границей множества S, но а + 1 является верхней границей. Рассмотрим числа а + (1/10), а + (2/10), ..., а + (9/10) и найдем такую цифру а* (из числа цифр 0, 1, ..., 9,), что а 4- 0,аг не является верхней границей множества S, но а + 0,04 4-0,1 является верхней границей.Продолжая этот процесс, приходим к действительному числу
х = а + 0,a1a2«a ...
такому, что для всех k = 1, 2, 3, ...
а 4- О,^^ ... аЛ не является верхней границей S, (4)
но
а 4- 0,0404 ... а* 4- 10"* является верхней границей S. (5)
(Мы могли бы записать также х = а^а.2 .... если бы было известно, что а^> 0; конечно, это не обязательно так.)
Пусть у — любое число, принадлежащее S. Из утверждения (5) следует, что у а + 4-0,04 ... 4- 1 СТ* (для всех fc=2, 3, ...). Поскольку а + 0,С4...аЛ<^ имеем х + 10“*,
или у — х^ 10“*, k = 2, 3.Это значит, что у — х^ О.по следствию 2 из аксиомы 17 (см.
§ 3.4); поскольку у — произвольный элемент множества S, то х — верхняя граница 5 ,
Допустим теперь, что w — верхняя граница S. Согласно (4), имеем w^>a4"0,C4... при k = 2, 3, ...; в самом деле, в противном случае а 4- 0,а^ ... сц, было бы верхней границей S. Поэтому х — ip”*, или х — 10“* для всех целых положительных k. Это значит, что
х — w 0, или х w. Тем самым х есть наименьшая верхняя граница1 множества S.
УПРАЖНЕНИЯ
21. Пусть S — множество всех рациональных чисел х таких, что х2 + 4< 6. Найдите наименьшую верхнюю границу (верхнюю грань) S.
±22. Пусть S — множество всех рациональных чисел г таких, что 2г3 — 1< 15. Найдите наименьшую верхнюю границу S.
1 В предыдущем доказательстве мы воспользовались принципом наименьшего целого числа.
Можно показать, что этот принцип является следствием аксиом 17 и 18. С другой стороны,
17 вытекает из 18 и I. Более того, если бы мы более тщательно сформулировали наше определение целых чисел (см. § 2), то мы могли бы доказать и I. Мы не доказываем здесь этих утверждений, поскольку нам это не понадобится в дальнейшем.
52
Приложение к главе 1
1 1 ]
» ТГ ’ ТТ ’ ” I ’ Найдите наибольшую ниж-
23. Пусть S — множество
1 ’ 7 нюю границу S.
24. Пусть S — множество всех действительных чисел, десятичное разложение которых начинается с 0,12 ... Найдите наименьшую верхнюю и наибольшую нижнюю границы S.
25. Пусть S — множество всех рациональных чисел х, удовлетворяющих неравенству х>/з+ + 2< 4. Найдите верхнюю грань S.
26. Пусть S — множество всех иррациональных чисел t таких что i < Z3 + 1^.3 Найдите верхнюю и нижнюю грани S.
27. Пусть S — множество всех иррациональных чисел п, удовлетворяющих неравенству о2 4- v<Z 2. Найдите верхнюю и нижнюю грани S.
6.5 . Аксиомы действительных чисел'
В J 5 мы рекомендовали читателю принять на веру предложение А. Теперь мы предлагаем ему другой выбор. Можно рассматривать утверждения 1 —18 как аксиомы системы действительных чисел, т. е. как исходные предложения, логические следствия которых мы намерены исследовать. Заметим кстати что обычно аксиомы 1—18 коротко выражают говоря, что действительные числа образуют полное архимедово упорядоченное поле.
Все огромное здание математического анализа покоится на аксиомах 1—18. На них же основана большая часть новых математических теорий, создаваемых в настоящее время. (Дальнейшее обсуждение этого вопроса см. в § 8.)
$ 7. Приближенные вычисления
7.1. Оценка точности
Пусть Л Y и х, у — такие числа, что X близко к г и Y близко к у. Тогда можно рассчиты вать, что X + Y близко кх + и X - Y близко кх - Можно также рассчитывать, что XY близко к ху> а при Y =/= 0 — что XIY близко к х!у. Пользуясь аксиомами 1—16, можно все это проверить и превратить в строгие предложения.
Теорема 1. Пусть
|Л-х|<а. |У— y\<b. (I)
Тогда
|Х + Y - (х+ у) | < а + Ь, |Л — Y — (л — у) | < a -f bt (2)
\XY — ху | < |х| b -f- | у | a 4- ab, (3)
L1 евла
Y 0, 1/4=0, b< ~ |y|, ’ (4)
mo, кроме того,
I2L x I 2(1 XIЬ I x/|cr) 2| XI 2
I y у I< Ы* I у I2 Id °’
Прежде чем перейти к доказательству теоремы, отметим ее значение Допустим, что мы хотим вычислить х + У, х — у. ху или х/у, причем числа х и у известны лишь приближенно напри мер с ошибками, не превосходящими соответственно а и Ь. Это значит, что мы знаем числа X и Y, удовлетворяющие неравенствам (I). Такое положение возникает, например, когда х и у — физические величины. Никакое измерение не может дать нам точных значений х и у, мы вынуждены довольствоваться приближенными значениями X и Y. Но даже если мы знаем точные значения х и у, мы их часто округляем для сокращения вычислений, а в случае использования вычислительных машин округление обычно неизбежно.
Наша теорема показывает, какова ошибка, если принять за требуемые точные значения х + 4- у,х — у ху и х/у доступные нам числа X + Y, X — У, XY и XIY. А именно, теорема утверж
§ 7. Приближенные вычисления
53
дает, что для вычисления суммы, разности, произведения и частного двух чисел х и у с ошибкой, не превосходящей некоторого заданного положительного числа (которое может быть сколь угодно малым), достаточно задать (или знать) числа х и у с определенной степенью точности.
Так, если мы хотим найти х + У или х — ус ошибкой, не превосходящей 1/100, то в силу неравенств (2) достаточно задать каждое из чисел х и у с точностью до 1/200.
Для произведений и частных положение несколько более сложно. Чтобы найти ху, скажем, с точностью в 1/100, в силу (3) достаточно знать х с ошибкой не больше а и у с ошибкой не больше d, где должно быть
'аЬ<157-
Если, например, известно, что |х| 10, |z/| 100, то достаточно иметь 1/30000, d<^
< 1/3000.
Чтобы найти х/у с точностью в 1/100, достаточно, чтобы допустимые ошибки а ид, как это видно из (4) и (5), удовлетворяли неравенствам
2d | х |___1 2а 1
|t/|2 С 200 ’ 11/1 С 200 ’
Если, например, известно, что |х| 100, |«/| 100 и |z/| 5, то достаточно иметь
5 _ 1 25___________1_
а 2-200 ” 80 ’ < 2 • 100 • 200 “ 1600*
Мы говорим для определенности о конкретных числах, но наши выводы носят общий характер. Выбрав а и b достаточно малыми, можно сделать правую сторону (3) или (5) меньшей любого наперед заданного положительного числа *.
Перейдем теперь к доказательству теоремы. Мы будем пользоваться без подробных пояснений правилами обращения с неравенствами и абсолютными значениями, выведенными в § 3. По условию, X = х + a, Y = #=?, где |а| а, |£| д. Отсюда, пользуясь неравенством треугольника [см. неравенство (11) из § 3.5], имеем
|(Х + Г) — (х + у) I = I (х + а + у + ₽) — (х + у)| = I а + р | < | а | + | р | < а + Ь, что и доказывает первое неравенство (2). Второе неравенство (2) устанавливается аналогично.
* В реальной технике вычислений простые правила (2) и более сложные правила (3) и (5) обычно формулируют близко друг к другу, пользуясь понятиями «абсолютной погрешности»
I % ' I
| х — X | и «относительной погрешности»-j---. При этом правила (2) утверждают, что аб-
I я |
солютная погрешность суммы или разности двух ^приближенных чисел» (т. е. X и Y) не превосходит суммы абсолютных погрешностей этих чисел. Аналогично, разделив обе части неравен-X ( X \
ства (3) на XI/, а неравенства (5) — на— мы здесь считаем xy=£Q, —={= 01 , получаем У \ У 7
\xy — XY\ a b а b_________а b
I *у1 <1*1+ 1г/1+ 1*1 1</1 1*1 + И
/ a b а b
ибо погрешности -------- и ---- обычно полагают малыми и, значит, произведение —- •--------
\ 1*1 |</| 1*1 |</|
а b \
можно считать много меньшим суммы —---------------4- ---- и
1*1 I У I /
: -^1 < 2 (-а- + -—
4 I у У у I \ I * | \ у\ )
откуда вытекает, что относительная погрешность произведения и частного двух ^приближенных чисел» не превосходит (удвоенной, в случае частного; впрочем, множитель 2 здесь обычно можно опустить) суммы относительных погрешностей этих чисел
54
Приложение к главе 1
Далее, снова пользуясь неравенством треугольника, находим \ХУ — ху I — I (X ч- а) (у 4- ₽) — ху | = | х₽ + уа + а0 | < | дф | + | уа | + | а₽ | = = 1*П₽1 + |!/11«Ц-|а|1?1<|х|6 + |!/|а+а6, что доказывает (3).
Допустим теперь, что соблюдаются условия (4). Тогда
|у| = | (</ + ₽)+ (-₽)К1«/ + М + 1М и
|y+₽l>lJH-IM>lFl-4- |У| = Т ы’ откуда
I»^ + WI = IfII» + ₽I>4" 1у12-
Поэтому 1 2
\У(У + ?) I \У I2 *
Пользуясь этим, получаем
X _ х I = I х -j-a _ х I |(х + а) I/ — (у + ft) х | = \ ху + уа — ух— $х\
у «/ I |!/4-Р у I I у (у+ ?) I - !//(</ + ₽)!
|У 11« I + I х Ц Р| 2|j/||a| + 2|x||M 2\y\a + 2\x\b
1Н</ + ₽)1 ' IУ I2 ' Ы2
что и доказывает (5).
УПРАЖНЕНИЯ
1. Найдите такое а, что если X отличается от 2 не более чем на а и У отличается от 6 не более чем на а, то X + Y отличается от 8 не более чем на 1/10.
2. Найдите такое Ь> что если X отличается от 5 не более чем на 0,1 и У отличается от 2 не более чем на Ь, то X—Y отличается от 3 не более чем на 0,15.
3. Найдите такое а, что если U, V, W, X, Y и Z отстоят от 3 не более чем на а, то U + + V + W + X + Y + Z отличается от 18 не более чем на 0,25.
А 4. Найдите такие а и Ь, что если X отличается от 5 не более чем на а, а У от 8 — не более чем на bt то XY отличается от 40 не более чем на 1.
5. Как близко должно быть X к 1, чтобы X2 отличалось от 1 не более чем на 0,01?
6. Найдите такое а, что если X отличается от 10 не более чем на а и У от 4 — не более чем на а, то ХУ отличается от 40 не более чем на 1/4.
7. Как близко должно быть X к 3, чтобы ХУ отличалось от 6 не более чем на 0,25 для любого У, удовлетворяющего неравенствам 1,95< У < 2,05?
8. Как близко должно быть У к 8, чтобы У/Х отличалось от 4 не более чем на 1,1 для любого X, удовлетворяющего неравенствам 1,75< Х< 2,25?
9. Пусть х и у — заданные числа, причем |х| < 100, 1 < Ы < 100. Найдите такое а, чтобы для X, отстоящего от х не более чем на а, и для У, отстоящего от у не более чем на За, частное Х/У отличалось бы от xty не более чем на 1/2.
10. Пусть X отстоит от х не более чем на 0,05, причем 1 х^ 2, а У отстоит от 1 не более чем на 0,001; оцените, насколько близко Х/У к х.
11. Найдите такие а и Ь, что если X отстоит от 4 не более чем на а, У отстоит от 8 не более чем на О 01 и Z от 2 — не более чем на Ь, то X + Y/Z отличается от 6 не более чем на 0,011.
12. Пусть х и у — заданные числа, причем 1< х< 10, 3< y<Z 5. Найдите такие а и b что если X отстоит от х не более чем на а, У от у — не более чем на а и Z от 1 — не более чем на 6, то XYZ отстоит от ху не более чем на 0,1.
§ 7. Приближенные вычисления
55
7.2. Округление десятичных дробей
Применим теорему 1 к случаю, когда х и у заданы в виде десятичных дробей, а X и У получаются простейшим способом округления, т. е. отбрасыванием всех знаков после запятой, начиная с (т 4- 1)-го. Тогда (как мы уже отмечали в § 4.5) имеем ]Х— 10~т, |У —у\
<5. \(Гт. Следующее предложение непосредственно вытекает из теоремы 1.
Теорема 2. Если при вычислении х + у, х — у, ху и х/у сохранять в десятичных разложениях х и у только т знаков после запятой, то
| ошибка в вычислении х 4~ У или х — у | < 2- 10”т,
| ошибка в вычислении ху | < 10"тх 4- \0~ту + 10“а/п,
а если 2- 10"т < | у |, то ошибка в вычислении
(6)
(7)
(8)
<2(|х| + |у|)Ю-т У Р I У I2
Из этих формул видно, что (как уже утверждалось в § 4.5) при достаточно большом т сумма, разность, произведение и частное двух действительных чисел могут быть найдены с любой требуемой степенью точности. Насколько большим следует выбрать т, зависит лишь от величины допустимой в результате ошибки, а в случае произведения и частного — также от величин заданных чисел.
Предыдущие рассуждения устанавливают лишь, что при вычислениях с десятичными дробями можно достигнуть любой желательной точности, сохраняя некоторое конечное число знаков, но не указывают, как это сделать наиболее эффективно.
При вычислении произведения ху, например, может оказаться невыгодным округлять х и у до одинакового числа знаков. Лучше сначала записать х и у в виде степеней десяти, умноженных на числа, по абсолютной величине меньшие единицы: х = Ю^г, у = 10?s, где |r|< 1, |s|< 1, а затем округлить г и s до одинакового числа знаков.
Наш способ округления простым отбрасыванием всех знаков после m-го также неэффективен. Например, округляя до двух знаков, можно уменьшить ошибку, заменяя 0,2345 на 0,23, а 0,2378 — не на 0,23, а на 0,24.
В действительности вычисления, выполняемые на современных вычислительных машинах, могут содержать сотни миллионов сложений и умножений. Контроль над вызванными округлениями ошибками при таких вычислениях оказывается трудной и интересной задачей, требующей утонченной математической техники в области анализа и других математических дисциплин.
УПРАЖНЕНИЯ
13. Вычислите 22,41 + 10,132 с ошибкой, не превышающей 2«10“4.
14. Вычислите 3,16387 — 1,025 с ошибкой, не превышающей 0,0001.
15. Вычислите 1,1673210—1,0672 с ошибкой, не превышающей 10“4.
16. Вычислите 2,86 + 0,998 — 0,98221 с ошибкой, не превышающей 0,001.
17. Вычислите (8,3) «(0,9988) с ошибкой, не превышающей 0,01.
Д 18. Вычислите (0,717) «(0,1819) с ошибкой, не превышающей 0,0001.
19. Вычислите (30,41) «(61,025) с ошибкой, не превышающей 1.
20. Вычислите 3,6/2,15 с ошибкой, не превышающей 10”2.
21. Вычислите 0,5/0,0002 с ошибкой, не превышающей 10.
22. Вычислите 998/1,01 с ошибкой, не превышающей 1.
56
Приложение к главе 1
§ 8. Рациональные и иррациональные числа
В этом параграфе доказываются и дополняются некоторые утверждения, сделанные в настоящей главе.
8.1. Геометрическое построение произведения и частного
Как было уже сказано в § 1.1, если некоторый отрезок выбран в качестве единицы длины, то произведение длин двух отрезков ab и частное этих длин а/b могут быть построены геометрически также в виде длины некоторого отрезка. Построение это основано на следующей теореме:
Пусть АВС — треугольник, D — точка отрезка АВ и Е — точка отрезка СВ, причем отрезок DE параллелен АС (рис. 1.16); тогда
| ВЛ | | ВС | | ЛС |
|BD| “ | BE | “ |DE|
Построение отрезков длин ab и а/b изображено на рис. 1.17, где принято, что 1
Чтобы найти х = ab, мы строим треугольник такого рода, как изображенный на рис. 1.16, где теперь |ВЛI = 1, |BD| = а и |ЛС| = Ь. Тогда х = |£>Е| есть требуемая длина, поскольку \/а =
Чтобы найти х = а/b, мы строим такой же треугольник, где |ВЛ| = a, |BD| = b и |£)Е| = = 1. Тогда х = |ЛС| есть требуемая длина, поскольку х/1 = а/Ь.
Приведенная выше основная теорема о подобных треугольниках может служцть иллюстрацией трудностей, связанных с несоизмеримостью. Она легко доказывается, если отрезки BD и DA соизмеримы. Доказательство указано на рис. 1.18, где |ВЛ|/|BD| = 5/3 и где все параллелограммы, а также все треугольники равны друг другу. В случае же, когда заданные отрезки несоизмеримы, самый смысл теоремы становится неясным.
Трудность устраняется введением действительных чисел. После этого теорема о подобных треугольниках приобретает ясный смысл также и в случае несоизмеримости отрезков; она может быть доказана. То же справедливо и для основных теорем о площадях. Так, площадь прямоугольника длины а и ширины b равна ab. Это значит, что прямоугольник можно разрезать на куски и затем, переставив их, сложить из них прямоугольник длины ab и ширины 1. Это может быть доказано как в случае рациональных, так и в случае иррациональных чисел а, Ь.
В «несоизмеримом» случае доказательства этих теорем не просты, и мы их здесь не приводим. В самом деле, после введения действительных чисел мы можем совсем оставить в стороне геомет
рические доказательства и свести все геометрические теоремы к некоторым утверждениям о числах. Подробнее этот вопрос рассматривается ниже, в гл. 2.
Все же поучительно припомнить, как преодолевали трудности, связанные с несоизмеримостью отрезков, древнегреческие математики. Вопрос состоял в следующем: если PQ,RS, и RiSi — четыре отрезка, не обязательно соизмеримых друг с другом, то какой смысл имеет IPQI IPiQil -ь утверждение, что 1 =-!—1_Ц1?
|/?S| |/?iSi|
Решающую роль здесь играет следующее соображение. Пусть т и п—целые положительные числа. Независимо от того, соизмеримы ли отрезки PQ и или нет, утверждение Z>— |/t 51 п
имеет простой геометрический смысл: отрезок, который в п раз длиннее PQ, имеет большую длину, чем отрезок, который в т раз длиннее RS\ символическая запись: nPQZ> mRS. В силу этого Евдокс назвал два отношения длин равными, если не существует таких целых чисел тип, что одно из этих отношений больше т/п, а другое — нет.
То же определение применимо и к отношениям других геометрических величин: площадей,
объемов и углов.
Как заметил читатель, определение Евдокса очень близко к нашему способу употребления действительных чисел. Мы «знаем» действительное число х, если известно, для каких рациональ-
ных чисел г выполняется неравенство х >г; эта информация и содержится в десятичном разложении числа х. Евдокс точно так же «знал» отношение двух геометрических величин а и 0, если ему было известно, для каких целых чисел тип величина та превосходит «0.
§8. Рациональные и иррациональные числа
57
Рис. 1.17
8.2. Следствия из аксиом поля
Как было сказано в § 2.3, все обычные правила алгебры могут быть выведены из аксиом 1—12. Выводы эти нетрудны; надо только тщательно обосновывать каждый шаг, ссылаясь на аксиомы или уже установленные следствия из них. Мы продемонстрируем это на нескольких примерах.
• Примеры. 1. — 0 = 0, —(—а) = а для всех а.
Первое утверждение справедливо, так как —0 есть, по определению, такое число х, для которого 0 4- х = 0, а в силу 4 имеем 0 + 0 == 0. Второе утверждение означает, что (—а) + а = = 0; но это вытекает из 2 и 5.
2. Вычитание, а + х = b тогда и только тогда, когда х — b — а.
Доказательство. Если а + х = Ь, то (а + х) + (—а} = b + (—а). Но, по определению, b + (—а) = b — а. Далее, в силу 2, 3, 4 и 5 имеем (а + х) + (—а)=(х + а)+(—а)= х Ч- (в-Н—а))= х + 0 = 0 + х = х. Таким образом, х = b — а.
Пусть теперь х = b — а = b + (—а). Тогда, пользуясь 2, 3, 4 и 5. имеем а 4" х = а 4" + (Ь + (—а)) = (( — а) + Ь) = (а 4- (- а)) 4- b = 0 + b = Ь.
3. Деление. Пусть а =/= 0. Тогда ах = b в том и только в том случае, когда х = Ьа~х (что, по определению, равно Ыа).
Доказательство. Пусть ах = Ь. Согласно 7, 8, 10 и 12, имеем (ах)а'1 = (ха)а-1 = = х(аа~1) = х-1 = 1 »х = х. Отсюда х = ЬаГ1.
Пусть теперь х = Ьа~\ Тогда ах = а^ЬсГ1) = а(аГ*Ь) = (ааГг}Ь = 1 *Ь = Ь, где использованы аксиомы 7, 8, 10 и 12.
4. 0а = 0 для всех а.
Доказательство. Дистрибутивный закон 9 в применении к случаю с = 0 дает в силу 7 а(Ь 4- 0) = ab + а0 = ab 4* 0а. Но, согласно 2 и 4, а(Ъ 4- 0) = а(0 + b) = ab. Отсюда ab 4- 0а = ab. В силу примера 2 и аксиомы 5 0а = ab — ab = ab 4" (—ab) = 0.
5. Закон сокращения. Если ab = 0, то либо а = 0, либо Ъ = 0.
58
Приложение к главе 1
Доказательство. Пусть b =/= 0, ab = 0. Тогда (аЬ)Ь~г = a(bb^) = а-1 = а = О, потому что в случае ab = 0 из примера 4 следует, что (ab)c = 0 для всех с.
6. (—а)Ь = —ab, (—а)(—b) — ab.
Доказательство. Первое утверждение означает, что ab + ((—а)Ь) = 0. В самом деле, согласно 9 и 7, имеем ab + ((—а)Ь) = (а + (—a))b = 0Ь = 0, где последний шаг следует из примера 4. Чтобы доказать второе утверждение, воспользуемся только что установленным результатом и примером 1: (—а)(—Ь) = —(а(—Ь)) = —((—Ь)а) = —(—ba) = Ьа = аЬ.ф
УПРАЖНЕНИЯ
Пользуясь аксиомами поля, проверьте, что следующие утверждения справедливы для всех a, b, с, d.
1. (а + Ь) + (с + d) = (d 4- а) 4- (с 4- Ь). Д2. (а 4- Ь) (с 4- d) = (ас 4- bd) 4- (be 4- ad).
3. Если о=£ 0 и а = аа, то а = 1.
4. (2 4- 3) (а 4- 1 + Ь) = [(2 4- 3) + (2 4- 3) Ь] 4- (2 + 3) а.
5 (ab 4- ac)d = a (bd 4- cd).
6Т-'- А12. —— = —- • -7— для а =4= 0, b =/= 0. ab а b (
’ ‘ =»• ab b 13. — =— для а=/=0, с#=0.
8. — а для а=/=0. а”1 ас с а 4- b а b 14. — 4“ Для с =/= 0.
9. — — для а =£ 0. а —>а с с с а с ad 4- be 15.— + — = для ЬфО, d*0. 0 a bd
10. = — 1 16. (а+&)а = а2 + 2а& + 62. 17. (а+Ь)(а — Ь) = а2 — Ь2.
— а а 11. — для 6=/=0. — b b 18. (—а)» = —а*. 19. (— а)4 = а4. 20. (а — Ь)3 = а3 — За2Ь + ЗаЬ2 — Ь3.
8.3. Периодичность рациональных десятичных дробей
Мы докажем теперь сделанное в § 4.4 утверждение о том, что в бесконечном десятичном разложении положительного рационального числа цифры обязательно периодически повторяются. Если число имеет конечное десятичное разложение, то его бесконечное разложение оканчивается бесконечным рядом девяток. Рассмотрим теперь число, которое нельзя представить конечной десятичной дробью, например 23/J8. Его десятичное разложение получается делением столбиком и начинается следующим образом:
§ 8. Рациональные и иррациональные числа
59
23,000... | 18
1®- 1,27
50
36
140
126
14
Остаток после трех шагов равен 14-ГО"2; предыдущий же остаток был равен 14-Ю"1, г. е. отличался от него лишь множителем, равным степени десяти. Это не случайно. Можно было бы и без вычислений предвидеть, что в конечном счете получится, в точностью до степени десяти, встречавшийся ранее остаток: в самом деле, каждый возможный остаток имеет вид «г, умноженное на степень десяти», где г — целое положительное число, меньшее 18. т. е. одно из чисел 1, 2, ..., 17. Поэтому самое большее через 17 шагов мы должны получить такое значение г, с которым мы уже встречались.
Проведенное только что рассуждение имеет общий характер. Пусть р и q — целые положительные числа, q > 1 и выполняется деление р на q; тогда все получаемые при этом остатки имеют вид «число г, умноженное на степень десяти», где г — одно из чисел 1, 2..q — 1. Поэтому
процесс деления самое большее через q — 1 шагов должен привести к тому же значению г, которое у нас уже встречалось.
Вернемся к нашему примеру — к 23/18. Мы прервали деление на остатке 14-Ю"2. Ранее нам встречался остаток 14-10”1, который дает в частном цифру 7. Поэтому, если продолжить деление, мы вновь получим цифру 7. Раньше эта цифра в .частном привела к остатку 14-10"2; поэтому следующий остаток будет 14-10"3, следующая цифра частного — опять 7, и т. д. Итак
23 -
----= 1,2777 ... (все семерки) = 1,27.
18
Здесь опять-таки рассуждение носит общий характер. Повторение остатков приводит к повторению знаков или последовательностей знаков. Поэтому каждое положительное рациональное число может быть представлено, и притом единственным образом в виде бесконечной периодической десятичной дроби. («Периодичность» означает, что повторение начинается либо непосредственно после запятой, либо через конечное число знаков после нее.)
Как мы видели в § 4.4, справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь представляет рациональное число. Мы проверим это утверждение на примере, одновременно продемонстрировав правило обращения периодической десятичной дроби в простую дробь\ метод, используемый при этом, очевидным образом применим во в с е х случаях.
Пусть сначала а = 0 и повторение начинается сразу после запятой. В этом случае правило гласит:
где в знаменателе стоят s последовательных девяток. Так, например, 0.7-4-' <'>
Чтобы в этом убедиться, применим формулу § 2.5 для суммы геометрической прогрессии к
числу 0,77... 7 с п семерками после запятой. Это число равно
7. ю-14-7 . IO’2 4- ... 4-7 • 10~л = (0,7) [1 4- (0,1) 4- (0,1)а 4- ••• 4-(0,1)л“1] =
7 1—(0,1)я 7 *7 1Л_Я
10 1-0,1 9 9
60
Приложение к главе 1
так что
п
п
. 7 ---—.
0,77 ... 7<—< 0,77 ... 7 4-Ю’”.
У
Это значит, что в десятичном разложении числа 7/9 первые п знаков после запятой — все семерки. Поскольку это верно для любого л, равенство (1) доказано.
Рассмотрим в качестве второго примера число 0,312 = 312/999 = 104/333. В самом деле, в этом случае имеем
0,312312...312 = 312 • 1000-! +312 • 1000“2 Ч---+ 312 • 1000"" =
Зп цифр
= 0,312 [1 4- (0,001) 4- (0.001)2 +----F (0,001)я->] =
312
1000
1 — (0,001)” 312 312 1о_зл
1—0,001
999 999
Таким образом, для любого п
0,312312...312
Зл
312
999
0,312312...312 4- 10“зл, Зп
так что в десятичном разложении 0,312312 ... 312.
Теперь нетрудно рассмотреть случаи, когда а #= 0 или зу после запятой. Например, легко проверить, что
числа 312/999 = 104/333 первые Зп знаков имеют вид
когда
повторение начинается не сра-
2,007 = 2 + 0,007 = 2 +
•0,7 = 2 +
1
100
7 1807 ’
9 “ 900
УПРАЖНЕНИЯ
Представьте заданные в упражнениях 21—26 числа в тичных дробей:
виде
конечных и бесконечных деся-
21. 3. 22. 11/2. 23. 1/1000. 24. 33/5. 2’5. 8/50.
26. 11/80.
Представьте заданные в упражнениях 27— -36 числа в виде десятичных дробей:
27. 30/11. 31. 2/7.' 34. 99/101.
28. 7/60. 32. 299/54. 35. 25/26.
29. 3/22. 30. 223/111. 33. 45/74. 36. 30/31.
$ 8. Рациональные и иррациональные числа
61
Представьте заданные в упражнениях 37—45 числа в виде простых дробей:
37. 0,4. 40. 0,41. 43. 0,0198
А38. 0.8Г. 41. 1,125. 44. 1,б0Н.
39. 3,9. 42 0,081. 45. 1,00П.
8.4. Плотность
Мы докажем теперь теорему 2 § 5.6, согласно которой каждый интервал (любого рода) с& держит бесконечно много рациональных чисел и бесконечно много иррациональных чисел. Это свойство чисел выражают еще иначе, говоря, что как рациональные, так и иррациональные числа расположены на числовой прямой плотно.
Каждый интервал содержит открытый конечный интервал; назовем его (а, Ъ). Пусть х — центр этого интервала, т. е. х = (а + 6)/2. Возьмем такое целое положительное число /п, чтобы было 10“m< b — х\ такое число существует в силу следствия 2 из аксиомы 17 (см. § 3.4). Заме тим, что если число у удовлетворяет неравенству |х — t/|< 10"OT, то у принадлежит (а, Ь) Пользуясь этим, мы найдем в (а. Ь) рациональное число с и иррациональное число d. Точнее пусть с — число, которое получается, если заменить нулями все знаки десятичного разложения числа х после m-го. Тогда с рационально. Далее, пусть d — число, которое получается, если заменить все указанные выше знаки непериодической последовательностью 101101110111101... Тогда d иррационально. (Можно построить d другим способом: если х иррационально, положить d = х; если же х рационально, положить d = х + 10~'n-1|/r2.)
Этот процесс можно продолжить. Можно найти рациональное число между а и с, другое рациональное число с2 между а и с± и т. д. Точно так же можно найти иррациональное число-dj между о и4, затем другое иррациональное число d% между а и d j и т. Д. Таким образом, теорема доказана.
8.5. Сумма и произведение действительных чисел
Мы утверждали в § 5.2, что можно определить сложение и умножение действительных чисел так, чтобы соблюдались аксиомы 1—18. Для полноты мы очень коротко объясним, как это можно сделать.
Предположим, что рациональные числа уже известны и что отношение «<> между действительными числами уже определено, как это сделано в § 5.1. Тогда легко проверить аксиомы 13. 14 и 17. Далее, что особенно важно, можно доказать и утверждение 18 (см. § 6.4). Принципом-точной верхней грани 18 мы и воспользуемся для определения сложения и умножения действительных чисел.
Пусть аир — положительные действительные числа. Пусть А ~ множество всех рациональных чисел а, удовлетворяющих неравенствам 0< a<Z а, В — множество всех рациональных чисел Ь, удовлетворяющих неравенствам 0<Р< b, S — множество всех рациональных чисел вида а + Ь, где а принадлежит А и b принадлежит В. Р — множество всех рациональных чисел вида ab, где а принадлежит А и b принадлежит В. Эти множества ограничены.
Далее доказывается, что если аир рациональны, то наименьшая верхняя граница S есть а +р, а наименьшая верхняя граница Р есть аР. Если же хотя бы одно из чисел а, р иррационально, то сумма а + Р и произведение аР определяются как верхние грани S. соответственно Р.
Затем доказывается, что 1 -а = а для всех а. где 1 — действительное число 0,9; что при 0< <Z а<р существует единственное действительное число л, для которого а + х == Р; что при 0< а. 0<fp существует единственное действительное число уу для которого ay = Р. (Число х получается как верхняя грань множества всех положительных рациональных чисел для которых а + с<Р при любом а из А. а у — как верхняя грань множества всех по*
«2
Приложение к главе 1
ложительных рациональных чисел d, для которых ad<P при любом а из Л.) Теперь уже нетрудно определить сумму и произведение двух произвольных действительных чисел и проверить все остальные аксиомы.
8.6. Другая точка зрения
Читателю, интересующемуся основаниями математики, следует знать, что некоторые математики (именуемые интуиционистами или конструктивистами*) отвергают теорию действительных чисел, заключенную в аксиомах 1—18. Они полагают, что любое утверждение о числе х имеет смысл лишь в том случае, если оно содержит фактическое предписание для вычисления этого числа. Доказательство существования корней (см. §5.4) удовлетворяет этому требованию, а доказательство существования верхней грани у любого ограниченного множества, проведенное в§6.4, не удовлетворяет. В самом деле, это последнее доказательство не содержит никакого предписания, которое позволило бы на каждом шаге решать, является ли рациональное число а верхней границей множества S. «Классический» математик полагает, что, во всяком случае, очевидно следующее: либо а является такой границей, либо нет! Однако этот достопочтенный принцип «исключенного третьего» отвергается интуиционистами.
Можно развить анализ также способом, приемлемым для конструктивистов, но это требует большего труда. Среди сторонников конструктивистской школы насчитываются некоторые из величайших математиков, например Кронекер, Пуанкаре. Брауэр и Вейль.
Леопольд КРОНЕКЕР (1823—1891), выдающийся алгебраист, выразил свое отношение к основаниям математики следующим афоризмом: «Господь бог создал целое число; все остальное — дело рук человека».
Анри ПУАНКАРЕ (1857—1912). В течение нескольких десятилетий неутомимый ум Пуанкаре властвовал над математикой и математической физикой. Он создал или преобразовал многие области математики, а также независимо от Эйнштейна пришел к уравнениям специальной теории относительности. Пуанкаре написал также несколько общедоступных книг о науке *, доставивших ему место во Французской Академии по разряду литературы **.
Л. Э. И. БРАУЭР (1881—1967) являлся одним из основоположников топологии, новейшей отрасли геометрии. Впоследствии этот голландский математик обратился к основаниям математики и стал одним из вождей «интуиционистовв.
Герман ВЕЙЛЬ (1885—1955) был одним из немногих поистине универсальных математиков нашего времени; интересы его простирались от философии до физики и заключали всю математику. Одна из ряда его знаменитых книг (Симметрия, 1952)*** доступна широкому кругу читателей.
После прихода к власти Гитлера Вейль покинул свою родину Германию и принял кафедру в Институте Высших Научных Исследований США (Принстон, штат Нью-Джерси).
Эти книги переведены и на русский язык: А. Пуанкаре, Наука и гипотеза, Спб., «Слово», 1906; Наука и метод. Спб., изд. Н. П. Карабасникова, 1910; ср. также А. П у а н к а-р е, Последние мысли, Пгр., Научное книгоиздательство, 1923.
Французская Академия (называемая также «Академией бессмертных», поскольку число ее членов, равное 40, никогда не меняется) отличается от Академии наук Франции, кратко называемой «Институтом» («LMnstutut»).
*** Русский перевод: М., «Наука», 1968.
«Интуиционисты» и «конструктивисты» — две различные (хотя и близкие по своим позициям) школы в области оснований математики, возникновение которых частично связано с теми трудностями в учении о бесконечных множествах, о которых вскользь упоминалось на стр. 41. По этому поводу см., например, книгу: А. Гей тин г, Интуиционизм, М., «Мир», 1965, автором которой является один из лидеров интуиционистской школы, а редактором и автором добавлении-—видный конструктивист А. А. Марков. См. также более доступную брошюру А А Мао-ко в, О конструктивной математике, М., «Знание», 1972. к
Задачи
63
ЗАДАЧИ
1. Целое число р > 1, не делящееся ни на какое целое положительное число, кроме 1 и самого р, называется простым. Таким образом, 2, 3, 5, 7, 11, 13, ... — простые числа. Две следующие теоремы доказываются в любой книге по элементарной теории чисел: существует бесконечно много простых чисел; каждое целое число 1 может быть записано в виде произведения простых чисел, и притом единственным способом (с точностью до порядка сомножителей). Последнее предложение иногда называют основной теоремой арифметики. (Пример! 12 = 2-2-3 = 2-3-2 = 3-2-2; очевидно, нет другого способа представить 12 в виде произведения простых чисел.) Пользуясь основной теоремой арифметики, покажите, что если k и п—целые положительные числа и k не является л-й степенью другого целого числа, то У~ k иррационален._
2. Пусть а, Ь, с, d — рациональные числа. Покажите, что если а + ьУ 2 = с + d,y 2 , то а = с и 6 = d.
3. Покажите, что для любых двух рациональных чисел a, Ь, не равных одновременно^улю, можно найти другую пару рациональных чисел с, d, такую, что (а + ЬУ2) (с + dy 2 )=1.
4. Множество всех чисел вида а + ЬУ 2 , где а и b— рациональные числа, образует поле,— даже упорядоченное архимедово поле. Докажите это, проверив аксиомы 1—1*7. _
5. Сохраняет ли силу утверждение задачи 4, если заменить У"2”на УЗ ? На)ИГ? Haj/^4 ? На /б~?
6. Пользуясь результатами задач 1—5, покажите, что для любого заданного целого числа г, не являющегося квадратом другого целого числа,- множество всех действительных чисел вида а + ьУг . где а, b рациональны, образует упорядоченное архимедово поле. Это поле обычно обозначается через Q(}/7~).
7. Пусть п>1 —целое число. Рассмотрим множество Zn целых чисел 0, 1, 2, ... . Определим сумму двух элементов Zn как остаток от деления их «обычной» суммы на п; аналогично определяется произведение. (Пример: если п = 3, то «новая» сумма 2 и I есть 0, так как 2+1 = 3 делится на 3, «новое» произведение 2 и 1 есть 2, «новая» сумма 2 и 2 есть 1, так как 2+2=4 = 3-1 + 1, и т. д.)
Составьте таблицы сложения и умножения для Za, Z3 и Z4. Проверьте, какие из этих множеств удовлетворяют аксиомам 1 —12.
8. Покажите, что Zn удовлетворяет аксиомам 1—11 при любом п.
9. Покажите, что Zb является полем, a Ze — нет.
10. Покажите, что Zp является полем, если р — простое число.
11. Покажите, что Zn не является полем, если п — не простое число; а именно, покажите, что в этом случае для Zn неверен закон сокращения.
12. Никакое поле Zp, где р — простое число, не может быть упорядочено. Докажите это. (Смысл этого предложения состоит в том, что для элементов Zp нельзя ввести отношение «<» таким образом, чтобы соблюдались аксиомы 1—16.)
13. Существует поле, содержащее ровно 4 элемента. Обозначив их через 0,1, а, Р, найдите для этого поля таблицы сложения и умножения.
14. Рационально ли число 0.123456789101112131415161718192021222324...? Мотивируйте Ваш ответ.
15. Приведите пример такого числа х, что прибавление к нему 1О“10000 меняет все знаки десятичного разложения х от запятой и вплоть до 10000-го знака.
16. Существует ли иррациональное число, в десятичном разложении которого лишь один знак? Лишь два знака? (Пример: в десятичное разложение 1/4 = 0,24999... = = 0,249 входят только три знака 2, 4 и 9.)
17. Верно ли, что любой интервал числовой прямой содержит рациональное число, которое можно записать в виде конечной десятичной дроби?
18. Верно ли, что любой интервал числовой прямой содержит число, десятичное разложение которого может быть записано лишь с помощью знака 3?
19. Пусть в качестве основания позиционной системы используется не десять, а другое число, например k. Тогда, точно так же как выше, можно изображать числа «fc-ичными» дробями. Останется ли в силе теорема, в силу которой рациональные числа, и только они, представляются периодическими дробями?
«4
Приложение к главе 1
20. Говорят, что интервал /* с концами а, b содержит интервал /2 с концами с, d, если а с<С d Ь.
Интервалы /р 12, /3, ... называются вложенными друг в друга, если каждый интервал /у содержит следующий интервал //+1 .
Принцип вложенных интервалов гласит, что для любой последовательности замкнутых и последовательно вложенных друг в друга интервалов существует точка (т. е. действительное число), принадлежащая всем без исключения интервалам нашей по следовательности.
Докажите принцип вложенных интервалов, пользуясь принципом верхней грани. (Можно также, хотя и с большим трудом, вывести принцип верхней грани из принципа вложенных интервалов.)
21. Покажите на примере, что утверждение принципа вложенных интервалов может быть неверно, если заменить замкнутые интервалы открытыми.
22. Постройте последовательность вложенных замкнутых интервалов с рациональными концами таким образом, чтобы никакая рациональная точка не принадлежала всем им.
23. Пусть все действительные числа разбиты на два класса — «левый» класс L и «правый» класс R—таким образом, что: (1) в каждом из этих классов имеются числа, (2) каждое число из L меньше каждого числа из R. Приняв принцип верхней грани, докажите принцип Дедекинда: либо L содержит наибольший элемент, либо R содержит наименьший элемент. (Можно также, хотя и с большим трудом, вывести принцип верхней грани из принципа Дедекинда.)
24. Покажите, что можно разбить все рациональные числа на два класса L и R, обладающие теми же свойствами, что выше, но так, что L не содержит наибольшего элемента, a R не содержит наименьшего элемента. Иными словами, приведите пример, показывающий, что принцип Дедекинда в поле рациональных чисел неверен.
2/КООРДИНАТЫ
Это также вводная глава; она содержит элементы аналитической геометрии, и читатель, знакомый с этим предметом, может пропустить ее или лишь бегло просмотреть. Построение аналитической геометрии будет нами продолжено в главах о векторах (см. гл. 9) и о квадриках (см. гл. 10). Эти главы можно читать непосредственно после гл. 2.
Приложение к этой главе состоит из двух параграфов. В § 5 приводится доказательство одной из исторически первых теорем анализа — принадлежащее Архимеду вычисление площади параболического сегмента. В § 6 речь идет о двух путях обоснования геометрии — об аксиоматическом методе и аналитическом методе.
66
2. Координаты
§ 1. КООРДИНАТЫ ТОЧКИ. ФОРМУЛА РАССТОЯНИИ
Понятие действительного числа развивалось постепенно и полная ясность здесь была достигнута лишь много позже того, как анализ превратился в процветающую математическую дисциплину. Иначе обстояло дело со вторым основанием, на котором строится здание анализа,— с аналитической геометрией, которая была придумана одновременно и независимо двумя учеными: философом Декартом и юристом Ферма; оба они принадлежат к числу величайших математиков всех времен.
Основная идея аналитической геометрии проста: положение точки на плоскости можно описать двумя числами и таким образом перевести любое утверждение о точках в утверждение о числах.
1.1. ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Проведем в плоскости две перпендикулярные прямые и назовем одну из них горизонтальной осью, а другую — вертикальной осью*. Точка пересечения осей называется началом координат. На каждой из осей мы выберем одно из двух возможных направлений: на горизонтальной оси это направление называется направлением «вправо», а на вертикальной — направлением «вверх»; противоположные же направления обозначаются словами «влево» и «вниз». Выберем также единицу длины. (Обычно оси изображаются так, как это показано на рис. 2.1.) Обе оси вместе с выбранной единицей длины образуют декартову систему координат на плоскости.
Пусть Р — точка плоскости; мы свяжем с ней два числа, называемых координатами этой точки. Первая координата равна нулю, если Р лежит на вертикальной оси; она равна расстоянию от Р до вертикальной оси, если Р лежит справа от вертикальной оси, и равна расстоянию от вертикальной оси, взятому со знаком минус, если Р лежит слева от вертикальной оси. Вторая координата Р равна нулю, если Р лежит на горизонтальной оси, и равна расстоянию Р от горизонтальной оси (или этому расстоянию, взятому со знаком минус), если Р лежит выше горизонтальной оси (соответственно ниже ее). Некоторые точки и их координаты показаны на рис. 2.2.
Первая координата точки часто обозначается буквой х, вторая — буквой у. Соответственно этому горизонтальную ось называют также осью х, а вертикальную — осью у. Отметим, что каждая из осей координат является числовой прямой в смысле § 5.3 гл. 1.
Укажем другое истолкование координат: чтобы достигнуть точки (а, Ь) исходя из начала координат, надо сначала пройти а единиц в направлении оси х, а затем b единиц в направлении оси у. Пройти а единиц в направлении оси х означает: вовсе не двигаться при а = 0; пройти расстояние а в направлении оси х при а > 0; пройти расстояние | а | в противоположном направлении при а < 0. Аналогично истолковывается движение в направлении оси у.
Точка Р определяется своими координатами, причем для любых двух чисел а, Ь существует точка Р, имеющая а своей первой координатой и Ь — второй. Таким образом, упорядоченную пару чисел (а, Ь) — координат точки Р — можно исполь-
* В нашей литературе приняты названия: ось абсцисс и ось ординат.
§ 1. Координаты точки. Формула расстояний
67
бберх
Рис. 2.1
бпрабо
У
зовать в качестве символа или «наименования» этой точки Р, что мы и будем делать в дальнейшем.
Когда мы говорим, что координаты точек образуют упорядоченную пару, то имеем под этим в виду, что порядок чисел здесь существен. Так, (2, 3) и|(3, 2)— это разные упорядоченные пары, обозначающие разные точки.
Все точки, расположенные справа от оси у, имеют положительную первую координату. Множество всех этих точек называется «множеством х > 0», или правой полуплоскостью. Аналогично, множество х < 0 есть левая полуплоскость (ее образуют все точки, расположенные слева от оси у), множество у > 0 есть верхняя полуплоскость (все точки выше оси х), множество у < 0 есть нижняя полуплоскость (все точки ниже оси х).
Рене ДЕКАРТ (1596—1650) — отец современного мучного мышления (во всяком случае, это вер* но для европейской культуры). Свою философию оо основал на независимом суждении и анализе явлений, а не на вере в авторитеты, характерной для религиозного мышления средневекового человека. Его философия содержит также попытку строго механического объяснения всех явлений природы, в том числе явления органической амзнн. Единственная книга Декарта по математике, ого «Геометрия» *, вышла в свет в 1635 г.
Молодым человеком Декарт много путешествовал и служил в армии. Затем он поселился в Голландии, которую покинул лишь незадоиго до смерти, направившись в Стокгольм в качестве наставника шведской королевы Христины.
Пьер де ФЕРМА (1601—1665) был советником парламента в Тулузе; зга связанная с юриспруденцией должность оставляло ому достаточно времени дм занятий математикой. Вместе с Декартом он явился основоположником аналитической геометрии л вместе с Паскалем — основоположником теории вероятностей; его можно также считать одним из предшественников математического анализа и великим творцом в обнести теории чисел.
Одной из наиболее известных нерешенных математических проблем является доказательство )или опровержение) тав называемой «великой теоремы Ферма»: если tt >3 — целое число и х.у — рациональные число, то хл_|_ 1. Ферма написал на полях книги: «Я нашел поистине
замечательное доказательство втой теоремы, оо по плюю здесь места, чтобы ого записать». (В настоящее время с использованием зяектронпых вычислительных машин удалось доказать, что теорема Форам, оо всяком случае, справедливо для всея Ж100 600).
* Русский перевод: М.—Д., Гостехлздат, 1938; см. также в книге: Р. Декарт, Рассуждение о методе, М., изд. АН СССР, 1953, с. 299—408.
68
2. Координаты
Пересечение верхней и правой полуплоскостей есть множество точек, обе координаты которых положительны; оно называется первым квадрантом. Второй, третий и четвертый квадранты — это множества, определяемые соответственно условиями: х < 0, у > 0; х < 0, у < 0; х > 0, у < 0 (рис. 2.3).
упражнения
Начертите систему координат и постройте точки со следующими координатами:
1. (2,3). 3. (0,4). 5. (—2,3).
7. (2, —3).
2. 1). 4. (-1.1). 6. (3.-2),
Для каждой из следующих задач выполните чертеж (лучше на бумаге «в клетку»).
9. Найдите координаты всех точек в третьем квадранте, находящихся на расстоянии 5 от начала и на расстоянии 3 от оси х.
10. Найдите координаты всех точек левой полуплоскости, находящихся на расстоянии 3 от оси х и на расстоянии 2 от оси у.
11. Найдите координаты всех точек верхней полуплоскости, находящихся на расстоянии 7 от оси х и на расстоянии 4 от оси у.
12. Найдите координаты всех точек второго квадранта, находящихся на расстоянии бот начала и на расстоянии 5 от прямой у = —1.
13. Найдите координаты всех точек правой полуплоскости, находящихся на расстоянии 2 от прямой у = 3 и на расстоянии 4 от прямой х = 5.
14. Найдите координаты всех точек, находящихся на расстоянии 13 от точки (1, 0) и на расстоянии 5 от оси х.
Найдите координаты веек точек четвертого квадранта, находящихся на расстоянии 8 от прямой у = 1 и на расстоянии JL от прямой х = 8.
&
15.
^16. Найдите координаты всех точек прямой х = 10, находящихся на расстоянии 5 от точки (7, -1).
1.2. ПЕРЕНОС СИСТЕМЫ КООРДИНАТ
Выбором декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это значит, что каждой точке соответствует единственная пара чисел и каждой упорядоченной паре чисел соответствует единственная точка.
Однако выбор системы координат на плоскости достаточно произволен. В другой координатной системе та же точка имеет, конечно, другие координаты. Мы рассмотрим здесь лишь простейший случай этой ситуации.
Выберем сначала одну систему координат, а затем другую, «новую», с другим началом, но с осями, параллельными старым осям и имеющими те же направления. В. этом случае говорят, что новая координатная система получается из старой посредством (параллельного) переноса (рис. 2.4).
Пусть точка Р имеет координаты (х, у) в старой системе и координаты (X, Y) — в новой и пусть (а, Ь) — координаты нового начала в старой системе. Тогда
х = а + X и у = b + Y. (1)
$ 1. Координаты точки. Формула расстояний
69
„новое" начало
Р
старые координаты нового начала:-2,2 старые координаты Р: -1,5 новые координаты Р: £3
-1 = 1 +(-
5 = 3+2
Это можно усмотреть из рис. 2.4, на котором новое начало лежит в первом квадранте и точка Р — в (новом) первом квадранте. Читатель может убедиться самостоятельно, что формулы (1) справедливы и во всех остальных случаях; один из них показан на рис. 2.5.
УПРАЖНЕНИЯ
В каждом из следующих упражнений новая координатная система получается из старой посредством переноса. Сделайте чертеж к каждому упражнению.
17. Пусть координаты нового начала в старой системе равны (0, 3), а координаты точки Р в старой системе равны (—1, 4); найдите координаты Р в новой системе.
18. Пусть координаты нового начала в старой системе равны (—1, 5), а координаты точки Р в старой системе равны (0, 8); найдите координаты Р в новой системе.
19. Пусть координаты точки Р в старой системе равны (1, —2), а в новой системе равны (3, 1); найдите координаты нового начала в старой системе.
±20. Пусть координаты старого начала в новой системе равны (—3, 2); найдите координаты
нового начала в старой системе.
Пусть координаты нового начала в старой системе равны (—1, —4), а координаты точки Р в новой системе равны (—6, 2); найдите координаты Р в старой системе.
Пусть координаты нового начала в старой системе равны (3, —2), а координаты точки
Р в новой системе равны (-L, —1); найдите координаты Р в старой системе.
2
21.
22.
1.3. ФОРМУЛА РАССТОЯНИЙ
Напомним теперь знаменитую теорему Пифагора. Квадраты, построенные на катетах прямоугольного треугольника, можно разрезать на части и затем заново сложить эти части таким образом, что получится квадрат, построенный на гипотенузе (см. рис. 2.6, где построенный на гипотенузе квадрат разбит на два прямоугольника, имеющие те же площади, что и построенные на катетах квадраты). Кстати, теорема Пифагора — это один из старейших математических результатов; открытие его принадлежит вавилонянам, а общая формулировка и доказательство— грекам.
70
2. Координаты
Рис. 2.7
Греки воспринимали теорему Пифагора как некоторое утверждение о п л ощ а-д я х. В наши дни, владея понятием действительного чирла, мы можем сформулировать ее как предложение о числах: если а и b — длины катетов прямоугольного треугольника и с — длина его 'гипотенузы, то а2 + Ь2 = с2.
Применим теорему Пифагора для вывода важной формулы.
Теорема 1. Расстояние d между точками (хь уд и (х2, г/2) равно
d = /(Xi — Хг)2 + (1/1 —{/г)2 (2)
{формула расстояний).
Чтобы доказать формулу (2), рассмотрим сначала частный случай, когда одна из точек является началом координат (0, 0). Пусть другая точка обозначается через (х, у)\ надо показать, что расстояние от (0, 0) до (х, у) равно Ух2 + f/2> или, что то же,
(расстояние от (0, 0) до (х, у))2 = | х |2 + I У I2-
Это очевидно в случае (х, у) = (0, 0), а также при х = 0 или у = 0. Во всех других случаях наше утверждение совпадает с теоремой Пифагора (рис. 2.7).
Обратимся теперь к общему случаю. Перенесем координатную систему так, чтобы новым началом стала точка (хь уд- Тогда новые координаты второй точки равны (х2 — Xi, у2 — #i)» как это видно из формул (1), где надо положить (а, Ь) = = (хь уд и (х, у) = (х2, уд- По только что доказанному, расстояние между нашими двумя точками равно
/(х2 —хх)2 + (1/2—t/J2 ,
как мы и утверждали в условии теоремы.
§ 1. Координаты точки. Формула расстояний
71
Рис. 2.8
Рис. 2.9
1.4. КООРДИНАТЫ В ПРОСТРАНСТВЕ
Следует предупредить читателя, что мы редко будем обращаться к стереометрическим построениям; однако все же полезно кратко обрисовать построение декартовой системы координат в пространстве.
Выберем снова единицу длины и точку в пространстве, называемую началом координат. Проведем через эту точку три взаимно перпендикулярные прямые и выберем на каждой из них направление. Назовем эти прямые осью х, осью у и осью г*; они обычно изображаются так, как показано на рис. 2.8. Каждая пара осей задает содержащую их координатную плоскость.
Положение то^ки Р в пространстве полностью описывается упорядоченной тройкой ее координат (а, Ь, с). Можно достигнуть точки Р, двигаясь от начала на а единиц в направлении оси х, на b единиц в направлении оси у и на с единиц в направлении оси г (рис. 2.8).
Множество х = а, т. е. множество всех точек с координатой х (первой координатой), равной а, есть плоскость, параллельная плоскости уг и, следовательно, перпендикулярная оси х. При а =0 она совпадает с плоскостью yz, в противном же случае отстоит от нее на расстояние | а |. При а > 0 плоскость х =а лежит по ту сторону от плоскости уг, куда указывает ось х, при а < 0 — по другую сторону. Аналогично, множества у = Ь (точек g координатой у, равной Ь) и г = с (точек с координатой z, равной с) — это плоскости, перпендикулярные соответственно осям у и г. Точка (а, Ь, с) есть пересечение трех плоскостей: х = а, у = Ь, г = с.
Три координатные плоскости делят пространство на 8 октантов; тот из них, все три координаты точек которого положительны, называется первым октантом.
Расстояние d точки Р с координатами (а, Ь, с) от начала координат равно
d = У а2 4- Ь2 4- с2 . (3)
* В русской учебной литературе: ось абсцисс, ось ординат и ось аппликат.
72
2. Координаты
Доказательство этой формулы в случае, когда точка Р лежит в первом октанте, указано на рис. 2.9. Пусть s — расстояние от О до PZ9 где Pz— точка в плоскости ху с координатами (а, Ь). По формуле расстояний на плоскости,
s2 = а2 + Ь2.
Поскольку ОР — гипотенуза прямоугольного треугольника с катетами ОРг и Р2Р и длина Р2Р равна с, из теоремы Пифагора имеем
d2 = s2 + с2.
Отсюда d2 = а2 + Ь2 + с2, и равенство (3) доказано.
Из равенства (3), как и в случае плоскости, получается формула расстояний для пространства: расстояние между точками (ai9 bi9 сд и (а2, b2t с2) пространства равно
d = /(а,- + (bi-b^+ (d-c. (4)
УПРАЖНЕНИЯ
В следующих упражнениях найдите расстояния между точками с заданными координатами:
23. (0,1) и (1,0).
24. (—1,-2) и (3,1).
25. (—2,0) и (— 1,1).
26. (0,1,1) и (—2,1,4).
27. (1,-6, 0) и (2, 3, 1). и-(2=т)и (з’-4)-29,( 3, — I) и (—1,3).
АЗО. (1,3,2) в (2,1,3).
§ 2. ПРЯМАЯ ЛИНИЯ
2.1. ЛИНЕЙНЫЕ УРАВНЕНИЯ
В этом и в следующих разделах мы предполагаем, что выбрана некоторая декартова система координат. Перевод геометрических утверждений в алгебраические формулы, т. е. в утверждения о числах, основан на формуле расстояний и на другом результате, который мы теперь сформулируем.
Теорема 1. Пусть А, В, С — числа, причем А и В не равны нулю одновременно. Тогда множество всех точек, координаты которых удовлетворяют уравнению
4х + Ву + С = 0, (1)
есть прямая линия. Обратно, каждая прямая линия есть множество всех точек, удовлетворяющих уравнению этого вида.
Доказательство. Заметим сначала, что вертикальная прямая, т. е. ось у или параллельная ей прямая, есть множество всех точек (х, у), удовлетворяющих уравнению х — а, при некотором фиксированном а. (Если прямая есть ось у, то а = 0; в противном случае | а | есть расстояние от оси у до прямой, и число а положительно или отрицательно в зависимости от того, лежит ли прямая справа или слева от оси у.} Отметим, что уравнение х = а имеет вид (1), где А = 1, В = 0 и С = —а. Точно так же горизонтальная прямая есть множество всех точек (х, у).
§ 2. Прямая линия
73
для которых у = Ь, где b — фиксированное число; это уравнение также имеет вид (1) при Д = О, В = 1 и С = —Ь.
Пусть I — прямая, проходящая через начало и не совпадающая ни с одной из осей. Если Р — точка пересечения I с прямой х = 1, то Р имеет координаты (1, т)9 где т > 0 или т < 0, в зависимости от того, проходит ли I через первый или четвертый квадрант (см. рис. 2.10, где zn>0).
Пусть Q — любая точка прямой Z, отличная от Р и О; обозначим ее координаты через (х, у) и заметим, что при т >0 х и у имеют один и тот же знак, а при т < 0 — противоположные знаки. Если R — точка (х, 0), то треугольники О\Р и 0RQ подобны (рис. 2.10), откуда имеем
или |f/| = |m||x|. 1 |х| 1 11 1
Учитывая сказанное выше о знаках х и у, заключаем, что у = тх как при т > 0, так и при т < 0.
Далее, все точки (х, у) плоскости такие, что у = /их, принадлежат Z. В самом деле, если точка (х, у) не принадлежит Z, то она лежит на другой прямой проходящей через начало. Эта другая прямая пересекает вертикальную прямую х = 1 в точке (1, mi), где mi =/= т. Рассуждая так же, как и выше, имеем у = mix, откуда у =/= тх. Итак, прямая Z есть множество всех точек (х, у), для которых у = тх. Это уравнение имеет вид (1), где А =т,В= —1 и С = 0.
Пусть, наконец, Z — прямая, которая не горизонтальна, не вертикальна и не проходит через начало. Тогда Z пересекает ось у в точке Q с координатами (0, ft), й =/= 0 (рис. 2.11, где b > 0). Проведем через начало прямую Zb параллельную I. Заметим, что Z лежит над Zt при b > 0 и под Zt при b < 0. Как мы только что видели, существует такое число т, что Zt есть множество всех точек (х, у), для которых у = = тх. Пусть Р — некоторая точка Z, отличная от Q, и /? — такая точка Zi, что прямая PR вертикальна. Тогда ORPQ — параллелограмм и отрезки OQ и RP равны. Точки Р и R имеют одинаковую первую координату, а вторая координата Р — =(второй коордйнате R) + Ь. Если Р и R имеют первую координату х, то вторая координата R равна тх, а вторая координата Р равна тх 4- Ь. Итак, I есть множество
74
2. Координаты
точек (х, у). для которых у = тх + Ь. Это уравнение имеет вид (1), где А = /и, В = — 1, С =Ь.
Мы показали, что точки (х, у) л ю б о й прямой удовлетворяют уравнению ви-да (1).
Будем теперь исходить из заданного уравнения вида (1), где А и В не равны од-Q
повременно нулю. Если В = 0, то Л 0 и в силу уравнения х -----; множество
точек (х, у). удовлетворяющих этому уравнению («множество решений» уравнения), А С
есть вертикальная прямая. Если В =# 0, уравнение (1) дает у -----х —&- ;
А С
полагая здесь —= т,---------= 6, получим
у = гпх-[~ Ь. (2)
При т = 0 множество решений есть горизонтальная прямая. При т =/= 0 и b = 0 множество решений есть, как мы видели выше, прямая, проходящая через О и через точку (1, /и). Если 6 =/= 0, то, как мы уже установили выше, множество решений есть прямая, проходящая через точку (0, Ь) и параллельная прямой проходящей через точки О и (1, т).
Теперь теорема 1 полностью доказана. Как показывает проведенное рассуждение, для заданной прямой I можно написать уравнение (1), которому удовлетворяют все ее точки. Это уравнение определяется однозначно, если не считать, конечно, того, что его можно умножить на любое отличное от нуля число.
Уравнение вида (1) называется линейным; доказанная нами теорема объясняет ©тот термин.
ф Примеры. 1. Начертить прямую, уравнение которой имеет вид 2х 4- Зу — 1 = 0.
Решение. Чтобы начертить прямую, достаточно знать две различные ее точки. Зададим вопрос, есть ли на прямой точка с х = 0? При х = 0 из уравнения следует Зу — 1 =0, или у = Поэтому точка (0, принадлежит нашей прямой. Точно так же при х = 5 из уравнения следует 10 4- Зу — 1 =0, или у = —3. Поэтому точка (5, —3) лежит на прямой. Теперь легко начертить прямую.
2. Лежит ли точка (—3, 2) на прямой 5х 4” ty — 7 =0?
Решение. Нет, поскольку 5- (—3) + 4*2—7 = —14 #= 0.
3. Найти точку пересечения прямых 2х — Зу =0 и Зх 4* 2# 4“ 13 =0.
Решение. Точка (х, д) принадлежит обеим прямым, если ее координаты удовлетворяют обоим уравнениям. Решая эти уравнения совместно, получаем х = —3, у = —2. Таким образом, искомая точка пересечения есть (—3, —2). Предлагаем читателю проверить это, вычертив обе прямые, ф
УПРАЖНЕНИЯ
1. Начертите прямую в уравнением 5х — 2у 4* I « 0. Начертите прямую g уравнением 5дг — 2у + 2 ® 0. Опишите еовекупнооть прямых — 2у 4“ с « 0, где а — любое действительное число.
2. Начертите прямую у « 4- 1. Начертите ври тех же евях координат врямую у =
«= —2х + 1. Где перевекаютвя эти прямые? Под каким углем?
§ 2. Прямая линия
75
3. Начертите прямую у = —-l-x — 2. Начертите при тех же осях координат прямую у = о
= Зх — 2. Где пересекаются эти прямые? Под каким углом?
4. Покажите, что уравнение у — 2 = 3(>г — 1) есть уравнение прямой. Принадлежит ли этой прямой точка (1, 2)?
Покажите, что уравнение = 1
5.
6.
7.
8.
есть уравнение прямой. Начертите ее. Где она
пересекает ось дг? Ось у?
Найдите точку пересечения прямых 4х — Зу — 2 = 0 и х — бу + 10 = 0.
Покажите без чертежа, что прямые 114дг — 2у — 26 = 0 и г/ = б7х + 57 не имеют об-
щих точек.
Поскольку оси х и у — прямые, они имеют уравнения вида (1). Найдите эти уравнения.
2. 2. НАКЛОН
Невертикальная прямая, как мы видели выше, есть множество всех точек (х, у), удовлетворяющих уравнению у = тх + b 1см. уравнение (2)]. Число т называется наклоном* этой прямой. Оно однозначно определяется прямой и системой координат. Если прямая задана уравнением Ах + By 4- С = 0, то ее наклон равен
(3)
(так как прямая не вертикальна, здесь В #= 0). Чтобы получить формулу (3), достаточно разрешить уравнение Ах + By + С =0 относительно у.
Предположим, что прямая, заданная уравнением у = тх + Ь, содержит точки (*ь г/i), (х2, У г)- Тогда
= тХ1 + b, у2 = тх2 + Ь.
Вычитая первое уравнение из второго, имеем
Уг~ У1 =т(хг — Xi). (4)
Поскольку прямая не вертикальна, здесь Xi ф х2; поэтому
т = «/г —У1 ' /5х
Х2 —*1
Эти формулы иллюстрируют геометрический смысл наклона. Если т = 0, то прямая горизонтальна; любые две точки ее имеют одну и ту же координату у. Если т > 0, то точка поднимается при движении вдоль прямой слева направо, причем координата у возрастает в т раз быстрее координаты х, как это видно из равенства (4). Таким образом, малый положительный наклон означает медленный подъем, большой же — крутой подъем. Если т < 0, то прямая опускается при движении слева направо; координата у убывает в | т | раз быстрее, чем возрастает координата х (рис. 2.12).
Наклон вертикальной прямой мы не определяем**.
* В русской учебной литературе принят термин «угловой коэффициент! прямой; в некото-рых книгах употребляется также термин «подъем».
** Иногда говорят, что вертикальная прямая имеет бесконечный наклон, и записывают его символом (не числом!) оо.
76
2. Координаты
упражнения
9, Пусть точка Qнаходится на 3 единицы выше и на 2 единицы правее точки Р; каков наклон прямой, проходящей через Р и Q?
10. Пусть точка Q находится на 6 единиц выше в на 1 единицу левее точки Р; каков наклон прямой, проходящей через Р и Q?
11. Пусть точка Р находится на 2 единицы ниже и на 10 единиц правее точки Q; каков наклон прямой, проходящей через Р и Q?
12. Прямая имеет уравнение Зу + 2х = 6, прямая /я — уравнение 5дг — 2 ® 2у. Какая из этих прямых опускается при движении слева направо?
13. Прямая It имеет уравнение Зу — 4х — 2 = 0, прямая /з — уравнение 2у — 40% + 7 = = 0, прямая /3 — уравнение 18у — 17х + 51 = 0. Какая из этих прямых поднимается быстрее всех? Медленнее всех?
2.3. ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
Теорема 2. Две различные прямые параллельны в том и только в том случае, если они либо обе вертикальны, либо имеют один и тот же наклон.
Доказательство неявно содержится в выводе теоремы 1. Как мы там видели, наклон невертикальной прямой Z равен наклону прямой /ь параллельной I и проходящей через начало координат. Поэтому две невертицальные прямые параллельны тогда и только тогда, когда они имеют одинаковый наклон*. С другой стороны, ясно, что вертикальная прямая и невертикальная прямая не параллельны друг другу.
Теорема 3. Две прямые перпендикулярны друг другу в том и только в том случае, если одна из них горизонтальна, а другая вертикальна или если их наклоны удовлетворяют условию
/И1/П2 =—1. (6)
Доказательство. Пусть и Z 2 — две прямые. Построим прямые и Z 2 (читается «/ один с шапочкой»,«/два с шапочкой»), проходящие через начало координат и параллельные соответственно Zi и /2 (рис. 2.13). Прямые /4 и /2 перпендикулярны тогда и только тогда, когда перпендикулярны Zi и /2. Поэтому достаточно доказать теорему для прямых, проходящих через начало.
* При этом совпадающие прямые здесь рассматриваются как частный случай параллельных.
§ 2. Прямая линия
77
Горизонтальная прямая перпендикулярна вертикальной, и обратно. Рассмотрим теперь две прямые, которые не вертикальны и не горизонтальны. Тогда обе они имеют наклоны nti и /и2, причем mi #= О, т2^= 0. Уравнения двух прямых можно записать так:
у = mix, у = т2х.
Если /Hi > 0, /и2> 0, то обе прямые проходят в первом квадранте, но тогда они
не перпендикулярны (рис. 2.14) и /П1/и2> 0, так что равенство (6) неверно. Если
< 0, т2 < 0, то обе прямые проходят через второй квадрант; снова они не перпендикулярны и /П1Аи2 > 0. Пусть теперь mi и т2 имеют противоположные знаки, например mi > 0 и т2 < 0, как на рис. 2.15. Две прямые перпендикулярны тогда и только тогда, когда углы а и 0 дополнительные (дают в сумме прямой угол). Это может быть лишь в том (и только в том) случае, когда два прямоугольных треугольника, показанных на рис. 2.15, подобны, а они подобны тогда и только тогда, когда
=-г-Ц, что равносильно соотношению | т^т2 I = 1- Поскольку mi и т2 1 |/Лг|
имеют противоположные знаки, это равносильно условию (6).
УПРАЖНЕНИЯ
14. Найдите уравнение прямой, проходящей через (0, 0) и параллельной прямой 2х — Зу + + 7 = 0.
15. Найдите уравнение прямой, проходящей через (0, 0) и перпендикулярной прямой 2х — Зу + 7 = 0.
16. Для каких значений а уравнение ах + Зд — 5 = 0 есть уравнение прямой, перпендикулярной прямой х — у + 9 = 0?
17. Для каких значений а уравнение 2их — Зд + 6 » Оесть уравнение прямой, параллельной прямой 6х + 4у — 3 = 0?
18. Для каких значений t уравнения tx — 2д + 8 = 0 и 3tx + Зд + 4 = 0 суть уравнения перпендикулярных прямых?
19. Найдите уравнение прямой, проходящей через точку (—1, 2) и параллельной прямой 4х + 12у + 3 = 0.
Д20. Найдите уравнение прямой, проходящей через точку (6, —3) и перпендикулярной прямой х — Зу + 12 = 0.
21. Найдите уравнение прямой, проходящей через точку (1/2, —1) и перпендикулярной прямой 18х + 12# — 1 = 0.
78
2. Координаты
2.4 . УРАВНЕНИЯ ПРЯМЫХ
Перечислим некоторые удобные способы записи уравнений невертикальных прямых. Если I пересекает ось х в точке (а, 0),то а называется следом I на оси х. Точно так же если I пересекает ось у в точке с координатами (0, ft), то b называется следом I на оси у.
А. Уравнение прямой с наклоном т и следом Ь на оси у имеет вид
у = тх + Ь.
Доказательство. При х = 0 из уравнения следует у = ft; поэтому точка (0, ft) принадлежит прямой. При этом прямая, имеющая это уравнение, параллельна искомой прямой и, значит, с ней совпадает.
Б. Уравнение прямой с наклоном т9 содержащей точку (xi9 у^9 имеет вид
y — yi =m(x — Xi). (7)
Доказательство. Уравнение (7) равносильно уравнению у = тх + ft, где ft = г/1 — mxt. Таким образом, это уравнение прямой с наклоном т. Легко проверить, что точка (хь r/i) удовлетворяет уравнению (7).
В. Уравнение прямой с наклоном т и следом а на оси х имеет вид у =т(х — а).
Это частный случай (Б) при (xl9 уд = (а, 0).
Г. Уравнение прямой, проходящей через две различные точки (xit уд, (х2, У г), имеет вид
(У — */г)(Х1 — х2) = 0/1 — у2)(х — х2). (8)
Доказательство. Уравнение (8) есть линейное уравнение, связывающее переменные х, у (поскольку xi9 yi9 х2, у2 — фиксированные числа). Поэтому множество решений уравнения (8) есть прямая. Легко проверить, что (xi9 уд и (х2, у2) удовлетворяют (8).
Д. Уравнение прямой со следом а=^= 0 на оси х и следом 0 на оси у имеет вид
— + 4г = 1- (9)
а b
Доказательство. Уравнение ,(9) есть линейное уравнение, которому удовлетворяют точки (а, 0) и (0, ft).
Нет никакой необходимости запоминать все эти формулы: если они понадобятся, то их легко вывести из уравнения (2) прямой, заданной наклоном и следом на оси у, или из общего уравнения прямой (1).
ф Пример. Найти уравнение прямой, проходящей через точки (3, 4) и (4, 3).
Первое решение. Согласно п. Г, имеем (у — 3)(3—4) = (4—3)(х — 4), или после упрощения х + у — 7 =0.
§ 3. Окружность
79
Второе решение. Искомое уравнение имеет вид Ах + By + С = О, и ему должны удовлетворять точки (3, 4) и (4, 3). Следовательно, должно быть
ЗЛ + 4В + С = О, 44 + ЗВ + С = 0.
Считая С заданным, решим эти уравнения совместно относительно А и В; находим
А = В = —. Уравнение прямой записывается в виде
С С , п л
7 7
Так как значение С несущественно, если только С У= 0, выберем С = —7, что приводит к тому же уравнению, что и выше, ф
УПРАЖНЕНИЯ
22. Найдите уравнение прямой с наклоном 4, проходящей через точку (—2, —3).
23. Найдите уравнение прямой с наклоном —1/2, проходящей через точку (1 7).
24. Найдите уравнение прямой, проходящей через точки (—6, 2) и (3, —2).
25. Найдите уравнение прямой, проходящей через точки (0, 2) и (—24, 0).
26. Найдите уравнение прямой с наклоном 3/4, проходящей через точку (100, 30).
27. Найдите уравнение прямой с наклоном 6 и следом 2 на оси у.
2х и
±28. Найдите следы на осях х и у прямой, уравнение которой имеет вид-— — = 1.
3 4
29. Найдите уравнение прямой со следом —2 на оси х и следом 2/5 на оси у.
30. Каков наклон прямой, не проходящей через начала, еледы которой на осях х и у равны друг другу?
31. Найдите уравнение прямой, проходящей через точки (36, —10) и (34. —4).
32. Прямая у = тх + b проходит через точки (1, 2) и (3, 5). Найдите т и Ь.
33. Найдите уравнение перпендикуляра, делящего пополам отрезок, соединяющий точки (3, —1) и (—2, —2).
34. Найдите уравнение прямой, отсекающей от третьего квадранта равнобедренный треугольник площади 4.
35. Найдите точку прямой 2х — у = 1 = 0, равноудаленную от точек (3, 2) и (2, 3).
36. Найдите уравнение прямой, проходящей через начало и параллельной прямой Зх — 2у — 1 = 0.
37. Точки X = (3, —2), Y = (4, 1), Z = (—3, 5) являются вершинами треугольника. Найдите уравнение прямой, проходящей через Y и перпендикулярной стороне XZ.
38. Покажите, что высоты треугольника XYZ из упр. 37 пересекаются в одной точке.
§ 3. ОКРУЖНОСТЬ
3.1. УРАВНЕНИЕ ОКРУЖНОСТИ
Окружность есть множество всех точек, отстоящих на одно и то же расстояние г от некоторой фиксированной точки Q. Точка Q называется центром окружности, а г — ее радиусом; радиус — всегда положительное число. Окружность радиуса 1 с центром в начале координат называется единичной окружностью.
Пусть центр Q имеет координаты (а, Ь). Расстояние от точки (х, у) до Q выражается формулой
У(х-аУ + (у-ЬГ.
80
2. Координаты
Таким образом, окружность с центром (а, Ь) и радиусом г > 0 есть множество решений уравнения
(x-aY + (y-b)*=r\ (1)
Точка (х, у) называется внутренней (соответственно внешней) по отношению к окружности*, если ее расстояние от центра (а, Ь) меньше (соответственно больше) радиуса г. Следовательно, множество точек, внутренних относительно окружности, есть множество решений неравенства (х — а)2 4- (у — Ь)2 < г2, тогда как множество внешних точек задается неравенством (х — а)2 + (у — Ь)2 > г2.
Теорема 1. Пусть А, В, С — числа. Тогда множество решений уравнения
х2 + у2 + Ах -ь By + С = 0 (2)
есть либо окружность, либо точка, либо пустое множество.
Доказательство. Мы применим метод дополнения до полного квадрата, являющийся одним из старейших математических приемов (он был известен еще в древнем Вавилоне). Имеем
, , . » . „ / А \ , . о / А \ , Аа А2 / . А А2
х2 + Ах = х2 2 — х| = х2 4- 2 I—х]4--------=[х4------------>
\ 2 ) \2. / 4 4 \ 2 ) 4
в । о I । В \а В2 у2 + Ву =[у + —\------,
так что уравнение (2) можно записать в виде
+ + + с = о,
\ 2 ) 4 * 2 ) 4
ИЛИ
(х + тУ + (у + т)2 = £’’ (3)
гдеР = (Л2 4* В2)/4 — С. ЕслиР > 0, положим г = Тогда (3) есть уравнение А В
окружности с центром (-----^-) и радиусом г. Если D = 0, то уравнение (3)
означает, что сумма двух неотрицательных чисел (х 4- А/2)2 + (у 4- В/2)2 равна нулю. Следовательно, оба числа должны быть равны нулю. Множество решений состоит из одной точки х = —Д/2, у = —В/2. Наконец, если D < 0, то уравнение (3) не может удовлетворяться никакой парой действительных чисел; множество решений пусто.
ф Пример. Описать множество решений уравнения
2х2 + 2у2 — 2х 4- — 10 =0.
Решение. Разделим сначала обе части уравнения на 2; получаем
х2 4“ У2 — * + 2у — 5 =0.
Дополняем до полного квадрата:
* Множество точек, внутренних по отношению к окружности, вместе со множеством точек самой окружности, называется кругом.
§ 3. Окружность
81
, 2 Q 1 2 0 1 . / 1 V / 1 V / 1 V 1
х2 — х =х2 — 2х • — = х2 — 2х --------Н — I — I — I = *-----1------>
2 2 \ 2 ) \ 2 ) \ 2 ) 4
У2 4- 2у = уг 4- 2у 4- I2 — I2 = (у 4- I)2 — 1;
теперь уравнение принимает вид
fx--LY + (!/+l)2-------J---1-5=0,
\ Z / 4
ИЛИ
/ I \2 I / I 1\2 25
(* ——J + <# + 0 = —•
1 5
Множество решений есть окружность с центром (-^-, —1) и радиусом —
УПРАЖНЕНИЯ
1. Найдите уравнение окружности радиуса 2 е центром в (О, 3).
2. Найдите уравнение окружности радиуса 3 G центром в (—1, 4).
3. Найдите уравнение окружности в центром в (1, 6) , преходящей через точку (—2, 2).
4. Найдите уравнение окружности в центром в (—3, 2), проходящей через точку (-*2, 1).
5. Найдите уравнение окружности радиуса 4, проходящей через точки (—3, 0) и (5, 0).
6. Найдите уравнение окружности радиуса 3 с центром в точке ( —10, 12).
7. Опишите множество решений уравнения х2 + у2 + 2х + 4р + 4 = 0.
Опишите множество решений уравнения х2 4- у2 + 4х — 4у+ 8 = 0.
9. Опишите множество решений уравнения х2 + У2 — х — у 4- 1=0.
10. Опишите множество решений уравнения ха 4- У2 4“ 6х — 2у —6 = 0.
11. Опишите множество решений уравнения 2х2 4~ %У2 + 2х — 2у — 1 =0.
12. Опишите множество решений уравнения 4х2 +4р2 + 8х— 4у 4- 5 = 0.
3.2. КАСАТЕЛЬНАЯ
В качестве примера применения аналитической геометрии мы докажем алгебраическими методами две геометрические теоремы.
Теорема 2. Пересечение прямой I и окружности С либо пусто, либо состоит из одной точки, либо состоит из двух точек.
Доказательство. Выберем координатную систему таким образом, чтобы окружность С была единичной окружностью (для этого надо принять центр окружности за начало координат и радиус — за единицу длины), а прямая / — горизонтальной (для этого надо выбрать ось х параллельной прямой I). Тогда уравнение прямой имеет вид у = Ь. Точка, общая Си/, имеет координаты (х, 6), для которых х2 + b2 = 1, или
X2 = 1 — Ь2. (4)
Если | b | > 1, то 1 — Ь2 < 0, и никакое число х не удовлетворяет (4); это значит, что С и I не имеют общих точек. Если | b | = 1, т. е. b = 1 или Ь = —1, то равенство (4) означает, что х = 0; в этом случае существует в точности одна точка пересечения, а именно (О, Ь), Если же | b | < 1, то 1 — Ь2 > 0, и равенство (4) означает, что либо х = ]/1 — Ь2. либо х = —]/ 1 — 62; в этом случае есть ровно две точки пересечения: (У 1 —Ь2. Ь) и (—]/1 —Ь2. Ь). Теорема доказана.
Диаметр окружности есть прямолинейный отрезок, проходящий через центр окружности, с концами, лежащими на окружности. Касательная к окружности есть прямая, имеющая с окружностью в точности одну общую точку (рис. 2.16).
82
2. Координаты
Теорема 3. Пусть Р — точка окружности С, I — прямая, проходящая через Р\ тогда I есть касательная к С в том и только в том случае, когда I перпендикулярна к диаметру, проходящему через Р.
Доказательство. Выберем координатную систему, как в предыдущем случае. Поскольку Р принадлежит С, уравнение I имеет вид у = Ь, где | b | <1 1. Если I — касательная, то в силу предыдущих рассуждений либо Ь = 1, либо Ь = = —1. Это значит, что либо Р = (0, 1), либо Р =(0, — 1). В обоих случаях^прямая ОР вертикальна и тем самым перпендикулярна /. Если / — не касательная, то в силу предыдущих рассуждений | < 1. Тогда Р есть либо точка (У 1—Ь2, Ь), либо точка (—У1—Ь2, Ь). Наклон прямой ОР равен либо &/]/ 1 — b2, либо —b/У 1 — Ь2\ она не вертикальна и потому не перпендикулярна /.
Заметим, что доказательства теорем 2 и 3 получились столь легкими потому, что мы надлежащим образом выбрали систему координат.
Вопрос о длине окружности и о площади круга пока не рассматривается: он отнссится не к аналитической геометрии, а к (математическому) анализу.
УПРАЖНЕНИЯ
13. Окружность с центром в (1, 2) проходит через точку (— 1, 1). Каков наклон прямой касающейся этой окружности в точке (—1, 1)?
14. Прямая проходит через точку окружности (0, 1), но ни через какую другую ее точку. Каков наклон прямой, если центр окружности находится в точке (—1, 3)?
15. Уравнение окружности есть х2 + у2 — 10х = 28. Найдите уравнение касательной, проходящей через точку окружности (3, 7).
16. Уравнение окружности есть х2 + у2 + 4х — 8у — 5=0. Каково уравнение касательной к окружности в точке (1,0)?
17. Уравнение окружности есть х2 + у2 — 2х — 24 = 0. В какой точке касательная к окружности в точке (1,5) пересекается с касательной к окружности в точке (4, —4)?
J^18. Пусть прямая у = х касается окружности в точке (3, 3), а прямая у = 2х проходит через центр окружности. Каково уравнение окружности?
19. Найдите уравнение прямой, касающейся окружности х2 + у2 = 1 и проходящей через точку (3, 1).
20. Найдите уравнения всех прямых, касающихся окружности х2 + у2 — 2х = 0 и проходящих через точку (4, 0).
§ 4. Парабола
83
§ 4. ПАРАБОЛА
Силу методов аналитической геометрии в полной мере можно оценить, лишь рассматривая кривые, более сложные, чем прямая и окружность. Мы рассмотрим в этом параграфе параболу — кривую, открытую древнегреческими геометрами. (Изучение параболы будет продолжено в гл. 10. Там мы рассмотрим также еще две новые кривые: гиперболу и эллипс.)
4.1. ОПРЕДЕЛЕНИЕ ПАРАБОЛЫ
Пусть I — прямая и F — точка, не принадлежащая I. Парабола с директрисой / и фокусом F определяется как множество всех точек, равноудаленных от I и F (рис. 2.17). Это значит, что точка Р принадлежит параболе в том и только в том случае, когда
расстояние от Р до F = расстоянию от Р до I. (1)
Мы хотим представить параболу как множество решений некоторого уравнения. Уравнение это будет зависеть от выбора системы координат; мы попытаемся выбрать ее таким образом, чтобы уравнение оказалось простым.
Опустим перпендикуляр из F на /; он пересекает I в точке R. Примем за начало координат середину отрезка FR, а горизонтальное направление будем считать параллельным /. Тогда F имеет координаты (0, р), где ру= 0, а / имеет уравнение у = —р (рис. 2.18). Пусть точка Р имеет координаты (х, у). Тогда по формуле расстояний (см. § 1.3) имеем
расстояние от Р до F = ]Лх2 + (у — р)2.
Далее, как видно из рис. 2.18,
расстояние от Р до I = | у + р)2.
(Можно рассуждать также следующим образом. Точка Q с координатами (х, —р) лежит на /, а прямая, проходящая через Р и Q, перпендикулярна /. Поэтому расстояние от Р до I равно расстоянию от Р до Q, а это последнее, по формуле расстояний, равно У (у + р)2 = | у + р |.] Теперь условие (1) можно записать в виде
У*2 4- (у — р)2 = |у 4- р|, а это значит (поскольку неотрицательные числа равны в том и только в том случае, когда равны их квадраты), что
х2 А-(у — р)2 = (у 4- р)2, или
х2 4* У2 — 2 РУ + Р2 = у2+ 2ру + р2,
т. е.
х2 = Ару.
(2)
84
2. Координаты
Тем самым мы доказали следующую теорему:
Теорема 1. Множество решений уравнения хг = 4ру при любом р =# О есть парабола с фокусом (0, р) и директрисой у = —р.
Если мы выберем в качестве единицы длины удвоенное расстояние между фокусом и директрисой, а вертикальное направление так, чтобы фокус лежал в верхней полуплоскости, то имеем р = ----и уравнение (2) принимает простой вид
У = х2. (3)
При изучении геометрических свойств параболы мы можем ограничиться этим уравнением.
Парабола (3) изображена на рис. 2.19. Этот чертеж получен путем вычисления координат многих точек (х, х2) и нанесения их на координатную плоскость. Другие параболы имеют ту же форму, хотя и другое расположение и размеры. В этом отношении параболы напоминают окружности. Для любой окружности существует координатная система, в которой уравнение этой окружности имеет вид х2 + У2 = 1: достаточно в качестве начала координат выбрать центр окружности, а ее радиус принять, за единицу длины. Точно так же для любой заданной параболы существует координатная система, в которой уравнение этой параболы имеет вид у = х2. Это можно выразить так: все окружности подобны друг другу, все параболы подобны друг другу. (Аналогично, все квадраты подобны друг другу, но для треугольников это уже, конечно, не будет верно.)
4.2. СВОЙСТВА ПАРАБОЛЫ
Прямая, проходящая через фокус параболы и перпендикулярная ее директрисе, называется осью параболы. Точка пересечения параболы с ее осью называется вершиной параболы. В случае, когда уравнение параболы имеет вид у = х2, ось совпадает с осью у, а вершина — с началом координат.
§ 4. Парабола
85
Рис. 2.19
Вершина ближе к директрисе^ чем любая другая точка параболы.
Чтобы доказать это, мы можем взять уравнение параболы в виде у = х2, выбрав надлежащим образом систему координат. Тогда вершина имеет координаты (0, 0), а директриса есть прямая у = —1/4. Расстояние от вершины до директрисы равно 1/4, а расстояние от любой точки параболы (х, у) до директрисы равно у + 1/4; поскольку у = х2> 0, оно всегда >>1/4.
Если точка (х, у) удовлетворяет уравнению у = х2, то и точка (—х, у) удовлетворяет тому же уравнению. Но точки (х, у) и (—х, у) симметричны друг другу относительно оси у. Это значит, что соединяющая их прямая перпендикулярна оси у и что обе точки равноудалены от оси у. Итак, парабола симметрична относительно своей оси.
Фокальная хорда параболы определяется как лежащий внутри параболы отрезок прямой, проходящей через ее фокус и параллельной директрисе. Точнее, парабола пересекает эту прямую в двух точках и тем самым делит ее на три части, две из которых имеют бесконечную протяженность; оставшийся конечный отрезок и есть фокальная хорда (рис. 2.20). Для параболы у = х2 фокус находится в точке (0, 1/4), а прямая, проходящая через фокус и параллельная директрисе, имеет уравнение у = 1/4. Она пересекает параболу в точках, в которых 1/4 = х2. Таким образом, конечные точки фокальной хорды — это (— 1/2, 1/4) и (1/2, 1/4), а длина ее равна 1.
УПРАЖНЕНИЯ
В упражнениях 1—6 начертите каждую параболу и изобразите на чертеже вершину, фокув, директрису и ось.
1. Найдите фокус и директрису параболы х2 = 8у.
2. Найдите фокус и директрису параболы 8ха '=» у.
3. Найдите уравнение параболы, Директрисой которой является прямая у = 3, а фокусом— точка (2, 1). Найдите вершину и ось симметрии этой параболы. [Указание. Сначала попытайтесь вывести уравнение прямым путем, как это сделано в тексте: вычислите рав-стояния от точки (х, у) до фокуса и до директрисы, приравняйте их друг другу и упростите уравнение. Затем попытайтесь вывести уравнение из уже имеющегося в тексте, пользуясь новой системой координат и формулами замены координат. Конечно, Вы должны получить обоими способами одно и то же уравнение.]
86
2. Координаты
J^4. Найдите уравнение параболы, директрисой которой служит прямая у = 1, а фокусом — точка (—2, —4). Найдите вершину и ось симметрии этой параболы.
5. Найдите уравнение параболы, директрисой которой служит прямая х = 2, а фокусом — точка (1, 1). Найдите вершину и ось симметрии этой параболы.
6. Найдите уравнение параболы, директрисой которой служит прямая х = 0, а фокусом — точка (—4, 2). Найдите вершину и ось симметрии этой параболы.
7. Найдите концы и длину фокальной хорды параболы х2 = 16^/. Начертите параболу и ее фокальную хорду.
8. Найдите концы и длину фокальной хорды параболы х2 == \ру.
9. Директрисой параболы является прямая у = 1, а фокусом точка (2, 9). Найдите концы фокальной хорды. Начертите параболу и ее фокальную хорду.
10. Директрисой параболы является прямая х = 2, а фокусом — точка (—1, 1). Найдите концы фокальной хорды. Начертите параболу и ее фокальную хорду.
4.3. ПАРАБОЛА С ВЕРТИКАЛЬНОЙ ОСЬЮ
Теорема 2. Пусть А, В, С — числа, причем В у= б. Тогда множество решений уравнения
хг + Ах+Ву+С=^ (4)
есть парабола с вертикальной осью.
Доказательство. Дополняя до полного квадрата, перепишем равенство (4) в виде
(А \2 Д2
*+“•) -^- + Ву + С=0,
или
(х + Л\* = _вв_0 + ±. = _BL_ .?.-«). (6)
\ 2 ) 4 V 4В )
Введем новую систему координат, полученную из нашей первоначальной системы посредством (параллельного) переноса, так что новые координаты X, Y связаны со старыми координатами х, у равенствами
В частности, новое начало имеет при этом в старой системе координаты
/___А_ Я2 —4С\
\ 2 ’ в
Положим также — В = 4р. Тогда уравнение (5) принимает вид
X2 = 4рГ, что, как мы знаем, есть уравнение параболы, ф Пример. Найти фокус и директрису параболы
Xй + 4х + 2у — 1 =0.
§ 4. Парабола
87
Решение. Запишем уравнение в виде
(х 4- 2)2 — 4 + 2у — 1 =6, или
- 2 (у-----7) = (* + 2)®.
5
Полагая *4-2 = X и у----------%- = У, приводим это уравнение к виду — 2Y = X2.
По теореме 1, это уравнение параболы с фокусом X = О, Y = —1/2 и директрисой Y =1/2. Следовательно, в первоначальной системе координат (х, у) фокус нашей параболы находится в точке (—2, 2), а директриса имеет уравнение у = 3. Парабола изображена на рис. 2.21. ф
УПРАЖНЕНИЯ
Найдите фокус и директрису для каждой параболы, уравнение которой указано ниже. Навертите параболу, отметьте вершину, фокус, директрису и ось.
11. х2 — 6л* — 7 — 8у = 0. 14. 4ха — 4х — 7 = 16f.
12. 2х2 + 4х + 5 + у = 0. 15. 4х2 — 4х + 1 = у.
13. х2 — 14х + 1 = 16у. 16. х2 + 8х + 17 = —4#.
4.4. КАСАТЕЛЬНАЯ
Рассмотрим теперь, что представляет собой пересечение параболы с прямой.
Теорема 3. Прямая либо вовсе не пересекает параболу, либо пересекает ее в одной точке, либо пересекает в двух точках.
Доказательство. Пусть координатная система выбрана таким образом, что уравнение параболы имеет вид у = х2.
Рассмотрим сначала вертикальную прямую, т. е. прямую, параллельную оси параболы. Такая прямая имеет уравнение х = а, где а — некоторое число. Она перетекает параболу в точке (а, а2) и ни в какой другой точке.
88
2. Координаты
Если невертикальная прямая у = тх + Ь пересекает параболу у = х2, то координата х точки пересечения удовлетворяет квадратному уравнению
тх + b = х2.
Дополняя до полного квадрата, имеем
(т \2 . . /и2
*--г) <6>
Если правая часть отрицательна, то точек пересечения нет\ если она равна нулю, есть одна точка пересечения; если положительна — две точки пересечения. Это и доказывает теорему.
Прямая, пересекающая параболу в одной точке и не параллельная ее оси, называется касательной к параболе.
Теорема 4. Через каждую точку параболы проходит в точности одна касательная. Если рассматриваемая парабола есть у = х2 и точка имеет координаты (х, х2), то касательная имеет наклон 2х.
Доказательство. Касательная есть прямая у == тх +- Ь, пересекающая параболу в точности в одной точке. Согласно предыдущему доказательству, коорди-.ната х точки пересечения удовлетворяет уравнению х — = О [см. формулу (6)].
Поэтому наклон т равен 2х.
Теорема 5. Пусть Р — точка параболы, отличная от ее вершины. Тогда касательная в точке Р пересекает ось параболы в такой точке Q, что Р и Q равноотстоят от прямой, проходящей через вершину параболы и перпендикулярной ее оси (рис. 2.22).
Доказательство. Можно выбрать координатную систему так, чтобы парабола имела уравнение у = х2. Пусть Р имеет координаты (а, а2), где а 0. Наклон касательной к параболе в точке Р равен 2а. Согласно п. Б § 2.4, уравнение касательной можно записать в виде
у — а2 = 2а(х — а).
При х = 0 получаем у = —а2. Следовательно, Q = (0, —а>2), откуда видно, что Р и Q равноудалены от оси х.
Сделаем одно замечание по поводу определения касательной. Мы определили касательную к окружности в точке Р как прямую, пересекающую окружность в точке Р и только в этой точке. В случае параболы такое определение непригодно. В самом деле, для каждой точки параболы существуют две прямые, пересекающие параболу только в этой точке: прямая, параллельная оси, и другая прямая («касательная»). Чувствуется, что эта другая прямая и есть «настоящая» касательная, она «как раз касается» параболы, тогда как прямая, параллельная оси параболы, просто пересекает параболу.
Теоремы 3 и 5 были известны грекам. Задача о разыскании касательных к другим кривым была одним из стимулов, приведших к развитию анализа.
ф Пример. Найти такую точку Q параболы у = х2, чтобы касательная в точке Q была перпендикулярна касательной в точке (2, 4).
Решение. Касательная в точке (2, 4) имеет наклон 4; касательная в точке Q = (х, х2) — наклон 2х. Должно быть 4- 2х = —1, откуда х =-g- и Q (— -g-, -^-).ф
$ 5. Квадратура параболы
89
УПРАЖНЕНИЯ
17. Найдите уравнение касательной к параболе у = х2 в точке (—2, 4).
18. Найдите точку, в которой касательная к параболе у = х2 в точке , -pg-j пересекает продолжение фокальной хорды параболы. Начертите параболу, ее фокальную хорду и касательную.
19. В какой точке пересекаются касательные к параболе у = х2, проведенные в точках (2, 4) и (4, 16)?
А 20. Найдите такую точку Q параболы у = х2, чтобы касательная к параболе в Q была перпендикулярна касательной к той же параболе в точке (—10, 100).
21. Касательная к параболе у = х2 в точке Q пересекает продолжение фокальной хорды в точке, где х = 1. Какие координаты может иметь Q?
22. Найдите наклоны всех касательных к параболе у = х\ проходящих через точку (4, —9)*. Начертите параболу и касательные.
Приложение к главе 2
§ 5. Квадратура параболы
5.1. Теорема Архимеда
Задача о касательных была одним из стимулов развития анализа. Другим стимулом была задача о площадях: как вычислить площадь области с криволинейной границей. Главный результат анализа состоите том, что эти две, казалось бы, очень разные задачи, теснейшим образом ввязаны между собой. (Эта связь будет пояснена в гл. 5.)
Греки пытались решить очень трудную задачу о площади: они хотели осуществить «квадратуру круга», т. е. построить с помощью циркуля и линейки квадрат, площадь которого была бы в точности равна площади заданного круга. Это невозможно; доказательство невозможности такого построения было дано лишь в XIX в. Но Архимед, величайший математик древности, сумел квадрировать область, ограниченную дугой параболы. Вот его знаменитая теорема:
Рассмотрим прямоугольник, одной ив вершин которого является вершина параболы, противоположной ей вершиной — другая точка параболы, а одна ив сторон принадлежит оси параболы. Тогда парабола делит площадь этого прямоугольника в отношении 2 : 1 (рис. 2.23).
5.2. Доказательство Архимеда
Мы изложим здесь (в современных обозначениях) одно из доказательств Архимеда. Пусть парабола задана уравнением у = х2 и вершины прямоугольника суть (0, 0) и (а, а2), где а >0 (рис. 2.23). Площадь прямоугольника равна а*а2 = а8. Пусть S — площадь части прямоугольника под параболой. Надо показать, что
s = V а3- (П
О
Заметим, что мы не задаемся здесь вопросом, чтб понимается под площадью фигуры, ограниченной некоторой кривой, а полагаемая на наше интуитивное представление е площадях.
Для доказательства равенства (1) используем формулу
Р + 2»+3«4-...+л« = -5-л’+4'л8+4"п* (2>
О Z о
90
Приложение к главе 2
Рис. 2.24
доказанную в гл. 1 (см. § 6.3). Другое доказательство этой формулы мы дадим ниже в этом параграфе.
Пусть п — целое положительное число. Разделим интервал (0, а) на п равных отрезков точками 0, ^2_ , ...» (n U?, а (см. рис. 2.24, где л=6). Каждый отрезок имеет длину-2- . Над
п п п п
каждым из этих отрезков мы строим «длинный» прямоугольник, верхний правый угол которого принадлежит параболе, и «короткий» прямоугольник такой, что параболе принадлежит его верхний левый угол; над отрезком (0,-2_) короткого прямоугольника, нет. Высоты длинных п прямоугольников равны
так что сумма их площадей равна
а3 Л а3 / п3 п2 п \
или, что то же,
о,3 a3 а3
Т+ 2п +-6п* *
(3)
Площадь каждого короткого прямоугольника равна площади соответствующего длинного прямоугольника минув площадь малого прямоугольника (густо заштрихованного на рис. 2.24). Каждый из этих малых прямоугольников имеет ширину-2-. Если поставить их друг на друга, п
то высоты их дают в сумме а2. Таким образом, их общая площадь равна-21. п
Сумма площадей коротких прямоугольников равна поэтому числу (3) минус — , т. е. п
§ 5. Квадратура параболы
91
а3 Т а3 । а3 1 а3 »| «1
2п 6п2 п 3 2п 6п2
Очевидно, S меньше (3) а3 и больше (4), а3 а3 т. е. д3 д3 д3
• — 4- 4— -
т 2п 6п2 3 2п бп2
Поскольку 1 1 2л 1 6л2 Зп + 1 6л2 <2 бп 1_ 6п2 п
и 1 2л + 1 6п2 -Зл+ 1 6п2 — бп — 1 6л2 п
имеем
(4)
а3 д3 д3 д3
3 п 3 п
Вычитая из всех членов этих неравенств д3 1
и умножая их на — , получаем д3
1 1
3 < п
1 S п < д3
Это справедливо при всех п = 2, 3, 4,
поэтому-^- = ,
д3 3
что и доказывает требуемое соот-
ношение (1).
Доказательство Архимеда было одним из первых результатов математического анализа. Мы увидим дальше, что с помощью более общего метода та же задача решается гораздо проще.
5.3. Сумма квадратов
Дадим теперь другое доказательство формулы (2). Для любого числа i имеем (1 +03 —*3 = 3/2 + з/+ 1.
Запишем это равенство для t = 1,2, ...» п — 1, п:
23 — I3 = 3.12 + 34 + 1,
З3 — 23 = 3-22 + 3-2 + 1, г
(п + 1)3 _ яз = 3.Я2 + з.„ + L
Складывая все п равенств, имеем
(п + I)3 — 1 = 3(12 + 22 + ... + л2) + 3(1 + 2 + ... + л) + л.
Заменяя здесь 1 + 2 + ... + л на разрешая полученное равенство относительно
I2 + 22 + ... + л2 и упрощая, приходим к формуле (2).
92
Приложение к главе 2
УПРАЖНЕНИЯ
1. Пусть вершины прямоугольника находятся в точках (0, 0), (2, 0), (0, 4), (2, 4). Найдите площадь каждой из двух областей, на которые этот прямоугольник делится параболой у = х2.
2. Найдите площадь области, ограниченной параболой у = х2 и ее фокальной хордой.
3. Найдите площадь прямоугольника, основанием которого является интервал [2, 3], а верхний левый угол принадлежит параболе у = №.
4. Найдите площадь прямоугольника, основанием которого является интервал [2, 3], а верхний правый угол принадлежит параболе у = №.
б. На каждом из интервалов [ ?] п0СТР°йте прямоуго-
льник, верхний правый угол которого принадлежит параболе у = х2. Найдите сумму площадей этих прямоугольников. Сравните ваши вычисления шаг за шагом с вычислениями в тексте для любых аи п и покажите, что они согласуются между собой.
6. На каждом из интервалов » [“£” » 1] > [ » [“f"’ 2] постройте прямоуголь-
ник, верхний левый угол которого принадлежит параболе у = х2 (высота прямоугольника над первым интервалом равна нулю, так что этим прямоугольником можно пренебречь). Найдите сумму площадей этих прямоугольников. Сравните ваши вычисления шаг за шагом с вычислениями в тексте для произвольных а и п и покажите, что их результаты согласуются.
7. Найдите площадь области в первом квадранте, ограниченной параболой у ® х2, осью х и прямой х = 2, и сравните ее с числами, полученными в упр. 5 и 6. Проверьте, что а3
разность между этими числами равна — и что рассматриваемая площадь действительно заключена между ними'.
§ 6. Геометрия и числа
6.1. Аксиоматическая геометрия
Слово «геометрия» буквально означает «измерение земли», т. е. землемерие. Первоначально геометрия была практическим ремеслом, а как наука носила чисто экспериментальный характер. Геометрия как дедуктивная наука создана греками. Фалесу, по преданию, первому греческому философу, приписывается также первое доказательство геометрической теоремы. В дедуктивной геометрии некоторые простые предложения о точках и прямых (а в случае пространственной геометрии — также и о плоскостях) принимаются в качестве аксиом; все остальные предложения суть теоремы, т. е. логические следствия аксиом.
Платон, на философию которого оказала влияние греческая математика, подчеркивал, что дедуктивная геометрия рассматривает не физические, а идеальные, абстрактные фигуры. Прямая геометра — не линия, начерченная на бумаге, не натянутая веревка и не луч света. Чертежи представляют собой лишь средство, помогающее памяти и стимулирующее воображение. Современные математики принимают точку зрения Платона, хотя, пожалуй, не в ее первоначальном смысле. Существенно здесь то, что никакие понятия или свойства, кроме явно перечисленных в аксиомах, не должны применяться в доказательствах.
Конечно, это не значит, что геометрия не имеет ничего общего с реальным миром. Аксиомы выбираются именно так чтобы они отражали некоторые свойства физического мира. Абстрактный же характер определений и доказательств обеспечивает справедливость теорем, если предположить, что верны аксиомы. Как показывает история науки, математика становится все более универсальным (а тем самым все более полезным) орудием исследования природы, по мере того как она приобретает все более абстрактный характер.
Строго логическое построение геометрии на основе аксиом было задачей «Начал» Евклида*, труда, подведшего итоги целого столетия развития греческой математики и ставшего второй по влиянию книгой в истории нашей цивилизации. Огромные достижения Евклида и его предшест-
* русский перевод (в трех томах): М.—Л., Гостехиздат, 1948—1950.
$ 6. Геометрия и числа
93
венников ни в коей мере не умаляются тем обстоятельством, что в точки зрения нынешних требований строгости они не достигли поставленной ими же цели. Система аксиом, действительно достаточная для построения всей евклидовой геометрии, была создана сравнительно недавно. Книга Гильберта «Основания геометрии**, содержащая такую систему, была опубликована в 1899 г.
6.2. Аналитическая геометрия
Мы не намерены перечислять аксиомы Гильберта. В этом нет надобности поскольку их можно резюмировать одной фразой: евклидова геометрия есть аналитическая геометрия, основанная на декартовой системе координат. Объясним это подробнее.
Допустим, что мы знаем действительные числа, либо построив, их из целых положительных чисел, например с помощью бесконечных десятичных дробей, либо приняв аксиомы 1—18 предыдущей главы. Определим плоскость как множество всех упорядоченных пар Кисел (х, у). Каждая такая пара называется точкой. Расстояние между точками (xj, у^) и (ха, yz) определяется как число (xj — хз)а + (yt — yz)2 . Прямой, по определению, называется множество всех точек (х, у), удовлетворяющих некоторому уравнению вида Ах + By + С = 0, где А, В. С — такие числа, что А2 + В2 =/= 0 (условие А2 4* В2 =/= 0 означает, что числа А и В не равны нулю одновременно).
Приняв эти соглашения, мы можем перевести каждую из аксиом Гильберта, поскольку они относятся к плоскости, в утверждение о числах; обнаруживается, что все эти утверждения можно доказать исходя из аксиом 1—18.
Обратно, исходя из аксиом Гильберта, можно построить декартову систему координат, вывести формулу расстояний и т. д. По существу, это мы и делали в § 1—4, но пользовались при этом геометрией неформально, не апеллируя во всех построениях к аксиомам Гильберта.
Точно так же можно строить геометрию в пространстве — стереометрию. Если считать стереометрию уже известной, то можно доказать следующее: множество точек (х, у, г) пространства, декартовы координаты которых удовлетворяют линейному уравнению
Ах + By + Cz + D = О,
где числа А, В, С не равны нулю одновременно, есть плоскость, и любая плоскость может быть представлена как множество точек (х, у, г), удовлетворяющих подобному уравнению (до-
ФАЛЕС (VI в. до и. ».J. Сведения о математических и астрономических достижениях Фалеса считаются исторически недостоверными.
ПЛАТОН (429—348 до и. ».), ученик Сократа и основоположник идеалистической философии, положил также начало университетскому образованию. Он учредил Академию — школу, просуществовавшую около тысячи лет.
Этот великий мыслитель и писатель восхвалял математику как путь к истинному знанию и предназначил ей видное место в программе Академйи. Хотя сам Платон и не был математиком и даже нет доказательств того, что он полностью владел математическими достижениями своего времени, традиция Платона сыграла видную роль в создании современной математической науки.
ЕВКЛИД (ок. 365—300 до и. ».|. До недавнего времени большая часть учебников геометрии для средней школы представляла собой более или менее упрощенные версии «Начал» Евклида. Но сама книга Евклида не была предназначена для элементарного образования. Это был ученый трактат по геометрии, а также по теории чисел, излагающий результаты предшественников Евклида и его собственные.
Давид ГИЛЬБЕРТ (1862—1943) был самым влиятельным математиком XX в. Он был профессором в Гёттингене, бесспорной столице мировой математики до ее разрушения нацистами в 1933 г. Гильберт обычно посвящал несколько лет интенсивной работе в одной из областей математики, а затем покидал ее, чтобы перейти в другую. Таким образом, он полностью изменил лицо многих областей математики. *
Русский перевод (последний): М.—Л., Гостехиздат, 1948.
94
Приложение к главе 2
казательств© этого будет дано лишь в гл. 9, § 4, поскольку раньше этот результат нам не понадобится). Тем самым мы имеем ключ к чисто аналитическому построению стереометрии. Пространство определяется при этом как множество всех упорядоченных троекчисел (х, у, г). Эти тройки называются точками. Расстояние между двумя точками определяется формулой (4) § 1. Множество всех точек, удовлетворяющих линейному уравнению Ах 4- By + Cz 4” D = 0, где 42 + В2 + С2 =£ 0, называется плоскостью. Прямая в пространстве есть, по определению, множество точек пересечения двух различных плоскостей, имеющих общую точку.
. Здесь снова оказывается, что-все аксиомы Гильберта для стереометрии могут быть выведены из аксиом 1—18 действительных чисел.
6.3. Алгебраический вывод аксиом
В следующих двух примерах геометрические аксиомы выводятся из свойств чисел.
1. Пусть Р и Q — две различные точки; тогда существует прямая, содержащая их.
Две различные точки — это две различные упорядоченные пары чисел (дгт, у^) и (лгг, «Прямой, их содержащей», называется множество решений линейного уравнения которому удовлетворяют пары (xY и txt, у Такое уравнение мы вывели в § 2 (уравнение (8)].
11. Две различные прямые имеют не более одной общей точки.
Эта аксиома означает, что если множества решений двух линейных уравнений
Др 4- ВАу -h Cf = 0 и А2х 4- В^у 4- Се = 0 (1)
не совпадают, то существует не более одной точки иг, у), удовлетворяющей обоим уравнениям. При этом предполагается, что Д? 4- Bf =/= 0 и А% + В$ Ф О- В самом деле если точка (лг, у) удовлетворяет обоим уравнениям, то она удовлетворяет также уравнениям, полученным: (а) умножением первого уравнения на В 2. второго на В^ и последующим их вычитанием; (б) умножением первого уравнения на Да, . второго на Дх и последующим их вычитанием. Полученные уравнения имеют вид
(А^В2 —- А2В^)х = — В26$ 4- (Дт.В2 — А2В$)у в Д2С{ *“ А^Ф^, (2)
Если AiB2 А2Вг =/= 0, то находим
__ — #2^1 4~ #10» * __ ^2^1 *— ^1С2
Х~ АхВг —А^В^ ’ У~ А^—А^ ’’
как единственно возможное решение уравнений (1). Как показывает подстановка значений (3) в эти уравнения, это .действительно их общее решение
Далее, если Д1#2 — А2В^ = 0 и если существует точка (х у), удовлетворяющая обоим уравнениям (2), то В2&? — в Av&t — А^2 = 0. Если Д^ 0, имеем
а это значит, что Д 2 =/= 0, поскольку не может быть А 2 в Да = 0. Теперь второе уравнение (1) приводится к виду
( Яг Сх\ л -'(‘+т,+т)-с’
или
Да
(Aix 4* В1У 4- Сх) в 0»
и оба уравнения (1) имеют, таким образом, одно и то же множество решений. То же заключение справедливо, как читатель может проверить, ори ДщВ2 — Да^г ™ 0 и Bj 0.
Задачи
95
6.4. Пространства более чем трех измерений
Изложенная выше арифметическая интерпретация геометрии сразу же приводит к понятию /l-мерного пространства, где п — любое целое положительное число. Точка этого пространства есть упорядоченная последовательность из п действительных чисел (xlt хг, ...» хп). Расстояние между точками, например точками (аг....аЛ) и (0Х, 0Л), определяется с помощью формулы
К(а!-М2 + ••• + (“»-?п)2 •
Далее, (п — 1)-мерной гиперплоскостью называется множество решений линейного уравнения
А1Х1 + ^2Х2 + • • * + Апхп "Ь = 0,
в котором не все коэффициенты А равны нулю. Множество точек, равноудаленных от фиксированной точки, называется [(п — 1)-мерной] сферой. Следуя этому пути, можно построить n-мерную геометрию. Эта геометрия не имеет ничего общего с теми тайнами, которыми окружают «четвертое измерение» философы и авторы научно-фантастических сочинений. Каждое предложение n-мерной геометрии есть попросту некоторое утверждение о числах. По аналогии с «видимыми» случаями п = 1, 2, 3, геометрический язык помогает ставить интересные вопросы и предугадывать правильные ответы на них.
Первоначальной мотивировкой построения n-мерной геометрии было стремление математиков к обобщению понятий до их естественных логических рамок. Однако n-мерные пространства, как и более сложные пространства бесконечного числа измерений, не являются всего лишь чисто математической игрой: они стали необходимым рабочим орудием современной физики.
На протяжении всей этой книги мы будем.пользоваться геометрическим языком и геометрическими рассуждениями. Но все наши утверждения будут такого рода, что их легко доказать как утверждения о действительных числах. Немногие .исключения будут особо оговорены.
УПРАЖНЕНИЯ
1. Принадлежит ли точка (0, 1, 3, —2) гиперплоскости Зхх + 2хг — х3 + х4 + 3 = О?
2. Принадлежит ли точка (2, 0, —1, 4) гиперплоскости Зхх — хъ + х4 — 2 = 0?
3. Принадлежит ли точка (0, 0, 0, 1, 0) гиперплоскости 5хх + хъ — х3 + 6х4 — 7х5 — 6 = = 0?
4. Каково расстояние между точками (0, 0, 0, 0) и (—2, —1, 3, 1)? [Заметьте, что нет смысла спрашивать о расстоянии между точками (0, 0, 0) и (2, —1. 3, 1). Почему?]
^5. Каково расстояние между точками (0, 1, 0 , 1) и (1, 1, 2, —3)?
6. Гиперплоскость хх = 2 пересекает трехмерную сферу
*1 + х% + х% + х% = 9
по обычной (двумерной) сфере. Найдите радиус и центр этой сферы.
ЗАДАЧИ
1. Покажите, что при любом выборе числа b уравнение х2 + у2 — 2by = 1 есть уравнение окружности, проходящей через точки (1, 0) и (— 1, 0). Где находится центр этой окружности?
2. Напишите, уравнение всех окружностей, проходящих через точки (а, Ь) и (с, d) (предполагая эти точки различными).
3. Дайте аналитическое доказательство теоремы о том, что через любые три точки плоскости, не принадлежащие одной прямой, проходит единственная окружность.
4 Обобщив рассуждения § 3, покажите, что множество решений уравнения
х2 + у2 + г2 + Ах + By + Cz + D = 0
есть либо сфера, либо точка, либо пустое множество.
96 Приложение к главе 2
5. Дайте аналитическое доказательство теоремы о том, что пересечение сферы с плоскостью либо пусто, либо состоит, из одной точки, либо является окружностью. [Указание: введите удобно расположенную систему координат.]
6. Для четырех точек в пространстве, не принадлежащих одной плоскости,существует единственная сфера, проходящая через эти точки. Докажите это аналитически. [Указа-н и е: введите систему координат, в которой одна из данных точек служит началом, другая принадлежит оси х, а третья — плоскости г = 0.J
7. Найдите параболу с вертикальной осью, проходящую через точки (1, 3), (2, —3) и (4, 6).
8 Докажите, что для трех заданных точек плоскости Р, Q, R и прямой I существует единственная парабола, проходящая через Р, Q, R, ось которой параллельна Z, если только ни один из отрезков PQ, QR и RP не параллелен /.[Указание: введите удобно расположенную систему координат.]
9. Рассмотрим параболу о вертикальной осью, вершиной О и фокусом F. Предположим, что прямая, проходящая через F, пересекает параболу в двух различных точках Р и Q. Отрезок PQ и дуга параболы ограничивают некоторую область R; обозначим ее площадь через А. Выразите А через длины OF и PQ.
10. Теоремы, доказанные в задачах 3 и в, имеют обобщения для четырехмерного, а также для любого л-мерного пространства. Сформулируйте эти обобщения.
3/ФУНКЦИИ
В этой главе начинается изучение математического анализа. Здесь развивается язык функций и пределов. Читатель, которому изучение этого нового языка покажется утомительным, может пропустить некоторые части главы, возвращаясь к ним по мере надобности.
Приложение к этой главе состоит из трех параграфов. Первый из них (см. § 5) посвящен односторонним пределам, бесконечным пределам и пределам на бесконечности; он может быть опущен при первом чтении. Остальные два параграфа содержат доказательства некоторых теорем, сформулированных, но не доказанных в основном тексте. Поскольку эти теоремы геометрически очевидны, читатель может пока принять их на веру.
98
3. Функции
§ 1. ФУНКЦИИ И ГРАФИКИ
В математическом анализе и во всех его разветвлениях господствуют понятие непрерывности и связанное с ним понятие предела. Нынешняя форма была придана этим понятиям в XIX в., главным образом Коши и Вейерштрассом. Поскольку основоположники анализа ими не владели,первые шаги анализа были как бы окутаны тайной; математики применяли новое мощное орудие для решения задач и открытия закономерностей, не будучи в состоянии обосновать свои методы.
Но при изложении анализа современному читателю можно обойтись без всякой таинственности. Мы будем свободно пользоваться понятием непрерывности с самого начала. Чтобы разъяснить его, определим сначала, что такое функция.
1.1. ФУНКЦИИ
Функцией в математике называется правило, сопоставляющее каждому элементу некоторого множества элемент того же или другого множества. В первой половине этой книги речь идет главным образом о функциях, сопоставляющих каждому действительному числу из некоторого множества чисел другое действительное число. Такие функции называются действительнозначными функциями действительного переменного; начиная с этого места мы будем называть их просто функциями. Множество чисел, которым сопоставляются другие числа, называется областью опре-' деления функции. Мы будем считать, что область определения функции представ-'Ляет собой интервал или совокупность нескольких интервалов. В частности, областью определения может быть вся числовая прямая. Мы обычно не будем указывать область определения, если в этом не будет необходимости; часто она будет видна из контекста.
Правило, сопоставляющее одному числу другое, может быть любого характера. Можно, например, сопоставить каждому числу его квадрат. Мы запишем эту функцию в виде
X 1-> х2
(читается: «х переходит в х2»). Здесь х — переменная; она представляет любое действительное число. Правило сопоставляет каждому числу другое число; областью определения в этом случае является вся числовая прямая.
Часто для обозначения числа, сопоставляемого другому числу по нашему правилу, пользуются другой переменной; обозначая такую переменную через yt можно записать
х »-► у = х2,
или, короче,
У = х*.
При этом х (представляющий число, которому сопоставляется другое число), называется независимой переменной, а у (представляющий число, сопоставляемое первому) — зависимой переменной.
§ 1. Функции и графики
99
Функция х ь-* х2 сопоставляет числу 2 число 4, числу — 7 число 49 ит. д. Мы будем говорить, что функция равна 4 в точке 2, или что она принимает значение 49 в точке — 7.
Символы, применяемые для обозначения переменных, конечно, несущественны. Записи
р=а2, w*-*u yt-*x=y2
описывают одну и туже функцию, ибо во всех случаях правило будет одним и тем же: числу ставится в соответствие его квадрат.
Функция
1 Хн>---
X
сопоставляет каждому числу (конечно, за исключением числа 0) ему обратное. Область определения состоит в этом случае из интервалов (—оо, 0) и (0, оо). Та же функция может быть записана в виде
1
*=т-
Правило, задающее функцию, может быть и более сложным, например
Х1-+У\ + х + 2 — х + х10.
Эта функция определена для х, удовлетворяющих неравенствам 1 + х > 0 и 2 — х > 0, т. е. при —1 х 2.
Мы воспользовались здесь следующим часто применяемым соглашением: если функция задана формулой, то при отсутствии особых оговорок областью ее определения считается наибольшее множество, на котором эта формула имеет смысл.
Первоначально математики рассматривали только функции, заданные формулами. Это, однако, оказалось неудобным, препятствуя развитию и приложениям математики. Мы не будем поэтому требовать, чтобы правило, задающее функцию, состояло из единственной формулы. Например, следующее правило:
— х при х-^0,
1 при 0<х< 3, Vx" при 3<^х
Огюстен Луи КОШИ (1789—1857) своей неутомимой продуктивностью, изобретательностью и ши* ротой математических интересов напоминает великих математиков XVIII в. Но Коши был математиком XIX столетия и уделял большое внимание логическому обоснованию математического анализа.
У Коши были стойкие религиозные и политические убеждения. После революции 1830 г. он последовал за Бурбонами в изгнание; вернувшись во Францию, он отказывался от должности в университете до тех пор, пока не была отменена присяга в лояльности правительству.
Карл ВЕЯЕРШТРАСС (1815—1897) начал свою деятельность в качестве учителя средней школы. Er© глубокие исследования, некоторые из которых печатались в таких неподходящих для зтого изданиях, как гимназические программы, доставили ему место профессора в Берлине. С зтого времени его лекции и семинары оказывали огромное воздействие на математику. Тенденция к сведению всей математики к числам и требование полной строгости в значительной мере являются результатами влияния Вейерштрасса.
100
3. Функции
вполне определяет функцию для всех значений х. Еще более странной кажется функция
{0 при рациональном х,
1 при иррациональном х;
она также определена для всех х.
1.2. ПЕРЕМЕННЫЕ, ОБОЗНАЧАЮЩИЕ ФУНКЦИИ
1 Точно так же, как мы пользуемся переменными для обозначения произвольных чисел, можно использовать их для обозначения произвольных функций. Когда мы говорим «пусть f — некоторая функция», то f представляет некоторое конкретное, но не указанное нами или даже неизвестное нам 'правило сопоставления чисел другим числам. Если мы хотим представить символом f некоторую известную нам функцию, например функцию х i-> х2, мы пишем: /(х) = х2. Символ /(х) читается: «/ от х», или «значение f в точке х»; он изображает число, сопоставляемое по правилу f числу х. Так, если /(х) = 2х3, то /(0) = 0, /(—1) = —2, /(/) = 2/3, f(2y) = 2(2z/)3 = 16г/3 и т. д.
Пусть f и g — функции; тогда утверждение f = g означает, что f и g — одна и т а ж е функция, а это в свою очередь значит, что fug определены на одном а том же множестве и что для всех х из этого множества /(х) = g(x). Вместо записи f = g часто пишут также /(х) = g(x).
Строго говоря, следует различать функцию f (т. е. правило) и число /(х), сопоставляемое по правилу f конкретному числу х. На практике, однако, смешение здесь возникает редко. Если, например, идет речь о функции х2, то имеется в виду правило соответствия х »-► х2.
Для каждого числа а можно определить функцию х н> а, сопоставляющую каждому числу ходно и тоже число а. Эту функцию обычно обозначают тем же символом, что и^число а\ такие функции называются постоянными функциями, , или константами.
•Примеры. 1. Какое значение сопоставляет числу 3 функция
Решение. Если и = 3, то (2u + l)/(u2 + 1) = (2-3 + 1)/(32 + 1) = 7/10.
Таким образом, наша функция сопоставляет числу 3 число 7/10.
2. Пусть f(t) =. (2t + 1)/(/2 +1); чему равно f (3)?
Решение. Это та же функция, что и выше, но с другим наименованием переменной; следовательно, опять /(3) = 7/10.
3. Для каких значений х определена функция xt+Vx — 1 + 1/)^2 — х?
Решение. Чтобы можно было вычислить ]Лх — 1, число х — 1 должно быть неотрицательно. Отсюда следует условие х 1. Точно так же ]/2 — х имеет смысл при 2 — х>0, т. е. при х<С2. Но чтобы можно было, далее, вычислить 1/]/2 — х, знаменатель должен быть отличен от нуля; таким образом, значение х = 2 здесь
§ 1. Функции и графики
101
исключается. Соберем вместе найденные условия: х >> 1, х 2, х #= 2. Итак, наша функция определена при 1 •< х < 2.
4. Для каких значений t определена функция h(t) = У/ У t — 1 ?
Решение. Очевидно, h (t) определена, если: Г определено значение ]/Т— 1 и 2° У t — 1 >> 0. Первое условие означает, что t >- 0, второе же — что 1, т. е. / >• 1. Итак, h(f) определена при 1 >- 1.ф
УПРАЖНЕНИЯ
1. Какое значение функция xi-*2x2— 1 сопоставляет числу 7? Числу 3/2? Числу —4?
2. Какое значение функция и к* (и + 1)/(«2 + 1) принимает в точке —1? В точке 1/4? В точке ]Л2 ?
3. Чему равна функция у 4#3 4- У2 + 1 в точке 2? В точке — 2? В точке 0? 1/3
4. Чему равно значение функции 4- h при h = —8? При h = 27? При Л= 1/125?
5. Какое значение функция а »-► (а2 4- 1) (а3 — 2а) сопоставляет числу —1? Числу 0,3? Числу 0,02?
6. Рассмотрим функцию i/ = 3x'24-x (т. е. х н>3х“24-*)- Какое значение эта функция сопоставляет числу —3? Числу 10? Числу —}^2 ?
7. Рассмотрим функцию у = 2и 2/3 4- (и 4- I)2. Каково значение у при и = 8? При и = = 0,027? При и =— 1?
8. Рассмотрим функцию f (х) = 1/(х 4- 1)—х3 [т. е. / есть наименование функции хн> 1/(х 4- 1) —х3]. Чему равно f (2)? f (1/2)? f (— 1/3) ?
9. Пусть h (0 = (—/) 3/24-(Г—I)2. Чему равно h (—4)? h (—9/4)? h ((—8),/3)?
4 .----
А Ю. Для каких значений х определена функция хн>1/(х — 1) + 1/(х 4-2) 4-у Зх— 2?
11. Для каких значений и определена функция f (и) = — 1 — и2 ?
/4и —1
12. Какова область определения функции у — ——-— 4- У (г + 1) (г 4- 2) ? г3 — 1
о г, /в2 — 9
13. Для каких значений в определена функция 6 >->• —— .....?
У 4 _ (0—8)2
14. Какова область определения функции f(z)=^z— У г2— г — 2?
15. Для каких значений v определена функция С (о) = и | — У I v | — р2 ?
1.3. СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ФУНКЦИЙ
Пусть f и g — две функции. Сумма f + g, разность f — g, произведение fg и частное fig этих функций суть функции, определенные соответственно правилами (предписаниями):
-t*->/(x) + g(x), x-*f (х) — g(x), «•*/(*) • g(x), . /(x)
g(x)
10?
3. Функции
Эти функции определены для всех тех х, для которых определены обе функции f и gf за исключением функции f/g, не определенной в точках х, где g(x) = 0. Для функций справедливы коммутативный, ассоциативный и дистрибутивный законы, поскольку они верны для чисел. Таким образом, f + g = g + f, fg = gf, (f + g)-\-h = = f + (g + Л), (fg)h = f(gh) и f(g + h) = fg + fh.
•Пример. Пусть f(x) = 2x2 + 3, g(x) = Ух — 1. Тогда f + g, f—g и fg определены для всех x > 1, a fig определена при x > 1. Например, (/g)(5) = /(5)-g(5) = = 53-2 = 106. Далее, 2/ есть функция х 4х2 + 6; —g = (—l)g есть функция х —Ух — 1; f — 3 есть функция х 2х2. ф
1.4. КОМПОЗИЦИЯ ФУНКЦИЙ
Пусть /, g — две функции; тогда их композицией, обозначаемой через fog, называется функция
* f(g(x)).
Она определена для тех чисел х, для которых определена g и для которых число g(x) принадлежит области определения f. Таким образом, функция fog, называемая также сложной функцией, есть следующее правило: сначала применитьg, а затем/. Вообще говоря, это функция отлична от gof (сначала применить /, а затем g).
фПример. Пусть / и g — те же, что в предыдущем примере. Тогда fog есть функция х 2g (х)2 + 3. Поскольку g(x) =У к—1, fog есть функция х»-> (Ух — 1)2 + 3 = 2х Ч- I, которая определена при х>1 и не определена при х<1. Функция gof есть функция х^У?(х) — I. Поскольку/(х) = 2х2 + 3, gof есть функция х ]/ 2х2 + 2 , определенная при веем. х. В частности, /(g(l))=3, a £(/(1))=2.ф
УПРАЖНЕНИЯ
16. Пусть /(х^ = х — 5, g(x) = х + 5. Какое значение Hrg еожоставляет числу 4? Какое значение fg сопоставляет числу 2? Какое значение l°g вопдставляет числу—1? Какое значение go1 сопоставляет числу 10?
17. Пусть / (х) = 2х — 1, g(x) = x2 Чему равны (/— g) (3), (Ий (3), (f/g) (—2), (/og)(3), (g о f) (5/2) ?
18. Пусть h, (s) = s2 — > 4- 1, L (s) = s/(s — 1). Чему разив (2h — 3L) (4), (bb/i)(2), (LoLofz)(— 1)?
19. Пусть a(t) = y^T9 p (О = . Чему равны (а о p) ф, (a<>p)(—2), (₽oa)(4),
(poa)(— 4)?
,4zO. Пусть F (u) = u2 4- 2u— 3, К(«)=!/(«— 1). Чему равны ^4-40(5), ((F + К) о F) (2),
(Fo(FK))(- 1), (F + (M))(3)?
21. Пусть / (x) = 2x 4- 5, g(x) = x24-l, h(x)=l/x. Найдите для жаждой функции в левом столбце равную ей функцию в правом:
(•) t + g — h, (a) w н* (2w 4-5) (w2 4- 1) 4- (2/w).
(2) fg+2h. (б) ^к>1/(^2+ 1).
(3) foh. (в) (2/w 4- 5)2 4- 1*
§ 1. Функции и графики
103
(4) hog.
(5) gof о ft.
(6) h of og.
(7) ft oft о/о/.
(8) ft о/о ft о/.
(9) ho(f + g).
(10) g°(gg)-
(г) и;»-* l/(wa -f- 2w 4- 6).
(д) wi-* (w2 4- I)4 4- 1.
(e) w»-* (2w 4-5)/(10w 4-27).
(ж) w »-► w2 4- 2w 4- 6 — (1/w).
(з) w »-* to 4- 15.
(и) wk* l/(2wa 4- 7).
(к) wi-* (2/w) 4- 5.
22. Пусть R (x) = 1 4- У x » aS (x)=l/(l 4- *)• Укажите непосредственные выражения для R4-S, RS, RoS, SoR, выбрав в качестве независимой переменной х.
2/3
23. Пусть A (s) = (s 4- 1) , В (t) = Р — 2. Чему равны (А о В) (v), (ВоД) (w) и (Д о (В 4- 2)) (х)?
24. Пусть f (х) = ха, g(x) = x4-l, Л(х)=1/х. Найдите выражение функции s к* (s 4- 3)“4, содержащее только /, gt h и операцию композиции функций (но не сложение и умножение). Найдите выражение функции / i-*/3 4-З/2 4-2/, /=/=0, содержащее только f, g, h, операцию композиции функций и умножение функций.
25. Где определена функция fog, если f (х) = ]Лх 4~ 3 и g (у) = 1 4- у2?
26. Где определена функция сот, если а (и) = l/J^l— и ит(о) = и3?
27. Какова область определения G о R, если G (s) = У$2 — 4 , R (у) = У у — 1 ?
28. Для каких значений и определена функция (gof)(u), если g(x) = )^9 — (х—I)2 и f (г) = = ]/25 —г2?
29. Где определена функция ho С, если h (у) = (| у | — 12,/6) и С (х) = х 4- 4?
30. Где определена функция А о В, если A (s) = s2 и В (/) = УI — t2 ?
31. Пусть хь*/(х) определена при х<0 и при 1<х<5, a g(y)=zbf(y2‘ — 4). Где определена функция fog?
1.5. ГРАФИКИ
В принципе функция f проще всего представляется таблицей, в первом столбце которой перечисляются все числа х, для которых определена /, а во втором — значения /(х), соответствующие каждому х. Часть такой таблицы для функции х н-> у = х2 имеет вид
X У
0 0
0,1 0,01
0,2 0,04
0,3 0,09
0,4 0,16
104
3. Функции
Рис. 3.2
Невозможно выписать все входные данные таблицы, поскольку область определения функции обычно представляет собой бесконечное множество. Тем не менее возможно и полезно представлять себе функцию как множество всех строк такой таблицы, т. е. множество всех упорядоченных пар (х, /(х)), по одной для каждого числа х, для которого определена функция.
Графиком функции f называется множество всех точек плоскости с координатами (х, /(х)). Таким образом, график есть полная таблица функции: в нем содержится вся информация о функции, и если вычертить график или его часть, то можно «увидеть» функцию.
Вот несколько примеров. Как мы уже знаем, график функции у = х2 есть парабола (рис. 3.1). График функции у ±= 1/х показан на рис. 3.2; этот график называется равнобочной гиперболой. График функции у = х3, показанный на рис. 3.3, называется кубической параболой. График функции
х + 1 при х<0,
х2 при 0 х 1,
2/х при 1 <х,
показанный на рис. 3.4, состоит из трех кусков.
Для функций, изучаемых в анализе, точки графика не рассеяны на плоскости, а составляют так называемую кривую или несколько кривых, как это видно из четырех только что рассмотренных примеров.
Не каждое множество точек плоскости является графиком функции. Для этого необходимо и достаточно, чтобы каждая вертикальная прямая пересекала множество не более чем в одной точке. Пусть это условие выполнено; тогда множество является графиком следующей функции: если вертикальная прямая х = а не пересекает множества, то f(a) не определено; если же х = а пересекает множество в точке (а, 6), то fid} = Ь.
§ 1. Функции и графики
105
Рис. 3.5 иллюстрирует это соглашение. Кривая слева удовлетворяет нашему условию и является графиком функции. Функция определена в интервале, состоящем из точек оси х, лежащих прямо под кривой или над нею, как точка а. (Число же находится вне области определения.)
С другой стороны, правая кривая не удовлетворяет нашему условию: имеются вертикальные прямые, пересекающие кривую в двух точках. Кривая не является поэтому графиком функции. В самом деле, если бы она была графиком, то какое значение следовало бы сопоставить числу а2?
•Пример. Единичная окружность (с центром в начале, радиуса 1) н е является графиком функции, поскольку в этом случае не выполнено предыдущее условие. Верхняя полуокружность, т. е. множество точек (х, у), для которых х2+ у2 = = 1 и у > 0, является графиком функции х /1 — х2. Точно так же нижняя полуокружность является графиком функции х »-> —У1 — х2. Обе функции определены при —1<х<1.«
Форма графика отражает свойства функции, как мы увидим на примерах.
1. 6. МОНОТОННЫЕ ФУНКЦИИ
Функция называется возрастающей, если
ЖХ/(*г) пРи хх<х2.
Это значит,что из двух любых точек графика правая лежит выше левой. При движении слева направо график поднимается; примером может служить график /(х) = = х3, изображенный на рис. 3.3.
Функция называется неубывающей, если
/(Л)</(хг) ПРИ
* Это значит, что из двух заданных точек графика правая не ниже левой. График при
106
3. Функции
движении слева направо не опускается. Например, такова функция Дх) = 0 при х -С 0, f(x) = х при х > О (рис. 3.6).
Подобным же образом функция f называется убывающей, если
f (xr) > f (Xg) при Xj < х2
(график понижается), и невозрастающей, если
/(хО > /(хг) при Xi < х2
(график не поднимается).
Функция называется строго монотонной, если она возрастающая или убывающая; монотонной, если она неубывающая или невозрастающая.
Функция Дх) = х2 не входит ни в один из этих классов. Она убывает при х < О и возрастает при х > 0. Это пример кусочно-монотонной функции. Функция называется кусочно-монотонной, если любой конечный интервал, на котором она определена, можно разбить на конечное число интервалов, в каждом из которых функция монотонна. Другим примером кусочно-монотонной функции служит функция х *-> sin х, изучаемая в гл. 6.
1. 7. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
Функция / называется четной, если
/(—х) = Дх), и нечетной, если
f(-x) = - f(x)
для всех х, при которых функция определена; в обоих случаях предполагается, что Д—х) определена одновременно о Дх). Например, х2 — четная функция, а х3 — нечетная
§ 1. функции и графики
107
График четной функции симметричен относительно оси у (рис. 3.7). График нечетной функции симметричен относительно начала координат. (Это значит, что если точка Р принадлежит графику, то ему принадлежит и точка Р' прямой, со* единяющей Р с О, причем О является центром отрезка РР*\ рис. 3.8.)
Заметим, что произвольно заданная функция не является, вообще говоря, н и четной, ни нечетной; такова, например, функция, изображенная на рис. 3.6.
УПРАЖНЕНИЯ
В упражнениях 32—37 установите, является ли заданная функция четной, нечетной, или же ни той, ни другой.
32. х*->%2 + 4. 35. i/ = /34-/2.
33. s н► ( s1/3 + 5)/s. ±36. //(z) = ]/?3+ 1.
34. / (a) = (u3 + I)3 — u4. 37. p>->/o2+ 1/| о |.
38. Может ли функция быть и четной, и нечетной? Если это возможно, попытайтесь найти все такие функции или хотя бы привести пример такой функции.
В упражнениях 39—44 установите, является ли заданная функция возрастающей, неубывающей, убывающей, невозрастающей или не принадлежит ни к одному из этих классов. [Естественно, возрастающая функция является, тем самым, неубывающей; дайте в этих случаях более сильный из двух ответов.]
39. 42. £(</) =
40. f (х) = \1Ух . 43. h (и) = | и \/и.
41. г = х3 4- х2. А 44. k (г) = г 4- 1 при г < 0; k (г) = г2 при г >0.
В упражнениях 45—48 каждая из функций кусочно-монотонна. В каждом случае разделите область определения функции на интервалы, в которых она монотонна, и для каждого из этих интервалов укажите, является ли в нем функция возрастающей, неубывающей, убывающей или невоз р аста ю ще й.
45. А (х) (х — I)4. 46. <р (у) = */2 4- у.
108
3. Функции
47. г н* t2 при t < 0; t и* 1 — t при t > 0.
48. g(h) = l/h при A <2 0; g (h) = (h — l)2 при 0 < h < 2; g (h) = 1/Л3 при h > 2.
В упражнениях 49—56 установите, является ли функция, график которой изображен, четной, нечетной или ни той, ни другой. Если функция кусочно-монотонна, отметьте на горизонтальной оси интервалы, в которых она монотонна. Для каждого такого интервала укажите, является ли в нем функция возрастающей, неубывающей, убывающей или невозрастающей.
Л 1> Функции и графики
109
1. 8. ПРИЛОЖЕНИЯ ФУНКЦИЙ *
В приложениях математики функции используются для представления соотноше- v ний между • измеряемыми величинами.
Предположим, что мы измеряем температуру в некотором месте в течение неко-. торого промежутка времени. Эти измерения можно изобразить в виде кривой, слу- • жащей графиком функции. В этом случае говорят, что температура является функ- < цией времени. Следует, однако, помнить, что математическую функцию, т. е. правило, сопоставляющее одно число другому, мы получаем лишь после того, как примем соглашения относительно единиц измерения и начальных точек отсчета. Если температура измеряется в градусах Фаренгейта, а время — в минутах, причем за начало отсчета принимается полдень, то получается одна такая функция. Если же температура измеряется в градусах Цельсия, а время — в секундах, причем за начало отсчета принимается 2 часа пополудни, то мы получаем совсем другую функцию, представляющую ту же физическую величину, тот же процесс измерения значений этой величины. Конечно, нетрудно перейти от первой функции ко второй.
Те же замечания можно сделать по поводу чисел (переменных), участвующих в измерениях расстояний, площадей, объемов, весов, давлений, интенсивностей, скоростей, ускорений, затрат, цен и т. п., связываемых друг с другом посредством функций. Один случай представляет особую важность.
Для заданной функции х у = /(х) можно истолковать х как время и у — как , координату точки, движущейся по числовой прямой. Постоянная функция, например, представляет покоящуюся точку, тогда как возрастающая представляет движение в положительном направлении. Как мы увидим, такое кинематическое ис-; толкование функции весьма важно.
УПРАЖНЕНИЯ
57. Расстояние между движущейся точкой и закрепленной начальной точкой измеряют в течение некоторого промежутка времени (т. е. расстояние рассматривается как функция времени). Если расстояние измеряется в метрах*, а время— в секундах (от начала промежутка), то получается функция t Z2 + 3t Какая функция получится, если измерять расстояние в сантиметрах, а время — в минутах (также от начала промежутка)?
58. Дом перемещают 1200 м по прямой дороге; движение начинается <в полдень. Если расстояние от дома до начальной точки перемещения измеряется в метрах, а время от полудня — в минутах, то получается функция
расстояние = f (0 =
I при 0 < t < 600, 600 при 600 < t < 660, 2t — 720 при 660 < i < 960.
Какая функция получится, если расстояние от дома до конечной точки перемещения измеряется в километрах, а время от полудня — в часах?
- .:аэ) Е‘ •
ТТ . к? л
♦ Здесь и дальше английские меры заменены метрическими.
110
3. Функции
59. Температуру проволоки длиной в 1 м измеряют в каждой ее точке. Если температура измеряется в градусах Цельсия, а расстояние от одного из концов — в сантиметрах, то получается функция
{s® при 0 < s < 50,
(100 —s)* пр. 50 <.<(00,
Какая функция получится, если температура измеряется в градусах Фаренгейта, а расстояние (от другого конца) — в метрах? Напомним, что температура по Цельсию С и температура по Фаренгейту F связаны соотношением F = 9/5 С + 32.
60. Зажигают печь и измеряют ее температуру в течение некоторого промежутка времени. Если температура измеряется в градусах Фаренгейта, а время (с начала промежутка) — в минутах, то получается функция
температура = h (t) =
/а при 0 < t < 30, о
10/ при 30 < t < 120, 1200 при 120 < /.
Какая функция получится, если температура измеряется в градусах Цельсия, а время (с начала промежутка) — в часах?
61. Скорость автомобиля измеряют в течение некоторого промежутка времени. Если скорость измеряется в метрах в минуту, а время — в секундах, то получается функция
скорость = v (t) =
20/ при 0 < / < 15, 300 при 15 < / .
Какая функция получится, если измерять скорость в километрах в час, а время — в минутах?
§ 2. МНОГОЧЛЕНЫ,
нальных функций, или многочленов; общих рациональных функций, или алгебраических дробей; иррациональных функций? образуемых из переменной х с помощью рациональных операций и операции извлечения корня — описываются в следующих разделах.
Определение функции в § 1.1 является общим. На прак-РАЦИОНАЛЬНЫЕ тике используются большей частью некоторые специаль-И ИРРАЦИОНАЛЬ-ные классы Функций. Три таких класса — целых рацио-НЫЕ ФУНКЦИИ. "°...... ’’’ ™
ВВЕДЕНИЕ В ТЕОРИЮ ПРЕДЕЛОВ
2.1. ЛИНЕЙНЫЕ ФУНКЦИИ
К простейшим и самым важным функциям относятся линейные функции
/(х) = тх + Ь.
График линейной функции есть прямая линия (см. гл. 2, § 2). Обратно, каждая невертикальная прямая есть график линейной функции. Если наклон т положителен,
§ 2. Многочлены, рациональные и иррациональные функции
111
то функция — возрастающая, причем наклон служит мерой быстроты возрастания функции. При т = 0 функция — постоянная; при т < 0 функция — убывающая. Тождественная функция х н-> х имеет наклон 1.
Для любой функции f число а, при котором /(а) = 0, называется корнем, или нулем /. Непостоянная линейная функция имеет в точности один нуль (так как тх + b = 0 при х = — Ыт и ни при каком другом значении х).
2.2. КВАДРАТИЧНЫЕ ФУНКЦИИ
Пусть а, 6, с — фиксированные числа, причем а =/= 0. Тогда функция
У = / (*) = а*2 + Ьх + с
называется квадратичной функцией со старшим коэффициентом а. График квадратичной функции есть парабола с вертикальной осью (см. гл. 2, § 4.3).
Дополняя до полного квадрата, запишем функцию в виде г / х г/ । । с b2 1
y = f(x)=a х+ — 4------------— ,
L\ 2а / а 4аа J
или
у = а (х 4- + —, где D = 4ас — &а.
\ 2а/ 4а
Предположим, что а > 0. Тогда наименьшее значение у соответствует значению х = —Ы2а. Поэтому точка (—является вершиной параболы. Если D > 0, то вершина и вся парабола лежат в верхней полуплоскости; корней в этом случае нет. Если D = 0, вершина лежит на оси х. В этом случае функцию можно записать в виде
/ (х) =а(х — г)2, где г= —
Таким образом, f оказывается квадратом линейной функции ]/га(х — г). Корень г называется при этом двойным корнем. Наконец, если D < 0, то вершина лежит в нижней полуплоскости. Парабола пересекает ось х в двух различных точках X = rt и X = г 2> где
— Ь + _ — Ь — У^Р
2а ’ 2 — 2а
и функция может быть записана, как читатель легко проверит, в виде произведения двух различных линейных функций:
Дх) = а (х — гх) (х — Гг).
112
3. Функции
Эти три случая показаны на рис. 3.9.
Читатель может также убедиться, что в случае а < 0 получаются те же результаты: наша функция имеет два различных корня, один двойной корень или ни одного корня в зависимости от того, будет ли D < О, D =0 или D > 0.
УПРАЖНЕНИЯ
1. Для каких значений а функция х х2 — 2адг + 10 имеет два различных корня?
2. Для каких значений s функция г »-* г3 + г + 4s не имеет корней?
3. Для каких значений а функция [(у) = ау2 + 2^+1 имеет один двойной корень?
А4. Для каких значений г график функций х *+ г2 + Здгг+4 пересекает график функции
х >-► 1 в двух различных точках?
5. Пусть каждая из функций х »-► х2 + rx + s и у »-► х2 + гх — s 4" ~ имеет лишь один
двойной корень. Что можно утверждать относительно г и s?
6. Для каких значений и функция s »-► s2 + 2u2s + и имеет два различных корня?
7. Запишите функцию х >-► х2 + Зх + 1 в виде произведения двух линейных функций.
8. Запишите функцию s 2s2 — 4s + 1 в виде произведения двух линейных функций.
2.3. МНОГОЧЛЕНЫ
Линейные и квадратичные функции — это частные случаи многочленов. Многочлен, или многочленная функция, или, наконец, целая рациональная функция, есть правило вида
f М = аохп + а^"-1 + а^хп~2 + • + а^х + ап,
где п — целое неотрицательное число и aQ, ai9 ап— заданные числа, причем а0 #= 0- Число п называется степенью многочлена, числа а0, ах, ... , ап — его коэффициентами, а число а0 — старшим коэффициентом.
Многочлен степени 0 есть постоянная; степени 1 — линейная функция; степени 2 — квадратичная функция.
Мьг рассмотрим некоторые свойства многочленов, вернее всего, знакомые читателю.
Теорема 1. Если fug — многочлены, то f + g, fg и fog — также многочлены.
Это утверждение очевидно. Вместо формального доказательства мы рекомендуем читателю рассмотреть несколько примеров.
§ 2. Многочлены, рациональные и иррациональные функции
113
2.4. ДЕЛЕНИЕ «УГЛОМ»
Напомним процесс деления «углом» в применении к многочленам; он во всем аналогичен процессу деления целых чисел. Пусть надо, например, разделить f(x) = = 4х4 — Зх + 15 на g(x) = 2х2 + 2х + 5. Вычисления имеют вид:
4Х4—Зх -f- 15 |2х2 + 2х4-5
4Х4 -и 4х3 -4- Юх2 2х2 — 2х — 3
— 4х3 — 10х2 — Зх -и 15
— 4х3 — 4х2 — !0х
— 6х2 + 7х + 15
— 6х2 — 6х — 15
13х 4- 30
Здесь мы останавливаемся, поскольку степень остатка (а именно, 1) оказывается ниже степени делителя (равной 2). Результат вычисления означает:
4х* — Зх 4- 15 = (2х2 + 2х 4- 5) (2х2 — 2х — 3) 4- (13х 4- 30). делимое целитель частное остаток
Этот процесс применим во всех случаях и приводит к следующей теореме.
Теорема 2. Пусть f(x) и g(x) — многочлены соответственно степени п и степени т, причем п^ т> 0; тогда существуют многочлен Q(x) степени п — т (частное) и многочлен R(x) степени меньше т (о с та то к) такие, что
fW = g(x)Q(x) + /?(х).
(Если /? = 0, то говорят, что f делится на g или что g делит f.)
Важный частный случай этой теоремы мы получаем, положив п > 1 и g(x) = = х — г, где г — некоторое число.
Теорема 3. Если многочлен f(x) степени п > 1 разделить на линейную функцию х — г, то остаток есть число f(f).
Доказательство. Применим теорему 2 к случаю п > 1, т = 1; тогда существуют многочлен Q(x) степени п — 1 (частное) и многочлен степени 0, т. е. постоянная /? (остаток), такие, что
f(x) = (х — r)Q(x) + /?
при любом х. При х = г получаем f(r) = O-Q(r) 4- /? = /?.
2.5. КОРНИ МНОГОЧЛЕНОВ
Из теоремы 3 можно сделать выводы о корнях многочленов. Пусть f(x) — многочлен степени п > 1 иг 4— корень /; это значит, что /(rj)= 0. В этом случае в силу теоремы 3 линейная функция х — fi делит /(х). Следовательно, f(x) = (х — ^i)Qi(x),
114
3. Функции
где Qi—многочлен степени п— 1. Пусть теперь Qt имеет корень гг. ТогДа опять получаем Qi(x) = (х — rJQdx), где Qa— многочлен степени п — 2. Если Q3 имеет корень г3, то Q3(x) = (х — r3)Q3(x), где Q3 — многочлен степени п — 3. Этот процесс должен прерваться после п шагов или раньше, если получится многочлен Q, не имеющий корней. (Так называемые комплексные корни здесь не рассматриваются.) Мы получаем, таким образом,
f(x) = (х — п)(х — rj...(x — rk)Q(x),
где Q(x) — многочлен степени п — k, не имеющий корней. (Если сам многочлен f не имеет корней, то k = 0 и линейные множители отсутствуют, так что f = Q.)
Конечно, числа гь ..., гк не обязательно различны. Пусть т — такое число, что среди чисел г1( ..., rk имеется в точности т равных г; тогда г называется тп-кратным корнем многочлена, или корнем кратности т. Иными словами, г является корнем f кратности т, если
f(x) = (х — гу*Р(х),
где Р(х) — многочлен, причем такой, что Р(г) ф 0.
Итак, мы доказали следующую теорему:
Теорема 4. Многочлен степени п имеет не более п (действительных) корней, если считать каждый корень столько раз, какова его кратность.
• Пример. Рассмотрим многочлен
f(x) = 2х8 — 10х7 4- 8х* 4- 8х® + бх4 + 18х®.
Очевидно, 0 является тройным (или трехкратным) корнем этого многочлена. Мы хотим найти другие корни. Деление на 2х® приводит к многочлену х6 — бх4 4-4- 4х® 4- 4х^ 4- Зх 4- 9. «Методом проб и ошибокэ убеждаемся, что —1 является корнем этого многочлена. Деление на х 4- 1 дает многочлен х4 — бх3 4- 10х? — 6x4-9; число —1 не является его корнем, но 3 является. Деление на х — 3 дает х3 — Зх2 + х — 3. Этот многочлен опять имеет корень 3; деля на х — 3, получаем х? 4- 1, т. е. многочлен, не имеющий корней. Итак,
/(х) = 2х*(х 4- 1)(х — 3)2(х2 4- 1).
Корни многочлена: 0 (кратности 3), 3 (кратности 2) и —1 (кратности !).•
УПРАЖНЕНИЯ
В упражнениях 9—16 выполните указанные деления, записав ответ в виде (делимое) — = (делитель) (частное) 4- (остаток):
9. Разделите f (х) = Зх3 4-х2 — х + 2 на g (х) = х2 + х — 2.
10. Разделите ft (s) = ss — 2s4 -|- s3 — 6s2 -f- s 4- 8 на ft (s) = c2 4- 1.
11. Разделите {/«-►у44-1/—1 на у»-*{/34-1.
12. Разделите A (0 = t6 4- 2f* —/ —г 2 на В (t) = t 4- 2.
13. Разделите f (x) = 2x4 на g (x) = 3r2 4- x.
14. Разделите (г) = г3 4- г2 — 1 на ₽ (г) = г — в, где с — постоянная.
15. Разделите xt-*x®4-2x— 5 на xt-*7.
16. Разделите ft (а) = и2 4- 2а — 3 на ft (а) = а2 — а — 1.
§ 2. Многочлены, рациональные и иррациональные функции
115-
В упражнениях 17—21 найдите с помощью деления углом значения многочлена в заданной точке г
17. /(х) = х3 4-х—1, г = 2.
18. g (х) — 2х4 — х2 + 2х — 1, г = — 1.
19. s»_>4 — 2s-|-s2 — s\ г = — 2.
20. h (у) = 2у3 4- 2у — 1, г =1/2.
21. гк>г3/3 —2z24-i4-6, г=3.
22. Найдите многочлен, имеющий двойной корень в точке 1, простые корни в точках —1 и О и никаких других корней. _
23. Найдите многочлен, корнями которого являются 2 (кратности 3) и ±"]/2 (каждый из них кратности 1).
24. Найдите многочлен, имеющий двойной корень в точке —2, двойной корень в точке 3, тройной корень в точке 1/2 и никаких других корней.
25. Многочлен f(x) = х4 + х3 — 7х2 — 13х — 6 имеет двойной корень —1; найдите остальные корни
А26. Многочлен у »-► у° — lif + 2#2 4- 12# — 8 имеет двойной корень —2 и простой корень 2; найдите остальные корни.
27. Найдите все действительные корни (и их кратности) многочлена (х — 2)10(х10 4" 2).
28. Найдите все действительные корни (и их кратности) многочлена
(х 4- З)3 (х — I)2 (х4 - 1)\
2.6. РАЦИОНАЛЬНЫЕ ФУНКЦИИ
Рациональная функция — это функция вида
ср(х) =
fix)
g(x)
где f и g — многочлены, причем g(x) Ф 0. Многочлен есть тоже рациональная функция, соответствующая g(x) = 1 (поэтому она называется целой рациональной). Функция ф определена для всех х, за исключением корней знаменателя g.
Справедливость следующего утверждения очевидна:
Теорема 5. Пусть fug — рациональные функции; тогда f + g, fg и f°g — также рациональные функции, а при g(x) 0 это же верно и для fig.
Отношение между многочленами (целыми рациональными функциями) и рациональными функциями формально аналогично отношению между целыми и рациональными числами. Рациональные числа образуют п о л е, т. е. удовлетворяют аксиомам 1—12 гл. 1, § 2. Целые же числа не образуют поля, поскольку частное двух целых чисел не обязательно целое число; они удовлетворяют, однако, аксиомам 1—11. Мы выразим это короче, говоря, что целые числа образуют кольцо. Подобным же образом рациональные фунции образуют поле; они удовлетворяют аксиомам 1—12, в которых слово «число» надо заменить словом «функция». С другой стороны, многочлены образуют кольцо. (Заметим, что в этой интерпретации роль 0 и 1 играют постоянные функции 0 и 1.) Каждая рациональная функция есть частное двух многочленов, подобно тому как любое рациональное число есть частное двух целых чисел.
116
3. Функции
УПРАЖНЕНИЯ
29. Пусть f (х) = (1 + — х) и g (х) = 1 + х2; найдите f+g. fog и gof. Покажите,
что эти функции рациональные.
30. Пусть R (у) = 1/(1 + у — у2) и S (у) — у/(1 + у)\ найдите R — S, R/S и S о R. Покажите, что эти функции рациональные.
31. Пусть А (t) = (t2 + 2)// и В (t) — tl(t — 3); найдите Д4-2В, АВ и А о В. Покажите, что эти функции рациональные.
32. Пусть a (z) = (z2 + г — 3)/(z + 2) и f(z) = 1 /г2; найдите а/Р и а о р. Покажите,
что эти функции рациональные.
33. Пусть f (х) = (х2 — х)/(х + 3), g (х)=1/(х + 1) и h (х)=х2/(х + 1); найдите ° (Я ° Л)]+/. Покажите, что эта функция рациональная.
2.7. ИРРАЦИОНАЛЬНЫЕ ФУНКЦИИ
Рациональную функцию можно определить как функцию, получаемую применением рациональных операций (сложения, умножения, вычитания, деления) к постоянным и тождественной функции х »-► х. Иррациональная функция есть функция, получаемая применением рациональных операций и операций композиции функций к постоянным и к функциям х х1/л , где п — целое положительное число. Иными словами, иррациональная функция есть функция, заданная формулой, содержащей символ независимой переменной (например, х), числа, знаки +, —, ., / (или :) и рациональные степени. Область определения такой функции есть интервал или несколько интервалов.
ф Пример. Функция
/(х) =2х-,л + (1 - х,/2),/4
есть иррациональная функция. Область ее определения задается условиями х^>0, х1/2>0 и 1—х1/2^0, или 0<х^1.ф
Следующее предложение по существу является повторением определения.
Теорема 6. Если fug — иррациональные функции, то f + g. fg. f/g и fog — также иррациональные функции в предположении, что эти функции определены.
Заметим, что, например, в случае, когда f(x) = ]/х — 2 и g(x) = —1 — х, невозможно определить ни одну из функций f + g. fg. f/g. fog.
Множество иррациональных функций содержит в качестве подмножества поле рациональных функций* (а последнее содержит кольцо многочленов).
УПРАЖНЕНИЯ
34. Пусть /(х) = (1 4- V* )fx и g (х) = х/У х — 1; найдите f + g, fig и fog. Найдите
35. Пусть h (у) —2у 2/3 + у2 н k (у) = (у3 + 2) Wу— 1; найдите h — k, hk и koh. Найдите (k о h) (9).
А 36. Даны функции f (х) = 1 + . g(x) = \ iyV и Л(х) = 4/х. Найдите функцию
/о go h of. Найдите значение этой функции в точке 225.
37. Даны функции A (z) = V г . В(г) = V — z , С (z) = 1/z. Определена ли функция А + + В + С? Д/В? ДоВ?
* Таким образом, каждую рациональную функцию можно считать также и иррациональной (что, конечно, свидетельствует о некотором неудобстве принятой терминологии). -
§ 2. Многочлены, рациональные и иррациональные функции 117
2.8. РАСШИРЕНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ РАЦИОНАЛЬНОЙ ФУНКЦИИ
Как мы отметили выше, рациональная функция (т. е. частное двух многочленов) определена везде, где знаменатель не равен нулю. Но иногда можно естественным образом расширить область определения такой функции, включив в нее некоторые точки, являющиеся корнями знаменателя.
Рассмотрим, например, очень простую функцию
с / ч х2 — 1
X — 1
Эта функция не определена при х — 1, так как подстановка в формулу х = 1 приводит к бессмысленному выражению Заметим, однако, что можно переписать функцию в виде
= (*+Д)(х—\)
Х—1
и сократить на х— 1; тогда она задается формулой /(х) = х + 1. Эта функция определена также в точке х = 1, где она принимает значение 2.
Работая с рациональными функциями, мы часто будем предполагать, что каждый линейный множитель, входящий одновременно в числитель и в знаменатель, уже сокращен и что область определения функции соответствующим образом расширена.
Например, функция
первоначально не определена при х = 1 и х = — 1. Но х3— 2х2 + х =х(х— I)2 и х2— 1 =(х— !)(*+ 1). Поэтому можно записать
Ф(х) = (2)
х-4- 1
и считать функцию определенной также при х = 1, причем <р(1) = 0.
2.9. ПРЕДЕЛЫ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Посмотрим теперь на предыдущие рассуждения критически. Мы утверждаем, что
х3 — 2ха х _ х(х— 1)а _ х (х — 1)
X2 — 1 ~ (х+ 1) (X — 1) X + 1 ' '
Законность первого шага не вызывает сомнений: какое бы число мы ни подставили вместо х, первая и вторая дроби либо представляют одно и то же число, либо обе не определены. Однако второй шаг, состоящий в делении числителя и знаменателя на х — 1, имеет смысл лишь при условии, что число х — 1 отлично от нуля, т. е. х отличен от 1. Вправе ли мы при этом сказать, что
х8‘-2ха + х х (х — 1)
х!— и хи-* — --------------
ха—1
х+1
118
3. Функции
одна и та же функция? Для значений х, отличных от —1 и 1,— безусловно вправе, но не для значения х = 1. Можно лишь сказать, что мыдоговари-в а е м с я изменить определение первой функции, приписав ей значение 0 в точке х = 1, где она первоначально не была определена.
Такой способ расширения области определения нашей функции естествен, тогда как любой другой способ задать значение функции при х = 1 был бы неестественным или даже противоестественным. В самом деле, если взять значение х, не равное 1, но близкое к 1, то все три дроби (3) равны друг другу. В последней дроби числитель близок к 0, знаменатель же — к 2; поэтому вся дробь близка к 0. Ясно также ( и этому можно придать точный смысл), что чем ближе х к 1, тем ближе общее значение трех дробей (3) к 0. Мы можем сделать дроби (3) столь близкими к 0, как нам угодно, если взять в качестве х числа, отличные от 1, но достаточно близкие к 1.
Таким образом, наш способ расширения области определения <р(х) путем включения в нее также и точки х = 1 является естественным в следующем смысле: когда независимая переменная «стремится к 1», значение функции «стремится к 0». Это утверждение кратко записывается в виде
lim<p(x) = 0
[читается: «предел <р(х), когда х стремится к 1, равен 0»1.
Можно смотреть на это и с другой точки зрения. Построим график функции (2). Это кривая, изображенная на рис. 3.10; у нее нет разрывов, за исключением разрыва при х = —1. Построим теперь график функции (1); мы получаем ту же кривую, но без точки (1, 0) (рис. 3.11).
Если бы мы приняли в качестве значения <р(1) любое число, отличное от 0, то график функции имел бы разрыв при х = 1.
2.10. ПРЕДЕЛЫ ДРУГИХ ФУНКЦИЙ
Описанный выше метод расширения области определения функции /(х) на точку х0, в которой функция первоначально не была определена, состоит в том, что находится то число, к которому «стремится» зависимая переменная, когда независимая переменная «стремится» к х0. Применимость этого метода не ограничивается одними лишь рациональными функциями. Рассмотрим, например, функцию
у |X| —4
Эта функция не определена при х = 256. Однако
У|7Г-16 = (/ |х| —4)(/|х| +4),
так что при х=/=256 можно записать
f(x) = |х| +4.
§ 2. Многочлены, рациональные и иррациональные функции
119
Теперь легко видеть, что
iim/(x) =8, х—256
и естественный способ определить /(256) состоит в том, чтобы принять за это значение число 8.
Не следует думать, что описанный метод действует во в в е х случаях — это не так. Например, функция
, . х3 — 2ха ч- я
<PW =------—
х2 — 1
рассмотренная нами выше, график которой изображен на рис. 3.11, не определена при х = —1, и хотя мы можем выбрать в качестве <р(—1) произвольное число, не существует никакого естественного способа выбрать его. Когда х стремится к —1, функция ф(х) принимает сколь угодно большие положительные и сколь угодно большие по абсолютной величине отрицательные значения. Не существует никакого числа, к которому функция при этом «стремилась» бы. В этом случае мы говорим, что функция не имеет предела в точке х = —1.
Понятие предела имеет для анализа'решающее значение. Мы дали пока лишь весьма краткое и неформальное введение в это понятие. Мы вернемся к этому понятию дальше и рассмотрим его, опираясь на тесно связанное а ним понятие непрерывности.
120
3. Функции
УПРАЖНЕНИЯ
В упражнениях 38—47 найдите точки, в которых заданная функция не определена и, если возможно, расширьте на эти точки область определения функции таким образом, чтобы график функции оказался непрерывным.
38. х »-* (х — 1)2/(х2 — 1).
39. х (2х2 4- х — 3)/(2х2 — х — 1).
40. х »-► (х2 — х)/[(х — 1)2х].
41. х *-► (х2А — 4)/(2х2/з — ЗхМЗ — 2).
42. х »-► (х — 2)/(х2 — 4).
43. х (Х2/3 — 5x1/3 + 4)/[(х2/з — 1)(л-2/з — 4)].
А 44. ан- (х2 — бх + 9)/[(х2 — 9)(х — 3)].
45. х (х3 + Зх2 — х — 3)/(х* + х2 — 2х):
46. х *—► _(х — 2)(х — 1)3/[х(х2 + х — 2)2].
47. х »-► х2/(|Лх2 4-1 — 1).
§ 3. НЕПРЕРЫВНЫЕ
ФУНКЦИИ
3.1. ПРИМЕРЫ
Непрерывность — важное свойство, которым одни функции обладают, а другие — нет. Грубо говоря, функция непрерывна, если ее график не имеет разрывов. Прежде чем перейти к точному определению, приведем несколько примеров.
Рассмотрим функции, графики которых изображены на рис. 3.12—3.17. Заметим, что на рис. 3.12 и 3.13 каждый из графиков состоит из одного куска. Напротив, графики остальных функций имеют разрывы. Для функции рис. 3.14 разрыв происходит при х = 0, для функции рис. 3.15 — при х = —1 и х = 1, для функций рис. 3.16 и 3.17 — при х = 0. Две последние функции не определены в точке х = 0, и при малых | х | числа у = f(x) становятся очень большими по абсолютной величине. Первые две функции называются непрерывными, а функции, подобные изображенным на рис. 3.14—3.17, — разрывными. Еще одним примером разрывной функции является функция, график которой изображен (вернее, символически показан) на рис. 3.18; этот график имеет разрыв в каждой точке*.
Если истолковать х как время и у = f(x) как положение точки, то первые две функции представляют то, что обычно называется непрерывным движением. Функция рис. 3.14 представляет движение точки, покоящейся до момента времени 0, затем переходящей скачком в новое положение и после этого движущейся непрерывно. Движение, изображенное функцией рис. 3.15, совершает два внезапных скачка в моменты времени —1 и 1. Остальные функции (рис. 3.16—3.18) трудно или даже невозможно истолковать как изображающие движение точки.
Разницу между первыми двумя функциями и остальными можно описать также : и другим способом. В случаях 1 и 2 для близких друг к другу значений х, например Xi и х2, соответствующие значения у, т. е. /(xt) и /(х2), также близки друг к другу. Для остальных функций дело обстоит иначе. Так, например, для функции рис. 3.14 При отрицательном xt и положительном х2, близких друг к другу, величина I /(хг)—/(xi) I близка к 1. Для функции рис. 3.16 при малом положительном %! всегда можно найти другое положительное число х2 такое, что 0 < х2 < и величина 1/(Хг)—/(*i) I сколь угодно велика; то же верно для функции рис. 3.17. Наконец,
* Эту функцию впервые рассмотрел немецкий математик конца XIX в. Поль Лежен Д и-рих л е; поэтому ее часто называют функцией Дирихле.
§ 3. Непрерывные функции
121
{~х - 1 при х^-1
- Vl~x2 ~1 при-1 <х<1 х—1 при Х&1
Рис. 3.16
Рис. 3.17
122
3. Функции
/tel - I еС/ш X иРРаи>иОна/,ь"9
1 Л если л рашшмм»
Рис. 3.18
в случае функции рис. 3.18 величина |/(х2) — f(x^ | = 1, если х2 рационально, а Xi иррационально, независимо от того, насколько велика разность | х2— jq |.
Заметим еще, что функции рис. 3.14 — 3.17 «разрывны» лишь в отдельных точках (х = 0 для рис. 3.14, 3.16 и 3.17; х = —b и х = 1 для рис. 3.15), а во всех других непрерывны, тогда как функция рис. 3.18 разрывна везде.
Непрерывные функции чрезвычайно важны в математике и ее приложениях. Чтобы можно было высказать о них общие утверждения, надо дать им точное определение. Это будет сделано в ближайшем разделе, где мы точно определим, что имеется в виду, когда говорят, что «функция f(x) непрерывна в точке х0». Мы будем при этом руководствоваться приведенными выше примерами. Однако для большинства функций, встречающихся в анализе, обычно можно и без формального определения сказать, где они непрерывны и где разрывны.
УПРАЖНЕНИЯ
В упражнениях 1—6 укажите точки оси х, в которых изображенная на графике функция имеет разрыв.
§ 3. Непрерывные функции
123
7. Укажите функцию х /(х), определенную при всех х и непрерывную везде, кроме точек — 1, 2 и 3. Попытайтесь задать такую функцию простой формулой.
8. Укажите функцию si-> g(s), определенную при всех s и непрерывную везде, кроме точек —1/2, 0 и 8.
9. Укажите функцию у = ft(z), определенную для всех г, за исключением г — 0, и непрерывную везде в своей области определения, кроме точек —1 и +1.
10. Укажите функцию х »-► /(х), определенную и непрерывную при всех х, равную хн-х2 при х<^ 0, но не равную 4 в точке 2.
3.2. ОПРЕДЕЛЕНИЕ НЕПРЕРЫВНОСТИ
Пусть х0 — точка числовой прямой, т. е. действительное число, их»-* /(х) — функция, определенная при х = х0. Мы хотим придать точный смысл утверждению: если х близко к х0, то f(x) близко к f(x0). Для этого сначала условимся, что выражение «вблизи х0» означает: «в некотором интервале с центром х0», или, что то же, «для всех х, удовлетворяющих неравенству |х — х0 |<б, где 6 —некоторое положительное число». (Почему мы не настаиваем на том, чтобы выражение «близко от х0» всегда означало «в некотором малом интервале с центром х0»? Дело в том, что нельзя сразу для всех случаев жизни определить, какие числа следует считать «малыми», а какие — уже «не малыми»: это зависит от обстоятельств.)
Теперь мы дадим основное определение непрерывности. Функция f(x), определенная в точке х = х0, называется непрерывной в топке х0, если она обладает двумя следующими свойствами:
(I) Если А — число, для которого /(х0) < А, то f(x) < А при всех х; близких к х0 {и таких, что /(х) определено].
(II) Если В — число, для которого /(х0) > В, то f(x) > В при всех х, близких к х0 {и таких, что f(x) определено].
Функция f(x), определенная на некотором интервале оси х, называется непрерывной на этом интервале, если она непрерывна в каждой его точке.
Это определение выражает геометрический смысл непрерывности: график не должен иметь разрывов. Если (х0, Дх0)) — точка графика, то график не может сразу перескочить в точку выше прямой у = А > /(х0) или ниже прямой у = В < Дх0). Это иллюстрируется рис. 3.19 и 3.20.
Как видно из нашего определения непрерывности, малое изменение х приводит к малому изменению у. В самом деле, пусть / непрерывна в точке х0 и е — положительное число, сколь угодно малое. Тогда /(х0) < /(х0) + е и /(х0) > /(х0) — е. Поэтому [пользуясь условием I при А = /(х0) + е и условием II при В = /(х0) — el имеем вблизи х0
Дх0) — е < Дх) < /(х0) + е, или | Дх0) — /(х) | < е.
«Вблизи х0» означает: в некотором интервале с центром х0. Обозначим длину такого интервала через 26; тогда интервал есть множество всех х, для которых Iх — хо I <б • Иными словами: если дано положительное е, то можно найти такое положительное 6, что для всех х, удовлетворяющих неравенству | х — х0 I < 6, имеем I /(х) — Дх0) | < е.
124
3. Функции
Как легко видеть, это утверждение равносильно условиям I и II; оно называется 8-6-определением непрерывности. Его геометрический смысл виден из рис. 3.21: если мы хотим, чтобы у изменился менее чем на е, достаточно изменять х менее чем на 6. Функция непрерывна в точке х0, если для каждого данного расстояния е можно найти соответствующее 6. (При этом нет надобности искать для данного е наибольшее возможное 6: например, величина 6, показанная на рис. 3.21, может быть увеличена.)
Ниже приводятся некоторые примеры и упражнения, в которых используется это определение. Во всех случаях использование определения подтверждает интуитивное представление о непрерывности как об отсутствии внезапных «скачков». Читателя может обескуражить то обстоятельство, что даже для доказательства непрерывности простых функций требуются довольно сложные рассуждения; впрочем, скоро мы познакомимся с более эффективными способами доказательств.
• Примеры. Два первых примера поясняют технический смысл термина «вблизи».
1. Положительна ли функция х »-* 1 — х2 вблизи О?
Ответ. Да, поскольку существует интервал с центром в точке 0, в котором функция положительна. Таков, например интервал —1 <х< 1.
Положительна ли функция 1—1010х2 вблизи 0? Да, она положительна при —0,00001 <х< 0,00001.
2. Если fug определены вблизи х0, то uf+g определена вблизи х0. В самом деле, если f определена при всех х, для которых | х — х0 | < а (где а > 0), и g — при всех х, для которых | х — х0 | < b (где b 0), то f 4- g определена в интервале | х — х0 | < с9 где с — меньшее из чисел а и Ь.
3. Постоянная функция непрерывна везде. В самом деле, если постоянная функция < А (или > В) в некоторой точке, то она < А (или > В) везде.
4. Тождественная функция /(х) = х непрерывна везде. В самом деле, если /(х0)< < А для некоторого заданного х0, то х0 < А, и, полагая 6 = А — х0, имеем х < А при |х — х0 |<6. Таким образом, выполнено условие I. Читатель сам проверит условие II.
§ 3. Непрерывные функции
125
5. Функция f(x) = 1/| х | (см. рис. 3.16) непрерывна во всех точках, кроме нуля.
Мы проверим условие I в точке х0 > 0, предоставив читателю остальную часть доказательства провести самостоятельно. Пусть А — число, для которого /(х0) < < А, т. е. 1/|х0| < А. Надо показать, что
— < А вблизи х0 1*1 0
при тех х, для которых функция определена, т. е. при х =/= 0. Поскольку для таких х имеем | х | > 0, требуемое утверждение принимает вид
I х I > — вблизи х0, что равносильно условию
l*| —l*ol>~r —1*о1 вблизи х0.
/1
Положим 5 = |х0|— 1/Л. Тогда 8>0, и мы покажем, что |х|— |х0|>— 3 вблизи х0. В самом деле, имеем
1*о1 = Iх — (*~ *о)| <1*1 + 1 * —*о1» так что
l*l~l*ol>—|*~*ol и
1*|—1*о1>—8 при I*— *ol<8-
6. Функция, изображенная на рис. 3.14, т. е. такая, что /(х) = 1 при х < 0 и f(x) = 2 — х при х 0, не является непрерывной в точке 0. Условие I в этом слу-
з
чае выполнено, а условие II — нет. В самом деле, /(0) = 2 > но каждый интервал с центром в точке 0 содержит отрицательные точки х, в которых f(x) = 1 и тем
126
3. Функции
о
самым /(х) < -у. Конечно, можно было бы взяяъ и любое другое значение В между 1 и 2 вместо -g-.
7. Функция f, для которой f(x) = 0 при рациональном х и f(x) = 1 при иррациональном х, не является непрерывной ни в какой точке.
Доказательство. Пусть х0 рационально. Тогда f(x0) = 0 < 1/2. Но каждый интервал с центром х0 содержит иррациональные точки х, в которых f = 1 я, таким образом, f не меньше 1/2. Условие I тем самым нарушено. Точно так же, как легко видеть, условие II нарушено в каждой иррациональной точке х0.®
УПРАЖНЕНИЯ
11. Пусть [(х) = х2 + 1. Верно ли, что f<Z 2 вблизи 0? Если это верно, найдите наибольшее такое а. что f(x)< 2 при | х |< а. (Конечно, а должно быть положительно. В других случаях может оказаться, что а = оо, т. е. неравенство справедливо везде.)
12. Пусть#(х) с= \/х2. Верно ли, что# > 1/4вблизи 1?-Если это верно, найдите наибольшее такое о, что g(x) > 1/4 при | х — 1|< б.
13. Пусть Л(/) = + 1. Верно ли, что А < 1 вблизи 3? Если это верно, найдите наиболь-
шее такое е что Л(/)< 1 при | t — 3 |<е.
14. Пусть L(z) = г2 при z < 1; £(z) = z + 1 при z > 1. Верно ли, что L<Z 3/2 вблизи 1? Если это верно, найдите наибольшее такоер, что L(z)< 3/2 при | z — 1 |<Р-
15. Пусть Н(и) = и при и 0; Н(и)= —2и при и >0. Верно ли, что Н >—1 вблизи 0? Если это верно, найдите наибольшее такое у, что Н(и) >—1 при | и |<Y-
JJ6 Пусть t(x)= х2 + 1; возьмем любое фиксированное число А > 1. Верно ли, что А вблизи 0? Если это верно, найдите наибольшее такое а. что £(х)<^ А при | лг |<С а. Каким образом здесь использовано условие А > 1? Почему без этого условия было бы наивно спрашивать, верно ли что ft<Z А вблизи 0?
•17. Пусть Дх) = х2 + 1; возьмем любое фиксированное число е >0. Верно ли, что 1 + + е вблизи 0? Если это верно, найдите наибольшее такое а. что /(*)< 1 +е при I х|< < а.
18. Пусть F(y) = 2у + 3; возьмем любое фиксированное число В< 5. Верно ли, что F > > В вблизи 1? Если это верно, найдите наибольшее такое0 . что F(y) > В при | у— 1
Р
/9. Пусть Л(0 = (t — 4)1/3-f- 2; возьмем любое фиксированное число у >0. Верно ли, что А < 2 +у вблизи 4? Если это верно, найдите наибольшее такоее . что A <Z 2+v при U —4|<в.
20. Пусть g(x) = l/xz; возьмем любое фиксированное число B<Z 1. Верно ли, что # >В вблизи 1? Если это верно, найдите наибольшее такое б, что g(x) > В при | х — 11< б.
51 Пусть f(a) = иА при 0; f(u} = и2 4- 1 при и >0. Верно ли. что А вблизи 0, каково бы ни было А >0?
Если это неверно, найдите наибольшее А, для которого £<А вблизи 0. (Символ < означает «не<». Для-чисел а < b равносильно Ь. Для функций, однако, g < h не равносильно h.)
22. Пусть G(z) e z3 + 2 при 1; G(z) 2z при 1. Верно ли, что А вблизи 1
для любого А >3? Верно ли что G > В вблизи 1 для любого В <2 3? В каждом случае, если ответ положителен, найдите наибольшее такое б, что при | х — 1|< б неравенство справедливо. Если же ответ отрицателен, укажите такое значение А или В. для которого неравенство не соблюдается вблизи 1.
23. Докажите, что функция Л(х) = 2х + 1 непрерывна в точке 3 (т. е. проверьте условия
24 Докажите, что функция #(х) = (х2 — 1)/3 непрерывна в точке 0.
25. Докажите, что функция [(у) = Зу — 2 при у <0 • f(y} = у 4- 1 при у >0 не является непрерывной в точке 0.
Д26 Докажите, что функция Л(0 = Z2 4- I при '< —I; h(t) = —2t при —1 непрерывна в точке —I.
§ 3. Непрерывные функции
127
27. Докажите, что функция К(и) = и3 — 1 при 1; К(и) = 2и при и > 1 не является непрерывной в точке 1.
Отметим, что е-б-определение очень распространено и приобретает все большее значение при переходе к более сложным вопросам анализа. Следующие упражнения иллюстрируют типичные вычисления, применяемые для проверки непрерывности согласно этому определению.
28. Пусть 1(х) = 9х — 5. Найдите такое б > О, что | Дх) — 4 | < 1/10 при | х — 1 | < б. 29. Пусть е(у) = 2у2 + 3. Найдите такое а >0, что | g(y) — g(0) |< 1/2 при | у |< а. 30. Пусть hit) t2 — t. Найдите такое X >0, что | h(t) — h(l) |< 1/5 при | t — 1 | < X.
31. Пусть 1(и) = и + 3 при м^2; j(u) = Зи — 1 при и >2. Найдите такое С >0, что ЬЙ) — f(2)| < 1/3 при |u — 2|< С
А32. Пусть ft(x) = (2х + 3)/5. Докажите, что fj непрерывна в точке 1, пользуясь е-о-оп-ределением. [У казан ие: начните с фразы «пусть даное >0».)
3.3 . НЕПРЕРЫВНОСТЬ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО
На практике непрерывность функции устанавливают не просто по определению, а с помощью некоторых общих правил, которые мы сейчас сформулируем.
Теорема I. Пусть функции fug непрерывны в точке х0- Тогда функции f + g, f — g. fg, а в случае g(x0)=^= 0 также и функция f/g непрерывны в той же точке.
Справедливость этой теоремы интуитивно очевидна, если вспомнить смысл непрерывности: малое изменение х вызывает малое изменение у. Формальное доказательство теоремы 1 дано в Приложении (см. § 6).
ЗЛ. НЕПРЕРЫВНОСТЬ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Теорема 2. Многочлен непрерывен везде.
Доказательство. Как мы уже видели, тождественная функция х »-► х непрерывна. Следовательно, по теореме 1, непрерывны функции х2 = хх, х3 = х2х и т. д. Таким образом, непрерывны функции хп при всех целых положительных п. Мы уже знаем, далее, что все постоянные непрерывны. Следовательно, по теореме 1, непрерывны все члены вида схп (где с — постоянная, п — неотрицательное целое число). Многочлен является суммой таких членов и поэтому непрерывен в силу той же теоремы 1.
Теорема 3. Рациональная функция непрерывна во всех точках, где она определена.
Доказательство. Рациональную функцию можно записать в виде f/g. где f и g — многочлены, не имеющие общих корней. По теоремам 1 и 2 она непрерывна в каждой точке, не являющейся корнем знаменателя.
3.5 . НЕПРЕРЫВНОСТЬ КОМПОЗИЦИИ ФУНКЦИЙ
Теорема 4. Пусть функция f непрерывна в точке xQ и yQ=f(xQ). Пусть g — функция. непрерывная в точке yQ. Тогда композиция этих функций gof непрерывна в точке х0. [Напомним, что gof есть функция X •-> g(f(x)).]
Обозначим композицию через h(x), так что h(x) = g(f(x)). Пусть х, близко к х0. Тогда yt = /(х,) близко к у0, так как f непрерывна в точке х0. Далее, Л(х,) = =?= g(f(xi)) = g{yt) близко к Л(х0)=£(у0), так как g непрерывна в точке у0. Как показывает это рассуждение, можно ожидать, что h непрерывна. Формальное доказательство приводится в Приложении (см. § 6).
128
3. Функции
УПРАЖНЕНИЯ
В упражнениях 33—39 предполагается, чтоф(х), ф(х) — непрерывные функции, определенные при всех значениях х. Каждая из перечисленных ниже.функций непрерывна; поясните, откуда это следует. [Указание: примените теоремы 1 2, 3. 4.]
33. f (х) = (х) 4- ф (х) 4- <? (х) ф (х).
37. / (х) = (ф (х2)).
34. / (х) = <р (ха 4- 2х).
38. f(xk= ха4-ф(1 4-Ф(ха)).
35. Пх) = ?(х)/(1+ха).
39. / (х) = х<р (2 4-Ф (х)2).
36. Нх) = ф(х)/(14-?(х4)).
3.6. ПРОМЕЖУТОЧНЫЕ ЗНАЧЕНИЯ
Теорема 5 устанавливает очень важное свойство непрерывных функций.
Теорема 5 (теорема о промежуточном значении). Пусть Г(х) непрерывна при а < х < ft; допустим, что f(a) =/= f(b). Если у — любое число, лежащее строго между f(a) и f(b). то существует такая точка с. где а < с < Ь. что f(c) = у.
Справедливость теоремы геометрически очевидна. Поскольку f непрерывна, график состоит из одного куска. Кривая эта соединяет точки (a. f(a)) и (6, f(b)). одна из которых лежит ниже прямой у = у, а другая — выше ее. Поэтому кривая должна где-то пересекать прямую у = у (рис. 3.22). Значит, существует по крайней мере одно с. для которого а < с < b и f(c) = у. Аналитическое доказательство теоремы 5 дано в Приложении (см. § 7).
Теорема 5 служит для локализации нулей непрерывных функций. Если такая функция положительна в некоторой точке а и отрицательна в точке Ь. то между а и Ь имеется корень функции. Следствием этого факта является следующая теорема:
Теорема 6. Многочлен нечетной степени имеет по крайней мере один (действительный) корень.
Доказательство. Пусть п — нечетное целое положительное число и f — многочлен степени п. Можно предположить, что старший коэффициент f равен 1 (в противном случае можно разделить f на его старший коэффициент, что не меняет корней). Таким образом,
f(x) = хп 4- а1хл"1 4- а^с^ 4- • • • 4- ап^х 4- ап.
где аг. аг.... ,ап — некоторые числа. Для х =/= О имеем
t (X) = хл (1 4- — Ч- — + • • • 4- Д«=1_ + ±1 \ X X2 X71"1 хп
Поскольку п нечетно, хл>0 при х>0 и хл<0 при х<0. но велико, каждый из членов at/x, ajx2,.... ап/хп меньше величине. Для такого х в силу неравенства треугольника
Если ]х| достаточ-1/п по абсолютной
2 п
2 п
.•ч- —= 1, п
+
§ 3. Непрерывные функции
129
так что
Поэтому f(x) > 0 при большом | х | и х > 0 и /(х) < 0 при большом | х | и х < 0. По теореме 2, функция /(х) непрерывна. Следовательно, в силу теоремы о промежуточном значении существует такое число с, что /(с) = 0.
Примечание. Для многочленов четной степени утверждение теоремы, вообще говоря, неверно. Например, многочлен х2 + 1 корней не имеет.
УПРАЖНЕНИЯ
40. Пусть функция f непрерывна в интервале [—1, 1], К—1) = 2, £(0) = —1 и f(l) = 3. Каково наименьшее возможное число корней в этом интервале? Начертите график функции, удовлетворяющей указанным условиям и имеющей это наименьшее возможное число корней. Начертите другой график, где число корней больше на два.
41. Пусть функция g непрерывна в интервале [—2, 3] и g(—2)=1/2, g(—1) = —1, g(ty=2, g(l) = 2, g(2) = —2, g(3) = 4. Каково наименьшее возможное число корней g в этом интервале? Начертите график функции, удовлетворяющей указанным условиям и имеющей это наименьшее возможное число корней.
42. Начертите график функции, непрерывной в интервале I—1. 2], положительной на его концах и имеющей в этом интервале ровно два корня.
43. Постройте функцию, непрерывную во всех точках интервала [—1, 1], за исключением одной точки 0, отрицательную в точке —1, положительную в точке 1, но не имеющую корней. (Сначала попытайтесь начертить график.) Не противоречит ли существование такой функции теореме о промежуточном значении?
^44. Применив метод доказательства теоремы 6 (о действительных корнях многочленов нечетной степени), найдите такое число К, чтобы многочлен £(х) = г9 — ЮОх4 + Зх3 — 2 имел действительный корень в интервале (—К, +К).
45. Найдите такое число К, что многочлен хъ — 18х3+ 333 имеет корень /-.абсолютной величины | г | < К.
3.7. ОБРАТНАЯ ФУНКЦИЯ
Пусть /(х) определена и непрерывна при а<х^На = /(а) < Р = f(b) (рис. 3.23). По теореме о промежуточном значении функции, / где-то в интервале (а, Ь) принимает каждое значение у между аир. Конечно, она может принимать это значение в нескольких и даже в бесконечно многих точках. Точно так же f может принимать зна-
130
3. Функции
а Ь
Рис. 3.23
чения а, 0 не только на концах интервала, нои во внутренних точках (см., например» график функции, изображенный на рио. 3.23).
Но если f(x) — возрастающая функция, то дело обстоит иначе. Для такой функции из xj<x2 следует /(xt)</(x2). Поэтому / принимает значение а только в точке а, значение 0 — только в точке Ь и каждое значение у между а и 0 — водной и только в одной точке, заключенной где-то между а и b (рис. 3.24). Тем самым f устанавливает взаимно однозначное соответствие между (замкнутым) интервалом 1а, Ь\ оси х и (замкнутым) интервалом la, 0J оси у. Правило
то к из интервала а х < Ь, для которого f(x) = у»
есть вполне определенная функция, заданная для всех у из интервала а < у < Р* Эта функция называется обратной по отношению к /. Если обозначить ее буквой g> то имеем
g(f(x}) = х для всех х, а х Ь, В самом деле, что такое ^(/(х))? Это единственное число, которому f сопоставляет значение /(х), т. е. х. Подобное же рассуждение (вспомните вопрос: «Кто похоронен в могиле генерала Гранта?») показывает, что
f(g(y>) = У для всех у, а < у < Р, так что / есть функция, обратная по отношению к g. Очевидно, g — возрастающая функция.
Подобное же рассуждение применимо к непрерывным убывающим функциям, 1 но при этом и обратная функция оказывается убывающей.
ф Примеры. 1. Функция /(х) = ха, рассматриваемая в любом интервале справа от 0, т. е. при 0 < х Ь, есть непрерывная и возрастающая функция, принимающая j неотрицательные значения. Обратная функция g(y) определяется как то неотрицательное число, квадрат которого равен у. Иными словами, g(y) = Уу.
2. х »-► х2 есть убывающая непрерывная функция в любом интервале а < х < 0 I слева от 0. Обратная функция в этом случае есть у — У~у (рис. 3.25).
3. Функция х х3— непрерывная и возрастающая при всех х. Обратная функция есть у »-► ifу. ф
§ 3. Непрерывные функции
131
Рис. 3.26
Предыдущие рассуждения содержат доказательство первой половины следующей теоремы:
Теорема 7 (теорема об обратной функции). Пусть f— не-прерывная, строго монотонная (возрастающая или убывающая) функция, определенная взамкнутом интервале [а, Ы. Положим а = f(a), (3 = [(b). Тогда:
1° существует строго монотонная (возрастающая или убывающая) функция g, называемая обратной по отношению к f, определенная в замкнутом интервале с концами а, (3 и такая, что g(f(x)) = х, f(g(y)) = у;
2° обратная к f(x) функция g(x) непрерывна.
Аналитическое доказательство утверждения 2° содержится в Приложении (см. § 6.3). Утверждение это становится геометрически очевидным, если заметить, что график g получается из графика f перестановкой осей х и у, т. е. зеркальным отражением (осевой симметрией) графика относительно биссектрисы первого координатного угла (рис. 3.26). Если / непрерывна, график / состоит из одного куска. Это свойство графика сохраняется при отражении; поэтому график g также состоит из одного куска, т. е. функция g непрерывна.
132
3. Функции
УПРАЖНЕНИЯ
В упражнениях 46—49 каждая из функций имеет обратную в указанной области. Найдите обратную функцию.
Д46. l(t) = (3t + D/Л t >0. 48. Л(дг) = (1 + /7)’, х >0.
47. g(y) = (1 -j/W. J/>1- 49. f(z) = 1/(1 — г®), г> 1.
В упражнениях 50 и 51 решите, имеет ли заданная функция обратную.
50. а) х I-* х2. определенная при всех лг; б) х аг2, определенная при х^> 0; в) аг *—► аг2. определенная при х < 0.
51. а) аг !-► аг2 + аг — 1, определенная при всех х; б) х ь->х2 + х — 1. определенная при
—1/2; в) х »-► х2 + х — 1, определенная при х^. —1/2.
В упражнениях 52—54 решите, имеет ли функция, изображенная на графике, обратную, и в утвердительном случае набросайте график обратной функции.
В упражнениях 55—60 для каждой из отмеченных точек горизонтальной оси найдите наибольший содержащий эту точку интервал, в котором функция строго монотонна. В каждом таком интервале функция (точнее, «сужение» функции) имеет обратную. Набросайте графики обратных функций.
3.8 . НЕПРЕРЫВНОСТЬ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
Мы можем теперь установить непрерывность третьего класса функций, введенного в § 2.
Теорема 8. Иррациональная функция непрерывна во всех точках, где она определена.
§ 4. Пределы
133
Доказательство. Функции х1/2, х1/4, х1/6, х1/8, ... определены при х>. 0. Они обратны непрерывным функциям х2, х4, хв, х8, ..., возрастающим при х>> 0. По теореме 7, функции х1/2, х1/4 и т. д. непрерывны.
Функции х1/3, х1/5, х1/7, ... определены при всех х. Они обратны непрерывным функциям х3, хб, х7, ... и, следовательно, непрерывны (снова по теореме 7).
Далее, xp/q, где р и q — целые числа и q > 0, есть композиция двух непрерывных функций x'/Q и хр [так как хрН = (х1^)^ ]. Следовательно, эта функция непрерывна везде, где она определена (по теореме 4).
Наконец, иррациональная функция непрерывна везде, где она определена, поскольку она получается из непрерывных функций (степенных функций с рациональным показателем степени) посредством рациональных операций и композиции, а эти процедуры, применяемые к непрерывным функциям, приводят снова к непрерывным функциям (теоремы 1 и 4).
Замечание. Как читатель, может быть, заметил, опираясь на теорему 7 о существовании обратных функций, мы могли бы доказать существование корня n-й степени из положительного действительного числа независимо от соображений § 5.4 гл. 1. ।
§ 4. ПРЕДЕЛЫ В этом параграфе систематически изучается понятие пре-
дела, которого мы уже касались в § 4. Это понятие естественно возникает из понятия непрерывности.
4.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА
Пусть функция Дх) определена вблизи х0, за исключением, возможно, самой точки х0. Мы ищем такое число а, что если определить (или переопределить) f в точке х0, положив Дх0) = а, то f становится непрерывнойв этой точке. Если такое а существует, оно называется пределом функции f в точке х0; это записывается так:
lim f (х) = а
х->х0
(читается: «предел f от х при х, стремящемся к х0, равен а»), или
Дх) ->а при х ~>х0
(читается: «Дх) стремится к а, когда х стремится к х0»).
Если Дх0) уже было определено вначале и функция была непрерывна в точке х0, то нет надобности в ее переопределении. Итак,
lim Дх) = Дх0) означает, что f определена вблизи х0 и непрерывна в точке х0.
Если не существует способа определить Дх0) так, чтобы функция стала непрерывной, то говорят, что f не имеет предела в точке х0 или что предел f в точке х0 не существует.
• Примеры. 1. lim х3 = 27, потому что функция х н>х3 непрерывна в точке 3 и х—*-3 *
З3 = 27.
134
3. Функции
2. Пусть f(x) = х3 при г 3 и /(3) = 26. Тогда lim f(x) = 27 (по той же причи-х<*0
не, что и выше).
3. Пусть f(x) = х при х< 0 и f(x)=x2 при х > 0 (рис. 3.27). Тогда lim f(x) = х-*0
= 0, так как выбор значения /(0) = 0 делает функцию непрерывной при х = 0.
4. Пусть f(x) = 2 при х < 0 и f(x) = 1/2 4- х при х > 0 (рис. 3.28). Тогда / не имеет предела в точке х = 0, поскольку нет способа так переопределить /(0), чтобы сделать функцию непрерывной в этой точке, ф
Заметим, что функция не может иметь двух различных пределов в данной точке. В самом деле, предположим, что /(х) имеет в точке х0 предел а, а также другой предел 0 > а. Это значит, что если приписать /(х0) значение а, то получается функция, непрерывная в точке х0, обозначим ее через если же приписать /(х0) значение 0, то получается другая функция /2(%)» также непрерывная в этой точке. Итак, Л(х0) = а, /2(хо) = Р, fM = f 2W при х =/= х0, и обе функции и /\ непрерывны в точке х0. Но это невозможно: в самом деле, в этом случае функция g(x) = = /2(х) — fM непрерывна в х0 (в силу теоремы 1 § 3.3). Если 7 — число, удовлетворяющее неравенствам р — а > 7 > 0, то g(x0) > у, а поскольку g(x) = 0 при х #= х0, то вблизи х0 не может быть g(x) > у, что противоречит условию II в определении непрерывности.
Повторим определение предела. Утверждение «lim f(x) = а» означает, что: х-*х<
Г функция f определена во всех точках вблизи х0 (кроме, возможно, самой точки х0, где она может не быть определена);
2° если определить или переопределить значение функции в точке х0, положив Z(x0) = а, то f становится непрерывной в точке х0.
Утверждение, что «lim f(x) = а», можно высказать еще иначе: функция f(x)
Х->Х0
определена для значений х, близких к х0, за исключением, может быть, точки х0, и для каждого числа е > 0 существует такое число 6 > 0, что для всех х, удовлетворяющих неравенствам 0 < | х — х0 | < б, имеем | f(x) — а | < е.
Это е-8-определение предела равносильно первоначальному определению: если только что указанное условие выполнено и если положить /(х0) = а, то получается функция, непрерывная в точке х0. В силу этого определения утверждение «/(х) -*-а при х ->х0» имеет тот смысл, что /(х) становится сколь угодно близким к а, если только х достаточно близко к х0, но отлично от х0.
§ 4. Пределы
135
Читатель может убедиться, что употребление термина «предел» в § 2 согласуется с принятым здесь определением.
УПРАЖНЕНИЯ
В упражнениях 1—15 выясните, вычислите их.
1. lim f (х), где f (х) = (х3 — 7х)/(х 4- 5) х-*з
±2. lim/:(/), где h (t) = (/Г — 1)/(/2 4- 1). /->4
3. Нт (у2 4-— 1)/(г/— 1). «/-*—I
4. Нт (и2 4- 1)/(1 4- /2и 4- 8). а-* 1/2
существуют ли указанные
пределы, и если существуют
5. lim (А2 4- 2Л — 1). h-*0
6. lim (Л3 4-2Л2 — h)lh.
7. lim («а — l)/(u — 1). u-*1
8. lim(z24-* —6)/(z2 —4). г->2
9. Предел функции <н>(4г< — Зг 4- 1)/(4г3 —4г2 4- г), когда г стремится к 1/2, ±10. lim (xjfjT — х4-/Г — 1)/(х— 1). х-*1
11. Iim/(x), где [ (х) = х2 4- 4 при х < 2; £(х) = х3 при х>2. х->2
12. lim | х \/х. х->0
13. limg(x), где g(x) = x —2 при *<0: g(x)==r3 —3 при х>0. х-*0
±14. lim И (у), где Н (у) = у2 + у при </<1/3; Н (У) = о при <,= 1/3; Н (у) = |2</« {/-*1/3
при у^> 1/3.
15. iimK(0, где Л (/) = t 4- 4 при t <; — 2; /((0=0 при ^ = -2; /((/) = /2
при t > — 2.
4.2 . ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Теперь мы сформулируем основные правила вычисления пределов.
Теорема 1 (предел суммы, произведения и частного).
Пусть функции /(х), g(x) имеют пределы в точке х0. Тогда
lim 4- gj = lim/ 4- limg, lim (tg) = (lim/) (lim g),
lim — = , если g=/=0
g lim g
(где все пределы берутся при х -*-х0).
Словами это можно выразить так: предел суммы (произведения, частного) равен сумме (произведению, частному) пределов. 7 р
Это утверждение сразу же вытекает из теоремы 1 § 3.3 и определения предела
136
3. Функции
Докажем его только для суммы, поскольку в других случаях рассуждения аналогичны. Положим
lim f (х) = a, lim g (х) =$. X-fX0 Х-*Х0
Это значит, что если определить или переопределить значения функций в точке х0, положив f(x0) = а и g(xQ) = 0, то функции f и g становятся непрерывными в точке х0. Но тогда функция /+ g. принимающая значение а + р в точке х0, также непрерывна в этой точке (теорема 1 § 3.3), так что lim [/(х) + g(x)] = а + ₽. А это к-*х0 нам и требовалось доказать.
Частным случаем теоремы является следующее правило: lim(c/) = с lim / (где с — постоянная);
в самом деле, постоянная—непрерывная функция. Далее, поскольку f — g = = f + (—g) = f + (—l)g, имеем также
lim(/ — g) = lim f — lim g.
Ясно, что можно применять это правило также к суммам, разностям, произведениям и частным более чем двух функций. Если, например, функции /, gnh имеют в точке х0 пределы а, (3 и 7, то функция f + g — h имеет в точке х0 предел а + (3 — 7.
•Пример. Легко видеть, что
lim ( = 0 при а> 1.
*->о \ х )
Поэтому, согласно теореме 1, имеем
Пт —(1 ~ х). =Нт [ Нт =0- — = 0. •
х->о х (2х + 3) х-*о \ х / \ х-о 2х 4- 3 / 3
Теорема 2 (предел композиции функций). Если lim/(x) = t/0, g(y) х->х0
непрерывна в точке у0 и g(y0) = а, то , lim g (/(%)) == а. х-*хс
Это предложение сразу же вытекает из теоремы 4 § 3.5 о непрерывности композиции функций.
•Пример. Чтобы вычислить
27х3 + 4х — 4 х10 4- 4х2 4- Зх
заметим, что функция у »-> у'/з непрерывна везде, так что искомый предел равен
3 /—Z----------- 3 Alim (27х3 4- 4х — 4) з г—~
Hm 1 / 27х34-4х-4 = Л х->1 = <//27 = 3 _
х<1 V х10 4 Ах2 4- Зх У lim (*10 + 4х2 4- Зх) I/ 8 2 ‘ *
§ 4. Пределы
137
УПРАЖНЕНИЯ
В упражнениях 18—20 и 22 предполагается, что,функция gB требуемых точках непрерывна.
Д16. Пусть lim f (х) = 12 и lim g (х) = 3; найдите lim y(fg)(x). х —>0 х-*0 х->0
17. Пусть lim / (х) = 1/3 и lim g (х) = 30; найдите lim (fg — f — g) (x).
х-И/2 x-*l/2 x-1/2
18. Пусть limf(x)=2 и lim g (x) = 8; найдите lim (gof) (x). x->l x->2 x->l
19. Пусть limf(x) = 9 и lim g (x) =5; найдите lim(goj/f )(x). x->l x->3 x->l
20. Пусть limf(x) = 4 и lim g (x) =36; найдите lim У gof (x). x->2 x->4 x->2
21. Пусть limf(x) = 30 и limg(x)= 1/2; найдите lim (f + g)/(f — g) (x). X->1 X->l X->1
22. Пусть lim f (x) = 3, lim g (x) = 1/3 и lim g (x) = 2; найдите lim (/ -f- (g of)/g) (x). x->2 x->2 x->3 x-*2
4.3. ОБОБЩЕНИЯ
Нам придется пользоваться некоторыми обобщениями понятия предела, которые мы здесь неформально поясним на примерах.
Рассмотрим сначала функцию
f (х) = -Ш- = Щ —— ; х 4- х3 х 14-х2
она определена при всех х #= 0, и график ее изображен на рис. 3.29. Заметим, что | х ]/х = 1 при х > 0 и | х \/х = —1 при’х < 0. Функция /(х) не имеет предела в точке х = 0, но для положительных и достаточно малых х значения /(х) сколь угодно близки к 1, а для отрицательных и достаточно малых по абсолютной величине х эти значения сколь угодно близки к —1. В этом случае говорят, что /(х) имеет в точке 0 односторонние пределы: предел справа 1 и предел слева — 1; это записывается так:
lim/(x) = 1, lim/(x) = — 1. x->Ch х->0~
(Символы х ->0+ и х ->0" читаются: «когда х стремится к нулю справа», «когда х стремится к нулю слева».)
Та же функция /(х) обладает тем свойством, что при достаточно больших х значения f(x) становятся сколь угодно малыми. Это можно выразить словами так: /(х) имеет предел 0 при х стремящемся к +оо (читается: «к плюс бесконечности»); соответствующая запись имеет вид
lim /(х) = 0.
х-*Ч-00
Точно так же очевиден смысл записи
lim /(х) = 0. \ ж-*—»
В подобном случае говорят, что функция f(x) имеет пределы на бесконечности.
138
3. Функции
Рис. 3.29
Рассмотрим теперь функцию
определенную для всех х Ф —1; ее график изображен на рис. 3.30. Никакое число нельзя назвать односторонним пределом этой функции в точке х = —1 или ее пределом на бесконечности. Можно, однако, утверждать, и ниже мы это проверим, что функция g(x) становится сколь угодно большой, когда х стремится к —1 справа или когда х стремится к 4- оо. Это записывают так:
lim g(x) = 4- оо,
limg(x) = 4-оо.
Точно так же сам собою понятен смысл записей
lim g(x) — — оо, lim g(x) = — оо.
Говорят, что g(x) имеет односторонние бесконечные пределы в точке х = —1, а также и бесконечные пределы на бесконечности.
Докажем теперь сделанное выше утверждение. Пусть сначала х близко к —1; положим х = — 1 4- t, так что | t | мало. Если х —1, то можно записать
Число 1/2/ положительно при х>—1 (т. е. при />0), отрицательно при х < —1 (когда t < 0); его абсолютную величину можно сделать сколь угодно большой, если взять | t | = | х — (—1) | достаточно малым. То же верно и для g(x), так как при малом | t | число —1 4- t/2 близко к —1.
Посмотрим, что происходит с g(x) при больших | х |: для этого заметим, что при хф 0,—1
Если | х | велико, то Их близко к 0, 24-2/х близко к 2, и дробь 1/(2 4- 2/лс) близка к 1/2. Поэтому для больших | х | функция g(x} имеет тот же знак, что и х, и
$ 4. Пределы
139
I g(x) | может быть сделано сколь угодно большим, если х достаточно велико. А это нам и требовалось доказать.
Символы 4- оо и — оо очень удобны; читатель должен помнить, однако, что они являются не наименованиями чисел или каких-либо других знакомых нам объектов, а просто чем-то вроде стенографических знаков, позволяющих сократить запись некоторых предложений.
Надо помнить также, что выражение «/ имеет предел в. точке х<р всегда употребляется в смысле утверждения существования числа а такого, что lim f(x) = а.
х-*х0
Если мы хотим сказать, что либо существует число а, служащее пределом f в точке х0, либо lim f(x) = + оо, либо lim f(x) = — оо, мы говорим: «/ имеет конечный х->х0 х->х0
или бесконечный предел в точке х0». То же соглашение относится к односторонним пределам и к пределам на бесконечности.
Формальные определения «пределов», описанных выше, и правила их вычисления содержатся в Приложении (см. § 5).
УПРАЖНЕНИЯ
В упражнениях 23—27 установите, какие из утверждений верны.
23. a) limx2=0, б) limx2=H-oo, в) limx2 =— оо.
«-►0+ х-*-4оо х->—оо
24. a) lim | х |3/х3 =1, б) lim | х |3/х3 = 0, в) lim | х |3/х3 = — 1. х-*0+ х-*0“ х—0“
25. a) lim (1 4- х)/( 1 — х) = 1, б) lim (1 4- х)/( 1 — х) = — 1, в) lim (14- х)/( 1 — х) = — оо. х->4-со оо X—>—ОО
Д26. a) lim х3/(1 4-х2) = 4-оо, б) lim х®/(1 4- х2) = — оо, в) Игл х3/(1 4-х2) = 8/5. х ->4со х->—оо х->2+
27. a) lim х2/( 1 — х) = — оо, б) lim х27( 1 — х) = 4- оо, в) lim х2/(1 — х) = 4- оо. Х->1"
140
Приложение к главе 3
Приложение к главе 3
$ 5. Односторонние пределы, бесконечные пределы и пределы на бесконечности
В этом параграфе на более высоком уровне математической строгости обсуждаются описанные выше различные видоизменения понятия предела.
5.1. Односторонние пределы
Определение односторонних пределов весьма напоминает определение предела. Утверждение lim f (х) = а
[читается: «предел [(х) при х, стремящемся к х0 справа, равен а»], или
f (х) —> а при х —> х0
[читается: «f(x) стремится к а, когда х стремится к х0 справа»] означает, что:
Г функция f(x) определена в некотором интервале с левым концом х0, т- е- пРи *o<Z x<Z b (она может быть определена или не определена в точке х0);
2° если определить или переопределить величину f(xQ), положив ее равной а, то функция, определенная таким образом прй х0Ь, непрерывна в точке х0. (Если такое значение а существует, то оно единственно, как видно из приведенного в § 4.1 рассуждения.)
Совершенно аналогично определяется предел f, когда х стремится к х0 слева, т. е. смысл утверждения1
lim / (х) = р.
X-Хо
Предположим, что /; определена вблизи х0, за исключением, возможно, самой точки х0, и что существуют оба односторонних предела
limf(x) = a и lim/(x) = ₽.
Х-*Х% X—Xq
Если а = р, то, как легко видеть,
lim f (х) = а. X—*х0
Если же а Р > то не существует способа сделать /j непрерывной в точке х0; в этом случае говорят, что f претерпевает конечный разрыв (или скачок) в точке х0. Рис. 3.29 объясняет этот термин.
• Примеры. 1. Пусть функция f(x) = 1 при х<_0, f(x) = 2 — х при х >0, a f(0) не определено; тогда /(х) —* 2 при х —► 0+, f(x) —► 1 при х —► 0“. В самом деле, функция 2 —х непрерывна в точке 0, 2 — 0 = 2, а постоянная функция 1 непрерывна в точке 0. Таким образом, наша функция в точке х = 0 имеет конечный разрыв.
1 Иногда вместо х~>х0 пишут xf х0, а вместо х~>х0 пишут хфх0. (В русской учебной и научной литературе употребляются также имеющие тот же смысл записи х~>х0—0, соответственно — Прим, ред.)
§ 5. Односторонние пределы, бесконечные пределы и пределы на бесконечности
141
2. Положим g(t) = \Ц при К 0, g(0) = 4, g(t) = 7 + при t >0. Тогда lim g(t) = 7 ng /-►си-
не имеет предела, когда t стремится к 0 слева.
3. Обозначим для каждого числа х через [х] наибольшее целое число, не превосходящее х; например, 1—5] = —5, [—5,3] = —6, [-L] = Оит. д. Пусть п — любое целое число; тогда lim [х] = п — 1, lim [х] = я. Все разрывы функции [х] — скачки, ф
Х->Л“ х->л+
УПРАЖНЕНИЯ
В упражнениях 1—8 установите, существуют ли указанные пределы, и в утвердительном случае найдите их.
1. lim/(x), где f (х) = х3 — 1 при х< 1; 1/2 при х= 1; х2 при х> 1.
х-И+
2. Нтй(х), где А (х>= (х2 4-I)2 при х < 0; 2х — 8 при х>0. x-(l/2)“
3. lim g(t), где g(t) = (/2 + 1) (/ — I)”1 при t < 1; /2— 1 при t > 1.
/-1-
Х4. lim А (и), где Л (я) = и 4-1 при и < 3; и2 « 1 при я>3.
н->3+
5. a) lim —* v2 , б) lim 1 =» и2 .
6. lim (е> 4-2) (4 — и2)1/2.
D-*-—2“
7. lim (х2 — (9 —х2)1/2)1/2.
х—►—3+
8. lim/(«/), где f (у) = У2 при 0,0001; у 4" 1 при — 0,0001 < у < 0;
У 2с/ — с/2 при 0 < #<4.
9. Начертите график функции G(s) = l при s > 1; 1/2 при l>s> 1/2; 1/4 при 1/2> >s> 1/4; 1/8 при l/4>s> 1/8, ... , 1/2л при H2n^>s> 1/2л и п= 1,2, 3, ...; 1 при s = 0; 0 при s < 0.
Установите, существуют ли lim G (s) и limG(s), и в утвердительном случае найдите их/ s->o+
Что можно сказать о поведении G в точке 0?
10. Начертите график функции Н (/) = 1 при i > 1; 2t — 1 при 1 > t > 1/2; 4/ — 1 при 1/2>/> 1/4; 8/ — 1 при 1/4>/ > 1/8, ... » 2nZ — 1 при 1/2л"х >t > 1/2л и п = = 1,2,3,...; 1 При t = 0; 0 при t < 0.
Установите, существуют ли lim Я(0 и lim Я(0» и в утвердительном случае найдите их. /-0+ . /-о-
Что можно сказать о поведении функции Н в точке 0?
5.2 . Бесконечные пределы
Функция f(x) = 1/1 х | не определена при х = 0 и не имеет в этой точке предела, причем разрыв не является конечным. Напротив, для любого сколь угодно большого числа А имеем f > Л вблизи 0 (за исключением самой лишь точки 0). Но сказанное равносильно следующему утверждению: Ц >0 вблизи 0, за исключением самой точки 0, и для любого сколь угод
142
Приложение к главе 3
но малого положительного числа е вблизи 0 мы имеем f/f<8 (за исключением разве что самой точки 0). Это подсказывает следующее определение бесконечного предела: утверждение
lim f (х) = + оо х->х0
(читается: «предел f в точке х0 равен плюо бесконечности»), или [ —> + оо при х -> х0
(читается! «J стремится к плюс бесконечности, когда х стремится к х&>) означает, что! 1° iW >0 вблизи х0 (кроме, возможно, самой точки х0);
2° lim 1/f (х) =0. х->х0
Подобным же образом придается точный смысл утверждениям lim f (х) = — оо , lim f(x) = 4- оо х-*х<г х->х0+
и т. д. Напомним еще раз (ср. с § 4.3), что символы +оо, —оо не являются наименованиями чисел.
• Примеры. 1. lim 1/х4= 4- оо, так как х4>0 при х=^0, х4 непрерывна в точке 0, 1//(х)= х-»-0
= х4 и lim х4 = О4 = 0. х->0
2. lim 1/х= 4-00, lim 1/х = — оо. В самом деле, 1/х>0 при х>0, 1/х<;0
х->0+ х->0“
при х < 0 и lim х = 0. х-о
3. lim (1 4- *)/(1 — х) = — оо. В самом деле, при х> 1 имеем 1 4- х> О, 1 — х<0, так х->1+
что (1 4-*)/(1 — х)<0 и функция (1 —х)/(1 4-х) непрерывна в точке х= 1, где она принимает значение 0. •
УПРАЖНЕНИЯ
В упражнениях 11—15 установите, имеет ли заданная функция в указанных точках предел (имеется в виду конечный предел), бесконечный предел или ни того, ни другого. В первых двух случаях вычислите предел (мы пользуемся этим общепринятым, хотя и не совсем точным выражением также в случае бесконечных пределов).
V, 11. a) lim (х24- 1)/(х —2), Х-+&
А12. a) lim(x4- 1)/|х-1|, х-И+
13. a) lim \/Ух , х->0+
14. a) lim (/3 4- 1)7(2/4-3), /->(-2/3)+
15. a) lim (иъ 4- 2ц)/(ц5/3 — и\, и->1+
16. Начертите график функции
б) lim (х2 4-1)/(х —‘ 2), x-+Z~
б) lim (х 4- 1)/| х — 11 , х->Г
б) lim (4 —х2)//4 —х». х-*2“
б) lim (/3 4-1)/(2/4-3), /->(-2/3)-
б) lim (и6 4- 2ц)/(и5/3 — м),
f (г) = 1 при г > 1; — 2 при
в) lim (х2 4- 1)/(х — 2). х->2
в) lim(x4- 1)/|х —1|. х->1
в) Нт р 4- 1)7(2/4-3).
2/3
в) lim (иъ 4- 2ц)/(цэ/3 — и). u-d
1>г> 1/2; 4 при 1/2 >z
> 1/4; —8 при 1/4 >z > 1/8..................
(— 1) • 2я при 1/2л"1 > 2 > \/2п и п=1, 2, 3,...
Установите, имеет ли f(z) предел, бесконечный предел или ни того, ни другого, когда г стремится к 0 справа. В первых двух случаях найдите предел.
§ 5. Односторонние пределы, бесконечные пределы и пределы не бесконечности
143
5. 3. Пределы на бесконечности
Язык пределов можно применить также для описания поведения функции f(x) при больших значениях х. Условимся, что выражение «вблизи 4-оо» означает: «для всех чисел х,. больших некоторого положительного числа». Мы будем говорить, что lim f(x) = а, если:
X’ >~|~00
1° / определена вблизи 4-°о,
2° при а < А вблизи 4- оо выполняется неравенство f < А, а при а > В вблизи + 00 — неравенство f > В.
В этом случае пишут также: f -> а при х -> 4- оо.
Точно также «вблизи — оо» означает: «для всех х, меньших некоторого отрицательного числа». Вряд ли необходимо после этого разъяснять смысл утверждения lim /(х) = {з.
г—>—оо
Заметим теперь, что если f(x) определена вблизи Ч-оо (т. е. для всех х, больших некоторого числа), то функция /•-*/(!//) определена для всех положительных t вблизи 0 (т. е. для всех положительных /, меньших некоторого числа). Если /(х) < А [или f(x) > В] для всех х вблизи H-оо, то /(1/0 < А [или /(!//) > В] для всех положительных t вблизи 0. Мы приходим, таким образом, к равносильному определению пределов на бесконечности:
lim f (х) = а означает, что lim f (—= а.
X->-|-OO \ t /
Подобным же образом
lim f (x) = 3 означает, что lim f (—) = ₽. x->—oo \ t /
Если оба предела существуют и равны, то мы пишем также*
lim f (х) = а, что означает lim f f—) = а. t—>оо ^->0 \ t J
Условимся распространять эти определения и на случаи, когда а и £ — не числа, а один из символов Ч-°°. —оо.
ф Примеры 1. lim (1/х) = 0. Действительно, заменив х на 1//, имеем lim / = 0.
Х->оо /->0
2. Имеем
1 + 2х 2
lim ---------= —----
х->4-<» 1 — Зх 3
В самом деле, это означает (если заменить х на 1//), что
14-2// 2
lim ---------= — — •
1 — 3/Z 3
Но
14-2// /4-2
i—з/ “ t — з 9
а эта функция непрерывна в точке / = 0 и ее значение в этой точке равно —2/3.
* В русской учебной литературе чаще в таких случаях пишут lim / (х) = а [сохраняя за записью lim /(х) = а смысл утверждения lim /(х)=а].
144
Приложение к главе 3
3. lim хп = + оо для любого целого положительного п. Действительно, lim 1//л = X—>~|-оо t~*-0^
~ + °°» так как /л>0 при />0, tn непрерывна в точке / = 0 и ОЛ = О.
4. lim хп = + оо для любого четного целого положительного числа п и lim хп = —оо Х-*—со х->—со
для любого нечетного целого положительного числа л. (Примените то же рассуждение, что в примере 3.) ф
УПРАЖНЕНИЯ
17. a) lim (14-6х)/(—2 4-х) = ? (Проставьте число, 4-оо или — оо или скажите, что х—>—|-оо.
функция не имеет ни конечного, ни бесконечного предела).
б) lim (1 4- 6х)/(—2 4-х) = ? в) lim (1 4- 6х)/(—24-х) = ? Х-> — СО Х~>00
,Л18. a) lim (1 4- у 4- 2р2)/(10 4- 5у - 4р2) = ?
А/-*Н-оо
б) Ji™ (1 + + 2^)/(10 + = ?.
в)П1т (1 +p + 2j/2)/(10+5i/ —4^) = ?
Z/->oo
19. a) lim 2/3/(6 4-1 4- 2f2 4- *3) = ? t-»--|-оо
б) lim 2/3Z(6 4-1 + 2Р 4- t3) = ? —00
в) lim 2/3/(6 4- t + 2/» 4- i3) = ?
20. Пусть x p(x) — многочлен степени п >0 со старшим коэффициентом г, ахн- q(x) — многочлен степени п со старшим коэффициентом s.
a) lim р (x)!q (х) = ? б) lim р (x)/q (х) = ?
' х->4-оо х->—со
в) lim р (x)/q (х) = ? х-*со
21. a) lim 3/(u3 4- и — 1) = ? б) lim 3/(и3 + и — 1) = ? И-*—(“СО U-*—со
в) lim3/(u34-u—1) = ?
22. a) lim (100г8 4-г 4-1)/г4 = ? б) lim (100г8 4-г 4-D/г4 = ? г->4~°° —°0
в) lim (100г3 4-г 4-I)/*4 = ? г-* со
23. a) lim (о100 4-f")/(v101 — f100) = ? б) lim (v100 4-v")/(o101 — t»100) = ?
в) '"Пт”»1004-t>->OO
a xi-*q(x)—многочлен степени в) lim р(х)/<?(х) = ?
lim (t»3 4- 1)Z(f2 — 1) = ? >-►—co
6) lim (2r3 4- '2 — l)/(r 4- 5) = ? r->—co
6) lim (j/4 — 2y3 4- у — l)/(y — 1) = ? p-*—co
24. Пусть x p (x) — многочлен степени n, a) lim p(x)/g(x) = ? 6)
x->-|-oo x->—co
25. a) lim (t»3 4-l)/(f2 — 1) = ? 6)
O-»+a>
в) lim (o34-l)/(a2 — 1) = ? V->00
26. a) . lim (2r3 4- r2 — l)/(r 4- 5) = ? r->-1-co
в) lim (2r3 4- r2 — 1)/ (r 4- 5) = ? r->oo
27. a) lim (y4 — 2i/2 4-1/— 1)/(1/— 1) = ?
в) lim (j/4 — 2y3 4- у — i)/(y — 1) = ? у-*-00
lim p(x)/q (x) = ?
§ 5. Односторонние пределы, бесконечные пределы и пределы на бесконечности
145
28. Пусть х^р(х)— многочлен степени n, a i->g(x)— многочлен (не тождественно рав. ный нулю) степени т<^п.
а) • lim р (x)/q (х) = ? б) lim р (x)/q (х) = ? в) lim р (x)/q (х) = ? Х-*+<Ю х-*-—оо х->оо
[Указание: рассмотрите отдельно случаи, когда п — т четно и п— т нечетно.]
5.4. Вычисление бесконечных пределов
Как мы показали в § 4.2 (см. теорему 1), пределы суммы, разности, произведения и частного двух функций, имеющих пределы в точке, равны соответственно сумме, разности, произведению и частному пределов этих функций (в случае частного надо предположить также, что предел делителя не равен 0). Легко убедиться в том, что все это верно и для односторонних пределов.
Как же обстоит дело с бесконечными пределами? Оказывается, можно применить те же правила вычисления пределов, если только при «операциях над пределами* пользоваться одним из следующих правил (в приводимых ниже формулах а означает число)!
4-оо + а= а +(+оо) = -Ьоо-|-(-f-оо) = 4-оо, — оо 4- л = а 4~ (— оо) = — оо 4- (— оо) = — оо, а (4- оо) = (4- оо) а = (— а) (— оо) = (— оо) (— а) = 4" 00 при а > О,
а (— оо) = (— оо) а = (— а) (4- оо) = (4- оо) (— а) = — оо при а > О,
(+ оо) (4- оо) = (— оо) (— оо) = 4- оо, (4- °0) (—оо) = (—оо) (4- оо) = — оо,
—— =—— = 0.
4“ оо — оо
(*)
Мы должны проверить, что каждое из этих правил приводит к верному результату. Это легко усмотреть из соображений здравого смысла. Например, первая из приведенных формул по существу утверждает, что если одна из функций становится очень большой (и положительной), когда независимая переменная стремится к некоторой точке, а другая функция непрерывна в этой точке, то и сумма их становится очень большой и положительной. Те’же соображения приводят и к формальному доказательству: надо только вместо «очень больших» значений говорить о «больших любого заданного числа». Предлагаем читателю «установить на уровне здравого смысла» и другие утверждения (♦). В одном из случаев они будут доказаны формально в § 6.4.
Заметим, что имеются случаи, не охватываемые нашими правилами. Не существует «формул» для выражений, подобных 0/0, 0-(4-оо) или (+оо)+ (—оо). Это вполне естественно. В самом деле, если, например, две функции £(х) и g(x) имеют в некоторой точке предел 0, то не существует общего способа предсказать, как будет вести себя в этой точке частное h(x) = f{x)lg{x). Чтобы убедиться в этом, рассмотрим случай, когда Цх) = х2, g(x) = хп, где п — целое число. Частное h(x) = х2гП может иметь в точке 0 предел 0 (при п ® 1), или 1 (при п = 2) или оо (при п = = 4), или может случиться, что предел слева в точке 0-равен —оо, а предел справа равен 4-оо (при п = 3).
Применимость правил (*) к случаю односторонних пределов и пределов на бесконечности не требует дальнейших пояснений.
Очевидно также, что правило вычисления предела композиции двух функций (сформулированное в теореме 2 § 4.2) применимо к односторонним пределам, пределам на бесконечности и бесконечным пределам.
• Примеры. 1. Пусть мы хотим вычислить lim (ха—Зх). Как известно, lim х2= +оо (пример х->ч-св х -►+«
3 § 5.3), и из правила (*) следует, что lim (—Зх) = (—3) (4-оо) = —оо., Однако, пользуясь х-*+°*
этой информацией, мы не можем вычислить lim (х^ — Зх), поскольку выражению (4“Оо) 4- (—оо) + «
не приписывается никакого смысла. Вместо этого применим правило (*) следующим образом!
146
Приложение к глазе
lim (х2 — Зх) = lim х (х — 3) = lim х • lim (х — 3) =
= (+ оо) (+ оо — 3) = (+ оо) (+ оо) = 4- оо .
2. Пусть мы хотим вычислить предел при х -> I функции
, I + *3 f (х) =-----------.
I _ 2х 4- ха
2
Мы не можем при этом воспользоваться бессмысленным выражением -у- . Вместо этого за метим, что
14-х8 . » ।
---- = (1 4- х3) . 1 —2x4-х2---------------(1— х)2
Поскольку при х=/= 1 имеем (1 — х)2>0, то
lim /1 1 \2 = + 00 • х-н (1 —X)2
• откуда получаем
lim f (х) = 2 (4- оо) = 4- оо .
х-Н
3. Точно так же в случае
' 1 — Зх + Зх2 — х»
имеем
lim
f(x) = — оо ,
lim f (х) = 4- оо .
В самом деле,
(1-Х)’
1
и нт —;--------------------------г = — оо , нт —----------— = + оо . ф
х-г (1 - х)3 х)3 w
УПРАЖНЕНИЯ
Хотя многие из следующих упражнений можно выполнить «в лоб», т. е. без всяких ухищрений, обычно оказывается проще воспользоваться некоторой комбинацией приведенных выше правил.
29. lim (х3 4- 2х — 5) (х8 4- 2х7 4- *3 — 1) = ? х->0
30. lim (г11 — 2г 4-З)6 (z7 4-z2 — 1)“8 = ? 2->1
31. lim (9 — уг)~1,2(уа + 2)1» = ?
±32. lim (2х + 1)1°° / (х2 + х — 2) = ? х->Г
33. lim (| х |/х)’ (х2 4- /Г+4)4 == ? х-»0+
34. hm (<2 + I)» (/Г— I)3 l(/2 + 1) / (2/2 — 5)]2 = ? <-►4-00
§ 6. Доказательства некоторых теорем о непрерывности
147
35. lim
(цз + 2ц — 1)*
(и2 -|- и — 6)'
36. lim
37. lim
—00
38. lim
/ (?3-2г+1)^ |/ (2z2+?—I)3
Г (иЯ -|- 2и04 W3
|_ j
1/х— 1/х*~
1/X3 — 1/X4
Некоторые выражения, содержащие +оои —оо «невычислимы», поскольку любая попытка остановить «вычислительное правило» была бы несовместима с теоремами предыдущего раздела. Ию иллюстрируют следующие упражнения.
39. Пусть/(х) = 2х, g(x) = —х. Вычислите lim f (х), lim g(x)9 lim (/+g)(x). Х-Н-со х-*+« r-*4-00
40. Пусть f (x) = 2x, h (x) = — Зх. Вычислите lim f (x), lim h (x), lim (f -f- h) (x). r-*4-00 X-*4-00 X-*4-00
41. Пусть A (t) = t~2, В (t)= t~l. Вычислите lim 4(f), limB(f), lim(A/B)(0, lim(B/A) (0. t ->()+ t-W
§ 6. Доказательства некоторых теорем о непрерывности
В этом параграфе доказываются некоторые из теорем, сформулированных без доказательств в § 3, а также правило вычисления бесконечных пределов из §5.4. Доказательства, по существу, представляют собой упражнения в применении определения непрерывности. Доказательство же теоремы о промежуточном значении, основывающееся на фундаментальных свойствах действительных чисел, откладывается до следующего параграфа.
В подлежащих доказательству теоремах заключение всегда одно и то же — что некоторая функция непрерывна, г. е. обладает свойствами I и II, составляющими определение непрерывности. Во всех случаях мы проверим лишь свойство I. Мы предлагаем читателю провести доказательство свойства II, следуя тому же образцу.
6.1. Сумма, разность, произведение и частное
Мы начнем с доказательства теоремы 1 § 3.3, согласно которой для любых двух функций tug, непрерывных в точке х0, непрерывны также f + g, f — g и fg, а если g(x9) =/= 0, то и f/g.
Доказательство мы разобьем на несколько шагов.
1) Пусть f — функция, непрерывная в точке ха, и с — постоянная. Тогда сумма f + с непрерывна в точке х9.
Доказател ьство. Пусть Дх0) + А. Тогда ^(хе)< А — е и так как f непрерывна, то А — с вблизи хе, так что f + А вблизи х9. Таким образом, j + с обладает свойством 1.
2) Пусть f и с — те же, что и в п. 1. Тогда функция cf непрерывна в точке ха.
Доказательство. Если с = 0, то функция cf(x) есть постоянная 0 и, следовательно, непрерывна везде. Предположим, что с>0. Если с/(х0)< А, то Дх0)< А/с. Поскольку / непрерывна, имеем Дх)< А/с вблизи х0. Поэтому cf<Z А вблизи ха. Таким образом, cf обладает свойством I. Случай c<Z 0 рассматривается аналогично.
3) Пусть fug непрерывны в точке х9\ предположим, что f(x9) = g(x0) = 0. Тогда сум м а f + g непрерывна в точке х0.
148
Приложение к главе 3
Доказательство. Пусть f(x0) + g(x0X Л. Тогда А > 0 и поэтому ДхоХу > А А А
g(x0) < "7j" Поскольку f и g непрерывны, f(xX-g-и g(xX“у вблизи х0. Следовательно. А А
I + g<Z ~2 + "2~ = вблизи х0- Таким образом, f + g обладает свойством I.
4) Пусть fi и g непрерывны в точке х9; тогда и су м ма f + g непрерывна в той же точке.
Доказательство. Положим fiY(x) = ft(x) — f(x0), gi(x) = g(x) — g(x§). Тогда и gi в силу п. 1 непрерывны в точке х0, причем £х(х0) = gi(*o) = 0- Согласно п. 3, функция ф = fi + gi непрерывна в точке хе. Но f(x) + g(x) = ф(х) + с, где с = £(х0) + g(x0). Согласно и. 1, и + g непрерывна в точке х9.
5) Пусть fug непрерывны в точке х0, тогда разность f — g непрерывна в той же точке.
Доказательство. Функция —<£ = (—l)g непрерывна в точке х0 согласно п. 2. Но тогда из п. 4 следует, что в той же точке непрерывна функция f — g = f + (—g).
6) Пусть fug такие же, как и в п. 3; тогда произведение fg непрерывно в точкех0.
Доказательство. Предположим, что f (х0) g (х0) < А. Тогда А > 0. Следовательно, f (х0) = 0 < А и f (х0) = 0 > — Л; поскольку f непрерывна, f (х)< Л и f (х) > — А вблизи х0, иначе говоря, | f | < Л вблизи х0.
Далее, g (х0) < 1 и g (х0) > — 1, а так как g непрерывна, то g< 1 и g>- 1 вблизи х0; иначе говоря, | g | < 1 вблизи х0,
Отсюда заключаем, что | fg | = | f 11 g | < Л • 1 = Л вблизи х0, и тем более fg<ZA вблизи х0. Тем самым функция fg обладает свойством I.
7) Пусть fug непрерывны в точке х0; тогда и произведение fg непрерывно в той же точке'.
Доказательство. Положим Л (х) = f (х) -^f (х0), gx (х) = g (х) — g (х0) и <p = figi-Тогда имеем f (х) g (х) = <р (х) + f (х0) g (х) 4- g (*0) f W +/ (х0) g (х0). Функции fi и в силу п. 1 непрерывны в точке х0. В силу п. 2 в той же точке непрерывны функции f(x^)g(x) и g(xe)f(x), а согласно п. 6, непрерывна и <р(х). Наконец, в силу п. 4 функция fg также непрерывна в точке х0 как сумма непрерывных функций.
8) Пусть функция f непрерывна в точке х0 и f(х0) = 1: тогда функция 1// непрерывна в точке х0.
Доказательство. Предположим, что Uf (xQ) <^А. Это значит, что Л>1. Следовательно, /(х0)>1/Л и, поскольку f непрерывна, />1/Л вблизи х0. Таким образом, 1//<Л вблизи х0, и функция \/f обладает свойством I.
9) Пусть f непрерывна в точке хои f(xo)=£O; тогда функция l/f непрерывное точке х0.
Доказательство. Функция [1// (х0)] f (х) в силу п. 2 непрерывна в точке х« и принимает в точке х0 значение 1. В силу п. 8 в точке х0 непрерывна функция f(xQ)/fMt и снова вследствие п. 2 — функция 1И (х) = [ 1 If (х0)] [f (xQ)/f (х)].
10) Пусть fug непрерывны в точке х0 и тогда и частное fig непрерывно
в той же точке.
Доказательство. В силу п. 9 функция 1/g непрерывна в точке х0, а вследствие п. 7 — и функция flg = (1/g) f непрерывна.
Теорема 1 вытекает из пунктов 4, 5, 7 и 10.
УПРАЖНЕНИЯ
1 Проверьте, что функция f + с п. 1 обладает свойством II.
2. Проверьте, что функция cfj п. 2 обладает свойством 1 при 0.
3. Проверьте, что функция cf п. 2 обладает свойством II.
4. Проверьте, что функция f + g п. 3 обладает свойством II.
5. Проверьте, что функция fg п. 6 обладает свойством II.
6. Проверьте, что функция l/f п. 8 обладает свойством II.
§ 6. Доказательства некоторых теорем о непрерывности
149
6.2. Композиция функций
Мы докажем теперь, что композиция двух непрерывных функций непрерывна (теорема 4 § 3.5).
Пусть даны функции f и g: f непрерывна в точке х0, f (х0) = yQ и g непрерывна в точке г/0. Трёбуется доказать, что = g of непрерывна в точке
Предположим, что <р(х0)<А. Это значит, что g (f (х0))<А, т. е. g (Уо) <2 А. Поскольку g непрерывна, имеем g<ZA вблизи yQ\ иначе говоря, существует такое положительное число6, что g (у) <Z А для всех у, удовлетворяющих неравенствам yQ— ^<^У<СУо + ^-
Далее, f (х0) =у^<Уо + ^ и f = Уо > Уо — 5- Так как? непрерывна, f < у^+ 6 и f>yQ—6 вблизи х0, и в силу сказанного выше g (f (х))< А вблизи х0. Тем самым свойство 1 соблюдается.
УПРАЖНЕНИЕ
7. Проверьте, что фун кция Ф = £ ° f обладает свойством II.
6.3. Обратная функция
Теперь мы установим непрерывность функции обратной по отношению к непрерывной строго монотонной функции. Это часть теоремы 7 § 3.7, оставленная там без доказательства. При этом мы не будем здесь касаться вопроса о существовании обратной функции: как было от*-мечено в § 3, она вытекает из теоремы о промежуточном значении.
Мы предполагаем, таким образом, что даны две строго монотонные функции f и g, взаимно обратные друг другу Пусть f определена при а х^ Ь. Допустим, что f непрерывна. Функция g такова, что g(f(x)) = х для всех х, а^ х^, Ь. Надо доказать, что g непрерывна.
Пусть для определенности f возрастает; положим f (а) = а и f(b) = $. Тогда g (у) определена при а < у < р и также возрастает, причем g (а) = а, g (р) = b.
Возьмем теперь число yQ, удовлетворяющее неравенствам а < у0 < р. Пусть число А таково, что g (у0) <Z А\ надо показать, что g (у) < А вблизи у0. Можно считать при этом, что А < 6; в противном случае доказывать нечего, поскольку g вообще не принимает значений, больших Ь.
Положим g(yQ) = Ао. Тогда, по определению g, имеем а < Ао < b и / (Ад) = у0. Положим f(A) = y1. Тогда yt < р. Поскольку Ао < А и f возрастает, имеем Если у удовлетво-
ряет неравенствам yQ<Zy <1У1^ то» по теореме о промежуточном значении, у = f (С) для некоторого С. Так как f возрастает, то из f (С) <Zf (А) следует С<А. Но если y = f (C)t то g (у) = С. Отсюда g (у) < А при у0 < у < yr. С другой стороны, поскольку g возрастает, g (g)< <А при у < yQ. Итак, g<A вблизи g0, и свойство 1 проверено.
УПРАЖНЕНИЕ
^8. Проверьте, что функция g обладает свойством II.
6.4. Вычисление бесконечных пределов
Мы докажем теперь один из случаев правил (*) вычисления бесконечных пределов (см. § 5.4). Эти правила относятся к разным случаям—и во всех случаях доказательство проводится сходным образом. Ограничимся лишь случаем, когда
lim f}= а >0, lim g = +оо
(1)
(здесь и дальше все пределы берутся при х —> х0).
В этом случае правила (*) в применении к суммам, произведениям и частным сводятся к следующим утверждениям:
lim (f+ g) = 4-оо, lim (/g) = 4- oo,
(2)
(3)
150
Приложение к главе 3
lim — = 0. g
Надо показать, что это действительно так. В силу (1) вблизи х0 имеем f > 0 и g > 0. Поэто-му t + g >0 вблизи хв. Далее, также вследствие (1) lim (1/g) = 0. Повторное применение теоремы 1 § 4.2 дает
Нт —-
(4>
1
lim — • lim g
1
lim--------------
g [1 + (f/g)]
1
= lim — • —
g 1 4-(limf) • (lim (1/g))
= lim — • , 1-Ь/(1/Я) g Hm|l+/(l/g)]
1 = 0,
= 0 •
а это равносильно (2). Далее, fg^>Q вблизи x0 и, по теореме 1 з 4. 2,
1 1 • lim — =--------
g lim /
1 I lim — = — -0=0, g *
lim = lim — fg f
что равносильно (3).
Наконец, по той же теореме,
lim — = lim (f • — | = (lim f) • (lim —= a • 0 = 0, g \ g / \ g /
так что верно и (4).
УПРАЖНЕНИЯ
9. Докажите, что если в некоторой точке х0 имеем lim f — -1-оои lim g = 4-оо, то lim (/ 4- g) = lim(/g) = + oo
10. Докажите, что если в некоторой точке х0 имеем lim £ = -f-oo и Um g = —оо, го 11пц/£)= = —сю.
§ 7. Доказательство теоремы о промежуточном значении
Пусть f(x) определена и непрерывна при а х Ь. Положим а = /(а), 0 = f(b) и допустим что а #= Р. Для определенности предположим, что а<0. Пусть число у удовлетворяет неравенствам а<у<Ср. Тогда в интервале (а, Ь) существует такое число с, что [(c) = у.
Это и есть теорема о промежуточном значении (теорема 5 § 3.6). Доказательство ее непосредственно опирается на принцип верхней грани (аксиома 18 гл. 1).
7.1. Доказательство
Обозначим через S множество всех чисел х, для которых а х b и f(x)<y Множество S не пусто, так как содержит число а; оно ограничено сверху, поскольку можно взять в качестве его верхней границы число Ь. Следовательно, существует некоторое число с, служащее наи меньшей верхней границей S (или верхней гранью). Это с есть наименьшее число, обладающее свойством: если f(x)< у, тох<^с. Ясно, что а с (так как а принадлежит S) и г<^д(так как Ъ есть верхняя граница S).
Здесь возможны три случая: f(c)<Z У , 1(c) >у и/(с) =у. Покажем, что два первых случая ведут к противоречию; тогда должен иметь место третий, т. е. [(c) = у , что и доказывает теорему
Допустим, что [(c) <У- Тогда /(с)<0; отсюда с =£ b и c<Z b Так как / непрерывна в точке с, имеем Дх)<у вблизи с (по условию I непрерывности). Поэтому имеются точки справа от с, где/<у; все такие точки принадлежат S. Но поскольку с есть верхняя граница S. такие
точки не могут лежать справа от с что и приводит к противоречию.
§ 7. Доказательство теоремы о промежуточном значении. Задачи
151
Допустим теперь, что Дс) >у. Тогда [(c) >а; отсюда с ¥= а и с >а. Так как t непрерывна в точке с, имеем f(x) >у вблизи с (по условию II непрерывности). Это значит, что существует число Cf, для которого a<Z <Z с и f(x) >у ПРИ всех х из интервала с± < x<Z с.
Поскольку ни одна точка S (множества, где 1<у) не лежит справа от с, то ни одна точка S не лежит справа от q. Но тогда С] — верхняя граница S, и притом меньшая с, что противоречит определению наименьшей верхней границы- S.
УПРАЖНЕНИЯ
1. Докажите следующую теорему: пусть f(x) непрерывна при—оо<х <4-оо; допустим, что lim Дх) = a, lim f(x) = 0 > а (где а,0 — числа). Если у — любое число, лежащее строго
X-*—со +
между аир, то сущевтвует число с, —оо< 4- оо, для которого f(c) =у- (Конечно, теорема справедлива и при Р < а.)
2. Сформулируйте и докажите теорему, аналогичную приведенной в упр. 1, для а = —оо и Р = -Ьоо.
7.2. Необходимость доказательств
В § 3.6 мы сделали вывод о справедливости теоремы о промежуточном значении, сославшись на геометрическую интуицию. График непрерывной функции состоит из одного куска; одна из его точек лежит ниже прямой у = с, а другая выше, и поэтому на графике должна быть точка, где он пересекает прямую у = с. Что может быть проще этого рассуждения? Зачем усложнять дело, ссылаясь на принцип верхней грани и предлагая довольно сложное непрямое доказательство?
Тот же вопрос относится ко многим «геометрически очевидным» теоремам, которым математики дают, однако, аналитические доказательства.
Ответ состоит в следующем: наша геометрическая интуиция — бесценный руководитель, но, к несчастью, не всегда непогрешимый. Встречаются утверждения, которые кажутся геометрически очевидными, а между тем они ложны.
Аналитические доказательства не заменяют интуицию, а подкрепляют ее. Лишь строгое доказательство может убедить нас в том, что интуиция не ввела нас в заблуждение.
ЗАДАЧИ
1. Пусть x*+g(x) —функция, для которой g(x) = 1 при рациональном х, g(x) = —1 при иррациональном х Положим Цх) = xg(x). В каких точках f(x) непрерывна?
2. Пусть ft(x) и g(x) —две непрерывные функции, заданные в интервале /. Положим в каждой точке х этого интервала h(x) = max (f(x), g(x)) и k(x) =min (f(x), g(x)), где max (a, b) означает большее из чисел a, b, a min (a. b) — меньшее из них. Покажите, что функции h и k непрерывны.
3. В условиях задачи 2 предположим, что функции fug — неубывающие. Следует ли отсюда, что и функция h — неубывающая? Ответьте на тот же вопрос для функции k.
4. Пусть f(x) и g(x)— нечетные функции и р, q — целые положительные числа; какова функция <р(х) = l(x)P g(x)q — четная, нечетная или ни та, ни другая?
5. Верно ли, что композиция двух монотонных функций также монотонна?
6. Четна или нечетна композиция двух нечетных функций? Четна или нечетна композиция четной и нечетной функции?
7. Покажите, что если функция x^f(x) непрерывна, то и функция xi-* | f(x) | непрерывна, но обратное утверждение неверно.
3. Постройте функцию F(x), которая не является непрерывной ни в какой точке, в то время как Г(х)2 непрерывна везде.
9. Пусть f(x) — рациональная функция; предположим, что оба утверждения, «lim ftx) = Х«*4- оо
= +оо» и «lim f(x) = —оо», ложны. Покажите, что в этом случае существует конеч-Х-*4-оо
ный предел lim f(x).
152
Приложение к главе 3
10 Пусть Дх) — рациональная функция, отличная от постоянной функции 0. Покажите, что существует такое число А, для которого либоДх)>0 прих>Д, либо Дх)< 0 при х > А.
11. Как было упомянуто в § 2.6, рациональные функции образуют поле. Для двух элементов j, g этого поля утверждение g» означает, по определению, что t(x)<Zg(x) для всех х, больших некоторого числа А (которое может зависеть от f и g). Покажите, что это определение превращает поле рациональных функций в упорядоченное поле, т. е. в поле, удовлетворяющее аксиомам 13—16 гл. 1.
12. Покажите, что поле рациональных функций с только что введенным упорядочением — не архимедово, т. е. не удовлетворяет аксиоме 17. (Заметим, что любое целое число, как и любое действительное, можно рассматривать как рациональную функцию, а именно постоянную.)
13. Верен ли принцип верхней грани для поля рациональных функций?
14. Для любой рациональной функции f(x) Ф 0 имеется такое целое число п (положительное, отрицательное или нуль), что существует конечный, не равный нулю предел lim (xnf(x)).
x—>-f-oo Докажите это предложение.
15. Для любой иррациональной функции Дх) Ф 0, заданной при всех х >4, имеется такое рациональное число г, что существует конечный, не равный нулю предел lim (xrt(x)).
дг-*-4-ео Проверьте это предложение на нескольких примерах.
16. Постройте функцию, непрерывную для всех значений независимой переменной, относительно которой Вы уверены, что она не является иррациональной функцией.
17 Предположим, что функция непрерывна в некотором интервале и принимает в нем лишь рациональные значения. Что можно сказать об этой функции?
18. Пусть f(x) определена при 0< х< 1. Пусть нам известно, что для всех этих значений х и для всех целых положительных п число 10я Дх) — никогда не целое. Что можно сказать о функции f?
19. Может ли нечетная функция иметь обратную? Если она имеет обратную, то является ли эта обратная функция нечетной? Поставьте такой же вопрос для четных функций и дайте на него ответ.
20. Постройте такие три функции Дх), g(x) и Л(х), чтобы при х -* 4-оо было £ Ч“оо. g->4"OO, h 4-оо, i — g —6o, i — h — 3, (Jg 1/2, fr/h -> 1.
ПРОИЗВОДНЫЕ
В этой главе развивается первое из двух основных понятий анализа — понятие производной. (Второе из них — понятие интеграла, рассматривается в гл. 5.) Читатель должен, с одной стороны, интуитивно освоить понятие производной, с другой же стороны, — научиться легко и правильно вычислять производные и пользоваться ими. Различные применения понятия производной, обсуждающиеся в этой главе, служат обеим целям.
В Приложении рассматриваются односторонние и бесконечные производные (см. § 7; этот материал вполне может быть опущен при первом чтении), а также доказываются некоторые теоремы о производных (см. § 6 и 8). К счастью, эти теоремы геометрически очевидны; поэтому если читатель готов довериться своей интуиции, то он может свободно опустить эти доказательства.
154
4. Производные
§ 1. ПРОИЗВОДНАЯ ФУНКЦИИ. КАСАТЕЛЬНАЯ. СКОРОСТЬ
Понятие производной возникло из двух на первых взгляд не связанных между собо.й задач: о построении касательной к некоторой линии и о вычислении скорости движущегося тела. Мы рассмотрим здесь обе эти задачи.
1.1. ПРОИЗВОДНАЯ — НАКЛОН КАСАТЕЛЬНОЙ
В предыдущей главе мы изучали непрерывные функции — функции, графики которых «не имеют разрывов» (т. е. состоят из одного куска). Теперь мы рассмотрим непрерывные функции, графики которых «не имеют изломов». Пример графика с изломами изображен на рис. 4.1; график же, изображенный на рис. 4.2, не имеет изломов. Через каждую точку последнего графика проходит единственная прямая, «тесно прилегающая» к кривой,— касательная к кривой.
Рассмотрим функцию х f(x). Производная функции f в точке х0 есть наклон касательной к графику / в точке (х0, f(x0)). Это по существу и есть описание производной, данное «Лейбницем в первой опубликованной им работе по анализу (1684 г.). В работе содержится чертеж, напоминающий наш рис. 4.3. Производная / в точке х0 обозначается через f'(xo) (читается: «/ штрих от х0»).
Для некоторых функций производная может быть найдена сразу же.
Так, график линейной функции х >-* тх + Ь есть прямая, которую следует рассматривать как свою собственную касательную. Таким образом,
если f(x) = тх + Ь, то f (х) = т. (1)
График функции х >-*]/1 — х2 есть верхняя полуокружность радиуса 1 с цен тром в начале координат (рис. 4.4). Касательная к этой окружности, проходящая через точку (х, у), где у= 1 — х2 , перпендикулярна прямой, соединяющей точки (О, 0) и (х, у), и имеет тем самым наклон —х/у (см. гл. 2, § 3.2). Поэтому
если j(х) = V1—ха, то f (х) = - . (2)
V 1—X2
График функции х i-> х2 есть парабола (рис. 4.5) и, как мы уже знаем (см. гл. 2, § 4.4), касательная к параболе, проходящая через точку (х, х2), имеет наклон 2х. Итак, если f (х) = х2, то f (х) = 2х. (3)
Чтобы применить-определение Лейбница к другим функциям, надо строго о п-ределить, что мы называем касательной. Для окружности касательной называется прямая, имеющая с окружностью в точности одну общую точку. Для параболы
Готфрид Вильгельм ЛЕЙБНИЦ (1646—1716) провел ббльшую часть свеей жизни на службе немецкой герцогской фамилии (один из его покровителей стал впоследствии королем Англии Георгом I). Он был одинаково знаменит как философ и как математик. Кроме того, он был юристом, дипломатом, теологом, историком, геологом, экономистом, библиотекарем и лингвистом. Лейбниц основал Берлинскую Академию наук и один из первых научных журналов В этом журнале он опубликовал свое первое исследование по анализу. Лейбниц изобрел анализ позже Ньютона, но .независимо от него.
Центральное место в размышлениях Лейбница занимали поиски «универсального метода» с целью сведения всех умозаключений к вычислениям; в этом отношении Лейбниц был предшественником математической логики. Он изобрел также определители и сконструировал вычислительную машину.
§ 1. Производная функции. Касательная. Скорость
155
Рис. 4.6
Рис. 4.5
156
4. Производные
касательная определяется как прямая, имеющая с параболой в точности одну общую точку и не параллельная ее оси. Ясно, что в общем случае подобные определения не годятся. Рассмотрим, например, линию, изображенную на рис. 4.6. Существует много прямых (например, прямые, помеченные цифрами /, 2, 5), пересекающих линию в точке Р и ни в какой другой, но ни одна из них не соответствует пониманию касательной как прямой, «тесно прилегающей» к кривой в точке Р. Прямая 4, напротив, этому пониманию соответствует, но она пересекает кривую также и в других точках.
УПРАЖНЕНИЯ
При выполнении упражнений 1—5 воспользуйтесь существующим у Вас интуитивным представлением о «касательной».
1. Проведите касательную в каждой точке, отмеченной на данном графике, и измерьте ее наклон.
2. Постройте график функции х f(x), определенной и непрерывной при —4^х^4, для которой f(—3) = 0, f (—3) = 1, f(0) = 1. f (0) = 0, f(3) = —3 и f'(3) = —2.
3. Постройте график функции v = g(u), определенной и непрерывной при —1/29/2, для которой g(0) = 0, g'(l) = 0. g(2) = 1, g'(2) = 1, g(3) = — 1 и g'(4) = — 1/2^
4. Постройте график функции х »-> h(x), определенной и непрерывной при —5/4 7/2, такой, что й(1) = 0, возрастающей в интервале [—1,0) и удовлетворяющей условиям h'(0) = 0, h(2) = —1, h'(3) = 3/2.
5. Постройте график функции у = g(x), определенной и непрерывной при—3^ 5/2,
такой, что g(—2) = 1, g'(—1/2) = —1. g(O) = 0, что график g не имеет касательной в точке (0, 0) и что: a) g нечетна; б) g четна.
1.2. ПОСТРОЕНИЕ КАСАТЕЛЬНОЙ
Итак, наша цель — придать точный смысл выражению «прямая тесно прилегает к кривой в данной точке». Как часто делают в математике, мы сначала допустим, что уже знаем, что такое касательная к графику, и зададимся вопросом, как вычислить наклон этой прямой. Затем метод вычисления мы превратим в определение.
Даны функция х »-> f(x) и точка Р = (х0, /(х0)); мы хотим вычислить наклон т касательной I к графику функции f в точке Р (рис. 4.7). Трудность состоит в том, что мы знаем лишь одну точку искомой прямой /, а именно Р, тогда как длд вычисления наклона требуется две точки (см. гл. 2, § 2.2). Решающее значение имеет здесь следующее наблюдение: если взять на кривой другую точку Q, близкую к Р, то наклон /И1 прямой соединяющей Р с Q, будет близок к т. Но mi можно вычислить. В самом деле, если координаты точки Q суть (хь /(х4)), то
§ 1. Производная функции. Касательная. Скорость
157
— ~~
Х1«—х0
Удобно положить h = — х0. Тогда
т _ f(xQ + h) — f(xQ)
1 h
Это число называется разностным отношением функции f в точке х0 для шага h. Для точки Q, близкой к Р9 это отношение приближенно равно т.
Предположение, что Q близка к Р, означает, что | h | мало. Мы можем рассчитывать, что при малом | h | наклон близок к т и что он тем ближе к т9 чем меньше | h |. Проверим это в случае параболы /(х) = х- и точки Р = (1, 1), где, как мы знаем, т = 2.
Сначала вычислим ггц для разных значений ft, малых по абсолютной величине:
h f(l +/1) = (1 +/1)2 (1 -М)2_ 1 mt = h,
0,1 1,21 2,1
—0,1 0,81 1,9
0,01 1,0201 2,01
—0.01 0,9801 1,99
0,001 1,002001 2,001
—0,001 0,998001 1,999
158
4. Производные
Рис. 4.9
Результаты подтверждают наши ожидания. Но мы можем сделать больше. Если /(х) = х*, х0= 1, то
_ ,04-»>-„) _ _ 2 + й („р„ Ь +0).
h fi
Заметим, что как функция от А имеет предел при h 0 (так как 2 + h есть непрерывная функция от Л). Предел равен 2, что в точности совпадает о наклоном т.
Мы рассчитываем поэтому, что если график функции f имеет касательную / в точке (х0, /(х0)), то наклон / можно найти, вычислив сначала разностное отношение т 1 функции f в точке х0 пРи переменном шаге й, а затем найдя предел mi при й ->0. Этот процесс иллюстрируется на рис. 4.8.
упражнения
6. Дана функция f(x) = х2 — 4; составьте таблицу значений разностного отношения (Д2 + Л) — f(2))//i при h = ± 1 ±1/2 и ± 1/4.
7. Дана функция g(Z) = 2/2 — /4- 1; составьте таблицу значений разностного отношения (g(t9 4- X) — g(lo))/k в точке «о = 1 при 1* ±1, ±0,1, ±0,01. (Представьте ответы в виде чисел, записанных в десятичной системе вчисления; если понадобится, в виде десятичных дробей.)
8. Дана функция h(z) ® г/(г 4- 1); составьте таблицу значений разностного отношения (Л(зо 4" б) — h(z0))/d в точке г* = 0 при ±1 ±0,1, ±0,01.
9. Дана функция Дх) = ЮООх8 — 900 х2 — 10х 4” I; составьте таблицу значений разностного отношения (Дх0 4“ &) —£(х<))/Л в точке х0 = 0 при h = ±1, ±0,1, ±0,01.
§ 1. Производная функции. Касательная. Скорость 159
1J. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Предыдущие соображения подсказывают следующее определение производной,, Пусть f — функция, определенная вблизи точки х0. Производная функции f в точке х0 есть число
f(xj = lira (4>
конечно в предположении, что стоящий в правой части равенства (4) предел существует.
Заметим, что полагая х0- -F равенство (4) можно записать также и в следующем виде:
= lim . (4'>
*1 — Ai
Частное
—Нх0) = f(x0 -к f (х0) , ч — х0 h
как мы уже говорили, называется разностным отношением (функции f в точке х^ для шага h}. Это наклон прямой, соединяющей точки (х0, /(х0)) и (х1э /(xj), где х1 = х0 + h,, 1г Ф 0 (такая прямая называется хордой кривой).
1.4. КАСАТЕЛЬНАЯ И НОРМАЛЬ
После определения производной мы можем дать определение касательной. Касательная к графину х >-♦ /(х) в точке х0 есть прямая с уравнением
У — /Uo) = Г (Хй)(х — х0). (6>
т. е. прямая, проходящая через точку (х0, /(х0)) и имеющая наклон Г(х0).
Прямая, проходящая через точку (х0, /(хп)) и перпендикулярная ка-
сательной, называется нормалью к графику в этой точке (рис. 4.9).
Следовательно (см. гл. 2, § 2.3), уравнение нормали имеет вид
у — f(x0) = — —(х — х0), (7>
f
если f'(xn) 0. и х = ха, если /'(х0) = 0.
Конечно, может случиться, что функция не имеет производной- в точке х0.
В этом случае ее график не имеет касательной* в точке (л0, /(х0)).
* Или имеет вертикальную касательную, если эта производная бесконечна [т. е. если
lim + Й) — Um ---------------------
h
оо или — оо .]
160
4. Производные
1.5. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ ИСХОДЯ ИЗ ЕЕ ОПРЕДЕЛЕНИЯ
Непосредственное вычисление производной для данной функции состоит в'том, что записывается4 разностное отношение
f(xo + h)—f(xQ) h
{где х0 — фиксированное число или символ, представляющий произвольное фиксированное число, a h представляет число, малое по абсолютному значению, но отличное от нуля), а затем с помощью надлежащих алгебраических преобразований этому отношению придается вид, позволяющий найти его предел (при h ->0).
Следует помнить, что х0 в процессе всего вычисления фиксировано (не меняется).
фПримеры. 1. Вычислить /'(2) для f(x) = х3— х.
Решение. Имеем
/'(2) = lim UL+!4^2). = lim ч-fe)3(2 + ft)] - (23 — 2) = h-*0 h h-+Q h
= ljm (8 + 12A + 6/г2 4- — 2 — /I) — (8 — 2) =
h-+0 h
= lim + = _|_ бЛ 4 Л2) = 1L
h-0 h h-0
2. Найти уравнения касательной и нормали к кривой f(x) = УТ в точке (4, 2).
Решение. Сначала вычислим производную функции f(x) = Ух в точке х = 4. Имеем
/(4-h/i)-/(4) /ГрГ-2 h ,h
Чтобы найти предел этой функции от h при h ->0, умножим числитель и знаменатель последней дроби на }/4 4- й Ч- 2. Это приводит к выражению
7(44-6)- /(4) = (УТ+h - 2) (VtTh" + 2) = 1 9
h h (УТ+7Г + 2) К4"+Л 4-2
которое является иррациональной функцией от Л, определенной и непрерывной при h = 0; ее значение при h = 0 равно 1/4. Отсюда
/i->o h 4
В силу уравнений (6) и (7) (см. выше) уравнение искомой касательной есть
у — 2 = — (х — 4), или х — 4у 4- 4 = 0,
4
а уравнение искомой нормали —
у — 2 =— 4(х— 4), или 4х 4- у—18=0. ф
§ 1. Производная функции. Касательная. Скорость
161
УПРАЖНЕНИЯ
В упражнениях 10—21 вычислите производные непосредственно, исходя из определения производной (как и в предыдущих примерах); правила, облегчающие процедуру нахождения производной, будут даны ниже.
10. Пусть ft(x) = х2 — х — 1; найдите f (1).
И. Найдите производную функции g(s) = (s + l)(s — 1) при s = 0.
12. Найдите наклон касательной к графику функции Н{х) = дг2/(дг + 1) при х == 1.
13. Найдите уравнение касательной к графику функции у = х + (1/дг) в точке (1, 2).
14 Найдите уравнение нормали к графику функции г = дг8 — 1 в точке (2, 7).
15. Пусть g(t) = “|Л2 + 4; найдите ^(3).
А 16. Найдите уравнение касательной к графику функции s = //(tf2 — 1) в точке (2, 2/3).
17 Найдите уравнение нормали к графику функции v = 2х + (3/х2) при дг = 1.
18. Пусть h(y) = (у + I)4 — у; найдите Ад—1).
19. Найдите уравнение касательной к графику функции х = и9 + и — 1 при и = 2.
20. Найдите, в какой точке касательная к графику функции K{s) = (s + 2)6 (s — I)2 в точке (—2, 0) пересекает вертикальную ось.
21. Найдите f(l), если Дх) = дг2 при х^ 1, 1{х) = 2х — 1 при х > 1.
1.6 . ПРОИЗВОДНАЯ — НОВАЯ ФУНКЦИЯ
Строго говоря, следует различать производную f'(xQ) функции х f(x) в некоторой точке х0 и правило х н* /'(*)• сопоставляющее каждому числу х из области определения f значение производной f'{x) в этой точке. Правило х *-+f'(x) есть новая функция, часто называемая производной функцией от /.
Обычно, однако, в обоих случаях применяется термин «производная». Так, в случае f(x) = х3 мы говорим: «производная этой функции есть функция х Зх2», но также: «производная /(х) в точке х = 2 есть число 12». Процесс вычисления производной называется дифференцированием.
•Примеры. 1. Пусть f(x)=mx 4- Ь\ вычислить производную в некоторой точке х.
Решение. Имеем
f (х) ~ тх 4- b, f(x 4- h) = т (х 4- й) 4- Ь
и
f (х + h) — f (х) {тх + mh + Ъ) — {тх + Ъ) __ h h
Разностное отношение постоянно. Поэтому
/' (х) = lim — + = iim т = т
h-0 h h^0
в соответствии с утверждением § 1.1.
2. Вычислить f'(x) для f(x) = 1/х (конечно, при условии х =/= 0).
Решение. Имеем
f(x + /i)-f (X) = 1 /1 1 \ 1 х-(х + Я) _ 1
h h \ х + А х/ h х(х + А) х (х + А)
Последнее выражение задает функцию от й, непрерывную в точке й = 0 (поскольку х #= 0). Следовательно, /'(х) = —1/Л
162
4. Производные
3. Вычислить f'(x) для f(x) = / х (при х> 0). Решение. Имеем
f(x + h)-f(x) /хТй —/х~
h h
Не сразу видно, что можно доопределить эту функцию Л до функции, непрерывной при h = 0. Здесь помогает следующий прием (ср. пример 2 из § 1.5):
/хТй —/х~ _ /х + й —/Г . /х+~й-ь/Г = (/х+~й)2 — (/Г)2 = 1
Л А /х + й4-/х" й(/хТй4-/Г) /х+Л4-/^.
Это иррациональная функция от h, определенная и непрерывная при h = 0. Поэтому
f (х) = lim 1------— = __ 1—— = —.
*-►0 /х4- h -|-/х Ух + Ух 2 Ух
4. Вычислить f'(х) для f(x) = У 1 — хг (при некотором х, где — 1<х<1).
Решение. Применим тот же прием, что выше. Имеем
f(x + h)-f(x) _ /1-(х + Й)2 /Т~^ = h й
= /1 —(x + ftj»~ —/1 —х2 /1—(х + Л)2 4-/1 —х2 ; Л у 1 — (х 4- Л)2 -Ь/П^Т
_ (1 — (х 4- й)2) — (1 —х2) 1 — х2 — 2хй — й2 — (1 — х2) _
й (/1 — (х 4- Л)2 4- /ТТ^) й (у 1 — (х 4- Л)2 + /Т^Т2)
__________—- 2х — h____________ /1 — (х -f- Л)а + / 1—х3
Это непрерывная функция от h при h = 0. Полагая h = 0, имеем
в соответствии с утверждением § 1.1. ф
УПРАЖНЕНИЯ
В упражнениях 22—29 вычислите производные непосредственно, исходя из определения (как и в предыдущих примерах).
А22. g(x) = 1/(2х — 3); найдите g'(x).
23. f(x) = х2 — (1/х); найдите f (х).
24. Я(х) = 1/|Лх; найдите Я'(х).
25. Найдите производную функции s и-► s3.
26. Найдите производную функции G(x) = (2х — 3)/(3х + 2).
27. Найдите производную функции t »-► (!//)_+ (1/г).__ _
28. Продифференцируйте функцию z »-► Д/г + (1/Vz) (т. е. найдите ее производную).
29. Продифференцируйте функцию h »-► 2Ла — ЗА + 5.
§ 1. Производная функции. Касательная. Скорость
163
1.7. ОБОЗНАЧЕНИЕ ЛЕЙБНИЦА
Обозначение f'(x) для производной функции у = /(х) было введено Лагранжем. Лейбниц обозначал ту же производную через
< df(x) df dy
- , или —, или — dx dx dx
(читается: «d/ no dx» или «dy no dx»).
В этих обозначениях результаты предыдущих примеров принимают вид:
d(mx+ft) =m _£U1=2x> = 3x2- 1,
dx dx dx
d (1/x) ____1_ d VT = 1 , d = _ x
dx x2 dx 2 У~х dx }^1__x2
Обозначение Лейбница можно пояснить с помощью «математического мифа», изображенного на рис. 4.10.
Согласно этому «мифу», кривая состоит из бесконечного множества «бесконечно малых» прямолинейных отрезков. (Конечно, последнее утверждение не имеет строго смысла, но именно поэтому мы и употребляем выражение «миф».) Касательная к кривой есть прямая, содержащая такой бесконечно малый отрезок. Пусть теперь кривая есть график функции у = /(х). Для вычисления наклона касательной в точке (х, у) увеличим х на бесконечно малую величину dx; этому соответствует увеличение у = /(х) на бесконечно малую величину dy такую, что /(х + dx) = у + dy. Кусок графика между бесконечно близкими точками (х, у) и (х + dx, у + dy) является бесконечно малым отрезком; его наклон равен
(У 4- dy) —у = dy_ (х + dx) — х dx
Именно так представляли себе анализ математики до выяснения точного смысла понятия предела; разумеется, они сознавали логические пробелы такого подхода, но следовали совету Даламбера: «Продвигайтесь вперед — и вера к вам придет».
В наше время dy и dx не считаются наименованиями бесконечно малых величин, а -----их отношением; тем не менее обозначение Лейбница все еще применяется.
Жозеф Луи ЛАГРАНЖ (1736—1813) был ведущим математиком XVIII столетия. Одна из его книг, знаменитая «Аналитическая механика» *, представляет собой систематическое построение механики методами анализа; в этой книге нет ни одного чертежа — все основано только на формулах. Лагранжу не исполнилось и двадцати лет, когда он стал профессором математики Артиллерийской школы в своем родном городе Турине. Позднее он был преемником Эйлера в Берлинской академии. С 1786 г. Лагранж жил в Париже; после Французской революции он преподавал во вновь учрежденных Ecole Normale (Нормальной школе) и Ecole Polytechnique (Политехнической школе).
Жан Лерон ДАЛАМБЕР (1717—1783) был в высшей степени влиятельным ученым, в частности математиком. Он принадлежал к группе философов Французского Просвещения, опубликовавших «Энциклопедию», и был непременным секретарем Парижской Академии наук. Наиболее значительный след Даламбер оставил в механике.
• Русский перевод: М.—Л, Госгехиэдат, 1950 (в двух томах).
164
4. Производные
Прежде всего оно имеет высокую эвристическую ценность. Символ является просто обозначением производной, но в то же время форма его напоминает, что производная есть предел разностного отношения (5), которое и в самом деле представляет собой дробь, с приращением х в качестве знаменателя и соответствующим приращением у в качестве числителя. Приращение х часто обозначается через Дх. (При этом важно заметить, что Дх есть цельный символ, а не произведение Д на х. Этот символ произносится «дельта х». Ранее мы обозначали то же приращение через Л.) Обозначим теперь приращение функции у = f(x) через Д#. Тогда \у = = f(x + Дх) —f(x). и разностное отношение можно записать в виде Отсюда имеем
dx дх-*о Ах
Это еще одно «оправдание» обозначения Лейбница. Главное же оправдание, как мы сможем убедиться в ряде случаев, состоит в его удобстве.
К сожалению, обозначение Лейбница не указывает точки х, в которой вычисляется производная. Этот недостаток преодолевают, указывая точку внизу в качестве «нижнего индекса»; таким образом, пишут
^)=2х, =4.
dx \ dx )х = 2
Такое обозначение будет использоваться там, где это окажется нам удобным. Имеются и другие обозначения производной, которыми мы не будем пользоваться: Df и (D/)(x).
УПРАЖНЕНИЯ
В упражнениях 30—37 вычислите производные либо непосредственно, со ссылкой на определение, либо с использованием предыдущих примеров и упражнений.
30. Пусть у = и2; чему равна (dyldu)^ _ ?
31. Пусть и — у2\ чему равна (du/dy)y^ ^3?
32. Пусть r=y2s—1; чему равна dr Ids?
. d (и2 — и)
33. Найдите —----.
dy
34. Найдите ------------.
du
or /d(2v3 + 3v2)\
35. Найдите -------------- •
\ dv )v=\
A 36. Пусть s= l/(/2 4-1 1); найдите (ds/df)t
37. Найдите dz*/dz.
§ 1. Производная функции. Касательная. Скорость
165
1.8. ТЕОРЕМА О ЛИНЕЙНОМ ПРИБЛИЖЕНИИ
Рассказанный выше «математический миф» содержит зерно истины. Чтобы усмотреть это, сформулируем заново определение производной.
Теорема 1. Пусть f — функция, определенная вблизи х0. Функция имеет производную т в точке х0 тогда и только тогда, когда
f(x)=f (х0) + т (х — х0) + г (х) (х — х0), (8)
где
lim г (х) = 0, (9)
х-*х0
или, что то же самое, г(х) непрерывна в точке х0 и r(xQ) = 0. (9')
Доказательств о. Если условия (8) и (9') выполнены, то
= т + г^
X —х0
и предел этого выражения при х ->х0 равен т. Обратно, если f'(xQ) = /ли если определить г(х) при х =/= х0 предыдущим равенством, то г непрерывна, удовлетворяет условию (9) и соблюдается (8).
Чтобы лучше понять смысл теоремы, заметим, что
x*-*f(xQ) + m(x — х0), где т = f (х0), если линейная функция, график которой представляет собой касательную к графику f в точке (х0, /(х0)). Число же
г(х)(х —х0) (10)
указывает ошибку, которую мы допускаем, если при вычислении значения /(х) в близких к х0 точках х заменяем график функции ее касательной в точке (х0, /(х0)). Геометрический смысл этого члена (10) ясен из рис. 4.11.
Ошибка эта мала при малых значениях х — х0 и, как видно из равенства (9), гораздо меньше х — х0. В самом деле, если х — х0 мало, то ошибка равна х — х0, умноженному на малое число г(х). В этом смысле можно заменить малую дугу кривой ее касательной.
166
4. Производные
ф Пример. Представить функцию f(x) =х3 — 2х—1 вблизи х = 2 как линейную функцию плюс малый член, указывающий погрешность такой замены.
Решение. Имеем /(2) = 3 и по методу § 1.5 находим /'(2) = 10. В силу теоремы 1 линейная функция, приближающая /(х) вблизи х = 2, есть
х ь-> 3 + 10(х — 2) = 10х — 17.
Погрешность замены определяется выражением
(х3 __ 2х — 1) — (10х — 17) = х3 — 12х + 16.
Мы хотим записать этот член в виде произведения х — 2 на множитель, малый вблизи х = 2. Деление «углом» дает
х3 — 12х 4- 16 = (х — 2) (х2 4- 2х — 8).
Заметим, что многочлен х2 4- 2х — 8, соответствующий г(х) из теоремы 1, в самом деле обращается в нуль при х = 2. Итак, получаем
х3—2х— 1 = 10х—17 4- (х—2) (х24-2х—8)
линейная функция погрешность = (х — 2) г (х)
и г(2) = 0. Можно записать также
х3 _ 2Х — 1 = 10х — 17 4- (х — 2)2(х 4- 4), поскольку х2 4- 2х — 8 = (х — 2)(х 4- 4).
Заметим, что при х = 2,1 член, указывающий величину погрешности, равен (0,1)2.6,1 = 0,061, а при х = 2,01 он равен (0,01)2-6,01 = 0,000601. ф
УПРАЖНЕНИЯ
В упражнениях 38—45 представьте заданную функцию в виде (8) близи заданной точки, указав, какие члены в выражении соответствуют т и г (конечно, при этом можно изменить обозначения, например, х на г или f на Л). Проверь?е, что г непрерывна в заданной точке и обращается в этой точке в нуль.
38. f(x) = 2х* — х вблизи точки х0 = 3.
39. g(s) — 1—3s 4“ s2 вблизи точки s0 = —1.
40. у i-> 2у — 1 вблизи точки yQ = 1/2.
41. H(z) = —2 вблизи точки г0 = 10.
^42. t i-> 1// вблизи точки /0 = 1.
43. f(u) = 10—2/3 и вблизи точки uQ = —3.
44. h(v) = v3 вблизи точки ц0 = 1.
45. Q(s) = s(s — 1) вблизи точки s0 = 0.
1.9 . ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ФУНКЦИЙ
Теорема 1 подсказывает метод приближенного вычисления значения /(х) для х, близкого к числу х0, если известны /(х0) и /'(х0). Пренебрегая указывающим погрешность членом, получаем
+ (И)
Знак » читается: «приближенно равно». В одной из следующих глав мы рассмотрим приближение (11) подробнее (см. гл. 8, § 1).
§ 1. Производная функции. Касательная. Скорость
167
фПримеры. 1. Пустьмыхотим вычислить 1,023?. Значение 1,023 близко к 1, и мы ищем /(1,023) = /(1 4- 0,023), где /(х) = х2.
Известно, что /(1) = 1 и /'(1) = 2. Поэтому из (11) имеем
1.0232 «14-2- 0,023 = 1,046.
Точно так же, поскольку 0,98 = 1—0,02 = 1 4- (—0,02),
(0,98)2 « 1 + 2 (— 0,02) = 1 — 0,04 = 0,96.
Вообще
(1 + ft)2 « 1 4- 2ft при малых | ft |.
В этом случае (1 4- ft)2 = 1 4- 2Л 4- ft2 и допущенная ошибка равна Л2: поэтому при малых | ft | она гораздо меньше | Л |.
2. Как мы знаем, для / (х) = ]/~х производная /'(х) = 1/(2}/~х ) (см. § J.7). Отсюда /(1) = 1, /'(1) = 1/2 и
1 4- Л « 14—ft при малых | Л |.
Например, ]/ 1,03 «1,015 и }Л),98 «0,99. Аналогично, в силу равенств /(100) = 10 и /' (100) = 1/20 = 0,05 имеем
У100 4- ft « 10 4- 0,05ft при малых | Л |.
Например, j/ToT « 10 4- 0,05 = 10,05, )/97« 10 —0,05-3 = 10 —0,15=9,85
3. Используя равенство
Id (1 /х)\ = _ j
\ dx 7jc=i
(см. пример 2 § 1.6), имеем
—Ц- «1 — Л при малых | Л |.
1 -|- п
Например, 1/1,02^0,98 и 1/0,99« 1,01. •
УПРАЖНЕНИЯ
В упражнениях 46—55 воспользуйтесь приближением (11).
46. Вычислите приближенно (3,05)\ /
47. Вычислите приближенно 7^49.1
48. Вычислите приближенно 1^35,99
49. Вычислите приближенно (1,988)2.
50. Вычислите приближенно (1,08)^.
51. Найдите приближение для (1 + h)3 при малых | h |.
52. Вычислите приближенно 1/]/^25,025.
53. Найдите приближение для 1/]^ 1004-Л при малых | Л \.
54. Пусть g(s) = (s 4- l)(s — 1); вычислите приближенно g(0,025)
55. Вычислите приближенно,. f2.95)4
168
4. Производные
1.1 0. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
Функция, имеющая производную, называется дифференцируемой. При введении понятия производной функции мы считали функцию непрерывной; это естественно: мы не можем рассчитывать на существование касательной там, где график терпит разрыв. Сделанное нами предположение оправдывается следующей теоремой:
Теорема 2. Если f имеет производную в точке х0, то f непрерывна в этой точке.
Доказательство. Если f'(xQ) = m, то справедливо равенство (8), в котором f представляется в виде суммы трех функций [постоянной, линейной функции и функции г(х)(х — х0)1, каждая из которых непрерывна в точке х0. Но сумма непрерывных функций всегда непрерывна (по теореме 1 § 3.3 гл. 3).
1.1 1. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Задача о касательной — лишь одна из двух задач, приведших к понятию производной. Второй была задача об описаний движения. Эта задача преимущественно и занимала Ньютона, создавшего анализ одновременно с научной механикой.
Рассмотрим частицу, движущуюся вдоль прямой (прямолинейное движение). Под частицей понимается тело, размерами которого в рассматриваемой задаче можно пренебречь, так что его можно считать математической точкой. Например, если речь идет о движении Земли вокруг Солнца, то Землю можно считать точкой. Выберем на прямой, по которой движется наша частица, точку О и выделим одно из ее направлений в качестве положительного. Выберем, далее, единицы длины, времени и момент, о которого отсчитывается время. Тогда частица движется вдоль числовой прямой, и это движение задает функцию
t >—► s(/),
сопоставляющую каждому значению времени t координату s частицы в этот момент.
График этой функции можно рассматривать как изображение движения. Конечно, надо иметь в виду, что график движения зависит от выбора единиц длины и времени. Мы получим графики разного вида, если будем измерять расстояние в метрах, а время — в часах, или если воспользуемся сантиметрами и секундами.
Исаак НЬЮТОН (1642—1727) учился, а затем преподавал в Кембриджском университете. Во вре-мя Великой чумы 1664—1665 гг. Ньютон, только что получивший звание бакалавра искусств, уехал в свою родную деревню Вулсторл. За эти два года он открыл, что белый свет может быть разложен на лучи различных цветов, изобрел математический анализ, сформулировал закон всемирного тяготения, а затем вывел из него кеплеровы законы движения планет. Эти великие открытия были опубликованы значительно позже. Так, «Математические основы натуральной философии», содержавшие ньютонову механику, появились в 1687 .году *: в этой книге анализ не применяется.
Интеллектуальные интересы Ньютона не ограничивались физикой и математикой, двумя областями, в которых он никогда не был превзойден. Он оставил также множество рукописей по теопо-гнн и алхимии. Кроме того, он успешно выполнял обязанности заведующего монетным двором, за что получил право именоваться «сэр»; несколько раз он представлял также свой университет в парламенте **.
* Последнее русское издание: Крылов А Н., Собрание трудов, т. VII, М.—Л.< Изд-во АН СССР, 1936.
В XVII в а Англии университеты имели право выдвигать своих депутатов в парламент.
$ 1. Производная функции. Касательная. Скорость
169
1.1 2. РАВНОМЕРНОЕ ДВИЖЕНИЕ
Движение называется равномерным, если расстояние, пройденное движущейся точкой (частицей), пропорционально истекшему времени. Допустим, что движение именно таково, и определим число а следующим образом: абсолютная величина | а | есть расстояние, пробегаемое точкой за единицу времени', а положительно или отрицательное зависимости от того, движется ли точка в положительном или отрицательном направлении. Мы говорим, что скорость нашей равномерно движущейся частицы равна
а единиц длины/единицу времени;
например, а см/с (читается «а сантиметров в секунду»). Предположим еще, что в момент t = 0 наша точка отстоит на расстоянии (3 от 0. Через t единиц времени ее расстояние от Р будет at, а от 0 — соответственно Р + at. Таким образом, движение изображается функцией
t ^s(f) = at + р.
Мы видим, что график равномерного движения есть прямая, наклон которой равен скорости движения.
1.1 3. СКОРОСТЬ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ
Рассмотрим теперь неравномерное движение частицы, например движение автомобиля по прямолинейной дороге. Что такое скорость движения частицы в данный момент времени? Можно, конечно, ответить на это: «число, показываемое спидометром». Но для того чтобы понять движение (и, в частности, чтобы сконструировать спидометр), надо свести понятие скорости к более простым понятиям расстояния («число, отсчитываемое на измерительной ленте») и времени («число, отсчитываемое по часам»).
Допустим, что в момент t частица находится в точке s = s(t), а в момент t + h —в точке Si = s(t + h). Это значит, что за h единиц времени частица проходит — s единиц длины. Конечно, отсюда нельзя заключить, что скорость в момент t была равна
si —s = s(t + h)—s (0 12
h h ' '
единицам длины в единицу времени, поскольку частица могла, например, двигаться очень быстро в течение первых й/2 единиц времени и очень медленно — в оставшееся время. Но, как подсказывает нам интуитивное представление о движении, при малом h «средняя скорость» (12) должна быть близка к «истинной», или «мгновенной», скорости частицы в момент времени t. Можно также предвидеть, что чем меньше h, тем ближе «средняя скорость за время й» к «мгновенной скдрости». Мы определим поэтому скорость v(t) движущейся точки в момент времени t как число (единиц длины в единицу времени), к которому сколь угодно приближается средняя скорость
170
4. Производные
в промежутке времени от t до t + ft, когда h становится достаточно малым. Иными словами, это (однозначно определенный) предел
P(Z) = lim = s' (/)t
л-*о h
или, в обозначении Лейбница, v =-^- .
at
Таким образом, скорость есть производная пройденного расстояния по времени, или, что то же, наклон касательной к графику функции: (время)*-+(пройденное расстояние).
Применив это определение к равномерному движению s = at + ($, получаем
+ ® = а, dt как и должно быть. .
Если задана произвольная дифференцируемая функция, то можно представить себе либо описываемую ею кривую (геометрическое представление), либо описываемой ею движение (кинематическое изображение); соответственно этому производную можно истолковать либо как наклон касательной, либо как (мгновенную) скорость. Эти представления дополняют друг друга.
УПРАЖНЕНИЯ
В упражнениях 56—62 заданные функции описывают движение частицы вдоль прямой.
56. Пусть s = Z3 — Л где расстояние s измеряется в метрах, а время t — в секундах. Чему равна скорость при t = 10?
57. Пусть s = t. где расстояние s измеряется в сантиметрах, а время t — в секундах. Чему равна скорость при t = 100?
58. Пусть s = 100—60/, где расстояние s измеряется в километрах, а время t — в часах Чему равна скорость при t = 1?
59. Пусть s = 1 /(1—t), 0< t< 1. где расстояние s измеряется в дециметрах, а время t — в минутах. Чему равна скорость при / = 0,75?
60. Пусть функция, связывающая время и расстояние, есть г »-► 1, где расстояние измеряется в сантиметрах, а время — в минутах. Чему равна скорость при t — 1,5?
61. Пусть г = t2 — /, где расстояние г измеряется в метрах, а время t — в секундах. Чему равна скорость при t = 0,25? При t = 0,5? При t = 0,75?
62. Пусть г = Зг2 — 2х, где г — расстояние, а х — время; каков промежуток времени, в течение которого частица движется в положительном направлении?
1.14. СВОБОДНОЕ ПАДЕНИЕ
Простейший пример неравномерного движения — падение тела, отпущенного на некоторой высоте и падающего на Землю. Открытие неравномерности этого движения было важным событием в истории науки.
Древние греки были превосходными математиками, они создали также остроум* ную статику (часть механики, изучающую покоящиеся тела и действующие на них силы). Однако их представления о динамике (механике движущихся тел) были очень наивны. Аристотель учил, что падение тел равномерно и что более тяжелые тела падают быстрее, чем более легкие. Поскольку авторитет Аристотеля приобрел почти религиозный характер, это его утверждение не оспаривалось до XVI столетия. Ис
§ 1. Производная функции. Касательная. Скорость
171
тинный закон падения тел был открыт Галилеем, чем была заложена основа современной физики. Галилею понадобилось при этом проанализировать понятие скорости; благодаря этому он стал одним из предшественников анализа.
Согласно закону Галилея, расстояние, пройденное свободно падающим телом, отпущенным из состояния покоя, пропорционально квадрату времени падения, причем коэффициент пропорциональности является одним и тем же для всех тел.
Сформулируем эти утверждения математически.
Рассмотрим направление падения как отрицательное направление на вертикальной оси, приняв за начало О точку, откуда было отпущено тело, и отсчитывая время с момента начала падения. Тогда, по Галилею, движение падающего тела описывается уравнением
s = — р/2. (13)
График этого движения — парабола. Значение 0 — одно и то же для всех тел; конечно, оно зависит от избранных единиц. Если пользоваться сантиметрами и секундами, то 0 приближенно равно 490. Знак минус в равенстве (13) поставлен для того, чтобы Р было положительно.
Вычислим скорость в момент /; имеем
V = — = _ 28/.
dt di
Таким образом, абсолютная величина скорости пропорциональна времени, истекшему с начала падения.
Частица, отпущенная в состоянии покоя и скользящая по наклонной плоскости (рис. 4.12), подчиняется, по существу, тому же закону. Если обозначить теперь через s расстояние, измеряемое вдоль пути движения, начиная от точки покоя, и снова принять за положительное направление вверх, то закон Галилея имеет вид
s =-----— /2, (14)
/1 + т2
АРИСТОТЕЛЬ (384—322 до и. ».) в течение двадцати лет был членом Академии Платона, после чего основал собственную школу — Ликей. Одно время он был воспитателем будущего полководца Александра Македонского. Аристотель не внес чего-либо нового в'математику (в собственном смысле этого слова), но заложил фундамент формальной логики, как и многим другим областей знания (учение о политике, литературная критика, описательная биология). Первое существенное продвижение в логике после Аристотеля произошло в XIX столетии, когда возникла символическая, или математическая, логина.
Примирение между платоно-пифагорейским мировоззрением и аристотелевским подмодом, требовавшим наблюдения реальным явлений, стало возможным лишь после возникновения математического естествознания на основе анализа.
Галилео ГАЛИЛЕЙ (1564—1642) явился основоположником современной науки, заявившим, что книга природы написана математическими символами. Он был математиком, физиком, астрономом, блестящим полемистом и талантливым писателем. Галилей сформулировал закон инерции, нашел законы движения маятника, падающим тел и снарядов. Он один из первым построил телескоп, открыв с его помощью спутники Юпитера и Сатурна, фазы Венеры, вращение СолнЦа и гористый рельеф лунной повермиости.
Галилей был профессором в Пизе и в Падуе, а потом «главным философом и математиком» при дворе великого герцога Флорентийского. В возрасте семидесяти лет Галилей подвергся допросу инквизиции из-за его «Диалога о двум великим системам мира» ♦. Его принудили отречься от системы Коперника; остаток жизни он провел под домашним арестом, продолжая работать и писать.
Последний русский перевод — в книге: Галилео Галилей, Избранные произведения в двум томах, т. I, М-, «Наука», 1964.
172
4. Производные
Рис. 4.12
где (J — то же число, что раньше, а tn — наклон плоскости скольжения. График движения — опять парабола; скорость равна
v = ds — t
& /14-т2
И в этом случае скорость пропорциональна времени, но при малом т она возрастает медленно. Это обстоятельство было весьма благоприятно для Галилея, поскольку он располагал лишь примитивными измерительными средствами (у него не было Часов) и не был в состоянии точно измерять быстрые движения.
Следует иметь в виду, что закон падения тел (13) пренебрегает эффектом сопротивления воздуха, а закон (14) пренебрегает трением между телом и плоскостью скольжения.
УПРАЖНЕНИЯ
63. Мяч сброшен с высоты 100 м. Какова его скорость через 2 с?
64. Камень сброшен с высоты 10 см. Какова его скорость через 0,1 с?
65. Книга сброшена с высоты 81 м. Через сколько секунд книга ударится о Землю? Какова будет ее скорость в этот момент? (Точнее, каков предел скорости при /, стремящемся слева к /0, где /в — момент удара?)
▲ 66. Кирпич свалился с дома. Какое расстояние он пролетел, когда его скорость стала равна —42 м/с?
67. Мяч катится по плоскости с наклоном 1/2. Расстояние измеряется в сантиметрах; ка-. кова его скорость через 2 с?
68. Частица скользит по наклонной плоскости, достигая скорости — 16 м/с через 10 с после начала скольжения. Каков наклон плоскости?
69. Мяч катится по плоскости с наклоном 1/4. Расстояние измеряется в сантиметрах; чему равна скорость через 4 с?
70. Частица, скользящая по наклонной плоскости длиной в 3 м, в конце ее достигает скорости — 2 м/с. Каков наклон плоскости?
1.15. БЫСТРОТА ИЗМЕНЕНИЯ
Скорость движения является примером быстроты изменения. Если функция х »-* у du описывает некоторое отношение между двумя количествами, то производную можно назвать быстротой изменения у по отношению к х. Так, скорость есть быстрота изменения расстояния по отношению ко времени.
• Примеры. 1. Быстрота изменения веса W куба из однородного материала по отношению к длине его стороны а равна Заа2, где а — вес куба со стороной 1.В самом деле, W = аа8, откуда -d^ - = 3 аа2.
Вспомнив теорему о линейном приближении (теорема 1 § 1.8), можно истолковать это следующим образом: если дан куб со стороной а и удельным весом а, то при
§ 2. Дифференцирование
173
увеличении стороны на малую величину h вес куба возрастает приблизительно на Заа2Л.
2. Рассмотрим пример из экономики. Если q(x) стоимость изготовления х экземпляров некоторого продукта, то q'(x) — скорость изменения стоимости при изменении количества продукта — называется предельной (маргинальной) стоимостью, а также предельными издержками. На практике обычно х — очень большое число, так что 1 мала по сравнению с х, и q'(x) приближенно равно q(x + 1) — q(x). Поэтому экономисты определяют предельные издержки также как стоимость изготовления «еще одного экземпляра» продукции.
3. Быстрота изменения скорости по отношению ко времени называется ускорением. В дальнейшем мы будем часто встречаться с этим важным понятием. Отметим здесь, что при свободном падении ускорение, т. е. производная от скорости — 2р/ по времени, есть постоянная — 2р. ф
УПРАЖНЕНИЯ
В этих упражнениях предполагаются известными некоторые простые геометрические фор мулы.
71. Найдите быстроту изменения площади круга по отношению к радиусу.
72. Найдите быстроту изменения поверхности куба по отношению к длине его стороны.
73. Движение частицы, движущейся по прямой, описывается уравнением $ = Z3 — /, где расстояние s измеряется в метрах, а время t — в секундах. Каково ускорение, когда скорость фавна 11 м/с?
74. Пусть h — высота, аг — радиус основания цилиндрической коробки. Если высота коробки 1 дм, то какова быстрота изменения объема по отношению к радиусу, когда радиус равен 1/2 дм?
75. Пусть h — высота, а г—радиус основания цилиндрической коробки. Если радиус равен 1/2 дм, то какова быстрота изменения объема по отношению к высоте, когда высота равна 1 дм?
76. Пусть стоимость q изготовления х экземпляров продукта задается формулой q = = 10 000 + 22х + х2/12 ООО 000; какова маргинальная стоимость при х = 120 000?
$ 2. ДИФФЕРЕНЦИРОВАНИЕ Процесс нахождения производной функции называется дифференцированием. При дифференцировании функций нет надобности возвращаться к определению производной. Вместо этого применяется ряд правил, с помощью которых дифференцирование функций, обычно встречающихся в анализе, сводится к чисто механическим процедурам. Приступим к выводу этих правил.
2.1. ОСНОВНЫЕ ПРАВИЛА
Теорема 1. Пусть fug — две функции, имеющие производные в точке х^ис — постоянная. Тогда в точке х0:
</=0, (1)
(cfY=cff. (2)
(f + g)' = f' + g', (3)
174
4. Производные
if-gY = f'-g', (4) (fgY = f'g + rg', (5)
и, если g(xo)=f=0, то (—Y = -~V’ (7) \ g / ga
Прежде чем доказывать теорему, запишем ее утверждения в обозначениях Лей-
бница: — = 0 (c — постоянная), (1') dx d(cf) df z . /nZ4 =€ — (c — постоянная), (2) dx x dx d(f + g) = /3л dx dx dx 9 d(f — g) =df__£g /4/4 dx dx dx 9 dx \ g / g2 dx dx \ S / g2 \ *x) v
Одно из преимуществ обозначения Лейбница состоит в том, что оно приводит к простым правилам (2'), (3'), (4'), напоминающим правила действий с дробями. Словесно эти правила формулируются так: постоянную можно вынести за знак производной} производная суммы равна сумме производных} производная разности равна разности производных.
Более сложны правила (5), (6), (7) для производной произведения (производная первого множителя на второй плюс первый множитель на производную второго), производной от единицы, деленной на функцию (взятая со знаком минус производная функции, деленная на ее квадрат), и производной частного (производная числителя на знаменатель минус числитель на производную знаменателя — и все это деленное на квадрат знаменателя). В этих случаях обозначение Лейбница не помогает запоминанию.
Правила (1) — (7) принадлежат к числу тех немногих фактов (математического) анализа, которые следует запомнить.
§ 2. Дифференцирование
175
Только что сформулированные правила можно применять и более чем к двум функциям. Например, если функции /, g, h имеют производные/', g', h', то
Pf-3g + h)' =2f'-Sg' + К
и
(fgh)' = f'gh 4- fg'h + fgh'\
в самом деле, например,
(fgh)' = \(fg) ЛГ = (fg)'h + (fg)h' = (f'g + fg')h 4- fgh' = f'gh 4- fg'h 4- fgh'.
УПРАЖНЕНИЯ
1. Пусть f(x) = 2x3 и g(x) = у x + 1. Вычислите f'(x), g'(x), (f + gY(*)> (fgY(*) непосредственно по определению. Проверьте, что (/; + gY = f + g' и (fg)' = fg + fg'-
2. Пусть h(s) = 2s + 1 и k(s) = 3s2 — 5. Вычислите Л'($), k'(s), (k — Af (s), (k/h)'(s) непосредственно по определению. Проверьте, что (k — hY = k' — h' и (k/h)' = (k'h — kh')lh2.
3. Пусть P(x) = x2 — x — 1 и Q(x) = x + 1. Вычислите ₽'(**)» Q'(x)> (2P — 3Q)'(*)>
(PQYM непосредственно по определению. Проверьте справедливость теоремы 1.
1 2
4. Пусть Л(/) = t2+ t и B(t) = t2 — t. Вычислите Л'(0» В'(0» (у Л — -у В)'(Л, (Л/В)'(0 непосредственно по определению. Проверьте справедливость теоремы 1.
5. Пусть f(x) = х2—2х и g(x) = х. Вычислите f (дг), g'(x), (f + g2Y(*Y (g/b'M непосредственно по определению. Проверьте справедливость теоремы 1.
^6. Пусть f(0) = 1, f(0) = 2, g(Q) = 1/2, g'(Q) = —3. Пользуясь теоремой 1, найдите (fe)'(0)'« (g/fY(O).
7. Пусть Л(3) = — 1, В(3) = —4, Л'(3) = 2, В'(3) = 5. Пользуясь теоремой 1, найдите (24 — ЗВ)'(З). (ЛВ)'(З) и (Л/В)'(3),
8. Пусть ф(10) = —1/2, ф(10) = 6, <р' (10) = 1/3, <р'(10) = 8. Пользуясь теоремой 1, найдите (5<р + ф<р)'(10) и (3<рФ — 10ф)'(Ю).
9. Пусть f(x) = х2, g(x) = х, h(x) = 1/х. Вычислите f'(x), g'(x), h'(x), (f + g + А)'(л-) и (fgty't*) непосредственно по определению. Проверьте, что (f + g + hY = f' + g' + h' и W = ffgh + fg'h + fgh'.
10. Пусть A(x) = x — 1, B(x) = x + 1, C(x) = x + 2. Вычислите Л'(*), B'(x), С'(х), (2A —В+ ЗС)'(х), (ЛВС)'(х) непосредственно по определению. Проверьте справедливость обобщения теоремы 1 на три функции.
11. Пусть f(l) = —2, I'(1) = 3, g(l) = —5, g'(l) = h лр) = Л'(1) = 4. Пользуясь пра-
вилами теоремы 1. найдите (fghY<\\ (tglhY(AY (t/ghY*l) и (g/f — ft)'(l).
12. Пусть Л(2) = 1, В(2) = 10, С(2) = —2. А'{2) = = 3» С'(2) = 4- Пользуясь
правилами теоремы 1. найдите (AB/CY(2)> (А2/(В + С))'(2), ((Л + В)/(В + С))'(2).
2.2. НАБРОСОК ДОКАЗАТЕЛЬСТВА
Как мы уже знаем, с' = 0, так что равенство (1) справедливо. Это частный случай примера из § 1.1, притом геометрически очевидный (поскольку горизонтальная прямая имеет наклон 0). Докажем теперь правило для суммы (3), правило для произведения (5) и правило (6).
Рассмотрим сначала случай, когда функции f и g линейны. Тогда (ер. с § 1.8) имеем:
f(x) =а4-а(х — %ь). где a =f(x0), а = f(x9),
g(x) =Z>4- р(х —х0), где b =g(xn), Р -=j?'(x0).
176
4. Производные
Отсюда
f(x) + g(x) = а 4- b + (а 4- Р)(х — х0).
Это опять линейная функция. Ее наклон (т. е. производная функции f + g) есть а + Р, что равно f'(x0) + g'(x0), в соответствии с (3).
Далее,
f(x)g (х) = [а 4- а (х — х0)] [Ъ 4 р (х — х0)] = ab 4 (ab 4 а?) (х — х0) 4 а? (х — х0)2.
Таким образом, fg есть сумма линейной функции с наклоном ab 4 аР и члена аР(х — х0)2 — (х — х0)г(х), где г(х) = аР(х — х0) — непрерывная функция, для которой г(х0) = 0. По теореме о линейном приближении (теорема 1 § 1.8) следует, что производная от fg в точке х0 есть ab 4- аР =/'g 4- fg', в согласии с (5).
Допустим теперь, что g(x0) = b ф 0, и положим
<р (х) = —-— ------------;
g(x) »4М*-^
вычислим <р'(х0), пользуясь определением производной. Имеем
<р (хЛ = —, ® (хв 4- А) --------------= —!—
* b t’4-₽(xe4-A-x0) &4₽Л
и
у(х0+Л)-<р(х0) = H(b + W-llb = _ ц Л Л 6(Ь-ЦЙ) ’
Это непрерывная функция от А; значение ее при Л = 0 есть ср'(лс0) = —р/А2. Итак, (l/g)' = —g'/g2 в согласии с (6).
Только что проведенные рассуждения можно повторить с небольшими изменениями и в том случае, когда функции не линейны. В самом деле, по теореме о линейном приближении имеем:
Дх) = а 4- а(х — х0) 4- г4(х)(х — х0), где а = Дх0), а = f (х0),
g(x) = b 4- Р(х — х0) 4- г2(х)(х — х0), где b = g(x0), Р = g'(x0);
здесь гДх), г2(х) — непрерывные функции, для которых ri(x0) — г2(х0) = 0.
Чтобы вычислить производные f 4- g, fg и Mg вблизи х0, достаточно рассматривать лишь значения х вблизи х0. Для таких х члены (погрешности, допускаемые при замене функций линейными) гДх)(х — хв) и г2(х)(х — х0) очень малы и не сказываются на конечных результатах.
Проведем это рассуждение для суммы (правило (3)1. Имеем
f(x) 4- g(x) = а 4- b 4- (а 4- Р)(* — *в) 4- 1п(х) 4- г2(х)](х — х0).
Таким образом, f 4- g есть линейная функция с наклоном а 4* Р плюс член (х — х0)г(х), где г(х) ( = г, (х) 4 rt (х)] непрерывна и г(х0) = 0. По теореме о линейном приближении заключаем, что производная от f 4 g в точке х0 есть а 4- Р = fixe) 4- g'(x0).
Полные доказательства (5) и (6) аналогичны, но занимают больше места; они отнесены в Приложение (см. § 6.1 и 6.2).
Из (5) и (1) выводим соотношение (2), т. е. утверждение (с/)' =cf'i
{cf)' =c'f + cf =Of + cf — cf •
L Дифференцирование
177
Далее, из (3) и (2) выводим соотношение (4):
(/-£)'=(/ + (- l)g)' = Г 4- ((-1)2)' = Г + = f-
Конечно, можно доказать (2) и (4) также прямым путем; пусть читатель попытается сделать это самостоятельно.
С помощью (5) и (6) можно теперь доказать правило дифференцирования частного (Jig)' = (j'g — fg')/g-\ именно
X g / \ g J g \ g J g g2 g g g
Это и есть формула (7), чем и завершается доказательство теоремы 1.
Можно также доказать теорему 1 прямым применением определения производной и правил вычисления пределов, установленных в гл. 3, § 4.2. Чтобы доказать правило (/ + g)' = f + g', положим <р(х) = f(x) + g(x). Тогда
ffi | lj\ CD / V
(p' (x0) = lim 0-------—~ (по определению производной] =
h-o h
= lim If (x0 + ft) + £ (Xq + h)] - [f (x0) + g (x0)l = h-0 h
= ]jm / f (Xp + h) —f (x0) I g (Xp + /t) — g (x0) \ = h-0 \ h h )
= lim ---1- lim [так как предел суммы равен сумме пределов) =
/1-0 h h-+Q h
= ff (xo) 4“ gr (xo) [ПО определению производной].
Доказательства правил (5) и (6) тем же методом проводятся в Приложении (см. § 6.1 и 6.2).
2.3. ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕНЕЙ
Теорема 2. Пусть f(x) = хп, где п — любое целое положительное число; тогда /'(х) = nx'’”1, т. е.
dX* /о.
---= пхп1. (8) dx
При п = 1 это значит, что производная функции х »-► х есть 1. Этот частный случай содержится в примере из § 1.1 и геометрически очевиден (график тождественной функции имеет наклон 1). Для п > 1 мы дадим три разных доказательства.
1. Воспользуемся правилом дифференцирования произведения (5) и тем фактом, что х' =1.
Имеем
(х2)' = (хх)' = х'х 4- хх' = х + х = 2х, (х3)' = (хх2)' = х'х2 4- х (х2)' = х2 4- х (2х) = х2 4- 2х2 = Зх2, (X4)' = (хх3)' = х'х3 4- X (X3)' = X3 4- X (Зх2) = х3 4- Зх3 = 4х3 и т. д. (Чтобы сделать рассуждение формально строгим, следовало бы применить математическую индукцию.)
178
4. Производные
II. Пусть f(x) = xnt где п > 1 — целое число. Тогда
г/ /л\ 1 • hn — О
/' (0) = lim—— п
= lim hn~l = 0,
что совпадает с (8) при х = 0. При х #= 0 запишем разностное отношение в точке х в виде
(х 4- h)n—xn = х”(1 4- (h/x))n — хп = хп (1 4- (h/x))n — 1 = (1 + (h/x))n—l =
h x(h/x) х h/x ~Х (1 4-(Л/х)) — 1
и . Г, , , h \ /, h \2 . , , h \Л-П [здесь используется формула для
= Xя-1 II 4-114- ------14-114- ------ г 4- • • • 4“ I 1 4- -1 I суммы геометрической прогрессии
[ \ X ) \ X / \ X / J при q= 1 4- (Л/х)].
Разностное отношение есть многочлен от Л, следовательно, непрерывная функция от ft; ее значение при h = 0 есть ax'1"1. Итак, /' (х) = /IXя"1, что и требовалось доказать.
п множителей
III. Поскольку (х 4- Л)л =Нх + ft) (х + А)... (х + Л) = (сумме произведений, каждое из которых содержит по одному множителю, х или ft, из каждой скобки) = = хп 4- пхп~{Н 4- ft2• (некоторый многочлен от h), имеем
= /IXя”1 + ft • некоторый многочлен от h.
Это непрерывная функция от ft, и значение ее при ft = 0, т. е. , равно
пхя”1.
Теорема 3. Формула (8), т. е.
= пх-‘
справедлива при всех целых п.
Доказательство. При п > 0 дело сводится к теореме 2. Для п == 0 надо показать, что производная функции х° = 1 есть 0; это верно в силу правила (1) теоремы 1. Если же п — целое отрицательное число, то т = — п — целое положительное число, и в силу правила (6) теоремы 1 и теоремы 2 имеем
что и требовалось доказать.
§ 2. Дифференцирование
179
2.4. ПРОИЗВОДНЫЕ МНОГОЧЛЕНОВ И РАЦИОНАЛЬНЫХ ФУНКЦИИ
Рассмотрим целую-рациональную функцию (многочлен), например
у = Зх6 + 2*3 — бх + 1.
Пользуясь равенствами (1), (2), (3), (4) и (8), вычисляем ее производную следующим образом:
tf = (Зх5 4- 2х3 — бх 4- 1)' = (Зх5)' 4- (2х3)' — (бх)' 4- Г =
= 3 (х5)' + 2 (х3)'— 6 (х)' 4- 1' = 3 • (5х4)4-2 • (Зх2) — 6 4-0 = 15х*4-6х2 — 6.
Точно так же в общем случае имеем
(аоХя 4- агхп^ 4- •• • 4- ап^х 4- ап)' = па^хп^ + (п — 1) а1хл"2 4- • • • 4- ап.г
Тем самым мы установили, что справедлива
Теорема 4. Производная многочлена степени п есть многочлен степени п— 1.
Теорема 5. Рациональная функция имеет производную везде, где она определена; эта производная снова есть рациональная функция.
Доказательство. Пусть f — рациональная функция; тогда f = plq, где р и q — многочлены, не имеющие общих корней, и f определена везде, где <?=/= 0. Во всех таких точках, согласно (7), имеем /' = (p’q — pq')lq2» По теореме 4, р’ ng' — многочлены; по теореме 1 § 2.3 гл. 3, p’q — pq’ и q2 — также многочлены. Следовательно, /' —отношение двух многочленов, т. е. рациональная функция.
• Пример. Вычислить производную функции у = (Зх2 + 5х — 7)/(х10 + 1) в точке х = 1.
Решение. Имеем
dy = (Зх2 4- 5х — 7Y (X10 + 1) — (Зх2 + 5х — 7) (х™ 4- 1)' __
dx ~ (х™ + I)2 ”
_ (6х4-5)(х1°4-1) —(Зх24-5х —7) • 10х» (Х10 1)2
далее можно упрощать это выражение или оставить в таком виде. Во всяком случае,
[du\ = И ♦ 2— 1 • ю = з _ \ dx 22 * •
УПРАЖНЕНИЯ
В упражнениях 13—32 вычислите производные, пользуясь доказанными выше правилами.
13. Пусть f (х) = х& — 2х9 4- 1.; найдите /' (х).
f dz
14. Пусть z=(yn—Ъу'+ЪНу— 1); найдите —.
dy
15. Пусть g (t) = (t9 4- 3) (f 4- З/4 — t2 4- 1); найдите g' (t).
16. Продифференцируйте функцию и (и2 — 2и 4- 3)/(м2 4- 2м — 3).
17. Пусть h (w) = (w9 — 2w)/(w2 —w — 1); найдите h' (1).
180
4. Производные
А18. Найдите уравнение касательной к графику функции у = (х2 4- 1)/(х3 + 1) в точке (0, 1).
19. Найдите — dx
1 — 2х 4- **
14-х2
20. Продифференцируйте функцию t »-> (/3 4- 2t2 — 4) (t2 — 2/4- 3)/(/3 — 1).
21. Найдите уравнение нормали к графику функции г = (/3 4- t)/(t — 1) в точке (2, 10).
22. Пусть $=(и44-н3 — 2«4-1)(н3 — 2и2 4- и 4- 6); найдите (— \ du /и=2
23. Найдите уравнение касательной к графику функции s=(t2 — 5/4- 10)/(3/> — 1) в точке /== 0.
24. Найдите производную функции (/3 — 2/4- 6) (/5 — З/3 — 1).
25. Продифференцируйте функцию г (г2 — 2г) (г10 4- 9г 4- 5)/(гь — 2г2 4- 2).
26. Продифференцируйте функцию w н* (бш3 4- и»2 — 1) (ш2 — 10ш 4- 6) 4- w — 1/(и> 4- 1).
27. Найдите уравнение касательной к графику функции х=(у4— 2)/(у64"0 в точке (0, —2).
dx
28. Пусть х = (z15 — Зг12 4- *6 — 1) (г3 4- 3z 4~ 1) (z3 4- 5); найдите — • dz
29. Пусть A (s) = (s 4- 1)/($4 — 3^ 4- $2 — 1); найдите Д' (1).
30. Найдите уравнение касательной к графику функции г= (1—Зу 4- у9) (1 4- У2) в точке (0, 1).
31. Продифференцируйте функцию х = [(х3 — Зх)/(х2 — 1)] 4" [(х6 — 3)/(х* 4" 2)].
32. Пусть f (х) — (хь — 2х4 4“ Зх3 — х 4~ I)2’, найдите [' (х).
2.5. ЦЕПНОЕ ПРАВИЛО
Мы переходим теперь к очень важному цепному правилу для дифференцирования композиции функций (т.е. сложной функции).
Теорема 6. Пусть функция и =/(х), имеет в точке х0 производную а функция у = g(u) имеет в точке и0 = /(к0) производную g'(/(x0)); тогда их композиция <р = gof, т. е. функция у = g(f(x))t имеет в точке х0 производную
^^)=g'(f(xQ))f'(x>). (9)
(Производная композиции равна произведению производных.) В обозначении Лейбница эта теорема формулируется более изящно:
= ^У_ /д/х
dx du dx
Возникает искушение сказать: «Здесь просто сокращается du», но это не имеет смысла, поскольку и 57--------не дроби, a du — не число. Однако формула (9')
легко запоминается и удобна в пользовании.
Прежде чем доказывать теорему 6, покажем на простом примере, как она применяется. Пусть мы хотим продифференцировать функцию х *—► (1 + х3)2. Поскольку (1 -f- х8)2 — 1 4- 2Х3 + хв, то производная, конечно, равна 6х2 + бх5. Чтобы примет нить цепное правило, положим Дх) = 1 4- х3 и g(u) = и2. Тогда <р(х) = g(f(x)) = = (1 + х3)2. Так как f(x) = Зх2 и g'(u) = 2u, то, согласно (9), имеем
ф' (х) = g' (f (х)) f' (х) = 2 (1 4- х3) • Зх2 = 6х2 4- бх5,
§ 2. Дифференцирование
181
что и следовало ожидать. В обозначениях Лейбница те же вычисления принимают вид
d(14-*’)9 d(14-x»)8 d(14-x3) du* d(l+xa) „ ....
dx d(l+xs) dx du dx
= (2u) (3x2) = 2 (1 + x3) (3x2) = 6x8 + 6x«.
При некотором опыте можно опустить шаг «положим и = 1 4" х*» и обращаться с 1 -j- х3, как с единым символом:
d(l+x8)8 = d(l + x*)* d(14-x») = 2(1+ х3)Зха. dx d (1 + х3) dx
[При еще большем опыте нет надобности вообще записывать член d(l 4- х8), а можно привычным образом дифференцировать «снаружи внутрь».]
Конечно, цепное правило можно применять повторно. Например, как мы показали в § 1.6,
d У~ _ 1
Лх 2/х"
Поэтому
d г 1 + /1 + х8 = d r 1 4- /1 + х» d (1 4- /1 4- х8) d У1±х* d(l 4-х8) = d(14-/l 4-х») d /1 4- x8 d(\+x*} dx
d Уй~ d(14-t>) d/®d(l + x>) ,___________ __
=-------- —-———- —----- ————- [полагаем и = 1 -f- У1 -f- x** о = У1 4- л* * o> = 1+ x*] =
du dv w dx
= • 1--• (2x) = -------- -------------------.
2 Уи 2 Уш 2 У1 4- /1 4-х8 /14-х2
Докажем теперь цепное правило, предполагая при этом, что обе функции f и g линейны. Тогда /(х) = а 4- ах, g(u) — ,b 4- Р« и
<р(х) = = g(f(x)) = b 4- р(а + ах) =(6 4- ра) 4- (₽а)х.
Это опять линейная функция. Ее наклон, т. е. производная функции <р, есть Ра, т. е. произведение производных g' и f.
Как мы уже заметили в § 2.2, при вычислении производных можно заменять функции их линейными приближениями. Полное доказательство цепного правила, отнесенное в Приложение (см. § 6.3), построено точно так же, как приведенное выше доказательство для линейных функций._________
•Примеры. 1. Продифференцировать ]/1 4* о*’ ,где а — постоянная (и, конечно, 1 4- ах3 > 0).
Решение. В силу теоремы 6 имеем
d (У 1 4- ах8) = d у 1 4- ах8 d(l+ax8) = 1 = ах .
dx d (1 4- ах8) dx 2 У 1 -|-ах8 у 14-ах8
При а = — 1 получаем равенство (2) § 1.
182
4. Производные
2. Пусть /(х) = (1+(1 4-х)100)1009. Вычислить /'(0) и f (—1). Решение. Применяя цепное правило, имеем
df = d (1 (1 -|-х)100)1000 d(l -Hl+x)100) d(l +х)1П0 d(l 4-х)
dx d(l 4- (1 4-*),0°) «/(l+x)1®0 d(l + x) dx ~~
= 1000(1 4- (1 + x)100)999 4 1 • 100(1 + x)99 • 1 = Ю5 [1 4- (1 4- x)100]999(1 4- x)99.
Отсюда
= 105 • 2s99 и /'(—1) = f—Y =0.
\ dx jx=Q \ dx )x=—\
3. Зная, что d(\/x) ________________________________________1_
dx x2
(это было доказано прямым путем в § 1) и пользуясь цепным правилом, можно вывести (6).
В самом деле, при g(x) =# 0 имеем d 1 d(\/g) dg =__j_ dg = ф
dx g dg dx g2 dx g2
УПРАЖНЕНИЯ
В упражнениях 33—52 вычислите производные, пользуясь доказанными выше правилами.
33. Пусть f (х) = (хБ — Зх3 2х2 4- х — I)100; найдите /' (х).
34. Пусть g (z) = (ze 4- 3z2 4- г — З)12: найдите g' (z). ;
Г------------ dz
35. Пусть z = у у4 — у2 4- 5 ; найдите — •
36. Продифференцируйте функцию х»-> х }Ах6 — 2х4 4- * .
37. Пусть g (s) = (s3 — s 4- Уе )б: найдите g' (s).
А38. Пусть / (/) = 4-2/ — V t ; найдите Г (О*
39. Пусть h (t) = — 2t2 + i — l)/(/4 4- t* 4- 1)ьо; найдите h' (0.
40. Продифференцируйте функцию у (ge 4- уА — 2у 4- I)16 (у2 4- I)10. dx
41. Пусть х = (уь 4- 2g — З)8 (у2 4- у — З)6; найдите — •
1 1
42. Пусть f = go Л, h (2) = 6, h' (2) = — 10, g' (6) = — — • Найдите У (2).
43. Пусть Л = Во С, С(0) = —2, С (0) = 1/2, В (0) = 3, В' (0) = 5, В(—2)=10, В' (— 2) = 6. Найдите Л' (0).
44. Пусть ? (12) = — 3, <р'(12)=10, ф (12) = 2, ф'(12) = 1/2, ф (— 3) = 12, ф' 3) = 4. Найдите (фо<р)'(12) и (<р«ф)'(— 3).
45. Пусть g (0 = ((/э — б/2 — З)10 + /2 — II3; найдите g' (Z). • ___________________________ dz
46. Пусть z = У (у2 4- 1)э — 1; найдите — • dy
47. Найдите d(t» + /l + /2)s/dZ.
48 Продифференцируйте функцию и »-► 4- (и2 — З)8]8 (и3 — I).
§ 2. Дифференцирование
183
49. Продифференцируйте функцию s »-► (s2 4- p^s2 4" 1 )4 (s 4“ 1).
50. Пусть Fi0)=l, F'(0) = —2, G(l) = 3, G'(D = —5, H' (3)=4. Найдите (H об oF)'(0).
1/2 dx
51. Пусть х=(/а — 3)< (Z3— О4 (/4-1) : найдите — . dt
52. Пусть г — <? н- s 4- Р4* I найдите - •
ds
2.6. ПРОИЗВОДНЫЕ ОБРАТНЫХ ФУНКЦИЙ
Напомнйм (см. гл. 3, § 3.7), что две функций х »-► f(x) и у g(y) называются обрат ними друг по отношению к другу, если g(f(x)) = х и f(g(y)) = у. Пусть даны две такие функции, причем известно, что обе они имеют производные. Тогда по цепному правилу имеем
^(/(х))Г(х) =-£• = 1-dx
Тем самым обе функции могут быть дифференцируемы лишь в том случае, если ни одна из их производных не равна нулю. Оказывается, верно и обратное: если одна из функций имеет ненулевую производную, то и вторая имеет производную, также отличную от нуля.
Теорема 7. Пусть у = f(x) и х =± g(y) — строго монотонные функции, обратные друг другу. Предположим, что f имеет в точке х0 производную f'(x0) =/= 0, и положим у о = f(x0). Тогда g имеет в точке yQ производную
S'W-yJ-- (10)
Это правило также выглядит изящнее в обозначении Лейбница:
— =—L_. (ioz)
dy dyjdx
Утверждение теоремы 7 легко проверить геометрически. Пусть I — касательная к графику функции x*-*f(x) = ув точке (х0, У о)- Тогда I есть график линейной функции
х тх + b = у, т = /'(х0).
График обратной функции у g(y) получается симметрией графика f относительно биссектрисы первого координатного угла, т. е. относительно прямой у = х (рис. 4.13). Если отразить также /, то получается прямая касательная к графику g в точке (г/о» *о)- Н° Л сеть график линейной функции, обратной по отношению к у = тх + Ь, т. е. функции
1 ь
X = —у--------.
т т
Поэтому
,, ч 1 1 g (%) = — = ГГТ т Г (х0)
Из этого рассуждения видно также, что происходит при f'(*o) = 0. В этом случае I горизонтальна и вертикальна; тем самым g не имеет производной в точке Уь (рис. 4.14). Аналитическое доказательство теоремы 7 содержится в Приложении (см. § 6.4).
184
4. Производные
Рис. 4.14
УПРАЖНЕНИЯ
В упражнениях 53—66 вычислите производные, пользуясь доказанными выше правилами.
53. Пусть у = [(х) и х = g(y) — строго монотонные функции, обратные друг другу. Дано, что /(0) = 3 и /' (0) = —1/4; найдите g'(3).
54. Пусть х н* h(x) и х »-> k(x) — строго монотонные функции, обратные друг другу. Дано, что Л(—1) = 2, Л'(—1) = 1/3 и Л'(2) = —3; найдите k'(2).
Примечание. Понятие обратной функции не зависит от того, какими символами обозначаются зависимая и независимая переменная, если такие обозначения вообще введены. Иногда удобно для обратной функции поменять местами символы зависимой и независимой переменных (в особенности это относится к случаям, когда функции возникают из некоторой физической задачи), но в этом нет надобности, если пользоваться надлежащими обозначениями.
55. Пустьф иФ — строго монотонные функции, обратные друг другу. Дано, чтоф(О) = 1 и ФЛ(О) ® —2/3; найдите ф'(1)В.
56. Функция /(дг) в дг3 + 2лг — возрастающая. Пусть g — функция, обратная /; найдите ?'(0) в g'(3).
§ 2. Дифференцирование
185
57. Функция у = 3 — х — 2г3 — убывающая. Найдите (dx/dy)y в з и (dx!dy)y _ о.
Примечание. Если пользоваться обозначениями Лейбница в чистом виде, как это сделано в настоящем упражнении, то приходится при переходе к обратной функции менять местами символы зависимой и независимой переменных: в самом деле, в этом случае нет другого способа обозначить обратную функцию
58. Функция s i-> s5 + 3s3 — 1 — возрастающая. Пусть j — обратная ей функция; найдите Г(—1) и Г(3).
59. Функция х 2х — 1 —возрастающая. Найдите производную обратной функции в точке 3.
60. Функция г »-► г + уТ" — возрастающая. Найдите производную обратной функции в точке 2.
61. а) Функция ft(z) = г2 — г + 1 — возрастающая при г . Пусть k — функция, обратная h в этом интервале; найдите £'(3) и
' 1
б) Функция h{z) — г2, — г 4- 1 — убывающая при г<^ Пусть I — функция, обратная
h в этом интервале. Найдите Г(3) и /'(7).
J^62. а) Функция у = f(x) = х4 + 1 — возрастающая при х>0. Пусть х «= g(y) — функция, обратная f в этом интервале; найдите (dgjdy)y -2 и (dg/dy)y — 82.
б) Функция у « = х4 + 1 —убывающая при х< 0 Пусть х ® h(y) — функ-
ция, обратная / в этом интервале. Найдите (dh/dy)t^2 и (dh/dy)y=*82.
Примечание. Обозначение Лейбница в чистом виде плохо подходит к этой си-dy du dh
туации. поскольку оно не указывает, имеется ли в виду или----.
dy dy
63. а) Функция Дг) = г3 — 9г — возрастающая при г< —1/3. Пусть g — функция, обратная ft в этом интервале; найдите g'(0).
б) Функция Дг) = г3 — 9г — убывающая при —]ЛЗ< г< )/Т. Пусть h — функция, обратная J в этом интервале; найдите ft'(0).
в) Функция Дг) = г3 — 9г — возрастающая при г > "\/3l Пусть k — функция, обратная f в этом интервале; найдите ft'(0).
64. Функция у = Дх) = 1 — х3 — х° — убывающая. Пусть х ® g{y) — функция, обратная 4; найдите g' о
65. а) Функция Д$) = s4 — 4s — возрастающая при s> 1. Пусть g — функция, обратная ц в этом интервале; найдите g' о Д
б) Функция f(s) = $* — 4s — убывающая при s< 1. Пусть ft — функция, обратная Ц в этом интервале; найдите h' ®
66. а) Функция P(s) = s3 — 2s2 + s — возрастающая при s< -1-. Пусть 4 — функция.
обратная Р в этом интервале; найдите Г о Р
б) Функция P(s) = s3 — 2s2 4- s — убывающая при -1 < s< 1. Пусть g — функция, о
обратная Р в этом интервале; найдите g' ° Р.
в) Функция P(s) = s3 — 2s2 4“ s — возрастающая при s > 1. Пусть ft — функция обратная Р в этом интервале; найдите ft' о Р.
2.7. ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕНЕЙ С РАЦИОНАЛЬНЫМИ ПОКАЗАТЕЛЯМИ
Теперь мы в состоянии доказать следующую теорему.
Теорема 8. Пусть г — рациональное число*, тогда dxr г*
dx
фля всех х, при которых определены функции хг~* и хГ).
186
4. Производные
Доказательство. Для целого г дело сводится к теореме 3 этого параграфа. Рассмотрим сначала случай, когда г = 1/п, где п — целое положительное число. Как мы покажем,
. 1/л
dx__ = 1 х(1/п)~1
dx п
т. е.
При п = 2 это вновь приводит нас к формуле дифференцирования ]/~х~, уже доказанной прямым путем и неоднократно применявшейся.
Для доказательства требуемого утверждения заметим, что функции у = хУа и х = уп
взаимно обратны. По теоремам 7 и 3 имеем
d*1/n _ dy _ 1 1 _ 1 _ 1 _ 1 _ 1 (i/n)_i
dx dx _dx_ == d£ nyn-i в(Л1'°)я-' n
dy dy
что и требовалось доказать.
Пусть теперь г = т/п, где т — целое число, ап — целое положительное число.
В силу теоремы 3, теоремы 7 и только что доказанного результата имеем
dx' _ d(xl/ny” _ d(xl'nYn dxUa _ ( 1 (I/O)—J _
дл dx (x1/”) dx n
m (m/n)—(l/n)-H!M)—1 .
= — x = rx^\
n
Тем самым теорема 8 доказана.
2.8. ПРОИЗВОДНЫЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
Доказанные выше правила дифференцирования достаточны, чтобы продифференцировать любую иррациональную функцию.
Теорема 9. Иррациональная функция имеет производную везде, еде она определена, за исключением, возможно, конечного числа точек. Производная снова есть иррациональная функция.
Доказательство становится очевидным из рассматриваемых ниже примеров, ф Примеры. 1. Продифференцировать /(х) = yf 1 + xVj/^xI Решение. Имеем
Их) = A =-£ (О + -
dx I /' J dx
§ 2. Дифференцирование
187
- .«О+«!'-» х-.,. + (| + xS).,3 И) =
dx dx
d (1 4- х2)173 d (1 4- %2) —i/4 . Z1 , 2л/з d(x""174)
= - -Л...^ ---L L x 4- (1 4- X2) —-----[по теореме 6J =
d (1 4- x2) dx dx
= — (1 + X2)“2/3(2x) X-l/4 + (1+ X2)1/3 f— —) Х“®/4 (ПО теоремам 1 И 8J = 3 \ 4 /
= -£(14- x2)-2/3 x3/4------£ (1 + x2)I/3 x~5/4.
При желании это выражение можно «упростить»:
Г (х) = (1 + ж2)"2'3 х3/4 (-?---L (1 + х2) хг2) =
\ о 4 /
___ /х3 /2 1 4- х 2 \ (5х2 — 3) jAx3
~ 3/--------- ( з 4х2 / э/ ~~
VU4-X2)2 , ' 12х2 у (1 4-х2)2
Это упрощение, впрочем, несущественно. Формула для Т'(х) справедлива при х> 0, т. е. во всей области определения f(x).
2. Продифференцировать f(x) = (1 + х3)475.
Решение. Имеем
r w _ £<I + J,>"5. _ + _ Д (1 + АГМ .за.
dx d (1 4- х8) dx 5
Это выражение имеет смысл лишь при 1 + х3 #= 0, т. е. при х =£ — 1. Однако функция f определена также при х =—1.
"1 ^/~~~ I
3. Продифференцировать f(x) = V Ух У х.
Решение. Имеем f (х) = ( х1/3 4- х1/5)172. Отсюда
Г(х) = (х1/3 х1/5)1/2 d(x1/34-*1/5) = 1 ( *1/3 XV5\~1,2/_L х~2/3 I 1 х~4/б\
Z d( х1/3 4-xl/5) dx 2 V ' V 3 "Г 5 f
Здесь /(0) =0 определено, а /'(0) — нет. ф
ЭадРАЖНЕНИЯ
В упражнениях 67—76 вычислите производные, пользуясь доказанными выше правилами. 67. Пусть f (s) = s2/3 4- 3s1/4 — 2s-3; найдите /'(s).
68. Пусть у = zbf2 — (г2 4- 1)2/3 ; найдите — dz
69. Найдите d (о372 4- (у2 — v 4- 1 )”"2/3)/dv.
188
4. Производные
uV3_2nl/2
70. Продифференцируйте функцию и н*----------------.
а2'5 + За
71. Пусть s = (г8 + 2г — 1)3^4 + г 2/5; найдите • dz
72. Пусть h (х) = (х + (1 — Xя)1/2)3/2; найдите h' (х).
73. Пусть g (/) = (/2 4- (£ — 1)1/5) (/1/2 — I)4; найдите g' (/).
74. Пусть k (z)
17з"; найдите *'<*)•
75. Продифференцируйте функцию у »-* [(4 — 2t/1/3)l/4 4-
76. Пусть g (w) = (ш2/3 4- 1) ( u>1/2 — и?/4)1/2; найдите g' (w).
2.9. НЕДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
Мы определили производную функции f в точке х0 как предел разностного отношения
f(^ + h)—f(xQ) h
при h ->0, предполагая, что этот предел существует. Конечно, предел может и не существовать: график не обязательно должен иметь касательную. Если /'(хо) существует, то функция f называется дифференцируемой в точке х0. Как мы уже знаем (теорема 2 § 1), каждая дифференцируемая функция непрерывна.
Однако не каждая непрерывная функция дифференцируема. Простейший пример представляет функция /(х) = | х |; график ее, изображенный на рис. 4.15, имеет излом в точке х = 0.
Говорят, что эта функция имеет в точке х = 0 правую производную (равную 1) и левую производную (равную —1); соответствующая запись имеет вид f'(0+) = 1, /'(0") = —1. Подобным же образом функция, график которой изображен на рис. 3.6 (гл. 3, § 1.6), имеет в точке х = 0 односторонние производные: 0 (слева) и 1 (справа).
График функции f(x) = у х (рис. 4.16) имеет в точке х = 0 вертикальную каса-тельную; говорят, что f'(0) = + оо. График функции /(х) = | у х |, изображенный на рис. 4.17, также имеет вертикальную касательную при х = 0. Однако, по очевидным геометрическим причинам, в этом случае говорят, что = —оо и = = 4- °о. Точка 0 называется острием графика, или его точкой возврата.
Точные определения односторонних и бесконечных производных, а также правила их вычисления имеются в Приложении (см. § 7).
Непрерывная функция может быть не дифференцируемой и в силу более сложных причин. Иллюстрирующим это утверждение примером может служить функция, гра-
§ 2. Дифференцирование
189
фик которой изображен* на рис. 4.18; значение рассматриваемой функции в точке О равно 0. График функции совершает бесконечное число колебаний между прямыми у = х и у = —х. Рассмотрим разностное отношение при х = 0, т. е. отношение f(h)lh. Существуют сколь угодно малые значения й, для которых разностное отношение равно 1, а также сколь угодно малые значения й, для которых разностное отношение равно —1. Поэтому разностное отношение при й->0 не имеет предела: здесь у него не существует даже односторонних или бесконечных пределов.
* Такой вид имеет график функции
^почему?).
к sin 1/х при х =£ 0, 0 при х = О
190
4. Производные
Во всех описанных примерах рассматривались лишь функции, не имеющие производной только в отдельных точках. Кажется естественным предположение, что непрерывная функция в большинстве точек должна быть дифференцируемой. Но здесь интуиция вводит нас в заблуждение. Существуют непрерывные функции, не дифференцируемые нигде. 'Построить такие функции нелегко, и их почти невозможно наглядно изобразить с помощью графика. Мы не будем углубляться в этот вопрос, так как предмет математического анализа составляет рассмотрение дифференцируемых (т. е. имеющих производные) функций.
§ 3. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ.
УСКОРЕНИЕ
3.1. ПРОИЗВОДНЫЕ ПРОИЗВОДНЫХ
Рассмотрим дифференцируемую функцию х •-* у = /(х) и ее производную х »-»• -£- = = /'(х). Правило, сопоставляющее точке х наклон f'(x) касательной к кривой у = = Дх) в точке х, само по себе есть функция. Можно вычислить производную этой функции, если только она существует. Производная производной функций f обозначается через fix.) и называется второй производной /; f часто называют также первой производной.
Этот процесс можно продолжить. Производная функции /"(х), т. е. производная второй производной, или производная производной производной, обозначается через f’"(x) и называется третьей производной /. Аналогично, четвертая производная f определяется как производная функции f"'\ ее можно было бы обозначить через но обычно пользуются символом /,v или /(4); пятую производную обозначают через f4 или /(5) и т. д.; k-я производная f, т. е. /<А)(х), называется также производной Л-го порядка.
Лейбниц обозначал производные высших порядков так:
Г(х)= = ' ' ' drf dx*
(читается: <d два f по dx в квадрате» или <d два у по dx квадрат»), /-"(о —5 - g-. /,vw =2-..........м =
Это обозначение можно мотивировать, заметив, что производная f (х) функции ₽/х) получается посредством применения к f процесса дифференцирования. Пос-z » df d
кольку мы записываем f в виде символ истолковывается как символ cone-
§ 3. Производные высших порядков. Ускорение
191
ратора» дифференцирования; пишут также f = • Вторая производная /"
получается двукратным применением процесса дифференцирования:
f =--------f, или / = I — | /;
dx dx \dx )
обращаясь c d и с dx как с числами, можно записать
= А_ / = ' dx2 ' dx2
Аналогично,
= А А А / = /AV f - d3f dx dx dx \ dx ) dx3
и т. д. для /IV, /v, ... .
Хотя последнее рассуждение выглядит несколько натянутым, на практике обозначения Лейбница оказываются весьма удобными.
Функция f называется Л-кратно дифференцируемой в некотором интервале, если в каждой точке этого интервала существуют производные f (х), /"(*)» •••» /^Неособенно важны функции, имеющие производные всех порядков. Таковы, например, многочлены, рациональные функции во всех точках, где они определены, и иррациональные функции, за исключением отдельных их точек.
ф Примеры. 1. Пусть /(х)=2--------^-х34-х5; тогда
f (X) = — А Х2 + 5Х4, г (х) = _ Зх _|_ 20х\ f'" (X) = — 3 + 60х2, о
/lv(x) = 120х, /v (х) = 120, Л' (х) = 0 и, разумеется,
/VII(x) = /vm (X)
2. Пусть у — х7/3; тогда
dy 7 4/3 d2y 28 i/3 d3w 28 -2/3
— = — х , —— = — х при всех х, --------------- = — х при х=£и.
dx 3 dx2 9 dx* 27
В интервале — оо< х<+ оо функция х7/3 дифференцируема дважды, но не трижды. В интервалах —оо <х<0и0<Х<Ц-сюта же функция имеет производные всех порядков, ф
УПРАЖНЕНИЯ
d*2w
1. Пусть у = х3 — ха -4- 2% 4- 1; найдите •
2. Пусть f (/) = /4 — 2f3/2 4- 3//; найдите fIV (/).
Отт** Л. 5/2 о 2/3
3. Найдите третью производную функции гн>7 — 2z -4- г.
4. Пусть h (s) = (s2 — I)6; найдите h" (s).
192
4. Производные
5. Найдите уравнение касательной в точке х = 2, у = 1 к графику производной функции у = )Лг2 — 3 . _
6. Найдите вторую производную функции —Yu )5« 5/2
7. Пусть /(х) = (2x4- 1) ; найдите f” (х). Имеет ли график острия или вертикальные касательные? do d2o d3o
8. Пусть о = (у + 2)6 (2у — 3)в; найдите — » —- » •
dy' dy2 dy3
dz
9. Пусть г = /4(1 —2/)5; какова быстрота изменения—— по отношению к /? dt
10. Найдите третью производную функции w*-*w6(2w—I)4.
11. Пусть h (и) = и/(и — 1); найдите Л"' (и).
1/-----
Пусть х = г 1 + V У ’» найдите ----— •
dy2
Пусть k (х) = x3h (х) и h (1) — 3, h' (1) = 1/2, h” (1) = 4. Найдите k" (1).
Пусть А (г) = (г — 1)‘/2В (г) и В (5) = — 1, В' (5) = 1/3, В" (5) = 2, В'" (5) = 10. Найдите А'" (5).
15. Пусть / (0) = 2. /' (0) = — 4, /" (0) = 1/5, g (0) = 10, g' (0) = 2, g" (0) = — 1. Найдите (/g)'(0).
А16. Пусть G (х) = (Н (х)]» и Н (1) = 2, Н' (1) = 1/3, Н" (1) = 1/4. Найдите G" (1).
12.
13.
14.
17. Пусть w (s) = У 1 — (s) и ф(—2) = — 3, ф'(—2) = 3, Ф" (—2) = 5. Найдите < (—2).
18. Пусть А (и) = В (и3 + 1) и В' (1) = 1/6, В" (1) = — 2, В' /2) = 3, В" (2) = 1/4. Найдите Л" (1). _
19. Пусть f (s) = sg (Уs ) и g' (3) = 6, g" (3) = — 1, g" (3) = 2. Найдите f'" (9).
20. Пусть G (0) = 1, G' (0) = 2, G"(0)=l/2, H' (0) = 0, Я" (0) = — 1, . H' (1) = 6, H" (1) = 10. Найдите (Я □ G)" (0).
21. Пусть f(0 = H; найдите (0 при k= 1, 2, 3, ... .
22. Пусть g(u) = (u+\) 1/2; найдите g^ (и) при k= 1,2,3.........
23. Пусть А (х) = (1—2х)2/3; найдите (х) при k= 1,2,3...........
24. Пусть /г (г) = г2 4- z + ; найдите (г) при k = 1,2, 3.......
3.2 . УСКОРЕНИЕ
Смысл второй производной становится особенно ясным, если представить себе функцию как описание движения по прямой. В соответствии с нашими предыдущими обозначениями мы запишем нашу функцию* в виде
t s(t),
где t означает время, as — пройденный путь. Первая производная v(t) = s'(f) есть (мгновенная) скорость (см. § 1.13).
Пусть h — малое число; разность v(t + й) — есть изменение скорости за промежуток времени от t до t 4- Л; это изменение, конечно, измеряется в единицах скорости, т. е. в единицах длины за’единицу времени (например, в см/с). Дробь
р(/ + /0-О(0
h
§ 3. Производные высших порядков. Ускорение
193
есть среднее изменение скорости в течение интервала времени [/, t + /г], или среднее ускорение. Оно измеряется в единицах длины за единицу времени, в расчете на единицу времени, например в см/с2 (читается: «сантиметр в секунду за секунду» или, короче, «сантиметр на секунду в квадрате»). Если брать все меньшие значения /г, последняя дробь приближается к производной:
а(0=-^=*'(0-at
Величина а(0 называется (мгновенным) ускорением; отметим, что
a(t) = s"(/) = —;
dt2
итак, ускорение есть вторая производная от пройденногр расстояния (пути) по времени движения.
Рассмотрим теперь свободно падающее тело (см. § 1.14). Согласно Галилею, имеем s = —р/2. Отсюда
Таким образом, закон Галилея принимает вид: ускорение всех свободно падающих тел имеет одно и то же постоянное значение. Число 20 обычно обозначается через gf так что предыдущее равенство переписывается в виде
d?s
W = -s- (.1)
Численное значение g зависит от используемых единиц измерения пути и времени; в частности, имеет место приближенное равенство
g « 980 см/с2.
3.3 . ЗАКОН НЬЮТОНА
Определив ускорение, мы можем теперь сформулировать один из важнейших законов физики, а именно (третий) закон Ньютона, управляющий движениями тел. В этот закон входят кроме ускорения еще два основных понятия: сила и масса.
Представление о силе происходит от субъективного ощущения усилия, которое мы испытываем, когда нам приходится изменять скорость тела, например при бросании камня. В физике сила определяется как то, что является причиной, вызывающей ускорение. В случае прямолинейных движений сила может быть задана числом.
Как известно из повседневного опыта, одно и то же усилие, приложенное к разным телам, вызывает разные ускорения. По этой причине мы сопоставляем каждой частице положительное число, измеряющее ее сопротивление действию силы и называемое массой. Опыт показывает, что это сопротивление ускорению есть свойство самой частицы, не зависящее ни от ее скорости, ни от величины приложенной
194
4. Производные
к ней силы. (Впрочем, для очень быстро движущихся тел это утверждение должно быть пересмотрено; см. ниже § 3.4.) Опыт показывает также, что масса тела, состоящего из двух частей, равна сумме масс этих частей. Поэтому мы считаем массу тела мерой содержащегося в нем количества вещества. Для измерения массы, конечно, надо выбрать единицу; обычно в качестве единицы массы выбирают грамм. Соответственно этому мы будем пользоваться в наших примерах большей частью системой единиц CGS (сантиметр, грамм, секунда).
Теперь мы сформулируем закон движения частицы массы т, перемещающейся вдоль прямой. В каждый момент времени ускорение а этой частицы и действующая на нее сила F связаны соотн ошением
та = F. (2)
Отсюда видно, что сила измеряется в единицах «масса на ускорение», например в г-см/с2 («грамм на сантиметр в секунду за секунду»).
При а > 0 сила положительна, т. е. толкает тело в положительном направлении. Поскольку ускорение есть производная скорости, закон Ньютона можно также записать в виде
т — = F. (2')
di '
Сила, вынуждающая тело падать на Землю, называется его весом. Согласно Галилею, свободно падающее тело имеет всегда одно и то же ускорение g. Обозначая вес тела через W, имеем поэтому
mg = W. (3)
Итак, вес тела зависит лишь от его массы. Массы двух тел можно поэтому сравнить, сравнив их веса, например поставив их на весы. Вес тела массой в 1 г является удобной мерой силы; он называется грамм-силой.
УПРАЖНЕНИЯ
25. Движущаяся частица массой 0,3 г имеет в некоторый момент ускорение 10 см/е2. Какова сила, действующая на частицу в этот момент?
26. Тело массой 10 г толкают по горизонтальному столу без трения в направлении некоторой прямой. Скорость тела выражается формулой о = (/2/10) + /, О^С 10, где и измеряется в см/с, a t — в секундах; чему равна сила, приложенная к телу при t =» 1? При t = 2? При t = 10?
27. Пуля массой 30 г вылетает из оружия в горизонтальном направлении и погружается в вязкую жидкость, где она движется прямолинейно. Расстояние, пройденное пулей, выражается формулой s = 100 — (100— О4 при 0*^ 100, где s измеряется в санти-
метрах, а время t — в секундах; какова сила сопротивления жидкости движению пули при t = 10? При I =» 50?
28. Тело массой 500 кр помещается в гидравлический лифт, толкающий его вверх. G какой силой лифт должен действовать на тело, чтобы оно двигалось с постоянным ускорением в 2- м/с2?
&
§ 3. Производные высших порядков. Ускорение
19S
3.4 . ЗАКОН ЭЙНШТЕЙНА
В начале нашего столетия Эйнштейн открыл, что физика Ньютона неприменима к движениям с очень большими скоростями. В теории относительности Эйнштейна дифференциальное уравнение прямолинейного движения частицы под действием силы F имеет следующий отличный от равенства (2) вид:
где /и0 — масса покоящейся (т. е. не движущейся) частицы*, а с — скорость света в пустоте (с = 3-1010 см/с).
Когда Эйнштейн сформулировал свой закон, последний имел лишь чисто теоретическое значение, поскольку физике не приходилось иметь дело с телами, движущимися со скоростью, сравнимой со скоростью света: Но если v/c очень мало, то число — (и2/с2) настолько близко к 1, что закон (4) можно заменить законом Ньютона (2')« Однако в современных ускорителях некоторые элементарные частицы достигают скоростей порядка 0,99 с..
Выполним в равенстве (4) дифференцирование, с тем чтобы прийти к ускорению а = Применяя правила § 2 (в том числе цепное правило дифференцирования сложных функций), находим
d v _______________Г d "] dv
л Y i — (о2/^) | л» Yi — (f2/c2) Л
Правую часть этого равенства можно переписать так:
Таким образом, (4) принимает вид w>° = F. (4')
(у 1 — Wc2»3 ' '
Отсюда видно, что отношение Fla зависит не только от массы тела, но и от его скорости. Чем больше скорость, тем большая сила требуется, чтобы вызвать задан-ное ускорение.
* Так называемая «масса покоя» частицы—дело в том, что в теории относительности принимается, что масса частицы зависит от ее скорости.
196
4. Производные
УПРАЖНЕНИЯ
В упражнениях 29—32 применяйте, если не оговорено противное, уравнение (релятивистское) движения Эйнштейна. В качестве системы единиц выбирается CGS с— скорость света.
29. Частица с массой покоя 0,001 г имеет в некоторый момент скорость 0,9 с и ускорение 1 см/с2. Какова сила, действующая на частицу в этот момент? Сравните ее с силой, предсказываемой законом Ньютона.
30. Частица с массой покоя 1 г имеет в некоторый момент скорость 0,1 с и ускорение 10 см/с2. Какова сила, действующая на частицу в этот момент? Сравните ее с силой, предсказываемой законом Ньютона.
31. Частица с массой покоя 0,003 г разгоняется таким образом, что скорость ее меняется по закону v = tc/(t + 100), 0. Когда скорость достигнет 0,5 с? Какова будет в этот
момент действующая на частицу сила? Когда скорость достигнет 0,9 с? Какова будет сила, действующая на частицу в этот момент? Сравните эти силы с силами, предсказываемыми законом Ньютона.
^32. Чтобы вызвать ускорение в 5 см/с2 у некоторой движущейся частицы, требуется сила в 10 г см/с2. Пусть скорость частицы равна 0,8 с; какова ее масса покоя? Сравните ее с массой, предсказываемой законом Ньютона.
3.5 . ПРЕДПОЛОЖЕНИЯ ДИФФЕРЕНЦИРУЕМОСТИ В ФИЗИКЕ
В (третьем) законе Ньютона (и в законе Эйнштейна) молчаливо предполагается, что положение движущейся частицы описывается дважды дифферецируе-м о й функцией времени $(/), так что понятия скорости s'(0 и ускорения $"(0 имеют смысл. Обычно это предположение оказывается вполне оправданным; встречаются, однако, и ситуации, где оно не соблюдается.
Микроскопическая частица, плавающая в жидкости, испытывает толчки (гораздо меньших ее!) молекул жидкости; эти бесчисленные толчки вызывают блуждающее движение частицы. Это явление было впервые замечено ботаником Брауном. В математической теории броуновского движения положение такой частицы описывается непрерывной, но не дифференцируемой функцией. Тем самым частица не имеет определенной мгновенной скорости.
Около сорока лет назад физики поняли, что входящие в состав атомов «элементарные частицы», такие как электроны, протоны или нейтроны, не подчиняются законам классической физики Галилея и Ньютона. В квантовой механике (так на-
▲льберт ЭЙНШТЕЙН (1879—1955), работавший с 1905 г. в Швейцарском Патентном бюро, опубликовал в этом году три работы, каждая из которых положила начало новой физической теории. Одна из них касалась так называемого броуновского движения помещенных в жидкую среду мельчайших частиц; в другой содержалось первое применение квантовой гипотезы Планка к взаимодействию излучения с веществом. Эта работа, вместе с другими сделала Эйнштейна одним из отцов квантовой теории, которую он, впрочем, так' никогда и не принял до конца. Третья работа содержала специальную теорию относительности. За нею последовала в 1916 г. общая теория относительности, а затем в течение десятилетий — напряженные поиски единой теории, которая должна была описывать одновременно и тяготение, и электромагнетизм*.
Эйнштейн прибыл в Соединенные Штаты в 1933 г. в качестве беженца из гитлеровской Германии и поселился в Принстоне, штат Нью-Джерси. В 1939 г. он подписал письмо, обращающее внимание президента Рузвельта на возможность создания атомной бомбы. В течение всей жизни Эйнштейн сохранял большой интерес к общественным вопросам, в особенности к поддержанию мира во всем мире и к защите гражданских свобод.
4 Основная идея общей теории относительности Эйнштейна состоит во включении гравитационных полей (т. е. явлений тяготения) в геометрическую структуру пространства-времени; гипотетическая «единая теория поля» должна была описывать в геометрических терминах наряду с этим также и явления электромагнетизма. Поиски такой «единой теории» привели к заметному прогрессу геометрии; что же касается физических результатов, то тут заметного успеха достигнуть не удалось, несмотря на многолетнюю напряженную работу многих выдающихся ученых.
§ 4. Знаки производных. Максимумы и минимумы
197
зывается теория движения таких частиц) скорость не является производной от положения частицы по времени, во всяком случае в том смысле, в каком это понимается в классической физике. Когда мы мыслим себе скорость как производную, мы предполагаем, что возможно измерить ее, точно определив положения частицы s(t) в различные моменты времени; затем расположить все эти положения частицы на одной кривой и, построив касательную к этой кривой, измерить ее наклон. При этом чем точнее нам известно положение, тем точнее получилась бы скорость. Однако в силу одного из основных принципов квантовой теории в любом эксперименте более точное измерение одной из двух величин — положения и скорости — приводит к менее точному измерению второй величины. А именно, если положение частицы измеряется с точностью до величины а, а ее скорость — с точностью до р, то, согласно принципу неопределенности Гейзенберга, <х(3 > h/m, где т — масса частицы, а h — универсальная постоянная (так называемая постоянная Планка}, Это вовсе не означает, что в квантовой теории неприменим математический анализ; напротив, математический аппарат квантовой механики целиком базируется на (математическом) анализе*.
§ 4. ЗНАКИ ПРОИЗВОДНЫХ. МАКСИМУМЫ И МИНИМУМЫ
Научившись вычислять производные, можно задаться вопросом о том, какую информацию о функции можно получить, если известно, что производная положительна или отрицательна, В этом параграфе мы ответим на этот вопрос и некоторые другие, с ним связанные.
4.1. ПРЕДВАРИТЕЛЬНЫЙ РЕЗУЛЬТАТ
Мы начнем с одного простого результата, утверждающего, что в точке, где касательная направлена вверх, кривая поднимается, а в точке, где касательная направлена вниз, кривая опускается.
Роберт БРАУН (1773—1858) • — английский ботаник.
Вернер ГЕЙЗЕНБЕРГ (род. в 1906 г.) — один и первооткрывателей квантовой механики. Принцип неопределенности Гейзенберга был изложен в работе, опубликованной в 1926 г.
Макс ПЛАНК (1858—1947) предложил в 1900 г. свою «квантовую гипотезу», согласно которой при электромагнитном излучении знергия может испускаться лишь порциями величины Nh тгдо N — целое число. V — частота излучения и h — некоторая универсальная постоянная..
• Английская фамилия Brown (Браун) долгие годы неправильно транскрибировалась в русской литературе как «Броун», откуда и возник широкораспространенный термин «броуновское движение» (правильнее было бы писать «брауновское движение»).
• Сказанное следует понимать лишь в том смысле, что методы описания движения, изло-женные в § 1.11, 1.13, 3.2, 3.3, 3.4, неприменимы в квантовой механике (последнее, однако, связано не с недифференцируемостью каких-либо функций, вроде тех, которые возникают при математическом описании броуновского движения, а обусловлено совсем иными обстоятельствами).
198
4. Производные
Теорема 1. Справедливы следующие заключения:
если то при х < х0 и вблизи х0 а при х>х0 и вблизи х0
Г(хо)>0 f(x)<Zf (х0) f (х0) < f (х)
Г (*о)<О ' /(*)>/(х0) /(х0)>/ (X)
Доказательство. Мы докажем только утверждения, содержащиеся в первой строке таблицы; вторая строка вполне аналогична первой. Производная f'(x0) есть предел разностного отношения
f (Хо + Л)—/(хо)
h V '
при h -> 0. Производная положительна; поэтому разностное отношение положительно при достаточно малых положительных й. Это значит, что если точка х = = xQ + h находится вблизи и справа отх0, так что h мало и по ложительно, то и числитель в (1) положителен, так что/(х) = f(xQ + h) > /(х0). Аналогично, если х0 + h — точка вблизи х0 и слева от х0, т. е. h мало по абсолютной величине и отрицательно, то f(x0 + h) < f(xQ),
Следующий результат относится уже не к отдельной точке, а к целому интервалу.
4.2. ФУНКЦИИ С ПРОИЗВОДНЫМИ ОДНОГО ЗНАКА
Теорема 2. Пусть f(x) непрерывна в замкнутом интервале а х < 6. Пусть во всех точках х, а < х < й, производная существует; тогда
если f' >0 то f в интервале а < Сх< С b возрастает
если /' < со то f в интервале а < С х < Z. b убывает
Это один из основных результатов анализа. Напомним, что функция f называется возрастающей, если для любых двух точек Xi и х2 интервала, где xt < х2, имеем Утверждение теоремы вполне убедительно: если касательная во всех точках направлена вверх, то кривая поднимается (рис. 4.19).
Строгое доказательство теоремы 2 требует, однако, более тонких рассуждений. Мы приведем его в Приложении (см. § 8.1). Пока же мы примем эту теорему как геометрически очевидную.
•Примеры. 1. Рассмотрим функции
f (х) = х3, g(x) = х1/3, h (х) = х при х <^0; 2х при х >0.
§ 4. Знаки производных. Максимумы и минимумы
1W
Рис. 4.19
Все эти функции непрерывны везде. При х #= 0 их производные существуют и положительны; однако = 0, в то время как g и h не дифференцируемы в точке х = 0. Однако все три функции возрастают при всех х (рис. 4.20, 4.21 и 4.22). Тем самым установлено, что неравенство f > 0 является достаточным, но не необходимым условием возрастания /.
2. Найти интервалы возрастания и убывания функции f(f) = (1 + 0/(1 + /2)-Решение. Имеем
(1 4- /*) — (1 4- /) . 2t 1 _ 2г — /2 _ 2 —(<+ I)2 (1 + Z2)2 “ (1+/2)2 (1+^2)2
Заметим, что (1 4- /2)2 положительно при всех t. Следовательно, /' (/) >• 0, если 2 — (t 4- I)2 > 0, т. е. при 11 4- 11 < |^2 , иначе говоря, при — 1 — 1^2 < < t <Z — 1 4- 1^2 . Далее, f (t) = 0 при t = — 1 4- У"2 и t = — 1 — ]Л2 ; для всех остальных t имеем /' (0 < 0. Мы заключаем, что f возрастает при — 1 — — ]f2 — 1 4~ 1^2 ; убывает при t <; — 1 —j/2 и при t > — I 4- У"2 .
3. Найти интервалы возрастания и убывания функции g (х) = Зх,/3 — 5х1/5. Решение. Имеем
g’ (х) = х-2/3 - х'4/5 = х-4/5 (х2'15 - 1)
при х=^=0, в то время как при х=0 производная не существует. Так как
х-4'5 = ( х ,/5)4 >• 6 при х =/= 0 и х2/15 — 1 > 0, если | х | >• 1, и х2/15 — 1 < 0,
если |х|< 1, то мы видим, что g возрастает при х<—1; убывает при —1 •< < х< 1; возрастает при х> 1.
4. Рассмотрим функцию f(x) = — при х =# 0, /(0) = 0. Мы видим, что f < 0 при всех значениях х, за исключением х = 0, при котором производная не существует. Но/не является убывающей при всех значениях х, так как, например,
200
4. Производные
f(—1) = —1 <z 1 = f(l). Этот факт не противоречит теореме 2, поскольку f не является непрерывной в точке х = 0. (Конечно, / убывает при х < 0 и при х > 0.)ф
4.3. ФУНКЦИИ С НЕОТРИЦАТЕЛЬНЫМИ И НЕПОЛОЖИТЕЛЬНЫМИ ПРОИЗВОДНЫМИ
Отметим для ссылок в дальнейшем одно следствие из теоремы 2.
Теорема 3. Пусть f(x) непрерывна в замкнутом интервале а х Ь и во всех точках х9 где a<Z х <Z Ь, существует производная f'(x). Тогда
если f' > 0 то f не убывает в этом интервале
если f < 0 то f не возрастает в этом интервале
§ 4. Знаки производных. Максимумы и минимумы
201
Мы докажем лишь первое утверждение. Второе может быть доказано аналогично или же можно получить его, применив первое к функции (—/). Примеры, иллюстрирующие теорему, изображены на рис. 4.20 и 4.23.
Доказательство теоремы 3. Нам надо показать, что если Xt<X2, ТО /(Xj)</(X2).
Пусть п — целое положительное число; положим g(x) = f(x) В каждой точке, где/' >• 0, имеемg' = f 4- > 0, поскольку сумма неотрицательного числа
и положительного числа положительна. Пусть xt и х2— любые две точки рассматриваемого интервала, причем xi<x2. Тогда по теореме 2 имеем g(xt) < g(x2). Это значит, что /(х,) + х,/п < f(x2) + х2/п, или, что то же, /(xf)—f(x2)< < (х2—xt)/n. Поскольку это верно при п = 1,2,3,..., отсюда следует, что /(xi) — /(х2) 0; итак, /(х,) <1/(х2), что и требовалось доказать. (Заметим, что здесь использована аксиома Архимеда.)
УПРАЖНЕНИЯ
В упражнениях 1—8 найдите интервалы везрастания и убывания заданных функций. Предполагается, что эти интервалы должны содержаться в области определения функций и быть максимальными (сколь возможно большими).
1. /(ж) = Г’+хв-А2. /(/) = (/ —2)/(; + 1).
3. s !—► (s2/2) Н- 3s*/3.
4. g (х) = х3 — 2ха х — 1
5. Л (г) = г2/уг2 4- 1 .
6. у (s) = s* — 2s2 4- 4.
7. £ (У) = (у/3) 4- У2/3 — 8«/1/3
8. /(х)=х2(х=-1)1/3.
4.4. ЛОКАЛЬНЫЕ МАКСИМУМЫ И МИНИМУМЫ
Говорят, что функция /, определенная вблизи точки х0, имеет в этой точке локальный максимум, если f.(x) < /(х0) для всех х вблизи х0. В этом случае xQ называется точкой локального максимума, а число /(х0) — локальным максимумом.
Если /(х) < /(х0) для всех х =/= х0 вблизи х0, то говорят, что максимум строгий. Различные возможные случаи показаны на рис. 4.24.
Говорят, что функция f имеет в точке х0 локальный минимум, если /(х) >• /(х0) для всех х ф х0 в б л и з и х0; строгий локальный минимум, если /(х) > /(х0) для в с е х х =£ х0 вблизи х0 (рис. 4.25). При этом х0 называется точкой локального минимума, а число /(х0) — локальным минимумом*.
♦ Концевые точки отрезка, на котором функция определена, обычно не считаются точками (локального) максимума или минимума.
202
4. Производные
Читатель без труда убедится, что если функция постоянна в некотором интервале, т. е. если ее график содержит горизонтальный отрезок, то в силу нашего определения каждая точка этого интервала, за исключением концов, является одновременно точкой локального максимума и точкой локального минимума.
Если f'(x0) > 0 или f'(x0) < 0, то f(x) не может иметь в точке х0 ни локального максимума, ни локального минимума, как это следует из теоремы 1. На геометрическом языке: в вершине или низине кривой касательная горизонтальна, если в этой точке она существует. Сформулируем последнее утверждение в виде теоремы.
Теорема 4. Если f(x) имеет в точке х0 (локальный) максимум или (локальный) минимум и дифференцируема в этой точке, то f'(x0) = 0.
Не следует думать, однако, что верно и обратное; из того, что f'(xQ) = 0, вовсе еще не следует, что функция f(x) имеет в точке х0 максимум или минимум (рис. 4.26). Точки, в которых производная функции f(x) равна нулю, называются критическими, или стационарными, точками функции. Таким образом, точка локального максимума или минимума дифференцируемой .функции всегда является
§ 4. Знаки производных. Максимумы и минимумы
203
критической точкой, но критическая точка (дифференцируемой) функции н е обязательно является точкой локального максимума или минимума.
Пусть /(х) определена при а < х < b и х0 — такая точка, что а < х0< Ь. Тогда можно высказать следующие очевидные утверждения, записанные ниже в виде таблицы:
если в [а, х0] функция f а в [х0, Ь] функция f то f имеет в точке х0
убывает не возрастает возрастает не убывает возрастает не убывает убывает не возрастает строгий локальный минимум локальный минимум строгий локальный максимум локальный максимум
В качестве приложения докажем следующий результат:
Теорема 5. Пусть функция f дифференцируема вблизи точки х0; тогда
если и то f имеет в точке х0 строгий локальный
Г (*о) = 0 Г(х0)>0 минимум
Г (х0) = 0 Г(Хо)<О максимум
Мы докажем лишь первое из этих утверждений. Доказательство второго аналогично; оно может быть, впрочем, получено из первого, если применить его к функции (-/).
Предположим, что /'(х0) = 0 и /"(*о) > 0- Напомним, что /"= (/')'. Применив теорему 1 к функции Г(х), заключаем, что для х < х0 и близких к х0 имеем /'(х) < < f'(xQ) = 0 и что для х > х0 и близких к х0 имеем f'(x) > /'(х0) — 0. Поэтому в силу теоремы 2 f убывает в некотором интервале, правым концом которого является х0, и по той же причине f возрастает в некотором интервале с левым концом х0. Из приведенной выше таблицы мы видим, что f имеет в точке х0 строгий локальный минимум.
ф Примеры. 1. Найти локальные максимумы и минимумы функции f(x) = 4х4 — х2 4- 5.
Решение. Сначала найдем критические точки f, т. е. точки, где /' = 0; затем определим знак /" во всех критических точках (этот прием называется критерием второй производной). В нашем случае /'(/)_= 16х3—2х =2х(8х2—1) для всех х. Критические точки суть х =0,х = 1/J/8 и х =—1/]/8. Далее, /"(х) = = 48х2—2. Отсюда /"(0)=— 2 < 0, /"(1//8У = /"(—1//8) = 4 > 0. Следова-тельно, по теореме 5, f имеет строгий локальный максимум в точке 0 и строгие локальные минимумы в точках х = 1/1/8, —1/}/8. Значение локального максимума /(0) =5, локальных минимумов /(1/]/8) = f(—1/]/8) =79/16.
204
4. Производные
2. Функция f(x) = — | х | имеет строгий локальный максимум в точке х = 0, но не имеет в этой точке производной. Этот локальный максимум не может быть обнаружен с помощью описанных выше приемов, ф
УПРАЖНЕНИЯ
В следующих упражнениях найдите все локальные максимумы и минимумы заданной функции.
9. f (х) = ж3 4- Зха — Зх 4- 4. 14. и | 1 4- и21.
10. g (х) = 2х» — 15жа — 36х — 1. 15. х | 4- Зх2 4- бх |.
11. /(х) = 2хЬ — 10х —7. 16. Н</) = Н + !/|.
А12. / (X) = х100 4- 17. (2 4“ ха)/( 1 4- ха)
13. <р (х) = бх* 4- 10»3 4- 161Г*. 18. «(0 = ^1 + /*.
4.5. КУСОЧНО-МОНОТОННЫЕ ФУНКЦИИ \
Напомним, что функция, определенная в некотором конечном интервале, называется кусочно-монотонной, если интервал ее определения можно разбить на конечное число частей, в каждой из которых функция монотонна (рис. 4.27).
Теорема 6. Если функция Дх), определенная в некотором интервале, имеет непрерывную производную Г(х), у которой в атом интервале есть лишь конечное число корней, то f[x) кусочно-монотонна.
Доказательство. Между двумя точками, в которых Д(х) принимает соответственно положительное и отрицательное значения, Лежит корень производной, как это следует из теоремы о промежуточном значении. Поэтому между двумя последовательными корнями производной знак ее не меняется: либо она везде положительна, либо везде отрицательна. Но тогда, по теореме 2, Дх) либо возрастает, либо убывает между двумя последовательными корнями f'(x).
§ 4. Знаки производных. Максимумы и минимумы
205
Из теоремы 6 вытекает теперь, что многочлены, рациональные и иррациональные функции кусочно-монотонны. То же относится и к большинству функций, обычно встречающихся в анализе. Непрерывная, но не кусочно-монотонная функция изображена на рис. 4.28; видно, что строение ее сложнее, чем у обычно встречающихся нам функций.
4.6. АБСОЛЮТНЫЕ МАКСИМУМЫ И МИНИМУМЫ
Пусть функция f(x) определена в некотором интервале и х0 — точка этого интервала. Если f(x) f(xQ) для всех точек х этого интервала, то говорят, что f имеет в точке х0 абсолютный максимум (для данного интервала), а значение /(х0) называется максимумом f в интервале [часто пишут /(х0) = max /]. Аналогично, функция f имеет в точке х0 абсолютный минимум, если /(х) ft*o) для в с е х х из данного интервала; значение /(х0) называется в этом случае минимумом f [запись: /(х0) = = min /1. Функция, определенная в интервале, необязательно имеет в нем максимум или минимум.
фПримеры. 1. Непрерывная функция /(х) == х не имеет в открытом интервале 0 < х < 1 ни максимума, ни минимума. В замкнутом же интервале 0 х 1 она имеет максимум 1 и минимум 0.
2. Положим /(х) = х2 при 0<х< 1, /(0) = /(1) = 1/2. Функция / определена в замкнутом интервале 0 х 1, но не является в нем непрерывной. Она не имеет в этом интервале ни максимума, ни минимума.
3. Непрерывная функция /(х) =1/]Л1—х2, определенная в открытом интервале —1 < х < 1, имеет минимум 1 в точке х = 0, но не имеет максимума, ф
УПРАЖНЕНИЯ
19. Постройте график функции, определенной и непрерывной в интервале [—2, 2], имеющей абсолютный максимум в трех точках и строгий локальный минимум в двух точках (возможно ли это?).
20. Постройте график функции, определенной и непрерывной в интервале [0, 5], имеющей абсолютный максимум в точках 1 и 3, строгий локальный минимум в точке 2 и не имеющей абсолютного минимума (возможно ли это?).
21. Постройте график фуйкции, определенной и непрерывной в интервале (—2, 2], имеющей абсолютный максимум в точке 1, острие в точке 1 и абсолютный минимум в точках —1 и 3/2 (возможно ли это?)
22. Ниже изображен график функции; укажите точки, в которых эта функция имеет локальный максимум или минимум, абсолютный максимум или минимум. Укажите также, где производная равна нулю и где не существует производной.
206
4. Производные
4.7. СУЩЕСТВОВАНИЕ МАКСИМУМОВ И МИНИМУМОВ
Непрерывная функция, определенная в замкнутом интервале, всегда имеет в этом интервале максимум и минимум. Это утверждение кажется правдоподобным, но доказывается не очень просто. Мы приведем это доказательство в Дополнении, помещенном в конце книги. Пока мы не будем пользоваться этой теоремой, поскольку для наших целей достаточен следующий, значительно более простой результат:
Теорема 7. Функция, определенная, непрерывная и кусочно-монотонная в замкнутом (конечном) интервале, имеет абсолютный максимум и абсолютный минимум.
Доказательство. Если f непрерывна и монотонна при а то ясно, что f принимает наименьшее и наибольшее значение в концах аир. Если f непрерывна и кусочно-монотонна при а С 6, то существует конечное число таких точек аь а2, ...»аЛ, что
а < оц < а2 < .. • < < b
и f монотонна в каждом из интервалов [a, aj, [аь а2], ...» [ай, Ь]. Поэтому наибольшее значение f равно наибольшему из чисел
/И, /(ax), /(а2),...,/(аЛ), /(6),
а наименьшее значение f — наименьшему из этих чисел.
4.8. РАЗЫСКАНИЕ МАКСИМУМОВ И МИНИМУМОВ
Одно из первых приложений анализа — разыскание максимумов и минимумов. Обычно встречаются функции, удовлетворяющие условиям теорем 6 и 7. В этом случае max f и min f могут быть найдены путем сравнения локальных максимумов и минимумов f и значений f в концах рассматриваемого интервала или же просто вычислением f в концах интервала и во всех критических точках (отвечающих корням производной /').
•Примеры. 1. Найти наибольшее и наименьшее значения функции
/(х)=-^-(х3 — 12х + 10)
в интервале — 3 < х < 3. /
Решение. Имеем /'(х) = (Зх2—12) =-^-(х + 2)(х— 2). Корни/' суть — 2 и 2. Так как /(— 3) = 1,9, /(—2) = 2,6, /(2) = — 0,6 и /(3) = 0,1, заключаем, что тах/=/(—2) = 2,6 и min/ = /(2) = — 0,6 (рис. 4.29).
§ 4. Знаки производных. Максимумы и минимумы
207
Рис. 4.29
2. Найти максимум и минимум функции f(x) =]/гх —2угх при О-^х-^ЮО. Решение. Имеем
1 __з_ / I \
„ 1 ~ 2 „ 1 ~ 4 1 4 / 4 , |
f (х) = — х — 2 • — х = — х I х — 11.
. ' ' 2 4 2 \ )
Заметим, что f не дифференцируема при х = 0. Единственный корень_производной f есть х — 1. Поскольку /(0) =0, /(1) — —1 и /(100) — 10—2]/10>0, имеем max f = 10—2уТ(Г, min / =—1. _______
3. Найти максимум и минимум функции f(x) = 1/]/ 1—х2,—1<х<1.
Решение. Вместо /(х) можно рассмотреть g(x) 1/(х)18 = 1/(1 — х8): в самом деле, поскольку / > 0 и и и8— возрастающая функция при и >> 0, функции / и g имеют максимумы и минимумы в одних и тех же точках.
Имеем g'(x) = 2х/(1 —х8)2. Следовательно, g'—G тогда и только тогда, когда х = 0. Минимум g достигается в точке х = 0; максимума g не имеет. Поскольку функция / определена в открытом интервале, нет надобности рассматривать конечные точки.
Еще проще было бы перейти к функции Л(х) = 1/[/(х)]2 = 1 —- х8, заметив, что максимум h достигается в той же точке, что и минимум /, а минимум h, если он отличен от нуля, — в той же точке, что максимум /. Яс но, что в заданном интервале h имеет максимум 1 и не имеет минимума, ф
Задачи о максимуме и минимуме часто имеют вид геометрических и арифметических теорем или возникают в заимствованных из практики проблемах. В этих случаях для решения задачи требуется некоторая п редварительная работа: исходной формулировке вопроса надо придать вид задачи о наибольшем или наименьшем значении некоторой функции, заданной в извес тном нам интервале. Мы проиллюстрируем эту процедуру рядом примеров.
фПримеры. 1. Доказать теорему: среди всех прямоугольников с данной диагональю наибольшую площадь имеет квадрат.
208
4. Производные
х
Рис. 4.30
Доказательство. Пусть х и у — стороны прямоугольника (мы имеем в виду, конечно, длины сторон; небольшие неточности этого рода не могут привести к недоразумению). Площадь S = ху. Примем диагональ за единицу длины (рис. 4.30). Тогда х2 t/2 = 1 и у = 1 — х2, откуда S = хУ 1 — х2. Интерес
представляют лишь значения 0 С х 1. Требуется найти максимум S в интервале [0, 1]. Рассмотрим вместо S функцию /(х) = S2 =х2(1 —х2) = х2—х4. Поскольку S положительна, функции S и f = S2 достигают максимума в одних и тех же точках. Имеем2\х) = 2х — 4х® = 2х(1 — 2х2). Корни /' суть 0 и 1/^2. Далее, /(0) = = 0, /(1/]/2)_= 1/2— 1/4 = 1/4, Д1) = 0. Следовательно, максимум достигается при х = 1/У2? В этой точке у — ]/1 — х2 — 1/]/2; таким образом, искомый прямоугольник — квадрат.
2. Показать, что при х^> —1 справедливо неравенство
Г1+х< 1 +^-.
Первое доказательство (методами элементарной математики). Утверждение равносильно неравенству
1+х<Н+—| =,+х + ~-
справедливость которого очевидна.
Второе доказательство (методами анализа). Положим 1 2 у
/(х)=(1 + х) -1--^-.
Тогда
Отсюда видно, что '(*) < 0 и / убывает при х > 0, в то время как /'(*)> 0 и / возрастает при —1 х < 0. Но /(О) '== 0. Следовательно, f(x) "С 0 при —1, что и требовалось доказать.
3. Показать, что при х > 0 для рационального числа г >2 справедливо неравенство
(1 + X)'> 1 + гх +
§ 4. Знаки производных. Максимумы и минимумы
209
Доказательство. Положим
/(х) = (1 + ху- 1 - гх -
Тогда
/' (х) = г (1 + х)т~1 — г — г (г — 1)х, f" (х) = г (г - 1) (1 + хГ2 - г (г — 1) = г (г — 1) К1 + ху~* - 1]. Поскольку г >2, имеем /"(х) > 0 при х>0. Поэтому f'(x) возрастает. Так как /'(0) = 0, имеем f (х) > 0 при х > 0. Поэтому /(х) возрастает. Поскольку /(0) = 0, отсюда следует, что /(х) > 0 при х > 0, что и требовалось доказать.
4. Какова наиболее выгодная форма жестяной банки? (Банка есть прямой круговой цилиндр радиуса г и высоты h. Количество использованной для изготовления банки жести измеряется площадью полной поверхности: 3 = основанию + боковая поверхность 4- крышка = -кг* 4- 2ягЛ + № = 2к(г2 4- rh). Объем банки V = Мы хотим сделать V возможно большим при заданном 3.)
Решение. Поскольку 3 = 2№ 4- 2«гй, имеем
й = и V = w2/i = -1- (Sr — 2№)= JLг (3 _ 2w2).
Нас интересуют лишь те значения г, при которых V не отрицательно, т. е.
Требуется найти точку этого интервала, в которой V достигает максимума. В конечных точках V = 0. Далее,
dV 1 /е с 24 с _-п
— = — (3 — 6w2), — = — 6w < 0. аг 2 dr*
Первая производная обращается в нуль в точности в одной точке; в этой точке вто-
рая производная отрицательна. Это точка локального максимума и V имеет в этой точке абсолютный максимум. Максимум достигается при условии S — 6кг2 =0, что равносильно 2кг2 + 2кгЛ — 6кг2 = 0, или h = 2г.
Ответ означает: диаметр банки должен быть равен ее высоте.
(Мы воспользовались здесь некоторыми элементарными результатами, касающимися площадей поверхностей и объемов. Эти формулы будут рассмотрены ниже.)
5. Найти наибольшую площадь прямоугольника, вершины которого находятся * начале декартовой системы координат, на оси х, на оси у и на параболе у == 4—х*
Решение. Пусть вершина, лежащая на параболе, находится в точке Л, 4 — х2). Тогда площадь прямоугольника равна S = (4 — х2)х = 4х — х3. Рас* :мотрим интервал [0, 21. Поскольку ~ = 4—Зх2, = —6х, максимум дости-их ах
2 16-
'ается при х = _, и требуемая наибольшая площадь равна 772-.. ф г 6 у 3
210
4. Производные
Рис. 4.31
УПРАЖНЕНИЯ
23.
24.
25.
26.
27.
а) Найдите максимум и минимум функции j(x) (ж2 + 5)Дх + 2) при O^x^lO. б) Найдите максимум и минимум функции Ц(х) « (аг2 + 5)/(х + 2) при 0, если оии
существуют.
Найдите максимум и минимум функции £(аг) х х^ при —1 хL Где / достигает
максимума и минимума?
Найдите максимум и минимум функции <р(у) » (2 + у —* у*)К% ** В + У1) при
—4 У 'С 4.
Найдите максимум я минимумлфункции »-► 1 — s3.
Найдите все точки где функции gW = и
21/Т+7
Л достигает максимума
или минимума.
28. Пусть ffy) = Зу4 — 4^ — 12уа + 12. Найдите интервалы возрастания и убывания f. Найдите все точки локального максимума и минимума j (если такие точки существуют). Найдите все точки абсолютного максимума и минимума I (если они существуют)
29. Пусть h(z) = z3/^ + 27). Найдите интервалы возрастания и убывания Л. Найдите все точки локального максимума и минимума h (если такие точки существуют). Найдите веж точки абсолютного максимума и минимума h (если они существуют).
30. Покажите, что функция х н* 3 + Заг — лг® положительна при 2.
31. Пусть хну — неотрицательные числа и аг2 + у2 в lj каково при этом наименьшее значение 2г3 + г/®? Каково при тех же условиях наименьшее значение kx* + у3, где k — положительная постоянная?
Д 32. Каковы должны быть размеры закрытой коробки с квадратным основанием, если объем ее должен быть равен V и требуется израсходовать наименьшее количество материала?
33. Каковы должны быть размеры открытой коробки с квадратным основанием, если объем ее должен быть равен V и требуется израсходовать наименьшее количество материала?
34. Художник решил нарисовать картину, изображающую красный прямоугольник, окру* женный белой каймой. Требуется, чтобы площадь красного прямоугольника была равна 12 дм2, а ширина каймы — 1 дм по сторонам и 2 дм сверху и снизу. Каковы должны быть размеры картины, чтобы общая площадь ее была наименьшей?
35. Стадион представляет собой прямоугольное поле е областями в виде полукруга, присоединенными к двум его противоположным стбронам. Периметр стадиона должен быть равен 330 м; найдите наибольшую возможную его площадь.
36. Открытую коробку изготовляют из прямоугольного куска жести 5 дм х 9 дм, для чего вырезают равные квадраты по углам и сгибают жесть вдоль линий выреза. Какие квадраты следует вырезать, чтобы получить коробку наибольшего объема?
§ 4. Знаки производных. Максимумы и минимумы
211
37.
Некоторая страна проектирует новый флаг, представляющий собой оранжевый прямо-о угольник, разделенный розовой полосой. Периметр всего флага должен быть равен 4—м,
О
38.
39.
40.
41.
оранжевая часть должна иметь площадь 1 ма. Один проект предлагает горизонтальную полосу, другой — вертикальную; какой следует избрать, чтобы полоса была возможно более широкой? (По обычаю, более длинная сторона флага — горизонтальная.) Каков прямоугольник наибольшей площади, вписанный в полукруг радиуса 1 таким образом, чтобы две его вершины лежали на диаметре полукруга?
Человек, гуляющий в лесу, находится в 5 км от прямолинейной дороги (предполагаемой бесконечно длинной) и в 13 км от дома, стоящего у дороги. Человек может пройти 3 км в час по лесу и 5 км в час по дороге. Он направляется по прямой линии к дороге, а затем по дороге к дому. Каково кратчайшее время, в течение которого он может достигнуть дома?
а) Фермер хочет расчистить поле в виде прямоугольного участка с присоединенным, к одной из его сторон полукруглым участком. Прямоугольный участок будет отведен под сено, дающее доход в 5 центов на м2, а полукруглый будет засеян рисом, дающим доход в 6 центов на м2. Периметр поля должен быть равен 800 м. Как должен фермер спланировать поле, чтобы получить наибольший доход?
б) Предположим, что цена риса возросла, так что участок, засеянный рисом, дает доход в 10 центов на м2. Какова будет теперь форма поля?
Проволока должна быть разрезана на две части. Одна часть будет изогнута в квадрат, а другая — в круг. Общая площадь обеих полученных фигур должна быть равна 16 дм2. Какова кратчайшая возможная длина проволоки? Какова наибольшая возможная длина?
42. У фермера имеется стадо в 100 коров, каждая массой в 200 кг. Содержание одной коровы обходится в 60 центов в день. Корова прибавляет 2,4 кг в день. Рыночная цена коров составляет теперь 2,5 доллара (250 центов) за фунт и падает на 1 цент в день. Как долго должен фермер откладывать продажу, чтобы получить наибольший доход? Сколько он выиграет по сравнению с немедленной продажей?
Примечание. Предполагается, что коровы прибавляют все равномерно в течение каждого дня. что стоимость содержания коровы равномерно распределена в течение дня и т. п.
43. Из точки Р с координатами (3, 0) проведена прямая, пересекающая в точке Q кривую, заданную уравнением у = х\ О^х^З. Каково должно быть направление прямой, чтобы площадь треугольника, ограниченного этой прямой, осью х (горизонтальной прямой, проходящей через Р) и вертикальной прямой, проходящей через Q, была наибольшей?
А44. Каково кратчайшее расстояние от точки (1, 0) до кривой, заданной уравнением у = = Кх2+ бх+ю?
45. Найдите кратчайшее и длиннейшее расстояние от точки (—2, 1) до кривой, заданной уравнением у = 1 + J<18 — 2х2.
46. Найдите трапецию наибольшей площади, вписанную в полукруг радиуса г и имеющую нижним основанием диаметр полукруга.
47. Освещенность, получаемая от точечного источника, прямо пропорциональна интенсивности источника и обратно пропорциональна квадрату расстояния от источника. Освещенность от нескольких источников равна сумме освещенностей от каждого из них. Пусть имеются два маяка на расстоянии в 12 км друг от друга, причем инФенсивность первого в 8 раз превосходит интенсивность второго. Какая точка отрезка, соединяющего маяки, наименее освещена? Обобщите результат на случай, когда первый маяк в Л3 раз сильнее второго.
48. Человек, страдающий сенной лихорадкой*, обнаружил, что достигающее его. количество пыльцы от данного источника (например, от леса, в котором растут нежелательные для больного деревья) прямо пропорционально интенсивности источника пыльцы (скажем, количеству этих деревьев) и обратно пропорционально расстоянию от источника. К сожалению, он вынужден жить где-нибудь на отрезке, соединяющем два источника пыль-
* Заболевание аллергического характера, вызываемое пыльцой определенного вида растений.
212
4. Производные
хорда y^^(x)
। касательная у- И
Рис. 4.32
Рис. 4.33
цы, отстоящие друг от друга на 1 км. Один источник в 4 раза сильнее другого. Где должен поселиться человек, чтобы испытывать наименьшее неудобство? Обобщите результат на случай, когда один источник в k2 раз сильнее другого.
49. Коксовая печь, работающая при 500 °C, производит 1 ОО^м3 газа в минуту. Это количество увеличивается на 1/5 м3/мин при увеличении температуры на 1 °C вплоть до 750 °C. Свыше 750 °C повышение температуры на 1 °C вызывает увеличение производительности
х на 1/4 м3/мин. Эксплуатация печи в течение часа при температуре Т 6С (Т^> 500) обходится в 1000+ (Т/10 — 100)2 центов. Какова наиболее выгодная температура эксплуатации печи, если 1 - м3 газа стоит 1 цент?
50. До введения усовершенствований в методах получения газа при высоких температурах количество газа, производимое описанной в упр. 49 печью, возрастало лишь на 1/10 м3/мин при повышении температуры на 1 °C свыше 750 °C. Какова была тогда наиболее выгодная температура эксплуатации при тех же прочих условиях?
51. Ребенок ростом в 1 м стоит в 8 м от лампы. Каково кратчайшее возможное расстояние от лампы до конца тени ребенка?
52. Коридор шириной в 1 м пересекает холл под прямым углом. По полу коридора тянут прямолинейный кусок водопроводной трубы длиной в 8 м (шириной трубы мы пренебрегаем). Какова должна быть ширина холла, чтобы в нем можно было развернуть трубу и вытянуть ее из коридора?
4.9 . ВЫПУКЛОСТЬ
До сих пор нас интересовал главным образом знак первой производной функции; однако и знак ее второй производной имеет простой геометрический смысл. Если в некотором интервале /" > 0, то fr возрастает. Это значит, что при движении вдоль кривой слева направо наклон касательной к графику возрастает: касательная поворачивается в направлении, обратном направлению вращения часовой стрелки (рис. 4.32).
График при этом «изгибается вверх», «выпячиваясь вниз». Такая функция называется выпуклой, а график ее — выпуклым вниз, или вогнутым вверх. Как видно из рис. 4.33, выпуклый график расположен «ниже своих хорд и выше своих касательных». Аналогично, если f" < 0, то /' убывает, касательная вращается по часовой стрелке, и график лежит «выше своих хорд, но ниже своих касательных» (рис. 4.34). Такая функция называется вогнутой, а график ее —вогнутым вниз, или выпуклым вверх.
§ 4. Знаки производных. Максимумы и минимумы *
213
Сформулируем эти наблюдения в виде следующей теоремы:
Теорема 8. Пусть f(x) дважды дифференцируема при а х 6. Пусть х «-► li(x )—линейная функция, для которой /Да) = f(a), li(b) = f(b). (График li есть хорда графика f.) Пусть х0 такая точка, что a<x0<bt и х »-► 12(х) — линейная функция, для которой /2(х0) = Л*о), (хо) =Г(хо)« (График 12 есть касательная к графику f.) В этих условиях
если при а<х<Ь ‘ то при a<Zx<Zb и при a<ix<Zb, х^х0
Г >0 f<k
/"<0 f>li t<Zh
Аналитическое доказательство будет приведено в Приложении (см. § 8.2).
Примечание. Пусть f дважды дифференцируема вблизих0. Еслиf"(x^ == = 0 и /" меняет знак в точке х0, то говорят, что (х0, Л*о)) есть точка перегиба графика (рис. 4.35). В такой точке меняется направление выпуклости.
4.1 0. ПОСТРОЕНИЕ ГРАФИКОВ
Информация, содержащаяся в этом параграфе, приводит к процедуре, позволяющей вполне точно изобразить ход графика функции /(х), вычислив ее значения лишь в сравнительно небольшом числе точек. Процедура эта, применимая ко многим функциям, заданным формулами, состоит из следующих шагов.
1°. Решают, является ли функция четной, нечетной или ни той, ни другой. Если функция четна или нечетна, достаточно рассмотреть ее значения лишь при х >• 0.
2°. Находят интервалы, где функция определена. Находят (одновременно) пределы функции при х->+°°,х->-------оо ив концах интервалов ее определения.
Если f имеет конечный предел с при х—> + о° или %—э оо, проводят прямую
214
4. Производные
у = с, полезную при построении графика; такая прямая называется горизонтальной асимптотой. Если f становится бесконечной при х = а, т. е. если f имеет бесконечные односторонние пределы при х = а, проводят прямую х = а как вспомогательное средство для построения графика; такая прямая называется вертикальной асимптотой.
[Мы пользуемся здесь понятиями односторонних и бесконечных пределов, неформально введенными в гл. 3, § 4.3. Точные определения и методы вычисления этих пределов содержатся в Приложении к гл. 3 (см. § 5). Для удобства читателей, опустивших это Приложение, мы сопровождаем следующие ниже примеры весьма подробными пояснениями.]
3°. Находят, если возможно, корни f (соответствующие точки отмечаются на графике).
4°. Вычисляют производную f' и находят, если возможно, ее корни. Находят интервалы убывания й возрастания /; для каждого корня а производной /' устанавливают, является ли а локальным максимумом, минимумом или ни тем, ни другим, и вычисляют /(а). Строят точки (а, /(а)) и проходящие через них горизонтальные касательные. (Отмечают также точки, где /' становится бесконечной или где существуют лишь односторонние касательные.)
5°. Вычисляют/"; находят, если возможно, корни /", а затем интервалы выпуклости и вогнутости /. Устанавливают, какие из корней' |3 второй производной являются точками перегиба; для каждого такого (3 вычисляют /(|3) и /'(|3). Строят точки (Р, /(р)) и проходящие через них касательные с наклоном /'(Р)-
6°. Пользуясь результатами шагов Г—5°, строят график функции. Для большей точности можно вычислить координаты добавочных точек графика и наклоны в этих точках*.
• Примеры. В нижеследующих примерах мы пишем /( + °°), /(— °°) в качестве сокращенных записей, обозначающих односторонние пределы lim/(х), lim/(х)
X » + <О X -» — 00 И Т. Д.
1. /(х) = —(х3/6) — (х/6) + 2. Функция fix') есть многочлен; она определена везде. При х #= О имеем /(х) = —(х3/6) [1 + (1/х?) — (12/х3)]. Если | х | достаточно велико, то член 1 + 1/х2—12/х3 близок к 1; следовательно, /(х) < О при х>0 и /(х) > 0 при х < 0. При достаточно больших | х | абсолютная величина Дх) становится сколь угодно большой; это значит, что /(х) -»— оо при х -► + оо и /(х) -> + оо при х — оо. Мы запишем это так: /(— оо) = + оо и Д4- оо) =? — оо. Далее, f'(x) = —(х2/2) — 1/6<0, т. е. f убывает. Отметим, что Д0)=2 и /'(0)= —1/6. Вторая производная f"(x) = —х; тем самым f выпукла при х< 0 и вогнута при х > 0. Имеется точка перегиба при х = 0. Ясно, что существует корень f между О и + оо. Вычисляем /(1) = 5/3, /'(1) = —2/3, /(2) = 1/3, /'(2) = —13/6, /(3) = = —3, /'(3) = —28/9. Таким образом, f имеет корень между 2 и 3.
График Дх) изображен на рис. 4.36.
2. Дх) = (х — 1)/(х — 2). Имеем /'(х) = — 1/(х — 2)2 и f(x) < 0 при всех х Ф 2; /"(х) = 2/(х — 2)3, и /"(х) < 0 при х < 2; /"(х) > 0 при х > 2. Функция определена при х =/= 2, убывает и вогнута при х < 2, убывает и выпукла при х > 2. Вычислим односторонние пределы в точках 2“, 2* и при +оо, —оо.
* В частности, полезно найти точку (О, ДО)) пересечения графика с осью ординат.
§ 4. Знаки производных. Максимумы и минимумы
21$
Рис. 4.36
Если х близок к 2, то х — 1 близко к 1, а х — 2 близко к 0, так что f(x) становится сколь угодно большой по абсолютной величине, когда х достаточно близко к 2. Далее, Дх) > 0 при х > 2 и f(x) < 0 при х < 2 и х, близком к 2.
Таким образом, Дх) -►+ оо при х -*-2+ (т. е. когда х приближается к 2 справа) и Дх) -»— оо при х —*• 2” (т. е. когда х приближается к 2 слева). Мы запишем это так: Д2") = — оо, Д2+) = + оо. Имеется вертикальная асимптота х — 2. (На рис. 4.37 и на других рисунках асимптоты проведены пунктиром.)
При х =£ 0 имеем
/(*) =
1 - (2/Х) ‘
Если х достаточно велико по абсолютной величине, то числитель и знаменатель этой дроби становятся сколь угодно близки к 1. Поэтому Дх) 1 при х -*-+ оо и при х ->— оо, или f(— оо) = Д + оо) = 1. Таким образом, график функции Дх) имеет горизонтальную асимптоту у=\. Далее, Д0)=1/2, /'(0) = —1/4, Д1) = = 0, /'(1) = —1, ДЗ) = 2, /'(3) = —1. График построен на рис. 4.37.
3. Дх) = х2/(1—хг). Эта функция четна; она определена при | х | =#= 1. При х 0 имеем
f (х) —------!— ,
' 1—(1/х2)
откуда видно, что Дх) становится сколь угодно близкой к —1 при достаточно больших значениях | х |. Итак, / ( Ч- оо) = —1, и мы получаем горизонтальную асимп- тоту у = —1.
Заметим далее, что
/ (х) = —----------—
' 1-4-х 1—X
216
4. Производные
Для х, близких к 1, первая дробь близка к 1/2. Вторая дробь велика по абсолютной величине и положительна или отрицательна в зависимости от того, будет ли х < 1 или х > 1. Следовательно, Д1~) = + оо и /(1+) = — оо. Прямая х « 1 является вертикальной асимптотой.
Далее,
§ 4. Знаки производных. Максимумы и минимумы
217
Г/Н - 2х f" /Н - 2(1 +2х2-3х4) Г 2(1 4-Зх2)]
>() (1—х2)2’ (1—х2)4. [ (1—х2)2 J ’
Имеем /(0) = /'(0) = 0 и /”(0) — 2; таким образом, х = 0 — точка локального минимума. График изображен на рис. 4.38; поскольку функция четна, он симметричен относительно оси у.
4. f(x)=y'r(x — 1)/(х — 2) = (х — 1)1/3(х — 2)~ 1/3. Эта функция определена при |х|=^=2. Как и в примере 2 или прямо пользуясь результатами примера 2, получаем /(—оо) = / (оо) — 1, /(1) = 0, /(2") =—оо и /(2+) = 4-оо. Имеются две асимптоты: х = 2 и у = 1. Далее,
Г(х) = у (х — 1)-2/3(х — 2)”1/3 — (х — 2)—4/3 (х — 1)*/3 =
= у (X - 1)"2/3 (X - 2)"4,3 [(х - 2) - (х - 1)] =-- ----------------.
з/ (х—1)2(х —2)4
Производная f' обращается в бесконечность при х=1; таким образом, х = 1— вертикальная асимптота. При х#=1, 2 имеем /'(х)<0. Затем находим
f" (х) = у (X - 1)-5/3 (X - 2)"4/3 + у (X - 2)-7/3 (X - 1)~2/3 =
= _1 (х _ J)-'3(х _ 2)"^ Г_1_ (х _ 2) + _1 (х _ 1)1 = (4/3)1 .
L J 3 /(х—1)*(х —2)7
Заметим, что /" > 0 при 1 < х < 4/3 и при х > 2, так что график оказывается выпуклым в этих интервалах. При х< 1 и 4/3 < х< 2 имеем /" < 0, и график является вогнутым. Имеется точка перегиба при х = 4/3.
Вычисляем /(4/3) = —0,15...,/'(4/3) = —0,22 ... . График построен на рис. 4.39.®
УПРАЖНЕНИЯ
Постройте графики функций, заданных в упражнениях 53—82. Должны быть найдены все точки разрыва кривой; интервалы возрастания и убывания; точки с горизонтальной касательной, с вертикальной касательной, с острием или изломом (более сложное поведение возможно, но в этих примерах вряд ли встретится); все локальные и абсолютные максимумы и минимумы; интервалы выпуклости и вогнутости; все точки перегиба и т. д. При построении этих графиков иногда может оказаться полезным выбрать разные единицы длины для двух координатных осей.
53. f(x) = Xs—Зх2 —24x4-20.
54. Нх) = х3 — 12x4- 11.
55. g (х) = х4 — 18х2 4- 17.
56. k (х) = Зх4 4- 8х3 — бх2 — 24х — 13.
57. F (х) = х4 — 4хэ 4- Ю.
А 58. /(х) = |х|/(х-|-1).
59. хь* (хБ/5) — (7/2) х4 4- 15х».
60. i/ = (x2 —7x4- 10)/(х — 1).
61. у = (х- 1) (х-J-1)2.
62. /(/) = (/4-1)2/(/2 4-1).
63. / (х) = х/(х2 — 1).
64. h (s) = (2 — s 4- s2)/(2 4- s — s2)
65. /ь* t Y~4- 5/ 4- 3 Y~.
66. />->- tV~ 4-4/—ЗуТ-.
218
4. Производные
67. f(u) = u/-fu+ 1 .
687 g (x) — xHx— I)2.
69. у = /и2 4- 2u 4- 2 .
70. f (x) = К (4 — x) (4 + x) .
71. g(z) = zVT+3"
72. h (x) = x2 /x 4- 5 .
73. g (x) = х/Уx2 4- 1 .
A 74. y = (8/x9) — (6/x).
75. y = x4 (IM).
76. g (x) = (x2 4- 3)/)<x2 4- 1.
.77. x^2x'/3-x2/b.
78. A (x) = Зх5/3 — 5x.
79. y=(x-l)2/34-(x4-l)2/3.
80. y=(x- l)‘/34-U+ D1/3.
81. F(z) = (z — l)2 г‘/3.
82. g (x) = (x« 4- x 4- l)l/3.
§ 5. ПЕРВООБРАЗНЫЕ ФУНКЦИИ
5.1. ОПРЕДЕЛЕНИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
Пусть Дх) и F(x) — две функции. Если F'(x) = Дх) в некотором интервале значений х, то F называется первообразной*, или примитивной функцией для функции f (или функции /). Например, функция F(x) = 1/х есть первообразная функции Дх) = — —1/(х2), так как
d / _1_\ 1_ dx \ х ) х2
При этом заданием функции /(х) ее первообразная функция не определена однозначно: так, наряду с F(x) функция F^x) = (1/х) + 73 также является первообразной той же функции —(1/х2).
Вообще, если F(x) — первообразная f(x), а С—любая постоянная, то F(x) Н- С также является первообразной /(х). Это очевидно и геометрически: график функции у = F(x) +С получается из графика F(x) переносом на С в направлении оси у вверх, если С > 0, и вниз, если С< 0. Но этот перенос не меняет наклона касательных (рис. 4.40).
5.2. ЕДИНСТВЕННОСТЬ
Если мы знаем одну первообразную F(x) функции /(х), то мы знаем и множество других, а именно все функции вида F(x) + С, где С — постоянная. Оказывается, что этим исчерпываются все первообразные. Чтобы доказать это, мы воспользуемся следующей теоремой.
* Эта терминология является совершенно естественной: функция f(x) = F'(x) называется производной для F(x) [т. е. «произведенной» или порожденной функцией F(x), полученной из F(x) q помощью процесса дифференцирования]; напротив, F(x) называется первообразной (т. е. исходной) для /(*)—это есть та функция, из которой получается функция /(х).
§ 5. Первообразные функции
219
Теорема 1. Если g'(x) = 0 при всех х из некоторого интервала, то функция g(x) постоянна в этом интервале.
Теорема утверждает, что линия, касательная к которой в каждой точке горизонтальна, есть горизонтальная прямая. Геометрическая интуиция подсказывает нам, что это так и есть. Утверждение теоремы становится также очевидным, если истолковать нашу функцию как описывающую движение точки: поскольку скорость всюду равна нулю, точка не движется. Конечно, доказательство все же необходимо. Оно легко получается из теоремы 3 § 4.3/ *
Пусть х2 > *1 — две точки нашего интервала. Так как g' >. О, g не убывает, а потому g(Xi) ^.g(x2). Но, с.другой стороны, g' 0, поэтому g и не возрастает, т. е. g(x^ >• g(x2). Таким образом, g(xi) = g(x2), и функция g принимает во в с е х точках одно и то же значение.
Теорема 2. Если F(x) и Fi(x) — первообразные одной и той же функции, то FM — F(x) есть постоянная функция; иначе говоря, существует такое число С, что FДх) = F(x) + С.
Доказательство. Пусть F(x) и Г^х) — первообразные функции /(х); положим g(x) = Fi(x) — F(x). Тогда g'(x) = F’}(x) — F'(x) = /(x) — /(x) = 0 и, по теореме .1, g(x) = С, что и требовалось доказать.
5.3. ПРОСТОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В качестве приложения найдем все функции <р(х), вторая производная которых тождественно равна нулю (т. е. равна нулю при всех х); иными словами, решим дифференциальное уравнение
<р"(х)=0. ' (1)
Это уравнение означает, что
220
4. Производные
но тогда, по теореме 1, существует такое число а, что
<р' (х) = а.
Итак, ф является первообразной постоянной функции а. Одной из таких первообразных является ах; все другие имеют вид ах4- (3, где р—любое число. Итак, функция ф линейна. Обратно, вторая производная каждой линейной функции тождественно равна нулю.
5.4. РАЗЫСКАНИЕ ПЕРВООБРАЗНЫХ
Естественно, возникает вопрос о том, любая ли непрерывная функция имеет первообразную. Как мы увидим в следующей главе, ответ на этот вопрос положителен.
Пока же мы можем лишь угадать некоторые первообразные функции. Каждое правило дифференцирования есть в то же время правило разыскания первообразной. Некоторые результаты в этом направлении, содержащиеся в нижеследующей таблице, вытекают из правил дифференцирования § 2.
каждая первообразная функции имеет вид (С — произвольная постоянная)
(а) cf' (х), с— постоянная Cf (X) + С
(б) Г (*) + §' (X) f(x) + g(x) + C
(В) Г (х) g (X) + f (X) g' (X) f (х) g (х) + С
(г) _ Г (X) f(x)2 /(х) 4 С
(д) xa , а рационально, a=f=—1 уа-Н + с « +1
ф Примеры. 1. Первообразная функции 2х3+х+1 есть функция-^-х2 + х + С [в силу (а) и (б)}. Этот результат^ как и любой результат о первообразных функциях, может быть проверен дифференцированием.
2. Вообще, первообразная функция многочлена степени п aQ + а±х + а2х2 Ч---------------------------h апхп
есть многочлен
с+ аох + 4*2 + • • • + -^-хя+1
7 о п -f- 1
степени п + 1.
§ 5. Первообразные функции
221
3. Найти первообразную функции f(x) =
хг
(x’ + l)2
Решение. Заметим, что (xa + 1)' = Зх2. Поэтому
— Зх2
(Xs + I)2
и в силу (а)
1 1
3 «зц-!
+ С
X
есть первообразная функции /.
4. Первообразная функции —==г есть j/1 4- х24- С. г 1 4~ t
5. Найти все решения дифференциального уравнения f' '(х) = 0.
Реш ен и е.Так как ///х = (/")' = 0 везде, /"(х) есть постоянная; обозначим ее через а. Тогда (/')' = a; f'{x) есть первообразная функции а. Отсюда заключаем, что /'(х)= ах 4- (3, где 0 — другая постоянная. Значит, / есть первообразная функции ах 4- 0. Одной из таких первообразных является функция -у-ах2 4- 0х. Следовательно, /(х) = -i-ax2 + (Зх + *[, где а, 0, т — произвольные постоянные; иными словами, /(х) — квадратичный многочлен.
6. Найти такую функцию ff что f'(x) = ]/л7 и /(1) = 2.
Решение. Поскольку /'(х)=х1/2, в силу (д) имеем /(х) = — х/2-}-С, Из 3
условия f(l)=2 имеем С — —.
3
Таким образом, /(х) = — (х Vx~ + 2). ф
3
УПРАЖНЕНИЯ
1. Найдите Ёсе функции ф, для которых ф'(х) = 1/2.
2. Найдите все функции ф, для которых ф'(х) = х2.
3. Найдите все функции ф, для которых ф"(х) = —1.
4. Найдите все первообразные функции хь>(%4- I)9.
5. Найдите все первообразные функции s s4 4- 4ss + 4s — 2.
6. Найдите все первообразные функции f (и) = и^3 4~ Зи1/2.
7. Найдите все первообразные функции f (г) = г/У г2 + 1 .
8. Найдите все первообразные функции G (х) = (]/"х 4- 1)5/2 У"х .
9. Найдите все первообразные функции гн- (z3 + z2 — 2z 4- З)10 • (3z2 + 2z — 2).
10. Найдите все функции f, для которых f"(s)= 12s2 4-$—1.
11. Найдите все решения дифференциального уравнения f" (х) = Ух .
12. Найдите функцию g, для которой g' (s) = s3 4- (1/«2) и g (1) = 1.
13. Найдите функцию Л, для которой п' (t) = t (tfa4 I)9 и Л (0) = 1/10.
Д14. Найдите функцию 4, для которой Д" (v) = 3v2, А' (0) — 1 и 4(0) = — 1.
15. Найдите функцию F, для которой F” (s) = 6s 4- 1, F (0) = 2 и F (1) = 0.
222
4. Производные
5.5. ИНЕРЦИЯ
Применим теперь понятие первообразной к (третьему) закону Ньютона. Для частицы с массой т, движущейся по прямой, этот закон имеет вид
та = F,
где F — приложенная сила и а — ускорение. Так как а есть первая производная от скорости v = v(t) и вторая производная от расстояния s = s(f), предыдущую формулу можно также переписать в виде
(2) at
ИЛИ
Чтобы найти движение из этого дифференциального уравнения, мы должны знать силу.
Рассмотрим некоторые простые случаи.
Предположим сначала, что на тело не действует никакая сила. Тогда F == = 0, и (2) принимает вид /п-^- = 0, или 0- Согласно теореме 1, v есть постоянная. Это закон инерции, установленный Галилеем: /пело, на которое не действует никакая сила, находится в состоянии покоя или равномерного движения по прямой.
5.6. ВЕРТИКАЛЬНОЕ ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
Пусть теперь тело движется вертикально под действием силы тяжести. Тогда, как мы видели в § 3.3, F = весу = —mg, где g — постоянная, одна и та же для всех тел. Уравнение движения имеет вид
cPs dv
т----= — mg, или т — = — mg;
dt2 6 dt 6
после сокращения на т оно принимает вид
d2$ dv
= — g, или — = — g. dt2------------------------* dt &
Мы снова пришли к закону Галилея. Но на этот раз мы применим его не к телу, свободно отпущенному в момент t = 0, а к телу, брошенному в момент t = 0 вверх или вниз с высоты s0 со скоростью р0.
Пусть v(t) — скорость в момент t. Тогда v(f) — первообразная постоянной функции — g\ следовательно, = —gt + а, где а — некоторая постоянная. Для того чтобы найти ее, заметим, что р(0) = а. Но мы обозначили начальную скорость нашего тела через о0. Поэтому а = и
f(0 = —gt + р0.
$ 5. Первообразные функции
223
Как мы видим, скорость состоит из двух частей; начальной скорости о®, которая была бы, по закону инерции, постоянной скоростью тела при отсутствии силы, и скорости —gt, возникающей в результате ускорения, вызываемого силой тяжести. (Можно сказать, что тело одновременно участвует в двух движениях: равномерном движении со скоростью t»0 по закону инерции и падении со скоростью — gt по закону Галилея.)
Какова высота тела s(t) в момент времени f? Поскольку s'(О = v(f), функция s(0 есть первообразная функции — gt 4- »0. Она имеет, следовательно, вид — -y-g/24-o®Z 4- 0, где 0—постоянная. Чтобы найти 0, заметим, что s(0)= 0. Поэтому 0 = s0, т. е. высоте (над точкой отсчета) нашего тела в момент t — 0. Отсюда
s(0 =-----j-g*2 4-Ц/4-s0. (3)
График движения есть парабола (или, точнее, часть параболы, соответствующая положительным значениям /)*
Предположим для определенности, что о® > 0 (тело брошено вверх при t = 0) и что з0 = 0 (высота тела над точкой отсчета при t = 0 равна нулю). Пусть, кроме того, точка отсчета взята на уровне Земли. Тогда движение описывается формулой
s(t)±=- -±-gt* + vot.
В какой момент тело ударится о Землю? Для этого надо решить уравнение s(0 = = 0, что дает t = 0 (начальный момент) и
t = ^-. g
Какова наибольшая высота, достигаемая телом? Для этого надо найти абсолютный максимум $(£) в интервале (0, 2o®/g]. По правилам, объясненным в § 4, находим точку, в которой s'(0 = 0. Поскольку s'(t) = —gt 4- v0, производная обращается в. нуль при t = v^g. Для этого значения t имеем s"(0 = —g < 0, а значение $ равно
«о
2g ’
Это и есть, следовательно, наибольшая достигаемая высота. В момент ее достижения скорость, конечно, равна нулю, поскольку тело меняет в этот момент направление движения. Это еще раз поясняет, почему производная (= скорости) обращается в нуль в точке максимума.
Представляет интерес вычислить скорость, с которой тело ударяется о Землю, т. е. значение v(t) = s'(f) = —gt 4- v0 при t = 2vo/g. Подстановка дает — о®. Таким образом, конечная скорость по абсолютной величине равна начальной. Как мы увидим в дальнейшем, это частный случай закона сохранения энергии.
224
4. Производные
УПРАЖНЕНИЯ
16. Частица вылетает из оружия вверх со скоростью 12 м/с. Предположим, что частица начинает движение с уровня Земли; какова наибольшая высота, достигаемая ею? Через какое время частица ударится о Землю?
17. Камень бросают вниз с высоты 160 м с начальной скоростью 2 м/с. Через какое время камень достигает Земли? С какой скоростью?
Д 18. Человек, стоящий на Земле, бросает вверх мяч. Какова должна быть максимальная скорость бросания, если он хочет, чтобы мяч поднялся по крайней мере на 18 м?
19. Камень отпускается на высоте 24 м. Второй камень бросают на секунду позже; какова должна быть его начальная скорость, если требуется, чтобы оба камня достигли Земли одновременно?
20. Камень брошен прямо вверх и ударился о Землю через t с. Как высоко он поднялся?
21. Частица массой в 2 г покоится в момент t = 0. К ней прилагается постоянная сила. Найдите эту силу, если скорость частицы через 4 с равна 8 м/с.
22. Автомобиль движется по 20-километровому испытательному треку, начиная испытание со скоростью 20 км/ч. Если время t измеряется в часах и отсчитывается от начала испытания, ускорение автомобиля выражается формулой а = 4 — 12/ (где t пробегает промежуток времени, в течение которого происходит испытание). Где находится автомобиль при t = 1/2 ?
23. Автомобиль движется по 20-километровому испытательному треку. Когда он достигает конца трека, он движется обратно к начальной точке. Время измеряется в часах от начала испытания. Автомобиль возвращается в начальную точку при t = 2, причем ускорение его выражается формулой а = — 120 (t — I)2. Где находится автомобиль при t = 1/2? Какова скорость автомобиля в начале испытания?
5.7. РЕЛЯТИВИСТСКОЕ ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ПОСТОЯННОЙ СИЛЫ
Рассмотрим теперь частицу е массой покоя т0, движущуюся в соответствии с уравнением Эйнштейна (4) § 3.4 (стр. 195) под действием постоянной силы F > 0 и начинающую движение с состояния покоя (и = 0 при t = 0). Тогда
v
У 1 — (и2/с2) есть первообразная функция постоянной функции F1mQ. Далее, эта первообразная принимает при t = 0 требуемое значение 0. Поэтому у____________________________________________ Ft
у \ _ (V2/C2) mQ
Возводя обе части в квадрат, находим о2 _ Г2/2 1_(Р2/С») “ *
Решая это уравнение относительно о2, получаем о2=с2--------------------------------------,
fflgc2 + F2/2 а так как скорость о = v(f) положительна, то
V (0 = с —— .
V mgc2 + F2/2
§ 5. Первообразные функции
225
В последней формуле знаменатель дроби всегда больше числителя. Следовательно, v(f) < с при всех /, т. е. тело никогда не может достигнуть скорости света. [Но при достаточной продолжительности движения скорость тела может стать сколь угодно близкойк скорости света; иными словами, lim v(t) = с.]
/-►-j-QO
УПРАЖНЕНИЯ
В упражнениях 24 и 25 примените релятивистское уравнение движения. Примите для скорости света значение с = 3 -1010 см/с.
24. Частица с массой покоя 0.02 г покоится в момент t = 0. К ней прилагается постоянная сила в 1010 г*см/са. Какова ее скорость через 10 с?
25. Частица с массой покоя 0,1 г имеет в момент t = 0 скорость с/2. К ней прилагается постоянная сила и через 10 с ее скорость достигает значения Зс/4. Найдите силу.
5.8. ПЛОЩАДЬ ПОД ПАРАБОЛОЙ
В качестве другого применения первообразных функций вычислим площадь области, ограниченной параболой у = х2, осью х и прямой х = t > 0. Обозначим эту площадь через £(/); она показана на рис. 4.41. В Приложении к гл. 2 (см. § 5) мы нашли эту площадь методом Архимеда, показав, что
S(0 = 4^ ‘ (4)
Теперь мы получим тот же результат с помощью производных. (На этой стадии изложения мы будем считать понятие площади интуитивно ясным.)
Вычислим производную где значение tQ закреплено. Пусть h > 0 — малое число. Тогда S(/o 4- А) — S(t0) есть площадь, показанная на рис. 4.42. Она меньше площади h(t0 4- А)2 «более высокого» прямоугольника и больше площади А/а0 «более низкого» прямоугольника. Таким образом,
А(о < S (Го 4- А) - S (/0) < А (/, 4- А)2.
Разделив эти неравенства на А, имеем
Г SVo.+ V-Stfo). < /2 4- 2toh + А2. (5)
Для отрицательного, малого по абсолютной величине h из рис. 4.43 получаем неравенства
f 4- 2/0А 4- А2 < 5 (<о + й)-3 (<0) < /2 . (6)
Из неравенств (5), (6) следует, что
,litn S«q + A)-S(<0) = /2. л-о Л 0’
Таким образом, S'(Q = t*. Так как это верно для любого t0, то S(f) есть первообразная функция для функции t2. Но тогда £(/) = -у/8 4- а, где а — некоторая
4. Производные
Рис. 4.43
постоянная. При t = 0 получаем 5(0) = а, а так как 5(0) = 0, то а = 0; таким образом, мы снова приходим к формуле (4).
Открытие Архимеда было одной из вершин греческой математики. Оно оставалось изолированным достижением в течение двенадцати столетий до тех пор, пока Кавальери с помощью метода, аналогичного методу Архимеда, не показал, что площадь, ограниченная кривой у = хп, осью х и прямой х = t, равна
/л+1
n-h 1
Бонавентура КАВАЛЬЕРИ (1598—1647) был учеником Галилея. Он принадлежал к группе блестящи! математиков, предвосхитивших многие идеи и результаты анализа до его пострения Ньютоном и Лейбницем.
§ 6. Доказательство правил дифференцирования
227
Впрочем, Кавальери сумел доказать это лишь для п = 3, 4, ..., 9. В настоящее время такие задачи, и /[аже гораздо более сложные, легко решаются каждым, владеющим элементами анализа. Ключом к этому вопросу является связь между двумя на первый взгляд совершенно разными задачами — об измерении площадей и о построении касательных.
Эта связь, иллюстрируемая предыдущим примером, будет систематически изучена в следующей главе.
УПРАЖНЕНИЯ
26. Примените метод этого пункта для вычисления площади области, ограниченной прямой у = X, х^ 0. осью х и прямой X = t >0.
27. Примените метод этого пункта для вычисления площади области, ограниченной кривой у = х3. 0, осью х и прямой х = t >0.
28. Примените метод этого пункта для вычисления площади области, ограниченной кривой у = осью х и прямой х = t > 0.
Приложение к главе 4
§ 6. Доказательство правил дифференцирования
В этом параграфе мы дадим полные доказательства правил дифференцирования, изложенных в § 2.
6.1. Производная произведения
Пусть f(x) и g(x) определены вблизи х0 и дифференцируемы в точке х0.
Тогда произведение f,(x)g(x) в точке х0 имеет производную, которая выражается по правилу (fgY = fg + fg' В § 2.2 мы доказали это для случая, когда fug линейны.
в Теперь мы покажем, что рассуждение, проведенное в § 2.2, легко распространяется на общий случай, как там и было сказано.
По теореме о линейном приближении (теорема 1 § 1.8), можно записать:
f (х) = а + а (х — х0) + ft (х) (х — х0), (1)
g (х) = b + ₽ (х — х0) -t- г2 М (х — х0), (2)
где
а = /(х0), <* = Г(х0), b=g(xoh Р = g' (х0) (3)
и Г1 (х), г2(х) — непрерывные функции, для которых
Н М = г2 (х0) = 0. (4)
Отсюда имеем
f (х) g (х) = [а + а (х — х0) + г, (х) (х — х0)] [& 4- ₽ (х — х0) + г2 (х) (х — х0) }
= аЬ + (а& + а₽) (х — х0) 4- г (х) (х — х0), где
г (х) = аг2 (х) + bt\ (х) 4- [а₽ 4- агг W 4- Рп (х) 4- г, (х) г2 (х)] (х —> х0).
228
Приложение к главе 4
Ясно, что г(х) непрерывна в точке х0, причем г(х0) = 0. Но тогда, по теореме о линейном приближении , fg имеет в точке х0 производную а0 + ab = f/g + fg'.
Дадим еще другое доказательство правила дифференцирования произведения, которое основано на правилах вычисления пределов. Пусть
<f(x) = f(x)g(x).
Тогда
? (*0 4-6) — <Р (Хр) _ f(Xo+/t)g(*o + ft)—f(Xo)g(Xo) Л Л
Применим здесь следующий простой и полезный прием: числитель правой части не изменится, если прибавить и вычесть число f (х0) g (х0 + Л). Имеем
,, . .. <р(Хо + А) —<Р(Хр)
<f (хр) = Пт -----------------=
л-о Л
f(Xp + A)g(x0+ft)—/(x0)g(x0 + A)+f (xp)g(x0 + A) —/(x0)g(x0) = lim ------------------------------------------------------------------- =
Л->о h
Г f (Xp + h) — /(x0) , ,4 , ,, . g (Xp 4-Л) — g (x0)l
= llm ----------7-------- g (x0 4- Л) 4- f (x0) ------------ =
h-0 L « n J
-Um Hrngcx. 4-»)+,!„/,...> llm »<». + *>-«<*>>_
Л-.0 n h-*0 h-*0 Л—0 h
= f' g (x0) 4- f (x0) g' (x0).
Мы воспользовались здесь правилами вычисления пределов § 4 гл. 3 и теоремой 2 § 1, согласно которой g(xQ + Л) — непрерывная функция от Л в точке h = 0. Кроме того, мы использовали здесь то обстоятельство, что f(xQ) не зависит от h (постоянная функция от h). Итак, <р' = f/g + fg' в точке х0, что и требовалось доказать.
6.2. Производная от функции, обратной данной в алгебраическом смысле
Мы покажем, что (1/gY = —g'lg2* точке х0, предполагая, что g дифференцируема и не равна нулю в этой точке. [Величины g и —- в арифметике и алгебре называются взамно обрат-1 н ы м и; поэтому функцию можно назвать «обратной» функции g(x) в алгебраическом смысле этого термина.] Представим g(x) в виде (2), где b =# 0 (см. стр. 227); тогда g(x)=£ 0 также и для х, близких к х0; поэтому функция
<? (х) = —j— g(x)
определена вблизи хд. Очевидно, <р(х0) = 1/Ь; мы хотим показать, что <p'(x<>) = —р//>2. Это значит, что если функция г(х) определяется равенством
1 Р
<Р(х)= — — — (х — х0) + г (х) (х — х0), О о*
то после доопределения ее в точке х0 с помощью условия г(х0) = 0 получается непрерывная функция (обращающаяся, конечно, в нуль в этой точке). Подставляя вместо g(x) выражение (2), получаем
г . . = [& — Р (х — х0)] r2 (X) 4- р2 (X — х0)
Z>2 [b 4- р (х — х0) + гг (х) (х — х0)] Отсюда видно, что г(х) обладает требуемыми свойствами.
§ 6. Доказательство правил дифференцирования
229
Приведем еще другое доказательство (читателю рекомендуется обосновать здесь все переходы):
1 __ 1
, , , <р(х04-Л)—<р(х0) „ g (*о + h) g(x<>)
<f (х0) = Um --------------------= lim ------------------------ =
h-0 n h-0 ft
_ g(*o+ ft) — g(x0)
... g (*o) — g (xo + Л) ft
= ujp - = Um =
Л-0 g (x0 4- ft) g (x0) ft <1-0 g (*o + ft) g (x0)
,, g (*0 + ft) — g (*o) — Um----------------------
= h = _ g' (x0) .
lim g (xQ -f- ft) hm g (xQ) g (x0)a
Л-+0 л-+о
УПРАЖНЕНИЯ
1. В § 2.2 мы вывели правила дифференцирования (с/)' = cf и (fi — g)' = К — / из других правил дифференцирования. Дайте их прямое доказательство с помощью теоремы о линейном приближении.
2. Докажите правила (cf)' = cf', (Z — g)' = /i' —g', пользуясь определением производной и правилами вычисления пределов.
3. Докажите правило вычисления производной частного, пользуясь определением прбиз-водной и правилами вычисления пределов.
6. 3. Доказательство цепного правила
Цепное правило (теорема 6 § 2.5) утверждает, что если функция х ьь f(x) дифференцируема в точке х0 и функция и ь* g(u) дифференцируема в точке uQ = f(x0), то композиция функций ф(х) = (g ° Dx = Дифференцируема в точке х9 и
<р'(х0) = g' (/ (х0)) f (Х0).
По предположению и в силу теоремы о линейном приближении (теорема 1 $ 1.8) имеем f (х) = и0 4- а (х — х0) 4-rt (х)(х —х0), g(u) = С + D (и — ио) + г2(и) (и — uQ), где непрерывна в точке х#, гч непрерывна в точке и0 и а (х0) = 0, г2 (и0) = 0.
Далее, f'(x0) = a. g(tt0) = C, g'(u0) = D.
Подставляя выражение функции / в выражение функции g, получаем
<? (х) = g (f (х)) = С + D [f (х) - u0] 4- r2 (f (x)) [/ (x) - «„] = = С 4- D [a (x — x0) 4- ri (x) (x — x0)] 4- r<i (f (x)) [a (x — x0) 4- 'i (x) (x — x0)] =s = C 4- Da (x — x0) 4- r (x) (x —x0), где
г (x) = Drt (x) 4- (f (X)) 4- r2 (f (X)) f! (X).
По теореме о непрерывности композиции функций (теорема 4 § 3 гл. 3), функция х r2(f(x)) непрерывна в точке х0. Поэтому г(х) непрерывна в той же точке в силу теоремы 1 § 3 гл. 3. Кроме того, г(х0) = 0. Следовательно, по теореме 1 § 1, <р'(х0) = Da = gZ(u0)i (х0) = g'(f(x,))f(х0). и цепное правило (правило дифференцирования сложной функции) доказано
230
Приложение к главе 4
6. 4. Производная обратной функции
Теперь мы дадим аналитическое доказательство теоремы 7 § 2.6 о производной обратной-функции (где в отличие от п. 6.2 термин «обратная функция» понимается так, как это принято в анализе, или в учении о функциях*). Эта теорема гласит:
Если у = f(x) и х = g(y) — строго монотонные функции, обратные друг другу, и функция имеет в точке х = х0 производную, причем f' (xQ) =£ Q то g имеет производную в точке у = = Уо = К*о) и g'{ya) = l/f(X0).
Чтобы доказать, это, заметим, что существует функция h определенная вблизи точки
h = 0, для которой
y<> + h = f(x<) + 't(h)).
В самом деле, требуемым свойством обладает функция
<f (А) = g (Уо + Л) — х0 = g (у0 + Л) — g (у0).
Легко видеть, что эта функция непрерывна и что<р(0) = 0, но при А =/= 0 и <р (А) =£ 0. Разностное отношение для функции g в точке yQ можно теперь записать так:
g (Уо + ft) — g (Уо) = g (f (Xq + <р (ft)) —g(f (x0)) = XO + <p (ft) — x0 =
ft f(xo + <f(h))-f(xt) t(Xo + <r(h))-t(x9)
__________1_________
f(Xo+<t (ft)) — f (x„)
<p(ft)
Предел этого выражения при h—>0 обратен (разумеется, —в алгебраическом смысле) пределу [/(х0 + <р (А))—f (х0)]/«р (А) при Л—>0, а этот последний (в силу теоремы 2 § 4.2 гл. 3) равен пределу [f (xQ + А)—f(xo)]/k ПРИ А—>0, т. е. /' (х0), что и требовалось доказать.
§ 7. Односторонние производные. Бесконечные производные.
Дифференцируемые и недифференцируемые функции
В этом параграфе рассматриваются различные видоизменения понятия производной, неформально изложенные в § 2.9. Он может быть опущен при первом чтении. Мы пользуемся здесь обозначениями, введенными в Приложении к гл. 3 (см. § 5 этой главы).
7.1. Односторонние производные
Пусть дана функция [(х). Правой производной функции fj в точке х0 называется предел
Г(<) = Пт
/(x0 + A)-f(x0) Л
если только он существует. Эта производная может существовать и в том случае, если функция f(x) определена лишь в точке х0 и в точках х, близких к х0 и лежащих справа от х0. Аналогично, левая производная в точке х0 определяется как предел
7(Xo + ft)-f(X0) — -— ---------,
А
если этот предел существует.
* В английском языке функция g(x), такая что f-g=l, называется reciprocal function; функция g(x)t такая что f°g — x, называется inverse function.
§ 7. Односторонние производные. Бесконечные производные
231
Рис. 4.44
•Примеры. 1. Пусть f(x) = х3/2 тогда ИО*) = 0. В самом деле, при h >0 имеем
Н0 + ^)-/(0) /i3/2-o .1/2
= = п , h-------------------h
а А1/2 непрерывна справа в точке 0 и обращается в 0 в этой точке. [Конечно, в этом случае функция не имеет левой производной, поскольку функция f(x) = Ух^ определена лишь при х^ 0.J
2. Пусть £(х) = 2х при 0, f(x) = х2 при х^> 0. Тогда f'(0“) = 2 (так как функция 2х имеет в точке х = 0 производную 2) и Г (О*) = 0 (так как функция х2 имеет в точке х = 0 производную 0). ф
Пусть f — такая функция, что f (х0) = a, {'(Xq) = 0. Если при этом а = р. то / дифференцируема в точке х0, и, как легко видеть, /'(х0) = а. Если а р, то f не дифференцируема в точке х0. Мы говорим в этом случае, что график / имеет излом в точке (х0. f(x0)). Типичный случай изображен на рис. 4.44.
Теорема 1. Если функция имеет в точке х0 правую (левую) производную, то она непрерывна в замкнутом интервале, имеющем эту точку своим левым (правым) концом. Точнее, такая функция есть сумма постоянной, линейной функции и функции (х — х0)г(х) где г(х) имеет в точке xQ правый (левый) предел, равный нулю.
Правила вычисления производных суммы, разности, произведения и частного (теорема 1 § 2), цепное правило дифференцирования сложной функции (теорема 6 § 2) и правило вычисления производной обратной функции (теорема 7 § 2) сохраняют силу и для односторонних производных.
Первое утверждение доказывается почти в точности так же, как соответствующие результаты § 1 (теоремы 1, 2). Остальные утверждения доказываются так же, как соответствующие результаты § 2.
УПРАЖНЕНИЯ
1. Пусть g (s) = s8 при s < 1 и s2 при 1; найдите g' (1") и g' (2+).
2. Пусть f (х) = (1 — х)3/2; найдите /' (1’).
5/2
3. Пусть h (t) = (t2— 4) . Установите, какие из односторонних производных h' (—2’), h’ (—2+), h' (2”), h' (2+) существуют, и вычислите их в случае существования.
А4. Пусть f (у) = ц + 1 при у < 3 и у2 — 2у 4- 1 при у > 3; найдите Г (3") и /' (3+).
5/2
5. Пусть f (х) = х при х < 0 и х при х > 0; найдите f' (О’) и f' (0+).
6. Пусть (и) = (и — 1)2/3 при и < 0 и (и 4- 1)2/3 при а>0; найдите ср' (О’) и у' (0+).
7. Пусть h (s) = s2— 1 при s < 1 и s при s> 1; найдите h' (1’) и h' (1+).
232
Приложение к главе 4
8. Постройте график функции / (х), непрерывной при | к | < 1, удовлетворяющей условиям /(0) = О, Г (0-) = 0 и f'(0+) = 1.
9. Постройте график функции g(x), непрерывной при—3/2<х<5/4, удовлетворяющей условиям g (— 1) = 0, g' (0“) = — 1, g' (0+) = 2 и g (1) = 1.
10. Постройте график функции h(t)t определенной и непрерывной при |/| < 1, удовлетворяющей условиям ft' (— 1+) = А (0)=0, А' (0) = 0, Л' = — 1, Л' - ) = 1 и
Л'(Г) = -
7.2 . Бесконечные производные
Непрерывная функция Цх) может не иметь производной в некоторой точке х0; например, возможен случай, когда разностное отношение в точке х0 можно сделать больше любого заданного числа, если взять А достаточно малым. Это значит, что
.. f (Хо + ft) — f (х9)
н m -----------------= 4-оо.
' h-o А
В этом случае мы пишем f' (х0) = 4- оо. Если же
.. f (*0 + Й) — / (*о) .
1 im -----------------= 4- оо,
Л
то говорят, что Г( х0) = 4- °0. Теперь ясно, в каком смысле понимаются записи вида f' (х0) = = — оо, /'( xj) = — оо, ['[ х0) =4-оо и f'[ х0) = — оо. Во всех этих случаях f не дифференцируема в точке х0. Если f' = 4- оо или f' = — оо в точке х0, то говорят, что график f имеет вертикальную касательную (рис. 4.45). Если в точке х0 одна из односторонних производных равна 4- оо, а другая — оо, то график f имеет острие (или точку возврата) с вертикальной касательной (рис. 4.46).
1/3
фПримеры. 1. Пусть [ (х) = х (рис. 4.47). Тогда f' (0) = 4- °°, так как
f(h)-f(O) Л1/3 ,-2/3 1
h - н ~h -уаг’
а эта функция неотрицательна при Л=£0 и limy^ft2 =0.
2. Пусть f (х) = | х1/31. Тогда подобным образом находим Г (0+) = 4- оо, f' (0") = — оо (острие; рис. 4.48).
3. Касательная к окружности х24-«/2 = L в каждой из точек (1, 0), (—*1, 0) вертикальна; поэтому можно ожидать, что для / (х) = 1 — х2 будет f' (— 1+) = 4- оо, /' (1“) = — оо. Это
действительно так, поскольку (при Л>0)
/ <— 1 4- ft) — f(— 1) V 1 - 1 4- ft)2 = /2А - А2 = /А (2 - А) =
А Л Л А
——— ->4-оо при Л —► 0+ /А
И (при ft <Z 0)
§ у. Односторонние производные. Бесконечные производные
233
/(1 + ft) —Hl) _ К1 - (1 -ьй)2 _ /— 2й — Й-' _ /-й(2 -г й) _
Л h. h ' h
j/Г+й" /2 + й- , _____
= ----------------= — ------- —> — оо при /г —>- О .А
— (— h)
7.3. Пределы производных
При вычислении производных (в том числе односторонних и бесконечных) может быть полезен следующий результат.
Теорема 2. Предположим, что функция [(х) имеет производную ['(х) при всех х, близких к точке xQi ва исключением, может быть, самой точки х0. Пусть существует конечный предел
lim f (х)
Х->Х0 и конечный или бесконечный предел а = lim f' (х). х—х0
Тогда существует
/' (х0) = а.
234
Приложение к главе 4
Соответствующее предложение об односторонних пределах и односторонних производных также справедливо.
Доказательство будет изложено в следующем параграфе (см. § 8.3).
• Пример. Рассмотрим функцию Ддг) = х1/3. При х =/= 0 она имеет конечную производную Дх”2/3. Следовательно,
lim/' (х) = 4- оо.
х-*о
Существует, далее, конечный предел lim (х1^3), равный 0. Таким образом, Р(0) = +оо« •
УПРАЖНЕНИЯ
В упражнениях 11—17 опишите поведение производной каждой функции возможно более полным образом, т. е. сначала установите, где производная существует, а затем вычислите ее во всех таких точках; далее, установите, где производная бесконечна, и вычислите ее значения +оо или —оо в этих точках; наконец, найдите все точки, где существуют лишь односторонние производные или где односторонние производные бесконечны, и вычислите значения односторонних производных.
И. /(х) = х2/3. 13. SH. (s— 1)3/7.
12. /(/) = —4 . 14. k (х) = х|/3 + ?/3.
2/3
15. g (и) = (8и — 1) при и < 1/8; (8и — I)2 при и > 1/8.
16- <Р (у) = (.У + 1)3/5 при у < 0; -у- (у — 1)2/5 — -у при у > 0.
17. Д (0 = У /|/3 + 1 .
18. Постройте график функции /(х), определенной и непрерывной при —1 <х< 2, удовлетворяющей условиям f (— 1) = 1, f' (— 1+) = — оо, f (1) = 2, /' (1“) = — 1, f (1+) = = 4-00.
19. Постройте график функции g(t), определенной и непрерывной при —3 < t < 9/8, удовлетворяющей условиям g' (— 2") = — — , g' (— 2+) = 1, g (0) = 0, g' (1) = 4- 00 •
20. Постройте график функции А (и), определенной и непрерывной при |н| < 1, удовлетворяющей условиям g' (— 1+) = 4- оо, g' /— —] = — оо, g' (0") = — 1, g' (0+ )=4~ 1 •
§ 8. Доказательства некоторых теорем о производных
В этом параграфе содержатся доказательства ряда сформулированных, но не доказанных выше теорем.
8.1. Функции с положительной производной
Сначала докажем основную теорему 2 § 4.2: функция, производная которой в некотором интервале положительна, возрастает в этом интервале', функция с отрицательной производной, напротив, является убывающей. Мы докажем только первое утверждение (первый ряд таблицы), предоставив читателю доказательство второго.
§ 8. Доказательства некоторых теорем о производных
235
Доказательство опирается на теорему 1 § 4.1 [если fi'(xQ) >0, то Дх0)< f[x) для х вблизи х0 и справа от х0 и f(x) < Дх0) для х вблизи х0 и слева от х0] и на принцип верхней грани.
Дано, что /(х) непрерывна при а < х < 6 и имеет положительную производную f'(x) при а < х < Ь.
Докажем сначала более слабое утверждение о том, что f не убывает при а < х < Ь\ отсюда уже без труда получится и строгое возрастание функции f. Допустим, что f не является неубывающей функцией, и приведем это допущение к противоречию.
Если f не является неубывающей функцией, то существуют такие хх, х2, что a<C^i<x2<6 и Дхх) >Дхг). Поскольку fj непрерывна в точке xlt для чисел с вблизи х/ и справа от хг имеем Дс) >Дхг); зафиксируем такое с. Точно так же из непрерывности в точке Х2 следует, что для чисел d вблизи хг имеем Дс) >£(d); зафиксируем одно такое d. Заметим, что а< с <2 d<2 Ъ, так что Ц дифференцируема в замкнутом интервале [с, d].
Обозначим через S множество всех х, х-^ d, для которых f(x) >f(d). Тогда с принадлежит S так что S не пусто. С другой стороны, d — верхняя граница S (не принадлежащая S). Пусть у — наименьшая верхняя граница (т. е. верхняя грань) S.
По теореме 1 § 4.1, существуют такие числа с' >с и d' < d, что при с<2 х<2 имеем f(c)<2 <2 f(x), а при df <2 х< d имеем Дх)< /(dk Отсюда ясно, что все х из интервала х< с' принадлежат S, а все х из интервала d'< х<^ d не принадлежат S. Тем самым с' у^ df, откуда с<2 y<Z d.
Покажем, что f(y)^t(d). В самом деле, если бы было f(y) X(d), (т. е. у £ S), то в силу непрерывности f вблизи у и справа от у было бы f >f(d) вопреки определению верхней грани.
По теореме 1 § 4.1, вблизи у и слева от у имеем Ц<21(у)- Следовательно, существует такое число z, с<2 z<2 У что при z<2 х<2 у имеем Дх) <J^Jjorfla тем более Дх)< f(d) для тех же х, и в интервале г<2 х<2 у (а также в интервале х<> d) нет точек множества S. Но тогда г является верхней границей S, и у не может быть верхней гранью S.
Полученное противоречие доказывает, что fj — неубывающая функция. Остается исключить случай, когда для некоторых и, v, где а^ и<2 6, имеет место равенство Да) = £(v).
Но в этом случае, очевидно, f постоянна в интервале [а, о], и f' = 0 во внутренних точках этого интервала вопреки условию теоремы. Тем самым теорема доказана.
Примечание. Теорему 2 часто доказывают исходя из так называемой теоремы о среднем значении. Этот подход мы рассмотрим в Дополнении в конце книги.
УПРАЖНЕНИЯ
1. Докажите вторую строку теоремы 2 § 4.2.
2. Функция Ц непрерывна в интервале [а, Ь] и имеет положительную производную во всех точках этого интервала, за исключением конечного их числа. Докажите, что утверждение теоремы 2 § 4.2 остается в силе.
8.2. Функции с положительной второй производной
Докажем теперь теорему 8 § 4.9. Эта теорема состоит из двух утверждений (два ряда таблицы). Мы докажем лишь первое утверждение, касающееся того случая, когда Дх) имеет положительную вторую производную fi'(x) в интервале х-^ Ь.
Рассмотрим две линейные функции: х /Дх) ихн- /з(х); график первой из них проходит через точки (а, Да)) и (Ь, Д6)); график второй есть касательная к графику j в точке (х0, Дх0)), где х0 — некоторое число из интервала а< х< Ь. Требуется доказать, что
h (*) </(*)< h (х)
при а^х^. 6, причем равенство справа возможно лишь при х = а или х = Ь, а равенство слева — лишь при х = х0.
Чтобы убедиться в этом, положим
gi (X) = f(x) — 1г (х), g2 (х) = f (х) — Z2 (х).
Так как /х и /2 линейны, имеем l\ (х) = 12 (х) = 0 и gj = > 0.
236
Приложение к главе 4
По теореме 2 § 4.2, функция g't(x) возрастает, поскольку (g/)' = gi" >0. По условию, gi(a) я gi(6)=0- Поэтому gx(x) не является ни возрастающей, ни убывающей функцией в [а,6]. По теореме 2, производная gj должна менять знак. Поскольку g\ возрастает и непрерывна, она имеет в интервале (а, Ь) в точности один корень; обозначим его через хр Тогда Xj< b и giM<C 0 *при a<Z x<Z g'i(x) >0 при Xj< x< По теореме 2, gi убывает в [a, xj, возрастает в [xx, 6J. Следовательно, gi(x)< 0 при*а< x<5> Xf и при Xi^C x< b, t. e. gi(x)< 0 при a<Z x< b, что равносильно Дх)< G(x).
Далее, ga— также возрастающая функция. Поскольку, по предположению, ga'(Xo) == 0» именем g/(x)< 0 при х< х0 и gz(x) >0 при х0< х^Ь. Одедовательно, ga(x) >0 при аЧх<;хо и при х0< х^> Ь. Тем самым /з(х)< Дх) при х-^ bt х =# х0.
УПРАЖНЕНИЕ
3. Докажите вторую строку теоремы 8 § 4.9.
8.3. Пределы производных
Докажем, наконец, теорему 2 § 7.3, утверждающую, что если Нт Дх) существует (и конечен) X^Xq
н Нт ^'(х) существует (причем здесь он может быть конечным или бесконечным), то Д(х0) =
= lim f(x).
х-*х0
Для упрощения записей допустим, что х0 = 0. Допустим также, что ДО) определено таким образом чтобы функция встала непрерывной в точке 0, причем ДО) = 0. Последнее предположение не нарушает общности доказательства: в самом деле, при ДО) 0 можно рассмотреть вместо f функцию fj(x) = Дх) — ДО), имеющую ту же производную, что и Д
Рассмотрим сначала случай, когда f'(x) имеет в точке 0 конечный предел. Можно считать этот предел равным 0. В самом деле, если он равен а 0, то можно рассмотреть вместо £ функцию 6(х) = Дх) — ах, производная которой f(x) — а имеет в точке 0 предел 0.
Итак, предполагается, что
f(0) = 0, lim/'(x) = 0, (1)
x-t-0
и надо показать, что
Г (0) = 0.
Пусть е — положительное число. Достаточно показать, что вблизи 0 для всех х =/= 0 разностное отношение Дх)/х лежит между—е ие. Но согласно второму равенству (1), имеем — е < <С 4'(х)<е при х 0 вблизи 0. Для таких х функции ех + Дх)и ех — Дх) возрастают, поскольку их производные в + Д(х) ие — f'(x) положительны. Обе функции обращаются в 0 при х = = 0. Следовательно, они положительны при х >0 и отрицательны при х<С 0. Для положительных х разделим на х два неравенства: ех + Дх) >0 и ех — Дх) >0. Для х < 0 разделим два противоположных неравенства на положительное число —х. В обоих случаях получаем — <Z Дх)/х<8; что и требовалось доказать.
Рассмотрим теперь случай, когда предел Г(х) в точке 0 бесконечен. Достаточно рассмотреть случай
lim Г (х) = + оо. (2)
Надо показать, что
Г (0)=4-оо.
Пусть? — заданное положительное число. Достаточно будет показать, что Дх)/х > 1/е при х+ 0 и вблизи 0. Из (2) видно, что У(х) > 1/е для х вблизи 0 и х 0. Для таких х функция f(x) — хк возрастает, поскольку ее производная f(x) — 1/е >0. Эта функция обращается в
Задачи
237
при х = 0. Следовательно, f(x) — х/е >0 при х >0 и f{x) — х/е, < 0 при х< 0. Отсюда заключаем, что при х ф 0 и в достаточной близости от 0 справедливо неравенство Дх)/х > 1/е. Это завершает доказательство.
Теорема 2 § 7.3 применима также к односторонним производным; доказательство то же.
УПРАЖНЕНИЕ
4. Докажите утверждение теоремы 2 в случае, когда Д(х) имеет предел —оо в точке х = 0.
ЗАДАЧИ
1. Пусть f(x) —функция, равная 1 для рациональных х и 0 для иррациональных х. Положим g(x) = xr f(x), где г — положительное рациональное число. Где эта функция непрерывна? При каких значениях х существует производная gf(x)^ Чему она равна?
2. Ниже предлагается «доказательство» теоремы о дифференцировании обратной функции. В чем его ошибка?
Предположим, что [(х) дифференцируема и имеет положительную производную f'(x). Пусть g(y) — функция, обратная Д Тогда #(Дх)) = х. По цепному правилу имеем, следовательно, g'(f(x))f'(х) — L откуда = 1/fOO-
3. Докажите следующее обобщение правила дифференцирования произведения. Пусть f(x) и g(x) определены и непрерывны вблизи х0, существует (конечная) производная Г(х^) и g'(xQ) = 4-оо; тогда для функции ф(х) = f(x)g(x) имеем: ф'(*о) = + оо при HxQ) >0 и ф'(х0) = —00 при W<0. Покажите также, что если Дх0) = 0, тоф'(*о) = A (*o)g(*o)-
4. Сформулируйте и докажите обобщение цепного правила на случай, когда одна из функций, композиция которых рассматривается, имеет бесконечную производную, а дру-
гая — конечную.
Пусть г — положительное рациональное число; положим Дх) = хг. Каково наибольшее целое число k, для которого f имеет в точке х = 0 (конечную) производную &-го порядка? Пусть функции Дх) и g(x) имеют производные всех порядков. Запишите формулу для (fg)" и для(/£)"'. Затем попытайтесь угадать формулу для (fe)IV; проверьте эту формулу. Продолжите это, если Вы сможете.
Определите непрерывную функцию, которая не является кусочно монотонной. [У к а-з а н и е: возьмите в качестве области определения х >0, положив функцию линейной в каждом из интервалов (1,4-оо), (1/2 1), (1/3, 1/2), (1/4, 1/3) и т. д.]
Пусть f(x) имеет непрерывную производную при всех значениях х и ДО) = 0, | Д (х) |< 1 для всех х. Покажите, что | Дх) |<С | х | при х ф 0. Дайте графическую иллюстрацию этого факта. [Указание: рассмотрите функции х — Дх) и х 4~ Дх); исследуйте, являются ли они монотонными.]
5.
6.
7.
8.
9.
Пусть Дх) имеет непрерывную вторую производную ДО) = 0, /'(0) = 0, | f"(x) |< 1 при
всех х. Покажите, что | Дх) | < -L х2 при всех х=/=0.
10 Покажите, что справедлива теорема, обратная теореме 3 § 4: если функция не убывает и имеет производную, то ее производная неотрицательна.
11. Покажите, что если ff = t" = 0 и — а =£ 0 при х = 0, то график Дх) имеет при х = 0 точку перегиба.
12. Покажите, что если = f," = ff" = 0 и fIV = а 0 при х = 0, то Дх) имеет в точке х = 0 локальный минимум или локальный максимум в зависимости от того, положительно или отрицательно а.
13. Обобщите результаты задач 11, 12 в следующем предложении: Если функция Дх) такова, что все ее производные порядков 1, 2, ..., k — 1 в точке х = 0 равны 0, а k-я производная принимает при х = 0 значение а. то ... . Дополните утверждение теоремы и попытайтесь доказать его.
14. Докажите, что всякая функция, четвертая производная которой есть постоянная 0, является многочленом не более чем третьей степени.
15. Пусть п — заданное целое положительное число. Каковы функции Дх), для которых ДлДх) = 0 при всех х?
238
Приложение к главе 4
16. Пусть две функции имеют одну и ту же вторую производную. Докажите, что их разность — линейная функция.
17. Найдите все функции, третья производная которых есть х.
18. Пусть 1(х) непрерывна при всех х и линейна в каждом открытом интервале между двумя последовательными целыми числами. Покажите, что f(x) имеет первообразную функцию, и укажите, как ее найти.
19. Докажите или опровергните утверждение: первообразная функция положительной функции, определенной в некотором интервале, имеет не более одного корня. Рассмотрите предложения, получаемые из предыдущего заменой слова «положительная» на «отрицательная»; на «неотрицательная».
20. Пусть [(х) и g(x) имеют соответственно первообразные F(x) и G(x). Найдите первообразную функцию t(x)G(x) + F(x)g(x).
21. Пусть ,u(x) имеет первообразную F(x). Найдите первообразную функции h(x) = = F(x)ki(x), где k —1 — целое число.
22. Пусть g(x) имеет первообразную G(x), Найдите первообразную для Л(х) ® g(xk}xk~\ где k — любое целое число, отличное от 0.
23. Существует ли такая функция /(х), что limf(x) = +оо и lim f'(x) = 0? Что lim f(x)=O r->4-a> х->4-оо
и lim h'(x) = +оо?
24. Что можно сказать о функции, вторая производная которой нечетна? Четна?
5/ИНТЕГРАЛЫ
В этой главе изучается второе основное понятие математического анализа — интеграл. Сначала мы определим интегралы и получим их основные свойства геометрическим путем; затем мы покажем, как можно дать чисто аналитическое определение интеграла. В § 2 разъясняется основная теорема о связи между интегралами и производными. В § 3 показано, как эта теорема используется для вычисления интегралов, а в § 4 излагаются основные геометрические приложения понятия интеграла.
Приложение к этой главе содержит пять параграфов: один посвящен физическим понятиям, другой содержит полезное обобщение понятия интеграла, а три остальных — доказательства теорем, принятые ранее как геометрически очевидные. Эти последние параграфы Приложения рассчитаны в первую очередь на читателя, желающего ознакомиться с вполне строгим изложением математического анализа.
240
5. Интегралы
§ 1. ИНТЕГРАЛ
ОТ ФУНКЦИИ.
ПЛОЩАДЬ
ПОД КРИВОЙ
1.1. ИНТЕГРАЛ ОТ НЕОТРИЦАТЕЛЬНОЙ ФУНКЦИИ
Рассмотрим непрерывную функцию у = /(х), не принимающую отрицательных значений, так что график ее целиком лежит выше оси х, хотя и может касаться оси х в некоторых точках (рис. 5.1). Пусть а и b — такие числа, что функция определена при а < х < Ь.
Кривая у = /(х) и прямые х = а, х = b и у ~ 0 ограничивают некоторую область плоскости, называемую областью под кривой у = f(x) от а до Ь, или криволинейной трапецией с (параллельными) «основаниями» х=аих=6и «боковыми сторонами» у = 0 и у = /(х). Эта область имеет определенную площадь S.
Верно ли последнее утверждение? Наша интуиция и наш опыт подсказывают что верно. Если требуется вычислить эту площадь, то можно, например, покрыть плоскость сетью мелких квадратов и сосчитать число квадратов, лежащих внутри нашей области (рис. 5.2). Это не дает еще всей площади, поскольку некоторые из квадратов лежат частично внутри, а частично вне рассматриваемой области. Но мы рассчитываем, что если сделать сеть достаточно густой, то можно будет вычислить S с л ю б о й требуемой степенью точности. Тот факт, что действительно существует число S, которое может быть вычислено таким способом, представляет собой математическое предложение, требующее доказательства, и мы займемся этим вопросом в дальнейшем. Пока же мы примем понятие площади в качестве известного. Число S зависит от функции / и от чисел а и Ь. Согласно Лейбницу, его записывают в виде
ь
S = J / (х) dx. а
Правая часть здесь читается: «интеграл от а до Ь функции Дх) по х» или «интеграл от а до & от/(х)^х». Символ J есть знак интеграла, функция f есть подынтегральная функция, или интегранд, а интервал (а, Ь) — интервал (промежуток) интегрирования. Числа а и Ь обычно называются нижним и верхним пределами интегрирования. («Пределы интегрирования» не имеют ничего общего с термином «предел», определенным в гл. 3.)
Обозначение Лейбница может быть оправдано еще одним «математическим мифом» (ср. с гл. 4, § 1.7). Область под кривой составлена из бесконечно многих бесконечно тонких прямоугольников (рис. 5.3). Каждый такой прямоугольник поднимается над точкой х интервала [а, 6]; он имеет высоту /(х) и бесконечно мадую ширину dx\ площадь его равна, следовательно, f(x)dx. Общая же площадь S есть сумма всех таких площадей. Символ J* и означает «сумму»; в действительности это удлиненная буква S.
«Миф» этот в буквальном смысле неверен, но содержит зерно истины. Мы увидим позже, в чем оно состоит.
§ 1. Интеграл от функции. Площадь под кривой
241
Рис. 5.2
Вот некоторые примеры. Символ
з
J xdx
2
представляет площадь, изображенную на рис. 5.4. Область, о которой идет речь, является (обычной, или прямолинейной) трапецией, площадь которой мы умеем вычислять. Итак,
з -
jxdx = -2
242
5. Интегралы
Результат Архимеда о площади под параболой, уже полученный в Приложении к гл. 2, § 5, а затем еще раз в § 6 гл. 4, можно записать так:
о
Переменная х, входящая в эти формулы (переменная интегрирования), представляет собой так называемую «немую переменную». Она служит лишь для указания вида функции, подлежащей «интегрированию», т. е. той, для которой вычисляется площадь. Немую переменную можно заменить любой другой буквой, например,
1
№dy
с . , 1
И I a2 da = —.
J 3
1.2. ИНТЕГРАЛ ОТ ФУНКЦИИ, ПРИНИМАЮЩЕЙ ОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ
Обобщим теперь определение интеграла на функции, принимающие и отрицательные значения. Если а < Ь9 то число
ь
J f (х) dx
§ 1. Интеграл от функции. Площадь под кривой
243
есть общая площадь области, ограниченной кривой у = /(х), осью х и прямыми х = а и х = Ь, причем площади, лежащие выше оси х, считаются положительными, а расположенные ниже оси — отрицательными.
Так, если f задана графиком, изображенным на рис. 5.5, то число ь
^f(x)dx равно сумме площадей 1 и III минус сумма площадей II и IV. а
1
Вычислим в качестве примера J2xdx (рис. 5.6). Треугольник под осью х имеет площадь 4, треугольник над этой осью — площадь Г. Таким образом,
1
J 2х dx = — 3.
УПРАЖНЕНИЯ
В упражнениях 1—10 вычислите заданные интегралы. Начертите график подынтегральной функции, заштрихуйте соответствующую площадь. [Указание: в упр. 3, 4, би 10 воспользуйтесь упомянутым в § 1.1 результатом о площади, ограниченной параболой.]
4 1. 3zdz. 2/3 1 3. j Pdt. 5. f | и 1 du. 0 —1
1/2 1 а . Л Г /1 .av а С _ О”2/3
2. 1(1— s)ds. А 4. j(l— y2)dy* J z2dz, где а = 2
—1 0 —а
1
7. С h (t) dt, где h (/) = 1 при t < 0; h (t) = t + 1 при i > 0.
4
8. I y{r)dr, где <p(r) = 2 — г при r < 2; <p(r) = 2r —4 при 2 <r < 3; <p(r) =2 при r>3.
3
9. j f (v) dv, —1
при о >2.
где
f (v) = « 2 при v < 0; f (v) = v — 2 при 0 < v < 2; f (v) = 2v — 4
4
10. §g(y)dy, где —4
при у > 1.
g (у) = 1 при у < —1; g (у) = у2 При — 1 < у < 1; g (у) = 3 — 2у
244
5. Интегралы
Рис, 5.8
1.3. ТРИ ОСНОВНЫХ СВОЙСТВА
Частный, но важный случай представляет функция /(х) = а, постоянная для всех х в рассматриваемом интервале. Очевидно,
ь
§adx = (b — а) а, (1)
а
так как прямоугольник ширины Ь — а и высоты | а | имеет площадь | а 1(6 — а). (Если а = 0, то прямоугольника в действительности нет и нуль является единственным значением, какое в этом случае можно приписать площади.]
Рис. 5.7 иллюстрирует эту формулу.
Основное и интуитивно очевидное свойство площадей состоит в следующем: если а< b < с, то
f (х) dx -Ь f f (х) dx = J f (x) dx. (2)
a b a
§ 1. Интеграл от функции. Площадь под кривой
245
Эту формулу иллюстрирует рис. 5.8: вся заштрихованная площадь есть сумма двух площадей, заштрихованных более светло и более темно. Это свойство называется свойством аддитивности* интеграла по отношению к интервалу интегрирования.
Функция, изображенная на рис. 5.8, положительна; однако, рассматривая изображенную на рис. 5.9 функцию, читатель сам убедится, что утверждение имеет общий характер. На этом рисунке
j/(x)dx = I —II, f/(x)dx = — III + IV, J/(x)dx =1 +IV —(11+III), a b a
так что равенство (2) справедливо и здесь.
Другое интуитивно очевидное свойство площади выражается следующим правилом (монотонность интеграла):
если а<Ь и f(x)^g(x) при a<Zx<b, то
ь ь
С f (х) dx f g(x) dx.
(3)
а
В словесной формулировке: «у большей функции больший интеграл (в одном и том же интервале, считая слева направо)». Это предложение иллюстрирует рис. 5.10. Площадь под f составляет в этом случае часть площади под g. Взглянув на рис. 5.11, читатель убедится, что утверждение сохраняет силу и для функций, принимающих отрицательные значения.
* От латинского слова addjtivus — придаваемый, присоединяемый (ср. «аддитивное свойство» — свойство, связанное со сложением).
246
5. Интегралы
Рис. 5.13
1.4. КУСОЧНО-НЕПРЕРЫВНЫЕ ФУНКЦИИ, ОГРАНИЧЕННЫЕ ФУНКЦИИ
Свойство аддитивности (2) подсказывает, как следует определить интеграл от некоторых разрывных функций.
Функция х /(х), определенная в интервале а<х< Ь, называется ограниченной в этом интервале, если существует такое число М, что | /(х) |< М. при всех х из интервала а < х < Ь. Если /(х) к тому же и непрерывна, то мы предполагаем ь
возможным однозначно определить площадь j* f(x)dx. а
Пусть теперь /(х) ограничена в конечном интервале (а, с) и существует такое число b между а и с, что /(х) непрерывна при а < х < 6, а также при Ь < х < с; тогда с b с
можно определить J f(x)dx по аддитивности как сумму J/(x)rfx + f/(x)dx (рис. 5.12). а а Ь
Тот же способ применяется и в общем случае, когда интервал (а, с) делится не на два, а на несколько интервалов, в каждом из которых f (х) ограничена и непрерывна.
Функция /, непрерывная в интервале, за исключением, может быть, конечного числа точек, называется кусочно-непрерывной в этом интервале. (Функция, определенная на бесконечном луче или на всей числовой прямой, называется кусочнонепрерывной, если она обладает этим свойством в любом конечном интервале из своей области определения.) Большинство функций, встречающихся в анализе, кусочно-непрерывны. (Конечно, непрерывная функция также рассматривается как частный случай кусочно-непрерывной.) ь
Итак, интеграл J/(x)dx мы считаем определенным, если (а, Ь) — конечный ин-а
тервал и функция /(х) ограничена и кусочно-непрерывна в (а, Ь).
Как мы покажем, свойства интегралов (1), (2), (3) позволяют приближенно вычислить значение интеграла от заданной функции.
§ 1. Интеграл от функции. Площадь под кривой
247
1.5. СТУПЕНЧАТЫЕ ФУНКЦИИ
Функция g(x), определенная при a<Zx <Z bt называется ступенчатой функцией, если интервал (а, Ь) можно разделить на конечное число частей, в каждой из которых g(x) постоянна. Например,
g(x) =
6 при —2<х<—1,5;
2 при — 1,5 < х <0;
3 при 0 < х < 1;
4 при 1 < х <2,5;
—,2 при 2,5 < х < 4
есть ступенчатая функция, определенная в интервале (—2, 4). Области ее постоянства суть (—2, —1,5), (—1,5, 0), (0, 1), (1, 2,5), (2,5, 4); значения, которые g принимает в концах этих областей, интереса не представляют. График функции g изображен на рис. 5.13; его вид объясняет термин «ступенчатая функция».
Конечно, ступенчатая функция ограничена и кусочно-непрерывна; интеграл от нее по любому конечному интервалу можно сразу же вычислить, либо пользуясь аддитивностью и формулой для интеграла от постоянной, либо, еще проще, пользуясь непосредственно определением интеграла как площади.
Так, например, для описанной выше функции g(x) имеем
4 —1,5 0 1 2,5 4
J g (х) dx = J 6dx + J 2dx + j* 3dx + J 4dx + J (— 2) dx =
—2 -2 —1,5 0 1 2?5
=6.4- + 2 . A + 3 .! + 4 • A + (_ 2) . A = 12,
как это можно усмотреть из рис. 5.13.
1.6. ВЫЧИСЛЕНИЕ ИНТЕГРАЛА
Пусть теперь /(х) — ограниченная кусочно-непрерывная функция, определенная в конечном интервале (а, &), и пусть <р(х) и ф(х) — две ступенчатые функции, для которых
Ф(х)</(х) <ф(х)
при а < х < Ь. Тогда, по свойству монотонности (3), b b д
J <р (х) dx < J f (х) dx < J ф (х) dx. а а а
Интегралы слева и справа могут быть вычислены, а зная их, мы знаем и ь ь
величину J/(x)dx, причем возможная ошибка не превосходит разности J<p(x)dx— ь а . а
— J<p(x)dx. Геометрический смысл только что сказанного поясняет рис. 5.14:
248
5. Интегралы
площадь под кривой больше суммы площадей «низких» прямоугольников и меньше суммы площадей «высоких». На рис. 5.15 показано, как обстоит дело для функции, принимающей и положительные, и отрицательные значения.
Если / задана, то легко найти ступенчатые функции ф и ф, удовлетворяющие неравенствам ф ф. Для этого достаточно разделить интервал (а, Ь) на части и в каждой из этих частей выбрать для ф и ф постоянные значения, удовлетворяющие тем же неравенствам. Оказывается, что таким путем можно вычислить значение ь
Jf(x)dx с любой требуемой заранее степенью точности, а
1.7. ОЦЕНКА ПОГРЕШНОСТИ ДЛЯ МОНОТОННОЙ ФУНКЦИИ
Проверим последнее утверждение для возрастающей функции. Разделим интервал (а, Ь) на N равных отрезков, каждый длиной в (Ь — d)/N. В каждой из этих частей всего интервала выберем наименьшее возможное значение для ступенчатой функции ф, а именно значение, которое функция / принимает в левом конце отрезка. Подобным же образом выберем для ф наибольшее возможное для каждого отрезка значение — значение, принимаемое f в правом конце (рис. 5.16).
ь ъ
Чему равна при этом разность J <p(x)dx— /ф(х)б/х? Очевидно, она равна сумме а а
N площадей заштрихованных на рис. 5.17 прямоугольников. Эта сумма равна (Ь — a)/N, умноженному на сумму высот, т. е. на f(b) — f(a). Тем самым мы знаем ь
\f(x)dx с погрешностью, не превосходящей а
Ь b
J ф (х) dx — J ф (х) dx = (b — a) [f (b) — f (а)].
а а
§ 1. Интеграл от функции. Площадь под кривой
249
Это число можно сделать сколь угодно малым, для чего только надо выбрать /V достаточно большим.
•Пример. Вычислить
0,5
J (1 + x^dx о
с ошибкой, не превосходящей 0,03.
Решение. Применим только что изложенный метод. Поскольку Ь — а = = 0,5—0 = 0,5 и f(b) — f(a) = 1,25—1 = 0,25, имеем (b — a) lf(b) — f(a)] = 0, 125, так что N должно удовлетворять условию 0,125/N < 0,03. Возьмем N = 5; тогда, действительно, 0,125ЛУ = 0,025 < 0,03. Из таблицы
X 0 0,1 0,2 0,3 0,4 0,5
f(x) 1 1,01 1,04 1,09 1,16 1,25
видно, что значения <р в пяти частях интервала равны 1; 1,01; 1,04; 1,09; 1,16, а значения ф равны 1,01; 1,04; 1,09; 1,16; 1,25. Длина каждого малого отрезка равна 0,5/5 = 0,1. Отсюда
0,5
( Ф
dx = (0,1)(1 -f- 1,01 4- 1,04+ 1,09+ 1,16) =0,530
и
dx =(0,1)(1,01 + 1,04+ 1,09+ 1,16+ 1,25) =0,555.
250
5. Интегралы
Итак,
0,5
0,530 <j (14-x2)dx< 0,555. о
В следующем параграфе мы узнаем, как точно вычислить этот интеграл; окажется, что
0,5 _
j (1 + х2) dx = 0,5416 (= 0,541666... ).< о
Выше мы показали, как можно вычислить интеграл от возрастающей функции с любой заданной точностью. Отметим, что то же рассуждение распространяется и на неубывающие функции. При этом лишь для краткости мы разбили интервал (а, Ь) на N р а в н ы х частей; существенно лишь, чтобы эти части были достаточно малы. То же рассуждение годится и в случае невозрастающей функции. Ввиду свойства аддитивности (2) мы заключаем, что интеграл от кусочно-монотонной функции вычислим с помощью ступенчатых функций с любой заданной точностью. Это охватывает все функции, обычно встречающиеся в приложениях анализа.
Как мы покажем в Приложении (см. § 8), метод вычисления интегралов посредством «зажимания» функции ‘между двумя ступенчатыми функциями действует столь же успешно и для функций, не являющихся кусочно-монотонными.
УПРАЖНЕНИЯ
2
11. Найдите приближенное значение I g (t) dt, где g— функция, график которой изображен
§ 1. Интеграл от функции. Площадь под кривой
251
3
12. Найдите приближенное значение \f{y)dyt где / — функция, график которой изобра-—1
жен ниже. Оцените возможную погрешность.
5/2
13. Найдите приближенное значениеJ h(v)dv> где h — функция, график которой изображен 1/2
ниже. Оцените возможную погрешность.
К упр. /5
252
5. Интегралы
2
14. Найдите приближенное значение J <p(t)dt, где ср— функция, график которой изобра-~ -1/2
жен ниже. Оцените возможную погрешность.
В упражнениях 15—25 вычислите заданные интегралы с указанной степенью точности, пользуясь ступенчатыми функциями. Если возможно, вычислите также точные значения рассматриваемых интегралов.
1
15. 1 (х2 4- 1) dx С погрешностью не выше 0,1.
16. 0,2 1 t2dt с погрешностью не выше 0,002.
17. 0.1 0.3 J Д У2 + У) dy с погрешностью не выше 0,03.
18. 0,3 J (1— у2) dy с погрешностью не выше 0,002.
19. 0.2 0 J (*’ + 2) di с погрешностью не выше 0,05.
§ 1. Интеграл от функции. Площадь под кривой
253
2
^20. J dx/x с погрешностью не выше 1/4.
0,36
21. J УТГ dv с погрешностью не выше 0,15. о
3/2
22. J [2х/(2х + 1)] dx с погрешностью не выше 1/10. 1/2
2
23. f (х) dx с погрешностью не выше 2,5, где /(х) = — х при 0 О < 1 и f(x) = = 1 4- х2 при х > 1.
1
24. J f (0 dt с погрешностью не выше 2,5, где / (/) = /3 при I < — 9 и f (/) = (t 4- Ю)2 при _1 t>-9.
3/2
25. f (z) dz с погрешностью не выше 1, где f (z) = 1/(2 4- 2) при z < 1 и f (г) = z3 при
1.8 . АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
До сих пор мы действовали таким образом, как будто знаем все о площадях, и использовали эти знания для определения интеграла. Теперь мы обратим этот ход мыслей. Мы дадим аналитическое определение интеграла, т. е. определение, основанное только на свойствах чисел.
Очень легко дать такое определение для ступенчатых функций: если ступенчатая функция ф(х), заданная в конечном интервале (а, 6), имеет k интервалов постоянства с длинами 1Ъ /2, ..., lk и принимает в этих интервалах значения ai, a2, •••» ал, то, по определению, полагаем.
ь
' J ф (X) dx = aj/j a2/? 4- ... 4- aklk. a
Теперь мы воспользуемся ступенчатыми функциями для определения интегралов от других функций. Предыдущее обсуждение подсказывает, что можно предполагать справедливость следующей теоремы:
Теорема 1 (теорема о существовании интеграла). Пусть f(x) — ограниченная кусочно-непрерывная функция, определенная в конечном интервале (а. Ь). Тогда существует одно и только одно такое число S, что. каковы бы ни были ступенчатые функции ф(х) и ф(х), удовлетворяющие неравенствам ф(х) < /(х) ф(х) при a<Z х < b. имеем
ь ь
j Ф (х) dx<C $ -С J ф (*) dx.
а а
254
5. Интегралы
Определение. Число S обозначается символом
ь
J f(x)dx а
и называется интегралом от функции f(x) по интервалу (а, 6).
Доказательство теоремы 1 будет дано в Приложении (см. § 8). Пока же мы предлагаем читателю принять эту теорему без доказательства, так же как и следующее предложение:
Теорема 2 (т 'е о р е м а об основных свойствах интегра-л а). Пусть (а, Ь) — конечный интервал. Тогда для любых двух ограниченных кусочно-непрерывных функций f, g:
ь
J а dx =a(b — а) при любой постоянной а; (1)
а
ebb
J f (x) dx 4- J f (x) dx = у f (x) dx при любом c, a<2c<2b; (2)
аса
b b
[/(x)dx< §g(x)dx при f(x)^g(x), a<zx<zb. (3) a a
Эта теорема лишь резюмирует геометрически очевидные свойства площадей, уже отмеченные выше. Аналитическое доказательство будет приведено в Приложении (СМ. § 8).
1.9. РАСШИРЕНИЕ ОБОЗНАЧЕНИЙ
Ь
Для дальнейшего удобно расширить наши обозначения. До сих пор число j f(x)dx а
было определено лишь при а < Ь. Мы хотим определить его также при а = b с тем, чтобы свойство аддитивности (2) осталось в силе. Таким образом, должно быть справедливо равенство
J f (х) dx 4- J f (х) dx = J f (х) dx. а а а
Этого можно достигнуть, лишь положив
а
У f (х) dx = 0. (4)
а
b
Далее, мы хотим определить J f (х) dx при b < а. При этом мы снова хотим а
сохранить правило (2). Но тогда должно быть
§ 1. Интеграл от функции. Площадь под кривой
255
J f (х) dx 4- С f (х) dx = j / (х) dx = О, aba
и нам приходится, по определению, принять
Ь а
j / (х) dx = — у f (х) dx.
(5)
Начиная с этого момента соотношение (2) можно считать справедливым для любых трех чисел а, Ь, с (читатель может проверить это на примерах).
УПРАЖНЕНИЯ
Вычислите следующие интегралы:
-I 2
26. у 2dx. 29. У (— 4) dx.
О ь
—3 1
27. J xdx, 30. J x2dx.
—1 2
5 2—2
28. У (Xi»0 — x)dx. 31. у 4- У x*dx. 5 —2 2
а—I
32. Найдите такое число а, чтобы было J 2dx = 5.
Ь—2
33. Найдите такое число 6, чтобы было J xdx = 6.
34. Пусть f (х) ограничена, непрерывна и неотрицательна при Покажите, что
ь
У f (х) dx > 0. а
35. Пусть f (х) такая же, как в упр. 34; с—число такое, что Покажите, что
Ь с
У f(x)dx> У f (х) dx. а а
36. Покажите, что 2 < 1(1 + х22) dx < 4.
256
5. Интегралы
§ 2. ОСНОВНАЯ ТЕОРЕМА АНАЛИЗА
2.1. ПЕРВАЯ ЧАСТЬ ОСНОВНОЙ ТЕОРЕМЫ
Пусть функция f(t) определена при a<t<Zb; предположим, что она ограничена и кусочно-непрерывна. Тогда для каждого числа х между а и b можно
X
вычислить число G (х) = J f (/) dt — площадь под кривой от а до х. Мы
а
получаем, таким образом, новую функцию х »-► G (х), определенную при а х Ь\ ясно, что G (а) = 0. Можно спросить, имеет ли эта функция производную и если имеет, то чему эта производная равна?
Рассмотрим сначала некоторые примеры. Пусть /(/)=//2+1 и а = 0 (рис. 5.18).
Из чертежа видно, что
G(x)=W_L+1'Uz = —+х;
<Л2 1 4
график G (х) изображен на рис. 5.19. Дифференцируя G (х), находим G' (х) = + 1,
или G' (х) = f (х). Мы возвращаемся, таким образом, к исходной функции f.
§ 2. Основная теорема анализа
257
Пусть теперь f (t) = /2 и а = — 1. Тогда
G(x) =
/М/
О х
проверим это для х > 0. По свойству аддитивности (2), G (х) = С /2 di + J /2 dt; это —1 о
сумма двух площадей под параболой, показанных на рис. 5.20. Из результатов § 5.8 гл. 4 мы знаем, что первая из них равна 1/3, а вторая х3/3. Г-рафик G изображен на рис. 5.21. Дифференцируя G(x), находим G'(x) = х2. И в этом случае G'(x) = /(х).
Прежде чем перейти к формулировке общей теоремы, рассмотрим еще один пример. Пусть f(t) = 2t при 0 < t < 1 и fit) =1 при t > Г, график f изображен на
258
5. Интегралы
х
рис. 5.22. Положим G(x) = f = площади под f от 0 до х. Из графика видно, о
что G(x) = хг при 0 х 1 и G(x) = 1 + (х — 1) = х при х > 1.
График функции G изображен на рис. 5.23. Как легко видеть, при 0 х < 1 имеем G'(x) = 2х = /(х), а при х > 1 имеем G'(x) = 1 = /(х). При х = 1 функция G не имеет производной. Функция / имеет в этой точке разрыв, а график G — излом.
Разобранные примеры подсказывают следующее предложение:
Теорема 1 (основная теорема анализа, первая часть). Пусть f(t), где a<.t < Ь,— ограниченная кусочно-непрерывная функция. Положим
а
Тогда G(x) — непрерывная функция и во всех точках х, где f непрерывна, имеем
G'(x)=f(x).
Последнее равенство играет центральную роль. Его можно записать в виде d х
— J f(t)dt = f(x), если f непрерывна в точке х. а
(Если х = а или х = Ъ, то под производной надо понимать одностороннюю производную.)
Рассуждение, доказывающее основную теорему, то же, что и в § 6 гл. 4, где с его помощью была вычислена площадь под параболой.
§ 2. Основная теорема анализа
259
Допустим для простоты, что /> 0. Пусть х0 — точка рассматриваемого интервала и h — малое положительное число. Тогда G(x0+&) есть площадь под кривой от а до х0 + Л, G(x0) — площадь под кривой от а до х0, а разность G(x0 + h) — G(xQ) есть вся заштрихованная на рис. 5.24 площадь. Если во всех точках |/(/) | М, то величина этой площади не превосходит Mh.
Следовательно, величина |G(x0 + Л) — G(x0)| мала при малых h. Подобные же рассуждения проводятся при отрицательных h. Таким образом, функция G непрерывна в точке х0. (Это верно даже в том случае, когда функция / не является непрерывной в точке х0.)
Но если / непрерывна в точке х0, то разность G(x0 + А) — G(x0) приближенно равна площади заштрихованного прямоугольника, т. е. hf(xQ). Это значит, что
=1Ы+...,
где точками обозначено «нечто», становящееся сколь угодно малым, если h достаточно мало. Такое же заключение получается для отрицательных Л. Итак, G'(*o) == /(*о)«
Формальное доказательство, приводимое в Приложении (см. § 8), представляет собой уточнение и проверку этого интуитивно ясного рассуждения.
Открытие математического анализа обычно приписывается Ньютону и Лейбницу; к сожалению, оно сопровождалось некрасивым и бессмысленным спором о приоритете между последователями этих двух ученых. В действительности неправильно связывать такое исключительное достижение, как создание новой большой науки, с именами всего лишь двух человек, даже такик гигантов, как Лейбниц и Ньютон. По существу содержание основной теоремы, играющей ключевую роль в анализе, было впервые сформулировано Барроу, учителем Ньютона.
УПРАЖНЕНИЯ
В упражнениях 1—5 проверьте, что для заданных функций справедлива теорема 1. х
1. G (х)= J h (0 dt, где h (0 = 1 при t < 0; h (t) = t + 1 при / >0. х
А2. G (х) = J ср (г) dr, где ср (г) = 2 — г при г < 2; ср (г) = 2г при г > 2.
3. Н(у) = С f(tf)dv, где /(0 = ^2 при v < 0; f(v) = v при0<о<2; f(v) = 2v при э>2.
V
4. К (v)= J g (и) du, где g (и) = 4 при и < — 1; g (и) = 2 при — 1 < и < 0; g (и) = при и>0.
Исаак БАРРОУ (1630—1677) был теологом и математиком. В 1669 г. он отказался от кафедры математики в Кембридже в пользу Ньютона, своего тезки и ученика.
260
5. Интегралы
z
5. F (z)=J h (/) dt, где Л (0=1— 2/ при t < 2; h (t) = 1 при 2 < t < 3; h (0 = 3/ — 8 1
при t > 3.
В упражнениях 6—8 функция f (t) считается ограниченной кусочно-непрерывной и определенной при а<^1<^Ь. При выполнении этих упражнений следует применить теорему 1.
Ъ
6. Пусть Н (t) = J f (t) dt. Покажите, что И непрерывна при а < х < b и что во всех точат
ках х интервала [а, Ь], в которых f непрерывна, Н' (х) = —f(x). [Указание: воспользуйтесь свойством (2) аддитивности интеграла, § 1.8.]
X
7. Пусть с — любая точка [а, 6] и К(х) = §f(t)dt. Покажите, что функция К непрерывна с
при а<х< Ь и что для всех точек х интервала [а, 6], в которых f непрерывна, К' (х) = f (х), [Указание: воспользуйтесь упр. 6 и равенством (5) § 1.9.]
8. Пусть Р(х), —дифференцируемая функция, значения которой принадлежат ин-
₽(х)
тервалу [а, 6]. Положим L (х) = j* f (t) di. Покажите, что L непрерывна при I < х<т с
и что во всех точках х интервала [Z, т\, для которых f непрерывна в точке ₽(х), имеем
£' (х) = р' (х) f (Р (х)). [Указание: запишите L (х) в виде композиции функций, одна из которых — функция К(х), заданная в упр. 7.]
2. 2. ВТОРАЯ ЧАСТЬ ОСНОВНОЙ ТЕОРЕМЫ
Основная теорема имеет еще и вторую часть; именно этой частью мы будем постоянно пользоваться.
Теорема 2 (основная теорема анализа, вторая часть). Пусть F(x) — непрерывная функция, определенная при а х Ь, и пусть f(x) — ограниченная кусочно-непрерывная функция, такая что
F'(x)=f(x),
кроме, быть может, конечного числа точек. Тогда ь
dt = F(b) — F(a).
а
Доказательство. Предположим сначала, что / непрерывна и F' (х) =/(х) для всех х. Положим а
требуется доказать, что G(b) = F(b) — F(a).
Положим, далее, Н(х) = G(x) — F(x) 4- F(a). Тогда дело сводится к доказательству равенства Н(Ь) = 0. В действительности, как мы покажем, Н(х) = 0. В самом деле, по теореме 1, G'(x) = f(x), так что Н'(х) =
§ 2. Основная теорема анализа.
261
=/(х) — /(х) = 0 во всех точках х. По основной теореме 1 § 5.2 гл. 4, функция Я(х) постоянна. Но Н(а) = G(a) — F(a) + F(a) = = 0. Отсюда H (х) = 0.
То же рассуждение применимо и в случае, когда f кусочно-непрерывна и равенство F'= f может нарушаться в конечном числе точек. Тогда интервал 1а, 61 можно разделить на конечное число частей, в каждой из которых Я'(%) = 0 и, следовательно, в каждой из которых функция Н постоянна. Но поскольку, как мы уже знаем, Н(х) непрерывна во всем интервале [а, Ь], она постоянна и в [а, 6], что завершает доказательство.
Для любой функции Г(х) принято писать
М = F(b)~F (а).
С помощью этого обозначения вторая часть основной теоремы может быть записана в виде
и ъ
J F' (х) dx = F (х) |а;
здесь предполагается, что F'(x) существует, ограничена и кусочно-непрерывна. С помощью этой формулы можно вычислить площадь под кривой у = /(х), если известна первообразная функции /.
ф Примеры. 1. Вернемся к примеру, рассмотренному в § 1. Первообразная для функции 1 + х2 есть х + (х3/3). Поэтому
1/2 / v9 \ i1/2 1 I 1Q _
. С (1 +x2)dx = (x+ — = — + — =—= 0,5416.
J v \ 3 / о 2 24 24
2. В качестве другого приложения решим задачу, рассмотренную Кавальери (см. гл. 4, § 6), т. е. вычислим площадь под кривой у = хп от 0 до t> 0 (где п — некоторое целое положительное число). Так как хп есть производная функции хл+1/(п + 1), то
Обратите внимание, с какой легкостью мы получили этот результат для всех п\
3. Только что найденная формула представляет частный случай следующей, более общей:
(а0 + (цх +-------1- апхп) dx = (аох + + • • • +
V 2 п 4- 1
Это соотношение сразу же вытекает из основной теоремы и правил дифференцирования. Оно позволяет найти площадь под графиком любого многочлена.^
262
5. Интегралы
УПРАЖНЕНИЯ
В упражнениях 9—23 вычислите интегралы с помощью основной теоремы.
0.3 0.3S
9. f (1 — у2) dy (ср. с упр. 18, § 1). 11. f Yv dv (ср. с упр. 21, § 1).
0,2 О
О 20
10. J (t2 + 2)dt (ср. с упр. 19, § 1). 12. J dt/P.
—1 10 к
1
13. J (2х24- *+ x~3)dx.
—2 '
14. Найдите площадь, ограниченную графиком функции Zh*/ 2/3, горизонтальной осью и прямыми t = 8 и / = 27.
1
15. J (и + I)5 du. о
А16. Найдите площадь, ограниченную графиком функции z Yz—1 , горизонтальной осью и прямыми г = 2 и г = 5.
2
17. f (2s—l)2/3ds.
18. Найдите площадь, ограниченную графиком функции и \!у и 4- 3 , горизонтальной осью
и прймыми и = 1 и и = 6.
з
19. J s(s2 — 2)5ds. о
^20. Найдите площадь, ограниченную графиком функции v н> v jAu2 + 9, горизонтальной осью и прямой v= 4.
2
21. J [s2/(s2 + 2)2] ds.
1
2
22. J f (х) dx, где f (х) = Yx + (1/х2)при 0<х<1; f (х) = 2х2^3 прих>1.
5
23. у g (/) dt, где g (t) = (1 —/)3/2 при t < 0; g (t) = 1 при t = 0; g (t) = (t + 4)1/2 при />0.
2.3. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Основная теорема отвечает на вопрос, поставленный в гл. 4, § 6. Каждая непрерывная функция является производной некоторой другой функции, т. е. имеет первообразную функцию. Точнее, непрерывная функция f(x) является производной функции
§ 2. Основная теорема анализа
263
Р(х\- f f(f) dt, и
измеряющей площадь под кривой f от некоторой фиксированной точки до х. По этой причине первообразную функции f часто называют неопределенным интегралом функции /; здесь прилагательное «неопределенный» подчеркивает, что верхний предел интеграла не закреплен, является переменным, или неопределенным. Вместо соотношения F\x) = f(x) часто пишут
J/(x) dx = F(x) + C
без пределов интегрирования, но с неопределенной постоянной С (постоянной интегрирования). Эта постоянная напоминает нам, что неопределенный интеграл определяется функцией f лишь с точностью до («аддитивной») постоянной. Важно иметь в виду, что если функция f задана с помощью формулы, таблицы значений или графика, то значения F(x) могут быть фактически вычислены.
ф Пример. Если гФ—1 —рациональное число, то
xrdx =-------h С. ф
г+1
УПРАЖНЕНИЯ
24. Пусть F' — 1 и F (0) = 4; чему равно F (6)?
25. Пусть G" (и) = и2 — Зи и G (0) = 1, G (1) = 7/12; чему равно G (— 1)? 2/3
26. Найдите для функции и 2и —иъ первообразную, обращающуюся в нуль при и= 1.
27. Найдите для функции гн>г(г2 — 5)6 первообразную, принимающую в точке 1 значение 2.
28. Найдите для функции t ( /3/2—1)4 первообразную, принимающую в точке 1 значение 0.
X
29. Пусть х3 4- 2х = J [ (/) dt} чему равно /(3)? о
। а(х)
30. Пусть(х10—1) = J (/ + I)4 dt} чему равно а (х)? о
31. Начертите графики функций хь-*х2, xi-> 2x4-1 и х >-► (х + I)2 = х2 + 2х + 1 при х > 0. а а а
Вычислите J x2dxt J (2х+ 1)^хи J (х2 4- 2х 4- 1) dx и покажите, что сумма двух- первых 0 0 и
интегралов всегда равна третьему.
X
А 32. Пусть f(x)—первообразная для функции хн- I (s3 — l)ds, принимающая в точке 0 зна-о
чение —1; чему равно f (—1)?
264
5. Интегралы
Рис. 5.25
2. 4. ИНЕРЦИОННАЯ НАВИГАЦИЯ
Рассмотрим в виде приложения инерционную навигацию. Представим себе закрытый ящик без окон, движущийся по прямой. Наблюдатель, находящийся в ящике, должен определять пройденное расстояние с помощью измерений и вычислений, выполняемых внутри ящика (таким образом, не разрешается пользоваться спидометром, который должен быть присоединен к колесам, касающимся земли).
Если ящик движется с постоянной скоростью, то наблюдатель, находящийся внутри него, не заметит движения и не будет способен обнаружить его никаким механическим опытом. Это классический принцип относительности, который был известен еще Галилею.
Равномерное движение не может быть обнаружено даже опытами внутри ящика, касающимися электромагнитных явлений, например распространения света. Это принцип относительности Эйнштейна, лежащий в основе так называемой специальной теории относительности.
Между тем, как знает каждый ездивший в движущемся экипаже, изменение скорости, т. е. ускорение, можно обнаружить и не смотря в окно. Это не только субъективное ощущение. Пружина, расположенная вдоль направления движения и прикрепленная одним из концов к задней стенке (рис. 5.25), сжимается при (положительном) ускорении и растягивается при замедлении (отрицательном ускорении). Измеряя длину пружины, наш наблюдатель сможет определить ускорение ящика a(t) в момент времени t.
Напомним, что ускорение есть производная мгновенной скорости v(t), т. е. a(t) = Следовательно, v(t) есть первообразная функции a(t). Допустим, что в начальный момент (/ '= 0) ящик покоится. Тогда значение v(t) при t = 0 равно нулю. Отсюда, по основной теореме,
i
v (/) = J а (т) dx.
о
(Здесь т, как мы знаем, «немая» переменная: ее можно заменить любым другим символом или буквой, за исключением о, а и t, уже использованных для обозначения других величин.) Таким образом, наш наблюдатель может вычислить для любого момента t мгновенную скорость яшика (например, вычертив кривую a(t) и измерив площадь под нею].
§ 2. Основная теорема анализа
265
Далее, скорость v(t) есть производная от расстояния $(/), пройденного за время t. Таким образом, $(0) = 0 и$'(/) = v(t). Согласно основной теореме,
t s(t) =
Этим способом наблюдатель может определить свое положение в любой момент времени.
Только что описанная ситуация никоим образом не является вымышленной. Она встречается в случае атомных подводных лодок, остающихся месяцами в погруженном состоянии, а также в случае ракет. Принцип инерционной навигации всегда один и тот же: измеряется ускорение, а затем интегрированием находятся скорость и положение. Конечно, ракеты и подводные лодки движутся не только по прямой, и ускорения в разных направлениях приходится измерять с помощью сложных, высокочувствительных приборов. Интегрирование же, т. е. вычисление площадей, выполняется быстродействующими электронными вычислительными машинами.
УПРАЖНЕНИЯ
33. Ракета покоится при t = 0. Как показывают измерения внутри ракеты, ее ускорение a(t) = + 1 при 0, где время t измеряется в секундах, а ускорение а — в м/с2.
Чему равна скорость при t = 64? Как далека ракета от точки старта в этот момент?
34. Пусть для ракетьь описанной в упр. 33, ускорение a(t) = + 1. Чему равна скорость
при t = 64? Как далека ракета от точки старта в этот момент?
35. Пусть ракета, описанная в упр. 33, испытывает ускорение, графически изображенное на рисунке ниже. Оцените скорость при t = 1, t = 2, t = 3, 10 и используйте
эту информацию для построения графика скорости при 0<^. 10. Оцените с помощью
этого графика, как далеко уйдет ракета от точки старта за 10 g.
см/с2
20
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIHSIIIIUIIHIIIIIIIISIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIMIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIHHIIIIIIIIIIIIIIIIIIIIIIIIIIIIIMIIIIIIIIIIII miiiiiiiiiiiiiiiiiiiiiiiEiiiiiiHiiiiiiiiiiiiimiiiiiiiiiiiiiiiiiiiiiiiHiiiiiirdiiiiiiiiiiiiii
15 ШИИИгЖЩВВшЖв
10
5
о
irjiiiiiiiiiiiiiiiiiiiiiiiHiiiiiiiiiiiiHiimiiiiiiiniiiiiiiiiiiiiiiiiiiiimiiHiiiiiiiiiiiiiii rillllllllHIIIIIIIIIIIIIIIIIIIIIIIIIIllllllilllllHIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII iiiiiiiiiiiiiiiiiiiiiHiiiiiiiiiiiiiiHiiaiHiiiiiiHiiiniiiiiiiiiiiHHiiiiiniiiiiiiiiHiiiiHii
1
К упр, 35
з
8
5
2
4
6
7
9
266
5. Интегралы
§ 3. ИНТЕГРИРОВАНИЕ
3.1. ЧИСЛЕННОЕ И ФОРМАЛЬНОЕ ИНТЕГРИРОВАНИЕ
Пусть f — заданная непрерывная функция. Проинтегрировать f — это значит вычислить ее интеграл, т. е. либо некоторый определенный интеграл, другими словами, ь
число ^f(x)dx, либо неопределенный интеграл, т. е. первообразную функцию F9 а
для которой F'(x) = f(x). Мы уже говорили, что этот интеграл может быть вычислен; для его вычисления существуют два способа: численное интегрирование и формальное интегрирование.
ь
Численное интегрирование — это приближенный подсчет величины $f(x)dx с а
помощью свойств интеграла, установленных в § 1. Можно, например, воспользоваться двумя ступенчатыми функциями ф и ф, для которых ср f ф, и вычислить ь ь
два интеграла J(p(x)rfx и j\|)(x)dx, что не представляет труда. Тогда известно, что ис-а а
b b b
комое значение \f(x)dx лежит между f<p(x)dx и j\p(x)dx. Дальше (см. гл. 8) мы позна-а а а
комимся с более эффективными численными методами. Если мы уже знаем, как вычислить определенные интегралы, то мы в состоянии найти также первообразные; в самом деле, если а — некоторое фиксированное число, то функция х F(x) = х
= является первообразной для /. а
Численное интегрирование применимо во всех случаях. Второй же метод, формальное интегрирование, действует лишь в некоторых случаях, но зато в этих случаях быстро и изящно ведет к цели. Метод состоит в разыскании первообразной функции F для заданной функции f среди «известных» функций. «Известными» считаются попросту такие функции, которые уже ранее были определены и названы и для которых мы располагаем либо хорошей таблицей, либо методом вычисления такой таблицы. Если мы знаем первообразную функцию Г, то можно вы-ъ
числить j7(x)dx, поскольку этот определенный интеграл равен F(b) — F(a). а
При отыскании первообразных функций пользуются так называемыми правилами интегрирования, которыми мы сейчас и займемся. Для простоты предположим, что все рассматриваемые функции ограничены и непрерывны в интервале, по которому производится интегрирование. Из нашего изложения будет ясно, как обобщить правила интегрирования на кусочно-непрерывные функции.
3.2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
В силу основной теоремы анализа каждое правило дифференцирования можно переписать как правило интегрирования. Особенно важно правило
§ 3. Интегрирование
267
b b b
§tf(x) + g(x)]dx=^f(x)dx+$g(x)dx. (1)
a a a
В словесной формулировке: интеграл от суммы функций равен сумме интегралов от этих функций. Чтобы доказать это, обозначим через F(x) и G(x) соответственно первообразные функций f(x) и g(x) (т. е. такие функции, что F' = /; G ' = g). Тогда F + G, по правилу дифференцирования суммы, есть первообразная f + g. Тем самым левая часть (1) равна [F(&) + G(d)l — I/7(а) + G(a)], правая же равна [F(b) — F(a)] + [G(6) — G(a)J, т. e. тому же числу.
Точно так же из правила дифференцирования разности следует: интеграл от разности функций равен разности интегралов'.
ь ь ь
J If (х) — g (х)] dx = J /(X) dx — J g(x) dx. (2)
a a a
Ясно, что правила (1) и (2) можно применить более чем к двум функциям. Например,
b b b ь
J [/(•*) + g(x) + h (х)] dx = J/(x) dx 4- j g(x) dx 4- J h (x) dx. a a a a
Правило дифференцирования произведения функции на постоянную приводит к равенству
ь ь
j cf (x)dx = с J f (x) dx (c — постоянная) (3)
a a
или словесно: стоящий при подынтегральной функции постоянный множитель можно вынести за знак интеграла. Доказательство равенства (3) предоставляется читателю.
Иногда записывают те же результаты для неопределенных интегралов, т. е. для первообразных:
§[f(x) + g(x)]dx = ^f(x)dx + j g(x)dx,
j If (x) — g (x)] dx = J f(x) dx — J g(x) dx,
J cf (x) dx = c J f (x) dx.
Эти формулы отличаются лишь обозначениями от строк (а) и (б) таблицы § 5.4 гл. 4.
Так как для любого рационального числа а =# —1» по теореме 8 § 2 гл. 4,
ь
b
J x*dx
а-Н X
а 4- 1
(4)
268
। 5. Интегралы
то мы можем проинтегрировать каждую функцию, представляющую собой сумму членов вида сх® (а —1 рационально, с — произвольно).
•Пример.
3 у^х + 4 у^х v----dx = 3 f х‘/3 dx + 4 j* х'/4 dx — х'2 dx =
УПРАЖНЕНИЯ
Найдите следующие определенные и неопределенные интегралы:
1. j (Зх10 + 5х7) dx. 1 2. — z34-z3 — г+ l)dz. 2 11. у [s3 + (s— l)’ + (s + 2)3] ds. 1
12. J [( z+I)3 — (2z + 3)4] dz.
1 3. J (100/” + 99/lo»)d/. f / z2 \ 13. | z 1 — + 1 j dz.
—1 1
4. J (“’ — 7и* — и2) du. 14. / (x3 + l)2 3x2dx.
5- J y^z’ dz. 15. у (z3 + Yz — 1) dz.
1
6. У (г2 + Vz — г-2) dz. 16. 1 [5 (s3 — s + 2) + 3s« (s3 + 1)’] ds.
7. J[^3-3^2 + 3I/-3/5]^# 17' J 1/2Z+ 1 + Y3t-l]dt.
8. У + у^~)<Й. 0 18. J 0 I k Yt2+ 1 +?/3]dL
9. у (1 +/)5<й. 19. J у у + dy. у Г (i'+J)2 J y
2 10. У [(X —4)4 + (х+ l)’l dx. 0 20. J. f(x)dx, где f(x) = j (fl^l)dt.
§ 3. Интегрирование
269
b
21. J [f(x) + g(x)]dx, a
b b
где Jf(x)dx=3, J g (x)dx = — 4. a a
22. j [2<p(x) — 3^(x)-f-x]dx, где j<?(x)dx=4 и ф(х) = I t2dt.
—1 ~1 ~1 1/2 ______
23. J [f (x) + g(x)]dx, где f (x) = )<2x +3 и g (x) = x2 при x < 0, x при x> 0.
—1 1 2 1
24. C [f (z) + g (z)] dz, где f (z) = J t3dt и g (z) = J ztdi. Q 0 0
1
25. f [?'(x) — Зф'(x) 4-(x)] dx, где ? (1) = ф (1) = 2, ?(0)=l, ф (0) = 0 и g (x) =
29. I [/(x) •*-2g (x)] dx, где f (x) = g(x)=x при x < 0 и f (x) = x2, g(x) = x3 при x > 0.
3.3. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Правило дифференцирования произведения
d[Z(*)g(*)] = f' (X) g (х) + f (X) g' (X) dx
(см. гл. 4, § 2) приводит к методу вычисления интегралов, известному под названием интегрирования по частям. Согласно (1), имеем
b Jr£ , b ь
j dx = j f> g (x) dx + j f (x) g'.(x) dx,
a a a
270
5. Интегралы
и по основной теореме анализа, ь ь
f(x)g(x) £ = f'(x)g(x)dx + J f(x)g'(x)dx, a a
ИЛИ b b
J f (X) g' (x) dx = f (x) g (x) £ — j f' (x) g (x) dx. a a
Чтобы применить это правило к вычислению интеграла ь J q>(x)dx, а
(5)
надо сначала суметь представить <р(х) в виде f(x)g'(x)9 а затем найти первообразную функции f'(x)g(x).
фПример. Пусть мы хотим вычислить
1
J (1 — х)100 xdx.
—1
Положим f (х) = х, g (х) = — (1/101) (1 — х)101; тогда (1 — х)100 х = f (х) g' (х) и f'(х)g(х) = — (1/101)(1—х)101. Заметим, что —(1/101)(1—х)101 есть производная функции (1/101 • 102) (1—х)102. Далее, в силу (5)
+ -^ /(!-№ ““1 — J -1
_L_ I _
101 101 J 101 101 • 102
— 1
__ 2101 2102 __ 2101 Л 2 \
1оГ + 101 • 102 ~ ioF \ 102*/ ‘ ®
Правило интегрирования по частям удобно запомнить и применять, пользуясь некоторым обобщением обозначения Лейбница, описанным ниже.
3.4. ЯЗЫК ДИФФЕРЕНЦИАЛОВ
Заметим, что
^>- = /'(х); (6)
ах
запишем формально
df(x) = F(x)dx. (7)
Слово «формально» означает, что (7) есть всего лишь сокращенная запись (6).
Символdf(x) называется дифференциалом /(х), a dx — дифференциалом х. Мы небу-
§ 3. Интегрирование
271
дем, впрочем, на этом этапе придавать символам df(x),dx какого-либо значения сверх только что указанного. В этих обозначениях основная теорема принимает вид
d J f(t)dt = f(x)dx а И b
J df(x) = f(x)|\ а
Правила дифференцирования суммы функций и произведения функции на постоянную записываются в виде
d(f + g) = df 4- dg, d(cf)=cdf, а правило дифференцирования произведения— в виде d(fg) =gdf + fdg, , и правило интегрирования по частям — в виде ь ь
J fdg = fg £ — J gdf. a a
ф Пример. Используя эти новые обозначения, получаем (ср. выше, стр. 270)
1 ’ , 1 к
j (1 — х)100 xdx = fx d (--jjp (1 — x)1MJ =
—1 —1
=------x(l —I _ r /----------L_ 0 _ X)1O1\ dx =
101 J 101 ’ }
1-1 —1
_____-2^ + _L_ fd-xrdx_______________----------------L- fd(i-x)™«
101 101 J ' 101 101 102 ’
2101_____л-x)10211 - 2101 I 2102 a
101 101 102 ' |-i 101 101 • 102 ’ W
Иногда правило интегрирования по частям применяется несколько раз подряд, например
f (1 + х)1/3 xadx = f xad (— (1 + х) ) = 4 Сx8d(l + х) «
J X \ 4 / 4 J
₽ ± x«(l + х)4/3 Iе —7 f (1+ x)4/3 d (x8) =
4 10 4 J
Ill
5. Интегралы
= Л ад(1 + а)4/3 — А С (1 + Х)4/3 2xdx -
4 4 J
= 4 а2 (1 + а)4/3---3~ К d(4 (1 + х)7'3 ) =
4 2 \ 7 '
=4 а2о + °)4/3 - 4 fх d(1 +х)7/3 = 4 14 J
3 9/. , \4/3 9 /I । \7/31° < 9г,.. >7/3 .
= —а2(1+а) — — х(1+х) 4- — (14-х) dx =
4 14 io 14 J
= 4а2 (*+а)4/з~4а(1+a)7/3+4J 4d(1+x),0/3 = о
3 2/1 , \4/3 9 , >73 , 27 , >Ю/3|а
= —а2(1+а) — — а(1+а) +—— (14-х) =
4 14 140 |о
3 2/1 . \4/3 9 . >7/3 27 , >10/3 27
= — а2(1+а) — — а(1+а) +ттг(1+а) — — •
4 14 140 140
Из этого примера видно также, как пользоваться интегрированием по частям для вычисления первообразных. В самом деле, как видно из нашего вычисления, функция
3 2/1 I ч4/3 9 /II \7/3 I 27 /1 . \10/3
— х2(14-х) — — х(1 4-х) 4-—— (14-х)
4 . 14 140
есть первообразная функции х2(1 + х)4/3, что можно проверить дифференцированием.
УПРАЖНЕНИЯ
31. Пусть d (5х2 + х3) = / (х) dx; чему равно f (2)?
А 32. Пусть d(2]/^x 4-я4— l) = /(x)dx; чему равно f (1)?
33. Пусть d [х (х + I)6] = g (х) dx; чему равно g (— 1)?
34. Пусть d (t2/(t — 1)) = h(t) dt; чему равно h (2)?
35. Пусть d (и I У и2 4- 1) = f (и) du; чему равно f (и)? S
36. Пусть d J Ух2 + 1 dx = h (s) ds; чему равно h (1)? 1
37. Пусть f, g и h — дифференцируемые функции от х. Какие из следующих утверждений справедливы во всех случаях?
a) d(fgh) = (df)(dg)(dh);
б) d (fgh) = d(fg)h + fg dh;
B) (fgh) = fgh [(1/f) df 4- (1/g) dg + (l/Л) dh]t если f9 g и h не обращаются в нуль;
г) d(fgh) = (g/h) df 4- (h/f) dg 4- (f/g) dht если f9 g и h не обращаются в нуль.
§ 3. Интегрирование
273
38. Найдите функцию f, для которой df = ( х Z — 2 (х + I)8) dx.
39. Пусть x2df = (х3 — 1) dx и f (1) = 0; чему равно f (2)?
40. Пусть d (f + g) = xdx, d (f — g) = (1 — x) dx и f (0) = g (0) = 1; чему равны f (x) и g (x)?
41. Пусть d (xf) = (2 -I- 3 Yx ) dx и f' определена в точке 0; чему равно f (0)?
42. Пусть / (х) = х3 — 1 и g (х) = Зх — 1; для каких значений х df = dg?
В упражнениях 43—57 найдите заданные интегралы При этом полезно применить интегрирование по частям. В каждом случае, когда требуется найти неопределенный интеграл, проверьте ответ дифференцированием.
2 2
43. j х (3 — 2х)9 dx. 1 51. J (х2 4- 1) (х — 1)2/3 dx. 0
44. J х У х 4- 1 dx. 52. У |х2 /]/х 4] dx. '
45. 1 J х (2х — I)6 dx. 0 53. У [(0 4- 1)2/(о- I)4] do.
А 46. У (2г —3) у г — 3dz. 54. У К*2 + 0/(s 4- 4)в] ds.
47. 3 j [(Зх+ 1)/(х 4- 2)3] dx. —1 55. 1 У (у — I)2 Vy~dy. 0
48. У [(3 — 2и)/(1 — и)3/2[ <1и. 56. У (З/2 — 1) (2/ 4- 3)1’ dt.
49. 50. 1 У (9/4-(3/4- 2) di. С (х-Н 1)2х1/3 dx. •57. У(г4-1)‘/3 (z-l)3d2.
3.5. ЗАМЕНА ПЕРЕМЕННЫХ
Если переписать цепное правило (см. теорему 6. § 2 гл. 4) как правило интегрирования, то получается важное правило подстановки для замены переменной интегрирования:
Если х = ср(/) — функция с непрерывной производной <р'(0» определенная при а 0, и если = а, = Ь, причем значения 'С ft)
ходят за пределы отрезка [а, Ь]9 то
или У / (*) dx = у f (ф (/)) ф' (0 dt, (8) а а Ф (3) 0 У f(x)dx = У/(ф(0)ф'(/)Л. (8') Ф (а) а
274
5. Интегралы
Доказательство. Пусть F(x) — первообразная функция для f(x), т. е. F' (х) = f (х); тогда, по основной теореме,
ь
F (b) —F (а) = f (х) dx.
а
Положим G (t) = F (<р (0). По цепному правилу, G' (0 = ?'(ф (t))<f'(t) = = 7(ф(0)?(0- Следовательно, по основной теореме,
F (b) - F (а) = F (ф (?)) - F (ф (а)) = G (?) - G (а) = J G' (0 dt = а
3
= р(ф(0)ф'(0^.
Сравнивая два выражения для F(b) — F(a), мы убеждаемся в справедливости правила подстановки (8). Отметим, что в равенстве (8) функция ф не обязательно должна быть монотонной.
фПример. Проиллюстрируем применение этого правила. Пусть требуется вычислить
где ф (0 не обращается в нуль на отрезке [а, ?]. Положив f (х) = х~ъ, имеем в силу (8)
3 , ₽ v (0)
С У dt — I f (ф(О)ф' (t)dt = С f(x)dx [согласно (8')] =
«J <?(Z)2 OJ T(«)
-2Я 1 |’(₽) > 1
— I X *иХ = —_________I = — —____ ,
J х 1? <«> ср (а) <р(?)
<Р (а)
В итоге получаем формулу
Г<»>.Л = _!---------------' , (9)
J <р(02 <р(а) <р(Р)
которую можно было бы проверить и непосредственно, воспользовавшись правилом дифференцирования функции, обратной (в алгебраическом смысле!) данной функции. ф
Перепишем правило подстановки, поменяв ролями хи/:
Ь ф (6)
J (Ф (X)) ф'(х) «= j g(t)dt-, (10)
а Ф (а)
здесь ф(х) — функция с непрерывной производной, определенная при а х < Ь»
§ 3. Интегрирование
275
При применении правила подстановки главная трудность состоит в том, что надо суметь представить подлежащую интегрированию функцию (скажем, функцию аргумента х) в виде ^(ф(х))ф'(х), где^— функция, первообразная которой известна. Обозначения Лейбница могут подсказать здесь правильную догадку. А именно, пользуясь обозначениями Лейбница, мй могли бы следующим образов угадать правило подстановки (8). Чтобы подчеркнуть, что речь идет о функции от х, мы запишем подлежащий вычислению интеграл в виде
х—ь
J f (х) dx.
х=а Если
х = ср (/), то dx Г - -<р(0
и «поэтому»*
dx = ср' (/) dt.
Далее, если t = а, то х = а; если t = р, то х = Ь. «Подставляя», получаем t=$ x=b
J /(ф(О)ф' (ffdt = j* f(x)dx, t=a x=a
что и следовало ожидать.
Конечно, это не доказательство. Мы действовали так, как если бы dx и dt были числами, между тем как осмыслено лишь (слитное) выражение , но не «числитель» и «знаменатель» последней «дроби». Однако формальная процедура ведет к правильным результатам и ею удобно пользоваться, применяя правило подстановки. Проиллюстрируем это на примере, показывающем одновременно, как с помощью правила подстановки находить первообразные функции.
фПример. Пусть мы хотим вычислить
{ f(H-5x)"*/3dx.
5 У 1 + 5* о
Первообразная функции (1 + 5х)—1/3 нам не известна, но мы можем вспомнить, з
что -^-/2/3 есть первообразная функции /_|/3. Поэтому пробуем применить подстановку
1 + 5х = t.
* На этой стадии последующее равенство следует воспринимать как имеющее чисто символический характер (что подчеркивается употреблением кавычек): ведь ни его левая часть [т. е. dx], ни правая часть [<p'(f)dZ] не имеют реального смысла. Однако если развить «язык дифферен-^циалов» (см. § 3.4), то этому рассуждению можно придать и совершенно строгий смысл.
276
5. Интегралы
Рис. 5.26
Имеем — = 5, dx = — dt ах о
И
t = 1 при X = 0, t = 6 при X = 1.
Отсюда
Г<1 + 5л)-« dx - f г'я -Ldt - -L • — Л’Г = A 6s’ — — - А (^36 -11.
J ' ' ]) 5 5 2 11 10 10 10 >
Просматривая вычисления, видим, что первообразная для (1 4-5х)—1/3 есть (3/10) t*3, т. е. (3/10) (14- 5х)2/3. Итак,
d / 3 R .2/з \ .. , _ .-1/3
ТТ7(1+5х) =(14-5х)
dx \ 10 /
Конечно, это можно проверить дифференцированием, ф
Излишне упоминать, что не каждая подстановка ведет к упрощению. Когда подстановка выгодна и какую именно подстановку следует применить — все это может подсказать лишь опыт.
3.6. ИНТЕГРАЛЫ ОТ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЯ
Укажем еще одно приложение правила подстановки. Напомним, что функция f(x) называется четной, если /(—х) = /(х), и нечетной, если /(—х) = —f(x).
Функция четна в том и только в том случае, когда ее график симметричен относительно оси у, нечетна в том и только в том случае, когда ее график симметричен относительно начала координат (см. гл. 3, § 1). Поэтому (рис. 5.26)
§ 3. Интегрирование
277
b —д
J f (x) dx — § f (x) dx, если f четна, a —b
b —a
J f (x) = — J f (x) dx, если f нечетна, a —b
(11)
(12)
Докажем (11) аналитически. Воспользуемся подстановкой х = —t, dx = —dt\ t = —а при x = a, t — —b при x = b. Тогда для четной функции f имеем
j f (x) dx = p (-1) d (- 0 = - p (/) dt = J f(t) dt. д — Д —ci —b
Та же подстановка доказывает (12); предлагаем читателю проверить это самостоятельно.
УПРАЖНЕНИЯ
В упражнениях 58—79 вычислите заданные интегралы. В каждом случае найдите надлежащую подстановку. Там, где требуется найти неопределенный интеграл, проверьте ответ дифференцированием.
58. 2 j (2х — 3) dx. 1 65. /2 C x<^x
J (^+1)3 ' — I
59. с * 66. f [ \ \ I 1 \l/2 J “
J /3+&
60. f (*-D3 67.
J (1 + (X- 1)*)» 1
61. + (\—2y)4dy. A 68.
i/t </ ' 0
Г £i+y,-. J Vy
62. § z/z2+ 4 dz. 0 69.
63. i p u2du 70. a
J (2-uV * J x3 У 1 4- x4 dx.
64. f ——г+1 и 71. C ( —3/5 1/5 \l/3 j J (У + У ) dy.
J (га 4-2z + 3)2/3 dZ*
[Указание: в упр. 71 перед выбором подстановки попробуйте сделать некоторое алгебраическое преобразование.!
278
5. Интегралы
J /i-yd + zr^)2’
c cd + K^^+l)3 л I ----- ' ---- dv.
J + 4
j* X3 + 6x
J (x3 + 2)3
9 ________
77 • j* j/1 + Vy~ dy-0
78. I —---------------— dt.
) l/з ш
3.7. ЗАМЕЧАНИЕ О НЕСОБСТВЕННЫХ ИНТЕГРАЛАХ
b
В некоторых случаях символ ^f(x)dx обозначает вполне определенное число, хотя а
функция / не ограничена или интервал (а, Ь) не конечен, так что определение, данное в § 1, неприменимо. Такие «несобственные» интегралы мы рассмотрим в Приложении (см. § 6).
§ 4. ПЛОЩАДЬ.
ОБЪЕМ. ДЛИНА
4.1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
Сначала мы рассмотрим площади плоских областей. Как мы знаем, площадь области («криволинейной трапеции»), ограниченной осью х, прямыми х = а и х—Ь и графиком неотрицательной функции у = f(x), равна
ь
J f (х) dx. а
Только что сделанное утверждение можно истолковать двояко. Мы можем считать, что нам известно, что такое площадь, и рассматривать предыдущее утверждение как определение интеграла; е другой стороны, мы можем считать интеграл определенным аналитически, как в § 1.8, и рассматривать это утверждение как определение площади для области под графиком функции. (Далее мы будем предпочтительно считать более удачной вторую точку зрения.)
Рассмотрим теперь площади иных областей, отличных от «криволинейных трапеций». Оказывается, эти площади также можно выразить интегралами. Сначала допустим: нам известно, что такое площадь и речь идет только о вычислении площадей. После этого обратим наш ход мыслей, превратив метод вычисления площадей в их определение.
§ 4. Площадь. Объем. Длина
279
Пусть 7? — «хорошая» плоская область, т. е. множество точек плоскости, лежащих внутри гладкой замкнутой кривой (рис. 5.27) или между несколькими такими кривыми (рис. 5.28; как уже указывалось выше, точного определения понятия площади мы пока не даем*). Мы хотим вычислить площадь S области 7?.
Возьмем прямую L, выберем на ней начало отсчета О и положительное направление, которое назовем направлением «вправо». Пусть Mt (где t — произвольно заданное число) — прямая, перпендикулярная L и пересекающая L в точке, удаленной от О на (положительное или отрицательное!) расстояние /. Предположим для простоты, что наша область R целиком расположена между прямыми Ма и Мь, где а < b (рис. 5.29). Обозначим через S(t) площадь той части /?, которая лежит слева от Mt\ тогда S(a) = 0, поскольку вся область R лежит справа от Ма, и S (b) = S, поскольку вся область 7? лежит слева от Мь. Отсюда S = S(b) — S(a) и в силу основной теоремы
ь s = j S' (/) dt, а
если функция S(t) имеет ограниченную, кусочно-непрерывную производную. Так как S(t) = 0 при t < а и 5(7) равна постоянной S при t > b, то £'(/) = 0 при t < а и t> Ь, так что последний интеграл можно записать и не уточняя пределов интегрирования:
S = J S' (О dt.
—со
Что же такое, однако, S'(0?
Пересечение области 7? с прямой Mt есть множество точек, принадлежащих и /?, и Mt (на рис. 5.29 это множество состоит из трех отдельных отрезков). Длина пересечения /(/) определяется во всех случаях, когда пересечение состоит из одного или нескольких отдельных отрезков и конечного числа точек: /(/) есть сумма длин составляющих пересечение отрезков (произолированные точки, входящие в состав этого пересечения, мы можем попросту забыть). Если пересечение пусто или сводится к конечному числу точек, то /(/) = 0.
Пусть h — малое положительное число. Тогда S(t + й) — S(0 есть площадь части 7?, заключенной между прямыми Mt и Mt+h. Если пересечение 7? и Mt состоит из одного или нескольких отрезков, то площадь S(t + h) — S(t) мало отличается от площади одного или нескольких прямоугольников общей высоты 1(1) и ширины й, как это видно из рис. 5.30 и 5.31. Следовательно, разность S(t + й) — S(t) приближенно равна /(/)й, так что
S(t + h)-S(t) z
* Читателей,^ заинтересованных в строгом определении (интуитивно ясного) понятия площади плоской области, не апеллирующем к понятию интеграла, можно отослать, например, к доступно написанной, хотя все же не очень простой для начинающего статье: В. А. Рохлин, Площадь и объем, «Энциклопедия элементарной математики», кн. V (геометрия), М., «Наука», 1966, с. 5—87.
280
5. Интегралы
Рис. 5.31
§ 4. Площадь. Объем. Длина
281
Рис, 5.34
Можно предположить поэтому,что S'(f) = l(t) и, следовательно,
со
S= j l(t)dt.
—со
(1)
Соотношение (1) мы назовем формулой площадей.
4.2. ОПРЕДЕЛЕНИЕ ПЛОЩАДИ
Теперь мы изменим нашу первоначальную точку зрения и определим площадь. За определение площади мы просто примем формулу (1). (Это законно, поскольку в § 1 мы дали аналитическое определение понятия интеграла, не обращаясь к понятию площади, а пользуясь только числами.) Множество R точек плоскости мы назовем областью с площадью S, если к R применима формула (1), т. е. если существует такая прямая L, для которой интеграл (1) имеет смысл и может быть вычислен.
Покажем, что в простых случаях формула площадей приводит к ожидаемым результатам.
Пусть область R ограничена осью х, прямыми х = оих = &>аи графиком положительной непрерывной функции g = f(x) (рис. 5.32). В качестве прямой L мы выберем ось х. Тогда l(t) = /(/) при а t Ь и /(/) = О при t < а и t > Ь. По формуле площадей
<$= J l(f)dt—^f(t)dt,
—<х> а
как и следовало ожидать.
Другой пример представляет площадь, заключенная между двумя графиками функций. Пусть функции /(х) и£(х) ограничены и кусочно-непрерывны при а х < Ь\ допустим, что g(x) /(х). Обозначим через R область, ограниченную графиками этих функций и прямыми х = а, х = 6; пусть S — площадь R. Тогда, как видно из рис. 5.33 (где и f и g положительны) или из рис. 5.34 (где f положительна, a g отрицательна), имеем
282
5. Интегралы
Рис. 5.35
b b
S = J fix) dx — j g (x) dx. a a
Это можно переписать так: b s = j U(x) — g(x)] dx. a
Если выбрать в качестве L ось х9 то /(/) = /(/) — g(f) при а < t < b, но 1(f) = о при t < а и t > Ь. Следовательно, последнее равенство эквивалентно формуле площадей.
Чтобы оправдать определение площади с помощью формулы (1), нам следовало бы показать, что определенная таким образом площадь обладает обычным свойством аддитивности площадей, т. е. что площадь области, составленной из двух неналегающих областей R{u равна сумме площадей Ri и R2. Далее, надо было бы показать, что вычисление площади одной области R по формуле площадей (1) при разных прямых L приводит к одному и тому же результату. Оба утверждения можно доказать, пользуясь аналитическим определением интеграла и обычными свойствами чисел. Но это легче сделать в контексте анализа функций нескольких переменных; поэтому мы отложим доказательство этих фактов до гл. 13.
В качестве иллюстрации вычислим двумя различными способами площадь, ограниченную параболой у = х2 и прямыми х = 0 и у = 1 (рис. 5.35, а). Если принять за прямую L ось х (рис. 5.35, б), то имеем
1(f) = 1 — /2 при 0 < / < 1, /(f) = 0 при t < 0 , t > 1,
и, следовательно, искомая площадь
I / /з \ 1 12
S= f(l-/2)^ = [t- -i-)1 = 1 - 4= 4-. j \ 6 J о о о
Если же принять за L ось у (рис. 5.35, в),
то 1(1) = ]/гГ~ при 0 < t < 1, /(/) =0 при /<0, /> 1, и
s= I* =_L,
J a l0 6
§ 4. Площадь. Объем. Длина
283
как и выше. Это совпадение вряд ли кого-либо удивит, но все же оно действует ободряюще, подкрепляя нашу уверенность в целесообразности принятого опреде
ления площади.
Из формулы площадей следует также, что две области с одной и той же функцией l(t) имеют одинаковую площадь. Это знаменитый принцип Кавальери. Его геометрическое истолкование можно усмотреть из рис. 5.36: две области на этом рисунке имеют одинаковые функции 1(1) и одинаковые площади.
Существуют и очень сложные области, к которым формула площадей неприменима; однако в обычных приложениях анализа такие области никогда не встре-
чаются.
ф Примеры. 1. Найти площадь S, заключенную между кривой у = х3 и прямой у = х (рис. 5.37).
Решение. Область состоит из двух кусков. Примем за прямую L ось х. Тогда
о X3— X X — X3
О
при x<Z— 1,
при — 1 < х < О, при 0<х<^ 1, при х> 1,
l W =
как это видно из чертежа. Следовательно, по формуле площадей/
1 о 1
S = J I (х) dx = f (х3 — х) dx 4- j (х — х3) dx = —1 —Г о
10 л- (—_—I1 = — (—_Ц д. (J._L3_L
(4 2 Л-1 + К 2 4 /1о~ \ 4 2 / + ( 2 ’ 4 2 ‘
284
5. Интегралы
2. Найти площадь, заключенную между параболой у = х2, осью у и касательной к этой параболе в точке (1, 1) (рис. 5.38).
Первое решение. Уравнение касательной есть у = 2х — 1. Следовательно, приняв за L ось х, имеем /(х) = х2— 2х + 1 при 0 х < 1 и /(х) = О при х<0 и х> 1. По формуле площадей
Второе решение. Площадь под параболой от 0 до 1 равна 1/3. Площадь треугольника I равна 1/4, и такова же площадь треугольника II. Отсюда
УПРАЖНЕНИЯ
В упражнениях 1—15 найдите площадь области, ограниченной заданными кривыми. До применения формулы площадей начертите заданную область. При этом может оказаться полезным воспользоваться различными единицами длины для двух координатных осей.
1. 1/3 У = х , х = 0 и у = 1. 6. у = — х2 и у = х* — 20.
2. у = X2 и 7. * 1 сч II S * II
3. у = X3 и У = х2. 8. </ = х2, у = (х — I)2 и у= 1/9.
4. 1/3 У = * 1/5 и у = х . 9. у—х, у = х2-\-\, х=0ир=2.
5. У = Vx , у = х— 2 и х=0. 10. х + У — 1 , х+у = —1, х — у = 1 И X—у
§ 4. Площадь. Объем. Длина
28$
11. у = х3, у = 0 и касательная к кривой у=х3 в точке (1, 1).
12. у = У~х , у = 1/4 х и нормаль к кривой у = х в точке (1, 1).
13. г/2 = х и y — Vx (*2 — О-
А14. (/ = №—12х и у=х2.
15. у =я х3 — хи касательная к кривой у = х3 — х в точке х = — 1. [Указание: учтите» что касательная и кривая заведомо пересекаются при х = 1. j
Г
f Уг2 _ /2 dt.
4.3. ПЛОЩАДЬ КРУГА. ЧИСЛО П
В качестве еще одного примера вычислим площадь круга, т. е. площадь области» заключенной внутри окружности
х2 + у2 = г2.
Ясно (рис. 5.39), что
I (0 = 2 У г2 — t2 при — г < / < г и 1(f) = 0 при 111 > г.
Поэтому площадь г 0 ______
2 У/-2 — /2 dt = 2 J /г2 — /2 dt + 2 —г
В первом интеграле сделаем подстановку:
/= — rx, dt = — rdx\ t= — г при х = 1, /=0прих=0.
Во втором интеграле сделаем подстановку: t = rx, dt = rdx-, t = 0 при x = 0, t — г при х = 1.
286
5. Интегралы
Окончательно получим
О . I
(2)
Определим теперь число л как площадь круга радиуса 1. Тогда имеем
к = 4 — х2 dx.
(3)
Заметим, что поскольку интеграл может быть определен аналитически, число л можно считать также определенным в помощью формулы (3), безотносительно к геометрии. Позже мы покажем, что л есть также отношение длины окружности к длине ее диаметра.
Теперь мы можем истолковать результат (2) следующим образом: площадь круга радиуса г равна лг?. _____
Заметим еще, что функция у = — х- убывает при 0 < х < 1, так как в этом
интервале = —x/]/^ 1 — х?< 0. Поэтому л можно вычислить а любой требуемой точностью, вычислив интеграл (3) по методу § 1,.Лучшие методы будут изложены в гл. 8.
Число л иррационально; его десятичное разложение имеет вид
тс = 3,1415926535
оно бесконечно и не имеет периода, чего мы здесь не станем, впрочем, доказывать. С помощью электронных вычислительных машин теперь нетрудно вычислить тысячи знаков этого числа. Иначе обстояло дело до появления машин и до изобретения логарифмов. Как показал Архимед,
а когда Лудольф около 1600 г. вычислил 35 знаков п, это достижение произвело на математиков столь сильное впечатление, что л долго называли «числом Лудольфа»*.
44. ВЫЧИСЛЕНИЕ ОБЪЕМОВ
Займемся теперь вычислением объемов. Пусть У? — плоская область площади S. Построим для каждой точки /? отрезок длины Я о началом в этой точке, перпендикулярный содержащей /? плоскости; пусть все эти отрезки лежат по одну и ту же
* По поводу истории числа к см., например, Ф. Кымпан, История числа тс, М.» «Наука», 1971.
§ 4. Площадь. Объем. Длина
287
Рис. 5.40
сторону /?. Тело в пространстве, образованное всеми этими отрезками, называется прямым цилиндром с основанием 7? и высотой Н (рис. 5.40). Элементарная геометрия учит, что объем такого цилиндра V = SH, во всяком случае тогда, когда 7? — многоугольник или круг. Мы покажем, как можно прийти к этой формуле, пользуясь формулой для объема прямого параллелепипеда, интуитивным понятием объема и основными идеями анализа.
Мы будем использовать декартову систему координат в пространстве (см. гл. 2, § 1.4). Пусть 7? — область плоскости хус площадью S; предположим, что она ограничена гладкой кривой. Прямой цилиндр с основанием 7? и высотой Н есть множество С всех точек (х, у, г), для которых (х, у) принадлежат 7? и 0 г (рис. 5.41).
Допустим, что область 7? заключена между прямыми х = а и х — Ь (где b > а). Обозначим через V(t) объем части С, лежащей слева от плоскости х = t. Тогда V(a) — 0, а У(6) есть полный объем С. Если функция V(t) имеет ограниченную, кусочно-непрерывную производную У'(7), то V =j V'(t)dt, что можно записать также а в виде
V= J V'(t)dt, —со
поскольку V'(/) = 0 при t <_ а и при t > b.
Пусть h — малое положительное число. Тогда V(t + /г) — V(t) есть объем слоя С, заключенного между плоскостями x=tnx=t-}-h. На рис. 5.41 мы изобразили случай, когда плоскость х= t пересекает 7? по одному отрезку длины /(/). Слой С между х =t и х= / + h приближенно можно считать параллелепипедом с площадью основания h- 1(f) и высотой И. Объем этого слоя приближенно равен Отсюда
288
5. Интегралы
Рис. 5.41
Это приводит к предположению, что
У'(О=Я/(/), и потому
J 1(f) dt.
V= J Hl(t)dt = H
ОО
Поскольку по формуле площадей f l(f)dt = S, имеем
V =SH.
В частности, если основание /? есть круг радиуса г, получаем известную формулу
V = кг2Н.
Теперь мы выведем формулу для объема тел более общего вида, действуя так же, как и в случае площадей. Сначала, свободно пользуясь нашей геометрической интуицией, мы предположим, что нам известно, что такое объем, и требуется только его вычислить. Затем мы превратим метод вычисления в определение понятия объема.
§ 4. Площадь. Объем. Длина
289
W)
Рис. 5.42
Рассмотрим «хорошее» тело В; пусть его объем равен V. Чтобы вычислить V, выберем прямую L, точку отсчета О на этой прямой и положительное направление на ней. Для простоты допустим, что пересечение с В любой плоскости Р, перпендикулярной L, состоит из одного куска. Пусть Pt — такая плоскость, t — расстояние этой плоскости от О (положительное или отрицательное). Обозначим через 5(0 площадь пересечения Pt с В (рис. 5.42).
Предположим, что В заключено между плоскостями Ра и Рь, где а < Ь. Пусть V(t) обозначает объем части В, заключенной между Ра и Pt. Тогда V(a) = 0 и V(b) = V.
Разность V(t + h) — V(t) есть объем тонкого слоя, приближенно представляющего собой цилиндр высоты Л, в площадью основания S(t) (рис. 5.42).
Поэтому V(t + h) — V(t) близко к S(t)h9 дробь
и можно рассчитывать, что
V"(0 = Hm + *> — = £(/).
fc-H) h
b
Но тогда, по основной теореме анализа, V = JS(0d/. a
Заметив, что S(t) = 0 при t < а и при t> b, можем записать это в виде
Js(t)dt. (4)
^—СО
Назовем равенство (4) формулой объемов. Из нее вытекает принцип Кавальери для (пространственных) тел: если два тела имеют одну и ту же функцию S(t), то их объемы равны.
290
5. Интегралы
4.5. ОПРЕДЕЛЕНИЕ ОБЪЕМА
До сих пор мы считали понятие объема известным, а к формуле (4) пришли с помощью целенаправленных догадок. Теперь мы изменим точку зрения и определим объем с помощью формулы объемов (4). Эта формула применима к таким множествам В точек пространства, для которых при надлежащем выборе прямой L пересечение Вс Pt есть область, имеющая площадь S(/), причем определен интеграл (4). Формула объемов применима не ко всем без исключения пространственным телам; однако тела, в применении к которым эта формула пасует, в приложениях не встречаются и их совсем не просто обнаружить — для этого надо солидно потрудиться.
Следовало бы показать, что определенный таким образом объем обладает обычными свойствами и не зависит от выбора прямой L, Это сделать можно, но доказательство упрощается, если применить технику анализа функций многих переменных; поэтому мы отложим его до гл. 13.
УПРАЖНЕНИЯ
В упражнениях 16—20 используется следующее обозначение: запись ((х, у) |...} обозначает множество точек (х, у), удовлетворяющих условию ...; так, например, {(х, у) | у = 0} — это ось х.
±16 Основание тела есть треугольник {(х, у) | О^х^. 1, 0<^%х) плоскости ху. Каждое сечение, перпендикулярное оси х, есть квадрат;. Вычислите объем тела
17. Основание тела есть треугольник {(х, у) | 0 х1, 0 у х) плоскости ху. Каждое сечение, перпендикулярное оси х, есть полукруг Вычислите объем тела. (Вспомните, что площадь круга радиуса г равна яг2.)
18. Основание тела есть квадрат {(х, у) | 0 < 1, 0у 1} плоскости ху. Каждое
сечение перпендикулярное оси х есть треугольник. Верхние вершины всех треугольных сечений лежат на прямой, соединяющей точку х = 0, у = 1/2, г = 2с точкой х = = 1, у — 1/2. г = 1 Вычислите объем тела.
19. Основание тела есть круг {(х, у) | х2 + 1). Каждое сечение, перпендикулярное
оси х есть квадрат Вычислите объем тела.
20. Основание тела есть треугольник {(х, у) I —1 х<С L | х | 1} плоскости г = 0.
Каждое сечение, перпендикулярное оси уУ есть треугольник Верхние вершины всех тре угольных сечений лежат на четверти окружности {у, г\у2Ч-г2=1, у > 0, г > 0} в плоскости х = 0. Вычислите объем этого тела.
21. Вычислите объем шара радиуса ft, пользуясь формулой объемов. (У к а з а н и е: воспользуйтесь тем, что плошадь круга радиуса г равна яг2.]
22. Вычислите объем прямого кругового цилиндра с радиусом основания ft и высотой Н пользуясь формулой объемов и приняв за L прямую, перпендикулярную оси цилиндра
23. Вычислите с помощью формулы объемов объем прямого кругового конуса с высотой Н и радиусом основания ft.
4.6. ТЕЛА ВРАЩЕНИЯ
Рассмотрим плоскую область R под графиком функции у = Дх) от а до b (рис. 5.43); функцию мы считаем здесь неотрицательной. Если область R поворачивается вокруг оси х на 360° (один полный оборот), то она «заметает» некоторое тело В, называемое телом вращения.
Чтобы вычислить объем V тела В, выберем в качестве L ось х. Тогда пересечение плоскости Pt с В есть кр\г радиуса /(() при a<Z К. Ь. Отсюда S(f) = л/(()2 при
§ 4. Площадь. Объем. Длина
291
У
Рис. 5.43
а < / < Ь и, очевидно, S(t) = 0 при t < а и при t> Ь. Общая формула объемов
принимает теперь вид
ь
V = « J/(О2 dt.
<5)
Это и есть формула для объема тела вращения. Конечно, ее можно применять и в тех случаях, когда ось вращения не совпадает с осью х.
Пусть, например, R — область, ограниченная кривой х = f(y), а у Ъ, осью у и прямыми у = ану = Ь, и В — тело, заметаемое R при повороте вокруг оси у на 360° (такое тело рассмотрено ниже, в примере 2). Тогда объем В выражается той же формулой (5); действительно, объем не зависит от наименований осей.
фПримеры. 1. Найти объем, полученный вращением вокруг оси х области под параболой у = х2 от х = 0 до х = 2 (рис. 5.44).
Решение. Имеем а = 0, b = 2, f(t) = t2 и
2
V = К f tkdt = К — |2 = —
J 5 Io 5
2. Найти объем, полученный вращением вокруг оси у области, ограниченной дугой параболы у = х2 от х = 0 до х = 2, осью у и прямой у = 4 (рис. 5.45).
Решение. В этом случае а == 0, Ь = 4, /(/) = УТ. В силу (5)
V = к С tdt = к — I4 = 8те.
J 2 10
292
5. Интегралы
3. Найти объем, полученный вращением вокруг оси д области под параболой у = х2 от х = 0 до х = 2 (рис. 5.46).
Первое решение. Применим формулу (5), приняв за L ось у. При О < / < 4 пересечение нашего тела с Pt есть круговое кольцо с радиусами граничных окружностей 2 и У t (рис. 5.47). Для таких t имеем £(/) = л-22 — nt = л(4—/); далее, S(t) = 0 при / < 0 и при t > 4. Следовательно,
4 4
V = —/)Л =«(4/ ——У = 8«.
о о’ \ 2 /0
§ 4. Площадь. Объем. Длина
293
Рис. 5.47
Второе решение. Рассматриваемое тело вместе с телом, объем которого вычислен в примере 2, составляет круговой цилиндр с радиусом основания 2 и высотой 4; объем цилиндра равен 16л. Поэтому искомый объем равен 16л—8л = 8л.ф
4.7. ШАРЫ И КРУГОВЫЕ КОНУСЫ
Шар радиуса г получается вращением вокруг оси х области под кривой у = = г2— х2 от —г до г (рис. 5.48).
Объем шара можно найти по формуле (5), полагая
а = — г, b = г, f(t) = /г2 — /2.
Он равен
V = К J (г2 — /2) dt = Л (r2t~ -у) |г ,
ИЛИ
v=4"w'3- <6>
Прямой круговой конус радиуса г и высоты Н получается вращением вокруг оси х области под прямой у = (г/Н)х от х =0 до х = Н (рис. 5.49). Из (5) находим объем конуса:
или
V = — г2Н.
3
(7>
294
5. Интегралы
Рис. 5.48
Рис. 5.49
Рис. 5.50
Рассмотрим теперь круговой цилиндр, радиус основания которого равен его высоте, вписанный в него полушар и конус, в свою очередь вписанный в полушар (рис. 5.50). Как вытекает из только что выведенных формул, объемы этих тел относятся как 3:2: 1. Этот прекрасный результат был получен еще Архимедом.
Древние греки всегда выражали формулы для длин, площадей и объемов как утверждения об отношениях «подобных» величин. Они справедливо причисляли формулы для объема шара и кругового конуса к высочайшим достижениям своей математики. Впервые эти формулы были открыты философом-материалистом Демокритом, но строгое доказательство их было дано лишь математиком Евдоксом, другом идеалиста Платона. (Термины «идеалист» и «материалист» применяются здесь в их философском смысле и вовсе не означают, что в этическим смысле Платон
§ 4. Площадь. Объем. Длина
295
был выше Демокрита.) Идеи Платона и его ученика Аристотеля в течение столетий господствовали в культуре Запада; между тем ни один из трудов Демокрита не сохранился*. Математики узнали об открытии Демокрита лишь благодаря случайной находке в 1906 г. рукописи давно утерянной книги Аристотеля. Из этой книги стало известно также, что метод Демокрита основывался на «математическом мифе», подобном описанному в § 1; этот метод был в некоторых отношениях родствен математическому анализу.
УПРАЖНЕНИЯ
24. Найдите объем тела, образованного вращением вокруг оси х области под графиком функции у= 1—х2 от х = 0 до х = 1
25. Найдите объем тела образованного вращением вокруг оси у области под графиком функции // = 1 — х2 от х = 0 до х = 1
26. Найдите объем тела, образованного вращением вокруг оси х области под графиком функции у — х3 от х = 0 до х = 1.
27. Найдите объем тела, образованного вращением вокруг оси у области под графиком функции у = (2х + 1^1/3 от х = 0 до х = 13.
28. Найдите объем тела, образованного вращением вокруг оси х области под графиком функции у = Мх от г — 1 до х = а > 1 (Что происходит с этим объемом при а-> оо?)
29. Найдите объем тела образованного вращением вокруг оси х области, ограниченной кривыми у = х х = 0 и у — 1
30. Найдите объем тела, образованного вращением вокруг оси у области, ограниченной кривыми у = ]Л. г = 0 и t/= I
31. Найдите объем тела образованного вращением вокруг оси х области ограниченной кривыми и = 1 — г2 у = х и и = 0. (Обратите внимание на то, что кривая у = 1 — х2
есть не что иное как верхняя половина окружности х2 + у2 = 1.)
32 Найдите объем тела, образованного вращением вокруг оси у области, ограниченной кривыми у = 1 — х2, у = х и у = 0.
33. Найдите объем тела, образованного вращением вокруг оси х области, ограниченной кривыми у = х2 + 1, х = 0 и касательной к кривой у — + 1 в точке х = 1.
Д34 Найдите объем тела, образованного вращением вокруг оси у области ограниченной кривыми у — х2/3 х = 0 и касательной к кривой у = х2/3 в точке < — I
35. Найдите объем тела, образованного вращением вокруг прямой у = —I области, ограниченной кривыми 0 = 4 — х2 п у = 3.
36. Найдите объем тела, образованного вращением вокруг прямой х = — 1 области, ограни генной кривыми у = 1/(х + 1), х = 0. х = 1 и у = 0.
37 Найдите объем тела, образованного вращением вокруг прямой х = —2 области, ограниченной кривыми у = х3 и у = х.
38. Найдите объем тела, образованного вращением вокруг прямой у = 2 области, ограни ченной кривыми у = х$ и у = I
39 Найдите объем тела, образованного вращением вокруг прямой х = —2 области, ограниченной кривыми и = х3 х — —1 г = 0 и и — 4.
ДЕМОКРИТ из Абдеры (он. 460—370 до н. в.) был основоположником греческого «атомизма», возможно, вместе с философом Левкиппом. Он внес свои вклад в большинство областей знания, но из его многочисленны работ до нас дошло лишь несколько отрывков.
Демокриту принадлежит смелая идея — объяснить мир движением неизменных, неделимых атомов в пустом пространстве.
* Видимо, не без участия в «исчезновении» всех работ Демокрита последователей Платона <а может быть, и его самого?) что может сложить дополнительной иллюстрацией к заключенному в скобках замечанию автора.
296
5. Интегралы
40. Найдите объем тела, образованного вращением вокруг оси у круга (х — 4)2 + у2 < 1 [т. е. круга с центром (4, 0) и радиусом 1]. (Такое тело называется тором.)
41. Найдите объем, заключенный внутри цилиндра дга + уй= 1, 0-^ 1 и находящийся
между плоскостью z = 0 и плоскостью z = х (т. е. плоскостью, пересекающей плоскость основания г = 0 по оси у под углом 45°).
42. Найдите объем, заключенный внутри сферы х2 + у2 + z2 = 1 и под плоскостью z = 1/2.
43. Две цилиндрические трубки, каждая диаметром в 2 см, пересекаются под прямым углом (так, что оси их лежат в одной плоскости). Найдите объем их общей части.
4.8. ДЛИНА
Как мы сейчас увидим, вычисление длин кривых также приводит к интегралам. Допустим сначала: нам известно, что такое длина кривой, — и воспользуемся этим для того, чтобы высказать разумную гипотезу о способе ее вычисления. Затем мы определим длину с помощью полученной формулы.(Вспомним, что точно так же мы поступали при определении площадей и объемов.)
Рассмотрим график гладкой функции у = /(х), а < х < Ь и обозначим его длину через I. Пусть 1(1) означает длину части кривой, соответствующей значениям х между а и t. Тогда 1(a) = 0, 1(b) = /, и если l(t) — «хорошая» функция, то, по основной теореме,
ь
1 = ^1' (О dt. а
Чтобы найти /'(/)» возьмем малое положительное число h и рассмотрим разност** ное отношение
/(/ -f-A)-Z(Z)
h
Числитель есть длина малой дуги кривой, лежащей над интервалом [/, t 4- h\. Сделаем теперь следующее предположение: если заменить дугу кривой, отвечающую значениям х, заключенным между t и t 4- h, ее касательнойв точке (t9 f(t))t то происходящая от этого погрешность в вычислении разностного отношения будет очень м гла (рис. 5.51).
Замена кривой ее касательной означает, что на этом рисунке длина дуги PQ заменяется длиной отрезка PQ'; последняя же, как видно из того же рис. 5.51, равна
4- (mh)2 = h ]/1 4- т2.
Но, по определению производной, т = /' (/). В силу этого отношение |/ (/ 4- h)— I (t)]/h приближенно равно
. ]Л1 _|_ f (/)3.
h
§ 4. Площадь. Объем. Длина
Предположим поэтому, что /'(/) = /I + /' тогда
I = J К1 +/'(02dt а
Мы назовем это равенство формулой длин.
Изменим теперь нашу точку зрения и определим длину участка графика функции у = /(х), отвечающего таким значениям х, что а < х < Ь, с помощью формулы (8). Эта формула применима, если рассматриваемая функция имеет ограниченную кусочногнепрерывную производную.
Если кривая не является графиком функции (как, например, кривая, изображенная на рис. 5.52), но может быть разбита иа несколько дуг, являющихся графиками функций (таковы дуги PQ, QR и RS на рис. 5.52), то мы определим длину кривой как сумму длин этих дуг. Остается показать, что наше определение длины не зависит от положения координатной системы; это будет сделано в гл. 11, § 3.10.
фПримеры. I. Вычислить длину прямолинейного отрезка, соединяющего точки (—2, 4) и (3, 5).
Первое решение. По формуле расстояний
I = /(—2 —З)2 4- (4 —5)2 = /26.
Второе решение. Уравнение прямой, соединяющей две точки, имеет вид (см. гл. 2, § 2)
5) (__ 2 — 3) = (4 — 5) (х — 3),
или
22 5
По формуле длин
298
5. Интегралы
как и следовало ожидать.
2. Найти длину графика функции х i-> у = х3/2 между х = 1 и х = 2.
Решение. По формуле длин
//2 4 л/ f 9 1 _ 4 / 2 /3,г\ I2274 _ 223/2 - 1з3/?
J/ • —d/ [полагая | + —ж-/]-— Щ------------------
УПРАЖНЕНИЯ
В упражнениях 44—53, применив формулу для длины дуги, найдите длину заданного графика между заданными точками.
44. f (х) = (х 4- 1)3/2 между х = 3 и х = 8. 2/3
45. g (х) = х — 1 между х = 8 и х = 27.
Замечание. Функции, заданные в упр. 44 и 45, взаимно обратны и, следовательно, кривые, длина которых подлежит вычислению, «одинаковы». (Точнее, одна кривая получается из другой отражением от прямой у = х.)
Л
46. f (х) = J У t2—1 dt между х=1 и х=3.
47. f (х) между х = 1 и х = а (а >> 1), где у = f (х) — любое решение дифференциального уравнения dytdx = (х4 — 1) /
48. f (х) = (1/3) (х2 4- 2)3/2 между x = V<2 и х=р<7.
49. f (х) = (2/3) х3/2— (1/2) х1/2 между х = 1 и х = 4.
50. f (х) = (5/6) х6/5— (5/8) х4/5 между х = 1 и х = 32.
51. f (х) = (5/48) ( х4/54- 1)3/2 между х=1/32их=1.
52. f (х) = х4/4 4~ х”2/8 между х—1 их=2. X
53. f(x) = j [t 4- l/t + 1]1/2 между х=1их = 4.
64. Пусть Р(а, Ь) и Q(c, d) — две различные точки плоскости; допустим для простоты, что а с и b d. Найдите уравнение прямой, проходящей через Р и Q, и, применив формулу для длины дуги, вычислите расстояние между Р и Q. Покажите, что Ваш ответ соглас уется с формулой расстояний.
§ 4. Площадь. С бьем. Длина
299
4.9 . КРУГОВЫЕ СЕКТОРЫ. ДЛИНА ОКРУЖНОСТИ
Мы докажем с помощью формулы длин две теоремы элементарной геометрии:
Площадь кругового сектора равна половине произведения его радиуса на длину его дуги.
Длина окружности равна 2л г, где г — радиус и л — число, следующим образом определяемое с помощью интеграла:
у = J У I — х2 dx
О
(см. § 4.3). (Поскольку мы уже знаем, что площадь круга равна лг2. а круг может быть разбит на секторы, вторая теорема следует из первой.)
Для упрощения записей рассмотрим случай круга единичного радиуса. Надо показать, что: (I) площадь кругового сектора радиуса I равна половине длины его дуги', (II) длина окружности радиуса 1 равна 2л.
Примем центр круга за начало координат О; пусть а и b — такие числа, для которых — I 1, и Р, Q — точки верхней полуокружности с первыми
координатами а, Ь. Тогда (рис. 5.53) Р = (а, ]/ 1 — a2), Q = (Ь, ]/1 — Ь2).
Верхняя полуокружность есть график функции
= /1 — X2
Чтобы применить формулу длин (8), вычислим
ау_ = __ * j + tdy_\2= 1 4- х* = 1
dx у \ х2 ’ \ dx / 1 — х2 1 — ха ’
1/1 + —!------
У \dx / у'1 — X2
Отсюда b dx длина дуги PQ окружности = С —- х -. (9)
J /1-х*
Очевидно, та же формула выражает длину дуги нижней полуокружности между х = а и х = Ь.
Верна ли формула (9) при а = —1 и (или) b = 1? При а = —1 или b = 1 определение интеграла, данное в § 1, неприменимо, так как подынтегральная функция (1 — х2)“,/2 не ограничена в интервале (—1, 1): она становится сколь угодно большой, когда х приближается к —1 или к 1. Но геометрически очевидно, что при фиксированном а длина дуги окружности PQ является непрерывной функцией от Ь, определенной также при b = 1, и что при фиксированном b длина PQ есть непрерывная функция от а, определенная также при а— —1. (Скоро мы проверим это аналитически.) Поэтому равенство (9) сохраняет силу также при а = —1 и при b = 1, 1
если, например, истолковать интеграл j(l—х2)~1/2 dx как предел интеграла а
b
j(l—x2)-IA dx, когда b ->-1 слева. (Это пример «несобственного» интеграла;
ср. с § 6.)
300
5. Интегралы
Вычислим теперь площадь сектора OPQ. Пусть сначала —1 < а < 0 < 6 < 1 (рис. 5.54). Тогда, обозначив площади областей, указанных на чертеже, через I, II, III, мы видим, что I 4- II + III есть площадь под кривой у = /1 — х2 от х = = а до х = 6, откуда ь
14- II + III = J /1 - х2 dx.
а
Далее, 1 =-------------------- а ]/1 — a2, III = — b
2 2 г
(поскольку а<0 и 6>0). Площадь сектора есть II. Итак, ь______________________________
площадь сектора OPQ = С К1 — х2 dx — — 6]Л1 — Ь2 —— ауЛГ— а2. (10) J 2 2
а
Та же формула справедлива в случае 0 < а < b < 1, показанном на рис. 5.55. В этом случае интеграл в (10) равен II 4- IV, и (1/2)а]/1 —а2 = I 4- III; (1/2)6 У1 —62= III 4- IV. Правая часть (10) равна
(II + IV) — (III 4- IV) 4- (I + Ш) = 11 + 1.
Это и есть площадь сектора. Читатель сам легко убедится, что равенство (10) справедливо и при а = —1 или а = 0, а также при 6 = 0 или 6=1.
Геометрическое утверждение (I), которое мы хотим доказать, сводится к равенству ь ь
fyT^dx--l-&/r^p4--5-a/r^=4 f —+ • (11)
J 2 2 2 J __ х2
[Заметим, что левая часть непрерывно зависит от а и 6 при | а | 1, |6|<^1.
Поэтому, как только мы докажем (11), тем самым будет проверено и сделанное выше утверждение о пределах интеграла (9) при а Ги 6 1".]
§ 4. Площадь. Объем. Длина
301
Перепишем (11) в виде
fl/1—x2dx — — 6/Г^Р + — а)/1 —а2 — — ( —=0,
J 2 2 г 2 'J угт^
будем считать а постоянным и рассмотрим левую часть как функцию от К Со гласно основной теореме, производная этой функции есть
(b ь
+ -La}/T=V—L f
а а
dx
= /1-6* _ +2.
..-?2_4.o__L 1—
/1 — 2 V1 — ьа
= 0.
Итак, наша функция постоянна. Но при b = а она равна 0. Значит. (11) верно при всех Ь.
При а = 0, b = 1 уравнение (11) принимает вид
( dx = 2 .[ /ПТх2 dx, о П-x» J
или, ввиду определения числа л, р dx __________________________________ те
J /1 — х2 2
Точно так же при а = —1, b = 1 получаем из (И)
Поскольку последний интеграл равен половине длины окружности единичного радиуса, мы доказали тем самым геометрическое утверждение (II): длина единичной окружности равна 2л.
УПРАЖНЕНИЯ
Упражнения 55—60 относятся к кругу радиуса г с центром в О.
55. Пусть L(a, b) — длина дуги верхней полуокружности от точки Р(а, Ут2 — а2) до точки Q(b, ]/г2 — 62), где,—г^а<^г, a S (а, Ь)— площадь сектора OPQ. Запишите две теоремы, сформулированные в начале этого раздела, в виде равенств содержащих L и S.
56. Запишите £(а, Ь) в виде интеграла.
57. Найдите формулу для S(a, b)t аналогичную (10).
58. Докажите, что S(a, b) = (1/2)г£ (а, Ь).
59. Покажите, что £(0, г) = (1/2)лг.
60. Вычислите £(— г, г).
302
Приложение и главе 5
Приложение к главе 5
§ 5. Энергия
5.1. Силы, зависящие от положения
Остановимся на механических применениях понятия интеграла. Рассмотрим частицу, совершающую прямолинейное движение, так что положение частицы описывается о д-н и м числом — координатой $ соответствующей точки прямой Предположим, ,что сила F, действующая на частицу (в направлении прямой, по которой движется частица), зависит лишь от положения частицы. Последнее означает, что
s •-* F (s)
есть некоторая заданная функция.
Примером может служить вес движущейся по вертикали частицы массы т. В этом случае
F(s) = — mg,
где g есть ускорение силы тяжести, и направление вверх считается положительным. Эта сила не зависит ©i s — она постоянна.
Другой пример представляет частица, связанная с пружиной (рис. 5.56). Значение s = Омы припишем точке, отвечающей ненапряженной пружине; следовательно, при $ = 0 к частице не приложена никакая сила. Таким образом, F(0) = 0. Если частица находится в точке s=#=0, то пружина действует на частицу, стремясь восстановить прежнее состояние, т е сжать пружину, если она растянута, и растянуть ее, если она сжата (восстанавливающая сила). Таким образом, F(s) отрицательна при$>0 и положительна при s< 0 (рис. 5.57). Точная форма линии F = F(s) — графика зависимости силы от положения частицы — задается физическими свойствами пружины. Особенно важен простейший случай линейной восстанавливающей силы
F = — ks
(рие 5.58). В большинстве случаев предположение о линейности восстанавливающей силы пружины при малых отклонениях s хорошо отражает реальное положение дел. В самом деле, если кривая F = F(s) имеет в точке s = 0 касательную и рассматриваются лишь малые значения s, то без большой погрешности можно заменить кривую F = F(s) ее касательной. Пружина с линейной восстанавливающей силой называется упругой, а постоянная k — постоянной пружины. Так как F измеряется в единицах силы (например, г-см/с2), as — в единицах длины (например, в см), то k измеряется в единицах массы на единицу времени за единицу времени (например, в г/е2' Тем самым численное значение k зависит от применяемых единиц.
УПРАЖНЕНИЯ
i. Упругая пружина имеет постоянную 3 г/g2. С какой восстанавливающей силой действует пружина на тело, прикрепленное к одному из концов пружины, если она оттянута на 2 см от положения равновесия?
2. Когда к вертикальной упругой пружине подвешен груз в -1- г, она оттягивается на 5 см
ниже положения равновесия. Какова постоянная пружины? (Пренебрегите весом пружины.)
3. Масса в 2 г подвешена к вертикальной упругой пружине, постоянная которой равна 100 г/с2. Как далеко отклонится пружина от положения равновесия? (Пренебрегите весом пружины.)
4. Пусть восстанавливающая сила пружины задается формулой F(s) = 5s — 16s3 + s5 Для малых отклонений s можно считать пружину упругой; какова ее постоянная k?
$ 5. Энергия
303
Рис. 5.56
Рис. 5.58
5.2. Работа Величина
►5
S
W = — J F (х) dx
So
называется работой против силы F, необходимой для перемещения частицы из положения s® в положение $. Это определение; его нельзя доказать, но можно мотивировать, что мы сейчас и сделаем.
Как известно из повседневного опыта, при перемещении частицы против действующей на нее силы, например при подъеме камня, затрачивается работа. Не имея еще никакого определения этого понятия, мы ясно ощущаем, что например, для поднятия камня вдвое большей массы понадобится вдвое большая работа и что работа, необходимая для подъема камня на 3 м, втрое больше, чем работа, требуемая для подъема его на ’1 м. Поэтому в случае постоянной силы мы можем определить работу как произведение силы на расстояние. При этом работа считается положительной, если частица движется в направлении, противоположном направлению силы, и отрицательной в противном случае.
Предположим теперь, что сила не является постоянной, и рассмотрим работу, необходимую для перемещения частицы из положения зь в положение х\ эту работу мы обозначим через №(х). Конечно, №(х) еще подлежит определению; но, разумеется, следует считать, что
W (s0) = 0,
304
Приложение к главе 5
поскольку при отсутствии перемещения частицы работа не затрачивается. Естественно также считать, что
W(x + h) — W(x) = w
есть работд, затрачиваемая при перемещении частицы из положения хв положение* + h. Допустим, что h мало; тогда при изменении s от значения х до (близкого к х) значения х + h сила F меняется мало и поэтому Мало отличается от значения силы в точке х. Рассматривая силу в интервале (х, х + h) как постоянную, имеем
w % — F (х) h.
Знак минус здесь выбран правильно: в самом деле, если Г(х) отрицательна (сила толкает влево), a h положительно (частицу перемещают вправо), то работа w должна получиться положительной. Из предыдущих равенств следует, что
W(x + h)-W(x) h
Это приводит к предположению о том, что
W' (х).= —F(x),
и в силу условия lF(s0) = 0 из основной теоремы анализа получаем
U7(s) = _ jf (X)dx. (1)
So
Работа измеряется в единицах «сила на расстояние», например г«см2/са.
5.3. Потенциальная энергия
Зафиксируем теперь значение s0 («нулевой уровень»); разумеется, это значение мы можем выбрать произвольно. Тогда W(s) называется потенциальной энергией частицы в положении s. Если тело находится под действием силы тяжести F = —mg. то удобно считать значение $0 = 0 отвечающим уровню Земли. В этом случае потенциальная энергия частицы на высоте s есть
s ч
W (s) = — С (— mg) dx = mgs. о
(2)
т. е. равна весу, умноженному на высоту.
В случае пружины мы также примем значение зь = 0 за «нулевой уровень^. Когда конец пружины находится в точке s, потенциальная энергия ее
№(s) = — F(x)dx.
Читатель проверит, что W(s) >0 при 0 и при s >0. Для линейной восстанавливающей силы F = —ks имеем
w (S) = ks».
(3)
§ 5. Энергия
305
Одно из повседневных значени й слова «энергия» — это «способность к работе», что и объясняет термин «потенциальная энергия» для №(s). Камень, поднятый на высоту s, совершит работу (упадет), если его отпустить; то же верно для натянутой пружины.
УПРАЖНЕНИЯ
5. Две положительно заряженные частицы с зарядом в 1 электростатическую единицу (CGSE) отталкиваются с силой, равной 1/г2, где г— расстояние между ними, измеряемое в сантиметрах. Одна частица закреплена, другая же перемещается по направлению первой из точки на расстоянии 100 см до точки на расстоянии 10 см от нее. Какова произведенная работа?
6. Какую работу надо затратить, чтобы поднять тело массой в 10 г с высоты 100 см на высоту 200 см?
7. Какую работу надо затратить, чтобы оттянуть на 3 см конец упругой пружины от положения равновесия, если постоянная пружины равна 15 г/с2?
8. Какова потенциальная энергия камня массой 10 кг на высоте в 50 м?
9. Какова потенциальная энергия упругой пружины, если она сжата на 1 см от положения равновесия и постоянная пружины равна 4,5 г/с2?
10. На сколько надо сжать упругую пружину с постоянной 3 г/с2, чтобы она имела потенциальную энергию в 13,5 г-см2/с2?
5.4. Кинетическая энергия. Закон сохранения энергии
Движущаяся частица может совершить работу. Например, падающий в воду камень вызывает волны. Мы хотим поэтому определить энергию движения, или кинетическую энергию К движущейся частицы. Поскольку К,должна измеряться в единицах работы, т. е. в г-см2/с2, масса— в граммах и скорость — в см/с, то естественно попытаться определить К как величину a то2, где а — численная постоянная. Оказывается, следует взять а = 1/2 и положить
К = “у (4)
Сейчас мы увидим, почему 1/2 — «правильная» постоянная.
Если частица движется по прямой под действием силы, зависящей только от ее положения, то сумма
Е= K+W
ее потенциальной и кинетической энергий в течение движения постоянна.
Величина Е называется полной энергией частицы. Тот факт, что Е постоянна, представляет собой частный случай закона сохранения энергии. Это — математическое следствие закона движения Ньютона и определений W и К. Следуя ходу доказательства, читатель заметит, что если бы мы взяли в определении кинетической энергии отличный от 1/2 множитель, то доказательство не прошло бы.
Заметим, что Е, W и К — функции времени. В частности,
„ 1 ds
К — — тхР, о =—
2 dt
и, по цепному правилу, dK 1 d(oa) 1 d(v*) do d2s
dt ~ 2 m dt ~ 2 m do -dt=mV~dP'
306
Приложение к главе 5
или
dK ----= mva, dt
где а — ускорение. С другой стороны, потенциальная энергия в момент t есть потенциальная энергия в точке $(/), т. е.
s(O Г (s (/)) = - J F(x)dx. So
По основной теореме анализа
и, снова по цепному правилу,
dW dW ds
= — = — Fv. dt-------ds dt
Следовательно,
dE dW dK
— =--------f----= mva — Fv — {ma — F) v.
dt dt dt
Но, по закону движения Ньютона,
та = F,
dF
следовательно, —1 = 0 для всех рассматриваемых / , и в силу теоремы 1 § 5 гл. 4 величина Е dt
постоянна, что нам и требовалось установить.
5.5. Свободное падение
Применим только что установленный принцип сохранения энергии к свободному падению. В этом случае W задается формулой (2) так что полная энергия
1
Е = — mv2 4- mgs.
Эта величина постоянна в течение движения. Если частица отпущена с высоты $0, то ее скорость в начале движения равна 0. Отсюда
mv2 4- mgs = mgsQ
в течение движения. Когда частица ударяется о землю, $ = 0. Поэтому конечная скорость, которую мы обозначим через может быть вычислена из равенства
1 2
— mvx = mgs^
таким образом,
fl = V 2gs0 .
(5)
§ 5. Энергия
307
Если частицу бросают вверх с уровня Земли со скоростью ос, то ее потенциальная энергия
в начальный момент равна нулю и, следовательно, полная энергия Е — Когда частица
вновь достигает Земли, ее кинетическая энергия равна -1- тц2ъ где Vj— конечная скорость, а
потенциальная энергия снова равна нулю. Следовательно, — mv2! = _Lmv20t и поскольку и0 >0 и < 0, имеем
= — Ц>, (6)
как уже было отмечено в гл. 4, § 5.
Результаты (5) и (6) можно получить также из общей формулы, задающей в момент t положение s свободно падающей частицы, имевшей в начальный момент t = 0 положение $0 и скорость у0. По этой формуле [см. формулу (3) § 5 гл. 4],
s (О = — - gt2 + vQt 4- s0-
С помощью той же формулы легко непосредственно проверить, что для рассматриваемого движения частицы справедлив закон сохранения энергии. В следующих разделах мы применим этот закон к двум случаям движения, для которых мы еще не в состоянии вычислить функцию s(/),
УПРАЖНЕНИЯ
11. Какова должна быть скорость снежка массой в 200 г, чтобы его кинетическая энерп я была такой же, как у автомобиля массой в 1200 кг. движущегося со скоростью 20 км/ч?
12. С какой высоты надо сбросить цветочный горшок массой в 1 кг, чтобы его кинетическая энергия в момент падения на Землю была такой же. как у автомобиля массой в 1200 кг, движущегося со скоростью 20 км/ч?
13. Частица массы т движется пр прямой. Если ее расстояние s от некоторой фиксированной точки измеряется в сантиметрах, а время t — в секундах то положение частицы при 0 задается формулой s = № 4- t -h 1. Какова кинетическая энергия частицы при t = 49?
А 14. Пусть K(t) — кинетическая энергия в момент t тела массы т, свободно падающего под действием силы тяжести. Покажите, что K"(t} постоянна, и найдите значение этой постоянной
15. Частица массы т движется по прямой под действием силы, не зависящей от ее положения. Пусть значение силы, действующей на частицу в момент t, равно 6/. Допустим еще, что в момент t = 0 частица покоится.
а) Найдите скорость частицы.
б) Найдите кинетическую энергию К частицы непосредственно, исходя из определения К.
в) Найдите положение частицы (приняв за начало отсчета положение при t = 0).
г) Найдите значение силы в момент, когда частица находится в точке s прямой.
д) Найдите потенциальную энергию W частицы, исходя из определения W (приняв положение при t = 0 за «нулевой уровень» энергии).
е) Проверьте справедливость закона сохранения энергии.
16. Частица массы 1 движется под действием силы, значение которой в каждой точке прямой не зависит от времени. Расстояние частицы от некоторой фиксированной точки прямой задается формулой $ = t^2t 0, где t — время.
а) Найдите кинетическую энергию К частицы, исходя из определения /(.
б) Найдите силу в каждой точке прямой s.
в) Найдите * потенциальную энергию IF частицы, исходя из определения W (приняв начало отсчета расстояний за «нулевой уровень» потенциальной энергии).
г) Проверьте справедливость закона сохранения энергии.
308
Приложение к главе 5
Рис. 5.59
5.6. Тяготение
Закон всемирного тяготения Ньютона гласит, что между двумя любыми частицами, массы которых равны Мити которые отстоят друг от друга на расстоянии г, действует сила притяжения, равная
^Мт г* ’
Здесь у — постоянная (гравитационная постоянная), одна и та же для всех тел. Поскольку сила измеряется в единицах массы, умноженной на длину и деленной на квадрат времени (например. в г-см/с2), а выражение Мт/г2 — в единицах квадрата массы, деленного на квадрат длины (например, в г2/см2). то у должна измеряться в единицах куба длины, деленного на массу и на квадрат времени (например, в см3/г«с2). Следовательно, численное значение у зависит от используемых единиц.
Применяя закон Ньютона к шаровым телам, таким как Солнце и планеты, можно считать общую массу тела сосредоточенной в его центре. (Последнее утверждение есть математическая теорема, которая будет доказана лишь в гл. 13*.)
Как мы увидим дальше, закон, тяготения может быть выведен из наблюдаемых движений планет. Применим его теперь к случаю, когда одна из «частиц» — Земля, другая же — тело, движущееся по прямой, проходящей через центр Земли (рис. 5.59).
* Здесь предполагается не только шарообразная форма тела, но и сферически симметричное распределение его массы, т е. плотность в точках, равноотстоящих от центра должна быть одинаковой. При этом условии еила тяготения между телами на любом расстоянии такая же, как между частицами тех же масс, сосредоточенными в их центрах. Если же расстояние между телами значительно больше их размеров, то закон Ньютона будет применим независимо от формы и распределения масс в тяготеющих телах; так, например, этот закон применяют к астероидам произвольных форм
§ 5. Энергия
309
Обозначим центр Земли через О, а расстояние от О до движущейся частицы — через s. Пусть Л1 — масса Земли, т — масса движущейся частицы. Наконец, пусть R — радиус Земли. По закону тяготения сила, с которой Земля действует на частицу, есть
она отрицательна, поскольку толкает тело к Земле. В повседневной жизни мы имеем дело с телами, расстояние которых от поверхности Земли очень мало по сравнению с радиусом Земли R. Для такого тела имеем
s= R + х и
^Мт = - (/? + х)2 *
Если x/R мало, то число \/(R + г)2 очень мало отличается от I//?2; в самом деле, при х >0
1 1 2Rx х2 2х х2
R^~ (/? + х)2 = (R + х)2 R2 <'~R^ + R* (8)
Приближенное значение R, по геодезическим данным, таково:
R 6,37 • 108 см = 6370 км.
Если х меньше 1/1000 земного радиуса, т. е. меньше 6,3 км, то разность (8) меньше 1/1019 см2.* Следовательно, для тел, близких к Земле, с малой погрешностью можно считать силу F постоянной:
_ _ fMm
~ R2
Полагая
получаем из закона движения
— = (а — ускорение).
Это закон постоянного ускорения Галилея: а = —g
(В действительности ускорение силы тяжести на поверхности Земли не всегда одинаково. Зависимость g от географической широты была обнаружена еще в 1672 г. Ньютон заключил отсюда, что Земля не является вполне правильным шаром: экватор отстоит от центра Земли дальше, чем полюсы*. Кроме того, как показали точные измерения, значения g меняются также в зависимости от местных особенностей строения земной коры. Этот факт используется в научном прогнозировании возможных месторождений нефти, минералов и i. п.)
5.7. Скорость убегания
Вернемся теперь к случаю, когда расстояние тела от поверхности Земли достаточно велико и, следовательно, надо пользоваться первоначальным уравнением (7). Закон движения такого тела имеет вид
уМт та = — ------- »
s2
* На значениях gt измеренных для пунктов, имеющих разную широту, сказывается также и вращение Земли вокруг оси, скорость (линейная) которого зависит от широты.
310
Приложение к главе 5
или
В гл. 11, § 5.1 мы изложим метод решения этого дифференциального уравнения, т. е. покажем, как найти из него функцию s(/). Поскольку однако, F зависит лишь от s, можно применить принцип сохранения энергии. Вычислим потенциальную энергию тела на расстоянии sot центра О приняв за нулевой уровень энергии точку ч = R (поверхность Земли). В силу (1) и (7) имеем
т р -pMm г ах / I 1 \
W = - J --------- *х = 1Л т J — = 1Мт \-^ - —) • (Ч>
R R Х '
Применим эту формулу для вычисления начальной скорости су которую следует сообщить гелу например ракете, чтобы оно поднялось на расстояние А от точки О и лишь затем начало падать обратно на Землю В начальный момент
К = 4- W* 1Г = 0.
2 о’
В момент максимального подъема имеем ' = А. и = 0. откуда
К. = 0, W = ^Мт
Но сумма К + W должна сохранять постоянное значение в течение движения Поэтому 1 2 / I 1 \
ИЛИ
Ро= •
В силу (9) имеем yM = gR2. Следовательно,
' (12)
Заметим, что о0 не зависит от т.
Когда А неограниченно возрастает, о0 стремится к пределу:
(13)
Тело, брошенное с этой (или большей) скоростью никогда не вернется на Землю: поэтому и0 называется скоростью убегания*. Подставив указанное выше значение R и значение g = =980 см/с2, получаем
о0 = 1,17* 10е см/с.
Конечно мы пренебрегаем в наших расчетах действием сопротивления воздуха и тяготением других небесных тел. Но полученное значение не очень отличается от действительной скорости убегания от Земли.
5 И „и первой космической скоростью.
§ 5. Энергия
311
УПРАЖНЕНИЯ
В упражнениях 17—21 примите значение гравитационной постоянной у = 6,67.10“® см3/г-с2.
17. Радиус Луны приближенно равен 1,74-10° см; масса ее приближенно равна 7.35- 1055 г. Вычислите скорость убегания частицы от Луны
^18. Радиус планеты Юпитер приближенно равен 70,96- 10е см, масса ее приближенно равна 1,88-1030 г. Вычислите скорость убегания частицы от Юпитера.
19. Радиус Солнца приближенно равен 692,32-10® см, масса его приближенно равна 1.97 . • 1033 г. Вычислите скорость убегания частицы от Солнца.
20. Пусть о0 — скорость убегания частицы от большого шарового тела массы М и радиуса R. Предположим, что R остается постоянным, а М меняется (например, метеоры, падающие из космоса, погружаются в тело, увеличивая его массу без заметного возрастания
радиуса). Найдите
(1М
21. Пусть в упр. 20 величина М остается постоянной, в то время как R меняется (например пульсирующие звезды — шаровые тела переменного радиуса; впрочем, масса такой
звезды также не постоянна). Найдите .
5.8. Энергия и масса в теории относительности
Пусть теперь частица движется столь быстро, что надо воспользоваться уравнением движения Эйнштейна 1см. уравнение (4) § 3 гл. 4], т. е.
d v _
/п0---------------------= р t
d/ у~ 1 — (и2/с2)
где с — скорость света и т9 — масса частицы в состоянии покоя /так называемая масса покоя,. Как мы показали в гл. 4. § 3, уравнение движения Эйнштейна может быть также записано в виде
/иоа dv
-- -— = г, где а = — • (/1 — (сЯ/с2)3
Кинетическую энергию движущейся частицы мы определим теперь формулой
У1 — (о2/с2)
(14)
. (15)
Это определение оправдывается тем, что сумма Е = К + W остается постоянной в течение движения. [Здесь W — потенциальная энергия, определенная по-прежнему равенством (1).]
В самом деле, в силу (14) имеем
dE dK dW dK dv dW ds
~~7~ = ”7“ = "77 f ПО ^пиому правилу i —
dt dt dt dv dt ds at
Имеются серьезные физические основания назвать величину
312
Приложение к главе 5
У 1 — (V2/са)
(16)
массой движущейся частицы. Сравнивая (15) и (16), заключаем, что возрастание (или убывание) энергии вызывает возрастание (или убывание) массы по закону
Е=тс*. (17)
Конечно, предыдущее рассуждение не доказывает, а лишь иллюстрирует на примере это знаменитое соотношение Эйнштейна.
§ 6. Несобственные интегралы
В этом параграфе мы рассмотрим полезное обобщение понятия интеграла. Мы уже им пользовались неформальным образом в § 4.9.
6.1. Неограниченные подынтегральные функции
Число
ь J fM dx а
было определено до сих пор лишь для ограниченных (и кусочно-непрерывных) функций и для конечных интервалов (а, Ь). Однако в некоторых случаях можно естественным образом приписать интегралу определенное значение, несмотря на то что функция f(x) принимает сколь угодно большие значения вблизи а и b или в случае, когда область интегрирования (а, Ь) б е с к о н е ч н а. Мы будем рассматривать такие несобственные интегралы лишь для неотрицательных функций и вместо общего определения приведем несколько типичных примеров.
График функции
1
У~ УТ’
определенной при х>0, показан на рис. 5.60. Если е — малое положительное число, то
f -7^ = 2 rrl1 = 2-2 уг.
Ух 1е
Поскольку Уё" — непрерывная функция оте при е > 0 и = 0, отсюда следует, что
lim f —= 2. (1)
•-О* J ух
(Вспомним, что «е 0+» означает: «когда 8 стремится к нулю, принимая положительные значения».) Естественно считать, что площадь, заключенная между осью у, прямой х = 1 и нашей кривой, имеет значение 2, хотя область простирается сколь угодно далеко вверх. Поэтому мы пишем
§ 6 Несобственные интегралы
313
Рис. 5.61
Рис. 5.60
Эту формулу следует понимать как сокращенную запись (1). Говорят также, что несобствен-1
ный интеграл J dx сходится и что он имеет (конечное) значение 2. о
Рассмотрим далее функцию
1 у==~
(определенную при х =£ 0). Как мы знаем, ее первообразной является функция —JL Если е — малое положительное число, то
С —— I1--!--!
J х2 X L е е 6
Это число становится сколь угодно большим (положительным), еслие достаточно мало; кратко только что высказанное утверждение записывается в виде
.. f dx lim I — = -|- оо. /
£-0+ J X2
6
(Напомним, что символ «оо» читается «бесконечность»; он не является наименованием какого-либо числа.) Поэтому мы не будем приписывать никакого числового значения символу
f —
J х2 о
f и будем говорить что несобственный интеграл J x^dx расходится.
о
314
Приложение к главе 5
6.2. Бесконечные области интегрирования
Вычислим сначала площадь под кривой = 1/дг2 от 1 до большого положительного числа а. Имеем
откуда
или в сокращенном обозначении
(2)
Мы говорим также, что несобственный интеграл | x^dx сходится (к числу 1). Точно так же
чтс означает
С другой стороны, несобственный интеграл
расходится иными словами этому символу не приписывается никакого числового значения Чтобы убедиться в этом, заметим, что при а >0 имеем
и предел этого выражения при а -> 4-оо есть -f-oo
6.3. Другие примеры
В предыдущих примерах «несобствен ность» всегда была сосредоточена в одном из концов области интегрирования. Однако так бывает далеко не всегда
Рассмотрим следующий пример. Смысл равенства
J Км
виден из рис. 5.6!. Это сокращенная запись утверждения: если ив 9— малые положительные
числа то
§ 6 Несобственные интегралы
315
сколь угодно близко к 4, есливт и я 2 достаточно малы. Иначе это можно записать так: несобственные интегралы
сходятся и
В § 4.9 мы показали что
(4)
это несобственный интеграл и равенство (4) можно рассматривать как сокращенную запись утверждения
ь
р dx • п
Пт | — = — •
J у 1 _ Х2 2
Правила интегрирования выведенные нами f § 3, сохраняют силу для интегралов от кусочно-непрерывных функций а также ъля несобственных интегралов. Доказательство этого факта почти очевидно и может быть опущено.
УПРАЖНЕНИЯ
В упражнениях 1—10 установите, существуют ли указанные несобственные интегралы (т. е можно ли им приписать конечное значение), и в случае утвердительного ответа вычислите их. ( Указание: если не удается сразу найти ответ выполните интегрирование по частям.)
и du
(и2 4- I)3
7. f
К (1-?/)2/3
/2
▲ь f и dv
0 (О2 - l)V5
9 । du
у (2у+ I)2 ’
10. со f. X dx
J 0 (х+ I)3
316
Приложение к главе 5
6 Л. Теорема сравнения <
Имеется полезный признак сходимости несобственных интегралов от неотрицательных функций.
Теорема 1 (признак сравнения для несобственных интегралов). Пусть f(x) и g(x)—dee функции, определенные при a<Z х <Zb, где а — число, а b — либо число, либо символ +оо. Предположим, что для любого с, удовлетворяющего неравенствам а<С с<С b функции I и g ограничены и кусочно-непрерывны в (а, с) и что
О <f(x) < g (х) для a<Zx<Zb. (5)
Тогда, если интеграл ь J g(x)dx
сходится, то сходится также интеграл , ь
J f (X) dx. а
Теорема охватывает два случая: b = 4~оо и b<Z 4*0°, причем в последнем случае подразу-мейается, что функции / и g обращаются в оо при х Ь~ Справедливость теоремы геометрически очевидна. Из условия (5) вытекает, что график функции заключен между осью х и графиком функции g. Поэтому если площадь под графиком g (от а до Ь) конечна, то и площадь под графиком I конечна. Аналитическое доказательство содержится в § 9.
Аналогичное предложение можно сформулировать и для случая, когда «несобственность» сосредоточена в левом конце области интегрирования.
Покажем, например, что несобственный интеграл
J 1 4- х2 00 сходится. Заметим сначала, что о° —1 ,-1 . +00 ,
р dx р dx р dx р dx
J 1 4- х2 J 1 4- х2 J 1 4- х2 J 1 4- х2
-----------------------СО —00 —1 1 Левая часть этого равенства имеет смысл, если имеют смысл все три слагаемых правой части. О среднем слагаемом можно не беспокоиться, поскольку функция 1/(1 4" х2) непрерывна, но имеют ли смысл первое и третье слагаемые? Иначе говоря, сходятся ли эти интегралы? По признаку сравнения они сходятся, поскольку
а интегралам (2) и (3) , как мы уже видели выше, можно приписать вполне определенные конечные значения (рис. 5.62).
В следующем пункте мы получим замечательный результат:
dx
1 + х2
(6)
где л — отношение длины окружности к ее диаметру. Геометрически очевидно также (и вытекает из приведенной теоремы), что в предположениях ь ь
теоремы 1 из расходимости интеграла £ f(x)dx следует расходимость интеграла J g(x)dx. а а
$ 6. Несобственные интегралы
317
УПРАЖНЕНИЯ
В упражнениях 11—20, применив один из рассмотренных в этом пункте признаков, установите, сходятся или расходятся заданные несобственные интегралы.
dx
15.
—!—do. V3
». f -£±!
б (г2—4)
----- d2. у
dx
4
1
13. f
dt
<+ v~
A16, f '/
(X— 1)
P (/ + 2)</3
) (4t-l)2
17.
dt.
19.
dy (H-j/2)2
„Л f dx
’ J (/*-0s
dt
&t — I)2 + I
6.5. Некоторые интегральные функции, содержащие ъ
Чтобы доказать соотношение (6), заметим сначала, что функция t = 1/х убывает при х >0-Зафиксируем число N >0 и применим к интегралу
dx
UN
подстановку
1 di 1
x = — , dx = — —-; при этом t = N, если x = , и t = 1, если x = 1.
t t* N
318
Приложение к главе 5
Мы получаем
и, поскольку t и х — «немые» переменные,
dx
1 + х2
Первый интеграл при неограниченном возрастании N может быть сделан сколь угодно близким 1
к f dx/(l 4- х2); то же верно, следовательно, и для второго интеграла. Поэтому
, +°° .
dx р dx
1 4- х2 J 1 4- х2
(7)
Теперь мы видим, что здесь можно было бы действовать и смелее: мы могли бы сразу применить к первому из интегралов (7) подстановку х = \/t. dx = —(dtlt2), «4 = 4"°°» при х = О, t — 1 при х = 1. Поскольку функция 1/(1 4“ х2) четна, имеем (см. § 3.6)
Итак, нам остается только показать, что
(8)
Для этого применим к интегралу (4) подстановку
24
X = -------г
1 4- /2
и заметим, что
х = 0 при 4 = 0, х = 1 г ри t = 1.
§ 6. Несобственные интегралы
31»
-1 1
Рис. 5.63
Л Я П РР
dx _ (1 4- /2) • 2 — 2/ • 2/ _ 2(1 — ?2) dt “ (1 + /2)2 = (1 + * *2)2
Отсюда видно, что х — возрастающая функция от t при 0< t<Z 1. Наконец,
V1 — X2 =
4/2
(1+/2)2
1 —/2
1 4- /2 ’
откуда
п р dx е 1 4- /2 2(1 — /2) , р dt
2 "" J у \ _Х2 “ J I — /2 (1 + /2)2^ ~ J 1 4- /2 *
что и доказывает (9). Рис. 5.63 геометрически иллюстрирует смысл равенств (6) и (9).
Манипуляции, произведенные в этом и предыдущих разделах, принадлежат к числу тех, о которых Эйлер сказал: «Мое перо умнее меня». Заметим однако, что читатель, который ознакомится с гл. 6, найдет, что соотношения (5) и (8) являются гораздо менее таинственными, чем они представляются менее искушенному читателю.
Леонард ЭЙЛЕР (1707—1789) родился в Базеле, в Швейцарии, и учился там у Иоганна Бернулли. Большую часть своей жизни он был членом Академий в Берлине и в Санкт-Петербурге. Эйлер был ие только плодовитейшим математиком всех времен, ио и одним из величайших математиков; ему принадлежат результаты, касающиеся всех математических дисциплин, а также и некоторых нематематических. Последние 13 лет жизни он работал в полной слепоте, диктуя свои работы ученикам.
Эйлер написал учебники анализа, от которых ведут начало все последующие пособия *. Собрание сочинений Эйлера все еще ие издано полностью; до сих пор вышло около 70 объемистых томов **.
* Многие книги Эйлера, в том числе его учебники анализа (Л. Эйлер, Дифференциальное исчисление, М.—Л., Гостехиэдат, 1949; Интегральное исчисление, тт. I—III, М., Физ-матгиэ, 1956—58), переведены на русский язык.
** Издание Полного собрания сочинений Л. Эйлера было начато еще в 1911 г.; завершение его потребовало гораздо больше времени и труда, чем первоначально предполагалось. Это издание является международным и осуществляется в весьма малом тираже, с тем чтобы каждая из стран-участниц получила один экземпляр; возможные сроки завершения всей работы все еще трудно предсказать.
320
Приложение к главе 5
УПРАЖНЕНИЯ
21. Найдите объем тела, образованного вращением вокруг оси х области под графиком функции у = 1/~[Л + х2 от х = 0 до х = 1.
22. Пусть Va обозначает объем тела, образованного вращением вокруг оси х области под графиком функции у = 1/Д/1 + от х = 1 до х = а (а > 1). Найдите lim Va, если а-+<х>
этот предел существует. [Можно считать его объемом тела, образованного вращением вокруг оси х области под графиком при 1 х< оо.]
со
23. Найдите интеграл J dx/(\ + лх2), если он существует, —со 00
24. Найдите интеграл J udu/(\ + а4), если он существует. [Указ а н и е: попробуйте применить подстановку и2 = х.]
1 _ ___________
25. Найдите интеграл ]Ли du/j/l—и, если он существует. [У казан и е: попробуйте применить подстановку и = x2.j
§ 7. Доказательство основной теоремы
Мы привели в § 2 наглядные соображения, подкрепляющие первую часть основной теоремы. Теперь мы дадим формальное доказательство.
Пусть (а, Ь) — конечный интервал и f(x) — ограниченная кусочно-непрерывная функция, определенная при х< Ь. Положим
X
G(x) = j а
Требуется доказать, что G(x) непрерывна при Ь и что G'(x^) = Дхв), если I непре-
рывна в точке х®.
7.1. Доказательство непрерывности
Пусть х0 и х — две различные точки в интервале [в. М. В силу аддитивности интеграла р (0 + р(0 Л,
а а х0
так что х
G(x)-G(x0) = p(M
*0
Поскольку f ограничена, существует такое число М, то |/(0 М для всех рассматриваемых значений t т е. такое, что
5 7. Доказательство основной теоремы
321
Пусть х>х0. По теореме 2 § 1 имеем X X
J(— MYdi <
х0 х> х.
или — М (х — х0) < G (х) — G (xe) < М (х — х0),
что равносильно неравенству | G (х) — (? (х0) | <М|х —х0|.
Точно так же доказывается, что это неравенство справедливо и при х< хе. Отсюда видно, что G непрерывна в точке хф; если х лежит в интервале длины 2d с центром х0, то G(x} отличается от 6(х0) не более чем на Mb (отметим, что хв здесь может быть также одним из концов (а,6)<|.
7.2. Вычисление производной
Пусть теперь х0 «— точка интервала (а, Ь), в которой f непрерывна, а е — некоторое (фиксированное) положительное число. Тогда, по определению непрерывности,
Z(x0) —е < f(f) < f(xQ) 4-е
для значений Л близких к х0, т. е. при хф — d< хф 4“ d, где d — достаточно малое положительное число. Пусть х настолько близко к х9, что | х — х0 |< d. Тогда предыдущие неравенства справедливы для всех t между хф и х. По свойству монотонности интеграла имеем
j — е1Л < fddt < J [f (x0) 4- e] при x>x0, X0 Xe X»
J If — s\dt < < J [f (x0) 4- e) при x<x0.
x r X
Вычислив интегралы от постоянных, получаем
х
I/ (-М — б] (X — х0) < J f (0 di < [/ (х0) 4- е] (х — х0) при х > х0 «о
И
[f (Хо) — е] (Хо — х) < J f(t) dt < [/(х0) 4- е| (х0 — х) при х < х0. х
Разделив первые неравенства на положительное число х — хв, имеем
1 *
/(х0> —е< ------ Г/(О<«</(хл) + ».
I
322
Приложение к главе 5
Тот же результат получается, если разделить вторые неравенства на х0 — х, поскольку
। Iх
------ П(0Л=---------- х0— х J *---------------------х0
Следовательно, во всех случаях
«, X G (*) — 0 (*о) .
I (*«) — « < ------------< f Оо) + в
X Xq
при х =£ х0 и I •* — *9 К Точнее, мы показали, что при любом е >0 существует такое б >0, что предыдущие неравенства справедливы при | х — х0 |< б. Это значит, что
lim — / (Xq)9
х->хо X — хо
или G'(x0) = f(*o)» что и требовалось доказать. Подобное же рассуждение применимо в случае, когда хф — один из концов интервала (а, Ь).
§ 8. Существование интегралов
В этом параграфе мы докажем существование интеграла и три его основных свойства, т. е. теоремы ! и 2 § 1. Доказательства просты, но довольно длинны; они основываются на принципе верхней грани.
Рассматриваемое ниже понятие интеграла было впервые дано в несколько иной форме Ри* маном в 1854 г.
8.1. Интегралы от ступенчатых функций
На протяжении этого раздела (а, Ь) означает нонечный интервал; все рассматриваемые функции предполагаются определенными в этом интервале и ограниченными в нем. Для функций ди g неравенство j g означает, что
£(*)-< g(x) вых x, a<Z x< b.
Буквыф, ф| х всегда будут обозначать ступенчатые функции. Напомним, чтоф называется ступенчатой функцией, определенной в (a, b)t если (а, Ь) можно разделить на конечное число частей (интервалов постоянства), в каждом из которых ф(х) принимает постоянное значение. Значения ф в концах интервалов постоянства для дальнейшего несущественны.
Бернард РИМАН (1826—1866) учился в ГБттингеиском университете, а затем преподавал а нем. В возрасте 33 лет Риман стая ординарным профессором и не должен был больше заботиться о заработке. В 40 лет он умер от туберкулеза.
Риман написал сравнительно немного работ; полное собрание его трудов * составляет небольшой том объемом около S00 страниц, примерно половина из которыж — вто посмертные публикации. Однако обширная область современны! исследований по математике и математической физике представляет собой развитие идей и методов Римана.
* Оно переведено о на русский язык: Б. Риман, Сочинения, М.—Л., Гостехиэдат, 1948.
$ 8. Существование интегралов
323
Рис. 5.65
Рис. 5.64
Пустьф— ступенчатая функция, определенная в (а, 6), имеющая п интервалов постоянства с длинами Zf, /а, ...» Zn и принимающая в них значения bf, оа, ...» Vn. Напомним, что интеграл ь
J Ф (x)dx был определен с помощью формулы а
Ь
j* <р (х) dx = Vilt + OaZ2 + • • • 4- (1)
a
Это и есть в точности «площадь между кривой у = ф (х) и осью х, где х заключено между а и 6», причем площади под осью х вчитаются «отрицательными» (рис. 5.64). Поскольку здесь площадь — это сумма площадей нескольких прямоугольников,то наше определение не вызывает никаких сомнений.
Замечание. Если дана ступенчатая функция, то можно разделить некоторые из ее интервалов постоянства на меньшие подынтервалы и назвать интервалом.постоянства к а ж-д ы й из них (см. рис. 5.64 и 5.65, где одна и та же функция ф рассматривается как имеющая 5, соответственно 8, интервалов постоянства). Легко видеть, что значение интеграла от этого не изменится. Для этого достаточно проследить, что происходит при делении одного из интервалов постоянства на две части.
Точно так же, еслиф принимает одно и то же значение в смежных интервалах постоянства, можно объединить их в один интервал постоянства, что опять не меняет значения интеграла.
Лемма А. Для ступенчатых функций справедливы следующие утверждения'.
Ь
если <р (х) = а, где а — постоянная> то § у (х) dx = а (Ь — а); (А1)
а
ebb
если а<^ с <Ь, то J <р (х) dx 4- J <р (х) dx = J <р (х) dx; (А2)
аса
b b
если <Р < ф, то У <р (х) dx < у ф (х) dx. (АЗ)
а а
Доказательство. (А 1). Можно считать, что функция ф имеет один интервал постоянства (см. замечание выше). Длина этого интервала равна 6— а. Следовательно, по определению интеграла от ступенчатой функции,
Ъ
j* !f(x)dx = a(b-a). а
324
Приложение к главе 5
(А2). Можно считать (см. замечание выше), что с — конечная точка некоторого из интервалов постоянства функции <р. Пусть (а, с) состоит из k первых интервалов постоянства, а (с, Ь) — из п — k остальных. Тогда
с b
J (х) dx = Oj/i Ч-----1- j <P (x) dx = Vb+ilb+i 4--1- vnln.
a c
Сравнивая это e (1), убеждаемся в справедливости (А2).
(АЗ). Можно считать, чтоф и ф имеют одни и те же интервалы постоянства (по сделанному выше замечанию). Тогда имеет место (1) и
Ь
j ф (х) dx = WX/1 + Wtla Ч----I-«Мл, <2>
а
где tt/f, ay а, ..., wm — значения ф в первом, втором, ..., n-м интервале постоянства.
Если ф < ф, то Uf < tt/f, v* Ша, ...» vn < юя, и поэтому < Wjlt, < tt>a/a, ... » vnln < шя/я. Сравнивая (1) и (2), убеждаемся в справедливости (АЗ).
8.2. Верхние и нижние интегралы
Пусть t — ограниченная функция и М — такое число, что | i | М Заметим, что если ф — ь
ступенчатая функция, для которой ф < М, то в силу (А1) и (АЗ) имеем |ф(х)Жг < М(Ь —а). а
Следовательно, если рассмотреть всевозможные ступенчатые функции ф. для которых ф ь
то числа Уф (x)dx ограничены сверху. Согласно принципу верхней грани, множество этих а
чисел имеет (наименьшую) верхнюю грань, которая называется нижним интегралом от t ь
по интервалу (о, Ь) и обозначается через J [(x)dx.
а
Таким образом, ь ъ
J f (х) dx = (наименьшей) верхней грани^ <р (х) dx для всех ступенчатых функций <р < f.
а а
Аналогично определяется верхний интеграл от £
Т ь
J f (х) dx = (наибольшей) нижней грани^ ф (х) dx для всех ступенчатых функций ф > /. а а
Ъ
Это определение законно, поскольку множество чисел J ф (x)dx для всех ф > t ограничено а
ь снизу: в самом деле, если ф > f, то ф > —М, откуда согласно (А1) и (АЗ), следуету ty(x)dx >
> __ М(Ь — а).
Заметим, что нижний и верхний интегралы определены для всякой ограниченной функции. При этом, как видно из следующей леммы, для ступенчатых функций мы не получаем ничего нового;
§ 8. Существование интегралов
325
Лемма Б. Если х — ступенчатая функция, то ь ь ~ь
j X (*) dx = j X (*) dx = J х (X) dx. a a a
b
Доказательство. Пусть S — множество всех чисел j\(x)dx, где <р < х» и / —• а
верхняя грань S. Поскольку у — ступенчатая функция и, конечно (по определению отношениж), ь
имеем х < X» то число §i(x)dx принадлежит S. Следовательно, a Ь
J X (*) < /• а
b Ъ
С другой стороны, если <р < х» то в СИЛУ (АЗ) имеем J* <р (х) dx < J х (*) dx, так что а а
О
JxWd* — верхняя граница S. Поскольку / ’—наименьшая верхняя граница, то а ь
/ < j X W dx. а
b
Так как, по определению / = J 4(x)dx, то половина утверждения леммы нами уже доказана. а
Вторая половина доказывается аналогично.
Лемма В. Для любой ограниченной функции I и для любого заданного числа е >0 существуют такие ступенчатые функции ф и ф, что ь ь ь
tp (х) dx 4- е,
а а. а
b ~b b
ф (х) dx — е.
а а а
<р < f U J <р (X) dx <
ф > f и j* ф (х) dx > J f (х) dx >
Доказател ьство. Лемма утверждает, что нижний (верхний) интеграл от / можно сколь угодно близко аппроксимировать интегралом от ступенчатой функции, лежащей ниже (выше) /. Мы докажем лишь существованиечф; для ф доказательство проводится аналогично.
ь
Пусть S —множество всех чисел J<p(x)dx для всевозможных <р < f. Положим а
А Ь
J f (х) dx =/. Поскольку /— наименьшая верхняя граница S, имеем J <р(х) dx < / при <р < /. а а
326
Приложение к главе 5
ь
Пусть задано е>0. Вели бы для всех у < f было справедливо неравенство J <р(х) dx</ —е, а
то / —е было бы верхней границей S, меньшей /, что невозможно. Следовательно, существует ь ь
такая функция <р, что (х) dx —е,т.е. / < J <р (х) dx 4- е; <р обладает требуемыми свойствами, а . а
[Заметим, что, вообще говоря, верхний и нижний интегралы от функции не совпадают. Например, если /(х) = 0 для рациональных х и /(х)=1 для иррациональных х, то
1 1
Jf(x)dx=O, a J о о
Лемма Г. Для каждой ограниченной функции f ь 7
J f (х) dx < J f (х) dx. а а
Доказательство. -Пусть <р и ф таковы, как в лемме, В. В силу (АЗ) имеем ь ь
^(x)dx < J ф (х) dx; следовательноi по лемме В, а а
ъ ь ь ~ь
J f (х) dx < J (х) dx + 8 < J ф (х) dx 4-е < J f (х) dx 4- 2е. а а а а
Так как это верно для любого положительного е, то искомое неравенство справедливо.
8.3. Свойства верхних и нижних интегралов
Мы можем теперь доказать, что верхние и нижние интегралы обладают тремя характерными свойствами интегралов:
Лемма Д. Пусть f и g — ограниченные функции. Тогда}
ь ь
если f(x) — a, где а — постоянная1 то J f (х) dx = J f (х) dx = а (6 — а); а а
с Ь b
если а<с<Ь, то J f (х) dx 4- J f (х) dx = J f (x) dx, а с а
~ ~b b
jf(x)dx+ p(x)dx= Jf(x)xd; а с a,
b b T T
если f<g, mo J t (x) dx < J g (x) dx, J f (x) dx < J g (x) dx. a a a a
(Д1)
(Д2)
(ДЗ)
§ 8. Существование интегралов
Доказательство. (Д1) следует из леммы Б и (А1).
(Д2). Пусть е>0 — заданное число. По лемме В, существуют ступенчатые функции и <ра, определенные соответственно в (а, с) и (с, Ь), для которых (х) < f (х) при а<х<с, <Р2 W < f (х) при с < х < b и
с с b b
J f (х) dx < J <Р1 (•») dx + е, J f (х) dx < J <ft (x) dx + e. a a с c
Определим ступенчатую функцию <p(x) условиями: <р(х) = <рх(х) при а<х<с, ср(х)== = <Р2(х) при с<х< ft. Тогда <р определена в (а, ft) и <р < f. Пользуясь предыдущими неравенствами (А2) и определением нижнего интеграла, имеем
с ь с ь
^f(x)dx+ J f (х) dx < J <р! (х) dx + J <f>2 (x) dx + 2e = аса c
c b b b
= J <p (x) dx + J tp (x) dx 4- 2e — J <p (x) dx 4- 2e < J f (x) dx 4- 2e. a c a a
\f (x)dx < у f(x)dx.
Поскольку e — произвольное положительное число, последнее означает, что ebb У f (х) dx 4-аса
С другой стороны, опять по лемме В, существует такая ступенчатая функция < / , что b ft
J f (х) dx < У?з (х) dx + е. а а
В силу (А2) получаем отсюда b e ft с ft
У f (X) dx < у <рз (X)dx+ У <p3(x)dx-|-e < (х) dx+ J Z(x)dx + »,
а а с а_ с
а так как е произвольно, ft с ь
f(x) dx+ у f (х) dx. а а с
Вместе с уже доказанным противоположным неравенством это завершает доказательство (Д2) для J. Для J* доказательство проводится аналогично.
(ДЗ). Пусть дано .Е>0. По лемме В, существует ступенчатая функция ?</, для которой ft ft
J f (x) dx < J <p (x) dx 4- e. a a
Но поскольку f < g, имеем <f < g и, следовательно, ft ft
У <f (x) dx < у g (x) dx. a a
328
Приложение к главе 5
так что
ъ ъ
J f (X) dx < Jg (х) dx ч- в. а а
Поскольку в произвольно, получаем требуемое неравенство для J . Для J неравенство до* называется аналогично.
Вспомним теперь доказательство первой части основной теоремы анализа, данное в §7.1 (теорема 1 §2). Доказательство это опиралось только на формулу для интеграла от постоянной и на свойства аддитивности и монотонности интеграла. Поэтому для нижних и верхних интегралов можно повторить доказательство из § 7.1. что приводит к следующему результату:
Лемма Е. Пусть ЙО — ограниченная функция, определенная при a<Z t<C>b. Положим
G(x) = $f(t)dt, G(x) = j f(t)dt, a a
для каждого x ив интервала a<Z x < b, а также 6 (a) =7? (a) = 0.
Тогда функции G(x) и G(x) непрерывны при a x b, и в каждой точке х, где £ непрерывна, имеем &(х) = G'(x) = Дх).
84. Интеграл Римана
Ограниченная функция j называется интегрируемой по Риману в интервале (а, Ь) если
с Т
(х) dx = у f (X) dx. а а
Например, ступенчатая функция интегрируема по Риману в силу леммы Б. Если j интегрируема по Риману, то общее значение нижнего и верхнего интегралов называется интегралом Ри-ь
мана функции i и обозначается через J t(x)dx. а
Теорема 1. Пусть h ограничена а кусочно-непрерывна в интервале (а, Ь). Тогда Ц интегрируема по Риману в этом интервале.
Доказательство. Пусть G(x) и С(х) определены, как в лемме Е; положим
tf(x) = G(x)-G(x).
Тогда Н(х) непрерывна везде, Н(а) = 0 и Н’(х) ® 0 для всех х, кроме, возможно, конечного числа точек, где j разрывна. По теореме 1 § 5 гл. 4 функция Н постоянна. Следовательно, Н(Ь)= = Н(а) = 0, откуда имеем
Т ь
G (Ь) = J f (*) dx = G(b) = §f(x)dx. a a
§ 8. Существование интегралов
329.
(4)
Лемма Ж. Пусть £ — ограниченная функция, определенная в интервале (а, Ь). Тогда f интегрируема по Риману в том и только том случае, если существует единственное число S, обладающее тем свойством, что для любых ступенчатых функций у и ф, для которых <р < f < ф, справедливы неравенства
Ъ b
J ф (х) dx < S < J (х) dx. (3)
а а
Доказательство. Число S обладает требуемым свойством в том и только том случае, если оно является нижней гранью для интегралов всевозможных ступенчатых функций а также верхней гранью для интегралов всевозможных ступенчатых функций < Д Иными словами, S обладает требуемым свойством тогда и только тогда, когда
ь ~ь
^f(x)dx<S< а а
Если fi интегрируема по Риману, то этим условиям удовлетворяет единственное число, а ь
именно $ » ^f(x)dx. Если же f не интегрируема по Риману, то из леммы Г вытекает существо-а
вание бесконечного множества чисел S, удовлетворяющих неравенствам (4).
Как показывает лемма Ж, интеграл Римана и интеграл, определенный нами в § 1, — это одно и то же.
В силу только что установленной теоремы 1 и леммы Д существование интеграла для ограниченной кусочно-непрерывной функции (т. е. теорема 1 § 1) и три свойства интеграла (теорема 2 § 1) доказаны исходя из свойств действительных чисел, без обращения к геометрической интуиции.
8.5. Вычисление интегралов с помощью ступенчатых функций
Теорема 2. Пусть Ц — ограниченная функция, определенная в интервале fa, Ъ). Функция f интегрируема по Риману в том и только в том случае, если для любого числа 8 > 0 найдутся такие ступенчатые функции фиф, что
Ъ ъ
<? < / < Ф. о < J ф (х) dx — j <Р (X) dx < в. (5)
а а
Доказательство. Пусть (риф обладают указанными свойствами. Поскольку
ь ь ь ь
$f(x)dx^> fo(x)dx и f t(x)dx ^$ty(x)dx, мы видим, что верхний интеграл отличается от нижнего а а а а
не более чем на8. Так как это верно для любого положительного е, то верхний и ннжяий интегралы совпадают и, значит, функция Ц интегрируема по Риману.
С другой стороны, если j интегрируема по Риману, то существование фифе требуемыми свойствами непосредственно следует из леммы В
В теореме 2 содержится утверждение, высказанное без доказательства в § 1» интеграл мо~ s;cem быть вычислен с любой требуемой точностью при помощи ступенчатых функций.
8.6. Монотонные функции
Теорема 3. Каждая монотонная функция интегрируема по Риману.
Доказател ьство. Рассуждение, проведенное в § 1. 7, показывает, что такая функция удовлетворяет условию теоремы 2.
Поскольку монотонная функция может иметь бесконечное множество точек разрыва, эта теорема свидетельствует о существовании интегрируемых по Риману функций, не являющихся кусочно-непрерывными.
330
Приложение к главе 5
УПРАЖНЕНИЯ
1. Докажите вторую половину леммы Б.
2. Докажите существование функции ф в лемме В
3. Докажите для J утверждение (Д2) леммы Д.
4. Докажите для j утверждение (ДЗ) леммы Д.
5. Докажите сделанное в тексте утверждение о верхнем и нижнем интегралах функции [(х), равной 0 и 1 в зависимости от того, рационально или иррационально х.
6. Приведите пример ограниченной монотонной функции, имеющей бесконечное множество скачкообразных разрывов в интервале (0, 1).
§ 9. Существование несобственных интегралов
В этом параграфе мы докажем теорему сравнения для несобственных интегралов (теорема 1 § 6). Доказательство основано на результате, который важен и сам по себе.
9.1. Пределы монотонных функций
Теорема А (о пределах монотонных функций). Пусть х ь* f(x) — неубывающая функция, определенная в интервале (а, Ъ), где а — число, b — либо число, либо символ H-оо. Допустим, что существует такое число М, что f(x) < М при а < x<Z b. Тогда существует конечный предел а = lim fax) (причем а < М).
х Ъ~
Иными словами, неубывающая функция, ограниченная сверху, имеет предел в правой точке интервала, где она определена. (Если Ь = +оо, то Ь" тоже означает оо.)
Доказательство теоремы опирается на принцип верхней грани. По предположению множество S всех чисел 1(х}, где х лежит между а и Ь, ограничено сверху; в самом деле, верхней границей служит М. Пусть а — наименьшая верхняя грань этого множества (так что а^М). Мы утверждаем, что а — предел слева функции ft в точке х = Ь. Таким образом, следует доказать справедливость двух утверждений: (1) если А — такое число, что а ,то [(х) < А при а<х<^; (2) если В— такое число, что а>В, то существует такое число d, a<^d<^b, что f(x) >В при d<Z х<С Ь.
Утверждение 1 справедливо по той простой причине, что если А > а, то [(x)<Z А при всех х из интервала а< х< Ъ, поскольку t(x) < а для всех этих х.
Чтобы доказать утверждение 2, заметим, что существует такое d, что f(d) >В, так как в противном случае В служило бы верхней границей для Дх), но а >В—наименьшая из верхних границ. А тогда при х< Ъ будет Дх) > В.
9.2. Доказательство теоремы сравнения
Теперь уже легко доказать теорему сравнения для несобственных интегралов. Пусть (а, Ь)— такой же интервал, как в § 9.1, и функции f, g определены в этом интервале. Дано, что для любого с между а и b обе функции ограничены и кусочно-непрерывны в интервале (а, с), что
О < Дх) < g(x) при а <х< b (1)
и что интеграл ъ
$ g(x)dx (2)
а
существует (возможно, как несобственный интеграл). Надо показать, что существует также интеграл &
f f (X) dx. (3)
а
Для каждого у между а в b положим
§ 9. Существование несобственных интегралов.
Задачи
331
У У
F (У) = f f (*) <3 (У) — f g (*) dx-
a a
Обе функции, очевидно, неубывающие; в самом деле, при yt<Z у2 имеем
у»
?(Уд~? (Уд = f f(x)dx>0
У1
в силу (1) и свойства монотонности интеграла; то же рассуждение применимо к G. Поскольку интеграл (2) существует, функция G (у) имеет конечный предел при у —* д”. Поэтому существует такое число Af, что G(y) < М. при а< у<С Ь. В силу (1) и свойства монотонности интеграла имеем F(y) < G(y) при Ь. Следовательно, F(y) < М для тех же у и, по теореме А, функ-
ция F(y) имеет конечный предел при у —► Ь~. Но это равносильно существованию интеграла (3).
УПРАЖНЕНИЯ
1. Сформулируйте и докажите теорему А для невозрастающей функции, определенной в (а, Ь) и ограниченной снизу.
2. Сформулируйте и докажите аналог теоремы А, утверждающий, что при некоторых условиях функция, определенная в интервале (а, 6), имеет предел в левом конце интервала (левым концом может быть —оо).
3. В доказательстве признака сравнения мы воспользовались тем фактом, что если G(y) — неубывающая функция, определенная в (а. 6), и существует конечный предел lim G(y), у -* b~
то G ограничена снизу. Дайте полное доказательство этого утверждения.
ЗАДАЧИ
В задачах 1—17 все функции предполагаются ограниченными и кусочно-непрерывными в любом интервале, по которому они интегрируются.
1. Пусть Дх) непрерывна при 0< х< 1 и принимает только неотрицательные значения.
1
Покажите, что jf(x)dx >0, если только Дх)— не постоянная, равная нулю.
о
Ь
2. Покажите, что | J7(x)dx | < М | b — а | , если |Дх)| < М для х между а и Ь. Проверьте, а
что в отличие от свойства монотонности (3) §1 это предложение не связано с услови-ема<Ь.
3. Пусть Дх) непрерывна и ограничена при а< х< Ь. Предположим, что Дх) не принимает
Ь ь
значения т. Покажите, что либо $t(x)dx > m(b —а), либо jf(x)dx< m(b —а), а а
[Указание: воспользуйтесь теоремой о промежуточном значении и свойством монотонности интеграла. ] Покажите, что соответствующее предложение для кусочно-непрерывных функций неверно.
4. Покажите, что если Дх) ограничена и непрерывна при a<Zx<Z b, то существует такое число Хо, что
Ь
л < *о < * и f (х0) (b — а) = J f(x)dx а
(это — разновидность так называемой теоремы о среднем значении для интегралов).
5. Докажите следующую теорему о среднем значении для интегралов.Пусть р(х) и q(x) — ограниченные непрерывные функции, определенные при а < х< Ь\ допустим, что для этих х имеем р(х) >0- Тогда существует такое число х0, что
ь ь
а < х0< Ь и J р (х) dx = q (х0) У р (х) q (х) dx.
а а
332
Приложение к главе 5
х
6. Докажите следующее обобщение основной теоремы анализа. Пус1ь F(x) = при а
а < х < Ь и в точке хе, а<х0<Ь, существует конечный односторонний предел m=lim Дх). Тогда односторонняя производная существует и равна т.
Х-*Хо“
7. Положим для непрерывной функции ДО
F(x) =|(x~-0/(/)<#.
Покажите, что F(x) дважды непрерывно дифференцируема и что
F"W = /(x).
8. Положим для непрерывной функции ДО
X
f W = 4"
О
Покажите, что F трижды непрерывно дифференцируема и что
F'"(x) = Дх).
9. Обобщая задачи 7 и 8, докажите с помощью математической индукции, что если ДО — непрерывная функция, то функция
х
fw-f U-0-VWd» о
п раз дифференцируема и F(«)(x) = Дх). Найдите также значения F(0), F'(0)» F"(0), .... F(«- D(0).
10. Из основной теоремы следует без каких-либо вычислений, что если даны ограниченная и непрерывная функция Дх) и целое положительное число k, то существует такая функция G(x), что G(*)(x) = Дх). Воспользуйтесь этим замечанием для доказательства утверждений, содержащихся в задачах 7, 8, 9. [У к а з а н и е: воспользуйтесь интегрированием по частям.]
11. Как следует изменить утверждения в задачах 7, 8, 9, если функция f предполагается ограниченной и кусочно-непрерывной?
12. Докажите неравенство Шварца для интегралов:
ь 1 / b ь
f f (x)g(x)dx < 1/ J f (x)2 dx • J g (x)2 dx. a * a a
[Указание. Пусть и — число.Рассмотрите интеграл ь
f [«/ (*) + g (*)Р dx а
и поставьте вопрос о том, может ли быть этот интеграл отрицательным.]
Герман Амакдус ШВАРЦ (1841—1921) был одним из оригинальнейшим математиков XIX столетия.
Задачи
зэз
13. Покажите, что для любых двух функций Ь и g
]/ f [f (*) + g (х)]а dx < \/ Г f (х)а dx + 1/ Г g (х)а dx. » а * а * а
[Указание: примените неравенство Шварца.]
14. Как мы знаем, дифференцируемая функция непрерывна. Если что-либо известно о производной, мы можем иногда сказать, «насколько» функция непрерывна. Это иллюстрируется следующей задачей. Пусть ff(х) непрерывна в интервале, причем для всех х из интервала | ff(x) | < К. Докажите, что для любых двух точек xj и ха из того же интервала имеем
l/Ui) — /(xeJKKIxj — х2|. (а)
15. Только одни постоянные «более непрерывны», чем функции с ограниченной производной. Точнее, если функция j(x) удовлетворяет в некотором интервале неравенству
|/(*1)I « К| *1 —Хг|й, fe>l,
для любых двух точек xj, ха этого интервала, то i постоянна. Докажите это. [У к а-з а н и е: для решения задачи не понадобятся интегралы, а только производные.]
16. Покажите, что при Ь для любой функции Ц имеем
ь / ь
У t (х) dx < V (b — а) j f (х)а dx а * а
[Указание: примените неравенство Шварца.]
Ь
17. Предположим, что/(х) имеет в интервале (а, Ь) производную и что J (х)я dx «С Л4. а
Покажите, что для любых двух точек xlt х2 этого интервала имеем
I f (*i) - Н*а) I « У Allxj-xal. (б)
Это еще один пример, когда можно сказать, «насколько» функция непрерывна, располагая некоторой информацией о ее производной. [Указание: воспользуйтесь результатом задачи 16.]
18. Постройте непрерывную функцию, удовлетворяющую условию (б) задачи 17 при некотором М, но не удовлетворяющую условию (а) задачи 14.
19. В тексте рассматривались несобственные интегралы лишь от неотрицательных функций. Можно, однако, рассматривать такие интегралы и для функций, принимающих как положительные, так и отрицательные вначения. Покажите, что если f(x) ограничена и кусочно-непрерывна в каждом интервале (а, Ь) и если несобственный интеграл
+<»
У lf(x)|dx а
сходится, то существует также несобственный интеграл
4-оэ ь
f f(x) dx = lim f f (x) dx,
a Ь-H- i
в
< У I f(x) I dx. a
334
Приложение к главе 5
[Указание: запишите f (х) = ft (х) — (х), где (х) = f (х) при f (х) > 0 и (х) = О при f (х) < О.]
20. Пусть х ь* Дх)(а < х < Ь) — положительная функция с непрерывной производной. Геометрически очевидно, что длина ее графика по меньшей мере равна расстоянию между точками (а, [(а)) и (6, 1(b)). Дайте аналитическое доказательство этого факта.
21. В тексте были доказаны две важные формулы
J cf (х) dx = о f f (х) dx.
j f (x) dx + | g (x) dx = J [f (x) + g (x)J dx
(I)
(ID
для ограниченных кусочно-непрерывных функций, причем была использована основная теорема анализа. Легко непосредвтвенно убедиться, что равенства (I) и (II) справедливы для ступенчатых функций. Пользуясь этим, докажите соотношения (I) и (II) для любых функций, интегрируемых по Риману, не применяя основной теоремы анализа.
22. Пусть i — ограниченная функция, не обязательно интегрируемая по Риману, и с — постоянная. Покажите, что
J cf (х) dx « с j* [ (х) dx при с > О,
J cf (х) dx = с J f (х) dx при с < 0.
23. Найдите две такие ограниченные функции Дх) и g(x), определенные в (0, 1) что
р (х) dx = р (х) dx = 0,
[/W + g(x)ldx=l.
6/ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
Эта глава посвящена важнейшим трансцендентным (т. е. не рациональным и не алгебраическим) функциям, применяемым в математике и ее приложениях. В число этих элементарных трансцендентных функций входят тригонометрические функции, логарифмические и показательные функции. Мы будем изучать их методами математического анализа, не предполагая у читателя никаких предварительных знаний об этих функциях.
Приложение к этой главе содержит три параграфа. В § 6 рассматриваются различные применения показательных функций, в § 7 — гиперболические функции, в § 8 — примеры некоторых неэлементарных функций.
336
6. Трансцендентные функции
§ 1. СИНУС И КОСИНУС
1.1. АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
Функция х I-* f(x) называется алгебраической, если по заданному числу х можно вычислить /(х) с помощью конечного числа сложений, умножений, вычитаний, делений и решения конечного числа алгебраических уравнений, т. е. нахождения корней многочленов.
Все многочлены, рациональные функции и иррациональные функции — алгебраические.
Рассмотрим в качестве типичного примера функцию
Пусть х = 4. Чтобы найти у, сначала надо решить алгебраические уравнения /a = 4Hf = 4H найти, таким образом, ]/~4 = 2 и у/~4. Затем надо вычислить число
3 • 2 — 2 4
5 • 2 + V 4 10 +
из которого у получается возведением в степень 3/7; для нахождения этого числа нам потребуются операции умножения, вычитания и деления. Наконец, у находится как решение алгебраического уравнения у1 = 14/(10 4)]3.
Функция, не являющася алгебраической, называется трансцендентной. Простейшими и наиболее важными трансцендентными функциями являются так называемые элементарные трансцендентные функции: логарифмические функции; показательные х ах, связанные с операцией возведения в степень; тригонометрические функции; функции, обратные тригонометрическим. Эти функции знакомы читателю; их обычно изучают в средней школе. Поскольку, однако, наиболее простой и поучительный подход к этим функциям связан о (математическим) анализом, мы не будем предполагать никаких предварительных знаний о логарифмах или о тригонометрии, а изложим все эти вопросы «ab ovo»*.
Доказательство того факта, что только что упомянутые функции действительно трансцендентные на этом этапе потребовало бы от нас очень сложных рассуждений; располагая же более развитой математической техникой, это можно доказать очень просто. Поэтому мы просим читателя принять на веру, что функции, называемые здесь трансцендентными, в самом деле являются таковыми.
* Буквально — «6 яйца» (лат.), т. в. е самого начала (выражение ab ovo есть сокращение латинского выражения» «ab ovo usque ad mala», т. e. «от яйца до фруктов», означавшего в древнем Риме «е начала и до конца» — здесь имеется в виду то, что у римлян обед обычно начинался с яиц и кончался фруктами)
§ 1. Синус и косинус
337
УПРАЖНЕНИЯ
1.
2.
3.
Опишите алгебраические операции, применяемые для вычисления у по данному х в случае функции у = 1 + х4 + "|/1 + х2. Вычислите у, если х = 2~\/^2.
Опишите алгебраические операции, применяемые для вычисления у по данному х в случае функции # = /?+ 4 4-— х + 1. Вычислите у, если х = 1.
Опишите алгебраические операции, применяемые для вычисления и по данному t в случае функции
з,
4.
и =
Опишите алгебраические операции, применяемые для вычисления $ по данному ф в случае функции
1
Вычислите $, если ф = 8.
5. Опишите алгебраические операции, применяемые при вычислении г по данному у в случае функции
_ ( у"1' + у Yz*
г '
Вычислите г, если у = 8.
6. Опишите алгебраические операции, применяемые при вычислении х по данному и в случае функции
— 3/—
/и 4-у и+ 1
х------ЗГ
У и2 4- и -f- 1
1.2. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Пусть р =/= 0 — число их»-* f(x) — функция. Говорят, что / имеет период р, или периодична с периодом р, если
/(х 4- р) = /(р).
График периодической функции изображен на рис. 6.1.
Если f имеет периоды р и р, то р + q — также период, поскольку f(x + р + q) = == f(x + р) = /(х). Таким образом, если / имеет период р, то все целочисленные кратные р, как, например, р, —р, 2р, —2р, Зр и т. д., также являются периодами /. Наименьший положительный период /, если таковой существует, называется просто периодбм функции / (или, лучше, примитивным периодом /).
Периодические функции играют важную роль в науке и технике, поскольку очень многие явления природы и искусственные устройства периодичны во времени: движения планет, приливы, звуковые волны, электромагнитные колебания, дыхание, движение часов и других механизмов и т. д.
Перечислим некоторые простые свойства периодических функций.
338
6. Трансцендентные функции
Г. Если f(x) имеет период р и g(x) = /(ах), то g имеет период p/а (здесь, конечно, предполагается, что а #= 0).
Доказательство. Очевидно, имеем g(x + (p/a)) = f [а(х + (р/а)] = f (ах + р) = f (ах) = g(х).
2°. Если f(x) имеет период р и дифференцируема, то f'(x) также имеет период р.
Доказательство. Ясно, что f(x 4- р 4- Л) — f(x + ,р) = f(x + h)— —f(x). Разделим это равенство на Л и перейдем к пределу при h -► 0; мы получим f'(x + р) = f'(x).
3°. Если функция f(x) определена и непрерывна в замкнутом интервале [х0, х0 + р] и f(x0)= f(x0 + р), то можно так определить f(x) для всех х вне этого интервала, чтобы f стала непрерывной функцией, периодической с периодом р. (Это 'можно сделать единственным способом.)
§ 1. Синус и косинус
33»
Доказательство. Каждое х можно записать в виде х = пр 4- у, где п — целое число и х0 -С У < + р. Величина f(y) нам известна; вследствие перио-
дичности мы должны положить f(x) = f(y). Условие /(х0) = /(х0 + р) гарантирует непрерывность полученной функции. Эта ситуация изображена на рис. 6.2.
1.3. ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СИНУСА И КОСИНУСА
Важнейшими периодическими функциями являются тригонометрические функции, в частности синус и косинус. Напомним геометрическое определение этих функций.
Рассмотрим единичную окружность х? 4- у2 = 1. Пусть 9 — неотрицательное число и Р (9) — точка единичной окружности, достигаемая в результате движения по окружности в положительном направлении (против часовой стрелки), начиная с точки (1, 0), после прохождения пути длины 9». Заключенное в кавычки выражение апеллирует скорее к общежитейским представлениям, чем к математике; оно имеет следующий точный смысл: при 9= 0 следует считать, что Р(9) есть точка (1, 0); при 0 < 9 С я символ Р(9) означает ту точку верхней полуокружности, для которой дуга полуокружности от Р(0) до Р(9) имеет длину 9, как это изображено на рис. 6.3 (геометрически очевидно, что существует в точности одна такая точка; в дальнейшем это будет доказано аналитически); при л < 9 2л под Р(9) понимается та точка нижней полуокружности, для которой длина дуги между Р(л) = = (—1, 0) и Р(9) равна 9— л, как это изображено на рис. 6.4; при 9 > 2л запишем 9 в видев = 2лп 4- <р, где п — целое положительное число и 0 ф < 2л, и положим Р(0) = Р(ф). Таким образом, для всех 0 имеем
Р(0 + 2л) = Р(0). (1)
Определим также Р(—0) как точку, симметричную Р(0) относительно оси х; это определение оправдывается рис. 6.5. Говорят, что точка Р(—0) достигается в результате движения на 0 единиц длины вдоль единичной окружности в отрицательном направлении (по часовой стрелке), начиная с точки (1, 0). Заметим, что соотношение (1) сохраняет силу и при отрицательных 0.
Пусть теперь 0 —любое число, и точка Р(0) имеет координаты (х, у). Тогда вводят следующие определения (рис. 6.6):
cos 9 = х, sin 9 = у.
Поскольку точка Р(9) всегда принадлежит единичной окружности, имеем (cos 9)а 4- (sin 9)2 = 1. (2)
д л pfi
sin 9 > 0 при 0 < 6 < те. (3)
Из нашего определения вытекает, что синус и косинус периодичны с периодом 2те; именно, вследствие (1)
cos (9 4- 2те) = cos 9, sin (9 4- 2те) = sin 9. (4)
Далее, P(0)=(l, 0), Р(те/2) = (0, 1), Р(те) = (—1, 0), так что
cos 0 = sin— = 1, sinO = cos — = sin те = 0, cos те =— 1. (5)
2 2
340
6. Трансцендентные функции
Рис. 6.7
Рис. 6.8
§ 1. Синус и косинус
341
Рис. 6.10
Поскольку точки Р (9) и Р (— 0) симметричны относительно оси х, имеем cos (— 0) = cos 9, sin (— 9) = — sin 9; (6)
таким образом, косинус — четная функция, а синус — нечетная функция.
Геометрически очевидно (и будет дальше доказано), что синус и косинус — непрерывные функции, а также что косинус убывает в интервале [0, л], а синус возрастает в интервале [0, у] и убывает в интервале л]. Графики функций sinO и cos 0, определенных в интервале [0, л], изображены на рис. 6.7 и 6.8. С помощью равенств (6) легко продолжить эти графики на интервал [—л, л] (рис. 6.9). Важно запомнить общую форму этих кривых; обратите внимание, в частности, на то, где функции синус и косинус положительны, отрицательны, убывают, возрастают.
На рис. 6.10 графики тех же функций изображены на большем протяжении; из него видно, что 2л является примитивным периодом синуса и косинуса.
УПРАЖНЕНИЯ
Установите, периодичны ли следующие функции, и в случае утвердительного ответа найдите ИХ примитивные периоды.
7. хн- sin Зх. 9. хь* (1 + cos3x)sin(x/8)
8. х cos х + cos 2х. 10. х н* sin(x/rt).
342
6. Трансцендентные функции
14. УГЛЫ
Мы определили синусы и косинусы чисел; в средней школе же обычно говорят о синусах и косинусах углов. Установим теперь связь между этими двумя понятиями.
Точка О на прямой I делит прямую на два луча; О называется началом обоих лучей. Углом называется пара лучей с общим началом', это начало называется вершиной угла, а лучи — его сторонами. Чтобы задать угол, достаточно указать его вершину О и две точки, отличные от О, на обеих его сторонах, например Р и Q (рис. 6.11). Заданный таким способом угол обозначается через ^POQ или ^.QOP. На данном этапе мы рассматриваем лишь ненаправленные углы, т. е. считаем стороны угла равноправными, не выделяя одну из них в качестве «первой».
Пусть дан угол, стороны которого различны, например построим окруж-
ность радиуса 1 с центром О и обозначим через А, В точки ее пересечения со сторонами угла.. Эти точки делят окружность на две дуги; длина меньшей из них, 0, называется мерой угла (рис. 6.11). Если обе дуги имеют равную длину, безразлично, какую из них выбрать; в этом случае мера равна л и обе стороны угла суть лучи одной прямой. Если же стороны угла совпадают, то, по определению, его мера рав
§ 1. Синус и косинус
343
на нулю. Мера ненаправленного угла всегда есть число 0, удовлетворяющее неравенствам ОС0 < л.
При 0 = л/2 угол называется прямым. Два угла с одинаковой мерой называются конгруэнтными. Часто вместо этого говорят, что два угла «равны», а вместо выражения «мера ^POQ есть 0» говорят: «угол POQ равен 0». Подобного рода языковые неточности безвредны, пока они не приводят к смешению понятий.
Если дан угол ^zPOQ меры©, то sin (^POQ), по определению, означает sin0, a cos (^POQ) означает cos 0. То же соглашение применяется дальше к другим функциям.
1.5. ТРЕУГОЛЬНИКИ
Пусть дан треугольник с вершинами А, В, С; обозначим для краткости длины его сторон ВС, СА, АВ соответственно через а, Ь, с, а меры его углов ^:ВАС, ^СВА, s'BCA — через А, В, С (рис. 6.12). Если, в частности, угол при вершине С — прямой (С = л/2, как на рис. 6.13), то имеем
sin А = — , cos А = —. (7)
с с
Чтобы в этом убедиться, введем координатную систему с началом в А такую, что С принадлежит положительному лучу оси х и единица масштаба такова, что с = 1. Тогда точка В имеет координаты (cos A, sin А), что и доказывает утверждение (7).
Заметим теперь, что в рассматриваемом треугольнике А + В — л/2 и что sin В = = Ыс = cos Л. Отсюда
sin 9 = cos (-2-о). (8)
Мы доказали это соотношение для О<0 < как видно из (5), равенство (8) справедливо также при 0 = 0 и 0 = л/2; в дальнейшем мы увидим, что (8) справедливо при в с е х 0. *
1.4. ГРАДУСЫ И РАДИАНЫ
Тригонометрические функции применяются в землемерии для вычисления элементов плоских треугольников, а в астрономии и навигации — для вычисления элементов сферических треугольников, т. е. треугольников, образованных дугами больших окружностей сферы. Применения в астрономии предшествовали всем другим. Таблицы функции синус были составлены уже во II в. до н. э. Старейшие сохранившиеся таблицы содержатся в труде Птолемея, известном под арабским названием «Альмагест»*. Латинское слово «синус» является искажением арабского слова, означающего хорду.
• Точнее, следовало бы писать «Аль-магест» — приставка «аль» придает арабизированную форму греческому слову це-ра-ст) (величайшая), хорошо выражающему отношение арабских ученых к книге Птолемея.
344
6. Трансцендентные функци
Рис. 6.14
Рис. 6.15
Принято делить полную окружность на 360 равных частей, называемых градусами, каждый градус — на 60 минут (1* = 60') и каждую минуту — на 60 секунд (Г = 60"). Эта традиция восходит к шестидесятиричной системе счисления, принятой в древнем Вавилоне. В повседневной жизни и в большинстве научных и технических вопросов углы измеряют не в числах, а в градусах; градусная мера угла используется практически во всех тригонометрических таблицах.
В математике же, напротив, почти неизбежно следует измерять углы «естественным» способом, т. е. числами. Простейший способ сопоставления этих методов состоит в том, что раз и навсегда уславливаются ечитахь ЗбО9 (360 градусов) другим наименованием числа 2л, Iе (один градус) — другим наименованием числа
и вообще k9 (k — градусов) — другим наименованием числа . Итак,
В частности,
(9)
Угол меры 1 часто называется радианом.
фПримеры. 1. Чему равен cos (—90°)?
Ответ. Поскольку 90°=^^= — , имеем cos(—90°) = cos 90° = cos — = 0.
180 2 ' 2
2. sin30° =-i-, sin60° = . sin45° = Jy-.
Первые два соотношения легко находятся из равностороннего треугольника (рис. 6.14) с помощью теоремы Пифагора, последнее — из прямоугольного равнобедренного треугольника (рис. 6.15).
§ 1. Синус и косинус
345
3. Чему равен sin 360 030°?
Ответ. В силу периодичности синуса и результата предыдущего примера имеем
sin 360 030° = sin (1000-360° + 30°) = sin 30° = 1/2.®
УПРАЖНЕНИЯ
11. Примените равенства (7) для вычисления cos(k/4) и sin(u/4).
12. Примените равенства (7) для вычисления косинуса и синуса к/3 и к/6.
В упражнениях 13—17 мера углов задается в градусах. Обратите ее в эквивалентное числовое (радианное) выражение.
13. 10°. 14. 15°. 15. 24°. 16. 36°. 17. 90°/те.
В упражнениях 18—22 мера углов задается численно (в радианах). Обратите ее в эквивалентное градусное выражение
18. к/9. 19. к/10. 20. к/30. 21. к/8. 22. 1/3.
23. Вычислите sin 2925°. 24. Вычислите cos 2925°.
1.7. ОБРАТНЫЕ ФУНКЦИИ ДЛЯ СИНУСА И КОСИНУСА
Наша ближайшая задача — выразить синус и косинус с помощью интегралов. Оказывается, это можно сделать, если рассмотреть вместо функций cos 0 и sin 0 им обратные.
Конечно, функции синус и косинус не монотонны. Чтобы определить, например, функцию, обратную х = cos 0, надо выбрать интервал, в котором эта функция возрастает илиубывает. Мы выберем с этой целью интервал [0, л]. Функция, обратная cos 0 в этом интервале, называется арккосинусом и обозначается через arccos. Таким образом,
0 = arccos х означает, что х = cos 0, 0 0 л,
или
arccos(cos 0) = 0 при 0^0 л, cos(arccos х) = х.
346
6. Трансцендентные функц^
Функция arccos х определена лишь при — 1 1, так как | cos 01 никогда не
превосходит 1. График функции, обратной косинусу, изображен на рис. 6.16; он получен отражением графика рис. 6.8 от биссектрисы угла между положительными лучами осей х и у.
Вспомним теперь (см. § 1.3), что при 0^0 < я величины cos0 и sin© суть координаты точки {х, у), для которой ха + Уг = 1 и у >• 0, так что длина дуги верхней полуокружности от (1, 0) до (х, у) (жирная линия на рис. 6.17) равна 0.
В силу формул § 4.9 гл. 5 длина такой дуги
0 =
du
/1 — и»
(Ю)
Она равна также удвоенной площади кругового сектора, опирающегося на эту дугу, т. е.
1
9= х]/1—х2+ 2J/1 — и* du. (10')
X
(Эти два выражения для 0 равны друг другу, поскольку оба представляют собой непрерывные функции от х, равные нулю при х = 1 и имеющие одинаковые производные. Первое выражение короче; второе же имеет два преимущества: оно не содержит «несобственного» интеграла и может быть получено без помощи формулы длин.)
Поскольку равенства (10) и (10') означают, что х. = cos 9, имеем 9 = arccos х. Следовательно, ,
1 р du arccos х= 1 — при |х|<1 (11)
У1 — иг
§ 1. Синус и косинус
347
И
______ 1
arccosх = х"К 1—х2 + 2 J J/ 1 — и2du при |х|^1. X
(11')
Геометрический смысл последней формулы виден из рис. 6.18.
Дифференцируя обе части равенств (11) или (1Г), получаем
d (arccos х) 1
dx у 1—х2
при — 1 < х < 1,
(12)
чем еще раз доказывается, что арккосинус — убывающая функция. Весьма замечательно, что производная трансцендентной функции арккосинус есть алгебраическая (а именно иррациональная) функция.
Найдем теперь функцию, обратную синусу. Как видно из графика, функция 0 >-► sin 0 возрастает при —л/2 0 В интервале [—л/2, л/2] синус имеет, следовательно, обратную функцию, называемую арксинусом и обозначаемую символом arcsin. Ясно, что эта обратная функция определена в интервале [—1, 1]; ее график изображен на рис. 6.19. Заметим, что
9 = arcsin х означает, что х = sin 9,---j- 9 "С •
Чтобы найти формулу для арксинуса, рассмотрим сначала такое число х, что О •< х < 1. Тогда (см. рис. 6.19) 0 arcsin х < и поэтому в силу равенства (8) § 1.5 имеем
sin -----arccos xj = cos (arccos х) = х. .
Отсюда
arcsin х = -^— arccos х, (13)
а так как 1 1 я р du Г du
—----arccos х = arccos 0 — arccos х = I ------ — I =
2 J yi — u2 J У 1 — u2
0 x
1 x x .
P du p du Г du
J /1 — J yi —«a J у 1m-W2 ’ o i о
получаем
arcsin x =
(14)
Мы доказали это для 0 < х < 1; но формула (14) верна и при —1 х < 0.
В самом деле, поскольку sin 0 — нечетная функция, arcsin х должен быть нечетен,
348
6. Трансцендентные функции
а правая часть (14) как легко видеть,— нечетная функция от х. Итак, формула (14) справедлива при —1 х 1, а тем самым справедлива при —1 1 и форму-
ла (13), равносильная (14). Правило дифференцирования
d (arcsin х) 1
------------ = ~~--------j при — 1 < х < 1
dx у 1 — х2
(15)
непосредственно следует из (14).
УПРАЖНЕНИЯ
В упражнениях 25 — 30 найдите указанные числа.
25. arccos (1/2). 28. arcsin (— Vzl 2).
26 arcsin (1/2). 29. arccos (—1/2).
27. arccos (1 / 30. sin (arcsin (1/27)).
В упражнениях 31 — 34 найдите f' (x).
31. f (x) = arcsin (2x), | x |< 1/2.
32. f (x) = (arccos x)3, | x |< 1.
33. / (x) = arcsin (sin 2x).
34. f (x) = sin [arcsin (2x)J.
35. Найдите -7— (arccos У 1 — xa), 0 < x < 1. dx
d
A 36. Найдите------((arccos u) (ntccQs 2a)].
du
37. Продифференцируйте t »-> У 1 — t2 arccos/.
P du
38. Найдите I — ----------.
J- У 1 — 16ua
39. Найдите j
P 3uh
40. Найдите I — - du.
J
о
41. Найдите J arccos xdx. [Указание: примените интегрирование по частям; будьте осторожны с несобственным интегралом.)
Найдите
dx
ya — bx2
где а и b —* положительные постоянные. Указание: восполь-
зуйтесь тем, что У а — Ьх2 = Уа
Vi
р dx
Вычислите I ---------- .
J у\ — х2 о
§ 1. Синус и косинус
.34*
44. Вычислите
45. Вычислите
arccos ©
46. Вычислите
[Указан и е: примените подстановку t— г2.]
1.8. ПОВТОРЕНИЕ
Каков же итог наших предыдущих рассуждений? Он, очевидно, сводится к следующей теореме:
Теорема 1. Существуют однозначно определенные непрерывные функции О |~* cos 0, 0 sin 0, заданные при всех значениях 0 и обладающие следующими свойствами:
(I) Функция cos 0 четна, имеет период 2л и является в интервале 0 < 0 < тс обратной для функции
arccos х =
du
/T^TI2
(16>
(так что х = cos 0 равносильно 0 = arccos х).
(II) Функция sin 9 нечетна, имеет период и
sin 0 = — (cos О)2 при О С 9 тс
(17)
(III) Каждая точка (х, у), для которой х2 + у2 = 1, может быть записана & виде х = cos 0, = sin 0, и это представление единственно, если потребовать, чтобы было О 0 < 2л.
При выводе этой теоремы мы приняли (в § 1.3) некоторые утверждения как геометрически очевидные. Этого легко избежать. Формула (16), определяющая arCcos х, показывает, что функция х »-> arccos х непрерывна, убывает при —1 х 1 и что arccos (—1) = л, arccos 1 = 0. Теперь мы можем считать утверждения (I) и (II) нашей теоремы определениями cos 0 и sin 0 и доказать непрерывность этих функций, опираясь на теорему 7 § 3.7 гл. 3 о непрерывности обратных функций. Как видно из формул для арккосинуса и арксинуса, можно было бы прийти к тригонометрическим функциям без всякого обращения к геометрии — просто изучив функцию, обратную для первообразной некоторой несложной иррациональной функции (а именно функции х 1/]Л 1 — х2).
350
6. Трансцендентные функции
1.9. ДИФФЕРЕНЦИРОВАНИЕ СИНУСА И КОСИНУСА
Теорема 2. Справедливы формулы
d cos 0 . „ d sin 6 л z i о\
= — sin 0, ---------- COS 0. (18)
М di
Доказательство. Предположим сначала, что 0 < 6 <; к. В силу равенства (12) и теоремы о дифференцировании обратных функций (теорема 7 § 2.1 гл. 4) имеем, полагая 6 = arccos х, х = cos 6:
4 cos 9 _ 1 __________________1 ___т/|__xz __
di di I d cos 9 d arccos x I dx — 1 / У 1 — x2
= — 1 — (cos 0)a = — sin 0,
что и требовалось доказать. Далее, в силу (17) по цепному правилу имеем
d sin 9 d К1 — (cos 9)2 4 /1 — (cos 9)a dcos9 _
di ~ di ~ dcos9 di
1 1 cos 9 sin 9
=-------— - (— 2 cos 9) (— sin 9) ------ cos 9.
2 /1 _ (cos 9)2 sin 9
Следовательно, в интервале (0, к) справедливы соотношения (18).
Для 9 из интервала (— к, 0) число — 9 заключено между 0 и я и в силу (6), по цепному правилу, dc^9 = dcos(-9) =---------------dcos(-6) _ _ _ = _
di di d (— 9)
d sin 9 d sin (—9) 4 sin (— 9)__ , 0
" "--- — ’- ——— = == CUb l- Ul — LUo U.
di di d (—9)
Вследствие периодичности [см. свойство (2) периодических функций в § 1.2J те же соотношения (18) верны и для всех значений 9, кроме, может быть, 9 = 0, л, — л, 2л, — 2л и т. д. Но поскольку косинус и синус везде непрерывны, формулы (18) сохраняют силу и в этих точках. В самом деле, пусть F(9) — первообразная функция для sin 9; положим G(9) = F(9) 4-cos 9. Тогда G(9) непрерывна везде и G'(9) = —
— sin 9, за исключением, может быть, значений 9 = пп, где п — целое число. Но тогда G(9) должна быть постоянной, так что G'(9) = 0 и, следовательно, (cos 9)' = = —sin 9 везде. Второе утверждение (18) доказывается подобным же образом.
•Примеры. Отметим два важных частных случая.
1. Показать, что
.. sin а . lim-----== 1
а->0 а
(так что для малых значений |а| синус а близок к а).
Решение. Поскольку sin 0 = 0, имеем
Um slne Um sin (0 + а) — sin 0 /dsin9\ _ *
lim---------- lim —1—!—-------= /------1 = cos 0=1.
а-*0 Л а-*>0 Л \ dO /0=0
§ 1. Синус и косинус
351
2. Показать, что
lim cosa-J = 0
а->0 Cl
Решение. Как и выше, доказывается, что искомый предел есть производная от cos 6 в точке 6 = 0, т. е. он равен sin 0 = О.ф
Примечание. К сожалению, принято писать cos^ 6 вместо (cos 6)2, sin3 6 вместо (sin 6)3 и т. д. и аналогично для других тригонометрических функций.* Мы придерживаемся этой традиции и пишем, например, cos2 6+sin26=l вместо простого и не могущего вызвать никаких разночтений равенства (cos 6)2 + (sin 6)^ = 1.
УПРАЖНЕНИЯ
47. Продифференцируйте t sin (2t + 1).
d
48. Найдите —— cos xa. dx
49. Найдите---cos2 x,
dx
60. Найдите —- cos cos x. dx
51. Продифференцируйте z к* sin (cos z).
dy
Найдите —— , где у = cos 0 sin 0. a0
53. Найдите-----sin (arccos u),
du du
± 54. Найдите ------, где и = cos2 (2г + 1) sin (2г + I)2.
dz
d2
55. Найдите — • cos3 (20). dO2
d2t/
56. Найдите , где у = arccos (sa). ds2
9n/2
57. Найдите J sin 3t di,
5it/2 c °
58. Найдите l cos-^- dO. &
59. Найдите J cos (xa) x dx.
* Иногда (в частности, в старых английских учебниках) символом f(x) обозначали суперпозицию j о f(x). Если принять эту систему обозначений, то выражение sinax должно было бы обозначать sin (sin х), а вовсе не (sin х)а.
352
6. Трансцендентные функции.
р dx
А 60. Найдите 1 cos (]^Т) —
61. Найдите J (sin2 0) cos 0 dO.
г / 1 \» sin 0 dO.
62. Найдите
63. Найдите J х cos х dx, [Указание: проинтегрируйте по частям.]
d?y х
64. Найдите решение дифференциального уравнения — = cos — .
сРу dy
65. Найдите решение дифференциального уравнения — 2 = 3 cos х. [Указание:
положите t/ = acosx4- bsinx, где а и b —»постоянные, и подставьте у в дифференциальное уравнение.]
66. Найдите lim -7- cos | — -f- .
Лм.о h \ 2 }
sin (л 0
67. Найдите lim----------- .
м) *
sin2 X
68. Найдите lim—— .
Х-0 X
cos 0 sin О
69. Найдите 11 m-------.
е-о 0
1.10. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ СИНУСА И КОСИНУСА
Хотя использование тригонометрических функций в геометрии сегодня так же важно, как и в старину, все же большое место функций синус и косинус в математике и в других науках в первую очередь связано с дифференциальным уравнением, которому удовлетворяют эти функции.
По теореме 2, (cos х)' = —sin х и (sin х)' = cos х, откуда (cos х)" = —cos х. Подобным же образом (sin х)" = —sin х, так как (sin х)" = (cos х)' = —sin х. Итак, обе функции х cos х и х »-► sin х удовлетворяют одному и тому же дифференциальному уравнению
ГМ + f(x) = 0. (19)
Мы найдем все решения этого дифференциального уравнения второго порядка. [Уравнение (19) называется уравнением второго порядка, поскольку в него входит вторая производная. Независимую переменную мы обозначаем здесь через х вместо 0, что, разумеется, несущественно. Мы предпочитаем такое обозначение, поскольку геометрическое происхождение синуса и косинуса отходит теперь на второй план.)
§ 1. Синус и косинус
353
Теорема 3. Пусть aub — два числа. Если
f(x) = a cos х + b sin х, (20)
то f(x) удовлетворяет уравнению (19):
Г(х)+/(х) = 0 и /(0) = а, /'(0) = Ь. (21)
Обратно, если функция f(x) удовлетворяет уравнению (19) а условиям (21), то она имеет вид (20).
Во второй части теоремы предполагается, что f(x) определена при всех х или по крайней мере в некотором интервале, содержащем х = 0. Отметим три важных частных случая:
если /" + / = 0 и /(0) = /'(0) = 0, то f = 0;
если /" + / = 0 и /(0) = 1, /'(0) = 0, то /(х) — cos х;
если /" + f = 0 и /(0) = 0, /'(0) = 1, то /(х) = sin х.
Доказательство теоремы 3. Если /(х) = a cos х + b sin х, то, как
легко проверить, /"(х) + /(х) = 0 и /(0) = а, /'(0) = Ь.
Второе утверждение мы докажем сначала в частном случае. Предположим, что /(х) удовлетворяет уравнению /" + / = 0 и что /(0) = /'(0) = 0. Мы покажем, что = 0.
Для этого рассмотрим функцию
<р(х) = [/(х)]2 + [/'W12
Ясно, что ф(0) = 0 и
<Р'(Х) = 2/(х)/'(х) + 2f (х)/"(х) = 2/'(х)[/(х) + Г(х)\ = 0.
Следовательно, функция ср постоянна, а поскольку <р(0) = 0, имеем <р(х)= 0. Так как 1/(х)]2 и [/'(х)]2 неотрицательны, отсюда следует, что [/(х)]2 = 0 и, значит, /(х) = 0.
Пусть теперь f (х) — заданная функция, удовлетворяющая уравнению f" -f- f=0 и условиям /(0)=а, /'(0) = 6. Положим g(x) = f(x)— acosx — b sin x; надо показать, что g(x) = 0. Но g(0) = /(0) — а = 0 и, далее,.
g'(x) = /'(х) + a sin х — b cos х, g'(0) = /'(0) — 6 = 0, g"(x) = f'(х) + a cos х + b sin х = —f(x) + a cos х + b sin х = —g(x).
Таким образом, g''(x) + g(x) = 0 и g(0) = g'(0) = 0; по доказанному выше g(x) = 0, что и требовалось доказать.
Содержание теоремы 3 иногда выражают, говоря, что /(х) = a cos х + b sin х есть общее решение дифференциального уравнения /"(х) + /(х) = 0. Это значит, что при любом выборе постоянных а, b функция a cos х + b sin х удовлетворяет уравнению и что любая функция, удовлетворяющая уравнению, может быть записана в виде a cos х + Ь sin х при некотором выборе а и Ь.
Теорема утверждает также, что решение /(х) уравнения /"(х) + 7(х) = 0 однозначно определяется так называемыми начальными условиями, т. е. значениями /(0) и /'(0), которые могут быть заданы п роизвольно. Можно задать также значения функ.
354
6. Трансцендентные функции
ции f и ее производной /' в любой точке х0. В самом деле, если /(х) — решение, удовлетворяющее условиям /(0) = а, /'(0) = то ЛОО = /(* — *о) есть решение, удовлетворяющее условиям /1(х0) = а, /'i(x0) = Ь.
УПРАЖНЕНИЯ
В упражнениях 70—75 найдите решение дифференциального уравнения (19), удовлетворяющее указанным условиям.
70. /(0) = /'(0) = 1. 73. £(л/2) = 0, f (л/2) = 1.
71. /(0) = 2f'(0) = 8. 74. /(-л) = Г(-л) = 3.
72. /(л) = 1, Г(л) = — 1. 75. £(3л) = Г(3л) = Зл.
1.1 1. ТЕОРЕМА СЛОЖЕНИЯ
Из теоремы 3 можно вывести все свойства синуса и косинуса . Важный пример представляет так называемая теорема сложения:
Теорема 4. Справедливы тождества
sin (х + у) = sin х cos у + cos х sin у,
(22) cos (x + у) = cos x cos у — sin x sin y.
Доказательство. Пусть /(x) = sin (x + у), где у фиксировано. Продиф' ференцируем эту функцию дважды, помня, что у следует рассматривать как поспит янную. Имеем f'(x) = cos (х + у) и f"(x) = —sin (х + у), так что f''(x) + /(х) = 0 при всех х. В силу теоремы 3 имеем /(х) = a cos х + Ь sinx, где а —/(0) и &=/'(0). Но /(0) = sin у и /'(0) — cos У- Подставляя эти значения а и 6, получаем первое из соотношений (22). Второе можно доказать аналогично или получить дифференцированием по х обеих частей первого соотношения, где у считается фиксированным.
Из теоремы сложения вытекает ряд интересных следствий. При х = у получаем формулы удвоения:
sin 2х = 2 sin х cos х, cos 2х = cos2 х — sin^ х.
Второе соотношение можно записать также в виде
cos2x = 2cos2x— 1 =s 1 —2sinax.
При у = л/2 и у = ъ получаем соотношения
sin (х + л) = — sin х, cos (х + л) = — cos х.
(23)
Из теоремы сложения вытекают также важные формулы
sin | —--х | = cos х, cos | —-x | = sin x;
V2 J \ 2 )
мы предоставляем читателю самостоятельно провести подробное их доказательство
§ 1. Синус и косинус
355
(раньше эти формулы были установлены лишь при О х л/2). Отсюда видно, что график косинуса может быть получен из графика синуса сдвигом влево на л/2.
ф Примеры.
что 0 9 к.
Решение.
« п -в 0 • Л Л о
1. Выразить sin — и cos — через sin 9 и cos 9, предполагая,
Применив теорему удвоения, считая 2х = 9, находим
П 20 -26
cos 9 = cos2----sin2 —.
2 2
Кроме того, 1 = cos2 —+ sin2—. 2 2
Складывая и вычитая два последние равенства, получаем
1 — cos 9 =2 sin2 —, 1 + cos 9 = 2 cos2 —.
2 2
Разделив на 2 и замечая, что sin— и cos — Д°лжны быть неотрицательны, имеем
2. Выразить cos Зх и sin Зх через cos х и sin х.
Решение. Применив теорему сложения и формулу удвоения, имеем cos Зх = cos 2х cos х — sin 2х sin х = cos3 х — cos х sin2 х — 2 sin2x cos х = = cos3 х — 3 cos х sin2 x.
Точно так же показывается, что
sin Зх = 3 cos2 х sin х — sin3 х.
3. Доказать формулы
cos х + cos у = 2 cos cos -, * 2 2
sin х + sin у = 2 sin * +-у cos —~ ~. 57 2 2
Решение. Мы докажем только первое из этих соотношений; второе получается аналогично. По теореме сложения,
cos (а + 0) = cos а cos 0 — sin а sin 0,
а так как а — 0 = а + (—0), то
cos (а — 0) = cos а cos 0 + sin а sin 0.
Сложив два последних равенства, получаем
cos(a + 0) + cos(a — 0) = 2 cos a cos 0.
356
6. Трансцендентные функции
Полагая здесь а + ₽ = х, а — ₽ = д, имеем а = х^~ и 0 = -у— , откуда и следует требуемое соотношение, ф
УПРАЖНЕНИЯ
76. Выразите sin 40 через cos0 и sin 0.
77. Выразите cos 5х через cos х и sin х.
78. Выразите cos (0/4) через cos0 и sin0, предполагая, что 0<0<2л.
79. Выразите cos(3f/2) через cos2 и sinf, предполагая, что 0«/ «л.
80. Найдите J sin2 х dx, [Указание: примените формулу удвоения.]
81. Найдите J cos2 Зх dx,
Д 82. Найдите J cos2 х sin2xdx. [Указание: примените повторно формулу удвоения.]
83. Найдите J cos4 2г dz. [Указание: примените повторно формулу удвоения.] тс/З
84. Найдите j sin 0 sin (0/2) d0. [Указание: примените формулу для половинного угла те/4
из примера 1.]
85. Найдите [* cos 5u cos Зи du, [Указание: решите относительно х и у уравнения (х + У)/% — Зи, (х— у)/2 = 3и и воспользуйтесь результатом примера 3.]
В упражнениях 86—91 начертите графики заданных функций. В частности, найдите точки, где касательная горизонтальна или вертикальна, точки перегиба, точки максимума и минимума (абсолютного и локального). Укажите также, где функция убывает и где она возрастает, где она выпукла вверх и где вниз.
86. 0 2 sin (0/2). Воспользуйтесь только рис. 6.9.
87. О »—► 3 sin 20. Воспользуйтесь только рис. 6.9.
88. О _1_ cos 40. Воспользуйтесь только рис. 6.9.
89. х I—► х + sinx при —л < х < л.
90. х cos2x при —л < х < л.
91. х ь* )^cosx при —л/2 < х < л/2.
1.12. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВТОРОГО ПОРЯДКА
Теорема 3 допускает простое, но важное обобщение.
Теорема 5. Пусть со > 0 — заданное число. Общее решение дифференциального уравнения
Г(х) + <»7(*) =0 (24)
имеет вид
f(x) = a cos шх + b sin сох. (25)
Эту теорему можно доказать так же, как теорему 3. Но, по-видимому, проще свести теорему 5 к теореме 3. Положим F(t) = /(Z/u>). Тогда /(х) = F(<dx), /'(х) = = (dF'((dx) и/"(х) = ^F''(&x). Таким образом, уравнение/" + со2/ = 0 равносильно уравнению F" + F = 0. Но мы знаем, что F" + F = 0 в том и только в том случае, если F = a cos t + b sin /. Следовательно, /" + <о2/ = 0 в том и только в том случае, если /(х) = a cos сох + b sin (их.
§ 1. Синус и косинус
357
Рис. 6.20
Постоянные а и b в равенстве (25) можно найти, если известны значения f и f в некоторой точке. Например, если /(0) = А и /'(0) = В, то а = А и Ь = В/<о.
Отметим, что общее решение уравнения (24) периодично о периодом 2л/а> [см. свойство (1) периодических функций, § 1.2].
1.13. ДВИЖЕНИЕ УПРУГОЙ ПРУЖИНЫ
Применим теперь теорему 5 к движению частицы, прикрепленной к упругой пружине.
Такая пружина изображена на рис. 6.20. Предполагается, что у пружины есть положение равновесия и что при смещении из этого положения на расстояние s возникает восстанавливающая сила F, приложенная к частице и стремящаяся вернуть пружину в положение равновесия. (Можно считать, что при s > 0 пружина растянута, а при s < 0 — сжата.) Пружина называется упругой, если восстанавливающая сила есть линейная функция смещения:
F = — ks,
где k — положительная постоянная (постоянная пружины*). На практике можно считать все пружины упругими, если только рассматриваются достаточно малые смещения. (Мы уже говорили об этом в гл. 5, § 5.)
Пусть т — масса частицы, прикрепленной к пружине. Если пренебречь массой самой пружины и заметить, что ds/dt, производная от s по времени, есть скорость, a d2s/dF — ускорение, То закон Ньютона запишется так:
т = — ks. (26)
Последнему уравнению можно также придать следующий вид:.
d2S | 2 Л
----------И s = 0, dt2
(26')
где
* Число k называют также отвечающим пружине коэффициентом восстановления, -или коэффициентом упругости.
358
6. Трансцендентные функции
Уравнение (26') совпадает с уравнением (24) с точностью до наименований входящих величин. Из теоремы 5 заключаем, что функция t s(/), описывающая движение, имеет вид
s(t) = a cos W + b sin ю/. (27)
В частности, движение периодично с периодом Т, где
Т = - = 21Г . (28)
Такое бесконечно повторяющееся движение возможно, поскольку мы пренебрегаем трением. Чтобы полностью найти движение, надо знать постоянные а и b в формуле (27). Это значит, что надо знать положение s(t) и скорость v(t) нашей пружины в некоторый фиксированный момент времени /0, например в н а ч а л ь • н ы й момент t = 0. Если эти начальные условия заданы, то можно вычислить постоянные а и b и тем самым положение s(t) и скорость s'(f) пружины в любой момент времени t.
Мы утверждаем, что s(t) можно записать также в виде
$(/) = 4cos[g)(/ —/0)], (29)
где Л > 0 и t0— постоянные, зависящие от начальных условий. Чтобы убедиться в этом, будем исходить из выражения (27) для $(/). Если а = b = 0, положим А = 0. Если а2 + 62 > 0, пусть А = ]/а2 + Ь2. По теореме I, существует такое число а, что а/А = cos а, Ь/А = sin а. Положим /0= а/<о; тогда по теореме сложения имеем
s(t) = а cos со/ 4- fcsinco/ = Acosu>/0 cost»)/ + A sinu)/0 sin co/ =
= A cos (u)/ — u)/0) = A cos [<d (t — /0)J.
Поскольку косинус колеблется между —I и I, число А есть наибольшее отклонение пружины от положения равновесия; А называется амплитудой колебания. Число /0 задает момент времени, когда достигается наибольшее отклонение; оно называется фазовой разностью. Между моментами tQ и tQ 4- Т пружина совершает полный цикл колебания.
Амплитуда -и фазовая разность зависят от того, как началось движений при t = 0; однако период колебания Т зависит лишь от пружины.
1.14. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Если ударить по камертону, то мы слышим всегда звук одного тона независимо от того, сильно или слабо мы ударяем. Точно так же, нажимая на одну и ту же клавишу фортепьяно, мы производим звуки различной интенсивности в зависимости от силы нажима, но одной и той же высоты. Эти и многие им подобные явления можно понять, рассматривая колеблющееся тело по аналогии с упругой пружиной. Дело в том, что дифференциальные уравнения, описывающие колебания камертона, струны фортепьяно и т. д., приближенно совпадают с уравнением движения упругой пружины, т. е. с уравнением (26). Иными словами, существуют число $, задающее отклонение колеблющегося тела от положения равновесия, постоянная k, изме
§ 1. Синус и косинус
359
ряющая жесткость тела, и постоянная /и, измеряющая инерцию тела. Эти три величины и время t связаны уравнением (26). Но тогда s как функция времени задается формулой (27) или (29).
Амплитуда и фазовая разность зависят от начальных условий; однако период Т задается формулой (28) и зависит лишь от жесткости k и инерции т колеблющегося тела, равно как и число
называемое частотой колебания: v есть число циклов колебания в единицу времени. В случае звука (слышимых колебаний воздуха) частота определяет высоту тона. В нашем случае
J_ 1/_L
2~ г т '
(30)
Таким образом, частота всегда одна и та же — она не зависит от амплитуды, в случае звука определяющей его интенсивность.
Движение, управляемое тем же дифференциальным уравнением, что и движение упругой пружины, называется гармоническим колебанием. Гармонические колебания встречаются не только в задачах о движениях упругих тел, но во многих других ситуациях, например в радиопередатчике или в теории атома. Важнейшим свойством их является постоянство тона. Этим объясняется и то, почему пружинные часы, которые Вы носите на руке, показывают правильное время, и то, почему атом всегда испускает свет определенной частоты (в случае видимых световых колебаний, определяющих воспринимаемый глазом цвет). Тот поразительный факт, что в формулу для частоты входит число л, подсказывает существование связи между гармоническими колебаниями и окружностью; подробнее мы займемся этим в гл. 11.
УПРАЖНЕНИЯ
В упражнениях 92—97 частица массы т прикреплена к одному из концов горизонтальной упругой пружины, постоянная которой равна k. Другой конец пружины закреплен, и частица колеблется вдоль оси пружины. Смещение частицы из положения равновесия обозначается через s= s(/), где s>0b растянутом состоянии пружины.
х 92. Пусть т = 5 г и s = 2 cos(?/3). Найдите постоянную пружины.
93. Пусть т = 2ги&=8 г/с2. Пусть, далее, в момент t = 0 пружина оттянута на 1 см от положения равновесия, а скорость частицы равна 4 см/с и возрастает. Найдите s(t). Найдите амплитуду.
94. Пусть tn = 1,5 г и k = 8 г/с2. Пусть, далее, в моменты t = 0 и t = л}^3/6 пружина сжата на 1 см от положения равновесия. Найдите выражение скорости частицы.
95. Пусть т = 0,2 г и k = 1,8 г/с2. Пусть, далее, в момент t — 0 пружина сжата на 2 см от положения равновесия. Найдите скорость частицы в момент t = тс/6. Для каких» значений t Вы можете вычислить скорость?
96. Пусть т = 1 г и k = 0,25 г/с2. Пусть, далее, в момент t = 0. пружина оттянута на 1 см от положения равновесия, а в момент t = л/2 скорость частицы равна У2/2 см/с. Найдите s(t). Найдите амплитуду.
97. Пусть период движения равен 2л/15 с. Пусть, далее, в момент t = 0 скорость частицы равна —15 см/с, а в момент i ® л/6 скорость частицы равна 3 см/с. Найдите s(t). Найдите амплитуду.
360
6. Трансцендентные функции
§ 2. ТАНГЕНС И АРКТАНГЕНС
В предыдущем параграфе мы отметили, что синус и косинус можно было бы определить исходя из первообразной функции ! В этом параграфе мы покажем, как эти функции
можно было бы определить исходя из еще более простой (рациональной!) первообразной функции В то же время мы изучим третью важную тригонометрическую функцию.
2.1. ТАНГЕНС
Мы начнем с того, что определим функцию 0 »—* tg G, называемую тангенсом:
tgO = -^. (1)
cos 6
Эта функция определена и непрерывна при всех значениях 9, для которых cos 9 =?£= 0, т. е. при 9 =/= к/2 + пп, п = 0, ± 1, ±2..
Тангенс является нечетной функцией, так как tg (- 9) = 8> - sin 9- = - tg 9. (2)
cos (— 0) cos в
Тангенс периодичен в периодом к, поскольку в силу равенств (23) из § 1 tg (8 + .> _ _ te 8. (3)
cos (6 4- те) —cos О
Тангенс строго возрастает в интервале ------у, и тем самым в любом
интервале -------и = 0, ±1, ±2..................... В самом деле, в интервале
(---Y, -у) тангенс имеет положительную производную:
__/ sine V _ (s*n в)' cos в — sin 8 (cos0)'_cos20 + sin29 _ 1
\ cos 0 / cos2 6 cos2 0 cos2 9
Эго можно записать либо в виде ;1 /4) dO cos2 9 ‘ либо в виде
-^p-=l + tg’9. (5)
аи
Поскольку st в (п/2) = 1, cos (тг/2) =0, a tg 9 положителен и возрастает при 0< 9<it/2, то tg 9 становится сколь угодно большим, когда 9 стремится к чс/2 слева. Это обстоятельство можно записать так:
§ 2. Тангенс и арктангенс
361
tgd
Рис. 6.21
lim tg9 = + oo. (6)
в-»(к/2Г
Точно так же мы убеждаемся, что tg 6 становится отрицательным и сколь угодно большим по абсолютной величине, когда 6 стремится к —л/2 справа:
lim tg Q = — оо. (7)
М-я/2)+
Поскольку tg 0 имеет период к, отсюда заключаем, что
lim tg 9 = 4- °°. lim tg9 = — оо, n = 0, ± 1, ± 2,.... (8)
6-*(гс/2-Ьтгс)~ 0->(—тс/2-Нтгс)+
График функции tg 0 изображен на рис. 6.21. Отметим, что л — примитивный период тангенса.
Примечание. Пока мы не имеем еще удобного наименования для первообразной функции 0 I-* tg 0. Мы вернемся к этому в § 4.7.
УПРАЖНЕНИЯ
d iP tj? х
1. Найдите —— tg(26 4-it) в точке в — я/8. ▲ 4. Найдите -------- в точке х = 9я/4.
аи dx3
d2
2. Продифференцируйте u»-*tg(ua). б. Найдите ——— sin (tg 0).
do2
d cPz
3. Найдите ——tg2z. 6. Найдите ------, где z = и tgn.
dz dua
362
6. Трансцендентные функции
2.2. ТЕОРЕМА СЛОЖЕНИЯ
Функция тангенс подчиняется своей теореме сложения:
+ = (9)
1 — tg a tg р
(Здесь предположено, что ни одно из чисел а, ₽ и а + ₽ не равно л/2 + пл.) Чтобы доказать это, воспользуемся определением (1) тангенса и теоремами сложения для синуса и косинуса. Имеем
л / sin a sin р \
« n n cos а cos Р ---------4-----7~
fg । р) ____ sin (а + Р) _ sin а cos р + cos а sin р ________\ cos а cos р /___
cos (а 4-Р) cos а cos ₽ —sin а sin р cos а cos В (1 — sina sin \ cos a COSp/
_ tg а + tg р
1 — tg a tg P что и требовалось доказать.
При a = р получаем формулу удвоения:
tg2a = 2tga . (10)
Б 1—tg2a V 7
(ID
(12)
2.3. ФУНКЦИИ sin 0 И cos 0 КАК РАЦИОНАЛЬНЫЕ ФУНКЦИИ ОТ tg(0/2)
Мы покажем теперь, что cos 0 и sin 9 могут быть представлены как рациональные функции от tg (0/2).
Теорема 1. При —имеем sin 9 = 2tg<6/2>., 1 + tg* (0/2)
COS0 = 1~ tg2(°—-.
1 + tg* (0/2)
Примечание. Поскольку обе части равенств (11) и (12) периодичны с периодом 2к, эти соотношения справедливы для всех значений 6, при которых определены их правые части, т. е. для всех 9, за исключением 6 = пк, где п — нечетное целое число. В этих исключительных точках пределы правых частей наших равенств равны 0 в случае (11) и в случае (12).
Первое доказательство. Полагая в формуле (10) a = 6/2, получаем
2tg(6/2) l-tg2(0/2) '
Далее, положим
. i 0
и запишем предыдущую формулу в виде
sin 0 2/ cos 0 1 — /2
(13)
(14)
§ 2. Тангенс и арктангенс
363
Возведя в квадрат и прибавив 1 к обеим частям, находим, что
1 — <2 \2 1 + Р J
(15)
1 4. ( sin6 У cosi> 6 + sin* 2 * 6 _ 1 _ j 4/2______/ 1 -На у
+ \ cos 0 / — cos2 0 cos2 0 ~ 1 - 2/2 + (4 "л 1 - /2 / ’
откуда
cos2 О
Если — к 0 — л/2, то cos 9 •< 0. Далее, в этом случае также — л/2 < 0/2
< — л/4 и, следовательно, tg(9/2)'—1, т. е. — 1, /2>1, 1—/2<С0 и (1 — /2)/(1 +/2) 0. Точно так же проверяется, что cos9 и (1—/2)/(14-/2)
имеют одинаковый знак, когда 9 лежит в интервалах [—л/2, 0], [0, л/2], [л/2, л]. Теперь из (15) можно заключить, что
Но тогда в силу (14) имеем также
sin9 = - И- (17)
14-/2 '
Формулы (16) и (17) равносильны (11) и (12)*.
Второе доказательство. Пусть функция /(9) определена с помощью
равенства (13). Тогда
/(0) = tgO =0
и, как видно из (5),
r(0) = _L(i + tg2A)=_2.(i + /2).
Положим
/(9) =—?£—, g(9)
'' ' 1 + Р s v 1 + г2
Тогда
2(1 + <2) —(2Q (2Q 2 fl — /2) 1
(1+Z2)2 - <16 (14-/2)2 ’ 2
1 —/2
I 4- 4а
=g (В).
Подобное же вычисление показывает, что
§,(0) = _/(0).
Отсюда Г (9) = / (9) = - /(9) и g" (0) = - f (9) = — g (9). Далее, f (0) = 0 и g(0) = 1, так что г (0) = g(0) = 1 и g' (0) = — /(0) = 0. Теперь из теоремы 3 § 1.10 следует, что f (9) — sin 9, g(9)=cos9.
* Можно также исходить из формул удвоения!
cos2 JL — sin2 -А. 2 sin -i- cos-4-
0 0 2 2 2 2
cos 0 = cos2 — —sin2— =------------------ и sin 0= --------------- (
2 2 co^-L+sin2 ® cos2-L 4-sin2-L
z z z z
0 разделив числитель и зжаменатель стоящих в правых частях дробей на cos2 — , получим форму
лы (16) и (17).
364
6. Трансцендентные функции
УПРАЖНЕНИЯ
_ я sin 2х
7. Покажите, что tgx =-------------.
1 + cos 2х
8. Найдите выражение tg 36 через tgO.
' л _ х _n sin 36 4- sin 6
9. Покажите, что tg 20 =---—-------— .
Б cos 36 + cos 6
10. Выразите sin х и cos х как рациональные функции от tg(x/4).
11. Применив теорему 1 и пользуясь периодичностью и нечетностью тангенса, покажите, что синус — нечетная функция, косинус — четная и что обе они имеют период 2л.
12. Пусть (х, у) — точка единичной окружности, не совпадающая с (—1, 0). Покажите, 1 ____________________________________________________________/2 О/
что существует действительное число t, для которого х = — , у = ___ . Одно-
значно ли определено такое f?
13. Покажите, что sin х и cos х можно выразить как иррациональные функции от tg х.
п/3
С tg о
14. Найдите | — ----——d6.
J 1 + tg2 6
о
к/4
С 1 — tga X
15. Найдите I -----------— dx.
J . l + tg2x
24. АРКТАНГЕНС
Поскольку функция и = tg 6 строго возрастает и имеет положительную производную в интервале —л /2 < 0 < л/2, она имеет дифференцируемую обратную функцию (см. теорему 7 § 3.7 гл. 3 и теорему 7 § 2.6 гл. 4). Назовем эту функцию арктангенсом и обозначим ее через arctg. В силу (6) и (7) уравнение tg 0 = и имеет решение в интервале—л/2 < 0 < л/2, каково бы ни было число и. Следовательно, функция и arctg и определена для всех значений и. График арктангенса (рис. 6.22) получается отражением от биссектрисы первого координатного угла центральной ветви графика, изображенного на рис. 6.21. Поскольку tg 0 = 0, имеем
arctg 0=0. (18)
Вычислим теперь производную арктангенса. По определению, arctg (tg 0) = 0 при —л/2 < 0 < л/2, откуда
(d arctg и \ ___ 1 _ 1
Ти 6 “ dtgO/d0 “ 1 4- tg2 6 ’
ИЛИ
d arctg и = 1 , j 9)
du 1 + и2
Из формул (12), (19) и основной теоремы анализа вытекает следующая.
Теорема 2. Функция
§ 2. Тангенс и арктангенс
365
рассматриваемая в интервале —я!<2< 9< гс/2, имеет обратную функцию
и . С dt и aretg и — I -------.
J 1+*а
(20)
Теорема 2 свидетельствует о возможности еще одного аналитического подхода к определению тригонометрических функций. Именно, мы могли бы определить tg 9, не пользуясь синусом и косинусом, как функцию, обратную функции (20), а затем определить синус и косинус с помощью соотношений (11) и (12).
Из теоремы 2 вытекает интересное
Следствие. Справедливы соотношения
(21)
(22)
Доказательство. Очевидно,
tg45° = tg^- = 1, 4
(23)
откуда
** = aretg и 1 + г2 6
л
= aretg А — aretg 1 = aretg А —-4
Поскольку в силу (6) и теоремы 1
Jim aretg Л =-^-»
366
6. Трансцендентные функции
имеем
7С
Т‘
Остальные соотношения (21) доказываются аналогично, а из них следует (22), так как интеграл в (22) является суммой четырех интегралов из (21).
В Приложении к гл. 5 (см. § 6.5) мы уже вывели формулы (21) и (22), не прибегая к тригонометрическим функциям. Только что приведенный вывод не кажется столь загадочным.
УПРАЖНЕНИЯ
1
. к, с dt rt
16. Покажите, что I -j-— = — , воспользовавшись функцией арктангенс,
о
d
17. Найдите----(aretg х3)2.
18. Продифференцируйте г »-► z aretg
19. Найдите —— aretg (У aretg /). dt
20. Найдите — aretg —.......
dz /z—1
I 1 \2
21: Найдите f" (s), где f (s) = [ aretg — I •
A 22. Найдите ----- lx aretg ——
dx2 \ Vx
23. Найдите g' (x), где g (x) = aretg x + aretg — . Что можно сказать о g? х
u2
24. Пусть f (и) = aretg —— . В каких интервалах [ возрастает? В каких интервалах f вы-
пукла вверх?
25. Покажите, что
sin (2 arc tg и) = t 1 + и‘
26. Покажите, что cos (2 aretg и) = ----
1 + и2
27. Покажите, что sin (aretg и) = — . [Указание: примените результат упр. 25 и
формулу для синуса половинного угла. Случаи «>0ии<0 рассмотрите отдельно.]
28. Покажите, что cos (aretg и) = — •
/1 + а»
§ 2. Тангенс и арктангенс
367
у 1 — «а .
29. Покажите, что tg (arccos и) =--------.
[Указания: 1°. Покажите, что обе части имеют одинаковую производную, а затем — что обе части совпадают при и 1. _____________
sin 6 У \ — cos2 6
2°. Запишите tg 0 =-----— = ±------------- и примените соотношение cos (arccos и) = и,
cos 6 cos О
Покажите, что знак минус невозможен.]
2.5. ПРИМЕНЕНИЯ АРКТАНГЕНСА К ИНТЕГРИРОВАНИЮ
Теорема 2 важна для интегрирования рациональных функций. Функция 1/(1 + х2) рациональна, но не является производной рациональной или даже алгебраической функции. В действительности она является производной трансцендентной функции arctg х. Пользуясь арктангенсом, можно записать в явном виде неопределенные интегралы для многих функций. Но мы пока не в состоянии указать удобную формулу для первообразной самой функции арктангенс. Этот вопрос мы рассмотрим дальше (см. § 4.7).
•Пример. Вычислить
г xdx
J 1 + *4’
Решение. Воспользуемся формулой дифференцирования (19) и тем фактом, что х является производной функции х2/2. Тогда получим
f х х- = — С —— = — С d arctg (х2) = — arctg (х2) | =
J l 4- х4 2 J l + (х2)2 2 J 6 v 7 2 6 v ' I
2 2 v ' x=2 x=2
= -y- arctg 9---arctg 4 « 0,13.
Примечание. Для отыскания значений арктангенса мы пользуемся таблицами тригонометрических функций. Если в таблице указаны тригонометрические функции от аргумента, заданного в градусах, то следует перевести градусы в радианы. ф
УПРАЖНЕНИЯ
Г dx
30. Найдите | -
J 1+(2х-I)2
Г dz
31. Найдите J 2Z 2 * к а за н и е: учтите, что z2 + 2z + 2 = 1 + (* + О2-]
32. Найдите С ———— . [Указание: учтите, что 2х2 — 6х 4- 5 = - (1+(2х—З)2). 1
J £хЛ — ох 4~ 5 L 2 J
368
6, Трансцендентные функции
33. Найдите Г У и du J 1 + а3 *
34. Найдите р t2 dt приближенно J j " • Воспользуйтесь таблицей значений арктангенса.
35. Найдите С x1/4dx J 4 + х5'2 *
36. Найдите С л . [Указание: учтите, что х4 + 2ха + 2 — 1 + (*а + I)2-] J г + 2ха + 2
37. Найдите (• du Г \ л , где а и b — любые положительные числа. У Казани е: учти- J а + bu2 L / Ъ \ [ 1/ Ь \2 1
те, что а + bu2 = а 1 1 + и21 = а 11 + у и j . J
38. Найдите arctg х все первообразные функции g (х) — • 1 + х
39. Найдите , (arctg t)2 + (arctg t)~2 все первообразные функции п (t) — 14-/2
40. Найдите dz u~3 такое решение дифференциального уравнения — , для которого du 1 и”4
lim z = u->oo 1.
41. Найдите d2x — t такое решение дифференциального уравнения — , для которого dt2 (1 + i2)2
к Х = ”8* при t = 0 и х = к при t = 1.
§ 3. ДРУГИЕ КРУГОВЫЕ ФУНКЦИИ
3.1. СЕКАНС, КОСЕКАНС, КОТАНГЕНС
В дополнение к трем изученным выше тригонометрическим функциям—синусу, косинусу и тангенсу, иногда применяются еще три—секанс, косеканс и котангенс:
1 1 . COS X . 1X
sec х =-----, cosec х =-------, ctg х -----. (1)
cos х sin x sin x
Их графики изображены на рис. 6.23, 6.24 и 6.25. Отметим, что, например,
tg х • ctg х = 1 (2)
всюду, где выписанное слева произведение имеет смысл.
§ 3. Другие круговые функции
369
Функции косеканс и котангенс нечетны, секанс же четен. Секанс и косеканс имеют период 2л, котангенс — период к. Ясно, что sec х не определен при пк + гс/2, где п — целое число; cosec х и ctg х не определены при х = /ш.
Отметим формулы дифференцирования:
d sec х sin х
dx (cos x)2
= tgxseax,
d cosec x dx
cos x
(sin x)2
== — ctg x cosec x,
= - 1 -(c,g - - <cosec '>*
<з>
(4)
= (sec x)2.
dx
(5)
370
6. Трансцендентные функции
Полезно помнить соотношения ,
sin -----= C°S Se° ("i--------= coseax’ tg ("^-------X) = (6)
(первое из которых было уже отмечено в § 1). Доказательства всех этих утверждений, вытекающие из определений (1), нетрудны и предоставляются читателю.
v ф Примеры. 1. Дан прямоугольный треугольник с вершинами Я, В, С, причем С — прямой угол. Тогда в обозначениях § 1 имеем (рис. 6.26):
sin/4 = —, cos4 = —, tgi4 = —, с с 6 ь
sec А = — , cosec А = — ,' ctg А = — , b а а
Первые два соотношения нам уже известны; остальные из них легко следуют.
2. Теорема сложения для котангенса имеет вид
Это можно доказать либо исходя из (2) и пользуясь теоремой сложения для тангенса, либо из (1), пользуясь теоремой сложения для синуса и косинуса.
3. Тождество
sec2 9 4- cosec* 0=4 cosec2 29
следует из определения секанса и косеканса и тождеств sin 20 = 2 sin 6 cos 0 и sin2 0 + + cos2 0 = 1. ф
УПРАЖНЕНИЯ
I. Найдите—tg((secx). dx
d r_____
2. Найдите—ysecz . dt
d2
б. Найдите —- cosec y. dy2
k/4
6. Найдите | sec54xdx.
3. Продифференцируйте и sec (arctg u). 7. Найдите I sec2 x tg x dx.
d —
4. Найдите (?tg2 у 6 . du
9, Найдите J tg»xdx. [Указан» e: учтите, что tg2 x = sec2 x —• 1. ]
A 8. Найдите I sec2xtg2xdx.
10. Начертите график функции у = sec2 х при ~ к
11. Начертите график функции j/ = ctg(x/2) при —«я « х « я.
12. Начертите график функции у = cosec (2х + я) при —я ч< х «
§ 3. Другие круговые функции
371
3.2. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Мы уже рассмотрели три так называемые обратные тригонометрические функции, а именно: функцию, обратную косинусу, или арккосинус, обратную синусу, или арк-синус, и обратную тангенсу, или арктангенс. Рассмотрим вкратце три остальные.
Функции (1) не монотонны. Чтобы определить обратные функции, надо выбрать для каждой из функций (1) интервал (или несколько интервалов), где она монотонна. Здесь возникает некоторый произвол, и разные авторы иногда делают это неодинаково.
Мы определим арккотангенс, арксеканс и арккосеканс как функции, обратные котангенсу, секансу и косекансу соответственно в интервалах (0, тс), [0, тс] и [—тс/2, тс/21*. Из графика ctg 9 (см. рис. 6.25) видно, что arcctg х определен везде. Его аналитическое определение гласит:
arcctg (ctg 0) = 0 при 0 < 0 < тс.
Принимая во внимание формулу (4) и соотношение ctg (arcctg х) = х, получаем
d arcctg х _1 ___________ 1 __ 1 _ 1
dx dx/d arcctg x d ctg (arcctg x)/d arcctg x 1 + ctg2 (arcctg x) 1 4- x2 ’
так что
d arcctg x _ _ Г
dx 1 + x2' * '
Далее, arcctg 0 = —. (8)
Функции arcsecx и arccosecx определены при |x|> 1. Имеем
arcsec (sec9) = 9 при 0<9<тс, 9^=-^-,
arccosec(cosec9) = 9 при-------<9<, 9 =y= 0,
sec (arc sec x) = cosec (arccosec x) = x при | x | 1
и
arcsec 1 = 0, arcsec (— 1) = тс,
(9)
arccosec 1 = —, arccosec (— 1) ----—.
2 ' 7 2
Принимая во внимание формулу (3), имеем
* При этом для секанса исключается точка 0 = -L, где он не определен, и, аналогично, для косеканса — точка 0 = 0.
372
6. Трансцендентные функции
d arcsec х 1 _ 1 _ 1 _
dx dx/d arcsec x d sec (arcsec x)}d arcsec x sin (arcsec x) / cos2 (arcsec x)
cos2 (arcsec x) 1 _ 1
У" 1 — cos2 (arcsec x) x2 У 1 — (1/x2) | x [ Yx2 — 1
ИЛИ d arcsec x __________________________________1_____
** । x i / ’
Аналогично доказывается, что d arccosec x 1 0
Графики функций арккотангенс, арксеканс и арккосеканс изображены на рис. 6.27—6.29.
В силу наших определений при | х | >• 1 arcsec х = arccos (—), arccosec х = arcsin (—). (12)
\ X } \ X /
В самом деле, если 0 < 0 < я и sec 6 = х, то cos 6 = 1/х, что и доказывает первое соотношение; второе доказывается аналогично.
Примечание. Рекомендуется из шести тригонометрических функций употреблять только sin х, cos х и tg х, а из шести обратных тригонометрических функций— только arctg х, arcsin х и arcsec х; эти функции являются соответственно первообразными функций 1 1 1
1 + *2 ’ /ПГр ’ । х । Y**^ *
(В некоторых книгах обратные тригонометрические функции обозначаются так: sin"1 х вместо arcsin х, cos"1 х вместо arccos х, tg"1 х вместо arctg хит. д.*)
УПРАЖНЕНИЯ
13. Найдите — arcsin У u 4-i • du
14. Найдите — arcsec Z2.
15. Продифференцируйте -------------
cosec О
dy г—
16 • Найдите —, где у = х2 arcsec У х . dx
d r__________
17. Найдите — tg У arcsec г . dz
18. Найдите — arcsin 3/2 ( .
du ' '
19. Найдите С — •
J У 1 — х4 ’
/Гл
_ тт f arcsin и
20. Найдите I — du.
i Yi-u2
* Такая символика используется в® многих старых английских учебниках (и иногда — в
их русских переводах); это соответствует иногда применяемому обозначению Гг(х) для функции, обратной (в смысле теории функций) функции [(х) (при этом функция, обратная f(x) в алгебраическом смысле, обозначается через (Лх)]"1, что, разумеется, отлично от f^(x)J.
§ 3. Другие круговые функции
373
Рис. 6.28
Рис. 6.29
374
6. Трансцендентные функции
21. Найдите i ------- [Указание: умножьте числитель и знаменатель подынте-
J г ^z4 — 1 тральной функции на г,
А 22. Найдите J х arcsec х dx. [Указание: проинтегрируйте по частям; соблюдайте осторожность при обращении с несобственным интегралом.]
1 t _
23. Найдите I ——arcsin ]/х dx. [Указание: Проинтегрируйте по частям; соблюдайте Vх осторожность при обращении с несобственным интегралом.)
24. Найдите J arcsec }^х dx. [Указание: проинтегрируйте по частям.]
25. Докажите второе из соотношений (12).
' 26. Докажите, что при х=/=0 справедливо соотношение arctgх = arcctg (1/х) + а, где а — постоянная. Найдите а.
§ 4. ЛОГАРИФМЫ
4.1. ПОТРЕБНОСТЬ В ЛОГАРИФМАХ
Логарифмы были изобретены Непером, опубликовавшим свои работы в 1614 г. (Другой математик, Бюрги, пришел к логарифмам независимо от Непера и примерно в то же время. Часто случается, что важные идеи одновременно и независимо возникают сразу у нескольких авторов.) Цель логарифмических таблиц состоит в облегчении вычислений, или, точнее, в сведении «трудных» операций (подобных умножению к «легким» (подобным сложению).
Еще до введения логарифмов математики пользовались с теми же целями тригонометрическими функциями. Ключом здесь являлась теорема сложения (см. § 1.11):
cos (а + Р) = cosa cos 0 —- sin a sin 0.
Заменив Р на (—Р), получаем
cos (а — Р) = cosa cosP + sin a sin р.
Джон НЕПЕР (1550—1617), шотландский дворянин, жил и работал в своем наследственном имении вблизи Эдинбургв. Он был ревностным сторонником протестантизма и автором трактата по теологии. До изобретения логарифмов Непер сконструировал другое средство для облег» чения вычислений —• «палочки Непера».
Ноет БЮРГИ (1552—1632), швейцарский часовщик, математик и изобретатель. ОН опубликовал свои таблицы в 1620 г.; обещанная же им книга инструкций и пояснений в атим таблицам так к не увидела свет.
§ 4. Логарифмы
375
Сложив эти формулы, получаем
2 cos a cos 0 = cos (а + 0) + cos (а — 0).
Допустим, мы хотим воспользоваться этим тождеством для умножения двух чисел а и Ь\ пусть 0<а<1 и 0 < d < 1. По тригонометрическим таблицам находим числа (или «углы») а и 0 такие, что a — cos а и b = cos 0. Затем вычисляем а -|- 0 и а — 0, ищем в таблице значения cos (а + 0) и cos (а — 0), складываем эти значения и берем половину их суммы. Это и есть искомое произведение ab = cos a cos 0.
Разумеется, раз приходится работать с таблицами, можно получить лишь приближенный результат. Если, например, задано некоторое а, то мы, вообще говоря, не найдем в таблицах такого а, что cos а = а, а лишь такое а, для которого cos а « а. Это замечание относится и к вычислениям с логарифмическими таблицами. Впрочем, чем обширнее таблицы, тем точнее получаемый с их помощью результат.
Таблицы логарифмов позволяют выполнять не только умножение, но и деление, возведение в степень и извлечение корня, и притом сравнительно легко. Вскоре после появления первых таблиц Непера, им же совместно с Бриггсом были составлены лучшие таблицы. Позже появились гораздо более обширные таблицы. В течение более трех столетий все сколько-нибудь сложные вычисления выполнялись с помощью логарифмов. Вряд ли найдется такое научное открытие или техническое достижение, которое не использовало бы^прямо или косвенно, изобретение Непера.
Лишь в самое последнее время, с появлением современных автоматических вычислительных машин, логарифмические (и другие) таблицы несколько устарели. Электронная вычислительная машина непосредственно выполняет умножение и деление, не сводя его к сложению и вычитанию; при этом числа в ней представляются в двоичной системе, и действия производятся с невероятной скоростью. Когда же вычислительной машине требуется логарифм или косинус какого-либо числа, она не ищет его в таблице, а получает его, выполнив необходимые вычисления. (Однако вычислительные машины пока еще не заменяют крайне дешевую и портативную логарифмическую линейку. Логарифмическая линейка — это просто таблица логарифмов, в которой некоторые числа представлены длинами отрезков.)
Но главную и непреходящую ценность открытия Непера представляет введение в математику новых крайне важных функций.
УПРАЖНЕНИЯ
В упражнениях 1—4 выполните указанные умножения с помощью косинусов.
1. 0,873 X 0,802 . 3. 0,904 X 0,75836.
2. 0,921 X 0,758. 4. 0.8577Р.
4.2. ПУТЬ К ЛОГАРИФМАМ
Цель таблиц логарифмов — свести умножение к сложению. Каков простейший способ достигнуть этого? Мы хотим связать с каждым положительным числом х другое число, называемое его логарифмом, таким образом, чтобы умножение двух чисел сво-
Генри БРИГГС (1561—1631) был профессором математики в Лондонском университете, а затем в Оксфорде.
376
6. Трансцендентные функции
далось к сложению их логарифмов. Обозначим (временно) логарифм числа х через <р(х). Мы хотим, чтобы логарифм произведения был равен сумме логарифмов сомножителей. Итак, нам нужна такая функция х »-> <р(х), для которой
<р(^) = ?(х) + <р(у). (1)
Мы назовем это равенство функциональным уравнением логарифмов. Подставив в это уравнение значения х = у = 1, находим, что ср(1) = 2ср(1), откуда
?(1) = 0. (2)
Конечно, мы не знаем еще, существует ли функция, удовлетворяющая условию (1). Допустим, однако, то такая функция есть, и предположим, далее, что она дифференцируема. Тогда, как мы увидим, удается найти ее производную. В самом деле, если <р'(х) существует, то
ф' (х) = lim - У [по определению] =
h->o h
<р(х) + <Р рч- —) — <р(х)
= Пт--------------------------------т— [согласно функциональному уравнению (1)] =
Л->0 А
h-0 h Л->0 X А
X
I A \
. <p(l+ —)
1 1. \ x / , i
= — Um [поскольку — здесь — фиксированное, число] =»
X h-+0 А х
х
= —— lim + ^2. [полагая — =□ А», замечая, что lim — = 0, ж пользуясь теоремой 4 § 3 гл. з],
X *->0 k х Л-0 *
Обозначая (не зависящее от х!) число lim *<* + *>-л->о А через с, имеем ф' (%) = —. (3)
X
Мы показали, следовательно, что если существует дифференцируемая функция х <р(х), удовлетворяющая условию (1), то ее производная равна с!х.
§ 4. Логарифмы
377
Выбор постоянной с зависит от нас. В самом деле, пусть ср — какая-либо функция, удовлетворяющая условию (1), и а — фиксированное число; тогда ф(х) = а<р(х) также удовлетворяет функциональному уравнению логарифмов, ибо
Ф (ху) = аф (ху) = а (Ф (х) + ф (у)) = ф (х) + ф (у).
При этом если ср'(х) = с/х, то ф'(х) = а с/х.
Самый простой и естественный (натуральный) выбор значения с — это положить с = 1. Поэтому функция х i-> ср(х), для которой ср(1) = 0 и <р'(х) = 1/х, называется натуральным логарифмом. Эта функция кратко обозначается через In х (а иногда через log х без всякого индекса снизу!). Мы будем придерживаться обозначения In х.
Непер сделал свое открытие до возникновения анализа. Но, по-видимому, он рассуждал подобно тому, как мы это делали выше, хотя и использовал совсем другие термины (ибо он ведь не владел понятием производной!). Непер понял, что свойство (1) функции ср(х) приводит к тому, что скорость изменения ?(х) пропорциональна 1/х, и выбрал в качестве коэффициента пропорциональности единицу. Действительно, его таблица 1614 г. — это таблица натуральных логарифмов*.
4.3. ОПРЕДЕЛЕНИЕ НАТУРАЛЬНЫХ ЛОГАРИФМОВ
Предыдущее обсуждение подсказывает следующее определение натуральной логарифмической функции (или просто логарифмической функции, если можно не опасаться смешения): х In х есть функция, удовлетворяющая условиям
In 1 = 0, - -- = — при х > 0. (4)
__________ dx х
* Опубликованная также и Бюрги в 1620 г. таблица являлась по существу таблицей натуральных логарифмов; первая же таблица десятичных логарифмов (более привычных большинству учащихся) была опубликована Г. Бриггсом в 1617 г. (год смерти Непера), в силу чего десятичные логарифмы в старину часто называли «бриггсовыми логарифмами», а натуральные логарифмы — «неперовыми логарифмами».
378
6. Трансцендентные функции
Что такая функция существует и единственна, следует из основной теоремы анализа; явная формула для нее имеет вид
In х = J -у- при х>0. (5)
1
- График функции у = 1/х изображен на рис. 6.30; он называется равнобочной гиперболой и состоит из двух ветвей. Натуральный логарифм числа х > 0 есть площадь под этой гиперболой от 1 до х (рис. 6.31). График функции у = In х представлен на рис. 6.32.
УПРАЖНЕНИЯ
В каждом из следующих упражнений укажите, для каких значений независимой переменной определена рассматриваемая функция. (Помните, что In х определен при лишь х>0.)
d
5. Найдите — In (1 4- и2). du d
6. Найдите -—Inin/. di
7. Найдите — In In In 2. dz du
8. Найдите —, где и = (In t/)3. dy
9. Найдите производную функции и i-> arctg(ln а).
10. Найдите f (х), где f(x) = ln(arctg х).
11. Продифференцируйте у = ln(sin 0.
▲12. Продифференцируйте у н* (In #)(arctg у*}
13. Продифференцируйте у = sin(ln 0.
14. Найдите производную функции v i-> и = cos In In V,
§ 4. Логарифмы
379
44. СВОЙСТВА ЛОГАРИФМОВ
Покажем теперь, что логарифмическая функция действительно обладает требуемым свойством (т. е. что логарифм произведения равен сумме логарифмов сомножителей).
Теорема 1. Функция х »->1п х непрерывна, возрастает, выпукла вверх и удовлетворяет функциональному уравнению
In (ху) = In х + In у, (6)
а также обладает следующими свойствами:
In — = In х — In у, (7)
У
In xr = г In х (8)
для любого рационального числа г и
lim In % =Ч-оо, limlnx = —оо. (9)
«-►4-oq х-*0+
Доказательство. Функция In х непрерывна, поскольку имеет производную 1/х; возрастает, поскольку эта производная положительна (1пх определен лишь при х>0); выпукла вниз, поскольку вторая производная (—1/х2) отрицательна. Что же касается равенства (6), то его мы докажем двумя способами.
Первый способ. Положим при фиксированном у
f(x) = 1п(ху) — In х — In у.
Надо показать, что f(x) = 0. Так как
/(1) == In у — In 1 — In у = —In 1 = О,
достаточно проверить, что f(x) — постоянная, тч. е. что f'(x) = 0. Имея в виду, что у следует считать постоянным, находим
г/ /х\ = d In (ху) d(xy) _ dlnx _ din t/ _ 1_1__0=0
d (xy) dx dx dx xy x ’
как и следовало ожидать.
Второй способ. Имеем
ху л х ху м
'”W= H'+Jr
1 1 X
Сделаем во втором интеграле подстановку t = xs; тогда dt = xds и s = 1 при t = х; s — у при t = ху; мы получим
f dt . л х ds с dt , с ds , . .
— + --- = ~Г + — = Inx + In у,
Ji J xs J t \ 8
что и требовалось доказать.
380
6. Трансцендентные функции
Продолжим теперь доказательство теоремы 1. При у = — из функционального х
уравнения следует In (х • —= In 1 = 0 = In х + In —, откуда \ х ) X
In — = — In х (10)
X
И
X / 1 \ 1
In--- = In I X • -I = In X + In — = In X — In y.
У \ У / У
Тем самым доказано свойство (7).
Далее, для целого положительного п имеем п раз п раз
In хп = In (х • X . . . х) = In X + In х + • • • + In X, или
1пхя = nlnx. (11)
То же верно при п = 0, так как х° = 1 и In 1 = 0.
Для целого отрицательного^ положим п = —т, где tn положительно; тогда
In хл = In x“m = In — = — In xm = — tn In x = n In x.
Таким образом, равенство (8) справедливо для всех целых значений г.
Поскольку х ) = х, имеем
In х = In х ) = п In х , или
In уПс = — Inx. (12)
п
Отсюда следует, что для целого положительного р и любого целого q
In xq,p = In (x'lP}q = q In x1/₽ = q In yGc = q [— In x) = — In x, \ p ) P
что и доказывает свойство (8).
Так как In х — возрастающая функция и In 1 =0, имеем
In х > 0 в том и только том случае, если х > 1. (13)
В частности, In 2 > 0. Далее, для х>2я
In х > In 2я = п In 2,
откуда видно, что lim In х = +°°-
Х->-|-оо
Наконец, покажем, что lim In х = —оо. В самом деле, In х = —In (1/х) и
lim In (1/х) = 4-оо, чем и завершается доказательство теоремы 1.
х—О*
§ 4. Логарифмы
381
Рис, 6.33
4.5. ЧИСЛО е
В силу (9) функция In х принимает сколь угодно большие и сколь угодно малые (т. е. сколь угодно большие по модулю и отрицательные) значения. Но тогда из теоремы о промежуточном значении (гл. 3, § 3.6) вытекает, что для каждого числа а существует такое положительное число х, что In х = а. Это число единственно, поскольку In х—возрастающая функция.
В частности, существует такое число е, что
1пе = 1. (14)
Это значит, что площадь под гиперболой ху = 1 от 1 до е равна 1 (рис. 6.33 и 6.34). Число е, как мы покажем дальше (гл. 8, § 2.9), — не рациональное*;
его приближенное значение равно**
е =2,718... .
Из дальнейшего выяснится важность числа е,_а также его поразительная связь с числом л.
УПРАЖНЕНИЯ
В упражнениях 15—20 выполните указанные вычисления, применяя натуральные логарифмы.
15. 4,53 х 3,09. 18. /4,12 х 0,138.
16. (8>56)1/3. 19. 0,389 х 12,2.
17. 6,12 : 5,59 20. (0,621 : 0,382)1/4.
* Можно даже доказать, что это число, более того, трансцендентное, т. е. не является корнем ни какого алгебраического уравнения с целыми коэффициентами (рациональное число х = — является корнем уравнения первой степени qx — р = 0).
Я
** Целый ряд первых десятичных знаков числа е легко запомнить: е = 2,718281828459045... •
Э82
6. Трансцендентные функции
О. ЛОГАРИФМЫ ПО РАЗНЫМ ОСНОВАНИЯМ
Как мы уже заметили выше, если нам известна некоторая функция, удовлетворяющая функциональному уравнению логарифмов, то из нее можно получить другие такие функции, умножая эту функцию на произвольные постоянные. Воспользуемся этим замечанием, чтобы для любого положительного числа а #= 1 определить логарифмы по основанию а. Именно, для положительных чисел х положим
loga% = -^ <15)
In а
(читается: «логарифм х по основанию а»).
Тогда, по определению,
logfl 1 = 0 (16)
и х 1 1 (17)
dx In а х .
Далее, по теореме 1,
loga (ху) = loga X + loge у, loga — = loge х — loga у (18)
У
и
logfl(xr) =rlogflx (19)
(где г рационально). Для любого положительного числа и существует единственное положительное число х, для которого logax =u. Поскольку In е = 1, из (15) находим
In. х = = In х; (20)
1пе
поэтому е называется основанием натуральных логарифмов*.
Для вычислений можно пользоваться таблицей логарифмов при любом основании а > 0. Чтобы найти ху (или х/у, или хт) находят а = logax, fl = logfl#, а затем число, логарифм которого по основанию а равен а + fl (или а — fl, или га). Однако если вычисления ведутся в десятичной системе, то удобнее всего оказываются логарифмы по основанию 10. Например, имеем
log10 22,34 = 1 + log10 2,234
(так как 10-2,234 = 22,34 и log1010 = 1),
log10 0,02234 = —2 + log10 2,234
(так как log1010"2 = —2) и т. д.
* В старину е часто называли также «неперовым числом»; это название можно встретить и в некоторых старых русских учебниках.
§ 4. Логарифмы
383
1дт
Рис. 6.35
Число logK>x называется десятичным логарифмом х. Большая часть таблиц логарифмов, составленных со времен Непера и Бриггса, содержат десятичные логарифмы*.
График функции х »-> log1Gx изображен на рис. 6.35.
УПРАЖНЕНИЯ
В упражнениях 21—28 выполните указанные вычисления с помощью десятичных логариф»
21. 10,8 х 2,91.
22. 108 : 0,0365.
23. (225)|/3.
24. 1,29 х 32,8.
25. 1,86 х 35,2.
26. (0,0178 : 0,138)1/3.
27. (327)6.
28. (1.89 : 1.87)*.
4.7. ПРИМЕНЕНИЕ ЛОГАРИФМОВ ДЛЯ ИНТЕГРИРОВАНИЯ
Функция х *-> 1/х есть простейшая рациональная функция, не являющаяся производной рациональной или алгебраической функции. В интервале (0, +<») эта функция имеет первообразную In х. Если х отрицательно, то —х положительно, так что функция х i-> 1п(—х) = 1п | х | определена при х < 0. В силу (4) имеем по цепному правилу
d In (— х) __d In (— х) d (— х)
dx d (— x) dx
Итак,
(21)
* См. сноску на стр. 377. Десятичные логарифмы в русской литературе обозначаются через 1g х; в иноязычной учебной и технической литературе для десятичных логарифмов обычно применяется обозначение log х, но в книгах математического содержания запись log х (вместо In х) зачастую обозначает натуральный логарифм.
384
6. Трансцендентные функции
Пользуясь логарифмической функцией, можно явно записать неопределенные интегралы (первообразные) целого ряда функций. Следующее правило заслуживает запоминания:
j A^dx = ln|<p(x)|4-C. (22)
Здесь С — постоянная интегрирования; при этом предполагается, что в рассматриваемом интервале функция х ф(х) не обращается в нуль. Если <р(х) положительна, имеем просто
С У. .(*) дх in ф
J у W
Для проверки этих утверждений заметим, что в силу (4), по цепному правилу,
J'"|;wi = прИ ф(х)+о. dx (х)
Проиллюстрируем применение логарифмов для разыскания интегралов на ряде примеров. В частности, мы сможем теперь записать явные формулы для первообразных функций арктангенс, тангенс, котангенс и др.
х"
ф Примеры. 1. Найти первообразную функции f(x) =-------------.
1 -|- х^оо
Решение. Заметим, что числитель этого выражения f «почти» равен производной знаменателя. В самом деле, если <р(х) = 1 + х100, то <р'(х) = 100х", откуда со' (х^ х" —,
Y — =-----------. Следовательно,
100<р(х) 1 + х1»0
f x*dx _ 1 Г IQOx^dx = 1 Г 1 А Л + X100) dx =
J 1 + X100 100 J 1 + х100 100 J 1 + х100 dx V ’
= —— ln(l +x100) + C. 100
To же можно записать в виде
1 Г 100x"dx 1 (• d(i+*100) _ 1 f d in (1 -i- r100l -
“ibcF J J 14-x*- J >~
= —L_ in(l +xioo) + c.
100
2. Найти первообразную функции 0 i-> tg 0.
Решение. Поскольку tg 9 = -—7- и d cos 0 = — sin 0 d0, имеем . cosb
f tg0d0 =— f =— ln|cos0| + C.
.) J cos e
§ 4. Логарифмы
385
3. Проинтегрировать функцию ctg 0.
Решение. Аналогично предыдущему находим
Jctg 0 d0 = In | sin 01 + C.
4. Найти J aretg x dx.
Решение. Интегрируем по частям:
J aretg x dx = x aretg x — J xd aretg x =
. C xdx . If d (x2) . 1 f d(l+xa)
= xaretgx — I -----= x aretgx-----| ——- = xaretgx--------I ——- =
J 14- x2 & 2 J 1 + %2 6 2 J 1 + x2
= x aretg x--— C d In (1 4- x2) = x aretg x-— In (1 + x2) 4- C.
2 J 2
5. Найти J In x dx.
Решение. Снова интегрируем по частям:
С In х dx = х In х — f x ln - dx = x In x — f dx = x In x — x 4- C.
J J dx J
6. Найти первообразную функции x»->xlnx.
Решение. Ив этом случае интегрируем по частям:
J х In х dx = J (In х) х dx = J (In x) d x — J ^x ~
= — Inx-------— f xdx = — Inx-------—(-C.
2 2 J 2 4
7. Найти C —.
J X In X
Решение. Имеем
f dx = f —--------— (In x) dx = In | In x | + С. ф
J x In x J In x dx
УПРАЖНЕНИЯ
29. Найдите f' (x), где f (x) = In (x3). i/3
30. Найдите h' (и), где ft (u) == (In (u2)) .
d2y 1
31. Найдите--— , где у = -------•
dx2 In x
32. Найдите g" (s), где g (s) = In In In s.
33. Пусть f (x) — положительная функция, удовлетворяющая условиям 1п/(х) = х1пхи /(2) = 4; найдите приближенно /' (2), пользуясь таблицами логарифмов.
1 + In | х |
34. В какой точке график функции у =----------- имеет горизонтальную касательную?
386
6. Трансцендентные функции
35.
Найдите
2х3 4~ *
dx.
36.
Найдите
все первообразные функции
1
1
37.
Найдите
1/У2
1 +(1/0) ЛУ‘
38.
Найдите
все первообразные функции
и + «~3 и2 4- а"2
39.
Найдите
все первообразные функции
г
2 г« + 1
1
In (z2 4- 1)
40. Найдите
41. Найдите
______dt
/ In (14-0
In и ---- du.
и
42.
Найдите
In Z
Z
dz.
43.
Найдите
44.
Найдите
при х =
все первообразные функции g (0 = Vt 1п7. dy r__
решение дифференциального уравнения — = х3 In У х , обращающееся в нуль
1.
45.
Найдите
_r secx + tgx
sec х dx. [Указание: запишите sec г = sec х -----и сравните про-
sec х -f- tg х
изводную знаменателя этой дроби с ее числителем.]
Найдите J sec2 х In (sec х) dx. [У к а з а н ие: воспользуйтесь интегрированием по частям.}
47. Найдите длину графика функции z/=ln(cosx) от пользуйтесь соотношением tg2 х 4- 1 = sec2 х. | sin и cos3 и
46.
48.
du. Указание: заметьте,
49.
50.
Найдите J (tg x 4- tg3 x) dx.
C u
Найдите 1 ---------- du.
J cos2 u2
51.
к
х = 0 до х = — . [Указание: вос-4
sin и 1
ЧТО -----— = tg и ------—
cos3 и cos2 и
Найдите j ——dx. [Указание: воспользуйтесь интегрированием по частям, а также примером 2.]
A 52. Найдите
l + tg2lnu , ------------ du.
и
§ 5. Показательная функция
387
53. Найдите решение дифференциального уравнения и в 1 — In 2 при t = 2.
d2v______1_
dt2 “ t2 ’
обращающееся в нуль при
6=1
54. Найдите I х In (х2 4- 1) dx.
55. Найдите
— In In t dt. t
1 1/2
C u
56. Найдите | --------— du.
J . , */2
о 1 4- и
x2 1
57. Пусть f (x) = — — — In x. Найдите длину графика f от x = 1 до x = 2. 2 4
A 58.
Указание, найдите такие постоянные а и Ь, что —---------= —4-
х2 4" х х
59. Найдите | — • [указание: найдите такие постоянные а, Ь, с, что —— = —• +
Jx34-x|_ хл + х х
Ьх-\- с 1
4- --!— •
х2+ 1 J
60.
dz
J (14-г2)(1-М)
1 a t bz 4- с
1 i
к а з а н и е: найдите такие постоянные at b
с, что
(1-М2) (14- z)
§ 5. ПОКАЗАТЕЛЬНАЯ
ФУНКЦИЯ
5.1. ИРРАЦИОНАЛЬНЫЕ ПОКАЗАТЕЛИ
Соотношение
In аг = г In а (1)
было установлено в § 4.4 для рациональных чисел г. Справедливо ли оно для иррациональных г? Верно ли, например, что 1п2^2 = уЗЛп 2? Пока этот вопрос лишен смысла, поскольку мы не определили, что такое аг\ в частности, на этой стадии нашего изложения символ 2^ не означает какого-либо числа. Но ничто не мешает нам определить степень с иррациональным показателем, потребовав, чтобы соблюл далось соотношение, аналогичное (1). Например, можно определить 2У2 как такое число, натуральный логарифм которого равен ]Л2 In 2.
13*
388
6. Трансцендентные функции
Вообще, условимся, что при а > 0 и при любом х символ ах обозначает то единственное число, натуральный логарифм которого равен xln а. Таким образом,
In ах = х In а. (2)
Это определение ах. Если х — рациональное число , то, разумеется, можно вычислить ах и иначе, причем в этом случае, как мы уже знаем, соотношение (2) выполнено. Итак, мы сделали соотношение (1) справедливым при всех г; теперь легко видеть, что для всех г справедливо также равенст во
loga(*r) =r\QgaX. (3>
При а = е соотношение (2) принимает вид
In ех = х (4)
(так как In е = 1). Пусть теперь и — любое положительное чис ло; применив формулу (4) к числу х = Ina, получаем ln(elnu) = In и.
Так как у двух разных чисел не может быть одинаковых логарифмов, отсюда следует, что
е1п“=а. (5)
Далее, для любого а > 0 имеем
ах = е . (6)
В самом деле, в силу (2) In ах = х Ina, а вследствие (4) lnexIna = х Ina. Наконец, для любого а > О
)ор и
logfl = хч а а = и. (7>
Действительно,
откуда и следует первое соотношение. Второе же вытекает из того факта, что обе части равенства имеют один и тот же логарифм по основанию а.
Следующее предложение представляет собой лишь другую формулировку соотношений (5) и (7).
Теорема 1. Для любого фиксированного а > 0 (a #= 1) функции
и l°ga и и х «-► ах
обратны друг другу, В частности, обратны друг другу функции
и *-* In а и х ех.
Теорема 1 знаменует возвращение к «школьному» определению логарифма: логарифм и по основанию а есть степень, в которую надо возвести а, чтобы получить и. Почему же мы не начали наше изложение с этого определения? Дело в том, что сна
§ 5. Показательная функция
389
чала надо было бы определить смысл ах для иррациональных х, а затем доказать, что уравнение ах = и при заданных а п и имеет единственное решение. Оба шага можно осуществить, оставаясь в рамках элементарной математики, но это потребовало бы от нас гораздо больших усилий.
УПРАЖНЕНИЯ
1. Чему равен logz2 z5/2? (Предполагается, что 0<г =£ 1.)
2. Чему равен logI/w2 u3/5? (Предполагается, что 1.)
3. Чему равен log^j (у4 4- 2v2 + 1)?
. ТТ п41°£23^
4. Чему равно 2 ?
- тт 1 ( 3iog„2\_
5. Чему равен log2 \ х х ) ?
6. Для каких значений х справедливо равенство logt(x + 6) = 2?
7. Для каких значений х справедливо равенство log4/x (х2— 6) = 2?
8. Для каких значений х справедливо неравенство logx [(х2/2) -f- 2] < 2? [Указание: рассмотрите отдельно случаи х> 1 и х< 1.]
5.2. СВОЙСТВА СТЕПЕНЕЙ
Теорема 2. Для положительных, а и b и любых х и у имеем:
ах+у = аха\ (8)
(9) а?
(аху=ахУу (Ю)
(ab)x==axbx. (И)
Это обычные свойства, уже известные нам в случае, когда х, t/-—рациональны е числа (см. гл. 1, § 5.5). Теперь мы докажем их в общем случае. Для этого достаточно проверить, что обе части каждого равенства имеют один и тот же натуральный логарифм. Мы сделаем это для равенства (11), предоставив читателю остальное проделать самостоятельно. В силу (2)
1п(а&)х = х ln(ab) =x(lna+lnb) = xln'a + х In Ь = 1пах + 1п Ьх = 1п(ах6х), откуда
(аЬ)х = ахЬх.
5.3. ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ
Определив степени с любым (рациональным или иррациональным) показателем, мы можем теперь изучить функции вида х >-► ах, где а — любое положительное число. Графики функций х н-> ех и х >-> 10х (полученные «отражением» от биссектрисы первого координатного угла графиков рис. 6.32 и 6.35) изображены на рис. 6.36 и 6.37.
390
6. Трансцендентные функции
Функция ех часто записывается символом ехрх:
ехр х = ех
и называется показательной (или экспоненциальной) функцией; это одна из важнейших функций математики.
Частный случай (8) представляет соотношение
02)
Зто так называемая теорема сложения, или функциональное уравнение, показатель* пой функции.
5.4. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Теорема 3. Имеем
(13)
и при а>0
- - = In а • ах. (14)
dx v '
Доказательство. В силу теоремы 1 и теоремы о дифференцировании обратных функций (теорема 7 § 2.6 гл. 4) имеем, полагая ех = и:
de* du 1 1 1
--- = — = -------=------- =-----= и = ех
dx dx dx din и \/u
du du
Аналогично можно доказать соотношение (14); но проще воспользоваться формулами
(6), (13) и цепным правилом:
§ 5. Показательная функция
391
dax dex}nx dexlna d (x In а) лх\па Л !_____________
= = ------- = e • In a = In a • a, dx-----------------------------dx-d (x In a) dx
ч то и требовалось доказать.
В гл. 4, §2.7 мы получили соотношение -^~= ах®*"1 для рациональных а.
Теперь мы покажем, что при х > 0 это ограничение несущественно.
Теорема 4. Для любого числа а при х > О dx* а—1 -37 = «х • (15)
Доказательство. Имеем dx* de* ln х de* ln x d (a In x) a In r a x* a—1
--- = ---- = ------- = e — = a - = ax • dx dx d (a In x) dx-------------------------x x
УПРАЖНЕНИЯ
9. Найдите f' (2), где f (x) = e2X.
10. Найдите f' (3), где f (/) = 5*.
11. Продифференцируйте sin(^).
12. Продифференцируйте e
13. Найдите пятую производную функции е2*.
14. Продифференцируйте еп\
15. Найдите j exdx.
16. Найдите I е~2Х dx.
17. Найдите, С х^7 dx.
J х2
18. Для каких значений х функция е возрастает?
5.5. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
Если функция х <р(х) положительна, то можно построить функцию х •-* 1п ф(х). Пусть ср дифференцируема; тогда, по цепному правилу,
dУ (х) = din? d? _ 1 ,. .
dx dff dx ? (x) ’
ИЛИ
/ / v / \ d In cp (x) ф'(х) = ф(х) —p-2 dx
(16)
Применениеэтой формулы вместе co свойствами логарифмической функции, иногда упрощает дифференцирование. Такой способ разыскания ср' называется логарифмическим дифференцированием. Нет надобности запоминать предыдущее равенство; достаточно знать, что требуемый результат обычно достигается, если положить ф(х) =е*(х), где ф(х) =1пср(х).
392
6. Трансцендентные функции
• Примеры. 1. Найти производную функции х <-► хх (при х > 0).
Первое решение. Положим у = Xх. Тогда в силу (16) du din u din хх d(xlnx) /. , 1 \ r ...
-T^y—T- = У —— =У———L = У Inx 4- x— =xx(lnx+ 1). dx dx dx dx \ x /
Второе решение. Имеем xx = exlnx\ отсюда
dx* dexinx rinr d(xlnx) rinr/i . 1\ rZ1 .
---- =-------- = ex ln * —i---L = ex 111 x (In x + x • —| = xx (In x 4- I),
dx dx dx \ x )
т. e. мы получили тот же результат, что и выше.
Третье решение. Положим у = хх\ тогда In у = х In х. Дифференцируя, имеем
1 X
— у' = In х 4-----, или у = #(1пх 4- 1) = хх (In х + 1).
У X
(1 *10 \ 1/10
----—-- I при X =0 и при X = к.
2 4- cos х /
Решение. Применим логарифмическое дифференцирование:
In# = In(1 4- х10)— In (2 4- cosx)j , d in у 1 10x9 1 (— sin x)
dx 10 14- x10 10 2 4- cos x
dy __ d In у _/ 1 -h x10 y/ю / x9 / sin x \
dx dx \2 4- cos x J \1 4- x10 20 4- 10 cos x/
И / dy \ ==0. (dy\ = ф
\ dx )x=o ’ \dx/x=ic \ (1 4- irl0)1/I0 /
3. Продифференцировать функцию f (x) = e* [ = Д ’
Решение. По цепному правилу
f' (х) = е*е ееХех.
С помощью логарифмического дифференцирования находим
х х х
. X dine** / de*x л6х dlne^ рех х
f'(x) = ее --------------- ее --------=ее • е --------------= ее • е^ • ех. А
dx dx dx
§ 5. Показательная функция
393
УПРАЖНЕНИЯ
В следующих упражнениях выражение вида сРС следует понимать в смысле , т. е. о 2 возводится в степень Ьс. Это число, вообще говоря, отлично от (аь)с = аос\ сравните 23 =
= 2(3>> = 2» = 512 с (23)2 = 82 = 64.
ж d In (1 + ех)
19. Найдите --------------
dx
it е d In (х + е*2)
20. Найдите ---------------
dx
dy
21. Найдите — , где у = cos (е^. dx
y^ln и
22. Продифференцируйте и*-+е
j /и
23. Продифференцируйте и 2U3
24. Продифференцируйте arctg е2.
d*es,n “
25. Найдите ------— .
du2
26. Найдите (0, где = l/x
27. Проверьте, что функция у = е является решением дифференциального уравнения х3 ---------4- х — — 2у = 0.
dx2 dx * d х» 28. Найдите — х . dx
29. Продифференцируйте v>-► (и2 4- 1)^.
dz
АЗО. Найдите — , где z = (х2 + 1)1п х. dx у
31. Продифференцируйте 61-> (cos 0)s,n 6 .
32. Продифференцируйте хн> tg ( х^х ) .
33. Найдите J cos 0 es,n 8 d0.
f*
34. Найдите I ------dx.
J Vx
35. Найдите | ------ dx.
] x2
394
6. Трансцендентные функции
36. Найдите J cos (е6 ) dO.
/Г
37. Найдите J 2*+lx3dx.
1
г8 4г,/3
38. Найдите I ---— dz.
J 2/3 1 z
39. Найдите J xexdx. [Указание: воспользуйтесь интегрированием по частям.]
Д40. Найдите J x2exdx. [Указание: воспользуйтесь интегрированием по частям и упр. 39.] 41. Постройте график функции х^х2е2Х при —4 < х < 1.
2х/3
42. Постройте график функции хь->хе при —3<х< 1.
43. Постройте график функции хь->/х е^х при 0 < х < 4.
44. Постройте^график функции хь->х3езх при —3 <х <1.
5.6. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Показательная функция х ех равна своей производной. В действительности она полностью определяется этим свойством и тем условием, что значение ее в точке х = 0 равно единице.
Теорема 5. Существует в точности одна функция х f(x), удовлетворяющая дифференциальному уравнению f'(x) =f(x) (17)
и условию /(0) = 1; (18)
это — функция f(x) = ех.
Доказательство. В силу теоремы 3 функция ех обладает требуемыми свойствами. Мы должны показать, что не существует другой функции, удовлетворяющей условиям (17) и (18). Пусть /(х)— такая функция; положим g(x) = e~xf(x).
Тогда g(0) = 1 и g'(x) = —e~xf(x) + e~xf(x) = 0 для всех х. Отсюда g(x) = 1, так что /(х) = ех.
Теперь мы несколько обобщим теорему 5. Это обобщение лежит в основе большей части приложений показательной функции.
Теорема 6. Пусть А и а — любые числа. Тогда функция
fix) = АеЛХ (19)
удовлетворяет дифференциальному уравнению fix) = а/(х) (20)
и начальному условию №)=А. (21)
Это — единственная функция, удовлетворяющая соотношениям (20) и (21).
§ 5. Показательная функция
395
Доказательство. Первое утверждение проверяется прямым вычислением. Пусть теперь функция Дх) удовлетворяет условиям (20) и (21). Положим g(x) = •= f(x)e'ax. Тогда
g'(x) = f'(x)e~ax — af(x)e~ax = e~ax(f'(x) — аДх)) = 0.
Следовательно, g — постоянная. Поскольку g(x) = g(0) = /(0) = Л, эта постоянная равна Л, откуда вытекает (19).
Теорему 6 можно формулировать также следующим образом: общее решение дифференциального уравнения f' + af = 0 есть Ае~ах. Из теоремы 6 можно вывести все свойства показательной функции. Покажем, например, как из нее получается новое доказательство теоремы сложения: ех+у = ех-еу.
Положим Дх) = ех+у, где у — фиксированное число. Тогда, по цепному правилу, dex+y = dex+y d(x + y) = dx d (х + У) dx
так что f'(x) = Дх). Далее, ДО) = е0+у = еу. Но тогда, по теореме 6, Дх) = еу-ех, что и требовалось доказать. (Сравните это рассуждение с доказательством теоремы сложения для синуса и косинуса, приведенным в § 1.11.)
УПРАЖНЕНИЯ
45. Найдите такую функцию Дх), что f(x) = f(x) и /(0) = 4.
^46. Найдите такую функцию f(x), что f.'(x) = 4Дх) и Д1) = е.
47. Найдите такую функцию f(x), что ЗД(х) = —2f(x) и ДЗ) = е.
48. Найдите такую функцию f(x), что f (х)/Дх) = 2/5 и f (1) = е.
В упражнениях 49—52 предположите, что существует решение вида Дх) = , и найдите
g(x). Затем проверьте, что eg(x) — действительно решение. Не забудьте ввести в Ваши вычисления постоянную интегрирования.
49. Найдите такую функцию Дх), что f'(x) = 2xf(x) и ДО) = 1.
50. Найдите такую функцию Дх), что f (х) = Зх2Дх) и Д0)= 2.
51. Найдите такую функцию Дх), что 2)/х Д(х) = Дх) и Д4) = 1.
52. Найдите такую функцию Дх), что х2Д(х) = —Дх) и lim Дх) = е.
Х-ИОО
5.7. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ
При использовании показательной функции следует иметь в виду, что при а > 0 функция е*х быстро возрастает. Пусть, например, а = Г, при этом е2 несколько больше 7, а е10 превосходит 22000. Вообще, если х растет «в арифметической прогрессии», т. е. принимает возрастающую последовательность значений
х = а, х = а + 6, х = а + 26, х = а + 36, х = а + 46, ..., то соответствующие значения еах образуют геометрическую прогрессию
Уо. УоУ, УоУ2> Уо<?. УоУ4.. где у0 = e*>, q = eab.,
Поскольку по предположение b > 0, имеем q> 1. Люди давно уже заметили, как быстро возрастают члены геометрической прогрессии при q> 1. (Вспомните восточную легенду о вознаграждении, потребованном изобретателем шахмат: он
396
6. Трансцендентные функций
попросил, чтобы ему положили 1 зерно пшеницы на первую клетку шахматной доски, 2 зерна на вторую клетку. 4 — на третью, 8 — на четвертую и т. д., наконец, 2е3 зерна — на последнюю клетку доски.)
Рассмотрим теперь точнее, как растет показательная функция.
Теорема 7. Пусть а — любое число; тогда
lim 4- = + (22)
X-*—}-оо X
Это выражают словами; «когда х—> +°°» функция ех стремится к бесконечности быстрее любой степени а переменной х». Теорема представляет интерес, конечно, лишь при а > 0.
Если а > 0, то lim ха = +оо. Поэтому знаменатель дроби (22) становится очень х-»-оо
большим при больших положительных х. Теорема утверждает,что ех,в конечном счете, становится еще больше. Слова «в конечном счете» здесь существенны. Если, например, взять а = 1010/1п 10, то при х = 1010 все еще х®> ех: в самом деле, (1010)а = = е10а1п1° = е1011 > е1010. Но даже для этого огромного а число ех при возрастании х становится в конце концов больше ха .
Доказательство теоремы 7. Рассмотрим сначала функцию ф(0 = = е* — 1 — t. Так как ф'(0 = е' — 1 и, следовательнр, ф'(0 > 0 при 0, то ф(/) — возрастающая функция от t при t > 0. Поэтому ф(/) > ф(0) = 0, откуда е* > > 1 + t и t
, > 1 + > 1 при t > 0. (23)
Пусть задано число а > 0. Возьмем целое число N > а и применим (23) к t = = x/N. Тогда при х > 0 имеем
x/N
-— > 1, или x/N
так что
Поскольку lim xN— = +<», отсюда следует утверждение (22). *•*+<» _
Отметим одно следствие теоремы 7.
Следствие. Для каждого а > 0
Л lim —----= Ч-оо.
In X
(24)
Это выражают словами: «при *-*+<» функция In х стремится к бесконечности медленнее любой степени х». ._
Доказательство. Положим In х = у. Тогда у -+ +°° при х -> -f-oo и ха _ / еу У,
1пх у у у1/а)
так что (24) вытекает из (22).
§ 5. Показательная функция
397
УПРАЖНЕНИЯ
53. Пусть а — положительное число. Начертите график функции хпри х>0. В частот
ности, найдите интервалы возрастания и убывания и все максимумы й минимумы, локальные и абсолютные.
ех
54. Вычислите —- при х = 1,2, 3, 4.
ех
55. Вычислите — при х=1,3,5,7. х3
56.
х2
57.
58.
Вычислите —-— при х= 1,2, 3, 4.
In х
X2
Начертите график функции хн------------- при х>0. В частности, найдите интервалы
in х
возрастания и убывания, а также максимумы и минимумы, локальные и абсолютные. ех х4
Найдите
такое значение х0, чтобы при х>х0
[Указание: восполь-
59.
60.
зуйтесь
Найдите
Найдите
неравенством
, положив
в нем N = 5. ]
такое значение х0, чтобы
было > 104.
такое значение х0, чтобы
х2 Г
было ---> 104. Указание: поло-
ln х I
N*
X2 / еУ V жите у = In х и воспользуйтесь соотношением —— = I .
5.8 . СЛОЖНЫЕ ПРОЦЕНТЫ
Якоб Бернулли предвосхитил открытие показательной функции своим вопросом: пусть заимодавец платит кредитору некоторое число процентов от занятой суммы в год; сколько он должен уплатить за год на каждую единицу занятой суммы, еслйГ ^Проценты нарастают непрерывно? Предположим, что выплачивается k процентов в год, и положим а = fc/100. Если вычислить долг в конце года, то он составит первоначальную сумму, умноженную на 1 + <*• Будем считать для простоты, что первоначальная сумма равна единице. Пусть теперь долг подсчитывается раз в полгода; тогда через полгода он равен 1 + у, а через год, следовательно,
(1 + т) (‘ +
Если долг подсчитывается раз в три месяца, то при каждом подсчете он возрастает в 1 + -2- раз, а к концу года — в (1 + у)4 раз.
398
6. Трансцендентные функции
Ежемесячный подсчет дает (1 4" В°°бш£> если разбить год на п равных
частей и вычислить долг в конце каждой части, то в течение года долг, равный 1, вырастет до
(1 + • (25)
Естественно считать, что при большом п число (25) будет близко к истинному результату, т. е. к величине долга при непрерывном наращении процентов.
Рассмотрим теперь вопрос с точки зрения математического анализа. Если проценты нарастают непрерывно, то величина долга должна быть возрастающей функцией протекшего времени; обозначим эту функцию через /(/). При этом время мы будем измерять в годах. Поскольку при t = 0 долг был равен 1, имеем
/(0) = 1. (26)
Допустим, что/дифференцируема, и попытаемся вычислить /'(/). Пусть А — малое положительное число. Рассмотрим некоторый момент времени tQ и малый промежуток времени от tQ до /0 + А. В течение этого малого промежутка f(t) изменится очень мало. Если пренебречь этим изменением, то сумма /(/0), которая принесла бы в год доход а/(/0), за малый промежуток времени h возрастет на haf(t0). Таким образом» приближенно имеем f(tQ + h) « /(/0) + haf(tQ) и, значит,
—-</°). = df (/0) 4- малая ошибка,
причем можно рассчитывать, что ошибка будет сколь угодно мала, если h достаточно мало. Но тогда
НО = а/(0. (27)
Вследствие теоремы 6 имеем
f(f) = е* (28)
и если t — 1, то /(1) = е*. Итак, ответ на вопрос Бернулли гласит: ел.
Процедура получения «решения» типична для приложений анализа. Она состоит из «интуитивной» части и «точной» части. Чтобы прийти к дифференциальному уравнению (27), мы свободно пользовались интуицией. Конечно, мы при этом не «доказали», что /(/) удовлетворяет уравнению (27). В самом деле, как мы могли это бы доказать? Ведь у нас нет на этом этапе даже отчетливого определения «непрерывно на-
БЕРНУЛЛИ. Эта семья из Базеля (Швейцария) породила в течение трех поколений ряд выдающихся математиков. Самыми знаменитыми из них были Якоб (1654—1705), его брат Иоганн (1667—1748) и сын Иоганна Даниель (1700—1784) *. Два старших Бернулли были первыми учеными. понявшими, применявшими и развивавшими дифференциальное и интегральное исчисление Лейбница. Якоб Бернулли был также автором первого трактата по математической теории вероятностей. Даниель известен прежде всего своими трудами по механике жидкости.
Бернулли поддерживали тесный научный контакт друг с другом, ио иногда яростно (и зачастую весьма пристрастно) спорили о приоритете в открытии того или иного математического факта.
* В русской математической литературе их зачастую именуют: Яков, Ивам (впрочем, в более новой литературе имя «Иван» почти не встречается) и Даниил. (Прим, перев.)
•§ 5. Показательная функция
399
растающего процента». В качестве такого определения как раз и естественно принять полученное дифференциальное уравнение.
Но как только мы пришли к дифференциальному уравнению, интуитивная часть рассуждения завершается. Следующий шаг, т. е. получение решения (28), осуществляется чисто математическим и вполне строгим методом — применением теоремы 6.
Если бы речь шла о естественном процессе, то мы могли бы после этого проверить правильность наших «интуитивных» догадок, сравнив решение дифференциального уравнения с наблюдениями. В нашем случае мы этого сделать не можем, поскольку вопрос Бернулли относится к чисто воображаемой ситуации. Но мы можем выполнить косвенную проверку. Если наше рассуждение было основательно, то число <1 + -^-)л должно быть при больших п очень близко к е°-; мы сейчас увидим, что это так и есть.
5.9. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ КАК ПРЕДЕЛЫ
Теорема 8. Для любого числа а
lim (1 4- —У = е . (29)
П 00 \ П J
Эта теорема подтверждает сделанную выше догадку. Ранее число п предполагалось целым, а а — положительным; оба этих ограничения оказываются излишними. Прежде чем перейти к доказательству, заметим, что (полагая п = у) можно записать (29) в виде
lim (1 + = еЛ .
Л->0+
Мы докажем большее, не требуя, чтобы h было положительным. А именно, установим что
lim (1 + ah)1/h = еа. (30)
Доказательс тво. Поскольку In х — непрерывная функция, непрерывна также и обратная функция ех\ поэтому (ср. с теоремой 2 § 4.2 гл. 3) вместо равенства (30) достаточно доказать, что
lim In (1 + ah),/h = In ea = a.
Ho
In (1 +a/i)1/h =—ln(l + ah) =— (ln(l +ah)— In 1} = h h
In (1 + ah) — In 1 = a
ah
400
6. Трансцендентные функции
И
lim а 11 , ||т " <+°*> ~1 = . цт
Л->0 ah h_Q ah k-+Q k
= а
что и требовалось доказать. Отметим частный случай а
/ dinх\ [ 1 \
I-------I = а I — I
\ dx )х=\ \ х Jx=\
= 1:
lim (1 4- —У = е.
n->-f-oo \ п /
(29')
Это соотношение часто служит определением е (но в этом случае надо доказать существование предела). Можно также принять (29) или (30) за определение показательной функции.
Аналогично можно определить и натуральные логарифмы:
Теорема 9. При а > 0
lim а ~~1 = In а. (31)
л->о h v
Доказательство. Имеем
1. ah — 1 t. ah — а°
lim ---= lim--------
л->о h h-*o h
= (Ina) aQ = In a,
что и требовалось доказать.
УПРАЖНЕНИЯ
/ 1 V+2
61. Найдите lim [ 1 + — .
\ x J
I 1 Vе
62. Найдите lim 1+------------| «
X->4-oo \ X + 1 )
63. Найдите lim (1 + 4x)3/x. x->0
X±1
A 64. Найдите lim (1—x) x . x->0
22“ _ 2«+l _|_ 1
65. Найдите lim ---------------
u->0 u2
5.10. ПОПУЛЯЦИОННЫЙ ВЗРЫВ
Существуют реальные ситуации, соответствующие представлению Бернулли о капитале, растущем со скоростью, пропорциональной его величине. Рассмотрим в качестве примера рост популяции бактерий. Бактерии, если их не убивать, продолжают жить сколь угодно долго, и заданная популяция из N бактерий через очень короткий промежуток времени h вырастает приблизительно на aNh, где a — некоторая положительная постоянная. Тем самым ~ ад^(/). Можно по-
этому предположить, что функция N(t). т. е. число бактерий в момент времени /, удовлетворяет дифференциальному уравнению
N'(t) = аЛф) (32)
§ 5. Показательная функция
40t
и потому задается (см. теорему 6) формулой
N(t) = NQe«, N« = N(0).
Быстрое возрастание еат при -J-co описывает «популяционный взрыв».
Только что рассмотренный пример иллюстрирует следующее важное обстоятельство. Число бактерий — целое; поэтому функция W(/) — ступенчатая и, строго-говоряще может рассматриваться как непрерывная. Но N — очень большое целое число, и возникновение новых бактерий меняет его очень незначительно*. Поэтому мы получим достаточно точное изображение действительности, обращаясь с N(t} так, как будто эта функция непрерывна и даже дифференцируема.
Дифференциальное уравнение, описывающее рост человеческой популяции, должно быть сложнее уравнения (32). Во всяком случае, оно должно содержать две постоянные, характеризующие рождаемость и смертность. Если предположить, что в популяции численности N за малый промежуток времени h происходит айМ рождений и $hN смертей, то мы получаем следующее дифференциальное уравнение:
[В самом деле, в момент t + h численность популяции приближенно равна Af(/) + + ahN(t) — $hN(t).] Это можно записать так:
N'(t) = (а - 0W). (33)
Решение имеет вид
N = ^0 = N (0). (34>
Форма популяционной кривой, описываемая формулой (34), зависит от знака а — 0. При а = 0 популяция сохраняет постоянную численность. При а < 0 она вымирает, поскольку lim N(t) = 0. Если же коэффициент рождаемости а превосходит коэффициент смертности, то популяция будет возрастать: вначале, может быть, довольно медленно, но через некоторое время неизбежно очень быстро.
Хотя имеющий в настоящее время место «демографический взрыв» представляет собой серьезную опасность для человечества, дифференциальное уравнение (33), разумеется, слишком упрощенно изображает реальную ситуацию, и его решение далеко от истинного течения процесса**. Например, коэффициенты рождаемости и смертности зависят и от величины популяции, и от распределения ее по возрастам,, и от других факторов***; они далеко не постоянны.
* Читателя, пожелавшего обдумать описанную ситуацию с самых общих позиций, можно отослать к довольно неконкретной, но выразительно написанной заметке: П. К. Рашев-с к и й, О догмате натурального ряда, «Успехи мат. наук», 28, вып. 4(172), 1973, с. 243—246.
** Не говоря уже о том, что сравнение совершенно безответственных бактерий со способными обдумывать свое будущее людьми вряд ли можно считать закономерным.
*** В случае человека — также и от уровня жизни и от образовательного ценза рассматриваемой группы людей (а в обществах с сильным влиянием религии — еще и от того, какая религия распространена в данном обществе).
402
6. Трансцендентные функции
УПРАЖНЕНИЕ
66. Пусть в виде опыта культуре из 100 бактерий предоставлена возможность размножаться при благоприятных условиях. Через 12 часов обнаруживается# что культура содержит 500 бактерий. Сколько бактерий будет через 2 дня после начала опыта?
5.11. РАДИОАКТИВНЫЙ РАСПАД
В качестве примера экспоненциального распада рассмотрим радиоактивный элемент, например радий. Пусть дано N атомов такого элемента; тогда через короткий промежуток времени h распадается приблизительно aNh из них. Поэтому количество радиоактивного вещества F(t), имеющееся в момент времени t (измеряемое его массой, или числом атомов, или иным способом), подчиняется дифференциальному уравнению
dt
(35)
Отсюда
F(t) = Foe~at, Fo=F(0).
(36)
Время /, в течение которого первоначальное количество вещества уменьшается вдвое, называется его периодом полураспада. Это время находится из уравнения е~°* = 1/2. Решая это уравнение относительно /, получаем
Период полураспада зависит лишь от природы вещества. Для радия он равен 1656 годам; для изотопов радия Л и С' он равен соответственно 2 мин 45 с и 1,4-10”6 с. Различные изотопы урана имеют период полураспада порядка 109 лет.
Универсальность закона распада (36) свидетельствует о том, что законы атомной и ядерной физики коренным образом отличаются от законов, описывающих объекты обычных размеров. Если дано N атомов плутония, то через 140 дней мы обнаружим, что примерно половина из них распалась (так как для плутония период полураспада около 140 дней). Разделим N атомов на несколько частей и будем наблюдать каждую в отдельности. Тогда за 140 дней распадется половина каждой части. Такое описание ситуации делает ясным тот факт, что не существует способа предсказать, когда распадется некоторый индивидуально выбранный атом.
Другие применения показательной функции (к ядерному делению, к атомным реакторам, к радиоактивному равновесию и к барометрическому давлению) рассматриваются в Приложении (см. § 6).
УПРАЖНЕНИЯ
67. Пусть период полураспада радиоактивного вещества составляет 1 год. Сколько времени пройдет, когда из 10 г вещества останется 1 г?
68. Пусть за 5 дней распадается 10% некоторого радиоактивного вещества; каков его период полураспада?
§ 5. Показательная функция
40*
Рис. 638
Рис. 639
5.12. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Поскольку функция 1равна своей производной, а функция t »-> отличается от своей производной лишь знаком, каждая из них удовлетворяет дифференциальному уравнению второго порядка
Г'(П - f(D = о. (38>
Это уравнение отличается от уравнения, решениями которого являются синусы и косинусы (/" + f — 0) «только» знаком. Это «небольшое» отличие имеет разительные следствия. Графики и совсем не похожи на синусоиды. Однако имеется далеко идущая формальная аналогия между тригонометрическими и показательными функциями. Эта аналогия становится особенно отчетливой, если рассмотреть следующие комбинации е* и
sh/ =
2 2
(39)
Функции 1»—► sh t и 1»—► ch£ называются соответственно гиперболическим синусом! и гиперболическим косинусом.
404
6. Трансцендентные функции
Графики гиперболического синуса и косинуса изображены на рис. 6.38 вместе с графиками функций Заметим, что
shO = 0, ch 0 = 1, (40)
sh(—/) == —sh t, ch(—/) = ch /, (41)
ch2 / — sh2/ = 1. (42)
(Мы пишем ch2 / вместо (ch /)2, и аналогично для других гиперболических функций.) Эти соотношения сразу же вытекают из определения (39) и напоминают соответствующие соотношения для синуса и косинуса. С другой стороны, функции sh / и ch/ не периодичны. Далее,
lim = lim = I. (43)
t-I t t » 4-со I .
-2 е1 ~e‘
В самом деле, stn = = j _ cht e j + Нт e_it = 0
1 t е* 1 , г-^-роо
— “7Г" е
Следовательно, при больших / функции sh t и ch t по существу сводятся к Заметим также, что
ch / >• 1 при всех /.
Действительно,
ch t - 1 = ± (е‘ + г* - 2) = -i- ( е"г - е-"2)2 > 0.
Поэтому гиперболический тангенс, определенный формулой
sh t _____
ch t e* -4- e-t *
(44)
(45)
непрерывен при всех значениях независимой переменной (в отличие от обычного тангенса). График гиперболического тангенса изображен на рис. 6.39. Гиперболический тангенс имеет пределы 1 при / -> 4-со и —1 при / —оо.
Следующие формулы дифференцирования аналогичны формулам для тригонометрических функций:
= Ch z, = Sh t, . (46)
df dt dt ch» t
§ 6. Другие применения показательной функции
405
{Здесь опять отличие в знаке: производная ch t есть sh t, а не —sh /.) Доказательства легко получаются из (39). Например, чтобы доказать первое из соотношений (46),
заметим, что / 1 . 1 Л d 1 — — — е~Ч •
dsht _ dt \ 2 2 / 1 t , 1 . . . = — = — ef H e‘ = ch t. dt 2 2
Остальные доказательства мы предоставляем читателю.
Имеются еще три гиперболические функции и шесть так называемых обратных гиперболических функций. Мы их опишем в Приложении (см. § 7), где будет разъяснен также термин «гиперболические».
УПРАЖНЕНИЯ
69. Покажите, что ------= shf.
dt d th t 1
70. Покажите, что-------= ——— •
dt ch21
71. Покажите, что sh (x y) — sh x ch у -f- ch x sh y.
72. Сформулируйте и докажите теоремы сложения для ch х и th х.
73. Упростите выражения chlnx и shlnx.
, d chl/2za Найдите------------
dz
„ ,, . d(xsh2x)
75. Найдите --------*
dx d
76. Выразите —In sh х через показательную функцию. dx
d
77. Найдите — (ch и sh u). du
78. Найдите d?z , где z = ch3 2i. dt2
79. Найдите C shu 1 “7— du-J ch u
80. Найдите J ch21 dt.
81. Найдите J ch3 z sh zdz.
82. Найдите J t sh t dt.
83. Найдите f (x), где f(x) = thtgx.
84. Найдите /' (x), где f (x) = sh x2 — ch /Г.
85. Докажите, что lim th t = — 1, lim th t = 1
406
Приложение к главе 6
Приложение к главе 6
§ 6. Другие применения показательной функции
В этом параграфе продолжается изучение дифференциального уравнения показательной функции. В частности, рассматривается так называемое неоднородное уравнение второго порядка [см. ниже уравнение (1)]. Это уравнение применяется к ядерному делению и к радиоактивному равновесию.
6.1. Общее решение неоднородного уравнения
Рассмотрим дифференциальное уравнение
1"{х) — aft(x) = Ф(х). (1)
гдеф — заданная функция. Чтобы решить это уравнение, т. е. чтобы найти все удовлетворяющие ему функции, мы применим прием, полезный также и для других дифференциальных уравнений. Еслиф= 0, то, как мы знаем, решение имеет вид Аеах , где А—постоянная (см. теорему 6-§ 5.6). Попытаемся решить уравнение (1), записав искомое решение в виде
f (х) = А (х) еах,
где Д(х) — функция, подлежащая отысканию. [Заметим, что если решение f(x) существует, то его всегда можно представить в этом виде: достаточно положить [(х):еах = Д(х).] Подставив, в уравнение (1) выражение для j, находим
f' (х) — af (х) = А'(х) еах 4- Д(х) аелх — аА(х) елх = ср (х), или
Д'(х) = е“ахср(х).
По основной теореме анализа
А (х) = J е ср (£) d£ 4- А, о
где А — постоянная, причем значение Д(х) при х = 0 равно А. Итак,
f (х) = Ае* 4- е* J е ср (£) (2>
о
Сформулируем этот результат в виде теоремы:
Теорема 1. Решение (единственное) дифференциального уравнения (1), удовлетворяющее начальному условию f(0) = А, имеет вид (2).
Отметим, что теорема 5 § 5.6 является частным случаем этой теоремы [приф(х) = 0].
УПРАЖНЕНИЯ
1. Найдите такую функцию f(x), что f (х) — 2/(х) = х и f(0) = 1/2.
2. Найдите такую функцию £(х), что /}'(х) 4- /(х) = е2* и f(0) = — 1.
3. Найдите такую функцию f(x), что Ц'(х) —= eXf2 и = 2*
4. Найдите такую функцию f(x), что f(x) 4- ftx) = cos(«ex) и f(0) = е.
5. Найдите такую функцию £(х), что (х) + 3/(х) — хех и f(0) = 4/е.
§ 6. Другие применения показательной функции
407
6.2. Ядерное деление
Ядерное деление, т.е. распад атомного ядра на несколько частей, может происходить у ряда элементов, например у U235 (изотоп урана с атомным весом 235); это происходит, когда в атомное ядро попадает нейтрон — незаряженная элементарная частица. Свободные нейтроны всегда присутствуют в веществе. Некоторые из них сталкиваются с атомными ядрами, вызывая их деление; часть из возникающих при этом нейтронов в свою очередь вызывает деление других ядер, а часть покидает вещество. (В атомном реакторе имеется также и независимый источник нейтронов.) Когда нейтроны возникают в результате ядерного деления, высвобождается большое количество энергии, главным образом в виде тепла.
Мы выведем дифференциальное уравнение, описывающее (разумеется, в сильно упрощенной форме) этот процесс. (В частности, в дальнейшем мы пренебрегаем используемыми в реальных атомных реакторах «замедлителями»— веществами, рассеивающими нейтроны и замедляющими процесс.)
Рассмотрим шар радиуса г равномерной плотности р из расщепляющегося вещества. Если N — число нейтронов в момент времени /, то через короткий промежуток времени h в результате деления возникнет добавочное число нейтронов, пропорциональное N и h, т. е. равное aNh. Положительный множитель а зависит от применяемого вещества и плотности, но не от размеров •и формы вещества. Объясняется это тем, что каждый индивидуальный акт ядерного деления происходит в объеме, размеры которого незначительны по сравнению с «обычным» размером куска металла.
В течение того же краткого промежутка времени h некоторое число нейтронов покинет вещество; это число равно 0 Ж. так как оно пропорционально числу имеющихся нейтронов N и прошедшему времени. Разумно предположить, что коэффициент пропорциональности 0 зависит ют радиуса г, поскольку лишь нейтроны, близкие к поверхности шара, способны покинуть его за короткое время h. Таким образом, 0 следует считать пропорциональным отношению площади поверхности шара к его объему, т. е. величине
4кг2 3
(4/3)лг3 г
Итак,
„ Ро
где положительная постоянная 0о зависит лишь от вещества и от плотности. Следовательно, число нейтронов через промежуток времени h будет примерно равно
N + aNh — $Nh.
Поэтому N как функция времени t удовлетворяет дифференциальному уравнению
dN
= (а —₽) N, а
решение которого имеет вид
N = V‘-₽,<
(3)
Если t измеряется в секундах, то размерность постоянных а, 0 есть 1/с; поэтому 0 о имеет размерность скорости (см/с, если радиус шара задается в сантиметрах). Величина радиуса г, при которой а = 0 = 0о/г> называется критическим радиусом; он равен гКр = 0о/а. Соответствующая масса расщепляющегося вещества /пКр —- у- л (гКр)3 р , гдер — плотность вещества, называется критической массой.
Количество энергии, высвобождающееся при делении, пропорционально числу возникших нейтронов. Если это число растет очень быстро, то огромное количество энергии выделяется в короткое время, что и происходит, как только масса превзойдет критическую. В самом деле, при г > гкр имеем а —0 > 0, и N возрастает «экспоненциально». Так происходит «атомный взрыв».
408
Приложение к главе 6
6.3. Атомные реакторы
Рассмотрим теперь случай, когда имеется также источник нейтронов, вводящий в шар q нейтронов в единицу времени. Теперь, если в момент времени t число нейтронов равно N, то в момент t + h при малом h число их приближенно будет равно
N + aNh —$Nh + qh.
Мы получаем, таким образом, дифференциальное уравнение dN — =(а-0)Л/ + <?. (4)
(№ .
Это частный случай уравнения (1), в котором «заданная функция»ф сводится к постоянной q. По теореме 1 имеем t
N = NQe -be I е q d£. (5)
о Так как t -(а—3) е t
'„s--’-г——I J а — р Io а — р
0 получаем отсюда
N = {1 - . (6)
г ®
Здесь предполагается, что а —0 =/=0. т. е. г =# гкр. Если а —0 = 0, то из (4) непосредственно следует, что N = No + qt.
Если а > 0 (сверхкритическая масса), то, как видно из (6), N растет экспоненциально, и в этом случае происходит взрыв. Если а < 0 (докритическая масса), то величина РК в равенстве (6) быстро приближается к нулю, и мы находим
0 —а
(7)
Это значит, что число нейтронов остается примерно одинаковым, и мы имеем постоянный источник тепла. Таков принцип работы атомного реактора. (Заметим, что для получения большого N при малом q надо, чтобы 0 — а было мало, т. е. требуется докритическая масса, близкая к критической; при этом необходимо тщательное управление работой реактора.)
6.4. Два радиоактивных вещества
Рассмотрим в качестве следующего приложения теоремы 1 радиоактивный элемент с периодом полураспада (In 2)/а. Если дано N атомов этого элемента, то через короткое время h приблизительно aNh из них распадется. Как мы показали в § 5.11, количество F(t) радиоактивного вещества, имеющегося в момент времени t, есть F(t) = F(0)e—a*.
Когда радиоактивное вещество распадается, оно превращается в другой элемент, обычно также радиоактивный. Мы предположим поэтому, что вещество I со временем полураспада (In 2)/а переходит в вещество II с другим периодом полураспада (In 2)/0. Обозначим через F(t) и G(t) количества веществ I и II, имеющиеся в момент /, и предположим, что
F(0) = G(0) = 0. (8)
Функция F уже вычислена. В течение короткого промежутка времени от t до t + h количество G(t) возрастет на aF(t)h в результате распада вещества I и убавится на0С(/)Л вследствие
§ 6. Другие применения показательной функции
409
распада вещества 11. Отсюда имеем G(t + h) — G(t) —06(/)Л + аГ(/)Л. и дифференциальное
уравнение для G имеет вид
G'(f) = —р(7 (0 + aF(0. или
G'(/) + pG(O=aFoe_a'. , (9)
Это частный случай уравнения, рассмотренного в теореме 1. Поэтому
t t (З-a) Е Е=/
- 3* С Р* - «Н ,, - зг с (Р—«) & „ - Р* е I
6 (/) = е 1 е aFoe d£ = aFoe | е d£ = aFQe —------------------- =
J J ₽-« 'e=0
ИЛИ
G(0 = T^-( (10)
p — a 4 '
Легко проверить дифференцированием, что G действительно удовлетворяет уравнению (9); при этом, очевидно, 6(0) = 0.
Рассмотрим два крайних случая, представляющих особый интерес. Предположим сначала, что вещество I недолговечно, а вещество II имеет большой период полураспада; тогда а очень велико по сравнению cf. Сравнительно скоро e~at станет близким к нулю, а G(t) будет приближенно равно [aF0/(a —0 )]е—Р*. Грубо говоря, вещество I полностью исчезнет, породив количество aFo/(a — 0) е—вещества II, а это последнее будет распадаться по свойственному ему закону.
Более интересен случай долговечного «материнского вещества» I и недолговечного «дочернего вещества» II. В этом случае а мало по сравнению с 0 , так что 0 — а приближенно равнор .
В начале процесса t очень мало. Для таких значений t можно с небольшой погрешностью заменить G(t) линейной функцией, равной 6(0) = 0 при t = 0 и имеющей наклон 6'(0) (см. теорему 1 § 1.8, гл. 4). Производная функции е—а* —е-Р* при t = 0 равна (—a е~л* + 0е~3#)t=o = = 0 — а. Таким образом, при малых t
G(t)^aFa. (И)
Рассмотрим теперь наш процесс через значительный промежуток времени t. Тогда член е—Р* в формуле (10) становится очень малым и им можно пренебречь по сравнению с е—Если заменить знаменатель формулы (10) на 0, то имеем
G4/)^-^-Fee-°'. (12)
р
Заметив, что Ffie~~at — F(t)у находим
G(0^4"fW- (13)
р
Таким образом, хотя количество вещества I медленно убывает, количество вещества II составляет фиксированную малую долю количества вещества I. Эта доля равна а/0, т. е. отношению периода полураспада вещества II к периоду полураспада вещества 1. В этом случае говорят, что вещества I и II находятся в радиоактивном равновесии.
•Пример. Закон распада радия имеет вид G(t) = бое"7/2400, где t измеряется в годах. В настоящее время средняя концентрация радия на Земле составляет КГ12 (это значит, что один из 1012 атомов нашей планеты есть атом радия). Пусть требуется найти концентрацию радия миллион лет назад. Из уравнения 10”12 = 6(О)е“1о6/2400 получается 6(0) = 10“12 е1о6/2400 = 65, что нелепо, так как ответ должен быть меньше 1. Решение этого кажущегося парадокса состоит в том, что радий, находимый в настоящее время, не является всего лишь остатком радия, имевшегося 10е лет назад. Радий Ra является потомком медленно распадающегося U238, т. е. урана с атомным весом 238 (впрочем, не прямым его наследником!), и находится с ним в состоянии радиоактивного равновесия. Нынешняя концентрация U238 составляет 3* 10“®, т. е. в 3 000 0000 раз выше концентрации радия; это число близко к отношению периодов полураспада урана и радия, ф
410
Приложение к главе &
6.5. Барометрическая формула
Приложения показательной функции к физическим вопросам не исчерпываются процессами роста и распада. В качестве примера иного рода мы выведем барометрическую формулу — формулу изменения атмосферного давления с высотой.
Барометр измеряет атмосферное давление р. Мы рассмотрим р как функцию высоты у над уровнем моря, исходя из следующих физических допущений.
1°. Давление р и плотность р связаны зависимостью
Р = ар (14}
2°. Атмосферное давление в любой точке равно весу столба воздуха сечения 1, простирающегося от этой точки вверх «до бесконечности».
Приступим к выводу дифференциального уравнения для функции р(у).
Пусть h — малое положительное число. По предположению 2°, разность р(у + h) — р(у) есть вес цилиндра воздуха сечения 1 между высотами у и у + Н (рис. 6.40). Объем этого цилиндра равен fi. Поскольку h мало, можно считать, что в рассматриваемом цилиндре плотность воздуха имеет постоянное значение:
I Р = —Р{у). а
Поэтому масса воздуха в цилиндре равна
/г рй =--р (у),
а
gh
Вес его равен —-----р (у), откуда
а
где b = g/a. Следовательно, функция р удовлетворяет дифференциальному уравнению p'W = — Ьр[у).
То же можно записать в виде
р' (У) t d In р (у)
= — д, или = — Ь. р (у)--------------------dy
Отсюда In р(у) ® —by + с, где с — постоянная; полагая у = 0, мы видим, что давление на уровне моря р(0) задается условием In р(0) = с. Итак.
1 Р(0)
и = — In--------.
Ь Р(у)
Эта формула позволяет определить высоту, измерив давление. Ее можно записать также в виде р(у) = р(0}е-»У. (16)
Отметим, что постоянная а в формуле (14) зависит от температуры. Поскольку мы молчаливо предполагали, что температура не зависит от высоты, формула (16) справедлива лишь приближенно.
(15)
УПРАЖНЕНИЯ
6. Пусть для данного расщепляющегося вещества а = 2- КЯс-1; допустим, что критический радиус равен 50 см. Шар из этого вещества радиуса 40 см содержит AZ0 свободных нейтронов в момент времени t = 0; сколько нейтронов он содержит при t = 1?
-§ 6. Другие применения показательной функции
411
Рис. 6.40
7. Пусть для данного расщепляющегося вещества а = 2-108 с-1 и Ро = 4-1010 см/с. Найдите критический радиус гкр. Далее, найдите наименьшее значение г, при котором шар радиуса г из этого вещества потеряет через 1 с не более половины своих свободных нейтронов. Найдите отношение rlrK^.
А 8. Пусть из вещества, описанного в упр. 7, сделан шар радиуса г = 1-гкр. Пусть в нем со-
держится источник нейтронов, вводящий в шар 100 нейтронов в секунду. В момент t шар содержит N(t) свободных нейтронов, причем ЛА(О) = Nq\ найдите N(t) и lim N(f).
/-*"{-00
В упражнениях 9—11 рассматривается радиоактивное вещество 1 с периодом полураспада <1п2)/а, превращающееся в радиоактивное вещество II с периодом полураспада (1п 2)/р. Количество вещества I, наличное в момент времени /, обозначается через F(t), а количество вещества II — через G(/); предполагается, что Г(0) = Го и 6(0) = 0.
9. Пусть р= 100 а. Обозначим через G (t) приближение—Гое“[см. уравнение (12)]. По-
кажите, что существует /0, для которого >> 1 при/ < /п,.^ = 1 и 1 >> > —
к G (0 G(tQ) G(t) 100
при найдите /0. Что можно отсюда заключить о проценте погрешности при замене
G (/) на G (/)?
10. Формула (10) справедлива лишь при допущении, что а=^=р. Найдите уравнение для G(t) при а = Р.
И. Укажите, где функция G(t) возрастает, где убывает, есть ли у нее, и в каких точках, максимумы и минимумы, локальные и абсолютные. Рассмотрите отдельно случаи а = р, а > Р и а < р .
12. Пусть имеется шар из расщепляющегося вещества (Р = 2а) с источником, вводящим в него qt2 нейтронов за промежуток времени [0, /]. Пусть 2V(Z) означает число свободных нейтронов в шаре в момент /; найдите дифференциальное уравнение для 2V(/) и решите это уравнение с помощью теоремы 1.
412
Приложение к главе 6
13. Пусть барометрическая формула имеет вид о = —Р(у) + где а — некоторая noct
стоянная. Найдите дифференциальное уравнение для р(у) и решите это уравнение с помощью теоремы 1.
14. Пусть имеется прямоугольный водяной бак с основанием в 1 ма. В основании имеется отверстие, через которое вода выливается со скоростью, пропорциональной высоте воды. Наконец, пусть в бак вливается вода, так что в течение промежутка времени [0, 4 прибавляется g(i) м8 воды. Обозначим через у(0 высоту воды в момент t\ у(0) = у0. Найдите дифференциальное уравнение для у(0 и решите его с помощью теоремы L [Примечание. Если вода вливается с постоянной скоростью в b м3/мин и t измеряется в минутах, то g(t) = bt.]
§ 7. Гиперболические функции
В этом параграфе мы рассмотрим подробнее гиперболические функции, определенные в§ 5.12. Две основные гиперболические функции — это
, е‘ — e~f е* 4-
sh t =-------, ch t = -------
2 2
Напомним, что обе функции определены для всех значений t\ что sh 0 = 0, ch 0 = 1; что sh t — нечетная функция, a ch / — четная функция; что ch2 t — sh2 t = 1.
ch t =
(1)
7.1. Дифференциальные уравнения
Можно было бы определить гиперболический синус и косинус как решения некоторых дифференциальных уравнений.
(а ) Имеем
Как мы уже отметили в § 5, это непосредственно следует из определений. Следующее утверждение аналогично теореме 3 § 1.10.
(б ) Общее, решение уравнения
Г(0 - КО = 0 (3)
есть
КО = a ch t 4- b sh t. (4)
Доказательство. (Обратите внимание, что оно отличается от доказательства теоремы 3 § 1.10.) Можно непосредственно проверить, что при любом выборе чисел а и b функция (4) удовлетворяет уравнению (3). Пусть теперь КО — заданное решение уравнения (3). Положим а = f(0), b = К(0) и
g(t) = КО — a ch t — b sh t.
Надо показать, что g(t) = 0- Легко подсчитать, что g"(t) = g(t) и g(0) = 0, g'(0) = 0. Пусть ф(4 = g(0 — g'(0- Тогда ср (0) = g(0) — ^'(0) = 0 и
ф'(0 = g'(t) — g"(0 = g'(0 — g(0 = — ф(0-
Применив теорему 6 § 5.6, заключаем, чтоф(/) = 0. Но это значит. что£(0 = g'(t). Поскольку g(0) = из теоремы 6 § 5.6 следует, что g(t) = 0.
(в ) Пусть со > 0 — заданное число. Тогда общее решение уравнения
ПО ~ &К0 = 0 (3*)
есть
КО — a ch со/ 4“ b shcot (4*)
§ 7. Гиперболические функции
413
Рис. 6.42
Справедливость этого утверждения выводится из формулы (4), точно так же как теорема 5 § 1.12 выводится из теоремы 3 § 1.10. Подробности предоставляются читателю.
УПРАЖНЕНИЯ
1. Найдите такое решение уравнения f"(f) — 4f(/) = 0, для которого /(0) = 8 и f'(O) = —4.
2. Найдите такое решение уравнения — 9/(0 = 0, для которого /(0) = 2л и Г(0)=
= л/2.
3. Найдите такое решение уравнения ["(f) — t(t) = 0, для которого £(0) = 1 и /(1) = е.
4. Найдите такое решение уравнения /"'(0 — Г(0 = 0» для которого f(0) = 1, /'(0) = 1»
/"(0) = 2. [Указание: найдите сначала f (0J
7.2. Обратный гиперболический синус
Поскольку гиперболический синус возрастает (его производная всегда положительна) и имеет пределы —оо при t —► —оо и +оо при t -► + оо, функция t sh t имеет обратную функцию, обычно обозначаемую* через arsh t. График этой функции изображен на рис. 6.41. Чтобы продифференцировать arsh у, полагаем t = arsh у, т. е. у = sh t\ тогда
d arsh у dt 1 11 1 1
dy dy dy/di dsht/dt chZ 1 + sh4 V \ + У2
или
d arsh у 1
---я = / — (5> dy--------------------------------------------------VT+y*
и, поскольку sh0=0,
У
p du
arsh у = I z . (6>
J "Иi + w2 о
* Эту функцию называют гиперболический арксинус или ареасинус: иногда ее обозначают символом areash.
414
Приложение к главе 6
Эта формула аналогична соответствующим формулам для арксинуса и арккосинуса (см. $ 1.17). Но, как и следует ожидать, существует еще тесная связь между гиперболическим арксинусом— обратной функцией гиперболического синуса'и логарифмом—обратной функцией показательной функции. Чтобы найти эту связь, заметим, что если t = arsh у, то i/=sh t, т.е.
2у = е* — e~f.
Умножив обе'части последнего равенства на е* и перенеся все члены влево, получим
e2t — 2уе* — 1=0,
откуда, по формуле решения квадратного уравнения,
= У + V I + уг .
(Здесь знак минус перед корнем отброшен, так как он привел бы к отрицательному значению е1, что невозможно.) Отсюда имеем
t = In (у 4- К1 + I/2) , «ли ______
arsh у = Ш (у 4- У 1 4- 4/а). (7)
7.3. Обратный гиперболический косинус
Функция I ch г возрастает при t > 0. В этом интервале она имеет обратную функцию, которую мы обозначим так: х arch х. Таким образом.
ch(arch х) = х при х > 1. arch (ch Л = | / |. (8)
График этой функции — гиперболического арккосинуса* — изображен на рис. 6.42.
Выразим arch х через логарифм. Если х = ch t, то
2х = е*4-
.или 2хе'4- 1=0;
имея в виду что мы хотим найти и, следовательно, 1, получаем
е1 = х 4- У к2 — 1
(знак минус привел бы к е1 < 1). Отсюда t = in (х 4- Ух2 — 1) , «ли ______
агсп х = In (дг V — 0 .
Далее, по цепному правилу
darchx I / х \
“ = I 1 4--. _ I ,
dx х + /х- — 1 \ /х* — 1 /
или d arch л 1
dx У х* — \
(9)
(Ю)
* Или ареакосинуса (иногда эту функцию обозначают через areach х).
§ 7. Гиперболические функции
415
Поскольку arch 1 = 0, имеем
arch х =
du
/ы2— 1 ’
(II)
УПРАЖНЕНИЯ
5. Найдите .d .
dz
, d arch (sec 0) л Л л
6. Найдите-----—------ при 0 < 0 < — .
а0 2
dy
7. Найдите----- , где у = (arccos х) (arsh2x).
dx
dz j.....
8. Найдите-----, где г = у 4t2 — t arch 2t.
di
d2u
9. Найдите —— , где u = и arsh v2.
dv2,
Г t2 dl
10. Найдите I —----.
J /т+v
11. Найдите | 1/ —L_ dz.
J r 1 4- z3
p ex dx
12. Найдите I - - .
J )/e2X — 1
P du
13. Найдите I — - .
J У u2 + 2u
14. Найдите J arch г dz. [Указание: воспользуйтесь интегрированием no частям.] p arsh и
15. Найдите i —2=" du.
J /1 4- u2
16. Найдите J <**•
7.4. Геометрическое истолкование гиперболических функций
Теперь мы дадим функциям гиперболический косинус и гиперболический синус геометрическое истолкование, аналогичное геометрическому смыслу функций синус и косинус. (Отсюда, в частности, станет понятным происхождение термина «гиперболический».)
(г) Каждая точка (х, у), удовлетворяющая уравнению
х2 — I/2 = 1 (12)
и неравенству х >0, может быть однозначно представлена в виде х — ch f, у = sh t.
416
Приложение к главе 6
Д о к а з а т е л ь с т в о. Найдем по заданному у значение t = arsh у\ тогда для х = ch t имеем х = УI -j- у2 т. е. х2 — у2 = 1.
Множество точек (х, у), удовлетворяющих соотношению (12), показано на рис. 6.43. Это равнобочная гипербола (мы проверим это в гл. 10; здесь это несущественно). Нас интересует лишь правая ветвь кривой. Пусть Р — точка этой ветви. Тогда Р = (ch t, sh/).
Мы утверждаем, что t равно удвоенной площади сектора, ограниченного осью х, отрезком ОР и дугой кривой от Р до (1, 0) (рис. 6.44), или при t < 0— этой площади, взятой со знаком минус.
Достаточно доказать это утверждение для />0. Пусть площадь, о которой идет речь, равна S(t). Ясно, что 5(0) = 0; если t >0, то S(t) есть площадь изображенного на рис. 6.44 прямоугольного треугольника минус площадь под кривой от х = 1 до х = ch t. Отсюда
ch г «hr
S (/) = ch t sh t — j* Ух2 — 1 dx = sh 2t — Уx2 — 1 dx,
1 i
Следовательно,
S' (/) = — (ch 2/) • 2 — (sh 0 Veh2/ — 1 = 4“ ch21 + 4>sh21 — shat = 4 2 2
= -y- (ch21 — sh2 0 = 4” .
Поэтому
S(0 = -L 4" const;
так как S(0) = 0, имеем
2S(0 = t, что и требовалось доказать.
Только что доказанное предложение следует сравнить с соответствующим предложением о точке P(cos /, sin t) единичной окружности (см. § 3). Если 0 < t<^ л, то / можно рассматривать либо как длину дуги окружности от (1, 0) до Р, либо как удвоенную площадь кругового секто-
§ 7. Гиперболические функции
417
ра, ограниченного этой дугой, осью х и отрезком ОР. Лишь это второе истолкование, показанное на рис. 6.45, обобщается на случай гиперболических функций*.
7.5. Обратный гиперболический тангенс
Напомним, что гиперболический тангенс определяется равенством sh t — е~* th t .
ch t e* +
и имеет пределы 1 при i -► +оо, —1 при t -* —оо; его производная равна dth/ 1
dt ~~ ch21
и везде положительна. Тем самым обратная функция arth t определена при [ t | < I: th(arth t) = t.
Легко обычным способом проверить, что d arth х 1 —---------------------------------------т~? I'K'-
(13)
(14)
* Аналогия между геометрическими определениями функций sin х и cos х, в одной стороны, и sh х и ch х — с другой, подробно прослеживается в доступно написанной брошюре: В. Г. Ш е р-в а т о в, Гиперболические функции, М., Физматгиз, 1958.
418
Приложение к главе 6
Поскольку th 0 = 0, имеем X к
С du Г / 1 1 1 1 \ 1 / \ |х
arth* = Jrz^ = j(TTT^+V— )^=т(1п(1+ «)-!"(1-и)) 0 = о о
так что 1 1 -j- %
arth х = — In -----— . (15)
График функции arth t изображен на рис. 6.46.
7.6. Выражение гиперболических синуса и косинуса через гиперболический тангенс
Следующее предложение аналогично теореме, 1 § 2.3.
(Д) Функции sh /, ch t и th t могут быть выражены как рациональные функции от th(//2):
2th(//2) с11Г~ 1 + th2 (Z/2) uu__ 2 th (//2)
S 1 — th2 (Z/2) ’ C 1 — th2 (Z/2) ’ 1 + th2 (t/2) *
(16)
et/2_e-t/2
Для доказательства достаточно заменить th (t/2) на --------— и выполнить очевидные упро-
?/2 + е“//2
щения.
7.7. Другие гиперболические функции и им обратные
Нам остается кратко рассмотреть гиперболический секанс, гиперболический косеканс и гиперболический котангенс. Они определяются следующим образом:
1 2 ,1 2 , 1 е‘ + е~(
sech t — —;— = —:-----т- , cosech t = —;— = — ---------— , cth t = , t = — ----— , (17)
ch/ sh/ e* — e“‘ th/ e* — e~‘
причем последние две функции определены лишь при t =/= 0. Графики их изображены на рис. 6.47—6.49. Отметим, что lim cth t = 1 и lim cth t = — 1, в то время как lim sech t =’ t->4-oo —co /->±00
= lim cosech t = 0. Читатель легко проверит, что /->±00
d sech / th t d cosech / cth / d cth / 1
dt ch/ dt sh/ dt sh2/ v 7
Из графиков видно, как определить обратные функции: arcth х (эта функция имеет смысл лишь при |х | > 1), arsech х (где 0 < х < 1; функция arsech х принимает лишь неотрицательные значения), arcosech х (определена при х ф 0). Ясно, что
arcth х = arth — , (19)
х
так как из cth / следует 1/х = th /. Точно так же
arsech х = arch — , arcosech х = arsh —- . (20}
X X
-§ 7. Гиперболические функции
419
Отсюда в силу предыдущих результатов получаем
d arsech х 1 d arcosech х 1 d arcth x 1
--------= —--------— , ----------= —------------ , ---------= ;------; (21,
dx x/1 — x2 &с |x|/14-x2 dx *— x
И _______ _________________________________
arsech x = In , arcoseh x = In fJL 1/ 1 + -L.Y arcth x = — In —^-7 ; (22)
x \ x Г x2 J 2 x — 1
формулы, содержащие функцию arsech, справедливы при 0 < х < 1; содержащие функцию arcosech — при х =#= 0; содержащие функцию arcth — при | х | > 1. Подробности мы предоставляем читателю.
Графики только что рассмотренных функций изображены на рис. 6.50 — 6.52.
Из предыдущего изложения видна далеко идущая формальная аналогия между показательными функциями, записанными в «гиперболической форме», и тригонометрическими функциями. Мы проследим ее еще отчетливее в гл. 8. Однако подлинная причина этой формальной аналогии выясняется лишь после введения комплексных чисел, при изучении функций комплексного переменного.
420
Приложение к главе 6
упражнения
17. Докажите первое из соотношений (16).
18. Докажите второе и третье из соотношений (16).
19. Покажите, что ch a ch 0 = -L {ch(a + р)-|-ch(a—Р)}.
20. Выведите формулу, выражающую shashp через гиперболические функции от a + Р и a — Р .
21. Выведите формулу, выражающую sh a chР через гиперболические функции от a + Р и a — р.
22. Упростите функцию earth ха (Т. е. выразите ее в виде иррациональной функции от х).
23. Упростите функцию earch ха (т< е. выразите ее в виде иррациональной функции от х).
24. Проверьте равенства (18).
25. Найдите J ch Зг ch 5г dz.
26. Найдите С —du.
J 1 — th 2и
Р dx
27. Найдите I ------- -.— .
J х /1 — 9х2
Р х dx
28. Найдите | — - .
J /1 — х4
29. Докажите соотношения (21).
ДЗО. Докажите соотношения (22).
§ 8. Некоторые неэлементарные функции
8.1. Элементарные и неэлементарные функции
Элементарные трансцендентные функции, рассмотренные в предыдущих параграфах, были открыты различными способами. Тригонометрические функции были введены исходя из нужд астрономии. Логарифмы были придуманы для того, чтобы облегчить вычисления. Функция х А- ах возникла как естественное обобщение операции возведения числа в рациональную степень. Однако, как читатель уже заметил, все эти функции могут быть получены единым методом— интегрированием рациональных функций. Все рассмотренные функции можно получить из первообразных функций -I и i-l. т. е. из функций логарифм и арктангенс. В самом деле, функция, обратная логарифму, есть показательная функция е*. Каждая функция х н* 0х может быть записана в виде где а = In а. Гиперболические функции суть простые комбинации показательных. Обращение арктангенса приводит к функции tg 0. Все остальные тригонометрические функции могут быть получены из тангенса рациональными операциями.
Можно было бы рассчитывать получить другие интересные функции, разыскивая первообразные других рациональных функций,—однако на самом деле здесь все обстоит иначе. Оказывается, с помощью функций логарифм и арктангенс можно записать явную формулу для неопределенного интеграла от л ю б о й рациональной функции. Этот замечательный факт будет установлен в гл. 7, § 2. Неопределенные интегралы от иррациональных и других алгебраических функций, вообще говоря, являются трансцендентными, и притом неэлементарными, функциями. Исключение составляют неопределенные интегралы от квадратных корней из квадратичных функций. Они приводят к функциям, уже изученным ранее. В самом деле, можно определить синус и косинус как функции, обратные неопределенным интегралам от 1/V 1 — х2, а гиперболические синус и косинус — как функции, обратные неопределенным интегралам от l/j^x2 + 1, соответственно от 1//х2— 1 .
§ 8. Некоторые неэлементарные функции
421
Интегралы от квадратных корней из многочленов третьей и четвертой степени называются эллиптическими интегралами. Типичным примером является функция
X I—►
du
обращение ее приводит к так называемой эллиптической функции* *.
Имеется много важных неэлементарных функций, определяемых совсем иными способами. Сейчас мы рассмотри^ три примера функций, определяемых с помощью показательной функции.
8.2. Нормальная кривая
Функция
2
х «-► е'
(график которой показан на рис. 6.53) играет важную роль в теории вероятностей и математической статистике.
Площадь между графиком функции и осью х к о н е ч н а, т. е. несобственный интеграл f e~x2dx существует. Чтобы доказать это, воспользуемся критерием, установленным в §6.4 гл. 5. Достаточно показать, что при больших | х | выполнено неравенство е~х* < | х |”2. Но в силу теоремы 7 § 5.7 при больших | х | имеем | х реМ >1, откуда < | х р; тем более е-*2 < | х р. Оказывается, что
(2)
Это — неожиданная связь между числами е и л; простейшее доказательство соотношения (2) использует функции Двух переменных (см. гл. 13, § 7.3).
График функции ё~х* имеет колоколообразную формул это значит, что он имеет единственный максимум (при х = 0) и две точки перегиба (прих= —1/рих = l/J/^2). Далее, график симметричен относительно оси у. С помощью функции е~х2 строится функция, зависящая от двух параметров — числа т и положительного числа о:
1 —е а
(х—ту 2а2
(3)
Ее график обладает следующими свойствами: (а) график симметричен относительно прямой х = т\ (б) полная площадь под графиком равна 1; (в) график является колоколообразной кривой с точками перегиба х= т + о и х — т — о. Как видно из последнего свойства, график функции (3) имеет острый пик при малом о и становится пологим при большом о.
у
Г
* Об этой функции, ее геометрическом смысле и родстве с функциями х= | — •-
J yi — W2 о
У
Р du
(т. е. с функцией p=sin х) и х = | ——--- (т. е. с функцией у = sh х) см. брошюру; А. И. Ма р-
J У 1 + и2 о
к у ш ев и ч, Замечательные синусы, М., «Наука», 1974.
422
Приложение к главе 6
Свойство (а) доказывается прямым вычислением. Если х/ = т + 6 и х2 == т — 6, то формула (3) в точках xj и Х2 определяет одинаковые значения функции. Для доказательства (б) положим (х — т)/У~2“(У = t; тогда имеем в силу (2)
СО 00
I - (к-т)* С \ 1 Р
— е dx =» I -— e~~t2 yTvdi =----- I = a-------------------------------------------------------J a /2z-J
—CO —co —co
Для доказательства (.в) найдем производную функции (3):
х— т ------е a3 /2z
2a2
(х-ту
(X — ги)2 2ст2 -----TZT" е
_ (х—т)*
X — ГП \2 1 2а2
------- — 1 > е
a
и ее вторую производную: _ (х—т)а 1 -------------е , ~ ______ а3/2л а5/2л а3 /2л
Очевидно, вторая производная положительна при | х—т |> а и отрицательна при |х — m| <а. График функции (3) называется нормальной кривой со средним значением т и стандартным
отклонением а (или дисперсией о2). На рис. 6.54 показаны нормальные кривые при т = 0 и 0=1.5 2 6 □
8.3. Закон ошибок Гаусса
Функцией нормального распределения со средним значением т и стандартным отклонением
<У называется функция
w dt.
F (г) =
а/2л
(4)
§ 8. Некоторые неэлементарные функции
423
Таким образом, F(x) есть площадь под нормальной кривой от —оо до х (рис. 6.55). Функция F(x), график которой (при т = 0, о = 1) изображен на рис. 6.56, не элементарна. Ее нельзя выразить через уже известные нам функции без помощи знака интеграла или равносильного приема. Очевидно,
lim F(x) = 0, lim F (x) = 1; (5)
x-* —co x-* 4-00
далее,
F(m) = -L, (6)
поскольку половина всей площади лежит слева от прямой х = т. Замена переменной интегрирования, подобная примененной выше при доказательстве (б), приводит к равенствам
-1 1
1 Г 1 Г
F (т— а) = — I e—^dty F (т + а) = • ; — | e~~t2I2 dt (7)
/2тс J /2^ J
—00 —со
и, как показывает численное интегрирование,
F (т—а) 0,159, F (т-}-с) 0,841.
Таким образом, слева от прямой х = т — о и справа от прямой х = т + а лежит примерно по 16% общей площади, тогда как между прямыми х = т — о и х = т + о — около 68%.
Предположим, что с помощью одного и того же прибора много раз измеряется некоторая величина, например вес некоторого предмета. Пусть истинное значение измеряемой величины равно а, а отсчет прибора равен 6. Конечно, мы не можем рассчитывать получить в точности значение 5 = а. Но если прибор «правильный», т. е. не делает «систематических ошибок», то мы получим в среднем столько же отсчетов с недостатком (£ < а), сколько с избытком (£ > а). Более того, оказывается, что доля тех случаев, когда получается отсчет $ < х, приближенно равна F(x), где F(x) — функция нормального распределения со средним значением а и некоторым стандартным отклонением о.
Чем меньше о, т е. чем более чувствителен прибор, тем большая доля всех измерений £ оказывается близкой к а.
Только что приведенное утверждение о распределении результатов измерений называется законом ошибок Гаусса, а также законом Лапласа. Область его применимости гораздо шире, чем может показаться на первый взгляд. Каждый раз, когда выполняется ряд измерений, результаты которых определяются многими независимыми случайными событиями, можно рассчитывать получить нормальное распределение. Так обстоит дело, в частности, с индексом умственных способностей (IQ-индекс) в обширной совокупности особей, с распределением роста у большого
424
Приложение к главе 6
числа людей одного возраста и т. п. Мы сформулировали закон ошибок как «интуитивное» эмпирическое правило. В математической теории вероятностей имеется и соответствующая «строгая» теорема, на чем мы, впрочем, здесь не можем останавливаться.
8.4. Гамма-функция
Приведем теперь пример неэлементарной трансцендентной функции, определенной с помощью несобственного определенного интеграла. Это — гамма-функция, открытая Эйлером:
х ь* Г (х) = f tx~x dt,
(8)
(Заметим, что немая переменная интегрирования здесь t, а не х. Кроме того, вместо +оо мы пишем, как это принято, оо.)
Интеграл в формуле (8) имеет смысл, поскольку вблизи верхнего предела (t = +оо) по теореме 7 § 5.7 имеем 1, откуда < Г2. Вблизи нижнего предела (t = 0) соблюдает-
ся неравенство е”*/*"1 < причем, по предположению, х > 0. При х у 1 интеграл в точке t = 0 оказывается собственным. Далее,
Г (1) = lim \ е~* dt = lim (—e”z)
ЛГ-*”{-00 Q ЛГ CO
= lim (— e~~N 4-0=1.
0 N-^4-00
Поскольку несобственный интеграл, задающий Г(1), существует, предыдущее вычисление можно записать короче:
со оо
Г (1) = J e~‘dt = — е~‘ =—0+1 = 1. (9)
о о
Соотношение
Г
(10)
Карл Фридрих ГАУСС (1777—1855] был сыном бедного крестьянина. Он вспоминал полушутя, что умел складывать, прежде чем выучился говорить. Наблюдательный учитель начальной школы заметил гений Гаусса. Он оказал ему покровительство, позволившее Гауссу продолжить свое образование. Молодой Гаусс колебался между филологией и математикой; он сделал выбор после своего первого выдающегося открытия — построения циркулем и линейкой правильного семнадцатиусольника *.
Еще при жизни Гаусса считали равным Архимеду и Ньютону. С него начинается слава Гбттии-гена как математического центра: он был там профессором и директором обсерватории. Интересы Гаусса охватывали всю математику, астрономию, физику и геодезию. Этот неутомимый, внушавший глубокое почтение исследователь несколько нерешительно публиковал свои работы; как обнаружилось из его записных книжек, он предвосхитил множество открытий, совершенных впоследствии другими математиками.
Пьер Симон ЛАПЛАС (1749—1827]. Два его крупнейших труда — многотомная «Небесная механика» и «Аналитическая теория вероятностей» **. Важность атих сочинений определяется в первую очередь наличием в каждом из них новых глубоких методов, играющих большую роль в современной математике.
Лаплас, как и Гаусс, происходил из крестьянской семьи. Он занимался также политической деятельностью и был осыпан почестями Наполеоном (которому он некоторое время служил в качестве министра), а после его падения — и Бурбонами, сделавшими его маркизом.
* См. по этому поводу доступно написанную статью: С. Г. Г и н д и к и н, Дебют Гаусса, журнал «Квант», 1972, N© 1, с. 2—11.
* * Введение в эту книгу переведено и на русский язык: см. П.-С. Лаплас, Опыт философии теории вероятностей, М. 1908.
§ 8. Некоторые неэлементарные функции
425
можно проверить с помощью правила подстановки: полагая t = у2, имеем dt = 2ydy = 2t№dy и r\j2dt = 2dy, откуда
Г = j е~* = 2 J у2 dy = J e~yi dy = .
О 0 —09
Здесь мы воспользовались четностью еу* и равенством (2).
Выведем теперь функциональное уравнение гамма-функции:
Г(х) = (х — 1)Г(х — 1) при х > 1. (11)
Доказательство в сокращенном виде состоит в следующем?
Г(х) = F <r‘ tx~! dt = — 7 de-‘ =—tx~i е~‘ + + f e~‘ dtx~' = (x — 1) f e~‘tx-*di, 0 0 0 0 0
откуда
Г (x) = (x — 1) £ е~Чх~2 dt = (x — \)V (x— 1).
Напомним известное обозначение:
О! = 1, Н = 1, 21 = 1*2. 31 = Ь2.3, 41 = 1.2-3.4 и т. д.
(л! читается «л факториал»). Так как Г(1) = 1, из соотношения (11) получаем Г(2) = ЬГ(1) = = 1, Г(3) = 2 Г(2) = 2=2-1, Г(4) = 3 Г (3) = 3- 2-1, и вообще
Г(л) = (л — 1)1 при л = 1,2, 3, ... . (12)
Мы коснулись лишь некоторых из замечательных свойств гамма-функций.
8.5. Функция, все производные которой в данной точке равны нулю
Построим теперь с помощью теоремы 7 § 5.7 функцию, имеющую производные всех порядков, причем такую, что все ее производные в точке 0 равны нулю. Конечно, этими свойствами обладает постоянная функция; но функция, которую мы построим, не постоянна ни в какой сколь угодно малой окрестности точки х = 0.
Теорема 1. Пусть л — любое целое число. Положим
хпе-1/х‘ при хфО,
(1О) 0 при х = 0.
fn (*) =
Тогда: (а) функция fn везде непрерывна: (б) функция /л имеет производные всех порядков: (в) все эти производные равны нулю в точке х = 0.
Доказательство. При х = 0 непрерывность очевидна и производная /д(х) может быть вычислена формально:
fn (х) = пх"-1 е~1/хг + хп -------------
= пхя-1 е 11x1 + хл е ^х‘ —— = лхя~1 е ^х* 4- 2хя-8 X3
Поэтому при х =/= 0 /;« = <-1(х)+2/я.зй. (14)
Чтобы доказать непрерывность [п в точке х = 0, надо проверить, что lim /д(х) =0, или, что х-*0
то же, Ит|^д(х) | = 0. Воспользуемся теоремой 7 § 5.7 и правилами вычисления пределов, ус-х—^0
тановленными в § 4.2 и 4.3 гл. 3. Полагая х”2 = tt так что | х | = Г1^2, имеем
426
Приложение к главе 6
Рис. 6.57
lim | fn (х) | = lim (I х |п е~1/хг) = lim Г~пП е~* = —-—* = —— = О,
х—о х-»о <-►+<» lim tnMe‘ оо
что и доказывает (а).
Теперь мы знаем, что правая часть (14) непрерывна при х = 0 и обращается в нуль в этой точке; в самом деле, достаточно применить (а) к jn—i и fn—з. Из теоремы 2 § 7.3 гл. 4 вытекает теперь, что равенство (14) справедливо также при х = 0, причем f>n'(0) = 0. Применяя еще раз (14) и только что доказанный результат, имеем
(п (х) = nfn_{ (х) + 2/я_3 (х) = п( (п— 1) fn_2 (х) + 2/„_4 (х) ) + 2 {(п 3) /я_4 (х) + 2/я_в (х) ( = = п (п — 1) /я_2 (х) + (4и — 6) /я_4 (х) 4- 4/я_в (х).
Следовательно, /д имеет вторую производную в точке х = 0, равную нулю. Таким же способом находится fn"' и доказывается, что(О) = 0, и т. д.
График функции у — ^о(х) = е~Ч*2 изображен на рис. 6.57.
ЗАДАЧИ
5.
7.
Хв+Р
1. Пусть [(х)— непрерывная функция с периодом р. Покажите, что J t(x)dx не зависит от хо. ч
2. Пусть t(x) — непрерывная периодическая функция с периодом р и г(х) — неопределенный интеграл от f(x). При каком условии F периодична с периодом р? (Найдя условие, проверьтё, что ему удовлетворяет функция £(х) = sin х, р = 2л.)
3. Пусть функции i(x) и g(x) — периодические с периодами р и q соответственно. Покажите, что если р и q — рациональные числа, то функция Л(х) = f(x) + g(x) — периодическая.
4. Пусть /(х) — периодическая монотонная функция. Что можно утверждать об /?
Пусть f(x) определена и непрерывна при всех х и любое из чисел р = 1, А, -у»--- является периодом Докажите, что f — постоянная.
Пользуясь геометрическим определением синуса и косинуса, докажите, что при О < | 6 | < л/2 справедливы неравенства 0 < | sin 0| < | 0 | < )tg 0 |. [Указание: пусть Р — точка с координатами (cos 6, sin0) и Q — точка с координатами (1, tg 0), Pj — точка с координатами (cos 0, 0) и Qx — точка (1. 0). Выразите площади треугольников OPPf и OQQx и кругового сектора OPQj через 0, sin 0, cos 0 и tg 0.]
i. sin 0
Не пользуясь сведениями о производных синуса и косинуса, докажите, что lim-— =1
и lim C°S----- =0. [Указание: примените результат предыдущей задачи.]
б-»>о 0
6.
Задачи
427
8. Считая известными теоремы сложения для синуса и косинуса, докажите,что функции sin О и cos 0 имеют соответственно производные cos 0 и —sin 0. [Указание: воспользуйтесь результатом предыдущей задачи.] Обратите внимание на то обстоятельство, что теоремы сложения могут быть доказаны геометрически. (Это есть традиционный вывод формул дифференцирования.)
9. Пусть f'(x) = g(x) и g'(x) = —[(х) для всех х вблизи х = 0, причем ДО) = 0, g(0) = 1. Покажите, что f(x) = sin х, g(x) = cos x.
10. Покажите, что функции синус и косинус — не иррациональные, установив, что никакая непостоянная периодическая функция не может быть иррациональной. [У к а з а н и е; воспользуйтесь результатом задачи 15 гл. 3.]
11. Функциональное уравнение для арктангенса имеет вид
А X + у arctg х + arctg у = arctg —--.
Докажите это, пользуясь теоремой сложения для тангенса.
12. Дайте прямое доказательство функционального уравнения для функции arctg х, исходя из определения: х н* arctg х есть первообразная функции х н*—!— , обращающаяся в 14-х2
нуль при х = 0.
13. Выразите полную энергию колеблющейся упругой пружины как функцию от амплитуды и скорости в моменты, когда отклонение от положения равновесия равно нулю. Выразите кинетическую энергию как функцию времени. (По поводу определения энергии см. гл. 5, § 5.)
14. Сформулируйте и докажите функциональное уравнение для арккотангенса, аналогичное уравнению для арктангенса (см. задачу И).
15. Докажите, что In х — не иррациональная функция. [У к а з а н и е: воспользуйтесь результатом задачи 15 гл. 3.]
16. Пусть 1(х) — положительная дифференцируемая функция и g(x) — дифференцируемая функция. Найдите производную функции х i-> F(x) = Дх)й<*).
17. Докажите теорему 5 § 5.6 (характеризация показательной функции ее дифференциальным уравнением и начальным условием) без каких-либо предварительных сведений о показательной функции. [Указание: сначала выведите из уравнения (х) = [(х), что Д—х)Дх)— постоянная. Затем покажите, что Дх)— решение этого уравнения, удовлетворяющее условию ДО) = 1, должно быть: 1® положительно; 2° строго монотонно. Положив у — f(x)t рассмотрите х как функцию от у, вычислите ее производную, примените основную теорему анализа и заключите, что Дх) — обратная функция для In.]
18. Дайте прямое доказательство теоремы 6 § 5.6. [Указание: воспользуйтесь планом, предложенным в задаче 17.]
19. Даны две функции Дх) и g(x), для которых lim Дх) = limg(x) = +оо; говорят, что g Х-*-{-00 х-^Ч-со
растет быстрее если lim [g(x)/f(x)] = +оо. Найдите функцию, растущую быстрее 6х ; х->+<»
быстрее ех ; быстрее ; быстрее произвольной заданной функции <р(х).
20. Найдите функцию, растущую быстрее е*, но медленнее хе**; быстрее любого многочлена, но медленнее е^х ; быстрее In х, но медленнее р^х; медленнее In In х. (Говорят, что f растет медленнее g, если g растет быстрее /.)
21. Найдите две такие непрерывные функции Дх) и£(х), что обе они растут быстрее ех, частное их t(x)lg(x) не имеет предела при х -* +оо и ни одна из функций Дх), g(x) не растет быстрее другой.
/2
22. Покажите, что > 1 + t +
при t > 0.
23. Оцените приближенное значение следующих чисел:
а = (1,00000001)10000000, b = (О,99999999)10000000, с = (1,00000001)100000, d = (0,99999999)10000000000.
Укажите основания вашей догадки.
428
Приложение к главе 6
24. Покажите, что функция /и* (1 + -L/возрастает при больших t (насколько больших?).
25. Прием, примененный в § 6.1 для решения неоднородного уравнения f/(x) — f;(x) = ф(х), называется «методом вариации постоянных». Примените ту же идею к неоднородному уравнению
f"(x) + £(х) = ф(х),
гдеф — заданная функция. [У к а з а н и е; дляф(х) = 0, как мы знаем, общее решение имеет вид f(x) = a cos х + b sin х, где а, b — постоянные. Попытайтесь решить неоднородное уравнение, положив f(x) = a(x)cos х + 6(x)sin ж, где а b — функции, подлежащие отысканию. Какие условия надо наложить на эти функции, чтобы их можно было найти интегрированием?].
26. Найдите общее решение дифференциального уравнения
f"(x) + Дх) = cos ®х.
[Указание: примените метод предыдущей задачи.] Это уравнение описывает движение гармонического осциллятора частоты 1/(2л) под действием внешней периодической силы частоты со/(2л). Исследуйте, что происходит в случае «резонанса», т. е. когда ш=1 (частота возмущающей силы совпадает о частотой осциллятора).
27. Теоремы сложения для гиперболических синуса и косинуса имеют вид sh(x + у) = sh х ch у + ch х sh у, ch(x + у) = ch х ch у + sh х sh у.
Выведите их из теоремы (б) § 7.1.
28. Найдите общее решение неоднородного дифференциального уравнения
I"W — Дх) «= ф (х),
гдеф — заданная функция, следуя указанию к задаче 26.
29. Покажите, что неоднородное дифференциальное уравнение предыдущей задачи равносильно системе двух уравнений первого порядка, а именно:
g'(x) 4- g(X) =<f(X), g(x) — [(x) = g(x).
Воспользуйтесь этим, чтобы заново доказать теорему б) из § 7.1; получйте, далее, новое выражение общего решения соответствующего неоднородного уравнения.
30. Покажите, что дифференциальное уравнение f"(*) — =ф (х) равносильно системе двух дифференциальных уравнений первого порядка.
31. Пользуясь геометрическим истолкованием гиперболических функций,найдите и докажите неравенства, аналогичные неравенствам задачи 6 но связывающие функции sh Л и th L
32 Пользуясь результатом предыдущей задачи и теоремами сложения для гиперболических синуса и косинуса, докажите, что производные sh t и ch t равны соответственно ch t и sh t. [У к а з а н и e: примите во внимание задачи 7 и 8.]
7/ ТЕХНИКА ИНТЕГРИРОВАНИЯ
Эта глава носит по существу технический характер. В ней излагаются методы вычисления интегралов и первообразных функций. В соответствии с современными требованиями численное интегрирование в этой книге предшествует так называемому «формальному» интегрированию.
В Приложении приводятся основные формулы интегрирования.
430
7. Техника интегрирования
§ 1. ЧИСЛЕННОЕ
ИНТЕГРИРОВАНИЕ
1.1. ФОРМАЛЬНОЕ ДИФФЕРЕНЦИРОВАНИЕ
Основные процессы анализа — дифференцирование и интегрирование или, на геометрическом языке, отыскание касательных и вычисление площадей. Основная теорема анализа обнаруживает тот поразительный факт, что эти процессы обратны друг другу. Между ними имеются, однако, существенные различия. Это становится очевидным, если Вам надо продифференцировать или проинтегрировать заданную функцию.
Функция х н* /(%) может быть «задана» разными способами. Она может быть определена явной формулой, содержащей конечное число рациональных операций,, извлечений корней и подстановок в некоторые «известные», или «элементарные», функции. Так называются обычно элементарные трансцендентные функции, изучавшиеся нами в гл. 6.
Отыскание производной такой функции представляет собой чисто механический процесс, если предположить, конечно, что нам известны производные «элементарных» функций. Сколь бы ни была сложна формула, мы придем через конечное число шагов к явной формуле для /'(*), систематически применяя выученные нами правила дифференцирования. Можно было бы даже запрограммировать все шаги операции дифференцирования и поручить делать это вычислительной машине. Сегодня в этой связи обычно говорят, что дифференцирование функций, заданных явными формулами, представляет собой «конечный алгоритм».
С интегрированием дело обстоит совершенно иначе. Из основной теоремы анализа мы знаем, что каждая непрерывная функция /(х) имеет первообразную функцию F(x); однако если непрерывная функция /(х) задана явной формулой, то нет никаких причин ожидать, что и первообразная функция F(x) может быть задана такой формулой. Как правило, это невозможно. Разыскивая первообразные от простых «известных» функций, можно прийти к интересным новым функциям. Вспомним в этой связи, как логарифм и арктангенс определяются с помощью интегралов.
Тем не менее весьма важны те исключительные случаи, когда функция /(х) может быть проинтегрирована в конечном виде, т. е. имеет первообразную (неопределенный интеграл), выражающуюся явной формулой. Иногда удается найти формулу для F(x) с помощью правил интегрирования § 3 гл. 5, в особенности заменой переменной (подстановкой) и интегрированием по частям. Этот процесс называется формальным интегрированием. Почти всегда этот процесс производится «методом проб и ошибок». Для формального интегрирования не существует «конечного алгоритма», и эта задача не может быть возложена на машину. Мы займемся формальным интегрированием в следующем‘параграфе этой главы.
1.2. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
В приложениях математики часто встречаются функции х^/(х),заданные неявной формулой, а каким-либо иным способом. Например, функция может быть «задана численно», т. е. может быть представлена таблицей некоторых ее значений. Так обстоит дело, например, когда/(х) возникает в итоге некоторого эксперимента
§ 1. Численное интегрирование
431
или измерения. Иногда измерительный прибор вычерчивает график функции, т. е. задает приближенную таблицу ее значений; в других случаях задается некоторый бесконечный процесс, позволяющий вычислить значение функции с любой требуемой точностью. В некотором смысле все элементарные функции определяются этим последним способом: в самом деле, если функция задана явной формулой, эта формула и есть не что иное как описание метода вычисления числа Дх) по заданному числу* х.
Отыскание производной функции Дх), заданной таблицей, т. е. численное дифференцирование функций, представляет, вообще говоря, малоприятную задачу. Эта задача может оказаться бессмысленной: если даже известно, что функция Дх) непрерывна, она может вовсе не иметь производной. Но даже если мы знаем, что производная существует, то вычисление ее в некоторой точке х зачастую бывает довольно затруднительно. Конечно, вычислив «разностное отношение»
f (XQ A) f (Xq) \
h ' 7
для малого А, мы можем принять его за приближенное значение Д(х0). Однако чтобы оценить, насколько точно это приближение, требуется дополнительная информация, о функции. Если известно, что функция имеет вторую производную Д'(х) и что | Д'(х) | М 2 для всех х, заключенных между х0 и х0 + А, то допускаемая погрешность не превосходит у M2h2 (это следует из формулы Тейлора, излагаемой в гл. 8). Таким образом, чтобы получить высокую точность, надо взять малое А, т. е. нужна подробная таблица значений функции.
Но если | А | мало, то малая ошибка в вычислении значений Дх0 + А) и Дх0) может привести к большой ошибке для частного (1).
Мы не останавливаемся дальше на численном дифференцировании, поскольку этот процесс применяется весьма редко. Некоторые новые руководства по численному анализу вовсе о нем не упоминают. ,
1.3. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Напротив, интегрирование функций, заданных численно, представляет собой часто используемую и важную технику. Даже в том случае, когда Дх) задана явной формулой, единственный способ вычислить интеграл
ь
J f (х) dx (2)
а
часто состоит в том, что Дх) рассматривают как функцию, заданную численно, и прибегают к численному интегрированию. Единственный способ вычислить первооб-
* При этом если явная формула содержит функции In, logfl, sin, aretg и т. д., то процесс вычисления числа 1(х) предполагает обращение к таблицам названных (элементарных) функций.
432
7. Техника интегрирования
разную F(x) может состоять в составлении таблицы ее значений путем вычисления а
для различных значений х. В дальнейшем мы предполагаем, что f(x) непрерывна при так что интеграл (2) имеет смысл.
Разделим интервал (а, Ь) на п равных подынтегрален, каждый длины п
Концы этих малых интервалов суть
х0 = a, Xi = а + й, х2 = а + 2й, ...» хп = а + лй = Ь (3) (рис. 7.1, где п =6). Допустим, что значения
Уо = f(x0), yi = у2 = /(х2), уп = /(*„) (4)
известны; мы хотим найти формулу для приближенного значения интеграла (2), выражающего это значение через 2п + 2 чисел х0, •••» хп; Уо> •••» Уп-
Приближенные формулы интегрирования часто называются квадратурными формулами. Ни одна из них не применима ко всем возможным непрерывным функциям. Так, любая разумная квадратурная формула ’ должна давать значение, равное нулю, в том случае, когда все значения функции (4) равны нулю. Но существуют непрерывные функции, для которых /(ху) = 0 при / = 0, 1, ...» п, в то время ь
как интеграл J/(x)dx имеет отличное от нуля большое значение; пример такой функ-а
ции приведен на рис. 7.2.'
§ 1. Численное интегрирование
433
1.4. ПРАВИЛО ТРАПЕЦИЙ
Мы уже рассматривали в § 1.6 гл. 5 одну приближенную формулу интегрирования для монотонной функции Дх). Она сводится к замене площади под кривой х >-► Дх) суммой площадей п прямоугольников ширины h с высотами у0 = Дх0), yi =/(xi),... ...,уп—\ = (рис. 7.3). Каждый прямоугольник имеет площадь hyj (отрицательную, если yj < 0). Поэтому приближенная формула имеет вид
ь
f f (х) dx « hy0 4г hyr + ... + hyn_! = (y0 + yt + ... + y^). (5)
J n
a
Можно воспользоваться прямоугольниками с высотами yit у2, ...» уп (рис. 7.4). Это приводит к формуле*
ь
f f(x) dx « hyi + hy2 + ... ч- hyn-= —a (y± + y2 + ... + yn). (6) J n
a
Для монотонной функции истинное значение интеграла лежит между приближенными значениями (5) и (6). Это обстоятельство подсказывает, что можно получить лучшую квадратурную формулу, взяв среднее арифметическое значений (5) и (6). Складывая (5) и (6) и деля на два, получаем приближенную формулу
Формулы (5) и (6) в учебной'литературе часто называют формулами прямоугольников.
434
7. Техника интегрирования
Рис. 7.5
b
f /(х)dx да ь~а (у0 + 2ух + 2уг 4-... 4- 2yn_j + уп) =
J хм
= ~(У° + 2ух 4- 2у2 4- ••• + 2yn_! 4- уп). (7)
правило трапеций.
Это так называемое
Та же формула может быть получена иным путем, объясняющим также ее название. Пусть ф(х) — непрерывная функция, совпадающая с /(х)при х = х0, *2, •••»
хл, но линейная между каждыми двумя последовательными значениями Ху и х/44' эта функция изображена на рис. 7.5 [где f(x) не монотонна!. Мы хотим воспользоваться ь ь ь
интегралом J<p(x)dx в качестве приближенного значения J а а
сумма п интегралов:
ь
есть
Ху
хя
Х0
п
•• + J <p(x)dx.
а
а
Ху
Поскольку С ср (х) dx есть площадь трапеции, то
Ха
Ху С h
J <P(*)dx = —(^4-^).
Хо
[Можно было бы вывести эту формулу более педантично, проинтегрировав линейную функцию ф(х).] Точно так же
§ 1. Численное интегрирование
435
ха
J cp(x)dx = *1
j <p(x)dx = -у(г/п-1 + Уп)-
*Л-1
Складывая эти равенства, получаем
ь
J <р(х) dx = А (^ + 2У1 + 2у2 + ... + 2уп_! + уп). а
Правая часть этой формулы—та же, что и в (7).
1.5. ОЦЕНКА ПОГРЕШНОСТИ ДЛЯ ПРАВИЛА ТРАПЕЦИИ
Пусть теперь Е — абсолютная величина погрешности, допускаемой при вычислении интеграла (2) по правилу трапеций, т. е.
ь
Е= ^f(x)dx— A(% + 2i/i + 2i/a +... + 2уп_1+уп) . а
Конечно, точное значение Е зависит от функции /, от а и Ь.
Справедливы следующие оценки:
Е = — | f (Ь) — f(a)\h, если f (х) монотонна, (8)
2п 2
Е < (Ь~?2^ЗА12 = ПТ(Ь - а} м*h2’ ~если If"м I < м* (9)
(Здесь и дальше предполагается, что наложенные на / условия выполнены при всех х, где а *О.)
Докажем неравенство (8), считая функцию /(х) монотонной. Тогда истинное значение интеграла заключено между (5) и (6), как это видно из рис. 7.3 и 7.4. Приближенное значение, заданное правилом трапеций, является средним арифметическим значений (5) и (6). Тем самым абсолютная величина погрешности не превосходит половины абсолютной величины разности:
I—— (У1 + Уг + ••• + Уп)--------(Уо + У1 + ••• + Уп-i) I = I ——~ (Уп — Уо) I =
I п П I I п I
п
Вторая оценка (9) будет доказана в приложении к гл. 8 (см. § 9.1).
436
7. Техника интегрирования
УПРАЖНЕНИЯ
Найдите приближенные значения следующих интегралов, пользуясь правилом трапеций при заданном значении п. Оцените ошибку с помощью формул (8) и (9), если только эти оценки возможны. Вначале запишите Ваш ответ в виде точной суммы, а затем его десятичное приближение, пользуясь в случае надобности таблицами. Конечно, число сохраняемых в вычислении десятичных знаков будет отчасти зависеть от Вашей оценки погрешности. (Можно, где это потребуется, применять оценку In 2 < 0,75, вытекающую из упр. 4.)
1
Р dx
I. I —---------— при п = 4.
J х* 4- 1
О
2
±2. J (хР 4- х) dx при п = 6.
тс/2
_ С dx
3. 1 ----------- при п = 4,
J 2 4- sin х
—тс/2
2
С dx
4. | ----- при п =э 6.
J х 1
1
5. f 16х dx при п = 4.
2
„ С 4х
6. | ~ dx при п = 4.
J х 4- 1
о
3 ____
7. J х Ух 4- 1 dx при /г = 6.
з
of Х
8. I ------ dx при /1 = 6.
J *4-1
о
з _____
9. J У4х2 4- 2х dx при п = 6.
з/2 _______
10. f (4х)1/3 У4х 4- 5 dx при л = 4.
-1/2
1.6. ПРАВИЛО СИМПСОНА
Есть почти столь же простая квадратурная формула, дающая в большинстве случаев лучшее приближение, чем формула трапеций. Это правило парабол, или правило Симпсона.
Пусть п ч е т н о, т. е. п = 2m; примем в качестве приближенного значения ь
число
а b J ф (х) dx, а
где ф(х) совпадает о f(x) при х = х0, х„ х2, .... хп и представляет собой квадратичный многочлен на каждом из т интервалов длины 2h : 1х0, хг1,1х 2, х41.1хгт_г, x^L
График функции ф(х), изображенный на рис. 7.6, состоит из дуг парабол.
Вычислим J<p(x)dx. В интервале (х0, х2] функция ф(х) есть многочлен второй х.
Томас СИМПСОН (1716—1T61J был по профессии ткачом по елку. Вго математические работы были по достоинству оценены и доставили ему место профессора в Вулвичском военном училище.
§ 1. Численное интегрирование
437
степени, т. е. ср(х) = Axi + Вх + С. Подставив вместо х выражение (х — х^ 4-хг приведем подобные члены и запишем
ф(х) = а(х — Xi)2 4- Р(х — Xi) + у.
Постоянные а, р, у находятся из условий:
ф(*о) =/(xi— Л) = /(х0) = у0,
<P(JCt) =f(Xi) = yit
ф(*г) =/(xi + /t) =/(х2) =уг.
Из второго соотношения имеем
Т = теперь можно записать первое и третье соотношения так: ah2 — fill =у0 — У! и ah2 + p/i = уг — yt. Складывая и вычитая эти равенвтва, находим а _ Уо + Уг—2yi о _ Уг —Уо 2ft2 ’ К 2ft Таким образом,
Ф (х) == У<>+^~2У1 (х — Xi)2 + -у?~ Уо (х— хг) + уг 2/г
при х0<^х^хг. Первообразной этого многочлена является Уг+^-.2У1_(х_Х1)3 + _^»_(Х_Х1)2 + ^Х.
Подставляя х = х2 = хх + й и х = х0 = хх — h, а затем вычитая, получаем
f ф (X) dx = go + ytr2y- - (- А>31 + У2^Уа- - <- №1 +y^h- (- А)1 = J 6Л2
х0
---y. + y2-2yi h + = / 1 % ц. 4 + \h J \ о о о /
438
7. Техника интегрирования»
Итак,
/ 1 ,4 , 1
\ j о оу
и точно так же
У 2 “+
4 । 1 U
7-У3 + — yAh. О Оу
J ^dx = ^y^ + -jyb-fr-jy^h, Х4
х2т
j Ф dx = (д- ytm_2 + -у- + -у y2m) h.
х2т-2
Сложив все эти равенства, получаем формулу Симпсона: ь
J f (х) dx а
Ь — аI 1 ,4 ,2 I 4 .
------7- У о + — У1 + "Г" У г + “Г" Уз 4
п \ 3 3 3 3
2 4 1 \
у4 + ...+ — Уп-2 + ”7'Уп-1 + ~Т~Уп ) = о о о у
= "7“ [(Уо + Уп) + 4 (У1 + Уз + ••• + Уп-i) + 2 (t/2 + #4 + ••• Уп-г)!- (Ю)
О
Применять ее почти так же просто, как формулу трапеций.
1.7. ОЦЕНКА ПОГРЕШНОСТИ ДЛЯ ПРАВИЛА СИМПСОНА
Пусть Е означает абсолютную величину погрешности, допускаемой при пользовании правилом Симпсона:
ь
Е = J f (х) dx — -j- [(у0 + уп) + 4 (t/j + у3'+ ... + у^) + 2(у2 + у4 + ... у^] |. а
Тогда для f(x), имеющей непрерывную четвертую производную, справедлива оценка
Е .(.ь - а)6 = (& — а) М4 й4, если |/IVW|<A14. (Ц)
180л4 180 i/i к /
Сравним это с оценкой (9); погрешность правила трапеций имеет порядок й2, тогда как погрешность правила Симпсона — порядок й4. [Из той же оценки (11) видно, что Е = 0, если f — многочлен степени не выше третьей.] Доказательство оценки (11) приводится в Приложении к гл. 8 (см. § 9.2).
§ 1. Численное интегрирование
439
ф Примеры. 1. Вычислить
6
x2dx Г = — 6 = 721, L 3 о J
пользуясь правилом трапеций, а также правилом Симпсона, в обоих случаях с 6 подынтервалами. Сравнить действительную ошибку с приведенными выше оценками.
Решение. Вычисления приведены в следующей таблице. В ней / означает индекс рассматриваемой точки, a v—«весовой множитель». Для правила трапеций v = 1 при / = 0 и j = п, v = 2 для других /. Для правила Симпсона v = 1 при / = 1 и / = п; для других j имеем v = 2 или v = 4 в зависимости от того, четно или нечетно /:
Правило трапеций П равилс > Симпсона
/ yj~xi *7*/
0 0 0 1 0 1 0
1 1 1 2 2 4 4
2 2 4 2 8 2 8
3 3 9 2 18 4 36
4 4 16 2 32 2 32
5 5 25 2 50 4 100
6 6 36 1 36 1 36
146 216
Итог сложения надо умножить на Л/2 (в- случае правила трапеций) или на Л/3 (в случае правила Симпсона). В нашем примере Л = 1, откуда
6
J х2 dx& Q
— • 146 =73 2 .
по правилу трапеций,
— • 216 = 72 3
по правилу Симпсона.
Для правила трапеций абсолютная ошибка Е равна 1. Оценки (8) и (9) дают при п = 6, а = О, b =6, f(b) — f(a) = 36 и М 2 = 2 соответственно неравенства Е 18 и £< 1.
> Для правила Симпсона, конечно, Е = 0 1см. формулу (11)1 и результат оказывается точным.
440
7. Техника интегрирования
2. Вычислить
з
"’-И
I
по правилу трапеций и по правилу Симпсона при п =4. Сравнить ошибку с оценками погрешности.
Решение. Вычисления имеют вид:
Правило трапеций Правило Симпсона
/ Ki "J °)
0 1,0 1,0000 1 1,0000 1 1,0000
1 1,5 0,6667 2 1,3334 4 2,6668
2 2,0 0,5000 2 1,0000 2 1,0000
3 2,5 0,4000 2 0,8000 4 1,6000
4 3,0 0,3333 1 0,3333 1 0,3333
4,4667 6,6001
Т ак как h = —, имеем 2
1пЗ«
• (4,4667) = 1,1167 по правилу трапеций,
. — • (6,6001) = 1,1000 по правилу Симпсона. 3 2
Для /(х) — 1/х имеем/"(х) = 2/х8, /IV(x) = 24/х®. При 1 х 3 можно применить оценку (9) при М2 = 2 и оценку (11) при Л14 = 24. Это дает (Ь — а = 2, п = 4):
£<
— = 0,0833 ... 12
— = 0,0166 ... 60
для правила трапеций,
для правила Симпсона!
В действительности In 3 = 1,0986..., а потому
0,0181 ...
0,0014 ...
для правила трапеций, для правила Симпсона.
Обе погрешности существенно ниже теоретических оценок, причем правило Симпсона дает более точный результат, ф
$ 1. Численное интегрирование
441
УПРАЖНЕНИЯ
Найдите приближенные значения следующих интегралов, пользуясь правилом Симпсона при заданном п. Оцените ошибки с помощью формулы (11).
dx _
------ при п = 4 (ср. с результатом упр. 1).
0
2
12. у (х4 + х) dx при п = 6 (ср. с результатом упр. 2). Какой результат получается при п = 2? о
тс/2
13- f
J 2 4-sin х
при п = 4 (ср. с результатом упр. 3).
2
(• dx
I -------- при
п = 6 (ср. с результатом упр. 4).
15. j 16х dx при
О
Вычислите точно каждый из следующих интегралов. Затем найдите его приближенные значения, сначала по правилу трапеций, потом по правилу Симпсона, при заданном значении п. Оцените ошибку в каждом случае с помощью формул (9) и (11). Сравните с действительной ошибкой, воспользовавшись соответствующими таблицами.
2
19. J V~xdx при л =4.
2/3
п = 4 (ср. с результатом упр. 5).
Г dx .) 2х + 1 о
при п « 6.
dx
при п = 2.
4
f хъ dx при п = 4.
о
4/5
18. J ех dx при п = 4. о
1.8. ПОГРЕШНОСТИ МЕТОДА И ПОГРЕШНОСТИ ОКРУГЛЕНИЯ
Мы рассмотрели только две квадратурные формулы и оценили лишь погрешности, происходящие от замены интеграла соответствующей суммой. Погрешности этого рода называются погрешностями метода. В фактйчески встречающихся вычислениях всегда имеется еще другой источник погрешности. Значения yj не могут быть вычислены совершенно точно; они находятся с некоторыми ошибками. Далее, производя арифметические действия, мы вынуждены округлять числа, т. е. отбрасывать знаки. Два приведенных выше примера были выбраны таким образом, чтобы погрешности округления были пренебрежимо малы. Но на практике приходится иметь с ними дело, и надо уметь их контролировать.
Однако эти вопросы, а также более сложные формулы квадратур лучше изучать вместе с техникой машинных вычислений.
442
7. Техника интегрирования
§ 2. ИНТЕГРИРОВАНИЕ Как мы уже говорили (в гл. 6), определив трансцендентные РАЦИОНАЛЬНЫХ Функции х »-► In | х | и х aretg %, имеющие соответствен-
ФУНКЦИЙ но производные l/х и 1/(1 + %2), мы можем записать явные формулы для неопределенных интегралов всех рациональных функций. Доказательство этого замечательного факта основывается на двух результатах. Прежде всего, существуют некоторые специальные рациональные функции, именуемые простейшими дробями, которые могут быть проинтегрированы в конечном виде. А затем оказывается, что любая рациональная функция может быть записана как сумма некоторого многочлена и простейших дробей.
2.1. ПРОСТЕЙШИЕ ДРОБИ
Простейшая дробь — это рациональная функция вида
h(x)n ’
где п — целое положительное число и либо (1) g — постоянная, а Л — непостоянная линейная функция, либо (2) g— постоянная или линейная функция, a h — непостоянная квадратичная функция (многочлен второй степени), не имеющая (действительных) корней.
Например, 2 6 7 4- Зх 3 —4х
х —3 ’ (X 4-100)1°° ’ 2х2 4- 2x4- 10 ’ (х2 + 2х 4-Ю)3
суть простейшие дроби. Дробь
______1______ (Х2 _ Зх 2)2
мы н е называем простейшей, так как ее знаменатель имеет корни х = 2 и х = 1.
Наша первая цель — научиться интегрировать простейшие дроби.
2.2. СТЕПЕНЬ ЛИНЕЙНОЙ ФУНКЦИИ В ЗНАМЕНАТЕЛЕ
Интегрирование простейших дробей первого типа, в знаменателе которых стоит степень линейной функции, не представляет труда. Надо только применить метод подстановки. Пусть задана подынтегральная функция вида а/(ах 4- Ь)\ где а У= 0, а =# 0. Положим ах + b = t, так что a dx = dt\ мы получим
a dx
(ах 4- Ь)п
Ca(\/d)dt
J 1п
---------------------------1- С при п =£ 1, а (1 — п) (ах 4- Ь)л"1
— In | ах + b | + С
при п = 1.
а J
§ 2. Интегрирование рациональных функций
443
Таким образом, первообразная функция есть либо рациональная, либо логарифмическая функция.
Запомнить следует метод интегрирования, а не результат. [Тот же метод сохраняет силу в случае не только целого, но и любого действительного показателя степени пЛ
5
f* 2 dx
•Примеры. 1. Вычислить |.
J Зх — 6
Решение. Положим Зх — 6=/, 3 dx = dt\ имеем
5 9
Г 2 dx = Г (2/3) dZ
J Зх-6 J t
3 з
= JL In 3 « — • 1,0986 = 0,7324.
3 3
—9
2. Вычислить С ------—------.
J (2х4-21)а —ю
Решение. Имеем
С dx = ' Г 9 (1/2) d(2x+21) _ =_____1__[_ 3
J (2х+21)2 J (2х + 21)2 J fl 2 t
—10 r=—10 1
3. Найти первообразную функции (2х — б)*"677. Решение. Имеем
J (2х — 5Г6/? dx = J (2х — б)"677 -_Ld(2x — 5) =2_J/-6/7d/ = = _L tw + С = -j-(2x — 5)'/? + C.
2
4. Найти C ———. J (2 —x)5
Решение. Подынтегральная функция в рассматриваемом интервале не ограничена. Интеграл не существует даже как несобственный интеграл. В самом деле, пусть 8 —число, удовлетворяющее неравенствам 0<8 <2; тогда, полагая 2 — х = /, dx = —dt, имеем
2—е f dX
J (2 —х)6 0
1 4/4
2
= J 1
“ 4е4 64
Это число становится сколь угодно большим при уменьшении g .ф
444
7. Техника интегрирования
УПРАЖНЕНИЯ
Найдите следующие интегралы»
. 3 С 1 1. 1 л dx. J (2х — I)2 1 1 2‘ J (2-х)’ dX-0 3 3- f-7 T~dX’ J Зх — 5 2 6/5 6’ j (5x_4)’dX-1 ’ J p 1 8. I dx. J /4 —3x 2
4. J (Зх — 8)2/5 dx. 9- f (2x + 4)I/3 0
5. J (3 — 2х)—2/3 dx. 10. f - L dx. J 8 — 7x
2.3. СТЕПЕНЬ КВАДРАТИЧНОЙ ФУНКЦИИ В ЗНАМЕНАТЕЛЕ. ПЕРВЫЙ СЛУЧАЙ
Покажем теперь, как найти первообразную функцию простейшей дроби, в знаменателе которой стоит степень квадратичного многочлена, не имеющего (действительных} корней. Займемся сначала дробью с постоянным числителем, т. е. попробуем вы-
числить f Где 4ac — b2 > 0. (1 \ J (ax2 + bx + c)n v r
Первый шаг состоит в сведении этого интеграла к интегралу вида
f — . (2> J (1 + Х2)л
Это выполняется следующим образом. Дополняя знаменатель до полного квадрата„ имеем
(ах2 + Ьх + с)п = ап (х2 Ч—- х + —Y* = ап[(х -I——+ —-------------—Р =
\ a a J | \ 2а ] а 4а2 I
„Г/ , b V . 4ac—b*Vt L\ 2a J 4a2 J
Далее, полагаем /4ac — Ьг x+(b/2a) q = —5 и — 2a q
§ 2. Интегрирование рациональных функций
445
Тогда имеем
(ах2 + Ьх 4- с)п = ап q2n (t2 4- 1)л, dx = q dt,
откуда P a dx ___________________________________ a C dt
J (ax2 -f- bx 4- c)n an q2n~* J (14"^2)я
И в этом случае следует запомнить метод, а не результат.
з
Г dx
ф Пример. Вычислить j 9"*
о
Решение. Имеем
/ 3 9 \ Г/ 3 \« 27 1
4х2 4- 6х 4- 9 = 4 (х2 4- *4- —] = 4IJx 4- + T6~J
где мы положили
откуда __
dx = dt и t = -Дг при х = 0, t = —Д2 при х =*= 3.
4 у 3 УЗ
Таким образом,
3 5//з"
С dx 4 /27 С dt 1 / , 5
J 4х“ + 6х+9 “ 27 4 J 1 + /’ ^27 \ /Т
УПРАЖНЕНИЯ
Найдите следующие интегралы:
11.
12.
dx
х2 4- х 4- 1 *
dx
х2 — х 4- 2 *
13.
14.
dx
2х2 4- 2х 4- 1 ’
о
о
446
7. Техника интегрирования
2.4. РЕКУРРЕНТНАЯ ФОРМУЛА
Вычисление интеграла (2) не представляет труда при п = 1: получается с точностью до постоянной интегрирования функция арктангенс. При п > 0 положим п = = т + 1 и выведем рекуррентную формулу, выражающую интеграл (2) при п = = т + 1 через подобный же интеграл при п = т. Повторив этот прием т раз, приходим к интегралу (2) с п = 1 и, следовательно, к арктангенсу.
Чтобы получить рекуррентную формулу, заметим, что
(1 4- х2)т _ 2тх
dx (14- х2)т*' ’
откуда ах 1 1
---------------------------- — а--. (14-х2)>и+1------------------------2тх (14-х2)"1
С другой стороны, 1 = 1 4-х2 1______u х2
(14-x2)m (14-x2)m+l (14-х2)/л+1 ‘ (14-х2)/и+1*
Поэтому, интегрируя по чаетям, имеем
Это и есть требуемая рекуррентная формула. В случае определенного интеграла она принимает вид
(Эта же формула верна и для нецелого /и, если только т Ф 0.]
Только что приведенный вывод основан на некоторой уловке. Но если рекуррентная формула (4) уже известна, ее легко непосредственно проверить дифференцированием. Формула утверждает, что
1
(1 4 х2)ш+1
1 \ 1 _ d 1 х
2т / (1 4- х2)т ~ dx ~2т (1 4- х2)т
и нетрудно убедиться в том, что это верно.
§ 2. Интегрирование рациональных функций
447
Читатель может по собственному выбору либо запомнить, что существует рекуррентная формула вида (4), которую можно найти в учебнике анализа или в таблице интегралов, либо запомнить метод получения этой рекуррентной формулы; саму формулу (4) запоминать не следует.
о
f dx
• Примеры. 1. Вычислить j (д.а + 2х + 2)’ ’
— 1
—§
1 t
4 “(ПЛ
1 1
3 1 t
+ 4 ’ 2 14-/2 о 0
Решение. Полагая z=x+l, dt = dx, имеем
о 1
____dx________ С ____________dx__________ Й dt (Х2 + 2х + 2)з ~ J [(х 4-1)2 4- II3 “ J (1 + /2)з —1_______________________________о
1 1 . 3 С dt > __ 1 t
F 4 J (1 4-/2)2 4 (1 4- t2)2
о о
1
I 3 1 С & 1 I 1 , з / 1 \ , 3 п 1,3%
. — । ---------— — I — — о I 4~ — I — — q ) 4“ — * — — — — •
4 2 J 1 + /2 4 \ 4 ) 8 \ 2 / 8 4 4 Г 32
о
2. Найуш первообразную функции (х2 + 2х + 2)“3. Решение. Повторяя предыдущие вычисления с неопределенными интегралами, получаем
С dx f dt 1 t f 3 t f 3
J (x2 4-2x 4-2)3 = J (1 4- /2)3 =••=— (14- /2)2 + “8 Г4Г/2 b arct2 z +
1 x 4“ 1 3 x 4- 13
+ C ~ (X2 4. 2x + 2)2 + T x2 + 2x + 2 + T arctg (x + b + •
УПРАЖНЕНИЯ
Найдите следующие интегралы:
1/2
17. f____-________. 20. f________
J (4x2+l)2 J (2xa-|-2x + I)2
_________dx
(z2 + /3 •
1/3
Г dx C dx
▲ 18. 21. I
J (*2 + 4)3 ’ J (9x24-1)4 ’
0
0 2
C dx Г dx
19. 22 \
J (X2 + 6x+ IO)2* —2 J (5x2 —2x+l)2 0
dx
J (4x2 4- 4x 4- б)3 ‘ 1/2
448
7. Техника интегрирования
2.5. СТЕПЕНЬ КВАДРАТНОЙ ФУНКЦИИ В ЗНАМЕНАТЕЛЕ. ВТОРОЙ СЛУЧАЙ
Рассмотрим теперь интегралы вида С ах + р J (ах2 + бх + с)" > ГДе а*0’ 4ас-&а>0.
Запишем (снова используя ту же уловку) а A a ab
С + Р Г_27(2ах + Ь)+₽__27 .
I ------------------ | -------------------ах =
J (ах2 + Ьх + с)п J (ах2 4- Ьх 4- с)п
__ а 1 (2ах + b)dx . /д _____ ab \ Г _____dx______ 2а J . (ах2 4- Ьх 4- с)л \ 2а ) J (ах2 4- Ьх 4- с)п
Мы уже умеем вычислять второй интеграл. Первый же получается методом подстановки. Полагая t = ах2 + Ьх + с, имеем
(2ах 4- Ь) dx (* d (ах2 4” Ьх 4- с) (* dt
J (ах2 4- Ьх 4- с)п “ J (ах2 4- Ьх 4- с)п J tn
In|Z| 4- С при n = l, In| ах2 4“ Ьх 4- с| + С прип=1,
= ----!------h С при n=/= 1 = ------------i-----------р С при n=f= 1.
r (1 — а) (ах2 4-Ьх 4-c)n-i К
Мы доказали следующее:
Первообразная функция любой простейшей дроби является суммой рациональной функции, логарифмической функции и функции арктангенс.
Конечно, при этом вовсе не всегда должны присутствовать одновременно все три типа функций. [Под логарифмической функцией здесь понимается функция вида х »-> aln \ах + 6| или х xln |ах2 4- Ьх 4- с|; под арктангенсом—функция вида х »-► a arctg(ax + fe).]
2
А Примеры. 1. Вычислить f —х + .
Jx2 4 2x4-2 о
Решение. Находим
2 2 1' 2 2
f (x + 3)dx f -у (2x4-2)4-2 ) Г (2x + 2)dx f dx
i --------- = i —=------------dx = — I ---------4-2 1 ----------=
J xa 4 2x 4 2 J X2 4- 2x 4- 2 2 J x2 4 2x 4 2 J x2 4 2x 4 2
r=2 x=2 10 3
_ 1 f <f(x24-2x4-2) f d(x+l) _ 1 C Jt_ C ds _
~ 2 .) x2 +2x4-2 J (x4-1)24-1 2 J t ' Z J sa4-l —
x=0 x=0 2 1
= TlnZ
10 |3 1 л
2 4-2 aretg = — In 54- 2arctg 3 — — « 1,7
(поскольку при x = 0 имеем хг + 2х + 2 = 2, х 4- 1 = 1, а при х = 2 имеем х8 + 2х 4- 2 = 10, х 4- 1 = 3].
§ 2. Интегрирование рациональных функций
449
2. Найти первообразную функции •
Решение. Имеем
(х 4- 3) dx (2х2 -j- 18)2
4 4“ 3 j г 4x dx Р dx
(2х2 + 18)2 dX== ~ J (2х24- 18)2 + 3 J (2х2 + 18)2 =
1 Г d(2x2 + 18) 3 Г dx
= 4 J (2х2 4- 18)2 + 4 J (х2 4~ 9)2 =
УПРАЖНЕНИЯ
Найдите следующие интегралы и результаты проверьте дифференцированием:
25. 1/2 1 (* Зх 4~ 2 f* х 4- 3 \ . dx. 30. о „ о dx (см. упр. 24). J 4х2 4- 1 J (4х2 4- 4х 4- б)3 0 1/2
26. Г Зх 1 О С Л ! J X2 4- 4х 4- 5 dx' J (9х2 4- бх 4- 2)« dX'
27. 2 (* 2х 4- 1 Г 4х — 3 J (S.. - 2, + !>. <“ 22)- 32' J 3,. + Зх + ! " 0 2 Р 1 — Зх _ Г X
28. 1 о dx. 33. \ dx. J 4х2 4- Зх 4- 1 .) 2х2 — 4х 4- 3 1 Г х — 2 Л Г 2 — х
29. .1 (2х. + 2,+ I)- 201 J (Х--2Х + 2).
450
7. Техника интегрирования
2.6. ОСНОВНАЯ ТЕОРЕМА ОБ ИНТЕГРИРОВАНИИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
Для интегрирования в конечном виде любых рациональных функций решающее значение имеет следующая
Теорема 1. Каждая рациональная функция, не являющаяся многочленом, может быть единственным образом представлена в виде суммы многочлена и одной или нескольких простейших дробей.
Если принять теорему 1, то в силу результатов § 2.2—2.5 сразу же приходим к следующей теореме.
Теорема 2. Первообразная рациональной функции всегда является суммой рациональной функции, логарифмической функции и функции арктангенс.
Чтобы получить явную формулу для первообразной рациональной функции, надо разложить эту функиию*на простейшие дроби. На практике это удается, однако, лишь в относительно простых случаях. Может оказаться, что даже для рациональных функций придется прибегнуть к численному интегрированию; таким образом, теорема 2 имеет главным образом теоретическое значение.
Мы не доказываем в этой книге теорему I. Ее доказательство опирается на так называемую основную теорему алгебры, согласно которой каждый многочлен (положительной степени, т. е. отличный от постоянной) имеет корни; если только расширить систему действительных чисел и допустить в качестве корней так называемые комплексные числа.
«Действительная» форма основной теоремы алгебры гласит:
Каждый многочлен (положительной степени, с действительными коэффициентами) может быть записан в виде произведения линейных и квадратичных многочленов.
Существует много доказательств основной теоремы алгебры; большинство из них принадлежат Гауссу, величайшему математику XIX века. Впрочем, справедливость этой теоремы подозревали задолго до Гаусса. Еще в XVI столетии итальянские математики открыли явные формулы для корней уравнений третьей и четвертой степеней (обычно связываемые с именем Кардано), продолжающие древнюю формулу для решения квадратных уравнений. Но поиски явной формулы, которая позволила бы решать всевозможные уравнения пятой степени, не увенчались успехом, и в конце концов Абель (в возрасте 22 лет) доказал, что такой формулы не существует *.
Еще более замечательное открытие было сделано Галуа (который погиб, не достигнув 21 года). Галуа показал, что если задано некоторое конкретное уравнение степени п >> 5, то, за исключением весьма специальных случаев, его корни нельзя получить из коэффициентов с помощью рациональных операций и извлечения корней.
• Не совсем полное доказательство того же факта несколько раныпе дал итальянский врач и замечательный математик-любитель Паоло Руффини (1765—1822).
§ 2. Интегрирование рациональных функций
4S1
2.7. РАЗЛОЖЕНИЕ НА ПРОСТЕЙШИЕ ДРОБИ
Пусть х /(х) — заданная рациональная функция. Тогда f(x) = ф(х)/ф(х), где Ф ф— многочлены. Мы можем допустить, что сама функция f—не многочлен, так как многочлены мы уже умеем интегрировать. Предположим поэтому, что степень многочлена ф(х) отлична от нуля и что ср не делится на ф.
Если степень ф не меньше степени ф, применим деление столбиком; получаем
ф(х) = 9(х)ф(х) + г(х), где q и г — многочлены и степень г меньше степени ф. Отсюда
Ф (X) (X)
Чтобы проинтегрировать Д достаточно найти интеграл от r/ф, поскольку интегрирование q не составляет труда. Таким образом, можно с самого начала считать, что степень ф м е н ь ш е степени ф и что эти многочлены не имеют общих линейных или квадратичных множителей.
Первый и самый трудный шаг разложения ф/ф на простейшие дроби состоит в том, чтобы представить знаменатель ф в виде произведения постоянной А и множителей, каждый из которых является либо степенью линейной функции х — а, либо степенью квадратичной функции х2 + ₽х + Ъ не имеющей (действительных) корней. Иными словами, мы должны найти разложение
ф (х) =А(х—aj’’ ... (x-a*)'* (х2 + ^х 4- ъ)14 ... (х2 + £,х + у У', (5)
где ^и — целые положительные числа, а,— различные числа, и все квадратичные функции х2 + + 7 различны. Числа ае—действительные корни ф, причем
— кратность корня af. Ясно, что сумма + ... + v* + 2рч + ... + 2^ равна степени ф. Тот факт, что мноючлен ф может быть единственным образом
Иеронимо КАРДАНО 1150*1—1576) — яркая фигура эпохи Возрождения и разносторонний ученый, опубликовал в 1545 г. метод решения кубических уравнений. Он признал, что частный случай этого метода ему сообщил при условии сохранения тайны другой итальянский математик Тартанья За этим последовала острая полемика между Тарталья и Феррари, учеником Кардано. Феррари и сам был талантливым математиком: он открыл, что уравнение четвертой степени может быть решено сведением его к кубическому уравнению.
Нильс Хенрик АБЕЛЬ (1802—1829). Его работа об уравнениях пятой степени — лишь одно из его великих достижений Абель внес свой вклад в создание строгой «еории бесконечных рядов; открытие им «эллиптических» и других трансцендентных функций послужило началом новой эпохи в математическом анализе.
В 16 лет Абель под влиянием чуткого учителя начал читать труды Ньютона, Эйлера и Лагранжа; через несколько лет он начал сам совершать открытия. Между тем умер его отец, и на Абеля легла ответственность за большую' семью, в течение всей остальной жизни он тяжко нуждался. Поддержка норвежского правительства дала ему возможность посетить Германию и Францию, но ведущие математики этих стран не сумели распознать его гений *. Абель умер от туберкулеза в возрасте 27 лет.
Эварист ГАЛУа (1811—1832) был преследуем правительством за радикальные взгляды, а некоторыми из преподавателей — за неуважительное поведение. Дважды он не был допущен в знаменитую Политехническую школу, был изгнан из Нормальной школы и провел несколько месяцев в тюрьме, 30 мая 1832 года Галуа дрался на дуэли <и был смертельно ранен. В ночь перед дуэлью он написал прощальное письмо другу, в котором изложил свои открытия. Это письмо содержало «теорию Галуа» — один из краеугольных камней современной алгебры.
* Впрочем, опубликованные в немецких математических журналах статьи Абеля доставили ему в самом конце жизни профессорскую кафедру в Берлине, которую он, однако, уже не успел занять (и даже не успел получить известия о своем избрании).
452
7. Техника интегрирования
представлен в этом виде, следует, как мы уже отметили, из основной теоремы алгебры. К сожалению, нет простого способа разложить заданный многочлен на линейные и квадратичные множители, так что числа а„ Ру, 7у приходился, вообще говоря, находить приближенно.
2.8. НЕОПРЕДЕЛЕННЫЕ КОЭФФИЦИЕНТЫ
Допустим, что знаменатель ф(х) уже представлен в виде (5). Можно считать, что А =1, так как для этого достаточно разделить числитель и знаменатель дроби f(x) на А. Требуется найти простейшие дроби, составляющие в сумме<р(х)/ф(х). В качествезна-менателей таких дробей могут фигурировать лишь линейные и квадратичные множители разложения (5), причем не в больших степенях, чем они входят в (5). Поскольку это известно, то фактическое построение разложения ф Л|? на простейшие дроби сводится к решению системы линейных уравнений. Этот метод неопределенных коэффициентов лучше всего разъяснить на примерах.
ф Примеры. 1. Рассмотрим рациональную функцию
х* 4- х2 4~ 2* 4~ 1
х4 (х 4- I)2
Множители х и х + 1 входят в знаменатель дроби соответственно в степенях 4 и 2. Поэтому если разложение данной рациональной функции на сумму простейших дробей существует, то знаменатели этих дробей могут иметь вид х4, х3^ х2, х, (х + I)2, (х -Ь 1) — и никакой другой. Поскольку множители х и х + 1 линейны (а не квадратичны), числители соответствующих им простейших дробей — постоянные (а не линейные функции). Следовательно, по теореме 1 существуют такие числа Д, В, С, D, Е, F, что
х4 4~ х2 4* 2х 4~ 1 =2L + JL + _C_+JL+ Е I F х4(хЧ-1)2 х4 х3 х2 х (х4-1)2 х 4- 1
(Мы еще не знаем, каковы числа А. В, С, D, Е\ F: отсюда идет и название «неопределенные коэффициенты».) Складывая шесть простейших дробей, получаем
Л (х 4- О2 Вх (х I)2 4~ С*2 (х 4- I)2 4- Dx3 (х 4- I)2 + Ex4 4- Fx4 (х 4- 1)
х4 (х 4- О2
Здесь числитель равен
(D + Е)х5 4- (С + 2D 4- Е 4- Е)х4 4- (В 4- 2С 4- D)x3 +
4- (А 4- 2В 4- С)х2 4- (2Д + В)х + А.
Требуется, чтобы этот числитель был равен х4 + х2 4" 2х 4" 1> т. е. чтобы было
D 4- F = О,
C + 2D + E + f = l,
В + 2С + D =0,
А + 2В 4- С = 1,
2А 4- В = 2,
А = 1.
§ 2. Интегрирование рациональных функций
453
Решая эту систему уравнений, находим A = 1,B=C=D=O, Е =1, F = 0. Таким образом, х4 + *2 + 2х + 1 • 1 ।_____1
?(х+ I)2 X4 + (х+1)а
2. Рассмотрим теперь дробь 2х* х4—1 *
Ее знаменатель можно записать так:
х4- 1 = (ха — 1)(ха + 1) =(х- 1)(х4- 1)(ха 4- 1).
Каждый множитель входит в знаменатель в первой степени; последний из них — квадратичный множитель, не имеющий действительных корней. По теореме 1 существуют, следовательно, такие числа А, В, С, D, что
2хэ 2х3 ____________________ А В Сх + D ________
х*—1 (х—1) (х + 1) (ха 4- 1) х—I *4-1 ха4-1
Л (х + 1) (х* 4- 1) + В(х-1)(*а4-1)4-(Сх4-О)(х-1)(х4-1) х4 — 1
т. е. что
Л(х® 4- ха + х 4- D 4- В(х® — ха 4- х — 1) 4- (Сх 4- П)(ха — 1) =
= (Л 4- В 4- Qx3 + (А — В 4- D)xa 4- (Л 4- В — С)х + А — В— D.
Чтобы числитель был равен 2Х3, необходимо соблюдение условий:
Л 4- В 4- С - 2,
Л — В 4- D =0,
Л 4- В — С = 0, A —B—D =0.
Решая эту систему уравнений, находим
Л=В= —, C = l, D=0. 2
Итак, искомое разложение имеет вад 1 I
2х3 _ 2 2 . х
х4—1 ~ х—1 х+1 х2+1 ‘ (6)
3. В качестве еще одного примера рассмотрим функцию л* + 2ха + х + 1
15—537
(ха + 1)э
4S4
7. Техника интегрирования
Здесь знаменатель — третья степень квадратичной функции, не имеющей действительных корней. Поэтому разложение может содержать лишь простейшие дрсби со знаменателями (х2 4- I)3, (х2 + I)2, х2 4- 1, а соответствующие числители должны быть линейными функциями (которые в частных случаях могут оказаться постоянными). Следовательно, по теореме 1, существуют такие числа А, В, C,D, Е, F, что
х4 4- 2х2 4- х 4-1 = 4x4-В , Cx4-D Ex+F (хг + 1)» (х2 4-1)2 + (х2 + I)2 + х2 + 1
Складывая стоящие справа простейшие дроби, находим числитель:
Ах 4- В 4- (Сх 4- О)(х2 + 1) + (Ех 4- Е)(х2 4- I)2 =
= Дх 4- В + (Сх + D)(x2 + 1) + (Ех 4- W + 2х2 4- 1) =
= Ех3 4- Ех4 4- (С + 2Е)х3 4- (D 4- 2Е)х2 4- (А 4- С 4- Е)х 4- (В 4- D 4- F)-
Он должен быть равен х4 4- 2ха 4- х 4- 1. Отсюда
Е =0,
F = 1,
С 4- 2Е = 0,
D 4- 2F = 2,
А 4- С 4- Е = 1, В + D 4- F = 1.
Решая эту систему, находим A =i, B=C=D=E=0, F = 1; значит, х4 4- 2ха 4- х 4- 1 _______________ х_______. 1
(х24-1)» ~ (ха4-1)’ + х2 4-1
Из рассмотренных примеров видно, насколько прост наш метод; часто он оказывается, однако, утомительным.
Мы умеем теперь интегрировать любую рациональную функцию.
•Примеры. 1. Найти первообразную функции •
Решение. Поскольку степень числителя превосходит степень знаменателя, производим деление; получаем
х1 + х3 = х^х4 — 1) 4- 2Х8.
Пользуясь соотношением (6), находим
( ..«’ + < ix = f k. + _ f р + _L_ + 1 +
J X"-1 J \ т «•-! ) J \ 20-1) 2<«+1)
। х \ j С я j । 1 (* dx । 1 С dx , С х dx
+ -?тг) “х - j dx + - J — + - J — + J “?тт -
§ 2. Интегрирование рациональных функций
455
1 Г d(x-l) , 1 С d(x+l) , 1 f d(x24 1)
2 J х-1 + 2 J х + 1 2 J х24
= -j-4-£-ln|x—11 4-yln|x4 114-|~ln(x24 1) 4С.
Заметим теперь, что в этом частном случае можно обойтись вовсе без простейших дробей; в самом деле,
fdg-1) „^Ini^-n + c.
J «•-! 2 J x4-! 2
Читатель легко проверит, что найденное этим методом решение совпадает с полученным выше.
2
2. Вычислить J 1
dx.
Решение. Знаменатель можно представить в виде (х2 4- 1)(х 4 1). Отсюда
Зх» 4- 2х 4- 5 _ A t Вх + С Xs 4 х2 4 х 4 1 «4-1 х» 4-1
с еще не определенными коэффициентами А, В, С. Складывая простейшие дроби, получаем числитель
Д(х2 4-D4- (Вх 4- С)(х 4- 1) =М + В)х2 4- (В + С)х 4- А 4- С,
равный Зх8 4- 2х 4- 5, если
Д 4- В = 3, В 4- С = 2, Л 4 С = 5,
т. е. А =3, В = О, С = 2. Следовательно, 2 2 2 2
+ =У(ТЛ~ + ^ + r)dX = 31П1Х+11 +2arctgX «0,66. 11 11
Ту же задачу можно решить и иначе. Заметив, что
«Цх3 4- х2 4- х 4- 1) = Зх2 4- 2х 4- 1, имеем 2 2 2
f_Зх24-2х + .5_. dx = Г_3х>+ 2»+1 dx + 4 С___dx____
J х3 4 ха 4 х 4 1 J х* 4- х» 4 х 4 1 х3 4 ха 4- х 4 1
Пользуясь простейшими дробями, получаем
1 = А Вх + С
х3 4 ха 4 х 4 1 «41 х2 41 ’
причем А =С = 1/2, В = — 1/2. Отсюда находим
456
7. Техника интегрирования
2 2
[<*(? + *’ + *+D + 4 Cf. 1 + 1-х =
J х* + х* + х+1 J \ 2 (х + 1) 2(х2 + 1)/
1 1
2
= In | х3 4- х2 4- х 4- 11
2 2 2
4- 2 aretg х — In (х2 4- 1) i i i
в соответствии с предыдущим решением, ф
УПРАЖНЕНИЯ
Найдите следующие интегралы:
35.
х2 —2 х3 — 4х
dx.
45.
5х2 — 4х 4“ 4
/з
Р х4 4- Зх2 4- х 4-1
ОО.
J х® + х 1
2
f X3 + 2х2 + 5х 4-1
О( . I dx.
J х2 4- 2х + 1
0
Р Зх2 — бх 4- 2
38. 1 о о dX*
J х3 — 2х2 4- х
ОГЛ Р х3 4- 4х2 4~ 5х — 2
ОУ. 1 л 1 dx. J х4 — 1
Р 2Х4 — х3 4- 2
J X2 (х2 4- 1)а
dx.
х3 — х2 4- Зх — 1 (х2 4- 4) (х2 + х+1)
48.
2х3 4- * ха — х 4- 1
dx.
Г 4Х4 4- 8хэ 4- 9х2 4- 4х
J (х 4- 1) (2х*4-2х+ 1Г’
2х2 4- 4х — 1 --------------------dx. (х2 4- 2х 4- 2) (х — 1)
х4 4- Зх3 4- 4х2 4- 4х 4-1
(х24-х4-1)3
51.
52.
С х3 — х2 4- 2х 1 --------------dx.
J X* + X2 + 1
Г 2х3 — Зх2 2х
J (х*+1)’
43.
2х2 4- 2х — 1
—з—;—dx-х3 — 1
х3 4~ 4х2 + 7х + 12
(х2 + х) (х2 + 3) dX‘
44.
Р 2х3 4- 7х2 + 4х — 3
J хз + Зх2 4- Зх Х>
Cl—4х + 8х2— 8х3
J х4(2х2 — 2х+ I)2 dX
§ 3. Рационализация интегралов
457
§ 3. РАЦИОНАЛИЗА- В этом параграфе перечисляются различные классы инте-ЦИЯ ИНТЕГРАЛОВ тралов, которые надлежащей подстановкой можно свес-- ти к интегралу от рациональной функции и, таким об-
разом, вычислить в конечном виде. В каждом случае, когда доказывается возможность такого сведения, доказательство одновременно доставляет и метод вычисления интеграла. Но часто целесообразнее вычислить интеграл каким-нибудь специальным методом, чем применять к нему общий «процесс рационализации» (т. е. приведения подынтегральной функции к рациональному виду). Мы проиллюстрируем это рядом примеров.
Изучая этот параграф, читатель должен по возможности развить в себе способность распознавать «рационализируемые» интегралы. Если уже известно, что заданный интеграл может быть вычислен в конечном виде (т. е. выражен формулой, содержащей элементарные функции), то интегрирование может быть произведено разными способами. В частности, можно воспользоваться таблицей интегралов*. Всегда желательно проверить результат интегрирования дифференцированием.
3.1. ОБОЗНАЧЕНИЯ
Для описания рационализируемых интегралов мы примем следующие обозначения. Символ R(u) будет всегда обозначать рациональную функцию переменной и. Символ R(u, о) будет всегда обозначать рациональную функцию двух переменных и и о, т. е. R(u, и) — это отношение двух многочленов от переменных u, v. Отметим, что если х f(x) и х g(x)— рациональные функции, то также и х »-> R(f(x)t g(x))— рациональная функция от х. Пусть, например,
тогда
R = (2х3, 4х2) = — х---— , R (cos /, sin 0 = ctg 2/.
4 х
В дальнейшем мы не указываем, где определены рассматриваемые функции, поскольку в каждом случае это будет ясно из контекста. Если, например, рассматривается функция —х2, то очевидно, что х означает число, удовлетворяющее
условию | х | 1.
* См., например, книги: И. Н. Бронштейн и К. А. Семендяев, Справочник по математике для инженеров и учащихся втузов, М., «Наука», 1967, или М. Л. Смо л я н с-к и й, Таблицы неопределенных интегралов, М., «Наука», 1967, или Г. Д в а й т, Таблицы интегралов и другие математические формулы, М., ИЛ, 1948, или, наконец, весьма обстоятельный справочник Й. М. Рыжик и И. С. Ррадштейн, Таблицы интегралов, сумм, рядов и произведений, М.—Л., Гостехиздат, 1951.
458
7. Техника интегрирования
ЗЛ. РАЦИОНАЛЬНЫЕ ФУНКЦИИ ОТ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Начнем с особенно простого случая интеграла, приводимого к рациональному виду. (I) Интеграл вида J R(e*)dx рационализируется подстановкой
у =ех.
Доказательство. Имеем х = In у, откуда dx = dyly и
f R(e*)dx = f R (y) — dy.
J J У
Это интеграл от рациональной функции.
ф Примеры. I. Найдем
f shx dx = -^~ f {ex — erx)dx = f (y------Ц (гле ((=еж) =
J 2J 2 J \ у ) у
1 С л \ C dy 1 . 1 , ' e* e~x , n
= — i dy-------* i — у — —|~ C — -j- — + C — ch x “f- C,
2 J * 2 J 2 * 2y 2 2
как и следовало ожидать.
2. Имеем
f У* — 1 С I А . в + Су \ .
J y(i + y2)dy J ( у + 1 Л-у2 ГУ’
после вычисления неопределенных коэффициентов А, В и С получим
((—L + -rrv-)dy = -f“ +.С^п1Йг = -,п1У1 + 1п(1+^) + с =
J \ У i + y2 J J У J (1 + У2)
= ln|-L±£-| + С = 1п|у + у| + С = ln(e* + t--r) + C = lnchx + C', где С* — новая постоянная; читатель легко может оправдать последний шаг. Конечно, можно найти тот же интеграл и проще:
f th х dx = f dx = f * = In ch x 4- C'.
J J ch x J ch x
Отсюда видно, что следовать общим правилам — это не всегда кратчайший путь к цели, ф
§ 3. Рационализация интегралов
459
УПРАЖНЕНИЯ
Найдите следующие интегралы:
2е2ДГ + е* + 1
2 ch х 4- 3 sh х — ---—-— dx.
3 ch x 4- 5 sh x
1 4~ sh x
1 4~ ch x
dx.
3.3. КОРНИ ИЗ ЛИНЕЙНЫХ ФУНКЦИЙ
(II) Интеграл вида J 7? (х, V ax4-p)dx, где q>l— целое число, а=#0, ра
ционализируется подстановкой
у = yfах 4- р.
Доказательство. Имеем
„ иЧ 8
ах 4- р = уч, х = —---—,
a a
откуда dx = dy a
И
J R (x, ax 4- p) dx = J.R ----dy.
а это интеграл от рациональной функции. 2 ______
ф Примеры. 1. Вычислить (* ху^2х__3dx
3/2
Решение. Полагаем з/--------------------- 1 3
у = У2х — 3, у3 = 2х — 3, х=—у3+—,
460
7. Техника интегрирования
так ЧТО . 3 о J
dx = —y*dy
и 2 ____ 1 1
2х — 3dx = fy = [(-4-у" + -^-yAdy =
3/2 б V 2 2 7 2 о k 4 47
= p-^ + _LH|' = _2L.
V 28 * 16 * / Io 112
ri P dx
2. Haumu I----— .
J l + /x
Решение. Положим у = ]/x, у2 = x, dx = 2y dy. тогда имеем
P dx P 2y dy P / 9 \ Л
----— = -rr^= (2-—-dy=2y-2 ln(l + y)+C =
J 1 + fx J 14-y J \ i + y/
= 2 V~x— 2In(1 4- ]/x) 4-C.
Проверим ответ дифференцированием:
— [2x,/2 - 2 In (1 + x,/2)] = x“1/2-----x^— =-------
dx 1 V t Л 1 + ?/2 1 + x,
что и следовало ожидать, ф
УПРАЖНЕНИЯ
Найдите следующие интегралы:
7. j х(2х — 1)1/3 dx.
о
Гх4-УТТТ .
8- I ----------dx.
J *+2
о f - 2х‘/3 4-1
J *4-1
Р ха
10. 1 о/п dX.
J (*4-4)3/2
f 2х+ЗГГ+1 .
11. I --------- dx.
J 2х — З/х+1
12 f xdx
J х 4- (х 4-1)3/5 4-1 ’
3.4. КОРНИ ИЗ ДРОБНО-ЛИНЕЙНЫХ ФУНКЦИЯ
(III) Интеграл вида
dx, где у > 1 — целое число иа& — 7?=/=0,
рационализируется подстановкой
т%Дх4- р V 7*4-5'
(1)
§ 3. Рационализация интегралов
461
Прежде чем доказать это, сделаем два замечания: 1) только что сформулированный результат содержит (II) как частный случай; 2) условие аб — Рч =И= 0 означает, что дробь (ах + р)/( ух + б) несократима (не является постоянным числом).
Доказательство. Из формулы (1) находим
Умножим обе части на ^х +б и разрешим полученное уравнение относительно х. Это дает
— 4q + 0 » — 07 .
х =----- . dx = и qy9 1 dy
УУ9 — а (УУ9 — “Г
и, значит,
f D( п%ах + ₽\ . f D(— W + ? \ (“5 — РТ) ЯУ9~' ,
I R (х, 1/ —-!-т) dx = I RI — -, у '—z---т dy,
J \ г 7хЧ-&/ J \ VJq —а / —а)2
что представляет собой интеграл от рациональной функции, ф Примеры. 1. Найти J dx.
Решение. Полагая
у2 __ J, так чт0 у2х = | х = J-----------У > fa = ---dy,
14-х 14- У2 (1 + ^2)2
имеем
J V т+т dx = I у (1 + У*у dy = J (г+7 + (1 + «/2)2) dy-
Чтобы найти этот интеграл, применим рекуррентную формулу (4), выведенную в § 2.4. Получаем
fdi/4-4 — f —— 2 f-JL_ + 2^^ =
J \1 +, W I 2 1 + у* 2 J 1+ W J 1 4- Уг \+уг
--2arOtg£+2r^ + C=-2arctg]ALp4 + (l + x) =
= — 2 arctg ]/ -j-pj- + У • — *2 + C.
Проверка дифференцированием предоставляется читателю.
2. Вычислить i----------л/ 1 ~х Av
J (1 + х)2 V 1 + х их-
Решение. Полагая
462
7. Техника интегрирования
имеем 1 — и3 , би2 , , 2
х —-----—, dx =--------------dy и 1 + х = —-—-,
1 + у3 (I + У3)3 1 + У3
откуда 1 о 1
f 1 Л1"* dx = _ С О + У3)2,, W—dy = — f ifldu =
J (1 + x)2 V 1 + x ax J 4 y (1 + i/2)2 ay 2 Jyay
0 1 0
2 4 y |o 8
co ______ »
3. Вычислить f_______!___iX.1 ~~~ * dx
J (1 + x)2 V 1 4- x ax' i
Решение. С помощью предыдущей подстановки находим, что этот несобственный интеграл равен
-A $y*dy=----------3~.
О
Детали выкладок предоставляются читателю, ф
УПРАЖНЕНИЯ
Найдите следующие интегралы:
3.5. РАЦИОНАЛЬНЫЕ ФУНКЦИИ ОТ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Перейдем к следующему важному результату.
(IV) Интеграл вида f /?(cos х, sin х) dx рационализируется подстановкой
• (2)
§ 2^3 ока^ательство* Воспользуемся соотношениями, установленными в
§ 3. Рационализация интегралов
463
2 tg —
8 2
sinx =
•+tg24-
1 - tg2 —
COS X =----------—
1 + tg2_r
Отсюда имеем
2y sin X =---------— ,
l + $/a
1- у2
cosx 1+ У2
Далее, в силу (2) = aretg у9 х =2 aretg у. Следовательно,
dx = —-— dy 1+y2
и
х, sinx)dx
1 — y* 2y \ 2 dy
1 + у2/1 4- у2
Таким образом, мы пришли к интегралу от рациональной функции.
Этот метод позволяет находить интегралы от функций, построенных с помощью рациональных операций из cos х, sin х, sec х = 1/cosx, cosec х = 1/sin х, tg х = = sin x/cos х, ctg x = cos x/sin x. Часто, однако, тот или иной частный прием оказывается выгоднее общего метода.
Примеры. 1. Найти J sec xdx.
Решение. Полагая у = tg , имеем
dx cosx
1+ j/a 2dy =
1 “ У2 ’ i + У2
1
1—у
= 1п|1 +у|-1п|1
1 + tgir
1 + у
1 —У
Проверим ответ дифференцированием:
— In dx
‘4-tg —
1 — tg —
* 2
1 — tg —
* 2
1
1+tgl
1 T
x 2 cos2-----
2
2___________
tg2 —) cos2 — cos2 -A- — sin2 — 6 2 J 2 2 2
1 -----= see x, COSX
2 w \2
что и следовало ожидать. Поскольку
464
7. Техника интегрирования
имеем
l+tg-£- cos-£-+sin-£-
cos-^-sin-L
X X
1 + 2 cos sin —-
2 2
cos2 ------sin2 -i-
2 2
XX XX
cos — 4- sin — cos — 4- sin — 2 2 2 2
cos -4----sin — cos -4- 4- sin -4-
2 2 2 2
1 + sin x cos x
= sec x 4- tg x,
J secxdx=ln|sec x4-tgx|4-C.
(3)
В таком виде этот интеграл и приводится в большинстве таблиц.
2. Найти § cosec х dx.
Решение. Этот интеграл можно было бы найти, пользуясь тем же общим методом. Но проще воспользоваться формулой (3):
I cosec х dx= I sec I —------x]dx = — \ sec I—----------x]d(—-------x | =
J J \ 2 / J \ 2 / I 2 /
= — In sec I—---------x) 4- tg (—------x ] 4- C = — In |cosec x 4- ctg x | + C,
I \ 2 / \ 2 li
что можно также записать следующим образом:
cosecxdx — In |cosecх — ctgx|4-C (4)
(в этом читатель легко убедится самостоятельно).
3. Найти J sin2 х dx.
Решение. Вместо того чтобы прибегнуть к общему методу, заметим, что
J cos2 х dx+ J sin2 x dx = J 1 • dx = x 4- Cv
J cos2 x dx— J sin2 xd-x= J cos 2x dx= -i- sin 2x 4- Сг.
Складывая и вычитая эти равенства, получаем:
J cos2 х dx= -i- х + -i- sin 2х 4- С, (5)
Jsin2xdx=-i- x----i-sin2x4-C. (6)
К тому же результату можно было бы прийти иным путем:
С . о j С 1 — cos 2х , 1 1-п . г-
I sin2 х dx= I--------ах = —х — — sin 2х + С.
J J 2 2 4*
§ 3. Рационализация интегралов
465
4. Найти I-----------.
J sin х + cos х
Решение. Вместо использования общего метода заметим, что
sin х 4- cos х = К 2 |-sin х 4-----cos х | = 1/2 I sin х cos-1- cos х sin —
\ /Г V2 / \ 4 4
= }/2 sin (х 4- .
Поэтому, пользуясь результатом примера 2, имеем
Р dx __ 1 Р______dx________
I sinx + cosx /2" I sin(x4-— 1 ”
J J \ 4 J
—-----In | cosec (x 4- 4- ctg (x 4- | 4- С.ф
УПРАЖНЕНИЯ
Найдите следующие интегралы. [Читатель может вместо общего метода (или наряду с ним) искать специальные приемы интегрирования.]
19. । 7 2 — cos л dx. ) 2 4- cos х 23. | a dx 27. P dx
) sin x 4- V"3 cos x J 4 cos2 x 4- 3 sin2 x
k20. 1 [* 1 — sin x ) 1 4- sin x 24 -j ’ sec x 28 J ' sec x
1 1 4- sin x * их, 1 — sec2 x
21. 0 cos3 x 25. * [* cosec x 29. 1 P sec x dx
। dx • J 1 4- cos2 x i _ dx. ) 34-4tgx 1 1 — 4 sec2 x
22. C 2 cos x — 5 sin x 26. C sec x cosec x 1 —————— Hr ж] 1 dx
i гч dxt ) 3 cos x -|- 4 sin x ) 34-6cosx * 9 cos2 x — 16 sin2 x
31. Покажите, что
J cosec х dx= In j tg -у-1 + С
(а) общим методом этого раздела;
(б) прямым дифференцированием;
(в) с помощью результата примера 2.
32. Покажите, как, используя тот же метод, что и в примере 4, вычислить ________________________________________dx______
a cos х 4- Ь sin х ’
где а и b таковы, что а2 + Ь2 =/= 0.
33. Покажите, как вышеуказанным методом вычислить
где a—любое число.
С q-f-tgx
J 1 — atgx
dxt
466
7. Техника интегрирования
3.6 . РАЦИОНАЛЬНЫЕ ФУНКЦИИ ОТ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
(V) Интеграл вида J7?(ch х, sh х) dx рационализируется подстановкой
</ = th-f-. (7)
Этот прием — прямой аналог (IV). Чтобы доказать (V), заметим, что из (7) следует (см. гл. 6, § 7.6 или проверьте непосредственно)
sh х = —, ch х = ’ + , 1 - у3 1 - у3
dx = ^-;
1- у3
отсюда
С R (ch х, sh х) dx = f R y , —) 2dy ,
J J v — y3 1 — y3h — y3
а это интеграл от рациональной функции.
Конечно, можно было бы обойтись без подстановки (7). Можно заметить,
что ch х — (ех + е~х), sh х = (ех — е~х) и применить подстановку у = ех [см. (I)
выше]. Какой из методов проще, зависит от рассматриваемого интеграла.
УПРАЖНЕНИЯ
Найдите следующие интегралы:
dx ch x + sh x
q- f hl* . . 35. I ——-—dx'
J 1 + ch x
36.
2 + 2 ch х — sh х ------ 1 — — dx.
2 + ch x + sh x
Рационализируйте следующие интегралы:
37.
ch x -------------dx. (1 + ch x)a
sh х dx
(4 + 3 ch х) (1 +2chx) *
3.7. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ j/l — X«
- (VI) Интеграл вида j/?(x, — x2) dx может быть сведен к интегралу от рацио-
нальной функции.
Доказательство. Мы укажем два способа приведения.
(а) Применяя тригонометрическую подстановку
§ 3. Рационализация интегралов
467
x = cosy, У 1 — х2 = sin у, dx= — sinydy, О^у^п,
имеем
J R (х, 'У 1 — х2) dx = — J R (cos yt sin у) sin у dy, что приводит нас к уже рассмотренному случаю (IV).
(б) Запишем тождество
откуда ____
J R (х, У 1 — х3) dx = J R (х, (1 4- х) У j ~ j dx,
что приводит нас к уже рассмотренному случаю (III).
ф Пример. Найти J У1 —х2 dx.
Решение. Применив метод (а), имеем
jyi—x2dx =
Далее, учитывая соотношение (6), находим
f У1 — х2 dx ---— у 4—— sin2y 4- С --— arccosх 4- — sinу cosy 4- С =
J 2 4 2 2
С sin у (— sin у) dy = — С sin2 у dy.
=------arccosх 4- хУ I — х2 4- С.
Метод (б) в этом случае приводит к более сложным вычислениям, ф
УПРАЖНЕНИЯ
Найдите следующие интегралы:
Г х2
39. I — 1 dx. [Примените метод (а).]
J У1 _ х»
Vi /2
40. х3 У1 — ха dx. [Примените метод (а).)
41.
dx.
[Примените метод (а) и воспользуйтесь соотношением
sin4 х (1 —cosax)a
cos2 к cos2 х
sec2 x — 2 4-cosa x.]
[Примените метод (a).]
468
7. Техника интегрировании
/1 — X2 х(1 +х)
dx.
[Примените метод (б).]
Д44. J х3 (1 —x2)lz* dx. [В этом случае подынтегральная функция — не рациональная, а иррациональная функция от х и У 1 — х2; несмотря на это, метод (а) все же применим.]
/2
45. J х3 У \ — х2 dx. [Примените метод (а).]
46. С 1 ~ dx.
J X2
[Примените метод (а).]
3.8. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ УХг — 1
(VII) Интеграл вида J R (х, Ух2— 1) dx может быть сведен к интегралу от рациональной функции.
Доказательство. Мы укажем три способа приведения.
(а) Применим тригонометрическую подстановку
х = sec у = —5—, cosy
откуда
l^x2— 1 = tg у, dx=tgy sec у dy
и
j R{x, Vх2 — l)dx = j R(secy, tgy)tgy sect/ dy.
Это интеграл типа (IV).
(б) Применим гиперболическую подстановку
х = ch у, Ух2 — 1 = sh у, dx = sh у dy,
откуда
j R (х, Ух2— 1) dx = JR(chу, shу)shу dy.
Это интеграл типа (V) или типа (I).
(в) Запишем данный интеграл в виде
J R (х, dx = J R (х, (х + 1) )/у=т) dx.
Это интеграл типа (III).
УГ
ф Пример. Вычислить
X«/x2— 1!'
§ 3. Рационализация интегралов
469
Решение. Используя метод (а), имеем
УТ п/4 тс/4
Г dx f tg w sec w dy C , .1 1
I ---- = I —-----— = | cos у dy= sin y\ = ——.
J xa _ i J sec2t/tgy J yT
10 0
УПРАЖНЕНИЯ
Найдите следующие интегралы;
47.
48.
49.
[Примените метод (а) и выразите новую подынтегральную функцию через
синус и косинус.]
х3 dx
—zzzzzr . [Примените метод (а), выразите новую подынтегральную функцию через /х2 — 1
синус и косинус и воспользуйтесь основным методом § 3.5.] dx
------- 3/2 . [Примените метод (а) и выразите новую подынтегральную функцию через синус и косинус.]
50. J /х2— 1 dx. [Примените метод (б). Примените также метод (а), выразив новую подынтегральную функцию через синус и косинус; затем воспользуйтесь основным методом § 3.5.]
УТ
51. | х3 У х2 — 1 dx. [Примените метод (а) и метод, используемый в упр. 29J
С V" х2 Т
52. | 2---------dx. [Примените метод (а).]
J х
3.9 . ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ fl+X2
(VIII) Интеграл вида J R (х, ]/1 + х2) dx может быть сведен к интегралу от рациональной функции.
Доказательство. Мы укажем два метода.
(а) Применяя тригонометрическую подстановку
х = tg у, ]/ 1 + х2 = sec у, dx = sec2 у dy, имеем
J R (х, 1 + х2) dx = J- R (tg у, sec у) sec2 у dy,
а это интеграл типа (IV).
(б) Применим гиперболическую подстановку
x — shy, J/4! + х2 — ch у, dx=chy dy,
470
7. Техника интегрирования
она приводит к интегралу типа (V) или типа (I):
J R (х, У1 4- х2} dx = J R (sh у, ch у) ch у dy.
УПРАЖНЕНИЯ
Найдите следующие интегралы:
53. j Ух2 + 1 dx. [Примените метод (б). Примените также метод (а), выразив новую подынтегральную функцию через синус и косинус, а затем — основной метод S 3.5.)
VT
f 1/ х2 _1_ J
±54. г —jL— dx. [Примените метод (а), выразив новую подынтегральную функцию через
!
синус и косинус.]
р х2 dx
55. j (’2"1)3/2 " • [Примените метод (а).]
Р dx
56. I — ------. [Примените метод (а) или (б).]
J /х2+ 1
р х2 dx
57. 1 — . [Примените метод (б).]
J /х2 + 1
f dx
“’J (х2+1)3/2 •
3.1 0. КВАДРАТНЫЕ КОРНИ ИЗ КВАДРАТИЧНЫХ ФУНКЦИЙ
Теперь мь! в состоянии доказать более общее предложение:
(IX) Любой интеграл вида j R (х, У ах2 + 2фх + 7) dx может быть рационализирован.
Можно считать, что а=/=0, поскольку в противном случае мы имели бы случай (II), для которого наше утверждение уже доказано. Положим
ах2 + 2(Эх + 7 = а (х + —) + °7 .
\ а / а
Пусть ау — ₽2 > 0; тогда У ах2 4- 2$х 4- I равен
Здесь <х> 0, так как иначе перзый квадратный корень не имеет смысла. Полагая
t °*4-₽ .. a dx
ч — , dt — >
/огГ-р2
преобразуем наш интеграл в интеграл вида (VIII).
§ 3. Рационализация интегралов
471
Пусть теперь oq — р2 < 0. Положим ах 4- р a dx
Е = - z=
и заметим, что У ахг 4- 2$х + 7 равен
1/ а (х 4- XY+ = 1/ |7-Д±О -11 = 1/ ($а- 1).
V \ а / а У а 1\/Р2 — аУ/ Jr а
Таким образом, наш интеграл превращается в интеграл типа (VI) или типа (VII) в зависимости от того, будет ли а < 0 или а > 0.
Наконец, случай а? — р2 = 0 не представляет интереса. В этом случае должно быть а > 0. Но тогда
\ а
и подынтегральная функция является рациональной. Итак, утверждение (IX) полностью доказано.
dx
ф Пример. Найти .
J У — 4х2 + 8х — 3
Решение. Имеем
—4х2 + 8х — 3 = — 4(х — 1)2 + 1 = 1 — (2х — 2)2.
Положим поэтому £ = 2х — 2, dt = 2 dx, что дает
Г dx 1 f dt 1 1
I —— — I —= — arcsin 5 + C = — arcsin (2x — 2) -4-C. J F — 4xa + 8x — 3 2 J у i _£2 2 2
УПРАЖНЕНИЯ
Приведите каждый из следующих интегралов к одному мэ видов (VI)—(VIII):
5ъ. J х3/9 —4x2dx.
64.
Р х3 dx 60. | --------- .
J /4х2 — 3
Р 1 — 4х + 4ха 61. I —dx.
J — 4х + 4х2
62‘ J (Зх2 + 8х + 5)3/2 '
Г 4 + 4х + х2
63. | -----dx.
J "К— 3 — 4х — ха
65.
66.
dx
/2х2 — бх + 5 (2х — х2)3/2 х2 — 2х + 1 “Х‘
dx. 4х + 2
1 — 4х 4“ 1
6 J (2х2-2х+5)3/2 dX-
Р dx
68- 1 ----
J У 9х2—30х+9
69.
ix—9х2)3</*’
472
7. Техника интегрирования
§ 4. ФОРМУЛЫ ПРИВЕДЕНИЯ
Формулы приведения применяются для вычисления некоторых интегралов, с трудом поддающихся изложенным методам. Пример этого рода уже встретился нам в § 2.4 при вычислении интеграла вида
1п = [----—-----, п = 1, 2, 3..
п J (1+х2)"
Подынтегральная функция зависит в этом случае от целого положительного числа п. При п = 1 неопределенный интеграл нам уже известен: это функция aretg х + С. Интегрирование по частям привело нас к соотношению, связывающему 1п и /п_г Применяя формулу приведения п — 1 раз, вычисляем /п. Как показывают рассматриваемые ниже примеры, только что описанная ситуация типична.
Напомним для .удобства читателя формулу интегрирования по частям (см. гл. 5, § 3.4):
J udv=uv— j vdu.
4.1. ИНТЕГРИРОВАНИЕ ФУНКЦИИ Хпех
Начнем с простого случая:
У хпех dx.
Интегрируя по частям, получаем
У хпех dx = у хп d(ex) — хпех — у е* d (хп) = хпех — п j xn~lex dx.
Итак,
У хпех dx = хпех — п у xn~lex dx. (1)
Это и есть требуемая формула приведения. (Формулу (1) и последующие формулы того же типа запоминать не следует.]
фПример. Найти первообразную функции х х3ех.
Решение. Применяя формулу (1), имеем
х3ех dx = х3ех — 3 у х2ех dx\
У хех dx — хех — у 6х dx = хе31 — ех +С.
Отсюда
f х3ех dx = х3ех — Зх2ел + 3- 2хех — 3- 2ех + С = (х3 — Зха + бх — 6)е* + С'.Л
х3ех dx = х2ех — 2 1 хех dx\
§ 4. Формулы приведения
473
УПРАЖНЕНИЯ
Найдите следующие интегралы:
1. J x4 e* dx. 5. J (3x3 — 2xi + x—\)evedx.
2. J (Зх4 —2x2)e*dx. 6. f x» (e3* 4- e3*) dx.
3. J x3e9Xdx. 7. J (2x3 4- *) ( e*/2 — 2ear) dx.
4. J (2x3 — x 4- 1) ex/2 dx. 8. J x5e*adx. [Положите и = x».]
4.2. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ х« (In х)п
Пусть мы хотим вычислить
J хя (In х)" dx, где — натуральное число, а а#=—1—любое число. Заметим, что dx“+1 = = (a+l)x“dx, откуда
f хя (In x)ndx — —5— С (In х)" с? (x“+I) =
J «4-1 J
= —— х“+'(1пх)л----------— C xa+‘ d(lnx)" =
«4-1 «4-1 J
= —— xa+1 (In x)n--------— f xa+1 (In х)л-> — dx.
a + 1 • + 1 J x
Следовательно,
J x“ (Inx)«dx = -------TTT J x* Х^Я~1 ^x’
Эго и есть требуемая формула приведения.
Случай a — —1 является более простым:
[ 1*22^ dx = f (lnx)nd(lnx) = (lnx)”"1 + C.
J X J n+1
УПРАЖНЕНИЯ
Найдите следующие интегралы:
9. | У~х In x dx. 13. j* ( x1'3 + x1/2 ) (In x)2 dx
Д10. f ?/3 In»xdx. 14. f ln2(a2x) dx.
J J x2
11. J 15. J +3^)[\n-L X^ dx.
P In» X „
12. I ---— dx. 16. f (2x)«(In(3x)]»dx.
J Yx J
474
7. Техника интегрирования
4.3 . ИНТЕГРАЛЫ ОТ х" cos х И хп sin х
Рассмотрим теперь интегралы
J хп cos xdx, J хп sin xdx.
Мы получим формулу приведения, связывающую интегралы обоих видов, а именно:
j хп cos х dx = j xnd (sin x) = xn sin x — j sin x d (xn), или
J xn cos x dx= Xя sin x — n J Xя"1 sin x dx. (3)
Точно так же доказывается, что
Xя”1 cos х dx.
(4)
п/2
ф Пример. Вычислить J х3 sin х dx.
о
Решение. Пользуясь формулами (3) и (4), имеем п/2
J х3sinxdx = — х3cosх о
к/2
п/2
С x2cosxdx= -^x3cosx
о
п/2
п/2
4-3x2sinx — о
2 J х sin х dx= (— х3 cos х 4- Зх2 sin х + бх cosх) о
= (— х3 cos х + Зх2 sin х + бх cos х — 6 sin х) Г/2 = |о
о п/2 п/2
о
Зк2 ~ ---------о.
4
О
О
УПРАЖНЕНИЯ
Найдите следующие интегралы: п/2
17. J ха cosxdx. о
п/2
18. [ х2 sin х dx.
п/3 n/i
19. f (Зх2— 2х + 1) cos х dx.
20. J x2 (cos x + sin x) dx.
21. j x»sin(2x)dx.
22. J x4sinxdx.
n/У
23. J (2x)a cos (3x) dx.
о
n/2
24. f x" (x cos x + 100 sin x) dx.
о
P __ dx _
25. I x3'2 cos }^x ——- . [Положите и = x .|
J P*
П1 \4
x---— nj cos x dx
§ 4. Формулы приведения
475
4.4. ПРОИЗВЕДЕНИЯ СТЕПЕНЕЙ СИНУСА И КОСИНУСА
Наша ближайшая цель — вычисление интегралов вида
J cos'1 х sin®1 х dx. (5)
Чтобы получить надлежащую формулу приведения, применим следующую уловку. Для любых чисел а и b имеем
d [cos® х sin* х) = (— a cos®"1 х sin*+1 х + b cos®+1 x sin*"1 x) dx.
cos®*1 x = cos®"1 x cos2 x = cos®"1 x (1 — sin2 x). Отсюда
d |cos® x sin* x] = (— (a + b) cos®"1 x sin*+1 x + b cos®"1 x sin*”1 x] dx.
Взяв неопределенные интегралы от обеих частей, получаем
cos® х sin* х = — (а b) J cos®"1 х sin*+1 х dx+ b J cos®"1 х sin*"1 х dx.
Положим теперь а — 1 =n, b + 1 =/п; тогда из предыдущего соотношения имеем
Г cos® х sin®1 х dx --?— cos®+1 x sin®1"1 x C cos® x sin®1"2 x dx. (6)
J » + tn n + m J
Это и есть требуемая формула приведения.
Выпишем еще частный случай (6), отвечающий значению п=0:
С sin®1 х dx=---— cos х sin®1"1 x + - I sin®1"2 x dx. (7)
J tn m J
С помощью формулы (7) можно свести вычисление уsin®1 х dx к случаю т =0 (если т четно) или т = 1 (если т нечетно); оба этих интеграла находятся без труда.
Соответствующая формула приведения для интегрирования cos®1x имеет вид С cos®1 х dx = — cos®1"1 х sin х + - ""-1- C cos®1"2 x dx. (8)
J tn tn j
Ее легко получить из (7), пользуясь соотношением cos(k/2 — х) = sin х; соответствующие вычисления предоставляются читателю. С помощью этой формулы приведения можно найти первообразную‘функции cosmx при любом целом т > 0.
Теперь ясно, что формула приведения (6) достаточна для вычисления интеграла (5) при любых целых т > 0, п > 0, поскольку она сводит этот интеграл либо к интегралу
J cos® х dx
(если т четно), либо к интегралу
J cos® х sin х dx=--cos®+1x + C
(если m нечетно). При отрицательных m или n формулы можно применять в обратном направлении.
476
7. Техника интегрирования
л/2
ф Примеры. 1. Вычислить J sin2*xdx, где k^O — целое. о
Решение. Соотношение (7), где т = 2k, принимает вид
к/2 я/2
f sin2*х dx— 2fe~1 С sin2*-2х dx
J 2ft J
о о
(9)
(поскольку cos x sin2*-*x принимает значение 0 при х = 0 и х = ir/2). С другой стороны, при k = 0 искомый интеграл равен л/2. Следовательно, повторное применение формулы приведения (9) дает:
«/2
j* sin2* х dx = — о
2ft —3 2ft —5
2k — 2 ’ 2k — 4
1 n
~2 ' ~2 '
ic/2
2. Вычислить J sin2**1 x dx, где A 0 — целое.
Решение. Прежде всего при k = 0 имеем п/2 «/2
fsinxdx =—cosx =₽ 1.
о о
Соотношение (7) при т = 2k 4- 1 принимает вид
п/2 п/2
С sin2*+1xdx =—f sin2**1 xdx.
J 2fe + 1 J
о о
(10)
Повторно применяя эту формулу, получаем
п/2
f sin2*+l х dx= —
J 2fe-j- i
о
2fe — 2 2fe — 4 2
2ft —1 * 2fe —3 3
3. Доказать, что
k/2
f sin2* x dx
lim k-+co
n/2
f sin2**1
x dx
§ 4. Формулы приведения
477
Решение. В интервале (0, л/2) функция sinx положительна и меньше 1. Отсюда
0< С sin2ft+1xdx<J sin2ftxdx< Jsin2*~xx dx. Q 0 0
k/2
Деля на J sin2*+1 x dx, получаем о ic/2 w/2
J sin2* x dx j sin2*-1 x dx
1 < —-------------< —---------------.
ic/2 ic/2
J sin2*+1 x dx f sin2*+1 x dx
0 0
Но последняя дробь, как это следует из формулы приведения (10), равна
2fe+i = j , 2k 2k
и при достаточно больших k становится сколь угодно близкой к 1, что и требовалось доказать.
Примечание. Из предыдущих примеров вытекает доказательство замеча-
тельной формулы Валлиса для числа л.
Чтобы вывести эту формулу, положим примеров 1 и 2 в виде
к/2
/п = С sin"x dx и запишем результаты
л 2
2 1
4 6 8 2k —2 2k j
з * 5 ’ 7 *“ 2k — 3 * 2k — 1 2ft’
5 7 2fe — 1 2fe + 1 ,
4 6 * 2^ — 2 2k 2ft+1*
Деля первое равенство на второе, имеем л _ 2 2 4 4 6 6 2fe 2fe Z2fe
2 ~ 1 ’ 3 ’ 3 * 5 ‘ 5 ’ 7 2k— 1 * 2k + 1
Принимая во внимание результат примера 3, приходим к соотношению
К .2 2 4 4 6 6 2k 2k
— = lim — . — • — • — • — • — ...----------.------... .
2 1 з 3 5 5 7 2k — 1 2/? +1
Обычно это записывают следующим достаточно понятным образом: те 2 2 4 4 6 6 2k 2k
2 “ 1 ’ 3 ’ 3 ’ 5 ’ 5 ‘ 7 ” 2k— 1 ’ 2k + 1 *
Это — бесконечное произведение Валлиса для числа -трф
Джои ВАЛЛИС * (1616—1703) был профессором математики в Оксфорде и одним из предшественников (математического) анализа.
В нашей литературе фамилия Wallis зтого математика транскрибируется как «Валлис», хотя более правильным было бы написание «Уоллес».
478
7. Техника интегрирования
УПРАЖНЕНИЯ
Найдите следующие интегралы с помощью формулы приведения (6):
27. J sin3x dx. 28. J cos6 х dx.
29. j sin4 x dx. [Примечание: другой способ приведения основан на соотношениях sin4 х dx=(sin2 х)а dx = --- (1 — cos 2х)2 d (2х) и т. д.] о
30. J cosax sinax dx. [Примечание: другой способ приведения основан на соотношениях
cos2 х sin2 х dx= — (1 — cos 2х) (1 + cos 2x) d (2x) = — sin2 2x d (2x) и т. д.)
' 8 8
31. J cos4 x sin3 x dx.
7C/3
Д32. j cos3x sin3x dx.
33. J cos3x sinax dx.
34. f cos3 (x 4- —) sin2 x dx. J 2
35. J cos3 (2x 4—y-) cos2 2х dx.
л/2
36. f cos3 3x sin6 3x dx.
4.5. ПРОИЗВЕДЕНИЯ СИНУСОВ И КОСИНУСОВ
Мы завершим этот параграф одним типом тригонометрических интегралов, которые могут быть найдены несколько иным способом, чем это делалось выше.
Типичным примером здесь является интеграл
J cos тх cos пх dx, где тип — два различных числа. Чтобы вычислить этот интеграл, воспользуемся тригонометрическим тождеством
COS a cos р = -у [cos (а + Р) 4- cos (а — p)J.
Отсюда
cos тх cos пх = -у [cos (т + п)х + cos (т — п) х] и
С sin (т + п) х . sin (т — п) х , п
\ cos тх cos пх dx = ——1—-—I ---------—h С.
J 2 (т 4- п) 2(т — п)
Заметим, что если тип — целые, то, повторно применяя теорему сложения, можно записать cos тх cos пх в виде рациональной функции от cos х и sin х. В этом случае из предложения (IV) § 3.5 можно было бы заключить, что рассматриваемый интеграл может быть найден. То же рассуждение применимо и в более общем случае, когда отношение т/п рационально. Но, конечно, прием, которым мы только что воспользовались, в этих случаях предпочтительнее общего метода (IV), а при иррациональном т!п оказывается единственно возможным.
§ 4. Формулы приведения
479
Точно так же вычисляются интегралы
J sin tnx sin пх dx9 J cos mx sin nx dx
с помощью тригонометрических тождеств
sin a sin p = -~ [cos (a — P) — cos (a 4- p)],
cos a sin P = -i- [sin (a + P) — sin (a — Р].
Читателю рекомендуется вывести эти тождества из теорем сложения. [Можно также свести два последних интеграла к ранее рассмотренному случаю с помощью соотношения cos(-^---х) = sin х.1
Ясно, что при помощи только что изложенного метода можно найти первообразную произведения любого числа функций, каждая из которых представляет собой синус или косинус некоторого кратного х.
ф Пример. Имеем
cos х cos 2х cos Зх = —- (cos Зх 4- cos х) cos Зх = -у- cos2 Зх 4- cos х cos Зх =
= cos Зх Ч—— cos 4х + — cos 2х = (— + — cos 6х^ 4- (— cos 4x4—— cos 2x^1 ,
2 4 4 к 4 4 / ’ \ 4 4
откуда
С cos х cos 2х cos Зх dx = — х + — sin 2х Ч—— sin 4х Ч—— sin бх Ч- С.
J 4 8 16 24
УПРАЖНЕНИЯ
Найдите следующие интегралы:
«/8 37. J cos3x cosxdx. 42. J cosa3x sin2xdx.
38. f cos5x sln3xdx. я/6 43, J cos2x sin 3x sin xdx.
39. J sin5x sin6xdx. 44. J (2 cos Зх 4-3 sin x) cos 2x dx.
40. J cos 2x sin3x sin4xdx. 45. j* (sin3x sin2x)adx.
41. J cos5x cos3x cosxdx. 46. J cos x cos 2x sin 3x sin 4xdr
480
Приложение к главе 7
Приложение к главе 7
§ 5. Сводка формул интегрирования
Мы соберем здесь важнейшие правила и формулы интегрирования. Для упрощения записей мы систематически опускаем постоянные интегрирования (как это обычно и делается в таблицах интегралов).
Опущены формулы, содержащие гиперболические функции и им обратные, так как эти функции могут быть выражены через показательные и логарифмические.
S.I. Основные правила
Пусть и и и — функции от дг; da н dv — сокращенные обозначения, соответственно, для u'(x)dx, v'(x)dx. В этих обозначениях основная теорема анализа имеет вид
J du = и, (1)
а правило подстановки (гл. 5, § 3.5) записывается в виде
У /'(«) du = f («). (2)
Имеем
Jfciz dx = и dx, k — постоянная, (3)
J (и + v) dx = j и dx -f- j v dx, (4)
У и dv = uv — J v du. (5)
Последняя формула есть формула интегрирования по частям (гл. 5, § 3.3, 3.4).
$.2. Степени. Рациональные функции
С хт+*
\ хт dx = --------- при т Ф — 1, (6)
J Щ И- 1
J -у- = In | х |, (7)
f -----£------= -*---------*---при (8)
J (1 4-%2)/я+1 2т (\ + х'2)т \ 2т ) J (1 + х2)т
Это формула приведения. При целом т повторное ее применение приводит к интегралу при т — 0, который равен
С dx
, = arctg * (9)
J 1 ~Т” Л
Каждую рациональную функцию можно проинтегрировать с помощью формул (6)—(9); ср. с § 2.
Имеются две формулы приведения, аналогичные (8):
С dx I х , Л 1 \ f dx
J (1 — x2)m+> 2m (1 — xa)m + ( 2m J J (1 — x»)m ПР“ ” * ’ 0)
§ 5. Сводка формул интегрирования
481
dx
(х2 —
1______х
2т (х2— 1)ш
----------f n dX ..гп ПРИ m °* \ 2m / J (x2 — l)m
Они представляют интерес, когда т — целое или полуцелое число (т. е. число вида п Н-А , где п — целое). При т = 0 имеем
S.3. Некоторые иррациональные функции
Р dx I — ' = arcsin х, (13)
J /1 — ха
J 'К 1 — X2 dx = -^-x y'l — X2 4- arcsin x. (14)
C —==r = In |x 4- /ГТ72!, (15)
J /1 + x2
J ут+т»dx = -y x кг+т* + -L in|x + /г+"Н (16)
P dx , , .----1
— In x+fx’-l , (17)
J /x2 — 1 r _______ ( _____ 1 ____
J /х2 — 1 dx = — X /x2— 1 — — In I x4- ]<x2— 1|. (18)
[Ср. c § 5.8, ниже.]
5.4. Тригонометрические функции. Основные формулы
j sin х dx = — cos xt (19)
J cos x dx = sin x, (20)
J tg x dx = — In | cos x |, (21)
j* sec x dx = In | sec x 4- tg x |, (22)
j cosec x dx = In | cosec x — ctg x |, (23)
j* ctgxdx= ln|sinx|, (24)
I sec2 x dx = tg x, (25)
482
Приложение к главе 7
J cosec2 х dx = — ctg х, J sec x tg x dx = sec x, cosec x ctg x dx = — cosec x.
(26)
(27)
(28)
5.5. Степени и произведения тригонометрических функций
f sin (a — b) x sin (a 4- b) x 1 sin ax sin bx dx= — (29) J 2(a-b) 2 (a + b) ' C . sin (a—b) x sin(a4-b)x i cos ax cos bx dx= —- - 4- —" » (30) J 2 (a — b) 2(a+b) ' ’ f . , cos (a — b) x cos (a 4- b) x | sm ax cos bx dx =— —- — -— » (31) J 2 (a — b) 2 (a 4- b)
если a2 — 62 0; J xk sin x dx= — x* cos x 4- k Jx*"1 cos x dx, (32) J xk cos x dx = x* sin x — k J x*’1 sin x dx, (33) С . b sin*“lx cos x k — 1 С j sin* xdx—— 4- j* j sin*“2xdx, (34) f . cos*"1 x sin x k — 1 С 1 cos* x dx— + . 1 cos*“2 x dx (35) J k k j
при Лг =^= 0; P t^*“1x C j tg*x dx = Y •— j tge-2x dx (36)
при fe=/=l. Формулы приведения (34) и (35) являются частными случаями следующей формулы: С т „ sin777"1 х cosn+1 х т — If 1 sin771 х cos'1 x dx = * 4- 1 sin771-2 x cos'1 x dx = J m 4- n m 4- n J sin771+1 X СО8Лв1Х n — If = 4 I sinm x cos'1"2 x dx, (37) m 4- n m + n J
где m=f= — n. [Ср. также c § 5.8, ниже.)
S.6. Обратные тригонометрические функции
J arcsin х dx = х’ arcsin x 4-У1 — x2 , arccos x dx = x arccos x — Vl — x2 ♦
(38)
(39)
§ 5. Сводка формул интегрирования
483
J arctg х dx =х arctg х — In (1 + х2), (40)
arcctg х dx = х arcctg х + In (1 + х2), (41)
Jarcsec х dx = х arcsec х — In |х + V х2 — 11, (42)
Jarccosec х dx = х arccosec х + In |х + J^x2 — 1|. (43)
В формулах (42) и (43) предполагается, что х > 1.
5.7. Показательная и логарифмическая функции
У exdx = ex,
= xkex — xk~1exdx,
sin ах dx=
(sin ах — a cos ах)
j e^cos ах dx= (cos ах + a sin ах)
J In х dx = х (In х — 1), У (In x)k dx= x (In x)k —
i*"1 dx,
ь . bL, Г X 1
xklnxdx = xk+1 -------- —
L ь -t-1 (* +
при k =£ — 1. При k = — 1 имеем
f In X 1
1 ------ dx = — (Inx)2.
J x 2
(44)
(45)
(46)
(47)
(48)
(49)
(50)
(51)
Интегралы, содержащие ax и logax, где a>0, вычисляются, если положить ax = exina и loga х = In x/ln a.
5.8. Рационализируемые интегралы
В этом разделе R(u) и R(u, v) означают произвольные рациональные функции. Следующие интегралы могут быть рационализированы (преобразованы в интегралы от рациональных функций) с помощью указанных подстановок:
(52)
(53)
R (8х) dx\ полагаем у = ех,
(здесь а, р, у, 8 — числа, для которых aS — fty=£0 и <?> 1 — целое),
484
Приложение к -главе 7
(* х
I R (sin х, cos х) dx; полагаем у = tg — (54)
[это равносильно подстановке sin х = 2у/(1 Ц- у2), cosx = (1 — у2)/( 1 + у2), при которой dx = = 2dy/(\ + y2)].
Следующие интегралы приводятся к виду (54) указанными подстановками:
J R (х, У 1 — х2) dx; полагаем х = cos у, (55)
J /?(х, У 1 4- х2) dx; полагаем x = tgj/, (56)
R (х, Ух2 — 1) dx; полагаем х ® sec у. (57)
(По поводу трех последних интегралов см. также § 3.7—3.9.)
Любой интеграл вида
J ₽(х, V ах2 + 2£х + ? ) dx (58)
может быть сведен к интегралам вида (53) [где q = 2], (55), (56) или (57) (ср. с § 3.W).
ЗАДАЧИ
1. Покажите, как найти первообразную функции хт[(х), где т >0 — целое и f(x) — обратная тригонометрическая функция.
2. Выведите формулы § 5.3 методом, описанным в § 5.8.
3. Выведите формулы, аналогичные формулам § 5.4, 5.5, для гиперболических функций.
4. Найдите неопределенные интегралы функций arcsec х и arccosec х в интервале лг<-4.
485
Решения упражнений, помеченных знаком ▲
Глава 1
§ 2
6. Имеем 7 + (—7) = 0 (аксиома 5); (—6) + 6 = 6 + (—6) (аксиома 2): 6 + (—6) = О (аксиома 5). Следовательно, 7 + (—7) = (—6) + 6.
14. В этих упражнениях нужно соблюдать осторожность — применять только такие законы и правила, которые уже были установлены. Так как апЬп = (ад)л то а5Ь5 = (ab)5 Применяя этот закон снова, получим а5дбсб = (ab)5c5 = ((ад)с)5 = (аде)5. Следовательно, a5b V = 2* = 32.
§ 3
16. Нет, при х = 0 это неравенство не справедливо. Оно верно при всех х =/= 0.
24. Мы должны рассмотреть два случая (при этом х — —3 исключается так как делить на 0 нельзя): (I) 3 + х>0 и 6 — 2х>> 2(3 + х); (11) 3 + г < 0 и 6 — 2х <Z 2(3 + х). В первом случае мы имеем х> —3 и 6 — 2х> 6 + 2х, т. е. х> —3 и x<Z 0; таким образом, здесь —3< x<Z 0. Во втором случае имеем х< —3 и 6 — 2х < 6 + 2л, т. е. x<Z —3 и х> 0, что невозможно Следовательно, решение неравенства имеет вид —3<х<0.
34. Это неравенство равносильно двум неравенствам
5х — 2 < 10х + 8 и 10х + 8< 2х — 8.
Первое из них справедливо в том и только в том случае, когда х > — 2. Второе — тогда и только тогда, когда х< —2. Но так как эти неравенства не могут выполняться одновременно, то данное неравенство решений не имеет.
44. С «квадратными неравенствами» обращаются так же, как с квадратными уравнениями: переносим все члены в левую часть неравенства а затем пытаемся разложить эту левую часть на множители (используя при необходимости формулу для корней квадратного уравнения). В нашем случае мы имеем х2 + Зх + 2>> 0. т е. (х + 1)(х-|-2)> 0 Так как произведение двух чисел положительно в том и только в том случае, если оба множителя положительны'или оба они отрицательны, то либо х + 1> 0 и х-|- 2>0 либо х + 1 < 0 и х + 2< 0. В первом случае х> —1 и х>> —2, т. е. х^> —1. Во втором х< —1 и х< —2. т. е. х< —2. Таким образом, решение неравенства имеет вид х> —1 или х< —2. (Другими словами, неравенство удовлетворяется для всех чисел х, за исключением тех, которые принадлежат интервалу [—2, -11.)
50. Это неравенство равносильно системе, состоящей из двух неравенств: 1) —Ю”-' < х—1; 2) х — 1 < 10"Л Применяя следствие 2 к неравенству 2) (при а = х — 1; А = 10 и п = /), мы находим что х — 1 <0, или х < 1. Неравенство 1) равносильно тому, что 1 —х <10“Л Снова используя следствие 2 (при а = 1 — х А = 10 и п = /), получаем 1 — х < 0, или х > 1. Применяя результат у пр. 9 из §3.2, мы видим, что единственным значением х, удовлетворяющим данному неравенству, является х = 1.
62. Так как । । а । — | b । | равно либо | а | — | b |, либо — (| а | — | д |) = 1^1 — I ° t то, для того чтобы доказать данное неравенство, мы должны показать, что:
1) | а - b 1 > | а | - | b |; 2) | а - b | > | b | - | а |.
486
Решения упражнений, помеченных знаком Д (глава 1)
Но 1) доказано в упр. 61, а 2) также следует из упр. 61, ибо
| а — 6 | = I — (а — &) | = | 6 — а | > | 6 | — | а |.
§ 5
3/—
10. Так как Р= 1, а23 = 8, то первая цифра числа у х равна 1. Испытывал 1,1 мы ви дим, что!,13 больше, чем 1,3, и, значит, больше, чем х\ следовательно, вторая цифра числа х есть 0. Так как (1,01)3>> 1,03 х. то третья цифра тоже есть 0. Наконец, угадывая нужные значения, а затем производя вычисления, мы находим, что (1 003)3< х, (1,004)3> х. Следовательно, десятичное разложение для у/"х начинается с цифр 1,003.
§ 6
6. Множество всех целых чисел, являющихся полными квадратами, бесконечно: {0, 1, 4, 9, 16, 25, ... }. Оно ограничено снизу числом 0, но не ограничено сверху. Следовательно, это множество не ограничено.
14. Пе р в ы й шаг. При п = 1 наше равенство сводится к следующему:
что, конечно, справедливо. Второй шаг. Предположим, что для некоторого (произвольного, но фиксированного) целого числа 0 справедливо равенство
Мы должны, используя равенство (1) (верное по предположению), показать, что данное утверждение справедливо и для k 4- 1, т. е. нам надо показать, что
(k + 1) (k 4- 2) (k 4- 3)
1 .24-2.3 4- ••• 4-М* 4-1)-Н* 4-1) (*4-2) = ---М Т М О
Докажем это. Прибавляя к обеим частям равенства (1) (k 4“ 1)(* + 2), мы получим
Л (Л ' 1) (k 4- 2)
1 . 2 4- 2 • 3 4- • • • 4- k (k 4- 1) 4- (* + 1) (* + 2) =-*-4- (* 4- 1) (* + 2). (2)
о
Но так как правая часть (2) равна
fe(fe +l)(fe + 2) + 3 (fe + I) (fe + 2) I) (fe + 2) (fe Ц- 3)
3 3
to (2) — это в точности то равенство, которое нам надо было доказать.
18. П е р в ы й шаг. При п = 1 наше утверждение сводится к неравенству 4 > 1, которое справедливо. Второй шаг. Предположим, что 4к k2 для некоторого (произвольного, но фиксированного) целого k> 0. Нам надо показать, что 4A+1 > (k -j~ I)2- Но 4*+i = = 4*-4; по предположению, 4А > k2, так что 4*. 4 > £а»4 = 4k2. Итак, мы знаем, что 4*+1 > > 4fc2. Но нам надо доказать, что 4^+1 > (k 4“ 1)а = &2 4“ 2Z? 4“ 1. В силу аксиомы 14 это будет сделано, если мы покажем что 4&2 > Z?2 4“ 2/г 4“ 1- Но последнее неравенство равносильно неравенству 3&2 > 2k 4- 1, справедливому в силу результата упр. 16. v
22. Неравенство 2г3 — 1< 15 равносильно неравенству ^<8. Если z— положительное число, то из обеих частей последнего неравенства можно извлечь кубический корень (§ 5.4, лемма); при этом мы получим 2. Если же г не положительно, то неравенство г3<8 справед
Решения упражнений, помеченных знаком А (главы 1, 2)
487
ливо всегда. Следовательно, S есть множество всех рациональных чисел г, удовлетворяющих неравенству г< 2. Число 2 является, очевидно, наименьшей из верхних границ (верхней гранью) множества S.
§ 7
4. Пользуясь неравенством (3) при х = 5 и у = 8, получим | ХУ — 40 | < 56 + 8а + ab Так как мы хотим, чтобы было справедливо неравенство | XY — 40 | < 1, то мы можем выбрать а и b достаточно малыми — так, чтобы выполнялось неравенство 56 + 8а 4- ab < 1. (В этом случае в силу аксиомы 14 будем иметь | XY — 40 I < 1.) Таи. если 6 < — и а < —.
то 56 < —. 8а < 3
— и ab < — • — < —, а значит 56 + 8а + ab < — 4- — + — = 1. 3 15 24 3 3 о о
18. Воспользуемся неравенством (7) теоремы 2. Так как | х | = | 0,717 |< 1 и \у | = = | 0,1819 । < 0,2, то мы имеем
10-m I jr I + ю-"11 U I 4- IO-2"1 < 1.10*m + 4- I0-”1 + KT2"*.
5
Следовательно, если выбрать m достаточо большим — так, чтобы было
10"m + 10~m/5 + 10“2т< 0,0001 = ЮЛ
то мы получим нужный результат (в ?илу аксиомы 14). Нетрудно видеть, что достаточно взять т = 5. Перемножая 0,71717 и 0,18191, мы получим 0,1304603947 0,1304.
§ 8
2. Имеем (a+6)(c+rf)= [а+цс+(в+>)(|я(.(в+м + (((в + б)я = (са + cb) + (da + db) = (ас + be) + (ad + bd) = ас + (be + {ad + 6d)) = ac + (be + (bd + ad)) == ac + ((be + bd) + ad) = ac + ((bd + be) + ad) =» = ac + (bd + (be + ad)) = (ac + bd) + (be + ad).
Справедливость этих равенств устанавливается последовательным применением аксиом 9, 7, 9, 7, 3, 2, 3, 2, 3, 3.
12. По определению, —- = (аб)”1 и — • = а-1бЛ По определению, (аб)”1 есть то
ab а b
единственное число, произведение которого на аб равно 1. Но а"г6“1 —это тоже такое число, прозведение которого на аб равно 1, гак как в силу 7, 8, 12, 10, 12 к
(аб) (a-16-1) = (ab) (Ь~ха~^) = а (66"1аЛ = а (1 • а-1) = аа"1 = 1.
Следовательно, (аб)"1 = а^б"1, или -у- = — • -у” • аб а 6
38. Как и в § 8.3, получаем, что 0.81 = 0.8 + 0,1-(0,1) = 8/10 + 1/10-О.Т. По правилу, установленному в тексте, 0,1 = 1/9. Следовательно, 0,81 = 8/10 + (1/10). (1/9) » 73/90.
Глава 2
§ 1
16. Как можно видеть, сделав рисунок, существуют две такие точки (а, 6) и (с, d). Если Р(7 —1) и Q( 10, —1), что ясно, что длина отрезка PQ равна 3. Пользуясь элементарными свой* ствами прямоугольных треугольников, находим. it.o расстояние точки Q как от (а, 6), так йот (с, d) равно 4, так что (а, Ь) = (10, 3) и (с, d) = (10, —5). 1 ; *
488
Решения упражнений, помеченных знаком Д (глава 2)
20. Пусть (а, Ь) — координаты нового начала в старой системе координат. Используя обозначения § 1.2, в которых теперь (х, у) — координаты старого начала в старой системе, а (X,Y)—координаты старого начала в новой системе, мы получим х=у = 0; X = —3, Y = 2. Следовательно, а — х — X — 0 — (—3) = 3 и b = у — У = 0 — 2 = —2. Таким образом, координаты нового начала в старой системе — это (3, —2).
30. Воспользуемся формулой (4) из § 1.4, где (alt blt q) = (1, 3, 2) и (az, bz, cz) = (2, I, 3). Мы получим
d = V (1 — 2)а 4-(3—1)а-Ь (2 —З)2 = /14-4 4-1 = /б“.
§2
20. Наклон заданной прямой равен 1/3 [ср. с равенством (3) из § 2.2]. Пусть / — прямая/ уравнение которой нам надо найти. Тогда наклон I будет равен—3 (§ 2.3, теорема 3). Мы знаем, что прямая I проходит через точку (6, —3). Пусть (х, у) — произвольная точка прямой /, отличная от точки (6, —3). Тогда, пользуясь равенством (5) из § 2.2, получаем (у 4“ 3)/(х — 6) = —3, или Зх 4- У —15 =0. Это—уравнение прямой, которая имеет наклон —3 и проходит через точку (6, —3), т. е. уравнение прямой /.
28. Данная прямая пересекает ось х при у = 0, т. е. когда х = 3/2, а ось у — при х = 0, т. е. когда у = —4. Мы можем решить эту задачу еще и следующим образом. Запишем уравнение прямой в виде х/а 4" у/b = 1. Так как 2х/3 — х/(3/2) и — #/4 =у/(—4), то наше уравнение приведется к х/(3/2)+ у/(—4) = 1. Согласно формуле (9) § 2.4, эта прямая пересекает ось х при х = 3/2 и ось у при у = —4.
§ 3
8. Выделим полные квадраты; мы имеем х2 + у2 4- 4х — 4у 4- 8 = 0, или (х2 4* 4х) 4-4- (у2 — 4у) = —8. Прибавим к первой скобке квадрат половины коэффициента при х [т. е. 22 = = 4], а ко второй скобке — квадрат половины коэффициента при у [т. е. (—2)2 = 4]. К правой части равенства прибавим 8, для того чтобы скомпенсировать это прибавление двух четверок к левой части. Теперь мы имеем (х2 4“ 4х 4“ 4) 4~ (у2 — 4у 4" 4) = —8 4~ 8, или (х 4" 2)2 4-4~ (у — 2)2 = 0. Мы видим, что сумма двух неотрицательных слагаемых равна нулю; следовательно, каждое из них равно нулю, так что х = —2 и у — 2. Таким образом, множество решений состоит из одной единственной точки (—2, 2).
18. Пусть I — диаметр окружности, проходящий через точку (3, 3). Так как касательная в точке (3, 3), прямая у = х, имеет наклон 1, то наклон прямой / равен —1. Поскольку точка (3, 3) принадлежит прямой /, мы можем.воспользоваться уравнением прямой, имеющей данный наклон и проходящей через данную точку [§ 2.4, формула (7)]. Так мы получим уравнение прямой /: у — 3 = (—1)(х — 3), или х 4" У — 6 = 0. Теперь мы знаем две различные прямые, проходящие через центр (а, Ь) нашей окружности: прямую I и прямую у = 2х. Так как точка (а, Ь) принадлежит каждой из этих прямых, то а 4“ — 6 = 0 и & = 2а. Решая эту систему урав-
нений, мы находим, что а = 2 и b = 4. Радиус окружности равен расстоянию между точками (2, 4) и (3, 3), т. е. равен /2 . Уравнение окружности имеет вид (х — 2)2 + (у — 4)2 = 2.
§ 4
4. Мы будем следовать указанию, данному после у пр. 3. __________________
1) Расстояние от тэчки (х, у) параболы до фокуса равно / (х + 2)2 4" (у + 4)2. Расстояние от точки (х, у) прямой у= 1 равно 1 —у. Действительно, так как вершина и фокус параболы расположены ниже оси х, то и вся парабола расположена там же. Расстояние от точки (х, у) параболы до оси х равно —у, а расстояние ее от прямой у = 1 равно —у 4“ 1» или 1 — у. Возводя полученные расстояния в квадрат и вычитая после этого одно число из другого, получаем х2 + 4х + 10# 4" 19=0.
2) Сдвинем параболу так, чтобы ее вершина совпала с началом координат. Вершина параболы — это точка (—2, —3/2); ее мы примем за новое начало координат. В обозначениях § 1.2 а =?= —2 и b = —3/2, а тогда х = а+Хну = b 4" Y [здесь (х, у) — старые, а (X, У) — новые координаты]. Если вершина параболы совпадает с началом координат, то можно воспользоваться
Решения упражнений, помеченных знаком А (главы 2, 3)
489
уравнением (2) из §4.1 при р = —5/2 [новый фокус находится в точке (0, —5/2)]; уравнение параболы в новых координатах будет иметь вид X2 = —10У. Положим теперь X — х + 2 и У = У + 3/2, мы получим (в старых координатах!) уравнение (х + 2)2 = —10(г/ + 3/2), или х2 + 4х + \0у + 19 = 0.
20. Наклон прямой, касающейся параболы в точке (—10, 100), равен 2-(—10), т. е. —20. Пусть точка Q имеет координаты (хо, хо2). Наклон прямой, касающейся параболы в точке Q, равен 2хо. Для того чтобы две прямые были взаимно перпендикулярны, необходимо и достаточно, чтобы произведение их наклонов было равно —1. Полагая (2х<>)(—20) = —1, мы находим хо = = 1/40. Таким образом, точка Q имеет координаты (1/40, 1/1600).
§ 6
5. Имеем /(0 — I)2 + (1 — I)2 + (0 — 2)2 + (1 + З)2 = У21~.
Глава 3
§ 1
10. Эта функция определена при всех значениях х, для которых х — I =#= 0, х + 2 =/= 0 и Зх — 2 > 0 (последнее необходимо потому, что не существует корня четвертой степени из отрицательного числа). Следовательно, мы должны иметь х =/= 1, х =/= —2 и х > 2/3. Но если х > 2/3, то, во всяком случае, х =/= —2, так что мы можем сказать, что наша функция определена при всех х > 2/3, ва исключением х = 1.
20. Имеем
(Р + К) (5) = F (5) + к (5) = (25 + 10 - 3) + 4- = 32-J- , 4 4
((F + K)°F) (2) = (F + К) (F (2)) = (F + К) (5) = 32-^-, 4
(F о (FK)) (- 1) = F (FK (-1)) = F ((F (- 1) К (-1)) = F ((- 4) (- 1 /2)) = F (2) = 5,
(F + К о К) (3)= F (3) + К (К (3)) = 12 + К (-М = 12 + 2) = 10-
36. Эта функция не является ни четной, ни нечетной. Она не является нечетной, так как, например, g(—1) = 0, а —g(l) = —У~2 ; она не является четной, поскольку, скажем, g(—1)= = 0. a g(l) =/2.
44. Область определения этой функции может быть разбита на два интервала [а именно: (—оо, 0] и (0, оо)], на каждом из которых эта функция возрастает. Так, в случае интервала (—оо, 0], если Zi<Z 22, то гх + 1 < 22 + 1, так что f(2xX £(22). Точно так же в случае интервала (0, оо), если гх<22, то 2i2<Z22 (ПОСКОЛЬКУ Zi И Z2 ПОЛОЖИТвЛЬНЫ), Т. е. /(21Х /(22). Однако если эту функцию рассматривать на всей прямой, то она уже не будет возрастающей (но не будет и убывающей), так как, например, 0 < — , но 1 = f(0)> f » в то время
как на интервале (—оо, 0), как мы уже видели выше, функция возрастает.
§2
4. График функции х х2 + Згх + 4 пересекает прямую у = 1 (т. е. график функции х»-> 1) в таких точках, что х2 + Згх + 4 = 1, т. е. х2 + Зхг +3 = 0. Наша задача состоит, следовательно, в определении таких значений г, для которых функция х х2 + Зхг + 3 имеет два различных корня. Но для этой последней функции D = 4* ЬЗ — (Зг)2 = 12—92я. Мы хотим узнать, когда D<0, и, значит, должны решить неравенство 12—9г2 <С 0, или 9г2 > 12* т. е. z2> 4/3. Таким образом, получаем гХ—З^Сз/З или г> 2^3/3.
490
Решения упражнений, помеченных знаком А (глава 3)
26. Так как число —2 является двойным, а число 2 — простым корнем многочлена, то этот многочлен делится на (у — 2)(у + 2)2 = у3 + 2^2 — 4у — 8. Разделим уъ — 7у3 + 2у2 + 4- 12^ — 8 на у3 + 2у2 — 4у — 8. Деление выполняется без остатка; частное равно у2 — 2у + + 1 = (У — В2» так что 1 будет двойным корнем нашего многочлена.
36. а) Находим
(/ogofto/) (х) = (Z»goA)(l + l^x )1/2= fog (4(1 + V х. )-|/2) =
= / (у (1 + /х )'/4)= (1 + Y /2 (1 + /х )1/8у/2 .
б) При х — 225 = 152 мы получаем ]Л“2.
44. Так как
-----<*.-3)<*-_3)_.
(х + 3> («-3) («-3)
то ясно, что функция fi не определена при х = 3 и при х = —3. Если х =/= 3, то х — 3 =/= 0, и мы можем, разделив чисЛитель и знаменатель на (х — З)2, получить функцию g(x)=l/(x + 3). Если х=£3, то Дх) и g(x) совпадают, т. е. принимают одинаковые значения для каждого действительного значения х. Но при х=3 имеем g(x) = 1/6, в то время как Дх) не определена. Как объяснялось в тексте, естественно положить, что ДЗ) = 1/6 по определению. Однако никакое «естественное» значение не может быть приписано функции Ц при х = —3, так как при приближении х к —3 функция Дх) принимает сколь угодно большие по модулю и положительные, и отрицательные значения.
§ 3
16. Мы покажем, что Дх)< А, если | х |< У А — 1. Неравенство х2 + 1 < А равносильно неравенству х2 < А — 1, которое, поскольку А> 1, равносильно системе неравенств — У А — 1 < х < У А — 1. А эта система (в свою очередь) равносильна тому, что | х | = = |х — 0 |< У А — 1. Следовательно, если а = У А — 1 и если | х | < а, то будет справедливо неравенство Дх)< А. Так как Дх)=х2+1>1 при всех х, то Дх) никогда не может стать меньше такого числа А, которое само не превосходит !.
Замечание. Далее в решениях мы будем пользоваться символом <-> для замены слова «равносильно».
26. Докажем, что выполняются свойства (I) и (II) определения непрерывности. (I). Пусть А > 2 == h(—1). Если />—1, то h(t) = —2t<Z 2< А. Предположим, что /< —1. Тогда h(t) = /2 + 1< А <-> t2< А — I +* — У А — I < /< УА — i — У А —14- 1 < t + 4- 1 < У А — 14" 1- Так как —1, то । t 4" 1 | = —(/ + 1). Левая часть последнего нера-
венства приводится к виду У А — 1— 1> | t 4" 1 I* Так как А> 2, то У А—1—1 > 0. Положим 6 = ]/А — 1 — 1. Тогда если | /4" 1 |<6, т. е. если t принадлежит интервалу длины 26 с центром в точке —1, то h(t)<Z А. (II). Пусть 2 = h(—1). Если —1, то h(t) =
= t2 4- 1 >> 2> В. Предположим, что —1. Тогда h (/) = —2/> В <-> /< — — В <->
t + 1< 1 —х—в.
Так как —1, то | t 4“ 1 | = Н" 1. Следовательно, пола-
гаем 6=1 — -у- 0. Тогда если | t 4- 1 | < 6, то имеем Л(/)> В.
32. Пусть заданое > 0; мы должны найти такое число 6 (которое в этом и в общем случае зависит от е), что для каждого х, для которого |х— 1 |<6, справедливо неравенство U(*)—/ (1) |<е. или|/ (х) —1 | < е.Но | / (х)—1 | < е <-> | — 1 |<е *+ |
2 5е «бе
< е о -у- |х — 1|<е <-> | х — 1 |< — Поэтому, если мы выберем 6 = —, то из неравенства । х — 1 |< 6 будет следовать, что | Дх) —Д1) |<в.
Решения упражнений, помеченных знаком (глава 3)
491
44. Мы будем следовать доказательству теоремы 6: Дх) = х9(1 —100/х° 4“ 3/х6 — 2/х9). Выберем | х | столь большим, чтобы каждое из значений | — 100/х6 |, |3/хв | и | — 2/х9 | было меньше, чем 1/4; с помощью небольшого числа проб убеждаемся в том, что достаточно взять |х| = 4. Положим К = 4. Тогда, рассуждая, как в последнем абзаце доказательства, мы видим, что если х>> 4, то Дх)> 0, а если х< —4, то Дх)< 0. Это означает, что функция Дх) имеет корень на отрезке [—4, 4]. Так как ни 4. ни—4 не являются корнями Дх) (проверьте это!), то f имеет корень в интервале (—4, 4).
46. Можно показать, что заданная функция непрерывна и монотонно убывает; поэтому для нее существует обратная функция. Однако нам нужно н а й т и эту обратную функцию. Пусть у = д/) = (3/ 4- 1 )/t = 3 + 1/t. Тогда у — 3 = 1//, или t = —. Таким образом, t =g(y) =
У — 3
= ------ и есть искомая функция (где у теперь является независимой переменной). Однако
У — 3
обычно независимую переменную обозначают той же буквой, что и в исходной функции, так что мы должны сказать, что «обратной функцией является функция t »-► ------». Применен-
ный здесь метод является вполне общим: если мы знаем, что для функции у = Дх) существует обратная функция, то для нахождения этой обратной функции достаточно решить уравнение у = Дх) относительно х. После того как это сделано, обычно меняют ролями х и у так, чтобы буква х обозначала независимую переменную.
§4
2. Функция А определена и непрерывна при /= 4 и h (4) =1/17. Следовательно, lim А (0 = h (4) = -^--^->4 17
f(x) = g(x) при по о пределе-
1 и, значит, по-
10. Положим f (х) = (хУх -x-j-Ух —1)/(х — 1). Функция f не определена при х=1. Мы попытаемся доопределить функцию f в точке х = 1 так, чтобы она была непрерывной и при х = 1. Как обычно мы это делаем, заменим функцию f такой функцией g, что х =/= 1, причем функция g определена и непрерывна при х = 1, и после этого, нию, положим f (1) = g (1). Мы имеем
Нх)=[(/Т - 1) (х 4- l)J/[(/T - 1) (УГ + 1)].
Это разложение допустимо^ поскольку нас интересуют значения х, близкие к ложительные, так что Ух определен. Еслих=/=1, то Ух —1 =/= 0, так что f (х) = g (х) = = х 4- 1/ух 4- 1. Функция g определена и непрерывна при х= 1, причем g (1) = 1. По определению, положим /(1) = 1. Тогда функция f будет непрерывна при х=1 и, значит, lim/(х) = / (1) = 1.
х—И
14. Так как обе функции у*-*у2-\-у и yt-+l2y3 непрерывны всюду и принимают при #= 1/3 одно и то же значение 4/9, то функцию Н (у) можно сделать непрерывной в точке у= 1/3, по-/ 1 \ 4
' лагая Н I —1 = — . Следовательно,
lim Н (у) = Н . 1
^"3
16. Нам надо найти предел lim yfg(x). Если положить А(х) = }/Гх', то функцию Уfg х—>о
можно рассматривать как функцию hofg. Мы знаем, что lim (fg) (х) = lim f (х) lim g (x) = x—M) x~*°
= 12-3 = 36 (теорема 1). Далее, можно воспользоваться теоремой 2 для того, чтобы найти 17*
492
Решения упражнений, помеченных знаком А (глава 3)
предел lim (hofg)(x), если известен предел lim Л(х). Это легко: функция h непрерывна в х—*о х—>36
точке 36 и Л (36) = 6. Следовательно, lim h (х) = 6. Теперь воспользуемся теоремой 2. (Функ-х—>36
ция /, фигурирующая в этой теореме, •— это функция fg нашего упражнения, а функция g теоремы— эта наша функция Л.) Так как lim (fg) (х) = 36 и lim h (х) = 6, то lim (h°fg) (х) = 6.
х->0 х-»36 х->0
26. а) Для определения предела на бесконечности рациональных функций (отношений многочленов) полезен следующий прием. Разделим числитель и знаменатель на член знаменателя, имеющий наивысшую степень. Так мы получим
уЗ уЗ / у2 у
lim----------= lim —— ------------= lim ----------------
х->4-00 14-х1 2 х->+» 1/х24-х2/х2 х-н-оо 1/х24-1
Ясно, что при х —► 4* оо знаменатель стремится к 1, в то время как числитель становится сколь угодно большим. Этим доказано утверждение а).
б) Имеем lim Х->—со
X3 X
= lim --------- 14-х2--------------------х->-с« 1/х24-1
оо.
в) Так как функция мы имеем
х3 14-х2
X3
Но тогда и lim -----------— = 8/5.
х->2+ 1 4- х2
непрерывна при х = 2и при х=2 принимает значение 8/5, то
lim х3/(1 4-х2) = 8/5. х->2
(Заметим следующее: из того, что «lim/(x) = a», вытекает, Х-^Хф
что верны оба утверждения: «lim f (х) = а» и «lim f (х) = а», но только одного какого-нибудь х-*х х->х
о о
из двух последних утверждений не достаточно для справедливости первого.)
§ 5
4. По определению, функция А при и = 3 принимает значение 3+1 = 4. Однако если и->3+, т. е. если и приближается к 3, принимая значения, большие, чем 3, то значения функции А вычисляются по формуле и2 — 1. Ясно, что при и—>3+функция Л(и) приближается к (З)2—1 = = 8. Но, по определению, Л(3) = 4. Однако мы можем переопределить А так, чтобы было 4(3) = 8. Так переопределенная функция Л, рассматриваемая при и > 3, непрерывна в точке и = 3. Следовательно, lim А(и) = 8.
«-*3+
12. Если х =£ 1, но х близко к 1, то (х + 1)/ |х — 1 |> 0. Далее, Нт | х — 1 | /(х + 1) = X—>1
= 0. Следовательно, lim(x + 1)/ | х — 1 | = + оо. Но из существования предела при х ->х0 х->1
вытекает существование предела (причем того же самого!) и при х -> х0+, и при х -> Хо”. Следовательно, все три рассматриваемые в этом упражнении предела равны + оо.
18. Пользуясь методом, проиллюстрированным на предыдущих примерах,получаем
1 + у + 2у2 = 1 + 1// + 2//2 = Пт ^ + / + 2 = _ _L.
10 4- 5у — 4г/2 10 + 5/Z — 4//2 >о Ю/2 +5/ — 4 2
1 Таким образом, и в пунктах а) и б) этого упражнения ответ равен — —.
Решения упражнений, помеченных знаком ▲ (главы 3, 4)
493
24. Пусть р (х) = rxn + rn_ix"-i J------F гхх + г0 и q (х) = sxm + sm_1x'n-‘ Н----f- sxx+ se.
Тогда
. PW = llm PQ/0 = iim ^', + r„-X/<"-» + -- - +rxy/ + r, .
хЛ» q (x) /-0 q (1 /0 r-o s/tm + H-------+ sjt + s0
Умножим числитель и знаменатель последней дроби на tm', мы получим
р (X) ,. rtm~n + гя_1/'»-'>-1 +-1- ritm-^ + г^т
11 m -----= lim ----------------------------—-------—--------
х—*оо q (х) /—*0 S 4- sm-^ 4“ • • ’ 4* 4- so^m
Так как т — п^> 0» то в каждом члене числителя t стоит в положительной степени. Следовательно, каждый член числителя при t -> 0 стремится к нулю. Так как знаменатель стремится к $, то искомый предел равен О/s = 0. Ответом на все три пункта этого упражнения будет 0.
32. Мы вычислим сперва Нт 1/(х2 4-х— 2) = lim 1/[(х4“ 2) (х—1)]. Если х<1, но х х—►!" х—>1“
близко к Ь, то х4-2 положительно, ах—1 отрицательно; следовательно, 1/(х24-х— 2) отрицательно. Так как х2 4- х — 2->0 при х->1“, то liml/(x24-x — 2) = — оо. Поэтому
lim (2x4-l)i°°/(x24-x —2)= lim (2х 4- I)100 lim 1/(х2 4- х — 2) = (З100) (— оо) = — оо.
X—►!" X—►]" х—И”
§ 6
8. Повторим доказательство, проведенное в тексте. Пусть уо удовлетворяет неравенству а < Уо < Р, а В — такое число, что g(#o)> В. Нам надо доказать, что g(yY> В для всех у, близких к уо. Мы можем считать, что В > а (поскольку функция g не принимает значений, меньших, чем а). Положим g(yo) = Bq. Тогда а < Bq < b и [(Bq) = уо. Пусть [(В) = у^. Тогда У! > а. Так как Во> В[Во = gG/o)> и функция j — монотонно возрастающая, то уо = = f(B0)> [(В) = yv Если, далее, у удовлетворяет неравенству yi<Z у<2 Уо, то, по теореме о промежуточном значении, у = [(C) для некоторого С, удовлетворяющего неравенству B<Z < C<Z Bq. Так как у = f(C), то g(y) = G. Следовательно, для всех у, удовлетворяющих неравенству f/f < y<Z уо, имеем g(y)Z> В. С другой стороны, поскольку g возрастает, то при у^> Уо и подавно g(y)> В. Следовательно, вблизи у о имеем g(y)Z> В, и свойство II доказано.
Глава 4
§ 1
16. Пусть f (i) = Z/(/2 — 1). Тогда
2 4-Л 2
xz Л .. (2 4- Л)2 — 1 — 3 .. — 26 — 5
f (2) = lim ---------------------= lim ------
л—>о h л—>о 362 4~ 126 4” 9
Уравнение искомой касательной
22. Имеем
1
имеет вид s — — = — — (t ~ 2), или 9s 4“ 5/ — 16 = 0. о 9
ггг 1>п. 2(х + й)-3 2х —3 (2х — 3) — [2(х + й) — 3]
g (х) = lim -----------------------------= lim --------------------------------- s=
h-*o ft h-H) Й (2x — 3) (2 (X + ft) — 3)]
ljm —2ft_______________[jm _____________—2__________________________2
h™ ft (2x — 3) [2 (x + ft) — 3| (2x — 3) [2 (x + ft) — 3] (2x — 3)a ’
494
Решения упражнений, помеченных знаком ± (глава 4)
36. Символ —— I означает: «производная (дайрой функции), вычисленная при значении
\ dt Jj
ds
t = — 1». Поэтому мы находим сперва производную — :
di
____________1__________ 1
ds (t + h)* 4- (t + h) + 1 ~ /a + / + l
—— — lim ------------------------------------ ==
dt h—*o h
= nm f2 + / + 1 - [(/ + ft)2 + (* + /0 + 1] _ Нт ____— 2//t —ft2—ft_______ =
h™0 h(t*+t + 1) [(/ + ft)2'+ (t + ft) 4- 1] ft-H) ft(/2 + /+ l)l(/ + ft)2 + (*+ft) + l]
__Hm ____________- 2/ - ft — 1________
ft^o (/2 +/+1) [(/+ft)2+(*+ ft) + 1]
— 2/ — 1
Так как последняя функция непрерывна при ft = 0, то искомый предел равен ^2"~ i)2~ * Следовательно,
/ ds \ _ — 2 (— 1) — 1___1___t
UJ/=_|= [(—I)2 — 1 4-I]2 ““ 1 ~
42. Пусть f (/) = — . Тогда (ср. с § 1.6) f' (/) = — — , т. е. f' (1) = — 1. Так как t F
/(1) = 1, то имеем [используя формулу (8) при х0 = 1]
f(0 = l-l(/-l)4-r(Z) (/-1).
Таким образом,
-р=2-/ + r(t)
и, значит,
Следовательно, r(t) непрерывна при t = 1 и г(1) = 0.
21
66. Пользуясь формулой v(t) = —20/, получаем —42 = —20/, или t = —-—, когда ско-Р
рость равна 42 м/с. Какое расстояние кирпич пролетит за это время? Пользуясь формулой s = — р/2, получаем
s = —0 • 441/0 2, или s = —441/0 « 90 м;
это означает, что кирпич будет на 90 м ниже той точки, с которой он падает.
§ 2 6. В силу формулы (5) имеем (fg)' = fg 4- fg' • Следовательно, (fe)'(0) = (Kg + fe')(0) = (f;g)(Q) + №')(0) = t'{O)g(O) + t(O)g'(O) = i + (-3) = -2.
g'/ — g/'
По формуле (7), (g/f)' =--------- и, значит,
P
( /h,(m = e'f-gf' 0 = (g'f) (Q)-(gD (0) = g' (Q)f(0)-g(0)f(0) = —3 — 1
ig/л (f f2 ( ) p (0) у (0)]21 j
Решения упражнений, помеченных знаком А (глава 4)
495
18. Пусть у = f(x). Для того чтобы найти наклон искомой прямой, вычислим Пользуясь правилом (7) для производной частного, находим
е 2х (х3 4- 1) — Зх2 (ха + 1)
f w =----------ГТТ’пз----------’
(х3 + 1)а
так что j5'(0) = 0 и уравнение искомой касательной имеет вид у — 1 = 0(х — 0), или у = 1.
38. Имеем f(t) = (/3 + 2/ — /1/2) 1/2 .Воспользуемся цепным правилом (правилом дифференцирования сложной функции), применив его к функции I = g°h, где g(u) = н1/2и h(t) = t3 + + 2t — tl/2. Мы получим
Г (t) = g' (Л (0) h' (t) = -— (P + 21 — l1/2)“1/2 (з12 + 2 — -j- t- = —+ 2 X№VT) K ’ W Р + ъ-уТ
( dg\
62. а) Производную —| можно обозначить через g' (2). Полагая yQ = 2, из утвер-\ dy )у=2
ждения теоремы 7 заключаем, что нам надо найти такое число х0, что /(х0) = 2, т. е. что мы должны решить уравнение х4 4-1 = 2. Ясно, что (вещественными) решениями этого уравнения
являются только значения х = ± 1, а так как область, в которой наша функция g (у) возрастает, — это только х>0, томы можем исключить значение х = — 1, так что интересующее нас значение х0 — это только х0= 1. Тогда, пользуясь теоремой 7, получаем g' (2) = 1//' (1) =
= 1/4, поскольку /' (х) = 4х3. Подробнее: g' (2) = g' (f (1)) = = — . Аналогично,
/ dg\ 11
я = (82) = V <3» = 7ГТЧГ = 17^ *
\ dy J у=82 f (3) 108
б) Рассуждая так же, как и выше, получаем:
( dh \ , 1 1
— = h'(2) = h (f = —— = - — .
\ dy ]у=2 Г (—1) 4
! dh\ 11
— =Л '(82) = h '(/(—3)) = ——-=- —
\ dy ]у=Ъ2 Г (— 3) 108
§ 3
16. Здесь мы воспользуемся цепным правилом [если положить F(x) = -г8, то G = F°H], в силу которого
G'(x) = 3[Я(х)]2Я'(х).
Далее, используя правило дифференцирования произведения двух функций, получаем
G"(x) = [6Я(х)Я'(х)]Я'(х) + 3[Я(х)РЯ"(х). Следовательно,
G" (1) = 6 • 2 • — • — + 3 • 22 • — = 4— • 3 3 4 3
32. Пользуясь («релятивистской») формулой этого параграфа, получаем г • см / см \ / у------------ см /
10-^—= /п0 ^5 — уK(l- 0.64)3 =5/п0 —/о,216,
или /по = 0,432 г. Классическая физика Ньютона дает значение массы, равное 2 г.
496
Решения упражнений, помеченных знаком А (глава 4)
§ 4
2. Эта функция не определена при t = —1. Если рассматривать f только в интервале 3
(—оо, —1), находим f'(0= ч 1ч2 >0- Следовательно, в интервале (—оо, —1) функция / воз-
т 1)
растает. Аналогично, если рассматривать f только в интервале (—1, оо), то f (0> 0 и / тоже возрастает.
12. Имеем £'(х) = ЮОх99 + 1 ОООх099 = 100дг99( 1 + 10х900). Так как х900 > 0 при всех х, то f'(x) = 0 только при лг=О. Следовательно, х = 0 является единственной критической точкой. Далее, f"(дг) = 9900 х98 + 999000 х998 и f"(0) = 0. Поэтому теорема 5 (исследование с помощью второй производной) здесь неприменима. Однако если мы заметим, что f'(x)<Z 0 при х<0 и f'(x)> 0 при х> 0, то мы можем воспользоваться первой строкой таблицы, непосредственно предшествующей теореме 5 (при хо = 0); мы получим тогда, что функция / имеет при х — 0 строгий локальный минимум. (Только что примененный нами прием, т. е. определение знака первой производной слева и справа от критической точки и использование затем соответствующей таблицы, называется исследованием с помощью первой производной.)
32. Пусть х — длина стороны основания, ah — высота коробки. Задача состоит в том, чтобы найти функцию [, выражающую площадь поверхности коробки через х, а затем «минимизировать» эту функцию f. Так как V фиксировано и V = х2Л, то h = —(Ясно, что значение х = 0 здесь бессмысленно.) Площадь поверхности коробки равна
4V
2х2 -|- 4xh = 2х2 +--•
х
4V -Положим f (х) = 2х2 4------ . Мы представили площадь
X
4V
f (х) = 4х — —— этой функции равна х2
поверхности коробки как функцию
нулю в том и только в том случае, ) = 12 > О и, значит, f
— , то х3
от х. Производная V если х = — , или х2
имеет при х = V локальный минимум. Для того чтобы убедиться в том, что это также и абсолютный минимум, заметим, что если 0< х < V , то /' (х) < 0 и f убывает, а если xZ>V^ , то /'(х) > 0 и / возрастает. Следовательно, размеры коробки должны быть такими: х — V и h = , т. е. коробка должна быть кубом. ___________
44. Пусть (х, у) — какая-то точка кривой. Тогда у = р^х2 4- 6х 4- 10. Расстояние d от точки (1,0) до точки (х, у) равно
d = /(х—l)24-(t/ —О)2 = V х2 — 2х 4- 1 4- !/а .
Мы попытаемся «минимизировать» d. Положив f = d2t мы можем вместо этого минимизировать /: f(x) = х2 — 2х 4- 1 + У2 = х2 — 2х 4- 1 + (ха + 6х 4“ Ю) = 2х2 4- 4х 4- Н.
Мы имеем f'(x) = 4х 4~ 4. Единственной критической точкой является х = —1 и f"(—1) = = 4> 0, так что при х = —1 будет локальный минимум. Ясно, что это будет и абсолютный минимум, поскольку кривая f является параболой. Так как при х=—1 функция d принимает значение ]/4 + 5 = 3, то наименьшее расстояние здесь равно 3.
х 1
58. Имеем f(x) = ------ при х > 0 и Г(х) =-------—0» так что ПРИ х > ° функция i
х4-1 ' (х4-1)2
возрастает. Далее,
2
Г W = -
(х+1)3
Решения упражнений, помеченных знаком Л (глава 4)
497
Рис. Р.1
Рис. Р.2
поэтому при х>0 кривая обращена выпуклостью вверх. При х>0 нет точек локального максимума или минимума, а также точек перегиба; f (+ оо) == 1. Если х < 0, то
Н-1+) =
1,
так что при
X
f (х) = —----- . Значение х =— 1 является точкой разрыва функции. При этом
х + 1
= 4-00 и / (—1 ”) = — оо. Производная /'(*) = —”--—
(х+ 1)а
2
х<0 функция f убывает; f" (х) = ----— положительна при х>—1 и отрицательна при
(х 4- I)3
х<—1 и, значит, f выпукла вниз при —1<х<0 и выпукла вверх при —оо<х<—1; f (— оо) = — 1 (рис. Р.1). 8 б
74. Положим / (х) =—-—— . Функция / не определена при х=0. При х=/=0 имеем х3 х
/ (х) = 2 (4 — Зх2)/х3, так что корни этой функции х = ± 2}^3 /3. Далее, /' (х) = 6 (х2 — 4)/х4 и /' (х) — 0 при х= ±2; f" (х) = 12 (8 — х2)/хБ и, значит, f" (2) >0, так что в точке (2, —2) имеем локальный минимум, а/" (—2) < 0 и, значит, в точке (—2, 2)—локальный максимум. Яри х= ± 2)^2 имеем /" (х) = 0, причем /" при переходе через эти значения меняет знак, и поэтому каждая из этих точек является точкой перегиба. Наконец, /(0+)= + оо, / (0~) = —оо, / (4-оо) = / (—оо) = О (рис. Р.2).
§5
14. Так как A"(v) = 3v2, то Л'(^) = Зи3/3 + С = v3 + С. Но поскольку Л'(0) =1» тс О3 + С = 1 и С = 1. Следовательно, Л'(^) = v8 + 1. Далее, A(v) = с4/4 + v + k, где k — некоторая постоянная. Но поскольку 4(0) = —1, то А = —1. Таким образом, искомой функцией будет A (v) = и*/4 + v — 1.
18. Если мяч достигает максимальной высоты 18 м, то его скорость будет равна нулю при том значении /, для которого s(/) = 18 м. Пусть этим значением t будет Тогда tx = v0/g,
498
Решения упражнений, помеченных знаком А (главы 4, 5)
или оо = gh [так как = —gtx + Do = 0]. Далее, s(fj) = — — gt\ + = 18. Заменяя Dq на gti, получим — ^4“ gt\ = 18, или tf = 6/ ]/~g. Так как ио = gti, то но =
= 6 Уg т 18,8 м/с2. Это есть минимальное значение требуемой скорости.
§7
4. Если у приближается к значению 3 слева, то f(y) = # + 1 Д» значит» /'(3”) = 1. Если у приближается к значению 3 справа, то f(y) = у2 — 2у + 1 и производная Здесь равна 2у — 2, т. е. при у — 3 ее значение равно 4: f (З4) = 4.
Глава 5
§ 1
4. Парабола 1 — у2 имеет в точности такую же форму, что и парабола у2, только последняя перевернута и смещена на единицу вверх. Таким образом, искомая площадь равна заштрихованной площади на рис. Р.З снизу, а эта площадь равна площади квадрата, верхняя правая вершина которого находится в точке (1, 1), минус площадь, ограниченная сверху кривой у2 в пре-
Г 1 2
делах от 0 до 1. Следовательно, данный интеграл равен 1 — I y2dy = 1 — — = —.
о
1 b —а
20. Поскольку функция у=— убывает на [1,2] (рис. Р.4), сосчитаем
/V \ 2 / 2N
тервал [1,2] на две равные дящая ниже нашей кривой,
2 Таким образом, J (х) dx =
N [f(a)-f(b)\ = Поэтому разделим ин-функция <р (х), прохо-
X
Если W = 2, то не превосходит — . показано на рисунке. Ступенчатая 1 и равна — на интервале
части, как 2 равна —
1 2
2 ' 3
на интервале
щая выше кривой, равна 1 на интервале р 1 12 5
но, <Hx)dx=T.l+T.T = -
2 . С dx \
показано, что | — = In 2 « 0,6931.
11 7
~ • — = — . Ступенчатая функция ф (х), проходя-
3 \ 2 / 3 \
• ~1 и — — на интервале I —, 21
7 с dx Ю
• Таким образом, — < I — < — .
12 J х 12
Следователь -
В гл. 6 будет
§ 2
С 1 х«
2. Если х < 2, то G (х) = — I <р (г) dr = — — (2 — х) (2 — х) = ^- 2 + 2х — — . (При
J 2 2
х вычислении интеграла мы воспользовались формулой площади треугольника.) При этом G' (х) =
X J
= 2 х = у (х). Если х > 2, то G (х) = f <р (г) dr = — (х — 2) (4 + 2х) = х2 — 4. (Здесь мы 2
Решения упражнений, помеченных знаком А (глава 5)
499
Рис. Р.4
Рис. Р.3
2
используем формулу площади трапеции.) При этом G' (х) = 2х ---------- --------- --------- ----------- —л ч той же
непрерывна, нетрудно проверить, построив в одной и ций — 2 4- 2х — — х2 при х < 2 и х2 — 4 при х > 2.
5
16. Искомая площадь равна J У^г—1 dz. Таким
2
первообразной для функции 1 и применении г------ 2 3/2
У г—1 является — (г — 1) . Следовательно, искомая площадь равна
3
-1 (5— 1)3/2 — -у (2—1)3/2 О о
(рис. Р.5). То, что функция G системе координат графики функ-
образом, задача состоит в определении
основной теоремы. Первообразной
для
2 2
т-8-т‘ =
11 3
20. Заметим, что график функции vt-*v ]/Ъ2 4-9 при 0 < и < 4
С v f/'v2 4- 9 do.
проходит через Следовательно, искомая
начало координат площадь
4 эта функция положительна.
Так как функция (сЯ 4- 9)3/2 является первообразной для vf^v2 4- 9 , 3
и что равна
то
г__________ 1 3/2 |4 125 27
v Kf2 + 9 dv = — (t>« + 9) ' = —— — —
3 Io 3 3
2
= 32Т-
h (x) = J (s3 — 1) ds. Тогда h (x) = — s|
о 0
X^ X®
первообразная для /г (x), т. e. (x) = Л (x). Следовательно, f' (x) = — —x, и f (x) =------
4 ‘ 20
— 4- С. Так как f (0) = — 1, то C = -l; поэтому [ (x) = — —— — 1 и f (— 1) =
Z ZU z
1 1 31
= — —— -------— 1 == — ---- •
20 2 20
32. Пусть
— x. Далее, f (x)
есть
500
Решения упражнений, помеченных знаком ± (глава 5)
§ 3
28. Сначала мы вычислим интеграл
4
I4
4
4 4
4
Следовательно,
1
' я х2 xdx — —
2
Р ( ])2 2 ~ 2
1 т=°-
2
* 32. Так как d (2 Ух 4-х4 — 1) = f (х) dx, то f (х) =
d(2}<x+x4-l) „
---------------. Следовательно,
dx
Н*)=—=- + 4*3 и f (>)= 1 +4 = 5. У*
46. Если произведение двух функций интегрируется по частям, то функция, принимаемая за f, должна быть такой, что интеграл от df «берется легче», чем интеграл от f. Ясно, что в нашем случае нам выгодно принять за f(z) = 2z — 3; тогда dfj = 2. Таким образом, полагаем f(z) = = 2z — 3 и dg(z) = У z — 3 dz. Мы имеем
f (2г — 3) Уг — 3dz = f (2г — 3) d [—(г — З)3/2 1 =-|- f (2г — 3) d (г — З)3/2 . J J L 3 J 3 J
Теперь мы можем применить формулу J f dg = fg — J g df\ при этом получаем
-2- f (2z — 3) d (г — З)3/2 = Г (2г — 3) (г — З)3/2 — f (г - З)3/2 d (2г - 3)1 =
- 4 [ (2г-3>(г-3)«- (<,-3),Л 23г1 = ” (2г — 3) (г — 3)3/! — А [(г-З)’" «г-
о L J J J о J
= -у (2г-3)(г-3)3/2- --------1- (г-3)5/2 +С = (г-З)3/2 (2г- 1) + С.
о о о о
68. Попробуем дрименить подстановку будет содержать #1/2. Функция ф(#) при 3
Так как ф'(у) = #1/2, то получаем у^2
= Ф (У) — !/3/2+ 1» оправдываемую тем, что ф*(у) 3 1/9
0 < у < 1 имеет непрерывную производную —
2
= ф'(у) и, следовательно,
о
j ( у1/2 (у3/2 + 01/2 лу = 4- [ [ф (у)]1/2 Ф' (у) <iy = t/ « J
о о
£
3
А Л2 2 = JL(2|42--i). о 1 у
Решения упражнений, помеченных знаком А (глава 5)
501
Рис. Р.8
74. «Очевидной* является здесь подстановка t = ф(г) = z + 1. Производная —-— = 1 dz
непрерывна на [0, 1]. Однако dt = dz, и может показаться, что наша подстановка мало облегчает дело. На самом же деле она оказывается полезной, так как если t = г + 1, то г = / — 1 и мы имеем
щадь
§ 4
14. Наши кривые пересекаются в точках (—3, 9), (0, 0) и (4, 16) (рис. Р. 6). Искомая
пло-
равна
4
(х3 — 12х — х2) dx 4- J (х2 — х3 4* 12х) dx = о
(х3 х4 \ |4 /Я1 \ / 64 \ 1
— -—4-6x4 =-( — -544-9) 4-1 4“ -644-96) = 78—.
3 4 J |о \ 4 J \ 3 ) 12
16. Основание тела изображено на рис. Р.7. Для каждого значения х, где 0 < х < 1, поперечное сечение представляет собой квадрат со стороной х. Следовательно, S(x) = х2 и
1 1
V = J S (х) dx = J х2 dx = .
о о
34. Касательная к нашей кривой в
точке
х = — I у — — 1; она пересекает ось объем У, можно вычислить объем ограниченной кривой х = у \т. е. у
2
(1, 1) имеет уравнение у — 1 = — (а? — 1), О
у = — (рис. Р.8). Чтобы получить искомый о
или
У при
Vlt получающийся при вращении вокруг оси у области, х2/3) в пределах от (/= 0 до у=1, и объем
502
Решения упражнений, помеченных знаком А (глава 5)
получающийся при вращении до у = 1; тогда
вокруг оси у прямой х = Окончательно получаем
1 в пределах от у — — о
следовательно,
V2 = « '
1/з‘
о
2 У4 I1 dy = = "7
4 10 4
|2 9
1 2тс
1/3 9
V = Vi-Vt.
и
U 2к U
= ~ ~ = *36
§ 5
К (0 = ~ rn[v (О]2 = ““ mg2t2 и, значит, К' (t) = mg2ft а
14. Так как
o(t) = — gt, то
следовательно, К" (О = mg2постоянна.
уМ
18. Заметим, что в формулу (13) входит g. Но g = —~ [ср. с формулой (9)], где М есть R2
масса планеты, а 7? — ее радиус. Формулу (13) можно, следовательно, переписать в виде о = = У 2?Л1/7?2 • R — У2у~ УМ/R , где теперь и есть скорость удаления частицы от тела массы М и радиуса R. В нашем случае v =]^13,34* 10”8 У 2,65 • 1020 = 1^35,35 • 10% или приближенно 6 • 10* см/с = 60 км/с.
§ 6
8. Подынтегральная функция обращается в бесконечность при v = 1. Следовательно, имеем
V2
Г2
—4/5do-|- f
r~4/bdv= lim f v(v2—1)
К2 5
f о(ог —l)-4/5do= lim — (о2—1)1/5
il. 2
2
5
+ lim — (v2 — l)1/s e-»o*- 2
0
— 2е),/5+1] +lim [1 — (е2 + 2е)1/51 = 5. е-О* 2
5 (
= lim — l(e2 £-*0+ 2
16. Заметим, что
1)"”2/3 dx = lim f (x — 1) 2/3 dx = lim3(x—1),/3 e-o* 5 e->0*
теграл сходится.
= lim (— Зе|/3 + 3) = 3.
0 e->&f
так что /(x — 1)2/3 < l/(x — 1)2/3 . Поэтому данный ин-
Решения упражнений, помеченных знаком Д (глава 6)
503
Глава 6
§ 1
„ d [(arccos u) (arccos 2«)1 36. Имеем ----------------------------- = arccos и •
du
— 1 —1
= arccos и •------ • 2+ arccos 2u • —------ — _______
У1 — 4u2 У1 — и2 У1 — 4u2
54. Положим t = 2г + 1. Тогда и = cos2 t • sin t2 и du d cos2 / ft d sin t2 d cos21 d cos t
di
d cos2 t
—-------sin t2 + cos21
di di
d arccos 2u
------------ + arccos 2u • du
2 arccos и
arccos 2и
У1 — и2
d sin t2
J , sin t2 4- cos21------------
d cos t dt d (t2)
darccos и du
dt
= 2 cos t (— sin t) sin t2 + cos21 • cos t2 • 2t = 2 cos t (t cos t cos t2 — sin t sin f2).
Итак, du dz dt dz
60. Положим и = Ух . Тогда du = 1/(2 Ух) dx. Следовательно,
J cos ]/xdx I /7 = 21 cos и du= 2 sin и + C = 2 sin x + C.
82. Имеем cos2 x sin2 x = — sin2 2x. Ho sin22x = ---S2L15 . значит sin2 x cos2x = —-
4 2 8
du dt
—-------— = 4 cos (2г + 1) [(2г + 1) cos (2г + 1) cos (2г + I)2 — sin (2г + 1) sin (2г + I)2].
а/
1
— cos 4х и , следовательно, наш интеграл равен 8
Л1 1 \ 1 1
— — — cos 4x1 dx = — х — —- sin 4х + С. 8 8 / 8 32
л _ d tg х
4. Так как —------
dx
§ 2
= 1 + tg2 x, то мы имеем
= 2 tg x (1-J-tg® x) = 2Igx + 2tgs x.
d3 tg x
-^-= 2 (1 + tg2x) + 6 tg2 x (1 + tg2 x) = 6tg4x + 8tg2x + 2. 9л При x =------получаем
4
6
+ 2=6+84-2= 16.
22. Имеем
( 1
d x arctg-------
dx
= х •
2_ «—3/2 2
, 1
1
4- arctg —
Ух" 1
—-----— + arctg---
2(x+l) S у
Следовательно, / 1 d2 х arctg-------;
dx2
_ — (х + 1) х 1/2 + 2х1/2
1
4(х+ I)2
4 (X +1)2 Ух
504
Решения упражнений, помеченных знаком Д (глава 6)
34. Положим и = (0 = 2/3. Тогда <?' (0 = 6/2 > 0, (0 непрерывна и du = 6/2 dt. Теперь
имеем
Пользуясь = 19,081.
2 16 16
f t2 dt 1 C du II 1 1
1 1 J-= V arctg “ =-7-arctg16 —'7‘arctg2-
J 1 + 4ie oJl + w о о 6
1 2 2
таблицами тригонометрических функций, находим, что tg 86° = 14,301 и tg 87° = 1 •
Интерполируя, получаем, что 16 % tg 86— % tg (259 л/540), или arctg 16 % 259л/540. <3
1 ° 1 Аналогично, 2^Xg63— = tg (127л/360), или arctg 2 % 127л/360. Следовательно, — arctg 16—-
— - arctg 2 % 137л/6480.
§ 3
d tg x
8. Так как sec2 x = —-— dx
, то
22. Имеем
/Г УТ
л х2 х2
1 х arcsec х dx = I arcsec х d -й-“ J J 2
С fg3 х
sec2 х tg2 х dx = I tg2 x d tg x = ——-•J «
— arcsec х
Т /Г
dx.
вычислить его, заметим, что /Г
Последний интеграл — несобственный. Чтобы
VT VT
С х С х dx
| ---—- — dx = lim I — = lim
J 2/^ZZJ J 2 Ух2—Г
= lim
2
2 ’
2
2
Следовательно,
/Г
x arcsec x dx =
1
x2
—— arcsec x
/2
1 1 t 1 л 1 л — 2
— — = arcsec У 2 — — arcsec 1 — — = — — — =--------------------
2 r 2 2 4 2 4
1
§4
12. Хотя arctg у определен для всех значений аргумента, In у определен только при у^> 0. Следовательно, наша функция имеет смысл только при у> 0. Производная ее равна
2у In у arctg у2
1 у
62. Так как Ни du — d In а и поскольку 1 + tg2(ln «) = sec2(ln и), наш интеграл равен J sec2 (In и) d (In и) = tg (In и) + С.
58. Следуя указанию, положим
1 а х24-х— х
вычислим а и Ъ. (Этот метод называется «разложением на элементарные дроби»; он будет рассмотрен в § 2 гл. 7.) Складывая дроби в правой части равенства, получим
1 ах 4- a -f- Ьх
b
х2 4* х
х2 4- х
Решения упражнений, помеченных знаком А (глава 6)
505
Поскольку эти дроби равны при всех значениях х (для которых х2 + х * 0), то их числители должны быть равны при всех значениях х. Полагая х = 0, находим, что а = 1. Далее, подставив х = 1, получим 1 = 2а + д = 2 + ^и, значит, b = —1. Мы нашли, что
1 1 1
а следовательно,
dx
— = ln[ x( — ln| x+ 1| +C.
§ 5
30. Так как г = (х2 4- 1)1п *, то г = е1п х 1п . Следовательно,
= е1п х 1ПСХЧ-1) Г 1п (X2 + о + 2х In *1 = (х2 + 1)1п х Г In + 1) 2xlnxl
dx [ х *2+lJ L х х2 + U *
40. Если подынтегральная функция представляет собой многочлен, умноженный на 6х, то применима формула интегрирования по частям, в которой надо многочлен принять за f, а е^х — за dg. Так мы получим
J х2ех dx = х2ех — J 2хех dx.
Снова применим метод интегрирования по частям, приняв на этот раз х за f, а e*dx за dg\ тогда мы получим
j x2ex dx = x2e* — 2 [xe* — J ex dxj = x2ex — 2xex 4- 2ex 4- C.
46. Рассмотрим функцию f(x) = е*х. Для нее справедливо равенство Ц'(х) = = 4f(x),
но f(l) =£ е. Заметим, однако, что если l'(x) = af(x) и если g(x) = С[(х), то и g‘(x) = ag(x). Следовательно, если функцию / заменить на Cf, то ее производная по-прежнему будет равна этой функции, умноженной на 4. Так как f(l) = е4, то надо принять С = 1/е3. Итак, мы заменим функцию е^х на — = е4*-3 и обозначим теперь через f новую функцию: f(x) = е4*"3.
Тогда равенства f'(x) = 4е4лг~3 = 4f(x) и f(l) = е будут справедливы. [Замечание: это есть частный случай общего метода, сформулированного перед упр. 49. Предположим, что искомая функция f имеет вид f(x) = тогда f'(x) = gf(x)e^x^=g'(x)t(x) = 4f(x). Следовательно, g(x) = 4х 4- С. Далее, f(x) = е4х+с и f(l) = е, а значит, С = —3. Далее проверяем, что функция [(х) = е4*-3 действительно обладает требуемыми свойствами.]
64. Как и при доказательстве теоремы 8, получаем
lim In (1 — х) х = lim <*+ l)ln<l ~= цт Г1п (1 — х)+ х->0 х-*0 X х->0 L
= lim In (1 — х) 4- Нт [— In (1 —- х)1 = 0 4 х->о Af->oL х J
Пользуясь тем же приемом, что, и в тексте, и полагая t= — х,
In (1-х) Г In (1+01 ln(l+/)-lnl
li m--------= lim I —----------I = — li m-----------------
x->o x t J м
Следовательно,
In (1 — х) lim —--------
х->о х будем иметь
k=i
1.
x-±l [ln(l-x)]£tl limln(l-x)2±l j
lim (1 — x) = lim e x = = e-1 = —
x-*o x->o e
t
1
506
Решения упражнений, помеченных знаком А (глава 6, 7)
74. Имеем
«<*‘/2г2 = — ch~1/2 = — ch-*'* г2 sh г2 = .
dz 2 dz 2 dz У ch z2
§ 6
8. Заметим прежде всего, что гкр = 4 • 1010/(2 • 108) = 2 • 102. Далее, г=-^-гкр=102 и р = р0/г = 4 • 1010/102 = 4 • 108. Следовательно,
= ^е-2-108' +е-240в'/ е2104 lOOdfc = о
= N(>e-2-lo,<+100e-21o,<l2'104 ‘ =Ыое~2Л04 + 1 , е~210,<
2 Ю» о +W 2-10» •
Искомый предел равен, второму члену.
§ 7
30. а) Используя равенства (20) и (9), получаем
arsech х = arch — = In (— + = In 1 K.! ~ ** .
X \ X f X2 J X
Мы пишем x, а не | x |, так как arsech х определен только при 0< х < 1.
б) Пользуясь равенствами (20) и (7) и замечая, что cosech х определен при 0 и при х< 0, получаем ______
arcosech х = arsh — = In j -L-j .
в) Пользуемся равенствами (19) и (15) и тем, что arcth х определен при | х |> 1.
Глава 7
§ 1
2. Имеем: х0 = 0, хг = 1/3, х2 = 2/3, х3 =1, = 4/3, хь = 5/3, = 2, h = 1/3.
Удобно составить таблицу этих значений х и соответствующих им значений у:
X 0 1/3 2/3 1 4/3 5/3 2
У 0 28/81 70/81 2 364/81 760/81 18
Мы можем сначала оценить погрешность. (Функция х4 + х монотонна на [0, 2].) Из равенства (8) следует, что Е < | 18—0 | • 1/3 = 6.
Из равенства (9) получаем Е < 1/12 (2—0)48* 1/9 = 8/9, так как | f'(x) | = | 12х2 | < 48 = = М 2. Мы можем теперь воспользоваться формулой трапеций:
2
J (хЧ- x)dx ж 1/6(0 + 56/81 + 140/81 + 4 + 728/81 + 1520/81 + 18) = 4226/486 « 8,69.
Конечно, нетрудно вычислить интеграл от функции х4 + х и непосредственно. Его точно значение равно 8,4.
Решения упражнений, помеченных знаком А (глава 7)
507
§ 2
18. Так как
+ 4 = 4[( )2 + 1] = 4(/2 + 1), где / = -£- и dt - у- ,
то
(* dx Г 2 dt____________1 Г dt______________1 Г 1 t / 1 \ С dt 1
J (х2 + 4)3 J 64 (Z2 + I)3 “ 32 J (/2 + I)3 ~ 32 [ 4 (1 + Z2)2 + V ~ 4 /J (1 + Z2)2 J=
1______I 3 Г 1 t / 1 \ Г dt ~[
= 128 (1 + Z2)2 + 128 [ 2 1 + Z2 + 2 / J 1 + <2 J “
1 * 3 t 3
~ 128 (1 4- Z2)2 + 256 1 + <2 + 256 aFCtg 1 + —
1 х 3 х 3 х
= “ЙТ (4 + х2)2 + 128 4 4-х2 + 256 aFCtg 2 + ’
34. Так как производная от дг2 — 2х + 2 равна 2х — 2, то нам полезно было бы иметь в числителе 2х — 2. Числитель нашей дроби равен 2 — х = —х + 2 = — —(2х — 2) + 1. Следовательно,
С 2-х С -у(2х-2)+1
I _______________dx = I ________________________dx =
J (x2 — 2x 4-2)3 J (x2 — 2x 4-2)3
1 I _______
2 J (x2 —2x4-2)» J (x2 —2x4-2)3
1 f d (x2 — 2x 4- 2) Г_________dx_______
‘T J (x2 — 2x 4- 2)3 + J (x2 — 2x 4- 2)3 *
Первый интеграл равен ми в двух предыдущих = (х — I)2 4“ 1 = /2 4-
— (х2 — 2х 4- 2)“2. Второй можно вычислить методами, рассмотренны-4
параграфах, следующим образом: х2 —2х 4- 2 = (х2 — 2x4- 1) 4- 1 =
1, где t = х — 1 и dt = dx. По формуле (4) второй интеграл равен
Г dt___________________1_ t 3 Г dt
J (Z2 4- I)3 “ 4 (Z2 4- I)2 + 4 J (Z2 4- I)2
1_ t ~ 4 (Z24- I)2 + 1 t 3 Г 4 L 3 1 t 1 r dt 1 2 Z24-l+2jz24-lJ=’ < 3 ’ » . 4- arctg t 4- k. /2 4- 1 8 -
4 (/2 4- I)2 1 8
Наконец,
f (2 — х) dx 1 X 3 x—1 3
J (x2 —2x4-2)3 4 (x2 — 2x 4- 2)2 + 8 x2 —2x4-2 + 8 arctg(x !) + C-
508
Решения упражнений, помеченных знаком А (глава 7)
§ 3
X
20. Пользуясь общим методом, т. е. полагая у = tg — , получим
1—
1 — sin X
1 + sin x
1 + #2 #2 — 2у -Н
! . 2У ~~ У2 + 2У + 1 1 4-
Так как
то наш интеграл приводится к виду
2 dx =------------dy,
1 + </2
Положим
y8~2* + 1 dy. (y+ l)a({/2 + l)
у2-2у+1
в___ Су + Р
(у + D2(У24- I) у + I ' (г/4-1)2 + у2 +1
Решая соответствующие уравнения, находим 4 = С = 0, В = 2, D = — 1. Далее, f 2 du С dy 4
2JV77F-2j7TT = -TM-2arct^ + c*
или
4
1 + tg"F
44. Полагая x = cos у, так что 1 — x2 = sin2 у и dx = — sin у dy, будем иметь j x3 (1 — x2)1/4 dx = J cos3 у sin3/2 у dy = — J (1 — sin2 y) sin3/2 у d sin у = = — f (1 — u2) u3/2 du [где U = sin У] = — “7“ u5/2 H- u9/2 4- c = J 5 9
9 9 9 9
= _ 4. sin5/2 У + 4- Sin9/2 y+ C = - 4- (1 - x2)5/4 + 4_ (1 _ x2)9Z4 + c 5 9 5 9
V x2 _1_ 1
54. Найдем сперва неопределенный интеграл от —---------X—. Пользуясь методом (а), получаем
sec у Л , — sec* =
cos у -гт-dy. sin4 у
А
Так как cos у dy = dsin у, последний интеграл равен — * — . Далее, если у = aretg xt то
3 sin3 у
sinj/ = 7iW“
1<3
dx-----+
Зх3
9У 3
з
Решения упражнений, помеченных знаком А (глава 7)
509
62. Так как ау —02= —1 < 0, то полагаем
Зх + 4
= Зх + 4.
Тогда
Зх2 + 8х + 5 = [(Зх + 4)а — 1] = 4" (62 — 1) и dt = 3dx. 3 □
Следовательно,
________dx_________
(Зх2 + 8х + 5)3/2
§ 4
а последний интеграл — интеграл вида VII.
10. Воспользуемся формулой (2):
С х1/3 1п2 х dx = -у- х4/3 1п2 х — - f х1/3 In х dx.
J 4 2 J
Последний интеграл берется по частям, если положить f = In х и dg = х1^3 dxt
С х1/3 In х dx— -7- х4/3 In х — f — х4^3 —— = -у- х4/3 In х — —— х4/3 + С,
J 4 J 4 х 4 16
Следовательно,
С х’/3 In2 X dx= — х4/3 In2 х - — х4/3 In х + x4'3 4- с.
J 4 8 32
32. Пользуясь формулой (6), получим*
ic/3
I cos3 х sin3 х dx = — — cos4 x sin2 x
J 6
n/4
k/3 k/3
+ --- J cos3 x sin x dx.
«/4 те/4
В последнем интеграле положим u = cos x. Тогда du = —sin xdx, и мы получим
с/3 1/2
J cos3 х sin х dx= — J u3 du =
«/4 VT h.
1/2
____3_
“ 64
VT/2
Следовательно,
«/3
C , . o , 1 1 3 111 I 11
I cos3 x sin3 x dx = e-r— • —— . — + —— • — . — 4- —— = —— .
J 6 16 4 6 4 2^ 64 384
* Здесь можно также воспользоваться тем, что cos3 х sin3 х = — sin3 2х.
Алфавитный указатель
Абель (Abel) 450, 451
Абсолютная величина 31
— погрешность 53
Аддитивность интегралов 244, 245, 267
— площадей 282
Аксиома 92
— Архимеда 30
— полноты для действительных чисел
50
Аксиоматическая геометрия 92
Аксиомы действительных чисел 52
— поля 22, 26
— —, следствия 23, 57, 58
— рациональных чисел 33
Алгебраическая функция 336
Амплитуда 358
Аналитическая геометрия 93
Ареа коси нус (гиперболический арккосинус) 413—415
Ареасинус (гиперболический арксинус) 413, 414
Аристотель (Aristotle) 170, 171, 286 , 295
Арккосеканс 371—373
Арккосинус 345—347
Арккотангенс 371—373
Арксеканс 371—373
Арксинус 346—348
Арктангенс 364—367
Архимед (Archimedes) 30, 89, 286, 294
Архимеда аксиома 30
— теорема 89. 225
Архимедово упорядоченное поле 41, 52
Асимптоты 213, 214
Ассоциативность сложения 18, 22
— умножения 19, 22
Атомный реактор 408
Барометрическая формула 410
Барроу (Barrow) 259
Бернулли Даниель (Bernoulli Daniel) 398
Бернулли Иоганн (Bernoulli Johann) 319, 398
Бернулли Дкоб (Bernoulli Jacob) 397, 398
Бесконечная десятичная дробь 35—38
— область интегрирования 314
— производная 232
Бесконечное десятичное разложение 36
— — —, периодичность 38, 58—60
Бесконечный интервал 46
— предел 138, 142. 145, 149, 150
Бинарная система счисления 34
Браун (Brown) 196, 197
Брауэр (Brouwer) 62
Бриггс (Briggs) 375, 377
Броуновское движение 196
Быстрота изменения 172
Бюрги (Burgi) 374, 377
Валлис (Wallis) 477
Валлиса бесконечное произведение 477
«Вблизи» бесконечности 143
— точки 123
Вейерштрасс (Weierstrass) 98, 99
Вейль (Weyl) 62
Вертикальная асимптота 213, 214
— касательная 232
— ось 66
Верхний интеграл 324—328
— предел интегрирования 240
Верхняя граница 47
— грань 50
Вершина параболы 84
— угла 342
Вес 194
Вложенные интервалы 64
Вогнутая функция 212, 213, 235, 236
Вогнутый график 212
Возрастающая функция 105, 198, 199, 234, 235
Вторая производная 190, 192
— —, приложения к исследованию
функций 203, 212, 213, 235, 236
Выпуклая функция 212, 213, 235, 236
Выпуклый график 212
Высота тона 359
Галилей (Galilei) 171, 226
Галилея закон 171, 193, 222, 309
Галуа (Galois) 450, 451
Гамма-функция 424, 425
Гармонические колебания 359
Гаусс (Gauss) 424, 450
Гаусса закон ошибок 423
Гейзенберг (Heisenberg) 197
Гейзенберга принцип неопределенности 197
Гильберт (Hilbert) 93
Гильберта аксиомы 93, 94
Гиперболические подстановки 466, 468, 469
Гиперболический косеканс 418, 419
— — обратный 418, 419
— косинус 403, 404, 412, 415, 416, 418
— — обратный 413—415
— котангенс 418, 419
— — обратный 418, 419
— секанс 418, 419
— — обратный 418, 419
— синус 403, 404, 412, 415, 416, 418
— — обратны.. 413, 414
— тангенс 404, 417, 418
— обратный 417. 418
Алфавитный указатель
511
Гиперплоскость 95
Горизонтальная асимптота 213, 214
— ось 66
Гравитационная постоянная 308
Градус 344
Грани множества 50
Границы множества 47
График 104
— вогнутый 212
— выпуклый 212
—, построение 213—217
Даламбер (D'Alembert) 163
Движение вертикальное под действием силы тяжести 222, 223
—, закон Ньютона 193, 194
—, — Эйнштейна 195, 311, 312
— неравномерное 169, 170
— периодическое 358
— прямолинейное 168, 169
— равномерное 169
— релятивистское под действием постоянной силы 224, 225
— упругой пружины 357, 358
Дедекинд (Dedekind) 41
Дедекинда принцип 64
Действительнозначная функция действительного переменного 98
Действительные числа, аксиомы 52
— —, вычисления 41, 52—55
— —, геометрическое истолкование 42, 43 — —, определение 40 — —, отрицательные 40 — —, положительные 39
— —, сложение и умножение 61
— —, сравнение по величине 40
(См. также Рациональные числа)
Декарт (Descartes) 66, 67
Декартова система координат 66
Деление столбиком 37
— «углом» 113
Демокрит (Democritus) 294, 295
Десятичная система счисления 33, 34 -
Десятичные дроби бесконечные 35—38
— —, вычисления 38, 39
— —, конечные 35, 37
— —, округление 38, 39, 55
— —, периодические 37, 38
Диаметр окружности 81 z
Директриса параболы 83
Дирихле (Dirichlet) 12b
— функция 120, 122
Дисперсия 422
Дистрибутивность 19, 22
Дифференциал 270
Дифференциальное уравнение 219
---- второго порядка 352
— — для гиперболического синуса и косинуса 412
— — — синуса и косинуса 352. 353, 356, 357
— — изменения атмосферного давления (барометрическая формула) 410 — —, начальные условия 353, 354
— —, общёе решение 353
— — показательной функции 394, 406
— — популяционного роста 401
— — процесса радиоактивного распада
409
— — — ядерного деления 407, 408
Дифференцирование 161
— гиперболических функций 404, 418
— иррациональной функции 186
— логарифмическое 391
— логарифмической функции 377
— многочлена 179
— обратной функции 183, 230
— — в алгебраическом смысле функции 228, 229
— обратных гиперболических функций
413, 414, 417, 419
— —тригонометрических функций 347, 348, 364, 371, 372
— —, основные правила 173, 174, 227, 228
— показательной функции 390
— рациональной функции 179
— сложной функции 180
— степени 177, 178, 185, 391
— тригонометрических функций 350, 360, 369
— формальное 430
— численное 431
(См. также Производная)
Дифференцируемая функция 168, 188
Длина, вычисление с помощью интеграла 296, 297
— дуги окружности 299
— интервала 46
— окружности 299, 301
— * определение 297
- т- пересечения 279
Дополнение до полного квадрата 80
Евдокс (Eudoxos) 21, 294
Евклид (Euclid) 92, 93
Единица 22
— длины 66
Единичная окружность 79
Жесткость 359
Зависимая переменная 98
Закон всемирного тяготения 308
512
Алфавитный указатель
Закон Галилея 171, 193, 222, 309
инерции 222
— Лапласа 423
— Ньютона 194
— ошибок Гаусса 423
— сохранения энергии 305
— Эйнштейна 195, 311
Замкнутый интервал 46
Излом 188, 231
Инерционная навигация 264, 265
Интеграл 240, 242, 243
—, аддитивность 244, 245, 267
—, аналитическое определение 253, 254
— верхний 324—328
— , вычисление 247, 248
— , монотонность 245
— неопределенный 263
— несобственный, см. Несобственный интеграл
— нижний 324—328
— определенный 266
— , основные свойства 254
— от постоянной функции 244
— — ступенчатой функции 247, 322—324
— , оценка погрешности для монотонной функции 248
— рационализируемый 457
— Римана 328
— , существование 253, 322—329
— эллиптический 421
(См. также Интегрирование)
Интегранд 240
Интегрирование 266
— в конечном виде 430
— гиперболических функций 466
— иррациональных функций 459, 460, 466—471. 481, 483. 484
— обратных тригонометрических функций 482, 483
—, основные правила 267, 271, 480
— показательных илогарифмических функций 472, 473, 483
— по частям 269—271, 480
— простейших дробей 442—448
—, рационализация интегралов 457—471, 483, 484
— рациональных функций 450—456, 480, 481
— с помощью арктангенса 367
— — — замены переменных 273—276
— — — логарифмов *383—385
— тригонометрических функций 474, 475, 478, 479, 481, 482
— формальное 266, 430
—, формулы приведения 472—475
— четных и нечетных функций 276, 277
— численное 266, 431, 432
Интервал 46
— бесконечный 46
— замкнутый 46
— интегрирования 240
— конечный 46
— открытый 46
— полуоткрытый 46
— постоянства 322
Интуиционисты 62
Иррациональная функция 116
— —, непрерывность 132
— —, основные формулы интегрирования 481
— —, производная 186
Иррациональные числа 40
Кавальера, (Cavalieri) 226, 227
Кавальери принцип 283, 289
Кантор (Cantor) 41
Кардано (Cardano) 450, 451
Касательная вертикальная 232
— к окружности 81, 82, 154
— — параболе 87, 88, 154
— , определение 159
— , построение 156—158
Квадрант 68
Квадратичная функция 111, 112
Квадратурные формулы 432
Квантовая механика 196, 197
Кольцо 115
Коммутативность сложения 18, 22
— умножения 19, 22
Композиция функций 102
— —, дифференцирование 180, 181
— —, непрерывность 127, 149
— —, предел 136
Конечный интервал 46
— разрыв 140
Константа 100
Конструктивисты 62
Координатные оси 66, 71
— плоскости 71
Координаты в пространстве 71
— на плоскости 66
— — прямой 42
Корень из числа 43
— функции 111
— — двойной 111
Корни многочлена 113, 114, 128, 450
Косеканс 368, 369
— гиперболический 418, 419
— обратный гиперболический 418, 419
Косинус, аналитическое определение 349
—, геометрическое определение 337
— гиперболический 403, 404, 412, 415, 416, 418
—, дифференциальное уравнение для синуса и косинуса 352, 353, 356, 357
Алфавитный указатель
513
Косинус, дифференцирование 350
—, интегрирование некоторых функций, содержащих синусы и косинусы 475, 478, 479 — обратный гиперболический 413—415
—, представление в виде рациональной функции от tg(0/2) 362
Котангенс 368, 369
— гиперболический 418, 419
— обратный гиперболический 418, 419
-Коши (Cauchy) 98, 99
Коэффициент восстановления (упругости) 357
— многочлена 112
Кривая 104
Криволинейная трапеция 240
Критерий второй производной 203
Критическая масса 407
— точка 202, 203
Критический радиус 407
.Кронекер (Kronecker) 62
Круг 80
Круговой конус 293
— сектор 299, 300
Кубическая парабола 104
Кусочно-монотонная функция 106, 204 250
Кусочно-непрерывная функция 246
Лагранж (Lagrange) 163
Лаплас (Laplace) 424
Лапласа закон 423
Левая производная 188, 230
Лейбниц (Leibniz) 154, 259
Лейбница обозначения 163, 164, 174, 190, 240
Линейная восстанавливающая сила 302, 357
— функция 110, 111
Линейное приближение 165, 166
— уравнение 74
Логарифмическая функция 377, 378
— —, дифференцирование 377
— — как предел 400
— —, основные формулы интегрирования 483
Логарифмы 374, 375
— десятичные 383
— натуральные 377
— по разным основаниям 382, 383
—, применение для интегрирования 383—385
—, свойства 379
— , функциональное уравнение 376
Лудольф (Ludolph) 286
Луч 342
Максимум 205
— абсолютный 205
— локальный 201
— — строгий 201
— , существование 206
— , разыскание 206
Масса 193
— в теории относительности 312
— «покоя» 195, 311
Математическая индукция 48, 49
Метод неопределенных коэффициентов 452—456
Минимум 205
— абсолютный 205
— локальный, 201
— — строгий 201
— , существование 206
— , разыскание 206
Минута 344
Многочлен 112
— , деление «углом» 113
—, корни ИЗ, 114, 128 450
— , коэффициенты 112
— , производная 179
' —, степень 112
Множество 47
— , грани 50
— , границы 47
— неограниченное 47
— ограниченное 47
— пустое 47
Монотонная функция 106
— —, интегрируемость по Риману 329 — —, оценка погрешности при вычислении интеграла 248
— —, предел 330
Монотонность интеграла 245
Наибольший элемент множества 47
Наименьший элемент множества 47
Наклон 75
Натуральные числа 18
Начало координат 66, 71
— отсчета 20
Начальные условия 353
Невозра.стающая функция 106, 200
Недифференцируемая функция 188, 231
Независимая переменная 98
«Немая» переменная 242, 264
Неограниченное множество 47
Непер (Napier) 374, 375, 377
Неперово число 382
Непрерывность 120
— , арифметические действия над непре-
рывными функциями 127, 147, 148
— в точке 123
— - дифференцируемой функции 1684
— , е-о-определение 124
— иррациональной функции 132
— композиции функций 127, 149
— на интервале 123
— обратной функции 131, 149
— рациональной функции 127
514
Алфавитный указатель
Неравенства 26
— , обозначения 26
— , правила 26, 27
— , решение 27—29
Неравенство треугольника 31
— Шварца для интегралов 332
Несобственный интеграл 278
— — от неограниченной подынтеграль-
ной функции 312, 314, 315
— — по бесконечной области интегрирования 314
— —, расходимость 313, 314
— —, сходимость 313, 314
— —, теорема сравнения 316, 330, 331
Несоизмеримые отрезки 20, 21
Неубывающая функция 105, 200
Нечетная функция 106, 107, 276, 277
Неэлементарные функции 421—425
Нижний интеграл 324—32&
— предел интегрирования 240
Нижняя граница 47
— грань 50
л-мерное пространство 95
Нормаль 159
Нормальная кривая 422
Нуль 19, 22
— функции 111
Ньютон (Newton) 168, 259
Ньютона закон всемирного тяготения 308
— — движения 194
Область определения функции 98
Обратная в алгебраическом смысле функция 228 — функция 130 — —, непрерывность 131, 149 — —, производная 183, 230
Обратное число 22
Обратные гиперболические функции, см, соотв. названия
Обратные тригонометрические функции 346—349, 364, 365, 371—373, 482, 483, см, также соотв. названия
Общее решение дифференциального уравнения 353
Объем, вычисление с помощью интеграла 286—289 — конуса 293
—, определение 290
— тела вращения 291
— шара 293
Ограниченная функция 246
Ограниченное множество 47
Односторонние пределы 137, 140
— производные 188, 230
Округление 38, 441
— десятичных дробей 55
Окружность 79
— , диаметр 81
— , длина 299
— единичная 79
—, касательная 81, 82
—, пересечение с прямой 81
—, радиус 79
— , уравнение 80
— , центр 79
Октант 71
Основание натуральных логарифмов 382
Остаток 113
Острие 188, 232
Ось абсцисс 66, 71
— аппликат 71
— ординат 66, 71
— параболы 84
Открытый интервал 46
Относительная погрешность 53
Отрезок 46
Отрицательные числа 19, 26, 40
Парабола 83, 104
— , вершина 84
— , директриса 83
— , касательная 87, 88, 154
— , ось 84
— , пересечение с прямой 87
— , площадь под параболой 89, 225, 226, 282, 283
— с вертикальной осью 86
— , уравнение 83, 84, 86
— , фокальная хорда 85
— , фокус 83
Параллельные прямые 76
Паскаль (Pascal) 67
Первая космическая скорость 310
Первообразная 218—220
Первый квадрант 68
— октант 71
Перенос системы координат 68
Переменная 22
— зависимая 98
— интегрирования 242
— независимая 98
— «немая» 242, 264
— , обозначающая функцию 100
Пересечение 279
Период 337
— полураспада 402
— примитивный 337
Периодическая десятичная дробь 37, 38, 58—60
— функция 337, 338
Перпендикулярные прямые 76, 77
Пифагор (Pythagoras) 21
Пифагора теорема 21, 69
Планк (Planck) 197
Алфавитный указатель
515
Планка постоянная 197
Платон (Plato) 92, 93, 294, 295
Плоскость 93, 94
Плотность 61
Площадь 240
—, аддитивность 282
—, вычисление с помощью интеграла 278—281
— круга 285, 286
— кругового сектора 299, 300
—, определение 281
— под параболой 89, 225, 226, 282, 283
Погрешность абсолютная 53
— линейного приближения 165, 166
— метода 441
— округления 441
— относительная 53
— , оценка для правила Симпсона 438
— , — — — трапеций 435
— , — — приближенных вычислений 52
Подынтегральная функция 240
— — неограниченная 312, 313
Позиционная система счисления 33, 34
Показательная функция 390
— —, дифференциальное уравнение 394,
406
— —, дифференцирование 390
— — как предел 399
— —, основные формулы интегрирования
483
— —, применения 397—402, 406—410
— —» функциональное уравнение 390
Поле 23
Положительные числа 18, 26, 39
Полуинтервал 46
Полуоткрытый интервал 46
Полуплоскость 67
Популяционный взрыв 401
— рост 400, 401
Постоянная интегрирования 263
— Планка 197
— пружины 302, 357
— функция 100, 244
Правая производная 188, 230
Правило подстановки 273, 480
— Симпсона (парабол) 436—440
— трапеций 433—435, 438—440
— цепное 180, 229
Предел 118, 133
— бесконечный 138, 142, 145, 149, 150
—, е-6 -определение 134
— композиции функций 136
— монотонной функции 330
— на бесконечности 137, 143
— односторонний 137, 140
—, правила вычисления 135, 136
— производной 233, 236, 237
Предельная стоимость 173
Пределы интегрирования 240
Примитивная функция 218
Принцип верхней грани 50
— вложенных интервалов 64
— Дедекинда 64
— «исключенного третьего» 62
— Кавальери 283, 289
.— наименьшего целого числа 48
— неопределенности Гейзенберга 197
— относительности классический 264
— — Эйнштейна 264
Произведение 18, 22
— , геометрическое построение 56
Производная бесконечная 232
— высшего порядка 190
* —, вычисление, см. Дифференцирование
—, — исходя из определения 160
—, знак производной 198—200
— как мгновенная скорость 170
— — наклон касательной 154
— левая 188, 230
— неотрицательная 200
— неположительная 200
—, обозначение Лейбница 163, 164
— односторонняя 188, 230
—, определение 159
— отрицательная 198, 200, 234, 235
— положительная 198, 200, 234, 235
— правая 188, 230
—, предел производной 233, 236, 237
—, применение для вычисления прибли-
женных значений функций 166, 167
— функция 161
Простейшие дроби 442
г — —, интегрирование 442—448
— —, разложение 451, 452
Простое число 63
Противоположное число 22
Прямая в пространстве 94
— на плоскости 72, 93
— — —, наклон 75
— — —, параллельность двух прямых 76
— — —, перпендикулярность двух прямых 76, 77
— — —, след 78
— — —, уравнения 72, 78
Прямой цилиндр 286, 287
Птолемей (Ptolemy) 34, 343
Пуанкаре' (Poincare) 62
Пустое множество 47
Работа 303, 304
Равнобочная гипербола 104, 377, 378, 416
Радиан 344
Радиоактивное равновесие 409
Радиоактивный распад 402. 408 409
Радиус окружности 79
516
Алфавитный указатель
Разделительная запятая 34
Разностное отношение 157, 159
Разность 18
Разрывная функция 120
Расстояние между двумя точками 70, 72, 93, 94
— — — — в л-мерном пространстве 95 Рациональная функция 115, 457
— —, интегрирование 450—456, 480,
481, см. также Интегрирование простейших дробей
— —, непрерывность 127
— — от гиперболических функций 466, 468—470
— — — показательной функции 458
— — — тригонометрических функций
462, 463, 466—469, 484
— —, первообразная 450
— —, предел 117, 118
— —, производная 179
— —, разложение на простейшие дроби
450—452
— —, расширение области определения
117
Рациональные операции 116
— точки 42
— числа 20
— —, определенные с помощью аксиом
33
— — отрицательные 19
— — положительные 18
— —, представление в виде бесконечных
десятичных периодических дробей 58—60 (См. также Действительные числа) Рекуррентная формула 446
Риман (Riemann) 322
Римана интеграл 328
Руффини (Ruffini) 450
Свободное падение 170—172, 306 307
Сегмент 46
Секанс 368, 369
— гиперболический 41 8, 419
— обратный гиперболический 418, 419
Секунда 344
Сила 193
— восстанавливающая 302, 357
—, зависящая от положения 302
—, работа против силы 303, 304
— тяжести 194, 222
Симпсоа (Simpson) 436
Симпсона правило 436—440
Синус, аналитическое определение 349
—, геометрическое определение 339
— гиперболический 403, 404, 412. 415, 416, 418
—, дифференциальное уравнение для синуса и косинуса 352, 353, 356, 357
—, дифференцирование 350
—, интегрирование некоторых функций, содержащих синусы и косинусы 475, 478, 479 — обратный гиперболический 413, 414
—, представление в виде рациональной функции от tg(6/2) 362
Скачок 140
Скорость 169, 222, 223
— мгновенная 169, 170, 192, 264
— средняя 169
— убегания 310
След 78
Сложная функция, см. Композиция функций
Сложные проценты 397 , 398
Сокращение 23, 57 , 58
Среднее значение 422
Стандартное отклонение 422
Степень, дифференцирование 177, 178, 185, 391
— многочлена 112
— с дробным показателем 46
— — иррациональным показателем 387—389, 391
— — целым показателем 24
Ступенчатая функция 247, 253, 322—324, 329 Сумма 18, 22
Сфера (в л-мерном пространстве) 95
Таблица 103
Тангенс 3.60, 361, 365
— гиперболический 404, 417, 418
— обратный гиперболический 417, 418
Тарталья (Tartaglia) 451
Тело вращения 290
Теорема 92
— алгебры основная 450
— анализа основная 258—261, 320—322, 430, 480
— арифметики основная 63
— Архимеда 89, 225
— о выпуклости и вогнутости графика функции 213, 235, 236
----дифференцировании композиции функций 180, 229
— — линейном приближении 165, 166 — — непрерывности дифференцируемой функции 168
— — первообразной рациональной функции 450
— — плотности 47, 61
— — пределе монотонной функции 330
— — представлении прямой линейным' уравнением 72—74
— — промежуточном значении 128, 129, 150, 151
— — среднем значении для интегралов 331
— - — существовании интеграла 253, 322—329
Алфавитный указатель
517
— — — корня из числа 43—45
—---------многочлена нечетной степени 128
— об обратной функции 131, 149 — — основных свойствах интеграла 254, 322—329
— Пифагора 21,69
— сложения для показательной функции 390
— сравнения для несобственных интегралов 316, 330, 331
Теоремы о возрастании и убывании функции 198, 200, 201, 234, 235 — — касательных 81, 82, 87, 88 — — максимуме и минимуме функции 202, 203, 206 — — непрерывности 127, 147—149 — — правилах дифференцирования 173—181, 183—186, 227—230 — —пределах 135, 136 — об оценке точности приближенных вычислений 52—55 — сложения для тригонометрических функций 354, 362, 370
Тождественная функция 111
Точка 93, 94
— возврата 188, 232
— критическая (стационарная) 202, 203 — локального максимума 201 — — минимума 201 — л-мерного пространства 95 — перегиба 213
Трансцендентная функция 336
Трансцендентное число 381 Тригонометрические подстановки 462, 466, 468, 469, 484 — функции 339—341, 360, 361, 368—370/ см. также соотв. названия — —, выражение через tg(6/2) 362 — — обратные, см. соотв. названия — —, основные формулы интегрирования 475, 478, 481, 482
Убывающая функция 106, 198
Угловой коэффициент прямой 75'
Угол 342
— , вершина, стороны 342
— , конгруэнтность углов 343
— , мера угла 342
— прямой 343
Упорядоченная пара чисел 67
Упорядоченное архимедово поле 41,52
— поле 26
Упругая пружина 302, 357
Ускорение 173
— мгновенное 193, 264
— . свободного падения 193, 309
— среднее 192, 193
Фазовая разность 358
Факториал 425
Фалес (Thales) 92, 93
Ферма (Fermat) 66, 67
Феррари (Ferrari) 451
Фокальная хорда 85
Фокус параболы 83
Формула длин 297
— объемов 289
— площадей 281
— расстояний 70, 72
— суммы квадратов первых т натуральных чисел 49
— — л членов геометрической прогрессии 25
Формулы приведения 472—475, 480—482
— прямоугольников 433
— удвоения 354, 362
Функции гиперболические, тригонометрические и им обратные, см., соотв. названия
Функциональное уравнение гамма-функции 425
— — логарифмов 376
— — показательной функции 390
Функция алгебраическая 336
—, арифметические действия над функциями 101, 102
— вогнутая 212, 213, 235, 236
— возрастающая 105, 198, 199, 234, 235
—, все производные которой в данной точке равны нулю 425, 426
— выпуклая 212, 213, 235, 236
—, вычисление приближенных значений функции с помощью производной 166, 167 — Дирихле 120, 122
— дифференцируемая 168, 188
—, — Л-кратно 191
— е-*2 421, 422
—, интегрируемая по Риману 328, 329
— иррациональная, см. Иррациональная функция
— квадратичная 111, 112
— кусочно-монотонная 106, 204, 250
— кусочно-непрерывная 246
— линейная НО, 111
— логарифмическая, см. Логарифмическая функция
— монотонная, см. Монотонная функция
— невозрастающая 106, 200
— недифференцируемая 188,. 231
—, не имеющая предела 133
— непрерывная 120, см. также Непрерывность
— .неубывающая 105, 200
— нечетная 106, 107, 276, 277
— неэлементарная 421
— нормального распределения 422, 423
— обратная, см. Обратная функция
518
Алфавитный указатель
Функция, обратная в алгебраическом смысле 228
— ограниченная 246
—, определение 98
— периодическая 337, 338
— подынтегральная 240
— показательная, см. Показательная функция
— постоянная 100, 244
— , приложения функций 109
— примитивная 218
— разрывная 1120
— рациональная, см. Рациональная функция
—, рациональные операции над функциями 116
— сложная 102, см. также Композиция функций
— строго монотонная 106
— ступенчатая 247, 253, 322—324, 329
— тождественная 111
— трансцендентная 336
— убывающая 106, 198
— четная 106, 107, 276, 277
— целая рациональная, см. Многочлен
— элементарная 420
— эллиптическая 421
Хорда 159
Целые числа 18, 24, 48
Центр интервала 46
— окружности 79
Цепное правило 180, 229
Частное 18
—, геометрическое построение 56
— при делении многочленов ИЗ
Частота колебания 359
Четная функция 106, 107, 276, 277
Числа, см. Действительные числа, Иррациональные числа, Рациональные числа
Число е 381, 400, 421
— л 286, 316, 421, 424, 477
Числовая прямая 43
Шар 293
Шварц (Schwarz) 332
Шварца неравенство для интегралов 332
Шестидесятиричная система счисления 34, 344
Эйлер (Euler) 163, 319, 424
Эйнштейн (Einstein) 195, 196
Эйнштейна закон движения 195, 311
— принцип относительности 195, 264
— соотношение 312
Экспоненциальная функция, см. Показательная функция
Экспоненциальный рост 395, 396
Элемент множества 47
Энергия в теории относительности 311, 312
— , закон сохранения энергии 305
— кинетическая 305
— полная 305
— потенциальная 304
Ядерное деление 407
Указатель основных обозначений
Некоторые постоянные
g ускорение свободного падения 193
С скорость света в пустоте 195
л площадь круга радиуса 1 286
7 гравитационная постоянная 308
е основание натуральных логарифмов 381
Функции (общие обозначения) символ, обозначающий функцию 98 /(*)«, « « 100
f (g (*)) композиция функций 102 1
—~ I [£(*)] 1 функция, обратная данной в gw
алгебраическом смысле 228, 372
Р(х) суперпозиция f°f(x) 351
f”1 W функция, обратная данной (в смысле теории функций) 372
Функции специального вида
arccos х арккосинус 345
arcsin х арксинус 347
arctg х арктангенс 364
arcsec х арксеканс 371
arccosec х арккосеканс 371
arcctg аг арккотангенс 371
arsh аг обратный гиперболический синус 413
arch аг « < косинус 414
arth аг « « тангенс 417
arsech х « « секанс 418
arcosech х « « косеканс 418
arcth аг « « котангенс 418
cos аг косинус 339
sin аг синус 339
tg аг тангенс 360
Указатель основных обозначений
519
secx секанс 368
cosec х косеканс 368 ctg х котангенс 368 ch х гиперболический косинус 403 sh х « синус 403
th х « тангенс 404
sech х « секанс 418
cosech х « косеканс 418
cthx « котангенс 418
In х логарифм по основанию е 377 logax « « « а 382
1g х, log10x « « « 10 383
ех, exp х показательная функция 390 со
Г (х) = J tx~r dt гамма-функция 424 о
f' ( х0 ) правая производная 230
/' ( х0 ) левая производная 230
Знаки интегрального исчисления ь
^f(x)dx интеграл 240 а
F (х) |£ символ двойной подстановки 261
J* f (x)dx неопределенный интеграл 263
Ь -j—оо
J f(x)dx, J f (х) dx несобственные интегра-—оо а
лы 314
Знаки теории пределов
х-> х0 стремится 118
lim/^x) предел 118
х -> х0, х f х0, х -> х0 — 0 стремится слева 140
х -* х0, х| х0, х -> х0 + 0 стремится справа 140
Знаки дифференциального исчисления
(х) производная 154
' du \
-у- ,Df,(Df)(x) « 164
< dx Jx=a
dx, dy дифференциалы 163
Дх, Дг/ приращения 164
d2/ г ТТ ’ dx2 d2y dx2 tPy вторая производная 190
dx3 третья < 190
flV(x). f(4> . d'f dx4 d*u четвертая « dx4 190
/<ft) (x),^- dky dx11 Л-я < 190
j f (х) dx нижний интеграл 324 а
7
J f (х) dx верхний интеграл 324 а
Некоторые другие знаки
= равно 18
4= не равно 22
= тождественно равно 100
тождественно не равно 115
приближенно равно 166
< , > < , > символы неравенства 26
| а | абсолютная величина 31
(а, Ь) открытый интервал 46
[а, 6] закрытый интервал 46
[а, Ь), (а, 6) полуоткрытые интервалы 46
(—оо, Ь), (а, 4-оо), (—оо, 4- оо) бесконечные интервалы 46,47
£ принадлежность элемента 47
max х наибольший элемент множества 47 xgS
minx наименьший элемент множества 47 xgS
sup х верхняя грань множества 50 хез
inf х нижняя грань множества 50
xgS
{(х, у) | ...} множество точек (х, у) 290
I факториал 425
Липман Берс МАТЕМАТИЧЕСКИЙ АНАЛИЗ
т. 1
Редактор А. М. Суходский. Художник-график Д. С. Котлов. Художественный редактор В. И. Пономаренко. Технический редактор Э. М. Чижевский. Корректор Г. И. Кострикова
Сдано в набор 6/VIII—74 г. Подп. к печати 18/VIH—75 Формат 70x90/i«- Бум. тип. Кв 2. Объем 32.5 печ. л. Усл. п. л. 38,02. Уч.-изд. л. 35,18. Изд. № ФМ-554 а. Тираж 33 000 экз. Зак. 537.
Цена 1 р. (2 к. БЗ-16-17-75.
Москва, К-51, Неглинная ул., д. 29/14, Издательство «Высшая школа»
Ярославский полиграфкомбинат «Союзполиграфпрома» при Государственном комитете Совета Министров СССР по делам издательств* полиграфии и книжной торговли, 150014. Ярославль, ул. Свободы. 97.