В. А. Зорин
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
Часть I
Издание второе,
исправленное и дополненное
Рекомендовано Министерством общего и профессионального образования
Российской Федерации в качестве учебника для студентов
математических и физико-математических
факультетов и специальностей
высших учебных заведений
Ф
ФАЗИС
Москва • 1997

ББК 22.16
386
УДК 517
Издание осуществлено при поддержке
>i/L Российского фонда, фундаментальных
исследований по проекту 96-01-14113
Зорич В. А.
Математический анализ. Насть I. Изд. 2-е, испр. и доп.
М.: ФАЗИС, 1997. - xiv + 554 с.
ISBN 5-7036-0031-6
В книге отражена связь курса классического анализа с современными
математическими курсами (алгебры, дифференциальной геометрии, диффе-
дифференциальных уравнений, комплексного и функционального анализа).
Основные разделы первой части: введение в анализ (логическая сим-
символика, множество, функция, вещественное число, предел, непрерывность);
дифференциальное и интегральное исчисление функции одной переменной;
дифференциальное исчисление функций многих переменных.
Органической частью текста являются примеры приложений развивае-
развиваемой теории, а также большое количество задач. Второе издание дополнено
вопросами и задачами коллоквиумов и экзаменов.
«Полная строгость изложения... соединена с доступностью и полнотой,
а также воспитанием привычки иметь дело с реальными задачами естест-
естествознания» (Из отзыва академика А. Н. Колмогорова о первом издании этой книги.)
Издательство ФАЗИС (ЛР N«064705 от 09.08.96)
123557 Москва, Пресненский вал, 42-44
Отпечатано в Московской типографии № 2 РАН
121099 Москва Г-99, Шубинский пер., 6
Заказ № 2543
ISBN 5-7036-0031-6 © ФАЗИС, 1997

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию IX
Из предисловия к первому изданию XI
Глава I. Некоторые общематематические понятия и обозначения 1
§ 1. Логическая символика 1
1. Связки и скобки A). 2. Замечания о доказательствах C). 3. Некото-
Некоторые специальные обозначения C). 4. Заключительные замечания C).
Упражнения D).
§ 2. Множество и элементарные операции над множествами 5
1. Понятие множества E). 2. Отношение включения G). 3. Простей-
Простейшие операции над множествами (8). Упражнения A0).
§ 3. Функция 11
1. Понятие функции (отображения) A1). 2. Простейшая классифика-
классификация отображений A5). 3. Композиция функций и взаимно обратные
отображения A6). 4. Функция как отношение. График функции A9).
Упражнения B2).
§ 4. Некоторые дополнения 25
1. Мощность множества (кардинальные числа) B5). 1. Об аксиомати-
аксиоматике теории множеств B6). 2. Замечания о структуре математических
высказываний и записи их на языке теории множеств B9). 'Упражне-
'Упражнения C1).
Глава П. Действительные (вещественные) числа 33
§ 1. Аксиоматика и некоторые общие свойства множества действительных
чисел 33
1. Определение множества действительных чисел C3). 2. Некоторые
общие алгебраические свойства действительных чисел C7). 3. Аксиома
полноты и существование верхней (нижней) грани числового множе-
множества D1).
§ 2. Важнейшие классы действительных чисел и вычислительные аспекты
операций с действительными числами 43
1. Натуральные числа и принцип математической индукции D3). 2. Ра-
Рациональные и иррациональные числа D6). 3. Принцип Архимеда E0). -
4. Геометрическая интерпретация множества действительных чисел и
вычислительные аспекты операций с действительными числами E2).
Задачи и упражнения F4).

IV ОГЛАВЛЕНИЕ
и и
§ 3. Основные леммы, связанные с полнотой множества действительных
чисел 68
1. Лемма о вложенных отрезках (принцип Коши — Кантора) F8).
2. Лемма о конечном покрытии (принцип Бореля — Лебега F9). 3. Лем-
Лемма о предельной точке (принцип Больцано — Вейерштрасса F9). Зада-
Задачи и упражнения G0).
§ 4. Счетные и несчетные множества 71
1. Счетные множества G1). 2. Мощность континуума G3). Задачи и
упражнения G4).
Глава III. Предел 76
§ 1. Предел последовательности 77
1. Определения и примеры G7). 2. Свойства предела последовательно-
последовательности G9). 3. Вопросы существования предела последовательности (83).
4. Начальные сведения о рядах (92). Задачи и упражнения A02).
§ 2. Предел функции 105
1. Определения и примеры A05). 2. Свойства предела функции A09).
3. Общее определение предела функции (предел по базе) A24). 4. Во-
Вопросы существования предела функции A28). Задачи и упражне-
упражнения A44).
Глава IV. Непрерывные функции 148
§ 1. Основные определения и примеры 148
1. Непрерывность функции в точке A48). 2. Точки разрыва A53).
§ 2. Свойства непрерывных функций 156
1. Локальные свойства A56). 2. Глобальные свойства непрерывных
функций A57). Задачи и упражнения A66).
Глава V. Дифференциальное исчисление 170
§ 1. Дифференцируемая функция 170
1. Задача и наводящие соображения A70). 2. Функция, дифферен-
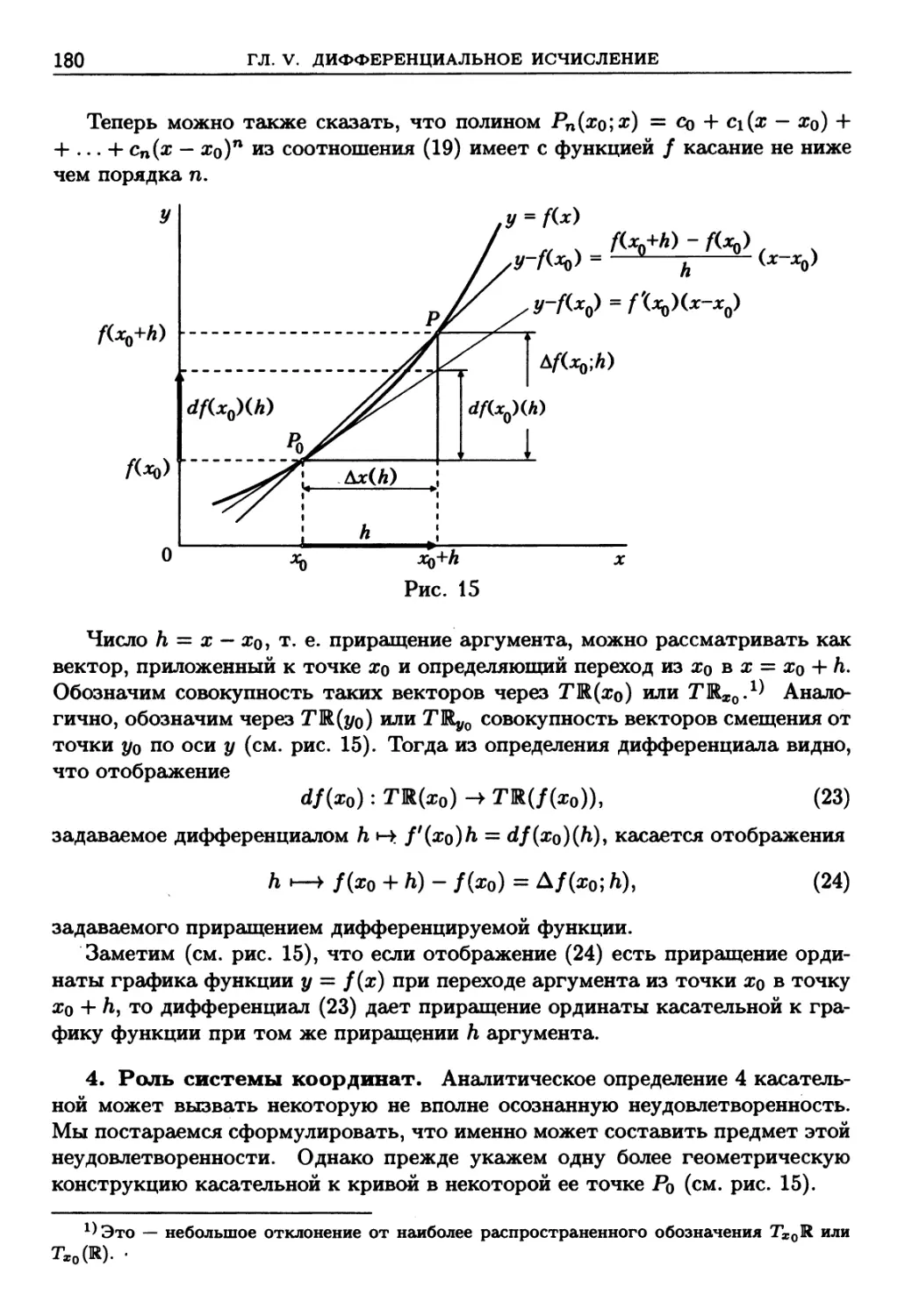
дифференцируемая в точке A75). 3. Касательная; геометрический смысл про-
производной и дифференциала A77). 4. Роль системы координат A80).
5. Некоторые примеры A82). Задачи и упражнения A87).
§ 2. Основные правила дифференцирования 189
1. Дифференцирование и арифметические операции A89). 2. Диф-
Дифференцирование композиции функций A92). 3. Дифференцирование
обратной функции A96). 4. Таблица производных основных элемен-
элементарных функций B00). 5. Дифференцирование простейшей неявно за-
заданной функции B00). 6. Производные высших порядков B05). Зада-
Задачи и упражнения B09).
§ 3. Основные теоремы дифференциального исчисления 210
1. Лемма Ферма и теорема Ролля B10). 2. Теоремы Лагранжа и Коши
о конечном приращении B12). 3. Формула Тейлора B15). Задачи и
упражнения B28).
§ 4. Исследование функций методами дифференциального исчисления ... 231

ОГЛАВЛЕНИЕ V
1. Условия монотонности функции B31). 2. Условия внутреннего экс-
экстремума функции B32). 3. Условия выпуклости функции B38). 4. Пра-
Правило Лопиталя B45). 5. Построение графика функции B46). Задачи
и упражнения B55).
§ 5. Комплексные числа и взаимосвязь элементарных функций 258
1. Комплексные числа B58). 2. Сходимость в С и ряды с комплекс-
комплексными членами B62). 3. Формула Эйлера и взаимосвязь элементарных
функций B67). 4. Представление функции степенным рядом, анали-
аналитичность B70). 5. Алгебраическая замкнутость поля С комплексных
чисел B75). Задачи и упражнения B81).
§ 6. Некоторые примеры использования дифференциального исчисления в
задачах естествознания 283
1. Движение тела переменной массы B83). 2. Барометрическая фор-
формула B85). 3. Радиоактивный распад, цепная реакция и атомный ко-
котел B87). 4. Падение тел в атмосфере B89). 5. Еще раз о числе е и
функции ехрх B91). 6. Колебания B93). Задачи и упражнения B97).
§ 7. Первообразная 301
1. Первообразная и неопределенный интеграл C01). 2. Основные об-
общие приемы отыскания первообразной C03). 3. Первообразные ра-
рациональных функций C09). 4. Первообразные вида / R(cos х, sin x) dx
C14). 5. Первообразные вида IR(x,y(x))dx C16). Задачи и упраж-
упражнения C19).
Глава VI. Интеграл 324
§ 1. Определение интеграла и описание множества интегрируемых функ-
функций : 324
1. Задача и наводящие соображения C24). 2. Определение интеграла
Римана C26). 3. Множество интегрируемых функций C28). Задачи
и упражнения C40).
§ 2. Линейность, аддитивность и монотонность интеграла 342
1. Интеграл как линейная функция на пространстве 71[а,Ь] C42).
2. Интеграл как аддитивная функция отрезка интегрирования C42).
3. Оценка интеграла, монотонность интеграла, теоремы о среднем
C45). Задачи и упражнения C52).
§ 3. Интеграл и производная 354
1. Интеграл и первообразная C54). 2. Формула Ньютона — Лейбница
C56). 3. Интегрирование по частям в определенном интеграле и фор-
формула Тейлора C57). 4. Замена переменной в интеграле C59). 5. Неко-
Некоторые примеры C61). Задачи и упражнения C65).
§ 4. Некоторые приложения интеграла 369
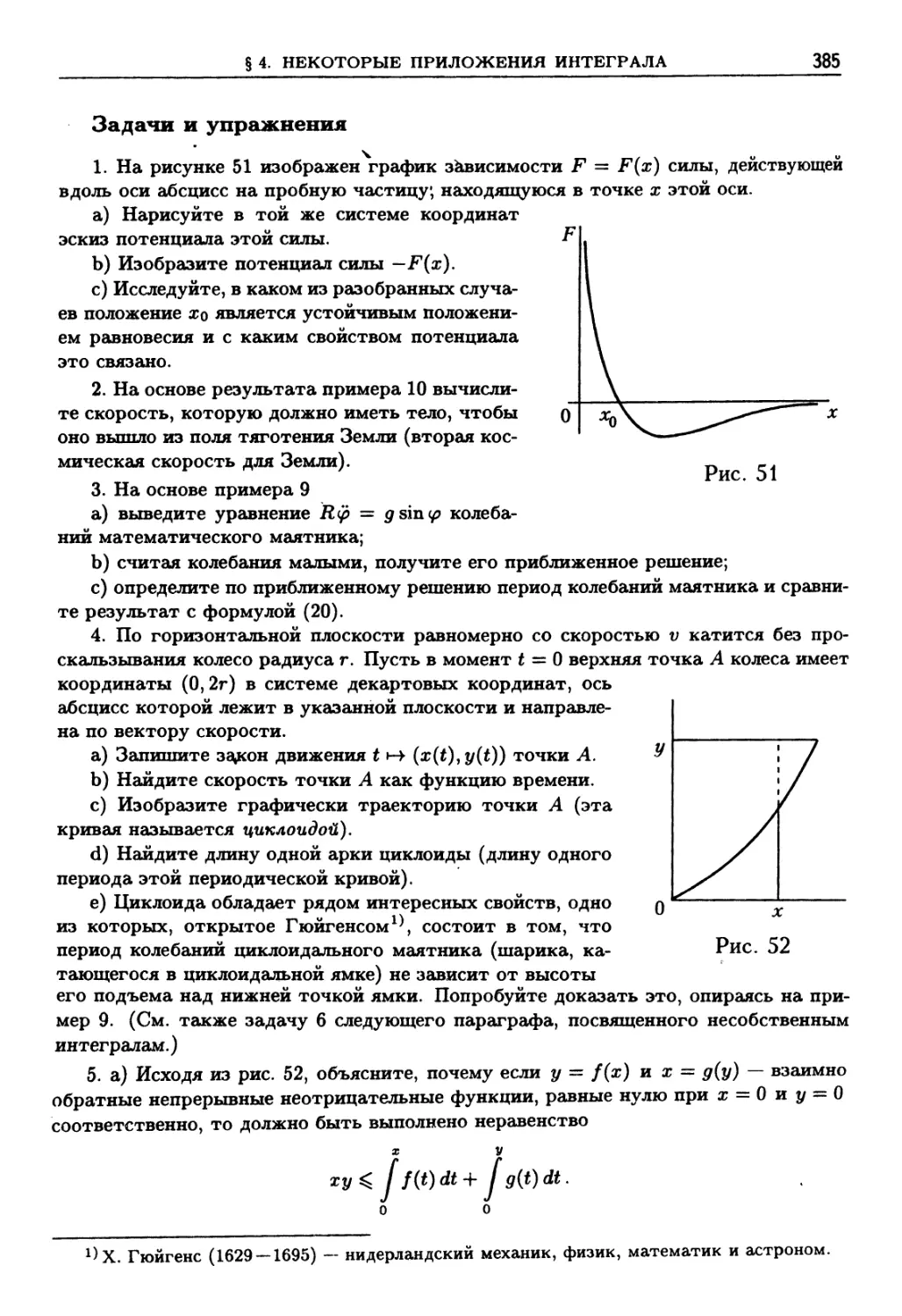
1. Аддитивная функция ориентированного промежутка и интеграл
C69). 2. Длина пути C71). 3. Площадь криволинейной трапеции C77).
4. Объем тела вращения C78). 5. Работа и энергия C79). Задачи и
упражнения C85).
§ 5. Несобственный интеграл 386

VI ОГЛАВЛЕНИЕ
1. Определения, примеры и основные свойства несобственных интегра-
интегралов C86). 2. Исследование сходимости несобственного интеграла C91).
3. Несобственные интегралы с несколькими особенностями C98). За-
Задачи и упражнения D01).
Глава VII. Функции многих переменных, их предел и непрерыв-
непрерывность 403
§ 1. Пространство Rm и важнейшие классы его подмножеств 403
1. Множество Rm и расстояние в нем D03). 2. Открытые и замкнутые
множества в Rm D05). 3. Компакты в Rm D08). Задачи и упражне-
упражнения D09).
§ 2. Предел и непрерывность функции многих переменных 410
1. Предел функции D10). 2. Непрерывность функции многих пере-
переменных и свойства непрерывных функций D15). Задачи и упражне-
упражнения D20).
Глава VIII. Дифференциальное исчисление функций многих пере-
переменных 421
§ 1. Линейная структура в Rm 421
1. Rm как векторное пространство D21). 2. Линейные отображения
L : Rm -» Rn D22). 3. Норма в Rm D23). 4. Евклидова структура
в Rm D25).
§ 2. Дифференциал функции многих переменных 426
1. Дифференцируемость и дифференциал функции в точке D26).
2. Дифференциал и частные производные вещественнозначной функ-
функции D27). 3. Координатное представление дифференциала отображе-
отображения. Матрица Якоби D30). 4. Непрерывность, частные производные
и дифференцируемость функции в точке D31).
§ 3. Основные законы дифференцирования 432
1. Линейность операции дифференцирования D32). 2.'Дифференциро-
2.'Дифференцирование композиции отображений D34). 3. Дифференцирование обрат-
обратного отображения D40). Задачи и упражнения D41).
§ 4. Основные факты дифференциального исчисления вещественнозначных
функций многих переменных 447
1. Теорема о среднем D47). 2. Достаточное условие дифференцируемо-
сти функции многих переменных D49). 3. Частные производные выс-
высшего порядка D50). 4. Формула Тейлора D53). 5. Экстремумы функ-
функций многих переменных D54). 6. Некоторые геометрические образы,
связанные с функциями многих переменных D61). Задачи и упражне-
упражнения D65).
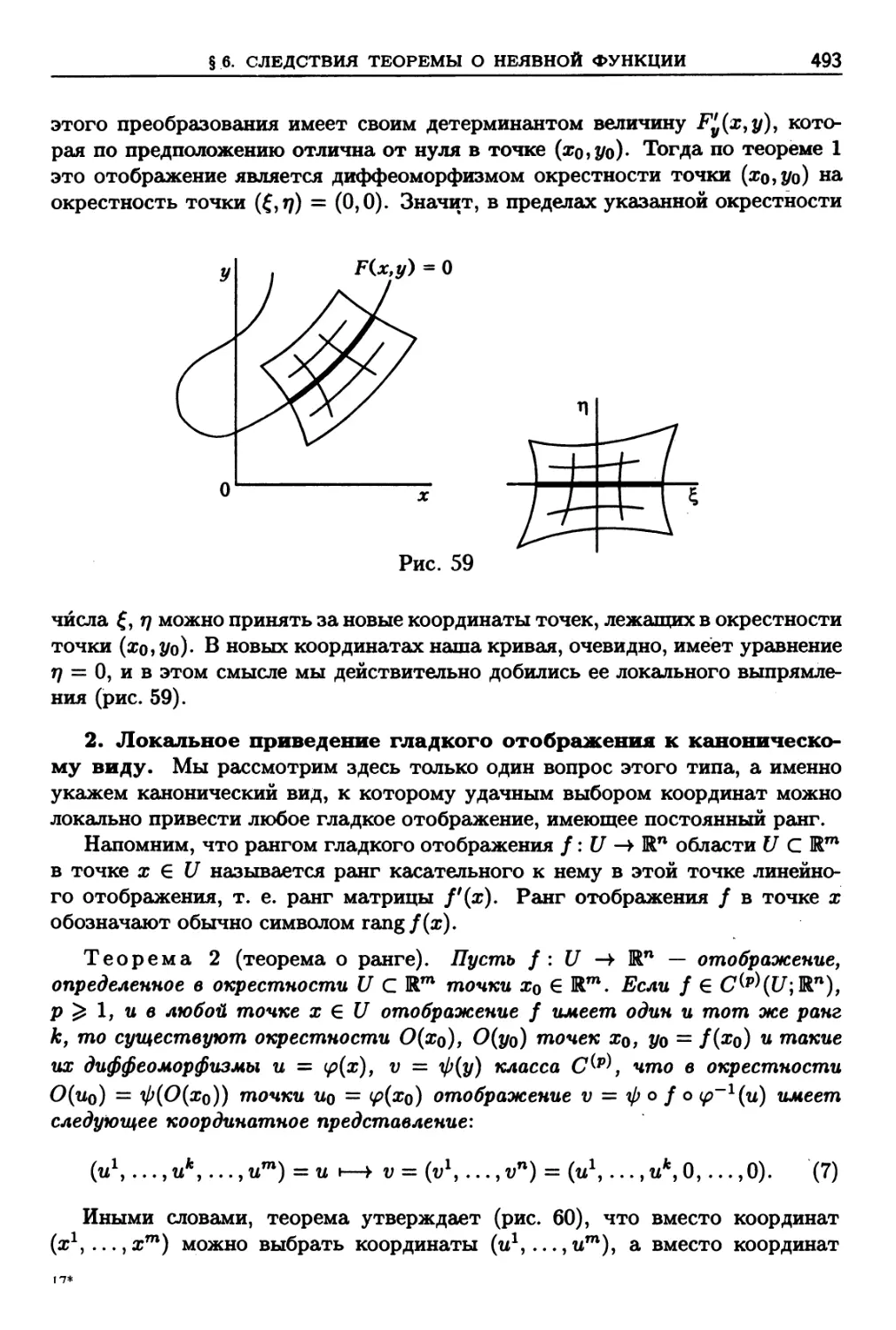
§ 5. Теорема о неявной функции 471
1. Постановка вопроса и наводящие соображения D71). 2. Простей-
Простейший вариант теоремы о неявной функции D73). 3. Переход к случаю
зависимости F(xl, ..., xm, у) = 0 D77). 4. Теорема о неявной функ-
функции D80). Задачи и упражнения D85).
§ 6. Некоторые следствия теоремы о неявной функции 489

VII ОГЛАВЛЕНИЕ
1. Теорема об обратной функции D89). 2. Локальное приведение глад-
гладкого отображения к каноническому виду D93). 3. Зависимость функ-
функций D97). 4. Локальное разложение диффеоморфизма в композицию
простейших D99). 5. Лемма Морса E01). Задачи и упражнения E05).
§ 7. Поверхность в Rn и теория условного экстремума 506
1. Поверхность размерности к в Rn E06).. 2. Касательное простран-
пространство E11). 3. Условный экстремум E16). Задачи и упражнения E28).
Некоторые задачи коллоквиумов 533
Вопросы к экзамену 538
Литература 542
Алфавитный указатель 545

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
В этом, втором издании книги, наряду с попыткой устранить опечатки пер-
первого1), сделаны отдельные изменения изложения (в основном это касается
вариантов доказательств отдельных теорем) и добавлены некоторые новые
задачи, как правило, неформального характера. В предисловии к первому
изданию этого курса анализа уже дана его общая характеристика, указаны
основные принципы и направленность изложения. Здесь я хотел бы сделать
несколько практических замечаний, связанных с использованием книги в учеб-
учебном процессе.
Любым учебником обычно пользуются как студент, так и преподаватель —
каждый для своих целей. Сначала и тот, и другой заинтересованы иметь
книгу, где, помимо формально необходимого минимума теории, имеются по
возможности разнообразные содержательные примеры ее использования, по-
пояснения, исторический и научный комментарии, демонстрируются взаимосвя-
взаимосвязи, указываются перспективы развития. Но в момент подготовки к экзамену
студент желает видеть тот материал, который выносится на экзамен. Пре-
Преподаватель точно так же, завершая подготовку курса, отбирает только тот
материал, который может и должен быть изложен в отведенное курсу время.
В этой связи следует иметь в виду, что текст данного учебника, конеч-
конечно, заметно шире того конспекта лекций, на базе которого он написан. Что
составило эту разницу? Во-первых, к конспекту добавлен, по существу, це-
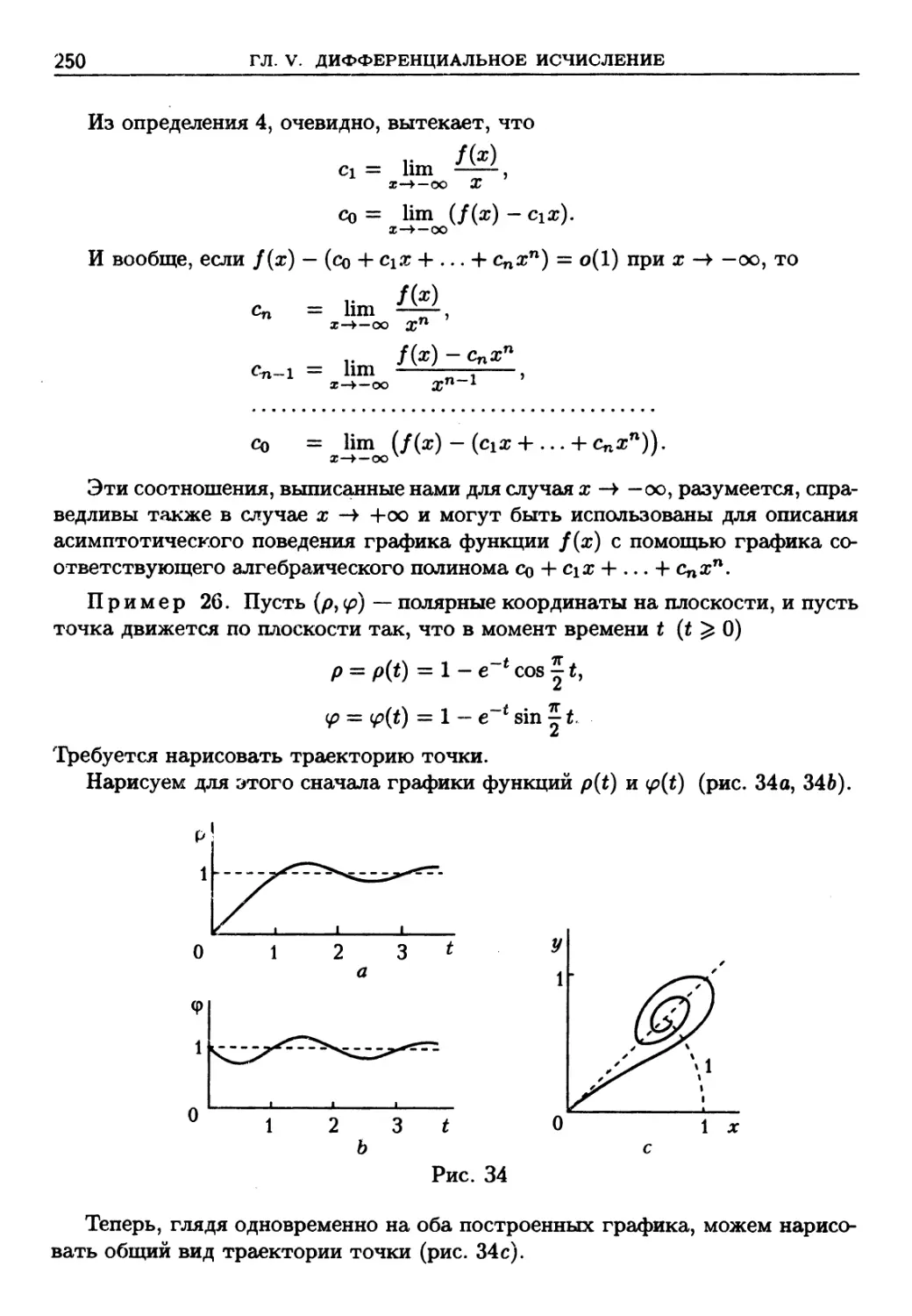
целый задачник, состоящий, не столько из упражнений, сколько из содержа-
содержательных задач естествознания или собственно математики, примыкающих к
соответствующим разделам теории, а иногда и существенно расширяющих их.
Во-вторых, в книге, конечно, разобрано много больше примеров, демонстри-
демонстрирующих теорию в действии, чем это удается сделать на лекциях. Наконец,
в-третьих, ряд глав, параграфов или отдельных пунктов сознательно написа-
написаны как дополнение к традиционному материалу. Об этом сказано в разделах
*' Не следует огорчаться: вместо исправленных опечаток не сохранившегося набора пер-
первого издания заведомо появится комплект новых опечаток, так оживляющих, по мнению
Эйлера, чтение математического текста.

X ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
«О введении» и «О вспомогательном материале» предисловия к первому изда-
изданию.
Напомню также, что в предисловии к первому изданию я желал предосте-
предостеречь и студента, и начинающего преподавателя от чрезмерно долгого сквозно-
сквозного изучения вводных формальных глав. Это заметно откладывает собственно
анализ и сильно смещает акценты.
Чтобы показать, что на деле остается в реальном лекционном курсе от
этих формальных вводных глав, и чтобы в концентрированном виде изложить
программу такого курса в целом, а также отметить возможные ее вариации в
зависимости от контингента слушателей, я в конце книги привожу некоторые
задачи коллоквиумов, а также экзаменационные вопросы последнего времени
за первые два семестра, к которым относится эта часть I.
По экзаменационным вопросам профессионал, конечно, увидит и порядок
изложения, и степень развития в нем фундаментальных понятий и методов, и
привлечение порой материала второй части учебника, когда рассматриваемый
в первой части вопрос уже доступен слушателям в более общем виде1).
В заключение хотел бы поблагодарить знакомых и незнакомых мне кол-
коллег и студентов за отзывы и конструктивные замечания к первому изданию
курса. Особенно интересно и полезно мне было прочитать рецензии А. Н. Кол-
Колмогорова и В. И. Арнольда. Разные по объему, форме и стилю, они в профес-
профессиональном плане имели так ободряюще много общего.
Москва, 1997 В. Зорин
1> Часть записей соответствующих лекций опубликована и формально я даю ссылку на
изданные по ним брошюры, хотя понимаю, что они уже малодоступны (лекции были прочи-
прочитаны'и изданы ограниченным тиражом в Математическом колледже МНУ и на механико-
математическом факультете МГУ).

ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Создание Ньютоном и Лейбницем три столетия тому назад основ дифферен-
дифференциального и интегрального исчисления даже по нынешним масштабам пред-
представляется крупнейшим событием в истории науки вообще и математики в
особенности.
Математический анализ (в широком смысле слова) и алгебра, переплета-
переплетаясь, образовали теперь ту корневую систему, на которой держится разветвлен-
разветвленное дерево современной математики и через которую происходит его основной
живительный койтакт с внематематическои сферой. Именно по этой причине
основы анализа включаются как необходимый элемент даже самых скромных
представлений о так называемой высшей математике, и, вероятно, поэтому
изложению основ анализа посвящено большое количество книг, адресованных
различным кругам читателей.
Эта книга в первую очередь адресована математикам, желающим (как и
должно) получить полноценные в логическом отношении доказательства фун-
фундаментальных теорем, но вместе с тем интересующимся также их внемате-
внематематическои жизнью.
Особенности настоящего курса, связанные с указанными обстоятельства-
обстоятельствами, сводятся в основном к следующему.
По характеру изложения. В пределах каждой большой темы изло-
изложение, как правило, индуктивное, идущее порой от постановки задачи и на-
наводящих эвристических соображений по ее решению к основным понятиям и
формализмам.
Подробное вначале, изложение становится все более сжатым по мере про-
продвижения по курсу.
Упор сделан на эффективном аппарате гладкого анализа. При изложении
теории я (в меру своего понимания) стремился выделить наиболее существен-
существенные методы и факты и избежать искушения незначительного усиления теорем
ценой значительного усложнения доказательств.
Изложение геометрично всюду, где это представлялось ценным для рас-
раскрытия существа дела.
Основной текст снабжен довольно большим количеством примеров, а почти
каждый параграф заканчивается набором задач, которые, надеюсь, сущест-

XII ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
венно дополняют даже теоретическую часть основного текста. Следуя ве-
великолепному опыту Полна и Сеге, я часто старался представить красивый
математический или важный прикладной результат в виде серий доступных
читателю задач.
Расположение материала диктовалось не только архитектурой математи-
математики в смысле Бурбаки, но и положением анализа как составной части единого
математического или, лучше сказать, естественно-математического образо-
образования.
По содержанию. Курс издается в двух книгах (части I и II).
Настоящая первая часть содержит дифференциальное и интегральное ис-
исчисление функций одной переменной и дифференциальное исчисление функ-
функций многих переменных.
В дифференциальном исчислении выделена роль дифференциала как ли-
линейного эталона для локального описания характера изменения переменной
величины. Кроме многочисленных примеров использования дифференциаль-
дифференциального исчисления для исследования функциональных зависимостей (монотон-
(монотонность, экстремумы), показана роль языка анализа в записи простейших диф-
дифференциальных уравнений — математических моделей конкретных явлений и
связанных с ними содержательных задач. Рассмотрен ряд таких задан (на-
(например, движение тела переменной массы, ядерный реактор, атмосферное да-
давление, движение в сопротивляющейся среде), решение которых приводит к
важнейшим элементарным функциям. Полнее использован комплексный язык,
в частности, выведена формула Эйлера и показано единство основных элемен-
элементарных функций.
Интегральное исчисление сознательно изложено по возможности на нагляд-
наглядном материале в рамках интеграла Римана. Для большинства приложений это-
этого вполне хватает1). Указаны различные приложения интеграла, в том числе
приводящие к несобственному интегралу (например, работа выхода из поля
тяготения и вторая космическая скорость) или к эллиптическим функциям
(движение в поле тяжести при наличии связей, маятник).
Дифференциальное исчисление функций нескольких переменных доволь-
довольно геометрично. В нем, например, рассмотрены такие важные и полезные
следствия теоремы о неявной функции, как криволинейные координаты и ло-
локальное приведение к каноническому виду гладких отображений (теорема о
ранге) и функций (лемма Морса), а также теория условного экстремума.
Результаты, относящиеся к теории непрерывных функций и дифференци-
дифференциальному исчислению, подытожены и изложены в общем инвариантном виде в
двух главах, которые естественным образом примыкают к дифференциаль-
дифференциальному исчислению вещественнозначных функций нескольких переменных. Эти
две главы открывают вторую часть курса. Вторая книга, в которой, кроме
х) Более «сильные» интегралы, как известно, требуют более кропотливых и выбиваю-
выбивающихся из основного русла теоретико-множественных рассмотрений, мало что прибавляя к
эффективному аппарату анализа, который и должен быть освоен в первую очередь.

ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ XIII
того, изложено интегральное исчисление функций многих переменных, дове-
доведенное до общей формулы Ньютона—Лейбница — Стокса, приобретает, таким
образом, определенную целостность.
Более полные сведения о второй книге мы поместим в предисловии к ней, а
здесь добавим только, что кроме уже перечисленного материала она содержит
сведения о рядах функций (степенных рядах и рядах Фурье в том числе),
об интегралах, зависящих от параметра (включая фундаментальное решение,
свертку и преобразование Фурье), а также об асимптотических разложениях
(они обычно мало представлены в учебной литературе).
Остановимся теперь на некоторых частных вопросах.
О введении. Вводного обзора предмета я не писал, поскольку большин-
большинство начинающих студентов уже имеют из школы первое представление о диф-
дифференциальном и интегральном исчислении и его приложениях, а на большее
вступительный обзор вряд ли мог бы претендовать. Вместо него я в первых
двух главах довожу до определенной математической завершенности предста-
представления бывшего школьника о множестве, функции, об использовании логиче-
логической символики, а также о теории действительного числа.
Этот материал относится к формальным основаниям анализа и адресован
в первую очередь студенту-математику, который в какой-то момент захочет
проследить логическую структуру базисных понятий и принципов, использу-
используемых в классическом анализе. Собственно математический анализ в книге
начинается с третьей главы, поэтому читатель, желающий по возможности
скорее получить в руки эффективный аппарат и увидеть его приложения, при
первом чтении вообще может начать с главы III, возвращаясь к более ранним
страницам в случае, если что-то ему покажется неочевидным и вызовет во-
вопрос, на который, надеюсь, я тоже обратил внимание и предусмотрительно
дал ответ в первых главах.
О рубрикации. Материал обеих книг разбит на главы, имеющие сплош-
сплошную нумерацию. Параграфы нумеруются в пределах каждой главы отдельно;
подразделения параграфа нумеруются только в пределах этого параграфа.
Теоремы, утверждения, леммы, определения и примеры для большей логиче-
логической четкости выделяются, а для удобства ссылок нумеруются в пределах
каждого параграфа.
О вспомогательном материале. Несколько глав книги написаны
как естественное окаймление классического анализа. Это, с одной стороны,
уже упоминавшиеся главы I, II, посвященные его формально-математическим
основаниям, а с другой стороны, главы IX, X, XV второй части,.дающие совре-
современный взгляд на теорию непрерывности, дифференциальное и интегральное
исчисление, а также глава XIX, посвященная некоторым эффективным асим-
асимптотическим методам анализа.
Вопрос о том, какая часть материала этих глав включается в лекционный
«
курс, зависит от контингента слушателей и решается лектором, но некоторые
вводимые здесь фундаментальные понятия обычно присутствуют в любом из-
изложении предмета математикам.

XIV ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
В заключение я хотел бы поблагодарить тех, чья дружеская и квалифи-
квалифицированная профессиональная помощь была мне дорога и полезна при работе
над этой книгой.
Предлагаемый курс довольно тщательно и во многих аспектах согласо-
согласовывался с последующими современными университетскими математическими
курсами — такими, например, как дифференциальные уравнения, дифферен-
дифференциальная геометрия, теория функций комплексного переменного, функцио-
функциональный анализ. В этом отношении мне были весьма полезны контакты и
обсуждения с В. И. Арнольдом и, особенно многочисленные, с С. П. Новико-
Новиковым в период совместной работы в экспериментальном потоке при отделении
математики.
Много советов я получил от Н. В. Ефимова, заведующего кафедрой мате-
математического анализа механико-математического факультета МГУ.
Я признателен также коллегам по кафедре и факультету за замечания к
ротапринтному изданию моих лекций.
При работе над книгой ценными оказались предоставленные в мое рас-
распоряжение студенческие записи моих лекций последнего времени, за что я
благодарен их владельцам.
Я глубоко признателен официальным рецензентам издательства Л. Д. Ку-
Кудрявцеву, В. П. Петренко, СБ. Стечкину за конструктивные замечания, зна-
значительная часть которых учтена в предлагаемом читателю тексте.
Москва, 1980 В. Зорин

ГЛАВА I
НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ
ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
§ 1. Логическая символика
1. Связки и скобки. Язык этой книги, как и большинства математи-
математических текстов, состоит из обычного языка и ряда специальных символов
излагаемых теорий. Наряду с этими специальными символами, которые бу-
будут вводиться по мере надобности, мы используем распространенные симво-
символы математической логики ->, Л, V, =>, <=> для обозначения соответственно
отрицания «не» и связок «и», «или», «влечет», «равносильно».1)
Возьмем, например, три представляющих и самостоятельный интерес вы-
высказывания:
L. «Если обозначения удобны для открытий ..., то поразительным обра-
образом сокращается работа мысли» (Г. Лейбниц2)).
Р. «Математика — это искусство называть разные вещи одинаковыми
именами» (А. Пуанкаре3)).
G. «Великая книга природы написана языком математики» (Г. Галилей4)).
*) В логике вместо символа Л чаще используется символ &. Символ =>• импликации ло-
логики чаще пишут в виде ->, а отношение равносильности — в виде « > или «—>. Однако мы
будем придерживаться указанной в тексте символики, чтобы не перегружать традиционный
для анализа знак —> предельного перехода.
2)Г. В. Лейбниц A646 —1716) — выдающийся немецкий ученый, философ и математик,
которому наряду с Ньютоном принадлежит честь открытия основ анализа бесконечно ма-
малых.
3)А. Пуанкаре A854 — 1912) — французский математик, блестящий ум которого пре-
преобразовал многие разделы математики и достиг ее фундаментальных приложений в мате-
математической физике.
4) Г. Галилей A564 — 1642) — итальянский ученый, крупнейший естествоиспытатель. Его
труды легли в основу всех последующих физических представлений о пространстве и вре-
времени. Отец современной физической науки.

ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Тогда в соответствии с указанными обозначениями:
Запись
L=>P
((L =>Р)Л (-.Р)) => (-.L)
^((L<^G)V(PoG))
Означает
L влечет Р
L равносильно Р
Если Р следует из L и Р неверно,
то L неверно
G не равносильно ни L, ни Р
Мы видим, что пользоваться только формальными обозначениями, избегая
разговорного языка, — не всегда разумно.
Мы замечаем, кроме того, что в записи сложных высказываний, соста-
составленных из более простых, употребляются скобки, выполняющие ту же син-
синтаксическую функцию, что и при записи алгебраических выражений. Как и
в алгебре, для экономии скобок можно договориться о «порядке действий».
Условимся с этой целью о следующем порядке приоритета символов:
-1, Л, V, =», <=».
При таком соглашении выражение -*А ABWС => D следует расшифровать
как (((-«A) AB)VC)=^D,a соотношение А V В => С — как (А V В) => С, но
не как А V (В => С).
Записи А => 5, означающей, что А влечет 5 или, что то же самое, В
следует из А, мы часто будем придавать другую словесную интерпретацию,
говоря, что В есть необходимый признак или необходимое условие А и, в
свою очередь, А — достаточное условие или достаточный признак В. Та-
Таким образом, соотношение А «Ф=> В можно прочитать любым из следующих
способов:
А необходимо и достаточно для В;
А тогда и только тогда, когда В;
А, если и только если В;
А равносильно В.
Итак, запись А <=> В означает, что А влечет В и, одновременно, В вле-
влечет А.
Употребление союза и в выражении А А В пояснений не требует.
Следует, однако, обратить внимание на то, что в выражении А V В со-
союз или неразделительный, т. е. высказывание А V В считается верным, если
истинно хотя бы одно из высказываний А, В. Например, пусть х — такое

§ 1. ЛОГИЧЕСКАЯ СИМВОЛИКА
действительное число, что х2 — За: + 2 = 0. Тогда можно написать, что имеет
место следующее соотношение:
(х2 - Зж + 2 = 0) <=> (х = 1) V (х = 2).
2. Замечания о доказательствах. Типичное математическое утверж-
утверждение имеет вид А => В, где А — посылка, а В — заключение. Доказательство
такого утверждения состоит в построении цепочки А => С\ =>...=> Сп => В
следствий, каждый элемент которой либо считается аксиомой, либо является
уже доказанным утверждением1).
В доказательствах мы будем придерживаться классического правила вы-
вывода: если А истинно и А =Ф- В, то В тоже истинно.
При доказательстве от противного мы будем использовать также принцип
исключенного третьего, в силу которого высказывание А V ->А (А или не А)
считается истинным независимо от конкретного содержания высказывания А.
Следовательно, мы одновременно принимаем, что -*(->А) <=> А, т. е. повторное
отрицание равносильно исходному высказыванию.
3. Некоторые специальные обозначения. Для удобства читателя и
сокращения текста начало и конец доказательства условимся отмечать знака-
знаками < и > соответственно.
Условимся также, когда это будет удобно, вводить определения посред-
посредством специального символа := (равенство по определению), в котором двое-
двоеточие ставится со стороны определяемого объекта.
Например,запись
[f(x)dx:= lim <т(/;Р,0
J А(Р)->0
а
определяет левую часть посредством правой части, смысл которой предпола-
предполагается известным.
Аналогично вводятся сокращенные обозначения для уже определенных вы-
выражений. Например,запись
п
вводит обозначение сг(/;Р, ?) для стоящей слева суммы специального вида.
4. Заключительные замечания. Отметим, что мы здесь говорили, по
существу, только об обозначениях, не анализируя формализм логических вы-
выводов и не касаясь глубоких вопросов истинности, доказуемости, выводимо-
выводимости, составляющих предмет исследования математической логики.
Запись А => В => С будет употребляться как сокращение для (А => В) Л (В => С).

4 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Как же строить математический анализ, если мы не имеем формализа-
формализации логики? Некоторое утешение тут может состоять в том, что мы всегда
знаем или, лучше сказать, умеем больше, чем способны в данный момент фор-
формализовать. Пояснением смысла последней фразы может служить известная
притча о том, что сороконожка даже ходить разучилась, когда ее попросили
объяснить, как именно она управляется со всеми своими конечностями.
Опыт всех наук убеждает нас в том, что считавшееся ясным или простым
и нерасчленяемым вчера может подвергнуться пересмотру или уточнению се-
сегодня. Так было (и, без сомнения, еще будет) и с многими понятиями мате-
математического анализа, важнейшие теоремы и аппарат которого были открыты
еще в XVII —XVIII веках, но приобрели современный формализованный, од-
однозначно трактуемый и, вероятно, потому общедоступный вид лишь после
создания теории пределов и необходимой для нее логически полноценной тео-
теории действительных чисел (XIX век).
Именно с этого уровня теории действительных чисел мы и начнем в главе II
построение всего здания анализа.
Как уже отмечалось в предисловии, желающие быстрее ознакомиться с
основными понятиями и эффективным аппаратом собственно дифференци-
дифференциального и интегрального исчисления могут начать сразу с III главы, возвра-
возвращаясь к отдельным местам первых двух глав лишь по мере необходимости.
Упражнения
Будем отмечать истинные высказывания символом 1, а ложные — символом 0.
Тогда каждому из высказываний ->А, А А В, А V В, А => В можно сопоставить
так называемую таблицу истинности, которая указывает его истинность в зави-
зависимости от истинности высказываний А, В. Эти таблицы являются формальным
определением логических операций ->, Л, V, =>. Вот они:
А
^А
0
1
1
0
АЛВ
А\
0
1
0
0
0
1
0
1
AV В
В
0
1
0
1
0
0
1
0
1
0
1
1
1
1
1
1

§ 2. МНОЖЕСТВО И ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
1. Проверьте, все ли в этих таблицах согласуется с вашим представлением о
соответствующей логической операции. (Обратите, в частности, внимание на то,
что если А ложно, то импликация А =>- В всегда истинна.)
2. Покажите, что справедливы следующие простые, но очень важные и широко
используемые в математических рассуждениях соотношения:
a) -.(Л AB)^-iAv -.?;
b) i(A V В) <=> -лА Л iB;
c) (А => В) <=> (-,? =>
d) (Л => Б) «=> -.А V Б;
e) -i(i4 => В) <=> А Л -iB
§ 2. Множество и элементарные операции
над множествами
1. Понятие множества. С конца прошлого — начала нашего столетия
наиболее универсальным языком математики стал язык теории множеств.
Это проявилось даже в одном из определений математики как науки, изу-
изучающей различные структуры (отношения) на множествах1).
«Под множеством мы понимаем объединение в одно целое определенных,
вполне различимых объектов нашей интуиции или нашей мысли» — так описал
понятие «множество» Георг Кантор2), основатель теории множеств.
Описание Кантора, разумеется, нельзя назвать определением, поскольку
оно апеллирует к понятиям, быть может, более сложным (во всяком случае, не
определенным ранее), чем само понятие множества. Цель этого описания —
разъяснить понятие, связав его с другими.
Основные предпосылки канторовской (или, как условно говорят, «наив-
«наивной») теории множеств сводятся к следующему:
1° Множество может состоять из любых различимых объектов.
2° Множество однозначно определяется набором составляющих его объ-
объектов.
3° Любое свойство определяет множество объектов, которые этим свой-
свойством обладают.
Если х — объект, Р — свойство, Р(х) — обозначение того, что 2; обладает
свойством Р, то через {х\Р(х)} обозначают весь класс объектов, обладаю-
обладающих свойством Р. Объекты, составляющие класс или множество, называют
элементами класса или множества.
*
1) Бурбаки Н. Архитектура математики. В кн.: Бурбаки Н. Очерки по истории
математики. М.: ИЛ, 1963.
2)Г. Кантор A845 —1918) — немецкий математик, создатель теории бесконечных мно-
множеств и родоначальник теоретико-множественного языка в математике.

ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Множество, состоящее из элементов #i, ..., хп, обычно обозначают как
{х\, ..., хп}. Там, где это не вызывает недоразумения, для сокращения записи
мы позволяем себе обозначать одноэлементное множество {а} просто через а.
Слова «класс», «семейство», «совокупность», «набор» в наивной теории мно-
множеств употребляют как синонимы термина «множество».
Следующие примеры демонстрируют применение этой терминологии:
множество букв «а» в слове «я»;
множество жен Адама;
набор из десяти цифр;
семейство бобовых;
множество песчинок на Земле;
совокупность точек плоскости, равноудаленных от двух данных
ее точек;
семейство множеств;
множество всех множеств.
Различие в возможной степени определенности задания множества наводит
на мысль, что множество — не такое уж простое и безобидное понятие.
И в самом деле, например, понятие множества всех множеств просто про-
противоречиво.
<4 Действительно, пусть для множества М запись Р(М) означает, что М
не содержит себя в качестве своего элемента.
Рассмотрим класс К = {М \ Р(М)} множеств, обладающих свойством Р.
Если К — множество, то либо верно, что Р(К), либо верно, что ->Р(К).
Однако эта альтернатива для К невозможна. Действительно, Р(К) невоз-
невозможно, ибо из определения К тогда бы следовало, что К содержит К, т. е.
что верно ~>Р(К); с другой стороны, -*Р(К) тоже невозможно, поскольку это
означает, что К содержит К, а это противоречит определению К как класса
тех множеств, которые сами себя не содержат.
Следовательно, К — не множество. >
Это классический парадокс Рассела1), один из тех парадоксов, к которым
приводит наивное представление о множестве.
В современной математической логике понятие множества подвергается
(как мы видим, не без оснований) тщательному анализу. Однако в такой
анализ мы углубляться не станем. Отметим только, что в существующих ак-
аксиоматических теориях множество определяется как математический объект,
обладающий определенным набором свойств.
Описание этих свойств составляет аксиоматику. Ядром аксиоматики те-
теории множеств является постулирование правил, по которым из множеств
1^Б. Рассел A872 —1970) — английский логик, философ, социолог и общественный
деятель.

§ 2. МНОЖЕСТВО И ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
можно образовывать новые множества. В целом любая из существующих ак-
аксиоматик такова, что она, с одной стороны, избавляет от известных проти-
противоречий наивной теории, а с другой — обеспечивает свободу оперирования
с конкретными множествами, возникающими в различных отделах матема-
математики, и в первую очередь именно в математическом анализе, понимаемом в
широком смысле слова.
Ограничившись пока этими замечаниями относительно понятия множе-
множества, перейдем к описанию некоторых наиболее часто используемых в анализе
свойств множеств.
Желающие подробнее ознакомиться с понятием множества могут просмо-
просмотреть пункт 2 из § 4 настоящей главы или обратиться к специальной литера-
литературе.
2. Отношение включения. Как уже отмечалось, объекты, составляю-
составляющие множество, принято называть элементами этого множества. Мы будем
стремиться обозначать множества прописными буквами латинского алфави-
алфавита, а элементы множества — соответствующими строчными буквами.
Высказывание их есть элемент множества X» коротко обозначают сим-
символом
х € X (или X Э х),
а его отрицание — символом
X (или X $ х).
х
В записи высказываний о множествах часто используются логические опе-
операторы 3 («существует» или «найдется») и V («любой» или «для любого»), на-
называемые кванторами существования и всеобщности соответственно.
Например, запись Wx ((x e А) <=> (х ? В)) означает, что для любого объек-
объекта х соотношения х ? А и х Е В равносильны. Поскольку множество вполне
определяется своими элементами, указанное высказывание
принято обозначать короткой записью
А = В,
читаемой «Л равно В», обозначающей совпадение множеств.
Аи В.
Таким образом, два множества равны, когда они состоят
из одних и тех же элементов.
Отрицание равенства обычно записывают в виде Аф В.
Если любой элемент множества А является элементом
множества В, то пишут А С В или В D А и говорят, что множество Д
является подмножеством множества В, или что В содержит А, или что В
включает в себя А. В связи с этим отношение А С В между множествами
В называется отношением включения (рис. 1).
Рис. 1

8
ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Итак,
{А С В) := Vz {{х еА)^(хе В)).
Если А С В и А ф В, то будем говорить, что включение А С В строгое
или что А — собственное подмножество В.
Используя приведенные определения, теперь можно заключить, что
(А = В) <=» {А С Б) Л (В С А).
Если М — множество, то любое свойство Р выделяет в М подмножество
{хеМ\Р(х)}
тех элементов М, которые обладают этим свойством.
Например, очевидно, что
. М - {х Е М\х Е М}.
С другой стороны, если в качестве Р взять свойство, которым не обладает
ни один элемент множества М, например Р(х) := (х ф х), то мы получим
множество
0 = {х е М \х ф х},
называемое пустым подмножеством множества М.
3. Простейшие операции над множествами. Пусть А и В — под-
подмножества множества М.
a. Объединением множеств А и В называется множество
A U В := {х ? М | (а: € А) V (х Е Б)},
состоящее из тех и только тех элементов множества М, юэторые содержатся
хотя бы в одном из множеств А, В (рис. 2).
b. Пересечением множеств А и В называется множество
А Г) В := {я Е М | (х Е А) Л (ж Е
образованное теми и только теми элементами множества М, которые принад-
принадлежат одновременно множествам А и В (рис. 3).
Рис. 2
Рис. 3
Рис. 4
Рис. 5

§ 2. МНОЖЕСТВО И ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
с. Разностью между множеством А и множеством В называется множе-
множество
А \ В := {х € М | (х € А) Л (х ? Б)},
состоящее из тех элементов множества А, которые не содержатся в множестве
В (рис. 4).
Разность между множеством М и содержащимся в нем подмножеством
А обычно называют дополнением А в М и обозначают через СмА или СА,
когда из контекста ясно, в каком множестве ищется дополнение к А (рис. 5).
Пример. В качестве иллюстрации взаимодействия введенных понятий
проверим следующие соотношения (так называемые правила де Моргана1)):
СМ(А U В) = См А П СМВ, A)
СМ(А ПВ) = См A U СМВ. B)
«^ Докажем, например, первое из этих равенств:
(х € Cm(AUB)) => (х ? {AU В)) =* ((х ? А) Л (х i В)) =*
=* (я € См А) Л (х € СМ5) 4(xG (СМА П СМ5)).
Таким образом, установлено, что
СМ(А U В) с (СмА П СмВ). C)
С другой стороны,
(х € (СмА П СМВ)) =* ((х е СмА) Л (х € См#)) =>
((х ? А) Л (х i В)) =* (х i (A U В)) =* (х € СМ(А U
т. е.
(СмА П СМЯ) С СМ(А U В). D)
Из C) и D) следует A). >
d. Прямое (декартово) произведение множеств. Для любых двух мно-
множеств А, В можно образовать новое множество — пару {А, В} = {В, А}, эле-
элементами которого являются множества А и В и только они. Это множество
состоит из двух элементов, если А ф В, и из одного элемента, если А = В.
Указанное множество называют неупорядоченной парой множеств А, В,
в отличие от упорядоченной пары (А, В), в которой элементы А, В наделены
дополнительными признаками, выделяющими первый и второй элементы пары
{А, В}. Равенство
(А, В) = (С, D)
А. де Морган A806 — 1871) — шотландский математик.

Ю ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
упорядоченных пар по определению означает, что А — С и В — D. В част-
частности, если А ф Б, то (А, В) ф (В, А).
Пусть теперь X и Y — произвольные множества. Множество
X х Y := {(х,у)\(х ? X) Л (у ? Y)},
образованное всеми упорядоченными парами (х, у), первый член которых есть
элемент из X, а второй член — элемент из У, называется прямым или декар-
декартовым произведением множеств X и Y (в таком порядке!).
Из определения прямого произведения и сделанных выше замечаний об
упорядоченной паре явствует, что, вообще говоря, X х Y ф Y х X. Равенство
имеет место, лишь если X = Y. В последнем случае вместо X х X пишут
коротко X2.
Прямое произведение называют также декартовым произведением в честь
Декарта1), который независимо от Ферма2) пришел через систему коорди-
координат к аналитическому языку геометрии. Известная всем система декартовых
координат в плоскости превращает эту плоскость именно в прямое произве-
произведение двух числовых осей. На этом знакомом объекте наглядно проявляется
зависимость декартова произведения от порядка сомножителей. Например,
упорядоченным парам @,1) и A,0) отвечают различные точки плоскости.
В упорядоченной паре z = (х1,хг), являющейся элементом прямого про-
произведения Z = Х\ х Х2 множеств Х\ и Хг, элемент х\ называется первой
проекцией пары z и обозначается через prx z, а элемент Х2 — второй проек-
проекцией пары z и обозначается через pr2 z.
Проекции упорядоченной пары по аналогии с терминологией аналитиче-
аналитической геометрии часто называют (первой и второй) координатами пары.
Упражнения
В задачах 1, 2, 3 через A, J5, С обозначены подмножества некоторого множе-
множества М.
1. Проверьте соотношения:
a) (АСС)Л(ВСС)<=> ((A U В) С С);
b) (С С А) А (С С В) <^> (С С (АП Б));
c) См(СмА) = А;
d) (А С СМВ) <^(ВС См А);
e) (А С В) <=> (СмА э СМВ).
^Р. Декарт A596 — 1650) — выдающийся французский философ, математик и физик,
внесший фундаментальный вклад в теорию научного мышления и познания.
2Ш. Ферма A601 — 1665) — замечательный французский математик, юрист по специ-
специальности. Ферма стоял у истоков ряда областей современной математики: анализ, анали-
аналитическая геометрия, теория вероятностей, теория чисел.

§ 3. ФУНКЦИЯ 11
2. Покажите, что
a) A U (В U С) = (A U В) U С =: A U Б U С;
b) АП(ВПС) = (АПВ)ПС=:АПВПС;
c) А П (В U С) = (А П Б) U (А П С);
d) A U (Б П С) = (A U Б) П (A U С).
3. Проверьте взаимосвязь (двойственность) операций объединения и пересече-
пересечения:
a) Cm(AUB) = СмАПСмВ]
b) СМ(А ПВ) = См A U СМВ.
4. Проиллюстрируйте геометрически декартово произведение:
a) двух отрезков (прямоугольник);
b) двух прямых (плоскость);
c) прямой и окружности (цилиндрическая поверхность);
d) прямой и круга (цилиндр);
e) двух окружностей (тор);
f) окружности и круга (полноторие).
5. Множество Л = {(xi,X2) 6 X2\xi = ?2} называется диагональю декартова
квадрата X2 множества X.
Проиллюстрируйте геометрически диагонали множеств, полученных в пунктах
а), Ь), е) задачи 4.
6. Покажите, что
a) (X xY = 0)<=>(Х = 0)V(Y = 0),
а если X х У ф 0, то
b) (А х В С X х Y) <t> (А С X) Л (В С Y),
c) (X х У) U (Z х У) = (X U Z) х У,
d) (X х У) П (X' х Уг) = (ХП X') х (У П У;).
Здесь 0 — символ пустого множества, т. е. множества, не содержащего элементов.
7. Сравнив соотношения задачи 3 с соотношениями а), Ь) из упражнения 2 к § 1,
установите соответствие между логическими операциями -«, Л, V на высказываниях
и операциями С, П, U на множествах.
§ 3. Функция
1. Понятие функции (отображения). Перейдем теперь к описанию
фундаментального не только для математики понятия функциональной зави-
зависимости.
Пусть X и У — какие-то множества.
Говорят, что имеется функция, определенная на X со значениями в У, если
в силу некоторого закона / каждому элементу х Е X соответствует элемент

12 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
В этом случае множество X называется областью определения функции;
символ х его общего элемента — аргументом функции или независимой пе-
переменной] соответствующий конкретному значению Xq € X аргумента х эле-
элемент уо € У называют значением функции на элементе Xq или значением
функции при значении аргумента х = хо и обозначают через f(xo). При из-
изменении аргумента х Е X значения у = f(x) Е У, вообще говоря, меняются в
зависимости от значений х. По этой причине величину у — f(x) часто назы-
называют зависимой переменной.
Множество
f(X) := {у 6 Y | Эх ((* 6 X) Л (у = /(*)))}
всех значений функции, которые она принимает на элементах множества X,
будем называть множеством значений или областью*значений функции.
В зависимости от природы множеств X, У термин «функция» в различных
отделах математики имеет ряд полезных синонимов: отображение, преобра-
преобразование, морфизм, оператор, функционал. Отображение — наиболее распро-
распространенный из них, и мы его тоже часто будем употреблять.
Для функции (отображения) приняты следующие обозначения:
/: X -» У, X -А У.
Когда из контекста ясно, каковы область определения и область значе-
значений функции, используют также обозначения х »-> /(х) или у = /(я), а чаще
обозначают функцию вообще одним лишь символом /.
Две функции /i, /2 считаются совпадающими или равными, если они име-
имеют одну и ту же область определения X и на любом элементе х ? X значения
Л(я), /2 (я) этих функций совпадают. В этом случае пишут /i = /2.
Если AcX,a,f:X-*Y — некоторая функция, то через f\A или /\а
обозначают функцию <р : А —? Y, совпадающую с / на множестве А. Точнее,
/|л(х) := р(х), если х Е А. Функция /\а называется сужением или ограни-
ограничением функции / на множество А, а функция / : X -> Y по отношению к
функции <р — $\а : А -> Y называется распространением или продолжением
функции (р на множество X.
Мы видим, что иногда приходится рассматривать функцию (р : А -> У,
определенную на подмножестве А некоторого множества X, причем область
значений (р{А) функции <р тоже может оказаться не совпадающим с У под-
подмножеством множества У. В связи с этим для обозначения любого множества
X, содержащего область определения функции, иногда используется термин
область отправления функции, а любое множество У, содержащее область
значений функции, называют тогда областью ее прибытия.
Итак, задание функции (отображения) предполагает указание тройки

§ 3. ФУНКЦИЯ 13
X — отображаемое множество, или область определения функции;
Y — множество, в которое идет отображение, или область прибытия
функции;
/ — закон, по которому каждому элементу х € X сопоставляется
определенный элемент у € У.
Наблюдаемая здесь несимметричность между X и Y отражает то, что
отображение идет именно из X в Y.
Рассмотрим некоторые примеры функций.
Пример 1. Формулы / = 2тгг и V = - тгг3 устанавливают функциональ-
ную зависимость длины окружности / и объема шара V от радиуса г. По
смыслу каждая из этих формул задает свою функцию /: П&+ —У IR+, опреде-
определенную на множестве П&+ положительных действительных чисел со значения-
значениями в том же множестве IR+.
Пример 2. Пусть X — множество инерцяальных систем координат, а
с: X -* Ш — функция, состоящая в том, что каждой инерциальной системе
координат х Е X сопоставляется измеренное относительно нее значение с(х)
скорости света в вакууме. Функция с : X -> Ш постоянна, т. е. при любом
х Е X она имеет одно и то же значение с (это фундаментальный эксперимен-
экспериментальный факт).
Пример 3. Отображение G : Ш2 -» Е2 (прямого произведения Ш2 = R х
х Ш = Rt х Rx оси времени IR* и пространственной оси Rx) на себя же, зада-
задаваемое формулами
х' — х — vt,
есть классическое преобразование Галилея для перехода от одной инерциаль-
инерциальной системы координат (x,t) к другой — (х;,^), движущейся относительно
первой со скоростью v.
Той же цели служит отображение L : Е2 -> Ж2, задаваемое соотношениями
х — vt
x1
t —
Это — известное (одномерное) преобразование Лоренца1\ играющее фунда-
фундаментальную роль в специальной теории относительности; с — скорость света.
^Г. А. Лоренц A853 — 1928) — голландский физик. Указанные преобразования были
найдены им в 1904 г. и существенно использовались в сформулированной в 1905 г. Эйн-
Эйнштейном специальной теории относительности.

14 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Пример 4. Проектирование ргх: Х\ х Х2 -» Х\, задаваемое соответст-
вием Xi х Хг Э (xi,?2) 1—^ х\ Е Х\, очевидно, является функцией. Аналогич-
Аналогичным образом определяется вторая проекция рг2 : Х\ х Х^ -> Х2-
Пример 5. Пусть V{M) — множество всех подмножеств множества М.
Каждому множеству А Е V(M) поставим в соответствие множество См А Е
Е V(M), т. е. дополнение к Ав М. Тогда получим отображение См ' V{M)
—> V(M) множества V(M) в себя.
Пример 6. Пусть Е С М. Вещественнозначную функцию \е ' М -»
определенную на множестве М условиями (хе{х) — 1, если х Е Е) Л (хе(х) =
= 0, если х Е СмЕ), называют характеристической функцией множества Е.
Пример 7. Пусть M(X\Y) — множество отображений множества X в
множество У, а х$ — фиксированный элемент из X. Любой функции / Е
Е M(X;Y) поставим в соответствие ее значение /(хо) Е Y на элементе яо-
Этим определяется функция F: М(Х; Y) -> У. В частности, если У = Е, т. е.
если У есть множество действительных чисел, то каждой функции /: X —> Е
функция F : М(Х;Е) -> Е ставит в соответствие число F(f) = f(xo). Таким
образом, F есть функция, определенная на функциях. Для удобства такие
функции называют функционалами.
Пример 8. Пусть Г — множество кривых, лежащих на поверхности
(например, земной) и соединяющих две ее фиксированные точки. Каждой
кривой 7 € Г можно сопоставить ее длину. Тогда мы получим функцию
F : Г -» Е, которую часто приходится рассматривать с целью отыскания
кратчайшей линии или, как говорят, геодезической линии между данными
точками на поверхности.
Пример 9. Рассмотрим множество М(Е;Е) всех вещественнозначных
функций, определенных на всей числовой оси Е. Фиксировав число а Е Е, ка-
каждой функции / Е М(Е;Е) поставим в соответствие функцию /а Е М(Е;Е),
связанную с ней соотношением fa(x) = f(x + a). Функцию /а(я) обычно на-
называют сдвигом на а функции f{x). Возникающее при этом отображение
А: М(Е;Е) -» М(Е;Е) называется оператором сдвига. Итак, оператор А
определен на функциях и значениями его также являются функции: fa = A(f).
Рассмотренный пример мог бы показаться искусственным, если бы мы на
каждом шагу не видели реальные операторы. Так, любой радиоприемник есть
оператор / •—> /, преобразующий электромагнитные сигналы / в звуковые /;
любой из наших органов чувств является оператором (преобразователем) со
своими областью определения и областью значений.
Пример 10. Положение частицы в пространстве определяется упорядо-
упорядоченной тройкой чисел (x,y,z), называемой ее координатами в пространстве.
Множество всех таких упорядоченных троек можно себе мыслить как прямое
произведение Е х Е х Е = Е3 трех числовых осей Е.
При движении в каждый момент времени t частица находится в некото-
некоторой точке пространства Е3 с координатами (x(t),y(t),z(t)). Таким образом,

§ з. функция 15
движение частицы можно интерпретировать как отображение j: Е —У Е3, где
Е — ось времени, а Е3 — трехмерное пространство.
Если система состоит из п частиц, то ее конфигурация задается положе-
положением каждой из частиц, т. е. упорядоченным набором (si,yi,2i; #2,2/2,^2; ...
• • • ; Хп,Уп, Zn) из Зга чиселч Множество всех таких наборов называется конфи-
конфигурационным пространством системы п частиц. Следовательно, конфигура-
конфигурационное пространство системы п частиц можно интерпретировать как прямое
произведение Е3 х Е3 х ... х Е3 = Е3п п экземпляров пространства Е3.
Движению системы из п частиц отвечает отображение 7 : R ~> ^Зп °си
времени в конфигурационное пространство системы.
Пример 11. Потенциальная энергия U механической системы связана с
взаимным расположением частиц системы, т. е. определяется конфигурацией,
которую имеет система. Пусть Q — множество реально возможных конфигу-
конфигураций системы. Это некоторое подмножество конфигурационного простран-
пространства системы. Каждому положению q Е Q отвечает некоторое значение U(q)
потенциальной энергии системы. Таким образом, потенциальная энергия есть
функция U: Q —> Е, определенная на подмножестве Q конфигурационного
пространства со значениями в области Е действительных чисел.
Пример 12. Кинетическая энергия К системы п материальных частиц
зависит от их скоростей. Полная механическая энергия системы Е = К + С/,
т. е. сумма кинетической и потенциальной энергий, зависит, таким образом,
как от конфигурации q системы, так и от набора v скоростей ее частиц. Как
и конфигурация q частиц в пространстве, набор v, состоящий из п трехмер-
трехмерных векторов, может быть задан упорядоченным набором из Зтг чисел. Упо-
Упорядоченные пары (q,v), отвечающие состояниям нашей системы, образуют
подмножество Ф в прямом произведении Е3п х Е3п = Е6п, называемом фазо-
фазовым пространством системы п частиц (в отличие от конфигурационного
пространства Е3п).
Полная энергия системы является, таким образом, функцией Е : Ф -» Е,
определенной на подмножестве Ф фазового пространства Е6п и принимающей
значения в области Е действительных чисел.
В частности, если система замкнута, т. е. на нее не действуют внешние
силы, то по закону сохранения энергии в любой точке множества Ф состояний
системы функция Е будет иметь одно и то же значение Eq 6
2. Простейшая классификация отображений. Когда функцию /:
X -» Y называют отображением, значение f(x) € У, которое она принимает
на элементе х € X, обычно называют образом элемента х.
Образом множества А С X при отображении /: X -> Y называют мно-
множество
f(A) := {у е Y | Эх ((* е А) Л (у = /(*))}
тех элементов У, которые являются образами элементов множества А.

16
ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Множество
r1(B)-{xeX\f(x)eB)
тех элементов X, образы которых содержатся в В, называют прообразом
(или полным прообразом) множества В С Y (рис. 6).
Про отображение /: X —У Y говорят, что
х х¦---- х у \ оно:
сюръективно (или есть отображение X
на У), если /(X) = У;
инъективно (или есть вложение, инъек-
инъекция), если для любых элементов xi, ?2 мно-
множества X
Рис. 6
т. е. различные элементы имеют различные
образы;
биективно (или взаимно однозначно), если оно сюръективно и инъективно
одновременно.
Если отображение /: X —> У биективно, т. е. является взаимно однознач-
однозначным соответствием между элементами множеств X и У, то естественно воз-
возникает отображение
Г1: У->*,
которое определяется следующим образом: если f(x) = у, то f~x(y) — х,
т. е. элементу у Е У ставится в соответствие тот элемент а; Е I, образом
которого при отображении / является у. В силу сюръективности / такой
элемент х Е X найдется, а ввиду инъективности / он единственный. Таким
образом, отображение f~l определено корректно. Это отображение называют
обратным по отношению к исходному отображению /.
Из построения обратного отображения видно, что f~l: У -> X само явля-
является биективным и что обратное к нему отображение (Z): X -> У совпа-
совпадает с /: X -> У.
Таким образом, свойство двух отображений быть обратными является вза-
взаимным: если f~l — обратное для /, то, в свою очередь, / — обратное для f~l.
Заметим, что символ f~l(B) прообраза множества В С У ассоциируется с
символом f~l обратной функции, однако следует иметь в виду, что прообраз
множества определен для любого отображения / : X -> У, даже если оно не
является биективным и, следовательно, не имеет обратного.
3. Композиция функций и взаимно обратные отображения. Бо-
Богатым источником новых функций, с одной стороны, и способом расчленения
сложных функций на более простые — с другой, является операция компози-
композиции отображений.

§ 3. ФУНКЦИЯ
17
Если отображения f:X-*Yng:Y->Z таковы, что одно из них (в
нашем случае д) определено на множестве значений другого (/), то можно
построить новое отображение
gof:X->Z,
значения которого на элементах множества X определяются формулой
Построенное составное отображение д о / называют композицией отобра-
отображения / и отображения д (в таком порядке!).
Рисунок 7 иллюстрирует конструкцию композиции отображений / и д.
С композицией отображений вы уже неоднократно встречались как в гео-
геометрии, рассматривая композицию движений плоскости или пространства,
так и в алгебре при исследовании
«сложных» функций, полученных ком-
композицией простейших элементарных
функций.
Операцию композиции иногда при-
приходится проводить несколько раз под-
подряд, и в этой связи полезно отметить,
что она ассоциативна, т. е.
ho(gof) = (hog)of.
Действительно,
ho (до /)(*) = h((g о
Рис. 7
= h(g(f(x))) =
= (hog)(f(x)) = ((hog)of)(x). >
Это обстоятельство, как и в случае сложения или умножения нескольких
чисел, позволяет опускать скобки, предписывающие порядок спаривания.
Если в композиции fn о ... о Д все члены одинаковы и равны /, то ее
обозначают коротко /п.
Хорошо известно, например, что корень квадратный из положительного
числа а можно вычислить последовательными приближениями по формуле
начиная с любого начального приближения Хо > 0. Это не что иное, как после-
последовательное вычисление /п(хо), где f(x) — - (х 4- —). Такая процедура, когда
вычисленное на предыдущем шаге значение функции на следующем шаге ста-
становится ее аргументом, называется итерационным процессом. Итерационные
процессы широко используются в математике.

18 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Отметим также, что даже в том случае, когда обе композиции д о / и / о д
определены, вообще говоря,
9° f Ф f °9-
Действительно, возьмем, например, двухэлементное множество {а, 6} и
отображения /: {а, 6} -> а, д : {а, 6} -* &. Тогда, очевидно, д о /: {а, 6} -* &,
в то время как /ор: {о,&}-4о.
Отображение /: X —>• X, сопоставляющее каждому элементу множества
X его самого, т. е. я i—> х, будем обозначать через ех и называть тождест-
тождественным отображением множества X.
Лемма.
(д о / = ех) => (<7 сюръективно) А (/ инъективно).
Ч Действительно, если f: X -> Y, д : Y -+ X и ро
X = ех(Х) = E ° f)(X) = g(f(X)) С
и, значит, д сюръективно.
Далее, если xi € X и х% € X, то
(«1 5^ «а) => (ex(a?i) # ех(х2)) => (E ° /)(*i) # (ff ° /)(x2)) =*•
следовательно, / инъективно. >
Через операцию композиции отображений можно описать взаимно обрат-
обратные отображения.
Утверждение. Отображения f: X -> Y', д : Y —> X являются биек-
биективными и взаимно обратными в том и только в том случае, когда g о / =
= ех и f og = eY.
Ч В силу леммы одновременное выполнение условий д о/ = ех и / од =
гарантирует сюръективность и инъективность, т. е. биективность каждого
из отображений /, д.
Эти же условия показывают, что у = f(x) в том и только в том случае,
когда х = д(у). >
Выше мы исходили из явного построения обратного отображения. Из до-
доказанного утверждения следует, что мы могли бы дать менее наглядное, но
зато более симметричное определение взаимно обратных отображений как та-
таких, которые удовлетворяют двум условиям: д о f = ех и / о д = еу (см. в
этой связи задачу б в конце параграфа).

§ з. функция 19
4. Функция как отношение. График функции. В заключение вер-
вернемся вновь к самому понятию функции. Отметим, что оно претерпело дли-
длительную и довольно сложную эволюцию.
Термин «функция» впервые появился в 1692 г. у Г. Лейбница (правда, в
некотором более узком смысле). В смысле, близком к современному, этот
термин употребил в письме к Лейбницу от 1698 г. Иоганн Бернулли1).
В формировании современного понимания функциональной зависимости
приняли участие многие крупные математики.
Описание функции, почти совпадающее с приведенным в начале парагра-
параграфа, встречается уже в учебниках математики С. Лакруа2^ A806 г.), переве-
переведенных на русский язык. Активным сторонником такого понимания функции
был Н. И. Лобачевский3^. Более того, Н. И. Лобачевский указал A834 г.),
что «обширный взгляд теории допускает существование зависимости только
в том смысле, чтобы числа одни с другими в связи понимать как бы данными
вместе»4^. Это и есть идея точного определения понятия функции, которое
мы теперь собираемся изложить.
Приведенное в начале параграфа описание понятия функции представля-
представляется весьма динамичным и отражающим суть дела. Однако с точки зрения
современных канонов оно не может быть названо определением, ибо использу-
использует эквивалентное функции понятие соответствия. Для сведения читателя мы
укажем здесь, каким образом дается определение функции на языке теории
множеств.
а. Отношение. Отношением 71 называют любое множество упорядочен-
упорядоченных пар (я, 2/).
Множество X первых элементов упорядоченных пар, составляющих 7?, на-
называют областью определения отношения 71, а множество Y вторых элемен-
элементов этих пар — областью значений отношения 71.
Таким образом, отношение 7Z можно интерпретировать как подмножество
К прямого произведения X х Y. Если X С X1 и Y С У, то, разумеется,
К С X х У с X' х У, поэтому одно и то же отношение может задаваться как
подмножество различных множеств.
Любое множество, содержащее область определения отношения, называют
областью отправления этого отношения. Множество, содержащее область
значений отношения, называют областью прибытия отношения.
)И. Бернулли A667 —1748) — один из ранних представителей знаменитого семейства
швейцарских ученых Бернулли; аналитик, геометр, механик. Стоял у истоков вариационно-
вариационного исчисления. Дал первое систематическое изложение дифференциального и интегрального
исчисления.
2> С. Ф. Лакруа A765 — 1843) — французский математик и педагог (профессор Нормаль-
Нормальной и Политехнической школ, член Парижской академии наук).
3'Н. И. Лобачевский A792 — 1856) — великий русский ученый, которому, наряду с вели-
великим немецким естествоиспытателем К. Ф. Гауссом A777 — 1855) и выдающимся венгерским
математиком Я. Бойяи A802 —1860), принадлежит честь открытия неевклидовой геомет-
геометрии, носящей его имя.
4) Лобачевский Н. И. Полное собр. соч. Т. 5. М.-Л.: Гостехиздат, 1951. С. 44.
2 Зорич В. Л.

20 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Вместо того чтобы писать {х,у) € 7?, часто пишут х TZy и говорят, что х
связано с у отношением 71.
Если 1Z С X2, то говорят, что отношение 1Z задано на X.
Рассмотрим несколько примеров.
Пример 13. Диагональ
Д = {(а,Ь) еХ2\а = Ъ}
есть подмножество X2, задающее отношение равенства между элементами
множества X. Действительно, а А Ь означает, что (а, Ь) Е А, т. е. о = Ь.
Пример 14. Пусть X — множество прямых в плоскости.
Две прямые а Е X и Ь Е X будем считать находящимися в отношении 7Z
и будем писать alZ 6, если прямая Ь параллельна прямой а. Ясно, что тем
самым в X2 выделяется множество 71 пар (а, Ь) таких, что aTZb. Из курса
геометрии известно, что отношение параллельности между прямыми обладает
следующими свойствами:
a 1Z а (рефлексивность);
a 1Z Ь => Ы1а (симметричность);
(a 1Z Ь) Л (Ь 71 с) => a 1Z с (транзитивность).
Любое отношение 7?, обладающее перечисленными тремя свойствами, т. е.
рефлексивное1), симметричное и транзитивное, принято называть отноше-
отношением эквивалентности. Отношение эквивалентности обозначается специаль-
специальным символом ~, который в этом случае ставится вместо буквы 7?, обозна-
обозначающей отношение. Итак, в случае отношения эквивалентности будем писать
а ~ Ь вместо a 1Z Ь и говорить, что а эквивалентно Ь.
Пример 15. Пусть М — некоторое множество, & X = V(M) — совокуп-
совокупность всех его подмножеств. Для двух произвольных элементов а и Ь мно-
множества X = V(M), т. е. для двух подмножеств а и Ь множества М, всегда
выполнена одна из следующих трех возможностей: а содержится в 6; Ь содер-
содержится в а; а не является подмножеством Ь и Ь не является подмножеством а.
Рассмотрим в качестве отношения 7Z в X2 отношение включения для под-
подмножеств X, т. е. положим по определению
alZb := (а С Ь).
Это отношение, очевидно, обладает следующими свойствами:
а 71 а (рефлексивность);
(a 7Z b) A (b 71 с) => aTZc (транзитивность);
(a 7Z Ь) Л (Ь 71 а) => а А &, т. е. а = Ь (антисимметричность).
1> Полезно для полноты отметить, что отношение 1Z называется рефлексивным, если его
область определения и область значений совпадают и для любого элемента а из области
определения отношения 1Z выполнено

§ з. функция 21
Отношение между парами элементов некоторого множества X, обладаю-
обладающее указанными тремя свойствами, принято называть отношением частично-
частичного порядка на множестве X. Для отношения частичного порядка вместо а 71Ь
часто пишут а^Ьи говорят, что b следует за а.
Если кроме отмеченных двух свойств, определяющих отношение частич-
частичного порядка, выполнено условие, что
Va Vb {{аПЪ)\/(Ы1а)),
т. е. любые два элемента множества X сравнимы, то отношение 1Z называется
отношением порядка, а множество X с определенным на нем отношением
порядка называется линейно упорядоченным.
Происхождение этого термина связано с наглядным образом числовой пря-
прямой Е, на которой действует отношение а ^ Ь между любой парой веществен-
вещественных чисел.
Ь. Функция и график функции. Отношение 7? называется функцио-
функциональным, если
(х П ух) Л{хП у2) => (j/i = у2)-
Функциональное отношение называют функцией.
В частности, если X и Y — два не обязательно различных множества, то
определенное на X отношение 7Z С X х Y между элементами х из X и у из
Y функционально, если для любого х € X существует и притом единственный
элемент у Е Y, находящийся с х в рассматриваемом отношении, т. е. такой,
для которого xTZy.
Такое функциональное отношение 1Z С X х Y и есть отображение из X в
Y, или функция из X в Y.
Функции мы чаще всего будем обозначать символом /. Если / — функция,
то вместо xfy мы по-прежнему будем писать у = f(x) или х \—> у, называя
у — f(x) значением функции / на элементе х или образом элемента х при
отображении /.
Сопоставление по «закону» / элементу х € X «соответствующего» элемента
у ? Y, о чем говорилось в исходном описании понятия функции, как видим,
состоит в том, что для каждого х Е X указывается тот единственный элемент
у е Y, что xfy, т. е. (х,у) е f С X х Y.
Графиком функции /: X —t Y, понимаемой в смысле исходного описания,
называют подмножество Г прямого произведения X х Y, элементы которого
имеют вид (x,f(x)). Итак,
T~{(x,y)€XxY\y = f(x)}.
В новом описании понятия функции, когда мы ее задаем как подмножество
/ С X х Y, конечно, уже нет разницы между функцией и ее графиком.

22 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Мы указали на принципиальную возможность формального теоретико-
множественного определения функции, сводящуюся по существу к отожде-
отождествлению функции и ее графика. Однако мы не собираемся в дальнейшем
ограничиваться только такой формой задания функции. Функциональное от-
отношение иногда удобно задать в аналитической форме, иногда таблицей зна-
значений, иногда словесным описанием процесса (алгоритма), позволяющего по
данному х € X находить соответствующий элемент у € Y. При каждом таком
способе задания функции имеет смысл вопрос о ее задании с помощью гра-
графика, что формулируют так: построить график функции. Задание числовых
функций хорошим графическим изображением часто бывает полезно тем, что
делает наглядным основные качественные особенности функциональной зави-
зависимости. Для расчетов графики тоже можно использовать (номограммы), но,
как правило, в тех случаях, когда расчет не требует высокой точности. Для
точных расчетов используют табличное задание функции, а чаще — алгорит-
алгоритмическое, реализуемое в вычислительных машинах.
Упражнения
1. Композиция 7Z2 о 7Z\ отношений 7Z\, 7Z2 определяется следующим образом:
П20П1 :={(x,z)\3y (x7Ziy)A(y7Z2z)}.
В частности, если TZi С X х У и 7^2 С У х Z, то 71 = 7^2 о TZi С X х Z, причем
х П z := 3 у {{у е У) Л (х Их у) Л (у П2
a) Пусть Ах — диагональ множества X2, а Ау — диагональ множества У2.
Покажите, что если отношения IZi С X х Y и 1Z2 С Y х X таковы, что G?г о И\ =
— Ах) Л AZi о 7^2 = Ау), то оба они функциональны и задают взаимно обратные
отображения множеств X, Y.
b) Пусть 1Z С X2. Покажите, что условие транзитивности отношения 71 равно-
равносильно тому, что 1Z о 7? С 71.
c) Отношение 7Z' С Y х X называется транспонированным отношением 7Z С
С X х У, если (у 71'х) <=> (х 71 у).
Покажите, что антисимметричность отношения 71 С X2 равносильна условию
тгптг'с а*.
d) Проверьте, что любые два элемента множества X связаны (в том или ином
порядке) отношением 7Z С X2, если и только если 7ZU7Z' = X2.
2. Пусть /: X -» У — отображение. Прообраз f~l{y) С X элемента у G У назы-
называется слоем над у.
а) Укажите слои для отображений
: Х\ xX2->Xi, рг2 : Х\ х Х2 -> Х2.
Ь) Элемент х\ G X будем считать связанным с элементом х2 G X отношением
7Z С X2 и писать xi7?x2, если f(x\) = f(x2), т. е. если х\ и х2 лежат в одном слое.
Проверьте, что 7Z есть отношение эквивалентности.

§ з. функция 23
c) Покажите, что слои отображения /: X —> Y не пересекаются, а объединением
слоев является все множество X.
d) Проверьте, что любое отношение эквивалентности между элементами множе-
множества позволяет представить это множество в виде объединения непересекающихся
классов эквивалентных элементов.
3. Пусть /: X —> Y — отображение из X в Y. Покажите, что:
если А и В — подмножества X, то
a) (А С В) => (f(A) С f{B)) ф (А С В),
b) (А ф 0) => (f(A) ф 0),
c) /(А П В) С/(А) Л/(В),
d) /(A U В) = f(A) U /(В);
если А' и В' — подмножества У, то
e) ;а' с в') =* (/-Ча') с
f) \ 1
g)
если УэА'э В', то
h) 1 1
для любого множества А С X и любого множества В' С Y
j) rVWJDA,
к) НГЧв1)) с в'.
4. Покажите, что отображение /: X —> Y
а) сюръективно, если и только если для любого множества В' С Y справедливо
Ъ) биективно, если и только если для любого множества А С X и любого мно-
множества В' CY справедливо
5. Проверьте эквивалентность следующих утверждений относительно .отображе-
.отображения / : X -» Y:
a) / инъективно;
b) f~l{f{A)) = А Для любого множества Л С Х\
c) /(А П В) = /(А) П /(В) для любой пары А, В подмножеств Х\
d) f(A) П /(Л) = 0^»ЛПВ = 0;
e) /(А \ В) = /(А) \ /(В), если X D A D В.
6. а) Если отображения f:X—>Yug:Y—>X таковы, что д о f = ex, где
ex — тождественное отображение множества X, то д называется левым обратным
отображением для /, а / — правым обратным для #. Покажите, что, в отличие от
единственного обратного отображения, может существовать много односторонних
обратных отображений.

24 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Рассмотрите, например, отображения f:X-+Yug:Y-+X} где X — одноэле-
одноэлементное, а У — двухэлементное множества, или отображения последовательностей
) • • • /)
B/2, ...,уп, ..) <-^-» B/1,2/2, ...,2/п, .-
b) Пусть /:Х—>Уи(?:У-»? — биективные отображения. Покажите, что
отображение д о / : X —> Z биективно и что (д о f)~l = f~l о д~1.
c) Покажите, что для любых отображений f : X —У Y, д : Y —> Z и любого
множества С С Z справедливо равенство
d) Проверьте, что отображение F:XxY-+YxX, задаваемое соответствием
(х,у) ь-> (у,х), биективно. Опишите взаимосвязь графиков взаимно обратных отоб-
отображений f: X —>Y ъ f~l\Y -* X.
7. а) Покажите, что при любом отображении / : X —> Y отображение F*: X —>
—> X х У, определяемое соответствием х i—У (х,/(х)), является инъективным.
Ь) Пусть частица движется равномерно по окружности У; пусть X — ось вре-
времени и х i—> у — соответствие между моментом времени х G X и положением у =
= /(ж) G У частицы. Изобразите график функции /:1чУв1хУ.
8. а) Для каждого из разобранных в § 3 примеров 1 — 12 выясните, является ли
указанное в нем отображение сюръективным, инъективным, биективным или оно не
принадлежит ни одному из указанных классов.
b) Закон Ома / = V/R связывает силу тока / в проводнике с напряжением V на
концах проводника и сопротивлением R проводника. Укажите, отображение О: X -»
—> У каких множеств соответствует закону Ома. Подмножеством какого множества
является отношение, отвечающее закону Ома?
c) Найдите преобразования С?, L, обратные к преобразованиям Галилея и
Лоренца.
9. а) Множество 5 С X называется устойчивым относительно отображения
/ : X -4 X, если /E) С S. Опишите множества, устойчивые относительно сдвига
плоскости на данный лежащий в ней вектор.
b) Множество I С X называется инвариантным относительно отображения
/: X —> X, если /(/) = /. Опишите множества, инвариантные относительно пово-
поворота плоскости вокруг фиксированной точки.
c) Точка р G X называется неподвижной точкой отображения /: X -» X, если
f(p) — Р- Проверьте, что любая композиция сдвига, вращения и гомотетии плоско-
плоскости имеет неподвижную точку, если коэффициент гомотетии меньше единицы.
d) Считая преобразования Галилея и преобразования Лоренца отображениями
плоскости на себя, при которых точка с координатами (x,t) переходит в точку с
координатами (ж',?'), найдите инвариантные множества этих преобразований.
10. Рассмотрим установившийся поток жидкости (т. е. скорость в каждой точке
потока не меняется со временем). За время t частица, находящаяся в точке х потока,
переместится в некоторую новую точку ft{x) пространства. Возникающее отобра-
отображение х »-> ft(x) точек пространства, занимаемого потоком, зависит от времени t и
называется преобразованием за время t. Покажите, что ft2 о ftl = ftl о ft2 = ftx+t2
и ft о f-t = /о =

§ 4. НЕКОТОРЫЕ ДОПОЛНЕНИЯ 25
§ 4. Некоторые дополнения
1. Мощность множества (кардинальные числа). Говорят, что мно-
множество X равномощно множеству У, если существует биективное отображе-
отображение X на У, т. е. каждому элементу х е X сопоставляется элемент у € У,
причем различным элементам множества X отвечают различные элементы
множества У и каждый элемент у Е У сопоставлен некоторому элементу мно-
множества X.
Описательно говоря, каждый элемент х € X сидит на своем месте у € У,
все элементы X сидят и свободных мест у Е У нет.
Ясно, что введенное отношение X 71Y является отношением эквивалент-
эквивалентности, поэтому мы будем, как и договаривались, писать в этом случае X ~ Y
вместо X 71Y.
Отношение равномощности разбивает совокупность всех множеств ла
классы эквивалентных между собой множеств. Множества одного класса
эквивалентности имеют одинаковое количество элементов (равномощны), а
разных — разное.
Класс, которому принадлежит множество X, называется мощностью мно-
множества X, а также кардиналом или кардинальным числом множества X и
обозначается символом cardX. Если X ~ У, то пишут cardX = card У.
Смысл этой конструкции в том, что она позволяет сравнивать количества
элементов множеств, не прибегая к промежуточному счету, т. е. к измерению
количества путем сравнения с натуральным рядом чисел N = {1, 2, 3, ...}.
Последнее, как мы вскоре увидим, иногда принципиально невозможно.
Говорят, что кардинальное число множества X не больше кардинального
числа множества У, и пишут cardX ^ card У, если X равномощно некоторому
подмножеству множества У.
Итак,
(cardX ^ card У) := CZ С У | cardX = cardZ).
Если X С У, то ясно, что cardX ^ card У. Однако, оказывается, соот-
соотношение X С У не мешает неравенству card У ^ cardX, даже если X есть
собственное подмножество У.
Например, соответствие х н-> -—г-г есть биективное отображение проме-
1 — \х\
жутка — 1 < х < 1 числовой оси Е на всю эту ось.
Возможность для множества быть равномощным своей части является
характерным признаком бесконечных множеств, который Дедекинд1) даже
предложил считать определением бесконечного множества. Таким образом,
множество называется конечным (по Дедекинду), если оно не равномощно
х)р. Дедекинд A831 — 1916) — немецкий математик-алгебраист, принявший активное
участие в развитии теории действительного числа. Впервые предложил аксиоматику мно-
множества натуральных чисел, называемую обычно аксиоматикой Пеано — по имени Дж. Пеано
A858 —1932), итальянского математика, сформулировавшего ее несколько позже.

26 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
никакому своему собственному подмножеству; в противном случае оно на-
называется бесконечным.
Подобно тому, как отношение неравенства упорядочивает действительные
числа на числовой прямой, введенное отношение неравенства упорядочивает
мощности или кардинальные числа множеств. А именно, можно доказать, что
справедливы следующие свойства построенного отношения:
1. (cardX ^ cardF) Л (cardУ ^ cardZ) => (cardX ^ cardZ) (очевидно).
2. (cardX ^ cardF) Л (card У ^ cardX) => (cardX = card У) (теорема
Шредера—Бернштейна1)).
3. VX УУ (cardX ^ card У) V (card У ^ cardX) (теорема Кантора).
Таким образом, класс кардинальных чисел оказывается линейно упорядо-
упорядоченным.
Говорят, что мощность множества X меньше мощности множества У, и
пишут cardX < card У, если cardX ^ card У и в то же время cardX ф card У.
Итак, (cardX < card У) := (cardX ^ card У) Л (cardX ф card У).
Пусть, как и прежде, 0 — знак пустого множества, аР(Х) — символ мно-
множества всех подмножеств множества X. Имеет место следующая открытая
Кантором
Теорема. cardX < card'P(X).
М Для пустого множества 0 утверждение очевидно, поэтому в дальнейшем
можно считать, что X ф 0.
Поскольку V(X) содержит все одноэлементные подмножества X, cardX ^
Для доказательства теоремы теперь достаточно установить, что cardX ф
Ф cardP(X), если X ф 0.
Пусть, вопреки утверждению, существует биективное отображение /:
X —У V(X). Рассмотрим множество А = {х Е Х\х $ f{x)} тех элементов
х Е X, которые не содержатся в сопоставленном им множестве f(x) E V{X).
Поскольку А € V(X), то найдется элемент а € X такой, что /(а) = А. Для
элемента а Е X невозможно ни соотношение а € А (по определению А), ни
соотношение а ? А (опять-таки по определению А). Мы вступаем в противо-
противоречие с законом исключенного третьего. >
Эта теорема, в частности, показывает, что если бесконечные множества
существуют, то и «бесконечности» бывают разные.
2. Об аксиоматике теории множеств. Цель настоящего пункта — дать ин-
интересующемуся читателю представление о системе аксиом, описывающих свойства
математического объекта, называемого множеством, и продемонстрировать про-
простейшие следствия этих аксиом.
. Бернштейн A878 — 1956) — немецкий математик, ученик Г. Кантора; Э. Шредер
A841 — 1902) — немецкий математик.

§ 4. НЕКОТОРЫЕ ДОПОЛНЕНИЯ 27
1° Аксиома объемности. Множества А и В равны тогда и только тогда,
когда они имеют одни и те же элементы.
Это означает, что мы отвлекаемся от всех прочих свойств объекта «множество»,
кроме свойства иметь данные элементы. На практике это означает, что если мы
желаем установить, что А = В, то мы должны проверить, что Vx ((x 6 А) <=>
<=>(хе В)).
2° Аксиома выделения. Любому множеству А и свойству Р отвечает
множество В, элементы которого суть те и только те элементы множества А,
которые обладают свойством Р.
Короче, утверждается, что если А — множество, то и В = {х G А \ Р(х)} — тоже
множество.
Эта аксиома очень часто используется в математических конструкциях, когда
мы выделяем из множеств подмножества, состоящие из элементов, обладающих тем
или иным свойством.
Например, из аксиомы выделения следует, что существует пустое подмножество
0х = {х G X | х ф х} в любом множестве X, а с учетом аксиомы объемности заклю-
заключаем, что для любых множеств X и Y выполнено 0х = 0у, т. е. пустое множество
единственно. Его обозначают символом 0.
Из аксиомы выделения следует также, что если А и В — множества, то А \ В —
= {х G А | х ? В} — тоже множество. В частности, если М — множество и А — его
подмножество, то См А — тоже множество.
3° Аксиома объединения. Для любого множества М множеств сущест-
существует множество UM, называемое объединением множества М, состоящее из техф
и только тех элементов, которые содержатся в элементах множества М.
Если вместо слов «множество множеств» сказать «семейство множеств», то ак-
аксиома объединения приобретает несколько более привычное звучание: существует
множество, состоящее из элементов множеств семейства. Таким образом, объедине-
объединение множества есть множество, причем iGUM <=> ЗХ ((X G М) А (х 6 X)).
Аксиома объединения с учетом аксиомы выделения позволяет определить пере-
пересечение множества М (семейства множеств) как множество
пм := {х ? им | \/х ((X ем)=>(хе X))}.
4° Аксиома пары. Для любых множеств X и Y существует множество Z
такое, что X и Y являются его единственными элементами.
Множество Z обозначается через {X, У} и называется неупорядоченной парой
множеств X nY. Множество Z состоит из одного элемента, если X = Y.
Как мы уже отмечали, упорядоченная пара (X, Y) множеств отличается от неупо-
неупорядоченной наличием какого-либо признака у одного из множеств пары. Например,
Итак, неупорядоченная пара позволяет ввести упорядоченную пару, а упорядо-
упорядоченная пара позволяет ввести прямое произведение множеств, если воспользоваться
аксиомой выделения и следующей важной аксиомой.
5° Аксиома множества подмножеств. Для любого множества X су-
существует множество V(X), состоящее из тех и только тех элементов, которые
являются подмножествами множества X.
Короче говоря, существует множество всех подмножеств данного множества.

28 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Теперь можно проверить, что упорядоченные пары (х,у), где х € X, а у € У,
действительно образуют множество
X х Y := {р е V(P(X) U V(Y)) |р = (х,у) Л (х 6 X) Л (у € У)}.
Аксиомы 1°—5° ограничивают возможность формирования новых множеств.
Так, в множестве V(X) по теореме Кантора (о том, что cardX < card'P(X)) имеется
элемент, не принадлежащий X, поэтому «множества» всех множеств не существу-
существует. А ведь именно на этом «множестве» держится парадокс Рассела.
Для того чтобы сформулировать следующую аксиому, введем понятие последо-
последователя Х+ множества X. Положим по определению Х+ = X U {X}. Короче, к X
добавлено одноэлементное множество {X}.
Далее, множество назовем индуктивным, если оно содержит в качестве элемента
пустое множество и последователь любого своего элемента.
6° Аксиома бесконечности. Индуктивные множества существуют.
Аксиома бесконечности позволяет с учетом аксиом 1°—4° создать эталонную
модель множества No натуральных чисел (по фон Нейману1'), определив No как
пересечение индуктивных множеств, т. е. как наименьшее индуктивное множество.
Элементами No являются множества
0, 0+=0U{0} =
которые и являются моделью того, что мы обозначаем символами 0, 1, 2, ... и назы-
называем натуральными числами.
7° Аксиома подстановки. Пусть Т(х>у) — такое высказывание (точнее,
формула), что при любом хо из множества X существует и притом единствен-
единственный объект уо такой, что Т(хо,уо) истинно. Тогда объекты у, для каждого из
которых существует элемент х 6 X такой, что J-(x,y) истинно, образуют мно-
множество.
Этой аксиомой при построении анализа мы пользоваться не будем.
Аксиомы 1°—7° составляют аксиоматику теории множеств, известную как ак-
аксиоматика Цермело — Френкеля 2\
К ней обычно добавляется еще одна, независимая от аксиом 1°—7° и часто ис-
используемая в анализе
8° Аксиома выбора. Для любого семейства непустых множеств сущест-
существует множество С такое, что, каково бы ни было множество X данного семей-
семейства, множество X ПС состоит из одного элемента.
Иными словами, из каждого множества семейства можно выбрать в точности по
одному представителю так, что выбранные элементы составят множество С.
Аксиома выбора, известная в математике как аксиома Цермело, вызвала горячие
дискуссии специалистов.
1^Дж. фон Нейман A903 —1957) — американский математик. Работы по функциональ-
функциональному анализу, математическим основаниям квантовой механики, топологическим группам,
теории игр, математической логике. Руководил созданием первых ЭВМ.
2)Э. Цермело A871 — 1953) — немецкий математик; А. Френкель A891 — 1965) — немец-
немецкий, затем израильский математик.

§ 4. НЕКОТОРЫЕ ДОПОЛНЕНИЯ 29
2. Замечания о структуре математических высказываний и запи-
записи их на языке теории множеств. В языке теории множеств имеются два
базисных или, как говорят, атомарных типа математических высказываний:
утверждение х Е А о том, что объект х есть элемент множества Л, и утвер-
утверждение А = В о том, что множества А и В совпадают. (Впрочем, с учетом
аксиомы объемности второе утверждение является комбинацией утверждений
первого типа: (х € А) <=> (х е В).)
Сложное высказывание или сложная логическая формула строятся из ато-
атомарных посредством логических операторов — связок -«, Л, V, =>• и кван-
кванторов V, 3 с использованием скобок ( ). При этом формирование сколь угод-
угодно сложного высказывания и его записи сводится к выполнению следующих
элементарных логических операций:
a) Образование нового высказывания путем постановки отрицания перед
некоторым высказыванием и заключение результата в скобки.
b) Образование нового высказывания путем постановки необходимой связ-
связки Л, V, => между двумя высказываниями и заключение результата в скобки.
c) Образование высказывания «для любого объекта х выполнено свойст-
свойство Р» (что записывают в виде Vx P(x)) или высказывания «найдется объект
х, обладающий свойством Р» (что записывают в виде Зх Р{х)).
Например, громоздкая запись
Зх (Р(х) Л (Vj/ ((P(y)) ^(у = х))))
означает, что найдется объект х, обладающий свойством Р и такой, что если
у — любой объект, обладающий свойством Р, то у = х. Короче: существу-
существует и притом единственный объект х, обладающий свойством Р. Обычно это
высказывание обозначают в виде Э!х Р(х), и мы будем использовать такое
сокращение.
Для упрощения записи высказывания, как уже отмечалось, стараются опу-
опустить столько скобок, сколько это возможно без потери однозначного толко-
толкования записи. С этой целью кроме указанного ранее приоритета операторов
-1, Л, V, => считают, что наиболее жестко символы в формуле связываются
знаками Е, =, затем 3, V и потом связками ->, Л, V, =>.
С учетом такого соглашения теперь можно было бы написать
Э!х Р(х) := Эх (Р(х) Л V</ (P(y) =>у = х)).
Условимся также о следующих широко используемых сокращениях:
(Vx е X) Р := Vx (x G X => Р(х)),
(Эх е X) Р := Эх (х е X Л Р(х)),
(Vx > а) Р := Ух (х G Ш Л х > а => Р(х)),
(Эх > а) Р := Эх (х G Ш Л х > а Л Р(х)).
Здесь Е, как всегда, есть символ множества действительных чисел.

30 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
С учетом этих сокращений и правил а), Ь), с) построения сложного выска-
высказывания, например, можно будет дать однозначно трактуемую запись
lim /(ж) = А := Уе > 0 38 > 0 Ух G E @ < \x - a\ < S =* |/(x) - Л| < е)
«>a
того, что число А является пределом функции /: Е —>• Е в точке о G
Быть может, наиболее важным из всего сказанного в этом параграфе явля-
являются для нас следующие правила построения отрицания к высказыванию, со-
содержащему кванторы.
Отрицание к высказыванию «для некоторого х истинно Р(х)» означает,
что «для любого х неверно Р(ж)», а отрицание к высказыванию «для любого х
истинно Р(х)» означает, что «найдется х, что неверно Р(х)».
Итак,
-.За; Р(х)
-•Уж Р(х) <=>3х -«Р(ж).
Напомним также (см. упражнения к § 1), что
На основании сказанного можно заключить, что, например,
¦ч((Уж > а) Р) <=> (Эх > a) -iP.
Написать в правой части последнего соотношения (Эх ^ а) ->Р было бы, ко-
конечно, ошибочно.
В самом деле,
((Уж > а) Р) := -I (Уж (xGEAx>a=> Р(ж)))
(хЕЕЛх>а=> Р(х))
Эх ((ж е ЕЛх > а)Л-«Р(ж)) =: (Эх > а) -«Р.
Если учесть указанную выше структуру произвольного высказывания, то
теперь с использованием построенных отрицаний простейших высказываний
можно было бы построить отрицание любого конкретного высказывания.
Например,
( lim /(ж) = А) <=> Зе > 0 У5 > 0 Эх G
G Е @ < |х - а\ < S Л |/(х) - Л| ^ е).
Практическая важность правильного построения отрицания связана, в
частности, с методом доказательства от противного, когда истинность не-
некоторого утверждения Р извлекают из того, что утверждение -«Р ложно.

§ 4. НЕКОТОРЫЕ ДОПОЛНЕНИЯ 31
Упражнения
1. а) Установите равномощность отрезка {гг€К|0^а;^1}и интервала {х 6
€R|O<?<1} числовой прямой R как с помощью теоремы Шредера — Бернштейна,
так и непосредственным предъявлением нужной биекции.
Ь) Разберите следующее доказательство теоремы Шредера — Бернштейна
(card X ^ card У) Л (card У ^ cardX) => (card* = card У).
< Достаточно доказать, что если множества Х) У, Z таковы, что X D Y D Z и
card Л* = cardZ, то cardX = card У. Пусть / : X —> Z — биективное отображение.
Тогда биекция д : X —ь У может быть задана, например, следующим образом:
/(х), если х € fn{X) \ /П(У) для некоторого п 6 N,
х в противном случае.
Здесь /п = / о ... о / — п-я итерация отображения /, а N — множество натуральных
чисел. >
2. а) Исходя из определения пары, проверьте, что данное в пункте 2 определение
прямого произведения X х У множеств X, У корректно, т. е. множество V(V(X) U
U V(Y)) содержит все упорядоченные пары (х, у), в которых х ? X и у € У.
b) Покажите, что всевозможные отображения f: X —> Y одного фиксированно-
фиксированного множества X в другое фиксированное множество У сами образуют множество
M(X,Y).
c) Проверьте, что если 11 — множество упорядоченных пар (т. е. отношение), то
первые элементы пар, принадлежащих множеству 11 (как и вторые), сами образуют
множество.
3. а) Используя аксиомы объемности, пары, выделения, объединения и беско-
бесконечности, проверьте, что для элементов множества No натуральных чисел по фон
Нейману справедливы следующие утверждения:
1° х = у => х+ = у+;
2° (VxGNo) (х+^0);
3° х+ = у+ =Ф- х = у;
4° (Vx e No) (х ф 0 => (Эу е No) (x = у+)).
Ъ) Используя то, что No — индуктивное множество, покажите, что для любых
его элементов х и у (а они в свою очередь являются множествами) справедливы
следующие соотношения:
1° cardx ^ cardx+;
2° card0 < cardx+;
3° cardx < card у <=Ф- cardx" < cardt/+;
4° cardx < cardx+;
5° card x < card у => card x+ ^ card y\
6° x = у <<=>> cardx = cardy;
7° (xCy)V(xDy).

32 ГЛ. I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
с) Покажите, что в любом подмножестве X множества No найдется такой (наи-
(наименьший) элемент хт, что (Vx 6 X) (cardxm ^ cardx). (В случае затруднений к
этой задаче можно вернуться после прочтения главы И.)
4. Мы будем иметь дело только с множествами. Поскольку множество, состоящее
из различных элементов, само может быть элементом другого множества, логики все
множества обычно обозначают строчными буквами. В настоящей задаче это очень
удобно.
a) Проверьте, что запись
Vx Зу Vz (z G у <=$- Зги (z G w Л w G х))
выражает аксиому объединения, по которой существует множество у — объединение
множества х.
b) Укажите, какие аксиомы теории множеств представлены записями
Vx Vy Vz ({z G x <<=>• z G у) <=>• x = у),
Vx Vy 3z Vt; (г; 6 z <=$> (v ~ x V v = y)),
Vx 3y Vz (z G у <=> Vu (u e z =Ф- и e x)),
Эх (Vy (-1З2 (z € y) => у G x) Л Vw (гу € 1 => Vw (Vv (г; G г* <=>
<=$> (v = w V г; G гу)) ^=Ф- it G x)).
c) Проверьте, что формула
Vz (z € f => Cxi 3yi (xi G x Л yi G у Л z = (xi, j/i))) Л
Л Vxi (xi G x =» 3yi 3z (yi G у Л z = (xi,yi) Л z € f)) Л
Л Vxi Vyi Vy2 Czi 3z2 (zi G /Л Z2 G /Л zi = (xi,yi) Л
Az2 = (xi,y2)) => yi = У2)
последовательно накладывает на множество / три ограничения: / есть подмноже-
подмножество х х у; проекция / на х совпадает с х; каждому элементу xi из х отвечает ровно
один элемент у\ из у такой, что (xi,yi) G /.
Таким образом, перед нами определение отображения /: х —> у.
Этот пример еще раз показывает, что формальная запись высказывания отнюдь
не всегда бывает более короткой и прозрачной в сравнении с его записью на разго-
разговорном языке. Учитывая это обстоятельство, мы будем в дальнейшем использовать
логическую символику лишь в той мере, в какой она будет нам представляться по-
полезной для достижения большей компактности или ясности изложения.
5. Пусть /: X —> У — отображение. Запишите логическое отрицание каждого из
следующих высказываний:
a) / сюръективно;
b) / инъективно;
c) / биективно.
6. Пусть X и Y — множества и / С X х Y. Запишите, что значит, что множество
/ не является функцией.

ГЛАВА II
ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ)
ЧИСЛА
Математические теории, как правило, находят свой выход в том, что позво-
позволяют перерабатывать один набор чисел (исходные данные) в другой набор
чисел, составляющий промежуточную или окончательную цель вычислений.
По этой причине особое место в математике и ее приложениях занимают чи-
числовые функции. Они (точнее, так называемые дифференцируемые числовые
функции) составляют главный объект исследования классического анализа.
Но сколь-нибудь полное с точки зрения современной математики описание
свойств этих функций, как вы уже могли почувствовать в школе и в чем вско-
вскоре убедитесь, невозможно без точного определения множества вещественных
чисел, на котором эти функции действуют.
Число в математике, как время в физике, известно каждому, но непонят-
непонятно лишь специалистам. Это одна из основных математических абстракций,
которой, по-видимому, еще предстоит существенная эволюция и рассказу о
которой может быть посвящен самостоятельный насыщенный курс. Здесь же
мы имеем в виду только свести воедино то, что читателю в основном известно
о действительных числах из средней школы, выделив в виде аксиом фундамен-
фундаментальные и независимые свойства чисел. При этом наша цель состоит в том,
чтобы дать точное, пригодное для последующего математического исполь-
использования определение вещественных чисел и обратить особое внимание на их
свойство полноты, или непрерывности, являющееся зародышем предельного
перехода — основной неарифметической операции анализа.
§ 1. Аксиоматика и некоторые общие свойства
множества действительных чисел
1. Определение множества действительных чисел
Определение 1. Множество Ш называется множеством действитель-
действительных (вещественных) чисел, а его элементы — действительными (веществен-

34 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
ными) числами, если выполнен следующий комплекс условий, называемый
аксиоматикой вещественных чисел:
(I) Аксиомы сложения
Определено отображение (операция сложения)
4-: К х ЛС ->
сопоставляющее каждой упорядоченной паре (х, у) элементов х, у из Ж неко-
некоторый элемент х + у Е Ж, называемый суммой х и у. При этом выполнены
следующие условия:
1+. Существует нейтральный элемент 0 (называемый в случае сло-
сложения нулем) такой, что для любого х Е
2+. Для любого элемента х Е Ж имеется элемент -iEl, называемый
противоположным к х, такой, что
х 4- (—х) = (—х) 4- х = 0.
3+. Операция 4- ассоциативна, т. е. для любых элементов х, у, z из
выполнено
х + (у~+ z) = (х 4- у) 4- z.
4+. Операция 4- коммутативна, т. е. для любых элементов ж, у из
выполнено
х 4- у = у 4- х.
Если на каком-то множестве G определена операция, удовлетворяющая ак-
аксиомам 1+, 2+, 3+, то говорят, что на G задана структура группы или что
G есть группа. Если операцию называют сложением, то группу называют
аддитивной. Если, кроме того, известно, что операция коммутативна, т. е.
выполнено условие 4+, то группу называют коммутативной или абелевойг\
Итак, аксиомы 1+— 4+ говорят, что Ш есть аддитивная абелева группа.
(II) Аксиомы умножения
Определено отображение (операция умножения)
сопоставляющее каждой упорядоченной паре (х,у) элементов я, у из Е не-
некоторый элемент х • у Е Ж, называемый произведением х и у, причем
так, что выполнены следующие условия:
1^Н. X. Абель A802 — 1829) — замечательный норвежский математик, доказавший не-
неразрешимость в радикалах алгебраических уравнений выше четвертой степени.

§ 1. АКСИОМАТИКА И СВОЙСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 35
#. Существует нейтральный элемент 1 Е Е \ О {называемый в случае
умножения единицей) такой, что Vx E
х •1 = 1 • х = х.
2#. Для любого элемента х Е Е\0 имеется элемент х Е Е, называемый
обратным, такой, что
х • х~1 — х~1 • х = 1.
3#. Операция • ассоциативна, т. е. для любых х, у, z из
х- (у- z) = (х-у) • z.
4#. Операция • коммутативна, т. е. для любых х, у из
х - у = у • х.
Заметим, что по отношению к операции умножения множество Е \ 0, как
можно проверить, является (мультипликативной) группой.
(I, II) Связь сложения и умножения
Умножение дистрибутивно по отношению к сложению, т. е. Vx, у, z G Ш
(х 4- y)z — xz + yz.
Отметим, что ввиду коммутативности умножения последнее равенство со-
сохранится, если в обеих его частях поменять порядок множителей.
Если на каком-то множестве G действуют две операции, удовлетворяющие
всем перечисленным аксиомам, то G называется алгебраическим полем или
просто полем.
(III) Аксиомы порядка
Между элементами Ш имеется отношение ^, т. е. для элементов х, у
из Ж установлено, выполняется ли х ^ у или нет. При этом должны удо-
удовлетворяться следующие условия:
. Vx G Е (х ^ х).
^ У) Л (у ^ х) => (х = у).
^y)A(y^z)=> (x^z).
. Vx G E V</ ? E (x ^ y) V (у ^ x).
Отношение $J в Е называется отношением неравенства.
Множество, между некоторыми элементами которого имеется отношение,
удовлетворяющее аксиомам 0^, 1^, 2^, как известно, называют частично упо-
упорядоченным, а если, сверх того, выполнена аксиома 3^, т. е. любые два элемен-
элемента множества сравнимы, то множество называется линейно упорядоченным.

36 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Таким образом, множество действительных чисел линейно упорядочено от-
отношением неравенства между его элементами.
(I, III) Связь сложения и порядка в
Если х, у, z — элементы Е, то
(х ^ у) => (х + z ^ у + z).
(II, III) Связь умножения и порядка в
Если х, у — элементы Е, то
х) Л ((К </) =>
(IV) Аксиома полноты (непрерывности)
Если X и Y — непустые подмножества Е, обладающие тем свойством,
что для любых элементов х Е X и у € Y выполнено х $С у, то существует
такое с Е М, что х ^ с ^у для любых элементов х (Е X и у Е Y.
Этим завершается список аксиом, выполнение которых на каком бы то ни
было множестве Е позволяет считать это множество конкретной реализацией
или, как говорят, моделью действительных чисел.
Это определение формально не предполагает никакой предварительной ин-
информации о числах, и из него, «включив математическую мысль», опять-таки
формально мы должны получить уже в качестве теорем остальные свойства
действительных чисел. По поводу этого аксиоматического формализма хоте-
хотелось бы сделать несколько неформальных замечаний.
Представьте себе, что вы не прошли стадию от складывания яблок, куби-
кубиков или других именованных величин к сложению абстрактных натуральных
чисел; что вы не занимались измерением отрезков и не пришли к рациональ-
рациональным числам; что вам неизвестно великое открытие древних о том, что диа-
диагональ квадрата несоизмерима с его стороной и потому ее длина не может
быть рациональным числом, т. е. нужны иррациональные числа; что у вас нет
возникающего в процессе измерений понятия «больше» («меньше»); что вы не
иллюстрируете себе порядок, например, образом числовой прямой. Если бы
всего этого предварительно не было, то перечисленный набор аксиом не только
не воспринимался бы как определенный итог духовного развития, но, скорее,
показался бы по меньшей мере странным и во всяком случае произвольным
плодом фантазии.
Относительно любой абстрактной системы аксиом сразу же возникают по
крайней мере два вопроса.
Во-первых, совместимы ли эти аксиомы, т. е. существует ли^множество,
удовлетворяющее всем перечисленным условиям. Это вопрос о непротиворе-
непротиворечивости аксиоматики.
Во-вторых, однозначно ли данная система аксиом определяет математиче-
математический объект, т. е., как сказали бы логики, категорична ли система аксиом.

§ 1. АКСИОМАТИКА И СВОЙСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 37
Однозначность здесь надо понимать следующим образом. Если лица А и В,
независимо, построили свои модели, к примеру, числовых систем Ед и Ев,
удовлетворяющие аксиоматике, то между множествами 1ЕЦ, Е# можно уста-
установить биективное соответствие, пусть /: Ед —> Rb ? сохраняющее арифмети-
арифметические операции и отношение порядка, т. е.
Я*-у) = /(*)¦/(у),
х ^ у О /(*) ^ /(у).
С математической точки зрения Ед и Ев в таком случае являются всего-
навсего различными (совершенно равноправными) реализациями (моделями)
действительных чисел (например, Ед — бесконечные десятичные дроби, а
Шв — точки на числовой прямой). Такие реализации называются изоморф-
изоморфными, а отображение / — изоморфизмом. Результаты математической дея-
деятельности относятся, таким образом, не к индивидуальной реализации, а к
каждой модели из класса изоморфных моделей данной аксиоматики.
Мы не будем здесь обсуждать поставленные выше вопросы и ограничимся
только информативными ответами на них.
Положительный ответ на вопрос о непротиворечивости аксиоматики все-
всегда носит условный характер. В отношении чисел он выглядит так: исходя из
принятой нами аксиоматики теории множеств (см. гл. I, § 4, п. 2), можно по-
построить множество натуральных, затем множество рациональных и, наконец,
множество Е всех действительных чисел, удовлетворяющее всем перечислен-
перечисленным свойствам.
Вопрос о категоричности системы аксиом действительных чисел имеет
положительный ответ. Желающие получат его самостоятельно, решив задачи
23, 24, помещенные в конце следующего параграфа.
2. Некоторые общие алгебраические свойства действительных
чисел. Покажем на примерах, как известные свойства чисел получаются из
приведенных аксиом.
а. Следствия аксиом сложения
1° В множестве действительных чисел имеется только один нуль.
< Если 0] и О2 — нули в Е, то по определению нуля
d = 0i 4- 02 = 02 + 0i = 02. >
2° В множестве действительных чисел у каждого элемента имеется
единственный противоположный элемент.
< Если х\ и Х2 — элементы, противоположные х Е Е, то
= х\ + 0 = х\ + (х 4- х2) = (xi 4- х) + Х2 = 0 4- х2 = х2. >

38 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Здесь мы использовали последовательно определение нуля, определение
противоположного элемента, ассоциативность сложения, снова определение
противоположного элемента и, наконец, снова определение нуля.
3° Уравнение
а 4- х = 6
в Ш имеет и притом единственное решение
х = 6 4- (—а).
< Это вытекает из существования и единственности у каждого элемента
а Е Ш противоположного ему элемента:
(а 4- х = 6) <=> ((ж 4- а) 4- (-а) = 6 4- (-а))
<Ф(х + (а + (-а)) = 6 4- (-а)) <=> (х + 0 = 6 4- (-а))
<=> (х = 6+ (-а)). >
Выражение 6 4- (—а) записывают также в виде 6 — а. Этой более короткой
и привычной записи мы, как правило, и будем придерживаться.
b. Следствия аксиом умножения
1° В множестве действительных чисел имеется только одна единица.
2° Для каждого числа х ф О имеется только один обратный элемент х~х.
3° Уравнение ах = 6 при а е Ш\0 имеет и притом единственное решение
х = 6 • а.
Доказательства этих утверждений, разумеется, повторяют доказательства
соответствующих утверждений для сложения (с точностью до замены символа
и названия операции), поэтому мы их опустим.
c. Следствия аксиомы связи сложения и умножения. Привлекая до-
дополнительно аксиому (I, II), связывающую сложение и умножение, получаем
дальнейшие следствия.
Г Для любого xeR
х • О = 0 • х = 0.
< (х • 0 = х - @ 4- 0) = х • 0 4- х • 0) => (х • 0 = х • 0 4- (-(ж • 0)) = 0). >
Отсюда, между прочим, видно, что если х е К \ 0, то х бМ\0.
2° (z-2/ = O)=>(z = O)VB/ = O).
< Если, например, у ф 0, то из единственности решения уравнения ху = 0
относительно х находим х = 0 у~х =0. >
3° Для любого xeR
—х = (—1) • х.
< х 4- (—1) • х = A 4- (—1)) х = 0х = х-0 = 0, и утверждение следует из
единственности противоположного элемента. >

§ 1. АКСИОМАТИКА И СВОЙСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 39
4° Для любого числа х
<< Следует из 3° и единственности элемента х, противоположного — х. >
5° Для любого числа жбМ
(—х)(—х) = х • х.
< (-*)(-*) = ((-1) • х)(-х) = (х • (-1))(-х) = х((-1)(-х)) = х • х.
Мы последовательно воспользовались двумя предыдущими утверждениями, а
также коммутативностью и ассоциативностью умножения. >
d. Следствия аксиом порядка. Отметим сначала, что отношение х ^ у
(читается ах меньше или равно ?/») записывают также в виде у ^ х («у больше
или равно х»); отношение х ^ у при х ф у записывают в виде х < у (чи-
(читается «х меньше у») или в виде у > х («у больше х») и называют строгим
неравенством.
1° Для любых х, у Е К всегда имеет место в точности одно из соотно-
соотношений:
х < 2/, х = 2/, х > у.
< Это следует из приведенного определения строгого неравенства и аксиом
и 3<. >
2° Для любых чисел х, у, z из
(х < у) Л (у ^ z) => (х < z),
^ у) Л (у < z) => (х < z).
^ Приведем для примера доказательство последнего утверждения.
По аксиоме 2^ транзитивности отношения неравенства имеем
х ^ у) Л (у < z) «Ф (х ^ у) Л (у ^ z) Л (у ф z) => (х ^ *).
Осталось проверить, что х ф z. Но в противном случае
(х ^ у) Л (у < г) О (z ^ у) Л (у <г)о^^у)Л(у<^г)Л(уф z),
В силу аксиомы 1^ отсюда следует
(у = г)/\{уф z)
— противоречие. >

40 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
е. Следствия аксиом связи порядка со сложением и умножением.
Если в дополнение к аксиомам сложения, умножения и порядка использовать
аксиомы (I, III), (II, III), связывающие порядок с арифметическими операци-
операциями, то можно получить, например, следующие утверждения:
1° Для любых чисел х, у, z, w из
(х < у) => (х 4- z) < (у + z),
@ < х) => (-ж < 0),
(х ^ у) Л (z ^ w) => (х 4- z ^ у 4- w),
(х ^ у) Л (z < w) =>> (х -f z < у 4- w).
< Проверим первое из этих утверждений.
По определению строгого неравенства и аксиоме (I, III) имеем
+ z).
Остается проверить, что х + z фу 4- z. В самом деле,
((ж 4- z) = (у 4- z)) =» (ж = (?/ + *) - z = у + (z ~ z) = 2/),
что несовместимо с условием а; < у. >
ж, у, z — числа из Е, шо
@ < х) Л @ < у) => @ < яг/),
(ж < 0) Л (у < 0) => @ < ху),
(х < 0) Л @ < у) => (ху < 0),
Л @ < z) => (xz < 2/z),
ж < 2/) Л (z < 0) => B/z < xz).
< Проверим первое из этих утверждений. По определению строгого нера-
неравенства и аксиоме (II, III)
@ < х) Л @ < у) => @ ^ х) Л @ ^ у) =» @ ^ Ж2/).
Кроме того, 0 ^ ^2/, поскольку, как уже было показано,
(х • у = 0) => (ж = 0) V (у = 0).
*
Проверим еще, например, и третье утверждение:
(х < 0) Л @ < у) => @ < -х) Л @ < у) =>
=» @ < (-»)_;») =>(<>< ((-1) • х)у) =>
,=>''@ < (-1) • (ху)) =»¦ @ < -(ху)) => (ху < 0). >

§ 1. АКСИОМАТИКА И СВОЙСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 41
Читателю предоставляется возможность доказать самостоятельно осталь-
остальные соотношения, а также проверить, что если в одной из скобок левой части
наших утверждений стоит нестрогое неравенство, то следствием его также
будет нестрогое неравенство в правой части.
3° 0 < 1.
<4 1 е R\0, т. е. Оф 1.
Если предположить, что 1 < 0, то по только что доказанному
A < 0) Л A < 0) =* @ < 1 • 1) =» @ < 1).
Но мы знаем, что для любой пары чисел х,у еШ реализуется и притом только
одна из возможностей: х < у, х = у, х > у. Поскольку 0 ф 1, а предполо-
предположение 1 < 0 ведет к несовместимому с ним соотношению 0 < 1, то остается
единственная возможность, указанная в утверждении. >
4° @ < х) => @ < х) и @ < х) Л (х < у) => @ < у'1) Л (у < ж).
< Проверим первое из этих утверждений.
Прежде всего, х ф 0. Предположив, что х < 0, получим
(х~х < 0) Л @ < х) => (х • х < 0) => (К 0).
Это противоречие завершает доказательство. >
Напомним, что числа, которые больше нуля, называются положительны-
положительными, а числа меньшие нуля — отрицательными.
Таким образом, мы доказали, например, что единица — положительное
число, что произведение положительного и отрицательного чисел есть число
отрицательное, а величина, обратная положительному числу, также положи-
положительна.
3. Аксиома полноты и существование верхней (нижней) грани
числового множества
Определение 2. Говорят, что множество X С Ш ограничено сверху
(снизу), если существует число с Е К такое, что х ^ с (соответственно, с ^ х)
для любого х Е X.
Число с в этом случае называют верхней (соответственно, нижней) грани-
границей множества X или также мажорантой (минорантой) множества X.
Определение 3. Множество, ограниченное и сверху и снизу, называ-
называется ограниченным.
Определение 4. Элемент а Е X называется наибольшим или макси-
максимальным (наименьшим или минимальным) элементом множества X С Е, если
х ^ а (соответственно, а ^ х) для любого элемента х G X.

42 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Введем обозначения и заодно приведем формальную запись определения
максимального и минимального элементов соответственно:
(а = maxX) := (а 6 X Л Vx е X (х ^ а)),
(а = min X) := (а € X Л Vx € X (а ^ х)).
Наряду с обозначениями maxX (читается «максимум X») и minX (чита-
(читается «минимум X»), в том же смысле используются соответственно символы
тахх и minx.
Из аксиомы 1^ порядка сразу следует, что если в числовом множестве
есть максимальный (минимальный) элемент, то он только один.
Однако не во всяком, даже ограниченном, множестве имеется максималь-
максимальный (минимальный) элемент.
Например, множество Х = {хЕЕ|0^х<1} имеет минимальный эле-
элемент, но, как легко проверить, не имеет максимального элемента.
Определение 5. Наименьшее из чисел, ограничивающих множество
1С I сверху, называется верхней гранью (или точной верхней границей)
множества X и обозначается supX (читается «супремум X») или sup x.
хех
Это основное определение настоящего пункта. Итак,
= supX:= VxeX ((x^s)A(Vs'<s Эх'еХ (s1 < х1))).
В первой скобке, стоящей справа от определяемого понятия, написало, что
s ограничивает X сверху; вторая скобка говорит, что s — минимальное из
чисел, обладающих этим свойством. Точнее, вторая скобка утверждает, что
любое число, меньшее 5, уже не является верхней границей X.
Аналогично вводится понятие нижней грани (точной нижней границы)
множества X как наибольшей из нижних границ множества X.
Определение 6.
z = infX:= VxeX ((г ^ х) Л (Уг < г' Зх1 е X (х'<г'))).
Наряду с обозначением inf X (читается «инфимум X») для нижней грани X
употребляется также обозначение inf x.
Таким образом, даны следующие определения:
supX :=min{cG R|Vx e X (х ^ с)},
infX :=max{ce R\Vx e X (с ^ х)}.
Но выше мы говорили, что не всякое множество обладает минимальным
или максимальным элементом, поэтому принятые определения верхней и ниж-
нижней граней числового множества нуждаются в аргументации, которую доста-
доставляет следующая

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 43
Лемма (принцип верхней грани). Всякое непустое ограниченное сверху
подмножество множества вещественных чисел имеет и притом единствен-
единственную верхнюю грань,
М Поскольку единственность минимального элемента числового множества
нам уже известна, необходимо лишь убедиться в существовании верхней гра-
грани.
Пусть X С Ш — данное подмножество, a Y = {у Е Ш\ Vx E X (х ^ у)} —
множество верхних границ X. По условию, X ф 0 nY ф 0. Тогда в силу ак-
аксиомы полноты существует число с Е К такое, что Vx G X Vj/ G Y (x ^ с ^у).
Число с, таким образом, является мажорантой X и минорантой Y. Как мажо-
мажоранта X, число с является элементом У, но как миноранта F, число с является
минимальным элементом множества У. Итак, с = иипУ = supX. >
Конечно, аналогично доказывается существование и единственность ниж-
нижней грани у ограниченного снизу числового множества, т. е. имеет место
Лемма. (X ограничено снизу) => C! inf X).
На доказательстве мы не останавливаемся.
Теперь вернемся к множеству X = {zGlR|0^#<l}. В силу доказанной
леммы оно должно иметь верхнюю грань. По самому определению множества
X и определению верхней грани очевидно, что supX ^ 1.
Для того чтобы доказать, что supX = 1, таким образом, необходимо про-
проверить, что для любого числа q < 1 найдется число х е X такое, что q < я,
т. е., попросту, что между q и 1 есть еще числа. Это, конечно, легко доказать
и независимо (например, показав, что q < 2~x(q + 1) < 1), но мы сейчас этого
делать не станем, поскольку в следующем параграфе подобные вопросы будут
обсуждаться последовательно и подробно.
Что же касается нижней грани, то она всегда совпадает с минимальным
элементом множества, если множество таковым обладает. Так что уже из
этого соображения в рассматриваемом примере имеем inf X = 0.
Другие, более содержательные примеры использования введенных здесь
понятий встретятся уже в следующем параграфе.
§2. Важнейшие классы действительных чисел
и вычислительные аспекты операций
с действительными числами
1. Натуральные числа и принцип математической индукции
а. Определение множества натуральных чисел. Числа вида 1, 1 + 1,
A + 1) + 1 и т. д. обозначают соответственно символами 1, 2, 3 и т. д. и
называют натуральными числами.
Принять такое определение может только тот, кто и без него имеет полное
представление о натуральных числах, включая их запись, например, в деся-
десятичной системе счисления.

44 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Продолжение какого-то процесса далеко не всегда бывает однозначным,
поэтому вездесущее «и так далее» на самом деле требует уточнения, которое
доставляет фундаментальный принцип математической индукции.
Определение 1. Множество X С К называется индуктивным, если
вместе с каждым числом х Е X ему принадлежит также число х 4-1.
Например, К является индуктивным множеством; множество положитель-
положительных чисел также является индуктивным множеством.
Пересечение X = f] Xa любого семейства индуктивных множеств Ха,
если оно непусто, является индуктивным множеством.
Действительно,
(x € X = П Ха) => (Va € A (x 6 Xa)) =>
^v ?• Уч
=» (Va Gi((x + 1N Xa)) =» ((я + 1) € П Xe = Л").
Теперь примем следующее
Определение 2. Множеством натуральных чисел называется наимень-
наименьшее индуктивное множество, содержащее 1, т. е. пересечение всех индуктив-
индуктивных множеств, содержащих число 1.
Множество натуральных чисел обозначают символом N; его элементы на-
называются натуральными числами.
С теоретико-множественной точки зрения, быть может, разумнее нату-
натуральные числа начинать с 0, т. е. вводить множество натуральных чисел как
наименьшее индуктивное множество, содержащее 0, однако нам удобнее на-
начинать нумерацию числом 1.
Следующий фундаментальный и широко используемый принцип является
прямым следствием определения множества натуральных чисел.
Ь. Принцип математической индукции
Если подмножество Е множества натуральных чисел N таково, что
1 6 Е и вместе с числом х Е Е множеству Е принадлежит число х 4-1, то
Итак,
(Е С N) Л A е Е) Л (Vx в Е (х е Е =» (х 4-1) € Е)) => Е = N.
Проиллюстрируем этот принцип в действии, доказав с его помощью не-
несколько полезных и постоянно в дальнейшем используемых свойств натураль-
натуральных чисел.
1° Сумма и произведение натуральных чисел являются натуральными чи-
числами.

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 45
4 Пусть m,n6N; покажем, что (т + п) Е N. Обозначим через Е множе-
множество тех натуральных чисел п, для которых (m + n) Е N при любом т Е N.
Тогда 1 Е Е, поскольку (m Е N) => ((ш + 1) Е N) для любого т Е N. Если
п Е Е, т. е. (m+n) Е N, то и (п+1) 6 Е, так как (m+ (n+1)) = ((m-hn) + l) Е N.
По принципу индукции Е = N, и мы доказали, что сложение не выводит за
пределы N.
Аналогично, обозначив через Е множество тех натуральных чисел п, для
которых (ш • п) Е N при любом т Е N, находим, что 1 Е Е, так как m • 1 = m,
и если п Е 13, т. е. т • n E N, то m • (п Н-1) = mn -f m есть сумма натуральных
чисел, которая по доказанному принадлежит N. Таким образом, (п Е Е) =Ф
=^ ((п 4-1) Е Е) и по принципу индукции 1? = N. >
2° Покажем, что (n E N) Л (п # 1) => ((п - 1) Е N).
< Рассмотрим множество Е натуральных чисел вида п — 1, где п — нату-
натуральное число, отличное от 1, и покажем, что Е = N.
Поскольку 1 Е N, то 2 := A + 1) Е N, а значит, 1 = B - 1) Е ?.
Если m Е Е, то m = п — 1, где п Е N; тогда т 4-1 = (п +1) — 1 и, поскольку
(п + 1) Е N, имеем (т + 1) Е J5. По принципу индукции заключаем: Е = N. >
3° Длл любого п Е N б множестве {х Е N | п < ж} есть минимальный
элемент, причем
min {ж Е N | п < ж} = п + 1.
<* Покажем, что множество JS тех n E N, для которых утверждение спра-
справедливо, совпадает с N.
Сначала проверим, что 1 Е Е, т. е.
min {ж Е N| 1 < х} = 2.
Это утверждение тоже будем проверять по принципу индукции. Пусть
По определению М имеем 1 Е М. Далее, если х Е М, то либо ж = 1и тогда
ж + 1 = 2 € М, либо 2 ^ х, тогда 2 ^ (ж + 1) и снова (х + 1) Е М. Таким
образом, М = N и, значит, если (ж ^ 1)Л(# Е N), то 2 ^ я, т. е. действительно
min{x Е N11 < х} = 2. Итак, 1 Е ?.
Покажем теперь, что если п Е JS, то и (п + 1) Е
В самом деле, если xE{xEN|n-hl< я}, то
.(ж — 1) =i/ € 0/EN|n <
ибо по доказанному все натуральные числа не меньше 1, поэтому (п + 1 < х)
=Ф A < х) => (х ^ 1), а тогда в силу утверждения 2° (х — 1) = ?/ Е N.
Если п Е Е, то min {2/ Е N| n < 2/} = n+1, т. е. ж-1 ^?
Значит,
Е {х Е N | п 4-1 < ж}) =*> (х ^ п + 2)

46 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
и, следовательно, min {х G N | п + 1 < х} = п + 2, т. е. (п + 1) G
По принципу индукции 2? = N, и утверждение 3° доказано. >
В качестве прямых следствий доказанных утверждений 2° и 3° получаем
следующие свойства 4°, 5°, 6° натуральных чисел:
4°
5° Число (п + 1) G N непосредственно следует в N за натуральным чи-
числом п, т. е. нет натуральных чисел х, удовлетворяющих условию п < х <
< п + 1, еслтг п G N.
6° #слг* n б N « п / 1, то число (n — 1) G N г* (п — 1) непосредственно
предшествует числу п в N, т. е. кет натуральных чисел х, удовлетворяю-
удовлетворяющих условию п — 1 < х < п, если п G N.
7° Покажем теперь, что в любом непустом подмножестве множества
натуральных чисел имеется минимальный элемент.
<4 Пусть М С N. Если 1 G М, то min М = 1, поскольку Vrc G N A ^ п).
Пусть теперь 1 ? М, т. е. 1 G Е = N \ М. В множестве Е должно найтись
такое натуральное число п Е Е, что все натуральные числа, не превосходя-
превосходящие гг, лежат в Е, а (п + 1) G М. Если бы такого п не было, то множе-
множество Е с N, содержащее единицу, вместе с п € Е содержало бы и (п + 1) и
по принципу индукции совпадало бы с N. Последнее невозможно, поскольку
N\E = M ф0.
Найденное число (n-f 1) G М и будет минимальным в М, поскольку между
пип + 1, как мы видели, уже нет натуральных чисел. >
2. Рациональные и иррациональные числа
а. Целые числа
Определение 3. Объединение множества натуральных чисел, множе-
множества чисел, противоположных натуральным числам, и нуля называется мно-
множеством целых чисел и обозначается символом Z.
Поскольку, как уже было доказано, сложение и умножение натуральных
чисел не выводят за пределы N, то эти же операции над целыми числами не
выводят за пределы множества Z.
< Действительно, если т^п G Z, то либо одно из этих чисел равно нулю
и тогда сумма т + п равна другому числу, т. е. (ш 4- п) G Z, а произведение
m • п = О G Z, либо оба числа отличны от нуля. В последнем случае либо
т, п G N и тогда (ш + п) G N С Ъ и (т • п) G N С Z, либо (-m), (-n) G N и
тогда mn = ((-l)m)((—l)n) G N, либо (—m),n G N и тогда (-m-n) G N, т. е.
m • n G Z, либо, наконец, m, —n G N и тогда (—т • n) G N и снова m • n G Z. >
Таким образом, Z есть аб&яева группа по отношению к операции сложения.
По отношению к операции умножения множество Z и даже Z \ 0 не являет-
является группой, поскольку числа, обратные целым, не лежат в Z (кроме числа,
обратного единице и минус единице).

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 47
•4 Действительно, если т Е Z и m ^ 0, 1, то, считая сначала т Е N,
имеем 0 < 1 < ш и, поскольку m • га = 1 > 0, должно быть 0 < т~1 < 1
(см. в предыдущем параграфе следствия аксиом порядка). Таким образом,
га ? Z. Случай, когда т — отрицательное целое число, отличное от — 1,
непосредственно сводится к уже разобранному. >
В том случае, когда для чисел m,n E Z число к = т • n~l Е Z, т. е. когда
т = к-Пу где к Е Z, говорят, что целое число ш делится на целое число п или
кратно п, или что п есть делитель т.
Делимость целых чисел путем надлежащих изменений знаков, т. е. домно-
жением на — 1, если в этом есть необходимость, немедленно приводится к
делимости соответствующих натуральных чисел, в рамках которых она и изу-
изучается в арифметике.
Напомним без доказательства так называемую основную теорему арифме-
арифметики, которой при рассмотрении некоторых примеров мы будем пользоваться.
Число р Е N, р ф 1, называется простым, если в N у него нет делителей,
отличных от 1 и р.
Основная теорема арифметики. Каждое натуральное число до-
допускает и притом единственное (с точностью до порядка сомножителей)
представление в виде произведения
п = pi... pk,
где piy ..., р^ — простые числа.
Числа m, n E Z называются взаимно простыми, если у них нет общих
делителей, отличных от 1 и —1.
Из приведенной теоремы, в частности, видно, что если произведение т • п
взаимно простых чисел т, п делится на простое число р, то одно из чисел т,
п также делится на р.
Ь. Рациональные числа
Определение 4. Числа вида т • п, где m, n E Z, называются рацио-
рациональными.
Множество рациональных чисел обозначается знаком Q.
Таким образом, упорядоченная пара (ш, п) целых чисел определяет рацио-
рациональное число q = т • п, если п ф 0.
Число q = т п~1 записывают также в виде отношения1) тип или так
называемой рациональной дроби —.
п
Правила действий с рациональными числами, относящиеся к такой фор-
форме их представления дробями, изучавшиеся в школе, немедленно вытекают из
х) Обозначение Q — по начальной букве англ. quotient — отношение (от лат. quota —
часть, приходящаяся на единицу чего-либо, и quot — сколько).

48 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
определения рационального числа и аксиом действительных чисел. В част-
частности, «от умножения числителя и знаменателя дроби на одно и то же от-
личное от нуля целое число величина дроби не изменяется», т. е. дроби —г- и
пк
— представляют одно и то же рациональное число. В самом деле, поскольку
(nk)(k-ln-1) = 1, т. е. (п • А;) = А; • п, то {тк){пк)-1 = (тк^к^п'1) =
= т • п~1.
Таким образом, различные упорядоченные пары (т,п) и (тк.пк) задают
одно и то же рациональное число. Следовательно, после соответствующих
сокращений любое рациональное число можно задать упорядоченной парой
взаимно простых целых чисел.
С другой стороны, если пары (mi,ni) и G712,^2) задают одно и то же
рациональное число, т. е. rai-nj = шг-п^1, то т\П2 = гп2П\, и если, например,
77ii и rii взаимно просты, то в силу упомянутого следствия основной теоремы
арифметики П2 • щ1 = т2 • mj = к € Ъ.
Мы показали, таким образом, что две упорядоченные пары (mi,ni),
G712,712) задают одно и то же рациональное число тогда и только тогда, когда
они пропорциональны, т. е. существует число к Е Z такое, что, например,
7712 = кт\ И П2 = kn\.
с. Иррациональные числа
Определение 5. Действительные числа, не являющиеся рациональны-
рациональными, называются иррациональными.
Классическим примером иррационального действительного числа является
\/2, т. е. число s € R такое, что s > 0 и s2 = 2. Иррациональность у/2 в силу
теоремы Пифагора эквивалентна утверждению о несоизмеримости диагонали
и стороны квадрата.
Итак, проверим, во-первых, что существует положительное действи-
действительное число s € М, квадрат которого равен двум, и, во-вторых, что s ? Q.
< Пусть X viY — множества положительных действительных чисел такие,
что Ухе X (х2 < 2), Vj/ € Y B < у2). Поскольку l€X, a2eF, тоХиУ —
непустые множества.
Далее, поскольку для положительных х и у (х < у) <^ (х2 < у2), то любой
элемент х € X меньше любого элемента у € Y. По аксиоме полноты сущест-
существует число s e R такое, что х ^ s ^ у для Vx 6 X и Vy € F.
Покажем, что s2 = 2.
9 — 2
Если бы было s2 < 2, то, например, квадрат числа s H ^-, большего
os
чем 5, был бы меньше 2. Действительно, ведь 1 б X, поэтому I2 ^ s2 < 2 и
= 2-52<1. Значит,

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 49
Следовательно, Is 4- r-J € X, что несовместимо с неравенством х ^ s для
любого элемента х € X.
2 _ л
Если бы было 2 < s2, то, например, квадрат числа s —, меньшего
oS
чем s, был бы больше 2. Действительно, ведь 2 € У, поэтому 2 < s2 ^ 22 или
= s2-2<3 и 0<у<1. Отсюда
и мы вступаем в противоречие с тем, что s ограничивает множество Y снизу.
Таким образом, реализуется только одна оставшаяся возможность: s2 = 2.
ТЭТ
ТЭТ
ТЭТ
Покажем, наконец, что s Ф Q. Предположим, что s € Q, и пусть
п
несократимое представление s. Тогда т2 = 2-п2, следовательно, т2, а значит,
и m делится на 2. Но если т = 2&, то 2&2 = п2 и по той же причине п должно
7Т7.
7Т7.
делиться на 2, что противоречит несократимости дроби —. >
п
Сейчас мы трудились над тем, чтобы доказать существование иррацио-
иррациональных чисел. Вскоре мы увидим, что в некотором смысле почти все дей-
действительные числа иррациональны. Будет показано, что мощность множества
иррациональных чисел больше мощности множества всех рациональных чисел
и совпадает с мощностью множества всех действительных чисел.
Среди иррациональных чисел выделяют еще так называемые алгебраиче-
алгебраические иррациональности и трансцендентные числа.
Вещественное число называется алгебраическим, если оно является корнем
некоторого алгебраического уравнения
а>охп •+... + ап-\х + ап = О
с рациональными (или, что эквивалентно, с целыми) коэффициентами.
В противном случае число называется трансцендентным.
Мы увидим, что мощность множества алгебраических чисел такая же, как
мощность множества рациональных чисел, а мощность множества трансцен-
трансцендентных чисел такая же, как мощность всех действительных чисел; поэтому
на первый взгляд кажутся парадоксальными и неестественными трудности в
предъявлении конкретного трансцендентного числа, точнее, в доказательстве
его трансцендентности.
Так, например, только в 1882 г. было доказано, что классическое геометри-
геометрическое число тг является трансцендентным1), а одна из знаменитых проблем
XJn — число, равное в евклидовой геометрии отношению длины окружности к ее диаме-
диаметру. Отсюда общепринятое с XIII века обозначение этого числа начальной буквой греческо-
греческого слова nepupepia — периферия (окружность). Трансцендентность тг доказана немецким
математиком Ф. Линдеманом A852 — 1939). Из трансцендентности тг, в частности, вытека-
вытекает невозможность построения циркулем и линейкой отрезка длины тг (задача о спрямлении
окружности), как и неразрешимость этими средствами древней задачи о квадратуре круга.

50 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Гильберта1) состояла в том, чтобы доказать трансцендентность числа а^, где
а — алгебраическое, (а > 0) Л (а ф 1), a /3 — алгебраическое иррациональное
число (например, а — 2, /3 = л/2).
3. Принцип Архимеда. Переходим к важному как в теоретическом от-
отношении, так и в плане конкретного использования чисел при измерениях и
вычислениях принципу Архимеда2). Мы докажем его, опираясь на аксиому
полноты (точнее, на эквивалентную ей лемму о верхней грани). При другой
аксиоматике множества действительных чисел этот фундаментальный прин-
принцип часто включают в список аксиом.
Заметим, что утверждения, которые мы до сих пор доказывали о натураль-
натуральных и целых числах, совершенно не использовали аксиому полноты. Как будет
видно из дальнейшего, принцип Архимеда, в сущности, отражает свойства на-
натуральных и целых чисел, связанные с аксиомой полноты. С этих свойств мы
и начнем.
1° В любом непустом ограниченном сверху подмножестве множества
натуральных чисел имеется максимальный элемент.
< Если Е С N — рассматриваемое множество, то по лемме о верхней грани
3! sup Е = s € М. По определению верхней грани, в Е найдется натуральное
число п € Е, удовлетворяющее условию s — 1 < п ^ s. Тогда п = max 2?,
поскольку все натуральные числа, которые больше п, не меньше п + 1, а
71+ 1 > 5. >
Следствия. 2° Множество натуральных чисел не ограничено сверху.
< В противном случае существовало бы максимальное натуральное число.
Но п < п + 1. >
3° В любом непустом ограниченном сверху подмножестве множества
целых чисел имеется максимальный элемент.
Ч Можно дословно повторить доказательство утверждения 1°, заменяя N
на Z. >
4° В любом непустом ограниченном снизу подмножестве множества
целых чисел имеется минимальный элемент.
< Можно, например, повторить доказательство утверждения 1°, заменяя
N на Z и используя вместо леммы о верхней грани лемму о существовании
нижней грани у ограниченного снизу числового множества.
х' Д. Гильберт A862 — 1943) — выдающийся немецкий математик, сформулировавший в
1900 г. на Международном конгрессе математиков в Париже двадцать три относящиеся к
различным областям математики проблемы, получившие впоследствии название «проблем
Гильберта». Вопрос, о котором идет речь в тексте (седьмая проблема Гильберта), был
положительно решен в 1934 г. советским математиком А. О. Гельфондом A906 — 1968) и
немецким математиком Т. Шнайдером A911 — 1989).
2) Архимед B87 — 212 гг. до н. э.) — гениальный греческий ученый, про которого один
из основоположников анализа Лейбниц в свое время сказал: «Изучая труды Архимеда, пе-
перестаешь удивляться успехам современных математиков».

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 51
Можно также перейти к противоположным числам («поменять знаки») и
воспользоваться уже доказанным в 3°. >
5° Множество целых чисел не ограничено ни сверху, ни снизу.
< Вытекает из 3° и 4° или прямо из 2°. >
Теперь сформулируем
6° Принцип Архимеда. Если фиксировать произвольное положи-
положительное число h, то для любого действительного числа х найдется и при-
притом единственное целое число к такое, что (к — l)h ^ х < kh.
< Поскольку Z не ограничено сверху, множество jn € Z г <п\ ~ непу-
непустое ограниченное снизу подмножество множества целых чисел. Тогда (см. 4°)
в нем есть минимальный элемент к, т. е. (& — 1) ^ x/h < к. Поскольку
h > О, эти неравенства эквивалентны приведенным в формулировке прин-
принципа Архимеда. Единственность к Е Z, удовлетворяющего двум последним
неравенствам, следует из единственности минимального элемента числового
множества (см. § 1, п. 3). >
Некоторые следствия:
7° Для любого положительного числа е существует натуральное число п
такое, что 0 < — < е.
п
Ч По принципу Архимеда найдется п € Z такое, что 1 < е • п. Поскольку
О < 1 и 0 < е, имеем 0 < п. Таким образом, пбМиО<-<е. >
п
8° Если число х € М таково, что О ^ х и для любого п 6 N выполнено
х < —, то х = 0.
71
Ч Соотношение 0 < х невозможно в силу утверждения 7°. >
9° Для любых чисел а, 6 G Ш таких, что а < Ь, найдется рациональное
число г € Q такое, что а < г < Ь.
< Учитывая 7°, подберем п 6 N так, что 0 < - < 6 — а. По принципу
п
Архимеда найдем такое число т € Z, что т ~ ^ а < —. Тогда — < 6, ибо в
п п п
противном случае мы имели бы ^ а < Ь ^ —, откуда следовало бы, что
п п
- > Ь - а. Таким образом, г=-еОио<-<6. >
71 71 71
10° Для любого числа х ? Ж существует и притом единственное целое
число к € Z такое, что к ^ х < к + 1.
< Это непосредственно вытекает из принципа Архимеда. >
Указанное число к обозначается [х] и называется целой частью числа.х.
Величина {х} := х — [х] называется дробной частью числа х. Итак, х =
= [х] + {я}, причем {х} ^ 0.
3 Зорич В. А.

52 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
4. Геометрическая интерпретация множества
действительных чисел и вычислительные аспекты
операций с действительными числами
а. Числовая ось. По отношению к действительным числам часто исполь-
используется образный геометрический язык, связанный с тем обстоятельством,
что, как в общих чертах известно из школы, в силу аксиом геометрии между
точками прямой L и множеством Е вещественных чисел можно установить
взаимно однозначное соответствие /: L —> Е. Причем это соответствие свя-
связано с движениями прямой. А именно, если Т — параллельный перенос пря-
прямой L по себе, то существует число t € Е (зависящее только от Т) такое, что
f(T(x)) = f(x) + t для любой точки xGL.
Число /(я), соответствующее точке х € L, называется координатой точ-
точки х. Ввиду взаимной однозначности отображения / : L —> Е координату
точки часто называют просто точкой. Например, вместо фразы «отметим
точку, координата которой 1», говорят «отметим точку 1». Прямую L при
наличии указанного соответствия / : L —> Е называют координатной осью,
числовой осью или числовой прямой. Ввиду биективности / само множество
Е вещественных чисел также часто называют числовой прямой, а его элемен-
элементы — точками числовой прямой.
Как отмечалось, биективное отображение /: L —> Е, задающее на L коор-
координаты, таково, что при параллельном переносе Т координаты образов точек
прямой L отличаются от координат самих точек на одну и ту же величину
t € Е. Ввиду этого / полностью определяется указанием точки с координа-
координатой 0 и точки с координатой 1 или, короче, точки нуль, называемой началом
координат, и точки 1. Отрезок, определяемый этими точками, называется
единичным отрезком. Направление, определяемое лучом с вершиной 0, содер-
содержащим точку 1, называется положительным, а движение в этом направлении
(от 0 к 1) — движением слева направо. В соответствии с этим соглашением
1 лежит правее 0, а 0 — левее 1.
При параллельном переносе Т, переводящем начало координат хо в точ-
точку Х\ — Т(хо) с координатой 1, координаты образов всех точек на единицу
больше координат прообразов, поэтому мы находим точку x<i — Т{х\) с ко-
координатой 2, точку х^ = Т(х2) координатой 3, ... , точку zn+i = T(xn) с
координатой п + 1, а также точку Х-\ = Т~г(хо) с координатой —1, ... , точ-
точку Х-п-1 — Т~1(х-п) с координатой — п — 1. Таким образом, получаем все
точки с целыми координатами m 6 Ъ.
Умея удваивать, утраивать, ... единичный отрезок, по теореме Фалеса
его же можно разбить на соответствующее число п конгруэнтных отрезков.
Беря тот из них, одним концом которого является начало координат, для
координаты х другого конца имеем уравнение п • х — 1, т. е. х =*—. Отсюда
m n
находим все точки с рациональными координатами — € Q.
п
Но останутся еще точки L, ведь есть же отрезки, несоизмеримые с единич-
единичным. Каждая такая точка (как и любая другая точка прямой) разбивает пря-

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 53
мую на два луча, на каждом из которых есть точки с целыми (рациональными)
координатами (это следствие исходного геометрического принципа Архиме-
Архимеда). Таким образам, точка производит разбиение или, как говорят, сечение Q
на два непустых множества X и У, отвечающие рациональным точкам (точ-
(точкам с рациональными координатами) левого и правого лучей. По аксиоме
полноты найдется чцсло с, разделяющее X и Y, т. е. х ^ с ^ у для ViGXh
\/у е Y. Поскольку X U Y = Q, то supX = s = i = inf F, ибо в противном
случае s < г и между s и г нашлось бы рациональное число, не лежащее ни
в X, ни в Y. Таким образом, s = г = с. Это однозначно определенное число с
и ставится в соответствие указанной точке прямой.
Описанное сопоставление точкам прямой их координат доставляет нагляд-
наглядную модель как отношению порядка в Е (отсюда и термин «линейная упорядо-
упорядоченность»), так и аксиоме полноты, или непрерывности Е, которая на геоме-
геометрическом языке означает, что в прямой L «нет дыр», разбивающих ее на два
не имеющих общих точек куска (такое разбиение осуществляется некоторой
точкой прямой L).
Мы не станем вдаваться в дальнейшие детали конструкции отображения
/ : L -> Е, поскольку геометрическую интерпретацию множества действи-
действительных чисел мы будем привлекать исключительно для наглядности и для
возможного подключения весьма полезной геометрической интуиции читате-
читателя. Что же касается формальных доказательств, то, как и до сих пор, они
будут опираться либо на тот набор фактов, который мы уже получили из ак-
аксиоматики действительных чисел, либо непосредственно на эту аксиоматику.
Геометрический же язык мы будем использовать постоянно.
Введем следующие обозначения и названия для перечисленных ниже число-
числовых множеств:
]а, Ь[ := {х € Е | а < х < Ь} — интервал аЪ\
[а, Ь] := {х € Е | а ^ х ^ 6} — отрезок а&;
]а,Ь]:={хбЕ|а<х^6} — полуинтервал аб, содержащий конец 6;
[а, Ь[ := {х € Е | а ^ х < 6} — полуинтервал ab, содержащий конец а.
Определение б. Интервалы, отрезки и полуинтервалы называются
числовыми промежутками или просто промежутками. Числа, определяющие
промежуток, называются его концами.
Величина Ь — а называется длиной промежутка ab. Если / — некоторый
промежуток, то длину его мы будем обозначать через |/| (происхождение та-
такого обозначения вскоре станет понятным).
Множества
]а,+оо[ := {х € Е|а < я}, ]-оо,Ь[ := {х € Е|х < 6},
[а, +оо[ := {х е Е | а ^ я}, ]-оо, Ь] := {х ? Е | х ^ 6},
а также ]—оо, +оо[ := Е, принято называть неограниченными промежутками.

54 ГЛ, II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
В соответствии с таким употреблением символов +оо (читается «плюс бес-
бесконечность») и —оо (читается «минус бесконечность») для обозначения неогра-
неограниченности числового множества X сверху (снизу), принято писать supX =
= +00 (infX = —оо).
Определение 7. Интервал, содержащий точку х € М, будем называть
окрестностью этой точки.
В частности, при 8 > 0 интервал ]х — 6, х + 6[ называется S-окрестностью
точки х. Его длина 28.
Расстояние между числами х, у € М измеряется длиной промежутка, кон-
концами которого они являются.
Чтобы не разбираться при этом, «где лево, а где право», т. е. х < у или
у < х, и чему равна длина, у — х или х — у, можно использовать полезную
функцию
х при х > О,
\х\ = < 0 при х = О,
k —х при х < О,
называемую модулем или абсолютной величиной числа.
Определение 8. Расстоянием между х, у € Ж называется величина
Расстояние неотрицательно и равно нулю только при совпадении х и у;
расстояние от х до у и от у до х одно и то же, ибо \х — у\ = \у — х\; наконец,
если z € М, то \х — у\ ^ \х — z\ + |z — j/|, т. е. имеет место так называемое
неравенство треугольника.
Неравенство треугольника следует из свойства абсолютной величины чи-
числа, которое также называется неравенством треугольника (ибо получается
из предыдущего при z = 0 и замене у на —у). А именно, для любых чисел х, у
справедливо неравенство
\х + у\ ^
причем равенство в нем имеет место в том и только в том случае, когда
оба числа х, у неотрицательны или неположительны.
Ч Если 0 ^ х и 0 ^ у, то 0 ^ х + у, \х + у\ = х + у, \х\ = х, \у\ = у и
равенство установлено.
Если х ^ 0 и у ^ 0, то х + у ^ 0, \х + у\ = -(х + ?/) = -х - ?/, |ж| = —ж,
|?/| = —2/ и опять равенство имеет место.
Пусть теперь одно из чисел отрицательно, а другое положительно, напри-
например, х < 0 < у. Тогда либо х < х + у ^ 0, либо 0 ^ х + у < у. В первом случае
\х + у\ < |я|, во втором \х + у\ < \у\, т. е. в обоих случаях \х + у\ < \х\ + \у\. >

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 55
Используя принцип индукции, можно проверить, что
\х\ + ... -Ь хп\ ^ \х\\ + • • • 4- \х
причем равенство имеет место, если и только если все числа х\, ..., хп одно-
одновременно неотрицательны или одновременно неположительны.
Число ^—— часто называется серединой или центром промежутка с кон-
цами а, 6, поскольку оно равноудалено от концов промежутка.
В частности, точка х € R является центром своей <5-окрестности ]х—<5, я+<5[
и все точки <5-окрестности удалены от х меньше чем на S.
Ъ. Задание числа последовательностью приближений. Измеряя ре-
реальную физическую величину, мы получаем число, которое, как правило, ме-
меняется при повторном измерении, особенно если изменить инструмент или
метод измерения. Таким образом, результатом измерения обычно является
некоторое приближенное значение искомой величины. Качество или точность
измерения характеризуется, например, величиной возможного уклонения ис-
истинного значения величины от ее значения, полученного в результате изме-
измерения. При этом может случиться, что точное значение величины (если оно
в принципе существует) мы так никогда и не предъявим. Встав, однако, на
более конструктивную позицию, можно (или следует) считать, что мы впол-
вполне знаем искомую величину, если в состоянии измерить ее с любой наперед
заданной точностью. Такая позиция означает отождествление числа с после-
последовательностью1) все более точных его приближений числами, получаемыми
при измерении. Но всякое измерение есть конечная совокупность сравнений с
некоторым эталоном или с соизмеримой с ним его частью, поэтому результат
измерения должен выражаться натуральными, целыми или, более общо, ра-
рациональными числами. Значит, последовательностями рациональных чисел в
принципе можно описать все множество вещественных чисел, построив после
должного анализа математическую копию или, лучше сказать, модель того,
что делают с числами люди, не подозревающие об их аксиоматическом описа-
описании. А они вместо сложения и умножения неизвестных им измеряемых вели-
величин складывают и умножают их приближенные значения (не всегда, правда,
умея сказать, какое отношение имеет результат таких действий к тому, что
получилось бы, если бы эти действия производились с точными значениями
величин; ниже мы обсудим этот вопрос).
Отождествив число с последовательностью его приближенных значений,
мы, таким образом, желая, например, сложить два числа, должны складывать
последовательности их приближенных значений. Получающуюся при этом но-
новую последовательность чисел надо считать новым числом, называемым сум-
суммой первых двух. Но число ли это? Деликатность вопроса состоит в том, что
1^Если п — номер измерения, а хп — результат измерения, то соответствие п ь-> хп
есть не что иное, как функция / : N —> R натурального аргумента, т. е., по определению,
последовательность (в данном случае последовательность чисел). Подробному изучению
числовых последовательностей посвящен § 1 гл. III.

56 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
не каждая случайным образом построенная последовательность служит по-
последовательностью сколь угодно точных приближений некоторой величины.
То есть необходимо еще научиться по самой последовательности узнавать,
представляет она некоторое число или нет. Другой вопрос, который возни-
возникает при попытке математического копирования операций с приближенными
числами, состоит в том, что разные последовательности могут быть последо-
последовательностями приближений одной и той же величины. Соотношение между
последовательностями приближений, определяющими число, и самими числа-
числами примерно такое же, как между точкой на карте и указкой, которая указы-
указывает нам эту точку. Положение указки определяет точку, но точка определяет
положение только конца указки, не мешая взять указку по-другому, поудоб-
поудобнее.
Этим вопросам дал точное описание и реализовал всю намеченную здесь в
общих чертах программу построения модели вещественных чисел еще О. Ко-
Коши1'. Надо надеяться, что после изучения теории пределов вы будете в состо-
состоянии самостоятельно повторить эти конструкции Коши.
Сказанное до сих пор, разумеется, не претендует на математическую стро-
строгость. Цель этого неформального отступления — обратить внимание читателя
на принципиальную возможность одновременного существования различных
естественных моделей действительных чисел; я пытался также дать некото-
некоторое представление об отношении чисел к тому, что нас окружает, и пояснить
фундаментальную роль натуральных и рациональных чисел; наконец, мне хо-
хотелось показать естественность и необходимость приближенных вычислений.
Последующая часть настоящего пункта посвящена используемым в даль-
дальнейшем и представляющим самостоятельный интерес простым, но важным
оценкам погрешностей, возникающих при арифметических операциях над
приближенными величинами.
Переходим к точным формулировкам.
Определение 9. Если х — точное значение некоторой величины, а х —
известное приближенное значение той же величины, то числа
:= \х — ж|,
8(x) :¦
х\
называются соответственно абсолютной и относительной погрешностью
приближения х. Относительная погрешность при х = 0 не определена.
Поскольку значение х неизвестно, значения А(х) и 8(х) также неизвест-
неизвестны. Однако обычно бывают известны оценки сверху Д(я) < А, 8(х) < 8 этих
величин. В этом случае говорят, что абсолютная или относительная погреш-
погрешность приближения х не превосходит Д или 8 соответственно. На практике
х) О. Коши A789 — 1857) — французский математик, один из наиболее активных творцов
современного языка и аппарата классического анализа.

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 57
приходится иметь дело только с оценками погрешностей, поэтому сами вели-
величины Д и S часто называют абсолютной и относительной погрешностями
приближения, но мы этого делать не будем.
Запись х = х ± Д означает, что х-Д^х^ж + Д.
Например,
гравитационная постоянная G = F,670 ± 0,007) • 10~п Н • м2/кг2,
скорость света в вакууме с = B99792,4562 ± 0,0001) км/с,
постоянная Планка h = F,62517 ± 0,00023) • 10~34 Дж • с,
заряд электрона е = A,60206 ± 0,00003) • 10~19 Кл,
масса покоя электрона те = (9,1083 ± 0,00003) • 10~31 кг.
Основным показателем точности измерения является величина относитель-
относительной погрешности приближения, обычно выражаемая в процентах.
Так, в приведенных примерах относительные погрешности не превосходят
соответственно
11-Ю; 35-Ю1; 35-Ю; 2-Ю; 33 • 10~7
или, в процентах от результата измерения,
11 • ИГ2 %; 35 • 10~9 %; 35 • 10 %; 2 • КГ3 %; 33 • КГ5 %.
Оценим теперь погрешности, возникающие при арифметических операци-
операциях с приближенными величинами.
Утверждение. Если
\х-х\ = Д(х), \у-у\ =
то
А(х + у) := |(х + »)-(* + jf)| ^ Д(х) + Д(Л), A)
А(х • у) := \х • у - х • у| ^ |?| Д(у) + |у|А(х) + Д(х) • Д(у); B)
если, кроме того,
уф 0, уф 0 и
то
/ ~* ч ^
дт ==
У У
1 - S(y)

58
ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
<4 Пусть х = ж + a, у = у + C. Тогда
А(х + у) = |(х + у) - (ж + у)\ = |а + /3| ^ |а| + Щ = Д(х) + Д(у),
Д(ж • у) = |я?у - ху\ = \(х + а) (у + /3) - жу | =
= \х/3 + уа + а/3\ ^ |х| \/3\ + \у\ \а\ + \а/3\ =
= \х\ А(у) + \у\
Д(у),
\У/
X
У
X
У
+ а
)у-
ху -ух
УУ
У2
1-
1
1 Т* 1 1 / ¦ 1 ^^— 1111 1 ?*\11 1
1 ™-J 1 1 r-J 1 I 1 *• 1 1 я_Д 1 j.
у2 1 - 6(у)
У2 1 ~ *5(у)
Из полученных оценок абсолютных погрешностей вытекают следующие
оценки относительных погрешностей:
/ Д(*) +
\х + у\
ж • ж-
8(-
У
5(х) + 6(у)
A')
B')
C')
На практике, при работе с достаточно хорошими приближениями, А(х) х
х А (у) « 0, S(x) • 5(у) « 0, 1 — E(у) « 1, поэтому пользуются соответствую-
соответствующими упрощенными, полезными, но формально неверными вариантами фор-
мул B), C), B'), C'):
\х\А(у) + \у\А(х)
У
У2
Формулы C), C') показывают, что надо избегать деления на близкие к ну-
нулю или довольно грубые приближения, когда у или 1 — 5(у) малы по абсолютной
величине.
Формула A;) предостерегает от сложения приближенных величин, если они
близки по абсолютной величине и противоположны по знаку, поскольку тогда
\х + у\ близко к нулю.

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 59
Во всех этих случаях погрешности могут резко возрасти.
Например, пусть ваш рост дважды измерили некоторым прибором. Точ-
Точность измерения ±0,5 см. Перед вторым измерением вам под ноги подложили
лист бумаги. Тем не менее может случиться, что результаты измерений будут
такими: #i = B00 ±0,5) см и Я2 = A99,8 ±0,5) см соответственно.
Таким образом, бессмысленно искать толщину бумаги в виде разности
#2 - #ь из которой только следует, что толщина не больше 0,8 см, что, ко-
конечно, очень грубо отражает (если это вообще можно назвать «отражает»)
истинное положение вещей.
Стоит, однако, обратить внимание и на другой, более оптимистичный
вычислительный эффект, благодаря которому грубыми приборами удается
провести сравнительно тонкие измерения. Например, если на том приборе,
где только что измерили ваш рост, измерили высоту пачки в 1000 листов
той же бумаги и получили результат B0 ± 0,5) см, то толщина одного листа
@,02 ± 0,0005) см= @,2 ± 0,005) мм, что вытекает из формулы A).
То есть с абсолютной погрешностью, не превышающей 0,005 мм, толщина
одного листа равна 0,2 мм. Относительная погрешность этого измерения не
превышает 0,025 или 2,5%.
Эту идею можно развить и предложить, например, способ выделения сла-
слабого периодического сигнала из превышающих его случайных радиопомех,
называемых обычно белым шумом.
с. Позиционная система счисления. Выше говорилось о том, что каж-
каждое число можно задать последовательностью приближающих его рациональ-
рациональных чисел.
Теперь напомним важный в вычислительном отношении метод, который
позволяет единообразно для каждого действительного числа строить такую
последовательность рациональных приближений. Этот метод ведет к позици-
позиционной системе счисления.
Лемма. Если фиксировать число q > 1, то для любого положительного
числа iGl найдется и притом единственное целое число k Е Ъ такое, что
qk~l ^ х < qk.
< Проверим сначала, что множество чисел вида qk, k Е N, не ограничено
сверху. В противном случае оно имело бы верхнюю грань 5 и по определению
верхней грани нашлось бы натуральное число т Е N такое, что - < qm ^ s.
Но тогда s < qm+l и s — не верхняя грань нашего множества.
Поскольку 1 < д, то qm < qn при т < n, m, n E Z, поэтому мы заодно
показали, что для любого числа с G R найдется такое натуральное число
N Е N, что при любом натуральном п > N будет с < qn.
Отсюда вытекает, что для любого числа е > 0 найдется число М Е N
такое, что при всех натуральных т > М будет — < е.

60 ТЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Действительно, достаточно положить c=-,aiV = M; тогда - < qm при
га > М.
Итак, множество целых чисел п Е Z, удовлетворяющих неравенству х < qm
при х > 0, ограничено сризу. Тогда в нем есть минимальный элемент fc,
который, очевидно, и будет искомым, так как для него qk~l ^ х < qk.
Единственность такого целого числа к следует из того, что если га, п Е Z
и, например, га < п, то га ^ п — 1, и поэтому если g > 1, то qm ^ д71.
Действительно, из этого замечания видно, что неравенства qm~l ^ х < qm
и qn~1 ^ х < qn, из которых следует qn~1 ^ х < qm, несовместны при
т ф п. >
Воспользуемся этой леммой в следующей конструкции.
Фиксируем q > 1 и возьмем произвольное положительное число х G Е.
По лемме найдем единственное число р Е Z такое, что
др^ж<др+1. A)
Определение 10. Число р, удовлетворяющее соотношению A), назы-
называется порядком числа х по основанию q или (при фиксированном q) просто
порядком числа х.
По принципу Архимеда найдем единственное натуральное число ар Е N
такое, что
apqp <^x<apqp +qp. B)
Учитывая A), можно утверждать, что apG{l, ...,g — l}.
Все дальнейшие шаги нашего построения будут повторять тот шаг, кото-
который мы сейчас сделаем, исходя из соотношения B).
Из соотношения B) и принципа Архимеда следует, что существует и при-
притом единственное число ap_i Е {0,1, ..., q - 1} такое, что
apqp + ap-i^ <С х < apqp + ар-^р~1 + qp~l. C)
Если уже сделано п таких шагов и получено, что
apqp
х < apqp + ap-nf-1 + ... + ap_n<f ~n + qp~n,
то по принципу Архимеда найдется единственное число ap_n_i E {0,1, ...
..., q — 1} такое, что
apqp + ... + ap-nqp~n
ж
Таким образом, указан алгоритм, по которому положительному числу х
однозначно ставится в соответствие последовательность чисел ap, ap_i, ...

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 61
..., ар_п, ... из множества {0,1,..., q — 1} или, менее формально, последова-
последовательность рациональных чисел гп специального вида:
rn = apgp + ... + ap_ngp-n, D)
причем так, что
rn^z<rn + —. E)
Иными словами, мы строим всё лучшие приближения снизу и сверху для
числа х посредством специальной последовательности рациональных чисел D).
Символ ар ... cxv-n - • • есть шифр всей последовательности {гп}. Чтобы по
нему можно было восстановить последовательность {гп}, необходимо как-то
отметить величину р — порядок числа х.
Условились при р ^ 0 после ао ставить точку или запятую; при р < О
слева от ар дописывать |р| нулей и после крайнего левого ставить точку или
запятую (напомним, что ар ф 0).
Например, при q = 10
123,45 := 1 • 102 + 2 • 101 + 3 • 10° + 4 • КГ1 + 5 • ИГ2,
0,00123 := 1 • 10 + 2 • 10 + 3 • ИГ5;
при q = 2
1000,001:= 1
Таким образом, значение цифры в символе ар ... ap_n ... зависит от пози-
позиции, которую она занимает по отношению к точке или запятой.
После этого соглашения символ ар ... ао,... позволяет однозначно восста-
восстановить всю последовательность приближений.
Из неравенств E) видно (проверьте!), что двум различным числам х, х' от-
отвечают различные последовательности {гп}, {г'п}, а значит, и разные символы
С*р ... С*О j • • • , ***я ... (Д>г\, • • •
Теперь решим вопрос, всякому ли символу вида ар ... ао,.. • отвечает не-
некоторое число х € Е. Оказывается, нет.
Заметим, что в силу описанного алгоритма последовательного получения
чисел ap_n Е {0,1,..., q — 1} не может случиться так, что все они, начиная с
некоторого, будут одинаковы и равны q — 1.
Действительно, если при п > к
гп = apqp + ... + ap-kqp-k + (q - ^
т. е.
то в силу E)
Г к Н г ^ X < 74
к~Р п~Р
qk—p qn—p qk~P

62
ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Тогда для любого п > к
О < гк + -1Г-7 -х <
,к-р
п—р *
что, как мы знаем из доказанной выше леммы, невозможно.
Полезно также отметить, что если среди чисел ар-к-\, • •, аР-п хотя бы
одно меньше q — 1, то вместо F) можно написать, что
1 1
qk-p qn-
или, что то же самое,
п +
,п-р
<Гк
1
*к-р '
G)
Теперь мы в состоянии доказать, что любой символ ап ... од,..., соста-
составленный из чисел ак Е {0,1,..., q — 1}, в котором как угодно далеко встреча-
встречаются числа, отличные от q — 1, соответствует некоторому числу х ^ 0.
В самом деле, по символу ар ... ар_п ... построим последовательность {гп}
вида D). В силу того, что го ^ т\ ^ ... ^ гп ^ ..., а также учитывая F) и
G), имеем
го
...<... ^ гп +
го +
(8)
Знак строгого неравенства в последнем соотношении следует понимать
так: любой элемент левой последовательности меньше любого элемента правой
последовательности. Это вытекает из G).
Если теперь взять х = sup rn (= inf (rn + q~^n~p^)I то последовательность
GN
rn будет удовлетворять условиям D), E), т. е. символ ар ... ар_п ... отвечает
найденному числу х G Е.
Итак, каждому положительному числу xGK мы взаимно однозначно со-
сопоставили символ вида ар ... од,..., если р ^ 0, или 0,0... 0 ар ..., если р < 0.
|р| нулей
Он называется q-ичной позиционной записью числа х\ цифры, входящие в сим-
символ, называют знаками] позиции знаков относительно запятой называются
разрядами.
Числу х < 0 условимся сопоставлять взятый со знаком минус символ поло-
положительного числа —х. Наконец, числу 0 отнесем символ 0,0... 0...
Тем самым завершено построение позиционной q-ичной системы записи
действительных чисел.
Наиболее употребительными являются десятичная система (в обиходе) и по
техническим причинам двоичная (в электронных вычислительных машинах).

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 63
Менее распространены, но также используются в элементах вычислительной
техники троичная и восьмеричная системы.
Формулы D), E) показывают, что если в g-ичной записи числа х оставить
только конечное число знаков (или, если угодно, заменить остальные знаки
нулями), то абсолютная погрешность получающегося при этом приближения
D) числа х не превысит единицы последнего сохраняемого разряда.
Это наблюдение позволяет в соответствии с полученными в подпункте b
формулами оценивать погрешности, возникающие при арифметических опе-
операциях над числами в результате замены точных значений чисел соответству-
соответствующими приближенными значениями вида D).
Последнее замечание имеет также определенную теоретическую ценность.
А именно, если в соответствии с идеей подпункта b мы отождествим веще-
вещественное число х с его g-ичной записью, то, научившись выполнять арифме-
арифметические действия непосредственно над д-ичными символами, мы построим
новую модель действительных чисел, по-видимому, наиболее ценную с вычи-
вычислительной точки зрения.
Основные задачи, которые пришлось бы решать на этом пути, таковы.
Надо двум g-ичным символам поставить в соответствие новый символ —
сумму исходных. Он, естественно, строится постепенно, а именно, складывая
все более точные рациональные приближения исходных чисел, будем получать
соответствующие рациональные приближения их суммы. Пользуясь сделан-
сделанным выше замечанием, можно показать, что по мере увеличения точности
приближений слагаемых мы будем получать все больше таких д-ичных знаков
суммы, которые уже не меняются при последующем уточнении приближений.
Тот же вопрос надо решать и относительно умножения.
Другой, менее конструктивный путь перехода от рациональных чисел ко
всем действительным числам принадлежит Дедекинду.
Дедекинд отождествляет действительное число с сечением в множестве Q
рациональных чисел, т. е. с разбиением Q на два не имеющих общих элементов
множества А, В таких, что Vo Е A V6 Е В (о < 6). При таком подходе
к действительным числам принятая нами аксиома полноты (непрерывности)
становится известной теоремой Дедекинда. По этой причине аксиому полноты
в принятой нами форме часто называют аксиомой Дедекинда.
Итак, в настоящем параграфе выделены важнейшие классы чисел. Показа-
Показана фундаментальная роль натуральных и рациональных чисел. Показано, как
из принятой нами аксиоматики1) вытекают основные свойства этих чисел.
Дано представление о различных моделях множества действительных чисел.
Обсуждены вычислительные аспекты теории действительных чисел: оценки
погрешностей при арифметических операциях с приближенными величинами;
g-ичная позиционная система счисления.
*) Почти в приведенном выше виде она была сформулирована на рубеже XX века Гиль-
Гильбертом; см., например, в кн.: Гильберт Д. Основания геометрии. М.: Гостехиздат,
1948. (Добавление VI: О понятии числа.)

64 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Задачи и упражнения
1. Опираясь на принцип индукции, покажите, что
a) сумма х\ +... +хп вещественных чисел определена независимо от расстановки
скобок, предписывающих порядок сложения;
b) то же для произведения х\ ... хп\
c) |Ж1 + ... + хп\ ^ \х\\ И- ... И- |хп|;
d) \х\ ... хп\ = |xi|... \хп\]
e) ((га, п е N) Л (га < п)) =» ((п - га) G N);
f) (l+z)n^l + nz при i > -1 и п 6 N, причем равенство возможно либо при
п=1, либо при х = 0 (неравенство Бернулли)\
g)
1! 2! (п — 1)!
(бином Ньютона).
2. а) Проверьте, что Z и Q — индуктивные множества.
Ь) Приведите примеры индуктивных множеств, отличных от N, Z, Q, R.
3. Покажите, что любое индуктивное множество не ограничено сверху.
4. а) Любое индуктивное множество бесконечно (т. е. равномощно своему под-
подмножеству, отличному от него самого).
Ь) Множество Еп = {х 6 N| x < п} конечно (caxdEn обозначают через п).
5. а) Алгоритм Евклида. Пусть га, п 6 N и т > п. Наибольший общий делитель
(НОД (ш, п) = d € N) можно за конечное число шагов найти, пользуясь следующим
алгоритмом Евклида последовательного деления с остатком:
га = qin + ri (ri < n),
п = qir\ +r2 (r2 < ri),
+ О,
и d = rk.
Ъ) Если d = НОД (га, п), то можно подобрать числа р, q 6 Z так, что pm + qn = d\
в частности, если га, п взаимно просты, то pm + qn = I.
6. Попробуйте самостоятельно доказать основную теорему арифметики (форму-
(формулировка в тексте § 2, п. 2а).
7. Если произведение га • п натуральных чисел делится на простое число р, т. е.
га • п = р • к, где А; 6 N, то либо га, либо п делится на р.
8. Из основной теоремы арифметики следует, что множество простых чисел бес-
бесконечно.
9. Покажите, что если натуральное число п не имеет вида fcm, где к, m 6 N, то
771 u
уравнение х =пне имеет рациональных корней.
10. Покажите, что запись рационального числа в любой д-ичной системе счисле-
счисления периодична, т. е., начиная с некоторого разряда, состоит из периодически по-
повторяющейся группы цифр.

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 65
11. Иррациональное число а € R назовем хорошо приближаемым рациональными
числами, если для любых натуральных чисел п, N 6 N существует рациональное чи-
число - такое, что
Я
ъ р
а
Я
1
Nqn
a) Постройте пример хорошо приближаемого иррационального числа.
b) Докажите, что хорошо приближаемое иррациональное число не может быть
алгебраическим, т. е. оно трансцендентно {теорема Лиувилля1').
12. Знал, что по определению дроби — := т • п, где т 6 Z, п 6 N, вывести
п
«правила» сложения, умножения, деления дробей, а также условие равенства двух
дробей.
13. Проверьте, что рациональные числа Q удовлетворяют всем аксиомам дейст-
действительных чисел, кроме аксиомы полноты.
14. Принимая геометрическую модель множества действительных чисел — чи-
числовую ось, покажите, как в этой модели строить числа а + b> a — Ь, aft, -.
15. а) Проиллюстрируйте аксиому полноты на числовой оси.
Ь) Докажите, что принцип верхней грани эквивалентен аксиоме полноты.
16. а) Если А С В С R, то sup A ^ sup Б, a inf A ^ inf В.
b) Пусть RDI/0 и R Э У # 0. Если Vx G X и Vy G Y выполнено х ^ у, то
X ограничено сверху, Y — снизу и supX ^ inf У.
c) Если множества X, Y из Ь) таковы, что X U Y — R, то supX = inf У.
d) Если X, У — множества, определенные в с), то либо 3maxX, либо ЗгшпУ
(теорема Дедекиида).
e) (Продолжение.) Покажите, что теорема Дедекинда эквивалентна аксиоме пол-
полноты.
17. Пусть А + В — множество чисел вида а + Ь и А • В — множество чисел вида
а • 6, где аб^СК и b e В CR. Проверьте, всегда ли
a) sup (А 4- В) = sup A -f supJ5;
b) sup (A • J5) = sup A • sup Б.
18. Пусть —А есть множество чисел вида —а, где a G А С R. Покажите, что
sup (—A) = —inf А.
19. а) Покажите, что уравнение хп = а при п 6 N и а > 0 имеет положительный
корень (обозначаемый ^/^или°1^п)-
Ь) Проверьте, что при а>0, Ь > 0 и п,
и V V5 = п•
c) (a1/n)m = (am)i/n =: am/n и ai/n • aVm = ai/n
d) (a™/71) = (aO71/71 =: a~m/n.
e) Покажите, что для любых ri, гг 6
ari -аГ2 =аГ1+Г2 и (аГ1)Г2 = аГ1Г2
. Лиувилль A809 — 1882) — французский математик; работы по комплексному ана-
анализу, геометрии, дифференциальным уравнениям, теории чисел, механике.

66 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
20. а) Покажите, что отношение включения есть отношение частичной (но не
полной!) упорядоченности множеств.
Ь) Пусть А, В, С — такие множества, что А С С, ? С С, А\В ф 0 и В\А Ф 0.
Частичный порядок в этой тройке введем, как в а). Укажите максимальный и мини-
минимальные элементы множества {А, В, С}. (Обратите внимание на неединственность!)
21. а) Покажите, что так же, как и множество Q рациональных чисел, множество
Q{y/n) чисел вида а 4 Ь\/п, где а, Ь 6 Q, a n — фиксированное натуральное число,
не являющееся квадратом целого числа, есть упорядоченное поле, удовлетворяющее
принципу Архимеда, но не удовлетворяющее аксиоме полноты.
b) Проверьте, какие из аксиом действительных чисел не будут удовлетворяться
для Q(^/rl), если в Q(^n) оставить прежние арифметические операции, а отношение
порядка ввести по правилу (а 4- Ьу/п ^ а' 4 Ь'у/п) := ((Ь ^ Ь') V ((Ь = Ь') Л (а ^ а'))).
Будет ли тогда для Q(-\/n) выполнен принцип Архимеда?
c) Упорядочите множество F[x] многочленов с рациональными или действитель-
действительными коэффициентами, считая
Рт(х) = ао + а\х 4 ... + amim >- 0, если am > 0.
d) Покажите, что множество Q(x) всех рациональных дробей
_ ao + а\х 4 ... 4 amxm
* ' Ьо + Ъ\х 4 ... +Ъпхп
с коэффициентами из Q или из R после введения в нем порядка Rm,n У 0, если
т21 > 0, и обычных арифметических операций становится упорядоченным, но не
Оп
архимедовым полем. Это означает, что принцип Архимеда не может быть выведен
из аксиом R, минуя аксиому полноты.
22. Пусть п G N и п > 1. В множестве Еп = {0,1, ..., п} определим сумму и про-
произведение элементов как остаток от деления на п «обычной» суммы и произведения
этих чисел в R. Множество Еп с так определенными в нем операциями обозначают
символом Zn.
a) Покажите, что если п не простое число, то в Zn есть такие отличные от нуля
числа га, к, что ш • к = 0. (Такие числа называются делителями нуля.) Это значит,
что из а Ь — с-Ь даже при Ь ф0 в Zn не следует, что а — с.
b) Покажите, что при простом р в Zp отсутствуют делители нуля и Zp есть
поле.
c) Покажите, что ни при каком простом р поле Zp нельзя упорядочить так,
чтобы этот порядок был согласован с арифметическими операциями Zp.
23. Покажите, что если RhR'- две модели множества действительных чисел,
а /: R -> R' — такое отображение, что f(x 4 у) = f(x) 4 f(y) и f(x • у) = f(x) ¦ f(y)
для любых х, j/ € R, то:
а)/@)=0';
b) /A) = 1', если f(x) ? 0', что мы дальше будем считать выполненным;
c) /(га) = га7, где га 6 Z и т' 6 Z', причем отображение /: Z -+ Zr биективно
и сохраняет порядок;
d) /(-) = ^т, где га, п € Z, п ф 0, га', n' G Z', п' ф 0', /(га) = гаг, /(п) = пг.
Таким образом, / : Q -> Q' есть сохраняющая порядок биекция.
e) /: R —> R' есть биективное, сохраняющее порядок отображение.

§ 2. ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ 67
24. Опираясь на предыдущую задачу и аксиому полноты, покажите, что акси-
аксиоматика множества действительных чисел определяет его полностью с точностью
до изоморфизма (до способа реализации), т. е. что если R и R' — два множества,
удовлетворяющие аксиоматике, то существует взаимно однозначное отображение
/: IR —> R', сохраняющее арифметические операции и порядок: f(x + y) = /(#) + /(j/)>
f(x ¦ у) = f(x) ¦ /(у) и (* < у) <=» (f(x) < /(у)).
25. В ЭВМ число х представляется в виде
к i
где р — порядок ж, а М = ?) —¦?• — мантисса числа х (- ^ М < 1).
n=i Я Я
При этом машина оперирует только с определенным диапазоном чисел: при q =¦ 2
обычно |р| ^64, а к = 35. Оцените этот диапазон в десятичной системе.
26. а) Напишите таблицу умножения (размера 6x6) для шестеричной системы
счисления.
b) Пользуясь результатом задачи а), перемножьте «столбиком» в шестеричной
системе
E32)б
A45N
и проверьте свои действия, повторив вычисления в десятичной системе.
c) Поделите «уголком»
A301N|B5)б
и проверьте свои действия, повторив вычисления в десятичной системе,
d) Проведите сложение «столбиком»
D052)
6
27. Запишите A00) ю в двоичной и троичной системах.
28. а) Покажите, что наряду с единственностью записи целого числа в виде
где at G {0,1,2}, возможна и также единственна его запись в виде
(Pnfin-l ¦ • • А))з,
где/? е {-1,0,1}.
Ь) Каково наибольшее число монет, из которых тремя взвешиваниями на чашеч-
чашечных весах можно выделить одну фальшивую, если известно только, что она отлича-
отличается от остальных монет по весу?
29. Какое наименьшее количество вопросов с ответами «да» или «нет» надо за-
задать, чтобы узнать любой из семизначных телефонных номеров?
30. а) Сколько различных чисел можно задать с помощью 20 десятичных знаков
(например, два разряда по 10 возможных знаков в каждом)? Тот же вопрос для
двоичной системы. В пользу экономичности какой из этих систем говорит сравнение
результатов?

68 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
b) Оцените количество различных чисел, которые можно записать, располагая п
знаками д-ичной системы. (Ответ: qn^q.)
c) Нарисуйте график функции /(х) = хп^х над множеством натуральных значе-
значений аргумента и сравните экономичность различных систем счисления.
§ 3. Основные леммы, связанные с полнотой
множества действительных чисел
Здесь мы установим несколько простых полезных принципов, каждый из ко-
которых можно было бы положить в основу построения теории вещественных
чисел в качестве аксиомы полноты1).
Эти принципы мы назвали основными леммами в соответствии с их широ-
широким использованием во всевозможных доказательствах теорем анализа.
1. Лемма о вложенных отрезках (принцип Коши — Кантора)
Определение 1. Функцию / : N —> X натурального аргумента на-
называют последовательностью или, полнее, последовательностью элементов
множества X.
Значение /(п) функции /, соответствующее числу п € N, ч&сто обозна-
обозначают через хп и называют n-м членом последовательности.
Определение 2. Пусть Х\, Х2, ... , Хп, ... — последовательность
каких-то множеств. Если Х\ Э Х2 Э ... Э Xn D ..'., т.е. Vn G N (Хп Э
Э Xn+i), то говорят, что имеется последовательность вложенных множеств.
Лемма (Коши — Кантор). Для любой последовательности 1\ Э I2 D • • •
... Э In D ... вложенных отрезков найдется точка 6 € R, принадлежащая
всем этим отрезкам.
Если, кроме того, известно, что для любого е > 0 в последовательности
можно найти отрезок /*, длина которого |/*| < е, то с — единственная
общая точка всех отрезков.
< Заметим прежде всего, для любых двух отрезков Im = [am,6m], In =
— [«n5bn] нашей последовательности имеет место ат $С Ьп. Действительно, в
противном случае мы получили бы ап ^ Ьп < ат ^ Ьт, т. е. отрезки /т, 1п не
имели бы общих точек, в то время как один из них (имеющий больший номер)
должен содержаться в другом.
Таким образом, для числовых множеств А = {ат \ т € N}, В = {bn \ n € N}
выполнены условия аксиомы полноты, в силу которой найдется число с € Ш
такое, что Vam E A, V6n Е В выполнено ат ^ с ^ Ьп. В частности, ап ^ с ^
^ Ъп для любого п € N. Но это и означает, что точка с принадлежит всем
отрезкам 1п.
. задачу 4 в конце параграфа.

§ 3. ОСНОВНЫЕ ЛЕММЫ, СВЯЗАННЫЕ С ПОЛНОТОЙ R 69
Пусть теперь С\ и С2 — две точки, обладающие этим свойством. Если
они различны и, например, с\ < С2, то при любом п ? N имеем ап ^ С\ <
< С2 ^ Ьп, поэтому 0 < С2 — с\ < Ъп — ап и длина каждого отрезка нашей
последовательности не может быть меньше положительной величины c*i — С\.
Значит, если в последовательности есть отрезки сколь угодно малой длины,
то общая точка у них единственная. >
2. Лемма о конечном покрытии (принцип Бореля-Лебега)
Определение 3. Говорят, что система 5 = {X} множеств X покрыва-
покрывает множество F, если Y С U X, (т. е. если любой элемент у множества Y
xes
содержится по крайней мере в одном из множеств X системы 5).
Подмножество множества 5 = {X}, являющегося системой множеств, бу-
будем называть подсистемой системы 5. Таким образом, подсистема системы
множеств сама является системой множеств того же типа.
Лемма (Борель—Лебег1)). В любой системе интервалов, покрывающей
отрезок, имеется конечная подсистема, покрывающая этот отрезок.
<4 Пусть S = {U} — система интервалов f/, покрывающая отрезок [а, Ь] =
= 1\. Если бы отрезок 1\ не допускал покрытия конечным набором интервалов
системы 5, то, поделив 1\ пополам, мы получили бы, что по крайней мере одна
из его половинок, которую мы обозначим через /г, тоже не допускает конеч-
конечного покрытия. С отрезком /г проделаем ту же процедуру деления пополам,
получим отрезок /з и т. д.
Таким образом, возникает последовательность 1\ Э h Э ... D 1п Э ... вло-
вложенных отрезков, не допускающих конечного покрытия интервалами систе-
системы 5. Поскольку длина отрезка, полученного на n-м шаге, по построению
равна |/п| = |ii| • 2~п, то в последовательности {/п} есть отрезки сколь угод-
угодно малой длины (см. лемму из § 2, п. 4с). По лемме о вложенных отрезках
существует точка с, принадлежащая всем отрезкам /n, n ? N. Поскольку
с € 1\ = [а, 6], то найдется интервал ]а,/3[ = U € 5 системы 5, содержащий
точку с, т. е. а < с < /3. Пусть е = min{c — а, /3 — с}. Найдем в постро-
построенной последовательности такой отрезок /п, что |/п| < е. Поскольку с € 1п
и |/п| < е, заключаем, что 1п С U = ]а,/3[. Но это противоречит тому, что
отрезок 1п нельзя покрыть конечным набором интервалов системы. >
3. Лемма о предельной точке (принцип Больцано-Вейерштрасса).
Напомним, что окрестностью точки х € Е мы назвали интервал, содержащий
эту точку; (^-окрестностью точки х — интервал ]х — 5, х + 6[.
Определение 4. Точка р € R называется предельной точкой множе-
множества X С IR, если любая окрестность этой точки содержит бесконечное под-
подмножество множества X.
Х)Э. Борель A871 — 1956), А. Лебег A875 — 1941) — известные французские математики,
специалисты в области теории функций.

70 ГЛ. И. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Это условие, очевидно, равносильно тому, что в любой окрестности точ-
точки р есть по крайней мере одна не совпадающая с р точка множества X.
(Проверьте!)
Приведем несколько примеров.
Если X = \— G I п € N >, то предельной для X является только точка
In J
0е R.
Для интервала ]а,6[ предельной является каждая точка отрезка [а, 6], и
других предельных точек в этом случае нет.
Для множества Q рациональных чисел предельной является каждая точ-
точка Е, ибо, как мы знаем, в любом интервале вещественных чисел имеются
рациональные числа.
Лемма (Больцано — Вейерштрасс1)). Всякое бесконечное ограниченное
числовое множество имеет по крайней мере одну предельную точку.
<4 Пусть X — данное подмножество Ж. Из определения ограниченности
множества X следует, что X содержится в некотором отрезке [а, Ь] = I С R.
Покажем, что по крайней мере одна из точек отрезка J является предельной
для X.
Если бы это было не так, то каждая точка х ? / имела бы окрестность
U(x), в которой либо вообще нет точек множества X, либо их там конечное
число. Совокупность {U(x)} таких окрестностей, построенных для каждой
точки х ? /, образует покрытие отрезка / интервалами f/(x), из которого
по лемме о конечном покрытии можно извлечь конечную систему U(x\), ...,
U(xn) интервалов, покрывающую отрезок /. Но, поскольку X С /, эта же си-
система покрывает все множество X. Однако в каждом интервале U(x{) только
конечное число точек множества X, значит, и в их объединении тоже конеч-
конечное число точек X, т. е. X — конечное множество. Полученное противоречие
завершает доказательство. >
Задачи и упражнения
1. Покажите, что
а) если / — произвольная система вложенных отрезков, то sup {а € R | [а, b] € /} =
и[а,C]= f| [а,Ц;
Ъ) если / — система вложенных интервалов ]а, 6[, то пересечение р| ]а, Ь[ может
оказаться пустым. ]л,Ь[е/
Указание: ]ап,Ьп[= 0, - .
2. Покажите, что
а) из системы отрезков, покрывающей отрезок, не всегда можно выделить ко-
конечную подсистему, покрывающую этот отрезок;
^Б. Больцано A781 — 1848) — чешский математик и философ; К. Вейерштрасс A815 —
1897) — немецкий математик, уделявший большое внимание логическому обоснованию ма-
математического анализа.

§ 4. СЧЕТНЫЕ И НЕСЧЕТНЫЕ МНОЖЕСТВА 71
b) из системы интервалов, покрывающей интервал, не всегда можно выделить
конечную подсистему, покрывающую этот интервал;
c) из системы отрезков, покрывающей интервал, не всегда можно выделить ко-
конечную подсистему, покрывающую этот интервал.
3. Покажите, что если вместо полного множества R всех вещественных чисел
взять только множество Q рациональных чисел, а под отрезком, интервалом и
окрестностью точки г € Q понимать соответствующие подмножества Q, то ни одна
из доказанных выше трех основных лемм не останется в силе.
4. Покажите, что если в качестве аксиомы полноты множества действительных
чисел взять
a) принцип Больцано — Вейерштрасса
или
b) принцип Бореля — Лебега,
то получится равносильная прежней система аксиом R.
Указание. Из а) следует принцип Архимеда и аксиома полноты в прежней
форме.
c) Замена аксиомы полноты принципом Коши —Кантора приводит к системе
аксиом, которая становится равносильной исходной, если кроме принципа Коши —
Кантора постулировать также принцип Архимеда (см. задачу 21 предыдущего па-
параграфа).
§ 4. Счетные и несчетные множества
Сейчас мы сделаем небольшое, полезное для дальнейшего добавление к тем
сведениям о множествах, которые уже были изложены в главе I.
1. Счетные множества
Определение 1. Множество X называется счетным, если оно равно-
мощно множеству N натуральных чисел, т. е. cardX = cardN.
Утверждение, а) Бесконечное подмножество счетного множества
счетно.
Ь) Объединение множеств конечной или счетной системы счетных мно-
множество есть множество счетное.
< а) Достаточно проверить, что всякое бесконечное подмножество Е мно-
множества N натуральных чисел равномощно N. Нужное биективное отображение
/ : N —>• Е построим следующим образом. В Е\ := Е имеется минимальный
элемент, который мы сопоставим числу 1 € N и обозначим е\ ? Е. Мно-
Множество Е бесконечно, поэтому Е2 := Е\е\ непусто. Минимальный элемент
множества ??2 сопоставим числу 2 и назовем его ег € Еч- Затем рассмотрим
Е<$ := iJ\{ei,ег} и т. д. Поскольку Е — бесконечное множество, то построение
не может оборваться ни на каком шаге с номером п € N, и, как следует из
принципа индукции, таким способом каждому числу п ? N будет сопоставле-
сопоставлено некоторое число еп ? Е. Построенное отображение /: N —> Е, очевидно,
инъективно.

72 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Остается проверить его сюръективность, т. е. что /(N) = Е. Пусть еб
Множество {п € N | п ^ е} конечно, и тем более конечно его подмножество
{п € Е | п ^ е}. Пусть к •— число элементов в последнем множестве. Тогда по
построению е = е^.
Ь) Если Х\, ..., Хп, ... — счетная система множеств, причем каждое мно-
множество Хт = {х^, ..., xjjj, ... } само счетно, то поскольку мощность множе-
множества X = U Хп, состоящего из элементов х^, где m, n ? N, не меньше мощ-
ности каждого из множеств Хт, то X — бесконечное множество. Элемент
х^ € Хт можно отождествить с задающей его упорядоченной парой (т, п)
натуральных чисел. Тогда мощность X не больше мощности множества та-
таких упорядоченных пар. Но отображение /: N х N —> N, задаваемое формулой
(га, n) i—> + т, как легко проверить, биективно (оно име-
имеет наглядный смысл: мы нумеруем точки плоскости с координатами (т,п),
последовательно переходя от точек одной диагонали, где т + п постоянно, к
точкам следующей, где эта сумма на 1 больше).
Таким образом, множество упорядоченных пар (га, п) натуральных чисел
счетно. Но тогда cardX ^ cardN и, поскольку X — бесконечное множество,
на основании доказанного в а) заключаем, что cardX = cardN. >
Из доказанного утверждения следует, что любое подмножество счетного
множества либо конечно, либо счетно. Если про множество известно, что оно
либо конечно, либо счетно, то говорят, что оно не более чем счетно (равно-
(равносильная запись: cardX ^ cardN).
Мы можем, в частности, утверждать теперь, что объединение не более
чем счетного семейства не более чем счетных множеств само не более чем
счетно.
Следствия. 1) cardZ = cardN.
2) cardN2 = cardN.
Этот результат означает, что прямое произведение счетных множеств
счетно.
3) cardQ = cardN, т. e. множество рациональных чисел счетно.
< Рациональное число — задается упорядоченной парой (га,п) целых
чисел.
Две пары (т,п), (т',п') задают одно и то же рациональное число в том
и только в том случае, когда они пропорциональны. Такимубразом, выби-
выбирая каждый раз для записи рационального числа единственную пару (т,п)
с минимальным возможным натуральным знаменателем п 6 N, мы получим/
что множество Q равномощно некоторому бесконечному подмножеству мно-
множества Z х Z. Но cardZ2 = cardN и, значит, cardQ = cardN. >

§ 4. СЧЕТНЫЕ И НЕСЧЕТНЫЕ МНОЖЕСТВА 73
4) Множество алгебраических чисел счетно.
< Заметим сначала, что из равенства cardQ xQ = cardN по индукции
получаем, что для любого А; € N выполнено cardQ* = cardN.
Элемент г ? Q* есть упорядоченный набор (п, ...,г*) к рациональных
чисел.
Алгебраическое уравнение степени к с рациональными коэффициентами
можно записать в приведенном виде хк + г\ хк~1 + ... + г* =0, где коэффици-
коэффициент при старшей степени равен 1. Таким образом, различных алгебраических
уравнений степени к столько же, сколько различных упорядоченных наборов
(п> • • •» гк) рациональных чисел, т. е. счетное множество.
Алгебраических уравнений с рациональными коэффициентами (произволь-
(произвольных степеней) тоже счетное множество как счетное объединение (по степе-
степеням) счетных множеств. У каждого такого уравнения лишь конечное число
корней, значит, множество алгебраических чисел не более чем счетно. Но оно
бесконечно и, значит, счетно. >
2. Мощность континуума
Определение 2. Множество R действительных чисел называют также
числовым континуумом1^, а его мощность — мощностью континуума.
Теорема (Кантор). cardN <cardK.
Теорема утверждает, что бесконечное множество R имеет мощность боль-
большую, чем бесконечное множество N.
<4 Покажем, что уже множество точек отрезка [0,1] несчетно.
Предположим, что оно счетно, т. е. может быть записано в виде после-
последовательности х\, Х2, ..., хп, ... Возьмем точку х\ и на отрезке [0,1] = /о
фиксируем отрезок ненулевой длины, не содержащий точку х\. В отрезке
1\ строим отрезок /2, не содержащий Х2, и если уже построен отрезок /п,
то, поскольку |/п| > 0, в нем строим отрезок /n+i так, что xn+i ? /n+i и
|Jn+i| > 0. По лемме о вложенных отрезках найдется точка с, принадлежащая
всем отрезкам /о, /i, ..., /п, • • • Но эта точка отрезка /о = [0,1] по построе-
построению не может совпадать ни с одной из точек последовательности х\, Х2, ...,
хП1 ... >
Следствия. 1) Q т^ Е и существуют иррациональные числа.
2) Существуют трансцендентные числа, поскольку множество алгебра-
алгебраических чисел счетно.
(После решения задачи 3, помещенной в конце параграфа, читатель, навер-
наверное, захочет переиначить последнее утверждение и сформулировать его так:
«В множестве действительных чисел иногда встречаются также и алгебраи-
алгебраические числа».)
Continuum (лат.) — непрерывное, сплошное.

74 ГЛ. II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
Уже на заре теории множеств возник вопрос о том, существуют ли мно-
множества промежуточной мощности между счетными множествами и множе-
множествами мощности континуума, и было высказано предположение, называемое
гипотезой континуума, что промежуточные мощности отсутствуют.
Вопрос оказался глубоко затрагивающим основания математики. Он был
окончательно решен в 1963 г. современным американским математиком П. Ко-
эном. Коэн доказал неразрешимость гипотезы континуума, показав, что и она
сама, и ее отрицание порознь не противоречат принятой в теории множеств
аксиоматике, а потому гипотеза континуума не может быть ни доказана, ни
опровергнута в рамках этой аксиоматики,— ситуация, вполне аналогичная не-
независимости пятого постулата Евклида о параллельных от остальных аксиом
геометрии.
Задачи и упражнения
1. Покажите, что множество всех действительных чисел равномощно множеству
точек интервала ]—1,1[.
2. Установите непосредственно взаимно однозначное соответствие между
a) точками двух интервалов;
b) точками двух отрезков;
c) точками отрезка и интервала;
d) точками отрезка [0,1] и множеством R.
3. Покажите, что
a) любое бесконечное множество содержит счетное подмножество;
b) множество четных чисел равномощно множеству всех натуральных чисел;
c) объединение бесконечного множества и не более чем счетного множества име-
имеет ту же мощность, что и исходное бесконечное множество;
d) множество иррациональных чисел имеет мощность континуума;
e) множество трансцендентных чисел имеет мощность континуума.
4. Покажите, что
a) множество {ni < 712 < ... } возрастающих последовательностей натуральных
чисел равномощно множеству дробей вида 0, акхг ...;
b) множество всех подмножеств счетного множества имеет мощность конти-
континуума.
5. Покажите, что
a) множество V(X) подмножеств множества X равномощно множеству всех
функций на X со значениями 0,1, т. е. множеству отображений / : X -> {0,1};
b) для конечного множества X из п элементов caidV(X) = 2П;
c) учитывая результаты задач 4Ь) и 5а), можно писать, что caidV(X) = 2cardx
и, в частности, cardP(N) = 2cardN = cardR;
d) для любого множества X
card X < 2 саг , в частности, п <2п при любом п ? N.
Указание. См. теорему Кантора в п. 1 § 4, гл. I.

§ 4, СЧЕТНЫЕ И НЕСЧЕТНЫЕ МНОЖЕСТВА75
6. Пусть Х\, ..., Хт — конечная система конечных множеств. Покажите, что
( U Хг ) = ]Г
card ( U Хг ) = ]Г cardXix - ^ card (Xh П
card №i n X<2 nXis) -••• + (-1O71 card (Xi П ... П
*1<*2<*3
причем суммирование ведется по всевозможным наборам индексов в пределах 1, ...
..., га, удовлетворяющих указанным под знаком суммы неравенствам.
7. На отрезке [0,1] С R изобразите множество чисел х ? [0,1], троичная запись
которых х = 0, ctict2OL3 .. •, где а» ? {0,1,2}, обладает свойством:
a) ol\ ф 1;
b) (ai ф 1) Л (а2 / 1);
c) Vi Е N (а» ^ 1) (кантпорово множество).
8. (Продолжение задачи 7.) Покажите, что
a) множество тех чисел х € [0,1], троичная запись которых не содержит 1, равно-
мощно множеству всех чисел, двоичное представление которых имеет вид 0, /?i/?2 • • •;
b) канторово множество равномощно множеству всех точек отрезка [0,1].

ГЛАВА III
ПРЕДЕЛ
Обсуждал различные стороны понятия действительного числа, мы, в частно-
частности, отметили, что при измерении реальных физических величин получаются
последовательности их приближенных значений, с которыми затем и прихо-
приходится работать.
Такое положение дел немедленно вызывает по крайней мере три следующих
вопроса:
1) Какое отношение имеет полученная последовательность приближений
к измеряемой величине? Мы имеем в виду математическую сторону дела,
т. е. мы хотим получить точную запись того, что вообще означает выражение
«последовательность приближенных значений» и в какой мере такая последо-
последовательность описывает значение величины; однозначно ли это описание или
одна и та же последовательность может отвечать разным значениям измеря-
измеряемой величины.
2) Как связаны операции над приближенными значениями величин с теми
же операциями над их точными значениями и чем характеризуются те опера-
операции, при выполнении которых допустима подмена точных значений величин
приближенными?
3) Как по-самой последовательности чисел определить, может ли она быть
последовательностью сколь угодно точных приближений значения некоторой
величины?
Ответом на эти и близкие к ним вопросы служит понятие предела функ-
функции — одно из основных понятий анализа.
Изложение теории предела мы начнем с рассмотрения предела функций на-
натурального аргумента (последовательностей) ввиду уже выяснившейся фун-
фундаментальной роли этих функций и потому, что на самом деле все основные
факты теории предела отчетливо видны уже в этой простейшей ситуации.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 77
§ 1. Предел последовательности
1. Определения и примеры. Напомним следующее
Определение 1. Функция /: N —> X, областью определения которой
является множество натуральных чисел, называется последовательностью.
Значения f(n) функции / называются членами последовательности. Их
принято обозначать символом элемента того множества, в которое идет ото-
отображение, наделяя символ соответствующим индексом аргумента, хп := f(n).
Саму последовательность в связи с этим обозначают символом {хп}, а также
записывают в виде х\, #2, • • •» хт ... и называют последовательностью в X
или последовательностью элементов множества X.
Элемент хп называется п-м членом последовательности.
Всюду дальше в ближайших параграфах будут рассматриваться только
последовательности /: N —> Е действительных чисел.
Определение 2. Число А € Ш называется пределом числовой после-
последовательности {хп}, если для любой окрестности V(A) точки А существует
такой номер N (выбираемый в зависимости от V(A)), что все члены последо-
последовательности, номера которых больше JV, содержатся в указанной окрестности
точки А.
Ниже мы приведем формально-логическую запись этого определения, но
прежде укажем другую распространенную формулировку определения преде-
предела числовой последовательности:
Число А Е 1 называется пределом последовательности {хп}, если для
любого е > 0 существует номер N такой, что при всех п > N имеем
\хп - А\ < е.
Эквивалентность этих формулировок легко проверить (проверьте!), ес-
если заметить, что в любой окрестности V(A) точки А содержится некоторая
е-окрестность этой же точки.
Последняя формулировка определения предела означает, что, какую бы
точность е > 0 мы ни задали, найдется номер N такой, что абсолютная по-
погрешность приближения числа А членами последовательности {хп} меньше
чем ?, как только п > N.
Запишем теперь приведенные формулировки определения предела в логи-
логической символике, договорившись, что запись « lim xn — А» означает, что
п—юо
А — предел последовательности {хп}. Итак,
lim хп = А := VV(A) 3NeN Vn > N (хп € V(A))
и соответственно
lim xn = А := Ve > О 3N <Е N Vn > N (\хп - А\ < е)
п—юо

78
ГЛ. III. ПРЕДЕЛ
Определение 3. Если lim хп = А, то говорят, что последовательность
П—?ОО
{хп} сходится к А или стремится к А и пишут хп -> А при п -> оо.
Последовательность, имеющая предел, называется сходящейся. Последова-
Последовательность, не имеющая предела, называется расходящейся.
Рассмотрим некоторые примеры.
Пример 1. lim — = 0, так как
п—ЮО 71
тт о v
Пример 2. lim
п—Юс
71
71
71
1, так как
71 +1
п
. 1.
n
при n>N= Г-
= — < е при п > N =
Пример 3. lim I 1 +
n—»-oc
при п > N = - .
Пример 4. lim
( (-l)n^
im I 1 + -—— 1=1, так как
__ y
= - < ?
п
sinn
П—ЮО 71
О, так как
sinn
-О
п
- < е при п> N = \ Ц.
n ^ UJ
Пример 5. lim — = 0, если \q\ > 1.
П—ЮО
Проверим это по определению предела. Как было доказано в гл. II, § 2,
п. 4с, для любого е > 0 можно найти число N G N такое, что -г-гг? < е. По-
скольку |#| > 1, то для любого п > N будем иметь
и определение предела удовлетворено.
qn
г?
Пример б. Последовательность 1, 2, -, 4, -, б, -, ... с п-м членом
^n=^^-1^ , nGN,— расходящаяся.
Действительно, если А — предел последовательности, то, как следует из
определения предела, в любой окрестности А лежат все члены последователь-
последовательности, за исключением, быть может, конечного их числа.
Число А ф 0 не может быть пределом данной последовательности, ибо вне
\А\ Л
^-окрестности А при е = J-r-L > 0 лежат все члены нашей последовательности
+ 12'
вида
для которых
Число 0 тоже не может быть пределом этой последовательности, посколь-
поскольку, например, вне единичной окрестности нуля, очевидно, тоже имеется бес-
бесконечно много членов нашей последовательности.
Пример 7. Аналогично можно проверить, что последовательность 1,-1,
+1, —1, ... , для которой хп = (—1)п, не имеет предела.
*) [х] — целая часть числа ж; см. следствие 10° принципа Архимеда, гл. II, § 2, п. 3.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 79
2. Свойства предела последовательности
a. Общие свойства. Мы выделим в эту группу те свойства, которыми
обладают, как будет видно из дальнейшего, не только числовые последователь-
последовательности, хотя здесь мы эти свойства будем рассматривать только для числовых
последовательностей.
Последовательность, принимающую только одно значение, будем называть
постоянной.
Определение 4. Если существуют число А и номер N такие, что хп =
= А при любом п > 7V, то последовательность {хп} будем называть финально
постоянной.
Определение 5. Последовательность {хп} называется ограниченной,
если существует число М такое, что \хп\ < М при любом п ? N.
Теорема 1. а) Финально постоянная последовательность сходится.
b) Любая окрестность предела последовательности содержит все члены
последовательности, за исключением конечного их числа.
c) Последовательность не может иметь двух различных пределов.
d) Сходящаяся последовательность ограничена.
М а) Если хп — А при п > TV, то для любой окрестности V(A) точки А
имеем хп ? V(A) при п > TV, т. е. lim xn = А.
П—ЮО
b) Утверждение непосредственно следует из определения предела последо-
последовательности.
c) Это важнейший пункт теоремы. Пусть lim хп = А\ и lim xn = А2.
п—юс п—юс
Если А\ ф Лг, то фиксируем непересекающиеся окрестности V(Ai), V(A2)
точек А\, Ач-
В качестве таковых можно взять, например, E-окрестности этих точек при
S < - \Ai — Лг]. По определению предела найдем числа N\ и Л^ так, что Vn >
> Ni (xn e V(Ai)) и Vn > N2 (xn e V(A2)). Тогда при п > max{NliN2}
получим хп € V{A\) П V(A2). Но это невозможно, поскольку V(A\) П V(A2) =
= 0.
d) Пусть lim xn = А. Полагая в определении предела е — 1, найдем номер
п—юо
N такой, что Vn > TV (\xn - А\ < 1). Значит, при п> N имеем \хп\ < \А\ + 1.
Если теперь взять М > max{|xi|, • • •, |яп|, \А\ + 1}, то получим, что Vn > TV
(|xn| < М). >
b. Предельный переход и арифметические операции
Определение 6. Если {хп}, {уп} — две числовые последовательности,
то их суммой, произведением и частным (в соответствии с общим определе-
определением суммы, произведения и частного функций) называются соответственно
последовательности

80 гл. ш. предел
Частное, разумеется, определено лишь при уп ф 0, п € N.
Теорема 2. Пусть {хпу, {уп} ~~ числовые последовательности. Если
lim xn = A, lim ?/п = В, то:
п—>оо п—юо
a) lim (жп + уп) = А + В]
п—юс
b) lim хП'уп = А В;
п—>оо
c) lim — = — еслгг упф^ (гг- =1,2,...) и В ф 0.
П—»-ОО 1/п -О
^ В качестве упражнения воспользуемся уже известными нам (см. гл. II,
§ 2, п. 4) оценками абсолютных погрешностей, возникающих при арифмети-
ческих операциях с приближенными значениями величин.
Положим \А — хп\ = Д(хп), \В — уп\ = А(уп). Тогда для случая а) имеем
\(А + В) - (хп + уп)\ ^ А(хп) + Д(уп).
Пусть задано число е > 0. Поскольку lim xn = Л, найдется номер TV' та-
п—»-оо
кой, что Vn > TV' (Д(ггп) < е/2). Аналогично, поскольку lim yn = Б, найдет-
п—»-оо
ся номер 7V" такой, что Vn > TV" (Д(уп) < ^/2). Тогда при n > max{7V', TV"}
будем иметь
что в соответствии с определением предела доказывает утверждение а).
Ь) Мы знаем, что
\(А • В) - (хпУп)\ < kn| Д(Уп) + Ш &(Хп) + Д(я?п); Д(Уп)
По заданному е > 0 найдем числа N' и N" такие, что
Vn>N' (Д(х„)
Vn>7V» (ДЫ
(|B|
Тогда при п> N = max {N',N"} будем иметь
|у„| < \В\ + Д(уп)
Д(х„)-

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
81
Таким образом, при п> N
\хп\ А(уп) < (\А\
\уп\ А(хп) < (\В\
3(|В|
?
3'
?
3'
поэтому \АВ — хпуп\ < е при п > N.
с) Воспользуемся оценкой
А х
п
хп\А(уп) -f \уп\А(хп)
где
А(уп)
При заданном ? > 0 найдем числа TV' и N" так, что
Vn>N'
Vn>N" (Д(уп)<ппп
Тогда при п > max {N',N"} будем иметь
\B
\уп\ > \В\ - А(уп)
¦<'<ь>-тйм§8;
1
2'
поэтому
\х
п\
± А(уп)< (\А\
Уп
Уп
А(хп) <
0<
в2 ¦
2 е|Б| _ е
?
4'
1
8
<2
4'

82 гл. ш. предел
и, следовательно,
4 - — < е при n > 7V. >
В уп
Замечание. Формулировка теоремы допускает и другой, менее кон-
конструктивный путь доказательства, вероятно, известный читателю по школь-
школьному курсу начал анализа. Мы напомним его, когда будем говорить о пределе
произвольных функций. Но здесь, рассматривал предел последовательности,
нам хотелось обратить внимание на то, как именно по ограничениям на по-
погрешность результата арифметической операции ищутся допустимые погреш-
погрешности значений величин, над которыми эта операция производится.
с. Предельный переход и неравенства
Теорема 3. а) Пусть {хп}, {уп} ~~ две сходящиеся последовательно-
последовательности, причем lim хп = Ar lim уп = В. Если А < В, то найдется номер
п—юо п—юс
N ? N такой, что при любом п > N выполнено неравенство хп < уп.
Ъ) Пусть последовательности {хп}, {уп}, {zn} таковы, что при любом
п > N ? N имеет место соотношение хп ^ уп ^ zn. Если при этом последо-
последовательности {хп}, {zn} сходятся к одному и тому же пределу, то последо-
последовательность {уп} также сходится и к этому dice пределу.
Л а) Возьмем число С такое, что А < С < В. По определению предела
найдем числа TV' и N" так, чтобы при любом п > N' иметь \хп — А\ < С — А
и при любом п > N" иметь \уп — В\ < В - С. Тогда при п > N = max {TV', N"}
получим хп < А + (С - А) = С = В - (В - С) < уп.
Ь) Пусть lim xn = lim zn — А. По е > 0 найдем числа N' и N" так,
п—>оо п—юо
чтобы при любом п > Nf иметь А — е < хп и при любом п > N" иметь zn <
< А+е. Тогда при п> N = max{7V', N"} получим А—е < хп ^ уп ^ zn < А+е
или \уп - А\ < е, т. е. А = lim yn. >
п—»-оо
Следствие. Пусть lim xn = А и lim yn = B.
Если существует номер N такой, что при любом п > N:
a) хп > уп, то
b) хп ^ уп, то
c) хп > В, то А^ В;
d) хп ^ Б, то А^ В.
Ч Рассуждая от противного, из пункта а) теоремы немедленно получа-
получаем первые два утверждения. Третье и четвертое утверждения суть частные
случаи первых двух, получающиеся при уп = В. >
Стоит заметить, что строгое неравенство в пределе может перейти в ра-
равенство. Например, - > 0 при любом п G N, но lim — = 0.
П П—ЮО П

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 83
3. Вопросы существования предела последовательности
а. Критерий Коши
Определение 7. Последовательность {хп} называется фундаменталь-
фундаментальной (или последовательностью Коши1)), если для любого числа е > О най-
найдется такой номер N ? N, что из п> N и т > N следует \хт — хп\ < е.
Теорема 4 (критерий Коши сходимости последовательности). Числовая
последовательность сходится тогда и только тогда, когда она фундамен-
фундаментальна.
< Пусть lim хп = А. По числу е > 0 найдем номер N так, чтобы при
п—юо
п > N иметь \хп — А\ < -. Если теперь т > N и п > N, то \хт — хп\ <
< |#т — ^4| + |#п"-^4| < о~*~о =б:и> таким образом, проверено, что сходящаяся
последовательность фундаментальна.
Пусть теперь {#*} — фундаментальная последовательность. По заданному
е > 0 найдем номер N такой, что из т ^ N и к ^ N следует \хт — Xk\ < г.
о
Фиксировав т = N, получаем, что при любом к > N
XN - ^< Хк < XN -\- -, A)
но поскольку имеется всего конечное число членов последовательности {хп}
с номерами,-не превосходящими N, то мы доказали, что фундаментальная
последовательность ограничена.
Для п G N положим теперь ап := inf #*, Ьп :=
Из этих определений видно, что ап ^ an+i ^ 6n+i ^ Ьп (поскольку при
переходе к меньшему множеству нижняя грань не уменьшается, а верхняя не
увеличивается). Последовательность вложенных отрезков [an,6n] имеет, по
лемме о вложенных отрезках, общую точку А.
Поскольку при любом п € N
ап ^ А ^ 6П,
а при к ^ п
ап = inf хк ^хк^ supxk = Ьп,
то при к ^ п имеем
|Л-х*| ^ Ьп -ап. B)
Но из A) следует, что при п > N
^ 25f ^Ьп = sup ж* ^ жлг 4- -,
к>п
х) Последовательности Коши ввел Больцано, пытавшийся, не располагая точным поняти-
понятием вещественного числа, доказать сходимость фундаментальной последовательности. Коши
дал такое доказательство, приняв за очевидное принцип вложенных отрезков, обоснованный
впоследствии Кантором.
4 Зорич В. А.

84 ГЛ. III. ПРЕДЕЛ
поэтому при п > т
2е
Ъп ~ а>п ^ -г- < е. C)
Сравнивая B) и C), находим, что при любом к > N
\А-хк\ <е,
и мы показали, что lim я* — А. >
к—юо
Пример 8. Последовательность (—1)п (п = 1, 2, ...) не имеет предела,
поскольку она не является фундаментальной. Хотя это и очевидно, но все
же проведем формальную проверку. Отрицание утверждения, что последова-
последовательность {хп} фундаментальная, выглядит так:
Эе>0 VTVeN 3n>N 3m>N (\xm - хп\ ^ е),
т. е. найдется е > 0 такое, что при любом N € N найдутся числа п, га, боль-
большие TV, для которых \хт — хп\ ^ е.
В нашем случае достаточно положить е — 1. Тогда при любом TV € N будем
иметь |ялг+1 - ялг+2| = |1 - (-1I = 2 > 1 = е.
Пример 9. Пусть
= 0,
— некоторая последовательность конечных двоичных дробей, причем каждая
следующая дробь получается дописыванием знака 0 или 1 к предыдущей. По-
Покажем, что такая последовательность всегда сходится. Пусть т> п. Оценим
разность хт — хп:
bm
2n+l 2m
+...+i
m
Таким образом, подобрав по заданному е > 0 число N так, что —^ < е для
любых т> п > N, получаем оценку \хт - хп\ < — < -^ < е, доказывающую
фундаментальность последовательности {хп}.
Пример 10. Рассмотрим последовательность {хп}, где
2 п
Поскольку для любого п € N
|#2п — Хп\ = + . . . Н > П • — = -,
1 ' п+ 1 п + п 2п 2
то в силу критерия Коши эта последовательность не имеет предела.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 85
b. Критерий существования предела монотонной
последовательности
Определение 8. Последовательность {хп} называется возрастающей,
если Vn € N (хп < ?n+i)l неубывающей, если Vn G N (хп ^ ?n+i); невозра-
стающей, если Vn G N (xn ^ xn_|_i); убывающей, если Vn G N (xn > xn+i)-
Последовательности этих четырех типов называют монотонными последова-
последовательностями.
Определение 9. Последовательность {хп} называется ограниченной
сверху, если существует число М такое, что Vn € N (хп < М).
Аналогично определяется последовательность, ограниченная снизу.
Теорема 5 (Вейерштрасс). Для того чтобы неубывающая последова-
последовательность имела предел, необходимо и достаточно, чтобы она была огра-
ограниченной сверху.
Л То, что любая сходящаяся последовательность ограничена, было дока-
доказано при рассмотрении общих свойств предела последовательности, поэтому
интерес представляет только второе утверждение теоремы.
По условию множество значений последовательности {хп} ограничено
сверху, значит, оно имеет верхнюю грань s = supxn.
n€N
По определению верхней грани, для любого е > 0 найдется элемент х^ G
G {хп} такой, что s — е < х^ ^ s. Поскольку последовательность {хп} не-
неубывающая, при любом п > N теперь получаем s — е < х^ ^ хп ^ s, т. е.
\s — хп\ = s — хп < е. Таким образом, доказано, что lim xn = s. >
7l-»OO
Разумеется, аналогичную теорему можно сформулировать и доказать для
невозрастающей последовательности, ограниченной снизу. В этом случае
lim хп = inf xn.
п-юо n€N
Замечание. Ограниченность сверху (снизу) неубывающей (невозраста-
(невозрастающей) последовательности на самом деле, очевидно, равносильна ограничен-
ограниченности этой последовательности.
Рассмотрим несколько полезных примеров.
Пример 11. lim — =0, если а > 1.
п-юо qn *
4 Действительно, если хп = —, то xn+i = хп, п G N. Поскольку
qn nq
= lim (l + -) - = lim f 1 + -) ¦ lim - = 1 • - = - < 1, то най-
n-+oo \ n/ q n—юо \ n/ n—foo q q q
lim ^±
n-?oo nq
дется номер TV такой, что при п > N будет < 1. Таким образом, при
nq
п > N будем иметь xn+i < хП1 т. е. после члена х^ наша последовательность
монотонно убывает. Поскольку конечное число членов последовательности,
как видно из определения предела, не влияет на сходимость последователь-
последовательности и ее предел, то достаточно теперь найти предел последовательности

86 ГЛ. III. ПРЕДЕЛ
Члены последовательности положительны, т. е. последовательность огра-
ограничена снизу. Значит, она имеет предел.
71 4" 1
Пусть х = lim хп. Из соотношения хп+\ = хп теперь следует
п-юо nq
т / \ т (п + 1 А т П + 1 ,. 1
ж = lim (яп+i) = lini I жп I = lim • lim xn = -ж,
n—юо п—юо \ ng / n-+oo 71^ n-+oo g
откуда находим A х = 0их = 0. >
V q/
Следствие 1. lim r\/n=l.
П—ЮО
M При фиксированном e > 0 по доказанному найдется N G N такое, что
при п > N будем иметь 1 < п < A + е)п. Тогда при п > N получим 1 ^
< 1 + е и, значит, действительно lim \fn = 1. >
п—юо
Следствие 2. lim V^ = 1 пРи любом а > 0.
Пусть а ^ 1. Для любого е > 0 найдем AT G N так, что при п > N
а < A + е)п, и тогда при п> N получаем 1 ^ \[а < 1 -he, т. е. lim V^ = 1-
П—+ОО
Если 0 < а < 1, то 1 < - и
а
lim \fa = lim —= =
V a
n
Пример 12. lim ^7 = 0; здесь q — любое действительное число, п €
п—юо п!
п! := 1 • 2 •... • п.
Если ^ = 0, то утверждение очевидно. Далее, поскольку
_n
71!
П!
»
то достаточно доказать утверждение для q > 0. Рассуждая в этом случае,
как и в предыдущем, замечаем, что хп+\ = —^—-хп. Поскольку множество
п + 1
натуральных чисел не ограничено сверху, найдется номер N такой, что при
п > N будет 0 < —2L- < 1. Тогда при п > N будем иметь жп+1 < хп и,
п -+-1
учитывая положительность членов последовательности, можно теперь гаран-
гарантировать существование предела lim xn = х. Но тогда
п—юо
х = lim a;n+i = lim -хп = lim • lim xn = 0 • х = 0. >
п—юо п—юо п + 1 п—юо п + 1 ^о
с. Число е
A \п
1 Н— 1 .
п/
Пределом в данном случае является число, обозначаемое после Эйлера
буквой е, столь же характерное для анализа, как для арифметики 1 или для
геометрии тг. К нему мы еще неоднократно будем возвращаться по очень
разным поводам.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 87
Проверим сначала следующее неравенство:
A + а)п ^ 1 + па при п € N и а > -1
(называемое иногда неравенством Я. Бернулли1)).
М При п = 1 утверждение справедливо. Если оно справедливо для n E N,
то и для п 4-1 тоже, поскольку тогда
A + a)n+1 = A4 а)A 4 а)п ^ A + а)A + па) =
= 1 4 (п 4 1)а 4 па2 ^ 1 4 (п 4 1)а.
По принципу индукции утверждение, таким образом, справедливо для любого
пе N.
Из выкладки, кстати, видно, что при а ф 0 имеет место строгое неравен-
неравенство. >
/ i\n+1
Покажем теперь, что последовательность уп = A Н— 1 убывающая.
М Пусть n ^ 2. Используя доказанное неравенство, находим, что
n-l/ _ п2п
Уп-1 V1 + n-l/ п2п п
Уп
n2-l/n4l \ n2-
Поскольку члены последовательности положительны, существует предел
A
14-)
Но тогда
lim A + -) = lim A + -) A + -) =
п-юо \ n/ n-+oo \ n/ \ П/
= lim A + -) lim T = lim A + -
П—?ОО \ 71/ П—ЮО i i_ П—ЮО \ fl/
П
Итак,
Определение 10.
Бернулли A654 — 1705) — швейцарский математик, представитель знаменитого
семейства ученых Бернулли; стоял у истоков вариационного исчисления и теории вероят-
вероятностей.

ГЛ. III. ПРЕДЕЛ
d. Подпоследовательность и частичный предел
последовательности
Определение 11. Если xi, Х2, ..., хп, ... — некоторая последова-
последовательность, а п\ < П2 < ... < rik < .!. — возрастающая последовательность
натуральных чисел, то последовательность хП1, хП2, ... , хПк, ... называется
подпоследовательностью последовательности {хп}.
Например, последовательность 1, 3, 5, ... нечетных натуральных чисел,
взятых в их естественном порядке, является подпоследовательностью после-
последовательности 1, 2, 3, ... Но последовательность 3, 1, 5, 7, 9, ... уже не
является подпоследовательностью последовательности 1, 2, 3, ...
Лемма 1 (Больцано —Вейерштрасс). Каждая ограниченная последова-
последовательность действительных чисел содержит сходящуюся подпоследователь-
подпоследовательность.
Ч Пусть Е — множество значений ограниченной последовательности {хп }.
Если Е конечно, то существуют по крайней мере одна точка х Е Е и после-
последовательность 7ii < п>2 < • • • номеров такие, что хП1 = хП2 = ... = х. Подпо-
Подпоследовательность {хПк} постоянна и, значит, сходится.
Если Е бесконечно, то по принципу Больцано — Вейерштрасса оно обла-
обладает по крайней мере одной предельной точкой х. Поскольку х — предельная
точка Е, можно выбрать rii Е N так, что \хП1 — х\ < 1. Если п& Е N уже
выбрано так, что \хПк — х\ < -, то, учитывая, что х — предельная точка Е,
найдем 71*+1 е N так, что п* < п*+1 и |xnfc+1 — х\ < .
Поскольку lim — = 0, построенная подпоследовательность хП1, хП2, ... ,
k—юо К
хПк, ... сходится к х. >
Определение 12. Условимся писать хп —> +оо и говорить, что после-
последовательность {хп} стремится к плюс бесконечности, если для каждого
числа с найдется номер N EN такой, что хп > с при любом п > N.
Запишем это и два аналогичных определения в логических обозначениях:
хп -> +оо := Vc € К 3NE N Vn > N (с < хп),
хп -> -оо := Vc € R 3Ne N Vn > N (хп < с),
хп ->. оо := Vc € R 3Ne N Vn > N (с < |ж
В последних двух случаях говорят соответственно: последовательность
{хп} стремится к минус бесконечности и последовательность {хп} стре-
стремится к бесконечности.
Заметим, что последовательность может быть неограниченной, но не стре-
стремиться ни к плюс, ни к минус, ни просто к бесконечности. Например, хп =

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 89
Последовательности, стремящиеся к бесконечности, мы не причисляем к
сходящимся.
Легко видеть, что в соответствии с этими определениями можно дополнить
только что доказанную лемму, сформулировав ее несколько иначе.
Лемма 2. Из каждой последовательности действительных чисел мож-
можно извлечь сходящуюся подпоследовательность или подпоследовательность,
стремящуюся к бесконечности,
Л Новым является только тот случай, когда последовательность {хп} не
ограничена. Тогда по k Е N будем выбирать rtk Е N так, что \хПк\ > к и
п*; < 7ifc+i. Получим подпоследовательность {xnfc}, которая стремится к бес-
бесконечности. >
Пусть {xk} — произвольная последовательность действительных чисел.
Если она ограничена снизу, то можно рассмотреть (уже встречавшуюся нам
при доказательстве критерия Коши) последовательность гп = inf х*. По-
к^
скольку in ^ гп+1 для любого п Е N, то либо последовательность {in} имеет
конечный предел lim in = /, либо in -У + оо.
п—>оо
Определение 13. Число / = lim inf х* называется нижним преде-
лом последовательности {xk} и обозначается lim Xk или lim inf х*. Если
in —> -Ьоо, то принято говорить, что нижний предел последовательности ра-
равен плюс бесконечности, и писать lim Xk — +00 или lim inf Xk = +00. Если
к
исходная последовательность {хь} не ограничена снизу, то при любом п Е N
будем иметь in = inf Хк = — оо. В этом случае говорят, что нижний предел
к^
последовательности равен минус бесконечности, и пишут lim х* = — оо или
к—>оо
lim inf Xk = —00.
Итак, с учетом всех перечисленных возможностей запишем теперь кратко
определение нижнего предела последовательности
:= lim inf Xk-
Аналогично, рассматривая последовательность sn = supx*, приходим к
определению верхнего предела последовательности
Определение 14.
:= lim supx*
Приведем несколько примеров.

90
ГЛ. III. ПРЕДЕЛ
Пример 14. хк = (-1)*, к € N:
lim
lim
к~?ОО
lim inf
П-?ООк>П
= lim inf(-l)'
n-юо • ~
lim (-1)
n->oo
= lim sup a;*. = lim sup(—1) = lim 1 = 1,
- •-- ry n->oo
Пример 15. я* = A;(-1)fc, A; € N:
lim
= lim inf
= lim 0 = 0,
n—>oo
lim
k—HX>
= lim supfc* ' = lim (+oo) = +oo
fl->OO
Пример 16. Xk = A;, A; G N:
lim к = lim inf к = lim n = +oo,
n—>oo fc>n n—>oo
lim к = lim sup к = lim (+oo) = +oo.
k—HX> - • -- - • --
Пример 17. хк =
, A; G N:
(-1)*
lim —;— = lim inf v y = lim ^
A; n->oo л>п к п->оо
' 1
—, если n = 2m -f 1
, если n = 2ra
lim —;— = lim sup .
к n-foo *.>„ к
= lim <
n—>oo
Пример 18. xfc =-А;2, к G N:
n-f 1
= o,
—, если п = 2ra
I 71+1
, если n = 2m + 1
lim (—A:2) = lim inf (—A;2) = —oo.
= 0.
Пример 19. хк = (~1)кк, A;GN:
lim(-l)*fc= lim inf(-l)*Jk= lim (-00) =-oo,
n—>oo ik>n n—>oo
= lim (+00) = +oo.
n->oo
lim (—1)*A;= lim
к-?ОО П->ОО
Чтобы разобраться в происхождении терминов «верхний» и «нижний» пре-
пределы последовательности, введем следующее

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 91
Определение 15. Число (или символ — оо или -Ьоо) называют частич-
частичным пределом последовательности, если в ней есть подпоследовательность,
стремящаяся к этому числу.
Утверждение 1. Нижний и верхний пределы ограниченной последо-
последовательности являются соответственно наименьшим и наибольшим из ее
частичных пределов1^.
< Докажем, это, например, для нижнего предела i = lim Xk- Про последо-
вательность гп = inf Xk нам известно, что она неубывающая и lim гп = г Е
к^ п-+оо
Для чисел п € N, используя определение нижней грани, по индукции подберем
числа кп е N так, что гп ^ Xkn < гп Н— и кп < A;n+i. Поскольку lim in =
п n+i у
П п->оо
= lim lin H—J = г, то, опираясь на свойства предела, можем утверждать,
что lim Xh = г. Мы доказали, что г — частичный предел последовательно-
п->оо
сти {х^. Это наименьший частичный предел, поскольку для каждого е > О
найдется число п е N такое, что г — е < гп, т. е. г - е < in = inf ж* ^ Xk при
любом А; ^ п. к^п
Неравенство г — е < Хк при к > п означает, что ни один частичный предел
нашей последовательности не может быть меньше г — е. Но е > 0 произвольно,
поэтому он также не может быть меньше г.
Для верхнего предела доказательство, разумеется, аналогично проведен-
проведенному. >
Заметим теперь, что если последовательность не ограничена снизу, то из
нее можно выделить подпоследовательность, стремящуюся к — оо. Но в этом
случае и lim х* = — оо и можно условиться считать, что снова нижний пре-
дел есть наименьший из частичных пределов. Верхний предел при этом может
быть конечным, и тогда по доказанному он является наибольшим из частич-
частичных пределов; он может быть и бесконечным. Если lim Xk = + оо, то последо-
к—>оо
вательность не ограничена также и сверху и можно выделить подпоследова-
подпоследовательность, стремящуюся к +оо. Если же lim х* = —оо, что тоже возможно,
к—-юо
то это означает, что supx^ = sn —> —оо, т. е. и сама последовательность
стремится к —оо, ибо sn ^ хп. Аналогично, если lim ж* = Ч-оо, то Xk -> +оо.
к—>оо
Учитывая сказанное, можно, таким образом, заключить, что справедливо
Утверждение 1'. Для любой последовательности нижний предел есть
наименьший из ее частичных пределов, а верхний предел последовательно-
последовательности — наибольший из ее частичных пределов.
1> При этом считаются принятыми естественные соотношения — сю < х < + оо между
символами —оо, -Ьоои числами iGM.

92 гл. ш. предел
Следствие 1. Последовательность имеет предел или стремится к
минус или плюс бесконечности в том и только в том случае, когда нижний
и верхний пределы последовательности совпадают.
<4 Случай, когда lim Xk = lim Xk = + оо, и случай, когда lim
= lim Xk = —оо, уже разобраны выше, поэтому можно считать, что lim Xk =
= lim Xk = A Е R. Поскольку in = inf х^ ^ xn ^ supx^ = sn и по условию
fc-юо к^
lim г'п = lim sn = Л, то по свойствам предела также lim xn = А. >
п—юо п-»оо п—юо
Следствие 2. Последовательность сходится тогда и только тогда,
когда сходится любая ее подпоследовательность.
< Нижний и верхний пределы подпоследовательности заключены между
нижним и верхним пределами самой последовательности. Бели последователь-
последовательность сходится, то ее нижний и верхний пределы совпадают. Тогда совпадают
нижний и верхний пределы подпоследовательности, откуда вытекает ее схо-
сходимость, причем, разумеется, к пределу всей последовательности.
Обратное утверждение очевидно, поскольку в качестве подпоследователь-
подпоследовательности можно взять саму последовательность. >
Следствие 3. Лемма Больцано — Вейерштрасса как в узкой, так и в
расширенной формулировке вытекает из утверждения 1 и утверждения V
соответственно.
< Действительно, если последовательность {xk} ограничена, то точки г =
= lim Xk и s = lim Xk конечны и по доказанному являются частичными
пределами последовательности. Только при г = s последовательность имеет
лишь одну предельную точку; при i < s их уже по крайней мере две.
Если последовательность не ограничена с какой-то стороны, то существует
подпоследовательность, стремящаяся к соответствующей бесконечности. >
Заключительные замечания. Мы выполнили (и даже с некото-
некоторым превышением) все три пункта намеченной перед началом параграфа
программы: дали точное определение предела последовательности, доказали
единственность предела, выяснили связь операции предельного перехода со
структурой множества действительных чисел, получили критерий сходимо-
сходимости последовательности.
Теперь рассмотрим один специальный часто встречающийся и очень по-
полезный вид последовательностей — ряды.
4. Начальные сведения о рядах
а. Сумма ряда и критерий Коши сходимости ряда. Пусть {ап} —
последовательность действительных чисел. Напомним, что сумму ар + ap+i +
я
+ ... + aq (p ^ q) принято обозначать символом YL ап- Мы хотим теперь
п=р

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 93
придать точный смысл выражению а\ 4- а2 4-... + ап 4-..., подразумевающему
суммирование всех членов последовательности {ап}.
Определение 16. Выражение а\ 4- Я2 4-... 4- ап 4-... обозначают симво-
оо
лом ]Г ап и обычно называют рядом или бесконечным рядом (чтобы подчерк-
п=1
нуть отличие его от суммы конечного числа слагаемых).
Определение 17. Элементы последовательности {ап}, рассматривае-
рассматриваемые как элементы ряда, называют членами ряда; элемент ап называют п-м
членом ряда.
п
Определение 18. Сумму sn = Ylak называют частичной суммой ряда
или, когда желают указать ее номер, n-й частичной суммой ряда1).
Определение 19. Если последовательность {sn} частичных сумм ряда
сходится, то ряд называется сходящимся. Если последовательность {sn} не
имеет предела, то ряд называют расходящимся.
Определение 20. Предел lim sn = s последовательности частичных
п—>оо
сумм, если он существует, называется суммой ряда.
Именно в этом смысле мы и будем в дальнейшем понимать запись
оо
п=1
Поскольку сходимость ряда равносильна сходимости последовательности
его частичных сумм {sn}> то применением к {sn} критерия Коши сразу полу-
получается
Теорема 6 (критерий Коши сходимости ряда). Ряд а\ 4- ... 4- ап 4- ...
сходится тогда и только тогда, когда для любого е > 0 найдется такое
число N Е N, что из т^ п > N следует \ап 4-... 4- ат\ < е.
Следствие 1. Если в ряде изменить только конечное число членов, то
получающийся при этом новый ряд будет сходиться, если сходился исходный
ряд, и будет расходиться, если исходный ряд расходился.
4 Для доказательства достаточно в критерии Коши считать число N пре-
превышающим максимальный из номеров измененных членов ряда. >
Следствие 2. Для того чтобы ряд а\ 4- ... 4- ап 4-.. • сходился, необ-
необходимо, чтобы его члены стремились к нулю при п —> оо; т. е» необходимо
lim an = 0.
п—юо
' Таким образом, на самом деле под рядом мы подразумеваем упорядоченную пару
(П ч
Sn = Yl ak )•

94 ГЛ. III. ПРЕДЕЛ
<4 Достаточно положить в критерии ш = пи воспользоваться определени-
определением предела последовательности. >
Вот другое доказательство: ап = sn—sn-i и, коль скоро lim sn = s, имеем
П-+ОО
lim an = lim (sn — sn-i) = lim sn — lim sn_i =5 — 5 = 0.
n—>oo n—»oo n—>oo n»oo
Пример 20. Ряд l + G + (jr + ... + gn + ... часто называют суммой
бесконечной геометрической прогрессии. Исследуем его сходимость.
Поскольку \qn\ = \q\n, то при \q\ ^ 1 будет \qn\ ) 1ив этом случае не
выполнен необходимый признак сходимости ряда.
Пусть теперь \q\ < 1. Тогда
1 — ап
sn = 1 + q + ... + qn~l = ч
и lim sn = , поскольку lim qn = 0, если \q\ < 1.
n—>oo 1 — q n—>oo
oo
Таким образом, ряд ]Г qn~x сходится тогда и только тогда, когда |д| < 1
п=1
и в этом случае его сумма равна .
Пример 21. Ряд 1 + - + ...Н h... называется гармоническим, по-
2 п
скольку каждый член этого ряда, начиная со второго, является средним гар-
гармоническим соседних с ним членов (см. задачу 6 в конце этого параграфа).
Члены ряда стремятся к нулю, но последовательность его частичных сумм
1 1
п'
как было показано с помощью критерия Коши в примере 10, расходится. Это
означает в данном случае, что sn —> + 00 при п —> оо.
Итак, гармонический ряд расходится.
Пример 22. Рассмотрим теперь следующий пример.
Ряд 1 — 1 + 1 — ... + (—l)n+1 + ... расходится, что видно и по последова-
последовательности 1, 0, 1, 0, ... его частичных сумм, и по тому, что чшены ряда не
стремятся к нулю.
Если расставить скобки и рассмотреть новый ряд
членами которого являются суммы, заключенные в скобки, то этот новый ряд
уже сходится, причем его сумма, очевидно, равна нулю.
Если скобки расставить иначе и рассмотреть ряд
+ (-1 + 1) + (-
то получится сходящийся ряд с суммой, равной 1

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 95
Бели в исходном ряде переставить все члены, равные —1, на две позиции
вправо, то получим ряд
расставив в котором скобки, придем к ряду
A + 1) + (-1 + 1) + (-1 + 1) + ...,
сумма которого равна двум.
Эти наблюдения показывают, что привычные законы обращения с конеч-
конечными суммами, вообще говоря, не распространяются на ряды.
И все-таки есть важный тип рядов, с которыми, как это потом выяснится,
можно обращаться так же, как с конечными суммами. Это так называемые
абсолютно сходящиеся ряды. Именно с ними мы главным образом и будем
работать.
Ь. Абсолютная сходимость; теорема сравнения и ее следствия
оо
Определение 21. Ряд ?) ап называется абсолютно сходящимся, если
оо n=1
сходится ряд Yj \anV
n=l
Поскольку \ап +... + ат\ ^ \ап\ +... + |ат|, из критерия Коши следует, что
если ряд сходится абсолютно, то он сходится.
То, что обратное утверждение, вообще говоря, не имеет места, т. е. что аб-
абсолютная сходимость есть требование более сильное, чем просто сходимость
ряда, можно продемонстрировать на примере.
Пример 23. Ряд 1 — 1 + т — г + г—«+..., частичные суммы которого
Z Z о о
равны либо —, либо 0, сходится к нулю.
71
Вместе с тем ряд из абсолютных величин его членов
расходится, что, как и для гармонического ряда, следует из критерия Коши:
1.1. .1.1
71 + 1 71+1 '" П + П П
= 2(—L- + ... + -J—)
\п + 1 п + п)
> 2п—— = 1
Для того чтобы научиться отвечать на вопрос, сходится ли ряд абсолютно
или нет, достаточно научиться исследовать на сходимость ряды с неотрица-
неотрицательными членами. Имеет место

96 ГЛ. III. ПРЕДЕЛ
Теорема 7 (критерий сходимости рядов с неотрицательными членами).
Ряд а\ Н-... + ап 4- •.., члены которого — неотрицательные числа, сходит-
сходится тогда и только тогда, корда последовательность его частичных сумм
ограничена сверху.
< Это следует из определения сходимости ряда и критерия сходимости
неубывающей последовательности, каковой в данном случае является последо-
последовательность S\ ^ «2 ^ ... ^ sn ^ ... частичных сумм нашего ряда. >
Из этого критерия вытекает следующая простая, но на практике очень
полезная
оо оо
Теорема 8 (теорема сравнения). Пусть ]Р аП1 ]Г] Ьп — два ряда с
п—1 п=1
неотрицательными членами. Если существует номер N Е N такой, что
при любом п > N имеет место неравенство ап ^ Ъп, то из сходимости
оо оо оо
ряда Yl bn вытекает сходимость ряда ]Р ап, а из расходимости ряда ]Р ап
п—1 оо п=1 п—1
вытекает расходимость ряда ?) Ьп.
п=1
< Поскольку конечное число членов не влияет на сходимость ряда, можно
без ограничения общности считать, что ап ^ Ьп для любого п G N. Тогда
п п оо
Ап = ]Г ak ^ Yl bk = Вп. Если ряд ]Г Ьп сходится, то последовательность
fc=l fc=l n=l
{Вп}, не убывая, стремится к пределу В. Тогда Ап ^ Вп ^ В при любом
оо
п € N и, следовательно, последовательность {Ап} частичных сумм ряда J2 ап
п=1
ограничена. В силу критерия сходимости ряда с неотрицательными членами
оо
(теорема 7) ряд ]Р ап сходится.
п=1
Второе утверждение теоремы, рассуждая от противного, немедленно по-
получаем из уже доказанного. >
Пример 24. Поскольку —, -г < т < т тт~ ПРИ п > 2, по теореме
п(п + 1) п2 (п1)п
ОО -1 ОО -I
сравнения заключаем, что ряды У) —г- и У" —7 гт сходятся или расходятся
п=1 п п=1 п(п + !)
одновременно.
Но последний ряд можно просуммировать непосредственно, заметив, что,
111 П1 1 °° 1
*(*+!) = *-(*+!) ипоэтому? MifcTl) = ^^ГГ- Значит'
ОО j
= 1. Следовательно, ряд Y1 ~ч также является сходящимся. Любопытно, что
по ¦ 2 П=1
1 7Г
У" —г = -г-. В дальнейшем это будет доказано.
п=1 П 6
Пример 25. Следует обратить внимание на то, что теорема сравнения
относится только к рядам с неотрицательными членами. Действительна^

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 97
оо
положим, например, ап = -п, а Ьп = 0, тогда ап < 6П, ряд ]Г &п сходится,
71=1
оо
но ряд 5^ ап расходится.
п=1
Следствие 1 (мажорантный признак Вейерштрасса абсолютной сходи-
оо оо
мости ряда). Пусть J2 ап и J2 Ьп — два ряда. Пусть существует номер
п=1 п=1
N ? N такой, что при любом п > N имеет место соотношение \ап\ ^ Ьп.
оо
При этих условиях для абсолютной сходимости ряда ]Р ап достаточно,
чтобы ряд 53 Ьп сходился.
п=1
< Действительно, по теореме сравнения тогда ряд ]Р \ап\ будет сходиться,
оо
п=1
оо
что и означает абсолютную сходимость ряда ]Г ап. >
п=1
Этот важный достаточный признак абсолютной сходимости часто форму-
формулируют кратко: если члены ряда (по абсолютной величине) мажорируются
членами сходящегося числового ряда, то исходный ряд сходится абсолютно.
оо
smn
smn
Пример 26. Ряд У2 —т~ абсолютно сходится, так как
°° 1 П=1
ряд 22 ~~2> как МЫ выяснили в примере 24, сходится.
п=1 п
оо
Следствие 2 (признак Коши). Пусть Y1 ап ~~ "данный ряд и а =
n=i
= lim Я/f^nI- Тогда справедливы следующие утверждения:
п—>оо
оо
a) Если а < 1, то рлс? ]Р ап абсолютно сходится.
п=1
со
b) ^слгл а > 1, то ряд ^2 ап расходится.
п=1
c) Существуют как абсолютно сходящиеся, так и расходящиеся ряды,
для которых а = 1.
4 а) Если а < 1, то можно выбрать число q 6 М так, что а < g < 1.
Фиксировав число q, в соответствии с определением верхнего предела найдем
номер N е N такой, что при п > N выполнено ^|an| < q. Таким образом,
оо
при п > N будем иметь \ап\ < qn и, поскольку ряд Y1 Яп ПРИ \я\ < 1 сходит-
оо n=1
ся, ряд ^2 ап (по теореме сравнения или признаку Вейерштрасса) сходится
п=1
абсолютно.

98 гл. ш. предел
b) Поскольку а является частичным пределом последовательности {ап}
(см. утверждение 1), то найдется подпоследовательность {anjt} такая, что
lim nSfa^k~ = а. Если а > 1, то найдется номер К € N такой, что при любом
Л—>оо
к > К будет \аПк\ > 1, тем самым необходимое условие сходимости (ап —»• 0)
оо
для ряда ?_) ап не выполнено и он расходится.
п=1
оо 1 оо -I
c) Мы уже знаем, что ряд Y1 — расходится, а ряд J2 ~ сходится
г г rfn~ г
(абсолютно, так как — = --). Вместе с тем lim 41 — = lim -7= = 1
71 71 П—>ОО у 71 П—>ОО^/71
и lim i/--- = lim л/-^ = lim (_гт= ) = 1. >
п—>оо и 71* п—>оо V 71^
Пример 27. Исследуем, при каких значениях х 6 IR ряд
П=1
СХОДИТСЯ.
Подсчитаем а = Шп VlB'+("^Г^! = И Пт |2 + (-1)п| = 3|х|.
п—>оо п—>оо
Таким образом, при |х| < - ряд сходится и даже абсолютно, а при |х| > -
1
ряд расходится. Случай |х| = - требует специального рассмотрения. В на-
о
шем примере оно элементарно, ибо при |х| = - для четных значений п имеем
о
B -+¦ (—1Jк)х2к = 32*(-J = 1 и ряд расходится, поскольку для него не
выполнено необходимое условие сходимости.
оо
Следствие 3 (признак Даламбера1)). Пусть для ряда Y1 ап существу-
п=1
ет предел lim
= а. Тогда справедливы следующие утверждения:
п—^оо
оо
a) Если а < 1, то рл<? ^ ап сходится абсолютно.
п=1
оо
b) ?сли а > 1, то рл(? ?_! ап расходится.
п=1
c) Существуют как абсолютно сходящиеся, так и расходящиеся ряды,
для которых а = 1.
•* а) Если а < 1, то найдется такое число д, что а < g < 1; фиксировав q и
учитывая свойства предела, найдем номер N ? N такой, что при любом п > N
будет —^— < q. Поскольку конечное число членов не влияет на характер
. Л. Даламбер A717 — 1783) — французский ученый, прежде всего механик, входив-
входивший в группу философов-энциклопедистов.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
99
сходимости ряда, без ограничения общности будем считать, что
при любом п € N.
Поскольку
а
п
<
Оп+1
On
•
on
on-i
• • •
о2
01
on+i
01
оо
мы получаем, что |on+i| ^ |ai| • qn. Но ряд J2 lail?n сходится (его сумма,
n=l
очевидно, равна ), поэтому ряд Y1 ап абсолютно сходится.
1~~ Я n=i
Ь) Если a > 1, то, начиная с некоторого номера N € N, при любом п > N
будем иметь
a
n
00
> 1, т. е. \ап\ < |on+i|, и, следовательно, для ряда Y1 ап
п=1
не выполнено условие ап -> 0, необходимое для сходимости.
с) Примерами в данном случае, как и в признаке Коши, могут служить
оо
ряды
п~1 п п=1 "
Пример 28. Выясним, при каких значениях х ? R сходится ряд
оо
^ п!
п=1
При х = О он, очевидно, сходится и даже абсолютно.
1x1
При х
имеем lim
п—юо
an
= lim
= 0.
п—>оо 71 -+- 1
Таким образом, этот ряд абсолютно сходится при любом значении х €
Рассмотрим, наконец, еще один более специальный, но часто встречающий-
встречающийся класс рядов: ряды, члены которых образуют монотонную последователь-
последовательность. Для таких рядов имеет место следующий необходимый и достаточный
признак сходимости.
оо
Утверждение 2 (Коши). Если а\ ^ а2 ^ •.. ^ 0, то ряд ]Г] ап схо-
п=1
оо
дится тогда и только тогда, когда сходится ряд ]Г] 2*а2* = Oi -f 2a2 -f
4- 4а4 4- 8ag 4-...
*=о
Поскольку
«2 ^ «2
«з
4а8 ^ а5 -f а6 4- ay -f
4а4,
. • . 4*

100 ГЛ. III. ПРЕДЕЛ
то, складывая эти неравенства, получим
1
с
где А* = ai 4-.. .+ a*, 5n = ai +2a2 +.. .+2na2« — частичные суммы рассматри-
рассматриваемых рядов. Последовательности {Ak} и {Sn} неубывающие, и потому из
полученных неравенств можно заключить, что они либо одновременно ограни-
ограничены, либо одновременно не ограничены сверху. Но по критерию сходимости
рядов с неотрицательными членами отсюда следует, что рассматриваемые два
ряда действительно сходятся или расходятся одновременно. >
Отсюда вытекает полезное
оо
Следствие. Ряд ]>3 — сходится при р > 1 и расходится при р ^ I.1)
Ч Если р ^ 0, то по доказанному наш ряд сходится или расходится вместе
с рядом
оо л оо
2* 1 = V B1~р)к
k=0 v ' *=0
а для сходимости последнего ряда необходимо и достаточно, чтобы было q =
= 21~р < 1, т. е. р> 1.
ОО -j
Если р ^ 0, то расходимость ряда V — очевидна, поскольку в этом случае
п=1 пР
все члены ряда больше 1. >
ОО |
Важность этого следствия состоит в том, что ряд ^3 — часто служит
п=1
основой для сравнения при исследовании сходимости рядов.
с. Нисло е как сумма ряда. Заканчивая рассмотрение рядов, вернемся
еще раз к числу е и получим ряд, доставляющий уже довольно удобный способ
вычисления е.
Мы будем использовать формулу бинома Ньютона при разложении выра-
A \п
1 Н— 1 . Те, кто не знаком с этой формулой из школы или не решил
задачу lg) из гл. II, § 2, могут, без потери связности изложения, опустить
настоящее добавление о числе е и вернуться к нему после формулы Тейлора,
частным случаем которой можно считать формулу бинома Ньютона.
Нам известно, что е = lim A Н— 1 .
*) Формально в нашей книге мы пока определили пр только для рациональных значений
р, поэтому читатель тоже пока вправе понимать это утверждение только для тех р, для
которых определено пр.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
101
По формуле бинома Ньютона
i
1! п
• • • I
2! n
n(n -
nk '" nn
14-777A 14- ••• 4- 77 I ^ ) \ ^ IX...
2! V п) к\\ п)\ п)
... х A ) + ...+—( 1 ) ••• ( 1 •
\ п ) п\\ п) \ п J
A\п
14— 1 =еп и
п/
1
-
2!
1
г = sn, таким образом, имеем
п!
Sfi \ Sfi yTl ~- X, а, ... у.
С другой стороны, при любом фиксированном к ип^ к, как видно из того
же разложения, имеем
<
При п —>• оэ левая часть этого неравенства стремится к^,а правая
поэтому мы теперь можем заключить, что Sk ^ е для любого А; 6 N.
Но тогда из соотношения
к е,
при п —> оэ получаем, что lim sn — e.
п—юо
В соответствии с определением суммы ряда мы теперь можем записать
Это уже вполне пригодное для вычисления представление числа е.
Оценим разность е — sn:
0 < е - sn =
(п + 1)! (п + 2)!
(n + 1)!
1
1
+
п + 1)!
1 +
(n + 2)(n
1 1
n + 2 (n + 2J
1 1
п + 2
1
(п + 1)! 1 L. п! (п + IJ п\п '
п + 2
Таким образом, чтобы абсолютная погрешность приближения числа е чи-
числом sn не превосходила, например, 10 , достаточно, чтобы было —г— <
Этому условию удовлетворяет уже $6-
п\п 1000

102 гл. ш. предел
Выпишем несколько первых десятичных знаков числа е:
е = 2,7182818284590...
Полученную оценку разности е — sn можно записать в виде равенства
n ^-> где О<0П<1.
71171
Из такого представления числа е немедленно следует его иррациональ-
ность. В самом деле, если предположить, что е = -, где р, q € N, то число q\e
Я
должно быть целым, а вместе с тем
ile = q\(i
+ ±)=4+± + ±+...+«
и тогда число — тоже должно быть целым, что невозможно.
Я
Для сведения читателя отметим, что число е не только иррационально, но'
даже трансцендентно.
Задачи и упражнения
1. Покажите, что число xGR рационально тогда и только тогда, когда его запись
в любой д-ичной системе счисления периодична, т. е., начиная с некоторого разряда,
состоит из периодически повторяющейся группы цифр.
2. Мяч, упав с высоты h, подскакивает на высоту qh, где q — постоянный коэф-
коэффициент, 0 < q < 1. Найти время, за которое он окажется покоящимся на земле, и
путь, который он к этому моменту пролетит.
3. На окружности отмечаются точки, получающиеся из некоторой фиксирован-
фиксированной ее точки поворотами окружности на всевозможные углы в п 6 Z радиан. Ука-
Укажите все предельные точки построенного множества.
4. Выражение
1
712 + -
+
7ljfe-l Ч
пк
где П{ 6 N, называется конечной цепной или непрерывной дробью, а выражение
1
Til Ч ;
712 +
713 + .
— бесконечной цепной дробью. Дроби, получающиеся из цепной дроби при отбрасы-
отбрасывании всех ее звеньев, начиная с некоторого звена, называют подходящими дробями.

§ 1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 103
Бесконечной цепной дроби в качестве значения сопоставляется предел последова-
последовательности ее подходящих дробей.
Покажите, что:
а) Каждое рациональное число —, где га, п 6 N, может быть разложено и притом
единственным способом в цепную дробь:
га _ 1
п
+ !
Яп
Указание. Числа q\, ..., qn, называемые неполными частными, получаются
алгоритма Евклида
га = п • qi Ч~ t*i,
п — т\ - дг + Г2,
Ч-
если его записать в виде
га 1
Т = 01 Ч-
n/ri ^2 Ч- .
b) Подходящие дроби Ri = gi, R2 = gi 4 , ... удовлетворяют неравенствам
Ri < Лз < ... < ifofc-i < — < R2k < Л2Л-2 < ... <
2Л
п
с) Числители Рд. и знаменатели Qk подходящих дробей Rk формируются по за-
закону
Рк = Pk-
d) Разность соседних подходящих дробей вычисляется по формуле
e) Каждая бесконечная цепная дробь имеет определенное значение.
f) Значение бесконечной цепной дроби иррационально.
g) —
h) Числа Фибоначчи 1, 1, 2, 3, 5, 8, ... (т. е. ип = un-i + ип-2 и ui = иг = .1),
получающиеся как знаменатели подходящих дробей в g), задаются формулой
'-(
\-у/Ъ
п

104 ГЛ. III. ПРЕДЕЛ
к
i) Подходящие дроби Rk = 77" в g) таковы, что
Q
к
Рк
2 Q
k
. Срав-
ните этот результат с утверждениями задачи 11, § 2, гл. И.
5. Покажите, что:
а) При п ^ 2 справедливо равенство
¦*- 4" тт 4* Т7 4" • • • 4" —г 4" —;— —• 3 —
1! 2! ¦" п\ п\п ~ 122! "' (n-l)n-n!
оо
с) Для приближенного вычисления числа е значительно лучше формула е « 1 4-
4- тт + • • • + ~т + ~Г~ > а не исходная формула ewlH-T7 + --- + -7 (оцените погрешности,
1! п! п\п 1! п!
посчитайте и сравните результат со значением е, приведенным на с. 102).
6. Если а и Ъ — положительные числа, ар — произвольное отличное от нуля
вещественное число, то средним порядка р чисел а и Ь называется величина
В частности, получаем при р = 1 среднее арифметическое, при р = 2 — среднее
квадратическое, при р = — 1 — среднее гармоническое чисел а, Ь.
a) Покажите, что среднее Sp(a,b) любого порядка заключено между числами а
и 6.
b) Найдите пределы последовательностей
{5n(a,fe)}, {5_n(a,fe)}.
7. Покажите, что если а > 0, то последовательность xn+i = « ( х™ "I ) ПРИ лю~
2 V а:п/
бом xi > 0 сходится к арифметическому квадратному корню из а. Оцените скорость
сходимости, т. е. величину абсолютной погрешности \хп — а\ = |АП| в зависимости
от п.
8. Покажите, что
а) S0(n)± l° + ... + n° =n,
и вообще
Sfc(n) = ak+\nk+1 4-... 4- а\п +
— многочлен от п степени к 4-1.
b) lim

§ 2. ПРЕДЕЛ ФУНКЦИИ 105
§ 2. Предел функции
1. Определения и примеры. Пусть Е — некоторое подмножество мно-
множества R действительных чисел и а — предельная точка множества Е. Пусть
/: Е -> Ш — вещественнозначная функция, определенная на Е.
Мы хотим записать, что значит, что при приближении точки х € Е к
а значения f(x) функции / приближаются к некоторому числу А, которое
естественно назвать пределом значений функции / или пределом функции /
при я, стремящемся к а.
Определение 1. Будем (следуя Коши) говорить, что функция /: Е
Ш стремится к А при х, стремящемся к а, или что А является пределом
функции f при х, стремящемся к а, если для любого числа в > 0 существует
число S > 0 такое, что для любой точки х € Е такой, что 0 < \х — а\ < ($,
выполнено соотношение \f{x) — А\ < е.
В логической символике сформулированные условия запишутся в виде
Ve > 0 36 > 0 VxeE @ < \х - а\ < S =» \f(x) - А\ < е).
Если А — предел функции f(x) при ж, стремящемся по множеству Е к
точке а, то пишут f(x) -t А при х —> а, х € Е, или lim f(x) = А. Вместо
х—va,x<zE
символа х —> a, iGB, мы, как правило, будем использовать более короткое
обозначение Е Э х -> а и вместо lim /(ж) будем писать lim f(x) = A.
>ЕЕ ЕЭх—ю.
Пример 1. Пусть Е = R \ 0, /(ж) = ж sin -. Проверим, что
lim х sin - = 0.
X
Действительно, при заданном е > 0 возьмем ($ = е, тогда при 0 < \х\ < S =
= ?, учитывая, что
. 1
sin -
, будем иметь
. 1
sin -
< е.
х
Из этого примера, кстати, видно, что функция / : Е —>¦ Ж может иметь
предел при Е Э х -> а, даже не будучи определенной в самой точке а. Как
раз эта ситуация чаще всего имеет место при вычислении пределов и, если вы
обратили внимание, это обстоятельство учтено в определении предела в виде
неравенства 0 < \х — а\.
Напомним, что окрестностью точки а ? Ж мы назвали любой интервал,
содержащий эту точку.
Определение 2. Проколотой окрестностью точки называется окрест-
окрестность точки, из которой исключена сама эта точка.
Если U(а) — обозначение окрестности точки а, то проколотую окрестность
о
этой точки будем обозначать символом U(а).

106 ГЛ. III. ПРЕДЕЛ
Множества
UE{a) :=
UE(a) :=EilU(a)
будем называть соответственно окрестностью и проколотой окрестностью
точки а в множестве Е.
о
Если а — предельная точка Е, то Ue{o) ф &, какова бы ни была окрест-
окрестность U (а).
Если на минуту принять громоздкие символы UE(a) и Vj^A) для обозна-
обозначения проколотой (J-окрестности точки а в множестве Е и е-окрестности
точки А в R, то приведенное выше так называемое «е-($-определение» Коши
предела функции можно переписать в виде
lim f{x) = A := VVjf(A) #j #j
Эта запись говорит, что А является пределом функции / : Е *-> R при
, стремящемся к а по множеству Е, если для любой е-окрестности ^
О г
точки А найдется проколотая (J-окрестность UE(a) точки а в множестве Е,
О г
образ которой f(UE(a)) при отображении f:E->R полностью содержится в
окрестности ^
Учитывая, что в любой окрестности точки числовой оси содержится так-
также некоторая симметричная окрестность ((J-окрестность) этой же точки, мы
теперь приходим к следующей форме записи определения предела, которую и
будем считать основной.
Определение 3.
lim /(*) = A := VVr(A) 3UE(a) (f(UE(a)) CVR(A)).
Итак, число А называется пределом функции f:E-+R при я, стремящемся
по множеству Е к точке а (предельной для Е), если для любой окрестности
точки А найдется проколотая окрестность точки а в множестве Е, образ кото-
которой при отображении f:E—>R содержится в заданной окрестности точки А.
Мы привели несколько формулировок определения предела функции. Для
числовых функций, когда а, А ? Е, как мы видели, эти формулировки экви-
эквивалентны. Вместе с тем для разных целей бывает удобна то одна, то другая
из них. Например, при численных оценках удобна исходная форма, указыва-
указывающая допустимую величину отклонения хото, при которой уклонение f(x)
от А не превысит заданной величины. А вот с точки зрения распространения
понятия предела на более общие функции, определенные не на числовом мно-
множестве, наиболее удобной является последняя формулировка, которую мы и
выделили. Из нее, кстати, видно, что мы сможем определить понятие предела

§ 2. ПРЕДЕЛ ФУНКЦИИ 107
отображения f:X-+Y, если нам будет сказано, что такое окрестность точки
в X и bY, или, как говорят, если в X и Y будет задана топология.
Рассмотрим еще некоторые, поясняющие основное определение примеры.
Пример 2. Функция
1 при х > 0,
sgn х = <
0 при х = 0,
k —1 при х < 0
(читается «сигнум ж»1)) определена на всей числовой оси. Покажем, что у нее
нет предела при х, стремящемся к 0.
Это значит, что
€E 3V(A) VL/(O) 3x?U@) (f(x)$V(A)),
т. е., какое бы А (претендующее на то, чтобы быть пределом sgnx при х -> 0)
мы ни взяли, найдется такая окрестность V(A) точки А, что, какую бы (ма-
о
лую) проколотую окрестность U@) точки 0 ни взять, в ней есть по крайней
о
мере одна точка х ? t/@), значение функции в которой не лежит в V(A).
Поскольку функция sgn ж принимает только значения —1, 0, 1, то ясно, что
никакое число А, отличное от них, не может быть пределом функции, ибо оно
имеет окрестность V(A), не содержащую ни одно из этих трех чисел.
Если же А € {—1,0,1}, то возьмем в качестве V{A) е-окрестность точки А
при е = 1/2. В такую окрестность заведомо не могут попасть одновременно
о
обе точки —1 и 1. Но, какую бы проколотую окрестность U@) точки 0 ни
взять, в ней есть как положительные, так и отрицательные числа, т. е. есть и
точки я, где f(x) = 1, и точки, где f(x) = —1.
о
Значит, найдется точка х € С/@) такая, что f(x) ? V(A).
Условимся, если функция /: 25 -» R определена во всей проколотой окрест-
о о о
ности некоторой точки а € R, т. е. когда Ue{o) = Ur(u) = U(a), вместо записи
Е Э х —> а употреблять более короткую запись х —у а.
Пример 3. Покажем, что lim IsgnaH = 1.
Действительно, при х € R \ 0 имеем |sgnx| = 1, т. е. функция постоянна
о
и равна 1 в любой проколотой окрестности U@) точки 0. Значит, для любой
окрестности V(l) получим /(G@)) = 1 € ^A).
Обратите внимание, что хотя в данном случае функция | sgn x \ и определена
в самой точке 0 и |sgn0| = 0, но это значение не имеет никакого влияния на
величину рассматриваемого предела.
Таким образом, не следует смешивать значение /(а) функции в точке а с
пределом lim f(x) функции при ж, стремящемся к а.
х—Уа
Signum (лат.) — знак.

108 гл. ш. предел
Пусть R_ и R+ — множества отрицательных и положительных чисел со-
соответственно.
Пример 4. В примере 2 мы видели, что предел lim sgnx не суще-
ствует. Замечая, однако, что ограничение sgn|R_ функции sgn на М_ есть
постоянная функция, равная — 1, asgn|R есть постоянная, равная 1, можно,
как и в примере 3, показать, что
lim sgn а; = —1, lim sgn a; = 1,
R90 R90
т. е. ограничение одной и той же функции на различные множества может
иметь различные пределы в одной и той же точке или даже не иметь его, как
это было в примере 2.
Пример 5. Развивая идею примера 2, можно аналогично показать, что
функция sin - не имеет предела при х —> 0.
Х „ о °
Действительно, в любой проколотой окрестности С/@) точки 0 всегда есть
точки вида г-—-— и ———-—, где п € N, в которых функция принима-
7Г/2 +¦ 2тгп 7Г/2 -+¦ 2тгп
ет значения —1 и 1 соответственно. Но оба эти числа не могут одновременно
содержаться в е-окрестности V(A) точки AgM, если е < 1. Значит, ни одно
число А ? К не может быть пределом этой функции при х ~> 0.
Пример 6. Если
x, nG
-тг/2 4-2тгп
и
Е+ = \х € К х = /о * о—, n€Ni,
I тг/2 4-2тгп J
то, подобно рассмотренному в примере 4, получаем, что
lim sin - = — 1 и lim sin - = 1.
Е-ЭХ-+0 X Е+Эх->0 X
Между изученным в предыдущем параграфе понятием предела последова-
последовательности и введенным здесь понятием предела произвольной числовой функ-
функции имеется тесная связь, которую выражает следующее
Утверждение I1). Соотношение lim fix) = А имеет место тогда
ЕЭх->а
и только тогда, когда для любой последовательности {хп} точек хп € Е\а,
сходящейся к а, последовательность {f(xn)} сходится к А.
иногда называют утверждением о равносильности определений предела по Коши
(через окрестности) и по Гейне (через последовательности).
Э. Гейне (Хайне) A821 — 1881) — немецкий математик.

§ 2. ПРЕДЕЛ ФУНКЦИИ 109
<4 То, что ( lim fix) = А) => ( lim f(xn) = А), сразу следует из опре-
V ЕЭх-*а ' \ п—юо /
делений. Действительно, если lim f(x) = А, то для любой окрестности
ЕЭ*
о
V(A) точки А найдется проколотая окрестность Ue{o) точки а в Е такая,
о
что для х € Ue{o) имеем f(x) € ^(^4)- Если последовательность {хп} точек
множества Е \а сходится к а, то найдется номер N такой, что при п > N
о
будет хп € Ue{o) и, значит, f(xn) ? ^(^4). На основании определения предела
последовательности, таким образом, заключаем, что lim f(xn) = A.
п—>оо
Перейдем к доказательству обратного утверждения. Если А не является
пределом f(x) при Е Э х —> а, то найдется окрестность V(A) такая, что при
любом п € N в —окрестности точки а найдется точка хп € Е\а такая, что
п
/(^п) & У {А). Но это означает, что последовательность {f(xn)} не сходится
к Л, хотя последовательность {хп} стремится к а. >
2. Свойства предела функции. Теперь установим ряд постоянно ис-
используемых свойств предела функции, многие из которых аналогичны уже до-
доказанным свойствам предела последовательности и потому, в сущности, нам
уже знакомы. Более того, на основании только что доказанного утвержде-
утверждения 1 многие важные свойства предела функции, очевидно, немедленно следу-
следуют из соответствующих свойств предела последовательности: единственность
предела, арифметические свойства предела, предельный переход в неравен-
неравенствах. Тем не менее мы вновь проведем все доказательства. В этом, как
выяснится, есть определенный смысл.
Мы хотим обратить внимание читателя на то, что для установления всех
свойств предела функции требуются всего два свойства проколотых окрест-
о
ностей предельной точки множества: Bi) Ue(o>) ф 0, т. е. проколотая окрест-
окрестность непуста, и В2) VUfE{a) VJ7?(a) 3UE(a)(UE(a) С U'E{a) П Щ(а)), т. е.
в пересечении любой пары проколотых окрестностей содержится проколотая
окрестность. Это наблюдение приведет нас к общему понятию предела функ-
функции и возможности в будущем использовать теорию предела уже не только
для функций, определенных на числовых множествах:. Чтобы изложение не
было простым повторением сказанного в § 1, мы используем здесь некоторые
новые полезные приемы и понятия, которые не демонстрировались в § 1.
а. Общие свойства предела функции. Сначала несколько определе-
определений.
Определение 4. Функцию /: Е —> R, принимающую только одно зна-
значение, будем, как и прежде, называть постоянной. Функция /: Е —у R назы-
называется финально постоянной при Е Э х —У а, если она постоянна в некоторой
проколотой окрестности Ue{o) точки а, предельной для множества Е.
Определение 5. Функция f:E-+R называется ограниченной, ограни-
ограниченной сверху, ограниченной снизу, если найдется число С € Ш такое, что для
любого х ? Е выполнено соответственно \f(x)\ < С, f(x) < С, С < f(x).

НО ГЛ. III. ПРЕДЕЛ
В случае, если первое, второе или третье из этих соотношений выполнено
о
лишь в некоторой проколотой окрестности Ue(o) точки а, функция /: Е —> R
называется соответственно финально ограниченной при Е Э х —> а, финаль-
финально ограниченной сверху при Е Э х —> а, финально ограниченной снизу при
Е Э х -> а.
Пример 7. Функция /(х) = (sin —\- х cos - ), определенная этой фор-
\ х х/
мулой при х ф 0, не является ограниченной на области определения, но она
финально ограничена при х —> 0.
Пример 8. То же самое относится к функции /(х) = х на
Теорема 1. a) (f : Е —У R при Е Э х -> а есть финально постоян-
постоянная А) => ( Ит /(х) = А).
b) C Ит /(х)) => (/: Е —> Е финально ограничена при Е Э х —> а).
c) ( lim )( )
\ ЕЭ
«4 Утверждение а) о наличии предела у финально постоянной функции и
утверждение Ь) о финальной ограниченности функции, имеющей предел, вы-
вытекают прямо из соответствующих определений. Обратимся к доказательству
единственности предела.
Предположим, что А\ ф Аъ- Возьмем тогда окрестности V(A\), V(A2) так,
чтобы они не имели общих точек, т. е. V(A\) П V(^2) = 0- По определению
предела имеем
lim f(x) = A1=>3U'E(a)
ЕЭх-+а
lim f(x) = A2=>3U?(a) (/(^(a)) С V{A2)).
ЕЭх->а
о
Возьмем теперь проколотую окрестность Ue(o>) точки а (предельной
о , о о о
для Е) такую, что Ue{o) С U'E(a) П U'i{a) (например, можно взять Ue{o) =
о о
= U'E{a) П UE(a), поскольку это пересечение тоже есть проколотая окрест-
окрестность).
о Ч °
Поскольку Ue{o) ф 0, берем х ? 'Ue{o)- Тогда /(х) € V(A\) П V(A2),
что невозможно, так как окрестности V(Ai), V{A2) по построению не имеют
общих точек. >
Ь. Предельный переход и арифметические операции
Определение б. Если две числовые функции /:?J->M, g : Е -»
имеют общую область определения J5, то их суммой, произведением и част-
частным называются соответственно функции, определенные на том же множестве

§ 2. ПРЕДЕЛ ФУНКЦИИ 111
следующими формулами:
(f +
если д(х) ф 0 при х € Е.
Теорема 2. Пусть f: Е -> R и д : Е -> R — две функции с общей
областью определения.
Если lim f(x) = A, lim g(x) = В, то:
ЕЭх-+а "
a) lim
b) lim
ЕЭх—Кг
c) lim ( — )(х) = —, если В ф 0 и д(х) ф 0 при х ? Е.
Еэх-+а \д/ В
Эта теорема, как уже отмечалось в начале пункта 2, непосредственно вы-
вытекает из соответствующей теоремы о пределах последовательностей, если
учесть утверждение, доказанное в пункте 1.
Теорему можно получить также, повторив доказательство теоремы об
арифметических свойствах предела последовательности. Все изменения в до-
доказательстве, которые при этом придется провести, сведутся к тому, что всю-
всюду, где раньше мы выбирали «N € N, начиная с которого...», нужно будет
о
выбирать некоторую проколотую окрестность Ue{cl) точки а в множестве Е.
Советуем читателю проверить это.
Здесь же мы получим эту теорему из ее простейшего частного случая,
когда А = В = 0 (утверждение с) при этом, разумеется, не рассматривается).
Функцию /: Е —> Е принято называть бесконечно малой при Е Э х —> а,
если lim f(x) = 0.
ЕЭх-+а V '
Утверждение 2. а) Если а: Е -> М и C: Е —У R — бесконечно малые
функции при Е Э х —> а, то их сумма а И- /3 : Е —> R — также бесконечно
малая функция при Е Э х -> а.
b) Если а: Е -+ R и /3: Е —> R — бесконечно малые функции при Е Э х ->
—У а, то их произведение а • C : Е -> R — также бесконечно малая функция
при Е Э х —У а.
c) Если а : Е —> R — бесконечно малая функция при Е Э х —> а, а /3: Е —>•
—> R — финально ограниченная функция при Е Э х —> а, то произведение
а • /3 : Е —> R есть бесконечно малая функция при Е Э х —> а.
< а) Проверим, что
( lim а(х) =о)л( lim /?(х) = 0W ( lim (а 4- /3)(х) =

112 ГЛ. III. ПРЕДЕЛ
Пусть задано число е > 0. По определению предела имеем
€ U'E(a)
x)= 0\ => (зи?(а) Vx € #?(а) (\0(х)\ < §))•
Тогда для проколотой окрестности Ue{o) С U'E(a) П i/#(a) получаем
Vz G UE(a) \(а + /3)(я:)| = |а(х) -I- /3(х)| ^ \а(х)\ + |/?(ж)| < ?,
т. е. проверено, что lim (а 4- /3){х) = 0.
ЕЭх—>-а
b) Это утверждение есть частный случай утверждения с), поскольку всякая
функция, имеющая предел, финально ограничена.
c) Проверим, что
( lim а(х) = о) Л (ЗМе R 3%?(a) Vx € %?(а) (|/3(х) < Af))
\ ЕЭх-+а /
( lim а(х)/?(х) =0).
\ЕЭх->а /
Пусть задано е > 0. По определению предела имеем
а(х) = О)
Тогда для проколотой окрестности U^(a) С {/^(а) П Ue{o) получаем
Vx € U?(a) |(а -/?)(х)| = |а(х)/?(х)| = |а(х)||/?(х)| < ^ ¦ М = е.
Тем самым проверено, что lim а(х) /3(х) = 0. >
ЕЭх->а
Теперь сделаем следующее полезное
Замечание.
lim f(x) = A <?=> (f(x) —Ал- <х{х)) Л ( lim a(x) =
ЕЗх—ya
Иными словами, функция / : Е —У R стремится к А тогда и только то-
тогда, когда она может быть представлена в виде суммы А 4- а(#), где а(х) —
бесконечно малая при Е Э х —> а функция (уклонение f(x) от 1^
*) Любопытная деталь: это почти очевидное, но очень полезное в вычислительном плане
и важное в идейном отношении представление особо отмечалось французским математиком
и механиком Лазаром Карно A753 — 1823), революционным генералом и академиком, отцом
родоначальника термодинамики Сади Карно A796 — 1832).

§ 2. ПРЕДЕЛ ФУНКЦИИ 113
Это непосредственно следует из определения предела, в силу которого
lim f{x) = А <=> lim (f(x) - А) = 0.
Приведем теперь доказательство теоремы об арифметических свойствах
предела функции, основанное на этом замечании и установленных свойствах:
бесконечно малых функций.
Ч а) Если ton f(x) = А и ton д(х) = В, то f(x) = А + а(х) и д(х) =
= В + ^З(х), где а(х) и /3(а;) — бесконечно малые при Е Э х —> а. Тогда
(/ + 0H*0 = /0*0 + д(х) = А + а(х) + В + /3(х) = (А + В) + 70*0, где 70*0 =
= а(х) 4- /?0*0> как сумма бесконечно малых, есть бесконечно малая функция
при Е Э х —> а. Таким образом, ton (/ 4- д)(х) = А 4- В.
ЕЭ
b) Вновь представив f(x) и д(х) в виде f(x) — А-\- а(х) и д(х) = В +
имеем
(/ ' 9){х) = f(x)g(x) = {А + а(х)){В 4- 0(х)) = А • В 4- 70*0,
где 7(я) = ^/?(^) + Ва(х) 4- а(х)^3(х) по свойствам бесконечно малых есть
бесконечно малая функция при Е Э х —> а.
Таким образом, ton (/ • д)(х) = А • В.
ЕЭх->а
c) Вновь запишем, что f(x) = А + а(х) и д{х) = В + /3(х), где lim a(x) =
ЕЭх->а
= 0, lim /3(х) = 0.
ЕЭх->а
Поскольку В^О, существует проколотая окрестность Ue(o), в любой точ-
точке которой \/3(х)\ < ф, и потому |^(х)| = |В + /3(ж)| ^ |В| - \/3(х)\ >
о 12 1
Тогда в UeM будем иметь также , , Ч| < -г:, т. е. функция —г-г финально
|Р(«I 1^1 9(х)
ограничена при Е Э х -> а. Теперь запишем
_ А + а(х)
В д(х) В
1 1
- д(х)
По свойствам бесконечно малых (с учетом доказанной финальной ограничен-
ограниченности —гт) функция 7(я) есть бесконечно малая при Е Э х —У а. Таким
д(х)' ^J
образом, доказано, что lim ( - )(х) = —. >
Еэх-+а \д/к J В
с. Предельный переход и неравенства
Теорема 3. а) Если функции f : Е -> Ш и д : Е —> R таковы, что
lim f(x) = A, lim g(x) = В и А < В, то найдется проколотая окрест-
Э+ 0 ЕЭх-+а
0
ноешь Ue{o) точки а в множестве Е, в любой точке которой выполнено
неравенство f(x) < g(x).

114 ГЛ. III. ПРЕДЕЛ
b) Если между функциями f: Е -> Е, g : Е -+R' и h: Е -+ R на множе-
множестве Е имеет место соотношение f(x) ^ g(x) ^ h(x) и если lim f(x) =
ЕЭх—ta
= lim h(x) = С, то существует также предел д(х) при Е Э х -> а, причем
ЕЭх->а
lim g(x) = С.
<* а) Возьмем число С такое, что А < С < В. По определению преде-
о о
ла найдем проколотые окрестности U'E(a) и UE(a) точки а в множестве Е
о о
так, чтобы при х € U'E{a) иметь \f(x) - А\ < С — А и при х € ?^(а) иметь
о
|у(х) — В\ < В — С. Тогда в любой проколотой окрестности Ue{o), содержа-
содержась о
щейся в UE{a) П UE{a), получим
f(x) < А + (С - А) = С = В - (В - С) < д(х).
Ь) Если lim f(x) = lim h(x) — С, то по любому фиксированному е > О
ЕЭх—>а ЕЭ>
0
найдутся такие проколотые окрестности UE{a) и ?/^(о) точки а в множестве
о о
??, что при х € {/^(а) имеем С — е < f(x) и при х Е UE{a) имеем Л(х) < С 4- ?.
о о о
Тогда в любой проколотой окрестности Ue(o>), содержащейся в UE(a) П С/^(а),
будем иметь С — е < f(x) ^ у(х) ^ Л(х) < С 4- ?, т. е. |у(х) — С| < е, и,
следовательно, lim g(x) = С. >
Следствие. Пусть lim /(x) = А и lim g(x) = В. Если в некоторой
ЕЭх-*а ЕЭ*
о
проколотой окрестности Ue{o) точки а:
a) выполнено f(x) > д(х)у то А^ В\
b) выполнено f(x) ^ у(х); то А^ В;
c) выполнено /(х) > В, то А ^ В;
d) выполнено f(x) ^ В, mo A ^ В.
^ Рассуждая от противного, из утверждения а) теоремы 3 немедленно
получаем утверждения а), Ь) доказываемого следствия. Утверждения с), d)
получаются из первых двух при д(х) = В. >
d. Два важных примера. Прежде чем переходить к дальнейшему изло-
изложению теории предела функции, продемонстрируем на двух важных примерах
использование уже доказанных теорем.
Пример 9.
Здесь мы будем апеллировать к школьному определению sin x как ордина-
ординаты точки, в которую переходит точка A,0) при повороте (с центром в начале
координат) на угол х (радиан). Полнота такого определения всецело зависит

§ 2. ПРЕДЕЛ ФУНКЦИИ 115
от того, насколько тщательно установлена связь между поворотами и действи-
действительными числами. Поскольку сама система действительных чисел в школе
не была описана достаточно подробно, надо считать, что нам необходимо
уточнить определение sin x (то же самое отно-
относится и к функции cosx). ^ ^б = (C0SXf sinx)
В свое время мы это сделаем и обоснуем те
рассуждения, которые сейчас будут опираться
на наглядность. ( q—г1Л = A, 0)
а) Покажем, что
2 sin я;., п ^ \ \ ^ п
cos х < < 1 при 0 < \х\ < — . рис g
X ?i
М Так как cos^ x и четные функции, то достаточно рассмотреть
х
случай 0 < х < тг/2. Из рис. 8 и определения cos я и sin я, сравнивая площади
сектора <OCD, треугольника АОАВ и сектора <ОАВ, имеем
= « \ОС\ • \CD\ = -(cosa;)(xcosx) = -2
? Z Z
< Saoab = \ \OA\ ¦ \BC\ = | • 1 • sins = | sinx <
< S<Oab = ±
Разделив эти неравенства на - ж, получаем то, что и утверждалось. >
b) Из а) следует, что
|sinx| ^ \х\
при любом xGl, причем равенство имеет место только для х = 0.
Ч При 0 < |х| < тг/2, как показано в а), имеем
|sinx| < \х\.
Но |sina:| ^ 1, поэтому для \х\ ^ тг/2 > 1 также выполнено последнее неравен-
неравенство. И только при х = 0 имеем sin х = х = 0. >
c) Из Ь) следует, что
lim sins = 0.
4 Поскольку 0 ^ |sinx| ^ |х| и поскольку lim |х| = 0, на основании тео-
х—Ю
ремы о связи предела функции с неравенствами получаем, что lim Isinxl = 0,
+0
следовательно, lim sinx = 0. >
0
d) Теперь докажем, что lim ^-^ = 1.
ж->0 X
5 Зорич Б. Л.

116 ГЛ. III. ПРЕДЕЛ
Считая, что |х| < тг/2, в силу полученного в а) неравенства имеем
- .2 ^ sin а:
1 — sin х < < 1.
х
Но lim(l — sin2 х) = 1 — lim sinx • lim sinx = 1 — 0 = 1, значит, по теореме о
»0 ж»0 х->0
1. sinx ^ .
предельном переходе в неравенствах можем заключить, что lim = 1. >
х—>О X
Пример 10. Определение показательной, логарифмической и степен-
степенной функций на основе теории предела. Мы продемонстрируем сейчас, чем
и как можно было бы дополнить школьное определение показательной и ло-
логарифмической функций, если располагать теорией действительного числа и
теорией предела.
Для удобства ссылок и полноты картины проделаем всё с самого начала.
а) Показательная функция. Пусть а > 1.
1° Для п Е N полагаем по индукции а1 := а, ап+1 := ап • а.
Таким образом, на N возникает функция ап, которая, как видно из опре-
определения, обладает свойством
° _ пт-п
ап
если т, п € N и т > п.
2° Это свойство приводит к естественным определениям
а0 := 1, а~п := — при п € N,
ап
после которых функция ап оказывается распространенной на множество Z
целых чисел и для любых m, n E Z
ат ап = ат+п
3° В теории действительных чисел мы отметили, что для а > 0 и п € N
существует единственный арифметический корень n-й степени из а, т. е.
число х > 0 такое, что хп = а. Для него принято обозначение al/n. Оно
удобно, если мы желаем сохранить закон сложения показателей:
По той же причине естественно положить am/n := (а1/71I71 и а/71 :=
= (а1/71) для п € N и m € Z. Если окажется, что a^mk)^nk) = am/n для
fc € Z,"to можно считать, что мы определили о? для г € Q.
4° Для чисел 0 < х, 0 <• у по индукции проверяем, что для п € N
(х < у) <=* (хп < у

§ 2. ПРЕДЕЛ ФУНКЦИИ 117
поэтому, в частности,
(х = у) *> (хп = у").
5° Это позволяет доказать правила действий с рациональными показате-
показателями, в частности, что
а(тк)/(пк) _ ат/п
И
Действительно, a(m*)/(n*) > 0 и ат/п > 0. Далее, поскольку
b ** = /i/(nfcl
=атк
И
то первое из проверяемых равенств в соответствии с 4° установлено.
Аналогично,
/ m2/n2\
И
поэтому второе равенство также доказано. >
Таким образом, мы определили аг для г € Q, причем аг > 0 и для любых
аГ1-аГ2 =аГ1+Г2.
6° Из 4° следует, что для п, г 2 € Q
<г2) => (ап <аГ2).
^ Поскольку A < а) <=» A < а1/71) для п € N, что сразу следует из 4°,
то (a1/11) = am/n > 1 при n, m € N, что опять-таки следует из 4°. Таким
образом, при 1 < а для г > 0, г Е Q имеем ar > 1.
Тогда при г\ < Г2 на основе 5° получаем
аГ2 = аГ1 • аГ2~Г1 > аГ1 • 1 = ari
5*

118 ГЛ. III. ПРЕДЕЛ
7° Покажем, что для го €
lim аг = аг°
< Проверим, что ар -> 1 при Q Э р -+ 0. Это следует из того, что при
< - имеем в силу 6°
а-1'* <ар < а1/».
Мы зн*аем, что al/n —>> 1 (и а~х1п -> 1) при п —^ оо. Тогда стандартным
рассуждением проверяем, что для е > 0 найдется ? > 0 такое, что при \р\ < S
будет
1-е<ар<1+е.
В качестве ? можно взять -, если 1 — е < аГх1п и а1//п < 1 -К ?.
п
Теперь докажем основное утверждение.
По е > 0 подберем ? так, что при |р| < S
Го <ар < Ц
Если теперь \г — го\ < ?, то
aro(l-ea-ro) <ar = ar°-ar-r° < аг°A
или
аго - е < аг < аг° + г. >
Итак, на Q определена функция аг со свойствами:
а1 = а > 1;
аГ1-аГ2 =аГ1+Г2;
аГ1 < аГ2 при ri < Г2;
аГ1 —> аГ2 при Q Э ri —>• гг.
Продолжим ее на всю числовую ось следующим образом.
8° Пусть х € Е, 5 = sup ar и г = inf ar. Ясно, что 5, г € R, так как
Q9>
при п < х < Г2 имеем аГ1 < аГ2.
Покажем, что на самом деле s = г (и тогда эту величину мы обозначим
через ах).
Ч По определению 5 и г, при г\ < х < г2 имеем
ari
Тогда 0 ^ i - s ^ аГ2 - аГ1 = аГ1(аГ2~Г1 - 1) < 5(ar2"ri - 1). Но ар -> 1
при Q Э р —> 0, поэтому для любого е > 0 найдется ? > 0 такое, что при

§ 2. ПРЕДЕЛ ФУНКЦИИ 119
О < Г2 — r\ < S будет аГ2~Г1 — 1 < е/s. Тогда получим, что 0 ^ г — s < e, и,
поскольку е > О произвольно, заключаем, что г = 5. >
Положим ах := s = г.
9° Покажем, что ах = lim ar.
Ч Учитывая 8°, для е > 0 найдем У < х так, что s — е < аг ^ 5 = ах,
и г" так, что ах — г ^ аг < % + е. Поскольку г' < г < г" влечет аг < аг < аг ,
для всех г € Q, лежащих в интервале ]г;, г"[, будем тогда иметь
а* - е < аг < ах + е. >
Займемся теперь свойствами построенной функции ах на R.
10° Для a?i,X2 € R при а > 1 (a?i < х2) =» (аЖ1 < аХ2).
Ч На интервале ]xi,a?2[ найдутся два рациональных числа г\ < гъ- Если
< г2 ^ X2, то по определению ах, данному в 8°, и свойствам функции
aXl <ari <аГ2 <аХ2. >
ах на О имеем
11° Для любых a?i, а:2 € R верно aXl • аХ2 = аХ1+Х2.
Л В силу известных нам оценок абсолютной погрешности произведения и
свойства 9° можно утверждать, что для любого е > 0 найдется число 6' > 0
такое, что при \х\ — r\\ < S', \х2 — гг| < <J' будет
? < ап
Уменьшая, если нужно, й;, можно подобрать S < 6' так, что при \х\ — r\\ < S,
— гг| < 6, т. е. при |(a?i + жг) — (ri + Г2)| < 2E, будем иметь также
Но аГ1 • аГ2 = аГ1+Г2 для ri,r2 € Q, значит, из полученных неравенств
вытекает, что
aXl • аХ2 - е < aXl+X2 < aXl • аХ2 + е.
Поскольку е > 0 произвольно, заключаем, что
а11-а*2 =аХ1+Х2. >
12° lim ах = ах°. (Напомним, что «ж -> хо» — принятое сокращение для
X—?Xq
Э х
Проверим сначала, что lim ах = 1. По е > 0 найдем n G N так, что -
х->0
1-?< а~1/п < а1/п <1 + е.

120 гл. ш. предел
Тогда в силу 10° при \х\ < 1/п будем иметь
1 - е < о/п <ах < al/n < 1 + е,
т. е. проверено, что lim ax = 1.
х—уО
Если теперь взять S > 0, чтобы при \х — хо\ < S было \ах~х° — 1| < еа~х°,
то получим
ахо - е < ах = аХо (ах~х° - 1) < ах° + е
и тем самым проверено, что lim ах = аХо. >
13° Покажем, что множеством значений построенной функции х н* ах
является множество R+ всех положительных действительных чисел.
М Пусть 2/о € R+. Если а > 1, то, как нам известно, найдется число п € N
такое, что а~п < уо < ап.
В силу этого оба множества
= {x?R\ax <у0} и В = {х €Ж\у0 < ах}
непусты. Но поскольку (х\ < х%) <=> {aXl < аХ2) (при а > 1), то для любых
чисел д?1, Х2 € К таких, что Xi € А и ^2 € В, имеем xi < #2. Следовательно,
к множествам А и В применима аксиома полноты, из которой следует суще-
существование числа хо такого, что х\ ^ хо ^ хг для любых элементов Xi € А и
Х2 € В. Покажем, что ах° = j/o-
Если бы было аХо < уо, то, поскольку а*0+1/п -> аж° при п -» оо, нашлось
бы число п € N такое, что аЖо+1/п < i/o- Получилось бы, что (жо + —) €
в то время как точка хо разделяет А и В. Значит, предположение аХо < у о
неверно. Аналогично проверяем, что неравенство ах° > уо тоже невозможно.
По свойствам действительных чисел отсюда заключаем, что ах° = j/0- >
14° Мы пока считали, что о > 1. Но все построения можно было бы по-
повторить и для 0 < а < 1. При этом условии 0 < аг < 1, если г > 0; по-
поэтому в 6°, а затем окончательно в 10° теперь получим, что при 0 < а < 1
(xi <х2) =*> (аХ1 >аХ2).
Итак, при а > 0, а ф 1 на множестве Е действительных чисел* мы постро-
построили действительнозначную функцию х н* ах со следующими свойствами:
1) а1 = а;
2) аХ1-аХ2 =а*
3) ах -+ аХо при х
'4) (а*1 < а*2) <=> (xi < х2), если а > 1,
(аХ1 > аХ2) <<=> (xi < х2), если 0 < а < 1;
5) множеством значений функции х н* ах является множество R+ = {у €
Е К. 10 < у} всех положительных чисел.

§ 2. ПРЕДЕЛ ФУНКЦИИ 121
Определение 7. Отображение х *-» ах называется показательной или
экспоненциальной функцией при основании а. Особенно часто встречается
функция х н-> ех, когда а = е, которую нередко обозначают через ехрх. В
связи с этим для обозначения функции х н* ах также иногда используется
символ ехра х.
Ь) Логарифмическая функция. Поскольку отображение ехра : Е -» Е+,
как видно из свойств показательной функции, биективно, оно имеет обратное
отображение.
Определение 8. Отображение, обратное к ехра : Е -> Е+, называется
логарифмической функцией при основании а (О < а, а ф 1) и обозначается
символом
loga : Е+ -+ Е.
Определение 9. При основании а = е логарифмическая функция, или
логарифм, называется натуральным логарифмом и обозначается In: Е+
Причина такой терминологии прояснится при другом, во многом даже бо-
более естественном и прозрачном подходе к логарифмам, который мы изложим
после построения основ дифференциального и интегрального исчисления.
По определению логарифма как функции, обратной экспоненциальной,
имеем
Чх е Е (loga(a*) = х),
V2/GE+
Из этого определения и свойств показательной функции, в частности, полу-
получается, что в области Е+ своего определения логарифм обладает следующими
свойствами:
1') logaa = l;
2') loga B/1' 2/2) = loga 2/1 -I- loga 2/2;
3;) bga у -> loga 2/0 при E+ Э у -> 2/o € E+;
4') (loga2/i < loga2/2) <=*> B/1 < 2/2), если a > 1,
(loga 2/1 > loga 2/2) «=> B/1 < У2), если 0 < a < 1;
5;) множество значений функции loga: E+ —> E совпадает с множеством Е
всех действительных чисел.
М Из свойства 1) показательной функции и определения логарифма полу-
получаем 1;).
*
Из свойства 2) показательной функции получаем 2;). Действительно, пусть
хг = loga 2/1 и х2 = loga 2/2. Тогда 2/i = a*1, 2/2 = aX2 и по 2) угУ2= aXl • аХ2 =
= аХ1+Ж2, откуда logaB/1 • 2/2) = хг + х2.

122
ГЛ. III. ПРЕДЕЛ
Аналогично, свойство 4) показательной функции влечет свойство 4;) лога-
логарифмической.
Очевидно, 5) => 5').
Осталось доказать 3').
В силу свойства 2') логарифма
loga у - loga 2/о = bga ( — ),
поэтому неравенства
-е < loga у - loga 2/о < е
равносильны соотношению
a (О = -е< loga( — ) < е = \oga(a?),
\2/о/
которое по свойству 4;) логарифма равносильно
У
-а? < — < а? при а > 1,
а? < — < а~? при 0 < а < 1.
2/о
У
\пх
В любом случае мы получаем,
что если
Уоа~? < у < уоа? при а > 1
или
Уоа? < у < уоа~€ при 0 < а < 1,
то
—? <С loga у — loga 2/о ^ ?•
Таким образом, проверено, что
рис. 9 На рис. 9 изображены графики
функций ех, 10х, In х, Iog10:r =
/1\х
=: logx, а на рис. 10 — графики функций ( - 1 , @,1)х,
Остановимся еще на одном свойстве логарифма, которым тоже часто при-
приходится пользоваться.

§ 2. ПРЕДЕЛ ФУНКЦИИ
123
Рис. 10
Покажем, что для любого ft > 0 и любого а € М справедливо равенство
6;) loga(ft«) = alogaft.
^ 1° Равенство справедливо при a = п 6 N, ибо из свойства 2') логарифма
по индукции получаем logaB/1... уп) = loga уг + ... + loga </п, значит,
loga(bn) = loga ft + ... + loga ft = n loga ft.
2° loga(ft~1) = - loga ft, ибо если /3 = loga ft, то
ft =
ft = or
и
loga (ft) = -/}.
3° Из 1° и 2° теперь заключаем, что для a € Z равенство loga(fta) = a loga ft
справедливо.
4° loga(ft^n) = - loga ft при п € Z. Действительно,
5° Теперь можно проверить, что для любого рационального числа а = — е
Е Q утверждение справедливо. В самом деле,
m
п
loga ft = mloga (ft1/-) = loga
= ioga (ft-/-).
6° Но если равенство loga ftr = r loga ft справедливо для любого г е Q, то,
устремляя г по Q к а, на основании свойства 3) показательной и свойства 3')

124
ГЛ. III. ПРЕДЕЛ
логарифмической функций получаем, что если г достаточно близко к а, то Ь
близко к Ьа и loga 6Г близко к loga 6a. Это означает, что
lim loga6r =loga6a.
9*
Ho loga br = r loga 6, поэтому
loga ba = lim loga br = lim r loga b = a loga 6. >
QBr—»a Q3r—toe
Из доказанного свойства логарифма можно сделать вывод, что для любых
а, /3 € К и а > О имеет место равенство
п\ (пос\C _J aocC
Ч При а = 1 считаем, по определению, 1а = 1 для а € Е. Таким образом,
в этом случае равенство тривиально.
Если же а ф 1, то по доказанному
= /31og>a) = /3 • aloga a = /3 • a = loge(aa*),
У
что в силу свойства 4;) логарифма доказывает справедливость указанного
равенства. >
с) Степенная функция. Если считать la = 1, то при любом х>0иаЕ1
мы определили величину ха (читается «х в степени а»).
Определение 10. Функция
i4xQ, определенная на множестве
R+ положительных чисел, называ-
ется степенной функцией, а число а
называется показателем степени.
1 Степенная функция, очевидно,
является композицией показатель-
показательной и логарифмической функций,
точнее,
1
0
-1/2
ха =
Рис. 11
На рис. 11 изображены графики
функции у = ха при различных зна-
значениях показателя степени.
3. Общее определение предела функции (предел по базе). Дока-
Доказывая свойства предела функции, мы убедились, что от проколотых окрест-
окрестностей, в которых были определены наши функции и которые возникали в
процессе доказательств, кроме свойств Bi), B2), указанных во введении к
предыдущему пункту 2, действительно ничего не потребовалось. Это обсто-
обстоятельство служит оправданием для выделения следующего математического
объекта.

§ 2. ПРЕДЕЛ ФУНКЦИИ
125
а. База; определение и основные примеры
Определение 11. Совокупность В подмножеств В С X множества X
будем называть базой в множестве X, если выполнены два условия:
Bi) VB € В {Вф 0);
в2) VBi € в vb2 ев зв ев (в с вг п в2).
Иными словами, элементы совокупности В суть непустые множества и в
пересечении любых двух из них содержится некоторый элемент из той же
совокупности.
Укажем некоторые наиболее употребительные в анализе базы.
Обозначение
базы
х —У а
X —У ОО
х —У а, х € Е
или
Е Э х -> о
или
х —> а
х —* оо, х G 2?
или
Е Э х -> оо
или
х —> оо
Чтение
обозначения
х стремится к а
х стремится к
бесконечности
х стремится к а
по множеству Е
х стремится к
бесконечности
по множеству Е
Из каких множеств
(элементов) состоит
база
База проколотых
окрестностей точ-
точки а € R
База окрестностей
бесконечности
База*) проколотых
окрестностей точки
а в множестве Е
База**) окрестностей
бесконечности в мно-
множестве Е
Определение и обозна-
обозначение элементов базы
Ща) :=
= {х € R о - 6i <
С ж / 1
где ^i > 0, ^2 > 0
С/(оо) :=
= {х е R\S < х|},
где S € R
1/я(оо) :=?7ПС/(оо)
*) Предполагается, что а — предельная точка множества Е.
*' Предполагается, что множество Е не ограничено.
Если Е = Е+ = {х € Щх > а} (Е = Е~ = {х € R| х < а}), то вместо
х -У а, х € Е пишут х —у а + 0 (х —У а — 0) и говорят, что х стремится
к а справа или со стороны больших значений (соответственно, слева или со
стороны меньших значений). При а = 0 принята краткая запись х -У +0
(я: -> -0) вместо х -> 0 + 0 (х -> 0 - 0).

126 ГЛ. III. ПРЕДЕЛ
Запись ? 3 а; 4 а + 0 (Е Э х -+ а — 0) будет употребляться вместо
х -* а, х Е 1? П 15+ (х -» а, хе^П -Б"). Она означает, что х стремится по
множеству Е к а, оставаясь больше (меньше), чем о.
Если
= {хе Ш\с<х} (Е = Е^ = {хеЩх < с}),
то вместо х -> оо, х Е 15 пишут # —>> +оо (я -> —оо) и говорят, что а: стре-
стремится к плюс бесконечности (соответственно, к минус бесконечности).
Запись Е Э х -> -Ьоо (?зж-^ —оо) будет употребляться вместо х -» оо,
хб?ПЕ+ (хчоо, жЕВПЕ").
При 1? = N вместо х -> оо, х Е N мы (если это не ведет к недоразумению)
будем, как это принято в теории предела последовательности, писать п -> оо.
Заметим, что все перечисленные базы обладают той особенностью, что пе-
пересечение любых двух элементов базы само является элементом этой базы, а не
только содержит некоторый элемент базы. С другими базами мы встретимся
при изучении функций, заданных не на числовой оси1).
Отметим также, что используемый здесь термин «база» есть краткое обо-
обозначение того, что в математике называется «базисом фильтра*, а введенный
ниже предел по базе есть наиболее существенная для анализа часть созданно-
созданного современным французским математиком А. Картаном понятия предела по
фильтру2\
Ь. Предел функции по базе
Определение 12. Пусть /: X —> Ш — функция на множестве X; В —
база в X. Число А Е Ш называется пределом функции f : X -> Е по базе
В, если для любой окрестности V(A) точки А найдется элемент В Е В базы,
образ которого f(B) содержится в окрестности V(A).
Если А — предел функции /: X -> R по базе В, то пишут
= А.
Повторим определение предела по базе в логической символике:
lim/(:r) = A:= \fV(A) ЗВ Е В (f(B)cV(A)).
Поскольку мы сейчас рассматриваем функции с числовыми значениями,
полезно иметь в виду и следующук>'форму этого основного определения:
lim/(x) = А := Ve > О ЭВ 6 В Уж € Б (|/(х) - А\ < е).
1' Например, совокупность открытых (без граничной окружности) кругов, содержащих
данную точку плоскости, является базой. Пересечение двух элементов базы не всегда круг,
но всегда содержит круг из нашей совокупности.
2) Подробнее об этом см.: Бурбаки Н. Общая топология. М.: ИЛ, 1958.

§ 2. ПРЕДЕЛ ФУНКЦИИ 127
В этрй формулировке вместо произвольной окрестности V(A) берется сим-
симметричная (относительно точки А) окрестность (е-окрестность). Эквивалент-
Эквивалентность этих определений для вещественнозначных функций вытекает из того,
что, как уже говорилось, в любой окрестности точки содержится некоторая
симметричная окрестность этой же точки (проведите доказательство полно-
полностью!).
Мы дали общее определение предела функции по базе. Выше были рас-
рассмотрены примеры наиболее употребительных в анализе баз. В конкретной
задаче, где появляется та или иная из этих баз, необходимо уметь расшифро-
расшифровать общее определение и записать его для конкретной базы.
Так,
lim /Or) = A:= Ve >O 36 > 0 Vx€]a-rf,a[ (|/(а?) - A\
x-*a—O
lim /(a?) = A := Ve > 0 35 € R Vz < 5 (|/(s) - A| < e).
X—*— OO
Рассматривая примеры баз, мы, в частности, ввели понятие окрестности
бесконечности. Если использовать это понятие, то в соответствии с общим
определением предела разумно принять следующие соглашения:
lim/(x) = oo:= VF(oo) ЗВ Е В (f (В)) С V(оо))
или, что то же самое,
lim/(а?) = оо := Ve > О ЗВ Е В УхЕВ (е <
lim/(ж) = +оо := Ve E R ЗВ ЕВ УхЕВ (е <
lim /Or) = -оо := Me Е Ж ЗВ ЕВ VxeB (f(x) < e).
Обычно под е подразумевают малую величину. В приведенных определе-
определениях это, разумеется, не так. В соответствии с принятыми соглашениями,
например, можем записать
lim /(я) = -оо := Ve E R 36 Е Ш Vx>6 (f(x)<e).
Советуем читателю самостоятельно написать полное определение предела
для различных баз в случае конечных (числовых) и бесконечных пределов.
Для того чтобы можно было считать доказанными и в общем случае пре-
предела по произвольной базе все те теоремы о пределах, которые мы доказали
в пункте 2 для специальной базы Е Э х -> а, необходимо дать соответствую-
соответствующие определения: финально постоянной, финально ограниченной и бесконечно
малой при данной базе функций.
Определение 13. Функция /: X -» Ш называется финально постоянной
при базе В, если существуют число А Е R и такой элемент В Е В базы, в любой
точке х Е В которого f(x) = A.

128 гл. ш. предел
Определение 14. Функция /: X —> Ш называется ограниченной при
базе В или финально ограниченной при базе В, если существуют число с € Ш
и такой элемент В ? В базы, в любой точке х € В которого \f(x)\<c.
Определение 15. Функция /: X -> R называется бесконечно малой
при базе В, если lim/(a:) = 0.
После этих определений и основного наблюдения о том, что для доказа-
доказательства теорем о пределах нужны только свойства Bi) и Вг) базы, можно
считать, что все свойства предела, установленные в пункте 2, справедливы
для пределов по любой базе.
В частности, мы можем теперь говорить о пределе функции при х —> оо,
или при х -> —оо, или при х -> + оо.
Кроме того, мы обеспечили себе возможность применения теории пределов
и в том случае, когда функции будут определены не на числовых множествах;
в дальнейшем это окажется особенно ценным. К примеру, длина кривой есть
числовая функция, определенная на некотором классе кривых. Если мы знаем
эту функцию на ломаных, то потом предельным переходом определяем ее для
более сложных кривых, например для окружности.
В данный же момент основная польза от сделанного наблюдения и введен-
введенного в связи с ним понятия базы состоит в том, что они избавляют нас от
проверок и формальных доказательств теорем о пределах для каждого кон-
конкретного вида предельных переходов или, в нашей нынешней терминологии,
для каждого конкретного вида баз.
Для того чтобы окончательно освоиться с понятием предела по произволь-
произвольной базе, доказательства дальнейших свойств предела функции мы проведем
в общем виде.
4. Вопросы существования предела функции
а. Критерий Коши. Прежде чем формулировать критерий Коши, да-
дадим следующее полезное
Определение 16. Колебанием функции /: X -> R на множестве Е С X
называется величина
(fE):= sup
т. е. верхняя грань модуля разности значений функции на всевозможных парах
точек Х\, Х2 G Е.
Примеры.
11) а,(*2;[-1
12) Цх;[-1,2]) =
13) w(x;]-1,20=3.

§ 2. ПРЕДЕЛ ФУНКЦИИ 129
14) u;(sgn:r;[-l,2])=2.
15) cj(sgna;;[0,2]) = 1.
16) cj(sgna;;]0,2]) =0.
Теорема 4 (критерий Коши существования предела функции). Пусть
X — множество и В — база в X.
Функция /: X -> R имеет предел по базе В в том и только в том случае,
когда для любого числа е > 0 найдется элемент В ? В базы, на котором
колебание функции меньше е.
Итак,
Э ton Дат) ** Ve > 0 ЗВ ? В И/; В) < e).
в
<< Необходимость. Если lim Да?) = А, то для любого е > 0 найдется
в
элемент В базы В, в любой точке х которого \f(x) — А\ < е/3. Но тогда для
любых х\, i2 из В
|/(ая) - Дх2)| < !/(*!) -А\ + |/(х2) - А\ < \е
и, значит, cj(f; В) < е.
Достаточность. Докажем теперь основную часть критерия, утвер-
утверждающую, что если для любого е > 0 найдется элемент В базы В, на котором
u(f) В) < ?, то функция / имеет предел по базе В.
Придавая е последовательно значения 1, -, ... , —, ..., получим последо-
2 п
вательность В\, 1?2» • • • » ВП1 ... элементов базы таких, что шЦ\Вп) < 1/п,
п € N. Поскольку Вп -ф 0, в каждом Вп можно взять по точке хп. После-
Последовательность f(x\), f(x2), ... , f(xn), ••• фундаментальная. Действительно,
Вп П Вт ф 0, и, взяв вспомогательную точку х G Вп П 2?т, получим, что
\f(xn) - f(xm)\ < \f(xn) - f(x)\ -f \f(x) - f(xm)\ < 1/n -f 1/m. По доказанному
для последовательностей критерию Коши, последовательность {f(xn), п ? Щ
имеет некоторый предел А. Из установленного выше неравенства при т —> оо
следует, что |/(хп) — А\ ^ 1/п, а отсюда, учитывая, что u(f;Bn) < 1/п, за-
заключаем теперь, что если п > N = [2/е] + 1, то в любой точке х € Вп будет
- А\ < е. >
Замечание. Проведенное доказательство, как мы увидим позже, оста-
остается в силе для функций со значениями в любом так называемом полном про-
пространстве Y. Если же Y = R, а этот случай нас сейчас в первую очередь и
интересует, то при желании можно пользоваться той же идеей, что и в дока-
доказательстве достаточности критерия Коши для последовательностей.
<< Полагая тв = inf Дя), М# = sup f(x) и замечая, что для любых эле-
хев хеВ
ментов В\, B<i базы В выполнено тпв1 ^ ™>в1пв2 ^ Мв1пв2 ^ Мв2-> по аксио-
аксиоме полноты найдем число A G R, разделяющее числовые множества {тв} и

130 ГЛ. III. ПРЕДЕЛ
{Mb}, где В € В. Поскольку u(f; В) = Мв—тв, то теперь можно заключить,
что как только о;(/; В) < е, так \f(x) - А\ < е в любой точке х Е В. >
Пример 17. Покажем, что в случае, когда X = N и В есть база га -> оо,
га Е N, доказанный общий критерий Коши существования предела функции
совпадает с рассмотренным ранее критерием Коши существования предела
последовательности.
Действительно, элементом базы га -> оо, га G N является множество В =
= N П ?/(оо) = {га G N | га > N} тех натуральных чисел га G N, которые больше
некоторого числа N ? Ш. Без ограничения общности можно считать, что
N G N. Соотношение u(f;B) < e в нашем случае означает, что Vrai,ri2 >
имеем |/(rai) — /(гаг)! < е-
Таким образом, условие, что для любого ? > 0 найдется элемент В €
базы, на котором колебание о>(/; В) функции / меньше ?., для функции /: N
равносильно условию фундаментальности последовательности {/(га)}.
Ь. Предел композиции функций
Теорема 5 (о пределе композиции функций). Пусть Y — множество;
— база в Y; д: Y —> Е — отображение, имеющее предел по базе By-
Пусть X — множество, Вх — база eXuf:X->Y— такое отображе-
отображение X в Y, что для любого элемента By G By базы By найдется элемент
Вх € Вх базы Вх, образ которого f(Bx) содержится в By.
При этих условиях композиция g о /: X -> R отображений fug опреде-
определена, имеет предел по базе Вх и \im(g о f)(x) = limg{y)>
В By
<4 Композиция g о /: X -> R определена, поскольку f(X) С Y.
Пусть limg(y) = А. Покажем, что lim (gof)(x) = А. По заданной окрестно-
окрестному Вх
сти V(A) точки А найдем элемент By € By базы By такой, что д(Ву) С V(A).
По условию найдется элемент Вх G Вх базы Вх такой, что f(Bx) С By. Но
тогда (д о f)(Bx) = g(f(Bx)) С д(Ву) С V(A) и мы, таким образом, прове-
проверили, что А является пределом функции (д о /): X —> R по базе Вх- >
Пример 18. lim = ?
ж-+о 7х
Если положить д(у) = 5S2, а /(х) = 7х, то (д о/)(х) = S1^ ж. В нашем
у (к
случае Y = R \ 0, X = R. Поскольку lim p(j/) = lim ^2J? = i? то для примене-
з/-+о j/-^o г/
ния теоремы надо проверить, что, какой бы элемент базы у —> 0 мы ни взяли,
найдется элемент базы х —у 0, образ которого при отображении f(x) = 7x со-
содержится в указанном элементе базы у —> 0. Элементами базы J/ —>• 0 являются
о
проколотые окрестности Uy@) точки 0 Е R.
Элементами базы х —> 0 также являются проколотые окрестности С/х@)
точки 0 G R. Пусть U у @) = {j/GR|a<j/</9, 2/^0} (где a, /? G R, причем

§ 2. ПРЕДЕЛ ФУНКЦИИ 131
а < О, /3 > О) — произвольная проколотая окрестность нуля в Y. Если взять
Ux@) = {х Е R| ^ <#< ^, х ^ 0}, то эта проколотая окрестность нуля в X
7 7 о о о
уже обладает тем свойством, что f(Ux)@) = Uy@) С Uy(O).
Условия теоремы выполнены, и теперь можно утверждать, что
,. sin7x ,. sin у л
hm —-— = hm —- = 1.
ж—>о 7х у-+о у
Пример 19. Функция д(у) — |sgnj/|, как мы уже видели (см. пример 3),
имеет предел lim |sgnj/| = 1.
у—уо
Функция у = f(x) = xsin -, определенная при х ф 0, также имеет предел
lim xsin - =0 (см. пример 1).
Однако функция (д о f)(x) = sgn (x sin ~
при х —> 0 не имеет предела.
Действительно, в любой проколотой окрестности точки х = 0 имеются ну-
нули функции sin -, поэтому функция
х
sgn
в любой такой окрестности
принимает и значение 1, и значение 0 и по критерию Коши не может иметь
предел при х —> 0.
Не противоречит ли это доказанной теореме?
Проверьте, как мы сделали это в предыдущем примере, выполнены ли здесь
условия теоремы.
Пример 20. Покажем, что
< Пусть
Y = N, By — база п -> оо, п Е N;
X = Ш+ = {х е R | х > 0}, Вх — база х -+ +оо;
f:X->Y есть отображение a: i—> [х],
где [х] — целая часть числа х (т. е. наибольшее целое число, не превосходящее
числа х).
Тогда для любого элемента By = {n € N|n. > N} базы п ->• оо, ?i G N,
очевидно, найдется элемент Bx = {xeE|x>iV + l} базы х ->• Н-оо, образ
которого при отображении х —>• [х] содержится в By.
A \п / 1 \п / 1 \n+i
1 + -J , gi{n) = A + ^J-jJ , дз(п) = (l + ^J , как
нам уже известно, имеют своим пределом по базе п —> оо, п G N число е.

132 гл. ш. предел
По теореме о пределе композиции функций можно утверждать, что тогда
функции
(92 о /)(*) = (l +
также имеют своим пределом по базе х —> +оо число е.
Теперь остается заметить, что при х
[Ж]
/
и так как при х —> +оо крайние члены стремятся к е, то по свойствам предела
(теорема 3) получаем lim A + — ) = е.
ж—>>+оо \ X/
Используя теорему о пределе композиции функций, покажем теперь, что
lim (l + -У = е.
ж—>>~оо\ X/
Запишем
im f I + -) = lim A -f т^^ = lim f 1 -
>-oo V XJ (-t)->-oo\ (-*)/ t-^+oo V *
= lim A + -—- ) = lim A + -—г ' lim
= lim f^l f)
frrl lim
Написанные равенства с учетом произведенных замен и = t — 1 и t = —х
обосновываются с конца (!) на основе теоремы о пределе композиции функ-
/ 1 \и
ций. Действительно, только тогда, когда мы пришли к пределу lim (l-f-1 ,
существование которого уже доказано, теорема позволяет утверждать, что
предыдущий предел тоже существует и равен этому. Тогда и стоящий перед
ним предел существует, и конечным числом таких переходов придем к ис-
исходному пределу. Это довольно типичный пример процедуры использования
теоремы о пределе сложной функции при вычислении пределов.
Итак, мы имеем
lim Г1 + -) =е lim
х/ ж-++оо
A + -) .
\ х/
A \х
1 Н— 1 = е.
х /
Действительно, пусть задано число s > 0.

§ 2. ПРЕДЕЛ ФУНКЦИИ
133
A \х
1 + - ) = е, найдется число с\ € R такое, что при х < с\
X /
будет
о+а
< ?.
A \х
1 И— 1 = е, найдется число С2 € R такое, что при c<i < х
х /
будет
- — e
< е.
A \
1 H—J — e
самым проверено, что lim A H— ) = e. >
Ж—^OO \ X/
Пример 21.
< е. Тем
М После замены х = \/t возвращаемся к пределу, рассмотренному в пре-
предыдущем примере. >
Пример 22.
х
х
lim — = 0, если а > 1.
>+ qx
< Мы знаем (см. § 1, пример 11), что lim — =0, если q > 1.
п—юо qn
Теперь, как и в примере 3, можно рассмотреть вспомогательное отобра-
отображение / : R+ —> N, осуществляемое функцией [х] (целая часть х).
Воспользовавшись неравенствами
[х]
х
q*
и учитывая, что по теореме о пределе сложной функции крайние члены стре-
от
от
мятся к нулю при х -> +оо, заключаем, что lim — = 0. >
ж-++оо qx
Пример 23.
lim
ж—>-foo
^ Пусть а > 1. Полагаем ? = logaar, находим ж = а*. По свойствам
показательной и логарифмической функций (учитывая неограниченность an,
п € N) имеем (х —>• +оо) -Ф=> (t —>• +оо). Используя теорему о пределе сложной
функции и результат примера 4, получаем
logax ?
lim —— = lim -r = 0.
Если 0 < a < 1, то положим — t = logax, x = а~ь. Тогда (х"-> +оо)
+оо), и так как I/a > 1, то снова
logax
lim —2S— = lim
= - lim
г = 0. >

134 ГЛ. III. ПРЕДЕЛ
с. Предел монотонной функции. Рассмотрим теперь один частный,
но весьма полезный класс числовых функций — монотонные функции.
Определение 17. Функция / : Е —> R, определенная на числовом мно-
множестве Е С К, называется
возрастающей на Е, если
E (xi < х2 => f(xx) < Дх2));
неубывающей на Е, если
Vxbx2 Е E (xi <x2=> f(xi) ^ Дх2));
невозрастающей на Е, если
Vxbx2 е Е (хг < х2 =* f(xx) ^ /(х2));
убывающей на i?, если
> f(x2)).
Функции перечисленных типов называются монотонными на множестве
Предположим, что числа (или символы —оо, +оо) г = inf Е и 5 = supi?
являются предельными точками множества Е и f : Е —> Ж — монотонная
функция на Е. Имеет место следующая
Теорема б (критерий существования предела монотонной функции).
Для того чтобы неубывающая на множестве Е функция f: Е -> R имела
предел при х —> 5, х G Е, необходимо и достаточно, чтобы она была ограни-
ограничена сверху, а для того чтобы она имела предел прих —> i, х Е Е, необходимо
и достаточно, чтобы она была ограничена снизу.
< Докажем теорему для предела lim f(x).
ЕЭх—ts
Если этот предел существует, то, как и всякая функция, имеющая предел,
функция / оказывается финально ограниченной при базе Е Э х —> s.
Поскольку / — неубывающая на Е функция, отсюда следует, что / огра-
ограничена сверху. На самом деле можно утверждать даже, что f(x) ^ lim f(x)
ЕЭх-ts
для любого х Е Е. Это будет видно из дальнейшего.
Перейдем к доказательству существования предела lim f(x) при условии
ЕЭх—?в
ограниченности / сверху.
Если / ограничена сверху, то существует верхняя грань значений, кото-
которые функция принимает на множестве Е. Пусть А = sup /(x); покажем, что
lim f(x) — А. По е > 0, на основании определения верхней грани множе-
ЕЭх—ts
ства, найдем точку хо G Е, для которой А — е < /(хо) ^ А. Тогда ввиду
неубывания / на Е получаем, что при xq < x G Е будет А — е < f(x) ^ А. Но

§ 2. ПРЕДЕЛ ФУНКЦИИ 135
множество {х Е Е\хо < х}, очевидно, есть элемент базы х -> s, х ? Е (ибо
5 = supi?). Таким образом, доказано, что lim f(x) = A.
ЕЭх—ts
Для предела lim fix) все рассуждения аналогичны. В этом случае имеем
ЕЭi
lim f(x) = inf /(яг). >
ЕЭх—>t €E
d. Сравнение асимптотического поведения функций. Этот пункт
мы начнем поясняющими тему примерами.
Пусть тг(х) — количество простых чисел, не превосходящих данного ве-
вещественного числа х ? R. Имея возможность при любом фиксированном х
найти (хотя бы перебором) значение 7г(ж), мы тем не менее не в состоянии
сразу ответить, например, на вопрос о том, как ведет себя функция тг(х) при
х —> + оо или, что то же самое, каков асимптотический закон распределения
простых чисел. От Евклида нам известно, что тг(х) —> +оо при х —>• +оо, но
доказать, что тг(х) растет примерно как -—, удалось только в прошлом веке
шх
П. Л. Чебышеву1).
Когда возникает вопрос об описании поведения функции вблизи некоторой
точки (или бесконечности), в которой, как правило, сама функция не опреде-
определена, говорят, что интересуются асимптотикой или асимптотическим по-
поведением функции в окрестности этой точки.
Асимптотическое поведение функции обычно характеризуют с помощью
другой, более простой или более изученной функции, которая в окрестности
исследуемой точки с малой относительной погрешностью воспроизводит зна-
значения изучаемой функции.
Так, 7г(ж) при х —у +оо ведет себя как -—; функция при х —> О
111 J0 X
ведет себя как постоянная функция, равная 1; говоря о поведении функции
х2 + х + sin - при х —> оо, мы, ясно, скажем, что она в основном ведет себя
как функция х2, а при х ->• 0 — как sin -.
х
Дадим теперь точные определения некоторых элементарных понятий, от-
относящихся к асимптотическому поведению функций. Этими понятиями мы
будем систематически пользоваться уже на первом этапе изучения анализа.
Определение 18. Условимся говорить, что некоторое свойство функ-
функций или соотношение между функциями выполнено финально при данной базе
В, если найдется элемент В е В базы, на котором оно имеет место.
Именно в этом смысле мы до сих пор понимали финальное постоянство или
финальную ограниченность функции при данной базе. В этом же смысле мы
дальше будем говорить, например, о том, что финально выполнено соотно-
соотношение f(x) = g(x)h(x) между некоторыми функциями /, g, h. Эти функций
1^П. Л. Чебышев A821 — 1894) — великий русский математик и механик, основатель
большой математической школы в России.

136 ГЛ. III. ПРЕДЕЛ
могут даже иметь разные исходные области определения, но если мы инте-
интересуемся их асимптотическим поведением при базе В, то нам важно только,
чтобы все они были определены на некотором элементе базы В.
Определение 19. Говорят, что функция / есть бесконечно малая по
сравнению с функцией д при базе В и пишут / = о(д) или f = о(д) при В,
в
если финально при базе В выполнено соотношение f(x) = а(х) • д(х), где а —
функция, бесконечно малая при базе В.
Пример 24. х2 = о(х) при х —> 0, так как х2 = х • х.
Пример 25. х = о{х2) при х —> оо, так как финально, когда уже х ф О,
1 2
X = - -X .
X
Из этих примеров надо сделать вывод, что указание базы, при которой
/ = о(д), совершенно необходимо.
Обозначение / = о(д) читается «/ есть о малое от д».
Из определения следует, в частности, что получающаяся при д{х) = 1 за-
запись / = оA) означает просто, что / есть бесконечно малая при базе В.
Определение 20. Если / = о(д) и функция 4д сама есть бесконечно
в
малая при базе В, то говорят, что / есть бесконечно малая более высокого по
сравнению с д порядка при базе В.
Пример 26. х~2 = —- при х —> оо есть бесконечно малая более высокого
х1
порядка по сравнению с бесконечно малой х~1 = -.
х
Определение 21. Функцию, стремящуюся к бесконечности при данной
базе, называют бесконечно большой функцией или просто бесконечно большой
при данной базе.
Определение 22. Если / и g — бесконечно большие при базе В и
/ = о(д), то говорят, что д есть бесконечно большая более высокого порядка
в
по сравнению с /.
Пример 27. - -> оо при х ->• 0, -г -> оо при х -> 0 и - = о( —?)
х х2 х \х2)
при х —>• 0, поэтому — есть бесконечно большая более высокого порядка по
сравнению с - при х —> 0.
' Вместе с тем при х —> оо функция х2 есть бесконечно большая более высо-
высокого порядка, чем х.
Не следует думать, что, выбрав степени хп для описания асимптотическо-
асимптотического поведения функций, мы сможем каждую бесконечно малую или бесконечно
большую характеризовать некоторым числом п — ее степенью.

§ 2. ПРЕДЕЛ ФУНКЦИИ 137
Пример 28. Покажем, что при а > 1 и любом п G
Ит %=0,
т. е. хп = о(аж) при х -* 4-оо.
^ Если п ^ 0, то утверждение очевидно. Если же п G N, то, полагая
g = ^/а, имеем д>1 и ^¦ = (¦7) > поэтому
хп (х \п х х
lim — = lim ( — I = lim — •... • lim — =0.
х-++ооах х—*+ooyqx J x—н-oo qx x—>>+oo qx
п раз
Мы воспользовались, по индукции, теоремой о пределе произведения и
результатом примера 22. >
Таким образом, при любом п G Ъ получаем хп = о{ах) при х —> +оо, если
а > 1.
Пример 29. Развивая предыдущий пример, покажем, что при а > 1 и
любом а € R
lim — = О,
х—>+оо аж
т. е. ха = о(аж) при х —> + оо.
^ Действительно, возьмем число n G N такое, что п > а. Тогда при х > 1
получим
Опираясь на свойства предела и результат предыдущего примера, получаем,
ха
что lim — = 0. >
х—>+00 ах
Пример 30. Покажем, что при а > 1 и любом a G Е
lim ^ = 0,
R+Эж-Ю Ха
т. е. а~1/ж = о(ха) при х -> 0, х G K+.
«^ Полагая в этом случае х = —l/t,no теореме о пределе сложной функции,
используя результат предыдущего примера, находим
lim = lim — = 0. >
ха
Пример 31. Покажем, что при а > 0
lim
ж—>>+оо Ха

138 гл. ш. предел
т. е. при любом положительном показателе степени а имеем logax = о(ха)
при х -> +оо.
< Если а > 1, то положим х = а*/а. Тогда по свойствам показательной
функции и логарифма, опираясь на теорему о пределе композиции функций и
результат примера 29, находим
logax (t/a) I t n
hm = hm . = — lim — = 0.
a1 a t—>+oo a1
Если 0 < a < 1, то I/a > 1 и после замены x = а~~ь/а получаем
hm —2— = hm -——— = hm 7 = 0. >
z->+oo xa t-н-оо a~l a t-n-oo (I/a)
Пример 32. Покажем еще, что при любом a > 0
ха loga х = оA) при х —>• 0, х G IR+.
^ Нам нужно показать, что lim xa loga х = 0 при a > 0. Полагая
RЭ^О
х = 1/?, применяя теорему о пределе композиции функций и результат пре-
предыдущего примера, находим
г а, ,. bga(l/t) logat
hm xa loga x = hm ° = - hm ° = 0. >
Определение 23. Условимся, что запись / = О(д) или f = О(д) при
базе В (читается «/ есть О большое от д при базе В») будет означать, что
финально при базе В выполнено соотношение /(х) = /3(х)д(х), где C(х) —
финально ограниченная при базе В функция.
В частности, запись / = 0A) означает, что функция / финально ограни-
ограничена при базе В.
Пример 33. (—(- sinxj х = О(х) при х —>• оо.
Определение 24. Говорят, что функции /ид одного порядка при
базе В, если одновременно / = О(д) и д = O(f).
Пример 34. Функции B + sinx)x и х одного порядка при х -> оо, но
A + sinx)x и х не являются функциями одного порядка при х -» оо.
Условие, что функции f и д одного порядка при базе В, очевидно, равно-
равносильно тому, что найдутся числа с\ > 0, С2 > 0 и элемент В базы В такие,
что на В имеют место соотношения
или, что то же самое,
1|/(х)| ^ \д(х)\
С2

§ 2. ПРЕДЕЛ ФУНКЦИИ 139
Определение 25. Если между функциями / и д финально при базе В
выполнено соотношение /(х) = j(x)g(x), где Imi7(#) = 1, то говорят, что при
базе В функция f асимптотически ведет себя как функция g или, короче,
что / эквивалентна g при базе В.
Будем в этом случае писать f ~ g или f ~ g при базе В.
Употребление термина «эквивалентна» оправдано тем, что
{f ~
(/ %9)*(9~h) => (/ - h).
Действительно, соотношение / ~ / очевидно, в этом случае *у(х) = 1. Да-
Далее, если Ит7(#) = 1, то lim —г—г = 1 и д(х) = —т-г/(х). Здесь надо только
В В ~ix) К\х)
объяснить, почему можно считать, что 7(я) Ф 0. Если соотношение /(х) =
= 7(#)#(#) имеет место на элементе В\ € S, а соотношение ^ < \j(x)\ < - —
на элементе Бг G В, то мы можем взять элемент В С 2?i П Дг, на котором
будет выполнено и то и другое. Всюду вне В, если угодно, можно вообще
считать, что у(х) = 1. Таким образом, действительно (f ~ g) => (g ~ f)-
Наконец, если /(х) = ji(x)g(x) на 5i G В и ^(х) = 72(#)М#) на -^2 € #,
то на элементе В е В базы В таком, что В С 5i П Б2, оба эти соотно-
соотношения выполнены одновременно, поэтому /(х) = 71 (#) 72(#) М#) на В. Но
lim 71 (х) 72 (#) = lim 7i (х) • lim 72 (#) = 1 и тем самым проверено, что f ~ h.
Полезно заметить, что поскольку соотношение Iini7(x) = 1 равносильно
тому, что j(x) = l-fa(x), где lim a(x) = 0, то соотношение f ~ g равносильно
тому, что /(х) = #(х) + а(х) #(х) = ^(х) + о(^(х)) при базе В.
Мы видим, что относительная погрешность |а(х)| =
f(x)-g{x)
прибли-
жения функции с помощью функции #(х), эквивалентной /(х) при базе S, есть
величина бесконечно малая при базе В.
Рассмотрим некоторые примеры.
Пример 35. x2+x=(l + -Jx2~x2 при х ->¦ оо.
Абсолютная величина разности этих функций
|(х2+х) -х2| = |х|
стремится, к бесконечности, однако относительная погрешность U- = — за-
xz \х\
мены функции х2 Ч- х на эквивалентную величину х2 стремится к нулю при
х —>• оо.

140 гл. ш. предел
Пример 36. В начале этого пункта мы говорили о знаменитом асим-
асимптотическом законе распределения простых чисел. Теперь мы в состоянии
записать его точную формулировку:
/ \ х , ( х \
тг(х) = ¦ Ь о\ -— 1 при х
lnx \1пх/
00.
S1X1 X
Пример 37. Поскольку lim = 1, то sinx ~ x при х -* О, что можно
х—>0 X
написать также в виде равенства sinx = х + о(х) при х -* 0.
Пример 38. Покажем, что InA + х) ~ х при х —> 0.
м lim ln(l + *) = Иш 1ПA + x)l'x = In( lim (I + хI'*) = lne = 1.
х->0 X *-*0 \х->0 ' )
Мы воспользовались в первом равенстве тем, что loga(fta) = alogaft, а во
втором тем, что lim loga t = logab = loga ( lim t). >
Итак, ln(l 4- x) = x + o(x) при x -> 0.
Пример 39. Покажем, что ех = 1 + x Ч- о(х) при х -> 0.
ex — 1 t
4 lim = lim -— г = 1.
x l(l t)
Мы сделали замену x = ln(l4-t), ex — 1 = t и воспользовались тем, что
ех —>• е° = 1 при х -> 0, причем е1 ^ 1 при х ^ 0. Таким образом, на
основании теоремы о пределе композиции и результата предыдущего примера
утверждение доказано. >
Итак, ех — 1 ~ х при х -> 0.
Пример 40. Покажем, что A + х)а = 1 + ах + о(х) при х -> 0.
lim
.. eolnA+I) -1 aln(l-hx)
= lim —— г- • ^ L =
l(l)
= lim г
х х->о aln(l-l-x) х
r el r ln(l-hx)
= a lim • lim — =»а.
t^o t х-уо х
В этой выкладке мы, предполагая а ф 0, сделали замену а1пA+х)=?и
воспользовались результатами двух предыдущих примеров.
Если же а = 0, то утверждение очевидно. >
Таким образом, A + х)а — 1 ~ ах при х -> 0.
При вычислении пределов иногда бывает полезно следующее простое
Утверждение 3. Если f ~ f, то lim f(x)g(x) = \imf(x)g(x), если один
из этих пределов существует.

§ 2. ПРЕДЕЛ ФУНКЦИИ 141
Действительно, коль скоро /(х) = j(x)f(x) и Iim7(#) = 1, то
в
x) jr(x)g(x) = Ii7() /()p()
Пример 41.
,. In cos x 1 .. In cos2 x 1 ,. ln(l-sin2x)
hm —: — = - hm r— = - hm — - =
2 2 xz 2 *
1 ,. -sin x 1 ,. x2 1
= — lim -— = — — lim — = ——.
2 x->o x2 2 x->o x2 2
Мы воспользовались тем, что ln(l + а) ~ а при а —> О, sin х ~ х при х ->- О,
• -г при Р —^ 0 и sin2 х ~ х2 при х -> 0.
sin /3
Мы доказали, что в одночленах при вычислении пределов можно заменять
функции на им эквивалентные при данной базе. Не следует распространять
это правило на суммы и разности функций.
Пример 42. у? + х ~ х при х -> +оо, но
lim (ух2 + х — х) Ф lim (х — х) = 0.
4+осЛ ' х±+оо '
В самом деле,
li
lim (v х2 -f x — х) = lim , = lim
-^+оо ж^+оо jx2 f X f X ж4+
lim .
-f X -f X ж-4+оо Д , 1 , i 2
V
Д , 1 , i
V X
Отметим еще следующие широко используемые в анализе правила обраще-
обращения с символами о(-), О(-).
Утверждение 4. При данной базе:
a) o(f) + o(f) = o(f);
b) o(/) есть также О(/);
c) о(/) + O(f) = O(f);
d) O(f) + O(f) = O(f);
g(x) \g(x)J g(x)
Обратите внимание на особенности действий с символами о(-), О(-), выте-
вытекающие из смысла этих символов. Например, 2о(/) = о(/), или о(/) + O(f) =
= O(f) (хотя, вообще говоря, o(f) ф 0), или о(/) = О(/), но Of/) ^ о(/).
Здесь знак равенства всюду имеет значение слова «есть». Сами символы о(),
О(-) обозначают не столько функцию, сколько указание на характер ее асим-
асимптотического поведения, которым, кстати, обладают сразу многие функции,
например, и /, и 2/, и т. п.

142 ГЛ. III. ПРЕДЕЛ
М а) После сделанного уточнения утверждение а) перестает выглядеть не-
неожиданным. Первый символ o(f) в нем означает некоторую функцию вида
c*i(x)/(x), где limai(x) = 0. Второй символ о(/), который можно (или нужно)
было бы снабдить пометкой, отличающей его от первого, означает некоторую
функцию вида аг(х)/(х), где Итаг(х) = 0. Тогда ai(x)/(x) -I- аг(х)/(х) =
= (ai(x) + a2(x))/(x) = a3(x)/(x), где Ита3(х) = 0.
b) Следует из того, что всякая функция, имеющая предел, является фи-
финально ограниченной.
c) Следует из Ь) и d).
d) Следует из того, что сумма финально ограниченных функций финально
ограничена.
_а(х)/(х)_^ч/(х)_У/(х)
9(х) 9(х)
Аналогично проверяется и вторая часть утверждения е). >
Пользуясь этими правилами и эквивалентностями, полученными в при-
примере 40, теперь можно следующим прямым методом искать предел из при-
примера 42:
lim (а/х2 + х - х) = lim x
—^ + ОО >¦ ' X—Ц-ОО
1+--1 =
= lim x(l + ±-± + o(±)-l) = lim
V 2 X \X
-Ч-хо(-)) =
9 V т / /
= lim (l+o(l)\
\2 v 7 2
Несколько позже мы докажем следующие важные соотношения, которые
уже сейчас стоит запомнить как таблицу умножения:
х = 1 + -гх+ —х2 + +
ех = 1 + -гх+ —х2 + ... + —%хп + ... при х G R,
1! 2! п\
1 1 (—1)*
cosx = 1 -*?т х2 + — х4 + ... + 77Г7ТГ х2Л + • • • ПРИ х
Z! 4! (^^'
при
1 2 1 3 ("I)
2 3 ' n
n—1
хп + ... при
п.! '

§ 2. ПРЕДЕЛ ФУНКЦИИ 143
Эти соотношения, с одной стороны, уже могут служить вычислительными
формулами, а с другой стороны, как будет видно, содержат в себе следующие
асимптотические формулы, обобщающие формулы, полученные в примерах
37-40:
hx+kx2+-+hxn+°(xn+1) прих^о,
при х —> 0,
1! 3! BA: -f 1)! v
— xn + O(xn+1) при x^O,
п
а(а-1)(а-п+1)х {хП+1) _^
Эти формулы обычно являются наиболее эффективным средством при отыс-
отыскании пределов элементарных функций. При этом полезно иметь в виду, что
O(xm+1) = xm+1 • O(l) = хт • х • ОA) = хт • оA) = о(хт) при х -> 0.
Рассмотрим в заключение несколько примеров, показывающих эти форму-
формулы в работе.
Пример 43.
x.sina. ( )
= ЙЬ —^ ? ^ = Ь ( + °W) = 3!
Пример 44. lim x2 (I/5i±* _ Cos i^ =?
Имеем при х —^ оо:
ТТхЗ = 1+х-3 " V1 + х2 J I1 + г3 J =
1,11
cos — = 1 — — • ~

144 ГЛ. III. ПРЕДЕЛ
откуда получаем
7/x3 +x К 9 1 , Гх. _ .
" Г = ТТ • -У + ° \-Ч при X -> 00.
Таким образом, искомый предел равен
14
Пример 45.
lim
SB-+OO
Ит ехр< х2 In A Н— ) — х\ =
-юо I \ X/ J
= lim ехр (х2 A - -L + Of-IY) - х} =
*->оо *^ t Vx 2х2 \х3// J
р(^
*-юо L 2 VX
Задачи и упражнения
1. а) Докажите, что существует и притом единственная определенная на R функ
ция, удовлетворяющая требованиям:
/A) = а (а > 0, а ф 1),
/(xi)-/(x2) ч= /(xi +х2),
/(х) -> /(хо) при х -> хо-
Ь) Докажите, что существует и притом единственная определенная на R+ функ
ция, удовлетворяющая требованиям:
/(а) = 1 (о > 0, а # 1),
/(*i) + /(*2) = /(xi -х2),
/(х) -> /(хо) при хо € R+ и R+ Э х ->
Указание. Просмотрите еще раз конструкцию показательной и логарифмиче-
логарифмической функций, разобранную в примере 10.
2. а) Установите взаимно однозначное соответствие у> : R -> R+ так, чтобы
для любых х, у € R было 1р(х + у) = у>(х) • у>(у), т. е. чтобы операции сложения
в прообразе (в R) отвечала операция умножения в образе (в R+). Наличие такого

§ 2. ПРЕДЕЛ ФУНКЦИИ 145
отображения означает, что группы (R, +) и (R+, •) как алгебраические объекты
одинаковы, или, как говорят, изоморфны.
Ь) Докажите, что группы (R, +) и (R \ 0+, •) не изоморфны.
3. Найдите пределы:
a) lim xx:
1 х++0
b) lim х
С) Вт
х+0
х-+0
пх — 1
d) lim .
4. Покажите, что
1 + - + ...Ч—= Inn -fc + o(l) при п —> оо,
где с — постоянная. (Число с = 0,57721... называется постоянной Эйлера.)
Указание. Можно воспользоваться тем, что
In 2-±-i = In (l + i) = !+ Of Л) при n->oo.
5. Покажите, что:
оо оо
a) если два ряда Y1 ап, ?Ьп с положительными членами таковы, что ап ~ Ьп
п=1 п=1
при п —> оо, то эти ряды сходятся или расходятся одновременно;
оо ^
b) ряд ^2 sin — сходится только при р > 1.
п=1 п
6. Покажите, что:
оо / 1 \
а) если ап ^ an+i > 0 при любом п € N и ряд ^ an сходится, то ап = о ( — ) при
п=1 Чп/
п -> сх>;
A \ °°
—), то всегда можно построить сходящийся ряд ^ ап
такой,
что bn = o(an) при п -> оо;
оо оо
с) если ряд ^2 ап с положительными членами сходится, то ряд Y1 Ап > гДе -^п =
п=1 п=1
оо / оо
a>k — a S afc» тоже сходится, причем an = о(Лп) при п —> сх>;
оо оо
d) если ряд ^2 ап с положительными членами расходится, то ряд ^ Ап, где
п=1 п=2
п /п-1
а* "" -\/ S afc» тоже расходится, причем Ап = о(ап) при п -> сх>.
V
Из с) и d) следует, что никакой сходящийся (расходящийся) ряд не может слу-
служить универсальным эталоном для установления сходимости (расходимости) других
рядов путем сравнения с ним.

146 ГЛ. III. ПРЕДЕЛ
7. Покажите, что:
оо
а) РЯД Е 1пап, где ап > О, п € N, сходится тогда и только тогда, когда после-
n=l
довательность {Пп = ai ... оп} имеет отличный от нуля предел;
оо
Ь) ряд Yl ln(l + an), где |an| < 1, абсолютно сходится тогда и только тогда,
оо
когда сходится абсолютно ряд Y1 а" •
п=1
Указание. См. задачу 5а).
оо
8. Говорят, что бесконечное произведение Yl e* сходится, если последователь-
k=1 w
ность чисел Пп = Yl е* имеет конечный, отличный от нуля предел П. Тогда пола-
к=1
оо
гают П = Yl
k=i
Покажите, что
а) если бесконечное произведение Yl еп сходится, то еп —> 1 при п -> оо;
оо
n=l
оо
b) если Vn € N (en > 0), то бесконечное произведение Yl en сходится тогда и
п=1
оо
только тогда, когда сходится ряд ^2 In en;
п=1
оо
c) если en = l-han и все ап одного знака, то бесконечное произведение Yl A+atn)
оо ~
сходится тогда и только тогда, когда сходится ряд ^2 ап •
п=1
9. а) Найдите П A +х2п).
п=1
оо
Ь) Найдите Yl cos ^г и докажите следующую формулу Виета1^:
п=1 2
7Г 1
- + - - + - Д
с) Найдите функцию /(ж), если
/@) = 1,
= cos2 ж •
/(х) -> /@) при х -> 0.
Указание: ж = 2 • —.
. Виет A540 — 1603) — французский математик, один из создателей современной
алгебраической символики.

§ 2. ПРЕДЕЛ ФУНКЦИИ 147
10. Покажите, что
h °°
а) если г-2— = 1 + /Зп, п = 1, 2, ..., и ряд 53 Рп абсолютно сходится, то суще-
Ол+1 п=1
ствует предел lim Ьп = Ь € R;
оо
b) если —— = 1 -f — + an, n = l, 2, ..., причем ряд 53 a" абсолютно сходится,
то fln ~ -г при п -> оо;
оо оо
оо оо
с) если ряд J2 ап таков, что —З— = 1 -f - +an и ряд У] an абсолютно сходится,
n=l an+l П ~!
оо
то ряд 53 о>п абсолютно сходится при р > 1 и расходится при р ^ 1 (признак Гаусса
абсолютной сходимости ряда).
11. Покажите, что для любой последовательности {ап} с положительными чле-
членами
Ш
ап
и эта оценка неулучшаема.

ГЛАВА IV
НЕПРЕРЫВНЫЕ ФУНКЦИИ
§ 1. Основные определения и примеры
1. Непрерывность функции в точке. Пусть / — вещественнозначная
функция, определенная в некоторой окрестности точки a G Ш.
Описательно говоря, функция / непрерывна в точке а, если ее значения
f(x) по мере приближения аргумента х к точке а приближаются к значению
f(a) функции в самой точке а.
Уточним теперь это описание понятия непрерывности функции в точке.
Определение 0. Функция / называется непрерывной в точке а, если
для любой окрестности V(f(a)) значения /(а) функции в точке а найдется та-
такая окрестность U(a) точки а, образ которой при отображении / содержится
в V(f(a)).
Приведем формально-логическую запись этого определения вместе с двумя
его вариациями, часто используемыми в анализе:
/ непрерывна в точке а := VF(/(a)) 3U(a) (f(U(a)) С
\/е > 0 3U(a) \/x e U(a) (\f{x) - f{a)\ < е),
Ve > 0 36 > 0 Vx е Ж (\х-а\<6=* \f{x) - f(a)\ < е).
Эквивалентность этих формулировок для вещественнозначных функций
следует из того, что (как уже неоднократно отмечалось) любая окрестность
точки содержит некоторую симметричную окрестность этой точки.
Например, если по любой е-окрестности Vе(f (а)) точки /(а) можно подо-
подобрать окрестность U(a) точки а так, что Vx G U(a) (\f(x) — /(a)| < е), т. е.
f(U(a)) С Ve(f(a)), то и для любой окрестности V(f(a)) тоже можно подо-
подобрать соответствующую окрестность точки а. Действительно, достаточно
сначала взять Vе(f (а)) С V(f(a)), а затем по Vе(/(а)) найти U(a). Тогда
f(U(a)) С Vе(f(a)) С F(/(a)).

§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ 149
Таким образом, если функция непрерывна в точке а в смысле второго из
приведенных определений, то она непрерывна в ней и в смысле исходного
определения. Обратное очевидно, поэтому эквивалентность первых двух фор-
формулировок проверена.
Дальнейшую проверку оставляем читателю.
Чтобы не отвлекаться от основного определяемого понятия непрерывности
функции в точке, мы сначала для простоты предположили, что функция /
определена в целой окрестности точки а. Рассмотрим теперь общий случай.
Пусть /: -Е -+ К — вещественнозначная функция, определенная на некото-
некотором множестве Е С К, и а — точка области определения функции.
Определение 1. Функция f: Е -+ Ж называется непрерывной в точ-
точке а € Е, если для любой окрестности V(f(a)) значения /(а) функции, при-
принимаемого ею в точке а, найдется такая окрестность Ue{o) точки а в мно-
множестве1) Е, образ которой /(С/я(а)) содержится в V(f(a)).
Итак,
/ : Е —> Ш непрерывна в a G Е :=
3UE(a) (f(UE(a))cV(f(a))).
Разумеется, определение 1 тоже можно записать в е - 5-форме, рассмотрен-
рассмотренной выше. Там, где нужны числовые оценки, это бывает полезно и даже не-
необходимо.
Запишем эти вариации определения 1:
/: Е —>- R непрерывна в a G Е :=
= Ve > 0 3UE(a) \/x (Е UE(a) (\f{x) - f(a)\ < е),
или
/: Е -+Ш непрерывна в a G Е :=
= Ve > О 3S > О V* е Е (\х - а\ < S => \f(x) - f(a)\ < e).
Обсудим теперь детально понятие непрерывности функции в точке.
1° Если а — изолированная, т. е. не предельная, точка множества Е, то
найдется такая окрестность U(a) точки а, в которой нет других точек множе-
множества Е, кроме самой точки а. В этом случае Ue{o) = а, и поэтому /(С/^(а)) =
= /(а) С F(/(a)), какова бы ни была окрестность V(f(a)). Таким образом, в
любой изолированной точке области определения функция, очевидно, непре-
непрерывна. Но это вырожденный случай.
Напомним, что Ue(o>) = Е П U(a).

150 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
t
2° Содержательная часть понятия непрерывности относится, таким обра-
образом, к тому случаю, когда а € Е и а — предельная точка множества Е. Из
определения 1 видно, что
(/: Е —>- Ж непрерывна в а € -Б, где а — предельная точка Е)
W lim f(
\ ЕЭх-+а
< В самом деле, если а — предельная точка Е, то определена база Е Э х —> а
о
проколотых окрестностей Ue{o) = Ue(o) \ о, точки а.
Если / непрерывна в точке а, то, найдя для окрестности V(f(a)) окрест-
окрестность Ue{o) такую, что /(t/e(a)) С F(/(a)), мы одновременно будем иметь
о
1(Уе{о)) С F(/(a)) и в силу определения предела, таким образом, lim f(x) =
Обратно, если известна, что lim fix) = /(а), то по окрестности F(/(a))
оо
найдем проколотую окрестность Ue{cl) так, что /({/^(а)) С F(/(a)). Но по-
поскольку /(a) G F(/(a)), то тогда и /(С/^(а)) С V(/(a)). В силу определения 1
это означает, что функция / непрерывна в точке a G Е. >
3° Поскольку соотношение lim f(x) = /(а) можно переписать в форме
ЕЭх—ю.
f(x) = /( li
мы теперь приходим к полезному заключению, что непрерывные в точке функ-
функции (операции) и только они перестановочны с операцией предельного пере-
перехода. Это означает, что то число /(а), которое получается при выполнении
операции / над числом а, можно сколь угодно точно аппроксимировать зна-
чениями, получаемыми при выполнении операции / над соответствующими
заданной точности приближенными значениями х величины а.
4° Если заметить, что при а € Е окрестности Ue{o) точки а образуют
базу Ва (независимо от того, является ли а предельной или изолированной
точкой множества), то мы увидим, что само определение 1 непрерывности
функции в точке а совпадает с определением того, что число f(a) — значение
функции в точке а — является пределом функции / по этой базе, т. е.
(/: Е -* R непрерывна в а € Е) <=> (\imf(x) = /(a)V
5° Заметим, однако, что если lim f(x) существует, то, поскольку a G Ue(o)
Da
для любой окрестности f/^(a), этот предел неизбежно оказывается равным
/(а).
Таким образом, непрерывность функции /: Е -* Ж в точке а € Е равно-
равносильна существованию предела этой функции по базе Ва окрестностей (но не
проколотых окрестностей) Ue{o) точки а в Е.

§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ 151
Итак,
(/: 25 -> R непрерывна в а € Е) <^ (З lim f(x)}.
6° В силу критерия Коши существования предела теперь можно сказать,
что функция непрерывна в точке a G Е тогда и только тогда, когда для
любого е > О найдется окрестность Ue{o) точки а в Е такая, на которой
колебание u(f; Ue(o>)) функции меньше е.
Определение 2. Величина u(f]a) = lim tj(/;[/j|(a)) (где U^(a) есть
S>Ю
5-окрестность точки а в множестве Е) называется колебанием функции f:
Е —> Ж в точке а.
Формально символ u{f\X) уже занят, он обозначает колебание функции на
множестве X. Однако мы никогда не будем рассматривать колебание функ-
функции на множестве, состоящем из одной точки (это колебание, очевидно, равно
нулю); поэтому символ cj(/;a), где а — точка, всегда будет обозначать то
понятие колебания функции в точке, которое мы только что ввели определе-
определением 2.
Колебание функции на подмножестве не превышает колебания функции
на множестве, поэтому величина u(f;U^(a)) есть невозрастающая функция
от 6. Поскольку она неотрицательна, то либо она имеет конечный предел при
S —> +0, либо при любом 6 > 0 выполнено u(f; U^(a)) = +oo. В последнем
случае естественно полагают u(f; a) = +оо.
7° Используя определение 2, сказанное в 6° теперь можно резюмировать
так: функция непрерывна в точке тогда и только тогда, когда ее колебание в
этой точке равно нулю. Зафиксируем это:
: Е -? R непрерывна в о Е В) ^ (^(/; а) = 0).
Определение 3. Функция f: Е —> Ж называется непрерывной на мно-
множестве Е, если она непрерывна в каждой точке множества Е.
Совокупность всех вещественнозначных функций, непрерывных на множе-
множестве Е, условимся обозначать символом С(Е;Ш) или, короче, С(Е).
Мы обсудили понятие непрерывности функции.
Рассмотрим теперь некоторые примеры.
Пример 1. Если f: Е -+ Ш — постоянная функция, то / G С(Е). Это
утверждение очевидно, ибо f(E) = с С V(c), какова бы ни была окрестность
V(c) точки с G
Пример 2. Функция / (х) = х непрерывна на
Действительно, для любой точки Хо G Ш имеем \f(x) — f(xo)\ = \x — хо\ < ?,
как только \х — xq\ < S = е.

152
ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
Пример 3. Функция f(x) = sin ж непрерывна на Ж.
В самом деле, для любой точки х0 € Ш имеем
sinx —
2 cos
+
sin
sin
X
X
2 ч
-Xq
2
2
= \X - Xq
?,
как только \х — a?o| < <J = s.
Мы воспользовались неравенством |sinx| ^ |x|, доказанным в гл. III, §2,
п. 2d, пример 9.
Пример 4. Функция f(x) = cos ж непрерывна на Ж.
Действительно, как и в предыдущем примере, для любой точки xq €
имеем
Icosx -
9
sin
X
+
2
Xq
2
sin
sin
X
—
2
2
Xq
как только \х — xq\<& — е.
Пример 5. Функция f(x) = ax непрерывна на
Действительно, по свойству 3) показательной функции (см. гл. III, § 2,
п. 2d, пример 10а) в любой точке xq G К. имеем
lim ах = ахо,
что, как мы теперь знаем, равносильно непрерывности функции ах в точке
Пример 6. Функция f(x) = logax непрерывна в любой точке xq G
области определения R+ = {х € Ш \ х > 0}.
В самом деле, по свойству 3) логарифмической функции (см. гл. III, § 2,
п. 2d, пример 10Ь) в любой точке xq € 1R+ имеем
lim
что равносильно непрерывности функции loga x в точке
Попробуем, кстати, по заданному е > 0 найти окрестность Ur+(xq) точки
так, чтобы в любой точке х G C/r+(xo) иметь
| loga х — loga xo| <е.
Это неравенство равносильно соотношению
Пусть для определенности а > 1; тогда последнее соотношение равносильно
условию
~? < х < хоаЕ.

§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ 153
Интервал ]хоа~е, xque[ и есть искомая окрестность точки Хо. Полезно
обратить внимание на то, что эта окрестность зависит как от величины е,
так и от самой точки жо, чего не наблюдалось в примерах 1 — 4.
Пример 7. Любая последовательность / : N —у Ж есть функция, непре-
непрерывная на множестве N натуральных чисел, поскольку каждая точка множе-
множества N является его изолированной точкой.
2. Точки разрыва. Для того чтобы лучше освоиться с понятием непре-
непрерывности, выясним, что происходит с функцией в окрестности той точки, где
она не является непрерывной.
Определение 4. Если функция / : Е -> Ж не является непрерывной
в некоторой точке множества Е, то эта точка называется точкой разрыва
функции /.
Построив отрицание к утверждению «функция / : Е —> Ж непрерывна в
точке a G Е», мы получаем следующую запись определения того, что а —
точка разрыва функции /:
a G Е — точка разрыва функции / :=
= 3V{f(a)) 4UE(a) Зх € UE(a) (/(*) I V(/(o))).
Иными словами, а ? Е — точка разрыва функции /: J3 —> R, если найдется
такая окрестность V(f(a)) значения /(а) функции в точке а, что в любой
окрестности Ue{o) точки а в множестве Е найдется точка х ? С/я(а), образ
которой не содержится в V(f(a)).
Be- J-форме это же определение выглядит так:
Зе > О V6 > 0 Зх е Е (\х - а\ < S A \f(x) - f(a)\ > e).
Рассмотрим примеры.
Пример 8. Функция f(x) = sgnx постоянна и, значит, непрерывна в
окрестности любой точки абМ, отличной от нуля. В любой же окрестности
нуля ее колебание равно 2. Значит, 0 — точка разрыва функции sgnx. За-
Заметим, что функция имеет в точке 0 и предел слева lim sgnx = — 1, и пре-
х->—О
дел справа lim sgnx = 1, но, во-первых, они не совпадают между собой, а
во-вторых, ни один из них не совпадает со значением sgnO = 0 функции в
точке 0. Это прямая проверка того, что 0 — точка разрыва функции.
Пример 9. Функция f(x) = |sgnx| имеет предел lim |sgnx| = 1 при
х -> 0, но /@) .= |sgnO| = 0, поэтому lim f(x) ф /@) и 0 — точка разрыва
ж->0
функции.
Заметим, однако, что в данном случае, изменяя значение функции в точке
0 и полагая его равным 1, мы получим функцию, непрерывную в точке 0, т. е.
устраним разрыв.

154
ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
Определение 5. Если точка разрыва а € Е функции f:E-> E такова,
что существует непрерывная функция f: Е -+ Е такая, что /|#\а = /\е\сп т0
а называется точкой устранимого разрыва функции f: Е -> Е.
Таким образом, точка устранимого разрыва характеризуется тем, что су-
существует предел lim f(x) = А, но А ф /(а), и достаточно положить
ЕЭх+а
f(x) при xGE, х ф а,
при х = а,
fix) =
как мы уже получим непрерывную в точке а функцию /: Е
Пример 10. Функция
= <
sin - при х ф 0,
X
0
при х = 0
разрывна в точке 0. При этом она даже не имеет предела при х —>- 0, ибо, как
было показано в гл. III, § 2, п. 1, пример 5, не существует предела lim sin -.
График функции sin - изображен на рис. 12.
х
Примеры 8, 9 и 10 поясняют следующую терминологию.
Определение 6. Точка а € Е называется точкой разрыва первого рода
для функции /: Е
если существуют пределы
1)
lim f(x) =: f(a
0),
lim
ЕЭх-+а+0
а — точка разрыва, то а — предельная точка множества Е. Однако может слу-
случиться, что все точки множества Е в некоторой окрестности точки а лежат по одну сторону
от точки а. В этом случае рассматривается только один из указанных в определении пре-
пределов.

§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ 155
но по крайней мере один из этих пределов не совпадает со значением /(а)
функции в точке а.
Определение 7. Если а € Е — точка разрыва функции /: Е —> Ж и
в этой точке не существует по меньшей мере один из пределов, указанных в
определении 6, то а называется точкой разрыва второго рода.
Таким образом, имеется в виду, что всякая точка разрыва, не являющаяся
точкой разрыва первого рода, является точкой разрыва второго рода.
Приведем еще два классических примера.
Пример 11. Функция
1, если х е Q,
Т>(х) = <
О, если х € R \ Q,
называется функцией Дирихле1^.
Эта функция разрывна во всех точках, причем, очевидно, все ее точки
разрыва — второго рода, так как на любом интервале есть как рациональные,
так и иррациональные числа.
Пример 12. Рассмотрим функцию Римана2^
Щх) = <
, если х = — € Q, где несократимая дробь,
п п п
О, если х еЖ\
Заметим, что, каковы бы ни были точка а € К и ее ограниченная окрест-
окрестность U(а) и каково бы ни было число N G N, в U(a) имеется только конечное
число рациональных чисел —, m G Z, п € N, таких, что п < N.
п
Уменьшая окрестность, можно, таким образом, считать, что знаменатели
всех рациональных чисел, попадающих в нее (кроме, быть может, числа а,
если а € Q), уже больше чем N. Таким образом, в любой точке х € U(a)
\Щх)\ < 1/N.
Мы показали тем самым, что в любой точке а € Ш \
lim Щх) = 0.
х+а
Значит, функция Римана непрерывна в любой иррациональной точке. В
остальных точках, т. е. в точках х € Q, функция разрывна, и все эти точки
являются точками разрыва первого рода.
1^П. Г. Л. Дирихле A805 — 1859) — крупный немецкий математик-аналитик, занявший
пост ординарного профессора Геттингенского университета после смерти К. Гаусса A855).
2>Б. Ф. Риман A826 — 1866) — выдающийся немецкий математик, фундаментальные ра-
работы которого легли в основу целых областей современной геометрии и анализа.

156 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
§ 2. Свойства непрерывных функций
1. Локальные свойства. Локальными называют такие свойства функ-
функций, которые определяются поведением функции в сколь угодно малой окрест-
окрестности точки области определения.
Таким образом, сами локальные свойства характеризуют поведение функ-
функции в каком-то предельном отношении, когда аргумент функции стремится
к исследуемой точке. Например, непрерывность функции в некоторой точке
области определения, очевидно, есть локальное свойство функции.
Укажем основные локальные свойства непрерывных функций.
Теорема 1. Пусть f: Е -> Ж — функция, непрерывная в точке а € Е.
Тогда справедливы следующие утверждения:
1° Функция f ограничена в некоторой окрестности Ue{o) точки а.
2° Если f(a) ф 0, то в некоторой окрестности Ue(o>) точки а все значе-
значения функции положительны или отрицательны вместе с f(a).
3° Если функция g: Ue{cl) —> Ж определена в некоторой окрестности точ-
точки а и, как и f : Е —> Ж, непрерывна в самой точке а, то функции:
а) (/ + $)(*) :=/(*)+$(*),
Ь)
(f\ /(я)
— )(х) := -у-^ (при условии, что д(х) ф 0)
определены в некоторой окрестности точки а и непрерывны в точке а.
4° Если функция g : Y —> Ж непрерывна в точке b G Y, а функция f
такова, что f:E-+Y, f(a) = b и f непрерывна в точке а, то композиция
(9 ° /) определена на Е и также непрерывна в точке а.
М Для доказательства теоремы достаточно вспомнить (см. § 1), что не-
непрерывность функции / или g в некоторой точке а области определения рав-
равносильна тому, что предел этой функции по базе Ва окрестностей точки а
существует и равен значению функции в самой точке a: lim/(x) = /(a),
limg(x) =g(a).
Таким образом, утверждения 1°, 2°, 3° теоремы 1 непосредственно вы-
вытекают из определения непрерывности функции в точке и соответствующих
свойств предела функции.
В пояснении нуждается только то, что отношение ^-7—7 в самом деле опре-
9(х)
делено в некоторой окрестности Ue(o>) точки а. Но, по условию, д(а) ф 0 и
в силу утверждения 2° теоремы найдется окрестность %(а), в любой точке
fix)
которой д(х) ф 0, т. е. ^~~ определено в Ue(а)-
9\х)

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 157
Утверждение 4° теоремы 1 является следствием теоремы о пределе компо-
композиции, в силу которой
Urn (д о f)(x) = limg(y) = g(b) = g(f(a)) = (g о /)(а),
что равносильно непрерывности (д о f) в точке a.
Однако для применения теоремы о пределе композиции нужно проверить,
что для любого элемента Uy(b) базы Вь найдется элемент Ue(o) базы Ва та-
такой, что /(С/#(а)) С С/уF). Но в самом деле, если Uy(b) = КП ?/(Ь), то по
определению непрерывности функции /: Е —>- У в точке а для окрестности
{/F) = U(f(a)) найдется окрестность Ue{o) точки а в множестве Е такая,
что /(f/^(a)) С U(f(a)). Поскольку / действует из Е в Y, то /(%(а))С УП
П U(f(a)) = Uy(b) и мы проверили законность применения теоремы о пределе
композиции. >
Пример 1. Алгебраический многочлен Р(х) = аохп + aix*1 + ... 4- an
является функцией, непрерывной на Е. х
Действительно, из пункта 3° теоремы 1 по индукции следует, что сумма и
произведение конечного числа непрерывных в некоторой точке функций есть
функция непрерывная в этой точке. Мы проверили в примерах 1 и 2 § 1,
что постоянная функция и функции f(x)=x непрерывны на Ш. Тогда на
непрерывны и функции ахт = а х... ж, а следовательно, и полином Р(х).
т раз
Р(х)
Пример 2. Рациональная функция R(x) = ; :
Q(x)
мов — непрерывна всюду, где она определена, т. е. где Q(x) ф 0. Это следует
из примера 1 и утверждения 3° теоремы 1.
Пример 3. Композиция конечного числа непрерывных функций непре-
непрерывна в любой точке области своего определения. Это по индукции вытекает
из утверждения 4° теоремы 1. Например, функция esin (lnlcos*l) непрерывна
всюду на R, за исключением точек ^B к -hi), fe€Z, где она не определена.
2. Глобальные свойства непрерывных функций. Глобальным свой-
свойством функции, описательно говоря, называется свойство, связанное со всей
областью определения функции.
Теорема 2 (теорема Больцано — Коши о промежуточном значении).
Если функция, непрерывная на отрезке, принимает на его концах значения
разных знаков, то на отрезке есть точка, в которой функция обращается
в нуль.
В логической символике эта теорема имеет следующую запись1):
(/ € С[а,Ь)) А {/(а) ¦ f(b) < 0) => Зс € [а,Ь] (/(с) = 0).
„, ч — отношение полино-
Q(x)
*' Напомним, что символ С(Е) обозначает совокупность всех функций, непрерывных на
множестве Е. В случае Е = [а,Ь] вместо С([а, Ь]) часто пишут сокращенно С[а,Ь].

158 гл. iv. непрерывные функции
Ч Делим отрезок [а, Ь] пополам. Если в точке деления функция не равна
нулю, то на концах одного из двух полученных в результате деления отрезков
функция снова принимает значения разных знаков. С этим отрезком посту-
поступаем теперь так же, как и с исходным отрезком [а, Ь], т. е. делим его пополам,
и продолжаем процесс дальше.
Тогда мы либо на каком-то шаге попадем в точку с € [а, Ь], где /(с) = О,
либо получим последовательность {/п} вложенных отрезков, длины которых
стремятся к нулю и на концах которых / принимает значения разных знаков.
В последнем случае на основании леммы о вложенных отрезках найдется един-
единственная точка с Е [а, Ь], общая для всех этих отрезков. По построению су-
существуют две последовательности {х'п} и {х„} концов отрезков 1п такие, что
f(x'n) < 0, /(#„) > 0, lim х'п = lim х„ = с. По свойствам предела и опреде-
п—юо п—Уоо
лению непрерывности получаем lim f(x'n) = /(с) ^ 0, lim f(x'^) = /(с) ^ 0.
П—ЮО П—?О0
Таким образом, /(с) = 0. >
Замечания к теореме 2. 1° Доказательство теоремы доставляет
простейший алгоритм отыскания корня уравнения f(x) = 0 на отрезке, в
концах которого непрерывная функция имеет значения разных знаков.
2° Теорема 2, таким образом, утверждает, что при непрерывном измене-
изменении нельзя перейти от положительных значений к отрицательным или наобо-
наоборот, не приняв по дороге значения нуль.
3° К описательным высказываниям типа 2° следует относиться с разум- *
ной осторожностью, поскольку в них обычно подразумевается больше, чем
высказывается. Рассмотрим, например, функцию, равную — 1 на отрезке [0,1]
и равную 1 на отрезке [2,3]. Ясно, что эта функция непрерывна на обла-
области своего определения, принимает там значения разных знаков, но нигде не
обращается в нуль. Это замечание показывает, что свойство непрерывной
функции, выраженное теоремой 2, действительно проистекает от некоторо-
некоторого свойства ее области определения (которое, как впоследствии выяснится,
состоит в том, что это множество должно быть связным).
Следствие теоремы 2. Если функция <р непрерывна на интервале
и в каких-то точках а и Ь интервала принимает значения <р(а) = А и
ip(b) = В, то для любого числа С, лежащего между А и В, найдется точка
с, лежащая между точками а иЬ, в которой (р(с) = С.
< Отрезок / с концами а, Ь лежит в нашем интервале, поэтому функ-
функция f(x) = <р(х) — С определена, непрерывна на / и, поскольку /(а) • f(b) =
= (А — С)(В — С) < 0, по теореме 2 между а и Ь найдется точка с, в которой
/(с) = ф) - С = 0. >
Теорема 3 (теорема Вейерштрасса о максимальном значении). Функ-
Функция, непрерывная на отрезке, ограничена на нем. При этом на отрезке есть
точка, где функция принимает максимальное значение, и есть точка, где
она принимает минимальное значение.

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 159
4 Пусть /: Е -* Ш — непрерывная функция на отрезке Е = [а, 6]. В силу
локальных свойств непрерывной функции (см. теорему 1) для любой точки
х G Е найдется окрестность U(x) такая, что на множестве Ue(x) = Е П U(x)
функция ограничена. Совокупность таких окрестностей U(x), построенных
для всех точек х G 2?, образует покрытие отрезка [а, 6] интервалами, из кото-
которого по лемме о конечном покрытии можно извлечь конечную систему U(xi),
..., U(xn) интервалов, покрывающих в совокупности отрезок [а, Ь]. Поскольку
на множестве ECiU(xk) = Ue(xic) функция ограничена, т. е. m* ^ f(x) ^
где т*, Мк €Ш и х € Е/#(я*), то в любой точке х G Е = [а, Ь] имеем
min{mi, ..., mn} ^ f(x) ^ max {Mi, ..., М„}.
Ограниченность функции на отрезке [а, Ь] установлена.
Пусть теперь М = sup/(я). Предположим, что в любой точке х G Е
(f(x) < М). Тогда непрерывная на Е функция М — f(x) нигде на Е не обра-
обращается в нуль, хотя (в силу определения М) может принимать значения, сколь
угодно близкие к нулю. Тогда функция ——77~т > с одной стороны, в силу ло-
М — j\x)
кальных свойств непрерывных функций, непрерывна на Е, ас другой — не
ограничена на Е, что противоречит уже доказанной ограниченности функ-
функции, непрерывной на отрезке.
Итак, существует точка хм € [а, Ь], в которой /(хм) = М.
Аналогичным образом, рассмотрев т = inf f(x) и вспомогательную
•I *Cii
функцию -77—г , докажем, что существует точка хт G [а, Ь], в которой
f(x) — m
f(xm) = т. >
Заметим, что, например, функции /i(#) = #, /г(^) = - непрерывны на
х
интервале Е = @,1), но /i не имеет на Е ни максимального, ни минимально-
минимального значений, а функция f2 не ограничена на Е. Таким образом, выраженные
теоремой 3 свойства непрерывной функции также связаны с некоторым свой-
свойством области определения, а именно с тем, что из покрытия множества Е
окрестностями его точек можно извлечь конечное покрытие. Такие множе-
множества мы впоследствии назовем компактами.
Прежде чем перейти к следующей теореме, дадим
Определение 1. Функция /: Е -» Ж называется равномерно непрерыв-
непрерывной на множестве Е С Ш, если для любого числа е > 0 найдется число S > О
такое, что для любых точек a;i,#2 € Е таких, что \х\ — х2\ < S, выполнено
- Д*2)| < е.
Короче,
f: Е -+ Ш равномерно непрерывна :=
= Ve > 0 3S > 0 Vxi G E Vx2 G Е (\хг - х2\ < S => \/(хг) - f(x2)\ < e).

160 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
Обсудим понятие равномерной непрерывности.
1° Если функция равномерно непрерывна на множестве, то она непрерыв-
непрерывна в любой его точке. Действительно, достаточно в приведенном определе-
определении положить х\ = х и Х2 = а и мы видим, что определение непрерывности
функции /:?->1в точке a Е Е удовлетворено.
2° Непрерывность функции, вообще говоря, не влечет ее равномерную не-
непрерывность.
Пример 4. Уже неоднократно встречавшаяся нам функция f(x) = sin -
на интервале ]0,1[ = Е непрерывна. Однако в любой окрестности точки 0 в
множестве Е функция принимает как значение —1, так и значение 1, поэтому
при е < 2 для нее уже не выполнено условие |/(#i) — /(#2)! < ?•
Полезно в этой связи записать в явном виде отрицание свойства функции
быть равномерно непрерывной:
/: Е —> Ш не является равномерно непрерывной :=
3хг еЕ Зх2 еЕ {\xi -x2\ < SA\f(x1)-f(x2)\ ^
Рассмотренный пример делает наглядным различие между непрерывно-
непрерывностью и равномерной непрерывностью функции на множестве. Чтобы ука-
указать то место в определении равномерной непрерывности, откуда проистека-
проистекает это различие, приведем подробную запись того, что значит, что функция
/: Е —? Ш непрерывна на множестве Е:
f: Е -*Ш непрерывна на Е :=
= Va G E V? > 0 36 > 0 Vs G Е (\х - а\ < S => \f(x) - f(a)\ < e).
Таким образом, здесь число S выбирается по точке а ? Е и числу е и
потому при фиксированном е может меняться от точки к точке, как это и
происходит в случае функции sin -, рассмотренной в примере 1, или в случае
функции loga х или аж, рассматриваемых на полной области их определения.
В случае же равномерной непрерывности гарантируется возможность вы-
выбора 8 только по числу е > 0 так, что во всех точках a G Е из \х — а\ < S при
х G Е будет следовать \f(x) — /(a)| < e.
Пример 5. Если функция /: Е —> R не ограничена в любой окрестности
фиксированной точки хо G Е, то она не является равномерно непрерывной.
Действительно, тогда при любом S > 0 в --окрестности хо найдутся точ-
ки д?1, Х2 Е Е такие, что \f(xi) - /(яг)! > 1» хотя \xi - х2\ < S.
Так обстоит дело с функцией f(x) = -, рассматриваемой на множестве
х
R \ 0. В данном случае xq = 0.
Так обстоит дело и с функцией loga x, определенной на множестве положи-
положительных чисел и неограниченной в окрестности точки xq = 0.

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 161
Пример 6. Функция f(x) = х2, непрерывная на К, не является равно-
равномерно непрерывной на R.
В самом деле, в точках х'п = у/п + 1, х1^ = у/п, где и Е N, имеем f(x'n) =
= и + 1, /«) = п, поэтому /(а?) - /«) = 1. Но
lim (у/п~+Т — у/п) = lim .
п-+оо n-юо ^/п + 1 +
поэтому при любом S > О найдутся точки д;^, ж^ такие, что |д;^ - х„\ < 6, в то
время как /(я;^) - f(xn) = 1-
Пример 7. Функция /(х) = sin я2, непрерывная и ограниченная на Е,
не является равномерно непрерывной на Ш. Действительно, в точках х'п =
, < = ^|п, где п е N, имеем |/«) - /(ж^)| = 1, в то время
как lim \х'п - х„\ = 0.
После этого обсуждения понятия равномерной непрерывности функции и
сопоставления непрерывности и равномерной непрерывности мы можем те-
теперь оценить следующую теорему.
Теорема 4 (теорема Кантора—Гейне о равномерной непрерывности).
Функция, непрерывная на отрезке, равномерно непрерывна на этом отрезке.
Отметим, что в имеющейся литературе эту теорему обычно называют тео-
теоремой Кантора. Чтобы избежать разночтений, мы в дальнейшем при ссылках
сохраняем это распространенное наименование.
Ч Пусть /: Е —> Е — данная функция; Е = [а, Ь] и / ? С{Е). Посколь-
Поскольку / непрерывна в любой точке х G Е, то (см. § 1, п. 1, 6°) по е > 0 можно
найти такую J-окрестность U5(x) точки я, что колебание u(f)U^(x)) функ-
функции / на множестве U^(x) = ED U6(x) точек области определения функции,
лежащих в IIs (х), окажется меньше е. Для каждой точки х € Е построим
окрестность Us(x), обладающую этим свойством. Величина S при этом мо-
может меняться от точки к точке, поэтому правильнее, хотя и более громоздко,
обозначить построенную окрестность символом Us^(x), но, поскольку весь
символ определяется точкой я, можно условиться в следующей сокращенной
записи: Щх) = Us^(x) и V(x) = U6^/2(x).
Интервалы V(x), x G Е, в совокупности образуют покрытие отрезка Е ==
= [а, Ь], из которого по лемме о конечном покрытии можно выделить конеч-
конечное покрытие V(xi), ..., V(xn). Пусть S = mini-S(xi), ..., -S(xn)\. Пока-
Покажем, что для любых точек х', х" Е Е таких, что \х' — х"\ < 6, выполнено
\f(x') — f(x")\ < е. Действительно, поскольку система интервалов V(x\),...
... , V(xn) покрывает Е, найдется интервал V(xi) этой системы, который со-
содержит точку х;, т. е. \х' — Xi\ < -6(х{). Но в таком случае
х" - Xi\ ^ \х' - х"| + \af - Xi\ < S + i

162 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
Следовательно, х', х" е и?*{)(х{) =ЕП Us^XiHxi) и потому |/(*') - /(х")|
Приведенные выше примеры показывают, что теорема Кантора сущест-
существенно опирается на некоторое свойство области определения функции. Из
доказательства видно, что, как и в теореме 3, это свойство состоит в том,
что из любого покрытия множества Е окрестностями его точек можно извлечь
конечное покрытие.
Теперь, после того как теорема 4 доказана, полезно вновь вернуться к
разобранным выше примерам непрерывных, но не равномерно непрерывных
функций и выяснить, как, например, функция sin я2, равномерно непрерывная
по теореме Кантора на каждом отрезке вещественной прямой, оказывается
не равномерно непрерывной на Ш. Причина здесь вполне аналогична той, по
которой вообще непрерывная функция может оказаться не равномерно непре-
непрерывной. На сей раз мы предоставляем читателю возможность самостоятельно
разобраться в этом вопросе.
Теперь перейдем к последней теореме параграфа — теореме об обратной
функции. Нам предстоит выяснить условия, при которых непрерывная на
отрезке вещественнозначная функция имеет обратную и в каких случаях эта
обратная функция непрерывна.
Утверждение 1. Непрерывное отображение f: Е —> Е отрезка Е =
= [а, Ь] в R инъективно в том и только в том случае, когда функция f
строго монотонна на отрезке [а, Ь].
< Если функция / возрастает или убывает на произвольном множестве
Е С М, то отображение /: Е —> М, очевидно, инъективно: в различных точках
множества Е функция принимает различные значения.
Таким образом, наиболее содержательная часть утверждения 1 состоит в
том, что всякое непрерывное инъективное отображение /: [а, Ь] -» Ж отрезка
осуществляется строго монотонной функцией.
Предположив, что это не так, мы найдем три точки х\ < Х2 < х$ отрезка
[а, Ь] такие, что /(#2) не лежит между f(x\) и /(#з)- В таком случае либо /(#з)
лежит между f(xi) и /(а^), либо f{x\) лежит между /(а^) и /(хз)- Пусть для
определенности имеет место последняя из двух указанных возможностей. По
условию функция / непрерывна на отрезке [2:2,0:3], и потому (см. следствие
теоремы 2) на нем есть точка х[ такая, что f(x[) = f(xi). Таким образом,
х\ < х[ и f(x\) = f(x[), что несовместимо с инъективностью отображения.
Случай, когда /(#з) лежит между /(#i) и /(#2), разбирается аналогично. >
Утверждение 2. Каждая строго монотонная функция /: X
определенная на числовом множестве ХсМ, обладает обратной функцией
/-1: Y -> М, которая определена на множестве Y = f{X) значений функции
/ и имеет на Y тот же характер монотонности, какой имеет функция f
на множестве X.

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 163
< Отображение /: X —? Y = f(X) сюръективно, т. е. является отображе-
отображением на множество Y. Пусть для определенности f:X->Y возрастает на X.
В этом случае
X V#2 € X (x\ < Х2 <=> f(xi) < /(#2)Ь A)
Таким образом, отображение f: X -> Y в различных точках принимает
различные значения, т. е. оно инъективно. Следовательно, f:X—>Y биектив-
биективно, т. е. / — взаимно однозначное отображение X на Y. Значит, определено
обратное отображение f~l: Y -* X, задаваемое формулой х = /~г(у), если
У = f(z).
Сопоставляя определение отображения f~l: Y -4 X с соотношением A),
приходим к соотношению
V»i € Y V2/2 e Y {Г1(Уг) < Г1Ш **У1< 2/2), B)
означающему, что функция f~l возрастает на области своего определения.
Случай, когда / : X ->> Y убывает на X, очевидно, разбирается анало-
аналогично. >
В соответствии с доказанным утверждением 2, если интересоваться не-
непрерывностью функции, обратной к вещественнозначной функции, полезно
исследовать условия непрерывности монотонных функций.
Утверждение 3. Функция /: Е —? IR, монотонная на множестве Е С
С Ш, может иметь на Е разрывы только первого рода.
М Пусть, для определенности, / — неубывающая функция. Предположим,
что а ? Е есть точка разрыва функции /. Поскольку а не может быть изоли-
изолированной точкой множества Е, то а — предельная точка по крайней мере для
одного из двух множеств Е~ = {х G Е \ х < а}, Е+ = {х 6 Е \ х > а}. Посколь-
Поскольку / — неубывающая функция, для любой точки х ? Е~ имеем f(x) ^ /(а)
и ограничение f\E- функции / на множество Е~ оказывается неубывающей
ограниченной сверху функцией. Тогда существует предел
lim (f\E-)(x)= lim /(*) =
~Эх^аУ *а/ ЕЭх^а-0
Аналогично доказывается существование предела lim f(x) = /(a + 0),
ЕЭх-+а+0
если а — предельная точка множества
Случай, когда / — невозрастающая функция, можно либо разобрать, по-
повторив проведенное доказательство, либо, перейдя к функции —/, свести дело
к уже рассмотренному случаю. >
Следствие 1. Если а — точка разрыва монотонной функции f: Е
то по крайней мере один из пределов
lim /(x) = /(a-0), lim /(*) =/(a + 0)
ЕЭх->а-0 ЕЭх-+а+0

164 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
определен; по крайней мере в одном из неравенств f(a — 0) ^ /(а) ^ /(а + 0),
если f — неубывающая (или /(а — 0) ^ /(а) ^ /(а + 0), если / — невозра-
стающая) функция, имеет место знак строгого неравенства; в интервале,
определяемом этим строгим неравенством, нет ни одного значения функции;
указанные интервалы, отвечающие различным точкам разрыва монотонной
функции, не пересекаются.
< Действительно, если а — точка разрыва, то она предельная для множе-
множества Е и в силу утверждения 3 является точкой разрыва первого рода. Таким
образом, по крайней мере одна из баз Е Э х —> а — 0, Е Э х -+ а+0 определена
и по ней (а в случае определенности обеих баз — по каждой из них) существует
предел функции /. Пусть, для определенности, / — неубывающая функция.
Поскольку а — точка разрыва, то по крайней мере в одном из неравенств
/(а — 0) ^ /(а) ^ /(а + 0) на самом деле имеет место строгое неравенство.
Поскольку f(x) ^ lim fix) = f(a — 0), если х Е Е и х < а, и, аналогично,
ЕЭх-+а—О
/(а + 0) ^ f(x), если х Е Е и а < х, то интервал, определяемый строгим
неравенством /(а — 0) < /(а) или /(а) < /(а + 0), действительно свободен от
значений функции. Пусть а±, п2 — две различные точки разрыва функции, и
пусть а\ < п2- Тогда, в силу неубывания функции /, имеем
/(«0 ^ /(<*1 + 0) ^ /(О2 - 0) ^ /Ы ^ /(О2 + 0).
Отсюда следует, что не содержащие значений функции интервалы, отве-
отвечающие различным точкам разрыва, не пересекаются. >
Следствие 2. Множество точек разрыва монотонной функции не бо-
более чем счетно.
< С каждой точкой разрыва монотонной функции свяжем, по следствию 1,
интервал, определяемый значением функции в точке разрыва и одним из пре-
пределов функции при приближении аргумента справа или слева к точке разрыва.
Эти интервалы не пересекаются. Но на прямой может быть не более чем счет-
счетное множество непересекающихся интервалов. В самом деле, в каждом из них
можно выбрать по рациональной точке, и тогда множество интервалов ока-
окажется равномощным подмножеству счетного множества Q всех рациональных
чисел. Значит, оно само не более чем счетно. Вместе с ним, таким образом, не
более чем счетно и равномощное ему по построению множество точек разрыва
монотонной функции. >
Утверждение 4 (критерий непрерывности монотонной функции). Мо-
Монотонная функция f: Е ->> IR, заданная на отрезке Е = [а, Ь], непрерывна на
нем тогда и только тогда, когда множество f(E) ее значений само явля-
является отрезком с концами1^ /(а) и /F).
*) При этом /(а) ^ /F), если / — неубывающая, и /F) ^ /(а), если / — невозрастающая
функция.

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 165
< Бели / — непрерывная монотонная функция, то ввиду монотонности
/ все значения, которые функция принимает на отрезке [а,Ь], лежат между
значениями /(а) и /(Ь), которые она принимает в концах отрезка. Ввиду не-
непрерывности функции она обязана принимать также и все промежуточные
значения между /(а) и f(b). Таким образом, множество значений функции,
монотонной и непрерывной на отрезке [а, Ь], действительно является отрезком
с концами /(а) и /(Ь).
Докажем теперь обратное утверждение. Пусть / — монотонная на от-
отрезке [а,Ь] функция. Бели она разрывна в некоторой точке с ? [а, 6], то по
следствию 1 утверждения 3 один из интервалов ]/(с — 0), /(с)[, ]/(с), /(с + 0)[
заведомо определен и в нем нет значений нашей функции. Но ввиду моно-
монотонности функции этот интервал содержится в отрезке с концами /(а), /(Ь),
поэтому если на отрезке [а, Ь] монотонная функция имеет хотя бы одну точ-
точку разрыва, то весь отрезок с концами /(a), f(b) не может лежать в области
значений функции. >
Теорема 5 (теоремаоб обратной функции). Функция /: X ->> Е, строго
монотонная на множестве X С Е, имеет обратную функцию f~l : Y —У
-у Е, определенную на множестве Y = f(X) значений функции f. Функция
/-1: Y —> Е монотонна и имеет на Y тот же вид монотонности, какой
имеет функция f: X —у Е на множестве X.
Если, кроме того, X есть отрезок [а, Ь] и функция f непрерывна на нем,
то множество Y = f(X) есть отрезок с концами f(a), f(b) и функция
f~x:Y-yR непрерывна на нем.
М Утверждение теоремы о том, что в случае X = [а, Ь] и непрерывности /
множество Y = f(X) есть отрезок с концами /(а), /(Ь), следует из доказанно-
доказанного выше утверждения 4. Остается проверить, что f~l: Y —> Е — непрерывная
функция. Но /~х монотонна на У, Y есть отрезок и f~x(Y) = X = [а,Ь] —
тоже отрезок. В силу утверждения 4 заключаем, что функция /~* непрерывна
на отрезке Y с концами /(a), f(b). >
Пример 8. Функция у = f(x) = sinx возрастает и непрерывна на от-
отрезке [—?»?]• Значит, ограничение этой функции на отрезок [—?»?] имеет
обратную функцию х = /~1B/), обозначаемую х = arcsiny, определенную на
отрезке f sin Г-~J, sin уРп = [—1,1], возрастающую от — ~ до ^ и непрерыв-
непрерывную на этом отрезке.
Пример 9. Аналогично, ограничение функции у = cos а; на отрезок
[0, тг] есть убывающая непрерывная функция, которая в силу теоремы 5 име-
имеет обратную функцию, обозначаемую х = arccosy, определенную на отрезке
[—1,1] и убывающую на нем от значения тг до значения 0.
Пример 10. Ограничение функции у = tgx на интервал X = 1—?, тН
есть возрастающая от —оо до +оо непрерывная функция, которая в силу пер-
первой части теоремы 5 имеет обратную функцию, обозначаемую х = arctgy,

166 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
определенную на всей числовой прямой у Е К и возрастающую на ней в пре-
пределах интервала 1""х»?| своих значений. Чтобы доказать непрерывность
функции х = arctg у в любой точке у о ее области определения, возьмем точку
хо = arctg j/о и отрезок [хо — е,хо + е], содержащий xq внутри и содержащийся
в интервале 1 -™, тг Г. Если х0 - е = arctg B/0 — <^i) и а?о + ? = arctg (у0 + <J2),
то ввиду возрастания функции х = arctg у можно утверждать, что при любом
yGl таком, что уо — 8\ < у < уо + <$2, будем иметь а?о — ? < arctgy < Хо + е.
Итак, \axctgy — aictgyo\ < е при — Ji < у — уо < <$2 и тем более при \у — t/o| <
< S = min{<Ji, J2}, что и проверяет непрерывность функции д; = arctg у в точке
Пример 11. Рассуждениями, аналогичными проведенным в предыдущем
примере, устанавливаем, что поскольку ограничение функции у = ctgx на
интервале ]0, тг[ есть убывающая от +оо до —оо непрерывная функция, то она
имеет обратную функцию, обозначаемую х = arcctgy, определенную на всей
числовой оси М, убывающую на ней в пределах интервала своих значений ]0, тг[
от тг до 0 и непрерывную на Ш.
Замечание. При построении графиков взаимно обратных функций у =
= f(x) и х = f~l{y) полезно иметь в виду, что точки плоскости с координа-
координатами (x,f(x)) = (х, у) и (у,/~г(у)) = (у,х) в одной и той же координатной
системе (в которой лишь указана первая и вторая оси координат, а не ось х
или ось у) симметричны относительно биссектрисы первого координатного
угла.
Таким образом, графики взаимно обратных функций, изображенные в од-
одной системе координат, оказываются симметричными относительно этой бис-
биссектрисы.
Задачи и упражнения
1. Покажите, что:
a) Если / G С(А) и В С А, то f\B G С(В).
b) Бели функция /: Е\ U 2?2 ->• R такова, что /\е{ ? C(Ei), г = 1, 2, то не всегда
f eC(EiUE2).
c) Функция Римана 7?, как и ее ограничение 7Z\q на множество рациональных
чисел, разрывна в каждой точке множества Q, кроме нуля, и все точки разрыва при
этом устранимые (см. § 1, пример 12).
2. Покажите, что если функция / G С[а,6], то функции
т(х) = min /(*), М(х) = max f(t)
также непрерывны на отрезке [а, 6].
3. а) Докажите, что функция, обратная функции, монотонной на интервале, не-
непрерывна на области своего определения.
Ь) Постройте монотонную функцию со счетным множеством точек разрыва.

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 167
с) Покажите, что если функции f : X -> Y и f~x: Y -> X взаимно обратны
(здесь X,Y — подмножества R) и / непрерывна в точке хо Е X, то из этого еще не
следует непрерывность функции f1 в точке уо = /(яо) € Y.
4. Покажите, что:
a) Если / е С[а,Ъ] л д € С[а,6], причем /(а) < р(а) и /F) > #(Ь), то существует
точка с Е [а, 6], в которой /(с) = р(с).
b) Любое непрерывное отображение / : [0,1] —> [О,1] отрезка в себя имеет непо-
неподвижную точку, т. е. точку х Е [0,1] такую, что f(x) = х.
c) Если два непрерывных отображения /ид отрезка в себя коммутируют, т. е.
/ о д = д о /, то они имеют общую неподвижную точку.
d) Непрерывное отображение /: R —> R может не иметь неподвижной точки.
e) Непрерывное отображение /: ]0,1[ —> ]0,1[ может не иметь неподвижной точки.
f) Если отображение /: [0,1] —> [0,1] непрерывно, /@) = 0, /A) = 1 и (fof)(x) =
= х на [0,1], то /(х) = х.
5. Покажите, что множеством значений любой непрерывной на отрезке функции
является отрезок.
6. Покажите, что:
a) Если отображение /: [0,1] —> [0,1] непрерывно, /@) = 0, /A) = 1 и при не-
некотором n G N fn(x) := ( /о... о/ )(х) = х на [0,1], то /(х) = х.
п раз
b) Если функция /: [0,1] —> [0,1] непрерывна и не убывает, то для любой точки
х G [0,1] реализуется по крайней мере одна из двух возможностей: либо х — непо-
неподвижная точка, либо fn(x) стремится к неподвижной точке (здесь fn(x) = /о.. .о/ —
п-я итерация /).
7. Пусть /: [0,1] —? R — непрерывная функция такая, что /@) = /A)- Покажите,
что
a) при любом п G.N существует горизонтальный отрезок с концами на графике
этой функции, длина которого равна —;
п
b) если число / не имеет вида —, то найдется функция указанного вида, в график
которой уже нельзя вписать горизонтальный отрезок длины /.
8. Модулем непрерывности функции /: Е —> R называется функция шF), опре-
определяемая при S > 0 следующим образом:
= sup \f(xi)-f(x2)l
Таким образом, верхняя грань берется по всевозможным парам точек xi, ж2 множе-
множества Е, удаленным друг от друга меньше чем на S.
Покажите, что:
a) Модуль непрерывности — неубывающая неотрицательная функция, имеющая
предел^ cj(+O) = lim ljF).
b) Для любого е > 0 найдется S > 0 такое, что для любых точек Ж1,Ж2 € Е
соотношение |xi — хг| < 6 влечет |/(xi) — /(хг)| < cj(H-O) + ?•
Поэтому модуль непрерывности обычно рассматривают при 8 ^ 0, полагая ш@) =

168 ГЛ. IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
c) Бели Е — отрезок, интервал или полуинтервал, то для модуля непрерывности
функции /: Е —> R имеет место соотношение
d) Модулем непрерывности функции х и sin ж2, рассматриваемых на всей число-
числовой прямой, являются соответственно функция шF) = 6 и постоянная и>F) = 2 в
области 8 > 0.
e) Функция / равномерно непрерывна на множестве Е тогда и только тогда,
когда ш(-1-0) = 0.
9. Пусть fug — ограниченные функции, определенные на одном и том же множе-
множестве X. Величина А = sup \f(x) — д(х)\ называется расстоянием между функциями
f и д. Она показывает, насколько хорошо одна функция аппроксимирует другую на
данном множестве X. Пусть X — отрезок [а, 6]. Покажите, что если /, д € С[а, 6], то
Зхо € [а, 6], где А = |/(жо) — <?(яо)|, и что для произвольных ограниченных функций
это, вообще говоря, не так.
10. Пусть Рп(х) — многочлен (полином) степени п. Будем приближать ограни-
ограниченную функцию /: [а, 6] —> R многочленами. Пусть
Д(РП)= sup |/(*)-Рп(*)| и Sn(/)=infA(Pn),
х€[а,Ь] рп
где нижняя грань берется по всевозможным многочленам степени п. Многочлен Рп
называется многочленом (полиномом) наилучшего приближения функции /, если
для него Д(Рп) = #п(/).
Покажите, что:
a) Существует многочлен Ро(х) = ао наилучшего приближения степени нуль.
b) Среди многочленов Q\(x) вида ЛРп(х), где Рп — фиксированный многочлен,
найдется такой многочлен Q\o, что
Д(<?Ло) =
c) Бели существует многочлен наилучшего приближения степени п, то существу-
существует также многочлен наилучшего приближения степени п + 1.
d) Для любой ограниченной на отрезке функции и любого п = 0, 1, 2, ... най-
найдется многочлен наилучшего приближения степени п.
11. Покажите, что:
a) Многочлен нечетной степени с действительными коэффициентами имеет по
крайней мере один вещественный корень.
b) Бели Рп— многочлен степени п, то функция sgnPn(«) имеет не более п точек
разрыва.
c) Бели на отрезке [а, 6] имеется п -I- 2 точки хо < х\ < ... < жп+1 такие, что
величина
постоянна при i = 0,..., п + 1, то En(f) ^ min |/(ж») — Рп(х%)\ (теорема Валле-
O^t^n+l
Пуссена1^). (Определение En(f) см. в задаче 9.)
. Ж. ла Балле-Пуссен A866—1962) — бельгийский математик и механик.

§ 2. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 169
12. а) Покажите, что при любом п € N функция Тп(х) = cos(narccos#), опреде-
определенная на отрезке [—1,1], является алгебраическим многочленом степени п (поли-
(полиномы Чебышева).
b) Найдите явное алгебраическое выражение полиномов Ti, Тг, Тз, Та и нари-
нарисуйте их графики.
c) Найдите корни многочлена Тп(х) на отрезке [—1,1] и те точки отрезка, где
величина |Тп(х)| достигает максимума.
d) Покажите, что среди многочленов Рп{х) степени п с коэффициентом 1 при хп
многочлен Тп(х) является единственным многочленом, наименее уклоняющимся от
нуля, т. е. Еп@) = max |Tn(#)| (определение En(f) см. в задаче 9).
13. Пусть / € С[а,Ъ].
a) Покажите, что если для полинома Рп(х) степени п найдутся п 4- 2 точки
хо < ... < хп+1 (называемые точками чебышевского алътернанса) такие, что
f(xi)-Pn(xi) = (-1)'Д(Рп)-а, где Д(РП) = max |/(x) -Pn(x)|, a а — постоянная,
х?[а,Ь]
равная 1 или —1, то Рп(х) является и притом единственным полиномом наилучшего
приближения функции / степени п (см. задачу 9).
b) Докажите теорему Чебышева: многочлен Рп(х) степени п тогда и только
тогда является многочленом наилучшего приближения функции / € С[а,Ъ], когда на
отрезке [а, Ь] найдется по крайней мере п + 2 точки чебышевского альтернанса.
c) Покажите, что для разрывных функций предыдущее утверждение, вообще
говоря, не верно.
d) Найдите многочлены наилучшего приближения нулевой и первой степени для
функции \х\ на отрезке [—1,2].
14. В § 2 мы обсуждали локальные свойства непрерывных функций. Настоящая
задача уточняет понятие локального свойства.
Две функции / и д будем считать эквивалентными, если найдется такая окрест-
окрестность U(a) фиксированной точки а € R, что Уж 6 U(a) имеем f(x) = g(x). Это
отношение между функциями, очевидно, рефлексивно, симметрично и транзитивно,
т. е. действительно является отношением эквивалентности.
Класс эквивалентных между собой в точке а функций называется ростком функ-
функций в данной точке а. Если рассматривают только непрерывные функции, то гово-
говорят о ростке непрерывных функций в точке а.
Локальные свойства функций — это свойства ростков функций.
a) Определите арифметические операции над ростками числовых функций, за-
заданными в одной и той же точке.
b) Покажите, что арифметические операции над ростками непрерывных функ-
функций не выводят из этого класса ростков.
c) Покажите, учитывая а) и Ь), что ростки непрерывных функций образуют
кольцо — кольцо ростков непрерывных функций.
d) Подкольцо / некоторого кольца К называется идеалом кольца К, если про-
произведение любого элемента кольца К и элемента под кольца / лежит в /. Найдите
идеал кольца ростков функций, непрерывных в точке а.
15. Идеал кольца называется максимальным, если он не содержится ни в каком
большем идеале, кроме самого кольца. Множество С[а, Ь] функций, непрерывных на
отрезке, образует кольцо относительно обычных операций сложения и умножения
числовых функций. Найдите.максимальные идеалы этого кольца.

ГЛАВА V
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 1. Дифференцируемая функция
1. Задача и наводящие соображения. Предположим, что, следуя Нью-
Ньютону1), мы хотим решить кеплерову2) задачу двух тел, т. е. хотим объяс-
объяснить закон движения одного небесного тела га (планета) относительно дру-
другого тела М (звезда). Выберем в плоскости движения декартову систему
координат с началом в М (рис. 13). Тогда положе-
положение га в момент времени t можно охарактеризо-
охарактеризовать численно координатами (x(t),y(t)) точки га
в этой системе координат. Мы хотим найти функ-
функции x{t), y(t).
Движением га относительно М управляют два
знаменитых закона Ньютона:
общий закон движения
т
Рис. 13
ma = F,
A)
связывающий вектор силы с вектором вызванного ею ускорения через коэф-
коэффициент пропорциональности га — инертную массу тела3), и
закон всемирного тяготения, позволяющий найти гравитационное воздей-
^И. Ньютон A642 —1727) — английский физик, механик, астроном и математик, круп-
крупнейший ученый, сформулировавший основные законы классической механики, открывший
закон всемирного тяготения, разработавший (наряду с Лейбницем) основы дифференциаль-
дифференциального и интегрального исчисления. Оценен был уже современниками, которые на его могиле
начертали: «Здесь покоится то, что было смертного у Ньютона».
2)И. Кеплер A571 —1630) — знаменитый немецкий астроном, открывший законы движе-
движения планет (законы Кеплера).
3^Мы обозначили массу символом самого тела, но это не приведет к недоразумениям.
Заметим также, что если т <^С Л/, то выбранную систему координат можно считать инер-
циальной.

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ171
ствие тел т и М друг на друга по формуле
г, B)
где г — вектор с началом в теле приложения силы и концом в другом теле,
|г| — длина вектора г, или расстояние между т и М.
Зная массы m, M, по формуле B) без труда выражаем правую часть урав-
уравнения A) через координаты x(t), y(t) тела т в момент ?, чем исчерпываем всю
специфику данного движения.
Чтобы получить теперь соотношения на x(t), y(t), заключенные в урав-
уравнении A), необходимо научиться выражать левую часть уравнения A) через
функции x(t), y(t).
Ускорение есть характеристика изменения скорости v(?), точнее, просто
скорость изменения скорости; поэтому для решения задачи прежде всего не-
необходимо научиться вычислять скорость v(?), которую имеет в момент t тело,
движение которого задается радиус-вектором г(?) = (x(t),y(t)).
Итак, мы хотим определить и научиться вычислять ту мгновенную ско-
скорость тела, которую подразумевает закон движения A).
Измерить — значит сравнить с эталоном. Что же в нашем случае может
служить эталоном для определения мгновенной скорости движения?
Наиболее простым видом движения является такое, которое совершает по
инерции свободное тело. Это движение, при котором за равные промежутки
времени происходят равные (как векторы) перемещения тела в пространстве.
Это так называемое равномерное (прямолинейное) движение. Бели точка дви-
движется равномерно, г@) и гA) — ее радиус-векторы относительно инерциаль-
ной системы координат в моменты t = 0 и t = 1 соответственно, то в любой
момент времени будем иметь
r(t) - г@) = v • *, C)
где v = гA) — г@). Таким образом, перемещение r(t) — г@) оказывается в
простейшем случае линейной функцией времени, причем роль множителя про-
пропорциональности между перемещением г(?)—г@) и временем t играет в данном
случае вектор v перемещения за единицу времени. Этот вектор и называется
скоростью равномерного движения. То, что движение прямолинейно, видно из
параметрического уравнения его траектории: r(t) = г@) + v • t, являющегося
(см. курс аналитической геометрии) уравнением прямой.
Мы знаем, таким образом, скорость v равномерного прямолинейного дви-
движения, задаваемого формулой C). По закону инерции, если на тело не дей-
действуют внешние силы, оно движется равномерно и прямолинейно. Значит,
если в момент t экранировать действие тела М на тело т, то последнее про-
продолжит свое движение уже равномерно с некоторой определенной скоростью.
Таким образом, естественно считать, что именно она является (мгновенной)
скоростью нашего тела в момент t.

172
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Однако такое определение мгновенной скорости оставалось бы чистой аб-
абстракцией, не дающей никаких рекомендаций для конкретного вычисления
этой величины, если бы не следующее обстоятельство первостепенной важно-
важности, которое мы сейчас обсудим.
Оставаясь в рамках того (как сказали бы логики, «порочного») круга, в
который мы вошли, написав уравнение движения A), а затем принявшись вы-
выяснять, что такое мгновенная скорость и ускорение, мы все же заметим, что
при самом общем представлении об этих понятиях из уравнения A) можно сде-
сделать следующие эвристические выводы. Если силы отсутствуют, т. е. F = О,
то ускорение тоже равно нулю. Но если скорость а(?) изменения скорости
v(?) равна нулю, то, по-видимому, сама скорость v(t) вообще не меняется со
временем. И мы приходим к закону инерции, по которому свободное тело
действительно движется в пространстве с постоянной во времени скоростью.
Из того же уравнения A) видно, что ограниченные по величине силы спо-
способны создать только ограниченные по величине ускорения. Но если на отрез-
отрезке времени [0, t] абсолютная величина скорости изменения некоторой величи-
величины P(t) не превышала некоторой постоянной с, то, по нашим представлениям,
изменение \P(t) — Р@)\ величины Р за время t не превышает с • ?, т. е. в этой
ситуации за малый промежуток времени величина мало меняется (во всяком
случае, функция P(t) оказывается непрерывной). Значит, реальная механиче-
механическая система за малый промежуток времени мало меняет свои параметры.
В частности, скорость v(t) тела т во все моменты времени t, близкие к
некоторому моменту to, должна быть близка к значению v(?q), которое мы
желаем определить. Но в таком случае само движение в малой окрестности
момента to должно мало отличаться от равномерного движения со скоро-
скоростью v(?o), причем тем меньше отличаться, чем меньше мы уходим от to.
Если бы мы сфотографировали траекторию тела га через телескоп, то в
зависимости от его силы мы получили бы примерно следующее:
Рис. 14
Представленный на фотографии с участок траектории соответствует
столь малому интервалу времени, что на нем уже трудно отличить истинную

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ 173
траекторию от прямолинейной, так как она и в самом деле на этом участке
похожа на прямолинейную, а движение — на равномерное прямолинейное. Из
этого наблюдения, кстати, можно заключить, что, решив задачу об опреде-
определении мгновенной скорости (а скорость — векторная величина), мы одновре-
одновременно решим и чисто геометрический вопрос об определении и нахождении
касательной к кривой (кривой в данном случае служит траектория движения).
Итак, мы заметили, что в нашей задаче должно быть v(t) « v(?o) при
?, близких к to, т- е. v(t) -» v(?q) при t —>• to или, что то же самое, v(t) =
= v(?o) + o(l) при t -> to- Тогда должно быть также
r(t) - r(t0) » v(*0) • (t - to)
при t, близких к to у точнее, величина смещения r(t) — r(to) эквивалентна
v(to)(t — to) при t -> to, или
r(t) - r(t0) = v(to)(t - to) + o(v(to)(t - to)), D)
где o(v(to)(t — ^o)) есть поправочный вектор, величина которого при t
стремится к нулю быстрее, чем величина вектора v(to)(t — fo)- Тут следует,
естественно, оговорить тот случай, когда v(?o) = 0. Чтобы не исключать
этот случай из общего рассмотрения, полезно заметить, что1) |v(?o)(? — *о)| =
= |v(^o)||* - *о|- Таким образом, если |v(to)| ф 0, то величина \v(to)(t - *о)|
того же порядка, что и |? — to\, и поэтому o(v(to)(t - *о)) = o(t — t0). Значит,
вместо D) можно записать соотношение
r(t) - r(to) = v(to) (t - t0) + o(t - t0), E)
которое не исключает также случая v(?o) = 0.
Таким образом, от самых общих и, быть может, расплывчатых предста-
представлений о скорости мы пришли к соотношению E), которому скорость должна
удовлетворять. Но из E) величина v(?0) находится однозначно:
v(*0) = Шп *Ь?&>, F)
t-+to t — to
поэтому как само фундаментальное соотношение E), так и равносильное ему
соотношение F) можно теперь принять за определения величины v(?o) — мгно-
мгновенной скорости тела в момент ?о-
Мы не станем сейчас отвлекаться на подробное обсуждение вопроса о пре-
пределе векторнозначной функции и ограничимся сведением его к уже рассмо-
рассмотренному во всех подробностях случаю предела вещественнозначной функции.
Поскольку вектор r(t) — г(*о) имеет координаты (x(t) — x(to), y(t) — y(to)), то
p(t) - p(t0)
t-t0
(x(t) - x(t0) y(t) - y(t0) \
= i _i-^— N \ -^—f±—z- J и, значит, если считать, что векторы
\ t — to t — to /
Здесь |t — to I — модуль числа t — to, a |v| — модуль, или длина вектора v.

174 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
близки, если их координаты близки, то предел в F) следует понимать так:
,. , r r(t) - г(*р) / x(t) - x(t0) y(t)-y(to)\
v(t0) = hm —— —- = ( hm —— —-, hm —— —- ,
7 t-+to t-t0 \ t->t0 t-t0 t-+t0 t-t0 )
a o(t — to) в E) надо понимать как вектор, зависящий от t и такой, что вектор
^- стремится (покоординатно) к нулю при t —> to.
t — Со
Наконец, заметим, что если v(to) ф 0, то уравнение
г - г(«о) = v(*0) • (* - to) G)
задает прямую, которая в силу указанных выше обстоятельств должна быть
признана касательной к траектории в точке (х(to), у (to))-
Итак, эталоном для определения скорости движения служит скорость
равномерного прямолинейного движения, задаваемого линейным соотноше-
соотношением G). Эталонное движение G) подгоняется к исследуемому так, как
этого требует соотношение E). То значение v(to), при котором E) вы-
выполнено, может быть найдено предельным переходом F) и называется ско-
скоростью движения в момент to- Рассматриваемые в классической механике
движения, описываемые законом A), должны допускать сравнение с таким
эталоном, т. е. должны допускать линейную аппроксимацию, указанную в E).
Если r(t) = (x(t),y(t)) — радиус-вектор движущейся точки т в момент ?,
r(t) = (x(t),y(t)) = v(?) — вектор скорости изменения г(?) в момент ?, а г(?) =
= (я@> ?К0) = а@ ~ вектор скорости изменения v(?), или ускорение в момент
?, то уравнение A) можно записать в виде
откуда для нашего движения в поле тяжести получаем в координатном виде
Это точная математическая запись нашей исходной задачи. Поскольку мы
знаем, как по г(?) искать r(t) и далее г(?), то уже сейчас мы в состоянии отве-
ответить на вопрос, может ли какая-то пара функций (#(?),$/(?)) задавать движе-
движение тела т вокруг М. Для этого надо найти x(t), y(t) и проверить, выполнены
ли соотношения (8). Система (8) является примером системы так называемых
дифференциальных уравнений. Пока что мы можем только проверять, явля-
является ли некоторый набор функций решением системы. Как искать решение
или, лучше сказать, как исследовать свойства решений дифференциальных
уравнений, изучается в специальном и, как уже сейчас можно понять, весьма
ответственном отделе анализа — теории дифференциальных уравнений.

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ 175
Операция отыскания скорости изменения векторной величины, как было
показано, сводится к отысканию скорости изменения нескольких числовых
функций — координат вектора. Таким образом^ эту операцию следует прежде
всего научиться свободно выполнять в простейшем случае вещественнознач-
ных функций вещественного аргумента, чем мы теперь и займемся.
2. Функция, дифференцируемая в точке. Начнем с двух предвари-
предварительных определений, которые мы чуть ниже несколько уточним.
Определение Oi. Функция /: Е -> К, определенная на множестве Е С
С К, называется дифференцируемой в точке a Е Е, предельной для множества
Е, если существует такая линейная относительно приращения х — а аргумента
функция А • (х — а), что приращение f(x) — /(а) функции / представляется в
виде
f(x) — f(a) = А • (х — а) + о(х - а) при х -> а, х G Е. (9)
Иными словами, функция дифференцируема в точке а, если изменение ее
значений в окрестности исследуемой точки линейно с точностью до поправки,
бесконечно малой по сравнению с величиной х — а смещения от точки а.
Замечание. Как правило, дело приходится иметь с функциями, опреде-
определенными в целой окрестности рассматриваемой точки, а не только на каком-то
подмножестве этой окрестности.
Определение Ог- Линейная функция А - (х — а) из (9) называется диф-
дифференциалом функции / в точке а.
4
Дифференциал функции в точке определен однозначно, ибо из (9) следует
hm ^-^-^—г-1-1 = lim А -I- — = А
ЕЭх->а Х — а ЕЭх->а\ X — О, )
и в силу единственности предела число А определено однозначно.
Определение 1. Величина
/(Х)/(О) . A0)
ЕЭх-+а Х — а
называется производной функции / в точке а.
Соотношение A0) можно переписать в эквивалентной форме
х — а
где а(х) —> 0 при х -> а, х Е Е, что в свою очередь равносильно соотношению
f(x) - f(a) = f'(a)(x - а) + о(ж - а) при х -> а, ж € ?. A1)
Таким образом, дифференцируемость функции равносильна наличию у нее
производной в соответствующей точке.

176 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Если сопоставить эти определения с тем, что было сказано в пункте 1, то
можно заключить, что производная характеризует скорость изменения функ-
функции в рассматриваемой точке, а дифференциал доставляет наилучшую линей-
линейную аппроксимацию приращения функции в окрестности рассматриваемой
точки.
Если функция f : Е -* R дифференцируема в различных точках множе-
множества Е, то при переходе от одной точки к другой как величина А, так и
функция о(х — а) в (9) могут меняться (к чему мы уже явно пришли в A1)).
Указанное обстоятельство следует отметить уже в самом определении диф-
дифференцируемой функции, и мы приведем теперь это основное определение в
его полной записи.
Определение 2. Функция /: Е -> К, заданная на множестве Е С
называется дифференцируемой в точке х G Е, предельной для множества Е,
если
1 ' A2)
f(x + ft) - f(x) = A(x)h + a(x; ft),
где ft н* A(x)h — линейная относительно ft функция, а a(x;ft) = o(ft) при
ft ->• 0, x + ft G E.
Величины
Ax(h) := (x -I- ft) — ж = ft
и
Д/(х; Л) := /(* + Л) - Дх)
называют соответственно приращением аргумента и приращением функции
(соответствующим этому приращению аргумента).
Их часто (правда, не вполне законно) обозначают символами Ах и Д/(х)
самих функций от ft.
Итак, функция дифференцируема в точке, если ее приращение в этой
точке как функция приращения аргумента ft является линейной с точностью
до поправки, бесконечно малой при ft —>• 0 в сравнении с приращением аргу-
аргумента.
Определение 3. Линейная по ft функция ft »-> A(x)h из определения 2
называется дифференциалом функции f: Е -> Е в точке х G Е и обозначается
символом df(x) или Df(x).
Таким образом, df(x)(h) = A(x)ft.
Из определений 2, 3 имеем
Д/(х; ft) - d/(x)(ft) = a(x; ft),
причем a(x; ft) = o(ft) при ft -> 0, я + ft G J5, т. е. разность между приращением
функции, вызванным приращением ft ее аргумента, и значением при том же ft

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ 177
линейной по h функции df(x) оказывается бесконечно малой выше чем первого
порядка по h.
По этой причине говорят, что дифференциал есть (главная) линейная
часть приращения функции.
Как следует из соотношения A2) и определения 1,
A(x) = f(x) = ton
/o
поэтому дифференциал можно записать в виде
df(x)(h) = f(x)h. A3)
В частности, если f(x) = ж, то, очевидно, f'{x) = 1 и
dx(h) = 1 • h = Л,
поэтому иногда говорят, что «дифференциал независимой переменной совпа-
совпадает с ее приращением».
Учитывая это равенство, из A3) получаем
df(x)(h) = f'(x)dx(h), ¦ A4)
т. е.
x) = f(x)dx. A5)
Равенство A5) надо понимать как равенство функций от h.
Из A4) получаем
df(x)
т. е. функция —— (отношение функций df(x) и dx) постоянна и равна f'(x).
По этой причине, следуя Лейбницу, производную часто обозначают символом
dfix) -v
—— наряду с предложенным впоследствии Лагранжем1^ символом f'(x).
В механике, кроме указанных символов, для обозначения производной от
функции (p(t) по времени t используется символ ф(г) (читается «ip с точкой
от t»).
3. Касательная; геометрический смысл производной и диффе-
дифференциала. Пусть /: Е -+ Е — функция, определенная на множестве ЕсЖ,
и !со — фиксированная предельная точка множества Е. Мы хотим подобрать
постоянную со так, чтобы она лучше всех остальных констант характеризо-
характеризовала поведение функции в окрестности точки xq. Точнее, мы хотим, чтобы
. Л. Лагранж A736 — 1813) — знаменитый французский математик и механик.

178 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
%
разность /(х) — со при х —? хо, х ? Е была бесконечно малой в сравнении уже
с любой не нулевой постоянной, т. е.
/(х) = со + оA) при х -^ х0, х е Е. A7)
Последнее соотношение равносильно тому, что lim /(х) = cq. Если, в
ЕЭх—>хо
частности, функция непрерывна в точке хо, то lim /(х) = /(хо) и, есте-
ЕЭх—?хо
ственно, со = f(xo).
Попробуем теперь подобрать функцию со 4- ci(x — хо) так, чтобы иметь
/(х) = со + с\(х - х0) + о(х - хо) при х -? х0, х е Е. A8)
Очевидно, это — обобщение предыдущей задачи, поскольку формулу A7) мож-
можно переписать в виде
/(х) = со + о((х — хо)°) при х -» хо, х е Е.
Из A8) при х —> хо, х G Е немедленно следует, что со = lim /(x), и если
ЕЭх—Ухо
функция непрерывна в точке, то со = /(#о)-
Если со найдено, то из A8) следует, что
/(х) - со
с\ = lim —— .
ЕЭх-+хо X — Хо
И вообще, если бы мы искали полином Рп(хо;х) = со + ci(x — хо) + ... +
+ сп(х — хо)п такой, что
/(х) = со + ci(x - хо) + ... + с„(х - хо)п +
+ о((х - хо)п) при х -> хо,- х е Е, A9)
то мы последовательно и вполне однозначно нашли бы
со = lim /(x),
ЕЭх—>хо
/(х) - со
= hm —— ,
ЕЭх-+хо X —
сп = lim ; -,
ЕЭх-*хо (X — Хо)п
при условии, что все указанные пределы существуют; в противном случае
условие A9) невыполнимо и задача решения не имеет.
Если функция / непрерывна в точке хо, то из A8), как уже отмечалось,
следует, что со = /(#о) и мы приходим к соотношению
/(х) - /(х0) = ci(x - х0) + о(х - х0) при х -? хо, х ? Е,
равносильному условию дифференцируемости функции /(х) в точке

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ 179
Отсюда находим
Cl= Um
ЕЭ
ЕЭх—?хо X — Хо
Таким образом, доказано
Утверждение 1. Функция / : Е -? R, непрерывная в точке хо G Е,
предельной для множества Е С R, допускает линейное приближение A8) в
толе м только в том случае, когда она дифференцируема в этой точке.
Функция
(р(х) = со + ci(x - хо) B0)
при со = /(#о) и ci = /'(хо) является единственной функцией вида B0), удо-
удовлетворяющей соотношению A8).
Итак, функция
4>(х) = f(xo) + /'(хо)(я - яо) B1)
доставляет наилучшее линейное приближение функции / в окрестности точки
Хо в том смысле, что для любой другой функции вида B0) /(х) — (р(х) ф
Ф о(х — хо) при х —? хо, х G Е.
Графиком функции B1) является прямая
проходящая через точку (хо,/(хо)) и имеющая угловой коэффициент /'(^о)-
Поскольку прямая B2) доставляет наилучшее возможное линейное прибли-
приближение графика функции у = /(х) в окрестности точки (xo,f(xo)), то естест-
естественно принять
Определение 4. Если функция /: Е —? R определена на множестве
?с!и дифференцируема в точке хо G Е, то прямая, задаваемая уравнением
B2), называется касательной к графику этой функции в точке (хо, /(хо)).
Рисунок 15 иллюстрирует все основные понятия, связанные с дифферен-
цируемостыо функции в точке, которые мы к настоящему моменту ввели:
приращение аргумента и соответствующие ему приращение функции и значе-
значение дифференциала; на рисунке изображены график функции, касательная к
графику в точке Ро = (so>/(#o)) и, для сравнения, произвольная прямая (на-
(называемая обычно секущей), проходящая через Ро и некоторую точку Р ф Ро
графика функции.
Развитием определения 4 является
Определение 5. Если отображения f: Е -? R, g : Е -? R непрерывны
в точке хо G Е, предельной для множества Е С R, и /(х) — д(х) = о((х — хо)п)
при х —? хо, х G Е, то говорят, что / и д имеют в точке хо касание порядка п
(или, точнее, порядка не ниже п).
При п = 1 говорят, что отображения / и g касаются друг друга в точке хо.
В соответствии с определением 5 отображение B1) касается в точке хо G Е
отображения /: Е —? R, дифференцируемого в этой точке.
7 Зорин В. Л.

180
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Теперь можно также сказать, что полином Рп(хо;х) = со + с\(х —
+ ... + сп(х — хо)п из соотношения A9) имеет с функцией / касание не ниже
чем порядка п.
У
о
У = fix)
- fix,)
df(xQ)(h)
Число ft = х — хо, т. е. приращение аргумента, можно рассматривать как
вектор, приложенный к точке хо и определяющий переход из хо в х = хо + h.
Обозначим совокупность таких векторов через ТМ(хо) или TUL^.1) Анало-
Аналогично, обозначим через ТЖ(уо) или ТШу0 совокупность векторов смещения от
точки J/0 по оси у (см. рис. 15). Тогда из определения дифференциала видно,
что отображение
d/(x0): TR(xo) -> TR(/(x0)), B3)
задаваемое дифференциалом h hj f'(xo)h = d/(xo)(/i), касается отображения
+ h) -
А/(х0;
B4)
задаваемого приращением дифференцируемой функции.
Заметим (см. рис. 15), что если отображение B4) есть приращение орди-
ординаты графика функции у = /(х) при переходе аргумента из точки хо в точку
хо + Л, то дифференциал B3) дает приращение ординаты касательной к гра-
графику функции при том же приращении h аргумента.
4. Роль системы координат. Аналитическое определение 4 касатель-
касательной может вызвать некоторую не вполне осознанную неудовлетворенность.
Мы постараемся сформулировать, что именно может составить предмет этой
неудовлетворенности. Однако прежде укажем одну более геометрическую
конструкцию касательной к кривой в некоторой ее точке Pq (см. рис. 15).
— небольшое отклонение от наиболее распространенного обозначения TXQR или

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ Ш
Возьмем произвольную точку Р кривой, отличную от Pq. Прямая, опре-
определяемая парой точек Ро, Р, как уже отмечалось, называется секущей по от-
отношению к кривой. Заставим теперь точку Р вдоль кривой стремиться к
точке Ро- Если при этом секущая будет стремиться к некоторому предель-
предельному положению, то это предельное положение секущей и есть касательная к
кривой в точке Ро.
Такое определение касательной при всей его наглядности в данный момент
для нас неприемлемо потому, что мы не знаем, что такое кривая, что значит
«точка стремится к другой точке вдоль кривой» и, наконец, в каком смысле
надо понимать «предельное положение секущей».
Вместо того чтобы уточнять сейчас все эти понятия, мы отметим основ-
основную разницу между двумя рассмотренными определениями касательной. Вто-
Второе было чисто геометрическим, не связанным (во всяком случае, до уточне-
уточнений) с какой бы то ни было системой координат. В первом же случае мы
определили касательную к кривой, являющейся в некоторой системе коорди-
координат графиком дифференцируемой функции. Естественно может возникнуть
вопрос, не получится ли так, что если эту кривую записать в другой системе
координат, то, например, соответствующая функция перестанет быть диф-
дифференцируемой или будет дифференцируемой, но в результате новых вычи-
вычислений мы получим другую прямую в качестве касательной.
Этот вопрос об инвариантности, т. е. независимости от системы коорди-
координат, всегда возникает, когда понятие вводится с помощью некоторой системы
координат.
В равной степени этот вопрос относится и к понятию скорости, которое мы
обсуждали в пункте 1 и которое, кстати, как это уже отмечалось, включает
в себя понятие касательной.
Точка, вектор, прямая и т. д. имеют в разных системах координат разные
численные характеристики (координаты точки, координаты вектора, уравне-
уравнение прямой). Однако, зная формулы, связывающие две системы координат,
всегда можно по двум однотипным числовым представлениям выяснить, явля-
являются ли они записью в разных системах координат одного и того же гео-
геометрического объекта или нет. Интуиция подсказывает нам, что процедура
определения скорости, описанная в пункте 1, приводит к одному и тому же
вектору независимо от системы координат, в которой проводились вычисле-
вычисления. В свое время, при изучении функций многих переменных, мы подробно
обсудим подобного рода вопросы. Инвариантность определения скорости от-
относительно различных систем координат будет проверена уже в следующем
параграфе.
Прежде чем переходить к рассмотрению конкретных примеров, подведем
некоторые итоги.
Мы столкнулись с задачей математического описания мгновенной скоро-
скорости движущегося тела.
Эта задача привела к задаче аппроксимации заданной функции в окрест-
окрестности исследуемой точки линейной функцией, что в геометрическом плане
7*

182 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
привело к понятию касательной. Функции, описывающие движение реаль-
реальной механической системы, предполагаются допускающими такую линейную
аппроксимацию.
Тем самым среди всех функций естественно выделился класс дифференци-
дифференцируемых функций.
Было введено понятие дифференциала функции в точке как линейного ото-
отображения, определенного на смещениях от рассматриваемой точки, которое с
точностью до величины бесконечно малой по сравнению с величиной смещения
описывает поведение приращения дифференцируемой функции в окрестности
рассматриваемой точки.
Дифференциал df(xo)h = f'(xo)h вполне определяется числом f'(xo) —
производной функции / в точке хо, которое может быть найдено предельным
переходом
ЕЭх—>хо X —
Физический смысл производной — скорость изменения величины f(x) в мо-
момент хо; геометрический смысл производной — угловой коэффициент каса-
касательной к графику функции у = f(x) в точке (хо,/(хо)).
5. Некоторые примеры
Пример 1. Пусть /(х) = sinx. Покажем, что /'(х) = cosx.
.. sm(x + /i)-sinx ,. 2sin(|)cos(X + l)
< hm - J. = hm 4Z/ ч LL =
h—>0 h h—>0 h
sin(h\
= lim cos(x -h — ) • lim —x^4 = cosx. >
/ V 2/ /i-чо
(i)
Мы воспользовались теоремой о пределе произведения, непрерывностью
функции cosx, эквивалентностью sin2 ~ t при t —> 0 и теоремой о пределе
композиции.
Пример 2. Покажем, что cos' х = — sin x.
.. cos(x + /i)-cosx r ~2sin(|)sin(:r + |)
< hm -1 = lim \±±- 1 ±L- =
h h-*o h
= — lim sin
/ . \ Sin ( - I
in I x + — • hm —/,v = — sin x.
\ 2/ /i-^o (h\

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ 183
Пример 3. Покажем, что если f(t) = rcosut, то /'(?) = — rusinut.
,. г cosu/(* + Л) - г cos u/* r sin(,Tj SmaV + 2 У
hm ~ = г lim —— =
л-ю h h->o h
—r hm sin ш 11 + — 1 • lim —/ Л = —ru sin ut. >
/i->o \ 2/ /i-^o /^^\
V 2 У
Пример 4. Если f(t) = rsmut, то f'(t) = rucosut.
^ Доказательство аналогично разобранным в примерах 1 и 3. >
Пример 5. Мгновенная скорость и ускорение материальной точки.
Пусть материальная точка движется в плоскости и в фиксированной системе
координат закон ее движения описывается дифференцируемыми функциями
от времени
х = x(t), у = y(t)
или, что то же самое, вектором
r(t) = (x(t),
Как мы выяснили в пункте 1 настоящего параграфа, скорость точки в мо-
момент t есть вектор
где x(t), y(t) — производные функций x(t), y(t) по времени t.
Ускорение а(?) есть скорость изменения вектора v(t), поэтому
a(*)=v(t) = f(t) = (*(*),»(*)),
где x(t), y(t) — производные по t функций x(t), y(t), или так называемые
вторые производные функций x(t), y(t).
Таким образом, по смыслу физической задачи функции x(t), y(t), описыва-
описывающие движение материальной точки, должны иметь и первые и вторые про-
производные.
Рассмотрим, в частности, равномерное движение точки по окружности
радиуса г. Пусть и — угловая скорость точки, т. е. величина центрального
угла, на который перемещается точка за единицу времени.
В декартовых координатах (в силу определений функций cos a;, sinx) это
движение запишется в виде
г(?) = (rcos(u;? + a), rsin(u;? + а)),
а если г@) = (г, 0), то в виде
= (rcosu>?, rsmut).

184 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Без ограничения общности дальнейших выводов и для сокращения записи
будем считать, что г@) = (г, 0).
Тогда в силу результатов примеров 3 и 4
v(t) = r(t) = (—г и smut, ги cos ut).
Из подсчета скалярного произведения
(v(t),r(t)) = — r2LJsmut cosut + r2ucosLjtsmLjt = 0,
как и следовало в этом случае ожидать, получаем, что вектор v(t) скорости
ортогонален радиус-вектору r(t) и направлен по касательной к окружности.
Далее, для ускорения имеем
а(?) = v(t) = r(t) = (—rLj2cosut, —ru2smut),
т. e. a(t) = — и2 • r(t) и ускорение, таким образом, действительно центро-
центростремительное, ибо имеет направление, противоположное направлению век-
вектора r(t).
Далее,
Г
" Подсчитаем, исходя из этих формул, например, величину скорости низкого
спутника Земли. В этом случае г совпадает с радиусом Земли, т. е. г «
« 6400 км, а |а(?)| « д, где д » 10 м/с2 — ускорение свободного падения у
поверхности Земли.
Таким образом, v2 = |а(*)| г » 10 м/с2 х 64 • 105 м = 64 • 106 (м/сJ и
v » 8 • 103 м/с.
Пример 6. Оптическое свойство параболического зеркала. Рассмот-
Рассмотрим (рис. 16) параболу у = r-х2 (р > 0) и построим касательную к ней в
Zp
точке (so,2/o) = ^)
Поскольку f(x) = 5~a;2, то
lim — — = — lim (х + х0) = -
>* X — Х 2р х>х Р
Значит, искомая касательная имеет уравнение
1 2 1 / ч
У -—х? =-хо(х - хо)
ИЛИ
- хо (х - хо) - B/ - Уо) = 0, B5)

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ
185
, если х Ф О,
если* = О.
Рис. 16
Рис. 17
Вектор n = f—хо,1), как видно из последнего уравнения, ортогонален
прямой B5). Покажем, что векторы еу = @,1) и е/ = (— хо, ~ —2/о) образуют
с п равные углы. Вектор еу есть единичный вектор направления оси Оу, а
е/ — вектор, направленный из точки касания (хо»2/о) = (яо> ^"^о) в ТОЧКУ
10, — 1 — фокус параболы. Итак,
cose/n =
In
р
р
2
1
е/||п
^
2р
1
п
Таким образом, показано, что волновой источник, помещенный в точке
(О, ~J — в фокусе параболического зеркала, даст пучок, параллельный оси
Оу зеркала, а приходящий параллельно оси Оу пучок зеркало пропустит через
фокус (см. рис. 16).
Пример 7. Этим примером мы покажем, что касательная является всего-
навсего лучшим линейным приближением графика функции в окрестности
точки касания и вовсе не обязана иметь с ним единственную общую точку,
как это было в случае окружности и как это вообще имеет место в случае
выпуклых кривых. (О выпуклых кривых будет специальный разговор.)
Пусть функция f(x) задана в виде
=
x2sin -, если х ф О,
х
О, если х = О.
График этой функции изображен на рис. 17.
' 2 • 1

186
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Найдем касательную к графику в точке @,0). Поскольку
/'@) = li
О • 1 л
xz sin О
X
. 1
л — = lim х sin - = 0,
х—?0 X — 0 ж—И) X
то касательная имеет уравнение
-0 = 0(х-0),
или просто
Таким образом, в нашем примере касательная совпадает с осью Ох, с
которой график имеет бесконечное количество точек пересечения в любой
окрестности точки касания.
В силу определения дифференцируемое™ функции /:?чМв точке хо Е
€ Е имеем
/(х) - /(х0) = А(хо)(х - хо) +о(х - х0) при х -> х0, х е Е.
Поскольку правая часть этого равенства стремится к нулю при х —? хо, х Е -Б,
то lim /(x) = /(хо), так что дифференцируемая в точке функция обязана
??Эх—?хо
быть непрерывной в этой точке.
Покажем, что обратное, конечно, не всегда имеет место.
Пример 8. Пусть /(х) = |х| (рис. 18). Тогда в точке хо = 0
х—ухо— О X —
/(*) - /(хо)
= lim
х|-0 _
—х
lim
*->—о х — 0
И-о
= lim
X —
*-и-о х — 0
lim
х—>— О X
lim — = 1.
х—>+0 X
— —1,
Следовательно, в этой точке функция не имеет производной, а значит, и
не дифференцируема в этой точке.
Пример 9. Покажем, что ex+h — ех =
= exh + o(h) при h -* 0.
Таким образом, функция ехр(х) = ех диф-
дифференцируема, причем dexp(x)h = exp(x)/i,
или de* = e*dx, и тем самым ехр'х = ехрх,
de*
или
dx
¦ f>x+h „x —
Мы воспользовались полученной в примере 39, гл. III, § 2, п. 4 формулой
eh - 1 = h + o(/i) при

§ 1. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ
187
Пример 10. ax+h — ах = axlnah + o(h) при h -> 0 и а > 0.
Таким образом, dax = ах \nadx и -г— = ах In а,
ах
ax+h ~ах = ax(ah - 1) = a*(eMne - 1) =
= ax(h\na + o(ftlna)) = a*lna/i + о(Л) при
Пример 11. ln|x + h\ — ln|x| = -Л + о(Л) при /i -4 0 и х ф 0.
Таким образом, dlnlxl = -dx и —у^—- = -.
х ах х
=ln
X
1+-, поэтому для достаточно малых значений
X
При \h\ < \х\ имеем
можно написать
= 1.
х
при h —>• 0. Мы воспользовались здесь тем, что, как показано в примере 38,
гл. III, § 2, п. 4, ln(l -f t) = t + o(t) при t —? 0. >
Пример 12. logjx + h\ — loga|x| = —:—h + o(h) при h -> 0, x ^ 0,
X 111 О
0< a^ 1.
" E1 = _J_.
h
1
Таким образом, dloga|x| = —-—dx и ,
01 ' xlna dx
loga|x + Л| - loga|x| = loga
In a
x
х
lnaVx
x
xlna
Мы воспользовались формулой перехода к другому основанию логарифмов
и соображениями, изложенными при рассмотрении примера 10. >
Задачи и упражнения
1. Покажите, что
а) касательная к эллипсу
в точке (хо,2/о) имеет уравнение
х2 v
х I У
ХХр
а2
б2
_ 1
Ь) световые лучи от источника, помещенного в одном из двух фокусов F\ =
= (—у/а2 — б2, 0), F2 = (л/a2 —б2, 0) эллипса с полуосями а > b > 0, собираются
эллиптическим зеркалом в другом фокусе.

188 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
2. Напишите формулы для приближенного вычисления значений
a) sin (^ + а) при значениях а, близких к нулю;
b) sinC0°+ а0) при значениях а0, близких к нулю;
c) cosf j + а) при значениях а, близких к нулю;
d) cosD5° + а0) при значениях а°, близких к нулю.
3. Стакан с водой вращается вокруг своей оси с постоянной угловой скоростью ш.
Пусть у = /(х) — уравнение кривой, получающейся в сечении поверхности жидкости
плоскостью, проходящей через ось вращения.
2
a) Покажите, что f{x) = — х, где д — ускорение свободного падения (см. при-
пример 5).
b) Подберите /(х) так, чтобы функция /(х) удовлетворяла условию, указанному
в а) (см. пример 6).
c) Изменится ли приведенное в а) условие на функцию /(х), если ось вращения
не будет совпадать с осью стакана?
4. Тело, которое можно считать материальной точкой, под действием силы тяже-
тяжести скатывается с гладкой горки, являющейся графиком дифференцируемой функ-
функции у = /(х).
a) Найдите горизонтальную и вертикальную компоненты вектора ускорения, ко-
которое имеет тело в точке (хо,уо)-
b) В случае, когда /(х) = х2 и тело скатывается с большой высоты, найдите ту
точку параболы у = х2, в которой горизонтальная составляющая ускорения макси-
максимальна.
5. Положим
х, если 0 ^ х ^ -,
1-х, если - ^ х < 1,
и продолжим эту функцию на всю числовую прямую с периодом 1. Эту продолжен-
продолженную функцию обозначим через <ро. Пусть, далее,
Ых) = -^оD"*).
Функция <рп имеет период 4~п и производную, равную +1 или —1 всюду, кроме
точек х = ——-, п 6 Z. Пусть
*> т 1
оо
п=1
Покажите, что функция / определена и непрерывна на R, но ни в одной точке не
имеет производной. (Этот пример принадлежит известному современному голланд-
голландскому математику Б. Л. Ван дер Вар дену. Первые примеры непрерывных функции,
не имеющих производной, были построены Больцано A830 г.) и Вейерштрассом
A860 г.).)

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 189
§ 2. Основные правила дифференцирования
Построение дифференциала заданной функции или, что равносильно, отыс-
отыскание ее производной называется операцией дифференцирования функции1).
1. Дифференцирование и арифметические операции
Теорема 1. Если функции f: X -> IR, g : X -> R дифференцируемы в
точке х € X, то
а) их сумма дифференцируема в х, причем
b) их произведение дифференцируемо в х, причем
(/¦9У(х)=Пх)-9(х)+/(х)-9'(х);
c) их отношение дифференцируемо в х, если д(х) ф 0, причем
9
<< В доказательстве мы будем опираться на определение дифференцируе-
дифференцируемой функции и свойства символа о(), установленные в гл. III, § 2, п. 4.
9)(х + Л) - (/ + ?)(*) = (/(* + К) + fl(x + Л)) -
- (f(x) + ^(х)) = (/(х + Л) - /(х)) + (д(х + К) - ^(х)) =
' + (g'(x)h +
b) (/ • ^)(х + Л) - (/. </)(х) = /(х + h)g(x + Л) -
= (/(яг) + /#(х)Л + о(Л))(^(х) + g'{x)h + o(h)) - f(x)g(x) =
= U'{x)g{x) + f{x)g'{x))h
c) Поскольку функция, дифференцируемая в некоторой точке х G
непрерывна в этой точке, то, учитывая, что #(х) ф 0, на основании свойств
непрерывных функций можем гарантировать, что при достаточно малых
1> При математической равносильности задачи отыскания дифференциала и задачи
отыскания производной, все же производная и дифференциал — не одно и то же, и поэто-
поэтому, например, во французском математическом языке имеются два термина: derivation —
«деривация», нахождение производной (скорости), и differentiation — «дифференцирование»,
нахождение дифференциала.

190 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
значениях h также д(х + h) ф 0. В следующих выкладках предполагается,
что h мало:
9
1
(/(as + h)g(x) - f(x)g(x + h)) =
д(х)д(х + h)
х) - f(x)(g(x) + g'(x)h
+ о(Л)) =
Мы воспользовались тем, что в силу непрерывности функции д в точке х
и того, что д(х) ф 0,
lim
д(х)д(х
т. е.
1 1
где оA) есть бесконечно малая при /ь-*0, x-f/iGX. >
Следствие 1. Производная от линейной комбинации дифференцируе-
дифференцируемых функций равна линейной комбинации производных этих функций.
М Поскольку постоянная функция, очевидно, дифференцируема и ее про-
производная всюду равна нулю, то, считая в утверждении Ь) теоремы 1, что
/ = const = с, имеем (сд)'(х) = сд'(х).
Используя теперь утверждение а) теоремы 1, можем записать
(Pi/ + с2д)'(х) = (ci/)'(x) + (с2дУ(х) = Clf'(x) + с2д'(х).
С учетом доказанного, по индукции проверяем, что
cnfn)'(x) = cif[(x) + ... + cnf'n{x). >
Следствие 2. Если функции /i, ..., fn дифференцируемы в точке х,
то
М Для п = 1 утверждение очевидно.
Если оно справедливо для некоторого п Е N, то в силу утверждения Ь)

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 191
теоремы 1 оно справедливо также для (п +1) € N. В силу принципа индукции
заключаем о верности приведенной формулы для любого п 6 N. >
Следствие 3. Из взаимосвязи производной и дифференциала следует,
что теорема 1 может быть записана также через дифференциалы. Именно:
a) d(f + g)(x) = df{x) + dg(x);
b) d(f ¦ g)(x) = g(x)df(x) + f(x)dg(x);
0 <*)(»)-'('W(%fX)*(g), еслид(х)*0.
Проверим, например, а). Действительно,
d(f + g)(x)h = (/ + g)'(x)h = (/' + g'){x)h =
= (/'(*) + 9'{x))h = /'(x)/i + 0
= df(x)h + dg(x)h = (d/(x) -f dg{x))h,
и совпадение функций d(/ + #)(x), d/(x) -f d^(x) проверено. >
Пример 1. Инвариантность определения скорости. Теперь мы в со-
состоянии проверить, что вектор мгновенной скорости материальной точки,
который был определен в п. 1 § 1, не зависит от выбора системы декартовых
координат. Мы проверим это даже для любой из аффинных систем координат.
Пусть (ж1, х2) и (ж1, х2) — координаты одной и той же точки плоскости в
двух различных системах координат, связанных между собой соотношениями
х1 =a\xl +a\x2 +
Поскольку любой вектор (в аффинном пространстве) определяется парой
точек, а его координаты суть разности координат начала и конца вектора,
то координаты одного и того же вектора в этих двух системах должны быть
связаны соотношениями
v1 = a\vl + ait;2,
B)
~1 1 Л 0 1 V /
Если закон движения точки в одной системе задается функциями
ж2(?), то в другой — функциями xl{t), x2(t), связанными с первыми посред-
посредством соотношений A).
Дифференцируя соотношения A) по времени ?, по правилам дифференци-
дифференцирования находим
ж1 = а\х1 +
~2 1 • 1
х2 =а\х1 +
^ '

192
Гл v ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Таким образом, координаты (v1, v2) = (ж1, ж2) вектора скорости в первой
системе и координаты (гI, гJ) = (ж1, ж2) вектора скорости во второй системе
оказались связанными соотношениями B), говорящими нам о том, что мы
имеем дело с двумя различными записями одного и того же вектора.
Пример 2. Пусть f(x) = tgx. Покажем, что f'{x) =
всюду, где
COS X
cos ж ^ 0, т. е. в области определения функции tgx =
В примерах 1 и 2 из § 1 было показано, что sin'ж = cos ж, cos'ж = —sin ж,
поэтому из утверждения с) теоремы 1 получаем при cos ж ф 0:
Vcos
— sin ж cos ж
COS2 Ж
cos ж cos ж + sin ж sin ж
COS2 Ж
COS2 Ж
Пример 3. ctg^
, , cos x
функции с!сж = ——.
sin x
Действительно,
sin2 x
ПРИ sin ж ^ 0, т. е. в области определения
sin
— cos ж sin ж
sin2 ж
— sin a; sin ж — собжсоэж
sin2 ж
sin2 ж
Пример 4. Если Р(х) = со + схж -f ... + спжп — полином, то -Р'(ж) =
= Ci 4-
п~1
+ ... + ncnx
J J П
Действительно, поскольку — = 1, то по следствию 2 -j— = пхп~1 и теперь
ci«Z/ ax
утверждение вытекает из следствия 1.
2. Дифференцирование композиции функций
Теорема (теорема о дифференциале композиции функций). Если функ-
функция f: X —> Y С Е дифференцируема в точке х ? X, а функция g : Y
'дифференцируема в точке у = /(ж) Е F, то композиция g о f : X
этих функций дифференцируема в тдчке х, причем дифференциал d{gof)(x)
ТЕ(ж) -> TR(g(f(x))) композиции равен композиции dg(y) о df(x) дифферен
циалов
df(x): ТЩх) -> ТЩу = /(ж)),
= /(ж)): ТВД -> ТЩд(у))
Условия дифференцируемости функций / и д имеют вид
/(ж + Л) -/(ж) = f'(x)h + o(h) при /ь-»0, ж +
при

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 193
Заметим, что в последнем равенстве функцию o(t) можно считать опреде-
определенной и при t = 0, а в представлении o(t) = 7@*) гДе 7@ -> 0 при ? ->• 0,
2/ + ? € У, можно считать 7@) ^= 0. Полагая f(x) = у, f(x + Л) = 2/ -f t, в
силу дифференцируемости, а значит, и непрерывности функции / в точке х
заключаем, что при h ->> 0 также ? ->> 0, и если я + h € X, то у -I-1 € Y. По
теореме о пределе композиции теперь имеем
7(/(х + Л) - /(ж)) = a(h) -» 0 при Л -> 0, ж + Л G
и, таким образом, если t = f(x + Л) — /(ж), то
о(«) = 7(/(х + h) - /(х))(/(х + Л) - /(*)) =
= a(h)(f'(x)h + o(h)) = a(h)f'(x)h + a(h)o(h) =
= o(h) + o(/i) = o(h) при ft -> 0, ж + ft € X
Далее,
о f){x + h)-{go f)(x) = g(f(x + h)) - g(f(x)) =
= g(y +1) - g(y) = g'(y) t + o(t) =
= »'(/(*))(/(* + h) - fix)) + o(f(x + ft) - Six)) =
= д'ЦШПФ + o(ft)) + o(/(« + ft) - /(*)) =
= 9'(№)(f'(x)h)+g'ifix))io(h)) + oiSix + ft) - /(*)).
Поскольку величину ^/(/(ж))(//(х)Л), очевидно, можно интерпретировать
как значение dg(f(x))odf(x)h композиции h \ 9 У °—% g'{f{x))-f'{x)h отоб-
ражении h \ > / (х)д, г i > 9ЛУ)Т на смещении д, то для завершения
доказательства теоремы остается заметить, что сумма
есть величина бесконечно малая в сравнении с h при /ь-*0, ж + ЛбХ, ибо,
как мы уже установили,
o(f(x + /i) - /(ж)) = o(/i) при /i -^ 0, ж + h €
Итак, показано, что
при Л -> 0, i +
Следствие 4. Производная (д о /)'(ж) композиции дифференцируемых
веществ еннозначных функций равна произведению ^/(/(ж))-//(ж) производных
этих функций, вычисленных в соответствующих точках.

194 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Большим искушением к короткому доказательству последнего утвержде-
утверждения являются содержательные обозначения Лейбница для производной, в ко-
которых, если z — z(y), а у = 2/(х), имеем
dz _ dz
dx dy dx'
dz dy
что представляется вполне естественным, если символ — или -j- рассматри-
ay clx
y
вать не как единый, а как отношение dz к dy или, соответственно, dy к dx.
Возникающая в связи с этим идея доказательства состоит в том, чтобы
рассмотреть разностное отношение
Az_ _ Az
Ах Ау Ах
и затем перейти к пределу при Ах —>• 0. Трудность, которая тут появляется
(и с которой нам тоже отчасти пришлось считаться!), состоит в том, что Ау
может быть нулем, даже если Ах ф 0.
Следствие 5. Если имеется композиция (fn о ... о /i)(x) дифференци-
дифференцируемых функций J/1 = /i(x), ..., уп = fn(yn-i), то
(fn О ... О ДУф = /;(»„-!)/;_! (уя-2) . . . /{(*)•
М При п = 1 утверждение очевидно.
Если оно справедливо для некоторого п Е N, то из теоремы 2 следует, что
оно справедливо также для п+1, т. е. по принципу индукции установлено, что
оно справедливо для любого п G N. >
Пример 5. Покажем, что при a G Ш в области х > 0 имеем —— = ах01,
ах
т. е. dxa = axa~1dx, и
(х + h)a - ха = аха~1Н + o(/i) при А -» 0.
^ Запишем ха = еа1пх и применим доказанную теорему с учетом резуль-
результатов примеров 9и11из§1и пункта Ь) теоремы 1.
Пусть д(у) = еу и у = f(x) = alnx. Тогда ха = (д о /)(х) и
(до/У(х) = ^B/) ' /Ч«) = еу- - = еа1пж • ~ = ха • 2 = ах*. >
X XX
t
Пример 6. Производная от логарифма модуля дифференцируемой функ-
функции часто называется логарифмической производной.
Поскольку F(x) = ln|/(x)| = (In о | | о /)(х), то в силу результата примера
11 из § 1 F'(x) = (ln|/|)'(x) =

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 195
Таким образом,
Пример 7. Абсолютная и относительная погрешности значения диф-
дифференцируемой функции, вызванные погрешностями в задании аргумента.
Если функция / дифференцируема в точке х, то
f{x + К) - fix) = f'{x)h + а(х; Л),
где а(х; /ь) = о(/ь) при /ь ->> 0.
Таким образом, если при вычислении значения f(x) функции аргумент х
определен с абсолютной погрешностью Л, то вызванная этой погрешностью
абсолютная погрешность |/(# + h) — f(x)\ в значении функции при достаточно
малых h может быть заменена модулем значения дифференциала \dfix)h\ =
= \f'{x)h\ на смещении h.
Тогда относительная погрешность может быть вычислена как отношение
\f'(*)h\ \df(x)h\
или как модуль произведения
/'(*)
\h\ логарифмической
производной функции на величину абсолютной погрешности аргумента.
Заметим, кстати, что если f(x) = In ж, то din х = — и абсолютная погреш-
погрешность в определении значения логарифма равна относительной погрешности в
определении аргумента. Это обстоятельство прекрасно используется, напри-
например, в логарифмической линейке (и многих других приборах с неравномерным
масштабом шкал). А именно, представим себе, что с каждой точкой числовой
оси, лежащей правее нуля, мы связали ее координату у и записали ее над точ-
точкой, а под этой точкой записали число х = еу. Тогда у = \пх. Одна и та же
числовая полуось оказалась наделенной одной равномерной шкалой у и одной
неравномерной (ее называют логарифмической) шкалой х. Чтобы найти lnx,
надо установить визир на числе х is. прочитать наверху соответствующее чи-
число у. Поскольку точность установки визира на какую-то точку не зависит от
числа х или у, ей отвечающего, и измеряется некоторой величиной Ау (длиной
отрезка возможного уклонения) в равномерной шкале, то при определении по
числу х его логарифма у мы будем иметь примерно одну и ту же абсолют-
абсолютную погрешность, а при определении числа по его логарифму будем иметь
примерно одинаковую относительную погрешность во всех частях шкалы.
Пример 8. Продифференцируем функцию и(х)у(х\ где и(х) и v(x) —
дифференцируемые функции и и(х) > 0. Запишем u(x)v^ = ev(x)*nu(x) и вос-
воспользуемся следствием 5. Тогда
dev(x)\nu(x) v(x)lnu(x)f ,, ч. /ч , ,и(х)\
= eHx)lnu^x)[v (x)\nu(x) + v(x) -f-f =
dx \ и(х))
= u(x)v^ •v'{x)\nu{x)+vix)u{x)vi<x)-1 'u'(x).

196 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
3. Дифференцирование обратной функции
Теорема 2 (теорема о производной обратной функции). Пусть функ-
функции f : X -? Y, f~x : Y -> X взаимно обратны и непрерывны в точках
х0 е X и f(xo) =y0 eY соответственно. Если функция f дифференцируема
в точке хо и f'(xo) ф 0, то функция f~l также дифференцируема в точке
уо, причем
4 Поскольку функции /: X —> Y, f~x :Y~*X взаимно обратны, то вели-
величины f(x) - /(яо), f~X(y) — /~Х(Уо) при у = f{x) не обращаются в нуль, если
х ф хо- Из непрерывности f в хо и f~l в уо можно, кроме того, заключить,
что (X Э х -> хо) <=> (Y Э у -> уо)' Используя теперь теорему о пределе
композиции функций и арифметические свойства предела, находим
X) — J{Xq)
= lim
ff(x)-f(xo)\ f'(x0)
\ X — J
Xo J
Таким образом, показано, что в точке у о функция f~l : Y -> X имеет
производную и
(Г'УШ = (/'(хо)). >
Замечание 1. Если бы нам заранее было известно, что функция f
дифференцируема в точке j/o, то из тождества (/~х о f)(x) = x по теоре-
теореме о дифференцировании композиции функций мы сразу же нашли бы, что
(ГЧ'Ы • ГЫ = 1.
Замечание 2. Условие f'(xo) Ф 0, очевидно, равносильно тому, что
отображение h *-> f'(xo)h, осуществляемое дифференциалом df(xo): ТЩхо) ->¦
-> ТЩуо), имеет обратное отображение [^/(хо)]: ТЩу0) -? TR(x0), зада-
задаваемое формулой т *-> (//(хо))~1т.
Значит, в терминах дифференциалов вторую фразу формулировки теоре-
теоремы 3 можно было бы записать следующим образом:
Если функция f дифференцируема в точке хо и в этой точке ее диффе-
дифференциал df(xo): ТЩхо) -> ТЩуо) обратим, то дифференциал функции f,
обратной к f, существует в точке уо = /(#о) и является отображением
1: ТЖ(у0)
обратным к отображению df(xo): TR(xq) —>• ТЩуо)

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 197
Пример 9. Покажем, что arcsin'г/ = , при \у\ < 1. Функции
у/1-у2
sin : [~тг/2, тг/2] -> [-1,1] и arcsin : [-1,1] ->• [-тг/2,тг/2] взаимно обратны и
непрерывны (см. гл. IV, § 2, пример 8), причем sin'a; = cos ж ф 0, если |х| < тг/2.
При |х| < тг/2 для значений у = sinx имеем |j/| < 1.
Таким образом, по теореме 3
arcsin у = . , =
sin x cosx у/1 _ sin2 x y/l-y2
Знак перед радикалом выбран с учетом того, что cosx > 0 при |х| < тг/2.
Пример 10. Рассуждая, как и в предыдущем примере, можно показать
(с учетом примера 9 из § 2 гл. IV), что
arccos'j/ = . при \у\ < 1.
л/1-2/2
Действительно,
arccos' у =
cos'x sinx у/1 - cos2 x y/\ - 2/2
Знак перед радикалом выбран с учетом того, что sinx > 0, если 0 < х < тт.
Пример 11. arctg'2/ = ——г, ye
1 + у*
Дй
Действительно,
1 1 2
arctg у = т-т— = т—-—г- = cos х =
tg'x / 1 ^
тт тг = cos х = гт =
tg'x / 1 ^ l-htg2x 1-fj/
Пример 12. arcctg'2/= - ——2, у €
Действительно,
arcctg' у = —— = 7 -—- = -sin2x = -
ctg'x ( ±_\
\ sin2 х /
1 -f ctg2 х 1 + у2 '
Пример 13. Мы уже знаем (см. примеры 10, 12 из § 1), что функции
у = /(х) — ах и х = f~~l{y) = logax имеют производные /'(х) = axlna и
Проверим, как это согласуется с теоремой 3:
= =
#(x) a* In a 2/ In a'
U) (У)
\y\naj

198
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 14. Гиперболические, обратные гиперболические функции и их
производные. Функции
называются соответственно гиперболическим синусом и гиперболическим ко-
косинусом1^ от х.
Эти в данный момент вводимые нами чисто формально функции, как вы-
выяснится, во многих вопросах появляются так же естественно, как появляются
круговые функции sin я, cosx.
Заметим, что
sh(—х) = —shx,
ch(—x) = chx,
т. е. гиперболический синус — нечетная функция,
а гиперболический косинус — функция четная.
Кроме того, очевидно следующее основное тож-
тождество:
ch2x — sh2x = 1.
= sh х
О
х
Рис. 19
Графики функций у = shx и у = chx изображе-
изображены на рис. 19.
Из определения функции shx и свойств функ-
функции ех следует, что shx — непрерывная строго
возрастающая функция, отображающая взаимно однозначно Е на Е. Обрат-
Обратная функция к shx, таким образом, существует, определена на Е, непрерывна
и строго монотонно возрастает.
Ее обозначают символом
arshy
(читается «ареа-синус^ от у»). Эту функцию легко выразить через уже из-
известные. Решая уравнение
относительно х, найдем последовательно
у +
(ех > 0, поэтому ех ф у — у/1 + у2) и
х = 1п(у -Ь
2/2)
*) От лат. sinus hyperbolici, cosinus hyperbolici.
2'Полное название — area sinus hyperbolici (лат.); почему здесь используется термин
«площадь» (area), а не «дуга» (arcus), как в круговых функциях, выяснится несколько позже.

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 199
Итак,
arshy = ln(y + y/T+ у2), у ? R.
Аналогично, используя монотонность функции у = ch x на участках Е_ =
= {х € М | х ^ 0}, R+ = {х € R | х ^ 0}, можно построить функции arch_ у и
arch+ у, определенные для у ^ 1 и обратные к ограничению функции chx на
_ и R+ соответственно.
Они задаются формулами
arch_ у = In (у - у/у2 - 1),
arch+ у = In (у 4- л/у2 - 1).
Из приведенных определений находим
sh'x = \(ех + е~х) = chx,
ch'x = ^(ex -e"x) = shx,
Zi
а на основе теоремы о производной обратной функции получаем
111 1
sh'x chx
arsh; у =
1 1 1 1
arch у = -—-j— = —— = . = = . , v > 1,
~У ch'a: shx -УЬ21 V^7!
1 1 1 1
arch. у = —г— = -— = . = = 7 , 2/ > 1.
+ ch'x shx /tfi fiF^l
Последние три соотношения можно проверить, используя явные выражения
для обратных гиперболических функций arshy и arch у.
Например,
2/ Н- \/1 + 2/
-hy2 \/l-fy2
Подобно tg х и ctg х можно рассмотреть функции
., shx ., chx
thx = —— и cthx = ——,
ch x sh x
называемые гиперболическим тангенсом и гиперболическим котангенсом со-
соответственно, а также обратные им функции ареа-тангенс:
|i±J \у\<1,

200
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
и ареа-котангенс:
arcthy= ±1п^—-, \y\ > 1.
? У — 1
Решения элементарных уравнений, приводящие к этим формулам, мы опус-
опускаем.
По правилам дифференцирования имеем
th х =
cth' x =
sh' x ch x — sh x ch; x _ ch x ch x — sh x sh x
ch2 x ch2 x
ch'xshx — chxsh'x shxshx — chxchx
1
ch2 x'
1
sh x sh x
По теореме о производной обратной функции
arth' х =
sh x
7
th'x
= сд2 х =
l-th2x
, M < i,
arcth' x =
cth'x ( 1_\
\ sh2xJ
= — sh x =
1
cth2x-l
Две последние формулы можно проверить и непосредственным дифференци-
дифференцированием явных формул для функций arth у и arcth у.
4. Таблица производных основных элементарных функций. Вы-
Выпишем теперь (см. табл. 1) производные основных элементарных функций,
подсчитанные в § 1 и 2 .
5. Дифференцирование простейшей неявно заданной функции.
Пусть у = y(t) и х = x(t) — дифференцируемые функции, определенные в
окрестности U(to) точки fo € R. Предположим, что функция х = x(t) име-
имеет обратную функцию t = ?(х), определенную в окрестности У(хо) точки
хо = х(?о)- Тогда величину у = y(t), зависящую от ?, можно рассматривать
также как функцию, неявно зависящую от х, поскольку y(t) = y(t(x)). Най-
Найдем производную этой функции по х в точке хо, предполагая, что х'(?о) Ф 0.
Используя теорему о дифференцировании композиции и теорему о дифферен-
дифференцировании обратной функции, получаем
= dy(t(x))
*x\x=x0 fa
X—Xq
= dy{t)
dt
t=to
dt(x)
dx
dy(t)
dt
dx(t)
dt
t=to
t=to
x't(t0)
(Здесь использовано стандартное обозначение f(x)\ _ := /(xq).)

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
201
Функция /(х)
1. С (const)
2. ха
3. ах
4. logjx|
5. sinx
6. COS X
7. tgx
8. ctgx
Q arcsin x
10 АГССОЧ T
11. axctgx
12. arcctgx
13. shx
14. ch x
К fit r
16. cthx
17. arshx ln(x + %/l + x2)
18. axchx-ln(x±v/x2-l)
10 n.rtb т .-in .f ."t.i?
0 <*• 1
Производная f'(x)
0
ax-"
axlna
1
xlna
cosx
— sinx
1
COS2X
1
• 2
иДХХ JU
1
¦v/ 1 — Of**
v ¦*• •*•
1
\/l — x2
1
14-x2
1
1 4-х2
chx
shx
1
1
1
+ 1
1
1-х2
1
1-х2
Таблица 1
Ограничения на область
изменения аргумента х G R
х > 0 при a G R
х G R при a G N
х G R (a > 0, а ф 1)
xGR\0 (a>0, аф 1)
хф^+пк, к G Z
x т^ 7Г&, fc G Z
• | -
|x|<l
M>i
Если одна и та же величина рассматривается как функция различных ар-
аргументов, то во избежание недоразумений при дифференцировании явно ука-
указывают переменную, по которой это дифференцирование проводится, что мы
и сделали.

202 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 15. Закон сложенгм скоростей. Движение точки в доли пря-
прямой вполне определяется, если в каждый момент t выбранной нами системы
отсчета времени мы знаем координату х точки в выбранной системе коорди-
координат (числовой оси). Таким образом, пара чисел (х,?) определяет положение
точки в пространстве и во времени. Закон движения точки запишется в виде
некоторой функции х = x(t).
Предположим, что движение этой же точки мы хотим описать в терминах
другой системы координат (ж,?). К примеру, новая числовая ось движется
равномерно со скоростью — v относительно первой (вектор скорости в данном
случае можно отождествить с задающим его одним числом). Будем для про-
простоты считать, что координаты @,0) и в той и в другой системе относятся к
одной и той же точке или, точнее, что в момент i = 0 точка х = 0 совпадала
с точкой х = 0, в которой часы показывали t = 0.
Тогда один из возможных вариантов связи координат (х, ?), (x,i), опи-
описывающих движение одной и той же точки, наблюдаемое из разных систем
координат, доставляют классические преобразования Галилея
х = х + vt,
D)
t=t.
Рассмотрим несколько более общую линейную связь
х = ах + Bt,
E)
t = + $?
разумеется, в предположении, что эта связь обратима, т. е. определитель ма-
трицы [ \ ) отличен от нуля.
\7 о)
Пусть х = x(t) и х = x(i) — закон движения наблюдаемой точки, записан-
записанный в этих системах координат.
Зная зависимость х = x(t), из формул E) найдем
x(t) = ax(t) +
t(t) = jX{t) + 6t,
а в силу обратимости преобразований E), записав
х = ах + fit,
t = 7x 4- Si, .
зная х = х(?), можно найти
i = dx(i) + pi,
Si.
Из соотношений F) и (8) видно, что для данной точки существуют взаимно
обратные зависимости i = i(t) и t = t(i).

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 203
Рассмотрим теперь вопрос о связи скоростей
V(t) = *gU it(t) и
нашей точки, вычисленных в системах координат (ж, t) и (х, ?) соответственно.
Используя правило дифференцирования неявной функции и формулы F),
имеем
dx dx ,
а+
или
где i и t — координаты одного и того же момента времени в системах (х, t) и
(x,i). Это всегда имеется в виду при сокращенной записи
формулы (9).
В случае преобразований D) Галилея из A0) получаем классический закон
сложения скоростей
V = V + v. A1)
Экспериментально с достаточной степенью точности установлено (и это
стало одним из постулатов специальной теории относительности), что в ва-
вакууме свет всегда распространяется с определенной скоростью с, не зависящей
от состояния движения излучающего тела. Это означает, что если в момент
t = t •=• 0 в точке х = х = 0 происходит вспышка, то через время t в систе-
системе (xyt) свет достигнет точек с координатами х такими, что х2 = (с?J, а в
системе (х, i) этому событию будут отвечать время i и координаты х точек
такие, что опять х2 = (с?J.
Таким образом, если х2 — <?t2 = 0, то и х2 - с2?2 = 0, и обратно. В
силу некоторых дополнительных физических соображений следует считать,
что вообще
х2-с2*2=х2-с2^, A2)
если (ж, t) и (x,i) отвечают одному и тому же событию в различных систе-
системах координат, связанных соотношением E). Условия A2) дают следующие
соотношения на коэффициенты а, /3, 7> S преобразования E):
A3)
2 2
a — с 7
aE — c27
/?2 - c2S
(J = 0,
2 = -c2

204 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Если бы было с = 1, то вместо A3) мы имели бы
откуда легко следует, что общее (с точностью до перемен знака в парах (а, /?),
G,<5)) решение Системы A4) может быть дано в виде
а = ch у>, 7 = sh Фч /3 = sh<^>, 6 = ch <р,
где ц> — некоторый параметр.
Тогда общее решение системы A3) имеет вид
(
а а\ /chip cshy
7 <V \-sh<z? clup
и преобразования E) конкретизируются:
х = clup x +
t = -sh<p x 4- ch<p t,
с
Это — преобразования Лоренца.
Чтобы уяснить себе, каким образом определяется свободный параметр <^,
вспомним, что ось х движется со скоростью —v относительно оси х, т. е. точка
х = 0 этой оси, наблюдаемая из системы (ж,?), имеет скорость — v. Полагая в
A5) х = 0, находим ее закон движения в системе (x,t):
х = — ctlup t.
Таким образом,
thy>=-. ' A6)
Сопоставляя общий закон A0) преобразования скоростей с преобразованиями
Лоренца A5), получаем
+ csh(p
- sh <p V + ch <p
или, с учетом A6),
A7)
c2
Формула A7) есть релятивистский закон сложения скоростей, который при
\vV\ < с2, т. е. при с -* оо, переходит в классический, выраженный форму-
формулой A1).

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 205
Сами преобразования Лоренца A5) с учетом соотношения A6) можно за-
записать в следующей более естественной форме:
X + Vt
х- . ,
t =
откуда видно, что при \v\ <^С с, т. е. при с —> оо, они превращаются в класси-
классические преобразования Галилея D).
6. Производные высших порядков. Если функция /: Е —> Е диффе-
дифференцируема в любой точке х ? Е, то на множестве ? возникает новая функция
/':?-* Е, значение которой в точке х Е Е равно производной f'{x) функции
/ в этой точке.
Функция /; : Е —>• Е сама может иметь производную (/')' : Е —> М на ?,
которая по отношению к исходной функции / называется второй производной
от / и обозначается одним из символов
"
а если хотят явно указать переменную дифференцирования, то в первом слу-
случае еще, например, пишут fxX(x).
Определение. По индукции, если определена производная /(п~х) (х) по-
порядка п — 1 от /, то производная порядка п определяется формулой
Для производной порядка п приняты обозначения
dnf(x)
dxn
Условились считать, что f^°\x) := f(x).
Множество всех функций /: Е —> Е, имеющих на Е непрерывные произ-
производные до порядка п включительно, будем обозначать символом С^(Е, Е),
а когда это не ведет к недоразумению — более простыми символами С^ (Е)
или Сп(Е, Е) и Сп(Е) соответственно.
В частности, С^0ЦЕ) = С(Е) в силу принятого соглашения, что f^(x) =
= /(*)•
Рассмотрим несколько примеров вычисления производных высших по-
порядков.

206
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
16.
17.
18.
19.
Примеры.
Дх)
ах
ех
sinx
cosx
я*)
ах In a
ех
COSX
— sinx
/"(х)
ах In2 a
ех
— sinx
20.
x)a a
ax In d
sin(x -h птг/2)
cos(x + птг/2)
a(a - 1) ...(a - n + l)x
21.
22.
23.
xa
loga j.
lnlx
ах
"-1
a(a — 1)... (a — n + l)x
xx
a~n
x
In a
X
-1
-2
х
-1
In a
In a
x
Пример 24. Формула Лейбница. Пусть и(х) и v(x) — функции, имеющие
на общем множестве Е производные до порядка п включительно. Тогда для
га-й производной от их произведения справедлива следующая формула Лейб-
Лейбница:
п
c;>(n-wVm)
V
A9)
m=0
Формула Лейбница очень похожа на формулу бинома Ньютона и на самом
деле с нею непосредственно связана.
4 При п = 1 формула A9) совпадает с уже установленным правилом диф-
дифференцирования произведения.
Если функции u, v имеют производные до порядка п +1 включительно, то,
в предположении справедливости формулы A9) для порядка п, после диффе-
дифференцирования ее левой и правой частей получаем
п
п
c;>(n-mVm+1) =
m=0
m=0
n+1
A;=0
Мы объединили слагаемые, содержащие одинаковые произведения произ-
производных от функций u, v, и воспользовались тем, что С* 4- С„~1 = С*+1.
Таким образом, по индукции установлена справедливость формулы Лейб
ница. >

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 207
Пример 25. Если Рп(х) = со + с\х + ... 4- спа:п, то
Рп@) = со,
^ 2с2х + ... + пспхп-1 и Р
+ 3 • 2с3х + ... + п(п - l)cnxn и Р^@) = 2!с2,
,<3>(а;) = 3 • 2с3 + ... + п(п - 1)(п - 2)спа:п-3 и Р^3)@) = 3!с3,
и Р^@) = п!сп,
^ = 0 при А;>п.
Таким образом, полином Рп(#) можно записать в виде
Р„(х) =
+ р@)« + p^Jx + ... +
Пример 26. Используя формулу Лейбница и то обстоятельство, что
производные от полинома, имеющие порядок вьппе его степени, тождественно
равны нулю, можно найти га-ю производную функции f(x) = х2 sinx:
">(*) = sin(n>a: • х2 + С* sin^^ • 2х + С^ sin(n*-2)x • 2 =
= х2 sin f а: + п ^ j 4- 2пх sin (ж + (п — 1) ~ J 4-
4- f — п(п - 1) sinfx 4- птг)) =
= (х2 — п(п — 1)) sin(х 4- n^ j — 2nzcosfz -h n^J.
Пример 27. Пусть f(x) = arctgx. Найдем значения /(п)@) (п = 1,2, ...).
Поскольку /;(х) = 1н| 2, то A + z2)/;(z) = 1.
Применяя формулу Лейбница к последнему равенству, находим рекуррент-
рекуррентную формулу
4- x2)f(n+4(x) + 2nxfW(x) 4- п(п - l)/*"-1^*) = 0,
из которой можно последовательно найти все производные функции f(x)
Полагая х = 0, получаем
При п = 1 имеем /B) @) = 0, поэтому вообще /Bп) @) = 0. Для производ
ных нечетного порядка имеем
= -2тBт -

208ГЛ. V, ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
и, поскольку /'@) = 1, получаем
Пример 28. Ускорение. Если х = x(t) — зависимость от времени коор-
координаты движущейся вдоль числовой оси материальной точки, то }. = x(t)
dx(t) d2x{t) .....
есть скорость точки, а тогда v = 2 = х(?) есть ее ускорение в мо-
момент t.
Если x(t) = at + /?, то я(?) = а, а х(?) = 0, т. е. ускорение в равномерном
движении равно нулю. Вскоре мы проверим, что если вторая производная
функции равна нулю, то сама функция имеет вид at + /?. Таким образом, в
равномерных движениях и только в них ускорение равно нулю.
Но в том случае, если мы желаем, чтобы наблюдаемое из двух систем коор-
координат движущееся по инерции в пустом пространстве тело в обеих системах
двигалось равномерно и прямолинейно, нужно, чтобы формулы перехода из
одной инерциальной системы в другую были линейными. Именно по этой
причине в примере 15 были выбраны линейные формулы E) преобразования
координат.
Пример 29. Вторая производная простейшей неявно заданной функ-
функции. Пусть у = y(t) и х = x(t) — дважды дифференцируемые функции. Пред-
Предположим, что функция х = x(t) имеет дифференцируемую обратную функ-
функцию t = t(x), тогда величину y(t) можно считать зависящей неявно от #, ибо
у = y(t) = y(t(x)). Найдем вторую производную ух'х в предположении, что
x'(t) ф 0.
По правилу дифференцирования такой функции, рассмотренному в пунк-
пункте 5, имеем
xt
поэтому
(у
" - г./V - Mil - UA _ «)
КУ)
Заметим, что явные выражения всех участвующих здесь функций, в том
числе и 2/^'д., зависят от ?, но они дают возможность получить значение у'х'х в
конкретной точке х после подстановки вместо t значения t = ?(#), отвечаю-
отвечающего заданному значению х.
Например, если у = е*, х = Int, то
' Ухх -
Мы специально взяли простой пример, в котором можно явно выразить t
через ж, t = еж, и, подставив t = ех в y(i) = e*, найти явную зависимость

§ 2. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 209
у = ее* от х. Дифференцируя последнюю функцию, можно проверить пра-
правильность полученных выше результатов.
Ясно, что так можно исккть производные любого порядка, последователь-
последовательно применяя формулу
Ухп ""
xt
Задачи и упражнения
1. Пусть <*о, Qti, ..., otn — заданные вещественные числа. Укажите многочлен
Рп{х) степени п, который в фиксированной точке хо G R имеет производные
Р^к)(х0)=ак} А; = 0,1, ..., п.
2. Вычислите /'(#)> если
ехр Г И при ж ^ 0,
0 при х = 0;
а) /(а) =
Ь) /() < *
При Ж = 0.
c) Проверьте, что функция из задачи а) бесконечно дифференцируема на R,
причем /(п)@) = 0.
d) Покажите, что производная функции из задачи Ь) определена на R, но не
является непрерывной функцией на R.
e) Покажите, что функция
0 при
бесконечно дифференцируема на R.
3. Пусть / € C(oo)(R). Покажите, что при х ф 0
4. Пусть / — дифференцируемая на R функция. Покажите, что:
a) Бели / — четная, то /; — нечетная функция.
b) Бели / — нечетная, то /' — четная функция.
c) (/' нечетна) <=>(/ четна).
5. Покажите, что:
a) Функция f(x) дифференцируема в точке хо в том и только в том случае, когда
f(x) — f(xo) = <p(x)(x — а?о), где tp(x) — функция, непрерывная в xq (и в таком случае
<р(х0) = f'(x0)).
b) Бели f(x) — f(xo) = tp(x)(x-xo) и <р € C(n~l\U(xo)), где U{xq) —окрестность
точки жо, то функция f(x) имеет в точке хо производную /*п^(жо) порядка п.

210
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
¦-1
6. Приведите пример, показывающий, что в теореме 3 условие непрерывности
/ в точке у о не является излишним.
7. а) Два тела с массами mi и гаг соответственно перемещаются в простран-
пространстве только под действием сил взаимного притяжения. Используя законы Ньютона
(формулы A) и B) из § 1), проверьте, что величина
Е = (I
\m2vl
)
-K + U,
где v\ и V2 — скорости тел, а г — расстояние между ними, не меняется при таком
движении.
b) Дайте физическую интерпретацию величины Е = К + U и ее составляющих.
c) Распространите результат на случай движения п тел.
§ 3. Основные теоремы дифференциального исчисления
1. Лемма Ферма и теорема Ролля
Определение 1. Точка хо G Е С Ш называется точкой локального
максимума (минимума), а значение функции в ней — локальным максимумом
(минимумом) функции f:E-+R, если существует окрестность Ue(xo) точки
х0 в множестве Е такая, что в любой точке х G Ue(xq) имеем f(x) ^ f(xo)
(соответственно, f(x) ^ f(xo)).
о
Определение 2. Если в любой точке х ? Ue(xo)\#о = Ue(xo) имеет
место строгое неравенство f(x) < f(x0) (f(x) > f(xo))> то точка х0 ? Е
называется точкой строгого локального максимума (минимума), а значение
функции в ней — строгим локальным максимумом
(минимумом) функции /: Е -> R.
Определение 3. Точки локального максиму-
максимума и минимума называются точками локального экс-
экстремума, а значения функции в них — локальными
экстремумами функции.
VI>Л 1 Пример 1. Пусть
У
4
-10 12
Рис. 20
х
№ =
х
4,
если -1 ^ х < 2,
если 2 ^
х
(рис. 20). Для этой функции:
х = -1 — точка строгого локального максимума;
х = 0 — точка строгого локального минимума;
х = 2 — точка локального максимума;
х > 2 — точки экстремума, являющиеся одновременно точками и локаль-
локального максимума, и локального минимума, поскольку здесь функция локально
постоянна.

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 211
Пример 2. Пусть f(x) = sin - на множестве Е = Ж \ 0.
X
Точки х = (^ 4- 2&7М , fc G Z, являются точками строгого локального
максимума, а точки х = (— ^+2&тг J , А: € Z, — точками строгого локального
минимума для f(x) (см. рис. 12).
Определение 4. Точку х$ € Е экстремума функции /: Е ->- R бу-
будем называть точкой внутреннего экстремума^ если #о является предельной
точкой как для множества ?_ = {х е Е\х < я0}, так и для множества
?+ = {х € #|я > хо}.
В примере 2 все точки экстремума являются точками внутреннего экс-
экстремума, а в примере 1 точка х = — 1 не является точкой внутреннего экстре-
экстремума.
Лемма 1 (Ферма). Если функция f: Е -? R дифференцируема в точке
внутреннего экстремума Хо ? Е, то ее производная в этой точке равна
нулю: f'(x0) = 0.
М По определению дифференцируемое™ функции в точке хо
f(x0 + К) - f(x0) = f'{xo)h + a(x0; h)hy
где а(хо] h) -> 0 при h -> 0, х0 + Л € Е.
Перепишем это соотношение в виде
f(xo + h)- f(x0) = [f(x0) + а(х0; h)]h. A)
Поскольку хо — точка экстремума, то левая часть равенства A) либо нео-
неотрицательна, либо неположительна одновременно для всех достаточно близ-
близких к нулю значений h таких, что Хо + h E Е.
Бели бы было f'(xo) Ф 0, то при h достаточно близких к нулю величина
/Ч^о) 4- a(xo;h) имела бы тот же знак, что и /'(#o)> ибо a{xo\h) -> 0 при
h -^ 0, хо + h € Е.
Что же касается самого значения Л, то оно может быть как положитель-
положительным, так и отрицательным, коль скоро хо — точка внутреннего экстремума.
Таким образом, предположив, что /'(^о) ф 0, мы получаем, что правая
часть A) меняет знак при изменении знака h (если h достаточно близко к ну-
нулю), в то время как левая часть A) не может менять знака (если h достаточно
близко к нулю). Это противоречие завершает доказательство. >
Замечания к лемме Ферма. 1° Лемма Ферма дает, таким образом,
необходимое условие внутреннего экстремума дифференцируемой функции.
Для невнутренних экстремумов (как точка х = — 1 в примере 1) утверждение
о том, что f'{xo) = 0, вообще говоря, неверно.
2° Геометрически лемма вполне очевидна, ибо она утверждает, что в точке
экстремума дифференцируемой функции касательная к ее графику горизон-
горизонтальна (ведь f'(xo) есть тангенс угла наклона касательной к оси Ох).
8 Зорич В. А.

212
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
3° Физически лемма означает, что при движении по прямой в момент на-
начала возврата (экстремум!) скорость равна нулю.
Из доказанной леммы и теоремы о максимуме (минимуме) функции, не-
непрерывной на отрезке, вытекает следующее
Утверждение 1 (теорема Ролля1)). Если функция f: [a, ft] ->• R непре-
непрерывна на отрезке [a, ft], дифференцируема в интервале ]а,Ь[ и f(a) = f(b), то
найдется точка f ? ]а, Ь[ такая, что /'(?) = 0.
М Поскольку функция / непрерывна на отрезке [a, ft], то найдутся точ-
точки хт,хм € [a, ft], в которых она принимает соответственно минимальное
и максимальное из своих значений на этом отрезке. Если f(xm) = /(хм), то
функция постоянна на [а, ft], и поскольку в этом случае /'(#) = 0, то утвержде-
утверждение, очевидно, выполнено. Если же f(xm) < /(хм), то, поскольку /(о) = /(ft),
одна из точек хт, хм обязана лежать в интервале ]а, ft[. Ее мы и обозначим
через f. По лемме Ферма /'(?) = 0. >
2. Теоремы Лагранжа и Копта о конечном приращении. Следую-
Следующее утверждение является одним из наиболее часто используемых и важных
средств исследования числовых функций.
Теорема 1 (теорема Лагранжа о конечном приращении). Если функция
f: [a, ft] —>• К непрерывна на отрезке [а, ft] и дифференцируема в интервале
]а,ft[, то найдется точка ?€]а,Ь[ такая, что
/F) - /(а) = f'(O(b - а).
B)
Для доказательства рассмотрим вспомогательную функцию
которая, очевидно, непрерывна на отрезке
[о, ft], дифференцируема в интервале ]a,ft[
и на его концах принимает равные значе-
значения: F(a) = F(b) = /(о). Применяя к F(x)
теорему Ролля, найдем точку ? G ]a, ft[, в
которой
Рис. 21
ПО = № -
f{bl" /(о)
ft — a
= о- >
Замечания к теореме Лагранжа. 1° Геометрически теорема
Лагранжа означает (рис. 21), что в некоторой точке (?,/@)» гДе ? € ]а,Ь[,
. Ролль A652 — 1719) — французский математик.

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 213
касательная к графику функции будет параллельна хорде, соединяющей точ-
точки (а, /(а)), (ft, /(ft)), ибо угловой коэффициент последней равен I •
2° Если х интерпретировать как время, a /(ft) — f(a) — как величину пе-
перемещения за время ft — а частицы, движущейся вдоль прямой, то теорема
Лагранжа означает, что скорость /'(#) частицы в некоторый момент f ? ]a, ft[
такова, что если бы в течение всего промежутка времени [о, ft] частица двига-
двигалась с постоянной скоростью /'@> то она сместилась бы на ту же величину
/(ft) — /(о). Величину /'(?) естественно считать средней скоростью движения
в промежутке [a, ft].
3° Отметим, однако, что при движении не по прямой средней скорости в
смысле замечания 2° может не быть. Действительно, пусть, например, части-
частица движется по окружности единичного радиуса с постоянной угловой скоро-
скоростью и = 1. Закон ее движения, как мы знаем, можно записать в виде
г(?) = (cos t, sin t).
Тогда
= v(t) = (— sin t, cost)
и |v| = vsin21 + cos21 = 1.
В моменты t = 0 и t = 2тг частица находится в одной и той же точке
плоскости г@) = гBтг) = A,0), и равенство
гBтг) - г@) = v@ Bтг - 0)
означало бы, что v(?) = 0, но это невозможно.
Однако мы сознаем, что зависимость между перемещением за некоторый
промежуток времени и скоростью движения все же имеется. Она состоит
в том, что даже вся длина L пройденного пути не может превышать мак-
максимальной по величине скорости, умноженной на время в пути. Сказанное
можно записать в следующей более точной форме:
|г(Ь)-г(а)|< sup |r(t)||6-e|.
t€]o,6[
C)
Как будет в свое время показано, это естественное неравенство действи-
действительно всегда справедливо. Его тоже называют теоремой Лагранжа о конеч-
конечном приращении, а формулу B), справедливую только для числовых функций,
часто называют теоремой Лагранжа о среднем значении (роль среднего в дан-
данном случае играет как величина /'(?) скорости, так и точка f, лежащая между
а и ft).
4° Теорема Лагранжа важна тем, что она связывает приращение функции
на конечном отрезке с производной функции на этом отрезке. До сих пор мы
не имели такой теоремы о конечном приращении и характеризовали только
локальное (бесконечно малое) приращение функции через производную или
дифференциал в фиксированной точке.
я*

214 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Следствия теоремы Лагранжа
Следствие 1 (признак монотонности функции). Если в любой точке
некоторого интервала производная функции неотрицательна (положитель-
(положительна), то функция не убывает (возрастает) на этом интервале.
<4 Действительно, если х\, х2 — две точки нашего интервала и Х\ < x2i
т. е. х2 — х\ > О, то по формуле B)
f(x2) - f(xi) = /'(?) (х2 - zi), где xi < ? < х2,
и, таким образом, знак разности, стоящей в левой части равенства, совпадает
со знаком /'(О- >
Разумеется, аналогичное утверждение можно высказать о невозрастании
(убывании) функции с неположительной (отрицательной) производной.
Замечание. На основании теоремы об обратной функции и следствия 1,
в частности, можно заключить, что если на каком-то промежутке / число-
числовая функция f(x) имеет положительную или отрицательную производную, то
функция / непрерывна на /, монотонна на J, имеет обратную функцию /-1,
определенную на промежутке Г = /(/) и дифференцируемую на нем.
Следствие 2 (критерий постоянства функции). Непрерывная на от-
отрезке [а, Ь] функция постоянна на нем тогда и только тогда, когда ее про-
изводная равна нулю в любой точке отрезка [а, ft] (или хотя бы интервала
<4 Интерес представляет только доказательство того факта, что если
f'(x) = 0 на ]a,ft[, то для любых Х\,х2 ? [а,ft] имеет место равенство f(x\) =
= /(#2)- Но это вытекает из теоремы Лагранжа, по которой
ибо ? лежит между х\ и х2, т. е. ? € ]а, Ь[ и /'(?) = 0. >
Замечание. Отсюда, очевидно, можно сделать следующий (как мы уви-
увидим, очень важный для интегрального исчисления) вывод: если производные
F[(x)t F^(x) двух функций F\(x), F2(x) совпадают на некотором промежут-
промежутке, т. е. F[(x) = F^x), то на этом промежутке разность F\(x) — F2(x) есть
постоянная функция.
Полезным обобщением теоремы Лагранжа, которое тоже основано на те-
теореме Ролля, является следующее
Утверждение 2 (теорема Коши о конечном приращении). Пусть х =
= x(t) и у = y(t) — функции, непрерывные на отрезке [а, /?] и дифференцируе-
дифференцируемые в интервале ]а,/?[.
Тогда найдется точка г б]а,/?[ такая, что
х'(т)(у@)-у(а))=у'(т)(х@)-Х(а)).

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 215
Если к тому же x'(t) ф 0 при любом t Е]а,/?[, то х(а) ф х(C) и справедливо
равенство
~ Via) = j/
=
х(/3)-х(а) х
< Функция F(t) = x(t)(y(C) - у (а)) - y(t)(x(/3) -x(a)) удовлетворяет усло-
условиям теоремы Ролля на отрезке [а,/?], поэтому найдется точка г €]а,/?[, в
которой F'(r) = 0, что равносильно доказываемому равенству. Чтобы полу-
получить из него соотношение D), остается заметить, что если x'(t) ф О на ]а,/?[,
то по той же теореме Ролля х(а) ф х(/3). >
Замечания к теореме Коши. 1° Если пару функций #(?), y(t) рас-
рассматривать как закон движения частицы, то (#'(?),2/'(?)) есть вектор ее ско-
скорости в момент t, а (х(/3) - х(а),у{0) — у(а)) есть вектор ее смещения за
промежуток времени [а,/?], и теорема утверждает, что в некоторый момент
г Е [а, Р] эти векторы коллинеарны. Однако этот факт, относящийся к движе-
движению в плоскости, является таким же приятным исключением, каким является
теорема о средней скорости в случае движения по прямой. В самом деле,
представьте себе частицу, равномерно поднимающуюся по винтовой линии.
Ее скорость составляет постоянный ненулевой угол с вертикалью, в то время
как вектор смещения может быть и вертикальным (один виток).
2° Формулу Лагранжа можно получить из формулы Коши, если в последней
положить х = x(t) = t, y(t) = у(х) = /(#), а = а, /? = Ь.
3. Формула Тейлора. Из той части дифференциального исчисления,
которая уже изложена к настоящему моменту, могло возникнуть верное пред-
представление о том, что чем больше производных (включая производную нуле-
нулевого порядка) совпадает у двух функций в некоторой точке, тем лучше эти
функции аппроксимируют друг друга в окрестности этой точки. Мы в основ-
основном интересовались и сейчас будем интересоваться приближением функции в
окрестности некоторой точки с помощью многочлена Рп(х) = Рп(#о;#) =
= со + с\(х — хо) + ... + сп(х — Хо)п- Нам известно (см. пример 25 из § 2, п. 6),
что алгебраический полином можно представить в виде
Рп(х) = Рп(х0) + Щ^-{х - хо) + ... + Р"|Хо)(х- хо)п,
1! п\
Р(к)(хо)
т. е. Ск = п ,,—- (? = 0,1, ..., п). В этом легко убедиться непосредственно.
Таким образом, если нам будет дана функция /(#), имеющая в точке хо все
производные до порядка п включительно, то мы можем немедленно выписать
полином
Рп(х0; х) = Рп(х) = /(х0) + ?^ (х - х0) + ... + ^^ (х - хо)п, E)
производные которого до порядка п включительно в точке xq совпадают с
производными соответствующего порядка функции f(x) в точке

216
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Определение 5. Алгебраический полином, заданный соотношением E),
называется полиномом Тейлора1^ порядка п функции f(x) в точке
Нас будет интересовать величина
f(x) - Рп(х0;х) = гп
F)
уклонения полинома Рп(х) от функции /(#), называемая часто остатком,
точнее, п-м остатком или п-м остаточным членом формулы Тейлора:
/(*) = /(Хо) +
1!
х - х0) + ... + /(П)(,Хо) (х - хо)п + г„(х0; х).
П!
G)
Само по себе равенство G), конечно, не представляет интереса, если о
функции гп(хо;х) не известно ничего, кроме ее определения F).
Сейчас мы воспользуемся довольно искусственным приемом для получения
информации об остаточном члене. Более естественный путь к этому даст
интегральное исчисление.
Теорема 2. Если на отрезке с концами хо, х функция f непрерывна
вместе с первыми п своими производными, а во внутренних точках этого
отрезка она имеет производную порядка п + 1, то при любой функции ip,
непрерывной на этом отрезке и имеющей отличную от нуля производную в
его внутренних точках, найдется точка ?, лежащая между Хо и х, такая,
что
(8)
На отрезке / с концами хо, # рассмотрим вспомогательную функцию
= f(x)-Pn{t;x)
от аргумента t. Запишем определение F(t) подробнее:
F(t) = /(х) -
(9)
m
A0)
Из определения функции F(t) и условий теоремы видно, что F непрерывна
на отрезке J и дифференцируема в его внутренних точках, причем
1!
1!
1!
2!
п!
П!
Тейлор A685—1731) — английский математик.

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
217
Применяя к паре функций F(t), (p(t) на отрезке J теорему Коши (см. со-
соотношение D)), находим точку f между хо и я, в которой
F(x)-F(x0) ^F'
(р(х) -
Подставляя сюда выражение для F'(f) и замечая из сопоставления формул
F), (9) и A0), что F(x) - F(x0) = 0 - F(x0) = -rn(z0;z)> получаем форму-
формулу (8). >
Полагая в (8) <p(t) = х — ?, получаем
Следствие 1 (формула Коши остаточного члена).
гп(х0;х) = ± /(п
* - *)"(* " «о).
(И)
Особенно изящная формула получается, если положить в соотношении (8)
Следствие 2 (формула Лагранжа остаточного члена)
гп(х0; х) =
A2)
Отметим, что формулу G) Тейлора при xq = 0 часто называют формулой
Маклорена1).
Рассмотрим примеры.
Пример 3. Для функции f(x) = ех при хо = 0 формула Тейлора имеет
вид
*2 + v. + l*" + rn@;*), A3)
и на основании равенства A2) можно считать, что
1 t
гп@;х) =
(п +1)!
где |?| <
Таким образом,
г„@;х)| =
(п +1)!
(п + 1)!
"-"
A4)
1*1
п+1
Но при любом фиксированном х € К, если п -> оо, величина ' ' ч , как нам
(п+1)!
известно (см. пример 12 из гл. III, § 1, п. ЗЬ), стремится к нулю. Значит, из
. Маклорен A698—1746) — английский математик.

218 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
оценки A4) и определения суммы ряда вытекает, что для х €
^x+x + ... + Un + ... A5)
1! 2л 71:
Пример 4. Аналогично получаем разложение функции ах для любого а,
О < а, а ф 1:
от =
1па , In2а 2 , , Ьа п
1! 2! п!
Пример 5. Пусть /(х) = sinx. Нам известно (см. пример 18 из § 2, п. 6),
что /(п)(х) = sinfx + тгп)> тг € N, поэтому из формулы A2) Лагранжа при
= 0 и любом х €. R находим
гп@;х) = -^-^ sin(c + |(n + I))*"*1, A6)
откуда следует, что для любого фиксированного значения х € R величина
гп@;х) стремится к нулю при п —? оо. Таким образом, при любом х €
справедливо разложение
. + |«... + ?^. + ... (it,
Пример 6. Аналогично, для функции/(х) = cosх получаем
rn@; х) = -^-^ cos ({ + | (n + 1)) х"+1 A8)
и
сект - 1 - i- <r2 4- i- т4 - 4- (~1)П Т2п
Пример 7. Поскольку sh' х = chx, ch' x = sh x, для функции f(x) = shx
при хо = 0 из формулы A2) получаем
где </?(?) = sh?, если п четно, и ip(?) = ch^, если п нечетно. В любом случае
\<р(€)\ ^ max{|shx|, |chx|}, ибо |^| < |х|. Значит, для любого фиксирован-
фиксированного значения х € R выполняется гп@;х) —? 0 при п —? оо, и мы получаем
разложение
| | ^ ..) B0)
справедливое для любого х € R.

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 219
Пример 8. Аналогично получаем разложение
* + * + ... + ^y* + ..., B1)
справедливое для любого значения х € R.
Пример 9. Для функции /(х) = 1пA+х) имеем f^nHx) — -—}Тл—Ц —,
A + х)п
поэтому формула Тейлора G) при хо = 0 для этой функции имеет вид
2 + i3+ ()П хп + гп@;х). B2)
xx + x...+
2 о п
На сей раз представим гп@;х) по формуле Коши A1):
ИЛИ
B3)
где точка ? лежит между 0 и ?.
Бели |х| < 1, то из условия, что f лежит между 0 и х, следует, что
1-|0|
Таким образом, при |х| < 1
|rn@;x)K|xP+1, B5)
и, следовательно, при |х| < 1 справедливо разложение
— хп + ... B6)
п
Заметим, что вне отрезка |х| ^ 1 ряд, стоящий справа в B6), всюду расхо-
расходится, так как его общий член не стремится к нулю, если |х| > 1.
Пример 10. Если /(х) = A + х)а, где а ? R, то /(п)(х) = а(а - 1) х
х ... х (а - п + 1)A + х)а~п, поэтому формула Тейлора G) при х0 = 0 для
этой функции имеет вид
71!

220 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Используя формулу Коши A1), находим
rn@;i) = Q(a - ^ •(а " П) A + О*-*-1 (х - Оwx, B8)
где f лежит между 0 и ж.
Если |х| < 1, то, используя оценку B4), имеем
(l + O*!*! • B9)
При увеличении п на единицу правая часть неравенства B9) умножается на
м ~Г7)Х • Но поскольку |х| < 1, то при достаточно больших значениях п,
независимо от значения а, будем иметь (l Jx < q < 1, если |х| < q < 1.
Отсюда следует, что при любом а € R и любом х из интервала |х| < 1 вы-
выполнено гп@;х) -> 0, когда п -> оо; поэтому на интервале |х| < 1 справедливо
полученное Ньютоном разложение (бином Ньютона)
\* * а а(а —1) о а(а — 1)... (а — п+ 1) п /ллЧ
х)а = 1 + -х + v ., } х2 + ... + -^ '- f ^хп + ... C0)
Заметим, что, как следует из признака Даламбера (см. гл. III, § 1, п. 4Ь),
при |х| > 1 ряд C0) вообще расходится, если только а $ N.
Рассмотрим теперь особо случай, когда а = п € N.
В этом случае функция /(х) = A + х)а = A + х)п является полиномом
степени п, и поэтому все ее производные порядка выше чем п равны нулю.
Таким образом, формула Тейлора G) и, например, формула Лагранжа A2)
позволяют записать следующее равенство:
x2 + ... + n(Tl-1V--1x", C1)
представляющее собой известную из школы формулу бинома Ньютона для
натурального показателя:
A + х)п = 1 + С* х + С2пх2 + ... + С%хп.
Итак, мы определили формулу Тейлора G) и получили вид (8), A1), A2)
остаточного члена формулы Тейлора. Мы получили соотношения A4), A6),
A8), B5), B9), позволяющие оценивать погрешность вычисления важных эле-
элементарных функций по формуле Тейлора. Наконец, мы получили разложения
этих функций в степенные ряды.
Определение 6. Если функция /(х) имеет в точке хо производные
любого порядка п е N, то ряд
/Ы + ~/'(яо)(х - *о) + ... + ~/(п)(х0)(х - хо)п + ...
1! п!
называется рядом Тейлора функции / в точке

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 221
Не следует думать, что ряд Тейлора каждой бесконечно дифференциру-
дифференцируемой функции сходится в некоторой окрестности точки хо, ибо для любой
последовательности со, ci, ..., Сп, ... чисел можно построить (это не совсем
просто) функцию /(х) такую, что /^пЦхо) = Сп, п € N.
Не следует также думать, что если ряд Тейлора сходится, то он обязатель-
обязательно сходится к породившей его функции. Сходимость ряда Тейлора к поро-
породившей его функции имеет место только для так называемых аналитических
функций.
Вот пример Коши неаналитической функции:
Г е~г/х , если х Ф О,
= \
О, если х = 0.
Исходя из определения производной и того, что хке~г/х -> 0 при х -> 0
независимо от значения А; (см. пример 30 из § 2 гл. III), можно проверить, что
/(п)@) = 0 для п = 0, 1, 2, ... Таким образом, ряд Тейлора в данном случае
состоит только из нулевых членов и его сумма тождественно равна нулю, в
то время как /(х) фО при х ф 0.
В заключение остановимся на локальном варианте формулы Тейлора.
Вернемся снова к задаче о локальном приближении функции / : Е ->> R
полиномом, которую мы начали обсуждать в § 1, п. 3. Мы хотим подобрать
полином Рп{хо\х) = со + с\{х — хо) + ... + сп(х — хо)п так, чтобы иметь
/(х) = Рп(хо;х) + о((х - хо)п) при х -» х0, х е Еу
или, подробнее,
f(x) = со + ci(x - хо) + ... + сп{х - хо)п +
+ о((х - хо)п) при х -> хо, х е Е. C2)
Сформулируем в явном виде по существу уже доказанное
Утверждение 3. Если полином Рп(хо;х) = со + с\(х — хо) + ... +
+ сп(х — Хо)п, удовлетворяющий условию C2), существует, то он единст-
единственный.
< Действительно, из условия C2) последовательно и вполне однозначно
(в силу единственности предела) находятся коэффициенты полинома
со = _ Jim /(яр),
/(х) - со
= hm
X —
f(x) - [со + ... -f cn_i(x
= lim ;
(Х —

222 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Докажем теперь следующее
Утверждение 4 (локальная формула Тейлора). Пусть Е — отрезок с
концом Хо € Е. Если функция f: Е -> Е имеет в точке Хо все производные
/'(хо), ..., f^n\xo) до порядка п включительно, то справедливо следующее
представление:
+ о((х - хо)п) при х-»хо, хеЕ. C3)
Таким образом, задачу локального приближения дифференцируемой функ-
функции решает полином Тейлора соответствующего порядка.
Поскольку полином Тейлора Рп(хо; х) строится из условия совпадения всех
его производных до порядка п включительно с производными соответствую-
соответствующего порядка функции / вточке хо, то /(кЦхо) — Рп{хо;хо) = О (А; = 0,1, ...
..., п) и справедливость формулы C3) устанавливает следующая
Лемма 2. Если функция (р: Е —> К, определенная на отрезке Е с концом
Хо, такова, что она имеет е точке хо все производные <?>'(хо), ..., <р(п\хо)
до порядка п включительно и <р(хо) = <^;(жо) = ... = (р^пЦхо) = 0, то <р(х) =
= о((х - Хо)п) при х -> хо, х G Е.
< При п = 1 утверждение вытекает из определения дифференцируемости
функции ip в точке хо, в силу которого
<р(х) = (р(хо) + <р'(хо)(х - х0) -I- о(х - хо) при х -> хо, х е Е,
и, поскольку (р(хо) = <р'(хо) = 0, имеем
ср(х) = о(х — хо) при х -> хо, х ? Е.
Предположим, что утверждение доказано для порядков п = fc — 1
Покажем, что тогда оно справедливо также для порядка п = А; ^ 2.
Заметим предварительно, что поскольку
(х0) = hm
х —
то существование v?^*^(xo) предполагает, что функция <^?^~1)(х) определена на
Е хотя бы вблизи точки хо. Уменьшая, если нужно, отрезок Е, можно заранее
считать, что функции <?>(х), (р'(х), ..., (р(к~гЦх), где к ^ 2, определены на
всем отрезке J? с концом xq. Поскольку к ^ 2, то функция </?(х) имеет на
производную (р'(х) и по условию
Таким образом, по предположению индукции
<р'(х) = о((х — хо)*) при х ->- хо, х е Е.

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 223
Тогда, используя теорему Лагранжа, получаем
ср(х) = (р{х) - (р(х0) = <р'{?)(х - х0) = а *1
где f — точка, лежащая между хо и х, т. е. |? - хо| < |х - хо|, а а@ ->> 0 при
->> 25, ? € Е. Значит, при х ->> хо, х € 2? одновременно будем иметь ? -» U,
G i? и а(?) ->> 0, и поскольку
* - хо\к"г\х - хо|,
то проверено, что
х) = о((х — хо)*) при х -> хо, х ? Е.
Таким образом, утверждение леммы 2 проверено принципом математиче-
математической индукции. >
Соотношение C3) называется локальной формулой Тейлора, поскольку ука-
указанный в нем вид остаточного члена (так называемая форма Пеано)
rn(x0;x) = o((x-xo)n) C4)
позволяет делать заключения только об асимптотическом характере связи по-
полинома Тейлора и функции при х ->> хо, х € Е.
Формула C3) удобна, таким образом, при вычислении пределов и описании
асимптотики функции при х —> Хо, х 6 ??, но она не может служить для при-
приближенного вычисления значений функции до тех пор, пока нет фактической
оценки величины гп(хо;х) = о((х — хо)п).
Подведем итоги. Мы определили полином Тейлора
х) = /(хо) + ?^(х - хо) + ... + /<;Хо) (х - хо)п,
JL ТЪ
написали формулу Тейлора
») = /(хо) + ^^ (х - хо) + ... + /^о) (х - х0)" + г„(хо; х)
и получили следующие ее важнейшие конкретизации:
Если f имеет производную порядка п + 1 в интервале с концами хо, х,
то
= /(хо) +
где ? — точка, лежащая между xq и х.

224 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Если f имеет в точке хо все производные до порядка п ^ 1 включительно,
то
f{x) = /(хо) + Щг^{х - *0) + ... + /(*о)(х - rro)n + о((х - хо)п). C6)
1! п\
Соотношение C5), называемое формулой Тейлора с остаточным членом
в форме Лагранжа, очевидно, является обобщением теоремы Лагранжа, в ко-
которую оно превращается при п = 0.
Соотношение C6), называемое формулой Тейлора с остаточным членом
в форме Пеано, очевидно, является обобщением определения дифференцируе-
мости функции в точке, в которое оно переходит при п = 1.
Заметим, что формула C5) практически всегда более содержательна, ибо,
с одной стороны, как мы видели, она позволяет оценивать абсолютную вели-
величину остаточного члена, а с другой, например, при ограниченности
в окрестности xq из нее вытекает также асимптотическая формула
f{x) = /(хо) + ?^(х - Жо) + . ¦. + /()(,*о) (х - so)" + О((х - хо)"+1). C7)
Так что для бесконечно дифференцируемых функций, с которыми в пода-
подавляющем большинстве случаев имеет дело классический анализ, формула C5)
содержит в себе локальную формулу C6).
В частности, на основании формулы C7) и разобранных выше примеров
3—10 можно теперь выписать следующую таблицу асимптотических формул
при х ->> 0:
ex =
1! 2! n!
I^ + I
shx = х + 1x3 +
n - "
O(xn+1)
n!

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 225
Рассмотрим теперь еще некоторые примеры использования формулы Тей-
Тейлора.
Пример 11. Напишем полином, позволяющий вычислять значения функ-
функции sinx на отрезке —1 ^ х ^ 1 с абсолютной погрешностью, не превышаю-
превышающей 10~3.
В качестве такого многочлена можно взять тейлоровский многочлен подхо-
подходящей степени, получаемый разложением функции sinx в окрестности точки
хо = 0. Поскольку
Sina; =х_ 1 3 + 1 5 _тиш+ ("I)" Х2"+1 + 0 . Х*п+2 + r2n+2(Q; д.),
о! О: (Zfl -г 1)\
где по формуле Лагранжа
Г2п+2@;х) =
то при |х| ^ 1
|г2п+2@;х)|< /9л . ом-
\Zn + о;!
Но jt— vf < 10~~3 при п ^ 2. Таким образом, с нужной точностью на отрезке
х\ ^ 1 имеем sinx « х — ~х3 + т:Хъ.
3! 5!
Пример 12. Покажем, что tgx = х + -х3 -f о(х3) при х -> 0. Имеем
о
tg' X = COS X,
tg/; x = 2 cos x sin x,
tg;// x = 6 cos x siri2 x -f 2 cos x.
Таким образом, tgO = 0, tg'O = 1, tg"O = 0, tg/;/0 = 2 и написанное
соотношение следует из локальной формулы Тейлора.
Пример 13. Пусть а > 0. Исследуем сходимость ряда У] In cos —.
п=1 п
При а > 0 — ~> 0, когда п -> оо. Оценим порядок члена ряда
п
1ПCOS = lnl 1 — — • -г- -hOl -r- = • -г- -НО! -г- .
па V 2! n2a \n2aJ 2 n2a Vn2a/
Таким образом, мы имеем знакопостоянный ряд, члены которого эквива-
00 —1
лентны членам ряда ?) т^~- Поскольку последний ряд сходится только при
п=1 1п '
а > -, то в указанной области а > 0 исходный ряд сходится лишь при а > -
z 2
(см. задачу 16Ь)).

226 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 14. Покажем, что lncosx = -«^ "" То х* "" 45х6 + ^(х8) при
х -+ 0.
На сей раз, вместо того чтобы вычислять подряд шесть производных, мы
воспользуемся уже известными разложениями cos а; при ж -f 0 и h(l + «)
при и -> 0:
lncosx = lnfl - 1 х2 + |jX4 - ~хв + O(x*)) = ln(l + u) =
- -ir2 - —t4 - —rr6 4
~~ 2 12 45
Пример 15. Найдем значения первых шести производных функции
In cos x при х = 0.
Имеем (lncosVx = ~sinx, и потому ясно, что в нуле данная функция име-
cosx
ет производные любого порядка, ибо cos 0^0. Мы не станем искать функ-
функциональные выражения этих производных, а воспользуемся единственностью
полинома Тейлора и результатом предыдущего примера.
Если
/(х) = со + с\х + ... + СпХп + о(хп) при х -> 0,
то
и
Таким образом, в нашем случае получаем
(Incos)@) = 0, (Incos)'(O) = 0, (Incos)"@) = -^ • 2!,
(In cos) <3> @) = 0, (In cos) W @) = - -^ • 4!,
(In cos)<5>@) = 0, (Incos)<6> @) = --^ - 6!.
45
Пример 16. Пусть /(х) — бесконечно дифференцируемая в точке хо = 0
функция, и пусть известно разложение
/'(х) = с? + с[х + ... + с'пхп + O(xn+1)
ее производной в окрестности нуля. Тогда из единственности тейлоровского
разложения имеем
(/')<*>«)) = к\с'к,

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 227
поэтому /(*+1)@) = к\с'к. Таким образом, для самой функции /(х) имеем
разложение
*) = /@) + f *
или, после упрощений
*) = /@) + $х + ^-х2 + ... + -^-xn+1 + О(х
1 Z П + 1
п+2).
Пример 17. Найдем тейлоровское разложение функции f(x) = arctga; в
нуле.
Поскольку f'(x) = —Ц = A + ж2)" = 1 - х2 + х4 - ... + (-1)пх2п +
+ О(х2п+2), то по соображениям, изложенным в предыдущем примере,
*) = /@) + \х - |х
т. е.
arctgx = х - ix3 4- ^х5 - ... + t^lx^1 + О(х2п+3).
3 5 2п +1 v 7
Пример 18. Аналогично, раскладывая функцию arcsin'х = A — ж2)"'
по формуле Тейлора в окрестности нуля, последовательно находим
7% I 77 * J ••• I 7» 71 т* 1
П!
1 • 3 • . . ¦ • BП - 1) 2п
" 2п-п!
arcsinx = х + ^х3 + ^г^зГэ х5 +...
Bп -1)!! 2п+1
или, после элементарных преобразований,
Здесь Bп - 1)!! := 1 • 3 •... • Bп - 1), Bп)!! := 2 • 4 •... - Bп)

228 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 19. Воспользуемся результатами примеров 5,12,17,18 и найдем
т axctgs-sins =
ж-+0 1
Задачи и упражнения
1. Подберите числа о и 6 так, чтобы функция f(x) = cos ж — Т Г*а при х
была бесконечно малой возможно более высокого порядка.
2. Найдите lim х\ ( ——) .
ж—к» Le \х -г 1 / J
3. Напишите полином Тейлора функции ех в нуле, который позволял бы вычи-
вычислять значения ех на отрезке -1^х^2с точностью до 10.
4. Пусть / — бесконечно дифференцируемая в нуле функция. Покажите, что
a) если / четная, то ее ряд Тейлора в нуле содержит только четные степени х\
b) если / нечетная, то ее ряд Тейлора в нуле содержит только нечетные степени х.
5. Покажите, что если/еС(оо)[—1,1], /(п)@) = 0 дляп = 0,1, 2, ... исуществует
число С такое, что sup |/(п)(ж)| ^ п!С, п € N, то / = 0 на [—1,1].
6. Пусть / в С(п)(]-1,1[) и sup |/(ж)| ^ 1. Пусть mk(I) = inf |/(fc)(*)|, где / -
-Kx<i хег
промежуток, содержащийся в интервале ]—1,1[. Покажите, что
a) если / разбит на три последовательных промежутка /i, /2, /3 и /г — длина /г,
то
mk(I) ^ -(m*_i(/i) + ra*_i(/3));
b) если / имеет длину Л, то
с) существует такое число ап, зависящее только от п, что если |/'@)| ^ ап, то
уравнение /(п^(х) = 0 имеет в ]—1,1[ по крайней мере п — 1 различных корней.
Указание. В Ь) используйте а) и принцип индукции; в с) используйте а) и по
индукции докажите, что существует такая последовательность xkl < хк2 < ... < хкк
точек интервала ]-1,1[, что f^k)(xki) • f(k)(xki+1) < 0 при 1 ^ г ^ к - 1.
7. Покажите, что если функция / определена и дифференцируема на интервале
/ и [о, Ь] С /, то
a) функция f (х) (даже не будучи непрерьшной!) принимает на [а, Ь] все значения
между /'(о) и f'(b) (теорема Дарбу1));
b) если еще f"(x) существует в ]а,Ь[, то найдется точка f € ]a,b[ такая, что
. Дарбу A842—1917) — французский математик.

§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 229
8. Функция f(x) может быть дифференцируемой на всей числовой прямой, но
при этом f'(x) может не быть непрерывной (см. пример 7 из § 1, п. 5).
a) Покажите, что функция f'(x) может иметь разрывы только второго рода.
b) Укажите ошибку в следующем «доказательстве» непрерывности f'(x).
< Пусть хо — произвольная точка на R и f(xo) — производная функции / в
точке хо. По определению производной и теореме Лагранжа
f{xo) = Ит /<*> " /(жо) = Ит /'(?) = Ит
? X — Х * ?
где f — точка между хо и ж, стремящаяся, таким образом, к хо при х —> хо- >
9. Пусть / — дважды дифференцируемая функция на промежутке /. Пусть Мо =
= sup |/(х)|, М\ = sup \f'(x)\, М2 = sup \f"(x)\. Покажите, что
1 l
а) если / = [—а, а], то
x2 + a'
Ь)
М\ ^ 2у/М0М2, если длина / не меньше
к Mi ^ y/2MoM2i если / = R;
c) в задаче Ь) числа 2 и %/2 не могут быть заменены меньшими;
d) если / дифференцируема р раз в R и если величины Мо и Мр = sup
хек
конечны, то при 1 ^ к ^ р конечны также величины М* = sup \f^k\x)\ и
хек
Указание. Используйте задачи 6Ь), 9Ь) и принцип индукции.
10. Покажите, что если функция / имеет в точке хо все производные до порядка
п ¦+ 1 включительно и /^п+1^(жо) ф 0, то в остаточном члене формулы Тейлора,
записанном в форме Лагранжа
гп(хо\х) = -т/(пЧжо + в(х — •'
п!
где 0 < в < 1, величина 0 = 0(ж) стремится к при х —>•
n -f 1
11. Пусть / — функция, п раз дифференцируемая на промежутке /. Покажите,
что:
a) Бели / в (п + 1) точках промежутка / обращается в нуль, то найдется точка
f G / такая, что /^(?) = 0.
b) Бели jci, Ж2, . • • , Хр — точки промежутка /, то существует и притом един-
единственный многочлен Ь(х) (интерполяционный полином Лагранжа) степени не выше
(п — 1) такой, что f(x%) = L(xi), i = 1, ..., п. Кроме того, для х € / найдется точка
€ / такая, что
х) - Цх) =
71!
!
с) Если Ж1 < Х2 < •.. < хр — точки промежутка /, гц A ^ гI ^ р) — натуральные
числа такие, что щ Н- п2 + .. • + пр = п и f(k)(xi) = 0 при 0 < & < п« - 1, то в
промежутке [ж1,жр] найдется точка ^, в которой /(п~1)({) = 0.

230 ГЛ. V, ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
с1)~Существует и притом единственный многочлен Н(х) (интерполяционный по-
полином Эрмита1^) степени п—1 такой, что f^k\xi) = H^(xi) приО ^ А: ^ п» — 1. Кро-
Кроме того, внутри наименьшего промежутка, содержащего течки жих,, г = 1, ..., р,
найдется точка f такая, что
= н(х) +
Эта формула называется интерполяционной формулой Эрмита. Точки ж», г =
= 1, ..., р, называются уздами гттерполлцгш кратности щ соответственно. Част-
Частными случаями формулы Эрмита являются интерполяционная формула Лагранжа
(задача Ь)) при р = п и rii = 1 (t = 1, ..., п), а также формула Тейлора с остаточ-
остаточным членом в форме Лагранжа, получающаяся при р — 1, т. е. при интерполировании
с одним узлом кратности п.
12. Покажите, что
a) между двумя вещественными корнями полинома Р(х) с вещественными коэф-
коэффициентами имеется корень его производной Р'(х)\
b) если полином Р(х) имеет кратный корень, то полином Р'(х) имеет тот же
корень, но на единицу меньшей кратности;
c) если Q(x) — наибольший общий делитель полиномов Р(х) и Р'(х), где Р'(х) —
производная полинома Р(ж), то полином , [ имеет в качестве корней корни поли-
Q(x)
нома Р(х), причем все они кратности 1.
13. Покажите, что
a) любой полином Р(х) можно представить в виде со +ci(a; — хо) +... +сп(х — хо)п;
b) существует единственный полином степени п, для которого f(x) — Р(х) =
= о((х — хо)п) при Е Э х —> xq. Здесь / — функция, определенная на множестве Е}
а хо — предельная точка Е.
14. С помощью индукции по А;, 1 ^ А;, определим конечные разности порядка к
функции / в точке
; hi) := Д/Oro; Ы) = f(x0 + hi) -
; hi, h2) := АД/Ого; huh2) =
= (f(x0 -I- hi + h2) - /(xo + h2)) - (/(a?o + Ы) -
= f(x0 + /ii + /12) ~ /(xo + /11) - /(жо + /12) +
A f(xo;hi, ...,
где gk(x) = A1/^; ^fc) = f(x
а) Пусть / 6 C^^^la^b] и существует /(п)(ж) по крайней мере в интервале ]а,6[.
Если все точки жо, ^о + hi, жо + h2, xo + hi +h2i хо Н- /ц + ... + hn лежат в [о, 6], то
внутри наименьшего отрезка, их содержащего, найдется точка f такая, что
; hu ..., hn) = /(n)(f) hi... hn.
. Эрмит A822 — 1901) — французский математик, занимавшийся вопросами анализа;
в частности, доказал трансцендентность числа е.

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 231
b) (Продолжение.) Если существует /^(жо), то имеет место оценка
|Ап/(ж0; /ii, • • •, К) - /(п)(*о) /ii • • • hn\ ^ sup \f(n)(x) - /(n)(*o)| • |/ii|... IM-
е)Ь[
с) (Продолжение.) Положим Anf(xo;h1...)h) =: Anf(xo\hn). Покажите, что
если существует /^(жо), то
d) Покажите на примере, что предыдущий предел может существовать даже
тогда, когда f^(x) в точке хо не существует.
Указание. Рассмотрите, например, А2/@;Л2) для функции
I О, х = О,
и покажите, что
lim r^r = 0.
•ZJ
15. а) Применив теорему Лагранжа к функции -^-, где а > 0, покажите, что при
п € N и а > 0 имеет место неравенство
1
< (
^ а\(п-1)а па
Ь) Воспользуйтесь результатом задачи а) и покажите, что ряд ^2 — сходится
П
при а > 1. n==1 П
§ 4. Исследование функций методами дифференциального
исчисления
1. Условия монотонности функции
Утверждение 1. Между характером монотонности дифференцируе-
дифференцируемой на интервале ]а,b[= E функции f:E->Ru знаком (положительностью)
ее производной /' на этом интервале имеется следующая взаимосвязь:
f'(x) > 0 => / возрастает => ff(x) ^ 0,
f'(x) ^ 0 => / не убывает => f(x) ^ 0,
/'(*) = 0 =» / = const => /'(я)=0,
/'(х) ^ 0 => / we возрастает => /'0е) ^ 0,
< 0 =*> / убывает => /'(ж) ^ 0.
«^ Левый столбец следствий нам уже знаком по обсуждению теоремы-Ла-
теоремы-Лагранжа, в силу которой /(жг) — f(x\) = F(Q(x2 — х\), где х\,Х2 G ]а,Ь[ и f —
точка между ^i и жг- Из этой формулы видно, что при х\ < х^ положитель-
положительность разности f(x2) — f(x\) совпадает с положительностью /'(О-

232 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Правый столбец следствий получается непосредственно из определения
производной. Покажем, например, что если дифференцируемая на ]а, Ь[ функ-
функция / возрастает, то f'(x) ^ 0 на ]а,Ь[. Действительно,
/'(х) = lim
Если h > 0, то f(x + ft) — f(x) > 0, а если ft < 0, то f(x + ft) — f(x) < 0; поэтому
дробь под знаком предела положительна.
Следовательно, ее предел ff(x) неотрицателен, что и утверждалось. >
Замечание 1. На примере функции f(x) = х3 видно, что возрастание
дифференцируемой функции влечет только неотрицательность производной,
а не ее положительность. В нашем примере /'@) = Зж2|ж=о = 0.
Замечание 2. В символе А => В, как мы уже в свое время отмечали,
А — условие, достаточное для JB, а В — условие, необходимое для того, чтобы
было выполнено А. Значит, из утверждения 1, в частности, можно сделать
следующие выводы:
функция постоянна на интервале тогда и только тогда, когда ее произ-
производная тождественно равна нулю на этом интервале;
для того чтобы дифференцируемая на интервале функция убывала на нем,
достаточно, чтобы ее производная была отрицательна в любой точке этого
интервала;
для того чтобы дифференцируемая на интервале функция убывала на нем,
необходимо, чтобы ее производная была неположительна на этом интер-
интервале.
Пример 1. Пустьf(x) =х3-Зх+2наR. Тогдаf'(x) = Зж2-3 = 3(ж2-1)
и, поскольку /'(#) < 0 при \х\ < 1 и f'(x) > 0 при \х\ > 1, можем сказать, что
на интервале ]—оо, —1[ функция возрастает, на интервале ]—1,1[ убывает, а на
интервале ]1, +оо[ вновь возрастает.
2. Условия внутреннего экстремума функции. Учитывая лемму
Ферма (лемма 1, § 3), можно сформулировать следующее
Утверждение 2 (необходимые условия внутреннего экстремума). Для
того чтобы точка хо была точкой экстремума функции /: U(xo) -> R, опре-
определенной в окрестности U(xo) этой точки, необходимо выполнение одного
из двух условий: либо функция не дифференцируема в Xq, либо fr(xo) = 0.
Простые примеры показывают, что эти необходимые условия экстремума
не являются достаточными.
Пример 2. Пусть f(x) = хг на Е. Тогда /'@) = 0, но в точке хо = 0
экстремума нет.
Пример 3. Пусть
{при х > Л'
при х < 0.

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 233
Эта функция с изломом в нуле, очевидно, не имеет в нуле ни производной,
ни экстремума.
Пример 4. Найдем максимум функции /(ж) = ж2 на отрезке [—2,1].
В данном случае очевидно, что он будет достигнут в конце —2 отрезка, но
регулярный способ его отыскания таков. Находим /'(ж) = 2ж и все точки ин-
интервала]—2, 1[, где /'(ж) = 0. В нашем случае это одна точка ж = 0. Максимум
/(ж) должен быть либо среди этих точек, либо в одной из концевых точек, о
которых утверждение 2 ничего не говорит. Таким образом, надо сравнить
значения /(—2) = 4, /@) = 0, /A) = 1, откуда заключаем, что максимальное
значение функции /(ж) = ж2 на отрезке [—2,1] равно 4 и принимается в точке
—2, являющейся концом этого отрезка.
Используя установленную в пункте 1 связь между знаком производной и ха-
характером монотонности функции, приходим к следующим достаточным усло-
условиям наличия или отсутствия локального экстремума в точке.
Утверждение 3 (достаточные условия экстремума в терминах первой
производной). Пусть /: U(xo) -* R — функция, определенная в окрестности
U(xo) точки хо, непрерывная в самой этой точке и дифференцируемая в ее
о о
проколотой окрестности ?/(жо). Пусть U~(xo) = {ж ? U(xo)\x < жо} и
U+(x0) = {ж € U(xo)\x > х0}.
Тогда справедливы следующие заключения:
a) (Уж € и~(хо) (f'(x) < 0)) Л (Уж € #+(ж0) (/'(*) < 0)) =>
=» (/ в хо экстремума не имеет);
b) (Уж G ?/-(ж0) (/'(*) < 0)) Л (Уж е ?/+(ж0) (/'(*) > 0)) =>
=>> (жо — точка строгого локального минимума /);
c) (Уж е и-(х0) (/'(*) > 0)) л (Уж е и+Ы (/'(ж) < о)) =>
=^ (жо — точка строгого локального максимума /);
d) (Уж е и~(х0) (f'(x) > о)) л (Уж е и+(х0) (/'(*) > о)) =>
=> (/ в хо экстремума не имеет).
Кратко, но менее точно, можно сказать, что если при переходе через точ-
точку производная меняет знак, то экстремум есть, а если ее знак при этом не
меняется, то экстремума нет.
Заметим сразу же, что эти условия, являясь достаточными, не являются
необходимыми для экстремума, в чем можно убедиться на следующем при-
примере.
Пример 5. Пусть
2ж2 + ж2 sin - при ж ф 0,
JC
0 при ж = 0.

234 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Поскольку х2 ^ f(x) ^ 2х2, то ясно, что функция имеет строгий локальный
минимум в точке хо = 0, однако ни в какой проколотой полуокрестности этой
точки ее производная ff(x) = 4х + 2xsin cos - не сохраняет знак. Этот
X X
же пример указывает на недоразумения, которые могут возникнуть в связи с
приведенной выше сокращенной формулировкой утверждения 3.
Теперь обратимся к доказательству утверждения 3.
о
< а) Из утверждения 2 следует, что функция / строго убывает на U~(xo).
Поскольку она непрерывна в хо, имеем о lim f(x) = f(xo) и, следова-
тельно, f(x) > f(xo) при х Е U~{xq). По тем же соображениям /(хо) > f(x)
о
при х Е U+(xo). Таким образом, функция строго убывает во всей окрестности
U(xo) и хо не является точкой экстремума.
о
Ь) Сначала, как ива), заключаем, что ввиду убывания f(x) на U~{xq) и
о
непрерывности / в Хо имеем f(x) > f(xo) при х Е U~(xo). Из возрастания / на
о о
U+{xq) и непрерывности / в xq заключаем, что /(хо) < /0е) при х Е U+(xo).
Таким образом, функция / имеет в хо строгий локальный минимум.
Утверждения с) и d) доказываются аналогично. >
Утверждение 4 (достаточные условия экстремума в терминах высших
производных). Пусть функция f : U(xq) -> R, определенная в окрестности
U(xo) точки хо, имеет в хо производные до порядка п включительно (п ^ 1).
Если Г{хо) = ... = f(n~l\xo) = 0 и fW ф 0, то при п нечетном в
хо экстремума нет, а при п четном экстремум есть, причем это строгий
локальный минимум, если f^(x0) > 0, и строгий локальный максимум, если
< 0.
Используя локальную формулу Тейлора
/(х) - /(хо) = /(п)(х0)(х - хо)п + а(х)(х - хо)п, A)
где ос{х) —> 0 при х ~> хо, будем рассуждать так же, как при доказательстве
леммы Ферма. Перепишем A) в виде
f{x) - /(хо) = (/(П>Ы + а(х))(х - хо)п. B)
Поскольку /*п)(хо) Ф 0, а а(х) -> 0 при х -> хо, то сумма f^(xo) + а(х)
имеет знак f(n\xo), когда х достаточно близко к хо. Если п нечетно, то при
переходе через хо скобка (х — хо)п меняет знак и тогда изменится знак всей
правой, а следовательно, и левой части равенства B). Значит, при п = 2к + 1
экстремума нет.
Если п четно, то (х — хо)п > 0 при х ф хо и, следовательно, в малой
окрестности точки хо знак разности /(х) — /(хо), как видно из равенства B),
совпадает со знаком /(п)(хо). >

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ
235
Рассмотрим примеры.
Пример 6. Закон преломления света в геометрической оптике (закон
Снеллиуса1)). Согласно принципу Ферма истинная траектория света между
любыми двумя точками такова, что на ней реализуется минимум времени,
которое необходимо свету, чтобы пройти из одной точки в другую по любому
фиксированному пути, соединяющему эти точки.
Из принципа Ферма и того, что кратчайшей линией между любыми двумя
точками является отрезок прямой с концами в этих точках, следует, что в
однородной изотропной среде (устроенной одинаково как в каждой точке,
так и в каждом направлении) свет распространяется прямолинейно.
Пусть теперь имеются две такие среды
и свет распространяется из точки А\ к Аг>
как показано на рис. 22.
Если с\, С2 — скорости света в этих сре-
средах, то время прохождения указанного пути Ш
таково: —
О
t(x) = —
С2
(а - ж)
а
А
Найдем экстремум функции t(x):
Рис. 22
t'(x) = 4-
X
+ х
1_
с2
а — х
+ (а - х)
= 0,
что в соответствии с обозначениями рисунка дает сг г sinai = с^1 sina2.
Из физических соображений или прямо из вида функции t(x), неограни-
неограниченно растущей при х ~> оо, ясно, что точка, где tf(x) = 0, является точкой
абсолютного минимума непрерывной функции t(x). Таким образом, из прин-
принципа Ферма следует закон преломления sinQl — —
Пример 7. Покажем, что при х > 0
х
а
ах + a — 1 ^ 0,
ха - ах + а - 1 ^ 0,
когда 0 < a < 1,
когда a < 0 или 1 < а.
C)
D)
< Дифференцируя функцию f(x) = ха - ах + a - 1, находим f'(x) =
= а(ха~г — 1) и f'(x) = 0 при х = 1. При переходе через точку 1 производная
переходит от положительных значений к отрицательным, если 0 < a < 1,
и от отрицательных к положительным, если а < 0 или 1 < а. В первом
случае в точке 1 строгий максимум, а во втором — строгий минимум (и не
только локальный, что следует из соображений монотонности / на участках
0 < х < 1, 1 < х). Но /A) = 0 и, таким образом, оба неравенства C), D)
. Снеллиус A580 — 1626) — нидерландский астроном и математик.

236 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
установлены. При этом показано даже, что оба неравенства строгие, если
хф 1. >
Заметим, что если заменить х на 1 + х, то мы обнаружим, что C) и D) —
это развитие уже знакомого нам при натуральном показателе а неравенства
Бернулли (гл. II, § 2, с. 64; см. также задачу 2 в конце настоящего параграфа).
С помощью элементарных алгебраических преобразований из доказанных
неравенств можно получить ряд классических и важных для анализа нера-
неравенств. Приведем их вывод.
а. Неравенства Юнга1). Если а> 0 и Ь> 0, а числар, q таковы, что
0,1 и ± + ± = 1, то
а1/р bl'q ^ i a + - Ь, если р > 1, E)
р q
а1/рbl'q >-a+ ~ft, если р < 1, F)
р q x '
причем знак равенства в E) г* F) имеет место только при а = ft.
^ Для доказательства достаточно в C) и D) положить х = - и а = -,
а также ввести обозначение - = 1 . >
q Р
b. Неравенства Гель дера2). Пусть Х{ ^ 0, у% ^ О (г = 1, ...,п) и
- + -¦= 1. Тогда
р q
~ ~ ~ G)
U
П / П \ 1/Р / П
i=l V»=l / V»=l
w / w \1/P / n
»=i \»=i / \t=i
(8)
В случае р < 0 в (8) предполагается, что ж» > 0 (г = 1, ..., п). Знак равен-
равенства в G) 1х (8) возможен только в случае пропорциональности векторов
п п
Проверим неравенство G). Пусть X = X! ж? > 0, У = 5^ 2/? > 0.
х? у?
Полагая в E) а = —, Ь = —, получаем
У» < 1 ?? , 1 У?
Х^В. Юнг (Янг) A882 — 1946) — английский математик.
2)<Э. Гёльдер A859—1937) — немецкий математик.

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 237
Суммируя эти неравенства по г от 1 до п, получаем
п
что эквивалентно G).
Аналогично, из F) получаем (8). Поскольку знак равенства в E) и F)
возможен лишь при а = ft, заключаем, что в G) и (8) он возможен лишь при
пропорциональности х? = А у? или у? = А ж?. >
с. Неравенства Минковского1). Пусть х% ^ 0, у% ^ 0 (г = 1, ...,п).
/ п \
I>i+2/*)p
1/р / п 41/р / п 4 1/р
t=l / \г=1
U
при р < 1, р ф 0. A0)
t=i / \t=i / \t=i /
Применим неравенства Гёльдера к членам правой части тождества
п п п
& + ViY = Е х> & + у^1 + Е w (ж*+ г/*)^1 •
t=l
Тогда левая часть будет оценена сверху или снизу в соответствии с нера-
неравенствами G), (8) величиной
г/р/п \i/« /п
?
(Е (Е
После деления полученных неравенств на ( J2 (xi 4- у%)р) приходим к (9)
и A0). Ki=1 J
Зная условия равенства в неравенствах Гёльдера, проверяем, что знак ра-
равенства в неравенствах Минковского возможен лишь в случае коллинеарности
векторов (хг, ..., хп), (уг, ..., уп). >
При п = 3 и р = 2 неравенство Минковского (9), очевидно, является нера-
неравенством треугольника в трехмерном евклидовом пространстве.
1^Г. Минковский A864 — 1909) — немецкий математик, предложивший адекватную ма-
математическую модель (пространство с индефинитной метрикой) специальной теории отно-
относительности.

238
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 8. Рассмотрим еще простейший пример использования высших
производных при отыскании локальных экстремумов. Пусть /(х) = sin х. По-
Поскольку f'{x) = cosx и f"(x) = — sinx, то все точки, где f'(x) = cosx = 0,
являются локальными экстремумами функции sinx, так как в них /"(х) =
= — sinx ф 0. При этом f"(x) < 0, если sinx > 0, и f"(x) > 0, если sinx < 0.
Таким образом, точки, где cos х = 0, a sin x > 0, являются локальными мак-
максимумами, а точки, где cosx = 0, a sinx < 0, — локальными минимумами
функции sinx (что, конечно, и так известно).
3. Условия выпуклости функции
Определение 1. Функция /: ]а,Ь[ ->• R, определенная на интервале
]а, Ь[ С К, называется выпуклой на нем, если для любых точек xi, х2 G ]а, Ь[ и
любых чисел а\ ^ 0, а2 ^ 0 таких, что а\ + с*2 = 1, имеет место неравенство
/(aixi + а2х2) ^ ax/(xi) -f a2/(x2). A1)
Если при Xi ^ X2 и ai • a2 ^ 0 это неравенство является строгим, то
функция называется строго выпуклой на интервале ]а, &[.
Геометрически условие A1) выпуклости
функции / : ]а, b[ -> R означает (рис. 23),
что точки любой дуги графика функции
лежат под хордой, стягивающей эту дугу.
В самом деле, в левой части A1) стоит
значение /(х) функции в точке х = a.\Xi -f
+ СК2Х2 G [х1,Хг], а справа — значение в
той же точке линейной функции, график
которой (прямая) проходит через точки
,/(xi)), (х2,/(х2)).
Соотношение A1) означает, что мно-
xv f{xx))
(х, fix))
х = a ^+
Рис. 23
жество Е = {(х,2/) G R2 |х G ]а,Ь[, /(х) < у} точек плоскости, лежащих над
графиком функции, является выпуклым, откуда и сам термин «выпуклая»
функция.
Определение 2. Если для функции /: ]а,Ь[ -> R в A1) имеет место
обратное неравенство, то говорят, что функция вогнута на интервале ]а, Ь[
или, чаще, что она выпукла вверх на этом интервале, в отличие от выпуклой
функции, которую тогда называют выпуклой вниз на интервале ]а,6[.
Поскольку все дальнейшие построения проводятся одинаково для функций,
вьшуклых вниз или вверх, мы ограничимся рассмотрением выпуклых (вниз)
функций.
Сначала придадим неравенству A1) другой вид, более приспособленный
наших целей.
Из соотношений х = а\Х\ + а2х2, а\ + а2 = 1 имеем
х — Xi
х2 — х
=
Х2 — Х\
а2 =
Х2 — Х\

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 239
поэтому A1) можно переписать в виде
/(яг)
Х2 — Xi X2 —
Учитывая, что Xi ^ х ^ Х2 и х\ < Х2, после домножения на Х2 — х\ получаем
(х2 - x)f(xi) + (xi - х2)/(х) 4- (х - xi)/(x2) ^ 0.
Замечая, что хг — х\ = (хг — х) + (х — xi), из последнего неравенства после
элементарных преобразований находим, что
/(*) - Пч) ^ /Ы - /(*) A2)
X — Х\ Х2 — X
при Х\ < х < Х2 и любых Xi, X2 € ]а,
Неравенство A2) является иной формой записи определения выпуклости
функции /(х) на интервале ]а,Ь[. Геометрически A2) означает (см. рис. 23),
что угловой коэффициент хорды /, соединяющей точки (xi,/(xi)), (x,/(x)),
не больше (а в случае строгой выпуклости — меньше) углового коэффициента
хорды II, соединяющей точки (х,/(х)), (х2,/(хг)).
Предположим теперь, что функция /: ]а, Ь[ -» R дифференцируема на ]а, Ь[.
Тогда, устремляя в A2) х поочередно к х\ и Х2, получаем
< /(a?2)"/(Jl) < ГЫ,
Х2 — X
что устанавливает монотонность производной функции /.
Учитывая это, для строго выпуклой функции, пользуясь теоремой Лагран-
жа, находим
Пх1) < т) = /(»)/(»!) < /ШМ = /'F) < /Ча;2)
X — Xi X2 — X
при xi < fi < x < & < ^2) т. е. строгая выпуклость влечет строгую монотон-
монотонность производной.
Итак, если дифференцируемая функция / выпукла на интервале ]а, Ь[, то
/' не убывает на ]а, Ь[, а в случае строгой выпуклости / ее производная /'
возрастает на ]а, Ь[.
Оказывается, это не только необходимые, но и достаточные условия вы-
выпуклости дифференцируемой функции.
В самом деле, для а < х\ < х < Х2 < Ь по теореме Лагранжа
~ /(X) _
х-х,
где xi < ^1 < х < ?2 < ^2, и если /'(fi) ^ /'(Сг), то выполнено условие A2)
выпуклости (или строгой выпуклости, если /'(fi) < /'(?2))-
Таким образом, мы доказали следующее

240 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Утверждение 5. Для того чтобы дифференцируемая на интервале
]а, Ь[ функция /: ]а,Ь[ —>• R была выпуклой (вниз) на ]а,Ь[, необходимо и до-
достаточно, чтобы ее производная f не убывала на ]а, Ь[. При зтом строгому
возрастанию f соответствует строгая выпуклость /.
Сопоставляя утверждение 5 и утверждение 3, получаем
Следствие. Для того чтобы функция /: ]а,Ь[ -* Ж, имеющая на интер-
интервале ]а,Ь[ вторую производную, была выпуклой (вниз) на зтом интервале,
необходимо и достаточно, чтобы на ]а, Ь[ было f"(x) ^ 0. Если же f"(x) > 0
на]а,Ь[, то этого достаточно, чтобы гарантировать строгую выпуклость
функции f: ]а, b[ -> R.
Теперь мы в состоянии объяснить, например, почему графики простейших
элементарных функций рисуют с тем или иным характером выпуклости.
Пример 9. Исследуем выпуклость функции f(x) = xa на множестве
х > 0. Поскольку f"(x) = а(а — 1)ха~2, то f"(x) > 0 при а < 0 или при
а > 1, т. е. при таких значениях показателя степени а степенная функция
ха строго выпукла (вниз). При 0 < а < 1 имеем f"(x) < 0, поэтому для
таких показателей степени она строго выпукла вверх. Например, параболу
f(x) = х2 мы всегда рисуем выпуклой вниз. Оставшиеся случаи а = 0 и а = 1
тривиальны: х° = 1, х1 =-,х. И в том и в другом случае графиком функции
является луч (см. рис. 30 на с. 247).
Пример 10. Пусть f(x) = аж, 0 < а, а ф 1. Поскольку f"(x) = ax In2 а >
> 0, показательная функция ах при любом допустимом основании а строго
выпукла (вниз) на Ж (см. рис. 24 на с. 247).
Пример 11. Для функции f(x) = logax имеем f"(x) = ———> поэтому
•Z/ ill О
функция строго выпукла (вниз), если 0 < а < 1, и строго выпукла вверх, если
1 < а (см. рис. 25 на с. 247).
Пример 12. Исследуем выпуклость функции f(x) = sin ж (см. рис. 26 на
с. 247).
Поскольку f"(x) = — sin ж, то f"(x) < 0 на интервалах тг • 2k < х < пBк 4-1)
и f"(x) > 0 на интервалах тгBА;— 1) < х < тг-2А;, где к € Z. Отсюда, например,
следует, что дуга графика функции sinx на отрезке 0 ^ х ^ — лежит над
стягивающей ее хордой всюду, кроме концевых точек; поэтому sin л; > — х
7Г П
при 0 < х < —.
Укажем теперь еще одну характеристику выпуклой функции, геометриче-
геометрически эквивалентную тому, что выпуклая область на плоскости лежит по одну
сторону от касательной к ее границе.
Утверждение 6. Дифференцируемая на интервале ]a,b[ функция /:
]о, Ь[ -* R выпукла (вниз) на ]а,Ь[ тогда и только тогда, когда ее график
всеми своими точками лежит не ниже любой проведенной к нему касатель-
касательной. При этом для строгой выпуклости функции необходимо и достаточно,

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 241.
чтобы все точки графика, за исключением самой точки касания, лежали
строго выше этой касательной.
<4 Необходимость. Пусть х0 ? ]а,Ъ[. Уравнение касательной к графи-
графику в точке (хо, /(#о)) имеет вид
У = f(xo) + f'(xo)(x -
поэтому
= f(x) - f(x0) - ?Ы{х - хо) = (/'(О - /'
где f — точка между х и Жо- Так как / вьшукла, то функция f'(x) не убывает
на ]а, Ь[ и знак разности /'(?) — /'(^о) совпадает со знаком разности х — Жо,
поэтому /(ж) — 2/(ж) ^ 0 в любой точке х ? ]а,Ь[. Если / строго выпукла, то
/' строго возрастает на ]а, Ь[ и, значит, f(x) — у(х) > 0 при хб]о,6[ и х ф xq.
Достаточность. Если для любых точек х, Хо € ]а,Ь[
/(ж) - у(х) = /(ж) - /(ж0) - f'(xo)(x - ж0) ^ 0, A3)
то
f(x) - /(хо) ^
X — Жо
/(ж) - /(хо) ^
Ж — Жо
Таким образом, для любой тройки точек х\, ж, жг € ]а,Ь[ такой, что Ж1 <
< ж < жг, получаем
Ж — Х\ Жг — Ж
причем строгое неравенство в A3) влечет строгое неравенство в последнем
соотношении, которое, как мы видим, совпадает с записью A2) определения
выпуклой функции. >
Рассмотрим примеры.
Пример 13. Функция /(ж) = ех строго вьшукла. Прямая у = ж 4- 1
является касательной к графику этой функции в точке @,1), так как /@) =
= е° = 1 и /'@) = еХ\х=о = 1. В силу утверждения б заключаем, что для
любого ж G
ех
причем если ж ф 0, то неравенство строгое.
Пример 14. Аналогично, пользуясь строгой выпуклостью вверх функ-
функции In ж, можно проверить, что при ж > 0 справедливо неравенство
In ж ^ ж — 1,
причем это неравенство является строгим, если ж ф 1.

242 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
При построении графиков функций бывает полезно выделять точки пере-
перегиба графика.
Определение 3. Пусть /: U(xo) -+ К — функция, определенная и
дифференцируемая в окрестности U{xq) точки хо ? Е. Бели на множестве
о
U~(xo) = {х € U(xo) \х < хо} функция выпукла вниз (вверх), а на множе-
о
стве ?/+(#о) = {х Е U(xo) \х > хо} выпукла вверх (вниз), то точка (хо,/(хо))
графика называется его точкой перегиба.
Таким образом, при переходе через точку перегиба меняется направление
выпуклости графика, а это, в частности, означает, что в точке (хо,/(хо))
график функции переходит с одной стороны касательной к нему в этой точке
на другую ее сторону.
Аналитический признак абсциссы Хо точки перегиба легко усмотреть, со-
сопоставляя утверждение 5 и утверждение 3. А именно, можно сказать, что
если / дважды дифференцируема в точке хо, то, поскольку /;(х) в точке хо
имеет максимум или минимум, необходимо /"(хо) = 0.
Если же вторая производная f"{x) определена в U{xq) и всюду в U~(xo)
о
имеет один знак, а всюду в U*(xq) — противоположный знак, то этого до-
о о
статочно для того, чтобы f'{x) в U~{xq) и в U+(xo) была монотонна, но
имела разный характер монотонности. Тогда в силу утверждения 5 в точ-
точке (хо,/(хо)) произойдет изменение направления выпуклости графика, т. е.
(хо,/(хо)) будет точкой перегиба.
Пример 15. В примере 12, рассматривая функцию /(х) = sin х, мы
нашли участки выпуклости и вогнутости ее графика. Покажем теперь, что
точки графика с абсциссами х = пк, к ? Z, являются точками перегиба.
Действительно, /"(ж) = — sin ж; /"(х) — 0 при х = тгк, к € Z. Кроме того,
при переходе через эти точки f"{x) меняет знак, что является достаточным
признаком точки перегиба (см. рис. 26 на с. 247).
Пример 16. Не следует думать, что переход кривой с одной стороны
касательной на другую ее сторону в некоторой точке является достаточным
признаком того, что эта точка является точкой перегиба. Ведь может так
случиться, что ни в левой, ни в правой ее окрестности кривая не сохраняет
определенный характер выпуклости. Пример легко построить, усовершен-
усовершенствовав пример 5, приведенный по схожему поводу.
Пусть
2х3 4- х3 sin — при х ф 0,
/(*) =
X2
0 при х = 0.
Тогда х3 ^ f(x) ^ Зх3 при 0 ^ х и Зх3 ^ /(х) ^ х3 при х ^ 0, поэто-
поэтому график этой функции касается оси абсцисс в точке х = 0 и переходит в
этой точке из нижней полуплоскости в верхнюю. В то же время производная

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 243
функции f(x):
6х2 4- Sx2 sin — — 2 cos — при х ф О,
f'(x) =
X2 Ж2
О при д; = О,
не монотонна ни в какой полуокрестности точки х = 0.
В заключение вновь вернемся к определению A1) выпуклой функции и до-
докажем следующее
Утверждение 7 (неравенство Иенсена1)). Если /: ]а,Ь[ —> К — вы-
выпуклая функция, xi, ..., хп — точки интервала ]а,Ь[, од, ..., ап — неошрт^
^отельные чгхсла такие, что а\ + ... + ап = 1, то справедливо неровенстйо
/(aiXi 4-... 4- апхп) ^ ai/(xi) 4-... + anf(xn). A4)
М При п = 2 условие A4) совпадает с определением A1) выпуклой функции.
Покажем, что если A4) справедливо для п = т — 1, то оно справедливо и
для п = тп.
Пусть, для определенности, в наборе од, ..., an имеем ап ф 0. Тогда
+ ...4-an>0 и — 4-... + -~ = 1. Используя выпуклость функции,
находим
+...4-anxn) = fUxiXi
поскольку од + /? = 1 и f -— ж2 4-... + -^ хп ) € ]а, Ь[.
Далее, по предположению индукции
Следовательно,
+ а2/(х2) + ... 4- anf(xn).
В силу принципа индукции заключаем, что A4) верно рдя любого п ? N. (Для
п = 1 A4) тривиально.) >
1^И. Л. Иенсен A859 — 1925) — датский математик.
9 Зорич В. А.

244 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Заметим, что, как видно из доказательства, строгой выпуклости отвечает
строгое неравенство Иенсена, т. е. если среди чисел а\, ..., ап по крайней
мере два отличны от нуля, то знак равенства в A4) может иметь место тогда
и только тогда, когда Х\ = ... = хп.
Для функции, выпуклой вверх, разумеется, получается обратное по отно-
отношению к неравенству A4) неравенство
f(aixi 4-... 4- апхп) ^ axf(xi) 4-... 4- anf(xn). A5)
Пример 17. Функция f(x) = lna: строго выпукла вверх на множестве
положительных чисел, поэтому в силу A5)
a\\iiX\ 4-... 4- о,пInxn ^ \n(oLiXi 4-... 4- <хпхп)
или
х... х%п ^ а\Х\ 4-... 4- апхп A6)
п
При Х{ ^ 0, (*i ^ 0 (г = 1, . . . , П) И Y1 аг =
г=1
В частности, если а\ = ... = ап = —, получаем классическое неравенство
n
Хг + ... + Xn
n
A7)
между средним геометрическим и средним арифметическим п неотрицатель-
неотрицательных чисел. Знак равенства в A7) возможен, как отмечалось выше, только при
= #2 = • • •= Хп- Если же в A6) положить п — 2, а.\ = -, а^ — -, #i = a,
= 6, то вновь получим уже известное нам неравенство E).
Пример 18. Пусть f(x) = жр, х ^ 0, р > 1. Поскольку такая функция
выпукла, имеем
П \р П
г=1 / г=1
Полагая здесь q = -^-, ai = bjf Е Ь?) , х{ = а{Ь~1/{р{~1] ? Ьг?, вновь
Р Vi=l / г=1
получаем неравенство G) Гёльдера
г=1 \г=1 / \г=1
где - 4- - = 1 и р> 1.
Р Я.
При р < 1 функция /(ж) = жр выпукла вверх, поэтому аналогичными рас
суждениями можно получить и другое неравенство (8) Гёльдера.

§ 4, ИССЛЕДОВАНИЕ ФУНКЦИЙ 245
4. Правило Лопиталя. Остановимся теперь на одном частном, но ино-
иногда полезном приеме отыскания предела отношения функций, известном как
правило Лопиталяг).
Утверждение 8 (правило Лопиталя). Пусть функции f : ]а,Ь[ —> R и
д : )а, Ь[ -* R дифференцируемы на интервале ]а, Ь[ (—со ^ а < b ^ +оо),
;( ^ 0 на ]а, Ь[ гх
/Чя)
^ * ^ пргх х-»а + 0 (-оо ^ А ^ 4-сх>).
Тогда в каждом из двух следующих случаев:
1° (/(ж) -> 0) Л (^(х) -^0) пргх х -> а + 0
или
2° ^(х) —> оо npw a; -> а 4- О
-> А пргх х -> а 4- 0.
Аналогичное утверждение справедливо и при х -> Ь — 0.
Коротко, но не вполне точно правило Лопиталя формулируют так: предел
отношения функций равен пределу отношения их производных, если послед-
последний существует.
М Если д'(х) ф 0, то на основании теоремы Ролля заключаем, что д(х)
строго монотонна на ]а, Ь[. Значит, уменьшив, если нужно, промежуток ]а, Ь[
за счет сдвига в сторону конца а, можно считать, что #(х) ф 0 на ]а,Ь[. Для
х, у G ]а, Ь[ по теореме Коши найдется точка f G ]а, Ь[ такая, что
fix) - f(y) = /40
Перепишем это равенство в удобном для нас сейчас виде
/(*) = Ну) , /'(О Л
9(х) 9(х) р'@ \
При х —> а •+• 0 согласованно с изменением х будем стремить у к о + 0 так,
чтобы при этом
/Ы _
и
. Ф. де Лопиталь A661 — 1704) — французский математик, способный ученик Ио-
Иоганна Бернулли, маркиз, длякоторого последний в 1691 — 1692 гг. написал первый учебник
анализа. Часть этого учебника, посвященная дифференциальному исчислению, в слегка из-
измененном виде была опубликована Лопиталем под своим именем. Таким образом, «правилом
Лопиталя» мы обязаны Иоганну Бернулли.

246 гл. v. дифференциальное исчисление;
В любом из данных нам двух вариантов 1° и 2° это, очевидно, можно сделать.
Так как ? лежит между х и у, то вместе с х и у также f -> а 4- 0. Значит,
правая, а следовательно, и левая часть последнего равенства при этом стре-
стремятся к А >
„ чл 1- sin a: ,. cos а; -
Пример 19. lim = lim —-— = 1.
ж—Ю X х-+0 1
Этот пример не следует рассматривать как новое, независимое доказатель-
sin х t t\ rt
ство того, что > 1 при х —> 0. Дело в том, что, например, при выводе
X
соотношения sin'x = cos x мы уже использовали вычисленный здесь предел.
В возможности применения правила Лопиталя всегда убеждаемся только
после того, как найдем предел отношения производных. При этом не следует
забывать о проверке условий 1° или 2°. Важность этих условий показывает
следующий
Пример 20. Пусть f(x) = cos ж, д(х) = sin x. Тогда f'(x) = —sin ж,
fix) fix)
д'(х) = cos а: и ^Ц-f -> +оо при х -> 4-0, в то время как ., : —> 0 при х -> 4-0.
9(х) 9'{х)
Пример 21.
Т ^ПХ 1« \Х/ 1- 1 п ^ п,
lim = lim т = lim = 0 при а > 0.
-++оо Ха s-++oo аха~1 ж-++оо ОсХа
Ха s-++oo аха~1 ж-++оо ОсХ
Пример 22.
,. ха r axa~l v a(a~l)...(a-n4-l)xa-n n
lim —- = lim = ... = hm —^ '- j-—гг = 0
+ ах ж-^+оо аж1па ж-^+оо ажAпа)
ха~п
при а > 1, ибо при п > а и а > 1, очевидно, > 0, если ж -» 4-со.
CLX
Заметим, что вся цепочка последних равенств носила условный характер
до тех пор, пока мы не пришли к выражению, предел которого смогли найти.
5. Построение графика функции. Для наглядного описания функции
очень часто используют ее графическое представление. Как правило, такое
представление бывает полезно для обсуждения качественных вопросов пове-
поведения исследуемой функции.
Для точных расчетов графики используются реже. В связи с этим прак-
практически важным оказывается не столько скрупулезное воспроизведение функ-
функции в виде графика, сколько построение эскиза графика функции, правильно
отражающего основные элементы ее поведения. Некоторые общие приемы,
встречающиеся при построении эскизов графиков функций, мы и рассмотрим
в этом пункте.
а. Графики элементарных функций. Напомним прежде всего, как
выглядят графики основных элементарных функций, свободное владение ко-
которыми необходимо для дальнейшего (рис. 24 — 30).

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ
247
У
У
у = cos х
[у = sin x
Рис. 25
Рис. 26
У
2
-1!
тс
= arcsocr
О 1 х
у = arcsm х
Рис. 27
тс
О JL
2
= tex
Рис. 28
Рис. 29
Рис. 30

248
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
b. Примеры построения эскизов графиков функций (без привле-
привлечения дифференциального исчисления). Рассмотрим теперь некоторые
примеры, в которых эскиз графика функции может быть легко построен, если
нам известны графики и свойства простейших элементарных функций.
Пример 23. Построим эскиз графика функции
2.
у
-Зя+2
Учитывая, что
Iog2(x2 - Зх + 2) Iog2(x - 1)(х - 2)'
строим последовательно график квадратного трехчлена у\ = х2 —3x-f2, затем
2/2 = log2 2/i (х) и затем у = —j^r (рис. 31).
«Угадать» такой вид графика можно было бы и иначе: выяснить область
определения функции loga.2_3a;-|_2 2 = (^og2(x2 — Зх + 2)), найти поведение
функции при приближении к граничным точкам области определения и на
промежутках, концы которых являются граничными точками области опреде-
определения, нарисовать «плавную кривую» с учетом найденного поведения функции
у концов промежутка.
О
1 2/2,5
271 X
Рис. 32
Рис. 31

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ
249
Пример 24. Построение эскиза графика функции
у = sin х2
видно из рис. 32.
Мы построили этот график по некоторым характерным для данной функ-
функции точкам — тем точкам, где sinx2 = — 1, sinx2 = 0 или sinx2 = 1. Между
двумя соседними точками такого типа функ-
функция монотонна. Вид графика в окрестности
точки х = 0, у = 0 определяется тем, что
sinx2 ~ х2 при х —> 0. Кроме того, полезно
заметить, что данная функция четна.
Поскольку мы все время будем говорить
только об эскизном, а не точном построении
графика функции, то условимся ради крат-
краткости в дальнейшем считать, что требова-
требование «построить график функции» для нас все-
всегда будет равносильно требованию «постро-
«построить эскиз графика функции».
Пример 25. Построим график функ-
функции
у = х + arctg (х3 — 1)
(рис. 33). При х ->• — оо график хорошо при-
приближается прямой у = х — ^, а при х —>
->• -foo — прямой у = х + —.
Введем следующее полезное
Определение 4. Прямая у == со + с\х
называется асимптотой графика функции
у = /(х) при х -* -оо (при х -* +оо), если
/(х) — (со + cix) = оA) при х -» —оо (при
х -> +оо).
Таким образом, в нашем случае при х
—оо график имеет асимптоту у = х — —,
а при х -» +оо — асимптоту у = х + —.
Рис. 33
Если при х -* а - 0 (или при х -* а + 0)
|/(х)| ->- оо, то ясно, что график функции
в этом случае будет по мере приближения х
к а все теснее примыкать к вертикальной
прямой х = а. Эту прямую называют вертикальной асимптотой графика,
в отличие от введенной в определении 4 асимптоты, которая всегда наклонна.
Так, график из примера 23 (см. рис. 31) имеет две вертикальные асимпто-
асимптоты и горизонтальную асимптоту (общую для х -* — оо и х —> +оо).

250
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Из определения 4, очевидно, вытекает, что
у
= hm
х—> —оо X
Со = lim (f(x) — с\х).
х-»-—оо
И вообще, если f(x) — (со 4- с\х 4- ... + спхп) = оA) при х ~> —оо, то
с„ =
сп„1 = lim
X—> —
х—>—оо X
/(а?) - спх"
.n—1
со
lim (fix) — (cix + ... 4- cnxn)),
-+—oox '
х—>—
Эти соотношения, выписанные нами для случая х —> — оо, разумеется, спра-
справедливы также в случае х -* 4- оо и могут быть использованы для описания
асимптотического поведения графика функции f(x) с помощью графика со-
соответствующего алгебраического полинома со 4- cix 4-... 4- СпХп.
Пример 26. Пусть (р, (р) — полярные координаты на плоскости, и пусть
точка движется по плоскости так, что в момент времени t (t ^ 0)
р = p(t) = 1 - е~г cos ^ t,
ip =
= 1 — e~l sin ^ t.
'Гребуется нарисовать траекторию точки.
Нарисуем для этого сначала графики функций p{t) и ip(t) (рис. 34а, 346).
0
Ф
0
12 3'
а
У
1
2 3 t
Ь
Рис. 34
0
1 х
Теперь, глядя одновременно на оба построенных графика, можем нарисо-
нарисовать общий вид траектории точки (рис. 34с).

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ
251
с. Использование дифференциального исчисления при построе-
построении графика функции. Как мы видели, графики многих функций можно
в общих чертах нарисовать, не выходя за пределы самых простых соображе-
соображений. Однако если мы желаем уточнить эскиз, то в случае, когда производная
исследуемой функции не слишком сложная, можно привлечь аппарат диффе-
дифференциального исчисления. Продемонстрируем это на примерах.
Пример 27. Построить график функции у = f(x) в случае
+ 2\е~1/х.
Функция f(x) определена при х ? R \ 0. Поскольку е 1//ж ~> 1 при х -> оо, то
'— (х + 2) при х —> — оо,
(х + 2) при х —> +оо.
Далее, при х —> —0, очевидно, имеем \х + 2| е^ —> +оо, а при х ~> 40
|х + 2| е~х1х ->- +0. Наконец, видно, что /(х) ^ 0 и /(-2) = 0. На основании
этих наблюдений уже можно сделать первый набросок графика (рис. 35 а).
У
-2-1 0
Рис. 35
Выясним теперь основательно, действительно ли данная функция монотон-
монотонна на промежутках ]—оо, —2], [—2,0[, ]0, + оо[, действительно ли она имеет
указанные асимптоты и правильно ли изображен характер выпуклости гра-
графика функции.
Поскольку
/ч*) =
х
е 1/ж, если х < —2,
, если — 2 < х и
и ?{х) ф 0, то можно составить следующую таблицу:
Промежуток
Знак f'(x)
Поведение /(ж)
]-оо,-2[
—
+оо\0
Ь2,0[
+
О/^+сх)
]0,+оо[
+
0/*+оо

252
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
На участках постоянства знака производной функция, как мы знаем, имеет
соответствующий характер монотонности. В нижней строке таблицы символ
+оо \ 0 означает монотонное убывание от + оо до 0, а символ 0 /* + оо —
монотонное возрастание значений функции от 0 до 4- оо.
Заметим, что f'{x) ->• —4е~1//2 при х ->• — 2 — 0 и f'(x) -> 4е~1//2 при х ->
-> — 2 -f 0, поэтому точка (—2,0) должна быть угловой точкой графика (излом
типа излома у графика функции |х|), а не обычной точкой, как это у нас изо-
изображено на рис. 35а. Далее, f'(x) —> 0 при х —> 4- 0, поэтому график должен
выходить из начала координат, касаясь оси абсцисс (вспомните геометриче-
геометрический смысл /'(х)!).
Уточним теперь асимптотику функции при х -* — оо и х ~> +оо.
Поскольку е~х1х = 1 — х 4- ^(а:) при х -> оо, то
|х + 2|е~1/ж
' —х — 1 4- оA) при х ~> —оо,
k х 4-1 4- оA) при х —> 4-оо,
значит, на самом деле наклонные асимптоты графика суть у = — х — 1 при
х ~> —оо и у = х 4-1 при х —> 4-оо.
По этим данным уже можно построить достаточно надежный эскиз гра-
графика, но мы пойдем дальше и, вычислив
/"(*) =
—Л/т
X
, если х <-2,
ел о
j—е/1, если —2<х и х
найдем участки выпуклости графика.
Поскольку /"(х) = 0 лишь при х = 2/3, то имеем следующую таблицу:
Промежуток
Знак /"(ж)
Выпуклость /(ж)
]-оо,-2[
—
Вверх
]-2,0[
4
Вниз
]0,2/3[
4
Вниз
]2/3,+оо[
—
Вверх
Поскольку при х = 2/3 наша функция дифференцируема, а при переходе
через эту точку /"(х) меняет знак, то точка B/3,/B/3)) является точкой
перегиба графика.
Между прочим, если бы производная /'(х) обращалась в нуль, то из табли-
таблицы знаков /'(х) можно было бы судить о наличии или отсутствии экстремума
в соответствующей точке. В нашем случае /'(х) нигде не обращается в нуль,
но в точке х = — 2 функция имеет локальный минимум: она непрерывна в
этой точке и при переходе через нее /'(х) меняет знак с — на 4-. Впрочем, то,
что при х = — 2 наша функция имеет минимум, видно уже из приведенного
в таблице описания изменения значений функции /(х) на соответствующих
промежутках, если, конечно, учесть еще, что /(—2) = 0.

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ
253
Теперь можно нарисовать более точный эскиз графика данной функции
(см. рис. 356).
В заключение рассмотрим еще один
Пример 28. Пусть (х, у) — декартовы координаты на плоскости, и пусть
движущаяся точка в каждый момент t (t ^ 0) имеет координаты
t-2t3
х =
t
I-*2'
У
I-*2 "
Требуется изобразить траекторию движения точки.
Нарисуем сначала эскизы графиков каждой из данных координатных
функций х = x(t) и у = y(t) (рис. 36а, 366).
У
0
У
1,2 0
У
4
-3
Рис. 36

254
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Второй из этих графиков несколько интереснее, поэтому поясним его по-
построение.
Поведение функции у = y(t) при ? -» +0, t —> 1 — 0, t -> 1 + 0 и асим-
асимптотику y(t) == 2t + оA) при t —> 4-оо усматриваем непосредственно из вида
аналитического выражения для y(t).
Вычислив производную
-5*24
находим ее нули: *i я» 0,5 и
Составив таблицу:
A - t2J J
1,5 в области t ^ 0.
Промежуток
Знак y(t)
Поведение y(t)
+
0 /¦ y(ti)
—
]M»l
—
+oo \ y(t2)
]<2,+OO[
+
y(t2) /* -hex)
находим участки монотонности и локальные экстремумы y{t\) » тг (max) и
у(^) » 4 (min).
Теперь, глядя одновременно на оба графика х = x(t) и j/ = y(^), строим
эскиз траектории движения точки по плоскости (см. рис. 36с).
Этот эскиз можно уточнять. Например, можно выяснить асимптотику
траектории.
Поскольку lim ~т( = — 1 и lim (y(t) + x(t)) = 2, то прямая у = — х + 2
является асимптотой для обоих концов траектории, отвечающих стремлению
t к 1. Ясно также, что прямая х = 0 есть вертикальная асимптота для участ-
участка траектории, отвечающего t -» + оо.
Найдем далее
^ 1
Функция
, как легко выяснить, монотонно убывает от 1 до — 1
при возрастании и от 0 до 1 и возрастает от — 1 до + оо при возрастании и от
1 до + оо.
Из характера монотонности у'х можно сделать заключение о характере вы-
выпуклости траектории на соответствующем участке. С учетом сказанного те-
теперь можно построить следующий, более точный эскиз траектории движения
точки (см. рис. 36d).
Если бы мы рассматривали траекторию также для t < 0, то, как следует из
нечетности функций x(t), y(t), к уже построенным на плоскости (х,у) линиям
добавились бы еще центрально симметричные им кривые.

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 255
Подведем некоторые итоги в виде самых общих рекомендаций относитель-
относительно порядка построения графика заданной аналитически функции. Вот эти
рекомендации.
1° Указать область определения функции.
2° Отметить специфические особенности функции, если они очевидны
(например, четность, нечетность, периодичность, совпадение с точностью до
простейших преобразований координат с графиками уже известных функ-
функций).
3° Выяснить асимптотическое поведение функции при подходе к гранич-
граничным точкам области определения и, в частности, найти асимптоты, если они
существуют.
4° Найти промежутки монотонности функции и указать ее локальные экс-
экстремумы.
5° Уточнить характер выпуклости графика и указать точки перегиба.
6° Отметить характерные точки графика, в частности точки пересечения
с осями координат, если таковые имеются и доступны вычислению.
Задачи и упражнения
1. Пусть х = (xi, ..., хп), а = («1,..., ап), причем х» ^ 0, а» > О при г = 1, ..., п
п
и J2 а% = 1. Для любого числа t ф О рассмотрим среднее порядка t чисел xi, ..., хп
с весами а%:
Me (:
(п
»=1
В частности, при оц = ... = ап = — и ? = —1,1,2 получаем соответственно среднее
гармоническое, среднее арифметическое и среднее квадратическое.
Покажите, что
a) lim Mt(x, a) = xj1... ar?n, т. е. в пределе можно получить среднее геометри-
ческое;
b) lim Mtix.a) = max X{\
t4+oo v ' 1<<п
с) lim Aft (ж, а) = min x%\
d) Mt(xya) — неубьшающая функция от t на Rx причем она строго возрастает,
если п > 1 и все числа Х{ отличны от нуля.
2. Покажите, что |1 •+• х\р ^ 1 4- рх + cpipp(x)y где ср — постоянная, зависящая
только от р, а
Г |х|2 при |х| ^ 1,
ipp{x) = < если 1 < р < 2,
I Irrl
\х\р при |х| > 1,
и ifp(x) — \х\р на R, если 2 < р.

256 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
3. Проверьте, что cos ж < f 2!!1? \ ПрИ о < |х| < ^.
4. Исследуйте функцию /(х) и постройте ее график, если
a) /(х) = arctg log2 cos (тгх + ^ J;
b) f(x) = arccos ( о — sin x 1;
c)
d) Постройте кривую, заданную в полярных координатах уравнением ip = —^-—,
р ^ 0, и укажите ее асимптоту.
e) Укажите, как, зная график функции у = /(х), получить графики функций
/(х)+В; А/(х); /(х + Ь); /(ах) и, в частности, — f(x) и /(—ж).
5. Покажите, что если / G С(]а, Ь[) и для любых точек xi, хг € ]а, Ь[ выполнено
неравенство
2 j
то функция / выпуклая на ]а, Ь[.
6. Покажите, что:
a) Бели выпуклая функция /: R —> R ограничена, то она постоянна.
b) Если для выпуклой функции /: R —> R
lim ^= Um
oo ar
то / — постоянная.
с) Для любой выпуклой функции /, определенной на промежутке а < х < +оо
/ ч /0*0
(или — сх) < х < а), отношение —1-- стремится к конечному пределу или к бесконеч-
ности при стремлении х к бесконечности по области определения функции.
7. Покажите, что если /: ]о, b[ -> R — выпуклая функция, то
а) в любой точке х € ]а, Ь[ она имеет левую /^ и правую /_|_ производные:
причем ?(х) <|
b) при xi, Х2 € ]а,6[ и xi < Х2 имеет место неравенство /[.(xi) ^ /!.(хг);
c) множество угловых точек графика /(х) (для которых /1(х) Ф f+(x)) не более
чем счетно.
8. Преобразованием Леокандра1^ функции /: / -> R, определенной в промежутке
/ С R, называется функция
x€J
х^ А. М. Лежандр A752 — 1833) — известный французский математик.

§ 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ 257
Покажите, что:
a) Множество /* тех значений t € R, для которых f*(t) € R (т. е. f*(t) Ф оо),
либо пусто, либо состоит из одной точки, либо является числовым промежутком,
причем в последнем случае функция /* (t) выпукла на /*.
b) Если / — выпуклая функция, то /* ф 0 и при /* ? С(/*)
(П*(х) = sup(s*- Г (*)) = /(*)
tei*
для любого х € /. Таким образом, преобразование Лежандра выпуклой функции
инволютивно (квадрат его есть тождественное преобразование).
c) Имеет место неравенство
xt ^ f(x) + /*(*) при х ? I и t ? Г.
d) В случае, когда / — выпуклая дифференцируемая функция, f*(t) = txt — f(xt),
где xt определяется из уравнения t = f(x)\ получите отсюда геометрическую ин-
интерпретацию преобразования Лежандра /* и его аргумента ?, показывающую, что
преобразование Лежандра есть функция, определенная на множестве касательных к
графику функции /.
e) Преобразованием Лежандра функции /(ж) = — ха при а > 1 их^О является
функция f*(t) = —t^j где <H и —^ — = 1; получите отсюда, с учетом с), уже
знакомое неравенство Юнга
^ 1 а , 1 /3
а
f) Преобразованием Лежандра функции /(ж) = еж является функция f*(t) =
-, ? > 0, и справедливо неравенство
при ж € R и * > 0.
9. Кривизна, радиус и центр кривизны кривой в точке. Пусть некоторая точка
движется в плоскости по закону, задаваемому парой дважды дифференцируемых
координатных функций ж = ж(?), у = y(t) от времени. При этом она описывает
некоторую кривую, про которую говорят, что кривая задана в параметрическом
виде ж = x(t)j у = y(t). Частным случаем такого задания является случай графика
функции у = /(ж), где можно считать, что ж = t и у = f(t). Мы хотим указать
число, характеризующее кривизну кривой в некоторой точке, подобно тому как ве-
величина, обратная радиусу окружности, может служить показателем искривленности
окружности. Этим сравнением мы и воспользуемся.
a) Найдите тангенциальную at и нормальную ап составляющие вектора а =
= (x(t),y(t)) ускорения точки, т. е. представьте а в виде суммы at 4- ап, где вектор
at коллинеарен вектору v(t) = (x(t),y(t)) скорости, т. е. направлен по касательной
к траектории, а вектор ап направлен по нормали к траектории.
b) Покажите, что при движении по окружности радиуса г имеет место соотно-
соотношение

258 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
с) При движении по любой кривой, учитывая Ь), величину
естественно назвать радиусом кривизны кривой в точке (x(t),y(t)).
Покажите, что радиус кривизны вычисляется по формуле
\ху-ху\
d) Величину, обратную радиусу кривизны, называют абсолютной кривизной
плоской кривой в данной точке (x(t),y(t)). Наряду с абсолютной кривизной рас-
рассматривается величина
k(t) _ хуху
B +
(х
называемая кривизной.
Покажите, что знак кривизны характеризует направление поворота кривой по
отношению к касательной. Выясните, какова размерность кривизны.
е) Покажите, что кривизну графика функции у = f{x) в точке (х, /(х)) можно
вычислить по формуле
кМ - »
Сопоставьте знаки к(х) и у"(х) с направлением выпуклости графика.
f) Подберите константы а, 6, R так, чтобы окружность (х — аJ 4- (у — bJ = R2
имела с данной параметрически заданной кривой х = х(?), у = y(t) в точке хо =
= х(?о), уо — У (to) касание возможно более высокого порядка. Предполагается, что
x(t)> !/(*) дважды дифференцируемы и (x(*o),y(to)) ф @,0).
Указанная окружность называется соприкасающейся окружностью кривой в
точке (хо, уо)' Бе центр называется центром кривизны кривой в точке (хо, Уо)- Про-
Проверьте, что ее радиус совпадает с определенным в Ь) радиусом кривизны кривой в
этой точке.
g) Частица без предварительного разгона под действием силы тяжести начинает
скатываться с вершины ледяной горки параболического профиля. Уравнение про-
профиля х 4- у2 = 1, где х ^ 0, у ^ 0. Рассчитайте траекторию движения частицы до
ее приземления.
§ 5. Комплексные числа
и взаимосвязь элементарных функций
1. Комплексные числа. Подобно тому, как в области Q рациональных
чисел алгебраическое уравнение х2 = 2 не имело решений, уравнение х2 = — 1
не имеет решений в области действительных чисел R, и подобно тому, как,
вводя внешний по отношению к Q символ л/2 в качестве решения уравнения
х2 = 2, мы увязываем его с операциями в Q и получаем новые числа вида
г\ + л/2 f, где ri, г2 € Q, можно ввести символ г в качестве решения уравнения
х2 = —1 и связать это внешнее по отношению к Ж число г с действительными
числами и арифметическими операциями в

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 259
Замечательной особенностью указанного расширения поля R действитель-
действительных чисел, кроме многого другого, является то, что в получающемся при
этом поле С комплексных чисел уже любое алгебраическое уравнение с дей-
действительными или комплексными коэффициентами будет иметь решение.
Реализуем теперь намеченную программу.
а. Алгебраическое расширение поля R. Итак, вводим (следуя обо-
обозначению Эйлера) новое число i — мнимую единицу, такое, что г2 = — 1.
Взаимодействие г с действительными числами должно состоять в том,
что можно умножать г на числа у ? М, т. е. необходимо появляются числа
вида гj/, и складывать такие числа с вещественными, т. е. появляются числа
вида х 4- ij/, где я, у ? Е.
Если мы хотим, чтобы на множестве объектов вида х + iy, которые мы
вслед за Гауссом назовем комплексными числами, были определены привычные
операции коммутативного сложения и коммутативного умножения, дистрибу-
дистрибутивного относительно сложения, то необходимо положить по определению,
что
+ (х2 + iy2) := {х\ + х2) + i(yi+ у2) A)
и
iyi) • (х2 + iy2) := (xxx2 - угу2) + i{xxy2 + х2уг). B)
Два комплексных числа х\ +iy\, x2 +iy2 считаются равными в том и только
в том случае, когда х\ = х2 и у\ — у2.
Отождествим числа iGlc числами вида ж + t-O, at — с числом 0 +1 • 1.
Роль нуля в множестве комплексных чисел, как видно из A), играет число
0 + i-0 = 0gR, роль единицы, как видно из B), — число l + t-O = lER.
Из свойств вещественных чисел и определений A), B) следует, что множе-
множество комплексных чисел является полем, содержащим R в качестве подполя.
Поле комплексных чисел будем обозначать символом С, а его элементы —
чаще всего буквами z и w.
Единственный не очевидный момент в утверждении о том, что С — поле,
который нуждается в проверке, состоит в том, что любое отличное от нуля
комплексное число z = x + iy имеет обратное г по отношению к умножению,
т. е. z • z~l = 1. Проверим это.
Число х — гу назовем сопряженным к числу z = х + iy и обозначим симво-
символом z.
Заметим, что z • z — (х2 + у2) + г - 0 = х2 + у2 ф 0, если z ф 0. Таким
образом, в качестве г~г следует взять —= • z= о х о — г* у о.
х2 + у2 х2 + у2 х2 + у2
Ь. Геометрическая интерпретация поля С. Заметим, что после то-
того, как алгебраические операции A), B) над комплексными числами введены,
символ t, который привел нас к этим определениям, перестает быть необхо-
необходимым.

260 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Комплексное число z = х + гу мы можем отождествить с упорядоченной
парой (х, у) действительных чисел, называемых соответственно действитель-
действительной частью и мнимой частью комплексного числа z (обозначения: х = Rez,
у = Imz1)).
Но тогда, считая пару (х, у) декартовыми координатами точки плоскости
R2 = Шх R, можно отождествить комплексные числа с точками этой плоскости
или с двумерными векторами с координатами (х,у).
В такой векторной интерпретации покоординатное сложение A) комплекс-
комплексных чисел соответствует правилу сложения векторов. Кроме того, такая ин-
интерпретация естественно приводит также к понятию модуля \z\ комплексного
числа z как модуля или длины соответствующего ему вектора (х, у), т. е.
z\ = у/х2 + у2, если z = х + iy, C)
а также к способу измерения расстояния между комплексными числами z\,
z<i как расстояния между соответствующими им точками плоскости, т. е. с
помощью величины
. D)
Множество комплексных чисел, интерпретируемое как множество точек
плоскости, называется комплексной плоскостью и также обозначается сим-
символом С, подобно тому, как множество вещественных чисел и числовая прямая
обозначаются одним символом R.
Поскольку точку плоскости можно задать также полярными координатами
(г, <?>), связанными с декартовыми координатами формулами перехода
p,
у = г sin <?,
комплексное число
z = х + г у F)
можно также представить в виде
z = r(cosip + г sin у?). G)
Записи F) и G) называют соответственно алгебраической и шригоноже-
трической формами комплексного числа.
В записи G) число г ^ 0 называется модулем комплексного числа z (ибо,
как видно из E), г = |z|), anp — аргументом числа z. Аргумент имеет смысл
только при z ф 0. В силу периодичности функций cos<?> и sin<?> аргумент ком-
комплексного числа определен с точностью до величины, кратной 2тг, и символом
Arg z обозначают множество углов вида <?+2тг&, к € Z, где <р — какой-то угол,
удовлетворяющий соотношению G). Если желают, чтобы комплексное число
лат. realis (вещественный) и imaginarius (мнимый).

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 261
однозначно определяло некоторый угол ц> € Argz, то договариваются заранее
о диапазоне, в котором его выбирают. Чаще всего это бывает полуинтервал
О ^ ц> < 2тг или полуинтервал —тг < у? ^ тг. Если такой выбор сделан, то гово-
говорят, что выбрана ветвь (или главная ветвь) аргумента. Значения аргумента
в пределах выбранного диапазона обычно обозначают символом argz.
Тригонометрическая форма G) записи комплексных чисел удобна при вы-
выполнении операции умножения комплексных чисел. В самом деле, если
z\ = г\ (cos ip\ + i sin
TO
Z\-Z2 = (ri COS<?>i + ir\ Sinipi)(r2 COSЦ>2 + 1Г2 Sin (?2) =
= (*ЧГ2 cos <?>i cos v?2 — Г1Г2 sin <?>i sin 4J) +
H- г (ri Г2 sin y?i cos y?2 + **i r2 cos </?i sin (^2) j
или
-f (^2) H-isin(y?i +y>2))- (8)
Таким образом, при умножении комплексных чисел их модули перемножа-
перемножаются, а аргументы складываются.
Заметим, что мы на самом деле показали, что если (р\ € Arg z\ и (f2 € Arg Z2,
то (ip\ -f- (^2) € Arg (zi • ^2). Но, поскольку аргумент определен с точностью до
2тг&, можно записать, что
Arg (zi -z2) = Arg zx + Arg z2, (9)
понимая это равенство как равенство множеств, правое из которых есть сово-
совокупность чисел вида (pi + v?2j где ?i"€ Argzi, a ^2 ^ Arg 2:2. Таким образом,
сумму аргументов полезно понимать в смысле равенства (9).
При таком понимании равенства аргументов можно, например, утверж-
утверждать, что два комплексных числа равны тогда и только тогда, когда соответ-
соответственно равны их модули и аргументы.
Из формулы (8) по индукции вытекает следующая формула Муавра1):
если z = r(cosy? + isinip), то zn = rn(cosn<p + isinrnp). A0)
С учетом разъяснений по поводу аргумента комплексного числа формулу
Муавра можно использовать, чтобы в явном виде выписать все комплексные
решения уравнения zn = a.
Действительно, если
а = p(cos ф + г sin ф)
и в силу формулы A0)
zn = rn (cos тар + i sin
А, Муавр A667 — 1754) — английский математик.

262 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Ф 2тг
то г = ц/р и тир = xj) + 2тгА:, к € Z, откуда у?* = — Н /г. Различные ком-
v 71 71
плексные числа получаются, очевидно, только при & = О,1,...,п — 1. Итак,
мы находим п различных корней из а:
= 0,1, ..., n - 1).
В частности, если а = 1, т. е. р = 1 и Ф = 0, имеем
zk = VTl = cosf — к] + isin( — к) (к = 0,1, ..., п — 1).
Эти точки находятся на единичной окружности в вершинах правильного
п-угольника.
В связи с геометрической интерпретацией самих комплексных чисел по-
полезно упомянуть о геометрической интерпретации арифметических действий
над ними.
При фиксированном b G С сумму z + Ь можно интерпретировать как ото-
отображение С в себя, задаваемой формулой z ь-> z + b. Это сдвиг плоскости на
вектор Ь.
При фиксированном а = \a\(cos(p + г sin<p) ф 0 произведение az можно ин-
интерпретировать как отображение z ь-> az С в себя, являющееся композицией
растяжения в \а\ раз и поворота на угол <р ? Arga. Это видно из формулы (8).
2. Сходимость в С и ряды с комплексными членами. Расстояние
D) между комплексными числами позволяет определить е-окрестность числа
zq € С как множество {z € C\\z — zo\ < e} — это круг (без граничной окруж-
окружности) радиуса е с центром в точке (хо, j/o)> если zq = xq 4- ij/o-
Будем говорить, что последовательность {zn} комплексных чисел сходит-
сходится к числу zq E С, если lim \zn — zo\ =0.
n-*oo
Из неравенств
тах{|жп - хо|, \уп - Уо\} ^ \zn - *о| ^ \хп - хо| + |i/n - Уо| A1)
видно, что последовательность комплексных чисел сходится тогда и только
тогда, когда сходятся последовательности действительных и мнимых частей
членов этой последовательности.
По аналогии с последовательностями вещественных чисел последователь-
последовательность комплексных чисел {zn} называют фундаментальной или последова-
последовательностью Кошщ если для любого е > 0 найдется номер N ? N такой, что
при п, га > N выполнено \zn — zm\ < e.
Из неравенств A1) видно, что последовательность комплексных чисел фун-
фундаментальна тогда и только тогда, когда фундаментальны последовательно-
последовательности действительных и мнимых частей членов данной последовательности.
Учитывая критерий Коши для вещественных последовательностей, мы,
таким образом, на основании неравенств A1) заключаем, что справедливо
следующее

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 263
Утверждение 1 (критерий Коши). Последовательность комплексных
чисел сходится тогда и только тогда, когда она фундаментальна.
Если сумму ряда
+ . . . + Zn + . . . A2)
комплексных чисел понимать как предел его частичных сумм sn = z\ +... + zn
при п —* оо, то получаем также критерий Коши сходимости ряда>A2).
Утверждение 2. Ряд A2) сходится тогда и только тогда, когда для
любого е > О найдется число N Е N такое, что при любых натуральных
п ^ т > N имеем
|zm + ... + zn|<e. A3)
Отсюда, как, впрочем, и из самого определения сходимости ряда A2), вид-
видно, что для сходимости ряда необходимо, чтобы zn -> 0 при п —* оо.
Как и в вещественном случае, ряд A2) называется абсолютно сходящимся,
если сходится ряд
Ы + Ы + ... + |*п| + ... A4)
Из критерия Коши и неравенства
\zm + ... + zn\ ^ \zm\ + ... + \zn\
следует, что если ряд A2) сходится абсолютно, то он сходится. .
Примеры. Ряды
о\ 1 1 2 i 1 4
3) 1-й* +4!* "•••
сходятся абсолютно при любом гбС, ибо ряды
1') * Х
3')
как мы знаем, сходятся при любом значении \z\ € М. Заметим, что здесь мы
воспользовались равенством \zn\ = |z|n.
Пример 4. Ряд 1 + z + z2 + ... сходится абсолютно при М < 1, и его
сумма равна s = . При \z\ ^ 1 он не сходится, так как в этом случае
общий член ряда не стремится к нулю.

264 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Ряды вида
со + ci(z - z0) + ... + cn(z - zo)n + ... A5)
называют степенными рядами.
Применяя признак Коши (см. гл. III, § 1, п. 4) к ряду
|со| + \cx(z - zo)\ + ... + \cn(z - zo)n\ + ... , A6)
заключаем, что он сходится, если
—1
/ \-1
и его общий член не стремится к нулю, если \z — zq\ > I lim у \сп\ ) .
Отсюда получаем следующее
Утверждение 3 (формула Коши — Адамара1)). Степенной ряд A5)
сходится в круге \z — zo\ < R с центром в точке zo, радиус R которого
определяется по формуле Коши — Адамара
Д = — " ¦ A7)
lim Я/сп|
n—foo
В любой точке, внешней по отношению к этому кругу, степенной ряд
расходится.
В любой точке этого круга степенной ряд сходится абсолютно.
Замечание. По поводу сходимости на граничной окружности \z — zq| =
= R в утверждении 3 ничего не говорится, поскольку здесь возможны все
логически допустимые варианты.
Примеры. Ряды
ОО
5) '
71=1
ОО
п=1
ОО
п=1
сходятся в единичном круге \z\ < 1, но ряд 5) расходится всюду при \z\ = 1;
ряд 6) расходится при z = 1 и, как можно показать, сходится при z = — 1;
ряд 7) сходится абсолютно при \z\ = 1, так как
п
2
1
71
2 *
. Адамар A865 —1963) — известный французский математик.

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 265
Следует иметь в виду не учтенный в формулировке утверждения 3, но
возможный вырожденный случай, когда в формуле A7) R = 0. В этом слу-
случае, разумеется, весь круг сходимости вырождается в единственную точку zq
сходимости ряда A5).
Из утверждения 3, очевидно, вытекает
Следствие (первая теорема Абеля о степенных рядах). Если степен-
степенной ряд A5) сходится при некотором значении z*, то он сходится и дао/се
абсолютно при любом z, удовлетворяющем неравенству \z — zo\ < \z* — zo\.
Те утверждения, которые пока были получены, можно рассматривать как
простое развитие уже известных нам фактов. Теперь докажем два общих
утверждения о рядах, которые мы раньше не доказывали ни в каком виде,
хотя частично обсуждали затрагиваемые в них вопросы.
Утверждение 4. Если ряд z\ + 22 + • • • + zn + • • • комплексных чисел
сходится абсолютно, то ряд zni + zn2 + ... + znh + ..., полученный переста-
перестановкой1^ его членов, также абсолютно сходится и к той же сумме.
оо
М Учитывая сходимость ряда ? \zn\, по числу е > 0 найдем номер N € N
оо n=1
так, что Yl \zn\ < e.
n=7V+l
Далее найдем номер К € N так, что среди слагаемых суммы s* = zni +
+ ... + znh при к > К содержатся все слагаемые суммы sn = z{ + ... + z^.
00
Если 5 = Yj zn, то мы получаем, что при к > К
п=1
оо оо
l*-e*l ^ \s~SN\ + \sN-sk\ ^ ]Г |*я|+ ]Г \zn\<2e.
n=7V+l п=ЛГ+1
Таким образом, показано, что ?* -> 5 при к —у оо. Если применить уже
доказанное к рядам \z\| + \z2\ + ... + \zn\ + ... и \zni \ + \zn2\ + ... + \znh\ + ...,
получим, что последний ряд сходится. Тем самым утверждение 4 доказано
полностью. >
Следующее утверждение будет относиться к произведению
+ с»2 + ... + ап + ...)• (bi + Ьг + ¦•• + Ьп + ...)
рядов. Вопрос состоит в том, что если мы раскроем скобки и запишем все-
всевозможные попарные произведения а»Ь^, то в них нет естественного порядка
суммирования, ибо есть два индекса суммирования. Множество пар (г,^), где
г, у ? N, как нам известно, счетно, поэтому можно написать ряд с членами
aibj, взятыми в некотором порядке. От того, в каком порядке эти члены
*) Членом с номером к (к-ъл членом) второго ряда является член znh с номером п* ис-
исходного ряда. Отображение N Э Jfe 1—> пь € N предполагается биективным отображением
множества натуральных чисел N.

266 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
брать, может зависеть сумма такого ряда. Но, как мы только что видели, в
абсолютно сходящихся рядах сумма не зависит от перестановки слагаемых.
Таким образом, желательно выяснить, когда ряд с членами a{bj сходится аб-
абсолютно.
Утверждение 5. Произведение абсолютно сходящихся рядов являет-
является абсолютно сходящимся рядом, сумма которого равна произведению сумм
перемножаемых рядов.
< Заметим сначала, что, какую бы конечную сумму Ylai^j членов вида
u{bj мы ни взяли, всегда можно указать N так, что произведение сумм Ар? =
= di + ... + aw и Bn = b\ + ... + bw будет содержать все слагаемые исходной
суммы. Поэтому
. N N N оо оо
i,jf=l 1=1 ,7=1 t=l j=l
оо
откуда вытекает абсолютная сходимость ряда JZ °ify> сумма которого, та-
таким образом, однозначно определена независимо от порядка слагаемых. В
таком случае ее можно получить, например, как предел произведения сумм
Ап = о>\ ¦+¦... + ап, Вп = Ь\ +... -f Ьп при п -4 оо. Но АпВп -> АВ при п —у оо,
оо оо
где А = J] оп и В = ^2 Ьп, что и завершает доказательство высказанного
п=1 п=1
утверждения 5. >
Рассмотрим важный
ОО -а ОО 1
Пример 8. Ряды У) —гап, 2 —тЬт сходятся абсолютно. В произ-
n=0 n! m=0 т!
ведении этих рядов будем группировать мономы апЬт с одинаковой суммой
п + т = к показателей степени. Тогда получим ряд
=O \n+m=Jb
Но
к
1
171+П=Л
поэтому мы получаем, что
!m! fc! ^-i n\(k -n)! fc!
n=0 v '
1 п v^ 1 ,m v^ 1
n=0 m=0

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 267
3. Формула Эйлера и взаимосвязь элементарных функций. В при-
примерах 1) —3) мы установили абсолютную сходимость в С рядов, полученных
распространением в комплексную область тейлоровских разложений функций
ех, sin х, cosx, определенных на R. По этой причине естественны следующие
определения функций е*, cosz, sin 2 в С:
^ |Z3 + ... , A9)
cosz:=l- hz2 +
mi •
Sin Z !-— Z —"" "tt Z "г "зт Z ~~ ... (?i\.)
3! 5!
Подставим, следуя Эйлеру 1\ в A9) z = гу. Группируя соответствующим обра-
образом слагаемые частичных сумм получающегося при этом ряда, найдем, что
г?{iy)+i{iyJ+h{iyK+i.{iyL + h{iy)b
l 1з_,_15 ^
т. e.
= cosy H- zsinj/.
B2)
Это и есть знаменитая формула Эйлера,
При ее выводе мы пользовались тем, что г2 = —1, г3 = —г, г4 = 1, г5 = г
и т. д. Число у в формуле B2) может быть как действительным, так и про-
произвольным комплексным.
Из определений B0), B1) видно, что
cos(-z) = cosz,
sin(—z) = — sinz,
т. e. cosz — четная функция, a sinz — нечетная функция. Таким образом,
e~ty = cosy — г sin у.
Сравнивая последнее равенство с формулой B2), получаем
1)JI. Эйлер A707 — 1783) — выдающийся математик и механик, швейцарец по происхо-
происхождению, большую часть жизни проживший в Петербурге. По выражению Лапласа, «Эйлер —
общий учитель всех математиков второй половины XVIII века».

268 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Поскольку у — любое комплексное число, то эти равенства лучше перепи-
переписать в обозначениях, не вызывающих недоразумений:
cosz=\{eiz+e-iz),
2 B3)
sin *= ^ (eiz - e~iz).
Таким образом, если принять, что expz задается соотношением A9), то
формулы B3) (равносильные разложениям B0), B1)), как и формулы
Л г -г B4)
можно принять в качестве определений соответствующих круговых и гипер-
гиперболических функций. Забыв все наводящие и подчас не вполне строго обосно-
обоснованные соображения, относившиеся к тригонометрическим функциям (кото-
(которые, однако, привели нас к формуле Эйлера), можно было бы теперь проделать
типичный математический трюк, приняв формулы B3), B4) за определения и
получить из них уже совсем формально свойства круговых и гиперболических
функций.
Например, основные тождества
cos2 г -fsin2 z = 1,
как и свойства четности, проверяются непосредственно.
Более глубокие свойства, как, например, формулы для косинуса или синуса
суммы, вытекают из характеристического свойства показательной функции:
exp (zi + z2) = exp (zi) • exp (z2), B5)
которое, очевидно, следует из определения A9) и формулы A8). Выведем
формулы для косинуса и синуса суммы.
С одной стороны, по формуле Эйлера
B6)
С другой стороны, по свойству показательной функции и формуле Эйлера
= (cos z\ cos 22 — sin z\ sin z<i) + i(sin z\ cos z<i + cos z\ sin 22). B7)
Бели бы z\ и z2 были действительными числами, то, приравнивая действи-
действительные и мнимые части чисел из формул B6) и B7), мы уже получили бы ис-
искомые формулы. Поскольку мы собираемся доказать их для любых zi, 22 ? С,

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 269
то, пользуясь четностью cos г и нечетностью sin г, запишем еще одно равен-
равенство:
B8)
Сравнивая B7) и B8), находим
cos(zi -I- z2) = i(ei(zi+Z2) -f e~iBl+Z2)) = cos*i cosz2 - sin*i sin*2,
sin(*r+ z2) = i;(e
Совершенно аналогично можно было бы получить соответствующие фор-
формулы для гиперболических функций ch z и sh z, которые, кстати, как видно из
формул B3), B4), связаны с функциями cos г, sin г простыми соотношениями
chz = cosiz,
shz = —г sin гг.
Однако получить такие геометрические очевидности, как sin?r = 0 или
cos(^ -f 2тг) = cos г, из определений B3), B4) уже очень трудно. Значит, стре-
стремясь к точности, не следует забывать те задачи, где соответствующие функ-
функции естественным образом возникают. По этой причине мы не станем здесь
преодолевать возможные затруднения в описании свойств тригонометриче-
тригонометрических функций, связанные с определениями B3), B4), а еще раз вернемся к
этим функциям после теории интеграла. Наша цель сейчас состояла только в
том, чтобы продемонстрировать замечательное единство, казалось бы, совер-
совершенно различных функций, которое невозможно было обнаружить без выхода
в область комплексных чисел.
Если считать известным, что для х G
cos (х + 2тг) = cos х, sin (x + 2тг) = sin x,
cos 0 = 1, sin 0 = О,
то из формулы Эйлера B2) получаем соотношение
B9)
в котором представлены важнейшие постоянные различных областей матема-
математики A — арифметика, тг — геометрия, е — анализ, г — алгебра).
Из B5) и B9), как и из формулы B2), видно, что
exp (z + г2тг) = exp z,
т. е. экспонента оказывается периодической функцией на С с чисто мнимым
периодом Т = г2тг.

270
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Учитывая формулу Эйлера, тригонометрическую запись G) комплексного
числа теперь можно представить в виде
где г — модуль числа 2, а ср — его аргумент.
Формула Муавра теперь становится совсем простой:
zn =
C0)
4. Представление функции степенным рядом, аналитичность.
Функция w = f(z) комплексного переменного z с комплексными значени-
значениями и>, определенная на некотором множестве Е С С, есть отображение
/: Е -> С. График такой функции есть подмножество вСхС = Е2хЕ2 =
и поэтому традиционной наглядности не имеет. Чтобы как-то компенсиро-
компенсировать эту потерю, обычно берут два экземпляра комплексной плоскости С и
в одном отмечают точки области определения, а в другом — точки области
значений.
В рассмотренных ниже примерах указаны область Е и ее образ при соот-
соответствующем отображении.
Пример 9.
Пример 10.
0
№.-:>
1 X
гу
ги
о
+ 1 = w
0
Рис. 37
|f=
+ г = w
и
IV
2г
i
0
Рис. 38

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
271
Пример 11.
х
XV
IZ — W
Рис. 39
и
Это следует из того, что г = е**/2, z = ret<p и iz =
тг
произошел поворот на угол —
т. е.
Пример 12.
О
©
г х
IV
Z2 = W
Рис. 40
Ибо если z = reiv?, то z2 = r2ei2<p.
Пример 13.
Рис. 41

272
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 14.
Рис. 42
Из примеров 12, 13 понятно, что в данном случае образом единичного
круга снова будет единичный круг, но только накрытый в два слоя.
Пример 15.
п = 3)
Рис. 43
Если 2: = гег(р, то в силу C0) zn = rnetn(f', поэтому в нашем случае образом
круга радиуса г будет круг радиуса гп и каждая точка последнего является
образом п точек исходного круга (расположенных, кстати, в вершинах пра-
правильного п-угольника).
Исключение в этом смысле составляет только точка w = 0, прообраз ко-
которой есть точка z = 0. Однако при z —>• 0 функция zn есть бесконечно малая
порядка п, поэтому говорят, что при z = 0 функция имеет нуль порядка п. С
учетом такой кратности нуля можно теперь говорить, что число прообразов
любой точки w при отображении z »-> zn = w равно п. В частности, уравнение
zn — 0 имеет п совпадающих корней z\ — ... = zn — 0.
В соответствии с общим определением непрерывности, функция f(z) ком-
комплексного переменного называется непрерывной в точке zq G С, если для лю-
любой окрестности V(f(zo)) ее значения /(>го) найдется окрестность U(zo) такая,
что при любом z € U(zq) будет f(z) e V(f(zo)). Короче говоря,
lim f{z) = /(го).
> Z
Производной функции f(z) в точке zq, как и для вещественного случая,
назовем величину
f'(z0) = lim
если этот предел существует.
Z - Zq
C1)

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 273
Равенство C1) эквивалентно равенству
/(*) - /Ы = f'(zo)(z - 2b) + o(z - z0) C2)
при z —>• го, соответствующему определению дифференцируемости функции в
точке го-
Поскольку определение дифференцируемости в комплексном случае совпа-
совпадает с соответствующим определением для вещественных функций, а ариф-
арифметические свойства поля С и поля R одинаковы, то можно сказать, что все
общие правила дифференцирования справедливы и в комплексном случае.
Пример 16.
(9ofy(z)=9'(f(z))-f(z),
поэтому если f(z) = z2, то f'{z) = 1 • z + z • 1 = 2z, или если f(z) = zn, то
f'{z) = nz*1, а если
Pn(z) = Co -I- ci(* - 20) -I-... -I- cn(* - 20)n,
TO
K + 2c2(z -
oo
Теорема 1. Сумма f(z) = 5Г Cn(^~^o)n степенного ряда — бесконечно
n=0
дифференцируемая функция во всем круге сходимости ряда. При этом
оо
n=0
U
nl
< Выражения для коэффициентов сп очевидным образом получаются из
выражений для f^k\z) при к = п и z = zq.
В свою очередь, формулы для f^k\z) достаточно проверить только при
к = 1, ибо тогда f'{z) снова окажется суммой степенного ряда.
оо
Итак, проверим, что функция tp(z) = ]Г] ncn(z — гоO1" действительно
п=1
является производной для f(z).
Прежде всего заметим, что в силу формулы Коши—Адамара A7) радиус
сходимости последнего ряда совпадает с радиусом сходимости R исходного
степенного ряда для f(z).

274
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
В дальнейшем для упрощения записи будем считать, что zq = 0, т. е. что
оо
оо
l-l
и ряды сходятся при \z\ < R.
f(z) = Z) cnZn, (p(z) = Y1
n=0 n=l
Поскольку внутри круга сходимости степенной ряд сходится абсолютно,
можно заметить, и это существенно, что при \z\ ^ г < R справедлива оценка
оо
1 = п|сл| l^l11" ^ nlcnlr11, а ряд ?) n\cn\rn~l сходится. Значит, для
л
п=1
любого е > О найдется номер N такой, что при \z\ ^ г
оо
Е
ncnz
n-1
оо
Таким образом, с точностью до | функция tp(z) в любой точке круга \z\ < г
о
совпадает с Л^-й частичной суммой определяющего ее ряда.
Пусть теперь (иг- произвольные точки этого круга. Преобразование
/(С) - /(*)
оо
~ Z
n
п-\
n'1
)
n=l
n
и оценка |сп((п * + .. .+zn x)| ^ |cn|nru x позволяют, как и выше, заключить,
что интересующее нас разностное отношение при |(| < г и \z\ < г совпадает,
с точностью до |, с TV-й частичной суммой определяющего его ряда. Значит,
при 1A < г и \z\ < г
/(С) - №
C-z
n=l
n=l
Если теперь, фиксировав z, устремить ? к z, то, переходя к пределу в ко-
конечной сумме, видим, что при С достаточно близких к z правая часть послед-
последнего неравенства, а с нею и левая становятся меньше е.
Таким образом, для любой точки z в круге \z\ < г < Л, а ввиду произволь-
произвольности г, и для любой точки круга \z\ < R проверено, что f'{z) = (p(z). >
Эта теорема позволяет точно указать тот класс функций, для которых их
ряды Тейлора сходятся к ним.
Говорят, что функция аполитична в точке zq E С, если в некоторой
окрестности этой точки ее можно представить в следующем («аналитиче-
(«аналитическом») виде:
оо
п=0
т. е. как сумму степенного ряда по степеням z —

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 275
Нетрудно проверить (см. задачу 7), что сумма степенного ряда аналитична
в любой внутренней точке круга сходимости этого ряда.
С учетом определения аналитичности функции, из доказанной теоремы
получаем
Следствие, а) Если функция аналитична в точке, то она бесконечно
дифференцируема в этой точке и ее рлд Тейлора сходится к ней в окрест-
окрестности этой точки.
Ъ) Ряд Тейлора функции, определенной в окрестности точки и бесконечно
дифференцируемой в точке, сходится к функции в некоторой окрестности
точки тогда и только тогда, когда функция аналитична в этой точке.
В теории функции комплексного переменного доказывается замечатель-
замечательный факт, не имеющий аналогов для вещественных функций. А именно, ока-
оказывается, что если функция f(z) дифференцируема в окрестности точки
zo € С, то она аналитична в этой точке. Это и в самом деле удивительно,
поскольку в силу доказанной выше теоремы отсюда следует, что если функция
f(z) имеет одну производную f'{z) в окрестности точки, то в этой окрестно-
окрестности она имеет также производные всех порядков.
На первый взгляд это так же неожиданно, как то, что, присоединив к R
корень i одного конкретного уравнения z2 = — 1, мы получаем поле С, в ко-
котором любой алгебраический многочлен P(z) имеет корень. Факт разреши-
разрешимости в С алгебраического уравнения P(z) = 0 мы собираемся использовать
и поэтому докажем его в качестве хорошей иллюстрации к введенным в этом
параграфе начальным представлениям о комплексных числах и функциях ком-
комплексного переменного.
5. Алгебраическая замкнутость поля С комплексных чисел. Бели
мы докажем, что любой полином P(z) = со + c\z + ... + CnZn, п ^ 1, с ком-
комплексными коэффициентами имеет корень в С, то уже не возникнет надоб-
надобности в расширении поля С, вызванной неразрешимостью в С некоторого
алгебраического уравнения. В этом смысле утверждение о наличии корня у
любого многочлена P(z) устанавливает алгебраическую замкнутость поля С.
Чтобы получить вполне наглядное представление о том, почему в С любой
полином имеет корень, в то время как в R его могло не быть, воспользуемся
геометрической интерпретацией комплексного числа и функции комплексного
переменного.
Заметим, что
и, следовательно, P(z) = CnZn + o(zn) при \z\ -? оо. Поскольку нас интересует
корень уравнения P(z) = 0, то, поделив- обе части уравнения на Сл, можно
считать, что коэффициент Сп многочлена P(z) равен 1 и потому
P(z) = zn + o{zn) при \z\-> oo. C3)
10 Зорич В. А.

276
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Если вспомнить (см. пример 15), что при отображении z *-? zn окружность
радиуса г переходит в окружность радиуса гп с центром в точке 0, то при
достаточно больших значениях г, в силу C3), с малой относительной погреш-
погрешностью образ окружности \z\ = г будет совпадать с окружностью |ги| = гп
плоскости w (рис. 44). Во всяком случае, важно, что образом будет кривая,
охватывающая точку w = 0.
Если круг \z\ ^ г рассматривать как пленку, натянутую на окружность
|г| = г, то при непрерывном отображении, осуществляемом полиномом w =
= P(z)} эта пленка перейдет в пленку, натянутую на образ окружности. Но
поскольку последний охватывает точ-
ку w = 0, то некоторая точка этой
пленки обязана совпадать с w = 0
и, значит, в круге \z\ < г найдется
точка ?о, которая при отображении
w = P(z) перешла именно в w = 0,
т. е. P(z0) = 0.
Это наглядное рассуждение при-
Рис. 44 водит к ряду очень важных и полез-
полезных понятий топологии (индекс пути
относительно точки, степень отображения) и с помощью этих понятий мо-
может быть доведено до полного доказательства, справедливого, как можно
понять, не только для полиномов. Однако эти рассмотрения, к сожалению,
отвлекли бы нас от основного предмета, которым мы сейчас занимаемся; по-
поэтому мы проведем другое доказательство, лежащее в русле тех идей, с кото-
которыми мы уже достаточно освоились.
Теорема 2. Каждый полином
и
;кп-2)
P(z) = Co -I" C\Z
CnZ
n
степени n^l с комплексными коэффициентами имеет в С корень.
М Без ограничения общности утверждения теоремы, очевидно, можно счи
тать, что сп = 1.
Пусть /1 = inf \P(z)\. Поскольку P(z) = zn(l + ^^- + ... + — V то
-1
и, очевидно, \P(z)\ > max{l,2/i} при \z\ > R, если R достаточно велико. Сле-
Сле— /х < -,
к
довательно, точки последовательности {г*}, в которых 0 <
лежат в круге \z\ ^ R.
Проверим, что в С (и даже в этом круге) есть точка zo, в которой
= /1. Для этого заметим, что если Zk—Xk-\- iyk^ то max{|z*|, \yk\} ^ \zk
R

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 277
•
и, таким образом, последовательности действительных чисел {хк}, {ук} ока-
оказываются ограниченными. Извлекая сначала сходящуюся подпоследователь-
подпоследовательность {xkl} из {хк}, а затем сходящуюся подпоследовательность {yklm} из
{ykt}, получим подпоследовательность zklm = xklm + ^Ук1гп последовательности
{zk\, которая имеет предел lim zkl = lim хк. +i lim ук. = x0 +iyo = zq,
m-юо m m—уоо m m—юо m
и поскольку \zk\ —> |zo| при A; —> oo, то \zq\ ^ й. Чтобы избежать громоздких
обозначений и не переходить к подпоследовательностям, будем считать, что
уже сама последовательность {zk} сходится. Из непрерывности P(z) в zq ? С
следует, что lim P(zk) = P(z0). Но тогда1) |Р(го)| = lim
Л—юо к—уоо
Теперь предположим, что \х > О, и приведем это предположение к про-
противоречию. Если P(zq) ф 0, то рассмотрим полином Q(z) = —7-7—г^. По
P\Zq)
построению, 0@) = 1 и \Q{z)\ = i^^ypi ^ 1.
Поскольку 0@) = 1, полином Q(z) имеет вид
Q(z) = 1 + qkzk +
где 1^1 5^ 0 и 1 ^ А: ^ п. Если ^ = рег^, то при ^ = п ~ ^ будем иметь
9л . (e^)fc = pj+e**-*) = pei7r = -р = -|gfc|. Таким образом, при г =
получим
qkzk\ + (\qk+1zk+1
1 " rk \qk\\ +
* - ... - rn-k\qn\)
если г достаточно близко к нулю. Но \Q(z)\ ^ 1 при z e С. Полученное
противоречие показывает, что P(z0) = 0. >
Замечание 1. Первое доказательство теоремы о разрешимости в С лю-
любого алгебраического уравнения с комплексными коэффициентами (которую
по традиции часто называют основной теоремой алгебры) было дано Гауссом,
который вообще вдохнул вполне реальную жизнь в так называемые «мнимые»
числа, найдя им разнообразные и глубокие приложения.
Замечание 2. Многочлен с вещественными коэффициентами P(z) =
= по +... + anzn, как мы знаем, не всегда имеет вещественные корни. Однако
по отношению к произвольному многочлену с комплексными коэффициентами
• *) Обратите внимание — мы, с одной стороны, показали, что из любой ограниченной по
модулю последовательности комплексных чисел можно извлечь сходящуюся подпоследова-
подпоследовательность, а с другой стороны, продемонстрировали еще одно из возможных доказательств
теоремы о минимуме непрерывной функции на отрезке, как в данном случае это было сде-
сделано в круге \z\ ^ R.

278 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
он обладает той особенностью, что если P{zq) = 0, то и P(zo) = 0. Действи-
Действительно, из определения сопряженного числа и правил сложения комплексных
чисел следует, что {z\ + z^) = z\ + z2- Из тригонометрической формы записи
комплексного числа и правил умножения комплексных чисел видно, что
. r2
Таким образом,
P(z0) =
= O
и если P(zo) = 0, то P(z0) = P(zo) = 0.
Следствие 1. Любой многочлен P(z) = cq -H ... -f CnZn cmenetiii n ^
с комплексными коэффициентами допускает, и притом единственное с точ-
точностью до порядка сомножителей, представление в виде
P(z) =cn(z-zl)...(z- zn), C4)
где Zi, ..., zn 6 С (и, может быть, не все числа zi,..., zn различны между
собой).
Ч Из алгоритма деления («уголком») многочлена P(z) на многочлен Q{z)
степени т ^ п находим, что P(z) = q(z)Q(z)+r(z), где q(z) и r(z) — некоторые
многочлены, причем степень r(z) меньше степени Q(z), т. е. меньше т. Таким
образом, если т = 1, то r(z) = г — просто постоянная.
Пусть z\ — корень многочлена P{z). Тогда P(z) = q{z)(z — z\) + г, и
поскольку P(z\) = г, то г = 0. Значит, если z\ — корень многочлена P(z),
то справедливо представление P(z) = (z — Zi)q(z). Степень многочлена q(z)
равна п-1,ис ним можно повторить то же самое рассуждение. По индукции
получаем, что P(z) = c(z — zi)...(z — zn). Поскольку должно быть czn =
то с = сп. >
Следствие 2. Любой многочлен P(z) = ао + ... + ап^п с
тельными коэффициентами можно разложить в произведение линейных и
квадратичных многочленов с действительными коэффициентами.
<< Это вытекает из предыдущего следствия 1 и замечания 2, в силу ко-
которого вместе с Zk корнем P(z) является также число z*. Тогда, перемно-
перемножив в разложении C4) многочлена скобки (z — Zk){z — Zk)i получим многочлен
z2 — {zk + Zk)z + |z*|2 второго порядка с действительными коэффициентами.
Число сп, в нашем случае равное ап, вещественное, и его можно внести в одну
из скобок разложения, не меняя ее степени. >
Перемножив одинаковые скобки в разложении C4), это разложение можно
переписать в виде
= cn{z-z1)k*...{z-zp)k*. C5)

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 279
Число kj называется кратностью корня Zj.
Поскольку P(z) = (z — Zj)k> Q(z), где Q(zj) ф О, то
P'(z) = kj(z - Zj)k'-lQ(z) + (z- Zj)k'Q'(z) = (z- z
где R(zj) = kjQ(zj) ф 0. Таким образом, мы приходим к следующему заклю-
заключению.
Следствие 3. Каждый корень Zj многочлена P(z) кратности kj > 1
является корнем кратности kj — 1 многочлена P'(z) — производной P{z).
Не будучи пока в состоянии найти корни многочлена P(z), мы на основании
последнего утверждения и разложения C5) можем найти многочлен p(z) =
= (z — z\)... (z — zp), корни zi, ..., zp которого совпадают с корнями P(z),
но все они уже кратности 1.
Действительно, по алгоритму Евклида сначала найдем многочлен q(z) —
наибольший общий делитель P(z) и P'{z). В силу следствия 3, разложения
C5) и теоремы 2, многочлен q(z) с точностью до постоянного множителя
равен произведению (z — Z\)kx~x... (z — zp)kp~x^ поэтому, поделив P(z) наq(z),
с точностью до постоянного множителя (от которого можно затем избавиться
дополнительным делением на коэффициент при zp) получим многочлен p(z) =
= (z - zi) ...{z - Z
P(x)
Рассмотрим теперь отношение R(x) = nf ' двух многочленов, где Q(x)
const. Если степень Р(х) больше степени Q(x), то, применив алгоритм
деления многочленов, представим Р(х) в виде Р(х) = p(x)Q(x) + г(х), где
р(х) и г(х) — некоторые многочлены, причем степень г(х) уже меньше, чем
степень Q(x). Таким образом, получаем представление R(x) в виде R(x) =
fix) 7*1 X 1
= р(х) + У, ., где дробь \, . уже правильная в том смысле, что степень г(х)
Q\x) Q\x)
меньше степени Q(x).
Следствие, которое мы сейчас сформулируем, относится к представлению
правильной дроби в виде суммы дробей, называемых простейшими.
Следствие 4. а) Если Q(z) = (z—z\)kl... (z—zp)kp и рг^ —правильная
дробь, то существует и притом единственное представление дроби f * в
Q\z)
виде
?
Ь) Если Р(х) и Q(x) — многочлены с действительными коэффициентами
и Q(x) = (х - xi)*1... (х - х/)*1 (х2 + ргх -h gi)mi... (х2 + рпх -h дп)Шп,

280 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
существует и притом единственное представление правильной дроби
в виде
Q(*)
C7)
где a,jk, bjk, Cjk — действительные числа.
Заметим, что универсальным, хотя и не всегда самым коротким способом
фактического отыскания разложений C6) или C7) является метод неопре-
неопределенных коэффициентов, состоящий в том, что сумма в правой части C6)
или C7) приводится к общему знаменателю Q(x), после чего приравнивают-
приравниваются коэффициенты полученного числителя и соответствующие коэффициенты
многочлена Р(х). Система линейных уравнений, к которой мы при этом при-
приходим, в силу следствия 4 всегда однозначно разрешима.
Поскольку нас, как правило, будет интересовать разложение конкретной
дроби, которое мы получим методом неопределенных коэффициентов, то кро-
кроме уверенности, что это всегда можно сделать, нам от следствия 4 пока ничего
больше не требуется. По этой причине мы не станем проводить его доказа-
доказательство. Оно обычно излагается на алгебраическом языке в курсе высшей
алгебры, а на аналитическом языке — в курсе теории функций комплексного
переменного.
Рассмотрим специально подобранный пример, на котором можно проил-
проиллюстрировать изложенное.
Пример 17. Пусть
Р(х) = 2х6 + Зх5 + 6х4 + 6х3 + Юх2 + Зх 4- 2,
Q(x) = х7 + Зх6 + Ъхъ + 7х4 + 7х3 + Ъх2 + Ъх + 1;
Р(х)
требуется найти разложение C7) дроби . '
Q(x)
Прежде всего, задача осложнена тем, что мы не знаем разложения мно-
многочлена Q(x). Попробуем упростить ситуацию, избавившись от кратности
корней Q(x), если таковая имеет место. Находим
Q'{x) = 7х6 + 18х5 + 25х4 + 28х3 + 21х2 + Юх + 3.
Довольно утомительным, но выполнимым счетом по алгоритму Евклида
находим наибольший общий делитель
d(x) = х4 + 2х3 + 2х2 + 2х + 1
многочленов Q{x) и Q*{x). Мы выписали наибольший общий делитель с еди-
единичным коэффициентом при старшей степени х.
Разделив Q(x) на d(x), получаем многочлен
q(x) =х3 + х2 + х +

§ 5. КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 281
имеющий те же корни, что и многочлен Q(x), но единичной кратности. Ко-
Корень —1 многочлена q(x) легко угадывается. После деления q(x) на х 4- 1
получаем х2 + 1. Таким образом,
q(x) = (x'+l)(x2 + 1),
после чего последовательным делением d(x) на х2 4- 1 и а; + 1 находим разло-
разложение d(rc):
2x2 + 1),
а вслед за этим и разложение
Р(х)
Таким образом, в силу следствия 4Ь) ищем разложение дроби nf > в виде
l2 l3 цХ f Сц
(я: -hiJ (x +1K x2 + l
Приводя правую часть к общему знаменателю и приравнивая коэффици-
коэффициенты полученного в числителе многочлена и соответствующие коэффициенты
многочлена Р(х), приходим к системе семи уравнений с семью неизвестными,
решая которую, окончательно получаем
Р{х) 1 2 1 гс-1 х +1
(x2-hlJ'
Задачи и упражнения
1. Используя геометрическую интерпретацию комплексного числа:
a) поясните неравенства \z\ + гг| ^ \z\\ 4- |гг| и |zi + ... + zn| ^ \z\\ + •. • 4-
b) укажите геометрическое место точек на плоскости С, удовлетворяющих со-
соотношению \z — 1| + \z -f 1| ^ 3;
c) изобразите все корни степени п из 1 и найдите их сумму;
d) поясните действие преобразования плоскости С, задаваемого формулой z к* z.
2. Найдите суммы:
a) 1+ q + ...-f gn;
b) 1 + g + ... 4- qn + • • • при Ы < 1;
c) l-^^
d) l+
e) 1 4- reitfi + ... 4- rneinip + ... при |r| < 1;
f) 1 4- r cos <p 4-.. ¦ 4- rncog n<p;
g) 1 4- r cos </> + ...+ rncos тир + ... при |r| < 1;

282 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
h) I -f r sin </>+... + rnsinny?;
i) 1 + rsin<p + ... +rnsinny? + ... при \r\ < 1.
(z \n
1 H— ) и убедитесь,
Ti/
что это число есть ez.
4. а) Покажите, что уравнение ew = z относительно w имеет решение w = In \z\ -f
-И Arg z. Естественно считать w натуральным логарифмом числа z. Таким образом,
w = Lnz не есть функциональное соотношение, поскольку Arg г многозначен.
b) Найдите Ln 1 и Ln t.
c) Положим za = eaLnz. Найдите Г и t\
d) Используя представление w = sinz = тр(е%г — e~**)> получите выражение для
z = arcsin z.
e) Есть ли в С точки, где |sinz| = 2?
5. а) Исследуйте, во всех ли точках плоскости С функция f(z) = непре-
непрерывна.
b) Разложите функцию ^ в степенной ряд при zo = 0 и найдите его радиус
сходимости.
c) Решите задачи а) и Ь) для функции -—Г2~~2> гДе А € R — параметр. Не
возникает ли у вас гипотезы относительно того, взаимным расположением каких
точек на плоскости С определяется радиус сходимости? Можно ли было понять это,
оставаясь на вещественной оси, т. е. раскладывая функцию Го~т> гДе ^ € R и
1 Н \*z*
6. а) Исследуйте, является ли непрерывной функция Коши
/(*) =
[О, z = О
в точке z = 0.
b) Будет ли непрерывно ограничение /|R функции / из задачи а) на веществен-
вещественную ось?
c) Существует ли ряд Тейлора функции / из а) в точке zo = 0?
d) Бывают ли аналитические в zo € С функции, ряд Тейлора которых сходится
только в точке ?
оо
е) Придумайте степенной ряд Yl cn (z—zo)n, который сходится только в точке
п=0
оо
7. а) Выполнив в степенном ряде ?} Ап (z — о)п формально подстановку z — а =
= (z — zo) + (zo — а) и приведя подобные члены, получите ряд J^ Cn(z — zo)n и
n=0
выражения его коэффициентов через величины A*, (zo — а)*, к = 0,1,...
Ь) Проверьте, чхо если исходный ряд сходится в круге \z — а\ < Я, a |zo — а| =
= г < Д, то ряды, определяющие Сп, п = 0,1, ..., сходятся абсолютно и ряд
оо
^2Cn(z — zo)n сходится при \z — zo| < R — г.
n=0

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 283
оо
с) Покажите, что если f(z) = ? An(z — а)п в круге \z — а| < Я, a \zo — а\ <
п=0
< Я, то в круге \z — го| <R — \zq — а] функция / допускает представление f(z) =
оо
п=0
8. Проверьте, что
a) когда точка z 6 С пробегает окружность \z\ = г > 1, точка tu = z + z~l
пробегает эллипс с центром 0 и фокусами в точках ±2;
b) при возведении комплексных чисел в квадрат, точнее, при отображении w ь->
>-t w2 такой эллипс переходит в дважды пробегаемый эллипс с фокусом в нуле;
c) при возведении комплексных чисел в квадрат любой эллипс с центром в нуле
переходит в эллипс с фокусом в нуле.
§ 6. Некоторые примеры использования
дифференциального исчисления
в задачах естествознания
В этом параграфе мы разберем несколько довольно далеких друг от друга
по постановке задач естествознания, которые, однако, как выяснится, име-
имеют довольно близкие математические модели. Модель эта — не что иное,
как простейшее дифференциальное уравнение для интересующей нас в зада-
задаче функции. С разбора одного такого примера — задачи двух тел — мы,
кстати, вообще начинали построение дифференциального исчисления. Иссле-
Исследование той системы уравнений, которую мы при этом получили, пока нам
недоступно. Здесь же будут рассмотрены вопросы, которые можно до конца
решить уже на нашем нынешнем уровне. Кроме удовольствия увидеть мате-
математический аппарат в конкретной работе, из ряда примеров этого параграфа
мы, в частности, извлечем также дополнительную убежденность как в есте-
естественности возникновения показательной функции ехра;, так и в пользе ее
распространения в комплексную область.
1. Движение тела переменной массы. Рассмотрим ракету, переме-
перемещающуюся прямолинейно в открытом космосе далеко от притягивающих масс
(рис. 45).
со
Пусть М(t) — масса ракеты (с топливом) в момент t\ V(t) — ее скорость
в момент t; ш — скорость (относительно ракеты) истечения топлива из сопла
ракеты при его сгорании.
Мы хотим установить взаимосвязь между этими величинами.

284 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
В силу сделанных предположений, ракету с топливом можно рассматри-
рассматривать как замкнутую систему, импульс (или количество движения) которой
поэтому остается постоянным во времени.
В момент t импульс системы равен M(t)V(t).
В момент t + h импульс ракеты с оставшимся в ней топливом равен
M(t + ft) V(t -f ft), а импульс Д/ выброшенной за это время массы |ДМ| =
= \M(t + ft) — M(t)\ = —(M(t + ft) — M(t)) топлива заключен в пределах
(V(t) -ш)\АМ\ < А/ < (V(t + ft) -о;)|ДМ|,
т. е. Д/ = (V(t) — и>)\АМ| + а(Л)|ДМ|, причем из непрерывности V(t) следует,
что а(Л) -+ 0 при ft ~+ 0.
Приравнивая импульсы системы в моменты t и t + /i, имеем
+ h) + (V(t) - w)|ДМ| + a(/i)|ДМ|,
или, после подстановки |ДМ| = — (M(t -f h) — M(t)) и упрощений,
+ ft) - M(t)) + a(h)(M(t -h ft) - M(t)).
Деля последнее равенство на ft и переходя к пределу при ft -> 0, получаем
A)
Это и есть искомое соотношение между интересующими нас функциями
V(t), M(t) и их производными.
Теперь надо найти связь между самими функциями V(?), M(t), исходя из
соотношения между их производными. Вообще говоря, такого рода задачи
много труднее задач нахождения соотношений между производными при из-
известных соотношениях между функциями. Однако в нашем случае вопрос
решается вполне элементарно.
Действительно, после деления на M(t) равенство A) можно переписать в
виде
V'(t) = (-u>]nM)'(t). B)
Но если производные двух функций совпадают на некотором промежутке,
то на этом промежутке сами функции отличаются разве что на некоторую
постоянную.
Итак, из B) следует, что
V(t) = -wlnAf(t)+c. C)
Если известно, например, что V@) = 1^), то это начальное условие вполне
определит константу с. Действительно, из C) находим

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 285
а затем находим искомую формулу1)
.
D)
Полезно заметить, что если тк — масса корпуса ракеты, тт — масса топ-
топлива, а V — конечная скорость, которую приобретает ракета после полной
отработки топлива, то, подставляя в D) М@) = гак -f гат и M{t) = mK, нахо-
находим
Последняя формула особенно ясно показывает, что на конечной скорости
сказывается не столько отношение гат/гак, стоящее под знаком логарифма,
сколько скорость истечения о>, связанная с видом топлива. Из этой формулы,
в частности, следует, что если Vo = 0, то, чтобы придать скорость V ракете,
собственная масса которой гак, необходимо иметь следующий начальный запас
топлива:
шт = тк(еу^ — 1).
2. Барометрическая формула. Так называется формула, указываю-
указывающая зависимость атмосферного давления от высоты над уровнем моря.
Пусть p(h) — давление на высоте ft. Поскольку p(h) есть вес столба воздуха
над площадкой в 1 см2, расположенной на высоте ft, то p{h -f Д) отличается
от p(h) весом порции газа, попавшей в параллелепипед с основаниями в виде
исходной площадки в 1 см2, расположенной на высоте ft, и такой же площадки
на высоте Л 4- А. Пусть р(Л) — плотность воздуха на высоте Л. Поскольку
р(Л) непрерывно зависит от ft, то можно считать, что масса указанной порции
воздуха может быть вычислена по формуле
р@ г/см3 • 1 см2 • Д см = р(?) Д г,
где ? — некоторый уровень высоты в промежутке от Л до ft + Д. Значит, вес
этой массы3) есть д • р(?) Д.
Таким образом.
Поделив это равенство на Д и перейдя к пределу при Д ~> 0 с учетом того,
что тогда и ? -> Л, получаем
P'(h) = -gp(h). E)
У Эта формула иногда связывается с именем К. Э. Циолковского A857 — 1935) — рус-
русского ученого, основоположника теории космических полетов. Но, по-видимому, впервые
она была получена русским механиком И. В. Мещерским A859 — 1935) в его труде 1897 г.,
посвященном динамике точки переменной массы.
2) В пределах наличия заметной атмосферы величину д можно считать постоянной.

286 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Таким образом, скорость изменения давления естественно оказалась про-
пропорциональной плотности воздуха на соответствующей высоте.
Чтобы получить уравнение для функции p(h), исключим из E) функцию
p(h). В силу закона Клапейрона1) давление р, молярный объем V и темпера-
температура Кельвина2) Т газа связаны соотношением
где R — так называемая универсальная газовая постоянная. Если М — масса
одного моля воздуха, а V — его объем, то р = —, поэтому из F) находим
Р V V М р М
R
Полагая А = — Т, таким образом, имеем
м.
р = \(Т)р. G)
Если теперь принять, что температура описываемых нами слоев воздуха по-
постоянна, то из E) и G) окончательно находим
(8)
Это дифференциальное уравнение можно переписать в виде
9
p(h) A
ИЛИ
(In р)'(ft) =(-f и)',
откуда
или
Множитель ес определяется из известного начального условия р@) = ро> в
силу которого ес = ро.
Итак, мы нашли следующую зависимость давления от высоты:
р = рое"(*/л)\ (9)
Для воздуха при комнатной температуре (порядка 300 К = 27 °С) известно
значение А « 7,7 • 108 (см/сJ. Известно также, что g « 103 см/с2. Таким
1^Б. П. Э. Клапейрон A799 — 1864) — французский физик, занимавшийся термодина-
термодинамикой.
2)У. Томсон (лорд Кельвин) A824—1907) — известный английский физик.

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 287
образом, формула (9) приобретает вполне законченный вид после подстановки
этих числовых значении д и А. В частности, из (9) видно, что давление упадет
в е (« 3) раз на высоте h = - = 7,7 • ДО6 см = 7,7 км. Оно возрастет во столько
if
же раз, если опуститься в шахту на глубину порядка 7,7 км.
3. Радиоактивный распад, цепная реакция и атомный котел.
Известно, что ядра тяжелых элементов подвержены самопроизвольному (спон-
(спонтанному) распаду. Это так называемая естественная радиоактивность.
Основной статистический закон радиоактивности (справедливый, следова-
следовательно, для не слишком малых количеств и концентраций вещества) состоит в
том, что количество распадов за малый промежуток времени Л, прошедший от
момента t, пропорционально h и количеству N(t) не распавшихся к моменту
t атомов вещества, т. е.
N(t + А) - N(t) « -
где Л > 0 — числовой коэффициент, характерный для данного химического
элемента.
Таким образом, функция N(t) удовлетворяет уже знакомому дифференци-
дифференциальному уравнению
N'(t) = -Atf (<), A0)
из которого следует, что
JV(*) = iVoe-A',
где No = N@) ¦*- начальное количество атомов вещества.
Время Т, за которое происходит распад половины из начального количе-
количества атомов, называют периодом полураспада. Величина Т находитсй, таким
образом, из уравнения е~АТ = -, т. е. Т = -^- « -—-.
& ДА
Например, для полония Ро210 Т « 138 суток, для радия Ra226 Г « 1600
лет, для урана U235 Т « 7,1 • 108 лет, а для его изотопа U238 Т « 4,5 • 109 лет.
Ядерная реакция — это взаимодействие ядер или взаимодействие ядра с
элементарными частицами, в результате которого появляются ядра нового
типа. Это может быть ядерный синтез, когда слияние ядер более легких эле-
элементов приводит к образованию ядер более тяжелого элемента (например, два
ядра тяжелого водорода дают, с потерей массы и выделением энергии, ядро
гелия); это может быть распад ядра и образование ядра (ядер) более лег-
легких элементов. В частности, такой распад происходит примерно в половине
случаев столкновения нейтрона с ядром урана U235. При делении ядра урана
образуется 2—3 новых нейтрона, которые могут участвовать в дальнейшем
взаимодействии с ядрами, вызывая их деление и тем самым размножение ней-
нейтронов. Ядерная реакция такого типа называется цепной реакцией.
Опишем принципиальную математическую модель цепной реакции в неко-
некотором радиоактивном веществе и получим закон изменения количества N(t)
нейтронов в зависимости от времени.

288 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Возьмем вещество в виде шара радиуса г. Бели г не слишком мало, то за
малый промежуток времени Л, отсчитываемый от момента ?, с одной стороны,
произойдет рождение новых нейтронов в количестве, пропорциональном h и
N(t), а с другой — потеря части нейтронов за счет их выхода за пределы
шара.
Бели v — скорость нейтрона, то за время h покинуть шар могут только те
из них, которые удалены от границы не более чем на расстояние г; ft, да и то
если их скорость направлена примерно по радиусу. Считая, что такие нейтро-
нейтроны составляют неизменную долю от попавших в рассматриваемую зону и что
нейтроны в шаре распределены примерно равномерно, можно сказать, что ко-
количество теряемых за время Л нейтронов пропорционально N(t) и отношению
объема указанной приграничной области к объему шара.
Сказанное приводит к равенству
() A1)
(ибо объем рассматриваемой зоны равен примерно 4тгг2г;Л, а объем шара
-тгг3). Коэффициенты а и /3 зависят только от рассматриваемого радио-
о
активного вещества.
Из соотношения A1) после деления на/in перехода к пределу при ft -> О
получаем
N1
откуда
'(*)= (а-¦?)*(«), A2)
N(t) = No exp <(a - @А t\.
Из полученной формулы видно, что при (а— — J > 0 количество нейтронов
будет экспоненциально во времени расти. Характер этого роста, независимо
от начального условия iV0, таков, что за очень короткое время происходит
практически полный распад вещества с выделением колоссальной энергии —
это и есть взрыв.
Если (а — —) < 0, то очень скоро реакция прекращается ввиду того, что
теряется больше нейтронов, чем рождается.
Если же выполнено пограничное между рассмотренными случаями условие
а — ^ = 0, то устанавливается равновесие между рождением нейтронов и
их выходом из реакции, в результате чего их количество остается примерно
постоянным.
Величина г, при которой а — — = 0, называется критическим радиусом, а
г
масса вещества в шаре такого объема называется критической массой веще-
вещества.

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 289
Для урана U235 критический радиус равен примерно 8,5 см, а критическая
масса около 50 кг.
В котлах, где подогрев пара происходит за счет цепной реакции в радио-
радиоактивном веществе, имеется искусственный источник нейтронов, который до-
доставляет в делящуюся массу определенное количество п нейтронов в единицу
времени. Таким образом, для атомного реактора уравнение A2) немного ви-
видоизменяется:
N'(t)= (a-?)N(t)+n. A3)
Это уравнение решается тем же приемом, что и уравнение A2), ибо
еСТЬ "Р<я»ОД«« ОТ Функции -^щ; In [(а - |)ВД + п],
(а - 0MN(t) + п
если а — — ф 0. Следовательно, решение уравнения A3) имеет вид
г
N(t) =
' ЛГ0 е<в-*/г>* %я- f 1 - е<в-*/г>*1 при а - ? ф 0,
а-0/rl 1 г
No + nt при а - — = 0.
Из этого решения видно, что если а — — > 0 (сверхкритическая масса), то
г
произойдет взрыв. Если же масса докритическая, т. е. а < 0, то очень
г
скоро будем иметь
? -а
г
Таким образом, если поддерживать массу радиоактивного вещества в до-
критическом состоянии, но близком к критическому, то независимо от мощ-
мощности дополнительного источника нейтронов, т. е. независимо от величины
п, можно получить большие значения N(t), а значит, и большую мощность
реактора. Удерживание процесса в прикритическои зоне — дело деликатное и
осуществляется довольно сложной системой автоматического регулирования.
4. Падение тел в атмосфере. Сейчас нас будет интересовать скорость
v(t) тела, падающего на Землю под действием силы тяжести.
Если бы не было сопротивления воздуха, то при падении с относительно
небольших высот имело бы место соотношение
v(t) = g, A4)
вытекающее из второго закона Ньютона ma = F и закона всемирного тяго-
тяготения, в силу которого при h <& R (R — радиус Земли)
Mm ~ Mm
G

290 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Движущееся в атмосфере тело испытывает сопротивление, зависящее от
скорости движения, в результате чего скорость свободного падения тяжелого
тела в атмосфере не растет неограниченно, а устанавливается на некотором
уровне. Например, при затяжном прыжке скорость парашютиста в нижних
слоях атмосферы устанавливается в пределах 50—60 м/с.
Для диапазона скоростей от 0 до 80 м/с будем считать силу сопротивления
пропорциональной скорости тела. Коэффициент пропорциональности, разу-
разумеется, зависит от формы тела, которую в одних случаях стремятся сделать
хорошо обтекаемой (бомба), а в других случаях (парашют) имеют прямо про-
противоположную цель. Приравнивая действующие на тело силы, приходим к
следующему уравнению, которому должна удовлетворять скорость тела, па-
падающего в атмосфере:
mv(t) = тд — av. A5)
Разделив это уравнение наши обозначив — через р, окончательно полу-
т
чаем
t)(t) = -/3v + g.
Мы пришли к уравнению, которое только обозначениями отличается от
уравнения A3). Заметим, что если положить —Cv(t) + д = /(?), то, поскольку
/'(?) = —/3v'(t), из A3;) можно получить равносильное уравнение
/'(*) = -?/(*).
которое с точностью до обозначений совпадает с уравнением (8) или уравне-
уравнением A0). Таким образом, мы вновь пришли к уравнению, решением которого
является экспоненциальная функция
Отсюда следует, что решение уравнения A3') имеет вид
— -r I e
а решение основного уравнения A5) имеет вид
где i?o = v@) — начальная вертикальная скорость тела.
Из A6) видно, что при а > 0 падающее в атмосфере тело выходит на ста-
стационарный режим движения, причем v(t) « —д. Таким образом, в отличие от
падения в безвоздушном пространстве, скорость падения в атмосфере зависит
не только от формы тела, но и от его массы. При а -> 0 правая часть равен-
равенства A6) стремится к i>o + gt, т. е. к решению уравнения A4), получающегося
из A5) при а = 0.

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 291
Используя формулу A6), можно составить представление о том, как бы-
быстро происходит выход на предельную скорость падения в атмосфере.
Например, если парашют рассчитан на то, что человек средней комплек-
комплекции приземляется при раскрытом парашюте со скоростью порядка 10 м/с, то,
раскрыв парашют после затяжного свободного падения, когда скорость паде-
падения составляет примерно 50 м/с, он уже через 3 секунды будет иметь скорость
около 12 м/с.
Действительно, из приведенных данных и соотношения A6) находим —д «
10, — « 1, vo = 50 м/с, поэтому соотношение A6) приобретает вид
«
v(t) = 10 + 40e-*.
Поскольку е3 « 20, то при t = 3 получим v « 12 м/с.
5. Еще раз о числе е и функции ехрх. На примерах мы убедились
(см. также задачи 3, 4 в конце параграфа), что целый ряд явлений природы
описывается с математической точки зрения одним и тем же дифференциаль-
дифференциальным уравнением
/'(*) = a f(x), A7)
решение которого f(x) однозначно определяется, если указано «начальное
условие» /@). Тогда
Число е и функцию ех = ехрх мы в свое время ввели довольно формаль-
формально, сославшись на то, что это действительно важное число и действительно
важная функция. Теперь нам ясно, что даже если бы мы не вводили раньше
эту функцию, то ее, несомненно, пришлось бы ввести как решение важного,
хотя и очень простого уравнения A7). Точнее, достаточно было бы ввести
функцию, являющуюся решением уравнения A7) при некотором конкретном
значении а, например при а = 1, ибо общее уравнение A7) приводится к это-
этому случаю после перехода к новой переменной t, связанной с х соотношением
х = 1 (а ф 0).
а
Действительно, тогда
dF(t)
dt
и вместо уравнения /'(х) = otf{x) имеем теперь aF'(t) = aF(t), или F'(?) =
Итак, рассмотрим уравнение
/'(*)'=/(*) A8)
и обозначим через ехрж то его решение, для которого /@) = 1.

292 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Прикинем, согласуется ли это определение с прежним определением функ-
функции ехрж.
Попробуем вычислить значение f(x), исходя из того, что /@) = 1 и / удо-
удовлетворяет уравнению A8). Поскольку / — дифференцируемая функция, то
/ непрерывна, но тогда в силу A8) непрерывна и функция /'(ж). Более того,
из A8) следует, что / имеет также вторую производную /"(ж) = f'(x), и во-
вообще из A8) следует, что / — бесконечно дифференцируемая функция. Так
как скорость /'(ж) изменения функции f(x) непрерывна, то на малом проме-
промежутке h изменения аргумента функция /' меняется мало, поэтому f(xo + h) =
= f(xo) + f'(?)h w f(xo) + f'(xo)h. Воспользуемся этой приближенной фор-
мулой и пройдем отрезок от 0 до ж с малым шагом h = —, где п € N. Если
п
= 0, Xk+i = Xk + h, то мы будем иметь
Учитывая A8) и условие /@) = 1, имеем
f(x) = f(xn) «
... к /(xo)(l + ft)n = /@)(l + /i)n = A + -У.
Представляется естественным (и это можно доказать), что чем мельче шаг
х ( х \п
h = —, тем точнее приближенная формула f{x) « A Н—] .
Таким образом, мы приходим к тому, что
fix) = lim
n-»c©
(Ж \ п
1 Н— 1 обозначить через е и
п/
показать, что е ^ 1, то получаем, что
/(*)= lim (H-^y = lim(l + t)*/t = limf(l + tI/'l=ex, A9)
ибо мы знаем, что ua ~> va, если u —> v.
Метод численного решения дифференциального уравнения A8), позволив-
позволивший нам получить формулу A9), был предложен еще Эйлером и называется
методом ломаных Эйлера. Такое название связано с тем, что проведенные
выкладки геометрически означают замену решения /(х), точнее, его графи-
графика, некоторой аппроксимирующей график ломаной, звенья которой на соот-
соответствующих участках [a^rcfc+i] (А; = 0, ..., п — 1) задаются уравнениями
у = f(xk) + f'{xk)(x - Xk) (рис. 46).

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ
293
Нам встречалось также определение функции ехрж как суммы степенно-
00 1
1
го ряда ХЗ ~7хП- К нему тоже можно прийти из уравнения A8), если вос-
п=о п-
пользоваться следующим часто применяемым
приемом, называемым методом неопределен-
неопределенных коэффициентов. Будем искать решение
уравнения A8) в виде суммы степенного ряда
f{x) = со + схх + ... + спхп + ... , B0)
коэффициенты которого подлежат определе-
определению.
Как мы видели (см. § 5, теорема 1), из B0)
следует, что сп =
У
1
0
hih
л
• •
j j
j •
j •
X
Рис. 46
. Но в силу A8) /@) = /'@) = ... = /W@)
и, поскольку /@) = 1, имеем cn = -г, т. е. если решение имеет вид B0) и
71.
/@) = 1, то обязательно
f(x) =
Можно было бы независимо проверить, что функция, определяемая этим
рядом, действительно дифференцируема (и не только при х = 0) и что она
удовлетворяет уравнению A8) и начальному условию /@) = 1. Однако мы не
будем на этом останавливаться, ибо наша цель состояла только в том, что-
чтобы понять, согласуется ли введение экспоненциальной функции как решения
уравнения A8) при начальном условии /@) = 1 с тем, что мы раньше подра-
подразумевали под функцией ехр х.
Заметим, что уравнение A8) можно было бы рассматривать в комплексной
области, т. е. считать х произвольным комплексным числом. При этом все
проведенные рассуждения останутся в силе, быть может, только частично
потеряется геометрическая наглядность метода Эйлера.
Таким образом, естественно ожидать, что функция
2isl 1 2
>* 1 _1_ у _1_ у^
1
п!
I! 2!
является и притом единственным решением уравнения
удовлетворяющим условию /@) = I.
6. Колебания. Если тело, подвешенное на пружине, отклонить от поло-
положения равновесия, например, приподняв, а затем отпустив его, то оно будет
совершать колебания около положения равновесия. Опишем этот процесс в
общем виде.

294 ГЛ. V, ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пусть известно, что на материальную точку массы га, способную переме-
перемещаться вдоль числовой оси Ох, действует сила F = — кх, пропорциональная1)
отклонению точки от начала координат. Пусть нам известны также началь-
начальное положение хо = х@) нашей точки и ее начальная скорость vo = х@).
Требуется найти зависимость х = x(t) положения точки от времени.
В силу закона Ньютона, эту задачу можно переписать в следующем чисто
математическом виде: решить уравнение
mx(t) = -kx(t) B1)
при начальных условиях xq = ж@), х@) = vo.
Перепишем уравнение B1) в виде
x(t)+ —*(*) = 0 B2)
га
и попробуем вновь воспользоваться экспонентои, а именно попробуем подо-
подобрать число А так, чтобы функция x(t) = ext удовлетворяла уравнению B2).
Подставляя x(t) = ext в B2), получаем
га
или
2 к
А2 + - = 0, B3)
га
т. е.
I к / к
= —4/ , А2 = \ . Поскольку га > 0, то при к > 0 мы имеем два
у тп у тп
Гк Гк
чисто мнимых числа: Ai =-Ы— и Аг = % у—. На это мь! не рассчитывали,
но тем не менее продолжим рассмотрение. По формуле Эйлера
= cos JEt _ t sin /г
V тп у m
Поскольку при дифференцировании по действительному времени t происхо-
происходит отдельно дифференцирование действительной и мнимой частей функции
eAt, то уравнению B2) должны удовлетворять порознь и функция cos 4/ — ?, и
V тп
функция sin 4/—t. И это действительно так, в чем легко убедиться прямой
V тп
*)В случае пружины коэффициент к > 0, характеризующий ее жесткость, называют
коэффициентом жесткости пружины.

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 295
проверкой. Итак, комплексная экспонента помогла нам угадать два решения
уравнения B2), линейная комбинация которых
x(t) = a cos 4 A-1 + с2 sin J— t, B4)
v ' у т у га
очевидно, также является решением уравнения B2).
Коэффициенты с\, с*ъ в B4) подберем из условий
Хо = аг(О) = Ci,
v0 = ж@) = [ -сг w — sin4/— ? 4- с2\/— cos W— t}
v/ у V"* V тп У т ушу
Таким образом, функция
x(t) = rcocosW — ? + vq\№t- sin4/—? B5)
v 7 у т у к \ т
является искомым решением.
Делая стандартные преобразования, B5) можно переписать в виде
x(t) = Jxl + v^sm[,/^t + a), B6)
где
а = arcsin
Таким образом, при к > 0 точка будет совершать периодические коле-
колебания с периодом Т = 2ttw^, т. е. с частотой — = — W—, и амплитудой
w
утверждаем это потому, что из физических соображений
ясно, что решение B5) поставленной задачи единственно. (См. задачу 5 в
конце параграфа.)
Движение, описываемое функцией B6), называют простыми гармониче-
гармоническими колебаниями, а уравнение B2) — уравнением гармонических колебаний.
Вернемся теперь к случаю, когда в уравнении B3) к < 0. Тогда две функ-
функции eAlt = ехр ( — у 11, eAat = exp ( J 1) будут вещественными реше-
решениями уравнения B2) и функция
B7)
также будет решением. Постоянные с\ и сч подберем из условий
= Х(О) = Ci +С2,
= i@) = С1А1 + C2A2.

296 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Полученная система всегда однозначно разрешима, ибо ее определитель
А2 - Ах ф 0.
Поскольку числа Ai и Аг противоположного знака, то из B7) видно, что
при к < 0 сила F = — кх не только не стремится вернуть точку в положение
равновесия х = 0, но со временем неограниченно уводит ее от этого положе-
положения, если хо или vq отлично от нуля. То есть в этом случае х = 0 — точка
неустойчивого равновесия.
В заключение рассмотрим одну вполне естественную модификацию урав-
уравнения B1), на которой еще ярче видна польза показательной функции и фор-
формулы Эйлера, связывающей основные элементарные функции.
Предположим, что рассматриваемая нами частица движется в среде (воз-
(воздухе или жидкости), сопротивлением которой пренебречь нельзя. Пусть сила
сопротивления среды пропорциональна скорости точки. Тогда вместо урав-
уравнения B1) мы должны написать уравнение
mx(t) = — ax(t) — kx(t),
которое перепишем в виде
ж(*) + —i(t)+ —»(*) = 0. B8)
mm
Бели вновь искать решение в виде x(t) = ел*, то мы придем к квадратному
уравнению
т т
корни которого Ai,2 = -^ ±
Случай, когда а2 — Атк > 0, приводит к двум вещественным корням
А2, и решение может быть найдено в виде B7).
Мы рассмотрим подробнее более интересный для нас случай, когда а2 —
— Атк < 0. Тогда оба корня Ai, A2 комплексные (но не чисто мнимые!):
а . у/Атк — а2
г
2т 2т
а , . у/4гпк — а2
2т 2т
Формула Эйлера в этом случае дает
eXlt = ехр( — y-tj (cos u>t — isinui),
eA2* = exp( — Y-
где и = v "*""* . Таким образом, мы находим два вещественных решения
expf—Y~t\ cosut, expl—Y^tj sinut уравнения B8), угадать которые было

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 297
бы уже довольно трудно. Затем ищем решение исходной задачи в виде их
линейной комбинации
x(t) = ехр Г-^~ t) (hi cos ut + c2 smut), B9)
подбирая с\ и С2 так, чтобы удовлетворить начальным условиям х@) = жо,
х@) = i>o.
Получающаяся при этом система уравнений, как можно проверить, всегда
однозначно разрешима. Таким образом, после преобразований из B9) полу-
получаем решение задачи в виде
x(t) =Aexp(-^t) sinM + a), C0)
где А и a — константы, определяемые начальными условиями.
Из этой формулы видно, что благодаря множителю ехр f — -— t), где a > 0,
т > 0, в рассматриваемом случае колебания будут затухающими, причем ско-
скорость затухания амплитуды зависит от отношения —. Частота колебаний
1 1 Гк / а \2
— и; = — \ ( -— 1 меняться во времени не будет. Величина ш тоже за-
тг 2тг у ™> \ 2ш /
т
1 Ik ( а \2
2тг
висит только от отношений —, —, что, впрочем, можно было предвидеть на
т т
основании записи B8) исходного уравнения. При a = 0 мы вновь эозвраща-
емся к незатухающим гармоническим колебаниям B6) и уравнению'B2).
Задачи и упражнения
1. Коэффициент полезного действия реактивного движения.
a) Пусть Q — химическая энергия единицы массы топлива ракеты, ш — скорость
истечения топлива. Тогда -w2 есть кинетическая энергия выброшенной единицы
массы топлива. Коэффициент а в равенстве -и2 — aQ есть коэффициент полезного
действия процессов горения и истечения топлива. Для твердого топлива (бездым-
(бездымный порох) и> = 2 км/с, Q — 1000 ккал/кг, а для жидкого (бензин с кислородом)
ш = 3 км/с, Q = 2500 ккал/кг. Определите в этих случаях коэффициент а.
b) Коэффициент полезного действия (к. п. д.) ракеты определяется как отно-
отношение ее конечной кинетической энергии тк -~- к химической энергии сгоревшего
топлива mTQ. Пользуясь формулой D), получите формулу для к. п. д. ракеты через
тк, гпт, Q и а (см. а)).
c) Оцените к. п. д. автомобиля с жидкостным реактивным двигателем, если ав-
автомобиль разгоняется до установленной в городе скорости 60 км/час.
d) Оцените к. п. д. ракеты на жидком топливе, выводящей спутник на низкую
околоземную орбиту.

298 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
e) Оцените, для какой конечной скорости реактивное движение на жидком топ-
топливе имеет наибольший к. п. д.
f) Укажите, при каком отношении масс тт/тк топлива и корпуса к. п. д. ракеты
с любым видом топлива становится максимально возможным.
2. Барометрическая формула.
a) Используя данные п. 2 настоящего параграфа, получите формулу поправочно-
поправочного члена для учета зависимости давления от температуры столба воздуха, если эта
температура подвержена изменениям (например, сезонным) в пределах ±40 ° С.
b) Найдите по формуле (9) зависимость давления от высоты при температурах
—40°С, 0°С, 40°Си сравните эти результаты с результатами, которые дает ваша
приближенная формула из а).
c) Пусть температура воздуха в столбе меняется с высотой по закону T'(h) =
= — аТЬ, где То — температура воздуха на поверхности Земли, а а « 7 10 см.
Выведите при этих условиях формулу зависимости давления от высоты.
d) Найдите давление в шахте на глубинах 1 км, 3 км, 9 км по формуле (9) и по
формуле, которую вы получили в с).
e) Воздух независимо от высоты примерно на 1/5 часть состоит из кислорода.
Парциальное давление кислорода составляет также примерно 1/5 часть давления
воздуха. Определенный вид рыб может жить при парциальном давлении кислорода
не ниже 0,15 атмосфер. Можно ли ожидать, что этот вид встретится в реке на
уровне моря? Может ли он встретиться в речке, впадающей в озеро Титикака на
высоте 3,81 км?
3. Радиоактивный распад.
a) Измеряя количество радиоактивного вещества и продуктов его распада в про-
пробах пород Земли и считая, что сначала продукта распада вообще не было, можно
примерно оценить возраст Земли (во всяком случае, с того момента, когда это ве-
вещество уже возникло). Пусть в породе имеется т г радиоактивного вещества и г г
продукта его распада. Зная период Т полураспада вещества, найдите время, про-
прошедшее с момента начала распада, и количество радиоактивного вещества в пробе
того же объема в начальный момент.
b) Атомы радия в породе составляют примерно 102 часть всех атомов. Каково
было содержания радия 105, 106 и 5 • 109 лет тому назад? E • 109 лет ориентировочно
считается возрастом Земли.)
c) В диагностике заболеваний почек часто определяют способность почек вы-
выводить из крови различные специально вводимые в организм вещества, например
креатин («клиренс тест»). Примером, иллюстрирующим обратный процесс того же
типа, может служить восстановление концентрации гемоглобина в крови у донора
или у больного, внезапно потерявшего много крови. Во всех этих случаях уменьше-
уменьшение количества введенного вещества (или, наоборот, восстановление недостающего
количества) подчиняется закону N = iVbe", где N — количество (или, иными сло-
словами, число молекул) вещества, еще оставшегося в организме по прошествии вре-
времени t после введения количества Аго, а г — так называемая постоянная времени:
это время, по прошествии которого в организме остается 1/е часть первоначально
введенного количества вещества. Постоянная времени, как легко проверить, в 1,44
раза больше времени полу жизни (или времени полураспада), по истечении которого
в организме остается половина первоначального количества вещества.

§ 6. ПРИМЕРЫ ПРИЛОЖЕНИЙ В ЗАДАЧАХ ЕСТЕСТВОЗНАНИЯ 299
Пусть радиоактивное вещество выводится из организма со скоростью, характе-
характеризуемой постоянной времени то, и в то же время спонтанно распадается с постоян-
постоянной времени тр. Покажите, что в этом случае постоянная времени т, характеризую-
характеризующая длительность сохранения вещества в организме, определяется из соотношения
г =ro-f т'1.
d) У донора было взято некоторое количество крови, содержащее 201 мг железа;
для того чтобы компенсировать потерю железа, ему было велено принимать три-
трижды в день в течение недели таблетки сернокислого железа, содержащие каждая
67 мг железа. Количество железа в крови донора восстанавливается до нормы по
экспоненциальному закону с постоянной времени, равной примерно семи суткам.
Полагая, что с наибольшей скоростью железо из таблеток включается в кровь сразу
же после взятия крови, определите, какая примерно часть железа, содержащегося в
таблетках, включится в кровь за все время восстановления нормального содержания
железа в крови.
e) Больному со злокачественной опухолью было введено с диагностическими це-
целями некоторое количество радиоактивного фосфора Р32, после чего через равные
промежутки времени измерялась радиоактивность кожи бедра. Уменьшение радио-
радиоактивности подчинялось экспоненциальному закону. Так как период полураспада
фосфора известен — он составляет 14,3 суток, — по полученным данным можно бы-
было определить постоянную времени процесса уменьшения радиоактивности за счет
биологических причин. Найдите эту постоянную, если наблюдениями установлено,
что постоянная времени процесса уменьшения радиоактивности в целом составляет
9,4 суток (см. выше задачу с)).
4. Поглощение излучения.
Прохождение излучения через среду сопровождается частичным поглощением
излучения этой средой. Во многих случаях (линейная теория) можно считать, что,
проходя через слой толщиной 2 единицы, излучение ослабляется так же, как при
последовательном прохождении через два слоя толщиной 1 каждый.
a) Покажите, что при указанном условии поглощение излучения подчиняется за-
закону / = /ое~ , где /о — интенсивность излучения, падающего на поглощающее
вещество, / — интенсивность после прохождения слоя толщиной /, а к — коэффици-
коэффициент, имеющий размерность, обратную размерности длины.
b) Коэффициент к в случае поглощения света водой в зависимости от длины
волны падающего света, например, таков: ультрафиолет, к = 1,4 • 10~2; синий, к =
= 4,6 • 10~4; зеленый, к = 4,4 • 10; красный, к = 2,9 • 10~3. Солнечный свет падает
вертикально на поверхность чистого озера глубиной 10 м. Сравните интенсивности
каждой из перечисленных выше компонент солнечного света над поверхностью озера
и на дне.
5. Покажите, что если закон движения точки х = x(t) удовлетворяет уравнению
тх + кх = 0 гармонических колебаний, то:
ч г, mx2(t) . kx2(t) /r, rs . тт
a) величина Е = ——— + —-" постоянна (Е = К + и — сумма кинетической
„ mx2(t) „ тт kx2(t) „ .v
К = ——— и потенциальной и = — энергии точки в момент t);
*> z
b) если х@) = 0 и х@) = 0, то x(t) = 0;
c) существует и притом единственное движение х = x(t) с начальными условиями
х@) = хо и х@) =

300 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
d) Проверьте, что если точка движется в среде с трением и х = x(t) удовлетво-
удовлетворяет уравнению тх + ai; + fcx = 0, a > 0, то величина Е (см. а)) убывает. Найдите
скорость этого убывания и объясните физический смысл полученного результата,
учитывая физический смысл величины Е.
6. Движение под действием гуковской1^ центральной силы (плоский осцилля-
осциллятор).
В развитие рассмотренного в п. 6 и задаче 5 уравнения B1) линейного осцилля-
осциллятора рассмотрим уравнение mr(t) = —fcr(t), которому удовлетворяет радиус-вектор
г(?) точки массы т, движущейся в пространстве под действием притягивающей цен-
центральной силы, пропорциональной (с коэффициентом пропорциональности к > 0)
расстоянию \r(t)\ от центра. Такая сила возникает, если точка соединена с центром
гуковской упругой связью, например пружиной с коэффициентом жесткости к.
a) Продифференцировав векторное произведение r(t) x r(t), покажите, что все
движение будет происходить в плоскости, проходящей через центр и содержащей
векторы го = г (to), го = r(to) начального положения и начальной скорости точки
(плоский осциллятор). Бели векторы г о = г(?о)> го = г (to) коллинеарны, то движение
будет происходить на прямой, содержащей центр и вектор го (линейный осциллятор,
рассмотренный в п. 6).
b) Проверьте, что орбитой плоского осциллятора является эллипс и движение по
нему периодично. Найдите период обращения.
c) Покажите, что величина Е = mv2(t) + kr2(t) сохраняется во времени.
d) Покажите, что начальные данные го = r(to), го = г(?о) вполне определяют
дальнейшее движение точки.
7. Эллиптичность планетных орбит.
Предыдущая задача позволяет рассматривать движение точки под действием
центральной гуковской силы происходящим в плоскости. Пусть это плоскость ком-
комплексной переменной z = х + it/. Движение определяется двумя вещественными
функциями х = х(?), у = y(t) или, что то же самое, одной комплекснозначной функ-
функцией z = z(t) времени t. Полагая для простоты в задаче 6т = 1, к = 1, рассмотрим
простейший вид уравнения такого движения z(t) = — z{t).
a) Зная из задачи 6, что решение этого уравнения, отвечающее конкретным на-
начальным данным zq = z(t0), io = я(*о), единственно, найдите его в виде z(t) =
= c\txt + C2e~lt и, используя формулу Эйлера, проверьте еще раз, что траекторией
движения является эллипс с центром в нуле (в определенных случаях он может пре-
превратиться в окружность или выродиться в отрезок — выясните когда).
b) Учитывая, что величина |i(t)|2 + |з(?)|2 не меняется в процессе движения точ-
точки z(t), подчиненного уравнению z(t) = — z(t), проверьте, что точка w(t) = z2(t) no
отношению к новому параметру (времени) г, связанному с t соотношением г = r(t)
dr i /.\i2 d w w
таким, что — = \z(t)\ , движется при этом, подчиняясь уравнению -т-у = —с
где с — постоянная, а w = w(t(r)). Таким образом, движения в центральном поле
гуковских сил и движения в ньютоновском гравитационном поле оказались взаимо-
взаимосвязаны.
*)р. ГУк A635—1703) — английский естествоиспытатель, разносторонний ученый и экс-
экспериментатор. Открыл клеточное строение тканей и ввел сам термин «клетка». Стоял у
истоков математической теории упругости и волновой теории света, высказал гипотезу
тяготения и закон обратных квадратов для гравитационного взаимодействия.

§ 7. ПЕРВООБРАЗНАЯ 301
c) Сопоставьте это с результатом задачи 8 из § 5 и докажите теперь эллиптич-
эллиптичность планетных орбит.
d) Если вам доступен компьютер, то, взглянув еще раз на изложенный в п. 5
метод ломаных Эйлера, для начала подсчитайте этим методом несколько значений
ех. (Заметьте, что кроме определения дифференциала, точнее, формулы f(xn) «
« /(xn_i) + f'{xn-\)h, где h = xn — xn-i, метод ничего не использует.)
r(t)
Пусть теперь г(*) = (*(*)>?/(*))> го = г@) = A,0), го = г@)=@,1) и *(') = -^
Опираясь на формулы
r(tn) « r(tn-i) +
V(tn) « v(tn-l) -f
где v(?) = r(t), a(?) = v(?) = r(?), методом Эйлера рассчитайте траекторию движе-
движения точки, посмотрите, какой она формы и как она проходится точкой с течением
времени.
§ 7. Первообразная
В дифференциальном исчислении, как мы убедились на примерах предыдуще-
предыдущего параграфа, наряду с умением дифференцировать функции и записывать
соотношения между их производными весьма ценным является умение нахо-
находить функции по соотношениям, которым удовлетворяют их производные.
Простейшей, но, как будет видно из дальнейшего, весьма важной задачей та-
такого типа является вопрос об отыскании функции F(x) по известной ее про-
производной F'(x) = f(x). Начальному обсуждению этого вопроса и посвящен
настоящий параграф.
1. Первообразная и неопределенный интеграл
Определение 1. Функция F(x) называется первообразной функцией
или первообразной по отношению к функции f(x) на некотором промежут-
промежутке, если на этом промежутке функция F дифференцируема и удовлетворяет
уравнению F'(x) = f(x) или, что то же самое, соотношению dF(x) = f(x)dx.
Пример 1. Функция F(x) = arctgx является первообразной для f(x) =
= 2 на всей числовой прямой, поскольку arctg'x = ^.
Пример 2. Функция F(x) = arcctg - является первообразной для функ-
1 Х
ции f(x) = 2 как на промежутке всех положительных чисел, так и на
полуоси отрицательных чисел, ибо при х ф О
F'(x) = __JL_ . (_±\ - _J_ - f(x)
r V**7/ /1\2 \ 2/" 1 j. 2 ~ J\x)'
Как обстоит дело с существованием первообразной и каково множество
первообразных данной функции?

302 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
В интегральном исчислении будет доказан фундаментальный факт о том,
что любая непрерывная на промежутке функция имеет на этом промежутке
первообразную.
Мы приводим этот факт для информации читателя, а в этом параграфе
используется, по существу, лишь следующая, уже известная нам (см. гл. V,
§ 3, п. 1) характеристика множества первообразных данной функции на чи-
числовом промежутке, полученная из теоремы Лагранжа.
Утверждение 1. Если F\(x) и F2(x) — две первообразные функции f(x)
на одном и том же промежутке, то их разность F\(x) — F2{x) постоянна
на этом промежутке.
Условие, что сравнение F\ и F2 ведется на связном промежутке, как от-
отмечалось при доказательстве этого утверждения, весьма существенно. Это
можно заметить также из сопоставления примеров 1 и 2, в которых производ-
производные функций F\(x) = arctgx и F2{x) = arcctg - совпадают в области R \ 0 их
совместного определения. Однако
Fi(x) — F2(x) = arctgx — arcctg - = arctgx — arctgx = 0,
если x > 0, в то время как F\(x) — F2(x) = —7г при х < 0, ибо при х < 0 имеем
arcctg - = 7г + arctgx.
¦С
Как и операция взятия дифференциала, имеющая свое название «диффе-
«дифференцирование» и свой математический символ dF(x) = Ff(x)dx, операция пере-
перехода к первообразной имеет свое название «неопределенное интегрирование»
и свой математический символ
//(*)
A)
называемый неопределенным интегралом от функции f(x) на заданном про-
промежутке.
Таким образом, символ A) мы будем понимать как обозначение любой из
первообразных функции / на рассматриваемом промежутке.
В символе A) знак / называется знаком неопределенного интеграла, f —
подынтегральная функция, a f(x)dx — подынтегральное выражение.
Из утверждения 1 следует, что если F(x) — какая-то конкретная перво-
первообразная функции f(x) на промежутке, то на этом промежутке
B)
т. е. любая другая первообразная может быть получена из конкретной F(x)
добавлением некоторой постоянной.

§7. ПЕРВООБРАЗНАЯ 303
Если F'(x) = /(я), т. е. F —- первообразная для / на некотором проме-
промежутке, то из B) имеем
d ff(x) dx = dF(x) = F\x) dx = f(x) dx.
C)
'(x) dx = F(x) + С.
Кроме того, в соответствии с понятием неопределенного интеграла как
любой из первообразных, из B) следует также, что
' D)
Формулы C) и D) устанавливают взаимность операций дифференциро-
дифференцирования и неопределенного интегрирования. Эти операции взаимно обратны с
точностью до появляющейся в формуле D) неопределенной постоянной С.
До сих пор мы обсуждали лишь математическую природу постоянной С
в формуле B). Укажем теперь ее физический смысл на простейшем приме-
примере. Пусть точка движется по прямой так, что ее скорость v(t) известна как
функция времени (например, v(t) = v). Бели x(t) — координата точки в мо-
момент ?, то функция x(t) удовлетворяет уравнению x(t) = v(t), т. е. является
первообразной для v(t). Можно ли по скорости v(t) в каком-то интервале вре-
времени восстановить положение точки на оси? Ясно, что нет. По скорости и
промежутку времени можно определить величину пройденного за это время
пути s, но не положение на оси. Однако это положение также будет полно-
полностью определено, если указать его хотя бы в какой-то момент, например при
t = 0, т. е. задать начальное условие х@) = хо. До задания начального усло-
условия закон движения x(t) мог быть любым среди законов вида x(t) = x(t) + с,
где x(t) — любая конкретная первообразная функции v(t), а с — произвольная
постоянная. Но после задания начального условия х@) = хо вся неопределен-
неопределенность исчезает, ибо мы должны иметь х@) = х@) + с = хо, т. е. с = хо — ?@),
и x(t) = хо -f [x(t) — х@)]. Последняя формула вполне физична, поскольку
произвольная первообразная х участвует в формуле только в виде разности,
определяя пройденный путь или величину смещения от известной начальной
метки х@) =
2. Основные общие приемы отыскания первообразной. В соответ-
соответствии с определением символа A) неопределенного интеграла, он обозначает
функцию, производная которой равна подынтегральной функции. Исходя из
этого определения, с учетом соотношения B) и законов дифференцирования
можно утверждать, что справедливы следующие соотношения:
а.
/ (аи(х) + 0v(x)) dx = a / и(х) dx + C fv(x) dx + с. E)
b.
/ (uv)'(x) dx = / u\x) v(x) dx+ I u(x)v'(x) dx + c. F)

304 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
с. Если на некотором промежутке 1Х
а (р : It -> Ix — гладкое (т. е. непрерывно дифференцируемое) отображение
промежутка It в 1Х, то
f° VW <р''(*) dt = (F о <p)(t) + с. G)
Равенства E), F), G) проверяются прямым дифференцированием их левой
и правой частей с использованием в E) линейности дифференцирования, в F)
правила дифференцирования произведения и в G) правила дифференцирова-
дифференцирования композиции функций.
Подобно правилам дифференцирования, позволяющим дифференцировать
линейные комбинации, произведения и композиции уже известных функций,
соотношения E), F), G), как мы увидим, позволяют в ряде случаев сводить
отыскание первообразной данной функции либо к построению первообразных
более простых функций, либо вообще к уже известным первообразным. На-
Набор таких известных первообразных может составить, например, следующая
краткая таблица неопределенных интегралов, полученная переписыванием та-
таблицы производных основных элементарных функций (см. § 2, п. 3):
f xadx = —1— xa+1+c (a#l),
J a + 1 v r ;,
/ — dx = ln|x| + c,
¦ л^
axdx= -— ax -h с @ < a ^ 1),
У In a
I exdx = ez + c,
/ sinxdx = — cosx + c,
cos x dx = sin x + c,
/ —r~dx = tgx-f c,
У cos^x
/—— dx = - ctgx + c,
surx
arcsinx-f c,
^/1 — x2 I — arccos x + c,

§ 7. ПЕРВООБРАЗНАЯ
305
f i f arctg хч4- с,
i ^^ ^х = j
i 1 + x2 ^ - arcctg x 4
/ sh x dx = ch x + c,
/ ch x dx = sh x + c,
ch x
dx — th x 4- c,
sh x
Vx2±l
dx = — cth x + c,
dx = In
X
1
1
+
4-
—
у
X
X
X2
+
±
c.
1
Каждая из этих формул рассматривается на тех промежутках веществен-
вещественной оси Е, на которых определена соответствующая подынтегральная функ-
функция. Если таких промежутков несколько, то постоянная с в правой части
может меняться от промежутка к промежутку.
Рассмотрим теперь некоторые примеры, показывающие соотношения E),
F) и G) в работе.
Сделаем предварительно следующее общее замечание.
Поскольку, найдя одну какую-нибудь первообразную заданной на проме-
промежутке функции, остальные можно получить добавлением постоянных, то усло-
условимся для сокращения записи всюду в дальнейшем произвольную постоянную
добавлять только к окончательному результату, представляющему из себя
конкретную первообразную данной функции.
а. Линейность неопределенного интеграла. Этот заголовок должен
означать, что в силу соотношения E) первообразную от линейной комбина-
комбинации функций можно искать как линейную комбинацию первообразных этих
функций.
Пример 3.
/
4- а\х 4-...
anxn) dx =
ао 11 dx 4- Q>i I х
dx
• 1 2 i
<^o^ ~r « Oix 4-..
n

306 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 4.
J X 6
Пример 5.
/ cos2 ~ dx = / - A + cosx) dx = - / A + cosx) dx =
= ~/ldx+x/ cos x dx = - x + - sin x + c.
b. Интегрирование по частям- Формулу F) можно переписать в виде
/г
Ail 1^ I fm^% 1 i Of* 1 *^^» Я ^ 1 I ^1^ I fm^i Й I O^ I ^^^» ^^
У
или, что то же самое, в виде
/ и(х) dv(x) = и(х)г/(х) — / v(x) du(x) + с. F')
Это означает, что при отыскании первообразной функции и(х)г/(х) де-
дело можно свести к отысканию первообразной функции v(x)u'(x), перебро-
перебросив дифференцирование на другой сомножитель и частично проинтегрировав
функцию, как показано в F;), выделив при этом член tt(x)i/(x). Формулу F;)
называют формулой интегрирования по частям.
Пример 6.
/lnxdx = xlnx— /xdlnx = xlnx— /x— dx =
= xlnx— /ldx = xlnx — x
Пример 7.
I x2exdx = x2dex = х2еж - exdx2 = x2ex - 2 xexdx =
= xV - 2 fxdex = x2ex - 2 (xex - fexdx) =
= (я2
= аг2еж - 2хеж + 2ex + с = (я2 - 2s + 2)ez -h с

§ 7. ПЕРВООБРАЗНАЯ 307
с. Замена переменной в неопределенном интеграле. Формула G)
показывает, что при отыскании первообразной функции (fo<p)(t) •</>'(*) можно
поступать следующим образом:
= ff(x) dx = F(x) + с = F(<p(t)) + c,
т. е. сначала произвести замену (p(t) = x под знаком интеграла и перейти к но-
новой переменной х, а затем, найдя первообразную как функцию от х, вернуться
к старой переменной t заменой х =
Пример 8.
tdt 1 f d(t2 + 1) i fdx
1 f d(t2
Пример 9.
Г dx Г dx Г dl
У sinx " J 2sin ? cos ? ~~ У tg ?
= / du /'rf(tgti) _ /4dv =
У tgtxcos2u J tgu J v
= ln|v| +c = ln|tgu| + с = In „o
Мы рассмотрели несколько примеров, в которых использовались порознь
свойства а, Ь, с неопределенного интеграла. На самом деле в большинстве
случаев эти свойства используются совместно.
Пример 10.
/ sin2x cos3x dx = - / (sin5x — sinx) dx =
= - ( I sin5x dx - / sinx dx J = i / i / sin5x dEx) -h cosx J =
= — / sintedte 4- -cosx = — — cosx + -cosx + c =
i-U J JL JLU !
JLU
11
= -z COSX — — COS 5X + C.
a JLU
11 Зорич В. А.

308 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 11.
/ arcsinx dx = х arcsinx — / х darcsinx =
f x 1 f d(l - x2)
= xaxcsinx — / . dx = x arcsinx + - / — —
J y/T^x2 2J
= x arcsinx + - l и l^2 du = x arcsinx + u1^2 + с =
= x arcsinx + v1 — x2 + c.
Пример 12.
/ eax cos bxdx= - cos bx deax =
= - eax cos bx - - /eax dcos 6x = - eax cos bx + - /eax sin bx dx =
a ay a ay
= - eax cos bx + 4- / sin bx efeax = i eax cos 6x+~ eax sin bx -
a az J a a1
b f ax j • l °cos Ьх Ч- Ь sin bx ax b2 f ax . ,
« / eax dsmbx = r eax T / eax cosbx dx.
a1 J a2 a2 J
Из полученного равенства заключаем, что
/ах г. j °> COS Ья? + 6 Sin Ьх ат ,
eax cos bx dx = 7:—-г еах + с.
а2 + б2
К этому результату можно было бы прийти, воспользовавшись форму-
формулой Эйлера и тем обстоятельством, что первообразной функции e(a+i6)x =
= еах cos bx + i eax sin bx является функция
б a2-hfe2
_ acosfex -f fesinfex ax . asinfex — bcosfex
e +
ax
Это полезно иметь в виду и в будущем. При вещественном х это легко прове-
проверить непосредственно, продифференцировав действительную и мнимую части
функции —^-тге(а+*6К
а + го
В частности, отсюда получаем также, что
• i. j a sin bx — b cos 6x лз.
sin bx dx = r—— eax + с
Уже этот небольшой набор разобранных примеров показывает, что при
отыскании первообразных даже элементарных функций часто приходится
прибегать к дополнительным преобразованиям и ухищрениям, чего совсем

§ 7. ПЕРВООБРАЗНАЯ 309
не было при отыскании производных композиции тех функций, производные
которых нам были известны. Оказывается, это не случайная трудность. На-
Например, в отличие от дифференцирования, переход к первообразной элемен-
элементарной функции может привести к функции, которая уже не является ком-
композицией элементарных. Поэтому не следует отождествлять фразу «найти
первообразную» с невыполнимым порой заданием «выразить первообразную
данной элементарной функции через элементарные функции». Вообще, класс
элементарных функций — вещь очень условная. Имеется еще много важных
для приложений специальных функций, которые изучены и затабулированы
ничуть не хуже, чем, скажем, sin ж или ех.
г
ж С1Т| ПГ
Например, интегральный синус Si х есть та первообразная / dx функ-
J х
ции , которая стремится к нулю при х —> 0. Такая первообразная суще-
х
ствует, но, как и любая другая первообразная функции , она не является
композицией элементарных функций.
Аналогично, функция
гл • / COS X л
Cix = / ах,
J х
выделяемая условием Cix -> 0 при х —> оо, не является элементарной. Функ-
Функция Cix называется интегральным косинусом.
/1 1
-— функции -— также неэлементарна. Одна из перво-
111 X Ш jC
образных этой функции обозначается символом И х и называется интеграль-
интегральным логарифмом. Она удовлетворяет условию И х -> 0 при х -> +0. (Подробнее
о специальных функциях Six, Cix, Их будет сказано в гл. VI, § 5.)
Учитывая эти трудности отыскания первообразных, составлены довольно
обширные таблицы неопределенных интегралов. Однако, чтобы успешно ими
воспользоваться или чтобы не прибегать к ним, если вопрос совсем прост,
необходимо иметь некоторые навыки обращения с неопределенными интегра-
интегралами.
Дальнейшая часть этого параграфа посвящена интегрированию функций
из некоторых специальных классов, первообразные которых выражаются в
виде композиции элементарных функций.
3. Первообразные рациональных функций. Рассмотрим вопрос об
интегралах вида / R(x) dx, где R(x) = тг^ есть отношение полиномов.
J Q{x)
'Если действовать в области вещественных чисел, то, не выходя за пределы
поля вещественных чисел, любую такую дробь, как известно из алгебры (см.
формулу C7) из § 5, п. 4), можно разложить в сумму

310
ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
где р(х) — многочлен (он появляется при делении Р(х) на Q(x), только если
степень Р(х) не меньше степени Q(x)), a,jk, bjk, Cjk — однозначно определяе-
определяемые действительные числа, a Q(x) = (х — xi)*1... {x — x{)kt (x2 +Pix + qi)mi...
. ..(х2 +pnx + qn)mn-
О том, как строить разложение (8), мы уже говорили в § 5. После то-
того как разложение (8) построено, интегрирование функции R(x) сводится к
интегрированию отдельных слагаемых.
Многочлен мы уже интегрировали в примере 1, поэтому остается рассмо-
рассмотреть только интегрирование дробей вида
(х - а)'
и
Ьх + С
(х
, где к € N.
Вопрос о первой из этих дробей решается сразу, ибо
[-L-
J (х - а
dx = <
-^ (х - а)-*+х + с при
(9)
С интегралом
In |x — а\ + с
Ъх + с
при к — 1
dx
(х2 +рх + q)k
поступим следующим образом. Представим многочлен х2 + рх + q в виде
(х + ^ р) + (q ~ IP)» гДе Я ~ 7^2 ^^ ^* так как многочлен ж2 +рх Ч- g не имеет
вещественных корней. Полагая х -\- -р — и и g — ip2 = а2, получаем
У (X
6х Ч- с
¦/
аи
(г/2 + а2)*
где а = Ь,
Далее,
1
с- -Ьр.
и
(u2 + о2)*
du=±
u2 + о2)
(и2 + о2)*
= <
2A — A)
i ln(«2 + a2)
2
при
при /: = 1,
A0)
и остается разобраться с интегралом
j _ f« du
* У («2+а2)*
(И)

§7. ПЕРВООБРАЗНАЯ 311
Интегрируя по частям и делая элементарные преобразования, имеем
du и i 2
= Г
J
= i2kf
(и2 4 а2)* (и2 + а2)* У (и2 + а2)**1
(и2 + а2) - а2 , и
/
(и2 И- а2)* У (и2 + а2)**1 (и2 4- а2)
откуда следует рекуррентное соотношение
(u2 4 a
позволяющее понижать степень к в интеграле A1). Но 1\ легко вычислить:
и
~arctg~4c; A3)
а а
таким образом, используя A2) и A3), можно вычислить также первообраз-
первообразную A1).
Итак, мы доказали следующее
Утверждение 2. Первообразная любой рациональной функции R(x) =
= n/r v выро»саетсл через рациональные функции, а также трансцендент-
ные функции In и arctg. Рациональная часть первообразной, будучи приведе-
приведена к общему знаменателю, должна в качестве такового иметь произведение
всех сомножителей, на которые раскладывается многочлен Q{x), только с
кратностями на единицу меньшими, чем кратность их вхождения в разло-
разложение Q(x).
тт 1 о о
Пример 13. Вычислим
Г
У
2х2 4- Ъх Л- 5
х2 - 1)(х + 2)
Поскольку подынтегральная функция является правильной дробью и, раз-
разложение знаменателя в произведение (х — 1)(гг + 1)(х + 2) тоже известно, то
сразу ищем разложение
А , В , С ,ЛА,
4- __ -f —— A4)
+ 2) х-
нашей дроби в сумму простейших дробей.
Приведя правую часть равенства A4) к общему знаменателю, имеем
2х2 + Ъх + 5 (А 4 В 4- С)ж2 4 (ЗА 4 В)ж 4 BЛ - 2Д - С)
(х - 1)(х 4 1)(аг 4 2) (х - 1)(х 4 1)(х 4 2)

312 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Приравнивая соответствующие коэффициенты числителей, получаем систему
А+ В + С = 2,
ЗА + В = 5,
{2А-2В - С = 5,
из которой находим (А, В, С) = B, — 1,1).
Заметим, что в данном случае эти числа можно было бы найти и в уме.
Действительно, домножая A4) на х—1 и полагая затем в полученном равенстве
х = 1, справа получим А, а слева — значение при х = 1 дроби, полученной из
нашей вычеркиванием в знаменателе сомножителя х—1, т. е. А = ——-— = 2.
Аналогично можно было бы найти В и С.
Итак,
/
2x2 + 5x + 5 , o f dx f dx f dx
x-f 1 / x + 2
= 21п|х - 1| - 1п|х + 1| + 1п|х + 2| + с = In
(х - IJ (х + 2)
с.
x-f 1
Пример 14. Вычислим первообразную функции
х7 - 2х6 + 4х5 - 5х4 + 4х3 - 5х2 - х
(х-1J(х2 + 1J
Прежде всего заметим, что дробь не является правильной, поэтому, рас-
раскрыв скобки и найдя знаменатель дроби Q(x) = хб—2х5+3х4—4х3Ч-Зх2—2х-|-1,
делим на него числитель, после чего получаем
D/ ч , х5 - х4 + х3 - Зх2 - 2х
щх) = х -I
а затем уже ищем разложение правильной дроби
х5 - х4 + х3 - Зх2 - 2х А В Cx + D Ex + F ( .
. (х - 1J(х2 + IJ (х - 1) + х - 1 (х2 + IJ х2 + 1 ' {Ь)
Конечно, разложение можно найти каноническим путем, выписав систему
шести уравнений с шестью неизвестными. Однако вместо этого мы проде-
продемонстрируем иные, иногда используемые, технические возможности.
Коэффициент А находим, домножив равенство A5) на (х — IJ и положив
затем х = 1: А = —1.
Перенесем дробь -( — с уже известным значением А — — 1 в левую часть
(х — 1)
равенства A5). Тогда получим
х4 + х3 4- 2х2 4- х - 1 В Cx + D Ex + F , ч
(х - 1)(х2 + IJ х - 1 + (х2 + IJ х2 + 1 ' [ }

§ 7. ПЕРВООБРАЗНАЯ 313
откуда, домножая A6) на х - 1 и полагая затем х = 1, находим В = 1.
Перенося теперь дробь г в левую часть равенства A6), получим
х — 1
х2 + х 4- 2 Сх + ?> JSx + F
(х2 + IJ " (х2 + IJ х2 + 1 "
Приводя правую часть равенства A7) к общему знаменателю, приравни-
приравниваем числители
х2 + х + 2 = Ex3 + Fx2 + (С + ?)х + (Z? + F),
откуда следует, что
JS? = О,
\^_J ^^^^ Jh« ^^^» J^ ^
D + F = 2,
или (C,D,E,F) = A,1,0,1).
Теперь нам известны все коэффициенты в равенстве A5). Первые две дро-
дроби при интегрировании дают соответственно и 1п|х — 1|. Далее,
[ Сх + Р _ /• х + 1 _
У (х2 + IJ Х ~ У (х2 + IJ X ~
X f С* I •?/ "Т" X у I ' UX ~~" X у
= 2 У (х2 + 1J+У (х2Ч-1J = 2(х2 + 1) 2?
где
J (х
х , 1 .
+ ^ arctg х,
2 + IJ 2 (х2 + IJ 2
что следует из A2) и A3).
Наконец,
у х2 Ч-1 у х2 Ч-1
Собирая все интегралы, окончательно имеем
= |х2 + -1у + _^_ +1п|х - 1| + |
R(x)dx = -х2 + Ч- о/ о , 1чо +Ь|х - 1| + -arctgx + c.
& X — 1 2ix* + IV 2
Рассмотрим теперь некоторые часто встречающиеся неопределенные инте-
интегралы, вычисление которых может быть сведено к отысканию первообразной
рациональной функции.

316 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
5. Первообразные вида / Я(ж, у(х)) dx. Пусть, как и в пункте 4,
R(x, у) — рациональная функция. Рассмотрим некоторые специальные перво-
первообразные вида
R(x,y(x))dx,
i
где у = у(х) — функция от х.
Прежде всего, ясно, что если удастся сделать замену х = x(t) так, что обе
функции х — x(t) и у = y(x(t)) окажутся рациональными функциями от ty то
x'(t) — тоже рациональная функция и
JR{x,y{x))dx =
т. е. дело сведется к интегрированию рациональной функции.
Мы рассмотрим следующие специальные случаи задания функции у = у{х).
/ лх I h лог I h
а. Если t/ = \ ;, где n ? N, то, полагая tn = :, получаем
уся + сг cx + rf
и подынтегральное выражение рационализируется.
Пример 19.
*!+!¦
* Л ' ' * " ' " 'й =
1-t3
1-^3 .
+ 4
з /X — 1
где t = -

§ 7. ПЕРВООБРАЗНАЯ
315
Пример 15.
Г dx _ Г 1
УЗ-fsinx У з + -
It
dt
du
3t2 + 2t
3tg24
Я + $и , /^ * 3t + l , /^ . 3tg2
= v2 arctg -7= + с = V2 arctg —=- -f с = v2 arctg 7=
л/2 \/2 л/2
Здесь мы воспользовались универсальной заменой t = tg ^
Пример 16.
-/
(sin x + cos xJ J cos2 x (tg x +1J
= f dtgx Г
У (tgx-ыJ У
=z с
tgx
Пример 17.
J
dx
da;
2 sin2 3x - 3 cos2 3x +
cos2 3x B tg2 3x - 3 + A 4- tg2 3x))
_ 1 Г
37
dtg3x
3tg23x
x _ 1 f dt = 1 /2 f^xh__
-2 ЗУ 3f2-2 ~3-2V3y 3<2_1 ~
3v/6 У «2 - 1 ~ бл/6
In
rt-1
In
Пример 18.
COS3X
sin7x
dx
¦/
/ / ±—т
J
cos2x dsinx f A —
= f
4 sin4 x 6 sin6 x
c.

314 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
4. Первообразные вида / Я (cos ж, sin ж) da:. Пусть fl(u,v) — рацио-
P(u,v)
нальная функция от и и v, т. е. отношение ¦— т полиномов, являющихся
Q(u, v)
линейными комбинациями мономов umvn, где т = 0,1, ..., п = 0,1, ...
Для вычисления первообразной JR(cos x, sin x) dx существует несколько
приемов, из которых один — вполне универсальный, хотя и не всегда самый
экономный.
а. Сделаем замену t = tg -. Поскольку
l-tg2f 2tg|
с = , sin x = —,
. dx 2d*
or = —¦, т. e. ax =
2cos2| l + tg21
то
2
и дело свелось к интегрированию рациональной функции.
Однако такой путь часто приводит к очень громоздкой рациональной
функции, поэтому следует иметь в виду, что в ряде случаев существуют и
другие возможности рационализации интеграла.
Ь. В случае интегралов вида [R(cos2x, sin2x)dx или fr(tgx)dx1 где г (и)
— рациональная функция, удобна подстановка t = tg x, ибо
2 1 -2
COS X = я—, Sin X =
lt2'
я,
l-htg2x'
# e#
COS2 X 1 + tg2 X
Выполнив указанную подстановку, получим соответственно
с. В случае интегралов вида
/ R(cos х, sin2 x) sin x dx или / i? (cos2 x, sin x) cos x dx
можно внести функции sinx, cosx под знак дифференциала и сделать замену
t = cosx или t = sinx соответственно. После замены эти интегралы будут
иметь вид
- f R{t, 1 - t2) dt или /яA - *2, t)

§ 7. ПЕРВООБРАЗНАЯ 317
b. Рассмотрим теперь случай, когда у = у/ах2 + bx -f с, т. е. речь идет об
интегралах вида
/ R(x, у/ах2 + Ьх + с) dz.
Выделяя полный квадрат в трехчлене ах2+Ьх+с и делая соответствующую
линейную замену переменной, сводим общий случай к одному из следующих
трех простейших:
[R(t,y/?T\)dt, JR{t,y/W^\)dt, JR{t,y/r^?)dt. A8)
Для рационализации этих интегралов теперь достаточно положить соот-
соответственно
y/t2+l = tu + 1, или y/t2 -hi = tu - 1, или \/t2 + 1 = t - и;
y/t2-l = u(t - 1), или >/t2-l = w(f+l), или л/*2 ~ 1 = t - u;
= u(l - t), ИЛИ VT^2 = u(l 4- t), ИЛИ VT-t2 = tu ± 1.
Эти подстановки были предложены еще Эйлером (см. задачу 3 в конце
параграфа).
Проверим, например, что после первой подстановки мы сведем первый ин-
интеграл к интегралу от рациональной функции.
В самом деле, если y/t2 + 1 = tu + 1, то t2 + 1 = t2u2 + 2 tu + 1, откуда
2u
t ~ i 2
1 — u^
и, в свою очередь,
Таким образом, t и y/t2 -f 1 выразились рационально через и, а следова-
следовательно, интеграл привелся к интегралу от рациональной функции.
Интегралы A8) подстановками t = sh <p, t = ch <p, t = simp (или t = cos ip)
соответственно приводятся также к тригонометрической форме
/ iJ(sh <py ch (p) ch <p dip, / jR(ch ц>, sh <p) sh y> dip
и
/ i?(sin у?, cos ip) cos у? dy? или — / R(cos <p, sin y?) sin y? d(p.
Пример 20.
dx __ Г dx _ f dt
x + y/x2 + 2x + 2" " У ж + л/(ж -f lJTl ~ У t-14

318 ГЛ. У. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
и2 — \
Полагая y/t2 +1 = и — ?, имеем 1 = и2 — 2tu, откуда t = ——. Поэтому
L
2J u2(u-l) 2
1
л ••• I »"» — I « л ——— 1
Теперь остается проделать обратный путь замен: u = t+\/t2 + \ vit = x
с. Эллиптические интегралы. Очень важными являются также пер
вообразные вида
где Р(х) — многочлен степени п > 2. Такой интеграл, как было показано
Абелем и Лиувиллем, вообще говоря, уже не выражается через элементарные
функции.
При п = 3 и п = 4 интеграл A9) называется эллиптическим, а при п > 4
Можно показать, что общий эллиптический интеграл элементарными под-
подстановками с точностью до слагаемых, выражающихся через элементарные
функции, приводится к следующим трем стандартным эллиптическим инте-
интегралам:
dx
I
I
- Х2)A
x2dx
I
- z2)(l - fc2x2)'
dx
B0)
B1)
hx2)yJ{\-X2){l-k2X2Y
где h и к — параметры, причем во всех трех случаях параметр А; лежит в
интервале ]0,1[.
Подстановкой х = cos <p эти интегралы можно свести к следующим кано-
каноническим интегралам или их комбинациям:
dtp
I
— k2sin2ip
A — Л sin2 у?) у 1 - к2 sin2(p
B3)
B4)
B5)

§ 7. ПЕРВООБРАЗНАЯ 319
Интегралы B3), B4), B5) называются соответственно эллиптическими ин-
интегралами первого, второго и третьего рода (в форме Лежандра). Через
F(Ar, ф) и Е(к, ф) обозначают эллиптические интегралы B3) и B4) первого и
второго рода соответственно, выделяемые условиями F(k, 0) = 0 и Е(к, 0) = 0.
Функции F(k, <р), Е(к, ф) часто используются, и потому составлены доста-
достаточно подробные таблицы их значений для 0 < к < 1 и 0 ^<р ^ тг/2.
Эллиптические интегралы, как показал Абель, естественно рассматривать
в комплексной области, в неразрывной связи с так называемыми эллиптиче-
эллиптическими функциями, которые соотносятся с эллиптическими интегралами так
л. Г dip .
же, как, например, функция sin <р с интегралом / = arcsin (p.
f dip =
Задачи и упражнения
1. Метод Остроградского1' выделения рациональной части интеграла от пра-
правильной рациональной дроби.
Пусть -; ' — правильная рациональная дробь; q(x) — многочлен, имеющий те
Q[x)
же корни, что и Q(x), но кратности 1; Q\{x) =
Щ.
q(x)
Покажите, что
а) Имеет место следующая формула Остроградского:
B6)
Pi(x) p(x) я fp(x) .
где n ( \» (~\ ~* правильные рациональные дроби, причем / ^у— ах — трансцен-
трансцендентная функция.
(В силу этого результата дробь - , { в B6) назьгоается рациональной частью
Qi(x)
интеграла
f
/
b) В формуле
Р(х) (Рг(х) V р(х)
Q(x) \Qi(x)J * q(x)>
полученной дифференцированием формулы Остроградского, дробь ( 1у\ ) после
\Qi\x)/
надлежащих сокращений приводится к знаменателю Q(x).
c) Многочлены q(x), Qi(a:), а затем и многочлены р(ж), Pi(x) можно найти ал-
алгебраическим путем, даже не зная корней многочлена Q(x). Таким образом, ра-
рациональную часть интеграла B6) можно полностью найти, даже не вычислив всей
первообразной.
l> M. В. Остроградский A801 — 1861) — выдающийся русский механик и математик, один
из инициаторов прикладного направления исследований в Петербургской математической
школе.

320 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
d) Выделите рациональную часть интеграла B6), если
Р(х) = 2х6 + Зх5 + 6х4 + 6х3 + 10х2 + Зх + 2,
Q(x) = x7 + Зх6 + Ъхъ + 7х4 + 7х3 + 5х2 + Зх + 1
(см. пример 17 в § 5 этой главы).
2. Пусть ищется первообразная
I R(cos х, sin x) dx, B7)
где K(u, v) = — — рациональная функция.
Q(UjV)
Покажите, что
a) если #(—и, v) = Я(щ v), то Я(и, v) имеет вид Ri(u2, v);
b) если Я(—ге, v) = — #(u, v)j то R(u, v) = u-H2(u2, v) и подстановка * = sinx
рационализирует интеграл B7);
c) если R(—u, —v) = #(u, v), то il(u, v) = R3 f-, v2j и подстановка ? = tgx рацио-
рационализирует интеграл B7).
3. Интегралы вида
[R(x, у/ах2 + bx + c)dx. B8)
а) Проверьте, что интеграл B8) приводится к интегралу от рациональной функ-
функции следующими подстановками Эйлера:
t = у/ах2 + Ъх + с dh ^/л^> если а > 0,
/ X -— Ж1 о
? = д / , если xi, X2 — действительные корни трехчлена ах + Ьх + с.
у I -X2
b) Пусть (хо, уо) — точка кривой у2 = ах2 + Ьх + с, a * — угловой коэффициент
прямой, проходящей через точку (хо,уо) и пересекающей кривую в некоторой точ-
точке (х,у). Выразите координаты (х,у) через (хо,уо) и t и свяжите эти формулы с
подстановками Эйлера.
c) Кривая, задаваемая алгебраическим уравнением Р(х, у) = 0, называется уни-
курсалъной, если она допускает параметрическую запись х = х(?), у = y{t) при
помощи рациональных функций x(t), y(t). Покажите, что интеграл jR(xry(x))dx,
где Я(и, v) — рациональная функция, а у(х) — алгебраическая функция, удовлетво-
удовлетворяющая уравнению Р(х,у) = 0, задающему уникурсальную кривую, приводится к
интегралу от рациональной функции.
d) Покажите, что интеграл B8) всегда можно свести к вычислению интегралов
следующих трех типов:
Ш r^I Tl I /fT
У Vax2 + Ьх + с J (x — xo)k • y/ax2 + bx + c
(Ax + B) dx
(x2 + px + g)m • >/ax2 -h Ьх + с

§ 7. ПЕРВООБРАЗНАЯ 321
4. а) Покажите, что интеграл
xm (a + bxn)p dx
от дифференциального бинома, где m, n, p — рациональные числа, приводится к
интегралу
'(а + bt)p tq dt, B9)
/¦
где Pi q — рациональные числа.
b) Интеграл B9) выражается через элементарные функции, если одно из трех
чисел р> q> p + q — целое. (П. Л. Чебышев показал, что других случаев, при которых
бы интеграл B9) выражался в элементарных функциях, не существует.)
5. Эллиптические интегралы.
a) Любой многочлен третьей степени с действительными коэффициентами име-
имеет вещественный корень xq и заменой х — хо = t2 приводится к многочлену вида
t2(at4 + btz + ct2 + dt + e), где а ф 0.
b) Функция R(xy y/P(x)), где R(u, v) — рациональная функция, а Р — полином
степени 3 или 4, приводится к виду Ri(t, >/atA + bt3+ ... + е), где а ф 0.
с) Многочлен четвертой степени ах4 + Ьх3 + ... + е представляется в виде про-
про2 + р\х + qi)(x2 + рх + д) и заменой х = a /у
изведения а(х2 + р\х + qi)(x2 + р2х + дг) и заменой х = a /у ^ всегда может быть
)
приведен к виду
t И-Л2
Q
d) Функция Я (ж, v"az4+ Ьж3+ ... + е) заменой х = Q ^ может быть приведена
к виду |
e) Функция Я(х, у/у) может быть представлена в виде суммы R\(x, у) + 2'ж',
у/У
где #i и #2 — рациональные функции.
f) Любая рациональная функция может быть представлена как сумма четной и
нечетной рациональных функций.
g) Бели рациональная функция R(x) четна, то она имеет вид г(х2), а если нечетна,
то вид хг(х2)у где г(х) — рациональная функция.
h) Любая функция R(x, у/у) приводится к виду
у/У у/У
i) Любой интеграл вида I R(x, y/P(x)) dz, где Р(х) — многочлен четвертой сте-
степени, с точностью до элементарных слагаемых приводится к интегралу
r(t2)dt
где r(t) — рациональная функция, А = ±1.

322 ГЛ. V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
j) Бели |mi| > |m2J > 0, то одной из замен вида y/m[t = х, y/rn[t = у/1 ~ х2,
х /—л 1 Г r(t2)dt
= . ., y/mit = . . интеграл / . ' . приводится к
VI-ж2 VI-х2 У v^(l + mit2)(l +Ш2*2)
v =, где 0<Л<1, а г — рациональная функция.
у^A — х2)A — А:2ж2)
к) Выведите формулы понижения показателей 2n, m для интегралов
Г х2п dx Г dx
У у/{\-х2){1-к2х2У J (x2-a)my/(l-x2)(l-
1) Любой эллиптический интеграл
R(x, у/рЩ dx,
где Р — полином четвертой степени, с точностью до слагаемых, представляющихся в
виде элементарных функций, приводится к одному из трех канонических интегралов
B0), B1), B2).
т) Интеграл / . . выразите через канонические эллиптические интегралы.
J у/\ + хъ
п) Выразите через эллиптические интегралы первообразные функций —=== и
vcoe2x
\/C0S Q — COS X
6. Используя вводимые ниже обозначения, найдите с точностью до линейной
функции Ах + В первообразные следующих неэлементарных специальных функций:
— dx (интегральная экспонента);
х
b) Si(x) = / dx (интегральный синус);
J x
dx (интегральный косинус);
d) Shi(x) = / dx (интегральный гиперболический синус);
e) Chi(x) = / dx (интегральный гиперболический косинус);
f) S{x) = J sin x2 dx Л
> (интегралы Френеля);
g) C(x) = / cos x2 dx J
e ~x dx (интеграл Эйлера—Пуассона);
i) li(x) = I-— (интегральный логарифм).
J lnx
7. Проверьте, что с точностью до постоянной справедливы следующие равенства:
a) Щх)=П(ех);
b) i

§ 7. ПЕРВООБРАЗНАЯ 323
с) Shi (*) = ±[Ei(*)-Ei (-*)];
d) Ei(ix) = Ci(x
e) ё*
8. Дифференциальное уравнение вида
dy = fix)
dx g(y)
называют уравнением с разделяющимися переменными, поскольку его можно пере-
переписать в виде
9(y)dy = f(x)dx>
в котором переменные я и у разделены. После этого уравнение можно решить:
вычислив соответствующие первообразные.
Решите уравнения:
a) 2ж3ууЧу2 = 2;
b) хуу' = TT^
c) у' = cos(y + х), положив и{х) = у(х) + ж;
d) ж2у' — cos 2у = 1 и выделите то решение, которое удовлетворяет условию
у(х) -> 0 при х -» +ос;
е) \y\x)=Si{x);
JO
f)
COSX
9. Парашютист прыгнул с высоты 1,5 км, а раскрыл парашют на высоте 0,5 км.
Сколько времени он падал до раскрытия парашюта? Предельную скорость падения
человека в воздухе нормальной плотности принять равной 50 м/с. Решите задачу в
предположении, что сопротивление воздуха пропорционально
a) скорости;
b) квадрату скорости.
Изменением давления с высотой пренебречь.
10. Известно, что скорость истечения воды из небольшого отверстия в дне сосуда
достаточно точно может быть вычислена по формуле 0,6д/2рЯ, где g — ускорение
силы тяжести, а Н — высота уровня воды над отверстием.
Цилиндрический бак поставлен вертикально и имеет отверстие в дне. Половина
воды из полного бака вытекает за 5 мин. За какое время вытечет вся вода?
11. Какую форму должен иметь сосуд, являющийся телом вращения, чтобы при
истечении из него воды уровень воды понижался равномерно? (Исходные данные
см. в задаче 10.)
12. В рабочее помещение вместимостью 104 м3 через вентиляторы в 1 минуту по-
подается 103м3 свежего воздуха, содержащего 0,04% СОг» и одновременно такое-же
количество смеси выводится из помещения. В 9 часов утра в помещение входят слу-
служащие, и через полчаса содержание СОг в воздухе повышается до 0,12%. Оцените
содержание углекислого газа в помещении к 2 часам дня.

ГЛАВА VI
ИНТЕГРАЛ
§ 1. Определение интеграла и описание множества
интегрируемых функций
1. Задача и наводящие соображения. Пусть точка движется вдоль
числовой оси, s(t) — ее координата в момент t, a v(t) = s'(t) — ее скорость
в тот же момент t. Предположим, что мы знаем положение s(to) точки в
момент to и к нам поступают данные о ее скорости. Располагая ими, мы
хотим вычислить s(t) для любого фиксированного значения t > to-
Если считать скорость v(i) меняющейся непрерывно, то смещение точки за
малый промежуток времени приближенно можно вычислить как произведение
v(r)At скорости в произвольный момент т, относящийся к этому промежут-
промежутку времени, на величину At самого промежутка. Учитывая это замечание,
разобьем отрезок [to,t], отметив некоторые моменты U (г = 0, ...,тг), так,
что to < h < • • • < tn = ?, и так, что промежутки [?»_!,?»] малы. Пусть
=ti — U-i и Ti € [?i_i,?i], тогда имеем приближенное равенство
n
s(t)-s(t0) «J^i
По нашим представлениям, это приближенное равенство будет уточняться,
если переходить к разбиениям отрезка [to, t] на всё более мелкие промежутки.
Таким образом, надо полагать, что в пределе, когда величина А наибольшего
из промежутков разбиения стремится к нулю, получим точное равенство
п
Шп ]Г v(n)Ati = s(t) - a(to). A)
Это равенство есть не что иное, как фундаментальная для всего анализа
формула Ньютона—Лейбница. Она позволяет, с одной стороны, численно

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ
325
находить первообразную s(t) по ее производной v(t), а с другой стороны,
по найденной каким-либо способом первообразной s(t) функции v(t) найти
п
стоящий слева предел сумм ?) у(т{) At{.
t=i
Такие суммы, называемые интегральными суммами, встречаются в самых
разнообразных случаях.
Попробуем, например, следуя Архимеду, найти площадь под параболой
у = х2 над отрезком [0,1] (рис. 47). Не останавливаясь здесь на подробном
обсуждении понятия площади фигуры, о котором речь будет идти несколько
позже, мы, как и Архимед, будем действовать мето-
методом исчерпания фигуры посредством простейших
фигур — прямоугольников, площади которых мы
вычислять умеем. Разбив отрезок [0,1] точками
0 = хо < х\ < ... < хп = 1 на мелкие отрезки
[ж*_1,а;*], мы, очевидно, можем приближенно вычи-
вычислить искомую площадь а как сумму площадей изо-
изображенных на рисунке прямоугольников:
п
t=i
i = Xi — Xi-\. Полагая f(x) = х2
здесь
ную формулу в виде
Рис. 47
и & = ж*_1, мы перепишем получен-
полученп
t=i
В этих обозначениях в пределе будем иметь
п
B)
где, как и выше, А — длина наибольшего из отрезков [ж*_1,ж<] разбиения.
Формула B) только обозначениями отличается от формулы A). Забыв на
миг о геометрическом смысле /(&), Да?» и считая х временем, а /(х) ско-
скоростью, найдем первообразную F(x) функции f(x) и тогда по формуле A)
получим, что а = F(l) — F@).
В нашем случае f(x) = ж2, поэтому F{x) = ~ж3 + сиа = F(l) — F@) = \.
о о
Это и есть результат Архимеда, который он получил прямым вычислением
предела в B).
Предел интегральных сумм называется интегралом. Таким образом, фор-
формула A) Ньютона—Лейбница связывает интеграл и первообразную.
Перейдем теперь к точным формулировкам и проверке того, что на эври-
эвристическом уровне было получено выше из общих соображений.

326 гл. vi. интеграл
2. Определение интеграла Римана
a. Разбиения
Определение 1. Разбиением Р отрезка [а,Ь], а < 6, называется конеч-
конечная система точек хо, ..., хп этого отрезка такая, что а = хо < х\ < ... <
< хп = Ь.
Отрезки [xi_i,a;i] (г = 1, ..., п) называются отрезками разбиения Р.
Максимум А(Р) из длин отрезков разбиения называется параметром раз-
разбиения Р.
Определение 2. Говорят, что имеется разбиение (Р,f) с отмеченными
точками отрезка [а, ft], если имеется разбиение Р отрезка [а, 6] и в каждом из
отрезков [si_i, Xi] разбиения Р выбрано по точке & € [я»-1, Х{] (г = 1,..., п).
Набор (&, ..., ?п) обозначается одним символом ?.
b. База в множестве разбиений. В множестве V разбиений с отмечен-
отмеченными точками данного отрезка [а, ft] рассмотрим следующую базу В = {-Brf}-
Элемент В^, d > 0, базы В есть совокупность всех тех разбиений (Р,?) с
отмеченными точками отрезка [а, Ь], для которых А(Р) < d.
Проверим, что {Brf}, d > 0, — действительно база в V.
Во-первых, Bd ф 0. В самом деле, каким бы ни было число d > 0, очевид-
очевидно, существует разбиение Р отрезка [о, Ь] с параметром А(Р) < d (например,
разбиение на п конгруэнтных отрезков). Но тогда существует и разбиение
(Р, f) с отмеченными точками, для которого А(Р) < d.
Во-вторых, если d\ > 0, d*i > 0 и d = min{di,d2}, то, очевидно, В
= Brf € fi.
Итак, В = {В^} — действительно база в Р.
c. Интегральная сумма
Определение 3. Если функция / определена на отрезке [о,6], а
— разбиение с отмеченными точками этого отрезка, то сумма
a(f;P, О :=?/&)Ахи C)
где Axi = Xi — Xi_i, называется интегральной суммой функции /, соответ-
соответствующей разбиению (Р,?) с отмеченными точками отрезка [о, 6].
Таким образом, при фиксированной функции / интегральная сумма
a{fiP,€) оказывается функцией Ф(р) = <r{f\p) на множестве V разбиений
р = (Р, ?) с отмеченными точками отрезка [о, 6].
Поскольку в V имеется база В, то можно ставить вопрос о пределе функции
Ф(р) по этой базе.
d. Интеграл Римана. Пусть / — функция, заданная на отрезке [а,Ь].
Определение 4. Говорят, что число J является интегралом Римана
от функции / на отрезке [а, Ь], если для любого е > 0 найдется число S > О

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 327
такое, что для любого разбиения (Р,?) с отмеченными точками отрезка [о, ft],
параметр которого А(Р) < <5, имеет место соотношение
п
*=1
Поскольку разбиения р = (Р, f), для которых А(Р) < ?, составляют элемент
введенной выше базы В в множестве V разбиений с отмеченными точками,
то определение 4 равносильно тому, что
J = ШпФ(р),
т. е. интеграл J есть предел по базе В значений интегральных сумм функции
/, отвечающих разбиению с отмеченными точками отрезка [а, ft].
Базу В естественно обозначить символом А(Р) —> О, и тогда определение
интеграла можно переписать в виде
п
D)
Интеграл от функции f(x) по отрезку [о, ft] обозначается символом
о
I f(x) dx,
в котором числа а, Ь называются нижним, и верхним пределом интегрирования
соответственно; / — подынтегральная функция, f(x)dx — подынтегральное
выражение, х — переменная интегрирования.
Итак,
о
I
п
fix) dx := lim
E)
Определение 5. Функция / называется интегрируемой по Риману на
отрезке [о, ft], если для нее существует указанный в E) предел интегральных
сумм при А(Р) -* 0 (т. е. если для нее определен интеграл Римана).
Множество всех функций, интегрируемых по Риману на отрезке [о, ft], бу-
будет обозначаться через Tl[a, ft].
Поскольку пока мы не будем рассматривать другого интеграла, кроме ин-
теграла Римана, условимся для краткости вместо терминов «интеграл Рима-
Римана* и «функция, интегрируемая по Риману» говорить соответственно «инте-
«интеграл» и «интегрируемая функция».

328 гл. vi. интеграл
3. Множество интегрируемых функций. В силу определения инте-
интеграла (определение 4) и его переформулировок в виде D) и E), интеграл есть
предел некоторой специальной функции Ф(р) = a(f; Р, ?) — интегральной сум-
суммы, определенной на множестве V разбиений р = (Р, ?) с отмеченными точка-
точками отрезка [a,ft]. Предел этот берется по базе В в?, которую мы обозначили
как А(Р) -+ 0.
Таким образом, интегрируемость функции / на [a, ft] зависит от наличия
указанного предела.
В силу критерия Коши этот предел существует тогда и только тогда, когда
для любого числа е > 0 найдется элемент В$ € В базы, в любых точках р', р"
которого выполнено соотношение
В более подробной записи сказанное означает, что для любого е > 0 най-
найдется S > 0 такое, что для любых разбиений (Р', ?'), (Р",?") с отмеченными
точками отрезка [a, ft], для которых А(Р') < 6 и А(Р") < J, выполнено нера-
неравенство
или, что то же самое, неравенство
п' п"
г=1
F)
Мы воспользуемся сформулированным критерием Коши для того, чтобы
получить сначала простое необходимое, а затем и достаточное условие инте-
интегрируемости функции по Риману.
а. Необходимое условие интегрируемости
Утверждение 1. Для того чтобы функция f, определенная на отрезке
[a, ft], была интегрируема на нем по Риману, необходимо, чтобы она была
ограничена на этом отрезке.
Короче,
(/ € ЩауЬ]) => (/ ограничена на [a, ft]).
< Если / не ограничена на [a, ft], то при любом разбиении Р отрезка [a, ft]
функция / окажется неограниченной по крайней мере на одном из отрезков
xi-i, Xi] разбиения Р. Это означает, что, выбирая различным образом точку
6 [xi-i,Xi], можно сделать величину |/(&)Джг| сколь угодно большой. Но
п
тогда и интегральную сумму ст(/;Р,^) = JZ f(d)^xi можно сделать по моду-
лю сколь угодно большой за счет изменений только точки & в этом отрезке.
Ясно, что в таком случае не может быть и речи о конечном пределе инте-
интегральных сумм, что, впрочем, видно и из критерия Коши, ибо соотношение

§ 1, ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 329
F) в этом случае, очевидно, не имеет места даже для сколь угодно мелких
разбиений. >
Как мы увидим, полученное необходимое условие еще очень далеко от необ-
необходимого и достаточного условия интегрируемости, однако оно уже позволяет
нам в дальнейшем исследовать только ограниченные функции.
Ь. Достаточное условие интегрируемости и важнейшие классы
интегрируемых функций. Начнем с нескольких обозначений и замечаний,
которые используются в дальнейшем изложении.
Условимся, когда задано разбиение Р
а = хо < Х\ < ... < хп = ft
отрезка [a, ft], наряду с символом Ах{, обозначающим разность Х{ — Х{-\, упо-
употреблять символ Дг для обозначения отрезка [xi-i,X{].
Если разбиение Р отрезка [a, ft] получено из разбиения Р только добавле-
добавлением к Р некоторых новых точек, то условимся называть разбиение Р про-
продолжением разбиения Р.
При построении продолжения Р разбиения Р некоторые (быть может, и
все) отрезки Д* = [#i-i> Xi] разбиения Р сами подвергаются разбиению Х{-\ =
= Xio < ... < Х{П{ = Х{. В связи с этим нам будет удобно нумеровать точки
разбиения Р двумя индексами. В записи х^ первый индекс означает, что
х^ € Дг, а второй индекс есть порядковый номер точки на отрезке Д*. Теперь
естественно положить Axij := х^ — Xij-i и Д^ := [xij-i,Xij]. Таким образом,
Axi = Ахц 4-... 4- Axini.
Примером разбиения, являющегося продолжением как разбиения Р', так и
разбиения Р", может служить разбиение Р = Р' U Р", полученное объедине-
объединением точек разбиений Р' иР".
Напомним, наконец, что, как и прежде, символ u;(/; E) будет обозначать
колебание функции / на множестве Еу т. е.
ц;(/;Я):= sup \f(x') - f{x")\.
х\х"€Е
В частности, u(f; A{) есть колебание функции / на отрезке Д*. Это коле-
колебание заведомо конечно, если / — ограниченная функция.
Теперь сформулируем и докажем следующее
Утверждение 2. Для того чтобы ограниченная на отрезке [a, ft] функ-
функция f была интегрируема на нем, достаточно, чтобы для любого числа е > О
нашлось число S > 0 такое, что при любом разбиении Р отрезка [а, ft] с па-
параметром А(Р) < S выполнялось соотношение
п

330
ГЛ. VI. ИНТЕГРАЛ
<4 Пусть Р — разбиение отрезка [а, ft] и Р
Оценим разность интегральных сумм cr(f; P,f)
ные выше обозначения, можем написать
— продолжение разбиения Р.
— <r(f; Р, ?). Используя введен-
ff (/; P,l)-o
—
n n»
(/; Л 0
* * 1 / » 'У * •
n n»
n
^b. ^k. ? I ш \ /\ ^k ? ? ш l /\
w ж I I r* * ' 1 / » m^ * * "«^— » f I f* • 1 / m 4t *
— ^ —
n n»
•* *• j ^
П fit
——
n
E E
n n»
n
= E w(/;
В этих выкладках мы использовали то, что
также то, что
, поскольку ^ G Ay С Д< и ^ G
Из полученной оценки разности интегральных сумм следует, что если
функция / удовлетворяет достаточному условию, сформулированному в
утверждении 2, то по любому числу в > 0 можно найти S > 0 так, что для
любого разбиения Р отрезка [а, 6] с параметром А(Р) < S и его продолжения
***** j->j-
Р при любом выборе отмеченных точек ? и ? будем иметь
Если теперь (Р',?;) и (Р",?") — произвольные разбиения с отмеченными
точками отрезка [о, ft], параметры которых удовлетворяют условиям А(Р') < <5,
А(Р") < 5, то, рассмотрев разбиение Р = Р' U Р;/, являющееся продолжением
обоих разбиений Р', Р", по доказанному будем иметь
Отсюда следует, что
как только А(Р') < S, А(Р") < 6. Таким образом, в силу критерия Коши
существует предел
п
А(Р)-+О J
=1
интегральных сумм, т. е. / € 7^[а, 6]. >

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 331
Следствие 1. (/€ C[a,ft]) => (/ G 7?[a,ft]), m. e. лю?ал непрерывная на
отрезке функция интегрируема на этом отрезке.
4 Если функция непрерывна на отрезке, то она ограничена на нем, так что
необходимое условие интегрируемости в этом случае, очевидно, выполнено.
Однако непрерывная на отрезке функция еще и равномерно непрерывна на
нем, поэтому для любого е > 0 можно найти S > 0 так, что на любом отрезке
Д С fa, ft] длины меньше S будем иметь о;(/;Д) < . Тогда для любого
о — а
разбиения Р с параметром А(Р) < 6 будем иметь
п п
5>(/;Д0Дх«<^?Дх« = ^(Ь-а) = е.
i=l i=l
В силу утверждения 2 теперь можно заключить, что / Е 1l[a, ft]. >
Следствие 2. ifrvm огранггчеянол на отрезке [о,Ь] ^ункг^ги / непре-
непрерывна на этом отрезке всюду, кроме, быть может, конечного множества
точек, то / G Ща,Ъ].
Ч Пусть u;(/; [a, ft]) ^ С < оо и / имеет к точек разрыва на отрезке [о, ft].
Проверим выполнимость достаточного условия интегрируемости функции /.
При заданном е > 0 возьмем число 6\ = и построим Ji-окрестности
8С -к
каждой из к точек разрыва функции / на [a, ft]. Дополнительное к объедине-
объединению этих окрестностей множество точек отрезка [a, ft] состоит из конечного
числа отрезков, на каждом из которых / непрерывна и, значит, равномерно
непрерывна. Поскольку таких отрезков конечное число, по е > 0 можно ука-
указать 62 > 0 так, что на любом отрезке Д, длина которого меньше 62 и который
полностью содержится в одном из указанных выше отрезков непрерывности
/, будем иметь u(f; Д) < . 6_ . Возьмем теперь число 6 = min{Ji, <5г}.
Пусть Р — произвольное разбиение отрезка [a,ft], для которого А(Р) < S.
п
Сумму Y1 шA\ Д*) Д^й отвечающую разбиению Р, разобьем на две части:
п
г=1
В сумму ^ включим те слагаемые, которые отвечают отрезкам Д$ раз-
разбиения Р, не имеющим общих точек с построенными Si -окрестностями точек
разрыва. Для таких отрезков Д* имеем u(f; Д») < -^тг-—г, поэтому
2(о — а)
§

332 гл. vi. интеграл
Сумма длин оставшихся отрезков разбиения Р, как легко видеть, меньше
(S + 2Si + S)к ^ 4^7^-г • А; = г-7, поэтому
С •
Таким образом, мы получаем, что при А(Р) < S
п
* Lj(f;Ai)Axi < ?,
т. е. выполнено достаточное условие интегрируемости и / Е Ща, Ь]. >
Следствие 3. Монотонная на отрезке функция интегрируема на этом
отрезке.
-4 Из монотонности функции / на отрезке [а, Ь] следует, что а;(/;[а, Ь]) =
= |/F) — f(a)\. Пусть задано е > 0. Положим S = тттг:—77~\\- ^ы считаем,
\f\P) ~ f\a)\
что f(b) — f(a) ф 0, поскольку в противном случае / постоянна и интегриру-
интегрируемость / не вызывает сомнений. Пусть Р — произвольное разбиение отрезка
[а, Ь] с параметром А(Р) < S.
Тогда для него с учетом монотонности / имеем
п п п
**) - /(««-01 =
n
Таким образом, / удовлетворяет достаточному условию интегрируемости,
т. е. / € Ща,Ь]. >
Монотонная функция может иметь уже бесконечно много точек разрыва
на отрезке (счетное множество). Например, функция, определяемая соотно-
соотношениями
f(x) = I 2П
, 1 при х =
на отрезке [0,1], не убывает и в каждой точке вида —, п 6 N, имеет разрыв.
Замечание. Отметим, что хотя мы сейчас имеем дело с вещественны-
вещественными функциями на отрезке, однако ни в определении интеграла, ни в дока-
доказанных выше утверждениях, за исключением следствия 3, мы по существу не
использовали то, что рассматриваемые функции вещественнозначные, а не
комплексно- или, например, векторнозначные функции точки отрезка [а, Ь].

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 333
Понятия верхней и нижней интегральной суммы, к которым мы переходим,
напротив, специфичны только для функций с действительными значениями.
Определение 6. Пусть /: [а,ft] -> Е — действительнозначная функция,
определенная и ограниченная на отрезке [а, ft]; Р — разбиение отрезка [а, ft];
Д^ (г = 1, ..., п) — отрезки разбиения Р. Пусть m* = inf f(x), Mi = sup f(x)
г = 1, ..., n).
Суммы
n
г=1
И
г=1
называются соответственно нижней и верхней интегральной суммой функции
/ на отрезке [a,ft], соответствующей разбиению Р этого отрезка1). Суммы
s(/;P) и S(f;P) называют также нижней и верхней суммой Дарбу, соответ-
соответствующей разбиению Р отрезка [a, ft].
Если (Р, ?) — произвольное разбиение с отмеченными точками отрезка
[а,Ь], то, очевидно,
s(f;P)^a(f;P,O^S(f;P). G)
Лемма 1.
5(/;Р) = sup
-* Проверим, например, что верхняя сумма Дарбу, отвечающая разбиению
Р отрезка [a, ft], является верхней гранью значений интегральных сумм, соот-
соответствующих разбиению с отмеченными точками (Р,?) отрезка [а,Ь], причем
верхняя грань берется по всевозможным наборам ? = (?i, ..., ?п) отмеченных
точек.
Ввиду G), для доказательства достаточно, чтобы при любом е > 0 нашелся
такой набор ? отмеченных точек, что имеет место неравенство
5(/; Р) < <r(/; P, |) + е. (8)
По определению чисел Mi, при каждом i € {1,..., п} найдется точка |t €
4i, в которой Mi < /(?) + -?-. Пусть ? = (&,..., ?„)• Тогда
О и
О
a/ =
x) Термин «интегральная сумма» здесь формально не вполне законен, так как не всегда
и Mi являются значениями функции / в некоторой точке ^ G Aj.

334 гл. vi. интеграл
что и завершает доказательство второго утверждения леммы. Первое утвер-
утверждение проверяется аналогично. >
Из доказанной леммы и неравенства G) с учетом определения интеграла
Римана заключаем, что справедливо следующее
Утверждение 3. Ограниченная вещественнозначная функция f: [а,Ь] —>•
-> Е интегрируема по Риману на отрезке [а, Ь] тогда и только тогда, когда
существуют и равны между собой пределы
1= lim s(/;P), /= lim S(f;P). (9)
A(P)->0 V f A(P)->0 V
При этом их общее значение 1 — 1 = 1 совпадает с интегралом
ь
f(x) dx.
1
-4 Действительно, если пределы (9) существуют и равны между собой, то
по свойствам предела из G) заключаем о существовании предела интеграль-
интегральных сумм, причем
С другой стороны, если / 6 И[а> Ь], т. е. существует предел
АИтоа(/;Р,0 /,
то из G) и (8) заключаем, что существует предел lim S(f; P) = J, причем
А(Р)->0
/ = /.
Аналогично проверяется, что lim s(f: P) = / = /. >
A(P)-+O
В качестве следствия утверждения 3 получаем следующее уточнение утвер-
утверждения 2.
Утверждение 2'. Для того чтобы функция /: [а,Ь] —> Ж, заданная
на отрезке [а, Ь], была интегрируема по Риману, необходимо и достаточно
выполнение соотношения
п
lim > w(f;Ai)Axi = 0. A0)
A(P)->0 ^
< Учитывая утверждение 2, нам остается лишь убедиться в необходимости
соотношения A0) для интегрируемости /.
Заметим, что а;(/; Д*) = Mi - m*, поэтому
п п
i = S(f;P) - s{f;P),
и теперь A0) следует из утверждения^, коль скоро / Е Ща, Ь]. >

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 335
с. Векторное пространство Tl[a,b]. Над интегрируемыми функциями
можно выполнять ряд операций, не выходя за пределы множества 72.[а, Ь].
Утверждение 4. Если /, д € 7?[а,6], то
a) (f + g)€H[a,b];
b) (a/) Е TZ[a,b], где а — числовой множитель;
c) |/| €Я[а,Ц;
d) f\[c,d) € ft[c,d], если [c,d] С [а, 6];
е)
Мы сейчас рассматриваем только вещественнозначные функции, но полез-
полезно отметить, что свойства а), Ь), с), d) окажутся справедливыми и для ком-
плекснозначных и векторнозначных функций. Для векторнозначных функций,
вообще говоря, не определено произведение / • д, поэтому свойство е) для них
не рассматривается. Однако это свойство остается в силе для функций с ком-
комплексными значениями.
Перейдем теперь к доказательству утверждения 4.
щ а) Это утверждение очевидно, поскольку
b) Это утверждение очевидно, поскольку
п п
г=1 г=1
с) Поскольку o;(|/|;i?) ^ ш(/;Е)} то можно написать, что
п п
г=1
и на основании утверждения 2 заключить, что (/ € 72.[а,Ь]) =$> (|/| G
d) Мы хотим проверить, что ограничение /f[c,d] интегрируемой на отрезке
[а, Ь] функции на любой отрезок [с, d] С [а, Ь] является функцией, интегрируе-
интегрируемой на [с, d]. Пусть тг — разбиение отрезка [с, d]. Добавив к тг некоторые точ-
точки, достроим тг до разбиения Р отрезка [а, Ь]у но так, чтобы иметь А(Р) ^ А(тг).
Ясно, что это всегда можно сделать.
Теперь можно написать, что
где 5^^. — сумма по всем отрезкам разбиения тг, а $^р — сумма по всем отрез-
отрезкам разбиения Р.

336 гл. vi. интеграл
При А(тг) -> 0 по построению также Х(Р) -> 0, и на основании утверждения
2' из полученного неравенства заключаем, что (/ € 7?[а, b]) => (|/| Е 7?[с, d]),
если [c,d] С [а,Ь].
е) Проверим сначала, что если / Е 7?[а, Ь], то /2 € 7?[а, ft].
Если / € 7?[а, ft], то / ограничена на [а, ft]. Пусть \f(x)\ ^ С < оо на [а,ft].
Тогда
- /2(Х2)| = !(/(*!) + Д*2)) • (/(*!) - /(*2))| ^ 2C\f(x1) - f(x2)\,
поэтому u(f2;E) ^ 2Cu(f;E)} если Е С [а,Ь]. Значит,
п п
откуда на основании утверждения 2' заключаем, что
Теперь перейдем к общему случаю. Запишем тождество
Из этого тождества с учетом только что доказанного утверждения и прове-
проверенных пунктов а) и Ь) утверждения 4 заключаем, что
(/ € П[а, Ь]) Л(де П[а, Ь}) => (/ ¦ д € Ща, Ъ)). >
Из курса алгебры вам уже известно понятие векторного пространства.
Вещественнозначные функции, определенные на некотором множестве, мож-
можно поточечно складывать и умножать на действительное число, получая при
этом снова функцию с вещественными значениями на том же множестве. Если
функции рассматривать как векторы, то можно проверить, что при этом вы-
выполнены все аксиомы векторного пространства над полем действительных чи-
чисел и указанное множество действительных функций является векторным про-
пространством относительно операций поточечного сложения функций и умноже-
умножения функций на действительные числа.
В пунктах а), Ь) утверждения 4 сказано, что сложение интегрируемых
функций и умножение интегрируемой функции на число не выводит за пре-
пределы множества 7?[а, Ь] интегрируемых функций. Таким образом, И[а, Ь] само
является линейным векторным пространством — подпространством вектор-
векторного пространства вещественнозначных функций, определенных на отрезке
[о, Ъ].

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 337
d. Критерий Лебега интегрируемости функции по Риману. В за-
заключение приведем пока без Доказательства теорему Лебега, дающую вну-
внутреннее описание интегрируемой по Риману функции.
Для этого введем следующее полезное само по себе понятие.
Определение 7. Говорят, что множество ?cR имеет меру нуль или
является множеством меры нуль (в смысле Лебега), если для любого числа
е > 0 существует такое покрытие множества Е не более чем счетной системой
оо
{Ik} интервалов, сумма Y1 1^*1 Длин которых не превышает е.
к=1
оо
Поскольку ряд 53 |Д| сходится абсолютно, порядок суммирования длин
*=1
промежутков покрытия не влияет на сумму (см. утверждение 4 из гл. V, § 5,
п. 2), поэтому данное определение корректно.
Лемма 2. а) Точка и конечное число точек суть множества меры нуль.
b) Объединение конечного или счетного числа множеств меры нуль есть
множество меры нуль.
c) Подмножество множества меры нуль само есть множество меры нуль.
d) Отрезок [о, Ь] при а < Ь не является множеством меры нуль.
< а) Точку можно покрыть одним интервалом длины меньшей, чем любое
наперед заданное число е > 0, поэтому точка является множеством меры нуль.
В остальном а) вытекает из Ь).
Ь) Пусть Е = (J Еп — не более чем счетное объединение множеств Еп меры
п
нуль. По е > 0 для каждого Еп строим покрытие {/?} множества Еп такое,
к ¦ *
Поскольку объединение не более чем счетного числа не более чем счетных
множеств само не более чем счетно, промежутки /?, к, п Е N, образуют не
более чем счетное покрытие множества Е, причем
!<- + — + + — + -Е
2 22 2П "' ™"
пук
Порядок суммирования ?) |^| по индексам пик безразличен, ибо ряд сходит-
п,к
ся к одной и той же сумме при любом порядке суммирования, если он сходится
для какого-то порядка суммирования. Последнее в нашем случае имеет место,
ибо любые частичные суммы нашего ряда ограничены сверху числом е.
Итак, Е есть множество меры нуль в смысле Лебега.
c) Это утверждение, очевидно, непосредственно следует из определения
множества меры нуль и определения покрытия.
d) Поскольку для любого покрытия отрезка интервалами можно выделить*
конечное покрытие, сумма длин промежутков которого, очевидно, не пре-
превосходит суммы длин промежутков исходного покрытия, то нам достаточно

338 гл. vi. интеграл
проверить, что сумма длин интервалов, образующих конечное покрытие от-
отрезка [a, ft], не меньше длины Ь — а этого отрезка.
Проведем индукцию по количеству интервалов покрытия.
При п = 1, т. е. когда отрезок [а,6] содержится в одном интервале (а,/?),
очевидно, имеем а < а < b < /3 и /3 — а > ft — а.
Пусть утверждение доказано до индекса А: € N включительно. Рассмотрим
покрытие, состоящее из к + 1 интервалов. Возьмем интервал (ai,a2), покры-
покрывающий точку а. Бели cli ^ ft, то а.^ — &\ > b — а и все доказано. Если же
а < а.2 < ft, то отрезок [а2,&] покрыт системой, состоящей уже не более чем
из к интервалов, сумма длин которых по предположению индукции не меньше
чем ft — Q2- Но
b — a = (b — аг) + (<*2 — а) < (ft — аг) + (<*2 — ai)
и, таким образом, сумма длин интервалов исходного покрытия отрезка [a, ft]
больше, чем его длина ft — a. >
Интересно отметить, что в силу пунктов а) и Ь) леммы 2 множество Q
всех рациональных точек числовой прямой R является множеством меры нуль,
что на первый взгляд выглядит несколько неожиданным при сопоставлении с
пунктом d) той же леммы.
Определение 8. Если некоторое свойство выполнено в любой точке
множества X, кроме, быть может, точек множества меры нуль, то говорят,
что это свойство имеет место почти всюду на множестве X или почти во
всех точках множества X.
Теперь сформулируем критерий Лебега.
Теорема. Функция, определением на отрезке, интегрируема по Риману
на этом отрезке в том и только в том случае, когда она ограничена на
этом отрезке и непрерывна почти во всех его точках.
Итак,
(/ € Ща>, ft]) <=^ (/ ограничена на [о, ft]) Л
Л (/ непрерывна почти всюду на [a, ft]).
Из критерия Лебега и свойств множеств меры нуль, изложенных в лемме 2,
очевидно, легко можно получить как следствия 1, 2, 3 утверждения 2, так и
утверждение 4.
Мы не станем сейчас доказывать критерий Лебега, поскольку при рабо-
работе с достаточно регулярными функциями, с которыми нам предстоит иметь
дело, он нам пока не нужен. Однако идейную сторону критерия Лебега вполне
можно объяснить уже сейчас.
Утверждение 2' содержало критерий интегрируемости, выраженный соот-
п
ношением A0). Сумма ?) u){f\ Д») Дх* может быть мала, прежде всего, за счет

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 339
множителей ы(/; Д*), которые малы в малых окрестностях точек непрерыв-
непрерывности функции. Бели же некоторые из отрезков Ах{ содержат точки разрыва
функции, то для них ш(/; А«) не стремится к нулю, сколь мелким бы ни было
разбиение Р отрезка [a, ft]. Однако u(f\ Д») ^ u;(/;[a,ft]) < оов силу ограни-
ограниченности / на [a, ft], поэтому сумма тех слагаемых, которые содержат точки
разрыва, тоже может оказаться маленькой, если только мала сумма длин от-
отрезков разбиения, покрывающих множество точек разрыва, или, точнее, если
рост колебания функции на некоторых отрезках разбиения компенсируется
малостью длин этих отрезков.
Точной реализацией и формулировкой этого наблюдения и является кри-
критерий Лебега.
Приведем теперь два классических примера, поясняющих свойство функ-
функции быть интегрируемой по Риману.
Пример 1. Функция Дирихле
{ О при х е R \ Q,
рассматриваемая на отрезке [0,1], не интегрируема на нем, поскольку для
любого разбиения Р отрезка [0,1] в каждом отрезке Д« разбиения Р можно
отметить как рациональную точку $, так и иррациональную точку ?". Тогда
п
1=1
в то время как
п
; р, «") = ? о • д*, = о.
Таким образом, интегральные суммы функции V(x) не могут иметь предел
при А(Р) -> 0.
С точки зрения критерия Лебега неинтегрируемость функции Дирихле
тоже очевидйа, поскольку функция V(x) разрывна в каждой точке отрезка
[0г 1], который, как было показано в лемме 2, не есть множество меры нуль.
Пример 2. Рассмотрим функцию Римана
П(х) =
г 1
—, если xGQhi = - — несократимая дробь,
п п
0, если х е Ш \ Q.
Мы уже рассматривали эту функцию в гл. IV, § 2, п. 2, и знаем, что функ-
функция И(х) непрерывна во всех иррациональных точках и разрывна во всех ра-
рациональных точках. Таким образом, множество точек разрыва функции Щх)
счетно и потому имеет меру нуль. В силу критерия Лебега можно заключить,
12 Зорич В. А.

340 ГЛ. VI. ИНТЕГРАЛ
что функция И(х) интегрируема на любом отрезке [а, Ь] С R, несмотря на то,
что точки разрыва этой функции попадают в любой отрезок любого разбие-
разбиения отрезка интегрирования.
Пример 3. Рассмотрим теперь еще один, менее классический вопрос и
пример.
Пусть /: [а, Ь] -> Ж — интегрируемая на [а, Ь] функция, принимающая зна-
значения на отрезке [c,d], на котором непрерывна функция д : [c,d] -> R. Тогда
композиция д о f : [a, b] -> R, очевидно, определена и непрерывна во всех точ-
точках отрезка [а, 6], в которых непрерывна функция /. В силу критерия Лебега
отсюда следует, что (g°f)G Ща, Ь].
Покажем теперь на примере, что композиция произвольных интегрируе-
интегрируемых функций — уже не всегда интегрируемая функция.
Рассмотрим функцию д(х) = |sgn|(x). Эта функция равна единице при
ж^Ои нулю при х = 0. Непосредственной проверкой убеждаемся, что если,
например, на отрезке [1,2] рассмотреть в качестве / функцию Римана 7?(х), то
на этом отрезке композиция (gof)(x) есть не что иное, как функция Дирихле
V{x). Таким образом, наличие даже одной точки разрыва у д(х) привело к
неинтегрируемости композиции до f.
Задачи и упражнения
1. Теорема Дарбу.
а) Пусть *(/; Р) и ?(/; Р) — нижняя и верхняя суммы Дарбу вещественнозначной
функции /, определенной и ограниченной на отрезке [а, 6], отвечающие разбиению
Р этого отрезка. Покажите, что для любых двух разбиений Pi, P2 отрезка [а,6]
справедливо неравенство
Ь) Пусть разбиение Р является продолжением разбиения Р отрезка [а, 6] и пусть
x, ..., Atj, — те отрезки разбиения Р, которые содержат точки разбиения Р, не
входящие в разбиение Р. Покажите, что справедливы оценки
0 ^ S(f\P) - S(f;P) ^ w(/;[a,6]) • (AXil + ... + Axih)}
0 ^ s(/; P) - s(f; P) ^ u(f; [a, 6]) • (Axix + ... + Axih ).
c) Величины / = sup s(f\ P), I = inf 5(/; P) называются соответственно нижним
p p
и верхним интегралом Дарбу функции / на отрезке [а, 6]. Покажите, что I ^ /.
d) Докажите теорему Дарбу:
/= lim s(/;P), /= lim S(f;P).
А(Р)-Ю ' А(Р)-Ю '
e) Покажите, что (/ € Ща,Ь]) <=> (I = /).
f) Покажите, что / € Щау Ь] тогда и только тогда, когда для любого е > 0 най-
найдется такое разбиение Р отрезка [а, 6], что 5(/;Р) — s(f\P) < e.

§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ИНТЕГРИРУЕМОСТЬ ФУНКЦИЙ 341
2. Канторов о множество лебеговой меры нуль.
a) Канторово множество, описанное в задаче 7 § 4 гл. И, несчетно. Проверьте,
что оно тем не менее есть множество меры нуль в смысле Лебега. Укажите, как
следует видоизменить конструкцию канторова множества, чтобы получить анало-
аналогичное всюду «дырявое» множество, не являющееся множеством меры нуль. (Его
тоже называют канторовым.)
b) Покажите, что заданная на отрезке [0,1] функция, равная нулю вне канторова
множества и единице в точках канторова множества, интегрируема по Риману на
этом отрезке, если и только если канторово множество имеет меру нуль.
c) Постройте неубывающую, непрерывную и не постоянную на отрезке [0,1]
функцию, которая имеет нулевую производную всюду, кроме, быть может, точек
канторова множества меры нуль.
3. Критерий Лебега.
a) Проверьте непосредственно (без ссылки на критерии Лебега) интегрируе-
интегрируемость функции Римана из примера 2 настоящего параграфа.
b) Покажите, что ограниченная функция / € Ща, Ь] тогда и только тогда, когда
для любых двух чисел е > 0 и 8 > 0 найдется разбиение Р отрезка [о, Ь] такое, что
сумма длин тех отрезков разбиения, на которых колебание функции больше ?, не
превосходит 6.
c) Покажите, что / € 7?[а, 6] тогда и только тогда, когда / ограничена на [а, 6]
и для любых чисел е>0и^>0 множество точек отрезка [а, 6], в которых / имеет
колебание больше чем е, можно покрыть конечным число интервалов, сумма длин
которых меньше 6 (критерий Дюбуа-Реймона1^).
d) Используя предыдущую задачу, докажите критерий Лебега интегрируемости
функции по Риману.
4. Покажите, что если /,g € Ща,Ь] и /, g действительны, то тах{/,р} € Ща,Ъ]
{
5. Покажите, что
ь ъ
a) если /, g е К[а, Ь] и f(x) = g(x) почти всюду на [о, 6], то J f(x) dx = Jg(x) dx\
a a
b) если / € Ща, b] и f(x)=g(x) почти всюду на [о, Ь], то g может не быть интег-
интегрируемой по Риману на [о, 6], даже если g определена и ограничена на [о, 6].
6. Интеграл от векторнозначной функции.
a) Пусть r(t) — радиус-вектор точки, движущейся в пространстве; го = г@) —
начальное положение точки; v(?) — вектор скорости как функция времени. Восста-
Восстановите r(t) по Го и функции v(t).
b) Сводится ли интегрирование векторнозначной функции к интегрированию
вещественнозначных функций?
c) Верен ли для векторнозначных функций критерий интегрируемости, выра-
выраженный в утверждении 2;?
d) Верен ли критерий Лебега для векторнозначных функций?
e) Какие из понятий и фактов этого параграфа переносятся на функции с ком-
комплексными значениями?
. Дюбуа-Реймон A831 — 1889) — немецкий математик.
12*

342 ГЛ. VI. ИНТЕГРАЛ
§ 2. Линейность, аддитивность и монотонность
интеграла
1. Интеграл как линейная функция на пространстве 7?[а
Теорема 1. Если fug — интегрируемые на отрезке [а,Ъ] функции,
то их линейная комбинация а/ 4- fig также является интегрируемой на [а, Ь]
функцией, причем
ь ь ь
/W + Pg)(x) dx = aff(x) dx + fifg(x) dx. A)
а
<4 Рассмотрим интегральную сумму для интеграла, стоящего в левой части
соотношения A), и преобразуем ее:
п п п
( гу / -4- fln\(?.\\i»' —— yv Л f^-|Лт- -4- й Л oiAiAt- ixi
VCJEI Т^ А? </Н Cl I *-** — Сх 7 I VCl/*-**"! \ Н 7 */\4t / **•*'• • \^/
i=l i=l t=l
Поскольку правая часть последнего равенства стремится к линейной ком-
комбинации интегралов, стоящих в правой части равенства A), если параметр
А(Р) разбиения стремится к нулю, то левая часть равенства B) тоже имеет
предел при А(Р) -> 0 и этот предел совпадает с пределом правой части. Таким
образом, (a/ -I- fig) E 7?[а,Ь] и выполнено равенство A). >
Бели множество И[а,Ь] рассматривать как векторное пространство над
б
полем действительных чисел, а интеграл f f(x)dx — как действительнознач-
а
ную функцию, определенную на векторах пространства И[а, 6], то теорема 1
утверждает, что интеграл есть линейная функция на векторном пространстве
Ща,Ь].
Во избежание возможной путаницы, функции, определенные на функциях,
называют обычно функционалами. Таким образом, мы доказали, что инте-
интеграл есть линейный функционал на векторном пространстве интегрируемых
функций.
2. Интеграл как аддитивная функция отрезка интегрирования.
ъ
Значение интеграла ff(x)dx = /(/;[а, Ь]) зависит как от подынтегральной
а
функции, так и от отрезка, по которому ведется интегрирование. Например,
если / € 7?[а,Ь], то, как мы уже знаем, /|[а,/?] € Щ&H]> если [а,/?] С [а,Ь], т. е.
определен интеграл I f{x) dx, который мы можем исследовать с точки зрения
его зависимости от отрезка [a, fi] интегрирования.

§ 2. ЛИНЕЙНОСТЬ, АДДИТИВНОСТЬ И МОНОТОННОСТЬ ИНТЕГРАЛА 343
Лемма 1. Если a<b<cuf€ Щаус], too f\[a,b] € Щ^Ь], f\[b,c) € ЩЬ,с]
и имеет место равенство1^
с Ь с
ff(x) dx = ff(x) dx + ff(x) dx. C)
a a b
Ч Отметим прежде всего, что интегрируемость ограничений функции /
на отрезки [а, 6] и [Ь, с] гарантируется утверждением 4 из предыдущего пара-
параграфа.
с
Далее, поскольку / € 7?[а,с], то при вычислении интеграла ff(x)dx как
а
предела интегральных сумм мы вправе выбирать любые удобные нам разбие-
разбиения отрезка [а, с]. В качестве таковых будем сейчас рассматривать только те
разбиения Р отрезка [а, с], которые содержат точку 6. Каждое такое разби-
разбиение с отмеченными точками (Р,?)> очевидно, порождает разбиения (Р',?') и
(Р">(") отрезков [о,Ь] и [Ь,с] соответственно, причем Р = P'UP" и f = f'Uf".
Но тогда имеет место следующее равенство между соответствующими ин-
интегральными суммами:
Поскольку А(Р') < А(Р) и А(Р") < А(Р), то при достаточно малом А(Р)
каждая из написанных интегральных сумм близка к соответствующему инте-
интегралу из C). Таким образом, равенство C) действительно имеет место. >
Чтобы несколько расширить применимость полученного результата, вер-
вернемся временно вновь к определению интеграла.
Мы определили интеграл как предел интегральных сумм
п
7F) Д*г, D)
г=1
отвечающих разбиениям с отмеченными точками (Р, f) отрезка интегрирова-
интегрирования [а, Ь]. Разбиение Р составляла монотонная конечная последовательность
точек хо, xi, ..., хп, причем точка xq совпадала с нижним пределом интегри-
интегрирования а, а последняя точка хп совпадала с верхним пределом интегриро-
интегрирования Ь. Эта конструкция проводилась в предположении, что а < 6. Если
теперь взять произвольно два числа а и Ь, не требуя, чтобы обязательно было
а < Ь, и, считая а нижним пределом интегрирования, а Ь верхним, провести
указанную конструкцию, то мы вновь получим сумму вида D), в которой на
сей раз будет Дх» > 0 (г = 1,..., п), если а < Ь, и Дж, < 0 (г = 1,..,, п)
^Напомним, что символ /|# обозначает сужение функции / на множество Е, лежащее
в области определения функции /. В правой части равенства C) формально полагалось бы
написать не /, а сужения / на соответствующие отрезки.

344 ГЛ. VI. ИНТЕГРАЛ
при а > 6, ибо Axi = Xi- Xi-i. Таким образом, сумма D) при а > Ь будет от-
отличаться от интегральной суммы соответствующего разбиения отрезка [6, а]
(Ь < а) только знаком.
По этим соображениям принимается следующее соглашение: если а > 6, то
Ь
ff(x)dx:=-ff(x)dx. E)
а
/¦
а Ь
В связи с этим естественно также положить, что
а
f(x) dx := 0. F)
а
После этих соглашений с учетом леммы 1 приходим к следующему важному
свойству интеграла.
Теорема 2. Пусть о, 6,с Е R и пусть f — функция, интегрируемая на
наибольшем из отрезков с концами в указанных точках. Тогда сужение f на
каждый из двух других отрезков также интегрируемо на соответствующем
отрезке и имеет место равенство
Ь с а
ff(x) dx + ff(x) dx + If(x) dx = 0. G)
a b с
< В силу симметрии равенства G) относительно а, 6, с, мы без ограничения
общности можем считать, что о = min{a, Ь, с}.
Бели max {а, Ь,с} = с и а < Ь < с, то по лемме 1
осе
ff(x) dx + ff(x) dx - ff(x) dx = 0,
что с учетом соглашения E) дает равенство G).
Бели max {a,b,c} = b и а < с < Ь, то по лемме 1
с о о
j f(x) dx + ff(x) dx - j f(x) dx = 0,
что с учетом E) вновь дает G).
Наконец, если какие-то две из точек а, Ь, с или все три совпадают, то G)
следует из соглашений E) и F). >
Определение 1. Пусть каждой упорядоченной паре (а,/?) точек а, C
отрезка [а, Ь] поставлено в соответствие число /(а,/3), причем так, что для
любой тройки точек а, /3, j € [о, Ь] выполнено равенство
J(a,7)= Да,

§ 2. ЛИНЕЙНОСТЬ, АДДИТИВНОСТЬ И МОНОТОННОСТЬ ИНТЕГРАЛА 345
Тогда функция /(а, 0) называется аддитивной функцией ориентированно-
ориентированного промежутка, определенной н$, промежутках, лежащих в отрезке [a, ft].
6
Если / € ЩА, В] и а, Ь, с € [А, В], тб, полагая /(a, ft) = j f(x) dx, из G) за-
а
ключаем, что
с Ь с
ff(x) dx = I' f{x) dx + ff(x) dx, (8)
a a b
т. е. интеграл есть аддитивная функция промежутка интегрирования. Ори-
Ориентированность промежутка состоит в данном случае в том, что мы упорядо-
упорядочиваем пару концов отрезка интегрирования, указывая, какой из них первый
(являющийся нижним пределом интегрирования) и какой второй (являющийся
верхним пределом интегрирования).
3. Оценка интеграла, монотонность интеграла, теоремы
о среднем
а. Одна общая оценка интеграла. Начнем с одной общей оценки инте-
интеграла, которая, как потом выяснится, справедлива не только для интегралов
от действительнозначных функций.
Теорема 3. Если а < ft и f € Ща,Ь], то |/| € Ща,Ь] и справедливо не-
неравенство
V
j
f(x)dx
(9)
Если при этом |/|(х) ^ С на [а, 6], то
о
f\f\(x)dx?C(b-a).
A0)
< При а = b утверждение тривиально, поэтому будем считать, что а <Ь.
Для доказательства теоремы достаточно вспомнить теперь, что |/| € Ща, ft]
(см. утверждение 4 из § 1), и написать следующую оценку интегральной суммы
п
п
п
п
Переходя к пределу при А(Р) -> 0, получаем
о о
ff(x)dx 4: f\f\(x)dx^C(b-a). >

346 ГЛ. VI. ИНТЕГРАЛ
Ь. Монотонность интеграла и первая теорема о среднем. Все даль-
дальнейшее специфично для интегралов от действительнозначных функций.
Теорема 4. Если а ^Ь, /ь /2 Е Ща,Ь] и /i(x) ^ ЛО^) в любой точке
х 6 [а,Ь], то
ь ь
Jfi(x)dx^Jf2(x)dx. A1)
а а
4 При а = Ь утверждение тривиально. Если же а < Ь, то достаточно
записать для интегральных сумм неравенство
п п
справедливое, поскольку Ах{ > О (t = 1, ...,п), и затем перейти в нем к
пределу при А(Р) —> 0. >
Теорему 4 можно трактовать как утверждение о монотонности зависимо-
зависимости интеграла от подынтегральной функции.
Из теоремы 4 получается ряд полезных следствий.
Следствие 1. Если а ^ ft, / е Ща,Ь] и т ^ f(x) ^ М на х € [а,Ь], то
ь
гП'(Ь-а) ^ ff(x)dx^M(b-a), A2)
а
и, в частности, если 0 < f(x) на [а, ft}, то
о
0 < ff(x) dx.
4 Соотношение A2) получается, если проинтегрировать каждый член не-
неравенств т ^ f(x) ^Ми воспользоваться теоремой 4. >
Следствие 2. Если f € Я[а,Ь], т = inf /(х), М = sup /(re), mo
найдется число /х € [т, М] такое, что
A3)
«* Бели а = Ь, то утверждение тривиально. Если а ф Ь, то положим д* =
= т ff{x) dx. Тогда из A2) следует, что m ^ р ^ М, если а < Ь. Но
а
обе части A3) меняют знак при перестановке местами а и ft, поэтому A3)
справедливо и при 6 < а. >

§ 2. ЛИНЕЙНОСТЬ, АДДИТИВНОСТЬ И МОНОТОННОСТЬ ИНТЕГРАЛА 347
Следствие 3. Если f € С[а,Ь], то найдется точка ? € [а,ft] такал,
что
ь
f A4)
<4 По теореме о промежуточном значении для непрерывной функции, на
отрезке [а, ft] найдется точка f, в которой /(?) = р, если только
m = min f(x) < \i < max f(x) = M.
€[6] €[&]
Таким образом, A4) следует из A3). >
Равенство A4) часто называют первой теоремой о среднем для интеграла.
Мы же зарезервируем это название для следующего, несколько более общего
утверждения.
Теорема 5 (первая теорема о среднем для интеграла). Пусть /, g ?
€ 7?[а,b], m= inf f(x), M= sup f(x). Если функция g неотрицательна
*?{а>Ь] х€[а>Ь]
(или неположительна) на отрезке [а,Ь], то
J J A5)
а а
где ii € [m, M].
Если, кроме того, известно, что f € C[a,b], то найдется точка ? € [а,Ь]
такая, что
ь ь
/(/ - «)(*) dx = №fg(x) dx. A6)
М Поскольку перестановка пределов интегрирования приводит к измене-
изменению знака одновременно в обеих частях равенства A5), то достаточно про-
проверить это равенство в случае а < Ъ. Изменение знака функции д(х) тоже
одновременно меняет знак обеих частей равенства A5), поэтому можно без
ограничения общности доказательства считать, что д(х) ^ 0 на [о, ft].
Поскольку m = inf f(x) и М = sup /(ж), то при д(х) ^
€М1
тд(х) ^ f(x)g(x) < Мд(х).
Поскольку т • д € 7J[a, ft], / • д € 7?[а,ft] и М д € Ща, ft], то, применяя тео-
теорему 4 и теорему 1, получаем
б & 6
т
а а а
оо о
Jg(x) dx ^ Jf(x)g(x) dx ^ M jg{x) dx. A7)

348 ГЛ. VI. ИНТЕГРАЛ
Бели fg(x)dx = 0, то, как видно из этих неравенств, соотношение A5)
а
выполнено.
ъ
Если же j g(x) dx ф О, то, полагая
g(x)dx) • f(f-g)(z)dx,
из A7) находим, что
т ^ [л ^ М,
но это равносильно соотношению A5).
Равенство A6) теперь следует из A5) и теоремы о промежуточном значе-
значении для функции / € С[а, 6], с учетом того, что в случае / Е С[ау Ь]
т = min f(x) и М = max f(x). >
Заметим, что равенство A3) получается из A5), если д(х) = 1 на [а, Ь].
с. Вторая теорема о среднем для интеграла. Значительно более
специальной и деликатной в рамках теории интеграла Римана является так
называемая вторая теорема о среднем1^.
Чтобы не осложнять доказательство этой теоремы, сделаем несколько по-
полезных заготовок, представляющих и самостоятельный интерес.
Преобразование Абеля. Так называется следующее преобразование
п к
суммы 5Г а»Ь»- Пусть А* = $^ а»; положим также Aq = 0. Тогда
t=i i=i
п п п п
n n—1 n—1
i=l t=0 t=l
Итак,
n n—1
2_2aibi = {Anbn — Aob\) + yj Ai(b{ — 6i+i), A8)
t=i i=i
и некотором дополнительном и часто вполне приемлемом условии на функции
основную теорему 6 этого раздела можно легко получить из первой теоремы о среднем.
См. по этому поводу задачу 3 к следующему параграфу.

§ 2. ЛИНЕЙНОСТЬ, АДДИТИВНОСТЬ И МОНОТОННОСТЬ ИНТЕГРАЛА 349
или, поскольку Aq = О,
n n— 1
афг = Anbn +
t=l t=l
A9)
На основе преобразования Абеля легко проверяется следующая
Лемма 2. Ясли числа A* = J2 a» (fc = 1, ...,n) удовлетворяют нера-
t=i
векствал* га ^ А* ^ М, а числа ft» (г = 1, ..., п) неотрицательны и ft» ^ fti+i
г = 1, ..., п —¦ 1, то
п
rafti ^
< Используя то, что ftn ^ 0 и
получаем
МЪ\.
B0)
t=l
0 при г = 1, ..., п — 1, из A9)
п
п—1
t=i
t=i
Аналогично проверяется и левое неравенство в соотношении B0). >
Лемма 3. Если / G 7?[a,ft], mo при любом х G [а,Ь] определена функция
X
F(x) = Jf(t) dt
B1)
uF(x) GC[a,ft].
< Существование интеграла B1) при любом х G [а,Ь] нам уже извест-
известно из утверждения 4 § 1, поэтому остается проверить непрерывность функ-
функции F(x). Поскольку / G 7ф,Ь], имеем |/| ^ С < оо на [а,Ь]. Пусть х G [a, ft]
и х + h G [a, ft]. Тогда в силу аддитивности интеграла и неравенств (9), A0)
получаем
\F(x + h) - F(x)\ =
х -t п х
J fit) dt - jfit) dt
fit) dt
X
j I/Wf
dt
Мы воспользовались неравенством A0) с учетом того, что при h < 0 имеем
х + h
j \fit)\dt = - j \№\A
\fit)\dt.

350 гл. vi. интеграл
Итак, мы показали, что если х, х + h G [а, Ь], то
x + h)-F(x)\^C\h\, B2)
откуда, очевидно, следует непрерывность функции F в любой точке отрезка
[а, Ь]. >
Теперь докажем лемму, которая уже является вариантом второй теоремы
о среднем.
Лемма 4. Если /, д G 1Z[a, Ь] ид — неотрицательная и невозрастающая
на отрезке [а, Ь] функция, то найдется точка ? G [а, Ь] такая, что
ъ Z
J(f-g)(x)dx = g(a)Jf(x)dx. B3)
а а
Прежде чем переходить к доказательству, отметим, что, в отличие от со-
соотношения A6) первой теоремы о среднем, в B3) под знаком интеграла оста-
осталась функция /, а не монотонная функция д.
< Для доказательства формулы B3), как и в уже рассмотренных выше
случаях, постараемся оценить соответствующую интегральную сумму.
Пусть Р — разбиение отрезка [а, Ь]. Запишем сначала тождество
= ^2 [ (f'9)(*)dx =
a t=l xU
n х* n Xi
i-i) J f(x)dx + J2 f [g(x) ~ g(xi-1)]f(x)dx
»—;1 *m . - 1—1 T •
и покажем, что при А(Р) -> 0 последняя сумма стремится к нулю.
Поскольку / € Ща, 6], то |/(ж)| ^ С < сх> на [а, Ь]. Тогда, используя уже
доказанные свойства интеграла, получаем
п
V
V
п
V
t=l ?_!
П Х* П
t=l хг-! г=1
при А(Р) -> 0, ввиду того, что д G 7?[а, 6] (см. утверждение 2 из § 1). Значит,
if' 9)(x)dx = lim > g(xi-i) / f(x)dx. B4)

§ 2. ЛИНЕЙНОСТЬ, АДДИТИВНОСТЬ И МОНОТОННОСТЬ ИНТЕГРАЛА 351
Оценим теперь сумму, стоящую в правой части равенства B4). Положив
X
F(x)=Jf(t)dt1
по лемме 3 получаем функцию, непрерывную на отрезке [a, ft].
Пусть
га = min F(x) и М = max F(x).
хе[а,Ь] €[6]
Xi
Поскольку j f(x)dx = F(x{) - F(xi-i), то
п *» n
B5)
г=1 ж^-1 t=l
Учитывая неотрицательность и невозрастание функции д на [a, ft] и полагая
сц =
по лемме 2 находим, что
п
(F(x») - F(xi-!)) gfa-г) ^ Мд(а), B6)
t=i
поскольку
к
Ak = J2"i = F(xk) - F(x0) = F(x,) - F(a) = F(xk).
t=i
Мы показали, что суммы B5) удовлетворяют неравенствам B6). Вспоми-
Вспоминая соотношение B4), теперь имеем
б
тд(а) ^ у (/ • д)(х) dx < Mg{a). B7)
а
Если д(а) = 0, то, как показывают неравенства B7), доказываемое соот-
соотношение B3), очевидно, справедливо.
Если же д(а) > 0, то положим
б
Из B7) следует, что т ^ /х ^ М, а из непрерывности функции F(x) =
= у f(t)dt на [а, Ь] следует, что найдется точка f G [a, ft], в которой F(?) = /х.
а
Но именно это и утверждает формула B3). >

352 ГЛ. VI. ИНТЕГРАЛ
Теорема 6 (вторая теорема о среднем для интеграла). Если /, д ? Ща, Ь]
ид — монотонная на [а, ft] функция, то найдется точка ? € [а, Ь] такая, что
ъ 4 ь
(/ ¦ g)(x) dx = g(a)ff(x) dx + g(b)Jf(x) dx. B8)
а
Равенство B8) (как, впрочем, и равенство B3)) часто называют формулой
Боннех\
М Пусть д — неубывающая на [a, ft] функция. Тогда G(x) = g(b) - g(x) —
неотрицательная, невозрастающая, интегрируемая на [a, ft] функция. Приме-
Применяя формулу B3), находим
ь С
/(/ • G)(x) dx = G(a)ff(x) dx. B9)
a . a
Ho
» 6 6
(/ • G)(x) dx = g(b)Jf(x) dx- JU- 9){x) dx,
a a a
(. i «
G(a)Jf(x) dx = g(b)Jf(x) dx - g(a)jf(x) dx.
a a a
Учитывая эти соотношения и свойство аддитивности интеграла, из B9) полу-
получаем доказываемое равенство B8).
Бели д — невозрастающая функция, то, полагая G(x) = д(х) — д(Ь), полу-
получим, что G(x) — неотрицательная, невозрастающая, интегрируемая на [a, ft]
функция. Далее вновь получаем формулу B9), а за ней и формулу B8). >
Задачи и упражнения
1. Покажите, что если / € 7?[a,ft] и f(x) ^ 0 на [a, ft], то
а) при условии, что в некоторой точке xq € [о, ft] непрерывности функция f(x)
принимает положительное значение /(яо) > 0, имеет место строгое неравенство
ь
/ f(x) dx > 0;
a
b
b) из условия / /(ж) dx = 0 следует, что f(x) = 0 почти во всех точках отрезка
*) П. О. Бонне A819—1892) — французский математик и астроном. Наиболее значитель-
значительные математические работы Бонне связаны с дифференциальной геометрией.

§ 2. ЛИНЕЙНОСТЬ, АДДИТИВНОСТЬ И МОНОТОННОСТЬ ИНТЕГРАЛА 353
2. Покажите, что если / € 7?[а,ф], т = inf /(ж), М = sup/(ж), то
]*>*[ ]а,Ь[
a) / /(ж) dx = /хF — а), где |г 6 [т, М] (см. задачу 5а) предыдущего параграфа);
а
b) при условии непрерывности / на [а, Ь] найдется такая точка f € ]а,6[, что
ъ
3. Покажите, что если / € С[а^Ь], /(ж) ^ 0 на [о, Ь] и М = max /(я), то
1/п
Hm[ fn(x)dx\ = М.
4. а) Покажите, что если / € Ща>Ь], то |/|р € Ща,Ь] при р ^ 0.
b) Исходя из неравенства Гель дера для сумм, получите неравенство Гель дера для
интегралов1^:
Ь S Ь х 1/р у 6 v 1/д
J(fg)(x)dx ^U\f\p(x)dx] ¦U\9\"(x)dx\ ,
если /, о € 7?[а,Ь] ир^1, д>1, - + - = 1.
c) Исходя из неравенства Минковского для сумм, получите неравенство Минков-
ского для интегралов:
/ * \1/Р / jl v 1/р , Ь v 1/р
И |/4-p|p(x)cixJ ^ И |/|p(x)dxj + fy MP(x)dxJ ,
если /, д € 7?[а,Ь] ир^1. Покажите, что это неравенство меняется на противопо-
противоположное, если 0 < р < 1.
d) Проверьте, что если / — непрерывная, выпуклая на R функция, а у? — произ-
произвольная непрерывная на R функция, то при сфО справедливо неравенство Иенсена:
х) Алгебраическое неравенство Гель дера при р = g = 2 впервые было получено в 1821 г.
Коши и носит его имя. Неравенство Гель дера для интегралов при р = q = 2 впервые нашел
в 1859 г. русский математик В- Я. Буняковский A804 — 1889). Это важное интегральное
неравенство (в случае р = q = 2) называют неравенством Бунлковского или неравенством
Коши — Бунлковского. Встречается иногда и менее точное его название «неравенство Швар-
Шварца» — по имени немецкого математика Г. К. А. Шварца A843 — 1921), в работах которого
оно появилось в 1884 г.

354 гл. vi. интеграл
§ 3. Интеграл и производная
1. Интеграл и первообразная. Пусть / — интегрируемая по Риману
на отрезке [а, Ь] функция. Рассмотрим на этом же отрезке функцию
X
F(x) = Jf(t) dt, A)
а
часто называемую интегралом с переменным верхним пределом.
Поскольку / е Ща, ft], то f\[a,x] € 7?[а,х], если [а,х] С [a, ft]; поэтому функ-
функция х н* F(x) корректно определена для х € [a, ft].
Если \f(t)\ ^ С < +оо на [a, ft] (a /, как интегрируемая функция, ограни-
ограничена на [a, ft]), то из аддитивности интеграла и простейшей оценки интеграла
следует, что
B)
если х, х + h € [a, ft].
Об этом мы, кстати, уже говорили, доказывая лемму 3 предыдущего пара-
параграфа.
Из неравенства B), в частности, следует непрерывность функции F на
[a, ft]. Итак, F еС[а,Ь].
Теперь мы исследуем функцию F более тщательно.
Имеет место следующая основная для всего дальнейшего
Лемма 1. Если / E 7?[a, ft] и функция f непрерывна в некоторой точке
х € [a, ft], то функция F, определяемая на [а, ft] формулой A), дифференциру-
дифференцируема в этой точке х, причем имеет место равенство
F\x) = /(*).
< Пусть х, х + h e [а, ft]. Оценим разность F(x + h) — F(x). Из непрерыв-
непрерывности / в точке х следует, что f(t) = f(x) + А(?), где Д(?) ->- 0 при t -> х,
t e [a, ft]. Функция A(t) = f(t) — f(x) интегрируема на [a,ft], как разность
интегрируемой функции t »-> f(t) и постоянной /(х), если х — фиксирован-
фиксированная точка. Обозначим через М(h) величину sup |Д(?)|, где I(h) — отрезок с
tei(h)
концами х, х + h e [a, ft]. По условию, М(К) -? 0 при h -> 0.
Теперь запишем
х -f h х х + h
F(x + h)- F(x) = f /(*) <ft - У/(«) <ft = / /(*) dt =
a a x
x + h x + h x + h
= f (/(») +Д(*)) dt = У f(x)dt + У A(t)dt = /(*)h 4- a(/i)h,

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ
355
где положено
У
Поскольку
x + h
I
A(t) dt
M(h) dt
= M(ft)|ft|,
то |a(ft)| ^ М(Л) и потому a(ft) -> 0, когда Л -> 0 (но так, что х -f ft G [a, ft]).
Таким образом, показано, что если функция / непрерывна в точке х G [a, ft],
то при смещениях ft от точки х таких, что x-f ft G [a, ft], имеет место равенство
F(x + ft) - F(x) = /(х)Л + a(ft)ft,
C)
где a(ft) -> 0 при ft -> 0.
Но это и означает, что функция F(x) дифференцируема на [a, ft] в точке
х G [а,Ь] и что F'(x) = /(x). >
Важнейшим непосредственным следствием леммы 1 является следующая
Теорема 1. Кат/сдоя непрерывная на отрезке [a,ft] функция /: [a,ft] -> R
имеет на этом отрезке первообразную, причем любая первообразная функции
f на [а, Ь] гшеет вид
= If{t) dt + с,
D)
где с — некоторая постоянная.
< (/ G <7[а,Ь]) =» (/ G Я[а,ft]), поэтому на основании леммы 1 функция
A) является первообразной для / на [a, ft]. Но две первообразные Fix) и F(x)
одной и той же функции на отрезке могут отличаться на этом отрезке только
на постоянную, поэтому F{x) = F(x) + с. >
Для дальнейших приложений удобно несколько расширить понятие перво-
первообразной и принять
Определение 1. Непрерывная на числовом промежутке функция х <->¦
Т{х) называется первообразной {обобщенной первообразной) функции х ь^
/(х), определенной на том же промежутке, если во всех точках промежутка,
за исключением, быть может, конечного их числа, имеет место соотношение
JF'(x) = /(*).
Учитывая это определение, можно утверждать, что справедлива следующая
Теорема 1'. Каждая определенная и ограниченная на отрезке [a, ft] функ-
функция /: [a, ft] -> R с конечным множеством точек разрыва имеет на этом
отрезке (обобщенную) первообразную, причем любая первообразная функции
f на [a, ft] имеет вид D).

356
ГЛ. VI. ИНТЕГРАЛ
< Поскольку / имеет конечное множество точек разрыва, то / Е И[а, ft] и
по лемме 1 функция A) является обобщенной первообразной для / на [а, ft].
При этом мы учли, что, как уже отмечалось, в силу B) функция A) не-
непрерывна на [а, Ь]. Если Т{х) — другая первообразная функции / на [a, ft],
то Т(х) — F(x) — непрерывная функция, постоянная на каждом из конеч-
конечного числа промежутков, на которые точки разрыва функции / разбивают
отрезок [a, ft]. Из непрерывности F(x) — F(x) на [a, ft] тогда следует, что
F{x) — F(x) = const на [a, ft]. >
2. Формула Ньютона—Лейбница
Теорема 2. Если /: [a,ft] -> R — ограниченная функция с конечным
числом точек разрыва, то / Е 7?[а, ft] и
E)
где Т \ [а, ft] —» Ж — любая из первообразных функции f на отрезке [а,Ь].
Щ Интегрируемость ограниченной на отрезке функции с конечным числом
точек разрыва нам уже известна (см. § 1, следствие 2 утверждения 2). На-
Наличие обобщенной первообразной Т{х) функции / на [a, ft] гарантирует тео-
теорема 1', в силу которой Т(х) имеет вид D). Полагая в D) х = а, получим, что
Т(а) = с, откуда
В частности,
а
что с точностью до обозначения переменной интегрирования совпадает с до-
доказываемой формулой E). >
Фундаментальное для всего анализа соотношение E) называется формулой
Ньютона — Лейбница.
Разность Т{Ь) — Т(а) значений любой функции часто записывают симво-
символом F{x)\a. В этих обозначениях формула Ньютона—Лейбница приобретает
вид
Поскольку обе части этой формулы одновременно меняют знак при переста-
перестановке а и ft, то формула справедлива при любом соотношении величин а и ft,
т. е. как при а ^ ft, так и при а ^ ft.

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ 357
На упражнениях по анализу формула Ньютона—Лейбница большей частью
используется только для вычисления стоящего слева интеграла, и это может
породить несколько искаженное представление об ее использовании. На са-
самом деле положение вещей таково, что конкретные интегралы редко находят
через первообразную, а чаще прибегают к прямому счету на ЭВМ с помощью
хорошо разработанных численных методов. Формула Ньютона—Лейбница
занимает ключевую, связывающую интегрирование и дифференцирование,
позицию в самой теории математического анализа, в которой она, в частно-
частности, получает далеко идущее развитие в виде так называемой общей формулы
Стоксах\
Примером того, как формула Ньютона—Лейбница используется в самом
анализе, может служить уже материал следующего пункта настоящего пара-
параграфа.
3. Интегрирование по частям в определенном интеграле
и формула Тейлора
Утверждение 1. Если функции и(х) uv(x) непрерывно дифференциру-
дифференцируемы на отрезке с концами а иЬ, то справедливо соотношение
[{и - v')(x) dx = {u- v){x)\ba - f{v - u')(x) dx. F)
Эту формулу принято записывать в сокращенном виде
6 6
udv = u-v\a— I vdu
a
и называть формулой интегрирования по частям в определенном интеграле.
Ч По правилу дифференцирования произведения функций имеем
(и • v)'(x) = {и1 • v){x) + (и • t/)(x).
По условию все функции в этом равенстве непрерывны, а значит, и интегри-
интегрируемы на отрезке с концами а и 6. Используя линейность интеграла и формулу
Ньютона—Лейбница, получаем
(и • v)(x)|^= / {и1 • v)(x) dx + Ни • v')(x) dx. >
a a
В качестве следствия получим теперь формулу Тейлора с интегральным
остаточным членом.
. Г. Стоке A819—1903) — английский физик и математик.

358
ГЛ. VI. ИНТЕГРАЛ
Пусть на отрезке с концами а и х функция t н-> f(t) имеет п непрерывных
производных. Используя формулу Ньютона—Лейбница и формулу F), проде-
проделаем следующую цепочку преобразований, в которых все дифференцирования
и подстановки производятся по переменной t:
X X
/(х) - f(a) = jf'(t) dt = -//'(<) (x - t)'dt =
a
x
= -f'(t)(x -t)\'a + ff"(t)(x -t)dt =
a
x
= f(a) (x - a) - \ Jf"(t) ((x -1J)' dt =
= /'(a)(x - a) - | /"(*)(* - Щ'а + \
= /'(a)(x - a) + | /"(a)(x - aJ - -^
X
x - tfdt =
((x - tK)'dt = ...=
где
= f'(a)(x - a) + \ /"(a)(x - aJ + ... +
2 • 3 •... • (n - 1)
G)
Итак, доказано следующее
Утверждение 2. ?сли функция t »-> /(t) имеет на отрезке с концами
а и х непрерывные производные до порядка п включительно, то справедлива
формула Тейлора
f(x) = /(a) + ^ /'(a)(x - a) + ... + -^^ f{n-l)(a)(x - a)
"
rn_x(o;x)
с остатком rn_i(a;s), представленным в интегральной форме G).
Отметим, что функция (ж — iI1 не меняет знак на отрезке с концами а и
ж, и поскольку функция t н* f^(t) непрерывна на этом отрезке, то по первой

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ 359
теореме о среднем на нем найдется такая точка ?, что
х
rn-i(a;x) = j^±— |/<n>(*)(* - t)n~ldt =
a
x
Мы вновь получили знакомую форму Лагранжа остаточного члена фор-
формулы Тейлора. (На основании задачи 2Ь) из предыдущего параграфа, можно
считать, что ? лежит в интервале с концами а, х.)
Это рассуждение можно было бы повторить, вынося из-под знака интегра-
интеграла G) f^@(x ~ 0n~*> гДе * € [1,п]. Значениям к = 1 и к = п отвечают
получаемые при этом соответственно формулы Коши и Лагранжа остаточно-
остаточного члена.
4. Замена переменной в интеграле. Одной из основных формул ин-
интегрального исчисления является формула замены переменной в определенном
интеграле. Эта формула в теории интеграла столь же важна, как в диффе-
дифференциальном исчислении формула дифференцирования композиции функций,
с которой она может быть при определенных условиях связана посредством
формулы Ньютона—Лейбница.
Утверждение 3. Если (р: [а,/?] -> [а,ft] — непрерывно дифференциру-
дифференцируемое отображение отрезка а ^ t ^ /3 в отрезок а ^ х ^ Ь такое, что
(р(а) = а и <^(/3) = Ъ, то при любой непрерывной на [а, Ь] функции f(x) функ-
функция f{(p{t))(p'(t) непрерывна на отрезке [а,/?] и справедливо равенство
ь
f
b
f(x)dx= I f(<p(t))(p'(t)dt (8)
4 Пусть Т(х) — первообразная функции f(x) на [a, ft]. Тогда, по теореме
о дифференцировании композиции функций, функция Т((р(г)) является пер-
первообразной для функции f((p(t))(p'(t)y непрерывной, как композиция и про-
произведение непрерывных функций на отрезке [а,/?]. По формуле Ньютона—
Лейбница ff(x)dx = Т{Ь) - ?{а) и J f(<p{t))<p'(t)dt = F(tp{p)) - T(ip(a)).
а а
Но, по условию, <р(а) = а и <р(C) = ft; таким образом, равенство (8) действи-
действительно имеет место. >
Из формулы (8) видно, насколько удобно иметь под интегралом не просто
знак функции, а дифференциальное выражение f(x)dx, позволяющее после

360 ГЛ. VI. ИНТЕГРАЛ
подстановки х = <p(t) автоматически получать правильное подынтегральное
выражение в интеграле по новой переменной.
Для того чтобы не осложнять дела громоздким доказательством, мы в
утверждении 3 умышленно сузили истинную область применимости форму-
формулы (8) и получили (8) из формулы Ньютона—Лейбница. Теперь перейдем к
основной теореме о замене переменной, условия которой несколько отличают-
отличаются от условий утверждения 3. Доказательство этой теоремы будет опираться
непосредственно на определение интеграла как предела интегральных сумм.
Теорема 3. Пусть <р: [а,/?] -> [а,ft] — непрерывно дифференцируемое,
строго монотонное отображение отрезка а ^ t ^ р в отрезок а ^ х ^ Ъ
с соответствием концов ip{at) = a, ip{/3) = ft или ip(a) = ft, <p@) = о- Тогда
при любой функции /(ж), интегрируемой на отрезке [а, ft], функция f(ip(i)) х
х (pf(t) интегрируема на отрезке [а,/?] и справедливо равенство
] f(x)dx=ff(V>(t))(p'(t)dt.
(9)
4 Поскольку (р — строго монотонное отображение отрезка [а, /3] на от-
отрезок [a, ft] с соответствием концов, то любое разбиение Р* (а = fo < • • <
< tn = /3) отрезка [а, /3] посредством образов ж» = <р(и) (i = 0,1,..., п) точек
разбиения Pt порождает соответствующее разбиение Рх отрезка [а, 6], кото-
которое можно условно обозначить как <p(Pt). При этом xq = а, если <р(а) = а, и
хо = ft, если (р(а) = ft. Из равномерной непрерывности <р на [а,/9] следует, что
если X(Pt) -> 0, то величина \(РХ) = \(ip(Pt)) тоже стремится к нулю.
Используя теорему Лагранжа, преобразуем интегральную сумму a(f; Рх,
следующим образом:
п п
*=1 *=1
*=i *=i
Здесь Х{ = ^(t»), ^ = </>(t»), ^» лежит на отрезке с концами x»_i, ж», а
точки г», г» лежат на отрезке с концами ?»_i, t» (t = 1,..., n).
Далее,
n n
П
t=i

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ 361
Оценим последнюю сумму. Поскольку / € ft[a,ft], функция / ограничена
на [а,Ь]. Пусть |/(х)| ^ С на [a, ft]. Тогда
п
*=1
п
*=i
где Д» — отрезок с концами ?<_i, t».
Последняя сумма стремится к нулю при X(Pt) —> 0, поскольку </?' — непре-
непрерывная на отрезке [а, /3] функция.
Таким образом, мы показали, что
п п
где а -» 0 при \{Pt) -+ 0. Как уже отмечалось, если \(Pt) -» 0, то и А(Ра;)
0. Но / € fc[a,ft], поэтому при А(Ра.) -» 0 сумма в левой части последнего
равенства стремится к интегралу f f(x) dx. Значит, при X(Pt) ->0и сумма
в правой части этого равенства имеет и притом тот же предел.
п
Но сумму Yl /(</?(r*))v?/(rt)^t можно считать совершенно произвольной
интегральной суммой функции f(<p(t))<p?(t), соответствующей разбиению Pt
с отмеченными точками г = (ri,..., тп), поскольку, ввиду строгой монотон-
монотонности <р% любой набор точек т можно получить из некоторого соответству-
соответствующего ему набора ? = (&,..., ?п) точек, отмеченных в отрезках разбиения
Таким образом, предел этой суммы есть, по определению, интеграл от
функции f{4>{t)L>'(t) по отрезку [а,/?], и мы доказали одновременно как ин-
интегрируемость функции f{<p{t))ip'{t) на отрезке [а,/?], так и формулу (9). >
5. Некоторые примеры. Рассмотрим теперь некоторые примеры ис-
использования полученных формул и доказанных в последних двух параграфах
теорем о свойствах интеграла.
Пример 1.
1 тг/2 7г/2
/ \/l — х2 dx = / v 1 — sin21 cos t dt = / cos21 dt =
-1 -тг/2 -тг/2
¦f-cos2*)ctt= ~
-тг/2

362
ГЛ. VI. ИНТЕГРАЛ
Для вычисления интеграла мы сделали замену переменной х — sin ?, а за-
затем, найдя первообразную получившейся после этой замены подынтегральной
функции, воспользовались формулой Ньютона—Лейбница.
Конечно, можно было бы поступить и иначе: найти довольно громоздкую
первообразную -z х л/1 — х2 -f -z arcsin х функции у/1 — х2 и затем воспользо-
it it
ваться формулой Ньютона—Лейбница. Пример показывает, что при вычисле-
вычислении определенного интеграла, к счастью, иногда удается избежать отыскания
первообразной подынтегральной функции.
Пример 2. Покажем, что
7Г
а) / sin mx cos nx dx = О, b) / sin2 mx dx = тг, с) / cos2 nx dx = 7г
— 7Г
— 7Г
— 7Г
при га, n 6 N.
7Г
а) / sin mx cos nxdx = - / (sin (n -f m)ж — sin (n - m)x) da; =
— 7Г
— 7Г
= « I cos(n + m)x H cos(n — m)x]
2 \ n + m n — m )
= 0,
если n — m ^ 0. Случай, когда n — m = 0, можно рассмотреть отдельно, и в
этом случае, очевидно, вновь приходим к тому же результату.
7Г 7Г
b) / sin2 mx dx = - I A - cos 2mx) dx = - ( x — ~— sin 2mx 1
7Г.
— 7Г
7Г
c) / cos2 nx dx = - I A + cos 2nx) dx = ~ (x + —- sin 2nx )
J 2 J 2 \ 2n J
= 7Г.
7Г
—7Г
Пример 3. Пусть / 6 7?[—a,a]. Покажем, что
/(x) dx = i
—a
a
2 / /(x) dx, если / — четная функция,
о
0,
если / — нечетная функция.
Если /(—х) = /(х), то
О
//(x)dx= [ f(x)dx+ [f(x)dx=
0
—a 0 a
a a a
a
[f(x)dx =
0
0
-*) d* + Jf(x) dx = J (/(-x) + /(*)) dx = 2//(x) dx.
0 0 0

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ 363
Бели же /(—х) = —/(ж), то, как видно из тех же выкладок, получим
а а а
f f(x) dx = f(f(-x) + f(x)) dx = fodx = 0.
-a 0
Пример 4. Пусть / — определенная на всей числовой прямой R перио-
периодическая функция с периодом Т, т. е. f(x + Т) = /(ж) при х € М.
Бели / — интегрируемая на каждом конечном отрезке функция, то при
любом a € М имеет место равенство
а + Т
о
т. е. интеграл от периодической функции по отрезку длины периода Т этой
функции не зависит от положения отрезка интегрирования на числовой пря-
прямой:
а+Т О Т а+Т
f f(x)dx= ff(x)dx+ [f{x)dx+ f f(x)dx =
a 0 T
T 0 a
= jf{x)dx + Jf(x)dx + Jf(t + T) Idt =
0 a 0
T 0
= ff(x) dx + ff(x) dx + Jf(t) dt = у7(ж
о о
Мы сделали замену х = t 4- Г и воспользовались периодичностью функ-
функции /(х).
1
Пример 5. Пусть нам нужно вычислить интеграл J sin x2 dx, например,
о
с точностью до 10~2.
Мы знаем, что первообразная /sinx2dx (интеграл Френеля) не выража-
выражается в элементарных функциях, поэтому использовать формулу Ньютона—
Лейбница здесь в традиционном смысле нельзя.
Поступим иначе. Исследуя в дифференциальном исчислении формулу Тей-
Тейлора, мы в качестве примера (см. гл. V, § 3, пример 11) нашли, что на отрезке
[—1,1] с точностью до 10~3 имеет место равенство
sinx « х - ^гх3 4- ^х5 =: Р(х).
о! 5!
Но если |sinx — Р(х)| < 10~3 на отрезке [—1,1], то верно также, что
|sinx2 - Р(х2)| < 1(Г3 при 0 < х ^ 1.

364
ГЛ. VI. ИНТЕГРАЛ
Следовательно,
1 1
2dx- lP(x*)dx
fsmx2dx-fp(x2)dx ^ [\smx2-P(x2)\dx < f IO~3 dx < 10.
0 0 0 0
X
Таким образом, для вычисления интеграла I sin x2 dx с нужной точностью
1 °
достаточно вычислить интеграл I P(x2) dx. Но
Jp(x2) dx = j(f - i x6 + ^x10) dx =
0
0
-Ax3 * x7 I *
~ V3 3!7 +5!11
1
0
зТ7

= °'310 ± 10'
поэтому
1
fsinx2dx = 0,310 ± 2 • 10~3 = 0,31 ± 10.
0
Пример 6. Величина /x = //(x) ^ называется интегральным сред-
a
ним значений функции на отрезке [a,b].
Пусть / — определенная на Е и интегрируемая на любом отрезке функция.
Построим по / новую функцию
х+6
= h I mdt>
I
х-6
значение которой в точке х есть интегральное среднее значений / в 5-окрест-
ности точки х.
Покажем, что функция Fs(x) (называемая усреднением /) более регулярна
по сравнению с /. Точнее, если / интегрируема на любом отрезке [a, ft], то
F6(x) непрерывна на М, а если /€ С(Е), то F6(x)e CA)(E).
Проверим сначала непрерывность функции Fs(x):
ж+Я+Л x-6
f f{t)dt + f f{t)dt
x-6+h
25

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ 365
если |/(t)| ^ С, например, в 2<$-окрестности точки х и |ft| < <5. Из этой оценки,
очевидно, следует непрерывность функции Fs(x).
Если же /€C(R), то по правилу дифференцирования сложной функции
Ь =
=Ь Im
dt-
f «г л r
a a
поэтому из записи
х+6 х—6
получаем, что
,м _ Six + S) - f(x - S)
{{X) ~ 2S •
Функцию Fs(x) после замены t = x + и переменной интегрирования можно
записать в виде
-6
Бели / € C(R), то, применяя первую теорему о среднем, находим, что
Fs(x) = ^ f(x + г) • 2<J = /(* + г),
где |r| ^ 5. Отсюда следует, что
lim F,ix) = Six),
о—>-+-U
что вполне естественно.
Задачи и упражнения
1. Используя интеграл, найдите
iim /т—гтТг +•¦¦ +
[(Н1J
пН-1J BnJJ
b) lim — ^,1 —, если а ^ 0.
п-юо Па+1
2. а) Покажите, что любая непрерывная на интервале функция имеет на нем
первообразную.
Ь) Покажите, что если / € СA)[а, 6], то / может быть представлена как разность
двух неубывающих на отрезке [а,Ь] функций (см. задачу 4 из § 1).
3. Покажите, что в предположении гладкости функции д вторая теорема о сред-
среднем (теорема 6 из § 2) интегрированием по частям непосредственно сводится к пер-
первой теореме о среднем.

366 ГЛ. VI. ИНТЕГРАЛ
4. Покажите, что если / 6 C(R), то для любого фиксированного отрезка [а, 6] по
заданному е > 0 можно так подобрать S > 0, что на [а, 6] будет вьшолнено неравен-
неравенство \Fs(x) — /(ж)| < ?, где F<5 — осреднение функции, рассмотренное в примере 6.
5. Покажите, что
.2
X
I
е* 1 з
— dt ~ — еж при ж —> +оо.
? х2
1
6. а) Проверьте, что функция f(x) = / sin^2d^ при х —> с» имеет следующее
представление:
cosx2 cos
b) Найдите Шп xf(x) и lim xf(x).
х-юо х-юо
7. Покажите, что если /: R —> R — периодическая, интегрируемая на каждом
отрезке [а, 6] С R функция, то функция
х
Г
dt
может быть представлена в виде суммы линейной и периодической функций.
8. а) Проверьте, что при х > 1 и h € N функция
п(х) = — / (ж
— 1 cos
есть полином степени, п (п-й полином Лежандра).
Ъ) Покажите, что
к J (х - у/х2 — 1 cos
О
п *
9. Пусть / — вещественнозначная функция, определенная на отрезке [а, Ь] С R,
a ?i > • • •, ?m — различные точки этого отрезка. Значения интерполяционного поли-
полинома Лагранжа степени m — 1
совпадают в точках ^i,..., f m (узлах интерполяции) со значениями функции /, при-
причем если / 6 С(т)[а,Ъ], то
т
где шт(х) = П (х ~ Ci)> а С(^) € К&1 (см. задачу 11 в § 3 гл. V)

§ 3. ИНТЕГРАЛ И ПРОИЗВОДНАЯ 367
Пусть ? = ^ + ^р ft, тогда ft € [-1,1], t = 1, ..., m.
а) Покажите, что
b
где
В частности,
/ Lo(x)dx = (Ь--а)/(а9 J, если т = 1, ft = 0;
Li(x)dx = ^—- [/(a) + f(b)], если m = 2, ft = -1, 02 = 1;
аз) lL2(x)dx=—5— /(a)+4/(—r—) + f(b) , если m = 3, ft = —1, ft = 0,
b) Считая, что / € С7^т^[а,Ь] и полагая Мт = max |/^тЧхI> оцените величину
х€[а,6]
Rm абсолютной погрешности в формуле
ь ь
jf(x) dx = JLm-i(x) dx + Rm (*)
и покажите, что |Ят| < —^ /
a
с) В случаях ai), аг), »з) формула (*) называется соответственно формулой пря-
прямоугольников, трапеций и парабол. В последнем случае ее называют также фор-
формулой Симпсона1). Покажите, что в случаях ai), аг), аз) имеют место следующие
формулы:
ШЛ ф^, л, = -
гДе €i> ^2> ^з € [а,Ь], а функция / принадлежит соответствующему классу С^[а,6].
d) Пусть / есть полином Р. Какова наивысшая степень полиномов Р, для кото-
которых точны формулы прямоугольников, трапеций и парабол соответственно?
. Симпсон A710 — 1761) — английский математик.

368 гл. vi. интеграл
Пусть h = -; Хк =a + hk, к = 0,1, ... , п; yfc =/(xfc).
Ь-а
п
е) Покажите, что в следующей формуле прямоугольников
ь
f(x) dx = h(yo + yi + ... + yn-i)
I
остаток имеет вид Ri = ^ (Ь — а)Л, где ? € [а, 6].
f) Покажите, что в следующей формуле трапеций
ь
f(x) dx=% [(уо + уп) + 2(yi + у2 + ... + yn-i)] + Яг
/
а
остаток имеет вид ifo = — Л F — a)h , где ? € [а, 6].
JL a
g) Покажите, что в следующей формуле Симпсона (формуле парабол)
ь
i
f(x) dx = - [(уо + Уп) + 4(yi 4- уз + ... 4- Уп-i)
+ 2(у2 + У4 + . • . + Уп-2)] +
которая пишется при четных значениях п, остаток Дз имеет вид
где$€ [а, 6].
h) Исходя из соотношения
1
dx
о
вычислите тг с точностью до 10~3, пользуясь формулами прямоугольников, трапеций
и парабол. Обратите внимание на эффективность формулы Симпсона, которая по
этой причине является наиболее распространенной квадратурной формулой (так
называют формулы численного интегрирования в одномерном случае, отождествляя
интеграл с площадью соответствующей криволинейной трапеции).
10. Преобразуя формулу G), получите следующие виды записи остаточного члена
формулы Тейлора, где положено h = х — а:
1
a) j^f
о
1
Ь) К [f(n)(x-hVi)dT.
n! J v '

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 369
§ 4. Некоторые приложения интеграла
Использование интеграла в приложениях часто происходит по одной и той же
схеме, которую по этой причине полезно изложить один раз в чистом виде.
Этому посвящен первый пункт настоящего параграфа.
1. Аддитивная функция ориентированного промежутка и инте-
интеграл. Обсуждая в § 2 свойство аддитивности интеграла, мы ввели поня-
понятие аддитивной функции ориентированного промежутка. Напомним, что это
функция (а,/?) н> /(а,/?), которая каждой упорядоченной паре (а,/?) точек
а, /? € [а, Ь] фиксированного отрезка [а, Ь] ставит в соответствие число /(а, /?),
причем так, что для любой тройки точек а, /?, 7 € [в> Ь] выполнено равенство
= J(a,/?) + /(/?, 7). A)
Из A) при а = /? = 7 следует, что 1(а,а) = 0, а при a = 7 получаем,
что /(а,/?) + /(/?,а) = 0, т. е. /(а,/?) = —/(/?, а). В этом сказывается влияние
порядка точек а, /3.
Полагая
в силу аддитивности функции / имеем
/(а,/?) =
Таким образом, каждая аддитивная функция ориентированного проме-
промежутка имеет вид
B)
где х н> Т{х) — функция точки отрезка [а, 6].
Легко проверить, что верно и обратное, т. е. что любая функция х *-> Т{х),
определенная на отрезке [а, Ь], порождает по формуле B) аддитивную функ-
функцию ориентированного промежутка.
Приведем два типичных примера.
х
Пример 1. Если / G Ща,Ь], то функция Т(х) = f f(t)dt порождает, в
a
силу формулы B), аддитивную функцию
р
/(a,/?) = ff(t)dt.
Заметим, что в данном случае функция Т(х) непрерывна на отрезке [а,Ь].
Пример 2. Пусть отрезок [0,1] есть невесомая струна с бусинкой еди-
единичной массы, прикрепленной к струне в точке х = 1/2.

370 ГЛ. VI. ИНТЕГРАЛ
Пусть Т(х) есть масса, находящаяся на отрезке [0, х] струны. Тогда по
условию
/ 0 при х < 1/2,
k 1 при 1/2 < х ^ 1.
Физический смысл аддитивной функции
при /3 > а — масса, попавшая в полуинтервал ]а,
Поскольку функция Т разрывна, аддитивная функция /(а, /3) в рассматри-
рассматриваемом случае не может быть представлена как интеграл Римана от некоторой
функции — плотности массы. (Эта плотность, т. е. предел отношения массы
промежутка к его длине, должна была бы равняться нулю в любой точке от-
отрезка [а, Ь], кроме точки х = 1/2, где она должна была бы быть бесконечной.)
Теперь докажем полезное для дальнейшего достаточное условие того, что
аддитивная функция порождается интегралом.
Утверждение 1. Пусть аддитивная функция /(а,/?), определенная
для точек а, /3 отрезка [а,Ь], такова, что существует функция / € Ща,Ь],
связанная с I следующим образом: для любого отрезка [а,/?] такого, что
а ^ а < /3 ^Ь, выполняется соотношение
inf f(x) (/? - а) < /(а, C) ^ sup f(x) (/? - а).
*е[а,/з] *е[а,/з]
Тогда
ь
/(а, 6) = ff(x) dx.
а
М Пусть Р — произвольное разбиение а = xq < ... < хп = Ь отрезка [а, 6];
Для каждого отрезка [xi-\,Xi] разбиения Р имеем по условию
Суммируя эти неравенства и пользуясь аддитивностью функции 1(а,/3),
получаем
п п
i=i t=i
Крайние члены в последнем соотношении суть знакомые нам нижняя и
верхняя суммы Дарбу функции /, соответствующие разбиению Р отрезка
[а, Ь]. При А(Р) —>> 0 обе они имеют своим пределом интеграл от / по отрезку
[а,Ь]. Таким образом, переходя к пределу при Х(Р) -> 0, получаем, что
1(а, Ь) = ff(x) dx.

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 371
Продемонстрируем теперь утверждение 1 в работе.
2. Длина пути. Пусть частица движется в пространстве R3, и пусть
известен закон ее движения r(t) = (x(t),y(t),z(t)), где x(t), y(t), z(t) — пря-
прямоугольные декартовы координаты точки в момент времени t.
Мы хотим определить длину I [а, ft] пути, пройденного точкой за промежу-
промежуток времени а ^ t ^ ft.
Уточним некоторые понятия.
Определение 1. Путем в пространстве R3 называется отображение
t н> (x(t),y(t),z(t)) числового промежутка в пространство R3, задаваемое не-
непрерывными на этом промежутке функциями x(t), у (t), z(t).
Определение 2. Бели 11-? (x(t),y(t),z(t)) есть путь, для которого об-
областью изменения параметра t является отрезок [a, ft], то точки
А = (x(a),y(a),z(a)), В = (x(b),y(b),z(b))
пространства R3 называются соответственно началом и концом пути.
Определение 3. Путь называется замкнутым, если он имеет и начало,
и конец и эти точки совпадают.
Определение 4. Бели Г: / -> R3 — путь, то образ Г(/) промежутка /
в пространстве R3 называется носителем пути.
Носитель абстрактного пути может оказаться вовсе не тем, что мы хоте-
хотели бы назвать линией. Существуют примеры путей, носители которых, на-
например, содержат целый трехмерный куб (так называемые «кривые» Пеано).
Однако если функции x(t), y(t), z(t) достаточно регулярны (как, например,
в случае механического движения, когда они дифференцируемы), то ничего
противоречащего нашей интуиции, как можно строго проверить, заведомо не
произойдет.
Определение 5. Путь Г: / -> R3, для которого отображение / -> Г(/)
взаимно однозначно, называется простым путем или параметризованной
кривой, а его носитель — кривой в R3.
Определение 6. Замкнутый путь Г: [а,Ь] -> R3 называется простым
замкнутым путем или простой замкнутой кривой, если путь Г: [а, Ь) -> R3
является простым.
Значит, простой путь отличается от произвольного пути тем, что при
движении по его носителю мы не возвращаемся в прежние точки, т. е. не пе-
пересекаем свою траекторию нигде, кроме, быть может, ее конца, если простой
путь замкнут.
Определение 7. Путь Г: / -> R3 называется путем данного класса
гладкости, если задающие его функции x(t), y(i), z(t) принадлежат указан-
указанному классу.
(Например, классу С[а,Ь], С^[а,Ь\или
13 Зорич В. А.

372 гл. vi. интеграл
Определение 8. Путь Г: [а,Ь] -> R3 называется кусочно гладким, если
отрезок [а, Ь] можно разбить на конечное число отрезков, на каждом из кото-
которых соответствующее ограничение отображения Г задается непрерывно диф-
дифференцируемыми функциями.
Именно гладкие пути, т. е. пути класса С^1\ и кусочно гладкие пути мы и
будем сейчас рассматривать.
Вернемся к исходной задаче, которую теперь можно сформулировать как
задачу определения длины гладкого пути Г: [а, Ь] —> R3.
Наши исходные представления о длине Z [а, /3] пути, пройденного в проме-
промежуток времени а ^ t ^ /?, таковы: во-первых, если а < C < 7, то
J[a,7] = *[<*,/?]-И [/?,7],
и? во-вторых, если v(t) = (x(t)yy{t),z{t)) есть скорость точки в момент ?, то
inf |v(t)| (/? - a) < J[a,/3] ^ sup |v(t)| (/? - a).
6[/3] [3]
Таким образом, если функции x(t), y(t), z(t) непрерывно дифференцируе-
дифференцируемы на [a, 6], то в силу утверждения 1 мы однозначно приходим к формуле
J\v(t)\dt = jjx*{t) + y*{t) + z*{t)dt, C)
которую и принимаем теперь как определение длины гладкого пути Г: [a, b]
Бели z(t) = 0, то носитель пути лежит в плоскости и формула C) приобре-
приобретает вид
б
I[а,Ь) = J^/x*(t)+y*(t) Л. D)
Пример 3. Опробуем формулу D) на знакомом объекте. Пусть точка
движется в плоскости по закону
х = jRcos2tt?,
(Б)
За промежуток времени [0,1] точка один раз пробежит окружность ради-
радиуса Д, т. е. пройдет путь длины 2тгД, если длина окружности вычисляется по
этой формуле.
Проведем расчет по формуле D):
1
/[0,1]= I y/(-2nRsm2ntJ + B7tjRcos27t*J dt = 2тг#.

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 373
Несмотря на ободряющее совпадение результатов, проведенное рассужде-
рассуждение содержит некоторые логические пробелы, на которые стоит обратить вни-
внимание.
Функции cos а и sin а, если принять их школьное определение, суть декар-
декартовы координаты образа р точки ро = A,0) при повороте на угол а.
Величина а с точностью до знака измеряется длиной дуги окружности
х2 + у2 = 1, заключенной между ро и р. Таким образом, при этом подходе к
тригонометрическим функциям их определение опирается на понятие длины
дуги окружности и, значит, вычисляя выше длину окружности, мы совершили
в известном смысле логический круг, задав параметризацию окружности в
виде E). '
Однако эта трудность, как мы сейчас увидим, не принципиальная, ибо
параметризацию окружности можно задать, вовсе не прибегая к тригономе-
тригонометрическим функциям.
Рассмотрим задачу о вычислении длины графика функции у = /(я), опре-
определенной на некотором отрезке [о, Ь] С Е. Имеется в виду вычисление длины
пути Г : [а, Ь] -> Ж2, имеющего специальный вид параметризации
из которого можно заключить, что отображение Г: [а, Ь] —> Е2 взаимно одно-
однозначно. Значит, по определению 5 график функции есть кривая в Е2.
Формула D) в данном случае упрощается, поскольку, полагая в ней х = t,
у = /(*), получаем
6
/ '2 F)
В частности, если рассмотреть полуокружность
У = V 1 — х2, -1 ^ х ^ 1,
окружности я2 + у2 = 1, то для нее получим
1
^_^ dx= I -^==. G)
VI ~ х*
Но под знаком последнего интеграла стоит неограниченная функция и,
значит, он не существует в традиционном, изученном нами смысле. Означает
ли это, что полуокружность не имеет длины? Пока это только означает,
что указанная параметризация полуокружности не удовлетворяет условиям
непрерывности функций х, у, при которых была выписана формула D), а
значит, и формула F). Поэтому нам следует либо подумать о расширении
понятия интеграла, с тем чтобы интеграл в G) получил определенный смысл,
либо перейти к параметризации, удовлетворяющей условиям применимости
формулы F).
13*

374 ГЛ. VI. ИНТЕГРАЛ
Заметим, что если взятую параметризацию рассматривать на любом от-
отрезке вида [— 1 + 8,1 — <J], где —1 < — 14- 8 < 1 — 8 < 1, то на нем формула F)
применима и по ней находим длину
1-6
dx
-1+6
дуги окружности, лежащей над отрезком [—1 + 6,1 — 8].
Естественно поэтому считать, что длина 2 полуокружности есть предел
lim /[— 1 + <J, I — 6]. В таком же смысле можно понимать и интеграл в соотно-
соотношении G). Этим естественно возникающим расширением понятия интеграла
Римана мы подробнее займемся в следующем параграфе.
Что же касается рассматриваемого конкретного вопроса, то, даже не ме-
меняя параметризацию, можно найти, например, длину '[—«'ol ДУГИ
ной окружности, опирающейся на хорду, конгруэнтную радиусу окружности.
Тогда (уже из геометрических соображений) должно быть 2 = 3-2 Г— -^, —1.
Заметим также, что
f dx _
поэтому
1-6
= 2 /
— х2 dx —
" -1+6
-1+6
Таким образом,
,1-S] = 2 f y/l - x2 dx.
-l
Длина полуокружности единичного радиуса обозначается символом 7г, и
мы приходим к следующей формуле:
тг = 2 /
— х2 dx.
-i
Последний интеграл есть обычный (а не обобщенный) интеграл Римана, и
его можно вычислить с любой точностью.

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 375
Бели для х Е [—1,1] величину / [х, 1] назвать arccosx, то в силу проведенных
выше выкладок
arccosx
/ dt
= / ,
ИЛИ
arccosx = x\/l — х2 + 2 / \/1 — ?2 dt
2 \\f\^
Если считать длину дуги первичным понятием, то первичными надо счи-
считать функцию х «-> arccosx, введенную только что, и функцию х \-ь arcsinx,
которую можно ввести аналогично, а функции х •-* cosx и х •-* sinx тогда
можно получить как им обратные на соответствующих отрезках. В. сущно-
сущности, именно это и делается в элементарной геометрии.
Пример с длиной полуокружности поучителен не только тем, что, разби-
разбирая его, мы сделали, быть может, небесполезное для кого-то замечание об
определении тригонометрических функций, но еще и тем, что он естественно
порождает вопрос о том, не зависит ли вообще определенное формулой C)
число от выбора системы координат х, у, z и параметризации кривой, когда
речь идет о длине кривой.
Оставляя читателю анализ роли пространственных декартовых коорди-
координат, рассмотрим здесь роль параметризации.
Уточним, что под параметризацией некоторой кривой в R3 мы подразуме-
подразумеваем задание простого пути Г: J —> R3, носителем которого является данная
кривая. Точку или число t Е / называют параметром, а промежуток J —
областью изменения параметра.
Если Г: I -+ С и Г: I -+ С — два взаимно однозначных отображения с
одним и тем же множеством значений С, то естественно возникают взаимно
однозначные отображения Г о Г :/->/, Г о Г : J -у I между областями
определения / и / этих отображений.
В частности, если имеются две параметризации одной кривой, то между
самими параметрами t G /, т 6 / устанавливается естественное соответствие
t = t(r) или г = т(?), позволяющее по параметру точки в одной параметриза-
параметризации определять ее же параметр в другой параметризации.
Пусть Г: [а, 6] -> С и Г: [а, /?]—>•? — две параметризации одной кривой
с соответствием Г(а) = Г (а), Г(Ь) = Г (/?) начала и конца. Тогда функции
t = ?(т), г = r(t) перехода от одного параметра к другому будут непрерыв-
непрерывными, строго монотонными отображениями отрезков а ^ t ^ Ь, а ^ г ^ 0
друг на друга с соответствием начал а +-? а и концов b «-> /3. «
Если кривые Г и Г при этом задавались такими тройками (x(t),y(t),z(t)),
(x(t),y(t),z(t)) гладких функций, что |v(t)|2 - ±2(t) -fy2(t) + ia(t) Ф 0 на [а,Ь]
и |v(t)|2 = ж2(г) 4- У2(т) + z2(t) ф 0 на [а,/?], то можно проверить, что в

376 ГЛ. VI. ИНТЕГРАЛ
этом случае функции перехода t = t(r) и г = r(t) будут гладкими функциями,
имеющими положительную производную на отрезке своего определения.
Мы не станем сейчас заниматься проверкой этого утверждения, оно бу-
будет в свое время получено как одно из следствий важной теоремы о неявной
функции. В данный же момент высказанное утверждение служит скорее мо-
мотивировкой следующего определения.
Определение 9. Говорят, что путь Г : [а,/?] —У Е3 получен из пути
Г: [а, b] -> R3 допустимым изменением параметризации, если существует та-
такое гладкое отображение Т: [а, /?] -+ [а, 6], что Т(а) = а, T{fi) = 6, Т'(т) > О
на [а,/?] и Г = ГоТ.
Проверим теперь следующее общее
Утверждение 2. Если гладкий путь Г: [а,/?] —> W получен из гладкого
пути Г: [а, b] -> R3 допустимым изменением параметризации, то длины этих
путей совпадают,
М Пусть Г : [а, /?] —> Е3 и Г : [а, 6] —> Е3 задаются соответственно трой-
тройками г t-? (x(r), у(т),г(т)) и t4 (x(t), y(t),z(t)) гладких функций, a t = t(r)
— допустимое изменение параметризации, при котором
х(т) = x(t(r)), у(т) = y(t(r)), г{т) = z(t(T)).
Используя определение C) длины пути, правило дифференцирования ком-
композиции функций и правило замены переменной в интеграле, имеем
2(t) + z2(t) dt = /V*2(*(r)) + y2(t(r)) + z2(t(T)) t'(r) dr =
a
[y(t(r))t'(r)J+ [z(t(T))t'(r)]2dr =
¦м
a
Итак, в частности, показано, что длина кривой не зависит от ее гладкой
параметризации.
Длину кусочно гладкого пути определяют как сумму длин гладких путей,
на которые он подразделяется; поэтому легко проверить, что и длина кусочно
гладкого пути не меняется при допустимом изменении его параметризации.
Заканчивая обсуждение понятия длины пути и длины кривой (о которой
мы после утверждения 2 теперь вправе говорить), рассмотрим еще один
Пример 4. Найдем длину эллипса, задаваемого каноническим уравне-
уравнением
|J i? (8)

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА
377
Взяв параметризацию х = asinV>, У = bcosip, 0 ^ ф ^ 2тг, получаем
2тг
2тг
= / >J{acQS\l)J + (—fesinVO2 dip = I у/а2 — (a2 - b2)sin2T/> dV> =
о о
тг/2 тг/2
= 4a / Wl - ^=^ sin2 V dxp = 4a f
о
о
где
= 1 2 ~~ квадрат эксцентриситета эллипса.
Интеграл
= /y/l-
о
не выражается в элементарных функциях и ввиду указанной связи с эллипсом
называется эллиптическим. Точнее, Е(к, ф) — эллиптический интеграл вто-
второго рода в форме Лежандра. Значение, которое он принимает при <р = тг/2,
зависит только от Л, обозначается через Е(к) и называется полным эллипти-
эллиптическим интегралом второго рода. Итак, Е(к) = 2?(fc,7r/2), поэтому длина
эллипса в этих обозначениях имеет вид Z = 4аЕ(к).
3. Площадь криволинейной трапеции. Рассмотрим фигуру аАВЬ
(рис. 48), называемую криволинейной трапецией. Фигура ограничена верти-
вертикальными отрезками аА, 6J3, отрезком [а, Ь] оси абсцисс и кривой АВ, являю-
являющейся графиком некоторой интегрируемой на [а, 6] функции у = f(x).
Пусть [a, ft] — отрезок, содержащийся в [а, 6].
Обозначим через 5(а,/?) площадь соответствую- у л В
щей ему криволинейной трапеции af(a)f(C)/3.
Наши представления о площади таковы: если
, то
(аддитивность площади) и
inf /(х) (/? - а) ^ 5(а,
€[0]
О
sup f(x) (/? - а)
ар
Рис. 48
Ъ х
(площадь объемлющей фигуры не меньше площади объемлемой).
Значит, в силу утверждения 1, площадь указанной фигуры надо вычислять
по формуле
б
[а, Ь) = / f(x) dx.
а
(9)

378 гл. vi. интеграл
Пример 5. Используем формулу (9) для подсчета площади эллипса, за-
заданного каноническим уравнением (8).
В силу симметрии фигуры и предполагаемой аддитивности площади, до-
достаточно найти площадь только той части эллипса, которая расположена в
первом квадранте, и затем учетверить полученный результат. Проведем вы-
вычисления:
п/2
S = 4 / Jb2(l - *р\ dx = 4ft / y/l - sin21 acost dt =
о о
tt/2 тг/2
= Aab I cos2 tdt = lab \ A - cos 2t) dt = nab.
о о
По дороге мы сделали замену х = asin?, 0 ^ t ^ тг/2.
Итак, 5 = nab. В частности, при а = b = R получаем формулу nR2
площади круга радиуса R.
Замечание. Необходимо отметить, что формула (9) дает площадь кри-
криволинейной трапеции при условии, что f(x) ^ 0 на [а, 6]. Если же / — про-
произвольная интегрируемая функция, то интеграл (9), очевидно, даст алгебра-
алгебраическую сумму площадей соответствующих криволинейных трапеций, лежа-
лежащих над и под осью абсцисс. Причем площади трапеций, лежащих над осью
абсцисс, будут суммироваться со знаком плюс, а площади трапеций, лежащих
под осью, — со знаком минус.
4. Объем тела вращения. Пусть теперь изображенная на рис. 48 кри-
криволинейная трапеция вращается вокруг отрезка [a, ft]. Определим объем полу-
получающегося при этом тела.
Обозначим через V(a,/3) объем тела, полученного вращением криволиней-
криволинейной трапеции af(a)f(/3)C (см. рис. 48), отвечающей отрезку [а,/?] С [a,ft].
По нашим представлениям об объеме, должны быть справедливы следую-
следующие соотношения: если a^a</3<j^b, то
И
тг [ inf fix) ] (/? — a) ^ V(a,/?) ^ п [ sup fix)) (/3 — a).
\xe[at0\ ) \xe[a,0) )
В последнем соотношении мы оценили объем V(a,/3) через объемы вписан-
вписанного и описанного цилиндров и воспользовались формулой объема цилиндра
(которую нетрудно получить, если уже найдена площадь круга).
Тогда в силу утверждения 1
6
ayb) = nff2(x)dx. A0)

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 379
Пример 6. Вращением вокруг оси абсцисс полукруга, ограниченного
отрезком [—R,R] этой оси и дугой окружности у = y/R2 — х2, -
можно получить трехмерный шар радиуса R, объем которого легко вычислить
по формуле A0):
R
(R2-x2)dx = ^
f
-Я
Подробнее об измерении длин, площадей и объемов будет сказано во II
части курса. Тогда же мы решим и вопрос об инвариантности данных опре-
определений.
5. Работа и энергия. Энергетические затраты, связанные с переме-
перемещением тела под действием постоянной силы в направлении действия силы,
измеряют произведением F • S величины силы на величину перемещения. Эта
величина называется работой силы на данном перемещении. В общем случае
направление данной силы и перемещение могут быть неколлинеарны (напри-
(например, везем за веревочку санки), и тогда работа определяется как скалярное
произведение (F, S) вектора силы и вектора перемещения.
Рассмотрим некоторые примеры вычисления работы и использования свя-
связанного с ней понятия энергии.
Пример 7. Работа, которую нужно совершить против силы тяжести,
чтобы поднять вертикально вверх тело массы т с уровня hi над поверхно-
поверхностью Земли на уровень /i2, в силу данного определения равна mg(h2 — hi).
Предполагается, что вся операция происходит у поверхности Земли, когда
изменением силы тяжести тд можно пренебречь. Общий случай разобран в
примере 10.
Пример 8. Пусть имеется идеально упругая пружина, один конец кото-
которой закреплен в точке 0 числовой оси, а другой находится в точке х. Известно,
что сила, с которой при этом приходится удерживать этот конец пружины,
равна кх, где к — коэффициент жесткости пружины.
Вычислим работу, которую надо совершить, чтобы переместить подвиж-
подвижный конец пружины из положения х = а в положение х = Ь.
Считая работу А(а,0) аддитивной функцией промежутка [а, /3] и прини-
принимая, что верны оценки
inf (кх) (/3 - а) ^ А(а,0) ^ sup (кх) (/? - а),
получаем в силу утверждения 1, что
Г кх2 ь
А(а, Ь) = / kxdx = —
J ?
а
Это работа против силы. Работа же самой силы пружины на том же пе-
перемещении отличается только знаком.

380 гл. vi. интеграл
кх2
Функция U(x) = -^—, которую мы нашли, позволяет, вычислять работу,
которую мы совершаем, меняя состояние пружины, а значит, и ту работу,
которую пружина может совершить при возвращении в исходное состояние.
Такая функция ?/(х), зависящая только от конфигурации системы, называется
потенциальной энергией системы. Из построения видно, что производная от
нее дает силу пружины с обратным знаком.
Если точка массы т движется вдоль оси под действием указанной упругой
силы, то ее координата x{t) как функция времени удовлетворяет уравнению
тх = —кх. A1)
Мы уже однажды проверяли (см. гл. V, § 6, п. 6), что величина
= K(t) + U(x{t)) = E, A2)
представляющая из себя сумму кинетической и (как мы теперь понимаем)
потенциальной энергий системы, остается во время движения постоянной.
Пример 9. Теперь рассмотрим еще один пример. В нем встретится
сразу целый ряд понятий, которые мы ввели и освоили в дифференциальном
и интегральном исчислении.
Заметим сначала, что по аналогии с функцией A2), записанной для кон-
конкретной механической системы, удовлетворяющей уравнению A1), для произ-
произвольного уравнения вида
s(t) = f(s(t)), A3)
где f(s) — заданная функция, можно проверить, что сумма
у + U(s) = Е A4)
не меняется со временем, если Uf(s) = ~f(s).
Действительно,
dE 1 ds2 ^ dU(s) ...dUds .... ., чч п
dt 2 dt dt ds dt
Таким образом, из A4), считая Е постоянной величиной, последовательно
находим
8 = ±y/2(E-U(8))
(где знак корня должен соответствовать знаку производной —), затем
си
dt _ 1
ds y/2(E-U(s))

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 381
и, наконец,
ds
у/2{Е-Щв))
Следовательно, используя закон сохранения «энергии» A4) уравнения A3),
нам удалось в принципе решить это уравнение, но найдя не функцию s(t), a
обратную к ней функцию t(s).
Уравнение A3) возникает, например, при описании движения точки вдоль
заданной кривой. Пусть частица перемещается под действием силы тяжести
по узкому идеально гладкому желобу (рис. 49).
Пусть s(t) — расстояние вдоль желоба (т. е. длина пути) от некоторой
фиксированной точки О — начала отсчета — до точки, в которой находится
частица в момент t. Ясно, что тогда s(t) есть
величина скорости частицы, a s(t) — величина
тангенциальной составляющей ее ускорения,
которая должна равняться величине тангенци-
тангенциальной составляющей силы тяжести в данной
точке желоба. Ясно также, что тангенциаль-
тангенциальная составляющая силы тяжести зависит толь- О
ко от точки желоба, т. е. зависит только от s, Рис. 49
ибо s можно считать параметром, параметри-
параметризующим кривую1), с которой мы отождествляем желоб. Если эту составляю-
составляющую силы тяжести обозначить через /(s), то мы получим, что
те = f(s).
Для данного уравнения сохраняться будет величина
где U'(s) = -
Поскольку слагаемое - те2 есть кинетическая энергия точки, а движение
вдоль желоба происходит без трения, то можно, минуя вычисления, догадать-
догадаться, что функция U(s) с точностью до постоянного слагаемого должна иметь
вид mgh(s)} где mgh(s) — потенциальная энергия точки, находящейся на вы-
высоте h(s) в папе тяжести.
Если в начальный момент t = О было s@) = 0, s@) = So и h(so) = Л<ь
из соотношения
— = s2 + 2gh(s) = С
т
^Параметризация кривой посредством ее же длины называется натуральной, а 5 в этом
случае называют натуральным параметром.

382
ГЛ. VI. ИНТЕГРАЛ
находим, что С = 2gh(so)y поэтому s2 = 2g(ho —
8
t =
ds
»o
- h(s))
A5)
В частности, если, как в случае маятника, точка движется вдоль окруж-
окружности радиуса Я, отсчет длины s ведется от нижней точки О окружности,
а начальные условия состоят в том, что при t = О
i@) = 0 и дан начальный угол — tpo отклонения
(рис. 50), то, как легко проверить, выражая s и h(s)
через угол отклонения <р, получим
8
-I
ds
ч>
«0
- h(s))
•I
~<PO
ИЛИ
Рис. 50
J */sin2 <?! _ oin2 t
-<po Vsm 2 2
Таким образом, для полупериода - Т качания маятника получаем
<Ро
-<ро
Vsm Т -sm ?
откуда после подстановки .
8
sin
= sin ^ находим
Напомним, что функция
A6)
A7)
A8)
называется эллиптическим интегралом первого рода в форме Лежандра. При
^р = тг/2 она зависит только от А;2, обозначается i^(fc) и называется полным

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА 383
эллиптическим интегралом первого рода. Таким образом, период колебаний
маятника равен
ГБ
A9)
Если угол <ро начального отклонения мал, то можно положить к = 0 и тогда
получим приближенную формулу
B0)
Теперь, когда формула A8) получена, все же следует проанализировать
весь ход рассуждений, и тогда мы заметим, что под знаками интегралов
A5)—A7) стоят неограниченные на отрезке интегрирования функции. По-
Подобная трудность нам уже встречалась при рассмотрении длины кривой, и
мы примерно представляем себе, как и какой смысл можно придать интегра-
интегралам A5) —A7).
Но раз этот вопрос возник вторично, то его следует разобрать в точной
математической постановке, что и будет сделано в следующем параграфе.
Пример 10. Тело массы т совершает подъем над поверхностью Земли
по траектории t »-> (x(t),y(t),z(t)), где t — время, а < t ^ ft, а х, у, z — де-
декартовы координаты точки в пространстве. Необходимо вычислить работу
тела против силы тяжести на промежутке времени [a, ft].
Работа А(а,/3) есть аддитивная функция промежутка [а,/?] С [а,ft].
Постоянная сила F при действии на тело, движущееся с постоянной скоро-
скоростью v, за время h совершает работу (F,v/i) = (F,v)h, поэтому представля-
представляется естественной оценка
inf <P(p(*)), v(t)) @ - а)< А{<*> Р) < sup <F(p(t))f v(t)) <fi - а),
[Д [0]
где v(t) — скорость тела в момент ?, p(t) — точка пространства, в которой
находится тело в момент ?, a F(p(t)) — сила, которая в точке р = p(t) дейст-
действует на тело.
Бели функция (F(p(t)),v(t)) окажется интегрируемой, то в силу утвержде-
утверждения 1 мы должны считать, что
В нашем случае \(t) = (x(t),y(t),z(t)), и если г(*) = (х(*),у(*), *(*)), то по
закону всемирного тяготения находим
GmM

384
ГЛ. VI. ИНТЕГРАЛ
где М — масса Земли, а ее центр предполагается совпадающим с началом
системы координат.
Тогда
, V)W=GmM
поэтому
I С
У (*"
а
Итак,
(X*(t) + V2(t) + *2(*)K/2
GmM
GmM
GmM GmM
Мы обнаружили, что искомая работа зависит только от величин |г(а)|,
г (Ь)| удаления тела т от центра Земли в начальный и конечный моменты
времени рассматриваемого промежутка [а, 6].
Полагая
получаем, что работа против силы тяжести по перемещению тела массы т из
любой точки сферы радиуса го в любую точку сферы радиуса г\ вычисляется
по формуле
Arori =m(U(ro)-U(ri)).
Функция U(r) называется потенциалом Ньютона. Если через R обозна-
обозначить радиус Земли, то, поскольку -^г- = д, функцию U (г) можно переписать
в виде
Учитывая это, можно получить следующее выражение для работы, необ-
необходимой для выхода из поля тяготения Земли, точнее, для увода массы m с
поверхности Земли на бесконечное расстояние от центра Земли. Под этой
величиной естественно понимать предел lim Art.
г—>+оо
Итак, работа выхода:
А =
= lim Art = lim m
+ +
r-»+oo
lim m (
r->+oo \ К
( —¦ —— ] =
Г J
= mgR.

§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА
385
Рис. 51
Задачи и упражнения
1. На рисунке 51 изображен график зависимости F = F{x) силы, действующей
вдоль оси абсцисс на пробную частицу; находящуюся в точке х этой оси.
a) Нарисуйте в той же системе координат
эскиз потенциала этой силы.
b) Изобразите потенциал силы — F(x).
c) Исследуйте, в каком из разобранных случа-
случаев положение xq является устойчивым положени-
положением равновесия и с каким свойством потенциала
это связано.
2. На основе результата примера 10 вычисли-
вычислите скорость, которую должно иметь тело, чтобы
оно вышло из поля тяготения Земли (вторая кос-
космическая скорость для Земли).
3. На основе примера 9
a) выведите уравнение R(p = g sin (p колеба-
колебаний математического маятника;
b) считая колебания малыми, получите его приближенное решение;
c) определите по приближенному решению период колебаний маятника и сравни-
сравните результат с формулой B0).
4. По горизонтальной плоскости равномерно со скоростью v катится без про-
проскальзывания колесо радиуса г. Пусть в момент t = 0 верхняя точка А колеса имеет
координаты @,2г) в системе декартовых координат, ось
абсцисс которой лежит в указанной плоскости и направле-
направлена по вектору скорости.
a) Запишите задсон движения t н* (я(?), y(t)) точки А. У
b) Найдите скорость точки А как функцию времени.
c) Изобразите графически траекторию точки А (эта
кривая называется циклоидой).
d) Найдите длину одной арки циклоиды (длину одного
периода этой периодической кривой).
e) Циклоида обладает рядом интересных свойств, одно q
из которых, открытое Гюйгенсом1^, состоит в том, что
период колебаний циклоидального маятника (шарика, ка-
катающегося в циклоидальной ямке) не зависит от высоты
его подъема над нижней точкой ямки. Попробуйте доказать это, опираясь на при-
пример 9. (См. также задачу 6 следующего параграфа, посвященного несобственным
интегралам.)
5. а) Исходя из рис. 52, объясните, почему если у = /(ж) и х = д(у) — взаимно
обратные непрерывные неотрицательные функции, равные нулю при х = 0 и у = 0
соответственно, то должно быть выполнено неравенство
X
Рис. 52
X У
Jf(t)dt + Jg(t)
dt.
о
. Гюйгенс A629 — 1695) — нидерландский механик, физик, математик и астроном.

386 гл. vi. интеграл
b) Получите из а) неравенства Юнга
_s> I v , 1 а
ХУ^ рХ +qV
при х, у J* 0, р, g > 0, - + - = 1.
c) Какой геометрический смысл имеет знак равенства в неравенствах задач а)
иЬ)?
6. Задача Бюффона1^. Число 7г можно вычислять следующим весьма неожидан-
неожиданным способом.
Берем большой лист бумаги, разлинованный параллельными прямыми с шагом
/i, и бросаем на него, никак специально не целясь, иголку длины I < h. Пусть мы
бросили иголку N раз и пусть п раз из них иголка после падения пересекала какую-
21
нибудь из прямых линий на листе. Если число N достаточно велико, то 7г « —, где
prt
р = — можно трактовать как приближенное значение вероятности того, что при
бросании иголка пересечет одну из линий.
Исходя из геометрических соображений, связанных с вычислением площадей,
попробуйте дать удовлетворительное объяснение этому методу вычисления тг.
§ 5. Несобственный интеграл
В предыдущем параграфе мы уже столкнулись с необходимостью несколько
расширить понятие интеграла Римана. Там же на разборе конкретной задачи
мы составили себе представление о том, в каком направлении и как это следует
сделать. Настоящий параграф посвящен реализации этих представлений.
1. Определения, примеры и основные свойства
несобственных интегралов
Определение 1. Пусть функция х »-> f(x) определена на промежутке
[а, +оо[ и интегрируема на любом отрезке [a, ft], содержащемся в этом проме-
промежутке.
Величина
+ОО 6
/f(x) dx := lim / fix) dx,
&-++oo J
a
если указанный предел существует, называется несобственным интегралом
Римана или просто несобственным интегралом от функции f no промежут-
промежутку [а, +оо[.
+0О
Сам символ I f(x)dx также называют несобственным интегралом и то-
а
гда говорят, что несобственный интеграл сходится, если указанный предел
. Л. Л. Бюффон A707—1788) — французский естествоиспытатель.

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
387
существует, и расходится в противном случае. Таким образом, вопрос о схо-
сходимости несобственного интеграла равносилен вопросу о том, определен ли
вообще этот несобственный интеграл или нет.
Пример 1. Исследуем, при каких значениях параметра а сходится или,
что то же самое, определен несобственный интеграл
+ОО
J Х<*
A)
Поскольку
о
/— —
х<* ~
1-Q
1-х»-
при а/1,
при а = 1,
то предел
f dx I
im / — =
>+оо J xa a — 1
lim
6-++OO
существует только при а > 1.
Итак,
оо
Г dx 1
J ха а - 1
если
а при других значениях параметра а интеграл A) расходится, т. е. не опре-
определен.
Определение 2. Пусть функция х »-> /(ж) определена на промежутке
[а, В[ и интегрируема на любом отрезке [а, Ь] С [а, В[. Величина
/fix) dx := lim / fix) dx,
если указанный предел существует, называется несобственным интегралом
от функции f no промежутку [о, В[.
Суть этого определения состоит в том, что в любой окрестности конечной
точки В функция / может оказаться неограниченной.
Аналогично, если функция х »-> f(x) определена на промежутке ]А, Ь] и
интегрируема на любом отрезке [а, Ь] С ]А, 6], то по определению полагают
//(ж) dx := lim / f(x)
Л а
dx

388 гл. vi. интеграл
и также по определению полагают
6
/fix) dx := lim / fix) dx.
a->-oo J
oo
Пример 2. Исследуем, при каких значениях параметра а сходится ин-
интеграл
/
J
Ч
ха
о
Поскольку при а € ]0,1]
1
dx
1-
1а
то предел
если а ф 1,
= j i - а а
lnxL, если а = 1,
lim
1 - а
существует только при а < 1.
Итак, интеграл B) определен только при а < 1.
Пример 3.
о о
fexdx= lim f exdx = lim (e*?) = lim A - ea) = 1.
у a-+—ooj a—>—oo V °/ a—>—oo
—oo a
Поскольку вопрос о сходимости несобственного интеграла решается оди-
одинаково как для несобственного интеграла по неограниченному промежутку,
так и для несобственного интеграла от функции, неограниченной около од-
одного из концов промежутка интегрирования, то в дальнейшем мы будем рас-
рассматривать оба эти случая вместе, введя следующее основное
Определение 3. Пусть [a,a;[ — конечный или бесконечный промежу-
промежуток, ахи f(x) — функция, определенная на нем и интегрируемая на каждом
отрезке [a, b] С [а,а;[. Тогда по определению
и; 6
ff(x)dx := lim [f(x)dx, C)
J Ъ-Ыл) J
если указанный предел при Ь -> ш, Ь € [a,a;[, существует.
В дальнейшем, если не оговорено противное, рассматривая несобственный
интеграл C), мы будем предполагать, что подынтегральная функция удовле-
удовлетворяет условиям определения 3.

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 389
Кроме того, для определенности мы будем пока считать, что несобствен-
несобственность интеграла связана только с верхним пределом интегрирования. Рас-
Рассмотрение случая, когда особенность интеграла связана с нижним пределом,
проводится дословно так же.
Из определения 3, свойств интеграла и свойств предела можно сделать
следующее заключение о свойствах несобственного интеграла.
Утверждение 1. Пусть х н-*> f(x) и а; и д(х) — функции, определен-
определенные на промежутке [а,а;[ и интегрируемые на любом отрезке [а, Ь] С [а,а>[.
Пусть для них определены несобственные интегралы
и>
/
a
/
f(x)dx, D)
g(x) dx. E)
Тогда
a) Если ш € К и / G И[а,и>], то значения интеграла D), понимаемого как
в несобственном, так и в собственном смысле, совпадают.
b) При любых Ai, A2 G Ш функция (Ах/ + Агр)(а:) интегрируема в несоб-
несобственном смысле на [а,а;[ и справедливо равенство
U) UJ
j (Ai/ + \2g){x)dx = Ai / f(x)dx + A2 / g(x)dx.
a a a
с) Если с G [a,o;[, mo
U> С Ш
I f(x)dx= I f(x)dx+ ff(x)dx.
a
d) Если (p : [a,7[ -> [a,u>[ — гладкое, строго монотонное отображение,
причем ip(a) = а и ip(/3) -> и при C -> j, /3 G [a,7[> mo несобственный инте-
интеграл от функции t н-» (/ о (p)(t)(pr(t) на [а,7[ существует и справедливо ра-
равенство
и; 7
Jf(x)dx = J (f ° <p)(t) ч>'(t) dt.
а а
< а) Следует из непрерывности функции
о
= If(x)
dx
на отрезке [a,a>], на котором / G 7?.[a,a>].

390 гл. vi: интеграл
b) Следует из того, что при Ь € [а, а;
6
а
dx = Ai / /(х) dx + А2 / ^(х) dx.
с) Следует из равенства
о с о
ff(x)dx=[f(x)dx+ff(x)dx,
справедливого при любых 6, с € [а,ш[.
d) Следует из формулы
ь = <р(/з)
f(x)dx^J(foip)(t)ipf(t)dt
а =
замены переменной в определенном интеграле. >
Замечание 1. К свойствам несобственного интеграла, выраженным в
утверждении 1, следует еще добавить весьма полезное правило интегрирова-
интегрирования по частям в несобственном интеграле, которое мы приведем в следующей
формулировке:
Если f,g€ СAЦа,и>[ и существует предел lim (f-g)(x), то функции
X-+UJ
f' • gf и f'-g одновременно интегрируемы или не интегрируемы в несобствен-
несобственном смысле на [а,ш[ и в случае интегрируемости справедливо равенство
= (f-g)(x)\ua-f(f'-g)(x)dx,
а а
где
(/•<?)(*)!?= Ит (f-9)(x)-(f-g)(a).
а
X-+LJ
Это следует из формулы
о о
J'(/ ¦ g')(x) dx = (/ • д)(х)\"а - J'(/'• д){х) dx
интегрирования по частям в собственном интеграле. >

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 391
Замечание 2. Из пункта с) утверждения 1 видно, что несобственные
интегралы
ш
Jf(x)dx, Jf{x)dx
а с
сходятся или расходятся одновременно. Таким образом, в несобственных ин-
интегралах, как и в рядах, сходимость не зависит от начального куска ряда или
интеграла.
По этой причине иногда, ставя вопрос о сходимости несобственного инте-
интеграла, вообще опускают тот предел интегрирования, около которого интеграл
не имеет особенности.
При таком соглашении полученные в примерах 1, 2 результаты можно за-
записать так:
Г dx ^i
интеграл / — сходится только при а > 1;
f dx ^1
интеграл / — сходится только при а < 1.
+о
Знак -f 0 в последнем интеграле показывает, что рассматривается область
х > 0.
Заменой переменной из последнего интеграла сразу получаем, что
Г dx ^л
интеграл / -t — сходится только при а < 1.
J (х- хо)
жо+0
2. Исследование сходимости несобственного интеграла
а. Критерии Коши. В силу определения 3, сходимость несобственного
интеграла C) равносильна существованию предела функции
6
Т{Ь) = f f(x) dx F)
а
при Ь -? шг Ье (а,а?[.
Поэтому справедливо следующее
Утверждение 2 (критерий Копш сходимости несобственного инте-
интеграла). Если функция х ^ f(x) определена на промежутке [а,ш[ и инте-
грируема на любом отрезке [а, Ь] С [а,а;[, то интеграл ff(x)dx сходится
а
тогда и только тогда, когда для любого е > 0 можно указать В € [а,ш[

392
ГЛ. VI. ИНТЕГРАЛ
так, что при любых 61,62
соотношение
Действительно, ведь
таких, что В <Ь\, В < Ьг, имеет место
ь2
f
f(x)dx
Jf(x)dx = Jf(x)dx - |/(*)d* =
поэтому выписанное условие есть просто критерий Коши существования пре-
предела функции Т(Ъ) при Ь -» ш, Ь € [а,о>[. >
Ь. Абсолютная сходимость несобственного интеграла
Определение 4. Про несобственный интеграл I f(x)dx говорят, что
U)
он сходится абсолютно, если сходится интеграл I \f\(x)dx.
а
В силу неравенства
62 &2
Jf(x)dx ^ f\f\(x)dx
bi
и утверждения 2 можем заключить, что если интеграл сходится абсолютно,
то он сходится.
Исследование абсолютной сходимости сводится к исследованию сходимо-
сходимости интеграла от неотрицательной функции. Но в этом случае имеем
Утверждение 3. Если функция f удовлетворяет условиям определе-
определения 3 и f(x) ^ 0 на [а,о>[, то несобственный интеграл C) существует в
том и только в том случае, когда функция F) ограничена на [а,ш[.
< Действительно, если f(x) ^ 0 на [о,а;[, то функция F) неубывающая на
[а,о>[ и потому она имеет предел при b -> a;, b G [а,а;[, если и только если она
ограничена. >
В качестве примера использования этого утверждения рассмотрим такое
его
Следствие (интегральный признак сходимости ряда). Если х н* f(x) —
определенная на промеоюутке [1,+оо[ неотрицательная, невозрастающая,
интегрируемая на каждом отрезке [1,6] С [1,+оо[ функция, то ряд
оо
? /(п) = /A) + /B) + ...
п=1

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 393
и интеграл
Т
I f(x)dx
1
сходятся или расходятся одновременно.
^ Из приведенных условий вытекает, что при любом п Е N выполнены
неравенства
п + 1
п
После суммирования этих неравенств получаем
n=l i п=1
ИЛИ
к Ь
где «л = Х^ /(гс)> а Т(Ъ) = ff(x)dx. Поскольку Sk и ^*F) — неубывающие
п=1 /
функции своих аргументов, то полученные неравенства и доказывают выска-
высказанное утверждение. >
В частности, теперь можно сказать, что результат примера 1 эквивалентен
тому, что ряд
00 1
, п<*
сходится только при а > 1.
Наиболее часто используемым следствием утверждения 3 является следую-
следующая
Теорема (теорема сравнения). Пусть функции х н* f(x), at н* g(x) опре-
определены на промежутке [a,cj[ и интегрируемы на любом отрезке [а, Ь] С [а,ш[.
Если на [а,ш[
О ^ f{x) ^
то из сходимости интеграла E) следует сходимость интеграла D) и спра-
справедливо неравенство
U)
I f(x) dx ^ / g(x) dx,
а
а из расходимости интеграла D) следует расходимость интеграла E).

394
ГЛ. VI. ИНТЕГРАЛ
М Из условий теоремы и неравенств для собственного интеграла Римана
при любом 6G [о,ш[ имеем
о о
Т(Ъ) = Jf(x) dx ^ jg{x) dx = д(Ъ).
Поскольку обе функции Т, Q неубывающие на [а,о;[, то теорема следует
из написанного неравенства и утверждения 3. >
Замечание 3. Если про функции /, д, участвующие в теореме, вместо
неравенств 0 ^ f(x) ^ д(х) известно, что они неотрицательны на [а,ш[ и
одного порядка при х -> ш, х ? [a,t<4> т. е. что найдутся такие положительные
константы ci, С2, что
то с учетом линейности несобственного интеграла из доказанной теоремы в
этом случае можно заключить, что интегралы D), E) сходятся или расходятся
одновременно.
Пример 4. Интеграл
+оо
/
dx
сходится, так как
yfxdx
/¦ч/
при х -» Н-оо.
Пример 5. Интеграл
+ОО
/
cos а:
dx
сходится абсолютно, ибо
cosx
х2
X
при х ^ 1. Следовательно,
-Ьоо
/
COSX
х'4
dx
-boo
/
COS Ж
х:
+оо
CKI7 ^> I ' « UhJU — X
Пример 6. Интеграл
+ОС
/<
е~ж dx

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 395
сходится, так как е х < е х при х > 1 и
+ОО +ОО
/ е х* dx < I e~~x dx = -
1 1
Пример 7. Интеграл
+ОО
dx
J
J lnx
расходится, ибо
lnx х
при достаточно больших значениях х.
Пример 8. Интеграл Эйлера
тг/2
/ In sin х
сходится, так как
|lnsinx|~ |lnx| < -7=
ух
при X -? +0.
Пример 9. Эллиптический интеграл
dx
при 0 ^ к2 < 1 сходится, поскольку
х2)A - Jb2x2)
при х ->• 1 — 0.
Пример 10. Интеграл
1
dip
\/cos в - cos <р
о v
сходится, так как
cos</> = W2sin ^—— sin ^—— ^ y/sirup (up
при в -> у? — 0.

396 ГЛ. VI. ИНТЕГРАЛ
Пример 11. Интеграл
/ • 2 ^0
4 / Sin •*¦; Sin
V 2
G)
при 0 < <ро < тг сходится, поскольку при ф -> у>0 — О
2
- sin21 ~ v^i^ (?>о - ФI'2. (8)
Соотношение G) выражает зависимость периода колебаний математиче-
математического маятника от его длины L и начального угла его отклонения, отсчитывае-
отсчитываемого от радиуса, идущего в нижнюю точку траектории качания. Формула G)
является элементарной вариацией формулы A7) предыдущего параграфа.
Маятник можно себе представлять, например, как невесомый стержень,
один конец которого шарнирно закреплен, а другой, с присоединенной к нему
точечной массой, свободен.
В таком случае можно говорить о любых начальных углах у?о € [О,тг]. При
<Ро = 0 и (ро = тг маятник качаться вообще не будет, находясь в первом слу-
случае в состоянии устойчивого, а во втором случае в состоянии неустойчивого
равновесия.
Интересно отметить, что из G) и (8) нетрудно получить, что Т -> оо при
(ро -> тг — 0, т. е. период колебаний маятника неограниченно растет по мере
приближения его начального положения </>о к верхнему положению (неустой-
(неустойчивого) равновесия.
с. Условная сходимость несобственного интеграла
Определение 5. Если несобственный интеграл сходится, но не абсо-
абсолютно, то говорят, что он сходится условно.
Пример 12. Используя замечание 1, по формуле интегрирования по ча-
частям в несобственном интеграле находим, что
+ОО ^ +ОО +ОО
/ [ cosx f cosx
X2
/sinx . cosx f cosa; , /"
Ж X n/2 J X J
n/2 ' тг/2 tt/2
тг/2 тг/2
коль скоро последний интеграл сходится. Но, как мы видели в примере 5, этот
интеграл сходится, поэтому сходится также интеграл
+оо
/S*n Х
—
тг/2
dx. (9)

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 397
Вместе с тем интеграл (9) не является абсолютно сходящимся. Действи-
Действительно, при b € [тг/2, +оо[ имеем
/sinx , . f sin2 х л __ 1 f dx If cos2x , ппч
""¦—~~~> CtX ^ I ——— ДХ — —¦ I —— — — I ————— дд;. ( AU)
x ' J x 2 J x 2 J x vy
тг/2
Интеграл
sin2x
X
/
тг/2
ix =
COS
X
1
2
2x
6
/
тг/2
dx,
dx
X
6
2 У
тг/2
cos2x ,
X
как можно проверить интегрированием по частям, является сходящимся, по-
поэтому при Ь -? -f оо разность в правой части соотношения A0) стремится к
-Ьоо и в силу оценки A0) интеграл (9) не является абсолютно сходящимся.
Приведем теперь один специальный признак сходимости несобственных
интегралов, опирающийся на вторую теорему о среднем и, значит, в сущности
на ту же формулу интегрирования по частям.
Утверждение 4 (признак Абеля—Дирихле сходимости интеграла).
Пусть х *-> f(x), х н* д(х) — функции, определенные на промежутке [а,а;[
и интегрируемые на любом отрезке [а, Ь] С [а,и;[. Пусть g — монотонная
функция.
Тогда для сходимости несобственного интеграла
и>
f(f'9)(x)
dx A1)
достаточно, чтобы выполнялась либо пара условий:
а\) интеграл I f(x)dx сходится,
а
Pi) функция g ограничена на [а,и>[,
либо пара условий:
ь
функция Т(Ь) = / f(x)dx ограничена на [а,ш[,
а
функция д(х) стремится к нулю при х -? ш, ж € [а,о;[.
Для любых 6i, 62 € [я,а;[ по второй теореме о среднем имеем
62 4 ^2
/ (/ • 9)(х) dx = д(Ъг) I /(x) dx + д(Ь2) I /(x) dx,
6i 6i ^

398 гл.-vi. интеграл
где ? — точка, лежащая между Ьх и &2 • Отсюда в силу критерия Коши (утвер-
(утверждение 2) заключаем, что интеграл A1) действительно сходится, если выпол-
выполнена любая из двух указанных выше пар условий. >
3. Несобственные интегралы с несколькими особенностями. До
сих пор мы говорили о несобственных интегралах с одной особенностью, свя-
связанной с неограниченностью функции у одного из пределов интегрирования
или с неограниченностью самого этого предела. Здесь мы укажем, в каком
смысле понимаются другие возможные варианты несобственного интеграла.
Если оба предела интегрирования являются особенностями того или дру-
другого из указанных выше типов, то полагают по определению
Jf(x)dx:= Jf(x)dx + Jf(x)dx, A2)
U/1 ~ U/1 С
где с — произвольная точка промежутка
При этом предполагается, что каждый из несобственных интегралов в пра-
правой части соотношения A2) сходится. В противном случае говорят, что ин-
интеграл, стоящий в левой части A2), расходится.
В силу замечания 2 и свойства аддитивности несобственного интеграла,
определение A2) корректно в том смысле, что оно на самом деле не зависит
от выбора точки с €
Пример 13.
1 О
/dx _ Г dx Г dx
vT^F ~ J vT^2 J ,/гзр
-1 О
= arcsmz + arcsmx L = arcsmz , = тг.
Пример 14. Интеграл
е х dx
— oo
называется интегралом Эйлера — Пуассона, а иногда еще и интегралом Гаус-
Гаусса. Он, очевидно, сходится в указанном выше смысле. Позже будет показано,
что он равен
Пример 15. Интеграл
+ ОО
J Z<*
О

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 399
расходится, поскольку при любом а разойдется по крайней мере один из двух
интегралов
+оо
/dx Г dx
х"' У х"*
О 1
Пример 16. Интеграл
+оо
/sinx ,
ах
х<*
о
сходится, если сходится каждый из интегралов
/sinx , f sinx ,
ax, / ax.
xa J x<*
О 1
Первый из этих интегралов сходится, если а < 2, ибо
sinx 1
XQ. rfOt— I
при х -> -1-0. Второй интеграл сходится при а > 0, что можно проверить
непосредственно интегрированием по частям, аналогичным проделанному в
примере 12, или сославшись на признак Абеля —Дирихле. Таким образом,
исходный интеграл имеет смысл при 0 < а < 2.
В том случае, когда подынтегральная функция не ограничена в окрестно-
окрестности одной из внутренних точек и> отрезка интегрирования [а,Ь], полагают
b и b
ff(x) dx := ff(x) dx + ff(x) dx, A3)
а аи
требуя, чтобы оба стоящих справа интеграла существовали.
Пример 17. В смысле соглашения A3)
dx л
= 4.
/
1
Пример 18. Интеграл / — неопределен.
J х
Существует и отличное от A3) соглашение о вычислении интеграла от
функции, неограниченной в окрестности внутренней точки и отрезка инте-
интегрирования. А именно, полагают
6 / и) — 6 b \
V. P.//(x) dx := tflimo I f f(x) dx + f f{x) dx ), A4)

400 гл. vi. интеграл
если стоящий справа предел существует. Этот предел называют, следуя Коши,
интегралом в смысле главного значения и, чтобы отличить определения A3)
и A4), во втором случае перед знаком интеграла ставят начальные буквы
V. Р. французских слов valeur principal (главное значение). В англоязычном
варианте используется обозначение Р. V. (от principal value).
В соответствии с этим соглашением имеем
Пример 19.
Принимается также следующее определение:
+оо R
V.P. Г f(x)dx:= lim f f(x)dx. A5)
J Я->+оо J
•oo -R
Пример 20.
+ОО
V
.P. Г xdx = 0.
—oo
Наконец, если на промежутке интегрирования имеется несколько (конеч-
(конечное число) тех или иных особенностей, лежащих внутри промежутка или со-
совпадающих с его концами, то неособыми точками промежуток разбивают на
конечное число таких промежутков, в каждом из которых имеется только од-
одна особенность, а интеграл вычисляют как сумму интегралов по отрезкам
разбиения.
Можно проверить, что результат такого расчета не зависит от произвола
в выборе разбиения.
Пример 21. Точное определение интегрального логарифма теперь мож-
можно записать в виде
X
/
О
X
J In*'
-—, если 0 < х < 1,
In с
V.P. / ;—:, если 1 < х.
о
В последнем случае символ V. Р. относится к единственной внутренней для
промежутка ]0,х] особенности, расположенной в точке 1. Заметим, что в
смысле определения A3) этот интеграл не является сходящимся.

§ 5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 401
Задачи и упражнения
1. Покажите, что функция
х
a) Six = / ——dt (интегральный синус) определена на R, нечетна и имеет
о
предел при х —>• +оо;
оо
b) si х = — / —— dt определена на R и отличается от функции Si x только на
X
постоянную;
оо
c) Ci х = — / —— dt (интегральный косинус) при достаточно больших значениях
х
ж может вычисляться по приближенной формуле Cia: « шж; оцените область тех
значений, где абсолютная погрешность этого приближения меньше 10~4.
2, Покажите, что
-foo -foo
ч Г sinx , /* cosx j ^ л
a) интегралы / —^~ аж, / —— dx сходятся только при а > 0, причем схо-
J X J X
1 1
дятся абсолютно только при а > 1;
b) интегралы Френеля
С(х) = -j= I cos t2dt, S(x) = -i= f sin t2dt
о
являются бесконечно дифференцируемыми функциями в промежутке ]0, +оо[, при-
причем обе они имеют предел при х —>• +оо.
3. Покажите, что
а) эллиптический интеграл первого рода
sin
/•
определен при 0^/с<1, 0^у?<^и приводится к виду
-/
dtp
Ъ) полный эллиптический интеграл первого рода
7Г/2
= /
dip
л/1 -A;2 sin2
0 v
неограниченно возрастает при к —> 1 — 0.

402 гл. vi. интеграл
4. Покажите, что
а) интегральная показательная функция (интегральная экспонента) Ei(a;) =
= / — dt определена и бесконечно дифференцируема при х < 0;
— ОО
b) - Ei(-x) = <Cl(l-! + -*-...+ (-!)»? + „( ?)) при х -> +оо;
ОО |
c) ряд 5^ (—1)п-^- не сходится ни при каком значении х € R;
n=0
d) lia: ~ -— при x —»• -1-0. (Определение интегрального логарифма Их см. в
примере 21.)
5. Покажите, что
X
1 Г 2
а) функция ф(х) = ~т= / е~Ь dt>i называемая интегралом вероятности ошибок
Л/ТГ J
— х
и часто обозначаемая символом erf (х) (от англ. error function — функция ошибок),
определена, нечетна, бесконечно дифференцируема на R и имеет предел при х
Ь) если упомянутый в а) предел равен единице (а это так), то
л 2 _Х2/ 1 1 13 1-3-5
1 и +
о
при а: —^ + оо.
6. Покажите, что:
а) Бели тяжелая частица под действием силы тяжести скользит вдоль кривой,
заданной в параметрическом виде х = х@), у = у@), причем в момент t = 0 частица
имела нулевую скорость и находилась в точке Хо = х($о), у = у@о)> то между пара-
параметром 0, определяющим точку на кривой, и моментом ? прохождения частицей этой
точки имеется связь (см. формулу A5) из § 4)
t-
в которой несобственный интеграл заведомо сходится, если у1 (во) ф 0 (знак выби-
выбирается в зависимости от того, имеют ли t и 0 одинаковый или противоположный
характер монотонности, причем если росту t отвечает рост 0, то, разумеется, сле-
следует брать знак плюс).
Ь) Период колебания частицы в ямке, имеющей профиль циклоиды
\в\ ^ тг,
у = -ДA +cos0),
не зависит от уровня уо = —ЯA + cos#o), с которого она начинает скольжение, и
равен 4тгу/R/g (см. задачу 4 из § 4).

ГЛАВА VII
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ,
ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
До сих пор мы рассматривали почти исключительно числовые функции х »->
i-> f(x), в которых число f(x) определялось заданием одного числа х из об-
области определения функции.
Однако многие величины, представляющие интерес, зависят не от одного,
а от очень многих факторов, и если сама величина и каждый из определяющих
ее факторов могут быть охарактеризованы некоторым числом, то указанная
зависимость сводится к тому, что упорядоченному набору (х1, ..., хп) чисел,
каждое из которых описывает состояние соответствующего фактора, ставит-
ставится в соответствие значение у = /(ж1, ..., хп) исследуемой величины, которое
она приобретает при этом состоянии определяющих величину факторов.
Например, площадь прямоугольника есть произведение длин его сторон;
объем данного количества газа вычисляется по формуле
Р
где R — постоянная, т — масса, Т — абсолютная температура и р — давле-
давление газа. Таким образом, значение V зависит от переменной упорядоченной
тройки чисел (т, Т, р) или, как говорят, V есть функция трех переменных га,
Тир.
Мы ставим себе целью научиться исследовать функции многих переменных
так же, как мы научились исследовать функции одного переменного.
Как и в случае функций одного переменного, изучение функций многих
числовых переменных начинается с описания их области определения.
§ 1. Пространство Шт и важнейшие классы
его подмножеств
1. Множество Ет и расстояние в нем. Условимся через Ет обозна-
обозначать множество всех упорядоченных наборов (я1, ...,хт), состоящих из т
действительных чисел хг G Е (г = 1, ..., т).
14 Зорич В. А.

404 гл. vii. функции многих переменных
Каждый такой набор будем обозначать одной буквой ж = (ж1, ..., хт) и
в соответствии с удобной геометрической терминологией называть точкой
множества Ет. Число ж* в наборе (ж1, . ..,жт) называют г-й координатой
точки х = (ж1, ..., хт).
Геометрические аналогии можно продолжить и ввести на множестве Ет
расстояние между точками х\ = (ж}, ..., ж}71), ж2 = (ж2, ..., ж™) по формуле
m
(!)
t=l
Функция
d: тат
определяемая формулой A), очевидно, обладает следующими свойствами:
a) d(xi,x2) ^ 0;
b) (d(xux2) = 0)<=> (Ж1 = ж2);
c) сг(жьж2) = d(x2,xi);
d) й(ж1,ж3) ^ d(xi,x2) + й(ж2,ж3).
Последнее неравенство (называемое опять-таки по геометрической аналогии
неравенством треугольника) есть частный случай неравенства Минковского
(см. гл. V, § 4, п. 2).
Функцию, определенную на парах (жх, х2) точек некоторого множества X
и обладающую свойствами а), Ь), с), d), называют метрикой или расстоянием
вХ.
Множество X вместе с фиксированной в нем метрикой называют метри-
метрическим пространством.
Таким образом, мы превратили Rm в метрическое пространство, наделив
множество Ет метрикой, заданной соотношением A).
Сведения о произвольных метрических пространствах читатель сможет
получить в главе IX (часть II). Здесь же мы не хотим отвлекаться от необхо-
необходимого нам сейчас конкретного метрического пространства Rm.
Поскольку в этой главе множество Ет с метрикой A) будет для нас един-
единственным метрическим пространством, составляющим объект изучения, то
общее определение метрического пространства нам по существу пока не нуж-
нужно. Оно приведено только для пояснения употребляемого по отношению к
множеству Ет термина «пространство» и по отношению к функции A) тер-
термина «метрика».
Из соотношения A) следует, что при г G {1,..., ш}
\х\ ~ х2\ ^ d(xi,x2) ^. у/т max \х\ — ж2|, B)
т. е. расстояние между точками х\, х2 G Em мало в том и только в том случае,
когда мало отличаются соответствующие координаты этих точек.

§ 1. ПРОСТРАНСТВО Rm И КЛАССЫ ЕГО ПОДМНОЖЕСТВ 405
Из B), как и из A), видно, что при т = 1 множество R1 совпадает с множе-
множеством действительных чисел, расстояние между точками которого измеряется
стандартным образом посредством модуля разности чисел.
2. Открытые и замкнутые множества в Шпг
Определение 1. При 6 > 0 множество
В(а; 6) = {х ? Шт \ d(a, х) < 6}
называется шаром с центром a Е Em радиуса 6 или также 6-окрестностью
точки a G тот
Определение 2. Множество G С Шт называется открытым в Rm,
если для любой точки х ? G найдется шар В{х; 8) такой, что В(х; S) С G.
Пример 1. Rm — открытое множество в Rm.
Пример 2. Пустое множество 0 вообще не содержит точек и потому
может считаться удовлетворяющим определению 2, т. е. 0 — открытое мно-
жество в lu)m
Пример 3. Шар В (а; г) — открытое множество в
Действительно, если х G В(а;г), т. е. d(a,х) < г, то при 0 < с$ < г — d(a,x)
будет В(х;6) С В(а;г), поскольку
=> (d(a, ?) < d(a, x) + d(x, ?) < d(a, x) + r — d(a, x) = r)
Пример 4. Множество G = {x e Mm|d(a,x) > г}, т. е. совокупность
точек, удаленных от фиксированной точки а ? Мт на расстояние, большее
чем г, является открытым, что, как и в примере 3, легко проверить, используя
неравенство треугольника для метрики.
Определение 3. Множество F С Шт называется замкнутым в Ет,
если его дополнение G = Ет \F в Ет является множеством, открытым в Ет.
Пример 5. Множество В(а;г) = {х € Rm\d(a,x) ^ г}, г ^ 0, т. е.
совокупность точек, удаленных от фиксированной точки а ? Шт не больше
чем на г, является замкнутым, что следует из определения 3 и примера 4.
Множество В{а; г) называют замкнутым шаром с центром а радиуса г.
Утверждение 1. а) Объединение |J Ga множеств любой системы
a, а ? А} множеств, открытых в Жт, является множеством, откры-
тым в IU>m
п
Ь) Пересечение f) Gi конечного числа множеств, открытых в Шт, явля-
г=1
ется множеством, открытым в т>гп
14*

406 ГЛ. VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
а') Пересечение f] Fa множеств любой системы {Fa, a € А} множеств
Fa, замкнутых в Rm, является множеством, замкнутым в тот
п
Ь') Объединение (J Fi конечного числа множеств F,, замкнутых в Rm,
г=1
является множеством, замкнутым в Rm.
М а) Если х ? U Ga, то найдется такое ао ? А, что х ? Gao, и, следо-
вательно, найдется такая <5-окрестность В(х;5) точки х, что В(х;6) С Gao.
Значит, В{х\8) С (J Ga.
п
b) Пусть х ? П Gi. Тогда х ? Gi (i = 1, ..., n). Пусть <$i, ..., Sn —
такие положительные числа, что B(x;Si) С Gi (г = 1, ... ,п). Полагая E =
n
= min{<5i, ..., <$n}, очевидно, получим, что <$ > 0 и В(х;6) С (°| Gj.
а') Покажем, что множество С( f] Fa), дополнительное к f] Fa в Rm,
является открытым подмножеством
Действительно,
= [j {СFa) = U
где Ga = CFa открыты в Rm. Теперь а') следует из а).
Ь') Аналогично, из Ь) получаем
Лг=1 ' г=1 г=1
Пример 6. Множество 5(а;г) = {х ? Rm|d(a,x) = г}, г ^ 0, назы-
называется сферой с центром а ? Rm радиуса г. Дополнение к S(a]r) в Rm в
силу примеров 3 и 4 является объединением открытых множеств. Значит, в
силу доказанного утверждения оно открыто, а сфера 5(а; г) есть замкнутое
подмножество Rm.
Определение 4. Открытое в Rm множество, содержащее данную точ-
точку, называется окрестностью этой точки в Rm.
В частности, как следует из примера 3, J-окрестность точки является ее
окрестностью.
Определение 5. Точка х ? Rm по отношению к множеству Е С Rm
называется:
внутренней точкой Е, если она содержится в Е вместе с некоторой своей
окрестностью;
внешней точкой Е, если она является внутренней точкой дополнения к Е
•т
В

§ 1. ПРОСТРАНСТВО Rm И КЛАССЫ ЕГО ПОДМНОЖЕСТВ 407
граничной точкой Е, если она не является ни внешней, ни внутренней
точкой множества Е.
Из этого определения следует, что характеристическое свойство граничной
точки множества состоит в том, что в любой ее окрестности имеются как
точки этого множества, так и точки, ему не принадлежащие.
Пример 7. Сфера 5 (а; г), г > 0, является множеством граничных точек
как открытого шара В (а; г), так и замкнутого шара В (а; г).
Пример 8. Точка а ? Rm является граничной точкой множества Rm \ а,
которое не имеет внешних точек.
Пример 9. Все точки сферы S(a;r) являются ее граничными точками;
внутренних точек множество S(a; r) как подмножество Rm не имеет.
Определение 6. Точка а ? Rm называется предельной точкой множе-
множества Е С Rm, если для любой окрестности О (а) точки а пересечение ЕГ\О(а)
есть бесконечное множество.
Определение 7. Объединение множества Е и всех его предельных то-
точек из Rm называется замыканием множества Е в Rm.
Замыкание множества Е обычно обозначают символом Е.
Пример 10. Множество B(a;r) = B(a;r) U S(a;r) есть множество пре-
предельных точек для открытого шара В (а; г), поэтому В (а; г), в отличие от
В (а; г), и назвали замкнутым шаром.
Пример 11. S(a;r) = S(a;r).
Вместо того чтобы обосновывать последнее равенство, докажем следую-
следующее полезное
Утверждение 2. (F замкнуто в Rm) <=> (F = F в Rm).
Иными словами, F — замкнутое в Rm множество тогда и только тогда,
когда оно содержит все свои предельные точки.
¦М Пусть F замкнуто в Rm, xGRm и x?F. Тогда открытое множество
G = Rm \ F является окрестностью точки ж, вообще не содержащей точек
множества F. Таким образом, показано, что если х ? F, то х — не предельная
точка F.
Пусть F = F. Проверим, что множество G = Rm \F открыто в Rm. Бели
х е G, то х ? F и потому х не является, предельной точкой множества F.
Значит, найдется такая окрестность точки х, в которой имеется только ко-
конечное число точек хь ..., хп множества F. Поскольку х $ F, то можно
построить, например, шаровые окрестности О\(х), ..., Оп(х) точки х так,
п
что Хг ? Oi(x). Тогда О(х) = П Qi(%) будет открытой окрестностью тонки
х, которая вообще не содержит точек F, т. е. О(х) С Rm \F и, следовательно,
множество Rm \ F = Rm \ F открыто, т. е. F замкнуто в Rm. >

408 гл. vii. функции многих переменных
3. Компакты в Ет
Определение 8. Множество К С Ет называется компактом, если из
любого покрытия К множествами, открытыми в Ет, можно выделить конеч-
конечное покрытие.
Пример 12. Отрезок [а,Ь] С Е1 является компактом в Е1 в силу леммы
о конечном покрытии.
Пример 13. Обобщением отрезка в Ет является множество
= {х € Ет | ах ^ хх ^ Ь\ г = 1, ..., т},
которое называется т-мерным промежутком, m-мерным брусом или т-мер-
ным параллелепипедом.
Покажем, что J — компакт в Ет.
< Предположим, что из некоторого открытого покрытия / нельзя выде-
выделить конечное покрытие. Разделив каждый из координатных отрезков Iх =
= {хх Е Е| ах ^ хг ^ 6*} (г = 1,..., т) пополам, мы разобьем промежуток J
на 2т промежутков, из которых по крайней мере один не допускает конеч-
конечного покрытия множествами нашей системы. С ним поступим так же, как
и с исходным промежутком. Продолжая этот процесс деления, получим по-
последовательность вложенных промежутков I = Д D h D ... D In Э ... , ни
один из которых не допускает конечного покрытия. Если 1п = {х Е Em |
ап ^ #* ^ Ьхп, г = 1, ..., т}, то при каждом г Е {1,..., т) координатные
отрезки ахп ^ хх < Ьхп (п = 1, 2, ...) образуют, по построению, систему
вложенных отрезков, длины которых стремятся к нулю. Найдя при каждом
г Е {1, ..., гп) точку f * € [ахп, Ьхп], общую для всех этих отрезков, получим точ-
точку ? = (f1, ..., ?m), принадлежащую всем промежуткам / = Ji, /г, ..., Jn, ...
Поскольку ? Е /, то найдется такое открытое множество G нашей систе-
системы покрывающих множеств, что (EG. Тогда при некотором S > 0 также
В(?]5) С G, Но по построению в силу соотношения B) найдется номер N
такой, что 1п С В(?; S) С G при п > iV, и мы вступаем в противоречие с тем,
что промежутки 1п не допускают конечного покрытия множествами данной
системы. >
Утверждение 3. Если К — компакт в Ет, то
a) К — замкнутое множество в Ет;
b) любое замкнутое в Ет множество, содержащееся в К, само является
компактом.
А а) Покажем, что любая точка а Е Ет, предельная для К, принадле-
принадлежит К. Пусть а ? К. Для каждой точки х Е К построим такую окрест-
окрестность G(x), что точка а обладает окрестностью, не имеющей с G(x) общих
точек. Совокупность {G(x)}, x E К, всех таких окрестностей образует от-
открытое покрытие компакта К, из которого выделяется конечное покрытие
G(x\), ... , G(xn). Если теперь Oi{a) — такая окрестность точки а, что

§ 1. ПРОСТРАНСТВО Rm И КЛАССЫ ЕГО ПОДМНОЖЕСТВ 409
п
G(xi) П Oi(a) = 0, то множество О(а) = f] Oi{a) также является окрест-
ностью точки а, причем, очевидно; КГ\О(а) = 0. Таким образом, а не может
быть предельной точкой для К.
Ь) Пусть F — замкнутое в Ет множество и F С К. Пусть {<?<*}, a e А,
— покрытие F множествами, открытыми в Rm. Присоединив к нему еще
одно открытое множество G = Шт \ F, получим открытое покрытие Мт и,
в частности, К, из которого извлекаем конечное покрытие К. Это конечное
покрытие К будет покрывать также множество F. Замечая, что G П F = 0,
можно сказать, что если G входит в это конечное покрытие, то, даже удалив
G, мы получим конечное покрытие F множествами исходной системы {Ga},
а € А. >
Определение 9, Диаметром множества Е С Ет называется величина
d(E) := sup
Определение 10. Множество Е С Шт называется ограниченным, если
его диаметр конечен.
Утверждение 4. Если К — компакт в Шт, то К — ограниченное
подмножество Шт.
М Возьмем произвольную точку а Е Мт и рассмотрим последовательность
шаров {В(а;п)} (п = 1, 2, ...). Они образуют открытое покрытие Rm, a
следовательно, и К. Если бы К не было ограниченным множеством, то из
этого покрытия нельзя было бы извлечь конечное покрытие К. >
Утверждение 5. Множество К С Мт является компактом в том и
только в том случае, если К замкнуто и ограничено в Ет.
4 Необходимость этих условий нами уже показана в утверждениях 3 и 4.
Проверим достаточность этих условий. Поскольку К — ограниченное мно-
множество, то найдется m-мерный промежуток J, содержащий* К. Как было по-
показано в примере 13, J является компактом в Ет. Но если К — замкнутое
множество, содержащееся в компакте /, то по утверждению ЗЬ) оно само
является компактом. >
Задачи и упражнения
1. Расстоянием d(E\,E2) между множествами Ei, E2 С Rm называется вели-
величина
= inf
Приведите пример замкнутых в Rm множеств J57i, E2 без общих точек, для которых
d{EuE2) = 0.

410 ГЛ. VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
2. Покажите, что
а) замыкание Е в Rm любого множества Е С Rm является множеством, замкну-
замкнутым в Rm;
b) множество дЕ граничных точек любого множества Е С Rm является замкну-
замкнутым множеством;
c) если G — открытое множество в Rm, a F замкнуто в Rm, то G \ F — открытое
подмножество Rm.
3. Покажите, что если К\ D Кг D ... D Kn D ... — последовательность вложен-
оо
ных компактов, то П К% ф 0.
§ 2. Предел и непрерывность функции многих переменных
1. Предел функции. В главе III мы подробно изучили операцию пре-
предельного перехода ддя вещественнозначных функций /: X —> Е, определенных
на множестве Х\ в котором фиксирована база В.
В ближайших параграфах нам предстоит рассматривать функции /: X
[п, определенные на подмножествах пространства Rm, со значениями в
= Е1 или вообще в En, n € N. Мы сделаем сейчас ряд добавлений к теории
предела, связанных со спецификой этого класса функций.
Начнем, однако, с общего основного определения.
Определение 1. Точка А € Еп называется пределом отображения
f : X —> Еп по базе В в X, если для любой окрестности V(A) этой точки
найдется элемент В € В базы В, образ которого f(B) содержится в V(A).
Короче,
\imf(x)=A:=VV(A) ЗВеВ (f(B)cV(A)).
в
Мы видим, что определение предела функции /: X —> Еп полностью со-
совпадает с определением предела функции /: X -у Е, если мы представляем
себе, что такое окрестность V(A) точки А € Еп для любого п Е N.
Определение 2. Отображение /: X —> Еп называется ограниченным,
если множество f(X) С Еп ограничено в Еп.
Определение 3. Пусть В — база в множестве X. Отображение /: X ->
—> Еп называется финально ограниченным при базе В, если найдется элемент
В базы В, на котором / ограничено.
Учитывая эти определения, нетрудно проверить теми же рассуждениями,
которые мы провели в главе III, что
функция f: X —>Шп может иметь не более одного предела по данной базе
В вХ]
функция f: X —> Шп, имеющая предел по базе В, финально ограничена при
этой базе В.

§ 2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 411
Определение 1 можно переписать также в иной форме, явно использующей
наличие в Еп метрики. А именно,
Определение 1;.
Aimf(x) = AeRn := Ve > 0 ЗВеВ Vs E S (d(f(x),A) < e)
или
Определение 1".
lim/(я) = А Е En := limd(/(x), A) = 0.
в в
Специфическая особенность отображения /: X —> Шп состоит в том, что
поскольку точка у Е Еп есть упорядоченный набор (у1, ..., уп) из п веществен-
вещественных чисел, то задание функции /: X —> Еп равносильно заданию п веществен-
нозначных функций /г: X —> Е (г = 1, ..., п), где f*(x) = у* (г = 1, ..., п).
Если А = (А1, ..., Ап) и у = (у1, ..., уп), то справедливы неравенства
* - А{\ ^ d(y,A) ^ V^ max \уг - А% A)
из которых видно, что
lim f(x) = А о lim /*(я?) = Л* (г = 1,..., п), B)
т. е. сходимость в Еп покоординатная.
Пусть теперь X = N — множество натуральных чисел, а В — база А; —> оо,
A; G N в нем. Функция /: N —>• Еп в данном случае есть последовательность
{ук}, к Е N, точек пространства Еп.
Определение 4. Последовательность {у*}, fc E N, точек у* Е Еп
называется фундаментальной, если для любого ? > 0 найдется такое число
N Е N, что при любых fci, &2 > iV выполнено ^(у^, у*2) < ?.
Из неравенств A) видно, что последовательность точек у* = (у?, ..., у?) Е
Е Еп фундаментальна тогда и только тогда, когда фундаментальна каждая из
последовательностей {yj.}, к Е N, г = 1, ..., п, их одноименных координат.
Учитывая соотношение B) и критерий Коши для числовых последователь-
последовательностей, можно теперь утверждать, что последовательность точек в Еп схо-
сходится тогда и только тогда, когда она фундаментальна.
Иными словами, критерий Коши справедлив и в пространстве Еп.
Впоследствии метрические пространства, в которых каждая фундамен-
фундаментальная последовательность имеет предел, мы назовем полными метрически-
метрическими пространствами. Таким образом, мы сейчас установили, что Еп при любом
п Е N является полным метрическим пространством.
Определение 5. Колебанием функции /: X ->¦ Еп на множестве Е С X
называется величина
Lj(f;E):=d(f(E)),
где d(f(E)) — диаметр множества f(E).

412 ГЛ. VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Как видно, это есть прямое обобщение определения колебания веществен-
нозначной функции, в которое определение 5 и переходит при п = 1.
С полнотой Rn связано то, что для функций /: X -* Rn со значениями в
Еп справедлив следующий критерий Коши существования предела.
Теорема 1. Пусть X — множество, В — база в X. Функция f: X —> Мп
имеет предел по базе В в том и только в том случае, когда для любого
числа е > 0 найдется элемент В Е В базы, на котором колебание функции
меньше е.
Итак,
3 lim/(a:) <ФФ Ve > 0 ЗВеВ (cj(/; В) < е).
в
Доказательство теоремы 1 дословно повторяет доказательство критерия
Коши для числовых функций (гл. III, § 2, теорема 4) с единственным измене-
изменением, сводящимся к тому, что теперь вместо |/(#i) — /(#г)| следует всюду
писать d{f(xi),/(#2)).
В справедливости теоремы 1 можно убедиться и иначе, если считать из-
известным критерий Коши для вещественнозначных функций и воспользоваться
соотношениями B) и A).
Для функций со значениями в Еп остается в силе также важная теорема о
пределе композиции.
Теорема 2. Пусть Y — множество, By — база в Y, g : Y -» En —
отображение, имеющее предел по базе By.
Пусть X — множество, Вх — база в X, f: X -+Y — такое отображе-
отображение X в Y, что для любого элемента By € By базы By найдется элемент
Вх € Вх базы Вх, образ которого f(Bx) содержится в By.
При этих условиях композиция g о f : X —>¦ Еп отображений fug опре-
определена, имеет предел по базе Вх и
lim(gof)(x)=limg(y).
Ox OY
Доказательство теоремы 2 можно провести, либо повторив доказательство
теоремы 5 из § 2 гл. III, с заменой там R на Еп, либо сослаться на указанную
теорему и воспользоваться соотношением B).
До сих пор мы рассматривали функции /: X —> Еп со значениями в Еп,
никак не конкретизируя область их определения X. В дальнейшем нас пре-
прежде всего будет интересовать случай, когда X есть подмножество простран-
пространства Ет.
Условимся, что, как и прежде:
U (а) — окрестность точки а Е Мт;
о о
U(а) — проколотая окрестность точки а Е Ет, т. е. U(a) := U(a) \ a;
Ue{o) — окрестность точки а в множестве Е С Мт, т. е. Ue(cl) := ЕПU(a)\
о • о
Ue{o) — проколотая окрестность точки а в множестве Е, т. е. Ue{o) •=
= EHU(a);

§ 2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 413
х —У а — база проколотых окрестностей точки а в Ет;
х —> оо — база окрестностей бесконечности, т. е. база, состоящая из мно-
множеств Ет \В(а]г);
х -? а, х Е Е, или (Е Э х -? а) — база проколотых окрестностей точки а
в множестве Е, если а — предельная точка для Е;
х —> оо, х € Е, или (Е Э х —>> оо) — база окрестностей бесконечности в
множестве Е, состоящая из множеств Е\В(а;г), если Е — неограниченное
множество.
В соответствии с этими обозначениями можно, например, дать следующие
конкретизации определения 1 предела функции, если речь идет о функции
/: Е -> Еп, отображающей множество Е С Мт в Еп:
( lim f{x) = А) := (Ve > 0 3Cfe(a) VxeUE(a) (d(f (x), А) < е)).
Это же можно записать и иначе:
lim fix) =
ЕЭх-+а V 7
0 3* > 0 Vx € S @ < d(a?,a) < S =» d(/(x), Л)
Здесь подразумевается, что расстояния d(x,a) и d(f(x),A) измеряются в тех
пространствах (Ет и Еп), в которых лежат указанные точки.
Наконец,
( lim f(x) = A) := (Ve > 0 3B(a;r) Vx € Rm\B(a;r) (d(f(x),A) < e)).
Условимся также, что запись «/(ж) —у оо при базе S» в случае отображения
/: X —> Шп всегда будет означать, что для любого шара В (А; г) С Еп найдется
элемент В € В базы В такой, что f(B) С En \В{А\г).
Пример 1. Пусть х i-> тгг(ж) — отображение тгг: Ет —> Е, состоящее в
том, что каждой точке х = (х1, ..., жт) пространства Ет ставится в соответ-
соответствие ее г-я координата хг. Итак,
7Гг(ж) = Xх.
Если a = (a1, ..., am), то, очевидно,
пг(х) —> аг при х —> а.
Функция а; ь^ ттг(а;) не стремится ни к конечной величине, ни к бесконеч
ности при х —У оо, если т > 1.
Вместе с тем
m
GГг(ж)) —>> СХ> При X —>• ОО
г=1

414 ГЛ УН. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Не следует думать, что предел функции нескольких переменных можно
найти, вычисляя последовательно пределы по каждой из координат. В этом
можно убедиться на следующих примерах.
Пример 2. Пусть функция /:Е2->1в точке (я, у) € Ш2 определена так:
f'(x\ У) "= <
если
О, если х2 + у2 = 0.
ТЪгда /@,у) = /(я?,0)"= 0, а /(х,х) = | при-яг 9* 0.
Таким образом, эта функция не имеет предела при (ж, у) -л @,0).
Вместе с тем
lim Y lim f(x, у)) = lim@) = 0,
lim f lim f(x,y)) = lim@) = 0.
Пример З. Для функции
о , 2, если х2 +у2 ф 0,
x1 +y2
x1
О, если х2 + у2 = О,
имеем
lim ( lim f(x,y)) = lim (~) = 1,
x—>О V у—>О / ж—>О \Х /
(\ ( V
lim f(x,y)) = lim I — ^
Пример 4. Для функции
a; H-1/ sin -, если х ф О,
О, если а; = О,
имеем
lim (lim/(ж,t/)) = 0,
ж—>0 V у—?0 /
(
ж—>0 V у—?0
и в то же время повторный предел
lim ( lim f(x.y))
вообще не существует.

§ 2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Пример 5. Функция
Х2у о , 2 v л
^^j, если х*+у>*0,
О, если ж2 -I- у2 = О,
имеет нулевой предел при стремлении к началу координат по любому лучу
х = at, у = /??.
Вместе с тем функция равна - в любой точке вида (а, а2), где а ф О, по
этому функция не имеет предела при (х,у) —> @,0).
2. Непрерывность функции многих переменных и свойства не-
непрерывных функций. Пусть Е — множество в пространстве Rm и /: Е -?
-> Мп — определенная на нем функция со значениями в пространстве Шп.
Определение б. Функция /: Е —> Еп называется непрерывной в точ-
точке а € Е, если для любой окрестности V(f(a)) значения /(а) этой функции,
принимаемого ею в точке а, найдется такая окрестность Ue(o) точки а в
множестве Е, образ которой /(С/е(о)) содержится в V(/(a)).
Итак,
(/ : Е -> Еп непрерывна boG?):=
Мы видим, что по форме определение 6 совпадает со знакомым нам опре-
определением 1 непрерывности вещественнозначнои функции, приведенным в § 1
гл. IV. Как и там, мы можем дать следующие вариации записи этого опре-
определения:
(f: Е -> Шп непрерывна в а € Е) :=
= (Ve > 0 36 > 0 Vx € Е (d(x,a) < 6 =» d(f(x),f(a)) < e)),
или, если а — предельная точка множества Е,
(f:E->Rn непрерывна в а е Е) := ( lim f(x) = f(a)).
\ЕЭх-+а /
Как уже отмечалось в главе IV, понятие непрерывности представляет ин-
интерес именно в том случае, когда речь идет о точке а Е Е, предельной для
множества Е, на котором определена функция /.
Из определения б и соотношения B) следует, что отображение fi
задаваемое соотношением
непрерывно в некоторой точке в том и только в том случае, когда каждая из
функций у1 = fi{x1^ ..., хт) непрерывна в этой точке.

416 ГЛ. VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
В частности, вспомним, что путем в Еп мы назвали отображение /: / -> Еп
промежутка I С Е, задаваемое непрерывными функциями /1(х), ..., fn(x) в
виде
х •-» у = (у\ ..., уп) = (f\x), ...,
Таким образом, мы теперь можем сказать, что путь в Еп есть непрерыв-
непрерывное отображение промежутка /cl вещественной оси в пространство Еп.
По аналогии с определением колебания вещественнозначной функции в
точке, вводится понятие колебания в точке функции со значениями в Еп.
Пусть Е — множество в Rm, а Е Е и Ве(п;г) = ЕПВ(а\г).
Определение 7. Колебанием функции /: ? ч Rn в точке а Е Е назы-
называется величина
ы(/;а):= lim u(f;BE(a;r)).
r-»+0
Из определения б непрерывности функции, с учетом свойств предела и кри-
критерия Коши, получаем совокупность часто используемых локальных свойств
непрерывных функций. Перечислим эти
Локальные свойства непрерывных функций
a) Отображение f : Е —У Шп множества Е С Шт непрерывно в точке
а Е Е тогда и только тогда, когда ы(/; а) = 0.
b) Отображение /:Е-+Жп, непрерывное в точке а Е Е, ограничено в
некоторой окрестности Ue{o) этой точки.
c) Если отображение g : Y —>• К* множества УсКп непрерывно в точке
Уо € Y, а отображение f: X —> Y множества X С Мт непрерывно в точке
хо Е X, причем f(xo) = уо, то определено отображение g of: X —У Шк и оно
непрерывно в точке xq E X.
Вещественнозначные функции, кроме того, обладают еще следующими
свойствами:
d) Если функция f: Е -> Е непрерывна в точке а Е Е и f(a) > 0 (или
f(a) < 0), то найдется такая окрестность Ue(cl) точки а в Е, что для
х Е Ue(o) справедливо f(x)>0 (соответственно, f(x) < 0).
e) Если функции f:E-+Rug:E-*R непрерывны в точке а Е Е,
то их линейная комбинация (af + /3g) : E —> R, где а, /? Е М, произведение
(/ -д): Е -> Е, а если д(х) фО на Е, то и частное ( — J : Е —> Е, определены
на Е и непрерывны в точке а Е Е.
Условимся говорить, что функция /: Е —> Еп непрерывна на множестве Е,
если она непрерывна в каждой точке этого множества.
Множество функций / : Е —> Еп, непрерывных на Е, будем обозначать
символом C(i?;En) или символом С(Е), если область значений функций од-
однозначно определяется по контексту; как правило, это сокращение будет ис-
использоваться в случае, когда Еп =

§ 2, ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 417
Пример б. Функции (я?1, ..., хт) ^ х{ (г = 1, ..., га), отображающие
Ет на Е (проекции), очевидно, непрерывны в любой точке а = (а1, ..., ат) е
Е Ет, ибо Ит тг^ж) = о* = тг^а).
Пример 7. Любую функцию х Н- /(ж), определенную на R, например
х 1-> sin ж, можно рассматривать и как функцию (х,у) •—> /(#), определен-
определенную, положим, на Е2. В таком случае, если / была непрерывна как функция
на Е, новая функция (х, у) i—> f(x) будет непрерывна как функция на Е2.
Это можно проверить либо непосредственно по определению непрерывности,
либо заметить, что функция F есть композиция (/ о п1)(х,у) непрерывных
функций.
В частности, отсюда с учетом с) и е) следует, что, например, функции
f(x,y) = sina? + e*y, f(x,y) = arctg(ln(|a?| + |у| + 1))
непрерывны на
Заметим, что проведенные рассуждения по существу своему локальны, а
то, что в примере 7 функции / и F рассматривались соответственно на всей
оси Е или плоскости Е2, является обстоятельством случайным.
Пример 8. Функция f(x,y) из примера 2 непрерывна в любой точке
пространства Е2, кроме точки @,0). Заметим, что, несмотря на разрывность
функции /(ж, у) в точке @,0), эта функция непрерывна по любой из двух своих
переменных при каждом фиксированном значении другой переменной.
Пример 9. Если функция /: Е -> Еп непрерывна на множестве Е, а
Е — подмножество Е, то ограничение*/\в функции / на это подмножество
есть функция, непрерывная на Е, что непосредственно следует из определения
непрерывности функции в точке.
Перейдем теперь к глобальным свойствам непрерывных функций. Чтобы
сформулировать их для функций /:Е—>Шп, дадим сначала два определения.
Определение 8. Отображение /: Е —У Еп множества.i? С Ет в про-
пространство Еп называется равномерно непрерывным на Е, если для любого
числа е > 0 найдется такое число S > 0, что для любых точек х\,Х2 € Е
таких, что d(x\,X2) < S, выполнено d(f{x\),f{x2)) < ?•
Как и прежде, подразумевается, что расстояния d(x\,X2), d{f{x\),f{x2))
измеряются соответственно в Ет и Еп.
При т = п = 1 мы возвращаемся к уже знакомому нам определению рав-
равномерной непрерывности числовых функций.
Определение 9. Множество Е С Ет называется линейно связным,
если для любой пары жо,'Х1 его точек существует путь Г : / —> Е с носителем
в Е и с концами в этих точках.
Иными словами, из любой точки хо € Е можно пройти к любой точке
х\ Е Е, не выходя за пределы множества Е.

418 ГЛ. VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Поскольку мы пока не будем рассматривать иного понятия связности мно-
множества, кроме понятия линейной связности, то для краткости условимся пока
линейно связные множества назвать просто связными.
Определение 10. Областью в пространстве Rm называется открытое
связное множество.
Пример 10. Шар В (а; г), г > 0, в Шт является областью. Откры-
Открытость В(а;г) в Шт нам уже известна. Проверим, что шар связен. Пусть
х0 = (#о, ..., х™) и х\ = (#}, ..., х™) — две точки шара. Путь, задаваемый
функциями xl(t) = tx\ + A — t)x%Q (г = 1, ..., m), определенными на отрезке
0 ^ t ^ 1, имеет своими концами точки xq и х\. Кроме того, его носитель
лежит в шаре В (а; г), поскольку, в силу неравенства Минковского, при любом
«€•[0,1]
d(x(t),a) =
i/
1=1
m / m
-«'))+
Пример 11. Окружность (одномерная сфера) радиуса г > 0 есть подмно-
подмножество в IR2, задаваемое уравнением (ж1J + (х2J = г2. Полагая ж1 = rcostf,
х2 = rsintf, видим, что любые точки окружности можно соединить путем с
носителем на окружности. Значит, окружность — связное множество. Однако
это множество не является областью в R2, поскольку оно не открыто в Ж2.
Сформулируем теперь основные
Глобальные свойства непрерывных функций
в) Если отображение f: К -> W1 непрерывно на компакте К С Шт, то
оно равномерно непрерывно на К.
b) Если отображение f: К -> Шп непрерывно на компакте К С Rm, то
оно ограничено на К.
c) Если функция f : К —> Ш непрерывна на компакте К С Жт, то она
принимает в некоторых точках К минимальное и максимальное из своих
значений на К.
d) Если функция f: Е —> Ш непрерывна на связном множестве Еу прини-
принимает в точках а, Ь € Е значения f(a) = A, f(b) = В, то для любого числа
С, лежащего между А и В, найдется точка с € Е, в которой f(c) = С.
Изучая в свое время (гл. IV, § 2) локальные и глобальные свойства число-
числовых функций одной переменной, мы дали такие их доказательства, которые

§ 2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 419
переносятся и на рассматриваемый здесь более общий случай. Единственное
изменение, которое при этом следует сделать в прежних доказательствах, со-
состоит в том, что выражения типа |xi — X2I или |/(xi) — /(^2)! надо заменить
на d(xi,X2) и d(/(xi), /B2)), гДе d ~~ метрика в том пространстве, где лежат
рассматриваемые точки. Это замечание относится в полной мере ко всему,
кроме последнего утверждения d), доказательство которого мы сейчас про-
проведем.
^ d) Пусть Г : J ->• Е — путь, являющийся таким непрерывным отобра-
отображением отрезка [а, /?] = / С R, что Г(а) = о, Г(/?) = Ь. В силу связности Е
такой путь существует. Функция /о Г : / ->• R, как композиция непрерывных
функций, непрерывна, поэтому на отрезке [а,/3] найдется точка у ? [а,/?], в
которой /о Г G) = С Положим с = ГG). Тогда сЕ Е и f(c) = С. >
Пример 12. Сфера 5@;г), задаваемая в Шт уравнением
является компактом.
Действительно, из непрерывности функции
следует замкнутость сферы, а из того, что на сфере |х*| ^ г (г = 1,..., ш),
следует ее ограниченность.
Функция
(х1, ..., хт) —> (х1J + ... 4- (х*J - (х*+1J - ... - (хтJ
непрерывна на всем пространстве Rm, поэтому ее ограничение на сферу есть
также непрерывная функция, которая в силу глобального свойства с) непре-
непрерывных функций имеет на сфере минимальное и максимальное значения. В
точках сферы A,0, ..., 0), @, ..., 0,1) рассматриваемая функция принимает
значения 1 и — 1 соответственно. Ввиду связности сферы (см. задачу 3 в конце
параграфа) на основании глобального свойства d) непрерывных функций мож-
можно утверждать, что на сфере есть точка, в которой рассматриваемая функция
обращается в нуль.
Пример 13. Открытое множество Ет \ 5@;г) при г > 0 не является
областью, так как оно несвязно.
Действительно, если Г: J -> Шт есть путь, один конец которого совпадает
с точкой хо = @,..., 0), а другой — с некоторой точкой xi = (xj, ..., х^1)
такой, что (х\J + ... + (xf1J > г2, то композиция непрерывных отображений
Г : / -» Шт и /: Rm -+ R, где
, . . . , X j • ) уХ j "г • • • г \Х
)

420 ГЛ. VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
есть непрерывная на отрезке / функция, принимающая на его концах значе-
значения, меньшее и большее чем г2. Значит, на этом отрезке найдется точка 7>
в которой (/ о Г)G) = г2. Тогда точка х7 = ГG) носителя нашего пути ока-
оказывается лежащей на сфере 5@; г). Мы показали, что нельзя выйти из шара
В@;г) С Шт, не пересекая его граничной сферы 5@; г).
Задачи и упражнения
1. Пусть / € C(Rm;R). Покажите, что
a) множество Е\ = {х 6 Rm | f(x) < с} открыто в Rm;
b) множество Е2 = {х 6 Rm | /(я) ^ с} замкнуто в Rm;
c) множество Ез = {х € Rm | f(x) = с} замкнуто в Rm;
d) если f(x) —> Н-оо при х —> оо, то Ет. и #з компактны в Rm;
e) для любой функции / : Rm —> R множество Е\ = {ж 6 Rm | w(/; x) ^ е}
замкнуто в Rm.
2. Покажите, что отображение /: Rm —> Rn непрерывно тогда и только тогда,
когда прообраз любого открытого в Rn множества является открытым в Rm мно-
множеством.
3. Покажите, что
a) образ f(E) связного множества Е С Rm при непрерывном отображении /: Е —У
—> W1 является множеством связным;
b) объединение связных множеств, имеющих общую точку, является связным
множеством;
c) полусфера (х1J + ... + (я171J = 1, хт ^ 0, является связным множеством;
d) сфера (ж1J Н-... -h (xmJ = 1 является связным множеством;
e) если Е С R и Е связно, то Е есть промежуток на R (т. е. отрезок, полуинтер-
полуинтервал, интервал, луч или вся числовая ось);
f) если Хо — внутренняя, а х\ — внешняя точка множества М С Rm, то носитель
любого пути с концами хо, х\ пересекает границу множества М.

ГЛАВА VIII
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
m
§ 1. Линейная структура в
1. Кт как векторное пространство. Из курса алгебры вам уже хо-
хорошо известно понятие векторного пространства.
Если в Шт ввести операцию сложения элементов х\ = (#*, ..., х™), х^ —
— (#2, • • • >x™) по формуле
ХХ + Х2 = (х\ + х\, . . . , X? + Х%), • A)
а умножение элемента х = (ж1, ..., хт) на число Л ? IR — соотношением
1 B)
то Ет становится линейным пространством над полем действительных чисел.
Его точки теперь можно называть векторами.
Векторы
d = @, ...,0,1,0, ...,0) (г = 1, ...,т) C)
(где единица стоит лишь на г-м месте) образуют максимальную линейно неза-
независимую систему векторов этого пространства, ввиду чего оно оказывается
m-мерным векторным пространством.
Любой вектор х € Шт может быть разложен по базису C), т. е. представлен
в виде
х = хгег + ... + хтет, D)
Индекс при векторе мы условимся писать внизу, а координаты, как и до
сих пор, будем отмечать верхним индексом. Это удобно по многим причинам,
одна из которых, в частности, состоит в том, что, следуя Эйнштейну1), можно
*) А. Эйнштейн A879—1955) — крупнейший физик нашего столетия, работы которого
по квантовой теории и особенно по теории относительности оказали революционизирующее
влияние на всю современную физику.

422
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
условиться выражения типа D) записывать коротко в виде
JL —^ JL С^
E)
считая, что появление одинакового индекса сверху и снизу означает суммиро-
суммирование по этому индексу в пределах диапазона его изменения.
2. Линейные отображения L : Шт —У Шп. Напомним, что отображе-
отображение L : X —> У" векторного пространства X в векторное пространство Y на-
называется линейным, если для любых ?i, #2 € X и Ai,A2 G М. выполнено
+ \2L(x2).
Нас будут интересовать линейные отображения L :
Если {ei, ..., ет} и {ei, ..., ёп} — фиксированные базисы пространств
m
и К71 соответственно, то, зная разложения
L(ei) = a]ei + ... + а%ёп = aJ{ej (i = 1, ..., m)
(в)
образов векторов базиса при линейном отображении L : Шт —> Шп, мы в силу
линейности преобразования L можем найти разложение по базису {ei, ..., ёп}
образа L(h) любого вектора h = h}e\ -f ... + hmem = hle{. А именно:
L(h) =
Значит, в координатной записи:
G)
(8)
Отображение L: Rm ->> En при фиксированном в Еп базисе можно, таким
образом, рассматривать как набор
= (L\...,Ln) (9)
из п (координатных) отображений LJ: Шт ->• R.
С учетом (8) легко заключаем, что отображение L : Ет ->• Еп линейно
тогда и только тогда, когда каждое отображение LJ набора (9) линейно.
Если записать набор (9) в виде столбца, то с учетом соотношения (8) имеем
L(h) =
( 1
a
\al
n
a
n
m/
h
m
A0)
Итак, фиксация базисов в Em и Еп позволяет установить взаимно одно-
однозначное соответствие между линейными отображениями L: Ет ->> Еп и т х п-
матрицами (а\) (г = 1, ..., m, j = 1, ..., п). При этом столбец с номером

§ 1. ЛИНЕЙНАЯ СТРУКТУРА В Rm 423
г матрицы (а^), отвечающей отображению L, состоит из координат образа
L{ei) вектора е* Е {ei, ..., em}. Координаты образа L(h) произвольного век-
вектора h = hlei € Rm могут быть получены из соотношения A0) умножением
матрицы линейного отображения на столбец координат вектора Л.
При наличии в Еп структуры векторного пространства можно говорить
о линейной комбинации Ai/i 4- А2/2 отображений /i: X -> Rn, /2 : X ->> En,
полагая
+ А2/2)(х) := Ai/i(a:) + А2/2(х). A1)
В частности, линейная комбинация линейных отображений L\ : Rm > Rn
L2 : Rm -> Rn есть, в соответствий с определением A1), отображение
h н—> AiZri(fc) + A2L2(/i) =
которое, очевидно, линейно. Матрица этого отображения есть соответству-
соответствующая линейная комбинация матриц отображений L\ и L2.
Композиция С = В о А линейных отображений А : Ет -> Еп, В : Еп -> R*,
очевидно, также является линейным отображением, матрица которого, как
следует из A0), есть произведение матрицы отображения А и матрицы ото-
отображения В (на которую умножаем слева). Кстати, закон умножения матриц
определен известным вам образом именно для того, чтобы композиции ото-
отображений отвечало произведение матриц.
3. Норма в Ет. Величину
^J A2)
назовем нормой вектора х = (ж1, ..., хт) € Rw.
Из этого определения с учетом неравенства Минковского следует, что
1° ||*|| ^ 0,
2° (||*|| = о) *» (* = 0),
3° ||А*|| = |А|.||*||, где AG
4°
Вообще, любую функцию || || : X -+ R на векторном пространстве X, удо-
удовлетворяющую условиям 1°—4°, называют нормой в векторном пространстве.
Иногда, чтобы уточнить, о какой норме идет речь, знак нормы вектора на-
наделяют символом того пространства, в котором эту норму рассматривают.
Например, можно написать ||*||цт или ||з/||цп, однако мы, как правило, не ста-
станем этого делать, ибо из контекста всегда будет ясно, о каком пространстве
и какой норме идет речь.
Заметим, что в силу A2)
A3)

424 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
где d(x\, Х2) — расстояние в Ет между векторами х\ и #2, рассматриваемыми
как точки метрического пространства Шт.
Из соотношения A3) видно, что следующие условия равносильны:
х ->> хо, d(x, #0) -* О» \\х — #о|| —> 0.
Ввиду A3), в частности, имеем
Свойство 4° нормы называют неравенством треугольника, и теперь ясно
почему.
Неравенство треугольника по индукции распространяется на сумму любо-
любого конечного числа слагаемых. А именно, справедливо неравенство
Наличие нормы вектора позволяет сравнивать по величине значения функ-
ции j . а —г ж. , д: л —г ik. .
Условимся писать, что f(x) = о(д(х)) или f = о(д) при базе В в X, если
||/(з)||цт = о(||0(я)||Кп) при этой базе В.
Если f(x) = (/1(ж), ..., fm(x)) — координатное представление отображе-
отображения /: X —У Шт, то ввиду неравенств
т
A4)
можно сделать следующее полезное для дальнейшего наблюдение:
(/ = °(д) ПРИ базе В) 4=Ф- (/г = о(д) при базе В; г = 1, ..., ш). A5)
Условимся также, что запись f = О(д) при базе В в X будет означать, что
з)||цт = О(||0(аО||и») при этой базе В.
Тогда из A4) получаем, что
(/ = 0{д) при базе В) <=$> (fl = О(д) при базе В; г = 1, ..., ш). A6)
Пример. Пусть L : Ет ->• Шп — линейное отображение и h = hle\ + ... +
+ hmem — произвольный вектор пространства Шт. Оценим ||L(/i)||Rn:
т
т / т
\\L(h)\\ =
Таким образом, можно утверждать, что
L(h) = O(h) при h -+ 0. A8)
В частности, из этого следует, что L(x — xq) = L(x) — L(xo) -> 0 при
x -> xo, т. е. линейное отображение L : Em -> En непрерывно в любой точке
xq G Em. Из оценки A7) видна даже равномерная непрерывность линейного
отображения.

§ 1. ЛИНЕЙНАЯ СТРУКТУРА В Rm 425
4. Евклидова структура в IRm. Из алгебры известно понятие ска-
скалярного произведения в вещественном векторном пространстве как числовой
функции (х,у), определенной на парах векторов пространства и обладающей
свойствами
, х) ^ О,
(хих2) =
(\xi,x2) = А(ж1,я2), где А €
Из этих свойств, в частности, следует, что если в пространстве фиксирован
базис {ei,..., em}, то через координаты (я1, ..., хт), (у1, ..., ут) векторов х
и 2/ их скалярное произведение (ху у) запишется в виде билинейной формы
(х,у) = дцх*у* A9)
(подразумевается суммирование по г и по j), в которой gij = (ei,ej).
Векторы называются ортогональными, если их скалярное произведение
равно нулю.
Базис {ei, ..., em} называется ортонормированным, если д^ = E^, где
0, если % ф j,
1, если г = j.
В ортонормированием базисе скалярное произведение A9) имеет самый
простой вид
или
B0)
Координаты, в которых скалярное произведение имеет такой вид, называ-
называют декартовыми координатами.
Напомним, что пространство Шт с определенным в нем скалярным произ-
произведением называется евклидовым пространством.
Между скалярным произведением B0) и нормой вектора A2) имеется оче-
очевидная связь
Из алгебры известно следующее неравенство:
(х,уJ ^ (х,х)(у,у),

426 ГЛ. VIIL ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
которое, в частности, показывает, что для любой пары векторов найдется
угол ip € [0, тг] такой, что
/ v 11 *i i 11 и
\ wL-f * %J / ™"~» I I ^J{_f II || \ш | | VrisV/O ^ш *
\ / Сг / || I I I I €7 I I •
Этот угол называют углом между векторами х и у. Именно по этой при-
причине естественно считать ортогональными векторы, скалярное произведение
которых равно нулю.
Полезным для нас будет также следующий известный из алгебры простой,
но очень важный факт:
любая линейная функция L : Шт —> Ж в евклидовом пространстве имеет
вид
L(x) = (?,х),
где ? € Шт — фиксированный и однозначно соответствующий функции L
вектор.
§ 2. Дифференциал функции многих переменных
1. Дифференцируемость и дифференциал функции в точке
Определение 1. Функция / : Е —> Еп, определенная на множестве
Е С Мт, называется дифференцируемой в точке х € Е, предельной для мно-
множества Е, если
1 ' A)
~ f(x) = L{x)h + а(я; /i),
где L(x) : Шт ->• Rn — линейная относительно h функция1), a a(x;h) = o(h)
при h -^ 0, x + h€ E.
Векторы
Ax(h) := (х + К) — х = /i,
; Л) :=
называются соответственно приращением аргумента и приращением функ-
функции (отвечающим этому приращению аргумента). Эти векторы пр традиции
обозначают символами Ах и Af(x) самих функций от h.
Линейная функция L(x) : Шт —> Шп в соотношении A) называется диф-
дифференциалом, касательным отображением или производным отображением
функции f: Е -> Еп в точке х е Е.
Дифференциал функции /: Е ->• Еп в точке х ? Е обозначается символами
, Df(x) или f'(x). *
аналогии с одномерным случаем, мы позволим себе писать L(x)h вместо L(x)(h).
Отметим также, что в определении мы подразумеваем, что Rm и Rn наделены указанной в
§ 1 нормой.

§ 2. ДИФФЕРЕНЦИАЛ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 427
В соответствии с введенными обозначениями, соотношение A) можно пе-
переписать в виде
f{x + h) - f{x) = f\x)h + a(s; h)
или
Д/(я; h) = dfix)h + a(x; h).
Заметим, что дифференциал, в сущности, определен на смещениях h от
рассматриваемой точки х ? Шт.
Чтобы это подчеркнуть, с точкой х ? Ет связывают свой экземпляр век-
векторного пространства Ет и обозначают его через ТжЕт, ТЕт(#) или ТЕ™;
ТШ™ можно трактовать как совокупность векторов, приложенных к точке
х € Ет. Векторное пространство ТШ™ называют касательным простран-
пространством к Шт в точке х € Rm. Происхождение этой терминологии прояснится
позже.
Значение дифференциала на векторе h € ТЕ™ есть вектор fix)h Е ТЕ", ч,
приложенный к точке fix) и аппроксимирующий приращение fix + К) — fix)
функции, вызванное приращением h аргумента х.
Итак, dfix) или fix) есть линейное отображение fix): TRJ1 -)• TRJ,y
Мы видим, что, в полном соответствии с уже изученным нами одномерным
случаем, функция многих переменных с векторными значениями дифференци-
дифференцируема в точке, если ее приращение A fix; h) в этой точке как функция прира-
приращения аргумента h линейно по h с точностью до поправки а(х; Л), бесконечно
малой при h —> 0 в сравнении с приращением аргумента.
2. Дифференциал и частные производные вещественнозначной
функции. Если векторы fix + /&), /(ж), L(#)/i, a(x;/i) из Rn записать в
координатах, то равенство A) окажется равносильным п равенствам
f\x + h)- f\x) = L\x)h + а\х; h) (i = 1, ..., n) B)
между вещественнозначными функциями, в которых, как следует из соотно-
соотношений (9) и A5) § 1, Llix): Шт -> Ж суть линейные функции, а al(x; h) = o(/i)
при |i-»0, x + h ? E для любого i = 1, ..., п.
Таким образом, справедливо
Утверждение 1. Отображение f:E->Rn множества Е С Кт диффе-
дифференцируемо в точке х € Е, предельной для множества Е, тогда и только то-
тогда, когда в этой точке дифференцируемы функции /*: Е —> Е (г = 1, ..., п),
задающие координатное представление данного отображения.
Поскольку соотношения A) и B) равносильны, то для отыскания диффе-
дифференциала L{x) отображения f: Е -* Шп достаточно научиться находить диф-
дифференциалы L%ix) его координатных функций fl: E ->R.
Итак, рассмотрим вещественнозначную функцию /: Е -> М, определенную
на множестве Е С Ew и дифференцируемую во внутренней точке х € Е этого
множества. Заметим, что в дальнейшем нам большей частью придется иметь

428 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
дело с тем случаем, когда Е будет областью в Ет. Если х есть внутренняя
точка множества J5, то при любом достаточно малом смещении h от точки х
точка х + h также будет принадлежать Е и, следовательно, будет находиться
в области определения функции /: Е —> Е.
Если перейти к координатной записи точки х = (ж1, ..., жт), вектора h =
= (Л1, ..., hm) и линейной функции L(x)h = ai(a;)/i1-|-... + am(x)ftm, то условие
f(x + Л) - /(re) = ?(ж)Л + o(h) при Л -+ 0 C)
перепишется в виде
Л1, ..., хт + hm) - Дж\ ...,xm) =
x + ... + am(x)hm + o(h) при h -> 0, D)
где ai(x), ..., ат(х) — связанные с точкой ж вещественные числа.
Мы хотим найти эти числа. Для этого^место произвольного смещения h
рассмотрим специальное смещение
* •
hi = hlei = 0 • ei + ... + 0 • e^-i + Wei + 0 • ei+i + ... + 0 • em
на вектор ft», коллинеарный вектору е^ базиса {ei, ..., em} в Em.
При h = hi, очевидно, \\h\\ = |Л*|, поэтому из D) при Л = hi получаем
• • r
= ai(x)W + о(Лг) при Л* —> 0. E)
Это равенство означает, что если фиксировать в функции /(ж1, ...,жт)
все переменные, кроме г-й переменной, то получаемая при этом функция г-й
переменной оказывается дифференцируемой в точке ж\
Из равенства E), таким образом, находим, что
/ \ i. Д* r " > * ,«i/-r/t,O/ ,...,x у j yj, , . . . , j, ? . . . , jj j
Л»Ю h*
Определение 2. Предел F) называется частной производной функции
f(x) в точке х = (ж1, ..., хт) по переменной ж\ Его обозначают одним из
следующих символов:
Пример 1. Если f(u,v) = и3 + v2sinu, то
dif(u,v) = -^~(u,v) = Зг/2
ait
ov

§ 2. ДИФФЕРЕНЦИАЛ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 429
Пример 2. Если f(x,y,z) = arctg(zy2) + ez, то
у2
ду
Итак, мы доказали
Утверждение 2. 2?слгг функция fiE-^Ш, определенная на множестве
Е С Мт, дифференцируема во внутренней точке х € Е этого множества, то
в этой точке функция имеет частные производные по каждой переменной и
дифференциал функции однозначно определяется этими частными производ-
производными в виде
^ ^. G)
Формулу G), используя соглашение о суммировании по повторяющемуся
снизу и сверху индексу, можно записать компактно:
df(x)h = dif{x)h\ (8)
Пример 3. Если бы мы знали (а скоро мы это узнаем), что рассмотрен-
рассмотренная в примере 2 функция /(ж, у, z) дифференцируема в точке @,1,0), то можно
было бы сразу записать, что
d/@,1,0) h = 1 • Л1 + 0 • h2 + 1 • h3 = h1 + h3
и, в соответствии с этим,
/(Л1,1 + Л2, Л3) - /@,1,0) = d/@,1,0)Л + o(h)
или
.3
arctg (Л1 A + Л2J) + eh = 1 + h1 + h3 + о(Л) при Л -> 0.
Пример 4. Для функции ж = (ж1, ..., жт) н^-> ж*, которая точке х G Em
ставит в соответствие ее г-ю координату, имеем
т. е. приращение этой функции само есть линейная по h функция h i—^ /i\
Таким образом, Ап{(х;Н) = Aтг{(х)к, причем отображение с1тг{(х) = dir1 на

430
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
т
самом деле оказывается не зависящим от х ? Ет в том смысле, что dnl(x)h =
= h1 в любой точке х € Rm. Если вместо тгг(гс) писать хг(х), то получаем, что
dxl{x)h = dxlh = h*.
Учитывая это обстоятельство и формулу (8), мы теперь можем предста-
представить дифференциал любой функции в виде линейной комбинации дифферен-
дифференциалов координат ее аргумента х € Шт. А именно:
df(x) = dif{x)dxi = ^{x)dxl + ... + ?t.(x)dxm, (9)
поскольку для любого вектора h ? ТШ™ имеем
df(x)h =
3. Координатное представление дифференциала отображения.
Матрица Якоби. Итак, мы нашли формулу G) для дифференциала веще-
ственнозначной функции /: Е —> R. Но тогда, в силу установленной эквива-
эквивалентности соотношений A) и B), уже для любого отображения /: Е —> Е"
множества Е С Мт, дифференцируемого во внутренней точке х € Е это-
этого множества, можно выписать координатное представление дифференциала
df(x) в виде
df(x)h =
fdf\x)h>
Kdfn(x)hj
dx1
(x) ...
df1
дхт
m
A0)
Определение 3. Матрица (difj(x)) (г = 1, ...,m, j = 1, ...,п) из
частных производных координатных функций данного отображения в точке
х € Е называется матрицей Якоби1^ или якобианом2^ отображения в этой
точке.
В случае, когда п = 1, мы возвращаемся к формуле G), а кргда п = 1 и
m = 1, мы приходим к дифференциалу вещественнозначной функции одного
вещественного переменного.
Из эквивалентности соотношений A) и B) и единственности дифференци-
дифференциала G) вещественнозначной функции следует
Утверждение 3. Если отображение /: Е-*Шп множества ф С Шт
дифференцируемо во внутренней точке х€Е этого множества, то оно име-
имеет в этой точке единственный дифференциал df(x), причем кфбрдинат-
ное представление отображения df(x) : TEJ1 -> TR?,_N задается соотно-
соотношением A0).
*)К. Г. Я. Якоби A804—1851) — известный немецкий математик.
2)Якобианом чаще называют определитель этой матрицы (когда она квадратном).

§ 2. ДИФФЕРЕНЦИАЛ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ 431
4. Непрерывность, частные производные и дифференцируемость
функции в точке. Мы закончим обсуждение понятия дифференцируемо-
сти функции в точке указанием на взаимоотношения между непрерывностью
функции в точке, наличием у нее частных производных в точке и дифферен-
цируемостью ее в этой точке.
В § 1 (соотношения A7) и A8)) мы установили, что-если L : Ет -» Еп —
линейное отображение, то Lh —>• 0 при h —> 0. Таким образом, из соотношения
A) можнв заключить, что функция, дифференцируемая в точке, непрерывна
в этой точке, поскольку
f(x + h)- f(x) = L(x)h + o(h) при h -> 0, x + h€E.
Обратное, конечно, не верно потому, что, как нам известно, это не верно
уже в одномерном случае.
Таким образом, взаимоотношение непрерывности и дифференцируемости
функции в точке в многомерном случае такое же, как и в одномерном.
Совсем иначе обстоит дело во взаимоотношениях частных производных
и дифференциала. В одномерном случае, т. е. в случае вещественнозначной
функции одного вещественного переменного, наличие дифференциала и на-
наличие производной у функции в точке были условиями равносильными. Для
функций многих переменных мы показали (утверждение 2), что дифферен-
дифференцируемость функции во внутренней точке области определения обеспечивает
существование у нее частных производных по каждой переменной в этой точ-
точке. Однако обратное утверждение уже не имеет места.
Пример 5. Функция
- 9 | 0, если ххх1 = 0,
f(x\xz) = <
1, если ххх1 ф 0,
равна нулю на осях координат и потому имеет в точке @,0) обе частные
производные:
в1/@>0) = lim /(^^)/@>0) = lim 0__0 =
= lim
h2 /12-ю h?
Вместе с тем эта функция не дифференцируема в точке @,0), поскольку
она, очевидно, разрывна в этой точке.
Приведенная в примере 1 функция не имеет одной из частных производных
в точках осей координат, отличных от точки @,0). Однако функция
У)
-?t_, earn z2+j/2#0,
2
0, если х1 + уz — 0

432 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
(которая нам встречалась в примере 2 из § 2 гл. VII), уже во всех точках
плоскости (х,у) имеет частные производные, однако она тоже разрывна в
начале координат и потому не дифференцируема в точке @,0).
Таким обра^Ьм, возможность написать правую часть равенств G), (8) еще
не гарантирует того, что это будет дифференциал нашей функции, поскольку
функция может оказаться не дифференцируемой.
Это обстоятельство могло бы стать серьезной помехой всему дифферен-
дифференциальному исчислению функций многих переменных, если бы не выяснилось
(это будет доказано позже), что непрерывности частных производных в точке
достаточно для дифференцируемости функции в этой точке.
§ 3. Основные законы дифференцирования
1. Линейность операции дифференцирования
Теорема 1. Если отображения /i: Е -> Еп, /г: Е -> Еп, определенные
на множестве Е С Ет, дифференцируемы в точке х € Е, то их линейная
комбинация (Ai/i + А2/2) : Е —> Еп также является дифференцируемым в
этой точке отображением, причем имеет место равенство
(Ai/i + А2/2)'(*) = (Ai/{ + Aa/JXs). A)
Равенство A) показывает, что операция дифференцирования, т. е. сопоста-
сопоставление отображению его дифференциала в точке, является линейной операци-
операцией на векторном пространстве отображений /: Е —> Еп, дифференцируемых
в фиксированной точке множества Е. Слева в A) стоит, по определению, ли-
линейное отображение (Ai/i + Аг/гУОО» а справа стоит линейная комбинация
(Ai/{ + A2/2X2O линейных отображений f[(x): Em -> En, ft(x): Rm 4 ln,
которая, как нам известно из § 1, также является линейным отображением.
Теорема 1 утверждает, что эти отображения совпадают.
А2/2)(х + h) - (X1f1 + А2/2)(х) =
h) + А2/2(а; + Л)) - (Ai/i(s) + X2f2(x)) =
+ h) - h{x)) + A2(/a(s + h) - f2(x)) =
+ о(Л)) + А2(/2»Л + o{h)) =
Бели рассматриваемые функции вещественнозначны, то над ними вьшол-
нимы также операции умножения и (при необращении знаменателя в нуль)
деления. Имеет место
Теорема 2. Если функции f : Е —> Ш, g : Е —> Ш, определенные на
множестве Е С Шт, дифференцируемы в точке х € Е, то

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ
433
a) их произведение дифференцируемо в х, причем
(f-9)'(x)=9(x)f(x)+f(x)g'(x);
b) их отношение дифференцируемо в х, если д(х) ф О, причем
B)
C)
Доказательство этой теоремы совпадает с доказательством соответству-
ющих пунктов теоремы 1 из § 2 гл, V, поэтому мы на нем не останавливаемся.
Соотношения A), B), C) можно переписать также и в иных обозначениях
дифференциала. А именно:
А2/2)(х) =
A2d/2)(x),
d(f • д)(х) = g(x)df{x) + f(x)dg(x),
Посмотрим, что означают эти равенства в координатном представлении
отображений. Нам известно, что если отображение <р: Е —> Еп, дифференци-
дифференцируемое во внутренней точке х множества Е С Ет, записать в координатном
виде
то его дифференциалу d(p(x): Rm -^1пв этой точке будет соответствовать
матрица Якоби
?>'(*) =
(х) =
При фиксированных базисах в Ет и Еп соответствие между линейными
отображениями L :
т
п
и т х п-матрицами — взаимно однозначное,
поэтому линейное отображение L можно отождествить с задающей его ма-
матрицей.
Для обозначения матрицы Якоби мы все же, как правило, будем исполь-
использовать символ f'(x), а не символ б?/(ж), ибо это больше соответствует тому
традиционному разделению понятий производной и дифференциала, которое
проводится в одномерном случае.

434 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Таким образом, в силу единственности дифференциала, во внутренней точ-
точке х множества Е получаем следующие координатные формы записи соотно-
соотношений A), B), C), означающие равенства соответствующих матриц Якоби:
/ + X2difi) (х) (i = l,...,m, j = 1,..., n), A')
{di(f ¦ g))(x) = g(x)dj(x) + f(x)dig(x) (i = l,...,m), B')
0) (x) = -^ {g(x)dif(x) - f(x)di9(x)) (i = l,...,m). C')
Из поэлементного равенства указанных матриц, например, следует, что
частную производную по переменной хг от произведения вещественнозначных
функций /(ж1, ..., хт) и д(хг, ..., хт) надо брать так:
9) ,г
(х х
тп\ °V („I Tm\ , f( I m\ °Ф / 1 m\
/ о ^ Vх ? • • • > л ) ' J V**' ? • • • ? ^ / о v Vх ? • • • ? ^ /•
Отметим, что как это равенство, так и матричные равенства A'), B'),
C') являются очевидными следствиями определения частной производной и
обычных правил дифференцирования вещественнозначных функций одного
вещественного переменного. Однако нам известно, что наличия частных про-
производных еще может оказаться недостаточно для дифференцируемое™ функ-
функции многих переменных. Поэтому наряду с важными и вполне очевидными
равенствами A'), B;), C;) особую роль в теоремах 1 и 2 приобретают утвер-
утверждения о существовании дифференциала соответствующего отображения.
Заметим, наконец, что по индукции из равенства B) можно получить со-
соотношение
dtfi • • • /*)(*) = (/2 • • • fk){x)dh(x) + ... + (/1... fk-i)(x) dfk(x)
для дифференциала произведения (/i... Д) дифференцируемых вещественно-
вещественнозначных функций.
2. Дифференцирование композиции отображений
а. Основная теорема
Теорема 3. Если отображение f: X ->Y множества X С Ет в мно-
множество Y СШп дифференцируемо в точке х € X, а отображение g:Y-}Rk
дифференцируемо в точке у = f(x) € Y, то композиция g о/ : X -> R* этих
отображений дифференцируема в точке х, причем дифференциал d(g of):
композиции равен композиции dg(y) о df(x) дифференциалов
df(x): ТЕ? -+ TW}{x)=y, dg(y):

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ
435
Доказательство этой теоремы почти полностью повторяет доказательство
теоремы 2 из § 2 гл. V. Чтобы обратить внимание на одну новую, появля-
появляющуюся теперь деталь, мы все же проведем еще раз это доказательство, не
вдаваясь, однако, в уже разобранные технические подробности.
Ч Используя дифференцируемость отображений / и д в точках х и у =
= /(ж), а также линейность дифференциала д'(х), можно написать, что
(д о /)(* + h) - (д о /)(*) = g(f{x + Л)) - g(f(x)) =
= »'(/(х))(/(х + Л) - /(*)) + o(f(x + h) - f(x)) =
= 9'{y){f'{x)h + o{h)) + o(f(x + h)- f{x)) =
= д'Ш'(Ф) + g'(y)№) + °(f(* + Л) - /(*)) =
+ а(х; Л),
где д'{у) о f'(x) есть линейное отображение (как композиция линейных ото-
отображений), а
a(x;h) = g'{y)(o(h)) + o(f{x + h) - /(*)).
Но, как показывают соотношения A7), A8) из § 1,
д'(у) (o(h)) = o{h) при h -+ 0,
f(x + h) - f(x) = f'(x)h + o(h) = O(h) + o(h) = O(h) при h -+ 0
и
o(f(x + ft) - f(x)) = o(O(h)) = o(h) при ft -> 0.
Следовательно,
a(x; ft) = o(ft) + o(ft) = o(ft) при ft —> 0,
и теорема доказана. >
Будучи переписана в координатной форме, теорема 3 означает, что если
х — внутренняя точка множества X и
U\J \Js) . • . UmJ Vх/
K8ifn(x) ... dmfn(x)j
а у = f(x) — внутренняя точка множества Y и
g'(y) =
15 Зорич В. А.
... dngk{y)j
= {dig1) (у),

436
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ТО
/)'(*) =
f){x),
= (di(9l о f))(x) =
д^1 (у) ... дпд1{у)^
Кд19к(у) ... дпдк(у);
п(х) ... dmfn(x)J
В равенстве
{di(glof))(x) = (dj9l(f(x))-difHx))
D)
справа имеется в виду суммирование по индексу j в пределах его изменения,
т. е. от 1 до п.
В отличие от равенств (I'), B'), C;), соотношение D) нетривиально даже
в смысле поэлементного равенства участвующих в нем матриц.
Рассмотрим некоторые важные частные случаи доказанной теоремы.
Ь. Дифференциал и частные производные сложной вещественно-
значной функции. Пусть z = д(уг, ..., уп) — вещественнозначная функция
вещественных переменных у1, ..., уп, каждое из которых в свою очередь есть
функция yj = fj(xl, ..., хт) (j = 1, ..., п) переменных ж1, ..., хт. В предпо-
предположении дифференцируемости функций д и f* (j = 1, ..., п) найдем частную
производную :? / (х) композиции отображений / : X ->• Y и д : Y
По формуле D), в которой при наших условиях I = 1, находим
di{gof){x)=djg{f{x))-diP{x)
E)
или, в более подробной записи,
d(gof)
дх{
dg
ду1
= д19(№) • dj1 (ж)
dng{f{x)) • ^/n(rr)
с. Производная по вектору и градиент функции в точке. Рас-
Рассмотрим установившийся поток жидкости или газа в некоторой области G
пространства Е3. Термин «установившийся» означает, что скорость потока
в каждой точке области G не меняется со временем, хотя в различных точ-
точках области G она, разумеется, может быть различной. Пусть, например,
f(x) = /(ж1, ж2, ж3) — давление в потоке в точке ж = (ж1, ж2, ж3) € G. Если мы
будем перемещаться в потоке по закону ж = ж(?), где t — время, то в момент
t мы будем регистрировать давление (fox)(t) = f(x(t)). Скорость изменения

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ 437
давления со временем вдоль нашей траектории, очевидно, есть производная
х)
— (t) по времени от функции (/ ож)(?). Найдем ее в предположении, что
/(ж1, ж2, ж3) — дифференцируемая в области G функция. По закону диффе-
дифференцирования композиции функций находим
§?{t) + ^L(x(t))iHt), F)
где i*(t) = ?(t) (г = 1,2,3).
Поскольку (я1, ж2, x3)(t) = и(?) есть вектор скорости нашего перемещения в
момент ?, a (c?i/, #2/, ^з/)(ж) есть координатная запись дифференциала d/(rr)
функции / в точке ж, то равенство F) можно переписать также в виде
= df(x(t))v(t), G)
т. е. искомая величина есть значение дифференциала df(x(t)) функции /(ж) в
точке x(t) на векторе v(t) скорости нашего движения.
В частности, если при t = 0 мы были в точке хо = ж@), то
t», (8)
где v = v@) — вектор скорости в момент t = 0.
Правая часть соотношения (8) зависит только от точки Хо € G и вектора
v скорости, которую мы имеем в этой точке, и не зависит от конкретного
вида траектории х = ж(?), лишь бы было выполнено условие х@) = v. Это
означает, что на любой траектории вида
(9)
где a(t) = o(t) при t —> 0, значение левой части равенства (8) будет одинаково,
поскольку оно вполне определяется заданием точки хо и вектора v € Т*Е^0,
приложенного к этой точке. В частности, если бы мы хотели непосредственно
вычислить значение левой (а значит, и правой) части равенства (8), то можно
было бы в качестве закона движения выбрать функцию
x(t) = хо + vt, A0)
отвечающую равномерному движению со скоростью и, при котором в момент
t = О мы находимся в точке ж@) = Жо.
Дадим теперь следующее
Определение 1. Если функция /(ж) определена в окрестности точки
Жо Е Em, a v € TR™0 — вектор, приложенный к точке Жо, то величина
А,/Ы := lim ^° + Vt) ~ /(Жо) I A1)
t->0 t
15*

438 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
(если указанный предел существует) называется производной функции f в
точке хо по вектору v.
Из проведенных рассмотрений следует, что если функция / дифференци-
дифференцируема в точке хо, то при любой функции x(t) вида (9) и, в частности, вида
A0) имеет место равенство
Dvf(x0) = ^^ @) = d/(x0) v, A2)
что в координатном представлении означает
Dvf(x0) = ^Ыу1 + ... + -^-(xo)vm. A3)
В частности, для базисных векторов е\ = A,0, ..., 0), ..., ет = @, ..., 0,1)
из этой формулы получаем
Deif(x0) = ^(^о) (г = 1, ..., га).
На основании равенства A2) в силу линейности дифференциала df(xo) за-
заключаем, что если / — дифференцируемая в точке xq функция, то для любых
векторов г>1, г>2 Е ТЖ™0 и любых Ai, A2 Е R функция имеет в точке хо произ-
производную по вектору (Ai^i -f A2V2) € TR™Q и при этом
= XiDVlf(x0) + A2-DV2/(«o). A4)
Если пространство Em рассматривать как евклидово пространство, т. е.
как векторное пространство со скалярным произведением, то (см. § 1) любую
линейную функцию L(v) можно будет записать в виде скалярного произведе-
произведения (?, v) фиксированного вектора ? = ?(L) и переменного вектора v.
В частности, найдется, вектор ? такой, что
df(xo)v = (€,v). A5)
Определение 2. Вектор ? Е TR™0, отвечающий в смысле равенства
A5) дифференциалу df(xo) функции / в точке х0, называется градиентом
функции в этой точке и обозначается символом grad/(xo).
Итак, по определению
df(xo)v = (grad/(xo),v).
A6)
Если в Ет выбрана декартова система координат, то, сопоставляя соотно-
соотношения A2), A3) и A6), заключаем, что в такой системе координат градиент
имеет следующее координатное представление:

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ 439
Выясним теперь геометрический смысл вектора grad/(xo)-
Пусть е Е TR™0 — единичный вектор. Тогда в силу A6)
Def(xo) = |grad/(z0)|cos<p, A8)
где ф — угол между векторами е и grad/(xo).
Таким образом, если grad/(xo) Ф 0 и е = || grad/(xo)||~1 grad/(xo), то про-
производная Def(xo) принимает наибольшее значение. То есть скорость роста
функции / (выраженная в единицах величины /, отнесенных к единице длины
в Ет) при движении из точки xq максимальна и равна || grad/(xo)tl> когда мы
смещаемся именно в направлении вектора grad/(xo). При смещении в проти-
воположном направлении значения функции наиболее резко уменьшаются, а
при смещении в направлении, перпендикулярном вектору ^rad/(x0), скорость
изменения значений функции равна нулю.
Производную по единичному вектору данного направления обычно назы-
называют производной по данному направлению.
Поскольку единичный вектор в евклидовом пространстве задается напра-
направляющими косинусами:
е = (cos ol\ , ..., cos am),
где oti — угол, который вектор е образует с базисным вектором в{ декартовой
системы координат, то
= (grad/(xo),e) = —(x0)cosai + ... +
Вектор grad /(xo) встречается очень часто и имеет многочисленные приме-
применения. Например, на отмеченном выше геометрическом свойстве градиента
основаны так называемые градиентные методы численного (на ЭВМ) поиска
экстремумов функций многих переменных. (См. в этой связи задачу 2 в конце
параграфа.)
Многие важные векторные поля, как, например, ньютоновское поле сил тя-
тяготения или кулоновское поле заряда, являются градиентами некоторых ска-
скалярных функций — потенциалов этих полей (см. задачу 3).
Многие физические законы в самой своей формулировке используют век-
вектор grad/. Например, в механике сплошной среды эквивалентом основного
закона Ньютона та = F динамики точки является соотношение
ра = — gradp,
связывающее ускорение а — а(х, t) в потоке свободной от внешних сил идеаль-
идеальной жидкости или газа в точке х в момент t с плотностью среды р = p(x,t) и
градиентом давления р = p(x,t), отнесенными к этой же точке и к этому же
моменту времени (см. задачу 4).
О векторе grad / мы еще будем говорить позже, при изучении векторного
анализа и элементов теории поля.

440 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
3. Дифференцирование обратного отображения
Теорема 4. Пусть /: U(x) -* V(y) — отображение окрестности U(x) С
С Rm точки х на окрестность V(y) С Шт точки у = f(x). Пусть f непре-
непрерывно в точке х и имеет обратное отображение f~l: V(y) -* U(x), непре-
непрерывное в точке у.
Если при этом отображение f дифференцируемо в точке х и касательное
к f в точке х отображение f'(x): ТЕ™ -> TWf имеет обратное отобра-
отображение [f'(x)]-x : ТШ? -> ТЩ?, то отображение f~l : V(y) -> U(x) диффе-
дифференцируемо в точке у = f(x) и справедливо равенство
Таким образом, взаимно обратные дифференцируемые отображения име-
имеют в соответствующих точках взаимно обратные касательные отображения.
<4 Положим
f{x) = у, f{x + К) = у + *, t = fix + К) - f(x);
тогда
Будем предполагать, что h столь мало, что i + /iG f/(x), а значит, у +1 E
€ V(y).
Из непрерывности /вхи/ х в у следует, что
t = f(x + h)- f{x) -> 0 при h -» 0 A)
и
h = f-1(y + t)-f-1iy)-+O при t->0. B)
Из дифференцируемоСти / в точке х следует, что
t = f'ix)h + o(h) при ft -> 0, C)
т. е. можно утверждать даже, что t = O(h) при ft —> 0 (см. соотношения A7),
A8) из § 1).
Покажем, что если f'(x) — обратимое линейное отображение, то и ft = O(t)
при t -> 0.
В самом деле, из C) последовательно получаем
'(x)]-1t = h+[f'(x)]-1o(h) при ft-» 0,- D)
при ft-» 0,
при Л-Ю,
при \\h\\<69

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ 441
где число S > 0 выбрано так, что ||о(Л)|| < х IHI ПРИ IM! < <*• Тогда с учетом
соотношения B) находим
)]||(||) при t
что равносильно соотношению
h = O(t) при t -> 0.
Отсюда, в частности, следует, что
o(h) = o(t) при t -» 0.
Учитывая это, из B) и D) получаем
h = [/'(ж)] ~* * + o(t) при * -> 0
или
ГЧ + *)Г1() [1'()Г1* + (г) при
Из алгебры известно, что если линейному преобразованию L: Rm -> Ет
отвечает матрица А, то обратному к L линейному преобразованию L: Em ->
-> Ет соответствует матрица Л, обратная к матрице А. Построение эле-
элементов обратной матрицы также известно из алгебры, следовательно, дока-
доказанная теорема дает прямой рецепт для построения отображения (/~1)/B/)-
Отметим, что при т = 1, т. е. при Ет = Е, якобиан отображения /:
U(x) -> V(y) в точке х сводится к одному числу /'(я) — производной функ-
функции / в точке х, а линейное преобразование f'(x) : ТЖХ —> ТЖу сводится к
умножению на это число: h i-> f'(x)h. Это линейное преобразование обра-
обратимо тогда и только тогда, когда f'(x) ф 0, причем матрица обратного пре-
преобразования [f'(x)]~ : ТЖу -> TRX также состоит из одного числа, равного
[/'(#)] ~ » т- е- обратного к f'(x). Значит, теорема 4 содержит в себе также
доказанное ранее правило отыскания производной обратной функции.
Задачи и упражнения
1. а) Два пути t ь-> xi(t), t ь-> X2(t) в Rm будем считать эквивалентными в точке
so € Rm, если ал@) = s2@) = х0 и d(xi(t),X2(t)) = o(t) при t -» 0.
Проверьте, что указанное отношение действительно является отношением экви-
эквивалентности, т. е. оно рефлексивно, симметрично и транзитивно.
b) Проверьте, что между векторами v 6 TW?0 и классами эквивалентных в точке
хо гладких путей имеется взаимно однозначное соответствие.
c) Отождествляя касательное пространство TR^ с множеством классов эквива-
эквивалентных в точке хо 6 Rm гладких путей, введите операции сложения классов путей
и умножения их на число.
d) Проверьте, зависят ли введенные вами операции от системы координат в
ЬТП

442 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
2. а) Изобразите график функции z = ж2 + 4у2, где (ж, у, z) — декартовы коорди-
координаты в R3.
b) Пусть /: С -> R — числовая функция, определенная в области G С Rm. Уров-
Уровнем (с-уровнем) функции называется множество Е С G, на котором функция при-
принимает одно значение (f(E) = с). Точнее, Е = /-1(с). Изобразите в R2 уровни
функции, указанной в а).
c) Найдите градиент функции f(x, у) = х2 + 4у2 и проверьте, что в любой точке
(ж, у) вектор grad/ ортогонален линии уровня функции /, проходящей через эту
точку.
d) Используя результаты задач а), Ь), с), проложите на поверхности z = х2 + 4у2
самый короткий, на ваш взгляд, маршрут спуска из точки B,1,8) поверхности в
низшую ее точку @,0,0).
e) Какой алгоритм, пригодный для ЭВМ, вы могли бы предложить для отыскания
минимума функции f(x, у) = х2 + 4у2? v
3. Говорят, что в области G пространства Rm задано векторное поле, если ка-
каждой точке х € G сопоставлен некоторый вектор v(a:) € TRJ1. Векторное поле v{x)
в G называется потенциальным, если в области G есть числовая функция U: G —> R
такая, что v(x) = grad U(x). Функцию U(x) называют потенциалом поля v(x).
(В физике потенциалом обычно называют функцию — U(x), а функцию U(x) на-
называют силовой функцией, если речь идет о поле сил.)
a) Изобразите на плоскости с декартовыми координатами (х, у) поле grad f(x, у)
для каждой из функций fi(x,y) = х2+у2; J2{x,y) = -(ж2+у2); h{x,y) = arctg (х/у)
в области у > 0; /*(х,у) = ху.
b) Согласно закону Ньютона частица массы т, находящаяся в точке 0 € R3,
притягивает частицу массы 1, находящуюся в точке х € R3 (х ф 0), с силой F =
= — т|г|~ г, где г — вектор 0а; (размерную постоянную G мы опустили). Покажите,
что векторное поле F(a;) в R3 \0 потенциально.
c) Проверьте, что массы гщ, (г = 1, ..., п), помещенные в точках (?», т;», ?г) (г =
= 1, ..., п) соответственно, создают вне этих точек ньютоновское поле сил, потен-
потенциалом которого служит функция
n
TTli
d) Укажите потенциал кулоновского электростатического поля напряженности,
создаваемого точечными зарядами д» (t = 1, ..., п), помещенными в точках (?», т)г, (%)
(г = 1, ..., п) соответственно.
4. Рассмотрим движение идеальной несжимаемой жидкости в пространстве, сво-
свободном от внешних (в том числе и гравитационных) сил.
Пусть v = v(x,y,z,t), a = 8i(x,y,z,t), p = p(x,y,z,t), p = p(x,y,z,t) суть
соответственно скорость, ускорение, плотность и давление в точке (х, у, z) среды в
момент времени t.
Идеальность жидкости означает, что давление в любой ее точке не зависит от
направления.
а) Выделите из жидкости объем в виде небольшого параллелепипеда, одно из ре-
ребер которого параллельно вектору gradp(a;,y, z,t) (где gradp берется по простран-
пространственным координатам). Оцените действующую на объем за счет перепада давления

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ 443
силу и дайте приближенную формулу для ускорения этого объема, считая жидкость
несжимаемой.
b) Проверьте, согласуется ли полученный вами в а) результат с уравнением
Эйлера
ра = — gradp.
c) Линия, в любой точке которой касательная имеет направление вектора'скоро-
вектора'скорости в этой точке, называется линией тока. Движение называется установившимся,
если функции v, a, р, p не зависят от t. Используя Ь), покажите, что вдоль ли-
линий тока в установившемся потоке несжимаемой жидкости величина - ||v||2 4- р/р
постоянна (закон Бернулли1^).
d) Как изменятся формулы в а) и Ь), если движение будет происходить в поле
тяжести вблизи поверхности Земли? Покажите, что в этом случае
ра = -grad(gz+p)
и потому вдоль каждой линии тока установившегося движения несжимаемой жид-
жидкости на сей раз постоянна величина r||v||2 -h gz 4- р/р, где д — ускорение силы
тяжести, a z — высота точки линии тока, отсчитываемая от некоторого нулевого
уровня.
e) Объясните на основании предыдущих результатов, почему несущее крыло име-
имеет характерный выпуклый вверх профиль.
f) В цилиндрический стакан с круглым дном радиуса R налита до уровня h
несжимаемая идеальная жидкость плотности р. После этого стакан стали вращать
вокруг его оси с угловой скоростью ш. Используя несжимаемость жидкости, найдите
уравнение z = /(ж, у) ее поверхности в установившемся режиме (см. также задачу 3
из гл. V, § 1).
g) По найденному в f) уравнению z = /(ж, у) поверхности напишите формулу
р = р(х, t/, z) для давления в любой точке (ж, у, z) объема, заполненного вращающейся
жидкостью. Проверьте, выполнено ли для найденной вами формулы полученное в d)
уравнение ра = — grad (gz + р).
h) He могли бы вы теперь объяснить, почему чаинки тонут (хотя и не слишком
быстро!), а при вращении чая собираются не у стенок стакана, а в центре дна?
5. Оценка погрешностей вычисления значений функции.
a) Используя определение дифференцируемой функции и приближенное равен-
равенство Af(x\h) « df(x)h, покажите, что относительная погрешность S = S(f(x);h)
в значении произведения f(x) = х1... хт т отличных от нуля сомножителей, вы-
вызванная погрешностями в задании самих сомножителей, может быть найдена в виде
m
S « Y1 &, где Si — относительная погрешность задания г-го сомножителя.
t=i
b) Используя то, что din f(x) = -jr-^-df(x), еще раз получите результат преды-
j\x)
дущей задачи и покажите, что вообще относительную погрешность дроби
, X
m
l> Д. Бернулли A700 — 1782) — швейцарский ученый, один из наиболее выдающихся фи-
физиков и математиков своего времени.

444 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
можно найти как сумму относительных погрешностей значений функций /i, ..., /п,
6. Однородные функции и тождество Эйлера. Функция /: G —> R, определенная
в некоторой области G С Rm, называется однородной (положительно однородной)
степени п, если для любых х 6 Rm и А € R таких, что х € G и Хх 6 B, имеет место
равенство
/(Ах) = А"/(«) (/(А.) = |А|п/(х)).
Функция называется локально однородной степени п в области С, если она явля-
является однородной функцией указанной степени в некоторой окрестности любой точки
области G.
a) Докажите, что в выпуклой области всякая локально однородная функция явля-
является однородной.
b) Пусть область G есть плоскость R2 без луча L = {(ж, у) G R2 | х = 2 Л у ^ 0}.
Проверьте, что функция
/ А1> если ^ > 2 Л у > 0,
д. ч = / У
^ у3 в остальных точках области,
локально однородна в G, но не является однородной функцией в этой области.
с) Укажите степень однородности или положительной однородности следующих
функций, рассматриваемых в их естественной области определения:
fi(x\ ..., хт) = х V + х V + ... + х™-1*™;
^z1 х2 х3 х4) - 12 34
-I- х2х3х
) = |ж ... а; |
d) Продифференцировав равенство f(tx) = tnf(x) no *, покажите, что если диф-
дифференцируемая функция /: G —? R локально однородна степени п в области G С Rm,
то она удовлетворяет в G следующему тождеству Эйлера для однородных функций:
Х Ит^ •> - • - Iх ) 4-... 4- х « m \х 1 - • > * х ) = ^/(х j • • •, х
е) Покажите, что если для дифференцируемой в области G функции / : G
R выполнено тождество Эйлера, то эта функция локально однородна степени п в
области G.
Указание. Проверьте, что функция ip(t) = t~nf(tx) при любом х € G опреде-
определена и постоянна в некоторой окрестности единицы.
7. Однородные функции и метод размерности.
1° Размерность физической величины и особенности функциональных связей
между физическими величинами.
Физические законы устанавливают взаимосвязи физических величин, поэтому
если для некоторых из этих величин принять какие-то единицы измерения, то едини-
единицы измерения связанных с ними других величин будут определенным образом выра-
выражаться через единицы измерения фиксированных величин. Так возникают основные
и производные единицы той или иной системы единиц измерения.
В системе СИ (Systeme International) за основные механические единицы изме-
измерения приняты единицы длины — метр (м), массы — килограмм (кг) и времени —
секунда (с).

§ 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФЕРЕНЦИРОВАНИЯ 445
Выражение производной единицы измерения через основные называется ее раз-
размерностью. Это определение ниже будет уточнено.
Размерность любой механической величины записывают символически в виде
формулы, выражающей ее через предложенные Максвелломх) символы L,M,T раз-
размерностей указанных выше основных единиц. Например, размерности скорости,
ускорения и силы имеют соответственно вид
Если физические законы не зависят от выбора единиц измерения, то отражени-
отражением этой инвариантности должны быть определенные особенности функциональной
зависимости
Хо = /(#1, . • • , Xk, Xk+1, • . • , Хп) (*)
между числовыми характеристиками физических величин.
Рассмотрим, например, зависимость с = /(о, Ь) = у/а2 + Ь2 между длинами кате-
катетов и длиной гипотенузы прямоугольного треугольника. Изменение масштаба длин
должно одинаково сказаться на всех длинах, поэтому для любых допустимых зна-
значений о и Ъ должно быть выполнено соотношение /(ао, аЬ) = </?(а)/(а,Ь), причем в
нашем случае <?>(а) = а.
Основная (на первый взгляд очевидная) предпосылка теории размерности состо-
состоит в том, что претендующая на физическую значимость зависимость (*) должна
быть такой, чтобы при изменении масштабов основных единиц измерения числен-
численные значения всех одноименных величин^ участвующих в формуле, менялись в одно
и то же число раз.
В частности, если a?i, жг, хз — основные независимые физические величины и
(xijX2yxz) *-? f(xi,X2,xz) — зависимость от них некоторой четвертой физической
величины, то, в силу сформулированного принципа, при любых допустимых значе-
значениях xi, #2, хз должно быть выполнено равенство
/{а1Х1уа2Х2,азхз) = <?>(<*!> а2,аз)/(я1,Ж2,яз)> (**)
с некоторой конкретной функцией (р.
Функция ip в равенстве (**) полностью характеризует зависимость численного
значения рассматриваемой физической величины от изменения масштабов основных
фиксированных физических величин. Таким образом, эту функцию и следует счи-
считать размерностью данной физической величины по отношению к фиксированным
основным единицам измерения.
Уточним теперь вид функции размерности.
a) Пусть х »->• f(x) — функция одного переменного, удовлетворяющая условию
f(ax) = (p(a)f(x)) где / и ip — дифференцируемые функции.
Покажите, что <р(а) = ad.
b) Покажите, что функция размерности (р в равенстве (**) всегда имеет вид
ах1 • а22 • а33, где показатели степени di, <Ь, ^з суть некоторые действительные
числа. Таким образом, если, например, фиксированы основные единицы L, М, Т,
. К. Максвелл A831 — 1879) — выдающийся английский физик; создал математи-
математическую теорию электромагнитного поля, известен также исследованиями по кинетической
теории газов, оптике и механике.

446 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
то набор (di,d2,<fe) показателей в степенном выражении LdlMd2Tdz также можно
считать размерностью данной физической величины.
с) В Ь) было получено, что функция размерности всегда имеет вид степенной
зависимости, т. е. является однородной функцией определенной степени по каждой
из основных единиц измерения. Что означает, что степень однородности функции
размерности некоторой физической величины по отношению к одной из основных
единиц измерения равна нулю?
2° Л-теорема и метод размерности.
Пусть [х{] = Х{ (г = 0,1, ..., п) — размерности физических величин, участвую-
участвующих в законе (¦).
Предположим, что размерности величин жо, #*+i, • • •, хп могут быть выражены
через размерности величин xi, ... , ж*, т. е.
[xk+i] = Хк+{ = X$ ...XPJ, (i = 1, ..., n - k).
d) Покажите, что тогда наряду с (*) должно быть справедливо соотношение
lj^ ... , а\п~к ... аРкп~к
хп)- (***)
е) Бели xi, ... , Хк независимы, то в (***) можно положить ot\ = xj, ..., а* =
х^1. Проверьте, что при этом из (***) получается равенство
_ ,Л Xk+1
г ^ V <rPl P
^l * * " "*^к ^
являющееся соотношением
П = /A, ...,1,П1,...,ПП_*) (****)
1 " ' ' к
между безразмерными величинами П, Пх, ... , Пп_&.
Таким образом, получается следующая
П-теорема теории размерности. Если в соотношении (*) величины
xi,...,Xjb независимы, то это соотношение сводится к функции (*¦**) от п — к
безразмерных параметров.
f) Проверьте, что если к = п, то на основании П-теоремы функция / из соот-
соотношения (*) может быть найдена с точностью до числового множителя. Найдите
таким путем выражение c(<po)y/l/g для периода колебаний маятника (т. е. подве-
подвешенной на нити длины I массы ш, качающейся у поверхности Земли; </?о — начальный
угол отклонения).
g) Найдите формулу Р = с y/mr/F для периода обращения тела массы ш, удер-
удерживаемого на круговой орбите центральной силой величины F.
Ь).Иэ закона Кеплера (Pi/РгJ = (ri/ггK, устанавливающего в применении к кру-
круговым орбитам связь между отношением периодов обращения планет (спутников) и
отношением радиусов их орбит, найдите, вслед за Ньютоном, показатель степени а
в законе F = G всемирного тяготения.

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 447
§ 4. Основные факты дифференциального исчисления
вещественнозначных функций многих переменных
1. Теорема о среднем
Теорема 1. Пусть f : G -> Е — вещественнозначнал функция, опре-
определенная в области G С Rm. Пусть отрезок [х,х + h] с концами х, х + h
содержится в G. Если при этих условиях функция f непрерывна в точках
отрезка [x^x + h] и дифференцируема в точках интервала ]x,x + /i[, то най-
найдется такая точка ^е]х,х + Л[, что имеет место равенство
x + h)-f(x)=f'(Oh.
l A)
Рассмотрим вспомогательную функцию
определенную на отрезке 0 ^ t ^ 1. Функция F удовлетворяет всем условиям
теоремы Лагранжа: она непрерывна на [0,1], как композиция непрерывных
отображений, и дифференцируема в интервале ]0,1[, как композиция диффе-
дифференцируемых отображений. Следовательно, найдется точка в Е ]0,1[ такая,
что
Но F(l) = Даг+ft), F@) = /(х), F'@) = Г{хЛ-вК)Н и, значит, выделенное
равенство совпадает с утверждением теоремы 1. >
Приведем теперь координатную форму записи соотношения A).
Если.х = (х1> ...,zm), h = (h\...yhm) и ?= (х1 + 9h\ ... ,xm + (9ftm), то
равенство A) означает, что
f{x + h)- f(x) = fix1 + Л1, ..., xm + hm) - /(x\ ..., xm) =
m
m
Используя соглашение о суммировании по повторяющемуся сверху и снизу
индексу, окончательно можно записать
fix1 + Л1, ..., xm + hm) - /(х1, ..., хт) =
= difix1 + 9h\ ...,xm + ehm)h\ (Г)
где 0 < в < 1, причем в зависит и от х, и от h.

448 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Замечание. Теорема 1 называется теоремой о среднем в связи с тем,
что существует некоторая «средняя» точка ? G ]х, х + ft[, в которой выполняет-
выполняется равенство A). Мы уже отмечали при обсуждении теоремы Лагранжа (см.
гл. V, § 3, п. 1), что теорема о среднем специфична именно для вещественно-
значных функций. Общая теорема о конечном приращении для отображений
будет доказана в главе X (часть II).
Из теоремы 1 вытекает полезное
Следствие. Если функция f: G —? R дифференцируема в области G С
С Кт и в любой точке х G G ее дифференциал равен нулю, то f постоянна
в области G.
М Равенство нулю линейного отображения равносильно обращению в нуль
всех элементов отвечающей ему матрицы. В нашем случае
поэтому d\f{x) = ... = dmf(x) = 0 в любой точке х G G.
По определению, область есть открытое связное множество. Воспользуем-
Воспользуемся этим.
Покажем сначала, что если х G G, то в шаре В(х; г) С G функция / по-
постоянна. Действительно, если (а: + h) G В(х;г), то и [х,х + h] С В{х\г) С G.
Применяя соотношение A) или A'), получаем
/(х + h) - /(*) = ?{?)h = О • h = О,
т. е. f(x -f h) = f(x) и значения / в шаре В(х;г) совпадают со значением / в
центре этого шара.
Пусть теперь жо, Х\ G G — произвольные точки области G. В силу связ-
связности G найдется путь t »-)> x(t) G G такой, что х@) = Хо, хA) = х\. Мы
предполагаем, что непрерывное отображение t ь» x(t) определено на отрезке
О ^ t ^ 1. Пусть В(хо;г) — шар с центром в жо, содержащийся в G. Посколь-
Поскольку х@) = хо и отображение t *-> x(t) непрерывно, найдется положительное
число S такое, что x(t) G B(xo;r) С G при 0 ^ t ^ S. Тогда по доказанному
(/ ox)(t) = f(xo) на промежутке [О,S].
Пусть Z = sup 6, где верхняя грань берется по всем числам S G [0,1] таким,
что (f о x)(t) = f(xo) на промежутке [О, S]. В силу непрерывности функции
f(x(t)) имеем f(x(l)) = f(xo). Но тогда / = 1. Действительно, в противном
случае можно было бы взять некоторый шар В(хA)',г) С С?, в котором f(x) =
= f(x(l)) = /(хо), затем в силу непрерывности отображения t »-> x(t) найти
Д > 0 так, что x(t) G B(x(l);r) при / ^ t ^ / + Д. Тогда (fox)(t) = f(x{l)) =
= /(хо) при 0^?^/ + Д и I ф sup 8.
Итак, показано, что (fox)(t) = /(хо) при любом t G [0,1]. В частности,
(/ох)A) = /(xi) = /(хо) и мы проверили, что в любых двух точках хо, Х\ G G
значения функции / : G —> Ж совпадают. >

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 449
2. Достаточное условие дифференцируемости функции
многих переменных
Теорема 2. Пусть f : U(x) -+ Ж — функция, определенная в окрестно-
окрестности U{x) С Rm точки х = (х1, ..., хт).
Если функция f имеет в каждой точке окрестности U(x) все частные
производные ^-~, ..., о~т^> то из их непрерывности в точке х следует диф-
ференцируемость функции f в этой точке.
< Без ограничения общности будем считать, что U(x) является шаром
В{х; г). Тогда вместе с точками х = (х1, ..., хт), х + h = (хх +h1, ..., хт + Лт)
области t/(x) должны принадлежать также точки (х1, х2 + Л2, ..., хш + Лт),
... , (я1, х2, ..., ж, хт + hm) и соединяющие их отрезки. Воспользуемся
этим, применяя в следующей выкладке теорему Лагранжа для функций одной
переменной:
f(x + h) - f(x) = fix1 + h\ ..., xm + /im) - /(x\ ..., xm) =
= fix1 -I- h\ ..., xm + /im) - /(s\ ж2 + Л2, ..., xm + hm) +
-f /(a:1, x2 + /i2, ..., xm + /im) - /(ж1, x2, я3 -I- /i3, ..., xm + hm) + ...
• • • i J\X ) X j • • • 7 X j X ~r #1 J у (X , . . . , X ) ——
= dxfix1 + ^/i1, x2 + /i2, ..., xm 4- /i771)/!1 +
• + d2fix\ x2 + 02/i2, x3 + /i3, ..., xm + hm)h2 + ...
• • • + dm fix1, x2,..., xm~\ xm -I- emhm)hm.
Пока мы воспользовались лишь наличием у функции / в области t/(x) част-
частных производных по каждой из переменных.
Теперь воспользуемся их непрерывностью в точке х. Продолжая предыду-
предыдущую выкладку, получаем, что
fix + h) - f{x) = di/(x\ ..., xm) h1 + alhx
• • • + dmfix\ ..., xm) /im + am/im,
где величины ai, ..., am в силу непрерывности частных производных в точке
х стремятся к нулю при h —> 0.
Но это означает, что
/(х + К) - fix) = L(x) h + o(/i) при /i -+ 0,
где L(x)/i = di/Cx1,...,x)^1 + ... + dm/(x\...,xm)/im. >
Из теоремы 2 следует, что если частные производные функции /: G -> Е
непрерывны в области С? С Rm, то функция дифференцируема в любой точке
этой области.

450 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Условимся в дальнейшем через C^(G;R) или, проще, через C^l\G) обо-
обозначать множество функций, имеющих в области G непрерывные частные
производные.
3. Частные производные высшего порядка. Бели функция /: G ->
, определенная в некоторой области G С Мт, имеет частную производную
ж) по одной из переменных ж1, ..., жт, то эта частная производная вновь
является некоторой функцией dif : G —> Е, которая в свою очередь может
иметь частную производную dj(d{f)(x) по некоторой переменной ж*7.
Функция dj(d{f) : G —> Е называется второй производной от функции f
по переменным ж% ж-7 и обозначается одним из символов
Порядок индексов указывает, в каком порядке производится дифференци-
дифференцирование по соответствующим переменным.
Мы определили частные производные второго порядка.
Если определена частная производная
порядка fc, то по индукции определяем частную производную порядка к ¦+• 1
соотношением
Здесь возникает специфический для случая функций многих переменных
вопрос о том, влияет ли порядок дифференцирований на вычисляемую част-
частную производную.
Теорема 3. Если функция f : G -? Ж имеет в области G частные
производные
d2f d2f
и J (Т) и J
mo в любой точке х G G, в которой обе зти производные непрерывны, их
значения совпадают.
<4 Пусть х eG — точка, в которой обе функции dijf: G —> R, djif :G
непрерывны. Дальнейшие рассмотрения будем проводить в некотором шаре
В(х; г) С G, г > 0, являющемся выпуклой окрестностью точки х. Мы хотим
проверить, что
* (х1 хт) - * (х1 хт
' ' ) дходхгК ' '
Поскольку во всех дальнейших выкладках меняться будут только перемен-
переменные хг и xJ, то мы для сокращения записи предположим, что / есть функция

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 451
двух переменных /(х1, х2), и нам надо проверить, что
если в точке (х1, х2) G I2 обе указанные функции непрерывны.
Рассмотрим вспомогательную функцию
F(h\ ft2) = /(х1 + Л1, х2 + /i2) - /(х1 + Л1, х2) - /(х\ х2 + /i2) + /(х\ х2),
где смещение ft = (ft1, /i2) предполагается достаточно малым, а именно таким,
что х 4- /i ? B(x;r).
Если F(hl, ft2) рассмотреть как разность
F(h\ ft2) = <рA) - <р@),
где <^(?) = fix1 + th1, x2-f Л2) — f{xl + thl, x2), то по теореме Лагранжа найдем,
что
F(h\ h2) = ^(^i) = (йД*1 -f- *iA1, x2 4 Л2) - ^/(х1 4 *!А1, х2))А1.
Применяя к последней разности вновь теорему Лагранжа, найдем, что
F(h\ h2) = 921/Сх1 + 0xh\ x2 + 02h2)h2h\ . B)
Если теперь F(/ix, h2) представить в виде разности
где (p{t) = f{xx + ft1, x2 -I- ?ft2) - fix1, x2 + tft2), то аналогично найдем, что
F(/i\ ft2) = d12fixx + Sift1, x2 + 02h2)h}h2. C)
Сравнивая равенства B) и C), заключаем, что
d2ifixx + 0!ft\ x2 4- 02ft2) = Sis/Cx1 4- Uft1, x2 4- ?2ft2), D)
где 0i, 02, #i, #2 € ]0»l[- Воспользовавшись непрерывностью рассматривае-
рассматриваемых частных производных в точке (х1, х2) при ft —^ 0, из D) получаем нужное
равенство
9/A2) 9/A2) >
Заметим, что без каких-либо дополнительных предположений, вообще го-
говоря, нельзя утверждать, что справедливо равенство 9^/(х) = ^/(х), если
обе указанные частные производные определены в точке х (см. задачу 2 в
конце параграфа).
Договоримся в дальнейшем через C^iG;R) или C^k\G) обозначать мно-
множество функций f : G -? Ж, все частные производные которых до порядка к
включительно определены и непрерывны в области G С та>т

452 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
В качестве следствия теоремы 3 получаем
Утверждение 1. Если f e C^(G;R)f то значение dix..mikf(x) част-
частной производной не зависит от порядка ti, ..., г* дифференцирования, т. е.
остается тем же при любой перестановке индексов ti, ..., г*.
М В случае к = 2 это утверждение содержится в теореме 3.
Предположим, что утверждение справедливо до порядка п включительно.
Покажем, что тогда оно справедливо и для порядка п + 1.
Но dnta.-in+i/O*) = dil(di2...in+1f)(x). Индексы г2, ..., tn+i по предположе-
предположению индукции можно переставлять, не меняя функции di2...in+1/(?), a следова-
следовательно, и функции di1,,.in+1f(x). Поэтому достаточно проверить, что можно
переставлять также, например, индексы i\ и г2, не меняя значения производ-
производной dili2...in^f(x).
Поскольку
то возможность этой перестановки непосредственно вытекает из теоремы 3.
В силу принципа индукции утверждение 1 доказано. >
Пример 1. Пусть f(x) = /(ж1, х2) — функция класса С(*)(С?;Е).
Пусть h = (ft1, ft2) таково, что отрезок [х,х ¦+• ft] содержится в области G.
Покажем, что функция
(p(t) = f(x + th),
определенная на отрезке [0,1], принадлежит классу С(*)[0,1], и найдем ее про-
производную по t порядка к.
Имеем
r1 + th\ x2 + Jft2)/!1 + d2f(x1 + *ft\ x2 + *ft2)ft2,
x + tft)ft1ft1 + d2if(x + tft)ft2ftx +
+ <9i2/(x + tft)ftxft2 + d22f(x +1 ft) ft2 ft2 =
x2 -I- 29i2/(x + ^ft)ftxft2 + a22/(a: + th){h2J.
Эти соотношения можно записать в форме действия оператора (hld\ -f h2d2)
на функцию:
+ h2d2)f(x + *ft) = fti9i/(a: + tft),
+ h2d2Jf(x + th) = ft^fti2 eilia/(x + th).
По индукции получаем
+ h2d2)kf(x + *Л) = ft^... ft** д^.лЛх + *ft)
(справа имеется в виду суммирование по всевозможным наборам t'i, ..., г* из
А; индексов, каждый из которых принимает значения 1 или 2).

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ
453
Пример 2. Если f(x) = /(х\ ...,xm) и / G CW(G;R), то, в предпо-
предположении, что [х,х + /i] С G, для функции <^(?) = /(x -f t/i), определенной на
отрезке [0,1], получаем
где справа имеется в виду суммирование по всевозможным наборам индексов
Чч • • • ? ikt каждьф из которых может принимать любое значение от 1 до m
включительно.
Формулу E) можно записать также в виде
... + hmdm)kf(x + th).
F)
4. Формула Тейлора
Теорема 4. Если функция /: U(x)
определена и принадлежит
классу C(n)(t/(x);R) в окрестности U(x) С Rm точки х е Шт, а отрезок
[х,х -f h] полностью содержится в U(x), то имеет место равенство
f(xl + Л1,
n-1
rn_i(a:;/i) =
о
- 1)!
• ¦ • + hmdm)nf(x
G)
(8)
Равенство G) совместно с соотношением (8) называется формулой Тейлора
с интегральной формой остаточного члена.
4 Формула Тейлора G) немедленно следует из соответствующей формулы
Тейлора для функции одной переменной. В самом деле, рассмотрим вспомо-
вспомогательную функцию
которая в силу условий теоремы 4 определена на отрезке 0 ^ t ^ 1 и (как мы
проверили выше) принадлежит классу С^[0,1].
Тогда при т G [0,1] в силу формулы Тейлора для функций одной переменной
можно записать, что
±
О

454 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Полагая здесь т = 1, получаем
1
„A) = „@) + 1 *>'@) + • • • + ^jjj У(п-Х)@) + | A(п"_'I"O V(n)«) A- (9)
0
Подставляя в полученное равенство, в соответствии с формулой F), зна-
значения
<pW@) = (tfdi + ... + hmdm)kf(x) (fc = 0, ..., n - 1),
hmdm)nf(x + th),
получаем то, что и утверждает теорема 4. >
Замечание. Если вместо интегральной формы остаточного члена в со-
соотношении (9) написать остаточный член в форме Лагранжа, то из равенства
*>'@) + + ^
где 0 < 0 < 1, получается формула Тейлора G) с остаточным членом
Гп-i(х; Л) = ~ (Л1^! 4-... 4- hmdm)nf(x + 0/i). A0)
Эту форму остаточного члена, так же как и в случае функций одной пере-
переменной, называют формой Лагранжа остаточного члена формулы Тейлора.
Доль скоро / G C(n)(t/(x);R), то из A0) следует, что
rn_i (x; /i) = ^ (/i1^! -f ... 4- /imam)n /(x) + o(\\h\\n) при /i -> 0,
поэтому имеет место равенство
..., xm + /im) - /(x\ ..., xm) =
n
k=l
называемое формулой Тейлора с остаточным членом в форме Пеано.
5. Экстремумы функций многих переменных. Одним из важней-
важнейших применений дифференциального исчисления является его использование
для отыскания и исследования экстремумов функций.
Определение 1. Говорят, что функция /: Е —»• E, определенная на
множестве Е С Кт, имеет локальный максимум (локальный минимум) во вну-
внутренней точке хо множества Е, если существует окрестность U(x$) С Е точки
хо такая, что /(х) ^ /(хо) (соответственно, /(х) ^ /(хо)) при х е U(xo).
Если при х ? U(xq)\xo имеет место строгое неравенство f(x) < /(хо) (или,
соответственно, /(х) > /(хо)), то говорят, что функция имеет в точке
строгий локальный максимум (строгий локальный минимум).

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 455
Определение 2. Локальные минимумы и локальные максимумы функ-
функции называют ее локальными экстремумами.
Теорема 5. Пусть функция f: U(xo) -+Ж, определенная в окрестности
U(xo) С Ет точки жо = (xj, ..., ж™), имеет в точке хо частные производные
по каждой из переменных ж1, ..., хт.
Тогда для того, чтобы функция имела в хо локальный экстремум, необ-
необходимо, чтобы в этой точке были выполнены равенства
A2)
Рассмотрим функцию ^(ж1) = /(ж1, ж§, ..., х™) одной переменной, опре-
определенную, в силу условий теоремы, в некоторой окрестности точки х\ ве-
вещественной оси. В точке Xq функция ^(ж1) имеет локальный экстремум, и
поскольку
Ч> (хо) =
Аналогично доказываются и остальные равенства системы A2). >
Обратим внимание на то, что равенства A2) дают лишь необходимые, но
не достаточные условия экстремума функции многих переменных. Примером,
подтверждающим это, может стать любой пример, построенный по этому
же поводу для функции одной переменной. Так, если раньше мы говорили
3 й й
о функции ж ь-> ж3, имеющей в нуле нулевую производную, но не имеющей там
экстремума, то теперь можно рассмотреть функцию /
/^ж , ..., ж ) = ^ж ) ,
все частные производные которой в точке жо = @, ..., 0) равны нулю, но
экстремума в этой точке функция, очевидно, не имеет.
Теорема 5 показывает, что если функция / : G,—> R определена на от-
открытом множестве G С Мт, то ее локальные экстремумы находятся либо
среди точек, в которых / не дифференцируема, либо в тех точках, в которых
дифференциал df(xo) или, что то же самое, касательное отображение /;(жо)
обращается в нуль.
Нам известно, что если отображение /: U(xo) —У Еп, определенное в окрест-
окрестности U(xo) С Rm точки жо G Em, дифференцируемо в Жо, то матрица каса-
касательного отображения /;(жо): Мт -у Еп имеет вид
A3)

456 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Определение 3. Точка хо называется критической точкой отобра-
отображения f : U(xo) —> Кп, если ранг матрицы Якоби A3) отображения в этой
точке меньше, чем min{m,n}, т. е. меньше, чем максимально возможный.
В частности, при п = 1 точка хо критическая, если выполнены условия
A2), т. е. все частные производные функции / : U(xq) —? R обращаются в
нуль.
Критические точки вещественнозначных функций называют также ста-
стационарными точками таких функций.
После того как в результате решения системы уравнений A2) найдены кри-
критические точки функции, их дальнейший анализ в отношении того, являются
они точками экстремума или нет, часто удается провести, используя форму-
формулу Тейлора и доставляемые ею следующие достаточные условия наличия или
отсутствия экстремума.
Теорема 6. Пусть /: U(xo) ->• R — функция класса C^(U(xo);R), опре-
определенная в окрестности t/(xo)cRm точки xq = (х©,. • • >#cT)€ ^mt и пусть
— критическая точка этой функции /.
Если в тейлоровском разложении
функции в точке Хо квадратичная форма
m
A4)
m
A5)
a) знакоопределена, то в точке Xq функция имеет локальный экстремум,
который является строгим локальным минимумом, если квадратичная фор-
форма A5) положительно определена, и строгим локальным максимумом, если
она отрицательно определена;
b) может принимать значения разных знаков, то в точке Xq функция
экстремума не имеет.
< Пусть /i^Onxo-f/iG f/(xo). Представим соотношение A4) в виде
/(х0) = 1
т
IN \\h\\
A6)
где оA) есть величина, бесконечно малая при h —У 0.
Из A6) видно, что знак разности /(хо ¦+• h) — /(хо) полностью определяется
знаком величины, стоящей в квадратных скобках. Этой величиной мы теперь
и займемся.

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 457
Вектор е = (/i7||/i||, ..., Лт/||Л||), очевидно, имеет единичную норму. Ква-
Квадратичная форма A5) непрерывна как функция h в Ет, поэтому ее ограни-
ограничение на единичную сферу S@; 1) = {х G Em | ||х|| = 1} также непрерывно на
S@;l). Но сфера 5 есть замкнутое ограниченное подмножество в IRm, т. е.
компакт. Следовательно, форма A5) имеет на S как точку минимума, так и
точку максимума, в которых она принимает соответственно значения т и М.
Если форма A5) положительно определена, то 0 < m ^ M и потому най-
найдется число 6 > О такое, что при ||Л|| < S будет |оA)| < т. Тогда при \\h\\ < S
квадратная скобка в правой части равенства A6) окажется положительной
и, следовательно, /(хо + h) — f(xo) > О при 0 < \\h\\ < 6. Таким образом,
в этом случае точка хо оказывается точкой строгого локального минимума
рассматриваемой функции.
Аналогично проверяется, что в случае отрицательной определенности фор-
формы A5) функция имеет в хо строгий локальный максимум.
Тем самым пункт а) теоремы 6 исчерпан.
Докажем утверждение Ь).
Пусть ет и ем — те точки единичной сферы, в которых форма A5) при-
принимает соответственно значения т, М, и пусть m < 0 < М.
Полагая h = ?em, где t — достаточно малое положительное число (настоль-
(настолько малое, что хо + tem E f/(xo)), из A6) находим
tem) - /(хо) = |f t2(m
где оA) —>• 0 при t —> 0. Начиная с некоторого момента (т. е. при всех доста-
достаточно малых значениях i), величина m -f o(l) в правой части этого равенства
будет иметь знак т, т. е. будет отрицательна. Следовательно, отрицательной
будет и левая часть.
Аналогично, полагая h — гем, получим
/(хо + teM) - /(хо) = j{ t2(M
и, следовательно, при всех достаточно малых t разность /(хо 4- гем) — /(хо)
положительна.
Таким образом, если квадратичная форма A5) на единичной сфере или,
что, очевидно, равносильно, в Rm принимает значения разных знаков, то в
любой окрестности точки хо найдутся как точки, в которых значение функ-
функции больше /(хо), так и точки, в которых оно меньше /(хо). Следовательно,
в этом случае хо не является точкой локального экстремума рассматриваемой
функции. >
Сделаем теперь несколько замечаний в связи с доказанной теоремой.
Замечание 1. Теорема 6 ничего не говорит о случае, когда форма A5)
полуопределена, т. е. неположительна или неотрицательна. Оказывается/ в
этом случае точка хо может быть точкой экстремума, а может и не быть
таковой. Это видно, в частности, из следующего примера.

458
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 3. Найдем экстремумы определенной в R2 функции f{x,y) =
В соответствии с необходимыми условиями A2) напишем систему уравне-
уравнений
г д?
дх
> ду
(ж, у) = 4х3 — \х — О,
,У) =
из которой находим три критические точки: (—1,0), @,0), A,0).
Поскольку
1
дх2
= 12х2
= 12х2-4,
д2/
(х,у) = 12у2,
дхдух""-"' ду2
то квадратичная форма A5) в указанных трех критических точках имеет
соответственно вид
т. е. во всех случаях она полуопределена (положительно или отрицательно).
Теорема 6 тут не применима, но поскольку f(x,y) = (х2 — IJ 4- у4 — 1, то
очевидно, что в точках (—1,0), A,0) функция f(x,y) имеет строгий минимум
— 1 (и даже нелокальный), а в точке @,0) у нее нет экстремума, поскольку
при х = 0 и у ф 0 /@, у) = у4 > 0, а при у = 0 и достаточно малых х ф О
=х4-2х2 <0.
Замечание 2. После того как квадратичная форма A5) получена, ис-
исследование ее определенности может быть проведено с помощью известного
из курса алгебры критерия Сильвестра1). Напомним, что в силу критерия
Сильвестра квадратичная форма
m
lxi
Q>ijXlxi c симметрической матрицей
\0>ml • ' • Q>
положительно определена тогда и только тогда, когда положительны все глав-
главные миноры этой матрицы; форма отрицательно определена тогда и только
тогда, когда ац < 0 и при переходе от любого главного минора матрицы к
главному минору следующего порядка знак значения минора меняется.
Пример 4. Найдем экстремумы функции
f(x,y) = xy\n(x2 + y2),
определенной в плоскости R2 всюду, кроме начала координат.
*) Дж. Дж. Сильвестр A814—1897) — английский математик; наиболее известные его
работы относятся к алгебре.

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 459
Решая систему
л.
§(х,у) = xln(x2 +у2) + -|?4 = О,
ду х2 + у2
находим все критические точки функции
(±1,0);
Поскольку функция нечетна относительно каждого из двух своих аргумен-
аргументов в отдельности, то точки @, ±1) и (±1,0), очевидно, не являются точками
экстремума нашей функции.
Видно также, что данная функция не меняет своего значения при одновре-
одновременном изменении знака обеих переменных х и у. Таким образом, если мы
исследуем только одну из оставшихся критических точек, например точку
( 1 1 \
I -=, —r= J, то мы сможем сделать заключение и о характере остальных.
\V2e \/2e/
Поскольку
дх2
х у) - \п(х2 + У2) + О _
'у) - ( + у '+
у2J'
то в точке (-^, -^=) квадратичная форма dijf(xo)hlh* имеет матрицу
т. е. она положительно определена, и, следовательно, в этой точке функция
имеет локальный минимум
В силу сделанных выше наблюдений относительно особенностей рассма-
рассматриваемой функции можно сразу же заключить, что
2е
также локальный минимум, а
2е

460 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
— локальные максимумы функции. Впрочем, это можно проверить и непо-
непосредственно, убедившись в определенности соответствующей квадратичной
формы. Например, в точке f —-=, -т=Л матрица квадратичной формы A5)
имеет вид
'-2 0
0 -2
откуда видно, что форма отрицательно определена.
Замечание 3. Следует обратить внимание на то, что мы указали необ-
необходимые (теорема 5) и достаточные (теорема 6) условия экстремума функции
лишь во внутренней точке области определения. Таким образом, при отыс-
отыскании абсолютного максимума или минимума функции необходимо наряду с
внутренними критическими точками функции исследовать также точки гра-
границы области определения, поскольку максимальное или минимальное значе-
значение функция может принять в одной из таких граничных точек.
Подробнее общие принципы исследования невнутренних экстремумов бу-
будут разбираться позже (см. раздел, посвященный условному экстремуму).
Полезно иметь в виду, что при отыскании минимумов и максимумов часто
наряду с формальной техникой, а иногда и вместо нее, можно использовать
некоторые простые соображения, связанные с природой задачи. Например,
если рассматриваемая в Rm дифференцируемая функция по смыслу задачи
должна иметь минимум и вместе с тем она не ограничена сверху, то, при
условии, что функция имеет единственную критическую точку, можно без
дальнейшего исследования утверждать, что в этой точке она и принимает
свое минимальное значение.
Пример 5. Задача Гюйгенса. На основе законов сохранения энергии и
импульса замкнутой механической системы несложным расчетом можно по-
показать, что при соударении двух абсолютно упругих шаров, имеющих массы
rai и гаг и начальные скорости v\ и v2, их скорости после центрального удара
(когда скорости направлены по линии центров) определяются соотношениями
~ _ (™>1 — m2)vi + 27712^2
rai + 7712
(m2 -
v2 =
+ 7712
В частности, если шар массы М, движущийся со скоростью V, ударяется
о неподвижный шар массы га, то приобретаемая последним скорость v может
быть найдена по формуле
v = -™- V, A7)
т + М v y
из которой видно, что если 0 ^ га ^ М, то V ^ v ^ 2V.
Каким же образом телу малой массы можно передать значительную часть
кинетической энергии большой массы? Для этого, например, между шарами

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ 461
малой и большой масс можно вставить шары с промежуточными массами
гп < т\ < Ш2 < • • < win < Af. Вычислим (вслед за Гюйгенсом), как надо вы-
выбрать массы mi, Ш2, ..., шп, чтобы в результате последовательных централь-
центральных соударений тело т приобрело наибольшую скорость.
В соответствии с формулой A7) получаем следующее выражение для иско-
искомой скорости как функции от переменных mi, Шг, ..., тпп:
V = -24 ^— ... ^ У—: -2"+1К A8)
m + m m + rri m + mn mn-i-M
Таким образом, задача Гюйгенса сводится к отысканию максимума функ-
функции
mi mn M
mn + M
Система уравнений A2), представляющих необходимые условия внутрен-
внутреннего экстремума, в данном случае сводится к системе
m • 7712 — mA = 0,
• 7713 — rnk = 0,
I mn-i-M -m2n = 0,
из которой следует, что числа m, mi, ..., mn, M образуют геометрическую
прогрессию со знаменателем д, равным п+^/М/тп.
Получаемое при таком наборе масс значение скорости A8) определяется
равенством
которое при п = 0 совпадает с равенством A7).
Из физических соображений ясно, что формула A9) указывает максималь-
максимальное значение функции A8), однако это можно проверить и формально (не
привлекая громоздких вторых производных; см. задачу 9 в конце параграфа).
Заметим, что из формулы A9) видно, что если m -> 0, то v -> 2n+1F.
Таким образом, промежуточные массы действительно заметно увеличивают
передаваемую малой массе m часть кинетической энергии массы М.
6. Некоторые геометрические образы, связанные с функциями
многих переменных
а. График функции и криволинейные координаты. Пусть х, у, z —
декартовы координаты точки пространства R3, и пусть z = f(x,y) — непре-
непрерывная функция, определенная в некоторой области G плоскости Ш? перемен-
переменных (ж, у).

462 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
В силу общего определения графика функции, график функции /: G
в нашем случае есть множество 5 = {(ж, у,z) € R3 | (ж, у) € G, z = f(x,y)} в
пространстве R3.
Отображение G —> 5, определяемое соотношением (ж,у) •-* (x,y,f(x,y)),
очевидно, есть непрерывное взаимно однозначное отображение G на 5, в силу
которого любую точку множества 5 можно задать, указывая соответствую-
соответствующую ей точку области G или, что то же самое, задавая координаты (х, у) этой
точки G.
Таким образом, пары чисел (х, у) € G можно рассматривать как некоторые
координаты точек множества 5 — графика функции z = f(x,y). Поскольку
точки 5 задаются парами чисел, то 5 будем условно называть двумерной по-
поверхностью в R3 (общее определение поверхности будет дано позже).
Если задать путь Г : / -> G в G, то автоматически возникает путь F о Г :
/ -> S на поверхности 5. Если х = x(t), у = y(t) — параметрическое задание
пути Г, то путь F о Г на S задается тремя функциями: х = x(t), у = y(t),
z = f(x(t),y(t)). В частности, если положить х = хо + t, у = уо, то мы
получим кривую х = х0 + t, у = t/o> z — f(xo + t, yo) на поверхности 5, вдоль
которой координата у = уо точек 5 не меняется. Аналогично можно указать
кривую х = х0, у = уо + t, z — f(xo, yo + t) на 5, вдоль которой не меняется
первая координата хо точек 5. Эти линии на S по аналогии с плоским случаем
естественно называть координатными линиями на поверхности 5. Однако, в
отличие от координатных линий в G С Н&2, являющихся кусками прямых,
координатные линии на 5, вообще говоря, являются кривыми в R3. По этой
причине введенные координаты (х,у) точек поверхности S часто называют
криволинейными координатами на 5.
Итак, график непрерывной функции z = f(x,y), определенной в области
GcK2, есть двумерная поверхность 5 в R3, точки которой можно задавать
криволинейными координатами (#, у) € G.
Мы пока не останавливаемся на общем определении поверхности, посколь-
поскольку сейчас нас интересует только частный случай поверхности — график функ-
функции, однако мы предполагаем, что из курса аналитической геометрии читате-
читателю хорошо знакомы некоторые важные конкретные поверхности в Ш? (плос-
(плоскость, эллипсоид, параболоиды, гиперболоиды).
Ь. Касательная плоскость к графику функции. Если функция z =
= f(x,y) дифференцируема в точке (хо,уо) € G, то это означает, что
, у) = f(x0, yo) + А(х -хо) + В(у-
+ о(у/(х - х0J + (у - уоJ) при (х,у) -> (жо,2/о), B0)
где А и В — некоторые постоянные.
Рассмотрим в R3 плоскость
z = zo + А(х - х0) + В(у - уо), B1)

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ
463
где zq = f(xo,yo). Сравнивал равенства B0) и B1), видим, что график нашей
функции в окрестности точки (хо>2/о>2о) хорошо аппроксимируется плоско-
плоскостью B1). Точнее, точка (x,y,f(x,y)) графика функции уклоняется от точки
(x,y,z(x,y)) плоскости B1) на величину, бесконечно малую в сравнении с ве-
величиной у/(х — хоJ + (у — уоJ смещения ее криволинейных координат (ж, у)
от координат (хо,уо) точки (xo,yo,zo).
В силу единственности дифференциала функции, плоскость B1), обладаю-
обладающая указанным свойством, единственна и имеет вид
B2)
Она называется касательной плоскостью к графику функции z = f(x,y) в
точке (xo,yoj(xo,yo)).
Итак, дифференцируемость функции z = f(x,y) в точке (жо,2/о) и наличие
у графика этой функции касательной плоскости в точке (хо, 2/о, /(#о> У о)) суть
равносильные условия.
с. Нормальный вектор. Записывал уравнение B2) касательной плоско-
плоскости в каноническом виде
Я 4
= f(xo,Vo) + fc
- х0) + -^-
x - х0) + -^
- уо) - (z - /(xo,yo)) = 0,
заключаем, что вектор
B3)
является нормальным вектором касательной плоскости. Его направление
считается направлением, нормальным или ортогональным к поверхности 5
(графику функции) в точке (яо,2/о,/(яо,2/о))-
В частности, если (жо, Уо) — критическая точка функции /(#, у), то в точке
(хо,Уо,/(хо,уо)) графика нормальный вектор имеет вид @,0,-1) и, следова-
следовательно, касательная плоскость к графику функции в такой точке горизон-
горизонтальна (параллельна плоскости (ж, у)).
Следующие три рисунка иллюстрируют сказанное.

464 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
На рис. 53а, с изображено расположение графика функции по отношению
к касательной плоскости в окрестности точки локального экстремума (со-
(соответственно, минимума и максимума), а на рис. 536 — в окрестности так
называемой седловой критической точки.
d. Касательная плоскость и касательный вектор. Мы знаем, что
если путь Г: / -> К3 в R3 задается дифференцируемыми функциями х = х(?),
У = 2/(*)> z = z(t), то вектор (x@),2/@),i@)) есть вектор скорости в момент
t = 0. Это направляющий вектор касательной в точке хо = х@), уо = 2/@),
zq = z@) к кривой в К3, являющейся носителем пути Г.
Рассмотрим теперь путь Г : / -> 5 на графике функции z = /(х,у), зада-
задаваемый в виде х = x(t), у = y(t), z = f(x(t),y(t)). В этом конкретном случае
находим, что
откуда видно, что найденный вектор ортогонален вектору B3), нормальному
к графику S функции в точке (хо,Уо,1(хо,Уо))' Таким образом, мы показали,
что если вектор (f, rj, ?) касателен в точке (хо, уо> /(#о, Уо)) к некоторой кривой
на поверхности 5, то он ортогонален вектору B3) и (в этом смысле) лежит в
плоскости B2), касательной к поверхности S в указанной точке. Точнее можно
было бы сказать, что вся прямая х = xq + f?, у = уо + r)t, z = /(xo>2/o) + С*
лежит в касательной плоскости B2).
Покажем теперь, что верно и обратное утверждение, т. е. если прямая
х = хо + ?t, у = уо -Ьr)t, z = /(хо, уо) + С* или? что то же самое, вектор (?,г/,()
лежит в плоскости B2), касательной к графику 5 функции z = /(x, у) в точке
(#о>Уо>/(яо>2/о))> то на 5 есть путь, для которого вектор (?>*?> С) является
вектором скорости в точке (хо,Уо»/(^о?Уо))«
В качестве такового можно взять, например, путь
х = хо + ?*, у = Уо + r)t, z = f(x0 4- ?t,y0 +
В самом деле, для него
Ввиду того, что
и по условию также
заключаем, что

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ
465
Итак, касательная плоскость к поверхности S в точке (xo,yo,zo) образо-
образована векторами, касательными в точке (жо,2/о>^о) к кривым, проходящим на
поверхности 5 через указанную точку (рис. 54).
Это уже более геометричное описание касательной плоскости. Во всяком
случае, из него видно, что если инвариантно (относительно выбора системы
координат) определена касательная к кривой, то
касательная плоскость также определена инвари-
инвариантно.
Для наглядности мы рассматривали функции
двух переменных, однако все сказанное, очевидно,
переносится и на общий случай функции
п
= f(x\...,xm)
B4)
m переменных, где т € N.
Плоскость, касательная к графику такой функ-
функции в точке (xq, ..., Xq1, f(xo,..., ^о1)), запишется
в виде
m
Рис. 54
У =
У* д*.(хЪ,...,х™)(х{
г=1
B5)
вектор
есть нормальный вектор плоскости B5). Сама эта плоскость, как и график
функции B4), имеет размерность т, т. е. любая точка задается теперь набо-
набором (ж1, ..., хт) из т координат.
Таким образом, уравнение B5) задает гиперплоскость в Rm+1.
Дословно повторяя проведенные выше рассуждения, можно проверить,
что касательная плоскость B5) состоит из векторов, касательных в точке
(xq, ..., ж™, /(#о, ..., ^о1)) к кривым, проходящим через эту точку и лежащим
на m-мерной поверхности S — графике функции B4).
Задачи и упражнения
1. Пусть z = /(х, у) — функция класса C^l\G\ R).
a) Бели -г~(х, у) = 0 в G, то можно ли утверждать, что функция / не зависит от
ау
у в области G?
b) При каком условии на область G ответ на предыдущий вопрос положителен?
2. а) Проверьте, что для функции
ж, У) =
ху
, О,
X2— У2
если х* + у'f О,
если х2 4- у2 = О,

466 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
имеют место следующие соотношения:
@,0) = 1
b) Докажите, что если функция fix, у) имеет частные производные — и —- в
ах оу
д2/
некоторой окрестности U точки (хо,2/о) и если смешанная производная ;? (или
ахау
) существует в с/ и непрерывна в (хо,уо)> то смешанная производная
дудх' -'——' •"-' ~ x-v,w, ^-- г,— дудх
d2f
(соответственно, ) также существует в этой точке и имеет место равенство
ОХ Су у
д2/
3. Пусть х1, ..., хт — декартовы координаты в Rm. Дифференциальный опера-
оператор
действующий на функции / € C^2\G;R) по правилу
т
t=i
называется оператором Лапласа.
Уравнение А/ = 0 относительно функции / в области G С Rm называется урав-
уравнением Лапласа, а его решения — гармоническими функциями в области G.
а) Покажите, что если х = (х1, ..., хт) и
m
то при m > 2 функция
m-2
является гармонической в области Rm \ 0, где 0 = @, ..., 0).
Ь) Проверьте, что функция
,...,
определенная при <>0их = (ж1, ..., хт) € Rm, удовлетворяет уравнению тепло-
теплопроводности
т. е. что -^7 = л2 5^ 2 в любой точке области определения функции.

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ
467
4. Формула Тейлора в мультииндексных обозначениях.
Символ а := (си, ..., ат), состоящий из неотрицательных целых чисел a», i
= 1, ..., m, называется мулыпииндексом а.
Условились в следующих обозначениях:
а\ :=
a! :=
наконец, если a = (ai, ..., am), то
... am!;
а) Проверьте, что если k € N, то
(О1+...+От)*=
e*i! ... am!
m
ИЛИ
a!
где суммирование ведется по всем наборам a = (ai, ..., am) неотрицательных целых
m
чисел, таким, что ^ |а»| = Л.
b) Пусть
Покажите, что если / € CW(G;R), то в любой точке х € G имеет'место равенство
гдеЛ = (Л1, ...,Л
с) Проверьте, что в мультииндексных обозначениях формулу Тейлора, например,
с остаточным членом в форме Лагранжа можно записать в виде
|a|=0
'
,
|a|=n
d) Запишите в мультииндексных обозначениях формулу Тейлора с интегральным
остаточным членом (теорема 4).
5. а) Пусть 1т = {х = (ж1, ..., хт) € Rm \ \х{\ ^ с\ г = 1, ..., т} - т-мер-
ный промежуток, а / — отрезок [а,Ь] С R. Покажите, что если функция /(х,у) .=
= /(ж1, ..., жт, у) определена и непрерывна на множестве Im x /, то для любого
положительного числа е > 0 найдется число ? > 0 такое, что если х € /m, yi, j/2 € /
- уз| < 6, то |/(ж,уО - /(ж,у2)| < е.

468 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Ь) Покажите, что функция
F(x) = j f(x, у) dy
а
rm
определена и непрерывна на промежутке 1т.
с) Покажите, что если / 6 C(Im;R), то функция
определена и непрерывна на Im x J1, где /1 =
d) Докажите следующую лемму Адамара.
Если / 6 CA)(Jm;R) и /@) = 0, то существуют функции ди ..., дт 6 С(/т;
такие, что
m
t=l
в /m, причем .
6. Докажите следующее обобщение теоремы Роллл для функций многих перемен-
переменных.
Бели функция / непрерывна в замкнутом шаре В@; г), равна нулю на его границе
и дифференцируема во внутренних точках шара 2?@; г), то по крайней мере одна из
внутренних точек этого шара является критической точкой функции.
7. Проверьте, что функция
Я*, У)=(У~ х2) (у - Зх2)
не имеет экстремума в начале координат, хотя ее ограничение на любую прямую,
проходящую через начало координат, имеет строгий локальный минимум в этой
точке.
8. Метод наименьших квадратов.
Это один из наиболее распространенных методов обработки результатов наблю-
наблюдений. Он состоит в следующем. Пусть известно, что физические величины х и у
связаны линейным соотношением
у = ах + 6, B6)
или пусть на основе экспериментальных данных строится эмпирическая формула
указанного вида.
Допустим, сделано п наблюдений, в каждом из которых одновременно измеря-
измерялись значения х и у, и в результате получены пары значений xi, yi; ...; хп, Уп-
Поскольку измерения имеют погрешности, то, даже если между величинами х и
у имеется точная связь B6), равенства
Ук = ахк -I- Ь
могут не выполняться для некоторых значений к 6 {1, ...,п}, каковы бы ни были
коэффициенты а и 6.

§ 4. ОСНОВНЫЕ ТЕОРЕМЫ
469
Задача состоит в том, чтобы по указанным результатам наблюдений определить
разумным образом неизвестные коэффициенты а и 6.
Гаусс, исходя из анализа распределения вероятности величины ошибки наблюде-
наблюдения, установил, что наиболее вероятные значения коэффициентов а и 6 при данной
совокупности результатов наблюдений следует искать, исходя из следующего прин-
принципа наименьших квадратов:
если 6k = (axk + Ь) —yk — невязка fc-го наблюдения, то а и 6 надо выбирать так,
чтобы величина
п
т. е. сумма квадратов невязок, была минимальной.
а) Покажите, что принцип наименьших квадратов в случае соотношения B6)
приводит к системе линейных уравнений
= [1,2/*]
для определения коэффициентов а и 6; здесь, следуя Гауссу, положено
= Х\Х\ + ... + хпхп; [х*,1] := xi-1 + ... +жп • 1; [хк,Ук] '= xiyi + ... + хпуп и т. д.
Ь) Напишите систему уравнений для чисел ai, ..., am, fe, к которой приводит
принцип наименьших квадратов в том случае, когда вместо равенства B6) имеется
соотношение
m
1=1
(или, короче, у = <цхг -I- 6) между величинами х1, ..., xm, у.
c) Как, используя метод наименьших квадратов, искать эмпирические формулы
вида
связывающие физические величины xi, ..., хт с величиной у?
d) (M. Джермен.) У нескольких десятков особей кольчатого червя Neries di
versicolor была измерена частота R сокращений сердца при различных температу-
температурах Т. Частота выражалась в процентах относительно частоты сокращении при
15°С. Полученные данные приведены в следующей таблице:
Температура, °С
0
5
10
15
Частота, %
39
54
74
100
Температура, °С
20
25
30
•
Частота, %
136
182
254
Зависимость Я от Т похожа на экспоненциальную. Считая Я = АеЬТ, найдите
значения констант Л и 6, которые бы наилучшим образом соответствовали резуль-
результатам эксперимента.
'/,16*

470
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
9. а) Покажите, что в рассмотренной в примере 5 задаче Гюйгенса функция A8)
стремится к нулю, если хотя бы одна из переменных mi, ..., тп стремится к бес-
бесконечности.
b) Покажите, что функция A8) имеет в Rn точку максимума и потому един-
единственная критическая точка этой функции в Rn должна быть ее точкой максимума.
c) Покажите, что величина и, определяемая формулой A9), монотонно возрастает
с ростом п, и найдите ее предел при п —> оо.
10. а) Во время так называемого круглого наружного шлифования инструмент —
быстро вращающийся шлифовальный круг (с шероховатой периферией), играющий
роль напильника, — приводится в соприкосновение с медленно (в сравнении с ним)
поворачивающейся поверхностью круг-
круглой детали (рис. 55).
Круг К постепенно подается на де-
деталь Див результате происходит съем
заданного слоя Н металла, доведение
детали до нужного размера и образо-
образование гладкой рабочей поверхности из-
изделия. Эта поверхность в будущем ме-
механизме обычно является трущейся, и,
чтобы увеличить срок ее службы, ме-
металл детали проходит предварительную
закалку, повышающую твердость ста-
стали. Однако из-за высокой температуры
в зоне контакта шлифовального круга с
деталью могут произойти (и часто про-
происходят) структурные изменения в некотором слое А металла и падение в этом слое
твердости стали. Величина А монотонно зависит от скорости s подачи круга на
деталь, т. е. А = <p(s). Известно, что существует некоторая критическая скорость
so > 0, при которой еще А = 0, а при s > so уже А > 0. Для дальнейшего удобно
ввести в рассмотрение обратную к указанной зависимость
s =
определенную при А > 0.
Здесь ф — известная из эксперимента монотонно возрастающая функция, опре-
определенная при А ^ 0, причем ф@) = so > 0.
Режим шлифования должен быть таким, чтобы на окончательно получаемой по-
поверхности изделия не было структурных изменений металла.
Оптимальным по быстродействию при указанных условиях, очевидно, будет та-
такой режим изменения скорости s подачи шлифовального круга, когда
S =
где S = S(t) — величина еще не снятого к моменту t слоя металла или, что то же
самое, расстояние от периферии круга в момент t до окончательной поверхности
будущего изделия. Объясните это.
Ь) Найдите время, необходимое для снятия слоя Н в оптимальном режиме изме-
изменения скорости s подачи круга.
Рис. 55

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ 471
c) Найдите зависимость s = s(t) скорости подачи круга от времени в оптималь-
оптимальном режиме при условии, что функция А ¦—> s линейна: s = so + А А.
В силу конструктивных особенностей некоторых видов шлифовальных станков
изменение скорости s может происходить только дискретно. Тут и возникает за-
задача оптимизации производительности процесса при дополнительном условии, что
допускается только фиксированное число п переключений скорости з. Ответы на
следующие вопросы дают представление о характере оптимального режима.
d) Какова геометрическая интерпретация найденного вами в Ь) времени t(H) =
я
dS
i
шлифования в оптимальном непрерывном режиме изменения скорости з?
e) Какова геометрическая интерпретация потери во времени при переходе от
оптимального непрерывного режима изменения з к оптимальному по быстродей-
быстродействию ступенчатому режиму изменения 5?
f) Покажите, что точки 0 = sn+i < хп < ... < х\ < хо = Н промежутка [О, Н], в
которых следует производить переключение скорости, должны удовлетворять усло-
условиям
1 L---(L\(X.)(X.-X. ) (i = l п)
и, следовательно, на участке от я* до я*+1 скорость подачи круга имеет вид з =
= i/>(xt+i) (г = 0, ..., п).
g) Покажите, что в линейном случае, когда ф(А) = so + А А, точки Xi (из зада-
задачи f)) на промежутке [О, Н] располагаются так, что числа
J<y+Xn<...<y+Xl<y+tf
образуют геометрическую прогрессию.
11. а) Проверьте, что касательная к кривой Г: / —> Rm определена инвариантно
относительно выбора системы координат в Rm.
b) Проверьте, что касательная плоскость к графику S функции у = /(ж1, ..., хт)
определена инвариантно относительно выбора системы координат в Rm.
c) Пусть множество S С Rm x R1 является графиком функции у = /(ж1, ..., хт)
в координатах (ж1, ..., жт, у) в Rm x R1 и графиком функции у = /(ж1, ..., хт) в
координатах (ж1, ..., жт, у) в Rm x R1. Проверьте, что касательная к S плоскость
инвариантна относительно линейного преобразования координат в Rm x R1.
m д2 f
d) Проверьте, что оператор Лапласа А/ = ^ —^(х) определен инвариантно
г=1 дхг
относительно ортогональных преобразований координат в Rm.
§ 5. Теорема о неявной функции
1. Постановка вопроса и наводящие соображения. В этом пара-
параграфе будет доказана важная как сама по себе, так и благодаря ее многочи-
многочисленным следствиям теорема о неявной функции.
Поясним сначала, в чем состоит вопрос. Пусть, например, мы имеем соот-
соотношение
х2 + у2 - 1 = 0 A)
16 Зорич В. А.

472
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Совокупность точек плоско-
плоскости Е2, удовлетворяющих этому соотношению, есть единичная окружность
(рис. 56).
Наличие связи A) показывает, что, фиксировав одну из координат, напри-
например ж, мы не вправе брать вторую координату произвольно. Таким образом,
соотношение A) предопределяет зависимость у от х. Нас интересует вопрос
об условиях, при которых неявная связь A) может быть разрешена в виде
явной функциональной зависимости у = у(х).
Решая уравнение A) относительно у, найдем, что
B)
Рис. 56
т. е. каждому значению х такому, что |ж| < 1, на самом деле отвечают два
допустимых значения у. При формировании функциональной зависимости
у = у(х), удовлетворяющей соотношению A),
нельзя без привлечения дополнительных тре-
требований отдать предпочтение какому-нибудь
одному из значений B). Например, функция
у (ж), которая в рациональных точках отрез-
отрезка [—1,1] принимает значение + у/\ — ж2, а в
иррациональных — значение —\/1 — ж2, оче-
очевидно, удовлетворяет соотношению A).
Ясно, что вариацией этого примера можно
предъявить бесконечно много функциональ-
функциональных зависимостей, удовлетворяющих соотно-
соотношению A).
Вопрос о том, является ли множество, за-
задаваемое в Е2 соотношением A), графиком
некоторой функциональной зависимости у = у(ж), очевидно, решается отри-
отрицательно, ибо с геометрической точки зрения он равносилен вопросу о воз-
возможности взаимно однозначного прямого проектирования окружности на не-
некоторую прямую.
Но наблюдение (см. рис. 56) подсказывает, что все-таки в окрестности от-
отдельной точки (жо,2/о) дуга окружности взаимно однозначно проектируется
на ось ж и ее единственным образом можно представить в виде у = у(х), где
ж ь-> у(х) — непрерывная функция, определенная в окрестности точки жо и
принимающая в жо значение уо. В этом отношении плохими являются только
точки (—1,0), A,0), ибо никакая содержащая их внутри себя дуга окружно-
окружности не проектируется взаимно однозначно на ось ж. Зато окрестности этих
точек на окружности хорошо расположены относительно оси у и могут быть
представлены в виде графика функции ж = ж(у), непрерывной в окрестности
точки 0 и принимающей в этой точке значение —1 или 1 в соответствии с тем,
идет ли речь о дуге, содержащей точку (—1,0) или A,0).

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ 473
Как же аналитически узнавать, когда наше геометрическое место точек,
определяемое соотношением типа A), в окрестности некоторой точки (хо>2/о)»
принадлежащей ему, может быть представлено в виде явной зависимости
У = У(х) или х = х(у)?
Будем рассуждать следующим, уже привычным способом. У нас есть
функция F(x,y) = х2 + у2 — 1. Локальное поведение функции в окрестности
точки (хо,уо) хорошо описывается ее дифференциалом
х - х0) + F^(xo,yo)(y - 2/o)>
поскольку
x, у) = F(xo,yo) + F'x{x0, yo)(x - х0) + i^(z0, уо)(у - у0)
+ о(\х-х0\
при (х,у) -> (хо,уо).
Если F(xo,yo) = 0 и нас интересует поведение линии уровня
нашей функции в окрестности точки (хо,$/(>)> т0 ° нем можно судить по рас-
расположению прямой (касательной)
К(хо,Уо)(х - х0) + Fy(xo,yo)(y - уо) = 0. C)
Бели эта прямая расположена так, что ее уравнение можно разрешить от-
относительно j/, то, коль скоро в окрестности точки (хо,2/о) линия F(x,y) = 0
мало уклоняется от этой прямой, можно надеяться, что ее в некоторой окрест-
окрестности точки (хоууо) тоже можно будет записать в виде у = у(х).
То же самое, конечно, можно сказать о локальной разрешимости уравнения
F(x, у) = 0 относительно х.
Записав уравнение C) для рассматриваемого конкретного соотношения
A), получим следующее уравнение касательной:
хо(х - х0) 4- уо(у - уо) = 0.
Это уравнение разрешимо относительно у всегда, когда j/o ф 0, т. е. во всех
точках (хо,2/о) окружности A), кроме точек (—1,0) и A,0). Оно разрешимо
относительно х во всех точках окружности, кроме точек @, — 1) и @,1).
2. Простейший вариант теоремы о неявной функции. В этом па-
параграфе теорема о неявной функции будет получена очень наглядным, но не
очень эффективным методом, приспособленным только к случаю веществен-
нозначных функций вещественных переменных. С другим, во многих отно-
отношениях более предпочтительным способом получения этой теоремы, как и с
более детальным анализом ее структуры, читатель сможет познакомится в
главе X (часть II), а также в задаче 4, помещенной в конце параграфа.
16*

474 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Следующее утверждение является простейшим вариантом теоремы о неяв-
неявной функции.
Утверждение 1. Если функцця F : ?/(жо,Уо) "~^ ^> определенная в
окрестности ?/(жо>2/о) точки (хо»2/о) € R2, такова, что
1° FeCM(U;R), гдер^ 1,
2° F(zo,yo)=O,
3°
то существуют двумерный промежуток I = Ix х 1У, где
Ix = {x? R||x-xo| <a}, Iy = {y ? R\\y-yo\ <
являющийся содержащейся в ?/(хо,Уо) окрестностью точки (хо,уо), и такая
функция f ? C^(Ix;Iy), что для любой точки (х,у) ? Ix x 1У
F(x,y) = O**y = f(x), D)
причем производная функции у = f(x) в точках х ? 1Х может быть вычи-
вычислена по формуле
E)
Прежде чем приступить к доказательству, дадим несколько возможных пе-
переформулировок заключительного соотношения D), которые должны заодно
прояснить смысл самого этогд соотношения.
Утверждение 1 говорит о том, что при условиях 1°, 2°, 3° порция мно-
множества, определяемого соотношением F(x,y) — О, попавшая в окрестность
I = 1Х х 1у точки (хо,уо)> является графиком некоторой функции /: 1Х —> 1У
класса С ^ AХ \1У).
Иначе можно сказать, что в пределах окрестности I точки (хо,уо) урав-
уравнение F(x,y) = О однозначно разрешимо относительно у, а функция у = f(x)
является этим решением, т. е. F(x,/(x)) = 0 на 1Х.
Отсюда в свою очередь следует, что если у = f(x) — функция, определенная
на 1Х, про которую известно, что она удовлетворяет соотношению F(x, f(x)) =
= 0 на 1Х и что /(хо) = 2/о> то при условии непрерывности этой функции в
точке Хо ? 1Х можно утверждать, что найдется окрестность Д С 1Х точки Хо
такая, что /(Д) С 1У и тогда /(х) = /(х) при х G Д.
Без предположения непрерывности функции / в точке хо и условия /(хо) =
= уо последнее заключение могло бы оказаться неправильным, что видно на
уже разобранном выше примере с окружностью.
Теперь докажем утверждение 1.
< Пусть для определенности F^(xo,yo) > 0. Поскольку F ? C^(U;R), то
Fy(x,y) > 0 также в некоторой окрестности точки (хо,уо)« Чтобы не вводить

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ 475
новых обозначений, без ограничения общности можно считать, что Fy(x,y) >
> 0 в любой точке исходной окрестности ?/(хо»2/о)-
Более того, уменьшая, если нужно, окрестность ?/(жо>Уо)> можно считать
ее кругом некоторого радиуса г = 2/3 > 0 с центром в точке (а?о,2/о)-
Поскольку F'y{x,y) > 0 в С/, то функция F(xo,y) от у определена и моно-
монотонно возрастает на отрезке уо — /3 ^ у ^ уо + /?, следовательно,
F(x0, Уо - Р) < F(xo,yo) - 0 < F(z0, Уо + 0).
В силу непрерывности функции F в С/, найдется положительное число
а < /3 такое, что при \х — жо| ^ а будут выполнены соотношения
F(x, 2/о - ?) < 0 <
Покажем теперь, что прямоугольник I = Ix x /у, где
является искомым двумерным промежутком, в котором выполняется соотно-
соотношение D).
При каждом хб/i фиксируем вертикальный отрезок с концами (ж, уо — /?),
(#, 2/о + /3)- Рассматривая на нем F(x,y) как функцию от у, мы получаем
строго возрастающую непрерывную функцию, принимающую значения раз-
разных знаков на концах отрезка. Следовательно, при х € 1Х найдется един-
единственная точка у(х) € lv такая, что F(xiy(x)) = 0. Полагая у(х) = /(ж), мы
приходим к соотношению D).
Теперь установим, что / € С^AХ;1У).
Покажем сначала, что функция / непрерывна в точке хо и что /(хо) = Уо-
Последнее равенство, очевидно, вытекает из того, что при х = хо имеется
единственная точка у(хо) € 1У такая, что F(xo,y(xo)) = 0. Вместе с тем по
условию F(oo,yo) = 0, поэтому /(х0) = уо-
Фиксировав число е, 0 < е < /3, мы можем повторить доказательство
существования функции f(x) и найти число 6, 0 < 6 < а, так, что в двумерном
промежутке / = Ix x /у, где
Ix = {z<ER||a;-zo| < 6}, Iy = {у€Е||у-уо| <
будет выполнено соотношение
(F(x,y) = 0 в /) <* (у = /(х), х € 1Х) F)
с некоторой вновь найденной функцией /: 1Х —> 1У.
Но /с С 1Х, /уС/у и / С /, поэтому из D) и F) следует, что f(x) = /(ir)
при х ? Ix С Ix. Тем самым проверено, что |/(х) — /(хо)| = \f(x) — уо| < е при
а: - хо| < S.

476 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Мы установили непрерывность функции / в точке xq. Но любая точка
(я, у) € J, в которой F(x,y) = 0, также может быть принята в качестве ис-
исходной точки построения, ибо в ней выполнены условия 2°, 3°. Выполнив это
построение в пределах промежутка /, мы бы в силу D) вновь пришли к со-
соответствующей части функции /, рассматриваемой в окрестности точки х.
Значит, функция / непрерывна в точке х. Таким образом, установлено, что
f€C(I9;Iy).
Покажем теперь, что / € С^1Ц1Х',1У), и установим формулу E).
Пусть число Дх таково, что х 4- Дх € 1Х. Пусть у = f(x) и у 4- Ау =
= f(x + Да;). Применяя в пределах промежутка / к функции F(x,y) теорему
о среднем, находим, что
О = F(x + Дх, f(x + Ах)) - F(x, f(x)) =
= F(x 4- Дх, у 4- Ay) - F(x, у) =
= Fx(x + в Ах, у + 0Ау)Ах + F'y{x 4- 0Дх, у 4- 6Ау)Ау @ < в < 1),
откуда, учитывая, что Fy(x,y) ф 0 в J, получаем
Д2/
Ах
Поскольку / € СAХ;1У), то при Ах —у 0 также Д$/ чОи, учитывая, что
F € С^^С/; R), из G) в пределе при Дх -> 0 получаем
где у = f(x). Тем самым формула E) установлена.
В силу теоремы о непрерывности композиции функций, из формулы E)
вытекает, что / € С^AХ;1У).
Если F € C^(U] R), то правая часть формулы E) допускает дифференци-
дифференцирование по х и мы находим, что
\F" + F" • fr(x)]Fr - F' \F" 4- F"
— *¦ xx XV J * 'lry rxjrxy ^ ryy
где Fx, F^ Fx'x, Fx'y, F%y вычисляются в точке (х,/(х)).
Таким образом, / € C^(Ix\Iy), если F € C^(U;R). Поскольку порядок
производных от /, входящих в правую часть соотношений E), E') и т. д., на
единицу ниже, чем порядок производной от /, стоящей в левой части равен-
равенства, то по индукции получаем, что / € C(p\lx;Iy), если F € С^(С/;Е). >
Пример 1. Вернемся к рассмотренному выше соотношению A), задаю-
задающему окружность в Е2, и проверим на этом примере утверждение 1.

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ
477
В данном случае
и очевидно, что F G C(°°>(R2;R). Далее,
Fly(x,y)=2y,
поэтому Fy(x,y) Ф О, если у ф 0. Таким образом, в силу утверждения 1, для
любой точки (яо,2/о) данной окружности, отличной от точек (—1,0), A,0),
найдется такая окрестность, что попадающая в нее дуга окружности может
быть записана в виде у — f(x). Непосредственное вычисление подтверждает
это, причем f(x) — у/1 — х2 или f(x) = — у/1 — х2.
Далее, в силу утверждения 1,
Непосредственное вычисление дает
=
, если /(х) = \/1-х
, если /(х) =
что можно записать одним выражением
Х
г/
вычисление по которому приводит к тому же результату
что и вычисление по формуле (8), полученной из утверждения 1.
Важно заметить, что формула E) или (8) позволяет вычислять /'(х), даже
не располагая явным выражением зависимости у = /(х), если нам только
известно, что /(хо) = 2/о- Задание же условия у о = /(хо) необходимо для
выделения той порции линии уровня F(x,y) = 0, которую мы намереваемся
представить в виде у = /(х).
На примере окружности видно, что задание только координаты хо еще не
определяет дугу окружности и, только фиксировав уо, мы выделяем одну из
двух возможных в данном случае дуг.
3. Переход к случаю зависимости F(xx^ ..., жт, у) = 0. Простым
обобщением утверждения 1 на случай зависимости F(xx,..., xm, у) = 0 явля-
является следующее утверждение.

478 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Утверждение 2. Если функция F : U -* R, определенная в окрестно
сти U С Km+1 точки (xOiyo) = (xq, ..., я™, yo) Е Km+1, такова, что
2°
3° F;(xo,yo) = i^D, ...,<, j/o)/О,
то существуют (m 4- 1)-лсериы# промежуток I = I™ x I*, где
I™ = {x = (ж1, ..., xm) € Rm | \x{ - a?j| < а*, г = 1, ..., m},
являющийся лежащей в U окрестностью точки (хо,уо), и такая функция
f € C(p)(/^;/i), что для любой точки (х,у) G I™ x IJ
1 1 (9)
частные производные функции у = /(ж1, ..., жт) в точках 1Х могут
быть вычислены по формуле
' [К* (*.
Доказательство существования промежутка /m+1 = I™ x /^, функции
( = /(ж1, ..., хт) и ее непрерывности в I™ дословно повторяет соот-
соответствующие части доказательства утверждения 1, с единственным измене-
изменением, которое сводится к тому, что теперь под символом х надо понимать
набор (ж1, ..., жт), а под символом a — набор (а1, ..., ат).
Если теперь в функциях ^(а;1, ..., хт, у) и /(ж1, ..., хт) фиксировать все
переменные, кроме хх и у, то мы окажемся в условиях утверждения 1, где
на сей раз роль х выполняет переменная ж*. Отсюда следует справедливость
формулы A0). Из этой формулы видно, что ~^т € СA™;1у) (г = 1, ..., т),
т. е. / G C^l\l™\ Iy). Рассуждая, как и при доказательстве утверждения 1, по
индукции устанавливаем, что / G C^(/J*;/y), коль скоро F € C^(U;R). >
Пример 2. Предположим, что функция F : G —* Ж определена в области
и принадлежит классу CA)(C?;R). Пусть ж0 = (ж?, ...,?сР) € G и
го, ..., Жд1) = 0. Если жо не является критической точкой функции
F, то хотя бы одна из частных производных функции F в точке жо отлична
OF
от нуля. Пусть, например, ^-^-(яо) Ф 0.
Тогда, в силу утверждения 2, в некоторой окрестности точки жо подмно-
подмножество Rm, задаваемое уравнением ^(ж1, ...,жт) = 0, может быть задано
как график некоторой функции хт = /(ж1, ..., ж), определенной в окрест-
окрестности точки (жо, ...,х™~1) € R, непрерывно дифференцируемой в этой
окрестности и такой, что

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ 479
Таким образом, в окрестности некритической точки хо функции F урав-
уравнение
задает (т — 1)-мерную поверхность.
В частности, в случае R3 уравнение
в окрестности некритической точки (хо, Jftb^o), удовлетворяющей ему, задает
двумерную поверхность, которая при выполнении условия -«—(ячъЗ/сь^о) ф О
локально может быть записана в виде
z = f(x,y).
Как мы знаем, уравнение плоскости, касательной к графику этой функции
в точке (жо, Vo,zo), имеет вид
z - z0 = — (х0,уо)(х - хо) 4- -д-(хо,Уо)(у - Уо)-
Но по формуле A0)
df
F?(xo,yo,zo) dy
поэтому уравнение касательной плоскости можно переписать в виде
, yo,zo)(y - Уо) 4- F'z(xo,yo,zo)(z - z0) = 0,
симметричном относительно переменных ж, у, z.
Аналогично и в общем случае получаем уравнение
m
гиперплоскости в Rm, касательной в точке хо = (хп,... ,Хс?) к поверхно-
сти, задаваемой уравнением ^(а;1, ..., хт) = 0 (разумеется, при условии, что
F(xo) = 0 и что хо — некритическая точка F).
Из полученных уравнений видно, что при наличии евклидовой структуры
в Rm можно утверждать, что вектор
dF
ортогонален поверхности r-уровня F(x) = г функции F в соответствующей
точке хо €

480
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Например, для функции
х2 у2 z2
F(x,y,z) = -5 + f; + -z,
определенной в R , г-уровнем являются: пустое множество при г < 0; точка
при г = 0; эллипсоид
! !
=г
+ +
а2 Ь2 с2
при г > 0. Если (жо,2/<ъ2о) ~~ т°чка на этом эллипсоиде, то по доказанному
вектор
j ev ч ^2а?о 2у0
gradF(:ro,yo,zo) = ^
ортогонален этому эллипсоиду в точке
точке плоскость имеет уравнение
, уо, zo), а касательная к нему в этой
Уо(у~Уо) Zq(z-Zq) _
Ь2 2
а2 Ь2 с
которое с учетом того, что точка (жо, yo,zo) лежит на эллипсоиде, можно пе-
переписать в виде
уоу zoz _
4. Теорема о неявной функции. Теперь перейдем к общему случаю
системы уравнений
F1(x1,...,xm,y\...,yn)=0,
k Fn(x\ ...,xm,y1,...,yn)=0,
(И)
которую мы будем решать относительно у1, ..., уп, т. е. искать локально экви-
эквивалентную системе A1) систему функциональных связей
у1 = /VT-.., хт),
k yn = fn(x\...,xm).
A2)
Для краткости, удобства письма и ясности формулировок условимся, что
х = (ж1, ..., хт), у = (у1, ..., уп); левую часть системы A1) будем записывать
как F(x,y), систему A1) как F(x,y) = 0, а отображение A2) как у = f(x).
Если
so = (xj, ..., zj1), уо = (Уо, • • •, У?)>
а = (а1, ..., ат), /3 = (/?\ ..., /?п),
то запись \х — хо\ < а. или |у — уо| < ft будет означать, что \хг — Xq\ < а1
(г = 1, ..., т) и, соответственно, |yJ — yjl < ft (j = 1, ..., n).

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ
481
Далее положим
/а/1
/% 1 • • •
dfn
/of1
f\ л • • •
dFn
t\ л • • •
дхш '
dF*\
дхт
dFn
дхт '
(*),
A3)
A4)
дуп
dFn dFn
дуп >
A5)
Заметим, что матрица Fy(x,y) квадратная и, следовательно, она обратима
тогда и только тогда, когда ее определитель отличен от нуля. В случае п = 1
она сводится к единственному элементу и в этом случае обратимость матри-
матрицы Fy(x,y) равносильна тому, что этот единственный ее элемент отличен от
нуля. Матрицу, обратную к F'y{x^ у), будем, как обычно, обозначать символом
n, опреде-
опредеТеперь сформулируем основной результат параграфа.
Теорема (о неявной функции). Если отображение F : U->
ленное в окрестности U точки (хо,Уо) € Rm+n, таково, что
1° FeCW(U;Rn), p^l,
2° F(rro,»o)=0>
3° Fy(xo,yo) — обратимая матрица,
то существуют (т 4- п)-мерный промежуток I = I™ x 1? С U, где
4m = {x€Em||x-xo|<a}, /vn = {»€Kn||j/-j/o|</3},
и такое отображение f € C(p\l™\Iy), что для любой точки (х,у) € I™ xl?
F(x,y) = 0 <=> y = f(x), A6)
причем
/'(*) = -[Щх,Пх))]-1№{х,№)]. A7)
< Доказательство теоремы будет опираться на утверждение 2 и простей-
простейшие свойства определителей. Разобьем его на отдельные этапы. Будем рас-
рассуждать методом индукции.
При п = 1 теорема совпадает с утверждением 2 и потому верна.

482 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Пусть теорема справедлива для размерности п—1. Покажем, что она тогда
справедлива и для размерности п.
a) В силу условия 3°, определитель матрицы A5) отличен от нуля в точке
(яо>Уо) € Ет+П, а значит, и в некоторой окрестности точки (я(ьУо)- Следо-
Следовательно, по крайней мере один элемент последней строки этой матрицы от-
отличен от нуля. С точностью до перемены обозначений можно считать, что
dFn
таким является элемент -=—.
дуп
b) Применяя тогда к соотношению
утверждение 2, найдем промежуток /m+n = (J™ х /у) х J* С U и такую
функцию / € С<р)G™ х J^;/у), что
(Fn(x\ ...,xm,y\...,yn)=0 в
11 A8)
с) Подставляя найденное выражение уп = /(я, у , ..., уп~ ) переменной уп
в первые п — 1 уравнений системы A1), получим п — 1 соотношений
т
= FV. • • •, хт, у1, ..., уп-\ f{x\ ...,xm,y\..., у"-1)) = О,
: A9)
ФП~1(Х1 Хт V1 ?7П~
_ pn-l/ I m I w11 f(xl Tm II1 ип~1)\ — П
—J7 \^х , .. . , х , у , ... , у , / ^j; , ..., j; ? У ) • ¦ ¦ ^ У /у — и.
Видно, что Ф* G CW(I™ х I*; И) (t = 1, ..., п - 1), причем
Ф*(а?, ..., xg, yj, ..., yj) = 0 (г = 1, ..., п - 1),
ибо /(xj, ..., xj1, yl, ..., yj) = у? и F*(xo,yo) =0 (г = 1,..., п).
В силу определения функций Ф* (к = 1, ..., п — 1),
дФк dFk 8Fk df '
^ +
Положив еще
фп( 1 m
т и1

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ
483
в силу A8) получаем, что в области своего определения Фп = 0, поэтому
дФп _ dFn dFn df _
ду* ~ ду1 + дуп ' ду{ ~
Учитывая соотношения B0), B1) и свойства определителей, можно заме-
заметить, что определитель матрицы A5) равен определителю матрицы
B1)
dF1
ду1
dFn
ду*
dF1
ду"
8Fn
ду"
.df
ay» ••
df
ду* ••
dF1
ду"~*
dFn
ду"~*
dF1
ду"
dFn
ду"
df
ду"-1
df
дуп~*
—
dF1 \
ду"
dFn
ду" /
( аФ1
ду*
дФп-
ду*
0
\
••• ду»-1
-1 аФп-х
0
dF1 >
ду»
dFn~l
ду»
dFn
ду» >
dFn
По предположению, -~-^- ф 0, а определитель матрицы A5) по условию от
личен от нуля. Следовательно, в некоторой окрестности точки (xj, ..., ж^1
\ч • • • 1J/?) отличен от нуля и определитель матрицы
дФ
п-1
дФ
п-1
т
Тогда по предположению индукции найдутся промежуток Jm+n~1 = I™ x
х Z^ С /^х/^, являющийся окрестностью точки (xj, ..., я™, Уо> • • • > Уо~1)
в R11*"*"*1, и такое отображение / € СМA™;1?~1), что в пределах проме-
промежутка /m+n-1 = I™ х J^ система A9) равносильна соотношениям
B2)
у
п—1 /п—
d) Так как J^ С Z^, a /f С /^, то, подставляя /\ .
сто соответствующих переменных в функцию уп = /(ж1, .
из соотношения A8), получаем зависимость
переменной уп от (х1, ..., хт).
, /п"х из B2) вме-
вме1 у71)
, жт, у1, ..., у71
B3)

484 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
е) Покажем теперь, что система равенств
B4)
задающая отображение / € С(рЦ1™;1?), где I^—I^ l x /*, равносильна в
пределах окрестности Jm+n = I™ x 1? системе уравнений A1).
В самом деле, сначала мы в пределах /m+n = (/™ х Iy~x) xi] заменили
последнее уравнение исходной системы A1) эквивалентным ему, в силу A8),
равенством уп = /(ж, у1, ..., yn-1). От так полученной второй системы мы
перешли к равносильной ей третьей системе, заменив в первых п — 1 уравне-
уравнениях переменную уп на /(ж, у1, ..., у71"). Первые п —1 уравнений A9) третьей
системы мы в пределах I™ х 1?~г c/fx I?~l заменили равносильными им
соотношениями B2). Тем самым получили четвертую систему, после чего пе-
перешли к равносильной ей в пределах I™ x I?~l x I* = Jm+n окончательной
системе B4), заменив в последнем уравнении уп = /(ж1, ..., жт, у1, ..., уп~1)
четвертой системы переменные у1, ..., уп~г их выражениями B2) и получив
в качестве последнего уравнения соотношение B3).
f) Для завершения доказательства теоремы остается проверить форму-
лу A7).
Поскольку в окрестности I™ х I™ точки (жо,Уо) системы A1) и A2) равно-
равносильны, то
^(ж, /(ж)) = 0, если ж € /?\
В координатах это означает, что в области Га
Fk{xl, ..., жт, fl(xl, ..., жт), ..., /п(ж\ ..., жт)) =0 (Jfc = 1, ..., п). B5)
X
Поскольку /€ C^(I^'Jy) и FeCM(U;Rn), где р ^ 1, то F(- ,/(¦))€
€ C(p)(J™;Rn) и, дифференцируя тождества B5), получаем
dFk ?A dFk dp
+ Е^ ° (* 11) B6)
Соотношения B6), очевидно, равносильны одному матричному равенству
в котором у = /(ж).
Учитывая обратимость матрицы Fy(x,y) в окрестности точки (жо,уо), из
этого равенства получаем, что
и теорема полностью доказана. >

§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ 485
Задачи и упражнения
1. На плоскости R2 с координатами х, у соотношением F(xyy) = 0, где F 6
? C^(R2, R), задана кривая. Пусть (жо, Уо) — некритическая точка функции F(x, у),
лежащая на кривой.
a) Напишите уравнение касательной к этой кривой в точке (жо,Уо)-
b) Покажите, что если (жо,уо) — точка перегиба кривой, то в этой точке выпол-
выполняется равенство
{F'x'xF'y2 - 2Fx'yF'xF'y + F^2)(xOiyo) = 0.
с) Найдите формулу для кривизны кривой в точке (а?о»Уо)-
2. Преобразование Лежандра для т переменных.
Преобразование Лежандра от переменных ж1, ..., хт и функции /(ж1, ..., хт)
есть переход к новым переменным ?i,..., ?m и функции /*(?i, • •., ?m)> задаваемый
соотношениями
B7)
ТП
a) Дайте геометрическую интерпретацию преобразования B7) Лежандра как пе-
перехода от координат (ж1, ..., хт, /(ж1, ..., жт)) точки на графике функции /(ж) к
параметрам (fi, ..., ?m, /*(fi,..., ?m)), задающим уравнение плоскости, касатель-
касательной к графику в этой точке.
b) Покажите, что преобразование Лежандра локально заведомо возможно, если
c) Используя для функции f(x) = /(ж1, ..., хт) то же определение выпуклости,
что и в одномерном случае (подразумевая теперь под х вектор (ж1, ..., хт) G Rm),
покажите, что преобразованием Лежандра выпуклой функции является выпуклая
функция.
d) Покажите, что
т тп тп
df = ?>'dfc + ?&dz' - df = JVdfc,
t=l »=1 »=1
и выведите отсюда инволютивность преобразования Лежандра, т. е. проверьте, что
(/*)•(») = /(«)•
е) Учитывая d), запишите преобразование B7) в симметричном относительно
переменных виде
m
<=1 B8)
/9 f /)/*

486
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
или, короче, в виде
где
vf(x) - (EL М
m
f) Матрицу, составленную из частных производных второго порядка функции
(а иногда и определитель этой матрицы), называют гессианом функции в данной
точке* at ar
Пусть da и dii — алгебраические дополнения элементов
гессианов
а2/
дх1дх1 ''' дх1дхт
d2f
d2f
к дхтдх1 ' дхтдхгп ,
f d*r
2г
07
т
2/*
а2/
2x*
д2
@
функций /(ж) и /*((), a d и d* - определители этих матриц. Считая, что d ф О,
покажите, что d • d* = 1 и что
g) Мыльная пленка, натянутая на проволочный контур, образует так называе-
называемую минимальную поверхность, имеющую наименьшую площадь среди всех поверх-
поверхностей, натянутых на этот контур.
Бели локально задать эту поверхность как график функции z = /(ж, у), то, ока-
оказывается, функция / должна удовлетворять следующему уравнению минимальных
поверхностей:
A + tfM'L - 2f'xfvfJv + (i + f^f'Jy = о.
Покажите, что после преобразования Лежандра это уравнение приводится к виду
A + г?) С + 4nf% + A + ?)№ = 0.
3. Канонические переменные и система уравнений Гамильтона1^.
а) В вариационном исчислении и фундаментальных принципах классической ме-
механики важную роль играет следующая система уравнений Эйлера—Лагранжа:
B9)
v = ?(*),
*) У. Р. Гамильтон A805 — 1865) — знаменитый ирландский математик и механик. Сфор-
Сформулировал вариационный принцип (принцип Гамильтона), построил феноменологическую
теорию оптических явлений; создатель теории кватернионов и родоначальник векторного
анализа (кстати, ему принадлежит сам термин «вектор»).

§ 5, ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ 487
где L(t,x,v) — заданная функция переменных t, ж, vy среди которых t обычно явля-
является временем, х — координатой, a v — скоростью.
Систему B9) составляют два соотношения на три переменные. Из системы B9)
обычно желают найти зависимости х = x(t) и v = v(t), что по существу сводится к
отысканию зависимости х = x(t), ибо v = -тт.
Запишите подробно первое уравнение системы B9), раскрыв производную -т-
с учетом того, что х = x(t) и v =¦ v(t).
b) Покажите, что если от переменных t, х, г;, L перейти к так называемым
каноническим переменным ?, ж, р, H, сделав преобразование Лежандра (см. задачу 2)
Н — pv — L
по переменным г/, L, заменяя их на переменные р, Ну то система Эйлера—Лагранжа
B9) приобретает симметричный вид
дН . дН
C0)
в котором она называется системой уравнений Гамильтона.
с) В многомерном случае, когда L = L(?, ж1,..., жт, v1,..., vm), система уравне-
уравнений Эйлера—Лагранжа имеет вид
дь . d дь uz x и}==и
C1)
где для краткости положено х = (ж1,..., жт), v = (v1, ..., vm).
Сделав преобразование Лежандра по переменным v1, ..., vm, L, перейдите от
переменных ?, х1, ..., xm, v1, ..., vw, L к каноническим переменным t, ж1, ..., жт,
Pi, • • •, Рт, Н и покажите, что в них система C1) перейдет в следующую систему
уравнений Гамильтона:
• t Ол1 *. - \ С\О\
dpi
4. Теорема о неявной функции.
Решение этой задачи дает другое, быть может, менее наглядное и эффектив-
эффективное, но более короткое в сравнении с изложенным выше доказательство основной
теоремы настоящего параграфа.
а) Пусть выполнены условия теоремы о неявной функции, и пусть
dF{ dF{
— г-я строка матрицы Fy(x, у).
Покажите, что определитель матрицы, составленной из векторов Fy(xi,yi), от-
отличен от нуля, если все точки (xiyyi) (г = 1, ..., п) лежат в некоторой достаточно
малой окрестности U = I™ х 1? точки (жо,уо)-

488 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Ь) Покажите, что если при ж G I™ найдутся точки yi, уг € /у такие, что F(xyy\) =
= 0 и F(x,y2) = 0, то для каждого i G {1, ..., п} найдется такая точка (ж, у»),
лежащая на отрезке с концами (x,yi), (ж,уг), что
- yi) = 0 (i = l,..., п).
Покажите, что отсюда следует, что у\ = уг, т. е. если неявная функция / : /™
существует, то она единственна.
c) Покажите, что если шар В(уо\ г) лежит в /?, то F(xo, у) ф О при ||у — yo||Rn =
= r >0.
d) Функция ||F(xo,y)||?n непрерывна и имеет положительный минимум /i на
сфере \\у - yo||Rn = г.
e) Существует S > О такое, что при ||ж — жо||кт < S
*> y)llRn > \fr если ||у - yo||Rn = г,
*>y)llRn< |м> если у = уо.
f) При любом фиксированном ж таком, что ||ж — жо|| < 6, функция ||^(#, y)||Rn
достигает минимума в некоторой внутренней точке у = /(ж) шара \\у — yo||Rn ^ г> и
поскольку матрица Fy(ж,/(ж)) обратима, то F(x,f(x)) = 0. Этим устанавливается
существование неявной функции /: В(жо; 8) —> ?(уо; г).
g) Если Ау = /(ж + Аж) - /(ж), то
где Fy — матрица, строками которой являются векторы F^(a;»,y») (i = 1, ..., n),
где (ж», у») — соответствующая точка на отрезке с концами (ж, у), (х 4- Аж, у + Ау).
Аналогичный смысл имеет символ Fx'.
Покажите, что из этого соотношения следует непрерывность функции у = /(ж).
h) Покажите, что
'(*) = -[F^x, fix))]-1 ¦
5. «Если /(«,»,*) = 0, то g ¦ g • g = -Ь.
a) Придайте точный смысл этому высказыванию.
b) Проверьте его справедливость на примере формулы Клапейрона
PV
= const
и в общем случае функции трех переменных.
c) Как выглядит аналогичное высказывание для соотношения /(ж1, ..., жт) = 0
между т переменными? Проверьте его справедливость.
6. Покажите, что корни уравнения
*n + cizn~l -f... 4- Сп =0
гладко зависят от его коэффициентов, во всяком случае, пока все корни различны.

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ 489
§ в. Некоторые следствия теоремы о неявной функции
1. Теорема об обратной функции
Определение 1. Отображение /: U -> V, где U и V — открытые под-
подмножества в Ет, называется С ^ -диффеоморфизмом или диффеоморфизмом
гладкости р (р = 0,1,...), если
2) / — биекция;
3) f^eC^HV
С (°)-диффеоморфизмы называют гомеоморфизмами.
Здесь мы, как правило, будем рассматривать только гладкий случай, т. е.
случай р € N или р = оо.
Следующая часто используемая теорема в идейном плане утверждает, что
если дифференциал отображения обратим в точке, то само отображение обра-
обратимо в некоторой окрестности этой точки.
Теорема 1 (теорема об обратной функции). Если отображение f:G-t
-+ Rm области G CRm таково, что
1° /eC<">(G;Rm), p^l,
2° Уо = /(zo) при хо е G,
3° /'(хо) обратимо,
то существуют окрестность U{xq) С G точки xq и окрестность V(yo)
точки J/0 такие, что f : U(xo) —> V(yo) есть С^-диффеоморфизм. При
этом если х € U{xq) и у = f(x) G V(yo), то
Соотношение у = f(x) перепишем в виде
A)
Функция F(x,y) = f(x) — у определена при х € G и у G Em, т. е. опреде-
определена в окрестности G x Rm точки (хо,^о) € Rm x Rm.
Мы хотим разрешить уравнение A) относительно х в некоторой окрест-
окрестности точки (яо,Уо)- В СИЛУ условий 1°, 2°, 3° теоремы отображение F(x,y)
таково, что
F e Cip)(G х Rm; Rm), p ^ 1,
обратимо.

490
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
По теореме о неявной функции найдутся окрестность Ix х 1У точки (хо,уо)
и отображение д Е C^p\ly\Ix) такие, что для любой точки (х,у) Е Ix х 1у
B)
и
-1
В нашем случае
F' (т iA — fUx} F'(т iA
где Е — единичная матрица; поэтому
я'(у) =
Если положить V = /у и t/ =
О)
, то соотношение B) показывает, что
отображения f:U->Vng:V-*U взаимно обратны, т. е. д = Z" на У.
Поскольку V = /у, то V — окрестность точки уо. Это означает, что при
условиях 1°, 2°, 3° образ уо = /(#о) точки хо € G, внутренней для G, является
точкой, внутренней для образа f(G) множества G. В силу формулы C) ма-
матрица д'(уо) обратима. Значит, отображение д: V ->• U обладает свойствами
1°, 2°, 3° относительно области V и точки уо € V\ Тогда по уже доказанному
хо = 9(Уо) — внутренняя точка множества U = <7(V).
Поскольку условия 1°, 2°, 3° в силу формулы C), очевидно, выполнены в
любой точке у G V, то любая точка х = р(у) является внутренней точкой
множества U. Таким образом, U — открытая (и, очевидно, даже связная)
окрестность точки х0 в Rm.
Теперь проверено, что отображение f:U->V удовлетворяет всем условиям
определения 1 и утверждению теоремы 1.. >
Приведем несколько примеров, иллюстрирующих теорему 1. Очень часто
теорема об обратной функции используется при переходе от одной системы
координат к другой системе координат. Простейший вариант такого пре-
преобразования координат рассматривался в аналитической геометрии и линей-
линейной алгебре и имел вид
У
а\
.. а
т
а
m
n
m
m/
«.яг
т
или, в компактной записи, у-7 = а\хх. Это линейное преобразование А: MJ* -4
"^ имеет обратное A~l: EJJ1 ->• RJ1, определенное во всем пространстве
, тогда и только тогда, когда матрица (af) обратима, т. е. при условии,
что det(af) ф 0.
Теорема об обратной функции является локальным вариантом этого утвер-
утверждения, опирающимся на то обстоятельство, что гладкое отображение в ма-

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ
491
лой окрестности точки ведет себя примерно так же, как его дифференциал в
этой точке.
Пример 1. Полярные координаты. Отображение /: R+ -> R2 полуплос-
полуплоскости R+ = {(р, ф) G Е2 | р ^ 0} на плоскость R2, задаваемое формулами
х = р cos <?,
у = р sin у?,
проиллюстрировано на рис. 57.
Ф
п_
2
D)
Ф
о
0
Ф
о
Рис. 57
Якобиан этого отображения, как нетрудно подсчитать, равен р, т. е. от-
отличен от нуля в окрестности любой точки (р, у?), где р > 0. Таким образом,
формулы D) локально обратимы и, значит, локально числа р, tp могут быть
приняты в качестве новых координат точки, которую раньше задавали декар-
декартовы координаты х, у.
Координаты (р, ф) являются хорошо известной системой криволинейных
координат на плоскости — это полярные координаты. Их геометрический
смысл виден из рис. 57. Отметим, что в силу периодичности функций cosy?,
sin if отображение D) при р > 0 только локально диффеоморфно, а во всей этой
области оно не является биективным. Именно поэтому переход от декартовых
координат к полярным всегда сопровождается выбором ветви (т. е. указанием
диапазона изменения) аргумента (р.
Полярные координаты (р, ф, ф) в трехмер-
трехмерном пространстве R3 называют сферическими
координатами. Они связаны с декартовыми
координатами формулами
z =
у = р sin ф sin
х = р sin ф cos (p.
E)
/ У
Рис. 58
Геометрический смысл параметров р, фу if
показан на рис. 58.
Якобиан отображения E) равен р2 sin ф и в силу теоремы 1 преобразование
E) обратимо в окрестности любой точки (р,ф, у?), в которой р > 0 и sin^ ф 0.
17 Зорин В. Л.

492 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Множествам, где р = const, ц> = const или г/> = const, в пространстве
(х, y,z), очевидно, отвечают соответственно сферическая поверхность (на
сфере радиуса р), полуплоскость, проходящая через ось z, и поверхность ко-
конуса с осью z.
Таким образом, при переходе от координат (х, у, z) к координатам (р, *ф, ф),
например, сферическая поверхность и поверхность конуса локально распрям-
распрямляются: им соответствуют куски плоскостей р = const и ф = const соответ-
соответственно. Аналогичное явление мы наблюдали и в двумерном случае, когда
дуге окружности на плоскости (х, у) отвечал отрезок прямой на плоскости с
координатами (p,ip) (см. рис. 57). Обратите внимание на то, что это именно
локальное выпрямление.
В m-мерном случае полярные координаты вводятся соотношениями
х1 = pcosy?i,
х2 = р sin <pi cos
Хт 1 = р sin ipi Sin y>2 • • • sin <?m-2 COS
xm = p sin <?>i sin y>2 ... sin <?m_2 sin
Якобиан этого преобразования равен
pm-l ginm-2^ sinm-
и в силу теоремы 1 оно тоже локально обратимо всюду, где этот якобиан
отличен от нуля.
Пример 2. Общая идея локального выпрямления кривых. Новые коор-
координаты обычно вводят с целью упростить аналитическую запись объектов,
участвующих в задаче, и сделать их более обозримыми в этой новой записи.
Пусть, например, на плоскости К2 некоторая кривая задана уравнением
Пусть F — гладкая функция, а точка (хо, уо) такова, что она лежит на кривой,
т. е. F(xo,yo) = 0, и не является критической точкой функции F, например,
пусть i^(xo,2/o) т*0.
Попробуем подобрать координаты ?, г/ так, чтобы в них дуге нашей кри-
кривой, содержащей (хо,Уо)> отвечал отрезок одной из координатных линий, наг
пример линии г) = 0.
Положим
Матрица Якоби

§6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ
493
этого преобразования имеет своим детерминантом величину Fy(x,y), кото-
которая по предположению отлична от нуля в точке (хо,уо)- Тогда по теореме 1
это отображение является диффеоморфизмом окрестности точки (xo,j/o) на
окрестность точки (?,т?) = @,0). Значит, в пределах указанной окрестности
У
F(x,y) = 0
Рис. 59
числа f, т) можно принять за новые координаты точек, лежащих в окрестности
точки (хо,Уо)- В новых координатах наша кривая, очевидно, имеет уравнение
г) = 0, и в этом смысле мы действительно добились ее локального выпрямле-
выпрямления (рис. 59).
2. Локальное приведение гладкого отображения к каноническо-
каноническому виду. Мы рассмотрим здесь только один вопрос этого типа, а именно
укажем канонический вид, к которому удачным выбором координат можно
локально привести любое гладкое отображение, имеющее постоянный ранг.
Напомним, что рангом гладкого отображения /: U -> Rn области U CRm
в точке х Е U называется ранг касательного к нему в этой точке линейно-
линейного отображения, т. е. ранг матрицы /'(ж). Ранг отображения / в точке х
обозначают обычно символом rang/(ж).
Теорема 2 (теорема о ранге). Пусть f : U -»• Rn — отображение,
определенное в окрестности U С Rm точки х0 е Rm. Если f G C^(C/;Rn),
р ^ 1, и в любой точке х G U отображение f умеет один и тот же ранг
к, то существуют окрестности О(х0), О(уо) точек х0, уо = f(xo) и такие
их диффеоморфизмы и = ip(x), v = гр(у) класса С^р\ что в окрестности
O(uq) = ф@(хо)) точки щ = ip(xo) отображение v = \j> о / о 1р~г(и) имеет
следующее координатное представление:
(и1, ...,u*, ...,um) =т—у v = (v1, ...,vn) = (и1, ...,ti*,0, ...,
G)
Иными словами, теорема утверждает (рис. 60), что вместо координат
(ж1, ...,хт) можно выбрать координаты (м1, ...,мт), а вместо координат
17*

494
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
(у\ • • •»Уп) — координаты (г?1,..., vn) так, что локально наше отображение
в этих новых координатах будет иметь вид G), т. е. канонический вид линей-
линейного отображения ранга к.
< Запишем координатное пред-
представление
У
у
к __
= fk{x\...,xm),
х1 хт)
(8)
нашего отображения /: U -4 R?, определенного в окрестности точки ж0 € R™.
Чтобы не менять нумерацию координат и окрестность V, будем считать, что
в любой точке х 6 U главный минор порядка к, стоящий в левом верхнем углу
якобиевой матрицы отображения /, отличен от нуля.
Рассмотрим отображение, определяемое в окрестности U точки хо равен-
равенствами
и1 = ^(ж1, ...,а;т) =
и =
= X
ит = ipm(x\ ...,хт) = хт.
Его матрица Якоби имеет вид
' dfl
дх1
д/к
дх1
9 Ш •
• • •
0
а/1 .
дхк ]
а/* :
дхк
а/1
QXk+\ ¦
dfk
; a**+i •
0
а/м
• ax-
a/*
•• a*-
0
и в силу сделанного предположения ее определитель отличен от нуля в U.
По теореме об обратной функции, отображение и = ср(х) является диф-
феоморфизмом гладкости р некоторой окрестности О(хо) С U точки хп на
окрестность О(щ) = у?(О(х0)) точки w0 = <р(хо)-

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ
495
Сравнивая соотношения (8) и (9), видим, что композиция д
O(uq) -> Ry имеет следующее координатное представление:
= f°<P
-1.
ук =
A0)
уп = fn о ^Г1 (u\ ...,u
п =
= дп(и
= дп(и\ ..., ит).
Поскольку отображение </? г : О(щ) -)> O(xq) в любой точке и G
имеет максимальный ранг т, а отображение / : О(хо) —>- R? в любой точке
х G 0(жо) имеет ранг А;, то, как известно из линейной алгебры, матрица
д'(и) = //(^(tx)) • (v7) (w) имеет ранг fc в любой точке и G
Прямой подсчет матрицы Якоби отображения A0) дает
1
0
dgk+1
ддп
dul
0
dgk+1 .
du" ;
dgn i
• ¦ au*
0
Quk+l ' ' '
dgk+1
dum
dgn
dum
Значит, в любой точке и Е О(щ) получаем -^(и) = 0 (г = к + 1, ..., ш;
j = А: + 1, ..., п). Считая окрестность О(ио) выпуклой (чего можно добиться,
уменьшив О(ио), например, до шара с центром г/о), отсюда можно заключить,
что функции gi при j = А: + 1, ..., п на самом деле не зависят от переменных
и
т
После этого решающего наблюдения отображение A0) можно переписать
в виде
У1 =ч\
Ук = ик,
A1)
уп = дп{и\...,ик).

496
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Теперь уже можно указать отображение ф. Положим
=: Г (У),
vk = yk
(у1,
=: ФЧУ),
=: Фк+1(У),
A2)
V
. 1 jL.
= v — d (t/ t/ )
Из построения функций gi (j = fc + 1,..., п) видно, что отображение
определено в некоторой окрестности точки у о и принадлежит классу С^ в
этой окрестности.
Матрица Якоби отображения A2) имеет вид
о
о
о
1
Бе определитель равен 1, и, значит, по теореме 1 отображение ф является
диффеоморфизмом гладкости р некоторой окрестности О(уо) точки у о Е R?
на окрестность 0{vq) = ^(О(уо)) точки vo € RJJ.
Сравнивая соотношения A1) и A2), видим, что в достаточно малой окрест-
окрестности О(щ) С O(uq) точки uq такой, что q{O(uq)) С О(уо), отображение
ф о f о ip~l: O(uo) -)• 1RJJ является отображением гладкости р этой окрестности
О(щ) на некоторую окрестность 0{vq) С O(vo) точки vo € R? и при этом
имеет канонический вид
V
и
vk = w*,
V
k+l =
= o,
A3)
V
п
= 0.
Полагая ц> 1@(ио)) = 0(хо), Ф x@(vo)) = 0(уо)> получаем указанные в
теореме окрестности точек хо, уо> ^ем и завершается доказательство. >

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ 497
Теорема 2, как и теорема 1, очевидно, является локальным вариантом со-
соответствующей теоремы линейной алгебры.
В связи с проведенным доказательством теоремы 2 сделаем следующие
полезные для дальнейшего замечания.
Замечание 1. Если в любой точке исходной окрестности U С Rm ранг
отображения / : U —>• Rn равен п, то точка уо = /(хо), гДе хо €• U, явля-
является внутренней точкой множества /A7), т. е. содержится в f(U) вместе с
некоторой своей окрестностью.
<4 Действительно, по доказанному отображение фо f oip~l: О(щ) ->• O(vq)
в этом случае имеет вид
(и1,..., ип,..., ит) = и i—> v = (v1,..., vn) = (и1,..., un),
поэтому образ окрестности точки щ = <^(хо) содержит некоторую окрест-
окрестность точки vo = *ф о f о ср~х (uq).
Но отображения ц>: О(хо) -> О(щ), г/> : О(уо) ->• O(vo) — диффеомор-
диффеоморфизмы, поэтому они переводят внутренние точки во внутренние. Записывая
теперь исходное отображение / в виде / = ф~х о (ф о f о <р~г) о ip, можем
заключить, что точка у о = /(хо) является внутренней точкой образа окрест-
окрестности точки хо. >
Замечание 2. Если ранг отображения /: U -? Rn в любой точке окрест-
окрестности U равен к и к < п, то, в силу равенств (8), A2) и A3), в некоторой
окрестности точки хо € U С Ет имеют место п — к соотношений
= gi(f1(x\...,xm),...,fk(x\...,xm)) A4)
Указанные соотношения выписаны в принятом нами предположении о том,
что главный минор порядка к матрицы /'(хо) отличен от нуля, т. е. что ранг
к реализуется уже на наборе функций Z1, ...,/*. В противном случае можно
было бы изменить нумерацию функций /г, ..., /п и снова иметь указанную
ситуацию.
3. Зависимость функций
Определение 2. Говорят, что система непрерывных функций /*(х) =
= /*(х1, ..., хт) (г = 1,..., п) является функционально независимой в окрест-
окрестности точки хо = (xj, ..., xj1), если для любой непрерывной функции F(y) =
= F(yx, ..., уп), определенной в окрестности точки Уо = (Уо > • • •, Уо) = (Z1
..., /п(хо)) = /(хо), соотношение
в окрестности точки хо возможно только в случае, когда Fty1,..., уп) = 0 в
окрестности точки

498 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Линейная независимость, рассматривавшаяся в алгебре, есть независи-
независимость по отношению к линейным соотношениям
Если система не является функционально независимой, то ее называют
функционально зависимой.
В случае линейной зависимости векторов один из них, очевидно, является
линейной комбинацией остальных. Аналогичная ситуация имеет место и в
отношении функционально зависимой системы гладких функций.
Утверждение 1. Если система f%(xl, ..., хт) (г = 1, ..., п) гладких
функций, определенных в окрестности U(xo) точки xq € Шт, такова, что
ранг матрицы
(x)
дх1 ''' дхт
dfn dfn
\ дх1 ''' дхт
в любой точке х € U один и тот же и равен к, то
a) при к == п система функционально независима в окрестности
b) при к < п найдутся окрестность точки xq и такие к функций си-
системы, пусть Z1, ..., fk, что остальные п — к функций системы в этой
окрестности представляются в виде
j \Х , ..., х ) = 9 \j \Х , ... 9 х J, ..., / [х , ..., х Jj,
где дг(ух, ..., ук) — гладкие функции, определенные в окрестности точки
2/о = (fl(xo), • • •, /п(#о)) и зависящие только от к координат текущей точ-
точки у = (у1, ...,2/п).
< В самом деле, если к = п, то в силу замечания 1 к теореме о ранге при
отображении
у1 =/V, •••,*"*),
A5)
уп =
образ окрестности рассматриваемой точки xq содержит целую окрестность
точки 2/о = /(#<))• Но тогда соотношение
в окрестности xq возможно только при условии, что
F(y\...,yn) = O
в окрестности точки 2/о- Этим утверждение а) доказано.

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ 499
Если же к < п и ранг к отображения A5) реализуется уже на функ-
функциях Z1, ..., /*, то в силу замечания 2 к теореме о ранге найдется такая
окрестность точки у о = /(хо) и п — к определенных в ней функций дг(у) =
— 9*{У1> • • • > Ук) (* = А + 1, ..., п) того же порядка гладкости, как и функции
системы, что в некоторой окрестности точки xq будут выполнены соотноше-
соотношения A4). Этим доказано утверждение Ь). >
Мы показали, что если к < п, то найдутся п — к специальных функций
F{(y) = уг — дг(у1, ..., ук) (г = к 4- 1, ..., п), устанавливающих соотношения
между функциями системы /*, ..., /*, ..., /п в окрестности точки
4. Локальное разложение диффеоморфизма в композицию про-
простейших. Здесь мы покажем, как, используя теорему об обратной функции,
можно локально представить диффеоморфное отображение в виде композиции
таких диффеоморфизмов, каждый из которых меняет только одну из коорди-
координат.
Определение 3. Диффеоморфизм д : U -> Rm открытого множества
U С Mw будем называть простейшим, если его координатное представление
имеет вид
уг = х\ ie {I, ...,m}, г
т. е. при диффеоморфизме д : U -> Ет меняется только одна из координат
отображаемой точки.
Утверждение 2. Если /: G -> Rm — диффеоморфизм открытого мно-
множества G С Ет, то для любой точки хо € G найдется такая ее окрест-
окрестность, в которой справедливо представление f ~ g\o.. .одп, где pi, ..., gn —
простейшие диффеоморфизмы.
< Проверим это по индукции.
Если исходное отображение / само является простейшим, то для него
утверждение тривиально справедливо.
Предположим, что утверждение справедливо для диффеоморфизмов, меня-
меняющих не более чем {к — 1) координату, где к — 1 < п.
Рассмотрим теперь диффеоморфизм /: G -> lRm, меняющий к координат:
У ==/(х,...,х ),
fk(xl Xm)
У —
ут = хт

500
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Мы приняли, что меняются именно первые к координат, чего можно до-
достичь линейными преобразованиями. Значит, это не умаляет общности рас-
рассуждений.
Поскольку / — диффеоморфизм, то его матрица Якоби /'(#) в любой точке
невырожденная, ибо
Фиксируем Xo 6 G и вычислим определитель матрицы f'(xo):
f1 . df df
df
dx1
df
dx1
0
df
dxk
df
dxk
df
\ dxk+l
\ df
\ dxk+l
1
' 0
df
dxm
df
• • 4 —^
0
1
df
dxk
dfk
(x0) ф 0.
Таким образом, один из миноров порядка к — 1 последнего определителя
должен быть отличен от нуля. Опять для упрощения записи будем считать,
что таким является главный минор порядка к — 1. Рассмотрим тогда вспомо-
вспомогательное отображение g : G -> lRm, определяемое равенствами
и
ик"г
uk
um
Поскольку якобиан
df1 df1 . df1
dx1
dfk~l
dx1
df-1
¦" ax*-1
0
: дхк
! dxk
. i
0
xm)
= /*(x1, ...,xm),
df
dx~
df-1
dxm
0
1
_4
(xo) =
a/-
dx1
dfk~l
dx1 '
df1
" dxk~l
df-1
ax*-1
A7)
(xo) Ф 0
отображения g : G -> Rm в точке xo G G отличен от нуля, отображение
является диффеоморфизмом в некоторой окрестности точки

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ 501
Тогда в некоторой окрестности точки tio = д(хо) определено обратное к
д отображение х = д~1(и), которое позволяет ввести в окрестности xq новые
координаты (и1, ..., um).
Пусть h = / о д~1. Иными словами, отображение у = h(u) есть наше
отображение A6) у = /(ж), записанное в координатах и. Отображение Л,
как композиция диффеоморфизмов, является диффеоморфизмом некоторой
окрестности точки щ. Его координатная запись, очевидно, имеет вид
У1 =
yk~l =
yk =
yk+l = uk+l^
ym = ixm,
т. e. h — простейший диффеоморфизм.
Но / = h о 0, а по предположению индукции отображение д, определенное
формулами A7), раскладывается в композицию простейших диффеоморфиз-
диффеоморфизмов. Таким образом, диффеоморфизм /, меняющий к координат, в некоторой
окрестности точки хо тоже раскладывается в композицию простейших диф-
диффеоморфизмов, что и завершает индукцию. >
5. Лемма Морса. К рассматриваемому кругу идей принадлежит также
красивая сама по себе и важная в приложениях лемма Морса1) о локальном
приведении гладкой вещественнозначнои функции к каноническому виду в
окрестности невырожденной критической точки.
Определение 4. Пусть xq — критическая точка функции / Е С ^ (?/; Ж),
определенной в окрестности U этой точки.
Критическая точка хо называется невырожденной критической точкой
функции /, если гессиан функции в этой точке (т. е. матрица Q L • (дго),
ОХ%ОХ3
составленная из частных производных второго порядка) имеет отличный от
нуля определитель.
Бели хо — критическая точка функции, т. е. /'(#о) = 0, то по формуле
Тейлора
/(х) - /(хо) =
К. М. Морс A892 —1977) — американский математик; основные труды посвящены
применению топологических методов к различным разделам анализа.

502
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Лемма Морса утверждает, что локально можно сделать такую замену х = д(у)
координат, что в координатах у функция / будет иметь вид
(/ о 9)(У) ~ /Ы = -(У1J - •••- (/J + (/+1J + • • • + (УтJ.
Если бы в правой части равенства A8) отсутствовал остаточный член
о(\\х — хо\\2), т. е. разность f(x) — /(хо) была бы просто квадратичной формой,
то, как известно из алгебры, линейным преобразованием ее можно было бы
привести к указанному каноническому виду. Таким образом, утверждение,
которое мы собираемся доказать, есть локальный вариант теоремы о приве-
приведении квадратичной формы к каноническому виду. Доказательство его будет
использовать идею доказательства этой алгебраической теоремы. Мы будем
опираться также на теорему об обратной функции и следующее предложение.
Лемма Адамара. Пусть /: U -> R — функция класса C^(f/;R), р ^ 1,
определенная в выпуклой окрестности U точки 0 = @, ..., 0) ? Rm и такая,
что /@) = 0. Тогда существуют функции Qi ? С^р"гЦи;Ш) (г = 1, ..., т)
такие, что в U имеет место равенство
т
f(x\ ...,xm) =
A9)
причем д{@) =
4 Равенство A9) — это, в сущности, иная полезная запись уже известной
нам формулы Тейлора с интегральным видом остаточного члена. Оно выте-
вытекает из равенств
/(х1, ...,xm) =
если положить
0
i=1
0
(tx\ ..., tx") dt,
9i{x\ ..., xm) = j |?(te\ ..., txm) dt (i = 1, ..., m).
о
To, что ф@) = ^4@) (i = 1,..., m), очевидно, а то, что # G
тоже нетрудно проверить. Но мы не будем сейчас заниматься этой проверкой,
поскольку в свое время будет доказано общее правило дифференцирования ин-
тегр'ала, зависящего от параметра, из которого нужное нам свойство функций
9г будет непосредственно вытекать.
Таким образом, с точностью до указанной проверки, формула Адамара
A9) установлена. >

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ 503
Лемма Морса. Если f : G -> R — функция класса C^(G;R), опреде-
определенная на открытом множестве G С Rm, a хо Е G — невырожденная крити-
критическая точка этой функции, то найдется такой диффеоморфизм g: V -> U
некоторой окрестности начала координат 0 пространства Rm на окрест-
окрестность U точки хо, что для всех точек у € V
(/ о 9)(у) = /(хо) - [(у1J + ... + (у*J] + [(у*+1J + ... + (утJ].
М Линейными заменами вопрос сводится к случаю, когда хо = 0 и /(#о) =
= 0, что мы в дальнейшем и будем считать выполненным.
Поскольку хо = 0 — критическая точка функции /, то в формуле A9)
gi@) = 0 (г = 1, ..., m). Тогда по той же лемме Адамара
m
i\x , ..., х ) — у ^ х fiij\Х , ..., х ),
где h^ — гладкие функции в окрестности точки 0, и, следовательно,
т
X , . . . , X ) — 7 X X Utj yjj , . . . , X ). V^U/
Подставляя здесь, если нужно, вместо hij функции h^ = x(/iij 4-
можем считать, что hij = Л^. Заметим также, что, в силу единственно-
единственности тейлоровского разложения, из непрерывности функций hij следует, что
^tj(O) = г, Л j(Q) и, значит, матрица (hij(O)) невырожденная.
Теперь функция / записана подобно квадратичной форме и мы хотим, так
сказать, привести ее к диагональному виду.
Как и в классическом случае, будем действовать по индукции.
Предположим, что существуют координаты гх1, ..., ит в окрестности U\
точки 0 € Rw, т. е. диффеоморфизм х = <р(и) такой, что в координатах
гх\ ..., ит
m
•-1\2
± ... ± КJ + ? и^Нц(и\ ..., ит), B1)
где г ^ 1, а ^ j
Заметим, что при г = 1 соотношение B1) имеет место, что видно из фор-
формулы B0), где
т
По условию леммы, квадратичная форма ?) x*x*hij@) невырожденная,
т. е. det (hij @)) ф 0. Замена переменных х = <?>(и) осуществляется диффео-
диффеоморфизмом, поэтому dety/(O) ф 0. Матрица формы ^(гх1J ± ... ± (ur~1J H-
m
-f X^ ulu^Hij@) получается из матрицы (/1^@)) домножением справа на ма-
матрицу (р'@) и слева на транспонированную по отношению к (р'@) матрицу,

504 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
поэтому она тоже невырожденная. Следовательно, по крайней мере одно из
чисел Hij@) (г, j = г, ..., т) отлично от нуля. Линейной заменой переменных
m
форму Yl ulu^Hij@) можно привести к диагональному виду, поэтому мож-
,j
но считать, что в равенстве B1) Нгг@) ф 0. Ввиду непрерывности функций
Hij(u) неравенство Нгг(и) ф 0 будет выполнено также в некоторой окрестно-
окрестности точки и = 0.
Положим ^(гх1, ..., ит) = у/\Нгг(и)\. Тогда функция ф принадлежит клас-
классу C^l\U2\ К) в некоторой окрестности U2 С U\ точки и = 0. Сделаем теперь
переход к координатам (v1, ..., vm) по формулам
Vх = иг, г ф г,
г if 1 m
Якобиан преобразования B2) в точке и = 0, очевидно, равен ф@), т. е.
отличен от нуля. Тогда в силу теоремы об обратной функции можно утвер-
утверждать, что в некоторой окрестности Щ С f/г точки и = 0 отображение
v = ф(и), заданное соотношениями B2), является диффеоморфизмом класса
C(l\Uz] IRm) и потому переменные (v1, ..., vm) действительно могут служить
координатами точек Щ-
Выделим в правой части равенства B1) все члены
m
iiriirH (ii1 i/m>\-I-9 \ ^ iiriiJH (iil iim\ (О*\\
содержащие иг. В записи B3) суммы этих членов мы использовали то, что
ЯТТ
«- ^— ГТ -*'
Сравнивая B2) и B3), видим, что выражение B3) можно переписать в виде
2
Знак ± перед vrvr появляется в связи с тем, что Нгг = ±(фJ, причем
берется знак плюс, если Нгг > 0, и знак минус, если Нгг < 0.
Таким образом, после замены v = ф(и) выражение B1) преобразуется в
равенство
??vVHiiiv1, ..., vm),
г=1
где Hij — некоторые новые гладкие функции, симметричные по индексам i,j.
Отображение (роф~1 является диффеоморфизмом. Таким образом, завершен
индуктивный переход от г - 1 к г и лемма Морса доказана. >

§ 6. СЛЕДСТВИЯ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ 505
Задачи и упражнения
1. Вычислите якобиан перехода F) от полярных координат к декартовым коор-
координатам в Rm.
2. а) Пусть хо — некритическая точка гладкой функции F: U —> R, определенной
в окрестности U точки хо = (xj, • •, х™) 6 Rm. Покажите, что в некоторой окрест-
окрестности U С U точки хо можно так ввести криволинейные координаты (?*, ..., fm),
что множество точек, выделяемое условием F(x) = F(xo), в этих новых координатах
будет задаваться уравнением ?т = 0.
Ь) Пусть (р, ф G C(k)(D;R) и пусть в области D (<р(х) = 0) => (ф(х) = 0).
Покажите, что если grad<^ / 0, то в D справедливо разложение ф — в • <р, где в ?
3. Пусть /: R2 —>• R2 — гладкое отображение, удовлетворяющее системе уравне-
уравнений Коши — Римана
df1 = df
Эх1 ~ дх2 ' дх2 ~ дх1'
a) Покажите, что якобиан такого отображения равен нулю в некоторой точке
тогда и только тогда, когда матрица f'(x) в этой точке нулевая.
b) Покажите, что если f'(x) ф 0, то в окрестности точки х определено обратное
к / отображение /""*, которое также удовлетворяет системе уравнений Коши —
Римана.
4. Зависимость функций (прямое доказательство).
a) Покажите, что функции пг(х) = хг (г = 1, ..., га) от точки х = (х1, ..., xm) G
? Шт образуют независимую систему функций в окрестности любой точки про-
пространства Rm.
b) Покажите, что, какова бы ни была функция / G C(Rn; R), система 7Г1, ..., 7rm, /
функционально зависима.
c) Если система гладких функций /х, ...,/*, к < т, такова, что ранг отобра-
отображения / = (/\ ..., fk) в точке хо = (xq, •.., xq1) € Rm равен А:, то в некоторой
окрестности этой точки ее можно дополнить до независимой системы / , ..., /
состоящей из т гладких функций.
d) Если система
*777
гладких функций такова, что осуществляемое ею отображение / = (/х, ..., /т) име-
имеет в точке хо = (xq, •.., х™) ранг га, то переменные (?*, ..., ?т) могут служить
криволинейными координатами в некоторой окрестности U{xq) точки хо и любая
функция (р: U(xo) —> R может быть записана в виде <р(х) = F(f1(xI ..., /m(x)), где
е) Ранг отображения, осуществляемого системой гладких функций, называют
также рангом этой системы. Покажите, что если ранг системы гладких функ-
функций /г(х\ ..., хт) (г = 1, ..., к) равен к и ранг системы функций /*, ..., /т, (р
тоже равен к в некоторой точке хо ? Rm, то в окрестности этой точки (р(х) =
= F{f\x),...,fk{x)).
Указание. Используйте с), d) и покажите, что F(f11 ..., /m) = F(f1, ..., fk).
5. Покажите, что ранг гладкого отображения / : Rm —> Rn является функцией,
полунепрерывной снизу, т. е. rang/(x) ^ rang/(xo) в окрестности точки хо ? Rm.

506 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
6. а) Дайте прямое доказательство леммы Морса для функций / : R
Ь) Выясните, применима ли лемма Морса в начале координат к функциям
3 -\ f{x) = e~1/z sin2-;
f(x,y) = x3-
c) Покажите, что невырожденные критические точки функции / €
являются изолированными: каждая из них имеет такую окрестность, в которой нет
других критических точек функции /, кроме самой этой точки.
d) Покажите, что число к отрицательных квадратов в каноническом предста-
представлении функции в окрестности невырожденной критической точки не зависит от
способа приведения, т. е. от системы координат, в которой функция имеет канони-
канонический вид. Это число называется индексом критической точки.
§ 7. Поверхность в Шп и теория условного экстремума
Для неформального понимания важной в приложениях теории условного экс-
экстремума весьма полезно иметь некоторые начальные сведения о поверхностях
(многообразиях) в пространстве Еп.
1. Поверхность размерности к в Жп. Обобщая понятие закона дви-
движения х = x(t) материальной точки, мы в свое время ввели понятие пути в
Шп как непрерывного отображения Г : / —> Шп промежутка / С Ш. Степень
гладкости пути определялась как степень гладкости этого отображения. Но-
Носитель ГG) С Rn пути мог быть довольно причудливым множеством в Еп,
которое иногда только с очень большой натяжкой можно было бы назвать
линией. Например, носитель пути мог оказаться просто точкой.
Аналогично, непрерывное или гладкое отображение f:Ik-> Шп к-мерного
промежутка 1к С Шк, называемое к-путем в Еп, может иметь в качестве
образа /(/*) совсем не то, что хотелось бы назвать А;-мерной поверхностью в
Еп. Например, это снова может быть точка.
Чтобы гладкое отображение /: G —> Шп области G С Жк определяло в Шп
к-меркую геометрическую фигуру, точки которой описываются к независи-
независимыми параметрами (tl, ... ,tk) ? G, достаточно, как мы знаем из предыдуще-
предыдущего параграфа, потребовать, чтобы в каждой точке t ? G ранг отображения
/ : G -> Шп был равен к (разумеется, к ^ п). В этом случае отображение
/ : G —> f(G) локально (т. е. в окрестности любой точки t E G) является
взаимно однозначным.
Действительно, пусть rang/(?o) = к и он реализуется, например, на первых
к из п функций
<
х =/(??
а)
xn = fn(t\...,tk),
задающих координатную запись отображения /: G —* Ш.п.

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА
507
Тогда по теореме об обратной функции переменные f1, ..., tk в некото-
некоторой окрестности U(to) точки to можно выразить через переменные х1, ..., хк.
Значит, множество f(U(to)) может быть записано в виде
~*+1 _ „&+1/ 1 к\ п _ (пп(~1 тк\
(т. е. оно взаимно однозначно проектируется на координатную плоскость
х1, ..., хЛ), и потому отображение /: U(to) -> f(U(to)) действительно взаимно
однозначное.
Однако уже на примере одномерного гладкого
пути (рис. 61) ясно, что подобная локальная вза-
взаимная однозначность отображения / : G -> Rn из
области G параметров в пространство Rn вовсе не
обязана быть взаимной однозначностью в целом.
Траектория может иметь многократные самопе-
самопересечения, поэтому если мы желаем определить
гладкую fc-мерную поверхность в Rn и видеть ее
как множество, которое около каждой своей точки
устроено как несколько деформированный кусок
Л-мерной плоскости (fc-мерного подпространства пространства Rn), то нам
не достаточно регулярно отображать канонический кусок G С Шк А;-мерной
поверхности в пространство Rn, но необходимо также следить за тем, как он
в целом оказывается вложенным в это пространство.
Рис. 61
X
п
tn
1
Iя
Рис. 62
Определение 1. Множество S С Шп будем называть к-мерной глад-
гладкой поверхностью в пространстве Rn (или k-мерным подмногообразием Rn),
если для любой точки xq ? 5 найдутся окрестность U(xo) вВпи диффеомор-
диффеоморфизм ц>: U(xq) -> In этой окрестности на стандартный n-мерный промежуток
In = {t € Rn | \t%\ < 1, i = 1, ...,n} пространства Rn, при котором образ
множества 5 П U(xo) совпадает с лежащей в / частью А;-мерной плоскости
пространства Rn, задаваемой соотношениями tk+l = 0, ... , tn = 0 (рис. 62).

508
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Степень гладкости поверхности 5 будем измерять степенью гладкости
диффеоморфизма (р.
Если смотреть на переменные tl, ..., tn как на новые координаты в
окрестности U(xo), то определение 1 в сокращенном варианте можно перефор-
переформулировать следующим образом: множество S С Rn называется ^-мерной по-
поверхностью (^-мерным подмногообразием) в Rn, если для любой точки хо € S
можно указать окрестность U(xo) и такие координаты t1, ..., tn в ней, что
множество 5 П U{xq) в этих координатах задается соотношениями
**+1 = ... = tn = 0.
Роль стандартного промежутка в определении 1 чисто условная и примерно
такая же, как роль стандартного размера или формы страницы в географи-
географическом атласе. Каноническое расположение промежутка в системе координат
t1, ..., tn также относится к области стандартизации и не более того, по-
поскольку любой куб в Rn дополнительным линейным диффеоморфизмом всегда
можно преобразовать в стандартный n-мерный промежуток.
Эти замечанием мы часто будем пользоваться, сокращая проверку того,
что некоторое множество 5 С Rn является поверхностью в Rn.
Рассмотрим примеры.
Пример 1. Само пространство Еп является п-мерной поверхностью
класса С^°°\ В качестве отображения </?: Rn -» In здесь можно взять, на-
например, отображение
— arctg хг
7Г
(г = 1, — , п).
Пример 2. Построенное в примере 1 отображение заодно устанавлива-
устанавливает, что подпространство векторного пространства Rn, задаваемое условиями
хЛ+1 = ... = хп = 0, является ^-мерной поверхностью в Rn (или ^-мерным
подмногообразием Rn).
Пример 3. Множество в Rn, задаваемое системой соотношений
а\х1 4-... 4- а\хк 4- а\ ,, х*+1 4-... 4- о>1>хп = О,
V 4-... 4- а%~кхк + а%
4-... 4- а%~кхп = 0
при условии, что ранг этой системы равен п — к, является ^-мерным подмно-
подмногообразием Rn.
Действительно, пусть, например, определитель
... а
п
Cli. II ... 0>п

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА
509
отличен от нуля. Тогда линейное преобразование
t1 = х\
хк,
t
п
a
ж + ... + a
п
очевидно, является невырожденным. В координатах tl, ..., tn наше множе-
множество задается условиями ?*+1 = ... = tn = 0, уже рассмотренными в при-
примере 2.
Пример 4. График определенной в некоторой области G С Шп~г гладкой
функции хп = /(ж1,..., ж") является гладкой (п — 1)-мерной поверхностью
>п
Действительно, полагая
= х*
(г = 1, ..., п — 1),
мы получаем систему координат, в которой график нашей функции имеет
уравнение tn = 0.
Пример 5. Окружность ж2 + у2 = 1 в R2 является одномерным подмно-
подмногообразием в R , что устанавливается разобранным в предыдущем параграфе
локально обратимым переходом к полярным координатам (р, </?), в которых
окружность имеет уравнение р = 1.
Пример 6. Этот пример является обобщением примера 3 и вместе с
тем, как видно из определения 1, дает общую форму координатной записи
подмногообразий пространства Мп.
Пусть ^(ж1, ..., жп) (г = 1, ..., п — к) — система гладких функций ранга
п — к. Покажем, что соотношения
•Г V**' j • • • } *** ) •** > * * * > *^ / "^
B)
задают в Еп подмногообразие S размерности к.
Пусть в точке жо G 5 выполнено условие
dF1 dF1
дхк+1 ''' дхп
dF
п-к
п-к
'" дхп
(ж0) ф 0.
C)

510 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Тогда преобразование
' ( fi _ ~i (А __ 1 1Л
<
t< = **-*(х\ ..., хп) {% = к +1, ..., п)
в силу теоремы об обратной функции является диффеоморфизмом некоторой
окрестности рассматриваемой точки.
В координатах t1, ..., tn исходная система будет иметь вид tk+l = ... =
= tn = 0; таким образом, 5 является fc-мерной гладкой поверхностью в Rn.
Пример 7. Множество Е точек плоскости W, удовлетворяющих уравне-
уравнению х2 — у2 = 0, состоит из двух прямых, пересекающихся в начале координат.
Это множество не является одномерным подмногообразием М? (проверьте!)
именно из-за указанной точки пересечения.
Если удалить из Е начало координат 0 ? R2, то множество Е \ 0 уже,,
очевидно, будет удовлетворять определению 1. Заметим, что множество Е\0
несвязно. Оно состоит из четырех не имеющих общих точек лучей.
Таким образом, удовлетворяющая определению 1 ^-мерная поверхность в
Еп может оказаться несвязным подмножеством, состоящим из некоторого
числа связных компонент (и уже эти компоненты являются связными А;-мерны-
ми поверхностями). Часто под поверхностью в Еп понимают именно связную
А;-мерную поверхность. Сейчас нас будут интересовать проблемы отыскания
экстремумов функций, заданных на поверхностях. Это локальные проблемы,
поэтому в них условие связности поверхности не проявляется.
Пример 8. Если гладкое отображение / : G -» IRn области G С Еп,
задаваемое в координатном виде соотношениями A), имеет в точке to € G
ранг к, то найдется такая окрестность U(to) С G этой точки, образ f(U(to)) С
С Шп которой является гладкой поверхностью в Rn.
Действительно, как уже отмечалось выше, в этом случае соотношения A)
могут быть в некоторой окрестности U(to) точки to & G заменены эквива-
эквивалентной им системой соотношений
х
D)
п = \ к
(для упрощения записи мы считаем, что уже система функций f1, ..., /*
имеет ранг к). Полагая
{(x\ ..., хп) = z*+i - ^(х1, ..., х*) (t = 1, ..., п - *),
записываем систему D) в виде B). Поскольку соотношение C) выполнено, то в
силу примера 6 множество f(U(to)) действительно является fc-мерной гладкой
поверхностью в Rn.

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА
511
2. Касательное пространство. При рассмотрении закона движения
х = x{t) материальной частицы в Е3, исходя из соотношения
x(t) = х@) + x'@)t + o(t) при t -> О E)
и считая, что точка t = 0 не является критической для отображения R9t4
»-> х(?) € Е3, т. е. х'@) ф О, мы определили прямую, касательную к траектории
в точке х@), как линейное подмножество в Е3, задаваемое в параметрическом
виде уравнением
х-хо=х'@)* F)
или уравнением
х - х0 = Z t, ' G)
где хо = х@), а ? = х'@) — направляющий вектор прямой.
В сущности, аналогичную вещь мы делали, определяя плоскость, касатель-
касательную к графику функции z = f(x,y) в R3. Действительно, дополнив соотно-
соотношение z = f(x,y) тривиальными равенствами х = х, у = у, мы получаем
отображение Е2 Э (х,у) ¦—> (х, у, /(x,j/)) G Е3, касательным к которому в
точке (хо,2/о) является линейное отображение
x —
У -2/0
1
О
О
1
X — Хо
У -2/0
(8)
гдег0 = /(хо,2/о).
Полагая здесь t = (х — хо, у — 2/о)> х = (х — хо, у — уо, z — zq) и обозначая
через х'@) указанную в (8) матрицу Якоби рассматриваемого отображения,
замечаем, что ее ранг равен двум и что в этих обозначениях соотношение (8)
имеет вид F).
Особенность соотношения (8) состоит в том, что из трех равенств:
х —
х —
(9)
У - 2/о = У - 2/о,
* - zo = Л(хо,2/о)(х - хо) 4- /у(хо,2/о)B/ - 2/о),
совокупности которых оно равносильно, только последнее нетривиально. По-
Поэтому именно оно осталось у нас как уравнение, задающее плоскость, каса-
касательную к графику функции z = f(x,y) в точке (хо, 2/о> ^о)«
Сделанное наблюдение можно использовать, чтобы теперь дать определе-
определение А:-мерной плоскости, касательной к А;-мерной гладкой поверхности 5 С Еп.
Из определения 1 поверхности видно, что в окрестности любой своей точки
Хо 6 5 А:-мерная поверхность S может быть задана параметрически, т. е.
с помощью отображения 1к Э (tl,..., tk) i—> (х1,..., хп) Е 5. В качестве
такового может выступать ограничение отображения ср~г: In —> U(xo) на
fc-мерную плоскость tk+x = ... = tn = 0 (см. рис. 62).

512 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Поскольку (р~г — диффеоморфизм, то якобиан отображения ip: In
-> U{xq) в любой точке куба 1п отличен от нуля. Но тогда ранг отображения
1к Э (t1, ..., tk) •—> (ж1,..., xn) € 5, полученного ограничением у? на ука-
указанную плоскость, должен быть равен к в любой точке куба /*.
Полагая теперь (J1,..., tk) = t 6 Ik и обозначая отображение 1к Э t •-+ ж 6 5
через х = х(?), получаем локальное параметрическое представление поверх-
поверхности 5, обладающее свойством, выраженным равенством E), на основании
которого уравнение F) принимаем в качестве уравнения касательного про-
пространства или касательной плоскости к поверхности S С Кп в точке хо Е 5.
Итак, мы принимаем следующее
Определение 2. Если fc-мерная поверхность 5 С Мп, 1 ^ к ^ п, в
окрестности точки хо G 5 задана параметрически с помощью гладкого ото-
отображения (tl, ..., tk) = 11—у х = (x1, ..., xn) такого, что хо = x@) и матрица
x'@) имеет ранг к, то А;-мерная плоскость в Rn, задаваемая параметрически
матричным равенством F), называется касательной плоскостью или каса-
касательным пространством к поверхности S в точке Хо € 5.
В координатной записи равенству (б) соответствует система уравнений
A0)
Пространство, касательное к поверхности 5 в точке х Е 5, будем, кок и пре-
прежде, обозначать1) символом TSX-
Важным и полезным упражнением, которое читатель может проделать
самостоятельно, является доказательство инвариантности определения каса-
касательного пространства и проверка того, что линейное отображение t »-> х'@) t,
касательное к отображению t »-> x(t), задающему локально поверхность 5,
осуществляет отображение пространства Шк = TMq на плоскость TSx(q) (cm.
задачу 3 в конце параграфа).
Выясним теперь, как выглядит уравнение касательной плоскости к fc-мер-
ной поверхности 5, заданной в Еп системой B). Будем для определенности
считать, что в окрестности рассматриваемой точки хо € 5 выполнено усло-
условие C).
Полагая (ж1, ..., хк) = и, (ж*+1, ..., xn) = v, (F1,..., Fn~*) = F, запишем
систему B) в виде
F(ti,t/) = O, A1)
а условие C) — в виде
^ A2)
— небольшое отклонение от наиболее распространенного обозначения TXS или
TX(S).

§ 7. ПОВЕРХНОСТЬ В Rn И ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА
513
В окрестности точки (txo, vo) = (xj, ..., х*, xj+1,..., х?) по теореме о не-
неявной функции перейдем от соотношения A1) к эквивалентному ему соотно-
соотношению
v = f(u), A3)
дополняя которое тождеством и = и, получаем параметрическое представле-
представление поверхности 5 в окрестности точки хо Е 5:
и = и,
v = f(u).
A4)
На основании определения 2, из A4) получаем параметрическое уравнение
и — uo = E t,
v - vq =
A5)
касательной плоскости; здесь Е — единичная матрица, a t = и — ио-
Подобно тому, как это было в случае системы (9), в системе A5) оставляем
только нетривиальное уравнение
которое и содержит в себе связи переменных х1, ..., хк с переменными х*+1,
..., хп, выделяющие касательное пространство.
Пользуясь тем, что по теореме о неявной функции
перепишем A6) в виде
u y = 0,
откуда после возвращения к переменным (х1, ..., xn) = x получаем искомое
уравнение
касательного пространства TSXo С Еп.
В координатном представлении уравнение A7) равносильно системе урав-
уравнений
- xh) + ... +
" - х?) = О,
A8)
п - х8) = 0.
Ранг этой системы по условию равен п — к, поэтому она задает ^-мерную
плоскость в
)П

514 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Аффинное уравнение A7) эквивалентно (если указана точка хо) вектор-
векторному уравнению
A9)
в котором ? = х —
Значит, вектор ? лежит в плоскости TSXo, касательной в точке xq E 5
к поверхности 5 С Sn, заданной уравнением F(x) = 0, в том и только в
том случае, когда он удовлетворяет условию A9). Таким образом, TSXo мож-
можно рассматривать как векторное пространство векторов ?, удовлетворяющих
уравнению A9).
Именно с этим обстоятельством и связан сам термин касательное про-
пространство.
Докажем теперь следующее, уже встречавшееся нам в его частном случае
(см. § 4, п. 6)
Утверждение. Пространство TSXo, касательное к гладкой поверхно-
поверхности S С Мп в точке хо € 5, состоит из векторов, касательных в точке xq к
гладким кривым, лежащим на поверхности S и проходящим через точку хо.
М Пусть поверхность 5 в окрестности точки хо Е S задана в виде системы
уравнений B), которую мы коротко запишем как
F(x) = 0, B0)
где F = (F1, ..., Fn"*), х = (х1, ..., хп). Пусть Г : I -» 5 — произвольный
гладкий путь с носителем на поверхности 5. Взяв / = {t€R||t|<l}, будем
считать, что х@) = хр. Поскольку x(t) € 5 при t G /, то после подстановки
x(t) в уравнение B0) получаем
F(x(t)) = 0 B1)
при t ? I. Дифференцируя это тождество по ?, находим, что
FUx(t))-x'(t) = 0.
В частности, при t — 0, полагая ? = х'@), получаем
т. е. вектор ?, касательный к траектории в точке хо (в момент t = 0), удовле-
удовлетворяет уравнению A9) касательного пространства TSXo.
Покажем теперь, что для любого вектора ?, удовлетворяющего уравнению
A9), найдется гладкий путь Г: I -> Sy который задает кривую на поверхно-
поверхности 5, проходит при t = 0 через точку хо и имеет вектор ? своим вектором
скорости в.момент t = 0.
Этим заодно будет установлено само существование гладких кривых, про-
проходящих на 5 через точку хо, которое мы неявно предполагали в уже прове-
проведенной первой части доказательства утверждения.

§ 7. ПОВЕРХНОСТЬ В Rn И ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 515
Пусть для определенности выполнено условие C). Тогда, зная первые к ко-
координат f\ ..., ?к вектора ? = (f1,..., ?*, ?*+\ ..., fn), мы из уравнения A9)
(равносильного системе A8)) однозначно определим остальныеего координа-
координаты ?*+1, ..., fn. Таким образом, если для некоторого вектора ? = (?*,..., f*,
?*+1, ...,fn) будет установлено, что он удовлетворяет уравнению A9), то
можно заключить, что f = ?. Воспользуемся этим.
Вновь, как это было сделано выше, введем для удобства обозначения и =
= (ж1, . ..,ж*), г; = (ж*+\ . ..,жп), ж = (ж1, . ..,жп) = (w,v), F(rr) = F(u,v).
Тогда уравнение B0) будет иметь вид A1), а условие C) — вид A2). В под-
подпространстве R* С Мп переменных ж1,..., хк возьмем параметрически задан-
заданную прямую
Ж* -Ж* =?4
с направляющим вектором (?*,..., ?*), который мы обозначим через ?w. В
более коротких обозначениях эта прямая может быть записана в виде
и = щ + ?ut. B2)
Решая уравнение A1) относительно v, в силу теоремы о неявной функции
получим гладкую функцию A3), подставляя в аргумент которой правую часть
равенства B2), с учетом самого равенства B2), получим гладкую кривую в
п заданную в следующем виде:
4 - ' —' *€t/@)cK. B3)
Поскольку F(uyf(u)) = 0, то, очевидно, эта кривая лежит на прверхно-
сти 5. Кроме того, из равенств B3) видно, что при t = 0 кривая проходит
через точку (t*o, vq) = (ж?,..., ж$, ж?+1, ..., ж?) = жо € S.
Дифференцируя по t тождество
F(u(t),v(t)) = *Х"о + &*,/(tio + &*)) = 0,
при ^ = 0 получаем
|t; =0,
где ^v = ^'@) = (^*+1, • • •, €п)' Это равенство показывает, что вектор ? =
= ((и, €v) = (f\ • • •, ?*, f*+1, • • • j fn) удовлетворяет уравнению A9). Таким
образом, в силу сделанного выше замечания заключаем, что ? = ?. Но вектор
? является вектором скорости при t = 0 для траектории B3). Тем самым
высказанное утверждение доказано полностью. >

516 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
3. Условный экстремум
а. Постановка вопроса. Одним из наиболее ярких и популярных до-
достижений дифференциального исчисления являются предлагаемые им реце-
рецепты отыскания экстремумов функций. Необходимые условия и достаточные
дифференциальные признаки экстремума, которые мы получили из формулы
Тейлора, относятся, как уже отмечалось, к внутренним экстремумам.
Иными словами, эти результаты применимы только к исследованию пове-
поведения функции Шп Э х (-> /(х) Е R в окрестности точки хо G Шп тогда, когда
аргумент х может принимать любое значение из некоторой окрестности в Жп
точки хо.
Часто возникает более сложная и с практической точки зрения даже бо-
более интересная ситуация, когда ищется экстремум функции при некоторых
условиях, ограничивающих область изменения аргумента. Типичным приме-
примером может служить изопериметрическая задача, когда ищется тело, имеющее
максимальный объем при условии, что ограничивающая его поверхность име-
имеет заданную площадь. Чтобы получить доступную нам математическую за-
запись такой задачи, упростим постановку и будем считать, что задача состоит
в том, чтобы среди прямоугольников, имеющих заданный периметр 2р, найти
тот, который имеет наибольшую площадь а. Обозначив через х и у длины
сторон прямоугольника, запишем, что
я + у = р.
Итак, надо найти экстремум функции сг(х, у) при условии, что переменные
х, у связаны соотношением х + у — р. Таким образом, экстремум функции
ищется только на множестве тех точек плоскости R2, которые удовлетворя-
удовлетворяют указанному соотношению. Эта конкретная задача, конечно, решается без
труда: достаточно, записав, что у = р — х, подставить это выражение в фор-
формулу для а(х,у) и найти обычными методами максимум функции х(р — х).
Она нам была нужна лишь для пояснения самой постановки вопроса.
В общем случае задача на условный экстремум обычно состоит в том, что-
чтобы найти экстремум вещественнозначной функции
у = f(x\ ...,xn) B4)
от п переменных при условии, что эти переменные удовлетворяют системе
уравнений
' F1(x\...yxn)=0,
B5)
Fm(x1, ...,хп) =0.
Поскольку мы собираемся получать дифференциальные условия экстрему-
экстремума, мы будем предполагать, что все рассматриваемые функции дифференци-
дифференцируемы и даже непрерывно дифференцируемы. Если ранг системы функций

§ 7 ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 517
F1, ..., Fm равен п — к, то условия B5) задают в Rn некоторую fc-мерную
гладкую поверхность 5 и с геометрической точки зрения задача на условный
экстремум состоит в отыскании экстремума функции / на поверхности S.
Более точно, рассматривается ограничение f\s функции / на поверхность S
и ищется экстремум функции /|s-
Смысл самого понятия точки локального экстремума при этом, конечно,
остается прежним, т.е. точка хо ? S считается точкой локального экстремума
функции / на 5 или, короче, функции /|s, если найдется такая окрестность
Us(xo) точки Хо в множестве1) S С 1П, что для любой точки х G Us(xo)
выполнено неравенство f(x) ^ f(xo) (тогда хо — точка локального минимума)
или f(x) ^ f(xo) (тогда хо — точка локального максимума). Если при х G
G Us(xo) \ хо указанные неравенства являются строгими, то экстремум, как и
прежде, будем называть строгим.
Ь. Необходимый признак условного экстремума
Теорема 1. Пусть f : D -> Ж — функция, определенная на открытом
множестве D сШп и принадлежащая классу C^(D;R). Пусть S — гладкая
поверхность в D.
Для того чтобы точка хо € 5, некритическая для функции f, была точ-
точкой локального экстремума функции f\s, необходимо выполнение условия
B6)
где TSXo — пространство, касательное к поверхности S в точке хо, а
TNXo — пространство, касательное к поверхности N = {х G D\ f(x) = f(xo)}
уровня функции f, которому принадлежит хо-
Заметим прежде всего, что требование, чтобы точка xq была некритиче-
некритической для функции /, в контексте обсуждаемой задачи отыскания условного
экстремума не является существенным ограничением. Действительно, если
уж точка хо G D является критической точкой функции / : D -> Е или точ-
точкой экстремума этой функции, то ясно, что она будет подозрительной точкой
или соответственно точкой экстремума и для функции f\s- Таким образом,
новый элемент в рассматриваемой задаче состоит именно в том, что функция
/|s может иметь критические точки и экстремумы, отличные от критических
точек и экстремумов функции /.
<4 Возьмем произвольный вектор ? G TSXo и такой гладкий путь х — x(t)
на 5, который проходит через точку хо при t = 0 и для которого вектор ?
является вектором скорости при t = 0, т. е.
B7)
*) Напомним, что U$(xq) = S П С/(яо), гДе ^(^о) ~ окрестность точки хо в Шп

518
ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Если хо — точка экстремума функции /|s, то гладкая функция f(x(t))
должна при t = 0 иметь экстремум. По необходимому условию экстремума ее
производная при t = О должна обращаться в нуль, т. е. должно выполняться
условие
/'(хо) • ? = 0, B8)
где
Поскольку хо — некритическая точка функции /, условие B8) равносиль-
равносильно тому, что ? Е TNXQ1 ибо именно соотношение B8) является уравнением
касательного пространства TNXQ.
Таким образом, доказано, что TSXQ С TNXQ. >
Бели поверхность 5 в окрестности точки хо задана системой уравнений
B5), то пространство TSXQ, как нам известно, задается системой линейных
уравнений
=
о,
B9)
Пространство TNXo задается уравнением
C0)
и, поскольку всякое решение системы B9) является решением уравнения C0),
последнее уравнение является следствием системы B9).
Из этих соображений вытекает, что соотношение TSXo С TNXQ в анали-
аналитической записи равносильно тому, что вектор grad/(xo) является линейной
комбинацией векторов gradF*(xo) (г =1, ..., ш), т. е.
C1)
Учитывая эту форму записи необходимого признака экстремума функ-
функции B4), переменные которой связаны соотношениями B5), Лагранж пред-
предложил при отыскании условного экстремума использовать следующую вспо-
вспомогательную функцию:
grad f(x0) =
m
L(x, А) = /(х) - ^ A, gradF*(*)
отп + m переменных (х, А) = (х1, ..., xn, Ai, ..., Am).
C2)

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 519
Эту функцию называют функцией Лагранжа, а метод ее использования —
методом множителей Лагранжа.
Функция C2) удобна тем, что необходимые условия ее экстремума как
функции переменных (х, А) = (х1, ..., xn, Ai, ..., Am) в точности совпадают с
условиями C1) и B5).
Действительно,
?
Ь» = &Ы-?ЪШМ = ° U = i,...,n),
Таким образом, при отыскании экстремума функции B4), переменные ко-
которой подчинены связям B5), можно написать с неопределенными множителя-
множителями функцию Лагранжа C2) и искать уже ее критические точки. Если есть воз-
возможность из системы C3) найти хо = (xj, ..., xJJ), не находя А = (Ai, ..., Am),
то с точки зрения исходной задачи именно это и следует делать.
Как видно из соотношения C1), множители А* (г = 1, ..., га) определяются
однозначно, если только векторы gradFl(xo) (г = 1, ..., т) линейно независи-
независимы. Независимость этих векторов равносильна тому, что ранг системы B9)
равен га, т. е. что все уравнения этой системы существенны (ни одно из них
не является следствием остальных).
Это обычно выполнено, ибо считается, что все соотношения B5) незави-
независимы и ранг системы функций F1, ..., Fm в любой точке х € S равен т.
Функцию Лагранжа часто записывают в виде
m
?,(*, A) =
г=1
который отличается от прежнего только несущественной заменой А^ на —
Пример 9. Найдем экстремумы симметрической квадратичной формы
п
aijxixj (oij = а#) C4)
на сфере
F(x) = JT И2 -1 = 0. C5)
г=1
Запишем функцию Лагранжа данной задачи:
п / п
L(x X) = V^ a t{tj - A I V^ (т{J - 1
i,j=l \г=1
*) По поводу необходимого признака условного экстремума см. также задачу 6 к § 7
гл. X (часть И).

520 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
и, с учетом того, что a,ij = а^, необходимые условия экстремума функции
L(x, А):
= 0 (г = 1,... ,n),
#
C6)
(х, А) = (?>*J - l) = 0.
i=l
Домножая первое уравнение на х* и суммируя затем все первые соотноше-
соотношения, с учетом второго уравнения получим, что в точке экстремума должно
быть выполнено равенство
п
C7)
Систему C6) без последнего уравнения можно переписать в виде
п
= Ах* (г = 1, ...,п), C8)
откуда следует, что А — собственное значение линейного преобразования А,
задаваемого матрицей (а^), а х = (х1, ..., хп) — собственный вектор этого
преобразования, отвечающий этому собственному значению.
Поскольку непрерывная на компакте S = {х € Rn ]С (#*J = 1 г Функция
C4) обязана принимать в некоторой его точке максимальное значение, систе-
система C6), а значит и система C8), должна иметь решение. Таким образом, мы
попутно установили, что любая вещественная симметрическая матрица (oij)
имеет по крайней мере одно вещественное собственное значение. Это хорошо
известный вам из линейной алгебры результат, являющийся основным в дока-
доказательстве существования базиса из собственных векторов симметрического
оператора.
Чтобы указать геометрический смысл собственного значения А, заметим,
что если А > 0, то, переходя к координатам tl = хг/у/\, вместо C7) получим
п
]> C9)
?
а вместо C5) —
Е ет=\- D0)
п
Но Y1 (^*J есть квадрат расстояния от точки t = (tl, ..., tn) квадрики C9)
до начала координат. Таким образом, если, например, соотношение C9) зада-

§ 7. ПОВЕРХНОСТЬ В Rn И ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 521
ет эллипсоид, то величина 1/А, обратная к собственному значению А, является
квадратом величины одной из его полуосей.
Это полезное наблюдение. Оно, в частности, показывает, что соотношения
C6), необходимые для условного экстремума, еще не являются достаточными:
ведь, например, в R3 эллипсоид кроме наибольшей и наименьшей полуосей мо-
может иметь промежуточную по величине полуось, в любой окрестности конца
которой есть как точки более близкие к началу координат, так и более дале-
далекие от него в сравнении с расстоянием от конца полуоси до начала координат.
Последнее становится совсем очевидным, если рассмотреть эллипсы, получа-
получающиеся в сечении исходного эллипсоида двумя плоскостями, проходящими
через промежуточную полуось и меньшую или большую полуоси эллипсоида
соответственно. В одном из этих случаев промежуточная полуось будет боль-
большей из двух полуосей эллипса сечения, а в другом случае — меньшей полуосью.
К сказанному следует добавить, что если 1/л/Х есть величина этой про-
промежуточной полуоси, то, как видно из канонического уравнения, эллипсоида,
величина А, очевидно, будет собственным значением преобразования А, поэто-
поэтому система C6), выражающая необходимые условия экстремума функции /|s,
действительно будет иметь решение, не дающее экстремума этой функции.
Полученный в теореме 1 результат (необходимый признак условного экс-
экстремума) проиллюстрирован на рис. 63 о, Ь.
Первый из этих рисунков поясняет, почему точка хо поверхности 5 не
может быть точкой экстремума функции /|s, если 5 не касается поверхности
N = {х € Rn | /(х) = /(xo) = со} в точке хо- При этом предполагается, что
grad/(xo) Ф 0. Последнее условие гарантирует то, что в окрестности точки
хо имеются точки как более высокого сг-уровня функции /, так и точки более
низкого Ci-уровня этой функции.
Рис. 63
Поскольку гладкая поверхность 5 пересекает поверхность N, т. е. со-уро-
вень гладкой функции /, то 5 будет пересекать как более высокие, так и более
низкие уровни функции / в окрестности точки хо. Но это и означает, что хо
не может быть точкой экстремума функции /|s-
Второй рисунок показывает, почему при касании N и S в точке хо эта
точка может оказаться точкой экстремума. На рисунке хо — точка локального
максимума функции f\s-

522 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Эти же соображения позволяют нарисовать картинку, аналитическая за-
запись которой может показать, что необходимый признак условного экстрему-
экстремума не является достаточным.
Действительно, в соответствии с рис. 64 положим, например,
/(я, у) = у, F(x, у) = х3 - у = 0.
Тогда очевидно, что на кривой 5 С Е2,
заданной уравнением у = х3, величина у
не имеет экстремума в точке @,0), хотя
эта кривая касается линии уровня /(х,у) =
Рис. 64 =0 функции / в этой точке. Заметим, что
grad/@,0) = @,l)/0.
Очевидно, это по существу тот же пример, который нам в свое время
служил для иллюстрации различия между необходимым и достаточным усло-
условиями классического внутреннего экстремума функции.
с. Достаточный признак условного экстремума. Докажем теперь
следующий достаточный признак наличия или отсутствия условного экстре-
экстремума.
Теорема 2. Пусть f : D -t R — функция, определенная на открытом
множестве D С Жп и принадлежащая классу C^(D;R)] S — поверхность
в D, заданная системой уравнений B5), где Fl E C^(D; Ш) (г = 1,..., т) и
ранг системы функций {F1, ..., Fm} в любой точке области D равен т.
Пусть в функции Лагранжа
т
L(x) = L(x; A) = /(х\ ..., хп) - ]Г A.F^x1, ..., хп)
,г=1
параметры Х\, ..., Ат выбраны в соответствии с необходимым признаком
C1) условного экстремума функции f\s в точке Хо ? S.1)
Для того чтобы при этом точка Хо была точкой экстремума функции
f\sy достаточно, чтобы квадратичная форма
Я2 Г
0
была знакоопределенной для векторов ? G TSXo.
Если форма D1) положительно определена на TSXo, то Хо — точка стро-
строгого локального минимума функции f\s'y если форма D1) отрицательно опре-
определена на TSXof то хо — точка строгого локального максимума функции f\s-
Для того чтобы точка хо не была точкой экстремума функции f\s, до-
достаточно, чтобы форма D1) принимала на TSXo значения разных знаков.
*) Фиксировав Л, мы получаем из L(x\ Л) функцию, зависящую только от х\ мы позволили
себе обозначать ее через L{x).

§ 7. ПОВЕРХНОСТЬ В Rw И ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 523
<4 Отметим прежде всего, что L(x) = /(х) для х е S, поэтому, показав,
что точка xq 6 5 является точкой экстремума функции L\s, мы одновременно
покажем, что она является точкой экстремума функции f\s-
По условию необходимый признак C1) экстремума функции f\s в точке
Хо ? S выполнен, поэтому в этой точке gradL(xo) = 0. Значит, тейлоровское
разложение функции L(x) в окрестности точки хо = (^о, • • • > хо) имеет вид
1 Я2Г
Цх) - L(xo) = ± о^ЬЫ (х* - х') (яР - х30) + о{\\х - хо\\2) D2)
при х —> хо-
Напомним теперь, что, мотивируя определение 2, мы отметили возмож-
возможность локального (например, в окрестности точки хо ? 5) параметрического
задания гладкой А;-мерной поверхности 5 (в нашем случае к = п — т).
Иными словами, существует гладкое отображение
R Э (t\ ..., tk) = t у—> х = (х\ ..., хп) е W1
(мы будем его, как и прежде, записывать в виде х = х(?)), при котором окрест-
окрестность точки 0 = @, ..., 0) € Шк биективно преобразуется в некоторую окрест-
окрестность точки хо на поверхности 5, причем хо = х@).
Заметим, что соотношение
x(t)-x@) = x'@)t+(\\t\\) при *->0,
выражающее дифференцируемость отображения t »-> х(^) в точке t = 0, рав-
равносильно п координатным равенствам
D3)
в которых индекс а пробегает целые значения от 1 до А; и по нему происходит
суммирование.
Из этих числовых равенств следует, что
) при
и,значит,
при i-X). D4)
Используя соотношения D3), D4), из равенства D2) получаем, что при
L(x(t)) - L(x@)) = ±дцЬ(хо) ЭахЩ дрх^О) t«t0 + o(\\t\\2). D2')
18 Зорич В. А.

524 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Отсюда при условии знакоопределенности формы
дахЩ d0xj(O) ta 1? D5)
следует, что функция L(x(t)) имеет при t = О экстремум. Если же форма D5)
принимает значения разных знаков, то L(x(t)) при t = О экстремума не имеет.
Но, поскольку при отображении t \-? x(t) некоторая окрестность точки О Е Шк
преобразуется в окрестность точки х@) = хо Е 5 на поверхности 5, можно
заключить, что тогда и функция L\s в точке хо либо будет иметь экстремум,
причем того же характера, что и функция L(x(t)), либо, как и L(x(t)), не
будет иметь экстремума.
Итак, остается проверить, что для векторов f Е TSXo выражения D1) и
D5) просто являются разными записями одного и того же объекта.
Действительно, полагая
мы получаем вектор f, касательный к S в точке хо, и если ? = (?*, ...,
x(t) = (ж\ ..., xn)(t), t = (t1, ..., **), то
откуда и следует совпадение величин D1), D5). >
Отметим, что практическое использование теоремы 2 затруднено тем, что
среди координат вектора ? = (?*, ..., fп) € TSXo только к = п — т незави-
независимых, поскольку координаты вектора ? должны удовлетворять системе B9),
определяющей пространство TSXo. Таким образом, непосредственное при-
применение к форме D1) критерия Сильвестра в нашем случае, вообще говоря,
ничего не дает: форма D1) может не быть определенной на TR?0, но оказать-
оказаться определенной на TSXQ. Если же из соотношений B9) выразить т коорди-
координат вектора ? через остальные к координат и полученные линейные формы
подставить в D1), то мы придем к квадратичной форме относительно к пере-
переменных, определенность которой уже можно исследовать с помощью критерия
Сильвестра.
Поясним сказанное простейшими примерами.
Пример 10. Пусть в пространстве R3 с координатами ж, у, z задана
функция
f(x,y,z) =x2-y2 + z2.
Ищется экстремум этой функции на плоскости 5, заданной уравнением
F(x,y,z) = 2x-2/-3 = 0.
Записав функцию Лагранжа
L(x,y,z) = (х2 - у2 4- z2) - АBх - у - 3)

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 525
и необходимые условия экстремума
тг— = 2х — 2А = О,
ох
= 2у + \ -О,
ау
-2z -О
= -Bх - j, - 3) = О,
находим подозрительную точку р = B,1,0).
Далее находим форму D1):
±дцЬ№ = (?)*-(?)*+(?)*. D6)
Отметим, что в данном случае параметр А не вошел в эту квадратичную
форму, поэтому мы его и не вычисляли.
Записываем теперь условие ? ? TSP:
D7)
Из этого равенства находим ?2 = 2?* и подставляем в форму D6), после
чего она приобретает вид
где на сей раз ?г и ?3 — независимые переменные.
Последняя форма, очевидно, может принимать значения разных знаков,
поэтому в точке р ? S функция f\s экстремума не имеет.
Пример 11. В условиях примера 10 заменим R3 на R2 и функцию / на
f(x, у) =х2-2/2,
сохранив условие
2х - у - 3 = 0,
которое теперь задает прямую 5 в плоскости Е2.
В качестве подозрительной найдем точку р = B,1).
Вместо формы D6) получим форму
а2 D8)
с прежним соотношением D7) между f1 и ?2.
Таким образом, на TSP форма D8) теперь имеет вид
т. е. является отрицательно определенной. Отсюда заключаем, что точка
р = B,1) является точкой локального максимума функции f\$.
!Я*

526 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Весьма поучительны во многих аспектах следующие простые примеры, на
которых можно отчетливо рассмотреть механизм работы как необходимых,
так и достаточных условий экстремума, в том числе роль параметра и нефор-
неформальную роль самой функции Лагранжа.
Пример 12. На плоскости Е2 с декартовыми координатами (я,у) дана
функция
f(x,y) = х2 + у2.
Найдем экстремумы этой функции на эллипсе, заданном каноническим со-
соотношением
где 0 < а < Ь.
Из геометрических соображений очевидно, что min f\s = a2, max/|s = Ь2.
Получим это, опираясь на рекомендации теорем 1 и 2.
Записав функцию Лагранжа •
jt п OL dL 0L г\
и решая уравнение аь = 0, т. е. систему — = — = — = 0, находим ее
решения:
= (±а,0,а2), @,±Ь,Ь2).
Теперь в соответствии с теоремой 2 выпишем и исследуем квадратичную
форму - d?L?2 — второй член тейлоровского разложения функции Лагранжа
в окрестности соответствующих точек:
В точках (±а, 0) эллипса 5 касательный вектор ? = (?*, ?2) имеет вид
@,?2), а квадратичная форма при А = а2 принимает вид
Учитывая условие 0 < а < Ь, заключаем, что эта форма положительно
определена и, значит, в точках (±а,0) € 5 имеется строгий локальный (а
здесь, очевидно, и глобальный) минимум функции /|s, т. е. min/|s = a2.
Аналогично находим форму
отвечающую точкам @, ±6) G 5, и получаем max /|s = b2.

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 527
Замечание. Обратите здесь внимание на роль функции Лагранжа в
сравнении с ролью функции /. В соответствующих точках на указанных ка-
касательных векторах дифференциал функции / (как и дифференциал L) обра-
обращается в нуль, а квадратичная форма xd2/^2 = (f1J + (f2J положительно
it
определена, в какой бы из этих точек ее ни вычислять. Тем не менее функция
/|s в точках (±а,0) имеет строгий минимум, а в точках (О, ±Ь) — строгий
максимум.
Чтобы понять, в чем тут дело, просмотрите еще раз доказательство те-
теоремы 2 и попробуйте, заменив в D2) L на /, получить соотношение D2').
Заметьте, что при этом у вас появится дополнительный член, содержащий
х"@). Он не исчезнет в связи с тем, что в отличие от dL дифференциал df
функции / в соответствующих точках не есть тождественный нуль, хотя на
касательных векторах (вида я'(О)) его значения действительно равны нулю.
Пример 13. Найдем экстремумы функции
f(x,y,z) =x2 + y2 + z2
на эллипсоиде 5, заданном соотношением
где 0 < а < Ь < с.
Записав функцию Лагранжа
в соответствии с необходимым признаком экстремума находим решения урав-
уравнения dL = 0, т. е. системы — = — = — = — =0:
ах ay oz дХ
,г/,г,А) = (±а,0,0,а2), @,±Ь,0,62), @,0,±с,с2).
Квадратичная форма
- А)
в каждом из этих случаев на соответствующей касательной плоскости имеет
вид
О»
(О

528 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Поскольку 0 < а < Ь < с, то на основании теоремы 2, дающей достаточный
признак наличия или отсутствия условного экстремума, можно заключить,
что в случаях (а) и (с) мы нашли соответственно min/|s = а2 и тах/|$ = с2,
а в точках @, ±6,0) G 5, отвечающих случаю (Ь), функция f\s экстремума не
имеет. Это вполне согласуется с очевидными геометрическими соображени-
соображениями, высказанными по этому поводу при обсуждении необходимого признака
условного экстремума.
Некоторые дальнейшие, порой весьма полезные стороны встретившихся в
этом параграфе понятий анализа и геометрии, в том числе физическая интер-
интерпретация самой задачи об условном экстремуме, а также его необходимого
признака C1) как разложения сил в точке равновесия и интерпретация мно-
множителей Лагранжа как величин реакций идеальных связей, представлены в
приведенных ниже задачах и упражнениях.
Задачи и упражнения
1. Путь и поверхность.
a) Пусть /:/—>- R2 — отображение класса C^(J;R2) интервала / С R.. Рас-
Рассматривая это отображение как путь в R2, покажите на примере, что его носитель
/(/) может не быть подмногообразием в R2, а вот график этого отображения в
R3 = R1 х R2 всегда является одномерным подмногообразием R3, проекцией которо-
которого в R2 является носитель /(/) указанного пути.
b) Решите задачу а) в случае, когда / — промежуток в R*, а / € C^(J;Rn).
Покажите, что в этом случае график отображения / : / —> Rn является гладкой
А:-мерной поверхностью в R* xRn, проекция которой на подпространство Rn совпа-
совпадает с /(/).
c) Проверьте, что если Д : Д —у S и /г : /г —> S — две гладкие параметризации
одной и той же /с-мерной поверхности S С Rn, причем ни /i в Д, ни /г в /г не имеют
критических точек, то определенные при этих условиях отображения
Г1 о / : h + Л /
/Г1 о /2 : h -+ Л, /г о /i : /i -^ /2
являются гладкими.
2. Сфера в Rn.
a) На сфере S2 = {х € R3 | ||ж|| = 1} укажите какую-нибудь максимальную
область действия криволинейных координат ((f,tp), полученных из полярных коор-
координат в R3 (см. формулу E) предыдущего параграфа) при р = 1.
b) Ответьте на вопрос а) в случае (ш — 1)-мерной сферы
в Rm и координат (y?i, ..., (pm-i) на ней, получаемых из полярных координат в Rn
(см. формулы F) предыдущего параграфа) при р = 1.
c) Можно ли сферу Sk С Rfc+1 задать одной системой координат (J1, ..., tk)y т. е.
одним диффеоморфизмом / : G —У Rk+1 области GCR*?
d) Какое наименьшее количество карт должно быть в атласе поверхности Земли?

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 529
e) Расстояние между точками сферы S2 С R3 будем измерять длиной кратчай-
кратчайшей кривой, лежащей на сфере S2 и соединяющей эти точки. Такой кривой является
дуга соответствующего большого круга. Может ли существовать такая локальная
плоская карта сферы, что все расстояния между точками сферы были бы пропор-
пропорциональны (с одним и тем же коэффициентом пропорциональности) расстояниям
между их изображениями на карте?
f) Углом между кривыми (лежащими или
не лежащими на сфере) в точке их пересече-
пересечения называется угол между касательными к
этим кривым в этой точке.
Покажите, что существуют локальные
плоские карты сферы, в которых углы меж-
между кривыми на сфере и соответствующими
кривыми на карте одинаковы (см. рис. 65,
изображающий так называемую стереогра- _ пг
л \ Рис. 65
фическую проекцию).
3. Касательное пространство.
a) Проверьте прямым расчетом, что касательное к гладкой А;-мерной поверх-
поверхности 5cRn в точке хо е S многообразие TSXQ не зависит от выбора системы
координат в Rn.
b) Покажите, что если при диффеоморфизме / : D —> D' области D С Rn на
область D' С Rn гладкая поверхность S С D отображается на гладкую поверх-
поверхность Sf С D\ а точка хо € S переходит в х0 € S', то при линейном отображении
/;(жо): Rn —> Rn, касательном к / в точке хо € -D, векторное пространство TSXQ
изоморфно преобразуется в векторное пространство TSX'Q.
c) Бели в условиях предыдущей задачи отображение /: D —> D' является любым
отображением класса C^(D;D'), при котором /E) С S', то f'(TSXQ) С TSX'Q.
d) Покажите, что ортогональная проекция гладкой /с-мерной поверхности S CRn
на касательную к ней в точке хо € S /с-мерную плоскость TSX0 является отображе-
отображением, взаимно однозначным в некоторой окрестности точки касания хо.
e) Пусть в условиях предыдущей задачи f € TSXQ и ||f || = 1.
Уравнение х — хо = ?t прямой в Rn, лежащей в TSXQi можно использовать, чтобы
каждую точку х € TSxo\xo характеризовать парой (*, f )• Это по существу полярные
координаты в TSXQ.
Покажите, что прямым х — хо = ?t нэ. поверхности 5 в окрестности точки хо от-
отвечают гладкие кривые, пересекающиеся только в точке xq. Проверьте, что, сохра-
сохраняя в качестве параметра на этих кривых величину t, мы получаем пути, скорость
вдоль которых при t = 0 совпадает с вектором ? € TSX01 определяющим прямую
х — хо = ?t, из которой получена данная кривая на S.
Таким образом, пары (?,?)> гДе € € TSXQ, ||?|| = 1, a t — вещественные числа из
некоторой окрестности U@) нуля в R, могут служить аналогом полярных координат
в некоторой окрестности точки хо € ? на поверхности S.
4. Пусть функция F € C^(Rn;R), не имеющая критических точек, такова, что
уравнение F(x2,..., хл) = 0 задает в Rn компактную поверхность ? (т. е. ? как
подмножество Rn является компактом). Для любой точки х ? S находим вектор
ff(x) = gradF(x), нормальный к 5 в точке х. Бели каждую точку х € S заставить

530 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
двигаться равномерно со своей скоростью т)(х), то возникает зависящее от времени
t отображение S Э х i—* х + ri(x)t € Rn.
a) Покажите, что при достаточно близких к нулю значениях t это отображение
биективно и при каждом таком значении t из S получается гладкая поверхность St.
b) Пусть Е — множество в Rn; ^-окрестностью множества Е назовем совокуп-
совокупность тех точек Rn, расстояние которых до Е меньше 6.
Покажите, что при значениях ?, близких к нулю, уравнение
F(x , ..., х ) = t
задает компактную поверхность St С Rn, и покажите, что поверхность St лежит в
?(?)-окрестности поверхности St, где S(t) = o(t) при t —У 0.
c) С каждой точкой х поверхности S = So свяжем единичный вектор нормали
п(х) =
и рассмотрим новое отображение S Э х i—> х + n(x)t € Rn.
Покажите, что при всех достаточно близких к нулю значениях t это отображение
биективно, получающаяся из S при конкретном значении t поверхность St гладкая
и если t\ ф *2, то Stx П S*2 = 0.
d) Опираясь на результат предыдущей задачи, покажите, что найдется число
S > 0 такое, что между точками ^-окрестности поверхности 5 и парами ($,а:), где
t € ]— 6,6[ С R, х € ?, имеется взаимно однозначное соответствие; если (J1, ..., tk) —
локальные координаты на поверхности S в окрестности Us(xq) точки хо, то вели-
величины (М\ •••>?*) могут служить локальными координатами в некоторой простран-
пространственной окрестности U(xo) точки хо € Rn.
e) Покажите, что при !*!<<$ точка х € S является ближайшей к (х + n(x)t) 6 Rn
точкой поверхности 5. Таким образом, поверхность St при \t\ < S есть геометриче-
геометрическое место точек пространства Rn, удаленных от поверхности 5 на расстояние |t|.
5. а) Пусть dp : S —У R — функция на /с-мерной гладкой поверхности 5 С Rn,
определенная равенством dp(x) = \\р — х||2, где р — фиксированная точка Rn, x —
точка S, а \\р — х|| — расстояние в Rn между этими точками.
Покажите, что в точках экстремума функции dp(x) вектор р — х ортогонален
поверхности S.
b) Покажите, что на любой прямой, ортогонально пересекающей поверхность
S в точке g б 5, имеется не более к таких точек р, что функция dp(x) имеет q
своей вырожденной критической точкой (т. е. точкой, в которой гессиан функции
обращается в нуль).
c) Покажите, что в случае кривой S (к = 1) на плоскости R2 (п = 2) точка р,
для которой точка q € S является вырожденной критической точкой функции dp(x),
совпадает с центром кривизны кривой S в точке q € S.
6. Постройте в плоскости R2 с декартовыми координатами х, у линии уровня
функции /(х,у) = хуи кривую
Используя полученную картинку, проведите полное исследование задачи об экс-
экстремуме функции f\s-

§ 7. ПОВЕРХНОСТЬ ВГИ ТЕОРИЯ УСЛОВНОГО ЭКСТРЕМУМА 531
7. На плоскости R2 с декартовыми координатами х, у определены следующие
функции класса C(oo)(R2;lR):
±t ч 2 с/ ч Г х2-j/ +e/x2sin-, если х # О,
/(х, j/) = х2- у; F(x,j/)=< о " *'
^ ж" — j/, если х = 0.
а) Нарисуйте линии уровня функции f(x,y) и линию S, заданную соотношением
b) Исследуйте на экстремум функцию f\s-
c) Покажите, что условие определенности формы dijf(xo)^1^ на TSX0, в отличие
от условия определенности формы dijL(xo)?l?* на TSXOi приведенного в теореме 2,
еще не является достаточным для того, чтобы подозрительная точка хо € S была
точкой экстремума функции /|s-
d) Проверьте, является ли точка хо = @,0) критической для функции / и можно
ли исследовать поведение / в окрестности этой точки только с помощью второго
(квадратичного) члена формулы Тейлора, как это подразумевалось в с).
8. В дифференциальной геометрии при определении главных кривизн и глав-
главных направлений бывает полезно уметь искать экстремум одной квадратичной фор-
формы hijifv? при условии постоянства другой (положительно определенной) формы
gijuxv?. Решите эту задачу по аналогии с разобранным выше примером 9.
9. Пусть А = [о}] — квадратная матрица порядка п такая, что
п
*=1
где Hi, ..., Нп — фиксированный набор из п неотрицательных действительных
чисел.
а) Покажите, что det2.4 при указанных условиях на матрицу А может иметь
только если строки матрицы А являются попарно ортогональными век-
векторами в Rn.
b) Исходя из равенства
где А* — транспонированная по отношению к А матрица, покажите, что при ука-
указанных выше условиях
max det2A = Hi... #n.
A
с) Докажите, что для любой матрицы [а}] имеет место неравенство Адамара
d) Дайте наглядно-геометрическое истолкование неравенства Адамара.
10. а) Нарисуйте поверхности уровня функции / ц плоскость S в примере 10.
Объясните на рисунке результат, полученный в этом примере.
Ь) Нарисуйте линии уровня функции / и прямую S в примере 11. Объясните на
рисунке результат, полученный в этом примере.

532 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
11. В примере 6 из § 4 главы V, исходя из принципа Ферма, был получен закон
Снеллиуса преломления света на поверхности раздела двух сред в случае, когда эта
поверхность — плоскость. Остается ли этот закон в силе для произвольной гладкой
поверхности раздела?
12. а) Материальная точка в потенциальном поле сил может находиться в положе-
положении равновесия (называемом также состоянием покоя или стационарным состояни-
состоянием) только в критических (стационарных) точках потенциала. При этом строгому
локальному минимуму потенциала отвечает положение устойчивого равновесия, а
локальному максимуму — неустойчивого. Проверьте это.
b) К какой задаче на условный экстремум (которую и решал Лагранж) сводится
вопрос о положении равновесия материальной точки, находящейся в потенциальном
поле сил (например, тяжести) и стесненной идеальными связями (например, точка
не может покидать некоторой гладкой поверхности, или бусинка — гладкой нити,
или шарик — желоба)? Связь идеальна (нет трения); это значит, что ее воздействие
на точку (реакция связи) происходит только в нормальном к связи направлении.
c) Какой физический (механический) смысл имеют в этом случае разложение
C1) — необходимый признак условного экстремума и множители Лагранжа?
Кстати, каждую из функций системы B5) можно поделить на модуль ее градиен-
градиента, что, очевидно, приводит к равносильной системе (если ее ранг всюду равен т).
Значит, все векторы gradF'(xo) в правой части соотношения C1) можно считать
единичными нормалями к соответствующей поверхности.
d) He становится ли после приведенной физической интерпретации самоочевид-
самоочевидным и естественным сам метод Лагранжа отыскания условного экстремума?

НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
Введение в анализ (число, функция, предел)
1. Длину стягивающего земной шар по экватору обруча увеличили на 1 метр.
Образовался зазор. Достаточен ли он для прохода муравья? Каковы величины абсо-
абсолютного и относительного увеличения радиуса Земли при таком увеличении длины
экватора? (Радиус Земли « 6400 км.)
2. Как связаны полнота (непрерывность) действительных чисел, неограничен-
неограниченность натурального ряда и принцип Архимеда? Почему любое действительное чи-
число можно сколь угодно точно приблизить рациональным? Объясните на модели
рациональных дробей (рациональных функций), что принцип Архимеда может быть
нарушен, и в таких числовых системах натуральный ряд ограничен и имеются бес-
бесконечно малые числа.
3. Четыре букашки, сидевшие в вершинах единичного квадрата, стали двигаться
друг за другом с единичной скоростью, держа курс на преследуемого. Нарисуйте
траектории их движения. Какова длина каждой траектории? Каков закон движения
(в декартовых и полярных координатах)?
4. Нарисуйте диаграмму вычисления у/а (а > 0) итерационным процессом
I •
Хп/
Xn+l = - [Хп
Как связано решение уравнений с отысканием неподвижных точек? Как нахо-
находить г\/а?
5. Пусть д(х) = /(ж) -I- o(f(x)) при х —> оо. Верно ли, что тогда и /(ж) = д(х) +
+ о(д(х)) при х —> оо ?
6. Методом неопределенных коэффициентов (или иначе) найдите несколько пер-
113
вых коэффициентов (или все) степенного ряда для A+х)а при а = —1, —-,0, -, 1, -.
(Интерполируя коэффициенты при одинаковых степенях х в таких разложениях,
Ньютон выписал закон образования коэффициентов при любом а € R — бином Нью-
Ньютона.)
7. Зная степенное разложение функции еж, найдите методом неопределенных ко-
коэффициентов (или иначе) несколько первых членов (или все) степенного разложения
функции In A + ж).

534 НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
8. Вычислите ехр Л, когда А — одна из матриц
)
00) (
o о/' Vo о
0
0
0
1
0
0
о/
/1
0
Vo
0
2
0
0
0
3
9. Сколько членов ряда для ех надо взять, чтобы получить многочлен, позволя-
позволяющий вычислять ех на отрезке [—3,5] с точностью до 10?
10. Нарисуйте эскизы графиков следующих функций:
a) log СО8. sin *; Ь) arctg A _ ж)*A + хJ -
Дифференциальное исчисление функций
одной переменной
1. Покажите, что если вектор ускорения а(?) в любой момент t ортогонален век-
вектору v(t) скорости движения, то величина |v(t)| остается постоянной.
2. Пусть (ж, t) и (ж, i) — соответственно координата и время движущейся точки
в двух системах отсчета. Считая известными формулы х = ах + /3t, t = *ух + St
перехода из одной системы отсчета в другую, найдите формулу преобразования
u dx — dx
скоростей, т. е. связь между v = — и v = —г.
at at
3. Функция /(ж) = х2 sin - при х ф 0 и /@) = 0 дифференцируема на R, но /'
разрывна при х = 0 (проверьте). «Докажем», однако, что если /: R —> R дифферен-
дифференцируема на R, то /' непрерывна в любой точке о 6 R. По теореме Лагранжа
x — a
где f — точка между о и ж. Тогда если х —? о, то f —У о. По определению,
Х-4О X — О
и поскольку этот предел существует, то существует и равен ему предел правой части
формулы Лагранжа, т. е. /'(?) —> /'(°) ПРИ ?—><*. Непрерывность /' в точке о
«доказана». Где ошибка?
4. Пусть / имеет (п + 1) производную в точке жо, и пусть f = жо + 0х(ж — #о) —
средняя точка в формуле Лагранжа остаточного члена —- f^n\%)(x — Жо)п, так что
О < вх < 1. Покажите, что 0Х —>• г при ж —>> жо, если /^п"|Чжо) 9^ 0.
п + 1
5. Докажите неравенство
of1... а*" ^ а\п\ -f ... +
где числа oi, ..., оп, c*i, . • •, скп неотрицательны и ol\ -I-... -I- ал = !•

НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ 535
6. Показать, что
lim A + - ) = ex(cos у + г sin у) (z = x + iy),
n-*oo \ П/
поэтому естественно считать, что ety = cos у + * sin у (формула Эйлера) и
ег = ехегу = ex(cos y + i sin у).
7. Найдите форму поверхности жидкости, равномерно вращающейся в стакане.
8. Покажите, что касательная к эллипсу -т + ^ = 1 в точке (хо,уо) имеет
от Ьл
ххо . т/т/о *
уравнение —~ + ^~ = 1 и что световые лучи от источника, помещенного в одном
из фокусов Fi = (—л/о2 — Ь2,0), Fi = {у/а2 — Ь2,0) эллипса с полуосями о > Ь > О,
собираются эллиптическим зеркалом в другом фокусе.
9. Частица без предварительного разгона под действием силы тяжести начи-
начинает скатываться с вершины ледяной горки эллиптического профиля. Уравнение
профиля: х2 + by2 = 1, г/ ^ 0. Рассчитайте траекторию движения частицы до ее
приземления.
Интеграл и введение в многомерный анализ
1. Зная неравенства Гель дера, Минковского и Иенсена для сумм, получите соот-
соответствующие неравенства для интегралов.
1
/ 2
е~х dxc относительной погрешностью в пределах 10 %.
о
х
1 Г 2
3. Функция erf (х) = — / е~* dty называемая интегралом вероятности ошибок,
— х
имеет пределом 1 при х —> +оо. Изобразите график этой функции и найдите ее
производную. Покажите, что при х —> +оо
_1 2 -х2( 1 1 .1-3 1-3-5 , / 1
_ 1 - -=е у + + °
Как продолжить эту асимптотическую формулу до ряда? Сходится ли этот ряд
хотя бы при каком-то значении х € R?
4. Зависит ли длина пути от закона движения (от параметризации)?
5. Вы держите один конец резинового шнура длиной 1 км. От второго его конца,
который закреплен, к вам со скоростью 1 см/с ползет жук. Каждый раз, как только
он проползает 1 см, вы удлиняете резинку на 1 км. Доползет ли жук до вашей
руки? Бели да, то приблизительно сколько ему на это потребуется времени? (Задача
Л. Б. Окуня, предложенная им А. Д. Сахарову.)
6. Подсчитайте работу по перемещению массы в гравитационном поле Земли и
покажите, что эта работа зависит только от уровней высот исходного и конечно-
конечного положений. Найдите для Земли работу выхода из ее гравитационного поля и
соответствующую (вторую) космическую скорость.

536 НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
7. На примере маятника и двойного маятника поясните, как на множестве соот-
соответствующих конфигураций можно ввести локальные координаты и окрестности и
как при этом возникает естественная топология, превращающая его в конфигураци-
конфигурационное пространство механической системы. Можно ли метризовать это простран-
пространство в рассмотренных случаях?
8. Является ли компактом единичная сфера в Rn? А в С[а,ЪI
9. Подмножество данного множества называется его е-сетью, если любая точ-
точка множества находится на расстоянии меньшем чем е от какой-либо точки этого
подмножества. Обозначим через N(e) наименьшее возможное число точек в е-сети
данного множества. Оцените е-энтропию log2 N(e) отрезка, квадрата, куба и огра-
ограниченной области в пространстве Rn. Дает ли величина , , \ при е —> 0 предста-
Iog2(l/e)
вление о размерности рассматриваемого множества? Может ли такая размерность
быть равной, например, 0,5?
10. На поверхности единичной сферы 5bR3 температура Т как функция точ-
точки меняется непрерывно. Обязаны ли на сфере быть точки минимума и максимума
температуры? При наличии точек с двумя фиксированными значениями температу-
температуры, должны ли быть точки и с промежуточными ее значениями? Что из этого верно
в случае, когда единичная сфера S берется в пространстве С[а,Ъ\, а температура в
точке / 6 S выражается в виде
Ь v -1
\f\(*)dx)
11. а) Взяв 1,5 в качестве исходного приближения для л/2, проведите две итера-
итерации по методу Ньютона и посмотрите, сколько верных знаков получилось на каждом
из двух шагов.
Ь) Найдите итерационным процессом функцию /, удовлетворяющую уравнению
х
f(x) = x + Jf(t)dt.
о
Дифференциальное исчисление функций
многих переменных
1. а) Какова относительная погрешность S = —у^ ПРИ вычислении значения
функции f(x,yyz) в точке (ж,2/,г), координаты которой даны с абсолютными по-
погрешностями Дж, Ду, Az соответственно?
b) Какова относительная ошибка в вычислении объема комнаты, размеры кото-
которой таковы: длина х = 5 ± 0,05 м, ширина у = 4 ± 0,04 м, высота z = 3 ± 0,03 м?
c) Верно ли, что относительная погрешность значения линейной функции совпа-
совпадает с относительной погрешностью значения ее аргумента?
d) Верно ли, что дифференциал линейной функции совпадает с ней самой?
e) Верно ли, что для линейной функции / справедливо соотношение /' = /?

НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ 537
2. а) Одна из частных производных функции двух переменных, заданной в кру-
круге, равна нулю во всех точках круга. Значит ли это, что функция не зависит от
соответствующей переменной в этом круге?
b) Изменится ли ответ, если вместо круга взять произвольную выпуклую об-
область?
c) А если взять вообще произвольную область?
d) Пусть х = x(t) — закон движения точки в плоскости (или в Rn) в промежутке
времени t € [а, Ь]; v(t) — ее скорость как функция времени, а С = convex {v(t) \ t G
6 [о, b]} — наименьшее выпуклое множество, содержащее все векторы v(t) (называе-
(называемое обычно выпуклой оболочкой того множества, на которое оболочка натягивает-
натягивается). Покажите, что в С найдется такой вектор v, что х(Ь) — х(а) = v • (Ь — о).
3. а) Пусть F(x,y,z) = 0. Верно ли, что —¦ • -^- • — = —1? Проверьте это на
зависимости — — 1 = 0 (соответствующей уравнению Клапейрона -— = R состоя-
Z JL
кия идеального газа).
ду &х
b) Пусть теперь F(x,y) = 0. Верно ли, что -^ ~ = 1?
ах ду
c) Что можно утверждать в общем случае зависимости F(x\i ..., хп) = 0?
d) Как, зная первые несколько членов тейлоровского разложения функции F(x, у)
в окрестности точки (хо, J/o), где F(xo, j/o) = 0, a F'y{xQ,yo) обратима, найти первые
несколько членов тейлоровского разложения неявной функции у = /(х), определяе-
определяемой в окрестности (xo,j/o) уравнением F(x,y) = 0?
X "U Z
4. а) Проверьте, что плоскость, касательная к эллипсоиду -^ + ттН—г = 1в
az bz с*
/ ч -. ххо , ууо , zzq л
точке (жо, 2/о,2о), может быть задана уравнением —^ + ^^- Н—^ = 1.
а* Ъг сг
Ь) Точка P(t)y= ( ~^=, —, — ) • t в момент времени t = 1 стартовала с эллипсо-
\ v 3 V 3 V 3 /
х2 у2 z2
ида —г- -I- ~ -f — = 1. Пусть p(t) — точка того же эллипсоида, ближайшая к P(t) в
аг Ъ* сг
момент времени t. Найдите предельное положение точки p(t) при t —> -foo.
5. а) В плоскости R2 с декартовыми координатами (х, у) постройте линии зфовня
функции /(ж, у) = ху и кривую S — {1&тУ) -€-Jfc^4^=t4'2 == 4}^-И€пользуя получен-
полученную картинку, проведите полное исследование задачи об экстремуме функции f\s —
ограничения / на окружность ?. * (
Ь) Какой физический смысл имеют множители Лагранжа в методе Лагранжа
отыскания условного экстремума, когда ищется положение равновесия материаль-
материальной точки в поле тяжести, если движение точки стеснено идеальными связями (на-
(например, вида Fi(x, j/, z) = 0, F2(x, у, z) = 0)?

ВОПРОСЫ К ЭКЗАМЕНУ
I семестр
Введение в анализ (число, функция, предел)
Дифференциальное исчисление функций
одной переменной
1. Действительные числа. Ограниченные (сверху, снизу) числовые множества.
Аксиома полноты и существование верхней (нижней) грани множества. Неограни-
Неограниченность множества натуральных чисел.
2. Основные леммы, связанные с полнотой множества действительных чисел R
(вложенные отрезки, конечное покрытие, предельная точка).
3. Предел последовательности и критерий Коши его существования. Критерий
существования предела монотонной последовательности.
4. Ряд и его сумма. Геометрическая прогрессия. Критерий Коши и необходимое
условие гходимости ряда. Гармонический ряд. Абсолютная сходимость.
5. Критерий сходимости ряда с неотрицательными членами. Теорема сравнения.
РЯД С(8)= 1Гп^.
п=1
6. Идея логарифма и число е. Функция ехр (х) и представляющий ее степенной
ряд.
7. Предел функции. Основные базы предельного перехода. Определение предела
функции при произвольной базе и его расшифровка в конкретных случаях. Беско-
Бесконечно малые функции и их своЙ€Т^?Ь—Сравнение _Фи?^льяого поведения функций,
асимптотические формулы и основные операции с символами о(-), О(-).
8. Взаимосвязь предельного перехода с алгебраическими операциями и отноше-
нием порядка в R. Предел при х -> 0.
9. Предел композиции функции и монотонной функции. Предел A н— ) при
\ х/
X —V ОО.
10. Критерии Коши существования предела функции.

ВОПРОСЫ К ЭКЗАМЕНУ 539
11. Непрерывность функции в точке. Локальные свойства непрерывных функ-
функций (локальная ограниченность, сохранение знака, арифметические операции, не-
непрерывность композиции). Непрерывность многочлена, рациональной функции и
тригонометрических функций.
12. Глобальные свойства непрерывных функций (промежуточные значения, мак-
максимумы, равномерная непрерывность).
13. Разрывы монотонной функции. Теорема об обратной функции. Непрерыв-
Непрерывность обратных тригонометрических функций.
14. Закон движения, перемещение за малое время, вектор мгновенной скорости,
траектория и касательная к ней. Определение дифференцируемости функции в точ-
точке. Дифференциал, его область определения и область значений. Единственность
дифференциала. Производная вещественнозначной функции вещественного пере-
переменного и ее геометрический смысл. Дифференцируемость функций sin ж, cos я,
ех, 1п|ж|, ха
15. Дифференцируемость и арифметические операции. Дифференцирование
многочлена, рациональной функции, тангенса и котангенса.
16. Дифференциал композиции функций и обратной функции. Производные
обратных тригонометрических функций.
17. Локальный экстремум функции. Необходимое условие внутреннего экстре-
экстремума дифференцируемой функции (лемма Ферма).
18. Теорема Рсддя. Теоремы Лагранжа и Коши о конечном приращении (о сред-
среднем).
19. Формула Тейлора с остаточными членами в формах Коши и Лагранжа.
20. Ряд Тейлора. Тейлоровские разложения функций ех, cos ж, sinx, ln(l + х),
A -f х)а (бином Ньютона).
21. Локальная формула Тейлора (с остаточным членом в форме Пеано).
22. Взаимосвязь характера монотонности дифференцируемой функции и положи-
положительности ее производной. Достаточные условия наличия или отсутствия ясда^
го экстремума в терминах первой, второй и высших производю* < -^~~^~
23. Выпуклая функция. Дифференциальные устов^^ьшуклости. Расположение
графика выпуклой функции по отнотртщю^^асательной.
24. Общее неравенство йеасена для выпуклой функции. Выпуклость (вогну-
(вогнутость) логарифма. ^Ь^ссические неравенства Копта, Юнга, Гёльдера и Минков-
ского. ^.
?5.. Комплексное число в алгебраической и тригонометрической записи. Сходи-
Сходимость последовательности комплексных чисел и ряда с комплексными членами. Кри-
Критерий Коши. Абсолютная сходимость и достаточные признаки абсолютной сходи-
сходимости ряда с комплексными членами. Предел lim A + - ) .
26. Круг сходимости и радиус сходимости степенного ряда. Определение функ-
функций е2, cos z, sin 2 (г € С). Формула Эйлера и взаимосвязь элементарных функций.
27. Дифференциальные уравнения как математическая модель явления, примеры.
Метод неопределенных коэффициентов и метод ломаных Эйлера.
28. Первообразная, основные общие приемы ее отыскания (почленное интегриро-
интегрирование слагаемых, интегрирование по частям, замена переменной). Первообразные
основных элементарных функций.

540 ВОПРОСЫ К ЭКЗАМЕНУ
II семестр
Интеграл (функции одной переменной)
Дифференциальное исчисление функций
многих переменных
1. Интеграл Римана на отрезке. Необходимое условие интегрируемости. Множе-
Множества меры нуль, их общие свойства, примеры. Критерий Лебега интегрируемости
функции по Риману (формулировка). Пространство интегрируемых функций и до-
допустимые операции над интегрируемыми функциями.
2. Линейность, аддитивность и общая оценка интеграла.
3. Оценки интеграла от вещественнозначной функции. Теорема о среднем (пер-
(первая).
4. Интеграл с переменным верхним пределом, его свойства. Существование пер-
первообразной у непрерывной функции. Обобщенная первообразная и ее общий вид.
5. Формула Ньютона —Лейбница. Замена переменной в интеграле.
6. Интегрирование по частям в определенном интеграле. Формула Тейлора с
интегральным остатком. Вторая теорема о среднем.
7. Аддитивная функция ориентированного промежутка и интеграл. Общая схема
появления интеграла в приложениях, примеры: длина пути (и ее независимость от
параметризации), площадь криволинейной трапеции, объем тела вращения, работа,
энергия.
8. Интеграл Римана —Стилтьеса. Условия сведения к интегралу Римана. Син-
Сингулярности и дельта-функция Дирака. Понятие обобщенной функции.
9. Понятие несобственного интеграла. Канонические интегралы. Критерии
Коши и теорема сравнения для исследования сходимости несобственного интеграла.
Интегральный признак сходимости ряда.
10. Локальная лине2ризация, примеры: мгновенная скорость и перемещение;
упрощение уравнения движения при малых колебаниях маятника; вычисление линей-
линейных поправок к значениям величин ехр(л), Л". det(E), (a, b) при малом изменении
аргументов (здесь А ~ обратимая, Е — единичная матрицы; а, Ъ — векторы; (•) —
скалярное произведение).
11. Норма (длина, модуль) вектора в векторном пространстве; важнейшие при-
примеры. Пространство L(X,Y) линейных непрерывных операторов и норма ? нем.
Непрерывность линейного оператора и конечность его нормы.
12. Дифференцируемость функции в точке. Дифференциал, его область опре-
определения и область значений. Координатная запись дифференциала отображения
/ : Rm —> Rn. Соотношения между дифференцируемостью, непрерывностью и нали-
наличием частных производных.
13. Дифференцирование композиции функций и обратной функции. Координат-
Координатная запись полученных законов применительно к различным случаям отображений
14. Производная по вектору и градиент. Геометрические и физические приме-
примеры использования градиента (уровни функций, градиентный спуск, касательная

ВОПРОСЫ К ЭКЗАМЕНУ 541
плоскость; потенциальные поля; уравнение Эйлера динамики идеальной жидкости,
закон Бернулли, работа крыла).
15. Однородные функции и соотношение Эйлера. Метод размерностей.
16. Теорема о конечном приращении. Бе геометрический и физический смысл.
Примеры приложений (достаточное условие дифференцируемое™ в терминах част-
частных производных; условие постоянства функции в области).
17. Высшие производные и их симметричность.
18. Формула Тейлора.
19. Экстремумы функций (необходимые и достаточные условия внутреннего экс-
экстремума).
20. Сжимающие отображения. Принцип Пикара—Банаха неподвижной точки.
21. Теорема о неявной функции.
22. Теорема об обратной функции. Криволинейные координаты и выпрямления.
Гладкая поверхность размерности к в Rn и касательная плоскость к ней. Способы
задания поверхности и соответствующие им уравнения касательного пространства.
23. Теорема о ранге и зависимость функций.
24. Условный экстремум (необходимый признак). Геометрическая, алгебраиче-
алгебраическая и физическая интерпретации метода Лагранжа.
25. Достаточный признак условного экстремума.
26. Метрическое пространство, примеры. Открытые и замкнутые подмноже-
подмножества. Окрестность точки. Индуцированная метрика, подпространство. Топологи-
Топологическое пространство. Окрестность точки, отделимость (аксиома Хаусдорфа). Топо-
Топология, индуцируемая на подмножествах. Замыкание множества и описание относи-
относительно замкнутых подмножеств.
27. Компакт, его абсолютность. Замкнутость компакта и компактность замк-
замкнутого подмножества компакта. Вложенные компакты. Метрические компакты,
е-сеть. Критерий метрического компакта и его конкретизация в пространстве Rn.
28. Полное метрическое пространство. Полнота R, С, Rn, Cn и пространства
С [а, Ь] непрерывных функций относительно равномерной сходимости.
29. Критерий непрерывности отображения топологических пространств. Сохра-
Сохранение компактности и связности при непрерывном отображении. Классические те-
теоремы об ограниченности, максимуме и промежуточном значении для непрерывных
функций. Равномерная непрерывность на метрическом компакте.

ЛИТЕРАТУРА
I. Классика
1. Первоисточники
Ньютон И.
a. Математические начала натуральной философии. Пер. с лат. В кн.: Кры-
Крылов А. Н. Собрание трудов. Т. 7. — Л.-М.: Изд-во АН СССР, 1936,
с. 57-662.
b. Математические работы. — M.-JL: ОНТИ, 1937.
Лейбниц Г. В. Избранные отрывки из математических сочинений. Успехи
машем, наук, 1948. 3A), 165-205.
2. Важнейшие систематические изложения предмета
Эйлер Л.
a. Введение в анализ бесконечных. В 2-х т. — М.: Физматгиз, 1961.
b. Дифференциальное исчисление. — М.-Л.: Гостехиздат, 1949.
c. Интегральное исчисление. В 3-х т. — М.: Гостехиздат, 1956-1958.
Коши О. Л.
a. Алгебраический анализ. — Лейпциг: Бэр и Хэрманн, 1864.
b. Краткое изложение уроков о дифференциальном и интегральном исчисле-
исчислении. — СПб.: Имп. Акад. наук, 1831.
II. Современные учебники1}
Ильин В. А., Позняк Э. Г. Основы математического анализа. В 2-х ч. —
М.: Наука, Ч. I. Изд. 4-е, перераб. и доп., 1982; Ч. И. Изд. 2-е, стереотип.,
1980.
Ильин В. А., Садовничий В. А., Сендов Б. X. Математический анализ.
В 2-х ч. Изд. 2-е, перераб. — М.: Изд-во Моск. ун-та, 1985, 1987.
^Приведенные в этом разделе книги допущены Минвузом СССР или рекомендованы
Комитетом по высшей школе Миннауки России в качестве учебников для студентов, обу-
обучающихся по специальностям «Математика», «Прикладная математика», «Механика», «При-
«Прикладная математика и информатика»

ЛИТЕРАТУРА 543
Камынин Л. И. Курс математического анализа. В 2-х ч. — М.: Изд-во Моск.
ун-та, 1993, 1995.
Кудрявцев Л. Д. Курс математического анализа. В 3-х т. — М.: Высшая
школа, 1988, 1989.
Никольский СМ. Курс математического анализа. В 2-х т. — М.: Наука,
1990.
III. Учебные пособия
Виноградова И. А., Олехник С. Н., Садовничий В. А. Задачи и
упражнения по математическому анализу. — М.: Изд-во Моск. ун-та, 1988.
Демидович Б. П. Сборник задач и упражнений по математическому анали-
анализу. — М.: Наука, 1990.
Макаров Б. М., Голузина М. Г., Лодкин А. А., Подкорытов А. Н.
Избранные задачи по вещественному анализу. — М.: Наука, 1992.
Рудин У. Основы математического анализа. Изд. 2-е. — М.: Мир, 1976.
Шилов Г. Б.
a. Математический анализ. Функции одного переменного. Ч. 1-2. — М,:
Наука, 1969.
b. Математический анализ. Функции нескольких вещественных переменных.
В 3-х ч. — М.: Наука, 1972.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления.
В 3-х т. Изд. 7-е, стереотип. — М.: Наука, 1969.
IV. Дополнительная литература
Александров П. С, Колмогоров А. Н. Введение в теорию функций
действительного переменного. — М.: ГТТИ, 1938.
Альберт Эйнштейн и теория гравитации: Сб. статей. К 100-летию со дня рожде-
рождения. — М.: Мир, 1979.
Арнольд В. И.
a. Гюйгенс и Барроу, Ньютон и Гук — первые шаги математического анализа
и теории катастроф, от эвольвент до квазикристаллов. —М.: Наука, 1989.
b. Математические методы классической механики. — М.: Наука, 1989.
Бурбаки Н. Очерки по истории математики. — М.: Изд-во иностранной ли-
литературы, 1963. (В частности, статья «Архитектура математики».)
Валле-Пуссен Ш.-Ж. Курс анализа бесконечно малых. В 2-х т. — Л.-М.:
ГТТИ, 1933.
В ей ль Г. Математическое мышление. — М.: Наука, 1989.
Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. — М.: Мир, 1967.
Гельфанд И. М. Лекции по линейной алгебре. — М.: Наука, 1971.
Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геоме-
геометрия: Методы и приложения. — М.: Наука, 1986.

544 ЛИТЕРАТУРА
Дьедонне Ж. Основы современного анализа. — М.: Мир, 1964.
Зельдович Я. Бм Мышкис А. Д. Элементы прикладной математики. —
М.: Наука, 1967.
Зорич В. А. Анализ. [Записки лекций для студентов Математического кол-
колледжа НМУ и механико-математического ф-та МГУ.] В 3-х вып. Вып. I.
Лекции 5-7: Дифференциал. Вып. П. Лекция 8: Теорема о неявной функ-
функции. Вып. III. Лекции 9-11: Приложения теоремы о неявной функции. — М.:
Изд-во механико-математич. ф-та МГУ, 1995.
К ар тан А. Дифференциальное исчисление. Дифференциальные формы.—М.:
Мир, 1971.
Колмогоров А. Н., Фомин С. В. Элементы теории функций и функцио-
функционального анализа. Изд. 4-е, перераб. — М.: Наука, 1976.
Кострикин А. И., Мании Ю. И. Линейная алгебра и геометрия. — М.:
Наука, 1986.
Кириллов А. А. Что такое число? — М.: Наука, 1993.
Курант Р. Курс дифференциального и интегрального исчисления. В 2-х т. —
М.: Наука, 1970.
Ландау Э. Основы анализа. — М.: Изд-во иностранной литературы, 1947.
Мании Ю. И. Математика и физика. — М.: Знание, 1979. — (Новое в жизни,
науке, технике. Серия: Математика, кибернетика; № 12.)
Милнор Дж. Теория Морса. — М.: Мир, 1965. — (Библиотека сборника «Ма-
«Математика».)
Нарасимхан Р. Анализ на действительных и комплексных многообразиях. —
М.: Мир, 1971.
Полна Г., Сеге Г. Задачи и теоремы из анализа. В 2-х ч. Изд. 3-е. — М.:
Наука, 1978.
Понтрягин Л. С. Обыкновенные дифференциальные уравнения. — М.: Нау-
Наука, 1974.
Пуанкаре А. О науке. — М.: Наука, 1990.
С пив а к М. Математический анализ на многообразиях. — М.: Мир, 1971.
Уиттекер Э. Т., Ватсон Дж.Н. Курс современного анализа. В 2-х ч. Изд.
2-е. — М.: Физматгиз, 1962-1963.
Успенский В. А. Что такое нестандартный анализ? — М.: Наука, 1987.
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике.
Т. I: Современная наука о природе. Законы механики. — М.: Мир, 1965.
Халмош П. Конечномерные векторные пространства. — М.: Наука, 1963.
Шварц Л. Анализ. В 2-х т. — М.: Мир, 1972.
Эйнштейн А. Физика и реальность: Сб. статей. — М.: Наука, 1965. (В
частности, статьи «Принципы научного исследования» — с. 8-10 и «Физика и
реальность» — с. 38-60.)

алфавитный указатель
Абель (Abel N. Н.) 34, 265, 318, 319,
348, 397
Абсолютная величина числа 54. См.
также Модуль действительного
числа
Адамар (Hadamard J.) 264, 468, 502, 531
Аддитивность интеграла 342
Аксиома Архимеда 50, 51. См. также
Принцип Архимеда
— бесконечности 28
— выбора 28
— выделения 27
— Дедекинда 63
— множества подмножеств 27
— непрерывности 36, 53
— объединения 27
— объемности 26
— пары 27
— подстановки 28
— полноты (непрерывности) 36, 41, 50,
53, 63, 65, 66, 68, 71
— Цермело 28
Аксиоматика действительных (вещест-
(вещественных) чисел 34, 50, 67
— категоричная 36
— непротиворечивая 36
— теории множеств 6, 26, 28
— Цермело — Френкеля 28
Алгоритм Евклида 64, 103
Альтернанс 169
Аргумент комплексного числа 260, 261
— функции 12
Архимед (АрхсцгNг)я) 50, 51, 325
Асимптота 249
— вертикальная 249
— горизонтальная 249
— наклонная 249
Асимптотика функции 135, 223
Атомный котел 287, 289
Ваза (базис фильтра) 125, 126
— в множестве разбиений 326
Базис 421
— ортонормированный 425
Бернулли Д. (Bernoulli D.) 443
Бернулли И. (Bernoulli J.) 19, 245
Бернулли Я. (Bernoulli J.) 64, 87
Бернштейн (Bernstein F.) 26, 31
Биекция 16
Бином дифференциальный* 321
— Ньютона 64, 206, 220
Бойли (Bolyai J.) 19
Больцано (Bolzano В.) 69, 83, 88, 157,
188
Бонне (Bonnet О.) 352
Борель (Borel E.) 69
Бунлкоеский В. Я. 353
Бурбаки (Bourbaki N.) 5, 126
Бюффон (Buffon G. L. L.) 386
Балле-Пуссен (La Vallee Poussin Ch. J.)
168
Ван дер Варден (van der Waerden В. L.)
188
Вейерштрасс (Weierstrass К.) 69, 85, 88
97, 158, 188
Вектор касательный 464, 465, 514
— нормальный 463, 465
Векторы ортогональные 425
Ветвь аргумента комплексного числа
261
Взрыв 288, 289
Виет (Viete F.) 146
Вложение 16
Выпрямление 492, 493
Галилей (Galilei G.) 1, 13
Гамильтон (Hamilton W. R.) 486, 487

546
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Гаусс (Gauss С. F.) 19, 147, 155, 259,
277, 398, 469
Гейне (Heine E.) 108, 161
Гёльдер (Holder О.) 236, 353
Гельфонд А. О. 50
Гессиан 486, 501, 530
Гильберт (Hilbert D.) 50, 63
Градиент 436, 438, 439
Граница числового множества верхняя
(мажоранта) 41
нижняя (миноранта) 41
точная верхняя 42
нижняя 42
Грань числового множества верхняя 42,
43
нижняя 42, 43
График функции 21, 22, 166, 246, 248,
251, 255
многих переменных 461, 462
Группа 34
— абелева 34, 46
— аддитивная 34
— коммутативная 34
— мультипликативная 35
Гук (Hooke R.) 300
Гюйгенс (Huygens С ) 385, 460, 461
Даламбер (D'Alembert J.) 98
Дарбу (Darboux G.) 228, 333, 340
Дробь непрерывная 102
— подходящая 102-104
— простейшая 279, 309
— цепная 102, 103
Дюбуа-Реймон (Du Bois Reymond P.)
341
Декарт (Descartes R.) 10
Делитель 47
— наибольший 64
— нуля 66
Диаметр множества 409, 411
Дирихле (Dirichlet P. G.) 155, 397
Диффеоморфизм 489, 499
— простейший 499
Дифференциал отображения 426, 430
-* функции 175-177, 182, 189
многих переменных 426, 427, 429,
430
Дифференцирование и арифметические
операции 189, 191, 273, 432, 433
— композиции функций 192-194, 434
— неявной функции 200, 208
— обратной функции 196, 440, 441
— степенного ряда 273
Длина кривой 14, 373, 375, 376
— пути 371-373, 376
— числового промежутка 53
— эллипса 376, 377
Дополнение множества 9
Евклид (ЕукХеьбщ) 64, 74, 135
Евклидова структура 424
Единица в множестве действительных
чисел 35, 38, 41
мультипликативной группе 35
— мнимая 259
Жесткости коэффициент 294, 300, 379
Зависимость функций 497, 505
Задача Бюффона 386
— Гюйгенса 460, 461, 470
— Кеплера (двух тел) 170
— Окуня 535
Закон Бернулли 443
— Кеплера 446
— Клапейрона 286, 488
— Ньютона 170, 210, 289, 442, 446
— Ома 24
— преломления 235, 532
-— сложения скоростей 202-204
235, 532
Замена параметризации пути 375Г37&
допустимая 376
— переменной в интеграле неопреде-
неопределенном 306
определенном 359
Замкнутость алгебраическая поля
комплексных чисел 275-277
Замыкание множества 407, 410
Значение главное несобственного
интеграла 400
— функции 12, 21
среднее 364
Идеал кольца 169
непрерывных функций 169
максимальный 169
Иенсен (Jensen J. L.) 243, 353
Изоморфизм 37, 145
Индекс критической точки 506
Интеграл вероятности ошибок 402
— Гаусса 398
— гиперэллиптический 318
— Дарбу верхний (нижний) 340
— неопределенный 302, 304-306

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
547
Интеграл несобственный 386, 387
расходящийся 387
— — с несколькими особенностями 398
сходящийся 386
абсолютно 392
условно 396
— определенный 324-326
— от векторнозначной функции 341
— Римана 326
— с переменным верхним пределом 354
— Френеля 322, 363, 401
— Эйлера 395
— Эйлера —Пуассона 322, 398
— эллиптический 318, 319, 321, 322, 377,
395
второго рода 319, 377
полный 377
первого рода 319, 382, 401
полный 382, 401
третьего рода 319
Интегрирование 301, 302, 324
— заменой переменной 306, 359
— по частям 306, 357
Интервал действительных чисел 53
Инъекция 16
Итерации 17, 31, 167
Кантор (Cantor G.) 5, 26, 73, 83, 161
Канторово множество 75, 341
Кардинальное число (кардинал) 25, 26
Карно Л. (Carnot L. N.) 112
Карно Сади (Carnot N. L. S.) 112
Картан (Cartan H.) 126
Касательная 174, 179-182, 213, 240, 471,
511
— плоскость 463-465, 471, 479, 511
— прямая, см. Касательная
Касательное отображение 426, 493, 512
— пространство 427, 511-514, 529
Квантор всеобщности 7, 30
— существования 7, 30
Кельвин, лорд (Kelvin), см. Томсон У.
Кеплер (Kepler J.) 170, 446
Клапейрон (Clapeyron В. Р. Е.) 286
Колебание функции в точке 151, 416
на множестве 128, 151, 329, 411
Колебания 293
— гармонические 295, 299
— затухающие 297
— маятника 382, 383, 385, 396, 402, 446
Кольцо непрерывных функций 169
— ростков непрерывных функций 169
Компакт 159, 408
-вГ 408, 409, 418
Композиция отношений 22
— отображений 17, 130, 156, 192, 194,
340, 412, 423, 434
Континуум 73. 74
Координаты декартовы 425
— криволинейные 461, 462
вГ 492
— полярные 491
— сферические 491
Координаты точки 52, 404
Корень многочлена 168, 275, 276, 278
кратный 230, 279
— n-й степени арифметический 65, 116
из комплексного числа 262
Косинус гиперболический 198
— интегральный 309
Котангенс гиперболический 199
Коши (Cauchy A. L.) 56, 68, 83, 93, 97,
99, 105, 106, 129, 157, 214, 217, 221,
264, 282, 353, 400, 505
Ксэн (Cohen P.) 74
Коэффициент жесткости 294, 300, 379
— полезного действия 297
Кратность корня многочлена 279
Кривая 371
— параметризованная 371
— простая замкнутая 371
— уникурсальная 320
Кривизна кривой 257, 258
Критерий Дарбу интегрируемости
функции 340
— Дюбуа-Реймона интегрируемости
функции 341
— Коши существования предела после-
последовательности 83, 263, 411
функции 129, 412
сходимости несобственного инте-
интеграла 391
ряда 93, 263
— Лебега интегрируемости функции
337, 338, 341
— непрерывности монотонной функции
164
— Сильвестра 458
— существования предела монотонной
последовательности 85
функции 134
— сходимости ряда с неотрицательными
членами 96
Круг сходимости степенного ряда 264,
265

548
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Лагранж (Lagrange J. L.) 177, 212, 217,
224, 229, 230, 486, 518, 519, 532
Л акру a (Lacroix S. F.) 19
Лаплас (Laplace P. S.) 267, 466
Лебег (Lebesgue H.) 69, 337, 338
Лежандр (Legendre A. M.) 256, 319, 366,
377, 382, 485
Лейбниц (Leibniz G. W.) 1, 19, 50, 170,
177, 194, 206, 324, 356
Лемма А дам ара 468, 502
— Больцано — Вейерштрасса 88, 92
— Морса 501, 502
— о верхней грани 42, 50
вложенных компактах 410
отрезках 68, 69
конечном покрытии 69, 70
предельной точке 69, 70
— Ферма 211
Линдеман (Lindemann F.) 49
Линейность интеграла 342
Линия геодезическая 14
— тока 443
— уровня 442, 473
Лиувилль (Liouville J.) 65, 318
Лобачевский Н. И. 19
Логарифм 121, 122, 187, 194, 195, 282
— интегральный 309, 322, 400
— натуральный 121, 282
Логарифмическая шкала 195
Лопитпаль (L'Hospital G. F. А.) 245
Лоренц (Lorentz H. А.) 13, 204
Маклорен (Maclaurin С.) 217
Максвелл (Maxwell J. С.) 445
Максимум 42, 66, 158, 418, 460
— локальный 210, 233, 234, 454, 456, 532
— условный 517, 522
Мантисса 67
Масса критическая 288
Матрица Якоби 430, 433, 434, 456
Маятник 382, 383, 385, 396, 446
— циклоидальный 385, 402
Метод градиентный 439
— исчерпания 325
— ломаных Эйлера 292
— множителей Лагранжа 519, 532
— наименьших квадратов 468
— неопределенных коэффициентов 280,
293
— Остроградского 319
— размерности 444, 446
Метрика 404, 405, 419
>га
404, 411
Мещерский И. В. 285
Минимум 42, 66, 158, 418, 460
— локальный 210, 233, 234, 454, 456, 532
— условный 517, 522
Минковский (Minkowski H.) 237, 353
Многочлен Лагранжа 229, 366
— Лежандра 366
— наилучшего приближения 168, 169
— Тейлора 216, 221-223
— Чебышева 169
— Эрмита 230
Множество 5, 6, 26
— бесконечное 26
— замкнутое 405-409
— инвариантное 24
— индуктивное 28, 44, 64
— интегрируемых функций 327, 328,
336
— канторово 754 341
— конечное 25
— меры нуль 337, 338, 341
— неограниченное 54, 413
— несчетное 73
— ограниченное 41, 409
сверху (снизу) 41
— открытое 405, 406, 408, 418, 420
— пустое 11, 27
— равномощное другому множеству 25
— связное 418, 420
линейно 417
— счетное 71, 72
— устойчивое 24
Модель действительных чисел 36, 37,
56, 63, 66
Модуль действительного числа 54
— (длина) вектора 171, 260. См. также
Норма вектора
— комплексного числа 260, 261
— непрерывности функции 167, 168
Монотонность интеграла 345
Морган (de Morgan A.) 9
Морс (Morse M.) 501, 502
Морфизм 12
Мощность континуума 73, 74
— множества 25, 26, 74
Муавр (de Moivre A.) 261
Мультииндекс 467
Нейман, фон (von Neumann J.) 28, 31
Неравенство Адамара 531
— Бернулли 64, 87, 236
— Гёльдера 236, 244, 353
— Иенсена 243, 244, 353
— Коши — Буняковского 353
— Минковского 237, 353, 404

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
549
Неравенство треугольника 54, 404, 424
числовое 54
— Шварца 353
— Юнга 236, 257, 386
Норма вектора 423, 425
Носитель пути 371, 375
Ньютон (Newton I.) 1, 64, 170, 220, 324,
356, 384, 446
Область в Rm 418
— значений отношения 19
функции 12
— определения отношения 19
функции 12
Образ 15, 21
Объединение множеств 8, 11
Объем тела вращения 378
Ограничение функции, см. Сужение
функции
Окрестность точки 54, 69, 105, 106, 406,
412
проколотая 105, 106, 412
Окружность соприкасающаяся 258
Окунь Л. Б. 535
Ом (Ohm G. S.) 24
Оператор 12
— Лапласа 466, 471
— сдвига 14
Операция ассоциативная 17, 34, 35
— дистрибутивная 35
— дифференцирования 189
— коммутативная 34, 35
— логическая 4, 11, 29
— над множествами 8, 11
— сложения 34, 35
— умножения 34, 35
Орбиты планет 300
Основание логарифма 121
— системы счисления 60
Осреднение функции, см. Усреднение
функции
Остаточный член формулы Тейлора 216,
220, 224, 368
в интегральной форме 357,
358, 453, 454, 467, 502
в форме Коши 217, 359
Лагранжа 217, 224,
229, 230, 359, 454, 467
Пеано 223, 224, 454
Остроградский М. В. 319
Осциллятор линейный 294, 299, 300
— плоский 300
Ось координатная 52
— числовая 52
Отношение 5, 19, 20
— антисимметричное 20, 22
— включения 7, 20, 66
— неравенства 21, 35, 36, 39
— порядка 21, 35, 53
линейного 21, 35, 36, 53
частичного 21, 35, 66
— равенства 7, 8, 20
— равномощности 25
— рефлексивное 20
— симметричное 20
— транзитивное 20, 22
— транспонированное 22
— функциональное 21, 22
— эквивалентности 20, 23, 25
Отображение 11, 12, 410. См. также
Функция
— биективное 16, 23
— взаимно однозначное 16
— инъективное 16, 23
— касательное 426, 493, 512
— линейное 175, 181, 182, 422-424, 433,
441, 490
— непрерывное 148-150, 415, 416, 418
— обратное 16, 18, 196, 440, 489, 490
левое (правое) 23
— ограниченное 109, 410, 418
— постоянное 109
— равномерно непрерывное 159, 417,
418
— сюръективное 16, 23
— тождественное 18
— финально ограниченное 110, 410
Падение тел 289
Пара неупорядоченная 9, 27
— упорядоченная 9, 27
Параметр разбиения 326
Параметризация кривой 375, 381
натуральная 381
Пеано (Peano G.) 25, 223, 224, 371
Первообразная 301, 302, 305, 307, 354,
355
— обобщенная 355
— рациональной функции 311, 313
Переменные канонические 487
Пересечение множеств 8, 11
Перестановка членов ряда 94, 265
Период колебаний маятника 382, 383,
385, 396, 402
— обращения 300
— полураспада 287, 298
— функции 188, 269, 363

550
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Плоскость касательная 463-465, 471,
479, 511
к поверхности 465, 479, 511, 512,
514
— комплексная 260
Площадь криволинейной трапеции 377,
378
— эллипса 378
Поверхность 462, 479, 506, 507, 511, 517
— минимальная 486
Поглощение излучения 299
Погрешность абсолютная 56-58, 77, 195
— относительная 56-58, 195, 443
Подмножество 7, 27
— пустое 8, 27
— собственное 8
Подпоследовательность 88
Подстановка Эйлера 317, 320
Поле алгебраическое 35
— архимедово 66
— векторное 442
— потенциальное 442, 532
— упорядоченное 66
Полуинтервал 53
Порядок касания 179, 180
— числа 60, 67
Последователь 28
Последовательность 55, 68, 77
— вложенных компактов 410
множеств 68, 70
отрезков 68, 70, 83
— возрастающая 85
— Коши 83, 262, 411
— монотонная 85
— невозрастающая 85
— неубывающая 85
— ограниченная 79
сверху (снизу) 85
— постоянная 79
— расходящаяся 78
— сходящаяся 78
— убывающая 85
— финально постоянная 79
— фундаментальная 83, 262, 411
— числовая 55
— элементов множества 68
Постоянная времени 298
— гравитационная 57
— Планка 57
— Эйлера 145
Потенциал векторного поля 439, 442, 532
— Ньютона 384, 442
— силы 380, 381, 384, 385, 442
Почти всюду 338, 341, 352
Правило Лопиталя 245, 246
Предел интегрирования верхний (ниж-
(нижний) 327, 345, 354
— композиции функций 130, 412
— отображения 410
— по базе 124, 126, 127
— последовательности 77-79, 83, 108
верхний (нижний) 89-91
частичный 91
— функции 105, 106, 108, 109, 112, 113,
126, 128, 129
Преобразование 12
— Абеля 348
— Галилея 13, 24, 202, 203, 205
— за время t 24
— инволютивное 257, 485
— Лежандра 256, 257, 485-487
— линейное 422, 423
— Лоренца 13, 24, 204, 205
Признак Абеля — Дирихле сходимости
интеграла 397
— Вейерштрасса сходимости ряда 97
— Гаусса сходимости ряда 147
— Даламбера сходимости ряда 98, 220
— достаточный условного экстремума
522
экстремума 233, 234, 456
— интегральный сходимости ряда 392
— Коши сходимости ряда 97, 99
— монотонности функции 214, 231, 232
— необходимый (достаточный) 2
сходимости ряда 93
условного экстремума 517, 519,
521, 532
экстремума 211, 232, 455
— постоянства функции 214, 231, 232
Принцип Архимеда 50, 51, 66, 71
— Больцано — Вейерштрасса 69-71
— Бореля — Лебега 69, 71
— верхней грани 42, 65
— Коши — Кантора 68, 71
— математической индукции 44
— Ферма 235, 532
Приращение аргумента 175, 176, 426
— функции 175-177, 426
Прогрессия геометрическая 94
Продолжение разбиения 329
— функции 12
Проектирование 14
Проекция 10, 417
— стереографическая 529
Произведение бесконечное 146
— множеств декартово 9, 10, 27, 31
прямое 9, 10, 27, 31
— рядов 265, 266
— скалярное 425

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
551
Производная 175, 177, 272, 426
— высшего порядка 205
— логарифмическая 194, 195
— односторонняя 256
— по вектору 438
направлению 439
— функции комплексного переменного
272
— частная 428
высшего порядка 450, 452
Промежуток многомерный 408
— числовой 53
неограниченный 53
Прообраз 16, 22
Пространство векторное 336, 342, 421
— евклидово 425, 426
— касательное 427, 511-514, 529
— конфигурационное системы п частиц
15
— метрическое 404
полное 129, 411
— фазовое системы п частиц 15
— Rm 403, 404, 411, 421
— Ща,Ь] 327, 335, 336, 342
Процесс итерационный 17
Пуанкаре (Poincare H.) 1
Пуассон (Poisson S. D.) 322, 398
Путь 371, 416, 441, 464, 506, 528
— гладкий 371
— замкнутый 371
— кусочно гладкий 372
— простой 371
замкнутый 371
Работа 379
— выхода 384
Равенство множеств 7
— функций 12
Радиус кривизны 258
— критический 288
— сходимости степенного ряда 264
Разбиение промежутка 326
с отмеченными точками 326
Разложение диффеоморфизма в
композицию простейших 499
— многочлена на множители 278
по формуле Тейлора 20\7, 215, 220
— рациональной дроби на сумму про-
простейших дробей 279, 280, 309
— функции в ряд Тейлора 218-220, 228,
274, 275
по формуле Тейлора, см. Формула
Тейлора
Размерность поверхности 506-508
— физической величины 444-446
Разность конечная 230
— множеств 8
Ранг отображения 493, 505
— системы функций 505
Распад радиоактивный 287, 298
Распространение функции, см.
Продолжение функции
Рассел (Russel В.) 6, 28
Расстояние (метрика) 404
о ]J$m 4П4
— между множествами 409
точками числовой оси 54
Риман (Riemann В.) 155, 326, 505
Роллъ (Rolle M.) 212, 468
Росток функции 169
Ряд 93
— гармонический 94
— расходящийся 93
— степенной 220, 264, 265, 273-275
— сходящийся 93, 263
абсолютно 95, 263, 265, 266
— Тейлора 220, 274, 275
— числовой 93
Сахаров А. Д. 535
Свойства непрерывных функций гло-
глобальные 157, 418
локальные 156, 169, 416
Свойство, выполненное финально (при
данной базе) 127, 128, 135, 136, 138,
139
— параболического зеркала 184, 185
Секущая 179, 181
Сильвестр (Sylvester J. J.) 458
Символ логический 1, 4, 7
— О большое 138, 141
— о малое 136, 141
Симпсон (Simpson Т.) 367, 368
Синус гиперболический 198, 268
— интегральный 309
— круговой 114, 268
Система счисления 59, 62, 68
позиционная 59, 62
— уравнений Гамильтона 487
Коши — Римана 505
Эйлера — Лагранжа 486, 487
— функций зависимая 498, 505
независимая 497, 505
Скорость вторая космическая 385
— мгновенная 171-173, 181, 183, 191
— света 13, 57, 203, 235
Слой 22

552
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Снеллиус (латинизир. Snellius, Snell van
Royen W.) 235
Среднее арифметическое 104, 244, 255
— гармоническое 94, 104, 255
— геометрическое 244, 255
— интегральное 364
— квадратическое 104, 255
— порядка р 104, 255
Стоке (Stokes G. G.) 357
Структура евклидова 424
— логическая математических высказы-
высказываний 29
Сужение функции 12
Сумма Дарбу верхняя (нижняя) 333, 340
— интегральная 325, 326
верхняя (нижняя) 333
— ряда 93
частичная 93
Сфера 406, 407, 419, 420, 529
Сходимость несобственного интеграла
386
абсолютная 392
условная 396
— последовательности 78
— ряда 93
абсолютная 95, 97, 263
Сюръекция 16
Таблица истинности 4
— первообразных (неопределенных
интегралов) 304
— производных 200
Тангенс гиперболический 199
Тейлор (Taylor В.) 215, 216, 220, 222,
223, 357, 358, 453, 466
Теорема Абеля 265
— алгебры основная 276, 277
— арифметики основная 47
— Больцано — Коши о промежуточном
значении 157
— Валле-Пуссена 168
— Вейерштрасса 85
о максимальном значении 158
— Дарбу 228, 340
— Дедекинда 63, 65
— Кантора 26, 73
о равномерной непрерывности 161
— Кантора—Гейне 161
— Коши 214, 215
— Лагранжа 212-214, 224
— Лиувилля 65
— о конечном приращении 212, 213, 448
неявной функции 471, 474, 481,
487, 489
ранге 493
среднем 213, 447, 448
для интеграла вторая 348, 351,
365, 397
первая 347, 365
— Ролля 212, 468
— сравнения (для несобственных инте-
интегралов) 393
(для рядов) 96
— теории размерности (П-теорема) 446
— Чебышева 169
— Шредера—Бернштейна 26, 31
Тождество Эйлера для однородных
функций 444
Томсон У. (Thomson W.), лорд Кельвин
(Kelvin) 286
Топология 107
Точка в Rm 404
— внешняя 406
— внутренняя 406
— граничная 406
— критическая 456, 532
вырожденная 530
невырожденная 501, 506
— — седловая 464
— локального максимума 210, 211,
232-234, 454, 455, 457
минимума 210, 211, 232-234, 454,
455, 457
— неподвижная 24, 167
— перегиба 242, 485
— предельная 69, 70, 407
— разрыва 153
второго рода 155
монотонной функции 163, 164
первого рода 154
устранимого 154
— стационарная 456, 532
— чебышевского альтернанса 169
Трапеция криволинейная 377, 378
Угол между векторами 426
кривыми 529
Узел интерполяции 230, 366
Упорядоченность линейная 35, 36, 53
— частичная 35, 66
Уравнение дифференциальное 174, 283,
286, 287, 289-291, 294, 295, 323
гармонических колебаний 294,
295, 299
с разделяющимися переменными
323
— Лапласа 466

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
553
Уравнение теплопроводности 466
— Эйлера (гидродинамическое) 439, 443
Уровень функции 442, 479, 517, 521
Ускорение мгновенное 170-172, 183, 188,
208, 257
Условие необходимое (достаточное) 2
Условия выпуклости функции 238-240
— дифференцируемости функции мно-
многих переменных 427, 429, 449
— интегрируемости достаточные
329-332
необходимые 328
и достаточные 334, 338, 340,
341
— монотонности функции 214, 231, 232
— экстремума функции 232-234
многих переменных 455, 456
Усреднение функции 364, 366
Ферма (Fermat P.) 10, 211, 235
Фибоначчи (Леонардо Пизанский)
(Fibonacci L.) 103
Форма записи комплексного числа алге-
алгебраическая 260
тригонометрическая 260, 261
Формула барометрическая 285, 286, 298
— Бонне 352
— Виета 146
— замены переменной в интеграле
неопределенном 307
определенном 359, 360
— интегрирования по частям в инте-
интеграле неопределенном 306
несобственном 390
определенном 357
— интерполяционная Лагранжа 229, 230
Эрмита 230
— квадратурная 367, 368
парабол 367, 368
прямоугольников 367, 368
Симпсона 367, 368
трапеций 367, 368
— Коши —Адамара 264
— Лейбница 206
— Маклорена 217
— Мещерского 285
— Муавра 261, 270
— Ньютона —Лейбница 324, 356
— Остроградского 319
— Тейлора 216, 223, 453, 456, 467
для функции многих переменных
453, 456, 502
в мультииндексных
обозначениях 467
локальная 222, 223, 454
с остаточным членом в интеграль-
интегральной форме 357, 358, 453, 467, 502
в форме Коши 217, 359
Лагранжа 217, 224,
230, 359, 454, 467
Пеано 223, 224, 454
— Циолковского 285
— Эйлера 267
Френель (Fresnel A. J.) 322, 401
Френкель (Fraenkel A.) 28
Функционал 12, 14, 342
Функция 11, 12, 19, 21
— аддитивная ориентированного про-
промежутка 345, 369, 370
— аналитическая в точке 221, 274
— асимптотически одного порядка с
другой функцией 138
эквивалентная другой функции
139
— бесконечно большая 136
более высокого порядка 136
— бесконечно малая 111, 112, 128, 136
более высокого порядка 136
по сравнению с другой
функцией 136
— вогнутая 238.
— возрастающая 134
— выпуклая 238
вверх (вниз) 238
— гармоническая 466
— гиперболическая 198, 199
— Дирихле 155, 339, 340
— дифференцируемая в точке 175, 176
— интегрируемая 327
— комплексного переменного 270
дифференцируемая 273
непрерывная 272
— Лагранжа 518, 519, 522, 527
— логарифмическая 116, 121, 122, 124
— локально однородная 444
— многих переменных 403
дифференцируемая 426
непрерывная 415
— монотонная 134
— невозрастающая 134
— непрерывная в точке 148, 149, 415
на множестве 151, 416
— неубывающая 134
— неявная 200, 208, 472, 474, 480, 481,
487
— обратная 16, 18, 162, 165, 166, 196,
440, 489
— ограниченная 109, 410
сверху (снизу) 109

554
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Функция однородная 444
— периодическая 188, 269, 363, 366
— показательная 116, 121, 124
— постоянная 109
— равномерно непрерывная 159, 161,
417, 418
— Римана 155, 166, 339, 340
— силовая 442
— степенная 116, 124
— строго выпуклая 238
— тригонометрическая 373, 375
— убывающая 134
— финально ограниченная 110, 128, 138,
410
— постоянная 109, 127
— характеристическая множества 14
— экспоненциальная 121, 186, 267, 290,
291, 293
— sgn (знак) 107
Центр кривизны 258, 530
Цермело (Zermelo E.) 28
Циклоида 385, 402
Циолковский К. Э. 285
Насть действительная комплексного
числа 260
— дробная числа 51
— мнимая комплексного числа 260
— рациональная интеграла 319
— целая числа 51
Чебышев П. Л. 135, 169, 321
Числа Фибоначчи 103
Число алгебраическое 49, 65, 73
— вещественное 33
— действительное 33
— иррациональное 48, 64, 73, 74
— кардинальное 25, 26
— комплексное 259
— натуральное 28, 43, 44
по фон Нейману 28, 31
— отрицательное 41
— положительное 41
— простое 47
— рациональное 47, 64, 72
— сопряженное 259
— трансцендентное 49, 65, 73
— целое 46
— е 86, 87, 100-102, 131-133, 269, 291,
292
— тг 49, 146, 269, 368, 372, 374
Числовая прямая 52
Шар 405
— замкнутый 405
— открытый 405
Шварц (Schwarz H. А.) 353
Шнайдер (Schneider Th.) 50
Шредер (Schroder E.) 26, 31
Эйлер (Euler L.) 86, 145, 259, 266, 267,
292, 317, 320, 322, 395, 398, 443, 444,
486
Эйнштейн (Einstein A.) 13, 421
Эквивалентность асимптотическая
функций 139
Экспонента 121, 186, 290-293
— интегральная 322, 402
— комплексная 267-269, 293, 295
Экстремум внутренний 211, 232-234
— условный 506, 516, 517, 522
— функции многих переменных 454-457
Элемент единичный 35, 38
— максимальный (минимальный) 41
— множества 5, 7
— наибольший (наименьший) 41
— нейтральный 34, 35
— нулевой 34, 37
— обратный 35, 38
— противоположный 34, 37
Энергия кинетическая 15, 299, 380, 381
— полная 15, 299, 380, 381
— потенциальная 15, 299, 380, 381
Эрмит (Hermite Ch.) 230
Юнг (Young W.) 236
Якоби (Jacobi С. G. J.) 430
Якобиан 430
— перехода к полярным координатам
в Rm 491, 492