Э. БЕККЕНБАХ, Р. БЕЛЛМАН
НЕРАВЕНСТВА

ERGEBNISSE DER MATHEMATIK
UND IHRER GRENZGEBIETE
Neue FolgeHeft 30
INEQUALITIES
by
Edwin F. Beckenbach and Richard Bellman
SPRINGER-VERLAG
BERLIN • GOTTINGEN • HEIDELBERG
1961

Э. БЕККЕНБАХ, Р. БЕЛЛМАН
НЕРАВЕНСТВА
Перевод с английского
Г. И. Басса, В. И. Левина,
Г. А. Шадрина
Под редакцией
В. И. Левина
ИЗДАТЕЛЬСТВО «МИР»
Москва 1965

УДК 517.0
Авторы книги, известные американские математики,
уже знакомы советскому читателю. Э. Беккенбах —
по сборнику «Математика для инженеров» (ИЛ, М ,
1958), Р Беллман — по книгам «Теория устойчивости
решений дифференциальных уравнений» (ИЛ, М , 1954),
«Динамическое программирование» (ИЛ, М , 1960)
и др. Основное содержание их новой книги
составляют неравенства, установленные за последние годы
и относящиеся к различным разделам математики
(матричная алгебра, теория операторов и т. д.) Особый
интерес представляет описание новых функционально-
аналитических методов поисков и доказательств
неравенств. Систематичность изложения и насыщенность
конкретным материалом позволяют использовать
книгу как своеобразный справочник для математиков
различных специальностей, а также для механиков,
физиков и инженеров-исследователей. Она будет
полезна преподавателям, аспирантам и студентам
математических и физических факультетов университетов,
пединститутов и технических вузов, а также
работникам вычислительных центров.
Редакция литературы по математическим наукам

ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Более тридцати лет назад, когда Харди, Литтлвуд
и Пойа писали свою известную монографию о
неравенствах, систематическое изложение оказалось возможным
только благодаря очень тщательному отбору
материала. Уже тогда обилие результатов, непосредственно
относящихся к тематике монографии, было таким, что
многие интересные и перспективные неравенства не
нашли в ней места. В качестве эпиграфа к своей книге
авторы избрали строфу Р. Браунинга (Saul. st. 39)
Oh, the little more, and how much it is!
And the little less, and what worlds away!x)
ярко характеризующую те трудности отбора, с
которыми им пришлось столкнуться.
За истекшие тридцать лет объем исследований по
неравенствам возрос во много раз и неравенства
завоевали много новых областей, в которых они играют
главенствующую роль. Тем более трудной была задача
отбора и расположения материала, вставшая перед
авторами. Они решили эту задачу, разбив, во-первых, книгу
на два тома (второй том еше не вышел), и используя,
во-вторых, возможность не доказывать многие из
приводимых результатов, которая предоставлена тем, что книга
вышла в известной серии «Ergebnisse der Mathematik und
ihrer Grenzgebiete» (Neue Folge, № 30), состоящей в
основном из обзоров отдельных областей математики.
Классификация неравенств в настоящей книге производится
не по методам доказательств (один из принципов
классификации Харди, Литтлвуда и Пойа), а в основном по
общности тематики и приложений.
!) О, чуть больше—и как много добавляется, а чуть меньше—
и какие миры исчезают!

6
Предисловие к русскому изданию
Следует еще отметить, что написана книга
«широкими мазками», изложение во многих местах не
затрагивает более тонких исследований, связанных с трудными
и интересными вопросами. Так, авторы далеко не всегда
приводят наилучшие неравенства (с точными константами),
ограничиваясь лишь фактом существования неравенства
и не устанавливая точных оценок. Это нельзя, однако,
поставить авторам в вину, так как детальная
разработка отдельных типов неравенств, какой бы интерес она
ни представляла для специалистов, действительно
невозможна в рамках такого издания, которое все же имеет
ознакомительно-справочный характер.
Книга Беккенбаха и Беллмана не является поэтому
монографией, по которой можно изучать неравенства
(как их можно изучать по книге Харди, Литтлвуда и
Пойа). Но она содержит такое богатство фактов (в
большинстве новых и новейших), притом умело
систематизированных, и столь обширную библиографию, что она без
сомнения окажется очень полезной для широкого круга
читателей. По ней можно навести справку, возможно ли
неравенство определенного типа, нужное как аппарат для
того или иного исследования, она может дать и много
стимулов для интересных исследований в области самих
неравенств.
Б. Я. Левин

Г. Г. Хардщ Дж. И. Литтлвуду и Д. Пойа
от двух последователей (на почтительном
расстоянии)
ПРЕДИСЛОВИЕ
Со времени выхода в свет классического труда Харди,
Литтлвуда и Пойа в 1934 г.1) математики приложили
колоссальные усилия к уточнению и обобщению
классических неравенств, открытию новых типов неравенств и
приложениям неравенств во многих разделах анализа.
В качестве примеров приведем теорию дифференциальных
уравнений, обыкновенных и с частными производными,
в которых доминирующую роль играют неравенства и
вариационные принципы, относящиеся к функциям и их
производным, многие приложения линейных неравенств
в теории игр и математической экономике, возродившие
интерес к вопросам выпуклости и пространствам
моментов, а также все новые и новые применения цифровых
машин, которые требуют систематического изучения оценок
погрешностей, опирающегося на сложные разделы теории
матриц и операторов.
Результаты, изложенные в настоящей книге, до
некоторой степени отражают все эти разветвления теории
неравенств в пограничные области анализа, но нашей
основной задачей было изучение неравенств как таковых.
Поскольку ясно, что невозможно дать связный отчет о
том взрыве аналитической активности, свидетелями
которого мы являлись на протяжении последних 25 лет, нам
пришлось ограничиться теми вопросами, которые нас
особенно интересовали, и в изучение которых нам
удалось внести некоторый вклад.
Мы приводим достаточное число литературных ссылок
как для того, чтобы заинтересованный читатель мог
х) Русский перевод: Харди Г. Г., Литтльвуд Дж. и
Полна Г., Неравенства, ИЛ, М., 1948.—Прим. ред.

8
Предисловие
проследить историю вопроса, так и для того, чтобы он
мог ознакомиться с более сложными аспектами
излагаемых результатов. Однако мы не стремились ни к энци-
клопедичности в подборе тем, ни к полноте
библиографических указаний по каждой из избранных тем.
Как и большинство авторов, мы эксплуатировали
наших друзей. Мы выражаем нашу сердечную благодарность
Фань Цзы за многократное чтение рукописи и за
подробнейшим образом разработанные предложения по тексту.
За многие ценные замечания и за чтение отдельных глав
мы выражаем нашу благодарность Р. П. Боасу, П. Лаксу,
Л. Ниренбергу, И. Олкину и О. Тауски.
Мы надеемся, что чтение этой книги доставит
столько же удовольствия другим, сколько получили мы, когда
ее писали.
Лос-Анжелес
и Санта Моника, 1961
Эдвин Ф.Беккенбах
Ричард Беллман

Глава I
ОСНОВНЫЕ НЕРАВЕНСТВА И РОДСТВЕННЫЕ ВОПРОСЫ
§ 1. Введение
В этой вступительной главе мы изложим ряд основных
результатов теории неравенств и их доказательства.
Некоторые из этих результатов важны сами по себе, другие
понадобятся нам в следующих главах. Наконец,
некоторые теоремы, так же как и разные варианты доказательств,
включены просто потому, что они очень красивы и
занимательны [1].
Мы начнем с неравенства Коши и тождества Лагранжа,
которые будут значительно обобщены в настоящей и
следующей за ней главах. Затем мы обратимся к вопросу,
который один заслуживает целой монографии, а именно
к знаменитому неравенству об арифметическом и
геометрическом средних п неотрицательных чисел. Мы приведем
двенадцать доказательств этого фундаментального
неравенства, конечно, не из-за недоверия к каждому из них
в отдельности, а для того, чтобы продемонстрировать
многообразие методов вывода неравенств, которыми
располагают алгебра и анализ. Особенно интересны доказательства
Коши, Гурвица и Бора.
Не без сожаления оставляя этот вопрос, мы займемся
установлением неравенств Гельдера и Минковского —этих
«рабочих лошадок» анализа —как в дискретном, так и в
континуальном вариантах.
Далее мы докажем некоторые родственные, но более
сложные результаты Беккенбаха и Дрешера. Здесь мы
используем важный прием квазилинеаризации, впервые
примененный Минковским, а затем разработанный Малером.
Этим приемом с успехом пользовались Юнг, Зигмунд
и Беллман.
Отсюда мы сделаем скачок к преобразованиям Шура
двояко стохастических матриц и к некоторым результа-

10 Гл. I. Основные неравенства и родственные вопросы
там Карамата, Островского и Харди, Литтлвуда и Пойа,
относящимся к мажорирующим последовательностям. Мы
упомянем также о континуальных аналогах,
принадлежащих Фаню и Лоренцу.
Следующей нашей темой является область
элементарных симметрических функций. Здесь имеются результаты
Маркуса и Лопеса, доказательства которых оказываются
гораздо более трудными, чем можно было думать. Самым
изящным доказательством этих неравенств является,
вероятно, то, которое опирается на теорию смешанных
объемов Минковского; эту теорию мы предполагаем
изложить во втором томе «Неравенств». Мы расскажем также
о результатах, принадлежащих Уайтли.
После этого мы перейдем к очень интересным
вопросам обращения и уточнения классических неравенств.
Вместо того чтобы следовать методам Бляшке и Пика или
Бюкнера, мы применим здесь (оставляя до гл. 3 и метод
моментов) метод Беллмана получения обратных неравенств,
основанный на дифференциальных уравнениях. Что
касается уточнения неравенств, то мы ограничимся только
упоминанием некоторых результатов, отсылая читателя
к соответствующим источникам.
Последняя часть главы посвящена некоторым
неравенствам, относящимся к суммам с знакочередующимися
членами, рассмотренным Вейнбергером, Сегё, Олкином, Беллма-
ном и другими. Все эти неравенства оказались частными
случаями нового неравенства Стеффенсена.
§ 2. Неравенство Коши
Самым фундаментальным неравенством является то,
которое выражает неотрицательность квадрата любого
действительного числа. Чтобы эффективно использовать
это утверждение, применим его к разности Ух — уъ, где yi
и Уч — действительные числа. Тогда неравенство (у± — у2)2 > 0
приведет к утверждению
У\+У2>2У1У2- (1)
Равенство имеет место тогда и только тогда, когда У\~Уъ
Это — простейший вид неравенства, связывающего
арифметическое и геометрическое средние. Следуя Коши, мы

§ 2. Неравенство Коши
11
будем в дальнейшем доказывать общий результат,
основываясь на этом частном случае.
Еще более эффективно можно применить
неотрицательность квадратов, образуя сумму
п п п п
2 (xtu+ybvf=ф 2 А + 2uv 2 ад +»" 2 уЪ (2)
г=1 г=1 г=1 г=1
в которой все входящие величины действительны.
Так как полученная квадратичная форма относительно
и т v неотрицательна для всех действительных значений
и и v, ее дискриминант должен быть неотрицателен,
что и дает неравенство Коши [1]:
(2^)<(2*f)(2tf)- (3)
M=l s М=1 У чг=1 у
Это неравенство можно рассматривать как выражение того
факта, что в евклидовом пространстве любого числа
измерений косинус угла по абсолютной величине не
превосходит единицы. Равенство имеет место тогда и только
тогда, когда системы чисел (хг) и (уг) пропорциональны,
т.е. тогда и только тогда, когда существуют числа К и [л,
не равные оба нулю, такие, что
^Ъ +№ =0, /=• 1, 2, ...,п.
Еще более общие результаты можно получить, применяя
предыдущее рассуждение не просто к n-мерному евкли-
довому пространству, а к общему линейному
пространству S, в котором для любых двух элементов х и у
определено скалярное произведение (х,у) со следующими
свойствами:
(а) (я, х)>0 для любого x£S, \
(б) (х,у) = (у,х), I
(в) (x,uy-\-vw) = u(x,y) + v(x,w) для любых |
действительных скаляров и и v. )
Эти свойства позволяют заключить, что квадратичная
форма относительно и и v
(их + ш/, га + vy) = и2 (х, х) + 2uv (х, у) + v2 (у, у) (5)
неотрицательна для всех действительных и и v.

12 Гл. I. Основные неравенства и родственные вопросы
Отсюда, как и выше, мы получаем неравенство
(х,у)2<(х,х)(учу)ч (6)
которое в свою очередь является частным случаем более
общих неравенств, рассматриваемых в гл. II; см. § 6 этой
главы.
Мы можем теперь вывести отсюда большое число
неравенств, выбирая S и скалярное произведение (х, у).
Так, мы можем положить
ь
(x,y)=^x(t)y(t)dG(t), (7)
а
где интеграл понимается в смысле Стильтьеса и G(t) не
убывает для а</<6, или
п
(х,у)= 2 aiJxiyji (8)
где А = (аи) — положительно определенная матрица и т. д.
§ 3. Тождество Лагранжа
Весьма интересной и трудной задачей со многими
неожиданными разветвлениями является доказательство
любого данного известного неравенства при помощи
тождества, которое делает это неравенство очевидным.
Неравенство (2.3) вытекает непосредственно из тождества
П П п 2 П
(2*?)(2^)-(2*!и) = 2 (*1»-^«)я; (1)
i=l г=1 г=1 i,j=l
последнее представляет собой также частный случай
более общего тождества, рассматриваемого в § 6 гл. II.
§ 4. Неравенство между арифметическим
и геометрическим средними
Мы начнем рассмотрение несколько более глубоких
результатов с одного неравенства —вероятно, самого

§ 5. Индукция вверх и вниз
13
важного и, несомненно, являющегося одним из столпов
теории неравенств, —именно с неравенства между
арифметическим и геометрическим средними. Это
исключительно красивое неравенство может быть сформулировано
следующим образом.
Теорема 1. Пусть х±, х2, ..., хп —неотрицательные
числа и п > 1. Тогда
Xl + X2+n--+Xn>(xlx2 ... xn)i,n. (1)
Здесь имеет место строгое неравенство, если только не
все xt равны между собой.
В §§5—16 мы изложим двенадцать доказательств
этого фундаментального неравенства, основанных на
разных принципах, или по крайней мере использующих
разные приемы. Существуют обобщения неравенства (1),
относящиеся к взвешенным средним. Интересно отметить,
что фактически они являются частными случаями этого
неравенства и его предельных случаев. См. § 14 ниже;
подробное изложение этих вопросов можно найти также
в [1.1].
§ 5. Индукция вверх и вниз
Следующее классическое доказательство теоремы 1
принадлежит Коши [2.1]. Как уже отмечено в (2.1), для
любых ух и у2 мы имеем
yl + yl>2yiy2. (1)
Полагая yl = xi9 yl = x2, мы получаем из (1), что
*±^>У5л, (2)
где jq и х2 — любые неотрицательные числа. Из (2.1) мы
уже знаем, что в (2) равенство имеет место тогда
и только тогда, когда х±=^х2.
Заменим теперь х1 новой переменной -^(х^х?) и х2—-
новой переменной у(я3 + *4)- Тогда из неравенства (2),

14 Гл. I. Основные неравенства и родственные вопросы
примененного дважды, мы найдем, что
4 >L"^ 2—J >
> [( W ( Wl^ = (*1*2*Л)1/4. (3)
Продолжая таким же образом, мы легко убеждаемся
в том, что неравенство (4.1) справедливо для п=1, 2,
4,..., и вообще для любого п, являющегося степенью
2. Это —индукция вверх.
Применим теперь индукцию вниз. Покажем, что если
неравенство справедливо для п, то оно справедливо
и для п— 1. Заменим в (4.1) хп на
х1 + х2 + • • • + хп-1 /л\
П—\ ' ^'
где п>2, и оставим другие xt неизменными. Тогда
по (4.1) мы получим неравенство
*i+*2+...+*n-i+*1+*2t--;+*n-1
= — >
> (*Л ... xU'n (*+*+-+^)1Л>, (5)
или
^zzi > (*i*2 - • • Xn-i) ^ ^zn J •
(6)
Упростив, найдем искомое неравенство
Xi+X2+:..+Xn^> {XiX2 Xnji^\ (7)
В сочетании с результатом, полученным для
степеней 2, мы имеем теперь индуктивное доказательство
теоремы.
Другим интересным неравенством, которое также
может быть доказано индукцией вверх и вниз, является
следующее неопубликованное неравенство Фань Цзы:

§ 7. Функциональные уравнения
15
если 0 < xt < -и- для / = 1, 2, ..., п, то
п п
"^— <Чг* . (8)
(S*0" [So-**)]"
г=1 г=1
причем равенство имеет место только в том случае, когда
все xt равны между собой.
§ 6. Анализ и множители Лагранжа
Подойдем теперь к неравенству между арифметическим
и геометрическим средними как к задаче из анализа. Мы
хотим найти наименьшее значение функции х1 + х2 +...
...+Хп в области неотрицательных хи удовлетворяющих
условию нормировки
Х^Хч ... хп = 1. (1)
Так как ясно, что искомое наименьшее значение не может
приниматься в граничной точке, то мы можем применить
метод множителей Лагранжа для определения локального
минимума. Для функции
/ \Х1ч х1ч • • • > Хп) = Х±%2 • • • Хп'— ^ \х1 ~Ь Х2 ~Ь • • • 4~ Хп) (2)
необходимые условия экстремума имеют вид
§1 = Х1Х2х\'Хп-Ь = 0' i=L 2 nt (3)
так что должно быть х1=х2= ... =хп. Отсюда мы
заключаем, что имеется единственная точка локально^
минимума Xi = \, i= 1, 2, ..., п и, следовательно, xt-\-
-\-х2+ ... +хп>п, что равносильно неравенству (4.1).
§ 7. Функциональные уравнения
Теорема 1 может быть также доказана методом
функциональных уравнений динамического программирования
[1]. Мы начнем с задачи отыскания наибольшего зна-

16 Гл. I. Основные неравенства и родственные вопросы
чения xtx2 ... хп при условиях
х1+х2+ ... +хп = а, хг>0.
Обозначим это наибольшее значение через fn(a), п =
= 1, 2, ..., а>0. Чтобы получить рекуррентное
соотношение между fn{a) и /n-i(a), заметим, что при
фиксированном выборе хп остается задача такого выбора хи х2, ...
..., хп-и подчиненных условиям
xt ±-х2 + ... +xn-i = a — хп, xt>0, (1)
чтобы произведение xtx2 ... хп-\ было наибольшим.
Отсюда следует, что
fn(a)= max [xnfn^(a — хп)], п = 2, 3, ..., (2)
О ^ хп ^ а
при fi(a) = a.
Произведя замену переменных х% = ауи i= 1, 2, ..., п,
мы будем иметь
fn(a) = a-fn(l). (3)
Подставляя это представление в (2), найдем, что
/.(1) = /н(1)[шах j/(l-^r1]=/-l(1)i;~1)"~1- (4)
Так как f1(l)=l, то ^(1)= 1/пл, что равносильно (4.1).
§ 8. Вогнутость
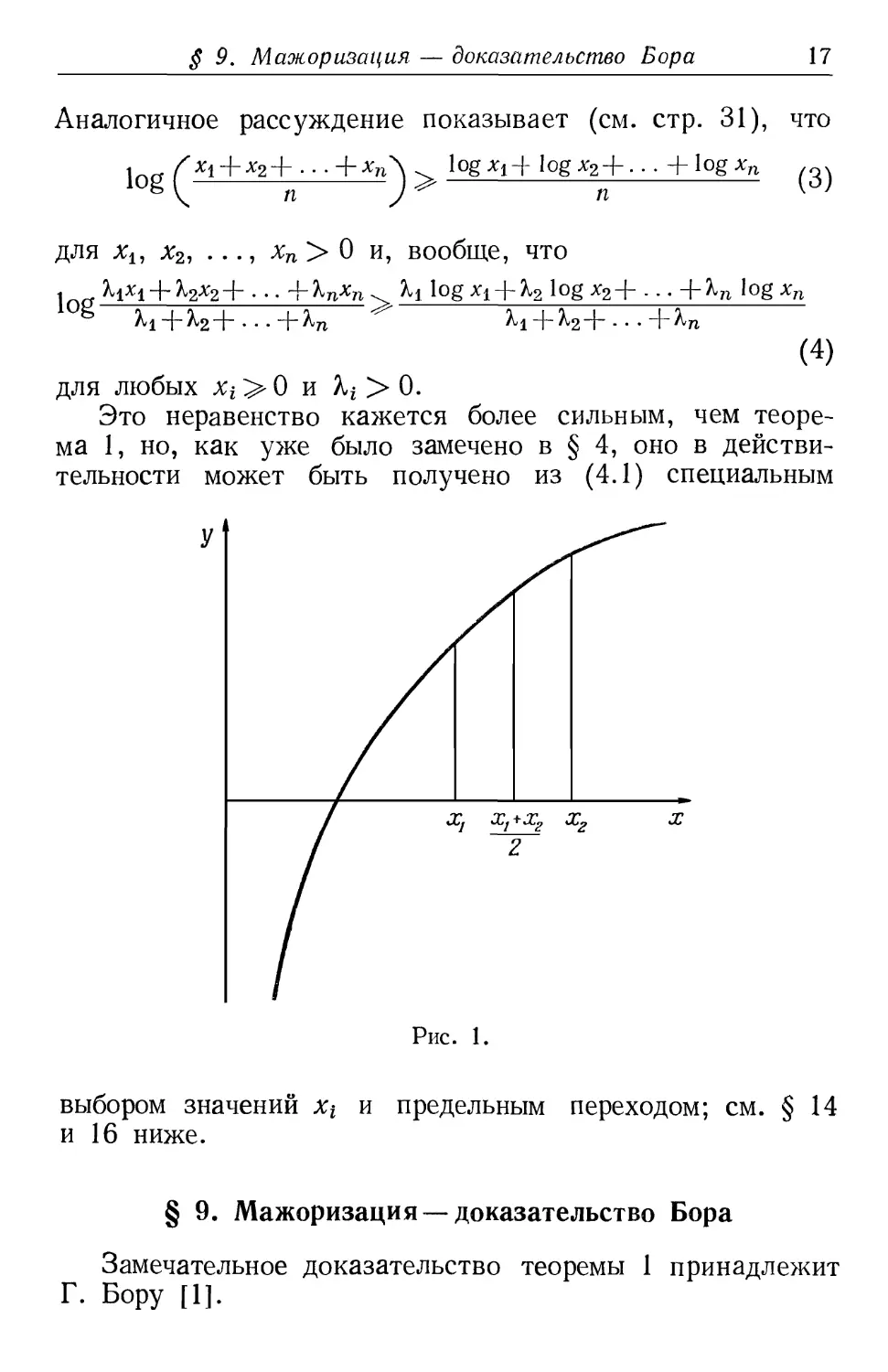
Предложим теперь доказательство теоремы 1,
основанное на геометрических рассуждениях [1, 2, 3, 4]. На
рис. 1 изображена кривая y = logx. Дифференцирование
показывает, что эта кривая вогнута, так что хорда,
соединяющая две любые ее точки, лежит под кривой.
Следовательно, для хи х2 > 0,
log^JEi±^^>i°gx1 + log^) (1)
причем равенство имеет место только при *1=х2-
Этот результат равносилен неравенству
X-^>VW~2- (2)

§ 9. Мажоризация — доказательство Бора 17
Аналогичное рассуждение показывает (см. стр. 31), что
l0g f *1 + *2+---+*тЛ
> l0g*l-f log*2+--- + log ^yi /3)
для хи х2, ..., хп > О и, вообще, что
iQg Ml + ^+ - • • +К*п ^ hi l0gX! + X2l0gA:2+ . ..+Хл log*n
^1+^2+ • • -+^71
^1+^2 + - • • +^7i
(4)
для любых a^>0 и Xf > 0.
Это неравенство кажется более сильным, чем
теорема 1, но, как уже было замечено в § 4, оно в
действительности может быть получено из (4.1) специальным
Рис. 1.
выбором значений хг и предельным переходом; см. § 14
и 16 ниже.
§ 9. Мажоризация —доказательство Бора
Замечательное доказательство теоремы 1 принадлежит
Г. Бору [1].

18 Гл. I. Основные неравенства и родственные вопросы
Сначала введем понятие мажоризации. Пусть f(y)
и g(y) — два формальных степенных ряда:
оо оо
!{у)=ЪапУп, g(y)=Hbnyn, (1)
п=0 гс=0
где ап, Ьп>0 для я>0.
Если ап>Ьп для п>0, то мы пишем
f(y)>g(y)- (2)
Если fi (у) > gt (у) и f2(у) > g2 (у), то, очевидно, и ft (у) х
хЫу)>Ыу)Ыу)-
Начиная с простой мажоризации
езд » *-&- (3)
для N = 1, 2, ... и х>0, у>0, мы находим, что
п
У 2 *i /- „ - xN nN
р i=i Чч ^1Х2 • • • *к) У (л\
* <*> (щп • KV
Отсюда, сравнивая коэффициенты при ynN, получаем
неравенство
(2 «Г ,
i=l 1*1*2 . • . Хп) /r\
(л#)1 ^ (N\)n ' W
ИЛИ
:> L(MrJ ' (b)
(2*0*
#1*2 * • • *7l
для всех положительных целых N.
Так как по формуле Стирлинга при k—>co
k\~kke-kV2nk, (7)
то
Из (6) и (8) следует теорема 1. Это — единственное из
приводимых нами доказательств, не позволяющее
усмотреть условия, при которых имеет место знак равенства.

§ 10. Доказательство Гурвица
19
§ 10. Доказательство Гурвица
Перейдем теперь к изложению интересного
доказательства Гурвица [1]. Оно было опубликовано в 1891
году, за шесть лет до его знаменитой работы о получении
инвариантов интегрированием по группам [2], но в нем
уже заложены некоторые идеи, получившие развитие
в его более поздних работах.
Пусть дана функция п действительных переменных
f(xu х2, ..., хп). Обозначим через Pf{xu х2, ..., хп)
сумму / по всем п\ перестановкам аргументов xt. Так,
например,
Р*Г = (п-1)! (*? + *?+ ...+*£),
г Х]Х2 ... Х-ц = tl! Х\Х2 ... Х-ц.
Рассмотрим функции фй, k = l, 2, .... п—1,
получаемые следующим образом:
Ф^РКх"-1-^-1)^-^)], |
ф2 = Р[(*Г2-*Г2)(*1—*2)*8], I
фз = Р К*?-*-*%-*) (Xi -х2)*Л], | (2)
фтг-1 = Р [(%! — %2) (#1 — XV -^3-^4 • • • хп\ • )
Мы ВИДИМ, ЧТО
Ц)1 = РХ'Ч + РХ^ — РХ^-1Х2-'РХ^-1Х1 =
= 2Рх™ — 2Рхп-1х2- (3)
Аналогично
ф2 = 2РХ*-*х2 - 2Рхъ-2х2х3, |
Фз = 2Рх™-2х2х3 — 2Pxni-42x^xk, I
фп_1 = 2Рх\х2х% ... xn_i — 2PxiX2 ... Хп. ]
Суммируя, получаем, что
ф1 + ф2 + • • • + фтг-1 = 2РХ? — 2РХ1Х2 ... Хп. (5)
(1)

20 Гл. I. Основные неравенства и родственные вопросы
Но в силу (1) это означает, что
*? + *§+..■+*£ __XiX2 т ш т Хп = 51_(ф1 + ф2+ . . . +фд-1). (6)
Легко видеть, что каждая из функций щ(х)
неотрицательна для Xj>0, так как
Щ = Р [(x?-k-x%-k) {х, ~х2) Х3Хь ... xk+1] =
= P[(x1-x2)»(*y-fe-i + яти +xn-K-i)XzXit ш ш 9 Xk+il (7)
Таким образом, разность в левой части тождества (6)
неотрицательна, что и доказывает теорему 1. Это
единственное из приводимых нами доказательств, которое сводит
неравенство (4.1) к тождеству.
§11. Доказательство Элерса
Мы докажем теорему 1, установив, что из
X\X<i . . . Хп — 1 ? Xi ^ и,
вытекает неравенство
*1+*2+ ...+Хп>П.
Допустим, что это справедливо для п и что
Х\Х^ . . . XnXn+i = 1.
Пусть xt и х2 — два из чисел хи такие, что a?i>1, а х2<
<1. Тогда (х± — 1)(х2— 1)<0, или
Xfa+^KXi+Xz. (1)
Отсюда вытекает, что
*l + *2 + X3+... -+Xn+l> 1+*1*2 + *3 + .. . +Xn+t>l+n
(2)
в силу неравенства для п чисел xtx2, х3, ..., хп, хп+1.
Далее, результат тривиален для п = 1, и теорема 1
доказана. См. [1.2].

§ 12. Лрифметико-геометрическое среднее Гаусса 21
§ 12. Арифметико-геометрическое среднее Гаусса.
Элементарные симметрические функции
Пусть а0, Ь0 — положительные числа и а0>Ь0-
Определим дальнейшие члены последовательностей {ап}, {Ьп}
соотношениями
a„+1 = ^±^, bn+1 = (anbn)1/2. (1)
Легко видеть, что
а0>а±> ...>ап>... >Ьп> . .. >b1>b0, (2)
и можно доказать, что последовательности {ап} и {Ьп}
имеют общий предел М(а0, Ь0). Эта функция М(а0, Ь0)
была впервые исследована Гауссом [1]. Она играет
важную роль в теории эллиптических функций; более того,
Гаусс показал, как вся эта теория может быть основана
на этой функции.
Сделанное выше утверждение относительно сходимости
последовательностей {ап} и {Ьп} допускает далеко идущие
обобщения. Например, если а0>Ь0>с0>0 и
пЛ~ Ьпсп
"n+1 — з > Vn+1 — I 3 J >
Cn+1 = {ClnbnCn)11*, (3)
то легко показать, что
lim an= lim bn= lim cn = M(a0, &0, c0); (4)
n->oo n-+oo n->oo
см. Шапиро [2], Шлезингер [3] и Беллман [4], где
устанавливается много других результатов относительно
симметрических средних.
Один из способов доказательства результатов о
симметрических средних состоит в применении некоторых
интересных неравенств между элементарными
симметрическими функциями п действительных переменных.
Оказывается, что неравенство между арифметическим и
геометрическим средними является лишь одним из звеньев
цепочки аналогичных неравенств.
Следуя изложению в [1.1], мы применим метод
доказательства, основанный на теореме Ролля. Этот метод

22 Гл. I. Основные неравенства и родственные вопросы
показывает, что полезные следствия можно извлекать (как
мы это сделали в § 2) не только из того факта, что
данный многочлен не имеет действительных корней, но и из
предположения, что все корни многочлена действительны.
Эта же идея будет развита нами ниже (см. § 36 — 38)
при изложении некоторых результатов, принадлежащих
Гордингу.
Необходимый нам результат является
непосредственным следствием из теоремы Ролля; он состоит в
следующем.
Лемма. Если все корни х/у уравнения
f(x, у)^с0хт + с1хт-1у+...+стУт = 0 (1)
действительны, то действительными будут также все
корни уравнений, полученных из (I) частными
дифференцированиями по х и по у.
Применим эту лемму к многочлену
/(*, У) = (х + hy)(х + г2у) ...(* + Гпу), (2)
где г% действительны. Полагая
f(x, у) ее x" + Pl ( J ) *п-*у + р2 ( J ) *"-2#2+ , ..+Рп!Г,
(3)
где
V k ) = k\ (n—k)\ ' ^4)
Ро=1 и (для й=1, 2, ..., п) ph является k-и
симметрической функцией с соответствующим весом чисел г и мы
видим, что уравнение
Pk-iX2+2pkxy + pk+1y2 = 0 (k=l, 2, ..., п— 1), (5)
которое может быть получено из f(x, у) = 0 повторным
дифференцированием, имеет два действительных корня.
Таким образом,
Pk-iPk+i<pt, k=l, 2, ...,м—1. (6)
Заметим, что это неравенство имеет место для любых ri%
положительных, отрицательных или равных нулю.

§ 13. Доказательство Якобсталя
23
Выведем теперь из неравенства (6) один результат,
принадлежащий Маклорену [5]. Для этого предположим,
что все гг положительны. Тогда в силу (6) имеет место
неравенство
(Р0Р2) (PiPs)2 (Р2Р4)3 ... (Pk-iPk+i)k < Р1Р2 • • • Pkk, (7)
или
p{'h>pif^\ k=\, 2, ..., я-1. (8)
Из (8) мы, в частности, получаем, что
Pi>Pnn,
т. е. неравенство между арифметическим и
геометрическим средними.
§ 13. Доказательство Якобсталя
Существует ряд доказательств неравенства между
арифметическим и геометрическим средними, основанных
на алгебраических соотношениях между этими средними.
Интересным примером таких доказательств является
следующее [1].
Начнем с тождества
*_&=![(„_„£+(£)■]. („
где
г=1 г=1
Далее применим неравенство
zn + n-l>nz, (2)
справедливое для г>0ип>1. Для целых значений п
соотношение (2) вытекает из тождества
zn-nz + n-l = (z—l)(zM + 2^+...+2 —Л+-1).
Если мы положим
z =
Gn-i'

24 Гл. I Основные неравенства и родственные вопросы
то получим из (1) неравенство
ИЛИ
^>^[(n-i)^-;-(.-i)+^], (3)
Д* - Gn > ^-i (4-i - Gn-J. (4)
По индукции мы находим отсюда искомый общий
результат:
An-Gn>0.
§14. Одно фундаментальное соотношение
Замечательные неравенства [ср. (13.2)]
ха — ах + а— 1 >0, а>1 или а < О, (1)
Я'а — ах + а— 1<0, 0<а<1, (2)
справедливые для х > О, являются фундаментальными для
всей теории, ибо из них непосредственно вытекает
неравенство между арифметическим и геометрическим
средними, а также основные неравенства Гёльдера и Минков-
ского (см. §§ 17 и 18 ниже).
Неравенства (1) и (2) легко доказываются простым
применением дифференциального исчисления. Равенство
имеет в них место только для х = 1.
Более длинное, но зато и более элементарное
доказательство этих неравенств состоит в следующем [1.1]: для
# > 0 и м= 1, 2, ... тождество
Уп+1— 1 уп— 1 У—1/nn-i 14
/2+ I Я /2(/2+1) V ^ ^ У J
показывает, что
/2+ 1 Я
причем равенство имеет место только при у = 1.
Следовательно, для любого целого m > я
//Ш 1 /7п 1
^ -~у- ->0,

§ 14. Одно фундаментальное соотношение 25
откуда при у = х1/п, х > О, вытекает неравенство
xm/n_1_j^(x_1)>0,
которое совпадает с неравенством (1) при рациональных
значениях а > 1, а именно
xm/n_Hx + fL_l>0 — >1, (3)
причем равенство имеет место только при л; = 1.
Неравенство (1) для иррациональных сс> 1 вытекает
из (3) при т/п—>а, но при предельном переходе строгое
неравенство для х Ф 1 теряется. Чтобы его восстановить,
положим a^rfi, где г>1 и Р>1, но г рационально.
Тогда
ха — ctx + ct— 1=(х$У — r$x + r$-l >гх$-г$х + г$-г>0,
и это завершает доказательство неравенства (1) при а > 1.
Подстановка
яа — ^-р^З-!, а> 1,
в (1) приводит к неравенству
r1(^-P^/+P-i)>o, Р<0,
так что (1) действительно имеет место и при а < 0.
Аналогичная подстановка
х? = х1М = у, а> 1,
показывает, что (2) имеет место при 0<а<1. Как
и прежде, равенство имеет место в (1) при а < 0 и в (2)
при 0 < а < 1 только при х = 1. В предельных случаях
сс = 0 и а=1 равенство тривиально для всех х > 0:
#а — ах + а — 1 ее 0, если а = 0 или а — 1.
Чтобы теперь вывести неравенство между
арифметическим и геометрическим средними, заметим, что для хи
х2 > 0 подстановка
Х\
*2

26 Гл. I. Основные неравенства и родственные вопросы
в (2) приводит к неравенству
Y_o-f- + a-l<0,
из которого вытекает, что
xuxi2-a<axi + (l—a)x2, 0 <a< 1,
а это и есть искомое неравенство для двух произвольных
чисел хи х2>0 и произвольных положительных весов а
и 1—ее. Равенство в нем имеет место только при Xi = x2.
Общий результат
EKf<2«i*» (4)
при
п
Xi>0, a*>0, 2ai=l (5)
легко получается по индукции. В этот результат входит
также утверждение, что равенство в (4) имеет место только
при xt = Xj для всех i, / = 1, 2, ..., п. В самом деле,
если (4) справедливо для п, то для
п+1
*i>0, сц>0, 2 a, = l
ПОЛОЖИМ
yt = Xt, Pi = af, /=1, 2, ..., я—1,
и
#n - х^/Рл^л_+1/Ри , p„ = a„ + ап+1.
Очевидно, что
n
Уг>о, рг>о, 2 P* = i,
и, следовательно, по индуктивному предположению
n-\-l n n
i=l i=l i=i
n n-fl
= 2 агхг + (аЛ + ап+1)(л«"/Р»^1/Рп)< 2 a,*,,

§ 15. Неравенство Юнга
27
причем равенство всюду имеет место только в том случае,
когда все хг равны между собой.
Таким образом, мы вновь (ср. с § 8) доказали
неравенство (4) для произвольных xt, cto удовлетворяющих
условиям (5); но на этот раз наше доказательство для
произвольных действительных (необязательно рациональных)
щ является предельно элементарным.
Неравенства (1) и (2) могут быть записаны в
симметричной форме, если положить х = -г{а > О, Ъ > 0) и
Тогда
1
Р
Сами ;
1
а = —
Р
+*-■
я-
, 1 —a =
<=&
-*-Ь
же неравенства (1)
aVp&i/a
Р я
-j (Р,ЯФ0 и Ф 1).
Я 1 Р \
(p-l)fa-l)=l. j
и (2) примут вид
ИЛИ fll/Pbl/9>iL_|_±
Р я
(6)
(7)
в зависимости от того, является ли р > 1 или р < 1
(р Ф 0). Равенство в неравенствах (7) имеет место только
при а = Ь. Легко проверить, что для р>0 второе
неравенство (7) имеет место при несколько более общих
предположениях а>0, Ь>0.
§ 15. Неравенство Юнга
Пусть у = ор(х) — непрерывная строго возрастающая
функция от х, х>0 и ф(0) = 0 (см. рис. 2).
Рассматривая площади, представленные соответствующими
интегралами, мы убеждаемся в том, что
а Ъ
аЪ < ^ <р(х) dx + ^ <f4y) dy, (1)
о о
где ф_1(у) — функция, обратная к ф(х). Легко видеть, что
равенство здесь имеет место только при b = tp(a). Это
неравенство называется неравенством Юнга [1].

28 Гл. J. Основные неравенства и родственные вопросы
Выбирая в качестве ф различные функции, мы
получаем ряд интересных результатов.
При у = хр~1, р> 1, (1) принимает вид
ab< .
Р Я
(2)
Это —первое из неравенств (14.7). Из него могут быть
легко получены другие результаты, приведенные в § 14.
У
№
У*¥
IX) у
(а,0)
Рис. 2.
Выбирая yz=q)(x) = \og(x+l) в неравенстве Юнга (1)
и заменяя а на а—1, мы получаем другой интересный
результат, а именно неравенство
ab<Ca\oga — а + еъ.
Это неравенство часто применяется в теории рядов Фурье.
§ 16. Средние Ж*(лг,а) и суммы St (х)-
В § 12 мы видели, что неравенство между
арифметическим и геометрическим средними является лишь одним
из цепочки неравенств, которым удовлетворяют
элементарные симметрические функции. Покажем теперь, что эти
средние включаются в целую непрерывную иерархию
средних значений. Хотя для рассматриваемых здесь неравенств
существуют элементарные доказательства, мы будем
в основном применять дифференциальное исчисление.
Нашим главным орудием будет теория выпуклых функций;
в частности, мы здесь изложим аналитическую основу тех
геометрических рассуждений, которые были приведены в § 8.

§ 16. Средние Mt (*, а) и суммы St (х) 29
Общая теория выпуклых функций и их приложений
рассматривается в работах Беккенбаха [8.3] и Грина [8.4].
Для любых положительных значений
(Х) EES (xi9 Хч, . . . , Хп)
и положительных весов
п
(a)==(alf a2, ... , an), 2 <*i=U
г=1
и любого действительного £ =£ 0 мы определяем среднее
порядка t, или t-норму, значений (х) с весами (а) как
М
,(*, a) =(2 a^)1/f-
В частности, средние порядков—1, 1 и 2 суть
соответственно гармоническое, арифметическое и квадратическое
средние.
При помощи правила Лопиталя легко устанавливается,
что
п
UmMt(x, a)= I]<S (1)
т. е. геометрическому среднему. Далее, если Xk = max(x),
то очевидно, что для t > О
откуда вытекает, что
limMf(x, a) = max (х). (2)
Но из соотношения
теперь следует, что
lim Mt(x, a) = min(x) (3)
t-*—oo

30 Гл. I. Основные неравенства и родственные вопросы
В силу этого мы полагаем
М0(х, а)=П *?',
г=1
Моо{х, а) = тах(х),
М-оо(х, а) = тт(л;).
Если относительно х% предполагается только, что они
неотрицательны и что по крайней мере одно из них равно
нулю, то для t < 0 среднее Mt (х, а) полагается равным нулю.
Однако мы будем рассматривать только положительные xt.
Покажем теперь, что для положительных х% среднее
Mf(x, а) является неубывающей функцией от t для
—оо<£<оо, причем если только не все xt равны между
собой, то Mt(x, а) даже строго возрастет. Неравенство
между арифметическим и геометрическим средними является
частным случаем этого утверждения.
Для обоснования этого общего факта сделаем сначала
одно замечание относительно выпуклых функций. Если
функция f(x) имеет вторую производную,
удовлетворяющую неравенству
s>» <«>
для а < х < 6, то график y = f(x) представляет собой
выпуклую дугу в этом интервале. Если значения
(х) = (#i, Хч, ..., хп)
лежат в интервале (а, 6), а
п
X = 2j ®iXi->
i=l
то х также лежит в (а, &), и по формуле Тейлора
f(xi) = f(x) + (xi-x)f'(x) + -^^^
Умножая на щ и складывая эти неравенства, мы получаем
2 atf (хг) = f (х) + 2 а^-х? Г (£,),
г=1 г=1

§ 16. Средние Mt (х, а) и суммы St(x) 31
а отсюда в силу (4) следует, что
2 <*,/(*,)>/( 2 а,*,), (5)
причем равенство имеет место только тогда, когда все х
равны между собой; см. § 8.
В частности, для функции
f(x) == х log х, х > О,
мы имеем
так что в силу неравенства (5) для положительных
значений (а:) справедливо неравенство
п п п
^]aixi\ogxi>(^]aixi) log(Sa^i); (6)
равенство имеет место только в том случае, когда все хг
равны между собой.
Нетрудно проверить, что
*2 V „ „t dMt(x,a)
2X4
Mt(x,a)£il~* dt
n n n
^^aiXJlogxj—f^aixnlogf^aiXjX
i=l 4i=l y 4i=l y
и неравенство (6), примененное к значениям (х*),
показывает, что
dMt (х, а) п.
равенство имеет место только в том случае, когда все xt
равны между собой.
Таким образом, если не все Xi равны между собой,
то Mt является строго возрастающей функцией от t и ее
график имеет две горизонтальные асимптоты. Можно было
бы в связи с этим предполагать, что график Mt имеет
только одну точку перегиба, т. е. состоит из одной
вогнутой и одной выпуклой части. Оказывается, что это не

32 Гл. I. Основные неравенства и родственные вопросы
всегда так [1], однако легко показать, что t\ogMt{x, а) —
выпуклая функция от t (для этого надо после дифферент
цирования применить неравенство Коши). Следовательно,
в силу (5) функция Mt(x, а) удовлетворяет неравенству
М?<ЦЛ1?Л (7)
г=1
для произвольных tt И
Г=2МЬ «г>0, 2а4 = 1. (8)
г=1 г=1
Сумма порядка t,
г=1
ведет себя как функция от t совсем по-другому. При t7
возрастающем от —сю до 0—, она монотонно убывает от
min(x) до 0, а при t, возрастающем от 0+ до +оо, она
монотонно убывает от со до max(x).
Неравенство
Sb(x)<Sh(x), 0<ti<t2,
иногда называют неравенством Иенсена [2, 3], хотя так
же называют неравенство (5), которое справедливо для
любых непрерывных выпуклых функций, а не только для
функций с положительной второй производной.
Из того факта, что t\ogMt(x, а) является выпуклой
функцией от t, легко следует, что t \ogSt (х) также является
выпуклой функций от t. Поэтому неравенство (7) имеет
место и для S вместо М.
Функция St(x) не обязательно вогнута для £<0 [5];
но она всегда выпукла для t > 0 [4, 5]. Соответственно St
удовлетворяет неравенству
п
i=l
для произвольных tt > 0 и Т и ttj, подчиненных
условиям (8). В действительности имеет место более сильное
утверждение, что logS* является выпуклой функцией от t

§ 17. Неравенства Гёльдера и Минковского S3
для t > О, так что в силу (5) даже
п
i=l
§ 17. Неравенства Гёльдера и Минковского
В силу (14.7)
aW/*<f + ±, (1)
если
|+|=i, p>i,
р я
если р < 1 (рФО).
Если мы здесь положим
Ф
Ь = -у-,
Х = 2*Г,
у^уЬ
г=1
/=1, 2, ..., п, и сложим получающиеся неравенства, то
получим неравенство
справедливое для p > 1, и обратное неравенство для р < 1
(р =£ 0). Равенство имеет место тогда и только тогда, когда
(xv) и (yq) пропорциональны. Таким образом, мы доказали
классическое неравенство Гёльдера [1].
Теорема 2. Если хи Уг>0, l/p+l/q=l, р> 1, то
2*у«<(2^)1Л,(2*?)1/в. (3)
г=1 г=1 г=1

34 Гл. I. Основные неравенства и родственные вопросы
Неравенство заменяется на противоположное, если р < 1
(р ф 0). (Для р < 0 следует предполагать, что хг, yt > 0.)
В каждом из этих случаев равенство имеет место тогда
и только тогда, когда (хр) и (yq) пропорциональны.
Для завершения перечня классических неравенств
приведем еще неравенство Минковского [2].
Теорема 3. Если х%, уг>0, р>\, то
[S(*«+^]1/i,<(S^)1/*+(S^r. (4)
Неравенство заменяется на противоположное, если р < 1
(р Ф 0). (Для р < 0 следует предполагать, что хи yt > 0).
В каждом из этих случаев равенство имеет место тогда
и только тогда, когда (х) и (у) пропорциональны.
Мы сначала дадим очень короткое доказательство этой
теоремы, а ниже, в § 20, выведем неравенство
Минковского при помощи квазилинеаризации.
В правой части равенства
2 (*i + ЫР= 2 xt (xi + yi)p-1+ 2 У. (*. +yty-* (5)
применим к каждой сумме неравенство Гёльдера с
показателями р и q, в результате чего получим неравенство
2(**+ыМ2</р[2(*г+*/0р]1/9+
г=1 г=1 г=1
+(2rf)1*[2(*i+*i)»]l/«.
г=1 г=1
равносильное (4). Неравенство заменяется на
противоположное, если р < 1 (р ф0). Равенство имеет место тогда
и только тогда, когда (хр) и (*/р) пропорциональны ((x-\-y)q),
или, что то же самое, когда пропорциональны (х) и (у).
Неравенство (4) иногда называется «неравенством
треугольника», так как для р==2 оно может быть
геометрически интерпретировано в n-мерном евклидовом
пространстве, где оно означает, что сумма длин двух сторон
треугольника не меньше длины третьей стороны. В этом
случае неравенство имеет место для всех действительных,
не обязательно положительных, значений х%, yt, причем

§ IB. Обобщения классических неравенств 35
условием равенства является положительная
пропорциональность (х) и (у), т. е. существование чисел Х>0
и [х>0, из которых по крайней мере одно отлично от
нуля, таких, что
кХг = \Ху1, 1=1, 2, . .., П.
§ 18. Обобщения классических неравенств
Рассмотренные выше неравенства могут быть обобщены
во многих направлениях. В этом параграфе мы кратко
коснемся некоторых наиболее важных из этих обобщений.
Укажем простое применение математической индукции
к следующим обобщениям неравенств Гёльдера и Минков-
ского.
Если Xtj^O для i=l, 2, ..., п и /=1, 2, ..., т,
т -
и если pj> I, причем 2 — = Ь то
з=1 Pi
п т т п
2.П/у<Д(2^Гг; (1)
г=1 з=1 7=1 г=1 '
равенство имеет место тогда и только тогда, когда т
систем чисел (x?i), (*£§), ..., (*?#) пропорциональны, т. е.
тогда и только тогда, когда существуют числа ^-, не
все одновременно равные нулю, такие, что
т
2 М#=0, 1=1, 2, ..., п.
3=1
Если хи>0 для i=l, 2, ..., п и / = 1, 2, ..., т
и если р> 1, то
n т т гг
[2(2*«)p]1A,<2(2*sr. (2)
г=1 j=l j=l г=1
Змдос неравенства меняется на обратный, если р < 1
(рфО). (Для р < 0 следует предполагать, что xi3- > 0.)
Б каждом из этих случаев равенство имеет место тогда
и только тогда, когда т систем чисел (хц), (xi2), ..., (xim)
пропорциональны (в смысле данного выше определения).

36 Гл. I. Основные неравенства и родственные вопросы
Существуют также обобщения этих неравенств на
кратные и бесконечные суммы. Как уже было, однако, указано
в § 14, при использовании предельных процессов особого
внимания требует формулировка случаев возможного
равенства. Подробнее этот вопрос изложен в [1.1].
Так как предыдущие неравенства «однородны
относительно 2», они имеют аналоги для средних. Таким
аналогом неравенства (1) является неравенство
п т т п vi/x>- т 1
г=1 з=1 з=1 v г~1 п=1 J
В неравенстве (2) также можно в соответствующих местах
вставить множители 1М и 1/т или один из них.
Неравенства, однородные относительно 2» всегда
допускают и интегральные аналоги. Так, неравенства Гёльдера
и Минковского приводят к следующим неравенствам
(неравенство Коши является частным случаем р = 2 дискретного
неравенства Гёльдера; его интегральный аналог называется
неравенством Коши —Шварца, или просто неравенством
Шварца, или неравенством Буняковского —Шварца).
Теорема 4. Пусть f(Р) иg(P) — функции,
определенные в некоторой области R, и пусть dV — элемент объема
этой области. Тогда, если только интегралы в правых
частях приведенных ниже неравенств существуют, то
существуют и интегралы в левых частях соответствующих
неравенств, и эти неравенства имеют место:
I fgdV<(l \f\*dVy/2 (J |£|W)V2 (3)
R R R
(Буняковский—Шварц);
R R R
(Гёльдер); (4)
(Jlf+ffl*^)1A,<(Jlfl'^)1A,+ (Jltfl'^)1
P>U (5)
(Минковский).

§ 18. Обобщения классических неравенств 37
Равенство имеет место в (3), (4) и (5) тогда и только
тогда, когда функции fug положительно пропорциональны
(за исключением множества меры нуль).
Неравенство Минковского может быть еще далее
обобщено заменой сумм в (5) интегралами:
[l\l№[**]1"<l[(l\f №*)**№*, Р>1-
R S S R
(6)
В неравенстве (2) можно также заменить интегралами
только суммы по /. В каждом случае неравенство
заменяется на противоположное, если р<1 (рфО), но при
р < 0 мы должны предположить, что функции нигде не
принимают значения нуль.
Существует несколько путей доказательств таких
интегральных неравенств. Мы можем их вывести как
предельные случаи дискретных неравенств, но можем также
доказать их непосредственно, применяя те же идеи, что и при
доказательстве дискретных аналогов.
Для иллюстрации первого из этих путей наметим
доказательство неравенства
1 1 1
($1/£И*)2<($1ЛМ*)($|£|2^). (7)
О 0 0
Сначала предположим, что f и g непрерывны. Тогда (7)
возникает в пределе при N —> оо из дискретного
неравенства
[2 \f(k/N)g(k/N)\/N]2<
< [ 2 | f (k/N) \VN] [ 2 I g (kIN) \VN], (8)
являющегося просто неравенством Коши (см. § 2).
Чтобы получить (7) в полной общности, используем
тот факт, что интегрируемые по Лебегу функции могут
быть в ZA-норме аппроксимированы многочленами. Ясно,
что этот путь доказательства не очень изящен и может
даже привести к серьезным трудностям, если мы имеем

38 Гл. I. Основные неравенства и родственные вопросы
дело с неравенством, относящимся к кратным интегралам
по области сложной природы.
Продемонстрируем теперь прямой подход к
доказательству неравенства (7) для произвольных областей R. Для
любых действительных и и и мы имеем неравенство
\u\* + \v\2>2\uv\. (9)
Рассматривая и и v как функции от Р и интегрируя
по R, находим, что
J \u\2dV+^ \v\2dV>2l \uv\dV. (10)
R R R
Заменим теперь и на \f\(\\f\2dVj 2 и v— на
R
\g\ (\ \g\i(Wj 2- Тогда из (10) будет следовать, что
R
l\f\2dV l\g\*dV l\fg\dV
что и дает обобщенное на произвольную область R
неравенство (7).
Далеко идущие обобщения неравенства Буняковского —
Шварца можно найти в книги Бохера [1] и в работе Огу-
ра [2]. Геометрические интерпретации, данные Огура для
неравенств в функциональных пространствах, являются
аналогами интерпретаций Бохера в евклидовом
пространстве.
Мы уже отмечали, что вследствие однородности
относительно 2 неравенства Гёльдера и Минковского допускают
аналоги для средних и интегральные аналоги. По той же
причине они допускают интегральные аналоги для средних.
Для этого надо только всюду заменить
J mesR J
R R
Неравенство
Sr(x)>St(x), r<t<0 или 0<r<t,

§ 19. Квазилинеаризация
39
из § 14, относящееся к конечным суммам, неоднородно
относительно 2 и не имеет интегрального аналога. Но
обратное неравенство
Мт (х) < Mt (*), — оо < г < t < со,
между средними, хотя также не является однородным
относительно 2» все же имеет интегральный аналог:
R R
Здесь под М-оо и М<х> мы должны понимать соответственно
существенный минимум и максимум (т. е. точные верхнюю
и нижнюю грани без учета множеств меры нуль), а под
М0—-геометрическое среднее
R
§ 19. Квазилинеаризация
Начнем наше рассмотрение метода квазилинеаризации
с замечания, что дискретный вариант неравенства Гёльдера
для р > 1 может быть сформулирован так:
Теорема 5. Для xt>0, р> 1, мы имеем
представление
(2*?)1/Р-тах2*^, (1)
г=1 Щу) г=1
где R (у) — область, определенная соотношениями
2У?=1, Уг>0. (2)
г=1
Важность этого представления заключается в том, что
мы можем представить нелинейную функцию, стоящую
в левой части неравенства (1), как огибающую линейных
функций. Таким образом, мы можем установить ряд
нетривиальных свойств нелинейной функции как простые
п
следствия тривиальных свойств линейной функции 2 ***/*•
г=1

40 Гл. I. Основные неравенства и родственные вопросы
Более подробное развитие этой идеи будет дано ниже
в § 25 и 26.
Приведем теперь несколько предварительных
соображений о понятии квазилинеаризации.
Пусть для начала L(x, */) — функция двух
переменных х и у, где х и (/ — элементы нормированных пространств,
соответственно R и S. Пусть \\у\\ обозначает норму
элемента y£S; определим новую функцию у(х) от одного
аргумента х соотношением
(р(х)= max L(x, у). (3)
Простые функциональные свойства L (х, у) как функции
от х, имеющие место при любых у, например
положительность, линейность и выпуклость, обусловливают
соответствующие свойства функции ср(х). Во многих случаях эти
свойства гораздо легче обнаружить у L(x, у), чем
непосредственно установить соответствующие свойства для ф(х).
Первым и наиболее важным случаем является тот,
когда функция L (х, у) линейна относительно х при любых
уч т. е. когда
L (axt + Р*2, У) = aL (*i> У) + № (*2, У)- (4)
Отсюда вытекает, что
ф (*i + х2) = max L(xi + x2, у) =
llvll^i
= max [L(xu y) + L(x2l #)]<
llvIKi
< max L(xi, y)+ max L(x2j y) =
llvIKi llvll^i
= <p(*i)-f <p(*2). (5)
Это — «неравенство треугольника» или «субаддитивность»
для ф(я).
Следующим важным случаем, играющим центральную
роль в гл. II, посвященной матрицам (см. также § 35
настоящей главы), является тот, когда
L(*, y)=^e-M(*>y>*)dG(y,z), (6)
R

§ 20. Неравенство Минковского
41
где dG>0, интегрирование производится по некоторой
области пространства z и функция М (х, у, г) линейна
относительно х при любых у и г.
Тогда мы имеем для 0 < X < 1
L (taq + (1 — X) х2, у) = \ е~ш^ у> 2>е-(1-л,)М(х2, у, 2)dQ (у> ^
к
(7)
Применяя неравенство Гель дера с показателями р = 1/Х,
g=l/(l— ^), мы получаем отсюда соотношение
L(^ + (1-^)^2, */)<
= L(*f, урЦхъуу-К (8)
Логарифмируя, мы видим, что logL(A:, у) является
выпуклой функцией от х при любых у.
В § 33 гл. IV мы применим квазилинеаризацию к
дифференциальному уравнению Риккати; в книге Беллмана,
Гликсберга и Гросса [1] даны некоторые приложения
формулы
\х\ = max ху (9)
к неклассическим задачам вариационного исчисления. Метод
квазилинеаризации широко применялся Зигмундом [2] в
теории рядов Фурье.
§ 20. Неравенство Минковского
В качестве первого примера рассуждений этого типа
приведем новое доказательство неравенства Минковского,
доказанного уже в § 17.
Теорема 6. Для хи yt>0, р> 1 мы имеем
[2(хг+^]1/р<(2^)1/р+(2^)1/р. (1)
г=1 г=1 г=1

42 Гл. I. Основные неравенства и родственные вопросы
Доказательство. Так как по неравенству Гёльдера
[1(** + У0р]1/Р = тах2 (*i + yj)2i, (2)
г=1 R(z) i=i
где R (z) — область, определенная соотношением
п
i=i г
мы находим, что
п п п
[ 2 (** + f/0p]1/Р < max 2 ■*%' + max 2 # А <
i=l R(z) i=i R(z) i=i
<(2*ГГ+(2</ГГ,
что и требовалось доказать.
Используя условие равенства в неравенстве Гёльдера,
нетрудно показать, что равенство имеет место в (1) тогда
и только тогда, когда либо р=1, либо (х) и (у)
пропорциональны.
§ 21. Другое неравенство Минковского
Применяя тот же метод квазилинеаризации, установим
еще одно неравенство, которое мы используем в § 34 и 35.
Теорема 7. Для хи */*>0 мы имеем
п п п
[П(*.+у,)Г>(П*.)1/я+(1Ь)1/я. (1)
г=1 г=1 г=1
Доказательство. Неравенство между
арифметическим и геометрическим средними утверждает, что
(П*01м=т1п2^' (2)
где /?(z) теперь обозначает область, определенную
соотношениями
П> = 1. 2*>0' (3)
г=1

§ 22. Неравенство Минковского для О < р < 1 43
Из (2) мы получаем искомое неравенство следующим
образом:
R(z) ffi n R(z) ^ n
Чг=1 У N=1 '
§ 22. Неравенство Минковского для 0<р<1
Вновь используя квазилинеаризацию, установим
следующий результат.
Теорема 8. Если xt, yt>0, 0 < р < 1, то мы имеем
[S(^+^r]1/p>(Sxfr+(S!/f)1/p. (1)
Доказательство. Пусть х% = иУр, у% = v\lv. В этих
обозначениях мы хотим доказать, что
S («,**+*W > KS "*)1/р+(2 ^)1/р]р. (2)
Так как для 0 < р < 1
[(2 «*)1/Р + (2 ^)1/р]р = тах[21(2«г) + ^(|] *,)], (3)
i=l г=1 £(z) г=1 г=1
где функция /? (z) определена соотношениями z\ + z\ = 1,
Zi, z2>0, а 9=1/(1—р), то
[(S ^)1/P+(S vi)^Y = m^[fi(z1ui + z2vi)}<
i=i г=\ R(z) i=i
< 2 max (гы + z2vt) < 2 {u}'* + v^f,
i=i R(z) i=i
что и требовалось доказать.

44 Гл. I. Основные неравенства и родственные вопросы
§ 23. Неравенство Беккенбаха
Докажем теперь следующий результат [1J.
Теорема 9. Пусть 1 < р < 2 и xt, уг>0 для i = 1,
2, ..., п. Тогда
S(**+s/op 2 Ч 2 ^
-^ <-^—+-^—. (1)
г=1 г=1 г=1
Доказательство. Для р = 1 неравенство
тривиально. Для р> 1 мы имеем, как в § 19, представление
(S*f)1/P = maxS^. (2)
г=1 R(z) i=l
Поэтому достаточно показать, что
<^ +-^ (3)
i=l i=l i=l
для всех Zj>0 (напомним, что здесь R (z) — область, опре-
деленная соотношениями 2 г? = 1, z$ > 0).
г=1
Для упрощения встречающихся в (3) выражений положим
(2*i*i)p (2НР
*Р™ • УР = ^ ■ (4)
2 *гг 2 уГ1
г=1 г=1
Находя отсюда суммы 2 xtzt и 2 У&г и подставляя все
г=1 г=1
это в искомое неравенство (3), мы придадим ему следую-

§ 24. Неравенство Дрешера
45
щую эквивалентную форму:
[*(2*Г1)1/Р+^(|^Г1)1/Р]Р
—^ ^ <х* + у>. (5)
г=1
Чтобы доказать справедливость неравенства (5),
применим неравенство Гёльдера для р > 1 к числителю левой
части, что даст
W2xr)1/p+HSf/r)1/p]p<
<(^+^)Ks^r^-^+ciir)*-11]^1. (6)
Таким образом, (5) имеет место, если имеет место
неравенство
(2 лГх)1/(р-о+(| yf-1)i/(P-i)< [I (^+^ri]i/<p-i>.
i=l i=l i=l
(7)
Но это — неравенство Минковского, справедливое для
О < р— 1 < 1, т. е. для 1 <р<2. Для р = 2 неравенство
(7) тривиально.
Для 0<р<1 знак неравенства в (1) должен быть
изменен на обратный.
§ 24. Неравенство Дрешера
Неравенство Беккенбаха было обобщено Дрешером [1],
который использовал для его доказательства метод
моментов.
Теорема 10. Если р>1>г>0, /, g>0, то
4l/+S|r*P/ < \Jf*P/ + [ iTd^l
(1)

46 Гл. 1. Основные неравенства и родственные вопросы
Этот результат может быть получен и квазилинеаризацией,
способом, аналогичным изложенному в § 23. Неравенство
(1) было также доказано Данскином [2], который применил
комбинацию неравенств Гёльдера и Минковского.
§ 25* Неравенство Минковского — Малера
Метод вывода неравенств, который мы применяли
в предыдущих § 19 — 24, основан на одной идее
Минковского [1]. Пусть F(x) — F(Xi, х2, ... , хп) — функция,
обладающая следующими свойствами:
(а) F(x)>0 для хфО,
(б) F(tx) = tF(x) для *>0,
(в) F(x) + F(y)>F(x + y).
(1)
Ясно, что F (х) является обобщенным расстоянием (от
начала координат), или обобщенной нормой n-мерного
вектора х\ см. § 2.
Если дана функция с указанными выше свойствами,
то мы можем ввести новую функцию G(y), называемую
полярной функцией, определенную соотношением
G(y) = max&$. (2)
В теории выпуклых тел (см. Боннесен и Фенхель [8.1])
G(y) называется «опорной функцией». Она Геометрически
определяется при помощи преобразования обратных поляр
относительно сферы (#, х) = 1. На этом основании можно
сделать предположение, что должно иметь место
двойственное соотношение
F(x) = max^-. (3)
Оно действительно было доказано Минковским [8.1,
стр. 24]. Отсюда вытекает, что
(х, y)<F(x)G(y). (4)
Это неравенство было, по-видимому, впервые явно указано
Малером [2] в геометрической теории чисел.

§ 26. Квазилинеаризация выпуклых и вогнутых функций 47
Некоторые интересные обобщения соотношения полюс—
поляра были рассмотрены Л. Юнгом [3], которому мы
следовали выше; см. также работу Фенхеля [4], которая
содержит другие литературные указания.
Подробно этот круг идей изложен Лорхом [5, 6, 7,
8.2], где можно найти много интересных результатов,
раскрывающих тесную связь между неравенствами,
выпуклостью и понятием «смешанного объема» Минковского.
Эти вопросы мы рассмотрим в нашем втором томе.
§ 26. Квазилинеаризация выпуклых и вогнутых функций
Представление F(x) в форме (25.3) содержит
квазилинеаризацию, которая была применена Л. Юнгом [25.3]
таким же образом, как это изложено выше в § 19 — 24.
Рассмотрим теперь квазилинеаризацию, которую можно
применить к выпуклым и вогнутым функциям и
функционалам, не являющимся обязательно однородными. Начнем
с одномерного случая. Пусть f(u) — строго выпуклая
функция от и для всех и в том смысле, что f" (и) > 0. Тогда
легко видеть, что
f(u) = max[f(v) + (u-v)f'(v)) (1)
v
и что единственный максимум достигается при v = u.
Точно так же, для строго вогнутой функции мы имеем
f(u) = min[f(v) + (u-v)f'(v)]. (2)
v
Общим результатом является следующий.
Теорема 11. Пусть f(x) = f(xi4 х2, ..., хп) — строго
выпуклая функция от х для всех х\ тогда
f(x) = max[f(y) + (x-y, <р(у))], (3)
У
где y(y) = (df/dy1, df/dy2, ..., df/dyn) —градиент f(y).
Единственный максимум достигается при у = х.
Этот тип квазилинеаризации широко применялся Белл-
маном [1, 2] и Калаба [3] в связи с аналитическим
исследованием функциональных уравнений и
приближенными методами их решений.

48 Гл. I. Основные неравенства и родственные вопросы
§ 27. Другой тип квазилинеаризации
Квазилинеаризация с применением случайных
переменных была использована Зигмундом [1] и Зигмундом и Мар-
цинкевичем [2]. В [2] они доказывают следующий результат.
Теорема 12. Пусть S = {ft} — линейное семейство
функций, принадлежащих Lp(a,b), р > О, и пусть Т —
линейное преобразование, обладающее тем свойством, что
Tft^LP(a,b) для каждого I. Если при этом существует
постоянная т, такая, что для всех i
ь ъ
l\Tfi\vdx<m^\fi\vdx, (1)
а а
то
5(2(Ш0Р/2^<Ч(2ЮР/2^ &
а а
для любой системы функций ft из S.
Соответствующий результат для вариаций приведен
в [1].
§ 28. Неравенство Карамата
В качестве примера представления функции из
теоремы И мы докажем один результат, принадлежащий
Островскому [1] и являющийся обобщением следующей теоремы
Карамата [2].
Теорема 13. Пусть даны 2п чисел {#&, у и}, k=l,
2, ..., п, удовлетворяющие условиям
(а) Xi>x2> ... >хп, yi>y2> ... >Уп,
(б) *!>*/!, |
Xi + Х2 > У\ + У2ч I /i\
Тогда для любой непрерывной выпуклой функции ф(л;)
имеем неравенство
<P(*i) + Ф(*г) +.. • + ф(*п) > фО/О + фЫ+ ... +фЫ- (2)

§ 30. Доказательство неравенства Карамата 49
Хотя условия теоремы кажутся весьма искусственными,
оказывается, что неравенства этого вида возникают во
многих самых разнообразных вопросах [3].
Доказательство теоремы 13 дано в § 30.
§ 29. Преобразование Шура
Теорема предыдущего параграфа была доказана
Карамата на основе следующей теоремы, представляющей
самостоятельный интерес.
Теорема 14. Необходимыми достаточным условием
для того, чтобы 2п чисел {хь, Уи) удовлетворяли
неравенствам (28.1), является наличие следующих
соотношений между ними:
п
Ук= 2 аыхи k=l, 2, ..., /г, (1)
где
а) аы>0, \
п I
б) 2aAi = L I /о.
П I
в) S 0ftz = l.
fe=l J
Преобразования типа (1) были впервые рассмотрены
Шуром [1]; следуя Островскому [28.1], мы будем
называть их преобразованиями Шура. В последнее время
матрицы (ам) с элементами, удовлетворяющими
условиям (2), называют двояко стохастическими. Они играют
важную роль в некоторых комбинаторных задачах; см.
Биркгоф [2]. Доказательство теоремы 14 можно найти
в книге Харди, Литтлвуда и Пойа [1.1], более простое
доказательство — у Островского [28.1]; см. также Шрей-
бер [3], Мирский [4], Райзер [5], Шур [1] и Фукс [31.1].
§ 30. Доказательство неравенства Карамата
Покажем теперь, как квазилинеаризация может быть
использована для доказательства теоремы 13. Нашим

50 Гл. I. Основные неравенства и родственные вопросы
исходным пунктом является представление
Ф (xi) + Ф Ы + . • . + ф (Хп) =
п п
= max[S ф(2|)+ S (xt-ZiWfa)] , (1)
z i=i i=l
причем мы пока предположим, что ф(г) строго выпукла.
Так как максимум достигается при z% = xt, a Xi>x2> ...
• -.>хп, мы можем ограничить область изменения (z)
неравенствами
Zi>z2> ...>гп. (2)
Чтобы доказать искомое неравенство, мы должны
показать, что для всех {хи, Ун}, удовлетворяющих условиям
(28.1), и для всех zu удовлетворяющих (2), имеет место
неравенство
xicp'(zi) + x2cp'(z2) + ... + xnq>'(zn)>
> УМ'Ы + Угф'Ы + • • - + УпЧ'(гп). (3)
Это неравенство, однако, непосредственно получается
суммированием по частям (формула Абеля —Бруначчи):
xiy'(zi) + x2q)'(z2)+ .. . + xny'(zn) =
= St №l) — ф'(%)1 + S2 [ф'(*2> — ф'(2з)] + • • • +
+ Sn-i to'(Zn-i) — ф'Ы 1 + snq>'(zn), (4)
где Sk = xi + x2+ ... +Хц. Так как cp"(z) > 0, мы видим,
что y'iZkXy'iZk-i). А так как, кроме того, Sk(x)>Sk(y),
k=l, 2, ..., п— 1, sn(x) = s„(y), то неравенство (3)
действительно должно иметь место.
§ 31. Неравенство Островского
Чтобы установить соответствующее неравенство для
более общего класса функций, рассмотрим функцию
F(Xi, х2,.. ,,хп), строго выпуклую, так что
Г (#1, Х2, . . . ,Хп) =
= imx[F(z1>22,...fz7l) + 2(^ —2|)^]. (1)

§ 32. Континуальные аналоги
51
Мы вновь можем считать, что максимум берется по области
Zi>z2> ... >Zn, (2)
так как мы заинтересованы только в таких значениях Хи
которые упорядочены подобным же образом. Рассуждения
предыдущего параграфа пройдут здесь только при
выполнении некоторых условий на dF/dzt. В частности,
целесообразно потребовать, чтобы
если Zt>Zj. Это естественное обобщение условия ф'(^г)>
><р/(2/) для zt>Zj. Если F удовлетворяет
сформулированному условию, то мы говорим, что F удовлетворяет
условию Шура; см. Островский [28.1] и Шур [29.1].
Легко видеть, что при этом условии доказательство
предыдущего параграфа проходит полностью, и мы можем
сформулировать следующую теорему.
Теорема 15. Если F удовлетворяет условию Шура
и {*и Уг} удовлетворяют условиям (28.1), то
F{xu х2,..., Хп) > F{yu у2,..., уп). (4)
Интересное доказательство этой теоремы,
использующее совершенно другую идею, дано Л. Фуксом [1].
Близкие результаты принадлежат Татаркевичу и Бисаку, см.
Бисак [4]. См. также Харди, Литтлвуд и Пойа [2] и Ру-
дерман [3].
§ 32. Континуальные аналоги
Континуальные аналоги теорем §§28 — 31 были получены
Фанем и Лоренцом [1]. Будем писать
f<g, (1)
если
X х
lf(t)dt<^g(t)dt, 0<а:<1 (2)
о о

52 Гл. I. Основные неравенства и родственные вопросы
1 1
lf(t)dt=lg(t)dt. (3)
О О
В цитированной выше работе [1] приводятся необходимые
и достаточные условия на функцию ф(£, щ, иг, ..., ип),
при которых
1 1
J Ф С AJ2, ... Jn) Л< J 4>C ft, ft* ...,gn)dt (4)
о о
для любой системы убывающих ограниченных функций ft
и gt, удовлетворяющих соотношениям ft -< gj, / = 1, 2,..., п.
§ 33. Симметрические функции
Перейдем теперь к некоторым интересным неравенствам
Маркуса и Лопеса [1]. Пусть xi9 х2> ... , хп —
неотрицательные числа; обозначим через Ег (х) r-ю элементарную
симметрическую функцию, образованную для этих чисел,
г= 1, 2, ..., п, т. е.
Ei(x)=xi + x2 + . ..+**, )
Е2 \Х) = 2j XiXji
гфз
hn \х) —Х\Х2 ... хп.
О)
Положим еще Е0 (я) = 1. Наконец, будем писать (х) ~ (у),
если существует число Я, такое, что
Xi = tyu / = 1, 2, ..., п. (2)
Первое утверждение, которое мы докажем, состоит
в следующем.
Теорема 16. Для г = 1, 2, ... , п, xt, уг > О
имеет место неравенство
Ег(х + У) ^ £г(*) , Ег(у) /оч

§ 33. Симметрические функции
53
если не все Хг и не все у-г равны нулю. Равенство имеет
место, если либо г = 1, либо (х) ~ (у) и по крайней мере г
чисел Xt и г чисел yt положительны.
Доказательство. Для г = 2 неравенство вытекает
из тождества
п п п
Е2(х+у) Е2(х) Е2(у) i=i 3=1 j=i r4v
Ei(x+y) E±(x) Ei (у) 2E1(x + y)Ei(x)E2(y) ' ™
Допустим теперь, что r>2 и что (x)<*f->(y). Обозначим
через (х'3) систему чисел хи х2, ..., xj-i, Xj+U ..., хп.
Мы имеем следующие два тождества:
(5)
2j Xi Er-i(Xi) — rEr(x),
i=l
XiEr-iixl) + Er{x\) = Er(x).
Суммируя второе из них по /, получаем
п п
пЕг{х) = 2 xtEr-i(Xi) + 2 Er(xi), (6)
i=l i=l
откуда в силу первого из них следует, что
%Ег(х$ = (п-г)Ег(х). (7)
г=1
Так как
Er(x) — Er(xi) = XiEr-i (х\) = XiEr-^x) —x-Er-2 (х\), (8)
мы находим соотношение
п п
гЕг(х) = 2 хгЕг-±(х) — 2 х*ЕГ-2(х\), (9)
г=1 г=1
ИЛИ
1 Г П П X? "I
=y 1-(§^"(§ ^+£mW)/^w) J' (10)

54 Гл. I. Основные неравенства и родственные вопросы
Отсюда вытекает, что для г=1, 2, ..., п и для всех х
мы имеем тождество
H(y /Л — Ег(х+У) Ег(х) Ег (у) _
а{х,У) - Er_i(x+y) Er_i(x) Ет_Лу) -
1 п ,- 2 2
= lv х'1 1 ^
(**+У*)2 "1 /11ч
где Fr(x) = JEr(x)/JEP_i(x).
Допустим теперь, что утверждение теоремы
справедливо для г—1, т. е., в частности, что
Fr-iixi + yi) > Fr-i(Xi)+FT-t(tii), (12)
если только не имеет места соотношение (xi) — (yi), когда
в (12) стоит знак равенства. Тогда при (xi)rj^(yi) для
некоторого /
1 п г 2 2
(^+w)!
,2
*i+#i+/V-i(**') + f,
-l(tf) J >
1 ^ [xifr-i(gi)-W^r-lW)l*
»'£'1[*| + ',r-iW)]IW + fr-i(«f)n** + W+^-i(«/) + ',r-i(w')] •
(13)
Таким образом, искомое неравенство справедливо
и для г, если только (xi) qP (yi) для некоторого i. Если же
(xi) — (yi) для каждого i, то это означает, что (xi) = Я^ (у*)
для каждого i, и тогда
[xifr-i^n-W^r-i W)]2 = (Xi-hyifFKiiyi). (14)
Но Fr-i(y'i) Ф О, так как по условию по крайней мере г
чисел yt положительны. Поэтому, хотя при (x'i) = Xi(yi)
первое неравенство (13) должно быть заменено равенством,
из (14) вытекает, что средний член (13) положителен при

§ 35. Некоторые результаты Уайтли
55
условии (х) г^ (у), так как из этого условия и (х[) — (yi)
для каждого i следует, что равенство xi = %\yi невозможно
при всех i.
§ 34. Еще одно неравенство
Еще одним результатом, относящимся к симметрическим
функциям, является следующий.
Теорема 17. Если {х} и {у} —системы, содержащие
по п положительных переменных, то
[Er(x + y)]i/r> [Er(x)]i/r + [Er(y)]i/r, г =1,2,..., п. (1)
Более сильный результат с исследованием случаев
равенства содержится в цитированной выше работе Лопеса
и Маркуса [33.1]. Мы ограничимся сформулированной
теоремой.
Доказательство основывается на комбинации теорем 7
и 16. По этим теоремам
1Ьг(Х + у)] ~lEr_l{x + y) Ег-2(х+у) ••• Г—J >
(Г Ет(х) . Ег(у) И Г£г-1(*) . fi-iMl
* \ L Яг-! (х) ^ £Г_А (у) J L Яг-2 (х) -I" Ег_2 (у)] • • •
+ [ Д jgfgy] '" = IE, Wlw+ 1ЕР to)!1". (2)
i=i
§ 35. Некоторые результаты Уайтли
Аналогичные и более далеко идущие результаты были
получены Уайтли [1.2]. Пусть
2 Т(п)(а) f
п=0
Д {l+a3t)k, если k>0,
5=1
П (1—fl;Oh. если £<°> ^
5=1

56 Гл. I Основные неравенства и родственные вопросы
где dj положительны. Тогда для k < 0 имеет место
неравенство
[T{n)(a + b)]i/n< [Tin\a)]i/n+ [7(n)(6)]1/n, (2)
а для &> 0 — неравенство теоремы 17.
Новый результат (2) легко получается методом
интегральных представлений, который мы разработаем глубже
в следующей главе. Для малых \t\ и k > 0 имеем
со
—ь =4гЛе~Н1 _а'V-1 ds, (3)
откуда
xJl s^dSidsz ... dsm. (4)
Следовательно,
со со m
т(п)и=шг -ш I • • • К 2 s^)" ф(8) ds' (5)
о о J^1
где
771
<p(s) ds = e *=1 Д s^-1 ds± ds2 ... dsm. (6)
Неравенство (2) является теперь следствием неравенства
Минковского.
§ 36. Гиперболические многочлены
Рассмотрим теперь важное понятие, введенное Гордин-
гом [1], а именно понятие гиперболического многочлена.
Пусть Р(хи х2, ..., хп) — однородный многочлен степени т
относительно хи и пусть а = {аи а2, ..., ап) — система

§ 37. Неравенство Гординга
57
действительных чисел. Если уравнение относительно s
Р(sa-{-x) = P(scii + Xi, sa2 + x2, ..., san + xn) = 0
имеет m действительных корней для всех
действительных xt, мы говорим, что Р(х) — гиперболический
многочлен относительно а. Эквивалентным определением является
следующее:
т
P(sa + x)=P(a) П [s + M*.*)]. (1)
где Р(а)фО и Я^(а,л:) действительны при
действительных х.
Как мы увидим, это понятие имеет непосредственное
отношение к ряду результатов настоящей главы, а также
играет важную роль в теоремах теории матриц, которые
мы рассмотрим в следующей главе; см. § 45 гл. II.
Исходя из одного гиперболического многочлена, мы
можем образовывать новые гиперболические многочлены
при помощи следующей леммы.
Лемма 2. Если многочлен Р(х) гиперболический
относительно а и m > 1, то многочлен
Q(x) = %°i£P(x) (2)
i=i OXl
также гиперболический относительно а.
Доказательство вытекает из теоремы Ролля, как в § 12.
Повторное применение этой леммы показывает, что
многочлены {Pk(x)}, определенные равенством
т
P(sa-+x)= S shPh(x), (3)
также гиперболические.
§ 37. Неравенство Гординга
Пусть М(хг, х2, ..., хт), где х1 представляет собой
я-мерный вектор хг = (х\, х\, ..., х]г), — полная полярная

58 Гл. I. Основные неравенства и родственные вопросы
форма многочлена Р(х):
1 т s п Л \
м(Х\ х\ ..., *m)=in(2*^>(A с1)
Теорема 18. Пусть многочлен Р(х) гиперболический
относительно а, Р(а) > О, т > 1, и пусть М — полная
полярная форма Р. Пусть, далее, x = (xi, х2, ..., хп) —
система таких хи что P(ta-\~x) ФО для t>0. Тогда
М(х\ х\ ..., xm)>{P(x')]i/m... [P(xm)]i/m. (2)
Так как доказательство этой теоремы с рассмотрением
случаев равенства требует подробного изложения, то мы
отсылаем читателя к работе Гординга [36.1].
§ 38. Примеры гиперболических многочленов
Двумя интересными примерами являются многочлен
P(x) = xl-xl-...-xl, (1)
гиперболический относительно а, если Р(а) > 0 (эту
квадратичную форму мы рассмотрим в § 39), и многочлен
Р{х) = х±х% ... хп, (2)
гиперболический относительно а, если Р (а) Ф 0. Так как
для функции (2) мы имеем соотношение
P(sa + x)=j]s^Ej(x) (3)
при а = (1, 1, ..., 1), то Ej(x) —элементарные
симметрические функции — гиперболические относительно (1,1,...,1).
Гординг заметил, что если многочлен Р(х)
гиперболический относительно а, то гиперповерхности Р(х) = с выпуклы
в области х, состоящей из тех хи для которых Р^а + х) Ф 0
при t > 0. Отсюда могут быть выведены некоторые
результаты § 33, 34.
Дальнейшие примеры приведены в гл. II в связи
с положительно определенными матрицами, и в гл. III
в связи с матрицами, введенными Лаксом. Некоторые
приложения неравенства Гординга в дифференциальной
геометрии даны Цзянем [2] и Гордингом [1].

§ 39. Пространства Лоренца
59
(2)
§ 39. Пространства Лоренца
В гл. II мы будем заниматься исключительно
положительно определенными формами. Покажем здесь, как могут
быть получены некоторые результаты для неопределенных
форм. Мы докажем следующую теорему.
Теорема 19. Пусть
ф(*) = (хГ-<-...-^)1/г\ р>1, (1)
для Xt из области R, определенной соотношениями
(a) xt>0,
(б)х1>« + ^+...+^)1/Р.
Тогда для x,y£R
ф(*+у)>ф(*)+ф(*/). (3)
Доказательство. Мы применим метод
квазилинеаризации, разъясненный выше. Покажем, что
п
<р(х) = тт^]хг2г, (4)
S(z) i=i
где S(z)— область, определенная соотношениями
(a) zt> 1, Zi>0,
(6)z«+...+z*<z?-l, Я = фгу
Применяя неравенство Гель дера, получаем
п п п
>ад-(^)1/рЙ-1)1/'. (6)
fe=2
Минимум последнего выражения как функции от zi в силу
условий (2) и (5) достигается в точке, где
п
1/4-1
(5)
*i=(S4r2j-!(2«-i)
h=2

60 Гл. I. Основные неравенства и родственные вопросы
и равен ф(х). Отсюда вытекает представление (4). Из этого
представления непосредственно вытекает теорема.
Приведенное доказательство принадлежит Беллману [1].
Дальнейшие замечания о неравенствах такого вида при
р = 2 можно найти у Мурнагана [2].
Эти результаты можно получить и другим путем,
используя представление, принадлежащее Бохнеру [3].
Они будут рассмотрены в гл. II, § 15 и 16.
Квадратичная форма х\-\-х\ +х\ —х\ играет
существенную роль в теории относительности (см. Синдж [4]).
Интересно отметить, что неравенство (3) участвует в
знаменитом «парадоксе близнецов».
Интерпретация этих неравенств с точки зрения
неевклидовой геометрии содержится в работе Ацела и Варги [5].
§ 40. Обратные неравенства
В предыдущих §§ 17, 18 мы рассмотрели неравенство
Буняковского — Шварца и его обобщение — неравенство
Гель дера. Ясно, что неравенство вида
(A uvdx)>k{\ u2dxY\^ v2dx) (1)
о оо
не может иметь места ни при какой положительной
абсолютной постоянной k для всех и и v из L2(0,1). Однако
такое неравенство имеет место, если и и v принадлежат
некоторым подпространствам L2(0,1).
Такие задачи рассматривались Франком и Пиком [1],
Бляшке и Пиком [2], Бюкнером [3] (см. Харди, Литтлвуд
и Пойа [1.1]), Фаваром [4], Бервальдом [5], Кнезером [6]
и Беллманом [7]. Хотя эти задачи допускают
систематическое рассмотрение методами теории моментов и теории
выпуклых множеств (см. Дрешер [24.1]) и могут быть
значительно обобщены методами Фавара и Бервальда,
мы следуем здесь изложению Беллмана [7], позволяющему
получить обобщения в другом направлении за счет
меньшей точности результатов.
Наш первый результат состоит в следующем.

§ 40. Обратные неравенства
61
Теорема 20. Пусть и(х) и v(x) — вогнутые
функции от х для 0 < х < 1, нормированные условиями
(а) \ иг{х) dx=l, [ v2(x) dx=\,
о о
(б)и(0) = и(1) = 0,
(в) о(0) = о(1) = 0.
(2)
Тогда
1
\u(x)v(x)dx>-^.
Минимальное значение 1/2 достигается для
и(х) = х}/3, 0<*<1, и(1) = 0,
v(x) = (l—x)Y3, 0<*<1, и(0) = 0.
(3)
(4)
Доказательство. Пусть и(х) принадлежит классу
функций, определенных и вогнутых для 0<л:<1 и равных
нулю на концах этого отрезка. Рассмотрим подкласс
функций, имеющих неположительную вторую производную:
tf(x)=-f(x), f(x)>0,
w(0) = w(l) = 0.
(5)
Минимизация по всем функциям более широкого класса
эквивалентна определению точной нижней грани по
классу функций, удовлетворяющих (5).
Пусть К(х,у) — функция Грина для оператора и"
с указанными в (5) граничными условиями, а именно
К(х,у) =
х(1—у), 0<*<у<1,
(1— х)у, 1>х>у>0.
Тогда и(х) можно представить в виде
1
u(x)=^K(x,y)f(y)dy.
(6)
(7)

62 Гл. I. Основные нёраёендтва и родственные вопросы
Используя это представление, определим минимум
линейного функционала
1
L (и) = \ и (х) h (х) dx
(8)
по всем вогнутым функциям и(х) с указанной
нормировкой, где h (х) — данная неотрицательная функция. Имеем
1 1
L(u)=^h(x)[^K(x,y)f(y)dy]dx =
= \f{y)[\h{x)K{x,y)dx~\dy, (9)
и мы должны определить точную нижнюю грань по всем
f(y)>0, для которых
1 11
lu*dx=^K2(y,z)f(y)f(z)dydz=l, (10)
00
где
1
К2{У,z) = § К(х,у)К{х,z)dx.
(И)
Рассуждая по аналогии с конечномерным случаем,
легко видеть, что точная нижняя грань по />0, т. е.
точная нижняя грань по и, дается формулой
\K(x,y)h(x)dx
minL(w) = min
УШ^У)
(12)
Доказательство этого утверждения мы здесь не
приводим, так как в § 41 мы проведем его в общем случае
для /Л
Из этого результата сразу вытекает теорема 20. Мы имеем
г*1
\ и (х) v (х) dx > min
«? У
^К(х,у) v(x)dx
(13)

§ 41 Пространство L
63
Применяя то же неравенство, но на этот раз для
неотрицательной функции К(х,у) и вогнутой функции v (х), мы
получаем окончательный результат в виде
I
\u(x)v(x)dx>mm\
е) У I
mm
lK(x,y)K(x,z)dx
j)
(14)
Остается показать, что это неравенство не тривиально.
Прямое вычисление, произведенное Гроссом,
обнаруживает, что минимум достигается при j/=l, z = 0 и в
симметричной точке у = 0, z=l, и равен 1/2. Экстремальные
функции были уже приведены выше.
§ 41. Пространство Lv
Докажем теперь //-обобщение теоремы 20; см. [40.7].
Излагаемое нами доказательство принадлежит Вейнбергеру.
Теорема 21. Пусть и{х) и v(х) — вогнутые
функции, нормированные условиями
1 1 \
(а) ^[u(x)]pdx=l, ^[v(x)]qdx=l, оо>р>1,
о о | (1)
(б) н(0) = г;(0) = 0, u(l) = v(l) = 0. )
Тогда
1
\ и (х) v (х)
dx>
(P+l)1/p(<7+l)1/q
(2)
Заметим, что максимум правой части достигается при
p = q = 2.
Доказательство. Как и выше, положим
1
и(х)= \K(x,y)ui(y)dy,
v(x)= ^K{x,y)vl(y)dy.
(3)

64 Гл. I. Основные неравенства и родственные вопросы
Тогда
1
Vи(х)v(x)dx=\\\ К(х,у)К(х,г)щ(у) v±(z)dxdy dz >
о
> [min k{y, z)\H{llK(x,y)]pdxyPx
x{[[K(x,z)]qdx\ Qui(y)vi(z)dydz, (4)
где
Ы w lK(x,y)K(x,z)dx
(У' Z) {llK(x, ytfdxy* { $[*(*, z)fdx}U« • W
Все интегралы берутся в пределах от 0 до 1. Применяя
неравенство Гёльдера, найдем, что
1
о
= I ui(y){lK(x9y)lu(x)]^1dx}dy<
= l4te){lmx,y)]pdx}i/Pdy. (6)
Аналогично
1 < I fi(z){J[/C(Jc,z)]« dx}1/Qdz. (7)
Неравенства (6) и (7) в сочетании с (4) показывают, что
1
\ и(х) v(x) dx > min k(y, z). (8)
0
Непосредственное вычисление, также произведенное
Гроссом, приводит к выражению в правой части (2).

§ 43. Обобщения Фавара — Бервальда
65
§ 42. Многомерный случай
Рассуждениями, аналогичными приведенным в § 40, 41,
можно доказать следующий общий результат.
Теорема 22. Пусть v(P) и и(Р) определены для
точек Р, принадлежащих некоторой области R, и
удовлетворяют трем следующим условиям:
(а) А и, Ду<0, Pg/?,
(б) и, v = 0 на 5, границе /?,
(в) ^u2dV=^v2dV=l.
R R
Пусть /С(Р, Q) —функция Грина для области R и
К2 (Р, Q) = IК (Р, Р') К (Р', Q) dV\ (2)
(1)
Тогда
uvdV> min К*{Р>®_=. (3)
Установить, что этот результат нетривиален (т. е.
что правая часть неравенства положительна),
по-видимому, не очень просто. Столь же непростой представляется
задача определения этого минимума для различных типов
областей.
§ 43. Обобщения Фавара—Бервальда
Далеко идущие обобщения результата Франка —Пика
из § 40 могут быть получены как частные случаи
неравенств, принадлежащих Фавару [40.4] и Бервальду [40.5].
Фавару принадлежит следующая
Теорема 23. Пусть f(x) —неотрицательная
непрерывная вогнутая функция на [а, Ь], отличная от
тождественного нуля. Положим
ь

66 Гл. f. Основные неравенства и родственные вопросы
Пусть т (у) — ограниченная неубывающая функция для
0<#<2/ и
у
^{y)=\m{t)dt, 0<*/<2/.
Тогда
2/
jf \ Ш*У>~ь=е\ *(/(*))dx. (2)
'О а
Фавар доказал соответствующие теоремы для
функций нескольких переменных, и указал также условия
равенства в (2). Обобщением теоремы 23 является
следующая теорема Бервальда [40.5].
Теорема 24. Пусть f(x) — неотрицательная
непрерывная вогнутая функция, не равная тождественно
нулю, на [а, Ь]. Пусть Ц)(у) строго монотонна и
непрерывна для 0<г/<У(ь где у0 достаточно велико. Тогда
уравнение
г Ъ
i\<P(y)dy=b=nl<t(n*))dx (3)
0 а
имеет в точности один положительный корень z = z.
Пусть т(у) ограничена и монотонна для 0<у<г;
положим
У
Ш=\т(*)<1чУ) (4)
о
(интеграл Стильтьеса). Тогда
z Ъ
j\^(y)dy>^=z\^(f(x))dx, (5)
0 а
если Ц)(у) и т(у) монотонны в одном и том же смысле, и
z ъ
j\№dy<bi=zlMf(x))dx, (6)

§ 43. Обобщения Фавара — Бервальда 6?
если эти функции монотонны в противоположных
смыслах.
Бервальд определил также возможные случаи равенства.
В качестве первого приложения теоремы 24 возьмем
Ф (У) = Уа> т {у) = Pf/e-°/a, q(y) = tfi, 0 < a < p. (7)
Тогда
z z
0 0
где
a
Тогда из неравенства (5) мы находим, что
a a
При a = 1, р = 2 получаем неравенство Франка — Пика,
тогда как при а=1, [3 = р> 1 — неравенство Фавара:
^limfdx^i^mdxj. (id
a a
Другими частными случаями являются следующие
неравенства:
ь
j\\ f(x)dx>± max f(x) (12)
a
И
1 b
"bZ^ J log/(*)(?»: b
a
принадлежащие соответственно Фавару и Бервальду. Оба
последних неравенства справедливы в предположениях
относительно /(*), сформулированных выше.

68 Гл. /. Основные неравенства и родственные вопросы
В цитированных работах Фавара и Бервальда
содержится много других результатов, включая обобщения
на многомерные случаи.
§ 44. Другие обращения теоремы Коши
В §40 — 43 мы рассмотрели один тип обращения
неравенства Коши. Сформулируем теперь другое
обращение этого неравенства, данное Швейцером и Пойа —Сегё
[1], где можно найти его доказательство.
Теорема 25. Если 0<m1<Xf<M1, 0<m2<#i<M2, то
(2d)(2rf)
(2*#*)а
Г MjM2 V/2 /" mtma Л
V ^1^2 /__\ M1M2 У
mlm2 Л^2
(i)
Имеет место также соответствующий континуальный
аналог.
Как было показано Дрешером [24.1], классические
неравенства Коши и Гёльдера вместе с их уточнениями
могут быть получены как следствия теорем теории
моментов методами, которые мы будем рассматривать в гл. III.
Теорема 25 относится к этому же типу и может быть
так же доказана. Обобщения на многомерный случай были
даны Маданским [2].
Неравенство (1) было улучшено Уотсоном [3],
доказательство было дано Касселсом (см. также Грейб и Рейн-
больдт [4]):
Теорема 26. Пусть хг,уг>0, Wt>0, /=1,2,...
..., п, но не все т% равны нулю. Тогда
(2*Я-)(2^0 , . ч2
к i=i п i=1—<™*(Xi!Lt^ • (2)
%=i
Еще один результат в этом направлении принадлежит
Фань Цзы и Тодду [5].

§ 45. Уточнения неравенств Коши — Буняковского — Шварца 69
Теорема 27. Пусть а-г, Ъ^ i = 1, 2, ..., п —
действительные числа, для которых аф^ — а^Ь^Ф^ (I Ф /). Тогда
(S/lM
i=l
{%\){%t)-{%ibi)
г=1 i=l i=l
Это неравенство является обобщением более раннего
результата Хассана [6].
§ 45. Уточнения неравенств
Коши—Буняковского—Шварца
Установив неотрицательность функционала
1 1 1
I(u,v)= (\ u2dt)(^ v2dt) - Q uvdtj, (1)
0 0 о
мы, естественно, заинтересованы в получении более
точной нижней границы для него, чем нуль. Мы можем
это сделать, если только рассматриваемые функции или
функционалы квадратичны в следующем смысле.
Применив понятие скалярного произведения,
рассмотрим функционал
J (и, v) = {и, и) (v, v) — (и, v)2, (2)
который будем считать неотрицательным для всех и и v.
Заменим и на rf + sg, где г и s — скаляры. Тогда
из условия J (и, v)>0 мы получим неравенство
г2 [(/, f) (t>, v) - (f, v)*\ + 2rs [(/, g) {v, v) - (/, v) (g, v)] +
+ &l(g,g)(v,v)-(g,v)*]>Q, (3)
которое в свою очередь приводит к неравенству
[(/, f) (и, v)-(f, vf] [(g, g) (v, v)-(g, vf] >
>[(f,g)(v,v)-(f,v)(g,v)}\ (4)
Это неравенство утверждает, что новое скалярное
произведение, определенное для фиксированного v и любых

70 Гл. 1. Основные неравенства и родственные вопросы
двух элементов f и g,
[/, g\ v] - (f, g) (v, v) - (/, v) (g, v), (5)
удовлетворяет тому же условию, что и старое скалярное
произведение (/, g), а именно
lf,f;v]lg,g\v]>[f,g; v]\ (6)
Этот процесс может быть, очевидно, повторен, и мы
получаем цепочку неравенств, каждое из которых сильнее
предыдущего. Эти неравенства эквивалентны
неравенствам § 5 гл. III.
§ 46. Теорема Мора и Нолля
Следующее уточнение неравенства (\f(t)dtj <
а
Ъ
<(b — a)^f2(t)dt было дано Мором и Ноллем [1].
а
Теорема 28. Если f (х) имеет непрерывную п-ю
производную в [а, Ь], то
Л \2 ^ (—l)h
фт*) =(*-я)2щ4тйх
a k=0
Ъ
xJlPW l(b-t)(t-a)]hdt + (-l)nRn, (1)
а
где
**=W И f{nKs)finKt)№-s)(t-a)]ndsdt. (2)
То, что Rn непрерывно, следует из другого его
представления:
Vi
Rn=S • • • S [ Ifin)(t) dt ]2 dXidyi -dXn dyru (3)
*1

§ 47. Вывод новых неравенств из старых 71
где интегрирование производится по области
Ж **<**-!< ... <*!<#!< ...<Уп-1<Уп<Ь. (4)
Более общие результаты могут быть получены, если
использовать обратные операторы, связанные с линейным
дифференциальным уравнением
L(u) = f(t), L(u) = dnu/dtn+pl(t)dn-iu/dtn-i + ...+pn(t)u.
§ 47. Вывод новых неравенств из старых
Неравенство (45.4) является частным случаем более
общих неравенств, которые могут быть получены
систематически. Пусть неравенство
F(u,v)>0 (1)
обладает тем свойством, что равенство имеет в нем место
тогда и только тогда, когда u = v. Мы рассмотрим теперь
возмущенное неравенство, возникающее из (1) в
результате подстановки
7 (2)
V — w + sg, J '
где w, fug — элементы той же природы, что и и и,
а г и s — скалярные величины. Разлагая F в степенной
ряд в окрестности точки r = s = 0, мы получим
следующее соотношение;
A(f,g,w)r* + 2B(f,g,w)rs + C(f,g,w)s* +
+ O(r3,r%rs\s3)>0. (3)
Выбирая г и s достаточно малыми, мы видим, что отсюда
следует неравенство
A(f, g, w) г2 + 2B(f, g, w) rs + C{f, g, w) s2 > 0 (4)
для всех г и s, так что должно быть
&(f,gM<Mf>g>w)C(f,g,w). (5)
Это рассуждение фактически было нами уже
применено при выводе неравенства Буняковского —Шварца.

72 Гл. К Основные неравенства и родственные вопросы
Другие интересные результаты могут быть таким образом
получены из неравенства Гёльдера и неравенства между
арифметическим и геометрическим средними.
§ 48. Уточнение неравенства между
арифметическим и геометрическим средними
Как известно, в этом неравенстве всегда имеет место
знак строгого неравенства, если не все xt равны между
собой. В связи с теорией алгебраических чисел
представляет интерес, измеряя «разброс» х% дискриминантом
dn= П (xi-xj)*, (1)
l^i<3^n
найти нижнюю грань отношения
(S*i)"
(2)
X\X^"'Xji
выраженную через dn. Результаты этого типа были
впервые получены Шуром [1]; дальнейшее исследование
вопроса принадлежит Зигелю [2], Коберу [3] и Дингхасу [4].
§ 49. Неравенства с чередующимися знаками
Следующий результат был получен Сегё [1].
Теорема 29. Пусть а{ > а2 > ... > a2n-i > 0, и пусть
f(x) — выпуклая функция на [0, а4]. Тогда
2п-1 2п-1
2(-ir1f(^)>f(2(-ir4-)- (о
3=1 3=1
Аналогичный результат был получен Беллманом [2]
путем простого сравнения площадей.
Теорема 30. Пусть а^ > а2 > ... > ап > 0, и пусть
f(x) —выпуклая функция на [0, aj. Тогда, если f (0)<0, то
2 (-1Г1 f(aj) >f(2 (-1ГЧ-)- (2)
3=1 3=1
Частный случай f(x) = xr, г> 1, был независимо
установлен Вейнбергером [3].

§ 50. Неравенство Стеффенсена
73
Эти две теоремы содержатся в качестве частных
случаев в следующей более общей теореме Олкина (4).
Теорема 31. Пусть 1 >Wi>w2> ... >wn> О,
а>\ > а2 > ... > ап > 0, и пусть f (х) — выпуклая функция
на [О, ах]. Тогда
[1-2Н)ьЧ]«о) +
+ 2(-1ГЧ/(^>/(2(-1ГЧ^). (3)
Вместо того чтобы доказывать эту теорему так, как
это делал Олкин, мы докажем другую теорему, которая
содержит неравенство Олкина; см. § 50, 51.
Несколько неравенств Олкина содержатся в работе
Брунка [6], где даны и более общие результаты. Они
родственны теоремам, доказанным выше в § 28 — 32.
§ 50. Неравенство Стеффенсена
Докажем следующее неравенство, принадлежащее
Стеффенсену [1]. При доказательстве мы следуем Белл-
ману [2].
Теорема 32. Пусть
(а) функция f(t) неотрицательна и монотонно ]
убывает в [а, 6],
(б) функция g(t) удовлетворяет условиям j ' ^
0<g(t)<l, a<t<b. j
Тогда
Ъ Ъ а+с
lf(t)dt<^f(t)g(t)dt<^f(t)dt, (2)
Ь—с а а
где
ъ
c=lg(t)dt. (3)

74 Гл. 1. Основные неравенства и родственные вопросы
Доказательство. Определим функцию u{s)
соотношением
s и
\f(t)g{t)dt=\f{t)dt. (4)
а а
Легко видеть, что в силу условий, наложенных на / и g,
и(а) = а, функция u(s) непрерывна и монотонно
возрастает при возрастании s от а до b и u(s)<s.
Дифференцируя, находим, что
№&=№g(s), (5)
откуда
ж-Ш)8(з)<8(8)- (6)
Следовательно,
S
u<a+^g(t)dt, (7)
а
и правое неравенство (2) доказано. Аналогично
доказывается и левое неравенство.
§ 51. Неравенство Брунка—Олкина
Чтобы получить неравенство Олкина (49.3) (заменив
в нем / на Л), положим в теореме 32
g(t) = Xk, ak+l<Ct<ah, ft=l,2, ...,n—1, (1)
где
%i = wi, K2 = wl — w2, Хз = ^1~^2 + ^з и т.д., (2)
и h(t)~f\t). Тогда мы получим даже несколько более
сильный результат, чем теорема 31.
§ 52. Обобщения неравенства Стеффенсена
Таким же образом можно доказать много других
неравенств. Например, имеет место следующее обобщение
неравенства Стеффенсена.

Библиография и дополнения
75
Теорема 33. Пусть
(а) функция f(t) неотрицательна и монотонно |
убывает в [а,Ь],
(б) f£U>[aM,
ъ
(в) g(t)>0, $£*Л<1,
(1)
где р> 1, q = p/(p—l). Тогда
Ъ a-fc
($fe#)P< j/**. (2)
а а
где
ь
с=0*л)Р- (3)
а
БИБЛИОГРАФИЯ И ДОПОЛНЕНИЯ
§ 1. Основным руководством по теории неравенств является
1. Хард и, Литтлвуд, Пойа (Hardy G. Н., L i t t-
lewood J. E., Polya G., Inequalities, London,
Cambridge University Press, 1951. Русский перевод издания 1934 г.:
Неравенства, ИЛ, М., 1948.
В этой книге можно найти много исторических замечаний,
ссылок и обобщений.
§ 2. Введенный здесь обобщенный косинус играет важную роль
в математической статистике, где он является корреляционным
коэффициентом.
1. К о ш и (Cauchy A. L.), Cours d'Analyse de PEcole Royale
Polytechnique, Ire partie, Analyse algebrique, Paris, Debure,
1821, Oeuvres completes, IIе serie, III.
§ 3. Cm. § 6 гл. II.
§ 7. Относительно других приложений этого метода см.
1. Беллман (Bellman R.), Dynamic programming,
Princeton, N. J., Princeton University Press, 1957. Русский перевод:
Динамическое программирование, ИЛ, М., 1960.
§ 8. Эти геометрические соображения, которых мы касаемся
только слегка, могут быть положены в основу теории неравенств.

76
Библиография и дополнения
Этот подход мы рассмотрим подробно в нашем втором томе. См.
Харди, Литтлвуд, Пойа [1.1] и
1. Боннесен, Фенхель (BonnesenT., Fenchel W.),
Theorie der konvexen Korper, Berlin, Springer 1951.
2. Л о p x (L о г с h E. R.), Differential inequalities and the theory
of convex bodies, Trans. Am. Math. Soc, 71 (1951), 243—256.
Общее рассмотрение выпуклых функций и их приложений
см. в работе
3. Беккенбах (Beckenbach Е. F.), Convex functions,
Bull. Am. Math. Soc, 54 (1948), 439—460.
4. Грин (Green J. W.), Recent applications of convex functions,
Am. Math. Monthly, 61 (1954), 449—454.
§ 9.
1. Бор (Bohr H.), The arithmetic and geometric means, J.
London Math. Soc, 10 (1935), 114.
§ 10.
1. Гурвиц (Hurwitz A.), Ober den Vergleich der arithrneti-
schen und des geometrischen Mittels, Math. Werke, 505—507,
Basel, Birkhauser, 1933.
2. Гурвиц (Hurwitz A.), Ober die Erzeugung der Invarian-
ten druch Integration, Math. Werke, 546—564, Basel,
Birkhauser, 1933.
§ И. На это доказательство наше внимание было обращено
Фань Цзы. См.
1.3л ере (Ehlers G.), в книге: Hayes W. D. (ed.), Colloquium
on linear equations, Office of Naval Research Technical Report
ONRL-35-54, 1954.
Другое простое индуктивное доказательство дано в работе
2. Диананда (Diananda P. Н.), A simple proof of the
arithmetic mean — geometric mean inequality, Am. Math.
Monthly, 67 (1960), 1007.
§ 12.
1. Гаусс (Gauss С F.), Werke, 10, 1, 172—292. Leipzig, Teub-
ner, 1917.
2. Шапира (Schapira H.), Bemerkungen zu der Grenz-
funktion algebraischer Iteration, S с h 1 6 m i 1 с h Z., 32 (1887),
310—314.
3. Шлезингер (Schlesinger L.), Ober Gauss'Jugend-
arbeiten zum arithmetisch-geometrischen Mittel, Deutsche Math.
Ver., 20 (1911), 396—403 (здесь можно найти много других
ссылок).
4. Беллман (Bellman R.), The symmetric mean, Math.
Mirror, Brooklyn College, 9 (1941), 5—6.
5. Маклорен (Maclaurin C), A second letter to Martin
: Folges, Esq.; concerning the roots of equations with the
demonstration of other rules in algebra, Phil. Trans., 36 (1729), 59—96.

Библиография и дополнения
77
§ 13.
1. Якобсталь (Jacobsthal Е.), Ober das arithmeti-
sche und geometrische Mittel, Norske Vid. Selsk. Fork. (Trondheim),
23 (1951), 122,
§ 14. Мы следуем Харди, Литтлвуду, Пойа [1.1].
§ 15.
1. Ю н г (Young W. Н.), On classes of summable functions and
their Fourier series, Proc. Roy. Soc. (A), 87 (1912), 225—229.
§ 16. Тот факт, что Mf(x,a) не обязательно выпукло-вогнутая
функция, был отмечен в работе
1. Шнайад (Shniad Н.), On the convexity of mean value
functions, Bull. Am. Math. Soc, 54, (1948), 770—776.
Неравенство St (x) ^ St (x), 0 < ti < t2, было установлено
Иенсеном в работе
2. Иенсен (Jensen J. L. W. V.), Sur les fonctions convexes
et les inequalites entre les valeurs moyennes, Acta Math., 30 (1906),
175—193, как приложение его новой теории выпуклых функций.
Как указывает, однако, Иенсен, это неравенство ранее было
доказано Прингсгеймом в работе
3. Прингсгейм (Pringsheim A.), Zur Theorie der
ganzen transzendenten Funktionen (Nachtrage), Munch. S.-B.t
32 (1902), 295—304.
Прингсгейм в свою очередь приписывает свое доказательство
Люроту (Luroth). Интересно, что, хотя Иенсен применял выпуклые
функции в своем доказательстве этого неравенства, он не показал,
что сама функция St (х) выпукла для t > 0; это было сделано
только позже в работе
4. Боннесен (Bonnesen Т.), En bemaerkning от konvekse
funktioner, Mathem. Tidsskr. (В), 1928, 18—20,
для t > 1 и другим методом в работе
5. Беккенбах (Beckenbach Е. F.), An inequality of
Jensen, Am. Math. Monthly, 53 (1946), 501—505,
для t > 0.
§ 17.
1. Гёльдер (Holder O.), Ober einen Mittelwertsatz, Getting.
Nachr., 1889, 38—47.
2. Минковский (Minkowski H.), Geometrie der Zahlen,
I, Leipzig, Teubner, 1896.
§ 18.
1. Бохер (Bocher M.), Introduction to higher algebra, New
York, Macmillan, 1907.
2. Orypa (Ogura K-), Generalizations of Bessel's and Gram's
inequalities and the elliptic space of infinitely many dimensions,
Tohoku Math. J., 18 (1920), 1—22.

78
Библиография и дополнения
§ 19. Этот метод был разработан независимо друг от друга
многими авторами, так что приоритет установить очень трудно.
См., однако, § 25.
1. Беллман, Гликсберг, Гросс (Bellman R.,
Glicksberg I., Gross О.), Some aspects of the
mathematical theory of control processes, Santa Monica, Calif., The
Rand Corporation, Report R—313, 1958. Русский перевод:
Некоторые вопросы математической теории процессов
регулирования, ИЛ, М., 1962.
2. Зигмунд (Zygmund A.), On certain integrals, Trans. Am.
Math. Soc, 55 (1944), 170—204.
§ 23.
1. Беккенбах (Beckenbach E. F.), A class of mean-
value functions, Am. Math. Monthly, 57 (1950), 1—6.
§ 24.
1. Дрешер (Dresner M.), Moment spaces and inequalities,
Duke Math. J., 20 (1953), 261—271.
2. Данскин (Danskin J. M.), Dresner's inequality, Am.
Math. Monthly, 49 (1952), 687—688.
§ 25.
1. Минковский (Minkowski H.), см. Боннесен —
Фенхель [8. 1].
2. M а л e p (Mahler К-)» Ein Ubertragungsprinzip fur konvexe
Korper, Casopis Mat. Fysik, 68 (1939), 93—102.
3. Юнг (Young L. C), On an inequality of Marcel Riesz, Ann.
of Math., 40 (1939), 567—574.
4. Фенхель (Fenchel W.), A remark on convex sets and
polarity, Comm. Sem. Math, de Lund, Tome Supp., 1952, 82—89.
5. Л о p x (L о г с h E. R.), On the volume of smooth convex bodies
in Hilbert space, Math. Z., 61 (1955), 391—407.
6. Л о p x (L о г с h E. R.), Convexity and normed spaces, Publ.
Inst. Math. Acad. Set. Serbe, 4 (1952), 109—112.
7. Л о p x (L о г с h E. R.), Su certe extensioni del concetto di
volume, Rend. Accad. Lincei (8), 16 (1954), 25—29.
§ 26. Этот вид кЁазилинеаризации мы вновь рассмотрим в гл. IV.
1. Беллман (Bellman R.), Functional equations in the
theory of dynamic programming, V, Positivity and quasi-linearity,
Proc. Nat. Acad. Set. USA, 41 (1955), 843—746.
2. Беллман (Bellman R.), On the representation of the
solution of a class of stochastic differential equations, Proc. Am.
Math. Soc.t 9 (1957), 326—327.
3. К а л а б a (K a 1 a b a R.), On nonlinear differential
equations, the maximum operation, and monotonic convergence, J.
Math, and Mech., 8 (1959), 519—574.

Библиография и дополнения
79
Неравенство
. п п 1 \ п
Vi=l УМ=1 гу г=1
дает квазилинеаризацию
1 г=1
где аг > 0 и минимум берется по всем
г=1
§ 27. См.
1. Зигмунд (Zygmund A.), Two notes on inequalities,
J. Math. Physics, 21 (1942), 117—123.
2. Марцинкевич, Зигмунд (Marcienkiewicz
J., Zygmund A.), Quelques inegalites pour les operations
lineaires, Fund. Math, 32 (1939), 115—121.
§ 28. Этот результат играет роль в теории матриц, как будет
показано в гл. II. См. также
1. Островский (Ostrow srk i A.), Sur quelques
applications des fonctions convexes et concaves au sens de I. Schur.,
J. Math. Pure AppL, 31 (1952), 253—292.
2. Карамата (Karamata J.), Sur une inegalite relative
aux fonctions convexes, Pub I. Math. Univ. Belgrade, 1 (1932),
145—148.
Так же, как и результат следующего параграфа, этот
результат играет важную роль в теории вероятностей и математической
статистике. См.
3. Блекуэлл (Blackwell D.), Comparison of experiments,
Proc. Second Berkeley Symposium on Mathematical Statistics and
Probability, 1950, 93—102, Berkeley, Calif., University of
California Press, 1951.
В этом докладе излагается неопубликованная работа Блекуэл-
ла, Боненбласта и Шермана.
§ 29. См.
1. Шур (Schur I.), Uber eine Klasse von Mittelbildungen mit
Anwendungen auf die Determinantentheorie, Sitzber. Berl. Math.
Ges., 22 (1923), 9—20.
2. Биркгоф (Birkhoff G.), Tres observaciones sobre el
algebra lineal, Rev. Univ. Nac. Tucuman (Л), 5 (1946), 147—151.
„2U
i=l

80
Библиография и дополнения
3. Шрейбер (Schreiber S.), On a result of S. Sherman
concerning doubly stochastic matrices, Proc. Am. Math. Soc, 9
(1958), 350—353.
4. Мирский (Mirsky L.), Proofs of two theorems on doubly
stochastic matrices, Proc. Am. Math. Soc, 9 (1958), 371—374.
5. P а й з e p (R у s e r H. J.), Matrices of zeros and ones, Bull.
Am. Math. Soc , 66 (1960), 442—464.
Ряд замечаний и других неравенств можно найти в книге Харди,
Литтлвуда и Пойа [11].
§ 31.
1. Фукс (Fuchs L.), A new proof of an inequality of Hardy —
Littlewood — Polya, Mat. Tidskr. (B), 1947, 53—54.
2. Харди, Литтлвуд, Пойа (Hardy G. H., L i t-
tlewood J. E., Polya G.), Some simple inequalities
satisfied by convex functions, Messenger of Math., 58 (1929), 145—152.
3. Рудерман (Ruderman H. D.), Two new inequalities, Am.
Math. Monthly, 59 (1952), 29—32.
4. Б и с а к (Beesack P. R.), A note on an integral inequality, Proc.
Am. Math. Soc, 8 (1957), 875—879.
§ 32.
1. Фань-Цзы, Лорентц (Fan К., Lorentz G. G.),
An integral inequality. Am. Math. Monthly, 61 (1954), 626—631.
§ 33.
1. Маркус, Лопес (Marcus M., Lopes L.),
Inequalities for symmetric functions andHermitian matrices, Canad.J.
Math., 8 (1956), 524—531.
2. Булле н, Маркус (Bullen P., Marcus M.).
Symmetric means and matrix inequalities, 1961.
§35.
1. Уайтли (Whiteley J. N.), Some inequalities concerning
symmetric functions, Maihematika, 5 (1958), 49—57.
Другие результаты, в том числе обобщения некоторых теорем
Ньютона, даны в работе
2. Уайтли (Whiteley J. N.), A generalization of a theorem
of Newton, Proc. Am. Math. Soc, 1961.
§ 36.
1. Гординг (Garding L.), An inequality for hyperbolic
polynomials, J. Math, and Mech., 8 (1959), 957—966.
§ 38. См. более раннюю работу
1. Гординг (Garding L.), Linear hyperbolic partial
differential equations with constant coefficients, Acta Math., 85
(1951), 1—62. Есть русский перевод.
2. Цзянь (С h е г n S.), Integral formulas for hypersurfaces in
Euclidean space and their application to uniqueness theorems,
J. Math, and Mech., 8 (1959), 947—956.

Библиография и дополнения
81
39. Теоремы этого типа были независимо друг от друга найдены
столькими авторами, что вопрос о приоритете решить очень трудно.
1. Беллман (Bellman R.), On an inequality concerning
an indefinite form, Am. Math. Monthly, 63 (1957), 108—109.
2. Мурнаган (Murnaghan F. D.), Schwarz's inequality
and Lorentz spaces, Proc. Nat. Acad. Set. USA, 36 (1950), 673—
676.
3. Бохнер (Bochner S.), Group invariance of Cauchy's
formula in several variables, Ann. of Math, 45 (1944), 686—707.
4. Синдж (SyngeJ. L.), Relativity, the special theory, New
York, Interscience Publ., 1956.
5. Ацел, Варга (Aczel J., Varga O.), Bemerkung
zur Cayley-Kleinschen Massbestimmung, Publ. Math., Debrecen,
4 (1955), 3—15.
§ 40.
1. Франк, Пик (Frank Ph., Pick G.), Distanzabschat-
zungen im Funktionenzaum, I., Math. Ann., 76 (1915), 354—375.
2. Бляшке, Пик (Blaschke W., Pick G.), Distanz-
abschatzungen im Funktionsraum, II, Math. Ann., 77 (1916),
277—302.
3. Бюкнер (Buckner H.), Untere Schranken fur skalare
Produkte von Vektoren und fur analoge Integralausdrucke, Ann.
Mat. Рига Appl. (4), 28 (1949), 237—261.
4. Фавар (Favard J.), Sur les valeurs moyennes, Bull. Set.
Math. (2), 57 (1933), 54—64.
5. Бервальд (Berwald L.), Verallgemeinerung eines Mittel-
wertsatzes von J. Favard fur positive konkave Funktionen,
Acta Math., 79 (1947), 17—37.
6. Кнезер (Kneser H.), Bemerkung uber die gemischten
Inhalte in vier Dimensionen, Math. Ann., 115 (1937), 132—135.
7. Беллман (Bellman R.), Converses of Schwarz's
inequality, Duke Math. J., 23 (1956), 429—434.
§ 44.
1. Пойа, Cere (Polya G., Szego G.), Aufgaben und
Lehrsatze aus der Analysis, I, 57, Berlin, Springer, 1925. Русский
перевод: Задачи и теоремы из анализа, ч. I, Физматгиз. М., 1956.
2. Маданский (Madansky A.), Bounds on the
expectation of a convex function of a multivariate random variable, Ann.
Math. Stat., 30 (1959), 743—746.
3. Уотсон (Watson G. S.), Serial correlation in regression
analysis, I, Biometrica, 42 (1955), 327—341.
4. Грэйб, Рейнбольдт (Greub W., R h e i n-
b о 1 d t W.), On a generalization of an inequality of L. V.
Kantorovich., Proc. Am. Math. Soc, 10 (1959), 407—415.
5. Ф а н ь Ц з ы, T о д д (Fan K-, Todd J.), A determinan-
tal inequality, J. London Math. Soc, 30 (1955), 58—64.
6. Хассан (Chassan J. В.), A statistical derivation of a pair
of trigonometrical inequalities, Am. Math. Monthly, 62 (1955),
353—356.

82
Библиография и дополнения
§ 46.
1. Мор, Н о л л ь (М о h г Е., N о 1„1 W.), Eine Bemerkung zur
Schwarzschen Ungleichheit, Math. Nachr., 7 (1952), 55—59.
§ 48.
1. Шур (Schur I.), Uber die, Verteilung der Wurzeln bei gewis-
sen algebraischen Gleichungen mit gauzzahligen Koeffizienten,
Math. Z., 1 (1918), 377—402.
2. Зигель (Siegel С L.), The trace of totally positive and
real algebraic integers, Ann. of Math., 46 (1945), 302—312.
3. Кобер (Kober H.), On the arithmetic and geometric mean
and on Holder's inequality, Proc. Am. Math. Soc, 9 (1958),
452—459.
4. Дингхас (Dinghas A.), Zur Abschatzung arithmetischer
Mittel reeler Zahlen durch Differenzprodukte derselben, Rend.
Mat. Palermo (2), 2 (1953), 177—202.
§ 49.
1. Cere (Szego G.), Uber eine Verallgemeinerung des Dirich-
letschen Integrals, Math. Z., 52 (1950), 676—685.
2. Б e л л м а н (Bellman R.), On an inequality of
Weinberger, Am. Math. Monthly, 60, (1953), 402.
3. Вейнбергер (Weinberger H. F)., An inequality with
alternating signs, Proc. Nat. Acad. Sci. USA, 38 (1952), 611 —
613.
4. Олкин (Olkin I.), On inequalities of Szego and Bellman,
Proc. Nat. Acad. Sci. USA, 45 (1959), 230—231.
5. P а й т (Wright E. M.), An inequality for convex functions,
Am. Math. Monthly, 61 (1954), 620—622.
6. Брунк (Brunk H. D.), On an inequality for convex
functions, Proc. Am. Math. Soc, 7 (1956), 817—824.
§ 50.
1. Стеффеьгсен (Steffensen J. E.), Bounds of certain
trigonometric integrals, Tenth Scandinavian Math. Congress 1946,
181—186. Copenhagen, Gjellerups, 1947.
2. Б e л л м а н (Bellman R.), On inequalities with alternating
signs, Proc. Am. Math. Soc, 10 (1959), 807—809.
Мы опустили здесь рассмотрение статистических метрических
пространств — понятия, введенного Вальдом и Менгером (Wald and
Menger), о которых см. работу
3. Швейцер, Скляр (Schweizer В., Sklar А.),
Statistical metric spaces, Pacif. J. Math., 10 (1960), 313—334.
Кроме того, мы не упомянули о неравенствах, возникающих
в теории вероятностей и теории информации, где важную роль
играет функция (энтропия) Vp?-logp?-; см. работу
i
4. Лейпник (Leipnik R.), The extended entropy
uncertainty principle, Information and Control, 3 (1960), 18—25.

Библиография и дополнения
83
5. Беллман, Кал аба (Bellman R., Kalaba R.),
Dynamic programming and statistical communication theory,
Proc. Nat. Acad. Sci. USA, 43 (1957), 749—751.
6. M о я л (M о у a 1 J. Е.), Quantum mechanics as a statistical
theory, Proc. Cambridge Phil. Soc, 45 (1949, Appendix I), 99—
124.
Изящные обобщения неравенства треугольника в виде
утверждений, относящихся к положительной определенности
некоторых квадратичных форм, содержатся в работе
7. Бейрлинг (Beurling A.), Sur quelques formes
positives avec une application a la theorie ergodique, Acta Math., 78
(1946), 319—334.

Глава II
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННЫЕ МАТРИЦЫ,
ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА И ПОЛОЖИТЕЛЬНЫЕ МАТРИЦЫ
§ 1. Введение
Как только мы покидаем хорошо пропаханные поля
действительных и комплексных чисел и оказываемся в
сравнительно мало исследованных областях гиперкомплексных
чисел, перед нами открываются многочисленные
возможности введения упорядочивающих соотношений. В этой
главе мы рассмотрим несколько интересных классов
неравенств, относящихся к матрицам. Как мы увидим,
основное понятие положительного числа может быть
распространено на матрицы разными содержательными
путями.
Самым простым и наиболее непосредственным из них
является понятие положительно определенной матрицы.
Мы начнем с того, что сосредоточим наше внимание на
характеристических числах матриц этого типа и на
некоторых функциях характеристических чисел. Самой
интересной такой функцией является произведение
характеристических чисел, определитель матрицы.
Из всех путей, которые ведут к нашей цели, т. е.
к изучению свойств определителя, мы выберем тот,
который основан на интегральных представлениях
определителя. После того как мы получим некоторые результаты
из элементарных представлений соответствующих
положительно определенных форм в виде суммы квадратов,
мы перейдем к более тонким результатам, получающимся
из интегральных представлений определителя,
принадлежащих Ингаму и Зигелю, и из их обобщений,
принадлежащих Беллману и Олкину.
Для того чтобы получить соответствующие результаты
для положительно определенных эрмитовых матриц, мы
выведем новое тождество для определителя эрмитовой
матрицы. Это представление даст нам возможность дока-

§ 1. Введение
85
зать ряд результатов для таких матриц методами,
пригодными и для симметричных матриц.
Некоторые из этих результатов принадлежат Фань Цзы,
который получил их, основываясь на вариационных
формулах, обобщающих классическое минимакс-определение
Фишера характеристических чисел. Это — еще один мощный
метод, заслуживающий систематической разработки.
Перейдя к изучению положительно определенных
матриц, мы далее рассмотрим положительные матрицы —
класс матриц, введенный Перроном и подробно
исследованный Фробениусом. В последние годы эти матрицы
приобрели выдающееся значение в связи с изучением
вычислительных алгоритмов для численного решения уравнений
с частными производными, встречающихся в
разветвляющихся процессах, в теории игр и линейного
программирования и в математической экономике.
В случае положительных матриц мы получим
вариационное определение наибольшего по абсолютной величине
характеристического числа, которое оказывается
действительным. Полученное таким образом представление даст
нам возможность доказать интересную теорему о поведении
этого характеристического числа как функции от матрицы.
Теория положительных матриц является лишь близкой
к поверхности разработкой двух исключительно богатых
жил: теории положительных операторов и теории лре-
образований, понижающих число перемен знака. Мы
сможем сделать только несколько небольших замечаний
по поводу этих теорий, в которых так много было сделано
Гантмахером, Крейном, Шенбергом, Карликом, Мак-Грего-
ром и др. Эти две теории заслуживают специальных
монографий.
Помимо понятия положительности, существует еще
понятие области положительности, введенное Кехером,
и связанное с интегралом Ингама и Зигеля, а также
понятие положительных преобразований Лёвнера. Эти
понятия играют большую роль в дисперсионной теории
в квантовой механике, а также в анализе линейных
электрических сетей.
Мы коротко остановимся на недавних результатах
Лакса, относящихся к классу матриц, важных для теории
гиперболических уравнений с частными производными.

86 Гл. //. Положительно определенные матрицы
Общие результаты Гординга, рассмотренные в § 36-38 гл. I,
обнаруживают причину сходства, существующего между
теорией характеристических чисел этих матриц и теорией
характеристических чисел эрмитовых матриц.
Наш краткий обзор некоторых результатов, упоминание
других и обилие ссылок ясно показывают, что изучение
многих различных типов отношений порядка, связанных
с конечномерными и бесконечномерными операторами, только
началось и что здесь можно открыть еще много красивых
идей и изящных результатов. Ввиду большого числа
неравенств, относящихся к определителям и
характеристическим числам матриц, наша цель может состоять только
в описании некоторых из многих возможных подходов.
Мы ни в коем случае не можем претендовать на сколько-
нибудь исчерпывающее изложение.
§ 2. Положительно определенные матрицы
Начнем с напоминания о некоторых основных понятиях
и изложения используемой символики.
Действительная квадратная матрица A = (aij)1 /, / =
= 1, 2, ..., п, называется симметричной, если а^ = ал.
Действительная симметричная матрица называется
положительно определенной, если квадратичная форма
п
Q(x)= 2 ciijXiXj (1)
положительна для всех нетривиальных систем значений
действительных переменных х%, т. е. для (х±, х2, ..., хп) Ф
Ф(0, 0, ..., 0) [1].
Комплексная матрица # = (/г^), /,/=1,2, ..., п,
называется эрмитовой, если htj и Нц комплексно сопряжены,
т. е. hij = hji. Эрмитова матрица называется положительно
определенной, если эрмитова форма
Р(г)= 23 hu**J (2)
положительна для всех нетривиальных систем
комплексных переменных zt. Очевидно, что эрмитова форма (2)
приводится к (1), если все г% и йу действительны.

§ 3. Необходимое условие положительной определенности 87
Если квадратичная или эрмитова форма только
неотрицательна, то соответствующая матрица называется
положительно полуопределенной или неотрицательно
определенной.
Как обычно, для двух n-мерных векторов хи у положим
п
(х,у) = 2*i#. (3)
г=1
и назовем это выражение скалярным произведением х и у.
Тогда имеют место компактные и весьма поучительные
соотношения
Q(x) = (x,Ax), |
Р(г) = (г,Нг). I (4)
Наконец, обозначим через \А\ определитель матрицы А.
Это обозначение применяется везде в гл. II; когда
вертикальные черточки применяются для обозначения
абсолютной величины, это будет каждый раз оговариваться.
При рассмотрении положительно определенных форм
мы сначала ограничимся действительным случаем, хотя
аналогичные результаты всегда имеют место и для
эрмитовых форм.
§ 3. Необходимое условие
положительной определенности
Докажем сначала, что если матрица А положительно
определена, то |Л|>0. Прежде всего, легко видеть, что
если А положительно определена, то |Л|=£0. Именно,
если бы было |Л| = 0, то мы могли бы выбрать
нетривиальную систему значений х%, такую, что выполнялись
бы уравнения
п
2яу*/ = 0. /=1, 2, ..., п. (1)
i=i
Для этих значений мы имели бы
п п
(х,Ах)= 2*i(2ay*/) = 0, (2)
i=l i=l
что противоречило бы положительной определенности.

&8 Гл. II. Положительно определенные матрицы
Утверждение |Л|> 0 теперь доказывается
рассуждением по непрерывности, которое часто применяется в
аналогичных ситуациях. Рассмотрим матрицу XI + (1-Х)Л,
где 0 < X < 1 и / — единичная матрица (для которой а^=0,
если 1ф] и ац = 1). Ясно, что эта матрица положительно
определена, если А положительно определена.
Следовательно, \Х1 + (1—Х)А\Ф0. Так как этот определитель
является непрерывной функцией от X, то его знак при
Х = 0 должен совпадать со знаком при Х=1, где этот
определитель положителен: |/| = 1.
Отсюда вытекает также, что если матрица А
положительно определена, то все определители
|Лл| = |а^|, *,/ = 1, 2, ..., k, k=\,2, ...,«, (3)
должны быть положительны.
Если известно только, что матрица А неотрицательно
определена, то XI + (1-Х) А положительно определена
только для 0<Я<1, и предыдущее рассуждение
показывает, что все определители (3) должны быть
неотрицательны.
§ 4. Представление в виде суммы квадратов
Посмотрим теперь, нельзя ли положительно
определенную квадратичную форму представить так, чтобы ее
положительность стала очевидной. Мы увидим, что такая
форма в самом деле может быть представлена как сумма
квадратов линейных функций. Этот результат связан
с некоторыми замечаниями, сделанными нами в гл. I, § 3, 10.
Представления такого типа не всегда возможны, если мы
имеем дело с более общими классами функций (см. [2.1],
где можно найти дальнейшие ссылки).
Для п = 2 имеет место тождество
auxl + 2а12х,х2 + а22х\ = аи(хх + ^~J +
если только апф0. Тождество (1) имеет, конечно, место
независимо от того, является форма определенной
или нет.

§ 5. Необходимое и достаточное условие 89
Отметим, что
#22 —
\ail fl12|
2
#12 I а12 а22 I
ап an
Важным обобщением (1) является
(2)
Теорема 1. (Лагранж, Бельтрами.) Если ни один из
определителей
\Ak\ =
#ц#12 • • • &1к
#21^22 • • • #2&
Uklak2 • • • Clkk
(3)
k = 1, 2, ..., п— 1, не равен нулю, то функция Q(x) == (х, Ах)
может быть представлена в виде
Q(
■&.
где |Л0| = 1,
i=.fe+i
я,
(4)
(5)
w by —рациональные функции от atj.
Эта теорема без труда доказывается по индукции.
§ 5. Необходимое и достаточное условие
положительной определенности
Непосредственным следствием представления (4.4) и
результатов § 3 является следующий фундаментальный
критерий.
Теорема 2. Необходимым и достаточным условием
положительной определенности симметричной матрицы А
является выполнение неравенств
|ЛЛ|>0, £=1,2,...,/*. (1)
Для необходимости даже не надо предполагать, что
матрица А симметрична, так как если А = В-\-С, где В —

90 Гл. II. Положительно определенные матрицы
положительно определенная, а С — кососимметричная
матрица, то, как показали Островский и Тауски [1],
\А\>\В\.
Легко видеть также, что матрица А неотрицательно
определена тогда и только тогда, когда все определители
\Ak\ неотрицательны.
Теорема 2 играет важную роль в изучении моментов.
Широко применяемый здесь метод состоит в сведении
положительности функции к положительной определенности
некоторой матрицы. Тогда соотношения (1) дают систему
необходимых и достаточных условий.
§ 6. Определители Грама
Теорема 2 содержит систематический метод получения
новых неравенств при помощи матриц, про которые заранее
известно, что они положительно определены. Рассмотрим,
например, действительную квадратную неособенную
матрицу X,
detX=|X|^0.
Если X'—транспонированная матрица, то XX'
симметрична и положительно определена. Это вытекает из
тождества
(х, ХХ'х) = (Х'х, Х'х) (1)
и из того, что Xfx~0 только для тривиального вектора
х = 0 (ввиду неособенности матрицы X).
Пусть X имеет вид
Х =
где x(i> —вектор-строка. Тогда
XX'=(№*»)), /,/
(2)
1,2,
, л.
(3)

§ 6. Определители Грама
91
Отсюда мы заключаем, что если векторы x(i> линейно
независимы, то все определители
Gk = \(**\ хЩ, /, /=1,2, ...,&,
(4)
&= 1, 2, ..., п, называемые определителями Грама,
положительны.
При & = 2 мы получаем следующее неравенство:
п п
п п
2 xtyi 2 у?
i=i
i=i
>o,
или
(5)
(6)
при условии, что векторы х и у линейно независимы. Мы
вновь получили неравенство Коши (см. § 2 гл. I).
Так же как существует тождество Лагранжа
(2*0(2tfM2W = S to-зд)2, (7)
г=1 г=1 г=1
из которого вытекает неравенство Коши, для любых k
существует представление Gk в виде суммы квадратов
[см. стр.28 книги Харди, Литтлвуда и Пойа ([1.1], гл. 1)].
В действительности для любой положительно
определенной матрицы А имеет место представление Л = 7X7",
где Т— действительная ортогональная матрица, a L
—диагональная матрица с положительными элементами на
главной диагонали. Это показывает, что любая положительно
определенная матрица по отношению к некоторому
обобщенному скалярному произведению может рассматриваться
как матрица типа Грама. Это замечание ведет к другому
доказательству теоремы 2.

92 Гл. II. Положительно определенные матрицы
Ряд интересных результатов может быть получен из
следующей теоремы представления:
ь
\\fi{x)gj{x)dx
и и
flM fi{X2) . . . МХп)
/2(^1) /2(^2) • • • Шп)
fn(Xt) fn(x2) . . • fn{Xn)
X
X
gi(*i) Siixz) . -. gi(xn)
gz{Xi) g2(X2) . . . g2(xn)
gn(Xi) gn(X2) . . . gn(Xn)
dx, (8)
где dx = dx1dx2 ... dxn; см. Пойа и Сегё ([44.1, стр. 48],
гл. I), а также Андреев [1], де Брейн [2], Джекобсон [3],
Мак-Даффи [4], Колмогоров [5]. Из (8) с очевидностью
вытекает, что если мы положим
и
lf>g] = \lfi(x)gj(x)dx
/,/ = 1,2, ...,п, (9)
то все неравенства, справедливые для обычного скалярного
произведения (f, g), остаются в силе и для этого
обобщенного скалярного произведения. Например, одно
неравенство Дэвиса, приведенное также Эвериттом [6], а именно
[f,g]'<[f,f][g,g],
(10)
сразу вытекает из сказанного выше. Другие неравенства
можно найти у Мофферта [7].
Мы будем, однако, избегать подробного рассмотрения
неравенств, связанных с определителями и минорами.
Читателя, интересующегося этими вопросами, мы отсылаем
к де Брейну [8].

§ 7. Вычисление одного несобственного интеграла 93
§ 7. Вычисление одного несобственного интеграла
Ряд приведенных ниже результатов основывается на
явном выражении многомерного интеграла
оо оо
/„= [...[ е-<-х-АхЫх, (1)
-оо —оо
где А — положительно определенная матрица, а
интегрирование производится по всему п-мерному действительному
пространству.
Теорема 3. Если А —положительно определенная
матрица порядка п, то
'-тЬК I «-**<)"-w- (2>
— ОО
Доказательство. Используя представление Q(x) =
= (х, Ах) в виде суммы квадратов (см. (4.4)), произведем
замену переменных
п
yk = xk + ^i bkjXj, k= 1, 2, ..., п, (3)
j=fe+i
в кратном интеграле. Так как якобиан преобразования
равен 1, мы находим, что
Jn =
оо
— оо
.А е h=i dy =
— оо
(!--*)"
п
ЦУШ/\Ам-1\
Я"/2
~ УЩ'
(4)
Точное значение постоянной V e~y2dy, между прочим,
—оо
для нас несущественно с точки зрения дальнейшего
использования значения Jn.

94 Гл. II. Положительно определенные матрицы
§ 8. Комплексные матрицы с положительно
определенной вещественной частью
Лишь немногим труднее доказательство следующей
теоремы.
Теорема 4. Если А и В — действительные
симметричные матрицы порядка п, причем А — положительно
определенная матрица, то
оо оо
J-J
т"/2
e-mmx)dx=W+wr (1)
где под квадратным корнем понимается его главное
значение.
Первым из следствий этого соотношения является
приводимая ниже теорема Островского и Тауски [5.1]; см.
также Тауски [1] и Беллман и Гофман [2].
Теорема 5. Если А и В — действительные
симметричные матрицы, причем А — положительно определенная
матрица, то абсолютная величина \\A + iB\\
определителя \A + iB\ удовлетворяет неравенству
\\A + iB\\>\A\, (2)
в котором равенство имеет место тогда и только тогда,
когда В — тождественный нуль.
Доказательство. Из предыдущего следует, что
оо оо оо оо
I f ... Г е-<*. (А+гВД dx I < Г ... f е-<*> А*> dx, (3)
— оо —оо
где вертикальные черточки означают абсолютную величину.
Отсюда вытекает утверждение теоремы 5.
§ 9. Одна теорема о вогнутости
Используя опять представление теоремы 3 методом,
намеченным в § 19 гл. I, докажем теперь один результат
Фань Цзы [1].

§ 10. Неравенство, относящееся к минорам 95
Теорема 6. Если А и В — действительные
положительно определенные матрицы, то
\Ы + {\-%)В\> \А\%\В\{~% (1)
для О < А, < 1.
Доказательство. Имеем
п/2 °° °°
П — С ...f e-4x,Ax)~(i-Wx,Bx)dXm (2)
У\КА + (\ — Х)В J J v '
— оо — оо
Так как результат очевиден для А, = О и К = 1, то
достаточно рассматривать значения А,, удовлетворяющие
неравенству О < X < 1. Применим к интегралу (2) неравенство
Гёльдера с показателями р = 1Д, д=1/(1—А). Тогда мы
получим неравенство
1/|Ы + (1 — Ь)Д ^
\1-Я
ОО ОО а ^ оо оо
< f С ... С е-(ж-Лж) Же) ( Г ... С в-о-в*) Же) <
— ОО —ОО —ОО —ОО
<yVlW1^)' (3)
равносильное (1). Это доказательство приведено в [2.1].
§ 10. Неравенство, относящееся к минорам
Продолжая рассуждать таким же образом, мы можем
доказать и следующий результат.
Теорема 7. Если А —действительная положительно
определенная матрица порядка п, то
\Ain\<\Aik\-\Ak+l,n\, (1)
где определители (Ars) определены так:
\АГ8\ = \аи\, '"> / = r> r+*> ---.s- (2)
В частности,
\А\<аиа22 • • • aw (3)

96 Гл. II. Положительно определенные матрицы
Доказательство. В интеграле Jn (7.1) произведем
замену переменных
Xi на — хи *"= 1, 2, ..., k
(4)
Х\ = Xf, I = К -\- 1, ... , tl, J
и полученный интеграл сложим с Jn. В результате получим
равенство
k п
» » - 2 аУжЛ ~ 2 аУжЛ ,
2J„= Г ...Г e *.i=i *.i=k+i (U + U^dx, (5)
— оо —оо
где
k п п k
-(2 2 ay***j+ 2 2а^Ы
Так как для всех положительных U
[/ + [/_1>2, (7)
то получаем неравенство
k
оо оо — ^j aijXtXj
— оо —оо
со со - 2 aijXiXJ .
х( $•■■$ е«=*-и rfxJ), (8)
-oo —oo
из которого вытекает (1).
Применяя (1) для k=l и рассуждая по индукции,
находим неравенство (3). Другое доказательство этого
неравенства, обобщаемое на положительно определенные
эрмитовы матрицы, можно найти в статье Беккенбаха [1];
см. также § 14 ниже.
§11. Неравенство Адамара
Неравенство (10.3) позволяет сразу установить самое
известное из всех неравенств для определителей.

§ 13. Теорема о представлении определителя эрмитовой матрицы 97
Теорема 8. Если \ху\ — действительный
определитель порядка п, то
1Ы<П(24)1/а- (О
i=i j=i
Доказательство. Пусть X = (xtj). Так как
результат тривиален для |Х| = 0, то предположим, что \Х\ ФО.
Тогда матрица XX' положительно определена. Применяя
(10.3), мы находим неравенство Адамара (1). См. Адамар
[1, 2]. Приведенное здесь доказательство следует Белл-
ману [3]. Другие доказательства можно найти у
Маркуса [4] и Островского [5].
§ 12. Неравенство Сасса
Неравенство Адамара, как и неравенство между
арифметическим и геометрическим средними, воспламенило
воображение математиков. Возникло много разнообразных
доказательств и обобщений этого неравенства. См. Фишер
[11, Уильямсон [2], Шур [3] и Буш и Олкин [41.
Особенно интересное обобщение принадлежит Сассу.
Оно состоит в следующем: если Pk обозначает
произведение всех главных миноров &-го порядка определителя
|Л|, где А — положительно определенная матрица, то
р^р^Кр^К.-^р^Г'Крп. (1)
Недавно Мирский [5] дал новое доказательство (1).
§ 13. Теорема о представлении определителя
эрмитовой матрицы
Докажем теперь теорему, аналогичную теореме 3.
Теорема 9. Если Н — положительно определенная
эрмитова матрица, то
оо оо
Jn{H)= J J e-^»*dxdy = nni\H\, (1)
— оо —оо
где z = x-\-iy, a dx и dy обозначают интегрирование по
вещественному n-мерному пространству.

98 Гл. II. Положительно определенные матрицы
Доказательство. Покажем сначала, что
Jn(H) = . яП1 . , (2)
\А\У\1 + А-1ВА-1В\ V J
если Н = А-{-1В1 а А и В —действительные матрицы. Так
как
(z, Hz) = (х, Ах) + 2{Вх, у) + {у, Ау), (3)
представление (2) получается двукратным применением
теоремы 3 (см. стр. 93).
Для завершения доказательства заметим, что
|//| = И+/я| = иц/+м-1в|, |
|Я'| = И-/5| = |Л||/-М_1Б|| J (4)
так что
|Я||Я/| = |Я|Я = ИН(/ + М-1В)(/-М-1В)| =
= |Ла||/ + Л"1ВЛ"15|. (5)
Эта формула была получена Беллманом [1]; она частично
обобщает один результат Хуа [2].
§ 14. Следствия
По аналогии с результатами, изложенными в § 7—12,
мы можем теперь, исходя из теоремы 9, вывести аналоги
этих результатов для эрмитовых матриц.
В следующем параграфе мы рассмотрим еще более
продуктивные представления, принадлежащие Ингаму,
Зигелю, Беллману и Олкину.
§ 15. Интегралы Ингама — Зигеля и их обобщения
В предыдущих параграфах мы видели, как ряд
интересных результатов получается из квазилинейного
представления |Л|1/2. Естественно теперь поставить вопрос
о том, какие результаты такого же типа можно получить
из других представлений.
Чтобы получить эти представления, обратимся к
интегралам, введенным Зигелем [2] в связи с его теорией

§ 15. Интегралы Ингама — Зигеля и их обобщения 99
матричных модулярных функций и Ингамом в связи
со статистическими задачами многомерного анализа.
Основой служит классический интеграл Эйлера
оо
^e'xvxs-1dx = T{s)y-\ Res, Re у >0. (1)
о
Зигель [2] дал следующее далеко идущее обобщение:
f esp(zy)|x|8-<w+1>/2dK =
= Яп(п-1У4 Г(з)Г(з-1/2)...Г(з-(п-1)/2) ( .
\Y\S ' V ;
где X и Y — положительно определенные матрицы
порядка п, Sp(X) обозначает след X, dV= Д йхц и инте-
грирование производится по всем положительно
определенным матрицам X. Предполагается, что вещественная
часть s больше (п— 1)/2. Аналог лапласовского
обращения (2) был дан Ингамом [1].
Интегралы Зигеля и Ингама могут быть в свою
очередь обобщены, как это заметил Сельберг (см. Белл-
ман [6] и Олкин [3]). Типичным результатом в этом
направлении является следующий:
2>*-(n+i)/2
\хГ *"Sp(ZYV
J |X(2)|^|X(3)|ft2...|X(n)|^-i
х>о
(3)
п
(Т^)п("-1)/2Г(й„)Г(/г„ + ^_1-1/2)...Г(2^-(»-1)/2)
г=1
|Уп1*п1Уп-11*Пг-1...1Щ*1
Здесь
\Xik'\ = \xv\, i,! = k, k + l, ...,я,1
\Yh\ = \yv\, *,/=!, 2,...,k. i ( }
Показатели kt должны удовлетворять условию, что все
выражения kn-\-kn-i-\-... -\-kT — г/2 положительны.

100 Гл. II. Положительно определенные матрицы
Ряд дальнейших результатов был дан Олкином [3];
см. также Бохнер ([39.3], гл. I), Гординг [4] и Айткен [5].
Мы не будем доказывать эти тождества, так как они
в дальнейшем не применяются. Ясно, что из
представления (3) вытекает ряд теорем о вогнутости. Однако
оказывается, что более общие результаты могут быть
получены более простым способом; см. Беллман [6].
Упомянем, наконец, об одном представлении,
принадлежащем Хуа, из которого получаются
дополнительные неравенства, содержащие определители. Некоторые
из его результатов вытекают также из представления,
приведенного в § 13 (см. Беллман [13.1]).
§ 16. Групповая инвариантность и формулы
представления
В своей работе [39.3], гл.1, Бохнер рассматривает
групповую инвариантность и ряд формул представления
приведенной выше общей формы, раскрывая их общее
происхождение. Так, например, он вывел формулу
J в-<*Л+ЗД + . • -+ЗДг> dXi ^ _ dXn =
R
= Сп{у\-у\-...-у1Гп/\ (1)
где R — область пространства (х, у), определенная
неравенствами
*iX4 + ... + *n)1/2, У1>(#2+ ...+№, (2)
а
сп=2п(п+1)/2Г(п-1)/Г[(п+1)/2]. (3)
Отсюда, между прочим, легко получается результат § 39
гл. I.
§ 17. Неравенство Бергстрома
В качестве другого примера применения метода
квазилинеаризации выведем следующий результат Бергстрома
[1]. Это доказательство принадлежит Беллману [2].

§ 18. Одно обобщение
101
Теорема 10. Пусть А и В — положительно
определенные матрицы, а At и Вг — подматрицы, возникающие
из А и В вычеркиванием i-й строки и i-го столбца.
Тогда
\А + В\ \А\ \В\ т
\Аг + ВгГ\Аг\^\Вг\' I1'
Доказательство. Рассмотрим задачу минимизации
положительно определенной квадратичной формы
п
Q(*)= 2 ауХМ = (х,Ах) (2)
по всем Xk, k= 1, 2, ..., п, подчиненным условию х% = \.
Легко видеть (например, при помощи неопределенных
множителей Лагранжа), что
minQ(*) = j^. (3)
Таким образом мы получаем квазилинейное представление
для |Л|/|Лг|, откуда неравенство (1) легко вытекает.
§ 18. Одно обобщение
Докажем теперь одну теорему, указанную Фань Цзы,
одновременно обобщающую теорему 10 и теорему 6 (из § 9).
Пусть А^д) обозначает главную подматрицу Л,
возникающую вычеркиванием из А первых (/—1) строк и
столбцов; в частности, A{i) = A. Пусть В0) и C(i) имеют
аналогичный смысл, причем С = ХА + (1—Х)В, 0<А,<1.
Предполагается также, что А к В положительно
определены. Тогда имеет место
Теорема 11. В сделанных выше предположениях
неравенство
nic(ilfej">nn(i14>(i)l(1~")fej" (О
имеет место для любых действительных чисел kj, таких,
что
2^>0, / = 1,2,..., п. (2)
г=1

102 Гл. II. Положительно определенные матрицы
Доказательство. В силу неравенства Бергстрома
из § 17
|С<»| > |Ы<*>| \(\-%)В^\ >
|С(;Ч1)| |Ы</+1)| ' |(1—Я)Б</+1)|
/ И<*>| Уу |Д{/>1 Л*~я
"Ч|Л(/+1У V|JB('+V '
причем в последнем случае мы применили неравенство
между арифметическим и геометрическим средними.
Утверждение (1) получается, если заметить, что
п \г<Ф - П^Ч1 r'c(2)iY1+fe2
И Iе I V|c(2V V|c(3V
и применить неравенство (3).
§ 19. Каноническая форма
До сих пор мы занимались только определителем
матрицы Л и его минорами. Сейчас мы обратимся к
изучению характеристических чисел Л как функций от Л.
Для этого мы должны установить основную связь между
Л и ее характеристическими числами, которые мы будем
обозначать через Я4, А/2, ..., 'к-а* Если Л — положительно
определенная матрица, то мы знаем, что все %t
положительны. Упорядочим их в невозрастающем порядке:
?4>Я2>...>^. (О
Известно, что тогда существует ортогональная
матрица 7\ такая, что
(2)

§ 20. Обобщение неравенства Бергстрома 103
Другими словами, существует ортогональное
преобразование х = Ту, такое, что
(х, Ах) = \yl + \у\ + ... + Kyi, (3)
— другое представление в виде суммы квадратов, если
А — положительно определенная матрица.
Аналогично, если Я —эрмитова матрица, то существует
такая унитарная матрица U, что
и*Ни=\ К . , (4)
\0 ''KJ
где СУ*— матрица, транспонированная к матрице,
сопряженной с U. Доказательства этих результатов можно
найти в [2.1].
Тождество (3) показывает, что положительность
характеристических чисел действительной симметричной
матрицы А является необходимым и достаточным условием
ее положительной определенности.
§ 20. Обобщение неравенства Бергстрома
Используя основную каноническую форму (19.2),
можно вывести следующее неравенство, частным случаем
которого является неравенство Бергстрома.
Теорема 12. Если действительная матрица А
положительно определена, то
(х,Ах)(у, А~1у)>(х,у)2 (1)
для всех действительных х и у.
Доказательство. Приведя А к диагональной форме
ортогональным преобразованием х = Ти и положив у = Tv,
мы должны доказать, что
(ll^Ylll.vi)>(Tu' Щ* = (и, vf. (2)
M=i ' м=1 * y
Это неравенство является, однако, частным случаем
неравенства Коши.

104 Гл. II. Положительно определенные матрицы
Так как равенство достигается при надлежащем выборе
Xt, мы можем записать, что
у(А)= (у, A^yf1 =тт{^. (3)
Отсюда вытекает, что
ф(Л + Я)>1КЛ) + ф(Я). (4)
Если в качестве у выбрать вектор с компонентами
yi=U yj=0, j Ф i, (5)
то мы получим теорему 10.
Теорема 12 допускает различные уточнения,
аналогичные тем, которые были изложены в гл. I (см. Грейб
и Рейнбольд [44.4], гл I). Так, например, имеет место
следующая
Теорема 13. Пусть А и В— действительные
положительно определенные матрицы порядка п. Если тА/<
<Л<т2/ и тьт2>0, то
(х, xf < (Ах, х) (А-*х, х) < ^±±^ (х, xf. (6)
Если АВ = ВА, т1/<Л<ш2/, т3, т4 > 0 и т3/<В<
<т4/, то
(Ах, Ах)(Вх, ВХ)< (^?OTtm?m?)2 {Ах, Bxf. (7)
§ 21. Теорема представления для |Л|1/П
Прежде чем перейти к одному неравенству Минков-
ского с его интересными обобщениями, докажем одну
теорему представления несколько иного типа, чем
соответствующие предыдущие теоремы.
Теорема 14. Если А — действительная положительно
определенная матрица порядка п, то
\А\*'«=т{пШт, (1)
|В| = 1 П
где В — положительно определенные матрицы.

§ 23. Обобщениеу принадлежащее Фань Цзы 105
Доказательство. В силу тождества Sp{Т'АТВ)=
= Sp (АТВТ') можно предположить, что А имеет
диагональную форму. Тогда
п
Sp(i4fl)=2 hbu. (2)
Используя неравенство между арифметическим и
геометрическим средними, мы находим, что
^Г>(ГЬ.)"*(Й»»)"* = 1л!""(Й »,,)"*• (3)
чг=1 у чг=1 у чг=1 у
Но из результатов § 10 вытекает, что
п
ЦЬц>\В\ = 1,
г=1
и неравенство (1) доказано.
§ 22. Одно неравенство Минковского
Из представления (21.1) непосредственно вытекает один
результат Минковского.
Теорема 15. Если А и В — положительно
определенные матрицы порядка п, то
\A + B\i/n>\A\i/n+\B\i/n. (1)
Обобщение этого результата на несимметричные
матрицы можно найти в работах Хейнсворта [1], [2], где
можно найти многочисленные литературные указания.
§ 23. Обобщение, принадлежащее Фань Цзы
Фань Цзы [1] установил теорему, одновременно
обобщающую неравенство (22.1) и неравенство Бергстрома,
приведенное выше.
Теорема 16. Пусть Ah обозначает главную
подматрицу Л, состоящую из k первых строк и k первых

106 Гл. II. Положительно определенные матрицы
столбцов А. Если С = А + В, где А и В — положительно
определенные матрицы порядка п, то
\m) >\w\) +kw\) • (1)
Доказательство основано на представлении,
обобщающем (17.3). См. также Фань Цзы [2] и Мирский [3].
§ 24. Обобщение, принадлежащее Оппенгейму
Обобщение в другом направлении было дано Оппен-
геймом [2]; см. также его более раннюю работу [1].
Теорема 17. Пусть А и В— положительно
определенные матрицы порядка п и Х1>Я2> ... >^п» [Ч>
> |i2 > • • • > И™, V! > v2 > ... > vn — характеристические
числа, соответственно А, В и А + В. Тогда
(П*Г>(Пя,)1Л+ПЪ.Г (1)
г=1 г=1 г=1
ДЛЯ k= 1, 2, . . . , П.
Этот результат может быть получен либо сведением
к диагональной форме, либо использованием
представления, аналогичного приведенному ниже в теореме 25, §34.
§ 25. Отношение Релея
Характеристические числа вводятся как корни
уравнения
\А-М\ = 0,
характеристического уравнения матрицы А. Если А
действительна и симметрична, то, как известно, все Xt
действительны.
Так как из этого определения нелегко получить
свойства %i как функций от Л, то обычно сначала
устанавливаются другие эквивалентные определения. Ключом к ним
является представление в диагональной форме, данное
в § 19, в сочетании с вариационными свойствами Хг. Как
из физических соображений (собственные частоты), так

§ 26. Мини макс-теорема Фишера
107
и с геометрической стороны (полуоси эллипсоида), мы
приходим к необходимости рассмотрения отношения Релея
(х, Ах)/(х, х).
Имеет место следующий замечательный факт.
Теорема 18. Если А — действительная
симметричная матрица, то
. (х, Ах)
?u = max , ч
х (х, х)
л . (х, Ах)
лЛ = тт^ -
(1)
Существует много доказательств этой теоремы. Одно
из них состоит в использовании представления § 16,
а именно тождества
(х, Ах) = \у\ + \у\ + ... + КУп,
где (х,х) = (у,у), х = Ту.
Если %i и %п рассматривать как функции от Л, то
квазилинейное представление (1) показывает, что для любой
неотрицательно определенной матрицы
Ь±(А + В)>Ь±(А),
К(А + В)Ж(А).
Кроме того, из (1) вытекают неравенства
Xi(KA + (l-'k)B)<'kX1(A) + (l-h)l1(B),
К (Ы + (1 - X) В) > ХК(А) + (1 - Щ„(£),
(2)
(3)
справедливые для любых двух симметричных матриц А
и В. Другими словами, ^(Л) является выпуклой
функцией от Л, а %п(А) вогнутой.
§ 26. Минимакс-теорема Фишера
Представления характеристических чисел %± и Хп
из теоремы 18 могут быть дополнены следующим
образом. Пусть ха) — характеристический вектор,
ассоциированный с ^ и нормированный условием (ха\ х(1))= 1. Тогда,

108 Гл. II. Положительно определенные матрицы
как из аналитических, так и из геометрических соображений
вытекает, что
где вектор х ограничен условием ортогональности
(х, ха)) = 0. Пусть х(2) — нормированный
характеристический вектор, ассоциированный с Я2, для которого в (1)
достигается максимум. Тогда
Хз-тах-^^-, (2)
где теперь уже х ограничен двумя условиями
ортогональности: (х, ха))=0, (х, х{2)) = 0, и т. д. Трудность
использования этих, казалось бы квазилинейных, представлений
%i заключается в том, что характеристические векторы
ха\ х(2\ ... сами зависят от Л. Поэтому вместо
указанных индуктивных представлений %% нам нужно
представление Хи не зависящее ни явно, ни неявно от %и Х2, ...
Такое представление было получено Фишером. Оно
играет важную роль в дальнейшем развитии
аналитической теории матриц. Обобщение этого представления
на широкие классы симметричных операторов было дано
Курантом [1]; исходное представление содержится в работе
Фишера [2].
Теорема 19. Характеристические числа %t>Х2> • • •
> %п любой действительной симметричной матрицы А
могут быть получены по следующим формулам:
(3)
Я4 = max (х, Ах),
(х, х)=1
Х2= min max (х
(V*V)=i (x,x)=l
(x,y)=0
Xk = min
(vli\ y(i))=i
i=i,2,..., k-l
, Ax),
max (x, Ax).
(x, x)=i
(x, 2/(i))=0
= 1,2,..., fe-1 )

§ 27. Еще одна теорема представления 109
Характеристические числа могут быть получены по
аналогичным формулам'.
Хп= min (х, Ах),
(х, х)=1
K-i= max min (х, Ах), (4)
(у, v)=i (x,x)=i
(*,!/)=0
и т.д.
Доказательство см. в [1] и [2.1].
Из этого результата легко вытекает, что
Xk(A + B)>Xh(A), /5=1, 2, ..., /г, (5)
для любой действительной симметричной матрицы А
и любой действительной неотрицательно определенной
матрицы В. Этот результат физически очевиден, так как
увеличение жесткости стержня или пластинки ведет
к повышению характеристических частот.
§ 27. Еще одна теорема представления
Введем обозначение
\A\k = Ki^n-i ... ^n-k+ii (1)
т. е. обозначим через \А\ь произведение k наименьших
характеристических чисел действительной положительно
определенной матрицы А.
Через Rk обозначим ^-мерное подпространство я-мер-
ного ^-пространства, определенное п — k соотношениями
(х,аг) = 0, i=l, 2, ..., п — k, (2)
где а\— это п — k линейно независимых векторов.
Докажем следующую теорему.
Теорема 20. Для любой действительной
положительно определенной матрицы А
-%- = max \ е-<*. **> dVk, (3)
где область интегрирования Rh определена
соотношениями (2), а максимум берется по всем таким Rh.

ПО Гл. II. Положительно определенные матрицы
Доказательство. Мы можем сразу предположить,
что (х, Ах) имеет вид \x\-\-\x\-\- • • • +^n*?l- Рассмотрим
объем Va(q) области, заданной условиями
(х,аг) = 0, i = 1, 2, ..., п — k. J
Очевидно, что
Va(Q) = Q^Va(\). (5)
Следовательно,
п
J в *=* dKA = J 6-PrfKa(Q)= у Va(l) \ e-PQ^/2-i rfg.
JRb —оо —оо
(6)
Чтобы завершить доказательство, мы должны показать,
что максимум Va(l) достигается для области Rk, для
которой определяющие условия (2) имеют вид
Xi = x2=... =xn-k = 0. (7)
Но этот факт непосредственно вытекает из формулы
объема эллипсоида
(х, Вх)=1, (8)
где В — положительно определенная матрица, и из
результатов Фишера, изложенных в § 26.
§ 28. Одно неравенство Фань Цзы
При помощи теоремы 20 и метода, использованного
в § 9, мы можем теперь доказать следующую теорему
Фань Цзы [1] о вогнутости.
Теорема 21. Если А и В — действительные
положительно определенные матрицы порядка п и 0 < X < 1, то
\%A-V{\--k)B\h>\A\l\B\{-\ (1)
Доказательство Фаня основывается на представлении,
изложенном в § 32 ниже.

§ 30. Результаты, относящиеся к характеристическим числам 111
§ 29. Аддитивный аналог
Мы можем также получить аддитивный аналог
теоремы 21. Вместо А рассмотрим матрицу I + гА и вместо
В—матрицу I + гВ, е > 0. Тогда утверждение теоремы 21
примет вид
\I + e(kA + (l-X)B)\k>\I + eA\Ul + zB\l-\ (1)
Характеристическими числами матрицы 7 + еЛ являются
1 + 8^! > 1 + 8^2 > ... > 1 + еХл; точно так же 1 + е^ >
> 1 + е[х2 > ... > 1 + е(хл — характеристические числа
матрицы I + гВ. Следовательно, для малых е>0 мы имеем
\1 + гА |£= 1 +1г(К + К-1+ ... + Wk) + 0(82), ^
|/+eB|i~x=i+ (1-^)8(^+^4 + ... (2)
...+^-*-ы) + 0(е2). J
В пределе при е —>0 из неравенства (28.1) мы
получим следующий результат.
Теорема 22. Пусть
Sk (А) = Хп + ^тг-1 + ... + hn-k+l (3)
для любой действительной симметричной матрицы А.
Если А и В—матрицы порядка п, то для 0<Я< 1
Sh(KA + (i-K)B)>KSk(A) + (l—%)Sh(B). (4)
Этот результат также принадлежит Фаню [9.1].
Доказательство, приведенное выше, дано Беллманом [2.1].
§ 30. Результаты, относящиеся
к характеристическим числам А, АА* и (А+А*)/2
Помимо результатов, изложенных в § 19 — 29,
известно много других соотношений между
характеристическими числами Л, с одной стороны, и
характеристическими числами АА* и (Л + Л*)/2 — с другой. Здесь Л*
обозначает матрицу, сопряженную к транспонированной
от А, т. е. А*=А'.
Эти соотношения, так же как и дополнительные ссылки,
читатель найдет в работах Вейля [1], Фань Цзы [2], Лид-

112 Гл. II. Положительно определенные матрицы
ского [3], Горна [4], Виландта [5], Амир-Моэза [6]
и Мирского [7].
Отметим, что, как и в предыдущих параграфах, любое
неравенство для А4* влечет за собой и соответствующее
неравенство для (А-\-А*)/2.
§31. Теорема разделения Коши — Пуанкаре
Из минимакс-теоремы Фишера (§ 26) непосредственно
вытекает следующий результат Коши [1] и Пуанкаре [2],
который мы используем в § 32.
Теорема 23. Пусть {х^}, j= 1, 2, ..., k, &<я,—
система ортонормированных векторов и
k
х=^] ujxM. (1)
i=i
Тогда
k
(х, Ах)= 2 иМх^, Ах«>). (2)
3,1=1
Рассмотрим k-мерную симметричную матрицу
B = ((^,iWO)), /, /=1, 2, ...,&. (3)
Тогда
^(В)<^(Л), *=1, 2, ..., fc
Я^(В) > ^.(Л), / = 0, 1, 2, ..., k - 1.
См. также Пойа [3] и Гамбургер и Гримшоу [4].
§ 32. Одно неравенство для ^nKn-i---^k
Применяя предыдущую теорему, можно доказать
следующий результат Фань Цзы [1].
Теорема 24. Пусть А —положительно определенная
матрица. Тогда
п
КК-1..Лк=т'т П (*(i), Ах№), k= 1, 2,..., л, (1)
причем минимум берется по всем п—k + l ортонормиро-
ванным векторам {хЩ.
(4)

§ 34. Аддитивное неравенство
113
Доказательство
Известно (см. теорема 7, § 10), что
ПМВ) = |В|<П(*(*>, ^>). (2)
г=1 г=1
Тогда %k(B)>K(A), K-i(B)>Kn-i(A) и т. д., поэтому,
как и в (31.4), (2) дает (1), так как равенство может
быть получено подходящим выбором векторов х^\ Ссылки
на дальнейшие результаты приведены в § 36.
§ 33. Обсуждение
Между полученными результатами данной главы
имеется много внутренних связей. Для удобства
читателей приведем следующую схему логических связей:
я теорема 21 —> теорема 6
теорема 24 ^
^ теорема 5
и, как будет видно из § 34,
теорема 24—■> теорема 25—> теорема 22
§ 34. Аддитивное неравенство
Заменяя Л на / + еЛ и рассуждая, как в § 21, легко
приходим к следующему аддитивному дополнению
теоремы 24, полученному Фанем [9.1]; см. также Мирский [1].
Теорема 25. Для любой действительной
симметричной матрицы А порядка п
2 h = max 2 (*<*>, Л*<*>).
Г1 i=1 п о)
2 V«+i = niin2 (*(i)> Ax(i))i
причем в обоих случаях вектор х^ пробегает всю систему
из k ортонормированных векторов.
Теорема 22 есть прямое следствие (1).

114 Гл. II. Положительно определенные матрицы
Заметим, что условие положительной определенности А
не является необходимым, так как 1-\-гА— положительно
определенная матрица для достаточно малых 8.
Из теоремы 25 непосредственно следует неравенство
п п
2 Я|<2 fl«, k = l, 2, ..., л, (2)
i=h i=k
аналогичное (10.3).
§ 35. Мультипликативное неравенство,
вытекающее из аддитивного
Оказывается, что не только аддитивное неравенство
можно вывести из мультипликативного, но и наоборот
(см. Беллман [1]). Предполагается, что матрица А
положительно определена.
Рассмотрим следующее суммирование по частям:
Ck^k + Ck+i^k+i + • • • + сп%п = Ck (Хд + Wi + ... + kn) +
+ (Ck+l—Ck) (Wi + • • • + К) + • • • + (Cn — Cn-i) К-
Предположим также, что 0<сд<£д-ц< .. . <сп.
Используя формулу (34.2), получим
п
ckU + ch+iXk+i+ ... +cnXn<ch [2 (*<*\ Ах(»)\ +
+ (cft+1-cft)[ 2 (*(i), Ax(»)} + ...
i=k+l
... + (c„-c„-1)(jkM, Л*<»))< (2)
< cfe (*<*>, iW>) + c*+1 (я<*+1>, ^x<fe+1)) + ...
для любой системы ортонормированных векторов {xS{)}.
Из (2) следует, что
п п
min(2c,Xj)<min [2 сг(х<*>, АхР>)], (3)

§ 36. Дальнейшие результаты
115
где R — область в пространстве с и которая определяется
соотношениями
(а) 0 <ck<ck+i< .. . <сп,
(Ь) П* = 1. (4)
Неравенство между арифметическим и геометрическим
средними, доказанное в гл. I, приводит к формуле
п
2 ctXi
tSV^WW' <5>
и таким образом минимум 2 ci^i достигается в точке
ct= г~к х> , l = fe,...,/l. (6)
Так как %k > Xk+1 > . . . > Яп, ограничение ck < £&+i < ...
... <£п. не исключает того, что минимум левой частью (3)
достигается. Это соображение было использовано в § 30
гл. I. Для того чтобы удержать это ограничение для
правой части (3), нужно дополнительно предположить
(*<*>, AxF>)>(**+!>, Axtk+U)>...>(xtn\ AxF>). (7)
При этом неравенство (3) приводит к соотношению
п п
Uh<U(*l>,Axm) (8)
для любой ортонормированной системы векторов {x(i)},
удовлетворяющих условию (7).
Из симметрии условия (7) видим, что оно не является
существенным ограничением.
§ 36. Дальнейшие результаты
Результаты Фань Цзы, касающиеся вариационных
характеристик таких функций, как Kn%n-i ... %п и Хп +
+ Xn-i+ • • • + ta» могут быть значительно обобщены.

116 Гл. II. Положительно определенные матрицы
Вначале можно задаться вопросом о представлении,
например, суммы ^1 + Я3 + Я10; затем о представлении
произведений вида Х^К^.
Далее можно рассматривать более общие
симметрические функции, такие, как 2 ^Ль и т- Д- РЯД
результатов этого типа приведен в работах Островского [28.1],
гл. I, Маркуса и Лопеса [32.1], гл. I, Маркуса и Мак-
Грегора [1], Маркуса и Мойлса [2], Маркуса, Мойлса
и Уэствика [3, 4], а также Али Р. Амир-Моэза [30.6],
где имеется обобщение результатов Виландта.
§ 37. Составные или присоединенные матрицы
Для эффективного изучения различных свойств
линейных преобразований у = Ах может быть использован ряд
полезных ассоциированных или индуцированных
преобразований. Из них наиболее важными являются
сопряженные преобразования.
Сопряженный оператор А' определяется соотношением
(Ах, у) = (х, А'у). Этим определяется матрица А' в
конечномерном случае, однако предыдущее равенство используется
и для бесконечномерного случая.
Другие важные так называемые «индуцированные»
преобразования можно получить, рассматривая некоторые
функции от х. Например, пусть заданы два преобразования
п п
#i = 2 CLijXj, Wi = ^ bijZj, t=l, 2, ...,n. (1)
3=1 j=l
Составим произведение
n
yiW3= 2 aikbJrxkzr. (2)
Если ввести два п2-мерных вектора с компонентами ytWj
и xtZj, i, j = 1, 2,.. ., п, то они будут связаны матрицей,
которая называется произведением Кронекера Л и Б; эта
п2-мерная матрица обозначается
АхВ = (аиВ). (3)
По этому поводу см. работы [2, 3, 2.1].

§ 38. Положительные матрицы
117
Вместо простых функций (2) можно рассматривать
более сложные; в частности, интересен случай функции
вида
i\/=l, 2, ...,n. (4)
XJ Уз I
Можно ввести произведения более высоких порядков,
например r-мерные определители типа (4). Таким образом,
вводятся составные или присоединенные матрицы (см.
Шур [1] и Мак-Даффи [2]).
Чтобы дать формальные определения, поступим
следующим образом. Пусть Л —квадратная n-мерная матрица,
г пробегает целые числа от 1 до п. Обозначим через Sr
множество совокупностей из г различных чисел, взятых
из 1, 2, ... п. Пусть s и t — два элемента Sr, As^
—матрица, получающаяся из А вычеркиванием всех строк
и столбцов, индексы которых не входят в s и t
соответственно. Нумеруя элементы Sr в некотором порядке
Si, s2, ... sm ^здесь т = rl£'__r^j , можно построить
m-мерную матрицу
CT(A) = (\AVJ\). (1)
Она называется r-й составной или присоединенной
матрицей к А.
Важность таких матриц обусловлена тем, что их
характеристическими корнями являются т выражений типа
kt ... кТ, составляющие r-ю элементарную
симметрическую функцию от кг. В приложениях эти матрицы
используются для вывода некоторых неравенств (см. Райзер [3]).
Дальнейшие применения приводятся в работах Беллмана
[4, 5], Кернера [6], Монтролла и У орда [7], Фейнмана [8],
Карлина и Мак-Грегора [9].
§ 38. Положительные матрицы
Перейдем к изучению других классов матриц, которые
также используются для получения некоторых неравенств.
Квадратная матрица Л, все элементы которой
положительны, называется положительной матрицей. Эти матрицы

118 Гл. II. Положительно определенные матрицы
были введены Перроном [1] в его диссертации по
многомерным непрерывным дробям Якоби. Им установлен
следующий фундаментальный результат.
Теорема 26. Положительная матрица А обладает
единственным наибольшим по абсолютной величине
характеристическим числом. Этот корень р(А) положителен
и имеет положительный характеристический вектор,
единственный с точностью до постоянного множителя.
Эта теорема остается в силе, когда элементы
матрицы А неотрицательны (см. Фробениус [2]). Фробениусом
был изучен широкий класс таких матриц. Важным
частным классом неотрицательных матриц являются матрицы
Маркова или стохастические матрицы теории вероятностей,
определенные условием, что ац являются вероятностями
перехода, т.е.
2fly = l, / = 1, 2, ...,л. (1)
г=1
Теорема 26 используется в различных областях
[теория дифференциальных уравнений (Гартман и Винтнер [3]),
алгебра (Брауэр [4], Гантмахер и Крейн [5], Перрон [1]),
метод неподвижной точки (Александров П. и Хопф [6],
Фань Цзы [7], Биркгоф [8], Беллман [9])]. Доказательство,
приводимое ниже, использует фундаментальные идеи
общей теории положительных операторов. Это
доказательство было сообщено нам Бонебластом и имеется в книге
Беллмана и Данскина [10]. Связь положительных матриц
с разветвляющимися процессами математической физики
указана в работах Беллмана и Гарриса [11], Гарриса [12];
связь с экономикой см. в следующих работах: фон
Нейман [13], Вальд [14], Леонтьев [42.1], Моргенштерн [42.2],
Эрроу и Нерлав [42.3], а также Дорфман, Самуэльсон,
Солоу [42.4], Карлин [15], Дебре и Херстейн [16],
Самуэльсон [17], Крейн и Рутман [18], Мьюборн [19].
§ 39. Вариационная характеристика р(А)
В этом параграфе будет получено представление для
р(А) как решения вариационной задачи. Это представле-

§ 39. Вариационная характеристика р (А) 119
ние даст возможность ввести некоторые основные
свойства р(А).
Теорема 27. Пусть А —положительная матрица,
S(А) —совокупность неотрицательных Я, для которых
существует неотрицательный вектор х, такой, что
Ах>Хх, Т(А) —совокупность положительных К, для
которых существует положительный вектор х, такой, что
Ax^clx.
Тогда
кроме того,
р(А) =
р(А) =
max Я,
min Я,
max min
х г
min max
х i
b£S(A),
ЯеГ(Л);
n
2 av*j
3 = 1
*i
n
2 av*i
3 = 1
*i
(1)
(2)
где в обоих случаях xt >0, 2 *i = l.
2=1
Этот результат был получен независимо рядом авторов.
Опубликован впервые Колатцом [1]; см. также Виландт [2].
Доказательство. Под положительным вектором
мы понимаем вектор, все компоненты которого
положительны; аналогично определяется неотрицательный вектор.
Соотношение х^у эквивалентно утверждению, что х — у
неотрицательно, или х — у>0, где 0 обозначает нулевой
вектор. Под нормированным вектором мы понимаем век-
п
тор, удовлетворяющий условию || х || = 2 хг = 1» норма
2=1
п
матрицы А определяется формулой ||Л||= 2 агз-
1,3=1
Из условия Кх^Ах получаем
Ш||<||Ае||<||Л|
(3)

120 Гл. II. Положительно определенные матрицы
где 0 < % < || Л ||. Следовательно, S (Л) — ограниченное
множество. Легко видеть, что ?t0 = supX, %£S(A), есть
действительно максимум. Пусть хт — вектор, отвечающий Я0,
т. е. %0х(0) < Лх(0). Покажем, что в действительности
это —равенство. В самом деле, не умаляя общности,
допустим, что
п
3=1
Рассмотрим вектор
di/2%0 \
0
о У
(4)
(5)
Ясно, что Ау > Я0#, так как все элементы матрицы А
положительны. Однако это противоречит тому, что к0 есть
максимум. Таким образом, предположение, что dx > 0,
приводит к противоречию. Аналогично доказывается, что
и остальные соотношения в (4) являются равенствами.
Остается показать, что Я0 — р(А). Пусть г
—характеристический вектор, отвечающий р(А), так что p(A)z = Az.
Обозначим через \г\ вектор, компоненты которого суть
абсолютные величины компонент г. Тогда неравенство
| р (А) | | z | < А | z | приводит к тому, что | р (А) | < Я0. Если
же |р(Л)| = Я0, то соотношение |р(Л)| |г|<Л |z| должно
быть равенством. Это значит, что | Аг \ = А \ z |, откуда
следует z = clw, где ^-—неотрицательный вектор,
удовлетворяющий условию Aw = p (Л)w. Поэтому число р (Л)
вещественно и равно к0.
Для выражения р(А) через минимум Я можно
поступить аналогичным образом либо воспользоваться более
изящным методом, основанным на транспонированных
матрицах или сопряженных преобразованиях и на том
факте, что р{А)^=р{А').
Доказательство единственности характеристического
вектора с точностью до множителя следует из
предыдущих рассуждений.

§ 40. Другая форма для р(А)
121
§ 40. Другая форма для р (А)
Биркгоф и Варга показали, что р(А) можно записать
в более изящной форме
п п
2 aijxtyj 2 aijxtyj
р(А) = max min ±Ц^ = min max -^^ .
xi^Q У^° 2j XWi yi^° Xi^° 21 Х*У*
(x,x)=l (y,y)=l i {y,y)=i (x,x)=l i
(1)
В этой форме равенство двух вариационных
выражений есть непосредственное следствие одного обобщения
теоремы о минимаксе фон Неймана, которую мы
рассмотрим в § 23 гл. III.
§ 41. Некоторые следствия
Приведенные выше вариационные выражения дают
непосредственно следующие результаты, которые
интуитивно ясны из экономических соображений.
Теорема 28. Если В— неотрицательная, а А
—положительная матрицы, то
р(А + В)>р(А). (1)
Если Ai — положительная матрица размерности п—\,
полученная выбрасыванием одной строки и одного столбца
произвольных индексов из матрицы А, то
p&XpiA). (2)
Используя неравенство (2), можно доказать, что р(А)
есть простой корень характеристического уравнения.
Другое следствие состоит в том, что наибольший
характеристический корень матрицы А мажорируется
наибольшим характеристическим корнем матрицы, элементы
которой есть абсолютные величины элементов матрицы Л.
В последние годы положительные матрицы играют
большую роль в математической экономике. Матричная
функция р(А) связана с концепцией развивающейся
экономики (см. фон Нейман [38.13]), а также с теорией
игр (§ 23 гл. III).

122 Гл. II. Положительно определенные матрицы
§ 42. Входные-выходные (input-output) матрицы
Рассмотрим класс квадратных матриц, определяемых
условиями
atj > 0, / ф /, ан —вещественны. (1)
Такие матрицы будем называть входными-выходными.
Экономические рассмотрения приводят к следующему
результату. (Леонтьев [1], Моргенштерн [2], Эрроу и Нер-
лав [3], Дорфман, Самуэльсон и Солоу [4].)
Теорема 29. Если А —входная-выходная матрица,
то она имеет характеристический корень г (А) с
наибольшей действительной частью, причем этот корень
действителен. Соответствующий характеристический вектор
положителен и единствен с точностью до множителя.
Доказательство. Этот результат будет получен
как предельная форма теоремы 27. Рассмотрим матрицу
е6А-/ + 6Л+..., (2)
которая положительна для малых значений 6. Очевидно
что
р(ебА)_ебг(А)# (3)
Это верно для некоторого интервала значений 6; поэтому
число г(А) действительно, причем г(А) > 0, так как
р(е6А)>1.
Для получения вариационной характеристики г (А)
используем формулу (39.2).
Имеем
п
еьг(А) = max min Ы 1_ о (б2). (4)
х i хг
Следовательно, при 6—>0 получаем
п
г(Л)=тах min— , (5)
х i хг
откуда и следует доказательство теоремы.

§ 44. Добавления
123
Легко показать, что
г(А+В)>г(А),
если А —- входная-выходная матрица, а В — положительная
матрица.
§ 43. Обсуждение
Тот факт, что р(А) представляется в виде (39.2)
следует из того, что положительная матрица А преобразует
область xt>0 в некоторую ее подобласть. Аналогично
имеется инвариантное преобразование, связанное с
входными-выходными матрицами (см. § 6 гл. IV). Именно,
необходимым и достаточным условием того, что решение
векторно-матричного уравнения
^ = Лх, х(0) = с9 (1)
неотрицательно для £>0 при любых с>0, состоит в том,
что А — входная-выходная матрица (см. Беллман, Гликс-
берг, Гросс [1]; Эрроу [2]).
§ 44. Добавления
Предшествующие результаты, касающиеся
положительных матриц, можно расширить по ряду направлений.
Прежде всего отметим результаты Фань Цзы [1]
относительно существования и характеристики величин,
удовлетворяющих п уравнениям
gi(X±, ..., Хп) = ЬЫ(Х1, ...,хп), /=1, ...,«, (1)
где gitthi — непрерывные функции, определенные на мно-
п
жестве S точек (хи ..., хп), х% > 0 и ^]xi=l; gt>0
2=1
и вогнутые на S, Aj<0 при х^Ои выпуклые на S.
Затем отметим результаты из динамического
программирования, в частности теорию разрешающих марковских
процессов, а также результаты Беллмана [38.9] и
Говарда [2], относящиеся к решениям уравнений
п
max [2 aij (д) xj] =xt, I = 1, 2, ..., и. (2)
q j=i

124 Гл. 11. Положительно определенные матрицы
§ 45. Матрицы и гиперболические уравнения
Лаксом [1] получен следующий результат.
Теорема 30. Пусть {X} — вещественное линейное
пространство n-мерных матриц, имеющих только
действительные характеристические корни. Тогда Ятах(Х),
наибольший характеристический корень, есть выпуклая
функция от X, a Jlmin(X), наименьший
характеристический корень, есть вогнутая функция от X.
Им также дано представление Ятах(Х) как верхней
грани по линейным функциям. Так как это представление
и доказательство теоремы связаны с теорией линейных
дифференциальных уравнений гиперболического типа, детали
мы будем опускать (см. Виландт [3], Герстенхабер [4]).
Простое и прямое доказательство монотонности
характеристических корней X(sXl + X2) при увеличении s
приводится у Вейнбергера [2]. Гординг установил, что этот
результат и соответствующий результат для
характеристических корней симметричных и эрмитовых матриц есть
частный случай его общей теоремы для гиперболических
полиномов (см. [36.1] и [38.1], гл. I).
§ 46. Определители, не обращающиеся в нуль,
и распределение характеристических чисел
Проблема определения верхней грани для |А | так же
важна, как и определение нижней границы, т. е.
верхней границы для |Л_1|. Желательно найти условия, при
которых определитель | А | отличен от нуля.
Возможно, что лучший результат этого типа состоит
в следующем.
Теорема 31. Если
\ац\> Slflift|» i"==1» 2> •- •> п> (О
кфг
то \А\фО.
Этот часто встречающийся результат вместе с многими
другими результатами содержится в обзорной статье
Тауски [1] (см. также Тауски [2]).
С теоремой 31 связана проблема определения области
на Я-плоскости, которая содержит все характеристические

§ 47. Монотонные матричные функции в смысле Лёвнера 125
корни матрицы А. Некоторые обобщения могут быть
найдены в работах Паркера [3], Брауэра [4], Фань Цзы [5],
Хейнсворта [6]. Дополнительные результаты имеются
у Островского [7], Слепяна и Вейнберга [8, 9] и Фань
Цзы [10].
Одно из следствий предыдущей теоремы состоит
в том, что характеристические корни матрицы А
содержатся в кругах, определяемых соотношениями Гершгорина,
|^ — ац\= 2|0ift|» i = l, 2,...,я. (2)
§ 47. Монотонные матричные функции в смысле Лёвнера
Если АиВ — вещественные симметричные матрицы и
матрица А —В неотрицательно определена, то будем писать
А>В. Легко показать на простых примерах, что Л>В
не является необходимым следствием соотношения А2>В2.
Задача исследования функций f(z), обладающих тем
свойством, что из А>В следует f(A)>f(B), была
впервые изучена Лёвнером [1,2]. Класс функций,
обладающих этим свойством для матриц всех измерений,
интересен тем, что он играет большую роль в математической
физике и теории электрических сетей, где его именуют
классом «положительных действительных» функций.
Легко видеть, что с&-\-Съ, где с± > 0, есть функция
такого типа; значительно труднее показать, что —г'1
обладает аналогичным свойством. Именно если Л>В>0, то
Л~1<В~1. Этот результат получается методами
квазилинеаризации. Вначале мы показываем, что равенство
-(у, A-1y) = min[(x, Ах)~2(х, у)] (1)
X
выполняется при А > 0. Так как минимум достигается
на векторах х, являющихся решением уравнения Ах = у,
мы легко получаем (1); сформулированный выше
результат есть простое следствие (1).
Заметим, что две функции с^г-\-с2 и —z~1 дают
возможность построить широкий класс монотонных матричных
функций. См. статьи Лёвнера [1,2], Бендата и Шер-
мана [3], где имеются обобщения на бесконечномерные
операторы и рассмотрен ряд других вопросов. Другие

126 Гл. II. Положительно определенные матрицы
ссылки и рассмотрения можно найти у Крауса [4], Доб-
ша [5], Вигнера [6], Лёвнера [7], Даффина [8],
Андерсона [9], Лейна и Томаса [10].
§ 48. Преобразование, уменьшающее число перемен знака
Естественным обобщением положительных
преобразований являются преобразования, уменьшающие число
перемен знака. Отличное изложение ряда проблем,
группирующихся около этой идеи, дается в работе Шенберга [1],
где приведена обширная библиография; см. также его
более раннюю статью [2], а также Мейерхубер, Шенберг
и Уильямсон [10].
Изучение линейных колебаний электрических цепей
привело Гантмахера и Крейна к понятию «полностью
неотрицательных матриц» (см. [5] и [38.5]). Эта концепция
была ранее развита Келлогом в связи с интегральными
уравнениями. Теория преобразований типа свертки,
начатая Гиршманом и Виддером [6], также приводит к
преобразованиям, уменьшающим число перемен знака. В
другом направлении, в теории марковских процессов, Карлин
и Мак-Грегор [8] получили дальнейшие результаты.
Примечательно, что имеется ряд геометрических связей (см.
Шенберг [7]). Здесь этих вопросов мы рассматривать не
будем, так как для освещения каждого из них требуется
целая монография.
§ 49. Области положительности
Положительно определенные матрицы тесно связаны
с определением их области положительности, R является
такой областью, если из х, y£R следует, что (х, Лу)>0.
Задачи, возникающие в связи с этим определением, были
изучены Кехером [1, 2].
Обобщением положительных преобразований является
преобразование Т, которое сохраняет отношение порядка,
т.е.
из х>у следует Тх>Ту. (1)
Другой способ введения понятия положительности
состоит в следующем. Пусть х и г/ —элементы двух

Библиография и дополнения
127
пространств Si и S2 соответственно, для которых
определено скалярное произведение (х, у) для любых x^Si
и y£S2.
Тогда, имея определение положительности для всех
xgSb можно определить положительность элемента у £ S2
соотношением
(*, у)>0, (2)
которое должно выполняться для всех положительных
x£Si. Эта идея является частным случаем основной темы
следующей гл. III.
Так, например, известно, что необходимым и
достаточным условием того, что симметричная матрица В является
положительно определенной, служит неравенство
Sp(^B)>0, (3)
которое должно выполняться для всех положительно
определенных матриц А. В этом примере А и В —элементы
одного и того же пространства и мы не получаем
обобщения понятия положительности.
Стрехмление обобщить понятие положительности на более
широкие классы матриц уводит нас далеко в сторону от
основной темы; здесь остается еще много невыясненного.
Интересующийся читатель может обратиться к работам
Беллмана [2.1] об устойчивости матриц, Филлипса [3],
рассматривавшего диссипативные операторы, Винера и
Мазани [4], Хельсона и Лоуденслагера [5], Маршалла
и Олкина [6,7], рассматривавших статистические и
вероятностные задачи.
БИБЛИОГРАФИЯ И ДОПОЛНЕНИЯ
§ 2. Введение в теорию симметрических матриц, содержащую
как изложенные выше, так и многие другие результаты, можно
найти в первых девяти главах книги
1. Беллман (Bellman R.), Introduction to matrix
analysis, New York, McGraw-Hill, 1960.
§ 5.
1. Островский, Тауски (Ostrowski A., Taus-
s k у О.), On the variation of the determinant of a positive
definite matrix, Nederl. Akad. Wet. Proc. (Л), 54, (1951), 383-385

128
Библиография и дополнения
§ 6. Оригинальные результаты Андреева можно найти в работе
1. Андреев (Andreief С), Note sur une relation entre les
integrates definies des products des fonctions, Mem. soc. sci.
Bordeaux (3), 2 (1883), 1—14.
В этой работе рассматривается непрерывный аналог формулы
Лагранжа. См. также
2. Д е Брейн (De Bruijn N. G.), On some multiple
integrals involving determinants, /. Ind. Math. Soc, 19 (1955), 133—
151.
Вопрос представления через сумму квадратов связан с
алгеброй квадратичных форм, а также форм высших порядков,
допускающих композицию. См.
3. Джекобсон (Jacobson N.), Composition algebras
and their automorphisms, Rend Circ. Math. Palermo (2), 7 (1958),
1—25.
В этой работе можно найти ссылку на одну из первых работ
Гурвица, а также ряд других. Обзор различных направлений
имеется в работе
4. М а к-Д аффи (Mac Duffee С. С), On the composition
of algebraic forms of higher degree, Bull. Am. Math. Soc, 51,
(1945), 198—211.
Более общие неравенства могут быть получены из теории
симметричных матриц Они были введены в следующих работах.
5. Колмогоров А. Н., Zur Theorie der Markoffschen Ketten,
Math. Ann., 112 (1936), 155—160.
6. Э в e p и т т (E v e г i t t W. N.), Inequalities for Gram
determinants, Quart. J. Math., (2), 8 (1957), 191—196.
7. Мофферт (Moffert C. F.), On the Gram determinants,
Quart J. Math., 10 (1959), 161—164.
8. Де Брейн (De Bruijn N. G.), Inequalities concerning
minors and eigenvalues, Nieuw. Arch. Wiskunde (3), 4 (1956),
18—35.
Последняя работа представляет собой превосходную обзорную
статью, в которой теория определителей используется для
унификации методов вывода ряда неравенств этой главы. Кроме того, эта
статья содержит некоторые новые результаты, а также обсуждение
теорем Карамата и Островского, которые в нашей книге
приводятся в § 28—31, гл. I.
§ 8.
1. Тауски (Taussky О.), Bibliography on bounds for
characteristic roots of finite matrices, National Bureau of Standards,
Washington, D. C, 1951.
2. Беллман, Гоффман (Bellman R., Hoffman A.),
A note on an inequality of Ostrowski and Taussky, Arkiu. Math.,
5 (1954), 123—127.
§9.
1. Фань Цзы (Fan K.)> On a theorem of Weyl concerning
eigenvalues of linear transformations, I, Proc. Nat. Acad. Sci.

Библиография и дополнения
129
USA, 35 (1949), 652—655; II, Proc. Nat. Acad. Sci ISA, 36 (1950),
31—35.
§ 10.
1. Беккенбах (Beckenbach E. F.), An inequality
for definite hermitian determinants, Bull. Am. Math. Soc, 35
(1929), 325—329.
§ 11-
1. Адамар (Hadamard J.), Resolution d'une question
relative aux determinants, Bull. Sci. Math., 2, (1893), 240—248.
Этот результат Адамара привлекает и продолжает привлекать
к себе большое внимание. Имеется около ста опубликованных
и неопубликованных доказательств. Адамар доказал этот
результат, не пользуясь теорией интегральных уравнений Фредгольма,
из которой этот результат получается мгновенно. В связи с этим
имеется следующая литература.
2. Адамар (Hadamard J.), The psychology of invention
in the mathematical field, Princeton, N. J., Princeton University
Press, 1949.
3. Беллман (Bellman R.), Notes on matrix theory, II. Am.
Math. Monthly, 60 (1953), 174—175.
Очень интересным методом неравенство Адамара выводится
в работе
4. Маркус (Marcus М.), Some properties and applications
of doubly stochastic matrices, Am. Math. Monthly, 67 (1960),
215—221.
Автор показывает, что тот же метод позволяет установить
неравенство Фань Цзы (см. § 32) и неравенство Минковского (см.
§ 22 этой главы).
5. Островский (Ostrowski А. М.), On some metrical
properties of operator matrices and matrices partitioned into blocks,
J. Math. Anal. AppL, 2 (1961).
§ 12. Различные обобщения можно найти в следующих работах,
1. Фишер (Fischer Е.), t)ber den Hadamardsche Determi-
nantensatz, Arch. Math. Phys. (3), 13 (1908), 32—40.
2. Уильямсон (Williamson J.), Note on Hadamard's
determinant theorem, Bull. Am. Math. Soc, 53 (1947), 608—613.
3. Шур (S с h u r J.), t)ber endliche Gruppen und Hermitesche
For men, Math. Z.f 1 (1918), 184—207.
4. Б у hi, О л к и н (Bush К. А., О 1 k A n J.), Extrema of
quadratic forms with applications to statistics, Biometrika, 46 (1959),
483—486.
5. Мирский (Mirsky L.), On a generalization of Hadamard's
determinantal inequality due to Szasz, Arch. Math., 8 (1957),
274—275.
§ 13.
1. Беллман (Bellman R.), Hermitian matrices and
representation theorems, Duke Math J., 26 (1959), 485—490.

130
Ёиблиография и дополнения
В следующей статье частично обобщаются результаты Хуа.
2, X у а Л о ■ г е н (Н u a L. К-)» Inequalities involving
determinants, Acta Math. Sinica, 5 (1955), 463—470.
Здесь дается совершенно другое представление определителей,
основанное на теории представлений групп.
§ 15. Обобщенный интеграл Эйлера был независимо открыт
Ингамом и Зигелем. По этому поводу см. следующие работы.
1. Ингам (Ingham А. Е.), An integral which occurs in
statistics, Proc. Cambridge Phil. Soc, 29 (1933), 271—276.
2. Зигель (Siegel C. L.), Ober die analytische Theorie der
quadratischen Formen, Ann. of Math., 36 (1935), 527—606.
Обобщение результатов Ингама и Зигеля дается в следующих
работах.
3. Олкин (Olkin J.), A class of integral identities with
matrix argument, Duke Math. J., 26 (1959), 207—213.
4. Гординг (Garding L.), The solution of Cauchy's problem
for two totally hyperbolic linear differential equations by means of
Riesz integrals, Ann. of Math., 48 (1947), 785—826.
5. Айткен(АЛкеп A. C), On the Wishart distribution in
statistics, Biometrika, 36 (1949), 59—62.
6. Беллман (Bellman R.), A generalization of some
integral identities due to Ingham and Siegel, Duke Math. J., 24
(1956), 571—578.
Интеграл, рассмотренный Зигелем, играет большую роль
в теории матричных модулярных функций. Комбинация последнего
с формулой суммирования Пуассона приводит к изящному
матричному варианту тождества Липшица. Аналогично обобщенный
интеграл Беллмана (6) может быть использован для получения
дальнейших обобщений результата Зигеля.
§ 17.
1. Бергстром (Bergstrom Н.), A triangle inequality
for matrices, DenElfte SkandinaviskiMatematiker-kongress,Trond-
heim, 1949, Oslo, Johan Grundt Tanums, 1952.
2. Беллман (Bellman R.), Notes on matrix theory, IV, An
enequality due to Bergstrom, Am. Math. Monthly, 62 (1955),
172—173.
§ 18. Обобщение частного результата, приведенного в § 15,
дается в следующей работе.
1. Беллман (Bellman R.), Notes on matrix theory, IX,
Am. Math. Monthly, 64 (1957), 189—191.
Результаты этого параграфа даются в (18.1). См. также § 44,
гл. I.
§ 21. Большое число подобных (но более сложных) результатов
может быть получено для других основных функций от А
(коэффициентов в разложении характеристического многочлена \Х1 +
+ А\) методом Гординга, использованного ранее для гиперболи-

Библиография и дополнения
131
ческих полиномов (см. § 36—38 гл. I). Из этих, а также аналогичных
им представлений может быть получен ряд неравенств.
Отметим также статьи [36.1,38.1] Гординга, [38.2] Цзяня
а также статью [8.2] Лорха, где дается связь этих результатов
с теорией связанных объемов Минковского. Несмотря на то что
эта теория имеет много точек соприкосновения с рассматриваемыми
здесь вопросами, мы детально изучим ее во втором томе.
Интересное обобщение теоремы 14 имеется у Тауски:
|W^= min M^l,
1*1=1 (J)
§ 22.
1. Хейнсворт (Haynesworth E. V.), Note on bounds
for certain determinants, Duke Math. J., 24 (1957), 313—320.
2. Хейнсворт (Haynesworth E. V.), Bounds for
determinants with positive diagonals, Trans. Am. Math. Soc, 96
(1960), 395—413.
Эти статьи содержат результаты Островского, Прайса, Шней-
дера, Бреннера. В них можно найти дальнейшие ссылки.
§ 23.
1. Фань Цзы (Fan К.)» Some inequalities concerning
positive-definite hermitian matrices, Proc. Cambridge Phil. Soc, 51
(1955), 414—421.
2. Ф а н ь Цзы (Fan К.), Problem 4786, Am. Math. Monthly,
65 (1958), 289.
3. Мирский (Mirsky L.), Maximum principles in matrix
theory, Proc. Glasgow Math. Assoc, 4 (1958), 34—37.
§ 24.
1. Оппенгейм (Oppenheim A.), Inequalities connected
with definite hermitian forms, J. London Math. Soc, 5 (1930),
114—119.
2. Оппенгейм (Oppenheim A.), Inequalities connected
with definite hermitian forms, II, Am. Math. Monthly, 61 (1954),
463—466.
§ 25. Дальнейшее обсуждение результатов §§ 25, 26 см. в
работе [2.1].
§ 26. Результаты Куранта относительно непрерывных
операторов можно найти в книге
1. Курант, Гильберт (Courant R., Hilbert D.),
Methods of mathematical physics, New York, Interscience
Publishers, 1953. Русский перевод второго немецкого издания: Методы
математической физики, т. I, II, Гостехиздат, М.—Л., 1951;
см. также перевод американского издания 1961 года; Р. К у-
р а н т, Уравнения с частными производными, «Мир», М., 1964.
Оригинальный результат Фишера можно найти в статье

132
Библиография и дополнения
2. Фишер (Fischer Е.), Uber quadratische Formen mit ree-
len Koeffizienten, Monatsh. Math. Phystk, 16 (1905), 234—249.
§ 27.
1. Беллман, Гликсберг, Гросс (Bellman R.,
Glicksberg I., Gross O.), Notes on matrix theory, VI,
Am. Math. Monthly, 62 (1955), 571—572.
§28
1. Фань Цзы (Fan K-), Problem 4430, Am. Math. Monthly
58 (1951), 194—195.
§ 29. См. часть II работы [9.1].
§30.
1. В e й л ь (W е у 1 Н.), Inequalities between the two kinds of
eigenvalues of a linear transformation, Proc. Nat. Acad. Set.
USA, 35 (1949), 408—411.
2. Фань Цзы (Fan К-)» Maximum properties and inequalities
for the eigenvalues of completely continuous operators, Proc.
Nat. Acad. Scl. USA, 37 (1951), 760—766.
3. Л и д с к и й В. Б., Собственные значения сумм и
произведений симметрических матриц, Докл. АН. СССР, 75 (1950), 769—772.
4. Горн (Horn A.), On the singular values of a product of
completely continuous operators, Proc. Nat. Acad. Scl. USA., 36 (1950),
374—375.
5. Виландт (Wielandt H.), An extremum property of sums
of eigenvalues, Proc. Am. Math. Soc, 6 (1955), 106—110.
6. А м и p - M о э з (A m i r - M о e z Ali R.), Extreme properties
of eigenvalues of a hermitian transformation and singular values
of the sum and product of a linear transformation, Duke Math. J.,
23 (1956), 463—477.
7. M и p с к и й (M i r s k у L.), Onaconvex set of matrices, Arch.
Math., 10 (1959), 88-92.
§ 31.
1. К о ш и (Cauchy A.), Sur l'equation a Paide de laquelle on
determine les inegalites seculaires des mouvements des planetes,
Oeuvres completes IIе serie IX, Paris, Debure, 1821, 174—195.
2. Пуанкаре (Poincare H.), Sur les equations aux
derivees partielles de la physique mathematiques, Am. J. Math.,
12 (1890), 211—294.
См. также следующие работы.
3. П о й а (Р о 1 у a G.), Estimates for eigenvalues, Studies in
Mathematics and Mechanics, New York, Academic Press, 1954.
4. Гамбургер, Гримшоу (Hamburger H. L,,
Grimshaw M. E.), Linear transformations in я-dimensional
vector space, Cambridge, Cambridge University Press, 1951.
Одна из простых формулировок теоремы разделения состоит
в следующем.
Пусть А — вещественная симметричная матрица порядка
п и В — матрица, полученная как главная подматрица А порядка k;

Библиография и дополнения
133
тогда %г(В) < %г(А), i=\t 2, ..., k, %n-j(B) Ж-№)> /=0, 1, ...
*.. , k — 1. (Эта формулировка принадлежит Фань Цзы.)
Работа [3] содержит несколько интересных замечаний
относительно эквивалентности теоремы разделения и теоремы о мини-
максе Фишера. Кроме того, приводятся некоторые приложения.
§32.
1. Фань Цзы (Fan К»), Problem 4429, Am. Math. Monthly,
58 (1951), 194.
§ 33. Результаты этого параграфа принадлежат Фань Цзы.
§ 34. Этот результат содержится в первой части работы [9.1],
1. Мирский (Mirsky L.), An inequality for positive definite
matrices, Am. Math. Monthly, 62 (1955), 428—430.
§ 35.
1. Беллман (Bellman R.), Note on matrix theory —
multiplicative properties from additive properties, Am. Math. Monthly,
65 (1958), 693—694.
§ 36.
1. Маркус, Мак-Грегор (Marcus M.,
McGregor J. L.), Extremal properties of hermitian matrices, Canad.
J. Math., 8 (1956), 524—531.
2. Маркус, Мойлс (Marcus M., M о у 1 s В. N.),
Extreme value properties of hermitian matrices, Dept. of Math.
Univ. of British Columbia, Vancouver, Canada, 1956.
3. Маркус, Мойлс, Уэствик (Marcus M., M о у 1 s
В. N., West wick R.), Some extreme value results for
indefinite hermitian matrices, II, Illinois J. Math., 2 (1958), 408—414.
4. Маркус, Мойлс Уэствик (Marcus M., Mo-
у 1 s В. N., Westwick R.), Extremal properties of
hermitian matrices, Canad. J. Math.
§ 37. Идея изучения различных классов присоединенных матриц
была введена Шуром в его диссертации.
1. Шур (Schur I.), Uber eine Klasse von Matrizen die sich einer
gegebenen Matrize zuordnen iassen, Dissertation, Berlin, Г901.
Детальное рассмотрение вопроса и дальнейшие ссылки см.
в работах
2. Мак-Даффи(МасОи!1ее С. С), The theory of
matrices, New York, Chelsea, 1946.
3. P а й з e p (R у s e r H. J.), Inequalities of compound and
induced matrices with applications to combinatorial analysis,
Illinois J. Math., 2 (1958), 240—253.
Отметим тот замечательный факт, что произведения Кронекера
для матриц, а также составные матрицы Шура возникают
естественным образом не только в теории групп и геометрии (см.,
например, Лорх [8.2], гл. I), но также и в других областях анализа. Так,
например, произведение Кронекера появляется в теории
устойчивости. См. по этому поводу

134
Библиография и дополнения
4. Беллман (Bellman R.), Kronecker products and the
second method of Lyapunov, Math, Nachr., 20 (1959), 17—19.
С произведениями Кронекера можно также встретиться в
теории стохастических процессов. См.
5. Ьеллман (Bell man R.), Limit theorems for
non-commutative operations, I, Duke Math. J., 21 (1954), 491—500.
6. Кернер (Kerner E. H.), The band structure of mixed
linear lattices, Proc. Phys. Soc, 69 (1956), 234—244.
Составные матрицы Шура, элементами которых являются
обобщенные координаты Плюккера, естественно возникают при
изучении процессов, включающих k частиц и обладающих тем
свойством, что никакие две частицы не могут одновременно
находиться в одном и том же состоянии. По этому вопросу см.
7. М о н т р о.л л, У о р д (М о n t г о 1 1 Е. W., Ward J. С),
Quantum Statistics of an electron gas, Bell Telephone Monograph
3036, New York, Bell Telephone Co., 1959.
8. Ф e й н м а н (F e у n m a n R. P.), The theory of positrons.
Space-time approach to electrodynamics, Phys. Rev., 76 (1949),
749—759, 769—789.
9. Карлин, Мак-Грегор(КагПп S.,McGregor J.),
Coincidence probabilities, Dept. of Statistics, Techn. Report No. 8,
Stanford, Calif., Stanford University Press, 1959.
Один из неисследованных здесь вопросов — это изучение
положительности или неотрицательности в связи с теорией
вероятностей. Отметим только, что этот вопрос в свою очередь тесно
связан с преобразованиями, понижающими число перемен знака,
о которых мы кратко говорили в § 48. Подобную методику можно
было бы использовать в гл. IV при обсуждении неотрицательности
функции Грина. Более подробного обсуждения этого весьма
мощного метода мы здесь не даем, так как это завело бы нас слишком
далеко.
§ 38. Только в последнее время был установлен приоритет
открытия фундаментального результата для положительных матриц,
который был получен Перроном.
1. Перрон (Perron О.), Zur Theorie der Matrizen, Math.
Ann., 64 (1907), 248—263.
Ряд результатов Фробениуса, который обобщил и развил
оригинальную теорему Перрона, можно найти в статье
2. Фробениус (Frobenius G.), Uber Matrizen aus nicht-
negativen Elementen, Sitzber. preuss. Akad. Wiss., 1912, 456—477.
Могут быть даны различные Доказательства теоремы 26. По
этому поводу см.
3. Гартман, Винтнер (Hartman P., Wintner А.),
Linear differential equations and difference equations with
monotone solutions, Am. J. Math., 75 (1953), 731—743.
4. Брауэр (Brauer A.), A new proof of theorems of Perron
and Frobenius on nonnegative matrices, I, Positive matrices,
Duke Math. /.. 24 (1957), 367—378.

Библиография и дополнения
135
5. Гантмахер Ф. Р., Крейн М. Г., Sur les matrices com-
pletament non-negatives and oscillatoires, Сотр. Math., 4 (1937),
445—476.
6. Александров П. С, Хопф (Hopf Н.), Topologie,
I, Berlin, Springer, 1935.
7. Ф а н ь Ц з ы (Fan K.)» Topological proofs for certain theorems
on matrices with nonnegative elements, Monatsh. Math., 62 (1958),
219—237.
8. Биркгофф (Birkhoff G.), Extensions of Jentzsch's
theorem, Trans. Am. Math. Soc, 85 (1957), 219—227.
9. Беллман (Bellman R.), On a quasi-linear equation,
Canada J. Math., 8 (1956), 198—202.
10. Беллман, Данскин (BellmanR., Danskin J.),
A survey of the mathematical theory of time lag, retarded control,
and hereditary processes, Santa Monica, Calif., RAND Corporation,
Report R-256, 1954.
Развитие теории положительных операторов обусловлено по
крайней мере тремя различными факторами. Это — внутренние
математические рассмотрения, математическая физика и
математическая экономика.
Отметим, что к изучению неотрицательных матриц можно
прийти, рассматривая различные инварианты, а не только через
теорию Перрона и Фробениуса. Подобно тому как ортогональное
преобразование сохраняет квадратичную форму (х, х), унитарное
преобразование сохраняет форму (х, х), матрицы Маркова сохра-
п
няют соотношения a:j>0, ^xt—1, так неотрицательное пре-
г=1
образование сохраняет область определения xt^>0. Изучая все
эти теории с подобной точки зрения, т. е. с точки зрения теории
инвариантов, мы видим, что многие интересные классы матриц
обладают различными видами «положительности».
С точки зрения математической физики теория
разветвляющихся процессов, которая описывает такие различные явления, как
нейтронный распад, каскады космических излучений,
биологический рост и мутации, представляет собой ряд проблем, связанных
с общей теорией положительных операторов. По этому поводу см.
11. Беллман, Гаррис (Bellman R., Harris Т. Е.),
On the theory of age-dependent stochastic branching processes,
Proc. Nat. Acad. Sci. USA, 34 (1948), 601—604.
12. Гаррис (Harris Т. E.), Branching processes, Ergebnisse
der Mathematik, Berlin—Gottingen — Heidelberg, Springer, 1961
готовится к печати русский перевод (изд-во «Мир»).
Отметим,наконец, работу фон Неймана, который начал изучение
экономики с математической точки зрения.
13. Фон Нейман (Von Neumann J.), Uber ein okono*
misches Gleichungssystem und die Verallgemeinerung des Bro-
uwerschen Fixpunktsatzes, Vienna, Ergebnisse eines Mathemati-
schen Kolloquiums, vol. 8 (1937), 73—83.

136
Библиография и дополнения
14. Вальд (Wald A.), Uber die Productionsgleichungen der
okonomischen Wertlehre, II, Vienna, Ergebnisse eines Mathema-
tischen Kolloquiums, vol. 7 (1936), 1—6.
С этими вопросами имеют связь входные-выходные модели
Леонтьева, которые рассматриваются в § 42, где изучается связь
этих матриц с математической экономикой. Входные-выходные
матрицы впервые изучались Минковским в несколько другой связи.
Детальный обзор результатов, полученных в этом направлении,
можно найти в следующих работах.
15. К а р л и н (К а г 1 i n S.), Mathematical methods and theory
in games, programming and economics, 1, 2, Reading, Mass,
Addison — Wesley, 1959. Русский перевод: Математические
методы в теории игр, программировании и экономике, «Мир»,
М., 1964.
16. Дебре, Херстейн (Debreu G., Hersteinl. N.),
Non-negative square matrices, Econometrica, 21 (1953), 597—607.
17. Самуэльсон (Samuelson H.), On the Perron — Frobenius
theorem, Michigan Math. /., 4 (1957), 57—59.
18. К p e и н M. Г., P у т м а н M. А., Линейные операторы,
оставляющие инвариантным конус в пространстве Банаха, Успехи
машем, наук, 3:1(23) (1948), 3—95.
19. Мьюборн (Mewborn А. С), Generalizations of some
theorems on positive matrices to completely continuous linear
transformations in a normed linear space, Duke Math. /., 27
(I960), 273—277.
§ 39. Как указывалось в тексте, вариационная характеристика
числа р (А) много раз открывалась заново. Мюррей в своей
неопубликованной работе использует этот результат и отмечает, что он
принадлежит фон Нейману. Доказательство этого результата можно
найти в следующих работах.
1. Коллатц (Collatz L.), Einschliessungssatz fur die cha-
rakteristischen Zahlen von Matrizen, Math. Z., 48(1946), 221—226.
Впервые этот результат установлен точно в статье
2. Виландт (Wielandt Н.), Unzerlegbare, nicht negative
Matrizen, Math. Z., 52 (1950), 642—648.
Доказательство, которое приводится здесь, было дано Бонен-
бластом в связи с проблемой, возникшей из исследований Беллмана
и Гарриса [38.11] по многомерным ветвящимся процессам.
§ 40.
1. Биркгофф, Варга (Birkhoff G., Varga R. S.),
Reactor criticality and nonnegative matrices, /. Ind. AppL Math.,
6 (1958), 354—377.
Теорема о минимаксе является ключевой в теории игр Бореля
и фон Неймана. Она рассматривается в гл. III, § 23.
§ 41. См. фон Нейман [38.131 и Вальд [38.141.
§ 42. Детальное обсуждение входных-выходных матриц можно
найти в работе [38.151, где приводятся дальнейшие ссылки. Отметим
в связи с этим следующие работы.

Библиография и дополнения
137
1. Леонтьев (Leontieff W. W.), The structure of American
economy, Cambridge, Mass., Harvard University Press, 1941.
2. Моргенштерн (Morgenstern О.), ред., Economic
activity analysis, New York, Wiley, 1954.
3. Эрроу, Нерлав (Arrow К. J., Nerlove M.), A note
on expectation and stability, Econometrica, 26 (1958), 297—305.
В каждой из этих работ можно найти многие дальнейшие
результаты и ссылки. По поводу общего обсуждения теории
линейного программирования и ее отношения к математической
экономике см. следующую литературу.
4. Дорфман, Самуэльсон, Солоу (Dorfman R.,
Samuelson Н., Solow R.), Linear programming and
economic analysis, New York, McGraw-Hill, 1958.
§ 43. Этот результат приводится в следующих статьях,
1. Беллман, Гликсберг, Гросс (Bellman R.,
Glicksberg I., Gross О.), On some variational problems
occurring in the theory of dynamic programming, Rend. Circ.
Mat. Palermo (2), 3 (1954), 1—35.
Изящное доказательство отрицательности —Л"1,
основании - , ,
ное на свойстве неотрицательности решении уравнения -rj—Au-f-b,
можно найти в работе
2. Эрроу (Arrow К. J.)» Price-quantity adjustments in
multiple markets with rising demands, Mathematical models in the
social sciences, Stanford, Calif., Stanford University Press, 1959.
§ 44.
1. Фань Цзы (Fan К.)» On the equilibrium value of a system
of convex and concave functions, Math. Z., 70 (1958), 271—280.
2. Горвард (Horward R.), Discrete dynamic programming,
New York, Wiley, 1960.
§ 45.
1. Л а к с (L a x P. D.), Differential equations, difference
equations, and matrix theory, Comm. Pure Appl. Math., 10 (1958),
175—194.
2. Вейнбергер (Weinberger H. F.), Remarks on the
preceding paper of Lax, Comm. Pure Appl. Math., 10 (1958),
196—197.
См. также статьи Гординга и Цзяня, на которые имеются
ссылки в § 36—38, гл. I.
Относительно связи между теорией симметричных матриц
и результатами Лакса см. работу
3. Виландт (Wielandt Н.), Lineare Scharen von Matrizen
mit reelen Eigenwerten, Math. Z., 53 (1950), 219—225.
По поводу обобщений см. работу
4. Герстенхабер (Gerstenhaber М.), Note on a
theorem of Wielandt, Math. Z., 71 (1959), 141—142.

138
Библиография и дополнения
§46.
1. Т а у с к и (Taussky О.), A recurring theorem on
determinants, Am. Math. Monthly, 56 (1949), 672—676.
2. Тауски (Taussky O.), Bibliography of bounds for
characteristic roots of finite matrices, Nat. Bur. Standards Report,
Washington, D. C, National Bureau of Standards, 1951.
3. Паркер (Parker W. W.), Characteristic roots and fields
of value of a matrix, Bull. Am. Math. Soc, 57 (1951), 103—108.
4. Брауэр (Brauer A.), Limits for the characteristic roots
of a matrix, I, II, III, Duke Math. J., 13, 14, 15 (1946, 1947,
1948), 387—395, 21—26, 871—877.
5. Ф а н ь Ц з ы (Fan K.), Note on circular disks containing the
eigenvalues of a matrix, Duke. Math. Z., 25 (1958), 441—445.
6. Хейнсворт (Haynsworth E. V.), Bounds for
determinants with dominant main diagonal, Duke Math. J., 20 (1953),
199—209.
Вещественные матрицы, удовлетворяющие условию
i*«i>2 ifl«ji.
иногда называются матрицами Адамара. Эти матрицы тесно связаны
с изучавшимися Минковским М-матрицами Островского.
7. Островский (Ostrowski A.), Note on bounds on
determinants, Duke Math. J., 22 (1955), 95—102.
В следующей работе можно найти ссылки на ранние работы,
а также теорию доминирующих матриц Слепяна и Вейнберга.
8. Слеп ян, Вейнберг (Slepian P., Weinberg L.),
Synthesis of paramount and dominant matrices, Los Angeles,
Calif., Hughes Research Laboratories, 1958.
9. Слепя н, Вейнберг (Slepian P., Weinberg L.),
Positive real matrices, /. Math, and Mech., 9 (1960), 71—84.
См. также
10. Фань Ц з ы (F а п К-)» N°te on M-Ma trices, Quart. J. Math.,
11 (1960), 43—49.
Матрицы этого типа играют большую роль в численных
решениях дифференциальных уравнений в частных производных и
возникают при различных разностных схемах. Отметим, что теорема,
утверждающая, что из Щг>^]\аи\ следует |Л|>0, допу-
екает доказательство по непрерывности, использованное в § 3.
Общий результат здесь состоит в следующем.
Пусть А принадлежит выпуклому множеству матриц,
содержащему единичную матрицу; тогда если |Л|=^0, то величина \А\ —
действительна и положительна.
§ 47.
1. Лёвнер (Loewner С), Uber monotone Matrixfunktionen,
Math. Z., 38 (1934), 177—216.
2. Лёвнер (Loewner С), Some classes of functions defined
by difference or differential inequalities. Bull. Am. Math. Soc,
56 (1950), 308-319.

Библиография и дополнения
139
3. Бендат, Шерман (Bendat J., Scherraan S.),
Monotone and convex operator functions, Trans, Am. Math.
Soc, 79 (1955), 58—71.
4. Kpayc (Kraus F.)f Uber konvexe Matrixfunktionen,
Math. Z., 41 (1936), 18—42.
5. Д о б ш (D о b s с h R.), Matrixfunktionen beschrankter
Schwankung, Math. Z., 43 (1937), 353—388.
6. В и г н е р (W i gner Е.), On a class of analytic functions
from the quantum theory of collisions, Ann. Math., 53 (1951),
36—37.
7. Лёвнер (Loewner C), On totally positive matrices,
Math. Z., 63, (1955), 338—340.
8. Д а ф ф и н (D u f f i n R. J.), Elementary operations which
generate network matrices, Proc. Am. Math. Soc, 6 (1955), 335—
339.
9. Андерсон (Anderson T. W.), The integral of a
symmetric unimodal function, Proc. Am. Math. Soc, 6 (1955), 170—
176.
10. Лей н, Томас (Lane A. M., Thomas R. G.), Я-
matrix theory of nuclear reactions, Rev. Mod. Phys., 30 (1958),
257—352.
§ 48.
1. Шенберг (Schoenberg I. J.), On smoothing operations
and their generating functions, Bull. Am. Math. Soc, 59 (1953),
199—230.
2. Шенберг (Schoenberg I. J.)» Uber variationsver-
mindernde lineareTransformationen, Math. Z., 32 (1930), 321—328.
Относительно теории строго положительных матриц Гантмахе-
ра и Крейна нужно заметить, что она представляет собой
алгебраическую аналогию ядер Келлога в теории интегральных
уравнений. См. по этому поводу работы
3. Келлог (Kellogg О. D.), The oscillation of functions
of an orthogonal set, Am. J. Math., 38 (1916), 1—5.
4. К e 1 1 о g (Kellogg O. D.), Orthogonal function sets arising
from integral equations, Am. J. Math., 40 (1918), 145—154.
См. также серию статей об этих ядрах Гантмахера и Крейна,
ссылки на которые можно найти в [38.5] и в книге.
5. Гантмахер Ф. Р., Крейн М. Г., Осцилляционные
матрицы, ядра и малые колебания механических систем, Физ-
матгиз, М.—Л., 1950.
6. Гиршман, Виддер (Hirschman I. L, Wid-
d е г D. V.), The convolution transform, Princeton, N. Y.,
Princetone University Press, 1955.
7. Шенберг (Schoenberg I. J.), An isoperimetric
inequality for closed curves convex in even-dimensional Euclidean
spaces, Acta Math., 91 (1954), 143—164.
Некоторые приложения этих идей к теории вероятностей и ста»
тистике можно найти в следующих статьях.

140
Библиография и дополнения
8. Карлин, Мак-Грегор (Karlin S.f McGregor
J. L.), The differential equations of birth-and-death
processes and the Stieltjes moment problem, Trans. Am. Math. Soc, 85
(1957), 489—546.
9. Карлин (Karlin S.)f Polya-type distributions, IV,
Ann. Math. Stat., 29 (1958), 1—21.
10. Мейрхубер, Шенберг, Уильямсон (Mair-
huber J. C, Schoenberg I. J.,
Williamson R. E,), On variation-diminishing transformations of the
circle, Rend. Circ. Mat. Palermo (2), 8 (1959), 241—270.
§ 49.
1. Kexep (Koecher M.), Die Geodatischen von Positivitat-
sbereichen, Math. Ann., 135 (1958), 192—202.
2. Kexep (Koecher M.), Positivitatsbereiche im Rn, Am.
J. Math., 79 (1957), 575—596.
Очень мало известно о так называемых устойчивых матрицах,
т. е. матрицах, все характеристические корни которых имеют
отрицательную действительную часть. Некоторые результаты по
этому поводу можно найти в [2.1], где имеются также дальнейшие
ссылки. Отметим, однако, что имеется весьма общая теория «дис-
сипативных операторов». См. следующие работы:
3. Филлипс (Phillips R. S.), On the integration of the
diffusion equation with boundary conditions, Trans. Am. Math. Soc.,
98 (1961), 62—84.
Несколько интересных неравенств для матриц можно найти
в статье
4. Винер, Мазани (Wiener N., Masani P.), The
prediction theory of multivariate stochastic processes, I, II, Acta
Math., 58 (1957), 111—148, 99 (1958), 93—130.
См. также работу
5. Хельсон, Лоуденслагер (Helson Н., Low-
denslager D.), Prediction theory and Fourier series in
several variables, Acta Math., 99 (1958), 165—202.
Ряд неравенств, которые выводятся из статистических и
вероятностных соображений, можно найти в статьях
6. Маршалл, Олкин (Marshall A., Olkin I.),
Technical Report No. 36, Applied Math, and Statistics, Stanford, Calif.,
Stanford University Press, 1960.
7. Маршалл, Олкин (Marshall A., Olkin I.),
Multivariate Chebyshev Type Inequalities, East Lansing, Mich.,
Michigan State University, 1959.

Глава III
ПРОСТРАНСТВА МОМЕНТОВ И РЕЗОНАНСНЫЕ ТЕОРЕМЫ
§ 1. Введение
Центральная идея анализа, которая может быть
использована для связи широкого круга вопросов, на первый
взгляд не связанных между собой, может быть выражена
в следующей простой форме.
«Элемент линейного пространства S часто может быть
охарактеризован довольно легко и явным образом путем
описания его взаимодействия с подходяще выбранной
группой элементов в двойственном пространстве S'».
Источник этого принципа находится в геометрии в
концепции полюсов и поляр; наиболее важным случаем этой
концепции является точечно-тангенциальная связь. Мы
уже в гл. I использовали эту идею при рассмотрении
неравенства Минковского — Малера, а также в
квазилинейных представлениях (гл. I и II). Взаимодействие между
точкой и линией характеризует алгебру, геометрию и
анализ. Вероятно, это единственная наиболее
разветвляющаяся концепция математики.
Многие примеры этого метода «проектирования» можно
найти в теории рядов Фурье, более общо в теории
ортогональных разложений. Наибольшего расцвета эта
концепция достигает в теории банаховых и гильбертовых
пространств. Изящные приложения имеются в теории
уравнений в частных производных, где метод ортогонального
проектирования слабых и обобщенных решений играет
основную роль. (См. Банах [1], Зигмунд [2].)
В этой главе мы будем рассматривать ряд теорем
«взаимодействия», привлекающих своей общностью,
многими внутренними связями, неожиданностью своих
отношений к теории неравенств. Эти отношения возникают
из того факта, что во многих важных случаях
взаимодействие между х £ S и у £ S' выражается посредством нера-

142 Pa. 1IL Пространства моментов it резонансные теоремы
венства
(х, у)>0 (1)
с подходяще выбранным определением внутреннего
произведения.
Иногда, например, в различных вопросах
квазилинейных представлений требуются более общие выражения.
Естественно, что здесь будет использован ряд теорем
и понятий из теории выпуклых множеств, с одной
стороны, и из теории линейных пространств — с другой.
Фундаментальную роль при этом будут играть метод
ортогональных проекций, теорема Банаха — Штейнгауза и
теорема расширения Хана —Банаха, а также понятие
разделяющей плоскости.
Важно отметить, что при изучении этих основных
вопросов математики искусственные границы между
алгеброй, геометрией и анализом стираются. Имеется ряд
определенных основных задач и методов решений, к
которым сводятся все эти разделы. Одним из наилучших
описаний решения ряда отдельных задач анализа с этой
объединяющей точки зрения является работа Розен-
блюма [3].
Для иллюстрации указанных выше идей перейдем
к рассмотрению отдельных примеров.
Начнем с обобщения неравенств Коши —Шварца —
Буняковского и Гёльдера.
Вместо частных результатов, которые мы раньше
получили для степенных сумм
sa=** + **+... +**, &=1, 2, ..., (2)
где х% — неотрицательные числа, желательно иметь так
называемую полную систему неравенств. Под полной
системой неравенств мы понимаем соотношения вида
Ri(su ..., sk)>0, f = l, 2,..., (3)
которые удовлетворяются всеми последовательностями
типа (2), наоборот, любая последовательность {s/J,
удовлетворяющая соотношениям (3), может быть представлена
в виде (2) (см., например, Урселл [2,1]).
Указанная проблема, конечно, является
фундаментальной в теории пространств моментов. В нашу задачу не
входит углубление в эту широкую область, а лишь рас-

§ 1. Введение
143
смотрение того, как эти вопросы связаны с изучением
неравенств, какие общие методы могут быть использованы
для их изучения и какого типа результаты могут быть
получены. Для детального изучения различных
результатов, которые здесь имеются, мы будем отсылать
читателя к ряду превосходных монографий и работ.
Далее будет рассматриваться более общая задача
определения полной системы неравенств для общих
«моментов»
mh=(x,yh), k = l, 2, ... . (4)
Здесь, как и выше, x£S, yk(zS', a S и S'— два
пространства, для элементов которых определено внутреннее
произведение.
Так сформулированная задача дает хорошую основу
для введения простых и интуитивных геометрических идей,
концентрирующихся около концепции выпуклости. Мы
выведем как непосредственное следствие отсюда хорошо
известную теорему Ф. Рисса, что является обобщением
неравенства Бесселя в теории ортогональных рядов, а
также неравенства Гёльдера.
Затем мы вернемся к задаче определения полной
системы неравенств для обыкновенных моментов
1
mk=^xkdG(x), (5)
о
а также для тригонометрических моментов
1
mk=^e2nikxdG(x). (6)
о
Детально будет рассмотрена связь между этими
задачами и задачей представления положительной в том или
ином смысле функции в виде квадрата или суммы
квадратов. Эти интересные и важные сами по себе вопросы имеют
тесную связь с положительно определенными
квадратичными формами, о которых шла речь в гл. IL
Неожиданным является результат о том, что полная
система неравенств может быть получена прямо из
установленных в гл. II, §§3 — 5, неравенств,
характеризующих положительно определенные квадратичные формы.

144 Гл. III. Пространства моментов и резонансные теоремы
Теория положительно определенных функций была
введена Матиасом [4] и уточнена Бохнером [5]; она играет
большую роль во многих частях современного анализа,
как следствие фундаментальных представлений теорем
Бохнера [5] (см. также Купер [6]). Некоторые обобщения
имеются в статьях Годемана [9], Картана и Годемана [10],
перекрывающих работы Гельфанда и Райкова. Мы будем
также отсылать читателя к некоторым работам Бохнера,
фон Неймана, Шенберга по гильбертовым пространствам
и положительно определенным функциям [15.4,15.5,
15.6], а также к работам Ароншайна и Смита по
воспроизводящим ядрам [16.1,16.2]. Дополнительный
материал имеется у Фань Цзы [7] и Виддера [8].
Теория моментов основательно и широко изложена
в доступных источниках; поэтому мы будем полностью
обходить принципиальные вопросы. Здесь будут
представлены некоторые результаты для тригонометрических
моментов, показывающих их связь с теоремами для
положительных тригонометрических полиномов. Эта теория
много проще для тригонометрических полиномов, чем для
обычных, благодаря простоте представлений, которые
существуют для тригонометрических полиномов (см. Виддер [8],
Шоат и Тамаркин [11], Карлин и Шепли [12]).
Попутно мы укажем более неожиданные связи между
группой этих задач и классическими результатами Пикара
и Ландау о целых функциях. В заключение этой главы
будут указаны отношения к теории теплицевых матриц
(см. книгу Гренандера и Сегё [13.11]).
Превосходный обзор обширного класса вопросов теории
моментов в рамках классической теории вероятностей
содержится в статье Маллоуза [13], там же приведена
библиография. В этой работе приводятся определения
пространств моментов, связанных с унимодальными
распределениями.
Мы рассмотрим задачу определения множества моментов,
заданных выражениями вида
1
mk=\cp(x)xkdx, & = 1, 2, ... , (7)
о
где функция ф(д:) является характеристической функцией

§ 1. Введение
145
множества SCZ[0, 1], т. е.
ф(*) = 1, *6S,
ф(х) = 0, xeS. ( }
В этой задаче будет использовано понятие выпуклости,
которое на первый взгляд кажется здесь неприменимым.
Далее будет приведена интересная теорема Ландау,
использующая неравенство Гёльдера. Ее содержание
состоит в том, что вектор х с компонентами хи х2, ..., хп, ...
принадлежит /р, т. е. пространству последовательностей
{хп}, для которых 2|^n|p<oo, Р>1, тогда и только
п
тогда, когда его проекции на векторы пространства
^ (0 = ~"zri) конечны. Указанный результат есть частный
случай теоремы Банаха —Штейнгауза [1], связанный также
с упомянутым выше результатом Рисса (он будет
приведен в § 7 данной главы).
Резонансные теоремы приводят к линейным
неравенствам, где аналог теоремы Ландау является основой
открытий Минковского; это в свою очередь дает
практические результаты в общей теории линейных неравенств,
нашедших в последнее время свое приложение в теории
игр Бореля и фон Неймана, а также в теории линейного
программирования. Так как имеется много работ по
указанным вопросам, в этой книге мы коснемся их кратко.
Основы теории и библиографию можно найти в работах
Карлина ([38.15] гл. II), Дорфмана, Самуэльсона и Солоу
([42.4], гл. II).
Между общей теорией выпуклых функций и линейными
неравенствами имеется очень много связей. Недавние
работы Фань Цзы [15,16], Фань Цзы, Гликсберга,
Гофмана [14] устанавливают связь между понятиями выпуклости
и теорией линейных и банаховых пространств. В частности,
теорема Хана — Банаха играет здесь основную роль и имеет
тесную связь с теоремой о разделяющей гиперплоскости.
Мы сформулируем и докажем лемму Неймана —Пирсона;
она иллюстрирует различие между используемой методикой
и результатами, полученными в теории линейных
неравенств, с одной стороны, и результатами классической
теории —с другой. Эта лемма, которая использовалась

146 Гл. Ill. Пространства моментов и резонансные теоремы
вначале в математической статистике, за последнее время
получила большое применение в экономике и в теории
управления процессами. (См. [17], а также [19.1], гл. I.)
В конце главы будут даны краткие замечания
относительно метода ортогональных проекций, разработанных
Зарембой и развитых Вейлем [18], Лаксом [19] и другими;
будут также указаны связи этого метода с
фундаментальной леммой Дю-Буа-Реймонда вариационного исчисления
(см. Грейвз [20], Бервальд [21]); наконец, будут указаны
отношения между этими идеями и теорией обобщенных
решений уравнений в частных производных, развитой
Бохнером и Фридрихсом и систематизированной в форме
теории распределений Л. Шварцем.
Нашей основной целью будет выделение
фундаментальных концепций и выяснение их связей и основных
приложений.
§ 2. Моменты
Рассмотрим выражения
sh = x% + xi+ ... + д£, £ = 1,2,..., (1)
где х% неотрицательны. Используя неравенство Коши —
Шварца для
sk+i = &х[ + х\х\ + ... + х*х1п, (2)
получаем
Sk-\-l^S2kS2l' (3)
Большое число неравенств дают соотношения
s1>s12/2> ... >s\ln> ... . (4)
Возникает вопрос, существует ли полная совокупность
неравенств, описанных в ведении к этой главе.
Интересно заметить, что эта нелинейная проблема может быть
преобразована в линейную. Для этого поступим
следующим образом. Запишем Sk в форме интеграла Римана —
Стильтьеса
оо
sk=^xhdG(x), (5)
о

§ 3. Выпуклость
14?
где G(x) ступенчатая функция со скачками, равными
единице в точках х = хи /= 1, 2, ..., я, причем ее можно
считать монотонно возрастающей (0 < л;1<*2< .. . <хп).
Если xt лежат на отрезке [0,1], то верхний предел
интегрирования в (5) равен единице. В общем случае,
допускающем совпадение хи можно рассматривать суммы вида
tk = К4 + hx$ + ... + Kxl, (6)
где %г > 0, a xt различны.
Исследуем связи, которые существуют между
элементами последовательности {т&}, определяемыми интегралами
1
mk=^xkdG(x), (7)
о
где G(x) — монотонно возрастающая функция,
ограниченная на [0,1]. Будем называть эту последовательность мо-
ментной и будем говорить, что mk составляют моменты
весовой функции G(x) (или функции распределения).
Рассматриваемая проблема, кроме большого
применения в теории вероятностей (см. Шоат — Тамаркин [1.11],
Маллоуз [1.13]), имеет много разветвлений и, конечно,
не может быть изложена в одной главе данной
монографии. Мы рассмотрим лишь основные ее аспекты,
подчеркивая частные случаи применения этой методики к
неравенствам. Задачи, связанные с последовательностями s&,
а также последние результаты приведены в работе Урсел-
ла [1].
Фундаментальная и изящная идея, которая будет здесь
использована, это — выпуклость, введенная Минковским,
Каратеодори и др.
§ 3. Выпуклость
Пусть (ть т2, ... , тп) — первые п моментов функции
G(x), и (т[, т'2, ... , ш;) — соответствующие первые п
моментов функции Н(х). Линейность интегралов (2.7) как
функционалов от G(x) и Н (х) позволяет принять, что
irtii + (1 — X) т[, ... , ктп + (1 -~ %) т'п составляют первые
п моментов для функции kG(x) + (l — 'к)Н(х). Более того,
когда 0 < X < 1, то XG (х) + (1 — гк)Н{х) — монотонно воз-

148 Гл. III. Пространства моментов и резонансные теоремы
растающая ограниченная функция х €[0,1]» если функции
G(x) и Н(х) обладают теми же свойствами.
Если вычислить первые п моментов для всех весовых
функций G(x), определенных на [0,1], где G(x) —
ограниченная монотонно возрастающая функция, и
рассматривать их как координаты точки в ^-мерном евклидовом
пространстве, то множество точек, полученных таким
образом, будет выпуклым. Это означает, как обычно, что если
Р = (тг, т2,..., тп) и Q = (m'1, т'2,..., т'п) принадлежат
данному множеству, то все точки kP + (l— K)Q при
0<Я<1 также ему принадлежат.
Заметим, что это не частное свойство моментов,
определяемых выше, а общее свойство большого класса
последовательностей, определяемых линейными
функционалами.
Пусть f — элемент пространства S, а {щ} —
последовательность в двойственном пространстве S', где S и S'
обладают тем свойством, что внутреннее произведение
(л:, у) может быть определено для любых xgS и любых
y£S'. Рассмотрим обобщенные моменты
trih=(f, Фл), k=l, 2, ... . (1)
Если элементы пространств S и S' не обладают
специальными свойствами, то нельзя ожидать, что какие-либо
интересные свойства будут обнаружены у
последовательности [гпь}. Предположим, однако, что S обладает тем
важным свойством, что из f£S и g£S следует, что
h(x)=Kf(x) + (l-X)g(x)
также являегся элементом S для всех 0<Я<1. Если S
обладает этим свойством, мы будем говорить, что оно
выпукло. (См. Боннесен и Фенхель [8.1], гл. I, Эглстон [1].)
Как и выше для обыкновенных моментов, получим,
что точки {ти га2, ..., тъ) образуют выпуклое множество
точек в /г-мерном евклидовом пространстве, когда /
пробегает S.
Рассмотрение проблемы моментов будет основано на
этом фундаментальном понятии выпуклости, а также на
фундаментальной идее положительности.

g 4. Примеры выпуклых пространств
149
§ 4. Примеры выпуклых пространств
Рассмотрим некоторые важные примеры выпуклых
пространств и связанные с ними моментные
последовательности.
1
A. fgS, если ^f2(x)dx<l; yk(x)£L2(0,l).
о
Из неравенства Коши —Шварца следует
существование моментов
1
mk=^f<phdx. (1)
о
Неравенство треугольника, т. е. неравенство Минковского
для р==2 дает выпуклость пространства S.
В большинстве важных случаев эти моменты являются
коэффициентами Фурье соответствующей ортонормирован-
ной последовательности функций {ц)и(х)}.
1
B. f€S, если J|/(*)|pd*<l; Ф*(*)€^(0,1),
о
р> 1, 1 + 1=1.
Из неравенства Гёльдера следует существование
моментов, а неравенство Минковского обеспечивает
выпуклость пространства S.
C. f£S, если vrai sup |f(x)|<l; ф*(*)б£(0,1).
i
D. fgS, если df>07 J rf/= = 1; yk(x) = e2nikx.
о
В последнем случае мы имеем пример комплексной
моментной последовательности,

150 Гл. III. Пространства моментов и резонансные теоремы
§ 5. Примеры невыпуклых пространств
Приведем два интересных примера невыпуклых
пространств.
A. f(x)£S, если f(x) принимает для 0<л:<1 только
два значения, 0 и 1; (pk(x) = xh.
B. f(x)£S, если f (х) — непрерывная унимодальная
функция на [0,1], т. е. функция, имеющая один экстремум
на [0, 1]; щ(х) = хК
Оба эти пространства различными способами могут быть
поставлены в зависимость от выпуклых пространств.
Один из них будет кратко рассмотрен в § 17 (Беллман,
Блекуэлл [1]), другой же обсуждается в обширной статье
Маллоуза [1.13] (см. также Ройден [2]).
§ 6. К определению выпуклых множеств
Как мы отметили ранее, наша цель состоит в том,
чтобы представить метод для получения полной системы
неравенств. Для этого изучается проблема определения
области вариации совокупности моментов (ть т2, ..., тп),
рассматриваемых как точки ^-мерного пространства, когда
f пробегает пространство S.
Область будет определена, если будет найдена ее
граница. Для этого мы должны использовать некоторые
внутренние свойства S. В частности, если пространство S
выпуклое, то множество соответствующих точек также
выпукло, и следующая простая геометрическая идея может
сыграть существенную роль.
Границу выпуклого множества точек R из ^-мерного
пространства можно найти так. Возьмем плоскость Р и
будем двигать ее параллельно самой себе до тех пор, пока
она не будет содержать крайних точек R. Множество
крайних точек для всех плоскостей и составляет
границу R. Эта интуитивная характеристика не всегда точна.
Более точное и детальное рассмотрение этого свойства
и другие применения можно найти в книге Боннесена
и Фенхеля [8.1], гл. I и статьях Розенблюма [1.3].
Рассмотрим, например, двумерный случай. Линии Le
и LE представляют крайние положения линии L, точки Р

§ 7. Пространство LP. Результат Ф. Рисса 151
и Р' принадлежат границе В выпуклой области R (см.
рис. 3)
В общем случае каждая точка границы R
обусловливается функцией f g S и определяет «касательную»
плоскость. Касательная плоскость в свою очередь
характеризуется тем простым фактом, что ее расстояние от начала
i^P
Л
ее
Рис. 3.
есть максимум или минимум среди множества расстояний
семейства параллельных плоскостей, содержащих элементы
области R. Трудности, возникающие при этом интуитивном
описании, имеют место, когда граница области имеет
острые углы или плоские части.
§ 7. Пространство Lp. Результат Ф. Рисса
В качестве первого примера использования метода,
изложенного в § 6, рассмотрим пространство S, содержащее
вещественные функции f(x), удовлетворяющие условию
\\f\Pdx<l, (1)
О
где р > 1.
Пусть {<Ph(x)} — последовательность функций,
принадлежащих La(0, 1). Рассмотрим моменты, определяемые

152 Гл. III. Пространства моментов и резонансные теоремы
интегралами
1
mk = ^fykdx, £=1, 2, ... . (2)
о
Обозначим через Яь Я,2, ... , Яп направляющие косинусы
семейства параллельных плоскостей
Mi + ^2+ ••• + ^71*71= Л (3)
где — оо < г < сю, (т4, т2, ..., тп) — координаты точки
в n-мерном моментном пространстве, определяемые
формулой (2). Тогда для функции f(x), удовлетворяющей
условию (1), имеем
1 п
JfW[S bk<Pk(x)]<bc = r- (4)
о k~i
Остается определить элементы S, дающие максимум
или минимум г —величине, пропорциональной расстоянию
плоскости (3) от начала координат. Используя неравенство
Гель дера, получаем, что экстремальное расстояние
обеспечивается функцией
п. * п.
2M^|p_1sgn(2^<p/0
" =1 ft="
1 п
(Л2^Ф*|в^)
/W = -*=4-s ~ (5)
причем
О k=i
1
\ S М>* dx) ' (6)
^*max :
б
Лит = ^"тах •
Чтобы использовать этот результат, заметим, что точка
принадлежит множеству R тогда и только тогда, когда
любая плоскость, проходящая через эту точку, находится
на расстоянии от начала, которое заключено между rmin
и rmax для семейства параллельных плоскостей.
Нами установлен, таким образом, следующий
результат (см. Рисс [1,3], Хелли [2], Банах [1.1]).

§ 8. Ограниченная вариация
153
Теорема 1. Точка (ти т2, ...,тп) является
элементом n-мерного пространства моментов,
определяемого (1) и (2) тогда и только тогда, когда
I 2 4mh I < (\ I 2 ЧЩ d^j,q (7)
для любой совокупности действительных чисел (^Д^,...
...Дп).
Хотя это и является интересным и изящным
результатом, но при р Ф 2 он применяется редко. (См. Боас [4].)
Если для некоторой бесконечной последовательности
{ти} соотношение (7) выполняется для всех п, то можно
утверждать, что существует функция fgLp[0,l],
удовлетворяющая условию (1), для которой имеет место
соотношение (2). Для доказательства рассмотрим
последовательность функций {fn}, таких, что
1
mh = ^fnq>hdx, £=1,2,..., п, (8)
о
1
причем \|fn|pdx<l при п= 1, 2, ... . Последовательность
о
{fn} содержит подпоследовательность {[те}, слабо
сходящуюся к некоторой функции f{x), причем
1 1
mh = lim \ fn<Pk dx=[ fykdx. (9)
0 0
§ 8. Ограниченная вариация
Пусть f(x) принадлежит пространству монотонно
возрастающих функций на [0,1], имеющих полную вариацию 1,
а {щ (х)} -— последовательность вещественных
непрерывных функций на этом же промежутке.
Моментную последовательность можно определить
интегралом Римана — Стильтьеса
1
mk = ^yk(x)df(x), £=1,2,.... (1)

154 Гл. III. Пространства моментов и резонансные теоремы
Для нахождения границы выпуклого множества в
га-мерном пространстве (mb т2, ..., тп) определим максимум
и минимум выражения
к п
r=][^Kyk(x)]df(x), (2)
о k~i
когда f(x) пробегает указанное выше пространство.
Ясно, что
п
Гтах = max Г 2 ЬАфА(*)1 ,
lin = min Г 2 ^аФл(лг)! ,
В любом случае экстремум достигается на функции f(x),
имеющей единичный скачок в точках максимума или ми-
п
нимума функции 2 ^лфл(*)» постоянной в остальных
k=i
точках. Если экстремумов несколько, то получим
семейство ступенчатых функций, дающих экстремум для (2).
Итак, получен следующий результат.
Теорема 2. Необходимым и достаточным условием
того, что точка (m4, m2,..., тп) принадлежит п-мерно-
му пространству моментов, определяемому формулой
(1), является соотношение
п п п
min 2 ^а<Ра(*)< 2 ^ktrtk < max 2 Kyk(x) (4)
для любой совокупности действительных параметров
(А,ь Я2, ... , Хп).
Нахождение границы зависит от возможного числа
максимумов и минимумов, принимаемых функцией вида
п
g(x)=2 **фл(*)- (5)
k=l
Задачи этого типа возникают в теории наилучших
приближений, развитой Чебышевым (см. С. Бернштейн [1],
Уолш [2]). Подробное исследование этих вопросов для

§ 9. Положительность
155
случая, когда (fh(x) = xh, имеется в работах Карлина
и Шепли [1.12], где приведена также библиография.
Интересные исследования связи между рассматриваемыми
вопросами и классическими неравенствами приведены в работе
Дрешера [24.1], гл. I.
Вопросы этого типа возникают также при изучении
оптимальных стратегий в теории игр (см. Дрешер и Кар-
лин [3], Карлин [38.15], гл. II.
§ 9. Положительность
Вопросы выпуклости связаны с теорией положительно
определенных квадратичных форм. Отметим вариант
теоремы 2.
Теорема 3. Для того чтобы точка (mb т2, ... , тп)
принадлежала n-мерному пространству моментов (8.1),
необходимо и достаточно выполнение условия
п
Ьо+2 Kmk>0 (1)
h=\
для всех значений Я0, Я1? ..., Хп, таких, что
&о+2 %W>0 (2)
k=i
для всех х£ [0,1].
Доказательство. Необходимость условия
очевидна. Покажем его достаточность. Для этого покажем,
что (8.4) следует из (1) и (2).
Предположим, что из (2) следует (1) и имеется
совокупность параметров (К\, К'2, ...,Я'П), таких, что
п п
2 ^mh > max 2 Xk<(k(x) • (3)
h=i O^x^l fc=i
Величину X'0 определим из условия, что
п
К + max У,К'т(х) = 0. (4)

156 Гл. III. Пространства моментов и резонансные теоремы
Получим последовательность значений (Я^, Х[, ...,к'п),
обладающих тем свойством, что
п
К + И Xkmk>0, (5)
но
п
^;+2%w<o (6)
для всех х£ [О, 1].
Это противоречит тому, что из (2) следует (1), так как
очевидным следствием этого условия является
п
К+Ц Kmk<0 (7)
для всех значений Я0, Ки ..., Хп, для которых
Ьо+2ЬаФа(*)<°- (8)
Аналогично доказывается, что
п п
min 2%W<2^mft. (9)
Интересно отметить, что этот результат может быть
получен из теоремы Хана —Банаха, как это сделано в [1.11]
Шоатом и Тамаркиным (см. также Банах [1.1]). Эта связь
теории выпуклости и проекций с фундаментальными
теоремами о расширениях линейных функционалов будет
наблюдаться и в дальнейшем (см. Лаке [1.19], Лорх [25.5],
гл. I, Вестон [1], Фань Цзы [1.15].
Доказательство того, что справедливость условий (1), (2)
для всех п обеспечивает существование функции f(x)
(ограниченной и монотонно возрастающей), проводится
так же, как и в § 7; при этом слабая сходимость в IF
заменяется сходимостью Хелли для функции ограниченной
вариации.
§ 10. Представление через квадраты
Для применения теоремы 3 нужно установить
некоторые необходимые и достаточные условия того, что функ-

§ 10. Представление через квадраты 157
ция вида
g(x) = Х0 + Я1ф1 (Х)+ ... + КуЛх) (1)
неотрицательна на [0, 1]. Для произвольной
последовательности {фй(х)} таких условий не существует, но для двух
очень важных случаев,
щ(х) = cos 2knx, cph(x) = xh, k = 1, 2, ... (2)
они легко находятся.
Эта проблема интересна сама по себе; ее основы лежат
в теории неравенств. А так как многие неравенства следуют
из того факта, что квадрат вещественного числа
неотрицателен, то нужно искать представление неотрицательных
величин через квадраты. В общем случае это тривиально,
так как для х>0
х={уЗс)\ (3)
Вопрос усложняется, когда на Ух накладывается
требование принадлежности его к той или иной системе
функций. (Например, к совокупности полиномов, полиномов
с вещественными коэффициентами, рациональным
функциям, тригонометрическим полиномам и т.д.)
Далее можно поставить вопрос о представлении
неотрицательных величин в виде суммы квадратов,
x=xl + xt+... . (4)
Примеры такого типа уже встречались в §§3 — 5 гл. II
в связи с квадратичными формами.
Подобные задачи возникают во многих областях
математики: проблема Варинга в аналитической теории чисел,
проблема Гильберта — Артина в алгебре, представления
неотрицательных гармонических функций в анализе
(см. книгу Сегё [1]). Мы укажем два простых результата;
один из них относится к последовательности {cos2&ttx},
другой —к {xk}. Их доказательства, а также другие
результаты читатель найдет в книге Пойа и Сегё ([44.1], гл. I); см.
также Карлин и Шепли [1.12], Шоат и Тамаркин [1.11].

158 Гл. Ill. Пространства моментов и резонансные теоремы
§11. Неотрицательные тригонометрические
и рациональные полиномы
В первую очередь нам нужен результат Ф. Рисса о
представлении неотрицательных полиномов.
Теорема 4. Если gn(x) — тригонометрический
полином вида
gn(x) = ^о + ^i cos 2пх+ ... + Яп cos 2ппх, (1)
неотрицательный для 0 < х < 1, то
gn(x) = \х0 + х^х + ... + хпе2лЫх\2, (2)
где все х% действительны.
Другой результат, являющийся следствием теоремы 4,
состоит в следующем.
Теорема 5. Если gn(x) — рациональный полином,
gn(x) =h + K*+...+ Кхп, (3)
неотрицательный в интервале — 1 < х < 1, то
gn{x) = p\x) + {\-x*)q*{x), (4)
где р(х) и q(x) — полиномы степени п и п— 1
соответственно с действительными коэффициентами.
Доказательства этих теорем приведены в книге Пойа
и Сегё ([44.1], гл. I). Результаты этого и предыдущих
параграфов могут быть использованы для получения ряда
необходимых и достаточных условий теории моментов.
§ 12. Положительно определенные квадратичные
формы и моментные последовательности
Основным результатом здесь является следующая
теорема Каратеодори.
Теорема 6. Для того чтобы последовательность
{mk} представляла собой последовательность
тригонометрических моментов
1
mk=\ cos 2nkx df(x), (1)
о

§ 13. Исторические замечания
159
где df(x)>0, необходимо и достаточно, чтобы
квадратичные формы
2т*( ^ *Л*) (2)
Ь=0 |i-j|=ft
были неотрицательны, что эквивалентно выполнению
следующих неравенств для определителей
|т|4_я|>0, *,/ = 0, 1, ..., л; л=1,2, ... . (3)
Необходимость условия очевидна: она следует из
рассмотрения квадратичной формы
\ I У,хке2зх111Х
2df(x). (4)
Достаточность установить сложнее.
Имеется ряд интересных доказательств этой теоремы
Каратеодори. Прямое доказательство основывается на
каноническом представлении положительно определенных
квадратичных форм (см. Фишер [1]). Оно приведено
в работе [2.1], гл. II, где имеются ссылки на работы
Сасса, Фейера, Шура и Каратеодори. Другие
доказательства имеются в книгах Фань Цзы [1.7], Шоата и Тамар-
кина [1.11].
§ 13. Исторические замечания
В небольшой статье [1] Пикар в очень простой форме
установил свои знаменитые теоремы о совокупности
значений, не принимаемых целыми функциями; эти теоремы
имеют большое значение для развития математического
анализа. Обобщению теорем и методов Пикара посвящен
ряд интересных работ (см. Борель [2], Ландау [3,9],
Бибербах [8]).
Так, в своем курсе [9], где уточняются теоремы Пи-
кара, Ландау изучает неотрицательные гармонические
функции внутри единичного круга. Другое направление
в исследованиях было дано в диссертации Адамара, где
решалась задача об этих свойствах функций по их
коэффициентам Фурье. Глубокие результаты получены здесь

160 Гл. Ill. Пространства моментов и резонансные теоремы
Фейером [4], Каратеодори [5], Каратеодори и Фейером [6],
Герглотцом [7], Фишером [12.1], Риссом [7.3].
Каратеодори указал, что рассматриваемые вопросы
относятся к проблеме моментов. Используя методы теории
выпуклости (см. § 3—12), он дал им строгое обоснование.
С упомянутыми выше работами тесно связаны
исследования Теплица. Пусть f(8) — действительная функция от 8,
где 0<6<2я, и пусть {сп}, п = 0, ±1, ±2, ... —
последовательность ее коэффициентов Фурье,
c» = ^rSf(8)e-inede- (1)
0
Конечные матрицы Тп= (Ck-i), k,l = 0, 1, ..., n—l,
называются тёплицевыми матрицами. Характеристические
корни этих матриц тесно связаны со значениями, которые
принимает функция f(8) на интервале [0, 2л;] (см. Пойа,
Сегё [44.1], гл. I).
Изучение этих матриц возобновилось в последние годы,
так как они играют большую роль в теории вероятностей
и статистической механике при изучении некоторых
идеализированных задач теории «порядка — беспорядка»
(см. статьи Каца, Map дока и Сегё [10], Вейсса [12] и
книгу Гренандера и Сегё [11]).
§ 14. Положительно
определенные последовательности
Последовательность комплексных чисел {ап}, п = 0,
±1, ±2, ... называется положительно определенной,
если
(а) а-п = ап,
п _ (!)
(б) 2 ak-3zkzj>0
для всех комплексных Zk-
Имеет место следующая фундаментальная теорема
Ф.Рисса [7.1].
Теорема 7. Для того чтобы последовательность
{ап} была положительно определенной, необходимо и до-

§ 15. Положительно определенные функции 161
статочно, чтобы
2я
an=^e^dV{^ (2)
о
где V(Q) — действительная монотонная неубывающая
функция ограниченной вариации.
По этому поводу интересно отметить статью Герглотца
[13.7], посвященную проблеме области Пикара-— Ландау—
Каратеодори. Далее, следствия этого результата,
использующего только представления теории положительно
определенных квадратичных форм, а также принцип
выбора Хелли, приводятся в статье Фишера [12.1]; другие
ссылки можно найти у Беллмана [2.1], гл. II.
Методы, основанные на указанном представлении,
играют большую роль в современном анализе (см. статью
Фань Цзы [1], в которой даются также ссылки на
применение их к теории вероятностей; см. также книгу
Гренандера и Сегё [13.11]).
§ 15. Положительно определенные функции
Естественным и наиболее важным обобщением
положительно определенных последовательностей является
понятие положительно определенной функции, введенное
Матиасом [1.4].
Комплекснозначная функция f(x) действительного
переменного х называется положительно определенной, если
она удовлетворяет следующим условиям:
(а) f(x) ограничена и непрерывна при — оо<х<оэ,
(б) f(-x)=W),
(в) для любых действительных х^ х2, ...,хп и любых
комплексных си съ ..., сп выполняется соотношение
п
2 crcsf(xr — xs)>0.
г, s=l
Укажем следующую основную теорему Бохнера (см.
Фань [1.7]).
Теорема 8. Если функция f(x) удовлетворяет
условиям (а), (б), (в), то существует неубывающая ограни-

162 Гл. III. Пространства моментов и резонансные теоремы
ченная функция g{y), такая, что
со
Kx)=lel"*dg(y)
—со
для всех действительных х.
Этот результат является главным в современной теории
гармонического анализа. Имеется много обобщений этой
теоремы (см. Купер [1.16], Люмис [1], Вейль [2], Шварц
[1.22], Годеман [1.9], Картан и Годеман [1.10], а также
статью Гельфанда и Райкова, упомянутую во введении
к этой главе). Последние результаты можно найти в
работе Девинатца [3].
Обобщенные положительно определенные функции
возникают в связи с задачей определения условий, при
которых скалярная комплексная функция, заданная на
элементах топологического пространства, является
гильбертовой функцией расстояния (см. Бохнер [4], Шенберг
[5], Шенберг и фон Нейман [6]).
Положительно определенные функции обобщенного
типа применяются также в теории интерполяций Пика —
Неванлинны (см. Секефальви-Надь, Кораньи [7]). Так как
эти задачи можно рассматривать также с точки зрения
теории моментов (см. Вейль [8]), то здесь опять видно
переплетение различных идей анализа.
§ 16. Воспроизводящие ядра
Комплекснозначная функция k(x,y) называется
воспроизводящим ядром, если
со
k(x,y)=lk(x,t)W^)dt (1)
—со
для всех действительных х и у. Эти ядра появляются
в анализе при изучении функций Грина (см. Ароншайн
и Смит [2])
Приведем теорему Ароншайна [1].
Теорема 9. Комплекснозначная функция k(x,y)
является воспроизводящим ядром тогда и только тогда,

§ 17. Невыпуклые пространства
163
когда
п
2 CiCjk(xuXj)>0 (2)
для всех комплексных ct и всех действительных xt.
§ 17. Невыпуклые пространства
Может случиться, что n-мерное пространство моментов
является выпуклым, хотя соответствующее ему
пространство S не является таковым. В этом отношении
интересным является первый пример, приведенный в § 5.
Рассматривается пространство S всех характеристических
функций, определенных следующим образом
«=u
если х£Е, Ed [0,1],
f(x)-\ п если xgEj (!)
и последовательность функций qk(x) = xh. Пространство
моментов состоит из точек
(\dx, [xdx, ..., \xndx\ (2)
ЕЕ Е
где Е—любое борелевское множество из [0,1].
Теорема Ляпунова [1] гарантирует, что это
пространство замкнуто и выпукло, хотя пространство
характеристических функций и не является выпуклым. Используя
это факт, легко получить следующий результат (см.
Беллман и Блекуэлл [5.1]).
Теорема 10. Пусть Xj — отрезок {a/<A:<a;+i} для
/ = 0, 1,...,л, где ао = 0<а!<а2< ... <ап+1 = 1.
Множества Е0, Е1ч определяемые с помощью формул
E0 = X0[jX2[j...,
£i = Xi(JXsll- ()
дают граничные точки пространства моментов, а
каждое Е, соответствующее граничной точке, совпадает
с точностью до множества меры нуль с множеством
одного из этих видов.

164 Гл. III. Пространства моментов и резонансные теоремы
Из этого следует, что параметрическое представление
границы, состоящей из двух частей, Di и D2, дается
формулами:
Dt: Xi = ri0(a) + ri2(a)+...,
D2: Xi = rH(a) + ri3(a) + ..., j= 0,1, ...,/z,
(4)
где
a*tj-a*+1
rti(fl)= i+\+1J . *,/=0,1,...,л. (5)
Доказательство. Функционал
минимизируется по всем E, определяемым условием
E =
<,2^<о|. (7)
Искомым множеством является либо Е0, либо Ei для
подходяще выбранных аг; обратно, каждое Е0 или Ei дает
граничные точки для подходяще выбранных %t. Заметим,
что в этом случае параметрическое представление
граничных элементов получается наиболее легко в координатах,
отвечающих различным %t.
Те же аргументы приводят к выводу, что пространство
моментов совпадает с множеством точек
(Лйх, Ixdx, ..., [xndx\ (8)
Е0 Ег Еп
где Е0, Еи...,Еп — непересекающиеся борелевские
множества, сумма которых равна [0,1]. Детали доказательства
можно найти в [5.1].
Во втором примере из § 5 рассматриваются непрерывные
на [0,1] функции, имеющие единственный экстремум. Как
и выше, этот пример может быть изучен рассмотрением
подпространства функций, имеющих единственный
экстремум в фиксированной точке х = а, с последующим
нахождением огибающей по а.

§ 18. «Резонансные» теоремы Ландау
165
О применениях проблемы моментов в теории
вероятностей см. цитированные выше статьи Маллоуза [1.13]
и Ройдена [5.2].
§ 18. «Резонансные» теоремы Ландау
Рассмотрим теперь теоремы несколько иного типа, в
первую очередь один результат, принадлежащий Ландау [1],
кажущийся довольно специальным, но имеющий много
неожиданно важных обобщений.
Теорема 11. Для того чтобы ряд
оо
2 шр, p>i,
п=1
сходился, необходимо и достаточно, чтобы ряд
оо
2 апЬп
п=1
сходился для всех последовательностей {Ьп}, для
которых сходится
оо
2l*»le, ?=т=т-
п=1 Р L
Необходимость непосредственно следует из неравенства
Гель дера. Достаточность доказывается сложнее. Нетрудно,
правда, дать доказательство от противного, используя
интересный результат Абеля, относящийся к сходимости
и расходимости рядов вида
оо
2%. 0<а<оо, (1)
n=l sn
где sn = Ui + u2-\- ... +ип- Однако, как мы увидим в § 19,
этот результат является частным случаем одной очень
глубокой теоремы анализа и любое непосредственное
доказательство лишь затемняет его (см. Банах [1.1]).
Отметим далее обобщение классического результата
относительно произведений Коши.

166 Гл. ///. Пространства моментов и резонансные теоремы
Теорема 12. Для того чтобы ряд
оо п
2 сп, где сп= 2 аФп-п, (2)
n=l k=0
ОО
сходился для всех сходящихся рядов 2 Ьп, необходимо и
достаточно, чтобы
оо
2 |Од|< ОО.
п=0
Имеется много обобщений на различные методы
суммирования. Все они являются частными случаями теоремы
суммирования Гурвица — Зильбермана — Теплица (см. Зигмунд
[1.2]), которая в свою очередь является прямым следствием
теоремы, рассматриваемой ниже.
Результаты этого типа были открыты и переоткрыты
многими математиками, так что авторство установить
трудно.
§ 19. Теорема Банаха—Штейнгауза
Рассмотрим банахово пространство /р, р>1,
состоящее из всех последовательностей {ап}, для которых
оо
2 |<МР<оо.
п=1
Для бесконечной последовательности Ъ = {Ьп}
рассмотрим линейный функционал, определяемый внутренним
произведением
оо
№ = (а,Ь) = 2яЛ. (1)
п=1
Теорема 11 утверждает, что ограниченность f(a) для всех
элементов Ь £ lq обеспечивает равномерную ограниченность
/(a) для Ъ всех в сфере ||6||<1, где
(2)
/со \ j

§ 20. Теорема Минковского
167
Это эквивалентно утверждению, что норма
/ °о \1/р
И=(21ЫР)
конечна.
В этой терминологии результат Ландау является
частным случаем теоремы Банаха — Штейнгауза относительно
линейных функционалов (см. Банах [1.1], Зигмунд [1.2]).
Этот результат является фундаментальным в теории
ортогональных рядов в связи с мультипликаторами и
константами Лебега, а также в теории суммируемости,
упомянутой выше, и в теории дифференциальных уравнений.
Беллман [1], Масс ера и Шеффер [2,3] охарактеризовали
решение однородных векторно-матричных уравнений, или
вообще уравнений в банаховом пространстве
%- = A(t)x (3)
в терминах решений всех уравнений вида
%-=A(t)y+f(t). (4)
Оригинальный результат в этом направлении был получен
Перроном. См. также Чезари [4], Кордуняну [5].
Дальнейшие ссылки можно найти в статьях, упомянутых выше.
§ 20. Теорема Минковского
Следующий изящный результат Минковского
принадлежит тому же направлению, но не является столь
всеобъемлющим.
Теорема 13. Пусть х и у — п-мерные векторы, А —
прямоугольная (т х п)-матрица. Необходимым и
достаточным условием того, что (х, у)>0 для всех у, для
которых Ау>0, является равенство х = А'Ъ, где Ь —
некоторый т-мерный вектор, причем Ь>0.
Доказательство теоремы приводится в недавно
вышедшей книге Гейла [1] и Г. Вейля [2]. Детальное
обсуждение дается в работе Фань Цзы [1.15].
Интересно отметить, что понятия и свойства выпуклых
множеств, играющие основную роль в указанных выше
работах, впервые были развиты Каратеодори в его статье,

168 Гл. ///. Пространства моментов и резонансные теоремы
посвященной проблеме тригонометрических моментов,
опорная же функция Минковского, используемая Вейлем
в его статье, в точности совпадает с функцией,
применяемой для квазилинеаризации в предыдущих главах. Здесь
мы опять видим, что эти методы между собою тесно
связаны и лежат в основе многих проблем теории
неравенств, а также классического и современного анализа.
Так же интересно отметить повторяющийся параллелизм
между теорией эрмитовых и положительных операторов.
§ 21. Теория линейных неравенств
Теорема Минковского 13 есть частный результат общей
теории линейных неравенств, большая часть которой
связана с проблемой нахождения максимума и минимума
линейной формы
п
Ц*)=2*Л (1)
г=1
по всем хи удовлетворяющим линейным неравенствам
п
^uijXj^bu /=1, 2, ...,ш. (2)
Известно громадное количество работ в этом направлении.
Некоторые важные результаты приведены в статьях
Минковского [1], Фаркаша [2], Штимке [3], Дайнса [4], Кар-
вера [5], Моцкина [6], Черникова [7], Фаня [1.15]
Никайдо [12].
В последние годы эти вопросы привлекают к себе
внимание своими многочисленными связями с прикладной
математикой, в частности с теорией игр. Внимание теперь
сосредоточено на проблеме определяющих алгоритмов
численного решения экстремальных задач описанного выше
вида, в особенности таких, которые могут быть точно и
быстро реализованы цифровыми машинами. Основным
является здесь симплексный метод, предложенный
Данцигом [8] и развитый и обобщенный Чарнсом, Лемке, Билом
и др. Для задач этого общего класса с различного типа
структурами существуют специальные алгоритмы (см. Форд
и Фулкерсон [9], Беллман [7.1], гл. I).

§ 23. Теорема фон Неймана о минимаксе 169
Область прикладной математики, изучающая алгоритмы
численного решения указанной экстремальной задачи,
называется теорией линейного программирования. Она
играет большую роль в исследовании операций и в
математической экономике (см. Данциг, Орден, Вольф [8],
Райли и Гасс [10], Карлин [38.15], гл. II, Дорфман, Самуэль-
сон и Солоу [42.4], гл. II). Имеются интересные
применения неравенств этого типа к вероятностной теории
«рационального пари» (см. Леман [11]).
§ 22. Обобщения
Результаты предыдущего параграфа обобщаются в двух
направлениях. Во-первых в направлении нелинейных
функций (см. Гейл, Кун и Таккер [1], Фань, Гликсберг, Гофф-
ман [1.14]) и, во-вторых, в направлении линейных
функционалов в более общих пространствах (см. Фань [1.15],
Даффин [2], Леман [3], Беллман и Леман [4]). В § 24
будут рассмотрены обобщения второго типа.
Работа Фаня [1.15] интересна в связи с § 18 — 21;
в ней вопросы линейных неравенств и теория
аппроксимации рассмотрены с точки зрения общей теории
линейных и банаховых пространств. В частности, обобщения
теоремы Хана —Банаха и теоремы выпуклости играют
здесь основную роль.
§ 23. Теорема фон Неймана о минимаксе
Как отмечалось в § 21, теория линейных неравенств
тесно связана с теорией игр, разработанной фон Нейманом
(см. фон Нейман, Моргенштерн [1], Уильяме [3], а
также раннюю работу Бореля [2]).
Краеугольным камнем теории игр является следующая
вариационная проблема (обманчиво простая по виду).
Теорема 14. Пусть {х} — совокупность векторов,
удовлетворяющих условиям
(a) xt > 0,
г=

170 Гл. III. Пространства моментов и резонансные теоремы
{у} — аналогичная совокупность. Если (а^) —любая
вещественная матрица, то
п п
min max J) ацх%у* = max min 2 аУ**#/- (2)
у х ij^i х у iyj==i
Доказательство теоремы приводится в [1,4]. Этот
результат можно рядом способов получить из теории
линейных неравенств (см. ссылки § 21—22) с помощью
теорем о неподвижной точке, а также индуктивно (см.
Люмис [4]) или как «установившееся состояние»
динамического процесса (см. Робинсон [5]). Интересное
доказательство, основанное на законах статики, приводится
в работе Гросса [6].
§ 24. Лемма Неймана — Пирсона
Классические неравенства могут быть установлены
стандартным вариационным методом благодаря наличию
нелинейностей. Эти нелинейности играют существенную
роль при выводе условий, характеризующих экстремум.
Ряд интересных вопросов анализа и приложений
(в частности, теория процессов управления) приводит
к задаче разыскания минимума линейного функционала
вида
1
\f{t)a{t)dt (1)
о
по всем функциям f(t), удовлетворяющим условиям
(а) 0</(/)<1, 0<*<1,
(б) lf(t)b(t)dt<c, (2)
о
где a(t) и b(t) — заданные функции, а с — известная
константа.
Как известно из предыдущего, эта задача эквивалентна
задаче определения области в двумерном пространстве

§ 24. Лемма Неймана — Пирсона
171
моментов
1
ml=^f(t)a(t)dt,
о
1
m2=^f{t)b(t)dt,
(3)
когда f(t) пробегает пространство S функций,
удовлетворяющих условию (2а).
Чтобы дать представление о результатах и методах,
применяемых в вариационных задачах этого типа,
приведем детальное доказательство следующей теоремы.
Теорема 15. Решение предыдущей задачи (1) —(2)
при дополнительных условиях
(а) b(t) > О,
(б) с>0 {)
определяется следующим образом.
Для каждого k (—оо<£<со) определяем множества
E~=E~(k) = {t; a(t)<kb(t)},
E=E(k) = {t; a(t)=kb(t)}, (5)
E+=E+(k) = {t; a(t)>kb(t)}.
Пусть k0 —верхняя грань всех неположительных k, для
которых выполняется неравенство
J b{t)dt<c, (6)
Е~
и пусть E~(k0) = Е~, Е (k0) = Е0, E+(k0) = Е*. (7)
Тогда множество минимизирующих функций f*
определяется так:
(а) ТО=1 на Е~0,
(б) f*(0=0 на £+ W

172 Гл. 111. Пространства моментов и резонансные теоремы
(в) функция f*(t) произвольна на E0i удовлетворяет
1
только условию (2а) и \f*(t)b(t)dt = c при k0 < 0, или
о
условию (2а) при kQ=0.
Подобным же образом определяются
максимизирующие функции.
Доказательство. Для любой функции f(t),
удовлетворяющей (2), можно написать
\f{t)a{t)dt = ^ +J+J =
О Ej е0 е+
= S f{t)a{t)dt + h^f{t)b{t)dt + l f(t)a(t)dt; (9)
Ч Щ Ef
так как
1
J f*(t) a(t) dt = J + I = I a(t) dt + k0 J f*(t) b(t) dt =
0 Eq E0 Eq Eo
= ^a(t)dt + k0[c-^b(t)dt], (10)
имеем
A = J f (t)a(t) dt-^ f*(t) a(t) dt =
о о
= l[f(t)-l]a(t)dt + k0lf(t)b(t)dt+ (11)
+ J f(t) a{t) dt - k0 [c - J 6(0 Л].

§ 25. Ортогональные проекции 173
Используя соотношение a(t)>k0b(t) на Е*,
последовательно получаем неравенство
Д >$[/(*)-1]а(*)Л +
+ k0[l f(t) b(t) eft + $ f(t) b(t) dt] - k0 [c - J b(t) dt] >
E0 e£ Bo
>^[f(t)-l]a(t)dt +
+ k0 [c - J f(t) b(t) dt] - k0 [c - J b{t) dt] >
>^\f{t)-\\a{t)dt+k^[\-f{t)\b{t)dt>
Eo Eo
>l\\-f{t)\\kQb(t)-a{t)\dt>0. (12)
Так как знак равенства имеет место тогда и только
тогда, когда f(t) совпадает с /*(/)» мы видим, что f*(t)
и есть совокупность минимизирующих функций.
§ 25. Ортогональные проекции
Ранее рассматривались вопросы, в которых функция /
характеризовалась моментами (/, (рп) по отношению к
некоторой последовательности функций {ф^}. Эти моменты
можно рассматривать как проекции f на «оси» фЛ. Теория
ортогональных рядов (см. Зигмунд [1.2], Качмаж и Штейн-
гауз [1]) есть частный случай исследований этого типа.
Эту идею можно значительно распространить. Наиболее
плодотворные применения концепции ортогонального
проектирования имеются в теории уравнений в частных
производных (см. Вейль [1.18]). Предварительный
результат в этом направлении был получен Зарембой (см. Розен-
блюм [1.3], Форсайт и Розенблюм [2]).
Основная идея состоит в следующем. Если и —
решение линейного уравнения L(u) = 0, то, очевидно,
(L(u),v) = 0 (1)

174 Гл. ///. Пространства моментов и резонансные теоремы
для всех v, для которых определено скалярное
произведение. Если дополнительно потребовать, чтобы v
принадлежало области определения сопряженного к L
оператора УИ, тогда (1) дает
(L(u),v)={u9M(v)) = 0. (2)
Предположим, что мы исходим из соотношения
(u,M(t>)) = 0 (3)
для всех v из подходяще выбранного множества. При
некоторых условиях это приводит к тому, что и является
решением уравнения Ци) = 0.
Интересно отметить, что ряд проблем, которые
решаются методом ортогональных проекций, могут быть решены
с помощью теоремы Хана —Банаха (см. Лаке [1.19]).
Метод ортогональных проекций является абстрактным
вариантом так называемой фундаментальной леммы
вариационного исчисления (см. Курант и Гильберт [26.1], гл. II,
Бервальд [1.21]). Целью здесь является вывод уравнения
Эйлера Е(и) = 0 из соотношений вида
(E(u),v) = 0 (4)
для всех v из некоторого множества функций.
Предыдущие рассмотрения естественно приводят к
развитому Бохнером и Фридрихсом понятию обобщенных
решений линейных и нелинейных операторных уравнений.
Систематизация этих идей привела к теории
распределений Шварца (см. Шварц [1.22]).
§ 26. Эквивалентность процессов минимизации
и максимизации
Тесно связанным с отмеченной и использованной нами
двойственностью является тот факт, что ряд
минимизирующих задач эквивалентен некоторым максимизирующим.
Важность этого для получения верхних и нижних границ
очевидна. Результаты Фридрихса в таких вариационных
задачах приведены в книге Куранта и Гильберта [26.1],
гл. II; применения и дальнейшие ссылки см. в работах
Лакса [1], Рогозннского и Шапиро [2].
Общее начало многих из этих результатов можно найти
в следующем простом геометрическом факте. Пусть R —

Библиография и дополнения
175
выпуклая область с границей В, и пусть р —внешняя
точка R (см. рис. 4). Рассмотрим задачу минимизации
расстояния \\р — q\\ между р и q£R. Минимум будет
достигаться в точке qo^B и прямая pq0 будет
ортогональна касательной плоскости в точке q0.
Рис. 4.
Рассмотрим множество касательных плоскостей к В
и расстояние от р до этих плоскостей (см. рис. 5).
Очевидно, что локальный максимум для этих расстояний
будет определяться расстоянием \\р — qo\\ к касательной
плоскости в точке q0.
Рис. 5.
Мы видим, что двойственность описания поверхности
с помощью точек и касательных плоскостей естественно
приводит к эквивалентности некоторых минимизирующих
и максимизирующих задач. Распространение этого факта
на абстрактное пространство приводит к ряду интересных
и важных результатов.
БИБЛИОГРАФИЯ И ДОПОЛНЕНИЯ
§ 1. Основной работой по теории банаховых пространств
является книга самого Банаха.
1. Банах (Banach S.), Theorie des operations lineaires,
Monografje Matematyczne, I, Warsaw, Z Subwencji Funduszu
Kultury Narodowej, 1932. Украинский перевод: Курс
функционального анал!зу. Кшв, 1948.

176
Библиография и дополнения
Ряд результатов, касающихся специальных приложений этой
теории к изучению ортогональных рядов, можно найти в гл. 4 книги
2. Зигмунд (Zygmund A.), Trigonometrical series. Monografje
Matematyczne V. Warsaw, Z Subwencju Funduszu Kultury Na-
rodowej, 1935. Русский перевод: Тригонометрические ряды,
ГОНТИ, 1939; перевод 2-го издания — «Мир», М., 1965.
3. Розенблюм (Posenbloom P.), Quelque classes de problemes
extremaux, Bull Soc. Math. France, 79 (1951), 1—58, 80(1952),
183—215.
Основными работами по теории положительно определенных
функций и последовательностей являются следующие.
4. Матиас (Mathias М.), Uber positive Fourier — Integrale,
Math. Z., 16 (1923), 103—125.
5. Бохнер (Bochner S.), Vorlesungen uber Fouriersche
Integrale, Leipzig, Akademische Verlagsgesellschaft, 1932.
6. Купер (Cooper J. L. В.), Positive definite functions of
a real variable, Proc. London. Math. Soc., 10 (1960), 53—66.
7. Ф а н ь Ц з ы (Fan K), Les fonctions definies — positives et
les fonctions completement monotones, Memorial Sci. Math., 64,
Paris, Gauthier-Villars, 1950.
8. Виддер (Widder D. V.), The Laplace transform,
Princeton, N. J., Princeton University Press, 1941.
Широкие обобщения этих понятий в абстрактном изложении
даются в работах
9. Годеман (Godemont R.), Les fonctions de type positif
et la theorie des groupes, Trans. Am. Math. Soc, 63 (1948), 1—84.
10. Карта н, Годеман (Cartan H., Godemont R.),
Theorie de la dualite et analyse harmonique dans les groupes abe-
liens localement compacts, Ann. Set. Ecole Norm. Sup. (3), 64
(1947), 79—99.
Обсуждение теории моментов можно найти в работе Виддер а
[8] (см. выше), а также в работах
11. Ш о а т, Тамаркин (Shohat J., Tamarkin J.),
The problem of moments, Mathematical Surveys, vol. 2, New
York, American Mathematical Society, 1943.
12. К a p л и н, HI e п л и (К а г I i n S., Shap ley L.),
Geometry of moment spaces, Memoirs of the American Mathematical
Society, 12, New York, American Mathematical Society, 1953.
Детальное обсуждение многих специальных классов задач
о моментах, превосходный обзор теории моментов в целом, а также
вскрытие связей с теорией вероятностей и статистикой дается
в работе
13. М а л л о у з (Mallows С. L)., Generalizations of Tceby-
cheff's inequalities, /. Roy. Stat. Soc. (£), 18 (1956), 139—176.
В этом томе мы систематически избегаем обсуждения большого
числа интересных и важных неравенств, выводящихся из
статистических соображений, так как это существенно увеличило бы объем книги.
14. Фань Цзы, Гликсберг, Гоффман (Fan К-,
Glicksberg I., Hoffman A.), Systems of inequalities
involving convex functions, Proc. Am. Math. Soc.t 8 (1957), 617—
622.

Библиография и дополнения
177
15. Ф а н ь Цзы (Fan К), On systems of linear inequalities,
Ann. Math. Stud., 38, 99—156, Princeton, N. J., Princeton
University Press, 1956. Русский перевод см. в сб. «Линейные
неравенства и смежные вопросы, ИЛ, М., 1959, 214—262.
16. Ф а н ь Цзы (Fan К ), Existence theorems and extrime
solutions for inequalities concerning convex functions or linear
transformations, Math. 2., 68 (1957), 205—216.
Отметим оригинальную статью, содержащую лемму Неймана —
Пирсона.
17. Нейман, Пирсон (Neyman J., Pearson Е.), On
the problem of most efficient tests of statistical hypotheses, Phil.
Trans. Roy. Soc. (A), 231 (1933), 289—337.
В связи с методом ортогональных проекций см. работы
18. В е й л ь (W е у 1 Н.), The method of orthogonal projection
in potential theory, Duke Math. /., 7 (1940), 411—444.
19. Л а к с (L a x P. D.), A remark on the method of orthogonal
projection, Comm. Pure Appl. Math., 4 (1951), 457—464.
Укажем одну из последних статей, в которой рассматривается
указанная фундаментальная лемма.
20. Г р е й в з (Graves L. М.), Extensions of the lemma of Haar
in the calculus of variations, Bull. Am. Math. Soc, 65 (1959),
319—321.
См. также работу
21. Бервальд (Berwald L.), Ober Haars Verallgemeine-
rung des Lemmas von Du Bois-Reymond und verwandte Satze,
Acta Math., 79 (1947), 39—49.
Отметим также следующие книги Лорана Шварца.
22. Шварц (Schwartz L.), Theorie des distributions, 1, II,
Actual Sci. Ind. 1091, 1122, Paris, Hermann, 1950, 1951.
Эти монографии содержат многочисленные ссылки на
основополагающие работы Бохнера и Фридрихса.
§ 2. Теме этого параграфа посвящена следующая работа.
1. Урселл (Ursell Н. D.), Inequalities between sums of
powers, Proc. London Math. Soc, 9 (1959), 432—450.
§ 3. Для изучения основ теории выпуклости отсылаем
читателя к работе [8.1], гл. I, а также
1. Эглстон (Eggleston Н. G.), Convexity, Cambridge
Tracts, No. 47, London, Cambridge University Press, 1958.
Мы используем здесь только простейшие идеи. В статьях Розен-
блюма, на которые мы ссылались выше [1.11, описано много других
методов, а также даются их приложения.
§5.
1. Беллман, Блекуэлл (Bellman R., Black-
well D.), On moment spaces, Ann. of Math., 54 (1951), 272—274.
2. Ройден (Royden H.), Bounds for distribution functions
when the first n moments are given, Ann. Math. Stat., 24 (1953),
361—376.

178
Библиография и дополнения
§ 7. Результаты этого типа впервые опубликованы в работе
Рисса.
1. Р и с с (R i е s z F.), Untersuchungen uber Systeme integrier-
barer Funktionen, Math. Ann., 69 (1910), 449—497.
2. Хелли (Helly E.), Uber lineare Ftinktionaloperationen,
Wiener Ber., 121 (1912), 265—297.
См. также книгу
3. P и с с (R i е s z F.), Les systemes d'equations lineaires a une
infinite d'inconnues, Paris, Gauthier — Villars, 1913.
Обычное доказательство можно найти в работе Банаха [1.12J.
Относительно приложений см. следующую литературу.
4. Б о а с (Boas R. P.), A general moment problem, Am. J.
Math., 63 (1941), 361—370.
§ 8. Очень интересным является тот факт, что проблемы
моментов тесно связаны с осцилляционными свойствами линейных
комбинаций базисных функций и, таким образом, с проблемами
наилучшей аппроксимации, которые впервые были поставлены Чебышевым.
Отдельные результаты этого типа можно найти в следующих
работах.
1. Бернштейн (Bernstein S.), Lesons sur les proprietes
extremales et la meileure approximation des fonctions analyti-
ques d'une variable reelle, Paris, Gauthier — Villars, 1926.
2. У о л ш (Walsh J. L.), Interpolation and approximation by
rational functions in the complex domain, American
Mathematical Society Colloquium Publications, vol. 20, New York, American
Mathematical Society, 1935.
3. Дрешер, Карлин (Drecher M., К a r 1 i n S.),
Solutions of convex games as fixed points, Ann. of Math. Stud., № 28,
75—86, Princeton, N. J., Princeton University Press, 1953.
Ряд дальнейших результатов можно найти в книге Карлина
[38.15], гл. II.
§9.
1. Вестон (Weston J. D.), A note on the extension of linear
functional, Am. Math. Monthly, 67 (1960), 444—445.
§ 10.
1. Cere (Szego G.), Orthogonal polynomials, American
Mathematical Society Colloquium Publications, vol. 23, New York,
American Mathematical Society, 1939.
§ 12.
1. Фишер (Fischer E.), Ober das Caratheodorysche Problem,
Potenzreichen mit positivem reelen Teil betreffend, Rend. Circ.
Mat. Palermo, 32 (1911), 240—256.
§ 13.
1. Пикар (Picard E.), Memoire sur les fonctions entieres,
Ann. Sci. Ecole Norm. Super. (2), 9 (1880), 147—166.

Библиография и дополнения
179
2. Борель (В orel Е.), Demonstration elementaire d 'un theoreme
de M. Picard sur les fonctions entieres, Compt. Rend. (Paris), 122
(1896,) 1045—1048.
3. Ландау (Landau E.), Ober eine Verallgemeinerung des
Picardschen Satzes, Sitz. ber. preuss. Akad. Wiss.y 1904, 1118—
1133.
4. Фейер (F e j e г L.), Ober trigonometrische Polynome, J.
Reine Angew. Math., 146 (1915), 53—82.
5. Каратеодори (Caratheodory C), Ober den
Variabilitatsbereich der Fourierschen Konstanten von positiven
harmonischen Functionen, Rend. Circ. Mat. Palermo, 32 (1911),
193—217.
6. Каратеодори, Фейер (Caratheodory С, Fejer L.),
Ober den Zusammenhang des Extremums von harmonischen Funk-
tionen mit ihren Koeffizienten und uber den Picard — Landau-
schen Satz, -Rend. Circ. Mat. Palermo, 32 (1911), 218—239.
7. Герглотц (Herglotz G.), Ober Potenzreihen mit posi-
tivem,reellem Teil im Einheitskreis, Sitz. ber. Sachs. Akad. Wiss.,
63, (1911), 501—511.
Обсуждение теоремы Пикара и ее обобщение с
теоретико-функциональной точки зрения имеется в книге
8. Бибербах (Bieberbach L.), Lehrbuch der Funktio-
nentheorie, Bd. 2, Berlin, Teubner, 1931, стр. 217 и далее.
Борель изучал теорему Пикара с точки зрения решений
функционального уравнения
«/<*>+1 =**<*>,
где f(z) и g(z) — целые функции. По поводу широких обобщений
в этом направлении см. книгу
9. Ландау (Landau G.), Darstellung und Begrundung eini-
ger neuerer Ergebnisse der Funktionentheorie, 2-е издание, гл. 7,
Ergebnisse der Math., Berlin, Springer, 1929.
Ссылки на статьи по этому вопросу Шура, Рисса, Фробениуса,
Сегё, Теплица имеются в работе Рисса [7.11 и в статье
10. К а ц, М а р д о к, С е г ё (Кае М., Murdock L., S z е-
go G.), On the eigenvalues of certain hermitian forms, /. Rat.
Mech. analysis, 9 (1953), 767—800.
Эти результаты, а также их обобщения и приложения к теории
вероятностей можно найти в книге
11. Гренандер, Сегё (Grenander U., S z е g 6 G.),
Toeplitz forms and their applications, Berkeley and Los Angeles,
University of California Press, 1958. Русский перевод: Тёплицевы
формы и их приложения, ИЛ, М., 1961.
Большой интерес к тёплицевым формам оправдывается их
сходством с некоторыми матрицами, применяемыми при
исследовании различных проблем статистической механики. В частности,
имеются тесные связи с проблемами теории «порядка —
беспорядка» (order-disorder). По этому вопросу см. следующую работу.
12. Марадудин, Beftcc(MaradudinA., Weiss G. Н.),
The disordered lattice problemes a review, /. Soc. Ind. Appl.
Math., 6 (1958), 302—329.

180
Библиография и дополнения
§ 14. Обзор теории положительных последовательностей и
функций можно найти в монографии Фань Цзы [1.5.] См. также
1. Фань Цзы (Fan К), On positive definite sequences, Ann.
of Math., 47 (1946), 593—607.
2. Левитан Б. M., Обобщенные положительно определенные
и обобщенные почти-периодические функции, Докл. АН СССР,
58 (1947), 1593—1596.
§ 15. Эта теорема Бохнера играет принципиальную роль
в анализе. Детальное обсуждение этого результата, а также
связанных с ним предшествующих результатов можно найти в
монографии Фань Цзы [1.11.
1. Люмис (Loomis L.), An introduction to abstract harmonic
analysis, New York, Van Nostrand, 1953. Русский перевод:
Введение в абстрактный гармонический анализ, ИЛ, М., 1956.
2. Вейль (Weil A.), L'integration dans les groups topologiques
et ses applications, Actual. Sci. Industr., 869, Paris, Hermann,
1940.
Несколько последних результатов можно найти в работе
3. Девинатц (Devinatz A.), Some contributions to the
extension of positive definite functions, Storrs, Conn.,
University of Connecticut, OSR—TN—55—421, 1955.
В книгах Фань Цзы [1.71 и Виддера [1.81 выясняется связь
между вполне монотонными функциями Хаусдорфа — Бернштей-
на — Виддера и положительно определенными функциями.
4. Бохнер (Bochner S.), Hilbert distances and positive
functions, Ann. of Math., 42 (1941), 647—656.
5. Шенберг (Schoenberg I. J.), Metric spaces and
positive definite functions, Trans. Am. Math.Soc, 44 (1938), 522—536.
6. Шенберг, фон Нейман (Schoenberg I. J., von
N e u m a n J.), Fourier integrals and metric geometry, Trans.
Am. Math. Soc.t 50 (1941), 226—251.
7. Секефальви-Надь, Кораяьи (S z. - N a g у В.,
Koran у i A.), Relatio/i d'une probleme de Nevanlinna et Pick avec
la theorie des operateurs de l'espace Hilbertian, Acta, Math. Hung.,
7 (1956), 295—305.
8. Вейль (Weyl H.), Ober das Pick — Nevanlinnasche Inter -
polationsproblem und sein infinitesimales Analogen, Ann. of
Math., 36 (1935), 230—254.
§ 16. Теория воспроизводящих ядер естественным образом
следует из теории интегральных уравнений математической физики,
которая основана на понятии функции Грина. В свою очередь
теория воспроизводящих ядер имеет значение для теории интегральных
уравнений. По этим вопросам отметим следующую литературу.
1. Ароншайн (Aronszajn N.), The theory of reproducing
kernels, Trans. Am. Math. Soc., 68 (1950), 337—404. Русский
перевод в сб. Математика, 7 : 2, 1963, 67—130.
2. Ароншайн, Смит (Aronszajn N., Smith К. Т.),
Characterization of positive reproducing kernels. Applications to
Green's functions, Am. J. Math., 79 (1957), 611—622

Библиография и дополнения
181
§ 17.
1. Ляпунов А. А., О вполне аддитивных вектор-функциях.
Известия АН СССР, сер. матем., 3 (1940), 465—478.
§ 18. Этот результат впервые дается в работе
1. Ландау (Landau Е.), Uber einen Konvergenzsatz, Gott.
Nachr., 1907, 25—27.
Кроме того, он приводится в книге Банаха [1.1]. Результат
Абеля приводится в книге Харди, Литтлвуда, Пойа [1.1, теорема 162,
стр. 120], гл. I.
§ 19.
1. Беллман (Bellman R.), On an application of the Banach—
Steinhaus theorem to the study of the boundedness of solutions
of nonlinear differential and difference equations, Ann. of Math.,
49 (1948), 515—522.
2. Массера, Шеффер (Massera J. L., Schaf-
f er J. J.), Linear differential equations and functional analysis,
I, Ann. of Math., 67 (1958), 517—573.
3. Массера, Шеффер (Massera J. L., Schaf-
fer J. J.), Linear differential equations and functional analysis,
II, Ann. of Math., 69 (1959), 88—104.
4. Чезари (Cesari L.), Asymptotic behavior and stability
problems in ordinary differential equations, p. 102, Ergebnisse
der Math., Berlin, Springer, 1959. Русский перевод:
Асимптотическое поведение и устойчивость решений обыкновенных
дифференциальных уравнений «Мир», М., 1964.
5. Кордуняну (Corduneanu С), Sur un theoreme de
Perron, Analele Stiintifice ale Univ. Jasi, 5 (1959), 33—36.
§ 20.
1. Гей л (Gale D.), Theory of linear economic models, New
York, McGraw-Hill, 1960. Русский перевод: Теория линейных
экономических моделей, ИЛ, М., 1963.
2. В е й л ь (W е у 1 Н.), The elementary theory of convex polyhe-
dra, Ann. Math. Studies, 24, 3—18, Princeton, N. J., Princeton
University Press, 1950.
§ 21.
1. Минковский (Minkowski H.), Zur Theorie der ein
heiten in den algebraischen Zahlkorpern, Gesammelte Abhand
lungen, I, Leipzig, Teubner, 1911.
2. Ф a p к а ш (Farkas J.), Uber die Theorie der einfachen
Ungleichungen, /. Reine Angew. Math., 124 (1901), 1—27.
3. Штимке (Stiemke E.), Uber positive Losungen homogener
linearer Gleichungen, Math. Ann., 76 (1915), 340—342.
4. Д а й н с (Dines L. L.), Systems of linear inequalities, Ann.
of Math., 20 (1919), 191—199.
5. Карвер (Carver W. В.), Systems of linear inequalities,
Ann. of Math., 23 (1920—1922), 212—220,

182
Библиография и дополнения
6. Моцкин (Motzkin Т.), Betrage zur Theorie der linearen
Ungleichungen, Diss., Basel, Azriel, Jerusalem, 1936.
7. Черников С. H., Системы линейных неравенств, Успехи
матем. наук, 8 (1953), 7—73.
См. также книгу Моргенштерна ([42.21, гл. 2.), в особенности
главы, написанные Вонгом и Вудбери. Симплексный метод
Данцига, который обычно используется для получения численных
решений, изложен в следующих работах.
8. Данциг, Орден, Вольф (Dantzig G. В., О г -
d е п A., Wolfe P.), The generalized simplex method for
minimizing a linear form under linear inequality restraints, Pacific J.
Math., 5 (1955), 183—195.
9. Ф о p д, Ф у л к e p с о н (Ford L. R. J., F u 1 k e r-
s о n D. R.), A simple algorithm for finding maximal network
flows and an application to the Hitchcock problem, Canad. /.
Math., 9 (1957), 210—218.
Дальнейшие ссылки можно найти в работах
10. Райли, Гасс (Riley V., Gass S. I.), Linear
programming and associated techniques, Baltimore, Md.f Operations
Research Office, John Hopkins University, 1958.
И. Леман (Lehman S.), On confirmation and rational
betting, /. Sympbolic Logic, 20 (1955), 251—262.
12. Никайдо (Nikaido H.), Sur un theoreme de Stiemke,
Osaka, Japan, Inst. Social Econ. Research, Osaka Univ., 1961.
§ 22.
1. Гейл, Кун, Таккер (Gale D., К u h n H., T u -
с k e r A. W.), Nonlinear programming, Second Berkeley
Symposium on Mathematical Statistics and Probability, Berkeley and
Los Angeles, University of California Press, 1951.
2. Д а ф ф и н (D u f f i n R. J.), Infinite programs, Pittsburgh,
Department of Mathematics, University of Pittsburgh, Technical
Report, № 20, 1955.
В статье Лемана развивается непрерывный вариант
симплексного метода.
3. Леман (Lehman S.), On the continuous simplex method,
Santa Monica,, Calif, The RAND Corporation, Research
Memorandum RM — 1386, 1954.
Проблемы, которые рассматриваются в этой работе, возникают
при исследованиях непрерывных производственных процессов;
см. [7.1.], [19.11, гл. I. Отметим в связи с этим следующую статью
4. Беллман, Леман (Bellman R., Lehman S.),
Studies on bottleneck problems in a production processes, Santa
Monica, Calif., The RAND Corporation, Paper P—492, 1954.
§ 23. В теории игр следующая работа является классической.
1. Фон Нейман, Моргенштерн (Neumann J.
von, Morgenstern О.), Theory of games and economic
behavior, Princeton, N. J., Princeton University Press, 1953.
Изучение игровых ситуаций для двух лиц было начато
независимо друг от друга Борелем и фон Нейманом. См.
2. Борель (В о г е 1 Е.), Applications aux jeux de hasard. Traite

Библиография и дополнения
183
du calcul des probabilities et deses applications, Paris, Gauthier—
Villars, 1913.
Наиболее доступное и занимательное введение в эти проблемы
можно получить, изучив следующую книгу.
3. Уильяме (Williams J. D.), The complete strategyst,
New York, McGraw-Hill, 1954. Русский перевод: Совершенный
стратег, Физматгиз, М., 1961.
4. Люмис (Loomis L. Н.), On a theorem of von Neumann,
Proc. Nat. Acad. Sci. USA, 32 (1946), 213—215.
5. Робинсон (Robinson J.), An iterative method for
solving a game, Ann. of Math., 54 (1951), 296—301.
6. Г p о с с (Gross О.), A mechanical proof of the min-max
theorem, Santa Monica, Calif., The RAND Corporation, Research
Memorandum RM-2320, 1960.
7. Никайдо (Nikaido H.), On a method of proof for the
minimax theorem. Proc. Am. Math. Soc, 10 (1959), 205—212.
8. Никайдо (Nikaido H.), Coincidence and some systems
of inequalities, /. Math. Soc. Japan, 11 (1959), 354—373.
9. HbK)MaH(NewmanJ.), Another proof of the minimax
theorem, Proc. Am. Math. Soc, 11 (1960), 692—693.
§ 24. Доказательство теоремы 15 содержится в
неопубликованной работе
1. Беллман, Шиффман (Bellman R.,Shiffman М.),
1
On the min-max of jj f(x)a(x)d(x)dt(x).
о
Кроме того, доказательство этой теоремы имеется в
монографии [19.1, гл. 12J, гл. I.
§ 25. Этот удивительно мощный метод развивался в течение
довольно длительного времени. Первоначальная идея Зарембы
легла в основу метода проекций в пространстве гармонических
функций. Этот метод был далее развит Бергманом и Шиффером,
Пиконе и Фикерой. Полный результат (полученный независимо
Шевалье и Хербрандом, которые, правда, не опубликовали свой
результат) был впервые дан Вейлем [1.181. Относительно
приложений и дальнейших ссылок см. следующую литературу.
1. Качмаж, Штейнгауз (Kaczmarz S., Stein-
h a u s H.), Theorie der Orthogonalreihen, Monografje Matematyc-
zne, VI, Warsaw, 1935. Русский перевод* Теория ортогональных
рядов, Физматгиз, М., 1958.
2. Форсайт, Розенблюм (Forsythe G. Е., Rosen-
bloom Р. С), Numerical analysis and partial differential
equations, Surveys in Applied Mathematics, New York, Wiley, 1958.
§ 26. См. результаты Фридрихса, на которые ссылаются в главе
об исчислении вариаций в работе [26. Ц, гл. II, а также работы.
1. Л а к с (Lax P. D.), Reciprocal extremal problems in function
theory, Comm. Pure Appl. Math., 8 (1955), 437—453.
2. Рогозинский, Шапиро (Rogosinski W. W.,
Shapiro H. S.), On certain extremum problems for analytic
functions. Acta Math., 90 (1953), 287—318,

Глава IV
ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ
§ 1. Введение
Эта глава посвящена следующему вопросу: дано
множество функций {и}, удовлетворяющих некоторым
граничным условиям, и оператор L, заданный на этом
множестве. Требуется выяснить, когда из неравенства
L(u)>0 (1)
следует, что и>0. Оператор L, удовлетворяющий этому
условию, назовем положительным, хотя более разумно
было бы называть так обратный оператор L-1. Мы
сосредоточим наше внимание на дифференциальных операторах,
обыкновенных и в частных производных.
Общие задачи такого типа широко изучались
Чаплыгиным [1], который с их помощью развил методы для
получения полезных аппроксимаций к решениям
дифференциальных уравнений довольно сложных типов. Ниже будут
рассмотрены некоторые из его результатов, а также
дальнейшие их уточнения.
Вначале мы рассматриваем дифференциальные
операторы первого порядка. Затем будут указаны результаты
Гронуолла [2], Беллмана [3], Бихари [4], Лангенхопа [5],
которые важны при изучении существования,
единственности и устойчивости решений обыкновенных
дифференциальных уравнений.
Для линейных дифференциальных операторов высших
порядков проблема положительности связана с
характеристическими корнями и двухточечной граничной задачей.
Здесь мы начнем с изучения дифференциального
неравенства второго порядка
"" + £(*)"> 0, и(0) = и(1) = 0. (2)

§ 1. Введение
185
Некоторые из многочисленных методов, применяемых
для уравнения (2), могут быть использованы и для
изучения операторов в частных производных.
Будут указаны некоторые простые рассуждения,
которые обычно применяются при изучении колебательных
и не колебательных решений обыкновенных
дифференциальных уравнений второго порядка. Обобщая эти
рассуждения, можно установить ряд принципов максимума
для решений уравнений в частных производных. Далее
будет дано доказательство Чаплыгина [1], основанное
на одном интегральном тождестве, а также
доказательство Беллмана [12.1], которое использует вариационные
методы. Другие доказательства можно найти в работах
Петрова [15.1] и Уилкинса [15.2]: они основаны на
уравнении Риккати. Наконец, доказательство, использующее
факторизацию оператора, имеется в работе Пуанкаре [6].
Метод факторизации операторов был использован
Пойа [7] для изучения обобщенной теоремы Ролля и
интерполяционной задачи для дифференциального уравнения
я-го порядка. Эти результаты Пойа рядом математиков
были обобщены на операторы в частных производных;
они объединены в статье Гартмана и Винтнера [8], где
приведена полная библиография.
Изучение этих вопросов приводит нас к естественному
обобщению понятия выпуклости, а также к исследованиям
Беккенбаха [17.1], Бонсалла [17.4], Пейсото [17.5] — [17.7],
Рейда [17.11], Гартмана [17.12] и др. В этих работах
уточняются некоторые из упомянутых выше результатов
Чаплыгина.
Отметим, что рассматриваемые вопросы тесно
связаны обобщениями рядов Тейлора (см. Пойа [7], Дель-
сарт [20.1], Петерссон [16.1], Левитан [20.2] Виддер,
[20.3]).
Будут приведены также некоторые результаты для
векторно-матричных дифференциальных уравнений вида
% = A(t)x, х(0) = с, (3)
где x(t) — векторная функция, A(t) — матричная
функция,

186
Гл. IV. Положительные операторы
Далее мы рассмотрим уравнения в частных
производных вида
ut — uxx — uyy — uzz — q(x, у,г)и = О,
Методы, применяемые для этих уравнений, могут быть
использованы для изучения более общих уравнений Бель-
трами. Положительность рассматриваемых
дифференциальных операторов эквивалентна положительности функции
Грина. К этим вопросам можно подходить различными
путями (см. Ароншайн и Смит [16.2], гл. III). Ряд этих
методов можно применить к изучению обыкновенных
дифференциальных операторов.
Для доказательства положительности функций Грина
изящна и удачна вероятностная интерпретация этих
функций. Превосходное изложение этого метода дано Кацом
[9]. Аналогичное применение теории вероятностей для
вывода положительности некоторых выражений имеется
в работе Карлина и Мак-Грегора [37.9], гл.II.
В данной книге вопросы положительности
дифференциальных операторов в частных производных мы
рассмотрим лишь кратко. Будут отмечены только основные
результаты Хаара [29.1], Вестфаля [29.2], Проди [29.3], Мла-
ка [29.5], имеющие большое значение в теории
устойчивости параболических уравнений в частных производных.
Эти результаты являются частными случаями «принципа
максимума» (см. Нюренберг [21.1], Вейнбергер [21.2],
Пуччи [29.4]).
Обобщения классической теории Штурма для
обыкновенных дифференциальных уравнений, данные Гартманом
и Винтнером [8] и Редхеффером [35.9], принадлежат
в большей степени теории уравнений в частных
производных, чем к теории неравенств, и поэтому не будут здесь
рассматриваться.
В конце главы мы кратко доказываем, как
положительные операторы используются при изучении нелинейных
функциональных уравнений в связи с методами
квазилинеаризации, упомянутыми в гл. I и П.
Очень трудно проследить все разветвления этой
основной линии анализа—теории положительных операторов.

§ 2. Линейные дифференциальные уравнения первого порядка 187
Указаны лишь некоторые главные направления развития
этой теории; для интересующихся читателей приводится
обширная библиография. Результаты для положительно
определенных операторов можно распространить на
операторы, уменьшающие число перемен знака (см. работы
Шенберга [10] и другие, на которые мы ссылались
в гл. II-[48.1,48.2,48.10]).
§ 2. Линейные дифференциальные уравнения
первого порядка
Наш первый результат относительно дифференциальных
операторов состоит в следующем.
Теорема 1. Если линейное дифференциальное
уравнение
— = «(*)", ы(0) = с, (1)
и линейное дифференциальное неравенство
^>a(t)v, v(0) = c, (2)
имеют место для промежутка 0 < t < Т, то
v(t)>u(t), 0<t<T. (3)
Доказательство. Оно является непосредственным
следствием того факта, что решение линейного
неоднородного уравнения
*L = a(t)v + f(t), о(0) = с, (4)
имеет вид
t t
\a(s)dss t \a(s)ds
v = ce° + [ er f(r)dr. (5)
о
Результат следует из положительности ядра
t
\a(s)ds

188
Гл. IV. Положительные операторы
§ 3. Обсуждение
Результат, приведенный в предыдущем параграфе,
хотя и очень простой, важен по двум причинам.
Во-первых, он иллюстрирует характер результата, который мы
желаем установить. Во-вторых, он дает следующий
образец типичного доказательства, который используется во
многих случаях.
Неравенство L(u)>0, где L — линейный
дифференциальный оператор, преобразуется в неоднородное
уравнение
L(u) = f(p), (1)
где функция f(p) неотрицательна. Решая (1)
относительно и, мы получаем соотношение вида
u = T(f). (2)
Таким образом, решение неравенства L(u)>0 сводится
к изучению положительной определенности оператора Т,
что эквивалентно положительной определенности функции
Грина для оператора L. В теореме § 2 это очевидно,
в общем же случае требуется дополнительное
доказательство.
§ 4. Фундаментальный результат теории устойчивости
С теоремой ] тесно связан следующий результат Белл-
мана [1.3].
Теорема 2. Если функции g(t) и u(t)
неотрицательны при £>0, то для с>0 из неравенства
t
u(t)<.c+[ g(s)u(s)ds, t>0, (1)
о
следует, что
t
^g(s)ds
u(t)<ce° , t>0. (2)
Этот результат может быть установлен либо
непосредственно, либо методом § 2 (см. Гронуолл [1.2], Гуилья-

§ 5. Неравенства Бихар и и Лангенхопа 189
но [3]). Ввиду того что теорема 2 часто используется,
приведем ее доказательство (см. Беллман [1]).
Доказательство. Из неравенства (1) имеем
—ттт—<т- (3)
с+ I g(s)u(s)ds
о
Интегрируя (3) от 0 до t, получаем
t t
ln[c+ \g{s)u(s) dsl — lnc< f g(s)ds. (4)
о о
Отсюда следует, что
t
t lg(s)ds
c+\g(s)u(s)ds<ce° . (5)
о
Требуемое неравенство (2) следует из (1) и (5),
Различные применения этого результата к изучению
устойчивости линейных и нелинейных дифференциальных
уравнений приведены в работе Беллмана [1].
Многочисленные применения к теории существования и
единственности дифференциальных уравнений можно найти в книге
Немыцкого и Степанова [2], а также Бихари [1.4],
Лангенхопа [1.5]; применения к априорным оценкам классов
решений уравнений в частных производных указаны в
работе Лакса [4].
§ 5. Неравенства Бихари и Лангенхопа
Бихари получил следующее обобщение теоремы 2
предыдущего параграфа.
Теорема 3. Если k, m>0 и функция g(s)
положительна для s > 0, то из неравенства
t
u(t)*ck + m \ v(s) g(u(s))ds, a<£<6, (1)

190
Гл. IV. Положительные операторы
следует,
где
что
i
u(t)<G'
G(u) =
~1(G(k) +
Р dt
щ
t
m\v(s)ds\
U > Uq > 0.
(2)
(3)
Применение этого результата Бихари см. в работе [1.4].
С теоремой 3 тесно связан результат Лангенхопа [1.5].
Пусть
(а) х—действительная переменная, z и F —
конечномерные комплексные векторы с п компонентами zt
и Ft соответственно;
(б) функция F непрерывна в точках (х, г) для всех z
и всех а:б [а, 6], т. е. а<#<Ь, а < &;
п
(в) при норме ||г||= 2 \гг\
г=1
\\F(x,z)\\<v(x)g(\\z\\),
где функция а (я) непрерывна, v(x)>0 для л: б [а, 6];
функция g(u) непрерывна и не убывает для и>0 я g(u)>
> 0 для и > 0.
Если функция z(#) непрерывна и является решением
dz
уравнения ^- = ^(#> z) Для *6[а, &], где jF
удовлетворяет указанным выше условиям, то для всех х£ [а, Ь]
функция г(х) удовлетворяет неравенству
\z(x)\> G^(b(\z(a)\)~^v(s)dsy
а
где
и
G(«)=J-|^y, «0>0,
щ
х
для всех я£[а,6], для которых G{\z{a)\) = \v(s)ds при-
а
надлежит области G~\

§ 6. Матричные аналогии
191
Сформулированные результаты Бихари и Лангенхопа
дают соответственно верхнюю и нижнюю границу решений
соответствующих уравнений.
§ 6. Матричные аналогии
Рассмотрим векторно-матричную аналогию теоремы 1.
Возьмем векторно-матричное неравенство
%L>A(t)x, *(0) = с, (1)
где A(t)—матричная функция, х —векторная функция
с п компонентами. В одномерном случае из этого
неравенства следует, что функция х ограничена снизу решением
уравнения
% = A(t)y, у(0) = с. (2)
В многомерном случае подобного результата нет. Для
случая же, когда Л —постоянная матрица, представляет
интерес один простой результат.
Теорема 4. Пусть Л=(ау) — постоянная матрица.
Для того чтобы решение неравенства
~>Ах, х(0) = с, (3)
было ограничено снизу для t>0 решением уравнения
^г = Ау, у(0) = с, (4)
необходимо и достаточно, чтобы было
Яу>0, ьф], ati—действительны. (5)
Доказательство. Так как решение неоднородного
уравнения
*L = Ax + f{t), х(0) = с, (6)
имеет вид
t
х = eAtc + J eA<*-i> f(s) ds, (7)

192 Гл. IV. Положительные операторы
где ел* — матричная экспоненциальная функция (см. [43.1],
гл. II), нам нужно определить, когда элементы eAt
неотрицательны для £>0.
Разложение
eAt = I + At+... (8)
для малых положительных t показывает, что условие (5)
необходимо. Для доказательства достаточности можно
использовать либо систему дифференциальных уравнений
^=2 «У». /=1,2,..., я, (9)
Уг(0) = а
(как будет сделано ниже в § 8), либо тождество
eAt = (eAt/Nf. (10)
Используем вначале тождество (10). Можно
предположить, что а у > 0, i Ф /, так как в этом случае результат
для ау>0 может быть получен предельным переходом.
Для фиксированного t и достаточно больших N из
разложения (8) следует, что матричная функция eAilN
положительна в том смысле, что все ее элементы положительны.
Так как произведение положительных матриц
положительно, то матрица eAt положительна, если ау>0, 1Ф j. Это
доказательство принадлежит Карлину.
Теорема 4 тесно связана с теоремой Перрона
относительно положительных матриц и с ее обобщением,
приведенным в гл. II (см. также [38.3], гл. II, где теорема
Перрона выводится из результатов теории линейных
дифференциальных уравнений). Отметим, что теорема 4
интуитивно очевидна из вероятностной или экономической
интерпретации уравнений (9) (см. Романовский [1],
Опиал [2]).
§ 7. Доказательство Тауски
Следующее короткое неопубликованное доказательство
Тауски обладает тем свойством, что оно применимо
к выводу ряда результатов относительно входных-выход-

§ 8. Переменные матрицы
193
ных матриц непосредственно из соответствующих
результатов для положительных матриц.
Пусть & — скаляр. Тогда
eAt _ e(A+kI)t e-kitm
Если выбрать k настолько большим, чтобы матрица
A-\-kI была неотрицательной, то £(A-W будет
неотрицательной матрицей* Так как e~kIt>0, то матрица eAt
неотрицательна.
§ 8. Переменные матрицы
Если A (t) — переменная матрица, то решение
линейного неоднородного уравнения
*^Л(0*+/(0. *(<>)=*, (1)
можно записать в виде
t
x = Y(t)c + lY(t) Y-\s) f(s) ds, (2)
о
где Y(t) —решение матричного уравнения
dX
dt
= A(t)X, X(0) = /. (3)
Из этого представления видно, что для того чтобы
из соотношения
£ = A(t)x, *(0)>0, (4)
следовало #>0 для £>0, необходимо и достаточно,
чтобы Y(t)>0\ необходимым и достаточным условием
того, что из
*L>A(t)x, *(0) = 0,
следует х>0 для £>0, является неравенство Y(t)Y~1(s)>
>0 для t>s>0.
Эти два условия не являются эквивалентными, как
в ел чае, когда A(t —постоянная мат ица.

194
Гл. IV. Положительные операторы
Простое достаточное условие того, что F(£)>0 для
£>0, состоит в том, что <%>0, / Ф /; это видно из
следующего соображения. Предположим, без потери общности,
что все xt(0) положительны, и пусть Xi(t) — компонента,
впервые обращающаяся в нуль в точке t0.
Тогда при t0 имеем
dx
-ft = ai2x2 + ... + ainxn > 0, (5)
а это противоречит тому, что х должно убывать, когда
t~>t0.
Это достаточное условие имеет большое значение при
изучении уравнения
■g- = max [A(q) х + %)], *(0) = с, (6)
возникающего в теории разрешающих марковских
процессов (см. [6.1], [7.1], гл. I и [44.2], гл. II), а также при
использовании метода квазилинеаризации.
§ 9. Обсуждение
Результаты § 8 касаются только одной частной задачи,
возникающей при изучении уравнения (8.1). Можно также
искать необходимые и достаточные условия того, что
решение x(t) ограничено для £>0 при любой функции
f(t), ограниченной для £>0, или что x(t)$L2(0,co) при
f(£)£L2(0,co) и т.д. Вообще, можно задаваться
вопросом, когда из /gS следует, что x£S', где S и S' —
банаховы пространства. Изучение этих проблем было начато
Перроном [1], который использовал прямые методы,
и продолжено Беллманом (см. [19.1], гл. III) методами
банахова пространства (см. также Массера [2, 3]).
Результаты Массеры применимы также к операторным
уравнениям.
§10. Результат Чаплыгина
Изучение линейных дифференциальных уравнений
второго порядка мы начнем с небольшого обобщения
результата Чаплыгина [1.1]. Первый применяемый нами метод
широко используется при изучении колебательности

§ 10. Результат Чаплыгина
195
решений линейных и нелинейных дифференциальных
уравнений второго порядка. Во многих случаях этот метод
может быть применен без изменений для установления
аналогичных результатов для уравнений в частных
производных.
Теорема 5. Если
(а) u" + p(t)u'-q(t)u>0, t>0,
(б) if + p(t)v'-q(t)v = 0, t>0,
(в) <7(0>0, *>0, (1)
(г) u{0) = v(0), u'(0) = v'(0);
тогда и > v для t > 0.
Доказательство. Вычитая (б) из (а), получаем
XBf + p(t)w' — q(t)w>0, (2)
где w = u — v, причем w(0) = w'(0) = 0. Отсюда следует,
что w > 0 в некотором интервале (0, t0]. Предположим,
что где-то функция становится отрицательной; тогда у w
должен иметься максимум в некоторой точке tt. В этой
точке ш' = 0, w > 0 и поэтому из (2) следует, что ш">0.
Это, однако, противоречит тому, что в точке f4 максимум.
Доказательство Чаплыгина для частного случая,
в котором p(t) = 0, основано на важном тождестве
о- а
\ u{u" — qu)dt=[uuX- I (u'2 + qu2)dt. (3)
о о
Пусть а — наименьшее положительное значение t, для
которого и = 0. Тогда из и(0) = 0 следует, что
а а
[ u(u" — qu)dt= — Uu'* + qu*)dt. (4)
о о
Если u"—qu>0 на отрезке [0,а] и &>0, то мы,
очевидно, получим противоречие* Таким образом, такой
точки а не существует.
Изучение обратной задачи, т. е. определение условий,
когда положительный оператор имеет указанный выше
вид, проведено в работе Феллера [1].

196
Гл. IV. Положительные операторы
§ 11. Конечные интервалы
Анализируя предыдущее доказательство, мы видим,
что условие q>0 может быть значительно ослаблено при
условии, что интервал является конечным. Это является
следствием того факта, что неравенство
а
\(u'2 + qu2)dt>0 (1)
о
может выполняться и для отрицательных q, малых по
абсолютной величине. Это утверждение следует из
неравенства Виртингера, которое детально будет рассмотрено
в следующей главе; оно, как будет показано, является
следствием обшей теории Штурма —Лиувилля.
Из формулы (10.4) легко может быть получен
следующий результат.
Теорема 6. Если
(а) u" — qu>0, 0<£<а,
(б) и(0) = и(а) = 0,
(2)
(в) \ (u'2 + qu2)dt>0,
о
то и<0 для 0<£<а.
Как будет видно из § 12 гл. V, достаточным условием
для (2в) является выполнение следующего неравенства
<7(')>—S- + *. S>0, 0<t<a. (3)
«Магическое» число п2/а2 является, конечно, первым
характеристическим числом, соответствующим задаче
Штурма — Лиувилля
и" + Хи = 0,
и(0) = и(а) = 0. ^
§ 12. Вариационное доказательство
Рассмотрим вариационное доказательство, которое
может быть использовано для получения ряда результатов,

§ 12. Вариационное доказательство
197
касающихся функций Грина для следующей задачи
ur + q(t)u = f(t),
и(0) = и(а) = 0. ( }
Мы изменили знак перед функцией q(t), чтобы
показать, что она является положительной в большинстве
важных случаев. Если q(t) = 0, то очевидно, что из
неравенства f(t)>0 для 0<£<а следует, что u(t)<0
в этом интервале. Более точный результат состоит в
следующем.
Теорема 7. Если
(а) q(t)<£—d, d>0, 0<t<a,
(2)
(б) f(t)>0, 0<*<а,
mo u(t)^0 для 0<t<a.
Доказательство. Рассмотрим задачу минимизации
функционала
а
J(u)= ^[u'2 — q(t)u2 + 2f(t)u]dt (3)
о
на функциях и, удовлетворяющих условиям и(0) — и(а) = О,
для которых интеграл (3) существует.
Из неравенства
ImuUt^-d^dtK^^lu'^t, (4)
о оо
которое получается из неравенства Виртингера, упомянутого
выше, с помощью обычных «вариационных» рассуждений
следует, что минимум функционала J (и) существует
и достигается на единственной функции и. Вариационное
уравнение Эйлера для этой функции есть уравнение (1).
Таким образом, чтобы убедиться в том, что решение
уравнения (1) неположительно для 0<£<а для любых
f(t)>0, t£[0, а], достаточно показать, что функция,
минимизирующая J (и), неположительна для любых
неотрицательных f(t).

198
Гл. IV. Положительные операторы
Последнее легко установить. Предположим, что найдется
некоторый отрезок [а±, 6J, лежащий внутри [0, а], такой,
что г/(/)>0 на [а4, Ь±]. Заменим u(t) новой функцией,
равной —u(t) на этом отрезке [а±, Ь±] и принимающей
прежнее значение в остальных точках. Эта вновь
введенная функция может иметь разрывы производной, однако
она остается /Линтегрируемой. Это изменение не скажется
на квадратичных членах, но оно уменьшает член,
включающий /(/); следовательно, если функция f (t) положительна
на множестве положительной меры отрезка [аи 64], то мы
получим противоречие (см. Беллман [1], Стильтьес [2]).
Чтобы доказать теорему, очевидно, достаточно
рассмотреть только положительные функции f (t) на отрезке [0, а].
§ 13. Обсуждение
Легко видеть, что результат теоремы 7 является не-
улучшаемым в том смысле, что если условие (12.2а)
не выполняется, то заключение теоремы может оказаться
неверным. Например, рассмотрим решение уравнения
u" + ku = sin—,
си
и(0) = и(а) = 0,
определяемое формулой
(2)
sin
k —
Tit
а
эт2
а2
Я2
Если k > —2~, то функция и положительна при 0 < t < а,
nt
хотя sin—>0 в [0,а].
я2
Как упомянуто выше, величина -^ является
наименьшим характеристическим числом уравнения Штурма — Лиу-
вилля
и"+Хи = 0, 0<£<а,
и(0) = и(а) = 0. (3)

§ 14. Линейные уравнения произвольного порядка 199
Результат теоремы 7 будет получен другим методом
в следующем параграфе.
Так как решение уравнения
"* + <7(0" = f(0.
и(0) = и(а) = 0, W
можно записать в виде
и= \ k(t, s)f(s)ds,
(5)
где k(t, s) — функция Грина, соответствующая задаче (4),
то очевидно, что любое утверждение относительно
решения (4) для всех неотрицательных f эквивалентно
утверждению относительно неотрицательности функции k(t, s).
Наконец, отметим, что аргументы, приведенные выше,
подобны используемым Стильтьесом [12.2] при
рассмотрении систем линейных уравнений и обращений матриц. Его
результаты могут быть сильно обобщены (см. 2.1, гл. II,
где приведены дальнейшие ссылки).
§ 14. Линейные дифференциальные уравнения
произвольного порядка
Рассмотрим теперь более общую задачу. Пусть L-
линейный дифференциальный оператор порядка п,
L(a) =
dnu
dtn
■fli(0
dn-*u
dtn-i
.+an(t)u,
(1)
где функции at(t) непрерывны на отрезке [0, t0] и пусть
щ,и2,..., ип — п линейно независимых решений
уравнения L(u) = 6.
Введем определители Вронского
\иМ) «2(01
Wl(t) = ul(t), W2(t) = \ 1W W|
Wn(t) =
Ui{t)
"1(0
«;(0
«1(0 "i(0
.. • «n(0
• • • Kit)
uf^Xt) «'"""(O ... u^-iy(t)
(2)

200
Гл. IV. Положительные операторы
Известно, что для вронскиана порядка п выполняется
соотношение
t
Wn(t) = e ° , (3)
которое принадлежит Якоби, причем мы полагаем, что
W„(0)ssl.
Наш результат относительно положительности
оператора L опирается на следующее интересное представление.
Теорема 8. Если Wi(t), i=l, 2, ..., я—1,
положительны для 0</<£()> то на этом отрезке
, wn d ТП-i d щ d щ d f и л ш
Wn_i dt Wn-2Wn '" dt WiWB dt WQW2 dt \WtJ' ^ }
Доказательство этой теоремы приведено в книге Пойа
и Сегё [44.1], гл. I.
§ 15. Положительность линейных
дифференциальных операторов высших порядков
Нетрудно получить следующий результат.
Теорема 9. Достаточным условием того, что из
неравенства
L(u)>0 u{0) = u'(0)=...=u(n-V(0) = 0 (1)
для 0<^<^, следует, что и>0 на [0, tfj, является
существование совокупности линейно независимых решений
ии и2, ..., ип, для которых Wt{t) > 0 (i = 1, 2, ..., п— 1)
на [0, t±].
Эта теорема обобщает соответствующий результат для
случая линейного дифференциального уравнения второго
порядка, полученный Петровым [1] и Уилкинсом [2].
В статье Уилкинса условие формулируется с помощью
соответствующего уравнения Риккати. Является ли
условие теоремы 9 необходимым, как в случае п = 2, не
известно.
Подробное обсуждение результатов этого типа
содержится в монографии Чаплыгина [1.1], где приводятся
аналитические и геометрические аргументы, а также даются
приложения.

§ 16. Некоторые результаты Пойа
201
§ 16. Некоторые результаты Пойа
Свойство, используемое в теореме 8, а именно
предположение о том, что существует п линейно независимых
решений иии2, ...,ип, для которых вронскианы Wt(t)
положительны на [0, ti\, было названо Пойа свойством W.
Используя указанное условие, он установил следующий результат.
Теорема 10. Если линейный дифференциальный
оператор
L(u) = uW + ai(t)u(n-U+ ...+an(t)u (1)
обладает свойством W, то для любой заданной функции
f(t), определенной на [0, tf4], п раз дифференцируемой
и обращающейся в нуль в п+l точке отрезка [0, fJ,
найдется внутренняя точка s, такая, что
L(u(s)) = 0. (2)
Это —широкое обобщение теоремы Ролля.
Теорема 11. Если свойство W выполняется, то
существует одно и только одно решение L (и) = 0, которое
принимает п заданных значений в п точках отрезка [0, tfj.
Эта теорема дает доказательство существования и
единственности для интерполяционной теоремы Лагранжа (см.
Петерсон [1]).
Теорема 12. Пусть выполняется свойство W, и пусть v
есть решение уравнения L(v) = 0, принимающее те же
значения, что и функция и в п заданных точках [0, ^].
Пусть, кроме того, w(t) —решение уравнения L(u)=l,
равное нулю в тех же п точках. Тогда найдется точка
s = s(t) на [0, ti]9 соответствующая каждому t из [0,1],
такая, что
u(t) = v (t) + w(t)L (и (s (t))). (3)
Этот результат является обобщением теоремы о среднем.
Частный случай для оператора
и" + и (4)
был установлен Пуанкаре [1, 6] и явился стимулом для
исследований Пойа. Дальнейшие результаты см. у Гарт-

202
Гл. IV. Положительные операторы
мана [17.12] и в статьях, цитируемых в § 19 и 20, имеющих
отношение к обобщенным разложениям Тейлора.
Интересным следствием этих результатов является тот
факт, что определитель \eXiVJ\ удовлетворяет условию
\ех^\ Ф 0, (5)
если Xi < х2 < ... < хп, yi<y2< .-• <Уп.
Результаты этого типа являются следствием теории
преобразований, уменьшающих число перемен знака, и, как
установил Шенберг [1.10], имеется много общего между
этими двумя направлениями.
§ 17, Обобщенная выпуклость
В этом параграфе, следуя идеям Беккенбаха [1], Бек-
кенбаха и Бинга [2], Валирона [3], Бонсалла [4], Пей-
сото [5, 6, 7], Моцкина [8],
Торнхейма [9], Куртиса [10],
»Ш ^^^ Рейда [11] и Гартмана [12],
кратко рассмотрим понятие
wu(t) обобщенной выпуклости,
введенной Беккенбахом [1], и его
рис. 6. связь с предыдущими
рассмотрениями.
Функция u(t), выпуклая на отрезке а < / < 6, может
быть описана следующим образом. Пусть a<ti<t2<b
и пусть v (t)— решение линейного уравнения
^- = 0, (1)
проходящее через две точки (tu u(ti)) и (t2, u(t2)). Тогда
u(t)<v(t) (2)
для ti<t<ct2 (см. рис. 6).
Для обобщения понятия выпуклости нужно обобщить
дифференциальный оператор (1); Бонсалл [4] рассматривал
линейное дифференциальное уравнение второго порядка
u" + p{t)u' + q{t)=0, (3)

§ 18. Обсуждение
203
Пейсото [7] использовал более общее нелинейное
дифференциальное уравнение
uT = g(t,u,u'), (4)
Приведем следующий результат Пейсото.
Теорема 13. Пусть уравнение (4) обладает
следующими свойствами:
(а) функция g(t, и, и') непрерывна по t,u,u' для a<t<Ь,
— оо <а< оо и — со < и' < оо; (5)
(б) для любой точки а < t0 < b, — оо < и0 < оо,
— оо < v0 < оо существует единственное решение
уравнения (4) для a<t<b, удовлетворяющее условиям
u(t0) = u0, u'(t0) = v0;
(в) для любых двух данных точек a<tt<b, — оо < ut < оо,
— оо < vt < оо, i = 1, 2, существует единственное
решение уравнения (4), удовлетворяющее условиям u(tt) = и$,
u'(ti) = Vi, £=1, 2.
£сли до (0 — любая дважды непрерывно равно
дифференцируемая функция при a <t <Ь, то необходимым и
достаточным условием того, что w(t)<cu(t), ^<^<^27 где
и определяется условиями (5в) и w(ti) = u(ti), г=1, 2,
является выполнение следующего соотношения
tif>g(t,w,w'), a<t<b. (6)
Бонсалл [4] установил соответствующий результат для
линейного уравнения (3) второго порядка без условия,
что w обладает непрерывной второй производной. В другой
статье [19] он рассмотрел соответствующую задачу,
связанную с дифференциальными операторами в частных
производных. Здесь мы сталкиваемся с гармоническими и
супергармоническими функциями и их обобщениями. Эти вопросы
будут рассмотрены во втором томе «Неравенств» (см. Рисс
[13], Радо [14], Беккенбах и Радо [15, 16], Беккенбах [17],
Рид [18], Таутц [20], Беккенбах и Джексон [21],
Джексон [22, 24], Айнон [23]).
§ 18. Обсуждение
Как указано во введении к этой главе, а также в § 15,
Чаплыгин [1.1] изучал связи между функциями, удовле-

204
Гл. IV. Положительные операторы
творяющими неравенству
t№-g(U и, и', ..., иС»-*>)>0, (1)
и функциями, удовлетворяющими уравнению
vW_gy9 VfV>9 ттт9 0(n-i))==o. (2)
Пусть w<ft>(0) = iKfe>(0) = cA для k^=0, 1, ..., п— 1.
Тогда, как установлено Чаплыгиным, имеется некоторый
f-интервал 0<£<£о» в котором и>и, так как можно
написать
а поскольку ^п>(0)>^(гг>(0) (в соответствии с (1) и (2))
и |Rn| = О(£п+1), \Sn\ = 0(tn+1) для малых *, то мы видим,
что наше утверждение справедливо.
Ряд приложений неравенств к проблеме получения
верхней и нижней границ для решения дифференциальных
уравнений был дан Чаплыгиным [1.1], а также рядом
других авторов (см. Пойа [1.7], Бонсалл [17.4], Петров
[15.1], Уилкинс [15.2], Гартман [17.12], Клямко [1],
Артемов [2], Пароди [3]).
§ 19. Обобщенная теорема о среднем
Гартмана и Винтнера
Теорема о среднем для линейных дифференциальных
операторов, сформулированная в § 16, имеет ряд аналогов
для уравнений в частных производных. Это было указано
Пойа [1], см. также Блейлер [2].
Обобщенная теорема о среднем, принадлежащая Гарт-
ману и Винтнеру [1.8] и являющаяся обобщением
результатов и методов Пойа, состоит в следующем.
Теорема 14. Пусть оператор L задан на множестве
функций {и(р)}, где р принадлежит области R. Обозначим
через В границу R, а через S множество функций,
удовлетворяющих фиксированным граничным условиям. Пусть

$ 20. Обобщенное разложение Тейлора 205
линейный оператор L обладает следующими двумя
свойствами:
(а) существует решение уравнения L(v)=l,
P£R, v£S; (1)
(б) если u£S и Ь(и)ф0 в R, то ифО в R.
Для любой данной функции и (р) пусть ui (р) является
решением уравнения L(%) = 0, таким, что u^ — u^S.
Тогда существует функция w (р), определенная для p£R,
такая, что
u(p) = ui(p) + v(p)L(u(w(p))). (2)
Доказательство. Так как v(р) не может
обращаться в нуль для p£R по условию (16), то для любого p£R
существует число а = а(р), такое, что
u(p) = ui(p) + av(p). (3)
Так как u(p) — ui(p) — av(p)^S, из (16) следует, что
L [и (р) — щ (p)—av (р)] = 0 в некоторой точке,
принадлежащей S. Обозначим эту точку через w(p). Тогда в этой
точке
0 = L[u(p) — u1(p) — av(p)]=L(u) — a. (4)
Отсюда видно, что a = L(u(w(p))), что и доказывает
теорему.
Отметим, что доказательство теоремы о среднем тесно
связано с установлением свойств положительности. В
деталях это будет обсуждаться в § 21.
Гартман и Винтнер в своей статье [1.8] привели ряд
интересных примеров, связанных с работами Бляшке [3],
Заремба [4] и др.
§ 20. Обобщенное разложение Тейлора
Обобщенная теорема о среднем —это, конечно, только
первый шаг в обобщении разложений Тейлора. Так как
эти вопросы не являются предметом изучения данной
книги, мы отсылаем читателя к статьям Дельсарта [1],
Левитана [2], Петерссона [16.1] и Виддера [3].

206
Гл. IV. Положительные операторы
§ 21. Положительность операторов
В остальной части главы мы сосредоточим наше
внимание на некоторых основных методах, которые обычно
используются при установлении положительности
классических операторов математической физики. Мы не будем
обсуждать здесь вопросы, связанные с проверкой точности
представления решения, а также не будем рассматривать
стандартные методы теории уравнений в частных
производных, основанные на принципах максимума (см. Нюрен-
берг [1] и Вейнбергер [2]); наконец, мы не будем
приводить интуитивных доказательств, основанных на связи
между функциями Грина и стохастическими процессами
(см. Кац [1.9]).
Вместо этого мы укажем обобщение вариационного
подхода, примененного в § 8, данное Беллманом — Бох-
нером [3, 4], а также набросок доказательства,
основанного на конечных разностях. Это последнее использует
идею процессов случайного блуждания без какого-либо
явного описания явления.
§ 22. Эллиптические уравнения
Легко видеть, что методы, представленные в § 20
в связи с дифференциальным уравнением второго порядка
(12.1), могут быть применены к дифференциальным
уравнениям с любым числом переменных
Uxx + uyy + q(x,y)u=f(x,y), x,y£R,
и = 0, х,у£В, (}
где В —граница области 7?.
Рассматривая квадратичный функционал
J(u)= ^[u% + ul—q(x,y)u2 + 2f(x1y)u]dxdy, ^)
R
можно легко получить следующий результат.
Теорема 15. Пусть ^ — наименьшее собственное
значение уравнения Штурма —Лиувилля
uxx + uyy + Xu = 0, x,y£R,
и = 0, х,у£В. * '

§ 24. Монотонность средних значений 207
Если
q(x, y)<K — d, d>0, x,y£R, (4)
то из неравенства
uxx + uyy + q(x, y)u>0, x,y£R,
и = 0, х, у£В, * '
следует, что
и<0, х, y£R. (6)
Этот результат, принадлежащий Беллману [12.1], легко
может быть обобщен на операторы Лапласа —Бельтрами
для общих областей.
§ 23. Положительные воспроизводящие ядра
Общая теория положительных воспроизводящих ядер
развита Ароншайном и Смитом (см. [16.2], гл. III).
Результаты относительно положительности функций Грина
являются ее следствиями.
В указанной работе можно найти библиографию по этим
вопросам, а также историю этой проблемы.
§ 24. Монотонность средних значений
Следующий результат Беллмана [21.3] нужно было бы
отнести к гл. V, однако он может быть использован при
установлении свойств положительности для
параболических операторов, как это делал, например, Бохнер в своих
исследованиях по квазианалитическим функциям.
Начнем с наиболее простого случая.
Теорема 16. Если
Щ = ихх, 0 < х < 1, t > 0,
и(0, t) = u(l, t) = 0, t>0, (1)
и(х, 0) = g(x), 0<х< 1,

208 Гл. IV. Положительные операторы
то
1
М0=$ И*. t)]2ndx, л=1, 2, ..., (2)
о
является монотонно убывающей функцией аргумента t
для t>0.
Отсюда следует, что
max\u(x, t)\ (3)
— монотонно убывающая функция для f>0.
Последний результат может быть расширен на
параболические уравнения общего типа. Это легко видеть из
доказательства теоремы 16 (см. также статью Бохнера
[21.4]).
Тот факт, что функция (3) является монотонно
убывающей, был ранее получен Пойа и Сегё [1], которые
использовали другой метод.
Доказательство. Имеют место следующие
формулы:
^ = 2п\[и (х, О]271"1 "* dx=
= 2п V [и (х, t)]71"1 ихх dx =
о
= 2n{[u(x,t)]**'1ux}- (4)
1
— 2/i(2n-l) J [и(х, t)]2n~2uxdx =
о
1
= - 2п (2/г - 1) J и2п~2 и% dx.
о
Следовательно,
dt ^и#

§ 25. Положительность параболических операторов 209
Для того чтобы показать, что функция (3) обладает
указанным свойством, используем следующую лемму,
которая интересна и сама по себе1).
Лемма. Если v(х) — непрерывная функция на
конечном отрезке [а,Ь], то
СЬ vl/2n
\v2n(x)dx) =max |i;(x)|. (5)
Соотношение (5) доказывается следующим образом.
Пусть m = max\v(x)\ на [а,Ь]\ тогда
ь d
m*n(b-a)>^v2n(x)dx>^v2n(x)dx, (6)
а с
где [с,d] — подинтервал [а,Ь], для которого \v(x)\^m — е.
Отсюда
СЬ \.1/2п
[v*n(x)dx\ >{т-г){й-с)тп. (7)
а
Так как
lim qV2n = 1 (8)
п->со
для любого q > 0, мы видим, что (5) выполняется.
Комбинируя эти два результата, получаем
доказательство теоремы. Доказанная лемма впервые была
использована М. Риссом.
§ 25. Положительность параболических операторов
Приведем следующий результат Бохнера [21.4],
использующий монотонное поведение функции
max \и(х, t)\
для доказательства положительности параболического
оператора с соответствующими граничными условиями.
г) Результат этой леммы напоминает квазилинеаризацию,
применяемую в гл. I: функционал сложной структуры записывается как
предел более простых функционалов.

210
Гл. IV. Положительные операторы
Решение уравнения
ut = uxx, u(x,0) = f(x), (1)
t > 0, / (х) — периодическая функция с периодом 2jt, дается
следующей формулой:
2я
"(*> 0 = ^$б(*-у,о/00«*У» (2)
о
где
со
G(x, f)-l+22 е~гЧ cosrx. (3)
Положительность G(x,t) следует непосредственно из
функционального уравнения для тэта-функции, а именно
из следующей фундаментальной формулы:
^,0 = m1/2Sexp(-fc^). (4)
4 ' Т=—СО '
Соотношение типа (4), однако, не имеет места для
общих областей. Приведем рассуждение, независимое от
области.
Предположим, что функция G(x,t) отрицательна для
некоторого />0 и некоторого х. Если эта величина t
фиксирована, то из условия нормировки
2я
±lG(y,t)dy = l (5)
о
следует, что должно существовать открытое множество,
такое, что
±[G(y,t)dy>l. (6)
R
Следовательно, существует интервал IClR, такой, что
±fay,t)dy>L (7)
I

§ 26. Конечно-разностные схемы
211
Используем теперь классическую процедуру теории
уравнений в частных производных. Можно
сконструировать гладкую функцию /(х), такую, что
(а) 0 < / (х) < 1 для всех х,
(б) f(x)=l, х£1, (8)
(в) f{x) = 0 вне R.
Для этой функции и для всех х и t мы имеем
|а(*,01<тах|/(*)| = 1. (9)
X
Однако для значений t, для которых функция G(x,f)
отрицательна, с помощью соотношения
2я
u(0,t) = -^\G(y,t)f(y)dy =
о (10)
^\G{y,t)dy>\
I
мы получаем противоречие.
§ 26. Конечно-разностные схемы
Рассмотрим в качестве аппроксимации к решению
параболического уравнения (25.1) следующую
конечно-разностную схему:
ц(*,* + 6»)=в(*+М + в(*-а'*), (1)
определенную на сетке
х = 0, б, ..., п8= 1,
t = 0 б2 ^
с граничными условиями
(а) u(0,t) = u(l,t) = 0, (3)
(б) u(x,0) = f(x),
выполняющимися в узлах сетки.

212
Гл. IV. Положительные операторы
Очевидно, что решение рекуррентного соотношения
неотрицательно, если f(x) > 0. Так как предел
рекуррентного соотношения при б—>0 есть уравнение в частных
производных, можно предположить, что предел решения
рекуррентного соотношения является решением этого
уравнения. Далее мы можем продолжить рассуждения
различными способами. Можно доказать сформулированное выше
утверждение либо при разумно выбранных ограничениях для
f(x) без предположения о существовании решения (см.
Йон [1]), либо предполагая, что решение существует (это
сделать много проще); наконец, можно показать, что ядро
оператора в дискретном случае сходится к ядру
непрерывного оператора при 6—>0. Этот последний способ
особенно удобен для уравнения с постоянными
коэффициентами.
Используя конечно-разностный алгоритм
x+qb
u{xJ + 62)=u0c±Mp(x-b1t1+ j u{yJ)dy^ (4)
x—qb
мы можем доказать следующий результат в
предположении, что нами уже установлено существование решения
для уравнения в частных производных.
Теорема 17. Если
(а) ut — uxx + q(x,t)u>0, 0<д:<1, £ > 0,
(б) и(*,0)>0, 0<х<1,
(в) u(0,t) = u(l,t) = 0, *>0, (5)
(г) q(x,t)>—k(T)> — cQ, 0<*<1, 0<f<7\
для любого Т > 0, то
u(x,t)>0, 0<х< 1, *>0.
Заметим, что преобразование вида и = еиу позволяет нам
предположить, что q(x,t)>0. Это замечание позволяет
легко доказать требуемое утверждение.
Ценность формулы (4) состоит в том, что с ее помощью,
выбирая подходящее разностное соотношение, мы можем
сделать неотрицательность решения очевидной. Этот
метод рассматривается в § 27.

§ 28. Обсуждение
213
§ 27. Уравнение потенциала
Метод, указанный в § 26, может быть использован для
изучения уравнения
uxx + uyy = f(x1y), (x,y)£R,
и = 0, (х,у)£В. ( }
Рассмотрим рекуррентное соотношение
, ч и(х+Ь,у) + и{х—6,у) + и(х,у + 6) + и(х,у — Ь)
-2f(x,y)8\ (2)
определенное на (х, #)-сетке, х, y=±k8, которое
формально сходится к (1) при б—>0.
Вместо этого статического рекуррентного соотношения,
из которого не следует непосредственно свойство
положительности, рассмотрим следующее динамическое
соотношение:
„ /v ,л_М*+в» У)+и>п(х—Ь, у)+ип(х1 у+&)+ип(х,у—д)
un+i\xi У)— 4
-2f(x,y)8\ (3)
Очевидно, что если ип(х,у)*сО и f(x, #)>0, то и
un+i(x, у)<0 На этом пути мы можем установить тот
факт, что из неравенства
uxx + uyy>0, (x,y)£R,
и = 0, (х,у)£В, ( )
следует, что а<0 при определенных предположениях
относительно границы В, причем опять предполагается,
что нам известен метод доказательства существования
решения уравнения в частных производных. Если же такого
метода нет, то требуются более жесткие ограничения.
§ 28. Обсуждение
Еще раз подчеркнем, что часто бывает удобно изучать
конечно-разностные уравнения вместо дифференциальных,
особенно при получении численных результатов.

214
Гл. IV. Положительные операторы
В качестве примера рассмотрим следующее нелинейное
уравнение:
щ = иих, u(x,0) = g(x). (1)
Для изучения последнего может быть использована
конечно-разностная схема
и(х, t + б) = и (х + 8и(х, t), t). (2)
Из уравнения (2) легко получить неотрицательность и
равномерную ограниченность решения уравнения (1).
Аналогичным образом можно изучать уравнение Берд-
жерса (Burgers)
щ = шх + еихх. (3)
Соотношение (2) с большим успехом можно использовать
для вычислительных целей [1].
§ 29. Неравенства Хаара — Вестфаля — Проди
Результаты § 24 — 26 относительно линейного
параболического уравнения — частные случаи более общих теорем,
связанных с нелинейным неравенством
Ut<g{uxx,ux,u,x,t), (1)
изучение которого было начато Хааром [1] и затем
продолжено Вестфалем [2], Проди [3], Пуччи [4] и Млаком
[5]. Неравенство (1) играет важную роль при изучении
устойчивости решений нелинейных параболических
уравнений (см. Беллмай [6], Нарасимхан [7] и Мак-Набб [8]).
§ 30. Некоторые неравенства Вендроффа
Результаты § 4 можно обобщить в нескольких
направлениях. Приведем несколько неопубликованных неравенств
Вендроффа. Если
У X
и(х,у)<Сс+ ^ v(r,s)u(r,s)drds, (1)
оо

§ 30. Некоторые неравенства Вендроффа 215
где О О, u(r,s), v(r,s)>0, то
ух
С %v(r,s)drds
и<се00 . (2)
Если
ух
и(х, у)<а(х) + Ь(у)+\\ v(r, s) u(r, s) dr ds, (3)
oo
где
a(x), b(y) > 0, a'(x), b'{y)>0, u,v> 0,
TO
yx
С %v(r,s)drds
„ ^ Ы0) + Ь(у)][а(х) + Ь(0)]е00 .
И^ a(0) + 6(0) * ^
Если
Я у
и(x, у) <с + a \ r/(s, j/)ds + 6 \ r/(x, s) ds, (5)
о о
TO
и(х,у)<сеах+Ъу+аЬху. (6)
Если
x у
u(x,y)<a(x) + b (y) + a[u(s,y)ds+b[u(x,s)ds, (7)
о о
то
u(x,y)<Q(x,y), (8)
где Q(x,y) есть следующая функция:
У X
[а(0) + Ь(0) + 1е-ьУЧ'(У1) dy±] [a(0) + 6(0) + $e-a**a'(*i) йхЛ X
о о
eax+by+abxy
[а(0) + 6(0)]-

216
Гл. IV. Положительные операторы
§ 31 • Результаты Вейнбергера — Бохнера
Как было показано Вейнбергером [21.2], результаты
Бохнера, которые являются в свою очередь обобщением
более ранних результатов Фейера относительно
неотрицательности тригонометрических полиномов, могут быть
интерпретированы в терминах свойств положительности
гиперболических уравнений и соответствующей им функции
Римана. Эти результаты связаны очень интересной
зависимостью с положительностью обычных тригонометрических
полиномов (см. § 10, 11, гл. III), а также со свойствами
положительности линейных дифференциальных операторов.
§ 32. Преобразования, понижающие число
перемен знака
Естественным обобщением понятия положительного
преобразования является понятие преобразования,
понижающего число перемен знака. Под этим мы понимаем
преобразование вида
ъ
v(x)= ^ k(x,y)u(y)dy, (1)
а
обладающее тем свойством, что число перемен знака v(x)
в интервале [а, Ь] меньше или равно числу перемен знака
и{у) в том же интервале.
Интересное и сравнительно подробное рассмотрение
различных проблем, возникающих на этом пути, можно
найти в работе Шенберга [1.10].
§ 33. Квазилинеаризация
Одной из причин нашего интереса к свойству
неотрицательности решений линейных неравенств является тот
факт, что результаты этого типа могут быть
использованы для получения представлений решений нелинейных
дифференциальных уравнений.
Рассмотрим, например, дифференциальное уравнение
Риккати
^ = ^ + а(0, и(0) = с. (1)

§ 34. Устойчивость операторов
217
Так как
и2 = max (2uv—v2) (2)
есть частный случай квазилинейного представления
выпуклых функций (см. § 26, гл. I), то мы можем переписать
(1) в виде
~ = rnax[2uv — v2 + a(t)], и(0)=^с. (3)
Таким образом, для любой функции v(t) можно
написать неравенство
^>2uv-v2 + a{t), и{0) = с. (4)
Сопоставляя последнее неравенство с теоремой 1 из § 2,
мы видим, что u>U, где [/ — решение уравнения
^ = 2Uv — v2 + а (f), U (0) = с. (5)
Так как для U можно выписать сразу решение, а именно
t t
2*\vds t 2$vds
U=ce° +l[a{h)-v2]e *i dtu (6)
о
то решение уравнения (1) может быть представлено в форме
t t
2*\vds t 2*\vds
о
Указанный максимум достигается на функциях v = u.
Более детальное обсуждение указанных идей можно
найти в работах Беллмана [1], Коллатца [2]. См. также
[26.1,26.2,26.3], гл. I, где приводится несколько
других типов функциональных уравнений.
§ 34. Устойчивость операторов
Уравнения, которые мы изучаем в этой главе, можно
рассматривать, как частные случаи еще более общего
класса задач, связанных с устойчивостью функциональных

218
Гл. IV. Положительные операторы
преобразований. Пусть дан оператор Т и класс {и}
соответствующих ему решений уравнения
Ти = 0.
Определить, когда из условия ЦТ^)!) < 8 (где || ||
обозначает некоторую подходящим образом выбранную норму)
следует, что || v — и || <6(е) для некоторого и.
Например, если /(х) —вещественная непрерывная для
xg(—оо, +оо) функция и
\f(x + y)-f(x)-f(y)\<s, (1)
то, как было показано Хайерсом и Уламом [1],
существует такая константа k, что
\f(x)-kx\<2e. (2)
По поводу некоторых результатов, имеющих
отношение к аппроксимации выпуклых функций, см. Грин [2].
Хотя основная часть работ в этом направлении относится
к дифференциальным уравнениям, обыкновенным и в
частных производных, все же имеется ряд работ и для
других типов функциональных уравнений. Классические
результаты читатель может найти в книгах Коддингтона—
Левинсона [3], Лефшеца [4], Чезари ([19.4], гл. III) и
Беллмана [1.3].
§ 35. Различные результаты
Тематика функциональных неравенств состоит из ряда
изолированных результатов, указывающих на
существование их общей теории, которая теперь еще несовершенна.
Имеется много связей с теорией Таубера, см. Виддер
([1.8], гл. III), Дейч [1] и статью Райта [2], в которых
дифференциальные неравенства приводят к теоремам о
простых числах (см. по этому поводу работы Эрдёша —- Сель-
берга, а так же работу Шапиро [3]).
Наиболее интересный результат, связанный с
непосредственными применениями неравенств к теории чисел,
состоит в следующем. Если ит>0, и
ttm+n ^ Mm i Un
(1)

Библиография и дополнения 219
для т, п>0, то
lim-^
п->оо П
существует. Доказательство можно найти у Пойа
и Сегё [44.1], гл. I; приложения рассматриваются в
работах Фюрстенберга и Кестена [4], а также Беллмана [5].
Дальнейшее развитие этих идей имеется в следующих
работах: Беккенбах и Радо [17.15, 17.16], Беккенбах
[17.17], Калаби [6], Яно и Бохнер [7], Оссерман [8],
Редхеффер [9,14], Сакстедер [10], Боас и Пойа [11],
Даффин и Сербии [12], Пейн и Вейнбергер [13], Лёвнер
([47.2], гл. II).
БИБЛИОГРАФИЯ И ДОПОЛНЕНИЯ
§ 1. Отметим интересные результаты Чаплыгина относительно
положительности операторов. Большинство из этих результатов
можно найти в следующей монографии.
1. Чаплыгин С. А., Новый метод приближенного
интегрирования дифференциальных уравнений, Гостехиздат, М.— Л.,
1950.
2. Гронуолл (Gronwall Т. Н.), Note on the derivatives
with respect to a parameter of the solutions of a system of
differential equations, Ann. of Math., 20 (1918), 292—296.
Обсуждение теории устойчивости и ее связей с неравенствами
дается в следующих работах.
3. Беллман (Bellman R.), Stability theory of differential
equations, New York, McGraw-Hill, 1954. Русский перевод:
Теория устойчивости решений дифференциальных уравнений,
ИЛ, М., 1954.
4. Bnxapn(Bihari I.), A generalization of a lemma of
Bellman and its applications to uniqueness problems of differential
equations, Acta Math. Hung., 7 (1956), 81—94.
5. Лангенхоп (Langenhop С. E.), Bounds on the norm
of a solution of a general differential equation, Proc. Am. Math.
Soc, 11 (1960), 795—799.
Основные результаты Пойа были стимулированы следующей
заметкой Пуанкаре.
6. Пуанкаре (Р о i п с а г е Н. L.), V Inter mediaire des Mat-
hematiciens, 1 (1894), 141—144.
См. также комментарии Деллака, Адамара, Ру и Дупорко на
стр. 69—70, 127, 172—173, 216—217 этого тома L'Intermediaire des
Mathematiciens.
7. П о й а (Р 6 1 у a G.), On the mean-value theorem
corresponding to a given linear homogeneous differential equation, Trans.
Am. Math. Soc. (1922), 312—324.
(2)

220
Библиография и дополнения
8. Гартман, Винтнер (Hartman P., Wintner А.)
Mean value theorems and linear operators, Am. Math. Monthly,
62 (1955), 217—222.
При кратком знакомстве с неравенствами, включающими
дифференциальные операторы, обыкновенные и в частных производных,
трудно провести границу между теорией неравенств и собственно
теорией дифференциальных уравнений.
9. К а ц (Кае М.), On some connections between probability
theory and differential and integral equations, Proc. Second
Berkeley Symposium on Mathematical Statistics and Probability,
Berkeley and Los Angelos, Calif., University of California Press,
1951.
10. Шенберг (Schoenberg I. J.), On
variation-diminishing transformations, Proc. Symposium on Numerical
Approximation, 1958, Madison, Wis., University of Wisconsin, 1959.
§ 4. Этот результат и его приложение к теории устойчивости
впервые были даны в статье
1. Беллман (Bellman R.), The stability of solutions of
linear differential equations, Duke Math. J., 10 (1943), 643—647.
Относительно других приложений имеется следующая литература.
2. Немыцкий В. В., С т е п а н о в В. В., Качественная
теория дифференциальных уравнений, ОГИЗ, М.—Л., 1949.
3. Гуильяно (Guilano L.), Generalazzioni di un lemma di
Gronwall, Rend. Accad. Lincei (1946), 1264—1271.
Вывод априорных оценок с помощью этих неравенств для
решений уравнений в частных производных дается в следующих работах.
4. Л а к с (Lax P. D.), The initial value problem for nonlinear
hyperbolic equations in two independent variables, Chapter 12,
Annals of Math. Studies, No. 33, Princeton, N. J., Princeton
University Press, 1954.
См. также
5. Л а к с (Lax P. D.), The scope of the energy method, Bull. Am.
Math. Soc, 66 (1960), 32—35.
6. Л а к с (L a x P. D.), On Cauchy's problem for hyperbolic
equations and the differentiability of solutions of elliptic equations,
Comm. Pure Appl. Math., 8 (1955), 615—633.
В этой работе можно найти дальнейшие ссылки.
Дифференциальные неравенства играют роль в применениях
второго метода Ляпунова для установления устойчивости.
7. Ласалль, Лефшец (LaSalle J. P., L е f-
s с h e t z S.), The stability theory of Liapunov. New York,
Academic Press, 1961. Русский перевод: Исследование устойчивости
прямым методом Ляпунова, «Мир», М., 1964.
8. Л и с (Lees М.), Appoximate solutions of parabolic equations,
Л Soc. Ind. Appl. Math., 7 (1959), 167—183.
§ 6. Этот результат дается в работе [43.1 J, гл II. Физический
смысл условия обнаруживается при изучении многоступенчатых
производственных процессов, упомянутых в гл. III, а также при
изучении марковских разрешающих процессов, см. [7.1], гл. I,
[44.21, гл. II. См. также следующие статьи.

Библиография и дополнения
221
1. Романовский Е. Р., Об одной теореме Р. Беллмана,
Теория вероятностей и ее применения, 4 (1959), 456—458.
2. Опиал (Opial Z.), Sur un systeme d'inegalites integrates,
Ann. Polon. Math., 3 (1957), 200—289.
§ 7. Это доказательство Тауски было сообщено в письме.
§ 8.
1. Лёвнер (Loewner С), A theorem on the partial order
derived from a certain transformation semigroup, Math. Z., 72
(1959), 53—60.
2. Гарнер, Бертон (Garner J. BM Burton L. P.),
Solutions of linear differential systems satisfying boundary
conditions in the large, Proc. Am. Math. Soc, 12 (1961), 100—106.
§9.
1. Перрон (Perron O.), Die Stabilitatsfrage bei Differential-
gleichungen, Math. Z., 32 (1930), 703—728.
2. Массера, Шеффер (Massera J., Schaffer J. J.),
Linear differential equations and functional analysis, 1, Ann. of
Math., 67 (1958), 517—573.
3. Массера, Шеффер (Massera J., Schaffer J. J.),
Linear differential equations and functional analysis, II, Equations
with periodic coefficients, Ann. of Math., 69 (1959), 88—104.
Работа Перрона была стимулирована ранними работами Боре-
ля и Харди в этой области.
§ Ю.
1. Феллер (Feller W.), On generalized Sturm — Liouville
operators, Proc Conference on Differential Equations, College
Park, Md., University of Maryland Press, 1955.
Результаты Феллера, приведенные в этой статье, а также в ряде
работ, на которые мы ссылались выше, имеют тесную связь с
понятием обобщенной выпуклости, о которой мы будем говорить дальше.
§ 12. Это доказательство дается в работе
1. Беллман (Bellman R.), On the nonnegativity of Green's
functions, Boll. Un. Math., 12 (1957), 411—413.
Эта работа тесно связана со следующей работой Стильтьеса.
2. Стильтьес (Stieltjes Т. J.), Sur les racines de Xn = 0,
Acta Math., 9 (1886—1887), 385—400.
Обширные обобщения этого метода, которые были даны Эрроу,
Вонгом, Вудбери и др., можно найти в ссылках к § 38 гл. II и
в [2.1], гл. П.
Таким же образом можно использовать вариационную
формулировку проблемы для установления того факта, что функция
Грина уменьшает число перемен знака. По этому поводу см. следующие
статьи.
3. Беллман (Bellman R.), On the variation-diminishing
property of Green's functions, Boll. Un. Math.
§ 15. Имеется огромное количество работ в этой области.
Отметим из них следующие.

222
Библиография и дополнения
1. Петров Б. Н., Пределы применимости теоремы С. А.
Чаплыгина для дифференциальных неравенств к линейным уравнениям
с обыкновенными производными второго порядка, Докл.
АН СССР, 51 (1946), 255—258.
2. Уилкинс (W i 1 k i n s J. Е., Jr.), The converse of a theorem
of Tchaplygin on differential equations, Bull. Am. Math. Soc, 53
(1947), 126—129.
См. также библиографию к § 18.
Теорема о разложении, использующая вронскианы, дает нам
возможность ясно увидеть связь между положительностью частных
решений, характеристическими корнями и положительностью
операторов для случая линейных уравнений второго порядка. Для
дифференциальных уравнений высших порядков эта связь не
исследована. Очень возможно, что имеется тесная связь с теорией
преобразований, понижающих число перемен знака, как это упоминается
в § 16.
§ 16.
1. Петерссон (Petersson Н.), Ober Interpolation durch
Losungen linearer Differentialgleichungen, Abh. Math. Sent.
Univ. Hamburg, 16 (1949), 41—55.
§ 17.
1. Беккенбах (Beckenbach E. F.), Generalized convex
functions, Bull. Am. Math. Soc, 43 (1937), 363—371.
2. Беккенбах, Бинг (Beckenbach E. F.,
В i n g R. H.), On generalized convex functions, Trans. Am.
Math. Soc, 58 (1945), 220—230.
3. Валирон (Valiron G.), Fonctions convex es et fonctions
entieres, Bull. Soc. Math. France, 60 (1932), 278—287.
4. Бонсалл (Bonsall F. F.), The characterization of
generalized convex functions, Quart J. Math., 1 (1950), 100—111.
5. Пейсото (Peixoto M.), Convexidas das curvas, Notas de
Matematica, No. 6, Livraria Boffoni, 1948.
6. Пейсото (Peixoto M.), On the existence of a derivative
of generalized convex functions, Sumtna Brasiliensis Math., 2,
No. 3 (1948).
7. Пейсото (Peixoto M.), Generalized convex functions
and second-order differential inequalities, Bull. Am. Math. Soc,
55 (1949), 563—572.
См. также следующие работы.
8. Моцкин (Motzkin Т. S.), Approximation by curves of a
unisolvent family, Bull. Am. Math. Soc, 55 (1949), 789—793.
9. Торнхейм (Tornheim L.), On n-parameter families
of functions and associated convex functions, Trans. Am. Math.
Soc, 69 (1950), 457—467.
10. К у p т и с (Curtis P. С, Jr.), W-parameter families and
best approximation, Pacific J. Math., 9 (1959), 1013—1027.
11. P e й д (R e i d W. Т.), Variational aspects of generalized convex
functions, Pacific J. Math., 9 (1954), 571—581.
12. Гартман (Hartman P.), Unrestricted л-parameter
families, Rend. Circ. Mat. Palermo (2), 7 1958), 123—142.

Библиография и дополнения
223
Применение этих идей к теории дифференциальных уравнений
в частных производных приводит естественным образом к
субгармоническим функциям и их обобщениям. По этим вопросам см.
следующую литературу.
13. Р и с с (Я i е s z F.), Sur les fonctions subharmoniques et leur
rapport a la theorie du potential, 1, II, Acta Math., 48 (1926),
329—343; 54 (1930), 321—360.
14. P а д о (R a d 6 Т.), Subharmonic functions, Ergeb. Math., Berlin,
Springer, 1937.
15. Беккенбах, Радо (Beckenbach E. F.,Rado Т.),
Subharmonic functions and minimal surfaces, Trans. Am. Math.
Soc, 35 (1933), 648—661.
16. Беккенбах, Радо (Beckenbach E. F.,Rado Т.),
Subharmonic functions and surfaces of negative curvature, Trans.
Am. Math. Soc, 35 (1933), 662—674.
17. Беккенбах (Beckenbach E. R), On subharmonic
functions, Duke Math. J., 1 (1935), 481—483.
18. P и д (R e a d e M.), Some remarks on subharmonic functions,
Duke. Math. J., 10 (1943), 531—536.
19. Б о н с а л л (В о n s а 1 1 F. F.), On generalized subharmonic
functions, Proc. Cambridge Phil. Soc., 46 (1950), 387—395.
20. T а у т ц (T a u t z G.), Zur Theorie der elliptischen Differen-
tialgleichungen, I, Math. Ann., 117 (1939—1941), 694—726.
21. Беккенбах, Джексон (Beckenbach E. F.,
Jackson L. K.)> Subfunctions of several variables, Pacific
J. Math., 3 (1953), 291—313.
22. Джексон (Jackson L. K-)> On generalized subharmonic
functions, Pacific. J. Math., 5 (1955), 215—228.
23. А й н о н (I n о n e M.), Dirichlet problem relative to a family
of functions, /. Inst. Polytech. Osaka City University (A), 7 (1956),
1—16.
24. Джексон (Jackson L. K.)> Subfunctions and the
Dirichlet problem, Pacific J. Math., 8 (1958), 243—255.
§ 18.
1. Клямко E. И., Некоторые применения метода Чаплыгина
к приближенному решению дифференциальных уравнений с
запаздывающим аргументом, Успехи матем. наук, 12 (1957), 305—312.
2. А р т е м о в Г. А., Применение метода Чаплыгина к решению
характеристической задачи Коши для уравнения в частных
производных параболического типа, Докл. АН СССР, 112 (1957),
791—792.
3. Пароди (Parodi М.), Determination de courbes planes
definies par une inegalite entre les valeurs absolues de fonctions
des elements de contact et un point courant, C. R. Acad. Sci.
(Paris), 245 (1957), 1871.
§ 19.
1. П о й a (P 6 1 у a G.), Quelques theoremes analogues au theoreme
de Rolle, lies a certaines equations lineaires aux derivees partiel-
les, C. /?. Acad. Sci. (Paris), 199 (1934), 655.

224
Библиография и дополнения
2. Блейлер(В1еи1ег К.)» Ober den Rolleschen Satz fur den
Operator Au-\-Xu und die damit zusammengangenden Eigenschaf-
ten der Greenschen Funktion, Geneva, Zurich Doct. Thes., 1942.
3. Бляшке (Blaschke V/.), Mittelwertsatz der Potentialtheo-
rie, Jber. Dtsch. Math. Ver., 27 (1918), 157—160.
4. Заремба (Zaremba S.), Sur une propriete generate des
fonctions harmoniques, Conference de la Reunion Internationale
des Mathematiciens, Paris, 1937, 171—176.
Таким образом, мы замечаем, что между двумя важными
концепциями, теоремой о среднем значении и положительной
определенностью существует тесная связь.
§ 20.
1. Дел ьсарт (Delsarte J.), Sur une extension de la formule
de Taylor, /. Math. Pures Appl. (9), 17 (1938), 213—231.
2. Левитан Б. M., Оценка остаточного члена в формуле
Тейлора — Дельзарта, Докл. АН СССР, 73 (1950), 269—272.
3. Виддер (Widder D. V.), A generalization of Taylor's
series, Trans. Am. Math. Soc, 30 (1928), 126—154.
§ 21.
1. Нюренберг (Nurenberg L.), A strong maximum
principle for parabolic equations, Comm. Pure Appl. Math., 6 (1953),
167—177.
2. Вейнбергер (Weinberger H, F.), A maximum
property of Cauchy's problem, Ann. oft Math., 64 (1956), 505—513.
3. Беллман (Bellman R.), A property of summation kernels,
Duke Math. J., 15 (1948), 1013—1019.
4. Б о x н e p (Bochner S.), Quasi-analytic functions, Laplace
operators and positive kernels, Ann. Math., 51 (1950), 68—91.
В этой статье аппарат, применявшийся Беллманом в связи
с уравнением щ= ихх\~ Ууу-\~ uzzi обобщается на общий оператор
Бельтрами и используется для волнового уравнения иц= иххт
+ uyy~\~uzz- Эти результаты тесно связаны с общей проблемой
получения априорных оценок для различных функционалов, связанных
с линейными операторными уравнениями.
Использование подходящей конечно-разностной аппроксимации
делает непосредственно ясными некоторые свойства решений
дифференциальных уравнений, обыкновенных и в частных производных
и является очень мощным методом. Отметим, что границы
применимости этого метода еще не исследованы достаточно полно. Кроме
того, этот метод имеет большое значение в связи с вопросами
численного решения уравнений. См. следующую работу.
5. Беллман (Bellman R.), On the nonnegativity of solutions
of the heat equation, Boll. Un. Math., 12 (1957), 520—523.
§ 24.
1.Пой a, Cere (Polya G.,Szego G.), Sur quelques proprie-
tes qualitatives de la propagation de la chaleur, C. R. Acad. Sci.
(Paris), 192 (1931), 1340—1342.
§ 26. Исчерпывающее изложение вопросов, связанных со
сходимостью разностных схем, см. в работе

Библиография и дополнения
225
1. Джон (John F.), On integration of parabolic equations by
difference methods, I, Linear and quasi-linear equations for the
infinite interval, Comm. Pure Appl. Math., 51 (1952), 155—211.
§ 28.
1. Б e л л м a Hf Черри, Уинг (Bellman R., Cherry I.,
Wing G. M.), A note on the numerical integration of a class
of nonlinear hyperbolic equations, Quart. Appl. Math., 16 (1958),
181—183.
§ 29. Статья Вестфаля [2] содержит обобщение результата,
который впервые получил Хаар для неравенств, содержащих частные
производные. Эти результаты в свою очередь были обобщены Проди
и использованы Млаком и Проди в теории устойчивости. Отметим
оригинальную статью Хаара.
1. Хаар (Haar A.), Ober Eindeutigkeit und Analyzitat der
Losungen partieller Differentialgleichungen, Atti Congresso Intern.,
Bologna, 3 (1928), 5—10.
2. Вестфаль (Westphal H.), Zur Abschatzung der Losungen
nichtlinearer parabolischer Differentialgleichungen, Math. Z., 51
(1949), 690—695.
3. Проди (Prodi G.), Questioni di stabilita per equazioni non
lineari alle derivate parziali di tipo parabolico, Acad. Naz. Lincei
(8), 10 (1952), 365—370.
4. Пуччи (Pucci C), Ordering and uniqueness of solutions of
boundary problems for elliptic equations, Technical Note BN-112,
College Park., Md., University of Maryland Press, 1957.
5. M л а к (M 1 a k W.), Differential inequalities of parabolic type,
Ann. Polon. Math., 3 (1957), 349—354.
Обсуждение проблем устойчивости для дифференциальных
уравнений в частных производных и выяснение границ применимости
результатов этого типа имеется в следующих работах.
6. Б е л л м а н (Bellman R.), On the existence and boundedness
of solutions of nonlinear partial differential equations of parabolic
type, Trans. Am. Math. Soc, 64 (1948), 21—44.
7. Нарасимхан (N a r a s i m h a n R.), On the asymptotic
stability of solutions of parabolic differential equations, /. Rat.
Mech. Analys., 3 (1954), 303—313.
Результаты этого типа были получены в 1950 году Лаксом
в одной неопубликованной работе по устойчивости решений
параболических уравнений. По этим вопросам отметим еще статью.
8. М а к-Н абб (McNabb A.), Notes on criteria for the stability
of steady-state solutions of parabolic equations, /. Math. Analys.
Appl.
§ 30. Эти результаты прежде не были опубликованы.
§ 31.
1. Бохнер (Bochner S.), Positive zonal functions on spheres,
Proc. Nat. Acad. ScL, USA, 40 (1954), 1141—1147.
2. Бохнер (Bochner S.), Sturm — Liouville and heat
equations whose eigenfunctions are ultraspherical polynomials of associa-

226
Библиография и дополнения
ted Bessel function, Proc. of the conference on differential equations
(посвященной А. Вайнштейну), 23—48, College Park., Md.,
University of Maryland Book Store, 1956.
3. Проттер (P rotter M. H.), A maximum principle for
hyperbolic equations in the neighborhood of an initial line, Berkeley
and Los Angelos, Calif., University of Califorma Press, 1956.
Основная проблема состоит в изучении множеств функций,
обладающих тем свойством, что из
в интервале —1 <; х < 1 следует, что
оо
п=1
в квадрате — 1 < л: < 1, —1 < # < 1 •
§ 32. См. ссылки к § 48, гл. II.
§ 33. Детальное обсуждение метода Ньютона для
функциональных уравнений и численные примеры даются в [26.3], гл. I.
Ряд результатов приводится в [26.1, 26.2], гл. I и в следующих
работах.
1. Беллман (Bellman R.), On monotone convergence to
solutions of u'^ q(u,t), Proc. Am. Math. Soc, 8 (1957), 1007—
1009.
Читатель может найти много ссылок по этим вопросам, а также
некоторые приложения в статье Кал аба [26.3], гл. I, и в следующей
Монографии.
2. Коллатц, Лангер (Collatz L., Langer R.),
Applications of the theory of monotonic operators to boundary value
problems. Boundary problems in differential equations, Madison,
Wis., University of Wisconsin, 1960.
§34.
1. Хайерс, Улам (Hyers D., U 1 a m S.), Approximately
convex functions, Proc. Bull. Am. Math. Soc, 3 (1952), 821—828.
2. Грин (G r e e n J. W.), Approximately convex functions, Duke
Math. J., 19 (1952), 499—504.
3. Коддингтон, JleBHHCoH(CoddingtonE., Levin-
son N.), Theory of ordinary differential equations, New York,
McGraw-Hill, 1955. Русский перевод: Теория обыкновенных
дифференциальных уравнений, ИЛ, М., 1958.
4. Лефшец (Lefschetz S.), Differential equations: geometric
theory, New York, Interscience Publishers, 1957. Перевод:
Геометрическая теория дифференциальных уравнений, ИЛ, М., 1961.
§35.
1. Дейч (Doetsch G.), Theorie und Anwendung der Laplace —
Transformation, New York, Dover Publications, 1943.

Библиография и дополнения
227
2. Р а й т (W г i g h t E. M.), Functional inequalities in the eleme-
tary theory of primes, Duke Math, J., 19 (1952), 695—704.
3. Шапиро (SchapiroH. N.), Tauberian theorems and
elementary prime number theory, Comm. Pure Appl. Math., 12 (1959),
579—610.
4. Фюрстенберг, Кестен (Furstenberg H., Kes-
t e n H.), Products of random matrices, Ann. Math. Stat., 31
(1960), 457—469.
5. Беллман (Bellman R.), Functional equations on the
theory of dynamic programming, Rend Circ, Mat. Palermo (2),
8 (1959), 1—3.
Мы не рассматриваем большое число интересных результатов
относительно дифференциальных неравенств в частных
производных вида ки > / (и) и их приложения к дифференциальной
геометрии и анализу. По этому поводу см. работы [17.15],
[17.16], а также следующие.
6. Калаби(Са1аЫ Е.), An extension of Е. Hopf's maximum
principle with an application to Riemannian geometry, Duke Math.
J., 25 (1958), 45—46.
7. Яно, Бохнер (Yano К., Bochner S.), Curvature and
Betti numbers, Ann. Math. Stud., No 32, Princeton, N. J.,
Princeton University Press, 1953. Русский перевод: Кривизна и -числа
Бетти, ИЛ, М., 1957.
8. О с с е р м а н (О s s е г га a n R.), On the inequality Aw > f(u),
Pacific J. Math., 7 (1957), 1641—1647. В этой работе имеются
ссылки на ранние работы Виттиха, Хэвиланда, Уолтера.
9. Редхеффер (Redheffer R.), On the inequality Au >
>/(«>|gradw|), /. Math. Analys. Appl., 1 (1960), 277—299.
10. Сакстедер (Sacksteder R.), On local and global
properties of convex sets and hypersurfaces, AFOSR TN 59-1294,
Baltimore, Md., Johns Hopkins University Press (1959).
В этой главе нами полностью опущено обсуждение вполне
выпуклых функций и важные результаты Бернштейна— Хаусдорфа—
Виддера, а также обобщения этих результатов. Для ссылок на
литературу по этим вопросам см. [1.81, гл. III, а также
И. Б о а с, П о й a (Boas R. Р., Р 6 1 у a G.), Generalizations
of completely convex functions, Proc. Nat. Acad. Sci. USA, 27
(1941), 323—325. Отметим также, что мы не делаем ссылок на
различные методы, опирающиеся на вариационные методы.
12. Д а ф ф и н, С е р б и н (D u f f i n R. J., S е г b у n W. D.),
Approximate solution of differential equations by a variational
method, J. Math. Physics, 37 (1958), 162—168.
13. Пей н, Вейнбергер (Payne L. E., Weinberger
H. F.), New bounds for the solutions of second order elliptic
partial differential equations,College Park.,Md., University of
Maryland, Tech. Note BN-108, 1959.
Наконец сошлемся на работу
14. Редхеффер (Redheffer R.), Inequalities for a matrix
Riccati equation, /. Math. Mech., 8 (1959), 349—367.
Кроме того, сошлемся еще раз на [47.21, гл. II. На эту статью
мы первый раз ссылались в связи с понятием монотонности
матричных функций.

Глава V
НЕРАВЕНСТВА ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ
§ 1. Введение
В этой заключительной главе мы рассмотрим ряд
вопросов из другой важной области анализа. Эту область
можно описать с помощью следующих общих понятий.
Рассмотрим множество обыкновенных дифференциальных
операторов {Тг} и множество функций {и}, являющихся
областью определения этих операторов. Введем далее
множество функций {Тги}. Мы уже решали вопрос о том,
когда из неотрицательности Тги следует аналогичное
свойство для и. В этой главе мы выясним, когда из
соотношения Тги£Ьр(0, со) следует, что u£Lr(0, со), где
величина г зависит, конечно, от р. Более общая задача:
дано 7]i/g LVi (О, со), /=1,2, ...,&, определить L-класс
для Tk+iU.
Эта задача в свою очередь является частным случаем
проблемы получения полного множества неравенств вида
оо оо оо
^гА+^гл<я($|г^|р1Л,...,^гА^л). (1)
О 0 0
Вопросы этого типа здесь не рассматриваются, хотя
иногда подобные неравенства будут указываться.
По-видимому, наиболее известным неравенством
предыдущего типа является классическое неравенство С. Берн-
штейна:
max \u'(t)\<N max \u(t)\, (2)
0^^2я ' 0^^2я' '
где
N
п=0
— тригонометрический полином степени N.

§ 1. Введение
229
Соответствующий результат Маркова справедлив для
обыкновенных полиномов на конечном интервале (см.
Мандельбройт [1]). Имеются многочисленные обобщения
этих результатов — для других норм, для общих
тригонометрических полиномов, для целых функций и т. д. Мы
не будем заниматься здесь этими вопросами, так как
элегантное и подробное их изложение имеется в книге
Боаса [2] и в обзорной статье Шеффера [3]. В этих
работах можно найти также обширную библиографию (см.
также Секефальви-Надь [4]).
Как и в других частях монографии, мы концентрируем
наше внимание на результатах и методах, которые до этого
вместе не рассматривались или не изучались детально.
Кроме того, мы хотим дать представление о методах,
которые могут быть широко использованы.
Так же как и в других частях книги, очень трудно
провести точную грань между неравенствами, которые
имеют интерес для анализа вообще, и теми из них,
которые используются в специальных областях. Несмотря
на элегантность и важность многих неравенств,
касающихся уравнений в частных производных, мы решили
(с некоторым сожалением) не рассматривать их на
страницах этой книги. Обсуждение неравенств Пуанкаре,
Корна, Фридрихса и др. можно найти в статьях Ароншайна
[5], Ниренберга [6], Фридрихса [7] (см. также
монографию Куранта и Гильберта [26.1], гл. II). Мы думаем,
что областью применения этих неравенств является
главным образом теория уравнений в частных
производных.
Мы рассмотрим вначале результаты, впервые
полученные Адамаром в его исследованиях, касающихся связей,
которые существуют между границами для u(t), и'(t),
u"(t) (t берется из конечного интервала). Детальное
обсуждение этих вопросов имеется в книге Харди, Литтл-
вуда и Пойа [1.1], гл. I. В книге Титчмарша [8]
рассматривается связь этих результатов с теорией Таубера.
Обобщения этих результатов были даны Экланьоном
и Ландау [9]. Проблема определения наилучших
возможных неравенств, связывающих различные нормы и, и', и",
была рассмотрена Колмогоровьш [10]. Как упомянуто выше,
мы не будем рассматривать вопросы этого типа.

230 Гл. V. Неравенства для дифференциальных операторов
Проблемы, с которыми мы будем иметь дело в этой
главе, тесно связаны с теорией линейных
дифференциальных уравнений (см. Бисак [11, 12], Колаутти [13], Рейд
[14], Беллман [15] и др.). Это обстоятельство используется
в книге.
Далее будут изучены результаты, касающиеся Lp-HopM
(см. по этому поводу Секефальви-Надь [16], Гальперин
[17], Гальперин и Питт [18], Беллман [15]). Затем мы
возвращаемся к классу неравенств, связанных с именем
Карлсона [19]. Как было установлено Надем [16],
имеется связь этих неравенств с неравенствами Адамара;
Кьелберг [20] установил также их связь с проблемами
моментов, рассматриваемыми в гл. III.
Обобщение неравенства Карлсона было дано Харди [21],
Габриэлем [22], Бейрлингом [23], Катоном [24], Надем [16],
Кьелбергом [20], Левиным [26] и Беллманом [25]. Не
затрагивая вопроса об определении наилучших возможных
констант (эта задача решена Левиным [26]), мы рассмотрим
здесь очень простой метод получения неравенств этого
типа.
Затем мы вернемся к неравенству Виртингера,
которое использовалось в гл. IV, и рассмотрим его
многочисленные обобщения. Для установления этих неравенств
будет использован интересный метод, основанный на
тождествах.
Хотя эти результаты легко могут быть выведены
из теории Штурма —Лиувилля, однако имеет смысл все
же использовать указанный выше элементарный метод
(Бисак [11,12]), так как он позволяет получить ряд
результатов, которые в противном случае потребовали бы для
своего доказательства применения солидного математического
аппарата. Эгот метод был усовершенствован Колаутти [13],
и Рейдом [14], которые получили с его помощью
многочисленные соотношения типа неравенства Виртингера.
В последней части главы нами будут установлены
некоторые частные неравенства указанного выше типа
(см. Норткотт [27], Беллман [28]), а также более
интересные дискретные варианты этих неравенств (см. Фань,
Тауски, Тодд [29]. Связанные с этими неравенствами
результаты можно найти в работах Островского [20.1]
и Блока [30].

§ 2. Некоторые неравенства Секефальви-Надя 231
Все эти проблемы, как будет кратко указано ниже
(детали можно найти в работах Харди, Литтлвуда и Пойа),
можно изучать методами вариационного исчисления; но по
ряду соображений эти методы не очень удобны для
использования.
Наконец, мы опустим из рассмотрения результаты
Борга [31], обобщение оригинальных результатов Ляпунова,
которые имеют большое значение в теории линейных
дифференциальных уравнений с периодическими
коэффициентами (см. Стажинский [32], где рассмотрены эти вопросы,
а также много других).
§ 2. Некоторые неравенства Секефальви-Иадя
Начнем наше обсуждение с некоторых интересных
неравенств Надя [1.16]. Аналогичные результаты были
установлены Э. Шмидтом [1] для случая конечных
интервалов.
Теорема 1. Пусть у(х) — определенная на всей оси
функция, для которой интегралы
оо оо
Ja=\\y\adx, KP=\\y'\pdx (1)
—оо —оо
существуют для некоторого а>0 и некоторого р>1.
Тогда
max |y|<(-n-) Ja Ap , (2)
-oo<x<oo V^/
где r=l + a(p—l)/p. Кроме того, для b>0
Ja+b< [±н(^)]ъ/гЛ+Нр-1Жрг)кГг), (3)
где
Н<Р>v)= ^г(1+Ц)Г(1+5 ' (4)
Доказательство. Рассмотрим вначале случай р = 1
и неравенство (2). Так как интеграл Ja конечен, то
существуют последовательности {ап}, {Ьп}, обладающие тем
свойством, что у(ап)-+0, у(Ьп)->0 при ап-+со, Ьп-+—со.

232 Гл. V. Неравенства для дифференциальных операторов
Отсюда
СО СО Z
\ | у' | dx > =р \ y'dx ± \ у' dx =
—оо z —оо
= lim (Т С ± П y'dx> ± 2y(z). (5)
z а„
п
Следовательно, для произвольного z
со
±2г/(2)< J |у'|Жс, (6)
— ОО
т. е. для р=1 неравенство установлено.
Рассмотрим случай р > 1. Используя неравенство
Гёльдера, получим
с» оо оо
J |y|(p-o«/p|y'|dx<( J \y\adxY P( $|у'|р<&)1Л,=
—оо —оо -—оо
= J(p-i)/v %1/р . (7)
Кроме того, имеем
оо оо О
J 0|(p-wp|#'k&> [ - J + j ](ssay)\y\(p-wpy'dx =
0 —оо
О
= ,+(Лф[-!+Я^^ЖИ1а/^ w
О -со
= уГ2|г/(0)Г-ит|£/(ап)Г-Нт|у(Ь„)|г]=уИ0)Г.
' L п-*оо п-э-оо J г
Так как интегралы инвариантны при преобразовании
у(х)—^у(х + 'к), мы видим, что (2) выполняется.
Доказательство соотношения (3) сложнее, и мы
отсылаем читателя к оригинальной статье [1.16].
§ 3. Неравенства, связывающие и, и\ и"
Выведем теперь некоторые неравенства, связывающие
и, и', и". Мы начнем с некоторых вводных рассуждений.,

§ 3. Неравенства, связывающие и, и', и" 233
а затем покажем, как их можно видоизменить для
получения искомых неравенств.
Теорема 2. Если и£Ьр[0, оо], р>1, u"£Lr[Q, оо],
г>1, то u'£Lm[0, оо] для m>max(p, г).
Если р=со, то условие и g Lp[0, оо] следует
интерпретировать как max | и | < а < оо.
Два наиболее интересных случая этого результата
р = г = т = со, р = г~т = 2 были рассмотрены Беллманом
в [1.3], гл. IV. Мы следуем здесь его методу.
Граница тах(р,г) может быть улучшена. Как было
показано Нюренбергом в неопубликованной работе,
метод, подобный методу, использованному Надем,
основанный на интегрировании по частям и элементарных
оценках, может быть использован для получения
обобщений следующих результатов.
Доказательство. Напишем
u"-u = f + g, (1)
где /£ U и g£Lp. Из уравнения (1) следует, что и можно
записать в виде
х
и = Cie% + с2е-* +1J [ег- -*-<'-•>] [f (s) + g (s)] ds. (2)
о
Из условия / £ Z/ и g£Lv вытекает, что интеграл
с»
le~s[f(s) + g(s)]ds
о
сходится и что величина
t
о
ограничена при t—>co. Следовательно, для того чтобы
выполнялось условие u£Lv, необходимо, чтобы
оо
ci + |$<rs[f(s)+g(s)]ds = 0. (3)
о

234 Гл. V. Неравенства для дифференциальных операторов
Используя это соотношение, мы можем представить (2)
в виде
, оо __. t
u^c2e-t-^e-4f + g]ds--^-leslf + g]ds, (4)
откуда
ОО I
u'=-c2e-i-^[e-*[f + g]ds + ^-[e*[f + g]ds. (5)
t о
Из этого представления легко получить требуемый
результат. Начнем со случая га = оо . На основании
неравенства Гель дера имеем
]*-fds \<fl\f №)1/р ( $*-«•*)"« < ,-<( ] \f\4sy/p,
' t t О
t \ t t oo
\e'fdsl < ( l е<*с18~)Ш (I | f \r>dsy,P < e< ( J |f |%)1/P,
о ' о о о
(6)
Аналогичные неравенства имеют место для g; отсюда
мы видим, что | и | и \и' \ равномерно ограничены для t > 0.
Если 1 <т<оо, то справедливо следующее неравенство:
оо
\u'(t)\m<ci(m)[e-mt + emt^e-s\f\dsyn +
оо ^
о о
t
+ e-mt(le>\g\ds)m]. (7)

§ 3, Неравенства, связывающие и, и', и" 235
Рассмотрим типичный член правой части соотношения (7),
проинтегрированной по / от О до со; имеем
^emt^e-s\f\dsydt<
о *
оо оо оо
< J ew<Q e-qs'4sY/q ( J е-*8'2 \ f \* ds)W/P dt <
о * '
OO OO
< c5 J em'/2 С J e-^2 I f \p ds Jm**dt. (8)
0 *
Интегрируя по частям, получаем
оо оо
Umm Qe-ps/21 f |p dsY/Pdt =
0 *
oo oo
= TIе<m~P)m^'" ( le~ps/21 f \PdsY/P~ dt < (9)
0 (
KCellfl^llffdsy^dt-
0 0
oo
= ce(lf\*dsyp<oo.
0
Мы видим, что условие т>р является существенным.
Таким образом, доказательство закончено.
Заметим, что мы получили более сильный результат,
чем сформулированный в теореме.
Условия и £ И и и" £ U не обязательны; достаточно,
чтобы выполнялись соотношения
п
fe=i
«'=2 «*• <10>
Л=1

236 Гл. V. Неравенства для дифференциальных операторов
где fk£Lpb, gk£L% рА, rk>l, и
m>max[pk, rk]. (11)
§ 4. Неравенства для и, u^k) и #<n)
Для того чтобы получить соответствующий результат для
более общего триплета производных и, i№ и и(п\ п > k> 1,
мы воспользуемся уравнением
a<«)_tt==f + £, (1)
если п = 4т+ 2 или ft —нечетное, и
a<n> + a = f + g, (2)
если п = 4т.
Причина такого раздельного рассмотрения состоит в том,
что мы хотим избежать случая, когда характеристическое
уравнение имеет корень с нулевой вещественной частью.
Результат, соответствующий теореме 2, формулируется
следующим образом.
Теорема 3. Если u£Lp, u(n)£Lr, р, г>1, ft>l,
то uW£Lm для яг>max [р, г] и k = О, 1, 2, ..., п— 1.
Доказательство проводится аналогично предыдущему.
§ 5. Другие неравенства для и, и и и"
Если вместо теоремы 2 мы хотим получить
действительные неравенства, то мы можем поступить следующим
образом. Из соотношения
-^r[e-t(u'+u)} = e-t(ii"-u) (1)
для функции u(t), удовлетворяющей условиям теоремы 2,
мы легко получаем, что
оо
и' = - и — е1 \е~* [и" — и] ds. (2)
Этот результат также можно получить из (3.5)
интегрированием по частям, используя тот факт, что
£2=[и(0) —ы'(0)]/2.

§ 5. Другие неравенства для и, и' и и" 237
Из (2) следует, что
max I и' I < 2 max I и I + max, и"\.
(3)
Заменяя u(t) на u(rt) для г > 0, мы получаем
соотношение
г max | и' | < 2 max \u\ + r2 max I и" I
*^0 *^0 *^0
для г > 0. Отсюда следует, что
(max I г/' |)2 < 8 (max I и I) (max I и"\).
(4)
(5)
Подобным же образом мы можем получить неравенство,
связывающее
ОО ОО ОО
J |н'|тЛ, J |а|р^ и J |^ТЛ
0 0 0
(см. [1.25]). Для того чтобы получить результат,
соответствующий (5), нужно использовать лемму § 9 этой
главы. К сожалению, этот метод не дает возможности
получить наилучшие константы.
Возможно, наилегчайший путь к получению
обобщений равенства (2) состоит в использовании векторно-
матричного соотношения
^•(е^х) = ^(Ах + х% (6)
где х—это я-мерный вектор, или
ОО
x = e~At ^ eAs (Ах f х') ds,
t
(7)
где Л —устойчивая матрица. Выбирая Л подходящим
образом и полагая
/ы >\
и'
х =
\ы<п-х7
(8)

238 Гл. V. Неравенства для дифференциальных операторов
мы можем получить различные соотношения, связывающие
u<k> с линейными комбинациями а и ее производных.
На этом пути можно вывести ряд обобщений неравенства (5).
§ 6. Неравенство Гальперина и фон Неймана
и его обобщения
Развивая предыдущие методы, можно получить
обобщения полученных ранее результатов.
Теорема 4. Если
(а) u" + ai(t)uf + a2(t)ueLpi
(б)иб1г, (1)
(в) \аЩ, |с2(*)1<с, < «>, 0</,
то и, u'£Lm для m>max(r, р).
Доказательство. Рассмотрим только случай т — со,
это означает, что мы изучаем равномерную ограниченность
для \и'\. Общий случай можно рассмотреть аналогично.
В дополнение к приемам, которые мы использовали
в предыдущих разделах, введем еще один.
Рассмотрим уравнение
и" — М2и = и" + О! (t) и' + а2 (t) и —
— la>i(t)u' + a2(t)u + M2u\ = f(t)--ai{t)u\ (2)
где f(t)£B [0, со] (В [0, со] — пространство функций,
равномерно ограниченных на [0, со] и удовлетворяющих
условию (1)), М — постоянная, которая будет выбрана позднее.
Решая уравнение (2) относительно и, получаем
t
и = с,е~ш + с2еш + ~ J [ем «~s> - е~м (*-*>] f (s) ds -
о
t
~ ш S[еМ (t~s) ~~ е~м а~8)] а* (s)"'(s) ds' (3)
о
Так как легко установить, что из соотношения
lu' + ax(t)u' + a2(t)u]eB[0,col ах (Об Я[0,со], /=1,2,

§ 6. Неравенство Гальперина и фон Неймана и его обобщения 239
следует, что
\u'(t)\<cebt
для некоторых постоянных с и Ь, мы видим, что интегралы
оо оо
^e~Msai(s)u,(s)ds и ^e-Maf(s)ds
о о
сходятся при достаточно большом /И. Следовательно,
решение (3) принимает вид
t
и = сф~ш — 2^ J e-MteM8f(s)ds +
о
t
о
+ ш \ е~ш If (s) - Qi (s)"' W ds' (4>
t
и соответственно
u'=—Mcie~Mi+j<\e-MteMef(s)ds —
о
t
- ^e-MteMeai (s)«'(«) <*s +
о
+ -2-y-M°[f(s)-ai(s)u'(s)]ds. (5)
*
Отсюда следует, что при подходящей постоянной с2
справедливо неравенство
t
\u'\<c2[e-Mt + e~MtleMs\f(s)\ ds +
о
t оо
+ e-Mtl eMs\u'(s)\ds + eMt^ e~M8\f(s)\ ds +
о *
oo
+ em[e-M*\u'(s)\ds\. (6)

240 Гл. V'. Неравенства для дифференциальных операторов
Таким образом, при некоторой постоянной с3
max |м'|< с3 + ( тах \и'\)М~1 +
(оо
eMt[e~Ms\u'(s)\ds); (7)
„^_^_ J /
отсюда при /И > 1
max |«'| < с3(1 — 1/М)~х +
(оо
eMt[e~Ms\u,{s)\ds)(l-l/M)-1. (8)
-^-^. ■ «] '
Считая, что М>3, получаем
оо
max |w'|<c4 + c4 max (eMt/*[e~Ms/2\uf(s)\ds). (9)
С другой стороны, возвращаясь к формуле (6), получаем
оо оо
Jg-*«/2 | и> (f) | ^ < С2 ^e-BMt/2 dt +
t t
оо t
« 0
oo t
+ J е-зд«/2 f J eMs|«'(s)|ds)^ +
« о
oo oo
+ JeM'/2 Q e-Ms |f(s)|ds)^ +
oo oo
+ JeJ«/2(Je-M«|«'(s)|rfs)df]. (10)

§ 7. Аналоги результатов Секефальви-Надя 241
Интегрируя по частям, получаем
оо
le-m'2\u'(t)\dt<c2 [Ае-зм«/2 +
t
+ Ше~ЗШ/2 I еШ l^s)l ds+m Ie~m/2 l/(s)l ds +
0 t
t
+ me~BMt/2 leMsW'(s)\ds + mle~Ms/2W(s)\ds +
0 t
2eMt/2 <g? 9 ^
+ T S^Msl/(s)|ds+ I- \e-"«*\f(t)\dt +
t t
+ T Se-^|^)|ds + 4Je-^|M'(s)|ds]. (11)
* t
Отсюда
gBft/2|е-м*/2|а^)|Л<Сз ^i + eZ^L J eMe|i/'(s)|ds]. (12)
* 0
Следовательно,
OO
max Гвм'/2{е-м'/2|а^)|л] <Cs+ 1 max |a'(OI- (13)
Комбинируя (8) и (13), мы видим, что величина max \u'(t)\
равномерно ограничена для 7>0. Этим доказательство
заканчивается.
Доказательство общего результата для линейных
дифференциальных операторов произвольного порядка можно
провести аналогично.
§ 7. Аналоги результатов Секефальви-Надя
Кратко укажем, как можно получить результаты,
подобные результатам Надя, приведенным в §2.

242 Гл. V. Неравенства для дифференциальных операторов
Пусть
u' + u=f + g, (1)
где f£Lp[—со, со], g£Lr[ — оо, со], р,г>1.
Тогда, рассуждая, как выше, находим, что функция и
должна иметь вид
t t
и = е~1^ f(s) es ds + e~l J g(s) es ds. (2)
-oo _oo
Условия, которым удовлетворяют fug, приводят
к равномерной ограниченности для и; поэтому из условий
u£Lp(—со, оо) и u'£U{—со, оо) следует, что u£Lp+b(—со, оо)
для 6>0. Однако этот результат слабее результата,
приведенного в § 2.
§ 8. Неравенство Карлсона
Неравенство Карлсона состоит в следующем.
Теорема 5. При g(t)>0
со со со
О 0 0
если второй интеграл в правой части существует.
Как установлено Над ем [1.16], этот результат
следует из теоремы 1 при
со
у (х) = j/| J g(t) cos xt dt, (2)
0
p = a = 2 применением формулы Парсеваля — Планше-
реля [1].
§ 9. Обобщения неравенства Карлсона
Неравенство Карлсона может быть существенно
обобщено. Общая задача состоит в определении границ для

§ 9. Обобщения неравенства Карлсона 243
оо
\f(x)dx, если задано, что существуют интегралы
о
оо оо
\xafbdx и \ xcfddx. Результаты в этом направлении полу-
о о
чены Харди [1.21], Габриэлем [1.22], Бейрлингом [1.23],
Катоном [1.24], Секефальви-Надем[1.16], Беллманом [1.25]
и Кьелбергом [1.20]. Как отметил Кьелберг, указанная
выше задача является проблемой моментов и может быть
изучена методами, описанными в гл. III (см. также
Боас [2]).
Здесь мы, следуя [1.25], дадим простой метод для
получения результатов этого типа для случая, когда
точные границы не представляют особого интереса. Вывод
точных неравенств приводится в работе Левина [1.26].
Докажем следующий результат.
Теорема 6. Если f(x)>0 и р, q >0, 0 < Я< р+ 1,
0<И><9 + 1, то
оо
(J
f(x)dxj <
о
оо ОО
\К(р, q, К ja)( Ja*-^1 dxy ^хч+^ч+Ыху. (1)
о "6
Доказательство. Очевидно, что
Используя неравенство Гёльдера, получаем
m Y(p-Wp+i)fdx
J ' W J ^-«ЛИ-1)(1+х) + ] хЪ+М*+»(1+1/х)' {2)
С x"
.. -fc)/(p+l)(1+x)
0 vi'
<
fl^/»-*)'^L.^,:>»)'™>
<
0 ' " 0

244 Гл. V. Неравенства для дифференциальных Операторов
x(q+m<l+i)fdx
<
6
)*<«+1*у<«+1>(1+1/*)
V/(<H-i>
(3')
(S^f,+^)^'(L^(,:,M).+,„)
О О \ I / /
Итак, получен предварительный результат:
оо оо
J / (*) Же < Cl (J *?-* fH-i Же)1/(Р+1) +
о о
оо
+ с2 Q х*^-1 /5+i dx)1/(Q+1), (4)
о
где С! и £2 — интегралы в (3) и (3'), не зависящие от /.
Используем теперь прием, который бывает полезным
во многих подобных ситуациях. Если заменить f(x) на
f (x/t), t > 0, то с помощью (4) после замены переменной
получим
оо оо
ф(х) dx< ^(p-M-DAH-dQxp-x fv+idx V/(p+1) +
о о
оо
+ c2#<H-H-2)/(<H-D ( J jce+iH-iffl+i ^Л1/(<z+1) , (5)
для всех t > 0.
Для получения требуемого в теореме 6 результата
используем следующую лемму.
Лемма. Если v > и> 0, а, 6, с>0 и
bxu<c + axv (6)
5ля всех х > 0, то
cv-uau>k(u,v)bl\ (7)
Лемма следует из (6) при подстановке х = (bu/av)l^v-u\
Итак, теорема доказана. Этот результат есть обобщение
известного факта, что 62<4ас, если Ьх^.с + ах2 для всех
x>0 и а, 6, с>0.

§10. Неравенство Вupтингера и связанные с ним результаты 245
Ясно, что соответствующее неравенство (1) может быть
получено для бесконечных рядов аналогичным образом.
§ 10. Неравенство Виртингера и связанные
с ним результаты
В ряде случаев в дополнение к включениям и явным
неравенствам можно вывести точные неравенства, а также
указать класс функций, для которых выполняется равенство.
Вообще это требует определенной изобретательности и лишь
иногда можно привлекать аппарат вариационного
исчисления. Иногда результаты могут быть получены несколькими
методами. Это, в частности, верно относительно неравенств,
содержащих квадратичные функционалы.
Возможно, что наиболее интересным примером, который
широко используется в анализе, является неравенство
Виртингера (см. Харди, Литтлвуд и Пойа [1.1], гл. I,
Бляшке [1], Фань, Тауски и Тодд [1.29]).
Теорема 7. Если u(t) имеет период 2я и
J u(t)dt = 0, (1)
о
то
2н 2Н
l[u(t)]2dt< ^[u'(t)]2dt, (2)
о о
причем неравенство будет строгое, если
и (t) = Ci cos t + c2 sin t. (3)
Приведем три доказательства. Из них первое основано
на теории рядов Фурье; этот метод использован Гурвицем
для установления изопериметрических неравенств в
плоскости и пространстве; второе основано на теории
Штурма—Лиувилля; третье —на интегральном неравенстве.
Последний метод был обобщен Бисаком [1.12]. Эти три
доказательства даются ниже в § 11 — 13.
Детальное обсуждение изопериметрических неравенств
будет дано во втором томе настоящей монографии. По

246 Гл. V. Неравенства для дифференциальных операторов
поводу обобщения этих неравенств см. работу [1.16] и статью
Шенберга [48.7], гл. II, на которые мы уже делали ссылки
в связи с неравенствами для определителей.
Обсуждение родственного неравенства Вейля см.
в работах Слепяна и Поллака [3], Ландау и Поллака
[4], Уитла [5].
§ 11. Доказательство с помощью рядов Фурье
Для вещественной функции u(t) составим ряд Фурье
u(t)~2ianein*, (1)
пфО
при этом п==0 в силу условия (10.1).
Тогда
и#(0~2 inaneint. (2)
пфО
Равенства Парсеваля для u(t) и и' (t) имеют вид
$И01»л= 2Ы2'
0 пфО
\[^(0]2^=2^2N2-
0 пфО
Отсюда следует соотношение (10.2), причем неравенство
будет строгим, если
ОпФО, \п\>2, (4)
хотя бы для одного п.
§ 12. Теория Штурма —Лиувилля
Пусть p(t) — ограниченная положительная функция.
Рассмотрим задачу получения неравенства, связывающего
интегралы
2Я 2Я
^p[u(t)]*dt и ^[u'(t)]2dt.
о о

§ 13. Интегральные тождества
247
Пусть и{0)--=и{2п) = 0\ найдем минимум функционала
2я
\ [u'(t)]2dt на функциях, нормированных с помощью
о
условия
2я
J pu2dt=\. (1)
о
Используя формально множители Лагранжа, мы сведем
эту задачу к минимизации квадратичного функционала
2я
J(u)= ^(u'2 — lpu2)dt (2)
о
на всех функциях u(t), для которых интеграл существует
и которые удовлетворяют условию (1) и указанным выше
граничным условиям.
Уравнение Эйлера имеет вид
и" + Хри = 0. (3)
Если и удовлетворяет этому уравнению, то мы имеем
2я 2я 2я
0= ^ u(u" + Kpu)dt = luu'f*-- I [u'(t)]2dt + ^ pu2dt,
0 0 0
(4)
или
K=^[u'(t)]2dt. (5)
о
Следовательно, требуемый минимум есть наименьшее
собственное число задачи Штурма — Лиувилля,
соответствующей (1) и двухточечному граничному условию
м(0) = м(2л;) = 0. (6)
Обсуждение этой задачи см. в работах Айнса [1],
Коддингтона и Левинсона [34.3], гл. IV.
§ 13. Интегральные тождества
Третий подход к рассматриваемой задаче и к ряду
аналогичных задач, включающим производные высших

248 Гл. V. Неравенства для дифференциальных операторов
порядков, основывается на классе тождеств Бисака [1.12]
(см. также Харди, Литтлвуд и Пойа [1.1], гл. 1).
Пусть v (t) — вещественная функция, удовлетворяющая
уравнению Риккати
v' + v2 + p(t) = 0 (1)
с некоторым начальным условием. С помощью формальных
вычислений получаем
2л 2л 2л
^[U'-V(U-b)¥dt= 5 u'2dt+ ^v2(u-b)2dt-
0 0 0
2л
— 2^vu'(u-b)dt. (2)
о
Интегрируя по частям, имеем
2л 2л
-^2vu'(u-b)dt = [-v(u — Ь)2]2*+ \v'{u-bfdt =
о о
2л
= 1 —1;(« — b)»jjrt_ \{v2 + p){u-b)2dt. (3)
о
Подставляя в (2), получаем тождество
2л
^[u' — v(u-b)]*dt =
о
2л
= \[u'2-p(u-b)2]dt + l-v(u-b)2]2*. (4)
о
Предположим, что v {и — Ь)2 = 0 при ( = 0 и что
функция v (t) существует и неотрицательна при 0<£<2я.
Тогда из (4) следует, что
2л
jj [u'-v(u-b)2]dt + v(2n)[u(2n) — b]2 =
о
2л
= \[u'*-p{u-bf]dt. (5)

§ 15. Дифференциальные уравнения в частных производных 249
Частный случай этого тождества приводится Харди,
Литтлвудом и Пойа при установлении неравенства Вир-
тингера. В своей статье [1.11] Бисак дает аналог этого
результата для уравнения четвертого порядка вида
и(™)±ри = 0 (6)
и использует его для установления ряда неравенств,
2л 2л
связывающих \ и"2 dt и \p{t)u2dt. Он также дает строгий
о о
вывод (4). Дальнейшие результаты для дифференциальных
уравнений, обыкновенных и в частных производных,
приводятся у Рейда [1.14] с применением к изоперимет-
рическим задачам.
§ 14. Результаты Колаутти
Как можно ожидать, тождество (13.6), связанное с
самосопряженным уравнением и"-\-ри = 0, есть частный
случай тождеств, которые могут быть получены с помощью
линейных дифференциальных уравнений L(u) и их
сопряженных уравнений L* (и) — 0. Эта тема очень
широко и искусно развита Колаутти [1.13], который
использовал разрешающие тождества для вывода
различных интересных неравенств. С этой работой связаны
результаты Хёрмандера [1].
§ 15. Дифференциальные уравнения в частных
производных
Бисаком [1.11] установлено, что тождества, подобные
[13.5], могут быть получены для уравнений в частных
производных.
Так, если
vxx + vyy + pv = 0 (1)
для (x,y)£R и v = 0 на границе, то мы имеем
l(u2x + u2y-pu2) dA=^[(ux-wu)2 + {uy — zu)2]dA, (2)
R R

250 Гл. V. Неравенства для дифференциальных операторов
где
— F- *"?• <3>
при условии, что « = 0 на R, и что все эти функции и
интегралы существуют. Подобным же образом могут
быть обобщены на уравнения в частных производных
и методы Колаутти. Заметим, что вместо уравнения
Риккати здесь используется уравнение
wx + zy + w2 + z* + p = 0. (4)
§ 16. Использование матриц
Систематический путь для получения аналогов
соотношения (13.5) для линейных дифференциальных
уравнений высших порядков и вообще для линейных операторных
уравнений состоит в использовании векторно-матричных
обозначений. Пусть х и Ь — это n-мерные векторы,
х—переменный, Ь — постоянный, Z — квадратная матрица порядка
л, удовлетворяющая уравнению
Z' + Z2 + P(0 = 0. (1)
Тогда, как и выше, получим
2я
$(*'— Z(x—b), x' — Z(x — b))dt =
о
2я 2я
= §(*', x')dt+ J (Z(x — b), Z(x — b))dt- (2)
о о
2я
-2 ^(x',Z(x — b))dt.
Так как
А
dt
4г((х-Ь), Z(x-b)) =
= 2(*'f Z(x-b)) + (x—b, Z'{x—b)), (3)

§ 17. Высшие производные и высшие степени 251
то после некоторых преобразований, как и в скалярном
случае, получим тождество
2я
\ [(*', *') — (*> P(t)x)]dt =
о
2я
= J (*'—Z(* —6), x' — Z(x — b))dt +
о
+ (*-&, Z(*-&)),=2«, (4)
при условии, что (x — b, Z(x—b)) = 0 при t = 0 и
матрица Z (2л;) — положительно определена.
Чтобы использовать тождество при получении
аналогов (13.5) для линейных дифференциальных уравнений
высших порядков, мы вначале записываем их в векторно-
матричной форме
x" + P(t)x = 0, (5)
используем (4) и возвращаемся к прежней записи. Ниже
мы будем использовать как исходное дифференциальное
уравнение, так и сопряженное.
§ 17. Высшие производные и высшие степени
Получив результат (2.10), естественно его обобщить
на высшие степени и высшие производные, т. е. на
неравенства, связывающие
2я 2л
J [u(t)]2rdt и \ [t№(t)]*rdt. (1)
о о
Проблемы этого типа являются принципиально простыми,
поскольку они относятся к вариационному исчислению,
однако при их решении возникают трудности, если нужно
получить точные неравенства. Детальный анализ многих
задач этого вида приведен в книге Харди, Литтлвуда
и Пойа и в статьях Колмогорова [1.10] и Бисака [1.11]
и [1.12].
Здесь мы приведем два легко получающихся
результата, принадлежащих Норткотту [1.27] и Беллману [1.28]
(см. также Островский [20.1]).

252 Гл. V. Неравенства для дифференциальных операторов
Теорема 8. Если u(t) — и (t + 2я), u(t), и'(t), ...
..., u^k~^{t) абсолютно непрерывны и
2я
\ u(s)ds = 0,
о
то
max \u(t)\^ak max \uh(t)\, (2)
где через {а&} обозначена следующая последовательность:
fli = y> а2—-g-» ^з — 24» .... (о;
Этот результат является наилучшим в том смысле,
что для любого k существует функция u(t), для
которой достигается равенство.
Теорема 8 может быть получена как предельный
случай следующего результата.
Теорема 9. Если u(t) = u(t + 2n), u'(t),..., uih"^{t)
существуют и и(к~1}(1) является интегралом некоторой
функции из L2r[0, 2л], а также
2я
\u(s)ds = 0,
о
то
2я 2я
J [и {t)]2rdt < alr I [uk(t)]2rdt. (4)
о о
Этот результат не является наилучшим в указанном
выше смысле.
§ 18. Дискретные аналоги Фаня, Тауски и Тодда
Как правило, дискретные аналоги неравенств более
интересны, хотя доказать их труднее и сложнее
определить точные постоянные и экстремальные функции.
Одним из первых результатов в этом направлении
является результат Бляшке [10.1].

19. Дискретный случай. Вторые разности 253
Теорема 10. Если L —периметр равностороннего
многоугольника с п сторонами и площадью Л, то
L«>[4/l1g£];4, (1)
причем неравенство строгое, если многоугольник не
является правильным.
Обсудим теперь ряд результатов Фаня, Тауски и Тод-
да [1.29], которые можно было бы отнести к гл. II,
где мы рассматривали неравенства, связанные с
матрицами. Их доказательства основаны на детальном анализе
характеристических корней и собственных векторов
различных специальных классов симметричных матриц.
Теорема 11. Если хи лг2, ..., хп действительны
и *! = (), то
п— 1 п
2 (** - W > 4 sin2 2{2*_{) 2 *?; (2)
при этом равенство может иметь место только в
случае, когда х% = сх\, /=1, 2, ..., я, где
*i = sin 2^Z-i > i=l, 2, —, /г. (3)
Структура симметричных матриц, которые здесь
встречаются, и соответствующие вариационные задачи,
рассмотренные Фанем, Тауски и Тоддом, были исследованы
Резерфордом [1] ввиду их большого значения для
ряда математических моделей химических и физических
процессов.
В дополнение к предыдущему получен ряд
результатов, соответствующих различным условиям, налагаемым
на Xi и хп.
§ 19. Дискретный случай. Вторые разности
Дальнейший анализ такого типа приводит к
следующему результату (см. статью Фаня, Тауски и Тодда [1.29]).

254 Гл. V. Неравенства для дифференциальных операторов
Теорема 12. Если х^ лг2,..., хп—вещественные числа
и х0 = xn+i = 0, то
2(^~2xm + ^+2)2>16sin427^i3^b (1)
г=0 \ Т ) 1=1
где равенство выполняется тогда и только тогда, когда
xi = csin^-l, i = l, 2, . . ., п. (2)
Существуют аналоги этого результата для других
граничных условий.
§ 20. Дискретный вариант неравенства
Норткотта — Беллмана
Рассмотрим теперь дискретный вариант некоторых
результатов, приведенных в § 17. Вначале укажем аналог
теоремы 9.
Теорема 13. Если хихг, .. .,хп — п комплексных
чисел, таких, что
п
2*f=o, (1)
то для любых положительных целых г имеют место
неравенства
п п
2|*«Г<[а1(п)]г2|*4-*1+1|г (2)
г=1 г=1
где
и
J1\xi\r<[a2{n)Y%xi-i-2xi^xi+i\\ (3)
г=1 г=1
%0 — Хт %1 — Хп+1 ? (4)
fli(/») = -2-, fl2(n) = -j2-. (5)

§ 21. Обсуждение
255
Неравенства (2) и (3) являются наилучшими из
неравенств такого вида.
Теперь отметим аналог теоремы 8, являющейся
некоторым обобщением результата Островского [1].
Теорема 14. Если п(п>2) действительных чисел
удовлетворяют условиям
п
(а) 2** = 0.
г=1
(б) max |*,| = 1, (6)
(в) Хп+1 = Х1,
то минимум функции
J(x)= max \xt — xi+i\ (7)
равен
4
, если n четное,
n
An
(8)
если n нечетное.
Доказательство этих результатов, так же как и их
обобщения, можно найти в статье Фаня, Тауски и Тод-
да [1.29].
§ 21. Обсуждение
Результаты, приведенные в § 18 — 20, важны в связи
с численным интегрированием обыкновенных
дифференциальных уравнений и уравнений в частных производных.
Так, например, если главное характеристическое число
для области R определяется как минимум функционала
и
[и% +и%] dxdy
\ \ и2 dx dy
/(ы)=_« (1)

256
Библиография и дополнения
на функциях, удовлетворяющих условию
и = 0 на В, где В — граница R (2)
(в [44.1], гл. I, систематически рассмотрены задачи этого
типа), то существенно знать связь между minJ(u)
и соответствующей постоянной, получающейся из
дискретного аналога задачи.
Вопросы этого типа рассматривались Форсайтом [1],
Крейном [2], Шварцем [3].
БИБЛИОГРАФИЯ И ДОПОЛНЕНИЯ
§ 1. Систематическая теория роста производных от функций
содержится в теории квазианалитических функций. В связи с этими
вопросами читатель может воспользоваться следующей литературой.
1. Мандельбройт (Mandelbrojt S.), Series de Fourier
et classes quasi-analytiques de fonctions, Paris, Gauthier-Vil-
lars, 1935.
Дальнейшие ссылки можно найти в книге
2. Б о а с (В о a s R. P.), Entire functions, New York, Academic
Press, Inc., 1954.
3. Шеффер (Schaeffer A. C), Inequalities of A. Markoff
and S. Bernstein for polynomials and related functions, Bull.
Am. Math. Soc, 47 (1941), 565—579.
4. Секефальви-Надь (Sz. -Nagy В.), Ober gewisse
Extremalfragen bei transformierten trigonometrischen Entwicklun-
gen, I, Periodischer Fall. II, Nichtperiodischer Fall. Ber. Math.
Phys. Kl., Sachs. Akad. Wlss. Leipzig, 90 (1938), 103—134, 91;
(1939), 3—24.
Результаты, относящиеся к дифференциальным уравнениям
в частных производных, можно найти в работе [26.1], гл. II, а также
в следующих статьях.
5. Ароншайн (Aronszajan N.), A unique continuation
theorem for solutions of elliptic partial differential equations or
inequalities of second order, /. Math. Pure Appl. (P), 36 (1957),
235—249.
6. Ниренберг (Nirenberg L.), On elliptic partial
differential equations, Ann. Scuola Norm. Sup. Pisa (3), 13 (1959).
115—162.
7. Фридрихс (Friedrichs К. O.), Symmetric positive
linear differential equations, Comm. Pure Appl. Math., 9 (1958),
333—418.
Обсуждение результатов Адамара, ссылки и обобщения можно
найти в работе [1.1], гл. I, а также в следующих работах.
8. Титчмарш (Titchmarsh Е. С), Theory of functions,
London, Oxford University Press, 1939. Русский перевод: Теория
функций, Гостехиздат, М., 1951.

Библиография и дополнения
257
9. Ландау (Landau Е.), Einige Ungleichungen fur zweimal
differentierbare Funktionen, Proc. London Math. Soc, 13, 43—49
(1913).
10. Колмогоров A. H., О неравенствах между верхними
гранями последовательных производных произвольной функции
на бесконечном интервале, Учен. зап. Ун-та, 30 (1939), 3—16.
И. Б и с а к (Beesack P. R.), Isoperimetric inequalities for the
nonhomogeneous clamped rod and plate, /. Math, and Mech., 8
(1959), 471—482.
12. Б и с а к (Beesack P. R.), Integral inequalities of the
Wirtinger type, Duke Math. J., 25 (1948), 477—498.
Ссылки на работы Пуччи и Фикеры читатель найдет в статьях
13. К о л а у т т и (С а 1 a u t t i М. P.), Sulla maggiorazione
«a priori» dellesoluzione delle equazione e del sistemi di equazioni
differenziali lineari ordinarie del secondo ordine, Matematiche,
Catania, 11 (1956), 8—99.
14. Рейд (Reid W. Т.), The isoperimetric inequality and associated
boundary problems, J. Math, and Mech., 8 (1959), 897—906.
15. Беллман (Bellman R.), On inequalities for differential
operators, Proc. Am. Math. Soc, 9 (1958), 589—597.
16. Секефальви-Надь (S z. - N a g у В.), Uber Integral-
gleichungen zwischen einer Funktion und ihrer Ableitungen, Acta
Sci. Math. Szeged, 10 (1941), 64—74.
Результат Гальперина — фон Неймана читатель найдет в статье
17. Гальперин (Halperin J.), Closures and adjoints of
linear differential operators, Ann. of Math., 38 (1937), 880—919.
Обобщение этого результата имеется в статье
18. Г а л ь п е р и н, П и тт (Halperin J., Pitt Н. R.),
Integral inequalities associated with differential operators, Duke
Math. /., 4 (1938), 613—625.
Неравенство Карлсона привлекло к себе большое
внимание. См.
19. Карлсон (Carlson F.), Une inegalite, Arkiv Mat. Astr.
och. Fysik, 25 B, 1 (1934), 1—5.
20. Кьелберг (К j e 1 1 b e r g В.), On some inequalities,
С R. Dixieme Congres des Mathematiciens Scandinaves, 1946,
333—340, Copenhagen, Jul. Gjellerups, 1946.
21. X a p д и (Hardy G. H.), A note on two inequalities, /. London
Math. Soc, 11 (1936), 167—170.
22. Габриэль (Gabriel R. M.), An extention of an inequality
due to Carlson, /. London Math. Soc, 12 (1937), 130—132.
23. Б e й p л и н г (В е u г 1 i n g A.), Sur les integrates de Fourier
absolument convergentes et leur application a une transformation
fonctionnelle, Neuvieme Congres des Mathematiciens Scandinaves,
1938, 345—366, Helsingfors, 1939.
24. К а т о н (C a t о n W. В.), A class of inequalities, Duke Math. J.,
6 (1940), 442—461.
25. Б e л л м а н (Bellman R.), An integral inequality, Duke
Math., J., 9 (1943), 547—550.
Проблема определения наилучшей постоянной в неравенстве

258
Библиография и дополнения
Карлсона была решена В. И. Левиным. Смотри приложение к
русскому переводу книги Харди, Литтлвуда и Пойа [1.1], гл. I, а также
26. Л е в и н В. И., Точные константы в неравенствах типа Карлсона,
Докл. АН СССР, 59, 635—638 (1948).
27. Норткотт (Northecott D. G.), Some inequalities
between periodic functions and their derivatives, /. London Math.
Soc, 14 (1939), 198—202.
28. Беллман (Bellman R.), A note on periodic functions
and their derivatives, /. London Math. Soc, 18 (1943), 140—142.
Дискретный случай подробно излагается в статье
29. Фань Цзы, Тауски, Тодд (Fan К- TausskyO.,
Todd J.), Discrete analogues of inequalities of Wirtinger,
Monatsh. Math. Physik., 59 (1955), 73—90.
Ссылки на ряд других результатов можно найти в работе [29],
в частности, там имеется ссылка на статьи Островского, Бюкнера
и Пойа.
30. Б л о к (В 1 о с k Н. D.), A class of inequalities, Proc. Am. Math.
Soc, 8 (1957), 844—851.
Полный обзор теории линейных дифференциальных уравнений
с периодическими коэффициентами, а также связей между
этой областью и неравенствами с дифференциальными операторами
дается в работе
31. Борг (В org G.), Ober die Stabilitat gewisser Klassen von
linearen Differential-gleichungen, Ark. Math. Astr. och.
Fysik, 31 A (1944), 460—482.
32. Стажинский (Starzinskii V. M.), Survey of works
on conditions of stability of the trivial solution of a system of
linear differential equations with periodic coefficients, Translation,
Am. Math. Soc. (2), 1, 189—239, New York, American
Mathematical Society, 1955.
Относительно неравенств, связывающих интегралы от
тригонометрических полиномов, см. статьи Секефальви-Надя, на которые
имеется ссылка в библиографии к работе [1.2]. Борг, исходя из работ
Бейрлинга, рассматривал связь, существующую между теорией
устойчивости и неравенствами вышеуказанного типа.
§2.
1. Шмидт (Schmidt Е.), Uber die Ungleichung, welche die
Integrate fiber eine Potenz einer Function und uber eine andere Po-
tenz ihrer Ableitung verbindet, Math. Ann., 117 (1940), 301—326.
§ 3. Cm. [1.3], гл. IV.
§ 6. Этот метод приводится в работе [1.15].
§8.
1. Титчмарш (Titchmarsh Е. С), Introduction to the
theory of Fourier integrals, Chapter 3, London, Oxford University
Press, 1937.
§ 9. Доказательство, которое приводится в этом параграфе,
изложено в работе [1.251. Результаты, связанные с результатами
этого параграфа, имеются в следующих работах.

Библиография и дополнения
259
1. Б о а с (Boas R. P.), Inequalities for monotonic Series, /. Math.
Analys. and Appl.
В этой статье обобщаются теоремы Лоясевича и Конюшкова.
Типичным является следующий результат. Если
ап>01 %>0, п-1ап\Ь>\,
то
N N
k=M k=Mb
N N
( 2 аку<А2(рЛ,Ь) 2 alb*'1- °<Р< 1-
k=M k=M/b
Отметим аналогию с результатом Гаусса, на который имеется
ссылка в конце этой библиографии.
§ Ю.
1. Бляшке (Blaschke W.), Kreis und Kugel, 13—20,
Leipzig, Veit u. Co (1916), New York, Chelsea, 1949.
В этой работе можно найти интересные геометрические
приложения для дискретного случая. См. также [48. 71, гл. II.
2. Г у р в и ц (Н u г w i t z A.), Sur le probleme des isoperimetres,
C. R. Acad. Scl. (Paris), 132 (1901), 401—403 (Werke, I, 490—491).
Неравенство Вейля (теорема 226, стр. 165, £1.11, гл. I)
со со оо
(I f2dx)2<C4(lx2pdx).(lf'*dx)
0 0 0
представляет собой количественное выражение принципа
неопределенности Гейзенберга в квантовой механике. Более детальное
обсуждение «принципов неопределенности» дается в следующих работах.
3. Слепян, Поллак(8 1ер1ап D., Pollak Н.), Prolate
spheroidal wave functions, Fourier analysis and uncertainty, I,
Bell. System Tech. /., 40 (1961), 43—64.
4. Ландау, Поллак (Landau H. J., Pollak H.),
Prolate spheroidal wave functions, Fourier analysis and
uncertainty, II, Bell System Tech. J., 40 (1961), 65—84.
5. Уиттл П., Непрерывные обобщения неравенства Чебышева,
Теория вероятностей и ее применения, 3 (1960), 385—394.
§ 12.
1. Айне (In се Е. L.), Ordinary differential equations, New
York, Dover Publications, 1944. Русский перевод 1 издания:
Обыкновенные дифференциальные уравнения, ГНТИ Украины,
Харьков, 1939.
§ 14.
1. Хёрмандер (Hormander L.), On the regularity of
solutions of boundary problems, Acta Math., 99 (1958), 225—264.
Русский перевод: О регулярности решений граничных задач, сб.
Математика, 4:4 (1960), 37—73.

260
Библиография и дополнения
§ 18.
1. Резерфорд (Rutherford D. R.), Some continuant
determinants arising in physics and chemistry, I, Hi Proc. Roy. Soc.
Edinburgh, 62A (1947), 229—236; 63A (1952), 232—241.
§ 20.
1.Островский (Ostrowski A. M.), Uber die Absolutabwei-
chung einer differentierbaren Funktion von ihrem Integralmittel-
wert, Comment. Math. Helv., 10 (1937), 226—227.
§ 21. Cm. [44.1], гл. I, а также
1. Форсайт (Forsythe G.), Asymptotic lower bounds for
the frequencies of certain polygonal membranes, Pacific J. Math.,
4 (1954), 467—480.
2. К p e й н M. Г., О некоторых задачах на максимум и минимум
для характеристических чисел и о ляпуновских зонах
устойчивости, Прикл. матем. и механ., 15 (1951), 323—348.
3. Шварц (Schwarz В.), On the extrema of the frequencies of
nonhomogeneous strings with equimeasurable density, AFOSR
TN 60—281, Haifa, Israel, Israel Institute of Technology, 1959.
Как мы указывали не раз, мы опускаем большое число
интересных неравенств, возникающих из теории вероятности и
статистики. Отметим, однако, одно неравенство Гаусса, имеющее
исторический интерес:
у2 \ u(x) dx < -Q- \ х2и(х) dx,
у 0
где у > 0, и (х) — невозрастающая функция. См.
4. Крамер (Cramer Н.), Methods of mathematical statistics,
p. 256, ex. 4, Princeton, N. Y., Princeton University Press, 1946.
Русский перевод: Математические методы статистики, ИЛ, М , 1948,
стр. 283, упр. 4.
Метод функциональных уравнений динамического
программирования может быть использован для получения нелинейных
дифференциальных уравнений в частных производных, определяемых
выражением вида
t
f(u, v, t) = max [ xaigbldx,
g
о
где g (x) должно удовлетворять условиям
t t
^xa*gb*dx^u, ^xa*gb3dx*Cv, g(*)>0.
о 0
Cm.
5. Беллман (Bellman R.), Adaptive control processes:
aguided tour, Princeton, N. J., Priceton University Press, 1961.
Русский перевод: Процессы регулирования с адаптацией, Физмат-
гиз, М., 1964.

ИМЕННОЙ УКАЗАТЕЛЬ
Абель 181
Адамар 97 , 129 , 159 , 219 , 229 , 256
Айнон 203 , 223
Айне 247 , 259
Айткен 100 , 130
Александров П . 118 , 135
Амир - Моэз 112 , 116 , 132
Андерсон 126 , 139
Андреев 92 , 128
Ароншайн 144 , 162 , 180 , 186 ,
229 , 256
Артемов 204 , 223
Ацел 60 , 81
Банах 141 , 152 , 156 , 165 , 167 ,
175 , 181
Бейрлинг 83 , 230 , 243 , 257
Беккенбах 4 , 6 , 9 , 29 , 76 , 77 ,
78 , 96 , 129 , 185 , 202 , 203 ,
219 223
Беллман 4 , 6 , 9 , 10 , 21 , 41 , 47 ,
60 , 72 , 73 , 75 , 76 , 78 , 81 , 82—
84 , 94 , 97 - 100 , 111 , 114 ,
117 , 118 , 123 , 127 — 130 , 132 —
135 , 137 , 150 , 161 , 163 , 167 —
169 , 177 , 181 , 182 , 184 , 185 ,
188 , 189 , 194 , 198 , 206 , 207 ,
214 , 217 — 221 , 224 — 227 , 230 ,
233 , 243 , 251 , 254 , 257 , 258 ,
260
Бельтрами 89
Бендат 125 , 138
Бервальд 60 , 65 — 68 , 81 , 146 ,
174 , 177
Бергстром 130
Берман 183
Бернштейн 154 , 178 , 180 , 221 ,
227 , 228
Бертон 221
Бибербах 159 , 179
Бил 168
Бинг 202 , 222
Биркгоф 49 , 79 , 118 , 121 , 135 ,
136
Бисак 51 , 80 , 230 , 245 , 249 , 251 ,
257
Бихари 184 , 189 — 191 , 219
Блейлер 204 , 224
Блекуэлл 79 , 150 , 163 , 177
Блок 230 , 258
Бляшке 60 , 81 , 205 , 224 , 245 ,
259
Боас 8 , 153 , 178 , 219 , 227 , 229 ,
243 , 256 , 259
Боненбласт 79 , 118
Боннесен 46 , 76 , 77 , 148 , 150
Бонсалл 185 , 202 — 204 , 222 , 223
Бор 9 , 17 , 76
Борг 231 , 258
Борель 145 , 159 , 169 , 179 , 182 ,
183 , 221
Бохер 38 , 77
Бохнер 60 , 81 , 100 , 144 , 146 , 161 ,
162 , 174 , 176 , 177 , 180 , 206 —
209 , 216 , 219 , 224 — 227
Браунинг 5
Брауэр 118 , 125 , 134 , 138
Брейн де 92 , 128
Бреннер 131
Бруни 73 , 82
Буллен 80 , 97 , 129
Бюкнер 81 , 258
Валирон 202 , 222
Вальд 82 , 118 , 135 , 136
Варга 60 , 81 , 121 , 136

262
Именной указатель
Вейль 111 , 132 , 146 , 162 , 167 ,
173 , 177 , 180 , 181 , 183 , 246
Вейнберг 125 , 138
Вейнбергер 10 , 63 , 72 , 82 , 124 ,
137 , 186 , 206 , 216 , 219 , 224 ,
227
Вейсс 160 , 179
Вендорф 214
Вестон 156 , 178
Вестфаль 186 , 214 , 225
Вигнер 126 , 139
Виддер 126 , 139 , 144 , 176 , 180 ,
185 , 205 , 218 , 224 , 227
Виландт 112 , 116 , 119 , 124 , 132 ,
136 , 137
Винер 127 , 140
Винтнер 118 , 134 , 185 , 186 ,
204 , 205 , 220
Виттих 227
Вольф 169 , 182
Вонг 182 , 221
Вудбери 182 , 221
Габриэль 230 , 243 , 257
Гальперин 230 , 238 , 257
Гамбургер 112 , 132
Гантмахер 85 , 118 , 126 , 134 , 139
Гарнер 221
Гаррис 118 , 135
Гартман 118 , 134 , 185 , 186 , 201 ,
202 , 204 , 205 , 220 , 222
Гасс 169 , 182
Гаусс 21 , 76 ; 259 , 260
Гейзенберг 259
Гейл 167 , 169 , 181 , 182
Гельфанд 144 , 162
Герглотц 160 , 161 , 179
Герстенхабер 124 , 137
Гёльдер 77
Гильберт 131 , 174 , 229
Гиршман 126 , 139
Гликсберг 78 , 123 , 132 , 137 , 145 ,
169 , 176
Говард 123
Годеман 144 , 162 , 176
Горвард 137
Гординг 22 , 56 , 58 , 80 , 86 , 100 ,
124 , 130
Горн 112 , 132
Гофман 94 , 145 , 169 , 175
Грейб 81 , 104
Грейвз 146 , 177
Гренандер 144 , 160 , 161
Гримшоу 112 , 132
Грин 29 , 76 , 218 , 226
Гронуолл 184 , 188 , 219
Гросс 64 , 78 , 123 , 132 , 137 , 170 ,
183
Гуильяно 188 , 220
Гурвиц 9 , 19 , 76 , 245 , 259
Дайнс 168 , 181
Данскин 78 , 118 , 135
Данциг 168 , 169 , 182
Даффин 126 , 139 , 182 , 219 , 227
Дебре 118 , 136
Девинатц 162 , 180
Дейч 218 , 227
Дельсарт 185 , 205 , 224
Джекобсон 92 , 128
Джексон 203 , 223
Джон 225
Диананда 76
Дингхас 72 , 82
Добш 126
Доллак 219
Дорфман 118 , 122 , 137 , 145 , 169
Дрешер 9 , 45 , 60 , 68 , 78 , 155
Дупорко 219
Дэвис 92
Заремба 146 , 173 , 183 , 205 , 224
Зигель 72 , 82 , 84 , 98 , 99 , 130
Зигмунд 9 , 41 , 48 , 78 , 79 , 141 ,
166 , 167 , 173 , 176
Иенсен 77
Ингам 84 , 98 , 99 , 130
Калаба 47 , 78 , 83 , 226
Калаби 219 , 227
Карамата 10 , 48 , 49 , 79 , 128
Каратеодори 147 , 158 — 161 , 167 ,
179
Карвер 168 , 181

Именной указатель
263
Карлин 85 , 117 , 118 , 126 , 134 ,
136 , 139 , 140 , 144 , 145 , 155 ,
157 , 169 , 176 , 178 , 186 , 192
Карлсон 230 , 257
Картан 144 , 162 , 176
Касселс 68
Катон 230 , 243 , 257
Кац 160 , 179 , 186 , 220
Качмаж 173 , 183
Келлог 126 , 139
Кернер 117 , 134
Кестен 219
Кехер 85 , 140
Клямко 204 , 223
Кнезер 60 , 81
Кобер 72 , 82
Коддингтон 218 , 226
Колаутти 230 , 249 , 250 , 257
Коллатц 119 , 136 , 216 , 226
Колмогоров 92 , 128 , 229 , 251 ,
257 , 259
Конюшков 259
Кораньи 162 , 180
Кордуняну 167 , 181
Корн 229
Коши 9 , 75 , 112 , 132
Крамер 260
Краус 126 , 139
Крейн 85 , 118 , 126 , 134 , 136 ,
139 , 256 , 260
Кун 169 , 182
Купер 144 , 162 , 176
Курант 108 , 131 , 174 , 229
Куртис 202 , 222
Кьелберг 230 , 243 , 257
Лагранж 89
Лаке 8 , 58 , 85 , 124 , 137 , 146 ,
156 , 174 , 177 , 183 , 189 , 220
Лангенхоп 184 , 190 , 191 , 219
Лангер 226
Ландау Г . 246 , 259
Ландау Э . 144 , 145 , 159 , 161 ,
165 , 167 , 179 , 181 , 229 , 257
Ласалль 220
Левин 230 , 243 , 257 , 258
Левинсон 218 , 226
Левитан 180 , 185 , 205 , 224
Лейн 126 , 139
Лейпник 82
Леман 169 , 182
Лемке 168
Леонтьев 118 , 122 , 136
Лефшец 218 , 220 , 226
Лёвнер 85 , 125 , 126 , 138 , 139 ,
219 , 221
Лидский 111 , 132
Литтлвуд 5 — 7 , 10 , 49 , 51 , 60 ,
75 — 77 , 80 , 91 , 181 , 229 , 231 ,
245 , 249 , 251 , 258
Лопес 10 , 52 , 80 , 116
Лоренц 10 , 51 , 80
Лорх 47 , 78 , 133 , 156
Лоуденслагер 127 , 140
Лоясевич 259
Люмис 162 , 170 , 180 , 183
Люрот 77
Ляпунов 181 , 231
Маданский 68 , 81
Мазани 127 , 140
Мак - Грегор 85 , 116 , 117 , 126 ,
133 134 139
Мак - Даффи 92 , 117 , 128 , 133
Маклорен 23 , 76
Мак - Набб 214 , 225
Малер 9 , 46 , 78
Маллоуз 144 , 147 , 150 , 165 , 176 ,
Мандельбройт 256
Mapадудин 179
Мардок 160 , 179
Марков 229
Маркус 10 , 52 , 80 , 97 , 116 , 129
133
Марцинкевич 48 , 79
Маршалл 127 , 140
Массера 167 , 181 , 194 , 221
Матиас 144 , 161 , 176
Мейрхубер 126 , 140
Менгер 82
Минковский 9 , 10 , 46 , 47 , 77 ,
78 , 105 , 129 , 145 , 147 , 167 ,
168 , 181
Мирский 49 , 80 , 97 , 106 , 112 ,
113 , 129 , 131 — 133
Млак 186 , 214 , 225
Мойлс 116 , 133
Монтролл 117 , 134
Мор 70 , 82
Моргенштерн 118 , 122 , 137 , 169 ,
182

264
Именной указатель
Мофферт 92 , 128
Моцкин 168 , 182 , 202 , 222
Моял 83
Мурнаган 60 , 81
Мьюборн 118 , 136
Нарасимхан 214 , 225
Нейман 177
Нейман фон 118 , 121 , 135 , 136 ,
144 , 145 , 162 , 169 , 180 , 182 ,
238 , 257
Немыцкий 189 , 220
Нерлав 118 , 122 , 137
Никайдо 168 , 182 , 183
Ниренберг 8 , 229 , 256
Нолль 70 , 82
Норткотт 230 , 251 , 254 , 258
Ньютон 80 , 183
Нюренберг 186 , 206 , 224 , 233
Огура 38 , 77
Олкин 8 , 10 , 73 , 82 , 84 , 97 — 100 ,
127 , 129 , 130 , 140
Опиал 192 , 221
Оппенгейм 106 , 131
Орден 169 , 182
Оссерман 219 , 227
Островский 10 , 48 , 49 , 51 , 79 ,
94 , 97 , 116 , 125 , 127 — 129 , 131 ,
138 , 230 , 251 , 255 , 258 , 260
Паркер 125 , 138
Пароди 204 , 223
Пейн 219 , 227
Пейсото 185 , 202 , 203 , 222
Перрон 85 , 118 , 134 , 135 , 192 ,
194 , 221
Петерссон 185 , 205 , 222
Петров 185 , 200 , 204 , 222
Пик 60 , 65 , 81
Пикар 144 , 159 , 161 , 178
Пиконе 183
Пирсон 177
Питт 230 , 257
Пойа 5 — 7 , 10 , 49 , 51 , 60 , 68 ,
75 — 77 , 80 , 81 , 91 , 92 , 112 ,
132 , 157 , 158 , 160 , 181 , 185 ,
204 , 208 , 219 , 223 , 224 , 227 ,
229 , 231 , 245 , 249 , 251 , 258
Поллак 246 , 289
Прайс 131
Прингсгейм 77
Проди 186 , 214 , 225
Проттер 226
Пуанкаре 112 , 132 , 185 , 201 ,
219 , 229
Пуччи 186 , 214 , 225
> Радо 203 , 219 , 223
Райзер 49 , 80 , 117 , 133
Райков 144 , 162
Райли 169 , 182
Райт 82 , 218 , 227
Редхеффер 186 , 219 , 227
Резерфорд 253 , 260
Рейд 185 , 202 , 230 , 249 , 257
Рейнбольдт 68 , 81 , 104
5 Рид 203 , 223
Рисс М . 209
Рисс Ф . 143 , 145 , 151 , 152 , 158 ,
160 , 178 , 179 , 203 , 223
' Робинсон 170 , 183
Рогозинский 174 , 183
Розенблюм 142 , 150 , 173 , 176 ,
177 , 183
Ройден 150 , 165 , 177
Романовский 192 , 221 , 222
Ру 219
i Рудерман 51 , 80
Сакстедер 219 , 227
Самуэльсон 118 , 122 , 136 , 137 ,
145 , 169
Сасс 159
Сегё 10 , 68 , 72 , 81 , 82 , 92 , 144 ,
157 , 158 , 160 , 161 , 178 , 179 ,
208 , 219 , 224
Секефальви - Надь 162 , 180 , 229 —
231 , 333 , 241 — 243 , 256 — 258
Сельберг 99 , 218
Сербии 219 , 227
Синдж 60 , 81
Скляр 82
Слепян 125 , 138 , 246 , 258
Смит 144 , 162 , 180 , 186
Солоу 118 , 122 , 137 , 145 , 169
Стажинский 231 , 258
Степанов 189 , 220

Именной указатель
265
Стеффенсен 10 , 73 , 82
Стильтьес 198 , 199 , 221
Таккер 169 , 182
Тамаркин 144 , 147 , 156 , 157 ,
159 , 176
Татаркевич 51
Таубер 218 , 229
Тауски 8 , 94 , 124 , 127 , 128 ,
131 , 137 , 138 , 192 , 230 , 245 ,
252 , 253 , 255 , 258
Таутц 203
Теплиц 160 , 179
Титчмарш 229 , 256 , 258
Тодд 68 , 81 , 230 , 245 , 252 , 253 ,
255 , 258
Томас 126 , 139
Торнхейм 202 , 222
Уайтли 10 , 55 , 80
Уилкинс 185 , 200 , 204 , 222
Уильяме 169 , 183
Уильямсон 97 , 126 , 129
Уинг 225
Уиттл 246 , 259
Улам 218 , 226
Уолтер 227
Уолш 154 , 178
Уорд 117 , 134
Уотсон 68 , 81
Урселл 142 , 177
Уэствик 116 , 133
Фавар 60 , 65 — 68 , 81
Фань Цзы 8 , 10 , 14 , 51 , 68 , 76 ,
80 , 81 , 85 , 94 , 101 , 105 , 106 ,
110 — 113 , 115 , 118 , 123 , 125 ,
128 , 129 , 131 — 133 , 135 ,
137 , 138 , 144 , 145 , 156 , 159 ,
161 , 167 — 169 , 176 , 177 , 180 ,
230 , 245 , 252 , 253 , 255 , 258
Фаркаш 168 , 181
Фейер 159 , 160 , 179 , 216
Фейнман 117 , 134
Феллер 195 , 221
Фенхель 46 , 47 , 76 , 78 , 148 , 150
Фикера 183
Филлипс 127 , 140
Фишер 85 , 97 , 108 , 110 , 129 ,
131 , 132 , 159 - 161 , 178
Форд 168 , 182
Форсайт 173 , 183 , 256 , 260
Франк 60 , 65 , 81
Фридрихс 174 , 177 , 229 , 256
Фробениус 85 , 118 , 134 , 135 , 179
Фукс 49 , 51 , 80
Фулкерсон 168 , 182
Фюрстенберг 219 , 227
Хаар 186 , 214 , 225
Хайерс 218 , 226
Харди 5 — 7 , 10 , 49 , 51 , 60 , 75 —
77 , 80 , 91 , 181 , 221 , 229 -
231 , 243 , 245 , 249 , 251 , 257 ,
258
Хассан 69 , 81
Хаусдорф 180 , 227
Хейнсворт 105 , 125 , 131 , 138
Хелли 152
Хельсон 127 , 140
Хербранд 183
Херстейн 118 , 136
Хёрмандер 249 , 259
Хопф 118 , 135
Хуа Ло - ген 98 , 100 , 130
Хэвиланд 227
Цзянь 58 , 80
Чаплыгин 185 , 194 , 195 , 200 ,
203 , 219 , 222
Чарнс 168
Чебышев 154 , 178
Чезари 167 , 181 , 218
Черников 168 , 182
Черри 225
Шапира 21 , 76
Шапиро Г . Н . 218 , 227
Шапиро Г . С . 174 , 183
Шварц Б . 256 , 260
Шварц Л . 146 , 162 , 174 , 177
Швейтцер 68
Швейцер 82
Шевалье 183
Шенберг 85 , 126 , 139 , 140 , 144 ,
162 , 180 , 187 , 202 , 216 , 220 , 246

266
Именной указатель
Шепли 144 , 155 , 157 , 176
Шерман 29 , 125 , 138
Шеффер А . 229 , 256
Шеффер И . 167 , 181 , 183 , 221
Шиффман 183
Шлезингер 21 , 76
Шмидт 231 , 258
Шнайад 77
Шнейдер 131
Шоат 144 , 147 , 156 , 157 , 159 , 176
Шрейбер 49 , 80
Штейнгауз 173 , 183
Штимке 168 , 181
Шур 9 , 49 , 51 , 72 , 79 , 82 , 97 ,
117 , 129 , 133 , 159 , 179
Эверитт 92 , 128
Эглстон 148 , 177
Экланьон 229
Элерс 20 , 76
Эрдёш 218
Эрроу 118 , 122 , 137 , 221
Юнг Л . 47 , 78
Юнг У . 9 , 77
Якоби 200
Якобсталь 23 , 77
Яно 219 , 227

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вариация ограниченная 153
Вектор неотрицательный 119
— нормированный 119
— положительный 119
Выпуклость 147
— обобщенная 202
Групповая инвариантность 100
Двойственность 175
Интеграл Зигеля 99
— Ингама 99
— Эйлера 99
Квазилинеаризация 39
— выпуклых и вогнутых
функций 47
Корень характеристический , по
абсолютной величине
наибольший 118 , 124
— — — — — наименьший 124
— — с наибольшей
действительной частью 122
Лемма Неймана — Пирсона 170
Мажоризация 18
Матрица Адамара 138
— входная - выходная 122
— двояко стохастическая 49
— доминирующая 138
Матрица комплексная с
положительно определенной
вещественной частью 94
— Маркова 118
— неотрицательная 135
— — полностью 126
— норма 119
— положительная 117
— положительно определенная ,
каноническая форма 102
— присоединенная 117
— симметричная 86
— — положительно
определенная 86
— — — полуопределенная 87
— составная 117 , 133
— стохастическая 118
— — двояко 49
— тёплицева 160
— устойчивая 140
— характеристическое
уравнение 106
— эрмитова 86
— — положительно
определенная 86
— — — полуопределенная 87
— — представление
определителя 97
Метод Беллмана получения
обратных неравенств 10
— Бляшке и Пика 10
— Бюкнера 10
Минимакс - определение
характеристического числа 85
Минимакс - теорема Фишера 108
Многочлен гиперболический 56 ,
57
— неотрицательный
рациональный 158

268
Предметный указатель
Многочлен неотрицательный
тригонометрический 158
— форма полная полярная 58
Множество выпуклое 148
Неравенства для
характеристических чисел матрицы 94 — 115
— с чередующимися знаками
72 , 73
Неравенство Адамара 97
— Беллмана 252
— — дискретный вариант 251
— Беккенбаха 44
— Бервальда 66
— Бергстрома 100
— — обобщение 103 , 105
— Бернштейна 228
— Бихари 189
— Брунка — Олкина 74
— Буняковского — Шварца
36
— — — обобщения 38
— — — обращение 60
— — — уточнения 69
— Вейля 259
— Вендорфа 214 , 215
— Виртингера 245 — 248
— Гёльдера дискретное 33 , 39
— — интегральное 35
— — обращение 60
— Гординга 57
— для миноров матрицы 95
— — многоугольника
равностороннего 253
— — уравнения матричного
дифференциального 191
— Дрешера 45
— Иенсена 32
— Карамата 48 , 49
— — континуальный аналог
— Карлсона 242
— — обобщения 243 , 244
— Коши 11 , 36 , 91
— — обращение 68
— — уточнения 69
— Коши — Шварца 36
— Лангенхопа 190
— линейное 168
— Маркуса — Лопеса 52 — 55
Неравенство между
арифметическим и геометрическим
средними 13 , 15 , 17 , 19 , 20 , 22 , 23 ,
25
— — — — — —
доказательство Гурвица 19
— — — — — — —
индукцией вверх и вниз 13
— — — — — — —
использующее вогнутость 16
— — — — — — — мажори -
зацией 17
— — — — — — — методом
множителей Лагранжа 15

функциональных уравнений
динамического программирования
15
— — — — — — — с
помощью симметрических функций
22
— — — — — — — Элерса
20
— — — — — — — Якобста -
ля 23
— — — — — — уточнение 72
— Минковского дискретное 34»
41
— — для произведений 42
0 < р < 1 43
интегральное 35
— — — обобщение 37
— Минковского — Малера 46
— Норткотта 252
— — дискретный вариант 255
— Оппенгейма 106
— Островского 50
— — континуальный аналог 51
— Островского — Тауски 89 ,
90
— Сасса 97
— Секефальви - Надя 231
— Стеффенсена 73
— — обобщение 74
— треугольника 34 , 40
— Уайтли 55 , 56
— Фавара 65 , 66
— Фань Цзы 110 , 111
— Франка — Пика 67
— Шварца 36
— Юнга 27

Предметный указатель
269
Норма обобщенная 46
Область положительности 85 ,
126
0£ъем смешанный 47
— эллипсоида 110
Оператор дифференциальный
187 , 188 , 199 , 200 , 228 — 260
— — порядка первого 187 , 188
— — — произвольного 199 ,
200
— параболический 209 — 212
— положительный 184
— сопряженный 116
Определитель 84
— Вронского 139
— Грама 91
Отношение Релея 107
Плоскость разделяющая 142
Положительная определенность
86
— — матрицы , условие
необходимое 87
_ — — — — и достаточное 89
— полуопределенность 87
Последовательность моментная
147
— положительно определенная
160
Преобразование
индуцированное 116
— положительное 85
— уменьшающее число
перемен знака 126
— унитарное 135
— Шура 49
— — континуальный аналог 51
Принцип неопределенности 259
Проекция ортогональная 173
Произведение Кронекера 116 ,
133
— скалярное 87
Пространство выпуклое 148
— — примеры 149
— двойственное 141
— невыпуклое , примеры 150
— Лоренца 59
Разложение Тейлора
обобщенное 205
Расстояние обобщенное 46
Свойство W 201
Связь точечно - тангенциальная
141
Система неравенств полная 142 ,
143
Соотношение рекуррентное
динамическое 213
— — статическое 213
Соотношения Гершгорина 125
Среднее арифметико - геометри -
ческое 21
— значение порядка t 29
Субаддитивность 40
Сумма порядка t 29
Схема конечно - разностная 211 —
213
Схемы логических связей 113
Теорема Банаха — Штейнгау -
за , частный случай 145 , 166
— Лагранжа — Бельтрами 89
— Ляпунова 163
— Мора и Нолля 70
— о вогнутости для матриц 94 ,
95
— — минимаксе фон Неймана
169
— — среднем обобщенная Герт -
мана и Винтнера 204
— представления для |A|Vn 104
— разделения Коши —
Пуанкаре 112
— резонансная Ландау 165
— Ролля , обобщение 201
— суммирования Гурвица —
Зильбермана — Теплица 166
Теория диссипативных
операторов 140
Тождество Лагранжа 12
— Липшица 130
Уравнение Берджерса 214
— дифференциальное векторно -
матричное 185 , 191 — 194

270
Предметный указатель
Уравнение потенциала 213
— Риккати 216 , 248 , 250
— характеристическое 106
— эллиптическое 206
Условие Шура 51
Форма квадратичная 86
— — каноническая 102
— — представление в виде
суммы квадратов 88 , 89
— — эрмитова 86
— полная полярная
многочлена 58
Формула представления 100
— Абеля — Бруначчи 50
Функция выпуклая 29 , 30
строго 47
— матричная монотонная 125
— — экспоненциальная 191 ,
192
Функция опорная 46
— положительная
действительная 125
— положительно определенная
161
— полярная 46
— симметрическая
элементарная 52 , 55
— субгармоническая 203
— супергармоническая 203
Число характеристическое , ми -
нимакс - определение 85
Ядро воспроизводящее 162
t — норма 29

ОГЛАВЛЕНИЕ
Предисловие к русскому изданию 5
Предисловие 7
Г л а в а I . Основные неравенства и родственные вопросы
§ 1 . Введение 9
§ 2 . Неравенство Коши 10
§ 3 . Тождество Лагранжа 12
§ 4 . Неравенство между арифметическим и
геометрическим средними 12
§ 5 . Индукция вверх и вниз 13
§ 6 . Анализ и множители Лагранжа . . . . . . . . 15
§ 7 . Функциональные уравнения 15
§ 8 . Вогнутость 16
§ 9 . Мажоризация — доказательство Бора 17
§ 10 . Доказательство Гурвица 19
§ 11 . Доказательство Элерса 20
§ 12 . Арифметико - геометрическое среднее Гаусса .
Элементарные симметрические функции 21
§ 13 . Доказательство Якобсталя 23
§ 14 . Одно фундаментальное соотношение . . . . . . 24
§ 15 . Неравенство Юнга 27
§ 16 . Средние Mt (х , а) и суммы St(x) 28
§ 17 . Неравенства Гёльдера и Минковского 33
§ 18 . Обобщения классических неравенств 35
§ 19 . Квазилинеаризация 39
§ 20 . Неравенство Минковского 41
§ 21 . Другое неравенство Минковского 42
§ 22 . Неравенство Минковского для 0<р<1 43
§ 23 . Неравенство Беккенбаха 44
§ 24 . Неравенство Дрешера 45
§ 25 . Неравенство Минковского — Малера 46
§ 26 . Квазилинеаризация выпуклых и вогнутых функций 47
§ 27 . Другой тип квазилинеаризации 48
§ 28 . Неравенство Карамата 48
§ 29 . Преобразование Шура 49
§ 30 . Доказательство неравенства Карамата 49
§ 31 . Неравенство Островского 50
§ 32 . Континуальные аналоги 51

272 Оглавление
§ 33 . Симметрические функции 52
§ 34 . Еще одно неравенство 55
§ 35 . Некоторые результаты Уайтли 55
§ 36 . Гиперболические многочлены 56
§ 37 . Неравенство Гординга 57
§ 38 . Примеры гиперболических многочленов 58
§ 39 . Пространства Лоренца 59
§ 40 . Обратные неравенства 60
§ 41 . Пространство Lv 63
§ 42 . Многомерный случай 65
§ 43 . Обобщения Фавара — Бервальда . . . . . . . 65
§ 44 . Другие обращения теоремы Коши 68
§ 45 . Уточнения неравенств Коши — Буняковского —
Шварца 69
§ 46 . Теорема Мора и Нолля 70
§ 47 . Вывод новых неравенств из старых 71
§ 48 . Уточнение неравенства между арифметическим и
геометрическим средними 72
§ 49 . Неравенства с чередующимися знаками 72
§ 50 . Неравенство Стеффенсена 73
§ 51 . Неравенство Брунка—Олкина 74
§ 52 . Обобщения неравенства Стеффенсена 74
Библиография и дополнения 75
Глава II . Положительно определенные матрицы ,
характеристические числа и положительные матрицы
§ 1 . Введение 84
§ 2 . Положительно определенные матрицы 86
§ 3 . Необходимое условие положительной
определенности 87
§ 4 . Представление в виде суммы квадратов 88
§ 5 . Необходимое и достаточное условие
положительной определенности 89
§ 6 . Определители Грама 90
§ 7 . Вычисление одного несобственного интеграла . . . 93
§ 8 . Комплексные матрицы с положительно
определенной вещественной частью 94
§ 9 . Одна теорема о вогнутости 94
§ 10 . Неравенство , относящееся к минорам 95
§ 11 . Неравенство Адамара 96
§ 12 . Неравенство Сасса 97

Оглавление 273
§ 13 . Теорема о представлении определителя эрмитовой
матрицы 97
§ 14 . Следствия 98
§ 15 . Интегралы Ингама — Зигеля и их обобщения . . . 98
§ 16 . Групповая инвариантность и формулы
представления 100
§ 17 . Неравенство Бергстрома 100
§ 18 . Одно обобщение 101
§ 19 . Каноническая форма 102
§ 20 . Обобщение неравенства Бергстрома 103
§ 21 . Теорема представления для \А\г/п 104
§ 22 . Одно неравенство Минковского 105
§ 23 . Обобщение , принадлежащее Фань Цзы 105
§ 24 . Обобщение , принадлежащее Оппенгейму . . . . 106
§ 25 . Отношение Рэлея 106
§ 26 . Минимакс - теорема Фишера 107
§ 27 . Еще одна теорема представления 109
§ 28 . Одно неравенство Фань Цзы 110
§ 29 . Аддитивный аналог 111
§ 30 Результаты , относящиеся к характеристическим
числам Л , АА* и (Л + Л*)/2 111
§ 31 . Теорема разделения Коши—Пуанкаре . . . . 112
§ 32 . Одно неравенство для %п%п— 1 . . . %k 112
§ 33 . Обсуждение . 113
§ 34 . Аддитивное неравенство 113
§ 35 . Мультипликативное неравенство , вытекающее из
аддитивного 114
§ 36 . Дальнейшие результаты 115
§ 37 . Составные или присоединенные матрицы . . . . 116
§ 38 , Положительные матрицы 117
§ 39 . Вариационная характеристика р(А) 118
§ 40 . Другая форма для р(А) 121
§ 41 . Некоторые следствия 121
$ 42 . Входные - выходные (input - output) матрицы . . 122
§ 43 . Обсуждение 123
§ 44 . Добавления 123
§ 45 . Матрицы и гиперболические уравнения 124
§ 46 . Определители , не обращающиеся в нуль , и
распределение характеристических чисел 124
§ 47 . Монотонные матричные функции в смысле Лёвнера 125
§ 48 . Преобразование , уменьшающее число перемен знака 126

274 Оглавление
§ 49 . Области положительности 126
Библиография и дополнения 127
Глава III . Пространства моментов и резонансные теоремы 141
§ 1 . Введение 141
§ 2 . Моменты 146
§ 3 . Выпуклость 147
§ 4 . Примеры выпуклых пространств 149
§ 5 . Примеры невыпуклых пространств 150
§ 6 . К определению выпуклых множеств 150
§ 7 . Пространство L9 . Результат Ф . Рисса 151
§ 8 . Ограниченная вариация 153
§ 9 . Положительность 155
§ 10 . Представление через квадраты 156
§11 . Неотрицательные тригонометрические и
рациональные полиномы 158
§ 12 . Положительно определенные квадратичные формы
и моментные последовательности 158
§ 13 . Исторические замечания 159
§ 14 . Положительно определенные последовательности . 160
§ 15 . Положительно определенные функции 161
§ 16 . Воспроизводящие ядра 162
§ 17 . Невыпуклые пространства 163
§ 18 . «Резонансные» теоремы Ландау 165
§ 19 . Теорема Банаха — Штейнгауза 166
§ 20 . Теорема Минковского 167
§ 21 . Теория линейных неравенств 168
§ 22 . Обобщения 169
§ 23 . Теорема фон Неймана о минимаксе 169
§ 24 . Лемма Неймана — Пирсона 170
§ 25 . Ортогональные проекции 173
§ 26 . Эквивалентность процессов минимизации и
максимизации 174
Библиография и дополнения . 175
Глава IV . Положительные операторы 184
§ 1 . Введение 184
§ 2 . Линейные дифференциальные уравнения первого
порядка 187
§ 3 . Обсуждение 188
§ 4 . Фундаментальный результат теории устойчивости 188

Оглавление 275
§ 5 . Неравенства Бихари и Лангенхопа 189
§ 6 . Матричные аналогии 191
§ 7 . Доказательства Тауски 192
§ 8 . Переменные матрицы 193
§ 9 . Обсуждение 194
§ 10 . Результат Чаплыгина 194
§11 . Конечные интервалы 196
§ 12 . Вариационное доказательство 196
§ 13 . Обсуждение 198
§ 14 . Линейные дифференциальные уравнения
произвольного порядка 199
§ 15 . Положительность линейных дифференциальных
операторов высших порядков 200
§ 16 . Некоторые результаты Пойа 201
§ 17 . Обобщенная выпуклость 202
§ 18 . Обсуждение 203
§ 19 . Обобщенная теорема о среднем Гартмана и Винт -
нера 204
§ 20 . Обобщенное разложение Тейлора 205
§ 21 . Положительность операторов 206
§ 22 . Эллиптические уравнения 206
§ 23 . Положительные воспроизводящие ядра 207
§ 24 . Монотонность средних значений 207
§ 25 . Положительность параболических операторов . . 209
§ 26 . Конечно - разностные схемы 211
§ 27 . Уравнение потенциала 213
§ 28 . Обсуждение 213
§ 29 . Неравенства Хаара — Вестфаля — Проди . . . . 214
§ 30 . Некоторые неравенства Вендроффа 214
§ 31 . Результаты Вейнбергера — Бохнера 216
§ 32 . Преобразования , понижающие число перемен
знака 216
§ 33 . Квазилинеаризация 216
§ 34 . Устойчивость операторов 217
§ 35 . Различные результаты 218
Библиография и дополнения 219
Глава V . Неравенства для дифференциальных операторов 228
§ 1 . Введение 228
§ 2 . Некоторые неравенства Секефальви - Надя . . . . 231
£ 3 . Неравенства , связывающие и , и' , и" 232
§ 4 . Неравенство для и , иШ и и(п) 226

276
Оглавление
§ 5 . Другие неравенства для и , и' и и" 236
§ 6 . Неравенство Гальперина и фон Неймана и его
обобщения 238
§ 7 . Аналоги результатов Секефальви - Надя 241
§ 8 . Неравенство Карлсона 242
§ 9 . Обобщения неравенства Карлсона 242
§ 10 . Неравенство Виртингера и связанные с ним
результаты 245
§ 11 . Доказательство с помощью рядов Фурье 246
§ 12 . Теория Штурма—Лиувилля 246
§ 13 . Интегральные тождества . * 247
§ 14 . Результаты Колаутти 249
§ 15 . Дифференциальные уравнения в частных
производных 249
§ 16 . Использование матриц 250
§ 17 . Высшие производные и высшие степени 251
§ 18 . Дискретные аналоги Фаня , Тауски и Тодда . . . 252
§ 19 . Дискретный случай . Вторые разности 253
§ 20 . Дискретный вариант неравенства Норткотта —
Беллмана 254
§ 21 . Обсуждение 255
Библиография и дополнения 256
Именной указатель 261
Предметный указатель 267
Э . Беккенбах , Р . Беллман
НЕРАВЕНСТВА
Редактор Е . М Дмитренко Художник А . , Г . Антонова .
Технический редактор В . П . Сизова
Сдано в производство 2/ХП 64 г . Подписано к печати 27/III 65 г .
Бумага 84хЮ81/з2=4 , 3 бум . л . 17 , 25 печ . л . Уч . - изд . л . 12 , 75 . Изд . № 1/3099
Цена I р . 9 к . Зак . 642
ИЗДАТЕЛЬСТВО «МИР»
Москва , 1 - й Рижский пер . , 2
Московская типография № 16 Главполиграфпрома Государственного комитета
Совета Министров СССР по печати . Москва , Трехпрудный пер . , д . 9