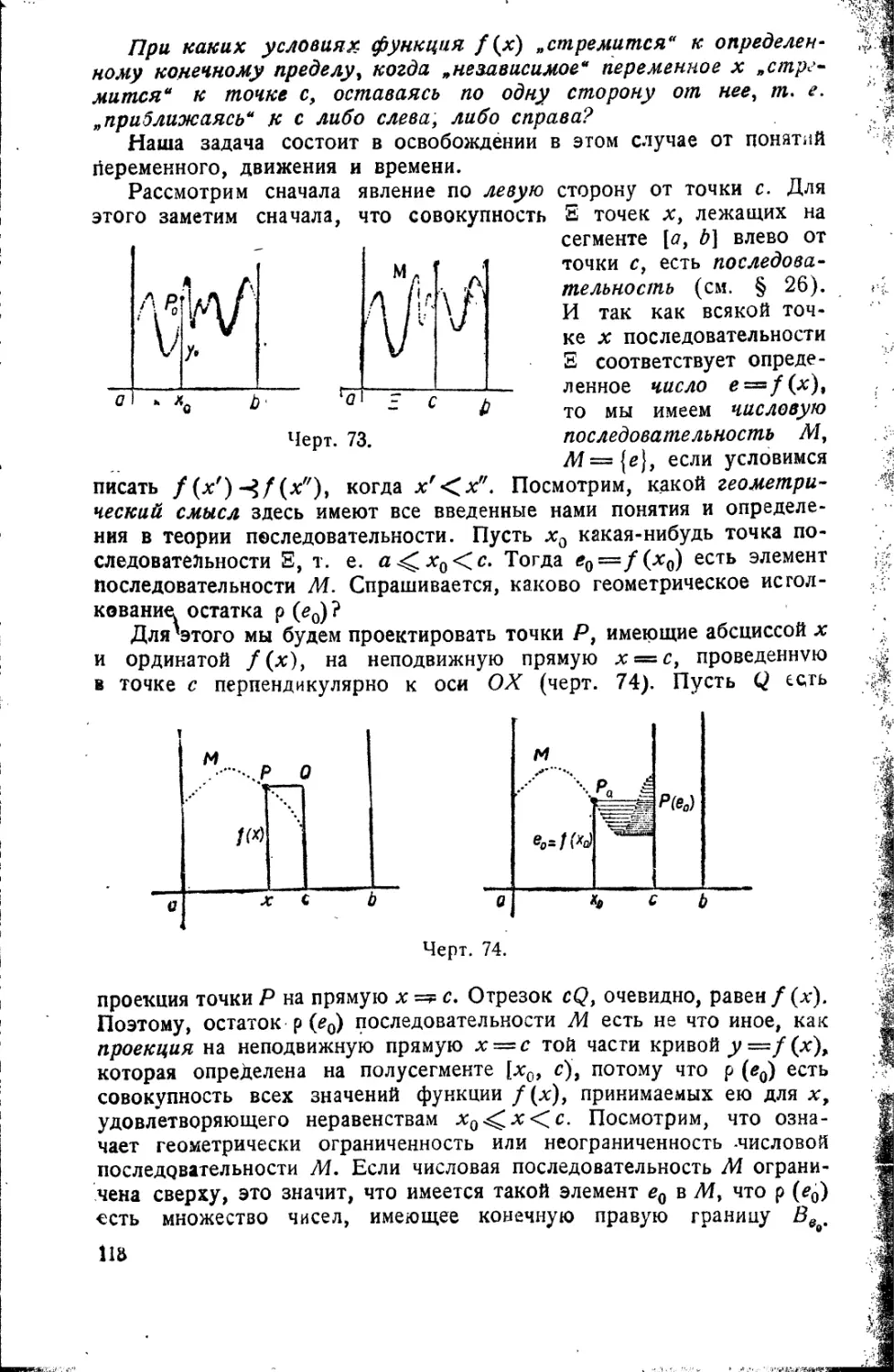
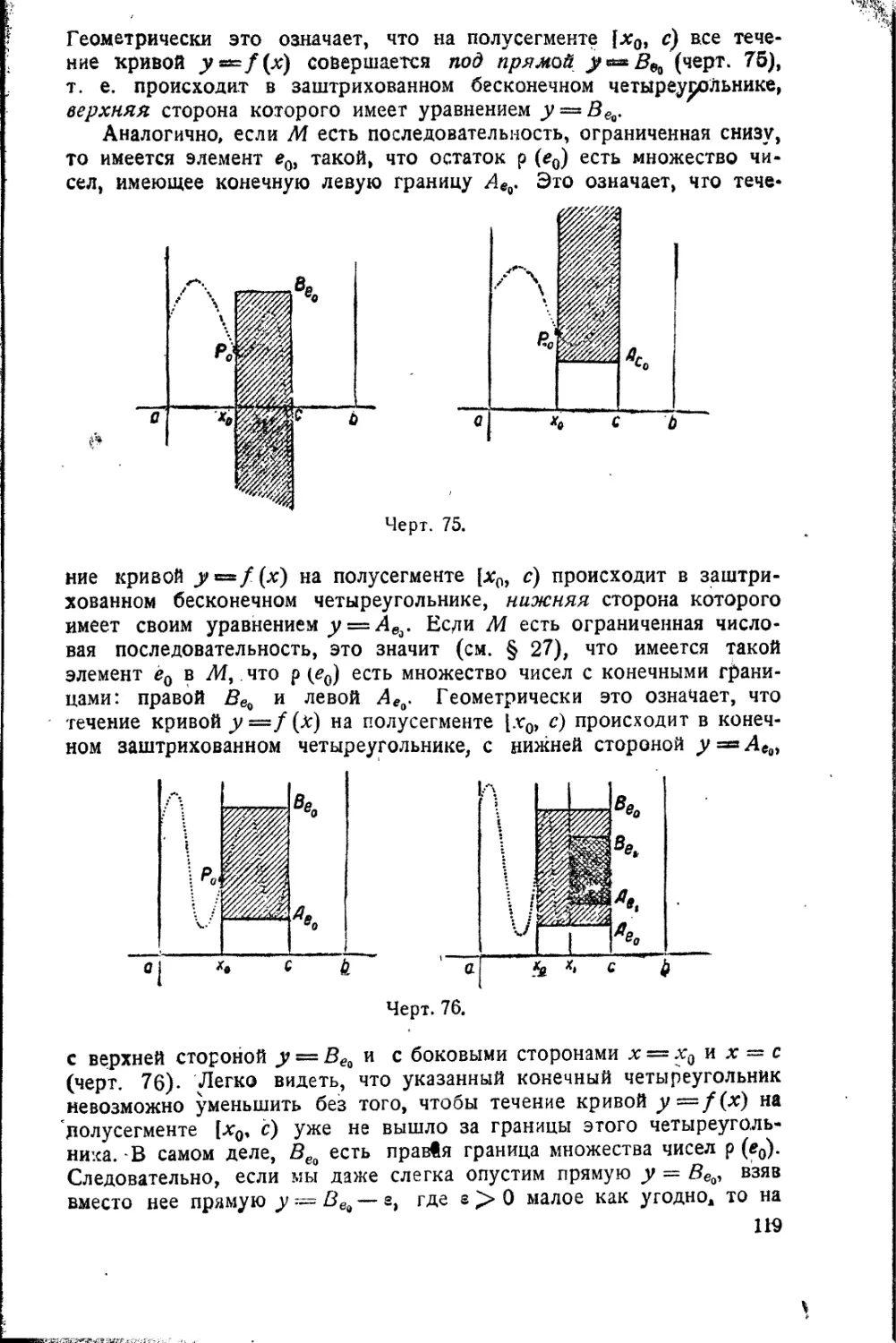
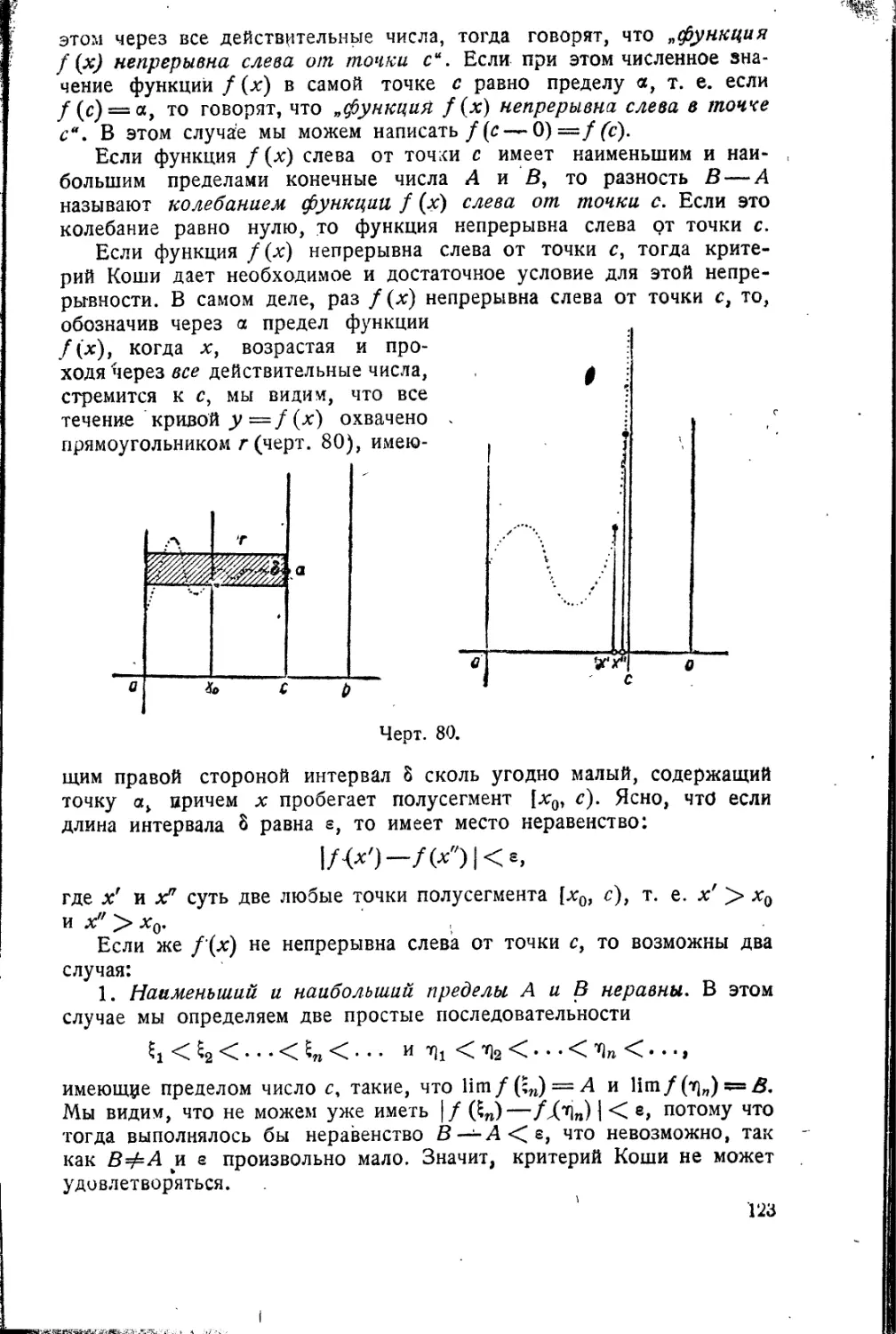
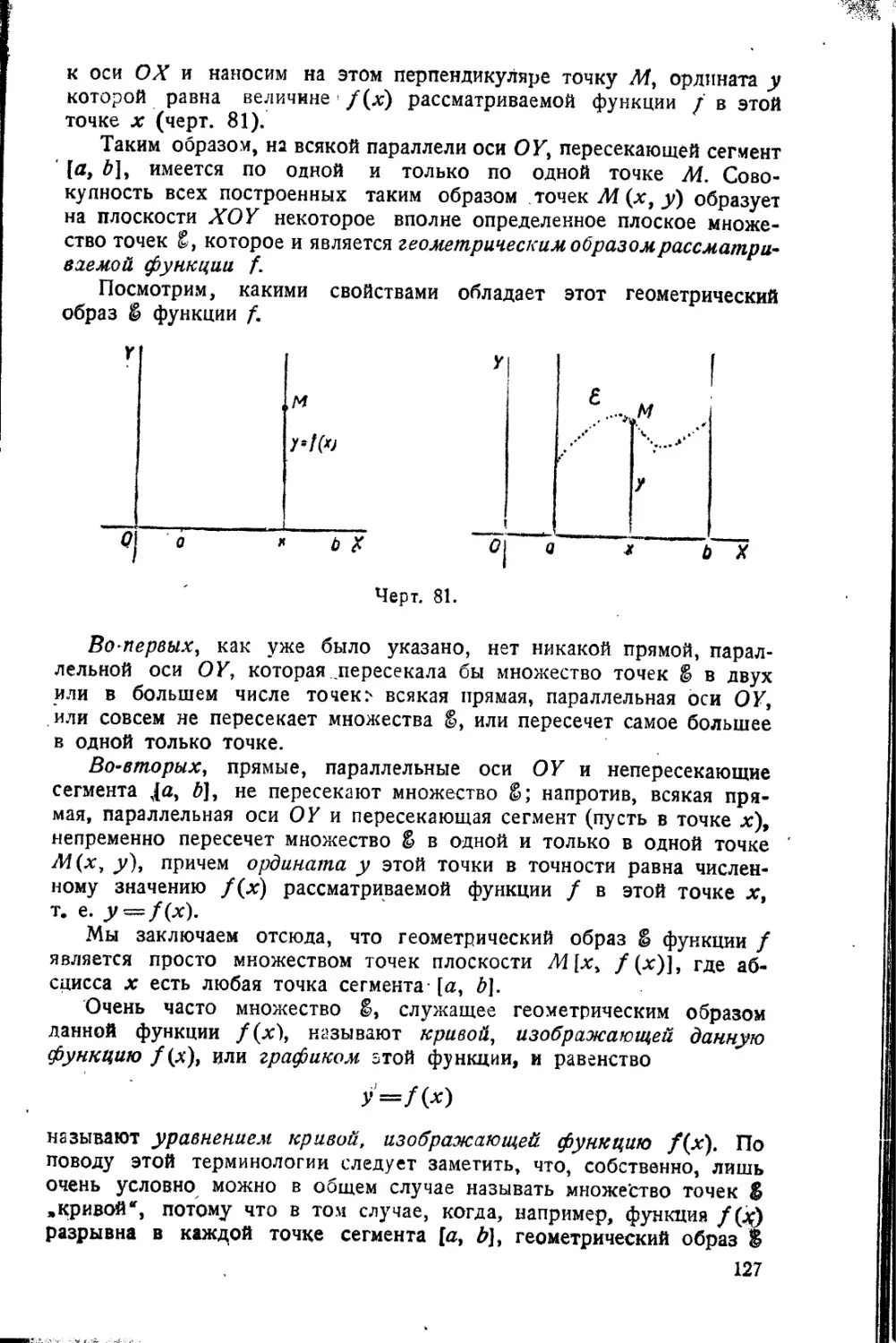
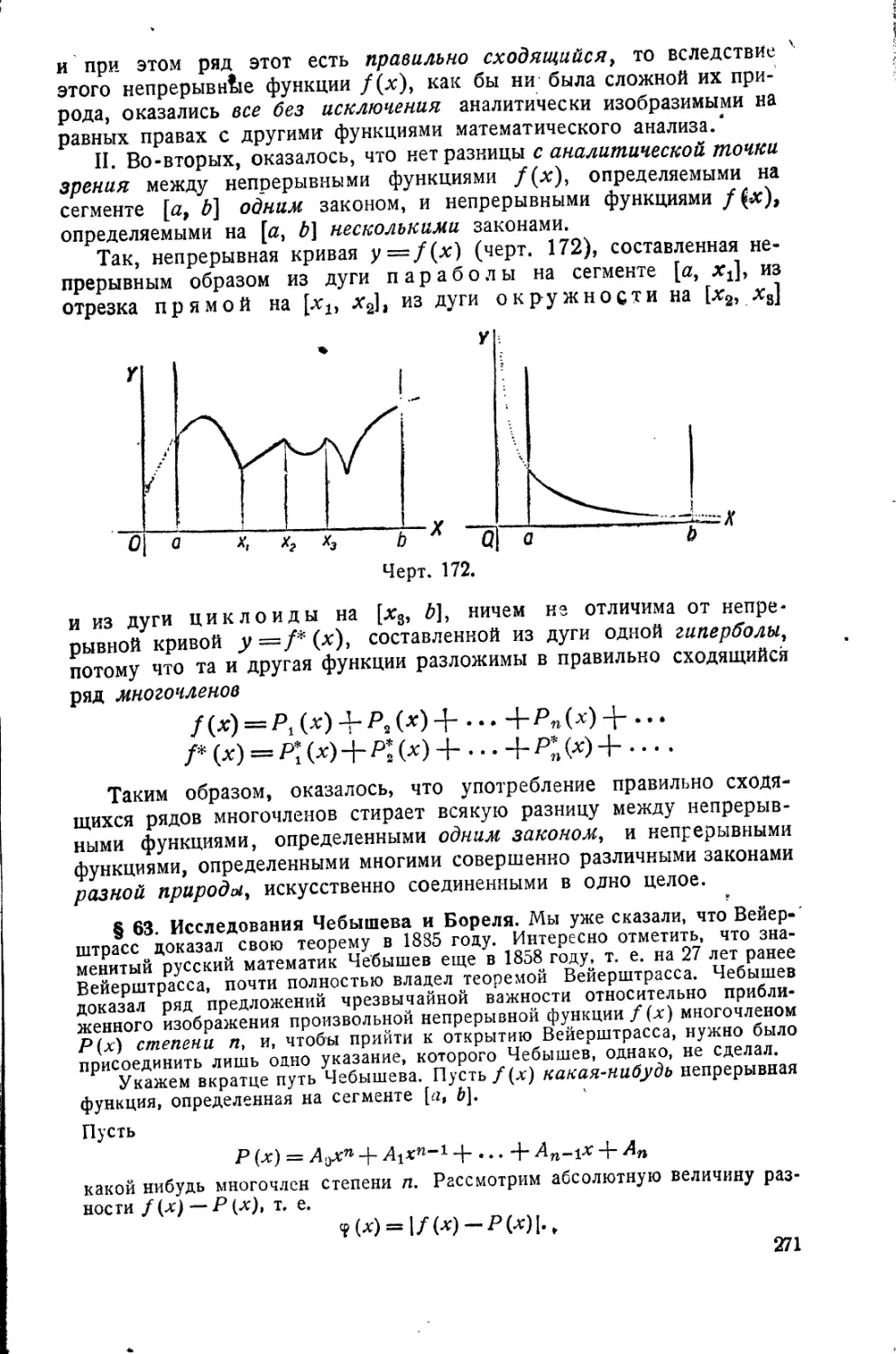
Текст
Акад. Н. Н. ЛУЗИН
ТЕОРИЯ ФУНКЦИЙ
ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
ОБЩАЯ ЧАСТЬ
УЧЕБНОЕ ПОСОБИЕ ДЛЯ ПЕДВУЗОВ
ИЗДАНИЕ ВТОРОЕ
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
. МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
М О С К В А * 1948
Утверждено
Министром просвещения РСФСР
и переизданию 4 апреля 1947 z.t протокол №165.
#
Предисловие
ОГЛАВЛЕНИЕ.
5
Стр.
Глава
ность •
I. Множество и мощ-
§ 9.
§10.
'§11.
7
9
И
15
Понятие множества . . .
Актуальная бесконечность.
Число и мощность • . . .
Счетные множества . . .
Арифметика счетной
мощности ~. . ♦ 25
Несчетные множества • . 26
Мощность континуума . . 28
Теорема о мощности про- *
межуточного множества . 37
Применение -критерия
равенства мощностей к
разысканию мощности
пространств многих измерений 43
Арифметика мощности
континуума 48
О существовании, высших
мощностей 49
Глава П. Множества точек* 55
Линейные множества . . 55
Сегменты и интервалы . * 56
Ограниченные и
неограниченные множества . • . , 57
Границы множества ... 58
Предельные точки и точки
конденсации 60
§ 17. Производное множество .
Замкнутые и совершенные
множества .С ♦ 63
§ 18. Строение замкнутых и
совершенных множеств ... 66
§ 19. Мера замкнутых и
совершенных множеств .... 69
§ 20. Мощность замкнутых и
совершенных множеств , , 73
§ 21. Категория ........ 84
§ 22. Множества точек в
многомерных пространствах» ♦ 85
1* .
Глава III. Теория пределов. 97
§ 23. Необходимость
обоснования теории пределов ... 97
§ 24. Упорядоченные множества 97
§ 25. Последовательности . . . 100
§ 26.-Последовательности чисел. 102
§ 27. Неограниченные и
ограниченные числовые
последовательности 103
§ 28.» Пределы число вой
последовательности 103
§ 29. Лемма Бореля-Лебега и ее
ближайшие следствия . . 105
§ ЗО.с Наибольший и наименьший
пределы числовой
последовательности 107
§ 31, Непосредственное
отыскание наибольшего и
наименьшего пределов . . . 109
§ 32. Сходящиеся числовые
последовательности .... 110
§ 33. Конфинальные
под-последовательности 112
§ 34. Критерий сходимости
числовой последовательности. 115
§ 35. Приложения критерия Ко-
ши . 117
Глава IV* Функция и
непрерывность 125
§ 36. Понятие функции". ... 125
§ 37. Геометрическое
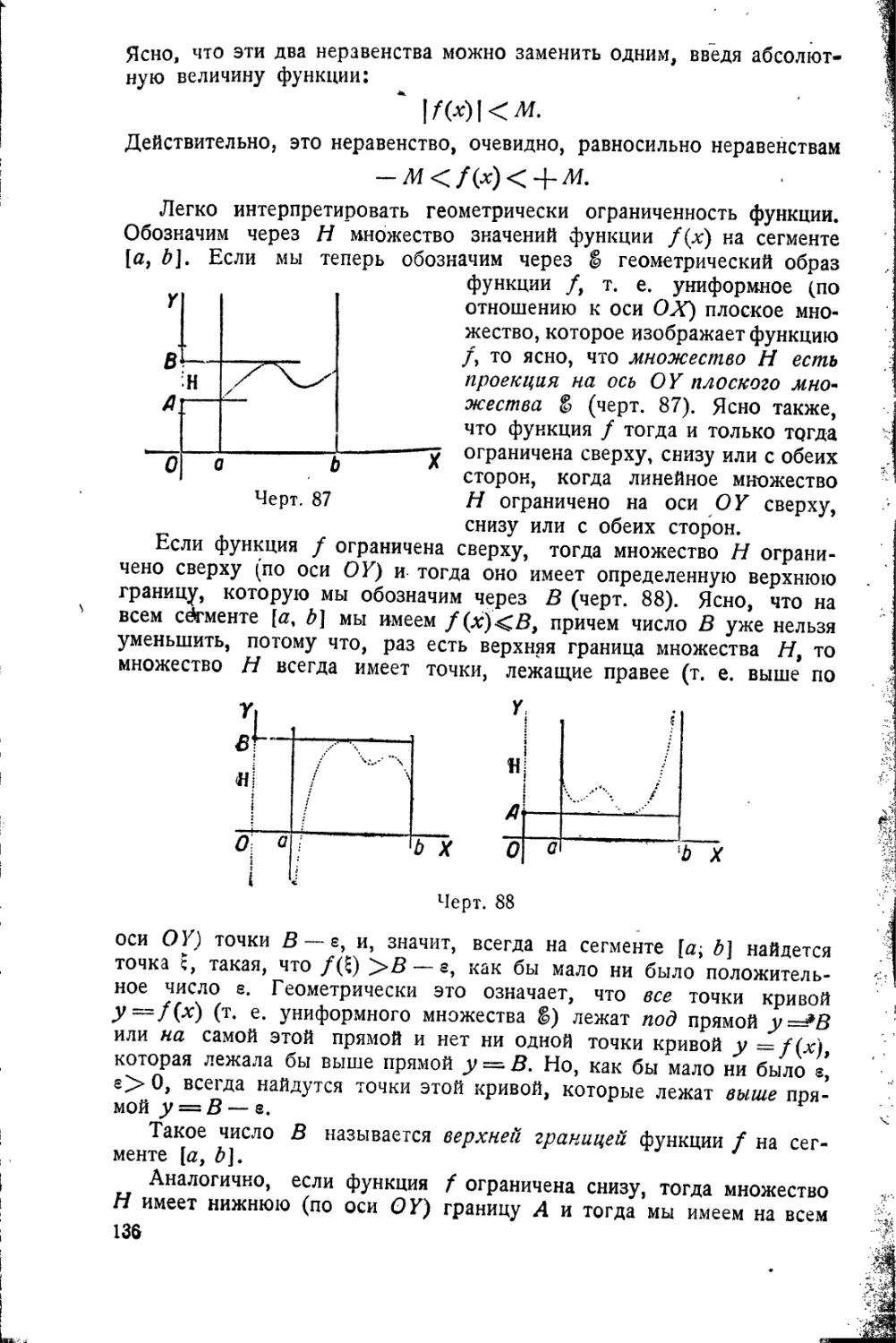
изображение функции 126
§ 38. Аналитическое выражение. 131
§ 39. Функции неограниченные
и ограниченные 135
§ 40. Верхняя и нижняя границы
функции в точке.
Колебание в точке 140
§ 41. Непрерывность 146
§ 42. Непрерывность справа и
слева •_*,•_,♦.•_.••,•.».,• 151
а
Стр.
§ 43. Непрерывность ц
стремление к пределу v 154
§ 44. Свойства непрерывных
функций 157
§ 45. Непрерывные функции
многих переменных 166
§ 46. Функции, непрерывные от
совокупности аргументов,
и функции, непрерывные
от каждого аргумента в
отдельности 172
§ 47ч. Пределы
последовательностей непрерывных функций. 181
Глава V. Непрерывные
кривые 193
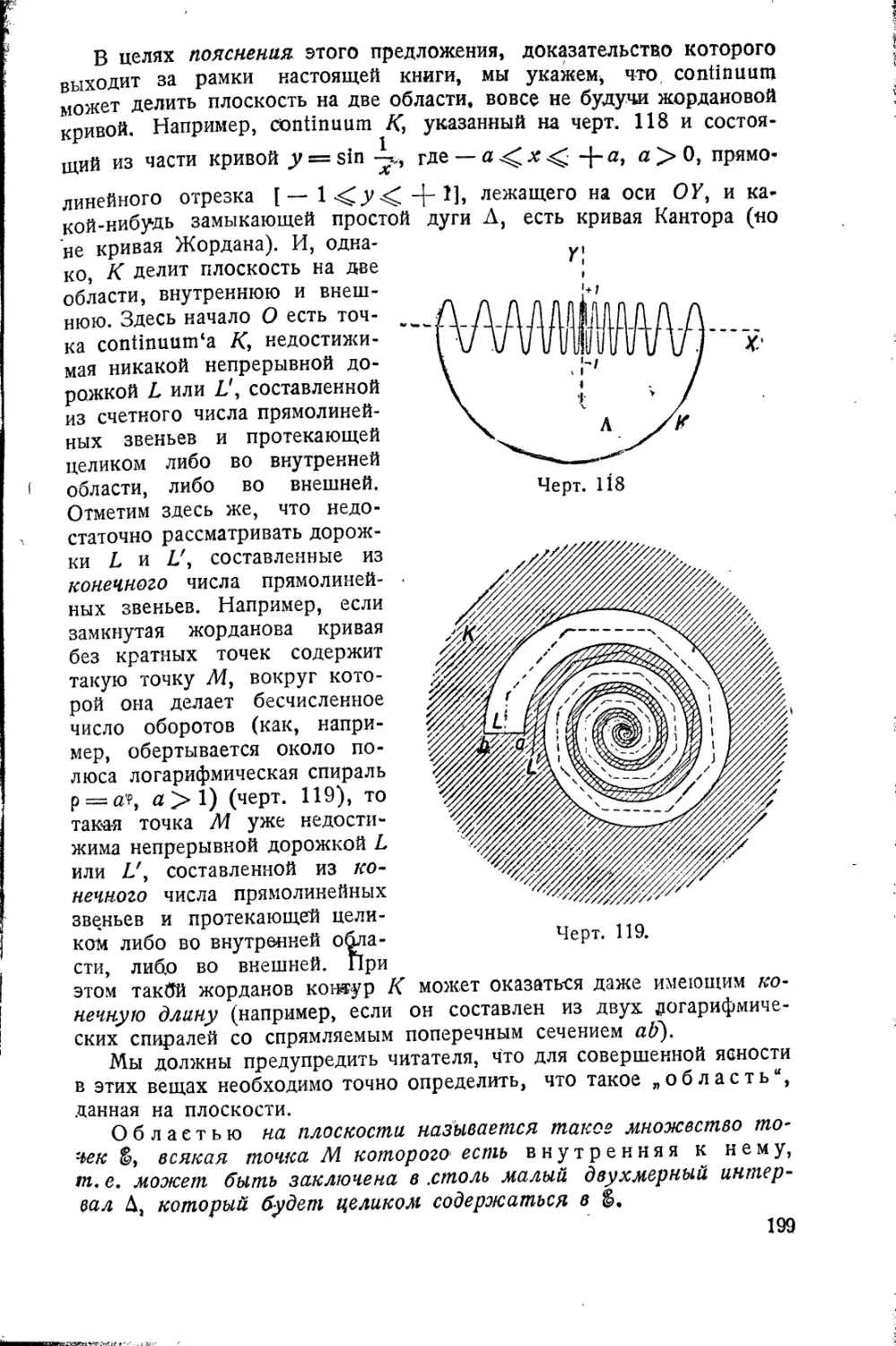
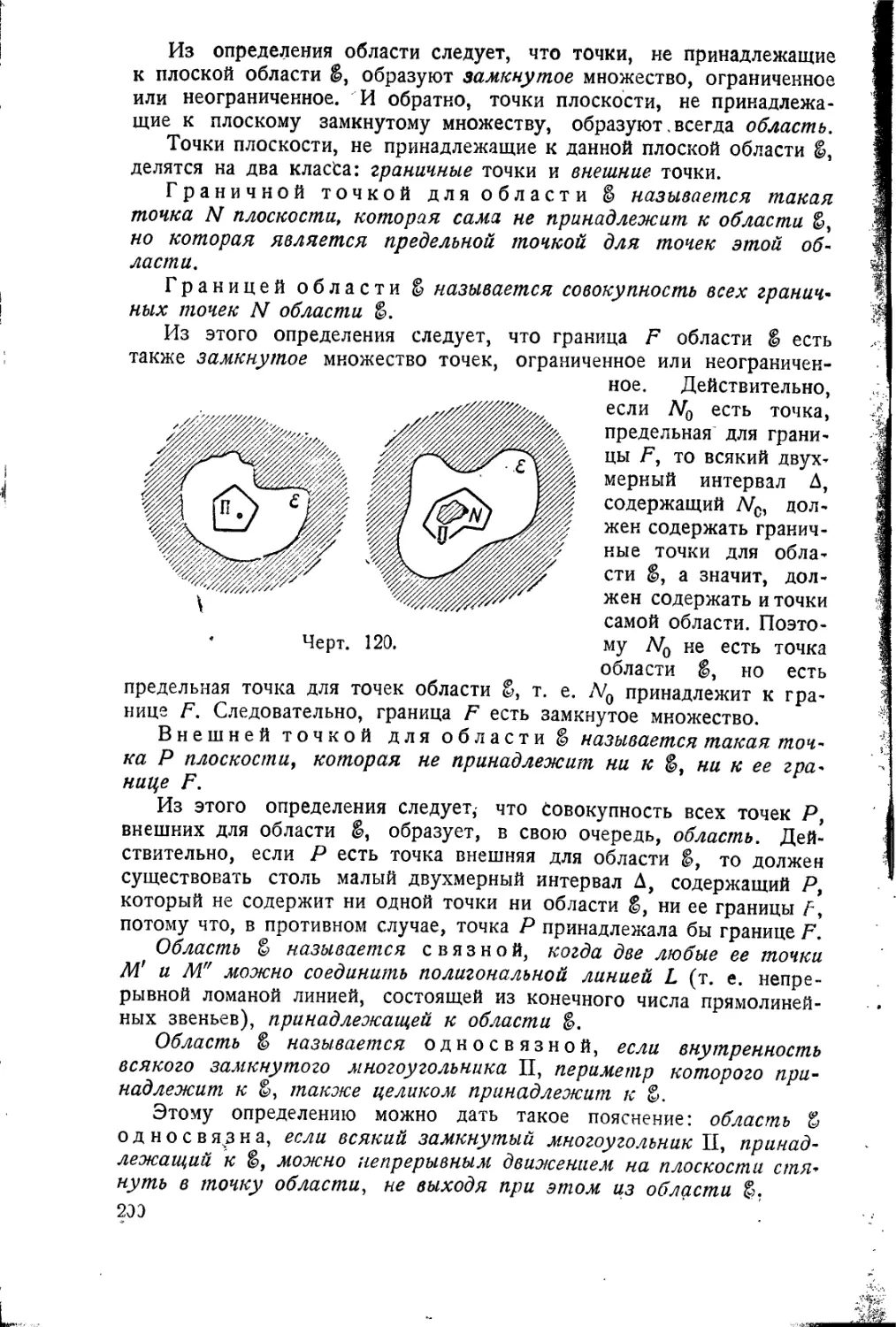
§ 48. Кривые Жордана и кривые
'Пеано 193
§ 49. Совершенные разрывные
множества 203
§ 50. Кривые Пеано 214
§ 51. Кривые Жордана и Пеано
в пространстве многих
измерении .*...,..•». 223
Г л а в а VI. Аналитическое
изображение непрерывных
функций . 227
§ 52. Функциональные ряды . . 227
§ 53. Правильно сходящиеся
ряды 228
§ 54., Усиление критерия пра-
' вильной сходимости
методом предварительной
группировки членов ряда 230
Стр.
Равномерная сходимость
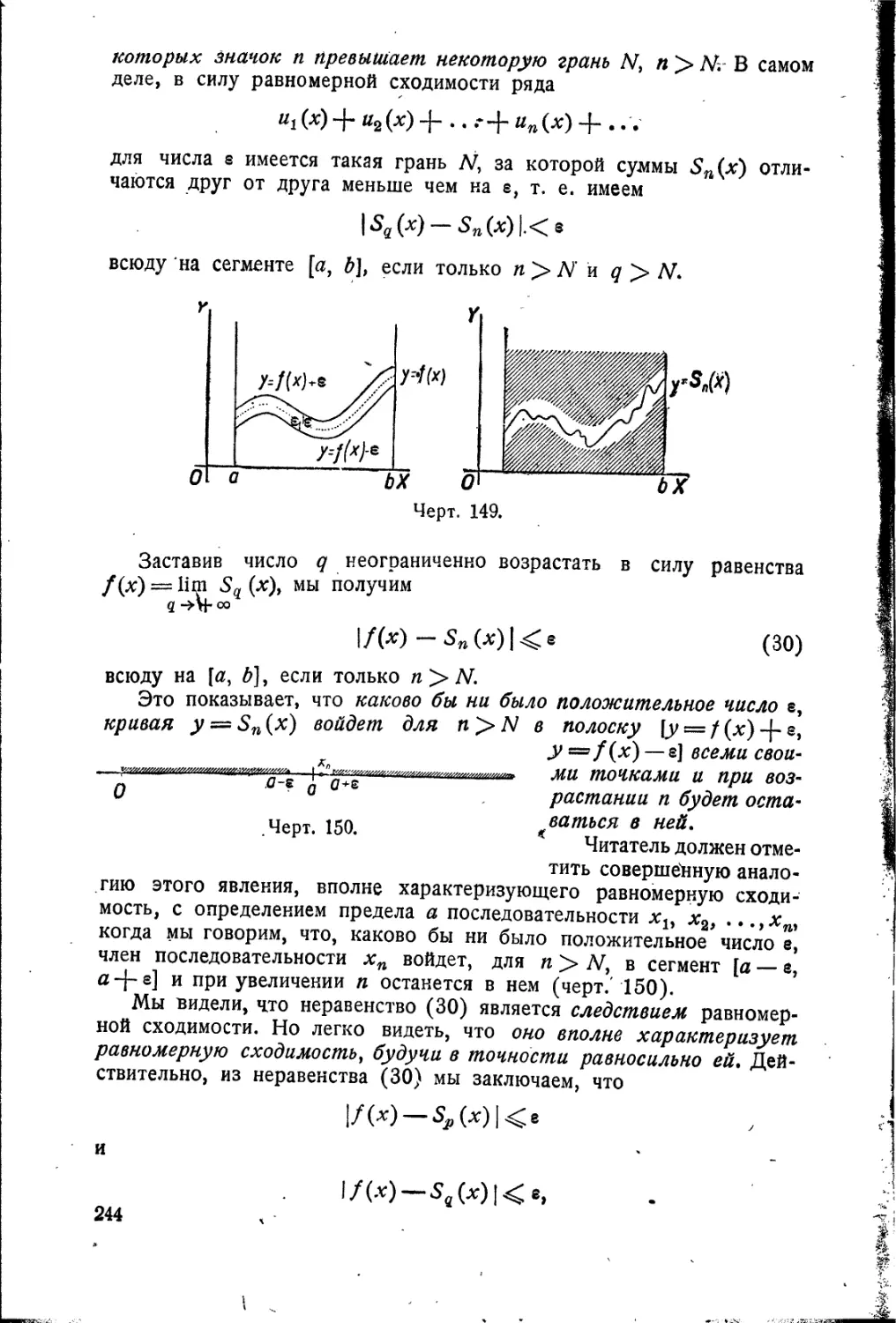
функциональных рядов . . 233
Равномерно сходящиеся
последовательности функций. 237
Исследование равномерной
сходимости . . 240
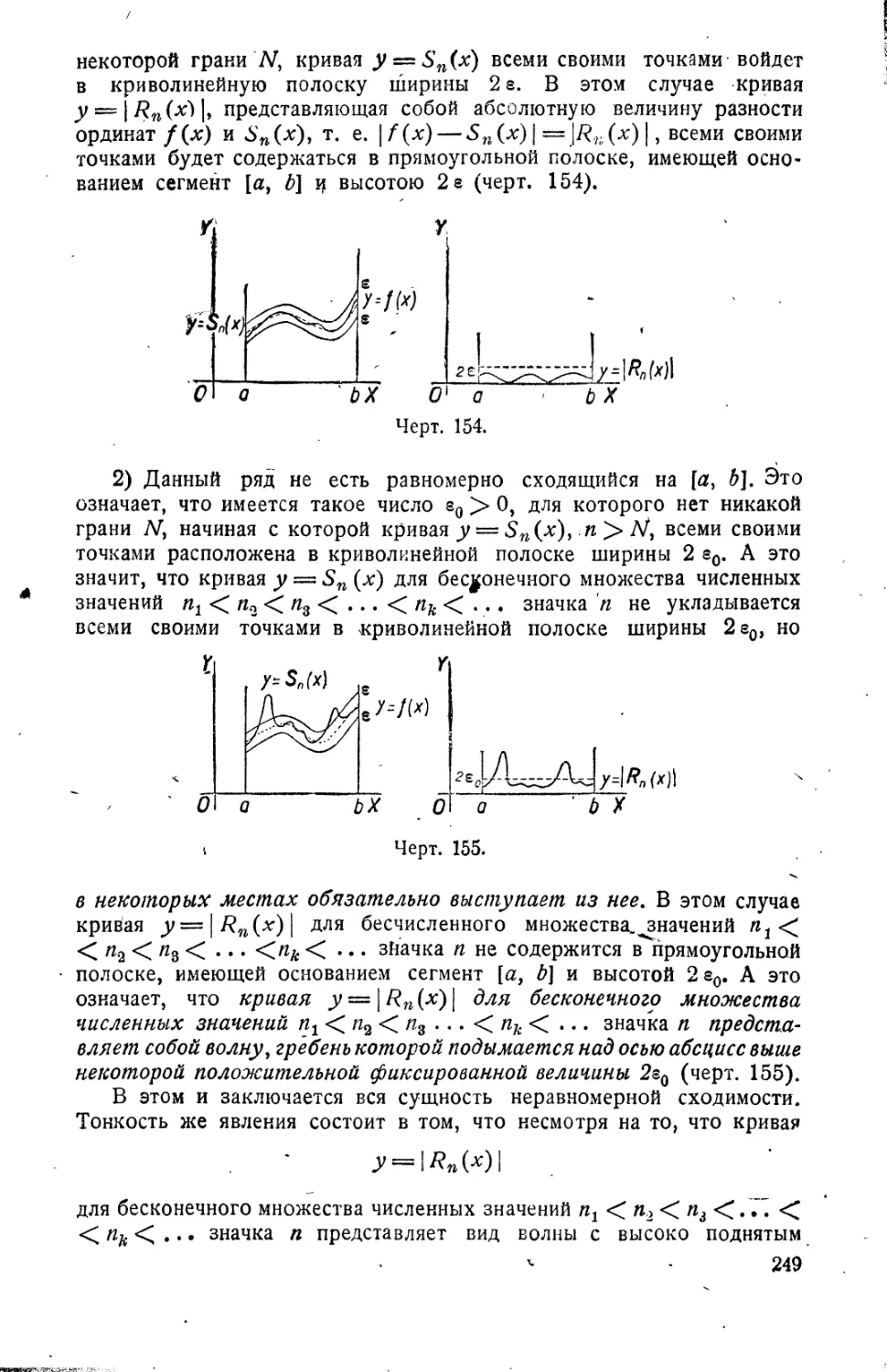
Исследование
неравномерной сходимости 248
Обобщенная равномерная
сходимость 252
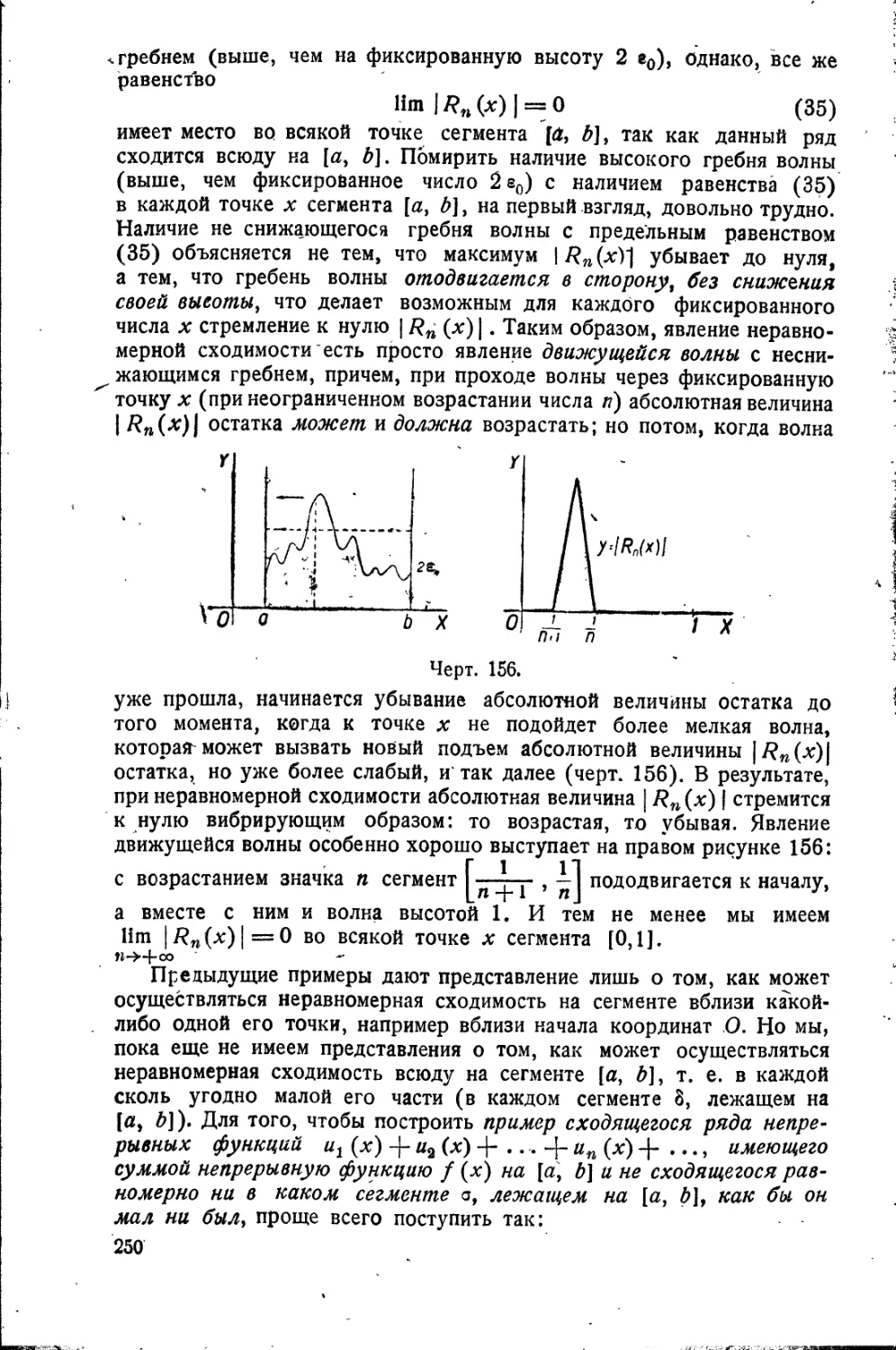
Квазиравномерная
сходимость 255
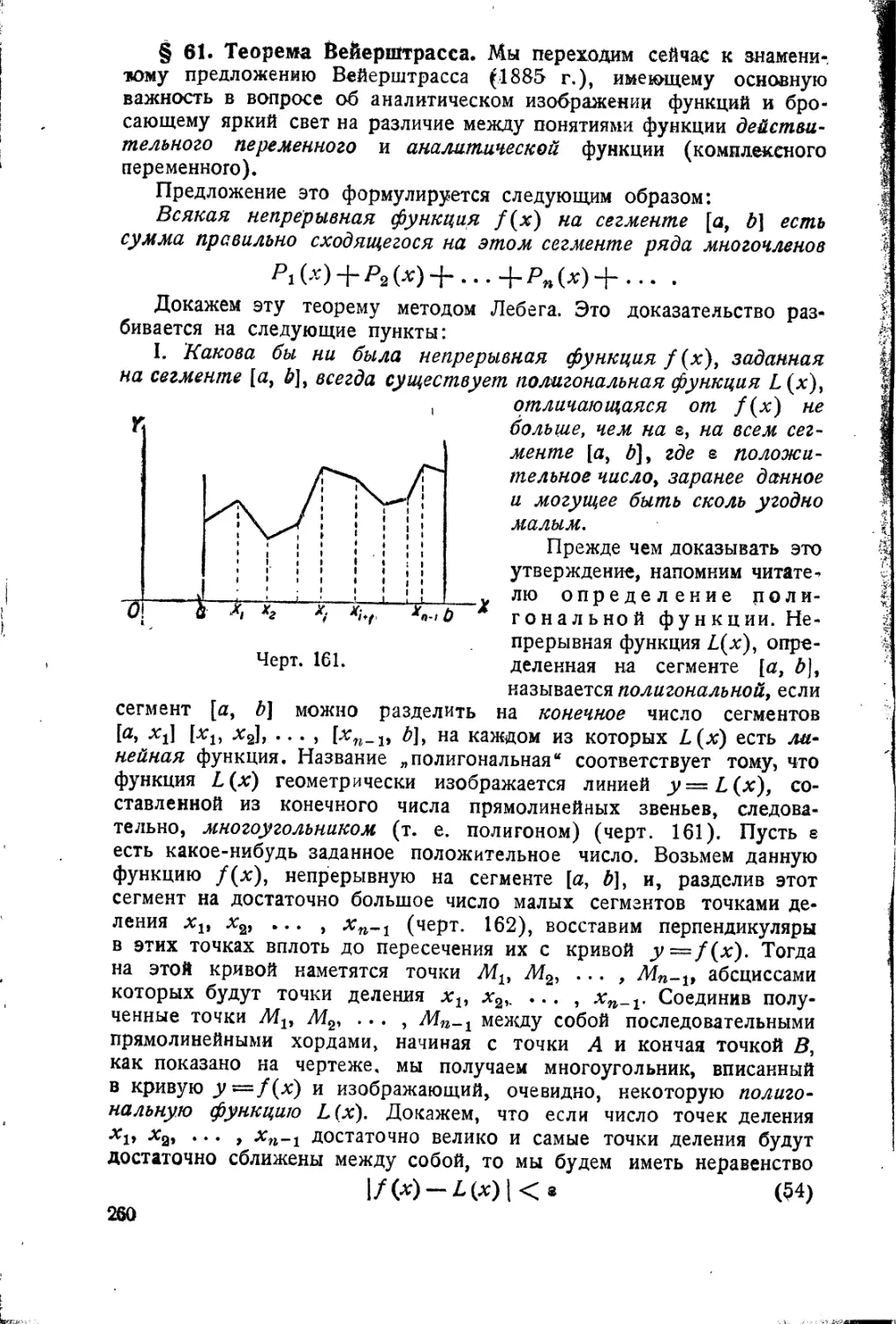
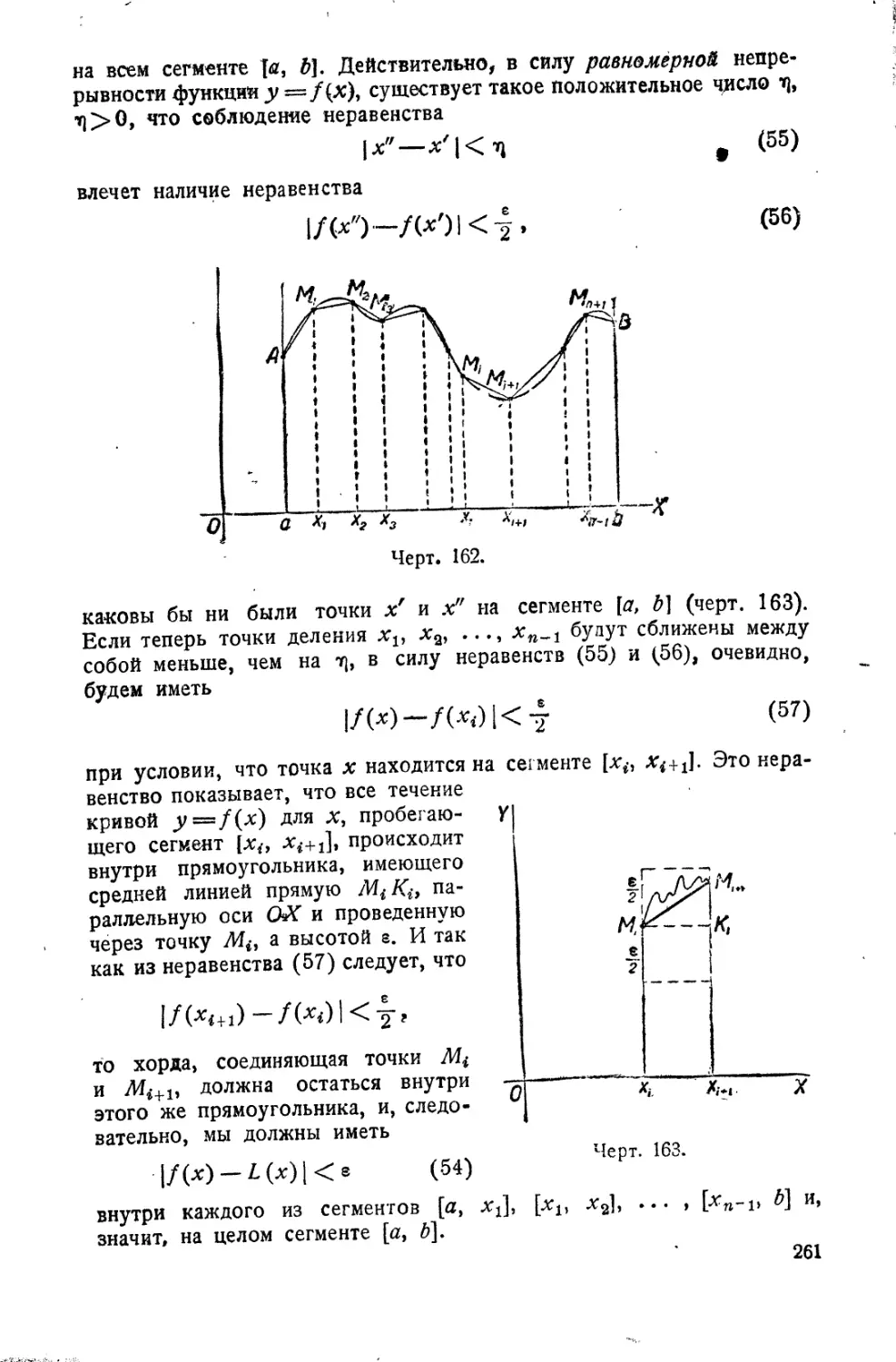
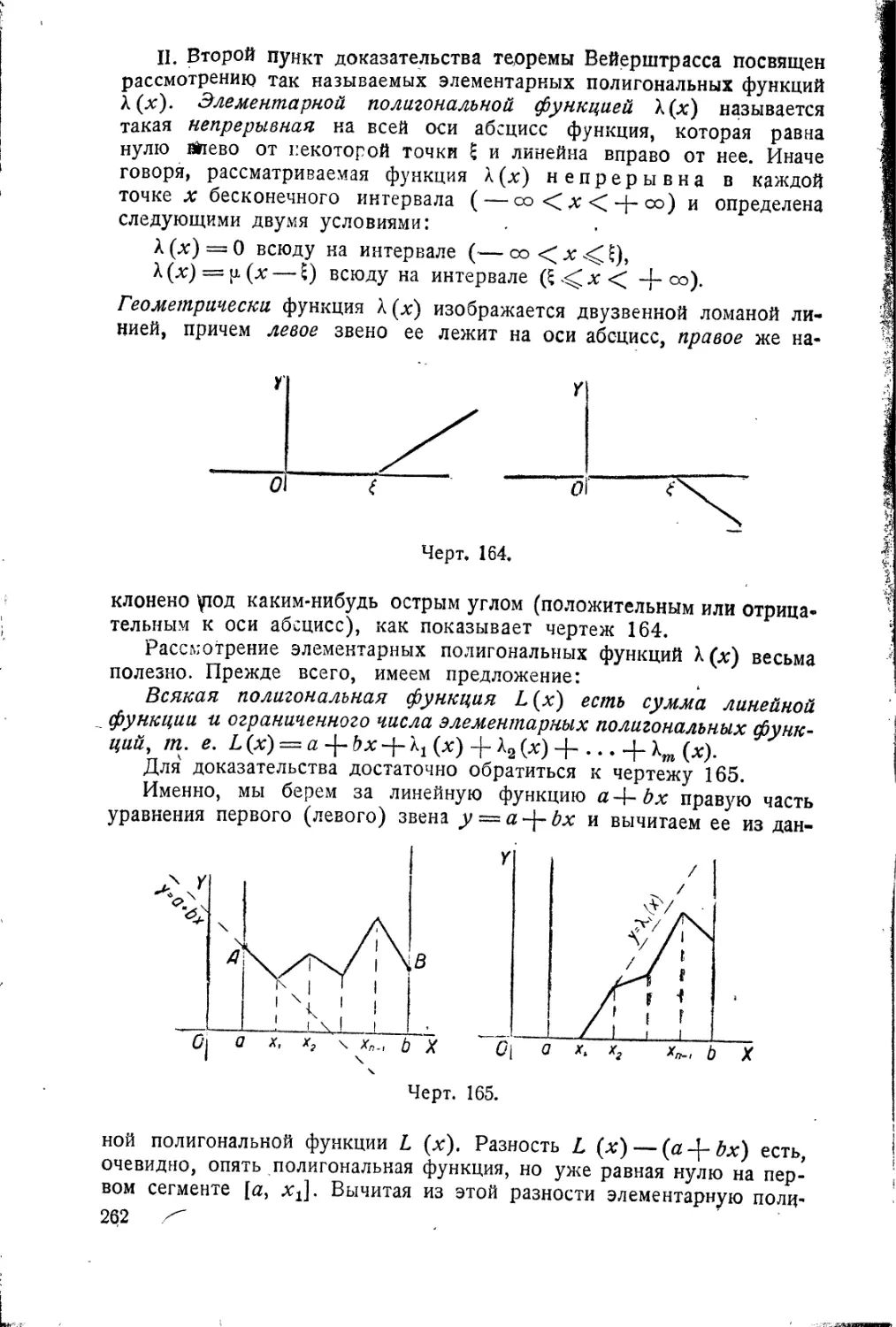
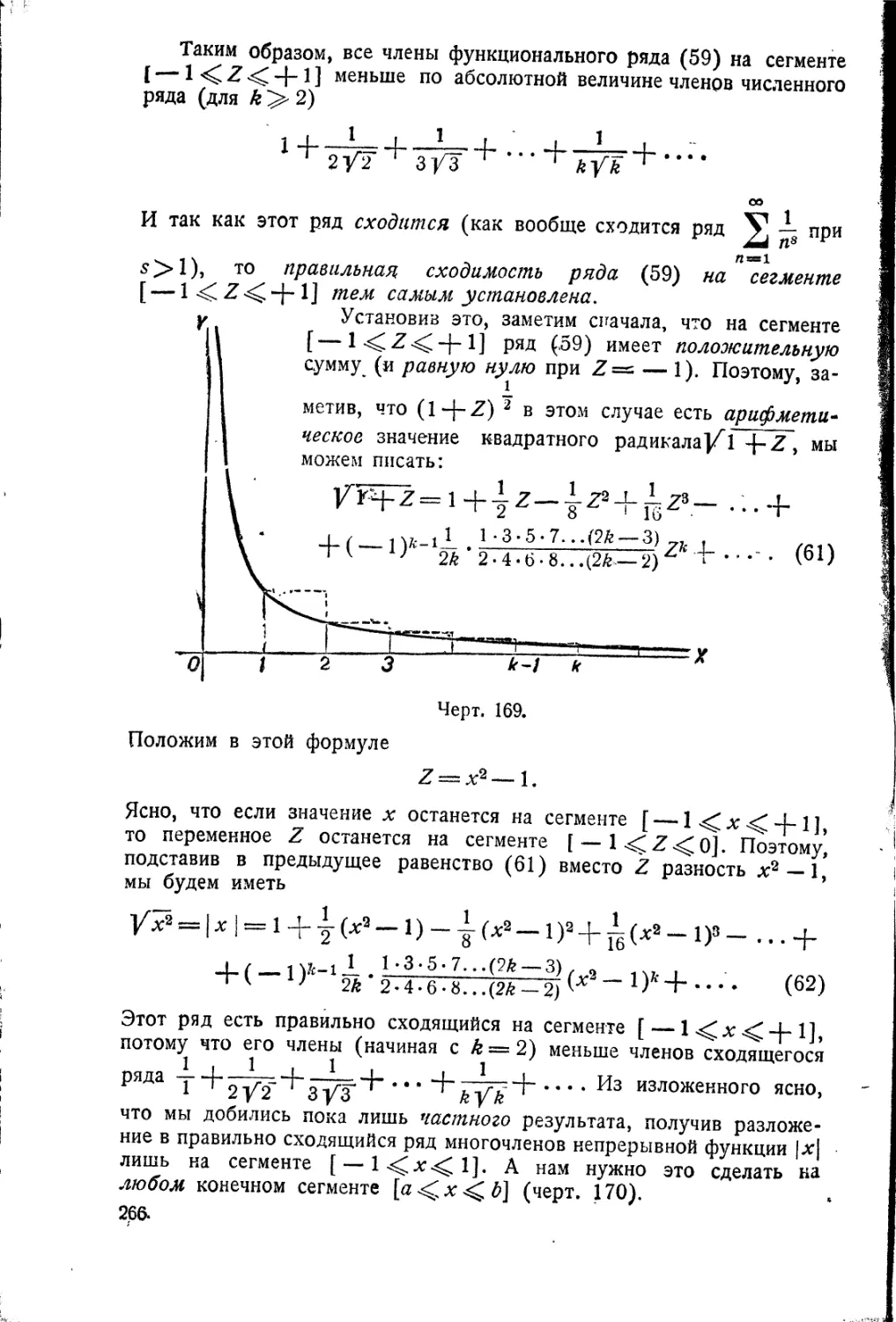
Теорема Вейерштрасса • 260
Следствия теоремы
Вейерштрасса 270
Исследования Чебышева
Уи, йореля . % „.*»., 271
Основная теорема
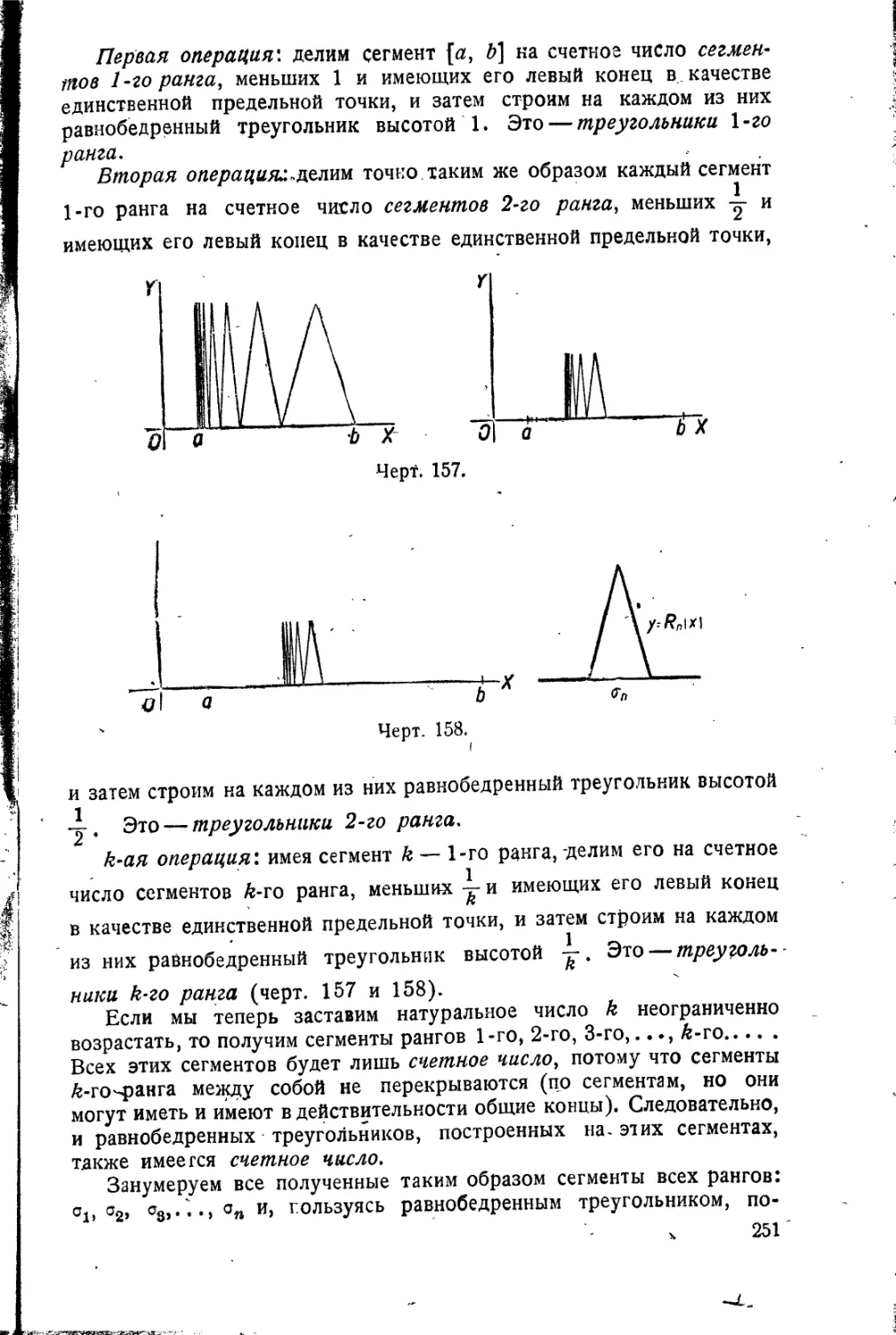
интегрального исчисления . . • 282
Приложение I. Теория иррацио.
нальных чисел 291
§ 65. Селения рациональной сети. 291
§ 66/Иррациональные числа. . 295
§ 67. Рациональные приближе-'
ния 302
§ 68. Положительные и
отрицательные действительные
числа 302
§ 69. Действия над
иррациональными числами ...... 303
§ 70. Принцип стягивающихся
отрезков ; .:.•/.... 305
§"55.
§56.
§57.
§58.
§59.
§60.
§61.
§62.
§63.
§64.
ПриЛоЯсёнйеЧТ. Классификация
Бэра '
30?
л
>
ПРЕДИСЛОВИЕ.
В настоящее время составление полного трактата по теории
множеств и по теории функций действительного переменного является
делом преждевременным, так как ведущиеся в различных
направлениях изыскания о принципах этих дясциплин легко могут заставить
быстро устареть самое добросовестное кропотливое изложение.
Ввиду этого, целью этой книжки является решение только чисто
педагогической проблемы преподавания начал теории функций.
Научная проблема, состоящая в подборе необходимого материала элементов
теории функций и приведении его в стройную логическую систему,
в достаточно удовлетворительной степени разрешена существующими
курсами, среди которых можно указать книгу Александрова и
Колмогорова или мелкий шрифт курса анализа Валле Пуссена.
Автор предлагаемой книги ставит целью разрешение лишь
педагогической проблемы, состоящей в том, чтобы, не увеличивая объема
научного материала, даваемого хотя бы Валле Пуссеном, представить
его в возможно более живой форме, делающей его доступным и
привлекательным для лиц, приступающих к углубленному изучению
математического анализа.
Теория иррациональных чисел помещена в Приложениях из
педагогических соображений, так как подробное логическое ее развитие,
помещенное в начале книги, могло бы затруднить читателя и повлиять
на его интерес к дальнейшему.
В заключение я не могу не упомянуть с глубокой признательностью
моих учителей: Б. К. Млодзеевского, выдвигавшего всегда на первый
план требование к художественной стороне научного изложения,
и Й. И. Жегалкина, постюянно настаивающего на доведении до
сознания учащегося малейших трудностей научного умозаключения и
предостережении его от рдзможных ошибок мышления,
8
В. И. Гливенко выражаю признательность за просмотр рукописи
и замечания. _
И, наконец, приношу глубокую благодарность редактору С. И.
Новоселову за детальный просмотр текста и за его ценные советы и
изменения, которые он внес в текст, некоторые части которого
принадлежат ему же.
Акад. Я. Лузин.
\
ГЛАВА I.
МНОЖЕСТВО И МОЩНОСТЬ.
§ 1. Понятие множества. Что такое „множество?" Мы не станем
доискиваться ответа на этот вопрос, потому что понятие множества '
является столь первоначальным, что затруднительно, по крайней мере
на сегодняшний день, определить его при помощи более простых
понятий.
Читателя это обстоятельство не должно удивлять. Действительно,
когда некоторое понятие Р определяется при помощи более простого
понятия Z), то само это понятие D также нуждается в определении
посредством более простого понятия С, а оно, в свою очередь,
нуждается в определении посредством еще более простого понятия В, и
так далее. Таким образом, в конце концов, мы должны будем прийти
к столь первоначальному понятию Л, которое не удается определить
помощью более простых понятий; все, что можно здесь сделать, — это
только разъяснить на ряде примеров смысл такого понятия Л.
Итак, мы не станем искать определения слова „множество".
Можно, разумеется, было бы сказать, что множество есть „собрание",
„коллекция", „класс", „система", „семейство", „комплекс", „ансамбль",
и так далее. Но такая замена одного слова другим никогда не может
дать самую идею множества тому, кто раньше не приобрел ее каким-
нибудь образом. Поэтому йы предпочитаем обратиться к примерам, -
разъясняющим смысл слова множество. Понимая под этим словом
совокупность, составленную из каких-нибудь предметов, мы можем
говорить о множестве всех букв на данной странице, о
множестве всех атомов серебра в данной монете, о множестве всех
корней данного уравнения, о множестве всех положительных чисгл,
.о множестве всех многочленов, о множестве всех непрерывных
функций, о множестве всех точек на данной окружности, о
множестве всех углов, имеющих иррациональное значение синуса, * и
так далее.
Предметы, составляющие данное множество, называются его
элементами. Для того, чтобы указать, что данное множество М состоит
из элементов е, обычно пишут:
в котором фигурные скобки {...} обозначают акт объединения
элементов е в одно целое для составления из них множества М.
Г
Из приведенных примеров видно, что элементами множества могут
быть самые разнообразные предметы: буквы, атомы, числа, функции,
точки, углы и так далее. Отсюда с самого начала ясна чрезвычайная
Широта теории множеств и ее приложимость к очень многим
областям знания (математике, механике, физике).
Читатель не должен упускать из виду, что самое существенное
в понятии множества — это акт объединения различных предметов
в одно целое, именно: в множество ЛТ, элементами которого (после
акта объединения) будут данные предметы. Этот существенный пункт
и желал подчеркнуть основатель теории множеств Георг Кантор, когда
он впервые высказал свое знаменитое положение:
„Множество есть многое, мыслимое нами как единое".
Чтобы прийти на помощь читателю, удобно будет прибегнуть
к такому несколько грубому образу. Представим себе некоторую
прозрачную непроницаемую оболочку, нечто вроде платно закрытого
прозрачного мешка. Предположим, что внутри этой оболочки
заключены все элементы е данного множества Л?, и что, кроме них, внутри
оболочки никаких других предметов не находится. Эта оболочка
с предметами е, находящимися внутри нее, и может служить образом
множества М, составленного из элементов е. Самая же эта
прозрачная оболочка, охватывающая все элементы (if ничего другого кроме
них), ^довольно хорошо изображает тот акт объединения элементов еу
в результате которого создается множество уИ. Обычно такой акт
объединения различных элементов в одно множество М совершается
путем формулирования некоторого характеристического свойства,
которым обладают элементы е (и только они одни). Например, когда мы
произносим фразу: „множество всех положительных чисел", мы
выявлением свойства „быть положительным" тотчас же выделяем из
всех действительных чисел одни лишь положительные числа и как бы
помещаем их все (и только их одних) в нашу прозрачную оболочку,
оставляя снаружи нее все другие числа (отрицательные и нуль), как
и все другие предметы.
Сделаем здесь зке последнее замечание: вовсе не обязательно, чтобы
множество содержало в самом деле много предметов. Множество
может иногда состоять всего из нескольких даже и из очень немногих
предметов. Читатель легко убедится в этом, если, например, возьмет
множество М всех корней какого-либо уравнения / (х)*=0. До
разрешения этого уравнения мы не знаем, сколько именно элементов
содержит наше множество М: может быть корней У него будет
бесконечно много, а мож«т быть и очень немного, например два или даже один.
Наконец, мощно мыслить и тот предельный случай, когдт
множеств© не содержит ни одного элемента. Это произойдет, например,,
тогда, когда уравнение f(x)=^=0 совсем не имеет корней. В этом*
случае можно представить себе одну прозрачную оболочку без
элементов внутри нее.
Множества, не содержащие ни одного элемента, называются ну**
Ътыми множествами.
S
Все пустые множества считаются тождественными между собой.
Два же непустые множества Мп Mt рассматриваются как
тождественные тогда и только тогда, когда они имеют одни и те же самые
элементы. В этом случае просто пишут: М = Мг.
§ 2. Актуальная бесконечность. Рассматривая приведенные выше
примеры множеств, читатель заметит, что в этом списке на одинаковых правах
поставлены рядом как множества конечные, так и множества бесконечные, Так,
множество всех букв на1 данной странице конечно, потому что буквы эти
легко пересчитать. Множество всех атомов серебра в данной монете хотя и
нельзя непосредственно пересчитать, однако физик тотчас же может
написать целое число, заведомо превосходящее число этих атомов; отсюда и
следует, что это множество атомов конечно. Но множество всех точек на
данной окружности, как и множество всех непрерывных функций, уже
бесконечно. Изучать какое-нибудь множество можно только тогда, когда оно
задано. Но что, собственно, означает фраза: „задать множество"? Если речь
идет о конечном множестве, дело может казаться более или менее ясным:
в этом случае фраза-„задать множестве*, естественно, означает „дать
все его элементы, не пропустив ни одного". Но можно ли
сохранить точно такое же толкование и для случая бесконечного
множества? Что в этом случае будет означать фраза „дать все его
элементы", раз этих элементов имеется бесконечность?
Когда впервые сталкиваются с этим вопросом, вот какой ответ
естественно приходит на ум;.дать бесконечность элементов—-это
значит дать сначала один элемент, потом дру'гой, затем
третий и так далее, пока мы не исчерпаем один по
одному их все. И следует тотчас же указать, что такое толкование,
несмотря на его очевидную наивность, все же имеет некоторые основания.
Действительно, спросим себя, что значит, например, задать какой-нибудь
бесконечный ряд
Ui + u2+u3+... + un+... •
Не значит ли это, в самом деле, сначала дать первый член ряда uh потом
второй член «2» затем третий щ% и так далее таким образом, что этими
последовательными заданиями в самом деле и будет исчерпано вполне
множество всех членов нашего ряда и, Следовательно, будет дан и весь этот ряд?
Таким образом, на первый взгляд данный ответ представляется весьма
убедительным. И, однако, он совершенно неправилен. Здесь уместно будет
указать читателю, желающему научиться самостоятельно мыслить в теории
функций, что во всех вопросах, в которых приходится встречаться с
бесконечными множествами, нужно в высшей степени остерегаться так называемой
очевидности: нет ничего здесь легче, чем быть вовлеченным в ложный
ход размышлений и, в результате, расплатиться одной лишь игрой слов.
Читатель в этом сейчас убедится.
Возьмем сначала хотя бы пример множества всех точек какой-нибудь
окружности. Оно, разумеется, бесконечно. Согласно намеченному выше
ответу, дать это множество означало бы дать сначала одну точку на этой
окружности, потом другую, затем третью и так далее, пока мы таким
образом не получим одну по одной их все. Но тогда спрашивается, в каком
порядке мы будем наносить на окружности эти точки, чтобы быть влолне
уверенными в том, что будем иметь их действительно &се? Правда, здесь
еще можно попробовать уйти от этого возражения, ответив так: чтобы иметь
действительно все точки окружности, достаточно просто, ее начертить при
помощи циркуля: тогда движущееся острие циркуля последовательно
пройдет через все эти точки.. Но уже здесь мы невольно останавливаемся/
замечай* разницу этого ответа по сравнению с тем, когда вопрос ставился для
случая бесконечного ряда членов ап. Там всякий элемент (кроме начального)
имел непосредственно предшествующий (и последующий) вполне
определенный элемент; это важное обстоятельство и облегчало нам возможность
говорить об исчерпании один по одному всех членов нашего ряда. Здесь
9
же мы не имеем ничего подобного, потому что точка на окружности не
имеет непосредственно соседней точки.
Как другой пример возьмем множество М всех непрерывных функций
f(x), M = {f (x)}. Оно также бесконечно. Но в то время как в
предыдущем примере точки окружности имеют определенный порядок, потому что
их все можно получить движением острия циркуля, чертящего эту
окружность и проходящего последовательно через все ее точки, —здесь элементы
/ (х) множества М представляются нам как бы никак не связанными между
собой или хаотически перемешанными и поэтому не имеющими никакого
естественного порядка: совершенно неясно, должна ли, например,
непрерывная функция log л: быть определенней раньше или позже непрерывной
функции sinx. Таким образом, здесь еще меньше оснований ожидать, что
действительно все элементы/(*) множества М могут быть даны один по
одному до полного исчерпания множества М.
Действительно, в дальнейшем будет строго доказано, что ни множество
всех точек окружности, ни множество всех непрерывных функций никогда
не могут быть получены заданием один по одному их элементов в том
смысле, как это кажется возможным для бесконечного ряда членов ип. Таким
образом, оказывается, что мы находимся на заведомо ложном пути. Чтобы
пойти по верному направлению, мы должны снова вернуться к поставленной
проблеме и пересмотреть намеченное первоначально решение. Это реше*
ние было подсказано рассмотрением бесконечного ряда. Но дать какой-ни*
будь бесконечный ряд
Щ + «2 + ^з+ ... + "«+••• _
вовсе не означает дать сначала его первый член иь потом второй щ> затем
третий «з и так далее, пока мы не исчерпаем один по одному всех его
членов* Этим приемом можно дать всегда лишь конечное число членов, и ни*
какой определенный бесконечный ряд никогда этим способом не может быть
дан. Истинная причина того, что какой-нибудь бесконечный ряд
рассматривается как данный, лежит в совершенно другом: бесконечный ряд задан
тогда и только тогда, когда мы умеем определить (в частности: вычислить)
его общий член ип% зная его значок п. Другими словами, бесконечный ряд
Щ + Щ + Щ + • • • + ип + • • • можно рассматривать как данный тогда и только
тогда, когда общий член дан как функция от л, йп=/(я). При этом не
надо упускать из виду, что ип может быть выражен не только к^к явная
• функция от /I, но, в общем случае, ип может чбыть определенным любым
законом (или правилом), например, каким-нибудь рекурентным
соотношением. Таким образом, бесконечный ряд задан вовсе^ не потому, что мы даем
один по одному все его члены, но потому, что известен тот закон*
которым определяются его члены. Закон этот, может случиться, является иногда
и сложным, но во всяком случае он должен быть выражен конечным обра-
зом, например, заданием общего члена ип как функции значка п. Именно
этот закон, будучи дан, и развертывает один за другим все члены ряда, не
пропуская ни одного и не повторяя несколько раз никакого из них; ой
является скрепляющим все его члены в одно целое. Таким образом,
относительно бесконечных рядов мы теперь приходим вот к какому заключению:
дать бесконечный ряд—это означает дать закон, определяющий его члены.
Сказанное применимо и к любому бесконечному множеству, ибо
множество есть многое, мыслимое как единое, в силу его закона.
Дать бесконечное множество — это означает дать его. закон, т. е.
дать характеристическое свойство его элементов.
Это характеристическое свойство, которым обладают элементы
рассматриваемого множества и которым не обладает никакой другой предмет, вполне
определяет это множество. Едва только мы сформулируем
характеристическое свойство элементов какого-нибудь множества, как этим самым тотчас же
и даются все его элементы, хотя бы их было бесконечно много. Если
обратиться к указанному выше очень грубому конкретному образу,
характеристическое свойство элементов множества является как раз той самой
прозрачной оболочкой, которая охватывает все элементы данного множества
(и только их одних). Например, множество М всех лепрерывных функций
10
f(x), M*={f(x)}t мы рассматриваем, как данное, потому что нам дано
характеристическое свойство его элементов: „быть непрерывной функцией*.
Ясно, что этим путем нам могут быть даны не только множества, фигури- '
рующие в указанном выше списке, но и беспредельно разнообразные иные -
бесконечные "множества. Но эта бесконечность элементов, „схваченная"
вместе в одно целое данным характеристическим свойством, является тем
самым уже данной вся целиком, уже сформированной и неизменной (раз мы
не меняем характеристического свойства) и, следовательно, как бы уже
неподвижной и замкнутой в себе.
Такую бесконечность принято называть актуальной бесконечностью.
Актуальная бесконечность имеет много общего с конечным: и та, и другое,
оба рассматриваются как неподвижные, постоянные, уже сформированные и,
как было сказано, замкнутые в себе.
§ 3. Число и мощность. Рассмотрим какое-нибудь множество М,
составленное из элементов е, М—{е]. Если множество М есть
конечное, мы имеем в этом случае возможность говорить о числе его
элементов. Когда множество М пустое, число его элементов есть
нуль; если же М непустое конечное множество, число его элементов
есть некоторое целое положительное число, т. е. натуральное число.
Натуральный ряд чисел 1, 2, 3,...я,., .начинается с числа Г;
за всяким числом п имеется другое число, непосредственно за ним
следующее. Когда хотят найти число элементов данного конечного
множества М, тогда их просто пересчитывают. Это означает, что
к элементам е множества М прикрепляют мысленно (т. е. делают
соответственными) по одному последовательно и без пропусков значки 1, 2,
3,..., так что элементы эти предстанут перед нами в
занумерованном виде: еь е2, е\,... И так как данное множество есть
конечное, то в ряду его элементов еи е2> е3,... непременно имеется
самыйГ последний ет так что множество М можно записать в виде
поместив в круглые скобки (...) все,эти элементы. В этих условиях
нумер п последнего элемента конечного множества М9
написанного в занумерованном виде, есть число элементов
множества М.
Всякое конечное множество Л4, содержащее больше чем один
элемент, можно, разумеется, занумеровать не одним только, но
несколькими способами; но каково бы ни было предпринятое
занумерована его элементов, всегда при этом приходят к одному и тому же
самому последнему нумеру п и, следовательно, к одному и тому же
числу элементов множества М. Таким образом, число элементов
какого-нибудь конечного множества М совершенно не зависит от
предпринятого способа его нумерования. Для того чтобы оценить
смысл этого, рассмотрим два каких-нибудь конечных множества
М=з{е} и М'~{е'}, имеющих одно и то же число элементов.
Такие конечные множества называются равночисленными. И для нашей
цели весьма важно найти условие, при котором' равночисленность
имеет силу. Раз множество М имеет п элементов, то это значит, что
все элементы множества М можно занумеровать без пропусков
натуральными числами 1, 2, 3,..., п. То же самое справедливо и для
множества М. Но тогда между элементами множеств М и М' уста-
11
навливается совершенно определенное взаимно-однозначное соот*
ветствие, потому что элементы этих множеств, получившие при
нумерации один и тот же нумер, мы можем рассматривать как
соответствующие друг другу. Это обстоятельство позволяет нам ввести
новое понятие в виде такого определения:
Два конечных множества МиМ' называются, эквивалентными
если можно установить взаимно-однозначное соответствие их
элементов.
Для того чтобы указать, что конечные множества М и М!
эквивалентны, обычно пишут символически AfcoAf. Ясно, что если два
каких-либо конечных множества М к М' эквивалентны каждое порознь
третьему конечному множеству Л1\ то М и М' эквивалентны между
собой. В символической записи это означает, что если А/соЛГ и в то
же самое время М'спМ", то и МсяМ'.
Возвращаясь теперь к равночисленным множествам, мы видим что
все они эквивалентны между собой. Но имеет место и обратное
предложение: два эквивалентные конечные множества М и М'
МсоМ'у сугпь равночисленные множества. Чтобы видеть это,
достаточно заметить, что нумерование элементов множества М натураль*
ными числами 1, 2, 3,...,я тотчас же влечет нумерование этими
числами и элементов множества М'% так как ничто не мешает нумер
полученный элементом множества ЛТ, отнести к- соответствующему
элементу множества М'. Это гТредложение имеет чрезвычайную важность
потбму что обнаруживает, что для установления равночисленности
двух каких-ЙИбудь конечных множеств М и М' нет надобности ни
уметь считан, ни даже обладать понятием натурального числа:
достаточно лишь уметь установить взаимно-однозначное 'соответствие
между множествами М и М\ что может быть достигнуто самыми
разнообразными приемами. Такими образом, логически нет никакой
надобности для установления равночисленности конечных
множеств в предварительном знании натуральных чисел.
Напротив, само натуральное число получает теперь новое
освещение: натуральное число ееъь количественная характеристика, общая
всем эквивалентным между собой конечным множествам. Так,
например, отвлеченное натуральное число 3 есть с этой точки зрения
характеристика каждого множеетаа, в состав которого входит тройка
каких-либо предметов, конкретных или отвлеченных. Все
эквивалентные между собой конечные множества М (и только эквивалентные
ме&ду собой) имеют одну и ту же зщрактериетику я, называемую
„числом элементов" множества М. Беля два конечные множества М
и М' не эквивалентны др/г другу, числа я и л' их элементов
различны: пфп'.
Таким образом, мы определили тождество и различие натураль-.
ных чисел исключительно на языке взаимно-однозначных соответствий.
Но этого мало: возможно на этом же языке логически определить
соотношения „больше* и „меньше* для натуральных чиеелГДля
того чтобы осуществить это, введем сначала определение: мы
говорим, что множество Mi есть точная часть (часть в собственном
смысле) множества М, конечного или бесконечного, если множе-
1S
ство Мх составлено из элементов множества М, но не
содержит их всех.
Пусть теперь М и Мг два какие-нибудь конечные множества,
имеющие в качестве числа их элементов п и п*. Введем такое
определение; мы говорим, что число п' больше числа п и пишем
п' > п, если множества М и М' не эквивалентны между собой и
если одновременно с этим^ множество М эквивалентно некото*
рой точной части М'х множества М'.
Из этого видно, что для решения вопроса о том, какое из двух *
различных чисел п и п одно больше другого, нет надобности
занумеровывать элементы множества М и М\ так как достаточно устано*
вить, во-первых, неэквивалентность множеств М и М' и, во-вторых,
эквивалентность одного из них точной части другого. Почти не
приходится указывать на то, что это определение вполне согласуется
с обычным представлением о натуральных числах: если, в самом деле,
число пг элементов множества М' больше числа элементов п множества
М, то, занумеровав элементы множестве и М\ M = (ev e2t...,en)
и M'~(e'v e'2,.. -,^,.. «>^/)> мы немедленно замечаем, что,
во-первых, М не эквивалентно М! и, во-вторых, что множество М! имеет
точную часть (^^'•'•»0' эквивалентную всему множеству Ж.
Читатель не должен удивляться тому, что мы уделили так много
внимания одним только конечным множествам. Дело в том, что многое
из только что сказанного о них без всякого изменения
распространяется также и на бесконечные множества.
В теории множеств почти не делают никакой разницы между
множествами конечными и бесконечными. Подобно тому, как всякое
конечное множество нами мыслится как уже данное нам сразу, со
всеми его элементами и, следовательно, как неизменное, теория
множеств мыслит также всякое бесконечное множество М, для
элементов которого нам указано характеристическое свойство (т. е. то,
которым обладают элементы множества М и только они одни), как
уже данное, со всеми его элементами.
Ввиду сказанного, теория множеств стремится обобщить на
бесконечные множества возможно больше закономерностей^ имеющих силу
для конечных множеств; обобщая на бесконечные множества понятие
„числа элементов" множества, введем важное понятие „мощности
множества".
Перенесем сначала на бесконечные множества понятие
эквивалентности :
Мы говорим, что два бесконечнее множества М и М'
эквивалентны, и пишем МсоМ\ если между элементами этих множеств
можно установить взаимно-однозначное соответствие.
Kai* и для случая конечных множеств здесь ясно, что' два мно-
лсества М и Мг, эквивалентные третьему М", эквивалентны между
собой, т. е. что имеем МсоМ', если имеем одновременно МсоМ" и
Конечные эквивалентные множества суть множества
равночисленные. Обобщением понятия равночисленности на случай бесконечных
13
множеств является понятие равно мощности* Подобным же образом
мощностью бесконечного множества М мы называем понятие,
относимое кЬ всякому бесконечному множеству М\ эквивалентному
множеству М.
Мощность бесконечного множества М есть понятие, связанное
со всяким бесконечным множеством М\ эквивалентным М, Воем
множествам, эквивалентным одному (и тому же множеству М,
можно отнести один и тот же символ у. Этот символ можно
рассматривать как обозначение мощности множества М. Если
два бесконечные множества М и М' не эквивалентны, мощности
их \ь и |/ различны, \ьф\ь'.
Таким образом, мы определили тождество и различие мощностей.
Но подобно тому, как мы. сделали для натуральных чисел, мощности
бесконечных множеств также можно сравнивать друг с другом,
определив для них соотношения „больше" и „меньше", т. е. установив для
мощностей неравенства.
о Если множества М и Мг не эквивалентны и множество М
эквцвалентно некоторой части множества М'9 то |л, мощность
множества М, меньше р/, мощности множества М'%
а \к' больше [х,
Читатель видит, что понятие „мощности" бесконечного множества
совершенно аналогично понятию „числа элементов" конечного множен
ства. Именно эту аналогию и стремился сохранить Георг Кантор,
когда он впервые давал свое определение мощности:
„Мощность множества есть то, что остается в нашем уме,
когда мы отвлечемся от качественной природы его элементов и
от их порядка, т. е. когда < мы мыслим эти элементы как
совокупность отвлеченных единиц".
Это определение психологически вполне соответствует идее
мощности, когда множество бесконечно, и идее натурального числа, когда
множество конечно.
Все данные нами выше определения не имели бы ни малейшего
смысла, если бы фактически оказалось в дальнейшем, что все
бесконечные множества эквивалентны между собой, потому что тогда мы
имели бы дело лишь с одной бесконечной мощностью и вводить
различные мощности и их неравенства было бы прямой бессмыслицей.
Но на самом деле этого нет, и одно из прекрасных открытий
Георга Кантора как раз и состоит в установлении того, что
имеются многие неравные между собой бесконечные мощности.
Чрезвычайно важным оказывается то обстоятельство, что среди
различных мощностей бесконечных множеств имеется наимень*
шая мощность. Ее Георг Кантор обозначает символом Ко-
Чтобы составить о нбй представление, проделаем следующий ум*
ственный эксперимент.
U
Возьмем натуральный ряд чисел
1, 2, 3, . .^ ,пу • шу
и рассмотрим какое-нибудь множество М> составленное из
элементов е, Af= {е}. Представим себе, что элементы е заключены все
в прозрачную плотно закрытую оболочку, не содержащую внутри себя
никаких других предметов. Проделаем в этой оболочке отверстие и
будем ее передвигать 'вдоль натурального ряда, и предположим, что
при проходе оболочки над натуральным числом из нее выпадает
элемент и прикрепляется к тому натуральному числу, на которое он упал.
Ясно, что при помощи этого механизма осуществляется нумерация
элементов с помощью натуральных чисел.
Логически представляются две возможности:
1. Или,^ при-движении оболочки, наступает такой момент, когда
все элементы множества М уже выпали, но еще остаются свободные
натуральные числа, незанятые элементами множества М, потому что
их уже больше нет. В этом случае ясно, что множество М конечно
и что числом его элементов будет последнее занятое натуральное
число.
2. Или этого не произойдет. Это значит, что все натуральные
числа окажутся занятыми, причем в оболочке, после прохода ее. над
всем натуральным рядом, могут остаться еще неупавшие элементы.
В этом случае ясно, что множес?во М бесконечно и что упавшие
элементы е образуют часть Мх множества М (точную или
совпадающую с М)у эквивалентную натуральному ряду чисел.
Отсюда, если мы обозначим через у. мощность множества М и
через Ко мощность натурального ряда, то в силу сказанного о
равенстве и неравенстве мощностей мы имеем
Н-Жо-
Обычно вместо этого умственного эксперимента выполняют
Другой, при котором просто вынимают из множества М сначала один
элемент и обозначают его через ev потом другой, обозначая его
через £2, потом третий ев и так далее, пока это еще возможно, т. ё.
пока в М остаются еще невынутые элементы. Ясно, что этим путем
мы в бесконечном множестве М определяем часть (точную или
совпадающую со всем Ж), занумерованную всеми натуральными числам*/
и, следовательно, эквивалентную натуральному ряду.
Будем считать данное объяснение достаточным основанием для
утверждения:
Мощность Ц0 множества всех натуральных чисел есть наи»
меньшая из бесконечных мощностей.
§ 4. Счетные множества. Раз мощность ц0 есть наименьшая
из всех бесконечных мощностей, естественно начать изучение теории
множеств с множеств именно этой мощности. Такие множества
называются счетными. Легко видеть причину такого названия: так как
всякое множество.М, М = {е}$ имеющее К0 своей мощностью, эк-
1&
бивалентно натуральному ряду, то существует, по крайней мере/
одно взаимно-однозначное ^соответствие между элементами е данного
множества и всеми натуральными числами. Эти натуральные числа мы
, можем рассматривать как нумера или как значки соответствующих
элементов; поэтому все без исключения элементы, е множества М
можно расположить в виде бесконечной последовательности
(М) *!, е9, еъ, ..., ею ..., . (I)
где они все являются пересчитанными. Отсюда и название: счетное
множество.
Одно и то же счетное множество М может быть расположено
в виде указанной бесконечной последовательности не одним только,
но многими разными . способами. Действительно, заставляя
обмениваться местами в последовательности (1) элементы е, мы будем
получать все новые и новые бесконечные последовательности,
состоящие из элементов того же множества М.
Свойства счетных множеств мы изложим в виде следующих
предложений.
Теорема 1. Всякая бесконечная часть счетного множества
есть счетное множество.
Для доказательства возьмем какое-нибудь счетное множество М,
Ж={^}. Пусть М'— данная бесконечная часть множества М* Так
каЬ М—счетное множество, его элементы можно расположить в виде
бесконечной последовательности
* Окрасим мысленно в какую-нибудь краску все элементы множества М,
* принадлежащие к части М\ оставив все прочие элементы множества М
неокрашенными. Тогда в последовательности (1) будут находиться
как окрашенные, так и неокрашенные элементы. Пусть в
последовательности (1) первый окрашенный элемент будет ещ\ обозначим его
через е.. Пусть первый следующий за ним окрашенный элемент
будет ещ, щ>пх\ обозначим его через е2. Пусть первый следующий
за еПл окрашенный элемент будет ещ, п2>п2; обозначим его через е3
и так далее.
Ясно, что последовательность
(Л*') <.«»'. «е.— /mf'- (2)
будет состоять только из окрашенных элементов; легко видеть, что
сна должна содержать их действительно все. Чтобы в этом убедиться,
возьмем какой-нибудь окрашенный элемент е\ В последовательности
(1) он занимает вполне определенное место, будучи некоторым ек.
С другой стороны, нумера окрашенных элементов, последовательно
определявшихся нами при составлении последовательности (2)> суть
пх < п2 < пъ < • • • • ^ак как этих нУмеРов бесконечно много и они,
не будучи равными друг другу, неограниченно возрастают, то
имеется такое число /, что п4<к^пм. Но так как окрашенный
элемент, следующий за ещУ есть ещ+и то & = fli+x.- Фто и обнару-
16
живает, что ек содержится в последовательности (2) и что она,
поэтому, содержит все окрашенные элементы. Из сказанного следует,
что вся рассматриваемая бесконечная часть Мг множества М
расположена в виде бесконечной последовательности (£). Значит, М'
есть счетное множество.
Для пояснения смысла этого предложения возьмем пример. Пусть
М есть натуральный ряд и Ж' — множество всех четных чисел. Так
как М! есть бесконечная часть счетного множества М, то, в силу
доказанной теоремы, М! есть счетное множество. Впрочем,
эквивалентность множеств М и М' можно и прямо доказать, заставив
соответствовать каждому натуральному числу п удвоенное число 2я.
Мы видим, насколько разнится понятие мощности от понятия
натурального числа: арифметическая аксиома — целое больше своей
часта— не имеет аналогии в теории мощностей. Так, четные числа
образуют правильную часть натурального ряда, и, однако, множество
их эквивалентно целому натуральному ряду.
Теорема 2. Если каждому элементу множества М можно
поставить в соответствие конечную систему натуральных чисел,
причем системы, соответствующие различным элементам
множества М\ различны, то М есть конечное, или счетное множество.
Эту теорему кратко сформулируем так:
Множество М элементов eM,r,...M,v, занумерованных конечными
системами натуральных чисел^ есть конечное^ или счетное
множество*
Числа р, q, г,..., я, г; суть натуральные, число их обозначим
через k. Притом совершенно безразлично, принимают ли числа р, qy
г,..., u,v и само k всевозможные или только некоторые целые
положительные значения.
Приведем несколько примеров таких множеств М.
Пример I. Множество, которое содержит:
1) один элемент
2) дв& элемента
3) три' элемента
ег,\ ег,2 ез,з
и так далее до бесконечности. Иначе говоря, это множество состоит
из элементов ерф число k = 2, первый из номеров р пробегает все
натуральные числа 1, 2, 3,..., второй q — лишь числа 1, 2,...,р.
Пример II. Множество, которое содержит:
1) два элемента
2) четыре элемента
eU\ ei,2 е2,\ %2
3) восемь элементов
*1,1, I *1,1, 2 *1,2,1 ^1,2,2 *2,1,1 *2, 1,2 *2, 2, 1 ^2,2,2
2 Эак. Ш4. 17
и так далее до бесконечности. Иначе говоря, это множество состоит
из элементов ер^^ г,.. .,и, v, число к номеров пробегает все
натуральные числа 1, 2, 3,..., каждый же из номеров принимает значения
1 или 2 независимо от остальных.
Пример II(. Множество, которое содержит:
1) бесконечное множество элементов
2) бесконечное множество элементов
£2,1 е>, 2 e2t з • • .,
3) бесконечное множество элементов
*з, 1 £о, 2 <?з, з • . .
и так далее до бесконечности. Иначе говоря, эго множество состоит
из элементов ер^д, число к = 2 и каждый из номеров пробегает все
положительные числа 1, 2, 3,... независимо друг от друга.
Для доказательства сформулированной теоремы поставим в
соответствие всякой системе к натуральных чисел р, q, г,..., #, v
некоторое вполне определенное натуральное число т и сделаем это так,
чтобы всяким двум различным системам p,q,r, ..., и, vup\ qf,r',.. .,
u\v\w\ состоящим соответственно из к и к! натуральных чисел,
отвечали два существенно неравные натуральные числа т и т\
тфт\ При этом две системы мы рассматриваем как различные,
если они нетождественные, т. е. если они отличаются друг от друга
или численностью их состава (значит, если имеем 'кфЬ'), или при
k = k' самим их составом (значит, либо рфр\ либо дфд\ либо гфгг
и так далее).
Для того, чтобы установить нужное нам соответствие для системы
р, q, г,.. ., м, v числа /я, мы определим это число т формулой
ТП~ \0Р + <11-Г+ • • •+ U+V _l_ Ю1 + Г + . .. + U + V J^
Ясно, что число т есть натуральное и "что оно пишется в
десятичной системе при помощи k единиц, отделенных друг о г друга нулями,
потому что число слагаемых в данной формуле равно, очевидно,
числу чисел р, q, г,. . ., и, v.
Докажем теперь, что двум различным системам p,q, г,. . .,u,v
и //, q', г,. . .,и\ v\ w\ состоящим соответственно из k и к7 чисел,
отвечают два существенно неравные числа т и т\ т. е., что тфт!'.
Действительно, если бы мы имели т = т\ то ввиду того, что всякое
натуральное число пишется- по десятичной системе единственным
образом, мы необходимо должны иметь прежде всего равенство
/с = к\ потому что число т имеет в десятичном изображении k
единиц. Таким образом, обе системы должны состоять из одинакового
числа составляющих их чисел, т. с. должны быть вида /?, q, г,... ,и,г>
11 Р > я\ г'т • • ? ti\v'. Далее л~п;о видеть, что v--=-v\ Действительно,
единица низшего разряда в десятичном изображении числа пг нахо-
18
дится на v-\-\ месте (считая справа); поэтому v -f-1 ■=» *>' + 1,
откуда « = ^. Затем, следующая единица числа т находится на
# -J- w -|- * месте; поэтому и-j- ^ +• * = и' -f- и' + 1; и так как v = г»',
то отсюда следует, что и = и'. Продолжая этот прием дальше, мы
получим равенства к=зк'^=*у\и = и',...,г = г', q — qr и р = рг.
А это и доказывает, что обе взятые системы р, q, r,..., и, v и
pr,q', /*',..., a', t/ тождественны, а не различны, как было
предположено. Таким образом, соответствие системе р, </, /%...,&,
^натурального числа яг таково, что двум действительно различным
системам р, q> г,..., и, ^ соответствуют два существенно неравные
числа т. Следовательно, множество систем р, qy r,..., я, г>
эквивалентно некоторой части натурального ряда, а значит, это
множество конечное или счетное. Поэтому, конечным или счетным должно
быть и множество элементов ePt q% г,.„,«, v, занумерованных этими
системами.
Доказанное предложение имеет многочисленные следствия, из
которых важнейшим является предложение:
Сумма конечного или счетного числа счетных множеств есть
счетное множество.
Так как это предложение употребляет не встречавшееся у нас
ранее понятие „суммы" множеств, то следует здесь же дать
необходимые разъяснения.
Пусть нам дано какое-нибудь множество множеств [М]. Тогда
множество, получающееся от соединения всех элементов всех
множеств М в одно целое, называется „соединением" множеств М.
При этом множества М могут иметь и общие элементы, которые
в соединении должны браться в одном только экземпляре. Если же
множества М не имеют попарно общих элементов, тогда соединение
множеств М называется „суммой" множеств М. Сумма множеств М
нередко обозначается символом £М*).
Эти определения относятся к самому общему случаю, т. е. какова
бы ни была мощность данного множества множеств {М). Если же
множество [М] есть конечное или счетное, тогда сумма множеств М
пишется (в первом случае) в виде: Мх-{- Ж2+ • • • +^п> если число
множеств М есть л, и, во втором случае, в виде бесконечного ряда
^1+^2 + ^3-К--+^4- —
Возвращаясь к доказательству теоремы, расположим счетное
множество Мг в виде бесконечной последовательности его элементов
\Ми ег\-> ~а'2> • • • > eij> • • • *
где первый значок i у всех элементов один и тот же, потому что
обозначает нумер множества М4, и где второй значок у, пробегая
все натуральные числа, дает все элементы этого множества. Отсюда
следует, что обе суммы: конечную М1 + М2 4" • • • + Щ 4- •.• + Мп
*) Впрочем, в математической литературе часто называют су мяо й
множеств всякое соединение, безразлично — имеют ли они общие элементы
или нет.
2* !9
и бесконечную Мх -f-M^-f- . •. + Мг 4- • • • можно рассматривать
как множество {е^\ элементов eiJy занумерованных системами двух
натуральных чисел / и j. В силу теоремы 2 это множество счетное,
что и доказывает предложение.
Заметим, что доказательство не теряет силы, когда дело идет
не о суммах, но о соединениях множеств, т. е. когда у соединяемых
множеств Mi имеются общие элементы. В этом случае мы сначала
рассматриваем их как различные, хотя бы потому, что они
принадлежат к различным множествам М$\ и затем, после нумерования
натуральными числами всех элементов соединения, мы опускаем в
получившейся таким образом бесконечной последовательности лишние
экземпляры одного и того же элемента.
В качестве другого следствия теоремы 2 укажем на одно из
важнейших предложений анализа:
Множество всех рациональных чисел счетно. Рациональное
число г имеет вид zt—, где р и q суть натуральные числа, причем
ч
числитель р равен нулю, если г = 0. Таким образом, множество R
всех рациональных чисел, /?=(г], разбивается на три множества:
гд^ р и q суть натуральные числа.
Рассмотрим сначала последнее множество {~}> где дробь —
несократима. Так как — можно представить в виде ер>д1 то отсюда
ясно, что множество <--> счетно. Ясно, что счетным будет и
множество | — -->, эквивалентное множеству {—>. Отсюда следует, что
R есть счетное множество. Таким образом, множество R всех
рациональных чисел г может быть занумеровано натуральными
числами, т. е. может быть расположенным в виде бесконечной
последовательности
(R) г\ > ^2> Г2> • • • > Гпч • • • •
В качестве третьего следствия теоремы 2 мы возьмем
алгебраические числа.
Алгебраическим числом называется любое действительное или
комплексное число, которое является корнем какого-либо
алгебраического уравнения с целыми коэфициентами.
Одной из важнейших теорем высшей алгебры является
предложение :
Корни алгебраического уравнения с алгебраическими
коэфициентами являются также алгебраическими числами.
В самом деле, рассмотрим уравнение
/(*, ос, р, ...,Х) = 0,
20
где /— многочлен с целыми коэфициенгами относительно неизвестного
х и данных алгебраических чисел л, (3,..., X. Так как а, {3,..., X
суть алгебраические числа, они удовлетворяют уравнениям с целыми
коэфициентами: о(ъ)~0, ty(j3) = 0,. . .. <о(Х) = 0. Но тогда ясно,
что, исключая а, ,3, ...,Х из уравнений /= 0, ср == 0, ty = 0,...,
ш = 0, мы получаем уравнение с целыми коэфициентами F (х) = 0,
имеющее своими корнями все корни уравнения /(х, a, J3,.. ., Х) = 0.
Значит, корни эти суть алгебраические числа. Отсюда следует, что
множество всех алгебраических чисел содержит все числау
которые можно определить при помощи конечного числа алгебраических
операций, производимых над натуральными числами.
К этому важному предложению высшей алгебры теория множеств
присоединяет следующее предложение:
Множество всех алгебраических чисел счетно.
Докажем это предложение. Пусть х есть какое-нибудь
алгебраическое число. Это значит, что х есть корень некоторого уравнения
рхп + qx" -1 + .^.+5X+/ = 0
с целыми коэфициентами р, д,.. ♦ , s^t. Но всякое число можно
представить в виде разности двух натуральных (т. е. целых
положительных) чисел. Отсюда предыдущее уравнение можно написать
в виде
(р' — p")**4-fo' — ?*)*«-!-]-... +(s' — sfr)x^r{t' — *") = 0.
Кроме того, всякое алгебраическое уравнение степени п имеет п
корней. Следовательно, все корни такого уравнения можно
пересчитать п значками: 1, 2, 3,..., п. В частности, и корень х получит
один из этих значков, например значок k, l^k^n. В результате
мы видим, что
рассматриваемый корень х мож- | о р ____________ у
но обозначить так: * * *~ ~ *
ep'>p"><i'*q"t.:4s',s,,,t,,t",ff Черт. 1.
Отсюда следует, что множество всех алгебраических чисел есть
множество элементов, занумерованных конечными системами
натуральных чисел. Следовательно, это ^множество счеШо.
Геометрические следствия. Рассмотрим прямую линию XX (черт. 1).
Рациональной точкой назовем всякую точку Р этой прямой,
расстояние которой до начала координат 0, измеренное с помощью данной
единицы масштаба, есть число рациональное. Это расстояние, взятое
со знаком ~|-, если точка Р лежит „вправо" от начала координат О,
и взятое со знаком —, если точка Р лежит „влево" от него,
называется абсциссой точки Р. Абсцисса самого начала координат О
равна нулю. Если отрезок ОР несоизмерим с принятой единицей
масштаба, точка Р называется иррациональной. Также и в этом случае
отношение отрезка ОР к единичному отрезку считается
положительным, когда Р лежит вправо от начала 0, и отрицательным, когда
21
Р лежит влево от начала 0, и называется попрежнему абсциссой
точки Р. Абсцисса иррациональной точки Р есть иррациональное
число. Точка Р называется алгебраической, если ее абсцисса х есть
алгебраическое число; в противном случае, точка Р называется
трансцендентной. Абсцисса трансцендентной точки есть неалгебраическое
число, т. е. такое, которое не является корнем никакого
алгебраического уравнения с целыми козфициентами; неалгебраические числа
называются трансцендентными.
Из геометрии известно, что каков бы ни был отрезок [а, Ь],
лежащий на прямой ХТX, внутри него имеется бесчисленное
множество рациональных точек (какой бы отрезок ни был принят за
единицу измерения) (черт. 2). Это предложение всегда справедливо,
каким бы малым ни был
У> 0 „?,...,.. .,/*, рассматриваемый отре-
г' г" зок [а, Ь\ и как бы
далеко он ни лежал (впра-
Черт. 2- во или влево) от начала
координат 0.
Если некоторое множество М точек прямой Х'Х расположено на
этой прямой так, что любой отрезок [а, Ь] (как бы этот отрезок ни
был мал) содержит точки данного множества, то говорят, что
множество М всюду плотно на прямой Х'Х.
Следовательно, можем сказать, что множество рациональных
точек всюду плотно.
И, однако, множество R есть лишь счетное, потому что
счетным является множество всех рациональных чисел. Это
обстоятельство, парадоксальное на первый взгляд, показывает, насколько нужно
быть осторожным при суждении о том, счетно или несчетно какое-
нибудь рассматриваемое множество точек: оно может быть вскдду
плотным на прямой ХГХ% и тем не менее оказаться всего лишь
счетным.
Так как всякое рациональное число есть частный случай
алгебраического числа, то множество R всех рациональных точек
образует лишь точную часть множества А всех алгебраических
точек. Во всяком отрезке [а, Ь\ имеется бесконечно много
алгебраических иррациональных точек. В этом легко убедиться, рассматривая,
например, точки, имеющие абсциссой числа вида /*1/Л2~ гДе г есть
любое рациональное число: множество точек этого вида, очевидно,
всюду плотно на прямой Х'Х, потому что всегда можнб так
подобрать рациональный множитель г, чтобы точка с абсциссой г
ухлопала в заданный заранее отрезок [а, Ь] *).
Это обстоятельство, на первый раз, заставляет усомниться вообще
в самом существовании трансцендентных точек, потому что можно
*) Если принять за новую единицу измерения диагональ квадрата,
сторона которого равна единице, ю точки с прежней абсциссой г У* 2 окажутся
теперь рациональными. По множество рациональных точек всюду плотно,
какой бы отрезок ни был выбран за единицу.
22
было бы думать, что всякая точка Р прямой Х'Х есть либо
рациональная, либо алгебраическая. Но Эрмит впервые доказал, что число
e=:lim (1 + —) ,
столь важное для анализа и приближенно выражающееся в виде
е = 2,718281828459045. .., не может служить корнем никакого
алгебраического уравнения с целыми коэфициентами. Этим впервые было
строго доказано существование трансцендентных чисел, а значит, и
трансцендентных точек. Интересно заметить, что год спустя после
появления работы Эрмита Георг Кантор опубликовал свое
знаменитое предложение о том, что мощность множества точек,
принадлежащих какому-нибудь отрезку [а, Ь], есть несчетная. При этом
оказалось, что множество всех трансцендентных точек имеет большую
мощность, чем множество алгебраических точек, и что трансцендентные
точки имеются на каждом отрезке [а, Ь], и притом з мощности
выше счетной.
В качестве второго геометрического следствия докажем важное
предложение:
Любое множество поперек} ывающихся отрезков,
расположенных на прямой, есть множество конечное, или счетное.
Заметим сначала, что два какие-нибудь отрезка Д и Д', лежащие
на прямой, называются неперекрывающимися, если они имеют самое
большее одну общую точку. Из этого определения следует, что если
отрезки Д и Д' не перекрываются, то или они отделены друг от
друга некоторым расстоянием, или имеют только одну общую
концевую точку и расположены от нее по разные стороны.
Для доказательства теоремы рассмотрим какое-нибудь множество
Ж попарно неперекрывающихся отрезков Д, М={Д}. Нужно
доказать, что М есть самое большее счетное множество.
Пусть R множество всех рациональных точек прямой XX, на
которой расположены отрезки множества Af, и пусть Д есть какой-
нибудь элемент множества М. Расположим множество R в виде
последовательности
v v 7*1 > ^2> ^3> ' • • >/п> • • •
Так как множество R всюду плотно на прямой ХгX, то внутри
отрезка Д находится бесчисленное множество рациональных точек г;
все такие рациональные точки /• образуют часть бесконечной
последовательности {jR), и среди таких точек г имеется одна с.
наименьшим нумером; пусть этот нумер есть I. Этот нумер / мы поставим в
соответствие рассматриваемому отрезку Д и обозначим отрезок Д через
Д*. Пусть теперь Д' е»ть какой-нибудь другой элемент множества М,
отличный от элемента Д. Согласно сказанному, Д' можно
обозначить в виде Д'^, где i' есть наименьшие нумер (в
последовательности (/?)) рациональной точки, содержащейся внутри отрезка Д'.
Так как отрезки Д и Д' не перекрываются, то внутренние их течки
(т. е. неконцезые) все различны. Следовательно, рациональные точки
23
ri и /у различны, т. е. 1ф1'. Поэтому, все элементы А множества М
оказываются снабженными существенно различными натуральными
значками /, т. е. множество М располагается в виде множества {AJ,
все элементы Д< которого занумерованы не равными друг другу
натуральными числами. Отсюда и следует, что множество М есть
счетное, или конечное.
Для дальнейших приложений сделаем следующее замечание:
Множество элементов еа> Ъ} Ct..., q, занумерованных конечными
системами, составленными из элементов какого-нибудь счетного
множества М, есть конечное, или счетное множество.
В справедливости этого убеждаемся так: раз множество М счетно,
то его элементы можно расположить в виде бесконечной
последовательности
(М) т{, т2, т
3>'
т.
в которой все элементы множества М будут занумерованы
натуральными числами. Отсюда следует, что конечная система а, Ь, с,. .., </
элементов множества М напишется в виде
тр, тд,
т0
mv, где
□
0
Черт. 3.
числа р, q, $>•"••» v СУТЬ натуральные. Поэтому элемент eat bi{
рассматриваемого множества можно написать в виде ет
или, короче, в виде е\
Р> Ъ •••. v
Так как теперь значки р, q,.. .,v
суть натуральные числа, то в силу теоремы 2 множество [е e^...ft?}
есть самое большее счётное. Следовательно, конечным или счетным
будет и множество [еа% ь% Cj. ..,g.}.
В частности: множество элементов eri r\r».,,. и множество
элементов еа> 0', в",..., занумерованных конечными системами
рациональных чисел г, гг, г",. . . или конечными системами
алгебраических чисел а, а', а",... есть самое большее счетное множество.
Поясним это следующим примером.
Предварительно введем такое определение:
Точка плоскости Р (х, у) или точка трехмерного пространства
P(x,y,z) называется рациональной, если ее координаты х, у, z
суть рациональные числа.
Рациональные точки плоскости и рациональные точки
трехмерного пространства образуют всюду плотные множества, первое — на
плоскости, второе — в пространстве. Это означает, что в любом
прямоугольнике на плоскости или в любом параллелепипеде в
пространстве содержится бесчисленное множеств? рациональных точек (^ерт.З).
24
Чтобы видеть это, достаточно спроектировать на оси координат
прямоугольник и параллелепипед: тогда на осях мы получим отрезки,
по одному на каждой оси, и внутри этих отрезков содержится
бесчисленное множество рациональных точек. Ясно, что эти точки
являются проекциями на оси координат рациональных точек,
содержащихся внутри прямоугольника или внутри параллелепипеда. Несмотря
на это свойство плотности множества рациональных точек плоскости
или пространства, это множество есть лишь счетное. Чтобы видеть
это, достаточно обозначить рациональную точку Р (х, у) плоскости
или рациональную точку пространства соответственно так: е х%у и е XtVtZ.
Ясно, что оба множества \е х% у) и [е ХлУ#), будучи занумерованными
конечными системами рациональных чисел, суть счетные множества.
Как следствие отсюда вытекает:
Множество М параллелепипедов, попарно не имеющих общих
внутренних точек, есть самое большее счетное множество.
Действительно, пусть М={тс}, где тс параллелепипед. Пусть R
есть множество всех рациональных точек Р трехмерного пространства;
так как R есть счетное множество, можно его элементы занумеровать:
(Я) Pr,P2,...,/V...
Пусть Р{ есть первая точка в последовательности (/?), содержащаяся
внутри тс; отнесем значок / к самому параллелепипеду тс, обозначив
его через гч. ' Если теперь мы возьмем другой параллелепипед тс',
отличный'от тс, то ему будет соответствовать другой значок if, когда
мы обозначим тс' через тс^. Действительно, если бы мы имели / = /',
то это означало бы, что точка Р{ находится и в параллелепипеде тс
и в тс', что невозможно, так как тс и тс' не имеют общей внутренней
точки. Отсюда следует, то множество М = {тс} есть множество {тч}
элементов тсг-, занумерованных различными натуральными числами, и,
значит, есть конечное или счетное множество.
§ 5. Арифметика счетной мощности. Пусть множества Ми
M2,..., Мъ где k натуральное число, не имеют попарно общих
элементов. Обозначим соответственно их мощность через ixj, jx2, . ..,jifc.
Обозначим через М сумму этих множеств, М = М{-\-М2-\- ... -\~Мк.
Естественно мощность \i множества Ж, зависящую лишь от мощностей
1*1 > V-& • • чРи и независящую от природы множеств Mv Af2, .. -,Мк,
назв'ать суммой мощностей <х1э р2, . . .,;ай и при этом писать равенство
^ = 1А1+Н'2-г ••• +Н-
Если множества ЛТХ, Л12,. . ., Ми.. . находятся в счетном числе и
не имеют попарно общих элементов, естественно сумму М зтих
множеств рассматривать как множество, имеющее своей мощностью
р- сумму мощностей ^ множеств Мг.
Таким образом, мы можем написать равенство
Н- = l^i -f" Н-2 + •• • -T-Vi-T
Но мы знаем, что сумма счетного множества и конечного
множества есть счетное множество, и далее, что сумма счетных мио-
25
жеств, взятых в ограниченном и;ш счетном числе, есть опять счетное
множество. В силу принятых теперь обозначений мы приходим к трем
следующим формулам:
КоЧ-л=Ко> * С3)
Ко-f «о+ «о + • • • + «о= «о» (4)
«о+«о+--- + «о+--. = «о- (5)
В первой формуле (3) число п есть любое натуральное число,
во второй формуле (4) число слагаемых К0 конечно, в третьей
формуле (5) число их счетно.
Чтобы идти по пути этой символики дальше, введем понятие
произведения мощностей.
Пусть M' — {ef\ и М" =-\ё') два какие-нибудь множества
соответственно мощности и/ и ц". Рассмотрим теперь множество Л/,
М=[е}, элементами е которого являются всевозможные пары (У, е")
элементов, взятых один из первого множества /И', другой — из
второго множества М". Таким образом, М=^\(е\ е")). Так как
мощность |х множества М не зависит от природы множеств М' и Мп\
но зависит лишь от их мощности *_<.' и и/', естественно
рассматривать мощность а множества М={(е'\ еп}\ как произведение мощ~
костей jj/ и \i? и писать равенство
Мы видели, что множество элементов ei h занумерованных
всевозможными парами натуральных чисел / и у,' есть счетное. Значит,
множестве {(/, j)} всевозможных пар натуральных чисел есть также
счетное. Тем более будет счетным множество пар (г, /) натуральных
чисел, где i принимает лишь значения 1, 2, 3,..., п и где j
пробегает весь натуральный ряд. Эщ замечание, в силу принятых
обозначений для произведения мощностей, дает формулы:
«о- «о=«о=«о- . (7)
В формуле (6) число п есть натуральное; в формуде (7) обозначение
&q есть просто сокращенный способ писать ^0 • &0- Равным образом,
мы сокращенно пишем К^— К0 • &1 и, вообще, ft* = &0. &J-1,
где п натуральное число. Но так как $2= &0, то отсюда следует,
что &* = К*= «0, а значит, «4 = К0 • «2 = tf* = К0 и так
далее. Таким образом, мы приходим к формуле
K;=No, (8)
где п число нзгуральное.
§ 6. Несчетные множества. Мы еще не доказали существования
несчетных множеств и, следовательно, несчетных мощностей. Этот
пробел будет восполнен в следующем параграфе. Пока ничто не
26
мешает нам установить взаимоотношения сметной и несчетной
мощности. Здесь важнейшие предложения таковы:
Прибавляя к какому-нибудь несчетному множеству М какое-
нибудь счетное множество Л, нельзя увеличить мсщности
множества М.
Действительно, раз М несчетно, оно бесконечно. Но всякое
бесконечное множество М содержит счетную часть М''. Заметив это,
мы можем представить данное множество М в виде суммы
М = N + M\
где N обозначает остаток множества М по удалении из М всех
элементов счетной части Мг. Ясно, что /Уесть несчетное множество;
в самом деле, если бы N было счетным, то счетной оказалась бы
и сумма NA-M' двух счетных множеств, что невозможно, потому
что М несчетно. Прибавив теперь к М счетное множество Л, мы
можем написать:
M-\rA = N-\-(Mf+A).
Но множество Af-f-Л есть счетное. Поэтому оно эквивалентно
счетному множеству М\ т. е. М'оэ М'-\-А. С другой стороны,
остаток N эквивалентен самому себе, т. е. NcoN. Отсюда следует,
что сумма N-{-М' эквивалентна сумме N-\%(М' -\-А).
Следовательно, множество М эквивалентно сумме М + Л, М со М-\- Л,
а значит, мощность обоих множеств: М и М~\-А, одинакова.
На языке арифметики мощностей эту теорему можно записать
так: если \ь есть мощность множества М, то
11+К0 = р. (9)
Дальнейшее предложение есть следующее: удаляя из какого-
нибудь несчетного множества М любую его счетную часть Mf,
невозможно уменьшить мощности множества М.
Действительно, обозначим через N остаток несчетного множества
М по удалении из М какой-нибудь его счетной части М!. Мы имеем
очевидное равенство
M = N + M*.
Остаток N есть, очевидно, несчетное множество, так как если N
есть счетное множество, то N-\-M' тоже счетно, что невозможно,
так как М несчетно. Но мы уже знаем, что прибавление к какому-
нибудь несчетному множеству любого счетного множества не
увеличивает мощности этого множества. Значит, мощность суммы N-\-Mr
есть та же самая, что и мощность остатка N. Но M~N-\-Mf;
поэтому мощности множества М и остатка N равны.
Предупредим читателя, что это предложение не следует
записывать на языке арифметики мощностей. В самом деле, при
попытке его так записать, пришлось бы ввести понятие разности
мощностей. Между тем даже в простом случае символ &0— К0 не
имеет никакого определенного смысла, потому что, удаляя из
счетного множества какую-нибудь его счетную часть, мы в остатке можем
27
получить и счетное множество, и конечное множество, и даже ничего I
не получить (т. е. иметь в остатке пустое хмножество): здесь все 1
зависит уже не от мощности удаляемой части, а от того, какова 1
именно удаляемая часть. I
Но сказанное отнюдь не препятствует тому, что понятие раз- 1
ности двух множеств есть совершенно точное понятие. I
В самом деле, пусть М есть какое-нибудь множество, содер- I
жащее в себе как часть множество Мх. В этих условиях под раз- I
ностъю М — Мх множеств М и Мх мы понимаем совокупность I
элементов множества М, не принадлежащих к Мх. Иначе говоря, 1
разность М — Мх есть остаток от множества М по удалении из I
него всех элементов части Мх. Как видим, разность множеств М — Мх I
есть совершенно точное понятие; но разность мощностей есть по- 1
нятие неопределенное, потому что уже на примере разности двух I
счетных множеств мы видели, что М — М1 имеет любую мощность, 1
не превышающую счетную .лощность. I
§ 7. Мощность континуума. Это есть первая несчетная мощ- 1
ность, которую встречает на своем пути математический анализ. Чтобы 1
определить ее, докажем сначала предложение: I
Теорема. Какова бы ни была бесконечная последователь- I
ность точек PL, Р.2, Р3, ..., Р/г,..., занумерованных натураль- 1
jhumu числами и принадлежащих данному отрезку [ау b\t всегда I
\чожно на этом отрезке найти такую точку Р, которая заве- 1
домо не принадлежит рассматриваемой бесконечной последова- .1
тельности точек. " I
Для доказательства возьмем множество У\ всех отрезков а, имею- 1
щих рациональные концы 2 = {з]. Заметим сначала, что множество I
2 счетно. Действительно, отрезок, имеющий рациональные концы 1
г и г\ можно рассматривать как элемент ert /, занумерованный си- I
стемой двух рациональных чисел. А выше мы видели, что множе- 1
ство таких элементов есть счетное. Таким образом, элементы мно- 1
жества V можно расположить в виде бесконечной последователь- 1
ности: Ш
(^j) °1> а2> а3' • • • ' °ю • • • • 1
Применим теперь следующий процесс. Пусть в последователь- 1
ности (2) 3/7Х есть первый отрезок, лежащий на [а, Ь] и не содер- 1
жащий точки Рх. Ясно, что такой отрезок <зП1 всегда существует, 1
1ак как рациональные точки образуют всюду плотное множество на |
{я, Ь]. Далее пусть а„2 будет первый отрезок в последовательности ]
V, лежащий на <зЛ1, не содержащий точки Р2 и такой, что его 1
длина будет меньше половины длины отрезка аПх. Ясно, чго сЯв не
содержит и точки Р1 (потому, что она не содержится в оп%) и что
''^2>ni (потому, что если w.2</z1, то <зП1 не будет первым отрезком, j
не содержащим точки Рх). Затем пусть аПъ будет первый отрезок \
в (V), лежащий на зИг) не содержащий точки Р3 и такой, что J
длина <зщ меньше половины длины аПь\ ясно, что a,h не содержит
ни Ри ни Р2, и что я3>я2. И так далее. Вообще, определив
отрезок оМЛ, не содержащий ни Ри ни Р2, ни РЛ, мы берем в (^)
первый отрезок <зПл+1, лежащий на a7?Jfe, не содержащий точки Pft_t
и такой, что его длина меньше половины длины отрезка оп&. Ясно,
что апк не содержит ни Р1э ни Р2, ни Р*, ни РЛ + 1 и что пк+х>пк
(потому, что если яЛ+1<л*, то aWfe не был бы первым отрезком,
не содержащим точек Р1э Ра, ... , Р&). Поступая таким образом
дальше, мы определим бесконечную последовательность отрезков
Ч' °v ' *#' 0?v
лежащих на данном отрезке [а, Ь] и вложенных один в другой,
причем всякий следующий меньше половины предыдущего. Но самое
важное свойство отрезка ЬПк — это то, что он наверное не содержит
k первых точек Рг, Р2, ... , Рн заданной бесконечной
последовательности точек Ръ Р2, . . . ,Рп
ПУ
Черт. 4.
Прежде чем идти дальше, укажем один основной принцип теории
точечных множеств:
Всякая бесконечная система отрезкоз ои os, ... , а^; ... ,
лежащих на прямой линии, вложенных осин в другой и имеющих
длины, стремящиеся к нулю, необходимо содержит одну и только
одну общую им всем точку I. Этот принцип является прямым
следствием теории иррациональных чисел и есть, в сущности, не что
иное, как утверждение непрерывности самой прямой линии.
В нашем случае отрезки зп, а*, ... , o)lk, ..., будучи вложенными
один в другой и имея длины стремящимися к нулю, стягиваются
к одной точке Р (черт. 4), которая принадлежит всем им
одновременно. Так как эта точка Р лежит на отрезке а , то она не может
быть ни Р3, ни Р2, ни Pk. Но здесь k есть произвольное натуральное
число. Значит, точка Р, которую мы нашли указанным процессом
и которая является точкой данного отрезка [а, Ь], не может
принадлежать данной бесконечной последовательности точек Р2, Р2,
^з» • • • > Pfe, . . . . А это и требовалось доказать.
Из доказанной теоремы вытекает чрезвычайно важное следствие:
Множество всех точек каждого отрезка прямой есть
несчетное множество.
Действительно, если бы нашелся некоторый отрезок [а, Ь],
множество всех точек которого было бы счетным, то, перенумеровав все
его точки при помощи натуральных чисел, т. е. расположив их
в виде последовательности Рх, Р2 .,., Ря,..., мы могли бы опре-
29
делить новую точку Р, заведомо отличную от любой точки
последовательности Pl5 Р2,..., Рг.,... и принадлежащую отрезку [а, Ь].
А это невозможно, так как последовательность Ри Р2,..., РЛ,...
предполагалась содержащей действительно все точки отрезка [а, Ь].
С другой стороны, важно заметить, что множества точек любых
двух отрезков равномош/ггы.
Это обстоятельство на первый взгляд кажется парадоксальным,
потохму что хочется думать, то „чем длиннее отрезок, тем больше
на нем лежит точек". Но это оказывается иллюзией, от которой
читатель должен освободиться. Чтобы видеть это, достаточно
рассмотреть чертеж 5. На нем концы двух параллельных неравных
отрезков [а, Ь] и [а , Ьг\ соединены прямыми, пересекающимися в точке О.
Проводя через О вращающуюся прямую OL, мы видим, что она
пересекает отрезки [а, Ь\ и \а\ b ] в двух точках Р и Р', которые
можно рассматривать как соответственные
друг другу. Когда точка Р при вращении
прямой OL описывает отрезок [а, Ь],
соответственная ей точка Р' описывает другой отрезок
[а', Ь']. Мы видим, что все точки отрезков
[а, Ь) и [а', Ьг] взаимно-однозначно
соответствуют друг другу, т. е. что множества точек
отрезков [а, Ь\ и [а\ Ьг\ эквивалентны. А это
и означает, что они равномощны.
Условимся называть мощностью континуума
мощность множества всех точек, лежащих на
отрезке [0, 1]. Мощность континуума обозначается буквой С. Так
как мощность эта несчетная, то имеем неравенство
С>Ко- (Ю)
На основании доказанной теоремы ясно, что мощность множества
всех точек всякого отрезка равна мощности континуума, т. е. равна
С. Но с другой стороны, мы видели, что множество всех
рациональных точек и множество всех алгебраических точек суть счетные
множества, и так как прибавление или выкидывание элементов в
счетном (или конечном) числе не изменяет мощности несчетного
множества, то отсюда следует, что:
Множество всех иррациональных точек, а также множество
всех трансцендентных точек всякого отрезка [а, Ь] имеют
мощность континуума, т. е. С,
Покажем теперь, что множество всех точек, лежащих на пря*
мой {бесконечной в обе стороны), имеет мощность континуума.
Для доказательства рассмотрим чертеж 6. Здесь на бесконечную
в обе стороны прямую Хг X положена сверху окружность,
касающаяся этой прямой в начале координат О. Йроводя через центр С
окружности полупрямые, мы пересекаем ими окружность и прямую
X'X в двух соответственных точках р и Р, q и Q. Когда точка Р
описывает всю прямую Х'Х, пробегая ее слева направо,
соответствующая ей точка окружности р описывает нижнюю полуокружность,
отсекаемую от окружности прямой АВ, проведенной через центр
30
окружности С и параллельной прямой XX. Поэтому точки прямой
Х'Х и точки нижней полуокружности ЛОВ находятся во
взаимно-однозначном соответствии; это означает, что множества точек прямой Х'Х
и нижней полуокружности ЛОВ суть эквивалентные множества.
Всякая полупрямая СР есть всегда наклонная прямая, т. е.
непараллельная прямой Х'Х. Отсюда следует, что точка /?,
соответствующая точке Р пьямой, лежит на нижней полуокружности ЛОВ так,
что никогда не совпадает ни с точкой Л. ни с точкой В. Это озна-
Черт. 6.
чает, что множества точек прямой Х'Х и нижней полуокружности
ЛОВ хотя и находятся во взаимно-однозначном соответствии, но при
этом нижняя полуокружность АОВ предполагается неполной, потому
что к ней не причисляются ее две концевые точки Л и В. Такая
полуокружность с исключенными концевыми точками называется
открытой. Спроектируем теперь открытую полуокружность ЛОВ на
прямую Х'Х, Мы получим как ее ортогональную проекцию
открытый отрезок ((2, Ь) прямой Х'Х, т. е. отрезок (а, Ь) с исключенными
х._ , О
Р-э Р-2 ^ Ро 8 £ в ff Х
Черт. 7.
концевыми точками а и Ь. Но проектируя полуокружность АОВ на
прямую Х'Х, мы, очевидно, устанавливаем взаимно-однозначное
соответствие между точками этой полуокружности и их проекциями,
лежащими на открытом отрезке (а, Ь). В результате, множество
точек прямой Х'Х эквивалентно множеству точек открытой
полуокружности ЛОВ и в то же самое время множество точек открытого
отрезка (а, Ь) эквивалентно множеству точек этой же открытой
полуокружности АОВ. Два множества, порознь эквивалентные третьему,
эквивалентны между собой. Значит, мощность множества всех точек
прямой Х'Х равна мощности множества точек открытого отрезка
(а, Ь). Но несчетная мощность не изменяется от присоединения к
несчетному множеству двух точек. Отсюда и следует, что мощность
множества всех точек бесконечной в обе стороны прямой Х'Х равна
мощности континуума, т. е. рав ia С.
Нанесем на прямой все целые точки Рт, т. е. точки, абсциссы
которых суть целые числа (черт. 7). Вся прямая Х'Х вследствие
этого будет разбита на счетное множество отрезков, длина каждого
из которых равна единице. Так как эти отрезки имеют общие концы,
31
то мы условимся присоединять ко всякому из этих отрезков его
левый конец, оставив этот отрезок открытым справа. Так как
несчетная мощность не изменяется от присоединения или от выкидывания
конечного или счетного числа элементов, то, очевидно, мощность
множества всех точек каждого такого отрезка (замкнутого слева и
открытого справа) есть мощность континуума. И так как эти отрезки
(замкнутые слева и открытые справа) не имеют попарно общих
точек и в сумме дают всю прямую Х'Х% то мы приходим к двум
следующим соотношениям:
C+C + C+...+C-f-...=C (П)
или
СК0=С. (12)
Тот факт, что мощность множества всех точек прямой равна
мощности континуума, дает возможность заключить о справедливости
предложения:
Мощность множества всех точек плоскости равна мощности
множества всех точек квадрата (включая точки его сторон).
Мощность множества всех точек трехмерного пространства равна
о яП
\ Черт 8.
мощности мнежгства всех точек куба {включая точки его
граней).
Действительно, раз множества точек бесконечной в обе стороны
-прямой Х'Х и отрезка длины единицы [0, 1] эквивалентны (черт. 8),
то между их точками Р и Р' можно установить в:аимно-однознач-
ное соответствие. Легко видеть, что это соответствие определяет
функцию. Действительно, обозначая абсциссу точки Р прямой через
х и абсциссу точки Р отрезка [0, 1] через х\ мы замечаем, что
каждому действительному числу х соответствует вполне
определенное действительное число х\ содержащееся между 0 и 1, причем
сами 0 и 1 также сюда включены. Но сказать, что всякому числу х
соответствует число х\ это и значит сказать, что хг есть функция
аргумента х> т. е. мы имеем
х = ср (х).
Важно обратить внимание на то, что х! не выходит за границы
О и 1, т. е. что [0^V<;1]. С другой стороны, рассматриваемое
соответствие точек Р и Рг, т. е. чисел х и х\ есть
взаимно-однозначное. Это значит, что х также является функцчеЯ, и именно
обратной функцией аргумента х\ т. е.
х = Ь(х'),
причем аргумент хг не выходит за границы промежутка [0О'<^1],
тогда как число х может быть каким угодно действительным числом,
32
Черт. 9.
7
/
0
vL
я;
1
t
А
* lL_
у/
при надлежащем подборе значения аргумента х\ На языке
уравнений это значит, что, решая уравнение х' — ®(х) относительно х, мы
получим x = ^(xf), и решая это последнее уравнение относительно
х', мы возвращаемся к первоначальному уравнению х' = ®(х).
Таким образом, в силу взаимной однозначности соответствия точек
Р и Р\ функции ои 6 суть взаимно обратные.
Заметив это, возьмем квадрат с вершинами в точках (0, 0), (0, 1),
(1,0), (1,1) и куб с вершинами в точках (0, 0, 0), (1, 0, 0), (0,1,0),
(0,0,1), (1,1,0), (1,0,1), (0,1,1,), (1,1,1). Такой квадрат и такой куб
называются соответственно единичным квадратом и единичным кубом.
Пусть теперь Р (х, у) есть какая-нибудь точка плоскости XOY
(черт. 9), имеющая х и у своими координатами. Ей мы поставим
в соответствие точку
Р (я', у'), координаты
х' и у' которой
определены уравнениями
*'=©(*), у' = о(у).
Ясно, что в силу
соотношений [0<>'<; 1 ]
и [0<У<!1] точка Р не
выйдет за пределы
единичного квадрата.
Обратно, если Р' {х\ yf) есть какая-нибудь точка единичного квадрата,
то ей соответствует единственная точка Р(х, у) плоскости,
координаты которой х, у определяются из уравнений хг = <р (х) и
у' =zy(y)y что дает х = <Ь(х') и у=:й(У). Мы видим, что
множества точек плоскости XOY и единичного квадрата суть
эквивалентные множества.
Точно так же слово в слово доказывается эквивалентность
множества точек трехмерного пространства OXYZ и единичного куба: для
этого достаточно установить взаимно-однозначное соответствие точек
Р(х, у, г) пространства и точек Р' (х\ у, г') единичного куба при
помощи уравнений
х' = о (лг), у' = с? (у), z = о (г\
из которых х, у, z определимы посредством обратной функции ty:
* = <К*')» У = 1ЛУ\ z = b(z').
Мы переходим теперь к изложению одного из самых глубоких
открытий Георга Кантора. Открытие это состоит в установлении того
кажущегося столь парадоксальным факта, что мощность множества
ссех точек квадрата равна мощности множества всех точек
отрезка. Если предложение „все отрезки равномощны" показывает, что
длина отрезка не играет никакой роли з величине мощности, то теперь
мы видим, что число измерений также не оказывает никакого
влияния на мощность, раз квтдрат имеет „столько же" всех точек, как
и одна его сторона.
3 Ът:. 1214. 33
Прежде всего, введем юдно вспомогательное определение:
Назовем символом Кенига о всякую конечную систему целых
чисел, из которых последнее есть натуральное число, все же
остальные, если они имеются^ суть нули.
Таким образом, а = (т) есть символ Кенига, если т натуральное
число; равным образом а = (000...О/я) тоже есть символ Кенига, если
т натуральнее число и если число нулей конечно.
Введя это определение, вспомним следующие положения
элементарной арифметики и алгебры:
I. Десятичным числом называется всякое рациональное число,
которое может быть представлено в виде дроби: -7—» где числитель/?
любое целое число и где а натуральное число или нуль. Так, напри-
3 3 3 15
мер, ^ десятичное число, ибо <Т: = -v g — tW ♦ Следовательно, де-
20 20 2*'О IV-
сятичным будет только таков рациональное число, знаменатель
которого можно написать в виде единицы с нулями, т. е. в виде:
или 1, или 10, или 100 и т. д.
II. Всякое недесятичное число лг, удовлетворяющее условию
0<Я^1, единственным образом разлагается в десятичную дробь:
х = 0, ах а2 яз • • • ап • * • >
которая необходимо будет существенно-бесконечной.
Этб значит, что буквы а^ а9,..., ап,... суть цифры 0, 1, 2, 3,
4, 5, 6, 7, 8 и 9, причем апфЬ для бесконечного множества значений п.
III. Всякое десятичное число х, удовлетворяющее условию
0<х<1, имеет два десятичных разложения:
х = 0, aL а2 а$...ап.••
и
л: = 0, b. b2 bs.. .bn.. .,
из которых одно существенно-бесконечно, имея бесконечное число
цифр ап, не равных нулю, а другое конечное, так как все его
цифры bnt начиная с достаточно большого п) суть нули.
Само число 1 также имеет два десятичных разложения: 1 =0,999...9...'
и 1 = 1,00000....
Из этих положений арифметики и элементарной алгебры мы
заключаем, что всякое действительное число х, удовлетворяющее
условию 0<л*^1, разлагается единственным образом
в существенно-бесконечную десятичную дробь:
х = 0, ах а2 а3. . . ап. ..,
т. е. имеющую бесчисленное множество цифр ач, не разных нулю.
Заметив это, возвратимся к символам Кенига. В силу самого
определения символа Кенига а, мы видим, что всякая
существенно-бесконечная десятичная дробь 0, ах а2 а3. . .ап. .. определяется
бесконечной последовательностью 0, ог о2а3. . .о„. . . символов Кенига ап,
имеющих своим последним числом одну из цифр: 1, 2,3, 4, 5, 6, 7,
8 и 9.
34
Обратно: всякая бесконечная последовательность 0, ах а3 а3'.. .з,г. ..
символов Кенига оп, последнее число которых есть одна из цифр:
1, 2, 3, 4, 5, б, 7, 8 и 9, определяет существенно-бесконечную
десятичную дробь, в которую разлагается некоторое
действительное число х, удовлетворяющее условию 0<лг^1.
Для того чтобы понять, каким образом делается превращение
бесконечной десятичной дроби в последовательность -символов Кенига
и также обратное превращение последовательности символов Кенига
в бесконечную десятичную дробь, достаточно взять один какой-нибудь
пример.
Бесконечная десятичны дробь
0,830519000320146000008001000003...
превращается, очевидно, постановкой круглых скобок
0, (8) (3) (05) (1) (9) (0003) (2) (01) (4) (6) (000008) (001) (000003). .7
в бесконечную последовательность символов Кенига. Для того чтобы
сделать обратный переход от последовательности символов Кенига
к бесконечной десятичной
дроби, достаточно просто **
стереть круглые скобки
у символов Кенига.
Перейдем теперь к
доказательству , теоремы
Кантора. Мы хотим уста- 0] / " 0 ~у
повить
взаимно-однозначное соответствие между Черт. 10.
всеми точками
единичного квадрата и всеми точками единичного отрезка [0,1],
лежащего на оси ОТ (черт. 10). Возьмем какую нибудь точку Р (ху у)
единичного квадрата, не лежащую на самих кях координат. Ясно,
что ее координаты х и у суть действительные числа,
удовлетворяющие условиям 0<х<1 и 0<О<1. Мы разлагаем х и у в
существенно-бесконечные десятичные дроби: х = 0, а^ а'2 а'3. . ,а'п... и
>' = 0, а[ а2 flg...a^.... и превращаем эти дроби в две
последовательности символов Кенига:
* = о, з; *; ^...*;...,
Из двух этих последовательностей символов Кенига мы составляем
одну последовательность, беря поочередно символы Кенига то из
первой, то из второй и выписывая их один за другим:
Ясно, что, уничтожив круглые скобки в этой последовательности
у всех символов Кенига, мы получим существенно-бесконечную дробь,
определяющую некоторое действительное число /, 0<£<1, которое
мы имеем право рассматривать, как абсциссу некоторой точки р>
3* 35
лежащей на отрезке [0,1] оси ОТ. Таким образом, всякой точке Р
единичного квадрата соответствует одна точка р единичного
отрезка [0,1].
Но верно и обратное: всякой точке р единичного отрезка [0,1],
не совпадающей с началом О, соответствует одна точка Р
единичного квадрата, не лежащая на осях координат. Действительно,
имея точку р, мы знаем ее абсциссу t, 0<£<;i. Имея t, мы имеем
существенно-бесконечное десятичное разложение /, которое
превращаем в последовательность символов Кенига. Затем * выписываем
символы Кенига, стоящие на нечетных местах, рядом друг за другом,
и стираем у них скобки. Это нам даст бесконечное десятичное
разложение абсциссы ху 0< х^ 1, точки Р. Наконец, выписываем
оставшиеся на четных местах символы Кенига рядом друг за другом.
Это дает ординату у, 0<^/<;i точки Р. Таким образом, точка Р
единичного квадрата находится единственным образом, раз дана
точка р единичного отрезка [0,1].
г\
/
\
о
! /
Р
У
~,,| *
г> \
\/ 1У
7
' /
/
f
X
4
Черт. 1Ь
Мы видим, что соответствие точек Pup есть
взаимно-однозначное. Но мы знаем, что мощность множества всех точек
прямолинейного отрезка с исключенным концом есть мощность континуума, т. е.
равна С. Следовательно, мощность множества всех точек Р
единичного квадрата, не лежащих на самих осях координат, равна С. И так
как присоединение к множеству мощности С конечного (и даже
счетного) числа множеств мощности С не изменяет его мощности, то,
присоединяя обе стороны единичного квадрата, лежащие на осях
координат, мы опять получим мощность С. ^
Таким образом, мощность множества всех точек единичного
квадрата, включая сюда его контур, есть мощность континуума.
Но мы видели, что множество точек всей плоскости эквивалентно
множеству точек квадрата, включая его контур. Следовательно:
Множество всех точек плоскости имеет мощность континуума.
Доказательство повторяется слово в слово и для трехмерного
пространства. В самом деле, достаточно рассмотреть единичный куб
и единичный отрезок [0,1], лежащий на оси ОТ (черт. 11). Если
точка Р принадлежит этому кубу и не лежит на плоскости коорди-
36
нат, мы имеем неравенства 0<л;^1, 0<д/<П, 0<г^1. Но
тогда, написав х, у и г в символах Кенига
0 11 И II It
.о а о ... а ... к
z = Q,ol o2 о3...оя...
и написав все эти символы Кенига в виде одной последовательности
/ = 0, о', о" а'" о' а" а'". . .о' а" а'". . .,
v> 1112 2 2' п п п ' *
мы определяем действительное число /, 0 < / ^ 1, которое
рассматриваем как абсциссу точки р прямолинейного отрезка [0,1] с
исключенным левым концом. Ясно, что соответствие точек Р куба и точек р
прямолинейного отрезка есть взаимно-однозначное. Отсюда после
присоединения к кубу трех его граней, лежащих на плоскостях координат,
мы видим, что мощность множества всех точек, принадлежащих
единичному кубу, включая сюда его грани, есть мощность
континуума.
Так как множество точек единичного куба эквивалентно
множеству точек всего трехмерного пространства, то отсюда следует, что:
Множество всех точек трехмерного пространства имеет
мощность континуума.
Для того чтобы идти дальше и рассматривать пространства
многих измерений, обратимся к общему вопросу разыскания мощностей.
§ 8. Теорема о мощности промежуточного множества. Для
удобства введем обозначение: если какое-нибудь множество В
составлено из элементов (некоторых или всех) множества Л, мы
условимся писать
Л>£.
Если даны три множества Л, В, С таких, что для них имеем
Л>С>£,
то в этом случае множество С называется промежуточным. Смысл
этого названия ясен: множество А объемлет множество С, а
множество С, в свою очередь, объемлет множество В] поэтому, С есть
промежуточное множество. Самые же множества А и В можно
назвать крайними множествами.
Чрезвычайно ценным инструментом для точного отыскания
мощности служит следующее важное предложение, получившее название
„критерия равенства мощностей" :
Если мощности крайних множеств равны, то и всякое
промежуточное множество имеет равную им мощность.
Это предложение кажется „очевидным". Но здесь читатель должен
быть весьма осторожен в своих умозаключениях.
Переходя к доказательству, сделаем сначала следующее замечание.
Сказать, что множество Л, А~\е}> эквивалентно множеству S, это
означает сказать, что между элементами множеств А и В можно
37
установить некоторое взаимно-однозначное соответствие ®,
заставляющее отвечать каждому элементу е множества Л вполне определенный
элемент множества В, который мы назовем отображением элемента е
и который мы обозначим через о (е), Если два какие-нибудь
элемента е и е множества Л различны, то различны будут и их
отображения о (*) и © (е'). Притом, множество отображений всех
элементов е множества А, очевидно, тождественно всему множеству В,
потому что соответствие <р есть взаимно-однозначное между всеми
элементами обоих множеств А и В
Пусть множество А/ есть какая-нибудь часть множества А;
естественно множество Bf отображений всех элементов ег множества А'
назвать отображением множества А' и обозначить его через <р (Л').
Таким образом, имеем:
<р(А') = В'.
Ясно, что если имеем две части А' и А" множества А и если А!'
объемлет Л', т. е. если '
то и отображение множества А", о (Л"), та.-ше объэмлет
отображение множества А', о [А'), так что имеем:
?(Л//)><?(4').
В частности, если А" совпадает с Л, то и о (А") совпадает с В;
следовательно, само множество В есть отображение множества Л,
и мы имеем:
9 (Л) = В.
Все эти определения и обозначения относятся к любым двум
множествам Л и В, эквивалентным между собой. В нашем случае само
множество В есть часть множества А,
А>В.
Отсюда следует, что отображение В = <р (Л) множества Л объем-
лет отображение £2 = ср (В) множества В, B^BV При этом
множество В рассматривается как часть множества Л, отображающегося
на В. Следовательно, отображение Вг = ^{В) множества В объемлет
отображение B% = v{Bx) множества В19
Продолжая дальше, мы видим, что отображение В.2 = <? (Вх)
множества Вх объэмлет отображение Вь = о (В2) множества В2 и так
далее. Таким образом, мы получаем бесконечную
последовательность множеств
Л>5>Я1>5а>В8>...>5яМ>в||>... ,
занумерованных натуральными числами, таких, что всякое из них
объемлет все следующие за ним, причем каждое из них (кроме на-
38
чального Л) есть отображение предыдущего:
■?(Д) = В, ?(S) = 5^9(8!) = fl2$?(ffa) = Se,..;,?(Sw_0 = Sn>...
Обозначим ч:рез D совокупность всех элементов s множества Л,
принадлежащих всем множествам Л, В, £j, В2,... Мп,. Л Множество
D может, в частности, оказаться пустым. Далее обозначим через Кп
разность Bn-i— Вп\ по определению, это есть множество всех
элементов, принадлежащих к Вп-\ и не принадлежащих к Вп. При
этом разность А — В будем обозначать через /С0, условившись писать
В = В0. Из сказанного ясно, что начальное множество Л можно
написать в виде бесконечной суммы
A = D + K0 + K1-\-Kz-\-...+Kn+...f
причем все множества, написанные в этой сумме, не, имеют попарно
общих элементов. Прибегнем для наглядности к следующей схеме.
Изобразим множества Л, В, Вх, В2,...,
Вп,... в виде системы концентрических
кругов, все меньших и меньших
радиусов, причем каждая окружность
причисляется к кругу, ею определяемому (черт.
12). Тогда множество D изобразится в
виде общей части, принадлежащей всем
этим кругам. Разность же /Ся = Вп_х —Вп
изобразится в зиде кругового кольца,
лежащего между окружностями кругов Вп_г
и B,h причем большая окружность
принадлежит к К„, а меньшая, наоборот,
исключена из Кп. Ясно, что К0 изобра- Черт. 12.
жает множество Л — В.
Докажем теперь, что все множества /Со, Kv Ко, • • •> Kni...
эквивалентны друг другу, т. е. что
Дг0 со /Сх со /С2 со /С, со ... со /(„_! со /Ся. . . .
Для этого докажем, что «кольцо» /С;г шиь отображение кольца
Kn-i, т. е. /С74 = ?(/С,1-1). В самом деле, раз какой-нибудь элемент*?
принадлежит к K}„v то он принадлежит к В,ь~2 и не принадлежит
к /in_j. Но тогда отображение у {е) элемента е должно, во-первых,
принадлежать к В1Ь_Х и, во-вторых, не может принадлежать к Вю
потому что если бы отображение <?(е) принадлежало к Вп, то
отображающий элемент е принадлежал бы к Вп_и а эгого нет в
действительности. Следовательно, если е есть элемент „кольца" Кп-и его
отображение с? (?) есть элемент „кольца" К)Г С другой стороны,
если е есть какой-нибудь элемент кольца /Сн, то с принадлежит
к Вп_1 и не принадлежит к Вп. Но тогда е есть отображение
некоторого элемента е, ef = ъ (г), и очевидно, что е принадлежит к Вп_2
и не принадлежит к Вп_х. Следовательно, отображающий элемент е
принадлежит кольцу КПтя1. Из сказанного мы заключаем, что кольцо
39
Кп есть отображение кольца Kn-U T- e- Ki = ?(Ял-1)- Таким
образом, мы имеем:
Ai = ? (АГ0), *а = ?(*,), ^ = ?(^)..--./См = ?(/Сй-1)»...
Это и показывает, что множества
К0 со /Cj со /С2 со /("з со . . . со Arw-1 со АГП...
эквивалентны друг другу и что взаимно-однозначное соответствие
устанавливается отображением <?> переводящим всякое множество
Кп_х в непосредственно следующее множество Кп.
Установив это, возьмем любое промежуточное множество С
и обозначим его последовательные отображения через Cv С2, С3,..м
ТаК ЧТО
Ясно, что переход от трех множеств Л,
С и В, связанных соотношением
к их последовательным отображениям
дает соотношения
В^С^В.
^1 ^> Q >- #2
Е>п-i^> Сп ^> #и
Черт. 13. * *
Наличие этих соотношений дает право изобразить на предыдущей
схеме множества С, Cv C2,..., Сй1... в виде замкнутых
многоугольников, охватывающих последовательно наши круги, начиная
с В, и лежащих в кольцах /С0, /С15 /С2,...5 /С»,... (черт. 13). При
этом контур многоугольника Си рассматривается как принадлежащий
этому многоугольнику.
Ясно, что из соотношения Вп-х^Сп^>Вп следует, что Сп есть
промежуточное множество между Bn~L и Вп и чго, поэтому, мы
имеем;
Вп-1 ~~ В>г ~ (Бп~1 — Сп) + (Q — #/*)•
Введем обозначения:
Кп —Bn-i— Сп и К"п~ Сп — Вп.
Ясно, что Л^ есть А — С, а Аг0' есть С—В. Вспомнив, что разность
Вп-Х — Вп есть «кольцо» Кп, мы имеем:
40
На схеме это означает, что круговое кольцо Кп есть сумма двух
неправильных колец К'п и К"п, из которых первое заключено между
окружностью и контуром многоугольника, а второе заключено между
контуром этого многоугольника и следующей меньшей окружностью.
Из того факта; что ъ{вп_%) = Вп„1 и ^(Вп^х) = Вп, мы вывели
заключение, что
Вп_х — Вп = о (Ва,2 —£n-i)>
т. е. что Kn^v{Kn_i). Другими словами, круговое кольцо Кп есть
отображение кругового кольца Kn.v Подобным же образом из
соотношений:
9(Вп_2) = Вп_и <?(Сп_1) = Сп и ?(S„-i) = 5„
мы заключаем, что
Bn.x-Cn^z{Bn_2-Cn^) и Сп — Вп^о(Сн^^Вп^Х
что можно написать в виде
К = ?(К-.)И К = НК-г)'
Это показывает, что все неправильные кольца, „одинаковым образом'
расположенные", эквивалентны между собой:
К'0 со ^со К!г со К^ со . . . со К'п_х со К'п со ...
/C0ff со /С/ со /Cj со К"ъ со . . . соД;,_1 со/С; со ...,
причем взаимно-однозначное соответствие осуществляется
отображением <?» переводящим всякое множество К' { в
непосредственно следующее множество К'п и всякое множество К'п_х в
следующее множество К\
Теперь, для того чтобы закончить доказательство теоремы о
мощности промежуточного множества, напишем очевидные равенства:
A = D + KrJ + K1 + K2+...+Kn+...
и
Разбивая каждое круговое кольцо Кп на сумму двух неправильных
колец К'п и К"п, мы находим
И
Обозначив через Е сумму
E=*D + Ki + Kl + FCa+. ..+*;+..., .
41
мы видим, что
с=£-[- K[-t-K2+K'3+... +/с;+....
Мы заметим, что все слагаемые множества каждой из этих обеих
сумм не имеют попарно общих элементов.
Заставим теперь соответствовать всякий элемент ?)
множества Е самому себе и всякому элементу е, принадлежащему сумме
множеств К1 о + К[ + К'2 + ... + К~\ "~Ь • • • его отображение о (е).
Ясно, что это соответствие переводит множество Е в самого себя и
что сумма #q 4-#i+■ А?2 + ... +/С-1+ '" перейдет в сумму
К+^ + **3+----Г*л+---> П010МУ ЧТ° ?(/Cl) = ^- СлеД°-
вательно, установленное таким образом соответствие есть
взаимнооднозначное. И так как оно переводит множество А в множество С, то
множество С эквивалентно
множеству Л, т. е. Л со С.
Это и доказывает
предложение.
Практически точное
отыскание мощности
множества лучше всего вести на
основании следующей
теоремы, являющейся простым
следствием только что
доказанного предложения.
Теорема. Если два какие-нибудь множества А и В таковы,
что каждое из них эквивалентно некоторой части другого, тогда
они эквивалентны между собой, т. е. А со В.
Пусть А ооБ1 и В со Л15 где At есть некоторая часть множества
А, и В1 есть некоторая часть множества В.
Раз множество А эквивалентно множеству Ви то между
множествами А и Вх можно установить взаимно-однозначное соответствие о,
переводящее А ъ Bv Следовательно, множество Bt есть отображение
множества Л, т. е.
С другой стороны, множество В эквивалентно множеству Дг Это
значит, что между множествами В и Ai можно установить
взаимнооднозначное соответствие 6, переводящее В в Л15
Указанное соотношение четырех множеств Л, В, Л1 и Вх можно
выразить схемой (черт. 14), в которой эти множества изображены
четырьмя кругами и в которой лучи, идущие от одного круга к
другому, указывают взаи но однозначные соответствия о и й, причем
направление отображений (т. е. отличие отображающего от ото-
42
Сражаемого указано стрелками. Множество В при отображении ф
переходит (в Av А1 = ^(В), ибо А1слВ. Но np i этом же
отображении ф множество Вг перейдет в некоторое множество А2,
являющееся, очевидно, частью множества Аг, т. е. А2 = ^(ВХ) и Л^Л^
Так как само Вх есть отображение множества А посредством <э,
B1^=to(A)i то имеем А2 = $[®(А)]. Итак, множество Лх есть
промежуточное между Л и Л2:
Л ^ А1^Ай,
и так как Л2 есть отображение множества А посредством комби-
iw\ овангого отображен, я tyy (где сначала нчд А производится
отображение <р> переводящее его в Bv и затем над .Bj выполняется
отображение ^, переводящее его в Л2), то множества Л и Л2
эквивалентны, т. е. ЛсоЛ2. Но Аг есть промежуточное множество
между А и Л2. Значит, в силу доказанного предложения, АсоАг] и
так как А1со В, то имеем окончательно А со В.
§ 9. Применение критерия равенства мощностей к
разысканию мощности пространств многих измерений.
Назовем точкой Р пространства п измерений (п — натуральное
число) всякую систему п действительных чисел хи х2>. .• , хп, которые
назовем координатами точки Р. Точка Я, имеющая хи х2,...,#w
своими координатами, будет нами обозначаться так: Р(хи х2,..мд:м).
Множество всех точек Р (дгг, х^...,хп) назовем пространством
п измерений и будем обозначать через Еп. При этом две точки
Р (atj, х2, . .. ,хп) и Р' {x'vx'v. ... ,х'п) считаются тождественными
тогда и только тогда, когда их координаты соответственно
тождественны, т. е. когда
Единичным n-мерным кубом мы называем множество всех точек
P(x1,x2,... ,хл), координаты которых удовлетворяют условию:
0<х1<1, 0<*а<1,..., 0<лгп<1.
Докажем, что множество точек всего п-мерчого пространства Eft
эквивалентно множеству внутренних точек п-мерного единичного
куба, т. е. множеству всех точек Р(х^х.2У.. ,,хп), для которых
0<^ < 1, 0 <х2 < 1,..., О < д-„ < 1.
Действительно, мы уже видели, множество точек прямой Х'Х
(бесконечной в обе стороны) эквивалентно множеству точек открытого
отрезка (а, Ь). При этом нужное нлм взаимно-однозначное соответствие
получалось геометрически посредством отображения прямой Х'Х на
нижнюю открытую полуокружность АОВу 2l эта последняя
отображалась на открытый отрезок (а, Ь). Ясно, что получившееся при этом
соответствие точек Р прямой Х'Х и точек Р' открытого отрезка
(я, Ь) есть не только взаимно-однозначное, но и взаимно-непрерывное,
потому что непрерывному движению точки Р по прямой отвечало
43
непрерывное движение соответственной точки р по открытой
полуокружности ЛОВ и, значит, непрерывное движение проекции Рг
точки р по открытому отрезку (а, Ь).
Легко, впрочем, освободиться от сложных геометрических
построений и чисто аналитически определить нужное нам соответствие. В самом
деле, пусть х есть любое действительное число. Определим
посредством него новое действительное число 5, написав формулу
1 + Щ '
где \х\ обозначает абсолютную величину действительного числа х.
Ясно, что £ есть функция аргумента х\ напишем, ради краткости, ее
в виде £ = ©(#). Ясно, что ©(0) = 0 и что <р( — х)=* —?(*)• Для
нас важно, что при безграничном непрерывном возрастании аргумента
л; от 0 до +оо, функция о(х) также непрерывно возрастает от О
и стремится к -\- 1 как к своему пределу. Значение +1 функция
о(х) никогда не принимает ни при каком действительном х.
Следовательно, уравнение £ = <?(х) устанавливает нужное нам
взаимно-однозначное и взаимно-непрерывное соответствие между множеством всех
действительных чисел х, —со < л: <-{-со, и множеством
действительных чисел 5, удовлетворяющих условию — 1 < 5 < -f-1 .
Наконец, чтобы не иметь дела с открытым отрезком (— 1, -}-1), но чтобы
рассматривать лишь открытый отрезок (0,1), мы делаем такое простое
преобразование:
s г' _ 1 + 6
х — 2 '
Ясно, что действительное число х' удовлетворяет условию 0 < х' < 1
и что при непрерывном возрастании £ от — 1 до -J- 1 значение х'
непрерывно возрастает от 0 до + 1. Следовательно, совокупность
двух формул
2 1 i- И
определяет х* как функцию аргумента х, т. е. как х' = ф (х), причем
при непрерывном возрастании аргумента х от — со до -j- со
значение хг непрерывно возрастает от 0 до -f-1. Сами же граничные
значения 0 и -f 1 никогда не будут получены числом х' ни при
каком действительном значении х. Следовательно, уравнение х' = ^ (л:)
устанавливает нужное нам взаимно-однозначное и взаимно-непрерывное
соответствие между множеством всех действительных чисел ху
— со < д; < -[- оо , и множеством действительных чисел х\
удовлетворяющих условию 0 < х' < 1.
Возвращаясь теперь к я-мерному пространству Ея, поставим в
соответствие всякой его точке Р (xv х2,. .., хп) точку Р (х[, х'2,.. .9х'п\
координаты которой x'v х'2, ..., х'п определяются уравнениями
*I = «K*i)> *; = «К*а)> •••> < = 'К^-
Ясно, что точка Pr (x'v х2, , •., хп) находится внутри единичного
/z-мерного куба, так как имеем 0 < х[<1, 0< х2< 1, ..., 0<*' <1,
44
При этом соответствие точек Р пространства Еп и точек Р'
внутренности единичного я-мерного куба есть взаимно-однозначное,
потому что уравнение х' = ty (х) всякому действительному числу х\
(0<^<1), заставляет отвечать лишь одно действительное число л:,
— эо<л;< + °°-
Таким образом установлена эквивалентность множества точек
я-мерного пространства Еп и множества точек внутренности
«-мерного единичного куба.
Чтобы идти дальше, обратимся к символам Кенига. Изобразим
числа x'v х', ..., х'п символами Кенига:
К = 0, оп о12 а|3 . . . а'
\т
х'2=0,
а21 °22 °23 * *
' а2т ' '
х'=0,
п '
л! «2 лЗ
Л/И '
Этих символов Кенига написано, очевидно, счетное множество, так
как мы видели, что всякое множество элементов o'ww,
занумерованных двумя натуральными числами, есть счетное. Поэтому, мы можем
написать все эти символы Кенига в виде одной последовательности:
<'=,6, о[ о'2 а; ... ?; ... ,
где всякий o'k есть некоторый а^, и, обратно, всякий з'ш написан
в виде некоторого з'к. Таким образом, каждой точке Pr (x'v xv.. .,х'п)
внутренности я-мерного единичного куба соответствует некоторое
вполне определенное действительное число t\ определенное
предыдущим равенством и, поэтому, удовлетворяющее условию
О < Г < 1 .
Если Р' (x'v x'v ..., х'п) и Р" {х[> х"2, ..'., хпп) суть две
различные толки внутренности я-мерного пространства Еп, то тогда они
отличаются друг от друга хотя бы одной координатой, например,
отличаются третьей координатой лг3, так что х'гф х"6. Но тогда
и разложения этой координаты по символам Кенига
^З^ °' а31 °32 °33 ' ' * %т • • • И Хз = О, о^ 3^ Ода . . . <£Л . . .
будут также различными. А это означает, что по крайней мере один
из символов Кенига o'Sm разложения х'3 будет различен от
соответствующего ему символа Кенига a£m, находящегося в разложении х"3 на
том же самом месте. Отсюда следует, что разложения
*' = о, 3;3; ... а; ... и t" = o, а;,; ... 0- ...
различны, так как некоторый о^ отличен от соответствующего ему зЛ.
Отсюда мы заключаем, что
45
Итак, дбум различным точкам Рг и Я7 внутренности л-мерного
единичного куба соответствуют две существенно-различные точки ( и t"
открытого отрезка (0 < t < 1).
Мы пришли к следующему выводу: множество внутренних точек
я-мерного единичного куба отображается взаимно-однозначным
соответствием на некоторое множество точек, принадлежащее открытому
отрезку (0</<1). Итак как множество точек пространства Еп
эквивалентно внутренности этого куба, то отсюда заключаем, что
множество точек всего л-мерного пространства Е^ эквивалентно
некоторой части множества точек открытого отрезка (0,1). С другой
стороны, множество точек отрезка (0,1) эквивалентно некоторой
части множества точек пространства Е}1: достаточно хотя бы взять
на оси ОХ открытый отрезок (0<х1<1). Мы видим, что находимся
в условиях применимости „критерия равенства мощностей".
Применив его, мы окончательно получаем чрезвычайно важное
предложение :
Множество всех точек пространства Еп, имеющего п
измерений, есть множество, эквивалентное множеству точек прямс-
линейного отрезка [0,1] и, значит, имеет мощность континуума^
т. е. мощность, равную С.
Это предложение имеет очень большую важность, так как
приводит к такому заключению:
Всякое множество точек М, лежащее в пространстве Ем п
измерений, есть множество мощности^ С. Оно имеет мощность,
равную С, гели возможно установить, что М содержит
некоторую часть Мх мощности С.
В справедливости этого мы убеждаемся на основании того, что
множество М будет тогда промежуточным множеством, так как
AV<M<E„
и крайние множества: Еп и Мх оба имеют мощность С.
В частности, если какое-нибудь множество точек М, лежащее
в пространстве Еп, содержит некоторый отрезок (а, Ь) или
хотя бы все его иррациональные точки, то отсюда следует, что
множество М имеет мощность континуума, т. е. равную С.
Вопрос о том, не будет ли вообще всякое несчетное
множество М точек, принадлежащих n-мерному пространству Е]Ъ
(в частности: трехмерному пространству, плоскости, прямой),
иметь мощность континуума,—еще не решен наукой. Это одна
из великих проблем; все усилия решить ее конструктивным
образом до сих пор оставались безуспешными и неубедительными.
Если бы проблема эта имела положительный ответ, т. е. что
всякое несчетное множество точек прямой имеет мощность
континуума, то это означало бы, что мощность континуума' С есть
непосредственно следующая за счетной мощностью &0, подобно тому
как натуральное число п имеет непосредственно следующее
натуральное число п 4-1, превосходящее его. Отрицательный ответ также
еще не получен. Несмотря на все сделанные усилия, до сих пор не
удалось отыскать несчетного множества точек мощности, меньшей
46
мощности континуума. Практически до сих пор все те несчетные
множества точек, с которыми анализ и теория функций имеют дело,
оказываются имеющими, каждое, мощность континуума.
То, что было сказано о пространствах конечного числа
измерений, без всякого изменения переносится на счетномерное
пространство.
Точкой Р счетно мерного пространства называется всякая
бесконечная последовательность действительных чисел
\Р) ' #1» -^2» -^3» * • • > Хп)'9Л1
занумерованных натуральными числами. Эти действительные числа
хи х2> ••♦> хп> ••• называются координатами точки Р. Две точки
Р [Xt, ^2' "•»*"'П)«")
И
ту/ / " " tr \
* wj.» •^2' " * *' *^w' * * **
различны, если отличаются друг от друга хотя одной парой
соответственных координат, т. е. когда для некоторого натурального п
имеем х'п-ф.х'п. Счетномерное пространство Е есть множество
всех точек Р (хи лг2, . .., хп> ...).
Точка Р принадлежит счетномерному единичному кубу, если имеют
место неравенства
0<^<1, 0О2<1, ..., 0<*й<1,...;
она лежит внутри куба, если знаки равенств исключены, т. е. если
имеем неравенства
0<х1<1, 0<х2<1, ..., 0<хп<1, ....
Множество точек счетномерного пространства Е эквивалентно
множеству внутренних точек счетномерного куба.
Доказательство остается тем же самым, как и в случае
пространства конечного числа измерений: достаточно подвергнуть коорринаты
хи х2, ..., хп, ... преобразованию хг = ^ (х), отображающему
множество всех действительных чисел х, —оо <я< -j- со, на
открытый отрезок (0<х'<1). Полагая *£ = Ф (*?»)> мы видим, что
точке Р {хих2, ..., хю ...) пространства Е соответствует точка
P'(x'v xv ..., х'п, .. .) внутренности счетномерного единичного куба, и
что соответствие это есть взаимно-однозначное. Наконец, написав
при помощи символов Кенига разложения чисел xfv x[^ ..., х'п, ...,
являющихся координатами точки Р' внутренности счетномерного куба,
Х1 = 0,а11а12. . .а^« .. .
x/. = 0oilcj2...oij...
47
и расположив эти символы (множество которых счетно как
занумерованное всеми парами натуральных чисел / и /) в простую
бесконечную последовательность, занумерованную натуральными числами
мы поставим в соответствие каждой точке Р' внутренности единич-"
ного счетномерного куба некоторую совершенно определенную
точку f открытого отрезка (0<^<1). Как и прежде, двум
различным точкам Р' и Р" ^отвечают две существенно-различные точки
f и *", ?' ф?\ открытого отрезка (0<*<1). Вследствие этого
множество всех точек счетномерного пространства Е эквивалентно части
множества точек открытого отрезка (0<7<1). И так как, с другой
стороны, множество точек- пространства Е имеет часть мощности
континуума, например, множество точек Р (хъ х2, ..., хп, ...),
где хх есть произвольное действительное число и где 0 = лга = х3 ==
= ... =хп = ..., то отсюда следует на основании „критерия
равенства мощностей'% что:
Множество всех точек счетномерного пространства есть
множество мощности континуума.
§ 10. Арифметика мощности континуума. Мы уже имели для
мощности континуума С формулы
s c+C + C+...+C+...=C (11)
и
С К0 = С. (12)
Теперь к ним можно присоединить дальнейшие формулы.
Для этого сначала заметим справедливость предложения:
Множество элементов eXi, х%, Хау . . ., занумерованных
конечными или счетными последовательностями действительных чисел,
имеет мощность не выше мощности континуума.
В самом деле, всякий такой элемент еХъ Xz> Хз>..., определяется
точкой Р (х1} х2, хв, ...) пространства конечного или счетного
числа измерений так, что двум разным элементам eXv Xty x .. .
соответствуют различные точки Р. Поэтому, множество элементов е
отображается на все или на часть пространства конечного или
счетного числа измерений. И так как множество точек пространства
имеет мощность континуума, то множество элементов eXl, ач, #.,,'...,
отображаясь на все или на часть этого пространства, имеет мощность
не выше мощности континуума.
Выше мы дали определение произведения двух мощностей.
Пусть А есть множество всех действительных чисел л;, А = {лг],-и пусть
В есть множество всех действительных чисел у, В — {у}. Тогда
множество М всех пар (х, у) действительных чисел х и у имеет,
согласно этому определению, мощность, равную произведению
мощностей С С, т. е. С2. Но, с другой стороны, всякая пара (х, у)
действительных чисел х и у соответствует точке Р (х, у) плоскости.
48
И так как множество всех точек плоскости имеет мощность
континуума, то имеем:
С.С = С* = С. (13)
Так как
с* = с*-с = с-с = с
и далее
с* = с*-с=с.с = с
и так далее, го вообще
Сп = С, (14)
где п есть число натуральное.
Расширим теперь понятие произведения мощностей. Пусть Ми М2,
уИ3, ..., МПУ ... есть конечная или счетная последовательность каких-
нибудь множеств, мощности которых соответственно суть |х1? ji9, ja3, ...
..., jxn, ... Пусть еп есть произвольный элемент, принадлежащий
к множеству Мп. Последовательность элементов
е = [е^ е%, £3, •. ., ею .. .)
можно рассматривать как новый предмет, и, значит, из этих новых
предметов можно составить некоторое множество Ж, являющееся
совокупностью всех таких предметов е. Мы можем определить
мощность jjl множества Ж как произведение мощностей pv ;x2, |х3, ...
и написать равенство
Пусть теперь всякая из мощностей \ьп равна мощности континуума,
т. е. |хх = С, |х2 = С, ..., {хп = С, .... В этом случае за множество
Мп мы можем взять множество всех действительных чисел хт.
— оо <д:м< + оо. Поэтому элемент e — (ev е2, е%$ . .., е, ...)
можно обозначить в виде бесконечной последовательности
действительных чисел {хх, х2, ..., xni ...). Другими словами, множество
Ж элементов е есть не что иное, как множество всех точек Р
счетномерного пространства. А так как оно имеет мощность
континуума, то отсюда выводим формулы:
С'С'С.С.^С (15)
или
§ 11. О существовании высших мощностей. Читатель может
подумать, что счетная мощность К0 и мощность континуума С суть
единственные бесконечные мощности. Такое мнение будет ошибочным,
как это вытекает из следующего предложения:
Каково бы ни было множество Ж, всегда можно определить
множество 9R, мощность m которого заведомо больше (и не равна)
мощности «а множества М,
m>u.
4 on к. 1241. 49
I
Множество SK, которое мы имеем в виду, есть множество всех
частей данного множесгвз М. При этом элементами множества 9К
являются не только все точные части множества М, но еще обе
взаимно-дополнительные неточные части: одной из них служит все
само множество М, а другая есть пустое множество. Обе эти
неточные части также рассматриваются как элементы множества Ж.
Самое доказательство теоремы весьма просто, мы проведем его
методом „от противного*-'. Пусть Ш со М. Тогда всякой части М'
множества М соответствует некоторый элемент этого множества,
который мы обозначим ew
Этот элемент ем1 может или принадлежать множеству /Л', или
не принадлежать ему. Обозначим через К множество всех элементов
емг, не принадлежащих соответстсующим им множествам М\ Так
как К есть ча:ть множества Л?, то К есть элемент множества 5Ш;
поэтому, множеству К соответствует некоторый элемент s
множества М, вследствие предположения об эквивалентности, дЯ со М. Но
здесь и наступает противоречие. В самом деле, во-первых] элемент е
не может не входить в К, потому что К есть множество всех
элементов <?дг', не входящих в соответствующие им множества М''. Поэтому,
е не может находиться вне множества К, т. е. не принадлежать
множеству /О Во-вторых, множество К не может и содержать
элемента г, потому что К есть множество только таких элементов е^/,
которые не принадлежат к соответствующим им множествам М\ и,
значит, среди них не может содержаться никакого элемента г,
входящего в соответственную ему часть К.
Итак, эквивалентности Ш со А1 быть не может.
С другой стороны, множество Ш имеет часть 99? 1э заведомо
эквивалентную множеству М, т. е. Qftjco М. За таковую достаточно
взять множество Ш единичных частей М" множества Мл т. е.
таких частей М", всякая из которых состоит лишь уз одного
элемента множества М. Заставляя каждой единичной части М"
множества М соответствовать ее единственный элемент, мы видим, что
Шх со М.
А это и показывает, что мощность m множества Ш больше
мощности {х данного множества М.
Если множество М конечно и состоит из п элементов:
М= (е1? с. 2,.. ., сп), тогда множество Ш есть также конечное и число
его элементов равно 2п. В этом легко убедиться методом
индукции: если /z=l, множество 5К состоит всего из 2 элементов:
неточная часть (с) и пустая часть. Пусть для п = k — 1 множество
Ш имеет 2к~г элементов. Докажем, что для /г = £ число элементов
множества Ш равно 2к. Действительно, если мы к множеству /И,
состоявшему из k—1 элементов еи е2, ..♦, £&-i> добавим
какой-нибудь новый элемент е*, то получим некоторое новое (дополненное
одним элементом) множество Л4*,
М\={е1У *2,. .., ек-и е*).
10
Ясно, что множество 3D?* всех частей множества М* состоит»
во-первых, из всех частей М' множества М, число которых 2fe-1.
Никакая из этих частей ЛГ не содержит добавленного элемента е*.
И, во-вторых, Ш состоит из частей М" множества М*,
содержащих элемент е*. Ясно, что все такие части М" получатся сразу,
простым присоединением к прежним частям Мг элемента е*.
Поэтому частей М' будет всего тоже 2к~1, и, значит, множество 5R*
состоит из 2к"1 -\-2к-1 = 2к элементов. Это и доказывает
предложение.
Когда данное множество М бесконечно и имеет мощность ix,
естественно обозначить мощность m множества Ш через 2^-.
Таким образом, имеет место равенство
m = 2i*>ji.. (17)
В частности, мы имеем
2*Чо>Ко.
Одним из замечательных предложений является равенство
мощностей:
2^0 = 0. (18)
Это предложение формулируется так: мощность множества всех
частей счетного множества равна мощности континуума.
Докажем это. За счетное множество М мы возьмем просто
натуральный ряд
(М) 1,2,3,...,/»,....
Множество SR есть множество всех' частей М! натурального ряда.
Мы знаем, что множество элементов <?#,</,..., и, v,
занумерованных конечными системами натуральных чисел /?,#,..., w, v9 есть
множество конечное, или счетное. Значит, множество всех
конечных частей натурального ряда есть счетное множество. А так
как множество Ш несчетно и так как мощность несчетного
множества не изменяется по удалении из него счетного числа элементов,
то для определения мощности множества Ш можно принимать во
внимание только бесконечные части натурального ряда. Итак, пусть Мг
есть бесконечная часть натурального ряда. Подпишем под каждым
натуральным числом п цифру 0, если п не входит в М\ и цифру 1,
если М' содержит число п. Ясно, что мы таким образом получим
существенно-бесконечную двоичную дробь
* = оле2е8...вя...,
где всякое Ьп есть либо 0, либо 1. Ясно, что действительное число
t принадлежит промежутку (0,1), так как имеем 0<^<;i.
С другой стороны, для двоичных бесконечных дробей имеет
место аналогичное предложение, как и для десятичных дробей, т.е.:
Всякое действительное число ty удовлетворяющее неравенству
0<г^1, разложимо единственным образом в существенно-
4* ' 51
бесконечную двоичную дробь, т. е. имеющую бесчисленное множе*
ство цифр 6Ш равных единице.
Таким образом, мы видим, что всякой бесконечной части Мг
натурального ряда соответствует некоторое действительное число t,
0<^1, и обратно, всякому действительному числу /, 0<^1,
соответствует бесконечная часть Мг натурального ряда, именно та самая,
которая образуется взятием тех натуральных чисел #, для которых
ея = 1.
Отсюда мы заключаем, что множество Tt всех частей
натурального ряда имеет мощность континуума, и} значит,
2 к о = С.
Это заключение тесно связано с понятием произведения мощностей.
Действительно, пусть каждое из множеств Ми М2% М3, ..., Мп,...
имеет только два элемента: Мп = (е'п> е'^). Рассмотрим бесконечную
последовательность e = (eh е2 ,..., £я,- ♦ -), составленную из
элементов множеств Ми М2,..., Л1П,..., выбранных соответственно по
одному в каждом из них, так что еп есть элемент множества Мп.
Е£ли мы обозначим множество всех таких последовательностей через
М, М = (е), то мы знаем, что мощность \i множества М равна
произведению мощностей множеств Mv М2, ..., Мп, ..., т. е.
\i = 2-2-2.. .. Но, с другой стороны, в качестве элемента еп может
быть выбран либо е^, либо е"п. Если еп = е' мы полагаем 8Л = 0; если
en=ze'^ мы полагаем 6П = 1. Ясно, что всякому элементу е
множества М соответствует вполне определенная двоичная дробь
(конечная или бесконечная):
и что соответствие это есть взаимно-однозначное. И так как
множество всех конечных двоичных дробей есть счетное множество,
то отсюда мы заключаем, что множество М имеет мощность
континуума, т. е.
2-2-2 ... 2 ... =С, (18)
что мы ранее написали в виде
2*^0= с. (19)
В качестве примера множества более высокой мощности, чем С,
рассмотрим множество М всех функций (непрерывных и
разрывных) аргумента х, М—{/(х)}, определенных на всей прямой X'X,
т. е. при аргументе х, могущем принимать всевозможные
действительные значения:—оо<х< ~|~ оо. Сначала мы рассмотрим лишь
часть множества М, именно: рассмотрим множество Ж* только таких
функций /* (х), чго для всякого действительного числа х функция
/*(х) равна либо 0, либо 1. Легко найти мощность множества Ж*.
Для этого заметим, что вся прямая X'X при помощи такой функции
/* (х) может быть разбита на две взаимно дополнительные части £*
и £*, причем для всех точек х множества £* имеем/* (х) —• 0 и для
52
всех точек х множества £* имеем /* (л:) = 1. Ясно поэтому, что
всякой функции /* (х) соответствует вполне определенная часть
прямой Х''Х, именно, множество Е\ всех корней уравнения /*(x) = l.
Обратно, если Е*2 есть какая-нибудь часть множества точек прямой
ХТХ, то, полагая /*(л;)=:1 на Е\ и/*(*) = 0 вне £*, мы имеем
функцию /* (х) как раз указанного вида. Отсюда мы заключаем,
что множество Л1 * = {/* (х)} указанных функций эквивалентно
множеству всех частей прямой XX и, следовательно, имеет мощностью
2е. С другой стороны, всякая функция f(x) изобразима
геометрически на плоскости в виде „кривой" _у=/(х). Значит,/(х)
соответствует часть множества точек плоскости, именно: множество всех
точек кривой _у =/(#). И так как мощность множества точек
плоскости XOY равна мощности континуума, то множество М всех
функций/(х), Af=-{/(*)}, эквивалентно части множества мощности 2е
(именно: части множества всех частей плоскости XOY). Применяя
теперь критерий равенства мощностей, мы немедленно заключаем,
что мощность множества М— {/ (х)} всех функций / (х) в точности
равна 2е (т. е. больше чем С).
Но большинство этих функций f(x) будут разрывные: таковы,
например, все функции /* (х), принимающие только два значения:
О и 1 в том случае, когда ни одно из множеств Е\ и £* не пусто.
Важно заметить, что для непрерывных функций f(x) дело обстоит
совершенно иначе.
Мноэюество всех непрерывных функций f(x) имеет мощность
континуума.
Для доказательства сначала отметим, что множество ЛГ, Л^ =
= {/(*)}> всех непрерывных функций f(x) содержит, как частный
случай, множество всех действительных констант С и, значит, имеет
часть мощности континуума. С другой стороны, всякая непрерывная
функция f(x) вполне определяется своими значениями в одних только
рациональных точках л:=зг, потому что, во-первых, всякая
непрерывная функция /(х), равная нулю во всех рациональных точках
д:=г, есть функция, тождественно равная нулю; во-вторых, две
непрерывные функции fx (x) и /2 (х), совпадающие своими значениями
для всех рациональных точек г, должны быть тождественными, потому
что разность их ftJ(x)—f\{x) есть непрерывная функция, равная
нулю для/ всех рациональных значений г аргумента л:. Но множество
всех рациональных чисел есть счетное. Перенумеровывая все
рациональные числа г натуральными числами
V?) г1> г2> Г3> ' • • > Гп > • • •»
мы видим, чго всякая непрерывная функция f(x) определяется
единственным образом (если только может определяться):
последовательностью действительных чисел уи у2, y3i .. ., yni ♦.., где
53
Таким образом, есякой непрерывной функции f(x) соотг,етстзует
единственная счетная последовательность е действительных чисел
^(Уи У-п Уг> •••, Уп, •••)
и двум существенно различимы непрерывным функциям fx(x) и /2(*)
соответствуют две различные последовательности ех и е%,
составленные из действительных чисел. Но всякая последовательность
Р(Уи У& • • •» Ут • • •) действительных чисел есть точка счетномер-
ного пространства. Следовательно, множество N всех непрерывных
функций f(x) отображается на часть счетномерного пространства.
И так как мощность множества точек этого пространства есть
мощность континуума, то, применив критерий равенства мощностей, мы
заключаем, что мощность множества N есть мощность континуума.
т
ГЛАВА II.
Черт. 15.
МНОЖЕСТВА ТОЧЕК.
§ 12. Линейные множества. Множество М, элементами которого
являются действительные числа, часто называют линейным
множеством, потому что это множество может быть изображено при помощи
соответствующего множества точек числовой прямой. Эту прямую
обычно называют осью абсцисс или осью ОХ.
Все свойства множества точек, лежащих на оси абсцисс ОХ,
вытекают только из двух следующих свойств этой оси.
I. Множество R всех рациональных точек г есть множество,
всюду плотное на оси ОХ.
Это означает, что на всяком отрезке [а, Ь] оси ОХ имеются
рациональные точки г, ему принадлежащие (черт. 15). Напомним,
что R есть счетное
множество.
JI. Всякая счет- £~——g
ная последовательность
°1>°2>-••>*»>•■•
замкнутых отрезков,
вложенных один в
другой и таких, что их
длины стремятся к
нулю, имеет одну и
только одну такую точку;,
которая принадлежит
всем этим отрезкам
(черт. 16).
Геометрически это означает, что вложенные друг в друга
замкнутые отрезки аПУ длины которых стремятся к нулю, стягиваются
к одной точке ?, принадлежащей всем этим отрезкам оп.
Оба свойства I и II числовой прямой ОХ суть простые логические
следствия определения действительного числа. Примем свойства I и
И оси абсцисс ОХ как постулаты, которым подчинена ось абсцисс
QX. Заметим только, что вовсе нет необходимости, чтобы отрезок оп
непременно лежал строго внутри отрезка оя_г. отрезок оп может
просто лежать на отрезке o„_i. Например, система замкнутых отрез-
55
ков ап = О,— стягивается к точке I = 0, являющейся левым концом
всякого из отрезков аЛ.
§ 13. Сегменты и интервалы. До сих пор мы говорили об
отрезках прямой и рассматривали их то как замкнутые, то как
открытые. Теперь мы должны значительно уточнить терминологию.
Назовем сегментом множество точек х оси абсцисс ОХ% для
которых выполнено условие
Геометрически это означает, что сегмент есть зам^гутый отрезок
(черт. 17), потому что оба его конца а и b в него включены. Точки
а и b называются концами сегмента. Сегмент, имеющий своими
концами а и Ь, обозначается [а, Ь]\ здесь квадратные скобки [ ]
х указывают, что концы
и ——-ь—* ■ ! ——— сегмента в него вклю-
п Си
и чены.
Черт. 17. Назовем
интервалом множество
точек х, для которых
О w J i f имеется условие
а аГ ' ' а<х<Ь.
^еРт- Ш- Геометрически это
означает, что интервал
есть открытый отрезок, потому что точки а и Ь из него исключены.
Обе точки а и b наз&ваются граничными точками интервала. Интервал,
имеющий своими граничными точками а и Ь, обозначается (а, Ь); здесь
круглые скобки ( ) указывают, что граничные точки не входят
в интервал.
Наконец, полусегментом [а, Ь) называется множество точек ху
для которых выполнено условие а < #<#. Полусегмент есть отрезок,
закрытый слева и открытый справа. Точка а есть конец полусегмента
и точка b есть его граничная точка. Замкнутость слева обозначена
постановкой квадратной скобки [, и открытость справа указывается
круглой скобкой ). Аналогично, полуинтервал (а, Ь] есть
множество точек ху для которых выполнено условие a<Cxz£b.
Полуинтервал есть отрезок, открытый слева и замкнутый справа. Точка а
есть граничная точка, точка b есть конец. Это обстоятельство
указано постановкой круглой скобки слева и квадратной — справа.
В таком же смысле можно употреблять обозначения для
несобственных (т. е. бесконечных) интервалов (— оо,~[-оо), (— оо, <:),
(с, + оо), полуинтервала (—со, с] и полусегмента [с, -J- оо); так,
например, бесконечный интервал (— оо, с) есть совокупность всех
точек л:, для которых выполнено условие #<с, и т. д.
•Читатель должен иметь в виду, что строгое различие сегмента
от интервала не есть бесполезная тонкость, но имеет громадное
значение для всего дальнейшего. Например, счзтная последовательность
5а
сегментов ох, з2, ..«, сп .. ., вложенных один в другой и имеющих
длины, стремящиеся к нулю, HMtei, как мы видели, точку £,
которая принадлежит им всем. Ничего подобного не имеется для
интервалов. Например, последовательность интервалов 81э 82, ..., 8Я,...,
где 5n = ( 0>"^)> есть последовательность тоже вложенных один в
другой интервалов, и длины их тоже стремятся к нулю, и, однако, не
существует никакой точки 5, принадлежащей всем этим интервалам
(черт. 18). Правда, они стягиваются к точке л- = 0. Но эта точка
есть граничная точка всякого интервала Ьп = (О,—\ а значит, как раз
в него и не входит.
§ 14. Ограниченные и неограниченные множества. Множество
М точек прямой ОХ называется ограниченным, если имеется сегмент
[a, ft], содержащий
все точки множества .__, , „ „ о _ 2 ,д_^пп, , , ,_ Й
М (черт. 19). В про- 0 ° Ь
тивном случае, множе- „
ство М есть неогра- ерт' *
ниченное.
Если М есть не- —. „ * . , . . ^
ограниченное множе- О £
ство, то никакой сег-
мент о, как бы велик ерт*
он ни был, не может
содержать всех точек ^
М
)>>1»г<,,1|ф.«
множества М. Значит,
вне каждого сегмента
о имеется, по крайней Черт. 21.
мере, одна точка
множества /И. Заметив это, возьмем сегмент <зЛ = [ — п, -\- п] (где
я>0). Раз множество М неограниченное, вне сегмента оп имеется
хоть одна точка множества М. Обозначим ее через хп. Ясно, что
1*п1>л- Отсюда следует, что последовательность точек хх, х2, ...,
*пэ... принадлежит множеству М и что lim \хп\ = + °°• Следова-
п -> +оо
тельно, если множество М неограяичено, то можно выделить из
него последовательность чисел хи *2, ..., х1П...у стремящихся
либо к -}- со, либо к —со. Поэтому всякое неограниченное
множество М есть множество бесконечное. Всякое конечное множество М
есть множество ограниченное.
Множество М называется ограниченным слева% если нл оси ОХ
имеется такая точка S, что все множество М лежит вправо
от Е (черт. 20).
Множество М есть ограниченное справа, если имеется такая
точка yj, по лев)ю сторону от которой лежит все множество М
(черт. 21).
Всякое ограниченное множество М есть вместе с тем
ограниченное и слева, и справа, т. е. ограниченное с обеих сторон. Обратное
57
утверждение также ясно: всякое ограниченное множество М с обеих
сторон (точками £ и ч\) есть ограниченное множество, потому что
оно все лежит на сегменте [$, т\].
Ограниченное множество М может быть бесконечным: в качестве
простого примера достаточно взять множество всех точек какого-
нибудь сегмента а.
§ 15. Границы множества. Пусть М есть множество,
ограниченное слева (черт. 22). Если множество М имеет самую левую точку Р,
т. е. такую точку Я, которая принадлежит множеству М и по левую
сторону от которой нет уже ни одной точки множества М, то такая
точка- Р называется ле-
Р м вым концом множества
"~U * ' -*--*——•—*--—« м. Если же множество М
ц 2? не имеет левого конца
(что, например, имеет
место, если М есть какой-
нибудь интервал), то тогда в этом случае можно определить левую
граничную точку для множества М. Делается это следующим
образом.
Возьмем какой-нибудь сегмент оь ах = [alf d1]i содержащий точки
множества М, и такой, что влево от точки аг нет ни одной точки
множества Ж.. Так как множество М ограничено слева, такой
сегмент Oj всегда существует. Разделим сегмент ах пополам; если его
левая* половина содержит точки множества М, мы берем ее как
сегмент и обозначаем через о2=[л2, Ь2]\ если левая половина не
содержит точек множества М, тогда мы берем правую половину, и ее,
рассматривая как сегмент, обозначаем через <з2. Ясно, что в обоих
Черт. 23.
случаях влево от точки а2 нет ни одной точки множества М и что
сегмент а2 = [а2, Ь2] содержит точки множества Ж. Таким образом,
мы перешли от начального сегмента ох = [а19 bt] к сегменту с2 =
= [^2* ^Ь ьдвое меньшему и в него вложенному. При этом оба они
содержат точки множества М и влево от их левых концов нет
ни одн(Й точки множества М (черт. 23). Ясно поэтому, что,
разделив пополам сегмент о2, мы точно так же получим новый сегмент
с3 = [я3, #зЬ вложенный в о2, вдвое его меньший, содержащий точки
множества Л1, и такой, что влево от него нет ни одной точки
множества М. Деля пополам о8, мы получим сегмент а4, и так далее
бесконечно. В результате мы определим бесконечную последовательность
сегментов
°1 > а2 > °3 > • • • > °п >
58
вложенных один в другой, причем каждый из них вдвое меньше
предыдущего. Самое важное сзойсгво сегмента <з„== [ап, Ьп) состоит
в том, что влево от точки ап нет ни одной тВчки множества М и
что сегмент ап наверное содержит точки этого множества. В силу
предыдущего, имеется точка ;, принадлежащая всем сегментам оп,
где #=1, 2, 3, .... Эта точка £ обладает, очевидно, следующими
двумя свойствами по отношению к множеству /И:
Во-первых, влево от Е нет ни одной точки множества М.
Действительно, если бы такая точка Р имелась (^черт. 24), то так
как сегмент оп = [ап, Ьп] стягивается к точке S, когда п
безгранично возрастает, то для достаточно большого п точка Р оказалась
бы влево от оп. А это
невозможно, потому Р ^ Ц^
что влево от любого о»
сегмента оп нет точек
множества М.
Во-вторых, любой
интервал 8,
содержащий точку 6,
содержит
бесчисленное множество точек
множества М.
Действительно, всякий
такой интервал 8 (черт. 25). содержа точку £ внутри, должен
содержать целиком и сегмент ow, когда число п достаточно большое,
потому что сегмент оп стягивается к точке £, когда п неограниченно
возрастает. А всякий сегмент оп содержит точки множества М.
Значит, и интервал 8 тоже содержат точки множества М. Легко видеть,
что о содержит точки множества М в бесконечном числе.
Действительно, если бы о содержал лишь конечное число точек
множества My то среди них имелась бы и самая левая, которая,
следовательно, была бы левым концом множества М. Но множество М не
имеет левого конца.
Такая точка S, которая сама не принадлежит множеству М и
влево от которой нет точек этого множества, но как угодно близко
вправо от которой лежит бесчисленное множество точек множества М,
называется левой граничной точкой для множества М.
Таким образом, всякое ограниченное слева множество М имеет
или левый конец, или левую граничную точку S, ему не
принадлежащую.
Аналогично всякое о?раниченное справа множество М имеет
или правый конец, или правую граничную точку т|, ему не
принадлежащую.
Для того чтобы убедиться в том, достаточно просто повернуть
чертеж около начала координат О так, чтобы отрицательная часть
оси ОХ легла на положительную часть. Тогда левый конец
множества М перейдет в правый конец, и если его нет, то левая
граничная точка для множества М перейдет в правую граничную точку
Аля Л1, т. е. в такую точку yj, которая ни сама не принадлежит к М9
59
ни вправо от которой не имеется точек множества ЛТ, но в
бесконечной близости В0С1Ю от которой точки множества М имеются
в бесконечном числе.
Если множество М ограничено слева, то часто объединяют в одно
оба случая и называют левый конец множества М ^если он имеется)
и левую граничную точку X для множества М (если левого конца не
имеется) общим названием: левая грань множества М. Левая грань
множества Ж, если она принадлежит к М, является его левым
концом; но если лев?я грань множества М не принадлежит к М9 тогда
она является левой граничной точкой для множества М.
Аналогично правой гранью множества М называется или его
правый конец, или правая граничная точка для М (при этом
предполагается, что множество М ограничено справа).
Если множество М ограничено (т. е. ограничено с обеих сторон),
то, обозначая через £ и ч\ границы множества Ж, мы видим, что
сегмент [£, т]] содержит множество М целиком и чго сегмент этот [£, у\]
нельзя уменьшить без того, чтобы вне его не оказались бы точки
множества М% Значит, сегмент [£, т)] есть наименьший из всех
сегментов, содержащих данное ограниченное множество М.
Принято также называть длину этого наименьшего сегмента [;, чг)|,
т. е. разность г\ — £, диаметром данного ограниченного множества М.
§ 16. Предельные точкя и точки конденсации. Какая-нибудь
точка £ называется предельной точкой для множества М, если
всякий интервал 8, содержащий $, содержит бесконечное
множество точек множества М. Точка с называется точкой
конденсации для множества /И, если всякий интервал 8, содержащий £,
q % содержит несчетное
—г вггг^——^--а множество точек
~Ь ' множества М.
Черт. 26. Первое
определение предполагает,
понятно, что множество М бесконечно; второе определение
предполагает, что множество М несчетно. Ясно, что конечное множество М
не имеет предельных точек и что счетное множество М не имеет
точек конденсации.
Введем еще важное определение: точка х0 множества М
называется изолированной (уединенной) точкой множества М, если х0
принадлежит к М и если имеется столь малый интервал 8,
содержащий лг0, который не содержит никакой другой точки, кроме х0,
множества М (черт. 26).
Относительно предельных точек и точек конденсации для
множества М имеет место чрезвычайно важное и основное предложение:
Теорема. Всякое ограниченное бесконечное множество М
допускает хотя бы одну предельную точку) всякое несчетное {не
обязательно ограниченное) множество М имеет точки
конденсации.
Первая часть этой теоремы носит название принципа Больцано-
Вейерштрасса. *
Lm*Y
,Л
Пусть М есть бесконечное ограниченное множество. Пусть ot есть
какой-нибудь сегмент, содержащий множество М. По условию,
сегмент ох содержит бесконечно много точек множества М. Разделим
сегмент аг пополам и возьмем ту его половину, которая заведомо
содержит бесконечно много точек множества М. Такзя половина
непременно существует, так как если бы обе половины сегмента ох
содержали каждая лишь конечное число точек множества М, то и
весь сегмент ох тоже содержал бы конечное число точек множества М,
что невозможно, так как М есть бесконечное множество. Обозначим
эту половину сегмента ох через а2. Это есть новый сегмент, вдвое
меньший начального сегмента ог и лежащий на о^, согласно
указанному выбору половины, сегмент а2 содержит бесконечно много точек
множества М. Деля сегмент о2 пополам и называя через ав ту из его
половин, которая содержит бесконечно много точек множества М,
мы имеем новый сегмент о3, вдвое меньший сегмента а2, на нем
лежащий и содержащий бесконечно много точек множества М. Деля
сегмент с3 пополам, мы получим новый сегмент о4, имеющий те же
самые свойства, и так далее бесконечно. Ясно, что таким образом
мы получаем бесконечную последовательность сегментов
а1>'2>С3>--. >3Я>...,
вложенных один в другой; каждый из них вдвое меньше
предыдущего и каждый из них содержит бесконечно много точек данного
множества М.
Обозначим через £ точку, при- q сп ;
надлежащую всем этим —»— —~" "^^zfS^ "
сегментам оп, где /г == 1 > о
2, 3, Легко видеть, Черт# 27.
что £ есть
предельная точка для множества М. Действительно, пусть S (черт. 27)
есть любой интервал, содержащий точку Е. Так как сегменты ал
стягиваются к точке Е, когда п безгранично возрастает, то для
достаточно большого числа п сегмент оп будет содержаться целиком
в интервале 8. А поэтому интервал Ь содержит бесконечно много
точек данного множества М. Следовательно, точка i есть
предельная точка для множества М. *
Заметим, что предельная точка множества М может и не
принадлежать самому данному множеству. Так, гапример, множество
Дробей —, -5-, -г,...,—,... имеет предельную точку О, не вхо-
2, о 4 ft
дящую в данное множество.
Точка конденсации определяется совершенно таким же образом,
как ^определяется предельная точка) только слова „бесконечно
много" заменены словами „несчетно много". Поэтому указанная
замена этих слов во всем предыдущем доказательстве о
существовании предельной точки для всякого ограниченного бесконечного
множества сразу дает теорему:
Всякое ограниченное несчетное множество М допускает точки
конденсации.
61
Но теорема о существовании точек конденсации для несчетного
множества М не предполагает ограниченности этого множества. Чтобы
освободиться от этого стеснения, покажем, что всякое несчетное
множество точек м, даже если оно не ограничено, непременно
содержит некоторую ограниченную часть М, которая также будет
несчетной. Действительно, обозначим через Мп совокупность всех
точек множества М, принадлежащую сегменту сп — [ — п,-\-п].
Ясно, что данное множество М есгь соединение счетного числа
множеств Л/1э М2, Afj, ..., Ж„,..., потому что, с одной стороны,
множество Мп содержится в М и, с другой стороны, всякая точка х0
множества М войдет в множество Мп для п достаточно большого.
Но множество М несчетно. Если бы всякое множество Мп было
четным, то счетным было бы и их соединение, т. е. и само
множество Ж, что невозможно. Значит, имеется, по крайней мере, одно
такое натуральное число &, что множество Мк есть несчетное. Но
множество Мк, содер-
о t £_ жась в сегменте [—k,
я.*** *г х> -f- *]»ограничено.
Значит, Мк допускает точ-
1/ерт. 28. ки конденсации £,
которые, очевидно,
явятся точками конденсации и для самого множества М, потому что
Мк содержится в М.
Т^ким образом, предложенная-теорема полностью доказана.
Заметим, что неограниченное бесконечное множество М может
не допускать ни одной предельной точки. Например, множество М
всех целых точек; M={v], где v = 0, dtl, :±2, ±3,...,
бесконечно, но для него, очевидно, нет ни одной предельной точки £.
Читатель видит, что это множество М неограничено (с обеих
сторон).
Мы видели, что всякое несчетное множество М должно
обязательно допускать точки конденсации и, значит, также и предельные
точки, потому что всякая точка конденсации непременно есть
вместе с тем и предельная точка, в силу определения этих точек.
Поэтому, неограниченное множество, не имеющее предельных точек,
является счетным.
Бесконечное ограниченное множество М может допускать и одну
только предельную точку, и конечное число их, и счетное
множество, и даже множество мощности континуума.
Например, множество М правых концов сегментов, полученных
делением пополам какого-нибудь сегмента з=[я, £], делением
пополам его левой половины, делением пополам полученной левой
половины, и так далее бесконечно, состоит из точек деления хи лга,
лг3, . •. (черт. 28). Ясно, что множество М счетно и что точка £ = я
есть единственная предельная точка этого множества М.
Если мы теперь произведем над сегментами [xv b], [лг2, л^],...,
[хк> хк-г] ту же самую операцию, какую мы выполнили над
начальным сегментом [а, Ь], и присоединим к новым точкам деления
прежние точки xv х2, . . •, хп, . . ., то получим счетное множество Ми
62
допускающее предельными точками точки дг1} дг2, #3, • ♦,, хк и а.
Значит, предельных точек у множества М окажется k-\-l.
Если мы выполним эту же самую операцию над, всяким
сегментом [#Л+1» хп], то получим счетное множество Ж2, допускающее
своими предельными точками точки xv х2, хв, ..., хт ... Значит,
множество М2 допускает предельные точки в счетном числе.
Наконец, если мы возьмем множество ЛГ3, состоящее из всех
рациональных точек сегмента [а, 6], то, очевидно, каждая точка Е
этого сегмента есть предельная точка для множества . Мъ. Значит,
здесь предельные точки для счетного множества Ж3 образуют
множество мощности континуума,
§ 17. Производное множество. Замкнутые и совершенные
множества. Пусть М есть какое-нибудь бесконечное множество.
Совокупность всех предельных точек £ для множества М называется
производным множа- ^
с те ом от
множества М и обозначается
символом М\ М' = {£}.
Множество М
называется всюду
плотным на сегменте
о=ф, *] (черт. 29),
если всякий
интервал 8, принадлежащий
сегменту о, содержит
точки множества М.
Ясно из этого опре- '""""" j£ T? х,
деления, что если
множество М всюду ЧеРт- 31-
плотно на
каком-нибудь сегменте о, то производное множество М' содержит
целиком этот сегмент. Действительно, раз М всюду плотно на
сегменте о, то всякая точка ; этого сегмента есть, очевидно,
предельная точка для множества М. Поэтому, производное множество
М' содержит о.
Множество М называется нигде неплотным на сегменте а
(черт. 30), если в каждом интервале 8, лежащем на а, имеется
такой меньший интервал 8'', который не содержит ни одной
точки множества М.
Всякое конечное множество М есть, очевидно, множество нигде
неплотное на всяком сегменте. Но множество может быть счетным
и вместе с тем нигде неплотным. Простой пример этого есть
множество М точек хп = ~ , где п — число натуральное, М — [хп].
Множество М есть последовательность точек лг^, а'^, х^ .. ., хПУ •. •
и допускает точку £=0 единственной предельной точкой (черт. 31).
В дальнейшем мы познакомимся с нигде неплотными*
множествами М, имеющими мощность континуума.
63
? -■"— -"■'-
О
а
0
Черт. 29.
о
Черт. 30.
b
О
.1
—.—1».
Ясно, что если какое-нибудь множество М нигде неплотно на
сегменте а, то производное множество Мг также нигде неплотно
на о. Действительно, раз интервал 8', содержащийся в 8, не имеет ни
одной точки множества М, то на 8' не имеется и предельных точек I
для множества Ж. Значит, 8' не содержит точек производного
множества М\ которое поэтому нигде неплотно на а.
Введем следующие три основные определения.
I. Множество точек М называется замкнутым, если оно со-
держат все свои предельные точки.
Так как совокупность всех предельных точек множества М
точек есть производное множество М', то, следовательно,
множество Ж замкнуто тогда и только тогда, когда множество М со-
tit* держит в себе свое
О JF 7 Т 7 \ производное
множество М'', т. е. когда
Черт. 32. мы имеем
соотношение М^М\
. Еще точнее было бы сказать, что множество точек М называется
замкнутым^ если нет предельных точек, которые ему не
принадлежали бы. Действительно, к замкнутым множествам причисляется также
всякое множество, вовсе не имеющее предельных точек, наприЛр
всякое конечное множество. В этом случае также справедливо
отношение М^М'. Только здесь Мг есть пустое множество.
II.\ Множество точек М называется плотным на себе, если
всякая его точка есть предельная {для М).
Ясно, что множество М плотно на себе самом тогда и только
тогда, когда имеет место соотношение М^М\
—- " -з -2 -/ а / 2 з~4~
Черт. 33.
III. Множество точек М называется совершенным, если оно
одновременно: и замкнуто и плотно на себе, т. е. когда оно
совпадает с своим производным множеством МТ\
М^М1.
Приведем примеры на все три случая.
1. Множество М, составленное из начала координат О и из
точек хп= — , где п — число натуральное, я=1, 2, З...(черт. 32),
есть множество замкнутое, потому что начало координат О
является единственной предельной точкой для множества М и оно
содержится в множестве М.
2. Множество М, состоящее из всех целых точек jrM = ±n, где
п натуральное число или нуль (черт. 33), есть множество
замкнутое, потому что оно вовсе не имеет предельных точек.
6i
3. Множество М, состоящее из всех рациональных точек какого*
либо сегмента о == [а,Ь] (черт. 34), есть множество плотное на себе
самом, потому что всякая его точка есть предельная для него самого.
4. Наконец, сегмент есть, очевидно, совершенное множество,
потому что производное множество сегмента тождественно с этим
сегментом.
Посмотрим, какое различие имеет место между замкнутым и
совершенным множествами. Прежде всего между этими множествами
имеется то общее, что всякое совершенное множество есть частный
случай замкнутого множества. Действительно, если М есть совершенное
множество, то оно совпадает с своим собственным производным
множеством М, т. е. щ^Л = М\ Но когда какое-нибудь множество А
Черт. 34..
совпадает с множеством В, А=В, то оно в нем и содержится, т. е.
А^В. В частности, равенство М = МГ логически влечет
соотношение: М' -*СМ. Следовательно, всякое совершенное множество М есть
множество замкнутое.
Принято обозначать замкнутое множество буквой F и
совершенное множество буквой Р.
Теперь, для решения вопроса о том, чем именно отличается
замкнутое множество F от совершенного множества Р, мы должны
обратиться к множествам неплотным на себе самих, потому что если
замкнутое множество
плотно на себе самом,
то оно, в силу самого ' j£
определения, есть со-
вершенное множество. Черт. 35.
Если какое-нибудь
множество М не есть плотное на себе самом, то это означает, что не всякая
его точка есть предельная. Следовательно, имеется хотя бы одна точка х0
множества М, которая не есть предельная точка М. Обращаясь
к определению предельной точки, мы видим, что должен иметься
столь малый интервал 8, содержащий точку х0 (черт. 35\ который
содержит лишь конечное число точек множества М, потому что
если всякий интервал 8, содержащий xQ, содержит бесконечно много
точек множества Ж, то это и значит, что х0 есть предельная точка
для Ж, что невозможно. Но если интервал 8, содержащий лг0,
содержит лишь конечное число точек множества М, то всегда найдется
такой еще меньший интервал Ь\ содержащийся в 8, который
содержит только одну точку множества Му именно самую точку х0 (черт. 36).
Действительно, раз в 8 имеется лишь конечное число точек
множества М и раз среди них обязательно находится точка х0, заведомо
принадлежащая к М, то ее можно окружить столь малым
интервалом 8', который будет иметь длину, меньшую расстояния xQ до бли-
5 Эак. 31244. §5
кайшей точки множества М. Ясно," что ётот интервал и будет таким*
который имеет точку х0 единственной точкой множества М.
Из всего сказанного следует, что всякая точка х0 множества
М, которая не является предельной для М% есть изолированная
точка множества М.
Обращаясь теперь к различию замкнутых множеств F от
совершенных множеств Р, мы заключаем, что замкнутое множество F,
не являющееся совершенным, непременно имеет хотя бы одну изо*
лированную точку. Совершенное множество Р не имеет
изолированных точек.
Действительно, если множество* F замкнуто, но не является
совершенным, то F не есть плотное на себе, и поэтому оно обязано,
иметь хоть одну изолированную точку.
- §18. Строение замкнутых и совершенных множеств.
Установим сначала, что всякое ограниченное слева замкнутое множество
имеещ левый конец и всякое ограниченное справа замкнутое мно*
жество имеет правый конец.
Действительно, если бы, например, ограниченное слева замкнутое
множество М не имело левого конца, т. е. самой левой точки, то
левая граничная точка 5 множества М (§15) rte принадлежала бы
к М. Н© это невозможно, потому что всякий интервал 6, содержа*
Черт. 37.
щий левую граничную точку Е множества М> необходимо содержи?
бесконечно много точек множества М. Следовательно, левая
граничная точка S множества М есть предельная точка для М и поэтому
должна принадлежать к AJ, потому что множество М замкнуто. Из
этого противоречия и следует, что всякое ограниченное слева,
замкнутое (в частности: ограниченное слева совершенное) множество М
имеет левый конец, т. е. самую первую точку £ (если проходить ось
абсцисс ОХ слева направо). Аналогично доказывается и вторая
половина нашего предложения.
Ясно, что всякое ограниченное (с обеих сторон) замкнутое
множество имеет оба конца: и левыйу и правый.
-->- Установив это, возьмем какое-нибудь замкнутое множество F*
Пусть хх (черт. 37) есть какая-нибудь точка, заведомо не
принадлежащая к F. Обозначим через /Сх совокупность всех точек
множества F, принадлежащих аолупрямой (~<х>, хх], и аналогично че*
т
pes 2^-*-совокупность всех точек Множества ^принадлежащих пб*
лупрямой [хи 4~°°)- Легко видеть, что К\ есть замкнутое
множество. Действительно, всякая предельная точка f для множества /Q
принадлежит полупрямой (—со, atJ. И так как & содержится
в F, то точка f есть предельная для F и, значит,* входит в F.
Поэтому точка т, будучи точкой и множества F, и полупрямой ( — оо,л::],
есть точка множества Kv Значит, множество Кх содержит в себе все
предельные для него точки, т. е. есть замкнутое. Аналогично и
множество Lx также есть замкнутое. Обозначим через ai правый
конец множества Кх и через Ьх левый конец множества Lt. Ясно,
что имеем
а1щ^.х1 <#!♦
Но точка хх заведомо не принадлежит к F, обе же точки ах и bt
принадлежат множеству F. Поэтому, знаки равенства невозможны, и
мы имеем а1<х1<Ь1.
Рассмотрим теперь интервал Ьх — (аи Ьх). Он обладает
следующими двумя свойствами:
Во-первых, его граничные точка ах и Ъх принадлежат к F.
Во-вторых, он не содержит на одной точки множества F.
В последнем легко убедиться, так как вправо от точки ах нет ни
одной точки множества К± и влево от Ьх нет ни одной точки
множества Lv Значит, на интервале 81==(а1, Ьх) нет ни одной точки ни
множества Ки ни множества Lv А так как F = Ki-\-Liy то на
интервале 8Х нет и точек множества F. Ввиду исключительной важности
построенного нами интервала Ьх, полезно ввести специальный термин,
предложенный Бэром:
Всякий интервал 8 = (a, Z?), обе граничные точки а и Ъ ко*
торого принадлежат замкнутому множеству F и который не
содержит ни одной точки множества F, называется смежным
интервалом к замкнутому множеству F.
Заметим, что в проведенном сейчас построении, при помощи
которого мы окружаем точку хх интервалом 81 = (д1, Ь{), может
случиться, что этот интервал окажется несобственным (т. е.
бесконечным), так что либо будет ах — —со, либо bx= -f-oo. Первое
произойдет тогда, когда множество F ограничено слева, а точка хг взята
левее всех точек этого множества (в этом случае множество Кх есть
пустое); второе — тогда, когда множество F ограничено справа и
точка хх взята правее этого множества (здесь множество Lx есть
пустое). Такие бесконечные интервалы мы тоже причисляем к
интервалам, смежным к множеству F. Ясно, что их либо совсем не будет —
если множество F не ограничено, либо будет один — если множество
F ограничено только слева или только справа, либо, наконец, их
будет два—если множество F ограничено (с обеих сторон). Все
остальные интервалы, смежные к множеству F, конечны.
Так как точка лгх была любой точкой, не принадлежащей к F,
то отсюда мы заключаем, что:
Всякая точка х, не принадлежащая замкнутому множеству F,
принадлежит к,некоторому смежному интервалу 8 к множеству F.
5* 67
ш
Ёажнейшим свойством смежных Кч/* интервалов является следующее!
Всякие два различных интервала 8 и 5', смежных к
замкнутому множеству F, не имеют никакой общей точки.
Действительно, если бы интервалы 8 = (а, Ь) и 8' = {а\ &'),
смежные к F, имели какую-нибудь общую точку х0 (черт. 38), то
граничные точ^и а! и Ьг интервала Ь\ как принадлежащие к F, не
могут принадлежать к 8, и поэтому интервал смежности 8' должен
содержать целиком интервал смежности 8, т. е. 8<*8'. Но роль обоих
интервалов смежности 8 и 8' одинакова. Значит, мы должны иметь
и обратное соотношение: 8'<8. Отсюда следует, что интервалы
смежности 8 и 8' тождественны, что противоречит предположению.
Из главы I известно, что всякая система неперекрывающихся по*
парно интервалов есть необходимо счетная (или конечная). Отсюда
мы заключаем, что:
Всякое замкнутое множество F получается посредством
удаления из оси ОХ счетного {или конечного) числа
неперекрывающихся попарно интервалов 81э 82,..#, 8Ш..Г, смежных к
множеству F.
Действительно, всякая точка х, не принадлежащая к F,
вынимается вместе с тем интервалом смежности 8, который ее содержит.
Значит, по удалении всех интервалов смежности 8!э 82,.*., 8т...
на оси ОХ останутся только точки множества F и останутся,
притом, все, потому что интервал смежности не содержит точек
множества F и, значит, удаление из оси ОХ интервалов смежности 8Х,
82,..., 8М|... не удалит ни одной точки множества F. Отсюда,
в частности вытекает, что:
Всякое ограниченное замкнутое множество F, имеющее своими
концами точки а и b, a<b, получается посредством удаления из
сегмента [а, Ь] счетного {или конечного) числа неперекрывающихся
попарно интервалов bv 82l.. . ,8W,..., смежных к множеству F.
Для окончательного уяснения строения всякого замкнутого
множества F остается изучить систему всех интервалов смежности 81э
89, • • •, J>n, •.. к множеству F. Легко видеть, что эта система
подчинена лишь одному условию: никакие два интервала 8* и 8^,
/=£/, системы интервалов Ьи 82, 83,.. .,8Л1.. .«* имеют общей
точки. Значит, нужно соблюдение одного лишь этого требования,
в остальном же интервалы bv 82, 88,.. . ,8Ш .. .-произвольны. Для
доказательства этого важного предложения установим предварительно
более общее предложение:
После удаления из оси ОХ произвольного множества {8}
{любой мощности) интервалов 8, перекрывающихся или
неперекрывающихся, всегда остается замкнутое множество.
Действительно, пусть по удалении из оси ОХ множества
интервалов {8} остается некоторое множество точек К. Покажем, что /Сесть
замкнутое множество. В самом деле, пусть Е есть предельная точка
множества К (черт. 39,). Если бы точка % не принадлежала к
множеству /С, она была бы удалена некоторым интервалом 80
множества {8}. Но тогда интервал 80, содержащий точку % внутри,
непременно должен был бьь содержать бесконечно много точек
множества К (потому что точка \ предельная к /С), и значит, было бы
а.
Черт. 39.
удалено бесконечно много точек множества /С, что невозможно. Итак,
предельная точка I к множеству К не удаляется вместе с
интервалами множества {8} и, значит, принадлежит к К. Поэтому, К есть
замкнутое множество.
Из доказанного следует, что всякое множество F, которое
получается удалением из оси ОХ конечной или счетной системы
неперекрывающихся попарно интервалов 8Х, 82, 83,..., замкнуто.
Интервалы 81э 82, 83,... являются смежными к F.
К этому предложению добавим следующее. Для того, чтобы
замкнутое множество F не было совершенным, необходимо и
5* ^~~^^
Черт. 40,
достаточно, чтобы в ряду смежных к нему интервалов Ьи 82, \, .77
имелись два смежных интервала 8^ и 8^, обладающих одной и той
же граничной точкой xQy от которой они расположены по разные
стороны (черт. 40).
Действительно, если это имеет место, то множество F имеет точку
х0 в качестве изолированной точки, значит, не есть совершенное.
С другой стороны, если множество F не есть совершенное, то
F имеет некоторую изолированную точку л:0 и к ней примыкают
(по разные стороны от нее) два смежных интервала 8г- и 8^,
имеющие эту точку своей общей граничной точкой.
Отсюда получается такой простой критерий для совершенных
множеств: Для того, чтобы замкнутое множество F было совершен*
ным множеством, необходимо и достаточно, чтобы смежные
к F интервалы 8Х, 82, 83,.. .не только не перекрывались попарно, но
и не имели бы общей граничной точки.
§ 19. Мера замкнутых и совершенных множеств. Оставляя
более полное развитие учения о мере множеств до другого тома
нашей книги, мы здесь коснемся лишь меры ограниченных замкну-
Щых множеств.
69
Частными случаями ограниченных замкнутых множеств являются:
сегмент, точка, конечное число неперекрывающихся попарно сегментов
и конечное число попарно различных точек. Естественно назвать
„мерой сегментаи его длину. Если рассматриваемый сегмент а есть
[а, Ь], то мера сегмента, следовательно, равна b — а. %
Принято обозначать меру какого-нибудь линейного множества Е
точек символом
mes E.
• Пользуясь этим обозначением, мы можем написать:
mes [a> b] = Ь — а.
Далее естественно считать меру точки, а также системы конеч»
ного числа точек равной нулю. Наконец, естественно считать меру
системы конечного числа неперекрывающихся сегментов ох, с2,..,, ок
равной сумме длин этих сегментов. Так как множество, состоящее
из соединения неперекрывающихся сегментов о1э с2,..., оЛ, пишется
в виде Oj -)- с2 -[- ... -f- оЛ, то мы имеем формулу:
mes (р1 4- а2 -f-... -j- оЛ) = mes ox + /rcesc2 -L , .7 -j- mes аЛ,'
Все эти разнообразные случаи тягостно рассматривать и запоминать
порознь. Поэтому, является желательным иметь общее правило для
вычисления меры любого замкнутого множества F и притом такое
правило, которое охватило бы все предыдущие случаи, которые мы рас*
сматривали лишь как
Ь2 дэ Jl hn служащие определе-
г ^~ч /-\.^-^/
^ Ь^ нию меры множества.
4 Естественно счи-
Черт. 41, тать, что отнятие у
сегмента одного или обоих
его концов не изменяет его меры; поэтому меры сегмента [а, #],
интервала (я, £), полусегмента [а, Ь) и полуинтервала (а, Ь] будем рас-?
сматривать как равные между собой, и именно равные их общей
длине b — а.
Заметив это, возьмем какое-нибудь ограниченное замкнутое
множество F, лежащее на некотором сегменте [а, Ь]. Пусть концами
множества F являются, точки £ и ?) (черт. 41).
Определение. Назовем мерой замкнутого множества
F разность между длиной сегмента [£, г\] и суммой длин всех
смежных к F интервалов 8П, лежащих на сегменте [S, rj\y т. е.
00
mes F == длина [;, г\]—2длина 8„. (1)
По поводу этого определения нужно заметить, что, во-первых, ряд
2 длина Ьп всегда сходится, потому что сумма любого конечного
числа п его членов
длина Ьх -f- длина 82 -{- .'.. + длина Ьп
70
не может перевысить ддииы *)—S сегмента IS, ij], содержащего интер*
валы 81э 82,..., 8Л. И, во-вторых, в силу только что сделанного
оо
замечания, сумма сходящегося ряда 2 Длина 8Л не может превысить
длины сегмента [&, т|]. Поэтому, мера wes F замкнутого множества
у, определенная согласно данному правилу, т. е. по формуле (1),
даст всегда либо положительное число, либо в крайнем случае нульх
так что
mes F^O.
Если замкнутое множество F не есть нигде неплотное на сегменте
[£, 1)], то тогда оно будет всюду плотным на некотором сегменте
с = [ос,р] (черт. 42), лежащем на [£,7|], и, значит, F содержит целиком
этот сегмент о, потому что F есть замкнутое множество. Отсюда
Черт. 42.
следует, что всякий интервал Ь{ или fy, смежный к множеству F,
будет находиться правее сегмента с, либо левее его. Из этого
следует, что сумма длин всех смежных к F интервалов 8^, лежащих
левее сегмента о, не превосходит длины сегмента [S, а]. Равным
образом, сумма длин всех интервалов Ъг, смежных кРи находящихся
правее сегмента о, не превосходит длины сегмента ф, ч\]. Поэтому,
сумма длин всех смежных к F интервалов Ьп не может превосходите
(а — £) + (*) — Р) = 0) — 5) — (Р— а) = длина[£, tj] — длина о.
Следовательно, мы имеем неравенство
со
2 длина Ьп <^ длина [£, yj] — длина о, откуда следует, что
со
длина [$, ч\] — 2 длина 8W>< длина а
««1
и, окончательно,
mes F^5 длина о > 0.
Итак, если замкнутое множество F всюду плотно на каком*
нибудь сегменте о, мера множества F не меньше длины этого
сегмента с, т. е. mes F есть число положительное.
Но обратное предложение неверно: замкнутое множество F
может иметь положительную меру, будучи ограниченным и нигде
неплотным множеством.
Легко, в самом деле, дать конкретный пример такого множества.
Для этого возьмем какой-нибудь сходящийся ряд положительных чисел
ц
сумма которого г йожет быть предположена сколь угодно малой,
С другой стороны, обозначим через
VAV ' Г1э Г2, /*3,. . ., Гп. . *
множество всех рациональных точек интервала (0,1).
Применим теперь следующий процесс: заключим первую рацио*
нальную точку гг в интервал Ъх длины <е1, имеющий
иррациональные граничные точки (черт. 43). Далее, удалив интервал Ьи мы
заключим первую rh из оставшихся рациональных точек
последовательности (Щ в интервал 82 длины<е2, имеющий иррациональные гра-
g ничные точки, не перекрывающий-
J^ s~~ч lk ся с 8, и не имеющий с 8, общей
q \. •/*! с,, ...j граничной точки. Затем, удалив 82,
мы заключим первую riz из остав-
Черт. 43. шихся в последовательности (/?)
рациональную точку в интервал 83
длины<е8, имеющий иррациональные граничные точки и не
перекрывающийся ни с 815 ни с 82 и не имеющий с ними общей
граничной точки. Удалив 88, мы таким же точно приемом строим 84, и так
далее до бесконечности. Описанный бесконечный процесс даст
систему интервалов
(д) 81э 82, 83,.. .,8ft>...,
лежащих на сегменте [0,1], не перекрывающихся попарно и не
имеющих попарно общей граничной точки. Значит, система (А) интервал
лов Ьк (k = 1, 2, 3,...) является системой смежных интервалов
к некоторому совершенному множеству Р, лежащему на сегменте [0,1].
Так как граничные точки интервалов 8Й иррациональны и так как
всякая рациональная точка гп содержится внутри некоторого интервала
смежности 8т (как это следует ' из самого построения системы (А)
интервалов 8Х, 82, 83,...), то отсюда заключаем, что совершенное
множество Р есть нигде неплотное на интервале (0,1). И так как
длина 8w<en, то, следовательно, mes Р>1 — е. Так как число в
можно выбрать заранее сколь угодно малым, то отсюда мы
заключаем, что на сегменте [0,1] имеются совершенные нигде неплот*
ные множества Р, мера которых сколь угодно близка к единице.
Этот результат кажется весьма замечательным, потому что
множество рациональных точек всюду плотно на сегменте [0,1], и
кажется непонятным, как это можно вынуть интервал, окружающий
каждую из них, и тем не менее все-таки оставить нечто на сегменте [0,1].
Как мы уже видели, для всякого ограниченного совершенного
множества Р имеет место неравенство mesP^Q. Естественно
возникает вопрос: существуют ля совершенные множества меры, равней
нулю?
Георг Кантор указал простой прием строить совершенные
множества Р меры, равной нулю. Возьмем для этого какой-нибудь
сегмент о, длину которого мы обозначим той же самой буквой о,
(черт. 44). Разделим о на три равные части и выбросим
центральный интервал Ъ[:У нас останутся два равные сегмента, каждый щ
7?
которых мы делим на три равные *!асти, и выбросим их центральные
интервалы 8"х ^и 8"а. У нас останутся четыре равные сегмента,
с каждым из которых мы поступаем опять попрежнему, т. е. делим
на три равные части и удаляем центральные -интервалы 8", Щ' 8д",
8"' и так далее до бесконечности. Первый вынутый интервал 8J имеет
4 *
длину -I. Сумма длин следующих двух интервалов 8J[ и 8£ равна
^= 4-•-|". Сумма длин следующих четырех интервалов 8'", 8"', 8'",
З2 «3 о ltd
22 • а / 2 \2 а
8"' равна ~оз~===(-о*) -$> Вообще, когда мы делаем &-й шаг в нашем
процессе и определяем равные интервалы 8<fe), 8^),..., Sj^, то их
Черт. 44.
сумма равна (~\ -~ • Следовательно, сумма длин всех вынутых
интервалов, при различных шагах нашего процесса, равна
*+4-т+(!)'*+-+(4Г*+--
_.! —
3
а 1
=■Гт = °.
3
Поэтому, мера полученного процессом Кантора совершенного
множества Р равна о — а = 0.
Таким образом, совершенное множество Кантора имеет меру,
равную нулю.
Можно поэтому усомниться, останутся ли, после удаления всех
смежных к Р интервалов, вообще невынугые точки на сегменте о.
Здесь, прежде всего, останутся нёвынутыми граничные точки каждого
смежного к Р интервала. Но, помимо этого, останется еще
множество мощности кэгагинуума невынутых точек, принадлежащих к
множеству Р. Это важное обстоятельство мы обнаружим в следующем
параграфе.
§ 20. Мощность замкнутых и совершенных множеств.
Установим, прежде всего, предложение:
Производное множество Мг от всякого множества точек М
есть замкнутое множество.
73
Действительно, пусть точка 5 (черт. 45) есть предельная для М\
Это означает, что всякий* интеррал 8, содержащий ?, содержит
бесконечно много точек.множества М'. Поэтому, интервал 8 содержит,
наверное, некоторую точку V множества М\ Но так как £' есть
предельная точка для М, то интервал 8, содержащий £', необходимо
должен содержать бесконечно много точек множества М. Отсюда,
г
Черт. 45»
точка \ должна быть предельной для М и, значит, принадлежать к М'.
Итак, производное множество М содержит все предельные для него
точки и поэтому есть замкнутое множество.
Теорема. Множество N всех точек конденсации для несчет'
ного множества М есть совершенное множество.
Действительно, обозначим через N множество всех точек
конденсации для данного несчетного множества М (черт. 46). Если §
S
i С
\ Черт. 46.
есть предельная точка для ЛГ, то всякий интервал 8, содержащий
точку £, содержит, наверное, точку (■' множества N. Но точка V есть
точка конденсации для множества Ж. Значит, о должен наверное
содержать несчетно много точек множества М. Поэтому, точка $
есть точка конденсации для М и, следовательно, принадлежит N.
Итак, множество N всех точек конденсации множества М есть
замкнутое множество. Но, более того: N есть совершенное мно-?
"о ( b
Черт. 47,
жество. Для этого достаточно показать^ что множество N не имеет
изолированной точки. Действительно, если N имеет изолированную
точку ?, ее можно сделать срединой столь малого сегмента о, о = [а, £],
который не имеет никакой другой точки множества N (черт. 47).
Поместим на сегменте [а, £] счетное множество точек xv х2,...,
хп,..., имеющее точку £ единственной предельной точкой; мы можем
предположить, что а <дг1 <^х^ <х3 < ... <хп < ... Аналогично
поместим на сегменте [£, Ь] последовательность точек # > ^i > J>2> .Уз>
> • • •>3/п>- • •» имеющую точку £ единственной предельной точкой
(черт. 48).
74
Ясно, что весь сегмент о есть соединение счетного числа
сегментов [а, хх]9 [хи х2),...у [хп, лг^],...; [yv b], [у2, л],...,
I^n+i» ЛЛ»-*- и точки 6. Но на каждом из сегментов [хп, хп+1] и
[уЛ+1, j/MJ множество N не имеет ни одной точки. Значит, на каждом
из этих сегментов множество М может иметь не более чем счетное
число точек. Отсюда ясно, что множество М имеет на всем
сегменте с, самое большее, лишь счетное множество точек. Поэтому,
точка £ не может быть изолированной точкой конденсации. Таким
образом, множество N есть совершенное.
о *, х, х, ( у3 уг у, Ь
Черт. 48.
Из предыдущего следует, что вне совершенного множества N
множество М Nимеет лишь счетное (или конечное) множество
точек.
Действительно, если в есть какой-нибудь сегмент, не содержащий
точек совершенного множества N, то на о данное множество М
имеет, самое большее, лишь счетное число точек, потому что в
противном случае сегмент о имел бы точки конденсации множества М.
Отсюда следует, что каждый интервал А, смежный к N, имеет лишь
счетное (или конечное) число точек множества М, потому что всякий
такой интервал А можно рассматривать как соединение счетного
числа расширяющихся сегментов аи о2, og,..., аь. .., вложенных
один в другой, и на каждом ofe множество М имеет лишь счетное
число точек (черт. 49). Отсюда и следует, что точки данного
множества Ж, не
принадлежащие к совершенному •
множеству iV, имеются
лишь в счётном (конеч- —-
ном) числе. С другой
стороны, всякий интервал 8,
содержащий точку^ со- Черт, 49
вершенного множества iV,
содержит несчетно много точек множества М, потому что § со*
держит точку конденсации для множества М.
Как следствие мы получаем:
Всякое замкнутое несчетное множество точек F содержит
совершенное множество.
Действительно, множество N точек конденсации множества F
есть совершенное. И так как всякая точка конденсации F есть
вместе с тем <и предельная точка F, то, в силу замкнутости, она
принадлежит к F. Отсюда следует, что множество F содержит
совершенное множество N.
Переходя теперь к установлению мощности замкнутых и
совершенных множеств, мы начнем с этих последних. Заметим, что здесь
75
интересны лишь совершенные нигде неплотные множества.
Действительно если совершенное множество Я. плотно на каком-нибудь
сегменте а, то оно содержит целиком этот сегмент, и значит, в силу
„ критерия для равенства мощностей", множество Р имеет мощность
континуума. Таким образом, все сводится к определению мощности
совершенного нигде неплотного множества.
Сделаем предварительно следующее замечание.
Из двух различных действительных чисел а и Ъ одно является
большим, а другое меньшим. Если a<CJb, то будем говорить, что а
предшествует д, a b следует за а. Переходя к изображению
действительных чисел на числовой прямой, скажем, что точка а
предшествует точке Ь. Предшествующая точка расположена на числовой
прямой „ левееи последующей.
Введем теперь следующее определение:
Два каких-нибудь множества точек А и В называются подобными,
если множества А и В допускают такое взаимно-однозначное
соответствие, которое сохраняет относительный порядок их точек. Это
Черт. 50.
\
означает, что если какая-нибудь точка а! множества А предшествует
какой-нибудь точке а" этого множества, то и для соответственных
им точек bf и Ь" множества В точка br тбже предшествует точкеч#".
Соответствие, устанавливающее подобие множеств А и В, называется
соответствием подобия или, просто, подобием множеств А и В.
Два подобных множества А и В равномощны. Но не всякие два
равномощные множества точек А и В подобны. Например, два счетные
множества: А = {-} и £ = <1—-j-j , где л=1, 2, 3,.,.,
неподобны, потому что элементы множества А убывают, так что влево
от каждого из них имеется бесконечная часть множества; элементы
же множества В, наоборот, возрастают, так что влево от всякого
из них имеется лишь конечная часть множества В. Поэтому, эти
множества А и В хотя и равномощные, но не могут допустить
соответствия подобия, если считать из двух различных точек ту
предшествующей, которая расположена левее.
Пусть Р есть нигде неплотное совершенное множество. Пусть
^i» ^2> ^s,..., ^п>-*« конечные смежные к Р интервалы. Обозначим*
через гп центр интервала Ьп (т. е. его средину) (черт. 50).
Докажем теперь следующее предложение:
Всякое счетное множество точек Z = {.%}* не имеющее кон*
цов и такое, что в нем нет никаких двух непосредственно
соседних точек (т. е. двух точек без промежуточной между ними),
подобно множеству 7?= [гп] всех рациональных точек интервала
(0,1).
76
Для доказательства выпишем все точки множеств Z и R в биДё
двух бесконечных последовательностей
(Z) ^1» -^2) ^8>' • • э ^ю» • • •
И
Мы хотим установить подобие между (Z) и (/?). Это подобие мы
будем устанавливать постепенно, составляя последовательно, одну за
другой, пары (г, г) соответственных точек гиг.
Первая пара (z'f r') соответственных точек составляется из самых
первых точек последовательностей (Z) и (R). Составив ее, мы
вычеркиваем из (Z) и (R) составляющие эту пару точки гх и rv Остальные
пары (г(*), г(*)) соответственных точек г4 и г< составляются
попеременным обращением*, то к последовательности (Z), то к
последовательности (/?).
^Обращаемся к (Z) и, взяв здесь первую невычеркнутую точку г"
(т. е. г2), подыскиваем в (/?) первую невычеркнутую точку г", такую,
что геометрический порядок точек г' и г" будет такой же, какой
имеется у точек z' и г". Пара (>", г") есть вторая пара
соответственных точек. Мы вычеркиваем ее точки из (Z) и (/?).
Обращаемся теперь к (R) и, взяв здесь первую невычеркнутую
точку г"', подыскиваем в (г) первую невычеркнутую точку zn\ такую,
что геометрический порядок точек г', z" и zm согласуется с
геометрическим порядком точек г\ г" и гш. Пара (г"\ г'") есть третья
пара соответственных точек. Мы вычеркиваем ее точки из (Z) и (/?).
Вообще^ имея уже составленными 2&-J-1 пар соответственных
точек > *
(*', г'), (Л О, (*", О.--» (*<*>, rW), (z№+i), /•<**+*>),
причем геометрический . порядок точек z\ z", zmy..., ,e(2ft+1)
согласуется с геометрическим порядком соответственных им точек г\ г",
г"',..., г(2Л+1), мы обращаемся к (Z) и, взяв первую невычеркнутую
точку г(2Л:+2>, подыскиваем в (/?) первую невычеркнутую точку г(2&+2),
такую, что относительный порядок точек r\ r", г'",..., гЧ27^1), ранее
определенных, и новой подысканной точки г(2А;+2) будет согласовываться
с относительным порядком прежних точек г/, г", У,..., <г(2&+1> и
новой взятой точки г(2Л+2>. Составив таким образом пару (<г(2/с+2), r(2fe+2)),
мы вычеркиваем ее точки из (Z) и (/?) и теперь обращаемся к (/?).
Пусть г(2Л+3) есть первая невычеркнутая точка в (R), Мы
подыскиваем в (Z) для нее первую невычеркнутую точку г(а*+8)э такую, чтобы
относительный геометрический порядок ранее определенных точек
z\ z", z"\..., £(2fe+2) и новой подысканной точки ,г(2Л+3) был
точно такой же, какой имеется у прежних точек г', г",
rw,..., r(27c+2) и новой взятой точки г(2Л+3>. Составив таким
образом пару (г(2Л:+3), r(2ft+8)) соответственных точек, мы
вычеркиваем эти точки из (Z) и {R) и продолжаем дальше
описанный нами процесс. Единственным препятствием продолжения
процесса и, значит, его остановкой был бы тот момент, когда
77
Ш, взяв первую невычеркнутую точку fe одной из
последовательностей (Z) или (/?), не могли бы подыскать во второй
последовательности никакой невычеркнутой точки, геометрический порядок
которой с вычеркнутыми точками этой второй последовательности
согласовался бы с геометрическим порядком вычеркнутых точек и
новой взятой точки, первой последовательности. Но этот момент не
может наступить, потому что и множество (Z), и множество (R) таковы^
что влево и вправо от каждой его точки лежит бесконечно много
точек, принадлежащих ему, и между всякими двумя точками каждого
из этих множеств лежит бесконечно много промежуточных точек.
Поэтому, взяв первую невычеркнутую точку в одной из
последовательностей (Z) и (R) и видя, что она находится между двумя уже
вычеркнутыми точками этой последовательности, мы в соответствующем
интервале, образованном вычеркнутыми точками другой
последовательности, заведомо будем иметь бесконечно много точек этой второй
последовательности. Среди этих точек имеется первая (т. е. с
наименьшим нумером), которую мы поставим в соответствие взятой точке
(первой) последовательности. Мы видим, что вычеркнутые точки и
новая точка той и другой из последовательностей (Z) и (R) имеют
одинаковое относительное геометрическое расположение. Таким
образом, описанный бесконечный процесс приводит к полному
установлению подобия множеств Z и /?, потому что относительное
геометрическое расположение точек z есть в точности то же самое, как
и отьюсительное геометрическое расположение соответствующих им
точек л
Как следствие доказанного предложения, получаем:
Множество всех конечных смежных интервалов Ь к север*
шенному нигде неплотному множеству Р подобно множеству
всех рациональных точек г интервала (0,1). ^
Действительно, множество центров ги z2, ..., гп> ... всех
конечных смежных к Р интервалов 8Ь 82, . *., 8П, •. • есть счетное
множество, не имеющее концов и такое, что между всякими двумя
его точками zm и zn имеется бесконечное число промежуточных то*
чек. В самом деле, раз Р есть совершенное нигде неплотное
множество, то между всякими интервалами Ьт и Ьп имеется бесконечное
число промежуточных интервалов 8Ь смежных к Р. Поэтому,
имеется бесконечное число центров zk, лежащих между двумя
любыми центрами zm и zn. На основании предыдущего, множество
центров zu г2, ..., zn> ... подобно множеству /? рациональных
точек интервала (0,1). Мы, поэтому, мржем установить соответствие
подобия центров zlf z2, ..., zn,.. * и рациональных точек интерн
вала ги г2, . .., гт ..., так что если гт<гп9 то гт<гп. «£-- :\
Если мы теперь поставим в соответствие конечному интервалу
смежности Ьп его центр zn, то мы видим, что всякому конечному
интервалу смежности 8^ соответствует рациональное число гп
интервала (0,1), что это соответствие есть взаимно-однозначное и
притом такое, что неравенство гт < гп равносильно тому, что интер»
вал Ьт лежит левее интервала 8П. А это и показывает, что
соответствие интервалов 8И и точек ги есть соответствие подобия. Для
78
установлений мощности совершенного множества мы нуждаемся еще
в одном определении:
Точкой первого рода совершенного множества Р называется такая
его точка $1э которая является предельной точкой для точек
множества Р лишь с одной стороны (черт. 51).
Это означает, что £2 есть граничная точка некоторого интервала 8,
смежного к Р. Понятно, что* по ту сторону точки Sj, где лежит
смежный интервал 8, граничной точкой которого является iv совсем
нет точек множества Р, как угодно близких к ?1# Но по другую
сторону точки £х есть непременно предельная для точек множества Р/
потому что совершенное множество не может иметь изолированной точки.
Часто называют точку ^ ч
первого рода совер- ^* **^\_
шенного множества Р - " >-т-1..и,.,- - -
граничной точкой (в
широком смысле) мно- Черт. 51.
жества Р. Заметим,
что все точки первого рода \ь за исключением только концов
множества Р, являются, очевидно, граничными точками конечных
интервалов 8, смежных к Р.
Точкой второго рода совершенного множества Р называется такая
его точка ?2, которая с обеих сторон является предельной точкой для
точек множества Р. Часто называют точку второго рода внутренней
точкой (в широком смысле) множества Р*).
Мы пока еще не знаем, имеет ли совершенное множество Р точки
второго рода. Но они действительно имеются и даже в несчетном
числе, как это видно из следующей теоремы:
Черт. 52.
Множество всех точек второго рода совершенного нигде
неплотного множества Р подобно множеству всех иррациональных
точек сегмента [0,1] и, значит, имеет мощность континуума.
Действительно, пусть Р есть совершенное нигде неплотное
множество, лежащее на оси ОХ. Пусть Ьи 8.2,..., 8Я>... есть множество
всех конечных интервалов, смежных к Р. Мы знаем, что оно подобно
множеству всех рациональных точек ги г2,.:., гп>••• интервала
(0<*<1). Это значит, что соответствие интервала 8^ и
рациональной точки гп можно предположить соответствием подобия (черт. 52).
Заметив это, возьмем какую-нибудь иррациональную точку т сегмента
(Ог^г-^1). Заключим т в систему интервалов Дх>Да>.. «>Дл>« • •>
*) Внутренней точкой (в узком смысле) какого-нибудь линейного
множества точек М называется всякая точка х$. для которой имеется некоторый
интервал Ь, ее содержащий и целиком содержащийся в М. Ясно, что
никакое нигде* непдотшэе множество М не. имеет внутренних точек в узком
смысле,
79
Имеющих рациональные граничные точки, сложенных один в другой
и стягивающихся к точке т (черт. 53). Так как граничные точки
интервала Ак рациональны, то им соответствуют, два некоторые
конечные интервала смежности к множеству Р, причем в силу подобия
множеств конечных интервалов смежности Ьп и рациональных точек
гп интервала (0<£<Г) левой граничной точке интервала АЛ
соответствует левый из этих двух интервалов смежности и правой
граничной точке отвечает правый интервал смежности. Но совокупность
всех точек оси ОХу лежащих между этими двумя интервалами
смежности, образует, очевидно, некоторый сегмент, который мы обозначим
через оА. Ясно, что система сегментов о1>оа> ... £>ofe>..., таким
образом определенных, есть система вложенных один в другой
сегментов, потому что граничные точки интервала ДЛм лежат внутри
интервала ДА и, значит, два интервала смежности, соответствующие
граничным точкам интервала Д*+1э находятся между двумя
интервалами смежности, соответствующими граничным точкам интервала Д^.
Легко\ видеть, что система сегментов а1>а2> ... >aft>.. . не может
стягиваться к сегменту, но стягивается к одной точке. Действительно,
если бы сегмент ок не стягивался к одной точке, то, обозначая через
ак и Ьк концы сегменса ол, мы бы имели две последовательности точек
Д1<а2<аз<-* •<#&<• *• и *1>&а>*8>-••>**>••'• *
Так как все точки ак и Ък принадлежат к Р, то предельная точка й
множества аи #2, а3» •••> #*>••• также принадлежит к Р. Точно
так же предельная точка b множества bv b2, b3, .♦., bki ...
принадлежит к Р. И раз о не стягивается к одной точке, то мы должны
иметь строгое неравенство а<#. Сегмент с=[я, &], очевидно,
принадлежит всякому сегменту ак, потому что ak<C.a<b<bk. Но
множество Р нигде неплотно. И так как концы а и b сегмента с
принадлежат множеству Р, то должен необходимо иметься интервал
смежности 8т к множеству Р, лежащий на о. Этому интервалу Ьм
соответствует некоторая вполне определенная рациональная точка гт.
И так как Лт лежит между интервалами смежности, определяющими
сегмент аь то в силу подобия рациональная точка гт должна лежать
между граничными точками любого интервала Ак. А это невозможно,
потому что интервалы Д!>Да. . .>ДЛ> . . . стягиваются к
иррациональной точке т и, значит, равенство т = гш невозможно. Таким
образом, система сешентов а1>о2>... >с&>. .. стягивается к
одной только точке, которую мы обозначим через х и которая
соответствует иррациональной точке т сегмента [O^/^l].
Точка х принадлежит к Р и (что важнее всего) является точкой
второго рода множества Р. Действительно, точка х принадлежит
80
всем сегментам з1>з2> ., .>ол., •, стягивающимся к ней, причем
сегмент ол+1 лежит строго внутри сегмента оА. Следовательно, точка х
является предельной с обеих сторон для множества концов
сегментов о#. И так как эти концы принадлежат к Р9 то х есть точка
второго рода множества Р.
Легко видеть, что всякая точка х0 второго рода множества Р
может быть получена указанным образом. Действительно, всегда
можно найти систему сегментов о1>о2> .. .>оА> .. „, вложенных
один в другой и стягивающихся к точке xQi где всякий из этих
сегментов ок есть часть оси ОХ, лежащая между некоторыми
двумя конечными интервалами смежности к множеству Р. Но
тогда этим двум конечным интервалам смежности соответствуют две
рациональные точки интервала (0</<1), определяющие интервал Дъ
соответствующий сегменту зА. Ясно, что система интервалов Aj>A2>,..
. ..>Д7с>... есть система вложенных друг в друга интервалов.
Легко видеть, что интервалы Д1? А2, . . ., д&,... стягиваются к одной
точке и что эта точка i есть иррациональная. Действительно, если бы
это было не так, то непременно имелась бы рациональная точка гт,
принадлежащая всем интервалам Д^. Но тогда интервал смеж-
Черт. 54.
ности 8W, соответствующий этой точке гШУ всегда лежал бы между
теми двумя интервалами смежности, которые определяли сегмент ort.
Значит, сегмент <зл содержал бы интервал смежности Ьш и поэтому
не мог бы стягиваться к одной точке х0. Из этого противоречия мы
заключаем, что интервалы Aj>A2> ... >Д&> ... стягиваются к
одной иррациональной точке т, и что, следовательно, всякая точка х
второго рода совершенного множества Р соответствует некоторое
иррациональной точке т сегмента [0^^^1].i
Легко, наконец, видеть, что это соответствие есть соответствие
подобия. Действительно, если z и т' (черт. 54) суть иррациональные
точки сегмента [0^/^1] и если ~<т', то имеется рациональное
число гт, удовлетворяющее неравенству х<гш<У. Но точка т
определяется системой стягивающихся интервалов Ай (&==1, 2, 3,...),
и точка ч/ определяется аналогичной системой стягивающихся
интервалов Д^(&==15 2, 3,...), причем граничные точки интервалов Afe
и Д^ рациональные. Значит, если натуральное число k достаточно
большое, то на сегменте [O^^^l] граничные точки интервала Aft
будут лежать левее точки rm, а граничные точки интервала А^ будут
находиться вправо от гт. В силу подобия рациональных точек
интервала (0<7<1) и конечных смежных к Р интервалов, сегмент о7.
будет находиться левее Ьту а сегмент о7/ правее 8W. Отсюда следует,
что точка второго рода, соответствующая иррациональному числу т,
лежит левее точки второго рода х\ соотве!Ствующейиррациональ-
6 Эаж. ША. S1
ному числу т', т. е. х < хг. Следовательно, неравенство т<4' влечет
неравенство лг<лг'. А это и устанавливает тот важный факт, что
множество всех точек второго рода совершенного нигде неплотного
множества Р подобно множеству всех иррациональных точек сегмента
[0<*<1Ь
Отсюда, как следствие, вытекает:
Все ограниченные совершенные нигде неплотные множества
подобны между собой.
Действительно, пусть Р и Р' два ограниченные совершенные нигде
неплотные множества. Прежде всего мы устанавливаем соответствие
подобия конечных смежных интервалов 815 82,..., 8Й,..« кРи ко-
нечных смежных интервалов 8J, &'2, ..., S^,.,, кР' с множеством
рациональных точек гъ г.2, ..., гп, ... интервала (0<7<1). Мы
видели, что это соответствие подобия устанавливает соответствие
подобия, с одной стороны, между множеством Е2 всех точек второго
рода множества Р и множеством / всех иррациональных точек
сегмента [0<^<Ч]> и аналогично, с другой стороны, имеем псдобие
между множеством Е всех точек второго рода множества Р' и тем же
самым множеством /. Если мы обозначим через х и х' точки второго
рода множеств Р и Р', соответствующие одной и той же
иррациональной точке т сегмента [0<^<!1], то легко заметить, что
соответствие точек х и х друг другу есть соответствие подобия. В
самом деле, пусть х и xt две различные точки второго рода
множества Р и пусть x<xt. Пусть х соответствует иррациональной точке
z и xt соответствует иррациональной точке т1# Вследствие подобия
между Е2 и /, имеем непременно 'и<т1. Вследствие же подобия между
Е'2 и / имеем х'<^х'ъ .где х' соответствует т и х\ соответствует т1#
Таким образом, множества Е2 и Ё2 подобны. Если теперь ^ есть
правая граничная точка какого нибудь конечного интервала
смежности Ьт к множеству Р, то ясно, что ^ есть левая граничная точка
для множества всех точек второго рода множества Р, находящихся
правее интервала Ьш. Но этим точкам второго рода множества Р
соответствуют иррациональные точки множества /, лежащие правее
рациональной точки гт. А этим иррациональным точкам
соответствуют, в свою очередь, точки второго рода множества Р', лежащие
правее интервала 8' , смежного к Р\ Таким образом, мы видим, что
если мы заставим соответствовать правой граничной точке £
интервала Ьт правую же граничную точку ^ соответствующего интервала
смежности Sm, то геометрический порядок точек ^ и точек
множества Е2 будет тем же самым, как и геометрический порядок
соответствующих точек % и Е'0. Ясно, что то же самое будет верно, если ^
есть левая граничная точка какого-нибудь конечного интервала
смежности множества Р. Если, наконец, мы заставим соответствовать
друг другу левые концы совершенных множеств Р и Рг и
аналогично сделаем то же самое с их правыми концами, то мы будем
82
иметь полное подобие друг другу совершенных нигде неплотных
множеств Р и Р'.
Заметим, что если исключить левые граничные точки каждого
конечного интервала смежности 8, то этим самым из ограниченного
нигде неплотного совершенного множества Р будет удалено лишь
счетное множество точек, и легко видеть, что оставшееся
множество Q точек множества Р подобно целому сегменту [O^t^.1].
Действительно, всякой иррациональной точке i сегмента [0<^<j; 1]
будет соответствовать единственная точка х второго рода множества Р,
и всякой рациональной точке гш сегмента [0<;^<;i] будет
соответствовать правая граничная точка интервала 3W) причем, в силу
доказанного выше, порядок соответствующих точек будет тем же
самым, как и у точек сегмента [0<^^1]. Следовательно, мы имеем
соответствие подобия.
Если прибегать к грубым образам, то после установления
подобия между конечными смежными интервалами Ьп ограниченного
совершенного нигде неплотного множества Р и между рациональными точками
гп интервала (0 < i < I)можно рассматривать смежный интервалЬп
просто как расплывшуюся {„разбухшую") рациональную точку /^,
потому что относительный геометрический порядок расположения
смежных интервалов 8 и точек второго рода х совершенно такой же,
какой имеется у соответствующих рациональных точек г и
иррациональных точек ? сегмента [СК<£<;1].
Теперь мы можем окончательно решить вопрос о мощности
совершенных множеств:
Всякое совершенное множество имеет мощность континуума.
Действительно, мы уже убедились выше в справедливости этого
предложения для всякого совершенного множества, плотного на
каком-нибудь сегменте. Если же совершенное множество Р нигде
неплотно, то, в силу доказанной теоремы, оно содержит часть,
имеющую мощность континуума; такой частью является множество всех
его точек второго рода. Отсюда на основании „критерия для равенства
мощностей" следует, что и само множество Р имеет мощность
континуума.
Мы видели выше, что всякое замкнутое несчетное множество F
содержит в себе совершенное множество Р: таким множеством Р
является множество всех точек конденсации множества F. Так как вся-
кое множество точек /И, содержащее в себе совершенное множество
Р, имеет, на основании „критерия для равенства мощностей",
мощность континуума, то отсюда следует, что:
Всякое несчетное замкнутое множество F имеет мощность
континуума.
Чрезвычайно важно заметить, что, несмотря на все попытки,
делавшиеся в течение больше чем тридцати лет, не удалось получить
ни одного индивидуального (т. е. определимого в одном лишь
экземпляре или определимого единичным образом) несчетного множества
точек М, которое было бы лишено совершенной части Р, в нем
содержащейся, Р<М. Отсюда следует, что всякое до сих пор
найденное несчетное множество точек М имеет мощность континуума.
6* 83
Всегда ли будет так, мы, понятно, не знаем. Но во всяком
случае, практически, всякое множество точек Ж, встреченное нами
в математическом анализе, есть либо счетное (или конечное), либо
содержащее совершенную часть Ръ т. е. обладающее мощн^тью
континуума.
§ 21. Категория. Какое-нибудь множество Маточек, лежащих на
сегменте а, называется множеством первой категории на а, если М есть
соединение конечного или счетного числа множеств Мъ Af2,..., Mni...t
каждое из которых ни-
б' где неплотно на а.
Если М есть
множество первой категории
на каком-нибудь
сегменте с, дополнение СМ
множества М до сегмента а
называется множеством
второй категории на с.
При этом дополнением множества М до с называется совокупность всех
точек сегмента а, не принадлежащих множеству М; это дополнение
множества М до с обычно обозначается символом СМ.
Докажем, прежде всего, что
Если удалить, из сегмента с какое-нибудь множество М первой
категории, на сегменте с остается всюду несчетно плотное на с
множество СМ неудаленных точек, не могущих образовать множества первой
категории *).
Действительно, пусть с' есть какой-нибудь сегмент, лежащий на ст. Пусть
М, будучи множеством первой категории на а, есть соединение нигде
неплотных множеств Мъ М\% М39..., Mw... • Так как М\ нигде неплотно на с',
Geo Oj» «б/о О/,
Черт. 55.
о/
то на с' можно найти два малых сегмента а'0 и ъ\ (черт. 55), не имеющих
общей точки (даже конца) и не содержащих точек множества М±. В каждом
из этих двух сегментов с'в (где 6} = О или 6j = 1) можно отыскать таким же
образом по два новых малых сегмента о'е * (где 62 = 0 или 62 = 1), не
содержащих точек множества Мъ причем эти четыре сегмента а'е ^ попарна
отделены друг от друга на конечное расстояние (черт. 56). И так далее.
Вообще, имея определенными 2ft сегментов с'8Л...0 , попарно отделенных
друг от друга и не содержащих точек множеств М±, Л1?,..., Мк, мы в
каждом из этих сегментов с'0 v . .6,^ отыскиваем два новых малых сегмента
си,..ий (jee ...g7<i , не перекрывающихся и не имеющих общего конца,
таких, которые не содержат точек множества Мк + Ь Этот процесс мы
продолжаем до бесконечности, не встречая остановки нигде, потому что мно*
жества Мь Л12,..., Мк> ... нигде неплотны на с
*) Множество Е называется всюду несчетно плотным на сегменте а9
если всякий интервал о, лежащий на с, содержит несчетно много точек
множества Е*
84
Обозначим через S^ систему 2к сегментов a'0i9,..Q где всякое в*
есть либо 0, либо 1. Ясно, что система S& содержит в себе систему S^.+1,
так что имеем:
Обозначим через Р совокупность точек х сегмента а, каждая из которых
принадлежит всем системам Sk (k = 1, 2, 3, .,.)• Так как система Si состоит
из двух отделенных сегментов, о/е (0i = 0 или = 1), то система SA получится
посредством удаления из сегмента о' трех интервалов и обоих концов
сегмента с'. Далее, так как система S2 состоит из четырех отделенных сегментов
с;0 е , то система S2 получится удалением из каждого сегмента с'е трех
интервалов и двух концов этого сегмента. Вообще система «S^-fi получается
удалением из всякого сегмента ^q^... по три интервала и удалением
концов этого сегмента. Из сказанного ясно, что множество Р всех точек х
сегмента о', каждая из которых принадлежит всем системам Sk(k — 1, 2, 3,...),
получится удалением из сегмента а' счетного числа неперекрывающихся
интервалов и удалением их общих граничных точек, каковыми служат концы
сегментов о'е ц •••б?,» Поэтому, в итоге, множество Р получается удалением
из с счетного числа неперекрывающихся интервалов, не могущих иметь
попарно общей граничной точки. Следовательно, Р есть множество совершен-
ног. Ясно, что на совершенном множестве Р нет ни одной точки ни одного
ив множеств Mi, М^... , Мп ... , потому что Р составляет часть системы
Sm а система Sn не содержит точек множеств Мъ М* ... , Мп. Поэтому,
совершеннее множество Р погружено целиком в дополнение СМ к
множеству М первой категории. И так как сегмент о' был взят произвольным
образом на сегменте с, то отсюда следует, что
Множество СМ второй категории на с есть множество всюду не-
счетню плотное на а и имеющее мощность континуума.
Важно заметить, что и множество М первой категории на а также мо-
;и,ет быть Есюду несчетно плотным на а. Например, взяв сегмент а и
занумеровав натуральными числами все лежащие на нем сегменты аь а2, ... ,
с?), ... , имеющие рациональные концы, иы можем поместить в сегмент <зп
какое-нибудь совершенное нигде неплотное множество. Ясно, что
соединение множеств Pi, Р2, ... , Р1Г ... есть множество М первой категории
на с, что оно всюду несчетно плотно на с.
И тем не менее существует огромная разница между множествами
первой и второй категории; эта разница заключается в том, что множество
второй категории нельзя истощить (исчерпать), вынимая из него
конечное или даже счетное число множеств первой категории.
Действительно, соединение конечного, или счетного числа множеств Еь £* ..., £&,...,
каждое из которых есть первой категории на с, есть, в конечном итоге,
соединение счетного числа нигде неплотных множеств на с. Поэтому,
вычеркнув из множества СЛ1, где М первой категории на с, множества Еь Е^,...,
Ekl.., мы вычеркнем из а только множество первой категории. Значит,
после удаления из СМ множеств Еь £?,..., Е^... на сегменте о заведомо
останется всюду несчетно плотное множество точек, которое вдобавок всегда
является опять множеством второй категории.
Из сказанного следует, что сам сегмент а есть множество второй
категории на а к что, напротив, всякое счетное множество точек есть
множество4 первой категории на с.
§ 22. Множества точек в многомерных пространствах.
Рассмотрим на плоскости XOY внутренность четырехугольника (черт. 57),
стороны которого параллельны осям координат; всякий такой
четырехугольник jR называется ориентированным по осям координат, и
совокупность всех точек плоскости, лежащих внутри R в строгом
$5
смысле, иногда называется двухмерным и тервалом. Если
вертикальные стороны четырехугольника R пересекают ось ОХ в точках а
и Ь, а горизонтальные стороны пересекают ось 07 в точках с и d,
то двухмерный интервал является совокупностью точек плоскости
М (х> У)> координаты которых х и у удовлетворяют неравенствам
(*<*<*, c<y<d).
Так как стороны х~а, x = b,y = c,y=zd рассматриваются
как не принадлежащие четырехугольнику /?, то R называется омхры-
тым четырехугольником. Аналогично в трехмерном пространстве
OXYZ рассмотрим совокупность точек пространства М(х.,у, z),
координаты которых удовлетворяют неравенствам
(a<x<b, c<y<d> g<z<h).
Ясно, что геометрически эта совокупность есть не что иное, как
внутренность параллелепипеда П, грани которого х = а, х = h} у = с$
y = d, г = g, z = h параллельны координатным плоскостям. Такой
параллелепипед П назы-
I *\ вается ориентированным
J - , Я S\ ^| по осям координат и
- Г 1 [^---U его часто называют трех-
V'\ \ 0р~— мерным интервалом.
~0\~~сГ1 t * ^У "—~—~Х Так как его грани пред-
У/* полагаются не
принадлежащими П, то паралле-
Черт. 57. лепипед II называется
открытым.
Какое-нибудь множество точек Е} лежащее в пространстве
нескольких измерений (двух, трех и т. д.), называется ограниченным, если Е
целиком содержится в некотором интервале того же числа измерений.
Точка М0 пространства называется предельной для множества £,
если всякий интервал (многомерный), содержащий точку М0,
содержит хотя бы одну точку множества Е, отличную от точки М0. Ясно,
что если М0 есть точка, предельная для Е, то всякий интервал,
содержащий М0, необходимо содержит бесчисленное множество точек
множества Е. Предельная точка М0 для множества Е есть точка
конденсации для Et если всякий интервал, содержащий MQ> содержит
несчетно много точек множества Е.
Совокупность всех точек, предельных для Е, называется
производным множеством от данного множества Е и обозначаете!
символом Е'.
Всякое ограниченное бесконечное множество Е допускает хшя
бы одну точку, предельную для Е; всякое несчетное множество
Е имеет точки конденсации для Е.
Это предложение доказывается совершенно так же, как оно
доказано для линейных множеств (см. § 16). Именно, сначала мы
вводим в рассмотрение многомерные сегменты, двухмерный сегмент
это есть закрытый двухмерный интервал, т. е. совокупность точек
Ж
М(х> у), координаты которых удовлетворяют соотношениям
Геометрически это есть прямоугольник R, ориентированный по осям,
к которому присоединены все его 4 стороны. Аналогично
трехмерный сегмент есть совокупность точек М{ху у, г), координаты
которых удовлетворяют соотношениям
[а<л:<£? с<у<</, £•<></*].
• Ясно, что это есть закрытый параллелепипед П, к которому
присоединены все его б граней. •
Если теперь мы имеем счетную последовательность
Rl>R*...>Rn>...
двухмерных сегментов, вложенных один в другой и длины сторон
которых стремятся к кулю, то имеется одна и только одна точка Ж0,
которая принадлежит всем этим сегментам Rn и к которой, таким
образом, стягивается сегмент Rn> когда п-> -{- со. Это легко
усматривается из того, что сегмент Rn= [ап < х < Ьп, £/г <.у ■< dn] имеет
проекцией на ось ОХ обыкновенный линейный сегмент [an, bn], откуда
Г,
ясно, что имеется одна и только
п л ~ »" " 1
1 1
1 гМ !
-;Х
Черт. 58.
одна точка х0, которая
принадлежит всем сегментам [ат £J, и
что сегмент [ап, Ьп] стягивается
к дг0, когда п -*~|- со.
Аналогично на оси OY имеется одна и
только одна точка уф
принадлежащая всем линейным сегментам
[сп, rfj, причем [ст dn]
стягивается к у0, когда л -> -f~ °°«
Ясно, что точка MQ (x0, у0) и есть
та единственная точка, которая
принадлежит всякому
двухмерному сегменту /?ш причем Rn
стягивается к Ж0, когда п -» ~j- со.
Аналогичное рассуждение справедливо для трехмерных сегментов.
Пусть теперь множество Е ограничено и бесконечно (или несчетно);
пусть Е содержится в двухмерном сегменте R. Деля проекции R на
оси координат пополам, мы делим R на четыре двухмерных сегмента,
причем один из них наверное содержит бесконечно (или несчетно)
много точек множества £ (черт. 58). Обозначим этот сегмент через Rv
Поступая с ним так же, как с /?, мы имеем новый меньший сегмент /?2,
содержащийся' в R и имеющий бесконечно (или несчетно) много
точек множества Е. И так далее бесконечно. Мы имеем
последовательность двухмерных сегментов
R>Ri>R2>...>Rn>..;
вложенных один в другой, стороны которых стремятся к нулю, когда
п -> ~j- og. Ясно, что течка Мф принадлежащая всем Rn, и есть точка,
предельная для Е.
w
Предлагаем читателю показать, что всякое неограниченное
несчетное множество содержит ограниченную несчетную часть. Тем самым
станет ясно, что теорема существования точек конденсации верна для
произвольного несчетного множества.
Множество Е называется замкнутым^ если оно содержит все^
предельные к нему точки. В этом случае мы имеем
Е^ЕГ.
Множество Е называется плотным на себе, если всякая его точка
есть предельная для него. В этом случае мы имеем
Наконец, множество Е называется совершенным, если оно
одновременно и замкнуто, и плотно на себе. В этом случае оно
совпадает со своим производным множеством, т. е.
Е = Е'.
Замкнутые множества обозначаются буквой F> совершенные —
буквой Р.
Если замкнутое множество F не является совершенным, то оно
имеет точку Му которая не есть предельная для Z7. Ясно, что такая
точка может быть заключена в такой интервал (многомерный),
который не содержит никакой другой точки множества F; такая точка М
есть изолированная точка множества F.
Пусть Е есть какое-нибудь множество точек, плоское или про-
'странственное. Пусть М есть какая-нибудь точка, принадлежащая к Е.
Мы называем М внутренней точкой множества Е, если имеется
интервал (многомерный), содержащий точку М и целиком
содержащийся в Е.
Точка N, не принадлежащая к Е, называется внешней точкой
для множества £", если имеется интервал (многомерный), содержащий
точку N и не содержащий никакой точки множества Е.
Наконец, точка Р называется граничной точкой для множества Е,
если Р не есть ни внутренняя точка множества Е> ни внешняя для
него. В этом случае всякий многомерный интервал, содержащий точку Р,
содержит точки как принадлежащие к £", так и не
принадлежащие к Е.
^Расстояние двух каких-нибудь точек М(х9у) и М' (х',у')
плоскости, как известно из аналитической геометрии, вычисляется по
формуле
ЛШ = У(х — x'f + {у—у'р.
Аналогично расстояние двух точек М(х,у,г) и М\х\у\гг)
трехмерного пространства вычисляется по формуле
1Ш = W — *')2 + (У — У)2+0?--О2-
В связи с этим, введем следующее определение. Пусть Е и Ef два
какие-нибудь множества точек, не имеющие общей точки. Мы назовем
расстоянием множеств Е и Е нижнюю (левую) границу расстояний
8а
ММ', где точка М пробегает все точки множества Е, а точка М
пробегает все точки множества Е'. Если одно из множеств Е или Е'
состоит из одной точки, тогда это определение дает расстояние
точки до множества, к которому она не принадлежит. Это
определение полезно для характеристики внутренней, внешней и граничной
точек. Действительно, пусть Е есть какое-нибудь множество и $ его
дополнение, т. е. совокупность всех точек, не принадлежащих к Е.
Ясно теперь, что если точка Му принадлежащая к Е, имеет
положительное (т. е. не нулевое) расстояние до множества $, то М есть
внутренняя точка множества Е. Если точка N> не принадлежащая
к Е, отстоит от Е на положительное (не нулевое) расстояние, то
TV есть внешняя точка для Е. Наконец, граничная точка Р для Е
принадлежит к одному из множеств Е или S и отстоит от другого
на нулевое расстояние.
Докажем, что два замкнутых ограниченных множества F и F\
которые не имеют общей точки, отдалены друг от друга на
положительное (не нулевое) расстояние.
Действительно, если бы расстояние множеств F и F' было равно
нулю, тогда можно было бы найти бесконечную последовательность
пар точек
(Ми М[), (М2, ЛГа), ..., (Мп, М'п),
таких, что точка Мп принадлежит к F, точка М'п принадлежит к F'
и расстояние МпМ'п стремится к нулю, когда п—►-(-со. Пусть гп
есть средина отрезка МпМп. Так как множества F и F' ограничены,
то последовательность точек zu z2> ..., zJlf... есть бесконечное
ограниченное множество. Пусть £ есть предельная для него точка *).
Так как М Мг-—* 0, когда я—*-]-со, то точка £, очевидно, является
предельной для каждого из множеств F и F' и, значит, принадлежащей
обоим этим множествам, что невозможно.
Если ограниченные замкнутые множества F и F' не имеют
общей точки, тогда множества F и F1 можно покрыть
системами £ и £', состоящими каждая из конечного числа многомер- ^
ных сегментов, причем эти системы не имеют общей точки.
Действительно, раз F и F' не имеют общей точки, то расстояние
этих множеств есть число положительное; мы его обозначаем через
т1> ^>0. Разделим теперь все наше пространство на сегменты (того
же числа измерений), такие, что диаметр каждого из них был бы
меньше, чем iq. Для этого, в случае плоскости, мы делим оси
координат ОХ и OF на равные сегменты, длины е, и проводим прямые,
параллельные осям координат. Тогда вся плоскость XOY разделится
на квадраты, имеющие своим диаметром (т. е. наибольшей хордой-
Диагональю) s]/2. В случае пространства 3-х измерений, мы делим
все три оси координат на сегменты длины е и проводим через точки
*) Если точки гь гг, ..., гп% ... находятся в конечном числе, будучи
геометрически тождественны, мы за точку £ берем одну из тех, которые
совпадают с бесконечным числом точек г^
$9
деления перпендикулярные к этим осям плоскости. Тогда все
пространство разделится на кубы, сторона которых равна « и, значит,
диаметр (наибольшая хорда-диагональ) которых есть е|/Б. Ясно, что
при достаточно малом е, сегменты, на которые разбито
пространство, будут иметь диаметр, меньший чем iq. Но никакой из этих
сегментов не может содержать одновременно и точки множества
F и точки множества F'', потому что в этом случае расстояние
множеств F и F' было бы меньше, чем yj. Следовательно, если
какой-нибудь сегмент содержит точку множестза F, то он уже не содержит
точки множества F', и обратно. Но множество F ограничено, значит,
оно покрывается конечным числом этих сегментов, образующих
систему 2* Аналогично множество F' покрывается конечным числом
сегментов, образующих систему J/. Ясно, что эти системы £ и £'
не могут иметь общей точки.
Доказанное предложение очень важно, так как из него следует,
что всякие два ограниченные непересекающиеся замкнутые
множества F и F' могут быть соответственно заключены в систему
конечного числа многоугольников (на
плоскости) или в систему конечного числа
многогранников (в пространстве 3-х измерений),
которые отстоят друг от друга на
конечное у ненулевое расстояние (черт. 59).
Действительно, сами системы £ и £' можно
рассматривать как такие многоугольники или
многогранники.
Введем, наконец, последнее определение,
относящееся к совершенным множествам.
Мы называем ограниченное совершенное
множество Р связным, если любые две
его точки М и М' можно соединить
ломаной линией Z,, составленной из прямолинейных звеньев длины <е,
точки соединения которых принадлежат к Р, где е>0 есть
любое положительное число, малое как угодно.
Докажем, что если совершенное множество Р связное, то его
нельзя разбить на два неперекрывающихся совершенных множества
Рг и Р2. В самом деле, в таком случае Pt и Р2 имели бы
расстояние т] положительное, т]>0, и тогда ясно, что нельзя соединить
никакую точку М1 множества Рх с какой-либо точкой М2 множества Р2
ломаной Z,, звенья которой были бы меньше, чем т(. •
Связное совершенное множество Р часто называют conti-
nuum'oM*).
Черт. 59.
*) Мы пишем здесь латинское слово „continuum" в отличие от русского
„континуум", которым мы пользовались ранее для обозначения мощности
множества.
Этот термин часто распространяют и на неограниченные совершенные
множества: именно, неограниченное совершенное множество Р называют
continuum'OM, если всякие его две точки М! и № принадлежат к ограни-
ченкомм coniinuum'y Pif содержащемуся в Р. Прежнее же определение,
которое мы только что дали для*ограниченного conanuuraa, перенести на
90
Согласно этой терминологии ясно, что замкнутый прямоугольник
и замкнутый параллелепипед суть continuum'bi, т. е. связные
совершенные множества. Но, например, два шара, отстоящие друг от друга
ка ненулевое расстояние, хотя и представляют собой совершенное
множество, но онб не есть continuum, так как не есть связное.
Напротив, тор есть continuum.
Противоположное предложение также верно: если ограничен-
ное совершенное множество Р не есть связное, то его можно
разбить на два непергкрывнощихся совершенных множества
Рг и Р2.
Действительно, раз множество Р не связно, то имеются две точки
М и М на Р, такие, которые нельзя соединить ломаной линией L,
звенья которой были бы не больше, чем е, г>0.
Пусть Рг множество точек множества Р, каждую из которых
можно соединить с точкой М ломаной линией, а звенья которой не
больше е.
Покажем, что Рг есть совершенное множество. В самом деле,
' во-первых, оно замкнуто. Действительно, если точка £ есть
предельная для множества Р1У то имеется точка ^ множества Ри такая,
что £?1<е. Но тогда ломаная линия Lu соединяющая точку ^ с М
и увеличенная на прямолинейное звено ^, дает как раз ломаную
линию, соединяющую М с ?, причем звенья этой ломаной все <^е.
Следовательно, точка Е принадлежит к Р1. Во-вторых, множество Рх
не может иметь изолированной точки, потому что всякая точка
множества Р, находящаяся на расстоянии ^s от точки множества Ри
очевидно, сама принадлежит к Ри так как соединима с точкой М
нужной нам ломаной линией I, имеющей звенья <; е. Итак, Рх есть'
совершенное множество. Оно не содержит точки М\ потому что М'
не соединима с М ломаной линией со звеньями ^ г. Пусть Р2 есть
множество точек, принадлежащих к Р и не принадлежащих к Ри
т. е. пусть Р2~Р— pv Ясно, что Р2 есть не пустое множество,
так как точка М' принадлежит к Р2. Легко видеть, что Р2 есть
совершенное множество. Действительно, если £ есть предельная точка
для Р2, то £ не может принадлежать к Ри потому что тогда к Рх
принадлежала бы и всякая точка множества Р, отстоящая от 5 меньше,
чем на е. Значит, Е принадлежит к Р2 и, значит, Р2 есть замкнутое
множество. Но Р2 не имеет изолированной точки, потому что, в
противном случае, эта точка должна быть предельной для множества Ри
т. е. принадлежащей к Pv что невозможно.
и ограниченный continuum невозможно, потому что, например, хотя
соединение S ветви гиперболы и ее асимптоты и имеет любые две его точки Ш
и А\" соединимыми полигональной линией П, звенья которой длины<е и *
вершины которой лежали на S, но П,**$ытя*ивается до бесконечности,
когда г->0. Соединение S не является continuum'OM, потому что точка
гиперболы М и точка асимптоты М" не соединимы ограниченным continuum'OM,
принадлежащим к 5. Нет поэтому ничего удивительного в том, что «S
разбивается на два совершенных множества без общей точки: на гиперболу и
на асимптоту. S не есть езязпое совершенное множество.
91
Таким образом, совершенное множество Р разбивается на два
неперекрывающиеся совершенные множества Р1 и Р2, Р = Р14-/У-)*
Мы знаем, что всякое линейное ограниченное замкнутое
множество Р получается из сегмента [a, h] удалением из него счетного
(или конечного) числа интервалов. Для плоских и пространственных
множеств мы уже не имеем понятия интервала смежности, даже если
мы слово „интервал" будем понимать в смысле многомерности.
Однако основное предложение все же останется верным, так как мы
имеем теорему:
Всякое ограниченное замкнутое множество F получается
удалением из сггмента, содержащего F, счетного или конечного числа
интервалов, не содержащих точек множества F. Обратно, всякое
удаление из сегмента счетного или конечного чист интервалов
приводит к замкнутому множеству, составленному из всех не-
удаленных точек.
Назовем рациональным всякий многомерный интервал или сегмент,
проекции которого на оси координат суть рациональные интервалы
или сегменты.
Так, например, интервал 3-х измерений
(fl<*<*, c<y<d, g<z<h)
есть рациональный, если все шесть чисел а, /?, с, d, g, h
рациональны. Ясно, что множество всех рациональных интервалов (или
сегментов) счетно, потому что мыожество конечных систем
рациональных чисел есть счетное множество.
Пусть теперь F есть какое-нибудь замкнутое множество и пусть
М какая-нибудь точка плоскости или пространства, не
принадлежащая к Р. Если всякий многомерный рациональный интервал А,
содержащий М, содержит точки множества F, то это означает, что
М есть предельная точка для Р, т. е. М принадлежит к Р, что
невозможно. Следовательно, всякая точка М, не принадлежащая
к F, есть точка внешняя для F, и ее можно удалить некоторым
рациональным интервалом (многомерным) А, не содержащим никакой
*) Эти обе теоремы распространимы и на неограниченные contitruum/ы.
Действительно» если неограниченный continuum Я разбивается на два
неперекрывающихся совершенных множества Рг и Р2, то же самое должно
происходить и с тем ограниченным continuum'OM Р', который соединяет точку М\
множества Pt с точкой М% множества Р2. А это невозможно. Таким образом,
прямая теорема доказана.
Обратно, если неограниченное совершенное множество Р не есть
continuum, то имеются в Р две точки М' и М", не принадлежащие никакому
ограниченному continuum'y К, содержащемуся в Р. Следовательно, часть Рс
множества Р, содержащаяся внутри некоторой окружности С и на ее
периферии, причем С содержит внутри обе точки М и М\ есть замкнутое
множество, не связывающее точек М' и М". А это означает, что Рс = PQ+P"C*
где Рс и Рс суть замкнутые множества без общей точки, причем Рс
содержит М! и содержится внутрц С, и Рс содержит М". Отсюда ясно, что
Р распадается на два неперекрывающиеся совершенные множества: Ре и
Р — Р'е, не имеющие общей точки,
92
в
точки множества F. В силу этого ясно, что если мы возьмем,
множество всех многомерных рациональных интервалов Д19 Д2, ... , Лл,...
и удалим из сегмента S, содержащего множество F, все
рациональные интервалы Д^, которые не содержат точек множества Z7, то
совокупность всех оставшихся точек на сегменте £ как раз и будет
тождественна замкнутому множеству F.
Обратно, если из какого-нибудь сегмента £ мы удаляем какое-
нибудь множество интервалов {Д}, то оставшееся множество F точек
на сегменте £ будет замкнутым. В самом деле, если £ есть точка,
предельная для Z7, то она непременно принадлежит к F, потому что
если бы £ была удалена из £ некоторым интервалом Д, то вместе
с £ было бы удалено бесконечно много точек множества F, что
невозможно. Следовательно, £ есть
неудаленная точка, т. е. принадлежит к F.
Назовем порцией какого-нибудь
множества точек Е совокупность всех его
точек, заключенных в каком-либо
многомерном интервале Д. Ясно, что порцией
плоскости или пространства будет
совокупность точек, лежащих внутри какого-
либо прямоугольника или параллелепи- -т&
педа. I
Какое-нибудь множество Е, лежащее Черт. 60.
на совершенном множестве Р, называется
всюду плотным на Р, если всякая порция П множества Р
содержит точки множества Е. Множество £, лежащее на Р,
называется нигде неплотным на Р, если всякая порция П множества Р
содержит такую порцию Г^ множества Р, которая не имеет никакой
точки множества Е. Здесь нужны некоторое внимание и
осторожность, так как термины „всюду плотныйи и „нигде неплотный" суть
термины относительные, т. е. имеющие силу лишь по отношению
к тому совершенному множеству Р, на котором рассматривается
множество Е. Например, замкнутый отрезок АВ прямой, лежащий
на плоскости (черт. 60), есть нигде неплотное множество по отношению
к плоскости, потому что всякий двухмерный интервал г плоскости
XOY содержит точки, не принадлежащие к отрезку А В. И в то же
самое время отрезок АВ есть всюду плотное множество на
прямолинейном сегменте [Л, В].
Какое-нибудь множество Е, лежащее на совершенном множестве Р,
называется множеством первой категории на Р, если Е есть соединение
счетного (или конечного) числа множеств Е\% Е%..., Еп,.. ♦♦ каждое из
которых Нигде неплотно на Р.
Дополнение СЕ к множеству Еу которое есть первой категории на
совершенном множестве Р, называется множеством второй категории на Р.
Совершенно таким же образом, как это было сделано для множеств
первой и второй категории на отрезке, доказывается, что всякое
множество второй категории на Р есть множество всюду несчетно плотное
на Р и что оно имеет мощность континуума.
Далее таким же образом устанавливается, что множество второй
категории нельзя истощить (исчерпать)^ вынимая из пего счетное число
множеств первой категории.
93
Отмстим, наконец, что производное множество Е' от всякого
ограниченного множества Е есть замкнутое множество и что
множество всех точек конденсации для ограниченного несчетного
множества Е есть совершенное множество. Доказательство этих
предложений такое же, как и раньше для случая линейных множествам. § 20).
Наконец, всякое совершенное множество Р имеет мощность,
равную мощности континуума.
В самом деле, раз Р есть совершенное множество, то оно
содержит по крайней мере две различные точки, которые мы можем
заключить внутрь (каждую в отдельности) многомерного сегмента, причем
эти оба сегмента Е0 и Ех мы предполагаем неперекрывающимися.
Многомерным сегментам Е0 и Ех поставим в соответствие линейные
неперекрывающиеся сегменты о0 и ои расположенные на прямой линии
ОТ (черт. 61)
"У
Черт. 62.
Повторим операцию, которую мы выполнили сейчас для всего
пространства, для каждого в отдельности многомерного сегмента Еох
где 6j равно или 0, или 1.
Именно, сегмент \ содержит бесконечно много точек множества
Р, так как содержит внутри точку множества Р, которая есть
предельная для Р. Значит, сегмент Еох содержит, по крайней мере, две
различные точки множества Я. Эти две точки мы заключаем в два
новых неперекрывающихся многомерных сегмента Eel0 и Eelb
содержащихся в Eet. Этим двум многомерным сегментам 1\о и E6ii мы
94
8 линейном сегменте щ± поставим в соответствие два новых
неперекрывающихся линейных сегмента оо0 и а^, содержащихся в а^. Таким
образом, мы получаем 4 многомерные сегмента Еед (где 6^ = 0 или
ss= 1) и 4 соответствующие им линейные сегмента о^, (черт. 62).
В каждом сегменте Бед мы повторяем ту же операцию, и так далее
до бесконечности. Ясно, что если первая операция дает нам два
многомерных сегмента Eet и два линейных сегмента а&1 (где Ьх = О
илИ = 1), то я-ая операция даст нам 2п многомерных сегментов Бед. , .Qn
и 2П линейных сегментов огчпз...9п, где 0^ = 0 или=1. Обозначим
через Sn систему 2п сегментов Бед...е„ и через sn систему 2№*ли-
нейных сегментов оед...9?1. Пусть II есть общая часть всех систем
St>S^>...>Sn>\..f т. е. n = SjX52X ■ • • X S« X .... Ясно,
что П есть совершенное множество, содероюащееся в данном
совершенном множестве. Действительно, всякая точка М9 не
принадлежащая к П, не принадлежит к некоторой системе Sk и,
следовательно, есть внешняя точка для Sk. Это значит, что эту точку М
можно заключить в многомерный интервал А, внешний для S&.
Следовательно, все точки интервала А будут внешними для Sk. Отсюда
следует, что ограниченное множество II получается исключением из
достаточно большого многомерного сегмента множества многомерных
интервалов А. Значит, II есть замкнутое множество. Но оно есть
совершенное множество, содержащееся в Р, потому что всякая точка
М множества II есть, очевидно, предельная и для множества Р,
и для самого множества II, потому что всякая точка М
множества П. есть предельная для бесконечного множества
пространственных сегментов Б6д...еш, содержащих точки множества Р и
множества П.
Обозначим через тг совокупность точек, принадлежащих всем
системам 5,1>52>- . ->$1Ь> • • •> T,==SiXSi2X • • -Х^Х ЯСНО, ЧТО 1С
есть линейное совершенное множество, так как оно получается
исключением из достаточно большого линейного сегмента
интервалов, смежных к системе sk, где А = 1, 2, 3 Так как
интервалы, смежные sA., не перекрываются, то тг есть совершенное
множество.
Следовательно, множество и имеет мощность континуума. Но
совершенное множество П, содержащееся в Р, находится во
взаимнооднозначном соответствии с совершенным линейным множеством it,
потому что всякой последовательности линейных стягивающихся
сегментов
O0t > 391ч|> 09Д9Я > • • • > 30ДЧв • • • 9я> • • •
соответствует последовательность пространственных стягивающихся
се [ментов
£et > Ее а > Еоа% > • • • > ^Ws • • «9n> • #.
и, значит, мы имеем две соответствующие друг другу точки т и /If,
причем т принадлежит множеству т.% а Л1~ множеству П.
95
Так как сегменты системы sn не имеют общей точки как и про-/
странственные сегменты системы Sn> то отсюда следует, что,
перемещая точку т по множеству тг, мы получим соответствующее
смещение точки М по множеству П. И так как всякая точка т
множества я принадлежит последовательности стягивающихся сегментов
oet>eel9l>--.>oele1,..e*>. .., т0 отсюда следует, что множества П
и ъ эквивалентны друг другу. Следовательно, множество П имеет
мощность континуума.
#■
Г Л А В А III
ТЕОРИЯ ПРЕДЕЛОВ
§ 23. Необходимость обоснования теории пределов. Всякий
математик знает, насколько важна теория пределов для
математического анализа. Ее значение столь велико, что без нее анализ
бесконечно-малых нельзя излагать лицам, еще незнакомым с высшей
математикой. Таким образом, на первый взгляд может показаться,
что теория пределов носит столь элементарный характер, что не
возникает и мысли искать ее обоснования. \
И тем не менее тщательное обоснование теории пределов
неизбежно. Причина этому лежит в следующем.
Элементарная теория пределов говорит о пределе переменной
величины. Переменной же величиной называется такая величина,
которая изменяет свое численное значение с течением времени. Таким
образом, теорией пределов сразу же вносится в математический анализ
совершенно чуждое ему понятие времени. Но, как это было впо*
следствии обнаружено, когда самое содержание анализа бесконечно-
малых уже сложилось — математический анализ нисколько не
нуждается ни в понятии времени, ни в понятии какого-либо изменения,
потому что весь он может быть обоснован без введения понятия
переменной величины и, значит, может быть обоснован стационарным
образом, т. е* построен на понятиях, не зависящих от понятий
изменения. Так как понятия изменения и времени вносятся в
математический анализ одной лишь теорией пределов, то отсюда и
возникает необходимость, при научном изложении математического
анализа, обосновать самую теорию пределов без введения понятия
переменной величины. Это и будет сделано в настоящей главе.
§ 24. Упорядоченные множества. Множество М, составленное из
каких-нибудь элементов е, уИ={е}, называется упорядоченным, если
в силу некоторого правила все его элементы е оказываются
расположенными в определенном порядке так, что из двух любых
элементов е' и е" множества М один „предшествует" другому.
,Для того чтобы указать, какой именно элемент предшествует
Другому, употребляют символу. Так, если элемент е' предшествует
элементу ег\ тогда мы пишем
1 Эак. ЪШ.
e'-if.
9?
/
0
pi ,:""
! f:V
p'k у ;
\ \ \
x' Г
f
Если элемент e' предшествует элементу епу то про элемент err
говорят, что он следует за элементом е\ и пишут е"Ь-е\
Здесь следует иметь в виду, что понятие „ предшествованияtf
должно обладать следующим свойством: если е' предшествует
элементу е", а е" предшествует элементу е"\ то тогда ег предшествует
элементу ет\ Это значит, что из двух соотношений е*' ~$е" и е"-$еш
вытекает соотношение ег-*>еш.
Чтобы вполне овладеть смыслом данного определения, читатель
должен иметь в виду следующие обстоятельства:
1. Что элементами е множества М могут служить какие угодно
предметы: числа, точки, функции и т. д.
2. Что данное множество М' при самом его задании часто со*
всем не является упорядоченным и лишь впоследствии становится
упорядоченным в силу какого-нибудь специального правила
(условия, соглашения), которое налагаем на все его элементы е и которое
заставляет из двух любых его элементов
один „предшествоватьа другому.
3. Что понятие „упорядоченности* мно*
жества можно не связывать ни с
расположением в пространстве его элементов^
ни с получением их во времени. Таким
образом, упорядоченность множества
зависит лишь от правила его упорядочивания.
Поясним это на простом примере.
Пусть М есть множество всех точек еди-
Черт. 63. ничного квадрата, включая и точки
периферии (черт. 63). Ясно, что при таком
задании множества М оно пока не является упорядоченным, потому что
совершенно неясно, какую из двух любых его точек Р' и Р" нужно
считать „предшествующейи и какую „последующейtf. Но примем
теперь следующее соглашение: согласимся считать из двух точек
Р' (xf у') и /^(л/'У) „предшествующейu ту, у которой абсцисса
меньше, а в случае равенства их абсцисс — ту, у которой ордината
меньше. Итак, согласимся писать Р'-^Р", если #'<*", или, в
случае равенства х' = х'\ если у' < у". Ясно, что это правило
удовлетворяет основному свойству „упорядочивания множеств", потому что
из соотношений Р1-2>Р" и Рп-$Р'" вытекает соотношение Р'-$Р"\
как мы в этом легко убеждаемся, исследуя взаимоотношения величин
абсцисс и ординат точек Р', Р" и Рш.
Итак, множество Af, первоначально заданное в неупорядоченном
виде, после принятия указанного правила сделалось упорядоченным
множеством. Вообще говоря, одно и то же множество М можно
сделать упорядоченным бесконечным числом способов, смотря по
тому, какое правило принимают для его упорядочивания. В данном же
случае правило это является очень простым: множество точек ед^
ничного квадрата рассматривается как составленное из вертикальных
прямолинейных отрезков, причем из двух любых таких отрезков тот
считается предшествующим, который лежит ближе к оси OY. Что же
касается до точек каждого из этих отрезков, то они считаются имею-
98
щими тот самый порядок, в каком они лежат на нем, т. е. снизу
вверх. Этим вполне устанавливается порядок точек квадрата.
Цриведенный пример чрезвычайно поучителен, потому что
множество М, хотя оно и сделано упорядоченным, т. е. расположенным
как бы в линейном порядке, однако его нельзя поместить все
целиком на одну из тех прямых, которые рассматриваются в анализе и
в обычной геометрии: действительно, всякая из этих прямых, как мы
видели, может содержать неперекрывающиеся отрезки лишь в
счетном числе. Наше же упорядоченное множество М, напротив,
содержит неперекрывающиеся отрезки внесчетном числе:
вертикальных отрезков, очевидно, столько же, сколько имеется различных
абсцисс, т. е. это есть мощность континуума. Поэтому, наше
множество М, сделанное упорядоченным согласно данному правилу, уже
невозможно поместить целиком на обыкновенную прямую, и если
его все-таки хотят вообразить помещенным на некоторую
отвлеченную „прямую", то прямая эта должна обладать совсем иными
свойствами, чем прямые линии анализа и обычной геометрии. В частности,
отвлеченные прямые, содержащие несчетно много неперекрывающихся
отрезков, часто называют нвархимедовыми прямыми*).
Но это же самое множество М можно упорядочить другим пра*
видом, и притом так, что оно после своего упорядочения может быть
помещено на обыкновенную прямую. Например, вспомнив, что
множеств© М имеет мощность континуума, мы можем привести во
взаимнооднозначное соответствие все точки Р множества М с точками
прямолинейного сегмента [0^£<[1]. И тогда мы можем уел овиться
считать все точки Р множества М имеющими тот же самый порядок,
который имеют на сегменте [0^/-^1] соответствующие им
точки L Итак, мы пишем Р'-^Р", если tr < tf". Ясно, что это правило
делает множество упорядоченным и что оно после такого
упорядочивания может быть помещено все целиком на обыкновенном
отрезке [0,1].
В качестве другого примера укажем на множество М всех
непрерывных функций f (х), М ={/(#)}. Ясно, что М есть пока неуио-
рядоченное множество. Однако, вспомнив, что мощность множества М
есть мощность континуума, мы можем установить взаимно-однозначное
соответствие между элементами / (л:) множества М и между точками
t сегмента [0 ^ t ^ 1 ]. Ясно, что множество М делается
упорядоченным, когда мы приписываем функциям f(x) тот же самый
относительный порядок, какой имеют соответствующие им точки, t.
*) Аксиомой Архимеда называют следующее положение: если даны две
величины / и L, L^>1, одной и той же природы, можно найти Taieoe
натуральное число т, что ml окажется больше L. Отвлеченные прямые, не
удовлетворяющие аксиоме Архимеда, называются неархимедовыми прямыми.
В начнем случае, мы как раз имеем дело с кеархимедовой прямой.
Действительно, если мы вообразим, что рассматриваемое упорядоченное множество
М лежит на прямой, то отрезок этой прямой, имеющий двоими концами дае
точки Р1 и Р" квадрата, не находящиеся на одном вертикальном отреэ^е,
заведомо содержит несчетно много неперекрывающихся отрезков длины
единицы.
L7* 99
§ 2S. Последовательности. Упорядоченное множество ЛТ, Л1=а
t= {#}9 называется последовательностью, если оно не имеет
самого последнего элемента, т. е. такого элемента е'$ по
отношению к которому каждый элемент е множества М (отличный
от ег) был бы „предшествующим", е-$е'.
Ясно, что всякое конечное упорядоченное множество М имеет
последний элемент и поэтому оно никогда не является
последовательностью в данном смысле. Отсюда вытекает, что всякая
последовательность есть бесконечное множество. Мощность последовательности
М может быть самой разнообразной, как счетной, так и несчетной.
Из счетных последовательностей простейшими являются те*
элементы которых следуют друг за другом в том же порядку, в
каком следуют друг за другом натуральные числа. Такова, например,
последовательность *
Но имеются еще и другие счетные последовательности Ж, такие, что
их элементы уже не могут следовать друг за другом так, как
следуют друг за другом натуральные числа. Такова, например,
последовательность
^1-3 02-303-2 • •"•-$ЯтН *•• -S*i-3*2-$*8""S ••'•"-$*я-3 •••*
в которой каждый элемент Ъп считается следующим за всяким
элементом ат. Эта последовательность, очевидно, счетная, но если ее
^ занумеровать натуральными чи-
*' *т ? слами, то тогда уже
разрушится тот порядок, в котором
Черт. 64. нам даны все элементы этой
последовательности:
действительно, до нумерации элемент Ь1 следовал за всеми элементами
аи а2, а3 , ат>..., которых бесконечно много. А после
нумерациа Ьг получит определенный конечный нумер и, поэтому, уже
не может следовать за всеми элементами аи а2, %>•••, которых
бесконечно много и которые, поэтому, получат нумера, наверное
превосходящие тот нумер, который получил элемент bv
Из несчетных последовательностей простейшими являются
последовательности мощности континуума. Из них отметим две
наиболее важные:
1. Последовательность всех точек х} лежащих левее данной точки а.
Здесь мы делаем естественное условие: из двух точек х' и х" считать
япредшествующей" ту, у которой абсцисса меньше, т. е. мы полагаем
х'-*>х", если х' <лг" (черт. 64). Ясно, что здесь мы имеем дело
с последовательностью точек (а не только с упорядоченным
множеством), потому что среди точек х, лежащих левее точки ал нет
самой последней (т. е. самой правой) точки.
2. Последовательность точек х> лежащих правее данной точки а
(черт. 65).
Здесь мы условливаемся считать из двух точек х' и хп ту из них
япредшествующей", у которой абсцисса больше. Таким образом, мы
190
пишем х' -$#", если хт > х". Ясно^ что и здесь мы имеем дело с
последовательностью, потому что среди точек х, лежащих направо от
точки а, нет самой левой точки.
Заметим, что сегмент [а, Ь\ не есть последовательность точек, если
порядок его точек есть порядок возрастающих или убывающих абсцисс,
потому что тогда имеется еамый последний элемент: всякий сегмент
содержит в себе свои оба конца. Но полусегмент [а, Ь) есть после-
довательность^, когда располагаем его точки в порядке возрастания
абсцисс. Точно так же, полуинтервал (а, Ь] есть последовательность,
если его точки располагать в порядке убывания абсцисс.
Мы видели, что самое существенное в определении
последовательности — это то, что „за всяким элементом какой-нибудь
последовательности непременно имеются дальнейшие элементы этой
последовательности *.
Но в математическом анализе вошло в обычай, при рассуждениях
над последовательностью, говорить о „переменноми. Под переменным
понимается какой-нибудь
символ, например х, про который
говорят, что он „ пробегает " - ? ? ?* У*
элементы последовательности
М так, что предшествующие Черт. 65.
элементы - будут „пройдены0
„раньше*, чем последующие. Таким образом, математический анализ —
по крайней мере в ранних стадиях своего изложения — прибегает
к понятию переменного, развертывающего перед нами все
элементы последовательности М во временном порядке. Не говоря уже о
том, что этот прием вносит в анализ чуждое ему понятие времени и
изменения, здесь мы находим еще то неудобство, что реальное
время обычно считают имеющим свои моменты расположенными
точно таким же образом, как расположены точки на прямой обыкно-;
венной геометрии. Но мы видели в предыдущем параграфе, что
имеются упорядоченные множества М, которые не могут быть
помещены на прямую обыкновенной геометрии. Если у таких множеств
отнять последние элементы, предполагая, что таковые там имеются
(например, у единичного квадрата М мы отнимаем ее самую
последнюю точку Я (1,1), то такое усеченное множество М становится
последовательностью, которую нельзя поместить на обыкновенную
прямую и которая требует для своего помещения неархимедовой
(воображаемой) прямой. Поэтому, если такую последовательность М;
мы хотим заменить рассмотрением „ переменногои ху то мы должны
признать, что изменение такого переменного х происходит в неархи-,
медовом времени, потому что его моменты t невозможно изобразить
на црямой обыкновенной геометрии. А так как говорить о кеархи-
медовом времена не представляется целесообразным ни с какой точки
зрения, то отсюда вытекает, что употребление „ переменного * х>
развертывающего перед нами все элементы последовательности М
в порядке реального времени (не фиктивного, т. е.
архимедова), сильно ограничивает класс рассматриваемых
последовательностей М.
101
Сказанное делает понятной необходимость освободиться от
употребления переменного и времени при общем рассмотрении
последовательностей.
§ 26. Последовательности чисел. В дальнейшем мы будем
рассматривать исключительно последовательности, элементами которых
явлшфгся действительные числа. Такие последовательности иногда
набивают числовыми последовательностями. Здесь прежде всего
нужно ед^лать одно замечание: числовая последовательность может
иметь некоторые элементы равными друг другу. Чтобы это понять,
рассмотрим сначала один частный пример. Пусть М простая счет*
н а я последовательность
(М) e1-$e2-^e3-3...$~en-i..~1
составленная из каких-нибудь элементов еъ е%,..., еп,..., следующих
друг за другом в том же порядке, в каком следуют их значки 1, 2,
3, ..., я,..., т. е. в порядке возрастания натуральных чисел. Мы
обращаем особое внимание читателя на то, что элементы е
последовательности М занумерованы натуральными числами, т. е.
расположены в виде еи £2,..., ею..., и что порядок элементов е
последовательности М согласуется с порядком их нумеров 1, 2, 3,.♦. . Если
мы теперь положим еп=*\у когда п есть нечетное число, и еп = О,
когда п четное, то получаем числовую последовательность
(М), 1, 0, 1, 0, 1, 0,..., .
состоящую только из чередующихся единиц и нулей. Мы видим, что
рассматриваемая числовая последовательность М имеет равные элементы,
так как все ее элементы е, стоящие на нечетных местах, равны друг
другу, как и все ее элементы <?, стоящие на четных местах.
В общем случае, образование числовой последовательности М>
М=>{е}, содержащей равные элементы, можно представить
следующим ©бразом: сначала берут последовательность А, А={а},
составленную из каких-нибудь нетождественных элементов а, и затем
образуют числовую последовательность М> Л1 = {#}, элементы е которой
'занумерованы элементами а последовательности Л, т. е. имеют вид
eai Af={£j, причем порядок элементов е последовательности М
согласуется с порядком их знаков а, т. е. мы пишем еаг-^еак, если
а'~$а". Ясно, что теперь нет ни малейшего неудобства, если
некоторые элементы еа числовой последовательности М окажутся и
равными между собой: в самом деле, если число еа равно числу еа>,
еа-=*е'лУ та это не представляет никакого неудобства, потому что
значки а и аг этих элементов нетождественны и, значит, мы хорошо
знаем, каркай из этих значков а к а' предшествующий и какой
последующий.
Таким образом, понятиечисловойпоследовательности, собственно,
совпадает с понятием функции, так как мы имеем некоторую
первоначальную последовательность Л={а}, составленную из
каких-нибудь элементов аъ и затем заставляем соответствовать всякому эле-
102
менту q, определенное действительное число е0, причем мы уславливаемся
писать еа*~$еа>, если а-$ а'. При этом, действительное чиеяо еа есть
функция элемента ащ определенная на послеювател^ности А, т. е,
^а=/(а), и что нет никакого основания требовать, чтобы значения
этой функции были бы все различными между собой.
§ 27. Неограниченные и ограниченные числовые
последовательности. Введем следующее определение: пусть е есть
какой-нибудь элемент данной последовательности М\ назовем сегментом
последовательности М, отсекаемым элементом et совокупность всех
тех элементов этой последовательности, которые предшествуют
элементу е; сегмент, отсекаемый элементом е, обозначается через о(е).
Далее, назовем остатком последовательности М, определенным
элементом е, совокупность всех тех элементов этой последователь-
кости, которые не принадлежат к сегменту о (е); остаток,
определенный элементом е> обозначают через р (е). Из определения остатка
следует, что р (е) состоит из самого элемента б и из всех тех
элементов е' последовательности М, которые следуют за элементом е.
Введя эти определения, годные для любых последовательностей,
возвратимся к изучению числовых последовательностей.
Числовая последовательность М называется ограниченной сверху,
если имеется такой элемент е, что остаток р (е) есть
множество чисел, ограниченное справа. Аналогично, числовая
последовательность М называется ограниченной снизу, если имеется
такой элемент ч е, для которого остаток р (е) есть множество
чисел, ограниченное слева.
Числовая последовательность М называется ограниченной
числовой последовательностью, ко$да она ограничена исв ерху и снизу.
Отыщем критерий ограниченности числовой последовательности.
Если числовая последовательность М ограничена сверху, имеется
такой элемент е'', что остаток р (ег) есть множество чисел,
ограниченное справа. Если та же самая последовательность М ограничена
и снизу, имеется такой элемент е", что остаток р (е") есть множество
чисел, ограниченное слева. Но последовательность М не имеет самого
последнего элемента. Значит, последовательность М содержит
элемент е, следующий и за элементом е", т. е. е' ^е ие"-$е. Ясно,
что остаток р (е) содержится и в остатке р(е')> и в остатке р (<?")•
Поэтому, остаток р (*) есть ограниченное множество чисел.
Обратно, если имеется в числовой последовательности М такой
элемент е% что остаток р (е) есть ограниченное множество чисел, то,
очевидно, числовая последовательность М ограничена.
Таким образом, необходимым и достаточным условием для того,
чтобы данная числовая последовательность М была ограниченной,
является существование такого элемента е в последовательности
Ж, что остаток р {е) есть ограниченное множество чисел.
§ 28. Пределы числовой последовательности. Введем
чрезвычайно важное понятие пределов числовой последовательности. Мы
должны предупредить читателяд что, вообще говоря, числовая по-
103
следовательность имеет не один только предел, но несколько, иногда
даже бесчисленное множество, так что, давая определение предела
числовой последовательности, мы определяем только один из
возможных ее пределов. Наше определение предела будет, таким образом,
более общим, чем то, с которым читатель до сих пор встречался
в анализе и относительно которого доказывалось, что
„последовательность может иметь только один предел".
Определение. Действительное число а называется пре*
делом числовой последовательности Му М — {е], если, каков бы
ни был интервал 8, содержащий точку а, всякий остаток р (е)
последовательности М
q ^*—^—*-^ имеет точку е' в интер*
*—= —■ е^Лд """—~ вале 8 (чеРт- 66-> *)•
ч бб До сих пор, в силу
F ' e самого определения, одни
лишь ограниченные
справа множества Е точек (или действительных чисел) имели правую
границу ?], которая есть конечная точка (или действительное число)
(см. стр. 60). Теперь мы приписываем формальным образом
правую границу всякому множеству./; чисел, полагая irj= +00»'
когда рассматриваемое множество точек неограничено справа. При
этом нужно иметь в виду, что символ -f- сю не есть число и что
мы, отказываясь производить над ним какие-либо арифметические
действиу, условимся считать его большим, чем всякое положительное
число. Аналогично, мы скажем, что множество чисел Е9 неограни*-
ченное слева, имеет левую границу £, равную символу —со, где
символ — со рассматривается как меньший всякого отрицательного
числа.
Таким образом, мы вводим два символа: -f °° и —оо и
предупреждаем читателя еще раз, что символы эти не суть действительные
числа (которые все конечны), что над этими символами нельзя
производить даже самых простых арифметических операций и что символы
эти введены нами исключительно ради словесного удобства разных
формулировок, чтобы не затрудняться многочисленными исключениями
из общих правил. Так, например, теперь всякое линейное множество Е
*) Читателю эт<* формулировка, без сомнения, в начале покажется
громоздкой и отвлеченной. Но чувство неясности исчезнет, если читатель
призовет на память привычное понятие „переменного" и „времени". В самом
деле, чего хочет добиться данная формулировка, если ее перевести на язык
„переменного" и „времени"? Для того, чтобы понять это,рассмотрим
переменное х, которое „пробегает* данную числовую последовательность М%
переходе от предшествующих чисел к последующим. Так как, согласно выще-
приведенной формулировке, всякий остаток р (в) имеет точки на интервале Ъ, то
это означает, что величина переменного х время от времени попадает на
интервал \ потому что за всяким „моментом времени tu (когда х = е) имеется
непременно^такой дальнейший „момент времени V* (когда х = е% что е*
уже заведомо принадлежит интервалу &. Таким образом, данная
формулировка на языке переменного и времени означает, что пределом числовой
последовательности М называется такое число я, от которого переменное л;
окончательно ? отделиться не может, так как впо временам* велилцыа
переменного х делается сколь угодао .близкой* к а.
Ш
чибел без исключения имеет правую и левую границы; но надо
помнить, что для случая неограниченных множеств границы эти
^фиктивны* в том смысле, что они суть символы -f- оо или —со,
которые не являются ни точками, ни действительными
числами.
Возвратимся теперь к числовым последовательностям М. Если
числовая последовательность М неограничена сверху, то ми
говорим, что ~{~ со есть один из ее пределов. Аналогично, если М
неограничена снизу, тогда —со есть один из ее пределов.
Это соглашение весьма естественно, так как, если, например, М
неограничена сверху, то это значит, что всякий остаток р (е)
последовательности М неограничен справа, и, значит, имеет точки на
любом бесконечном интервале (с, + °°)> где с есть какое-нибудь
действительное число. Этим и оправдывается соглашение
рассматривать символ + °° как °ДИН из пределов такой последовательности М.
На языке переменного и времени это означает, что каково бы ни
было положительное число сг с>0, за всяким моментом времени t
имеется такой момент ^
времени /', /' > t, когда __ ^-г —^ щ
переменное х получит я &'
значение х\ большее чи- qepT< 57.
ела с% хг>е.
Докажем теперь предложение: Множество всех конечных
пределов данной числовой последовательности М есть замкнутое
множество.
В самом деле, пусть Е есть множество всех конечных пределов
последовательности М. Пусть а есть какая-нибудь точка, предельная
для множества Е (черт. 67).
Заключим а в произвольный интервал 8. Так как а есть
предельная точка для Е, то 8 содержит наверное некоторую точку а'
множества Е. Так как аг есть один из пределов последовательности М,
то отсюда следует, что 8 содержит точки всякого остатка р(е).
А это^и означает, что а есть один из пределов последовательности Ж.
Заметим, что в доказательстве мы определяем замкнутое
множество как множество, содержащее все предельные к нему точки.
В этом смысле, замкнутое множество может быть и неограниченным.
Мы до сих пор еще не доказали, что ограниченная числовая
последовательность М имеет хотя бы один предел. Это предложение
очень важное, мы его докажем, пользуясь замечательной леммой
Бореля-Лебега.
§ 29. Лемма Бореля-Лебега и ее ближайшие следствия.
Установим одно замечательное и совершенно общее предложение,
имеющее принципиальную важность для многих отделов анализа и
носящее название племмы Бореля-Лебега41:
Лемма. Каково бы ни было множество Д = {8} интервалов 8,
имеющее то свойство, что всякая точка сегмента [at b\ принад-
леэюит по крайней мере к одному интервалу 8 множества А,
всегда можно выделить из Д конечную систему интервалов
105
8j, 82,T.., Ьк9 обладающую тем же самым свойством по
отношению к этому сегменту [а, Ь].
Допустим, что весь сегмент [а, Ь] невозможно покрыть конечным
числом интервалов 8, взятых из множества Д. Тогда мы делим
сегмент [а, Ь] пополам и получаем, таким образом, два половинных
сегмента, имеющих общий конец. Мы утверждаем, что по крайней
мере один из этих половинных сегментов невозможно покрыть
конечным числом интервалов 8, взятых из Д. Действительно, если
бы каждый из этих сегментов можно было покрыть конечным
числом интервалов 8, взятых из Д, то и весь сегмент [а, Ь]
покрывался бы конечным числом интервалов 8, что мы отрицаем. Итак,
пусть [аи Ьх] будет тот из половинных сегментов, который заведомо
не покрывается конечным числом интервалов 8. Делим его опять
пополам и обозначаем через [а2, Ь2] ту из его половин, которая
не покрывается конечным числом интервалов 8; затем мы опять
делим пополам сегмент [а2, Ь%] и обозначаем через [ав, Ь3] ту из
его половин, которая
^—?<L^^^ не допускает покры-
<^^гсг^^<^^^^,.. ,. тия конечным числом
"Л *° "П интервалов 8, и так
далее неограниченно»
Черт- б8' Таким образом, мы
имеем бесконечную
последовательность сегментов [a, b],laubt], [а2> £2],..., [ak, *J,.-...,
вложенных один в другой, причем каждый из них есть
половина предшествующего сегмента. Но в этих условиях мы
знаем, что имеется точка лг0, принадлежащая всем этим сегментам.
В частности, точка х0 принадлежит сегменту [а, Ь], и, согласно
условию, она принадлежит хотя бы одному интервалу 80 множества Д
(черт. 68). Этот интервал 80 содержит точку х0 строго внутри.
И так как сегмент [ап, Ьп] также содержит точку х0 и кроме того
стягивается к ней, когда п безгранично возрастает, то имеется
столь большое натуральное число п, что сегмент [апу Ьп] весь
находится внутри интервала 80. Но это невозможно, так как сегмент
1апу bnl нельзя покрыть конечным числом интервалов 8, взятых из
множества Д, а он оказался покрытым не только конечным числом
интервалов 8, взятых из множества Д, но даже одним таким
интервалом 80.
Из обнаруженного противоречия следует истинность леммы Бореля-
Лебега.
Как простое следствие леммы Бореля-Лебега, имеем:
Теорема. Если какой-нибудь сегмент [а, р] прямой не содер-
жит ни одного предела числовой последовательности Му то суще»
ствует такой элемент е в последовательности М, что остаток
р(е) не имеет ни одной точки на сегменте [<х, J3].
Пусть д:0 есть какая-нибудь точка сегмента [а, [3]. По условию
х0 не есть предел последовательности М. Это означает, что имеется
такой интервал 80, содержащий точку х0> и в последовательности М
такой элемент eQ9 что остаток р(е0) не имеет никакой точки на
106
интервале 80. Так как лг0 есть произвольная точка сегмента [ос, р]>
то множество А = {8} всех найденных таким образом интервалов 80
покрывает целиком весь сегмент [а, Р] и, значит, удовлетворяет
условию леммы Бореля-Лебега. Отсюда, из множества Д можно
взять конечное число интервалов 8^ 82,..., 8ft, покрывающих весь
сегмент [а, р]. Пусть еи e2i...9 ek элементы последовательности М,
выбранные так, что 8^ не содержит ни одной точки остатка р(^).
Так как последовательность М не имеет самого последнего элемента,
то существует в М такой элемент е, который следует за всеми
элементами еи е2> . .,, ек. Поэтому, остаток р (е) содержится в
каждом из остатков р(^), р(г2)>---> ?(ек)- Но остаток р(е{) не имеет
никакой точки на интервале 8г.. Значит, остаток р(е) также не
имеет никакой точки на интервалах 81э 82,..., Ьк и, поэтому, не
имеет никакой точки на сегменте [a, PJ.
Отсюда следует основная теорема о пределе последовательности:
Всякая ограниченная числовая последовательность имеет по
крайней мере один предел.
Пусть М есть ограниченная последовательность, не имеющая ни
одного предела. Раз М есть ограниченная последовательность, имеется
такой элемент е0, что остаток р(е0) есть ограниченное множество,
т. е. содержащееся целиком в некотором сегменте [а, р]. Но так
как М не имеет вообще никакого предела, то нет предела, привад»
лежащего к сегменту [а, р]. Это означает, в силу предыдущей тео-
ремы, что имеется элемент ev такой, что ocfaTOK p(et) не имеет
никакой точки на [а, р]. Если теперь е есть элемент, следующий
за е0 и за еи то остаток р (е) должен и содержаться в [a, р], и не
иметь никакой точки в [а, р], что невозможно.
Таким образом, всякая числовая последовательность имеет по
крайней мере один предел, конечный или бесконечный.
§ 30. Наибольший и наименьший пределы числовой
последовательности. Если последовательность М неограничена сверху, то
будем говорить, что наибольшим пределом является -j- oo. В этом
случае справедливо то свойство этого предела, что каков бы ни
был бесконечный интервал 8 = (г, -f-oo), где с есть любое
действительное число, всякий остаток р(е) последовательности М имеет
точки на 8. На языке переменного и времени это означает, что за
всяким моментом времени Т имеется дальнейший момент времени t
такой, что для него переменное х будет больше, чем с, дг>с; здесь
с есть любое действительное число, как угодно большое.
Пусть теперь М есть последовательность, ограниченная сверху.
Если М имеет конечные пределы, среди них есть наибольший,
потому что, как мы видели, множество Е всех пределов
последовательности М замкнуто и, значит, его правая граница принадлежит ему,
т. е. является правым концом множества Е. Пусть В есть
наибольший из пределов. Заключим его в интервал 8 = (#,£) как угодно
малый (черт. 69). Так как последовательность М ограничена сверху,
имеется такой элемент е0, что остаток р(е0) есть множество,
ограниченное справа, т. е. лежащее все целиком левее некоторой конечной
107
точки {3. Так как сегмент [£,В] не содержит предела для М9 то
имеется такой элемент еи что остаток р02) не имеет точки на [Ь$\.
Если теперь возьмем любой элемент егг, следующий за е0 и за ^,
то остаток р(е"), очевидно, не будет иметь ни одной точки направо
от интервала 8. Напротив, всякий остаток р(е) имеет точки,
принадлежащие к 8, потому что 8 содержит предел последовательно*
сти М.
Таким образом, наибольший предел В последовательности М
характеризуется тем свойством, что как бы мал ни был интерн
вал 8, содержащий В, имеется элемент е" такой, что остаток р(е")
не имеет точек направо от 8, но всякий остаток р(е) последо»
стельности М имеет точки в 8.
На языке переменного и времени это означает, что каково бы
ни было малое положительное число з, имеется такой момент
времени Т, начиная с которого, т. е. для />Г, сохраняется
неравенство л;<В-|-е, и вместе с тем, каков бы ни был момент времени
В , /, всегда имеется даль«-
*—, —^ iT^" 5Г"~ нейший момент вре*
О о ? мени ^ когда заве*
Черт. 69. домо имеем неравен*
ство х>В— s.
Рассмотрим, наконец, последний оставшийся случай, когда
последовательность М, ограниченная сверху, не имеет конечных
пределов. В. этом случае М имеет единственным пределом —со, Из пре*
дыдущих рассуждений ясно, что, каково бы ни было конечное число с,
последовательность М содержит такой элемент е, что остаток
р{е) не имеет никакой точки на бесконечном полусегменте [с, + со)
и, значит, будет содержащимся целиком в бесконечном интервале
(—оо,с).
На языке переменного и времени это означает, что каково бы
ни было действительное число х% имеется такой момент времени Т\
начиная с которого будет иметься и будет сохраняться неравенство
х<с. Это обстоятельство и выражают словами, говоря, что
„переменное стремится к пределу—со".
Чтобы изучить наименьший предел А последовательности М,
нет необходимости столь же детально рассматривать все возможные
случаи: достаточно данную числовую последовательность М, М= {е},
заменить другой М'— {г'}, где *'= —е. Тогда, очевидно,
наибольший предел В' числовой последовательности Мг равен — А, В1 = —А,
где А есть наименьший предел последовательности М. Так кай
наиболее важным случаем является тот, когда данная числовая
последовательность М имеет конечные наибольший и наименьший пределы,
то мы ограничиваемся этим случаем и формулируем все сказанное
следующим образом:
Последовательность М, имеющая конечные наибольший и
наименьший пределы В и А, есть ограниченная последовательность;
заключая эти пределы в два интервала 8" и 8' (черт. 70), как
бы они малы ни были, в последовательности М мы получим
такой элемент е0, что остаток p{eQ) не имеет никакой точки пра-
108
вее 8* и левее 8'. Наоборот, всякий остаток р(е) содержит точки,
лежащие и в 8' и в Ъп.
С точки зрения переменного и времени это означает, что,
начиная с некоторого момента времени Т% значения переменной величины
лежат на сегменте
[Л —е, В-Hi, как 5' а»
бы мало е(г>0) ни ~+ ^ Т~^ # ^ Т7^^-.,.^
было. Но за всяким ^ 3
моментом времени t Черт. 70.
найдутся такие
моменты if и t\ tf>t и *">/, когда значение переменного л: попадей
соответственно в 8' и в 8".
§ 31. Непосредственное отыскание наибольшего и наимень*
шего пределов. Мы сейчас укажем процесс, приводящий к
фактическому отысканию крайних пределов А и В числовой
последовательности М; М={е]. Возьмем для этого какой-нибудь элемент е
последовательности М и соответствующий ему остаток р(е). Этот
остаток есть некоторое множество чисел; пусть Ве есть его
правая граница. Ясно, что если е'~$е'\ то Ве'^Ве», потому что
остаток р {е") содержится в остатке р(е). Обозначим через В*
левую границу чисел Ве> где е есть любой элемент
последовательности М.
Покажем, что определенное таким образом В* (действительное
Число или один из символов-|- со или —со) есть наибольший
предел последовательности М. В самом деле, пусть наибольший и
наименьший пределы данной последовательности М суть В и А. Если
jB = -j- оо, последовательность М есть неограниченная сверху. В этом
случае р(#) есть множество чисел, неограниченное справа и, значит,
мы имеем всегда Ве = Ч- оо. Поэтому, В* = Ве и, значит, В* = -|- оо.
Поэтому, В*— В. Если В = —со, то, как мы видели, имеется
такой элемент е, что остаток р (е) не имеет никакой точки на
полусегменте [с, + со), где е есть любое действительное число. Поэтому,
имеется такой элемент еу что Ве < с, где с любое действительное
число. Значит, В*==—оо и, поэтому, мы опять имеем В* = В.
Наконец, если В есть конечное (т. е. действительное) число, мы
можем его заключить в интервал 8, произвольно малой длины. Из
характеристического свойства наибольшего предела мы знаем, что
имеется такой элемент е последовательности М, что остаток р (е) не
имеет никакой точки направо от о. Следовательно, Ве не лежит
направо от 8, И, поэтому, В* также не лежит направо от 8. Но,
с другой стороны, в интервале 8 наверное лежат числа всякого
остатка р (е), каков бы ни был элемент е последовательности М,
Значит, Ве наверное находится в 8; поэтому, В* также принадлежит
интервалу 8. Следовательно, две точки В и В* находятся в одном
и том же интервале 8, произвольно малой длины. Но это может
быть только тогда, когда В**=*В.
Итак, во всех случаях В* есть наибольший предел
последовательности М, В* = В.
109
Аналогично, наименьший предел А последовательности М
отыскивается следующим образом: пусть е есть какой-нибудь элемент
последовательности М и р(е) определяемый им остаток. Пусть Ае есть
левая граница множества чисел р (е) и Л* есть правая граница
множества чисел Ле, где е есть любой элемент последовательности Ж.
Определенное таким образом Л* и есть наименьший предел
последовательности М, Л* = А'.
Таким образом, мы приходим к заключению:
Для того, чтобы отыскать наибольший и наименьший пределы
числовой последовательности М, возьмем какой-нибудь ее элемент е
и обозначим через Ве и Ае правую и левую границы остатка р(#),
Ае < Ве. Если е' -§ е"9 то Аег < Ле» < Ве" < #©'• в этих условиях
правая граница А чисел Ае и левая граница В чисел Ве и
являются наименьшим и наибольшим пределами последовательности
М. Сказанное справедливо и в тех случаях, когда Ае и Ве не
суть числа, но символы -f-co или —со.
Читатель видит, что мы имеем всегда Ае^А^В^Ве, каков
бы ни был элемент е последовательности М.
§ 32. Сходящиеся числовые последовательности. Введем
следующее чрезвычайно важное определение:
Числовая последовательность М называется сходящейся, если
она имеет единственный предел и этот предел конечен.
Из предыдущего ясно, что для того, чтобы JA была сходя*
щейся* последовательностью, необходимо и
достаточно, чтобы ее наименьший и наибольший пределы
А и В были оба конечными и равными друг другу,
т. е. чтобы Л = £ = а.
Всякая сходящаяся последовательность ограничена. Это еле*
дует из того, что оба крайние ее предела А и В конечны, будучи
равны действительному числу а.
Для того, чтобы данная числовая
последовательность М была сходящейся, необходимо и достаточно,
чтобы существовало такое действительное ч и*с л о а,
что, каков бы ни был интервал 8, содержащие а, в
последовательности имеется такой элемент е, для
которого остаток р(е) содержится целиком в 8. В этом
случае, число а есть предел (единственный)
последовательности М.
В самом деле, если последовательность М сходится, то она огра*
ничена и ее крайние пределы А и В равны между собой. Пусть
А из В = а. Тогда, заключая точку а в любой интервал 8, мы видим,
что должен существовать элемент е0, такой, что остаток р(е0)
содержится в 8, как и остатки для всех элементов е, следующих за eQ.
Таким образом, формулированное условие необходимо.
Но указанное условие вместе с тем и достаточно. В самом деле,
во-первых, последовательность М является ограниченной, так
как ее остаток р (е0) содержится целиком в интервале 8,
охватывающем точку а. Следовательно, М имеет конечные крайние
пределы А и В9 содержащиеся в 8. И, во-вШрыхм крайние эти пределы
ПО
Л и В должны быть равны друг другу и совпадать с тонкой а,
потому что интервал 8, содержащий точку а, может быть взят сколь
угодно малым.
От сходящихся последовательностей надо отличать
последовательности М, имеющие только один предел: такие
последовательности сходятся, когда этот предел конечен (т. е, есть
действительное число). Но если этот предел есть -{- со или — со,
последовательность М уже не будет сходящейся. Однако, иногда такие
последовательности продолжают .называть „сходящимися" в
расширенном (несобственном) смысле.
Переводя на язык переменных величин, мы получаем:
Для того, чтобы переменная величина х стремилась к пределу а
{а конечно), необходимо и достаточно, чтобы, начиная с некоторого
момента времени Г, все численные значения переменного х лежали
на интервале (а— е, a-f-e), где в > 0 как угодно малое число, т. е.
чтобы выполнялось неравенство
| х — а | < е.
Таким образом мы приходим к классическому определению
предела переменкой величины.
Предел переменной величины х обозначается символом lim х.
Если же переменная величина х не имеет ^единственного предела, то
ее наибольший Предел обозначают в виде lim x и наименьший предел
в' виде lim л;. Таким образом, если переменное х получило свое
происхождение от рассмотрения числовой последовательности М,
имеющей своими наибольшим пределом В и наименьшим пределом Л, то
мы пишем:
lim * = Л и ИпГх = В.
Если числовая последовательность М сходится и ее предел (конеч*
ный) есть а, мы пишем:
lim я = д.
В заключение настоящего параграфа докажем весьма важную
теорему о пределе монотонной последовательности.
Прежде всего введем следующее определение: числовая
последовательность {е} называется неубывающей, если для любых двух
ее элементов е' и в" предшествующий элемент не превосходит
последующий^ иначе говоря, если имеет место соотношение е' -3 е",
то е' < е".
Последовательность называется невозрастающей, если для любых
двух ее элементов е' и ег\ связанных соотношением е' -$ ег\
выполняется соотношение е ^ е".
Невозрастающие и неубывающие последовательности называются
монотонными последовательностями.
Докажем следующую основную теорему: Всякая монотонная
ограниченная последовательность является сходящейся.
Докажем теорему для случая неубывающей последовательности.
Так как неубывающая последовательность ограничена, то существует
Ш
4>
&ж
конечная верхняя грань а для ее элементов. Любой сегмент [д —-е, й]
содержит элементы данной последовательности, где е>0 наперед
заданное как угодно малое число. Пусть е какой-нибудь элемент
последовательности, расположенный на этом сегменте, а — s<^>^a.
Так как последовательность является неубывающей, то любой ее
элемент е'; следующий за <?, расположен на том же сегменте:
а — s<;eO'<X
ОтсЪда и следует, что а является единственным пределом после*
довательности.
§ 33. Конфинальные под-последовательности. Пусть М есть
последовательность, составленная из каких-нибудь элементов е% М = {е\, могущих
и не быть числами. Пусть М есть часть последовательности М. Ясно, что
М есть упорядоченное множество, если мы согласимся сохранить для эле*
ментов, принадлежащих к М\ тот же самый относительный порядок, какой
имелся у элементов последовательности М. Если среди элементов этой
части Ш нет самого последнего, тогда' М есть последовательность и
тогда мы называем М под-последовательностью последовательности М*
Может случиться, что под-последовательность М вся целиком входит в
сегмент с (е), отсекаемый некоторым элементом е последовательности М. В этом
случае Ш состоит только из определенных элементов е'
последовательности М, предшествующих этому элементу е, и, значит, вся целиком
предшествует элементу е. Такие „короткие" под-последовательнрсти не
представляют ни малейшего интереса. В самом деле, если М есть числовая
последовательность, то мы можем отрезать от нее любой сегмент а (е) и,
значит, начать последовательность М с любого элемента е, без того, чтобы
при эт^м изменился какой-нибудь предел последовательности Щ, потому
что такая усеченная последовательность^ очевидно, имеет те же самые
пределы, как и неусеченная последовательность М. В этом мы немедленно
убедимся, заметив, что предел зависит лишь от остатков р (е)
последовательности М и отнюдь не зависит от ее сегментов о (е). Итак, интерес
представляют лишь те под-последовательности М\ которые не помещаются
ни в каком сегменте с (е) данной последовательности М.
Назовем под-последовательность М'% не
помещающуюся ни в каком сегменте последовательности М', кон*
финальной последовательности М.
Под-последовательность М', конфинальная последовательности М.
обладает, очевидно, тем свойством, что за всяким элементом е
последовательности М имеются элементы е\ принадлежащие к Мг. Ясно, что, если М есть
числовая последовательность, то под-последовательность М', конфинальная
последовательности М, может иметь своим пределом только такое число а
(или символы + со,— со), которое является пределом данной
последовательности М. В самом деле, если а есть предел под-последовательности М'9 то
всякий интервал 6, содержащийся, содержит точки всякого остатка
под-последовательности М'ь Но очевидно, что всякий остаток р (е) первоначальной
последовательности М содержит в себе целиком некоторый остаток
под-последовательности М'. Поэтому, интервал 5 содержит точки всякого остатка
последовательности М и, значит, а есть предел для М*
Итак: Всякий предел под-последовательности М', конфинальной к М,
есть предел последовательности М.
Обратное утверждение неверно, потому что под-последовательность М\
конфинальная к М, вполне может не иметь своим пределом тот или иной
предел последовательности М. Таким образом:
Множество всех пределов под-последовательности Мг, конфинальной
к М, есть^ вообще говоря, лишь часть множества всех пределов
последовательности М.
Возникает поэтому важный вопрос: если а есть какой-нибудь
предел числовой последовательности М, можно ли оп
редели тьв,Мта,кую под-последовательность Ш% ков финал ь-
112
vMwrr, * -ijuiwsa
я у ю к М, которая была бы сходящейся и имела а своим
пределом?
Ответ на этот вопрос отрицательный: вообще говоря, такого выбора
под-последовательности М', конфинальной к М, сделать нельзя, причем это
отнюдь не зависит от мощности последовательности М: среди
последовательностей Af; для которых этот выфор возможен или для
которых этот выбор невозможен, имеются такие, мощность которых как угодно
велика.
Возможность или невозможность выбора указанной под-последователь-
#ости М! обусловлена вовсе не мощностью последовательности М, а ее
строением (структурой). Мы сейчас укажем тот класс
последовательностей М, где этот выбор заведомо возможен. С этим классом
последовательностей М только и имеет дело математический анализ.
Введем сначала следующий термин: назовем простой последователь-
костью всякую последовательность вида
элементы которой еп расположены в том же порядке, как и
возрастающие их значки л, т. е. натуральные числа 1, 2, 3, ..., я, ...
Докажем теперь основную теорему:
Если данная числовая последовательность М содержит простую
под-последовательность М\ конфинальную к М, тогда всякий предел
а последовательности М есть предел сходящейся простой
под-последовательности А конфинальной к М.
Пусть М есть простая под-последовательность
(М') *'Н е'% -? в/-5 •.. -8 в п-5 • • м
конфинальная к Af. Далее, пусть а есть предел последовательности Af.
Предположим сначала, что а есть действительное (т. е. конечное) число.
Заключим а в интервалы о!>о2>.. .>оп>. «*„ вложенные один в
другой, причем предполагаем их длины стремящимися к нулю, так что Ьп
стягивается к точке а, когда п безгранично возрастает.
Применим теперь следующий процесс:
1. Берем &i и отыскиваем в остатке р (ех) какой-нибудь элемент aXt
содержащийся в Ьх. Имеем е t-$ ax. Сделав это, ищем в М' первый элемент
е'п t следующий за а\. Имеем ePi -%ai~$en%, где для однообразия
обозначений мы полагаем ni = 1.
2. Берем Ь2 и отыскиваем в остатке р(е'п+\) какой-нибудь
элемент а2, содержащийся в о2. Имеем eh -^ а2. Сделав это, ищем в М' первый
элемент еПъ, следующий за я2- Имеем eHl -^^i-§^'„8 -$a%-$e'n "
3. Берем Ьг и отыскиваем в остатке р (enz+i) какой-нибудь элемент аъ$
содержащийся в Ъг. Имеем еп^а3. Сделав это, ищем в М! первый элемент
е 'пС следующий за я3. Имеем е'Пх -§ ах -§ еПл -§ а2 -$ еп% -$ аь -§ е^. •
И так далее.
Читатель видит, что описанный процесс может быть продолжаем
неограниченно.
Следовательно, мы получаем в результате бесконечную строку
которая показывает, что простая последовательность А
(A) *iH*2-$*eH ••.-$*«-$...
8 оак. 1Э41. J1Q
конфинальна к последовательности М. В самом деле, если е есть какой-
нибудь элемент последовательности Му то, в силу конфинальности М к М,
существует такой элемент ет в М'9 что е-$еш. Но числа
ni < щ < л3 < .. • < nk < •..
неограниченно возрастают, значит, имеется пк такое, что ял,>т.
Следовательно, имеем е-$ет-$еп%-$аъ откуда £-$ д^ А это и показывает, что
простая под'Последовательность А конфинальна к данной
последовательности М. Наконец, число ак содержится в интервале о*. И так как Ьк
стягивается к точке а% когда k неограниченно возрастает, то отсюда и
следует, что число а есть единственный предел под-последовательности А н
что. поэтому, под-последовательность А сходится и имеет число а своим
пределом.
Мы видим, что теорема доказана для того случая, когда предел а
последовательности М есть действительное (конечное) число. Если же а есть
один из символов 4- со или— со, то надо только вместо интервала Ьп взять
бесконечный интервал (п, -J-oc), когда я = +со, и вместо интервала Ьп
бесконечный интервал (— оо, — п), когда а =—оо. Полагая в первом
случае bJ=(nt + °°) и в0 втором случае Ьп = (— оо, — /г), мы попреж-
нему проводим только что данное доказательство, повторяя его слово
в слово,
В математическом анализе ценность имеют лишь такие
последовательности М, которые допускают простые под-последовательности, конфиналь-
ные к М. Есе другие последовательности М, т. е. не содержащие простых
под-последовательностей, им конфинальных, для математического анализа
не представляют интереса. Поэтому, ценным для математического анализа
является предложение:
Те ар ем а. Всякая сче тная последовательность М имеет
простую под-последовательность Мг, конфинальную кЁВ самом деле,
если М есть счетная последовательность, то, занумеровывая все элементы е
последовательности М натуральными числами, мы имеем строку
(М) * еь ebe9t...9ent... . (!)
Читатель должен иметь в виду, что хотя эта строка (1) и содержит все
элементы последовательности Af, но, вообще говоря, отнюдь не в том по>
рядке, в к 'ком эти элементы расположены в самой последовательности М:
здесь вполне может случиться, что при р < q мы будем иметь ep-^eq, a
при другой паре чисел pr < q' мы уже будем иметь ер* $-eq'. Однако
легко выделить, пользуясь написанной строкой И), в последовательностям
конфинальную ей простую под-последовательность М':
(Af) «IS*£^*3-J----5«i-S-" «
Для этого поступим так: обозначив ех = еь мы идем вдоль строки (1) до
тех пор, пока не встретим первого элемента еп„ п% > яг =» 1, следующего
в последовательности М за элементом ех\ такой элемент е непременно
будет найден, так как е± не может быть самым последним элементом в
последовательности М. Найдя ev и обозначив его через е % / = еп* мы идем
дальше вдоль строки (1) до тех пор, пока не встретим первого элемента ещ
п3>я2, следующего за ещ в последовательности М; обозначим £3 = £ю»
и, идя вдоль строки (1) дальше, отыскиваем первый элемент еп„ пА>щщ
следующий за еПз в последовательности М; написав еА = env идем по строке
(1) дальше, и т. д. безгранично далеко. Ясно, что таким образом мы
образуем простую под-подс,ледовательность М!
(М') ^н4^4-5--Н^ • ••>
содержащуюся в последовательности М- Легко видеть, что М
конфинальна к М. Действительно, пусть € есть какой-нибудь элемент последо-
114
/V-wt
ватеяьности Af. В строке (1) он занимает определенное место, т. е.
написан там в .виде вт, е = ет> Теперь, так как натуральные числа 1 =* щ<^
<С Щ < • • • я&< • •. неограниченно возрастают, то существует такое
натуральное число kt что имеем соотношение nft<m <.л*-и. Если имеем иЛ= т,
то * =£ь в да = 0„Л = *Л. В этом случае, за элементом е следует элемент ek+\
под-последовательности М'. Если имеем пк < т < n^+i» то, так как епк*\
есть первый элемент в строчке (1), имеющий значок яЛ+ь больший значка
лй и следующий за элементом еПк, мы, очевидно, имеем: е?»—j£Wft. Но
^Пй=г^' и ет~ е. Значит, е-^е'
Во всех, поэтому, случаях за произвольным элементом е
последовательности М следует некоторый элемент ег простой
под-последовательности Л. Значит, А конфи-
нальна к М. J£ g; й . . . , вв. . ._1П
В силу указанного свой- а
ства, счетные
последовательности имеют весьма Черт. 71.
большое употребление в
анализе, даже если они не
простые. Что же касается до несчетных последовательностей, то
некоторые из них, обладающие указанным свойством содержать простую кон-
финальную под-последовательность, весьма употребительны в анализе,
таковы, например, обе последовательности мощности континуума, которые
мы уже привели выше:
1. Последовательность М точек х, лежащих левее данной точки.
В самом деле, пусть А какая-нибудь простая последовательность точек
(А) ах < а2 < аъ <... < ап...,
имеющая предельной точкой точку а (черт. 71). Так как сегмент [ап, a]
убывает по длине и стягивается к точке а, когда п безгранично
возрастает, то какова бы ни была точка дг, принадлежащая к М, мы имеем для
достаточно большого натурального числа п неравенство х < ап. А это
показывает, что А е^ть простая под-последовательность,
принадлежащая к М и конфинальная к М.
ft b3 Ь2 Ь,
а
Черт. 72.
2. Последовательность М точек х, лежащих правее данной точки а
(черт. 72).
Если через В обозначим простую последовательность точек, лежащих
направо от а и имеющих точку а предельной точкой
(В) *1>**>*8....>**>•...
то так же точно легко убедиться в том, что В есть простая
под-последовательность, конфинальная к М.
§ 34. Критерий сходимости числовой последовательности. То
условие для сходимости последовательности М, которое мы дали
в § 32, хотя и является полным, т. е. необходимым и
достаточным, однако оно еще неудобно для пользования на практике.
Поэтому его заменяют другим. Эту другую форму условия сходимости
часто называют критерием Коти.
Критерий Кош и. Для того, чтобы числовая
последовательность М была сходящейся, необходимо и достаточно, чтобы,
каково бы ни было заранее выбранное малое положительное число г,
8* 115
в последовательности М содержался такой элемент е, что для
всяких двух за ним следующих элементов е' и е" этой после*
довательности имеет место неравенство \е" — е'\ < е.
Условие необходимо. В самом деле, если последовательность М
сходится, то заключая ее предел а в интервал 8 длины е, мы в
последовательности М найдем элемент е, такой, что остаток р(е) весь
целиком содержится в 8. Поэтому, всякие двз элемента е* и е"
последовательности М, принадлежащие к остатку р (г), будут содержаться
в 8. Поэтому, разность е" — ег этих элементов по абсолютной величине
всегда меньше, чем е, т. е. \е" — £'|<е.
Условие достаточно. Если для s в последовательности М
содержится такой элемент е0, что имеем \е" — е'\ < в для всяких двух
элементов е' и е", следующих за е0, то имеем, в частности,
неравенство \е' — е\<& для всякого элемента £, следующего за е'. Поэтому,
заключив элемент е' в интервал 8', имеющий длиной 2е и серединой
элемент ef% мы видим, что остаток р (е') весь целиком содержится
в 8'. Поэтому, последовательность М ограничена и ее оба крайних
предела А я В конечны и содержатся в 8'. И так как длина
интервала 8' равна 2е, то имеем 0 <; В — А < 2г. Но пределы А и В
суть постоянные числа, а е может быть взято как угодно малым.
Отсюда следует, что Л = £, т. е. последовательность М есть
сходящаяся. /
Как частный случай имеем так называемый малый критерий Коши:
Для\сходимости числовой последовательности
(М) л*1э х.2у -хг3, . .., хпУ
необходимо и достаточно, чтобы для всякого е, г > 0, имелось
такое натуральное число п, что для всяких двух натуральных
чисел р и q, превосходящих или равных я, удовлетворялось бы
неравенство
\Хр Xq\ <C[ 8.
Читатель видит таким образом, что „малый" критерий Коши
рассматривает лишь счетные числовые последовательности и, притом,
только простейшие из них, имеющие порядок, устанавливаемый
возрастанием натуральных чисел (т. е. значков элементов хп
последовательности М), тогда как „большойа критерий Коши рассматривает
какие угодно числовые последовательности, в том числе и несчетные.
На язык переменных величин критерий Коши можно перевести
следующим образом:
Для того, чтобы переменное х стремилось к конечному
пределу, необходимо и достаточно, чтобы, каково бы ни было малое
положительное число ё, имелся такой момент времени Г,
начиная с которого всякие два численных значения х' и х"
переменной величины в два любые момента времени ? и f% следующие за
Т, f > Т и f > Ту отличались бы одно от другого меньше, чем
на е, т. е.
116
§ 35. Приложения критерия Коши. В качестве первого
приложения к теории рядов пусть имеем какой-нибудь числовой ряд
«1 + *9 + «з+ • ■' + »/* + •••; (2)
отыщем необходимое и достаточное условие его сходимости. Для
этого обозначим через sn сумму его п первых членов
Sn = .''i + tf2-f •••+«п
и рассмотрим бесконечную последовательность
sl* s2* 53> • • ч $ю • • * • («)
Как известно, ряд (2) называется сходящимся, если числовая
последовательность (3) будет сходящейся. В этом случае, предел s
последовательности (3) называют суммой ряда (2) и пишут равенство
S — U\ + и2 + "я ~ • • • 4~ Пп
Применим к последовательности (3) „малый" критерий Коши.
Необходимым и достаточным условием сходимости последовательности (3)
будет соблюдение неравенства \sq — sp\ < е, где г есть произвольно
выбранное малое положительное число и где натуральные числа р и qy
р < q, превосходят (или равны) некоторое натуральное число я,
величина которого определяется выбранным числом е, в остальном
же р и q произвольны. Так как sq — sp = ир + х -f- wp + 2 + • • • + "<р
то, заменив для удобства число р числом р— I, мы получаем пред*
ложение:
Для того, чтобы числовой ряд иг -f- %-Ь из ~f" • • • ~Ь ttn+ • • •
сходился, необходимо и достаточно, чтобы для всякого
выбранного г, s > 0, имелось такое натуральное число п, что для любых
двух натуральных чисел р и q, бЬльших или равных п}
удовлетворялось неравенство
К + «л + 1+•••+««!<«• .
Словесно это формулируют иначе:
Необходимым и достаточным
условиемсходимости ряда ttj-f-tfa-j" • •'ап~Ь • • • является, чтобы за
некоторой гранью п любойотрезокир-г-^ + 1-|-~'*-+м£ряДа
был бы по абсолютной величине меньше, чем е, где
е>0 как угодно малое наперед заданное число.
В качестве второго приложения критерия Коши обратимся к
функциям. Общее понятие функции будет рассмотрено в следующей
главе. Здесь же мы удовольствуемся теми познаниями, которые
читатель получил в курсе диференциального и интегрального исчислений.
Пусть/(х) какая-нибудь функция, определенная на сегменте [#<><;#]*
Это значит, что каждому числу х0 этого сегмента соответствует
определенное число у0, являющееся значением функции / в точке х0ш
т. е. y0=f{x0) (черт. 73).
Возьмем какую-нибудь определенную точку с, лежащую внутри
сегмента [а^х^б], и спросим себя;
117
ф\1)
v/1
При каких условиях функция f(x) „стремится" к
определенному конечному пределу, когда „независимое" переменное х
„стремится" к точке с, оставаясь по одну сторону от нее, т. е.
„приближаясь" к с либо слева, либо справа?
Наша задача состоит в освобождении в этом случае от понятий
переменного, движения и времени.
Рассмотрим сначала явление по левую сторону от точки с. Для
этого заметим сначала, что совокупность Е точек х, лежащих на
сегменте [а, Ь] влево от
М г 1 точки с, есть
последовательность (см. § 26).
И так как всякой
точке х последовательности
Е соответствует опреде-
л енное число е=/ (х),
0 и ~ " V то мы имеем числовую
Черт. 73. последовательность М,
М={е], если условимся
писать /(*')"3/(*")э когда х'<х". Посмотрим, какой
геометрический смысл здесь имеют все введенные нами понятия и
определения в теории последовательности. Пусть xQ какая-нибудь точка
последовательности Е, т. е. а<;лг0<с. Тогда eQ—f(xQ) есть элемент
последовательности М. Спрашивается, каково геометрическое
истолкование остатка р (е0) ?
Для^этого мы будем проектировать точки Р, имеющие абсциссой х
и ординатой /(#), на неподвижную прямую л: = £, проведенную
в точке с перпендикулярно к оси ОХ (черт. 74). Пусть Q есть
1
Q
/м
> (
1
! х с Ь
м
\Ра
«ев/Гад
Р(е0)
Черт. 74.
проекция точки Р на прямую х =? с. Отрезок cQ, очевидно, равен / (х).
Поэтому, остаток р (е0) последовательности М есть не что иное, как
проекция на неподвижную прямую *==<: той части кривой у —f (x),
которая определена на полусегменте [х0> с), потому что р (е0) есть
совокупность всех значений функции f(x), принимаемых ею для х,
удовлетворяющего неравенствам х0^х<.с. Посмотрим, что
означает геометрически ограниченность или неограниченность -числовой
последовательности М. Если числовая последовательность М
ограничена сверху, это значит, что имеется такой элемент е0 в Ж, что р (*0)
есть множество чнеел, имеющее конечную правую границу Ве.
Ш
Геометрически это означает, что на полусегменте [#0, с) все
течение кривой y*£zf{x) совершается под прямой у&жВ^ (черт. 75),
т. е. происходит в заштрихованном бесконечном четыреусоЛьнике,
верхняя сторона которого имеет уравнением у = Ве^.
Аналогично, если М есть последовательность, ограниченная снизу,
то имеется элемент е0, такой, что остаток р (е0) есть множество
чисел, имеющее конечную левую границу Л$0. Это означает, что тече-
Черт. 75.
ние кривой ysszf(x) на полусегменте [х0у с) происходит в
заштрихованном бесконечном четыреугольнике, нижняя сторона которого
имеет своим уравнением у = Аеу Если М есть ограниченная
числовая последовательность, это значит (см. § 27), что имеется такой
элемент ё0 в Ж, что р (eQ) есть множество чисел с конечными
границами: правой Ве0 и левой Ае^ Геометрически это означает, что
течение кривой у —f (X) на полусегменте [л:0, с) происходит в
конечном заштрихованном четыреугольнике, с нижней стороной у =» Лео,
с верхней стороной у = Вео и с боковыми сторонами х — х0 и х = с
(черт. 76). Легко видеть, что указанный конечный четыреугольнйк
невозможно уменьшить без того, чтобы течение кривой у=/(х) на
Полусегменте [*0, с) уже не вышло за границы этого четыреуголь-
ни:са. В самом деле, Вео есть прав!я граница множества чисел р (е0).
Следовательно, если мы даже слегка опустим прямую у = Вео, взяв
вместо нее прямую у^=Вей — г, где в > 0 малое как угодно^ то на
119
\
сегменте \Ве^—у, Be\ наверное имеются точки множества р (*0).
Это значит, что на полусегменте [х0, с) наверное имеется такое
число х', что / (х') >- В% —у * Следовательно, если мн опустим
прямую у = Ве0 до положения у==Ве0 — е, то уже в точке х = х'
кривая у=:/(х) выйдет за верхнюю граничную сторону четыреуголь-
ника. Точно так же, невозможно поднять нижнюю сторону у = Ле0
без того, чтобы течение кривой у=/(х) на полусегменте [л:0, с) не
вышло за контур четыреугольника.
Итак, четыреугольник, имеющий горизонтальными сторонами
у = Ве0 и у = Ае0, есть наименьший, охватывающий течение кривой
y=zf(x) на полусегменте [лс0, с).
Если теперь точку х0 заменить другой точкой хи находящейся
ближе к точке с, x0<*i<£, то ясно, что Яв1<Ввв и Ае%> Ае#
потому что остаток р (ег) содержится в остатке р (*0) (здесь мы через
ег обозначаем элемент /(jcj)
последовательности М). Таким образом, указанный
наименьший четыреугольник, содержащий
все точки кривой y=f (x) на
полусегменте [х, с), составит часть прежнего
четыреугольника, построенного для
полусегмента [л:0, с). Из неравенства
Ле0^Аег-СВ€1^Вв0 мы видим, что ле-
_ вая граница В чисел Вех и правая
граница А чисел Лег удовлетворяют
соотношению
Ле0<Л<В<£*0.
В силу § 31, числа А и В суть наименьший и наибольший
пределы числовой последовательности М.
Следовательно, мы можем написать
Ит/(х) = Л и Пт/(*)■= Я,
когда х возрастает и стремится к числу с как к пределу, „пробегая*
все действительные числа, меньшие числа с.
Из тех геометрических соображений, которые мы здесь дали,
ясно, что, если мы имеем какой-нибудь прямоугольник R>
вертикальная сторона которого лежит на прямой х = с и содержит
внутри сегмент [Л, 5], и который лежит по левую сторону от
прямой х = с, то имеется такая точка xQ% хь < с, что на полу-
сегменте [xQy с) все точки кривой у— f (x) содержатся внутри
прямоугольника R (черт. 77). В самом деле, из § 30 ясно, что
в числовой последовательности М имеется такой элемент eQ—f(x0\
что остаток р (е0) последовательности М целиком содержится на
сегменте [Л-—е, В-\~е], где з>0^и сколь угодно мало.
Мы должны здесь еще дать геометрический смысл любому
пределу а числовой последовательности М. Мы знаем, что если а есть
предел последовательности М% то заключая а в любой интервал Ь\
120
*0
Черт. 77.
cr*e'
•a
a-e'
сколь угодно малый, в каждом остатке р (с) последовательности М
имеется элемент е\ содержащийся в 8'. Поясним это геометрически.
Отметим на прямой х~с (черт. 78) две точки a— s' и a + s'
и проведем прямые у = а — г' и jfsra-f-e'. Обозначим через гг
прямоугольник, ограниченный прямой х^=а, .прямой л; = с и
горизонтальными прямыми у = а — г и у = а-^ъ'. Так как всякий
остаток р (в) последовательности Л1 имеет
точки на 8', то отсюда следует, что
имеется точка х', такая, что f(x')
будет удовлетворять неравенствам
а —е'</(*')< <%+ е'.
Важно заметить, что такая точка х'
может быть найдена сколь угодно
близко от точки с, потому что всякий оста- —
ток р (е), e=f(x)9 имеет точки на 8',
т. е. для любого х} л;<с, имеется х;,
х<х' < с, такое, что
a — s'</(*')<«+e'-
Возьмем теперь, вместо одного интервала 8' бесконечно много
таких интервалов
8'>8">8'"> ... >8<*)>...,
где 8М = [а — е(*0, а-}-еЩ и где числа e'>s" > .. . > s(fe)... ♦
стремятся к нулю.
Мы уже нашли такое л:', что a — г' </(V) <a-|-e/. Подобно
этому, мы найдем числа х' < х" < xw <.. . < *(*) < ..., такие, что
будут удовлетворены неравенства
Черт. 78.
а — е" </(*")< a-J-•"
а _s(fc) </ (*(*)) < а + e(*>,
(4)
причем, ввиду того, что каждая точка х^) может быть взята сколь
угодно близкой к точке с, мы имеем право предположить, что
х < х" < хт <. .. < *<*><... (5)
и что эта простая последовательность имеет точку с своей
предельной точкой. Если мы теперь рассмотрим простую последовательность
чисел
то из неравенств (4) мы тотчас же усматриваем, что последовательность
сходится и имеет а своим пределом. Таким образом, каков бы
ни был предел а числовой последовательности М, происходящей
от рассмотрения значений функции f(x) влево от точки с,
существует такая простая возрастающая последовательность
121
x' < x" < x"r < ... < лг<*> < ... значений аргумента х, имеющая
пределом число с, что соответствующие значения функций
f{£r)> f(x")> • • •> /(*(л))> • • • образуют сходящуюсй
последовательность^ имеющую, своим пределом а.
Это предложение имеет силу и тогда, когда а = -j- со или а а» — с».
Доказательство остается прежним, но надо вместо интервала 8<ft)
рассматривать интервал. (%,-{-оо) или (— оо, k)t В частности, для
наименьшего и наибольшего пределов Л и В последовательности М
имеются соответствующие простые последовательности ^ < Sa < • • •
.. . < 6* <... и *4i <%<•••< *1* <•••» такие, что пределами их
служит точка с, пределами же последовательностей/^), /(£2), • • • >/(%%),
•. • и /fa), /(7ia)f..., /Ы,... служат Л и В (черт. *9).
Если числовая последовательность М сходится, т. е. имеет своим
единственным пределом действительное число а, то мы знаем, что
тогда А = £ = а. В этом случае, каким бы малым ни был ин-
\
*~~0
s~-
..-••"'[
—1
<
'» ^
*/,
^
'"i
<
Ь <
ъ
>а
А
ш
t
> ""i
л
»
,/
Г
ш
•
Ao i
а
г 6
Черт. 79.
тервал 8, содержащий точку а, прямоугольник г, имеющий
правой вертикальной стороной интервал Ь, содержит все точки
кривой у= f(x) на полусегменте [хф с), где х0 выбрано достаточно
близким к с (черт. 79).
В этом случае мы говорим, что функция / (х) стремится
к конечному пределу, когда аргумент х стремится
к неподвижнойточке с, оставаясь, все время влево
от нее и пробегая все действительные числа,
меньшие числа с.
Соответствующая запись этого будет:
lim f(x) = a,
где предполагается, что х < с и что х проходит все действительные
числа, меньшие с. Иногда этот предел а функции / (х) обозначают
символом /(с — 0), так что lim f(x)=f(c — 0), где х возрастает
Х-+С
до с, проходя через все действительные числа.
Если функция f(x) стремится к определенному конечному
пределу а, когда х стремится, возрастая, к пределу с, проходя при
122
этом через все действительные числа, тогда говорят, что „функция
f (х) непрерывна слева от точки си. Если при этом численное
значение функций f (х) в самой точке с равно пределу а, т. е. если
/(с) = а, то говорят, что „функция f(x) непрерывна слева в точке
с". В этом случае мы можем написать /(г —0)=/fc).
Если функция f{x) слева от точки с имеет наименьшим и
наибольшим пределами конечные числа А и В, то разность В — А
называют колебанием функции f (x) слева от тонки с. Если это
колебание равно нулю, то функция непрерывна слева qt точки с.
Если функция f{x) непрерывна слева от точки с, тогда
критерий Коши дает необходимое и достаточное условие для этой
непрерывности. В самом деле, раз / (х) непрерывна слева от точки с, то,
обозначив через а предел функции
/(*), когда х, возрастая и
проходя через все действительные числа, ф
стремится к с, мы видим, что все
течение кривой у — / (х) охвачено
прямоугольником г (черт. 80), имею-
Ш
'ШЖ
'Шж
Q
1
.'"'"\ f
V
у'г
ч
if
I G
С
|
Черт. 80.
щим правой стороной интервал 8 сколь угодно малый, содержащий
точку а> причем х пробегает полусегмент [лг0> с). Ясно, что если
длина интервала 8 равна s, то имеет место неравенство:
где /и/ суть две любые точки полусегмента [л:0, с), т. е. х' > х0
и х" > дг0.
Если же f(x) не непрерывна слева от точки с, то возможны два
случая:
1. Наименьший и наибольший пределы А и В неравны. В этом
случае мы определяем две простые последовательности
?1<£2< ••<£«<• •• и *»л < Ча < — < Ч» < — 9
имеющие пределом число с, такие, что Нт/(;П) = Л и Mm f (ч\п) *= В.
Мы видим, что не можем уже иметь |/(£те)—/Х*Чп) I < 8> потому что
тогда выполнялось бы неравенство В—-Л<е, что невозможно, так
как ВФА и е произвольно мало. Значит, критерий Коши не может
удовлетворяться.
123
2. Наименьший и наибольший пределы А и В равны, но
бесконечны (черт. 80)» В этом случае критерий Коши опять
удовлетворяться не может, потому что, как бы близко точка х' ни лежала
к с9 всегда можно найти, точку л;", еще более близко лежащую
к точке г, в которой значение функции /(*") будет, по абсолютной
величине, как угодно велико, так что опять не может выполняться
неравенство
I/(*')-/(*")!<«•
Все, что мы сказали о поведении функции / (х) влево от точки с,
переносится и на поведение функции справа от точки с: и здесь
мы имеем непрерывность справа от точки су если f(x) стремится
к единственному конечному пределу, когда аргумент х
стремится к точке су убывая и проходя через все действительные числа,
большие числа £. иногда этот предел обозначают символом f {с 4-0).
Если имеем /(c-f-0)=/(c), тогда говорим, что / (х) непрерывна
справа в точке с. **
Наконец, если имеэм/(£ — 0) ===/(£:)==/(с+ 0,), тогда говорим,
что фуцщия Ых) непрерывна в точке с.
В этом случае мы пишем
причем не делаем никакой оговорки, по какую сторону от точки с
расположено значение х.
В качестве заключения укажем еще раз, что употребление
движения, изменения переменных'и времени.есть просто сокращенный
способ выражаться, так как, на деле, речь идет лишь о
последовательностях и их пределах. А эти понятия не имеют нужды в
понятиях времени и переменной величины. В дальнейшем мы, для
краткости изложения, все же будем иногда пользоваться понятием
переменной величины, так как, после данного обоснования теории
пределов, это уже не может повлечь недоразумений.
ГЛАВА IV
ФУНКЦИЯ И НЕПРЕРЫВНОСТЬ
§ 36. Понятие функции. По своему идейному содержанию
понятие функции вполне совпадает с понятием соответствия. Именно,
если мы имеем два любые множества М= [е] и N = {y|} какой угодно
мощности, составленные, притом, из каких угодно элементов е
и т], и если каждому элементу е множества М соответствует
некоторый впфлнё определенный элемент т] множества N, то мы
говорим, что имеем функцию, определенную на множестве М, и пишем
символическое равенство
где f| есть тот самый элемент множества N, который соответствует
элементу е множества М.
Символ е, который обозначает любой элемент множества Мл
называется аргументом функции; символ г\, обозначающий тот
элемент множества Ny который соответствует
рассматриваемому элементу е множества М, называется значением функции.
При этом, когда аргумент е функции действительно обозначает
произвольный элемент множества М> то мы говорим, что аргумент е
функции изменяется и пробегает все данное множество М.
В зависимости от этого изменения аргумента е изменяется и
„значение" т) функции, потому что разным элементам е\ е", е"-9 ...
множества М соответствуют, вообще говоря, различные элементы ?]', г{\
Tj'",..- множества N; здесь г{ =/(*'), if =/(*")> ^=/(А«--
Читатель должен иметь в виду, что вовсе нет необходимости, чтобы
множество значений функции совпадало обязательно с множеством
N: значения iq функции f(e)y Y] =/(£), могут пробегать лишь часть
множества N и притом так, что различным элементам е'9 е"}...
множества М может соответствовать один и тот же элемент ч\0
множества N; это говорит о том, что значения функции f(e) в
различных элементах е\ е",... множества М могут оказаться „равными
друг другу". Наконец, часто употребляют выражение „точка е
множества М" и „точка TJ множества А/", когда говорят об элементах
е и г\ множеств М и N.
Возвращаясь теперь к понятию функции, читатель видит, что
оно вполне совпадает с общим понятием соответствия, потому что
125
функция f(e\ определенная на множестве М, есть не что иное, как
просто соответствие / различным элементам множества М
некоторых элементов (различных или тождественных) множества N.
Мы говорим, что функция действительного переменного /(х)
определена на сегменте [а, Ь], если всякому действительному
числу х, принадлежащему этому сегменту, соответствует вполне
определенное действительное число у, которое мы обозначим
через /(х), причем мы пишем равенство
Отметим, что здесь вовсе нет необходимости, чтобы различным
численным значениям аргумента х соответствовали непременно
различные численные значения у функции / (х); эти численные
значения могут, вообще говоря, оказываться и равными между собой.
Самое существенное во фразе: „функция f(x) определена на
сегменте [я, Ь]и состоит в том, что численное
значение функции /(х), y=f(x), вполне определено, когда
вполне определено численное*значение аргумента х,
произвольно взятое на се гм ен те [а, Ь]\ эта полная
определенность действительного числа уу y=f(x), как только нам дано
действительное число х, и означает полную определенность функции
/(л;), на сегменте [а, Ь\. Вместо того, чтобы всякий раз отдельно
определять, что значит „задать функцию" f(x) на интервале
(а, Ь), полусегменте [а, д), полуинтервале (a, b)k мы введем йбщее
определение:
Функция /(х) действительного переменного х определена на
множестве Е действительных чисел, если всякому
действительному числу х, принадлежащему к Е, соответствует вполне
определенное действительное число уг называемое значением функции f
в точке х, причем мы пишем равенство y=f(x).
Совершенно аналогично мы определяем функцию / (х, у) или
/ (х, у у z) двух или трех действительных переменных, говоря:
функция f(x,y) или /(х, у, г) двух или трех
действительных переменных определена на множестве точек Е, лежащем на
плоскости XOY или в пространстве OXYZ, если всякой точке
Р (х, у) или Р(х,у,^), принадлежащей к Е, соответствует
вполне определенное действительное число и, называемое
значением функции f в точке Р> при этом мы пишем равенство
и = /(хуу) или u = f(x, у, z).
Читатель без труда сообрази г, как определить функцию /(х, у, г, t)
четырех и большего числа независимых переменных.^
§ 37. Геометрическое изображение функции. Понятие функции
одного действительного переменного f (x) и двух действительных
переменных /(х, у) можно интерпретировать геометрически. "Чтобы
изобразить геометрически функцию f(x) одного действительного
переменного х, возьмем плоскость и ,в ней прямоугольную систему
координат XGY. Если функция у =/(х) определена на сегменте [а, Ь],
мы восставляем во всякой точке х этого сегмента перпендикуляр
126
к оси ОХ и наносим на этом перпендикуляре точку М, ордината у
которой равна величине - /(х) рассматриваемой функции / в этой
точке х (черт. 81).
Таким образом, на всякой параллели оси OY, пересекающей сегмент
' [а, Ь\, имеется по одной и только по одной точке М.
Совокупность всех построенных таким образом точек М (л:, у) образует
на плоскости XOY некоторое вполне определенное плоское
множество точек g, которое и является геометрическим образом
рассматриваемой функции Л
Посмотрим, какими свойствами обладает этот геометрический
образ S функции /.
м
Ъ *
У
е..м
2 ■•»...>
г'
/
[
b X
Черт. 81.
Во-первых, как уже было указано, нет никакой прямой,
параллельной оси OY, которая ^пересекала бы множество точек $ в двух
или в большем числе то чек > всякая прямая, параллельная оси QY,
или совсем не пересекает множества §, или пересечет самое большее
в одной только точке.
Во-вторых, прямые, параллельные оси OY и непересекающие
сегмента ,{а, Ь], не пересекают множество S; напротив, всякая
прямая, параллельная оси OF и пересекающая сегмент (пусть в точке x)f
непременно пересечет множество § в одной и только в одной точке
М(ху у), причем ордината у этой точки в точности равна
численному значению /(х) рассматриваемой функции / в этой точке лг,
т. е. у^/(х).
Мы заключаем отсюда, что геометрический образ $ функции /
является просто множеством точек плоскости М\х> f (х)\, где
абсцисса х есть любая точка сегмента [а, Ь].
Очень часто множество $, служащее геометрическим образом
данной функции f(x\ называют кривой, изображающей данную
функцию /(х), или графиком 5 той функции, и равенство
называют уравнением кривой, изображающей функцию f(x). По
поводу этой терминологии следует заметить, что, собственно, лишь
очень условно можно в общем случае называть множество точек $
^кривой", потому что в том случае, когда, например, функция /(;$
разрывна в каждой точке сегмента [а, Ь), геометрический образ S
127
функции f(x) лишь очень отдаленно напоминает „кривую линию*,
так как множество § является скорее „облаком точек", но, правда,
таким, которое прорезается каждой прямой, параллельной оси О К,
самое большее в одной только точке М (черт. 82).
Название: „кривая, изобр ажающая функцию f(x)"
заимствовано из того случая, когда функция f(x) непрерывна и имеет
непрерывную первую производную f (х); в этом случае
геометрический образ $ функции f(x) представляется, действительно, в виде
непрерывной кривой, имеющей непрерывно изменяющуюся
касательную при непрерывном перемещении точки М по кривой. Название
же: „уравнение кривой, изображающей функцию /(*)%
У
0
М
а х t
.
> X
Y
~
С
£.,,.
4;v::;/.;::v%.
р^:ШШ$$
^•Л"•*^^C^,'•■'^^•«:'*"•V•^
Ч-?$~"'
4
\&Ш-:
":*.'•.':;.■..•
*'ДЧ."''*'
1/
. л;,'с
Ш^
!
~1
N
~Х
\ Черт. 82.
даваемое равенству з> =/(*), происходит от того, что
геометрическое место точек М (х, у) плоскости, координаты которых
удовлетворяют уравнению y=f(x), есть геометрический образ $ функции f(x).
Перенесем теперь наше внимание на само плоское множество §,
являющееся геометрическим образом функции /. Введем следующее
общее определение: Плоское множество § точек называется
униформным {однозначным) по отношению к оси ОХ> если всякий
перпендикуляр к этой оси пересекает множество Ь самое
большее в одной только точке. !
Пусть Е есть ортогональная проекция на ось ОХ плоского
множества $, униформного по отношению к этой оси. Ясно, что всякий
перпендикуляр ъх, восставленный в точке х к оси ОХ, совсем не
пересечет множества И, когда х не принадлежит к £", и пересечет
в одной только точке М это множество $, если х принадлежит
к Е (черт. 83).
Введя эту терминологию, мы замечаем, что геометрический
образ какой-нибудь заданной функции действительного переменного
/(#), определенной на сегменте [а, Ь], есть униформное по
отношению к оси ОХ плоское множество точек §, имеющее своей
проекцией на ось ОХ сегмент [а, Ь].
Но не только всякая функция действительного
переменного f(x), определенная на сегменте [а, ft], имеет своим
геометрическим образом плоское униформное множество 8, проекцией
которого на ось ОХ служит сегмент [а, 6], но верно и обратное:
128
всякое униформное множество S, проектирующееся на ось ОХ
в виде сегмента [а, Ь\, определяет на этом сегменте функцию
действительного переменного f{x), геометрическим образом коте*
рой оно является; чтобы иметь эту функцию /(л:), достаточно
поставить в соответствие всякой абсциссе х, принадлежащей
к [а, Ь], численную величину f(x) ординаты у той единственной
точки множества S, которая проектируется в точку х, т. е.
достаточно положить /(x)=j/.
Все, что было сказано о функциях f(x), определенных на
сегменте [а, Ь], слово в слово приложимо к функциям действительного
переменного /(#), определенным на любом точечном множестве Е,
лежащем на оси ОХ, потому что в сказанном нет ничего специфич-
Е
щ
х х О а
Черт. 83.
Ь X
ного, которое относилось бы только к сегментам, а не к
каким-нибудь множествам.
Таким образом, всякая функция действительного
переменного /(х), определенная на каком-нибудь точечном множестве Еу
лежащем на оси ОХ, имеет своим геометрическим образом
плоское униформное множество точек $, проектирующееся в Е\ обратно^
всякое плоское униформное множество $, проектирующееся в Е,
служит геометрическим образом некоторой функции
действительного переменного f(x): эту функцию получают, ставя в
соответствие точке х множества Е ординату у точки М множества $,
проектирующейся в точку х множества Е.
После сказанного не представляет ни малейшего труда
интерпретировать геометрически функцию f(x, у) двух действительных
переменных х и у*
Введем для этого определение: назовем униформным по
отношению к координатной плоскости XOY всякое пространственное
множество точек $, которое пересекается каждой параллелью оси OZ
не более, чем в одной точке. Пусть Е есть проекция да плоскость
XOY униформного множества S. Обозначим через Р какую-нибудь
точку, лежащую в плоскости XOY, и через Ир перпендикуляр
в точке'Р, восставленный к плоскости XOY. Ясно, что Пр не
пересечет множества S, если Р не принадлежит к плоскому
множеству Е, и что Пр пересечет множество § в единственной точке М,
9 Эак. Ш4. 129
если Р принадлежит к Е (черт. 84). "Установив это, возьмем кз*
кую-нибудь функцию f(x, у) двух независимых действительных
переменных хну, определенную на плоском множестве точек Е. Это
означает, что всякой точке Р(х, у) множества Е соответствует вполне
определенное действительное число f(x, у), которое мы называем
значением функции / в точке Р(х, у). Если мы теперь восставич
перпендикуляр Пр в этой точке Р к координатной плоскости XOY
и на этом перпендикуляре отметим точку Ж, такую, что РМ=з/(х, у),
тогда получим некоторое униформное множество точек §.
Полученное униформное множество $ имеет следующие свойства:
1. Проекция множества $ на плоскость XOY есть множество Е.
2. Координата г точки М{х, у, z) множества $ равна значению
f(x, у) функции / в точке Р (х, у\ служащей проекцией точки М
на плоскость XOY.
Черт. 84.
Униформное множество и есть геометрический образ 'функции
f{x, у) двух действительных переменных х и у. Очень часто мно*
жество S, служащее геометрическим образом данной функции f(x9 у),
называют поверхностью, изображающей функцию f(xt y)t и
равенство 2==;/(A% у) называют уравнением поверхности, изображающей
функцию f(x, у).
Название „поверхность" заимствовано из того случая, когда
функция /(х, у) непрерывна и имеет непрерывные первые частные
df df
производные -L и ~- внутри некоторого замкнутого контура,
расположенного на координатной плоскости XOY. Геометрический образ
§ такой функции f(x> у) представляется на самом деле в виде
непрерывной поверхности, имеющей непрерывно изменяющуюся
касательную плоскость, когда точка прикосновения М непрерывно
перемещается по поверхности.
130
Заметим, наконец, чго справедливо и обратное положение: всякое
униформное множество S>, проектирующееся на плоскость XOYb виде
плоского множества Е, определяет на Е функцию /(#, ji), имеющую $
своим геометрическим образом; чтобы получить эту функцию/(х,у),
достаточно определить координату z точки М множества §,
проектирующейся в точку Р(х, у) множества £, и обоэначить численную
величину этой координаты г через f{x, у), т. е. положить f(x, у) = г.
§ 38. Аналитическое выражение. Следует тщательно различать
функцию и аналитическое выражение, В начале наиболее
естественным приемом строить различные функции с теми или иными
^свойствами кажется задание функций посредством формул, т. е.
посредством аналитических выражений. Под формулой или под
аналитическим выражением мы разумеем совокупность тех
аналитических действий, которые нужно проделать
в определенном порядке и последовательно над
численной величиной х аргумента, чтобы получить
соответствующую численную величину f(x) функции.
Относительно аналитических выражений необходимо сделать ряд
замечаний.
Во-первых, в то время как всякая функция f(x) имеет лищь
одно геометрическое изображение, аналитических выражений, ее
изображающих, имеется *) всегда бесчисленное множество.
Читатель в этом легко убедится хотя бы из того известного факта,
что для любой численной величины х мы имеем равенство
lim ^. = 0.
Отсюда, полагая
s1=*uu ^2 = ai + tfa> 53Mtfi + tfa + tf8i ••'•»
sn — ui + ll2 + "з • ■ • + uw • • •
и
— *1
s»~~n\ >
мы имеем
Значит, имеем равенство
СО уП-1
*) Сказанное справедливо, понятно, лишь тогда, когда рассматриваемая
функция f(x) допускает хоть одно аналитическое выражение, ее
изображающее, т. е. дающее численную величину /(*), когда известна численная
величина л\
S* " 131
и, следовательно, функция, тождественно равная нулю, изобразила
сходящимся рядом многочленов^ из которых ни один не
тождественен нулю.
Прибавляя это аналитическое выражение к любому другому
аналитическому выражению, мы, очевидно, получим новое аналитическое
выражение, изображающее ту же самую функцию f(x).
Во-вторых, аналитическое выражение, вообще говоря, перестает
существовать, т. е. перестает иметь численный смысл при некоторых
численных значениях аргумента х; это чаще всего случается
вследствие того, что при этих численных значениях аргумента х те или иные
части рассматриваемого аналитического выражения А(х) теряют смысл.
Если мы обозначим через Н множество тех точек х, где данная
формула А(х) утрачивает смысл, то называя через Е множество*,
дополнительное к Н, мы видим, что в каждой точке х множества Е
рассматриваемое аналитическое выражение А(х) имеет вполне
определенное численное значение, т. е. опреде!яет на Е функцию
действительного переменного /(х).
оо
Например, ряд 2 х11 сходится в интервале (—1,+ 1) и рас-
холится вне его; в данном случае, множество Е есть интервал
(—1, + 1).
В-третьих, нельзя говорить, что какое-нибудь „аналитическое
выражение А(х) определяет на разных областях
разные функции". Этот способ выражения, употребительный в
теории функций комплексного переменного, грубо неверен в теории
функций действительного переменного. Нужно иметь в виду, что
множество Е, на котором данное аналитическое выражение А (х)
имеет смысл, есть область, на которой аналитическое выражение А (х)
определяет всегда единственную функцию f(x), именно ту самую,
численные значения которой в точности равны численным значениям
аналитического выражения А (х), т. е. такую, что имеем всюду на
Е равенство
f(x) = A(x).
Функция f(x), определенная аналитическим выражением А(х)
на Е, есть единственная, и ни о каких других функциях речи быть
не может. Правда, может иногда случиться, что область Е
разбивается на части, на каждой из которых / (л;) может быть
определена своим собственным законом, но это обстоятельство отнюдь
не мешает рассматривать f(x) на Е как единую функцию.
Например, аналитическое выражение:
A(x) = hm j-—
имеет, очевидно, численное значение, равное -9- при д: = 0, равное 1,
если л;>0, и равное 0, когда х <С 0. Геометрическим образом
функции / (л;), определенной этим аналитическим выражением;, является
униформное множество £, состоящее из куска оси ОХ, точки и куска
132
прямой ^=1 (черт. &5), т. е. в этом случае /(л:) = 0 влево от
начала О и /(х)=1 вправо от начала 0; но нельзя говорить, что
рассматриваемое аналитическое выражение А (х) определяет раэные
функции для х < 0 и для х > 0. В этом смысле, геометрический
образ £, составленный, например, из куска прямой, куска
окружности, куска параболы и куска циклоиды, определяет единую
функцию /(х), но не четыре различные функции.
_______ I 1
0\ X
Черт. 85.
В-четвертых, очень часто функция действительного переменного
задается соглашением, что /(х) равна тому-то там-то и тому-то там-то.
И вначале большое изумление вызывает тот факт, когда, оказывается,
можно подобрать аналитическое выражение А (х), дающее целиком
эту функцию.
Рассмотрим пример.
Пусть f{x) определена так:/(х) = 1, если х рационально и
f (л:) = 0, если х иррационально. Эта функция известна под
названием функции Дирихле. Гео- у\
метрически такая /(х) изо- | _
бразима в виде оси ОХ, " ' ~""~ Т ~~ ™
из которой вынуты все pa- J
циональные точки и поме *■ |« -.
щены выше нее на расстоя- ™ *
нии 1 (черт. 86). Несмотря Черт. 86.
на кажущуюся сложность и
искусственность такой функции /(х), она имеет аналитическое
выражение А (х), изображающее ее.
Действительно, положим: <
А (х) = lim • lim [cos 2 тс п\ х]-ш.
П -> 4" оо т->»-}-оо
Если х рациональное число, то х = ~, где д^>1 есть целое
ч
число. Но тогда п\х при я > # делается целым; поэтому cos2TCn!x
равен, при я > q , плюс или минус единице. Значит, [cos 2 тся!х]2т = 1
при всяком т. Поэтому lim [cos2tc/z!x]'2w = 1 и, следовательно,
от->4*оо
Л(х) = 1.
Если же х есть число иррациональное, то при всяком
фиксированном п мы имеем jcos 2 тс п\х\ < 1. Значит, lim [cos 2 тс /z!x]2w = 0,
т -> + оо
и поэтому /_(х) = О*
ш
Мы видим, что фуМкция Дирихле получила аналитическое
изображение А(х), /(х)жА(х).
К сказанному добавим, что на первый взгляд кажется, что
аналитические выражения А(х) представляют бесконечное разнообразие,
потому что можно в качестве действий, кроме первых четырех дей*
ствий арифметики, вводить еще логарифмирование, взятие синуса и т< д.
и т. д. На самом деле действия классического математического
анализа сводятся только к трем следующим действиям:
I. Сложение.
II. Умножение.
III. Переход к пределу по натуральным числам.
Это важное обстоятельство на первый взгляд кажется
парадоксальным. Тем не менее.его легко установить. Здесь основным является
предложение, которое мы докажем дальше и которое формулируется
так:
Всякая функция f {х), имеющая самое большее счетное число
точек разрыва, разложима в сходящийся всюду ряд многочленов,
оо
т. е. Да:)г= ^Рп(х), где Рп{х) есть многочлен от аргумента х.
W = 1
Это предложение показывает, прежде всего, что вся такая функция
f(x) изобразима указанными тремя действиями I, 41 и ///,
потому что, обозначив через Qn (х) сумму Р}(х) -{- Яа (х) -f- ... -f~ Pn(x)>
мы видим, что f(x) = \lm Qn(x), и так как всякий многочлен от
аргумента х составляется только при помощи действий I и II,
проделанных над аргументом х, то утверждение доказано *). Отсюда
немедленно вытекает, что действие деления сводится к трем
действиям I, II и III, потому что функция /(х) = - имеет лишь одну
точку разрыва, х = 0, и, значит, изобразима сходящимся к ней рядом
многочленов:
Такие же разложения мы имеем и для log x} sin jt, ах и т. д.
Действие диференцирования также приводится к действиям I, II
и III, потому что
F(x)= Urn —к- Ц
я-» -f оо Л
v п
и так как в числителе стоит непрерывная функция от х, т. е.
разложимая в сходящийся ряд многочленов. Интегрирование опять при*
*) Действия, проделываемые не над аргументом, т. е. проделываемые
над константами, в счет не идут, потому что совокупность всех констант
мы считаем нам данной. По этой причине действие вычитания сводится
к действиям I и III, так как вычесть аргумент л это означает прибавить
его, предварительно помножив на — 1, т. е, —л; = ( — 1) X •*•
134
водит к непрерывным функциям, т, е. разложимым в сходящийся ряд
многочленов, и т. д. и т. д.
Таким образом можно утверждать, что каждая функция f(x%
встречающаяся в классическом анализе, допускает аналитическое
выражение A(x), ее изображающее, т. е. такое, что
f{x)=*A{x)
на всем множестве £, где определена функция f(x\ причем аналити*
ческое выражение Л(х) построено лишь из трех действий /, //, ///,
употребленных в конечном или в счетном числе раз и
последовательно проделываемых друг над другом, отправляясь от аргумен*
та х и от численных констант, причем последние также входят
лишь в счетном числе.
Такие функции f(x) называются аналитически изовразимыми.
Приведем пример функцчи, неизОбразимой аналитически в
указанном выше смысле. Если х есть какое-нибудь иррациональное число,
разложение которого в непрерывную дробь есть
1
ДГ = Я0+-: j
а А
+ «п +-•••
то полагая f(x) =а 1, если среди неполных частных а}, аъ аъ ... имеется бес*
конечное множество делящихся друг на друга без остатка, и полагая f(x) ^0
для всех иных случаев, мы, как можно доказать, имеем функцию /(*)» не*
изобразймую аналнтн**ески.
Впрочем, и такая f(x) также становится изобразимо и, если
к трем действиям I, II и III, указанным выше, присоединить действие \imF{i)
i -> -t- оо
взятия наибольшего предела по непрерывно возрастающему
действительному переменному /(а не только по натуральным числам).
§ 39. Функции неограниченные и ограниченные. Пусть
функция /(х) определена на сегменте [я, Ь]. Мы называем функцию f(x)
ограниченной сверху на сегменте [а, Ь], если существует такое
действительное число В} что для всех точек х сегмента [а, Ь\ имеет
место неравенство
f(x)<B.
Соответственно этому, функция f(x) называется ограниченной
сЯизу на сегменте [а, о], если существует такое действительное
число Л, что для всех точек сегмента [а, Ь\ имеет место неравенство
№>А.
Функция /(х) называется ограниченной на сегменте [а, Ь], если
она ограничена одновременно и сверху и снизу, т. е.- если на всем
сегменте [а} Ь\ соблюдаются неравенства
А</(х)<В.
135
Ясно, что эти два неравенства можно заменить одним, введя
абсолютную величину функции:
* \№\<М.
Действительно, это неравенство, очевидно, равносильно неравенствам
-М</(х)<+М.
Легко интерпретировать геометрически ограниченность функции.
Обозначим через Я множество значений функции fix) на сегменте
[а, Ь\. Если мы теперь обозначим через $ геометрический образ
функции /, т. е. униформное (по
отношению к оси ОХ) плоское
множество, которое изображает функцию
/, то ясно, что множество Я есть
проекция на ось О Y плоского мно«
жества $ (черт. 87). Ясно также,
что функция / тогда и только тогда
^ ограничена сверху, снизу или с обеих
сторон, когда линейное множество
Я ограничено на оси OY сверху,
снизу или с обеих сторон.
Если функция / ограничена сверху, тогда множество Я
ограничено сверху (по оси OY) и тогда оно имеет определенную верхнюю
границу, которую мы обозначим через В (черт. 88). Ясно, что на
всем сегменте [а, Ь\ мы имеем f(x)<B, причем число В уже нельзя
уменьшить, потому что, раз есть верхняя граница множества Я, то
множество Я всегда имеет точки, лежащие правее (т. е. выше по
Черт. 87
1
А
0
а
5
_.
Ь X
оси OY) точки В — е, и, значит, всегда на сегменте [а; Ь] найдется
точка £, такая, что /(?) >£ — s, как бы мало ни было
положительное число е. Геометрически это означает, что все точки кривой
yz=f(x) (т. е. униформного множества $) лежат под прямой у=^В
или на самой этой прямой и нет ни одной точки кривой у =/(х),
которая лежала бы выше прямой у=^В. Но, как бы мало ни было е,
е> 0, всегда найдутся точки этой кривой, которые лежат выше
прямой у = В— 8.
Такое число В называется верхней границей функции / на
сегменте [а, Ь].
Аналогично, если функция f ограничена снизу, тогда множество
Я имеет нижнюю (по оси OY) границу А и тогда мы имеем на всем
136
сегменте [а, Ь] соотношение f(x)^A. Геометрически это означает,
что все точки кривой у=/(х) лежат или выше прямой у = А> или
на самой этой прямой, но никогда не лежат ниже ее. Но, как бы
мало ни было положительное число е, всегда имеется такое ?, что
/*(&)<Л-j-г, и, значит, всегда на кривой v=/(*) найдутся точки,
лежащие ниже прямой у = А-\-е.
Такое число А называется нижней границей функции / на
сегменте [а9 Ь].
Если В есть верхняя граница функции / на сегменте [а, Ь] и
если не существует абсциссы £, что / (£) = В, то легко доказать, что
на сегменте [а, Ь\ имеется такая последовательность точ§к \и £2,...,
%п9* • •> чт0 ^га f($n) = В. Действительно, возьмем числа Sj>s2>s3>
>•. .> ега>-• •> такие, что limen = 0, когда п неограниченно
возрастает. Мы видели, что всегда имеется такая точка lnf что /(Ел) >
> В — еп. И так как, по условию, нет такой точки £, что /($) = В,
то мы обязательно должны иметь строгие неравенства £>/(£„)>£ — гп
для всякого п. При неограниченном возрастании я, гп стремится
к нулю, и, значит, мы имеем
Нт /(?я) = В.
Легко видеть, что среди точек ?lf ;<>,..., $п,... мы имеем
бесконечно много различных точек. Действительно, если бы среди них было
лишь конечное число геометрически различных точек, то
бесчисленное множество точек %п совпадали бы с некоторой точкой £. А это
означало бы, что в этой точке имело бы место равенство /(£) = В,
что противоречит сделанному предположению. Вычеркивая из
последовательности Sj, £2, •••>*«» ••• геометрически тождественные
точки, мы получим бесконечное множество геометрически различных
точек этой последовательности.
Аналогично, если А есть нижняя граница функции / на сегменте
[я, Ь] и если нет такой точки $, что /(;)== А, то существует
бесконечная последовательность различных точек &1э $2, ..., ?я> ... на
сегменте [а, Ь\у такая, что lim /(;„) = Д.
П -» -{- оо
Эти обстоятельства могут казаться очень сложными; чтобы
пояснить логическую простоту самого дела, введем определение:
^ Если на сегменте [а, Ь\ имеем f (х) <; В и если существует
такая точка I, что /(£) = £, тогда такое число В называется
максимумом функции f на сегменте [а> £], а самая точка \
называется точкой максимума. Аналогично, если на [а, Ь] имеем
f(x)^A и если /(5) = Л, то А называется минимумом функции
/ на сегменте [а, Ь ] и £ точкой минимума.
Ясно, что всякий максимум есть в то же самое время и верхняя
граница функции. Но обратное неверно: верхняя граница В функции
/ будет максимумом тогда и только тогда, когда найдется такая
абсцисса 5, для которой /(5) = В. Таким образом, верхняя граница В
функции / является максимумом этой функции тогда и только тогда,
когда она достижима на сегменте [а, Ь\, т. е. тогда, когда среди
137
абсцисс х, принадлежащих этому сегменту, существует такая
абсцисса S, в которой величина /(£) функции в точке I строго равна
верхней границе B,/(£)=±=£.
Всякая ограниченная сверху функция / на сегменте [а, Ь] овя~
зательно имеет верхнюю границу В на этом сегменте. Но манси*
мума она может и не иметь. Например, разрывная функция f(x),
определенная условием: /(0) =/(1) = — и /(*) = х для 0 <я* < 1,
ограничена; ее нижняя граница есть 0, верхняя граница есть 1, но
она не имеет ни максимума, ни минимума на сегменте [0,1] (черт. 89).
Введя эту терминологию, мы можем сказать, что если функция /
ограничена сверху на сегменте [а, д] и не имеет на нем максимума*
то в этом случае на сегменте имеется бесконечная последовательность
точек 61эев. ,..,«„»•••. таких, что/(^) </(fa)< ... </(?«)< ••>
причем /{Ьп)-~у В, когда п-+-\~оо; здесь В есть верхняя граница
функций / на сегменте [а, Ь].
t X 01
Черт. 89.
i X
Аналогичное можно сказать и о нижней границе А функции /.
Заметим, наконец, что если функция / имеет максимум на
сегменте [а, #]> то последовательности различных абсцисс Ъи 12, ...,
1т .**, таких, что f(ln) стремится к максимуму, когда п -+*j~ са>
может и не существовать. Например функция f(x), равная 0 везде,
кроме x — ir (черт. 89), и такая, что /гй') — ** имеет, очевидно,
максимум на сегменте [0,1]; но последовательности различных абсцисс
$!, Eg,- •-,€*!>• • ч такой, что f(in) ~>1, не существует, так как всегда
имеем /(£) = 0, если %пф-^т ,
Если функция /ограничена на сегменте [а, Ь\> тогда она имеет
нижнюю и верхнюю границы; пусть А есть нижняя граница и В
верхняя граница. В этом случае, разность В — А называется
колебанием функции / на сегменте [а, Ь).
Понятие колебания функции чрезвычайно важно, как увидим из
дальнейшего. Пока же мы лишь отметим, что колебание В — А
функции есть не отрицательное число, потому что В >• Л. Ясно, что
колебание В-~А функции/на сегменте [а, Ь] равно нулю тогда и только тогда,
когда функция / постоянна на сегменте [а, &], /(лг) = const.
Это обстоятельство ясно из того, что колебание В — А есть,
очевидно, длина наименьшего отрезка [Д, Б], содержащего множество И
138
значений функции. И раз эта длина равна нулю, то все множество,/?
состоит лишь ив одной точки, т* е. f(x) постоянна на сегменте
[а, ft]. К этому мы прибавим еще следующее: функция / имеет на
[а, ft] максимум, если множество Н содержит свою правую границу.
Если же Н не содержит в себе своей правой границы, тогда / не
имеет максимума на [а, ft]. Аналогичное нужно сказать и о нижней
границе: если И содержит в себе свою левую границу, тогда /имеет
на [а, ft] минимум.
Если функция / неограыичена сверху на сегменте [а, ft], тогда мы
говорим, что ее верхняя граница есть -j- со. Аналогично, если /
неограничена снизу на [а, ft], мы говорим, что ее нижняя граница
есть — со.
Если / неограничена сверху на [а, ft], то это означает, что
кривая y==zf(x) имеет точки, лежащие выше прямой j/ = n, каково бы
ни было натуральное п. Пусть \п есть абсцисса одной из таких
точек, т. е./(£п)>я. Как и прежде, последовательность точек \ъ
Еа, *.., ?„, ... содержит бесконечное множество геометрически
различных точек сегмента [ау ft]. Из сказанного следует: если/
неограничена сверху па [а, ft], тогда существует бесконечная
последовательность точек ^. £2> . .., £п, ... сегмента [а, ft], таких> что
ftiXf (&<•■•</&)<••;
причем /(Sw)-> -j- О0> когда п-~>-\- со. Аналогично, если f
неограничена снизу на [a, ft],' тогда существует бесконечная
последовательность точек 51% ?2, ..., (•„, ..., такая, что
/(5i)>/(У >... >/(?»> >-..,
причем /(£»t) -* — оо, когда п -* -j- со.
Заметим, что верхняя граница функции f(x) на сегменте (a, ft]
является нижней границей для функции—/(#)> и обратно. Ввиду
этого многие теоремы о верхней границе автоматически переносятся
на нижнюю границу.
В заключение мы отметим, что данные в этом параграфе
определения „верхней границы", „нижней границы" и
„колебания" функции / без малейшего изменения распространяются на
тот самый общий случай, когда функция / задается не на
каком-нибудь сегменте [a, ft], но на произвольном множестве точек £.
Если рассматриваемая функция / определена во всякой точке
множества Е и не определена нигде вне этого множества Е, мы можем
говорить про „верхнюю границу Be", „нижнюю границу Ав* и
„колебание Ф£и функции / на множестве /:, определяя их совершенно
таким же образом, как и в случае, когда рассматриваемое множе*
ство Е является сегментом [a, ft].
И здесь мы имеем те же самые соотношения
и те же самые заключения, что и раньше: для того, чтобы функция/
была ограниченной сверху на множестве Е, необходимо и
достаточно, чтобы Be была конечным числом. Для того, чтобы / была
139
ограниченной на Еу необходимо и достаточно, чтобы числа Ае и Be
были оба конечными числами; в этом и только в этом случае
колебание a>js7 функции / на Е является конечным числом, большим или
равным нулю. Если функция / неограничена на Е хотя бы только
с одной стороны (сверху или снизу), мы имеем <o# = -j-co. Чтобы
/была постоянной на Е, необходимо и достаточно, чтобы ш^ = 0.
Наконец, если в какой-нибудь точке х0 множества Е мы имеем
/С*о) = Яг,
тогда л*0 есть точка максимума / на Е. Если Е есть множество,
состоящее из конечного числа точек, тогда / имеет обязательно
максимум и минимум на Е. Если / не имеет максимума на Е} тогда
всегда можно определить такую бесконечную последовательность
точек Sj, ?2, ..., %ю ..., лежащих на Е, что будем иметь /(£п)-+Ве
при п-+-\-оо.
Таким образом, нет никакого различия в общих свойствах границ
функции и ее колебания для сегмента [а7 Ь] и лля произвольного
множества Е.
§ 40. Верхняя и нижняя границы функции в точке.
Колебание в точке. Пусть / есть функция, определенная на сегменте
[а, Ь],их0 точка, лежащая внутри (в строгом смысле) этого сегмента.
В дальнейшем, если о есть какой-нибудь сегмент, лежащий на
[а, Ь]у \иы через Аа, В9 и оа будем обозначать нижнюю границу,
верхнюю границу и колебание функции / на сегменте о, <оа = Вд — А5,
ш5^0. Если /неограничена на а, мы полагаем <юа— -f-oo.
Заключим теперь точку х0 внутрь (в строгом смысле) сегмента а,
лежащего на [а, Ь], и покажем, что когда а стягивается к точке х0,
то величины А09 Д, и <оа стремятся к вполне определенным пределам,
которые мы обозначим через AWo, В^ и соГо и которые будем называть
нижней границей, верхней границей и колебанием функции / в точке х0.
Чтобы доказать это, возьмем последовательность ot > о2 >...
... > ап >... сегментов, стягивающихся к точке х0, которую они
содержат внутри (в строгом смысле), и таких, что каждый
следующий содержится в предыдущем. Ясно, что последовательность чисел
A9l^А0ъ^ .. .<y4g <;... не убывает и последовательность
чисел £ai!>e<jt^.. .^*Яв ^ не возрастает, так же как и
последовательность чисел <о51 ^5 o)Ja >... ;> <овд >- Поэтому, когда п
неограниченно возрастает, все три величины А0п, BZ)% и ю стремятся
к определенным пределам, которые мы обозначим через А> В и со.
Если теперь а есть какой-нибудь малый сегмент, содержащий точку
х0 внутри, то он будет содержаться в некотором сегменте ару
причем когда длина о будет стремиться к нулю, число р можно
предположить неограниченно увеличивающимся. Но раз о содержится
в api мы имеем" i43>i4ff, Bff<53p и ©3<<оу С другой стороны,
сегмент о содержит в себе некоторый сегмент oq, так как оя,
стягиваясь к точке х0> для достаточно большого п окажется
расположенным в сегменте а.
140
I
Следовательно
A9q^A„ В9д^В9 и «вв<«в.
Так как #>р, то мы имеем неравенства
A9q**Ae>Av B9q^B9^B9p и ш,а<шя<ш^;Р<д.
Если теперь длина сегмента с стремится к нулю, то натуральные
числа р и # можно предположить неограниченно увеличивающимися.
Но тогда крайние члены каждой из трех групп неравенств
стремятся к одному и тому же пределу. Поэтому мы будем иметь:
ИтА9 = А, 1\тВ9 = В и Нтсо3=со.
Следовательно, пределы А9, В9 и а>„ не зависят от способа
уменьшения длины сегмента а.
В дальнейшем, как было указано, мы будем соответственно
обозначать эти пределы через АХс9 ВХй и аХо, чтобы указать
зависимость их от точки х0, т. е. мы положим А*0 = А, Вх0 = Вн а>^ = <»
и будем называть эти числа соответственно нижней границей,
верхней границей и колебанием функции / в точке лг0.
Отметим основные свойства верхней границы ВХо функции /
в точке лг0. Прежде всего мы имеем неравенства
Are</(*0)<&re. (2)
Действительно, если о есть сегмент, содержащий точку л:0 внутри,
то мы, очевидно, имеем неравенства
Л,</(*о)<Я,-
Отсюда, заставляя а стягиваться к точке х0, мы переходом к
пределу убеждаемся в справедливости неравенств (2).
Если имеем равенство / (*0) = ВХб, то оно означает, что Вх0 есть
значение функции в точке лг0.
Если имеет место неравенство f(x0)<Bx0, то и подавно
справедливо неравенство f{x0)<B9. Но в силу уже знакомых нам
свойств верхнего предела функции на сегменте, мы имеем,
во-первых, на всем сегменте а неравенства Л3</(л:)<Вв и, во-вторых,
при*любом е, е>0, имеем такую точку 6, лежащую на сегменте о,
что /(£)>Я,— е. Но раз /(%)< в*> то точка 6 может быть взята
на сегменте *о так, чтобы она не совпала с точкой х0, т. е. 1фх0.
Заставим теперь сегмент а стягиваться к точке х09 для чего
рассмотрим последовательность сегментов
а1 > °2 > а3 > • • • > а« > * ' * *
Пусть 5П есть выбранная нами точка на зг„ такая, что
ЯаЛ>/С5п)>Ввл-вЯ1 (3)
где еп стремится к нулю, когда п -» + °°- Так как точка ^ отлична
от точки л-0, то последовательность точек \ъ 52, . . ., ?„, ...
содержит бесчисленное множество геометрически различных точек; выбра-
141
сывая тождественные точки, мы можем предположить, что
оставшиеся точки, геометрически различные м^жду собой1, опять
обозначены через Sj, 52, ..., Sn,
Но при п -> + оо мы имеем Вап -> ВХо и еп -* 0. Значит,
неравенство (3) даст;
Таким образом, или мы имеет ВХо—/(х0), или существует по-
следовательность геометрически различных точек Ьи £2,..., £п,.. ,,
таких, что f(ln) -* 5^, причем лри всяких значениях х, достаточно
близких к xQy имеем f{x)<C.Bxl-\-s. Аналогично: или мы имеем
Ла.о«5=/(#0), или существует последовательность геометрически
различных точек 1и £2,..., ?Л,.. ., таких\ что f (in) -> АТь% причем
мы имеем f{x)>AXQ—s при любом г, е>0, когда точка х
достаточно близка к л'0.
Следовательно, или f(x0) есть единственная максимальная
точка в некотором сегменте а для кривой y = f(x), или
существует последовательность точек £1э £а>. .., ?п,..., стремящихся
к х0, такая, что f ($п)-+ВХо. Аналогично, или f (x0) есть
единственная минимальная точка в а для кривой y=f(x)9 или имеем
fftn)-+Ax* когда 1п-+х0.
Сказанное имеет силу и для того случая, если АХо или ВХо равны
Ц-со !Ци. —- со. Для этого случая полезно ввести определение: мы
говорим, что / неограничена в точке х0, если / неограничена во
всяком сегменте о, содержащем точку х0 внутри.
Легко видеть, что множество Е точек, в которых / неограничена,
образует замкнутое множество. Действительно, если точка х0 есть
предельная для множества £", то всякий сегмент а, содержащий внутри
х0, будет содержать точку множества Е и потому / будет на а не-
ограничено. Следовательно, х0 принадлежит к Е.
Заканчивая этот параграф, мы должны отметить, что все данные
здесь определения распространяются и на тот случай, когда функдия/
определена не на сегменте [а, Ь], но на произвольном множестве
точек Е.
Действительно, если х0 есть какая-нибудь точка
рассматриваемого множества Е, мы можем заключить х0 в интервал 8 и
рассматривать только ту часть множества Е, которая содержится в 8;
назовем ее порцией множества Е, высеченной интервалом 8, и
будем обозначать через Е?1. Обозначая через А;> Дз и ^s нижнюю и
верхнюю границы / на Е?} и колебание / на Еъ> мы, повторив слово
в слово предыдущее доказательство, видим, что Аъ В6 и ш5
стремятся к вполне определенным пределам, когда длина интервала о
стремится к нулю. Эти пределы, обозначаемые через АХоУ ВХо и <оЛо,
и суть нижняя граница, верхняя граница и колебание функции f
на множестве Е в его точке х0.
Ясно, что попрежнему имеем I
142
Ясно также, что попрежнему для всякой точки х0>
принадлежащей к Ef имеет силу сделанное выше заключение: или л*0 есть
единственная точка максимума для некоторой порции Еь множества Е>
содержащей х0, или имеется на. Е бесконечная последовательность
точек !„ £2>--*> 5П,..., стремящихся к #0 и таких, что /(^)-*ВЩ>
когда я—►-J-"00* Аналогичное предложение сохраняется для точки х0
по отношению к числу АХь.
Доказательства этих предложений остаются прежними, достаточно
только заменить выше слово „сегмент [а, Ь\а словом: „множество £".
' Таким образом, все остается по-старому как в случае сегмента
[а, Ь], так и в случае произвольного множества Е. Мы должны,
однако, отметить некоторые особенности, которые не представляет
сегмент, но которые могут оказаться в случае произвольно взятого
множества Е.
Во-первых, сегмент не имеет изолированной точки, но таковая
легко может оказаться у множества Е. Если х0 есть изолированная
точка множества Е, то мы в ней необходимо имеем
Are = B,e и«,0яО.
Действительно, х0 есть единственная точка множества Е,
содержащаяся в интервале 5, когда длина 8 станет достаточно мала; поэтому,
еще до перехода к пределу мы будем иметь Az == Ва и <оа = 0.
Во-вторых, если точка х0 не принадлежит к Е и не является
предельной точкой для Е, тогда числа АХо, ВХо и <ьХо просто
не существуют, так как при достаточно малом 8 будет отсутствовать
самая порция £5. Но если х0 не принадлежит к Я и является
предельной точкой для Е, тогда при любом 8, содержащем х0,
существуют Аь Вь и ш6, и данное выше рассуждение показывает, что
существуют пределы этих чисел, когда длина о стремится к нулю.
Естественно пределы эти попрежнему обозначить через АХьУ ВХо и о)^, хотя
в этом случае точка х0 и не принадлежит к Е. Ясно, что числа Л#в1
Вщ и о)#0 не имеют никакого отношения к значению функций / в
самой точке хОУ потому что такового в ней не имеется, но учитывают
характер изменения функции / в бесконечной близости к точке xQi
множеству £, однако, не принадлежащей.
Это последнее замечание можно иллюстрировать следующими
весьма полезными построениями. Пусть Е какое-нибудь множество,
на котором дана функция /, вне которого она не существует.
Замкнем множество Е, присоединив к нему все невходящие предельные
для него точки. Известно, что после такого пополнения данное мно*
жество Е становится замкнутым:
F=zE-rE',
здесь Ег обозначает производное множество от /Г, и F есть
замкнутое множество. Ясно, что данное множество Е является частью
замкнутого множества F, всюду плотной на нем. После всего
сказанного очевидно, что вне замкнутого множества F ни в какой течк^
х0 прямой не существует чисел AXq, В^ и фх&. Напротив, если точка
х0 принадлежит к замкнутому множеству F, числа AXq, BXq и со^яв-
143
ляются вполне определенными, если даже л:0 и he будет принадле-
жать данному множеству Е.
Таким образом, на замкнутом множестве F в каждой его точке
х0 числа АХо, В-Со и <йХо существуют, несмотря на то, что функция/
определена не на всем этом множестве F, но лишь на его часта Е
(всюду плотной на F).
Это обстоятельство вынуждает нас спросить, нельзя ли дополнить
определение данной нам функции /, существовавшей ранее лишь на
множестве £, доопределив ее теперь на множестве-разности F — Е
таким образом, чтобы полученные выше числа Ах^ ВТ<> и аьХо
остались попрежнему нижней, верхней границами и колебанием
дополненной функципи / на всем замкнутом множестве F? Легко видеть,
что если такое пополнение / определения функции / возможно, то
его приходится делать очень осторожно, так как при неудачном
пополнении определения функции / числа АХ0 ВХ9 и ш^ могут сильно
изменяться, когда мы примем во внимание эти появившиеся новые
значения функции /. Например, если / имела на Е отрицательные
значения, то очевидно, что Ла?0<;Ои 5а?0<;0 во всякой точке xQ
замкнутого множества F. Поэтому, если мы пополним определение
функции / на Z7, положив /==4-1 всюду на множестве-разности
F—£, то теперь мы во всякой точке х0 этой разности будем иметь
#^ = + 1» а не В^0<;0, как имели раньше.
Легко видеть, что такое пополнение и не всегда возможно. Пусть,
например, точка л:0 множества F не принадлежит к Е и пусть
значения функции f(x) безгранично возрастают, когда х-*х0, В этом
случае до пополнения мы, ^очевидно, имеем Ах9 — Вх0 = 4- со. И
какое бы значение функции / мы ни выбрали для точки дг0, оно всегда
будет конечным; поэтому, после всякого пополнения функции /
мы должны получить для точки х0 нижнюю границу конечной, и,
значит, уже не равной -|- оо.
Но если функция / ограничена на Б, тогда такое
пополнение всегда возможно. Действительно, в этом случае оба числа А»0.и Вх0
всегда конечны, причем Ах0^.Вг0. Поэтому, если мы в каждой точке
х0 множества F, не принадлежащей к £, выберем произвольно значение
J(x0), но так, чтобы оно удовлетворяло неравенствам
A*.<7(*o)<&v
то тогда верхняя и нижняя границы пополненной функции / на
порции Fb замкнутого множества F> высеченной каким-либо интервалом 8,
очевидно, соответственно равны верхней и нижней границам функции
/ на £s. Отсюда ясно, что и пределы их во всякой точке х0
множества F должны оказаться равными.
Здесь же мы отметим, что случай с е гм е нта- \а> Ь] и
случай замкнутого множества Е почти неотличимы, так как
почти все свойства, относящиеся к случаю сегмента, автоматически
переносятся с теми же самыми доказательствами и на случай
замкнутого множества Е и, тем более, на случай совершенного множества Б.
144
Так например, предложение о том, что множество точек х0, в
которых данная функция / неограничена, есть замкнутое множество,
одинаково имеет силу и для случая/, заданной на сегменте [а, Ь], и
для случая /, заданной на каком-нибудь замкнутом множестве Е.
Но оно, разумеется, перестает быть верным, если Е не есть
замкнутое множество.
В заключение мы укажем на необходимость придерживаться здесь
точной терминологии: если рассматриваемая функция определена только
на множестве Е и, следовательно, просто не существует вне Е нигде,
мы можем говорить о нижней, верхней границах АХо> BXq и о
колебании о)о70 функции f в точке х0 множества £, не прибавляя
более ничего. Но если функция / определена на каком-нибудь
множестве Я, содержащем Е, Е < Я, то разумеется, нам никто не может
запретить рассматривать то или" иное явление только на множестве Е,
но при этом тщательно должно быть оговорено, учитываются ли здесь
величины функции / вне Е, или же совершенно оставляются без
внимания.
Так, например, пусть f(x) определена только на множестве R
всех рациональных чисел и равна -f 1, если х = — несократимая дробь
ч
с четным числителем р, и равна —1, если числитель р нечетный.
Обозначим множество R через Я и множество указанных
рациональных чисел -- с четным числителем через Е. Ясно, что £<Я.
q .
Мы можем рассматривать функцию / на всем множестве Я, но
можем рассматривать ее также только на его части Е. Пусть теперь
точка х0 движется по множеству Е, нигде не сходя с него, и пусть
мы желаем определить в этом случае числа АХо, ВХо и ша?0. Очевидно,
что вопрос неясно поставлен и что, поэтму, точный ответ на него
невозможен. В самом деле, если мы принимаем во внимание значения
функции во всех точках множества Я, то ясно, что
Но если мы, перемещая х0 вдоль множества Еу принимаем во
внимание значения функции / только на Е, то имеем уже
Агв= + 1, #*в= + 1, «*„ = (>.
Мы видим, что, рассматривая нижнюю, верхнюю границы и
колебание функции / на каком-нибудь множестве Е, необходимо заранее-
условиться, принимаются ли при этом во внимание величины функции
/только на Еу или вообще все возможные значения этой функции.
В первом случае рассмотрение есть релятивное и числа Ла?0,
£То, «'да называются „нижней, верхней границами" и „колебанием"
функции /на Е относительно Е. Следовательно, в этом случае
функция / рассматривается так, как если бы она не существовала
совсем вне Е, иначе говоря, мы имеем здесь „усечение функции /
множеством Я".
Во втором с л у ч а е рассмотрение абсолютное и, если точка х0
пробегает множество ЕЛ числа АХо, ВХо, юХо можно называть просто
Ю Эак. 1244. 145
„нижней, верхней границами" и „колебаниеми функции / на Е без
прибавления слов „относительно Е".
Ясно, что относительное и абсолютное определения совпадают,
если функция / не определена вне £, или если Е есть интервал (а, Ь).
§ 41. Непрерывность. Функция f(x) называется непрерывной
в точке х0, лежащей внутри сегмента [а, Ь], если ее колебание
а)^ в этой точке равно нулюу т. е. если ю^ —0.
Эта форма определения непрерывности функции в точке часто
называется определением Бэра (Baire).
Легко видеть, что это стационарное (без введения понятия
переменной величины) определение равносильно классическому
определению непрерывности функции в точке (определению Коши).
Действительно, во-первых, если функция f(x) непрерывна в
классическом смысле в точке л0, то ее колебание ®х0 в этой точке равно
нулю, т. е. шж0 = 0.
Чтобы доказать это, предположим, что f(x) непрерывна в точке х0
в классическом смысле. Это означает, что для любого положительного
е найдется такое положительное число % что имеет место неравенство
|/(*)-/Ы1-о, (4)
когда будет соблюдено неравенство
\ |x-.r0!<Y]. (5)
Но неравенство (4) можно переписать в виде неравенств
/(*о)-«</(*)</(*<>) + «» (4*)
говорящих о том, что нижняя и верхняя границы функции / (х) на
сегменте [х0~- тг), х04~^] подчинены неравенствам
Следовательно, для нижней и верхней границ в точке х0 мы и
подавно будем иметь неравенства
Я*о)- S< Aro< S», </(■*<>) + ••
Но здесь s есть число произвольно малое, числа же Ах0, Вх0 суть
постоянные. Отсюда следует, что Ах0 = Вх^ т. е. оз^ = 0. Поэтому,
функция /, непрерывная в классическом смысле в точке д:0, является
непрерывной в смысле Бэра.
Во-вторых, легко заметить, что если имеем <&х0 = 0, то функция
f(x)' непрерывна в точке х0 в классическом смысле. В самом деле,
если <ож0==0,. то Ахй = Вх^ т. е. числа Ах0 и Вх0 конечны и равны
друг другу. Если мы теперь заключим точку х0 внутрь сегмента о, то
видим, что при достаточной малости сегмента а величины Л, и В9
будут сколь угодно мало отличаться от соответственных чисел АХй и
Вх0. И так как Ах0 = Вх0, то при достаточной малости сегмента о
мы будем иметь
0<£а-Ла<е, (6)
146
me e > 0 как угодно малое число. Из неравенства же (6) следует,
что справедливо неравенстве
l/(**j-/(*')!<•• (Г)
если точки х' и х" содержатся на сегменте е. Положим лг'=»лг0 и
х" = х, тогда неравенство (7) перепишется в виде
' |/(*)-/(*о)1<«. (4)
причем оно. будет удовлетворено, если точка х будет принадлежать
сегменту о. В частности оно будет удовлетворено, если будет
удовлетворено неравенство
|дг —лг0|<4, (5)
где Y] означает расстояние ближайшего конца сегмента а до точки х0
(черт. 90).
Но неравенства (4) и (5) как раз и обозначают непрерывность
функции в классическом смысле в точке х0.
Таким образом оба определения непрерывности: в смысле Бэра и
в смысле Коши эквивалентны.
« Г
Черт. 90.
Заметим, что функция f(x), неограниченная в точке х0, не может
быть непрерывной. Действительно, если / неограничена в точке дг0,
то на всяком сегменте о, охватывающем х0, по крайней мере одна из
границ Д,'и Ва бесконечна и, значит, <ов===-|-оо. Поэтому мы имеем
и ша>0=~|- со. Кроме того, раз /неограничена в точке х09 не может
соблюдаться неравенство (4),
|/(*)-/(*о)1<«. (4)
потому что f(x0) есть конечное постоянное число, а абсолютная
величина /(х) может быть сделана сколь угодно большой при
надлежащем выборе точки х на сегменте [х0 —t\9 #04-4Qj, т. е. при
соблюдении неравенства (5)
!* — хо\<Ч-
Выше мы определили непрерывность функции /, заданной на
сегменте [ау Ь] в точке х0, которая лежит внутри этого сегмента. Но
мы ничего не сказали о том, как определяется непрерывность
функции /, если х0 является концом сегмента [а, Ь).
Чтобы не иметь дело с массой различных частных случаев, мы
обратимся теперь к самому общему определению.
Пусть /есть функция, заданная на каком-нибудь множестве точек
Е и несуществующая нигде вне его. Пусть х0 есть точка множества Е.
10* 147
Определение. Функция f называется непрерывной в точке
х0 множества Е, если ее колебание ®хй в этой точке равно нулю>
0)070 = 0.
Мы .обращаем внимание читателя на абсолютный характер этого
определения, ибо рассматриваемая ^функция /предполагается не
существующей нигде вне множества Е. Если же функция / хотя и
рассматривается на множестве £, но имеет значение еще и в точках х, не
принадлежащих к Е, тогда предыдущее абсолютное определение
следует заменить определением релятивным:
Функция f называется непрерывной в точке х0 множества Е
относительно множества Е, если ее колебание оц, в этой
точке относительно этого множества равно нулю, 0)^=0.
Это релятивное определение применяется, когда функция /
задается на более широком множестве Н, содержащем в себе
множество Е как часть, т. е. если £ <//. Например, в рассмотренном выше
примере функции /(х), определенной только на множестве R
рациональных точек и равной -р 1 или — 1 смотря по тому, будет ли
числитель р несократимой дроби л; = — четным или нечетным; если
мы обозначим через Е множество всех рациональных точек х с
четным р и через Н множество всех рациональных точек, мы видим,
что / непрерывна во всякой точке х0 множества Е относительно Е,
так как на Е рассматриваемая функция постоянна (/=-|-1) и> зка"
чит, ее\колебание о>^с в каждой точке множества Е относительно Е
равно нулю, ш,я0 =0. Но в то же самое время, в каждой точке х0
множества Е функция / относительно множества И разрывна,
потому что всякая точка х0 множества Е является, очевидно, пределом
рациональных точек х как принадлежащих к Еу так и не
принадлежащих к Е, и, следовательно, в каждой точке х0 множества Е
нижняя и верхняя границы функции / относительно Е будут
Ах0 — — 1, Вх0=-\-1.
Следовательно, мы имеем а>Го = 2 во всякой точке х0 множества Е
относительно множества Н, что и показывает разрывность
функции / во всякой точке множества Н относительно Н.
В дальнейшем мы часто будем рассматривать различные
совершенные множества Р, лежащие на сегменте [а, Ь], и, имея какую-нибудь
функцию /, определенную всюду на [а, Ь], будем изучать ее
непрерывность относительно тех или других совершенных множеств Р:
относительно некоторых / явится непрерывной в тех или иных его
точках, относительно же других она може1 явиться разрывной во всех
его точках.
Ясно, что относительное и абсолютное определения совпадают,
если f(x) нигде не определена вне Е или если fix) не может быть
определенной вне Е, например, когда Е тождественно всей оси ОХ,
Е = (~- оо < х<С + оо).
Особый интерес представляет тот случай, когда рассматриваются
функции f, определенные на замкнутых множествах и не
существующие вне их. В этом случае каждая точка xQ, не принадлежащая
143
к этому замкнутому множеству, удалена от него на некоторое
конечное отличное от нуля расстояние и, следовательно, в точке х0
совсем не может иметься чисел Ах0, Вх0 и ш^. Если же множество Ел
на котором определена функция /, не замкнутое, то, присоединив
к нему недостающие в нем предельные к нему точки, мы получаем
замкнутое множество F
F = E-\-E',
на котором Е всюду плотно. Мы уже видели, что в каждой точке
х0 этого множества F имеются числа AxQ} BxQ и ш.г0, причем ш^^О.
Если мы имеем
1 «Ч = О,
мы говорим, что f непрерывна в точке х0 множества F, хотя бы
xQ и не принадлежала к Еу на котором {и только на котором)
определена функция f.
На первый взгляд может -показаться, что это какое-то новое
определение непрерывности, так как здесь говорится о непрерывности
функции в таких точках, которые и не лежат на множестве, где
задана функция. Легко, однако, видеть, что это определение можно
свести к прежнему.
Действительно, дополним определение данной нам функции /(х),
определив в каждой точке х0 замкнутого множества F, не
принадлежащей к Еу значение f(x0) так, чтобы
Во всякой точке х0 непрерывности функции / на F это возможно,
потому что мы в ней имеем ш,Го = 0 и, значит, числа AxQ и Вх0 суть
конечные и равные друг другу, Ах0 = Вх0.
Полагая
У(х0) = Ах0^Вх0
во всякой точке непрерывности и полагая в точках разрыва
Аг0<7(х0)<&г0,
мы дополняем определение данной нам функции /(х), причем
дополненная функция/ (х) и первоначальная/(л:), разумеется, будут равны
на Е:
f{x) = J{x\x<E.
Ясно, что дополненная функция / (х) непрерывна относительно F
в прежнем смысле во всякой тоске х0 непрерывности данной
функции f(x).
Мы видели выше, что если функция / (х) ограничена на Е,
то пополненная функция / (а:) существует в каждой
точке х0 замкнутого множества F.
149
В этом случае мы скажем, что данная функция f{x) высечена а$
функции / (л;), определенной на всем замкнутом множестве f, с по*
мощью множества Е, содержащегося в F9 Е < F.
Действительно, мы имеем f(x)=f (х) всюду на Е,
Здесь уместно указать на одно предложение, весьма полезное для
многих построений.
Теорема. Всякая функция /(х), определенная только на
замкнутом множестве F и непрерывная в каждой его точке
(относительно F)y есть сечение с помощью множества F некоторой
непрерывной на всей оси ОХ функции / (х). Обратно: сечение
с помощью замкнутого множества F всякой, всюду на оси ОХ
непрерывной функции f (x) есть функция /(лг), определенная только
на F и непрерывная в каждой его точке (относительно F).
Пусть функция f(x), определенная на замкнутом множестве F,
непрерывна в каждой его точке х0 (относительно F). Пополним
определение функции f(x) линейной интерполяцией. Это означает, что
внутри всякого интервала oi = (ah b4), смежного к замкнутому
множеству F9 мы полагаем 5
Геометрически это означает, что мы просто.соединяем прямой линией
две точки Ai [ait /(а4)\ и Bt [bt, f(bi)] и затем принимаем за величины
пополненной функции f(x)
\
К
}(*)
А-
1(<ч)
а с
№
ерт,
91.
в интервале 8^ ординаты
точек прямолинейного
отрезка, концами которого
служат точки А$ и В$
№)\ | (черт. 91).
Ясно, что этим спосо-
$А II бом мы получим фуик-
Of b: d ЬГ~~* Дию f(x), определенную
на всей оси ОХ, т. е.
всюду на (— оо < х <
< + оо). Это
обстоятельство очевидно, если замкнутое множество F простирается
бесконечно в обе стороны. Если же оно ограничено, имея левым или
правым концом точки с и d, мы можем положить f(x) перед точкой с
и за точкой d, равной ординатам двух каких-нибудь кривых,
непрерывных в бесконечных полуинтервале (—оо<х^с] и
полусегменте [^<[х <-]-- °°) и имеющих в точках end своими ординатами
/(e) и /(d).
Покажем, что построенная таким образом
пополненная функция/(л;), равная на F данной функции /(*)>
непрерывна в каждой точке х0 оси ОХ.
Если х0 не принадлежит к множеству F, предложение очевидно,
так как в этом случае J(x) есть линейная в смежном интервале bkf
содержащем точку х0. Если х0 принадлежит множеству Ff тогда, по
150
условию, данная функция f(x) непрерывна в точке х0 относительно
/\ Это значит, что при любом малом положительном е, в > 0, можно
отыскать столь малый интервал 8, содержащий рассматриваемую точку
xQi что все значения функции f(x) на порции Fb будут отличаться
друг от друга не более, чем на е. Это показывает, что значения эти
содержатся целиком в некотором сегменте о длины ^з. И так как
при всякой линейной интерполяции интерполирующие значения всегда
содержатся между интерполируемыми, то отсюда следует, что, при
достаточно малом интервале 8, все значения на 8 пополненной функции
/ (х) будут принадлежать определенному выше сегменту о длины <1 е.
Отсюда следует, что колебание &Хо функции / (х) в точке xQ не
превосходит s. И так как е произвольно малое число, то имеем в
точности шХо = 0; отсюда и следует непрерывность / (х) на всей оси
ОХ.
Обратно, если f(x) есть функция, всюду определенная на оси
ОХ и непрерывная в каждой ее точке, то сечение ее1 произвольным
множеством точек Е определяет на Е функцию f(x), непрерывную
в каждой его точке (относительно Е).
Это обратное предложение является почти тривиальным. В самом
деле, раз /(х) непрерывна в точке х0> множество S5 ее значений
на каком-нибудь интервале 8, содержащем х0> имеет диаметр
стремящимся к нулю, когда 8 стягивается- в точку х0. Поэтому, тем более
множество $е8 значений функции f{x) на порции Еь будет иметь
диаметр стремящимся к нулю. А это и показывает, что функция fix),
равная на Е функции f{x)> непрерывна в точке xQ множества Е
(относительно Е).
В частности, если Е — F есть замкнутое множество, f(x)
непрерывна на F (относительно F).
§ 42. Непрерывность справа и слева. Мы выше определили
непрерывность функции / в точке х0, окружая эту точку сегментом
с, содержащим х0 внутри. Такая непрерывность называется непре-
li,.o
Черт. 92.
рывностыо в точке х0 с обеих сторон или дзухсторонней
непрерывностью. Теперь определим одностороннюю непрерывность.
Рассмотрим сегмент з, левым концом которого является точка х0
(черт. 92). Пусть попрежнему Ла и Ва нижняя и верхняя границы
функции / на сегменте с, и <о3 колебание ее на а, т. е. шб==^а — Аа.
Если сегмент о имеет длину, стремящуюся к нулю, тогда числа Ла
и BQ стремятся к вполне определенным пределам А^ и В^9 потому
П>1
что при убывании длины о Аа может только возрастать, а Вд
может только убывать, причем имеем неравенство Ад <; Ва. Следовательно,
пределы Л+ и £+ величин А9 и В0 удовлетворяют неравенству
К < ВХ •
Величины Л+ и S+ называются правыми нижней и верхней
границами функции / в точке х0. Величина ш+ = £+-—Л+ есть коле-
^J J и Xq Х0 Х0
бание функции / справа в точке х0.
Функция f(x) называется непрерывной справа в точке х0, если
«+ = 0.
Xq
Аналогично, взяв сегмент о с правым концом в точке х0 (черт. 93),
мы определяем на о обе границы функции AQ и BQ> AQ^Bg и коле-
Черт. 93.
бание со0 = Вс — Аг Если длина сегмента о стремится к нулю, то
величины^ и Ва стремятся к пределам, которые мы обозначим через
А~ и В~~ и назовем левыми нижней и верхней границами функции /
Xq Xq
в точке хп. Величина а>- = £-— А- есть колебание функции / слева
V Xq Xq Xq * ■* *
б точке х0.
Функция f(x) называется непрерывной слева в точке х0, если
xQ
Если функция f(x) непрерывна в точке х0 с обеих сторон, то
она непрерывна также справа и слева в этой точке. Обратное
также верно: если f(x) непрерывна в точке х0 справа и слева, то
она непрерывна (в обычном смысле, т. е. двусторонне) в этой точке.
Действительно, если о> = 0, то тем более имеем <о+ = 0 и от- = 0.
Xq ' Xq Xq
В самом деле, если а есть сегмент, содержащий х0 внутри (строго),
то, разбивая сегмент о точкой х0 на два сегмента: правый о+ и
левый о-, мы, очевидно, имеем:
Л,->А0> А^>А, и £а_<£а, £б+<Лб,
откуда
ша_Оа и о)0+ < соа.
И так как имеем, по условию, lim ша = 0, когда длина а стремится
к нулю, то lim а>а_ = 0 и lim шд+= 0, т. е. ш~ = 0 и а>+ = 0.
Обратно, если имеем ш~ = 0 и ш+ = 0, то для достаточно малого
Xq Xq
сегмента а, содержащего х0 внутри, имеем т,_ <4 и ш5+ < ~.
152
И так как, очевидно,
ТО
значит,
«>а<е;
Но а) есть постоянное неотрицательное число, е как угодно
малое число. Значит, о> «= 0.
От непрерывности справа в точке х0 следует различать
непрерывность справа от точки х0. Эта последняя определяется, как мы
знаем, не посредством сегмента, но посредством интервала о,
имеющего левой граничной точ- t
кой х0 (см. гл. III).
Мы, попрежнему, обозначим —
через Л§, Вь и о^ нижнюю и
верхнюю границы функции / на интер- Черт. 94.
вале Ь и колебание/на Ь (черт. 94).
Заставляя длину Ь убывать до нуля, мы видим, что Л8, Въ и а>5
стремятся к определенным пределам, потому что Лй возрастает, Вь
убывает и, следовательно, ш3 = Б?; — Л3 также убывает. Если
limo)5 = 0, функция / называется непрерывной справа от точки х0.
Т\эчно так же, если интервал 6 имеет х0 своей правой граничной
точкой (черт. 95), то мы определяем попрежнему Л5, В5 и os =
Если имеем iim о)5 = 0, когда длина 8 стремится к нулю, функ
Ция / называется непрерывной слева от точки х0.
Ясно, что функция /, непрерывная справа в точке х0, является
непрерывной справа от точки х0. Но обратное утверждение
неверно, как показывает чертеж 96. На левом чертеже изображена
функция /, непрерывная справа
в точке х0, на правом чертеже
изображена функция /,
непрерывная справа от точки х0: она
Черт. 95. / уже не является непрерывной
справа в точке х0.
Непрерывность «справа в точке х0» и непрерывность «справа
от точки х0» легко определить сразу релятивным способом.
Действительно, пусть Е какое-нибудь множество точек, на
котором определена функция f(x). Мы рассмотрим самый общий случай,
когда функция f(x) определена на более широком множестве Я,
содержащем множество Е9 Е < Я. «
Пусть х0 есть какая-нибудь точка множества Е. Мы обозначаем
через * Е+ множество всех точек х множества Е, которые лежат
направо от х0, и соответственно через £~ множество его точек,
лежащих левее xQ.
153
Мы говорим, что /(х) непрерывна справл в точке х0 множества
Е относительно Е, если / (х) непрерывна в точке х0 множества
{•*(» ^t} относйтельно этого множества. Аналогично, f(x)
непрерывна слева в точке х0 множества Е относительно Еу если f(x)
непрерывна в точке х0
з1-
множества
-^ относительно этого
множества.
Если х0 есть
предельная точка справа
. ,____ для множества £, то
" *> X 0\ *» X f(x) называется непре-
Черт. 95. i рывной справа от точ-
_ ки х0 относительно Ел
если функция /*(*), получающаяся пополнением функции (см. стр. 149)
f{x), рассматриваемой только лишь на множестве Е+, непрерывна
в точке х0 замкнутого множества £+4-(Zf-r)' относительно этого
множества. Аналогично, f(x) непрерывна слева от точки х0 множества
Е относительно Е, если У (х) непрерывна в точке х0 замкнутого
множества Е~~-\-*(Е~У относительно этого множества.
§^43. Непрерывность и стремление к пределу. Эти два явления
тесно связаны между собой, как показывает следующее предложение:
Для*того, чтобы функция f(x) была непрерывной в обычном
смысле в точке х0, необходимо и достаточно, чтобы функция f{x)
имела своим пределом f (х0), когда аргумент х стремится к х0
безразлично с какой стороны и принимая или нет само значение
х0. Если f(x) имеет
своим пределом f(x0), х0
когда точк! х прибли- ^---.___-J^"i " '
жается к х0 справа, °
тогда функция f(x) не- Черт. 97.
прерывна справа в
точке х0. Если f(x) стремится к определенному пределу, когда х
приближается справа к точке х0, но предел этот неравен /(%),
тогда f(x) непрерывна справа от точки х0. Аналогичное имеет
место для непрерывности слева. (Точный смысл выражений
„аргумент стремится", «х приближается» выяснен в конце § 35.)
Если функция f(x) непрерывна в точке х0 в обычном смысле,
то колебание функции f(x) в точке х0 равно нулю, т. е. odXo = 0.
Это же означает, что для любого е, е > 0, имеется такой сегмент
о, содержащий х0 внутри (строго), что колебание функции / на g
меньше в (черт. 97).
Б частности отсюда следует, что мы имеем
|/(*)—/(*о)1<е, ("О
если точка х принадлежит к а, например, если имеем
\х — Хо\<*П (5)
154
для т] достаточно малого. А неравенства (4) и (5) как раз и
обозначают, что имеем
Нт/(л) =/(*<>), (6)
когда лг~> л*0.
Обратно, если мы имеем соотношение (6), то это означает, что
справедливо неравенство (4) при выполнении (5); отсюда и следует,
что ш^==0, т. е. что / непрерывна в точке х0 в обычном смысле.
Если / непрерывна в точке х0 справа, то тогда колебание ш
справа в точке х0 равно нулю, т. е. ш^ = 0. Это означает, что для
любого s, s > 0, имеется сегмент о, левым концом которого служит
точка х0 (черт. 98), такой, что колебание функции / на z меньше s.
Потому, мы имеем неравенство
l/(-v)-/(*<>)!<«, (***)
когда х принадлежит к з, т. е. когда *
0*Сх — х0<ч\, (5**)
где т] достаточно малое. Неравенства же (4**) и (5**) указывают на
то, что мы имеем
НтЛ*)«=/(л;0), (6**)
когда х -* л:0, причем х приближается к хс, оставаясь все время
справа от точки х0 или совпадая с ней.
Ясно, что верно и обратное: если имеем соотношение (6**), когда
х-*х0> причем х^хф то справедливо неравенство <Ч**) при
выполнении (5**), что
означает, что'а>+=0. Отсюда - ^ ^__——-^—. -—■—
следует, что / непрернв- с °
на справа в точке х0. Черт. 98.
Наконец, если /
непрерывна справа от
точки xQi то это означает,
что для любого s, s > 0,
можно отыскать такой ин- Черт. 99.
терзал 8 (черт. 99),
имеющий х0 своей левой граничной точкой, что колебание функции f
на интервале 6 меньше, чем г. Отсюда, применяя критерий Коши
(см. § 34), мы видим, что функция /(х) стремится к вполне
определенному пределу, когда аргумент х, убывая, стремится к х0, при-
чем он никогда не принимает самое значение xQ. Этот предел,
вообще говоря, вовсе не обязан быть равным величине функции f(x)
в самой точке xQ; выше (§ 35) мы этот предел обозначали символом
f(x0 + 0), причем lira f{x) —f(x0 -f- 0) и; вообще говоря, f(x0 -f- 0) ф
ф/(х0). Обратно, если функция f(x) такова, что имеется предел
функции /(*), когда аргумент х% убывая, стремится к х0, то из
критерия Коши (§ 34) мы видим, что колебание функции / на ин-
155
тервале 8 стремится к нулю, когда длина интервала 8 убывает
до нуля. А это и означает, что функцил / непрерывна справа от
точки х0. *
Доказанная теорема справедлива не только для непрерывности
в обычном (абсолютном) смысле, т. е. для непрерывности функций /
всюду определенных, но и для непрерывности относите л ьной.
Если Е есть какое-нибудь множество точек, на котором
определена функция / и вне которого она также может существовать, и
если точка х0 есть предельная справа точка множества Е, то
необходимым и достаточным условием непрерывности функции, f справа
от точка х0 относительно множества Е является стремление
функции f(x) к определенному конечному пределу, когда точка х
безгранично приближается к точке x0f оставаясь все время на
множестве Е, т. е. существование предела limДат), когда х-+х0,
х < Е.
Если точка х0 принадлежит к Е и если мы имеем \imf(x)=f(x0),
когда точка х приближается к точке х0 справа, оставаясь все время
на множестве Еу тогда функция f(x) непрерывна справа в точке х0
на множестве Е относительно Е. Аналогичное справедливо для
непрерывности слева от точки х0 и в точке х0.
Для того чтобы функция f была непрерывна в точке х0
множества Е относительно Е> необходимо и достаточно, чтобы
существовал предел lim/(*), когда точка х безгранично
приближаете^ к точке x0i оставаясь все время на множестве Еу
безразлично с какой стороны, и чтобы мы имели Iim/(x) =/(x0).
Когда множество Е есть сегмент, мы получаем прежнее
предложение как частный случай, так как относительная непрерывность
переходит в абсолютную, когда речь идет о функциях, всюду
определенных.
Ясно, что доказательство для относительной непрерывности
является повторением данного выше доказательства для непрерывности
абсолютной.
Примечание. Пусть f(x) функция, определенная всюду на
сегменте [а, ft], и пусть х0 есть какая-нибудь точка, лежащая внутри
этого сегмента.
Часто называют функцию f(x) непрерывной в точке х0 в смысле
Гейне (Heine), если мы имеем равенство
lim f(xn)=f(x0),
какова бы ни была счетная сходящаяся последовательность точек
х19 лг2, • •. ,хп> • • •> имеющая х0 своим пределом.
Весь смысл этого определения в том, что рассматриваются все
время лишь счетные последовательности хи дг2,. . .хп,..., имеющие
х0 своим пределом, тогда как в непрерывности в смысле Коши или
Бэра рассматриваются две последовательности чисел х (всех
предшествующих х0 vi всех последующих за л:0) мощности континуума.
Непрерывность в смысле Гейне эквивалентна непрерывности
в смысле Коши или в смысле Бэра,
156
♦
Действительно, если f(x) непрерывна в точке х0 в смысле Коши
или Бэра, тогда, в силу доказанного, мы всггда будем иметь равенство,
Нт/(л:п)=/(л:0).
Обратное доказывается уже труднее: если f(x) непрерывна в точке
х0 в смысле Гейне, то она непрерывна в этой точке и в смысле Коши
(или Бэра). Доказательство обычно проводят так: если бы f(x) была
разрывной в смысле Коши или .Бэра, то нижняя граница АХо и верхняя
граница ВХо функции f(x) в точке xQ были бы или различными, или
обе равными и совпадающими либо с -f-oo, либо с —оо.
Если Ат^фВх^ тогда строят две последовательности
хх> х2>* * ->Xn>* * *
И
х\> Х2> * ' '>^л'* " *»
имеющие xQ своим пределом, такие, что имеем одновременно:
lim f(xh) = AXa
lim f(x"n) = Bx<).
Если же AXq<=z ВХо = ± со, тогда строят одну последовательность
х1 > х% > • • •> хп > • * • >
имеющую д:0 своим пределом, такую, что имеем
lim /(<)== :±:оо.
п -> -f оо
Оба эти вывода показывают, что в точке х0 нет непрерывности
в смысле Гейне.
Таким образом устанавливают эквивалентность обоих определений
непрерывности: Коши-Бэра и Гейне.
§ 44, Свойства непрерывных функций. Мы определили
непрерывность функции в точке; это свойство есть, поэтому, свойство
диференциальное (^точнее: локальное). Определим теперь
непрерывность функции на сегменте [а, Ь] и, вообще, на каком-нибудь
множестве Е относительно Е; это будет уже свойство интегральное
(точнее: глобальное).
Мы говорим, что функция f(x) непрерывна на сегменте [а, Ь],
если она непрерывна(двусторонне)вкаждойвнутрен-
ней его точке и непрерывна (односторонне) в его
обоих концах.
Более общее определение имеет релятивный характер и
формулируется так:
Функция f(x) непрерывна на множестве Е относительно Е,
если она непрерывна в каждой точке л:0 множества Е
относительно Е.
157
Г- Свойства непрерывных'функций в точке,.
Теорема 1. Сумма о ~f- ф, разность <? — ф, произведение ®b a
частное |- д*ул; непрерывных функций о и ф 5 точке х0 есть не-
прерывная функция в точке х0, если только знаменатель &(х0)
отличен от нуля.
Это свойство непрерывности функции в точке есть простое
следствие начальных предложений теории пределов о пределе суммы,
разности, произведения и частного. \,
Не останавливаясь более\на этом предложении, мы лишь заметим,
что оно имеет силу как для функций <?, ф, непрерывных на сегменте
[а, Ь] в точке х0> так и для функций <р, 6, непрерывных в то ч к е х0
*на множестве £ относительно Е, потому что в этом случаешы также
имеем оба равенства:
Пто(х)=о(х0)
и
Нт ф(*) == $ (*0),
когда х -» х0, оставаясь все время на множестве Е.
Теорема 2. Ясли; функция u = F(y) непрерывна в точке у
на оси OY, если функция у = f(x) непрерывна в точке х0 на оси
ОХь и если у0=/(х0), то тогда функция от функции u==F[f(x)]
непрерывна в точке х0 на оси ОХ.
Действительно, раз f(x) непрерывна в точке х0 на оси ОХ, мы
имеем \imf(x) =/(х0) =^0, когда х->х0. И, раз F(y) непрерывна
в точке у0 на оси OY, мы имеем lim F{y) = F (y0) = F lf(x0)]y
когда у->у0* Отсюда следует, что lim F[f(x)] = F [f(x0) ], когда
x -> xQy что и обнаруживает непрерывность функции от функции
F[f(x)\ в точке х0.
Заметим, что доказательство молчаливо предполагает
непрерывность функций f(x) и F (у) в точках х0 и j/0, содержащихся
соответственно в интервалах Ь и А, лежащих на осях ОХ и OF, причем
эти функции рассматриваются определенными всюду на 8 и на Д.
Но ясно, что в этом нет необходимости: достаточно, если функции
f(x) и F(y) будут определены соответственно на множествах Е н $,
лежащих на оси ОХ и на оси OF и содержащих точки х0 и yQy
причем не только имеем у0—/(х0), но и предполагаем, что
множество значений функции y = f(x) на Е содержится в множестве &
и, кроме того, функции / и F предполагаются непрерывными в
точках х0 и у0 относительно множеств Е и $. В самом деЛе, в этом
случае мы имеем попрежнему равенство
UmFlf(x)]=Fl/(xQ)]t
когда х -*■ хф оставаясь на множестве Е; это и показывает, что
рассматриваемая функция от функции непрерывна в точке х0
множества Е относительно Е.
II. Свойства непрерывных функций на сегментах
и, вообще, на замкнутых множествах.
158
Теорема 3. Всякая функция f(x% непрерывная на сегменте
(на замкнутом ограниченном множестве), есть функция,
ограниченная на этом сегменте (на этом замкнутом
множестве).
В самом деле, если функция f(x) непрерывна в точке х0 сегмента
[а, Ь], она ограничена на достаточно малом интервале 8,
содержащем точку х0. Справедливость этого мы видели в § 41, когда
доказывали, что функция /, неограниченная в точке д:0, не может
быть в ней непрерывной. Это обстоятельство имеет силу для любой
точки х0 сегмента [а, Ь]\ если х0 совпадает с одним из концов
сегмента [а, Ь], тогда .интервал 8 частью выйдет за сегмент [а, Ь],
но тем не менее ограниченность / на 8 имеет место, потому что мы
рассматриваем / только на сегменте [а, Ь] и совсем не рассматриваем
функцию / вне этого сегмента, считая ее вне [at b\ несуществующей.
Интервалы 8 образуют семейство А, А ={8}, обладающее тем
свойством, что всякая точка xQ сегмента [а, Ь] принадлежит, по
крайней мере, одному интервалу 8 этого семейства. Но тогда, согласно &
лемме БЪреля-Лебега, из семейства А можно отобрать конечное
число т интервалов 8Х) 82, ..., 8Ш, обладающих этим самым свойством.
Следовательно, весь сегмент \а, Ь\ содержится целиком в соединении
интервалов 8j + 82-f- ...-[- 8m. И так как на каждом из них
функция / ограничена, то она ограничена и на всем сегменте [а, Ь].
Теорема немедленно распространяется на всякое
замкнутое множество/7, содержащееся в каком-нибудь сегменте
[cfd]. В самом деле, если функция / определена только на/ и
непрерывна на этом множестве, то мы видели, что функцию / можно
дополнить линейной интерполяцией так, что получится непрерывная
функция f(x) на сегменте [с, d]9 совпадающая с/на*/7. Но согласно
только что доказанному, функция / ограничена на [с, d].
Следовательно, / должна быть ограниченной на F.
Теорема становится ложной для других множеств (незамкнутых).
Например, функция /(*) = •— непрерывна на интервале (0,1), но,
очевидно, не есть ограниченная на нем.
Теорема 4. Верхняя граница непрерывной функции f(x) на
сегменте (на замкнутом ограниченном множестве) есть
ее максимум; нижняя граница функции fix) есть ее минимум
на этом сегменте (на замкнутом множестве).
Это предложение утверждает, что всякая функция f(x),
определенная на некотором замкнутом множестве F и непрерывная на нем
относительно него, действительно достигает своей верхней
и нижней границ А и В на этом множестве в двух каких-то его
точках £ и Y], так что мы имеем /(£) = Л и /(?}) = /?.
Докажем сначала это предложение для случая сегмента. Пусть
f(x) непрерывна на сегменте [а, Ь]. Если бы f(x) не достигала на
эюм сегменте своей верхней границы В, тогда функция
159
была бы непрерывной на сегменте [a, ft], так как знаменатель есть
непрерывная функция на [a, ft], не равная нулю ни в какой точке
этого сегмента. Но тогда о (х) была бы ограниченной функцией
на [а, ft]. А это невозможно, потому что, раз В есть верхняя
граница значений функции f (х) на [a, ft], всегда можем найти на этом
сегменте такую точку лг0, что значение f(x0) будет сколь угодно
близким к В> например, чтобы мы имели
|/*0)-я|<~,
где N сколь угодно большое положительное число. Сравнивая это
н^плЕегство с предыдущим определением функции о (лг), мы
получаем неравенство
\?(x0)\>N,
противоречащее ограниченности функции о (х) на [a, ft].
Следовательно, знаменатель f(x) — В должен быть равным нулю
% в некоторой точке г\ц так что мы будем иметь
Аналогично доказывается необходимость наличия точки £ на [a, ft]
такой, что имеем
/О = л.
А это и показывает, что/(г*) действительно достигает своих
границ 4 и В на сегменте [a, ft], т. е. имеет на нем минимум и
максимум.
Более общее предложение о достижении функцией /(*),
определенной на замкнутом ограниченном множестве F и непрерывной на
F относительно F> своих нижней и верхней границ А и В на этом
множестве, получается немедленно как следствие из предложения о
достижении границ на сегменте.
Действительно, называя cud самую левую и самую правую
точки замкнутого множества F (предположенного ограниченным),
мы интерполируем линейно данную нам функцию /, определенную
только на F и непрерывную на нем. Полученная функция /(х),
пополняющая данную функцию/, непрерывна на сегменте [с, d].
Поэтому, она достигает на [с, d] своих границ, являющихся
максимумом и минимумом f(x) на сегменте [с, d]. Но f(x) линейна в
смежных к F интервалах. Поэтому ее максимум и ее минимум не могут
достигаться внутри смежных интервалов Ъь 8Л,. .. (кроме,
разумеется, тривиального случая, когда / есть постоянная в смежном
интервале 8^, но тогда/ имеет то же самое значение и в граничных
точках интервала 6^) и, поэтому, они могут быть достижимы лишь
на самом замкнутом множестве F (черт. 100).
Итак, имеем
/(5) = Л и/(к|)=»Я,
где ; и т) принадлежат множеству F.
100
Заметим, что теорема неверна для незамкнутых множеств.
Например, функция f(x)=x непрерывна на любом интервале 8 оси ОХ>
но, очевидно, не достигает своих границ и, значит, не имеет на 8
ни максимума, ни минимума.
Теорема 5. Если f непрерывна в точке х0 и если /(х)фО,
тогда существует такой интервал 8, содержащий х0, что всюду
на 8 функция / имеет такой же знак, как и в точке х0.
В самом деле, раз \/(х0)\>0, всегда можно найти столь малый
интервал, содержащий точку дг0, что всюду на 8 имеем
- |/(*)-/(*о)1<т1/(*о)1.
Ясно, что это неравенство, если / (х0) > 0, равносильно двум
обыкновенным неравенствам:
5/(*о)</(*)<|/(*о)
и, если f(x0) < 0, эквивалентно двум неравенствам
|/(*о)</(*)<у/(*о)-
Это и показывает, что f(x) имеет на 8 всюду тот же самый знак,
как и число f(xQ).
Теорема доказана для функций /, непрерывных на сегментах.
Но очевидно, что она имеет силу для относительной
непрерывности функции / на ка- у
ком-нибудь множестве Е.
Действительно, раз / непрерывна
в точке х0 множества Е
относительно Еу то все
предыдущие неравенства сохранятся на
порции Еь множества Е,
высекаемой из Е интервалом 8,
содержащим х0 и достаточно
малым.
Теорема 6. Если
непрерывная на сегменте [д, Ь]
функция f(x) имеет в двух его точках разные знаки, между
этими двумя точками она необходимо в некоторой точке имеет
значение, равное нулю.
Действительно, пусть функция/(х), непрерывная на сегменте [а, Ь],
имеет в двух его точках, cud, разные знаки. Ограничиваясь
рассмотрением сегмента [с, rf], мы видим, что всегда можно предположить
функцию/(л:), имеющей в концах сегмента разные знаки. Итак, пусть
например /(а) < 0 и/(£)>0. Если функция f(x) не обращается
в нуль ни в какой точке х0 сегмента [а, &], то всякую точку х0
этого сегмента можно заключить в некоторый интервал 8, столь
малый, что всюду на 8 функция f(x) будет иметь знак числа f(x0),
f(x0) ф 0. Иначе говоря, функция / сохранит свой знак на всем
интервале 8.
И Зак* .11244. 161
<f\
\hj
^L
я*и
Черт. 100.
Г Ь
Семейство Д, Д = {8}, таких интервалов 8 удовлетворяет, очевидно,
условию применимости леммы БореляЛебега. Поэтому из семейства Д
можно выделить конечное число, т, интервалов Ьи 82, ,,,, 8W,
покрывающих целиком сегмент [а, Ь].
Окрасим мысленно в синюю краску всякий интервал 8*, на
котором функция / отрицательна, и в красную краску всякий интервал 8^,
на котором / положительна. Ясно, что среди интервалов Ьи 82,..., Ьт
самый левый будет
синий, а самый правый
±-^ ^ % ^ь будет красный (черт,
101).
а Ор ир
Черт. 101. jaK как интервалов
Ьи 82,..., 8W имеется
лишь конечное число (т), то среди синих имеется самый правый;,
пусть это будет интервал %p==(api Ьр). Правая граничная точка Ьр
интервала Ьр не может быть синей, так как в этом случае она должна
была бы принадлежать некоторому синему интервалу 8^ и, значит, Ьр
не был бы самым правым синим интервалом. Но точка Ьр не может
быть и красной, так как тогда она была бы покрыта некоторым
красным интервалом 8^, причем 8^ и bq непременно перекрывались
бы, что невозможно, потому что окраска у них разная.
Из противоречия следует, что функция / (х) необходимо
обращается в нуль в некоторой внутренней точке сегмента [а, Ь].
Примечание. Доказанное важное предложение верно лишь
для сегментов, оно ложно даже для замкнутого множества*
если оно не является сегментом.
Черт. 102.
Действительно, пусть F есть какое-нибудь ограниченное замкну-
тое множество, не являющееся сегментом. Это означает, что имеется
по крайней мере один смежный к F интервал 8, по левую и по
правую стороны от которого имеются точки множества F (черт. 102).
Полагая f(x) = — 1 для точек множества F, лежащих цалево от
8, и /(л;) = ~|~ 1 для точек множества F, лежащих направо от 8, мы
получаем функцию / (х), определенную на F и непрерывную на F
относительно F. Эта функция изменяет свой знак на F% но нигде на
нем в нуль не обращается.
Теорема 7. Непрерывная функция на сегменте принимает
на нем все значения, промежуточные между ее максимумом и
минимумом на этом сегменте.
В самом деле, пусть А и В суть минимум и максимум
непрерывной функции f{x) на сегменте [а, Ь]. Пусть С есть какое-нибудь
число, удовлетворяющее неравенству
162
А<С<В.
Полагая
o(x)=f(x)-~C,
мы видим, что о{х) непрерывна на сегменте [а, Ь] и заведомо
изменяет на нем свой знак, так как в точке хь где f(xt)=A> мы имеем
?(*!)=/(*!) — С==Л — С<0
и в точке Хо, где /(дг2) = #, мы имеем
о {х2) —f(x2) — С = £ — С> 0.
Следовательно, в некоторой точке 5 сегмента [а, £] непрерывная
функция <рМ обращается в нуль, т. е.
Это и показывает, что /(£)== С.
Обычно это предложение выражают словами: непрерывная
функция не может перейти от одного значения к другому^ не пройдя
при этом через все промежуточные значения.
Действительно, если С есть число промежуточное между числами
f(a) и /(b), то имеем Л<С<# и, следовательно, С есть значение
функции f(x) на сегменте [а, Ь].
Отметим, что теорема не верна для замкнутых множеств, не
являющихся сегментами.
Теорема 8. Если f(x) непрерывна на сегменте [а, Ь], тогда
для каждого г, г>0, существует такое положительное tq, ?|>0,
что для любых двух точек х' и х" сегмента \а,Ь], сближенных
между собой меньше, чем на число т), |лг" — х'\ <yj, будет удовле*
творяться неравенство
\/(х")-/(х')\<г.
Эта замечательная теорема, носящая имя теоремы о равномерной
непрерывности, была впервые доказана Георгом Кантором. Чтобы
понять ее сущность, необходимо обратить внимание на следующее
обстоятельство: раз/(^непрерывна на сегменте [а, Ь], то это значит
только то, что f(x) непрерывна в каждой отдельно взятой точке х0
этого сегмента. Но раз f(x) непрерывна в точке х0У то это
означает, что для каждого е, е > 0, будет удовлетворено неравенство
\f(x)—f(x0) | < е, лишь бы точка х была приближена к
рассматриваемой точке х0 ближе, чем на некоторое числом, т. е, если справедливо
неравенство \х — х0|<т]. Но здесь число % подбираемое для
взятого s, зависит от положения точки х0, И если мы точку х0
возьмем в другом месте сегмента [я, Ь]> то, вообще говоря, и число г[
придется подбирать уже другим, может быть гораздо меньшим.
Следовательно, предполагая непрерывность функции f(x) в каждой
отдельно взятой точке х0 сегмента [а> Ь], мы видим, что число *}
зависит не только от г, но и от точки х0, т. е. это число i\ нужно
отметить значком дг0, написав его в виде ^.г0,%0 > 0. Итак, из
непрерывности функции f(x) в точке х0 следует лишь только то,
что мы имеем \f(x) —/(х0) | < е при справедливости неравенства
11* ' 163
1#—#оКЧа!ь. Если мы теперь начнем изменять х0) двигая х0 по
сегменту [а, Ь]% то изменяется и число %.о1 причем нисколько не
очевидно, что нижняя граница числа г\Го будет больше нуля.
Следовательно, нисколько не очевидно, что может быть найдено
единое число ?), годное для всех точек х0 сегмента [а, Ь], такое,
что будет удовлетворяться неравенство \f{x)—f(x0)\ < e, если
удовлетворено неравенство \х — х01<г\.
Поэтому, в высшей степени замечательно существование
положительного числа т), годного для всех точек сегмента [а, Ь] и
вызывающего справедливость неравенства \f(x")—f(x')\<le ПРИ сближении
точек х' и д;" ближе, чем на Y], | д;" — дг' | < т), где бы ни
находились эти точки х' и хп на сегменте [я, Ь]. Можно еще пояснить
указанное свойство равномерной непрерывности следующим образом: при
непрерывности функции f(x) в любой точке х0 сегмента [а, Ь] мы
имеем равенство lim \f(x)—/(д:0)] = 0, когда lim (д: — д:0) = 0. Но
здесь точка х0 предполагается хотя и произвольно выбранной, но
неподвижной. Теорема же о равномерной непрерывности говорит
о том, что мы имеем равенство lim [/(У)—/(д;')]=0, когда
lim (х"— х') = 0, причем отнюдь не предполагается, что одна из
точек х' и х" есть неподвижная или стремящаяся к какому-нибудь
предельному положению: обе эти точки х и д;'7 могут быть подвижными
и притом могут двигаться по сегменту [а, Ь) каким угодно способом,
не стремясь ни к какому пределу. Существенно лишь то, что при
\ ш г
ъ~,\ Л I..J 1..8 L-J 1 I 1,1 ,1 I I I A J—
\q К' X" X' X" \Ь
Черт. 103.
своем движении по сегменту точки х' и х" безгранично сближаются
между собой, так что их расстояние \х"—х' | стремится к нулю.
Перейдем к доказательству теоремы о равномерной непрерывности.
Возьмем какую-нибудь точку х0 сегмента [а, Ь]. Пусть а—сегмент,
содержащий точку х0 внутри, и такой, что колебание функции / на
о меньше, чем- • Обозначим через 8 интервал, полученный удалением
из о обоих его концов; интервал 8 содержат точку х0. Ясно, что
семейство. А, А = {о}, всех таких интервалов 8 удовлетворяет условию
леммы Бореля-Лебега. Отсюда весь сегмент [а, д] покрывается ко-
нечным числом интервалов o^Og,.. ,,8Ш, выбранных из семейства Д.
Граничные точки этих интервалов образуют конечную систему точек,
разделяющих сегмент [а, Ь] на конечное число малых сегментов
(черт. 103). Обозначим через г\ длину наименьшего из этих малых
сегментов. Пусть теперь х и х" две какие-нибудь точки сегмента
[а, *], отстоящие друг от друга меньше, чем на % т. е. пусть
\Х" — Х'\ <Y].
Ясно, что эти две точки х' и х" или лежат обе вместе на одном из
этих малых сегментов, или находятся в двух соседних сегментах.
Ь4
В первом случае мы, очевидно, будем иметь неравенство
|/(**)-/(*') К !<*,
потому что в этом случае х! и хг/ обе принадлежат одному из
сегментов oiy полученных от присоединения к интервалу 8tf обоих его
граничных точек. И так как колебание функции /на а4- меньше, чем ~, то
отсюда и следует справедливость предыдущего неравенства. Во втором
случае мы, обозначив точку деления, лежащую между х' и х"% через z>
имеем
I/(*')—/(*)!<-J и |/(**)-/0О1<£»
потому что пары точек х' и г, х" и г принадлежат, каждая, одному
из сегментов ои колебание на которых функции / меньше -к • Но из
этих двух неравенств следует одно неравенство
откуда и следует справедливость теоремы Кантора о равномерной
непрерывности.
Доказательство дано для случая непрерывной функции f(x) на
сегменте. Чтобы видеть, что теорема сохраняет свою силу и в общем
случае, когда функция / определена лишь на замкнутом ограниченном
множестве F и непрерывна на нем, достаточно пополнить данную
функцию/ (хотя бы линейной интерполяцией) так, чтобы дополненная
функция / (совпадающая с /на f) была бы непрерывной на
некотором сегменте [а, 0], содержащем ограниченное множество F
(данное замкнутое множество F заранее предполагается
ограниченным). Тогда в силу доказанного, функция /равномерно
непрерывна на [а ,#]. Это значит, что для всякого s, e > 0, имеется
положительное % т) > 0, таксе, что неравенство | х"—xr | < Y) влечет
за собой неравенство |/(/)-/(^)1<8' Здесь точки х! и х"
предполагаются любыми на [а, Ь\ и в частности они могут принадлежать
замкнутому множеству F. Нона множестве .рмы имеем всюду/ = /.
Следовательно на F предыдущее неравенство становится
|/(Л-/(*')!<••
А это и требовалось доказать.
Примечание. Для других множеств эта замечательная теорема
становится ложной. Например, на интервале (0,1) функции /(л)==
= sin— есть всюду непрерывная и ограниченная, но равномерной
непрерывности на (0,1) нет.
Далее, на бесконечном замкнутом множестве (— со, -f-oo)
функция /(*) = sin (x2) есть всюду непрерывная и тоже
ограниченная, но равномерной непрерывности на (—со, -f-со) нет. Однако,
функция f(x) = sin x есть ограниченная и равномерно непрерывная
на ( — ©о, -f со). Приведем примеры рациональных функций:
105
функции f(x) = < , 2 и /(.*) = л: равномерно непрерывны на
(— <ю, 4"°°) (заметим, что вторая функция не есть ограниченная);
функция f(x) = x2 не есть равномерно непрерывная на (— оо, -j- со).
§ 45. Непрерывные функции многих переменных. Обратимся
теперь к рассмотрению функций /, непрерывных на совершенном
множестве Р нескольких измерений.
Пусть М есть какая-нибудь точка, принадлежащая к
совершенному множеству Р (плоскому или пространственному). Пусть А есть
многомерный интервал, содержащий точку М и отсекающий от Р
порцию тг. Пусть Лг и Вк нижняя и верхняя границы на тг какой-
либо функции /, определенной лишь на совершенном множестве Р.
Это означает, что /не определена ни в одной точке, внешней для Р.
Пусть шп есть колебание функции / на порции тг, т. е.
»Я = ЯЯ — AKi шп>0.
Если диаметр порции тг стремится к нулю, тогда оба числа Az
и Вк стремятся к соответственным определенным пределам, которые
мы обозначим через Лм и Вм и которые будем называть верхней и
нижней границей функции f в точнее М совершенного множества Р.
Разность <*>М~ВМ — Ам называется колебанием / на
совершенном множестве Р в точке М.
Функция / называется непрерывной на совершенном множестве
Р в тЬчке М, если колебание <лм функции /на Р в точке М равно
нулю, т. е. если &м = 0.
Мы должны заранее сообщить читателю, что все без
исключения теоремы о функциях, непрерывных на линейных
совершенных множествах, доказанные нами, переносятся без всякого
изменения на функции, непрерывные на многомерных совершенных
множествах Р. Но если самые теоремы, т. е. их формулировки,
переносятся без изменения, то отсюда вовсе не следует еще, что
переносятся без изменения и доказательства. И, действительно,
мы увидим, что при доказательствах ряда теорем нам придется
придерживаться прямого метода, потому что косвенный метод,
основанный на употреблении теоремы о пополнении непрерывной функции /,
определенной только на Р, на любой сегмент, содержащий Р, здесь
трудно проводим, так как эта теорема трудно доказывается для лю*
бых многомерных множеств Р.
Прежде всего, предложения 1, 3, 4 и 8 параграфа 44 перено-
сятся на случай многомерного совершенного множества Р без
изменения в доказательствах, потому что в этих доказательствах
линейность совершенного множества Р не играет никакой роли. Следует
лишь указать на необходимость^изменения в обозначениях: величину
функции / в точке х оси ОХ мы обозначили через f(x); теперь
величину функции / в точке М (х, у) плоскости XOY или в точке
М(х, у, г) пространства OXYZ мы обозначаем через /(дг, у) или
f(x,y, z) илиа что еще проще, через f(M), полагая для случая
плоскости
166
и для случая пространства
/(Л)-/(*,* г).
Поэтому неравенства (4) и (5) в § 41 должны писаться так:
1 Д*> У у *)— /С*о> Л» *о) 1 <8>
когда
I* — *ol <Ъ \У—Уо I <Ч и | г — г0\ О.-
Итак, нам остается лишь оправдать свойства функций /,
непрерывных на совершенных (многомерных) множествах.
Сначала дадим определение: Функция /, определенная на
совершенном (многомерном) множестве Р, называется непрерывной
на Р, если она непрерывна на Р в каждой его точке.
Мы начинаем с обобщения леммы Бореля-Лебега на случай
любого ограниченного замкнутого (многомерного) множества F.
Это обобщение читается так: Каково бы ни было множество
{Д} многомерных интервалов Д, имеющее то свойство, что всякая
точка ограниченного замкнутого множества F принадлежит по
крайней мере к одно ну интервалу Д множества {Д}, всегда можно
выделить из {Д} конечную систему интервалов Дь Д2,..., Дш,
обладающую по отношению к F тем
же самым свойством, что и все
множество {Д}.
Доказательство этой леммы
совершенно аналогично тому, какое дано
в § 29 для того простейшего случая,
когда F есть линейный сегмент [а, о].
Мы ограничимся случаем плоского
множества F. Пусть F содержится в
замкнутом четыреугольнике (т. е. двухмерном
сегменте) /?0,
(#о) №<*<*» £<„У<д1.
Предполагая, что лемма Бореля-Лебега неверна, т. е. что F нельзя
покрыть конечным числом двухмерных интервалов Д, отобранных из
данного множества {Д}, мы делим четыреугольник R0 на 4 равных
аЛ-Ь
замкнутых четыреугольника, проводя прямые х — —~— и у =
Г.
и
с
0
С
"R"
1
7
Черт.
1
104.
R0
1
I
) X
У=*
= ^к—, делящие его противоположные стороны пополам (черт. 104).
Ясно, что множество F разделится на 4 замкнутых множества (среди
них могут быть и пустые), содержащиеся в этих четыреугольниках.
И ясно, что, по крайней мере, одно из этих 4 замкнутых множеств
нельзя покрыть конечным числом двухмерных интервалов д, взятых
из {Д}, потому что в противном случае, вопреки предположению, и
целое множество F можно было бы покрыть конечным числом
интервалов Д. Пусть R1 есть тот замкнутый четыреугольник, который
содержит часть множества F> не покрываемую конечным числом ин-
167
тервалов А, отобранных из (Л). Поступая с четыреугольником /?,
точно так же, как мы поступили с начальным четыреугольником RQi
и так далее, мы образуем бесконечную последовательность
замкнутых четыреугольников
R0>R1>R2> ...>/?„>...,
содержащихся один в другом, причем стороны всякого следующего
вдвое меньше сторон предыдущего. Значит, четыреугольник Rn
стягивается в некоторой точке М0, когда п-~> + °°. Точка М0
принадлежит к множеству F, потому что всякий четыреугольник Rn
содержит точки множества F, а множество F замкнуто. Существенно то,
что часть множества F, содержащаяся в Rm не допускает покрытия
конечным числом интервалов А, взятых из {А}. Но, с другой
стороны, по условию теоремы существует в множестве {А} такой
двухмерный интервал А0, который содержит точку М0. Так как
интервал А0 открытый, а четыреугольник Rn стягивается к точке Мф
то для достаточно большого значения натурального числа я, Rn
содержится целиком в интервале А0. Но это невозможно, так как, с
одной стороны, Rn содержит часть множества F, не покрываемую
конечным числом интервалов А, взятых из данного множества {А},
а, с другой стороны, эта часть оказалась покрытой одним
интервалом.
Из этого противоречия и следует справедливость леммы Бореля-
Лебега^
Для случая трехмерного пространства OXYZ доказательство
остается тем же самым, только приходится замкнутый начальный
параллелепипед /?0== [я<д:<£, c^y-^d, g^Cz^Ch] делить на
8 параллелепипедов плоскостями
а -\- Ь с-\- d ___g-\~k
Из этой леммы Бореля-Лебега сразу следуют все основные
свойства непрерывных функций / на совершенном (многомерном)
множестве Р. Эти свойства следующие.
- Функция /, непрерывная на Р,
1) ограничена на Р,
2) достигает своей нижней и верхней границы и равномерно
непрерывна на Р.
Действительно, пусть М есть какая-нибудь точка множества Р.
Раз / непрерывна на Я в точке М, то имеется многомерный
интервал А, содержащий М, и такой, что на порции П, высекаемой из Р
интервалом А, функция / ограничена. Ясно, что множество {А}
таких многомерных интервалов А удовлетворяет лемме Бореля-Лебега.
Следовательно, все целиком множество Р можно покрыть конечным
числом таких интервалов Д1э А2, ...., Aw, выбранных из
множества {А}. Но это и показывает, что функция / ограничена на Р.
Далее, функция f достигает своих границ: нижней А и
верхней В. Действительно, если бы / не достигала на Р, например,
168
своей нижней границы Л, тогда функция <р, определенная на Р
равенством
1 ^
была бы непрерывной на Р, потому что знаменатель /—А есть
непрерывная функция, нигде на Р не обращающаяся в нуль. Но
отсюда следовало бы, что о ограничена на Р. А это
невозможно, так как А есть нижняя граница функции / на Р и, значит,
имеется такая точка Af, в которой
0<|/(М) —Л |<е,
откуда и следует неравенство
1?И*)|>|,
что (в силу произвольной малости s) невозможно, так как <р должна
быть ограниченной на Р функцией. Из того, что <р не может быть
непрерывной функцией везде на Р, следует, что имеется на Р такая
точка М0У в которой /(Л10) = Л. А это и показывает, что граница
Л достижима функцией / на Р. Точно так же граница В является
достижимой.
Наконец, функция f равномерно непрерывна на Р. Это означает,
что для любого г, г>0, найдется такое положительное число ч\
(зависящее только от е), что всякий раз, как две какие-нибудь
точки Мг и М" множества Р сближены между собой меньше, чем
на ?), т. е. если М'М"<% будет справедливо неравенство
\f(M')-f(M»)\<e.
Действительно, пусть / не есть равномерно
непрерывная функция на А Это значит, что существует такое
фиксированное положительное % число е0, для которого не имеется
соответствующего положительного числа ч\. А это обозначает, что
как бы мало ни было положительное число тг), всегда найдутся две
такие точки Мг и М' множества Р, что, хотя они и являются
сближенными между собой меньше, чем на ?|, т. е. хотя мы и имеем
однако, для них справедливо неравенство
|/(Ж')-/(М'')|>г0.
Так как число е0 фиксировано, a -rj произвольно, то мы примем
7| = — (где п натуральное число). Пусть М'п и М"п та пара
различных друг от друга точек множества Р, которые удовлетворяют
условию
п п ^ ц
и для которых иг
1/(М'п)-/(М°П)\^ч. (8)
169
Пусть точка zn есть средина, прямолинейного отрезка М'п Afn. Мы
имеем бесконечную последовательность точек
Zb ^2>' * '» ^»> • • • •
Пусть \ есть предельная точка для этой последовательности.
Точка \ может быть также геометрически тождественной с
бесконечным множеством точек последовательности гъ гъ ..., znj....
Этот случай представится, когда последовательность состоит из
конечного числа геометрически различных точек.
Ясно, что £ принадлежит к Р, так как в бесконечной близости
к 6 скопляется бесчисленйое множество точек множества Р, именно,
концов М'п и М"п отрезков МгпМ"п. Пусть А есть многомерный
интервал, содержащий точку £, и такой, что имеем
где Л4—любая точка множества Я, принадлежащая А. Здесь е есть
произвольно выбираемое положительное число.
Так как имеется бесчисленное множество натуральных чисел п>
для которых весь отрезок №'пМ*п попадает целиком в интервал А,
то для таких натуральных чисел п мы имеем
I/W-/(0|<«
Отсюда мы заключаем, что должны иметь
|/(ЛГ)-/(ЛГ)|<2г.
Но если мы выберем е < 4^ , то будем иметь
l/W-/(Af;i<.0, (9)
а это неравенство (9) противоречит неравенству (8).
Обнаруженное противоречие доказывает истинность теоремы о
равномерной непрерывности функции / на Р.
Сделаем к теореме о равиомернойнепрерывности следующее
замечание. Длина отрезка М' Мп для случая плоскости выражается
формулой
WM" = V{xf — xfy + (У — ff
и для случйя пространства
Здесь х\у\ г' и х",у",г" суть координаты точек М! и М".
Ясно, что если
1*'-Л<-Ь,|/-У'[<-з-Ч и |У_*-|<^Ч,
170
то мы имеем
MrW<7\
и для случая плоскости, и для случая пространства.
Отсюда следует, что теорему о равномерной непрерывности
функции /(л:, у) или функции /(*, уу г) двух или трех аргументов можно
сформулировать так:
Если функция /(л:, у) непрерывна на совершенном множестве Р,
то для всякого е, е > 0, найдется такое положительное число yj,
что неравенства
I*' —*"|<tt [У—Я<4
влекут справедливость неравенства
' |/(x'fy>-/(^f Л |< г,
причем точйи М'(х', у') и ЛГ (*",/') должны находиться на Р.
Для случая пространства неравенства
\хГ — х?\<% |У —У1<Ъ I*' —г'Кч
влекут справедливость неравенства
|/(Л/^)-ЖУ,ОК«.
Мы видим, что, действительно, все предложения § 44 о
непрерывных функциях на линейных совершенных множествах Р
переносятся на случай любых многомерных совершенных множеств Р.
Единственная теорема о пополнении функции /, определенной только
на Р и непрерывной на Р, такими значениями вне множества Р,
чтобы дополненная функция / оказалась непрерывной на всем
многомерном сегменте 8, содержащем Р, еще не получила своего
доказательства. Не касаясь в этой книге доказательства этого предложения,
мы возвращаемся к тому важному предложению § 44, которое
говорит, что:
Непрерывная на линейном сегменте [а, Ь] функция /(#),
принимающая в двух точках этого сегмента значения разных знаков,
обращается в нуль по крайней мере в одной точке этого сегмента.
Эта теорема, кажущаяся столь „очевидной4* для случая сегмента
[а, Ь), уже неверна, когда дело идет о функции /, непрерывной на
линейном множестве Р, не являющемся сегментом: в этом случае
функция / может менять свой знак на Р, не принимая нигде на Р
значения нуль. Но линейный сегмент [а, Ь] есть частный случай
связного совершенного множества, т. е. continuum'a. И
действительно, здесь мы имеем важное предложение:
Непрерывная функция / на связном совершенном множестве Р
(т. е. continuum'e Р), имеющая в двух точках множества Р
значения противоположных знаков, необходимо обращается в нуль
по крайней мере в одной точке множества Р.
Действительно, пусть f(M') > 0 и f(M") < 0, где М! и М" суть
две некоторые точки многомерного совершенного множества Р. Так
как мы предполагаем Р связным (т. е. continuum'ом), то для лю-
171
бого s, e > О, имеется ломаная линия L, состоящая из конечного
числа прямолинейных звеньев длины < е, точки соединения которых
Ли А%, . . . , Ап принадлежат к Р (черт. 105). Так как в концах
М' и М" ломаной линии L значения функции / имеют разные знаки,
то должно иметься звено А{А{ + и в концах которого значения /
также имеют разные знаки, например /(Л^) > 0 и /(Л/ \ J< 0.
Обозначим через z средину этого звена.
До сих пор мы предполагали число в любым. Положим теперь
е = —, где п натуральное число. Соответствующую точку z обозначим
через zn. Бесконечная последовательность точек zu z2i ..., zn,...
или имеет бесконечно много
геометрически различных точек, или имеется
точка, тождественная с бесконечно многими
точками zn. В обоих случаях имеется
точка с, являющаяся или предельной для
множества точек гъ г2, ... , zm ..., или
тождественной бесконечно многим точкам
последовательности zu z2, ... , zn, . ♦.
Эта точка $ принадлежит к Р, потому
что служит предельной точкой для
бесконечного множества точек, принадлежащих
к Р концов звеньев А{Ащ. Легко видеть,
что /(5) = 0. Действительно, если бы
/(;) ф 0, то имели бы, например, /(£) >0.
Но тогда функция / была бы положительной на всей порции П,
высекаемой из Р достаточно малым многомерным интервалом А,
содержащим точку S. Но это невозможно, так как внутри
многомерного интервала А должно содержаться целиком звено AiAi+1 при
некотором достаточно большом значении натурального числа п. И
так как в концах звена AiAi + i функция / имеет противоположные
знаки, то / не может быть положительной на Р всюду внутри Д.
Из полученного противоречия вытекает справедливость теоремы*).
Точно так же, как и при доказательстве теоремы 7 § 44, мы
убеждаемся в том, что:
Непрерывная функция f на связном совершенном множестве Р
не может перейти от одного значения к другому\ не пройдя при
этом через все промежуточные значения.
§ 46. Функции, непрерывные от совокупности аргументов,
и функции, непрерывные от каждого аргумента в отдельности.
Мы остановимся на случае функции двух аргументов f(x,y).
Сначала предположим, что функция f(x,у) непрерывна на самом
*) Теорема верна и для неограниченных continuum'oB, потому что если
/ изменяет знак в двух точках М и М неограниченного, continuum'a P, то
/ изменяет знак в точках М/ М" того ограниченного continuum'a Kt
содержащегося в Р, который содержит М' и М".' Но тогда / обращается
в нуль на К и, значит, / обращается в нуль на Р,
172
простом из всех двухмерных совершенных мно-
жест в, именно на двухмерном сегменте /?,
/?=[а<х<&, c^y^Cd],
Такая функция /(#,у), как мы знаем из предыдущего параграфа,
обладает свойством равномерной непрерывности во всем сегменте R,
включая сюда и его стороны. Это означает, что для всякого
положительного числа е
можно отыскать такое
положительное Y], 7) > О, ЧТО
на каждом квадрате Д,
имеющем стороной %
колебание функции f(x,y)
меньше чем е (черт. 106).
При этом совершенно
безразлично, где на R лежит
этот квадрат Д. В целях
выяснения важного
различия между функциями
/(л:, у), непрерывными
Y
(j
0
с
t
R
Черт. 106.
от совокупности аргументов, и функциями f(x,y),
непрерывными от каждого аргумента в отдельности, докажем
предложение:
Для того, чтобы функция f(x,y) была непрерывна на всем
(включая и стороны) прямоугольнике R, необходимо и
достаточно, чтобы f была непрерывна на каждой непрерывной кривой
у = о(х) и x=zty(y)> где о и ф суть произвольные непрерывные
функции, определенные соответственно
на сегментах [а, Ь) и [с, d] и
удовлетворяющие условиям а ^ <р (х) ^ £,
Иными словами, для непрерывности /
на замкнутом прямоугольнике R
необходимо и достаточно непрерывности / на
каждой непрерывной линии, униформной по
отношению к той или другой оси
координат и содержащейся в R.
1. Условие необходимо. В самом деле, если f(x,y) непрерывна
на замкнутом прямоугольнике R (черт. 107), то обе сложные
(составные) функции f[xy ср (х)] и /[ф(.у),.у] суть непрерывные функции
аргумента х и аргумента у, если только непрерывные кривые у = о (х)
и х = ф (*у) не выходят за пределы многоугольника R. Действительно,
раз функция <?(х) определена на сегменте [а <;#<;#] и непрерывна
на нем, она равномерно непрерывна на сегменте [а, Ь]. Это
означает, что имеется такое а, а > 0, что при соблюдении неравенства
\х" — х' | < а мы непременно имеем
Черт. 107.
!?(*") —?(*')!< Ч-
(10)
173
Здесь мы всегда имеем право предположить, что «<*], потому что
если бы мы имели a>Yj, то всегда можно уменьшить число a
и считать его меньшим ч\. Но раз мы имеем | х" — х* | < yj и
\о{х") — ©СО|< т], то это означает, что точки М и М"у имеющие
координаты
ЛП*', ?(*% М"1х",<?(х")]щ
находятся на одном и том же некотором квадрате Д, сторона
которого равна *¥). А тогда, в силу равномерной непрерывности
функции f(x,y) на замкнутом прямоугольнике /?, мы имеем
1/К, ? (*")] —Я*', ? (-')] К з, (11)
потому что колебание функции / на квадрате Д меньше, чем е.
Но неравенство (11) и показывает, что сложная функция / [л:, о (х)]
непрерывна на сегменте [а^х^С *]•
Это же самоа доказательство годится и для непрерывной кривой
x = ty(y): сложная функция f[<\>(y), у] есть непрерывная функция
на сегменте [с ^у <]d].
II. Условие достаточно. Предположим, что оно выполняется,
ко что принтом функция /(л*, у) все-таки не непрерывна на зам-
у нутом прямоугольнике /?. Покажем, что это предположение ведет
к противоречию. Действительно, раз /(х, у) не есть непрерывная
на замкнутом прямоугольнике W, то в /? имеется течка разрыва
\М0(х0,у0) функции f(x9y). Если Лэ и В0 суть нижняя и верхняя
границк функции f{xyy) в точке М0) то по крайней мере одно из
этих двух чисел Л0 и Б0 отлично от числа f(x0,y0). А мы знаем,
что в этом случае существует бесконечная последовательность
геометрически различных точек Л^, Л/3, ..., Nk% ... прямоугольника
/?, имеющая точку М0 своей единственной предельной точкой, и такая,
что значение f{Nk) функции/ в точке Nk стремится как к пределу
как раз к тому из двух чисел (или символов) Л0 и В0> которое
отлично от числа f(xc,yQ), когда k—>~j-co.
Обозначим через хк, ук координаты точки Nk и через Z0 то из
двух чисел (или символов) А0 и В0, которое отлично от числа
f(xQ,y0). В этих обозначениях мы имеем:
lim лгЛ = х0, lim yk*=*y0, lim f(xk>yk) = Z0, причем г0ф/(х0,у0).
Теперь сделаем следующее замечание: мы всегда имеем право
предположить, что никакая из точек Л^, No, ..., Nk не лежит на
вертикальной прямой дг = а:0. Действительно, если бы какая-нибудь
точка Nfc оказалась случайно лежащей на прямой х=*х09 то это
значило 6иу что хк^=х0. Но функция f(x,yk) есть непрерывная
функция аргумента х на сегменте [*<;х<^£]. В самом деле, мы
предположим функцию f(x,y) непрерывной на всякой непрерывной
линии, униформной по отношению к оси ОХ; в частности, f(xyy)
должна быть непрерывной и на горизонтальной прямой у-=*ук9 т. е.
f(x,yk) есть непрерывная функция аргумента х. Но раз f(x,yk)
непрерывна, всегда можно найти такое число лгТ, близкое к х0, но
174
ему неравное, чтобы выполнялось неравенство j/(x*k,>yk) — f(x0,yk) I <
< -г- . Точка Nl (xl,yk) близка к точке Nk (xQ, ук)9 но уже не лежит на
прямой xz=*x0. Заменяя в последовательности Л^, Nq> ..., Nk, ...
те из точек Nkt которые случайно лежали на прямой х==л:0,
точками N*, близкими им, но заведомо сдвинутыми но горизонтальным
прямым у=ук и, значит, уже не лежащими на вертикали х = х0,
мы будем иметь тот же самый предел Ит/(х*ь,ук) Для сдвинутых
точек Л£, как и для прежних точек Nh% т. е„ \\mf{x*k,yk) =
= Hm/(jrjjfc), когда k -* + со. Итак, будем предполагать, что
хкфх0. Установив это, мы ищем в замкнутом прямоугольнике R
так^ю непрерывную линию L, выражаемую уравнением
У =<?(*)>
где о(х) есть непрерывная на сегменте [а^х^.Ь], которая заведомо
бы прошла через бесконечно много точек последовательности Nu
iV2, ..., Nk, ... .
Чтобы построить такую линию L, поступим так: прежде всего
сохраним в последовательности Nv N2, . .. , MJv> . .. только такие
точки, которые находятся в бесконечном числе по одну
определенную сторону вертикали х = х0 (например, вправо от нее, если это
возможно), остальные точки, лежащие по другую сторону этой
вертикали, мы просто выбросим из этой последовательности. Сделав
это, возьмем какую-нибудь из сохраненных точек и обозначим ее
через N'9 N'(xf,yf). Далее, из оставшихся сохраненных точек
последовательности Nv N2i ..., /Vj., ... находим такую точку ЛГ,
N"(xr\y"), проекция которой х" на ось ОХ лежит ближе к точке
x0, чем проекция х' точки N' на эту же ось. Затем, из оставшихся
сохраненных точек последовательности Nu iVg, ... , Nki ... мы
отыскиваем тхакую точку N"' (х"\у'")9 проекция которой хт на ось
ОХ лежит ближе к точке х0> чем проекция х" ранее найденной
точки N" на эту же ось. И так далее. Вообще, имея уже
отысканными точки N\ AT, N"'\ ... , ЛЛ^-1*, мы ищем среди оставшихся
сохраненных точек последовательности Л^, ЛГ2, ... , Nk, ... такую
точку ЛЛ», ЛЛ(лгИ, yW), проекция которой х^ на ось Облежала бы
ближе к точке ха, чем проекции х', х", ..., л;^-1) всех ранее найденных
точек ЛЛ, N", ... , iV(v~3> на эту же ось. Таким образом мы
получаем вполне определенную бесконечную последовательность точек
ЛГ, N", ... , ЛД*>, ... , абсциссы которых х\ х", ..., jeO>), ...
монотонно (т. е. убывая или возрастая) стремятся к точке дг0 как
к своему пределу, т. е. lim хм = х0. Так как точки Л/', ЛГ, ...,
V -» + ОО
Af(v), ... принадлежат последовательности Nu N2> •.• , Nki ...,
то мы имеем
Нт у^)=у0 и Hm f{xb\ J**) —Z0 ф/(х0,у0). (12)
v -> -j- со v -> J- °°
Рассмотрим теперь пары точек (AW), (Л^'ЛГ'), .. .ДЛ/^-^Л/^),...
и соединим каждую пару точек прямолинейным отрезком. Мы полу-
173
чим, таким образом, бесконечною последовательность
прямолинейных отрезков N' N", ЛГ N"\ ..., №>-*) Mv), ... , совокупность
которых образует ломаную линию, состоящую из бесконечного числа
прямолинейных звеньев, соединенных друг с другом в точках N",
N"\ ... , N^\ ... (4tpr. 108). Линия эта униформна по
отношению к оси ОХ, так как абсциссы х\ х"> ... , *(*'), ... стремятся
монотонно к точке лг0. А в силу
того, что точка Mv) стремится
к точке М0 как к своему
пределу, когда v-> -f* °°» т0
построенная ломаная линия, по
присоединении к ней точки MQf
является непрерывной; концами
— к ней служат точки М0 и N'.
* Пополняя построенную лома-
Черт. 108. НУЮ линию двумя
произвольными непрерывными кривыми,
лежащими в /?, униформными по отношению к оси ОХ и
примыкающими своими концами к точкам М0 и N\ мы будем иметь
непрерывную линию L, изображаемую уравнением
L — ? (x)f
где <?(х) есть непрерывная функция на всем сегменте [#<!*<;#].
Т^к как, по условию, функция f (х, у) непрерывна на кривой L,
го сложная функция / [х, <р (х)} есть непрерывная функция
аргумента х на сегменте [а, Ь]. Следовательно, мы должны иметь
llmf[x<?\ <р (*<*>)] = /[*0> ф(х0)] =f(xQ% у0). (13)
Но, с другой стороны, равенство (12) нам дает
Нт/[*Ч ?(*<*))] =Нт /[*<*), yM]=Z0zfzf(x0,yQ). (14)
v->-f- со v ->■ 4- оо
Получилось противоречие, и мы можем считать теорему доказанной*).
Естественным кажется, на первый взгляд, думать, что если мы
потребуем непрерывности функции /(*,у) на любой алгебраической
кривой /,, содержащейся в R (черт. 109), то отсюда автоматически
будет следовать непрерывность функции f(x, у) во всем замкнутом
прямоугольнике JR.
Оказывается — это не верно. Чтобы убедиться в этом, заметим
сначала, что никакая алгебраическая кривая L, касаясь
какой-нибудь прямой D, не допускает прикосновения бесконечно высокого
*) Из доказательства, собственно, следует нечто большее, чем
содержится в самой формулировке теоремы, а именно: так как мы в этом
доказательстве нигде не пользовались предположением непрерывности функции
fix, у) на непрерывных кривых х = <1>(у), униформных по отношению к оси
ОХ, то отсюда следует, что: для непрерывности функции f (х, у) на
замкнутом многоугольнике R необходимо и достаточно непрерывности
функции f(x,y) на любой непрерывной линии у=ху(х), униформной по
отношению к оси ОХ и содержащейся в R,
Н(У
M0^vW
\....S
У*
. N*. 1
А/-7
^Jn"
\
>v-
176
порядка (черт. ПО). Это означает, что если алгебраическая
кривая L касается прямой D в точке АТ0, то как бы тесным ни было
это прикосновение, отрезок MQ перпендикуляра, опущенного на
прямую D из точки М, близкой к точке касания М0, не есть
бесконечно-малое бесконечно высокого порядка по отношению к отрезку
M0Q, когда точка М приближается по кривой к точке касания М0.
Более точно порядок бесконечной малости отрезка MQ по
отношению к отрезку M0Q выражается вполне определенным
положительным рациональным числом —, где р и q натуральные числа. Это
q p
значит, что существует такое положительное рациональное число—,что
имеет место точное равенство
lim-
р.
(15)
где k есть положительное число (следовательно, неравное нулю) и
где точка М предполагается безгранично приближающейся к точке
М0 по кривой L. Мы не
станем доказывать равенства (15),
отсылая для этого читателя к
R курсу теории функций ком-
01 о
Черт. 109.
Черт. 110.
плексного переменного *). С другой стороны, существует сколько
угодно непрерывных трансцендентных кривых, имеющих с прямой
прикосновение бесконечно высокого порядка. Например, кривая Z,
определенная уравнением
y-e-i, (16)
есть непрерывная линия; правда, для х — 0 ордината у не
определена предыдущей формулой, но, условившись считать у — 0, когда
х = 0, мы получим непрерывную линию, лежащую выше оси ОХ и
*) Обычный путь для этого доказательства следующий. Сначала,
предполагая свободный член многочлена Р(ху у) равным нулю, доказывают, что
ветвь алгебраической кривой Р(х,у) = 0, проходящая через начало координат,
. иэобразима сходящимся степенным разложением у = at-\- bfi-^cfi + ...,
где t = Xя-% р и q суть натуральные числа кафО. Затем,, принимая прямую D за
ось ОХ и точку jWq за начало координат, полагают MQQ s* x, QM =у и | а\ = k.
12 Эак. Ш4. 177
касающуюся оси ОХ в начале координат. Как известно из теории
пределов, это есть прикосновение бесконечно высокого порядка,
потому что справедлива формула
_ 1
Нт'
хъ
= 0,
(17)
как бы велико ни было натуральное число п.'
Заметив это, начертим на плоскости XOY две кривые L0 и Lu
определенные уравнениями (черт. 111)
(А>)
(М
г_
' X*
Мы уже знаем, что обе эти кривые непрерывны в каждой точке х
бесконечного интервала (— оо, -}- oo) и что они имеют в начале
координат прикосновение бесконечно высокого порядка к оси ОХ.
~~х -^^
Г"—-»-^^
. _ »
0
С-"-"
»
А
'о
"-""С
"Т
X
Черт. ПК
Определим теперь функцию /(лг, у) следующими условиями:
1)/(0,0) = 0;
2) /(л:, у) = 0 на кривой L0 и везде выше нее;
3) f(x, у) —0 на omf ОХ и везде ниже нее;
4)/(л:, у) — 1 на кривой Ll9 кроме начала координат;
5) на всякой вертикальной прямой х =» дг0, не проходящей через
начало координат (т. е. при х0ф0), определение функции /(лг, у)
пополняется линейной интерпеляцией.
Последнее условие означает, что, обозначив три точки встречи
вертикальной прямой х — х0 с осью ОХ, кривой Lx и кривой L0
соответственно через А, В и С, мы имеем на этой вертикали /=0
в точке С и выше нее (условие 2), /=0 в точке А и ниже нее
(условие 3), /==1 в точке В (условие 4); в силу же условия 5,
функция / линейна на сегменте [А, В) и на сегменте [В, С]. Ясно,
что определенная этими пятью условиями функция / непрерывна во
всякой точке MQ (x0, у0) плоскости, кроме начала координат,
которое является точкой разрыва функции /(дг, у), так как колебание
функции / в начале координат равно единице. Чтобы убедиться
178
в последнем, достаточно заметить, что всякий двухмерный интервал,
содержащий начало О, содержит и точки кривой Lu но / (0,0) = 0
и/=1 на кривой Lly в точках, отличных от начала; значит, это
колебание равно 1.
Легко теперь доказать, что построенная таким образом
функция /(х, у) является непрерывной во всех точках каждой без
исключения алгебраической кривой. Действительно, пусть Р(х,у) = 0
какая-нибудь алгебраическая кривая; обозначим ее, для краткости,
через Л. Если кривая Л не проходит через начало О, функция / на
Л непрерывна, потому что / всюду непрерывна на плоскости XOY%
кроме начала координат. Если кривая Л проходит через начало О,
но не касается в начале О оси абсцисс, то тогда касательная к
кривой Л в начале О пересекает ось абсцисс под некоторым углом,
неравным нулю; в этом случае кривая Л вблизи начала О переходит
из области, лежащей выше линии Z,0, в область, лежащую под осью
ОХ, пройдя через начало О. И так как в этих областях /=0, и
так как в начале О мы также имеем /==0, то на малой дуге
кривой Л, содержащей начало О, функция f(x, у) равна О и
следовательно прерывна всюду на линии Л. Наконец, если линия Л касается
оси ОХ в начале О, то вблизи начала О та ее часть, которая
расположена выше оси ОХу непременно должна лежать выше кривой L0,
потому что кривая L0 имеет с осью ОХ в начале О прикосновение
бесконечно высокого порядка, а алгебраическая кривая Л имеет
прикосновение конечного порядка. Отсюда и следует, чго вблизи начала
О алгебраическая кривая Л или лежит выше кривой L0i или лежит
ниже оси ОХ. Так как в этом и другом случае функция / равна
нулю, так как /(0,0) =*0, то отсюда следует, что функция/ (х, у)
непрерывна вдоль кривой Л.
Таким образом, функция f(x,y) может быть непрерывной на
всякой алгебраической кривой и, вместе с тем, не быть непрерывной
в некоторой конечной точке плоскости. Так как прямые линии суть
алгебраические линии, то отсюда следует, что функция /(х, у) может
быть непрерывной на всякой вертикальной прямой х== const и на
всякой горизонтальной прямой у = const, и, вместе с тем, все-таки
не быть непрерывной в некоторой конечной точке плоскости.
Введем такую терминологию: если некоторая функция
f(x,y), определенная на замкнутом прямоугольнике
R [a^Cx^b,c^y^d], непрерывна в каждой точке /?,
мы скажем, что „функция f(x, у) непрерывна на R от
совокупности аргументов х и уи.
Если же некоторая функция f(xf у)> определенная
на замкнутом прямоугольнике Rla^x^b, с^.у<^d],
непрерывна по любому одному аргументу, при
постоянном значении другого, мы скажем, что „функцияf(x,у)
непрерывна на R от каждого аргумента в отдельности".
На первый взгляд можно думать, что если функция f(x,
^непрерывна от переменного хЛ считая у неизменяющимся, и если она
в то же самое время непрерывна от переменного у, считая х
неизменяющимся, тогда она будет непрерывной в обычном смысле, т. е.
12* 179
азу от двух аргументов х и у, каким бы образом они ни
изменялись. Оказывается, на самом деле это не верно, так как функция
fix, у) может быть непрерывной от каждого аргумента в
отдельности без того, чтобы оказаться непрерывной от их совокупности,
другой, вполне элементарный, но более грубый, пример дает
функция /(*, у), определенная формулой
/(*,/>= iffy,, (18)
причем ее определение в начале координат О дополняется условием
/(О, 0)-0. (19)
Ясно, что функция f(x, у), определенная формулами (18) и (19),
ограничена и при этом не только в любом прямоугольнике /?, но и
на всей плоскости. Действительно, мы имеем (х—,у)2!>0. Отсюда,
х2-\-у2—2ху'^>0 и, значит,
*9+J>2>2xy.
Поэтому, мы имеем неравенство
\f(x,y)\<U (20)
справедливое для любой точки М (л:, у) плоскости XOY.
Ясно, что f (х, у) непрерывна в любой точке М^ (х0,у0)
плоскости, кроме начала координат. Действительно, если М0 не есть
начало координат, то х2-\-у2>0.
Следовательно, / есть частное двух
непрерывных функций, причем знаменатель не
обращается в нуль, и поэтому / непрерывна
в точке М0 (х0, у$ на плоскости XOY.
Следовательно, функция /(х, у)
непрерывна на любой прямой D, не проходящей
через начало О. Но / (ху у) непрерывна
и на самих осях координат ОХ и ОУ,
так как на них мы имеем / (х, у) = 0.
1ерт 112 И' одиако> Функция f(x, у) разрывна
в начале координат О. В самом деле,
на прямой D'D, делящей пополам угол
между положительными частями осей координат и, следовательно,
имеющей уравнение (черт. 112)
У = *> (21)
мы имеем, в силу (21), равенство
Следовательно, функция/(л;, у) равна 1 всюду на прямой DD\
кроме начала О, где / равна нулю. Поэтому, f (х, у) имеет начало
О точкой разрыва.
Читатель видит, как следует быть осторожным в рассуждениях
даже над непрерывными функциями двух аргументов.
180
, I 47. Пределы последовательностей непрерывных функций. Пусть
функция f(x) определена на некотором сегменте [а, Ь\. Если функция f (х)
не непрерывна в точке х& тогда мы говорим, чю f (х) разрывна в точке
х0 и что х0 есть точка разрыва функции / (х).
Мы уже знаем, что / (х) непрерывна в точке х0 тогда и только тогда,
когда колебание о^ функции f(x) в точке х0 равно нулю, <ох = 0. Если
х0 есть точка разрыва для f(x), тогда колебание функции / (х) в точке х0
есть число положительное, (лХо >> 0.
Теорема L Множество Е точек разрыва х0, для которых имеем
^х ~>к> z$e k положительное постоянное число, есть множество
замкнутое.
Пусть £ есть предельная точка для Е. Нужно показать, что £
принадлежит к Е. Возьмем какой-нибудь интервал о, содержащий точку £. Ясно,
что о содержит точки множества £". Отсюда следует, что колебание щ
функции / на интервале о не может быть меньше, чем k, так как из неравенства
щ < k вытекает, что колебание / в каждой точке интервала о также
меньше чем k, что невозможно, потому что Ъ содержит точки множества Е.
Итак, необходимо имеем неравенство щ^>к, откуда и следует, что
колебание / в самой точке 6 также >#. Следовательно, ш^>& и точка £
принадлежит к множеству Е.
Теорема II (Бэ р,а). Если в каждой точке х сегмента [а, Ь]
колебание <лх функции /меньше k, <&х<^к, то существует столь малое
положительное число -/], ч\ > 0, что на всяком интервале Ь, имеющем
длину меньше, чем q, колебание щ функции f также меньше, чем k,
w8<£. .
Пусть теорема неверна. Это значит, что имеется бесконечная
последовательность интервалов оь Ц..., оп,..., принадлежащих сегменту [а, Ь],
имеющих длину стремящейся к нулю при безграничном возрастании числа
п, и таких, что колебание функции / на Ьп всегда > k, щ > k. Обозначим
через сп средину интервала 5М. Множество точек сь с^ сп ..., имеет по
крайней мере одну предельную точку £. Если же точки сп геометрически
совпадают с конечным числом точек сегмента [а, Ь], имеется точка £,
совпадающая с бесконечным числом точек сп. Пусть о есть какой-нибудь
интервал, содержащий точку ?. Ясно, что о содержит целиком некоторый
интервал Ьп* Поэтому мы должны иметь ш5 ;>/?. Отсюда следует, что мы
должны иметь также оз^!> k, что противоречит предположению.
Заметим, что из теоремы Бэра тотчас же следует теорема Г. Кантора
о равномерной непрерывности. Действительно, раз / непрерывна в
каждой точке х сегмента [а, Ь], то для всякого положительного числа е, заранее
заданного, мы имеем <ах < е. А тогда, по доказанной теореме II Бэра,
следует, что имеется столь малое положительное число •/), что для всякого
интервала о, длина которого не превосходит величину yj, имеем <о3 < е. Но
это и есть теорема Г. Кантора о равномерной непрерывности.
Заметим, что обе доказанные теоремы I и II распространяются на
функции / многих независимых переменных, определенные на любом замкнутом
множестве F.
Теорема I. Если f определена на замкнутом множестве F, тогда
множество Е точек М, в которых колебание <о м функции f не меньше
положительной постоянной k, <оЛ1>^, замкнуто.
Теорема II. Если в каждой точке М замкнутого множества F
колебание <*>м функции f меньше k, о> м < k, то существует такое
положительное число yj, Y] > 0, что на всякой части F± замкнутого
множества F, имеющей диаметр меньше yj, колебание wFi функций f также
меньше, чем k, o>Fi < k.
Мы не останавливаемся на доказательствах обеих этих теорем, потому
что эти доказательства без существенных изменений тождественны уже
изложенным доказательствам теорем I и II для случая сегмента [а, Ь].
Определение. Функция /, определенная только на совершенном
множестве Р, называется точечно разрывной наР, если точки
181
непрерывности функции f на Р образуют множество Е, всюду
плотное на Р.
Вся важность понятия точечной разрывности будет видна из
дальнейшего. Покамест же мы ограничимся указанием на то, что множество Е всех
точек непрерывности какой-либо функции / на совершенном множестве Р
имеет исключительно важные свойства. Среди них особенную важность имеет
свойство, формулируемое в виде предложения:
Теорема Ш. Если множество Е всюду плотно на каком-
либо совершенном множестве тс, содержащемся в Р, то тогда Е есть
множество второй категории на тс.
Обозначим через Dn множество всех точек разрыва М функции / на Р.
в каждой из которых колебание юж!> -—. Согласно теореме I, множество Dn
замкнуто. Так как всякая точка разрыва М функции / на совершенном
множестве Р характеризуется тем, что колебание шж функции / в ней
(относительно совершенного множества Р) есть число положительное, <о^>0, то
отсюда следует, что соединение D всех множеств Dlt D2, .... Dnf ..♦
D = D1 + D2 + Dd+...+Dn+...
есть не что иное, как совокупность всех точек разрыва функции / на
совершенном множестве Р. Следовательно, множество-разность Р — D есть в
точности множество Е всех точек непрерывности функции / на совершенном
множестве Р (относительно Р), т. е. имеем
E=P — D.
Теперь» по условию, множество Е всющ плотно на совершенном
множестве я, содержащемся в Р. Отсюда следует, что множество Dn нигде
неплотно на тс, так как если бы Dn было где-нибудь плотным на тс, то
имелась бы порция тс' совершенного множества тс (высеченная из Р
некоторым пространственным интервалом Д')» на которой множество Dn было бы
всюду плотным. И так как Dn есть замкнутое множество, то Dn содержало
бы целиком эту порцию тс' и, значит, на тс' не могло иметься ни одной точки
множества Е, что невозможно. Итак, всякое множество Dn нигде неплотно
на совершенном множестве тс. Отсюда следует, что соединение Ds=£>i4"
+ D2 + ... + Dn + ... есть множество первой категории на тс и, значит,
Е = Р— /) есть множество второй категории на «.
Из доказанного предложения следует замечательное свойство
множества Е всех точек непрерывности функции / на совершенном множестве Р
(относительно Р): достаточно этому множеству Е быть всюду плотным на
каком-нибудь совершенном множестве тс, содержащемся в Р, как в силу
одного лишь этого обстоятельства, множество Е оказывается не только
несчетным на тс, но даже второй категории на тс и, следовательно, во всякой
порции тс' множества тс оно имеет мощность континуума. Отсюда
следует, что если множество Е всех точек непрерывности функции / на Р
(относительно Р) счетно, то это не есть произвольное счетное множество, но
оно должно быть нигде неплотным на всякой совершенной части тс
множества Р.
Действительно, если бы рассматриваемое множество Е было всюду
плотным на какой-нибудь совершенней части тс множества Р, то в силу теоремы
III оно было бы второй категории на тс, т. е. несчетным, что противоречит
предположению.
Введем следующее новое определение:
Какое-нибудь множество точек Еназывается рассеянным*), если
оно нигде неплотно на всяком совершенном множестве.
Рассеянное множество точек £ н е может быть не^чет:
ным. Действительно, если Е несчетно, то точки конденсации для Е
образуют, как мы знаем, некоторое совершенное множество Р, на котором Е
всюду плотно, что противоречит предположению рассеянности множества Е.
*) Понятие, введенное A. Denjoy: clairseme,
182
;
Всякое конечное множество точек Е есть, очевидно, рассеянное множество.
Но не столь просто построить бесконечное рассеянное множество £ и, в
особенности, выяснить строение произвольного рассеянного множества:
с одной стороны, ясно, что счетное множество точек Е, имеющее конечное
производное множество Е, есть рассеянное, но, с другой стороны, имеется
сколько угодно рассеянных множеств Е, имеющих производное множество
Ег не только бесконечным, но даже совершенным. Например, если Р есть
совершенное множество, содержащееся в сегменте [0, lj"и нигде неплотное
на нем, то счетное множество Е, составленное из центров сь с2,..., сп,...,
смежных к Р интервалов Ьь о2, о3 оЛ,..., есть, очевидно, множество,
имеющее множество Р своим производным множеством, т. е. Е' = Р. И
однако, очевидно, что Е есть рассеянное множество.
Введение понятия рассеянного множества позволяет
формулировать предыдущее в виде предложения: если множество Е всех точек
непрерывности функции f на Р счетно, тогда оно необходимо есть
рассеянное множество.
Пример. Легко указать пример функции /(л), имеющей на сегменте
[О, 1] наперед заданное конечное множество Е точек своим множеством всех
точек непрерывности.
Действительно, пусть Е={аь аъ..., ак}, где a.t суть точки сегмента
[0-<*-<11. Пусть 9 (х) есть функция Дирихле, равная 1, если х
рационально, и равная 0, если х иррационально. В этих условиях ясно, что
функция/(лг), определенная формулой т
/М = (* —<*i) (x — at)... (х — ак)-ч(х),
непрерывна в каждой точке а и разрывна всюду вне множества Е.
Возвращаясь к точечно разрывным функциям, мы видим, что
всякая точечно разрывная функция f на совершенном множестве Р
имеет на всякой его порции Р* множество мощности континуума
точек непрерывности относительно Р.
Значение понятия точечной разрывности становится ясным
из важного предложения, получившего название „прямой теоремы Бэра*:
Если функция /, определенная на совершенном множестве Р, есть
предел последовательности функций fb /2,..., /w,..., непрерывных на Р, <
/=siim /w, тогда/ точечно'разрывная на всякой совершенной части те
я->4-оо
множества Р (относительно те).
Заметим прежде всего, что для полного доказательства нам достаточно
установить точечную разрывность функции / лишь на основном
совершенном множестве Р. Действительно, раз это будет сделано, то этим самым
точечная разрывность функции / будет установлена и на всякой совершенной
части те множества Р (относительно %), потому что п также можно
рассматривать, как основное множество, и потому что на нем мы также имеем
/= lim fn, где fn есть непрерывная на те функция (относительно те).
Ввиду трудности доказательства, мы заранее укажем его принцип. Мы
допустим, что / не есть точечно разрывная функция на Р (относительно Р)
и после этого найдем на Р такую точку ЛГ0> в которой последовательность
непрерывных функций fb /2,..., /w... расходится.
Рассмотрим множество D всех точек разрыва функции / на Р
(относительно Р). Мы уже знаем, что
D = DL+Di+...+Dn+...9
где Dn есть множество всех точек М разрыва, в которых колебание
функции /на Р*&м> больше или равно —, т. е. шж>.—. Мы также знаем, что
т п п
Dn есть замкнутое множество. Так как, согласно, гилотезе, / не есть
точечно разрывная на Р (относительно Р), то среди множеств Dn
имеется такое Din> которое не есть нигде неплотное на Р. Это значит, что
Ш
имеется такой многомерный интервал А, что высекаемая им порции Рд
совершенного множества Р вся целиком содержится в Dm.
Докажем сначала, что для любого натурального числа кидлялюбдго
интервала 5, содержащегося в Д а содержащего точки множества Р,
найдется такой интервал о', содержащийся в Ь и содержащий точки
множества Р, и такие числа nf и п", &<Х<#", что на порции Р3'
всюду будет иметься неравенство
Для того, чтобы доказать это, возьмем натуральное число k и какую-
нибудь точку Л1* совершенного множества Р, принадлежащую интервалу о
(черт. 113). Так как
последовательность /i, /о, ... , /п...- сходится
д к / в точке M*t то для некоторого
числа л'>& мы имеем неравенство
|/(Л1*) —/Л'(Л**)|<е. (21)
Но/я/ непрерывна на Р. Поэтому
можно найти столь малый
интервал 6*, содержащийся в о вместе со
своими граничными точками и
содержащий точку М*, что колебание
функции fn, на S* будет меньше,
Черт. 113. чем s# с другой стороны, колебание
функции / в точке М* не
меньше—. &то означает, что на порции Р§* можно отыскать такую точку М**9
что для нее справедливо неравенство
|/(Л1*)-/(Ж**)|>1. ' (22)
Так как последовательность fb fb ... , fn, ... сходится к / в точке М**,
имеется число п"^>п\ для которого справедливо неравенство
\f(M**)-fn.(M**)\<*. (23)
Но функция /п„ непрерывна на Р. Поэтому можно найти столь малый
интервал 6', содержащийся в 5* вместе со своими граничными точками и
содержащий точку М**, что колебание функции fn„ на о' меньше, чем е.
Сопоставим полученные неравенства. Раз колебание функции fn„ на о* меньше,
чей е, и раз о* содержит точку М*, то мы из неравенства (21) выводим
неравенство
|/(ЛР)-/я, (М)\<2г, (24)
где подвижная точка М пробегает всю порцию Р§*. С другой стороны, раз
колебание функции /Л„ на о' меньше чем s, и раз о' содержит точку Л4**, то
мы из неравенства (23) выводим неравенство
I/ (Л1») —/я. (Af) | < 2t, (25)
где подвижная точка М пробегает всю порцию Р$' .
Сравнивая теперь неравенства (22), (24) и (25), где подвижная точка М
пробегает лишь порцию Рь, , мы получаем неравенство
14' W-/„»W<>~-4e' (26>
184
Здесь число s предполагалось заранее фиксированным, но сколь угодно
малым. Принимая £=-£--, мы получаем окончательно
Это неравенство справедливо на всей порции Р$', где k < п' < п".
А это и требовалось доказать.
Возвращаясь к основному доказательству, теперь уже нетрудно найти
точки расходимости М0 последовательности/!,/^...,/^ В
самом деле, положив сначала о = Д и k = 1, мы определяем интервал о'^ и
числа пг > пх > 1« такие, что
1
i
/п, — Л*" I > 2/я
на порции Рь,.
Положив, далее, S = о' и k = n\ мы определяем интервал о' и числа
К > Л1 > Л" такие, что
2 2 1
|/«"2—Л/21> 2т-
на порции Р^ •
Положив, затем, о = &а и k = я2, мы определяем интервал 03 и числа
пз ^ пз > л2 такпе» что
|/»з ^я
> 2/л
на порции Р%\ и тал: далее до бесконечности.
Последовательность интервалов
д>о; >о;>в;> ...>*;>...
стягивается к точке Af0> заведомо принадлежащей к множеству Р, потому
что диаметр интервала \ можно предположить убывающим до нуля, когда
4->-f-oo, и потому что интервал ov, содержась в интервале о^__1 вместе со
своими граничными точками, наверное содержит точки совершенного
множества Р. С другой стороны, мы имеем бесконечную последовательность
возрастающих натуральных чисел
1 < п[ < п{ < щ < л2 < пъ < «J <.. • <п[ < п\ <...
и неравенство
[/< (ЛГ0) —/W^ (Af0) l>2ST- (28>
справедливое для *v = 1, 2, 3,.... Но неравенство (28) невозможно, если
последовательность /1г /2,..., /п,... сходится в точке М0.
Итак, отрицание точечной разрывности на Р функции /, служащей
пределом на Р сходящейся последовательности непрерывных на Р функций
fb/ъ- •., /я» ♦••» /= ^*га /п» приводит к заключению, что на Р имеется
гс-> -Ь оо
точка Мо расходимости этой последовательности. Поэтому, функция / не
может не быть точечно разрывной на Р. Это и требовалось доказать,
V::
Р качестве приложения прямой теоремы Бэра рассмотрим
производную f (х) некоторой непрерывной диференцируемой функции F(x), т. е.
Мы предполагаем, что производная f(x) определена во всякой точке х
некоторого сегмента [#, Ь]. Заранее нам ничего неизвестно относительно
производной / (х). Более того, в самом общем случае мы обязаны
предполагать производную f(x) разрывной функцией. Действительно, если, мы
рассмотрим непрерывную функцию F[x)
F(x)==x*sin—f
то тотчас же заметим, что эта функция F(x) во всякой точке сегмента
[ —1» + 1] имеет производную. В самом деле, если х ф О, эта производная
/ (х) = F'(x) вычисляется согласно правилам диференциального исчисления:
f(x) = F'(x) == 2x sini — cos! # f29)
Если же х = 0, производная /(0) = F'(0) вычисляется прямым образом, т. е.
посредством непосредственного перехода к пределу:
о /t2 sin —
/(0) = F(0) = Hm F (h) — F^) ^ нт _£- = llm h sin-r-^0.
Итак, Y (0) = 0. Формула (29) показывает, что производная / (л*) есть
разрывная функция и имеет точкой разрыва х = 0. Действительно, если аргумент
х стремится к нулю, то первый член 2х sin— формулы (29), очевидно,
стремится к нулю, а второй член cos— совершает бесконечное число раз
колебания между — 1 и + Ь Поэтому, производная / (х) имеет колебание 2
в точке дг = 0.
Итак, вообще говоря, производная / (х) непрерывной функции F (х)
есть функция разрывная. Но доказанная прямая теорема Бэра говорит нам,
что наряду с возможными точками разрыва, производная функция f(x)
непременно имеет точки непрерывности*
Действительно, так как мы имеем
F(*+i)-Fw
f (x) = F' (x) = lim —- 1 »
П -> + ОО J*.
П
то производная /(*) есть предел последовательности непрерывных функций
/i (x)i Л(х)>•--> /п (*), • • •> гАе мы полагаем
F(* + i)-F(*)
л»м=— -—т
п
когда /г-> 4"°°» Поэтому, согласно прямой теореме Бэра, производная
функция f(x) есть точечно разрывная на сегменте [a, h\t как и на всякой
совершенной части я этого сегмента (относительно я),
186
Итак, всякая производная функция f (х) необходимо имеет множество ,
мощности континуума точек непрерывности. Без прямой теоремы Бэра
мы не знаем доказательства этого интересного предложения.
Прежде чем перейти к обратной теореме Бэра% мы введем
вспомогательные определения.
Функция /*, определенная на совершенном множестве Р, называется
ступенчатой на Р, если Р можно разбить на счетное число
неперекрывающихся порций замкнутых множеств Р = ех + *2 + • • • + еп + • • •> на
каждой из которых f* есть постоянная.
Функция /, определенная на Р, называется ступенчатой до е в точке Мо,
если имеется такая ступенчатая на Р функция /*, что имеет место неравенство
I/—/*1 < е> справедливое на порции Р$, высеченной некоторым интервалом Ь,
содержащим точку М0.
Функция / называется ступенчатой в точке Mq% если она есть
ступенчатая в точке Mq до любого положительного числа е.
Лемма I. Множество точек Е, в каждой из которых функция f
не есть ступенчатая до е, есть совершенное множество.
Во-первых, Е есть замкнутое множество. Действительно, если точка N
есть предельная для множества £, то функция / не может быть в ней
ступенчатой до е, потому что тогда она, согласно самому определению, была бы
ступенчатой до е во всех точках порции Р§, высеченной некоторым
интервалом &, содержащим точку N. А это невозможно, так как такой интервал Ь
необходимо содержал бы точки множества Е.
Во-вторых, Е не может иметь изолированной точки. В самом деле,
пусть Mq есть такая точка. В этих условиях имеется интервал Д,
содержащий М$ и не содержащий никакой другой точки множества Е. Пусть теперь М
есть какая-нибудь точка порции Р^, отличная от точки Mq. Так как М не
принадлежит к Е, то имеется интервал Ь, содержащий М9 и некоторая
ступенчатая на Р функция ср*, такая, что имеем |/—<р*| < z, на всей П0РЦИИ Pfr
Мы заметим, что имеем право предположить интервал 5 рациональным,
потому что уменьшение его размеров, лишь бы он содержал М, не нарушит
написанного неравенства. По этой же причине мы вправе предположить,
что о содержится в Д. Заметим еще, что точка М0 не может входить в
рассматриваемый рациональный интервал 5, потому что иначе Mq не входила бы ъЕ.
Но множество всех рациональных интервалов в о счетно. Поэтому, мы можем
занумеровать все интересующие нас рациональные интервалы Б, написав их
в виде простой бесконечной последовательности Ьь Ъ* о3,..., Ьп,. ... К тому
же мы имеем право предполагать, что всякий интервал Ьп содержит точки
порции Рд, не принадлежащие предыдущим интервалам blt o2,..., оп_1в
Обозначим через <рп* ступенчатую функцию, соответствующую интервалу ол.
Построим теперь" новую функцию/*, определенную следующими
условиями:
1° /*(ЛТо)=ДЛ10);
2°/* = <рп*вточках порции Р6л, не принадлежащих предыдущим
интервалам 0^ ^2tb**» &П—1>
3° /* = О всюду на Р вне интервала Д.
Ясно, что функция /*, определенная на Р этими условиями, есть
ступенчатая на Р. Это следует из того, что порция е замкнутого множества, на
которой уп постоянная, если сохранить от нее лишь точки, принадлежащие
к Р$п и не принадлежащие к bv o^,..., Ъп„ь распадается, очевидно, на
ограниченное число порций замкнутых же множеств. Это важное обстоятельство
обусловливает ступенчатость на Р построенной функции /*. И так как мы,
очевидно, имеем [/—/*| < г на всей порции Р^, то точка MQ, содержащаяся
в Д, не может принадлежать к Е. Таким образом, множество Е не может
иметь изолированной точки и, значит, оно есть совершенное.
Лемма II. Функция f не имеет на совершенном множестве Е ни
одной точки непрерывности (относительно Е)%
М7
Если бы /оказалась непрерывной на Ев какой-нибудь точке М0
множества Е% то тогда можно отыскать интервал Д, содержащий MQ, и столь
малый, что колебание функции / на порции £д будет меньше, чем е. Далее
рассуждение происходит точно так же, как в лемме I. Именно, если М есть
какая-нибудь ючка порции />д не принадлежащая к Е, тогда точку М можно
заключить в рациональный интервал о, содержащийся в Д, и такой, что
имеется ступенчатая функция ср*, для которой имеем 1/—9*l<£ Ha BCe**
порции Р8. Мы всегда можем предположить интервалы занумерованными:
h> h> оз.---1 sw»-" и такими, что о^ содержит точки порции Рд, не
принадлежащие предыдущим интервалам oh 02,..., 8Л_г. Ясно, что никакой из
интервалов ^ не может содержать точек множества Е, так как в них /не
есть ступенчатая до е. Из сказанного ясно, что точки множества Р,
попавшие в интервалы о„,суть все точки порции Рд, не принадлежащие к Е.
Отсюда следует, что функция /*; определенная условиями:
1° /*=/(лЦ) на порции £д;
2° /* = cpw в точках порции Р§;г, не принадлежащих предыдущим
интервалам \у о2,..., on_j;
3° /* = 0 всюду на Р вне интервала Д,
есть функция, определенная всюду на совершенном множестве Р и
ступенчатая на нем, И так как мы, очевидно, имеем |/ — /*| < е на всей
порции Рд, то точка М0, содержащаяся в Д, не может принадлежать к Е.
Полученное противоречие доказывает справедливость леммы.
Из доказанного предложения вытекает справедливость предложения:
Лемма III. Функция /, точечно разрывная на всякой совершенной
части ъ множества Р, необходимо есть ступенчатая во всякой точке
множества Р.
В cafeoM деле, если / не есть ступенчатая в каждой точке множества Р,
тогда имеются точки, в которых / не есть ступенчатая до е при надлежаще
подобранном е. В силу леммы I, множество Е таких точек есть совершенное
и, в силу леммы II, функция / не есть точечно разрывная на Е, так как не
имеет на Е ни одной точки непрерывности (относительно Е). Это и
доказывает наше предложение.
Теперь мы можем доказать обратную теорему Бэра.
Функция /, точечно разрывная на всякой совершенной части я
множества Р, есть предел последовательности непрерывных на Р функций
/ь /?»••• t fn
Если / точечно разрывная на всякой совершенной части я множества Р,
тогда, по лемме III, / есть ступенчатая а каждой точке М совершенного
множества Р. Это означает, что каково бы ни было заданное число е, е>0,
имеется интервал о, содержащий точку М, и некоторая ступенчатая на Р
функция ср*, такая, что имеем |/— ср*| << е на всей порции Р§. Согласно лемме
Б о р е л я-Л е б е г а, все совершенное множество Р можно покрыть конечным
числом таких интервалов Ь. Мы обозначаем эти интервалы через bit 62,./.,5й
и соответствующие им ступенчатые функции через 4V ^з"»-» ¥&• К сказанному
прибавим, что мы отбрасываем всякий несущественный интервал Ьт, т. е. не
содержащий точек множества Р, которые не принадлежали бы уже к одному
из предыдущих интервалов Ьь 62,..., 5m-i«
Пусть, попрежнему, /* есть функция, определенная на Р условиями;
10 /* = 9* на Л-
2е /* = ср* в точках порции Р8п, не принадлежащих предыдущим интервалам
оь о2,..., о?г_1. Как и ранее, мы видим, что определенная таким образом
функция /* есть ступенчатая на Р и что мы имеем неравенство
135
справедливое на всем совершенном множестве Р. Дадим теперь числу г
значения ei, е2, ... ew... , образующие сходящийся ряд sj -f- ч + • • "• + £п + • • •
и обозначим через fn ступенчатую функцию, соответствующую числу г .
Имеем всюду на Р
|/-/*|<%- (30)
Сопоставляя неравенство (30) с неравенством
|/—/я-J <*„-!, (31)
мы получаем неравенство
1/"л—/«-il<*«-i+S« (32)
справедливое всюду на Р для я = 2, 3, 4,... .
Из неравенства (30) мы заключаем, что имеем
/ = lira /*
п ->4-°°
всюду на Р. Отсюда следует справедливость разложения
'/=А+(/1-/Ь+(Л-Л)+ --+<K-/n-i)+ •••
всюду на Р. Введя обозначения
мы получим разложение, справедливое всюду на Р:
/=£+£+£+ •••+ in+ •••• (33)
причем имеем на Р неравенство
№n!<en-i + £я (32*)
для я = 2, 3, 4, ... , показывающее, что разложение (33) есть абсолютно
оо
сходящееся, так как ряд 2(V-i + eM) сходится.
11-= 2
Всякая функция Ъп есть ступенчатая на Я. В самом деле, это
очевидно для я = 1, потому что &! —/i- Для я > 1 мы имеем ^ = /м— /»—i-
Пусть 4Я)#4Я). -.. • «in) » • • .и4я""1}. 4П""1}. ^у""1. • • • те порции зам-
кнутых множеств» на которых /;i и / w_i суть постоянные. Ясно, что
множества е^ X fiy*""""1*, Где ' и ./ пробегают независимо один от другого весь
натуральный ряд, имеются в счетном числе, что они не перекрываются попарно и
заполняют все множество Р. Так как общая часть двух интервалов
(пространственных) есть опять интервал, то всякое из этих множеств e^x*/1""1*
есть порция некоторого замкнутого множества (высекаемая из
произведения двух замкнутых множеств, порциями которых являются е™ие^п~~1\
произведением двух высекающих интервалов). И так как /^и/*в1 суть
постоянные на е\п} X ^f^1^ то <1* также есть постоянная на этом множестве.
Таким образом, уп есть с ту пек чата я функция на Я. Обозначим через аМ,
а^\ .. . , а(^ , . . . порции замкнутых множеств, на которых d>* постоянна;
пусть величина 6^ на а(£} равна постоянной С[£К Возьмем натуральное число/?,
189
не превосходящее числа п, р < я. Функция фр постоянна на порциях замкнутых
множеств а^\ а^,..., а(£\ .... Пусть интервалы, высекающие эти порции,
суть 5^, tffK .. . о^,. . . Мы обозначим через р^ совокупность всех
точек множества «^\ отстоящих от границы интервала Ь(р не ближе
чем на -. Ясно, что ^п есть замкнутое множество и что при безграничном
возрастании числа п замкнутое множество гр$ь увеличивается и стремится
к совпадению с множеством а(р) . Но множества а[р\ dJ^ а$\ .., Не
имеют общих точек. Следовательно, замкнутые множества
р$./»$ С <34>
(взятые только в числе п), будучи заключены в множествах afK o.(f\.,.;
,.., а (р\ не имеют попарно общих точек. Следовательно, множества (34)
попарно отдалены друг от друга на конечные (ненулевые) расстояния. При
этом, функция ^р равна на множествах (34), соответственно, постоянным
С[р), С(2Р),..., Clf\ Так как замкнутые множества (34) попарно отдалены
друг от друга, то мы всегда можем построить функцию fp, ПУ
непрерывную на всем пространстве, равную функции 6* на множествах
(34,) и на всем пространстве удовлетворяющую неравенству *)
\fp,n\<*p-i + zp, (35)
где р = 1, 2, 3,..., п.
Функция /п, определенная равенством
/»=/l, П+Д W +Д П + ••• +fptn-" +/»,№» (36)
непрерывна на всем пространстве.
Докажем, что во всякой точке Af совершенного
множества Р имеет место равенство f~\\mfn.
П -> -ЬОО
Действительно, пусть М есть какая-нибудь точка совершенного
множества Р и пусть р есть натуральное фиксированное число- Тогда точка М
принадлежит совершенно определенному множеству а^. Так как п -> + со» то
наступит такой момент, когда я > т, потому что число т есть
фиксированное. Ясно, что, начиная с достаточно большого значения числа п% точка М
будет находиться на множестве $Ц]п* содержащемся в а<£> Но раз точка М
принадлежит множеству* $Ц]п% мы имеем в этой точке равенство
/**=& (37)
*) Мы не входим в сущность этого построения, к тому же совершенно
ясного. Например, можно все пространство разделить на кубы, имеющие
ребро s. Этого достигаем, деля оси координат на сегменты длины е. Затем
мы полагаем /р,п равной постоянной C(jf* на тех кубах, которые содержат
(внутри или на границе) точки множества fy^. Так как множества (34)
отдалены друг от друга, то функция fp,n определена (и постоянна) на конечном
числе кубов, причем кубы, имеющие разные значения функции fPtn%
отдалены друг от друга, когда е достаточно мало. В этих кубах неравенство (35)
удовлетворено в силу неравенства (32*). Не представляет теперь ни
малейшего труда пополнить определение функции fp, n во всем пространстве так,
чтобы она была непрерывной на всем пространстве и удовлетворяющей
везде неравенству (35),
190
потому что fpn на множестве $£п равна постоянной (?£\ т, е. равна как
раз величине ступенчатой функции <Ьр.
Составим разность формул (33) и (36):
/-/»«(Ф1-/1.п)+(Й-/2.п) + ... + (Ф;-А.я) +
+ ...+(ф;-л.»>+4;+1+ *»+,+-. (38)
Так как для всякого фиксированного числа jy мы имеем, в силу (37),
равенство 4^—/p,w== 0, лишь бы я было достаточно велико,
то для всякого фиксированного числа q мы будем иметь q равенств
Ф*—/ь п =» °> Фг —Л» я = 0,. • •, Ф* — fq, n = О, (39)
лишь бы п было достаточно велико. Поэтому формула (38) дает
/--/п = (Ф«+1-/^+1,^ + ---+(Ф*--/^п)+Ф«+1 + Фп+2+.-. (40)
для п достаточно большого; из неравенства (32*) и (35) и равенства (40)
следует;
1/-АК1Ф;+1-/в+1.яГ + ..-+1Фя-/|..»1 +IO +
+ (ел+1 + еп+2> + ••• <3(eg-f £a + i+ s^+2+---)«
оо
Так как ряд 2 % есть сходящийся, то для q фиксированного, но до-
статочно большого, мы будем иметь
Ч + ££+* + ££+г + • • • < -|>
где е > 0 как угодно мало. Следовательно, мы имеем окончательно
\f — fn\<* (41)
при п достаточно большом. Неравенство (41), имеющее силу для любой
точки М совершенного множества Р, обнаруживает, что последовательность
непрерывных функций
J1 * /2» /з» • • •» /л» • • •
сходится на Я и имеет функцию / своим пределом.
Это и доказывает обратную теорему Бэра.
Соединяя прямую и обратную теоремы Бэра вместе, мы получаем
теорему Бэра:
Условие, необходимое и достаточное для того, чтобы какая-нибудь
функция /, определенная на некотором совершенном множестве Р, была
пределом сходящейся последовательности /i, /2, .. .,/м, ... непрерывных
на Р функций, f = Hm fm заключается в том, чтобы f была точечно
п -> + оо
разрывной на всякой совершенной части тс множества Р.
С этой теоремой связан критерий Бэра, заключающийся в том, что
на всякой совершенной части тс множества Р мы можем
отыскать одну точку непрерывности функции/нал
(относительно я).
Если нам это удается сделать, тогда / заведомо есть предел
последовательности непрерывных на Р функций. Действительно, если какая-нибудь
функция / не есть предел непрерывных функций, тогда она не есть
ступенчатая в каждой точке М совершенного множества Р, потому что все
доказательство обратной теоремы Бэра как раз и построено на том, что фун-
191
кция f, ступенчатая в каждой точке М множества Р, есть предел
непрерывных функций. Но раз / не есть ступенчатая в каждой точке множества
р, то должен существовать такой е, & > 0, что множество Е всех точек,
в 'которых / не есть ступенчатая до е, действительно существует (т. е. не
есть пустое множество). В силу леммы I множество Е есть совершенное* и,
в силу леммы II. на Е не имеется ни одной точки непрерывности функции /
(относительно Е).
Итак, для того, чтобы f была пределом непрерывных функций,
необходимо и достаточно, чтобы на всякой совершенной части тс множества Р
имелась по крайней мере одна точка непрерывности функции f
(относительно nj.
Это и есть критерий Бэра. Укажем наиболее типичные примеры.
Пример 7. Функция /, равная 0 всюду на Р, кроме одной точки, где
она равна 1, есть предел непрерывных функций. В самом деле, в этом
случае на всякой совершенной части п множества Р имеется точка
непрерывности функции /.
Пример 2. Пусть / равна 0 всюду на Р, кроме точек счетного
множества Е> в которых f равна \. Спрашивается, когда /будет пределом
непрерывных функций? Если Е есть рассеянное множество, тогда / имеет
точк# непрерывности на всякой совершенной части тс множества Р. Если
же Е не есть рассеянное множество, тогда имеется совершенное
множество Q, на котором Ь есть всюду плотное. А на таком множестве Q
функция / не имеет, очевидно, ни одной точки непрерывности (относительно Q).
Итак, рассеянность множества Е есть необходимое и достаточное
условие для того,' чтобы / была пределом непрерывных функций.
В частности функция Д ир ихл е /(лг), равная 0 Ьдя х иррационального
и равная 1 для х рационального, не есть предел непрерывных функций,
потому что f(x) не имеет точек непрерывности на сегменте [0<!.*<1].
Пример 3. Функция /, равная 0 для х иррационального и равная ~
в рациональной точке -у, гДе Дробь - несократима, есть предел
непрерывных функций, потому что эта / непрерывна во всякой иррациональной
точке, и, значит, всякое совершенное множество тс имеет точки
непрерывности.
Пример 4. Функция /(#), равная 0 вне некоторого совершенного нигде
неплотного множества Р, лежащего на [0<л:<1] и равная 1 на Р, хотя
и имеет на [0,1] бесконечность мощности континуума точек разрыва, однако,
есть предел непрерывных функций. Действительно, если тс есть какое-ниоудь
совершенное множество, лежащее на [0<л:<;1], когда тс имеет точку, не
принадлежащую к Р, то / (х) равна 0 на некоторой порции множества тс,
когда же тс содержится в Р, то f(x) = 1 на тс. В обеих случаях f(x) имеет
на тс точку непрерывности (относительно 7с).
Пример о. Если Р есть совершенное нигде не плотное множество,
лежащее на [0,1], то f(x), равная 1 в точках первого рода множества Р и
равная 0 вне их, не есть предел непрерывных функций на [0,1]. И, однако,
f(x) есть точечно разрывная на [0,1].
Примере. Пусть Рь Р2, ..., Рп, ... нигде неплотные
неперекрывающиеся совершенные множества, лежащие на [0,1], и такие, что каждый
интервал о, лежащий на [0,11, содержит точки некоторых из этих множеств.
Пусть £ = Pi + Р2 + ... -f- Рп + • • •• Ясно, что Е есть множество, всюду
несчетно плотное на [0,1]. , ,
Обозначим через f(x) функцию, равную 0 вне Е и равную ~ на
совершенном множестве Рп\ здесь я = 1, 2, 3. Определенная указанным образом
функция f(x) есть предел непрерывных функций. И, однако, f(x) имеет
несчетно много точек разрыва в каждом интервале о, лежащем на [0<ле<1].
Г Л А В А V.
НЕПРЕРЫВНЫЕ КРИВЫЕ.
§ 48. Кривые Жордана и кривые Пеанф. Когда мы говорим о
„кривой, начерченной на плоскости", наше воображение вызывает
образ тонкого штриха, вьющегося на плоскости, иногда
пересекающего, иногда не пересекающего самого себя. Если мы употребляем
терминологию теории множеств, законно спросить себя, какие свойства
должны быть приписаны множеству точек плоскости £, чтобы оно
могло рассматриваться как кривая, лежащая на плоскости?
Естественно искать то, что нам хочется называть кривой на
плоскости, среди ограниченных совершенных плоских множеств и,
чтобы говорить об одной кривой, а не о нескольких, естественно
рассматривать лишь связные совершенные множества, т. е. сопШшиш'ы.
Это и есть то первое общее определение кривой на плоскости,
которое было дано в науке Георгом Кантором и которое было им
выражено в словах:
Условимся понимать под кривой на плоскости всякое связное
совершенное множество Р, лежащее на плоскости и нигде неплотное
на ней.
Следовательно, для Г. Кантора плоская кривая есть простояло*
ский continuum, не содержащий никакой внутренней точки. Это
определение, совершенно точное, послужило в дальнейшем источником
многочисленных работ. Но нельзя не заметить, что оно не совсем
отвечает тому представлению о тонком штрихе, вьющемся на
плоскости, которое подсказывается нашим воображением. И хотя это
определение охватывает все алгебраические кривые, но оно охваты*
вает также и такие случаи, которые мы лишь с трудом можем
рассматривать как кривую, начерченную на плоскости. Например, если
мы удалим из квадрата счетное число открытых кругов, внешних
друг для друга, разбросанных всюду плотным образом по площади
квадрата, причем периферии этих кружков не касаются ни друг друга,
ни сторон квадрата, то неудаленная часть внутренней области
квадрата явится „кривой" в смысле Г. Кантора (черт. 114).
Всякий плоский continuum, лишенный внутренних точек, будем
называть кривой Кантора.
Ввиду некоторого несоответствия определения Георга Кантора
с нашим представлением „кривой", Камилл Жор дан дал другое
определение „кривой":
13 &ак. Ш4. 193
Плоская кривая есть совокупность точек плоскости,
координаты х и у которых даны двумя уравнениями
* = ?(#, У = Ф#Л
где <? и ф две какие-нибудь непрерывные функции переменного f9
определенные на сегменте [0<;/<;i].
В силу этого определения, если переменное t понимать как
„время", то движущаяся по плоскости точка М (ху у)у координаты
которой х и у даны уравнениями x=^o(t) и y = ty(t), где о и ф
непрерывны на [0, 1], описывает „кривую линию", когда
t возрастает от 0 до 1 (самые 0 и 1 сюда
включаются). ТЪкие кривые получили название кривых
Жор<^на. Определение, предложенное Жорданом,
есть столь же точное, как и определение Кантора,
и также послужило источником многочисленных
работ. Оно явилось безусловным прогрессом в науке,
потому что, в частных случаях, прекрасно
согласуется с нашим представлением о кривой как о
тонком штрихе, вьющемся по плоскости: например,
когда функции 9 и ф имеют непрерывные
производные <р' и ф', тогда кривая Жордана x=®(t)y y?=ty(t)
действительно является тонким штрихом, имеющим, вдобавок, определенную
длину S, даваемую известной формулой интегрального исчисления:
1
s=/|/^)+V2(o^-
Черт. 114.
Тем не менее определение Жордана скорее запутало вопрос о
кривой, чем выяснило его: в 1890 году итальянский математик Пеано
открыл, что кривая Жордана лг = <р(/), y = ty(t)y где <р и ф суть
непрерывные функции на [0, 1], может „заполнить площади* при
надлежащем подборе непрерывных функций <р и ф. Это означает, что
имеются такие пары непрерывных функций <р и ф, что множество
точек М(ху у) плоскости XOY, координаты. которых х и у даны
уравнениями д; = ?(/), ^аФ(0» содержит целиком множество всех,
внутренних точек некоторого квадрата. Одновременно с этим нужно
заметить, что всякая кривая Жордана, не состоящая из одной только
точки плоскости (это есть случай, когда непрерывные функции хр и
Ф суть постоянные), есть связное совершенное множество, т. е. con-
iinuum. Действительно, кривая Жордана есть замкнутое множество.
В самом деле, если Е есть кривая Жордана и М(%, ч\) есть точка,
предельная для Е, то имеется последовательность точек Мг> М2, ...,
Мк> ..., принадлежащих к Е и таких, что Мк -+ М, когда k -> + со.
Но раз точка Мк принадлежит к Е, то, обозначив координаты ее
через хк и ук, мы имеем лгЛ = ср(/Л), и .Ул = ф(/Л), где tk есть
некоторая точка сегмента [0, 1]. Последовательность точек tu t2, ..., tk, ...
имеет по крайней мере одну предельн}оо точку т, так как точки Мк
геометрически различны, следовательно, геометрически различны и
191
точки 4 сегмента [0, 1]. Пусть tkl9 tkv*.^ ik ,... точки, находя*
щиеся в последовательности tl9 /2> •••» 4» • • • и такие, что 4п-*т,
когда /г-* -j-oo. В силу непрерывности функций <р и ^ имеем
lim ? ('*«) = ? (lim hn) = ? (*)
и
Ит И'О = ♦(««*'О вФ(*).
Но <?(4j = ^ и ty(tkn)=ykni* мы, очевидно, имеем
Итл:ЙЛ = $ и lim ,уЛ|1 = ц.
Значит,
т. е. точка Ж принадлежит к Е.
Далее, кривая Жордана (не состоящая из одной точки) есть свяЗ*
нов замкнутое множество. Действительно, из равномерной
непрерывности функций ср и ф на [0,1] следует, что сегмент [0<С/^1] можно
рдзбить точками tut2i . . .,tm на столь малые сегменты [0,^], [t1} t2]y
'••> \U% ^+il> •••> I^w> 1] (ч"рт. 115), что колебание о&?нл;
функций с? (/) и 6 (*) на
каждом из них будет ........ ... , , t »
меньше наперед задан- 0 Ь Ъ t £*> 4 /
ного малого числа е,
е>0. В самом деле, Черт. 115.
для функции ср имеется
такое число ч\\ что неравенство \? — t"\ <ч\ влечет неравенство
1?Ю — ?(OI<s- Точно так же для ф имеется число r{\ r\r/ > 0,
что неравенство \f — f \ < ч\" влечет | ф (*') — 6 (Г) | < г.
Обозначая через т] наименьшее из двух положительных чисел ч\' и г[\ мы
имеем при соблюдении неравенства \tr—tn | <y) выполненными два
неравенства \у(¥) — ?(0| <е и |Ф(0 — т*(0|<е- Выбирая теперь
точки деления ^, t2, ..., tfw так, чтобы все сегменты [/г., /г.+1] были
по длине меньше, чем т), мы получим искомое деление сегмента [0,1]
на малые'сегменты [0, tt], [tut2], . . ., [tm, 1]. Пусть Pi точка кривой
Жордана Еу координаты которой суть х{ и yit где х^==о(^) и
^ = ^(^.). Ясно, что полагая £0 = 0 и tfw+] = l, мы имеем точки
^о» ^i» • • •' Ли* Л»+1» лежащие на кривой Жордана Е, причем
расстояние точек Pi и Pi+1 очень мало, так как
Пусть теперь Л/^, i^) и N2(l2> Ъ) Две какие-нибудь точки
кривой Жордана £. Это значит, что мы имеем
^ = 0(7^) и %««КП)
и
где Тг и Т2 две некоторые точки сегмента [0<Г/<;1]. Если Тг
принадлежит сегменту [t{, ti+1] и Г2 принадлежит сегменту [^-, ^+11,
мы имеем
I ?(<«) —?(7"i) |< • и 1<К'«)-<К7\)К«
13* 195
ii так же
I ?(';) — ?(П) ! <£ и | ф(*,) — 0(Т2) 1 <£,
потому что колебания функций о и ^ па сегментах [0, /^ [/2, /2], ... ,
• ••> [А>г> 1] меньше числа е. Отсюда мы заключаем, что расстояние
точек Р4 и Nt, и тякже точек Pj и N2 будут тоже меньше, чем
е]/2, т. е. PiNx <з|/2 и ;ЧА^ <s]/2. Значит, система точек
Nv P^ Pi+1, ЯгЧ2, . . . , Pj% N2 (мы предполагаем, что 7\<Г2 и что,
поэтому, г^у) такова, то прямолинейные отрезки
NxPuPiPiw Р<цР<ы ... , PjN2
.образуют ломаную непрерывную линию /, состаплепную из
прямолинейных звеньев, длины которых меньше е]/2 и которые соединяют
две точки А^ и N2, взятые произвольно на кривой Жордана Е} при-
Чсрт. 116.
чем концы всех этих звеньев Рь Р<м, ... , Pj принадлежат к Е.
А это и показывает, что кривая Жордана Е есть связное замкнутое
(и, значит, совершенное) множество, т. е. есть continuum. Таким
образом, всякая кривая Жордана x = ®(t), y=zO(t), не
заполняющая целиком никакого квадрата (т. е. не являющаяся кривой
Пеано), есть непременно кривая Кантора,
Действительно, в этом случае кривая Жордана есть нигде
неплотное на плоскости связное совершенное множество, т. е. кривая
Кангора. Но отекла нельзя заключать, что всякая кривая Кантора
является ьризой Жордана. Например, две криеые (черт. 116), из
которых первая есть окружность С с навертывающеюся на нее
изнутри спиралью 5, а вторая дается уравнением у = sin — для хфО,
причем к ней присоединен замкнутый отрезок [ — 1 <^<С +1],
лежащий на оси OY,—обе суть кривые Кантора, но не кривые
Жордана. В самом деле, если бы, например, первая кривля была
жордановой дг = 9(/), y = b(t), то точки, лежащие на о; р жности С,
соответствовали бы точкам t сегмента [0^^1], принадлежащим
некоторому замкнутому множеству F. Но существует спираль «S и
она должна также получаться, когда переменному t даем соответ-
196
ствующие значения. Значит, замкнутое множество F не может быть
тождественным с сегментом [0<;^<]1] и, значит, имеется некоторый
интервал (я, fr), смежный к F и соответствующий только точкам
спирали 6\ Но точки ^ = а и t=b соответствуют точкам
окружности С. Если мы теперь заставим переменное t, оставаясь в
интервале (а, &), стремиться к точке а или к Ъ, тогда точка М [?(t),^(/)]
должна по спирали S стремиться как к пределу к
точке окружности С, что невозможно при непрерывности
функций 9(0 и ДО).
Ввиду этого естественно было искать тех дополнительных
условий, наложенных на кривую Кантора, при которых она является
кривой Жордана. Таких условий было найдено несколько. Приведем
одно из них.
Пусть на плоскости XOY лежит некоторый continuum К (т. е.
ограниченное связное совершенное множество). Пусть М' и М" две
какие-нибудь точки, принадлежащее continuum'y К- Они могут быть
соединимы не только continuum'oM К (к которому они обе
принадлежат), но еще и другими сопйпиит'ами К', К", К"\ ... %
содержащимися в continuum}e К. Например, если continuum I( состоит
из окружности С и спирали S, K=C-{-S, то две точки М' и М'\
принадлежащие к К и находящиеся на окружности С, соединимы
друг с другом не только при помощи целого continuum'a К, но
еще и при помощи его части: дуги ММ" окружности С, К' = М' М'\
равным образом, если из двух точек М\ М" одна лежит на
окружности С (пусть /И'), а другая на спирали S (пусть Ж"), то Мг и М"
соединимы друг с другом при помощи continuum'a K\ составленного из окруж"
нэсти С и из той части S' спирали 5, концом которой служит точка М*
и которая навертывается на окружность С, /C/ = C-f-6v. Вообще го*
Еоря,. если точки Mf и Ml continuum'a К неограниченно сближаются
между собой (гтгигаясь по continuum'y /О, то диаметр соединяющего
их continuum'a К' не может стремиться к нулю. Это есть типичный
случай канторовоп нежордаповой кривой. Например, если М' есть
неподвижная точка окружности С и точка /И^ находясь на спирали S *
безгранично приближается к точке М\ когда п—> со, то диаметр
соединяющего их continuum'a K'n не может стремиться к нулю,
так как continuum K'n содержит окружность С.
То дополнительное условие, при котором канторова кривая
является жордаповой, может быть сформулировано в виде
следующего предложения:
Для того, чтобы плоский continuum К был кривой Жордана
x = v{t), y=z6(t)t необходимо и д:стапгочно, чтобы всякие две
безгранично сблиэшющиеся между собой точки Мг и Mr/ continue
inria К были соединимы continuum''ом К\ содержащимся в К,
диаметр которого стремится к нулю вместе с отрезком М' Мп\
Этот к р и тер и й, д л я т о г о ч т о б ы любой плоский
continuum К был кривой Жордана, сразу показывает, что
данный нами выше пример площади квадрата с удаленными из нее
открытыми кружками в счетом числе есть кривая Жордана. Не
}97
*
останавливаясь на доказательстве этого критерия, мы отметим, что
в матемаъическом анализе преимущественно рассматриваются кривые
Жордана.
Если мы имеем кривую Жордана x~<o(t), у = ф(7), где QO<l,
и если для всяких двух различных значений f и f\ t'=£t", соответ-
ствующие точки плоскости М' [? (f), Ф(01 и М" [о (t), ф (?')]
различны, тогда рассматриваемая кривая Жордана называется кривой
Жордана без кратных точек, или простой дугой. Если начальная
точка М0 [<?(0), ф(0)1 и конечная точка /^[^(И), ф(1)] кривой
Жордана совпадают, т. е. если ®(0) = u(ty и ф(0) = ^(1), то
кривая Жордана называется замкнутой. Если при этом движущаяся
точка M[o(t), <Н0]> когда * возрастает от 0 до 1, возвращается
в прежнее положение, в котором была раньше, лишь при£=1,
тогда кривая Жордана не пересекает самоё себя; про такую
замкнутую кривую Жордана мы скажем, что она образует простой за*
мкнутый контур, или что она есть
замкнутая кривая Жордана без кратных точек.
Как простые дуги, так и замкнутые жорда-
новы кривые без кратных точек составляют
предмет многочисленных работ. Из свойств
замкнутых жордановых кривых без кратных
точек важнейшим является то, которое вы-
Черт. 117. ражается предложением, кажущимся „оче-
\ видным":
Всякая замкнутая кривая Жордана без кратных точек делит
плоскость на две области, из которых одна есть внутренняя по
отношению к этой кривой, а другая — внешняя {черт. 117).
Мы не станем доказывать этого предложения, так как действа
тельно строгое доказательство его представляет трудности и занимает
много места. Заметим, что строгое доказательство теоремы Жордана
даже в том случае, когда контур есть обыкновенный многоугольник
(с конечным числом сторон), не столь простое, каким кажется на
первый взгляд, и требует для своего осуществления, отправляясь
от системы аксиом элементарной геометрии, указанной Гильбертом,
более трех десятков предварительных теорем, правда, довольно
элементарных. Таким образом, мы ограничимся тем, что просто сошлемся,
там, где это нужно, на истинность этого предложения, впервые
доказанного самим Жорданом.
Как на характеристику замкнутых кривых Жордана без кратных
точек следует указать на предложение: Для того, чтобы ограни*
ченный continuum К, делящий плоскость на две области,
внутреннюю и внешнюю, был замкнутой кривой Жордана без кратных
точек, необходимо и достаточно, чтобы всякая точка М,
принадлежащая continuum'у К, была концом двух непрерывных линий
L и V, составленных из счетного числа прямолинейных звеньев,
последовательно скрепленных своими концами, причем одна из этих
линий, L, составлена из точек (кроме точки М) внутренней
области, а другая линия, L% составлена (кроме точки М) из точек
внешней области.
|98
Ж
**£■-■
Черт. Ii8
В целях пояснения этого предложения, доказательство которого
выходит за рамки настоящей книги, мы укажем^ что. continuum
может делить плоскость на две области, вовсе не будучи жордановой
кривой. Например, continuum К, указанный на черт. 118 и
состоящий из части кривой .y = sin —., где — а<*< ~}-я, я>0,
прямолинейного отрезка [ — 1<з>< + 1], лежащего на оси OY, и
какой-нибудь замыкающей простой дуги А, есть кривая Кантора (но
не кривая Жордана). И, одна-
ко, К делит плоскость на две ' |
области, внутреннюю и
внешнюю. Здесь начало О есть
точка continuum'a /С,
недостижимая никакой непрерывной
дорожкой L или Z/, составленной
из счетного числа
прямолинейных звеньев и протекающей
целиком либо во внутренней
области, либо во внешней.
Отметим здесь же, что
недостаточно рассматривать
дорожки L и Z/, составленные из
конечного числа прямолиней- -
ных звеньев. Например, если
замкнутая жорданова кривая
без кратных точек содержит
такую точку Ж, вокруг
которой она делает бесчисленное
число оборотов (как,
например, обертывается около
полюса логарифмическая спираль
p = a'f, я>1) (черт. 119), то
такая точка М уже
недостижима непрерывной дорожкой L
или Z/, составленной из
конечного числа прямолинейных
звеньев и протекающей
целиком либо во внутренней
области, либр во внешней. При
этом такФй жорданов кошур К может оказаться даже имеющим
конечную длину (например, если он составлен из двух
логарифмических спиралей со спрямляемым поперечным сечением afi).
Мы должны предупредить читателя, что для совершенной ясности
в этих вещах необходимо точно определить, что такое „область",
данная на плоскости.
Областью на плоскости называется такое множество
точек §, всякая точка М которого есть внутренняя к нему,
т. е. может быть заключена в .столь малый двухмерный
интервал Д, который будет целиком содержаться в $ч
199
Из определения области следует, что точки, не принадлежащие
к плоской области $, образуют замкнутое множество, ограниченное
или неограниченное. И обратно, точки плоскости, не
принадлежащие к плоскому замкнутому множеству, образуют, всегда область.
Точки плоскости, не принадлежащие к данной плоской области $,
делятся на два класса: граничные точки и внешние точки.
Граничной точкой для области §> называется такая
точка N плоскости, которая сама не принадлежит к области S,
но которая является предельной точкой для точек этой
области.
Границей области $ называется совокупность всех
граничных точек N области S.
Из этого определения следует, что граница F области % есть
также замкнутое множество точек, ограниченное или
неограниченное. Действительно,
если N0 есть точка,
предельная для
границы F, то всякий двух-
мерный интервал А,
содержащий Nc,
должен содержать
граничные точки для
области §, а значит,
должен содержать и точки
самой области.
Поэтому ^Ч> не есть точка
области $, но есть
предельная точка для точек области S, т. е. Л/0 принадлежит к
границе /\ Следовательно, граница F есть замкнутое множество.
Внешней точкой для области $ называется такая
точка Р плоскости, которая не принадлежит ни к $, ни к ее
границе F.
Из этого определения следует, что Совокупность всех точек Я,
внешних для области $, образует, в свою очередь, область.
Действительно, если Р есть точка внешняя для области S, то должен
существовать столь малый двухмерный интервал А, содержащий Р,
который не содержит ни одной точки ни области $, ни ее границы /=,
потому что, в противном случае, точка Р принадлежала бы границе F.
Область § называется связной, когда две любые ее точки
М' и М" можно соединить полигональной линией L (т. е.
непрерывной ломаной линией, состоящей из конечного числа
прямолинейных звеньев), принадлежащей к области $.
Область $ называется односвязной, если внутренность
всякого замкнутого многоугольника П, периметр которого
принадлежит к S, также целиком принадлежит к §.
Этому определению можно дать такое пояснение: область б
од но связна, если всякий замкнутый многоугольник II,
принадлежащий к $, можно непрерывным движением на плоскости
стянуть в точку области, не выходя при этом из области §.
20Э
L
Черт. 120.
Из этого определения следует, что если область $ не есть
односвязная, то имеется замкнутый многоугольник П, контур которого
принадлежит к § и который содержит внутри по крайней мере одну
граничную точку N для $ (черт. 120). Отсюда же следует важное
предложение: Граница всякой односвязной ограниченной области
есть continuum. Действительно, если односвязная ограниченная
область $ имеет своей границей замкнутое множество F, которое не
есть continuum, , то тогда F разбивается на два замкнутых
множества F1 и F%> не имеющие общей точки. А тогда на плоскости можно
найти два такие замкнутые многоугольника Ut и П2, содержащие,
соответственно, внутри точки множеств Fx и F2> периметры которых не
Черт. 121.
имеют общей точки и содержат граничные точки области (черт. 121).
Так как многоугольники Па и П2 заведомо содержат внутри себя
точки области g (раз они содержат внутри граничные точки для g),
то две такие точки М! и М" можно соединить ломаной I,
принадлежащей к S. Эта ломаная L непременно пересечет периферию по
крайней мере одного из многоугольников Efj и IL>, и точки
пересечения должны принадлежать к $. Но тогда и все точки этого
периметра принадлежат к g, иначе на нем должны бы иметься граничные
точки для g, что невозможно. А отсюда следует, что g не есть одно-
связная область, так как этот периметр принадлежит к|, а
внутренность его не принадлежит целиком к g. *)
*) Предложением, до некоторой степени обратным, является
следующее: вынимая уз плоскости какой-нибудь continuum /<", мы получаем
конечное или счетное число неперекрывающихся связных областей-, если
К есть неограниченный continuum, все эти области о д н о с в я з н ы; если
К есть ограниченный continuum, все эти области ограниченные и
о дно связны, кроме одной, которая есть неограниченная связная
область.
Простой пример этому дает изображенный здесь continuum Л,
составленный из окоужностей, убывающих до края радиусов, соединенных
прямолинейными отрезками (черт. 122) и имеющими предельную точку N. Каждая
из внутренностей этих окружностей есть ограниченная односвязная область.
Единственная не односвязная область, остающаяся после вынутил coitmuum'a
К из плоскости — это неограниченная часть плоскости, внешняя для всех
кругов и соединяющих их прямолинейных отрезков. Если мы вынем из
плоскости XOY оси координат, то получим, очевидно, четыре неограниченные
односвязные области. Вынимая из плоскости какую-нибудь замкнутую жор-
данову кривую К без кратных точек, мы получаем две области: одна из
них $ есть ограниченная односвязная область, лежащая внутри кривой К*
2.01
Пусть g есть какая-нибудь область, лежащая в плоскости,
Назовем разрезом области g всякую простую дугу Жор-
дат L> концы которой находятся на границе F области &г все
же другие точки которой принадлежат области g (черт. 123).
Одним из важнейших свойств односвязных областей g является
следующее: Всякая односвязная область &/ какою ни. была бы ее
N К
^-^coqoooQOOO^
Черт. 122.
граница F, каждым разрезом L разбивается на две
неперекрывающихся области $' и g"; наоборот, если связная область $
не есть односвязная, всегда можно провести такой в ней разрез Li9
(Г)
Черт. 123.
после удаления которого из плоскости область Ъ продолжает
оставаться связной.
Например, область g, составленная ^совокупностью точек, нахо"
дящихся между двумя окружностями С и С', вложенными одна
другая из них g' есть неограниченная связная область, лежащая вне области,
ограниченной К', эта область g' уже не есть односвязная-, потому что
достаточно большой многоугольник П, содержащий кривую К внутри, имеет
периметр, принадлежащий к g', и внутри этого многоугольника имеются
точки, не принадлежащие к g'. r
Читатель видит, что всякая замкнутая жорданоза кривая К без кратных
точек есть точная граница только двух областей: внутренней g и
наружной g'. Но канторова кривая, вообще говоря, этим важным свойством не
обладает. Голландский математик Брауер построил точную канторову
кривую К> которая является точной границей одновременно трех одноевязных
областей g, g' и g". Мы не можем дать здесь это построение Брауера и
ограничиваемся лишь указанием на то, как следует быть осторожным там,
где вещи кажутся на первып взгляд, „очевидными8, потому что на первый
взгляд continuum AT, служащий точной границей одновременно трех
областей, представляется невозможным.
202
в другую не есть односвязнай (черт. 124). Разрез аЪ этой области!
сохраняет связность области §. Разрез же L\ проведенный в И, уже
заставляет утрачиваться связность.
' Введем следующее определение:
Неодносвязная область & называется ягвусв'язной, если после
одного надлежаще проведенного разреза она становится односвяз-
Черт. 124. Черт. 125.
ной. И, вообще, неодносвязная область S называется Уг-связной,
если она становится односвязной после надлежащего проведения
k — 1 разрезов.
Например, удаляя из внутренней области круга С систему k — 1
неперекрывающихся кругов Си С2,-.., СЛ-.1э мы получаем
^-связную область (черт. 125).
Эти свойства областей имеют большую важность для теории
функций комплексного переменного. В частности отсюда следует, что
внешняя область §,
определенная замкнутой жорда-
новой кривой К без кратных
точек, есть область двусвяз- К
ная (черт. 126), потому
что разрез этой области S
по линии L, содержащейся
в Si кроме своего конца N,
уходящей в бесконечность Черт. 126.
и такой, что всякий ее
отрезок NP есть простая жорданова дуга, — превращает, очевидно,
область S в одкосвязную. Это представление вполне соответствует
идеям геометрии, склонной вводить „бесконечно удаленные точки",
которые ока рассматривает как граничные точки плоскостей.
§ 4{Ь Совершенные разрывные множества. Для дальнейшего
нам необходимо рассмотреть один особо важный класс плоских
совершенных множеств Р.
Совершенное множество Р точек плоскости называется
разрывным, если оно не содержит в себе никакого continuum'а.
Из этого определения следует, что какова бы ни была точка М
совершенного разрывного множества Р, ее можно всегда заклю-
?03
нить внутрь замкнутого многоугольника п, диаметра сколь угодно
малого, периферия которого не содержит ни одной точки
множества Р*
действительно, пусть С—окружность радиуса, е, е > 0, имеющая
точку М своим центром (черт. 127). Обозначим через Рс
множество точек множества Л лежащих внутри С и на „ее периферии.
Пусть М' какая-нибудь точка множества Р, лежащая внутри С. Мы
утверждаем, что имеется такое положительное число т], ч\ > 0, что
нет никакой полигональной линии L, соединяющей точки М и М'
и имеющей длины всех прямолинейных звеньев меньшими yj,
вершины которой (т. е. точки соединения звеньев) принадлежат к Рс.
В самом деле, если для всякого ч\ имеется такая линия Ц то пола-.
гая %==—» гДе я натуральное число, и обозначая через Ln
соответствующую полигональную линию для- ч\п, мы можем обозначить
через К совокупность всех точек плоскости, служащих предельными
точками для множества вершин линий Ln> /г = 1,
2, 3, Ясно, что множество К содержится в Р}
потому что всякая вершина линии Ln принадлежит
к Р и Р есть совершенное множество. Ясно, далее,
что К есть замкнутое множество, содержащееся в
круге С ^включая его периферию) Наконец, К есть
continuum, так как в противно i случае К разбивалось
бы на два замкнутых множества F1 и F2> что
невозможно, потому что звенья линии Ln имеют длину < — ,
и, значит, найдутся точки множества К на периф?рии всякой
конечной системы замкнутых многоугольников О, содержащей Ft внутри
и имеющей F2 снаружи. Итак, К есть conrnuum, содержащийся в Я.
А так как, в силу определения разрывного множества Р, никакой
continuum не может содержаться в р, то отсюда и вытекает суще*
ствование положительного числа т], для которого нет полигональной
линии I, соединяющей М и Мг и имеющее звенья < т]. Обозначим
через F множество всех точек множества Рс, которые соединимы
с точкой М полигональными линиями L, имеющими звенья ^—-tj,
вершины которых лежат на Рс. Множество F замкнуто и
содержит точку М. Действительно, если £ есть предельная точка для
множества F, то мы всегда можем взять точку М" множества F,
лежащую к £ ближе, чем на -у т]. И тогда полигональная линия //',
соединяющая М с Мп (со звеньями < у ?) и с вершинами на Рс),
увеличенная на звено МГ,1У доказывает, что \ принадлежит к F.
Множество-разность F' — Pc— F содержит тот:ку М\. не содержит
точки М и, очевидно, состоит из всех тех точек множества Рс,
которые несоединимы с М указанными полигональными линиями L.
Легко видеть, что Fr <*сть замкнутое множество. В самом деле,
если точка \ есть предельная точка для Ff и если £ принадлежит
к Z7, то тогда к F должны принадлежать и все точки множества F\
204
, лежащие к точке £ ближе, чем на -^ ъ что невозможно. Итак, f й
F' суть два замкнутые неперекрывающиеся множества^ соответственно
содержащие точки М и М\
В силу §■ 22 можно отделить F от F' посредством конечной
системы (2) замкнутых многоугольников, содержащей F внутри,
имеющей F* стружи, лежащей внутри окружности С и не имеющей
на своей периферии ни одной точки множества Р.
Многоугольник П системы (УЛ содержащий точку М, очевидно,
удовлетворяет теореме.
Доказанное предложение очень важно, потому что дает
возможность выявить структуру разрывного совершенного множества Р.
Предположим сначала, что Р есть ограниченное совершенное
множество. Пусть М есть какая-нибудь точка множества Р. Заключим
ее внутрь замкнутого многоугольника П, диаметр которого < е и
периферия которого не содержлт точек множества Р. Пусть А есть
двумерный интервал, содержащий точку М и содержащийся в П.
Множество {Д} указанных двумерных интервалов А удовлетворяет^
очевидно, условиям леммы Есреля-Лебега. Поэтому все совершенное
множество Р можно покрыть конечным числом замкнутых
многоугольников П, диаметра < е,
периферии которых не
содержат точек множества. Р.
• Обозначим эти
многоугольники через rTj, По, . .., Пш
(черт. 128). Произведем
теперь следующую операцию:
берем целиком
многоугольник nif затем берем по
порядку многоугольники П2,
113,. • •, И/,-, если ни их
внутренниз области, ни периферии не перекрываются между собой,
а также с внутренней областью и периферией многоугольника Нг.
Идя, таким образом, по конечному ряду многоугольников П1э
112, . . .,Иь мы встретимся с таким многоугольником llfc.fi>
внутренняя область или периферия которого имеет общие точки с
внутренними областями или перифериями предшествующих
многоугольников П19 1Т2, ...,П7;. В этом случае мы заменяем
многоугольник Ilvfi другим многоугольником n*7t--fi, который не перекрывается
с многоугольниками IIj, П2, ...,П7<. и который содержит внутри
(строго) те же самые точки множества Р, которые лежат внутри
lI.Y-f 1 и которые не принадлежали ни внутренним областям, ни
перифериям многоугольников Пь 1Т2, ...,П£. Так как мы всегда можем
считать заменяющий многоугольник П*£_{_ х лежащим внутри
многоугольника Щ-fi, то диаметр многоугольника П*£ + 1 также < е.
Сделав замену многоугольника II*+i многоугольником IP^-f ь мы пере-
ходим к многоугольнику Щ + 2., заменяя его, если нужно,
многоугольником n*fef2, и так далее до тех пор, пока не пройдем всех
многоугольников IIl5 П2) . . ., Пш. Следовательно, каково бы ни было ма-
205
Лое положительное число б, ограниченное разрывное совершенное
множество Р можно покрыть конечным числом многоугольников
П*л, П*2, . •., П*ш, диаметров < г, ни внутренние об ласти у
ни периферии которых не имеют общих точек.
Установив это, дадим числу & значение гх и обозначим через Гг
совокупность конечного числа замкнутых многоугольников,
неперекрывающихся между собой, покрывающих все.множество Р и
имеющих диаметр <е1# Многоугольники совокупности Гг мы будем
называть многоугольниками первого ранга. Дадим теперь числу е
значение $з, ег > е2> и обозначим через Г2 совокупность конечного числа
замкнутых многоугольников вто*
рого ранга, имеющих диаметр
< г2, неперекрывающихся между
собой, содержащих множество Р
и содержащихся целиком в
многоугольниках совокупности Г*!, и
так далее до бесконечности (черт* ,
129).
Легко показать, что:
Черт. 129. Всякое ограниченное разрыв*
ное совершенное множество Р
можно получить, взяв конечно г число каких-нибудь замкнутых
неперекрывающихся многоугольников Оиаметра < е2, затем, взяв внутри
каждого из них конечное число каких-нибудь замкнутых
неперекрывающихся многоугольников диаметра < s2, и так далее до
бесконечности, причем гп стремится к нулю, когда я->со;
называя многоугольники, соответствующие числу ея, многоугольниками
„п-го ранга* и обозначая совокупность всех их точек {включая
периферию) через Тт мы можем рассмотреть данное разрывное
ограниченное совершенное множество Р как пересечение (т. е. как
обилую часть) всех множеств Г1э Г2, ..., Тп, ..»
Я^ХГаХ-.Х^Х....
В самом деле, любое множество Тп содержит все точки данного
, совершенного множества Р, следовательно Р содержится в
пересечении 1\ X Г2 X Гз X • • • X -Гп X • • • • Легко видеть, что произведение
1\ X Га X. .. X Тп X • • • не содержит ни одной точки, не
принадлежащей Р. Пусть М какая-нибудь точка, не принадлежащая к Р;
обозначим через tq расстояние до множества Р. Число ?) > 0, ибо
множество Р замкнуто. Выберем п настолько большим, чтобы
выполнялось неравенство еп<?]. Ясно, что точка М не может
принадлежать множеству Тп, ибо каждый из многоугольников, входящих
в состав Г, содержит точки множества Р и имеет диаметр, меньший г\.
Обратное также верно: Каким бы образом мы ни
выбирали многоугольники рангов 1, 2, 3, ..., пересечение суммы их
геометрических площадей Tlf Г2, Г3,... есть ограниченное раз-
рывное совершенное множество.
Легко видеть, что всякое неограниченное совершенное разрывное
множество Р может быть получено аналогичным образом, стоит лишь
205
взять счетное число многоугольников первого ранга, продолжая в то
же время брать в каждом из них конечное число многоугольников
следующих рангов. Действительно, неограниченное совершенное
разрывное множество Р может быть охвачено счетным числом
неперекрывающихся замкнутых многоугольников диаметра < еь причем эти
многоугольники не накопляются в бесконечном числе ни в какой точке
плоскости (лежащей на конечном расстоянии). И так как часть
множества Р, лежащая внутри всякого из них, есть ограниченное
разрывное совершенное множество, то дальше процесс протекает по-
старому, т. е. берется конечное число многоугольников следующих
рангов внутри всякого многоугольника первого ранга.
Выявленная структура совершенного разрывного множества Р
позволяет доказать весьма важное предложение:
Через все точка ограниченного совершенного разрывного
множества Р можно провести простую дугу Жордана.
\ Пусть Р есть какое-нибудь ограниченное совершенное разрывное
множество. Пусть Тп есть совокупность точек плоскости, принадле-
Черт. 130.
жащих замкнутым многоугольникам я-го ранга. Мы можем
рассматривать Тп как «я-ое приближение» совершенного разрывного
множества Р. Ясно, что множество Гп образовано конечным числом
многоугольников, диаметра < еп, удаленных один от другого на конечное
расстояние. Обозначим теперь через 0 операцию, состоящую в
следующем: всякий раз, когда на плоскости мы имем конечное число v
каких-нибудь замкнутых многоугольников Uti П2, ..., Hv, удаленных
один от другого на конечное расстояние, а на сегменте [0<;/<!1]
каквйчгабудь сегмент [а, &], поступаем так: во-первых, соединяем
многоугольники Hj, П2,..., IIV непересекающимися между собой про-
стыми дугами Жордана Си Сд,..., Cv + 1, причем простая дуга Q
соединяет два многоугольника Н^ и Пй дуги же Сх и Cvhl имеют
207
одни концы ни первом й последнем многоугольниках, а другие крнць*
их свободны (черт. 130); во-вторых, данный сегмент [я, Ь]>
лежащий на сегменте [0<;*<;i]„ делим на 2v -j~ 1 равных сегментиков,
которые и приводим во взаимно-однозначное соответствие с дугами
Жордана С1У С2, ..., Cv+1 и с многоугольниками П19- П2, ..., Ц,
так, чтобы при пробеге сегмента [а> Ь] слева направо были бы
пройдены дуги и многоугольники в том порядке, в каком они
соединены, начиная с дуги Сх и кончая дугой Cvfl. На чертеже
сегментики, соответствующие многоугольникам П^ П2, ..., Uv, отмечены
штрихами; в-третьих, установив соответствие простой дуги Жордана
С4 и сегментика оь о4=[а{, Ь4], мы детализируем это соответствие,
заставляя взаимно-однозначно и взаимно-непрерывно соответствовать
друг другу и самые точки простой дуги С4 и сегментика а4. Такое
взаимно-однозначное и взаимно-непрерывное соответствие точек дуги
С4 и сегментика <з1 вполне возможно осуществить, потому что
простая дуга С4 дается уравнениями х = о4(и) и y = ty4(u), где <р* и
$4 суть непрерывные функции параметра и, определенные на сегменте
[O^M^lJ; поэтохму, чтобы иметь нужное нам соответствие точек
дуги С4 и сегментика о4у достаточно лишь установить соответствие
точек сегмента [0О<;1] и сегментика o4=[a4^.t^b4]i что
достигается установлением соотношения между параметрами и и t
Описанную нами операцию 0 мы назовем для удобства операцией
связывания многоугольников П15 П2, ..., IIV, Но читатель видит,
Что, в действительности, не одно только связывание многоугольников
JIj, П2, ..., IIV осуществляет операция 0, но и отображение на
сегмент [#<^<С#], причем связывающие простые дуги Сг, С2, ..«,
С+1 отображаются взаимно-однозначно и взаимно-непрерывно своими
точками на сегментики olf o2, ..., ov+1, а многоугольники П^, П2,
. .., П, отображаются на сегментики хи та, ..., tv, но не своими
точками, а пока только суммарно (т. е. без разложения на точки,
но лишь поштучно): всему многоугольнику П4- соответствует целый
сегментик z4.
Введя, таким образом, операцию 0, мы приступаем к проведению
через все точки ограниченного совершенного множества Р простой
дуги Жордана. С этой целью заменим сначала совершенное множество Р
его первым приближением Тх и применим операцию 0 связывания
многоугольников, образующих Гь отображая всю фигуру на сегмент
[0<;/<]1] (черт. 131). В этом отображении всякая простая дуга С
соответствует сегменту о, причем соответствие точек дуги С и сегмента о
есть взаимно-однозначное и взаимно-непрерывное. Всякому же
многоугольнику П соответствует некоторый сегмент т. Возьмем теперь
второе приближение Г2 совершенного множества Р и выполним
операцию 0, связывая на этот раз многоугольники второго ранга,
содержащиеся в каждом многоугольнике первого ранга Я, и отображая
Каждую фигуру на соответствующий сегмент первого ранга т. При
этом мы будем соблюдать лишь ту осторожность, чтобы все простые
208
дуги Жордана, связывающие многоугольники второго ранга,
содержащиеся в П1э не выходили за периметр П и чтобы свободные концы
обеих дуг Жордана второго ранга, содержащихся в П, совпадали
с концами дуг первого ранга, примыкающих к многоугольнику П.
Сделав это, мы берем третье приближение Г8 множества Р и
выполняем операцию 0, связывая многоугольники третьего ранга,
содержащиеся в многоугольнике второго ранга и отображая каждую
такую фигуру на соответствующий сегмент т второго ранга. При этом
остается в силе та же самая осторожность о невыходе дуг Жордана
третьего ранга за периметр соответствующего многоугольника П*
второго ранга и о скреплении обоих свободных концов дуг третьего
ранга с концами дуг второго ранга, примыкающих к
многоугольнику П*. Продолжим этот процесс неограниченно.
Ясно, что взятие я-го приближения Тп совершенного множества Р
и его отображение на соответствующие сегменты х я-го ранга, ле-
Черт. 131.
жащие на [0<£<1], определит взаимно-однозначное и
взаимно-непрерывное соответствие точек всех простых дуг Жордана рангов 1,
2, 3,.. .,/г и сегментов о рангов 1, 2, 3,...,«, лежащих на [0<]^<; 1J.
Не участвуют в этом соответствии лишь сегменты х ранга я,
лежащие на [0<^-<1], но всякому такому сегменту х соответствует один
и только один многоугольник П ранга я, входящий в я-ое
приближение Тп совершенного множества Р. Следует указать на то, что
свободные концы простых дуг Жордана рангов 2, 3, . •., п являются
скрепленными с соответствующими концами дуг Жордана рангов 1,
2, ..., я— 1 так, что вся фигура, получившаяся при взятии я-го
приближения Гл, совершенно аналогична фигуре, построенной для
первого приближения Тг; только теперь многоугольники я-го ранга,
образующие я?ое приближение Гл, связываются простыми дугами
Жордана, вообще составленными из дуг Жордана различных рангов,
связанных концами одна с другой. При этом важно заметить, что дуга
Жордана &-го ранга не выходит за периметр многоугольника k — 1-го
ранга и, значит, имеет диаметр < eft-1. Ясно, что сегменты т ранга
я -f-1 содержатся в сегментах х ранга я, причем в каждом сегменте х
ранга я содержится ровно столько же сегментов х* ранга я -}-1,
сколько в соответствующем многоугольнике П ранга я содержится
14 *«. ШЬ 209
многоугольников II* ранга л + 1, составляющих приближение Tnhl.
И так как разрывное множество Р есть совершенное (а не только
замкнутое), то в каждом многоугольнике П ранга п можно
предположить по крайней мере два различных многоугольника П*
ранга л-f-l. Действительно, раз Р есть совершенное множество, то
оно не имеет изолированной точки. Поэтому, часть Я, содержащаяся
в П, имеет диаметр д?, отличный от нуля, d > 0. Но всех
многоугольников П ранга п конечное число. Следовательно, среди диаметров d
имеется наименьший отличный от нуля. Предполагая число ew+1
меньшим этого минимального диаметра d, мы видим, что в каждом
многоугольнике П ранга п содержится не один, а несколько
многоугольников П* ранга п -f-1. Это обстоятельство показывает, что в каждом
сегменте z ранга п содержится несколько сегментов т* ранга л-f-l.
Обозначим через Тп множество точек, принадлежащих сегментам т
ранга п. Множество точек тс, принадлежащих одаовременнб всем
множествам
«^ПХ^Х-.-ХГпХ...,
есть совершенное множество, лежащее на сегменте [0г^/^1]. Легко
видеть, что всякой точке t совершенного множества тс соответствует
определенная точка М совершенного множества Р и что это
соответствие есть взаимно-однозначное и взаимно-непрерывное.
Действительно, ^бесконечной последовательности IT, П", . . ., Шп\ ...
многоугольников рангов 1, 2,. .., я,,.., вложенных один в другой,
соответствует бесконечная последовательность сегментов т, z'\.. ., %(п\...
рангов 1, 2,..., я,..., также вложенных один в другой, потому что
соответствие многоугольников П и сегментов z ранга п есть взаимно-
однозначное^ каково бы ни было натуральное число п. Отсюда и:
следует, что совершенные множества Р и тс находятся во
взаимнооднозначном и взаимно-непрерывном соответствии, так как двум
близким между собой точкам t1 и /2 совершенного множества тс
(т. е. принадлежащим одному и тому же сегменту т*'*)) соответствуют
две близкие друг к другу точки М1 и М2 совершенного множества Р
(так как они обе должны принадлежать к многоугольнику 1№п\
соответствующему сегменту z(n)). Покажем теперь, что через все
точки совершенного множества Р уже проведена простая дуга Жор-
дана С. С этой целью мы заставляем соответствовать всякой точке t
сегмента [0^^<!1] определенную точку М плоскости XOY по
следующему закону:
1. Если / не принадлежит совершенному множеству тс, тогда /
принадлежит к некоторому сегменту а* какого-нибудь ранга &, и тогда
мы заставляем соответствовать этой точке t точку той простой дуги
Жордана С* ранга А, которая отображается на этот сегмент а*.
2. Если t принадлежит к совершенному множеству тс, тогда мы
заставляем соответствовать этой точке t точку совершенного
множества Р (как это описано выше).
Если точка t пробегает весь сегмент [0<;/<;1] слева направо,
тогда соответствующая точка М (я, у) плоскости пробегает некоторое
210
множество С точек плоскости, и ясно что координаты х и у точки М
суть функции переменного tt т. е.
* = ?(9. у°= «КО-
£Ъш /' ф fy то точка Мг, соответствующая /', отлична от
точки М\ соответствующей t".
В самом деле, пусть V ф t"\ Если tr и f принадлежат одному
сегменту о* ранга &, то точки М' и Мг различны, потому что простая
дуга Жордана С* не может иметь кратной точки. Если V и t"
принадлежат различным сегментам а* (одного или различных рангов),
тогда точки М' и М" также различны, потому что соответственные
простые дуги Жордана С* могут иметь только одну общую точку. •
Если одна из точек V и f принадлежит к тс, а другая не
принадлежит к тс, точки Мг и М" различны, потому что простая дуга
Жордана С* и совершенное множество Р не имеют общей точки.
Наконец, если V и f обе принадлежат к тс, мы уже видели, что
соответствующие точки Мг и М" (принадлежащие к Р) существенно
различны.
Итак, найденное геометрическое место точек М{х, у) на
плоскости XOY
* = ?('), Д^ФО
заставляет соответствовать различным значениям параметра t
существенно различные точки плоскости.
Легко теперь видеть, что функции о и <!> непрерывны на всем
сегменте [O^tf^l], Действительно, если£->£0, то точка уИ,
соответствующая tf, стремится, как к пределу, к точке М09 соответствующей tQ>
В самом деле, это очевидно, если t0 не принадлежит к П, так как
в этсм случае точка М0 находится на некоторой простой дуге С
(внутри или на конце ее), по которой и будет приближаться точка М
к точке М0, когда t-+t0. Если же t0 принадлежит к II, то точка t
будет принадлежать к сегменту т* ранга п, содержащему /0, когда t
будет расположено достаточно близко к точке t0. Отсюда следует,
что подвижная точка М попадет и будет оставаться внутри того
многоугольника II* ранга я, который содержит неподвижную точку М0.
И так как диаметр многоугольника II* меньше, чем еп, и число п
можно взять сколь угодно большим, то отсюда следует, что точка М
неограниченно приближается к точке М0, когда t-+iy Отсюда
вытекает, что обе функции y(t) и ty(t) непрерывны в точке t0i и так
как t0 есть любая точка сегмента [0<!^^1], то они непрерывны
на всем этом сегменте.
Таким образом, найденное соответствие х = ? (t), у = ty ОУ»
где 0<^<11, определяет простую дугу Мордат С, заведомо
проходящую через заданное ограниченное разрывное совершенное
множество Р.
Заметим, что концы А и В простой дуги Жордана С,
проходящей через данное разрывное совершенное множество Р9 были две
произвольные точки, не принадлежащие к Р. Заставляя их совпасть
друг с другом, мы получаем предложение:
14* 211
Через всякое ограниченное разрывное совершенное множество Р
можно провести замкнутую кривую Жордана С, не имеющую
кратных точек.
Это предложение может показаться читателю столь очевидным
и малоинтересным, что он будет недоумевать, зачем всему этому
предложению было отведено столько места. Но следующий простой
пример покажет всю глубину этого предложения.
Мы сначала построим разрывное совершенн9е множество Р таким
образом: берем квадрат, имеющий сторону 1 (черт. 132). Над этим
ф77/777Г/77/7777/77/7\ ¥7/77777777/77/77/7/7?,
LJ LJ
/£//4/£U£/£//Z//£ 1Х//4'&&Ха/21С£/<
у/7/7>/7777/7?77/77/7^ 977/7777?7T/7777777?i
1 Г
1
ШШ&7^6!//М/Л/6У&
III
U//^/jL/Oy^U£/^/JU/6 У/£7/;Ц/4£/Ш//<Цли/Ь
LI fc I
^N^bbss! tissue
I I i N
п n
kA Ъ/A te/A Ь/А Ъ/А ъЖ
г/А faA
□
Ь/аЫ
WW
w/A w/A
а а
о о
от
Оря v/y w^
#&£& О^й
ЯЩ &"% РР &7*
Черт. 132.
квадратом мы совершим ряд операций. Прежде всего мы вырезаем
из него крест площади ег; мы получаем 4 квадрата первого ранга,
общая площадь которых равна 1 -- sv Вторая операция состоит
в вырезывании в каждом из четырех квадратов креста так, чтобы
общая площадь всех четырех вырезанных крестов была е2; мы
получаем 16 квадратов второго ранга, общая площадь которых равна
1 — е2—е2. Третья операция состоит в вырезывании в каждом из
212
шестнадцати квадратов креста так, чтобы общая площадь всех
шестнадцати крестов была е3; мы получаем 64 квадрата третьего
ранга, общая площадь которых равна 1 — ег — S2~e3. и так
далее до бесконечности. Ясно, что, повторяя эту операцию удаления
крестообразной части из каждого остающегося целым квадрата
счетное число раз, мы в результате получим некоторое вполне
определенное плоское совершенное множество Р. Это совершенное
множество Р разрывно, потому что две любые его точки Мг и М\
сначала принадлежащие к одному и тому же квадрату ранга 1, 2,
3,..., попадут в два различные квадрата какого-нибудь ранга k и,
следовательно, не имеется никакого continuum'a /С, связывающего
эти точки М' и М" и принадлежащего к Р, потому что любые два
квадрата одного и того же ранга отделены друг от друга на
конечное расстояние. Наконец, этому совершенному множеству Р
естественно приписать „ площадьи, равную 1 — гх — г2 — е3 — . ..
... —еп— ..., потому что общая площадь всех вынутых
крестообразных частей есть е = ег -\- г2 -f- s3 -j- . .. -f- гп Л~ • • •» причем этот
ряд не только сходится, но даже его сумму s мы можем
предположить сколь угодно малой, потому что всякое из чисел «е^ е2, ...,
еп, ... находится в полном нашем распоряжении, так как мы можем
крестообразные части вырезать сколь угодно тонкими. И раз
площадь первоначальной квадратной пластинки была 1, а общая площадь
всех вырезанных частей была е, естественно рассматривать площадь
самого совершенного множества Р как 1 — з. Теперь, предыдущая
теорема говорит о том, что даже через такое совершенное
множество Р можно провести замкнутую непрерывную линию С, не
Черт. 133.
имеющую кратных точек (черт. 133). Такая замкнутая линия С,
содержащая на себе все точки совершенного множества Р, имеющего
меру, большую нуля, сама должна рассматриваться, как обладающая
мерой (т. е. площадью), болъшзй нуля. Если мы теперь обозначим
через А совокупность точек, находящихся строго внутри замкнутой
кривой С, то множеству А, являющемуся, очевидно, областью, мы
обязаны приписать также определенную положительную меру а (т. е.
площадь), потому что область А всегда может быть „триангулирована",
т. е. разбита на счетное число треугольников т1? т2, т.,,. . ., . т„,.. .,
неперекрывающихся между собой и становящихся все более и более
мелкими по мере приближения к границе С области А. Меру области А
получают, беря общую площадь всех этих треугольников in\ сулша
площадей этих треугольников образует заведомо сходящийся ряд
213
потому что все члены этого ряда положительны и потому что
никакая частная (усеченная) сумма -г1-Ьт2+ . . • + *»,
остановленная на я-ом члене, не может превысить величины площади
какого-нибудь фиксированного квадрата Q, содержащего внутри
кривую С.
Таким образом, и рассматриваемый контур С, и
ограничиваемую им внутреннюю область А приходится рассматривать
как имеющие положительные меры {площади). Ясно поэтому, что
когда речь идет об измерении „площади, охватываемой
замкнутой непрерывной линией С", то вовсе не одно
и то же, причисляют к этой площади самый контур С или не
причисляют: ясно, что площадь области плюс контур, А-\-С, будет
больше, чем площадь одной лишь внутренней области А. При
этом надо иметь в виду, что контур С есть непрерывная замкнутая
линия, отнюдь не заполняющая сплошь своими извивами никакого
куска плоскости. Этот факт абсолютно нов для читателя, потому
что при измерении площадей криволинейных фигур он никогда
раньше не останавливался перед вопросом, включать ли самый контур,
ограничивающий фигуру, в ее площадь или нет: для него было ясным,
что площадь круга С радиуса г останется той же самой тгг2, будем
ли мы причислять или нет к ней самую окружность С. То же самое
было ранее при измерении площади эллипса, имеющего полуосями
а и Ь\ площадь его, ъаЬ, останется неизменной, включим ли мы
или нет ^кривую эллипса в его площадь.
Таким образом, среди замкнутых непрерывных линий, не имеющих
кратных точек, приходится теперь различать кривые „утолщенные*',
включение которых в ограничиваемую площадь увеличивает ее
величину, и „обыкновенные* кривые, этим свойством не обладающие.
Кривые первого рода, обыкновенно, называются неквадрируемыми
кривыми; кривые второго рода, т. е. неутолщенные, называются
квадрируемыми. К квадрируемым кривым принадлежат окружности,
эллипсы и, прежде всего, все кривые, имеющие конечную длину
(т. е. „спрямляемые" кривые), но, кроме них, имеются еищ и
другие квадрируемые кривые. Квадрируемая кривая обладает тем
свойством, что может быть покрыта конечным числом квадратов, общая
сумма площадей которых как угодно мала: это есть необходимое
и достаточное условие для квадрируемости кривой. К этим
вопросам мы возвратимся в другой части нашей книги. Пока же мы
укажем лишь на то, что раз в такого рода вещах, казалось бы,
ясных с первого взгляда, имеются неожиданные фдкты, то тем более
приходится быть осторожным и необходимо строго доказывать даже
совсем очевидные вещи: например, теорема Жордана о том, что
всякая непрерывная замкнутая линия делит плоскость на две
области, внутреннюю и внешнюю,
§ 50. Кривые Пеано. Под кривой Пеано мы разумеем всякую
кривую Жордана
* = ?(')■ .у-«КО.
214
заполняющую внутренность какого-нибудь квадрата Q, лежащего на
плоскости XOY, Следовательно, кривая Пеано С, рассматриваемая
как плоское множество точек, не есть множество, нигде неплотное
на плоскости. Относительно кривых Пеано мы прежде всего имеем
следующее предложение, имеющее огромную принципиальную важность
для геометрии, так как оно показывает, в чем именно кроется самая
геометрическая сущность различия числа измерений двумерного
образа --**• плоскости и одномерного образа — прямой:
Теорема. Всякая кривая Пеано имеет кратные точки.
Предположим противное, а именно, что есть кривая Пеано
* = ?('), у = */(*),
не имеющая кратных точек и заполняющая внутренность некоторого
квадрата Q (черт. 134). Начертим внутри Q фигуру, состоящую из
д'—.
Ж\
-<k
V
Черт. 134.
трех замкнутых прямолинейных отрезков MQA\ MQA'\ MQAr/\
имеющих общую точку М0. Так как кривая лг — ср (t), y — ty (t) не имеет
кратных точек, то имеется взаимно-однозначное соответствие между
точками прямолинейных отрезков М0А\ М0А'\ М0А"' и точками
некоторых трех линейных множеств Е\ Е"', Е"\ принадлежащих
сегменту [0<^<;i]. Ясно, что множества Е\ Е", Е"' имеют только
одну общую точку, принадлежащую им всем: это есть точка t0 сегмента
10<£*'^1], соответствующая общей точке М0 трех отрезков М0А\
М(уАг\ М0А"Г, все же остальные их точки попарно различны. Легко
видеть, что множества Е\ Ег\ Еш замкнутые. В самом деле, если f
есть, например, предельная точка для множества Е\ то в силу
непрерывности функций 9Ht точка Мг [ср (£'), ф (О! есть предельная
для точек сегмента М0А' и, значит, сама принадлежит этому сегменту.
Поэтому, точка ? принадлежит множеству £', и, значит, Ef есть
замкнутое множество. Покажем, что множества Е\ Е'\ Ет суть
сегменты. Действительно, если бы, например, Ег не было сегментом,
то Е! разбивалось бы на два замкнутых множества Е{ и £2' без
общей точки Е' = £/ + £2'- Пусть 2К/ есть множество точек
Ж[х(0» .УСОЬ соответствующее множеству £/ и, аналогично,
пусть 2Й2' есть множество точек М (х, у), соответствующее
множеству Е2'. Ясно, что ЗК/ и ЗИ27 замкнутые множества, потому что Et'
и Е% —замкнутые множества и функции ср, ф непрерывны. Так как
Е' =£1/ + £,2/> т0 Mqa' ^ 3R/ + ЗЯ*'- А это равенство невозможно,
потому что MqA' есть сегмент, а никакой сегмент не может быть
разбит на два неперекрывающихся замкнутых множества. Итак, множе-
215
ства Ef, Е'\ Ет суть*сегменты, лежащие на сегменте [0<!*<Ч]
и имеющие общую точку /0, принадлежащую одновременно им всем
трем. /Последний же результат является невозможным, потому что
если два какие-либо сегмента имеют только одну общую точку, то
это означает, что она есть концевая и что оба сегмента лежат по
разные стороны от нее. Но тогда третий сегмент, содержащий ту же
самую точку, необходимо должен содержать бесчисленное множестро
точек одного из этих двух сегментов. А между тем множества Е\
Е", Еш не должны иметь никаких общих точек, кроме tQ, потому
что все точки сегментов МА\ MA", MA'" попарно различны, кроме
точки M0i принадлежащей им всем. Из обнаруженного противоречия
следует справедливость теоремы.
Доказанное предложение дает возможность вполне определенно
понять, в чем состоит сущность числа измерений и чем отличается,
например, плоскость (как множество точек) от прямой линии (как
множества точек). В отношении мощности между ними отличия нет,
потому что плоскость и прямая, рассматриваемые как множества
точек, равномощны. Но если между их точками и имеется взаимно-
однозначное соответствие, то такое соответствие не может никогда
быть непрерывным: предполагая взаимно-однозначное
соответствие д; = ©(*), у = <р (t) точек М (лг, у) квадрата Q и точек t
сегмента [0,1], мы видели, что предположение непрерывности
функций <р (t) и ф (t) ведет к противоречию. Мы не будем
останавливаться ни доказательстве более общего предложения:
Взаимно-однозначное соответствие между точками областей
различного числа измерений не может быть непрерывным.
Равным образом, мы не станем углублять предыдущего
предложения, доказывая, что:
Не существует кривой Пеано, всякая точка которой была бы
простой или двукратной. Это означает, что если уравнения х = <р (/),
yz=.ty\t), где 0<^<;i, определяют кривую Пеано, то наверное
имеются точки М0 (x0i y0) плоскости, проходимые по крайней мере
три раза, когда переменное t возрастает от 0 до 1. Аналитически
это означает, что система двух уравнений
имеет по крайней мере три корня: tu t2 и £3, таких, что
*о = ?('*)> Л)=<Н^)» ™e *'=1, 2 и 3.
Не останавливаясь на доказательстве этого интересного
предложения, мы сейчас дадим построение кривой Пеано, имеющей самое
большее трехкратные точки.
Для этого возьмем сначала фигуру, образованную некоторым
прямоугольником Q с отмеченными на нем двумя вершинами А и В9
одну из которых А мы будем называть начальной, другую же
В—конечной (черт. 135). Начальную вершину А будем
рассматривать как точку входа кривой Пеано в прямоугольник Q, а
конечную вершину В—как точку выхода кривой Пеано из этого
прямоугольника. Отмеченные вершины А и В могут иметь любое распо*
216
ложениё, т. е. могут быть как концами диагонали, так и концами
одной из сторон прямоугольника Q. Одновременно с
прямоугольником Q нам дан некоторый сегмент [а, Ь\, принадлежащий сегменту
[0<*<1]. Введем теперь операцию О, состоящую из следующих
действий.
Во-первых, прямоугольник Q разобьем на конечное число
прямоугольников Qu Q2>---> Qm (ка чертеже 136 m = 7),
перенумерованных так, чтобы всякий прямоугольник Qi с предшествующим
Qi-i и с последующим QiJrl был бы смежным, т. е. имеющим по
та с
+в-
Черт. 135.
куску общей стороны. Далее, мы предполагаем, что начальная
вершина А принадлежит к первому прямоугольнику Q, а конечная
вершина В к последнему прямоугольнику Qm. Затем, прямоугольники
Qu Q& • • • » Qm мы предполагаем так расположенными, что всякая
точка М прямоугольника Q принадлежит или одному, или двум, или
самое большее — трем различным прямоугольникам Q^ которые
предполагаем замкнутыми, т. е. включающими в себя свою границу.
Наконец, прямоугольники Q* предполагаются столь мелкими, что
диаметр каждого из них меньше половины диаметра всего
прямоугольника Q. Такое разбиение прямоугольника Q всегда можно
осуществить, как показывает чертеж 136.
j}0>
WE
—Is
23
a
.*''Qi
ZEE
,^-yfl;|
Z23u
' ---Osl
^-Qg
r~^j
Oi.QgpJ...
07,.
Черт. 136*
Во-вторых, мы отмечаем на каждом прямоугольнике Q^ точку
входа Ai и точку выхода £г-, руководствуясь тем правилом, чтобы
точка выхода Bi из прямоугольника Q{ совпала с точкой входа Ai+1
в прямоугольник Qi+V При этом вершина А должна быть точкой
входа в первый прямоугольник Qu а вершина В — точкой выхода
из последнего прямоугольника Qm. Такое указание точек входа и
выхода для прямоугольников Qi вполне возможно, так как
достаточно просто обойти все прямоугольники по пунктирной линии,
указанной на чертеже, следуя стрелкам и отмечая всякий раз точку
входа в прямоугольник Q{ и точку выхода из него.
В-третьих, мы разбиваем данный нам сегмент [а, Ь] на т
равных сегментов о , о2,.
занумерованных на сегменте [а, Ь]
слева направо, и ставим их в соответствие с прямоугольниками
Qi >Qa>«»#> Qm так> что прямоугольник Qi и сегмент а4
соответствуют друг другу.
217
Введя таким образом операцию О, мы отправляемся от
единичного квадрата (?[0<лг< 1, 0<^< 1] и от сегмента [0</<1],
За точки А и В входа и выхода кривой Пеано мы принимаем
концы диагонали (черт. 137). Применим операцию О, разбив
указанным выше способом квадрат Q на т(т = 7) прямоугольников
Qv Qa»---» Qm первого ранга, разбив сегмент [0<;/<;1] на т
равных сегментов первого ранга ot, o2,..., от и поставив в
соответствие прямоугольник Qi и сегмент-^, где /=1, 2, 3,..., т.
Так как всякий прямоугольник первого ранга Qt снабжен точкой
входа Аг и точкой выхода Biy то мы можем повторить операцию О,
разбив ^ на т прямоугольников второго ранга Qn, Q*2>---> Qim>
I » 1 'i
El
r -i
1 1
1 1
r-i
-1 r- -
1—1
.J.,. J
1 1
1 '
- J~uJ
' ' '1
ill
lit
1 f '
' >
1 <
П
1 ' J
Черт. 137.
разбив соответствующий ему сегмент первого ранга <з4 на т равных
сегментов второго ранга оп, ой,..., oiw и поставив в соответствие
прямоугольник Qy и сегмент о^. Так как всякий прямоугольник
второго ранга Qij снабжен точкой входа Ац и точкой выхода Вф то
мы можем повторить над Q^ и о^- операцию О, и так далее до
бесконечности. При этом мы должны соблюдать лишь ту
осторожность, чтобы, при разбиении квадрата Q на прямоугольник Цу...к
ранга я, никакая точка М квадрата Q не оказалась принадлежащей
сразу к четырем прямоугольникам л-го ранга, что, разумеется,
всегда можно сделать, передвинув, если это необходимо, слегка
линии деления прямоугольников (п—1)-го ранга на прямоугольники
п-го ранга. Покажем теперь, что это построение дает искомую нами
кривую Пеано. Действительно, пусть t какая-нибудь точка сегмента
[0<;/<;i]. Она принадлежит, по крайней мере, одному сегменту о'
ранга 1, далее, по крайней мере, одному сегменту о" ранга 2,
содержащемуся в а', затем, по крайней мере, одному сегменту о'"
ранга 3, содержащемуся в о", и так далее до бесконечности.
Последовательности сегментов рангов 1, 2, 3...
о'>а">о'"> ...>а(*>>...,
вложенных один в другой, соответствует бесконечная
последовательность прямоугольников
Q'>Q">Qf"> ...>Q<»>..M
также вложенных один в другой. И так как диаметр
прямоугольника QW меньше половины диаметра предыдущего прямоугольника
Q{n-Dt то имеется одна и только одна точка М(х9 у) квадрата Q,
218
принадлежащая всем этим прямоугольникам Q(n), к которой они
стягиваются. Координаты х и у этой точки М зависят только от t
и, следовательно, являются функциями' параметра t.
* = ?(0. ^ = <К0. о<*<1.
Покажем, что ср и ф суть непрерывные функции параметра /.
Действительно^ если t0 есть какая-нибудь фиксированная точка сегмента
[0<;t<;i] и если /-W0, то ясно, что точка t и точка t0 окажутся
в одном и том же сегменте о* ранга п. Но это означает, что и
соответствующие им точки М и MQ квадрата Q окажутся в одном
и том же прямоугольнике Q* ранга я. А так как диаметр
прямоугольника О* ранга п стремится к нулю, когда я-> + оо, то
отсюда следует, что расстояние обеих точек М0 и М стремится к нулю,
когда я~> -f- со. Следовательно, мы имеем М-~>М0> когда t->tCy
Иначе говоря,
lim?(0=?(<0) и Итф(*)=<К*о),
когда t->tQ. А это и значит, что функции <р и ф непрерывны в любой
точке £0 сегмента [0<^<Г1].
Итак, кривая
х = ?(0, jr - «О, где 0 < It < 1, (1)
есть кривая Жордана, так как ср и ф непрерывны на сегменте
[0<;*<; 1]. Покажем, что эта кривая Щордана есть кривая Пеано,
так как она проходит через любую наперед заданную точку М0(х0, у0)
квадрата Q (включая и периферию). Действительно, раз точка М0
принадлежит квадрату Q, то ока принадлежит по крайней мере одному
(и самое большое трем) прямоугольнику Q(») ранга я. Пусть
Q' > Q">Qm >...> QW > ... (2)
последовательность прямоугольников рангов 1,2,3,..., вложенных
один в другой и содержащих данную точку М0. Этой
последовательности прямоугольников соответствует последовательность сегментов
о'>о">о'"> ...>о(»)> ... (3)
рангов 1, 2, 3,..., также вложенных один в другой. Так как длина
сегмента о(») ранга п стремится к нулю, когда п -*-{- оо, то имеется
одна и только одна точка t0 сегмента [0 <; t <; 1 ], принадлежащая
всем этим сегментам. Из сказанного ясно, что точке tQ соответствует
как раз данная точка MQ квадрата и что, поэтому, мы имеем
дг0 ===== ср(^о) и Уо = №о)* где хо и Уо СУТЬ координаты точки Ж0,
произвольно заданной на квадрате Q. Это и показывает, что кривая
Жордана (1) есть кривая Пеано.
Легко видеть, что кривая Пеано (1) имеет, самое большее, лишь
трехкратные точки.
Действительно, так как всякая точка MQ (xQ, у^) квадрата Q
(включая и периферию) принадлежит одновременно, самое большее, трем
четыреугольникам ранга и, то имеются самое большее лишь три
различные последовательности (2) прямоугольников Q(n\ вложенных
219
о
[ i
1
l
1 ;'
О 1
1*7
]4
один в другой и содержащих точку М0. Поэтому, может иметься не
больше трех последовательностей (3) сегментов о(»), вложенных один
в другой и определяющих соответствующее точке ЛГ, значение /■
параметра *. Значит, система уравнений х0 = с (7), д/0 = 6(7) где хп и у°
даны, имеет самое большее три корня *'0, Г0, Г0 для неизвестного t
Полученные результаты доказывают существование кривой Пеано
* = 'f(0> y = W\ заполняющей квадрат, и наличие у нее счетного
множества трехкратных точек: это, очевидно, суть вершины
прямоугольников рангов 1,
2, 3. . . . Что же касается
до двукратных точек, то
мощность множества их
равна мощности континуума,
потому что всякая точка Ж,
лежащая на стороне
какать го-нибудь прямоугольника
QW ранга « и не
являющаяся его вершиной, есть,
„ ^ очевидно, двукратная
точка кривой Пеано. Точки же, не лежащие на сторонах
прямоугольников Q(n\ суть простые точки (т. е. однократные).
Так как сделанное построение несколько сложно, мы укажем еще
построение кривой Пеано, данное Гильбертом. Оно много проще но
получаемая при помощи него кривая Пеано имеет четырехкратные
точки. Единичный квадрат Q[0<*<1, 0<у<1] делится на
четыре равных квадрата первого ранга; сегмент [О<*^Г 1] так же делится
на четыре равных сегмента первого ранга; квадраты и сегменты
приводятся в попарное соот- — F
ветствие, причем это
попарное соответствие диктуется
пробегом сегмента [0<7<;1]
в положительном
направлении и обходом квадратов
ранга по пунктирной линии
(черт. 138). Следующее
применение операции состоит
в делении каждого квадрата
О
Черт. 138.
\в\
Lj
П-7
8
"1з
J
2 ]
«Г
9
«Г
i
ц
.... \т
_j I
1б\
«р
Черт. 139.
7
первого ранга на четыре равных квадрата второго ранга; каждый
сегмент первого ранга делится на четыре равных сегмента второго
ранга; квадраты и сегменты второго ранга ставятся в попарное
соответствие, причем это попарное соответствие диктуется положительным
пробегом сегмента [0<*<1] и обходом всех квадратов второго
ранга по пунктирной линии (черт. 139). Повторение этой операции
даст нам 64 квадрата третьего ранга, получаемых делением всякого
квадрата второго ранга на четыре равных квадрата; аналогично, всякий
сегмент второго ранга мы делим на четыре равных сегмента третьего
ранга; попарное соответствие всех квадратов и сегментов третьего
ранга осуществляется обходом всех квадратов третьего ранга по
пунктирной линии (черт. 140).
2?0
Продолжая неограниченно этот процесс и соблюдая ту осторожность,
чтобы п£и обходе всех квадратов я-го ранга четыре квадрата,
составляющие квадрат (п— 1)-го ранга, обходились не в разбивку, а подряд,
один за другим, мы будем иметь такое попарное соответствие
квадратов Q* и сегментов о* я-ранга, при котором квадрату (n-^-l)-ro
ранга, содержащемуся в Q*, будет отвечать сегмент (п-\-\) го ранга,
содержащийся в о*, и обратно. В этих условиях бесконечной
последовательности сегментов <з1 > о2 >.,. > оп >... рангов 1, 2, 3, •..,
вложенных один в другой, соответствует бесконечная последовательность
квадратов Qt>Q2> .. • > Qn > • • • рангов 1, 2, 3, ..., так же
вложенных один в другой. Поэтому, всякой точке t сегмента [0 ^ t ^ 1]
соответствует одна и только
одна точка М (а*, у)
квадрата, т. е. мы имеем
уравнения
* —9(0, У=*Ш
где 0<*<1.
Подобно тому, как мы
сделали выше для случая пря- б ' i *
моугольников, так же точно
и здесь доказывается, что Черт. 140.
9 (^) и 6 0) СУТЬ
непрерывные функции параметра t на сегменте [0^tf<;i] и что кривая
Жордана x — o{t)y ^ = ^V (0 действительно проходит через всякую
точку М0 (д:0, у0) единичного квадрата, и, следовательно, является
кривой Пеано. Здесь в единичном квадрате имеются точки Л10 (х0>у0),
принадлежащие одновременно четырем квадратам я-го ранга.
Поэтому, рассматриваемая кривая Пеано имеет четырехкратные точки:
1 1 и
такова, например, точка д:0 = -^, у0 = -г- ™ Центр квадрата,
#0=.— у0=~ , есть уже трехкратная точка*).
Относительно этой плоской кривой Пеано
* = ?('). .У-ФС).
заполняющей единичный квадрат Q (черт. 141), нужно отметить
следующее: на первый взгляд может казаться, что отнюдь нельзя
говорить в этом случае про „кривую", так как это слово
связывается с представлением о беспредельно тонком кривом штрихе,
вьющемся внутри квадрата Q и совершенно заполняющем своими
извивами всю его площадь так, что нет ни одной точки М квадрата
Q, через которую не прошел хотя бы один извив рассматриваемой
кривой линии. Именно, может казаться, что в действительности
вовсе нет никакой вьющейся кривой линии, а есть лишь формальное
*) Это обстоятельство, как мне заметил проф. В. Серпинский, было
упущено знаменитым Пикаром, утверждавшим что эта кривая Пеано имеет
наряду с простыми точками только двукратные и четырехкратные. См.
Picard— ТгаШ d* Analyse, t. 1. p. 30.
~Ь сг I '-р rr
_ u >___] j i_L
i"Ti 1 "Г ~ ~ '
221
соответствие всякой точке г сегмента [0<;^<;ij некоторое точки
М (■**, у) площади Q, соответствие, даваемое аналитическими
формулами (1), причем нисколько не обязательно представлять себе это
соответствие в виде извивов именно кривой линии. Однако, это не
совсем так. Чтобы подойти ближе к пониманию сущности явления,
открытого Пеано, присоединим к уравнениям (1) еще одно
уравнение: z*=t, и, следовательно, рассмотрим для трехмерного
пространства OXYZ систему трех уравнений
* = ?(*), ^ = Ф(0. * = '• (4)
Вполне естественно совокупность точек /V (х, у, z) трехмерного
пространства OXYZ, получаемую при помощи системы уравнений
2
/'
\х*у№/£*
1 J%0
\ / / х/
^S V-
1 :С/ у
N ?
1' /7 У^"/
/у'А-
М //
у о (/
J
г
)/
4
Черт. 142.
Z
0
р.
1
<
/V"
'N'
/ м~ /
оу
1
/ У
(4), когда параметр t пробегает сегмент [0</<1], рассматривать
как непрерывную линию, потому что двум различным точкам tr и t"
соответствуют различные точки N' {х\ у', zr) и N" (хг\ у", z")
кривой, так как z/ = t/ и z" = t" и, значит, zf фг". Таким образом,
система уравнений (4) действительно изображает траекторию
движущейся точки N (х, у, г), подымающейся все выше и выше, когда
численная величина параметра t возрастает. //, однако, эта несом*
ненно пространственная кривая линия (4) проектируется на
координатную горизонтальную плоскость XOY в виде
222
сплошной площади квадрата Q, потому что всякая точка М (х, у)
плоскости, даваемая уравнениями (1), есть проекция точки N (х,у, г)
простой дуги (4), где z — t (чеот. 142). Итак, имеются
пространственные простые дуги, проектирующиеся на плоскость в виде
сплошных площадей.
Можно подумать, что раз проекция простой дуги (4) есть квад-^
рат Q, то эта простая дуга (4) есть на самом деле „ поверхность V
На первый взгляд это кажется правдоподобным, раз всякий
перпендикуляр MP, восставленный в точке М квадрата Q, непременно
пересечет простую дугу (4) в одной, двух или трех точках ЛГ, Л/", AjW,
(если кривая Пеано (1) не имеет точек кратности выше трех).
Однако, простая дуга (4), хотя и непрерывка, вовсе не есть
непрерывная поверхность z = F(x, у), потому что малейшее перемещение
точки М по квадрату Q ведет к скачкообразному резкому
перемещению точек ЛЛ, N", N"\ так как кривая Пеано (1) не дает ни
взаимно-однозначного ни взаимно-непрерывного соответствия точек
квадрата Q и сегмента [0<1^1]. Притом, пространственная
простая дуга (4) проектируется на вертикальную плоскость х = 0 в виде
обыкновенной непрерывной кривой у = ф {г) и на вертикальную
плоскость j/ = 0 в виде непрерывной кривой x~v (z),
§ 51. Кривые Жордана и Пеаио в пространстве многих измерений.
Пространственную кривую
* = ?('). 3> = М0' * = «>(&
где 9» ^ и ш СУТЬ некоторые непрерывные функции параметра t на
сегменте [6<!£<1], называют кривой Жордана в пространстве трех
измерений. Кривая жордана называется простой дугой, если она не имеет
кратных точек. Кривая Жордана в пространстве трех измерений называется
кривой Пеано, если она заполняет внутренность некоторого куба.
. Как и в случае плоской кривой Пеано, для пространственной кривой
Пеано можно доказать, что она непременно имеет кратные точки и, притом,
кратности не менее четырех, С другой стороны, имеется кривая Пеано, все
точки которой имеют кратность не более четырех.
Если пространственная кривая Пеано
* = ?М. .У = Ф(0. *«"М. (5)
где 0</<1, заполняет единичный куб, не выходя за его поверхность, то
аналитически это означает, что непрерывные функции ср (t)9 ф (t)> со (t)
обладают следующими двумя свойствами: s
1. Удовлетворяют неравенствам 0 <ср (/)<1, 0<ф(/)<1, 0 < со (/)<1.
2. Система трех уравнений х0 =■• 9 (t), yQ — ф (t), z0~<* (t) имеет по
крайней мере один корень /0, 0 < /0 < 1. Здесь числа xQ, у0, z0 произвольные,
принадлежащие сегменту [0, 1].
Это аналитическое определение кривой Пеано переносят на
многомерные пространства. Именно, называют кривой Жордана систему
равенств
*i = <Pi (0. *2 = ¥2 (/), . •., хт = 9т (0.
где 9г(0 СУТЬ непрерывные функции на сегменте [0</<Ц.
Кривая Жордана называется кривой Пеано, заполняющей единичный
т-мерный куб, если функции ^i(t) удовлетворяют условиям:
1. Справедливы неравенства
0<9i(0<U 0<92(0<Ь .... °<¥т(0<1.
223
2. Система т уравнений
*х = ?i W. *2 = Ъ (*)> • • •» *т = 9m М
имеет по крайней мере один корень /0, каковы бы ни были числа *f *§,
..., *^, принадлежащие сегменту fO, 1].
Это определение переносится даже на „пространство, имеющее счетное
число измерений". Именно, бесконечную последовательность непрерывных
функций yn{t) на сегменте [0</<1]
*l = ?l(0> ^2 = ?2(0 -«П-ЫО. ••• (6)
называют кривой Пеано, заполняющей единичный счетномерный куб, если
соблюдены два условия:
1. Имеют место неравенства
0<¥i(/)<l, 0<%(/)<1, .... 0<9Л(/)<1
2. Бесконечная система уравнений
■*i = 9i(0. 4 = <М0, .... *2«Ы0. ...
имеет по крайней мере один корень /0, 0<;/0< 1, каковы бы ни были числа
х\> х% ..., х®п, взятые на сегменте [0,1].
Чтобы получить кривую Пеано, заполняющую единичный куб Q т
измерений, Q=[0<a*1<1, 0<л'2<1, . ..♦ 0 <jc^< 1], проще всего поступить
путем построения, аналогичного построению Гильберта для плоской кривой
Пеано.
Для этого мы сначала разбиваем куб Q на 2шправных кубов Q(n)
ранга п, для чего делим каждый из сегментов [0<лг^< 1], /= 1, 2, 3, ..., т,
лежащих на осях координат, на 2п равных сегментов bW ранга п,
рассматривая систему S сегментов а^, <*М, ..., <з&\ как проекцию куба Q(n)
на оси координат. Ясно, что всех таких кубов Q(n) ранга п будет столько
же, сколько имеется всех систем S, т. е. 2тп. Ясно, далее, что в
каждом кубе Q(n) ранга п содержится 2т кубов Q(n+^ ранга п + l н что все
они получаются делением пополам проекций а^1\ а%1\ ..., с$ куба Q(n) на
оси координат. Одновременно с этим мы делим сегмент [0<;*<1] на 2тп
сегментов х(») ранга п и ставим кубы Q(n) и сегменты тО) во
взаимнооднозначное соответствие, для чего предварительно мы располагаем все
2тп кубов Q(n> в определенном порядке, делая их обход в надлежащем
порядке, намеченном в единичном кубе Q. Это соответствие такого рода,
что кубу Qn'rl ранга л-}-1, содержащемуся в Q(n), соответствует сегмент
т(»+1) ранга п-\-\, содержащийся в том из сегментов z(n), который
соответствует кубу Q(n), и обратно. Как было показано выше, по этому
соответствию всякой точке /сегмента [0</-<1] соответствует точка М (хь
хъ ..., хт) единичного куба Q. Доказывают, попрежнему, что достигнутое
таким образом соответствие
*1 = Ъ (*). *> = Ъ V) хт = 9т (t) (7)
непрерывно на всем сегменте [0 < /< 1] и что полученная кривая Жордана
(7) есть кривая Пеано, заполняющая т-мерный куб Q.
Почти такой же прием пригоден и для построения кривой Пеано*
заполняющей единичный счетномерный куб Qt
<? = [0<*i<l, 0«,*а<1, .... 0<л-п<1, ...].
224
Для этого мы сначала разбиваем куб Q на 2 - 2 счетномерных па*
раллелепипедов П(те) ранга п,
п(») в [,(»). а<«), 4»)..., <#>, 0%,...., ■$*... ].
следующим образом: мы делим первый осевой сегмент [0<л:1<1] на 2^
равных сегментов <//Ч второй осевой сегмент [0<д:2<1] на 2м-1 равных
сегментов c'2w\ третий осевой сегмент [0 <лга < 1] на 2^-2 равных сегментов
а(3^ и так далее; я-ый осевой сегмент [0<;гп<1] делится лишь пополам,
т. е. всего на 2 сегмента o(ff; что же касается до дальнейших сегментов
[0<*fc< 1], где &>л, то они совсем не делятся. Каждый из сегментов
ву\ а^Ч..., с^*\л. м <f£\ .., рассматривается как проекция счетномерного
параллелепипеда ПО) на оси координат ОХь (XY2,..., ОХп,..., ОХк
Ясно, что всех таких параллелепипедов Шп) ранга п будет столько же,
сколько имеется всех последовательностей о{{1\ сг^,..., а£*\..., c(few) .. .и,
значит, сколько имеется всех систем о^\ а^} с„\ потому что все
дальнейшие члены с^Л) последовательности имеются лишь в одном экземпляре.
Следовательно, число параллелепипедов П(п) ранга п равно 2wX2n~~1X
Х2П"*'2Х« • * Х2 == 2 2 . Ясно, далее, что в каждом параллелепипеде
ПО) ранга п содержится 2n+1 параллелепипедов Шп+1) ранга л + 1 и что
все они получаются делением пополам проекций а[п\ а^п\ ..., с^ , и<п + г
параллелепипеда П (п) на оси координат ОХь ОХ% ..., ОХп> OXn+i. Одно-
временное этим мы делим сегмент [0<*<1]на2 2 сегментов т(м)
ранга п и ставим параллелепипеды П (п) и сегменты iin) во
взаимно-однозначное соответствие, для чего предварительно мы располагаем все
3 2 я-мерных параллелепипедов П^*,
Ып) _ | (п) 0(п) (л) 1
В определенном порядке, делая их обход по надлежащим образом намечен*
ной линии, в единичном л-мерном кубе [0<лг!< 1, ..., 0<лгп<1]. Этот
обход дает нам взаимно-однозначное соответствие параллелепипедов п!Л* и
сегментов %(п); а так как -всякий /г-мерный параллелепипед П^
соответствует одному и только одному счетномерному параллелепипеду П^
ранга /2, ортогональной проекцией которого на пространство п измерений
ОХ\Х%. ,.Хп он является, то ясно, что указанный обход дает нам
взаимно-однозначное соответствие всех счетномерных параллелепипедов П^
и сегментов % (») ранга п. Ясно далее, что это соответствие такого рода,
что параллелепипеду П(те+1) ранга л + 1, содержащемуся в П
^/соответствует определенный сегмент х(Л+1) ранга л+U содержащийся в том из
сегментов t \ который соответствует параллелепипеду П О), и обратно.
В этих условиях, бесконечной последовательности сегментов t'>x">...
>i(w)... рангов 1, 2, 3,..., вложенных один в другой, соответствует
бесконечная последовательность счетномерных параллелепипедов 1Г>11">...
> Шп) >... рангов 1, 2, 3, ..., также вложенных один в другой. Поэтому
всякой точке/ сегмента [0</<1] соответствует одна и только одна
точка М (хъ Хъ ..., хт...) счетномерного единичного куба.
Q=[0<at1<1, 0<лг2<1, ... 0<^я<1,...1.
15 Эак. 1!Ш< 225
Значит, бесконечная последовательность чисел хь x%t..'.']\ хп, ..^
определяется единственно знанием числа t А " это и значит, что мы имеем
равенства
*1 = ?i W» *2 = 92 (*), • •• > хт = ерш (4 .. ♦ , (8)
где 9w суть функции параметра/, определенные на сегменте [0</<l]fc
Если t стремится к t0 как к пределу, то обе точки: подвижная / и
неподвижная /0 принадлежат одному и тому же сегменту i(n) ранга п. А это
означает, что обе соответствующие точки счетномерного пространства:
подвижная М(хь х*>, ...,хт, ...) и неподвижная MQ(x°v х\% ..., х£, ...)
принадлежат одному и тому же параллелепипеду П^ ранга п. Это значит,
что обе точки: подвижная хт и неподвижная х^ принадлежат одному и
тому же сегменту с^]» в который проектируется параллелепипед ПО) на
ось ОХж Но длина сегмента а^ равна -w+i , потому что для
получения сегментов а^ мы делили осевой сегмент [0<^W<1] на 2п~т+1
равных частей, и сегмент off есть одна из них. Поэтому, если натуральное
число т фиксированоt а число п неограниченно возрастает (когда t
стремится к /0), то мы имеем limc^ = 0H, следовательно, Umxm = х^. А так
как xm = <?m(t) и *2, = <рт(4>). то имеем Нш срш (t) = срт (t0), когда /->/0.
Следовательно, каждая из функций <р™(0 есть непрерывная на всем
сегменте [0 <*< 1].
Таким образом, кривая (8) есть кривая Жордана. Чтобы видеть, что
кривая (8) есть кривая Пеано, достаточно взять какую-нибудь точку
Mq(x^ a^t .... хтч •* •) счетномерного куба Q. Из предыдущего ясно, что
точка т0 принадлежит по крайней мере одному счетномерному
параллелепипеду П(п> ранга п и, значит, имеется по крайней мере одна бесконечная
последовательность
П'>П">...>П<^ >...
счетномерных параллелепипедов рангов 1. 2, 3,..., содержащих точку М0
и стягивающихся к ней (в том смысле, что проекция т;М параллелепипеда
П(п) на ось ОХт стягивается к точке х^9 которую она содержит, когда
/z->+oo). Но этой последовательности параллелепипедов П/>П'/>...
. ..> П^)>... соответствует последовательность стягивающихся в точку tQ
сегментов %' > т" > ,.. > т;^ >... рангов 1, 2, 3, ... .
Из предыдущего ясно, что имеем
*1 = П (/о), 4 - <Р2 (/о). • • •, *£ = *т Со\ .... ' (9)
Это обнаруживает, что кривая Жордана (8) есть кривая Пеано,
заполоняющая счетномерный куб Q.
ГЛАВА VI.
АНАЛИТИЧЕСКОЕ ИЗОБРАЖЕНИЕ НЕПРЕРЫВНЫХ
ФУНКЦИЙ.
§ 52. Функциональные ряды. Функциональным рядом или
рядом функций мы называем бесконечный ряд * -
и1(х)~\-и2(х)+...+ип(х)-\-...\ С1)
в котором u1(x)J и%{х)$ ..., ип(х), .. . суть данные функции
независимого переменного х, называемые „членами" ряда.
Если данный ряд (1) сходится в каждой точке х некоторого
сегмента [а, &], то скажем, что он сходится всюду на сегменте [а, &].
Из элементов теории рядов известно, что именно следует
понимать под „суммой" f(x) сходящегося ряда (1). Она определяется
следующим образом: берется сумма Sn(x) первых п членов ряда (1), т. е.
Sn (х) = ut (х) + аа (*) -f- .. s+un (x) (2)
и рассматривается предел f(x) этой конечной суммы при
безграничном возрастании индекса п
f(x)=.limSn(x).
П -> + СЮ
Эта предельная функция f(x) и называется суммой сходящегося
бесконечного ряда (1); при этом мы пишем равенство
/W— н (*) + ч (ХУ+ • •• +«*(*) + — <3)
Здесь важнейшим вопросом является следующий вопрос:
сохраняются ли свойства конечных сумм Sn для суммы ряда f(x).
Мы знаем, например, что сумма конечного числа
непрерывных функций есть непрерывная функция. Но
можно ли утверждать, что если все члены ип(х) данного ряда суть
непрерывные функции на сегменте [а, 6], то непрерывной будет на [а, Ь]
и сумма f(x) этого ряда? А если это не верно, то при каких
необходимых и достаточных условиях свойство непрерывности
членов ип(х) переносится на сумму f(x) этого ряда?
Вопрос о непрерывности суммы ряда есть один из основных
вопросов этой главы. О том, что вопрос этот не простой, читатель
легко может судить уже хотя бы по одному тому факту, что
15* * 227
Ши даже ряд (1) абсолютно сходится всюду на сегменте [а, Ь]>
то сумма f{x) этого ряда может оказаться разрывной функцией
при непрерывности каждого члена ип(х).
Вот пример этому. Возьмем внутри сегмента [а, Ь] какую-нибудь
точку Е (черт. 143) и поместим на сегменте [£, Ь] счетное множество
точек хг > х2 > х$ > ... >*w > . • •, имеющих точку ? предельной
точкой, Нтд;п = £. Ясно, что сегмент [£, Ь] этим самым разделится
п-> -f- оо
на счётное число сегментов [х{, Ь]} [х2, хх], [д:3, дг2], ..., lxn+u xn\*
..., примыкающих один к другому своими концами. Обозначим
через ип{х) непрерывную функцию, равную нулю вне сегмента [хп,хп_г],
равную 1 в его середине и линейную в левой и в правой его
половине. Геометрически линия у=ап(х) изображается боковыми
сторонами равнобедренного треугольника, имеющего [хп> хп^х]
основанием и 1 своей высотой, и осью абсцисс, из которой вынут интервал
(хп> хп~\)- Ясно, что имеем ип{х)^% так что ряд ^(x) + B2(x)-f
+ •• • +ttn(^)+ ••• не имеет отрицательных членов. И так как
• G}£ *Рль& Ъ*гх1 Ь
А
Q £ */> Xn-i
т~.х
Черт. 143.
никакая точка х оси абсцисс не может находиться внутри двух
различных сегментов [хп, хп„г], п— 1, 2, 3, ..., то для каждого х в ряде
щ (лг) + и2 (х) + ... + ип (х) + ...
может оказаться, самое большее, только один член, отличный от
нуля. Это показывает, что ряд
«i 00 + «а (*)+••• + «п (*)+•• •
абсолютно сходится» Ясно* что его сумма /(*) есть разрывная
функция в точке 5, потому что/(х) равна нулю во всех точках хп
и равна 1 в середине сегмента [х„, хПтт1], которая также бесконечно
приближается к точке 5, когда п безгранично возрастает и, таким
образом, предел Нт/(х) не существует,когда л;-»£ справа.
Следовательно, сумма сходящегося ряда непрерывных
неотрицательных функций может оказаться разрывной функцией.
§ 53. Правильно сходящиеся ряды. Приведенный пример
естественно заставляет искать тех условий, когда сумма сходящегося ряда
непрерывных функций заведомо является непрерывной функцией.
Классическим условием для этого служит правильная сходимость.
228
Функциональный ряд
ux{x)+a%(x)+:~.*:-\-ttn(x)-\-..v (l)
называется правильно сходящимся на сегменте [а, Ь],
если имеется численный знакоположительный сходящийся ряд
члены которого превосходят абсолютные величины соответствен*
ных членов ряда (1), |«п(*)|<впэ при всех значениях х на
сегменте [а, Ь]> если только значок п достаточно велик.
Таким образом, правильная сходимость состоит в возможности для
членов ип(х) рассматриваемого функционального ряда(1) быть
превзойденными на всем сегменте [а, Ь] при достаточно большом п по
абсолютной величине соответственными членами $п некоторого
численного сходящегося ряда гх -j- s2 -\-.., -\~ гп -[- ... .
Ценность понятия правильной сходимости обнаруживается, прежде
всего, из предложения:
Сумма правильно сходцщегося ряда непрерывных функций есть
непрерывная функция.
Пусть f(x) есть сумма правильно сходящегося ряда
/(х)=*их{х)-}~и2(х)-\-...+ип(х)-{- .... (3)
По условию правильной сходимости, имеем неравенства
(х) | < ew+3> • • • (4)
на всем сегменте [а, Ь] при достаточно большом т. По условию
же сходимости ряда ех 4~г2 + ез4~ • * • +sn+ ♦ • • пРи достаточно
большом т имеет место неравенство
где в > 0 есть произвольно малое заранее заданное число.
Сопоставляя неравенства (4) и (5), мы видим, что неравенство
справедливо всюду на сегменте [а, Ь] для достаточно большого фи-
ксированного числа т. С другой стороны, всякий член ип(х) есть
непрерывная функция на [а, Ь]. Следовательно, непрерывной
функцией на [а, Ь] будет и функция Sm(x), определенная равенством
Sm(*) = Ul W + "2W + • • • +"»(4
так как т есть фиксированное конечное число.
В силу же непрерывности функции Sw(x), в точке I сегмента
[а, Ь\ имеет место неравенство
\Sm{x) — Sm$)\<^, (7)
229
которое выполняется, если «точка х достаточно близка к точке {, т. е.
если ,. ч
где ч\ некоторое положительное число.
Здесь £ есть любая фиксированная точка сегмента [а, Ь].
Из равенства (3) имеем
f(x) = Sm (*) + «»-Ц (х) + "ты(х) + ит+Ь(х) -f • • .
/(E) =■ 5W (?) + И^+jlE) -f «m+a (9 + "m+8 (*)•••*
откуда, вычитая, получаем
— [«m+j (0+ «»+»(&)+•••]•
Следовательно,
|/(*)-/(0 Kis«(*)-s«(e)i+!«m+i (*)-t-«*ie(*)-f • •• 1 +
+1«»+j (0 -h и«+й (5) + ... |. (9)
В силу неравенств (7) и (6), имеем неравенство
которое Справедливо, если будет удовлетворено неравенство (8).
А это и доказывает непрерывность сум^ы правильно сходящегося ряда
f(x) в точке £ сегмента [а, Ь]. И так как (• есть любая точка этого
сегмента, то f(x) непрерывна на всем сегменте [а, Ь].
Таким образом,* мы получаем критерий для непрерывности суммы
ряда в виде правильной его сходимости. Правда, критерий этот есть
лишь достаточный и отнюдь не необходимый, но самая его простота и
легкость применения позволяют широко пользоваться им в
математическом анализе. К сожалению, критерий этот довольно слабый, так
как применение его ограниченное.
§ 54. Усиление критерия правильной сходимости методом
предварительной группировки членов ряда. Мы уже заметили,
что критерий правильной сходимости является слабым, так как далеко
не все функциональные ряды
«i (*) + *«(*) + •••+ ип (*) + ■- (1)
сходятся правильным образом. Такими будут, например, все не
абсолютно сходящиеся * функциональные ряды, потому что правильная
сходимость на каком-нибудь сегменте [а, д] функционального ряда (1)
влечет за собой абсолютную сходимость этого ряда на сегменте [а, £],
т. е. сходимость всюду на [а, д] ряда абсолютных величин
| М*)1 + М*) I + • • •+K0OI+• • •>
что не для всех рядов имеет место.
230
Например, критерий правильной сходимости не приложим к
функциональному ряду
£ „4-£ ~ 4- 4-( 1V1+1~4-
хотя его сумма xlog2 есть непрерывная функция. В самом деле;
£_£4-~ — -4-... -4-(— 1V1+1~-!- .. —
=4r-i+-l-T + ---+(-i)"+^+---)=^0§2-
Ввиду этого очень часто и весьма успешно комбинируют метод
правильной сходимости с методом группировки членов ряда, причем
начинают с этой последней. Метод группировки членов ряда состоит
в следующем:
Пусть дан какой-нибудь бесконечный сходящийся ряд, числен*
ный или функциональный'
I/==«i + tta + «e+•••+«!!+•••> (10>
сумму которого обозначим через U. Не изменяя нигде порядка его
членов, соединим некоторые рядом стоящие члены в группы и
заменим каждую группу членов их суммой
(«i + «a+---+"*i) + («*i+i + "fcu-2+ •■• + **,)+•••
• • • + («*v-l+1 + fl*v-l + * + • • • + tf*v) + • • • • (И)
Для этого проще всего назначить заранее, какими должны быть
последние члены в каждой группе, например, выбрать последним
членом в первой группе член ukl, последним членом во второй
группе член uki, и т. д., вообще последним членом в v-ой группе
член %v и т. д., где числа kt < &2< &з < • • • < ^ < - •. образуют
возрастающую последовательность натуральных чисел. Ясно, что
в частном случае, когда за числа kly k2, kb> .. ., &v, ... мы выби-
раем^ самые натуральные числа, идущие без пропусков: 1, 2, 3, ...,
v, . .., тогда в каждой группе будет содержаться лишь по одному
члену и тогда сгруппированный ряд (11) ничем не будет отличаться
от данного ряда (10). Заметим, наконец, чта числа kv &2, ♦ •., Av,...
для группировки данного ряда (10) можно выбирать совершенно
произвольным образом, лишь бы они были возрастающими.
Отметив это, назовем сумму членов первой группы через Uv сумму
членов второй группы через U2 и, вообще, сумму членов v-ой группы
через UH. В этом случае сгруппированный ряд (1) перепишется
просто в виде
I/i + t/a+...+^+--.. (12)
Легко доказать, что сгруппированный ряд (12) сходится и имеет
ту же сумму U, как и первоначальный ряд (10).
231
Чтобы доказать это, обозначим через ov сумму v первых членов
сгруппированного ряда (12). Имеем
^ = Ц + "я+--. + Ц-
Но при вычислении конечной суммы av мы можем сначала
раскрыть скобки и возвратиться, путем уничтожения этих скобок, к
членам первоначального ряда (10). При этом, ввиду того, что v-ая группа
£/v оканчивается членом ик^ ясно, что сумма ov = Ux -j- U% -f-... + (7V
есть сумма подряд идущих членов данного ряда (10), начиная с его
первого члена их и кончая &,-ым его членом икч. Если мы
обозначим через Sn сумму п первых членов данного ряда (10), то ясно,
что имеем тождество
°,=»V (is)
Из равенства (13) следует, что
lim ov = lim SkH,
и так как натуральное число &v неограниченно возрастает с возра^
станием значка v, &v-*«4-oo при v-*4~°°> T0 мы имеем
v ->4-°° n -> + оо
потому \гго, раз имеется предел Sn при возрастании п по всем (без
пропуска) натуральным числам 1, 2, 3, ..., то предел этот будет
иметься и тогда, когда число п возрастает неограниченно не по всем
натуральным числам, но по некоторым из них ku k2, ..., &v, .Л,
т. е. с пропусками.
Итак, из предыдущих равенств мы заключаем, что
Hmo, = I/. (14)
V -> -f СО
Из доказанного предыдущего предложения вытекает следующий
усиленный критерий правильной сходимости.
Усиленный критерий правильной сходимости. Если
данный функциональный ряд
f(x) = u1(x) + u2(x)+...+un(x)+...i (3)
составленный из непрерывных функций и сходящийся на сегменте
[а, Ь]у не есть правильно сходящийся на этом сегменте, но
становится таковым при надлежащей группировке его членов, то
его сумма f(x) есть непрерывная функция на сегменте [а9 Ь],
В самом деле, группируя члены данного ряда (3), получаем но-
вый ряд
yiW + t/2W + ...+^W + ..., (15)
члены которого непрерывны и сумма которого есть функция f(x).
И так как по условию ряд (15) есть правильно сходящийся, та
/(х) непрерывна на [агЬ\.
232
Усиленный критерий правильной сходимости есть уже
чрезвычайно сильный критерий и большинство употребляющихся в
математическом анализе доказательств непрерывности суммы тех или
иных функциональных рядов основано на применении как раз именно
этою усиленного критерия правильной сходимости.
К сожалению, нет общего правила применения этого усиленного
критерия и в каждом отдельном случае приходится по-разному
подбирать числа ku &2» • • •» &п> определяющие полезную группировку
членов данного функционального ряда.
§ бб. Равномерная сходимость функциональных рядов. Исто*
рически стоящим в стороне и исходящим из иного круга идей является
критерий равномерной сходимости, мимо которого не может в на*
Стоящее время пройти ни один курс математического анализа.
Определение. Функциональный ряд
BlM+«2(*)+-"+M*)+*-7
называется равномерно сходящимся на сегменте [а, Ь], если для
каждого положительного числа е имеется такое число N,
независящее от х, что всякий отрезок
М*) + «р + 1 (*)+••• + UQ (*)» Р < $>
рассматриваемого ряда по абсолютной величине меньше чем е,
если только р > N,
\Яр (*) + Up 4- 1 (*) + •••+«* (*)1 < *• (16)
Так как всякий функциональный ряд для каждого численного
значения х становится, разумеется, числовым рядом, то ясно, что
равномерная сходимость какого-нибудь функционального ряда
ut (х)+ tfa (*)+••• +«п (*)+•♦ •
на сегменте [а$ Ь) влечет за собой, вместе с тем, и обыкновенную
сходимость его всюду на этом сегменте, потому что в этом случае
для каждого численного значения х, принадлежащего сегменту [а, Ь],
соблюдается критерий Коши. Таким образом, всякий равномерно
сходящийся на сегменте [а, Ь\ функциональный ряд
Ч (*) + "2 (*) + • • • + "п С*) + • • ♦
имеет на этом сегменте определенную сумму f (х), т. е.
/ (*) = Ч О) + «а (*) + • • • + «п (*) +
Из самого определения равномерной сходимости мы замечаем,
что оно в точности копирует малый критерий сходимости Коши, и
будь рассматриваемый ряд
»i (*) + Ч (*) + - • + ип (*)+•••
не функциональным рядом, а просто численным^ определение
равномерной сходимости не дало бы нам решительно, ничего нового,
так как в точности совпало бы с самим критерием Коши и выражало
233
бы только то обстоятельство, что рассматриваемый ряд Сходится*
Но благодаря тому, что рассматриваемый ряд
щ (х) + «а (■*)+... +ип {*)+" *
не численный, а функциональный, определение равномерной
сходимости, требуя от грани N независимости от аргумента х,
дает кое-что новое, но ценой того, что из всевозможных
функциональных рядов
«1 (*) + Ч (х) + • • • + ип (*)+•••,
сходящихся всюду на сегменте [а, Ь], выбрасывается бесчисленное
множество неравномерно сходящихся рядов: это суть те самые
ряды9 в которых грань N не может быть взята независящей от х
(по крайней мере для некоторых чисел е). Таким образом, в то
время как малый критерий Коши, примененный к численным рядам,
не выбрасывает из рассмотрения ни одного сходящегося численного
ряда, но сохраняет их все (и тЬлбко их одних), в это самое время
определение равномерной сходимости {которое есть не что иное,
как малый критерий Коши, но только с гранью N, не зависящей
от х) выбрасывает из рассмотрения бесчисленное множество
функциональных рядов, сходящихся всюду на сегменте [а, Ь\> заставляя
ограничиться рассмотрением весьма узкого их класса. Так, например,
функциональный ряд может быть абсолютно сходящимся всюду
на сегменте [а, Ь] и, вместе с тем, не быть равномерно
сходящимся на [а, Ь].
Чтобы убедиться в этом, достаточно обратиться к примеру
абсолютно сходящегося ряда неотрицательных непрерывных функций
ui (х) + Ч О) + • • • + ип (х) + .. .,
рассмотренного на стр. 228. В нем функция ип (х) равна 1 в центре
сегмента [хП1 xn^t], лежащего на [а, Ь]. Поэтому, как бы велико ни
было число р для всех значений аргумента х, расположенных на
сегменте [а, Ь], невозможно выполнение неравенства:
\ир (X) +1Гр + 1 (*)+•••+«« (*)1 < S>
так как уже в центре сегмента [хр, хр^х] член ир (х) обращается в 1,
а прочие неотрицательны.
Из сказанного следует, что равномерная сходимость какого-
нибудь функционального ряда
их (х) -f и2 (х) + .. . + ип (х) ~f- ...
на сегменте [а, Ь] влечет за собой вместе с тем и
обыкновенную сходимость его в каждой точке х этого сегмента] но
обратное не верно: даже абсолютная сходимость функционального ряда
всюду на сегменте [а, Ь] еще не влечет за собой его
равномерную сходимость.
Для того, чтобы сделать ясным смысл слова „ равномерная % не
лишне заметить следующее: функциональный ряд
«i (х) -f Ч (х) -f . .. + ип (х) -f ... „
234
просто сходящийся всюду на сегменте [а, Ь], имеет, разумеется, для
каждой тонки х этого сегмента грань N, такую, что е?ли р > N, то
выполняется неравенство:
' К с*)+up+i (*) + ••• + «а (*)| <е>
потому что для каждой фиксированной точки х функциональный ряд
обращается в численный сходящийся ряд, к которому применим
малый критерий 'Коши. Но, в общем случае, грань N есть своя
собственная для каждой точки хчи, поэтому, ее надо обозначить не
через N, а через Л^., и лишь в * случае равномерно сходящегося
функционального ряда грань Nx может быть установлена независимо
от х и, поэтому, ее можно обозначить просто буквой N без значка х,
ибо она становится пригодной однообразно (т. е. „равномерно") для
всех точек х сегмента [а, Ь].
Те'орема. Всякий правильно сходящийся функциональный ряд
на сегменте [а, д] есть вместе с тем и равномерно сходящийся
на этом сегменте.
Если ряд
«1 С*) V«a (*) + "• '• '• + ип С*) + • • •
есть правильно сходящийся на [а, 6], то мы должны иметь для
достаточно большого Ш неравенства •
(х)\<
всюду на сегмекге [а, Ь]. С другой стороны, численный ряд £i + s2 +
—1— - - - —I— в»» —1~" • • • сходится. Поэтому, на основании малого
критерия Коши, мы имеем неравенства
lsP + si> + .t+--- +e«l<8
при условии, что pug больше некоторого числа v, p > v и q > v.
Выбрав какое-нибудь фиксированное натуральное число TV,
превосходящее оба числа т и v, мы имеем для р > N и q> N неравенства
\ир (х) + upArX W + ...+egW|< \ир (х) \+\ир+! (х) | + ... +
на всем сегменте [а, 6]. А это и есть равномерная сходимость на
Теорема. Всякий равномерно сходящийся функциональный
ряд на сегменте [а, Ь] при надлежащей группировке его членов
становится правильно сходящимся на [а, Ь].
В самом деле, если функциональный ряд
их (х) + М*) + •-•+ «п (*) + •• •
равномерно сходится на [а, Ь], то для всякого числа еЛ, е;. > О,
имеется такая грань Л^, за которой (т. е. при р > Nk и q > Nk)
справедливы неравенства
\ир (х) + Vh (*)+••• + «<r (*) I < е*
235
на всем сегменте [а, Ь]. Таким образом, положительным числам еи
*2> • • • > гь • • • соответствуют грани Nu /v2,..., Nk, .., . Так как
числа elf е2, ... , еА,. .; произвольны, то мы можем взять их такими,
чтобы численный ряд, составленный из них, е2 4- s24~ • • • 4"sw4~ • • • »
был сходящимся, С другой стороны, мы имеем право предположить
грани Л/j, Л/"2, ... , Nkt ... возрастающими. Действительно, если
бы мы уже нашли грани Nu N2, •.., Nk_u то за грань Nk мы
всегда можем взять число, большее ранее найденных граней Л^,
N2, ... , Nk_v так как если бы грань Nk для ек оказалась бы меньше
какой-нибудь из граней Nu Л^,..., Nk_u то ничто не мешает нам
увеличить Nk на сколько угодно единиц, потому что от такого
увеличения число Nk нисколько не утратит свойства грани для eft, ввиду
того что неравенства
\ир(х) + ир+1 (х)+ ... + uq(x)]<sk
тем более будут удовлетворяться за увеличенной гранью Nk,
Итак, ряд
ei + Ч + • • • + Ч 4" • • •
сходится, а грани
Ni<Na<...<Nk<.;;
безгранично увеличиваются с возрастанием значка 6, Nk-+-{-co,
если /5-*4"°°* Заметив это, обозначим через UQ(x) начальную
группу
через U\(х) — первую группу [ttNl+1(x)+...uNt(x)]9
через U2 (х) — вторую группу [uNi+1 (х) + ... + ищ (х)] ,
и, вообще, через Uk(x)—&-ую группу (%+iW-f...+%ft+1Wb
Ясно, что данный ряд иг (х) 4- #2 (л:) 4~ ... 4* ял (л:) 4- • • •
перепишется в виде
[иг(х) +^2 (х) + • • • + «ffi (*)] + [«JTi+i W + • • • + «лг, (*)] +
+ ... + [в^л+1 (*)+••■ 4- «tf*+i (*)] + • • • (17)
или в виде
U0(x) + Ux{x) + U%(x) 4- • • • + %(*)4- • • - (18)
Так как
Uk (х) = вуЛ+1 (*) 4- «2ГЛ+а (*) 4- • • • 4" «Jfy+i (*)*
то i/ft(jc) есть бтрезок данного ряда
«i(*)4-M*)-f- •••4*кп(^)+ • •>
находящийся за гранью Nk. Значит, | Uk(x)\ < гк на всем сегменте
[а, Ь\. Поэтому сгруппированный ряд (17) или (18) имеет все члены,
начиная со второго, по абсолютной величине соответственно мень-
236
шими членов Сходящегося ряда &t -}- Ц + • • • -f- Ч + • •* > а эт0 й
показывает, что сгруппированный ряд есть правильно сходящийся.
Из полученного результата следует, что если равномерно
сходящийся ряд --.: - . —. .,
на сегменте [а, Ь] составлен из непрерывных функций, то к нему
всегда применим усиленный критерий правильной сходимости, так
как при надлежащей предварительной группировке его членов он
.превращается в правильно сходящийся ряд непрерывных функций.
Отсюда мы заключаем, что сумма равномерно сходящегося ряда
«i (*) + Ч И + • • • + ип (*) + • • •
непрерывных на сегменте [а, Ь\ функций есть непрерывная на сеГ~
менте [а, Ь] функция.
§56. Равномерно сходящиеся последовательности функций»
До сих пор мы говорили лишь о равномерно сходящихся рядах
функций. Теперь мы будем рассматривать последовательности
функций. Дадим следующее определение.
Определение. Последовательность каких-нибудь функций
St(x), S2(x}, ...,5п(лг), ..., определенных на сегменте [а, #],
называется равномерно сходящейся на [а, Ь\Л если для каждого
положительного з имеется такая грань N, независящая от х>
за которой две любые функции Sp (x) и Sq (x) последовательно-
сти (т. е. при р > N и q> N) отличаются друг от друга на
всем сегменте [а, Ь] меньше, чем на з,
\Sq(x) — Sp(x)\<*. (19)
Так как каждая последовательность функций ^(л:), 52(лг), . ..>
..., Sn(x), ... при численном значении аргумента х становится
численной последовательностью, то наличие грани N и неравенства (19)
означает, что выполнен малый критерий сходимости Коши для
последовательности чисел; поэтому эта последовательность должна
сходиться, т. е. мы должны иметь, lim Sn(x)=f(x). Отсюда, вся-
кая равномерно сходящаяся на сегменте [а, Ь] последователь*
ность функций Sx(x), S2(x), ..., Sn(x), ... есть вместе с тем
сходящаяся последовательность на [а, Ь] в обыкновенном смысле,
т. е. имеет определенный предел lim Sn(x)=f(x) в каждой
п -> + оо
точке х сегмента [а, Ь).
Но нельзя делать обратного заключения: последовательность
функций Sx(x), S2(x), ..., Sn(x),... может сходиться в каждой
точке х сегмента (а, Ь) и в то же самое время вовсе
не быть равномерно сходящейся на этом сегменте. Чтобы
убедиться, достаточно взять за функцию Sn(x) непрерывную
функцию, равную нулю вне сегмента I—^цт» — | (черт. 144), рав-
8?7
яую 1 в его центре й линейную & левой и в правой его пбловинах.
Ясно, что имеем lim Sn(x) = 0 в каждой точке любого сегмента
п -» + со
[а, Ь]у содержащего начало координат О внутри. И, однако, не
может иметь место ни за какой гранью N, какой бы далекой она
ни была (т. е. Д#я р > N и q > N), неравенство
■ \Sq{x) — Sp{x:)\<^
потому что разность Sq(x) — Sp(x) равна-fl в центре сегмента
Г—— , — и равна — 1 в центре сегмента —:—р, — . - —,.
Ltf+1 * Я\ J L^ + i /? J
Таким образом^ равномерная, сходимость последовательности
функций SaО), S2(x), .. .,Sn(x), . .. на сегменте [а, Ь] влечет за
собой вместе с тем и обыкновенную сходимость ее в каждой
точке х этого сегмента; но обратное неверно: даже сходимость
последовательности непрерывных функ-*
ций Sx О), S2 (х), • • *, Sk (#), ... к
непрерывному пределу f(x) еще не еле-
чет за собою равномерную сходимость
этой последовательности на
сегменте [а, Ь).
Когда последовательность просто
—г-—/ сходится на сегменте [а, &], тогда для
х I />+/ п всякого численного значения х она
Черт. 144. является сходящейся численной
последовательностью и поэтому к ней
применим малый критерий Коши; это означает, что для каждого
положительного s имеется такая грань Nx, за которой две любые
функции Sp (х) и Sq (х) последовательности (т. е. при p>Nx и q > Nx)
отличаются друг от друга на всем сегменте [а, Ь] меньше чем на з.
Но, в общем случае, грань эта Nx есть своя собственная у каждой
точки х. И только в случае равномерной сходимости
рассматриваемой последовательности St (x)t S2 (х), . •., Sn(x), ... грань Nx
можно выбрать независимо от х.
Зависимость грани Nx от х в случае неравномерной сходимости
выступает очень рельефно в предыдущем примере. В этом случае мы
имеем (черт. 145)
lim Sn(x) = 0
п -> + °о
на всей оси абсцисс, причем функция Sn(x) изображена на левом
чертеже, а разность Sq(x)—Sp (x) на правом.
Читатель видит, что разность Sq(x)—Sp(x), q >/?, имеет две
волны амплитудой в одну единицу, причем левая положительна, а
правая отрицательна. Обе эти волны находятся направо от начала
координат О, и так как правая волна оканчивается в точке — , то
при р очень большом, обе волны очень тесно прижаты к оси ордн-
238
0*
нат. Если мы через %р обозначим центр сегмента ——у, - I, то
имеем при q > p равенство
Vy—s,(^)=—1.
(20)
Из сказанного вытекает, что при г < 1 грань Nx для точки х = Е&
непременно должна быть больше числа k — 1. Действительно, если бы
гранью при s < 1 для точки \к служило число Л/j, <Г. ^ — 1, то
совокупность функций Sk (х)у лежащих за гранью Л^ (т. е. при п > iVg ),
sn, +1(*). %+2 (*)>•••> sB(4-.
содержала бы функцию Sk(x). И тогда мы должны бы иметь:
1М&*)-5*(У|<.<1, <21)
тогда как, в силу* (20), имеем наверное
|5в0*)-5*(6»)| = 1>«. (22)
Из полученного противоречия заключаем, что Л^Л>А — 1 и, значит,
что Ищ Л^л = + оо. (23)
Таким образом, грани Л/^, Л^2, ..., Л/^,... в точках Е1э52, ..., Ел,...
(для фиксированного числа е<1) возрастают до бесконечности,
■«.до
/7+1 4 /)
/ / /\ j / /
Черт. 145.
когда k неограниченно возрастает и, значит, невозможна какая-нибудь
общая конечная грань iV, пригодная сразу для всех них. Вследствие
этого, рассматриваемая последовательность функций S^x), S2(x),.. .,
Sn(x)y... не может быть равномерно сходящейся ни на каком
сегменте [а, Ь]9 содержащем начало координат внутри.
Мы видим полную аналогию. равномерной сходимости рядов и
последовательностей. Легко усмотреть причину этого, заключающуюся
в том, что
последовательные суммы
Sj(x), S2(x)y S3(*),..., Sn(x),...
239
первых одного] двух, трех, и т. д., А членов равномерно
сходящегося ряда
их(х) + щЦх) + Ч(х) + •; • + ип (*) + • •'•
на сегменте [а, Ь) образуют равномерно сходящуюся на этом
сегменте последовательность функций; обратное также верно:равно*
мерно сходящаяся на [а, Ь] последовательность функций
может быть рассматриваема как последовательность сумм первых
одного, двух, трех, и т. д., п членов равномерно сходящегося ряда
Si(x)+lSAx)-S1(x)l + lSAx)-SAx)}+.. -WSn{x)-Sn-i{x)] + - • •
на этом сегменте.
Действительно, если ряд
равномерно сходится, на [а, Ь]> для всякого е, е>0, мы имеем
грань ЛГ, за которой (для p>N, #>Л/) всегда справедливо
неравенство
I «iW + ^+i (*) + • • • -f ««(*)I <е .
на всем сегменте [а, £]. И так как это неравенство может быть
переписано в виде
|Se(*)—%_,(*)!<•, (24)
где 5п(х) обозначает сумму первых п членов ряда
и\{х) + и2(х) + ... + Hn(*) + ..'.,
го последовательность сумм ^(х), SaC*)» • • •» Sn(x)9 ... равномерно
сходится на [а, £], причем пределом f{x) этой последовательности
служит сумма данного ряда.
Введя обозначения ui(x) = S1(x)t щ(х) = 52(х) — 5\(л:), ...,
«*♦> Kn(4=Sn(x)-ViW» мы видим, что неравенство
\Sq(x) — Sp(x)\<e1 (25)
выражающее равномерную сходимость последовательности St (x),
$2(х)) .*., Sn(x), ..., переписывается в виде неравенства
1«*+1 (*) + **+*(*) + •.•+««(*)!<•» (26?
выражающего равномерную сходимость ряда #! (дг) + #2 (*) + • • • +
+ *»(*) + •••• • *
Таким образом, равномерная сходимость ряда и
последовательности есть одно и то же.
§ Б7. Исследование равномерной сходимости. Возьмем какой'
нибудь равномерно сходящийся ряд
«i (X) + Ч (х) + Ч(*) +••• *р «Л (*)+•• • (О
240
на сегменте [я, Ь] и нанесем на плоскостиУ ХОУ все кривые
y = Sn{x)% (п = 1, 2, 3, ...), (27)
где Sn(x) обозначает сумму п первых членов данного ряда (черт. 146).
Таким образом, мы будем иметь на плоскости XOY счетное
множество, кривых y = Sa(x); (я = 1, 2, 3, ...), занумерованных
натуральными числами. На чертеже эти кривые мы изображаем пунктиром,
так как они могут быть разрывными в Аждой точке. Если мы
ч
01 а
Г SA*)
ЬХ
q\ а х
Черт. 146.
ьхо
*
ЬХ
проведем в какой-нибудь точке х сегмента [я, Ь] перпендикуляр
к оси абсцисс, он пересечет каждую из этих кривых в одной и только
в одной точке. Таким образом, на этой прямой имеется счетное
множество точек *), имеющих ординатами значения функций Sx(x)y
S%(x)} ..., Sn(x)> ... . Для наглядности мы вычерчиваем отдельно
эту прямую горизонтально (черт. 147) вместе с расположенными на
-4-
О
SJx)
Sn(x) S,(x)
Черт. 147.
ней точками St (x), Sa (*), • • • , Sn(x), ..., обозначая эту прямую
как OY, причем точка О на ней играет роль точки х сегмента
[а, *].
Явление равномерной сходимости состоит в том, что для каждого
фиксированного г, е > О, имеется такая грань N, независящая
от а:, за которой любые две суммы Sp(x) и Sq(x) (т. е. при р > N
и q > N) отличаются друг от друга меньше чем йа е, т. е. имеем
I sq (х)— $р (х) I < s на 6Сем сегменте [а, Ь\. Чтобы понять это явле*
ние, удалим с плоскости первые N кривых y = St (х), у = «Sa (■*)*• ..,
... ,у = 8я(х). Оставшиеся кривые yz=SN^1(x)yy = 5^ 2(лг), ... ,
..., y^iS^x), ... образуют счетное множество кривых, и
на прямой, проведенной через точку х перпендикулярно к оси
абсцисс,' останется счетное
5Я(*),..., где n>N.
множество точек SN+1(x), 5^+2(л), .'
*) В случае совпадения друг с другом некоторых точек S^ (х), S2(x),..V ,
, Sn(x), ..., мы рассматриваем совпавшие точки как сратные, считая
■-~- S?(x),
одну и ту же точку столько раз, сколько совпадает с нею точек
S2 (х), ... , Sn (л-),
15 Зак. ША*
241
В силу неравенства
-' \Sq(x)Sp(x)\<e ^ (28)
любая пара этих оставшихся на прямой точек имеет
расстояние меньше чем е. А это важное обстоятельство равносильно тому,
что все множество оставшихся точек~SN+1(x), $я+2(х)> ••• > Sn(x),
... содержится в не^тором малом сегменте [а, [3] длины не больше
чем е (черт. 146 и 148). Действительно, если бы диаметр
множества точек SN j (л:), S_y+2(#)> .. ♦ , Sn(x), ... (т. е. длина
наименьшего сегмента, содержащего все эти точки) был больше е, то можно
было бы отыскать среди этих точек две точки Sp (х) и Sq (л:), рас-
____________ Sn(x)
о « р г
Черт. 148.
стояние которых было бы также больше е, что невозможно в силу
неравенства (28).
Таким образом, если мы удалим с плоскости первые- N кривых,
то оставшиеся кривые
y = SN+1(x), y = SN+2(x)y... , y = Sn{x), ...
будут пересекаться всякой прямой, параллельной оси ординат OY>
по совокупности точек, содержащейся в малом сегменте ]<х, $\
длины не больше чем е.
Предположим, что этот малый сегмент [а, 0] является
наименьшим, содержащим все оставшиеся точки .SN+t(x), SN (x),...t
Sw(a:),. .. и предположим,что он построен на всякой прямой,
перпендикулярной к оси абсцисс и пересекающей сегмент [а, Ь]. Тогда
верхние концы J3 и нижние концы а этих сегментов [а, 48]
образуют две кривые линии
; = *2W и j/= <*>_(*), где Фв(*)>Ф_(лО,
одна из которых лежит выше {не ниже) другой и которые сбли*
жены между собой не дальше чем на е.
Поэтому, часть плоскости XOY, содержащаяся между этими
кривыми (речь идет о точках, лежащих на параллелях оси ординат и
содержащихся между ординатами кривых у = Ф2(х) и у«=Ф_(л;)),
образует полоску ширины не больше чем е, вырезанную из
плоскости двумя кривыми у = Ф%(х) и у==Ф1(х).
В силу очевидных неравенств Ф_ (лО<5п(д;)<Ф2(л;) Для n=N-\-l9
N + 2, ..., имеющих силу на всем сегменте, [а, Ь]> эта полоска
содержит в себе все оставшиеся кривые
-V = ^4i(at), y = SN+2(x), ..., _y = Sw(x), .-...
Таким образом, если функциональный ряд
UX (x) -f tfg(x) + . . . +"»(*) + • . •
242
сходится равномерно На сегменте [а, Ь], то каково бы ни было
данное положительное число е, имеется такая грань N, завися*
щая только от е, за которой все кривые y=zSn (л:), п > N,
содержатся в полоске ширины, не большей чем е.
Обратное также верно: если для сегмента [а, Ь] при любом
положительном е кривые yz=zS1(x),y = S2 (х)~... , у = Sn (х),...,
за некоторой гранью N, все содержатся в полоске ширины, не
большей чем е, тогда ряд их (х) -\- и2 (х) -f- ♦.« + ип (х) -\- ...
равномерно сходится на [а, Ь].
Действительно, в этом случае суммы St (x), S2(x), ..., Sn(x),.'.\,
за гранью N не могут отличаться друг от друга более, чем на е.
Следовательно, мы имеем неравенства \Sq(x) — Sp (x) |<> для
всяких p>N, q>N на всем сегменте [а, Ь], которые и указывают,
что последовательность сумм St(x), S2(x), ..., Sn(x), ... равно*
мерно сходится на [а, Ь), ас ней и данный ряд «iW + ^Wt
+ ...+«»(х) + ... . , ^
\ Таким образом, равномерная сходимость функционального
ряда иг(х) -+-ti2(x) -f- • • • + ип(х) ~Ь • • • равносильна наличию по*
лоски ширины ^е, содержащей в себе все кривые у = Sx(x)y y =
z=S%(x), ... , y=>*Sn(x), ... за некоторой гранью N.
Этот результат очень важен, но еще очень не полон, так как мы
не знаем, где лежит эта полоска. Чтобы построить ее, отметим
сначала, что сумма f(x) равномерно сходящегося ряда есть функция,
предельная для суммы Sn(x), т. е. /(#) = lim Sn{x). Поэтому, раз
П ->-f*°9
мы имеем на сегменте [а, Ь\ неравенство
ФгО0<SnО) <Ф2(х) для п > N,
то, 'очевидно, имеем и неравенство
Ф* (*)</(*)< <М*)> ' (29)
обнаруживающее, что сама предельная функция f(x) также
должна находиться в рассматриваемой полоске ширины <>. Это
простое» замечание закрепляет на плоскости положение
рассматриваемой полоски, так как показывает, что она при уменьшении числа &
до нуля не может произвольным образом перемещаться по
плоскости, но должна стягиваться к предельной кривой у *=/(х).
Чтобы окончательно построить нужную нам полоску, мы сначала
вычерчиваем на плоскости XOY предельную кривую у=/(х) и,
начертив ее, будем непрерывным образом передвигать ее по плоскости
вверх и вниз параллельно самой себе на расстояние е. Передвигаемая
таким образом предельная кривая у=/(х) своим движением обра-
вует полоску шириной 2s, причем верхним краем этой полоски
будет кривая у=/(х)-\-г> а нижним краем — кривая у = f(x) — в
(черт. 149). Поэтому, средней линией этой полоски служит
предельная кривая y=f(x). Легко убедиться в том, что построенная
таким образоц полоска содержит в себе все кривые у =Sn(x), у
16* 243
которых значок п превышает некоторую грань N9 п > М В самом
деле, в силу равномерной сходимости ряда
«1 (*)+ Ч (*) +•••*+ «nW + •
для числа s имеется такая грань N, за которой суммы Sn(x)
отличаются друг от друга меньше чем на е, т. е. имеем
\Sq(x)-Sn(x)\.<*
всюду 'на сегменте [а, Ь]> если только я > N и q > М
Черт. 149.
Заставив число # неограниченно возрастать в силу равенства
/(*) = lim Sq (*), мы получим
|/(*)-5»(*)|0 (30)
всюду на [а, Ь], если только я > Л/".
Это показывает, что каково бы ни было положительное число е,
кривая y = Sn{x) войдет для n>N в полоску 1у = /(лг) + в,
j; z=f(x) — е] 0££Л*й ШЖ-
wAwr/wfsj*AM^^ yJ^KMwwsmw^mmmtmMmim MU m04KaMU U ПрЦ в03т
q Q-* а о+г растании п будет оста-
UanT 1f.n ваться в ней.
Черт. 150. € тт
Читатель должен
отметить совершённую
аналогию этого явления, вполне характеризующего равномерную
сходимость, с определением предела а последовательности хи хъ . ..,#я,
когда мы говорим, что, каково бы ни было положительное число е,
член последовательности хп войдет, для n > N, в сегмент [а — е,
а-\-г] и при увеличении я останется в нем (черт.' 150).
Мы видели, что неравенство (30) является следствием
равномерной сходимости. Но легко видеть, что оно вполне характеризует
равномерную сходимость, будучи в точности равносильно ей.
Действительно, из неравенства (30) мы заключаем, что
|/(*)—s, (*)!<•
и
244
I
если только р > N и q > Af на всем сегменте [а, ft]. Отсюда,
сопоставляя эти неравенства, мы имеем
|5д(^)-5р(д:)|<2в
(31)
на [а, Ь] и прири #, больших грани М Ясно, что неравенство (31)
и выражает равномерную сходимость, потому что число е можно взять
сколько угодно малым, в частности можно его заменить на ~, что
приводит к замене 2г через е. Таким образом, равномерная сходимость
получает следующее определение, равносильное прежнему:
сходящийся ряд
»i (*) + Ч(х) Ч +»!»(*)+•••"
££/w& равномерно сходящийся на сегменте [а, ft], если его остаток
Rn(x) = ww+1 (х) + ип+2(*) -J- ... равномерно стремится к нулю
на [а, ft]; это означает, что для любого е, е > 0, ^имеется такая
грань N, за которой остаток Rn(x) меньше по абсолютной
величине, чем е, на всем сегменте [a, ft],
т. е. если имеет место неравенство
|Я»(*)К«. (32)
на [a, ft] яри всяком п > ЛГ.
До сих пор мы предполагали члены
ип(х) равномерно сходящегося ряда
иг(х) + и2(х) + ... -f «„(*) -f- ^ .
какими-нибудь (вообще разрывными)
функциями на [a, ft]. Теперь мы предпо- L;e)T# 151
ложим их непрерывными на [a, ft].
Мы уже знаем, что в этом случае сумма ряда f (х) есть
непрерывная функция на [a, ft]. Это важное предложение мы выше (в§ 55)
доказали аналитическим методом. Легко теперь геометрически
истолковать причину этого. В самом деле, если бы сумма f(x) была
разрывной функцией хотя бы в одной точке х0 сегмента [а> ft], мы
имели бы колебание ш функции f(x) в точке х0 большим нуля,
со>0 (черт. 151); Это означало бы, что в сколь угодно тесной
близости с точкой х0 можно найти две такие различные точки V и £",
в которых значения функции f(x) отличаются друг от друга более,
чем на -£ . С другой стороны, в силу равномерной сходимости мы
имеем неравенство \f(x) — Sn (х) | < г всюду на [a, ft] при всяком
n>N. Это неравенство указывает, что предельная кривая y=f(x)
должна содержаться в полоске ширины 2 s, имеющей кривуюy=Sn(x),
/z>/V, своей центральной линией (т. е. в полоске, получаемой сдвигом
вверх и вниз кривой y = Sn(x) на s). Это же является абсурдом,
так как кривая у = Sn (x) непрерывна и полоска имеет ширину 2 е,
причем всегда можно предположить е < -| , так что 2s<-j-. Точки
же V и 6" могут быть взяты сколь угодно близкими в точке х0
245
и величины /(£') и /(£") отличаются друг от друга больше, чем
на^, Поэтому, если одна из двух точек М' [V, /(Г)] и /И"[$,/ (Г')1
попадает в эту полоску, то другая (вследствие большой разности
ординат) наверное не попадает в полоску, что невозможно, так как
предельная кривая у=/ (х) должна лежать в этой полоске всеми
своихми точками.
Другое аналитическое доказательство проводится все целиком
в нескольких строках: если f(x) есть разрывная функция в точке х0,
то ее колебание ш в этой точке должно быть положительным, со > 0.
Но тогда и колебание разности f{x) — Ф(х)} гДе Ф(*) есть любая
непрерывная функция, также равно в точке х0 ч'ислу ш. В частности,
колебание любой э разности /(х) — Sn (x) в точке xQ также должно
быть равным со, что невозможно, потому что при п > N имеем
| f(x) — Sn{х) | < y на всем сегменте [а, Ь].
Таким образом, при непрерывности членов ип (х) ряда их (х)-\-
4~ и2 (х) 4~ • • • + ап(х) "Ь • • • равномерная сходимость его на [а, Ь]
является достаточным условием
непрерывности его суммы f(x) на
[а, 6).
Это условие отнюдь не является
необходимым. Так, например, если
непрерывная функция Sn (x) равна
нулю вне сегмента 0,-1, равна 1
в его средине и линейна в левой и
в правой."его половине (черт. 152),
то ясно, что имеем lim Sn(x) = Q
Черт. 152, на всей оси абсцисс, а
последовательность S2 (х), 52(а:),' *.. ,
неравномерно сходится на сегменте [0,1], потому что
на всем сегменте [0,1] не имеет место неравенство
|0-Sn(*)|-|Sn(*)|<t
ни при каком п} если s < 1.
Таким образом, функциональный ряд
ut(x) + u2(x)-\-...+un(x) + .;:, -
составленный из непрерывных функций, может иметь суммой f (x)
на [а, Ь] непрерывную функцию и, вместе с тем, не быть
равномерно сходящимся на [а, Ь].
Есть, однако, случай, когда равномерная сходимость является
необходимым условием для "непрерывности суммы /(х) ряда при
непрерывности его членов. Это случай, когда все члены ип (х) ряда
имеют один и тот же знак.
Если все члены ряда отрицательны, то, переменив знак у каждого
члена, мы получим ряд с положительными (точнее: неотрицательными)
членами. Поэтому достаточно исследовать случай ряда иг (х) -[- и2 (х) +
'246 : " " "~ " ~ . . .
Sn(*)>
JJ-7.. -\-un(x)-\- •"••с неотрицательными членами ип(х) на сегменте
\а, Ь], ип(х)^*0. Пусть этот ряд сходится и имеет непрерывную
сумму f(x) на сегменте [a, b\\ :
f(x) = u1(x) + u2(x)-\-...-\-un(x) + ... (3)
Обозначим
Sn(x) = u1(x) + u2(x)+...^un(x)
и
Так как имеем
/(*) = 5Я(*) + ЯП(*)8
то в силу непрерывности функции Sn(x), остаток Rn(x) есть
непрерывная на [а, Ь\ функция. И в силу того, что ип(х)^0 на [а, Ь]%
остаток Ru(x) есть неотрицательная функция аргумента х на [а, £],
убывающая (точнее:, невозрастающая) при возрастании значка п и
стремящаяся к нулю, когда я -> -|~ оо,
iim Rn(x) = 0'
всюду на [а, Ь\. Пусть е есть какое-нибудь положительное число,
заранее данное, и пусть л:0 какая-нибудь точка сегмента [а, Ь]. В силу
сходимости ряда в точке л;0, имеем lim Rn(x0) = Q. Значит, имеется
столь большое натуральное число пХс, что имеем неравенство
0</?^ (х0)<4. В силу же непрерывности функции Rn (л:), можно
найти столь малый интервал сц, содержащий точку х0, на котором
Черт. 153.
имеет место неравенство 0<[/?^ (*)<« (черт. 153). Система
интервалов £ = {8о?0\} удовлетворяет, очевидно, теореме Бореля-Лебега,
так как всякая точка л:0 покрыта по крайней мере одним
интервалом 8, принадлежащим системе 2. Отсюда, можно взять из системы
Е такое конечное число k интервалов bv §2,..., 8Ъ которые
покрывают весь сегмент [а, Ь]. Но каждому интервалу 8 системы 2
соответствует определенное натуральное число п: это число такое, что на
всем интервале 8 остаток Rn(x) меньше, чем е. Если nv n2»--*»%
суть числа, соответствующие интервалам 81э 82,..., 8Л, то мы
имеем
.- Ящ(х) < е на »< (где / =. 1, 2, 3,..., £). (33)
Пусть теперь N есть натуральное число, превышающее все числа
пь я2,..., пи. Ясно, что имеем
RN(x)4CRni(x) на [at b]
247
и, следовательно, в силу неравенства (33) - • '-«■.*
Rn(x)<q на 8* ('= 1, % 3,..., k).
И так как 8^; 82 , 8^ покрывают весь сегмент [а, ft], то имеем
Rn(x)<.* н* всем ^гменте [а, ft].
В силу же убывания положительного остатка Rn (x) в любой точке х
сегмента [а, ft] при возрастании значка п, имеем и подавно
Rn {x) < s на [а, ft] при п > N.
А это значит, что данный ряд равномерно сходится.
Итак, если сходящийся ряд их (х) -f ^2(х) ~f" • • • + ип(х) Л~ • • •
непрерывных функций имеет все члены одного и того же знака
на всем сегменте [а, ft], то необходимым и достаточным условием
непрерывности суммы f(x) этого ряда на [а, ft] является
равномерная сходимость его на [а, ft].
§ 68. Исследование неравномерной сходимости. Мы сейчас
переходим к изучению неравномерной сходимости функциональных
рядов.
Обозначая попрежнему через Sn(x) сумму первых п членов этого
ряда и через Rn{x) остаток его, мы имеем
* sn (*) = ч (■*) 4- ч 00 + • • • + «п (■*)>
Rn(x) = яя+1 (x) -f unh2(x) -f ...
и
Так как данный ряд предполагается сходящимся всюду на сегменте
[а, ft], то имеем f(x) = lim 5w(x) на [a, ft], откуда находим основ-
ное равенство
Ит /?„(*) = 0, (34)
справедливое на всем сегменте [л, ft].
Для уяснения равенства (34) начертим на плоскости все кривые
y = \Ri(x)\,y = \R2(x)\,'.-,y = \Rn(*)\,--- .
Мы получим, таким образом, бесконечное множество кривых,
занумерованных натуральными числами и не имеющих нигде отрицательных
ординат.
Начертим сначала предельную кривую у*= f(x) и образуем около
нее криволинейную полоску ширины 2s, средней линией которой
является эта предельная кривая. Затем мы чертим кривую y='Sn(x).
Здесь имеются только две возможности. -
1) Данный ряд есть равномерно сходящийся на [a, ft]. Это
означает, что для любого положительного числа е, при значке я, большем
24S
некоторой грани ЛГ, кривая y=*Sn(x) всеми своими точками войдет
в криволинейную полоску ширины 2 е. В этом случае кривая
y = \Rn(x)\, представляющая собой абсолютную величину разности
ординат/(х) и Sn(x), т. е. \f(x) — Sn(x)\=\Rn(x)\y всеми своими
точками будет содержаться в прямоугольной полоске, имеющей
основанием сегмент [а, Ь] и высотою 2е (черт. 154).
=1*ям1
2) Данный ряд не есть равномерно сходящийся на [я, Ь]. Это
означает, что имеется такое число е0 > 0, для которого нет никакой
грани Л/, начиная с которой кривая y = Sn(x), n > А/, всеми своими
точками расположена в криволинейной полоске ширины 2 е0. А это
значит, что кривая y = Sn (x) для бесконечного множества численных
значений пх < щ < пг < ... < пк < .. • значка п не укладывается
всеми своими точками в криволинейной полоске ширины 2е0, но
/-7М
01 О
<?е,
d/=|ffn(*)»
ЬХ 0\ а
Черт. 155.
b X
в некоторых местах обязательно выступает из нее. В этом случае
кривая y—\Rn(x)\ Для бесчисленного множества, значений п1 <
< п2 < пь < ... <пк < ... значка п не содержится в прямоугольной
полоске, имеющей основанием сегмент [а, Ь] и высотой 2s0. А это
означает, что кривая y = \Rn(x)\ для бесконечного множества
численных значений пг < п% < п3 ... < пк < ... значка п
представляет собой волну, гребень которой подымается над осью абсцисс выше
некоторой положительной фиксированной величины 2г0 (черт. 155).
В этом и заключается вся сущность неравномерной сходимости.
Тонкость же явления состоит в том, что несмотря на то, что кривая
для бесконечного множества численных значений пх < п2 < п3 <. 7Т <
<%<••• значка п представляет вид волны с высоко поднятым
249
..гребнем (выше, чем на фиксированную высоту 2 е0), однако, все же
равенство
lim |/?Л*)1 = ° (35)
имеет место во всякой точке сегмента [4, *], так как данный ряд
сходится всюду на [ау Ь]. Помирить наличие высокого гребня волны
(выше, чем фиксированное число 2е0) с наличием равенства (35)
в каждой точке х сегмента [#, Ь], на первый взгляд, довольно трудно.
Наличие не снижающегося гребня волны с предельным равенством
(35) объясняется не тем, что максимум \Rn(x)'\ убывает до нуля,
а тем, что гребень волны отодвигается в сторону, без снижения
своей высоты, что делает возможным для каждого фиксированного
числа х стремление к нулю | Rn {х) |. Таким образом, явление
неравномерной сходимости есть просто явление движущейся волны с несни-
жающимся гребнем, причем, при проходе волны через фиксированную
^ точку х (при неограниченном возрастании числа п) абсолютная величина
I Rn(x)\ остатка может и должна возрастать; но потом, когда волна
У'Шх)!
ь х
0\ ± ~~Т
I X
Черт. 156.
уже прошла, начинается убывание абсолютной величины остатка до
того момента, когда к точке х не подойдет более мелкая волна,
которая может вызвать новый подъем абсолютной величины |/?w(x)|
остатка, но уже более слабый, и так далее (черт. 156). В результате,
при неравномерной сходимости абсолютная величина | Rn(x) | стремится
к нулю вибрирующим образом: то возрастая, то убывая. Явление
движущейся волны особенно хорошо выступает на правом рисунке 156:
с возрастанием значка п сегмент —— , — пододвигается к началу,
а вместе с ним и волна высотой 1. И тем не менее мы имеем
lim |/?те(л;)|=0 во всякой точке х сегмента [0,1].
Предыдущие примеры дают представление лишь о том, как может
осуществляться неравномерная сходимость на сегменте вблизи какой-
либо одной его точки, например вблизи начала координат О. Но мы,
пока еще не имеем представления о том, как может осуществляться
неравномерная сходимость всюду на сегменте [а, Ь], т. е. в каждой
сколь угодно малой его части (в каждом сегменте 8, лежащем на
[ау Ь]). Для того, чтобы построить пример сходящегося ряда
непрерывных функций их (х) + я9 (х) -{-..-. + йп (*) + ..., имеющего
суммой непрерывную функцию f (х) на [а] Ь] и не сходящегося
равномерно ни в каком сегменте а, лежащем на [а, Ь]9 как бы он
мал ни был, проще всего поступить так:
250
Первая операция: делим сегмент [а, Ь] ка счетное число
сегментов 1-20 ранга, меньших 1 и имеющих его левый конец в. качестве
единственной предельной точки, и затем строим на каждом из них
равнобедренный треугольник высотой 1. Это — треугольники 1-го
ранга.
Вторая операция:«делим точно таким же образом каждый сегмент
1-го ранга на счетное число сегментов 2-го ранга, меньших -^ и
имеющих его левый конец в качестве единственной предельной точки,
Г! Г\
ЬХ
/--/?„IXl
Черт. 158.
и затем строим ка каждом из них равнобедренный треугольник высотой
-у. Это — треугольники 2-го ранга.
k-ая операция: имея сегмент k — 1-го ранга, делим его на счетное
число сегментов &-го ранга, меньших -т- и имеющих его левый конец
в качестве единственной предельной точки, и затем строим на каждом
из них равнобедренный треугольник высотой -£-. Это —
треугольники k-го ранга (черт. 157 и 158).
Если мы теперь заставим натуральное число k неограниченно
возрастать, то получим сегменты рангов 1-го, 2-го, 3-го,.. ♦ , &-го
Всех этих сегментов будет лишь счетное число, потому что сегменты
&-гон?анга между собой не перекрываются (по сегментам, но они
могут иметь и имеют в действительности общие концы). Следовательно,
и равнобедренных треугольников, построенных на. этих сегментах,
также имеется счетное число»
Занумеруем все полученные таким образом сегменты всех рангов:
°i> °2» 0з>'«'>°пи> пользуясь равнобедренным треугольником, по-
25Г
-1-
строенным на aft* определим непрерывную функцию Rn (х), равную
нулю вне ап и равную ординатам боковых сторон построенного на
нем равнобедренного треугольника, когда х принадлежит к оЛ. Таким
образом, мы имеем последовательность неотрицательных непрерывных
функций:
С одной стороны, мы имеем
lim/?„(*) = О
всюду на сегменте [а, Л], потому что высоты треугольников,
основания которых содержат фиксированную точку х, стремятся к нулю,
когда их ранг безгранично возрастает. С другой стороны,
последовательность R1(x),R2(x)>.. .;Rn(x),— не может сходиться
равномерно ни на каком сегменте [а, (3], лежащем на [a, b].
Действительно, как бы мал ни был сегмент [&, р], он содержит целиком
некоторый сегмент ош. Но ни на каком сегменте ар не может быть
равномерной сходимости, потому что сегмент ар имеет определенный
ранг q и разделен на бесконечно много сегментов непосредственно
следующего ^-f-1-го ранга, высота треугольников на которых равна
. . Поэтому имеется бесконечно много функций Rni (x), Rn%(x),
Ч т~ ■*■
..., Рщ (х),..., п1<Сп2К ... < flv < ..., максимумы которых на
ор равны ., что противоречит равномерной сходимости на ор. •
Ч ~Т~ *■
§ 59. Обобщенная равномерная сходимость. Мы видели, что
равномерная сходимость является лишь достаточным условием для
непрерывности суммы ряда, составленного из непрерывных функций.
Мы знаем далее, что равномерная сходимость заключается в
требовании, чтобы для каждого данного положительного е имелась такая
грань N, за которой все остатки Rn{x) ряда по абсолютной
величине меньше, чем е, на сегменте [a, b]9
\Rn (*)]<*, (32)
для всякого значка я>А/г на всем сегменте [а, Ь].
Дини первый обратил внимание на то, что это условие слишком
сильное. Он выставил требование, чтобы множество значков п, при
которых неравенство (32) имеет место на всем сегменте [a, &], было
просто бесконечным, хотя бы и с пропусками. Исходя из этой мысли,
Дини пришел к простому достаточному условию, названному им
„обобщенной равномерной сходимостью"*).
Определение Дини. Сходящийся на сегменте [а, Ь]
функциональный ряд их (х) -f- и2 (х) -f- • • • + ип (х) -f- ... называется
имеющим на этом сегменте обобщенную равномерную
*) Точный термин самого Дини был: „простая равномерная сходимость".
Во избежание возможных недоразумений, мы избегаем термина „простая",
заменяя его на термин «обобщенная\
252
сходимость, если для каждого положительного числа е имеется
бесконечное множество чисел п> при которых неравенство
имеет место всюду на [а, Ь].
Докажем теорему Дини: Если сходящийся на сегменте [а, Ъ\
функциональный ряд их (л;) + и2 (х) +...+"«(*) + • • • с
непрерывными членами имеет на этом сегменте обобщенную
равномерную сходимость^ его сумма f(x) есть непрерывная функция
на [а, Ь].
Доказательство крайне просто. Имеем f(x) = Sn (x) -f Rn (x)>
В силу непрерывности на всем сегменте [а, Ь] суммы Sn{x) первых
п членов ряда, если точка х0 есть точка разрыва для функции/(лс),
то она должна служить точкой разрыва и для функции Rn(x). При
этом, если со есть колебание функций f(x) в точке х0, то таким же
должно быть колебание и функции Rn(x) в точке х0. Но, в силу
обобщенной равномерной сходимости, имеем, при подходящем
выбранном значении п> \Rn(x) |<e на сегменте [а, Ь]. Значит,
колебание функции Rn(x) в точке xQ самоё большее равно 2е и поэтому
О < а) ^ 2е. Но это невозможно, так как ш есть фиксированное
положительное число, а е произвольно малое положительное число.
Заметим, что при доказательстве предложения Дини не было
использовано то обстоятельство, что для кажйого е имеется
бесконечно много значений я, при которых 1/?п(*)|<е, так как
достаточно наличия для всякого е лишь одного значка я,
удовлетворяющего этому условию.
Докажем справедливость предложения: Обобщенная равномерная
сходимость Дини эквивалентна усиленному критерию правильной
сходимости. 0
Доказательство, естественно, распадается на две части.
1. Всякий функциональный ряд их (х) + «2 (*)+...+ «п (х) +
+ •••> сходящийся на сегменте [а, Ь\ и удовлетворяющий на нем
усиленному критерию правильной сходимости^ имеет на [а, Ь]
обобщенную равномерную сходимость Дини.
В самом деле, раз рассматриваемый ряд удовлетворяет на [а, Ь]
усиленному критерию правильной сходимости, то это означает, что
он становится правильно сходящимся на [а, Ь] при надлежащей
группировке его членов. Пусть будет
и1(х) + и2(х) + иь(х) + ...+иЛх)+-..:' (36)
сгруппированный нужным образом данный функциональный ряд
«i(*)+"M*H— + «nW+ •••, где
Ut = [«i (*)+••• + «fa (*)L U2 = [uki +1 (*) + ... + икш(х)],
причем &1<&2<^з« • • <Ж< Мы предполагаем, 'что имеем на
[а, Ь] неравенство
\VAx)\<** (37)
*253
для всякого v, превышающего некоторое натуральное чиСло*\>0, и что
ряд et -f. н + • * • Н~ 8v + • • • сходится. Обозначив через cv (х)
сумму первых v членов ряда (36) и через pv(x) соответствующий
его остаток, получим:
^MrsU1(x) + U2(x)+... + Ult(x) = Slh(x) (38)
и
Pv (*) = Unt (x) + <7v+2 (*) + ... = tfAv (л:). (39)
В силу неравенств (37) имеем для всякого v> v0 неравенство для
всякого х на сегменте [я, Ь]
//?b(^)|<|^+1W|4-|C/v+2(x)|-f-...<e,+1 + Sv+2-f-.... (40)
Установив это, возьмем какое-йибудь положительное число е и
определим такое натуральное число т, для которого
+ «„,+8+ •••<*• (41)
Из неравенства (40) мы заключаем, что при каждом 'индексе v,
большем двух чисел v0 и т, мы имеем
lfy(*)|<* (42)
всюду на [я, Ь]. И так как таких чисел v бесконечно много, то
бесконечно много и индексов п = &v, удовлетворяющих неравенству
\ \Rn{x)\<^m[a, Ь]. .
Следовательно, данный ряд иг (х) + «9 (*) + • • •'+ ип (х) +
имеет на [а, £] обобщенную равномерную сходимость Дини.
II. Всякий функциональный ряд их (х) + и2(х)-\-... -\-ип(х) + •..,
сходящийся на [а, Ь] и имеющий на этом сегменте обобщенную,
равномерную сходимость Дини, удовлетворяет на [а, Ь]
усиленному критерию правильной сходимости.
Пусть числовой ряд ®i + е2 + гз ~Ь • • • 4" sv + • • • > имеющий
положительные члены, сходится. В силу обобщенной равномерной
сходимости Дини, имеется бесконечно много натуральных чисел
я[у> < n<v> < п^) < ... < п$ <..., таких, что справедливо при '
каждом индексе и в любой точке на [а, Ь] неравенство
1К»£> (*)!<«,, /43)
каково бы ни было натуральное число т (т = 1, 2, 3,. •.). Установив
это, образуем из натуральных чисел п^) таблицу двойного хода,
написав в v-й строке числа п^\ п^\.. .,л($>*.. Имеем: .
Ф) Л«) л«... и»...
I во Я»
254
Отметив, что натуральные числа п^> < п<$ < п^ < . 7., написан
ные в v-ой строке, неограниченно возрастают, определим возрастаю*
щую последовательность натуральных чисел* kt < k% < kB < .. #
•.. < ft, < ... следующим образом: &х = nW, &2 равНФ наименьшему
числу второй строки, превосходящему А1э А3 равно наименьшему числу
третьей строки, превосходящему &2, и г. д. Вообще, Учесть
наименьшее число v-ой строки, превосходящее число kHwmV По самому
определению чисел v-ой строки, имеем неравенство
I^WKS " (44)
всюду на [а, 6], причем это неравенство справедливо для всех
натуральных чисел v (v = l, 2, 3,...). Рассмотрим теперь разность
&кч(х)—Rkv+x(x)- Ясно, что эта разность есть не что иное, как
группа членов первоначального ряда, именно
Я», (*) — Я*;+1 (*) = [ «*v+1 (*) -f **v+2 (*) + . • • +**v+1] = tfv+i (*)<
В силу неравенства (44) имеем
l^+1Wl<l^(*)l+^*H1(*)l<«i + «.tie<n.+ii (45)
причем неравенство (45) имеет силу всюду на [а, £] и для v = l,2,
3,4,...; ясно, что численный ряд Y|a + tj3 -j- тц4- • • • + 4*+ • • • есть
сходящийся. Обозначим через Ux(x) начальную группу членов
данного ряда [ их (л:.) -J- и2 (х) -\- ... -|- щ%]. Первоначально данный ряд
ui (х) + w2 (*) "т • • • НЬ й» (*) 4~ • • • теперь является
сгруппированным в виде
£/iW + yaW + Ui W + - + ^W+.. м (46)
причем во всякой точке сегмента [а, Ь] имеют место неравенства
Так как ряд ча+ %+•••+ Ч*+•• • сходится, то данный ряд
удовлетворяет усиленному критерию правильной сходимости.
§ 60. Квазиравномерная сходимость. Определение Дини не
в состоянии охватить всех случаев сходящихся функциональных
рядов их (х) -f- щ(х) -}- ... -J- ип(х) + .. •, сумма / (л;) которых
непрерывна на сегменте [а, 6]. В самом деле, легко видеть, что суще*
ствуют сходящиеся ряди иг (х) -4- и% (х) -\-... -f- ип (х) Ц- ... на
[а, Ь] с непрерывными членами ип(х) и непрерывной суммой /(л:),
которые не имеют на [а, Ь] обобщенной равномерной сходимости
Дини.
Самым простым примером такого ряда будет следующий: пусть
Rn(x) есть функция, равная 0 вне сегмента I , — и равная
ординатам боковых сторон равнобедренного треугольника, имеющего
этот сегмент основанием, а высотой 1 (черт. 159).
Ясно, что имеем l\mRn(x)~Q всюду на оси абсцисс. Если
Rn(x) рассматривать как я-ый остаток функционального ряда
255
/
иг (х) -f- и2(х) ~f- .\ . -f- #л (х) + ... , члены которого определяются
равенствами:
- .iij (л:) = 0, «2(а:) = /?! (л:) — /?з(*)> в8(а:) = /?2 (х) — /?3(*),...,"
..., ип(х) = Rn_t (х) — #м (л;), •..,
то ясно, что никакая группировка членов этого ряда не превратит
его в равномерно сходящийся ряд на сегменте [а, Ь], содержащем
начало координат внутри. В самом деле, всякая группировка членов
этого ряда даст сгруппированный ряд
Ux(x) + U2 (х)+... + ич(х)'+- •., (36)
остатки которого pv {x), как мы видели из формулы (39), суть
не что иное, как остатки /?ь (х) первоначального ряда. А так как
всякий остаток Rn (x) представляет собой волну с максимумом,
равным 1, то отсюда ясно, что
остатки pv (x) не могут удовлетворять
неравенству | pv (х) | < е и,
следовательно, сгруппированный ряд
(36) не может быть
равномерно сходящимся на [а, Ь].
Предыдущий пример, однако,
представляет вот какую особенность:
построенный ряд их (х) -}- #2 (х) -f-
\JL 1 ь Х - • • + ип (х) + ' • • • есть en*e Рав~
м п номерно сходящийся на всяком
Черт. 159. сегменте [а, р], не содержащем
начала координат О ни внутри,
ни на конце. В самом деле, при п достаточно большом, волна
просто уйдет из сегмента fa, р] и, значит, на [ее, р] мы будем~ иметь
ЛЛ(*) = 0.
Но можно, пользуясь рядом с непрерывными членами, имеющим
всюду непрерывную сумму и не сходящимся равномерно ни в каком
сегменте [х, р], каким бы малым этот сегмент ни был (см. пример
в конце § 58), так видоизменить построение, что получится ряд
с непрерывными членами, имеющий всюду непрерывную сумму и не
являющийся равномерно сходящимся ни в каком сегменте [а, р] и
ни при какой группировке членов. Мы предоставим читателю построить
этот пример. Таким образом, обобщенная равномерная сходимость
Дини далеко не решает еще проблемы об отыскании Необходимого
и достаточного условия для того, чтобы сходящийся ряд с
непрерывными членами имел непрерывную сумму. Первый разрешил эту
проблему Арцела сложным методом. Стремясь внести наибольшую'
простоту в определения и ясность в рассуждения Арцела, Борель
подверг целесообразному изменению определение Дини и, таким
образом, пришел к новому виду сходимости, названной им квазиравномерной.
Первое замечание, которое сделал Борель, было следующее:
определение Дини требует для всякого е наличия бесконечно многих
таких^ значений п} при которых неравенство |/?п(#)1<е соблюдается
на всем сегменте [а, Ь]. Но требовать существования бесконечно
256
многих значений п — это означает требовать, чтобы для всякого на*-
туралъного N имелось превышающее его натуральное число N\
такое, что отрезок [N, N'J натурального ряда содержат число п,
при котором имеет место неравенство |#я(л:)|<в. В этом и
заключается сущность обобщенной равномерной сходимости Дини.
Борель ослабил требование Дини, чтобы отрезок [N, WJ
натурального ряда содержал индекс, при котором неравенство | Rn (х) | < s
справедливо на всем сегменте fa, ft], и потребовал только того",
чтобы отрезок [TV, ЛГ| натурального ряда содержал индекс п9 не
постоянный, как у Дини, но изменяющийся в зависимости от х,
при котором попрежнему справедливо неравенство | /?я (х) | < е. Это*
индекс Борель'обозначает через пх. В этом и заключается вся суц|*
ность квазиравномерной сходимости Бореля.
Сформулируем определение Бореля:
Функциональный ряд, сходящийся всюду на сегменте [a, b]:
«iW + ffeW+ —+ «nW+-- (l)
называется сходящимся на. [р> Ь] квазиравномерно, если
для каждого положительного числа е и для всякого натурального
числа N имеется такое превышающее его - натуральное число N\
что отрезок [N, Л/'] натурального ряда для любой точка х,
принадлежащей сегменту [a, ft], содержит индекс пх\ при котором
имеет место неравенство |/?Па.(лг)|<в.
Теорема 1. Если сходящийся всюду на [a, ft] функциональный
ряд иг (х) -|- а2 (х) ~{- — + ипМ+"« с непрерывными членами
сходится на [a, fr] jc в а з ир а в н ом е р н о, то сумма / (л:) этого
ряда есть непрерывная функция на [at ft]. ^
Для доказательства непрерывности функции / (х) на [а, ft}
достаточно доказать, что колебание функции f(x) в каждой точке £
сегмента fa, ft] меньше чем 3s, где з произвольно малое положительное
число. Возьмем, прежде всего, натуральное число N столь большем,
что для всех чисел я>Л/г в данной точке 6 мы имеем
I Я.(«)!<••
Это законно, так как ряд иг (х) -f- щ (х) + ... -j- un (х) + • • • сходится
в точке S. С другой стороны, он сходится квазиравномерно на [а> ft].
Это означает, чго существует натуральное число N', превышающее
число N,N'>N, такоэ, что отрезок [N, N'] натурального ряда
содержит для всякого х индекс пХУ удовлетворяющий условию
\ I^WK». .(47)'
Так как nx>N, то имеем
I Я*,(«)!<•• ' С*8)
Теперь, написав равенства
/(*) = £»«, (0+яЯш0),
17 Эак. 12«.
257
вычтем втброе из первого. Имеем:
/(*) ~f$) = Snx(x)-Snx(\) + Rnx (*) -/?„„(&),
откуда
или, вследствие неравенства (47) и (48),
1/(*) -/(О I < I Snx (х) - «у, (?) | + 2е. (49)
Но имеем
•S»* (*) = в, (*) + и2 (*) + • • • + иПх (х)
и
S** (?) = и, (?) + «а (?) + -.. + ««» (?)•
Отсюда
S*. (*) - Srix (?) = fa, (х) - и, (?)] + [Щ (х) - и2 (?)] + • • • +
+ {ипх(х) - Uhx{%)\.
Беря абсолютные величины, мы находим
i^jf)-^eoi<i«iW-^(?)i+i"2w-«2(0!+..- +
+ \UnxM—Unx(^\.
Но, с другой стороны, индекс пх по условию квазиравномерной
сходимости должен быть меньше числа TV', яж<ЛГ. Поэтому, мы
лишь усилим предыдущее неравенство, добавив к нему новые
неотрицательные слагаемые:
i5„a!(x)-5„SB(?)!<|«1(x)-«1(?)|4-l«a(^-«2(5)|+...+
+ 1 %-(•*:)-%,(?)(. (5°)
Сопоставляя неравенства (49) и (50), находим
J/C*)-/(S)K I «I(*)-«i(91+l«i(*)-М01 + • • • +
+ |Яу,(*)-вК1(?)| + 2в.
Так как число Л/7 постоянно, то мы можем так приблизить х к Z,
что всякая из абсолютных величин разностей \иг{х) — их (;) |,...,
\uN, (х)—uN,(£)\ сделается меньше, чем ~. Поэтому, для х, близких
к £, мы получим
\№-f{\) к лг.-^ + 2. = з«.
Это и показывает, что колебание функции /(х) в точке £ не
превышает 3 s, т. е. есть нуль, потому что е произвольно мало. Таким
образом, f (х) не имеет точек разрыва на [а, д].
253
Теорема П. Если сумма f (х) сходящегося всюду на [а, Ь\
функционального ряда иг (х) -\- и2 (х) + ... -|- ип (х) -f-... с
непрерывными членами непрерывна на [а, Ь], то этот функциональный
ряд сходится на [а, Ь] квазиравномерно.
Возьмем какое-нибудь фиксированное положительное число в и
какое-нибудь фиксированное натуральное число N. Пусть х0 есть
произвольная фиксированная точка сегмента [а, Ь]. Так как ряд
сходится в точке х0, то имеем
lim Rn (x0) =* 0.
Следовательно мы можем найти такое натуральное число пХо> большее
числа М, пхо > N, что имеем
\RnXo(xQ)\<*. (51)
Но имеем тождество f(x) — Sn(x)-\~Rn(x), и так как, по условию,
f(x) непрерывна на [а, Ь] и члены ряда также непрерывны на [а, Ь]9
то остаток Rn (x) (при фиксированном и) есть непрерывная
функция аргумента х на [а, Ь]. В частности RnXo(x) есть непрерывная
функция на [а, Ь]9 В силу
неравенства (51) можно найти интервал ЬХо, ВУ?
содержащий точку х0 (черт. 160), "~J *~К0~ """~g—
во всякой точке которого
выполняется неравенство Черт. 160
I*»* (*)!<•• (52)
Но, раз произвольная точка х0 сегмента [а, Ь] покрыта
интервалом 8*0, ее содержащим, то по теореме Бореля-Лебега весь сегмент
[ау Ь] можно покрыть конечным числом k интервалов,83, 82, ..., 8Ь
принадлежащих системе интервалов {8*0}. И так как на каждом из
8$ будет удовлетворено неравенство
\Rni (*)!<• (53)
для некоторого фиксированного числа пь то беря за N' натуральное
число, превышающее все k фиксированных чисел пи я2, ... , пкУ
мы как раз и получаем отрезок [N, N'] натурального ряда,
удовлетворяющего требованию квазиразномерной сходимости на [а, Ь]
данного функциональное ряда.
Сопоставляя доказанные теоремы I и II, мы приходим к
предложению: Теорема Арцела-Бореля. Необходимым и
достаточным условием непрерывности суммы f (х) на [а, Ь]
функционального ряда иг (х) -|~ и2 (х) -}- . .. -\- ип (х) -|- ... с непрерывными
на [а, Ь] членами является его квазиравномерная сходимость на [a,b].
Заметим еще раз, что все определения и теоремы без
затруднения переносятся на любые замкнутые множества в пространстве
любого конечного числа измерений и на ряды непрерывных функций,
действительных или мнимых, определенных на этих множествах.
17* 259
§ 61. Теорема Вейерштрасса. Мы переходим сейчас к знамени-.
-юшу предложению Вейерштрасса (1885 г.), имекнцему основную
важность в вопросе об аналитическом изображении функций и
бросающему яркий свет на различие между понятиями функции
действительного переменного и аналитической функции (комплексного
переменного).
Предложение это формулируется следующим образом:
Всякая непрерывная функция f{x) на сегменте [а, Ь\ есть
сумма правильно сходящегося на этом сегменте ряда многочленов
Докажем эту теорему методом Лебега. Это доказательство
разбивается на следующие пункты:
I. Какова бы ни была непрерывная функция f(x), заданная
на сегменте [а, Ь]у всегда существует полигональная функция L(x)>
, отличающаяся от f(x) не
больше, чем на s, на всем
сегменте [а, Ь]9 где е положи-
тельное число> заранее данное
и могущее быть сколь угодно
малым.
Прежде чем доказывать это
утверждение, напомним читате*
лю определение роли-
гональной функции.
Непрерывная функция L(x),
определенная на сегменте [а, Ь],
называется полигональной, если
сегмент [а, Ь] можно разделить на конечное число сегментов
Черт. 161.
[а, хг\ [хъ х2],
[хп_1У Ь]9 на каждом из которых L(x) есть
линейная функция. Название „полигональнаяи соответствует тому, что
функция L(x) геометрически изображается линией y—L(x),
составленной из конечного числа прямолинейных звеньев,
следовательно, многоугольником (т. е. полигоном) (черт. 161). Пусть е
есть какое-нибудь заданное положительное число. Возьмем данную
функцию f(x), непрерывную на сегменте [а, Ь], и, разделив этот
сегмент на достаточно большое число малых сегментов точками
деления xlt x%, ... , хп~г (черт. 162), восставим перпендикуляры
в этих точках вплоть до пересечения их с кривой y=f(x). Тогда
на этой кривой наметятся точки Мь М2, ... , Мп-и абсциссами
которых будут точки деления хъ x2v ... , xn_v Соединив
полученные точки Ml9 М^ ... , Мп-Х между собой последовательными
прямолинейными хордами, начиная с точки А и кончая точкой В,
как показано на чертеже, мы получаем многоугольник, вписанный
в кривую у = f(x) и изображающий, очевидно, некоторую
полигональную функцию L(x). Докажем, что если число точек деления
х1У х2, ... , xn~t достаточно велико и самые точки деления будут
достаточно сближены между собой, то мы будем иметь неравенство
1/W-iWK» (Щ
260
на всем сегменте \а, Ь\. Действительно, в силу равномерной
непрерывности функций у =/(х), существует такое положительное число ч,
•*1>0, что соблюдение неравенства
\х"-х'\<ч 9 (55)
влечет наличие неравенства
1/(Л-/(*') K-J. (56)
Черт. 162.
каковы бы ни были точки х' и х" на сегменте [я, Ь] (черт. 163).
~~ будут сближены между
"п~1
Если теперь точки деления хг, х^
собой меньше, чем на г\, в силу неравенств (55) и (56), очевидно,
будем иметь
|/(*)-/(*<) К-у (57)
при условии, что точка х находится на сегменте [х^ xi+i]. Это
неравенство показывает, что все течение
кривой y=zf(x) для х, пробегаю- Y\
щего сегмент [х{у xi+1], происходит
внутри прямоугольника, имеющего
средней линией прямую М{К^
параллельную оси ОХ и проведенную
через точку Miy а высотой г. И так
как из неравенства (57) следует, что
то хорда, соединяющая точки Mi
и Mi+U должна остаться внутри
этого же прямоугольника, и,
следовательно, мы должны иметь
2
М,
М,.
К
Хы
■|/(*)-1(*)|<е
(54)
Черт. 163.
внутри каждого из сегментов [а, л^], [хи л*21,
значит, на целом сегменте [а, Ь\.
, [xn-v b] и,
261
II. Второй пункт доказательства теоремы Вейерштрасса посвящен
рассмотрению так называемых элементарных полигональных функций
Х(х). Элементарной полигональной функцией X (л:) называется
такая непрерывная на всей оси абсцисс функция, которая равна
нулю BfreBO от кекоторой точки £ и линейна вправо от нее. Иначе
говоря, рассматриваемая функция л(х) непрерывна в каждой
точке х бесконечного интервала ( — оо < х < + оо) и определена
следующими двумя условиями:
X (х) = 0 всюду на интервале (— со < х <; £),
X (х) = \i (х — £) всюду на интервале (S <; х < -f- оо).
Геометрически функция Х(х) изображается двузвенной ломаной
линией, причем левое звено ее лежит на оси абсцисс, правое же на-
Черт, 164,
клонено угод каким-нибудь острым углом (положительным или отрица^
тельным к оси абсцисс), как показывает чертеж 164.
Рассмотрение элементарных полигональных функций \(х) весьма
полезно. Прежде всего, имеем предложение:
Всякая полигональная функция L(x) есть сумма линейной
функции и ограниченного числа элементарных полигональных
функций, т. е. L(x)==a^bx + 'k1(x)-\~X^(x) + Ь^тС*)-
Для доказательства достаточно обратиться к чертежу 165.
Именно, мы берем за линейную функцию а 4- Ьх правую часть
уравнения первого (левого) звена у = а~\-бх и вычитаем ее из дан-
b X
G[
b X
Черт. 165.
ной полигональной функции L (х). Разность L (х) — (а-\-Ьх) есть,
очевидно, опять полигональная функция, но уже равная нулю на
первом сегменте [а, хх]. Вычитая из этой разности элементарную поли,-
262 /^
тональную функцию кг(х), образованную двумя первыми (левыми)
звеньями функции L (х) — (а-\-Ьх), мы получаем полигональную
функцию L(x) — (a-\~bx) — \х (х), равную нулю на сегменте [а, х2]
(черт. 166). Вычитая из этой функции элементарную полигональную
функцию Х2 (х)у образованную двумя левыми звеньями функции
L (х) — (а -f- Ьх) — кх (х), мы получаем полигональную функцию
(черт. 166) L (х) — (а-\~Ьх) — Хг (х) — А2 (#), равную нулю на
сегменте [а, хд]. И так далее. Продолжая этот процесс, мы через
п — 2 шагов дойдем до полигональной функции L (х) — {а-{-Ьх) —
— ^i(x) — ^2 (х)— •»• —^п-^С*)* равной нулю на сегменте [а, хПтт1]
и линейной на сегменте [хп„и Ь] (черт. 167). Следовательно, эта
а К, $
Хо-Лб X
0\ а
Xi X*
*»,. ь х
ГХ*М\
Черт. 166.
функция сама есть элементарная полигональная функция; обозначив
ее через Хв j (х), имеем желаемое тождество L(x) = (a-\-bx)-\-
III. Третий пункт доказательсгва теоремы Вейерштрасса посвящен
рассмотрению непрерывной функции у = \х\, где \х\ обозначает абсо-
лютную величину аргумента х. Как легко видеть, \х\ = У"*2» гДе
квадратный радикал берется в арифметическом смысле. Геометрически
функция |д:| изображается двузвенной ломаной линией, образованной
диагоналями первой и второй четверти прямоугольной системы
координат (черт. 168).
Докажем следующую лемму:
Каково бы ни было малое положительное число е и каков бы
ни был сегмент [a, £], всегда можно отыскать такой многочлен
Р (х), который отличается от \х\ менее, чем на е, на всем сегменте
[а, *].
Известно, что формула бинома Ньютона
(1 +2)»- 1 + Ср + С*р + -. • +С*2*+ ... +CJZ»,
где
г* /*(tt-l)(tt-2)...(ft~fe + l)
Оя — 1 Л О U
1-2-3...Л
263
есть конечная, если я-~- число натуральное, потому что дальнейшие
биномиальные коэфициенты C*+1, С%+'\ С*+3 в этом случае все равны
нулю.
Известно далзе, что если показатель бинома п не есть
натуральное число, то, хотя биномиальное разложение и будет в этом случае'
бесконечным, однако, суммой
его для значений Z,
меньших по абсолютной
величине единицы, |Z|< 1, будет
служить все то же выражение
\
Щ х
Черт. 167. Черт. 168.
(l-j-Z)№. Это означает, что мы имеем равенство
(1 4-Z)»=l-fC>Z + C*Z«+...-f- ckn Z*+•"•'-,
справедливое для всякого числа Z, для которого г \Z\ < 1. В част-
1
ности при п = ~, мы получаем
0+z)T«i+ clz + clz2+ ... + ciz*-f ... (58)
или, приняв во внимание равенства
2
имеем
Ь2-3 ... Л
_г ,ч^1 1 1-3.5-7 ... (Ч-З)
~к iJ 2k 2.4-0-8 ... (2& —2) >
г /_n* l J ЬЗ-5-7 .... f2^ —3> fc .
^К > '2k'2-4-b-8....(2k — 2)^~l~'"
(59)
В этой формуле важно заметить, что написанный в правой части
ряд есть правильно сходящийся ряд на сегменте [—1<;Z<; +1].
264
Чтобы убедиться в этом, оценим приближенную величину
произведения
п Ь3-5-7 ... (2А-3)
Имеем
-п (*-£)•
Отсюда
iosr<2w —Si<^(i —i).
Принимая во внимание, что
ft fri hs _
log (l — /0= —у— ^— з ~ ••• < —А
для 0<А< 1, имеем log^l — _^<_i•
Поэтому
А—I
Но известно, что
4+ г+т+ ••• +*зт>,ог*- (бо)
В справедливости неравенства (60) легко убедиться, рассматривая
площадь криволинейной трапеции, ограниченной гиперболой у = — ,
осью абсцисс и прямыми х = 1 и л: = А; эта площадь равна (черт. 169)
k
/>•
Чертеж показывает, что криволинейная трапеция содержится
в ступенчатой фигуре, площадь которой есть -у -(- ■— + -§■+ • • • +
+ Х^Т' откУда и следУет неравенство (60) . Из этого неравенства
следует, что
log Q*< — ±\ogk±=logy^9
откуда заключаем, что
Q*<7F
для k = 2, 3, 4, ... .
266
Таким образом, все члены функционального ряда (59) на сегменте
(— 1 <; Z <; +1 ] меньше по абсолютной величине членрв численного
ряда (для А>2)
И так как этот ряд сходится (как вообще сходится ряд V — при
s>l), то правильная сходимость ряда (59) на сегменте
[ — 1<;Z<[ + 1] тем самым установлена.
v Установив это, заметим скачала, что на сегменте
[—l<;Z<;-f--l] ряд (59) имеет положительную
сумму (и равную нулю при Z = — 1). Поэтому, за-
I
метив, что (1 + Z) 2 в этом случае есть
арифметическое значение квадратного радикалаj/l \-Z , мы
можем писать:
Положим в этой формуле
Черт. 169.
Z = X*—1.
Ясно, что если значение х останется на сегменте [ — 1 <^<;-{-^Ь
то переменное Z останется на сегменте [ — 1 <; Z <; 0]. Поэтому,
подставив в предыдущее равенство (61) вместо Z разность л;2 —1,
мы будем иметь
/л.в|* | = 1+ !(*'-!)-|(*«-1)а + А(
2 *~ -' 8
О.Г —iVt-iI b3-5-7...(?fc-3)
"•"^ ч 2й'2-4-6-8...(2А —2)
0!
|3_
(х»_1)*+..
• +
(62)
Этот ряд есть правильно сходящийся на сегменте [ — 1 <;лг<[-}-1],
потому что его члены (начиная с 4 = 2) меньше членов сходящегося
ряда -г4-- /--И т=-+ • • • Н г^Ч" • • • • Из изложенного ясно,
что мы добились пока лишь частного результата, получив
разложение в правильно сходящийся ряд многочленов непрерывной функции \х\
лишь на сегменте [ — l^x^l]. А нам нужно это сделать на
любом конечном сегменте [а<^<^#] (черт. 170).
266.
Для того, чтобы этого достигнуть, заключим заданный сегмент
[а, Ь] внутрь охватывающего его сегмента [ — iV, -\- N] и сделаем
преобразование независимого переменного
x=*N-t9
где t остается на сегменте [ -г-1 ^tf^-j- 1]. Мы, очевидно, имеем
iJC|=w.H=A/[44(^i)-{(^"i)4fb(^ir-'-+
-H-D*-1
JL_ Ь3.5.7...(2^3)
х
(t>
i)*+...],
откуда получаем, заменив t через ^:
..- ,1 1.3.5.7...(?ft-3) J* _ \* , "I
+ 1 1) , 2k 2-4.6.8...(2А-2) U2 %: *^ J
Этот ряд есть правильно сходящийся на сегменте [ — ЛГ<л;<; Н-Л/],
так как его члены на этом сегменте не превосходят (начиная с k — 2)
(63)
по абсолютной величине членов ряда Affy + —рН Т^Н*""*** ~Ь
-I = +...\ Установим это, предположив число N целым
1 kVk х 1
и положительным. Остановим ряд у + —-«= + ~^==
на таком члене —„, чтобы остаток ряда
тут
1,1,
+ ■■• +
kYk
(т + 1)У"^ + 1 (w + 2)Vm + 2 {
был меньше, чем -r^r • Если мы остановим на этом же члене беско-
нечный ряд (63), то будем иметь многочлен Р(х) степени 2 т,
отличающийся "на сегменте [ — N, •+■ N] от функции \ х | менее,
чем на ^* л/з^л/Ь т- е- будем иметь неравенство
267
справедливое на всем сегменте [ — Л^ л: <-f-NJ и, значит, на
данном сегменте [а, д]. Лемма доказана, так' как всегда можно
подобрать N столь большим, что будем иметь щ<*-
Следствие. Существует бесконечный ряд многочленов
Pi (х) + р2 (х) + • • • + рп (х) + • • • > правильно сходящийся на
всяком сегменте [а, Ь] к функции \х\.
В самом деле, в силу только что доказанной леммы, для каждого
натурального числа п имеется многочлен Qn(x), такой, что
справедливо неравенство
-й»<И-<?*(*К+;з
на всем сегменте [—п^х^-^^-п]. #
Положим
Pi (*) — Qi (*). р2 (*) = Q2 С*)—Qi (x),.; .*.
Pn(jf) = Qn(x) — Ся-^дг),
Ясно, что на сегменте [—/г, -\-п] имеем
]Л.(*)1
M-Q«-i (*) + <?«(*)■
1
<
+ \\X\ — Qn(x)
<
f-^<
1*1 —Gn-i(*)| +
2
(/г — 1)2 J Л2 ^ (л—1)2 •
Так как ряд p- + ^4~g7~f,»**+^2 + *»* есть сходящийся, то ряд
pi(х) + ^aW"h«*-+^«W+«" есть правильно сходящийся на
всяком сегменте [а> Ь], потому что при п достаточно большом
сегмент [я, Ь] содержится в сегменте [—п,-{-п] и, значит, его
общий член Рк{х) будет на [а, Ь] меньше, чем __ 2. С другой
стороны, ясно, что сумма п первых членов ряда Pi(x)-\-P2(x) -f-
+ • • • -\~рп(х) + • • • равна Qw(x), и так как на (— я, +я] имеем
f|*| —<?»(*) 1<й»> то на fa» ^ бУдем иметь
lim <2Я(*) = |*1-
IV. Четвертым пунктом оканчивается доказательство теоремы
Вейерштрасса.
а) Прежде всего отметим, что в всюду правильно сходящийся
ряд многочленов разлооюима не только функция \х |, но и функция
\х — ?|, где 6 есть какое-нибудь фиксированное действительное
число. В самом деле, равенство
I* \=*Pi(x) + P*(x)+- • • + Рп(х)+..., (64)
справедливое на всей оси абсцисс ОХ> после замены х через х—5
дает
\х-1\ = Г*(х)+1*(х)+...+Р'п(х)+..
(65)
268
где Р*п(х) обозначает многочлен Рп(х—£). Ясно, что ряд (65) есть
правильно сходящийся на всяком сегменте [а, Ь]9 если ряд (64)
имеет это свойство.
Геометрически функция \х—Ц изображена на чертеже 171.
Ь) Всякая элементарная полигональная функция X (х)
разложима в всюду правильно сходящийся ряд многочленов.
В самом деле, так как рассматриваемая функция к.(х) равна нулю
влево от точки £ и линейна вправо от нее, то мы, очевидно, имеем
тождество
M*) = p(l*-6| + *-5)..
(66)
где |л есть некоторое постоянное число. Действительно, выражение
в скобках, будучи всюду непрерывным, равно нулю влево от £ и
есть линейная функция вправо от нее. Ясно, поэтому, что выбором
числа \ь мы достигнем осуществле- у
ния тождества (66): для этого
достаточно, чтобы угловой коэфи-
циент правого звена двузвенной
линии у — X (х) был равен 2jx, так
как направо от точки £ мы имеем
\х — Е| = л: — % и, значит, \(х) =
==2|х (х — £). Тождество (66)
показывает, что функция \{х) изобрази-
ма всюду правильно сходящимся
рядом многочленов.
c) Всякая полигональная функция L(x), определенная на
сегменте [а% Ь]у азобразима правильно сходящимся на сегменте
[а, Ь] рядом многочленов.
Это ясно из того, что функция L(x) есть сумма линейной
функции и ограниченного числа элементарных полигональных функций,
т. е. из тождества
L (х) = а + Ьх -f \х (х) + hi*) + • • • + кт (*)•
d) Какова бы ни была непрерывная функция f(x),
определенная на сегменте [а, Ь], существует многочлен Р(х),
отличающийся от f(x) не более, чем на е, на всем сегменте [а, Ь\у
где з означает положительное число, заранее данное и могущее
быть сколь угодно малым. Действительно, всегда можно определить
полигональную функцию Ь(х), отличающуюся на [а, Ь] от
функции f(x) не больше, чем на ~, т. е. такую, что имеет место
неравенство
|/(a:)-L(a:)|<-o на сегменте [а, Ь].
(67)
С другой стороны, функция L(x) разложима в ряд многочленов,
правильно сходящейся на [а, Ь]. Останавливая этот ряд многочленов
на достаточно удаленном члене, мы получаем многочлен Р(х)> от-
269
личающийся от L (х) на сегменте [а, Ь) не больше, чем на -^ , т. е.
|Z.(*)-P(*)|<f. (68)
Сопоставляя неравенства (67) и (68), мы заключаем, что
|/(л) — Р(х) | <> на сегменте [а, Ь].
е) Всякая непрерывная функция f(x), определенная на
сегменте [а, Ь]9 есть сумма правильно сходящегося на этом сегменте
ряда многочленов»
Действительно, согласно предыдущему, существует многочлен
Qn{x), отличающийся от f(x) на всем сегменте [а, Ь] не более, чем
на -д-т2. Следовательно, имеем
lim Qn(x)=f(x).
я-> + оо
С другой стороны, полагая
Р± {х) = Qt (*), Р* (х) =* <?s (x) - Qt (x),
,..., Pn(x) = Qn(x) — Qn^1(:x)> ...,
мы видим, что ряд многочленов
* Pi 00 + р2(х)^...+рп(х)+. .: (бщ
есть правильно сходящийся на сегменте [а, Ь], так как имеем на
этом4сегменте при достаточно большом значении п
\Pn(x)MQn(x)-Qn-i(x)\<\A*)-Qn-i(x)\ + \/(x)-Qn(x)\<£
И так как сумма га первых членов ряда (69) есть Q„(x), то имеем
f(x) = P1{x) + Pa(x)+...+Pn{x)+ ...,
а это и есть теорема Вейерштрасса.
§ 62. Следствия теоремы Вейерштрасса. Теоретические
следствия теоремы Вейерштрасса огромны и вполне соответствуют тому
сильному впечатлению, которое произвело в свое время это открытие
Вейерштрасса.
I. Во-первых, оказалось, что всякая непрерывная функция есть
функция аналитически изобразимая.
Действительно, изображение функций сходящимися рядами есть
обычный и излюбленный метод математического анализа. И так как
всякий член этого сходящегося ряда в рассматриваемом случае есть
многочлен
270
и при этом ряд этот есть правильно сходящийся, то вследствие v
этого непрерывнее функции f(x)y как бы ни была сложной их
природа, оказались все без исключения аналитически изобразимыми на
равных правах с другими функциями математического анализа/
II. Во-вторых, оказалось, что нет разницы с аналитической точки
зрения между непрерывными функциями f(x), определяемыми на
сегменте [а, Ь] одним законом, и непрерывными функциями f{x)9
определяемыми на [а, Ь] несколькими законами.
Так, непрерывная кривая у=/(х) (черт. 172), составленная
непрерывным образом из дуги параболы на сегменте [a, хг]у из
отрезка прямой на [хи x2]t из дуги окружности на [л:2, #3]
о х, х2 х3 ь л Q\
Черт. 172.
и из дуги циклоиды на [л:3, Ь], ничем кэ отличима от
непрерывной кривой y=f*(x), составленной из дуги одной гиперболы,
потому что та и другая функции разложимы в правильно сходящийся
ряд многочленов
/(*)=/\(*)4- Р2 (*)+••• +/>»(*) +...
f*{x) = Pl(x) + Pt(x) + ...+P*n(x)-}-....
Таким образом, оказалось, что употребление правильно
сходящихся рядов многочленов стирает всякую разницу между
непрерывными функциями, определенными одним законом, и непрерывными
функциями, определенными многими совершенно различными законами
разной природы, искусственно соединенными в одно целое.
§ 63. Исследования Чебышева и Бореля. Мы уже сказали, что Вейер-
штрасс доказал свою теорему в 1885 году. Интересно отметить, что
знаменитый русский математик Чебышев еще в 1858 году, т. е. на 27 лет ранее
Вейерштрасса, почти полностью владел теоремой Вейерштрасса. Чебышев
доказал ряд предложений чрезвычайной важности относительно
приближенного изображения произвольной непрерывной функции f (х) многочленом
Р(х) степени я, и, чтобы прийти к открытию Вейерштрасса, нужно было
присоединить лишь одно указание, которого Чебышев, однако, не сделал.
Укажем вкратце путь Чебышева. Пусть/(л;) какая-нибудь непрерывная
функция, определенная на сегменте [а, Ь],
Пусть
Р (х) = А0хп + Axxn-i + ... + Ля-!* + Ап
какой нибудь многочлен степени п. Рассмотрим абсолютную величину
разности f(x) — P(x)t т. е.
¥(*) = l/(*)-P(*)k
271
Ясно, что 9 (x) есть непрерывная неотрицательная функция аргумента х*
определенная на сегменте [а, Ь]. Как всякая непрерывная функция,
функция <р(дг) достигает на [a, tr] maximum! a% который мы обозначим через Вр
и назовем „уклонением многочлена Р от данной непрерывной функции f*
£Р>0.
Если рассматривать коэфициенты А0, Аъ А2,.... Ап_ъ Ап многочлена Р(х)
как координаты точки М в пространстве /г-j-l измерений, ясно, что
уклонение Ер есть функция переменных A0f Ah ..., Ап_ь Ап, т. е. есть
функция точки Af(A0, Аь ...,y4„_i, An).
Каждой точке М соответствует свой собственный многочлен Р(х) и,
значит, свое собственное уклонение Ер. Если точка М непрерывно
перемещается в пространстве л+1 измерений, уклонение Ер изменяется также
непрерывно.
Чебышев поставил и разрешил задачу об отыскании наименьшего
уклонения Ер многочлена п-ой степени от заданной непрерывной
функции /(х) на сегменте [а, Ь].
Черт. 173.
В этой задаче речь идет об определении нижней границы
положительных чисел Ер, когда мы всячески изменяем коэфициепты Аь, А^ ..., An_h
Лп многочлена Р (х). Эта нижняя граница, очевидно, существует и есть
конечное число, но не очевидно, что она достижима выбором некоторого
многочлена тс (х) степени п
тс (х) ~а0*п + аххп-1 + ... + а^х + ап.
Чебышев преодолел эту трудность, доказав следующую замечательную тео-
реиу:
Теорема Чебышев а. Для всякой непрерывной функции /(лг),
заданной на сегменте [а, Ь\, существует один и только один многочлен
тс (дг) » aQxn^-haiXn-^ + ...-+- aflmml x + an степени п, который уклоняется
от f(x) на [а, Ь] строго меньше, чем всякий иной многочлен Р(х) втой
же степени.
С тех пор принято называть такие многочлены п (х) многочленами
Чебышева и уклонение. я (х) от/(дг) называть наименьшим уклонением
п-ой степени: оно обозначается через Еп.
Если мы изобразим функцию f{x) в виде непрерывной линии y = f(x)
и сдвинем вертикально вверх и вниз эту кривую на расстояние Еп (черт 173),
272
то получим криволинейную полоску ширины 2Еп, срединой которой является
данная кривая у =/(х). Многочлен Чебышева те (х) изображается кривое
y=zn(x), содержащейся в этой полоске. Всякий иной многочлен Р(х)
степени п изображается кривой у = Р (х), заведомо выступающей за
граничные линии этой полоски.
Важным является следующее предложение (приводим его без
доказательства). Многочлен Чебышева те (х) степени п характеризуется только
одним тем свойством, что данный сегмент [а, Ь\ можно разделить по
крайней мере на п + 2 (или еще более) последовательных сегментов
[а, хг], [хь дг2], ...,[*г-, **+i], ..., [хрч Ь], р^п + 1, в концах которых те(дт)
уклоняется от f (х) в точности на Еп, причем уклонения эти суть строго
разных знаков) самые концы а и Ь здесь во внимание не принимаются.
Так как всякий многочлен степени п — 1 есть частный случай многочлена
степени п (когда старший коэфициеит Дэ обращается в нуль), то ясно, что
наименьшее уклонение Еп убывает (или, по крайней мере, не возрастает),
когда натуральное число п увеличивается, т. е.
£о S> Ei ]> Еъ ... !> Еп !> ... .
Для того чтобы получить теорему Вейерштрасса, Чебышеву
достаточно было показать, что наименьшее уклонение Еп стремится к нулю,
когда п безгранично возрастает. Но занятый точным отысканием
„наилучшего приближения" п(х) для заданного числа п, знаменитый ученый
прошел мимо этого вопроса.
Другое замечание, которое можно сделать по поводу теоремы Вейер-
штрасса, состоит в следующем. Мы указали, что для всякой непрерывной
функции /(*), определенной на каком-нибудь сегменте._[а, Ь], имеется
такой многочлен Р(х), который отличается от f(x) на всем этом сегменте
не более чем на е, т. е.
1/(*)-Р(х)|<в.
Собственно, к этому утверждению существования многочлена Р(х) и
сводится вся теорема Вейерштрасса. Но, хотя мы и обнаружили
существование этого многочлена Р(х) и показали, как он получается, однако для
всякой заданной непрерывной
функции f(x) многочлен О ,
Р(х) получается no-свое- л * i j c/c3 l ' I ' ' С н ^
му, так что не ясно, а 1 * п &
как зависят коэфициенты Черт. 174.
многочлена Р(х) от вида
заданной функции f(x). Иначе говоря, зависимость коэфициентов
многочлена Р(х) от вида функции f(x) хотя и имеется, но она носит
лишь чисто логический характер, не будучи выраженной явно. Это
обстоятельство побудило Бореля желать освободиться от этой неявной
зависимости коэфициентов многочлена Р(х) от f(x) и стремиться выразить
явным образом эти коэфициенты через значения заданной
функции f(x) на сегменте [а, Ь]. И так как значений этих бесчисленное
множество, то речь должна идти о значениях функции f(x) лишь в
некоторых точках сегмента [а, Ь], которые, притом, можно взять даже в
конечном числе. В самом деле, в силу непрерывности рассматриваемой
функции /(*)» ее значения в близких друг к другу точках отличаются весьма
мало одно от другого, так что, приняв во внимание, что нужно отыскать
многочлен Р(х) лишь с точностью до е, вполне можно ограничиться только
конечным числом значений функции f(x) на сегменте [а> Ь] и именно
в каких-нибудь его точках сь с2, св, ...,с , (черт. 174).
Первое, что приходит на мысль в этом направлении, это —
воспользоваться известной формулой Лагранжа.
О ( И - V f (n \ (x-Cl)(X-C*)-~(X-CL'-J(X-Ck+l)---(X~' СП) /7ач
Рп-1 W- 2*kT {Ck) (с*-*) {ск-с,)...{ск-ск-1){ск-ск+1)...{ск-сп) ' КШ)
к = 1
обычно называемой интерполяционной формулой Лагранжа*•
18 Эак. 1244. ' 273
\
Эта формула, в самом деле, имеет совершенно явный характер и опре*
деляет многочлен Рп-\(х) степени п — 1, в точности равный величине
f {Ч) функции f{x) в точке х*=ск.
На первый взгляд кажется, что если*заставить точки clt г2, •••» сп за"
висеть от п (обозначив их в этом случае, разумеется, не через cit c2 сш
но через с^, с^,..., с***) та^цш образом, что при безграничном
возрастании числа п эти точки будут делить сегмент [а% Ь] на части все более
и более мелкие, так что длина наибольшей из этих частей будет стремиться
к нулю, — то в этом случае ivh ;> го член Лагранжа Pn-i(x) будет равномерно
стремиться к заданной функции /(*), при помощи значений которой он
У строится, т. е. что мы не только будем
'* иметь
lim Pn-i(x)«*f(x),
Я-> + 00
но еще и
l/(*)-P«-i(*)|<e
у при достаточно большом числе п в любой
к-) к к+? ' точке сегмента [а, Ь\. Такая гипотеза
~ТГ!)~1Г вполне естественна, но исследования Бо-
реля и Рунге обнаружили, что она совер-
Черт. 175. шенно неверна. Именно, Борель построил
• такую функцию f(x\ непрерывную на
сегменте [—1<!.г< + 1]» которая при делении этого сегмента на 2п равных
частей дает многочлен Лагранжа /V^-if*), заведомо не могущий
стремиться к f(x), когда п безгранично возрастает, потому 4то вычисления
обнаруживают, что верхний предел адсел
\
*(*)'M*Wt) *^(т)'
есть + со, а не/Гу). Таким образом, употребление интерполяционной
формулы Лагранжа не может привести к теореме Вейерштрасса.
Ввиду этого и в целях явного построения приближенного многочлена
Р(х) при помощи значений задаваемой функции /(*), Борелем была
поставлена проблема:
построить такие многочлены Ркп (х), зависящие лишь от двух на*
туральных чисел кип, что для полинома
и для произвольной непрерывной на [0,1] функции f(x) имеет место
на [0,1] неравенство ^ v
|/(*)-Я« (*)]<•
при всяком достаточно большом п.
Борель определяет многочлены. PUn (x) следующим образом: обозначим
через <$%п(х) непрерывную функцию (черг. 175), равную нулю вне сегмента
Г£_! %+ii
-*, I, равную 1 в его центре и линейную в обеих половинах этого
сегмента. Покажем, что имеем на сегменте [0,1] неравенство
/<: = »
|/<*)~ 2/(£)•**,« <■*>(<• (71)
274
при всяком достаточно большом л. В самом деле, пусть *0^сть какая-нибудь
точка сегмента [0,1]. Если она принадлежит к сегменту ■■, — ,-тОгкак
L n n J
показывает предыдущий чертеж, все функции 9а-,п(*о) равны нулю, кроме
только двух функций: уь%п{х) и Чн-1,п(х)> пРичем на сегменте —— , — I
имеет место тождество
VW + ^-i,«W = b (72)
потому что если <рЛ п (х) = 6, где 0 < 6 < 1, то !рй_, п (х) •■= 1 — 0.
Г/г — 1 h~\
Поэтому, если Л'о принадлежит к сегменту I , — ,
то
S f (!) • **л{Хй) = f (*ir) • **-».»(*о)+/ (I) * М*>- <73>
fr-=0
Но в силу равномерной непрерывности функции f(x) на сегменте [0,1]
выполняются неравенства
<i
<т.
если п достаточно большое натуральное число. Написав вместо этих
неравенств два равенства:
v - ,(*=-') =,м-и, f
и /(4)=/(*o)+e*"J'где 16jl|<1 и^к1-
из равенств (72) и (73) получим:
2/(£) • **,« С*о) = /(*о) + б3в, (74)
где 63 = 2^1'fft-1^^ + 02'f^n^0^ и' СлеД°вательн0» где|081<1| откуда:
7с=п
|/(*o)-2/(J)-?*,e(*to)|<«
fc==0
Следовательно, неравенство (71) справедливо, так как х0 есть произвольная
точка сегмента [0,1].
Чтобы прийти к многочленам Рьп(х0), Борель пользуется теоремой
Вейерштрасса и определяет многочлен ^w(^) из требования
18* 275
Рассмотрим теперь многочлен Рп(х)> определенный равенством
А«0
Мы имеем неравенства
^w=2/(t),p*.»'w- (76)
| рп w- 2/(1) **. «w I=12 /(4) [p*.. w - »*. n wi I <
fc==0
* = 0 ft==0
fc«*0 '
Так как функция f(x) ограничена на сегменте [0,1], то имеем !/(#)|<Af,
гДе М есть постоянное число и где лг есть любая точка сегмента [6,1.] В силу
этого замечания и в силу неравенства (75), при достаточно большом п получим
|р.м- 2/(т>м<*>| <*|~=^^<f <«■ сп)
Сопоставляя неравенства (71) и (77), получим
\f{x)-Pnix)\<** (78)
на всем сегменте [0<л:<1] при достаточно большом л.
Таким образом, многочлен Рп(х)% определенный по формуле
p»w=if/(£)-ft.*(*). (76)
разрешает проблему Бореля.
Следует, однако, заметить, что выражение, дающее многочлен Pk,n(x)
с двумя значками k и я, является несколько сложным ввчду того, что
функция укп(х) с двумя значками есть сумма трех элементарных полигональных
функций
Ъ, п(*) = Ч*'П) W + х?'П) (*) + Хз*'П) (х)
и, значит, для отыскания многочлена Pk п(х) приходится находить методом
Лебега приближенные для них многочлены Pf* n\x)t Pf' п)(х), Р^ п\х),
сумма которых
Pk, nW - Pf П) (*) + Pf П) (*) + Pf П) W
и даст многочлен Pk n (х).
Позже акад. С. Н. Бернштейн (1912 г.) в связи, повидимому, с другими
соображениями, пришел к простому и изящному выражению, для
многочленов Р^п(х) с двумя значками. Его многочлены Pk n(x) лишутся в виде
pk% n W = сп хк & - *)л~*. (79)
где С* есть целое число, биномиальный коэфициент, выражающий число со- -
четаний из п предметов по k.
Многочлен Рп(х), составленный из них по формуле
Рп(*)= if/(~)Ф*(1-*)*-*> (80)
276
также разрешает проблему Бореля. Чтобы убедиться в этом, достаточно
установить, что мы имеем равномерно на [О, 1] х
UmPn(*)-/(*) (81)
в том частном случае, когда функция f(x) есть натуральная степень аргу»
мента дг, т. е. когда f{x) = х\ где v = 1, 2, 3
Действительно, прежде всего мы имеем тождественно
1 = [(1 -х) + х]п а 2 С*«*(1 -х)п-К (82)
ыо
Поэтому, во-первых, равенство (81) для натуральных степеней буквы х,
равномерное на [0, 1], будет в этом случае иметь силу и тогда, когда функция
/(дг) есть произвольный многочлен те (х), т. е. когда f(x)=iz(x), так как
всякий многочлен есть конечная сумма степеней лг*, v = 0, 1, 2, 3, ...,
умноженных на постоянные числа.
Во-вторых, выбрав, на основании теоремы Вейерштрасса, какой-нибудь
многочлен тс* (л:), удовлетворяющий на [0, 1] неравенству
!/(*)-«*(*) K-J-, (83)
и обозначив через Рп{х) и Р„{х) многочлены степени я, образованные по
формуле (80) для f(x) и д*, т. е., положив
£=0
мы имеем
ftt=0
fc=0
<|-£с* **(!-*)»-*= f- <84>
fcsssO
на всем сегменте (Ф, 1].
И так как для достаточно большого п должно иметь место на сегменте
[0, 1] неравенство, справедливое для всякого многочлена тс* (х):
i«*(*)-p;wi<T. <ю>
то, сопоставив неравенства (83), (84) и (85),' убеждаемся в справедливости
неравенства
\f(x)-Pn(*)\<*
разрешающего проблему. Бореля для многочленов акад. С. Н. Бернштейна
Рп (х). Таким образом, все сводится к доказательству равенства (81),
имеющему место равномерно на [0, 1] для функций f(x) = х\ где ч = 1, 2, 3,... .
С этой целью возьмем какую-нибудь функцию Ф (х)9 имеющую v первых
d
производных, и проделаем над ней последовательно v раз операцию х -^ ,
277
состоящую в диференцировании по аргументу х и, затем, в умножении
полученного результата на аргумент х. Если мы выполним эту оцерацию v
раз, то результат можно записать так:
(-£)(*£)•••(*£)•
или символически, \х — } Ф .
Так, для v = 1, 2, 3, и т. д. имеем
(х ~) Ф = хФ' (х). (х £ J Ф = **Ф" (х) + х& (х\
(х~\ф^ хЩ"> (х) + 3**Ф7 (л:) + хФ' (х),
и т. д.; ясно, что в общем окончательном выражении для (х j-j Ф будут
содержаться линейным образом v первых производных Ф'(лг), Фг,(х),..щ%
Ф^ (л:), причем коэфициентом при старшей производной Ф^\х) будет лг\
Таким образом, получим
(х^)Ь)ф = х"ф(у)(х) + '- (86)
причем не написанные члены содержат лишь низшие производные.
Применив эту формулу к частному случаю бинома (x-\-y)nt где у
рассматривается как аргумент, независящий от х, имеем
причем коэфициенты не написанных членов содержат букву п в степенях,
, меньше чем v. Таким образом, мы имеем окончательно формулу ~
(x^)iV(x+y)n^x*n"(x + y)n-" + Q(n)> (87)
где Q(n) содержит букву п в коэфициентах в степени, не больше, чем
v— 1.
Возвратимся теперь к многочлену акад. Ct H. Бернштейна для функции
f(x) = х\ Обозначая этот многочлен через Рп(х), цмеем
*»с*>~ 2 (!) <fr*(i-*)-*.
fc=0
Положим ,у=1—х и согласимся временно рассматривать у как букву,
независящую от *. В этом случае, очевидно, можно написать
й«0 ft«0
1 / <^(v)/ • u.
Поэтому, согласно формуле (87), имеем
Рп (*) = -^ [х>т (х + jr)»-» + S (я)] = *' (.г + у}*- + -^,
278
Вспомним теяерь, что.у=«1—• х, и заставим п безгранично увеличиваться,
я-^-f-oo. Так как в этом случае мы имеем х +^ = 1, то
lim Pn (х) 5= xHt
потому что Q (п) есть многочлен от буквы п степени v —1 и, следовательно,
Q(n)
отношение ——должно равномерно стремиться к нулю на всем сегменте
[0,1]. Таким образом, многочлены Рп(х) акад. С. //. Бернштеина
разрешают проблему Бореля. \
Читатель не преминет отметить, что доказательство этого свойства
многочленов акад. С. Н. Бернштеина проведено при помощи теоремы
Вейерштрасса. Легко, впрочем, освободиться от этого и дать прямое
доказательство свойства этих многочленов *).
С этой целью разобьем многочлен
на две части: первую,оспо вну ю, Sn(x)t состоящую из членов, для
которых число k содержится в пределах -~ — х <е, и вторую, остаточную,
Rn(x), состоящую из членов, для которых k удовлетворяет неравенству
п I
Мы отмечаем, что как Sn(x)t так и Rn(x) отнюдь не являются ни
многочленными, ни даже просто непрерывными функциями, но суть функции,
разрывные на сегменте [0,1].
Оценим -вторую функцию Rn (x). Приняв во внимание то, что f(x) есть
ограниченная функция на сегменте [а, Ь], 1/0*0 | < Мг имеем
\Rnw\<M^ с;**(1-*)»-*<52|1-гГс»**(1""х)""*<
X \>9.
Л—п
к = п f
~^^(&-2кпх + п*х*)СкпхЦ\--хГ-Ъ~
к-Н
к=п к=п
~ 2пх 2 *с£ хЪ (1 - х)п-А + /Л*2 Л С* л*(1-.*)п-*|, (88)
7с==0 fc«0
*) Мы сохраняем идею доказательства, изложенного в книге В. И.
Гончарова „Теория интерполирования и приближения функций", Москва, ГТТИ,
1934 гч стр. 137.
279
Все три суммы легко вычислить. В самом деле, в силу данных выше тождеств,
имеем • » ~
(*h) ф=хф'(х) и {хТхТф={хШхтх) ф-*ч^ (*>•+**-(*).
Отсюда, заменяя функцию Ф (х) через бином (х + уу\ гту рассматривается
как аргумент, независящий от х% имеем
\ХаЬ) (*+У)п~хп(х+у)п-1
и
Но ясно, что
к = п к*=п
2 АЧ***(1 -*)»-*- 2^^"-й= (*^YV+.y)—
= дг2л (л - 1) (л: +^)w-2 + хп (х +y)n-i = д;2/г (л — 1) + лт*
и
#г=П & = ft
2*с*** (1-*)»-*« ЪкСпхкуП~к={хГх) <Х+УУ"*
к=0 к~0
= ХП (X +у)П-1 = д;Л.
Читатель здесь не должен удивляться тому, что сначала буква у лред-
полагается\ независящей от х, а потом на деле оказывается, что х -\-у = 1,
т. е. что ,у=1—•*• Дело в том, что независимость от х буквы у нужна
лишь для формального вывода нужной формулы, причем во время него
производится формальная операция х -т—» которая не должна затрагивать
буквы у. Но когда операция -*-г- совершена и результат получен, ничто
не мешает нам восстановить в нем первоначальное значение буквы у.
К этим двум найденным суммам нужно присоединить тождество
к = п
2 С*«*(1 —^)«-* = [(1 —*) + х]«=1. (82)
к = 0 Л
Введя вычисленные суммы в формулу (88), мы имеем
М
\Rn М\< — [х*п (п — 1) + хп — 2nW + п*х*\ »
= Л.х(\-х). (89)
Неравенство (89) показывает, что имеем lim Rn (x) = 0 равномерно на всем
сегменте [QJJ.
В частности, имеем
280
равномерно на [0,1]. Отсюда на основании тождества (82) заключаем, что
.^Н?.. ,2 , ф*о-*)■-*-i
равномерно на [0,1].
Возвратимся теперь к многочлену Рп(х). Имеем
Pn(*) = Sn(x) + Rn(x)t
1авномерно на [0,1]. С др]
причем lim Rn (х) = 0 равномерно на [0,1]. С другой стороны, имеем
П -> -f- оо
-~Х\<г
= 2, [/W-1*,»] СУ(1-дг)я-* =
I- — х\<*
п-к
Но первая сумма равномерно стремится к 1 на [0,1]. Вторая же сумма,
вследствие равномерной непрерывности функции / (х) на сегменте [0,1],
будет меньше, чем
Ч 2 Cknxk{\-~x)n-k<4
I л I
где f[ есть сколь угодно малое положительное число, потому что для
всякого малого y], yj > 0, можно найти столь малое положительное е, что
неравенство |лг'—.*|<е влечет неравенство |/(лг') — /(лг)|<^. В нашем же
случае мы как раз имеем
f( \ ) =/(дг) + Ъ* Т' е- ч*.<» = '( I )-/(^'
причем * <s. Следовательно, все ч\кп по абсолютной величине
меньше, чем v).
Итак, при достаточно большом л, имеем на всем сегменте [0,1]
1/(*)-5п(*)1<2ч
и, одновременно с этим, при п достаточно большом имеем на всем сегменте
|R»Wl<il. Отсюда имеем |/(л:) — Рп(х)| <3tq,
что и требовалось доказать.
Таким образом в этом рассуждении свойство многочленов, акад.
С. Н. Бернштейна доказывается не на основании теоремы Вейерштрасса,
но, наоборот, из теоремы Бернштейна вытекает теорема Вейерштрасса.
Заметим, что сам Вейерштрасс впервые доказал свою теорему при
помощи интегрального исчисления, рассматривая формулу
/(*)= lim —7= Г /(a)* da.
—00
381
§ 64. Основная теорема интегрального исчисления. В каче»
стве приложения предыдущих результатов мы рассмотрим основную
теорему интегрального исчисления, формулируемую в виде
утверждения.:
Всякая непрерывная функция f(x) есть производная от не*
которой непрерывной функции F(x), т. е.
В некоторых учебниках до настоящего времени можно встретить
следующее геометрическое „доказательство" этой теоремы, не
представляющее никакой научной ценности. Идея его состоит в том, что
чертят на плоскости XOY непрерывную линию, уравнение которой
есть у=/(х) (черт. 176), и обозначают через F(x) площадь, огра-
\°1а
ж /
ничейную кривой, осью ОХ, неподвижной ординатой аА и
подвижной ординатой хМ. Далее, из чертежа следует, что производная
непрерывной функции F{x) есть в точности данная функция /(#).
Однако, доказательство это основано лишь на „ наглядности" и это
рассуждение просто опирается на то, что всякая часть плоскости и,'
в частности, фигура аАМха, имеет „площадь", выражаемую вполне
определенным числом F{x). С логической точки зрения
доказательство это является сплошным недоразумением, основанным на
смешении понятий: „часть плоскости" и „площадь". Первое понятие
„части плоскости* есть совершенно определенное и вполне законное,
не могущее повлечь за собой никаких логических ошибок: „часть
плоскости" есть просто некоторая вполне определенная совокупность
ее точек. Эта совокупность определяется каким-нибудь данным нам
законом, например, указанием на ее „границы*, „внутри" которых
содержится рассматриваемая нами часть плоскости. Так, в нашем
случае, мы рассматриваем часть плоскости, заключенную внутри
границы, составленной из дуги AM кривой, сегмента ах оси абсцисс и
двух ординат а А и хМ. Второе же понятие „площади" есть
чрезвычайно сложное понятие, имеющее численный характер. В силу
него, данной части плоскости приписывается некоторое
неотрицательное число, называемое „площадью" или „мерой" этой части
плоскости. Это ч-исло должно быть вполне определенным из того
самого закона, который определяет рассматриваемую часть плоскости.
282
Когда часть плоскости дана, требовать единственность ее площади
(т. е. меры) — вполне естественно, потому что иначе мы должны
были бы признать наличие геометрической фигуры с двумя
различными площадями. Но процесс, посредством которого из задания
фигуры выводится ее площадь (т. е. ее мера), крайне сложен и
является предметом специальной теории.
Черт. 177.
Вопрос о том, что именно считать за „площадь" данной
геометрической фигуры, далеко не так прост, как это кажется на первый
взгляд, даже в том простом, случае, когда границей фигуры служит
замкнутая кривая Жордана без кратных точек.
Чтобы показать это, достаточно сделать следующее построение:
возьмем на плоскости XOY простой замкнутый многоугольник (т. е.
м - Р
Черт. 178.
не имеющий кратных точек) М, площадь которого равна 3, и
рассмотрим какую-нибудь простую дугу Жордана L, примыкающую
к нему своими концами (черт. 177). Возьмем внутри М конечное
число простых замкнутых многоугольников М^\ М?\ ... ,жр,
не имеющих попарно общих точек, диаметр каждого из которых < 1
и сумма площадей которых >l-j-l. Эти многоугольники
мы будем называть многоугольниками 1-го ранга. Продолжим
теперь простую дугу L внутри начального многоугольника МЛ
Заставив ее примкнуть концами к каким-нибудь двум разным много-
.283
угольникам первого рангами соединим все остальные простыми дугами,
не имеющими общих точек, так, как показано на чертеже, т. е. чтобы
они оказались скрепленными друг с другом и нанизанными один за
другим на одну нить. С каждым из этих многоугольников МО пер-
вого ранга мы проделаем то же самое, что и с начальным
многоугольником Ж, т. е. поместим внутрь каждого из них конечное число
простых замкнутых многоугольников 2-го ранга, имеющих диаметры
меньшими -^, не имеющих попарно общих точек и таких, чтобы
сумма площадей всех их была > 1 -j~ j (черт. 178). Продолжим дуги,
примыкавшие концами к многоугольникам 1-го ранга внутрь их, так,
чтобы все многоугольники 2-го ранга оказались скрепленными друг
с другом и нанизанными один за другим на одну нить. Этот процесс
мы продолжаем неограниченно. Таким образом, многоугольники п-го
ранга не имеют попарно <общих точек, имеют диаметры меньшими
— и сумму площадей больше 1 -f- ~ • Если мы теперь обозначим
через Р множество всех точек плоскости, каждая из которых
принадлежит многоугольникам всех рангов, то, как известно, Р есть
совершенное всюду разрывное множество. Присоединив к нему
дугу L и все дуги, скрепляющие все многоугольники всех рангов, мы
имеем замкнутый контур С Жордана без кратных точек.
Полученная замкнутая кривая Жордана С, не имеющая кратных точек,
проходит через все точки совершенного множества Р. Часть
плоскости, ограниченная контуром С, является некоторой фигурой. И,
однако, совершенно не ясно, что называть „площадью" этой фигуры
и какова численная величина этой площади. Если понятие „ площади *
отнести к внутренности (в строгом смысле) контура С, получим
одно число. Если же под „площадью" этой фигуры будем разуметь
понятие, отнесенное не только к внутренности контура С, но и
охватывающее ее контур С, то 'будем иметь совершенно другое число,
превосходящее прежнее по крайней мере на единицу: совершенное
множество Я, лежащее на этом контуре, являясь общей частью
систем многоугольников всех рангов, имеющих плошадь большую
единицы, само должно рассматриваться, как имеющее яплощадь" (т. е.
меру), большую или равную единице.
Таким образом, в случае фигур, ограниченных замкнутыми
линиями Жордана без кратных точек, понятие „площади" не является
простым, так как самый контур фигуры может явиться настолько
„утолщенным" (будучи, однако, непрерывным и без кратных точек),
что его участие в фигуре может сильно повысить численную
величину ее площади и, значит, пренебрегать самыми контурами никак
не приходится. С такими пне квадрируемыми" контурами мы ранее
уже встречались (см. главу V, § 49).
Возвращаясь теперь к вопросу о существовании функции F(x),
первообразной для данной непрерывной функции f(x), т. е.
имеющей ее в качестве своей производной,
мы должны сразу же признать, Что данное выше „доказательство*
существования первообразчой функции F(x) для f(x) нисколько
не является убедительным. Понятие плсщади ^(а:) фигуры аАМха,
ограниченной осью абсцисс, кривой линией, кеп^вижной ординатой
в ючке^ а и подвижной ординатой в точке х, совершенно ясно,
когда имеем дело с полигональной функцией f(x)9 потому что
рассматриваемая фигура является в этом случзе многоугольником,
площадь которого определяется и измеряется элементарной
геометрией. Но мы знаем, что дажз в случае площади круга
приходится прибегать к предельному процессу при помощи вписанных
правильных многоугольников. В случае же произвольной непрерывной
кривой y=f(x), делающей бесконечно много извивов (как это
показывает чертеж 176), понятие площади F(x) становится неясным
уже хотя бы по одному тому, что сначала приходится решить вопрос
относительно включения или исключения самого контура y—f(x)
и доказывать, что в рассматриваемом случае присоединение контура
не может сопровождаться увеличением численного значения площади.
, Аналитическое доказательство существования первообразной
весьма совершенно с точки зрения строгости, но и оно имеет
следующие два недостатка.
Во-первых, оно вносит много лишних элементов, прибегая к
понятиям, совершенно излишним для установления самого факта
существования первообразной функции F(x). Таким образом, оно не
ограничивается принципами, строго необходимыми для доказательства
существования первообразной функции, и это обстоятельство делает
это доказательство несколько затруднительным для начинающих.
Во-вторых, оно не только не следует историческому пути
развития анализа бесконечно-малых, но идет как раз по обратному
пути, чем путь, пройденный наукбй.
Сущность этого доказательства состоит в том, что сначала до-
ь
казывают существование определенного интеграла \f(x)dx> т. е.
а
существование предела „интегральной суммы" 5,
S=f(x0) A*0+/(*i) A*i+ ... +/(*») Д*я-1.
при разбиении данного сегмента [а, Ь] на малые сегменты [д, хх],
[xv х2], ..., [хп-ь *]> имеющие своими длинами Дл;0, Дл^, Ддг2,...,
Черт. 179.
• ..,Д#П_1 и в предположении, что длина наибольшего из них
стремится к нулю, когда п->-{-со (черт. 179).
Что в этих условиях интегральная сумма 5 стремится к
совершенно определенному пределу, не зависящему от способа разбиения
основного сегмента [а, Ь] на сегменты Дд:0, Lxb ..., ЬхПш.и лишь
285
бы все Они (и среди них самый крупный) стремились по длине к нулю,
это доказывается в каждом хорошем курсе математического анализа*
Затем, когда доказательство существования предела интегральной
суммы 5 проделано и, следовательно, существование определенного -
ъ
интеграла \f(x)dx установлено, тогда его верхний предел b
Предка
полагают переменным, обозначая его буквой х (а переменное
интегрирования лучше обозначить какой-нибудь другой буквой,
например а), т. е. рассматривают выражение
X
ff(a)d*
а
как функцию его верхнего предела х. Обозначив эту функцию через
^(л:), т. е. написав равенство
F(x)=*ff(*)da,
а
затем без труда доказывают, что F(x) и есть первообразная функция
для данной f(x)> х. е. имеет своей производной
\ /"(*)=/(*).
Таким образом, с}гществование первообразной для всякой
непрерывной функции/(л:) является установленным. Но здесь и
заключается главный недостаток этого приема доказательства основной
теоремы интегрального исчисления: и исторически, и фактически
вычисление определенного интеграла обычно происходит благодаря
предварительному знанию первообразной, по формуле
ь
ff(x)dx=F(b)-F(a)>
а
но не наоборот. В указанном же приеме первообразная
получается при помощи определенного интеграла.
Ввиду этого Лебег и предложил свой интересный прием
доказательства основной теоремы интегрального исчисления, не опираясь
на теорему существования определенного интеграла.
Лемма Лебега. Сумма и (х) правильно сходящегося ряда
ui (х) + и2 0*0 + • • • + ип (х) ~Ь • • • производных есть производная»
Пусть функциональный ряд *
и{х) — их (х) + и2 (х) -+- • • • + ип 00 -Ь • • • (91)
есть правильно сходящийся на сегменте [а, Ь]. Это означает, что
имеется сходящийся ряд положительных постоянных чисел
286*
^1тЛт • • • "т Аппг • * • $
(92)
таких, чтб для всех достаточно больших чисел п имеет место ни
всем сегменте [а, Ъ] неравенство
l«nWI<4" ' (93)
По условию, всякая функция ип(х) есть производная на всем
сегменте [а, Ь\ от некоторой непрерывной функции Un(x), т. е. имеем
££(*) = «„(*)•
Требуется доказать, что существует такая непрерывная функция U(x),
производной которой служит сумма и(х) данного правильно
сходящегося ряда (91). Рассмотрим ряд
+ ["»(*)-tf»(01+ •••. (94)
где с есть какое-нибудь постоянное число, взятое на сегменте [я, Ь].
♦ По теореме Лагранжа о конечном приращении имеем
Unix) ~ Un (с) = (х—с) Un (*я) = (х - с) И||(5Я),
где $п есть некоторая точка, промежуточная между точками сихи,
следовательно, принадлежащая сегменту [я, Ь]. Поэтому, в силу
неравенства' (93), имеем для достаточно большого числа п неравенство
\Un{x)-Un{c) \<(Ь — а) -Ап,
откуда и следует, что ряд (94) есть правильно сходящийся и,
следовательно, его сумма U (х)
U {х) = [U, (х) - U, (с)} -f [U2 (х) - U, {с)) + ...+ '
+ [£/»(*) —£/„(*)]-Ь-. (95)
есть непрерывная функция на сегменте [а, Ь]. Докажем, что эта
функция U(x) и есть первообразная для суммы и(х) данного
ряда ("91).
Иными словами, докажем, что
Urn U(x + h)-U(x) ( .
на всем сегменте [я, Ь]. Для этого докажем, что имеет место
неравенство
\Ш±±*±=±М.-и(х)\<* (96)
для всякого фиксированного х и для всякого s, s > 0, лишь бы | А |
было достаточно малым. Так как ряд (92) сходится, его можно
остановить на столь далеком члене Ат, чтобы остаток ряда удовлетворял
неравенству
287
Введем обозначения
f'm (*) = «т ь 1 (*) + «т+2 (*) 4" • . •
Sm (х) = | £/, (X) — t/, (с)] + ... 4- [£/m (д) - £/„, (C)];
Rm (x) = [t/m+1 (л) — Um+1 (с)] + ....
Имеем
и (*) = вт О) + Р», (*)
£/(*) = 5Ж(*)-НЪ(*).
Следовательно,
^* + у-^>_в(х)а.^(* + *)-Д,(дг)_о<|>(х)-| +
Так как /я есть число фиксированное и от h независящее, то
вследствие того, что S'm(x) = о^(лг), мы можем взять |А| столь малым,
что будем иметь
\Sm{x+htSm(x)-^^\<h №
С другой стороны, имеем
/4д*+А)-/?„,(*)= 2 {[*>*(* 4-*)-*>* to]—
ft = m -4-1
-Wk (ж) -Uk (c)]\ = 2 P* (* + *) — ^ (x)] =
& = m 4- l
oo oo
& = /rc -f 1 ft = ?« + l
где ЕЛ есть число, промежуточное между х и л:-[-А и, значит,
находится на сегменте [a, ft]. Поэтому, в силу неравенства (93) имеем
К(У|<4 и, значит,
I /?w(*+JQ —/?«,(*)
Наконец, имеем
OO
|рт(*)1 = |2М*)|<2л*<т. (loo)
/сс=»*4-1 Л s=s w + 1
Сопоставляя три неравенства (98), (99) и (100), находим
окончательно
U(x + h)— U(x) , Л I .
h———«w |<е
для достаточно малого |А|. Отсюда следует справедливость леммы
Лебега.
288
/
Из теоремы Вейерштрасса и "леммы Лебега следует, что
Всякая непрерывная функция/ (х) есть производная от
некоторой непрерывной функции F (х).
Действительно, в силу теоремы Вейерштрасса мы знаем, что всякая
функция f{x\ непрерывная на сегменте [a, £J, есть сумма правильно
сходящегося ряда многочленов
f(x) = P1(x) + P2(x)+... + Pn(x) + ....
Но всякий многочлен есть конечная сумма членов вида ачх\ где v есть
одно из чисел 0, 1, 2, 3, .... И так как этот член а^хн есть, оче-
видно, производная от непрерывной функции ач -—Т, то отсюда еле-
дует, что всякий многочлен есть производная и, следовательно, на
основании леммы Лебега, и непрерывная функция/(лг) есть производная.
А это и есть основная теорема интегрального исчисления.
Но можно на основании леммы Лебега, не пользуясь теоремой
Вейерштрасса, доказать основную теорему интегрального исчисления
следующим образом:
1) Всякая непрерывная функция f(x) на сегменте
[а, Ь] есть сумма правильно сходящегося ряда
полигональны х функций, т. е.
/(*)-М*)+М*)+ —+ М*)-!-::: •"
2) Всякая полигональная функция L(х) есть конечная
сумма линейной функции и элементарных
полигональных функций
L (х) = a -f- bx + *i {x) + Х2 (х) -J- . ТТ + Хт (х).
3) Всякая элементарная полигональная функция
Х(л:) есть производная
В самом деле, элементарная полигональная функция X (х) есть такая,
которая равна 0 влево от точки I и равна линейной функции р (х — £)
У-°
Черт. 180.
вправо от точки &, где (i = tgcp (черт. 180). Ясно, что функция Д(#),
определенная условием: Л (х) равна 0 влево от точки £ и равна -^ (*— I)2
вправо от точки $, есть непрерывная функция, имеющая свою
производную функцию Х(л;), т. е. Л' (л;) = X (л;).
19 3<ак. Ш4. 289
В этом убеждаемся на основании равенства
£%ХХ-Ф~Г(Х-1) = \(Х)
вправо от S и на основании равенства
d\(x)
dx
= 0 = X (х)
влево от точки 5, причем в самой точке х = ? мы, очевидно, также
имеем Л'(?) = 0 = А(е).
Геометрически, линия у = \ (х) есть двузвенная ломаная с левым
звеном, располагающимся по оси абсцисс, а линия у = А (л:) составлена
из части оси абсцисс, простирающейся влево от точки $, и параболы,
прикасающейся в точке £ к оси абсцисс. Ясно, что мы, в самом деле,
имеем равенство
А'(х) = \(х)
на всей оса абсцисс.
4) Из предыдущих пунктов следует, что всякая полигональная
функция L{x) есть производная и, на основании леммы Лебега,
отсюда вытекает, что всякая непрерывная функция f(x) есть
производная.
Этим основная теорема интегрального исчисления о существовании
первообразной функции F (х) для всякой непрерывной функции f(x)
доказана со всей строгостью без ссылки на теорию определенного
интеграла.
ПРИЛОЖЕНИЯ.
Приложение I.
ТЕОРИЯ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ.
§ 65. Сечения рациональной сети. Обозначим через R совокупность
всех рациональных чисел и, ради краткости, будем называть
Rрациональной сетью, не связывая этого названия ни с какими геометрическими
представлениями, от которых освобождаемся ради строгости рассуждений. Таким
образом, рациональная сеть R есть совокупность отвлеченных рациональных
чисел г. Это мы будем записывать в виде условного равенства R -= {г}, где
фигурные скобки { } обозначают акт собирания элементов г в одно целое.
Мы предполагаем известным, что рациональная сеть R есть множество
упорядоченное, т. е. все' элементы £ рациональной сети R расположены
в строго определенном порядке, сообразно их численным
величинам: из двух неравных рациональных чисел гиг' одно число (и только
одно) меньше другого, r<V. Наконец, мы предполагаем известным, что
рациональная сеть R не имеет двух непосредственно соседних
элементов: между всякими двумя неравными рациональными числами гиг' содер-
г+г''
жится промежуточное рациональное число, например —~—.
Мы будем рассматривать различные множества, элементы которых
суть рациональные числа. Чаще всего будем рассматривать пары таких
множеств: А = {а} и В = {Ь}, где всякое число а, принадлежащее
множеству Л, строго меньше всякого числа Ь, принадлежащего множеству В, т. е.
а<^Ь. Всякий раз, как мы имеем такую пару Л, В множеств, мы будем
называть множество А предшествующим множеству В или просто левым
множеством; множество В в этом случае называется правым или следующим
за множеством А. Такое расположение на рациональной сети R множеств
А и В будем записывать в увиде
А-$В.
Два множества А и В, А --? В, называются отделимыми, если имеется
рациональное число /-, большее всякого числа а, принадлежащего множеству Л,
и, одновременно с этим, меньшее каждого числа Ь, принадлежащего
множеству В. Такое рациональное число л не принадлежащее, понятно, ни к
множеству Л, ни к множеству ВУ называется отделяющим множества Л и В
друг от друга или промежуточным между этими множествами. Такое
расположение на рациональной сети R множеств Л, В и отделяющего числа г
будем записывать в виде
Если отделяющего рационального числа г не существует, то
рассматриваемые множества Ли В, А~$В, называются неотделимыми друг от друга.
Когда даны на рациональной сети R два какие-нибудь множества Л и В,
А -%В, могут представляться следующие три случая:
1) множества Л, В не отделимы;
2) множества Л, В отделимы только одним отделяющим числом г;
19* 291
3) множества А, В отделимы несколькими отделяющими числами.
Легко видеть, что в третьем случае отделяющих чисел г существует
бесконечное множество. В самом деле, если множества Л, В допускают
два различных отделяющих числа У и г", г'<С/", то имеем A<ir'<r"<^B>
и мы сразу замечаем, что всякое рациональное число г, содержащееся
между числами гг и rf/, r'< r<r//t также будет отделяющим. Легко дать
критерий для того, чтобы для множеств At В осуществлялся третий случай.
Теорема. Необходимым и достаточным условием дпя того, чтобы
множества А = {а} и В = {Ь} допускала более одного отделяющего числа,
является требование% чтобы разность Ь — а двух любых их элементов
а и Ь превосходила некоторое фиксированное положительное
рациональное число о, о>0, т. е. чтобы имели b — <2>о.
Условие необходимо. Если множества А и В допускают два различные
отделяющие числа г' и г", r'<^rr\ то имеем А-$rf-*Jr"-^В, откуда
следует неравенство я<£/•'<>"<£, справедливое для всяких элементов а и Ь%
соответственно принадлежащих множествам АиВ. Ясно, что b — #>r"— /•'.
Но разность г" — г есть фиксированное положительное рациональное число,
не зависящее от выбора элементов а и b в множествах А и В. Обозначив
через 8 эту разность г" — r\ Ь~г" —r\ мы приходим к неравенству
Ь — а>Ъ.
Условие достаточно. Пусть неравенство b — д>о удовлетворено при
всяком выборе элементов а к b в множествах А и В; здесь о есть
некоторое фиксированное положительное рациональное число, не зависящее от
выбора элементов а я Ь. Возьмем два какие-нибудь фиксированных элемента
а0 и Ь0, принадлежащих соответственно множествам А н В, и рассмотрим
бесконечную арифметическую прогрессию
» 8 , О 5 , О 5 I Ь
ао> Яо+з"» ao + 2~j> «о + з-тр ..., tfo + n-g-, ...»
начинающуюся с элемента #0- Ясно, что все члены этой прогрессии суть
рациональные числа. Первый член #о этой прогрессии предшествует всему
множеству В, т. е. имеем а0~$ В, потому что а0 принадлежит к множеству А
Случайно предшествовать множеству В могут и некоторые дальнейшие
члены, следующие за начальным членом а0, например, До + -^. а0-\-2-^9...
о о
и т. д. Но идя по членам прогрессии достаточно далеко от начального
члена #0' мы непременно встретимся с членами, уже не могущими
предшествовать множеству В, Например, если мы возьмем натуральное число п столь
большим, чтобы иметь неравенство #о+ п о>^о» то ясно, что ни этот член
ао~гп~о> ни все следующие за ним члены уже не могут предшествовать
множеству В. Поэтому, среди членов рассматриваемой арифметической
прогрессии имеется лишь ограниченное число членов, предшествующих
множеству В. Следовательно, среди таких членов прогрессии имеется самый по-
следний) обозначим его через д0 + &т»ао + k-=- -^ В. Так как следующий
о о
член прогресии aQ H-(£-f-1)-~- уже не межет предшествовать множеству В,
то имеется элемент bt множества В, удовлетворяющий неравенству
*о+ *-з <А<"о + (* + !) -3-.
С другой стороны, член a3r\- (k — 1) -5- прогрессии следует за множеством А,
т. е. удовлетворяет соо!ношению А^а0 +(&—-1)-^-. В самом деле, если
292
бы* это было не так, то имелся бы элемент at множества Л, удовлетворяющий
неравенству aQ + (^ —1)^-<#1- И так как дх < Ьь то имело бы место
нерашенство
*o + (*-l)}<*i<*i<*o+(* + l)^,
откуда следовало бы, что
h - cti < -| Ь < Ь,
что невозможно,так как мы предположили справедливым неравенство Ь ~ а>о
при всяких а и £, принадлежащих к множествам А и В. Таким образом, имеем
А это показывает, что рациональные числа a0 + (k — l)-^- и а0 + к-~
различны и каждое из них отделяет множества Л и В друг от друга.
Как следствие доказанного предложения имеем:
Неодходимым и достаточным условием для того, чтобы два
множества А — {а} и В— {b}, A-3В, были неотделимы или допускали не
более одного отделяющего числа г, А-$г-$В, является существование
для всякого положительного рационально?о е, s>0, двух элементов
а и Ь этих множеств, отличающихся один от другого меньше чем
на г, т. е. *
b — a<s.
Введем теперь следующее важное определение: Множество А~{а},
принадлежащее рациональной сети R, называется нижним классом,
если всякое рациональное число г, меньшее какого-нибудь элемента а
множества Л, принадлежит к множеству А. Аналогично, множество
В={Ь}, принадлежащее рациональной сети R, называется верхним
классом, если всякое рациональное число г, превосходящее какой-нибудь
элемент Ь множества В, принадлежит к множеству В.
Если какое-нибудь множество чисел ЭД1 = <{» принадлежит рациональной
сети R, то множество У1 = {м} всех рациональных чисел, не принадлежащих
к рассматриваемому множеству $Щ, называется дополнением множества Ш.
Ясно, что дополнение нижнего класса есть верхний класс) и обратно: до-
дополнение верхнего класса есть нижний класс.
Единственное множество рациональных чисел, являющееся о дно
времен н о и нижним, и верхним классом, есть сйма рациональная сеть R.
Дополнение ее есть „пустое" множество, т. е. не содержащее ни одного
элемента. Мы никогда не будем, рассматривать этих двух классов. Поэтому,
дополнения всех рассматриваемых нами классов никогда не будут пустыми
и будут, следовательно, классами, действительно содержащими
элементы.
Нижний класс %А{а} называется открытым, если он не содержит
наибольшего числам в противном случае, нижний класс называется
закрытым, и это максимальное (т. е. последнее) число а0 в классе А
называется граничным числом. ч
Аналогично, верхний класс В = {Ь} называется открытым, если он не
содержит наименьшего числа; в противном случае, верхний класс В
называется закрытым, и это минимальное (т. е. начальное) число Ь0
в классе В также называется граничным числом.
Ясно, что если какой-нибудь класс (нижний или верхний) закрыт,
дополнительный к нему класс непременно открыт. Иначе говоря, не
существует двух взаимно-дополнительных закрытых классов. Это есть
очень важное предложение, вытекающее из того, что рациональная сеть R
293
не имеет двух непосредственно соседних элементов. В самом деле, если бы
классы Л и В были взаимно-дополнительные и оба закрытые граничными
числами а0 и Ь0, то мы имели бы а0<^Ь0, и между этими рациональными
числами а0 и Ь0 не содержалось бы никаких
промежуточных рациональных чисел, что невозможно.
Введем следующее определение:
Два взаимно'дополнительные класса образуют сечение рациональной
сети. Сечение рациональной сети обозначается символом
(А, В),
где классы А и В суть взаимно-дополнительные, причем А есть
нижний класс и i5 есгъ верхний класс.
Мы видели, что не может существовать сечения (А, В) с двумя
закрытыми классами. Следовательно, имеются лишь две возможности:
1) или один из классов А и В закрыт, а другой открыт;
2) или оба класса А и В открыты.
Так как закрывающее класс граничное число есть число рациональное*
то сечения (Л, В) с закрытым классом сами называются рациональными
сечениями. Рациональные сечения строятся чрезвычайно легко и просто:
для этого достаточно взять какое-нибудь рациональное число г и отнести
к верхнему классу В его самого и также все рациональные числа г",
превышающие число г, rr/^>r. Дополнительный класс А, очевидно, будет
состоять из всех рациональных чисел /•', меньших числа г, /J'<>.
Ясно, что рациональное число г есть наименьшее в классе В, который
тем самым является закрытым классом. Нижний же класс Л, очевидно,
открыт.
Таким образом, мы имеем способ строить рациональные
сечения (Л, В) с открытым нижним (левым) классом Л и
с закрытым верхним (правым) классом В.
Этот способ даст все рациональные сечения с закрытым правым
классом и только такие сечения.
В дальнейшем мы не будем рассматривать сечений с закрытым левым
классом Л, так как всегда можно рациональное число г, закрывающее класс Л,
отчислить от этого класса и причислить к классу В, чтобы получить
сечение с закрытым правым классом. Поэтому без нарушения общности мы
можем условиться впредь рассматривать только лишь те рациональные
сечения, которые имеют открытый левый класс Л и закрытый правый класс В.
Остается теперь решить вопрос, существуют ли сечения (Л, В) с
обоими открытыми классами А и В. Мы называем такие сечения
иррациональными. Покажем, что иррациональные сечения действительно
существуют.
Рассмотрим в качестве примера сечение (Л, В), определенное следующим
законом: к верхнему классу В отнесем все положительные рациональные
числа Ь, квадрат которых превышает 2, ^->2,к нижнему классу Л отнесем
все остальные рациональные числа а. Этим законом сечение (Л, В) вполне
определено. Требуется определить тип этого сечения. Прежде всего
следует убедиться, что В действительно есть класс (а не только множество)
и именно верхний класс. Но это очевидно. В самом деле, если
рациональное число Ь принадлежит к В, то, согласно определению множества В, имеем
Ь^>0 и #2>2. Но тогда ясно, что если, г есть рациональное число и если
г>£, то имеем r^>0 nr2>^2>2. Значит, рациональное число г войдет в В
и, следовательно, В есть верхний класс. Отсюда вытекает, что его
дополнение, т. е. Л, есть нижний класс. Покажем, что класс В есть открытый.
Для этого достаточно показать, что в классе В нет наименьшего
числа. Ъ самом деле, пусть b есть наименьшее число класса В. Имеем
#>0 и £2>2. Посмотрим, нельзя ли найти столь малое положительное
рациональное число h, чтобы мы имели попрежнему b — /г>0 и (Ь — /г)2>2.
Если удастся найти таксе /г, то, очевидно, число b — /г также войдет в класс В,
и так как b — h<^b, то, значит, число b не могло быть наименьшим в класе В.
Неравенство (6 — /г)2>2 перепишется в виде £* — 26/2 +&2>2, что
равносильно неравенству 2£/г~^/г2<^:— 2, Если мы теперь определим доложи-
2Н
тельное рациональное число h столь малым, чтобы Л<—^—, то будем иметь
2bh<£№—2 и, значит, тем более будем иметь 2Ыг — №<Ь2 — 2. Мы видим,
что при выборе рационального положительного числа h меньшим чем —^т—
удовлетворяется неравенство (Ь — Л)2>2. Выбирая h еще более малым, чтобы
иметь Ъ — Л>0, мы устанавливаем, что число Ь не есть минимальное
в классе, В (вопреки предположению) и, следовательно, что класс В есть
открытый.
Покажем, наконец, что класс А также открыт. Для этого достаточно
показать, что в классе Л нет наибольшего числа. Пусть а есть
наибольшее число класса Л. Так как мы имеем 12=1<2, то наибольшее
число а класса Л (если оно там есть) дож^кно превосходить единицу, а>1.
Покажем, что всегда, попрежнему, можно найти столь малое положительное
рациональное число Н, что будем иметь (a -f- /г)2<^2. Если удастся отыскать
такое Л, то число а + h также войдет в класс А, и так как а+ /*>#, то,
значит, число а не могло быть максимальным в классе Л. Неравенство
(а + Л)2<2 перепишется в виде а2-4-2а/г-{- /г2<2, что равносильно
неравенству 2яй + /г2<2 — а2. Выберем сначала положительное рациональное
число h меньшим, чем 2а. Мы имеем h<2a, откуда Л2<2я/г. Следовательно,
если выбрать h кроме того так, чтобы 2а/г4-2аЛ<2 — а\ то тогда тем
более получим, в силу неравенства #2<2аЛ, неравенство 2а/г + /г2<2— а2
и, значит, неравенство (а + /г)2<2 будет удовлетворено. Итак, нужно
выбрать рациональное h так, чтобы 0<fr<2a и одновременно с этим, чтобы
2 cfi
2а/* + 2я/*<2 —а2, т. е. чтобы 4д/г<2 — я2 или, наконец, чтобы й<—^—•
что, понятно, всегда возможно, потому что числитель 2 — а2 есть
положительное рациональное число. Таким образом число а не есть максимальное
в классе А (вопреки предположению) и, следовательно, класс А есть от-
крытый.
Наличие конкретных сечений (А, В) рациональной сети Re обоими
открытыми классами Л и В есть следствие арифметических
неравенств и нисколько не зависит от каких-либо" достулатов
или аксиом геометрии.
§ 66. Иррациональные числа. Мы вводим основное определение
(Дедекинд, Рессель):
Всякое сечение (Л, В) рациональной сети R с открытым нижним
классом А называется действительным числом. Если сечение (Л, В)
есть рациональное, т. е. если верхний класс В закрыт некоторым
рациональным числом г, действительное число (Л, В) называется
рациональным числом и обозначается знаком этого рационального числа /%
г = (Л, В). Если сечение (А, В) есть иррациональное, т. е. если верхний
класс В есть открытый, действительное число (Л, В) называется
иррациональным числом.
По поводу данного определения иррационального числа следует заметить,
что для обозначения рациональных *) действительных чисел (Л, В) мы имеем
планомерное условие обозначать их тем же самым знаком г, как и
закрывающее верхний класс В рациональное число г, но у нас нет никаких правил
для планомерного обозначения иррациональных чисел. Вообще говоря, редко
бывает, чтобы иррациональное число было изображено формулой) чаще
всего иррациональное число обозначается каждое особым знаком или
буквой, короче говоря, новым символом, например У2 , тс, е> ... .
После того, как действительное число получило определение, установим,
что такое равные действительные числа и что значит, что одно
действительное число меньше или больше другого действительного числа.
*) Напомним, что мы условились рассматривать рациональные сечения
всегда с открытым левым классом Л и закрытым правым классом В.
295
Определение. Два действительных числа с = (А, В) и с''« (Л',В)
называются равными тогда и только тогда, когда их нижние классы
А и Аг (а стало быть и верхние классы В и В) совпадают друг с другом^
т. е. когда А~ А* (а стало быть и В = В')\ в этом случае пишем
равенство с— с'.
По поводу этого определения заметим, что „равные действительные
числа*1 это только различные символы, относящиеся к одному и тому же
сечению (А, В). В самом деле, если мы имеем тождество нижних классов
А~А\ то отсюда автоматически следует тождество и верхних классов
В = В\ дополнительных к ним и, поэтому, мы, собственно, не имеем двух
„равных" сечений (Л, В) и (Л', В')> но имеем, строго говоря, лишь одно
сечение (Л, В), к которому и относятся различные обозначающие его
символы с, с', ..., определяющиеся поэтому как „равные".
Заметим, далее, что установление равенства двух действительных чисел
с = (Л, В) и с' = (Л', В') есть, вообще говоря, одна из самых трудных задач.
В самом деле, для установления равенства с = с' двух действительных чисел
с и с' нужно установить тождественность состава нижних классов Л и А\
иначе говоря, надо доказать, что если какое-нибудь рациональное число г
входит в класс Л, то оно же войдет и в класс Л', а также и обратно: если г
входит в Л', то г входит и в Л. Но классы Л и Л' содержат, каждый,
бесконечно много рациональных чисел и перепробовать их один за другим
непосредственным образом не представляется возможным.
Современный математический анализ не имеет общего метода даже для
решения такой, на первый взгляд, простой задачи, какова: „Дано
действительное число с = (Л, В); узнать, рационально оно или иррационально* t
так как не имеется общего приема устанавливать, /шляются ли классы
сечения открытыми или один из них закрыт.
Прежде чем перейти к неравенствам для действительных чисел, сделаем
следующее замечание. Пусть с = (Л, В) ис' = (Л\ В') два неравные
действительные числа. Раз они не равны, их нижние классы Л и Л' нетожде-
Черт. 181.
ственны. Это значит, что в одном из них содержится рациональное число,
которого нет в другом. Пусть же в классе А содержится некоторое
рациональное число г\ не принадлежащее к классу Л (черт. 181). Раз г' не
принадлежит к классу Л, то г' входит непременно в верхний класс В. Поэтому,
всякое рациональное число а нижнего класса Л оказывается меньше этого
числа г\ а < г'. С другой стороны, число г' входит в нижний класс А;
поэтому всякое рациональное число, меньшее числа г', также должно
принадлежать к нижнему классу Л'. Отсюда следует, что нижний класс А
действительного числа с целиком содержится в нижнем классе А'
действительного числа с\ причем класс А является правильной частью класса А\
как легко видеть, имеется бесчисленное множрство рациональных чисел,
входящих в класс А' и не входящих в Л. Ввиду важности последнего
пункта, докажем его строго Рациональное число г', содержащееся в классе Л',
не принадлежит к классу Л. Значит оно принадлежит к верхнему классу В.
Следовательно, к этому верхнему классу В будет принадлежать всякое
рациональное число, большее чем /•'. Но класс А открытый. Поэтому,
в классе А имеется бесконечно много чисел, бдльших чем г\ Согласно
сказанному, они все должны принадлежать к верхнему классу В и,
следовательно, не могут входить в класс Л. Следовательно, имеется бесконечно
много чисел класса Л', не принадлежащих к классу Л.
2Э6
Таким образом: если действительные числа г = (Л, В) и с'=(Л', В')
не равны, то нижний класс, пусть А', одного числа не только целиком
содержит в себе нижний класс А другого числа, но он содержит
бесконечное множество элементов, не принадлежащих Л. Это свойство нижних
классов действительных чисел и кладется в их основу определения их
неравенства.
Определение. Мы говорим, что действительное число с = (А, В)
меньше действительного числа с' = (А', В') и пишем с < с\ если нижний
класс А числа с образует правильную часть нижнего класса А' числа с'.
Легко видеть, что такое определение неравенства действительных
чисел сохраняет все обычные свойства неравенств. Среди них важнейшим
является свойство транзитивности: из неравенств c<V и c'<V' следует
неравенство с<^с". В самом деле, если c<V, то это означает, что нижний
класс А действительного числа с = (Л, В) содержится в нижнем классе А'
действительного числа с\ причем, совпадение классов исключено. С другой
стороны, так как с'<С?*, то класс Аг содержится в нижнем классе А" числа
с" = (Л", В"). Отсюда заключаем, что класс А содержится в классе А", не
совпадая с ним. А это и означает, что с<^с".
Если два действительных числа с = (Л, Л)ис' = (А/, Вг) не равны и с
меньше, чем с', т. е. с<с', то действительное число с' называется большим
действительного числа с, и в этом случае пишут неравенство с'^>с. Ясно,
что если с'>с, то класс А' содержит как правильную часть класс А
Если два действительных числа с и с' не равны, то имеет место одно
из неравенств: с <У, или с'<<\
В дальнейшем мы будем обозначать через / совокупность всех
действительных чисел, как рациональных, так и иррациональных.
Из всего изложенного следует важное предложение: Совокупность I
всех действительных чисел есть упорядоченное множество,
В самом деле, если два действительные числа с и с' не равны, сфс\
то одно (и только одно) из них строго меньше другого: или с<^с\ или с'<^с,
причем одно из этих неравенств исключает другое. С другой стороны, если
с<Сс' и если с'<с", то с<^с". Это и доказывает, что множество / всех
действительных чисел есть упорядоченное множество.
В высшей степени важно отметить, что относительный порядок
расположения рациональных действительных чисел {А, В) на совокупности!
всех действительных чисел тождествен с расположением рациональных
чисел г на совокупности R всех рациональных чисел.
Смысл этого утверждения следующий: рациональное действительное
число есть, строго говоря, пара классов (Л, В) с закрытым верхним клас.
сом В. Эту пару классов ыы обозначили символом рационального
действительного числа г, закрывающего класс В, т. е. написали условное
равенство
служившее для выражения лишь той мысли, что знание обыкновенного
рационального числа г вполне определяет рациональное действительное число
(Л, В), к а к и о б р а т но. Но порядок расположения обыкновенных
рациональных чисел г на рациональной сети R дается непосредственно их
численными значениями-, порядок же (относительный) расположения
действительных рациональных чисел (Л, В) на совокупности / всех
действительных чисел диктуется теми правилами неравенства действительных чисел,
которые мы только что наложили на действительные числа. И, поэтому,
нисколько не очевидно, что оба эти порядка согласуются, когда мы
отождествляем (вернее сказать: считаем равносильными, или, еще лучше:
ставим в соответствие) рациональное действительное число (Л, В) и
обыкновенное рациональное число г, закрывающее верхний класс В, так как
может случиться, что порядок (относительный) рациональных пар (А, В) на
совокупности /—один, а порядок закрывающих верхние классы
обыкновенных рациональных чисел на рациональной сети R — совсем другой. Тем не
менее оба эти порядка согласуются. Чтобы доказать это, допустим, что ра-
297
циональное действительное число с = (А, В) меньше рационального
действительного числа с* =г (Л', В')> т. е. что имеем
с<с'.
Согласно нашим правилам, это означает, что нижний класс А числа с
образует правильную часть нижнего класса Л' числа с'. С другой стороны,
действительные числа с и cf суть рациональные действительные числа и,
следовательно, обладают закрытыми верхними классами В и В. Пусть г есть
закрывающее класс В обыкновенное рациональное число и, аналогично,
пусть г' закрывает класс В'. Согласно указанному выше условию, мы
обязаны обозначить пару (Л, В) через г и пару (А\ В') через г', написав
равенства
г = (Д5) и r'=z(A',B')m
Теперь докажем, что из соотношения (Л, £)<(Л', В') следует г</^
в смысле обычного понимания неравенства рациональных (обыкновенные)
чисел г и г'т В самом деле, класс А составляет, как мы видели, правильную
часть класса А'. Это означает, что в классе А/ имеется рациональное
Черт. 182.
число р, не принадлежащее к классу А (черт. 182). Следовательно, это число
р должна принадлежать к классу В. Поэтому мы имеем неравенство (в смысле
неравенства рациональных чисел) г< р, потому что г есть наименьшее число
класса В. И так как р принадлежит к классу Л', то, вследствие того, что
к этому же классу А' должны принадлежать все.рациональные числа,
превзойденные каким-нибудь числом, входящим в класс Л', то число г также
принадлежит к классу А' и, поэтому, оно меньше, чем рациональное число
г', принадлежащее к классу В, т. е. мы имеем г< г' в смысле неравенства
рациональных чисел. Таким образом, мы видим, что относительный порядок
рациональных действительных чисел г = (А, В) тождественен с порядком
численных величин соответствующих им рациональных чисел г. Поэтому мы
имеем право произвести полное отождествление рациональных
действительных чисел с обыкновенными рациональными числами и, следовательно,
рассматривать рациональную сеть R как часть совокупности 1 всех
действительных чисел.
Но эта возможность сразу же влечет за собой ряд новых
вопросов. И первым среди них является важный вопрос: каким образом
расположена рациональная сеть R на совокупности 1 всех действительных
чисел?
Чтобы ответить на него, необходимо доказать некоторые
предварительные предложения.
Лемма I. Каково бы ни было данное действительное число с,
с = (А, В), всякое рациональное число г0, принадлежащее к его нижнему
классу А, определяет рациональное действительное число г0 = (Ло, Bq),
которое меньше данного действительного числа с, /*о<£ (черт. 183).
В самом деле, согласно предположению, рациональное число г0
определяет рациональное действительное число (Л0, Bq). Это значит, что г0 служит
минимальным числом верхнего класса В0 и что, поэтому, нижний класс Aq
состоит из всех рациональны^ чисел, меньших чем г0. С другой стороны,
число г0 принадлежит к нижнему классу А; это значит, что к классу А
принадлежат также и все рациональные числа, меньшие чем г0. Отсюда
следует, что класс Aq составляет какую-то часть класса Л, т. е. имеем Ло<Л.
Здесь знак равенства <, добавленный к знаку неравенства, выражает мыс-
298
лимость тождества классов Ло и Л, мыслимость равенства Л0 = А. Но, на
самом деле, это равенство невозможно, так как уже само рациональное
число г0, принадлежащее к классу Л, является числом (минимальным)
класса Во и, значит, не находится в классе Л0. Таким образом, класс Ллесть
правильная часть класса Л и, значит, мы имеем Ао<А, откуда, и следует,
что г0<Сс.
Лемма II. Каково бы ни было данное действительное число с,
с = (Л, В), всякое рациональное число rQt принадлежащее к его верхнему
Черт. 183.
классу В, определяет рациональное действительное число г0 =а (Л0, В0),
превосходящее данное действительное число с, или% в крайнем случае,
равное ему с < г0; при этом, равенство с = г0 возможно лишь тогда,
когда данное действительное число с рационально и когда за число г0
взято минимальное число верхнего класса В.
Мы оставляем в стороне, кик очевидный, тот случай, когда данное
действительное число с, с = (Л, В)у есть рациональное, и когда г0 есть
минимальное число его верхнего класса В. В этом случае мы имеем
очевидное равенство с = г0, потому что определяемое рациональным числом г0
действительное рациональное число г0 = (Ло, В0) также имеет rQ
минимальным числом в верхнем классе В0 и следовательно
Л = Л0 и В = Во.
Итак, пусть данное действительное число с = (Л, В) есть какое угодно
рациональное или иррациональное, и пусть рассматриваемое
рациональное число г0 принадлежит к его верхнему классу В (черт. 184),
Черт. 184.
но не является минимальным числом этого класса (если класс В
закрытый). Обозначим через (Л0, ^действительное число, равное r0, rQ = (Л0, В0).
Это значит, что рассматриваемое рациональное число г0 есть минимальное
число верхнего класса BQ. Поэтому, класс.Л0 есть совокупность всех
рациональных чисел, меньших чем г0. Но число г0 принадлежит, по условию,
к верхнему классу В данного действительного числа с = (Л, В).
Следовательно, его нижний класс, будучи составлен только из рациональных чисел,
меньших чем г0, должен содержаться в классе Л0, т. е. мы имеем Л < Л0.
Но равенство А = А0 невозможно, так как, раз г0 не есть минимальное
число класса В, имеется в этом же классе число гь меньшее чем г0, г1<г0.
Это число гь очевидно, принадлежит к Л0 (будучи меньше чем г0) и
заведомо не принадлежит к Л (так как входит в В).
Поэтому класс Л0 содержит класс Л и, следовательно, A<^A0t откуда и
следует, что с<г0.
Из этих двух лемм вытекает важное предложение:
299
Теорема. Между всякими двумя неравными действительными
числами с* и с", сг<с", содержится бесконечное множество рациональных
действительных чисел г, с'<г<с".
В самом деле, раз действительное число с', сг = (А\В')> меньше
действительного числа с", с" = (Af/, В'% то это означает, что нижний класс А"
содержит в себе как правильную часть нижний класс А' и что, поэтому,
имеется бесконечное множество рациональных чисел г, принадлежащих
к А" и не входящих в А' (черт. 185).
Так как число/- не принадлежит к А', то оно входит в верхний класс В\
И раз таких чисел г, принадлежащих к А" и не принадлежащих к Л',
Черт. 185.
имеется бесконечное множество» мы всегда имеем право предположить, что
рассматриваемое рациональное число г не является минимальным числом
класса В' (которое, если вообще имеется в классе В\ есть единственное).
Но тогда, обозначая через (А> В) действительное рациональное число,
определяемое рациональным числом г, г=(А, В), мы видим, что /*<с", так как
г принадлежит к А", и что имеем £'<г, так так г принадлежит к В' и не
является его минимальным числом (если оно там есть). Следовательно, имеем
<•'< г< с". Доказанное предложение имеет исключительную важность, так
как оно показывает, что:
Рационильная сеть R есть всюду плотное множество на
совокупности I всех действительных чисел.
Важность имеют и обе доказанные леммы I и II, так как из них
следует, что каждое действительное число с = (А,В) больше всякого
рационального числа а, принадлежащего к нижнему классу А, А = {а}, а
меньше всякого рационального числа Ь, принадлежащего к верхнему классу
В, В~{Ь},не являющегося минимальным числом этого класса (если
этот класс имеет вообще минимальное число), т. е. мы имеем строгие
неравенства:
а<с<Ь.
В случае, каг£а Ь0 есть минимальное число класса В, данное
действительное число с есть рациональное, и мы имеем
а < £ и с = bo < £.
В частности, для иррациональных чисел c = (A,B) мы имеем более
простую формулировку:
Всякое иррациональное число с = (А, В) больше любого рационального
числа а, принадлежащего к его нижнему классу А,А = {а}, и меньше
любого рационального числа Ь, принадлежащего к верхнему классу
В,В = {&}, т. е. мы имеем
а<с<Ъ,
каковы бы ни были рациональные числа а и Ь, соответственно
принадлежащие классам А и В.
Из этого предложения мы заключаем, что иррациональное число
с = (At В) есть число промежуточное, превышающее все рациональные
числа а класса А и меньшее всех рациональных чисел b класса В и, еле'
довательно, отделяющее оба эти класса друг от друга% *
А < с < В.
300
Легко видеть, что между классами А и В нет никакого другого
действительного числа с\ отличного от с, В самом деле, если бы мы
имели Л<с,<5ис'^:с, то (вспомним, что между всякими двумя
различными действительными числами содержится бесконечное множество
промежуточных рациональных чисел г) существовало бы рациональное число г,
промежуточное между классами Л и В, т. е. А < г < В, что невозможно,
так как всякое рациональное число принадлежит непременно либо к классу Л,
либо к классу В,
Таким образом, иррациональное число с = (А,В) есть единственное,
содержащееся между обоими классами А и В.
Мы видим, что иррациональные числа заполняют просветы
(отверстия) в рациональной сети R.
Теперь возникает другой, .столь же важный вопрос: имеет ли
совокупность I всех действительных чисел желаемую нами сплошность
(непрерывность), достигнуть которой мы стремились, вводя
иррациональные числа? Другими словами, не представляет ли совокупность I всех
действительных чисел где-нибудь отверстий, которые придется
выполнять введением еще каких-нибудь новых .чисел"?
Прежде всего сформулируем определение непрерывности
упорядоченного плотного множества/ Упорядоченное плотное множество называется
непрерывным, если при любом сечении в этом множестве, т. е. при
разбиении всех элементов на два непустые класса А и В такие, что каждый
элемент класса А предшествует любому элементу класса В, один из
классов является закрытым (оба класса не могут быть закрытыми в силу
плотности данного упорядоченного множества).*)
Поставленный вопрос допускает вполне точный утвердительный ответ:
Совокупность I всех действительных чисел в самом деле является
непрерывной.
Чтобы показать это, будем рассматривать всевозможные сечения (А, В)
в множестве I всех действительных чисел, где А и В суть классы
действительных чисел, т. е. такие множества действительных чисел, что всякое
действительное число а, принадлежащее к классу А, меньше каждого
действительного числа р, принадлежащего к классу В, т. е. А = {а} иб = {р},
1*де непременно а<р. Класс А называется нижним, класс В называется
верхним. При этом мы предполагаем, что всякое действительное число y
непременно будет принадлежать либо к нижнему классу А, либо к
верхнему классу В. Иными словами, мы будем предполагать, что
1 = А + В.
Нижний класс А является закрытым, если в нем имеется наибольшее
(самое последнее) действительное число; в случае отсуствия в А
максимального действительного числа, класс А является открытым. Аналогично,
верхний класс В есть закрытый, если в нем имеется наименьшее
(начальное) действительное число; в случае отсутствия в В минимального числа,
класс В называется открытым. Ясно, что оба класса и нижний А и
верхний В не могут быть одновременно закрытыми, так как множество
действительных чисел является плотным.
Таким образом, по крайней мере один из классов А или В сечения
(А, В) есть класс открытый.
Если бы было констатировано наличие хотя бы одного случая,
когда оба вместе класса А и В сечения (А,В) открыты, тогда совокупность
/ всех действительных чисел имела бы просвет (отверстие) и,
следовательно, не была бы непрерывной. Но этого случая здесь никогда не
может представиться, так как легко доказать, что один из классов А или
В сечения (Л, В) непременно будет уже закрытым.
*) Это определение непрерывности упорядоченного множества является
весьма важным и имеющим принципиальное значение, так как оно применимо
к упорядоченным множествам-какой угодно мощности. Следовательно, оно
применимо и к неархимедовой прямой. Но в тексте речь идет о
непрерывности лишь множества всех действительных чисел (обыкновенной прямой).
301
В самом деле, пусть А0 есть совокупность всех рациональных чисел,
'принадлежащих к нижнему класс*}' действительных чисел А, и, аналогично,
В0 есть совокупность всех рациональных чисел, принадлежащих к верхнему
классу действительных чисел В. Ясно, что всякое рациональное число а%
принадлежащее к А?, меньше каждого рационального числа Ь,
принадлежащего к Bq. Ясно, далее, что всякое рациональное число будет принадлежать
непременно либо к Ло, либо к В0. Отсюда следует, что (Л0, В0) есть сечение
рациональной сети R и что Aq и В0 суть классы, причем А0 есть нижний
класс, Во есть верхний класс этого сечения. Оба класса Aq и В0 не могут
быть одновременно закрытыми, так как рациональная сеть R не имеет двух
непосредственно соседних чисел. Поэтому, tena один из них закрыт, Ми
оба класса открыты. В первом случае обозначим через Cq закрывающее
один из классов А0 и BQ рациональное число; во втором случае,
сечение (А0,В0) есть иррациональное и мы обозначаем через с0
иррациональное число (Л0, В0). Определенное таким образом действительное
число с0 будет принадлежать одному из классов А или В сечения (Л, В)
в совокупности / всех действительных чисел. Мы утверждаем, что с0 есть
закрывающее число того класса А или В. в который оно входит. Если с0
содержится в классе А, то в классе А не может содержаться никакое
действительное число clt большее чем с0, с0<^с1т В самом деле, между с0 и
с\ тогда имелось бы промежуточное рациональное число л которое, будучи
меньшим числа с\% должно содержаться в классе А0 и в то же самое время,
будучи больше числа с0, должно входить в класс Z?0, что невозможно.
Точно так же докажем, что если с0 содержится в классе В, тогда
в классе В не может содержаться никакое действительное число сь меньшее
чем c0t Ci<c0-
Таким образом, во всех случаях действительное число с0 закрывает
тот класс А или В, куда входит; это и обнаруживает, что классы эти
оба одновременно открытыми быть не могут и, значит, совокупность I
всех действительных чисел, не представляя нигде никакого просвета^
является непрерывной.
§ 67. Рациональные приближения. Мы уже видели, что рациональная
сеть R есть множество всюду плотное на совокупности всех
действительных чисел. Это свойство рациональной сети R позволяет говорить о
рациональных приближениях к произвольно данному иррациональному числу с%
с = (А,В).
Так как каждое рациональное число г, входящее в нижний класс А
данного иррационального числа с, меньше этого числа с, г<^с, то естественно
рассматривать г как приближение по недостатку для числа с. Аналогично,
всякое рациональное число /*, входящее в верхний класс В, естественно
рассматривать как приближение по избытку для числа с. Легко видеть,
что эти приближения могут быть взяты с любой точностью. Этим мы хотим
сказать, что для любого положительного рационального числа е существуют
два рациональных числа: а из нижнего класса A b из верхнего класса В%
такие, что разность Ъ — а меньше числа е, Ь — д<е. В этих условиях
естественно назвать числа а и Ь приближениями к с с точностью до е.
Чтобы убедиться в существовании таких чисел а и Ь> достаточно
заметить, что в рассматриваемом случае классы А и В представляют собой
неотделимые множества. Но, тогда в силу доказанного в § 65 предложения,
в классах А и В имеются соответственные элементы а и Ь, для которых
Ъ— а<г.
§ 68. Положительные и отрицательные действительные числа.
Действительное число с = (А, В) называется положительным, если оно больше
нуля, £>0, и отрицательным, если оно меньше нуля. Так как между
двумя действительными числами имеется бесконечно много промежуточных
рациональных чисел, то положительное действительное число с превышает
некоторое положительное рациональное число, и отрицательное действитель*
ное число с меньше некоторого отрицательного рационального числа.
302
Два рациональные числа, равные по абсолютной величине и отличающиеся
только их знаками — и — —, называются симметричны ни. Легко
перенести это определение на иррациональные числа. Пусть с = (Л, В) есть
какое-нибудь иррациональное число. Обозначим через — В совокупность
всех чисел — Ь% симметричных для чисел £, составляющих класс В, В = {Ь}.
Легко видеть, что — В есть нижний класс, не имеющий наибольшего числа.
Дополнительный к нему верхний класс Составлен из чисел — я,
симметричных для чисел а, составляющих класс А, А — {а}. Естественно поэтому его
обозначить через — Л. Класс—Л, очевидно, не имеет наименьшего числа.
Таким образом, сечение (—В, — Л) есть сечение с двумя открытыми
классами. Поэтому оно определяет некоторое новое иррациональное число,
мы обозначаем это иррациональное число через — си называем
симметричным для данного положительного иррационального числа с. Если имеем
£>0, тогда число 0 содержится в классе Л, Ясно, что класс — Л также будет
содержать число 0, и, поэтому, — с<^0. Ясно, что если с<0, то — с>0. Из
-двух симметричных чисел с и — с то число, которое положительно, называется
абсолютной величиной числа с и обозначается символом i с'.
' Заметим, наконец, что — (—- с) = с.
Если с есть какое-нибудь рациональное число, отличное от нуля, тогда
число — называется обратным числом для числа с. Легко перенести это
с
определение на иррациональные числа. Пусть с = (Л, В) какое-нибудь
иррациональное число. Если иррациональное число с положительно, с>0,
мы обозначаем через В-1 совокупность всех чисел -—, обратных числам Ь,
составляющим класс В, В = {Ь}. Присоединив к В-1 все отрицательные
рациональные числа и, также, число нуль, мы получаем некоторый открытый
нижний класс, который обозначим через В—1. Дополнение к нему есть,
очевидно, некоторый открытый верхний класс, являющийся не чем иным,
как совокупностью обратных чисел для положительных рациональных чисел,
содержащихся в классе Л; мы обозначим этот новый верхний класс через
А~* Сечение (^"J"1, ^7l) определяет некоторое новое иррациональное число,
которое мы обозначим через — и назовем обратным иррациональному
числу с. Если иррациональное число с отрицательно, с<С0, мы определяем
обратное ему число — по формуле — = — ("1—СУ *
§ 69. Действия над иррациональными числами. Мы рассмотрим теперь
определение действий над действительными числами.
Сложение. Пусть даны два какие-нибудь действительные числа с' = (Л', В')
и с"«(Л", В"). Пусть а' есть какое-нибудь число класса Л' и а"~какое-
нибудь число класса А". Ясно, что их сумма, а'+ а", есть число
рациональное; мы обозначим эту сумму через а%
а = а' + а".
Совокупность всех рациональных чисел а, составленных указанным образом,
где за слагаемые а' и а" берутся любые рациональные числа,
принадлежащие соответственно классам А1 и А", составляет некоторый новый нижний
класс, который мы обозначим буквой Л'. Ясно, что класс Л есть открытый%
так как, очевидно, он не может иметь максимального числа, раз классы
А и А" не имеют максимальных чи^сел. Обозначим через В дополнение
к полученному таким образом классу Л. Сечение (Л, В), имеющее
открытый нижний класс, определяет некоторое новое действительное число с,
которое мы назовем суммой действительных чисел с' и с" и которое
обозначается так:
с=*с' + с".
303
Легко видеть, что если слагаемые с' и с" представлены приближенно
с точностью до -н- рациональными числами:
а'<€?<Ь'щ Ь'-а><^
то сумма с = с'+с" представлена приближенно с точностью до е
соответствующими суммами приближений по недостатку и по избытку:
а' + а''<с' + с"<Ь' + Ъ\ (V + Ь») - (а' + а") < е.
Возможность приблизиться к определенному таким образом
действительному числу с суммами приближений оправдывает его название суммы
действительных чисел с' и с", а также его обозначение через с' + с".
Из данного определения суммы действительных чисел тотчас же
следуют равенства
(с + с') + с" = с + (с' + с")
с + 0=5 с; с + ( — с) = 0,
а также неравенство
Вычитание. Назовем вычитанием с' — с" двух действительных чисел
сг и с" брожение числа с с числом ( — с"), где-е" есть симметричное
число для сп. Введя обозначение
(К— С" = С' + ( — Ctr)t
находим
(с'-с'0 + С"=С' + (--С") + С''==С'+1(~С") + С"]г=:С' + 0=:С'
или
(с' — с") + сп = с'.
Отсюда ясно, что вычитание есть действие, обратное сложению.
Умножение. Пусть с' = (Л',£') и сг' = (А", Ва) два какие-нибудь
положительные действительные числа. Обозначим через А совокупность всех
отрицательных рациональных чисел, нуля и тех положительных
рациональных чисел а% каждое из которых есть произведение двух каких-нибудь
положительных рациональных чисел а' и а'', соответственно
принадлежащих к нижним классам А' и А", АТ = {а'} и А" = {я'7}. Ясно, что А
есть некоторый новый нижний класс, и ясно, что А не имеет
максимального числа, так как классы А и А" не имеют максимальных чисел.
Обозначим через В дополнение к полученному таким образом классу А.
Сечение (At В), имеющее открытый нижний класс, определит некоторое новое
действительное число с, которое мы назовем произведением
действительных чисел сг и с" и которое мы обозначим через символ d • сп\
Легко видеть, что если множители сг и сп представлены приближенно
с точностью до s рациональными числами а*'< с''< Ь\ Ь' — аг<^ г и а"< с"<^ bf\
Ь" — а"< е, то произведение с'• с" представляется приближенно
соответствующими произведениями приближений по недостатку и по избытку
а'а"< с'с"< Ъ'Ъ"%
304
причем точность этого приближенного изображения безгранично
увеличивается, когда число в убывает до нуля.
Возможность приблизиться к определенному таким образом
действительному числу с произведениями приближений оправдывает его название
произведения действительных чисел с' и с'\ а также его обозначение
через с' «с".
Если одно из данных чисел с' и с" или оба эти числа отрицательны,
то нахождение произведения сг * с" приводится к предыдущему случаю при
помощи добавочного определения — правила знаков:
с'-с"=* — с'-(— с")= — ( — сг).с"=*(~с')-( — с"). '
Эти определения тотчас же позволяют проверить сохранение основных
свойств умножения рациональных чисел, выражаемых формулами
ее' = сгс% (се')»^ = С'(с'с").
с(с' + сп)=сс' + сС9 c.L = l, c.l«c, |сс'| = ]с1-1с'|.
с
а также тот закон, в силу которого произведение нескольких множителей
отличных от нуля, всегда само отлично от нуля.
Деление. Назовем делением ~ двух действительных чисел с' и с",
c"dzOt умножение чисел </ и--, где JL есть число, о б р а т н о е для с''.
с' с"
Введя обозначение
с" \с") >
мы находим
(р)-с"!=с'-(р)-с"=зс'-Ш'с"]вс',1=!С'
или
(£)•"-'.
Отсюда ясно, что деление есть действие, обратное умножению.
§ 70. Принцип стягивающихся отрезков. Рассмотрим два множества
действительных чисел Л = {д} и £ = {£}, удовлетворяющих следующим
двум условиям:
I. Любое число а первого множества меньше любого числа Ь $то?
рого множества, а < Ь.
II. Для любого как угодно малого числа е > 0 можно найти такие
два числа а и Ьл что разность Ь — а меньше г, Ь — а < г.
Повторяя слово в слово рассуждения § 65, можно показать, что
множества А и В не могут допускать двух различных отделяющих
действительных чисел.
В § 65 мы видели, что множество рациональных чисел не обладает
достаточной полнотой для того, чтобы всякие два множества А и Я, удовле*
творяющие условиям I и II, допускали отделяющее их рациональное число:
такого числа может не быть. Легко видеть, что для любых двух множеств
А и В действительных чисел, удовлетворяющих условиям I и II, существует
единственное отделяющее их или граничное к одному из них
действительное число. Это число определяется следующим сечением: к нижнему классу
относятся все действительные числа, меньшие любого числа множества В%
а к верхнему классу — все остальные действительные числа. Ясно, что при
таком сечении все числа множества А относятся к нижнему классу, а все
числа множества В—к верхнему классу.
Отсюда, как4частный случай, вытекает принцип стягивающихся
отрезков, которым мы неоднократно пользовались, оставляя в стороне доказа-
20 а» ШЬ 305
тельство. Пусть имеется система вложенных стягивающихся сегментов \ait Ьх\\
[а$г Ьг]"- [ап*Ьп]-—'> это значит, что выполнены следующие условия:
* а) «1 <а%< аъ • • • < ап < • • •;
Ь) ^1>^2^>^з> ••• >^п> •••;
С) при любом значении п имеем ап < £л;
d) каким бы малым ни было взято число е, при достаточно большом п
выполняется неравенство bn — an<i е.
Из сформулированных условий ясно, что множества А = {аи aZt. ..an,...}
и 5 = {^i» b2...bn> • ••} удовлетворяют условиям I и II. Отсюда и следует
Существование единственного действительного числа £, принадлежащего всем
сегментам [аъ bi],[a2t b2 ],... [я^, bn]t... . Это и есть принцип стягивающихся
отрезков.
Приложение II.
КЛАССИФИКАЦИЯ БЭРА,
Бэру принадлежат глубокие идеи по классификации функций. Пусть Р
есть какое-нибудь совершенное множество. Бэр рассматривает непрерывные
на Р функции/как самые п р о с т ы е. Он называет их функциями класса О
и обозначает их совокупность через /С0.
С/едующий класс 1 состоит из функций/, которые, будучи разрывными,
являются пределами последовательности непрерывных на Р функций
/ь /2» •••» /п» •*•» т- е- /=Ип1 fn. Совокупность всех функций / класса 1
п -> -f- 00
Бэр обозначает через Къ
Следующий за ним класс 2 состоит из функций /, не принадлежащих
ни к /Cm ни к Къ ко которые являются пределами последовательности
функций /i, /2,..., /п> ♦••> принадлежащих к предыдущим классам /Со и Къ
т. е./ = Iim/n. Совокупность всех функций класса 2 Бэр обозначает через /£>.
Следует заметить, что последовательность функций Д,/2, ...,/те, ...,
дающая в пределе функцию / класса 2,/ = lim/w, должна содержать лишь ОГра-
га ~> -t- со
ничейное число функций класса 0, так как иначе /, будучи пределом
функций класса 0, была бы функцией класса 1, а не класса 2,
И так далее, неограниченно далеко.
Этим путем приходим к конечным классам Бэра
Ко* Къ Кг% •••» Кп% •••• (I)
причем класс О, т. е. Къ как было указано, состоит из всех непрерывных
на Р функций/. Имел определенными классы 0, 1, 2, ..., п — 1, т. е, имея
Ко* Къ K^t • •♦, Кп-ь мы определяем класс п как совокупность функций /,
не принадлежащих к ранее определенным классам /С0, Къ • • •» Кп-ъ но
которые являются пределами последовательности функций Д, Л» • • -Лг» • • •
входящих в эти предыдущие классы К> Къ • • •» Кп-ь т« е* /=^m/n
Совокупность всех функций класса п Бэр обозначает через Кп*
Следует точно так же отметить, что последовательность Л,Л,- •.» /п» •• •»
дающая в пределе функцию класса я, должна содержать лишь ограниченное
число функций классов <л — 2, потому что иначе/была бы функцией клас
са < п — 1, а не класса п. (
Цепочка конечных классов Бэра (1) обладает необыкновенной
стройностью замысла. И основная теорема Бэра (гл. IV, § 47) относится как раз
к этой классификации, именно, к классу Къ Действительно, эту теорему
Бэра можно формулировать так:
Для того, чтобы разрывная функция f была функцией класса], необ*
ходимо и достаточно, чтобы / была точечно разрывной на всякой
совершенной части множества Р.
Таким образом в критерии Бэра класс К\ получил полную характеристику.
Все попытки найти столь же полную характеристику для функций /
класса 2 пока остались бесплодными.
По поводу конечной классификации Бэра (1) следует заметить, что
она является чисто формальной до тех пер, пока мы не докажем
фактического существования функций / в каждом классе Кп* Действительно, если
бы какой-нибудь класс Кт оказался пустым, то ясно, что и все дальнейшие
классы Кт+и Кщ+ъ ••• окажутся также пустыми, т. е. они не содержали бы
ни одной функции, а при этих условиях и вся классификация Бэра окажется
построенной напрасно. На самом де\йе этой опасности нет: действительно
существуют функции / в каждом классе конечной классификации
Бэра (I).
Примеры функций классов 1, 2 и 3 были даны самим Бэром. Пример
функции класса 4 был дан Л. В. Келдыш. Формальное доказательство
непустоты конечных классов было дано Б о р е л е м. Наконец, формальное
доказательство непустоты всех классов было дано Лебегом.
Здесь мы установим существование лишь функций класса 2, потому что
не приходится говорить о существовании функций класса!:
функция/,равная единице в какой-либо точке М и равная нулю во всех остальных точках,
есть очевидно функция класса 1. Докажем, что функция Д ир ихл е/(дг),
равная единице для ^рационального и равная нулю для х иррационального,
есть функция в точности класса 2. Действительно, с одндй стороны, /(лг)не
имеет ни одной точки непрерывности на осиО^ и. поэтому, не может быть
класса < 1. С другой стороны, если мы занумеруем все рациональные точки
оси ОХ, расположив их в виде последовательности гь гь ..., гп, ..., и если
обозначим через fn (x) функцию, равную единице в первых п рациональных
точках гь гъ ...,гп и равную нулю в остальных точках, то ясно, во-первых^
что функция /п(х) есть класса 1 и, во-вторых, что имеем/ (*) — Ит/„(х).
п -> + °°
Отсюда и следует, что функция Дирихле f(x) есть функция класса 2.В§38
мы видели, что функция Дирихле /(дг) изобразима формулой
/(д:) = Нш Нш (cos 2кп\х¥т.
Тогда это изображение могло казаться искусственным. Теперь мы видим
какие глубокие основания лежат в изобразимости функции Дирихле
двумя переходами к пределу, будучи функцией класса 2, функция Дирихле
и не может быть изображена никогда при помощи одного перехода к
пределу перед знаком непрерывной функции.
Возвратимся к классификации Бэра. В строке (1) выписаны конечные
классы Бэра. Сам Бэр расширил свою классификацию за конечные классы
и дал так называемые трансфинитные классы. Так как полное
изложение их невозможно без предварительного изложения учения о так называемых
трансфинитных числах, то мы ограничимся здесь лишь тем, что
дадим самые простые понятия об этом.
Рассмотрим операцию О, которая, будучи применена к сходящейся
последовательности каких-нибудь функций
/l» /г» /з» • • •» Лг» • • • i
дает предел/ этой последовательности /—lim/n. Символически это мы
можем написать в виде схемы
0(Л,/2,/3, ...,/я, ...)=/, (2)
где
/=Нт/„.
Применим теперь операцию О к сходящейся последовательности функций
/ь Л>---» fn*--* конечных, но не ограниченных классов, так что в этой
последовательности найдутся функции как угодно высоких классов. Если
функция /, получающаяся при совершении операции О над этой
последовательностью, не является сама функцией конечного класса, тогда мы
говорим, что такая / есть функция класса со и обозначаем через Кф
совокупность всех функций / класса ш. Здесь значок ш следует рассматривать
308
как порядковое бесконечное число, непосредственно следующее за веема
натуральными числами, т. е. как непосредственно большее всех их.
Определив класс /Сш, мы совершаем операцию О над функциями этого
класса и предыдущих классов (конечньГх). Всякую получающуюся
функцию /, которая не есть ни класса К&> ни предыдущих классов, мы назовем
функцией класса «о + 1 и обозначим через АГш--1 совокупность всех функций
% класса ш+ 1.
* Затем *), определив класс K^t-i* MbI совершаем операцию О над
функциями этого класса и предыдущих классов. Всякую получающуюся в
результате операции О функцию /, которая не входит ни в класс К^+г
и ни в предыдущие классы, мы называем функцией класса ш-)-2й
обозначаем совокупность всех таких функций через К^^^
И так далее, безгранично далеко.
Ясно, что этим путем создается продолжение конечной классификации
Бэра в виде строки
Ац)) ^ш+1» Кы^Ь •••> AoDfftj • ••• (3)
Но эта строка (3) вовсе не представляет собой завершения
классификации Бэра, а является лишь ее „куском". В самом деле, обращаясь к схеме (2)
операции О, мы можем заменить функции fb /2, ..., fni ... этой схемы
какими-нибудь функциями ранее построенных классов, написанных в
строчках (1) и (3). Й если операция О даст функцию /, не содержащуюся ни
*) Предостерегаем читателя здесь от обычной начальной ошибки
мышления, коренящейся в непривычке ума к такого рода вещам. Именно, обычно
пытаются рассудить так: „Число со есть бесконечное, а прибавив к
бесконечности одну единицу, мы нисколько не увеличим бесконечности; значит, ш
и (o + l есть одно и то же, т. е. со = со + 1 и поэтому продолжение
классификации Бэра за конечные классы, бессмысленно и невозможно". На самом
же деле здесь надо умозаключение направить в точности по обратному
руслу и нужно рассудить так: „Раз класс Кф+\ содержит фактически
функцию /, заведомо не входящую ни в какой конечный класс и ни в класс Кф*
то отсюда как раз и следует, что классы. Кф и K^+i не тождественны,
т. е. что порядковые числа ш й ш + 1 неравны, и, значит, что мы имеем
(о + 1]>(о, причем равенство исключено. Здесь важно отметить, что
порядковые числа вовсе не являются мощностями и неудивительно, что они
увеличиваются от прибавления единицы. Разумеется, если бы было доказано,
что класс /Сю-ы не содержит никакой функции /, то все доказательство
о неравенстве <о и со + 1 прекратило бы свою силу. Ни в силу теоремы
Лебега никакой класс классификации Бэра не есть пустой.
Факт существования порядкового числа со и отличия его от порядкового
числа со + 1 можно иллюстрировать так: предположим, что на сегменте [0; 1}
имеется счетная последовательность точек Мх —$ Л12 -^ ... -$ Мп -$ ....
из которых всякая следующая лежит правее предыдущей, и предположим,
что такая же точно последовательность точек лежит яа сегменте [1, 2],
т. е. что на сегменте [1, 2] мы имеем Л^ —£ Лг2 Н ••• -3 Nn -$ .... Ясно,
что всякая точка Mi лежит левее всякой точки Nj. Предположим, что мы
пожелали точки обеих этих последовательностей обозначить одной и той
же буквой, например, буквой А с разными значками так, чтобы значки эти'
совершенно ясно указывали, какая точка лежит левее, а какая лежит правее/
Естественно для этого обозначить точки Mlt AU, •.., Мп, ... через А^
А* ..., Ап-Ь ..., а точки Nb Nb .. .♦ Nn, ... обозначить через Аф> Лш+1» ...
Аф+п-и
» Здесь значок со является первым бесконечным порядковым числом,
т. е. непосредственно следующим за всеми натуральными числами, иначе
говоря, наименьшим трансфинитным числом. Это порядковое число
существует* потому что существует точка N±. И порядковое число ш -J-1 отлично
от числа ш, потому чзго точки N% и N% различны,
2QD
в одном из ранее определенных классов *), мы можем назвать такую
предельную функцию / функцией класса о)2 и совокупность всех таких
функций / обозначить через /Гш2. Но едва лишь определен класс К^ъ как тотчас
же классификация может быть продолжена еще далее, т. е, за кусок (3)
в виде строчки
причем этот новый кусок классификации образуется из возглавляющего
его класса К^ повторным применением операции О, т. е. совершенно
таким же образом, как кусок (3) был образован из класса Кш-
Строкой (4) мы вовсе не закончили нашу классификацию, но лишь
прибавили к двум имевшимся ее кускам (1) и (2) еще новый кусок (4), ничего
не сделав больше. Действительно, мы видим, что кусок (4) еозник из куска (3)
повторным применением операции О. Но ведь точно так же, повтор-'
'ным применением операции О может быть получен еще новый кусок:
а за ним и дальнейшие куски.
И тгк дллее, безгранично далеко.
Читатель видит, что указанный процесс определения все новых и новых
кусков классификации приводит к бесконечной последовательности кусков,
идущих один за другим:
(АТо> Кь • • •)» (^ш> АГоЧ-З* • • •)» (К&Ъ #u>2-bli • • •)» • • •» (#и>ш» Кит + Ь • • •)»••• (6)
Легко, однако, видеть, что и эта бесконечная последовательность кусков
не составит окончания классификации, но является просто лишь „куском"
ее. В самом деле, если мы напдшем последовательность классов кусков (6)
в виде таблички
\
Kq K\ Ki* • *
^тт К-шт + 1 Au)?n+2» • •
, J
то немедленно замечаем, что составляющие ее классы К находятся в счет-
ном числе. А тогда, обращаясь к схеме (2) операции О, мы можем заменить
функции fb /2, .. .,/п, ... этой схемы какими-нибудь функциями, входящими
в классы таблички (6*). И когда операция О даст функцию /, не
содержащуюся ни в одном классе этой таблички**), тогда мы можем назвать такую
функцию / функцией класса со2 и совокупность всех таких функций
/обозначить через /СцД Но раз класс /<ш2 определен, как тотчас же
классификация может быть продолжена еще далее повторным применением операции О,
*) Для этого, очевидно, необходимо, чтобы последовательность/i,/2....i
• ••» /и» ••• содержала функции, принадлежащие к какому-нибудь ранее
определенэому классу К* в ограниченном числе, так как иначе предельная
функция /, по самому определению, принадлежала бы этому классу К» раз
она не входит в предыдущие классы.
**) Здесь мы предполагаем справедливость теоремы Лебега о непустоте
каждого вновь определяемого класса, когда ранее определенные классы
образуют самое большее счетное множество. Как мы увидим дальше, если
множество классов К несчетно, тогда операция О, совершенная над
функциями /i, /s,.. ,,/w, ..., входящими в классы этого несчетного множества,
может давать пустые классы, т. е. постоянно приводить к функции /,
содержащейся в одном из классов множества. '
Поэтому, существенным обстоятельством является спешность классов
таблички ф%]
Щ
/д*\
Бесполезно затруднять читателя, утомляя его внимание повторением
одних и тех же самых слов. К принципиальной стороне дела,
обусловливаемой однообразием приема, мы вскоре перейдем, пока же нам следует
остановить внимание на чисто символической стороне дела, именно, на
обозначениях классов /jft т. е. на способе писать их значки. Мы видели,
что за конечными классами К0, К\ ЛГП»--- непосредственно следует
первый трансфинитный класс К&. Это даст нам право рассматривать значок ш
как порядковое число, непосредственно следующее за всеми
натуральными числами 1, 2. 3, ..., я, .. .,т. е. как бы, в своем роде, предел
натуральных чисел,рассматриваемых как конечные порядковые числа:
ш = Игл /7.
п -> + со
В этом смысле, если Я1<я2< • • • <я&< • • • есть какая-нибудь
возрастающая последовательность натуральных чисел, мы можем продолжать писать
ш = Нт Яд.,
потому что порядковое число, непосредственно следующее за всеми
натуральными числами пь я2, ... , пк, ... , очевидно, тождественно порядковому
числу, непосредственно следующему за всем натуральным рядом. Заметив
это, введем особого рода символы те, являющиеся многочленами от буквы ш,
коэфидиенты которых суть натуральные числа или нули:
ЗГ ss ш%0 + 0>P-ltf j + • • • + «># р_1 -f- ар
и где а0фО. Мы уславливаемся всегда писать в этих символах численные
коэфидиенты а\ после соответствующих степеней <&?-*.
Будем рассматривать эти символы те, фактически, содержащие
букву <о, как бесконечные порядковые числа. С этой целью мы уславливаемся
из двух различных символов те' и те'7 считать предшествующим или
меньшим тот, у которого степень рг меньше р" или, при равенстве
степеней р'= р"= р, тот, у которого меньше первый по счету (слева направо)
коэфициент. Так, например, мы имеем ш52 + ш27 + ш8 + 3< о>52 + <&*9 + ш8 + 3,
потому что 7< 9; точно так же же о>52 + со27 + ш8 + 3< о>&2 -\- ш3 -{-•ш + 2.
потому что 0< 1. Благодаря этому условию, символы те образуют
упорядоченное множество, потому что, если те'<те" ите"<те"', то отсюда следует,
что те'<те'".
Введем следующее определение: Какое-нибудь упорядоченное
множество называется вполне упорядочен н ым, если всякая его часть
имеет начальный элемент.
Например, множество натуральных чисел 1,2, Я, ... , /т, ... есть вполне
упорядоченное, потому что в каждой части натурального ряда имеется
наименьшее число. Напротив, множество всех рациональных чисел,
содержащихся в интервале (ОД), будучи упорядоченным множеством (при этом
«предыдущим" считается меньшее число), не есть вполне упорядоченное,
111
потому что имеются части этого множества, например, .. . <^_<-__<^,_-1
не содержащие первого элемента (т. е. наименьшего числа). Легко теперь
видеть, что множество символов те есть вполне упорядоченное. Действительно,
если {те} не есть такое множество, то должна иметься его часть, лишенная
первого элемента. Иначе говоря, множество {те} должно иметь
последовательность те' >те" >• .. >те(*) >.. .убывающих порядковых чисел. В силу
самого определения неравенства порядковых чисел, степени р(*)
многочленов теД) должны удовлетворять неравенствам pf >/?"!> р(А) ;> ... . Атак
как р(«) суть неотрицательные числа, то мы необходимо должны иметь
точные равенства р(&) = p{k~v> = ... для натурального числа k, .'достаточно
большего. Значит, все многочлены те(#>, начиная с некоторого числа k,
будут одной и той же степени р. Но в силу этого же самого определения
т
неравенства порядковых чисел, старшие коэфициенгы а$ должны удовле-*
творять неравенствам cffi > a^+l^ >л^+2) > ... для достаточно большого
значения числа k, потому что тогда степени многочленов тс ДО равны друг
другу. А так как числа а$ суть неотрицательные целые числа, то отсюда
следует, что для достаточно большого числа k мы имеем точные равенства
аМ = oSq +1) = a[f+2) = ... , т. е. многочлены тсДО при достаточно боль*
том k имеют не только одинаковые степени, но и одинаковые старшие
члены. Точно так же доказывают, что у многочленов л ДО при достаточно
большом k будут одинаковые следующие за старшими коэфициенты аф =
= af+1) = af+2) = ... , и так далее. Мы видим, что все многочлены тс ДО
при достаточно большом k будут тождественны друг другу. А так как это
невозможно, раз мы имеем неравенства rJ >тс" ... >тсДО >..., то отсюда
следует, что убывающие бесконечные последовательности порядковых чисел
невозможны и, значит, множество {тс} порядковых чисел тс есть вполне
упорядоченное.
Заметим, что множество {тс} порядковых чисел счетно, потому что
многочлены с целыми коэфициентами образуют счетное множество.
Введем следующие определения: мы называем фундаментальной цепью
всякую возрастающую последовательность тс1<тс2<... <тсА<..
.порядковых чисел, степени рь р$—,рк,... которых ограничены: порядковое
число я называется пределом фундаментальной цепи тсх<тс2<... <тсА<...,
если тс есть порядковое число, непосредственно следующее за всеми
порядковыми числами Tclf тс«,...,тг£, ..., т. е. если не существует никакого
порядкового числа тс', которое превосходило бы все порядковые числа Tclf тс2,
,.#тс^,... и которое было бы меньше числа тс.
Докажем существование предела для каждой фундаментальной цепи.
В самом деле, раз степени многочленов ък> образующих фундаментальную
цепь тс!<тс2<... ^^к^ • • •» о г р а н и ч е н ы, то заведомо имеются
порядковые числа тс', превосходящие все числа ъь тс2,..., т^,... . Эти порядковые
числа тс' образуют часть множества {тс}. Но множество {тс} есть вполне
упорядоченное; поэтому среди чисел тс' имеется наименьшее число тс. Ясно,
что тс есть предел фундаментальной цепи ^^^^... <^<C • • • •
Порядковое число тс', имеющее непосредственно предшествующее ему
порядковое число тс, называется порядковым числом яе/мого рода.
Порядковое число *', не имеющее непосредственно предшествующего "ему
порядкового числа и отличное от нуля, называется порядковым числом второго рода
пли предельным числом. Если тс' есть число первого рода, тогда тс' имеет вид
тс' ess ц>р' а'0 + <йр'~г аг + ... <o#'p'-i + а'р\
где а'р' отлично от нуля, а'рг > 0. В этих условиях ясно, что непосредственно
предшествующее ему число тс есть
п = <**'а'0 + ^-1а\+...+ь>а'р<_1 + (а'р*--1).
Следовательно, всякое число тс' первого рода имеет вид тс + 1, т. е. тс' = тс -{- 1.
Если тс' есть число второго рода, то оно имеет вид
тс' = «*' а'0 + ш*'-1 а[ + ...+ *р'~1 a'it
где a'i>§ и где р'>/. В этом случае ясно, что последовательность чисел
*1<*2< • • • <Т'7с< • • • » гДе
тсл = *>? а0 + и*'"1 а[ + ...+ <»Р'- «-i)*'*-! + <»2>'-<К — 1) + *>*>'- <<+1) й
есть фундаментальная цепь, и что число тс' есть ее предел. Итак, всякое
число тс' второго рода есть предел фундаментальной цепи, которую
можно построить, зная это число «'•
312
Это вычисление пределов фундаментальных цепей приводит нас, в
частности, к формулам:
lim п =*со, lim (ш -f- п) = w2, lim (com + я) = со (/я -f- 1)
2i-»4-°° w->-t-oo n -» -f- oo
lim (соя) = со2, lim (со2 -f- со/г) = co52, lim (о^л) = о>з
lira (cow/i) = ©w+i.
ft -> + oo
Из математического анализа известно, что можно пользоваться
натуральными числами 1, 2, 3,...,я, ... как значками при выписывании один
за другим членов какого-нибудь ряда и1 + н2 +кз» •• . Также точно и здесь
можно пользоваться всеми введенными нами порядковыми числами
О, 1, 2, ... ,/Z, ... 1 со, со + 1, . .. | 0)2, ... | соЗ, . .. | со/2, ... | со2, ... |
0)3, .. . |<j)Wf ... |
как значками при определении один за другим последовательных классов К
классификации Бэра. Действительно, вообразим израсходованными на значки
часть порядковых чисел те для обозначения класса К и предположим, что
они не израсходованы все. Пусть те' есть первое еще неизрасходованное
число. Оно непременно имеется, потому что имеются неизрасходованные
порядковые числа, и среди них имеется наименьшее, потому что
множество {те} есть вполне упорядоченное. Если те' есть число первого рода,
рода те' = те-|-1, и мы видим, что раз число те было употреблено для
обозначения класса Кк, то число те' будет употреблено для обозначения
непосредственно следующего за ним класса Kn+i> Если те' есть число второго рода,
тогда ,те' есть предел некоторой вполне определенной фундаментальной цепи
Тл <С ^2 <С • • • < ^п < • • •» т- е- я' — lim теп. Мы видим, что раз эти числа
п-»-Ь со
были употреблены для обозначения классов/^* #in •••»/Cw •••» то число
те' будет употреблено для обозначения непосредственно следующего за ними
класса К Шкп.
ft->-|- со
Но легко заметить громадную разницу между обоими способами
выписывать один за другим члены и сходящегося ряда и обозначать
последовательные классы К классификации Бэра.
В первом случае запас натуральных чисел 1,2,3,... оказывается
достаточным для того, чтобы выписать все члены «i +#2 + из-г" ...
сходящегося ряда. Во втором случае запасете} порядковых чисел те
оказывается явно недостаточным: этот запас есть только счетный, и когда он
будет израсходован весь, то мы будем цметь определенными (и
обозначенными) счетное число классов:
не имеющих самого последнего. Тогда по теореме Лебега применение
операции О к последовательностям функций /,, /2, ..., /п, ..., принадлежащих
к этим занумерованным классам, дает функции /, не содержащиеся в этих
классах и составляющие новый класс К> который мы можем рассматривать,
как непосредственно следующий за всеми занумерованными классами. Этот
класс К является, очевидно, непосредственно следующим за простой
последовательностью классов
и, поэтому, естественно обозначить его через К^ - В этом случае значок
ш^ следует рассматривать как новое порядковое'.число,
превосходящее введенные раньше порядковые числа со- (где я-натуральное число)
и непосредственно следующее за ними. Поэтому естественно продолжать
рассматривать последовательность прежних порядковых чисел
с», *\ с»*, ♦ ,., »»,.♦.
313
как фундаментальную цепь, а новое порядковое число <о^ как ее предел,
lim (&п = <»ф*
'•• Н/ -> -f~ °°
Но следует заметить, что символ ш» уже не находится среди
введенных ранее порядковых чисел {п\ и что, таким образом, создавая символов,
мы заведомо выходим из прежнего запаса символов %.
Для того, чтобы расширить запас порядковых чисел за число ю^,
обычно рассуждают так: мы определили класс /fww, а с ним и порядковое
число <оЧ Допустим, что мы дошли до класса А"шТ» определив и этот класс.
Тогда мы можем отправляться от этого класса К^ точно так же, как
вначале мы отправлялись от класса Кс Это замечание дает нам возможность
определить все классы К^ +«, где « < шт. Но мы предполагаем, что все
классы, предшествующие классу К^ , суть в счетном числе. Поэтому^в
счетном числе будут и классы /CJ+K, где о < ш?. Кроме того, среди этих
классов нет самого последнего, так же, как нет, по предположению, класса, не*
посредственно предшествующего классу Д^т. Поэтому, применив к
классам Кфч,а операцию О, мы получаем новый класс, непосредственно
следующий за классами /Гшт+в, Этот новый класс естественно обозначить
через Кфт.2*
Вообще, если мы дошли до класса Кф1 , где п натуральное число,
то имеем и классы Аг0)тя + аэ где а <аЛ. А тогда применение операции О
дает нам класс К^ (п+\у
Определив классы К т,ЛГч,/Ст,..., АГт ..... мы применением оде-
рации О определяем новый класс, непосредственно следующий за ними.
Этот новый класс естественно обозначить через К у*1. Таким образом, от
s ч у+г
порядкового числа со1 мы перешли к новому порядковому числу <*>• •
Применим сказанное к порядковому числу о>">. Придя к нему, мы вводим
порядковые числа ojw -\- а, где а < ш^ и, следовательно, а есть символ из
запаса {тс}. Затем, мы приходим к числам о/°/г -{- а, где п пробегает все
натуральные числа 1, 2, 3... . И, наконец, мы приходим к числу w^+K
Повторяя все те же самые рассуждения над числом ш^+i, мы приходим
последовательно к числам со^+у, ... &ы+п} Здесь мы отметим, что
показатели <о, «о + I, <o-f-2, ... суть порядковые числа, уже введенные нами;
ранее (они в этом случае принадлежат к запасу символов {тс}. Допустим,
что мы ввели порядковые числа
где показатели at < а2 <.. ,<аЛ < ... принадлежат к ранее введенным.
нами порядковым числам, так же как и их предал. Если предел
последовательности показателей аь а2, ... обозначен через lim an, то естественно
п -> + °°
обозначить предел *) последовательности порядковых чисел ш«1,ша*|##«
через a)/z'^00. Это обозначение является законным, потому что если две
фундаментальные цепи ах < а2 < ... и рА < р2 <С • • • имеют одно и то же
предельное число у, Ига ап = у и lim $п = у, тогда обе последовательности
« -» + со '/г -* + со
a>ai < ш«я < ... и ш?! < оз?2 <^ ... имеют одно и то же предельное число,
потому что из неравенств ат < $п и ар > $q следуют неравенства <а*м < а$р
И шаР > ш^а. Вследствие этого, последовательность порядковых чисел
*) Этот предел существует, потому что, по теореме Лебега, существуем
класс, непосредственно следующий за классами К „* К „ *••. % К ~ й>%*
314
w«t 0>** < ... может быть рассматриваема как фундаментальная цепь,
litn a
п
имеющая своим пределом новое вводимое порядковое число <оп "* °° = оЛ.
Выше мы сказали, что порядковое число ш"5 является первым,
выходящим за границы запаса символов {тс}. Таким образом, приведенное только
что рассуждение дает нам порядковые числа <Л где ? < о03» т. е. где число y
принадлежит еще к запасу символов {я}. Следовательно, мы имеем
порядковые числа
И так как последовательность показателей
О), ш'2, О-3, . . . , (£)«,. . .
имеет пределом число а>ш, то предел порядковых чисел <о<*>, ш^2,.... a>u>nt...
должен быть обозначен через оз^ш. И так далее.
*Мы видим, что принятая система обозначений позволяет написать числа
<0, 0)^, ^%^ ###>
но предел этой последовательности уже не может быть написанным
даже в расширенной системе обозначений. И, однако, операция О,
примененная к последовательности классов /С, К , К и».... дает вполне опре-
деленный класс К> непосредственно следующий за ними. Обычно принято
вводить букву е для обозначения предела чисел со, а>и>, ш^,.... С этой
буквой е мы, разумеется, можем двинуться дальше в образовании
последовательных классов классификации Бэра. Но как бы ни казалось нам, что мы
ушли далеко, все же запас новых обозначений, получаемых
комбинированием двух букв: ш и е, не очень велик, будучи всего лишь счетным.
Следовательно, он должен вскоре исчерпаться, и мы будем поставлены перед
необходимостью вводить еще нозый третий знак. И тик далее. Этот
процесс должен длиться даже, собственно, не безгранично далеко, но, если
можно так выразиться, еще гораздо дальше, потому что счетного
числа знаков, очевидно, уже недостаточно для обозначения всех классов
классификации Бэра, так как всякий новый вводимый знак продвигает
классификацию вперед лишь на счетное число новых классов. Следовательно,
применение операции О оплть дает новый класс, для обозначения которого
требуется новый знак, неприводимый к прежним знакам, т. е. невыразимый
чер§з них.
*Это обстоятельство, обыкновенно, словесно выражают, говоря, что
процесс развертывания классификации Бэра идет „трансфинитно далеко".
Принципиальная сторона дела состоит в выявлении громадной разницы
последовательного образования натуральных чисел 1, 2, 3,..., л, /j-j-1,...
и трансфииитных чисел
ш, « + Ц.,. |ш2,... |шл,... |<о*,... |o>V.. | ««>,... 1оХ*\... Js,....
Натуральные числа образуются последовательно на основании
принципа:
«за всяким натуральным числом п имеется непосредственно
следующее за ним натуральное число п ~- 1».
В силу этого принципа множество всех натуральных чисел не может ,
быть конечным, потому что тогда за последним числом имелось бы
еще дальнейшее натуральное число. Траисфинитные же числа образуются
последовательно на основании совсем иного принципа, именно:
«за всяким счетным множеством трак с финитных чисел {а} имеется
непосредственно следующее за ними трансфинитное число р».
В силу этого принципа, множество всех трансфинитных чисел не
может быть счетным, потому чхо тогда имелось бы еще дальнейшее транс-
финитное число.
315
*
Это обстоятельство делает до известной степени оба принципа
похожими друг на друга. Но вот где начинается существенная разница между
ними. Принцип образования натуральных чисел обладает совершенным
автоматизмом1: за числом п путем прибавления единицы автоматически
образуется следующее число я + 1, причем совершенно неважно, какие
числа были образованы до числа п. Такого автоматизма уже нет у
принципа образования трансфинитных чисел: хотя за числом а автоматически
образуется следующее число а + Ь однако этот автоматизм не полон, так
как, когда у нас накопится множество {а} трансфинитных чисел, не
имеющее наибольшего числа, то непосредственно следующее за ними
трансфинитное число р уже не получается автоматически, но требует
занумеровать натуральными числами всех до этого момента полученных
трансфинитных чисел или требует указания фундаментальной цепи для множества
полученных чисел {а}. А такое занумерование или такое нахождение
фундаментальной цепи не делается автоматически, т. е. каким-либо
закономерным процессом *), но всякий раз есть результат той обстановки,
в какой было получено множество {а}. А так как эта обстановка все время
изменяется по мере расширения множества {а}, то в результате мы не
имеем никакого единообразного обозначения для всех трансфинитных
чисел.
Мы видим, какая имеется громадная разница между натуральным рядом
и последовательностью трансфинитных чисел. Но за всем тем, если мы
сделаем гипотезу о существовании всех рассматриваемых трансфинитных
чисел, мы сможем рассуждать над ними без того, чтобы уметь определить
и обозначать их все,
С этой точки зрения мощность мнржества всех рассмотренных нами
трансфикитных чисел есть первая несчетная мощность, т. е. мощность,
непосредственно следующая за счетной мощностью^о*
Действительно, если М есть какое-нибудь несчетное множество,
составленное из*каких-нибудь элементов т, М = {т}, то, нумеруя их сначала при
помощи натуральных чисел (включая сюда число нуль): О, I, 2, 3,... и затем
помощью траксфинитных чисел со, to -\- 1 , ш<*>,..., мы, очевидно,
израсходуем все рассматриваемые трансфинитные числа для нумерации элементов
т множества М. В самом деле, если бы мы были остановлены истощением
элементов т множества М при оставшихся еще неиспользованными
трансфинитных числах, то это значило бы, что элементы множества.М все
занумерованы трансфинитными числами ос, меньшими некоторого
трансфинитного числа 3, а <8; а так как множество {а} трансфинитных чисел а,
меньших чем р, есть заведомо счетное, то отсюда вытекало бы, что множество
М есть счетное. Итак, при нумерации элементов т какого-нибудь
несчетного множества М сначала будут использованы конечные числа 0, 1, 2,....
а затем и все рассматриваемые трансфинитные числа со, оз-j-l, ..., <о">,...,
причем у множества М могут еще остаться ненумерованные элементы.
Отсюда заключают, что всякое несчетное множество М имеет часть Мь рав-
номощную множеству всех этих трансфинитных чисел. Поэтому-то и
рассматривают мощность множества всех указанных трансфинитных чисел,
как наименьшую из всех несчетных мощностей,, т. е. как мощность
непосредственно высшую мощности Ко- Обычно вследствие этого обозначают
мощность множества всех трансфинитных чисел через Ni- Имеем, таким
образом, &о< ^г Проблема о мощности континуума состоит в
выяснении того, имеем ли мы С= &i, или же С> Kj.
Последовательность всех рассмотренных нами трансфинитных чисел
обычно пишется в виде
О, 1, 2, ..., и, ... , ю, со + 1,... , а, ... | Q,
*) Заметим, что все поцски такого закономерного процесса до сих пор
не увенчались успехом.
316
где п обозначает произвольное натуральное число и а обозначает
произвольное трансфинитное число. Буква Q ставится как символ,
обозначающий, что перед ним выписаны все рассмотренные нами трансфинитные
числа. Обычно принято называть 0, 1, 2, ..., п, ... порядковыми числами
класса I. Трансфинитные же числа о>, ш-М,..., а,..., образованные нами
при развертывании классификации Бера помощью операции О и теоремы
Лебега, называют порядковыми числами класса II. Символ Q называют
наименьшим порядковым числом класса III.
В дальнейшем, чисто формальнологически строят теорию чисел класса III
и высших классов и создают последовательность соответствующих им
мощностей
Ng? sS з> • • • > »^ n' • • •» Nu)) N од !>•••? N 2»• • ••
Мы не будем входить в детали этих абстрактных рассмотрений и
ограничимся лишь указанием на то, что математический анализ, по крайней мере
на сегодня, не имеет дело ни с трансфинитными числами класса III, ни с
мощностью j^2. В принятых обозначениях, вся классификация Бэра напишется
в виде
причем классы К образуют несчетное множество мощности j$j.
Чем выше класс функции /, тем она более сложную имеет природу.
Операция О, примененная к функциям /ь /2, ... , /п,..., входящим
в классификацию Бэра, уже не выводит нас за границы этой
классификации, но дает в результате функцию/, /= lim /п, непременно содер-
жащуюся в этой классификации. Действительно, если функция /п
принадлежит к числу класса ЛГ« , то называя через £ порядковое число,
непосредственно следующее за множеством чисел {ап}, мы видим, что или функция
/ входит в один из классов /С предшествующих классу К§, ила она не
входит ни в один из них. Если имеется налицо это последнее обстоятельство,
тогда / заведомо входит в класс Кл tio самому определению этого класса,
как совокупности функций /, являющихся пределами функций предыдущих
классов и не входящих ни в один из них. Таким образом, операция О не
выводит уже нас за классификацию Бэра.
Этот факт имеет чрезвычайную важность. Действительно, из него следует,
что всякая функция /, аналитически изобразимая (тремя операциями
+ ,Х* lim), принадлежит к классификации Бэра,
В самом деле, аналитически изобразимая функция / получается помощью
операций Н-,Х и lim, проделанными последовательно, одна за другой,
в счётном числе, исходя из многочленов с постоянными коэфициентами от
независимых переменных. Но многочлены, будучи непрерывными
функциями, входят в класс Ка- И далее, ни одна из указанных трех операций
не выводит за пределы классификации Бэра. Для операции lim мы это только
что показали. Операции же + их, совершенные над функциями класса Kq>
дают функции этого же класса и совершенные над функциями классов,
предшествующих какому-нибудь классу Ка, дают функции также классов,
предшествующих классу АГа. Отсюда и следует, что указанные три операции
никогда не выведут нас за границы классификации Бэра и, значит, всякая
аналитически-изобразимая функция / обязательно входит в эту
классификацию.
i С другой стороны, эта классификация содержит одни только
аналитически изобразимые функции, так как, во-первых, в силу теоремы
Вейерштрасса (§ 61), всякая функция / класса 0 аналитически-изобразима
(рядом многочленов) и, во-вторых, всякая функция / класса Ка получается
из функций предыдущих классов по формуле /=lim /n, причем все пред-
я->оо
шествующие классы, согласно предположению, содержат только
аналитически изобразимые функции. Значит, /С« состоит только из таких же функций.
317
Легко видеть, что каждый класс Д*« классификации Бэра содержит лишь
множество функций / мощности континуума. Действительно, это верно
относительно класса /С0, содержащего лишь одни непрерывный функции.
Если среди классов ' Кл имеются классы мощности, выше чем С\ пусть
класс К$ есть первый из таких классов. Всякий класс К9, где о < р, имеет
мощность С, И, кроме того, всех классов Ка, предшествующих классу /G.
а <р, есть счетное множество. Значит, всех функций /, входящих в классы,
предшествующие классу ЛТд, есть множества мощности &0 X С = С. Поэтому
всех счетных последовательностей fb /2, ... , /п, ... функций, входящих
в классы Ка, а < |3, есть множество мощности С (см. главу I о счетномер-
ных пространствах), так как всякую такую последовательность можно
рассматривать как точку счетномериого пространства. И так как каждая
сходящаяся последовательность fv /2> • • • » /п* • • • имеет только один предел /,
/slim fn, то отюда следует, что множество этих пределов / имеет мощ-
ность невышеС.
Таким образом, всякий класс К классификации Бэра имеет мощность не
выше С И так как $ 3 <С, то отсюда следует, что всех функций /,
входящих в классификацию Бэра, будет не больше чем СХ £= £2:= £•
Итак, классификация Бэра содержит лишь множество мощности
континуума функций /. А так как всех функций / имеется множество мощности
2е > С, то имеются функции /, не входящие в класс Бэра.
В § 38 мы указали индивидуальным образом функцию f(x)t не
входящую в классификацию Бэра; это была приведенная в конце § о8 неизобрази-
мая аналитически функция f(x).
\
Редактор В. С. Капустина
Техн. редактор В. В. Соколовская
Подписано к печати 25/Ш 1948 гч А0197Ц ,
Печ. л. 20 Уч.-изд. л. 23,41
Тираж 25 000 экз. Заказ 1244.
4«я типография им. Евг. Соколовой треста
„Полиграфкнига" ОГИЗа при Совете
Министров СССР, Ленинград, Измайловский
пр., 29.
L,™