г,
гъ -• *
«^ -J-
^7-t У^ —-
~s
I ****
f*4
v^v
=^4
^^,
"^
г^ж
. Л ^f>I?,,v. j
-.-.*, -jpf!^
л^^Г^ч^
A

ЛАБаранов
КВАНТОВАНИЕ
ПО УРОВНЮ
И ВРЕМЕННАЯ
ДИСКРЕТИЗАЦИЯ
в цифровых
системах
управления
МОСКВА
ЭНЕРГОАТОМ ИЗДАТ
1990

ББК 32.965
Б 24
УДК 681.51.09
Рецензент Ю. И. Грибанов
Баранов Л. А.
Б 24 Квантование по уровню и временная
дискретизация в цифровых системах управления. — М.:
Энергоатомиздат, 1990. — 304 с: ил.
ISBN 5-283-01520-3
Предложены модели и методы расчета оценок
погрешностей и помехоустойчивости квантования по уровню и
временной дискретизации сигналов, учитывающие способ получения
цифровых эквивалентов, методы восстановления дискретных
сигналов.
Для инженерно-технических работников, связанных с
разработкой, внедрением и эксплуатацией цифровых систем.
„ 2402010000-274 _,
Б 051(00-90 196-90 ББК 32'965
Производственное издание
БАРАНОВ ЛЕОНИД АБРАМОВИЧ
Квантование по уровню и временная дискретизация
в цифровых системах управления
Редактор А. Ю. Черкашин
Редактор издательства В. И. П е т ух о в а
Художник переплета С. А. К и р е е в
Художественные редакторы Т. А. Дворецкова,
А. А. Белоус
Технический редактор Н. В. Чиранова
Корректор Л. С. Тимохова
ИБ № 2581
Сдано 1
Формат
Печать
Тираж
в набор 14.03.90.
60X88'/ie
высокая
6000 экз.
Энергоатомиздат.
Подписано в
печать 31.03.90.
Бумага типографская № 2 Гарнитура
Усл. печ. л. 18,62
113114,
Москва, М-
Усл. kd.-ott.
Заказ 6036
-114, Шлюзоваз
18,62
а наб.,
литературная
Уч-изд.
Цена
10
л. 18,77
1р.40к.
2гг?ДПа Октябрьской Революции и ордена Трудового Красного Знамени
г^й-г» «Первая Образцовая типография» Государственного комитета
<-<-t,P по печати. 113054, Москва, Валовая, 28.
ISBN 5-283-01520-3 © Автор, 1990

ПРЕДИСЛОВИЕ
Разработка и внедрение автоматических систем
управления технологическими процессами, применение цифровых
систем управления и телеметрии обусловили создание
технических средств, обеспечивающих преобразование аналоговых
сигналов в цифровую форму—аналого-цифровых
преобразователей.
Значительно расширяется использование аналого-цифровых
преобразователей в микропроцессорных системах. Вопросы
сопряжения средств микропроцессорной техники с объектом
управления определяют работоспособность системы в целом,
так же как выбор закона управления и правильность
разработки математического и программного обеспечения. По
существу аналого-цифровые преобразователи являются
своеобразными органами чувств цифровых систем.
Преобразование аналогового сигнала, имеющего
бесконечное множество значений, в сигнал с конечным множеством
значений называют квантованием по уровню. Операция
квантования связана с .округлением непрерывной величины.
Преобразование сигнала, описываемого функцией непрерывного
аргумента (времени), в сигнал, представляемый функцией
дискретного аргумента, называют временной дискретизацией или
дискретизацией аналогового сигнала.
Операция квантования в соответствии с приведенным
определением нелинейна. В то же время процесс временной
дискретизации может быть описан линейным оператором,
поэтому в данной книге термин «квантование по времени», обычно
применяемый в технической литературе, не используется.
Процесс преобразования функции дискретного времени в функцию
непрерывного времени называют восстановлением.
Цель данной книги — изложение на едином
методологическим уровне моделей и методов определения погрешностей
преобразования детерминированных и случайных сигналов при
временной дискретизации и квантования по уровню.
Особенностью предлагаемых моделей является учет способа получения
цифрового эквивалента при определении точности и помехоус-
3

тойчивости трактов квантования по уровню, дискретизации и
восстановления. Описываемые методы расчета позволяют
решать задачу анализа погрешностей при заданных способе
квантования по уровню, шаге дискретизации (как
равномерной, так и неравномерной), шаге квантования по уровню и
способе восстановления, дают возможность синтезировать
тракт квантования по уровню и дискретизации при заданной
оценке погрешности.
В книге рассмотрены функции и принципы построения
аналого-цифровых преобразователей, определены методические
погрешности и оценки помехоустойчивости при квантовании по
уровню, дискретизации аналогового сигнала и его
восстановлении.
Модели аналоговых'сигналов представлены
детерминированными и случайными стационарными функциями.
Помехоустойчивость тракта преобразования анализируется при аддитив^
ных стационарных помехах, некоррелированных с сигналом.
В моделях тракта аналого-цифрового преобразования
рассматриваются квантование по уровню идеальным
квантователем и особенности квантования при преобразовании временных
интервалов и частоты в цифровой эквивалент, описываются
идеальная (квазимгновенная) временная дискретизация и
особенности дискретизации для способов получения цифрового
эквивалента при промежуточном преобразовании аналогЬвого
сигнала во временной интервал и частоту, учитывается
интегрирование аналогового сигнала в устройствах выборки и
хранения (УВХ).
Восстанавливающие операторы представлены интер- и
экстраполирующими многочленами, совпадающими со
значениями квантованного сигнала в точках временной дискретизации,
и многочленами, определенными по критерию наименьших
квадратов, а также фильтрами нижних частот (автоматическое
восстановление).
Получены выражения оценок методических погрешностей и
помехоустойчивости как при работе тракта преобразования
в реальном времени, так и при исключении погрешности от
запаздывания в случаях равномерной и неравномерной
временной дискретизации. Разработана инженерная методика
расчета методических погрешностей и помехоустойчивости
преобразования.
С учетом перспективности использования частотных датчик
ков в цифровых системах управления в книге приведены
способы уменьшения методических статических и динамических
погрешностей преобразования частотно-импульсного сигнала
в цифровой эквивалент, описаны инженерные методы анализа
и синтеза трактов преобразования частота — цифра на базе
моделей аналого-цифрового преобразования.
4

При построении комплексных цифровых систем
телемеханики используется общий тракт передачи сигналов
телеизмерений и телесигнализации, что определяет особенности расчета
методических погрешностей телеизмерений. Для этого случая
приведены модели и методы расчета методических
погрешностей преобразования.
Для иллюстрации моделей и методов расчета в тексте дано
большое число примеров, которые должны помочь читателю
в понимании основного содержания книги.
Конечные выражения оценок погрешностей о
помехоустойчивости сведены в таблицы, что позволит разработчикам
трактов аналого-цифрового преобразования использовать их в
своей деятельности.
Изложение материала рассчитано на специалистов,
занимающихся вопросами цифровых измерений, системами
автоматического управления и контроля, цифровой передачи
аналоговой информации, а также на студентов соответствующих
специальностей.
Автор благодарит Г. Я. Черкасову и Л. Г. Белякову за
помощь, оказанную ему при подготовке настоящей книги к
изданию. Слова признательности автор адресует доц. М. Н. Ар-
шинову, проф. Ф. И. Карпелевичу и канд. техн. наук С. С. Лыз-
лову, совместная работа с которыми повлияла на содержание
данной книги.
Автор выражает благодарность рецензенту Ю. И.
Грибанову и научному редактору А. Ю. Черкашину за
доброжелательную, принципиальную критику, позволившую улучшить
содержание книги.
Отзывы и пожелания по книге просьба направлять по
адресу: 113114, Москва, М-114, Шлюзовая наб., 10, Энергоатом-
издат.
Автор

Глава 1
ОБЩИЕ СВЕДЕНИЯ О КВАНТОВАНИИ
ПО УРОВНЮ И ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
АНАЛОГОВЫХ СИГНАЛОВ
1.1. ФУНКЦИИ УСТРОЙСТВ КВАНТОВАНИЯ ПО УРОВНЮ
И ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Техническое устройство, осуществляющее преобразование
сигнала, описываемого функцией непрерывного аргумента
(времени), имеющей бесконечное множество значений, р
сигнал, определяемый функцией дискретного аргумента, а также
функцией, имеющей конечное множество значений, называют
аналого-цифровым преобразователем (АЦП). Этот
преобразователь по существу реализует операцию квантования
аналогового сигнала и, как правило, вместе с управляющим
устройством осуществляет временную дискретизацию. Управляющее
устройство может быть как частью АЦП, так и составным
элементом системы, содержащей тракт аналого-цифрового
преобразования.
В соответствии с выполняемыми функциями АЦП можно
классифицировать следующим образом:
цифровые приборы, используемые для измерения
непрерывных величин и выдающие цифровой эквивалент в форме,
удобной для восприятия оператором;
преобразователи в системах телеметрии, используемые для
согласования аналоговых сигналов датчиков непрерывных
величин с кодо-импульсными устройствами передачи
информации;
элементы приемного тракта каналов связи, аппаратуры и
приборов для научных исследований, используемые для
преобразования аналогового сигнала в цифровую форму с целью
осуществления в дальнейшем цифровой фильтрации;
преобразователи измерительной информации в цепи
обратной связи цифровых систем автоматического управления
(САУ);
преобразователи аналоговой информации в цифровую
форму с записью на носитель, дающий возможность в
последующем обрабатывать эти данные с помощью средств
вычислительной техники;
цифровые преобразователи аналоговых (ЦПА) сигналов'
как пороговые устройства систем автоматического контроля.
6

1.2. МОДЕЛИ СИГНАЛОВ И ПОМЕХ
На вход аналого-цифрового преобразователя поступают
сигналы и помехи, являющиеся случайной функцией времени
(случайным процессом). Полной характеристикой случайной
функции является ее многомерная плотность распределения
вероятностей, получение которой представляет известные
трудности, поэтому такое описание случайных процессов
неприемлемо для анализа методов аналого-цифрового преобразования.
К выбору моделей сигналов и помех предъявляются
следующие требования:
максимальное приближение к реальным процессам в тракте
преобразования;
возможность получения характеристик случайных
процессов экспериментально или на основании априорного анализа
свойств объекта, генерирующего сигнал;
наличие необходимой информации для анализа методов
аналого-цифрового преобразования.
Этим требованиям в определенной степени удовлетворяет описание
случайных процессов в рамках корреляционной теории [1, 2, 3].
Характеристиками случайного процесса x(t) в этом случае являются
математическое ожидание тх, корреляционная функция Rxx(t) входного
сигнала или его спектральная плотность мощности S*x(co).
Набор типовых корреляционных функций и соответствующих им
спектральных плотностей мощности приведен ниже:
Корреляционная функция
RxxW = Сд (х)
„ , % n sincoox
Я**М=а** L
со0т
Rxx(t) — °*2 ~, ^ (sin ™.Щт> —
— sin /гсо0т)
Rxx(t) = Ox2 cos co0x
RxxW = Ox*eT*'xt
Спектральная плотность
случайного процесса
Sxx(«>)
1°х2/Щ
1 о
= c/(2n)
при |
при
Sxx (со) =
0,5o*2
при
со | <со0;
1 со | > со0
/1СОо<
(1.1)
(1.2)
Sxx(co)
(m—л)со0
< I co0 | < тц;
. О в остальных случаях
5xx(co)=0,5ax2[Mco-cod) +
+ Чсо + со0)] (1.4)
e-(»/20»
(1.3)
с / ч q*
2aJ/7c
Sxx(u>) ■■
Ox2
n a)2+a2
(1.5)
(1.6)
Приведенные выражения не исчерпывают всего
многообразия корреляционных функций. Однако линейная комбинация
Rxx(t) позволяет аппроксимировать подавляющее большинст-
7

во корреляционных функций, встречающихся в технических
приложениях.
Введем понятие дифференцируемого случайного процесса
[1, 2]. Случайная функция x(t) дифференцируема, если
существует такая случайная функция y(t)9 что
Ит м |Г*(, + ао-*(0_ •
где М — математическое ожидание случайной величины,
заключенной в фигурных скобках.
Случайную функцию y(t) называют производной случайной
функции x(t). Из определения (1.7) следует, что производная
случайной функции есть предел в среднеквадратическом
отношении приращения случайной функции к приращению
аргумента.
Доказано [1, 2], что дифференцируемыми стационарными
случайными процессами являются случайные функции
времени, у которых существует вторая производная от RXx(x) при
т=0.
Корреляционная функция производной стационарного
случайного процесса x(t) определяется выражением
Rvv(x)=—(PRxX(%)/di*.
Анализ данных (1.1) — (1.6) показывает, что (1.1)
соответствует случайному процессу с постоянной спектральной
плотностью мощности в полосе частот от —оо до -j-oo.
Корреляционная функция этого процесса Rxx (т) = сд (т) свидетельствует
об отсутствии статистической связи между сечениями
случайного процесса. Случайный сигнал, обладающий такими
свойствами, принято называть «белым шумом». Выражения (1.2) и
(1.3) соответствуют случайному процессу с постоянной
спектральной плотностью мощности в полосе частот от 0 до соо и от
псоо до moo.
Корреляционная функция (1.4) соответствует случайному
гармоническому сигналу с частотой соо, имеющему случайные
фазу и амплитуду.
Выражения (1.5), (1.6) соответствуют случайным
^процессам с убывающей спектральной плотностью мощности.
Корреляционные функции (1.2) —(1.5) имеют вторую
производную при т=0 и, следовательно, характеризуют
дифференцируемые случайные функции. Случайные процессы,
имеющие корреляционную функцию (1.6), являются недифферен-
цируемыми.
Очевидно, что случайные процессы характеризуются
законами распределения случайных величин, которые получаются
в данном сечении совокупности реализаций случайного процес-
= 0,
(1.7)
8

са. При гауссовом распределении случайный процесс называют
гауссовским.
Такой случайный процесс полностью описывается первыми
двумя моментами — математическим ожиданием и
корреляционной функцией, позволяющими получить многомерную
плотность распределения вероятностей [3]. Так, двумерная
плотность распределения вероятностей случайных величин хх и х2
определяется выражением
х
ИхК Ъ г) 2поХ1оху\-г* Н\
(*i — пгх{)2 2г(хг — тХ1) (х2—тХ2)
+
1
2(1-
(*2~
2\ ^
Г2)
«5, °*1<>х2 <
)■ (1.8)
где тх , тХл, QX,GX — соответствующие математические ожидания
и дисперсии; r = Rxx(tl9 ^/К^).
Для стационарного гауссовского процесса ох = ох =? ох\ тх. =
= щх% = тх\ Rxx (t1% t2) = Rxx (%), где * = 12 — tv
Для определения статистической связи между двумя
случайными функциями (например, между входной и выходной
функциями тракта аналого-цифрового преобразования)
используют второй смешанный центральный момент — взаимную
корреляционную функцию:
+ О0 +00
Rxzik, Q= j J H^-'M'iMfzfo)—mz(t2)]p(x, z, tx, Qdxdz,
—00 —00
где mz(/2)—математическое ожидание случайной функции
z(t) при t=t2\ p{x9 z, tu t2)—двумерная плотность
вероятности случайных величин x(t) и z(t) соответственно при t=t\ и
't=t2.
Для стационарных и стационарно-связанных x(t) и z(t)
взаимная корреляционная функция зависит только от
промежутка времени между сечениями [1]:
+ 00 +00
ЯхгСО — J J (* —*и*)(г —me)/?(x, z, t)dxdz. (1.9)
—00 00
Стационарный процесс называют эргодическим, когда
средние по множеству реализаций равны средним по времени одной
реализации.
В общем случае аналоговые сигналы являются
нестационарными функциями времени. Однако на интервалах времени,
достаточно продолжительных, эти функции могут рассматри-
9

ваться как квазистационарные или приводимые к
стационарным путем получения центрированного случайного процесса.
В качестве моделей помех обычно используют
стационарные случайные процессы [1]. Анализ физики воздействия
мешающих факторов на процесс аналого-цифрового
преобразования позволяет во многих практических случаях считать
помеху K(t) аддитивной и некоррелированной с сигналом x(t).
В этом случае на вход АЦП поступает сумма случайных
процессов х(t) +K(t) nRxk(i)=0.
Если преобразованию подлежат медленно изменяющиеся
функции времени и разработчика тракта аналого-цифрового
преобразования интересует точность, с которой каждое
отдельное преобразование представляет аналоговый сигнал, то
моделями входного сигнала и помехи являются случайные
величины, заданные своими законами распределения. В этом случае
решается задача статики аналого-цифрового преобразования.
Если разработчика интересует точность представления
аналогового сигнала на выходе тракта аналого-цифрового
преобразования по всей временной оси, то моделями входного сигнала
и помехи являются случайные функции времени и решается
задача динамики преобразования.
Методам получения статистических характеристик
случайных функций и величин посвящено значительное количество
работ, поэтому в данной книге эти вопросы не будут
рассмотрены. В дальнейшем принято, что случайные процессы и
помехи заданы своими корреляционными функциями (или
спектральными плотностями). При преобразовании случайных
величин известными считаются законы распределения.
При случайных моделях преобразуемых сигналов
возникает вопрос определения диапазона изменения этого сигнала. Под
диапазоном будем понимать интервал изменения
преобразуемой величины х от *min до xmax при условии, что вероятность
попадания х в этот интервал не менее заданной:
*тах
J px(x)dx>F, (1.10)
где F — заданная вероятность.
Диапазон изменения входного сигнала может быть выражен
через его дисперсию:
•*чпах -^min == X V -^л»
где х выбирают из условия выполнения' неравенства (1.10).
Так, при нормальном распределении преобразуемый параметр
с вероятностью 0,997 расположен в интервале, равном буДс
При равномерной плотности вероятности преобразуемый сиг-
10

нал с вероятностью, равной 1, расположен в интервале ^\2^DX
при треугольном законе (законе Симпсона) — Убу/)*.
Для оценки предельных характеристик тракта
аналого-цифрового преобразования входные сигналы могут быть заданы
детерминированными функциями времени, например линейной
функцией, соответствующей максимальной скорости изменения
входного сигнала. При заданном максимальном ускорении
преобразуемого параметра входной сигнал может быть принят
параболическим. Максимальная скорость и ускорение, как
правило, могут быть получены при анализе объекта,
генерирующего данный сигнал.
Рассмотренные в данном параграфе модели сигналов и
помех используются в дальнейшем для анализа методов
аналого-цифрового преобразования.
1.3. ПОГРЕШНОСТИ ПРИ КВАНТОВАНИИ ПО УРОВНЮ
И ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Процесс преобразования непрерывной информации в
дискретную осуществляется с конечной точностью, определяемой
методическими и инструментальными» погрешностями [4].
Минимизация инструментальных погрешностей связана с
прогрессом в области полупроводниковой электроники и технологии
приборостроения.
Идеальная операция квантования описывается статической
характеристикой нелинейного элемента НЭ, на вход которого
подключен аналоговый сигнал хвх, а на выходе получаем
квантованный Хвых (рис. 1.1,а). Погрешность квантования А=
Если нелинейный* элемент округляет аналоговый сигнал
л:Вх в соответствии с характеристиками, приведенными на
рис. 1.1,6 и ву то максимальная погрешность квантования
равна q — шагу квантования по уровню. В том случае, когда
округление реализуется нелинейным элементом, имеющим
характеристику, симметричную относительно оси ординат
(рис. 1.1,г), максимальное значение погрешности определяется
величиной q/2. Эту характеристику можно принять за базовую,
так как она уменьшает вдвое максимальную методическую
погрешность и может быть получена из первых двух путем
подачи на вход НЭ постоянного смещения, равного соответственно
±4/2.
Погрешность квантования по уровню для базовой
характеристики НЭ функционально связана с входной величиной
в соответствии с рис. 1.1,г следующим образом:
A=kq—xBli при kq—0,5<7<*BX<fe<7+0,5<7, (1.11)
где к — номер интервала квантования.
11

xbx
«)
*6ых *6ых
■ч
■ч
Iнэ к®^*~
-Ч-Ч -т.,
лВых
г ?Н
j i i 1 i i i _j i i i
■Ч 5) —' 'Ч\
-9ЧЧ-
■ в)
Рис. 1.1. Характеристики идеального квантующего устройства
Л'8ых
ч
ч
9
' Ч* -Ц-ЦЛ
-ч
\-Ч г)
Рассмотренные характеристики НЭ имеют постоянный шаг
квантования по уровню. В общем случае это необязательно.
При использовании АЦП как измерителя случайных
величин сумма погрешностей квантования и инструментальной
полностью определяет точность преобразования. Здесь под
измеряемой случайной величиной понимают неизвестный сигнал,
значение которого не изменяется в процессе измерения. Это,
конечно, идеализация. Однако если измеряемый сигнал
изменяется* достаточно медленно по сравнению с временем
преобразования, то его можно принять постоянным. Для
обеспечения постоянства сигнала во время преобразования в ряде
случаев используются устройства выборки и хранения (УВХ),
основная функция которых — выбор мгновенного значения
входного сигнала (стробирование) и хранение его в течение
времени преобразования. Если длительностью стробирующего
импульса можно пренебречь, то временная дискретизация
является квазимгновенной. В том случае, когда требуется учесть
время выборки, УВХ может быть представлен запоминающим
интегратором, сигнал на выходе которого определяется
средним значением преобразуемой функции за время стробирова-
ния.
Если АЦП используется как преобразователь информации
в цепи обратной связи системы автоматического управления
(САУ) или для записи реализаций некоторого случайного
процесса, то возникает задача оценки точности преобраз9вания
случайной функции. Пусть входной сигнал хвх(0 через отрезки
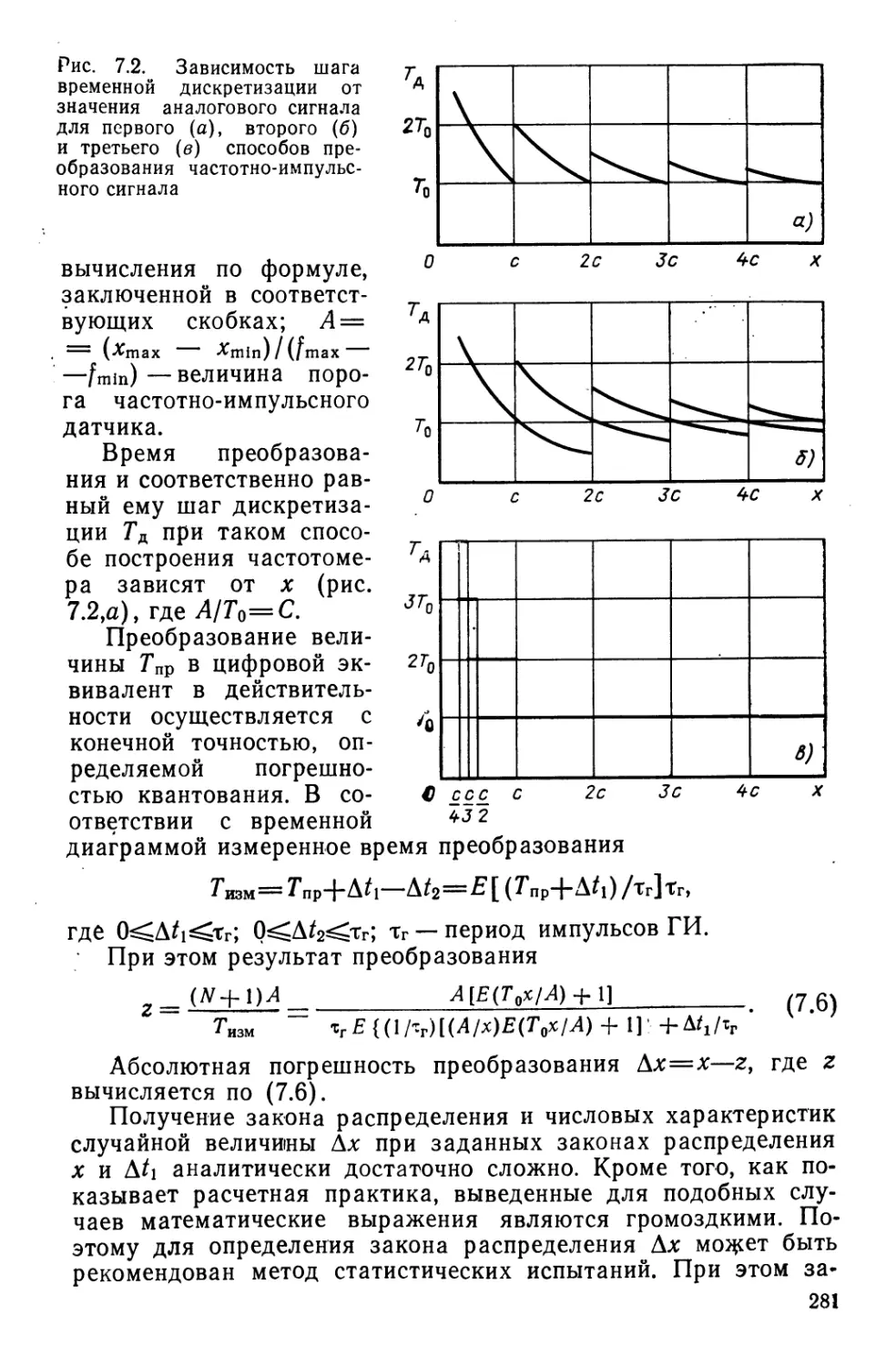
времени Т преобразован в цифровой эквивалент (рис. 1.2). На
выходе АЦП получаем последовательность ординат
случайного процесса х*[пТ]=хвх[пТ]+Асу где п— номер отсчета; Г —
шаг дискретизации по времени; Ас — суммарная погрешность
преобразования, определяемая инструментальной
погрешностью и квантованием.
Операцию представления сигнала x*(t) сигналом х*[пТ]
называют временной дискретизацией, В данном случае
рассмотрена равномерная дискретизация, так как принято, что
12

I9
H
н
4
4
. ?
x*(nT),z
— 'i^^^T
— „-I
"* jT
— -
x*(r)
\*(ZT)
i^I
*r
*6x
X*(nT)
T ZT JT 4Г 57" ^Г 7Г £
Рис. 1.2. Восстановление непрерывного сигнала z(t) из дискретизированного
х*(пТ) экстраполятором нулевого порядка
Т=const. В общем случае возможна неравномерная
дискретизация.
Оценка точности представления входного сигнала хВх дис-
кретизированным х*[яГ| может быть осуществлена только при
t=nTf так как последний не определен в промежутках между
отсчетами. Для получения сигнала z(t)f определенного между
точками дискретизации, необходимо осуществить
аппроксимацию х*[/гТ]. Процесс получения z(t) из х*[/гГ] называют
восстановлением и осуществляют восстанавливающими
устройствами. Простейшим методом аппроксимации является
ступенчатая аппроксимация, иначе — экстраполяция нулевого
порядка (штриховая линия на рис. 1.2). В этом случае значение
функции z(t) при nT^t<.(n-\-l)T принимается равным х*[яГ],
т. е. значение функции z(t) в рассмотренном интервале
времени экстраполируется по одному отсчету. Роль
восстанавливающего оператора при данном простейшем методе
аппроксимации играет память АЦП, куда записывается цифровой
эквивалент на время между преобразованиями. Другие способы
восстановления будут рассмотрены в дальнейшем.
Аппроксимированный сигнал z(t) сравним с xBX(t) на всей оси времени.
Текущее значение погрешности преобразования в этом случае
e(0=*BX(/)-z(0.
Если АЦП используется в разомкнутых системах
(например, для записи случайных процессов), когда задержки
информации не играют роли, то текущее значение погрешности
преобразования можно определить, исключив погрешность от
запаздывания. В этом случае
Q(t)=xBX(t—t3an)—z(t),
где /Зап — время запаздывания в АЦП и восстанавливающем
устройстве.
В качестве оценки точности преобразования случайных
величин используются максимальные, средние и среднеквадрати-
13

ческие абсолютные, относительные и приведенные
погрешности. Оценки погрешностей приведены ниже:
Абсолютные: максимальная Дтах = sup | N (x)]q— х | ;
+ 00
средняя Д= J \N(x)q — x\px(x)dx\
среднеквадратическая Кд2 =У J {N(x)q — x — A)2px(x)dx.
—оо
Относительные: максимальная Д0тах =Апах (*)/*;
^ +00
средняя Д0 = (1/*) J Д/7(Д | x)dk\
среднеквадратическая
/+00
j (Д-Д)^(А|л)ЙД.
ПрИВедеННЫе.*__МаКСИМаЛЬНая Дтах пр = Дтах/(*max—Xmin);
средняя ДПр=Д/(*тах—*тт);
среднеквадратическая
/(•^max *min)'
Здесь A=N(x)q—x — погрешность преобразования; рх{х) —
закон распределения преобразуемой величины; р(Д/х) —
условный закон распределения Д при заданном х; N(x)
—значение числового эквивалента, соответствующего х\ sup \N{x)q—
х
—х\—наибольшее значение величины, взятой по модулю по
всем х\ Xmax—-^min — диапазон изменения случайной величины.
В качестве оценки точности преобразования случайных
функций используются среднеквадратические погрешности,
которые можно вычислить в рамках корреляционной теории.
Введем обозначения оценок: б2, У б2— соответственно
абсолютные значения дисперсии и среднеквадратическои погрешности
преобразования; б2 = b2/Rxx{0)t к б2—относительные значения диспер.
сии и среднеквадратическои погрешности преобразования; &1Р=,
= в*/[ха/?**(0)], у SnP — приведенные значения дисперсии и
среднеквадратическои погрешности преобразования. Здесь Rxx(0) —
значение корреляционной функции преобразуемого сигнала
при нулевом значении аргумента, т. е. дисперсия входного сиг-
14

Рис. 1.3. К определению
вероятностей необнаруживаемого и ложного
отказов
нала; % — коэффициент,
определяющий диапазон
изменения входного сигнала.
При использовании АЦП
в системах автоматического
контроля [5], когда в
результате измерения параметра
принимается решение о
«годности изделия», о
принадлежности изделия
определенному сорту (либо о
нахождении параметров сигнала в
допуске) и т. д., применяются
оценки погрешности:
Рн.о — вероятность необнаруживаемого отказа,
определяемая тем, что из-за погрешности АЦП параметр, вышедший из
допуска, принят находящимся в допуске;
Рл.о — вероятность ложного отказа, определяемая тем, что
параметр, находящийся в допуске, принят вышедшим из
допуска.
Пусть х и А — соответственно входной сигнал и абсолютная
погрешность преобразования, c^x^.d — интервал,
соответствующий нахождению параметра х в допуске, рх{х)—закон
распределения ху р(А/х)—условная плотность распределения
вероятностей погрешности преобразования. В плоскости А, х
(рис. 1.3) площадь D\ соответствует нахождению параметра
в допуске и величинам погрешностей, при которых
принимается правильное решение; площади D4j D5i DSy D9 — нахождению
параметра вне допуска и величинам погрешностей, при
которых принимается также правильное решение; площади D6,
D7 — необнаруживаемому отказу, площади D2t D3 — ложному
отказу.
Поясним этот рисунок. Пусть измеряемый параметр равен
хх и расположен в поле допуска. Тогда диапазон изменения
погрешности измерения А, при котором принимается
правильное решение о нахождении параметра в поле допуска, будет
Ai<A<A2. При этом c<x1+A<d, т. е. при любом c<xx<d
и погрешности А внутри четырехугольника Dx принимается
правильное решение относительно нахождения хх в поле
допуска. В том случае, когда c<.xx<.d, A>d (площадь D2) и Д<£
(площадь £з), *i+A уже вне поля допуска. При этом
параметр, находящийся в поле допуска, из-за погрешности в конт-
15

ролирующем тракте считается вышедшим из поля, что
соответствует ложному отказу.
Далее допустим, что измеряемый параметр равен х2 и
расположен вне поля допуска, т. е. — оо<х2<с. Тогда при Д4<
<Д<оо и —оо<Д<А3 (площади Ds и DA) решение о
нахождении параметра вне поля допуска правильно. Если Аз<А<А4,
а —<х><Х2<.с (площадь D7)y то c<x2-\-A<dy что
соответствует необнаруживаемому отказу. Иначе: параметр,
находящийся в действительности вне поля допуска, принят находящимся
в нем.
И, наконец, рассмотрим случай, когда d<.xb<oo. Если
Аб<А<оо или —оо<Д<Аб (площади D5 и Z)9), то с<*з+
+A<d, т. е. принимается правильное решение о нахождении
параметра вне допуска. Если Дб<Д<Д5 (площадь D6)t то
£<*з+А<^, что соответствует необнаруживаемому отказу.
Искомые вероятности Рл.о и Рн.о определяются
интегрированием плотностей вероятности по - соответствующим
площадям:
Р*.о = $$Рх(х)Р(д/*)dxdb+^px(х)р(Мх)dx<ft; (1.12)
K.o=llPx{x)p{Nx)dxdb+ Црх(х)р(Ь1х)йх<1Ь. (1.13)
В том случае, когда погрешность преобразования не
зависит от параметра ху т. е. р(Д/х)=р(Д), выражения (1.12) и
(1.13) имеют вид
d Г +оо Т d Г с—х *1
Рм = $Рх(х)П p(b)dA\dx + jpx(x)\j p(&)db\dx; (1.14)
оо rd—x "I c rd—x "I
P«.0=\px{x)\ J p(b)db\dx+ J px(x)\ J p(b)dA\dx. (1.15)
d Y.C—X J —oo [_c—*' J
Вычисления двойных интегралов в (1.14) и (1.15) при
известных законах распределения х и А обычно выполняются
численными методами.
При независимых х и Д и учете реальных соотношений
величин погрешностей с диапазоном изменения преобразуемой
величины выражения (1.14) и (1.15) можно упростить [5],
получив тем самым более простую вычислительную процедуру.
Изменив порядок интегрирования, найдем
оо Г" оо "1 оо Г~оо "|
р*о=$\ J Px{x)dx\p(b)db-U\px(x)dx\p(&)db-
о U-Д J о Ld J
16

во Г с "I 0 Гс-Д "1
-J J pxix)dx\p(t)db+ J j px(x)dx\p(b)dL-
с \_d—Д J »—oo l—oo J
ОГс "1 Г с с—А "I
-J J Px(x)dx p(A)dA- J j M*)d* />(Д)<*Д =
—oo L—oo J L «^oo 5 J
= /,_/,_/,+/4_/5_Ув; (1,16)
^.0=4 J P„ (*)<** p(A)«to-f f px(x)dx\p(&)d&-
0 Lf-Д J 0 Ld-Д J
oo Too -I 0 rd—Д "I
. -J $px(x)dx \p(A)dA+ j j" px(x)dx\p(b)db-
0 U I —oo L—<» J
0 Гс-Д "I О Г d "I
- M j px{x)dx\p(b)db- J I px{x)dx\p(b)dL-
—oo \_ d J —oo L—°° J
= /1_/i-/i + /i_/i_/le. (1.17)
Так как при исправном и правильно выбранном АЦП
погрешность преобразования не может быть больше диапазона
изменения измеряемой величины, то /?(Д)=0 при b^d—c и
/3=/б=0.
Интегралы /2, /4, h и /ю не содержат переменных в
пределах интегрирования. Обозначив через Р — вероятность того,
что погрешность А положительна, определяем
(1.18)
h = p\px (x) dx; Jt = (1 - Р) j px (x) dx;
d —00
00 d
Jt = P§Px(x)dx; У10=(1 — P) J px(x)dx9
С —00
oo 0
где P= Jp(A)dA; 1 —P= j p(A)dA.
Далее рассмотрим интегралы /ь /4, /7 и /9. Умножив и
разделив J\ на Р, получим
ОО 00 00 00
JX = P§ j (l/P)p(b)px(x)dbdx=>P§ J(l/P)p(A)jM«—&)dzdb =
0 d-Л
0 d
00 Гоо
d LO
(1/Р)р(Д)р,(2
-Д)<*Д dz = .PJ
2—6036
/>,(г)&, 0.19)
17

где z=x+k при А^О; (1/Р)р (А)—усеченный закон
распределения А с точками усечения 0 и оо; p2(z)—плотность
распределения вероятностей суммы х с положительными
погрешностями.
Аналогично
С ОО
/4 = (1 -Р) \ Pt(z)dz; J, = \p2{z)dz;
/, = (1-Р) j Р-г(г)<Ь, (1.20)
— ОО
где p-z(г) — плотность распределения вероятностей суммы х
с отрицательными погрешностями.
С учетом (1.18) —(1.20) выражения (1.14) и (1.15)
преобразуем к виду
Гоо оо ~1
Ря.о = Р\ \pz(z)dz-$px(x)dx\ +
L'd d J
+ (1 -P) J P-Z(z)dz- j px(x)dx ; (1.21)
[_—oo —oo J
Ph.o = P\ j Px(x)dx- f pz{z)dz +
L—oo —oo J
Гоо оо ~Л
'+(\-P)\\px{x)dx-lP^z(z)dz\. (1.22)
Выражения (1.21) и (1.22) эквивалентны (1.14) и (1.15) и
во многих практических случаях приводят к . более простой
вычислительной процедуре.
Полученные формулы позволяют рассчитывать показатели
качества цифровых систем автоматического контроля —
вероятность необнаруживаемого отказа (Рн.о) и вероятность
ложного отказа (Рл.о), определяемые плотностями распределения
вероятностей контролируемой величины х и погрешности
квантования по уровню А. Приведенная постановка и решение
задачи характеризуют статический режим работы системы
автоматического контроля. Это*объясняется тем, что
аналого-цифровой преобразователь задан статической характеристикой
идеального квантователя. Такой подход справедлив в том
случае, когда временем преобразования можно пренебречь.
18

Глава 2
ПРИНЦИПЫ ПОСТРОЕНИЯ УСТРОЙСТВ
КВАНТОВАНИЯ ПО УРОВНЮ И ВРЕМЕННОЙ
ДИСКРЕТИЗАЦИИ
2.1. КЛАССИФИКАЦИЯ СПОСОБОВ КВАНТОВАНИЯ
ПО УРОВНЮ И ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Квантование по уровню является процессом
преобразования сигнала непрерывного по множеству в сигнал с конечным
числом значений. Как указывалось в § 1.3, процесс
квантования непосредственно связан с операцией округления,
реализуемой нелинейным элементом. Способ построения этого
элемента определяется принципом построения аналого-цифрового
преобразователя, ставящего в соответствие аналоговому
сигналу определенное значение цифрового эквивалента. Временная
дискретизация определяется как процесс преобразования
функции непрерывного аргумента (времени) в функцию
дискретного аргумента. Шаг временной дискретизации снизу
ограничивается длительностью получения цифрового эквивалента.
Поэтому принцип построения аналого-цифрового преобразователя
является существенным классификационным признаком,
позволяющим рассматривать различные способы квантования и
временной дискретизации.
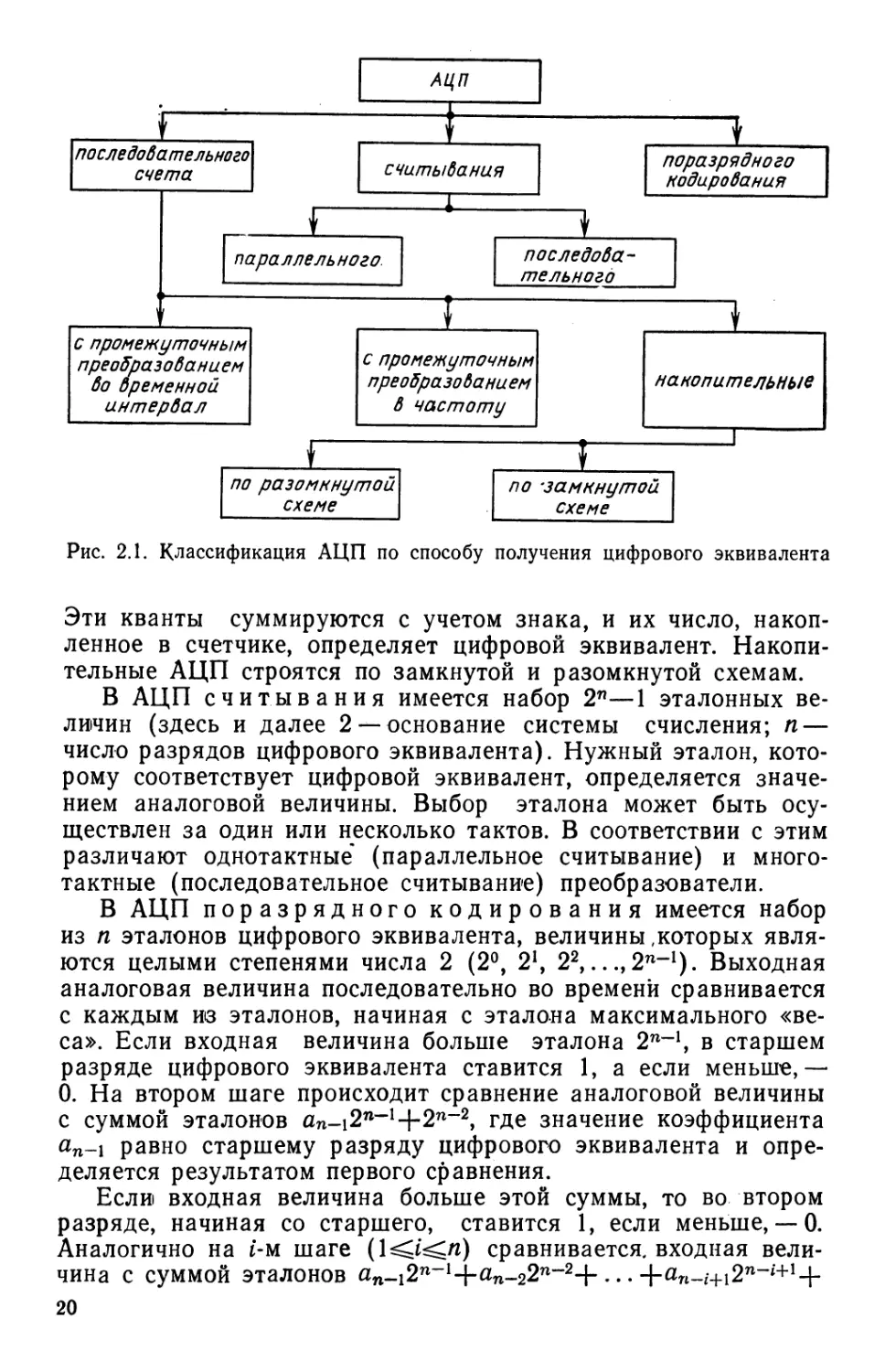
В соответствии с выбранным классификационным признаком
принято [6, 7] разделять АЦП на три группы (рис. 2.1):
последовательного счета, считывания, поразрядного кодирования.
В АЦП последовательного счета входная
аналоговая величина преобразуется в число квантов, сумма которых
определяет цифровой эквивалент. В том случае, когда
аналоговая величина преобразуется в пропорциональную ей
длительность импульса, которому ставится в соответствие число
квантов, определяющих цифровой эквивалент, получаем АЦП
последовательного счета с промежуточным преобразованием во
временной интервал.
В том случае, когда аналоговая величина преобразуется
в пропорциональную ей частоту следования импульсов, сумма
которых за заданное эталонное время определяет цифровой
эквивалент, получаем аналого-цифровой преобразователь
последовательного счета с промежуточным преобразованием в
частоту.
В АЦП последовательного счета накопительного типа квант
формируется каждый раз, когда аналоговая величина
изменяется на достаточно малое заданное значение, определяющее
точность представления непрерывной величины дискретной.
2* 19

последовательного]
счета
АЦП
считывания
X
поразрядного
иодирования
параллельного-

последовательного
с промежуточным
преобразованием
во временной
интервал
с промежуточным
преобразованием
в частоту
по разомкнутой
схеме
по -замкнутой
схеме
Рис. 2.1. Классификация АЦП по способу получения цифрового эквивалента
Эти кванты суммируются с учетом знака, и их число,
накопленное в счетчике, определяет цифровой эквивалент.
Накопительные АЦП строятся по замкнутой и разомкнутой схемам.
В АЦП считывания имеется набор 2^—1 эталонных
величин (здесь и далее 2 —основание системы счисления; п —
число разрядов цифрового эквивалента). Нужный эталон,
которому соответствует цифровой эквивалент, определяется
значением аналоговой величины. Выбор эталона может быть
осуществлен за один или несколько тактов. В соответствии с этим
различают однотактные* (параллельное считывание) и много-
тактные (последовательное считывание) преобразователи.
В АЦП поразрядного кодирования имеется набор
из п эталонов цифрового эквивалента, величины,которых
являются целыми степенями числа 2 (2°, 21, 22,...,2п~1). Выходная
аналоговая величина последовательно во времени сравнивается
с каждым из эталонов, начиная с эталона максимального
«веса». Если входная величина больше эталона 2п~1, в старшем
разряде цифрового эквивалента ставится 1, а если меньше,—
0. На втором шаге происходит сравнение аналоговой величины
с суммой эталонов ап-\2п-1+2п-2, где значение коэффициента
ап-х равно старшему разряду цифрового эквивалента и
определяется результатом первого сравнения.
Если входная величина больше этой суммы, то во втором
разряде, начиная со старшего, ставится 1, если меньше, — 0.
Аналогично на t-м шаге (К*<л) сравнивается, входная
величина с суммой эталонов ап-12п-1+ап-22п-2+ ... +o„_w2n-'+1+
20

+2Л-*, где значения коэффициентов определены на
предыдущих тактах. Если входная величина больше этой суммы,
значение в t-м разряде принимается равным 1, а если меньше,—
0. Таким образом, через п тактов будет получен цифровой
эквивалент.
2.2. КВАНТОВАНИЕ ПО УРОВНЮ И ВРЕМЕННАЯ
ДИСКРЕТИЗАЦИЯ ПРИ ПРОМЕЖУТОЧНОМ
ПРЕОБРАЗОВАНИИ АНАЛОГОВОГО СИГНАЛА
ВО ВРЕМЕННОЙ ИНТЕРВАЛ
Преобразователь данного типа (рис. 2.2) состоит из широт-
но-импульсного модулятора (ШИМ), преобразующего входной
аналоговый сигнал х в прямоугольный импульс, длительность
которого /и пропорционально значению х, и преобразователя
длительности импульса в цифровой эквивалент.
Широтно-импульсные модуляторы. Обычно применяют ши-
ротно-импульсные модуляторы двух типов: с линейной
разверткой и с интегральной широтно-импульсной модуляцией
(ИШИМ), обладающие высокой точностью, простотой
реализации и необходимой помехозащищенностью [4, 6].
Широтно-импульсные модуляторы с
линейной разверткой (рис. 2.3,а) состоят из генератора
пилообразного напряжения ГПН, порогового устройства ПУУ
срабатывающего, когда напряжение мгпн на выходе ГПН равно
напряжению входного сигнала иХу триггера-формирователя ГФ,
осуществляющего формирование модулированного импульса.
Триггер перебрасывается в состояние 1 при срабатывании ПУ
и в 0 на обратном фронте импульса ГПН. Из временной
диаграммы, иллюстрирующей работу ШИМ с линейной
разверткой (рис. 2.3,6), следует
ux(ti)=A[ti-(i-l)T]lTf
где Л —амплитуда пилообразного импульса; ti — i-й момент
времени, в который выполняется равенство ux(t) == игпн-у Т —
период следования этих импульсов; i — номер импульса.
Выражение в квадратных скобках представляет собой
длительность прямоугольного импульса на выходе ШИМ: ti—(i—
— l)T=tni. Поэтому можно записать
tni=Tux(ti)lA. (2.1)
Рис. 2.2. Схема АЦП
последовательного счета с промежуточным
преобразованием во временной интервал
ШИМ
и

Преобразователь
А
21

JL ^глн . ,
^х J
? Т"-
■ Т I
*Ч ТФ Ь*-
иГПН1их 1
Выход
Г7У1
Гф1
1 ^ГПН ЦЧ) "*
ff*^
1*» <
i
tfj
*;
Рис. 2.3. Структурная схема время-импульсного модулятора с линейной
разверткой (а) и временная диаграмма его работы (б)
Отсюда следует, что длительность импульса на выходе
ШИМ с линейной разверткой пропорциональна мгновенному
значению модулирующей функции в момент окончания
импульса.
Условие ux(t)>0 не явля'ется ограничением, так как при
—В1^их^.В2 на вход модулятора может быть подано
постоянное положительное смещение £/см> |#i|. При этом
^1=ТиСм1А+Тих(и)!/[-=
= tm+Tux(ti)lAy (2.2)
где tno=TUCM/A.
Из описания принципа действия ШИМ следует, что
необходимо одно пересечение модулирующего сигнала с
пилообразным напряжением. Это накладывает ограничение на
максимальную скорость изменения Ушах входного сигнала: Vmax<.Vn,
Где Vn — скорость изменения пилообразного напряжения.
Помехоустойчивость ШИМ с линейной разверткой оценим,
приняв, что на входе преобразователя подан постоянный
сигнал их и поступает аддитивная некоррелированная с сигналом
стационарная случайная помеха K(t), для которой m*,=0.
В этом случае абсолютная погрешность преобразования
Ми=Т[их+Х(и)]/А-
—Тих/А = П(и)/Ау
(2.3)
относительная погрешность
b = Mi/Ui=%{U)luXy (2.4)
откуда выражение дисперсии относительной погрешности имеет
вид
Ь2 = Х2(^)/и2х^о1/и2х,
(2.5)
где а2л — дисперсия помехи на входе модулятора.
22

+WL
=*4
кг
_LL
yy
/
ФУ
Выход
^»
^ис. 2.4. Схема время-импульсного модулятора,
осуществляющего интегральную модуляцию
Как следует из (2.5), отношение мощности помехи к
мощности сигнала на выходе модулятора равно отношению их на
его входе. Это означает, что ШИМ с линейной разверткой не
отфильтровывает помехи, так как длительность импульса на
его выходе зависит от мгновенного значения модулирующей
функции в момент отсчета.
Широтно-и м пульсные модуляторы с
интегральной широтно-импульсной модуляцией (рис.
2.4) содержат интегратор J\ фиксирующее устройство ФУ и
устройство управления У У ключами К1 — КЗ [7].
На первом такте преобразования за образцовое время /0б
происходит интегрирование модулирующего сигнала их^0
(ключ К1 замкнут, ключи К2 и КЗ разомкнуты). В начале
следующего такта на вход интегратора подается опорное
напряжение Г/оп, имеющее знак, противоположный их (ключ К1
разомкнут, ключи К2 и КЗ замкнуты).
* Процесс интегрирования длится до тех пор, пока значение
интеграла не станет равным нулю. Фиксацию этого времени U
и формирование импульса соответствующей длительности
осуществляет ФУ.
Определим зависимость между длительностью импульса и
значением модулирующей функции. В соответствии с
алгоритмом работы ШИМ
]Ч(о
dt-
J UJlv.
о,
где 0<г</об, 0<т<*и, откуда
'об
Цш'и= J МОЛ^^ср'об. 'и = 'об^*ср/£/оп.
о
где C/jc Ср — среднее значение модулирующей функции за
время fofc.
23

Отсюда следует, что длительность импульса на выходе
ШИМ с интегральной широтно-импульсной модуляцией
пропорциональна среднему значению модулирующей функции за
время интегрирования.
При —Bi^.ux^B2f как и для ШИМ с линейной разверткой,
на входе модулятора подается постоянное смещение £/см>
>|Bi|. Тогда
t„ =
^U
V0
х ср
+
'об
£/с- =
<об
UxcP + tt
и0>
где tm=t06UcM/Uon.
Если процесс интегрирования сигнала на входе ШИМ
начинается сразу же после окончания формирования импульса,
то период работы модулятора Т=/и+/об, причем значение /и
зависит от вида модулирующей функции. В этом случае
широтно-импульсной модуляции сопутствует паразитная частотно-
импульсная модуляция. При работе ШИМ с внешней
синхронизацией, когда процесс интегрирования входного сигнала
начинается через равные промежутки времени Г, величина
которых должна превышать /Итах+^об, частотно-импульсная
модуляция отсутствует.
Наличие интегратора на входе ШИМ повышает его
помехоустойчивость. Это можно показать следующим образом. Пусть
на вход ШИМ подаются постоянный сигнал их и аддитивная
некоррелированная с сигналом стационарная помеха K(t) при
/72^=0. Тогда длительность импульса на выходе ШИМ
'об
"on Uqtl J
Второе слагаемое этого выражения определяет абсолютную
погрешность А/и от действия помехи. Относительная
погрешность 6=Д/и/*и. Дисперсия этой погрешности определяется
следующим образом:
82 = М
'об
[ K(t)dt
о
%*об J
«U2
м
х 'об
'об 'об
j АСУ*! j■*(/,)Л.
'об 'об
их 'об «/ «/
0 0
где М — математическое ожидание выражения в квадратных
скобках.
24

Сч
Сброс
УУ
Считывание
ГОЧ
В* од
ГОЧ
счетчищ
Считывание
Сброс
'Ж
lift Л ' '
'l-ulL
-At, t
-L
а) 5) t
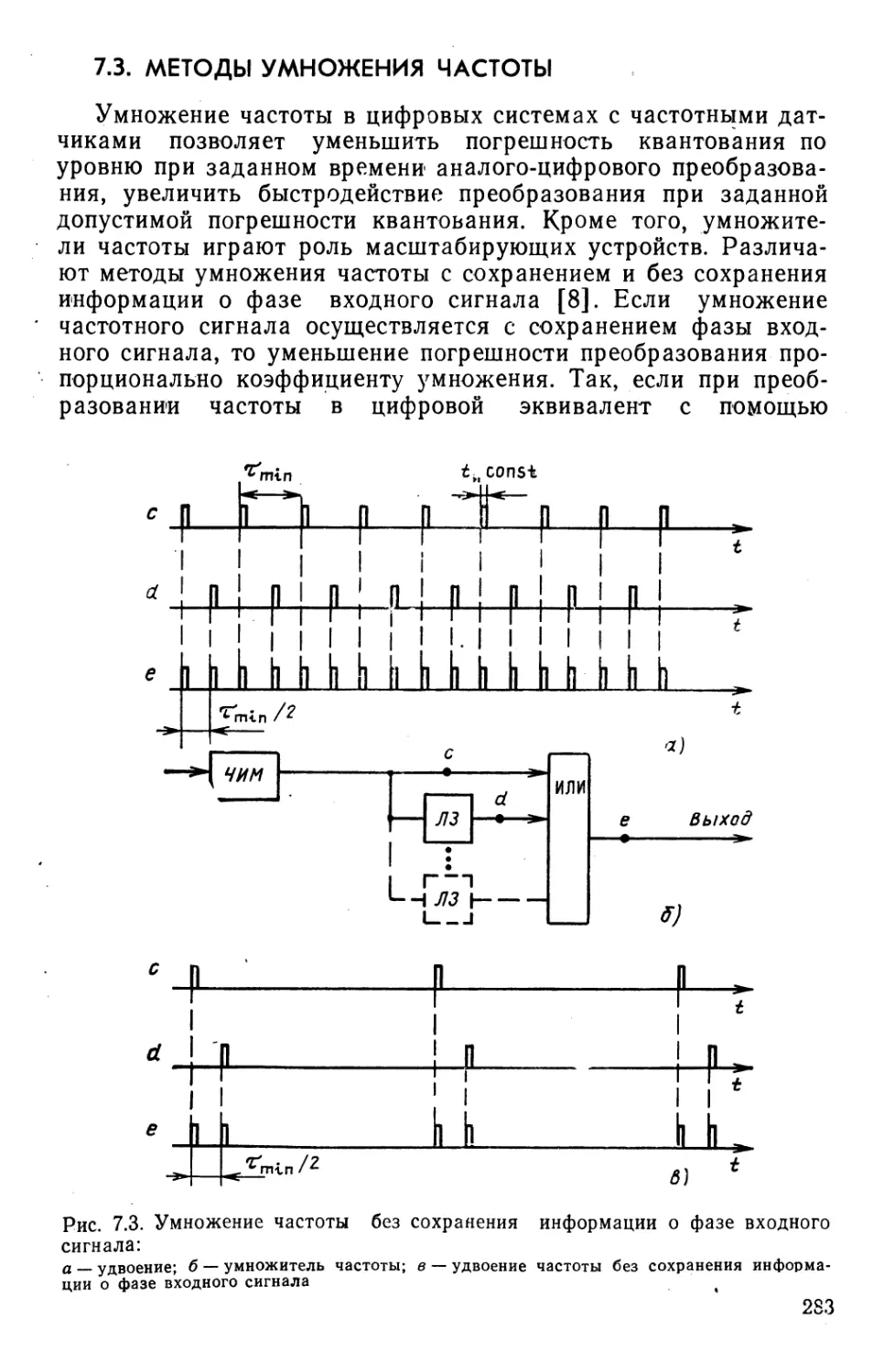
Рис. 2.5. Схема лреобразователя длительности импульса в цифровой
эквивалент (а) и временная диаграмма его работы (б)
Учитывая, что Af [*,(*,) A, (f2)] представляет собой
корреляционную функцию помехи Ru(ti—t2), можно записать
0 0
Для монотонно убывающих положительно определенных
корреляционных функций [4]
'об 'об
J $ RMti-tz)dtxdt2<о{уоб,
о о
+ 00
где а| = /?хх (0) — дисперсия помехи; ^ = J Яхх (*) dx//?Xx (0) —
—00
интервал корреляции.
В этом случае I2<о{ ч/(и2х to6),
Так как соотношение мощностей помехи и сигнала на входе
ШИМ определяется выражением 620=oh/u2x, то б*2<г0б"2о/^б.
Отсюда у ШИМ с интегральной частотно-импульсной
модуляцией отношение мощности сигнала к средней мощности
помехи на выходе в /Об/т0 раз больше, чем на входе. Близкие
результаты получаются и для высокочастотных помех с
корреляционными функциями других типов.
Преобразователь длительности импульса в цифровой
эквивалент. Преобразуемый импульс открывает клапан К
(рис. 2.5,а), при этом счетные импульсы с генератора
образцовой частоты ГОЧ поступают на вход суммирующего счетчика
Сч. После окончания импульса в Сч записано число JV,
являющееся цифровым эквивалентом длительности. Устройство
управления УУ после окончания импульса осуществляет
считывание числа и сброс счетчика в исходное положение. Как
следует из временной диаграммы работы преобразователя
25

(рис. 2.5,6), длительность временного интервала
T=N%—Atl+M29 (2.6)
где т — период следования импульсов ГОЧ; О^А^^т —
отрезок времени, обусловленный отсутствием синхронизации
последовательности счетных импульсов и преобразуемого
временного интервала; О^А^^т — отрезок времени,
обусловленный ошибкой определения целой части. Обозначив 1/т=/,
A£i/t=6i и Д^2/т=б2, из выражения (2.6) получим
Ar=77-i6i+62, (2.7)
где 0<6i<l; 0<62<1.
Отсюда следует, что цифровой эквивалент с погрешностью
квантования по уровню Д=62-^61 пропорционален
длительности интервала.
Учитывая ограничения, накладываемые на б2 и бь можно
считать, что суммарная погрешность А заключена в интервале
— 1^А^+1, т. е. определяется единицей младшего разряда
счетного устройства.
При синхронизации переднего фронта временного
интервала и счетной последовательности Д^ = 0. В этом случае Д=бз
и уменьшается диапазон изменения погрешности: O^A^l.
Шаг временной дискретизации при использовании АЦП
последовательного счета с промежуточным преобразованием во
временной интервал ограничивается снизу длительностью
временного интервала. В том случае, когда цифровой эквивалент
считывается в момент окончания импульса, получаем
неравномерную временную дискретизацию, шаг которой связан с
видом преобразуемого сигнала. Если считывание цифрового
эквивалента и запуск АЦП осуществляется внешним
устройством управления, то может быть реализована равномерная
временная дискретизация, шаг которой ограничивается снизу
максимальной длительностью временного интервала и,
следовательно, максимальным значением аналогового сигнала.
2.3. КВАНТОВАНИЕ ПО УРОВНЮ И ВРЕМЕННАЯ
ДИСКРЕТИЗАЦИЯ ПРИ ПРОМЕЖУТОЧНОМ
ПРЕОБРАЗОВАНИИ АНАЛОГОВОГО СИГНАЛА В ЧАСТОТУ
Схема АЦП данного типа (рис. 2.6) состоит из
частотно-импульсного модулятора ЧЙМ, преобразующего входной
аналоговый сигнал в частоту следования импульсов, и
преобразователя частота — цифровой эквивалент [8].
Частотно-импульсный модулятор. Как правило, частотно-
импульсный модулятор реализует интегральную
частотно-импульсную модуляцию (ИЧИМ). Принцип действия такого мо-
26

Рис. 2.6. Схема АЦП последователь их
ного счета с промежуточным преоб э
разованием в частоту
дулятора иллюстрируется его математической моделью
(рис. 2.7,а).
Входной сигнал x(t)^0 поступает на вход интегратора,
представленного первым звеном с передаточной функцией
/d(jo) = l/p. При достижении параметром у на выходе
интегратора порога А на выходе нелинейного блока формируется
6-функция, поступающая на второе линейное звено с переда-
точной функцией /(2(/?)= е и,формирующее прямо-
Р Р
угольный импульс длительностью /и, и по цепи обратной связи
сбрасывающая интегратор в нуль. После этого процесс
преобразования повторяется.
U
Пусть tt — момент возникновения t-го импульса, т. е. f x(t)dt =
6
U
= iA, где /= 1, 2 и т. д. При этом f x (t)dt = Л, откуда
XcV\ti—h'—l) z==Ai
где Хер—- среднее значение входного сигнала за время л=
= ti—U-\ И
l/Xi=fi=xCplA=kxcp. (2.8)
Таким образом, на выходе ЧИМ получаем
последовательность импульсов, время xi между передними фронтами которых
обратно пропорционально среднему значению модулирующей
функции за xi. При x(/)=const частота следования
прямоугольных импульсов f=kx. Очевидно, что на величину tu
накладывается ограничение /и<Спт1п, откуда следует tn<A/xmaxt
где хтах — максимальное значение входной величины.
Входной сигнал не обязательно должен быть
положительным, так как при —Bi^x^B2 на вход модулятора может быть
подано постоянное смещение £/CM>|5i|, при котором входной
сигнал x-ff/см будет положителен. В этом случае
f=(x+\U(m)/A=kx+f(h
где£=1/Л; /0=£/см/Л.
Временные диаграммы, приведенные на рис. 2.7,6,
иллюстрируют работу модулятора. При x=const частота
следования импульсов постоянна и пропорциональна модулирующему
сигналу. При x=var величина /<=1/т< пропорциональна сред-
ЧИН
f
^»

Преобразователь
N
27

*»6U
*Vy *
"1
Р
<А
У
7\ i
\_А _
i
У
z
1
J
а)
- Le-P*»
Р
Выход
"L"
*!
А
Выходу
ЧИМ
—>■
I
А
/
\l
*и
*7
А
/
*г
Г
*2
Л
/
<j
П
А
/
ч
Л
i <
г^^
л л L
м
t5\ t6\
i h t"
i 1— -A-
4 а,а|а|
' 1 1
1' II
Ш
t7\tekj \t:0
1 1 1
ihhnn
т—t T 1^
t
t
t
t
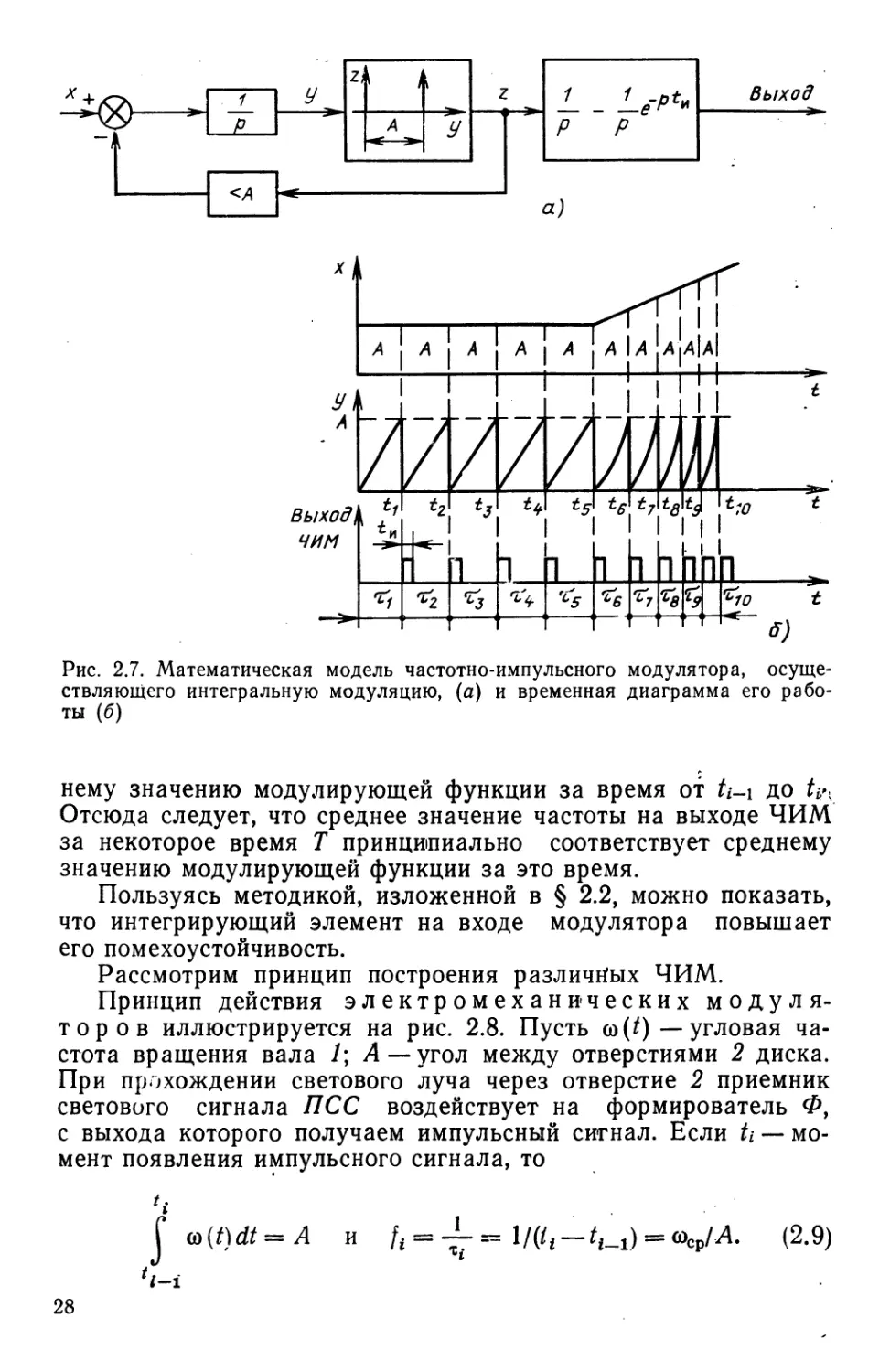
Рис. 2.7. Математическая модель частотно-импульсного модулятора,
осуществляющего интегральную модуляцию, (а) и временная диаграмма его
работы (б)
нему значению модулирующей функции за время от fr_i до t^
Отсюда следует, что среднее значение частоты на выходе ЧИМ
за некоторое время Т принципиально соответствует среднему
значению модулирующей функции за это время.
Пользуясь методикой, изложенной в § 2.2, можно показать,
что интегрирующий элемент на входе модулятора повышает
его помехоустойчивость.
Рассмотрим принцип построения различных ЧИМ.
Принцип действия электромеханических
модуляторов иллюстрируется на рис. 2.8. Пусть со (t) — угловая
частота вращения вала 1\ Л —угол между отверстиями 2 диска.
При прохождении светового луча через отверстие 2 приемник
светового сигнала ПСС воздействует на формирователь Ф,
с выхода которого получаем импульсный сигнал. Если U —
момент появления импульсного сигнала, то
28
1
Ч-i
<o(t)dt=A
/• = —
l/(<i-'i_i) = «fepM- (2.9)

пес
—^»
ф
Выход
Рис. 2.8. Электромеханический частотно-импульсный
модулятор частоты вращения ротора
Выражение (2.9) соответствует (2.8) при новых
обозначениях модулирующей функции. В случае со=const получим /=
= (о/Л.
Принцип действия конденсаторных
модуляторов напряжение — частота [4] базируется на свойстве
конденсатора интегрировать токовый сигнал. Пусть
u(t)—модулирующая функция, поступающая на вход управляемого
генератора тока УГТ (рис. 2.9). На выходе УГТ токовый
сигнал i=ku.
Напряжение на выходе конденсатора С
dt.
При достижении uc{t) величины А — напряжения
срабатывания порогового устройства ПУ—замыкаются контакты ПУ,
разряжается конденсатор, т. е. возвращается в исходное
состояние интегратор и поступает сигнал на формирующее
устройство ФУ, на выходе которого получается импульсный
сигнал.
По принципу действия трансформаторные модуля-
горы практически аналогичны конденсаторным. В этих
модуляторах в качестве интегратора используют трансформатор,
выполненный на магнитном материале с прямоугольной петлей
гистерезиса. Время перемагничивания tnep сердечника такого
У/Т
с]^пу\
i ].
г1
ПУ
<РУ
лпл.
>
Рис. 2.9. Схема конденсатного частотно-импульсного модулятора
29

трансформатора определяется вольт-секундной площадью
входного напряжения их:
*пер
f ux{t)dt = 2BrSy
6
где Вг — остаточная индукция; S —площадь поперечного
сечения тороидального сердечника трансформатора.
Из этого выражения следует, что
l/tnep=Uxcp/(2BrS)t
где их Ср — среднее значение входного напряжения за время
перемагничивания.
Момент перемагничивания обычно фиксируется
пороговыми устройствами. При этом т*=*пер/ и fi=l/xi=uXCpil (2BrS).
Из модуляторов подобного типа наибольшее распространение
получил мультивибратор Роера [4].
Сигнал интегральной частотно-импульсной модуляции
может быть также получен в результате
формирования импульсного сигнала частотной
модуляции (ЧМ) с гармоническойнесущей.
Частотно-модулированная гармоническая функция
иЧм (*)= U0 cos \«)0t + Дсо J к(it)dt ,
где x(t) —модулирующая функция.
После прохождения ЧМ-сигнала через усилитель-дграничи-
тель с большим коэффициентом усиления (теоретически
бесконечным) получаем последовательность импульсов, передние и
задние фронты которых совпадают с пересечением ЧМ-сигнала
с осью абсцисс. Если формировать положительные импульсы
на переднем и заднем фронтах сигнала на выходе усилителя
ограничителя, то интервал т/ между ними определяется из
следующих соотношений:
0)п'
i)0^ + Дсо Г x(t)dt — <o0fj_i + Aw f x (t) dt = it,
откуда
0),
,(*i-'i-i) + *<° J *(t)dt=>K9
т. e.
соЛ + Д<о*ср = *; /* = — = — *cP + — = k*cp + 2/0,
30

/
<p
н
1
•
ГОВИ
Сч
N
-*:—
Считывание
Сброс
°)
УУ
гови\
ЧИМ
Вход
Сч

Считывание
Сброс
к , /
г ^ ^
гМ
1 i мМм
МММ
i м i ж
^ " ■ "^
IINIIIIIIIIIIM,
t
МММ МММ .
1 1 I ^
1 1 1 1*
*)
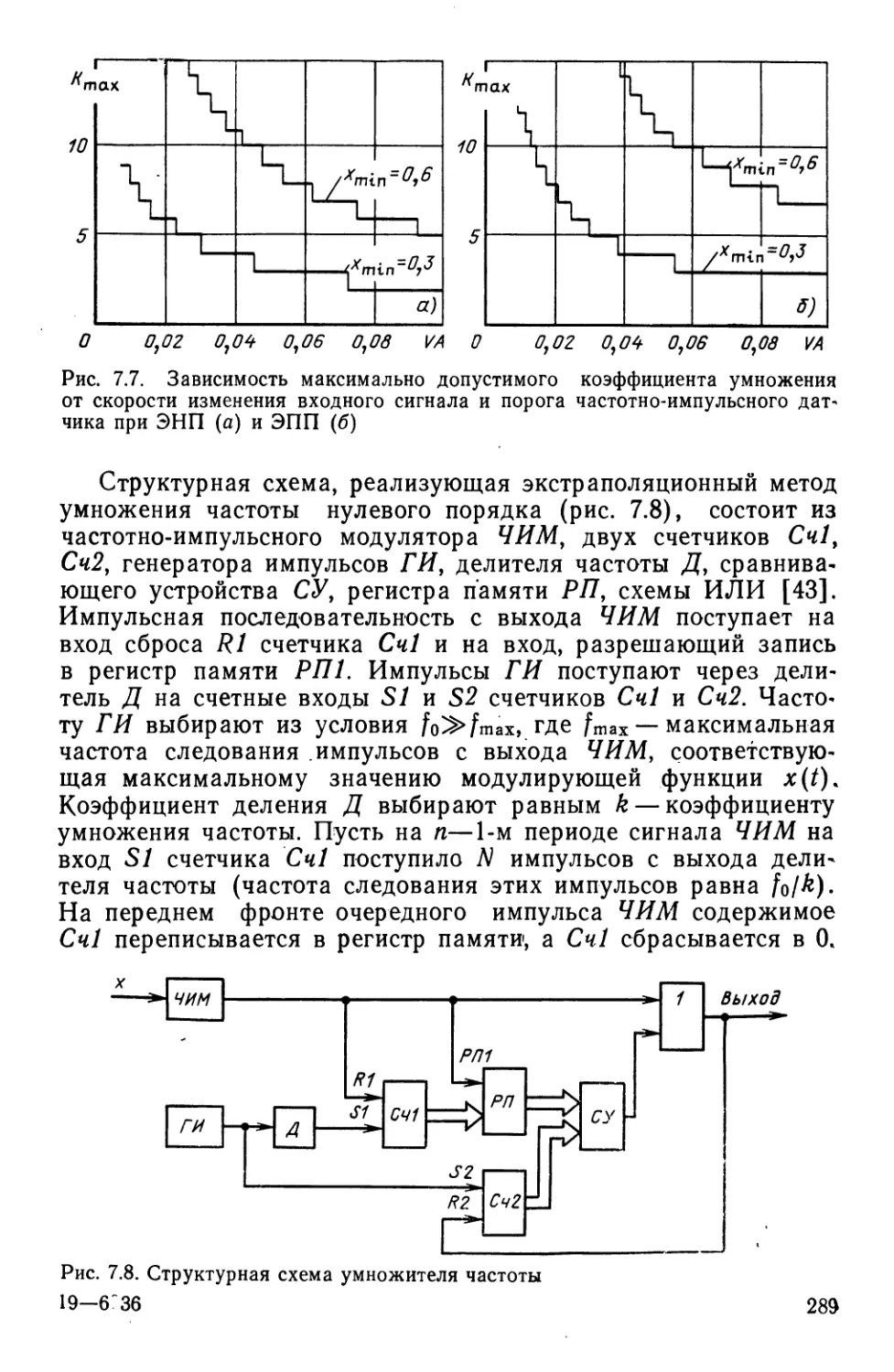
Рис. 2.10. Структурная схема циклического преобразователя частоты в
цифровой эквивалент (а) и временная диаграмма его работы (б)
где ^ср —среднее значение модулирующей функции на
интервале Ti.
Это выражение соответствует ИЧИМ.
При описании различных частотно-импульсных модуляторов
рассматривались лишь принципы их построения. В частности,
электромеханический ЧИМ может быть реализован
генерированием импульсного сигнала как при прерывании светового
потока, так и при модуляции магнитного поля [9]. В
конденсаторных ЧИМ в качестве управляемого генератора тока,
применяют усилители напряжения с большим выходным
сопротивлением. Пороговые устройства не выполняются на релейно-
контактных элементах, они используют современную
схемотехнику.
По способу измерения частоты различают [8] циклические
цифровые частотомеры, частотомеры непрерывного действия
с линией задержки, следящего уравновешивания и с
измерением по «k периодам».
В циклическом цифровом частотомере
(рис. 2.10,а) измеряемая частота поступает на ключ /С,
управляемый генератором образцовых временных интервалов ГОВИ.
Ключ К открывается на время Г, и на суммирующий счетчик
Сч поступают импульсы с выхода формирователя. Число этих
импульсов определяет среднюю частоту за время измерения.
После окончания импульса ГОВИ управляющее устройство
УУ обеспечивает считывание цифрового эквивалента и сброс
счетчика в исходное состояние.
31

Как видно из временной диаграммы (рис. 2.10,6),
зависимость цифрового эквивалента N от измеряемой частоты /
определяется выражением
N=Tf-6l+82f (2.10)
где Т — длительность образцового временного интервала; 6i =
=Atifc 62=Л*2/т; т= 1/f; 0<6i<l; 0<«2<1.
Отсюда следует, что цифровой эквивалент пропорционален
измеряемой частоте с погрешностью квантования по уровню
д=б2—8\.
Длительность временного интервала Т связана с
разрядностью счетчика. Если /max—максимальное значение
преобразуемой частоты, то Г/тах=2Л—1±Д«2П—1 и
7= (2*-1)//max, (2.11)
где 2 —основание системы счисления; л — разрядность
счетчика.
Выражение (2.10) полностью совпадает с (2.7), полученным
при рассмотрении принципов построения преобразователя
временного интервала в цифровой эквивалент. Это определяется
тем, что число N пропорционально произведению Tf с
точностью до —1^Д<;+1. При r=const рассматривается
преобразование в цифровой эквивалент частоты, при /=const—
длительности временного интервала. Следовательно, анализ
статической точности преобразования частоты и временного
интервала в цифровой эквивалент можно проводить относительно
переменной Tf (см. гл. 3).
Шаг временной дискретизации при использовании АЦП
последовательного счета с промежуточным преобразованием
в частоту и циклическим частотомером ограничивается снизу
длительностью образцового временного интервала. В том
случае, когда временной интервал не синхронизирован с
последовательностью счетных импульсов и считывание цифрового
эквивалента осуществляется на заднем фронте этого интервала,
реализуется равномерная временная дискретизация.
В цифровом частотомере непрерывного
действия с линией задержки [8] (рис. 2.11,а)
последовательность импульсов измеряемой частоты / подается
непосредственно на суммирующий вход реверсивного счетчика ЙСч,
а через линию задержки ЛЗ — на его вычитающий вход.
Числовое значение кода, содержащееся в реверсивном счетчике,
N=E\$f(t)dt-lf(t-T3)dt\ (2.12)
L0 0 J
где Е — знак выделения из выражения, стоящего в квадратных
скобках, целой части; Т3—время задержки.
32

f +,
Ц >7J [-3-
РСч
Суммируй
LLLUU 6X0
At7
тг
*;
#4^# Вход
РСч
Вычитаю-
щии Вход
РСч
N
5\-
4-
At<
цишл-
в)
8)
tf tZ t3 tif. t5t5t6 t7 tg tg t10tif t
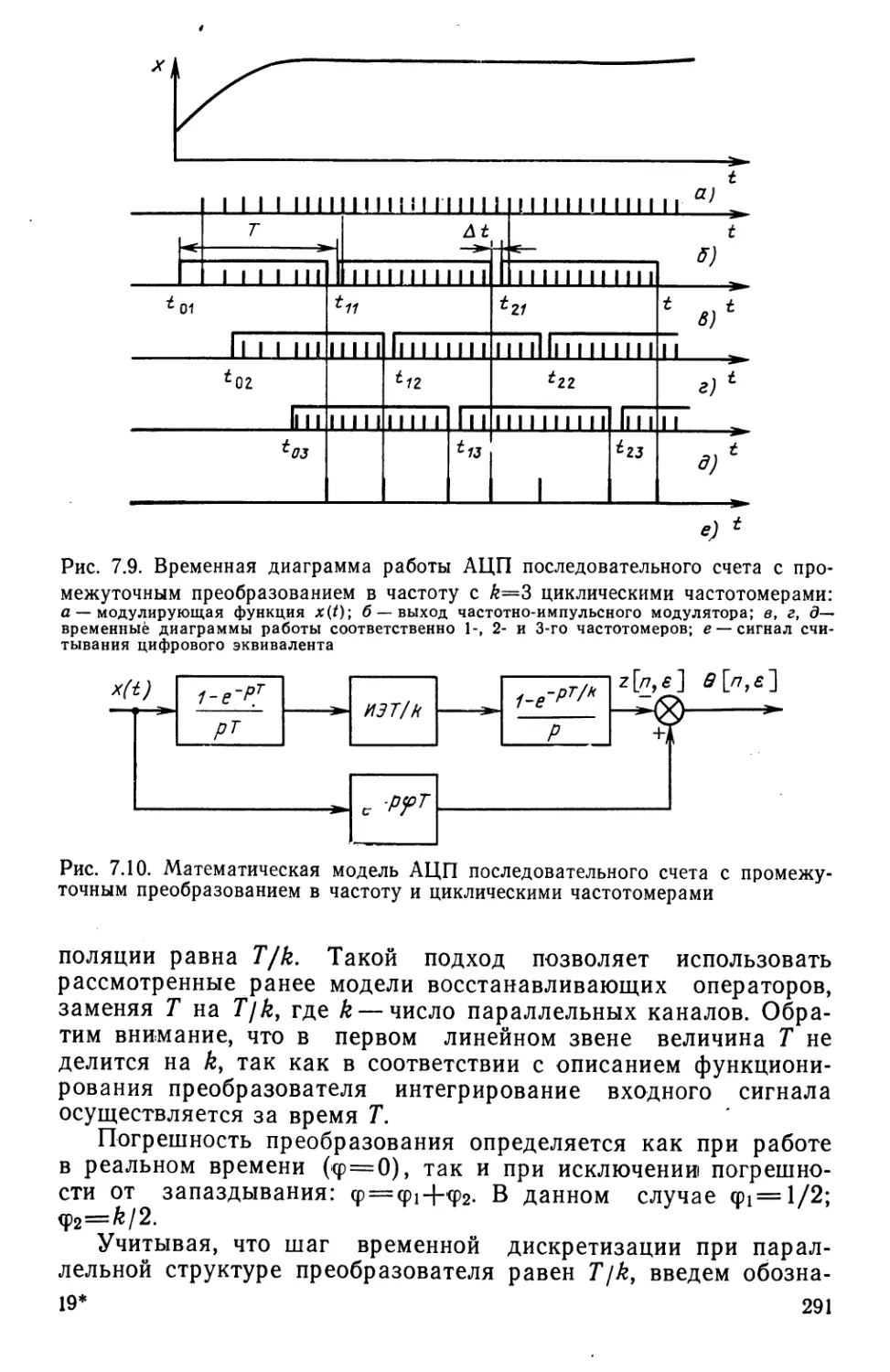
Рис. 2.11. Схема цифрового частотомера с линией задержки (а), временные
диаграммы его работы (б, в) и зависимость цифрового эквивалента N от
времени (г)
На временной диаграмме работы цифрового частотомера
(рис. 2.11,6) показана последовательность импульсов на
суммирующем и вычитающем входах РСч и зависимость
цифрового эквивалента от времени. Время задержки равно Т3.
Входной сигнал представлен последовательностью импульсов с
частотой /= 1 /т. Величина цифрового эквивалента,
соответствующая истинному значению частоты, обозначена ЫИ.
Установившийся режим наступает при t>h. В этом случае величина
цифрового эквивалента Nx с временем задержки на участке
fe^<^5' связана выражением
T*={Nx-\)x+titu
где O^A^i^t.
Разделив обе части равенства на т, получим
TJt=Nx-\+bu
где bx=AUlx и 0<fii<l.
Отсюда, погрешность квантования по уровню
д1 = Г^—Л^! = в1—1. (2.13)
Так как 0<81<1, то — КЛ^О. Аналогично на участке
tb' < t < t9 имеем Т = N^ + Aflf где N2 = Nx — 1 — значение цифро-
3-6036 33

вого эквивалента, откуда T3f=N2+8\ и
A2=T3f—N2=8i при 0^Д2<1. (2.14)
Таким образом, максимальные значения погрешностей
квантования по'уровню в непрерывном цифровом частотомере с
линией задержки, так же как в циклическом частотомере,
определяются единицей младшего разряда.
Длительность задержки связана с разрядностью
реверсивного счетчика частотомера следующим образом:
rafmax = 2»—1; Гз=(2»-1)/^тах. (2.15)
Из (2.15) и (2.11) следует, что при одинаковых А и /max
длительность временного интервала в циклическом
частотомере и время задержки в частотомере с линией задержки
совпадают.
' Название «непрерывный» цифровой частотомер в данном
случае оправдано тем, что значения цифрового эквивалента
с точностью до погрешности квантования по уровню
постоянно записаны в реверсивном счетчике.
Временная дискретизация при использовании АЦП
последовательного счета с промежуточным преобразованием в
частоту с цифровым частотомером непрерывного действия с
линией задержки реализуется внешним устройством управления,
осуществляющим подачу команды считывания числа,
записанного в реверсивном счетчике.
Цифровой частотомер следящего
уравновешивания (рис. 2.12) представляет собой замкнутую
систему следящего уравновешивания измеряемой частоты [8].
Элементом сравнения является реверсивный счетчик РСч, на один
из входов которого (сложения) подаются импульсы
измеряемой частоты f, на второй (вычитания) — импульсы
регулируемой частоты обратной связи /0.с с выхода двоичного делителя
Д, управляемого кодом счетчика РСч. Регулируемая частота
генерируется совоиупностью генератора образцовой частоты
ГОЧ, двоичного делителя частоты Д,< группы импульсно-потен-
циальных ключей К1—Кп и схемы ИЛИ. На управляемые
входы ключей подаются импульсы, формируемые фронтами
сигналов триггеров двоичного делителя. Частоты этих
импульсов относятся как 21 :22:...
...:2п (п—число разрядов
двоичного делителя), образуя
группу из п частотных
компонентов выходного сигнала
управляемого генератора. Триг-
/•-
fox
1
ГОЧ
^Т—
"* |/
L
РСЧ
т -4
|
\нп\
т
А
=HSr>/V
Рис. 2.12. Схема цифрового
частотомера следящего уравновешивания
34

геры реверсивного счетчика управляют импульсно-потенциаль-
ными ключами.
В результате суммирования частотных компонентов в
схеме ИЛИ образуется выходной сигнал, средняя частота
которого fox=f0Nf2n (где N — текущее значение числа в реверсивном
счетчике; 2п — емкость счетчика; f0 — частота образцового
генератора) определяется состоянием счетчика РСч и может
принимать 2п дискретных значений. Таким образом, в реверсивном
счетчике фиксируется число
N = E^[fx(t)-Lc(t)m. (2.16)
Очевидно, что частота fo должна быть не меньше
максимальной частоты входного сигнала.
В установившемся режиме частота обратной связи с
точностью до шага квантования равна входной частоте и, таким
образом, числовое значение кода, содержащееся в РСчу
пропорционально измеряемой частоте.
Название «непрерывный» для цифрового частотомера
следящего уравновешивания имеет тот же смысл, что и для
частотомера с линией задержки.
Временная дискретизация в АЦП последовательность счета
с промежуточным преобразованием в частоту и частотомером
следящего уравновешивания реализуется внешним
устройством управления.
Цифровые частотомеры с измерением по «^
периодам» по существу являются преобразователями вре-
k
менного интервала Тг = 2^^ соответствующего ДЛИТеЛЬНО-
сти «k периодов», в число (измерение «k периодов») с
последующим выполнением операции деления для получения
величины 1/7Y
Временная дискретизация в этом случае принципиально
неравномерна. Цифровой эквивалент считывается по окончании
временного интервала, равного «k периодам».
2.4. КВАНТОВАНИЕ ПО УРОВНЮ И ВРЕМЕННАЯ
ДИСКРЕТИЗАЦИЯ В НАКОПИТЕЛЬНЫХ
АНАЛОГО-ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЯХ
В накопительных АЦП цифровой эквивалент измеряют в тот
момент времени, когда аналоговый сигнал изменяется на 1,
соответствующую младшему разряду цифрового эквивалента.
Принцип действия накопительного АЦП без
обратной связи легко показать на примере нереверсивного
3* 35

Рис. 2.13. Схема накопительного АЦП угловых перемещений без обратной
связи (а) и с обратной связью (б)
преобразователя угловых перемещений (рис. 2.13,а). Пусть
требуется получить цифровой эквивалент угла поворота а
вала 1. При попадании луча источника света через отверстие 2
в диске на преобразователь светового сигнала в электрический
на выходе последнего формируется импульс, поступающий
в счетчик, который фиксирует число «элементарных углов» —
квантов, равных q=S60°/nf где п — число отверстий.
В счетчике фиксируется число N, соответствующее с
точностью до q угловому перемещению. К достоинству подобного
преобразователя относится высокое быстродействие, вызванное
тем, что на счетчик подается число импульсов, зависящее от
разницы предыдущего и данного значений преобразуемой
величины, в то время как в АЦП последовательного счета с
промежуточным преобразованием во временной интервал или
частоту преобразование аналогового сигнала осуществляется
каждый раз заново.
Однако в накопительном АЦП подобного типа при
подавлении помехой счетного импульса возникает ошибка, которая
запоминается (если не принято каких-либо дополнительных
мер) на все время работы преобразователя. Кроме того, в
накопительном АЦП без обратной связи отсутствует фиксация
нулевого состояния.
В накопительных АЦП с обратной связью эти
недостатки могут быть устранены [7]. Такой преобразователь
(рис. 2.13,6) содержит сравнивающее устройство СУ, цифро-
аналоговый преобразователь ЦАП, реверсивный счетчик РСчу
генератор импульсов ГИ и два ключа К1 и К2. Сравнивающее
устройство сравнивает входной сигнал хвх с сигналом
обратной связи уо.с, поступающим с выхода ЦАП. Последний
осуществляет преобразование цифрового эквивалента N,
записанного на РСч, в аналоговый сигнал. Если xBX>y0,Cf на выходе а
сравнивающего устройства появляется сигнал, открывающий
ключ /С/, который обеспечивает поступление импульсов ГИ на
суммирующий вход РСч. При хъх<у0.с в СУ на выходе b
формируется сигнал, открывающий ключ К2, благодаря чему им-
36

пульсы ГИ поступают на вычитающий вход РСч. В установив-
шемся режиме на РСч с точностью до погрешности
квантования по уровню записан цифровой эквивалент аналогового
входного сигнала.
Временная дискретизация при использовании
накопительных АЦП осуществляется, как правило, от внешнего
устройства управления.
2.5 КВАНТОВАНИЕ ПО УРОВНЮ И ВРЕМЕННАЯ
ДИСКРЕТИЗАЦИЯ В АНАЛОГО-ЦИФРОВЫХ
ПРЕОБРАЗОВАТЕЛЯХ СЧИТЫВАНИЯ
Принцип действия. К АЦП считывания относятся
преобразователи, у которых значению входной величины соответствует
определенный цифровой эквивалент, считываемый
непосредственно с кодирующего устройства, на которое нанесена вся
совокупность цифровых эквивалентов. Широко применяют такие
АЦП при преобразовании перемещений (в основном угловых)
в код [6, 10, 11].
Принцип действия этих преобразователей иллюстрируется
схемой, приведенной на рис. 2.14. Здесь входная величина а —
угол поворота вала 2. На диск нанесена «маска»
трехразрядного двоичного кода (в общем случае число разрядов п). Токо-
проводящая заштрихованная часть маски соответствует сигна*
лу 1, а часть маски, не проводящая ток (незаштрихованная),—
сигналу 0.
Поворот диска осуществляется валом, угловое
перемещение которого преобразуется в цифровой эквивалент.
Положительное напряжение на диск подается через кольцо / и
снимается щетками 3—5. Каждому угловому положению вала
соответствует код, который записан положительными потенциалами
относительно минуса источника питания на щетках. При
одновременном считывании информации со щеток получаем АЦП
параллельного считывания, при разделении во времени
элементов кода —АЦП последовательного считывания [7].
Считывание информации с диска может быть осуществлено
не только контактными устройствами. Широко используются
фотоэлектрические [6] и индукционные [10] способы. Так как
метод считывания не влияет на принцип действия
преобразователя, в дальнейшем любое считывающее устройство будем
называть щеткой.
Как следует из приведенного описания, методическая
погрешность ^преобразования в АЦП подобного типа
определяется ошибкой квантования по уровню и не превышает единицы
младшего разряда q=360°/2n (где п—разрядность цифрового
цифрового эквивалента) кодирующей маски. Однако это ут-
37

^ Цифровой
эквивалент
О 12 3 4 5 6 7 Разряды
I
%
У/.
ж
V/,
V,
У/У/л
шш
и
иг
Рис. 2.14. К объяснению принципа Рис. 2.15. Развертка маски АЦП счи-
действия АЦП считывания тывания с двоичным кодом
верждение справедливо лишь при точечном контакте
считывающего устройства и идеально изготовленной маске. Очевидно,
что эти условия практически невыполнимы.
Невыполнение этих условий приводит к погрешностям неод-.
нозначности считывания, которые могут быть значительными.
На рис. 2.15 приведена развертка маски с расположением
щеток на границе цифровых эквивалентов ПО и 011 (числа
записаны, начиная с младшего разряда). Из-за технологических
погрешностей в выполнении маски, неточности в расположении
щеток могут быть считаны числа 111, 000, 001 и т. д.
Для ограничения значения погрешности единицей младшего
разряда разработаны методы предотвращения
неоднозначности считывания [6, 7, 11].
Методы предотвращения неоднозначности считывания.
Наиболее распространены [6, 11] метод двойной щетки, метод
Баркера (У-код) и метод, основанный на использовании кода
Грея.
Метод двойной щетки основан на применении во
всех разрядах, кроме младшего, двух щеток, расположенных
относительно линии считывания на расстоянии 0,5?.
Выбор ряда считывающих щеток определяется значением
младшего разряда. Если с младшего разряда считывается 0,
то значения старших разрядов определяются правым рядом
щеток (Л-щетками), если 1, —левым рядом (В-щетками). При
этом неоднозначность возникает только в младшем разряде.
Так, при расположении щеток, показанном на рис. 2.16,а,
могут быть считаны числа 001 или 110 (коды записаны, начиная
с младшего разряда), соответствующие числам 3 и 4 в
десятичной системе счисления. При этом ошибка неоднозначности не
превышает единицы младшего разряда.
В том случае, когда по конструктивным соображениям
необходимо расположить щетки по одной линии, соответственно
видоизменяют рисунок маски (рис. 2.16,6). Все разряды,
кроме младшего, разделяют на два подразряда. Подразряды А
сдвинуты влево на 0,5(7 относительно своего положения в дво-
38

Рис. 2.16. Развертка маски АЦП со считыванием методом двойной щетки (а)
и со считыванием методом двойной щетки при расположении считывающих
элементов на'одной линии (б)
ичном коде, подразряды В — вправо на 0,5#. При этом
алгоритм выбора считывающих элементов остается прежним.
Модуль погрешности преобразования при методе двойной
щетки можно уменьшить на 0,5#, установив начало отсчета на
середине младшего разряда нулевой комбинации. При этом
допускаемые инструментальные погрешности, связанные с
неточным изготовлением маски и установкой щетки,
обеспечивающие суммарную погрешность, равную </, не должны
превышать 0,25<7 по каждому из разрядов [11].
Метод Баркера (V-код) во всех разрядах, кроме
младшего, использует два ряда щеток. Расстояние щеток в /-м
разряде (*=2, 3,...) от линии считывания определяется
выражением
. U=±095q-21-2.
Выбор считывающей щетки определяется значением
предыдущего (младшего по сравнению с данным) разряда. Если
в младшем по сравнению с данным разряде считывается 0, то
в данном разряде снимается информация с А-щетки, если 1,—
то с 5-щетки.
Например, при расположении маски, указанном на
рис. 2.17,а, могут быть считаны коды ПО или 001 (коды
записаны, начиная с младшего разряда), что соответствует числам
3 и 4 в десятичной системе счисления. Таким образом, ошибка
неоднозначности не превышает единицы младшего разряда.
Название V-код определяется тем, что расположение щеток
подобно написанию буквы V.
Если необходимо расположить щетки по одной линии,
соответственно видоизменяется рисунок маски (рис. 2.17,6) [6].
Все разряды, кроме младшего, разделяют на два подразряда.
"l~i\k Ро?-2ЯДе ^=2, 3>---) подразряды А сдвигаются влево
на 0,5*7 -2' относительно своего положения в двоичном коде,
подразряды В —вправо на 0,5<7«2'-2. При этом алгоритм
выбора считывающего элемента остается прежним.
Модуль методической погрешности преобразования при
У-коде уменьшается на 0,5# смещением начала отсчета так же,
39

О 1 2 3 Л 5 6 7 Разряды
ж
ЗВ<
ш
шм
1ш
ZA
УШ
О 1 2 J 4 S 6 7Под разряды
А
В
Рис. 2.17. Развертка маски АЦП считывания с V-кодом (а) и с У-кодом и
расположением считывающих элементов на одной линии (б)
как в методе двойной щетки. Однако требования к
допускаемым инструментальным погрешностям здесь не являются
постоянными, они менее жесткие для старших разрядов.
Действительно, при суммарной погрешности, равной qy для
младшего разряда инструментальная погрешность не должна
превышать ?/4, для следующего разряда —#/2, для t-ro разряда —
<7/23-*' при i>l [11].
Метод, основанный на использовании кода
Грея, обеспечивает ограничение ошибки, вызванной
неоднозначностью считывания, величиной младшего разряда. В коде
Грея соседние комбинации различаются только в одном
разряде. Пусть an-i#nb-2- • .во — число в двоичном коде; ему
соответствует число в коде Грея, полученном следующим образом:
Здесь Ф — знак суммирования по модулю два без переноса.
Так, если 01101 —двоичное число, то число в коде Грея
получается так:
,01101
0 110
®У
0 10 11
Здесь 01011 — число в коде Грея.
В табл. 2.1 приведены десятичные, двоичные числа и их
изображение в коде Грея.
Таблица 2.1
Десятичное
число
0
1
2
3
Двоичное
число
000
001
010
011
Изображение
в коде Грея
000
001
011
010
Десятичное
число
4
5
6
7
Двоичное
число
100
101
по
111
Изображение
в коде Грея
ПО
111
101
100
40

Разряды 0 113 4 5 6 1 Разряды 0 12 3 4 5 6 7
1
11
ш
УМ
1
Ж.
Ш/¥Ж
V//
//
V/V//
*)
I
II
III
б) IV
•
(
\
У/у
(
У
Ш
1
I
У/,
т
УМ
'УШШ
»
1
_ \
Рис. 2.18. Развертка маски с кодом Грея (а) и с двоичным кодом и
расположением считывающих элементов в соответствии с кодом Грея (б)
Соответствующая данной таблице развертка маски
изображена на рис. 2.18,а. Так как каждое последующее число в коде
Грея отличается от предыдущего не более чем в одном
разряде, ошибка от неоднозначности считывания не превышает q.
Анализ алгоритма построения кода Грея позволяет
сформулировать его свойства.
1. Старший разряд кода Грея равен старшему разряду
двоичного числа.
2. Сумма разрядов кода Грея по модулю два равна
младшему разряду двоичного числа, т. е.
п-1
£ я/ = К
/=о
Докажем это свойство. В соответствии с алгоритмом
построения кода Грея
а{ = а,фа|+1.
Отсюда
п-1
п-1
Так как at + аь =-- 0, то 2 а\ = ао, что и требовалось дока-
1=0
зать.
3. Двоичное число ап-\ап~2 ... До по заданному коду Грея
fln~ifl/n-2...^o может быть получено с помощью следующих
алгоритмов:
первый алгоритм позволяет получить двоичный код,
начиная со старшего разряда, на основании рекуррентных
соотношений.
fl/z-i^^C-! (см. свойство 1); ап_2 = ап__г@а'п_2\...
an_t = а„_е+1ф <_,;...; а0 = ах©а;;
41

второй алгоритм позволяет получить двоичный код,
начиная с младшего разряда. Задаемся произвольно
значением а0. Тогда, как следует из способа построения кода Грея,
#/2—2 = #-п__з© ап—з'у ап—1 ^ Лп+2© а«—2-
Суммируем по модулю два все разряды кода Грея. Если
после суммирования получим число (либо 0, либо 1),
совпавшее с тем оо, которым произвольно задались вначале, то
полученное двоичное число истинно, в противном случае следует
инвертировать (единицы заменить нулями, а нули —
единицами) все разряды двоичного числа;
третий алгоритм по существу совпадает со вторым, но
не требует суммирования разрядов кода Грея. При этом
алгоритме ап-\ вычисляется как сумма а'п-2®ап-2. Если Яп-1 =
= а'п_ь то а0 задались верно и полученное двоичное число
истинно. Если же Оп-\фо>'п-и все разряды полученного
двоичного числа инвертируются.
Пример 2.1. Дано в коде Грея число a/4a/3a'2a/ia/o = 10110; требуется
найти, какому двоичному чмслу оно соответствует.
Первый алгоритм: ай = а4' = 1 > аъ = Ч® Яз' = 1® 0 = 1; а2 = я3® а2 =
= 101=0; fl1 = aa©a1' = 0©l= 1; ао = а10ао' = 1фО=1, откуда
а9аъа2а1а0= 11011.
Второй алгоритм, пусть а0 = 0. Тогда ах = а0 0 a0f = 0 0 0 = 0; а2 =
= fli0<V = O01-= 1; а9 = а2<$а2' = 10 1-0; я4 = «з9«з'=0ф0=0,
4
но 2 <V = 1 0 0 © 1 0 1 0 1 = 1, т. е. значением а0 вначале задались не-
верно. Поэтому действительное значение двоичного числа получаем после
инвертирования всех разрядов: 11011.
Третий алгоритм: выполняем рекуррентную процедуру в соответствии со
вторым алгоритмом; а4 сравниваем с а\. При неравенстве а4 и а\
необходимо инвертировать разряды полученного двоичного числа.
Приведенные алгоритмы позволяют строить на типовых
логических элементах преобразователи кода Грея в двоичный
код.
Код Грея может быть получен при считывании с маски,
выполненной в соответствии с двоичным кодом [11]. При этом п
считывающих элементов не находятся на одной прямой, а
сдвигаются вправо наполовину весов соответствующего разряда
(рис. 2.18,6).
Дополнительно вводится я+1 считывающий элемент, уста^
навливаемый в исходном состоянии в начало отсчета. Таким
образом, с я-разрядной маски, выполненной в обычном
двоичном коде, считываем я+1 разрядный код Грея.
42

Требования к допускаемому значению инструментальных
погрешностей при суммарной погрешности, равной q, для
маски с кодом Грея совпадют с требованиями,
сформулированными при описании метода двойной щетки [11].
Временная дискретизация при использовании
рассматриваемого типа АЦП осуществляется устройством управления при
считывании цифрового эквивалента.
2.6.' КВАНТОВАНИЕ ПО УРОВНЮ И ВРЕМЕННАЯ
ДИСКРЕТИЗАЦИЯ ПРИ ПОРАЗРЯДНОМ КОДИРОВАНИИ
АНАЛОГОВОГО СИГНАЛА
Аналого-цифровые преобразователи. Структурная схема
АЦП поразрядного кодирования (рис. 2.19,а) состоит из
порогового устройства ПУ, весовых триггеров ГО, П,..., 7\,..., Тп-и
преобразователя ЦАПУ управляющего устройства УУ и набо-
. ра схем И.
Пороговое устройство сравнивает входной сигнал их с
сигналом обратной связи и0.с. При их<.и0.с на выходе ПУ будет
сигнал 1, при их>и0.с будет 0.
Управляющее устройство представляет собой кольцевой
распределитель, на нечетных выходах которого
последовательно во времени переключаются в состояние 1 весовые триггеры,
начиная с триггера старшего разряда. На сигналах с четных
выходов УУ весовые триггеры переключаются в состояние 0
при наличии на выходе ПУ сигнала 1, т. е. при их<и0.с.
Сигналом с 2я+ 1-го выхода УУ осуществляется считывание
цифрового эквивалента, а с 2м + 2-го — сброс весовых триггеров
в состояние 0.
Цифро-аналоговый преобразователь преобразует код,
записанный на весовых триггерах, в напряжение и0.с. При этом
п—\
где щ=\ и щ=0 при состоянии t-го весового триггера
соответственно 1 и 0; С/оп — опорное напряжение.
Последовательность работы преобразователя,
иллюстрируемую временной диаграммой (рис. 2.19,6), рассмотрим на
примере четырехразрядного АЦП (п=4) с диапазоном
преобразуемых напряжений от 0 до 16 В. При Uon=l В имеем 24£/оп=
= 16 В. Пусть входной сигнал их=3,5 В.
При сигнале 1 на выходе 1 УУ в состояние 1
переключается триггер ТЗ и и0.с = 23£/оп=8 В. Так как uQ.c>ux, то при
сигнале 1 на выходе 2 УУ через схему И триггер ТЗ
сбрасывается в состояние 0. Когда будет сигнал 1 на выходе 3 УУ,
43

Лп+2
-На считывание а)
~На сброс весовых триггеров
Рис 2.19. Структурная схема АЦП поразрядного кодирования (а) и
временная диаграмма его работы (б)
тогда в состояние 1 перебросится триггер Т2 и и0.с=24С/0п=
==4 В.
Так как и0.с>их, то сигнал 1 с выхода 4 УУ через схему И
сбрасывает триггер Т2 в состояние 0. При сигнале 1 на выходе
5 УУ в состояние 1 перебрасывается триггер 77 и u0.c—2lUon=
=2 В. Так как u0.c<uXi то сигнал .с ПУ на выходе 6 УУ
запрещает сбор схемы И и триггер 77 остается в состоянии 1.
При сигнале 1 на выходе 7 УУ в состояние 1 перебрасывается
триггер ТО и «о.с=21С/оп-Ь2°(/оп=3 В. Так как и0.с<их, то,
когда на выходе 8 У У будет сигнал 1, и схема И не собирается
и ТО остается в состоянии 1.
На этом по существу кончается процесс преобразования.
На весовых триггерах записан цифровой эквивалент ООН.
Сигналом 1 с выхода 9 УУ осуществляется считывание цифрового
эквивалента, а с выхода 10 сбрасываются в исходное состояние
все весовые триггеры.
Точность преобразования АЦП поразрядного кодирования
определяется единицей младшего разряда. В данном случае
2°£/оп=1 В.
Из описания принципа действия АЦП видно, что обеспечить
статическую точность, не превышающую единицы младшего
разряда, можно в том случае, когда за время преобразования
входной сигнал не изменяется больше чем на эту величину.
Для выполнения этого требования в ряде случаев АЦП
поразрядного кодирования дополняют устройствами выборки и хра-
44

в
I
+
**'
I*
+
'О*
II Y
^
-—•
^
1
1
*:
^
^
1
,i—;
Ik
1
^-t
, Г"
IK
«M
i
л ^
}*—f
SI ,
F-
CM
1 л
19
1
J
F*
\^.
1 л
Lis»
|
JI
Ik
CD
^'"T
-0
C\|
IS
l>4
«M
CM
CM
Q
CM
^ 6
с*
C5
45

нения (УВХ) преобразуемой величины, которые, как правило,
интегрируют входной сигнал за небольшое время стробирова-
ния. Далее результат интегрирования преобразуется в
цифровой эквивалент. По существу преобразованию подлежит
среднее значение аналогового сигнала за время интегрирования.
В том случае, когда используется УВХ и временем строби-
рования пренебречь нельзя, будем рассматривать АЦП
поразрядного кодирования с запоминающим интегратором.
Цифроаналоговые преобразователи. Широкое
распространение получили цифроаналоговые преобразователи
параллельного типа, преобразующие цифровой код с пространственным
разделением элементов в аналоговую величину [12, 13].
Так как основой для современных цифровых
автоматических и телемеханических устройств являются двоичные коды,
то принцип преобразования заключается в суммировании
аналоговых величин, которые относятся как целые степени
двойки. Выражение, являющееся формальной записью,
определяющей принцип преобразования, имеет вид
где и — аналоговая величина, получаемая в результате
преобразования; Uon — опорное напряжение, определяющее
единицу младшего разряда; а,— весовые коэффициенты,
определяемые соответствующими разрядами двоичного кода.
Так, при /г=4; a3^2^i^o=0011 и £/оп= 1 В имеем
«=1-2°-1 + Ь21-1+0-22-1+0-22-1= 3 В.
Преобразование двоичного кода в напряжение или ток
осуществляется схемами, приведенными в табл. 2.2. Здесь же
указаны зависимости выходных величин от значения кода,
записанного в весовых триггерах TOf...,Tn-u коммутирующих
соответствующие ключи К, которые подключают либо источник
опорного напряжения С/оп (при 1 в данном разряде), либо
шину «земля» (при 0 в данном разряде) [12], а также значения
/i—i
десятичного эквивалента Я= JJ ахТ преобразуемого
ДВОИЧНО
п-г-\
ного кода а^ах.,,ап-х и его максимальная величина/7тах = £2\
46

Глава 3
ОЦЕНКИ МЕТОДИЧЕСКИХ ПОГРЕШНОСТЕЙ
КВАНТОВАНИЯ ПО УРОВНЮ
3.1. КВАЗИМГНОВЕННОЕ КВАНТОВАНИЕ ПО УРОВНЮ.
ОЦЕНКИ МЕТОДИЧЕСКИХ ПОГРЕШНОСТЕЙ
В том случае, когда за время аналого-цифрового
преобразования аналоговый сигнал изменяется незначительно, процесс
квантования по уровню можно считать мгновенным. Такая
идеализация допустима в АЦП считывания, поразрядного
кодирования и накопительного при получении цифрового
эквивалента по стробирующему сигналу устройства управления.
Квантование по уровню в указанных АЦП при допущении
неизменности аналогового сигнала за время преобразования
будем называть квазимгновенным. Модель квазимгновенного
квантования представляется нелинейным элементом, имеющим
статическую характеристику, приведенную на рис. 1.1.
, Оценки погрешностей квантования случайных величин
(статика). Максимальная абсолютная погрешность Атах=^/2, где
q — шаг квантования по уровню., При выводе выражений
средних и среднеквадратических оценок заданным является закон
распределения рх(х).
В этом случае условная плотность распределения
вероятностей погрешности квантования при фиксированном цифровом
эквиваленте z=kq на выходе преобразователя имеет вид
/kq+0,Sq
J px(x)dx, (3.1)
kq—0,5?
kq+0,5q
где j px(x)dx = Pk вероятность того, что kq — 0,5^<
kq—0tbq
<x<kq + 0,5q.
Из (3.1) следует, что условная плотность распределения
вероятностей А совпадает с точностью до постоянного
множителя l/Pk с законом распределения случайной величины х.
При заданном х погрешность квантования A=kq—x
является детерминированной величиной при kq—Ofiq^x^Zkq+Ofiq.
Поэтому вероятность вычисленного А при фиксированном х
равна 1, откуда условная плотность распределения вероятности
А при известном х имеет вид
р(Ь/х) = £ b[A-kq + x]t
47

где б [A—kq-\-x]—дельта-функция от соответствующего
аргумента.
Двумерная плотность распределения вероятностей Аид:
будет
р(А, х)=р{А1х)рх(х).
При этом безусловная плотность распределения
вероятностей погрешности квантования по уровню
+ 00 £=+00 +00
Рд(д)= j Р(д, x)dx= £ j b[A~kq + x]px(x)dx.
—00 k=—00 —00
+ 00
Используя известное соотношение j 8 [х — a] f (х) dx = / (а),
'—оо
получаем
Ра(Д)« £°Рх№-Ь). (3.2)
£=—00
Выражения оценок абсолютных погрешностей квантования
определяем в соответствии с § 1.3:
Дтах=<7/2; (3.3)
<7/2 +<?/2
Д= j д2Рх(Л/-Д)^Д = 2 J bpx(kq~b)db (3.4)
—<?/2 £ fc — q/2
]/д2 = l/ f (Д-Д)»53Л(*9-А)^Д. (3.5)
-<?/2 Л
Если преобразованию подлежит фиксированная величина х,
относительная погрешность преобразования определяется как
(kq—x)/x.
Оценки приведенных погрешностей получаются путем
деления значения оценок абсолютных погрешностей на величину
диапазона.
Для анализа свойств закона распределения погрешностей
квантования рассмотрим характеристическую функцию
случайной величины А [14].
Известно [1], что характеристическая функция случайной
величины А определяется выражением
?ди = 1рд(д)е/юЛ^-
48

0,5<? 0,5?
= f Рд(А)е/<оДйД = Е J Р,(^-Д)е/ш4йД. (3.6)
—0,5? k —6,5?
Используя фильтрующее свойство б-функции при -—0,5д^
^x^0,5q, находим
2М*?-Л) = J PA*)\24x-kq + b)dx\. (3.7)
k -оо L * J
Сумму б-функций разлагаем в ряд Фурье [14]:
£ 8 (х - fy + Д) = --L £ ехр [/ *±- (х + Д)]. (3.8)
Подставив (3.7) в (3.6) с учетом (3.8), получаем
выражение характеристической функции погрешности квантования:
0,5? +оо
-0,5? -оо fc '
= Jj-i-lj" рЛ^)е/2^^ + |5?е/шЛе^А/^Ди
k —оо —0,5?
_*1JD / 2nk \ s\n0,bq(m+2fik/q) ,g дч
"~L * I <7 J OfU7(©+2i*/?) '
где Px{2nkjq) —характеристическая функция преобразуемой
величины jc при значении аргумента, равном 2nkjq.
Прежде чем проводить анализ выражения (3.9), рассмотрим
характеристическую функцию некоторой центрированной
случайной величины у, распределенной равномерно на
интервале ±а:
а
1 fry . 1 e/a>fl~e^/<ofl sincoa /Q 1ЛЧ
— e dy = г =: . (3.10)
2a 2a J® <oa
—a
Имея характеристическую функцию равномерно
распределенной случайной величины, можно утверждать, сравнив
выражения (3.10) и (3.9), что погрешность квантования
распределена равномерно при выполнении условия
Px{2nk/q)=0y когда &=^0. (3.11)
Рассмотрим ряд распределений, характеристическая
функция которых удовлетворяет этому условию [14]. Прежде всего
это закон равномерной плотности вероятности при условии,
4—6036 49

что диапазон изменения случайной величины кратен q.
Действительно, как следует из (3.10),
P,p^)«sin^/(2«*a/<7) = 0
при 1гФ0 и а, кратном q.
Пусть преобразуемая случайная величина х есть сумма т
независимых случайных величин и хотя бы одна из
составляющих, например xif распределена равномерно, а ее диапазон
изменения кратен q.
Известно [1], что характеристическая функция суммы
независимых случайных величин равна произведению
характеристических функций составляющих. При этом
^^©) = ftl(co)P,i(a>)...PX/(co)...ftm(co)f .
где Рх. (со) — характеристические функции составляющих xt.
Так как х-ь распределена равномерно и ее диапазон кратен
<7, то Рх. (о)=2я&/<7)=0 при k=£0t откуда
характеристическая функция случайной величины х удовлетворяет условию
(3.11).
Рассмотренные примеры распределений строго
соответствуют равномерной плотности вероятностей погрешности
квантования по уровню.
Распределение А приближается к равномерному, если
Px{2nk/q)<^.\ при k¥=0.
Так как характеристическая функция есть по существу
изображение по Фурье закона распределения, то с ростом
дисперсии случайной величины закон распределения становится
«шире», а его изображение по Фурье достаточно быстро затухает.
Когда дисперсия х хотя бы на порядок больше q2 (а это
обычно имеет место), то Px(2nk/q) ж0 при 1гф0. Отсюда следует,
что распределение погрешности квантования приближается
к равномерному при условии, что среднеквадратическое
отклонение преобразуемой величины значительно больше
погрешности квантования по уровню. При этом
pA(A) = \/q при -<7/2<Д<<7/2 и Д=0; Д2=<72/12.
Оценки погрешностей квантования случайных функций
(динамика) [14, 15]. Если на вход нелинейного элемента,
имеющего статическую характеристику, приведенную на рис. 1.1,г,
подан случайный процесс, то на его выходе получаем случай-,
ную последовательность дискретных отсчетов. Погрешность
квантования в этом случае (рис. 1.1,а) также является
случайной функцией. Так как зависимость А от х является периоди-
50

Рис. 3.1. Зависимость статической
погрешности квантования от
преобразуемой величины
/-faVzoV^Xvqv'a
чп
Ч V2<i х
-у/?
ческой функцией (рис. 3.1), ее разложение в ряд Фурье имеет
вид
(3.12)
Тогда математическое ожидание случайной функции Д(/)
можно представить в виде
+ 0О
Л {t) = I "7 S "Чг-sin ("Т"х)Рх {Х' ° dx' (3J3)
—00 k=l
При стационарных случайных процессах закон
распределения х не зависит от времени, следовательно, А также не
зависит от времени. Однако даже при центрированной случайной
функции x(t) в общем случае математическое ожидание
погрешности не равно нулю. Только при выполнении условия
(3.11) Д=0.
Второй смешанный начальный момент случайного процесса
А(/) по определению имеет вид
Яд &, А) = И Д1 &> А* ('«> Р <Ль А- 'ь Q <**,<**„ (3. Н)
At Аз
где р(Аь Аг, t\t t2) —двумерная плотность распределения
вероятностей.
Выражение отличается от корреляционной функции
(второго смешанного центрального момента) отсутствием
центрирования Ai(/) и А2(^).
Корреляционная функция случайного процесса Д(/) будет
ЯааРь g = J J[M'i)-M«][MU-M'.)] X
Ai Да
Хр(Дь Д„ *i, Qd^d^. (3.15)
Нетрудно получить связь между 5д(^, *2) и #дд(/ь ^):
Ядд &, ',) = Вд &, О - А (/г) I (t2). (3.16)
51

В случае стационарного входного сигнала, как следует из
(3.13), Д(^) = Г . -Д.
Рассматривая Д как функцию х, в соответствии с
выражением (3.12) получаем
—00 —00 k=l П=\
X sin Г—*2(д1/?(*!, x2> h, ti)dxldxi — ~R(t1)l(t2) =
00 OO +00 + OO
«=1 fc=l —oo —oo
X sin Г— x2 (gl /7 (jc15 xf, <ь g dxxdx2 — A (^) Д &)• -
(3.17)
Подставив в (3.17)
2ш
sin
sin
2tcAi
1 I2imxl(ti)lq -n*nxx(tx)lq
ге — е
l . j2nkx2(t2)/q —j2nkx2{t2)fq
e — e I
и учитывая, что двумерная характеристическая функция
определяется следующим выражением:
+ оо +оо
/>(*i> *2> *i. t2)dx,dx29 (3.18)
PxlXA®i, ®«, 'ьУ= J J e
определяем
оо оо
Ялл (*lf у - — >, ^ —-— [pXi
2пп 2nk , . \
Xi I , , h> h
n=lk=l
2nn 2nk
+ Pxxx2
2m
-p.
XiX,
2wi
2nk
, tu *,)
M'i)M'2) =
«=+oo &= + oo
(3:i9)
rt=—oo &=—oo
52

где PXlx2 ( , , tl9 tA—двумерная характеристическая
\ q q I
функция случайного процесса x(t) при t=t{ и t=t2,
определяемая выражением (3.18) при (u\ = 2nn/q, (u2=2nk/q.
Таким образом, при произвольном законе распределения
плотности вероятностей квантуемого сигнала для определения
корреляционной функции погрешности необходимо знание
двумерной плотности распределения вероятностей x(t).
Для гауссовских центрированных стационарных процессов
двумерная плотность распределения вероятностей
определяется выражением (1.8) при
mXi = тх% = 0, aXi = оХ2 = оХУ г = Rxx (т)/о/ = рхх (т),
где рхх{х) — нормированная корреляционная функция;
Рхгхш К, 0)2, t± — t2 = z) = exp j— -i- q/ « + G)22 + 2(^fDjfxx (x)]J.
(3.20)
Подставив (3.20) в (3.19), получим
/г=—оо /г=—оо
-* =: IT £ £ '"Т^Гe-2^<"*+*J)^ sh [4Aifa,- Рхх (,)/Л - д«.
/1=1 £=1
(3.21)
Если принять допущение, что ь2хх^>Я2> то, как было показано
выше, А = 0.
Кроме того [15],
/?лл (,) ^ -£- fl -Ь е-^'^Р^) Vrt«e (з.22)
V 2ТС2 ^J Л2 V
rt=l
В частности, при т=0 #дд(0)=<72/12, что соответствует
результатам, полученным при статическом расчете.
Получим далее взаимную корреляционную функцию
входного сигнала x(t) и погрешности квантования А(0:
+ оо +оо
Rxb(h, t2) = j ][Х^)-Х(^]\^)-1^)]Р^(Х, Д, tlt t2)dxdb =
—ОО —00
+ оо +*оо
= j J *(*i)A(',Jp(*. Д, tlt tidxd&-x(tt)I(tt), (3.23)
—ОО —00
53

где Рха(х, A, tu t2) —двумерная плотность распределения
вероятностей.
При центрированном входном сигнале x(t\)=0 и второе
слагаемое (3.23) обращается в нуль. Так как Д является
функцией х, то выражение взаимной корреляционной функции»
представим в виде
+ 00 +00
Ял (к, к) = J (' х1 (д Д [xt (g| р(xlt хг, tlt g dXldx2. (3.24)
—оо —оо
Подставив в (3.24) зависимость Д[х2(/2)], заданную рядом
(3.12), получим
k=i
—ОО —00
X
[2nk I
— х2 (/,) р (хъ хШ9 tl912) dxxdx2. (3.25)
Так же как при выводе формулы корреляционной функции
погрешности квантования, можно показать [14, 15], что
&= + оо
RxA(tlt t2) =
(-D*+1
2тс
k=—оо
, (3-26)
Jco1=0
где сомножитель в квадратных скобках представляет собой
частную производную двумерной характеристической функции
входного сигнала при coi = 0 и'о)2=2яй/^.
Если квантуемый сигнал — гауссовский центрированный
случайный процесс, заданный своей корреляционной функцией
о2хрхх (т), то
dP (cox, 2nk/q, t = /1 — t2)
XtX2
dtox
2nk
°*Ш9М*-**'4*.
|tt>!=o q
Подставив это выражение в формулу (3.26), получим
взаимную корреляционную функцию погрешности квантования и
входного стационарного гауссовского центрированного сигнала:
ЛлМ = 2ох»р„М2(-1)*е"8"^Т
(3.27)
k=\
Анализ этого выражения показывает, что абсолютная
величина взаимной корреляционной функции — порядка 10~8
значения корреляционной функции входного сигнала. Поэтому
погрешность квантования гауссовского стационарного
центрированного входного сигнала x(t) при o2x/q2>l можно считать
54

некоррелированной с x(t). В этом случае нелинейный элемент
может быть заменен сумматором, на один из входов которого
подан сигнал x(t)f на второй — помеха А, некоррелированная
с сигналом, корреляционная функция которой определяется
выражением (3.22).
Оценки погрешностей квантования случайных сигналов и
помех. Если на вход нелинейного элемента поступают случайный
сигнал и аддитивная помеха K(t)f статистически не связанная
с сигналом, то погрешность преобразования в фиксированный
момент времени
Д = /нэ (х 4- 1) — х = /нэ (X + Я)- (х + Я) + Я, (3.28)
где /нэ (•) —ФункЦия> описывающая статистическую
характеристику НЭ (см. рис. 1.1,г) при соответствующем значении
аргумента.
При известных х и X величина А является
детерминированной, поэтому ее условную плотность распределения
вероятностей можно записать в виде б-функции:
р (Д/х, Я) = 8 [А - /нэ (х + Я)- Я], (3.29)
откуда трехмерная плотность-распределения вероятностей
р(А, х, Я)=р(Д/х, К)р{х9 1) =
=р(А/х, К)рх(х)рь{к)9 (3.30)
где рхСк) —плотность распределения вероятностей помехи.
В (3.30) учтена статистическая независимость х и Я.
Интегрируя р (A, xf К) по х и Я, получаем закон распределения
погрешности квантования при наличии помехи:
Рь(*) = Цр(Ь>х> QdxdX. (3.31)
Введем обозначение хх=х-\-Х. Тогда Ыэ(х{) = kq при kq—
—0t5q^Xi^kq+0,5q и
Pl(л) = 1 1 2 »[4-*?+ *i-*lрх(■*!-*)Рх(Я)dxj Л=
—оо [_kq—0,5q k~—oo J
&7+0,5<? fc= + oo
= J 2 iM*i — Д + Л/— Xi)Px(b — kq + xJdXi^
kq—Q,5'q k=—oo
fc= + oo A+0,5?
= S j PxW^M*<7-A)- (3.32)
&=—oo Д—0,5q
Переход от плотности распределения вероятностей (3.32)
к характеристической функции осуществляется так же, как и
55

в случае отсутствия помехи на входе нелинейного элемента.
В результате [14] получаем
?A(») = V4 (-Шрх^ + ^Ц *чо,№+**тш (з.зз)
U \ q ) \ Я I 0,5<7(со + 2^/?) . V
Если выполняется условие (3.11), или при а2*><72 имеем.
Яд (аз) = рх (аз) sin 0,5<7G)/(0,5<7cd), . (3.34)
откуда следует, что характеристическая функция погрешности
квантования сигнала и помехи равна произведению
характеристических функций помехи и величины, равномерно
распределенной в пределах интервала квантования.
Таким образом, при выполнении условия (3.11) или при
o2x*>q2 закон распределения погрешности квантования сумм
независимых случайных величин х и Я равен композиции
законов распределения случайной величины Я и статистически не
связанной с ней случайной величиной, равномерно
распределенной в пределах интервала квантования.
При использовании аппарата характеристических функций
подобно тому, как это осуществлялось при отсутствии помехи,
в [14] показано, что при выполнении (3.11) или при o2x^>q2
погрешность квантования центрированных гауссовских
процессов x(t) и Я (О практически не коррелирована с этихми
процессами. Тогда при выполнении указанных условий НЭ может
быть заменен сумматором, на "один вход которого подан сигнал
х(t), на другой — помеха Я(0, а на третий — погрешность
квантования, корреляционная функция которого определяется
выражением (3.22) после замены [1—рхх(т)]о2х на [o2x-{-oh—
—о2хрхх (т) — Лрп (г) ].
3.2. ОЦЕНКИ МЕТОДИЧЕСКИХ ПОГРЕШНОСТЕЙ
НЕРАВНОМЕРНОГО КВАНТОВАНИЯ ПО УРОВНЮ
Неравномерное квантование.по уровню реализуется НЭ,
статическая характеристика которого приведена на рис. 3.2.
Диапазон изменения входного сигнала — от х0 до **, число
уровней квантования zu z2,...,zk равно k. В общем случае
#«+1 —Xi ^Xj+i —Xf.
При Xi-i^x^JCi текущее значение погрешности квантования
на t-м шаге At=Zi—x. Условная плотность распределения
вероятностей Д/ при фиксированном z/ определяется выражением
pA(^tlzi) = 1p—px(zi — Ll) при zj —*|<Д,<г, —*|_ь (3.35)
56

Рис. 3.2. Кривые, поясняющие
неравномерное квантование по уровню
xfz2
*-
-?-
ж~г
э2
7&
Г
II I I
*г хз хь х5 х*
где Р(гг)= f px(x)dx — вероятность появления уровня гь отку-
ч-1
да математическое ожидание абсолютной погрешности
^квантования на i-M шаге дискретизации имеет вид
Д,*= Г -^-px(zt — A,)dA,= Г ^^px(x)dx =
J P(2t)HxK ' l) ' J P(Z,) PXV '
"' ^(z,
ry J V,W
d* = Z| — хь
(3.36)
где &— математическое ожидание х на i-м шаге квантования.
Математическое ожидание абсолютной погрешности
квантования на всем диапазоне изменения входного сигнала
определим путем усреднения А,:
_ k k i=k xi
1 = 1 / = 1
t=l л:
i-1
= 2г* J Px(x)dx— J хр(л:)
dx.
/ = 1 JC
Второе слагаемое этого выражения является
математическим ожиданием х входного сигнала. Отсюда
<
= У г% Г рх (х) dx —х.
i=l x
i—l
(3.37)
57

Дисперсия абсолютной погрешности на i-м шаге
квантования имеет вид
_ *r*i-i
V = j (b-WpiuJzddbt. (3.38)
z.-x.
Подставив (3.35) и (3.37) в (3.38), имеем
*i -
J P(zt)
xi-i
Усреднив величину Д2,- по всему диапазону входного
сигнала, получим дисперсию погрешности неравномерного
квантования:
Д«= 2p(zi)^= % j (x-xirPx(x)dx. (3.39)
t = l i=\ x._1
Таким образом, при заданном законе распределения
входного сигнала и • фиксированной статической характеристике
квантующего устройства математическое ожидание абсолютной
погрешности квантования вычисляем по (3.37), дисперсию — по
(3.39). При расчетах погрешности неравномерного
квантования используются также оценки, основанные на критерии
среднего риска [16, 17, 18]. Пусть ср(х, zt) — функция,
указывающая, какой «штраф» платится за представление квантуемой
величины Ху находящейся в интервале от x,_i до хи величиной
zt. Тогда средний «штраф», полученный при условии, что на
выходе квантования формируется сигнал zt, определяется
выражением
Ji = р(^у j Ф (х9 zt) px \x) dx. (3.40)
Средний «штраф» (средний риск) по всему диапазону
величины х получим как математическое ожидание Jr.
к k xi
1=1 <=1 xt-1
Если положить (f(x, Zi) = (zi—x)2, то определим
квадратичную оценку погрешности квантования [16]:
^, = ,2 j (zi-x)tpx{x)dx. (3.41)
'-1 **-!
58

Так как в общем случае Х{фг'1у оценки (3.39) и (3.41) не
совпадают. Однако если дисперсия входного сигнала много
больше квадрата максимального шага квантования и z,-=
= (Xi_i-\-Xi) /2, то распределение погрешности внутри шага
квантования может быть принято равномерным. При этом xi=
=zi и, следовательно, /Кв=А2.
3.3. ОЦЕНКИ МЕТОДИЧЕСКИХ ПОГРЕШНОСТЕЙ
КВАНТОВАНИЯ ПО УРОВНЮ ПРИ ПРОМЕЖУТОЧНОМ
ПРЕОБРАЗОВАНИИ АНАЛОГОВОГО СИГНАЛА В ЧАСТОТУ
И ВРЕМЕННОЙ ИНТЕРВАЛ
Квантование сигнала в АЦП последовательного счета
осуществляется при преобразовании частоты или временного
интервала в цифровой эквивалент.
В АЦП с промежуточным преобразованием во временной
интервал и в АЦП с промежуточным преобразованием в
частоту при наличии циклического частотомера преобразование
осуществляется однотипными устройствами, в основе которых
лежит подсчет числа периодов импульсного сигнала за некоторый
временной интервал (см. § 2.2 и 2.3).
Зависимость цифрового эквивалента N от длительности
временного интервала Т или частоты f при использовании
циклического частотомера определяется в соответствии с рис. 2.5,6
и 2.10,6 выражением (2.10).
С учетом ограничений, накладываемых на 6i и 62 в (2.10),
суммарная статическая погрешность Д заключена в интервале
— 1<Д<+1. (3.42)
При этом с учетом (2.10)
A=62_6i = 77-N, (3.43)
где
N=E[Tf+8{b .(3.44)
Е означает взятие целой части числа, полученного в результате
вычислений по формуле, заключенной в квадратных скобках.
После подстановки (3.44) в (2.10) получаем
A=62_61 = r/-£[rf+6i]. (3.45)
Выражение (3.45) устанавливает детерминированную
зависимость между бг и Ь\ при заданной величине Tf. Отсюда
суммарная погрешность преобразования не может
рассматриваться как разность независимых случайных величин.
Статистически независимыми случайными величинами
являются Tf и Si. Очевидно, что для случайной величины 6i спра-
59

/wA'l)={(
ведлив закон равномерной плотности вероятности
1/х, если 0<Д^<х;
О в остальных случаях;
A.ft>-lj'"",0<'l*l! (3.46)
10 в остальных случаях.
Возникает задача определения закона распределения
величины А [19]. В общем случае она формулируется следующим
образом: дана детерминированная зависимость Д=<р(Г/, 6i),
определяемая выражением (3.45); задан закон prf(Tf)
распределения измеряемой величины Tf и определен закон (3.46)
распределения составляющей погрешности бг, требуется
определить закон Рд(А) распределения Д.
Рассмотрим решение этой задачи. Так как А=бг—6i и 0^
^бг^1, то имеем при O^A^l
0<6i<l— A, (3.47)
при — КД<0
—A<6i<l. (3.48)
Условная плотность распределения вероятностей
р(Д/6ь Tf)=*[b-Tf+E{Tf+6x)]9 (3.49)
где б[...]—дельта-функция от соответствующего аргумента.
По теореме умножения плотностей распределения
вероятностей получаем
р(Д, Tf, 6i)=p(A/6b Tf)p(8u Tf), (3.50)
где р(Д, Г/, 6i), p(6i, Tf) —соответственно трехмерная и
двумерная плотность распределения вероятностей.
Так как случайные величины 6i и Tf независимы, то
р(бь Tf)=p6l(8l)pTf(Tf). (3.51)
После подстановки (3.49) и (3.51) в (3.50) и
интегрирования по области изменения 6i и Tf получаем
р (Д) = J f 8 [Д - Tf + Е (Tf + 8,)] р (8,) pTf (Г/) MydTU (3.52)
8i Tf
откуда с учетом (3.46), (3.47), (3.48) определяем
1 ]А / J 8 [ Д - Tf + E(Tf + 8l}] pTf (Tf) dTj\ dtl9
0 Tf '
,.. i если 0<Д<1;
/'jf^i , (3.53)
j | J 6 [Д - Tf + E (Tf + bj] pTf (Tf) dT}J dtlt -.
-A v77
если — К Д < 0.
60

+ 00
Так как j f(x)8(x — a)dx = f(a)9 а такл.е с учетом того,
— 00
что из физических соображений l^Tf^oo, взятие интеграла
в фигурных скобках сводится к определению корней
следующего уравнения по переменной Tf:
A-Tf+E(Tf+6x)=0.
Это уравнение преобразуется в тождество при
Tf-A=E(Tf+80=ky k=l, 2,...
Отсюда
Tf=A+k. (3.54)
После подстановки (3.54) в (3.53) получаем
РЛ*)=\
2/77,/(^ + Д)(1-Д), если 0<Д<1;
k=i
(3.55)
%pTf(k+ &)(! +А), если -1<Д<0.
Анализ выражения (3.55) позволяет утверждать, что
плотность распределения вероятностей погрешности
рассмотренного преобразования в общем случае зависит.от закона
распределения измеряемого параметра.
Для определения некоторых общих свойств плотности
распределения вероятностей погрешности получим ее
характеристическую функцию:
ЯаИ= f /7д(Д)е/(оЛЙД= j %pTf(k + A)(l + A)ei<oAdb +
-00 —1 k=\
1 00
+ j £pr[(& + k)(l-b)e"*db. (3.56)
0 k=\
При этом
00 00 00
2prf(A + *)= $PT,{x) 2>4x-k-A)dx.
k=l О k=\
Так как pTf(x)=0 при *<1, то
00 + ОО £=-fOO
%Ртг(Ь + к)= I Рт№ S 4x-k-A)dx.
k—\ — оо k=—оо
61

Рис. 3.3. График закона распределения
Симпсона
ft=+oo fc= + oo
Учитывая, что 2 8(;с —Л —А) = 2 е/2*(*~Л)*, находим
&=—00 &.=—ОО
fc= + oo +оо
2^г/(А + д)= 2 1 ^/Ие
/2itfc(*—А)
Л=1
&=—оо — оо
£=оо
*=-оо
(3.57)
где PTf(2nk) —характеристическая функция измеряемой
величины при значениях аргумента, равных 2nk.
После подстановки (3.57) в (3.56) и несложных
преобразований выражение характеристической функции погрешности
примет вид
&= +оо
Рд(ю)= V PTf(2vk)\sm "~2nk /(со—2^)/2l2. (3.58)
fc=-oo
Прежде чем перейти к анализу выражения (3.58),
рассмотрим характеристическую функцию треугольного закона
распределения (закона Симпсона), график которого приведен на
рис. 3.3.
Характеристическая функция закона Симпсона
о 1
Рс (©) = J (1 + Д) е/юА dA + J (1 — Д) e/wAdA = sin2 со/со2. (3.59)
-i о
Выражение (3.59) совпадает с (3.58), если
PTf(2nk)=0 при 1гфО.
(3.60)
Как следует из материалов, приведенных в предыдущем
параграфе, условию (3.60) удовлетворяют распределения Tf
с равномерной плотностью вероятности при целом {Tf)max и
распределения Tfy полученные как сумма нескольких
случайных величин, одна из которых имеет равномерный закон
распределения при целом Tf. Если среднеквадратическое
отклонение Tf много больше единицы, то закон распределения
погрешности квантования приближается к закону Симпсона. -
Этот же результат при выполнении условия (3.60) можно
получить, используя методику, рассмотренную в предыдущем
62

параграфе. Положив Tf=x и заменив взятие целой части Е(х)
на операцию —<7/2+/нЭ{*), где fH$(x) описывается
статической характеристикой нелинейного элемента, приведенной на
рис. 1.1,г при q=\y преобразование временного интервала
(частоты) в цифру сведем к квантованию суммы случайных
величин х и Я=—1/2+бь Так как 6i равномерно распределена
от 0 до 1, то Я равномерно распределена от —1/2 до +1/2 и
характеристическая функция имеет вид Р\ — sinW > Тогда
со/2
характеристическая функция случайной величины погрешности
квантования в соответствии с (3.34) имеет вид
sin(co/2)
/V©)-
<о/2
что соответствует закону распределения Симпсона.
Анализ выражения характеристической функции
погрешности позволяет сформулировать следующее положение:
математическое ожидание погрешности рассматриваемого
преобразования равно 0 и не зависит от закона распределения
случайной измеряемой величины.
Докажем это положение. Известно [1, 2].определение
математического ожидания по характеристической функции
случайной величины
" dP(u>)
II асо J(o=o
(3.61)
Из (3.58) получаем
dPA (со)
dco
fc=+°° sin
V PTf(2*k)2
*=-oo
со— 2nk
(со — 2тг^)/2 d(o
Tsin^
2nk
2nk)j2
sin-
= 2-
©/2 da
[sin— "I fc=+oo
k=—oo
PV*k)X
sin
со — 2nk
со— 2nk
X2
sin
—— •
(со —2тс/г)/2 J
(3.62)
(со— 2*£)/2 dco L(w —2тс/г)/2.
Пусть теперь со = 0. Тогда все слагаемые в последней сумме
обращаются в нуль. Кроме того, известно, что -
dx, I
sin-
sinx
.] =0.
J*=0
, Г s'n— 1
— —-
dm L to/2 Jw=0
Поэтому
dm L 0)/2
требовалось доказать.
0. Значит,
4PA (о)
dco
= 0.
|w=0
что и
63

Так как А — центрированная случайная величина, дисперсия
погрешности определяется выражением [1]
--[■
<№д И
dco2
Подставив (3.58) в (3.63), найдем
£= + 00
(3.63)
(о=0
A2 = J У! PTf(2rM)^—t (3.64)
*=-оо
При выполнении (3.60) А2= 1 /6, что соответствует
дисперсии при треугольной плотности вероятности.
Одним из способов уменьшения абсолютной погрешности
является синхронизация переднего фронта импульса
временного интервала со счетным импульсом. При этом 6i=0 и Д=8г=
= Tf-E(Tf).
Закон распределения А определяется следующим
выражением:
/>а(Л)= ZPTf(k + b) приО<Д<1. (3.65)
k=\
Учитывая соотношение (3.57), получаем
Рь (*) = "if е"/2те"А Ртг (2«ft). (3.66)
Отсюда закон распределения погрешности преобразования
при синхронизации передного фронта импульса временного
интервала и счетного импульса зависит от закона распределения
измеряемой величины.
При выполнении (3.60) рд(Д) = 1 при O^A^l, что
соответствует равномерной плотности распределения вероятностей
погрешности квантования по уровню.
Характеристическая функция погрешности преобразования,
закон распределения которой имеет вид (3.66),
W- %рмы) '„.->*)• <3'67)
k=—ОО
Выражение средней погрешности преобразования получаем
после подстановки (3.67) в (3.61):
2 ^ U 2nk Л '
*=-оо
64

Аналогично, выражение второго начального момента
погрешности преобразования определяется подстановкой (3.67)
в (3.63):
Mn = i-"fpM2,k)^±L. (3.69)
fc=-00
При выполнении условий (3.60) А=1/2; Л1(Д2) = 1/3 и
А2=1/12, что соответствует моментам равномерного
распределения.
Для вычисления погрешности преобразования в некоторой
точке Tf требуется определить условную вероятность А при
заданном Tf.
Пусть 77=&+р, где & — целая часть, (bgfb^l.
В этом случае
b=Tf-N=k+$-E(k+$+8l) =
=*+Р-*-Щр+61)=р-£(р+61). (3.70)
Отсюда следует, что при заданном Tf=k-{-$ величина А
может принимать только два значения:
д fP при 0<р + 81<1;
1р—1 при КР + 8^2.
Учитывая, что 0^6i^l и распределена равномерно,
получаем
Р(А=р/(Г/))=Р(0<б1<1-р) = 1-р; (3.71)
Р(А=р-1/(Г/))=Р(1-р<б1<1)=р, (3.72)
где Р(А=р/(Г/)), Р(Д=р—1/(77)) —условные вероятности
А при заданном Tf.
Тогда максимальная, средняя и среднеквадратическая
погрешности квантования при заданном Tf=k-\-$ определяются
следующим образом:
Г ft ппн R>*0 К-
(3.73)
(3.74)
/ V = КР2(1-Р) + (Р-1)2Р = КР(1-Р). (3.75)
В том случае, когда квантование осуществляется АЦП
последовательного счета с промежуточным преобразованием во
5—6036 65
^а max
\ =
-{
= Р(1
Р
1Р-И
при
при
-Р) + Р(Р-
Р>0,5;
Р<0,5;
1) = 0;

временной интервал с широтно-импульсным модулятором,
имеющим статическую характеристику
Ти = /■"»*"*""" х + Ги0, (3.76)
и max Hmin
где Xmax—хтщ — диапазон изменения входного сигнала; ГИтаХ—
—^итт —диапазон изменения длительности импульсов на
выходе модулятора; Ти0 — длительность импульсов на выходе
ШИМ при х=0, шаг квантования по уровню определяется
выражением
я= (ТХтяСтт1п»> (3-77>
v и max йт!п''
где f — частота следования счетных импульсов.
Тогда погрешности квантования по уровню определяются как
<7Д, q V А2, <7Дтах, flA» qV V, <7Д a max»
Аналогично, если квантование осуществляется АЦП
последовательного счета с промежуточным преобразованием в
частоту с частотно-импульсным модулятором, имеющим
статическую характеристику
/*= ?maxZ!m'"* + /o, ■ (3.78>
'max 'min
то шаг квантования по уровню определяется выражением
V > V
п max mln /о 7Q\
4=Tf—~f—W' ( '
v,max 'min'
где T — длительность эталонного временного интервала.
Тогда оценки погрешности квантования по уровню при
данном значении q определяются так же, как и в предыдущем
случае.
Приведенный анализ точности преобразования временных
интервалов (частоты) в цифровой эквивалент осуществлен на
идеальной модели, не учитывающей конечной длительности
счетных импульсов и быстродействия счетного устройства.
Ниже рассмотрены характеристики погрешности квантования без
принятых выше допущений.
Пусть tn — длительность счетного импульса; tn —
длительность паузы; т=/и+^; to — минимальная длительность
импульса на входе счетного устройства, при которой этот импульс
успевает фиксироваться счетным устройством.
Как следует из рис. 3.4, импульс будет зафиксирован
первым в трех случаях: а) начало tH временного интервала Т
совпадает с нулевым импульсом, причем время между tH и задним
66

т
tn
*
0
*и
** '
A*1
-e
*C
1
*H
-~~
in
^ -**
T\—
—1«|
»
_,
4i
4 ^*2
Й1 t
к
*0
/i^T]
t
Рис. З.4. Временная диаграмма работы преобразователя частота — цифровой
эквивалент с учетом конечной длительности импульсов счетной
последовательности
фронтом нулевого импульса меньше, чем t0\ б) tH совпадает
с паузой между импульсами нулевым и первым; в) /н совпадает
с 1-м импульсом, причем время между tH и концом этого
импульса больше t0. Импульс N будет зафиксирован в трех
случаях: а) конец временного интервала *к совпадает с N-м
импульсом таким образом, что время между передним фронтом
этого импульса и задним фронтом временного интервала
больше /0; б) tK совпадает с паузой между Af-м и .V+1-м
импульсами; в) tK совпадает с Af+1-м импульсом, причем время между
передним фронтом N-j-1-го импульса и tK меньше t0.
Введем обозначения: Д^ — интервал времени между
передним фронтом временного интервала Т и моментом времени,
в который нулевой импульс уже не фиксируется счетным
устройством; А/2 — промежуток времени между задним фронтом
временного интервала Т и предельным моментом времени,
в который ЛЛ-й импульс еще фиксируется счетным устройством.
Тогда связь между длительностью временного интервала Т и
цифровым эквивалентом для любых положений tH и £к
относительно счетной последовательности при фиксации счетным
устройством числа N определяется выражением
T=N%-Ml+At2-tli+2to9 (3.80)
где 0^A/i<t; 0<Д*2<т, откуда
Tf=N-8l+b2-tnf+2t0f и
(T+tK—2t0)f=N-6l+82=N+A. (3.81)
Из этого выражения следует, что для обеспечения точного
преобразования частоты (временного интервала) в цифровой
эквивалент требуется стабилизировать длительности /и и t0f
а также учесть их при калибровке АЦП. При использовании
современных быстродействующих элементов счетного
устройства можно обеспечить t0= 1(Нч-10-67\ поэтому временем
срабатывания триггера младшего разряда счетчика можно
пренебречь. Стабилизацию ^и получают, используя
высокостабильные хронирующие элементы. Возможно и другое решение —
5* 67

обеспечение постоянной относительной длительности импульса
Э = /и/т=/и/ на выходе частотно-импульсного модулятора. Так,
при использовании в качестве ЧИМ мультивибратора Роера
0=1/2; при любом другом модуляторе можно получить 8=1/2,
осуществив деление на два частоты модулятора триггером со
счетным входом. В этом случае при условии, что t0<^Ty
77+е=ЛГ—61+62. (3.82)
Величина 0 = const легко компенсируется при построении
АЦП. Из (3.82) следует, что статические оценки погрешности
квантования А=б2—6i совпадают с полученными при
рассмотрении идеальной модели. В случае ^=const и t0<g.T оценки А
совпадают с полученным на идеальной модели при замене Т
на Г=Г+/И.
Квантование в АЦП последовательного счета с
промежуточным преобразованием в частоту и частотомером с линией
задержки. Квантование осуществляется в соответствии с
временной диаграммой, приведенной на рис. 2.11,е. Погрешность
квантования по уровню Aj на участке длительностью A^i
определяется выражением (2.13), погрешность квантования А2 на
участке длительностью т—A/i — выражением (2.14). Как
указывалось в § 2.3, максимальное значение погрешности
преобразования А равно ±1 младшего разряда реверсивного счетчика.
Если определить среднюю погрешность квантования как
.и подставить в это выражение Ai и Д2 из (2.13) и (2.14), то
д = М ГС^1—i)A/1 + a1(x—A/^-j = ^
где М — математическое ожидание случайной величины
в квадратных скобках.
Аналогично определим дисперсию квантования по уровню:
Из (2.13) и (2.14) следует, что Ai = A2— 1, а так как А2 и Ai
различаются только на детерминированную величину, то их
дисперсии равны. Отсюда
V = Д?; Д"2 = Л/ [Д22] = Д?- (3.83)
Как следует из (2.14), Д2=в'ь что соответствует
погрешности квантования по уровню в циклическом частотомере при
наличии синхронизации счетных импульсов с передним
фронтом временного интервала. В связи с этим закон распределе-
68

ния A2=6i совпадает с выражением (3.65) и Л1(А2)
определяется по формуле (3.69):
Д2=Л1(Д2)-[ДР,
где ^ — математическое ожидание погрешности
преобразования, вычисляемое в соответствии" с (3.68).
При выполнении условия (3.60) получим Д=1/2; А2= 1/12.
Если преобразованию подлежит некоторая фиксированная
частота /, то погрешность квантования является
детерминированной величиной, определяемой выражениями (2.13) и (2.14).
У АЦП последовательного счета с промежуточным
преобразованием в частоту и частотомером следящего
уравновешивания оценки погрешности квантования зависят от его
конкретной схемной реализации. Максимальная погрешность
квантования определяется единицей младшего реверсивного счетчика.
3.4. ОПТИМАЛЬНОЕ НЕРАВНОМЕРНОЕ КВАНТОВАНИЕ
ПО УРОВНЮ
Смысл оптимального неравномерного квантования по
уровню заключается в уменьшении шагов квантования для более
вероятных значений входной величины х за счет увеличения
их для менее вероятных с целью минимизации оценки
погрешности преобразования. Если проводить аналогию с
измерительным прибором, то неравномерное квантование эквивалентно
введению нелинейной шкалы, позволяющей более точно
измерять входной сигнал на одних участках шкалы за счет менее
точного измерения его на других.
Формализуем постановку задачи оптимального
неравномерного квантования [16, 17, 18]: заданы одномерный закон
распределения рх(х) квантуемой величины х, находящейся в
диапазоне от х0 до xk (см. рис. 3.2); число уровней квантования —
k\ фиксирована оценка погрешности преобразования /,
определяемая функционалом (3.41); требуется найти такие
параметры zu z2i...,zky xu x2t xZf...,xd-u чтобы обеспечить минимум
функционала (3.41).
Необходимые условия минимума функционала (3.41)
составляет система уравнений
dJ/dxi=0f i=\y 2,...,fe-l; (3.84)
dj/dzi=0t i=l, 2,...Л Ч (3.85)
В этой системе содержится 2k— 1 уравнений и столько же
неизвестных. При квадратической оценке погрешности условия
69

(3.84) имеют вид
dJ
дхс дх;
Г (x — zt)2px(x)dx + f (x — zi+1)2px(x)dx
= 0.
После дифференцирования по xt получаем
(xi—zi) 2px (xi) — {xt-Zi+t) *px (xt) = 0. (3.86)
Если принять физически оправданное допущение рх{х1)фЪ\П\)К
Xo<x<xky то с учетом поставленной задачи при г{Фг\+\ из
(3.86) находим
Xi={zi+zi+l)/2. (3.87)
Переходим к рассмотрению условчй (3.85):
f=.p
2(x — zi)px(x)]dx = 0; (3.88)
Г {х — Zi)px(x)dx = 0. (3.89)
xi-i
Введем обозначения с учетом уравнения (3.87): х*0—х0,...,
x*i= (Zi+ziH)/2,.. .,x*k=xk, i=l, 2,...,k— 1.
При этом (3.89) имеет вид
f (x — Zi)px(x)dx = 0. (3.90)
<-i
Условия (3.90) содержат k уравнений и k неизвестных.
Решить эту систему уравнений аналитически, как правило,
не удается за исключением тривиального случая,
соответствующего равномерной плотности вероятности» квантуемой
величины при х0<^х^хк. Поэтому обычно используются либо
итеративные вычислительные процедуры, сходящиеся к решению
этой системы уравнений [16, 17], либо аналитические
выражения, приводящие к приближенному решению задачи. Методы
решения системы уравнений (3.90) приведены в [17]. В [16]
указано, что при выполнении накладываемого на плотность
вероятности квантуемой величины, ограничения вида
d2\npx(x)/dx2<0 (3.91)
для всех Хо^х^хк система уравнений (3.90) содержит
единственное решение, соответствующее минимуму функционала
70

Рис. 3.5. Кривые, поясняющие
нелинейное преобразование параметра с
целью получения неравномерного
квантования по уровню
(3.41). При невыполнении
этого условия возможны
несколько решений, составляющих
локальные экстремумы.
Задача оптимального
неравномерного квантования
значительно упрощается при
большом числе уровней
квантования, когда квадратиче-
ская оценка ' погрешности квантования значительно
больше квадрата максимального шага квантования по
уровню. При этом допущении, соответствующем малости
погрешности квантования и равномерной плотности вероятности
погрешности между порогами квантующего устройства, задача
оптимального квантования сводится к задаче оптимального
нелинейного преобразования параметра [20]. Рассмотрим эту
задачу. Пусть у есть некоторая нелинейная функция
квантуемой величины х. Тогда равномерное квантование у
соответствует неравномерному квантованию величины х (рис. 3.5).
Выбор зависимости у{х), доставляющей минимум дисперсии
погрешности квантования по всей шкале, соответствует
решению задачи оптимального неравномерного квантования.
С учетом условий малости погрешности величин у и х
можно записать
Ay^=Ax^dyjdxy (3.92)
где ДуКв, Ax™ — соответственно погрешности квантования
величин у и х.
В этом случае дисперсия погрешности квантования между
порогами квантующего устройства
D{AyKB) =D(AxKB) (dy/dx)2. (3.93)
Усредненная по всей шкале дисперсия погрешности
квантования
Д2.-=
=J D (Дхкв) рх (х) dx = § -g£§^ рх (х) dx =
= 0(tyjj
Рх(х)
(dy/dxf
dx.
(3.94)
При заданном рх(х) требуется найти такую зависимость
y=f(x), при которой минимизируется оценка Д2 и выполня-
71

ются условия уо=х0 и t/fe=Xfe. Определение f(x) сводится к
задаче с закрепленными концами классического вариационного
исчисления.
Запишем функционал (3.94) в следующей форме:
A2=j F(x9 y,y')dx, (3.95)
где F (х, у, у')= рх (х) I [у' (х) ]2 при *<><*<**. • '
Для функций у{х)у дифференцируемых на интервале х0^.
^x^.xky функция F непрерывна по аргументу у\ у и х.
Уравнение Эйлера для функционала (3.95) имеет вид
F —F', = О
у дх у '
где Fu = = 0; Fu, = = — 2рх (х) —
ду у ду' [</'(*) I3
С учетом введенных обозначений получаем
дифференциальное уравнение относительно экстремали:
дх* (у'Т ^ХК ' {у')* *
откуда
3*lpAx)-*£*WJL=o.
dx2 rxx ' дх dx
Обозначив dy/dx=zf получим
dx дх
xk
У{*) = с<>) VPx(*)<bc + cu
где Со и С\ вычисляются из условия закрепления концов
х° xh
У0 = Ч = с0 J VPx (■*) dx + сг; yk = xk = \ yrpx(x)dx + ci>
откуда
сг = х0; с0 = ^^ ; У(х)= Ч *° х
?* за * 3/
Я« За . Л 3/
j ypx(x)dx j V/bOOdx
л;
xJVpTw^ + ^o. (3-96)
72

Здесь у\х)—функция оптимального нелинейного
преобразования параметра х, обеспечивающая при равномерном
квантовании у неравномерное квантование ху при котором достигается
минимум дисперсии погрешности квантования. Справедливость
данного утверждения распространяется лишь на тот случай,
при котором дисперсия случайной величины х не менее чем на
порядок больше квадрата максимального шага квантования
величины у. При этом закон распределения погрешности
внутри шага квантования по уровню может быть принят
равномерным (см. § 3.1).
Уменьшение дисперсии погрешности квантования за счет
оптимального нелинейного преобразования может быть
оценено следующим образом.
Пусть k — число уровней^ квантования. Тогда при
отсутствии нелинейного преобразования и условии равномерного
распределения погрешности внутри шага квантования дисперсия
погрешности квантования
7Пi = JL - (*fe~ *р)2 _ (Ук-Уо)2 =
12 Л* 12 Л* 12
V-
Я(Д0м).
Отношение дисперсии погрешности квантования при
наличии нелинейного преобразования к дисперсии погрешности при
отсутствии нелинейного преобразования имеет вид
В =
D(byKB)] РхШу1)-*** *k
=\ Рх{х)(у'уЧх,
V
где у(х) определяется выражением (3.96).
Дифференцируя (3.96), получаем
У'(*)-
*k—x*
г. Л 3/
J VPx(x)dx
-VPx{*)>
откуда
В
*k 3
J VPx(*)dx
(ч—ч)2
\Px(x)[VPx(x)] *dx. (3.97)
Рассмотрим пример оптимального неравномерного квантования.
Пример 3.1. Квантованию подлежит случайная величина х,
распределенная по закону Симпсона, диапазон изменения квантуемой величины ±1.
Требуется определить оптимальное -нелинейное преобразование у(х)у
доставляющее минимум дисперсии погрешности квантования, найти дисперсию
погрешности квантования х при числе уровней квантования, равном 10, и определить
выигрыш В.
73

У
•4-1
z
Li
L
zi
7
-1 L
У
/
V
/
Y
л
/
<£±
A
S
з\
У
t\
/'
Л Y
>л
ч у\
\А
У' '
/
+ 1
& Х1 Хг Xj Xif. Х$ X
Л-Zi
J~22
J
~yz3
-Л - 71
1 *
-\-7c
Рис. З.6. Пример нелинейного преобразования
параметра
В соответствии с условием
11 + х при — 1<х*^0;
1-х при 0<х< 1;
О в остальных случаях;
Хо = у0=—1; *л=*/а = 1.
Подставив рх (х) в (3.96) и учтя значения у0 и г/а, получим
(
*(*)="
2 Г zr
"о i \yl + xdx — 1 при" — 1<
j-j^l +xdx+ f-j^l—xdx -i <x<0;
О х
\ y^l +хdx + \ j/'l —хdx
J yT+xdx+ \frT^xdx L~i о
-l 6 при 0<х<1;
в остальных случаях,
откуда
( (х+1) y^x + l — l при —1<х<0;
У(*)
—(1 — x)-j/"l — х + I при 0<х<1;
О в остальных случаях.
График у(х) приведен на рис. 3.6.
74

Определим выигрыш, получаемый в результате оптимального нелинейного
преобразования. Подставляя рх(х), Хь, и х0 в (3.97), имеем
т 12
j-j/l +xdx + J-j/l — xdx\
Б =
2a J
—1
Г (1+x) (l + x)~2/3dx +
+j(I-x)(l-x)-wJ.-|-.
n ' • J
0
Таким образом, в результате проведенного нелинейного преобразования
дисперсия погрешности квантования равна 27/32 соответствующей дисперсии
при равномерном квантовании.
На рис. 3.6 указаны 10^уровней квантования (z,) величин у и х.
Максимальный шаг квантования х по уровню, как следует из рисунка, будет
Яхтах = #5—#4, #5=1.
Значение хА определим из (3.98), получий t/=z4 = 0,7:
0,7= — (1—х4) y^l_x4+l,
откуда 0,3= (1 т— х4) -|/"1 —х4 их4=1- /"(0,3)3.
При этом qmax = -/(0,3)3.
Дисперсия величины х равна
в 1 '
D* — f (i-fx)^dx— j (l-x)2dx:= 1/6,
-1 0
откуда Dx/^ax > 10, что удовлетворяет сформулированным выше
требованиям.
Рассмотренный пример иллюстрирует решение задачи
оптимального неравномерного квантования по уровню, когда
дисперсия преобразуемого сигнала много больше'квадрата шага
квантования по уровню, что, как правило, имеет место во
многих технических приложениях. В том случае, когда это условие
не выполняется, оптимальное квантование по критерию
минимума квадратичной оценки погрешности требует решения
системы уравнений (3.90).

Глава 4
ВРЕМЕННАЯ ДИСКРЕТИЗАЦИЯ
И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
4.1. МОДЕЛИ РАВНОМЕРНОЙ ВРЕМЕННОЙ
ДИСКРЕТИЗАЦИИ, УЧИТЫВАЮЩИЕ СПОСОБ ПОЛУЧЕНИЯ
ЦИФРОВОГО ЭКВИВАЛЕНТА
Выбор модели временной дискретизации определяется тем
математическим аппаратом, который будет использован в
дальнейшем для определения погрешностей, возникающих при
преобразовании аналогового сигнала. Удобные методы для
решения подобных задач представляет теория импульсных систем
[21, 22], использующая для описания дискретизированного по
времени сигнала решетчатые функции, именно этот путь
формализации и будет принят в дальнейшем.
В данной главе рассматривается временная дискретизация
в трактах аналого-цифрового преобразования без учета
погрешностей квантования по уровню.
Решетчатой функцией, соответствующей некоторой функции
e(t) непрерывного аргумента t, называется последовательность
б-функций 8{t\)f б(^2),••-,б(//),..., веса (коэффициенты)
которых определяются значениями e(t) в моменты времени tu
t2y..., U,... Интервал между находящимися рядом б-функция-
ми называют шагом временной дискретизации. Отсюда
следует, что дискретизированный по времени сигнал можно получить
на выходе множительного устройства (рис. 4.1,а), на один вход
которого подан сигнал e(t)9 а на второй — последовательность
б-функций. Отсюда решетчатая функция
y(tt) = e(t) 2 8(*-/,), /=0,± 1, ±2,... (4.1)
Очевидно, что в этом случае шаг временной дискретизации
Ti-x = ti—ti-l. Величина 7Vi может быть как постоянной, так
и переменной, что соответствует равномерной и неравномерной
временным дискретизациям. Переходя на терминологию функ-
«W '
■—*Q
Рис. 4.1. h
i = -oo
1 y(ii) ) eft)
§ -—
a)
Модель временной дискретизации
ИЗ
y(ii) -.
В)
76

ционального анализа имеем, y(ti)=L[e(t)\, где L — оператор,
преобразующий функцию e(t) в y{ti). В том случае, когда U
не зависит от e(t), оператор временной дискретизации
является линейным. Докажем это. Пусть e(t)=e{(t)-\-e2(t). Тогда
У Ci) = L [e, (t) + е2 (01 = \ег (t) + e2 (t)] ~f 8 (t - tt) =
i=oo /=+oo
= ex(/) £ 4t — tj) + et(t) S 8(*-*,) = ![*!(91+£[*,(91.
/=—oo l=—oo
(4.2)
Если e(t)=cex(t), то ,
УVi) = L\cex(О] = ^(/) "2°°8(/-/,) = cL[ex{t)\. (4.3)
/ =—00
Выражения (4.2) и (4.3) удовлетворяют определению
линейного оператора, откуда следует возможность применения
метода суперпозиции при рассмотрении задач прохождения
сигналов через элемент, осуществляющий временную
дискретизацию.
Принято элемент, преобразующий функцию непрерывного
времени в решетчатую, (временной дискретизатор), называть
идеальным импульсным элементом ИЭ (рис. 4.1^5). В
соответствии с (4.1) этот элемент выполняет умножение e(t) на
последовательность б-функций. При равномерной дискретизации
ti=nT (где п — целое число; Т — шаг равномерной
дискретизации) и решетчатая функция
У (',) = У \пТ] = в (/) П~£° 8 (t - nT). (4.4)
п=—оо
Выражение (4.4) соответствует мгновенному
преобразованию функции непрерывного времени в решетчатую.
АЦП последовательного счета с промежуточным
преобразованием в частоту. В преобразователях последовательного
счета с промежуточным преобразованием в частоту и
циклическим частотомером цифровой эквивалент пропорционален
среднему значению модулирующей функции за время
преобразования. Такой способ получения цифрового эквивалента может
быть представлен как временная дискретизация функции e(t)y
значения которой, в каждый фиксированный момент времени
равны среднему значению сигнала x(t) на входе АЦП за
время от t—T до t.
77

x(t)
«1(p)
eft)
ИЭт
У(Ч)
Рис. 4.2. Модель равномерной временной дискретизации, учитывающая
способ получения цифрового эквивалента
В этом случае сигнал, поступающий на вход ИЭ,
еЦ) = у- Г x(t)dt = (lfT)nx{t)dt—^ x(t)di\. (4.5)
t-T L0 0 J
Учитывая, что x(t)=0 при /<0, имеем
t—т t
J x(t)dt = \x(t — T)dt, (4.6)
о о
откуда, взяв преобразование Лапласа от левой и правой
частей (4.5) с учетом (4.6), получим
е(р) = {\-*г*т)х(р)1(рТ). (4.7)
Приведенная формализация позволяет представить
математическую модель временной дискретизации в АЦП
последовательного счета с промежуточным преобразованием в частоту и
циклическим частотомером в виде последовательного
соединения линейного звена с передаточной функцией
iCi(p) = (l-e-PO/(pr) (4.8)
и импульсного элемента (рис. 4.2). Импульсная
характеристика &i(t) этого звена находится как обратное преобразование
Лапласа от К\{р):
М*) = [1(т)-1(т-Г)]/7\ (4.9)
|0прих<0; (Опри*<Г;
где l(x) = {f п 1(т — Т)= , -
v ' 11 при х > 0; v ' [ 1 при х > Т.
Процесс временной дискретизации для данного способа
преобразования иллюстрируется на рис. 4.3,а. Решетчатая
функция условно представлена последовательностью
вертикальных отрезков, высота которых равна весу соответствующей
б-функции. Стрелка в конце вертикального отрезка
символизирует условность изображения б-функции. Такая условность
в изображении последовательности б-функции будет принята
везде. Значения весов б-функций определяются средними
значениями функции x(t) за время Т при (п—\)Т^Л^пТ. Так как
средние значения x(t) на интервалах дискретизации равны
78

,x(t)
_., у\лП
у{(п+1)т\
} y[(n+Z)f]
(n-Z)T (n-1)T nT
(n-2)T (n-1)T nT (n+1)T (ni-Z)T
(n-Z)T
(n-1)T
Рис. 4.З. Временная дискретизация сигнала x(t) с учетом способа получения
цифрового эквивалента:
а — временная дискретизация АЦП последовательного счета с промежуточным
преобразованием в частоту; б — временная дискретизация АЦП последовательного счета с
промежуточным преобразованием во временной интервал с ИШИМ; в — временная
дискретизация АЦП, когда временем интегрирования можно пренебречь; г — временная
дискретизация АЦП поразрядного кодирования с запоминающим интегратором; д — временная
дискретизация АЦП, временем преобразования в котором можно пренебречь
соответствующим мгновенным значениям этой функции, то
можно говорить о том, что результат временной дискретизации
«запаздывает» по отношению к тому мгновенному значению
x(t), которому он соответствует.
Модели временной дискретизации в АЦП
последовательного счета с промежуточным преобразованием в частоту и
частотомерами с линией задержки, следящего уравновешивания бу-
79

/
дут рассмотрены в гл. 7, с преобразователями частота —
цифровой эквивалент по «k периодам» — в § 4.5.
АЦП последовательного счета с промежуточным
преобразованием во временной интервал. В АЦП этого типа при
интегральной широтно-импульсной модуляции (ИШИМ)
длительность импульса на выходе модулятора, а следовательно, и
цифровой эквивалент, ей соответствующий, пропорциональны
среднему значению входного сигнала x(t) за время
интегрирования tQ6=yT (см. § 2.2), где 0<y<1. Учитывая, что
считывание числового эквивалента осуществляется в конце шага
временной дискретизации, получаем.
*-(1-Т)Г
e{t)==ir J x^dT>
t-T
откуда
e{p)=Ki{p)x(p),
где
К, (р) = (e-O-v^-e-pr) J (pyT). (4.10)
При этом импульсная характеристика рассматриваемого
линейного звена
A;1(x) = L-[/C1(/;)] = -L{1^-(l-T)n-lh-n}, (4.11)
У1
где
0 при *<(1_Т)Г; (0прих<Г;
1 при t>(1—у)Г; [Z J 11прит>7\
Таким образом, математическая модель временной
дискретизации для АЦП последовательного счета с промежуточным
преобразованием во временной интервал при интегральной
широтно-импульсной модуляции Т= const может быть
представлена последовательным соединением линейного звена с
передаточной функцией, определяемой выражением (4.10), и
импульсного элемента (см. рис. 4.2). Обратим внимание на то,
что при у=\ выражение (4.10) совпадает с (4.8).
Процесс временной дискретизации для данного способа
преобразования иллюстрируется на рис. 4.3Д Здесь вес 6-функ-
ции на каждом шаге дискретизации равен среднему значению
x(t) при (n—l)T<cit^:(n—l)T+yT за время уТ, а
следовательно, равен соответствующему мгновенному значению x(t) на
рассматриваемом временном отрезке. Поэтому результат
временной дискретизации «запаздывает» по отношению к тому
мгновенному значению x(t)t которому он равен.
1[х_(1_т)Г]
80

В том случае, когда временем интегрирования входного
сигнала x(t) в модуляторе можно пренебречь (рис. 4.3,в) при
Y<1, получаем
e(t)=x(t-T); КЛр)=е-*т; ^(т)=б(т-Г). (4.12)
Результат временной дискретизации «запаздывает» по
отношению к соответствующему мгновенному значению x(t) на
время Г.
Математическая модель временной дискретизации в АЦП
с ШИМ, полученная методом линейной развертки, не совпадает
с рассматриваемой.
АЦП поразрядного кодирования. В преобразователях
поразрядного кодирования при наличии устройства выборки и
хранения с интегрированием входного сигнала за время стро-
бирования цифровой эквивалент пропорционален среднему
значению этого сигнала за время интегрирования (рис. 4.3,г).
Тогда
t
.*(0 = ^г ] *(*)*> (4-13)
t—vT
где 0<v<l; vT — время интегрирования, откуда
e(p)=Ki{p)x(p)t (4.14)
Здесь
Ki(p) = -T7-(l-<rPVT), (4.15)
/Оприх<0; |0прит<уГ,
1(t)==(l прих^О; M'-vr)»^ npH,>vr
При этом способе преобразования (рис. 4.3,г) веса 6-функ-
ций. на выходе импульсного элемента определяются
мгновенным значением входного сигнала, равного среднему значению
x(t) за время т, где nt—^об^т^пГ, п=0, 1, 2 ... Здесь также
имеет место «запаздывание» дискретизированного сигнала по
отношению к соответствующим мгновенным значениям x(t).
АЦП, временем преобразования в которых можно
пренебречь. В преобразователях считывания и накопительных,
поразрядного кодирования с пренебрежимо малым временем строби-
рования входного сигнала цифровой эквивалент определяется
мгновенным значением x(t) (рис. 4.3,(3), т. е. e(t)=x\t). В этом
случае временной дискретизацией является модель
мгновенного преобразования непрерывной функции в решетчатую в соот-
6—6036 81

ветствии с (4.4). С целью получения общих результатов для
случая мгновенного преобразования запишем
е(р)=Кх(р)х{р), . (4.16)
где
Kx(p) = U *i(t)=6(T). (4.17)
Модель равномерной временной дискретизации [23].
Обобщая изложенное, можно сделать следующий вывод: модель
равномерной временной дискретизации может быть
представлена последовательным соединением линейного звена К\{р),
учитывающего способ получения цифрового эквивалента и
импульсного элемента ИЭ, с постоянным шагом дискретизации Т
(рис. 4.2).
Связь у[пТ] с x(t) получим, воспользовавшись интегралом
свертки. Так как е(р)=К\(р)х(р), то
t t
e(t)= [ ^(х)^^—x)dx={^(x)*1(/ — x)d% (4.18)
о о
откуда
t 00
y\nT\^lx^)k1(t — %)dz^b(t — nT). ' (4.19)
6 п=0
Оператор, определяемый выражением (4.19), является
линейным, что доказывается так же, как линейность оператора
(4.1).
Модели временной дискретизации при работе АЦП в
многоканальном режиме. Рассмотренные модели равномерной
временной дискретизации получены при работе АЦП в однока-
нальном режиме. В случае преобразования N аналоговых
сигналов одним АЦП при временном разделении (рис. 4.4)
канала преобразования передаточные функции звена К\(р) должны
учитывать режим получения цифрового эквивалента. Так, для
АЦП с промежуточным преобразованием в частоту и
циклическим частотомером преобразование по первому каналу
осуществляется за время от t\ до (п—1)Г (рис. 4.5,а), по второму —
*i(t) У1
xz(t)
АЦП
Уг
xnW , Уы
Рис. 4.4. Преобразование N аналоговых сигналов одним аналого-цифровым
преобразователем
82

XtftK
1
I
*/
. r
^ 1
\ 1
1
i
(n-f)T tz
■*
T
1
1
1
1
1
h
^^~~"
^»
и^Ц
пТ t
1 1
1 1
*1
y[(n-i)f\\
f/»-^7" *2 r
I
I
I
*J
I
|
"^
vCtT]
лГ t
Ю
Рис. 4.5. Временная дискретизация аналогового сигнала при работе АЦП
в многоканальном режиме (ЛГ=3):
а —^временная дискретизация АЦП последовательного счета с промежуточным
преобразованием в частоту; б — временная дискретизация АЦП последовательного счета
с ИШИМ
от (п—1)Г до t2y по третьему — от U до ^з и опять по первому —
за время от tb до пТ. Время преобразования равно TjN. В этом
сдучае временной дискретизации подлежит функция e(t),
значения которой равны средним значениям входного сигнала
X\(t) за время от t—TjN до /, т. е.
e(t) = j- \ *i(t)dt,
t—T/N
откуда
„ е(Р) i-e-?r/N, . , , [,, , , / Т \
где
l(t):
{J
О при т<0;
при х > 0;
: ю
f о
0 при х < Г/ЛГ;
при х>Г/Л^.
(4.20)
(4.21)
(4.22)
Для АЦП с промежуточным преобразованием во временной
интервал с интегральной широтно-импульсной модуляцией
(рис. 4.5^5) временной дискретизации подлежит функция e(t),
6* 83

значения которой равны средним значениям входного сигнала
x{(t) за время от t—T/N до t—(TjN—to6)f т. е.
откуда
где
e{t) =
*tM--S
*-(Г/АГ-<ов.
0 <-r/;v
р) e-a-VpTIN_e-pT/N
р) ~ pyT/N
<об = Т-£~. 0<^<-^-; М') =
^{'H'-^I-'I-t]!'.
t__d_Y)iL]_|0 ПРИ '<(1-Т)П^;
Л? J (l при *>(1 — y)W
(0 при i<T/N;
~\l при х>(1 —у)Г/^. •
(4.23)
(4.24)
(4.25)
Если временем интегрирования можно пренебречь (при
to6<TlN)9 то e(t)=xx{t—T/N)y откуда
/C1(p)=e-P^; kl(x)=8(t-T/N).
Частотные характеристики, первого звена. Комплексную
частотную характеристику звена К\(р)у определяющего способ
получения цифрового эквивалента, найдем заменой р на /со.
Так, для АЦП с промежуточным преобразованием в частоту
К* (/C0) = WIN = соГ/(2N) e • (4'26)
„ , ч sincor/(2V)
где Кх (со) = ——- — амплитудно-частотная характеристика
звена /Ci(p); 91(0) =— (uT/(2N)—фазочастотная
характеристика звена /Ci(p). Для данного способа получения цифрового
эквивалента АЦП является фильтром нижних частот.
Линейность зависимости фазочастотной характеристики
свидетельствует о запаздывании на <p\T=T/(2N), вносимым трактом
временной дискретизации.
В табл. 4.1 сведены выражения К\{р), /Ci (/со), k{(x) для
рассмотренных способов получения цифрового эквивалента.
Здесь же указаны величины запаздывания ср\Т, вносимые
трактом временной дискретизации. При N=1 найденные выра-
84

9-
*.§
^ ^
M^
1* ^r
^h
^ fe
~ ^
Э
.3^
Tfe
CN I™
3
(N
3
>-
к.
3
3
5
к
«,
^
^
s
ч
VO
<
s
"■£ * &
л S ~ Si
^ * S §
ffl о « ь
^
?-
*,
8.
д о*
cS д s
о<я ч5
ffl ~ §3
©о S
CQ д
- i * S
2 Н о S И fl>
« я * с5 о л
ля д о,ю
ffl ,-г g я «
ж »я ч ^ о, д
о о «в CD u a)
DQ д PQ Q, ф Q*
дне
g2
ч о
оде
О л
с ч о
с eg
Ч о ?
о 2
3
я о
о л
*§•
о л а)
«дм
д
о S »я
и о О
° с 2
я л а»
°* г) Л
5 л
5*к о
о5а
с я с 3
Дядя
< е< Я Ч
6 Я сЬ со
* S « ра
5 м Энн S
С S С з в
c§Ses
< >=С. Д ч Я
85

жения совпадают со случаем одноканального использования
АЦП.
Аналого-цифровые преобразователи, в модели временной
дискретизации которых ^Ci (со) ===== 1, будем называть АЦП с
амплитудно-импульсной модуляцией (АЦП с АИМ). Аналого-
цифровые преобразователи, в модели временной дискретизации
которых имеется усреднение (оператор интегрирования), будем
называть АЦП с интегральной амплитудно-импульсной
модуляцией (АЦП с ИАИМ).
Итак, приведенный в данном параграфе анализ позволяет
представить модель равномерной временной дискретизации
при использовании АЦП в многоканальном режиме в виде
последовательного соединения линейного звена К\(р)у
определяемого числом каналов и способом получения цифрового
эквивалента, и идеального импульсного элемента (ИЭ).
Для АЦП с АИМ импульсную характеристику первого
звена удобно представлять в виде ki(x)=i(x—<f\T). Так, при
Ф1==0 &i(t) соответствует АЦП с мгновенным съемом; при
Ф1 = 1 &i(t) описывает процессы в АЦП с промежуточным
преобразованием во временной интервал, когда временем
интегрирования можно пренебречь. Такой же «универсальностью»
для АЦП с ИАИМ обладает импульсная характеристика
(4.25). Так, при y=1 k\(x) соответствует АЦП с
промежуточным преобразованием в частоту; далее при y=1 и 1/N=v
выражение (4.25) определяет импульсную характеристику
первого звена для модели временной дискретизации АЦП
поразрядного кодирования с запоминающим интегратором (табл. 4.1).
Поэтому при дальнейшем изложении именно эти две
импульсные характеристики будут использованы как базовые.
4.2. МОДЕЛИ ПРОСТЕЙШИХ ВОССТАНАВЛИВАЮЩИХ
ОПЕРАТОРОВ
Процесс преобразования дискретизированной по времени
функции в функцию непрерывного аргумента называют
восстановлением. По существу восстановление может быть
определено как аппроксимация функции дискретного, аргумента y{to)>
y(t\)>---9y{tt)9--- функцией непрерывного аргумента z(t). Так
как модель дискретизированного по времени сигнала была
введена как решетчатая функция, восстановлением будем
называть преобразование решетчатой функции в функцию
непрерывного аргумента. Восстановление может осуществляться
в реальном времени^ когда сигнал z(t) получается на выходе
восстанавливающего устройства по мере поступления на его
вход дискретизированного сигнала. Эта ситуация, в частности,
характерна для систем управления, когда АЦП используется
86

иэт
кг(р)
г [/?,£]
Рис. 4.6. Математическая модель вре- eft)
менной дискретизации и восстанов- «^^
ления
в виде датчика в цепи обратной связи. Восстановление может
осуществляться также после получения необходимого числа
значений решетчатой функции. Такой случай имеет место,
например, при восстановлении телеметрической информации для
исследовательских задач. Широко применяют в технике экстра-
поляционные и интерполяционные процедуры восстановления.
Восстанавливающий элемент осуществляет экстраполяцию
М~го порядка, когда по значениям решетчатой функции #(^_м),
y(ti+M+\)9 y(ti-M+2),--.,y{ti) определяют значение z(t) при
Восстанавливающий элемент осуществляет интерполяцию
М-то порядка, когда по значениям решетчатой функции
y(ti-M)y y{ti-M+\),...9y(ti) определяют значение z(t) при /г-м<
^^:/,. При равномерной дискретизации U—U-\ = T=const.
Простейший пример ступенчатого восстановления уже был
рассмотрен в гл. 1 (см. рис. 1.2). При этом способе
аппроксимации результат восстановления z(t)=e[nT] получается путем
экстраполяции на шаг вперед значений дискретизированного
сигнала. Такой восстанавливающий оператор называется экст-
раполятором нулевого порядка (ЭНП).
Операция временной дикретизации при Т=const с
последующим восстановлением может быть осуществлена
разомкнутой импульсной системой — последовательным соединением ИЭ
с линейным звеном (рис. 4.6), передаточная функция которого
определяется способом аппроксимации решетчатой функции.
Экстраполятор нулевого порядка (ЭНП). Ступенчатое
восстановление на выходе импульсной системы обеспечивается
в том случае, когда импульсная характеристика /Сг(т)
линейного звена с передаточной функцией k2(p) является
прямоугольным импульсом длительностью Т и амплитудой, равной 1
(рис. 4.7,а). Действительно, при поступлении в момент t=nT
на вход /Сг(р) б-функции с весом, равным е[пТ], на выходе
этого звена получаем прямоугольный импульс длительностью Т
с амплитудой е[пТ].
Таким образом, в случае ЭНП
Мт) = 1(т)-1(т-Г),
где 1(х) = {° ПРИ т<°'> 1(,_Г) = /° ПрИ Х<Г;
[ 1 при х > 0; 1 lj при х > Т
и передаточная функция линейного звена
00
КЛР)= S ll'(')-l('-T)Ie-i" d*=(l-e-pT)/p. (4.27)
87

1
A—
2T t -T
a)
B)
Рис. 4.7. Импульсные характеристики экстраполятора нулевого порядка (а),
интерполятора первого порядка (б), экстраполятора первого порядка (в)
Для формального получения выражения восстановленного
сигнала z воспользуемся формулой свертки [21]
z[n> SI= S Мт> *]е[п — /я],
(4.28)
т=0
где
k2[my е] = 1[(т+е)Г] —l[(m—1+е)Г] (4.29)
— импульсная характеристика k2(x) при r=(tn+e)T9 m=0, l,
2,...; 0<е<1.
Подставив (4.29) в (4.28), получим ожидаемый результат:
z[n, в]=е[п]. . (4.30)
Комплексную частотную характеристику линейного звена,
осуществляющего ЭНП, найдем после замены р на /со в
выражении (4.27):
*,(/©) =
1—е"
-i<oT
sin (©772) ^J(oT/2
= i —чпк—е
(4.31)
/со соГ/2
Отсюда следует, что ЭНП является фильтром нижних
частот, вносящим запаздывание на 7/2.
Линейная интерполяция. При этом способе восстановления
(рис. 4.8,а) последующий и предыдущий отсчеты соединяются
прямыми линиями. Иначе этот способ восстановления
называют интерполяцией первого порядка.
Передаточная функция интерполятора первого порядка
ИПП
*2(р) = (1-е-*г)2/(Р2Г). (4.32)
откуда получаем импульсную характеристику ИПП
2 \ / гр Т Т
(4.33)
где второе слагаемое равно 0 при х<Т9 третье слагаемое
равно 0 при т<27\
Заменив т/Г на т+е, имеем
k2[m, в]=т-+е—2(т—1+е) + (т—2+в). (4.34)
88

Рис. 4.8. Кривые, поясняющие интерполяцию первого порядка не в реальном
(а) и в реальном (б) времени
'Как следует из (4.33) или (4.34), импульсная
характеристика ИПП имеет вид равнобедренного треугольника с высотой,
равнрй 1, и основанием, равным 2Г (см. рис. 4.7,6).
В соответствии с (4.28)
z([ny г]=ее[п] + (1—г)е[п—1]. (4.35)
Комплексную частотную характеристику ИПП получаем
заменой р на /со в выражении (4.32):
(4.36)
К2(!<») = - Sln2((0772) e-'"r.
2V/ ' Т (соГ/2)2
Отсюда следует, что ИПП является фильтром нижних
частот, который вносит запаздывание на Т. Это очевидно, так как
при работе в реальном масштабе времени необходимо ожидание
последующего отсчета для того, чтобы провести
аппроксимирующую прямую между амплитудой этого отсчета и
предыдущего (рис. 4.8,6). Поэтому выражение (4.35) соответствует
работе ИПП в реальном масштабе времени. При исключении
запаздывания (не в реальном масштабе времени)
Z[n-1, e]=ee[n] + (l-e)e[n-l]. (4.37)
Линейная экстраполяция. Восстанавливающее устройство
на шаг вперед от пТ до (az-J- 1)7" линейно экстраполирует дис-
кретизированную по времени функцию, считая, что наклон
аппроксимирующей линии равен
'. А е[пТ]-е[(п-\)Т] Q<A<\
т ^
На рис. 4.9 показан процесс .экстраполяции при ,Л=1.
В этом случае восстанавливающий оператор называют экстра-
89

rftkk
z\n,s\
^ ^A
/ \^fZ-~ """"*
/^^v*
1 S^,**^^^
^
S
l/Z[/7,e]
^^-—
ем
-Г 0 . T 2T TT
Рис. 4.9. Экстраполяция первого порядка
полятором первого порядка ЭПП. Коэффициент А может быть
выбран исходя из статистических свойств преобразуемого
процесса с целью минимизации погрешности преобразования.
Передаточная функция линейного экстраполятора (ЛЭ)
имеет вид [35]
откуда импульсная характеристика
(4.38)
Kb) = AJr-M1=
I _|_ A^^L + 1 (,) _ /il [x — Т\ —
-1[*-Т] + А\[*-2Т\,
(4.39)
где значения слагаемых при отрицательном значении
аргумента равны 0. На рис. 4.7,6 показана импульсная характеристика
ЭПП (пунктиром — способ ее построения). Переходя к
относительному времени, получаем
k2[m, г]=А{т+г)—2А(пг—1+е) +
+Л(т—2+e) + l[w+e]-i4l[m-l+e] —
— 1[т—1+е]+Л1[т-2+е].
С учетом (4.28) найдем
z[n, г] = (Ае+1)е[п]—Аее[п-1].
Анализ фазочастотной характеристики ЛЭ показывает, что
этот способ восстановления не вносит запаздывания.
Выражения передаточных функций рассмотренных трех
видов восстанавливающих операторов могут быть записаны в
общем виде [22]:
(4.40)
(4.41)
Кш{р) =
-^(1-е-^)2 + у(1-е-^)(1-Ле-^), (4.42)
90

где значения коэффициентов А и Б для каждого из
восстанавливающих операторов приведены ниже:
Вид восстанавливающего оператора .... ЭНП ИПП ЛЭ, ЭПП
Коэффициенты:
А О 1 0<Л<1
В 1 0 1
Общий вид импульсной характеристики
k2[mf е]=Л(т+е)— 2А{т— 1+е) +
+Л (т-2+е) +51 [т]— АВ\ [т-1] —
—В\[т— \]+АВ\[т—2]. (4.43)
Откуда
£2[0, г]=Аг+В; k2[\f е] =А(1-е)— АВ; k2[m>2f e]=0.
При этом
2[пу г] = (Аг+В)е[п]-[А(1-е)-АВ]е[п-1]. (4.44)
Из (4.44) при соответствующих значениях коэффициентов
легко могут быть получены выражения (4.30), (4.35) и (4.41).
Автоматическое восстановление. Восстанавливающие
операторы могут быть построены с использованием фильтров
нижних частот (ФНЧ). Технически это соответствует
последовательному соединению цифроаналогового преобразователя ЦАП
и ФНЧ. Такой способ восстановления называется
автоматическим.
На выходе ЦАП получаем прямоугольный сигнал,
амплитуда которого соответствует цифровому эквиваленту.
Длительность этого сигнала при использовании АЦПводноканальных
устройствах равна шагу временной дискретизации. Если АЦП
обслуживает N каналов, длительность сигнала на выходе ЦАП
равна T/N. При этом передаточная функция
восстанавливающего оператора
Кш(Р) = (1-<ГрТ/Ы)Кфнч(р)1Р, (4.45)
где Кфнц(р)—передаточная функция ФНЧ; (l—e~pTIN)/p —
изображение сигнала с амплитудой, равной 1, и длительностью T/N
на выходе ЦАП.
Простейшим ФНЧ является звено первого порядка. В этом
случае
Кфнч(р)=Ц(Гфр+ 1);
К М - L-1 [К2 (/?)] = (1 - е-т/7Ф) - (1 - e-*-TIN)/ГФ).
91

При этом
1 _. е-(«+«>г/1ф при 0 < s < 1/N;
К\т, е] |_е_(т+е)Г/7.ф + е_(т+е_1/Л0Г/Гф при l/N<s<l
Отсюда
г \п, е] =
t e[hi][\-t-(n-m+t)TITb\ при 0<е<1/ЛГ;
п
S -<п-т + г-1/Н)Т/Т. -(п-пг)Т/7\
е[ш][е ф—е ф] при l/N<e<l-.
(4.46)
При N=1 имеем
2 И, е] - 2 e[fra][l —е"
т=0
-(л-т+077Гф"|
-|],[m-l][l-e-(n-m+t)r/4 (4.47) .
т=1
Восстановление идеальным фильтром нижних частот
(ИФНЧ). Импульсная характеристика такого фильтра
^(T)=sina)maxt/((omaxT) при — оо<т<оо. (4.48)
Комплексная частотная характеристика /(г (/<*>) • ИФНЧ
определяется как преобразование Фурье от k2(x):
v /• ч Т а / ч -/-л J2* прИ Iе0' <0W; Га жл
К»(/(о) = Мх)е Л = <Л 14.49)
_Гоо [0 в остальных случаях.
Известно, что идеальный- фильтр физически не реализуем,
так как его импульсная характеристика начинается в -—оо, т. е.
до того, как на вход фильтра при т=0 подана б-функция.
Воспользовавшись формулой свертки для решетчатых
функций, вычислим результат восстановления:
т=+оо
z[n, s] ^= £ e\m\k2\n — m, e] =
т=—оо
т=+оо
= 2 « N sin gw [(л + 8) Г _тГ]/(отах[(л + г) Г _тГ]. (4.50)
т=—оо
Полученный результат называют рядом Котельникова.
92

Котельниковым В. А. доказана теорема, имеющая
фундаментальное значение для решения многих задач теории
цифровых систем управления [24]: непрерывная функция времени
e(t), не содержащая частот выше граничной сотах, полностью
определяется отсчетами мгновенных значений е[т] в точках,
отстоящих друг от друга на интервалы Т'=я/;а)тах. При
выполнении условий теоремы и восстановлении идеальным фильтром
нижних частот z[n, г]=е[п, е].
4.3. ВОССТАНАВЛИВАЮЩИЕ ОПЕРАТОРЫ Af-ГО ПОРЯДКА
НА ОСНОВЕ ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ ЛАГРАНЖА
Аппроксимация некоторой функции e(t), заданной в М-\-\
точке e(t0)t e(t{)f...fe(tM-)f может быть осуществлена
многочленом М-и степени
м
z(t)= %Lt(f)e(tt),
значения которого при аргументах to, tu...ftM соответственно
равны e(to), e(t\)y...ye(tM). Выражение
МО
'-м /-/
Л 1 пряМ>1;
/=о и~*1 (4-51)
1 при М = О,
где t0^t^tM.
Многочлен z(t) называют интерполяционной формулой Ла-
гранжа. В соответствии с этой формулой строят
восстанавливающие операторы. Порядок оператора определяется степенью
аппроксимирующего многочлена. Так, интерполятором М-го
порядка по Лагранжу (ИМП) называют восстанавливающий
оператор, осуществляющий аппроксимацию решетчатой
функции многочленом Л1-й степени внутри промежутка |70, *м],
причем значения этого многочлена в точках t0f tu...,tM равны
значениям соответствующих «весов» решетчатой функции.
Экстраполятором М-го порядка по Лагранжу называют
оператор, восстанавливающий решетчатую функцию на шаг
вперед на промежутке |7м, tM+\] многочленом М-& степени,
значения которого в точках t0f tu...,tM равны соответствующим
«весам» решетчатой функции.
Очевидно, ,что при аппроксимации интерполяционной
формулой Лагранжа многочленов, степень которых не превышает
М, результат аппроксимации полностью совпадает с
аппроксимируемой функцией. В дальнейшем везде термин «по Лагран-
93

жу» будем опускать, за исключением особых случаев, когда это
необходимо.
Интерполятор Л1-го порядка [25]. Пусть Ти — длительность
замкнутого интервала интерполяции, начало которого
совпадает с t0, а конец —с fob T11=tM-—U. Тогда при постоянном шаге
временной дискретизации Т=ТИ/М и ^/Ги=т+е, где т=0, 1,
2,...; 0<£е<1.
При этих обозначениях аппроксимация e(t) осуществляется
на замкнутом интервале от to=(n— 1)ГИ до tM = nTl[:
e(tt)=e[(n-l+ilM)TM];
/=м ^ /=м
Д (n-l+.)TM-(n-l+„M)tM ^TTeJbj- M>,
хх(л — l+i/AfjrM — (n— 1 +j/M)TM XX i — /
/=o /=o
1 при Л4 =i 0;
(4.52)
м
z (0 = г [(я -1) ГЖ + вГМ] = J в [ [п - 1 + -L) Гм] I,- [0, в].
(4,53)
Для удобства записи воспользуемся символикой, принятой
в теории импульсных систем, опуская ТМ в квадратных
скобках. Тогда
м
z [п — 1, б] - .2 * [л — 1 + «7М] V [0,9е]. (4.54)
/=о
Выражение (4.54) соответствует интерполяционной
процедуре не в реальном времени. Сигнал можно восстановить в
реальном времени лишь после того, как будут известны значения
e(ti)y т. е. с запаздыванием на ТИ=ТМ, откуда при работе
восстанавливающего- оператора в реальном времени
м
г [п, е] = 2 е \п - 1 + ЦЩ L? [0, г]. ' (4.55)
/=о
Здесь результат восстановления относится к промежутку
времени [пу е] вместо [п— 1, е]. Поэтому левая часть (4.55)
записывается как z[n, е] вместо z[n—1, е] в (4.54).
В этом случае процесс временной дискретизации и
восстановления интерполятором УИ-го порядка может быть описан
моделью несинфазной импульсной системы (рис. 4.10). При
таком представлении временная дискретизация с шагом Ти осуще-
94

e(t)
ъ&
-\-T«
*-рт*
-p£(»-i)\
*0 W
Фр)
ZI
lUp)
Рис. 4.10. Модель временной дискретизации и восстановления
интерполятором М-то порядка
ствляется идеальными импульсными элементами, период
работы которых равен ТИ=МТ. Запаздывание в f-м импульсном
элементе Ei=iT=iTJM учитывает номер отсчета. Звенья с
передаточной функцией е~~р(м—1)Тц1м введены для получения
физически реализуемых импульсных характеристик
восстанавливающих операторов. Действительно, интерполяция
решетчатой функции по М-\-1 отсчету может быть произведена лишь
после того, как эти отсчеты поступят на восстанавливающий
оператор, поэтому звенья с запаздыванием учитывают
реальную временную последовательность отсчетов. Отсюда очевидно,
что интерполятор Л1-го порядка обладает запаздыванием,
равным Тп=МТ. Восстанавливающие устройства представлены
линейными звеньями Li(p), импульсные характеристики
которых в соответствии с интерполяционной формулой Лагранжа
определяются выражением (4.52). Суммирование слагаемых
интерполяционного многочлена осуществляется сумматором
(рис. 4.10).
Зависимость между результатом интерполяции z[n, e] и
дискретизированным сигналом e(t) получаем, используя
теорему свертки для решетчатых функций
М М f n
г[п, е]= S *|[л> sl = E< S e[n — m, *i = i/M]X
/=0 /=0 lm=0
м
'. = Е^МО, е}е[п— 1, et=i/M]. (4.56)
i=o
Выражение (4.56) по существу является интерполяционной
формулой Лагранжа, записанной в терминах теории импульс-
95

ных систем для случая равномерной временной дискретизации.
Процедуру восстановления рассмотрим далее для ряда
частных случаев.
Интерполятор нулевого порядка (ИНП). В соответствии с выражениями
(4.52), (4.54) и (4.55) при М = 0 получаем
L0h [0, е] = 1, е [п— l+L/M]=e [я—1]; г [n, е]=е [л—1], (4.57)
когда ИНП работает в реальном масштабе времени, и
2[л—1]=е[л—1], (4.58)
когда ИНП работает не в реальном масштабе времени.
Интерполятор первого порядка (ИПП). При М=1 по (4.52) получаем
£ои[0, е] = (е—1)/(0—1) = 1—е; L,- [0, е] = (е—0)/(1—0) =е;
далее по (4.54), (4.55)
z[n, г]=е[п— 1, «о = 0] (1—е)+е [л—1, 8i = l]e=e [п— 1] (1— е) +е [п]г, (4.59)
когда ИПП работает в реальном масштабе времени, и
z [л—1, е] =е [/г—1] (1— е)+е[п]е, (4.60)
когда ИПП работает не в реальном масштабе времени.
Выражение (4.59), полученное из (4.54), полностью совпадает с (4.35).
Интерполятор второго порядка (ИВП). При М=2 по (4.52) получаем
L0« [0, В] = (2е—1) (2&-2)/[(—1) (—2).] = (в—1) (2е—1);
L,h[0, e] = (2е-0) (2е—2)/[1 (-1)] =4е(1-е);
L2h [0, е] = (2е-0) (2е—1)/[(2—0) (2—1)] =е(2е— 1).
Далее по (4.54), (4.55) определяем результат восстановления:
г[п, е]=е[л—1](е—1)(2е—1)+в[л—1 + 1/2]4е(1—е)+в[л]е(2е—1), (4.61)
когда ИВП работает в реальном времени, и
г[л —1, е] = е[п-\] (е — 1)(2£ 1) + ^[Л— ^"Г
4е(1—е)+
+ *[л]е(2е— 1), (4.62)
когда ИВП работает не в реальном времени.
Экстрйполятор М-го порядка [25]. Экстраполяционная
процедура восстановления определяет функцию z(t) на интервале
t-My /м+i по значениям дискретизированного сигнала в точках
^о> ^ь • • •> 1мУ т. е. tM^t<CtM+\-
Введем следующие обозначения: при 7,=const t/T=n-\-z,
где я=0, 1, 2,...; O^e^l. Обратим внимание на то, что в
данном случае относительное время получаем из отношения t/T
в отличие от процедуры интерполяции, где относительное
время определялось как t/Tvl=tl(MT). Это различие объясняется
тем, что в случае ИМП интервал интерполяции равен Ги, тогда
как при энтерполяции М-го порядка (ЭМП) интервал
экстраполяции равен Т.
96

eft)
иэт
(
^
> >■
e-P"Tl
e-p№)l
1 ^
4fA>
'оДО
i'w
2°*
'/,
1 Zm *
i
1
Z
Рис 4.11. Модель временной дискретизации и восстановления экстраполято-
ром М-го порядка
На интервале экстраполяции
t=(M+e)T; U=iT;
' /=М
W[o. •] =
/=0
M
l — \
1
при M = 0;
г [/i, e]= SL,e[0, e]e[/i —Af+i].
i=0
(4.63)
(4.64)
Так как экстраполяция сигнала осуществляется на
интервале MTf (М-\-\)Т по предыдущим отсчетам, выражение (4.64)
описывает процедуру восстановления в реальном времени.
В этом случае процесс временной дискретизации и
восстановления экстраполятором Л1-го порядка может быть
представлен моделью импульсной системы, приведенной на рис. 4.11.
Импульсный элемент имеет шаг временной дискретизации Т
(в отличие от модели интерполяторов Л1-го порядка, где Ти=
=МТ). Совокупность передаточных функций линейных
звеньев, расположенных после импульсного элемента, по правилу
получения эквивалентной передаточной функции параллельного
соединения определяется выражением
м
*=0
откуда эквивалентная импульсная характеристика
м
К Ь) = I- [Кш (р)} = S V [t-Ш- i) T),
/=о
где 1гх — операция обратного преобразования Лапласа.
7—6036 97

Переходя к относительному времени tjT=m-\-zy получаем
м
Мю, £1= SVH-Af + f + e].
*=о
Имея это выражение, определим сигнал на выходе
импульсной системы, используя формулу свертки для решетчатых
функций
Ф> £]= 2) ^^9[т-М + 1+е]\е[п-т].
Если функция L3i[m, g] имеет вид (4.63) и соответственно
не равна 0 только при т—M+i=0, то
м
г[п, е]= SVIO, в]* [л-Ж-Hi,
что совпадает с (4.64).
Процедуру восстановления рассмотрим далее для ряда
частных случаев.
Экстраполятор нулевого порядка (ЭНП). В соответствии "с (4.63) при
М=0 найдем L03 [0, е] = 1; z [n, е]=е [п], что совпадает с результатом,
полученным в предыдущем параграфе [см. (4.30)].
Экстраполятор первого порядка (ЭПП). При М=1 по (4.63) получаем
(1~14--е) (1 — 0 + е)
V[o.«] = (0_7) "е; Li9[Q> «1- {l_J0) = н-«: *[*.•]-
= —ee[n — \] + (l+e)e[n—l + \] = {l + s)e[n]—\e[n-- l], (4.65)
что совпадает с результатом, полученным в предыдущем параграфе при Л=1
[см. (4.41)].
Экстраполятор второго порядка (ЭВП). Значения L,3 [0, е] получаем из
(4.63) при М=2:
Лгп 1 2-1 + s 2-2 + е «(! + «) .
V [0, е] = —— —-—= ; 1хэ [0, е] =
=2_0+е2-2 + е
1-0 1 — 2 v ^
„.„ . 2-0+е2-1+* (2 + е)(1 + 0
"• i°> •] - -i=o—^~Г= Т. ' (4-66)
(1+е)е (2 + е)(1+е)
(4.67)
98

4.4. МОДЕЛИ ВОССТАНАВЛИВАЮЩИХ ОПЕРАТОРОВ,
ОПРЕДЕЛЕННЫХ С ПОМОЩЬЮ КРИТЕРИЯ
НАИМЕНЬШИХ КВАДРАТОВ
Аппроксимация функции e(t), заданной в Л4+1 точках
£(^о), e{t\),...,e(ti)9...te(tM), может быть осуществлена
линейной комбинацией заранее выбранных функций фо(0>
ф1(0»-'->фЛ0>--->Ф'(0> число которых /+1<М+1.
Таким образом, результат аппроксимации
2(0= З^фЛО. t0<t<tM, (4.68)
/=о
где Aj — коэффициенты. ~
На систему функций <р/(0 необходимо накладывать
следующее ограничение: никакая линейная комбинация вида (4.68)
не может иметь I различных корней на отрезке
аппроксимации. Системы функций, обладающие указанным свойством,
называют системами Чебышева [26]. В частности, систему Чебы-
шева образуют следующие функции:
Фо(о = 1; Ф1(0=<; Ф2(0=<я;---;ф'(0='1- (4.69)
При этом
■*(*) = %А;Р'. (4.70)
/=о
т. е. аппроксимация осуществляется линейной комбинацией
многочленов (4.69). В том случае, когда коэффициенты Л/
выбирают из условия.минимума суммы квадратов разности
.=м
Е= ?>[е{}д-гШ\ (4.71)
i=0
данный способ называют приближением линейной комбинацией
функций, определенной с помощью наименьших квадратов
[26]. С учетом (4.68)
М Г / -12
Е= Ые&)-2А,<р,{Щ. (4.72)
<=о L i=o J
Из условия минимума Е запишем
dEjdA/^0, /==0; 1;...;/.
7* 99

После несложных преобразований получаем систему
линейных уравнений:
мм м
а 2 фо it,) <(j (ti) + л S ч>1 &) <?>• (<«) + - + ax 2 ъ vd <rj (td =
/=o *=o /=o
M
,= 2*(f,)<p,(f|), / = 0; 1; 2;...; /. (4.73)
/=o
Решение (4.73) для чебышевской системы функций
однозначно определяет значения коэффициентов Л/.
Если ф;- (t) = Vy то
м . м мм
A2'i + A2^+1 + ... + ^2''+/= %e{tt)t{,
/ = 0; 1; 2;,..; / (4.74)
и аппроксимирующая функция имеет вид (4.70).
Результатом интерполяции 1-го порядка по критерию
наименьших квадратов на основе линейной комбинации
многочленов вида (4.69) является функция z(t), полученная после
определения коэффициентов Л/. Восстанавливающий оператор,
реализующий приведенные вычисления, будем называть
интерполятором 1-го порядка по критерию наименьших квадратов и
обозначать как И1ПКВ. При работе данного интерполятора в
реальном масштабе времени восстановление может быть
реализовано только после того, как будут известны все отсчеты
e(ti), т. е. имеет место запаздывание на время Ги=/л*—^о-
Результатом экстраполяции 1-го порядка jio критерию
наименьших квадратов на основе линейной комбинации
многочленов вида (4.69) является функция z(t)f полученная после
определения коэффициентов Л/, при /м^^м+ь
Восстанавливающий оператор, реализующей приведенные вычисления, будем
называть экстраполятором 1-го порядка по критерию
наименьших квадратов и обозначать Э1ПКВ. Таким образом, Э1ПКВ
определяют функцию z(t) на отрезке tM до tM+\ по Л1+1
предыдущим значениям решетчатой функции.
Если степень аппроксимирующего многочлена совпадает
с числом шагов дискретизации (т. е. /=Л1), то минимум Е
равен 0 и достигается при z(ti)=e(ti). В этом случае
восстанавливающие операторы, построенные на основе критерия
наименьших квадратов и по Лагранжу, совпадают.
И1ПКВ при равномерной временной дискретизации. Введем
следующие обозначения: ti—^•_1 = 7,=const — шаг временной
дискретизации; Тк=МТ — отрезок интерполяции; tjTn=t/MT =
= п+в9 где л=0, 1, 2,...; 0<е<1; и=(п—1)Тл+1Тл/М=
100

= (n—\)MT+iT. При этом система уравнений (4.74) имеет
вид
м м
А0 > [{tl-\)MT + iT}i + A12[{n-\)MT + iT\^ + ...
м
... + Al2[{n-l)MT + iT\l+t =
м
= %e[(n-l)TM + iT][(n-l)TM + iT]i9j = 0- 1; 2;...;/. (4.75)
/=о
Результаты восстановления будут
z [пу е] - 2 А2 К* — 1) ГАГ + *Щ' (4.76)
/=о
при работе восстанавливающего оператора в реальном
времени и
z [л — 1, е] -= S Л, [(л — 1) ГМ + еТМ]1 (4.77)
/=о
при исключении запаздывания.
Коэффициенты Л/ в (4.76) и (4.77) получаем из решения
системы уравнений (4.75). Обратим внимание, что при
рассмотрении И1ПКВ, так же как в случае интерполятора М-го
порядка по Лагранжу, период идеального импульсного элемента
принят равным Т^=МТ.
Интерполятор первого порядка по критерию наименьших
квадратов (ИППКВ). Этот восстанавливающий оператор
является частным случаем И1ПКВ, если 1=1.
При работе ИППКВ в реальном масштабе времени
z[n9 е]=Ао+Ах(п—1+г)ТМ, (4.78)
при исключении запаздывания
z[n-l, г]=А0+А1(п— 1+е)ТМ. (4.79)
Система уравнений (4.75) для ИППКВ имеет вид
мм м
-VSl + Л 2[(n-l)MT + iT]=2>e[(n-l)MT + iT];
i=0 /=0 *=0
м м
Ао 2\(n-l)MT + iT\ + A1 2[(п-1)МТ + 1Т]* =
i=0 i=0
м
= 2>e[(n—])MT + i][(n—l)MT + i], (4.80)
/=o
101

откуда
Ai =
£[(n-l)MT+iT]
Y,e[(n-\)MT+iT]
/=о
м
%e[(n-\)AT-{-iT][(n-\)MT + i] %[(n—l)MT+iT]*
i=0
i=0
М
i=0
м
M + l
м
%l(n-l)MT+iT]
i=0
5j[(n-l)MT+iT]
i=0
М
%[{n-l)MT + iTl*
i=Q
м
/=о
r(jW + l)»(iW+2)/12
Аналогично
S6[(n-l)rAf + /r](M+i)(t/iW-i/2) ■
^ = _iz°
1 Г (iW -f -1)2 (>И + 2) /12
Подставив (4.81) и (4.82) в (4.78) и (4.79), получим
м
Z [П9 S] - — у ; е I I II — 1 -J 1 У УК1 I V
L ' J (M+DlM + 2) L± П ШЙ ' '
»=0
2М + 1 /
(4.81)
(4.82)
х
[е(-1г-т)+-^^--^1: (483)
6М
2М Г
z[n—l, e]
\2М
X
X
(М + \)(М + 2) U [\ ^ М ) J
*=о
I V ^ 2 / ' 6iW 2М J v '
Схема разомкнутой импульсной системы, реализующей
восстанавливающий оператор ИППКВ в реальном времени,
совпадает со схемой на рис. 4.10 после замены звена L*i(p) на
Ьрмв l=l (p), импульсная характеристика которого
определяется выражением
.§*±i_ U (4.85)
1Дкв/=1[0,е] =
102
12М
(М + 1)(М+2)
■f.f-i_JL
L U 2

ПриЛ1=/=1
l.h.kb/=i[0, e]==2[e(i—l/2) + (l—0/2];
LoH.KB/=i==_e+1; l^b^^O, e]=e. (4.86)
При ИПП в соответствии с (4.52)
Loh[0, е]=_е+1; 1Л[0, е]=е.
Таким образом, LfHKB/=1 [0, e]=L/H[0, e] при Л1=/=1.
Э1ПКВ при равномерной временной дискретизации. В
отличие от задачи интерполяции, где период работы импульсного
элемента ТИ=МТ, в данном случае, поступим так же, как при
восстанавливающем операторе-экстраполяторе Л1-го порядка
(по Лагранжу), приняв t/T=n-\-ef-n=0, 1, 2...; 0^е=^1.
При этом система уравнений (4.74) имеет вид
м м
AoliKn-M + W + Ai % [(n-M + i)T\i+>+...
M M
...+At 2 [(«-М + /)П/+'= 2>e[(n-M + i)T]X
X[(n~M + i)Ty\ 1 = 0; 1;...; /. (4.87)
Результат восстановления:
z[n, е]= З^К" + е)П;'. (4-88)
/=о
где коэффициенты А/ получаем из решения системы уравнений
(4.87).
Экстраполятор первого порядка по критерию наименьших
квадратов (ЭППКВ). Этот восстанавливающий оператор
является частным случаем Э1ПКВ при 1=1.
Результат экстраполяции определяется выражением
z[n, e]=A0+Al(n+e)T. (4.89)
Система уравнений (4.87) для ЭППКВ имеет вид
мм м
VSl-M! %(n-M + l)T = 2e[{n-M + i)T];
м м
A ^(n — M + i)T+A1 %{n — M + i)2T2 =
t=0 i=o
м
= 2 e [(n — M + i) T] (n — M + i) T. (4.90)
103

Решение этой системы определяют значения коэффициентов:
м
[(п—М/2)2 + М(1/6 + М/12)] %e[(n-M + i)T)
М(М+\)(М+ 2)/\2
м
(п—М/2) %e[(n—M + i)T](n—M + i)
/=о
М(М + \)(М + 2)/\2
м
Аг = [У e[(n — M + i)TUn — M + i) —
/=о
м
-(»-jf)Sel(/*-A,+°4
Подставив Л0 и Л1 в (4.89), получим
м
2[Л> s]= 12 уе[(п-м + 1)Т]\- — +
L J (M + I)(M+2) Lt LV L 6 ' .
*=o
+ т+т+"(т-т)1- " <4-91»
Схема разомкнутой импульсной системы, реализующей
восстанавливающий оператор ЭППКВ, совпадает со схемой на
рис. 4.11 после замены звена Li3(p) на 1гэкв/==1(р), импульс- '
ная характеристика которого определяется выражением
1 J (M + l)(M + 2) [ 6 6 2
■ +'hi-f)]- (4-92»
ПриМ=/=1
L;9KB'=1[0,
s
i-+,(,-№)];
L09'**/=1 [0, e].= - e; L{3KB /=1 f0, s] = 1 + e,
что равно соответствующим L03[0, e], £i3[0, e] для ЭПП.
Недостаток выбранной чебышевской системы многочленов
(4.69) виден из рассмотренных примеров восстанавливающих
операторов ИППКВ и ЭППКВ. Даже при использовании
аппроксимирующих многочленов первой степени для получения г[пу г]
необходимы достаточно громоздкие выкладки. Увеличение
степени аппроксимирующего многочлена приводит к
необходимости решения системы линейных уравнений порядка Z+1, что
104

при больших I в общем виде затруднительно. Указанный
недостаток успешно преодолевается путем выбора другой чебышев-
ской системы многочленов q>j(0 [26], ортогональных на
множестве точек дискретизации при Т=const.
Система многочленов, ортогональных на множество точек
равномерной дискретизации. Начнем с введения обозначений.
Пусть Л1+1 точки дискретизации соответствуют моментам
времени t0i tu...ftM, причем tt+\—/,= const==7\ Проделаем
следующую замену переменных: ?= (t—t0)/T. Тогда точки t0,
/i,...,/m перейдут соответственно в О, 1,...,Л4, т. е. O^i-^M.
В [26] доказано, что равномерно дискретизированная по
времени функция e(t) может быть аппроксимирована по
критерию наименьших квадратов линейной комбинацией
многочленов, обладающих свойством ортогональности на множестве
точек *(0, 1,...9А1), т. е.
м
2ч,*.м('К.м(0 = 0 ПРИ*^Г> (4-93)
где ky г—соответственно стейени многочленов <р*,де(7) и <рг,м'(7).
Эти многочлены могут быть вычислены из следующего
рекуррентного соотношения [26]:
1 <Р/.Л1 ^ = 2(2/+D ф/+1.м W + ~Т ф/.м ^ —
Ф/-1.м(0 (4-94)
2(2/ + 1) т/-ьм
при
Фом(?) = 1; фш(?) = 1-2?/.Л1. (4.95)
В частности, при /=2 имеем
^M^l-jfjr^^Z^' (4.96)
При./=3
2(6^2 — ЗМ+2) -
фзм (0 = 1 М(М—\)(М—2) t +
| 30 72 20 р (497)
7Г(^-1)(М-2) М(М— \)(М—2) v '
И Т. Д.
Таблицы многочленов, ортогональных на множестве точек
/=0, 1,...,Л1, приведены в [28].
105

Результат аппроксимации, оптимальный в смысле критерия
наименьших квадратов при фиксированном 1<.МУ
определяется, как показано в [26], следующим выражением:
_ / _
(4.98)
/=о
где
J ~
г(0= £ ^Ф/,м(0.
/=о
(2j + l)W.M\ у rf
{M-j)\(j+M+\)\ a
i=-0
Получение моделей И1ПКВ при использовании многочленов
Ф/,м [27]. Интерполятор /-го порядка по критерию наименьших
квадратов аппроксимирует функцию e(t)f заданную в точках
/0= (п-1)Ти= [п—\)ТМ9 tx= {п—1 + 1/М)7714,..., /,-= (я—
— l+ilM)TM9...JM=nTM. Тогда
Г t—t0 t—(n—\)TM (n—\+e)TM — (n — l)TM .„
I zzz — =: = SM\
T T T
e[t=i]=e[{n—l+ijM)TM]t
откуда при работе И1ПКВ при исключении запаздывания
получим
z\n— 1, е] =
• / м
_ъ |!i+l'"ijj<|»-i+i)™|,,.,n,/,,w=
U (Л*-/)!(/ + Л1+ .
/=0 i=0
М I
• - /=о
М '
£ <? [(я- 1 + -i.) ГМ]1,ИКВ/ [О, .J, (4.100)
«=о /=о
М
/=0
где
l""' i°' -i - s <^;;ThU w'w,>. «i- иле.)
/=o
При работе И1ПКВ в реальном времени
м
z [п, в] = 2 е [(л — 1 + //А1) Щ1ЛКВ ' [0, в]. (4.102)
106

Схема разомкнутой импульсной системы, реализующая
И1ПКВ в реальном времени, совпадает со схемой на рис. 4.10
после замены звена LiK(p) на LiMi{Bl(p)f импульсная
характеристика которого определяется выражением (4.101).
При необходимости увеличения порядка интерполятора с I
на /+1 импульсная характеристика £,-и-кв/+1 [0, е] в
соответствии с (4.101) определяется по следующей рекуррентной
формуле:.
LH.KB/+1 г/Л 1 Г И.KB / г<Л л ,
/ [0, е] =Li [0, е] +
+ Ы1+1) + 1\МШ\ щ ф {Ш1 (4Л03)
Отметим, что при 1=М 1,я-кв/[0, е] равна соответствующей
импульсной характеристике £;и[0, е] при интерполяции по Ла-
гранжу.
С целью иллюстрации данного подхода получим еще раз
выражение z[n, e] для ИППКВ. При 1=1 в соответствии с
формулами (4.94) и (4.95)
<Po,m[J] = 1;" Ч>о,м[еМ] = \\
ф1 M[i] =A—2ijM\ (fUM[zM] = 1—2гМ/М = 1—2е,
откуда
и.кВ/=1[0 ]== mm + змм /,_и\ (!_*)=
1 ' J М\(М + \)\ (М—1)!(М+2)! \ Af Уv '
1 . ЗМ Л 2/
Af + 1 (М+ \)(М+2) \
(l-JL)(l-2e) (4.104)
м
1=0
+ ЗЛ*_ Л «_Wi_2.)
(М+\)(М + 2) \ М )у '
/=0
что совпадает с результатом, полученным ранее [см. (4.84)],
Интерполятор второго порядка по критерию наименьших
квадратов (ИВПКВ). Импульсную'характеристику £*икв z=2[0, e]
107

получаем в соответствии с выражениями (4.103) и (4.104):
L,HKB/=2[0, e] =
= Z/KB /=1 f 0, в] + S^W %м Щ %м [в, М].
Выражения фгм[*] и ф2м[еМ] следуют из (4.96) после
замены t соответственно на i и на гМ.
При этом
Lh.kb/=2[0 J = _L_ + ЗЖ / JM(l_2e)+ "
(М + \)(М + 2){М + Ъ)[ ' M-l. M(M-\) Iх
x[l—»*.+ **м ]; (4.105)
м
г[п,е] = ^[(й-1+^) ГЛ*] L,H кв '=2 [0, в] (4.106)
при работе интерполятора в реальном масштабе времени;
м
г[л —1, е]= 2* К* — 1+ЦМ)ТМ]Цкв1=2[0, е] (4.107)
при исключении запаздывания.
Рассмотренный пример иллюстрирует удобство
использования рекуррентной процедуры получения
математической-модели интерполятора порядка /+1 при известной модели
интерполятора /-го порядка.
Получение моделей Э1ПКВ при использовании многочленов
Ф^м(?). Экстраполятор 1-го порядка по критерию наименьших
квадратов по заданным М-\-1 отсчетам функции e(t) e[(n—
—М)Т\, e[(n—M+l)T\9...,e[(n—M+i)T\9...,e[nT]
определяет функцию z(t) на временном отрезке nT^t^.(n-{-l)T.
Обратим внимание на то, что в отличие от моделей И1ПКВ здесь
период идеального импульсного элемента равен шагу
дискретизации Т (а не ТИ=МТ).
При этом
t=e+My где 0<е<1, e[l=i]=e[(n-M+i)T];
г [я, е] =
/ м
-S <*%""*+■» S«n«-*+ont,..HW+*i-
/=0 *=0
108

M I
-2.|(—л+оп2тиЗД¥лтт1г»/-и*/-"+*,|-
i=Q /=0
М
= 2e[{n-M+i)T]Lt9'ml[09e]9 (4.108)
i=Q
где
ь"' Р-ч-Д(<.-Уц'Х.).^"'^'-+^ <4-|09>
/=0
Схема разомкнутой импульсной' системы, реализующей
Э1ПКВ, совпадает со схемой на рис. 4.11 после замены звена
Li3(p) на 1*э-кв/(р), импульсная переходная характеристика
которого определяется выражением (4.109). При необходимости
увеличения порядка экстраполятора с I на /+1 импульсная
переходная функция Lf3KB/+1 [0, е] в соответствии с (4.109)
определяется по следующей рекуррентной формуле:
£Лкв|+,[0, в]=-
гэ.кв/[П . \_ [2(/ +1) + l]Af!Af! r;1 r . -,,
= Ь( (J, eM ——-1 ф,^. ми]©,,. „U+M.
L' J^ (М —/-l)l(M+/+2)! /+,iMl J /+1'Ml
(4.110)
Отметим также, что при 1=М импульсная переходная
характеристика 1,-элсв/[0, е] равна соответствующей импульсной
характеристике L*3[0, е] при экстраполяции М-го порядка по
Лагранжу.
В качестве примера получим еще раз модель ЭППКВ из
общего выражения (4.108). При 1=1 в соответствии с (4.94) и
(4.95)
Фом W = l; %М[* + М]=1; Ф1М М- 1—2//АГ;
Отсюда
ls.kb/=i 0 8l = _L__ ЗМ Л AW1 + iLY (4.111)
м
•z[n9 *] = J*e[(n-M + i)T]\
/=о
ЗМ
М+\
("*) ('+-£-)]=
(Af+1) (Af + 2)
109

м
(Af+1) (M + 2) U lV ' Ч 6
1=0
+ T + 7 + '(ir-T)]- <4-"2»
Данная модель ЭППКВ соответствует формуле (4.92),
полученной иным способом.
Экстраполятор второго порядка по критерию наименьших
квадратов (ЭВПКВ). Импульсную переходную функцию'
Li9MBls=s2[0, e] получаем в соответствии с выражениями (4.110)
и (4.111):
L,9'KB/=2[0, e] =
Э.КВ/ = 1ГА _т , БМ1М1
(Af—2)! (Af + 3)!
г э.кв/=1т 1 , ЪМ\М\ гл г . Л/Л
Выражения фгм[(| и ф2м[е+Л1] следуют из (4.96) после
замены t соответственно на i и на е-\-М. При этом
L J M + l (Af+l)(iW + 2) \ MJ\ M /T
, b(M—\)M j^ 6/ , 6i2 1
(iM + l)(iM + 2)(iW+3)L iW—1 Af(M-l)JX
Г j _ 6(е+Л4) , 6(s^M)2 1
X [ M-\ ~ M (Af—1) J'
м
г[«, e]= 2e[(«_M + On^KB/=2[0- e]. (4.113)
Используя рассмотренную рекуррентную процедуру,
аналогично можно построить модели экстраполяторов более
высоких порядков.
4.5. НЕРАВНОМЕРНАЯ ВРЕМЕННАЯ ДИСКРЕТИЗАЦИЯ
Неравномерная [4] (или другой термин —«нерегулярная»
[29]) временная дискретизация определяется как
преобразование функции непрерывного аргумента e(t) в решетчатую y(U)
при Tfi-i = ti—ti_l=var в соответствии с оператором (4.1).
Учет способа получения цифрового эквивалента опишем,
подобно тому как это проведено в случае равномерной временной
дискретизации, соответствующим линейным оператором
110
e(t)=k[x(t)]y

где x(t)—процесс, подвергающийся аналого-цифровому
преобразованию.
В этом случае решетчатая функция y(ti) имеет вид
/= + 00
y(tt)= 2 k]x(t)]b{t-tt). (4.114)
/=—оо
Оператор, учитывающий способ получения цифрового
эквивалента для АЦП с АИМ, может быть представлен в виде
/=+00
У(*д= 2 *('-',«) 8(<-'f). (4Л15)
/ = -00
где 4ап — время запаздывания.
Оператор, определенный способом получения цифрового
эквивалента для АЦП с ИАИМ, учитывает факт усреднения
функции x{t).
Для АЦП последовательного счета с преобразованием в
частоту или временной интервал с ИШИМ (рис. 4.12,а)
/= + оо to6
У(*д= J] -^"j * С-Tw + U + xJAS (<-/,), (4.116)
/= — 00 О
где /об — время интегрирования входного сигнала; /зад
—длительность интервала между предыдущим отсчетом и началом
аналого-цифрового преобразования.
Для АЦП поразрядного кодирования при наличии
запоминающего интегратора на его входе (рис. 4.12,в)
i=^T 1 №
УУд= £ -7^-) *('-'*+*)*»('-',). (4.117)
/=—оо ° О-
При работе АЦП не в реальном масштабе времени отсчет
в момент /,■ можно относить к моменту t*i (рис. 4.12,6 и г), что
соответствует исключению запаздывания, определяемого
способом получения цифрового эквивалента.
Приведенные модели позволяют сформулировать
ограничения на минимальный интервал дискретизации Ггшп для случая
АЦП с ИАИМ:
^пПп^^пр+^зад", 7\п1п^^об, (4.118)
где /пр — длительность аналого-цифрового преобразования
в АЦП последовательного счета; t06 — время интегрирования
в АЦП поразрядного кодирования.
Восстановленный сигнал
м
*(<) = 2-У('|)М0. (4.119)
/=о
111

где Li(t) —функции, определяемые видом восстанавливающего
оператора.
При экстраполяции z(t) определяется при /л^^/м+ь ПРИ
интерполяции — при to^t^M* Отметим, что в отличие от
равномерной дискретизации в данном случае невозможно осущест-
x(t
гэодМ
y(t*0
п
| 1
1
| j
\Т-1 _
l I
I I
т
)\ y(*V
+*
т-1 1
I
I yfti)
1
1
\
1
1
1
1
\
1
у(Ф
+ *
■W—_-_
1
»
\
*
У(*н-1)
y(h)
у(Ф
Рис. 4.12. Неравномерная временная дискретизация при использовании АЦП
с ИАИМ:
а> б —для АЦП последовательного счета; в, г — для АЦП поразрядного кодирования
с запоминающим интегратором
112
11
11
1
1
1
J
ем-1
'!
I
А
у(*«-л)
■*——*i
1
t

W /
/i
\/
0 t0
I
x(*i)S
T7*
T tf
т0
«^ *-
I
У
гт
-^ >•
\
^'y/^i
У
t2 jt t3
-< ^
\
T
l-^
^7
/
4-T t+
T3
-^ »-
\
\
<*)
\
A
'
t
x(t)
b^~
о tB
f^-
T
7^
ti
i^^-
2Г
-G *»
/
4
\
JT
l/
/
<j
'
^3
"--■5^—T^
4Г
-* >•
5T
\
A
f
t
6)
Рис. 4.13. Временная дискретизация аналого-цифровым преобразователем
последовательного счета с промежуточным преобразованием во временной
интервал методом линейной развертки:
а—считывание цифрового эквивалента в момент окончания импульса; б — считывание
цифрового. экв,ивалеата при t=nT
вить интерполяционную процедуру восстановления в реальном
времени. Поясним это на примере ИПП по Лагранжу. Пусть
в момент времени ti известны значения цифрового эквивалента
z(U) и z(ti-i), известен также шаг дискретизации Ti-\ = ti—ti-\.
Интерполятор, начиная от t=ti, восстанавливает непрерывный
сигнал в виде прямой с углом наклона, тангенс которого
[z(tt)—z(ti-i)]/Ti-\. Момент окончания интерполяции равен
^+7i_!. Но в этот момент лишь с вероятностью, равной 0,
возможно возникновение нового опроса, т. е. интерполяции при
переменном шаге дискретизации и работе аналого-цифрового
преобразователя в реальном масштабе времени невозможна.
Следующей особенностью описания процессов при
неравномерной дискретизации является отказ от относительного
времени, принятого при равномерной временной дискретизации,
что, очевидно, следует из непостоянства 7У
Изменение шага дискретизации может быть вызвано
различными причинами. В частности, в аналого-цифровых
преобразователях последовательного счета с промежуточным
преобразованием во временной интервал методом линейной
развертки (см. § 2.2) значение цифрового эквивалента может быть
определено по окончании импульса (рис. 4.13,а). В
рассматриваемом случае п-и цифровой отсчет появляется тогда, когда
*п = ~А *(*»)'
пТ
(4.120)
8—6036
113

xft\
Si
0
f*
Ьо5
к
*об
"^•^^1
±1
*И1
7"o
\
+06
r^
^
ioB
I
&
^
1
t
a)
x*
'0
i
1
X'
I
V
"1 ,
V *
S)
Рис. 4.14. Временная дискретизация аналого-цифровым преобразователем
последовательного счета с промежуточным преобразованием во временной
интервал с ИШИМ при считывании цифрового эквивалента в момент
окончания импульса (а) и с промежуточным преобразованием в частоту и
преобразователем частота — цифра по «k периодам» (&=1) (б)
я длительность интервала временной дискретизации
_f - т
' п—\ — *п
^-•jlxitj-xit^], 0<Тп_г<Т. (4.121)
Если цифровой эквивалент формируется в фиксированные
моменты времени пТ (рис. 4.13,6), то шаг дискретизации
постоянен. Однако имеет место запаздывание хп цифрового
отсчета по отношению к моменту времени tn-u которому он
соответствует:
■(«-l)Nr-^(U (4Л22)
А
я0<тп<7\
В аналого-цифровых преобразователях последовательного
счета с промежуточным преобразованием во временной^
интервал с интегральной широтно-импульсной модуляцией (см.
■§ 2.2) при отсутствии синхронизации работы АЦП внешним
генератором цифровой эквивалент считывается в конце
сформированного импульса (рис. 4.14,а), после чего начинается
новое преобразование. Длительность шага временной
дискретизации
'об
T'/z-i — *п 'я-i — ^зт +
ип
1'л-1' *п
(4.123)
где Xf 9 f _ среднее значение модулирующей функции за
эталонное время интегрирования /0б.
Наименьший и наибольший шаги временной дискретизации
■соответственно будут
(4.124)
Т min = to6T"fo6-^min/^'oni
i max= *o6-f-toQXmax/ ^on.
(4.125)
114

В аналого-цифровых преобразователях последовательного
счета с промежуточным преобразованием в частоту и
преобразованием частота — цифра «по k периодам» (см. § 2.3)
длительность интервала дискретизации определяется суммой
длительностей k периодов частотно-импульсного сигнала
(рис. 4.14,6).
Так кяк Г x(t)dt = kA, то
Тп-1 = К - tn^k = kAlxtn_x, ,n; (4.126)
* min==^^/-^maxj •» max==^^/-^min« (4.12/)
В адаптивных цифровых телеизмерительных системах
изменение величины Ti определяется самим принципом построения
этих систем. Рассмотренные примеры иллюстрируют процесс
неравномерной временной дискретизации, в котором
длительность шага дискретизации зависит от дискретизируемой
функции. - .
• Возможны и другие случаи. В частности, при равномерной
дискретизации аналогового сигнала и передаче цифровой
информации по каналам с помехами ряд сообщений может быть
не воспринят приемником (например, при использовании кодов,
обнаруживающих ошибки), что приведет к изменению шага
временной дискретизации на входе восстанавливающего
оператора независимо от вида аналового сигнала.
Анализ причин неравномерной дискретизации позволяет
рассматривать три модели:
первая —шаг временной дискретизации является
случайной величиной; независимой от дискретизируемого процесса;
вторая — шаг временной дискретизации функционально
связан с дискретизируемым процессом;
третья—шаг временной дискретизации является
случайной величиной, статистически связанный с дискретизированным
процессом.
В настоящее время развиты методы определения
методических погрешностей восстановления дискретизируемого сигнала
при первой модели неравномерной дискретизации [4, 29, 30].
При второй и третьей моделях аналитически могут быть
получены верхние и нижние оценки погрешностей
преобразования в том случае, когда определены максимальный Гтах и
минимальный rmin шаги дискретизации.
В данной книге описываются модели неравномерной
временной дискретизации, в которых шаг дискретизации может быть
представлен случайной величиной, независимой от
дискретизируемого процесса. В остальных случаях ниже разобрана мето-
8* 115

дика определения верхней и нижней оценок погрешности
преобразования При ЗаДаННЫХ Гтах И Tmin.
При фиксированных моментах дискретизации /о, £ь...,/;,...
..., tM результат восстановления полностью определяется
значениями дискретизированного сигнала y{U) и способом
построения восстанавливающего оператора.
Рассмотрим выражения функций на выходе
восстанавливающего оператора при заданных способе получения цифрового
эквивалента, дискретизируемой функции x(t) и моментах
дискретизации.
Аналого-цифровое преобразование с АИМ.
Восстанавливающий оператор-интерполятор Л1-го порядка по Лагранжу. Per
зультат восстановления (не в реальном времени) определяется
выражением
м
z(0= 2*(<i-UV(9. (4Л28)
где t^t^tM\ Lp(t) вычисляется в соответствии с формулой
(4.51).
При интерполяции первого порядка
L0«(t) = (t-tl)/(to-ti); LiMO = ('-M/('i-'o). (4.129)
Обозначив t\—t0=T0, t—tQ=%y получим на интервале
интерполяции
zb) = -^ * (t0-t3J + ^- xitt-tsJ, 0«т<Г0. (4.130)
1 о 1 о
При интерполяции второго порядка
T4t) = ±zL 1—Ь-. L"(t) = i=^L ±zi.; £ »(/) = till. Lzk.m
lQ —l1 l0 — f2 *l l0 L\ '2 L2 *0 *2 *1
(4.131)
Обозначив ti—t0=T0i t2—t\ = Tu t—tQ=x9 получим на
интервале интерполяции
Wt/ (t-TJix-Wo+Tj] (f _f v ,
2 (*=) = * lr0 ~ 'aanJ i"
y o-ry i
+ -v x~(r;+ri) *d-',j +
— / о ' l
+ 1^Г7-Х-=Г1^-^' 0<<<Г, + 7'1. (4.132)
Учитывая, что в дальнейшем при анализе точности
преобразования случайных процессов будет использована статистика
116

интервалов дискретизации, функцию Lp(t) представим в виде
М—1
Li"(x, Г0 Гм-О приО<т< £7,
Очевидно, что
h-to =
Аналогично
*«-'>=ч
2^
1 о
2 г*
/-1
и Tk-=tk+1-
при />0;
при / = 0.
при / > /;
при /</.
-f*
(4.133)
(4.134)
Обозначив tj — t0— 2iTk и tt — </= 2 ^*» получим
/.о
'./
V(*. ?V 7"M-,) = n [(^-2^)/(2^J. (4-135)
y = t
откуда
м
2(*)= 2^(',-yV(', V-. Тм-x), ^t-t0. (4.136)
При интерполяции третьего порядка проиллюстрируем
использование формул (4.133) — (4.136):
zU) = xlt—t )Х~Т° т~(7'° + 7'^ '-(г» + г1 + г2) |
' зап/-Г0 -(Г0+Гх) -(Г.+ ^+Г,)^
+ *('.-'эап)
-Л -(^+7-,)
(4.137)
Tu + T1 + Ti T-i+Г, Та
Аналого-цифровое преобразование с ИАИМ.
Восстанавливающий оператор-интерполятор М-го порядка по Лагранжу.
При неравномерной дискретизации этот способ восстановления,
как указывалось выше, неприменим при работе АЦП в
реальном времени. При исключении погрешности от запаздывания
117

возможны два способа восстановления. Первый соответствует
интерполяции по точкам /0, /ь...,*м (см. рис. 4.12). При
втором способе отсчеты y(ti) сдвигаются влево к середине
интервала интегрирования, после чего осуществляется интерполяция.
В первом случае исключается запаздывание, вносимое
восстанавливающим устройством, во втором — запаздывание всего
тракта. Очевидно, что второй способ восстановления является
предпочтительным, так как обеспечивает уменьшение
погрешности преобразования.
Рассмотрим вначале первый способ. Результат
восстановления для АЦП последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ
получаем из (4.128):
м to6
*(0 = S"^f х(?*-Т*-1 + '™ + ^ах*1*'®' *о<*««- (4-138)
/=о о
Аналогично для АЦП поразрядного кодирования с
запоминающим интегратором определим результат восстановления
после подстановки (4.117) в (4.128):
М 'об
z (0 = S 1о7 j x {ti ~to6 + Ти) dz» L'" (0' (4'139)
1=0 0
Соответствующие выражения восстановленных функций на
интервале интерполяции имеют вид
м to6
i=0 0
(4.140)
м to6
2(t) = J]i^-j" *(<»-<об + ^)*.^"К Т0,..., Гм_,);
i=0 0
0<x<r0 + 711+...+rM_1. (4.141)
Выражения для. ИПП, ИВП, ИТП получаем из (4.130),
(4.132), (4.137) после замены x(ti—t3an) на
'об
О/'об) j *(U — Ti-1 + 'аап + Хи) *и Либо H3
(Шов) J *('i-'o6+'Odv
о
118

При втором способе восстановления для АЦП
последовательного счета с промежуточным преобразованием в частоту
или временной интервал с ИШИМ в соответствии с рис. 4.12
получаем
м
Z(o= 2v(o*('i*),
м
где If" (0 = Д [(* - f/)/('i* - 'Л1; ** = и-Тг.г + tM + W2;
/=о
/*/
^*—о* = U-1 — 0-1'
Введем обозначения:
М— 2
'-С+^'о-Г-г + 'зад + 'ов/З+Ч 0<х< 2 T*5
As=—1
i-2
*=/-1
/-2
I— 2 г* при <</;
/-2
*—1./—I
Тогда
м
1-(0 = ^(гГ_1;Го_Гм_2) = Г|Г/ _ 2г»)/ 2 тХ
/=0 L \ / — 1,-1 /' /—1,«-1 J
Выражение результата восстановления получаем после
замены 1ги(т, Г0,..., ТМ-\) в формуле (4.140) 'на L,h*(t, T-u Г0,...
..., Тм-2) при 0<т^71_1+Г0+ ... + ТМ-2.
Для АЦП поразрядного кодирования с запоминающим
интегратором исключение запаздывания на *0б/2 (см. рис. 4.12),
вызванного интегрированием аналогового сигнала, не приводит
к изменению нумерации шагов дискретизации. Выражение
результата восстановления на интервале интерполяции от /*о до
t*M определяется формулой (4.141).
Аналого-цифровое преобразование с АИМ.
Восстанавливающий оператор-экстраполятор Л1-го порядка по Лагранжу, Ре-
119

зультат восстановления в реальном времени определяется
следующим выражением:
м
г(х)= ^lx(ti-t3JLl3(tM+,), (4.142)
* = 0
где
м
Li3(tM+*) = UWM-tj + ^Wi-tj)]; 0<х<Гм; TM = tM+l-tM.
/=о
(4.143)
Обозначив, так же как и выше, ti — tj = 4^Tk и положив tM-
м—1
tj = ^ ткъ получим
V
(4.144)
м
"z(t)= S^ft-U^fvT, ГЛ_,), 0<х<Гл,. (4.145)
Рассмотрим частные случаи. При экстраполяции нулевого порядка (М=0)
2(*)=*(*0—*зап), 0<Т<Г0. (4.146)
При экстраполяции первого порядка (М==1)
^оэ(т, Го)=т/-Го; Li3(t, Г0)=.(Г0+т)/Го; (4.147)
*W = ~^^Л-^зап)+-^~!"х(/1"-/за^' 0<х<Г1. (4.148)
7 о у о
При экстраполяции второго порядка (М=2)
Ьэ(т, Го, 7,,) = (Г1+т)т/[7,о(7,о + 7,1)]; Ii»(t, Го, 74) = (Го + Г1+т)т/[(Г0 +
+ Z,i)(-7,i)]; L23K Го, Г,) = (Го + Г1+т)(Г1+т)/[(Г0+Г1)Г1]; (4.149)
г (х) = х (/0 - *.ап) ; ДЛ,[ + х & - *3.п) ' ,Tw Л + * (^-^зап)Х
x(VfW(r1+.)
Аналого-цифровые преобразователи с ИАИМ.
Восстанавливающий оператор-экстраполятор М-го порядка по Лагранжу.
Результат восстановления при работе АЦП в реальном време-
120

ни определяется выражениями \4.145), (4.146), (4.148),
(4.150) после замены в них x(ti—t3an) на (1/*0б) I x(ti—Ti-i +
о
<об
+ ^зад+Ти)^Ти ЛИбо На (1//об) f *(**—А>б +Ти)^Ти.
0
Если имеется возможность исключить погрешность от за-
лаздывания, то отсчеты относятся к середине интервала
интегрирования (см. рис. 4.12). Результат восстановления для АЦП
последовательного счета с промежуточным преобразованием
в частоту или временной интервал с ИШИМ определяется
выражением
м
г(,)= EV(U+ *)*(*,),
'м-'/*+■»
где
м
Так как
, t*M=tM—7,М-1 + £зад+^об/2=/м-1 + £зад+^об/2;
t*j = tj— 7,/-1 + ^зад+^об/2=//_1 + /3ад+^об/2;
V = V = и_л - t,_x = S Tkf то Lf- (fM + х) =
м
z(x)=£LJM(x,r_1>Te,...,7'M_8):
1 Г
X -j— J X (*j — T'j-i + ^зад + ти) ^и-
о
Для АЦП поразрядного кодирования с запоминающим
интегратором исключение запаздывания на /сб/2 (см. рис. 4.12),
вызванного интегрированием аналогового сигнала, не приводит
к изменению нумерации шагов дискретизации. Выражение
результата восстановления на шаге экстраполяции от t*M до t*M+{
121

определяется формулой (4.145) после замены x(ti—t3an) на
'об
(1Доб) | X(ti—/об+Ти)^Ти.
О
Аналого-цифровой преобразователь с АИМ.
Восстанавливающий оператор-интерполятор первого порядка по критерию
наименьших квадратов. В соответствии с (4.70) при 1=1 не
в реальном времени результат восстановления
z(t)=A{t+A0y (4.151)
где to^,t^tM\ А\ и А0 получаем как решение системы
уравнений (4.74):
Аг =
м м 1 /Г м м 1
{М+1) ]£*(*,)- Y,e(tt)tt \ (М+1) XV- %<* ;
1=0 *=0 J/ L ' 1 = 0 /=0 J
(4.152)
мм мм 1 /Г м мп
Л= Sv E«ft>- 2<f Е«(<|)>1 / (м+i) Sv- S v .
f=0 (=0 (=0 (=0 J/ L '=0 1=0 J
(4.153)
где e(ti)=x{ti—/3an). - s
Рассмотрим пример интерполятора первого порядка при
М=2. Учитывая, что ti = t0+T0 и ^2=<о+^о+7'ь получаем
2 W = o/T.-t-r1.^- гтм й- * ^ (2Г° + ГЛ + * &) (Го - *\) +
2(Г02 + 7'12+7'0Т1)
+ е (Q (27\ + Т0)) t + e (t0) [t0 (2T0 + 7\) + Т02 + (Г, + 7\)2] 4
+ е (У ft (^ - Го) +7\ (Г0 + 7\)] +
+ e{ti)[-tu{T0 + 2T1)-TuT1)}, t0<t<tt. (4.154)
Введем обозначения: t—tu-\-x, 0г£Ст<^м—*о>
Lo„.kb;=I(T) Г()) Г1) = [Ро+(Го+71)2-
-(2Го+Г,)т]/2(72о+Г2,+7'о7'1);
Ll«.K.i-i(Tt Го> Г,) = [Г1(Го+Г1) +
+ (7'o-7,1)t]/2(Po+7'2i+7,o7'i);
12и.квг=1(т> Го( Г1) = [(2Г,+Го)т-
-Г07'1]/2(Г2о+Г1+7'о7'1).
Тогда
/=о
122

Если Т=const, т/Ги=т/27,=е, то это выражение совпадает
с (4.84) при"Л1=2.
Описанный случай иллюстрирует методику аналитических
преобразований, позволяющих представить результат
восстановления как функцию длительности шагов дискретизации.
В общем случае интерполяции /-го порядка по М-\-1 отсчету
по критерию наименьших квадратов
м м—\
«(,)= 2L'KBl^> Т<»-> Тм-ОеЬ), 0<х<2т*- (4-155)
Функции 1/икв/[т, Го,..., ТМ-\] находятся так же, как
1/икв/=1[т, Го, Ti] в рассмотренном примере.
Аналого-цифровое преобразование с АИМ.
Восстанавливающий оператор-экстраполятор 1-го порядка по критерию
наименьших квадратов. Начнем так же, как в предыдущем случае:
при 1=1 результат восстановления
z{tM+t) =Ai (/м+т) +А0,
где 0^т^м+1—^м = Гм; А{ и А0 соответственно равны (4.152)
и (4.153).
Рассмотрим пример экстраполятора при М = 2:
2(Т,?-1-Т1*+ТьТ1)
+ е (h) (Г0 - 7\) + е (Q (27\ + Т0)] (t0 + Т0 + 7\ + ,) +
+ е (д [/0 (2Г0 + 7\) + Г02 + (Г0 + Гх)21 + е (^ [*0 (7\ - Т0) +
+ T1(T0 + T,))+e(t2)[-t0(T0 + 2T1)-T0T1l} =
2
= 2L?:KBl=l(^ T0, Тх)е(и), (4.156)
/=о
где
Lo9«b'=1(t, Го, Г1)==[7,20+(Го+Г1)2-
-{2T0+Tx)(T{sJtTl+H)\l2{T\+T\^TJl);
Li3.kbJ=1(t> Го> 7'1) = [7'1(7'о+7'1) + (Го-Г1)(Го+
+?,1+-г)]/2(Р0+р1+7'оЛ);
£2э.кв,=1(т> Го( т'1) = [2Г1+Го)(Го+Г1+т)-
-Г07,1]/2(Г20+7,21+7'о7'1).
При 7'=const, M=2 и е=т/Г выражение (4.156)
совпадаете (4.112).
123

Используя данный способ вывода результата
восстановления для общего случая — экстраполятора /-го порядка,
запишем
м
z(tM + -)= IU/-KB/b> Т0,..„ Тм_{]е{и). (4.157)
Функции Цэкв1[Ху Го, ..., ТМ-\] находятся так же, как
Li9MBlssl[%9 Г0, Т\] в рассмотренном примере.
Аналого-цифровой преобразователь с ИАИМ.
Восстанавливающие операторы ИПП и ЭПП по критерию наименьших
квадратов (М=2). Выражение результата восстановления при
АЦП последовательного счета с промежуточным
преобразованием в частоту или временной интервал в случае, когда не
исключается запаздывание, вызванное способом получения
цифрового эквивалента, получаем путем замены e(ti) в (4.155)
'об
для ИПП и в (4.156) для ЭПП на (1//0б) J x(U—Г^+^адН-.
о
+Ти)б?ти. Если запаздывание исключается, то в (4.155) и
(4.156) Г0 заменяется Т-и Тх — на Т0 и e(ti) — на (1/^об)Гх
о
Х^(^/—Г/-1+^зад+ти)^ти. При этом для ИПП О^т^Г^ь+Го,
для ЭПП 0<t<7Y
Выражение результата восстановления при АЦП
поразрядного кодирования с запоминающим интегратором в случае,
когда не исключается запаздывание, вызванное интегрированием
аналогового сигнала, получаем путем замены e(ti) в (4.155)
'<*
для ИПП и в (4.156) для ЭПП на (1/£0б) f x(U—^об+ти)^Ти.
о
Если указанное запаздывание на /0б/2 исключается, то
выражения (4.155) для ИПП и (4.156) для ЭПП после
соответствующей замены е(и) не изменяются. Однако текущее значение
времени т при ИПП рассматривается на интервале 0^1т<^*2—
t*0=T0-\-Tu при ЭПП на интервале 0^x^*3—^*2=^2 (см.
рис. 4.12).
Получение выражений z(tM-\-i:) при любом числе отсчетов
и заданном порядке восстанавливающего оператора
аналогично.
4.6. МОДЕЛИ ПОТОКОВ ОТСЧЕТОВ ПРИ
НЕРАВНОМЕРНОЙ ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Рассматривая факт получения отсчета при временной
дискретизации как случайное событие, последовательность
отсчетов будем трактовать как поток случайных событий или, про-
124

ще, случайный поток отсчетов. Структура потока событий
наиболее полно определяется многомерным (в общем случае
бесконечномерным) законом распределения интервалов 7\- между
событиями (отсчетами). С учетом известных трудностей,
которые встречаются на пути получения многомерных законов
распределения, случайные потоки событий представляются более
простыми моделями, хорошо разработанными и позволяющими
во многих технических приложениях получать
удовлетворительные результаты [29—32].
Рассмотрим ряд моделей потоков, которые достаточно часто
встречаются при решении технических задач.
Простейший поток. Этот поток событий, обладающий
следующими свойствами: стационарностью, отсутствием
последействия, ординарностью [31, 32].
Поток событий называется стационарным, если вероятность
попадания того или иного числа событий на участок времени
От зависит от длины участка и не зависит от того, где именно
на оси времени расположен этот участок.
Поток событий называется потоком без последействия, если
для любых непересекающихся участков времени число событий,
попадающих на один из них, не зависит от того, сколько
событий попало на другой.
Поток событий называют ординарным, если вероятность
попадания на один элементарный участок Ат двух и более
событий пренебрежимо мала по сравнению с вероятностью
попадания одного события при Ат->0.
Интегральный закон распределения случайного интервала
(в данном случае шага дискретизации) между моментами
дискретизации для простейшего потока определяется выражением
P(T<Ti) = l—e-*-T. (4.158)
Плотность вероятности случайного интервала
дискретизации
рт(Т) =dP(T<Ti) /dT=te-+T. (4.159)
Математическое ожидание и дисперсия случайной величины
Т соответственно будут
оо"
mT = f Трт (T)dT = 1/Я; (4.160)
о
00
DT = §(Т— \Ц)2рт (T)dT = 1/Я2. (4.161)
о
Величина Я — параметр закона распределения— обратно
пропорциональна математическому ожиданию — средней
длительности интервала дискретизации. Отсюда К определяет сред-
125

нее число событий в единицу времени и называется
интенсивностью потока событий (в данном случае — потока отсчетов).
Простейший поток отсчетов применим при анализе АЦП
с АИМ и не может быть использован при анализе АЦП
с ИАИМ, потому что учет способа получения цифрового
эквивалента при ИАИМ требует выполнения условия (4.118),
которое определяет минимальный шаг дискретизации. При
простейшем потоке сколь угодно малое значение интервала
дискретизации имеет конечную вероятность.
Потоки Эрланга. Если в простейшем потоке сохранить
только каждую k-ю точку, исключив все остальные, то получим *
новый поток, называемый потоком Эрланга &-го порядка.
Плотность вероятности интервалов между событиями для
этого потока определяется следующим образом [32]:
'т<П-*&£*-". (4.162)
Очевидно, что при Л=\ поток Эрланга совпадает с
простейшим.
Математическое ожидание и дисперсия случайного
интервала дискретизации при распределении Эрланга k-то порядка
определяются выражениями
mTw=kl%\ £М*)=£Д2. ' ' ' (4.163)
Так как длительность интервала дискретизации в потоке
Эрланга ограничена снизу нулем, эта модель потока отсчетов
может быть использована для анализа АЦП с АИМ.
Регулярный поток. По существу данный поток не является
случайным. Он соответствует потоку отсчетов при постоянном
шаге дискретизации r0=const. Однако, при использовании
аппарата б-функций детерминированные величины могут быть
представлены как случайные со следующим законом
распределения:
рт(Т)=8(Т-Т0). (4.164)
Математическое ожидание интервала между отсчетами
гпт-
„=^T5(T — T0)dT = T0. (4.165)
о
Дисперсия интервала
оо
DT = j (Т - Т0) 8 (Т - Т0) dT = 0. (4.166)
о
Эти результаты очевидны. Действительно, математическое
ожидание детерминированной величины равно ей самой, а
дисперсия (разброс) равна 0.
126

Рекуррентные потоки (потоки Пальма). Поток событий
называется рекуррентным (или потоком с ограниченным
последействием), если промежутки времени между
последовательными событиями представляют собой независимые одинаково
распределенные случайные величины [32]. Простейший поток,
потоки Эрланга, регулярный поток являются случаями
рекуррентных потоков.
Так как величина интервала между отсчетами является
положительной, в качестве плотности распределения интервала
могут быть использованы распределения, равные 0 при Г<0.
Еще раз подчеркнем, что для АЦП с ИАИМ необходимо,
чтобы время преобразования было меньше Тт\п. Этому
требованию, в частности, могут удовлетворять распределения:
равномерное, Симпсона, усеченное нормальное, регулярное.
Альтернирующий поток [29, 30]. В данном потоке
длительности интервалов между событиями независимы. Плотности
распределения длительности интервалов чередуются: за
интервалом с распределением Р\{Т) следует интервал с
распределением Р2(Т), а за интервалом с распределением Р2{Т) следует
опять интервал с распределением Р\(Т).
Поток, полученный из рекуррентного путем его просеивания
[29, 30]. В данном рекуррентном потоке каждое событие с
вероятностью Р остается, а с вероятностью 1— Р выбрасывается.
Такая модель удобна при описании цифровых
телеизмерительных систем. Пусть Т — постоянная длительность передачи
кодового слова по каналу связи. При передаче используются
коды с обнаружением ошибок. Вероятность обнаружения ошибки
в кодовой серии равна Р. Вероятность трансформации кодовой
серии пренебрежимо мала. В этом случае модель потока
отсчетов, поступающих на восстанавливающий оператор, есть
просеянный регуляторный поток, в котором с вероятностью 1—Р
отсчет остается, а с вероятностью Р выбрасывается (приемник
отказывается от декодирования).
В этом случае длительность интервала Гпр между
отсчетами, поступающими на восстанавливающий оператор, является
случайной величиной и кратна 7\ Вероятность того, что
длительность интервала Р(ТПр=Т)'=1—Р. Если в первый раз
произошло подавление кодового слова, то вероятность того,
что 7,пp=27,, определяется выражением
Р(Гпр=27,) = (1—Р)Р.
Аналогично, вероятность того, что Tnp=mTy определяется
выражением
Р(Гпр=тГ)=Р^1(1—Р).
127

Это выражение соответствует геометрическому закону
распределения. Плотность вероятности длительности интервала
имеет вид
00
' Р(Тпр)=1!ЦТпр-тТ)Р'"(\-Р).
Математическое ожидание и дисперсия соответственно
будут
Гпр=Г/(1-Р); (4.167)
оо оо
Т% = 1(7^-77(1 _Р))»р«-(1_Р) 2 b(Tnp-mT)dT =
= РГ/(1—Р)2. (4.168)
Перечисленные модели включают целую гамму потоков
с различной степенью упорядоченности — от «полного
беспорядка» (простейший поток) до «полной определенности»
(регулярный поток). Очевидно, что выбор модели потоков следует
из результатов обработки статистики интервалов
дискретизации либо из априорных соображений, вытекающих из природы
неравномерности (например, случай с подавлением кодовых
серий, описанный выше). Различные примеры потоков «подробно
изложены в [29, 30, 31].
Глава 5
МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ
ПРЕОБРАЗОВАНИЯ СИГНАЛОВ ПРИ ВРЕМЕННОЙ
ДИСКРЕТИЗАЦИИ
5.1. ПОГРЕШНОСТИ ПРЕОБРАЗОВАНИЯ
ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ ПРИ РАВНОМЕРНОЙ
ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Математические модели равномерной временной
дискретизации при заданных способе получения цифрового эквивалента
и восстанавливающем операторе без учета квантования по
уровню представляются синфазными (а) и несинфазными (б)
линейными импульсными системами (рис. 5.1). Синфазные
модели описывают процесс временной дискретизации при экстра-
поляционных процедурах восстановления и автоматическом
восстановлении, несинфазная — интерполяционных
процедурах [4].
128

."Tw4
ЧР)\
\иэт
Шр;\
I ! г-л Q
ИЭ
I "^l T
[ >■
-*
<И
ИЭ
r
'и
(TJM)i
I*
ИЗ
Ги ,
< ^-|
Э»>
!_~
е-рт»
гГР^(М-ь)
•
ф)
Ll(p)
WP)
—»•
—*-
"
AjW
*;
Рис. 5.1. Синфазная (а) и несинфазная (б) модели временной дискретизации
й восстановления
Синфазная модель. Входной сигнал x(t) и аддитивная
помеха X(t) поступают на первое звено с передаточной функцией
К\(р)у определяемой способом получения цифрового
эквивалента (см. табл. 4.1). Идеальный импульсный элемент ИЭ
осуществляет временную дискретизацию. Второе линейное звено
с передаточной функцией Аг(Р) соответствует
восстанавливающему оператору. Погрешность преобразования 8 получена на
выходе вычитающего устройства. Преобразуемый сигнал x(t)
подается на вход вычитающего устройства через звено Кз{р),
позволяющее при необходимости исключить погрешность от
запаздывания.
Передаточная функция К2(р) при ЭНП, ИПП и ЭПП (по
Лагранжу) определяется формулой (4.38), а соответствующая
ей импульсная характеристика— формулой (4.40).
При экстраполяции Af-го порядка по Лагранжу или /-го
порядка по критерию наименьших'квадратов импульсная
характеристика звена /С2(р) с учетом параллельного включения
звеньев Lf3[0, e] имеет вид
м
. k%[m, e]= 2V[/k —Af + i + iJf
i=0
(5.1)
где ЦЭ[0У е] при экстраполяции М-го порядка по Лагранжу
определяется формулой (4.63), при экстраполяции /-го поряд-
9—6036 129

ка по критерию наименьших квадратов —формулой (4.109).
Если 1=МУ выражения (4.63) и (4.109) совпадают.
В случае автоматического восстановления ^[т, е] имеет
вид (4.45) при /=(т+е)Г.
Передаточная функция третьего звена при исключении
погрешности от запаздывания определяется выражением
Я8(р)=е-рч*-. (5.2)
Здесь <pT=yiT-\-<p2Ty где (р\Т, ф2Г —запаздывания, вносимые
первым и вторым звеньями. При работе АЦП в реальном
времени ф=0 и Аз(р) = 1.
Несинфазная модель отличается от синфазной наличием М
идеальных импульсных элементов с периодом работы Ти=
= МТ (в синфазной модели период ЭИ равен Т) и
соответствующих звеньев с запаздыванием, определяющим
последовательность отсчетов. Выражения LfH[0, e] приведены в
предыдущей главе: формулы (4.52) или (4.101).
Результат восстановления z[nf e] для синфазной модели
получаем, используя теорему свертки для непрерывных и
решетчатых функций:
п (п—ш)Т
г К £] = 2 К К sl \ К (*) х [(л — т) Г — x] di. (5.3)
m=0 0 "
В случае экстраполяции Л1-го порядка по Лагранжу или /-го
порядка по критерию наименьших квадратов
п (п—ш)Т
г[п,в]= 2 Li\m — M + i + e] J k^x^n — т)Г —x]dx.
m=0 0
(5.4)
Учитывая, что LiB[m—М-\-1+г]ф0 только при m—M-\-i=
= 0, получаем
М {n—M+i)T
z [п, в] = 2 V [0, в] j kx (х) х [{п — М + 0 Т — х] А. (5.5)
/=о о
Аналогично в случае несинфазной модели
М (n-l + i/M)MT
г[п, в]= 2V[0. sl J k1(z)x[(n-l+i/M)MT-z]d^
/=0 0
(5.6)
где LiH[0, е] определяется выражением (4.52) при
интерполяции Л1-го порядка по Лагранжу, выражением (4.101) при
интерполяции /-го порядка по критерию наименьших квадратов.
Если l=Mt то (4.52) и (4.101) совпадают.
130

Пример 5.1. Определить функцию на выходе ЭНП, ЭПП, ИПП (по Лаг-
ранжу) при равномерной временной дискретизации сигнала x(t) = Vm&xt
аналого-цифровым преобразователем последовательного счета с промежуточным
преобразованием в частоту. Число каналов преобразования N, время
интегрирования уТ.
Импульсная характеристика первого звена, определяющего способ
получения цифрового эквивалента, в соответствии с данными табл. 4.1 имеет вид
^W = ^{lfx-(l-,)^]-l[x-^]}. (5.7)
Импульсная характеристика второго звена, описывающая способ
восстановления, определяется выражением (4.38).
Подставив (5.7) и (4.38) в (5.5), получим
пт
г[п,*] = (Ае + В)^-^ |i^(l^v)^J-l[x^~-]}xlnr-x]^ +
о
п Т
6
(\/N)T
-1)Г-~т]А = (Ж + Д)-^- "j x[nT-z]dz +
(1-7) T/N
" . (\/N) T
+ [А(1-ш)-АВ]— j х[(л-1)Г-*]А.
(1-7) TIN
m. (\/N) T
(5.8)
(\-{)T/N
Для восстанавливающего оператора г—ЭНП (по Лагранжу)—в
соответствии с данными § 4.2 Л=0; В=\. В этом случае
(l/N)T
' ■ *[я, «] = — f x[nT-i\dz. (5.9)
(l-T) TIN
Подставив в (5.9) x(t) = Vmzxt, получим
(\/N) T
Пп,*] = — f . Vmax(nr-x)dx. (5.10)
(1-Tf) TIN
Так как *(/)=0 при /<0, то z [0, e]=0. Общий результат имеет вид
!0 при п = 0;
(5.11)
Vmaxn"-(2-Y)/2/V] прил>1, К '
откуда следует, что переходный процесс на выходе тракта преобразования
длится один такт.
9* 131

Для восстанавливающего оператора — ИПП (по Лагранжу) — в
соответствии с данными § 4.2 Л=0; В=1. В этом случае
(1/ЛО Т (1/N) Т
г[А1, е] = —е J x[flT—z]dx + — (1-е) f x[(/l-4
-l)r-xjdx. (5.12)
Подставив в (5.12) *(f) = Vmax*, получим
N (1/Г) Г
*[*•] = —« J Vmax(nT-z)<b +
(1-7) 77*
(1/iV) Г
+vF(1~£) l ^axt(«-l)^-T]dx. (5.13)
a-T)m'
Так как x(t)=0 при f<0, то z [0, e]=0. По той же причине при п=\
второе слагаемое выражения (5.13) равно 0. Только при п>2 оба слагаемых
составляют результат, откуда
Z [П, е] =
0 при п = 0; •
l/maxr£[1-(2~Y)/2/V] при/1=1; (5.14)
К«мхП/1-!+«-(2-т)/2ЛГ] при л > 2.
Следовательно, переходный процесс на выходе ИПП длится два такта,
в установившемся режиме при п>2 сигнал на выходе ИПП повторяет
входной с запаздыванием на 1 + (2—y)/(2N).
Для восстанавливающего оператора — ЭПП (по Лагранжу)—в
соответствии с данными § 4.2 Л = 1; 5=1. При этом
*[",*] = — (• + !) J x[nT-z]dx--j' J х[(я-1)Г-т]Л.
(5.15)
Подставив в (5.15) x=Vmaxt, получим
(1/Ю т
(1-Т) 77*
(1/ЛО Г
1
(1-Т) TIN
-YT8 J ^.x^-n^-'lA- (5.16)
132

Таж как x(t)=0 при /<0, то z [0, e]=0; по той же причине второе слагаемое
выражения (5.16) равно 0 при п=\. Только при п>2 оба слагаемых
определяют результат, откуда
I 0 при п -= 0;
zln,*]=!VmJ (*+l)[l-(2-y)im при/i=l; (5.17)
' vmaxr 1л +«— (2 — Y)/2V1 при л 2* 2.
Здесь также в установившемся режиме имеем линейный сигнал на выходе
зкстратюлятора с запаздыванием на (2—y)/(2N). Длительность переходного
режима составляет два такта.
Пример 5.2. Для условий предыдущего примера определить z [n, е] при
временной дискретизации аналого-цифровым преобразователем поразрядного
кодирования с запоминающим интегратором.
Импульсная характеристика первого звена, определяющего способ
получения цифрового эквивалента в соответствии с данными табл. 4.1, имеет вид
*iW-^T{lW-K*-vn}. (5-18)
Подставив (5.18) в (5.5), с учетом (4.38) получим
v7-
z[n,s] = jjr(Ae+B) ^ х[лГ-т]<*т +
о
vT
+^T[i4(l--t)-i4B] ^xl(n~l)T-z)dx. (5.19)
Для ЭНП.(Л = 0; В=\)
(5.20)
Для ИПП (А= 1; # = 0)
10 при л = 0;
^шах7^1-^2) ПРИ " = 1; (5.21)
Kmax7,[rt-1+e-"v/2J при м^2.
Для ЗПП(Л= \\ В= 1)
i0 при п = 0;
УтахГ(1+е)0 ~v/2) при я=1; (5.22)
Vmaxr(rt + e-V/2) ПРИ П^%
Анализ полученных результатов показывает, что при ЭНП и линейном
входном сигнале длительность переходного процесса составляет один такт,
при ИПП и ЭПП — два такта, в установившемся режиме восстановленный
133

сигнал при ИПП и ЭПП повторяет входной сигнал с запаздыванием
соответственно на 1 +v/2 и на v/2.
Если в выражениях z [/z, е] примера 5.1 устремить N-+oo, а в примере
5.2 v->-0, то получаем одинаковые результаты, соответствующие АЦП с АИМ.
Пример 5.3. Определить функцию на выходе ИППКВ при равномерной
временной дискретизации сигнала х= V'max/ аналого-цифрового
преобразователя поразрядного кодирования с запоминающим интегратором, время
интегрирования v7\
Подставив в (5.6) выражения (5.18), (4.104) и x=VmaJ1 получим
?'":"=E(ST7+:
ЗМ!
(М + \)(М+2)
('-£)<'->]*
\Т
Х;И к-[(п-
1+-ММ
— х dz.
(5.23)
Учитывая, что х (t) = 0 при *<0, получаем
0
м
1 ЗМ
г [л, е] =
при п = 0;
V ТМ
max
*=0
iM + l^ (Af+I)(Af-f-2) К М
IX
X(1-2e)](lri~) при^1:
(5.24)
V ТМ
max
Af-f- 1 ' (M + l) (M + 2)
I
('-2'^)':
X(l-*)](»-.! +■jr-^r) при »>2.
Если положить М=1, получаем результат, совпадающий с ИПП по
Лагранжу (см. пример 5.2).
Текущее значение погрешности преобразования
детерминированного сигнала x(t) при отсутствии помехи, т. е. при K(t) =
=0, в соответствии с импульсными моделями (рис. 5.1)
определяется выражением
в [л, в]=х[(п+ъ)Т—<рТ]—г[п9 в]. (5.25)
При <р=0 получаем погрешность при работе в реальном
времена При ф=ф!+ф2 погрешность от запаздывания
исключается.
Аналого-цифровое преобразование с АИМ.
Восстанавливающие операторы-интерполяторы М-го порядка по Лагранжу
(погрешность от запаздывания исключается). В этом случае
134

£i(t)=6(t), ф=1. Известно [33, 34], что погрешность
преобразования
м
i=0
<
<(M7y+1
м
П(—г)
/=0
rAf+l
(М+ 1)! '
(5.26)
где 'Рм+\ — верхняя граница модуля (Л1+1)-й производной
функции х(0 в интервале, содержащем точки 0, 1/Af, 2/Af,...
Из неравенства (5.26) следует, что верхняя оценка
погрешности преобразования в рассматриваемом случае
6тах = 5ир(МГ)'
м+\
i=M
П(—ir
М+1
(М+1)!
(5.27)
Пример 5.4. Прямая задача. Найти 6таХ для АЦП с АИМ при
исключении погрешности ст запаздывания и восстанавливающих операторах ИПП и
ИВП по Лагранжу. Заданы величины Р2, Рг и Т.
Обратная задача. Найти максимально допустимый шаг дискретизации
при заданной величине Этах.
1. Интерполяция первого порядка, Af=l, P2=amax — наибольшее
значение модуля второй производной. Это по существу максимальное ускорение
(замедление) сигнала, подвергающегося временной дискретизации, которое
обычно может быть получено при изучении- объекта, генерирующего сигнал.
Из (5.27) следует
8 [я, e}<sup
.(.-i)£n
С целью определения 9тах исследуется на экстремум е(1—е).
Наибольшее значение модуля, в чем легко убедиться, соответствует е=0,5, откуда
emax=0,125amaxr2, (5.28)
и, следовательно, при заданной величине 8тах максимально допустимый шаг
дискретизации
Г = 1/89 Та (5.29)
У max' max* \«.*%//
2. Интерполяция второго порядка, М=2,
9 [*, е] <
(-i)<-
О
Y ОТ-
Исследуем на экстремум | е (е — 1/2) (е — I) [ :
V Г~~Т) (е-п] /^ = 3е2-3е+ 1/2 = 0,
135

откуда eli2 = —±—p==; ei=0,79; e2 = 0,21;
(~г)<->
_ j 1—0,051 при е1==0,79;
~~ 10,048 при е2 = 0,21/
Выбираем наибольшее значение модуля при ei = 0,79. При этом
етах=0,068РзР. (5.30)
Есл)И задала величина 8тах, то максимально допустимый шаг
дискретизации
з
^/Н^в^/Рз.
(5.31)
Аналого-цифровое преобразование с АИМ.
Восстанавливающий оператор-экстраполятор М-го порядка по Лагранжу
(погрешность от запаздывания в первом звене исключена). В этом
случае в соответствии с (5.25) и (5.5) при ф=0
м
Ь[п9 в] = х\(п + е)Т]- %Lt9[09 в]х[(п-М + 1)Т], (5.32)
/=о
где L/3[0, e] определяется по (4.63); М=0, 1, 2,...
Известно [33, 34], что погрешность преобразования
б И, в]<Г
>М + 1
JJ[(„ + e)-(n_Af + 01
*=0
М + 1
(М+1)\
= тм+ ]
м
Л(* + М-1)
i=0
М+1
(М+1)!
Верхняя оценка погрешности
м
втах = 8ирГ
М+1
П(в+^—о
i=0
М+1
(М+ 1)!
-j— jh,4m-i>-£3--pk„t-»
i=0
(М+1)!
(5.33)
Пример 5.5. Прямая задача. Найти 8тах для АЦП с АИМ при
исключении погрешности от запаздывания и восстанавливающих операторах ЭНП,
ЭПП и- ЭВП по Лагранжу.Заданы величины Рь Р2, Р3 и Т.
Обратная задача. Найти максимально допустимый шаг дискретизации
при заданной величине Gmax.
Л 36

1. Экстраполяция нулевого порядка, М=0, Pi=Vmax—наибольшее
значение модуля первой производной функции x(t), что соответствует
максимальной скорости изменения дискретизируемого сигнала.
Из (5.33) следует
етах- УтахГ, (5.34)
откуда максимально допустимый шаг дискретизации при заданной величине
Этах определяется выражением
r = emax/Vmax. (5.35)
Выражения (5.34) и (5.35) полз'чены без учета того факта, что ЭНП
вносит запаздывание на 1/2. Это следует из анализа его фазочастотной
характеристики, полученной в § 4.2. При работе тракта преобразования не в
реальном времени, когда погрешность от запаздывания может быть исключена,
ф2 = 1/2 и
6 [п, е]=х [(л+ 8-1/2) Г]-* [пТ], (5.36)
откуда
9 = sup Т
max /
т т
Я,-— /\= — V ; Т=^2В IV . (5.37)
1 2 2 max max' max* vu,c"/
Таким образом при исключении погрешности от запаздывания, вносимого
вторым звеном (экстраполятором нулевого порядка), величина 8тах при Г=
= const уменьшается вдвое, что соответствует увеличению вдвое
максимального шага дискретизации при заданной максимальной величине погрешности.
2. Экстралолятор первого порядка, M=l, P2 = amaх — наибольшее
значение модуля второй производной функции x(t)
втах^ЛтахГ2, (5.38)
откуда максимально допустимый шаг дискретизации при заданной величине
Отах определяется выражением
Г=Кв"^ЛГх- (5.39)
3. Экстраполятор второго порядка, М = 2,
етях=Р3Р; (5.40)
T = V»mJP*' (5.41)
Равномерная временная дискретизация линейно
возрастающего и параболического входного сигнала при
восстанавливающих операторах ЭНП, ЭПП и ИПП по Лагранжу. Выбор вида
детерминированного сигнала для анализа динамических
свойств АЦП определяется возможностью получения его
показателей при анализе системы, генерирующей сигнал, и
свойствами восстанавливающего оператора.
При использовании в качестве восстанавливающих звеньев
интерполяторов и экстраполяторов, порядок которых не
превышает единицы, свойства тракта преобразования можно проана-
137

лизировать при линейно возрастающем и параболическом
входном сигнале.
Пусть x=Vmaxt и x=amaxt2/2. Величины V max И Umax COOT-
ветствуют максимальной скорости и максимальному ускорению
аналоговой величины.
Текущее значение погрешности 8 [я, е] определяется по
(5.25), где z[n, е] вычисляется для рассматриваемых способов
восстановления при линейно возрастающем входном сигнале
в соответствии с выражениями (5.11), (5.14), (5.17); (5.20) —
(5.22). При x(t) = VmaXt функция 0[я, е] в установившемся
режиме при ЭНП, ЭПП и ИПП по Лагранжу не зависит от п.
Поэтому наибольшее значение погрешности в этом случае
находится как sup 6 [п, ej.
8
Выражения погрешности Qy[nf г] в установившемся режиме
для различных АЦП при учете и исключении погрешностей* от
запаздывания сведены в табл. 5.1.
Анализ данных этих таблиц показывает, что при линейно
возрастающем сигнале восстанавливающие операторы ИГТП и
ЭПП (по Лагранжу) обеспечивают равенство нулю
погрешности преобразования только при исключении погрешности от
запаздывания, в ином случае — при работе АЦП в реальном
времени—текущая погрешность преобразования не зависит от
времени и полностью определяется запаздыванием.
При параболическом входном сигнале после подстановки
x(t)=cimaxt2l2 в (5.8) далее по (5.25) получаем:
для АЦП с АИМ при Л,(т)=6(т)
цп, е}= а™*Т* (п + е — ф)2— (Ае + В)^-п*Г —
_Л(1-е — В)^Щ (л—I)2; (5.42)
для АЦП с ИАИМ при k^^JLU ft_(i_Y) — ] —
-'(--и}
а NT» Г/ 1 — у\* ( 1 \»1
_(Ле+В)-^__ 1(«—тг) -("-ТТЛ-
а NT* Г/ 1 — v\* / 1 \31
-А(1-,-В)-^-[(п-1—^) _(„—1—-^) J;
(5.43)
138

Таблица 5.1
С пособ

восстановления
ЭНП ПО
Лагранжу
ИПП по
Лагранжу
ЭПП по
Лагранжу
СО
to 1
АЦП последовательного сч ета с промежуточным
преобразованием в частоту, временной интервал с ИШИМ
Ф
0
2-Y , 1
2/V ~т~ 2
0
2""Y + 1
2N +1
0
2-Y
2iV
. у.ч
2iV у
^ax^(e--r)
^ax^(lF + 1)
0
2 —Y
r max1 2V
0
"max
<w(i+|r)
—- V' T
2 max
^maxT у "2ДГ + * J
0
2 —y
V T -
ктах' 2N
0
АЦП поразрядного кодирования с запоминающим
интегратором
<Р
0
—+—
2^2-
0
V
0
V
*у[П.ш]
^««^(•+"f)
^max^(^-T-)
^max^l+^J
0
V
V Т
1 max' 2
0
"max
»w(i+ir)
V T
2 rmaxJ
^max^(l+x)
0
v
V T
max1 2
0

а б л и ц а 5.
Способ
восстановления
АЦП с ИАИМ, kt (т) = —
1 (т - (1-т) JLJ _ 1 ^, _ -I-j] , *»W/2
а, 0» С, d
ЭНП
по Лагранжу
ИПП
по Лагранжу
ЭПП
по Лагранжу
2 + N
2.V
1 Y
1 + УУ ~~ 2iV
JL JL.
N 2N
a = 2; P= (2 —y)/^: c = 0\ ^= [(1 _T)3_ l]/(3iV2Y)
Y — 2
a = 2; p= — l; с = -др--
1 / Y \2 1 1—Y i
1 , l-Y , (1—Y)3—1
3#2y
2—y
a = 0; P = 2+-^; c =
. Q-f)3
"3y^2
+£[(•+*)'-(i+!^)
+
^'--i[('+T)'-('+1^)l
2—y 1 ЛМ / 1 3 (1 — Y)3
•=0;P = 0; ,__2—5J-3jvT+»rl('+-ff-|+-TF^-
1 \s
« ft. A 2 Y-, (1-Y)8-1 ,N\{.,L\
-('♦^"J"-
(1 — Y)3— 1
3yA/2
•a = o; p==0; c =
2 — y . (1 —Y)3 —1 , У
3y^V2
I— Y\31 1 / • Y \2 1
1+ту j; d=-/vr(i--r) +i^-[(i-Y)8-n

для АЦП с ИАИМ при кг (х)
vr
.[l(T)_l(,_vr)]
\Т
О
V7-
_[Л(1_в)_^]-1.|^И5.[(«-1)Г—«]«Л. (5.44)
О
.Анализ выражений (5.42) — (5.44) показывает, что
переходный процесс при параболическом входном сигнале
заканчивается не более чем за два такта. Число тактов п0 переходного
процесса сведено в табл. 5.2 и 5.3. В установившемся режиме
при п^2
а П
ОЛл, *] = ■ 2
• (аеп + fk + s2 + ев + d),
(5.45)
где а, р, с, d — коэффициенты, значения которых для АЦП
с ИАИМ приведены в табл. 5.2 и 5.3. Коэффициенты
определяются способом аналого-цифрового преобразования, методом
восстановления, возможностью учета запаздывания.
Та б л иц а 5.3
Cndco6
t восстановления
энп
по Лагранжу
ИПП
по Лагранжу
ЭПП
по Лагранжу
АЦП с ИАИМ, kx (т) = J- [1 (т) - 1 <т-v7)]. x =атах/*/2
Ф
0
1+v
2
0
V
0
V
т
«0
1
1
2
2
2
2
а, 0, f, d
а = 2; Р = v; с = 0; d = — v«/3
а = 2; р= -1; с= -(l + v);
(1+v)» v2
d== 4 -~
а = 0; p = 2 + v; с = 1 + v;
a = 0; p=0; c= —1; d= — v2/l2
a = 0; p = v; c=l + v; d = — v«/3
a = 0; p = 0; c = l; d = — v*/12
141

Анализ данных табл. 5.2 и 5.3 показывает, что а=0 и р=0,
т. е. погрешность не зависит от номера такта только при ЭПП
и ИПП при исключении запаздывания.
Значения коэффициентов для АЦП с АИМ могут быть
получены не только из (5.42). % Очевидно, что при JV->oo АЦП
с ИАИМ преобразуется в АЦП с АИМ.
Отсюда lima, HmP, lime, limd для АЦП с ИАИМ, когда k^z)
#_►«, W-юо /V-WV N-+00
определяется из (5.7), становятся равными соответствующим
коэффициентам для АЦП с АИМ, что позволяет проверить
полученные результаты.
Так, для АЦП с ИАИМ при ИПП и ср=0 (см. табл. 5.2)
•-*[(•+*№)■-(
1-У\
N /J
Зу№
Предельное значение с при N-+oo определим,
воспользовавшись правилом Лопиталя: lim с = 1, что соответствует АЦП
/V->oo
с АИМ.
Аналогично для АЦП с ИАИМ, когда &i(t) определяется
из (5.18), а, р, с, d становятся равными соответствующим
коэффициентам для АЦП с АИМ при v=0. Кроме того, так как
при v=l импульсная переходная характеристика модели
временной дискретизации для АЦП поразрядного кодирования
с запоминающим интегратором совпадает с моделью первого
звена АЦП последовательного счета с промежуточным
преобразованием в частоту, когда число каналов N равно'1 (см.
§4.1), то значения коэффициентов а, р, с, d при v=l из
табл. 5.3 совпадают со значениями коэффициентов из табл. 5.2
при y=1 и N=1.
Для оценки погрешности АЦП при детерминированных
входных сигналах удобно использовать критерии, имеющие
наибольшее применение в инженерной практике:
ftnax = SUP
/1,8
М*. £]
ц =
п«ГХ 1
п=п0 0
Xmax(re'"-Wo)
/
/ "т-1 1 \ "2
п=п0 О
4 («m-«o)rf
(5.46)
(5.47)
(5.48)
112

где p.max, р,, у р.2 —соответственно максимальная, средняя и сред-
неквадратическая приведенные погрешности преобразования;
по — номер такта, начиная с которого переходный процесс
закончен; Хтах — максимальное значение входного сигнала; Пт=
=У^тах/,(^тах7,2/2)—номер такта, при котором
параболический сигнал достигает максимального значения.
Кратность диапазона х величине атахТ2/2 принята для
упрощения выкладок и при больших п™, что обычно имеет
место, практически не является жестким ограничением. Так как л™
обычно много больше п0у то в выражениях (5.46) — (5.48)
можно считать /г0«0.
При а=0 и (3=0 Qy[n, e] не зависит от п и формулы
(5.46) —(5.48) упрощаются (не требуется суммирование и
деление на /гт—/г0).
При этом
>W = sup '**+/ + <*' ; (5.49)
• max
, . 1
~= ^e* + ec+d)de/xmax; (5.50)
6
_ / 1 \l/2
V^=\\(^+Ce + d)^slxl\ . (5.51)
Анализ выражения (5.45) показывает, что наибольшее
значение погрешности получаем при п=пш—1, величина бтах
определяется способом построения АЦП и методом
восстановления. Значение е, при которых jLi=jxmax, получаются
исследованием на экстремум функции |i(e) при п=Пт—1.
Для определения влияния величин N, у и <р при
параболическом входном сигнале проведены расчеты при вариациях
этих параметров, включающих практически полностью весь
диапазон их изменения:
N=1, 5, 10, 100; v=0,l; 0,5; 1.
Значения ф рассматривались-при исключении погрешностей
от запаздывания, а также при работе АЦП в реальном
времени (ф = 0).
На рис. 5.2 приведены зависимости \imax (сплошные линии),
|ы (штрихпунктирные линии), у р.2 (штриховые линии) от
обобщенного параметра пт, определяемого диапазоном ху
ускорением входного сигнала и шагом временной дискретизации
при параболическом входном сигнале.
Анализ полученных зависимостей позволяет сделать
следующие выводы:
143

l/2l,V^/*max,°/°
Рис. 5.2. Зависимость приведенных оценок погрешностей преобразования для
нулевого порядка (б), первого порядка (в), интерполятором первого порядка
ная приведенная оценка погрешности (сплошные линии); \ц\— модуль средней
оценка (штриховые линии) /
144

I/*',/* max
100
10
0,1
0,01t
A I'll II Г
N = i;y = Q,i—
10
A
S)
100
1000 Пт
АЦП с АИМ (a), для АЦП с ИАИМ при восстановлении экстраполятором
(г) при детерминированном входном сигнале x=at2/2 : Цтах — максималь-
приведенной оценки (штрихпунктирные линии); VV2 —среднеквадратичная
10—5036
145

100
1000 Пп

l/*';/*maxi%
100 С
0,01
Рис. 5.2
10*
1000 Пп
147

1. С ростом Пт погрешность преобразования падает. При
этом зависимости оценок погрешностей от пт практически
линейны в логарифмическом масштабе; следовательно, [i=f(nm)
может быть аппроксимирована степенной функцией.
2. При исключении погрешности от запаздывания с ростом
числа каналов при r=const погрешность преобразования
увеличивается.
3. При работе АЦП в реальном времени (<р=0) с ростом
числа каналов при Т=const погрешность преобразования
падает. Это объясняется тем, что с ростом N уменьшается
запаздывание.
4. При работе АЦП в реальном времени (ф=0)
экстраполяция нулевого порядка обеспечивает большую точность, чем
ИПП.
5. При работе АЦП в реальном времени определяющей
составляющей погрешности является погрешность от
запаздывания.
5.2. ПОГРЕШНОСТИ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ
СИГНАЛОВ, ЗАДАННЫХ КОРРЕЛЯЦИОННЫМИ
ФУНКЦИЯМИ, ПРИ РАВНОМЕРНОЙ ВРЕМЕННОЙ >
ДИСКРЕТИЗАЦИИ
В качестве моделей входного сигнала и помехи используем
центрированные стационарные в широком смысле случайные
процессы. Условие центрированности не нарушает общности
результатов. Это объясняется следующим образом. Допустим,
о
центрированный случайный процесс x(t) получен из
нестационарного x(t) путем вычитания из x(t) математического
ожидания mx(t) как функции времени. Так как тракт временной
дискретизации и восстановления' описывается линейным
оператором (см. §5.1), что позволяет применять метод суперпозиции, то
текущая погрешность преобразования определяется как сумма
погрешностей при детерминированном mx(t) или случайном
■э
x(t) входном сигнале. Методика оценок погрешностей при
детерминированном входном сигнале рассмотрена в предыдущем
параграфе. В данном случае через x(t) и A,(tf) будем
обозначать центрированный стационарный случайный процесс.
Описание входных сигналов и помех в рамках
корреляционной теории случайных процессов позволяет получать средне-
квадратические оценки погрешности преобразования.
Рассмотрим вначале свойства случайного процесса на выходе тракта
преобразования, заданного синфазной моделью (см. рис. 5.1).
Сигнал z[/z, e] в установившемся режиме при наличии помехи
J48

X (t) в соответствии с (5.5) имеет вид
00 ОО
*„[«.«]= 2*.И. e].fM')M(«-m)7,-*] +
т=0 6
+ Я [(я — т) Т — х]} dx. (5.52)
Математическое ожидание сигнала на выходе синфазной
модели
{оо t оо
2*,[m, e]S^(x){x[(«-m)T-x] +
m=0 0
+ Я[(л —т)Г—x]}dx|.
После внесения знака математического ожидания под знак
суммирования и интегрирования, учитывая, что M[x(t)]=0 и
А1[Я(/)]=0, получаем
М{гу[п9 е]}=0.
Корреляционная функция гу[п, e] при фиксированном е
с учетом равенства нулю математического ожидания zy[nt e] и
некоррелированности сигнала и помехи определяется
следующим образом:
Rzz(x + X) \g, в] = М {Zy [Л, в] Zy [П + g, в]} =
/ ОО 00
= М \ 2 Л,[т, в] j ^(^^[(/z-mjr-XiH- Я[(я-т)Г —
'чт=0 6
оо оо
-*i]*i} 2 Mr, в] j*iK){x[(n+g-r)T-x1]+i[(n+g-
г=0 О
_r)7-x2]dx2} .
После внесения знака математического ожидания под знак
суммирования и интегрирования
оо оо оо оо
Rzz(x+i)[g, е]= 2 %kt[m, e]kt[r, e]JJft1(x1)ft1<x1)X
m=Or=0 . 0 0
ХМ{х[(л-т)7'-т1]х[(п-г + £)Т-х21 +
+ Я1(я-т)7'-т1]Я[(й-г + ^)7,-х2] +
+ *[(/г_т)7'-х1]Я[(п-г + £)7'-х2] +
+ Я [(n — т) Т — хх] * [(п — г + g) Т — х2]} dtjdts.
Учитывая, что
M{x[(n—m) T—ti]x[ (n—r+g)T—т2]} =
=Д«'[ (g-r+m) Г—т2+т,];
149

М{Ц (п-т) Г-т, \Х[ (n-r+g) Г-т2]} =
=#n[(£-r+m) Г-гг+Т!];
М{х[]Ц-]}=0 в силу условия некоррелированности сигнала
и помехи, находим
00 00 ОО 00
&г{х+ ц [g, е] = J! ^ К [т, в] К [г, в) J { kx К) ^ К) X
m=Or=0 О О
X #„ [(g—r + m)T — т2 + хх] dtydit +
ОО ОО ОО ОО
m=Or=0 0 О
где RXx[']9 Ru.[m] — корреляционные функции сигнала и
помехи при соответствующих значениях аргумента.
Анализ выражения (5.53) показывает, что при Х=0
корреляционная функция Rzz[gf e] сигнала zy[nf е] определяется
первым слагаемым этого выражения.
Корреляционная функция сигнала zy[nt e], вызванного
только воздействием помехи, при x(t)=0 определяется вторым
слагаемым выражения (5.53). Существенным при анализе
выражения (5.53) нри фиксированном е является факт
зависимости корреляционной функции zy[nt e] от промежутка времени
gT и независимости от тТ и гТу откуда следует, что
последовательность отсчетов zy[n, e] при фиксированном е стационарна.
При этом можно трактовать величину е как континуальный
номер стационарной последовательности отсчетов с шагом Т
функции zy[n, e]. Однако отсюда также следует
нестационарность zy[nf е] как функции непрерывного аргумента в силу
зависимости RZz(x-\-X) от е. Полученный вывод может быть
проиллюстрирован при рассмотрении ступенчатого восстановления
дискретизированного случайного процесса x(t) (рис. 5.3).
Момент корреляции между случайными величинами z[T-\-e\T]
и z[T-\-z2T] равен /?**[0]. В то же время момент корреляции
между случайными величинами г^Г+езТ1] и z[2T-\-eAT] при
Т+Ы—£з)Т=(е2—г\)Т=х равен RXx(T). Отсюда
корреляционная функция случайного процесса z[n, е] зависит не только
от промежутка времени- между его сечениями, но и от
расположения этого промежутка на оси времени. В то же время
коэффициент корреляции между случайными величинами -г[/п7,+
+ei7f], z[rt-\-e\T] при фиксированном ei равен RXx[(m—r)T]>
т. е. последовательность отсчетов с шагом Т и при
фиксированном ei стационарна.
150

=(£2~e7)r хт+егт хТ+е3т ^ZT+e^T
Рис. 5.3. К определению нестационарности zy [n, е]
Выражение дисперсии случайного процесса на выходе
восстанавливающего оператора получаем из (5.53) при g=0:
ОО 00 00 ОО
Яв(,+ м[0, *]= 2 2K\m, e\kt[r, «]| J*iK)*iK)X
m=OC=0 0 6
X Rxx [(m - г) Г - x2 -f- xj] dxlCfT2 при Я = С; (5.54)
ОО 00 ОО ОО
w>[о, в] = 2|*.к в]л,[г, в] f jftx(х,)*х(х2)х
m=Or=0 6 О
XR \[(m — r)T— ^2 + H\dHdz2 пРи * = 0, (5.55)
где RZz[Of e]—дисперсия сигнала на выходе
восстанавливающего оператора; #22ш[0, е] —дисперсия помехи на выходе
восстанавливающего оператора.
Взаимную корреляционную функцию между случайными
процессами х[(п-\-г—ф)Г] и z[n+g, е] при фиксированном е
и %=0 определим следующим образом:
Rxz[g, *) = М{х[(п + e-y)T]z[n + gt е)} =
( оо оо Ч
= М{х[(п+е—9)TJ"2 К\т, e]§k1(x)x[{n—m + g)T — *\dx\ =
( m=0 О J
оо оо
= S *.K *]$k1{i)M{x[in + e-<,)T\x[(n-m+g)T-*]}dx =
т=0 О
151

« 2*.К вjJлх(-с)/?жх[(от—g + e—<p)T+x]dz9
m=0 6
откуда при g=0
ОО 00
Д«[0. е1= 2 М»и, в] J^(х)/?„[(« +в-9)7*+ ']Л. (5-56)
т=0 О
Полученные выражения являются исходными для
определения дисперсии погрешности /?ее<*+л)[0, е] преобразования на
синфазных моделях. Действительно,
Ь2х+х[0,г} = М{х[п + в-<р)Т}-гу[п,е]у =
= Л„(0)-2ЯЛ[0, в] + Л„[0. Н + ^г(х)[0, е], (5.57)
где первые три слагаемых определяют собственно дисперсию
погрешности преобразования при Я=0, последнее — дисперсию
сигнала, вызванного воздействием помехи. После подстановки
формул (5.54) и (5.56) в (5.57) получаем выражение
дисперсии погрешности преобразования при Я=0:
00 00
в5[0,«1 = Я„(0)-2 2М'и, <)$kiWxx[('n + *-4>)T + x]dx +
m=0 О
ОО ОО ОО ОО
+ 2 2М"*, *\b\r, '\\\kMhMR,x\(m-r)T-
m=Or=0 О О
— т2 + TiJ di-ydi^ (5.58)
Дисперсия,шума 82а,[0, е] на выходе тракта преобразования
определяется выражением (5.55). Если провести аналогичные
выкладки для несинфазной модели (см. рис. 5.1,6), легко
получить
М оо
F[o, b] = rxx(0)-2 si,"[о, «]Jai(*)*J(i-
м м
_-I_ + e_9J7AI+t]^+ SS1'"10, е11гИ[0, S]X
/=0r=0
oo oo '
X J J К W ki К) Л, Л (г -i)T + xx-x2] dx^,,; (5.59)
О О
ММ оо оо
6х[0( е] = ^ 2 W e]VfO, e]J J M'i)*iW +
t=or=o 6 о
X Дхх [(г — /) 7" + ^ — х2] <М*.. (5.60)
152

где L;H[0, e] определяются выражением (4.52) при
интерполяции М-го порядка по Лагранжу и выражением (4.101) при
интерполяции /-го порядка по критерию наименьших квадратов.
Анализ полученных формул свидетельствует о зависимости
дисперсии погрешности преобразования от е, способа
получения цифрового эквивалента, восстанавливающего оператора,
режима работы тракта преобразования. Так, при
невозможности исключения погрешности от запаздывания ф = 0. В
противном случае Ф=ф1+ф2, где ф1Г и щТ — соответственно
запаздывание в первом звене и восстанавливающем операторе.
В качестве оценок.погрешности удобно исцользовать
относительные величины. В частности, при фиксированном е сред-
неквадратическое отклонение (погрешность) преобразования
(СКО)
/>[0, в]==|/>[0, *]IRXX(% (5.61)
а отношение мощности помехи на выходе тракта
преобразования к мощности сигнала на его входе
82х[0, е]^Щ0у e]/Rxx(0). (5.62)
Суммарная относительная среднеквадратическая
погрешность преобразования при фиксированном е следует из (5.57):
/Й+х [0, .в] = /?[0, в] + «[0, в]. (5.63)
Для оценки погрешности преобразования на интервале
восстановления можно применять усредненную СКО и ее
наибольшее значение:
У¥=У]ё[0,ш)<Ь; (5.64)
о
уТ= i/supa^O, в]. (5.65)
Аналогично, отношение средней мощности помехи и ее
максимального значения на выходе тракта преобразования к
мощности сигнала на входе определяется следующим образом:
§! = J8?[0(S]de; (5.66)
о
8i = sup8l[0, e]; (5.67)
8
-|As + x=l/"62 + 5!; V%+i = Ye+bl. (5.68)
153

Таблица 5.4
1
ЭНП по Лагранжу
.
Линейная экстраполяция
(0<М<1); .
ЭПП по Лагранжу (Л = 1)
ИПП по Лагранжу
ф
2
0
•
<Pl+ —
0
*1
0
fi + 1
АЦП с АИМ, kx (т) = Ь (т — ф1П
Ъ* [0, 8]
3
9
. . f 1 D Г f,- 1 ,. \ Т1)
««(0) O-^xKb + fi)^}
2
€ л Г) Г/с 1 /П\ Tl 1
RxxiO) 0-Д**1(*-1/2)П)
2
1 f / И., j n d IU т M \ Tl Л г Р Г/1 ! г 1 m ^ Tl) 1
1— д> /q\ 1(Лс г 4 *<xx i\b T"¥iM J — лб/чди: К 1 -f- ь -j- <p1;> / jj -j-
1 / Г / A _L 1 \2_1 Л2-Я1 n> ml о Л~ / Л,, г i\D Г Til
~r д> /q\ ШЛь т~ ч ~r A fc J AjpclUJ—^Ль 1Ле -+- l) Ajc» L' J)
2 1
1 Г / /1- 1 1 \ П Г..Т1 Л-D Г/1 1 -\ Tl") 1. f Г/ Л- ! 1 \2 1
/?** (0) ПЛь "Г U AAjcbi J — л*Кд;д: 1(1 + *) i J) ■+• Rxx(0) \\.\A*~rl)-r
+ АЧ*] Rxx (0) - 2Ле (As + 1) /^ [T]}
2
1 . (PD Г/<- 1 ,« \T1 | /1 -\ D Г/1 1 <- 1 » \ ТЛ\ i
#**(0) l**** КЬ+Ы' J -r (1 v axxLU i- t_h <Ы l J/ +
1 .-■1'Г1.2 1 /1 -^21 D /Л\ l О- l\ -\ П ГТП
#x (0) Ub -T-(l—6)J a** (U; + Je Ц — t) t\xx У J)
2 1
1 ,_ (.D Г/1 .\ Tl _L /1 -\ D Г„Т1\ 1 .. ■- СГо.2 1 /1 o\21T4/
ХЯ**(0)+М1-«>***[Г1>

ЭМП по Лагранжу, Э1ПКВ
ИМП по Лагранжу, И1ПКВ
1+ М
м
1 ~~ Rxx(O) S Li*[°' elR*xUM-l+e + ^Tl +
1
/=о
м м
Rxx (0)
S И v t0, е] v [0, ei ***t(r ~~ °n
/=0r=0
M
/=0
M M
t=0r=0
■Ж7(оГ5]1«'И[о'е,^[(1-"^"+е+
f=0
*H
+
M M
Rxx (0) S S Lf"[0' e] V [0' e] Rxx w■"r) T]
i=0r=0
Rxx (0)
M
i=0
M M
1
Rxx (0)
"JJJJVIO. ']Lr*[0,M]RxxUi-r)T]
*=0r=0

~ Таблица 5.5
Способ восстановления
•
ЭНП по Лагранжу
Линейная экстраполяция
(0<Л<1);
ЭПП по Лагранжу
М = 1)
ф
0
1 2 — 7
2 + 2/V
0
АЦПсИАИМ. fel(,)=JL /l Г,-(1-т)^-|-.1Гт-.^.1\
Ь* [О, е]
l/N l/N l/N
1 ., . _ l D Г/« 1 « \T1 ^ |_...„. \ 14/
1 ««(0) Y J *"!<•+4> rlJ^+/?„(0) Y2 J 3 х4
<i-K)/w (l-t)/w (l-t)/tf
X««[(«i-«i)n*i*i
1/ЛГ
!-тет>гт 1 ^[(e-^""2^1+ei)T]d£i+
<l-7)/N
l/Л^ l/N
1 A2 f f
+ Rxx (0) T5" J J RxX l(£l ~ ч) T] **1***
(l-7)/N(l-7)/N
l/N l/N
!~../?*!(0) t{(A+1) I R«[« + Ji)n*i-A j Rxxl(i +
(1-7)/^ (1—7)//V
l/N l/N
(1—7)/^ (l—T)/iV
l/N l/N
- *«) Tl del*> - 2 (A + 1) A J f #** [(ex - *a + 1) T] d^deX
! 0-7)/^ (l-7)/N

Продолжение табл. 5.5
Способ восстановления
АЦПсИАИМ. fel(*)~{l [-«—О —7> -^-J —.1 [х —-^-]}
Ъ* [О, е]
ИПП по Лагранжу
(1—Т)/Л^
\(N
-A\i..fxA{i+e-'2^+H)T]dei}+^^{i{Ae+i)*+
l/N UN
\/N MN
+ A42] J I Rxx[(h-*2)T]dHd4-2(A*+l)A* j j X
(l-D/N (l-D/N
Х^«[(«1-В1 + 1)Л^4
(l-?)/W (l-T)/^
2 ЛГ
#**(0)
1/ЛГ 1/W
(1-1)/N
1 W*
1/W X/N
(1-Т)/ЛГ (1-т)/ЛГ
l/N l/N
-е2)Т[йе^е2 + 2е(1-е) J ^ Й«[(«1-«, + 1)ЛАа}

55 Продолжение табл. 5.5
00
Способ восстановления
•
ИПП го Лагранжу
ЭМП по Лагранжу, Э1ПКВ
<р
1+2""Y
1_г" 2N
0
ацпсИаим, kx rt = -ff h h-d-т) ж]-,1[т~~"г]}
Ъ* [0, е]
1/W
1 2 V (ь Г R \(ь + ь 1 2_1ГЫл 4-
(1-T)/W
1/ЛГ
(1-7)/^
1/Л7 1/Л/"
<l-T)/tf(l-7)/JV
i/лг i/yv
+ 2e ( 1 - e) j j Д,, [(.x — «. + !) T] de^
M l/N
1 \ /,ЧП rl 1 f? KM . f 1 e -1 с ^ 7*1 We 1
~" /?** (o) v Zj I *
1=0 (i-T)/^
M M l/N l/N
+ idwr?"SSVIO-*1Lr4o>tl ^ J R«I(r-' +
Ыг=0 (1-7)/^ (1-7)/ЛГ
+ ех—e2) rjdsjdea

Продолжение табл. 5.5
Способ восстановления
АЦП с ИАИМ, fel(T)=^- /l Г(т- (1 — Ч) -^-1 — 1 [т-7г]}
52 [0, 8]
М 1/N
,-^-tSvio>'1 I «**[(M-i+e-2~^+ei)T)h+
'=0 (1-7)/Л^
1 • W*
м м
X/N XJN
Rxx (0) y2 S S V [°' el V[°' 6l J f ***[(Г ~
(1-
i +
ИМП по Лагранжу, ИШКВ
1 Л/а
t=0
м м
TIN
I
Т (\--{)IN
М TIN
l—R^o)wYiLi"[°' e] I ^[(1~^Г+е)7'УИ+Т]Л +
Rxx(0) rv
/=0r=0
Г/JV Г/JV
I J
S 53L'"i°' eivto, ■] f j я«[(г-
— /) Г + «^ — т2] dx^Tjj

S Продолжение та$л. 5.5
Способ восстановления
ИМП по Лагранжу, И1П*в
1 Т" 2NM
АЦПсИАИМ, ^(x)=^~ /l r,-(i-7)Z-l_lN--I.jJ
г« [О, е]
2 ЛГ
м
Л«(0) Y^
5] v to, e]
X
/=0
7-(1-Т)/Л^
1 W*
м м
Я« (0) Г2у2
БЕ1-"10'
•] V' Ю- «] X
(=0 г=0
Г/Л? Г/Л».
X
Г , Г Л«[(г-0Н'1-^]ЛА
Т {i-D/N Т 0-V/N

В том случае, когда оценку погрешности преобразования
удобней приводить к диапазону изменения входного сигнала,
соответствующая относительная оценка делится на величину
%= (Xmax—Xmin) /УЯхХ(0); оценки (5.66) и (5.67) делятся на %2.
В частности, для гауссовского случайного процесса при,
определении диапазона изменения входного сигнала в пределах
±SyRxx(0) величина %=$, для закона равномерной плотности
вероятности %=yi2, для закона Симпсона х=У6-
Ниже будут приведены формулы оценок погрешностей
преобразования случайных сигналов для различных способов
получения цифрового эквивалента и восстанавливающих
операторов при X(t)=0. Анализ помехоустойчивости тракта
преобразования рассматривается в § 5.4.
Выражения оценок погрешности преобразования 62[0, е]
для АЦП с АИМ при k\(x)=6(x—(p\T)f выведенные путем
подстановки соответствующих выражений импульсных переходных
функций восстанавливающего оператора в (5.58) и (5.59)
с учетом (5.61) и (5.64), приведены в табл. 5.4. Аналогично
полученные выражения 62[0, е] для АЦП с ИАИМ при k\(r) =
=={NlyT){l[x—(l—y)TiN\—l[x-T/N]} приведены в табл. 5.5.
Эти формулы охватывают случаи учета (ф=0) и
исключения (ф = ф!+ф2) погрешности от запаздывания. При y=1 и
l/N=\ приведенные выражения соответствуют АЦП
поразрядного кодирования с запоминающим интегратором. Если 7=1,
рассматривается АЦП последовательного счета с
промежуточным преобразованием в частоту. Использование данных оценок
для анализа точности.трактов временной дискретизации и
восстановления рассмотрим на конкретных примерах, имеющих
самостоятельное значение в практике анализа и синтеза
трактов аналого-цифрового преобразования.
Пример 5.6. При использовании АЦП считывания определить оценки
погрешности тракта аналого-цифрового преобразовния случайного входного
сигнала с постоянной спектральной плотностью мощности в полосе частот от
О до Ютах при восстанавливающем операторе экстраполяторе нулевого
порядка по Лагранжу. Рассмотреть случаи работы тракта преобразования
в реальном времени и при исключении погрешности от запаздывания.
Импульсная переходная характеристика первого звена для указанного
способа получения цифрового эквивалента &i(t)=6(t) (cm. табл. 4.1).
Корреляционная функция заданного случайного сига ал а в соответствии
с данными табл. 1.1 имеет вид '
Rxx(t)=Rxx(0) sina)maxT/(a)maxT).
Подставив Rxx (т) в ^формулу, соответствующую АЦП с АИМ при ЭНП
и ф1 = 0 (табл. 5.4), получим
11—6036
161

2 {1 -sin eomax7V(o)maxre)} при у = 0;
i[0,c] =
И'
.g""Wr(—1/2):
' %.хП«-1/2) I
при у = ■
1
(5.69)
Проанализируем оценку погрешности преобразования. Точка (0тах7,=я
соответствует 0 корреляционной функции сигнала. В том случае, когда
восстанавливающий оператор — идеальный фильтр нижних частот, шаг
дискретизации по теореме Котельникова (см. § 4.2) выбирается равным Jt/wmax.
В данном случае идеальный фильтр нюкнлх частот заменен реальным (см.
амплитудно-частотную характеристику ЭНП в табл. 4.1). Входной сигнал
имеет ограниченный спектр, что соответствует условию теоремы Котельникова.
Подставив Г=л/о)таХ в (5.69), получим
82 [0, е]
| 2 [1 — sin 7ce/(7us)] при <р = 0;
Sin тс (е— 1/2)
2 1
1
(5.70)
ПрИ ?=—,
(5.71)
п (« -1/2)
откуда максимальное, значение СКО преобразования определится при 8=1:
yW=lv^Zl>41 при * = 0;
|[/l,68= 1.3 при <р= 1/2.
Таким образом, изменение условий теоремы Котельникова,. состоящее
в замене идеального фильтра нижних частот экстра пол ятором нулевого
порядка, при шаге временной дискретизации Т=п/ыт&х приводит к недопустимо
большим погрешностям преобразования (соответственно 141 и 130% при ф=0
и ф=1/2).
Максимальное значение СКО преобразования при Г<а)тах/л
определяется выражением
$2 =
1/2[1-81пГсотах/(Го)тах
)]
при у = 0;
]/2[l-sin-i-rcomax/(-|7rcomax)] при ?—L
(5.72)
Вычисления по (5.72) при малых (йт&хТ удобней проводить, разложив
в ряд Маклорена функцию sin х/х.
sinx y^
Так как = V
т=0
(—1)мхат|
(2т+1)!
то
v«l=
/•Б
162
(-0"Ч1Ка/)
(2/и + 1)!
%т
(-1)^Ч0,5сотахГ)^
(2т+ 1)!
при
= 0;
при ¥ = —• (5.73)

При малых (Dmax7\ что соответствует реально удовлетворяющим
значениям погрешностей, достаточно использовать первый член ряда (5.73). Так, при
7,= Ю-2л/0)тах
У'Р= |1/2(10-»я)»/6 = 0,054;
\|/2 (0,510~2n)2/6 = 0,027. (5.74)
Усредненная дисперсия погрешности с учетом разложения sin*/* в ряд
Маклорена имеет вид
д*= I
(-0" + 1КахП^
(2/72+1)! (2/72 + 1)
0 т=1
jSM0,elde = 2j; ______^-__ „р„? = Т. (5.75)
(О т=\
Для СКО до 20% достаточно пользоваться только одним членом ряда.
В этом случае относительная погрешность в определении ]/р с учетом
запаздывания не превышает 1%, при исключении запаздывания—10%.
Усредненная СКО преобразования
^=|Ш«ах7'/3 при ¥ = 0;
КахГ/6 при у =1/2.
Пример 5.7. При использовании АЦП поразрядного кодирования с
запоминающим интегратором определить оценки погрешности тракта аналого-
цифрового преобразования стационарного входного сигнала, заданного
корреляционной функцией Rxx(z) = Rxx(O) е~~а2т2, ПРИ восстанавливающем
операторе — интерполяторе первого порядка по Лагранжу.
Импульсная характеристика первого звена для указанного опособа
получения цифрового эквивалента в соответствии с данными табл. 4.1 имеет
вид ki(x) = (\/vT){\(i)—1(т—V7")}. Подставив заданное выражение
корреляционной функции в формулу б2[0, е] (ом. табл. 5.5) для АЦП с ИАИМ при
ИПП и положив l/JV=v, y=l, получим
Р[0, е] = 1 -2-J- е Г е-2 <е+8>>8 ™(U1+(l —) Ге~а2 <1 + i+e»)f7,,d.1L
* 0 6 '
V V
+-£- [£2+« - е)12 J j*e~~a2 (81"8I) 2T*delde*+
о о
+ 2"^"e(1-£) fl e~a8($1""82+1)8^eide2 при j = 0; (5.76)
'00
11* ' 163

«МО, «1 = l-2-J- It j e"ei<i+i»-1-v/2)irirf.I + (1 + .) X
* о
V J V V
xj ,-*(.+.,-v/2)^«deiL-L[t, + (,_e)2] j j"e-.'(..-^)'r.dhd4 +
О 0 0
v v
+ 2^е(1~е^|е~а1(в1~в2+1),Г^е1^ПРИУ=1+-7- (5'77)
0 0
Так как интеграл от еГаШТиг Не берется в квадратурах, разложим * эту
функцию в ряд Маклорена:
После подстановки (5.78) в (5.76) и (5.77), проведя интегрирование
равномерно сходящихся степенных рядов, получаем
(—\)т(аТ)*'п i i г (e + v)2^+i_62^vi
у (-\Г(*Т)^ ( i г
2т+ 1
+ (1—0 1-Л1^ + " : [е2 +
' l ' "~ ' • F (2m+l (m+1) Ll ^
2/n + l
+ (1— e)ajv2"— 4"8(1— e)[2-(l + v)2"+2_(l_>)2-'!+2j|j. при ? = 0;
']!
(5.79)
v\2r71+ *
«40, •] =
m! I v L 2m + 1
,_.,(•+т) -1-7) .
_-(l_v)i«+i]lj при 9=1 + -^-. (5.80)
164

Далее проведем преобразования, связанные с разложением по Синому
Ньютона ряда слагаемых:
2т
(« + у)1"-Н-,1»+1 ^
c27i+le v >
= 0
1 = 0
2т
(1+е + у)2^1^(1+е)2Л + 1 -~ /f,ev/*n-/.
/=о
т+1
2,(1+у)^1-(1-уГ. ^ }
/=1
+ 1
(е— 1+ v/2)2^+1 — (е —1 — v/2)2 z
*=0
Подставив полученные формулы в (5.79) и (5.80), получим
m=l ■ L i=0
4
[И+ (!-.)«] *•* + .(! _е) J] 2C|JH.2v2<'-I> +
+ (l+e)'(l_e)]v^-'-2[e2, + l + (l +e)«"( J _ e)] | +
1
(2m+l)(m + l)
i"=2
+ 2e(l-e)C2n+J при ? = 0; (5.81)
Pl„.,14<=iip^j__^_["j'2C&ti,i)^.-.H.x
"1=1 l f=o
X V»C"-') [c (e_ l)H + (l+e)i']-(2m+ 1) [e (1—e)»"» + (l _.)"]! +
Г m+l
I [t«+ (l_.).Jv"+«(.l -e) Jj 2C|'n+2v2C'-1) +
i'=2
+ e(l-e)2C22.n+2 1 при <p = l+y. (5.82)
+ !
(2m+l)(m+l)
1=2
165

Усредненное значение относительной дисперсии погрешности
преобразования получаем по (5.64):
оо / 2т— 1
у. У (-1Г(аГГ* 2 \1 ■ i .^-/ 2'*»-2
m! I 2m+ 1 Zj 2m+1 (t + i)(f + 2)
m=l *=o
2"н*—-2 1
(m + I) (2m + 1) + (2m + i) (m + 1) I 3 *~ "r 3 j£j "272+2
£=2
[OT+1
/ о
,v2'-2+
Ф— (2m+l) (m+l> |> при ¥ = 0; (5.83)
x- '
(/+ 1) (2i+l) ' m4-l
i
[m-l
2ScMt)
'-=0
з з U
i о
1 I * ■ .-. . i %lr2/ V2(*-1J_
(2m+l)(m + l) I 3 ■ ! 3 iJ ^2/72+2
*=2
+j(2m+l)(m + l)> при *=*.1+Д-. (5-84)
Учитывая, что результат получен в виде знакочередующихся сходящихся
степенных рядов, проведем анализ приведенных выше выражений,
ограничиваясь первыми двумя ненулевыми членами ряда:
57 \
+ 6v + —J при <р = 0; (5.85)
У } 2 \.24т 6 5 У 6 \ 32 ^336
+~3~"2 + ~42~) ПРИ У==1+Т;. (5,86)
Проведенный по (5.85) .и (5.86) расчет для худшего случая при v=l
показал, что результат вычисления "j/d2 при использовании первого
ненулевого »члена ряда в практически приемлемом диаоазоне СКО до 30% имеет
относительную погрешность не хуже 10%. *
Выражение максимальной дисперсии погрешности б2 должно быть
найдено после исследования на экстремум по е функций (5.76) и (5.77) либо
(5.81) и (5.82). В первом случае получаем трансцендентное уравнение
*/62[0, e]/de = 0, во„ втором — алгебраическое уравнение в общем случае
степени 2т при /п-^оо. Так как аналитическое решение этих уравнений не пред-
166

ставляется возможным, перейдем к приближенному определению б2. Анализ
выражений усредненной дисперсии погрешности свидетельствует о том, что
при реальных значениях СКО преобразования первый член ряда по существу
определяет сумму ряда.
С учетом этого обстоятельства, максимальное по периоду дискретизации
значение СКО .преобразования может быть приближенно оценено по первому
ненулевому члену выражений (5.81) и (5.82).
Так,
Ш
в*= SUp _!^X2^__S_2J <V[e'-n + (! + «)'(1-«)J V2"'-
(=0
-2[^ + (l + ej4l-e)]+4-[[s2+(l-s)2]v2+Ml-0 2v2 +
О
+ 2е(1-е).3] при у=0; (5.87)
1
— (»П4 2 СЧ . / 1 \ 2 (2-0 + 1
S2 = SUP^- \-Yli2Cb2t (ТУ V»<»-')[t(.-l)« +
+ (!-.)£»']—у [s(s-l)4+(l_e)e4] + -L[c2+(l^e)2]v4 +
•-; о
:(1 V ' %1|2Св2^2(/-1) + 2Св2
15
~'i=2
при у = 1 +v/2. (5.88)
Исследование на экстремум показывает, что дисперсия погрешности
достигает максимума при е = 0,5. В этом случае
— (<*П2
*2^— -(0,5v2 + 2v+2,02) при у = 0; (5.89)
■e,*iT-("i4+T*,+T) при "1+Т- (5-90)
Эта оценки распространяются -на АЦП с АИМ при v = 0 и на АЦП
с промежуточным преобразованием в частоту при v=l.
Результаты, полученные в данных примерах, позволяют
сделать ряд важных выводов: методика определения СКО
преобразования путем разложения корреляционной функции в ряд
Маклорена является- эффективным способом решения задачи;
усредненная и максимальная оценки СКО преобразования
с высокой точностью (не хуже 10%) в практически приемлемом
диапазоне СКО (до 20—30%) могут рассчитываться по
формуле первого ненулевого члена ряда; рост шага временной
дискретизации приводит к увеличению погрешностей преобразова-
167

ния; запаздывание в трактах преобразования приводит к
значительному увеличению погрешности.
Модель тракта временной дискретизации аналого-цифровым
преобразователем последовательного счета с промежуточным
преобразованием во временной интервал методом линейной
развертки и считыванием результата при t=nT. Учитывая
доминирующую составляющую запаздывания в оценке
погрешности, можно предложить модель тракта указанного
преобразования, позволяющую оценить сверху величину СКО. Так как
в АЦП с линейной разверткой при считывании цифрового
эквивалента в моменты пТ имеет место запаздывание на величину
Ф1Г, где ф1 зависит от дискретизируемого сигнала x(t) (см.
§ 2.2), то, положив ф1 = 1 в выражениях 82[0, е], б2, 6^,
выведенных для АЦП с АИМ, получим искомые верхние оценки.
Учет случайного запаздывания отсчетов на входе
восстанавливающего оператора для АЦП с АИМ. В том случае, когда
ф1 является случайной величиной (O^cpi^l) и не зависит от
дискретизируемого сигнала, оценки погрешности
преобразования могут быть получены путем усреднений 62[0, е] и б2 по фЬ
Выражения оценок погрешностей, учитывающих случайное
запаздывание, имеют вид
_ 1
«"■[О, *]= fSMo, «l/^*!)^; (5.91)
о
1
?i= рЫ/^Ы^ъ . (5.92)
6
где рФ1 (фО — плотность вероятности величины запаздывания.
Пример 5.8. Определить усредненную по шагу дискретизации СКО
преобразования случайного сигнала аналого-цифровым преобразователем с АИМ
прл восстанавливающем операторе — ЭНП. Корреляционная функция
входного сигнала RXx(f)=Rxx(0) cos (Зт. Закон распределения фА равномерный:
11 при 0< ft < 1;
ф1 10 в остальных случаях.
В соответствии с данными табл. 5.4
Ъ2 [0, e]=2{l-cosP [(б-Ьф1)Г]},
откуда
г
а» §[(■ + ?,) Г] ^ = 2— ~ [sin P (1 + Vl) Г — sin р?гГ].
62 =
:[2{1-
168

Искомая оценка имеет вид
1
?2= [ (2~ р|- [sin Р (1 + *) Г-sin Р?1Г]} dfl = 2 +
(1 —2cospr+cos2pr).
1 ФТ)
5.3. ПОГРЕШНОСТИ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ
СИГНАЛОВ, ЗАДАННЫХ СПЕКТРАЛЬНОЙ ПЛОТНОСТЬЮ,
ПРИ РАВНОМЕРНОЙ ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Случайный спектральный входной сигнал может быть описан
своей спектральной плотностью. В этом случае требуется
получить формулы для расчета среднеквадратических погрешностей
преобразования, в которых в отличие от соответствующих
выражений предыдущего параграфа вместо корреляционной функции
входного сигнала будет фигурировать спектральная плотность.
При заданных спектральных плотностях входного сигнала
Sxxi®) выражения б2[0, е] получаем, подставляя с учетом (5.61)
в формулы (5.58) для синфазной модели и (5.59) для
несинфазной, корреляционную функцию входного сигнала в виде
00
Я«М= jSxx((o)e-'mda. (5.93)
— 00
Синфазная модель. В результате подстановки (5.93) в (5.58)
+ 00
с учетом деления на Rxx(0)= J S^(co)do), четности RXx{t)
>—-00
и выражения (5.61) получаем
00 00
ЩО, .] = 1 —-J £ k2 [m, в) j k, (x) X
—oo
X [ j Sxx ((o) ew-<M + -^' dcol dx +
l
+ oo
J Sxx(<u)d(u m=Or=0 О О
X П^Н^-мг^,! doldx.dx, (534)
169

Изменим порядок суммирования и интегрирования во втором
слагаемом этого выражения:
00 ОО Г 00 "~1
2l К [Щ A j К (т) j Sxx (СО) е/шЬ(т-М-ф)Г-г] ^1 ^ =
т=0 О L— оо J
= J S^ (СО) 2: Mm» s]e J #l(T)e "T e "co-
m=0
Так как ^f! &2[яг, e]e " =/C2*[/co71, e]—комплексная частот-
m=0
ная характеристика разомкнутой импульсной системы, состоящей
ОО
из импульсного элемента и второго линейного зиена, J kx (т) е dx =
о
= ^i(/(0) — комплексная частотная характеристика первого звена,
то второе слагаемое формулы (5.94) имеет вид
+ 00
- т^-1 J Sxx (со) Кг (/со) К* ЦшГ, в) e4a('~*)Td«>.
J 5и(и)(/ш-»
— ОО
Изменим далее порядок интегрирования и суммирования
в третьем слагаемом выражения (5.94):
ОО ОО ОО 00
2 2А.К «]A,[r. «ij J*i('i)*iWX
m=Or=0 0 0
X J Sxx(<o)e dco d^T2 =
+ oo / oo ow oo
= J SXJL*)\2 А, К "le"7""17, ИМ'. ^]е/шГГ f^WX
\m=*C /-=0
Так как
. —/штУ W hrT
^ А,И. «]ё ' 2KV, Ф = *,*[/< «]*,*[-'К, «1 =
m=0 r=0 -
' ' -|*.*[К.«П\
170

j^K)e ^'dxj J*1(,Je/*I,dv=^i(/fi>>/Ciih->):= I M/a>)l*.
третье слагаемое (5.94) имеет вид
j Sxx((u)d(d
Js«HlC[/^,e]|,|^(ito)|,diB,
откуда текущая дисперсия погрешности
ffrn .i_ i_: 2 j s„He~/<"(,_lf)7'K1(/(o)^[/-(or) e]dco +
6^0, s]= 1 —-
j S^(<o)d<o-o
+ ^
J-OO
J S„ (со) | K\ (/©) |2 | K2* [/co7\ s] |2 do. (5.95)
j Sxx((d)d(d-
— 00
Несинфазная модель. В результате подстановки (5.93)
+оо
в (5.59) с учетом деления на Rxx(0) = J S(co)rf(o, четности
—оо
Rxx(i) и выражения (5.61) получаем
М оо +оо
j S(©)da
*=o
М_(1_//ЛЦ^-<р)ГЛ1-т]
M M
i +o
f ^(cojdco /=о'г=о
JJ]V[0, 4X
X
ОО ОО Г + 00 J
VIO..]JJ*1(t1)ftI(t1). j S„(»)e*'I-(r-|,r-"+",(to К
0 0 L-oo J
(5.96)
Та_к.же.как в случае синфазных моделей, изменим порядок
интегрирования и суммирования во втором и третьем слагае:
мых:
М оо Г + оо " ' ■ ' -1
i=o о L-~ J
171

-Г"
M
= J 5и(4Е^[0,^М')е ""*e .'"""'
/М+8—ф)7'М .
aw.
/=о
Г* —/(ox itoTi *
Так как J Ах (х)е ^ = КХ{^)\ Lt*[0, e]e =K2i [—/<о7\ sj,
то второе слагаемое имеет вид
+00 М
+ 00
J SxxMd®'
—oo 1=0
Аналогично третье слагаемое приводим к виду
+ оо
j 5Л.*(<о)Жо-<
+ оо М
> — oo I i=0
dco,
Таблица 5.6
Способ восстановления
Комплексная частотцая характеристика
М '
*.*[/»7\ •]. J] Я*. [/«Г, е]
/=0
ЭНП по Лагранжу
Линейная экстраполяция, ЭПП
по Лагранжу
Экстраполяция Af-ro порядка по
Лагранжу, /-то порядка по
критерию наименьших квадратов
ИПП по Лагранжу
Л+1-
м
1=0
-Ле-'шГе
-/со (М-
1)Т
1+е-'ш7"(1-е)
Интерполяция М-то порядка по
Лагранжу, /-го порядка по
критерию наименьших квадратов
2 V». «]е->вГ'
/=о
172

откуда
j 5^(<o)d(o-'
+ 00 М
J SXX(<*)KAM J] Kli [-jaT, e] X
, —00 *=0
Xe
—/ш(1+е—ф)ГЛ1
*>++=
J 5j«(<D)da>
+00
X
X
M
%Kli[ja>T, e]
d(o.
(5.97)
Таблица 5.7
Вид АЦП
МО, •]
АЦП с АИМ
+ —
] S*x (со) dco -ев
^■00
j S*x (со) dco -1
■e —B)|2d(0
А ЦП с ИАИМ
+ 00
2 Tq / i sin(Ycor/2/V) _
J ^^ ?соГ/2Л/ X
J Sjcx (со) dco -°
+ 00
Хе"-/ш7,в dco + -
1
l
S** (©) X
j Sxx (со) dco —•
X I ."I'tT^T'7 I I Л + 5 -Me-'*7, (1-е-B)|2rfco
[ y(x>T/2N \
173

Значения /Ci (/со) представлены в табл. 4.1, выражения
м
K*2[hT, e], 2 К** [/юГ, е] — в табл. 5.6.
При восстановлении по Лагранжу £*и[0, е] и £*э[0, e]
определяются формулами (4.52) и (4.63), при восстановлении по
критерию наименьших квадратов — формулами (4.101) и.
(4.109). Для простейших способов восстановления выражения
б2[0, е] сведены в табл. 5.7.
Полученные в данном параграфе выражения позволяют
рассчитывать среднеквадратические погрешности преобразования
при задании входного сигнала его^спектральной плотностью.
5.4. ПОМЕХОУСТОЙЧИВОСТЬ ПРЕОБРАЗОВАНИЯ
ПРИ РАВНОМЕРНОЙ ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Помехоустойчивость тракта временной дискретизации и вос-
тановления сигнала определяется как способность этого
тракта противостоять вредному действию помех. Наличие на входе
АЦП аддитивной помехи приводит к увеличению погрешности
преобразования. Текущее, среднее и максимальное значения
относительной дисперсии погрешности, как было показано
в § 5.2, определяются выражениями
Й+х[0, *\ = V[0, з] + б![0, •]; (5.98)
5f+x = 8*+s!; - . (5.99)
•Й+х ==? + §, (5.100)
где индекс X указывает на составляющую погрешности,
вызванную воздействием помехи.
Текущая относительная дисперсия б2я[0, е] в соответствии
с (5.62) и (5.55) определяется как отношение математического
ожидания квадрата результата восстановления помехи K(t) при
х=0 к дисперсии полезного сигнала:
б\[0, e]=M{z\[0t b])IRxx{0). (5.101)
Синфазные модели. Выражение текущей относительной
дисперсии помехи на выходе тракта преобразования в
соответствии с (5.55) и (5.62) имеет вид
ОО ОО 00 ОО
m=0r=*0 0 0
X Яхх [(т — г) Т — xt + Tl] dxjdx,. (5.102)
174

Подставив в (5.102) соответствующие значения £2[/я, е] и
£i(t), получим:
в случае АЦП с АИМ
оо оо
6^0, sJ==W(or SS^lm' e]KVt •l/?uK'»-r)7']'' (5Л03)
m=0r=0
при экстраполяционной процедуре восстановления
__ мм
б!1°' s]==^(orSSL'9[0, S1V10, е1^х[И-г)Г], (5.104)
. /=0г=0
где Lf3[0, e] определяется в соответствии с выражением (4.63)
при экстраполяции по Лагранжу и с выражением (4.109) при
экстраполяции по методу наименьших квадратов;
в случае АЦП с ИАИМ
оо оо
5i[0'е] = idior ЕЕ*'[п1, е]к[г'е] х
m=0r=0
MN IJN
-^- j J '/?хх[(г-Л-в1-в1)Г]Л1Л1; (5.105)
m=0r=0
1//V 1//V
X
у-
при экстраполяциойной процедуре восстановления
м м
8|f°'si=-d(orEEV[()'8,VIO'e]><
=0.г=0
[JN 1/N
J' Г # хх [(Г -« + *!- s2) Г] d?1de2. (5.106)
Л/2
Y2
(1-НГ)/# (1-T)/W
Несинфазные модели. Выражение текущей относительной
дисперсии помехи на выходе тракта преобразования в
соответствии с (5.60) и (5.62) имеет вид
м м
ь1[0' el=-^rEELiHI0, s]V[0, e]JJ*iw*i^x
*=lr=0 0 0
X /?хх [(* — г) Г — т2 + tJ А^г (5.107)
Подставив в (5.107) соответствующие выражения &i(t),
в условиях интерполяционной процедуры восстановления
получим:
175

в случае АЦП с АИМ
_ мм
ь1 [0's ]=~idw £ S L*H [0'8] Lr [0'sJ Rxx f(i ~r) T]> (5-108)
i=Or=0
в случае АЦП с ИАИМ
мм
6'[0' е] = ^ЛоГ Ц S L*"[0* е1 ^^ 1°' х
/=0 г=0
1/N 1/ЛГ
Х-^ j j «xxKf-Or+tex-ejnAi*., (5.109)
(1-T)//V (1-T)//V
где функция LiH[0, е] определяется выражением (4.52) при
интерполяции по Лагранжу и выражением (4.101) при
интерполяции по критерию наименьших квадратов.
Выражения (5.105), (5.106) и (5.109) получены при
временной дискретизации аналого-цифровым преобразователем
последовательного счета с промежуточным преобразованием во
временной интервал с ИШИМ. Если принять у=\9 то эти
выражения соответствуют временной дискретизации АЦП с
промежуточным преобразованием в частоту. При 7=1 и 1/N=v
рассматривается временная дискретизация АЦП поразрядного
кодирования с запоминающим интегратором.
Тракт аналого-цифрового преобразования с
восстанавливающим оператором можно рассматривать как динамическую
систему, осуществляющую фильтрацию помехи. Эта система
состоит из последовательного соединения звена К\(р) и
разомкнутой импульсной системы (синфазной и л и несинфазной). При
К\(р) = \ (случай АЦП с АИМ) фильтрация помехи
определяется восстанавливающим оператором. В случае АЦП
с ИАИМ имеет место дополнительная фильтрация, вызванная
наличием интегрирования в звене К\{р). С целью определения
фильтрующих свойств восстанавливающих операторов
получение оценок помехоустойчивости начнем со случая временной
дискретизации АЦП с АИМ. После подстановки в (5.103),
(5.104) и (5.108) соответствующих значений k2[m, e], £г9[0, е],
£/и[0, е] получим выражения 62я[0, е], сведенные в табл. 5.8,
Формулы усредненной относительной дисперсии h •■= J b\ [0,
о
e]de также сведены в эту таблицу.
176

53 Таблица 5.8
1 i
£? Вид
8? аЦп
1
АЦП
сАИМ
177
Способ восстановления
2
ЭНП по Лагранжу
Линейная экстраполяция
. (0<Л<1);
ЭПП по Лагранжу
. (А=1), Л1=»1
ЭПП по критерию
наименьших квадратов,
Ж = 2
ЭПП по критерию
наименьших квадратов,
М = 3
ь%\ №. «1
з
Яхх(0)/Я**(0)
Яхх(0)
l2^,+ 2Ag + l)-—w-
- Rxx(T)
( \ 5 \ Яи(0)
{-2-ei + e + -6-)-Rx7W+ '
+ "9--^Г(оГ_1^"е 8-"i2-JX
Лхх (2Г)
Яж* (0)
/1 3 7 \ Яи (0)
l-5-82+-T8+-ioj Rxx(O) +
, / 1 3 3 >\ ЯХх (П
+ ll0"e2 + l0-8 + -5-/ iWO) "
/ 3 9 I \Rix (2У)
\25 s*+ 10 e+5oJ Rxx(0) ~
t 9 ^ 27 19 \ i?xx (37")
V50 e +200e + 50 / RxxiO)
»4
4
#хх(0)/Я«(0)
/2 1 \ Яи(Г)
\ 3 Л + 2 ^ Я*, (0)
1 Г Rxx(0) Rxx(T)
36 L54 Rxx (0) + 16 Rxx (0)
*xx (2Г) 1
34"tf**(0) J
16 Rxx (0) , 47 «xx (*")
15 Rxx (0) + 60 Я*, (0)
6 Rn(2T) 61 «xx (37")
25 Rxx(0) 100 Rxx(0)

!^ Продолжение табл. 5.8
00
Вид ;
АЦП
1
АЦП
сАИМ
Способ восстановления
2 '
ЭВП по Лагранжу,
М = 2
ЭВП по критерию
наименьших квадратов,
Af = 3 '
»Ч [0. »]
3
/3 15 \ Яи (0)
Rxx(T) ,
- (2е*+ 8s» + 10е* + 4е) -Щ^Щ- +
, (1 ,5 \ Ди(2Г)
f1 ,. 3 ,.59„,21 Ю)Ли(0)
U fc ^2* +20* +10fc + 20/ Rxx(0) +
, / 1 3 , 305 . 6 , 9\
+ (-¥б4-Т£3-200£2-5-е+4о)Х
v Rxx (Г) , / 1 3 287
Х- + I ——£4 £3 ,2
/!«(0)Т1 4' 2 е 100 е
186 27 , Яи (2Г) / 1 3
100 е 10б/ Rxx (0) ~Ч 8 И + 4 £3 +
289 192 19 \ Яи (ЗТ)
+ 200г" + 200 е + 200) ~R~x7W
%х
4
*хх (0) Яи (?■) ,
6,8 Я** (0) ~"7,73 Д**(0) +
+ 1,93 /г«(о)
409ЯХХ(0) 263 ЯХХ(Г)
120 Я*, (0) 240 Я** (0)
__ 1549 ЯХХ(2Г) 1523ЯХХ(ЗГ)
600 Я**(0) "^ 1200 Я**(0)

Продолжение табл. 5.8
Способ восстановления
Ь\ [О, е]
54
ИПП по Лагранжу,
М= 1
ИПП по критерию
наименьших квадратов,
М = 2
ИПП по критерию
наименьших квадратов,
М= 3
(1_2е + 2е2)-^
А.
*хх (0)
— е2
,1).
хх (0)
*хх (Г)
Я** (0)
+-2(.-
/ 5\ *
хх (0) , 4 ЯХХ(Г)
(0)
+
(-
2е*+2е —-
9 Rxx(0)
Rxx (2Г)
Rxx (0)
[— 2 _i _|М *u (0) ,
I 5 е _ 5 е + 20 / Rxx (0) +
, / 2 2 19 \
** (0)
Rxx (Г) ,
Я**(0) +
п(27-)
~^\ 25 4 + 25 8 + 50 / #** (0)
\ 25 е + 25 е - 20 ) Rxx (0)
36 L24 Я
Яхх (0)
(0)
+ 12-
Rxx(T)
Rxx (0)
1 Г _Rxx
35 L18 Rxx
(0)
16-
*xx (?)
XX (0) "T"*" Ли(0)
*xx (2Г)]
+ 2 #**(0) J
19 i?xx(0) , 49 Rn(T)
60 Я** (0) ~l~ 120 K** (0) +
91 Яи(2Г) 13 /?хх(ЗГ)
h 100 Я**(0) "*" 200\R^tO)

^ Продолокение табл. 5.8
9 J »
Способ восстановления
"* [0. »]
ИВП по Лагранжу,
М = 2
«хх (0)
(24е*_48еЗ + ЗОе* - 6. + 1) ^ (Q) "
«ML (Г)
+ ( - 32И + 64еЗ _ 40е2 + 8е) ^ (Q)
«хх(2Г)
+ (Зе* _ 16=3 + Юе2 _ 2е) -^-^70—
ИВП по критерию
наименьших квадратов,
М = 3
.4 2 ^ 20
63
10
* +
+
19 \ «хх (0)
20 J Rxx (0)
2755
Тоо-ег +
\ «хх (0) , / 81
J Rxx(0) +V 8
18 9 V
~5"e+l0/
•* + ■
81
«хх (Т)
Rxx (0)
+
/ О] 01
\_«j
I «хх(0)
•0,27
+
«XX (27)^
2601 19 \ «и(ЗГ)
Л81
81
Т
200
е2—2,86е +
200/ Rxx(0)
ъ*\
\ 4
4 Кхх(0) 4 ЯХХ(Г)
5 Rxx (0) "t~ 16 «хх (0)
1 «хх (2Г)
15 Яхх(0)
23 Дхх<0) . 27 ЯХХ(Г)
40 Rxx (0) "*" 80 «хх (0)
27 «ХХ(2Г) 19 ЯХХ(ЗГ)
"•" 200 «хх (0) 400 Rxx (0)

Анализ данных таблицы позволяет сделать следующие
выводы для АЦП с АИМ:
при экстраполяции по Лагранжу дисперсия помехи на
выходе восстанавливающего оператора при е=0 равна дисперсии
помехи на входе тракта преобразования. Этот вывод следует
из совпадения результата восстановления и аналогового
сигнала при е=0; при е>0 происходит увеличение дисперсии
помехи на выходе восстанавливающего оператора по сравнению
с дисперсией помехи на входе тракта преобразования;
увеличение порядка экстраполяционной процедуры при Г=
= const увеличивает усредненную дисперсию помехи на выходе
восстанавливающего оператора; при ЭНП усредненное
значение дисперсии на выходе равно дисперсии помехи на входе;
при фиксированном порядке экстраполяции увеличение
числа отсчетов (увеличение числа М)у когда экстраполяция
осуществляется по критерию наименьших квадратов, приводит
к повышению помехоустойчивости преобразования;
при интерполяционной процедуре восстановления по
Лагранжу дисперсия помехи на выходе восстанавливающего
оператора р&вна дисперсии помехи на входе тракта
преобразования при s=i/M> где t=0, 1,...,Л1. Этот вывод следует из
совпадения восстановленного и аналогового сигналов в узлах
интерполяции; усредненное значение дисперсии помехи на
выходе восстанавливающего оператора при 7,=const меньше
дисперсии помехи на входе тракта преобразования; с ростом
порядка интерполяции по Лагранжу увеличивается усредненная
дисперсия помехи на выходе восстанавливающего оператора;
при интерполяционной процедуре восстановления по
критерию наименьших квадратов при фиксированном порядке
интерполяции, усредненная дисперсия помехи на выходе
восстанавливающего оператора уменьшается с ростом числа отсчетов
(с ростом М);
увеличение порядка интерполяции по критерию наименьших
квадратов при фиксированном числе отсчетов (УИ=const)
приводит к увеличению усредненной дисперсий помехи на выходе
восстанавливающего оператора.
При осуществлении временной дискретизации АЦП с ИАИМ
оценки помехоустойчивости могут быть получены из (5.105),
(5.106) и (5.109). Однако возможен и последовательный способ
решения задачи. Если по заданной корреляционной функции
/?яя(т) помехи на входе первого звена определить Rl\{t) —
корреляционную функцию помехи на его выходе, то, подставив
Rt\h) в формулы для АЦП с АИМ вместо #м(т), получим
искомые оценки.
Пусть X(t) —помеха на входе К\{р). Тогда установившееся
значение помехи на выходе К\(р) в соответствии с интегралом
181

свертки определяется выражением
оо
А* (/) = J кг К) X(t — ix) &г. (5.110)
6
Корреляционная функция помехи на выходе К\(р) имеет вид
/ttxW = Af[a*(Oi*(' + '0l, (5.111)
где М — знак математического ожидания.
Подставив X*(t) из (5.110) в (5.111), получим
ОО 00
Яп (х) = j J4 (хх) kx (х2) Rn (xt - ч - х) Л^,,, (5.112)
О О
откуда при ^(х) = -^|1[х--(1-7)-^|-1[х-^-]|
T/N TIN
N2 С С
Til-1)/N T(l-t)/N
1//V \/N
= ^r J J /гххК^-вО Г-,]&!&,. (5.113)
<1-Т)/ЛГ (1-T)/^V
Помехоустойчивость тракта преобразования при временной
дискретизации аналого-цифровым преобразователем с ИАИМ.
Помеха задана в виде белого шума. В рассматриваемом
случае #ля(т)=с«(т) и
(1-T)//V (1-K)/W
О при — оо<х<— yT/N;
cftT/N + x) N2l(fT2) при — уТ/Л/ < х < 0;
с ЦТ IN—*) ЫЧ(чЧ*) при 0<x<yT/N;
О при у77#<х <оо,
откуда следует, что #*и(т) является треугольником. При этом
ЯЬ (0) = dV/frr); /fa [пТ\ = О при я > 0. (5.114)
Подставив (5.114) в (5.103), (5.104), (5.108), получим для
АЦП с ИАИМ и помехи в виде белого шума:
й.1°' е, = таоГ t[kAm'e]Yc^ (5Л15)
т=0
182

__ М
^•Нт^Е^0'*11'^- (5Л17)
1=0
Кроме того, так как /?*х[0] = cN/(^T) и Rt\[nT] = 0 при /г>0,
то, подставив в формулы, приведенные в табл. 5.8, вместо
Якк(0) величину cN/(yT), вместо Яхк[пТ] при я>0 нули,
получаем соответствующие выражения б\[0, е] и dh. Таким
образом, нервые члены выражений, приведенных в табл. 5.8 при
/?u(0) =cNJ(уТ), определяют помехоустойчивость тракта
аналого-цифрового преобразования с ИАИМ при помехе,
заданной белым шумом. Осюда следует очевидный вывод,
дополняющий приведенные выше: для АЦП с ИАИМ и помехе,
заданной в виде белого шума, увеличение времени интегрирования
(уменьшение N и увеличение у) приводит к повышению
помехоустойчивости тракта преобразования.
Помехоустойчивость тракта преобразования при временной
дискретизации с АИМ. Помеха слабо коррелированная. Под
слабо коррелированной помехой будем понимать случайную
функцию X(t), у которой Ru[nT] «0 при я>0. В частности,
аналогичный случай уже рассматривался выше, когда помеха
являлась результатом прохождения белого шума через
линейное звено /Ci(p), осуществляющее текущее интегрирование.
В случае слабо коррелированной помехи с АЦП с АИМ
в соответствии с выражениями (5.103), (5.104), (5.108)
получаем
00
*i°'s|=тетг S{K[m's]}°; (5Л18)
m=0
М
Ж[0' s,==-^rS(Vl°'8l}2- (5Л20)
_ Если в табл. 5.8 рассматривать только первые слагаемые
б2я[0, е] и б2я, то получим искомые оценки помехоустойчивости
тракта преобразования для АЦП с АИМ и слабо
коррелированной помехой. В этом случае легко определяется б2 — макси-
183

Таблица 5.9
Способ восстановления
ЭПП по Лагранжу,
М = 0
Линейная
экстраполяция (0<Л<1),
ЭПП по Лагранжу
(А= 1), М = 1
ЭПП по критерию
наименьших
квадратов, М = 2
ЭПП по критерию
наименьших
квадратов, М = 3
ЭВП по Лагранжу,
М =2
ЭВП по критерию
наименьших
квадратов, М = 3
ИПП по Лагранжу,
М= 1
ИПП по критерию
наименьших
квадратов, М = 2
ИПП по критерию
наименьших
квадратов, М = 3
ИВП по, Лагранжу,
М = 2
ИВП по критерий
наименьших
квадратов, jW = 3
У'х
Rxx (0)/Rxx (0)
(2Л«+2АН)Яи(0;/Я«(0)
7 «хх<0)
3 Я« (0)
3 «хх«>)
2 К**(0)
«хх (0)
19 «**<0)
Rxx (0)
8,7 «,*(0)
«xx (0)
Rxx (0)
5 Яхх(0)
6 Rxx (0)
«хх (0)
°-45^ЛоГ
RxxiO)
Rxx (0)
«хх (0)
0,95 Rxx(0)
»x
Rxx (0)/RxxiO)
{lA*+A+lj RxxiO)/RxxiO)
9 Rxx (0)
8 RxxiO)
16 «xx (0)
15 *,* (0)
0 «xx (0)
6)8 RxxiO)
Rxx (0)
3,08 *««»
2 «xx (0)
3 «**(0)
1 «xx (0)
,2 £** (0)
19 «xx (0)
60 RXxi0)
Rxx (0)
0,8 RxxiO)
23 Яхх(0)
40 Rxx (0)
184

мальное значение относительной дисперсии помехи на выходе
восстанавливающего оператора. Действительно, при экстрапо-
ляционной процедуре восстановления с ростом е монотонно
увеличиваются первые члены 62я[0, е]. Поэтому при
экстраполяции оценки б\ определяются первыми членами выражений
б\[0, е] при е=1.
При интерполяционной процедуре восстановления требуется
найти наибольшее значение по е' соответствующих» первых
членов 6\[0, е], приведенных в табл. 5.8. Проведенный анализ
показывает, что в этом случае первые члены б2я[0, е] достигают
наибольшего значения при е=0 и е=1. Оценки б2 и б2 для
АЦП с * АИМ и слабо коррелированной помехой сведены
в табл. 5.9. Выводы, которые можно сделать из анализа этой
таблицы, полностью совпадают, со сформулированными выше.
В случае АЦП с ИАИМ при условии, что помеха на выходе
первого звена слабо коррелирована [т. е. Rix(z)9
определяемая выражением (5.112), может быть принята равной 0 при
х=пТ, тС^\\, оценки помехоустойчивости вычисляют по
(5.118) — (5.120) после замены Rkl(0) на /?£х(0).
. Используя свойства чебышевскоЗ системы многочленов q>. м (t)
ортогональных на множестве равноотстоящих точек (см. § 4.4), уп-
м м
ростим выражения 2 {Lai [0, е]}2 и J! {L9i [0, е]}2, необходимые для
/=0 1=0
расчета оценок помехоустойчивости [38].
В соответствии с (4.101) при интерполяционной процедуре
восстановления
М .Ml 2
1=0 i=0 7=0 '
Jj U (M—r)\(M—s)\(r + M + l)\(s+M+))\ Vr.Ml^Ws.Ml5 'JA
(2r+l)(2s+ 1)(M!)*_
[M—r)\{i
r=os=o
M
i=0
В силу ортогональности многочленов cpyAf
м
Зфг.мМф^м^^О, если г^5.
185

При r=st как показано в [26],
м
So щ = (г + М + \)(г+М)...(М+\)
г>м [ (2г+\)М(М-\)... (М-г + 1)
Тогда
м i
Y {!,.»- ' [0, si}' = \1 (2r + l)^-l)-(Af-,+ l)
£* '' ZJ (Af+r + l)(Af + r)...(Af+l) ^r'Ml '
/=0 r=0
В частности, при ИППКВ (/=1) имеем
72 m , *хх(0) Г 1 3Л* I
% ^хх(О) 2 , 72 ^)х(О) Г 1 ЗАГ 1
' Л«(0) Л4+2' х Rxx(0) [M + 1+(М+1)(М+2)\'
при ИВПкв(/=2)
8)[0' £] = Х(Г[^+Т+ (Af+l)(M + 2) (1~2e) +
_| ЬМ(М— 1) /. 6еЛ4 6бШ\«1
§2 = Кхх(О) 3(ЛР + Л1» + М-2)
Х Д**(0) (A* + l)(Af+ 2)(Л4+3)(Л1 —I) '
72 _ Ди(0) Г 1 ЗМ 5М(М-1) |
Х_ Я*х(0) liW + 1-Г (М+1)(Л1 + 2) "' (М + 1)(Л*+2)(Л1 + 3) J*
В соответствии с выражением (4.109) тем же способом,, что
и для случая интерполяции, получаем для экстраполяционнои
процедуры восстановления
м м
У {Ыь1 [0, .1}* = V (2i + i)M(M-i)..:(M-r + i) щ
UX l ' ' U (M+r + l)(M+r)...(M+\) ^Ml ^
1=0 <"=0
откуда при ЭНПКВ (/=0)
уДгп ei r2 Гг ^хх(О) _J_.
8,.[0, в] = 5Х = 5x^-5^5-^7-,.
при ЭППКВ (/=1)
^n'.'i . ^хх(О) [ 1 , ЗА* /М + 2.\'|.
ox 14 «J - Лж((0) [м + , f (Af+1)(^+2) \ Л1 / J'
~2 *хх(0) 4(Af+l) . 7J _ ^хх(О) [ 1 , 3(M+2)J.
8х_ Rxx(0) М(М+2) ' йх_ Я*ж(0) U + 1+ Af (Af+D J'
186

при ЭВПКВ(' = 2)
W\0 1- ^хх(О) / 1 ЗУИ / Af + 2'Y ,
1 ' SJ RxxW W+l^ (M + l,(M + 2) \ M ) ^
ЪМ(М-\) Гj _ 6(e + iM) 6(t+Af)«,»»-
(M+l)(M+2)(M+3)[ M-\ + M(M-\y}''
H + lT+w)
8х = -о-7Дг]^-7-:-г ,„ M +
Rxx(0) \M + l (M+\)(M+2)
ЪМ(М-\) |j 12['(Af+ 1)»—Af«] 36 [(Л1+1)»—Af»]
(.M + l)(iW + 2)(iW + 3)L (M —1)2 л l 5A4»(iW— l)2
6 f(Af+ 1)2—^2] 4[(M + l)3_Afl>J 18 [(Af + l)4—M*]
M—\ ' M(M— 1) Af (M—1)2
72 __ *u(0) / 1 ' I 3(M+2)
X #**(0) Wl "^ M(M + \) "*"
5M(M-1) Г-j _ 6(M+1) 6(iM+l)2 ]2)
+ (Af+-l)(iW + 2)(iW+3) I M—\ + Af(Af—1) J /'
Если в выведенных выражениях принять М=/, то получаем
оценки помехоустойчивости при интерполяционной и экстрапо-
ляционных процедурах восстановления по Лагранжу.
Помехоустойчивость тракта аналого-цифрового
преобразования с ИАИМ. Помеха задана в виде сигнала с постоянной
спектральной плотностью мощности в полосе от /zcoo до mcoo и
равной нулю вне этой полосы. Способы восстановления:
линейная экстраполяция, ИПП, ЭПП по Лагранжу. Корреляционная
функция указанной помехи имеет вид
/?xx(^) = tf? (sin//*(D0T — sin#(D0T). (5.121)
т(т—л)<°о
Корреляционная функция помехи на выходе К\(р) с учетом
(5.113) определяется выражением
XjN 1/N
#ЭД = С2— j J (т_п)(0о[Г(е1^в2)-с] X
<1_T)/JV (1-T)//V
X [sin{m<o0[T(st — e2) — z]} — sin{tm0[T(sx — s2) — z]}]ds^.
' • (5.122)
Для вычисления оценок помехоустойчивости б\ при
указанных способах восстановления в соответствии с формулами,
приведенными в табл. 5.8, нам необходимо вычислить /?*х(0) и
187

R*\(T). Разложив подынтегральную функцию вряд Мак-
лорена, получаем решение в виде степенных рядов:
К ' xm-n 7j\ > \N ° ) l(2i-l)(2i-l)\ ' V '
*[0+ij'*-('-ir-4 <5-124>
По данным формулам рассчитаны зависимости Rh(0) = /i[co07\
W, у, m, n] и /?*x [T] = /2 (со0Г, JV, y, m, /г) при о| = 1 (рис. 5.4
и 5.5). В соответствии с табл. 5.9 при ЭНП по Лагранжу
Й = Й = /йх(0)//?^(0);
при линейной экстраполяции
%=*^Г±АШ + А+Л_(±Аш+Л
Rxx(O) \ 3 ) \ 3 / Rxx(0)
61= AAV (2Л2 + 2Л+ 1)_2Л(Л+ 1).
#**(0) #**(0)
при ИПП по Лагранжу
~2 2 *п<0) 1 Яп(П з *и(0) '
3 RxxiO) 3 #**(0) Rxx(O)
откуда искомые оценки являются линейными комбинациями величин
/?и(0) и/?п(Г). На рис. 5.6 приведены зависимости o\Rxx(0)lRw(0)
й ^^?л:лг(0)//?хх (0) для рассматриваемых способов восстановления.
Анализ полученных зависимостей позволяет сделать
следующие выводы для случая равномерной временной
дискретизации аналого-цифровым преобразователем с ИАИМ при помехе
с равномерной плотностью мощности в полосе от ясоо до mcoo:
увеличение времени интегрирования при Т=const
(уменьшение N и увеличение у) приводит к повышению
помехоустойчивости [величины Rt\ (0) и /?n (T) уменьшаются];
при линейной экстраполяции с увеличением А растет
дисперсия помехи на выходе восстанавливающего оператора;
при W=const и y= const в случае ЭНП и ИПП с ростом Т
увеличивается время интегрирования и, следовательно,
увеличиваются показатели помехоустойчивости;
188

5-10~5ffL 1СГги£ 5-WzUt 10~1tf
Рис. 5.4. Зависимости R{x (0) и /?*х (Т) от со07\ /л, п при Af=l, v=^l
189

при Af=const и v=const в случае линейной экстраполяции
с ростом Т оценки помехоустойчивости при малых тип
монотонно увеличиваются и имеют явно выраженный максимум
при больших тип. Это объясняется тем, что с ростом Т при
постоянных N и у, помехоустойчивость, с одной стороны,
улучшается за счет увеличения
времени интегрирования, с
другой—ухудшается за счет увели- |
чения интервала
экстраполяции. При малых тип влияние
увеличения времени интегри- Qg5
рования меньше сказывается, '
чем увеличение шага
дискретизации.
Ьа/^АЛ
(V
Рис. 5.5. Зависимость #*х (0)
(сплошные линии) и Rn (T) (штриховые
линии) от щТ при т = 20, л = 0,3 и
при работе АЦП в режиме временного
разделения каналов
Рис. 5.6. Зависимость показателей по.
мехоустойчивости a=$\Rxx (0)/#u(0)
nb=I\Rxx(0)/Rlx(0)
при восстановлении ЭНП, ИПП (а),
ЭПП (б, в) от G)07\ rn, n при у=\,
.JV=1, /i=0,5/n в случае ш=Ъ
(сплошные кривые) и m=15 (штриховые)
к Г
Мч
Ml
\к
г\\
\
\\\
ц\
\Л
ш
№
г\
К\
х\'
\\
44
\
II
=
Wffl
.# /ki-n * I I I I
ч^//"
v/
ru,V
- 1 -
К
S N
\
1,3
\
Ч "
"?' I 111
^#5-Ш
-j -MJJJ
vl 11II
Ч Ы 111
TnJ kill
...LfcliL
0,3
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
-0,1
-0,2
-0,3
-ол
5-W5Ut W~2Vl
5-10~2Ut 10'2Ut
10'ztf 0,5-10-2иГ 10'1UC 10'2Ut' 0,5-W~2rt " 10~2Ul 09МГЪС
190

Разложение корреляционной функции помехи в ряд Мак-
лорена с последующим двойным интегрированием ряда
позволяет получить простые формулы для анализа
помехоустойчивости тракта преобразования с ИАИМ.
Помехоустойчивость тракта преобразования при помехе,
заданной спектральной плотностью мощности. Пусть Su (со) —
спектральная плотность мощности аддитивной помехи на
входе тракта равномерной временной дискретизации и
восстановления. Корреляционная функция помехи связана с Su(co)
известным соотношением
ЯххМ- f Sn((o)e/a)Tdx. (5.125)
—60
Подставив (5.125) в (5.103), (5.104) и (5.108) и повторив
выкладки, проведенные в § 5.3 для полезного сигнала,
получим текущую относительную дисперсию помехи на выходе
восстанавливающего оператора:, для АЦП с АИМ
8240, «] = -т^ J 5хх(в>) | К/(К, *)12Ж>; (5.126)
j Sxx(u)d<o —
—ОО
для АЦП с АИМ и.экстраполяционной процедуре
восстановления
+ о6 I М
1 Г о / ч И т эгл 1 -/«(Af-ОГ
dco;
tf[0, «1 = -^ j Su(<o) JJVIO, «]ег
Г Sxx(to)d<>> -~ l'=0
(5.127)
для АЦП с АИМ и интерполяционной процедуре
восстановления
+оо г- М -•
82х [0, з] = -^ j S„ (0) J] I,- f0, в] е~/#'Г X
—ОО
. . X 2V[0, e]e/e'rL. (5.128)
Выражения ^[O, е] для АЦП с ИАИМ получаем после
подстановки в (5.126), (5.127) и (5.128) вместо Su(co)
выражения Sm(od) |/Ci(/со) |2 — спектральной плотности мощности
помехи на выходе звена К\ (р).
191

5.5. ПОГРЕШНОСТИ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ
СИГНАЛОВ ПРИ НЕРАВНОМЕРНОЙ ВРЕМЕННОЙ
ДИСКРЕТИЗАЦИИ
В рамках корреляционной теории случайных процессов
в качестве оценок погрешностей преобразования случайного
сигнала при неравномерной временной дискретизации и
восстановлении линейным оператором вычисляемыми оценками
являются среднеквадратические. Общепринятый путь вывода этих
оценок — определение математического ожидания квадрата
текущей погрешности, полученной для детерминированного
сигнала. В случае неравномерной временной дискретизации
появляются дополнительные трудности, связанные с учетом
нерегулярности потока отсчетов. Кроме того, нестационарность
случайной функции на выходе восстанавливающего оператора,
как это имело место даже при равномерной дискретизации,
в совокупности с переменным шагом дискретизации определяет
необходимость выбора различных среднеквадратических
оценок. Поэтому задачу получения оценок погрешностей разделим
на ряд этапов: первый — определение текущей дисперсии
ошибки преобразования при фиксированных (в общем случае
различных) шагах дискретизации 7\; второй — выбор и
обоснование способов определения различных среднеквадратических
оценок погрешностей при заданной математической модели
потока отсчетов и известных, полученных на первом этапе
текущих дисперсиях погрешности преобразования; третий —
вывод выражений среднеквадратических оценок погрешностей
преобразования, учитывающих, в каких системах управления
и как будет использован восстановленный сигнал.
С целью иллюстрации методики решения задачи начнем
с наиболее простого случая, соответствующего АЦП с АИМ и
восстанавливающему оператору-экстраполятору нулевого
порядка. Пусть /Зап — время запаздывания аналогового сигнала
x(t) (в^ случае равномерной дискретизации t3an=q>iT). Тогда
текущее значение погрешности преобразования на интервале
дискретизации фиксированной длительности Ti=ti+{—ti при
детерминированном входном сигнале x(t) имеет вид
e,(o=*(o-*(0, (5Л29)
где z(t)—результат восстановления, определяемый по (4.146).
Обозначив Xi='t-—ti, O^Lto^Ti, получим
Qi(%)=x(ti+%i)—x{ti—tM). (5.130)
192

Дисперсия погрешности преобразования при
фиксированном Ti и стационарном центрированном входном сигнале x(t)
имеет вид
¥i(x)==M{[x(ti+ri)-x(ti—t3all)]2},
где М — знак математического ожидания.
Раскрывая скобки, получаем
Wi(x)=M[jfl{U+xi)]-
-2M[x(ti+b)x(tt—tm)] +
+M[x*(U-t3an)]=Rxx(0)-
—2RXx(-u+tM)+Rxx(0) =
= 2Rxx(0)—2Rxx(xi+tB*n)9 (5.131)
где Rxx(0)=M[x2(ti+xi)]=M[x2(ti—t3an)] — корреляционная
функция стационарного входного сигнала при значении
аргумента, равном нулю, т. е. дисперсия входного сигнала; Rxx(xt+
+£зап) =M[x(ti4-Xi)x(ti—t3an)] — корреляционная функция
входного сигнала при соответствующем значении аргумента
Относительную дисперсию погрешности на интервале 7\
получаем 02г(т) на Rxx(0):
^(т)=2[1-/?зсзс(Тг+^зап)]/^(0). (5.132)
Из этого выражения следует, что дисперсия погрешности
дискретизации при ступенчатом восстановлении равна 0, когда
т,=0, £зап=0, и достигает наибольшего значения при т/+4ап,
соответствующем минимальному значению Rxx(xt-{-t3aTl). Для
монотонно убывающих корреляционных функций 62i(x)
достигает максимума при xi=Ti. В случае знакопеременной
корреляционной функции подобное утверждение в общем случае
неправомочно. Однако при практически приемлемых значениях
погрешностей максимальный период дискретизации обычно
меньше временного интервала от т/=0 до то, где то — точка
первого пересечения корреляционной функции с осью абсцисс,
что соответствует учету корреляционных связей между
отсчетами преобразуемого процесса при восстановлении. В этом
случае монотонность корреляционной функции на участке Ото
сохраняется и выражение остается справедливым.
Таким образом, на первом этапе получено выражение
дисперсии погрешности при фиксированном шаге дискретизации
7\, показана нестационарность погрешности дискретизации. На
втором этапе выбирают среднеквадратические оценки
погрешности.
13—6036
193

Верхняя и нижняя максимальные оценки:
Vb2max = Hm /§2(^ + ^ап); (5.133)
VCn= Hm l/V(,t + *san), (5.134)
где Гтах и Гпип — соответственно максимальный и
минимальные интервалы дискретизации.
Этот вид оценок [35] можно использовать для случайных
процессов с монотонной корреляционной функцией, а также
со знакопеременными корреляционными функциями, когда to<
<Ттах при модели потока отсчетов с усеченным законом
распределения интервала дискретизации. По существу эти
оценки получены при замене процесса неравномерной
дискретизации процессом равномерной дискретизации с шагом
соответственно Гтах И! Гтт. В общем случае (5.133) и (5.134)
получаются из выражений для равномерной дискретизации при
Т=Ттах (верхняя оценка), Т=Тт[п (нижняя оценка). В АЦП
с ИАИМ время интегрирования t06 не зависит от 7\. Поэтому
при расчете верхней оценки погрешности принимают у=
= to6/Tmax, при расчете нижней — v=^6/^min-
К недостаткам данных оценок относятся трудности,
встречающиеся при определении величин максимальных значений
дисперсии для более сложных способов восстановления. В
частности, для экстраполяции и интерполяции Л1-го (М>1) по Ла-
гранжу или /-го порядка по методу наименьших квадратов
уравнение d62i(x)/dx=0t которое приходится решать для получения
б2,-, как показано в § 5.2, является 'трансцендентным.
Верхняя и нижняя усредненные квадратичные оценки.
Вначале определяют среднее значение дисперсии погрешности при
фиксированном шаге дискретизации:
rt __
Wi) = -M VW*. (5.135)*
' о .
после чего верхняя и нижняя оценки принимают вид [35]
V*L* = lim VWv\Y> (5.136)
/"£ = Hm Уь?(Т%). (5.137)
Ti-*Tmin
По существу здесь, так же как в предыдущем случае,
неравномерная дискретизация заменяется равномерной соответст-
194

венно с максимальным и минимальным шагами дискретизации.
Для вычисления оценок погрешности могут быть использованы
формулы, полученные для равномерной дискретизации.
Оценки V 8тах и у S^in обычно используются при моделях
потока отсчетом, в которых шаг дискретизации функционально
связан с дискретизируемой функцией.
Усредненная максимальная квадратичная
оценка [35]
vON
8* = У. \b>,m<T,)PTAT,)ir„ (5.138)
О *
где 8? тах — максимальное значение дисперсии погрешности на
шаге дискретизации длительностью Г,; рт (Tt) — закон распределения
интервалов дискретизации.
Величина >62 является математическим ожиданием
максимальной дисперсии погрешности.
Такой способ усреднения 8?тах правомочен в том случае,
когда результат восстановления используется системой
управления на каждом шаге дискретизации. Иной способ усреднения
будет рассмотрен ниже. Сложности определения этой оценки
в общем случае связаны с получением выражения
максимальной дисперсии на шаге дискретизации.
Усредненная квадратичная оценка [35]
Уъ-\/]ъ
?(Tt)pTlTt)dTt. (5.139)
__ Данная оценка получена двойным усреднением. Вначале
^•(т) усредняют по длине некоторого фиксированного
интервала Ti в соответствии с (5.135), затем 82i(Ti) —по
всевозможным интервалам 7\. Усредненная квадратичная оценка
определяет погрешность преобразования по всем шагам
дискретизации, когда результат восстановления используется системой
управления на каждом шаге 7\\
Усредненная квадратичная оценка с учетом случайного
момента сравнения [29, 35]. Пусть на ось времени (рис. 5.7)
«брошена» точка, попавшая в интервал 7\ в момент t*. Значение
квадратичной оценки на интервале Т{ при %,i=t:¥—ti
определяется выражением (5.132). В этом случае т'* является случайной
величиной; /* —случайный момент сравнения x(t) и z(t).
13* 195

Рис. 5.7. К определению дисперсии погрешности
в случайный момент сравнения
Тогда искомая оценка имеет вид
/V = |/Jv(V)j*Tj(V)*i', (5Л40)
где 62i(r'i) определяется формулой (5.132) при т=т'/; PvCt'i) —
закон распределения т'/, полученный с учетом факта
попадания точки на интервал Tt.
Из независимости положения точки tf* от распределений
событий в потоке отсчетов следует, что условный закон
распределения случайной величины т'/ при фиксированном 7\-
является равномерным:
p(ft/Ti) = llTt.
Пусть р* (7\) — плотность вероятности длительности шагов
дискретизации, содержащих брошенную наугад точку. Тогда
двумерная плотность распределения вероятностей величин %'\
и Ti имеет вид
p(Vt, Ti)=ptfilTi)p*(Tt)9 (5.141)
откуда закон распределения т'< при 'известном двумерном
законе распределения (5.141) с учетом того, что Ti>x'i> запишется
так:
*,W) = J РЫ> Ti)dTt = J JLp^dT,. (5.142) .
Выведем выражение p*(Tt) [36]. Пусть D — длительность
интервала наблюдения, содержащего N шагов дискретизации,
Z из которых имеют длительность от 7\- до 7\+А7У Тогда
частость появления таких шагов дискретизации на интервале
наблюдения есть 1/N, а соответствующая вероятность
рт (Г,) A^-lim (//#), (5.143)
196

где рт (Tt) — плотность распределения вероятностей длительности
шагов дискретизации потока отсчетов.
Частость того, что на шаг длительностью от 7\ до Tt-\-ATi
попадает брошенная наугад точка, очевиднр, следует из
выражения ITi/D. Разделив числитель и знаменатель этой дроби
на N и устремив Л^оо, получаем с учетом (5.143) вероятность
того, что на шаг длительностью от Г/ до 7\+Д7\- попадает точка
7\//Л/ TiPr,{Ti)
лг-eo D/N M[Tt]
где Л1[7\]— математическое ожидание длительности шагов
дискретизации.
Отсюда следует искомый закон распределения
tr(Td~tTiPTt(Tt)lM[Tt). (5.144)
Математическое ожидание длительности тех шагов
дискретизации, в которых находится брошенная точка,
оо
J M[TtyTiK " l
Учитывая, что f Tt2pT (7\) dTt = D [Tt] + M2 [Г,],
о '
где D[Ti]—дисперсия длительности шага дискретизации,
получаем
M[T*i]=M[Ti]+D[Ti]lM[Ti],
откуда следует, что средняя длительность шагов
дискретизации с находящейся в них точкой больше средней длительности
просто шага дискретизации. Этот факт очевиден, так как
брошенная* наугад на временную ось точка с большей
вероятностью попадает на шаг дискретизации большей длительности.
Подставив (5.144) в (5.142), с учетом (5.140) получаем
выражение искомой оценки:
Г ' о Ч'
Преобразуем полученное выражение:
1
M[Tt]
j>(V) Г J pTi (го д-Л dv= J Г-JL j* e»(V)*,' 1
X
197

х йТгГ] prt {Ti) dTi = J ^2 (Ti) P*(Ti) dTi'
УК = у J V (7-|) />* (^i) <&V (5-146)
0
Отсюда следует, что оценка 62о дисперсии погрешности
является усреднением оценки б2/(7\) по всем шагам
дискретизации, в которые попадает наугад брошенная точка. Оценка б2
отличается от 6?о только тем, что первая получена путем
усреднения по всем шагам дискретизации, а вторая—по шагам
«сточкой».
Рассмотрим область использования оценки "J/8V Выражение
плотности вероятности р*(7\) получено при редких бросаниях
точки. Интервалы времени между «бросаниями» точки
выбирают из условия их статистической независимости. Отсюда
оценка (5.146) должна быть использована в случаях редкого
обращения к результату восстановления. В то же время оценка
(5.139) учитывает сравнение функций x(t) и z(t) на каждом
шаге дискретизации. Поэтому ее применяют в задачах,
связанных с использованием результата восстановления на каждом 7\.
Представим себе, что «инспектор», проверяющий точность
преобразования, случайным образом достаточно редко (по
сравнению с шагом дискретизации) определяет погрешность
x(t)—z(t). Результаты поверки обрабатываются, и
вычисляется среднеквадратическая погрешность. В этом случае
результат при большом числе наблюдений стремится к оценке (5.146).
Если «инспектор» осуществляет измерение погрешности на
каждом шаге дискретизации в произвольной точке внутри 7\-,
после чего результаты измерения статистически
обрабатываются, то при большом числе измерений полученный результат
стремится к оценке (5.139).
Если дискретизация неравномерна, то редко приходящий
«инспектор» с большей вероятностью попадает на более
длительный шаг 7\, поэтому оценка (5.146) при прочих равных
условиях превышает оценку (5.139).
В случае равномерной временной дискретизации
вероятность попадания редко приходящего «инспектора» на любой
шаг дискретизации одинакова, "оценки (5.139) и (5.146)
совпадают.
Рассмотрим еще один случай. Пусть x(t)—стационарный
центрированный эргодический процесс, z(t) — результат
восстановления. Для оценки погрешности преобразования
непрерывно записывается текущее значение Q(t)=x(t)—z(t), затем
198

определяется среднее по времени значение относительной
дисперсии погрешности преобразования:
*--C5r£lT^l*w-'wr- (5-147>
где N «— число шагов дискретизации; Т—математическое
ожидание длительности шага дискретизации; NT— длительность
интервала наблюдения.
Перепишем это выражение в несколько ином виде:
n тг n
8~*= lim -L-\] f 8«(,)Л- Urn -J-V?(Г,)Гг> (5.148)
/V->oo NT ^ J N-+00 NT U
i=) 0 1 = 1
где ЬЧ*)=^Г7^-[х(и + -)-Ни + *)Г.
Kxx\y)
Если /f — число шагов -дискретизации длительностью от Tt
до Т% + Д7\ то /j/iV — частость этих шагов дискрети зации и
lim ltlN = р {T^dTi. При этом
N-*oo i
k
? = lim —5=- У* /,8s (Г,) TJt
jv-oo NT U y V l'
/=0
/г
где 2/, = ЛГ.
/=o
Преобразуем это выражение с учетом малости Д7\:
fc оо
N^oo Ш N Т J T i
i=0 О
откуда следует, что в рассматриваемом случае 62='82о.
Перейдем далее, рассматривая ряд примеров, к третьему
этапу — получению расчетных соотношений для АЦП с АИМ и
восстанавливающим оператором-экстраполятором нулевого
порядка.
Пример 5.9. Заданы максимальные и минимальные длительности шагов
дискретизацию. Корреляционная функция случайного процесса Rxx(z)=z
Для АЦП с АИМ и ЭНП требуется определить верхнюю и нижнюю
максимальные квадратичные оценки преобразования, верхнюю и нижнюю
усредненные квадратичные оценки при /Зап=0.
Так как /?*х(т) — знакопостоянная, то
К«!ах=К2(1-е-аГ™х): /'lL=/2(l-e-a7'm1");
199

/T'max
Г- f 2(l-e-ni)dx =
max J
0
-|/г,1,-*=-(,-~г~Ф
/T'min
уЛ- f 2(1——I")*-
min J
0
Эти оценки получены без исключения погрешности от запаздывания.
Если АЦП работает в условиях, когда погрешность от запаздывания может
быть исключена, то воспользовавшись данными табл. 5.4, найдем
maxl£-l/2| jds =
_J ,. -«Ггаах/2
/•L-y^
2 /. -^mln/v
■<*7\ U~~e ''
knin
Пример 5.10. Математическая модель потока отсчетов задана простейшим
потоком:
Рт( (Ti) = Ре"*7"'.
Корреляционная функция случайного процесса RXx М = вх е~~а • Для АЦП
с АИМ и ЭНП требуется определить усредненную максимальную
квадратичную оценку при /Зап=0 и работе АЦП в реальном времени.
Так как Кхх (т) — знакопостоянная функция, то
«Lax(^)=2(l-e""4
При этом выражение искомой оценки имеет вид
]/"?»= I/ J 2 < 1 - е~а^) Ре~Э3^7\. = |/"2 [1 — 1/(»/Р + 1)].
о .
200

* Пример 5.1.1. Для условий предыдущего примера найти усредненную
квадратичную оценку. В соответствии с (5.139) и с учетом (5.135) получаем
/*-j/rJ[i7?8<,-^",>*]
ре РГ«<*Г,=
i
б
-/«(■-^Тйй)-
Пример 5.12. Для условий примера 5.10 найти усредненную квадратичную
оценку с учетом случайного момента сравнения.
В соответствии с выражением (5.146)
«!/.»(
г р—1-
а 1 -f Р'а/
Пример 5.13. Математическая модель потока отсчетов задана регулярным
потоком: pTi(Ti)=fi(Ti—T). Для АЦП с АИМ и ЭНП требуется определить
усредненную квадратичную оценку б2 « усредненную квадратичную оценку
6о2 с учетом случайного момента сравнения.
В соответствии с выражением (5.144)
р*(Ti)=Ипгл д (Т~~Ti) = *{Т ~ Ti)f
откуда следует, что pTi(Ti)=p*{Ti)1 оценки б2 и б02 совпадают и
определяются формулами, полученными для равномерной дискретизации.
Изложенное иллюстрирует методику, дающую возможность
получить выражения квадратичных оценок погрешностей при
неравномерной временной дискретизации и восстановлении
линейным оператором. Так как оценки б^, 8min, б^ах, smin
определяются соответствующими выражениями для
равномерной дискретизации при T=TmaXi T=Tmin; y=to6/Tmax\ «у=
= *o6/Jmin, то ниже будут получены формулы только для
оценок б2 и V.
Аналитически для общего случая вывод оценок б2 не
представляется возможным из-за трудностей в определении б2/(Г/).
Аналого-цифровое преобразование с АИМ.
Восстанавливающий оператор-интерполятор М-го порядка по Лагранжу. Как
указывалось в § 4.5, восстановление дискретизированного
сигнала при неравномерной временной дискретизации может
осуществляться только не в реальном времени. В этом случае
текущее значение погрешности преобразования на /-м интервале
интерполяции с учетом (4.136) и при исключении погрешности
201

от запаздывания в восстанавливающем операторе
определяется выражением
м
M^^^ + ^-^w^K г0,..., 7-м-,),
ГАеО<т^:То+Т1+...+Тм-1.
Относительная дисперсия погрешности преобразования на
фиксированном интервале Т0-\-Т{-\-... +Тм-\ имеет вид
м
1=0
м м
1=0 г=0
XVK Гв,..., ГА1-1)/г,х('|-'г). (5Л49)
С учетом того, что U—U и U—U определяются как
алгебраическая сумма величин Г/, б2/(т) является функцией т, Т0,...
..., Гм-ь
Получим вначале усредненную квадратичную оценку.
Среднее значение дисперсии на /-м фиксированном интервале
интерполяции имеет вид
r.+r1+...+rAf
V(7o,..., ?V-i)= T , ' г Г 8?(*)Л. (5.150)
о
Усредняя б2/ по всевозможным Го, 7*1,..., Тм-и находим
искомую оценку:
/ 'max * max
VT*=\/ \ ... ( Wo TM_,)p(Tu Тм^йТ^Жм-и
/^max ^max
j... ( w.,...
T T
min min
(5.151)
где р(Г0, Гь...,Гм-i) —совместная плотность распределения
вероятностей длительностей шагов дискретизации. В случае
рекуррентного потока отсчетов
М—1
p(T0,Tl9...tTM-l)=\lpTm(Ti). (5.152)
Перейдем далее к выводу выражения усредненной
квадратичной оценки с учетом случайного момента сравнения. Будем
м—1
рассматривать весь интервал интерполяции ТИ = 2j Tt как
202

один интервал потока отсчетов. Плотность распределения
вероятностей такого интервала определяется как рт (Ги=7,0+
и
+Т{-\- ... +Тм-\). Рассуждая так же, как при рассмотрении
случая экстраполяции нулевого порядка, и заменяя шаг
дискретизации интервалом интерполяции, запишем выражение
плотности распределения вероятностей интервалов
интерполяции, содержащих наугад брошенную точку, иначе — плотность
распределения вероятностей интервалов интерполяции, на
которые попадает редко приходящий «инспектор»:
Л (Г. = Т0 + Т1 + ... + Гм-0 = „ ' , 1 ""' , X
И
М[Т, + Т1+...+Т„_1]
Хрт(Тя = Т0 + Т1+...+ ТМ-1). (5.153)
Условная плотность распределения вероятностей шагов
дискретизации внутри интервала интерполяции длительностью Ги
определяется выражением
~( М_1 •>\
Р I Т09-Тъ...,*Тм-.1 \TU= 2j Tt I =
/ м—2 >
PIT*. Tl>--> TM-2> Ги- 2 Ti
\ *=0 у
оо оо / М—2 \
О О \ 1=0 /
• (5.154)
i=0 J
Плотность распределения вероятностей интервалов
интерполяции
Рт (т* = To + Ti + .- + Тм-\) =
и
оо оо / М—2 \
= \-$Р\То, Ти..., Тм_2, Тя- 2 Tt )dT0...dTM_2. (5.155)
6 0 \ i=0 /
Среднее значение относительной дисперсии погрешности на
/-м фиксированном интервале интерполяции [считаем, что точка
t* сравнения функций x(t) и z(t) попала на этот интервал]
определяется выражением (5.150). Тогда дисперсия
погрешности имеет вид
оо оо / М—2 \ /
V = I--Jvk>, т\ тм_2, ти- 2 тЛЦт* тх,..., тм_2\та=
о о \ <=о / \
М-1 \
= 2 Г, /£ (7,и=7-0 + 7'1 + ... + 7'л,_1)^0..>й7'м_2^и. (5.156)
<=о / и
203

После подстановки в эту формулу соответствующих законов
распределения и несложных преобразований получаем
искомую оценку:
+ ТМ-1
+ rM-il х
V о о
"ХР(Г0, Ти...9 TM„l)dT0...dTM_l. (5.157)
Рассмотрим частные случаи интерполяции первого^и
второго порядка по Лагранжу, воспользовавшись выражениями L,H,
полученными в § 4.5.
При восстановлении интерполятором первого порядка
+^{1^+^]*"<0)-2^*"Ч (5158>
V(7,o) = T7JV(-)dx; (5.159)
' О
/^ ОО
b2 = $bi2(T0)PTo(T0)dT0; (5.160)
о
оо
^o^jVWf/'r.W^. (5.161)
о
При восстановлении интерполятором второго порядка
_ х[х-(Г, + Гх)1 д (_ Т +х)+ ^~То) R (_Т _Т + T)U.
7Vi (T'o + T'i)^! J
i 1 (\ (i-Ttflt-lTi + TJP
■ - i- х-, .--i/i i г1(х-Г.)1 Тд (0,
г2[х-(7'о+7'1)Р
+2^-w-^+;i)iT^(7-o+rl)-
204

— 2 T^T~7'o)['c~(r»+7'i)J R (T )\. (5 162)
TJi4Ti + T,) xxK ly y ' '
V (T0, Л) = —J— f 8? (*) <fc; (5.163)
7 о -г 7 i •/
0
S2 = f f V (Г0) 7\) p (Г0, 7\) d7-0dri; (5.164)
0
OO 00
V = f JV^e. Tjls^piT,, T^dT.dT,. (5.165)
0 0
Аналого-цифровое преобразование с А ИМ.
Восстанавливающий оператор-экстраполятор Л1-го порядка по Лагранжу.
Текущее значение погрешности преобразования на /-м шаге
дискретизации с учетом (4.142) определяется выражением
м -
вм W = X(tM+ x)- 2^(^-^зап) V(^0, ^1,..., ^M-l, *), (5.166)
где (Хт^Гд,.
При возможности исключения погрешности от запаздывания
*зап = 0.
Относительная дисперсия погрешности преобразования на
фиксированном шаге дискретизации Тм имеет вид
М М
/=0г=0
XV(^o, Л,-, TM^)Rxx(tt-tr). (5.167)
С учетом того, что tM—ti и\ ti—£/равны алгебраической
сумме величинТ/, б2м(т) является функцией т, Т0,...уТм-\.
Среднее значение дисперсии на М-м фиксированном шаге
дискретизации имеет вид
& (^о, Tl9...9 Тм) = ^\ Ь2М (z) dz. (5.168)
М J
о
205

Усредняя Ь2М по всевозможным Т0, 7\,..., TMt получаем
усредненную квадратичную оценку:
У*.-]/]..
оо ^
\ 8м(Г0. Tlt...f Тм)р(Т0,...9 TM)dT0...dTM. (5.169)
о
Перейдем теперь к получению усредненной квадратичной
оценке с учетом случайного момента сравнения. Пусть брошен:
ная наугад точка попала в момент времени t* на шаг
дискретизации Тм и р*(Г0, Ти...9Тм-и Тм)—плотность
распределения вероятностей соответствующих шагов дискретизации, Л1-й
из которых содержит точку. Тогда искомая оценка
определяется выражением
/ОО 00
1"^м(Т0у...9 Тм)р*{Т0У 7\,..., Тм-и TM)dT0...dTM.
о о
(5.170)
Для вычисления у 802 необходимо получить закон
распределения р*{Т0, Гь.„, Тм-и Тм) по известной многомерной плотности
распределения вероятностейр(Го, Гь..., Гм). В случае
экстраполяции нулевого порядка эта задача уже решена в начале
параграфа. Рассмотрим теперь экстраполяцию первого порядка.
Пусть D — длительность интервала наблюдения, состоящего из
N шагов дискретизации. Тогда имеется N—1 рядом лежащая
пара шагов дискретизации» Г/-ь Г/.
Пусть далее на участке наблюдения находится / пар рядом
лежащих шагов дискретизации, длительности которых
заключены в промежутке от 7V-i до 7\_i+A^-i и от Г/ до Гг+Д^>
Частость появления таких пар составляет l/(N—l).
Тогда lim = lim — = р (Tt_l9 Tt) dTi_1dTi — вероятность
N-+ooN—\ #-»oo N
соседних пар шагов дискретизации, имеющих длительность от
7V-1 до 7V-i+A//-i и от Tt до Т{-\-Ш{. Частость попадания
брошенной точки на шаг Г, определяется из следующего
очевидного отношения: ITi/D. Разделив на N числитель и
знаменатель этой дроби и устремив Af->oo, получаем вероятность того,
что длительность каждого из двух соседних шагов
дискретизации заключена в интервале от 7\-i до 7Y-i+Af/-b от Г/ до 7\+
+А^ и во втором интервале находится «брошенная» точка, т. е.
Р*<7V-i. *7>dh-гdTt = lira ?£- = W^-WW^ §
N-+oo D/N M[T{[
206

откуда
р*(77-ь Г,) = Г,р(77-ь Ti)lM[Ti]. (5.171)
Аналогично рассуждая для экстраполяции третьего
порядка, получаем
р*(Г/-2, Гц, Ti) = TiP{Tt-2, 7\-ь r,)/Af[r/] (5.172)
и в общем случае
Р*(Т0, Ти..,Тм) = Тмр(Т0, Гь...,7,м)/М[7,/]. (5.173)
Подставив (5.173) в (5.170), получим искомую оценку,
выраженную через закон распределения шагов дискретизации
потока отсчетов:
VAv=i/ J...J8f(7-„....
rob
Тм
тм)—— Р(7о,-> TM)dT0...dTM*
M[Tt]
(5.174)
Рассмотрим частные случаи (экстраполятор первого и
второго порядков по Лагранжу), воспользовавшись выражениями
Li3, полученными в § 4.5.
При восстановлении экстраполятором первого порядка
^)=\---^—{--}-Rxx{T0 + t3m + -)^
Кхх\у) I ' о
-2i^2i*„(7Y)}; (5.175)
«V., rj^-i-j &(')*; (5.176)
о
* = J ] S8 (To, TJ р <Т0, 7\) dT0dTi; (5.177)
о о
ОО 00
К = $$»(Г»Т1)-Ь-р&0,Т,)11Т<р1, (5.178)
0 0
где Т=М[7\] — математическое ожидание шага
дискретизации.
При восстановлении экстраполятором второго порядка
% (Т) = 1 "" IT^Ti Лг+4-ТГ 1 *» ^ + Г* + '- + х) -
207

(Г0+/г1+Т)Х^(^+/зап + х) +
1 О1!
2
^ (Л, + Г1)Г1 зап ^ 7 ^ Rxx(O) \ L Г*(Г, + Тг
■ (Гр+^+х)^ _| (7'о + 7'1+х)2(7'1+^ [р ,Q)_
Т у,^., Т (Ть + Т^Т^ \ ххУ '
_ 2 (7\+х)(Го+Г1 + Ф2 о ,г ч ,
о (ro+^i + ^'^i + tjt.p л^1 Г5 179)
ToWo+r,) **^/' 1 * ;
-Т,_
& О"., 7\, Г J = ТГ j & (,) dx; (5.180)
о
0 0 0
00 00 ОО
V= .JJf^Ve. *\. Т^р(Т0. T^TjdT^dTt. (5.182)
0 0 0
Аналого-цифровое преобразование с ИАИМ.
Восстанавливающий оператор-интерполятор Afro порядка по Лагранжу.
Текущее значение ошибки преобразования на 1-м интервале от
*о до tM-\, когда исключается запаздывание, вызванное
процедурой интерполяции, и не исключается запаздывание,
определяемое способом получения цифрового эквивалента, с учетом
(4.140) и (4.141) определяется выражением
М 'об
/=о о
(5.183)
для АЦП последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ и
выражением
М 'об
ez(x)=x(^0 + x)--l-^L,H(x, Г0 rM)J *(*гЛб+\)*и (5-*84)
/=о о
для АЦП поразрядного кодирования с запоминающим
интегратором.
208

В этих формулах, так же как в случае АЦП с АИМ, 0^т<
Относительная дисперсия погрешности преобразования на
/-м интервале интерполяции имеет вид
М 'об
8?(х) = М£Ш = L_^_ jW То_ Тм_1} С RxAto_
Rxx(O) RxxWttf Ш J
. /=о о
м м
-ti + Ti_1-t3m + ,-,1)d4 + -±-rVVLi^,, Т0 ГМ_,)Х
*<xx\v) *об #■ *■■
1=0 г=0
'об 'об
XV('Je ^M-Oj J Л«Л^-'г-1 +'i-^*iA. (5Л85)
о о
для рассматриваемых АЦП последовательного счета;
м
Rxx (0) #хх(0)*об *J
i=0
XJ -Я«('о-'| + 'об + *-Ч)*- +
0
м м
+ р 1/2 US1''**» r» r*-i)V(«. г. Гм-ОХ
Ахдс(О) Гоб iarf ^
*=-0 r=0
£об 'об
X J J ««й-'г+ 'i-^*i*. (5.186)
о о
для АЦП поразрядного кодирования с запоминающим
интегратором.
Учитывая, что U—^r+7\-i и U-\—tr-\ являются
алгебраическими суммами величин 7\-, б2/(т) для выражения (5.185) есть
функция от т, Г-1, Г0,..., ТМ-\. Аналогично, б2/(т) для
выражения (5.186) является функцией т, T0i..., ТМ-\. Обратим
внимание на то, что в последнем случае отсутствует шаг
дискретизации. Т-\. Тогда
Т0+... + ТМ—1
УА'-ьЛ,...,.^-!)^ т , ' т Г V(x)dx, (5.187)
о
14—6036 209

где V(T) определяется выражением (5.185);
О
где б2/(т) определяется выражением (5.186).
Усредняя б2/ по всевозможным 7\-ь Г0,..., Тм-\ для
рассматриваемых АЦП последовательного счета и б2/(т) по Го, Ти..„
..., Гм-i для АЦП поразрядного кодирования, соответственно
получаем
, / Лпах ^тах
7,0,..., Гм_1)р(7,_1, Г0,..., Тм_х)Х
М + \ раз
XdT_1dT0...dTM-i. (5-189)
К 82=l/ j... J Wo,-,
» ^min ^mi n
7,M_1)p(7,0,..., 7,M_1)dro...d7,M_i.
(5.190)
Перейдем теперь к выводу выражений усредненной
квадратичной оценки с учетом случайного момента сравнения. В
случае использования АЦП последовательного счета с
промежуточным преобразованием в частоту или временной интервал
с ИШИМ считаем, что наугад брошенная на ось времени
точка попадает на интервал интерполяции 7,И=7,0+Г14-... +Гм-ь
перед которым находится шаг дискретизации Т-\.
Рассматривая два соседних интервала 71-ь Г0+ ...+Тм-\ и используя
способ рассуждений, приведенный выше, получаем
Т -4- Т «4- -1- Т
Р*{Т-и ТИ=Т0 + Тх +...+ Тм-х) =М1то + т1+... + ТМ~^] X
ХР<Т-и ^^Го + ^+...+ Гм-i), (5.191)
где р(Т-и 7'и=7,о+Г1+...+7,л1-1)—совместная плотность
распределения вероятностей длительностей Г-i и суммы Т0-{-
+7\-|-... +Гл1-1. При этом
р(?'-1Ди = Г0 + ?'1+...+ Гм.,)=
Тт&х 7тах / М—2 \
= j ... | р[Т_и Т0,..., Тм_2, Тя- 2 Г, ЫГ0..Жм-2. (5.192)
'min 'min
210

Условная плотность распределения вероятностей шагов
дискретизации внутри интервала интерполяции Ги, перед которым
'находится шаг дискретизации длительностью Т-\, имеет вид
'(т-19тй9...9 тм-г\тЕ= Sr#) =
/ М~2 \
PK-lJo ^V2 Ti)
^тах ^тах / . М 2
^ ... j р[Т-г, Т0,..., 7*м__2» Ги— И Ti)dT0...dTM_2
Относительная усредненная дисперсия погрешности с учетом
случайного момента сравнения
» ^тах Ттах
I M—1 \
XP ^-1, ^O»---, '^Af-l
2 ^i = ^и dT-i dT0... dTM-2dTn,
/=o J
откуда после подстановки соответствующих законов
распределения получаем
,Tmax ^max
Х MlTt + T^.+T^Lil Р{Т~^ Т*>-> TM-i)dT^dT0...dTM^
(5.193)
Если временная дискретизация осуществляется АЦП
поразрядного кодирования с запоминающим, интегратором, то б2/ не
зависит от Т-\ и оценка погрешности имеет вид
// ^тах Т'тах т \ \ т
— _/(» п ~ ' о + • • • Т" ' М-1
б°2 = 1/ J -' J V(V..,^-l) Л*[Гд + Г1+...+Гм_11Х
4Xp(V.Jm-i)^-,^-i, (5.194)
где б2/(7"о,••., ^ai-i) определяется выражением (5.188).
Текущее значение погрешности преобразования на /-м
интервале интерполяции от Р0 до t*Mmmi (см. рис. 4.12,6), когда
14* 211

исключается запаздывание, вызванное процедурой
интерполяции и способом получения цифрового эквивалента,
определяется выражением
0,W= х(<* + х)-JJ^-K 7Llf Г0,..., Гм_2) j X(tt-
i=Q О
-Vi + U+^)^h (5.195)
для АЦП последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ, где 0^
^т^Г-^ ... +7V-2, и выражением
М 'об
i=0 0
(5.196)
для АЦП поразрядного кодирования с запоминающим
интегратором, где 0<t<fM— tl-
Получим вначале выражение относительной дисперсии
ошибки на шаге интерполяции при рассматриваемых типах
АЦП последовательного счета:
м—1
1 ' RxAO) Rxx(0) Li '«л ' v U °'
WO) RxxW
U
о
м м
+ ,» ' /m-S £ L**K r-i. V», Гм-») VK т^Л,-., Ь-jO X
'об 'об
х§ § Rxx(tt-i-tr-1 + *i-*ld*i*v (5Л97)
о о
Так как для случайного стационарного потока отсчетов
безразлично, как рассматривать М—1-й шаг дискретизации — от
(—1)-го до (М—2)-го или от 0-го до (Л1—1)-го, то, поменяв
индексацию шагов дискретизации и заменив i на i+1 и г на
/+1, получим
U«* (т, Г_1, ..., Тм-ъ) =Ь? (т, Го, ..., Тм-\),
212

откуда следует
' м
X \RXX (t,-U +1 + If- -x „) dxH +
6
мм"
-3^SSW г- rM-,)V(x'г- ^x
r=0r=0
XJ r^ft-'r + 'i—",)*!*,. (5.198)
0 0
В случае использования при дискретизации АЦП
поразрядного кодирования с запоминающим интегратором при
исключении запаздь1зания, вызванного интегрированием аналогового
сигнала, получим
м
S< (х) - RM0) = 1 RM0T L~^Li ( ' Т°'-> Гм-°Х
1=0
xfRxx[t0-tt + x + ^—^d4 +
о
м м
06 «=0г=0
1об 'об
XJ j Rxx(ti-tr + H-\)d4d^. (5.199)
о о
Сравнение выражений (5.198) и (5.199) показывает их
тождественность. Этот результат понятен и следует из того, что
при исключении погрешности от запаздывания, вызванного
способом получения цифрового эквивалента, в обоих случаях
восстановление осуществляется по отсчетам, определяемым
средним значением x(t) за эталонное время интегрирования,
когда значение отсчета перенесено в середину участка
интегрирования (см. рис. 4.12).
С учетом того, что и—и и ti—tr являются алгебраическими
суммами Ti, $2i(%) в соответствии с выражениями (5.196) и
(5.197) является функцией т, Г0, ..., Тм-\.
213

Тогда выражение Ь2{Т0,..., ТМ-\) получаем по (5.150),
выражение Кб2— по (5.190), выражение Кб20 —по (5.194) при
относительной дисперсии погрешности преобразования,
определяемой по (5.197).
Рассмотрим частный случай (интерполятор первого
порядка), воспользовавшись выражением LtH из § 4.5.
При временной дискретизации аналого-цифровым
преобразователем последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ, когда
ошибка от запаздывания, определяемого способом получения
цифрового эквивалента, не исключается, получаем
0
+ ^Г 77 Г ***<-/3« + '-*i)*i} +
0
^ RxxWXl г.* п 77 A, J J
об о 0
*об *об
-2^^-^-J J *„(7U+<x-v)*i*.};. (5.200)
о о
т° _
V^-b^^-^jVW^; (5.201).
8»= j | KiT^T^piT^TJdT^dT,- (5.202)
^max Лпах
87= J j V(T_1,7'e)-^-p(r_1,re)dr_1rf7'e. (5.203)
T'min ^min
Если погрешность от запаздывания, определяемого
способом получения цифрового эквивалента, исключена, то
о
214

О
+ Rxx(0)\[ V ^ r,» \ & } j
-j- f f RXX(T0 + 4-*,)Airf'.|; (5.204)
/ t» \ i />o6 лоб
_ 2 (^—^о)1 *
О О
V(r0) = (l/r0)SV(x)d,, (5.205)
О
где 62*(т) определяется выражением (5.204):
82= J Si4T0)p(T0)dT0; (5.206)
^тах
V= J V (Го)-=?-/> (П) <*7V (5-207)
■ ' При временной дискретизации аналого-цифровым
преобразователем поразрядного кодирования с запоминающим
интегратором, когда погрешность от запаздывания, определяемого
способом получения цифрового эквивалента, не исключается,
имеем
VW-,-555){i(-'-^)J-«-«-+'-^*- +
о
о
'обо о
2 х—Го * 1
*2
J j Л«(7,в +'1-^*1*.}. (5-208)
Г' Г* '"о о
Оценки погрешности получаем в результате подстановки
выражения (5.208) в (5.205) с последующим определением б2
по (5.206) и б2о — по (5.207).
215

Если погрешность от запаздывания, определяемая
интегрированием аналогового сигнала, исключается, выражения 62/(т),
62/(iTo), б2, б2о полностью совпадают с соответствующими
формулами (5.204), (5.205), (5.206) и (5.207).
Аналого-цифровое преобразование с ИАИМ.
Восстанавливающий оператор-экстраполятор Л1-го порядка по Лагранжу.
Текущее значение ошибки преобразования на М-и шаге
дискретизации, когда не исключается запаздывание, вызванное
способом получения цифрового эквивалента, определяется
выражениями
йм(*) = хЦм + *) —
М 'об
-J]^K^0,...^m-i)-^J xiU-T^ + t^+.^d^ (5.209)
*=0 0
для АЦП последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ. Здесь
0^т^м+1—tM = ТМ'у
Ьм (т) = X (tM + «0 —
М 'об
5]VK V..^m-i)-^J xiU-t^ + ^dn (5.210)
*=о
для АЦП поразрядного кодирования с запоминающим
интегратором.
Относительная дисперсия погрешности преобразования на
М-м шаге экстраполяции имеет вид
1 = 0
, и
X -£- j Rxx VM-ti + Tt_t -tm + x - x,) </,, +
0
M M
+-^rESL'3K t-- Tm-i)V(t' r°-- Tm-i)x
/=0r=0
'об 'об
*°6 if oJ
216

для рассматриваемых АЦП псоледовательного счета;
1=0
0
М М
/=ог=о
£об 'об
x4~f f ««('i-'r+^-'J^*. (5.212)
для рассматриваемого АЦП поразрядного кодирования.
С учетом того, что ^м = 2 ^м, (м — U и ^_х— tr_x являются
алгебраическими суммами величин 7\, б2м(т) для выражения
(5.211) есть функция от т, Г-ь Г0,.,., ТМ-\. Аналогично б2м(т)
для выражения (5.212) является функцией от т, Г0,..., Тм-\
(в последнем случае отсутствует шаг дискретизации 7\-i).
Тогда
тм_
8м (^-ь 7V--> ^м-ь Тм) == -=;— I 8м(^)dx,
'м J
о
где 8м (•*) определяется выражением (5.211),
т
8м^о>-»" ^м-1, Т'м) = -=— \ 8М(^)Л,
о
*2
где 8м (^) определяется выражением (5.212).
Усредняя 8м по всевозможным Т_ъ T0i..., Тм—\, Тм для
рассматриваемых АЦП последовательного счета и 8м по Т0,..., Гм-ь
Тм Для АЦП поразрядного кодирования, соответственно получаем
/
т т
шах max ~
J* ... j &м{Т_1,Т^...,ТМ-\,Тм)р{Т_.ъ..., TM)dT_v..dTMf
(5.213)
217

r-zr- I max 'max ~
У * = 1/ J - J 8^o,..., TM-u Tm)P<T09..<9 Tм)dr0...dT^
м-
(5.214)
Для получения среднеквадратичных оценок V 802 с учетом
случайного момента сравнения в (5.213) закон распределения
Р{?-и Т0,...,Тм-и Тм) заменяем на Тмр(Т-и.. ,TM)/M[Ti\y
а в (5.214) закон распределения p{T0i..., Тм) — на Тмр(Т0у...
...Jm)/M[Ti].
При исключении запаздывания, вызванного способом
получения цифрового эквивалента (см. рис. 4.12), текущие
значения погрешности
вм-i СО = *(& + *)—
М 'об
-J]i,"(*, r_lf r0,..., ^M-^r^J ^ft-r^ + ^ + ^^i
(=0 0
для АЦП последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ, где
м 'об
6m(^) = xAm-^ + xJ-^V(^ + ^)^-J .*(f|-4>6 + 'i)*i
/=о о
для АЦП поразрядного кодирования с запоминающим
интегратором, где О^т^Тм-
Относительная дисперсия погрешности преобразования на
(М—-1)-м шаге дискретизации при использовании рассматри-
ваемых АЦП последовательного счета имеет вид
м
r$ M [6M_i (%)] 2 V) Г э*/г Т Т W
/=0
'об
о
М М
+ —^— У!УЛЭ*К Т-1 тм-№(*, т_и..., Гм-2)Х
Rxx\0) 4яШ hU
t=0r=0
'об 'об
'обб о
218

Как уже указывалось, для случайного стационарного
потока отсчетов безразлично, как рассматривать Л1+1 шагов
дискретизации—от (—1)-го до (М— 1)-го или от 0-го до Af-го.
Поэтому, заменив индексацию шагов дискретизации i на i+l
иг на г+1, получим L/9*(t, T-u T0y...,TM-2)=U3{x^ Г0,...
.-.Jm-i), откуда
__ м
85,<')-,-^rS-^L',('-r» r"-i,x
'об
X j Rxx(tu-tt + - + Jf-n)d4 +
О
м м
+"«iwSSLi9(T' :Гo,••', Гм-1)^9(х' 7,°'-- Гл,-,)х
/=0г=0
'об 'об
X-з- f Г *~(U-tr + H-^Mv (5.216)
Относительная дисперсия погрешности преобразования на
М-м шаге дискретизации при использовании АЦП
поразрядного кодирования с запоминающим интегратором, когда
исключается погрешность от запаздывания, определяется также
выражением (5.216). Этот результат очевиден. После исключения
погрешности от запаздывания при временной дискретизации
АЦП с ИАИМ восстановление реализуется по отсчетам x(t)y
равным среднему значению функции зй время t0Q и отнесенным
к середине участка интегрирования (см. рис. 4.12). При этом
способ построения АЦП с ИАИМ не оказывает влияния на
дисперсию методической погрешности.
м-\
С учетом того, что tM = 2 ^м, tM—tt и tt — tr являются ал-
гебраическими суммами величин Ти Ь2м(ъ) есть функция т, Т0у...
..., ТМ-\. Тогда
т
$(Т0,..,, Т„) = -J- Гal(x)dt, (5.217)
м J
где b2M(z) определяется выражением (5.216).
219

Искомые оценки вычисляются по следующим формулам:
г-хг- . I ^тах ^тах
Кв| = 1/ J... J b2(To,..-,TM)p(T0,..t,TM)dT0...dTM] (5.218)
r min min
/ ^тах ^тах
г 'min min
Г
TM)-=r p(T0,...f TM)dT0...dTM.
(5.219)
Рассмотрим частные случаи — экстраполяторы нулевого и
первого порядков. Соответствующие выражения L*9 приведены
в § 4.5.
При временной дискретизации аналого-цифровым преобра--
зователем последовательного счета с промежуточным
преобразованием в частоту или временной интервал с ИШИМ
выражение относительной текущей дисперсии погрешности
преобразования на Af-м шаге дискретизации определяется
следующим образом:
при ЭНП без исключения запаздывания, вызванного
способом получения цифрового эквивалента,
^(x)=i-«uwr^(r-i~u+t~xi)dxi+
о
hw~h)) Rxx (Xi ~,J dzA» (5,220)
06 о о
при ЭНП с исключением запаздывания, вызванного
способом получения цифрового эквивалента,
о
+ -/етг15- j J *«K-*,)*i*,; (5.221)
'об о б
при ЭПП без исключения запаздывания, вызванного
способом получения цифрового эквивалента,
Я<"-,-й5){-Г.-С-1-ч-(Г'4'г-'-^ + '-^*1 +
О
220

О
+ —l—№ + ^±^!l_f. f06 'f R^-^d^
Rxx(0) UV^ V J t% J J
о о
- 2т(ут) -j-j Г в"*7"-1+Xl~t,)dXldX2 }: (5,222)
'об о о
. при ЭПП с исключением запаздывания, вызванного
способом получения цифрового эквивалента,
t^
W Rxx(0) \ Т0 U J "V ° 2 V
о
о
л«(0) U V w J & J J
о о
2х(Г0 + х) _1
'об 'об
-£-J J Rxx(T-t + 4-s)dHd^. (5.223)
0 о о
В случае восстановления экстраполятором нулевого
порядка, когда ошибка от запаздывания не исключается,
То
82м (Т_ъ Т0) = JL j 8^ (х) dx; (5.224)
f' = J j 8», (7^, Г0) p (T_u T0) с1Т_гс1Г0; (5.225)
max 'max
V= j j ^(7*-!, У,) TbP(TZ1' To) dT^dT» (5.226)
^min ^min
где Ьм (*) определяется выражением (5.220).
221

При исключении погрешности от запаздывания,
вызванного способом получения цифрового эквивалента, и ЭНП
82м (Т0) = (1/Т0) j 82м (,) dx; (5.227)
~ шах ^
52= j 8^(Г0)р(Г0)йГ0; (5.228)
^max ^
V = j 82M(r0)^Lp(T0)dr0, (5.229)
где b%(z) определяется выражением (5.221).
В случае восстановления экстраполятором первого
порядка, когда погрешность от запаздывания не исключается,
^ г,
& (Т_ь 70, 7\) « -1- J 82м (х) dx; (5.230)
о
^ ^тах ^тах ^тах ^
82 = J j j 8^(Г_Ь Г,, Т1)р(7'_1, Г0> T^dT^dTtdT» (5.231)
^min ^min ^min
^ ^max ^max ^max ~ _,
80s = j j J 82M (T_ 1( T0, 7\)-b-"p(T_lf Г0, 7\) dT^dT^T,,
Tmin ^min ^min
(5.232)
где 8^(x) определяется выражением (5.222).
При исключении погрешности от запаздывания, вызванного
способом получения цифрового эквивалента, и ЭПП
г* _
8м (T0f Тг) = -i- j 62M (x) dx; (5.233)
о
^ ^max ^max ^
*= j j 82,(Г0,Г1)р(Г0, 7^7^; (5.234)
^ ^max ^max ~ r
802= j j MT0,T1)JfpiJu,Tt)dTudT1, (5.235)
T'min ^min
где 8м (т) определяется выражением (5.223).
222

В случае временной дискретизации аналого-цифровым
преобразователем поразрядного кодирования с запоминающим
интегратором выражения квадратичных оценок при исключении
запаздывания на £0б/2 совпадают с выражениями,
полученными для рассматриваемых АЦП последовательного счета при
исключении запаздывания, вызванного способом получения
цифрового эквивалента.
Если запаздывание не исключается, то выражения
квадратичных оценок имеют вид:
при ЭНП
Rxx(Q) ttf J
о
+ p ' 2 f Гя„К—ч)*1*.; (5.236)
0 0
~ Го ^max
& (7,) = -£-j" &(')*; 8»= J b2M(T0)p(T0)dT0; (5.237)
0 fmtn
^max ^
V= J SM(T0)-j-P(T0)dT0;
при ЭПП
a** (o; i ^o fo6 J
о
t б
+J^-^.r^(/o6+x~xi)dTi}+
0
T Я«(о)\ V £, ) J ххУ1 г) l г
_2^^_i_jo6j'%^(ro+Ti_tj)dXidT| (5238)
'обо о
Выражения 8м (Т0, 7\), 82, 802 совпадают с (5.233) —(5.235)
после подстановки в (5.233) 8м(т) в виде (5.238).
223

Аналого-цифровое преобразование с АИМ и ИАИМ.
Восстанавливающий оператор-интерполятор и экстраполятор 1-го
порядка по^крите£ию наименьших квадратов. Квадратичные
оценки К б2 и г 802 получаем после замены в выражениях,
полученных при восстановлении по Лагранжу, функций LtH и
U9 соответственно на L,HKB/ и Li9JXBl.
5.6. ПОМЕХОУСТОЙЧИВОСТЬ ПРЕОБРАЗОВАНИЯ
ПРИ НЕРАВНОМЕРНОЙ ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Дисперсия помехи на выходе тракта преобразования при
заданном способе получения цифрового эквивалента и
фиксированных (в общем случае различных) шагах дискретизации 7\
определяется как математическое ожидание квадрата z(t) на
выходе восстанавливающего оператора. Выражение дисперсии
полезного сигнала на выходе восстанавливающего оператора
при заданной его корреляционной функции на входе тракта
преобразования уже получено в предыдущем параграфе при
вычислении дисперсии погрешности. Оно представляется
третьим слагаемым в формулах б2/(т) и $м(т) соответственно
при интерполяционной и экстраполяционной процедурах
восстановления. Поэтому заменив в этом слагаемом /?**(т)//?**(0)
на Rm(t)IRxx(0), получим текущее значение относительной
дисперсии на /-м (или М-м) участке восстановления при
фиксированных шагах дискретизации. Обозначим эти дисперсии
sfx(x) и «Leo.
Формулы 8?г(т) и бмх(т) для различных видов АЦП и способов
восстановления сведены в табл. 5.10.
Обращает на себя внимание факт зависимости дисперсии
помехи на выходе восстанавливающего оператора при
временной дискретизации аналого-цифровым преобразователем
последовательного счета с промежуточным преобразованием в
частоту или временной интервал с ИШИМ от того, исключено или
не исключено запаздывание, определяемое способом получения
цифрового эквивалента. Это объясняется тем, что только при
данном типе АЦП в случае неравномерной дискретизации
отсчет, полученный на заданном расстоянии от начала Т-\ шага
дискретизации, появляется в начале шага Го и, следовательно,
дисперсия помехи на выходе восстанавливающего оператора
зависит от Т-и когда запаздывание не исключено. В
противном случае, когда отсчет относится к середине интервала
интегрирования, результат восстановления не зависит от
предыдущего шага (см. рис. 4.12).
224

£ Таблица 5.10
о
О)
Вид АЦП
Способ

восстановления
АЦП и АИМ
АЦП последовательного счета
с промежуточным
преобразованием в частоту или временной
интервал с ИШИМ
(запаздывание, определяемое способом
получения цифрового
эквивалента, не исключено)
ЭМП,
Э1ПКБ
ИМП,
И1ПКВ
ЭМП,
Э1ПКВ-
ИМП,
И1Пкв
to
to
ел
«?х<*>- ^И"
ММ
1 *Я л.\ . .. \ • \ « тъ it Т .1 f» ГТ Т т1 v
°Mx(L) — Rxx(0) 2j 2j ' "", M~l9 ' rl °' "' **-!' ] A
i=0r=0
1 ХЯхх^-'г!
M M
/=0r=0
1 X*ixVt-tr]
M M
~*& (x> = ir-S S L3< ir° T«-f x] L9' |r* •- T"-i't] x
'об 'об
X J ] Д**(0) ^XXL'l-l — 'г-1 + 4~ L2J"VC2
1 о о
MM
~*(хЫ=-Ж-У)У)1И11То Гм_„ t]L"r[r„, ...,ГМ_„,]Х
06 iTor=0
'об 'об
1 N/ 1 I .._... П Г* * _l _ _ 1 Air A*
A J J #xx (0) *xx 14-i — h-i + 4 — L2J d\dT,2
• 0 0

£§ Продолжение табл. 5.10
Вид АЦП
АЦП с ИАИМ
(запаздывание исключено)
АЦП поразрядного
кодирования с запоминающим
интегратором
'
Способ

восстановления
ЭМП,
Э1ПКВ
ИМП,
И1ПКВ
«?х«- ^> •
м м
'об 'об
Г Г 1
A J /^ (0j Я\х [Г; — Г г + Ч — X2J ^xi«T2
0 0
VW 3—Т1 TI ^"'t^ ^Af—1- ^"rFo. .... Гм_„ т]Х
'об 'об
Г • Г 1
^ J J Rxx (0) ^u [ l* ~ r+ Zl""l2* * 2
0 0

5t Таблица 5.11
Вид АЦП
АЦП с АИМ. АЦП с ИАИМ
(запаздывание исключено)
АЦП поразрядного
кодирования с запоминающим
интегратором
Способ
восстановления
ИМП,
И1ПКВ
ЭМП,
Э1ПКВ
го
ю
' *Ч. ^ох
^-j-J[r. + ...!+rM_, -f ^(ИХ
0 0 0
ХР(Г TM_l)dTfi...dTM__x
оо оо То + ..Тм_ i
0 0 0
То + --- + тм-\
i0 + ... + ^M-i
оо оо * N
^x = I""\f["5T.f ^W^^' ...,TM)dT0...dTM
об о
оо оо ЗГм _
«Ix = J - j* Г-Т^Г J "«W^l^^o TM)dT0...dTM
0.0 0

52 Продолжение табл. 5.11
Вид \АЦП
АЦП последовательного
счета с промежуточным
преобразованием в частоту или
временной интервал с ИШИМ
^запаздывание, определяемое
способом получения цифрового
эквивалента, не исключено)
4Способ
восстановления
ЭМП,
Э1ПКВ
имп,
И1ПКВ
**• 7ох
|«V= J ---J [f^.J Жх^)^Р(Т-г, Г0,..., TM)dT1dT9...dTM
^min Mnin 0
Лпах ^max *M
^= J ■••■J [lyj 4('»*]^(^ r„ .... гм)Х
^min ^min 0
XdT-1dT0...dTM
~^2 f f Г * Г "?»" / \ /1
Ux~ J -J lr.+ ...+rM_I J "a(^j-
XP (T-i, T0, ... Гм_,) dT-JT, ... dTM_,
^max ^max T0 + ... Ч-^м—!
^" J - J. U+ ••■+■*«-. I "SfxW*]x
x — P (T , ТЛ Т Л Л dT >йТЛ dT J ■
Т л т f l ~b °» ' A!—1' u —1" о ••• ai Л1—1

Выражения усредненной относительной дисперсии помехи
на выходе тракта преобразования (б2я) и усредненной
относительной дисперсии помехи с учетом случайного момента
сравнения (Sqx) сведены в табл. 5.11. В таблице принято
обозначение математического ожидания в виде черты над случайной
величиной, например М[Т0+ ... +7,m-i]=7,o+ . • • +ТМ-\.
Оценка б\ характеризует помехоустойчивость тракта
преобразования при обращении к результату восстановления на каждом
шаге экстраполяции и интервале интерполяции, оценка 80\ —
при редких обращениях к результату восстановления либо при
усреднении дисперсии эргодическои помехи по оси времени
(см. § 5.5).
Функции Lf(xy T0f..., Тм-х) и Li*(x, Т0,...,ТМ-\) при
восстановлении по Лагранжу определяются выражениями (4.135)
(4.144). При экстраполяции и интерполяции /-го порядка по
критерию наименьших квадратов методика получения этих
функций показана в § 4.5. -
Пример 5.14. Требуется получить выражения 8jf и djjx при АЦП с АИМ
и восстанавливающем операторе ЭНП.
В случае экстраполяции нулевого порядка (М=0) функция 10э (х, Т0)=\
Отсюда
*1хН = Яхх(0)/Я**(0).
Следовательно,
о L о ■
Яхх(О)
***(0) '
о
оо
так как j p(T0)dT0 = 1.
о
Усредненная относительная дисперсия помехи при случайном моменте
сравнения имеет вид
Г *хх(0) Т9 ^х(О)
так как \ -=-р (Т0) dT0= l.
о
Таким образом, в рассматриваемом случае ^| =^qx =* ^хх(°) /#хх(0).
229

Глава 6
ИНЖЕНЕРНАЯ МЕТОДИКА РАСЧЕТА ОЦЕНОК
ПОГРЕШНОСТЕЙ ПРЕОБРАЗОВАНИЯ
СЛУЧАЙНЫХ СИГНАЛОВ ПРИ ВРЕМЕННОЙ
ДИСКРЕТИЗАЦИИ И КВАНТОВАНИИ ПО УРОВНЮ
6.1. РАСЧЕТ ОЦЕНОК ПОГРЕШНОСТЕЙ
ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ СИГНАЛОВ
ПРИ ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ
Расчет погрешностей, вызванных временной дискретизацией
и восстановлением случайного сигнала, в соответствии с
выражениями (5.58), (5.59), (5.61), (5.64), (5.65) связан с
необходимостью интегрирования корреляционных функций и вычис-'
лением двойных сумм. Во многих случаях эти интегралы не
берутся в квадратурах. Путь решения задачи в таких условиях
намечен в примерах 5.6 и 5.7 и заключается в использовании
разложения RXx{i) в ряд Маклорена [4.38].
Широкий класс дифференцируемых случайных процессов
описывается корреляционными функциями*, допускающими
представление в виде
00
*«(*)= 2С°(0)*2'/(2/)!, (6.1)
где RX2P (0) — 2/-я — производная корреляционной функции при
т = 0.
В частности, такое разложение допускают корреляционные
функции дифференцируемых сигналов, приведенные в табл. 1.1.
Аналогично для широкого класса недифференцируемых
случайных процессов справедливо разложение
00
*«(*)= 2О0)| *!'//!. . (6.2)
/ = 0
Ряды (6.1) и (6.2) являются равномерно сходящимися и
допускают почленное интегрирование. Более того, можно
показать, что степенной ряд, полученный после интегрирования,
также равномерно сходящийся и допускает почленное
интегрирование.
В данном параграфе приведены методика расчета
погрешностей, вызванных временной дискретизацией, и
восстановление случайных процессов, корреляционные функции которых
допускают разложение (6.1) и (6.2).
230

В качестве базовых импульсных характеристик первого
звена, определяющего способ получения цифрового эквивалента,,
используем: для АЦП с АИМ
*1(т)=й(т—чр1Г), (6.3)
для АЦП с ИАИМ
k 1(x) = _l_ii \x — IJ\ — \U — )—Xt\ (6.4)
Данные fci(x) являются «универсальными» в том смысле,*
что позволяют получить при соответствующих подстановках
(см.-§ 4.1) весь набор импульсных характеристик, приведенных
в табл. 4.1.
С целью получения достаточно удобных для расчетов СКО
преобразования аналитических выражений рассмотрим внача-.
ле свойства k\(x) и импульсных характеристик
восстанавливающих операторов, описанных в гл. 4 (см. § 4.2—4.4).
Свойства *i(x), k2[m9 е], Lt9[0, e], £,-и[0, e]:
(6.5)
(6.6)
(6.7)
(6.8)
JA
0
ос
2*
w=0
М
2 L,
1=0
м
Ж
(x)d-
г[т,
э(0,
и[0,
с =
е] =
']-
ф
1;
= 1;
= 1;
= 1,
/=0
где L,H[0, e] и Ц*[09 е] определяются соответственно при
интерполяции и экстраполяции по Лагранжу выражениями
(4.52) и (4.63), при интерполяции и экстраполяции по
критерию наименьших квадратов — выражениями (4.101) и (4.109).
Равенство (6.5) следует из непосредственного интегрирования
выражений (iS.3) и (6.4).
Равенство (6.6) для восстанавливающих операторов,
заданных (4.43), имеет вид
оо 2
21 kt[m, •]=■ Jl kt[m, г] = Ае+В + А(1 — е) — АВ. (6.9)
т=0 т=0
Непосредственной подстановкой можно показать, что при
любых Л и В, приведенных в § 4.2, правая часть выражения
(6.9) равна 1.
231

Рассмотрим далее автоматическое восстановление
фильтром нижних частот при работе аналого-цифрового
преобразователя в одноканальном режиме. Согласно равенству (4.45) при
N=1 передаточная функция восстанавливающего оператора
имеет вид
1 — е-*>т Мр)
где А(р) =a0+aiP+ ..• +ampm; В(р) = Ь0+Ьх(р)+... +Ьпрп;
п>т.
Статический коэффициент усиления фильтра а0/&о=1 из
условий одинакового масштаба сигналов на входе и выходе
тракта преобразования. Число полюсов передаточной функции
А(р)/В(р)
/=1
где г — число различных полюсов; // — кратность /-го полюса
Р/ (при отсутствии кратных полюсов г=л, //=1).
Импульсная характеристика восстанавливающего
оператора определяется на основании теоремы о вычетах:
*.W -1- [К.(Р)] = 1(*) + g 17pVplim ^r[(P-
_yi_J_lim4=Vf(p-p^^-eP(T-r)l,
откуда, переходя к относительному времени, получим
00 ОО
т=0 т=1
h (U-\)\ Р+Р, dp1 г' Г " рв(р) Г
р-*Р: dp i
232

Меняя порядок суммирования, имеем
т=0 /=1 '
^ U (//-1)! P^dp'r'lL
-р')1'7вш*"] jjle^-e'""-1^]}. (6.11)
J ет=1
Так как имеет смысл использовать только устойчивый
фильтр нижних частот, т. е. фильтр, полюсы которого имеют
отрицательную действительную часть /?б>Р/<0, то, рассматри-
00
вая 2 е как сумму бесконечно убывающей геометрической
прогрессии, получим
00
2[e'mr-e'(m-,)7'j = -l. (6.12)
ет=1
После подстановки (6.12) в (6.11) непосредственно следует
равенство (6.6).
При работе АЦП в многоканальном режиме (#>1)
утверждение (6.6) несправедливо.
Перейдем теперь к доказательству равенств (6.7) и (6.8).
Пусть x(t) = l(t) —дискретизируемый сигнал. Тогда результат
интерполяции и экстраполяции Л1-го порядка по Лагранжу или
1-го порядка по критерию наименьших квадратов также равен
1, т. е.
м
zln> е1= 2*[n\Li[0, е1 = 1.
/=о *
м
но х[п] *= 1, откуда 2 А1°>£] = 1,
что и требовалось доказать.
Расчет оценок погрешности равномерной временной
дискретизации и восстановления случайного входного сигнала. Расчет
получим после подстановки (6.1) или (6.2) в (5.58), (5.59)
с учетом (5.61).
233

Для синфазных моделей
э(2/)
/=0 т=0
" 1 A R{21)(0) *
О /=0
ОО ОО 00 00 \
m=Or=0 0 0' J
(6.13)
при дифференцируемых входных сигналах;
82[0, в] = 1 - _1_ £ -^1 £ А2 [от, г] f *х (х) | (т. + г-^р)Г+
00 г>(/)/л\ 00 00 ' 00 00
/=0 т=Ог=о О О
Х1(/п-г)Г + х,—..I'*!*. * (6-14)
при дифференцируемых входных сигналах;
Преобразуем выражение (6.13). Его второе слагаемое
(обозначим его как С) при 7—0 имеет вид
00 * ОО
я*,(0) о! ZJ 2l JJ 1V '
= (0)
m=0 0
Воспользовавшись равенствами (6.5) и (6.6), получаем
С=—2. Третье слагаемое (D) выражения (6.13) при /=0
определяется следующим образом:
D =
1 Rxx(0)
^ S S *• (m' s> *» lr' el J J ** ('») *» ('«) dz^> =
Д**(0)
m=Or=0 О О
OO 00
= 2 ft, [«, t] 2 К [Г, t] J" kx (xx) dxx j ^ (xf) dx2 = 1,
m=0 г=0 О О
откуда
/=1 v m=0 0
234

х [(ю + в - ф) г + х]3' dz + 2 2 м«, eJ fe2кs) x
m=0 r=0
OO 00 00
Xf 1КЫК{^[{т-г)Т + H-,2\dHd^U SajfoW, (6.15)
oo ' *=i
где
at=RfJ(0)l[Rxx(0)(2l)\] (6.16)
— коэффициент, зависящий от вида корреляционной функции
сигнала; /г/(е) —выражение, записанное в фигурных скобках и
определяемое способом построения АЦП с видом
восстанавливающего оператора.
Для недифференцируемых случайных сигналов
00
&\0, .J- 2«ib(«), (6Л7)
где
at = R&(0)l\Rxx(O)l\]; (6.18)
00 00
/i(«)«-2S*.l"». е1 Wx)l {m + t-4)T+x\ld* +
m=0 0
00 00 00 00
+ 2 2*.И. 81 *> l'. el 11*iK)*K)I(«-0T + xi~'.I'«M1-
m=0r=0 0 0
(6.19)
Для не синфазных моделей
1 J U Rxx(0)(2l)\ ^
/=0
M oo
X Щ Vjo, .] j\ (,) [(i _-L_ +, _Лгм + ,f dxj +
/=0 0
+Ё^шг{11!1^10-'1^10'«1Я*.(">*.<'=>|(г-''>г+
/=0 S=Or=0 0 0
+ *i~*ci]<fri£bii (6.20)
при дифференцируемых входных сигналах.
235

Учитывая равенства (6.5) и (6.7), получаем
/=1 v /=0 О
м м
x[(1~"^"+8-"<p)rA1+xrdx+SSIi"l0'slvl0,s]x
/«О r=0
оо оо % оо
XJJ^iW^iWKr-O^ + ^i-^^i^U 2*i/.iW. (6.21)
0 0 ) 1=1
где а^ = R{xx] (0)/[Rxx(0) (2/)!]; f2l (e) — вырая ение, стоящее в
фигурных скобках. Аналогично в случае недифференцируемых
случайных сигналов
оо
^[0,е]= 2«i.fi(«), (6.22)
где а, = Я# (())/[/?„ (0)/!];
М оо
/, (s) = —2 J] /,,и[0, s] J ^(х) Ц1 — -1- + е — Фj ГЖ +
/=0 О
ММ оо оо
:=0r=0 0 0
. (6.23)
Усредненные и максимальные дисперсии погрешностей
преобразования определяются выражениями
оо 1
1 = 1 0 f=l
^2= 2*i J/.iW*= 2fli/.i; (6-24)
6"=sup2fli/.i(e) (6.25)
для дифференцируемых входных сигналов и выражениями
ОО 1 00
s"2= 2« J/.(»)* = 2«»/«; (6.26)
/ = 1 0 / = 1
оо
6^= sup 2^//и (6-27)
е t=i
для недифференцируемых входных сигналов.
236

Таблица 6.1
Корреляционная функция
Rxx W
sin awe
av2
* со0т
охЧ-^>
зх2cos |3т
о^-М
Разложение корреляционной
функции в ряд Маклорена
2 г\ (-D' (М2'
°х U (2/+1)!
°*22j—я—
1=0
, Г! (-D' ((*)■'
a* £ (2/)!
(=0
a/
(-D4»'
(И+ 1)1 |
(—1)' a*' i
л ':
(-i)'P2'
(2/)!
V.
>
Типовые корреляционные функции и их разложение в ряд
Маклорена (коэффициенты щ) приведены в табл. 6.1. Знач|е-
ния /V(e), /г/ при дифференцируемом входном сигнале сведены
в табл. 6.2. В этой таблице £<и[0, е] и L,3[0, е] определяются
соответственно выражениями (4.52) и (4.63) при интерполяции
и экстраполяции Л1-го порядка по Лагра-нжу, (4.101) и (4.100)
— при интерполяции и экстраполяции /-го порядка по критерии
наименьших квадратов. Значения //(е) и fi при недифференци-
руемом входном сигнале и использовании АЦП с АИМ сведены
в табл. 6.3. Результирующие расчетные формулы величин б2
для типовых корреляционных функций при временной
дискретизации АЦП с АИМ и- простейших способов восстановления
сведены в табл. 6.4.
Рассмотрим задачу определения fi(e) и // для АЦП с ИАИМ
и недифференцируемом входном сигнале в частном случае
экстраполяции нулевого порядка [4].
Подставив соответствующие k2[my е] и &i(t) в (6.19),
получим
T/N
/l(e)=-2^r j |(в_ф)Г + ,|'* +
(1-VT/N
237

9-
+
9-
N
9-
S
Г
сч
*2 mS?
+ •?
r +
e* ...
r +
+
л\
в
a
с
я
238
Я"
<
я

АЦП
с ИАИМ
ЭНП по Лагранжу
+ 2Г»' gTTilfid + b)2/+1-?i2/+2-
fit (e)
2/-1
(=0
X
X Y \N) +
+ (2/-Ц)е^] + Г2'(2г + 1)1(/+1)Х
2/ —1
X
t=0
X
,-0-D^-J.^--' + l] +
+ T2/
1
(2/ + 1) (/+1)
W
2/-1
i=0
1_V 1 — (1—Y)a/+1~f (J__
-9
(*Г-
+
+ (2/+l)(e-^--f)a] +
+ T*1
(21 + 0(1+1)
2/-1
i_/V r.L
hi- -27'2'2T+l\2j C2/+1 <+l
X
(=0
i/ , 2-yV+1 / _L 2=I\' + 11
X[^"2"-^ATj - V~ 2 - 2JV j J
i -q-v)2*41-' (_L\
X
1 \«-'
X
+
+ V-2 ~ 2N ) -\~ 2~ 2N ) f+
+ Гг' (2/ + l)(f + l) ("AT)

.jjg Продолжение таб/i. 6.2
О :
Вид АЦП
Способ восстановления
f2/(e)* hi ПРИ<Р=°» ^
f2l (*)f f2l ПРИ <P=<Pi + <P2' &l
АЦП
с ИАИМ
Линейная
экстраполяция (0<Л<1)
ЭПП по Лагранжу
(Л=1)
Ы («) - -2-у-Г»* 2Пм{(Ле+ ° Х
-^[(1+е+ж)2'+2-
•(1+е+т)2'+2]}+(2ГТ
+ (Ле + 1)Ле[2-(1+-^-у +2-
fit
1) (f+1)
2/ —2
+
Г/ 2-у , 1 V'+1 f 2-Y ,
X •
1 _ у. a'+i
+ 4г1)"'"-А[(1+—
2-Y
2W
+
14-е
2-Y
2W
+
72/ y\/2
X
2/—1
{Sc^+i
X
2Г2/
fa/= ""2/+l\^j ^2/ + l
1 — (1 — Y)2^H-l—/ fj^yl-i
У
x—*-^ (-Jr)' x
_L\ (
N ) -{
i-v\2/+2]\
* / J/"r(2/ + l)(/ + l) Y2
x|[(A + i)» + ^2e2](-^-)2/ 2 +
f2/ - 2« + 1 \ £j 2C2/+i ^ 2 j x
(1)"-'Г
XI \r ) I л о; _i_ о — л о/ _i_ о 1г
2/ + 2 2i-»-2

+
CM
+
+
+
X
WW
^.^
+
(2/+1
5И.1
■ч;|(м
+
+
D(
+
CM
+
H*
+
4-
5
X
+
CM '
+
X
CM
+
X
r +
1 w ~l
1- + 1
+ --т-1?!
1 '*4 «"H
f |
1 CM н
lib
•** I
с
~ CM 1
+ "«
x~ Г -1
f 1
4" см| со ^ I см
CM >—
+■
CM
+
CM
+
CM
I
55
X
+
+
CM
+
X
X
X
+
+
° 'Tl
. >-
CM
+ JL
l
•4 "^
X
о
e
a
a
s
+
л,- +
CM ^
X_ X
+ I
- <N
+ +
= t *
+
+
+
U)
IT
16—6036
241

jg Продолжение табл. 6.2
Вид АЦП
Способ восстановления
f2l (б)* Ul ПРИ ф = °' /5? 1
f2l (е)* ^2/ ПРИ ф = ф1+ ф2* 1^]
АЦП с
И А ИМ
ИПП по Лагранжу
/ + 1
X
£^+2 (if 2+2e(l-e)(2/ +
/=2
f if = - Г2'
2/ +1
*=2/—1
Е с*/+
iX
t=0
1 \2/-« 1—(1--Y)2/ + 1"/
х-
2'+а-2 ) _ Г1| 22М2-2
(i + 1) (Л-2) / (* + 1)(2/ +
22^4 2 2
(2/ +
1)
Т*1 ( 2 /_Y_\2'
■ О (/ + 1М з \ w / +'
/+i
/ ^ \2i—2
xSC2'+2(i)
(=2
+—(2i+ !)(/ +
+
■'}
X j[«* + (1 - •)»] (^-)2' + 2e (1 - .) X
xJ]'C22/+2(^r)2l"2+2e{l+e)X
i=2
X(2/ +!)(/ + !)
}
Ы= -Г2'
2/ +1
/—I
Sr2i
X
j=0
/1 »2/ + l—2i / у \2'-2i |
X\TJ • ("iv"j (i + 1) (21
+ D
1 \+ I!! /AfJLf,
'"' • -41+1) \ 3 \nJ T
(/+1)/ (2/ + 1)
3 Jj C2'+2 ( yy ) +
(=2 '
+-£-(2*+I) </+!)}

АЦП
с АИМ
-
АЦП
с ИАИм
ЭМП по Лагранжу,
Э1П по критерию
наименьших
квадратов
ИМП по Лагранжу,
И1П по критерию
наименьших
квадратов
ЭМП по Лагранжу,
Э1П по критерию
наименьших
квадратов
М
м м
+е+?1)2/+Г2/2 2 vfo, ejx
/=0r=0
XVГО, «Иг-О1'
м
fa/ (•) = - 2Г»' JJ L,« [0> е] ^ _ J_+ -
/=0
м м
/=0г=0
XVfO, е](г-02/
Л! 1/yV
f2/= -2Т*1— JJvtO, «] J (M-
*=0 <1-Т)/Л7
N2
Af Af
xSSVf0, e]Lr9[0, e]x
f=0r=0
Af
fa/ (*) = - 2Г2/ ^ V fO, s] (Af - * +
Af Af
+ e)2i+T2t ^ 2 V [0, *] V [0, *] ('-O2'
/=0r=0
Af
f./(«)= -2^ Jvro, «] X
/=0
Af Af
4_^Г+Г2'11Е£'И[0'е1х
/=0r=0
XV40, e](r-i)2t
M
fa/W= -2Г»' — £]V[0, «JX
*=0
Г / 2 —Y\2/
x J (m-; + *i+*-—J *i+

J£ Продолжение табл- 6/2
•&. ____
Вид АЦП
•
АЦ
с ИАИМ
АЦП
с ИАИМ
Способ восстановления
ЭМП по-Лагранжу,
Э1П по критерию
наименьших
квадратов
ИМП го Лагранжу,
И1П по критерию
наименьших
квадратов
f2l (e), f2l при ф = 0, 1>\
1/N UN
(1-T)/N (1—Tf)//V
М
м м
t=0r=0
1/N 1/N
X ( ] (Г —t+e1 — ea)»/de1dea
(1-T)/N(1-T)/N
1
Ul (6) » ^2* "РИ ф = ^1+ ф2' ' > '
+г2/^тББ^Э10, e,VI0, e]X
/=0f=0
1/N 1/N
X I f (г-/ + ^1~е2)2^Ме2
(1-t);N(1-t)/n
M
f./W= -2T*1 — J]V[0,»]X
t=0
(1—7>/^V
Af Af
x *x+г2/ ^- Б БLjH l0, el LfH [0,e ] x
/=0 r=0
1/N 1/N
X Г I (r—i + ej—82)2^6^2
(l-T)/N(l--r)/N

Таблица 6.3
ki(x)

Восстанавливающий
оператор
//(О» //. /^ 1
*(t~lj)
ЭНП по
Лагранжу
ИПП по
Лагранжу
ЭПП по
Лагранжу
(Л=\),
линейная

экстраполяция
(0<Л<1)
f/(«)= -гг'] * + ?!-? \1
f/= -TTTl ?;4+ifi + l I при ? = 0
1
f/ =
-£[ij<f«H
L/=l J
1+Л 2 )
при (p = <Pl+-
+ V1—9 \1]+2T1e(\-e)
_2Tl j2(\+9i)l+2-fil + 2-(2 + n)l+t_,
4 1 + 2 ~t~
f/
Г
+
(2 + Tl)/+i_?1(i+?1)'+i+fl'+i_
r+
-(l + yi)'+42 + yi)_J_| при ? = Q
f/ = - 2Г' [
f/
= -2Г' [
+ 1
2г+2 —2
I (/+l)(J + 2)
= 0, 9 = 0
2
-t]
ПрИ yx =
-i]
при у =
f/(e> = -2T'[(At+l) h+?!-?! '-
-A'| 1+• + ?!-» I']-2r'i4«(t+l)
\' + 2
2Л
/ + 1
tVld + f!)'41-?!'4-2-
-(l + ?i)(2 + ?1)/+1+(l+«P1)'+a]+ —X
X[(l+<fi)'+1-?i'+1]+2^(-j-f-^-)} при ¥ = 0
i.
2
+ 3 ^ 2 / / + 1
ПРИ у = ?!
245

Таблица 6.4
Rxx Ы
sin о)0т
(Ух2
С00Т
<^~а'х2
ох2 cos 0т
«*-'"
Г*
ЭНП по Лагранжу
Ф = 0
(*>оП2 (со<Л_4
9 300
— (ar)2.__J-(ar)4
3 10 V
(Ю2 (РП4
3 60
1 (аГ)з
аТ — (аГ)2 + - }—
3 V ' ^ 12
Ф= J/2
(а)0Г)2_(со0Г)4
36 4800
(аГ)я' (аГ)4
6 ~~ 80
(РГ)2_(РГ)4
12 960
аТ (аГ)2 (аГ)3
2 ~~ 12 96
Г/ЛГ TIN
il-VT/N il-VT/N
\/N
= -2 —Г' J |*_ф + в1|'<
+
(1-D/W
i/yv 1/лг
где ф = 0 при работе АЦП в реальном масштабе времени
(ошибка от запаздывания не исключается), ф=ф1+ф2=1/Лг—
—y/(2/V) + 1/2 для АЦП с ИАИМ и ЭНП при исключении
погрешности от запаздывания.
Рассмотрим вначале случай ф=0. При этом в интервале J{
подынтегральное выражение всегда положительно, поэтому
знак модуля может быть опущен. Отсюда
N
1/N
_ о N p (s+l//V)/ + 1-(e+l/^-Y/A^ + 1
Y '+1
246

ИПП по Лагранжу
ф = о
I
ф = 1
ЭПП по Лагранжу
(сооП2
— 0,032 (со0Г)4
1,7.10-3(со0П4 —
-5,2-10-5(со0П8
5,210-2(со0Г)4_-
— 5-10-3(со0Г)в
2(аТ)2 — 1,9 (аГ)*
(РП2-о,1б(РП4
3' ' 9
0,1 (аГ)4 — 0,044 (аГ)в
3,1 (аГ)*~4,21(аГ)в
8,3-10-3(РГ)4_
— Ьб-НГ4^)6
0,26 (Р7у - 0,03 (РГ)«
3 "~ 15 + 120
5 7
3 18 V ^
+—(аГ)*
120
У интеграла /2 область интегрирования разбиваем на две:
8i>82 и 8i<62. В этом случае
У2 =
(1—T)/^V I L еа (l-T)/tf J I
Y2 J / + 1
(l-T)AV
iV
£,
/+1
(b-^n
de2.
Здесь подынтегральное выражение всегда положительно,
так как (1—Y)M^e2^l/N, и знак модуля может быть опущен.
Отсюда
№•
a+iw+2)
Итак, при <р=0
/ (g)^ о_у Tt(•+iml*i-(—nif+-(/tf)t+v I
+ 2Ш'т" 1
\N ) (/ + l)(/-h2)
(6.28)
(6.29)
247

о
(1+l/JV)'+g-(l/Af)'-b8_(1_1/Af-f-Y/^)'+8-(y/^-l/iV)4a
2)
Tl
Х (/+!)(/+ 2)
+ 2Ш'
(/ + 1)(/ + 2)
(6.30)
Рассмотрим определение fi(e) для случая исключения
погрешности от запаздывания. Интеграл /2 не зависит от ф и
определяется выражением (6.28). Подынтегральное выражение
/i разбиваем на области с положительным значением
аргумента. Обозначим ф—е=у. Тогда
1/N
/1 = _2^7* J \*1-y\ld*1%
У (1-1) IN
/V 2# 2 # 2<V ^ 2
Разделим плоскость г\у на области со знакопостоянным
значением г\—у (рис. 6.1,а). В областях 1 и 2 е\^у, в областях
3 и 4 ei<t/. При N=1 и у—1 плоскость ei# разделяется на две
области (рис. 6.1^5): в области 1 ei^y, в области 2 г\^у.
Если Ыф1, то
ЛЧ
—2 — Т1 f («! —у^Лх при-!- — Л -<у<
(1—Т)/л^
1/ЛГ у
-2JLP ^{§1-yydB1-2±Ti J (»-•!)'*!
ПРИ ^?<у< -L;
1/АГ
2
,_2.£г< J (y—j'Ax при -f^^-^H-
Если #= 1 и y= 1» т0
1 У
Jx = —2—Tl {(e1 — y)lds1—2—Tl [{y — ex)ld4 при 0<f/<l.
Y J Y J
у о
248

н
N ~2N 2
*)
Рис. 6.1. Разбиение области интегрирования на подобласти с положительным
значением аргумента корреляционной функции
Учитывая, что е=<р—у, и проводя интегрирование,
получаем: при Ыф\
л={
— 2
N Т1
Y /+1
[(ч-*ЧП+Н-+£-П
при —
2
2М
_2А Tl
■[(•
1
2 Г 2V '
J+1
Y / + 1 1Л 2V 2/ V 2-V 2 / J
— 2
Y *+l
При J- + _2_<,<1;
F 2 2N
(6.31)
[(т+^-) -('
2/V
/+i
при 0<e<-±--
2
2iV '
при N=l и y=1
/1==
2Tl
/+1
[el + I + (l—«)/ + 1l.
(6.32)
Таким образом, ft (e) = /x -f /2 и /, --= ] /xde + /2 определяются
о
соответственно выражениями (6.29) и (6.30) при <р=0. Если
Ф^=0, то /i рассчитывают по (6.31) при Ыф1 и по (6.32) при
N= 1 и у= 1. При этом
/i =
а+
DC + 2) Г v \ 2 2W j T \ 2 '
+^ГЧШ'] °»w- *-±-ir+T-№
/,=-
2Г'
a + D(/+2)
приЛГ=1; y=l; <p= 1. (6.34)
249

Пример 6.1. Прямая задача. Определить среднеквадратическую
погрешность преобразования случайноро стационарного сигнала, имеющего
корреляционную функцию Яхх(т)= Gx2e"~a^^9 ПРИ временной дискретизации
аналого-цифровым преобразователем последовательного счета с
промежуточным преобразованием в частоту и восстановлении экстраполятором нулевого
порядка по Лагранжу. Шаг дискретизации равен Т. АЦП работает в одно-
канальном режиме. Восстановленный сигнал используется для исследования
процесса x(t).
Обратная задача. При заданных выше условиях найти максимально
допустимый шаг дискретизации — такой, чтобы СКО преобразования не
превышала 10 % СКО входного сигнала.
Начнем с решения прямой задачи. В соответствии о условием N=\,
у=\ погрешность от запаздывания можно исключить, так как
восстановленный сигнал используется для исследования процесса x(t)t т. е. <р=1.
При этих условиях fi определяется выражением (6.34), а усредненная
дисперсия погрешности преобразования в соответствии с (6.26) и данными
табл. 6.1 имеет вид
~ \Л / «' Г 2Т1 1 11 , (аТ)1
•,-S«-"'- [-ттш^г -2Е<-|,,+'7Ьлг(6!И
/=1 / = 1
Вычислим значение СКО преобразования как сумму первых двух членов
ряда V& =1/аГ/6 —(аГ)2/24. При аГ=0,24 VW= |/о,04—2,4-10~3-100==
= 19,4%. Если оценивать СКО только первым членом ряда, то ]/52^=20%.
Таким образом, при практически приемлемых значениях погрешности
СКО преобразования можно вцчислять по первому члену ряда (6.35):
V*2=V~^nb- (6.36)
.Непосредственно из (6.36) получаем решение обратной задачи: 0,1 =
= l/af/6, откуда Г=6 10~21/а.
Для приведенных в табл. 6.1 корреляционных функций и
рассмотренных способов восстановления при 0^М^4 были
проведены расчеты величин б2 и б2, которые позволяют сделать
следующие выводы:
при невозможности исключения систематической
погрешности от запаздывания ступенчатая аппроксимация обеспечивает
более в'ысокую точность, чем интерполирующие устройства.
При этом с ростом числа каналов при r=const погрешность
снижается, так как уменьшается запаздывание, вносимое АЦП;
при исключении погрешности от запаздывания повышение
порядка интерполирующего полинома обеспечивает
уменьшение СКО;
#погрешность от запаздывания, вносимая АЦП и
восстанавливающими устройствами, превышает погрешности от
аппроксимации и усреднения;
250

при N-+oo зависимость СКО от параметров корреляционной
функции у АЦП с ИАИМ стремится к погрешности АЦП
с АИМ;
зависимость СКО преобразования от Т для рассмотренных
входных сигналов с высокой точностью при практически
приемлемых СКО до 20%, как правило, может быть
аппроксимирована одним членом ряда при разложении корреляционной
функции в ряд Маклорена.
Получение расчетных соотношений для экстраполяционных
и интерполяционных процедур восстановления высоких
порядков будет рассматриваться в § 6.3.
6.2. РАСЧЕТ ОЦЕНОК ПОМЕХОУСТОЙЧИВОСТИ
ПРЕОБРАЗОВАНИЯ СИГНАЛОВ ПРИ ВРЕМЕННОЙ
ДИСКРЕТИЗАЦИИ
Когда корреляционная функция помехи допускает
разложение в ряд Маклорена вида (6.1) или (6.2), расчетные
соотношения оценок помехоустойчивости бя2[0, е] получаются после
подстановки (6.1) или (6.2) в (5.102) и (5.107).
Для синфазной модели
/=1 m=0r=0
оо оо Ч
X J J К Ы К К) [(« - г) т + хх - ,,]•' dHfcS =
при дифференцируемой помехе, где
а,-^х°(0)/[/?хх(0)(2/)!]; (6.38)
72 гп , *u(Q) , v Я$(0)
{ОО '! ОО ОО ОО
2 2 К \m, s J k2 [r, e] J" f k, К) kx (х.) | (да - г) Т + хх -
т=0Г=0 0 6
(6.39)
(6.37)
,/ . . 1 Дхх(0)
1+J]a,f/x(e)
/ = 1
251

при недифференцируемои помехе, где
az = /?lV(0)/[/?xx(0)/!]. (6.40)
Здесь и далее /а(е)—выражение, записанное в фигурных
скобках.
Для несинфазной модели
' *хх(0)
*2 гП 1 *XXW , «71
R& (0)
•X
м м
1=1
оо оо
Rxx{0)(2l)\
X { 2 2 ^ [0, в] L? [О, .] \ \ k, К) кг (тг) [(r-i)T +
U=Or=0 О О
+ 4-\]il <М*,} = -^- [l + J a, /2,х (•)] (6.41)
при дифференцируемой помехе, где щ определяется
формулой (6.38);
,2 га _, *xx(0) , fi R\!1(0)
м м
/=1 *=0г=0
оо оо Ч
о о
*хх«»
Д**(0)
[l+£<*,/,*(«)] (6.42)
при недифференцируемои помехе, где щ% определяется
формулой (6.40).
Усредненные оценки помехоустойчивости в соответствии
с (5.66) определяются следующим образом:
% Дхх(О)
х~~ Rxx(O)
оо 1
L /=i о -^
(0)
*(0)
1 +
» -1
JWs/x
i=i J
(6.43)
при дифференцируемой помехе;
00 1
/=10
при недифференцируемои помехе.
252
х_ Л*»(0)
Rxx(O)
Я**(0)
l+JJflJ/xlce.
;=i J
44)

Таблица 6.5
Вид
АЦП
АЦП
сАИМ
АЦП
ИАИМ
Способ
восстановления
ЭНП по Лагранжу
ЭПП по Лагранжу
(А= 1), линейная
экстраполяция
(0< Л< 1)
ИПП по Лагранжу
ЭМП, Э1ПКВ
ИМП, И1ПКВ
ЭНП по Лагранжу
ЭПП по Лагранжу
(А = 1), линейная
экстраполяция
(0<Л<1)
ИПП по Лангаржу
ЭМП, Э1ПКВ
f2/X (•>• f2/X* /^l
f2/x= 0, f2/x(e)=0
f2/xW=-2i4r»'i(A+l)
f2/x=»-2i47»'(i4/3+l/2)
f2a(e) = ^2/2e(l-e); f2/x = T«//3
M M
*=0r=0
M M
f2/x(e) = ^2/S 2 L< f°- "IVfO, «Hr-01'
/=0r=0
f2/x(e) = f2/= ^2/(YM02//[(2/+ 1) (/ + 1)]
f2/x(*) = r2/ |[(А+1)2 + Л2е2] (-~-)2/-
, #2 Г / Y \2/+2
-(A+l)A-[2-(l+|) -
* \1-T/ J(2/+1)(/ + 1)J
t ( / Y \2/ yV2
f2/xH=^2/^2+(l-02](^) +— «О-
-)[2-(V^)2/+2-(-i)2'+1x
x ! I
(2/+l)(/ + l)(
м м
f2ix(') = T21 ^ J] J] V [0, .] V [0, •] X
|-=0r=0
I/JV 1/ЛГ
X j j (Г-/ +»i-e,) *'*!&,
(l-K)/iV(l-T)/Af
253

Продолжение табл. 6.5
Вид
АЦП
Способ
восстановления
/2/Х (О. f2lb I > 1
ИМП, И1ПКВ
м м
f2/xW = Г2/ ^7 J] S V [0, el V l°'el X
X [ Т (г —f + e! —e^/dt^sj
Выражения Ьа(е) при временной дискретизации АЦП
с АИМ и АЦП с ИАИМ сведены в табл. 6.5.
Когда интервал корреляции помехи больше шага
временной дискретизации, коэффициенты рядов (6.37), (6.39), (6.41)
и (6.42) убывают достаточно быстро и описанная методика
расчета эффективна. В случае «слабо коррелированной» помехи,
когда значение интервала корреляции того же порядка, что
у шага временной дискретизации, вычисления удобно
проводить в соответствии с методикой, изложенной в § 5.4.
Пример 6.2. Определить б2х тракта аналого-цифрового преобразования,
использующего АЦП. последовательного счета с промежуточным
преобразованием в частоту и работающего в одноканальном режиме.
Корреляционная функция помехи RkX(T) = G2xsm а)0т/((о0т). Шаг временной
дискретизации равен Т\ 0)0^=0,9; дисперсия сигнала Rxx(0) = G2x\
восстанавливающий оператор — ЭНП по Лагранжу.
(__!)/ со02/
В соответствии с данными табл. 6.1 а1Х = —— —; функцию f2a(e)
[21 -f- I).
находим для АЦП с ИАИМ по табл. 6.5. В соответствии с условием
примера N=1, 7=1. При этом
f2/x(«)=f2/X = ^2//I^+1)(/+I)].
Тогда
Gx2
G2 °°
1=1
Учитывая, что щТ=0,9, находим
(ш0Г)2 ,.(о)0Г)«1
(-1)>(<о0Г)2;
(2/+l)!(2/-f 1)(/ + 1)
1-
36
1800
= 0,98
21
Ох2
[1—2,25-Ю-2+ 3,645-10-*] =
GJ
254

6.3. РАСЧЕТ ОЦЕНОК ПОГРЕШНОСТЕЙ ПРИ РАВНОМЕРНОЙ
ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ СЛУЧАЙНЫХ СИГНАЛОВ
С ВОССТАНОВЛЕНИЕМ ПО МЕТОДУ НАИМЕНЬШИХ
КВАДРАТОВ*
Расчет среднеквадратических погрешностей
аналого-цифрового преобразования даже при разложении корреляционных
функций входного сигнала в ряд Маклорена остается
достаточно громоздким для высоких порядков интерполяционных и экс-
траполяционных процедур восстановления, поэтому
дальнейшее совершенствование методики расчета необходимо [38].
Выражения дисперсий погрешности преобразования будем
рассматривать при интерполяционных и экстраполяционных
процедурах восстановления по методу наименьших квадратов. Это
вызвано тем, что соответствующие формулы при
восстановлении многочленами Лагранжа являются частным случаем
формул, полученных для метода наименьших квадратов, если
степень / аппроксимирующего многочлена равна М, где М-\-1 —
число отсчетов, аналогового сигнала.
Получение расчетных соотношений для АЦП и АИМ при
интерполяционной процедуре восстановления
дифференцируемых случайных сигналов. Текущее значение относительной
дисперсии погрешности при интерполяционной процедуре
восстановления, когда /Ci(т) =б(т—ц>[Т), определяется выражением
- (6.21).
Введем обозначения **:
м м
АИт(з) = 2 2^Икв/[0, s]Z,fHKB' [0, е](г-;Г; (6.45)
1=0 г=0
М М
BL (*) = 2 2 ЬГВ' [0, I] Lr" кв' [0, «] {ЧМ - I)2"; (6.46)
/=0 г=0
ei = 1+е—Ф/Л*+Ф1/А1. (6.47)
Погрешность от запаздывания исключается при ei = e.
При этих обозначениях дисперсии погрешности имеют вид
00
8"2[0, е] = 2- атГт\А1т{в)-2В1п(в)]. (6.48)
т = \
* § 6.3 написан совместно с М. Н. Аршиновым.
** Здесь и далее в этом параграфе буква т заменяет / из выражения
(6.21), так как / в § 6.3 используется для обозначения степени многочлена.
255

Усредненная дисперсия погрешности
со
? = 2amP*H$m-2£U (6.49)
где
. ^=J^2m(*)de; B2rn-jBL(e)de. (6.50)
Рассмотрим теперь процедуру вычисления А%т(е) и В2т(е). Из
(6.45) и (6.46), очевидно, следует
2т М М
А1п{*) = li-iycU 2 Vкв' [0, «К 2^гикв1[0, t]r»~;
s=0 /=0 Г=0
2m M
Я"тИ = 2 (-irCL^O2"1-5 2^?KB' [0, «К- (6.51)
5=0 1=0
Полагая
м
£>,"= 2^"КВ'[0. «I*-*, (6.52)
будем иметь
2т
AL (■) == 2 (~ !)*<&, Я,и (s) D,- (2/» - s); (6.53)
BL(s)= S(-l)'CS»(A'«ir-*A"(5). (6.54)
5 = 0
Запишем (6.52), используя (4.101):
м i
ZJ Zj (Af-/)!(/+A* + l)l /,m l J /,mM
(=0/=0
/ м
(2/ + 1)(Л«)'
/=0 i'=0
/4=0
где
м
/=0
256
*i(ft>= 2 фл„И'*- (6-56)

Умножив обе части (4.94), рассматриваемой при /=/, на
i*"1 и просуммировав по 1=0, 1,...,Л1, получим следующее
рекуррентное (по k) соотношение:
P,(k)-—LL+0(^-/)p {k_l) + JLP{k_l)_
М ' 2(2/+1) '+1V ' 2 П '
ЦМ+l + i) _р^(Л_1). (6.57)
2(2/+1)
При этом начальными значениями P/(k) будут следующие:
м м
/=о /«о
Первое равенство следует из фо,м= 1, второе — из
ортогональности многочленов ф/,м. Действительно, так как фо,м=1, то
м м
2 Ф/,м w = 2 ф/рм м ф0,м ш = ° при /=^°.
/=0 /=0
откуда Яу(0)=0 при /=5^0.
м
Кроме того, Р0 (k) = 2 ik находится по известным формулам
для степенных сумм [39].
Для излагаемого метода расчета более удобно равенство
. Pj(k)= Pj{k).
При этом из (6.57) легко получается рекуррентность для
^(fe)==,(/+o(^/)^+/+^^l(^-1) +
М } 2(2/ +1) П1К '
+ *LPi(k — \) ]- Р;_х(£- 1) (6.58)
2 М 2Г2/ + 1) J V
с начальными значениями
р0(0)=1; />,(0)-0, /^=0; Ро(*)=-А-/>„(£). (6.59)
Соотношения (6.58) и (6.59) показывают, что pj(k) nptu-
ставляют собой многочлены от М. Результаты решения
рекуррентного соотношения (6.58) при начальных условиях (6.59)
17—6036 1Ы

Таблица 6.6
k
0
1
2
3
4
5
о
Многочлены Pi(k)t
0
1
Ml 2
M(2M+l)fb
M*(M+ l)/4
M (2M + 1) (3M* + 3M— 1)
30
M*(M+1)(2M*+2M—1)
12
M (2M+\) (зМ*+бМЗ—ЗМ+\)
42
l
0
-1/6
—Af/6
-(9Л*а+ЗМ —2)/60
М(Ш* + ЗМ— 2)
30
10Af* -f 12jW3—7iW2—ЗЛ1 +2
84
M (9AM+ 15M3—7Af«—9M+6)
84
для значений /, &=0, 1, ..., 6 сведены в табл. 6.6. При этом из
(6.55) следует, что
^(*)=E-t^w^im^
(6.60)
/=о
Используя последнюю формулу, выведем рекуррентное
соотношение для Din(k).
Подставив (6.58) в (6.60), получим
(1+1НМ-ЩМ + 1+2)
X
/=о
/=о
/=о
/—1
1 Г? ^1(5+1)1
tS
s=0
(Af—8—1)
ф.+1[«л«]рЛ*-1).
(6.61)
258

+■
/ = 0 6
2
О
О
1/30
Af/20
\2М*+ЗМ—Ь
210
Af(SAf»+3M—6)
84
25^ 4 + 25Af з
420
—4QM*— \QM + 14
+
420
з
0
0
0
— 1/140
—M/70
5M* + M — 3
252
M (2M*+M— 3)
84
0
0
0
0
1/630
Л4/252
18M*+3M—14
2772
-1/2772
—Л1/924
0
0
0
0
0
0
1/12012
Второе слагаемое этого выражения получено при s=/+l,
третье — при s=/—1. Положив <p-i,M=0, перепишем (6.61)
в следующем виде:
^^^) = Y^B^-1)-TSl^j!Ps(fe_1){s(M + s+1)X
s=0
X %-г,м [°М\ + (s + 1) (М - s) ф,+ЬД| [шЩ -
+ -Т ^(,,+ 1^1.м[^1л(*-1).
2 (Л1—г — 1)!
Воспользуемся теперь равенством
а+щм-п
(6.62)
^еЩ = щЬг){-
2(2/+l)
fy+l.M 1еЛ,1 +
^ 2(2/ +1) */-»•« l J/
(6.63)
которое получается из (4.94) при /=еЛГ. С учетом (6.63) имеем
Dl4k)=^Dnk-l)-^^j]^^%,M[sM]pAk-l) +
5=0
+ Т (^-/+0! K,,MH]P.(^l)-(^ + ^2)^[6MtX
17*
259

ХР,+х(^-1)} = у£»«и(*-1)-^1^А,,(*~1) + ^и(*-1).
(6.64)
где
Ег"(к-1) = ± ^_« + » {%+UM[eM]Pl(k-l)-
-(M + l + 2) ь>м [M]pt+1 (k - 1)}. (6.65)
Таким образом,
Ди (£) = щ е) D/- (*— 1) +£,« (k— 1). (6.66)
При этом Х>,и(0) = J] Ш+Ш-Чм[еМ)р}(0). Учитывая, что
/>у(0) = 0 при 1ф0, а Я0(0) = М + 1, получим р0(0) = —^— Х
(ЛН-1)!
X {М + 1) = 1. Следовательно, £>,и(0) = -^!_ q>0M [еМ] = 1.
Далее
_(М + / + 2)<р/>м[еМ]рг+1(0)}.
Выше было доказано, что р/(0)=0 при /^0. Отсюда и
£{■(0)^0, если /=^=0.
Ко'гда /=0,
£ои (°)= т 1^=77{фьм IsM] Ро (0) ~(М + 2) ф°'м [sM] Pl (0)} =
= -4L(l_2.).
2 v
Таким образом, начальные значения для рекуррентного
соотношения (6.66) имеют вид
( 0, если /^ 1;
D,H(0) = 1; £iH(0)= ллп ' w0 , п
1 v ' f v ; [ yVf (1—2s)/2, если / = 0.
Отметим, что при k^.1 из (6.65) следует Ei(k—1)=0,
поэтому Di*(k) = (Me)Di*(k—l) при 1<й</.
С учетом Аи(0) = 1 получим Dy(k) = (Me)k при &</.
Согласно (6:53) при 2т^Л будем иметь
2т
^(е) = (МеГ 2(-l)sC*, = 0.
, 5=0
260

Аналогично равенство при исключении погрешности от
запаздывания справедливо и для В\т (е). В самом деле, из (6.54)
при ei = е и 2т^1 вытекает
#п(*) = (Me)*" 2 (~ 1)SC|, = 0.
- Соотношение (6.66) вместе с равенствами (6.48) и (6.53),
(6.54) дает удобный численный метод определения
погрешности преобразования.
Можно получить также и явные формулы для вычисления
А2т(е) и ££п(е). В самом деле, из (6.66) следует
Ди(1)=Л1е+£/и(0);
Ди(2) = (Л1е)2+(Ме)£/и(0)+£/и(1);
k
Df{k) = (Me)k + 2 (Aft)*^£•,■(/- 1), k - 1,*2,...,
или q учетом (6.65)
/У(*)-(м«)» + -1- ^^1), {gM^M'-OwM-
ft
- (Af + / + 2) 2 (Me)*"' pJ+i (f - 1) Ф/>А| [sM]}. (6.67)
Введем для краткости следующие обозначения:
._ 1 (t+l)Af! . r w,
. p.__L (l + l)(M + i+i)Mi [шЩ (6 gg
r» 2 (Л/_/_1)| T'«Ml J v '
Равенство (6.67) перепишется в виде
k k
0|"(A) = (Aft)* + ai 2(Л4*)*-'Р,(<-1)-Р*и 2(Me)*-'pI+i('-l)-
(6.69)
Из (6.53) и (6.69) с учетом D,"(0) = 1 получаем [38]
2" Г s
Л£» (s) = 2 (- 1)SCU 2a," 2 (Ms)2"1"' p, (f -1) -
s-i L t=i
261

s "\ 2m Г
-W2№)^pM{t-l)\ + 2(-l)'Ci, -г^'Х
/=i J s=i L
s 2>я—s
x 2 2 (Msr—'p,<'-,)ft+1(r-i) +
/=1 r=i
s 2ю—s
+ WT2 2 (Aie)1№-r-'p,(<-i)ft(r-i) +
/=1 r=l
s 2tfi—s "I
+ (РЛ2 2 2 (Afcr~-'pl+1(*-i)pl+1(r-i) . (6.
*=1 r=l J
70)
Далее из (6.54) и (6.69) получаем [с учетом £)<и(0) = 1]
[38]
2'"п
^5»(.) = м*"(е1-гг + 2 (-lr^n^^r-* х
X\«i* %(М*У-'Pl(t-])-W % (Ме)*-'Р1,Л- 1)1. (6.71)
L *=i *=i J
При исключении погрешности от запаздывания (ei = e)
первое слагаемое в предыдущей формуле равно 0, и она
запишется в виде
2т s
ви*)= 2(-i)'ci» 2(^)2m-'[«iHpI(^-i)~P«,,p.+i(<-i)].
5=1 * = 1
(6.72)
Из (6.70) и (6.72) следует, что при ei = e выражение,
необходимое для вычисления погрешности преобразования,
имеет вид
2я—I 5 2 л—s
4U«)-2B5n(e)= 2 (-1ГО, 2 2 №)*"-'-<х
X[(a,TPI-i(^-l)P/('--l)-2aJ,!PIV, (/—l)p,+i(r— 1) +
+ (Pj'),Pi+i('-1)Pi+i('--1)1. (6.73)
Заметим, что при 1^т выражение (6.73) дает
Л^(8)-2В^(е) = 0.
262

Тогда согласно (6.48) дисперсия погрешности
интерполяции при исключении запаздывания
оо
?[0, е]= 2 атТ*"[Аи2т(е)-2В1„(*))
и, следовательно, имеет порядок величины Г2(/+1>.
Ниже приведены выражения главного члена ряда б2,
позволяющие рассчитывать относительную усредненную дисперсию
погрешности интерполяции для АЦП с АИМ при ki(x)=8(i)
и <$=МТ и при исключении погрешности запаздывания:
/=0 62=—а1(МТ)Щ;
1=1 ~6*=а2(МТ)*{1+5/М*)/30;
1=2 62=- [аъ (МТ)7420] (3+63/Л12—84/М3+28/Л14).
Здесь ат=#/ — из табл. 6.1 при m=l.
Получение расчетных соотношений для АЦП с АИМ при
экстраполяционной процедуре восстановления
дифференцируемых случайных сигналов. Текущее значение относительной
дисперсии погрешности при экстраполяционной процедуре
восстановления [38], когда &1(т)=6(т—ц>\Т), определяется
выражением (6.15). Обозначив ei = e—q>+q>i (ei = e при исключении
ошибки от запаздывания в первом звене), получим
82 [0, • ] = 2 От ТШ И*» (•) - 2ВЪп (.)]; (6.74)
m=l
00
?= Sfl»r"Hi,-2B»w]f (6.75)
m=l
где
мм
Aln(*)= 2 2^Г"[0, e]Z,;-KBZ[0, s](r-ir»; (6.76)
1=0 r*=0
м
b^(s)= 2^fKB'[0, tlK + л*-/)""; (6.77)
1
i4|i«=Jift.(e)&; (6.78)
о
l
B2m= §Bln(e)de. (6.79)
263

Из (6.76) и (6.77) следует
2т М М
au*)= 2(-i)*ci..2i/-e'[o, e]is2^9Ke'[o,ejr^-s;
5=0 /явО Г=гО
2т М
Яп(')= 2(-i)5^(^ + ^r_s 2^9KB''[o. •]«".
5=0 /=0
Полагая по аналогии с (6.52)
м
Di9(k)= 2^Ли/[0.«]'* (6.80)
/«о
будем иметь
ЛЬМ = 2 (-ir^D,9 (sWpm-sj; (6.81)
5=0
2т
Bin(e)= 2(-l)s<4,(M + eir-sA9(s). (6.82)
5=0
Запишем (6.80) в ином виде, используя (4.109):
где величины Pj(k) даются выражением (6.56).
Переходя, как и в случае интерполяции, к более удобным
для вычислений величинам Pj(k), получаем
/=о
Выведем теперь для Df{k) рекуррентное соотношение,
аналогичное (6.66). Согласно (6.58) имеем, подобно случаю
интерполяции,
#),•/* V <2/+l)MI , ш (j + i)(M-j)(M + j+2) ^
/=o
iJ (Л*-/)! 2(2/+1) 1V ' 2 ' V '
264

5=0
+ At|ftH(*-l) + -l. ■^|+_1>)' Tw,M|. + iMlft(*-l).
Воспользуемся теперь равенством
T/lMl J iM + 2e \ 2(2/ +1) //+«•«l T J^
T 2(2/+1) HJ" /
которое получается из (4.94) при F=e+M.
С учетом его найдем
*=0
XA(^-l)+4- ^Xl)! {Ф/+1.м[« + Л1]а^-1)-
-(Л1+/ + 2)(р,(Л1[е + Л1]р1+1(А-1)} = ^-А9(^-1) +
+ _М±*_/),•(*_!)+ £,•(*_!),
где
-(М + / + 2)Ф/1М[8 + М]А(*-1)}. (6.83)
Окончательный вид рекуррентного соотношения таков:
ZV (ft) = (Л1+е) Д* (ft-1) +£/э (ft— 1). (6.84)
При этом
I — (М + 2е)/2, если / = 0.
Из (6.84) вытекает, что
к
Dt'(k)=(M + e)k + 2(A* + «)*"'i?ie(ft-l). *=L 2,..,
*=i
265

или с учетом (6.83)
k
Х2(М + .)*-* Pi(t-l)-(M + l + 2)bt„[, + M\X
X 2(M + t)*-*ft+x(*-l)}. (6.85)
Обозначая для краткости
V-± »+»££{+*,„Ь + Мк (6.86,
перепишем равенство (6.85) в виде
k
D? (k) = (М + .)* + «,« 2 (М + е)*"' р, (* - 1) -
k
-Л9 2(М + 0*-<Л+1(*-1); *« 1, 2,... (6.87)
Из (6.81)-, (6.82), (6.86) и (6.87) определяем
2m s
Л»» (в) = 2 2! (-!)*<£. 2 (Af+e^la.Vi^-n-P/Vi-H ('-!)]+
5=1 f = l
2ю s 2m—s
+ 2(-i)*ci» 2 2 (^ + ^)2ff-'-r[(V)V{(^-i)P/(r-i)-
5=1 f = l Г = 1
-WWPi (t - 1)pm (r-1) +W)V<+i('-1) Pl+1 (r-1)]; (6.88)
2tfi s
^»(«) = [ai («!-•)]*"+ 2(-i)scl. 2(^+nr~'x
s=l f=l
X(M-H)s-'[a9p^-l)-P«9P/+i('- 1)]. (6.89)
При исключении погрешности от запаздывания (ei=e)
предыдущее выражение упрощается:
2т s
«»(•)« 2(-l)'CJn 21 (^ + •Г-'КЛ С-l)-P/*Pm ('-!)]•
5=1 ■ • * = 1
(6.90)
266

В этом случае необходимое для вычисления погрешности
экстраполяции выражение имеет вид
2т s 2n—s
А1п(в)-2в11(в)^ 2(-1)'с£» 2 2 (м + вг—<х
s=\ t=\ r=l
XI(OfP/('-l)ft(''-l)-2«iePieft('-l)ft+i('-l) +
+ (Pi3)2 Pi+i (^ — 1) Л-м (^ — 1)1- (6.91)
Ниже приведены выражения главного члена ряда б2,
позволяющие рассчитывать относительную дисперсию
погрешности экстраполяции для АЦП с АИМ, k\ (т) =f> (т) при
исключении погрешности от запаздывания в первом звене:
/ = 0 ? = —<*! (ТМ)2 (3 + 6/М + 4/М2)/6;
/ = 1 ? = а2 (МТ)А (5 + 20/М + 55/М2 + 70/М3 + 36/М4)/30;
/==2 М = Дз(^^)6 /о j . 126 . 819 _j_ 2436 » 4620 , 4704 , 640\
Расчетные соотношения при интерполяционной процедуре
восстановления дифференцируемых сигналов для АЦП с ИАИМ.
Используя методику вывода расчетных формул, рассмотренную
для АЦП с АИМ, получим [38] расчетные соотношения для
АЦП с ИАИМ, которые приводим без вывода.
Выражение относительной текущей дисперсии погрешности
преобразования имеет вид
00 00
8*10, ш) =1 + 2 %' Т*А& (в) -2 2 а/Г'В&К), (6.92)
fe=0 А=0
где
a.e.. а**ММ" <%*+>+!)
(2*+2s + D(A+s + l) ' * '
s=0
а* ~ 2j 22S№ + 2s+l) ' (°^>
ei=e+l—у/М-{-(2—у)/(2MN) (если погрешность от
запаздывания исключить нельзя, то ф=0, в противном случае <р=1 +
+ (2—y)/(2MN) и e=ei); ^(е) и В1к(ч) определяются
соответственно формулами (6.45), (6.46); Л0и(е)=5ои(е) = 1.
При исключении погрешности от запаздывания (e=ei) вы-
267

ражение (6.92) можно получить в виде
6Т[0, 8]^а272[ЛиИ-252и(в)] +
+ аГ{[А:(е) -2В/(.)] + (JL)e М/(.)-В/(.)] + (fj-z) +
+ в,Г {[Л,- (в) - 2ВДв)] + J- (JL)' [Л/ (.) - В4» (.)] +
+ (^IWM-WM1 + (-I-)\JL}. (6.95)
Здесь выписаны члены порядка до Г\ Для вычисления
усредненной дисперсии погрешности Л^(е) и £§*(*) в выражении (6.95)
заменяют на Л5* и В£*. Ниже приведены выражения для главного
члена ряда б2, позволяющие рассчитывать относительную
дисперсию погрешности интерполяции для АЦП с ИАИМ при
M'>-£{'['-e-flf]-i[-£]}. ,-*=*т+мг и
исключении запаздывания:
/ = 0 ?« — OiiMTy/S;
30 L Af8 ^ Af» \ N ) T 4M« \ N ) \
/ = 2 f'-^VY У- «»W [3 . 63 _ 84 28 _
24 V W j 420 [ AP M» "'" M*
— Зо(Л-У(1 ! Mi l05 M У!
\ N J \ M M* M» ) 8M« \ N ) \
Если запаздывание не может быть исключено, выражение
главного члена ряда при />0 имеет вид [38]
*£<о)
(МТу^ + ^у (6.96)
Rxx(0)
где ф1 для различных АЦП определяется по табл. 4.1.
Как следует из (6.96), главная часть б2 вообще не зависит
от / и остается порядка (МТ)2, в то время как при исключении
запаздывания б2 имеет порядок (МГ)2(/+1). Следовательно, при
невозможности исключения запаздывания увеличение порядка
интерполяции неэффективно. Более того, оно может привести
к уменьшению показателя помехоустойчивости.
Расчетные собтйЬшения при экстраполяционной процедуре
восстановления дифференцируемых сигналов для АЦП с ИАИМ.
2 68

Относительная дисперсия погрешности экстраполяции с учетом
обозначений (6.76) и (6.77) имеет вид [38]
00 00
6*10, е] = 1 + 2 ак' Гк A\k (s)-2 2 V ™92* (в), (6.97)
k=0
k=0
где a'k и a"k определяются соответственно выражениями (6.93),
(6.94).
Выражение (6.97), записанное в развернутом виде с
точностью до членов порядка Г6, при. исключении погрешности от
запаздывания (ei = e) имеет вид, аналогичный (6.95):
840, е]^а2Га[Лг»(з)-25г9(е)1 + а4Г|[Л49(е)-2В49(6)] +
+ (JL)-W(.)-B/(.„ + ^(JL)) +
+ а,Г |[V (t) - 2В; (.)I + ± (-1.)2 [Л4* (г) - В4* (е)1 +
-f(f)4[8^(e)-3B/(e)] + ^(-l-)} (6.98)
+
Ниже приведены выражения главного члена ряда б2,
позволяющие рассчитывать относительную усредненную
дисперсию погрешности экстраполяции для АЦП с ИАИМ при
МЧ~£{1 ['-0-T)-Jr]-i[«-f]}.f-*=1'- ч»-
ключении погрешности от запаздывания, вносимого первым
звеном:
/==0 у— ^^У^3+- + —1;
/== j ~2_ л2(Шу Г5 20 55 70 36
30 L ^ ^2 ^3 М«
" * 5f Ч \2( l JL 2 л- 2 Vl 5 М У
1 = 2 Ь2 = З74
24
4620
Ж*
48
аь(ГМ)*
+
4704
+
420
640
21
126 , 819 , 2436 ,
"г-т^г + —т" +
М
№
105
.3 Ш7_2_ , JL + JL +
48 , _2?_Л i 105 (j__ \
Методика расчета погрешностей интерполяции и
экстраполяции для различных типов АЦП при недифференцируемом
случайном входном сигнале аналогична рассмотренной.
269

6.4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРЕОБРАЗОВАНИЯ
АНАЛОГОВЫХ СИГНАЛОВ ПРИ КВАНТОВАНИИ
ПО УРОВНЮ И ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ.
РАСЧЕТ ПОГРЕШНОСТЕЙ
Математическая модель преобразования может быть
представлена нелинейной синфазной (рис. 6.2,а) и несинфазной
(рис. 6.2,6) импульсными системами, на вход которых
поступают сигнал x(t) и аддитивная помеха X(t). Первое звено
К\(р) определяет способ получения цифрового эквивалента
(см. гл. 4). Нелинейный элемент НЭ совместно с помехой %\(t)
определяет квантование по уровню. При квазимгновенном
квантовании по уровню |/Ci (/со) | = 1, Xi (0 =0, статическая
характеристика НЭ приведена на рис. 1.1,г. В АЦП
последовательного счета с промежуточным преобразованием в частоту и
циклическим частотомером, в АЦП с промежуточным
преобразованием во временной интервал (с ИШИМ) X\(t) учитывает
отсутствие синхронизации временного интервала и импульсов
счетной последовательности (см. § 2.2, 2.3), 0^ii(0^7>
статическая характеристика НЭ приведена на рис. 1.1,6. По
существу нелинейный элемент реализует операцию взятия целой
части, что соответствует определению целого числа импульсов за
временной интервал. Шаг квантования q по уровню для АЦП
последовательного счета с промежуточным преобразованием
I 1 yZ L0<f2pJ<}-
С
• >
иэт
Кг(р)
а)
т&А
Kl(P)
с
bf-<l/2
V
4Ж?
У/ \ О а
ИЭу
г J—
rpT*
L»\
I
%/"К
Br
iP%№
$(P>\
т-и£п
4<W
б)
т&А
\«1(p)
b
У1
Iя*
JL с
иэт
Э№>
*1(PJ\
г)
Рис. 6.2. Модели квантования по уровню и временной дискретизации
270

в частоту определяется выражение (3.79), для АЦП с
промежуточным преобразованием во временной интервал с ИШИМ —
с выражением (3.77). При осуществлении квантования АЦП
поразрядного кодирования с запоминающим интегратором
Xi{t)=0, статическая характеристика НЭ приведена на
рис. 1.1,г. Остальные звенья такие же, как в моделях,
приведенных на рис. 5.1.
Для стационарных центрированных гауссовских сигналов и
помех при а2*^><72 (что обычно имеет место) приведенные
нелинейные модели с учетом изложенного в гл. 3 сводятся к
линейным. При этом текущая и усредненная среднеквадратиче-
ские погрешности преобразования определяются
соотношениями
V^IjO, *] = /V[0, s] + 8? [0, s] + 8| [0, •]; (6.99)
: /V = l/ |8"2f0> »I* + J8?[0f ■]& + j8|[0, e]A, (6.100)
о о о
в которых выражения для расчета первых двух слагаемых под
знаком радикала приведены в § 6.1—6.3, 62д[0, е] — текущая
относительная дисперсия погрешности на выходе
восстанавливающего оператора, вызванная квантованием по уровню.
Квазимгновенное квантование по уровню и временная
дискретизация. Для указанных выше гауссовских моделей
сигнала и помехи в соответствии с выводами § 3.1 при |/Ci(/co) | = 1> •
k\(t)=0 нелинейный элемент можно заменить сумматором, на
первый вход которого подан сигнал x(t)9 на второй — помеха
Х(0э на третий — погрешность квантования А(0» равномерно
распределенная в интервале от —q/2 до q/2. Корреляционная
функция /?дд(т) определяется выражением (3.22) после замены
в показателе степени
[1—рхх(г)]о2х на [о2х+о\—о2хрхх{т;)— а2фхя(т)], где р**(т)
и рм(т) —нормированные корреляционные функции сигнала и
помехи; о2х и ah — дисперсии сигнала и помехи.
При этом для синфазной модели
m=0 r=0 л=1
Хехр[-^К2 + а2-а|р,Л[(т-г)Г]-а2ри[(от_г)7]}];
(6.101)
271

для несинфазной модели (при восстановлении
интерполяторами М-го порядка по Лагранжу или по критерию наименьших
квадратов)
__ ММ оо
«№«i-idraEEvl0',]VIM-£-E-3rx
/=0г=0 п=\
Х ехр [ - iji {о* + а* - а2 Рхх [(щ - г) Т] - о{ ?п [(щ - г) Г]}].
(6.102)
Пример 6.3. Определить б2д[0, е] при восстанавливающем операторе —
ЭНП по Лагранжу.
При ЭНП по Лагранжу k2[0, e]=l, k2[my е]=0, если т>1. Учитывая,
что р*х(0) = 1, ри(0) = 1, и подставляя &2[>я, е] в (6.101), определяем
А J #**(0) 2;i2 £J я* 12Л«(0)
п=1
где <72/12 — дисперсия погрешности квантования.
Пример 6.4. Определить 62д[0, е] при восстанавливающем операторе —
ИПП по Лагранжу.
При ИПП по Лагранжу 10и[0, е]=1— 8, LiH[0, е]=е. Подставив эти
выражения в (6.102), получим
А
оо
1 Г Q2 Q2 1 Q2 ¥4 1 -
)>s]=^(o)[(1-e)2i-+eai-+2e(,-e)ji^S^-x
n=i
X'expj- —[Ох2+Ох--°х2Рхх(Т)-о£рхх(Т)]У
При е = 0 и е = 1 относительная дисперсия д2А (0, е=0) = ^д (0, е = 1) =
— <72/[Я**(0)12], где ^2/12—дисперсия погрешности квантования.
Квантование по уровню и временная дискретизация в АЦП
последовательного счета с промежуточным преобразованием
в частоту (с циклическим частотомером) и временной интервал
(с ИШИМ) в АЦП поразрядного кодирования с
запоминающим интегратором. Статическая характеристика НЭ,
приведенная на рис. 1.1,6, совместно с помехой X\(t) реализует
операцию квантования по уровню в рассматриваемых способах
аналого-цифрового преобразования. Так как эта характеристика
может быть получена путем сдвига вправо на q/2 зависимости,
приведенной на рис. 1.1,г, то, заменив участок be синфазной и
несинфазнрй моделей (см. рис. 6.2,а и б) на схему,
приведенную на рис. 6.2,в, получим модель, близкую к модели квази-
мгновенного квантования. Такое преобразование позволит
воспользоваться результатами, приведенными в § 3.1.
272

Обозначим Х\—q/2=k*. Случайная величина X*
равномерно распределена в интервале от —q/2 до q/2, так как к\
распределена равномерно в интервале от 0 до q. Если далее x(t)
и Я(0 — стационарные гауссовские центрированные процессы,
то yi(t)—сигнал на выходе линейного звена К\(р), также га-
уссовский и центрированный. Кроме того, если дисперсия х
много больше q2, то при правильном выборе (или
проектировании) АЦП дисперсия у\ также много больше q2. При этих
условиях в соответствии с результатами § 3.1 нелинейный
элемент может быть заменен сумматором, на первый вход
которого'подан сигнал y\(t), на второй — помеха Я* (0, на третий —
погрешность квантования А(0> равномерно распределенная
в-интервале от —q/2 до q/2 (рис. 6.2,г).
Корреляционная функция y\(t) в соответствии с (5.113)
определяется выражением
Ry^-^ ) J {««[(•! —О^ — 'И-
(1_T)//V {\-i)N
+ /?хх [(ег - et) T — i]} dsxd4. (6.103)
Корреляционная функция погрешности квантования Д(^)
определяется выражением (3.22) после замены в показателе степени
[l-P^WK'Ha.fl-p^x)]^, где ol=Ryiyi(0); p,iVl(x) =
Дисперсия помехи X*(t)—Ri*\*(0) = q2/12, так как Я*
распределена равномерно в интервале от —q/2 до q/2.
При этом текущая усредненная дисперсия погрешности на
выходе восстанавливающего оператора, вызванная
квантованием по уровню, определяется выражениями
00 00
^I0,«l-iCT)J]J3*.[*.«]ft.[r..l^-X
оо оо
+ RMW SS^[m' el*tlr* «^^[(«-ОЛ (6.104)
m=Or=0
для синфазной модели и
__ мм
18—6036 273

x J -h- exp [- -^ <<*„ -1, p., *K» - '> n>]+
M M
+тш S S v [0, e] Lr" l°'sl *m'l(i" ~r) T] (6-I05)
/=or=o
для несинфазной модели.
Прио/></2 (см. § 3.3) Rw[(i — r)T]**0 при г фи Кроме
М оо
того, 2^|И[0, е]=1 и 2 ^2 И, s] = 1 Для экстраполяционных
продело т=0
дур восстановления, а также при автоматическом
восстановлении, когда N=1 (см. § 6.1). Тогда выражения б"2д[0, е]
имеют вид
si [о, в] = d, [в] + дч\ тхх (0)] (6.106)
для синфазной модели;
S|[0, B)^.DM + qV[l2Rxx(0)} (6.107)
для несинфазной модели, где А[е] и D2[e] определяются
первыми слагаемыми соответственно формул (6.104) и (6.105).
Если в тракте преобразования используется АЦП
последовательного счета с промежуточным преобразованием в частоту
и циклическим частотомером, в котором образцовый временной
интервал синхронизируется с импульсами счетной
последовательности, то Ai(0=0. Относительная дисперсия погрешности
квантования на выходе восстанавливающего оператора
определяется только первыми слагаемыми выражений (6.104) и
(6.105). В этом случае математическое ожидание погрешности
квантования на выходе тракта преобразования равно q/2.
Пример 6.5. Определить у дс2 на выходе тракта аналого-цифрового
преобразования.
Входной сигнал x(t) — стационарный, гауссовский, центрированный с
корреляционной функцией Rxx('X)=o2xsm со0т/(о)от), где со0=0,2, диапазон
изменения входного сигнала с вероятностью 0,997 принимается равным
±10 В, т. е. 3ov=10 В.
Помеха k(t) — стационарная, гауссовская, центрированная с
корреляционной функцией #хх (т) = ах2е—а2х2, где ах2 = 10~~2, а — 0,1; диапазон изменения
помехи с вероятностью 0,997 принимается равным ±3ая= 10 В.
Тракт преобразования состоит из одноканального (N=1) АЦП
исследовательского счета с промежуточным преобразованием в частоту и
циклическим частотомером. Число разряда АЦП n—S. Статическая характе-
274

ристика частотно-импульсного модулятора (задана) f=kx+f0, где 6=10.
Максимальная и минимальная частоты модулятора /max=3(ov-f-0x)&+
-j-/o; fm:n=—3(ox-\-oK)k-{'fo; нулевая частота модулятора /0={Ш(о>+-
+ох), где р—1,1-
Восстанавливающий оператор-экстраполятор — нулевого порядка по Ла-
гранжу. Информация с выхода экстраполятора используется для
управления (т. е. погрешность от запаздывания не должна исключаться).
Определим вначале длительность образцового временного интервала,
равную периоду временной дискретизации, и шаг квантования по уровню
соответственно
2п— 1 2я—1 2х— 1 28 — 1
"*" fmax ~ 3(a*-J- o,)£4-fn ~~ 3k(o*±0,)(l + В) " Q.in.in i .О i ~~°'4 C»
3(a,+ «}.)* + f0 3*(cf* + ox)(1-t-P) 3-10-10.1-2,1
Xmax"~Xmin 3(Тл(1 + Р) л лоо D
q ^ (f -f -If = ~~ 2"-l = ° '°82 B-
v'max 'mm' * i
. Дисперсия сигнала z/i(/) определяется в соответствии с (6.103) при
#=1, Y=l и т=0:
11 11
D /m Г Г о 5'"СО0[(вг-е2)Г] t , f Г 2 -а«[(ч-*.)Л> л л
■*Vi( > = J J °* «ь[(«1—2)П dM£2 + J J xe £M'1 =
0 0 0 0
-«.■s
(—1)'+1WP"2 +
/=i
+ а^(-1)ЧаГр,Ч2/ + ;)о + 1Г (6..03)
i=0
Так как to0T = 0,2-0,4=0,08, а аГ=0,1-0,4 = 0,04, то первые два члена
знакочередующегося ряда (6.108) с высокой точностью определяют
дисперсию:
(аГ)!1
ч», *»-•>[- ^h °! [■■ е
/ 10 \2 Г 0,082 1 Г 0,042 1
Отсюда RtJ ,, (0)^>q2 и, следовательно, (6.104) может быть использова-
на для'вычисления бд [0, е].
При восстанавливающем операторе-экстраполяторе нулевого порядка по
Лагранжу первое слагаемое (6.104) равно q2/\[\2Rxx(0)]. Отсюда
*д [0. «] = ^ = q*/[\2Rxx(0)\ + q*/[\2Rxx(0)] = q2/№xx(0)}. (6.109)
Дисперсию б2 определяют по (6.24) при f2i, приведенной в табл. 6.2
для АЦП с ИАИМ при JV=1; y=\t ср=0, когда восстанавливающий опера-
18* 275

тор — ЭНП по Лагранжу; коэффициент щ для данного вида
автокорреляционной функции Rxx(x) приведен в табл. 6.1, откуда
Л1-\
**~Ц (2/ + 1)! \~2Tal2l + { [}j C2'+U + l+ l
/=1 ч *-(=o
+
+ Т* (2/ + 1)(/+1)[^^б—• <6Л10>
Получим оценку помехоустойчивости б2я. При использовании экстрапо-
лятора нулевого порядка в соответствии с. выражением, приведенным для
рассматриваемого случая при a^^l,
1 °ь2 V\ (—\)1(*Т)21
«5[o,.]-?x-35iWJ?x,x,(o)=^2
%^?L 6 J'
/!(2/ + l)!(/ + l)
/=o
(6.111)
где #x,x,(0)—дисперсия помехи на выходе первого звена. Выражение (6.1 И)
соответствует второму слагаемому (6.100).
Таким образом, искомая усредненная относительная среднеквадратиче-
ская оценка определяется следующим выражением, полученным после
постановки (6.109)—(6.111) в (6.100):
лГ=- л/ 13(0)0Г)2 0. | (аГ)2| 3(1 + Р)а , _ 1П__3
При использовании в тракте преобразования АЦП поразрядного
кодирования с запоминающим интегратором Я*(/)=0; q= (xmax—xmin)/(2n—1);
относительная дисперсия погрешности квантования на выходе
восстанавливающего оператора определяется только первыми слагаемыми выражений
(6.104) и (6.105). В этом случае Ryiyi(z) рассчитывают по (6.103) при
Y=l и 1/N=v, где \T=t06 — время интегрирования.
Глава 7
МЕТОДЫ УМЕНЬШЕНИЯ ПОГРЕШНОСТЕЙ
ПРЕОБРАЗОВАНИЯ В СИСТЕМАХ
С ЧАСТОТНЫМИ ДАТЧИКАМИ
7.1. МЕТОДЫ И МОДЕЛИ ПРЕОБРАЗОВАНИЯ
ЧАСТОТНОГО СИГНАЛА В ЦИФРОВОЙ ЭКВИВАЛЕНТ
Частотные датчики обладают известными достоинствами,
связанными с высокой помехоустойчивостью, удобством ввода
информации в цифровые системы управления. Преобразование
276

частота— цифра реализуется циклическим частотомером,
.преобразователем по «k периодам», частотомерами следящего
уравновешивания и с линией задержки (см. гл. 2). Последние
два частотомера принято называть непрерывными цифровыми
(см. § 2.3), так как временная дискретизация при
использовании этих преобразователей осуществляется внешними
устройствами управления при считывании информации.
Математические модели временной дискретизации в
трактах преобразования с циклическим частотомером и по «k
периодам» рассмотрены соответственно в § 4.1 и 4.5, методы
определения оценок погрешностей преобразования—в § 2.3, 3.3
(статика), в § 5.1—5.3, 5.5 (динамика, при детерминированном
и случайном входном сигнале), анализ помехоустойчивости —
в § 5.4, 5.6. Анализ статических погрешностей квантования по
уровню для частотомеров следящего уравновешивания и с
линией задержки проведен в § 2.3.
В данном параграфе будут получены математические
модели, описывающие временную дискретизацию и способ
восстановления сигнала в системах с частотными датчиками и
непрерывными цифровыми частотомерами [8].
Модель тракта преобразования, содержащего частотомер
с линией задержки. Если пренебречь погрешностью
квантования по уровню [8], то связь цифрового эквивалента на выходе
рассматриваемого частотомера и частоты на его входе
определяется выражением (2.12) без учета символа взятия целой
части:
t t
N = \l(t)dt-\\{t-T3)dl (7.1)
6 О
Переходя к изображениям при условии, что f{t)=0 при t<.
<0, получаем
N(p) = (\-e-pT°)f(p)lp. (7.2)
Допуская отсутствие инерционных свойств частотного
датчика (а это можно сделать, так как Г3 обычно много больше
времени интегрирования сигнала в частотном датчике), имеем
f(t)=kx(t),
где x(t)—входной сигнал; & —коэффициент
пропорциональности.
При этом, учитывая, что измеренное значение частоты
определяется как N/T3 и цифровой эквивалент z нормируется
в единицах модулирующей функции x(t)t т. е. z=N/,(kT3),
найдем
z(p) = N (р) л (р)/Т3 = (1 -е-"^) х (р)/(рТ3). (7.3)
277

Таким образом, математическая модель тракта аналого-
цифрового преобразования с промежуточным преобразованием
в частоту без учета погрешности квантования по уровню и
временной дискретизации может быть представлена линейным
звеном, передаточная функция которого
К1(р) = 0-е-рТ>)1(рТ3). (7.4)
Когда цифровой эквивалент считывается с выхода
частотомера с линией задержки устройством управления через время
Т, математическая модель тракта преобразования в
зависимости от способа восстановления представляется синфазной или
несинфазной разомкнутой импульсной системой (см. § 5.1),
первое линейное звено которой имеет передаточную функцию
(7.4). Если время задержки Т3 равно шагу равномерной
временной дискретизации Г, то формулы расчета погрешности и
помехоустойчивости тракта преобразования с АЦП
последовательного счета с промежуточным преобразованием в частоту и
циклическим частотомером и частотомером следящего
уравновешивания полностью совпадают. В противном случае при Т>
>Т3 методика расчета помехоустойчивости погрешности от
временной дискретизации не изменяется с учетом
соответствующей импульсной характеристики первого звена.
Модель тракта преобразования, содержащая частотомер
следящего уравновешивания. При допущениях, принятых выше
(пренебрежение инерционностью частотного датчика и
погрешностью квантования по уровню), тракт преобразования
аналоговый сигнал — частота — цифровой эквивалент может быть
описан линейным дифференциальным уравнением. Пренебрегая
дискретностью цифрового эквивалента (опускаем знак Е —
взятие целой части) и дифференцируя обе части выражения
(2.16), определяем
dN/dt = f(t)-foc(t).
Так как /oc(0=W)/2n, T0 dN/dt+f0/2^=f(t).
Учитывая, что при допущении безынерционности частотного
датчика f(t)=kx(t), и обозначая z(t) = (l/k)N(t)f0/2n,
получаем
-*LJL + 2{t) = x(t).
fo at
^ереходя к изображениям, имеем
г(р)=К\(р)х(р)9
где
*1(р) = 17(7фР+1); 7ф=2»//о. (7.5)
278

Таким образом, при оговоренных выше допущениях и
отсутствии временной дискретизации тракт частотный датчик —
непрерывный цифровой частотомер следящего
уравновешивания описывается апериодическим звеном первого порядка с
постоянной времени Тф=2п/}о. С учетом того, что /0 выбирается
равной максимальному значению частоты датчика (см. § 2.3)
при п>\ (а это всегда имеет место), постоянная времени Гф
практически совпадает с длительностью временного интервала
циклического частотомера и частотомера с линией задержки.
В том случае, когда цифровой эквивалент считывается
е-выхода частотомера следящего уравновешивания устройством
управления через время Г, математическая модель тракта
преобразования в зависимости от способа восстановления
представляется синфазной или несинфазной импульсной системой
(см. § 5.1), первое линейное звено которой имеет
передаточную функцию (7.5). Методика расчета помехоустойчивости и
погрешности от временной дискретизации при заданном
способе восстановления в этом случае ■ остается такой же как
описанная выше.
7.2. МЕТОДЫ УМЕНЬШЕНИЯ СТАТИЧЕСКИХ
ПОГРЕШНОСТЕЙ ПРЕОБРАЗОВАНИЯ ПРИ ЗАДАННОМ
ВРЕМЕНИ ПРЕОБРАЗОВАНИЯ И ДИАПАЗОНЕ
ИЗМЕНЕНИЯ ЧАСТОТЫ
В гл. 2 был проведен анализ максимальных оценок
методических погрешностей преобразования частота — цифра. Когда
задано время преобразования Т (например, из условной
динамики), минимальная и максимальная частоты датчика (после
выбора датчика из конструктивных, технологических или
экономических соображений), рассмотренные способы
преобразования могут не обеспечить допустимого значения максимальной
статической погрешности. Поэтому в данном параграфе
приведены* несколько усовершенствованные способы
преобразования, позволяющие при заданном Т и диапазоне изменения
частоты датчика уменьшить наибольшие значения оценок
статических погрешностей. Реализация этих способов становится
целесообразной на базе применения микропроцессорнрй
техники.
Так как при использовании циклического частотомера
источником погрешности преобразования частота — цифра
является отсутствие синхронизации эталонного временного
интервала и счетных импульсов, а также отсутствие учета
временного интервала между последним импульсом счетной
последовательности и концом временного интервала Г, то
усовершенствование преобразования будет направлено на дополнительное
279

ги\ 111111111111111111111111111111111111111111
и i i i Mm i i nil и и
I 1 2 N
[1234... I I |
II li I Mill M Ml! I U I ill
At,
T"pi-1
V
N+1
г.... ki
JLLL
At
1 Z J
III11 ill 1111 ill I l,.l 11
■ЧР-
I I l I l I
ngt_
*)
2 H
' I ' ' ' 'I' ' ',,' ' I"
J_L
Ati-,
ли
M II llll I I I I ill II II I
' npi
Ю
\1 \z
I I I I III I I I I ill I U I I
I llll
^a-1)
At,
Рис. 7.1. Временные диаграммы способов преобразования
частотно-импульсного сигнала в цифровой эквивалент с учетом уменьшения погрешности
квантования по уровню
измерение этих временных отрезков с целью учета при
получении цифрового эквивалента [40].
Временные диаграммы, поясняющие различные способы
преобразования, приведены на рис. 7.1. При первом способе
образцовый временной интервал Т0 формируется генератором
импульсов ГИ с кварцевой стабилизацией. Синхронизация
импульсов счетной последовательности (на временной диаграмме
они нарисованы с большей амплитудой) с передним фронтом
импульса образцового временного интервала осуществляется
на первом импульсе ГИ, следующем после счетного. По
окончании образцового временного интервала измеряется
длительность Д^ —временной отрезок между задним фронтом
образцового временного интервала и первым после него импульсом
счетной последовательности. Если время преобразования Гпр
(рис. 7.1,а), может быть измерено идеально точно, то
статическая методическая погрешность отсутствует и преобразуемой
аналоговой величине х соответствует цифровой эквивалент
N+1:
x=(N+l)A/TnP,
где N=E[T0x/A]; Тпр= (А/х) [£(7Wi4) + l]; E определяет
операцию взятия целой части числа, полученного в результате
280

щ
Рис. 7.2. Зависимость шага j
временной дискретизации от А
значения аналогового сигнала
для первого (а), второго (б) 2Т0
и третьего (в) способов
преобразования
частотно-импульсного сигнала Т0
вычисления по формуле,
заключенной в
соответствующих скобках; А =
== (Ятах «£min)/(/max —
—/mm) — величина
порога частотно-импульсного
датчика.
Время
преобразования и соответственно
равный ему шаг
дискретизации Гд при таком
способе построения
частотомера зависят от х (рис.
7.2,а), где А/Т0=С.
Преобразование
величины Гпр в цифровой
эквивалент в
действительности осуществляется с
конечной точностью,
определяемой
погрешностью квантования. В со- € сс£
ответствии с временной *J2
\
[\
ч
а)]
2с
Зс
4с
\\
\
V
^
"^-^.
*7|
2с
Зс
4С
ТА
Jrn
2Тп
'в
sjj
2с
Зс
4с
диаграммой измеренное время преобразования
7,изм=7,пР+А^1—Д^2=£[(7,пр+Л*1)/тг]тг,
где O^A/i^Tr; 0^А^^тг; тг — период импульсов ГИ.
При этом результат преобразования
А[Е(Т0х/А) + \]
1 иям
z__(N+l)A
*ГЕ {(Ц1г)ЦА/х)Е(ТМА) + I]:- +&*!/*,
(7.6)
Абсолютная погрешность преобразования Дл:=*—г, где z
вычисляется по (7.6).
Получение закона распределения и числовых характеристик
случайной величины Ах при заданных законах распределения
х и A^i аналитически достаточно сложно. Кроме того, как
показывает расчетная практика, выведенные для подобных
случаев математические выражения являются громоздкими.
Поэтому для определения закона распределения Ал: мо^сет быть
рекомендован метод статистических испытаний. При этом за-
281

кон распределения At\ принимается равномерным, т. е.
f 1/
1/хг при 0<^1<хг;
в остальных случаях.
Закон распределения х определяется при анализе объекта,
генерирующего сигнал.
При втором способе (рис. 7.1,6) отсутствует синхронизация
переднего фронта Го и импульсов счетной последовательности.
В этом случае измерению подлежат величины Atf^-i, Д//, а
преобразуемая величина х связана с цифровым эквивалентом N
следующим соотношением:
x=AN/XTo+Ati-Ati-{).
Время преобразования Гпр и соответственно равный ему
шаг дискретизации Гд зависят от х и определяются
выражением
Т jAE(T0x/A)/x;
"р д \А[Е(Т0х/А)+Ц/х.
Источником методической погрешности в этом случае
является погрешность квантования при преобразовании временных
интервалов А^- и Ati-\ в число.
При третьем способе (рис. 7.1,в) измеряют временные
интервалы, определяемые моментом появления последнего
импульса счетной последовательности, попавшего в данный цикл
измерения, и моментом окончания Т0 данного цикла измерения.
В этом случае
x=AN/(To-Ati+Ati-{).
Время преобразования Гпр определяется так же, как и при
способе, показанном на рис. 7.1,6. Шаг временной
дискретизации
| Т0 при л: >С;
Гд =\Т0Е(А/хТ0) п[и 0<л<С;
[Т0[Е(А/хТ0)+ 1] приО<л<С.
График Тл=у(х) приведен на рис. 7.2,0. Источником
методической погрешности является погрешность квантования при
преобразовании временных интервалов AU и Ati-\ в число.
Последний способ преобразования, имеющий методическую
погрешность такую же, как второй, обладает рядом достоинств.
При х>С шаг временной дискретизации постоянен, что
удобно при синхронизации устройства аналого-цифрового
преобразования с микропроцессорной системой управления и
позволяет использовать один вход требования прерываний.
282

7.3. МЕТОДЫ УМНОЖЕНИЯ ЧАСТОТЫ
Умножение частоты в цифровых системах с частотными
датчиками позволяет уменьшить погрешность квантования по
уровню при заданном времени аналого-цифрового
преобразования, увеличить быстродействие преобразования при заданной
допустимой погрешности квантования. Кроме того,
умножители частоты играют роль масштабирующих устройств.
Различают методы умножения частоты с сохранением и без сохранения
информации о фазе входного сигнала [8]. Если умножение
частотного сигнала осуществляется с сохранением фазы
входного сигнала, то уменьшение погрешности преобразования
пропорционально коэффициенту умножения. Так, если при
преобразовании частоты в цифровой эквивалент с помощью
л а
thconst
ил
-Р4+
i i i
i i
-K-f
bbhh h hhb hbhhhh
L min /*
—Ц ним V
лз
d
L-4./7J | 1
L.-J
ИЛИ
a)
Выход
в)
с
d
е
-9—
[)
1
(1
\
^£min/2
Л
п
1
1
6
1 >
t
0 >
J *
Рис. 7.3. Умножение частоты без сохранения информации о фазе входного
сигнала:
а _ удвоение; б — умножитель частоты; в — удвоение частоты без сохранения
информации о фазе входного сигнала
2S3

циклического частотомера максимальная погрешность
преобразования определяется единицей младшего разряда счетчика,
то при умножении преобразуемой частоты в k раз с
сохранением фазы при неизменном времени преобразования в к раз
уменьшается значимость единицы младшего разряда и,
следовательно, в k раз уменьшается максимальная погрешность
такого преобразования. Если умножение входного частотного
сигнала осуществляется без сохранения фазы, то при широком
диапазоне изменения преобразуемой частоты существенного
повышения точности преобразования не достигается [8].
Умножение частоты без сохранения информации о фазе
входного сигнала. Пусть сигнал на выходе частотного датчика
(точка с на рис. 7.3,6) представлен последовательностью
импульсов постоянной длительности tK (рис. 7.3,а). Используя
линии задержки ЛЗ или регистры сдвига (рис. 7.3,6), можно
всегда сформировать импульс, расстояние которого на
временной оси от переднего фронта импульса ЧИМ равно Tmin/2, где
tmin=l//:max, и получить на выходе схемы ИЛИ (точка е)
сигнал удвоенной частоты. При f=/max импульсы на выходе
схемы умножения следуют друг за другом с интервалом 1/2/тах.
Однако при /</тах (рис. 7.3,в) информация о фазе исходного
сигнала пропадает. При этом увеличение точности за счет
удвоения частоты тем меньше, чем больше / отличается от fmax.
Аналогичные рассуждения могли быть проведены при
умножении частоты на произвольное число. Принцип построения
множительного, устройства при этом не изменяется (см.
штриховые линии на рис. 7.3,6). В частности, в [41] на изложенном
выше принципе разработан блок умножения частоты на любое
целое или дробное число. Несмотря на то что при широком
диапазоне изменения преобразуемых частот схемы умножения,
не сохраняющие информацию о фазе входного сигнала, не дают
существенного выигрыша в точности преобразования
частота-—цифра, они могут быть использованы как
масштабирующие устройства.
Умножение частоты с сохранением информации о фазе
входного сигнала. Умножение может быть осуществлено с помощью
экстраполяционного метода [42]. В этом случае максимально
допустимый коэффициент умножения, при котором умножитель
будет работать правильно, зависит от порядка экстраполяции,
параметров частотно-импульсного датчика и свойств
модулирующей функции. Рассмотрим экстраполяционный метод
умножения частоты для общего случая — экстраполяции Л1-го
порядка и методику определения максимально допустимого
коэффициента умножения при заданной детерминированной
модулирующей функции на входе частотно-импульсного
датчика, реализующего интегральную частотно-импульсную
модуляцию (ИЧИМ).
284

<Г[/7-2]
*[n-1]
*M
-[/7-/]
<Г[/7]
'["♦я
*["-*]
i [/7-7]
И
*["*Я
Рис. 7.4. Умножение частоты на 4
Экстраполяционный метод умножения частоты базируется
на прогнозировании длительности (я+1)-го интервала т*[я+
+ 1] частотно-импульсного сигнала при известных я, п—1,...
. ..,я—М интервалах, где М — порядок экстраполяции. Знание
т*[я+1] позволяет дополнить (я+1)-й интервал импульсной
последовательности &— 1 импульсами так, чтобы временной
интервал между дополненными импульсами был равен т*[я+
+ 1]/&. Полученная последовательность соответствует
умножению частоты в k раз. Если т*[я+1] равен
т[я+1]—действительной длительности интервала, то сохранение фазы
осуществляется. В общем случае т*[я+1]#т[я+1]. Однако,
учитывая свойства модулирующей функции, можно обычно
выбрать порядок экстраполяции, обеспечивающий выполнение
неравенства
|т*[я+1]-т[я+1]|<т*[/1+1]/А, (7.7)
что соответствует практически приемлемому сохранению фазы
при умножении частоты.
Для иллюстрации метода рассмотрим простейший способ
.умножения, использующий экстраполяцию нулевого порядка
(ЭНП) при прогнозировании длительности я+1 временного
интервала по п-му [42]. В этом случае т*[я+1] =х[п]. На
временной диаграмме (рис. 7.4) рассматривается умножение частоты
в 4 раза (&=4).* Сигнал частотно-импульсного датчика показан
жирными линиями, дополненные импульсы — тонкими. При
|т?[л] —-т[я+1] | <Ст[я]/4 получаем умножение частоты с
практически приемлемым сохранением фазы.
В общем " случае экстраполяции М-го порядка величина
T*[n-fl] вычисляется в соответствии с выражением,
базирующимся на интерполяционной формуле Лагранжа [33]:
м /=м
'•[«+U-J]n^7ZTJ'[«--M + fl.
(7.8)
*=0 /=0
где П — символ умножения.
285

После преобразования выражения (7.8) получаем
м
4J (Af + 1 —t)(Af—t)! t!
/=0
В частности, при ЭНП экстраполяции первого (ЭПП) и
второго (ЭВП) порядков т*[я+1] определяются
соответственно следующими выражениями:
т*[/1+1]=т[я]; (7.10)
х*[п+1]=2г[п]-ч[п-1]; (7.11)
т*[Аг+1]=Зт[Аг]— Зт[п—1]+т[лг—2]. (7.12)
Максимально допустимый коэффициент умножения /(max
определяется из условия, что /(max—1 импульсов,
дополняющих входную частотную последовательность и отстоящих друг
от друга на ч*[п-\-1]/КтаХ, размещаются на временном
интервале т[я+1]. Это условие выполняется всегда при т[я+1]^
^т*[я+1], в противном случае необходимо выполнение
следующего соотношения:
>f -ьп["Т!1,1л.Г > *»" при Ч« + 1К '* [« + 11, (7.13)
где ^и — длительность импульсов входной и дополненной
частотных последовательностей. Вторым ограничением на /(max
является условие
ktfmax<Tmm|>], (7.14)
где tmin[n] — минимальный временной интервал между
соседними импульсами входной частотной последовательности.
Условие (7.14), как правило, выполняется, так как длительность
счетных импульсов может быть реализована
схемотехническими способами достаточно малой.
Из условия (7.13) максимально допустимый коэффициент
умножения
/tmax= min Е\ *ln+.l]u^t 1 при**[*+1]>т[я+1],
М<п<оо L* [Л + 1]—*[l-|- 1]-Ии I
(7.15)
где Е — знак выделения целой части числа, полученного при
вычислении по формуле, заключенной в скобках; Л1<я<«>,
так как переходный процесс в умножителе при экстраполяции
Л1-го порядка заканчивается через М тактов.
Для определения величины /(max необходимо найти
зависимость между модулирующей функцией и величинами т[я]. При
286

/A/xmin
1^ »
-#-
t
ГЦ] Г[2] Г [/77+/] *
N *[/] *М...*[/17]*[/П^]*[/77^]
Рис. 7.5. К решению уравнений (7.16)
Рис. 7.6. Модулирующая функция (а) и соответствующая ей
частотно-импульсная последовательность (б)
ИЧИМ эта связь определяется системой уравнений
t[n[
f x(t)dt = nA; i[n] = t[n] — t[n—l]9 (7.16)
где л=1, 2, 3,...; ^[я]—момент, соответствующий переднему
фронту п-го импульса входной счетной последовательности; А—
порог модулятора.
Для иллюстрации методики решения системы уравнений
(7.16) рассмотрим рис. 7.5. Здесь у = J x(t)dt, параметр дис-
6
кретизируется с шагом Л, на оси ординаты получаем величины
t[n], разность между которыми определяет т[я].
Таким образом, при заданной модулирующей функции
величины х[п] определяются из решения системы уравнений
(7.16); при вычисленных значениях х[п] и выбранном порядке
экстраполяции в соответствии с выражением (7.15)
определяется /(max-
В качестве примера рассмотрим определение величины /(max
при детерминированном входном сигнале и экстраполяции
нулевого и первого порядков, пренебрегая длительностью
счетных импульсов ta.
Пусть модулирующая функция
*(<) = {
^min
при 0<t<t0;
■t0) при />/0,
(7.17)
где V соответствует максимальной скорости изменения
модулирующей функции; хтт— минимальное значение модулирующей
функции.
287

Обычно #min и V могут быть получены при априорном анализе
системы, генерирующей модулирующую функцию. Вид
модулирующей функции (7.17) и соответствующий ей
частотно-импульсный сигнал на выходе датчика представлены на рис. 7.6.
Пусть *[т]<*о<*[/и+1]. где m=M+l9 M+2,..., тогда
t0=yAlxm[n+mA/xmin=A(m-\-y) /*mIn, (7.18)
где 0*^у^1.
На выходе датчика длительности интервалов между
импульсами
M/*min при л= 1, 2,..., т\
T^/^min+ [-^min+K^in+ 2VA(l-T)JIV при п = т + 1;
ЛП]~ [Vx^ + WAin-m-V - yxlin+WA{n-m-l-=T)]/V
[ при п > m + 2.
(7.19)
Для ЭНП и ЭПП минимальное значение по п максимально
допустимый коэффициент умножения принимает при n=m+l.
С учетом (7.10), (7.11) и (7.19) максимально допустимый
коэффициент умножения при ЭНП и ЭПП
Кшк=" mJn Е(В)> Kmax= ПИП Е(С),
0sSt<l 0<Т<1
где
в= tAV/xltln-l+Vl + 2VA(l—()/4iln
ТГ AVtf*in ~ 1 + 2Vl+2VA(l—i)/x2mln-V\+2VA(2—i)Jx2mJ
(7.20)
с = _: Л1/(2г-1)/л^,п-2+2К1+2ГМ(1-у)/х2т1п
^/(2Y-l)/x^In-2 + 3Kl4-2^(l-Y)/^in-l/l + 2V>l(2-Y)/xSlln
(7.21)
Анализ» зависимости максимально допустимого
коэффициента умножения при входном сигнале вида (7.17) от VA для
ЭНП и ЭПП соответственно (рис. 7.7,а и б) показывает, что
с увеличением максимальной скорости изменения
модулирующей функции х и порога модулятора А максимально
допустимый коэффициент умножения /(max уменьшается, Ктах
увеличивается с увеличением jtmin. Экстраполяция первого порядка
обеспечивает коэффициент умножения выше, чем ЭНП. Это
объясняется тем, что ЭПП обеспечивает более точное
прогнозирование длительности интервала.
288

Km
10
5
ax
\
\
1
1
1
4.
~l
- /xmiT\ = 0i6
L
'Xrr\: " =0.J
H
a)
0,02 0,04 0,06 0,06
\
^max
in 1 '
1U
j
\
... j
\,
l
4
—1
ЦЛтйп=4*
/xmtr
=0,J
*;
M
0,02 0,04 0,06 0,08 VA
Рис. 7.7. Зависимость максимально допустимого коэффициента умножения
от скорости изменения входного сигнала и порога частотно-импульсного
датчика при ЭНП (а) и ЭПП (б)
Структурная схема, реализующая экстраполяционный метод
умножения частоты нулевого порядка (рис. 7.8), состоит из
частотно-импульсного модулятора ЧИМ, двух счетчиков Сч1,
Сч2, генератора импульсов ГИ, делителя частоты Д,
сравнивающего устройства СУ, регистра памяти РП, схемы ИЛИ [43].
Импульсная последовательность с выхода ЧИМ поступает на
вход сброса R1 счетчика Сч1 и на вход, разрешающий запись
в регистр памяти РП1. Импульсы ГИ поступают через
делитель Д на счетные входы S1 и S2 счетчиков Сч1 и Сч2.
Частоту ГИ выбирают из условия /о^/тах, где fmax—-максимальная
частота следования импульсов с выхода ЧИМ,
соответствующая максимальному значению модулирующей функции x(t).
Коэффициент деления Д выбирают равным k — коэффициенту
умножения частоты. Пусть на п— 1-м периоде сигнала ЧИМ на
вход S1 счетчика Сч1 поступило N импульсов с выхода
делителя частоты (частота следования этих импульсов равна folk).
На переднем фронте очередного импульса ЧИМ содержимое
Сч1 переписывается в регистр памяти, а Сч1 сбрасывается в 0.
\чим
"
г и
д
R1
J7
"*
СЧ1
/77
=ч>
1
РП Г
S2
R2
СчГС
=0
су\
1
Выход
» :»■
Рис. 7.8. Структурная схема умножителя частоты
19-6 36
289

На п-м периоде сигнала ЧИМ на вход S2 счетчика Сч2
поступают импульсы с ГИ. После того как Сч2 досчитает числа,
записанного в РП, на выходе СУ формируется единичный
импульс, поступающий на один из входов схемы ИЛИ, Далее этот
сигнал поступает на выход схемы ИЛИ и сбрасывает Сч2 в 0.
Счетчик Сч2 опять суммирует импульсы ГИ (напомним, что
частота следования импульсов на входе Сч2 в k раз выше, чем
на входе Сч1), и при появлении на выходе Сч2 числа, равного
записанному в РП, формируется единичный сигнал на выходе СУ,
который поступает на выход схемы ИЛИ и сбрасывает Сч2
в нуль. При правильно выбранном коэффициенте умножения на
л-м периоде сигнала ЧИМ сравнивающее устройство сработает
k—1 раз. С учетом того, что на второй вход схемы ИЛИ
поступают сигналы ЧИМ, на ее выходе будет формироваться
последовательность импульсов с частотой в k раз выше, чем на
выходе ЧИМ. Содержимое РП стирается импульсом ЧИМ в
конце п-то периода. Так как k—\ импульсов с выхода СУ
формируются в зависимости от длительности п— 1 периода ЧИМ,
рассматриваемая схема реализует экстраполяционный метод
умножения частоты нулевого порядка.
7.4. УМЕНЬШЕНИЕ ДИНАМИЧЕСКИХ ПОГРЕШНОСТЕЙ
ПРЕОБРАЗОВАНИЯ
Для уменьшения динамической погрешности при выбранном
из условий допустимой статической погрешности времени
преобразования Т частоты в цифровой эквивалент можно
использовать параллельную структуру преобразователя, состоящего
из одного частотно-импульсного модулятора и k циклических
частотомеров.
В моменты времени tou tn, t2i>.-. (рис. 7.9) формируется
эталонный временной интервал первого частотомера, в
моменты t02=t0i-\-T/k, tl2=tn-\-T/k, t22=t2\ + TIk —второго и т. д.
За время At управляющее устройство считывает по каждому
каналу преобразования со счетчиков циклических частотомеров
цифровой эквивалент, а затем сбрасывает счетчики в 0.
Отсюда следует, что шаг дискретизации аналогового сигнала в этом
случае равен T/k.
Рассмотрим, какое уменьшение погрешности в случае
восстановления экстраполятором нулевого порядка обеспечивает
параллельная структура преобразования. Математическая
модель (рис. 7.10) временной дискретизации и восстановления
экстраполятором нулевого порядка по Лагранжу при At<^.T
учитывает уменьшение шага дискретизации в k раз, что
обеспечивается периодом идеального импульсного элемента,
равного Тjfc. Передаточная функция второго звена учитывает
экстраполяцию на шаг вперед с тем, что в ней длительность экстра-
290

*\
1 1 1 1! Ill
|^
<01
T
MM Nil
ll 1 1 III
tQl
ITTit
<« 1
t
\ MUM! ГМ1 1 1 III MM II III Ml a) ^
At
1
II II II 1 II II 1 III
*ff 1
MM
MM
ll 1 1 Mill
Чг 1
Mill
hi
IT*^
t
IlllMMM MM
4i
111 ll ll I I 11 MM
tlz
11111111 ■ I
_J 1
llll
±гъ
o)
' S)'
M >
г)'
M >
»*
ш
Рис. 7.9. Временная диаграмма работы АЦП последовательного счета с
промежуточным преобразованием в частоту с k=3 циклическими частотомерами:
а — модулирующая функция x{t); б — выход частотно-импульсного модулятора; в, г, д—
временные диаграммы работы соответственно 1-, 2- и 3-го частотомеров; е — сигнал
считывания цифрового эквивалента
z[/7,«] *|>,fl]
x(t)
1-е~Рт
иэт/м
с -PfT
1-е-Рт?к
Р
z\n,e
>6<
Рис. 7.10. Математическая модель АЦП последовательного счета с
промежуточным преобразованием в частоту и циклическими частотомерами
поляции равна T/k. Такой подход позволяет использовать
рассмотренные ранее модели восстанавливающих операторов,
заменяя Т на T/k, где k — число параллельных каналов.
Обратим внимание, что в первом линейном звене величина Т не
делится на k> так как в соответствии с описанием
функционирования преобразователя интегрирование входного сигнала
осуществляется за время Т.
Погрешность преобразования определяется как при работе
в реальном времени (<р==0), так и при исключении
погрешности от запаздывания: <p = <p1-f<p2. В данном случае cpi=l/2;
ф2 = &/2.
Учитывая, что шаг временной дискретизации при
параллельной структуре преобразователя равен T/k, введем обозна-
19* 291

чения n-\-s=kt/T, я=0, 1,..., Osgresg: 1. Тогда
n T
*[*, sl= 2 K[m, e](l/^) J л [(/г — m)T/k — z]dz,
m=0 0
где k2[m, e] —импульсная функция второго звена.
При экстраполяции нулевого порядка k2[m, е] =1 [т] — 1 [т—1]
т
и г[п, e] = (l/T)$x[nT/k — z\cb.
о
При детерминированном входном сигнале x(t) погрешность
преобразования
т
б[л, в] = л[(д + е —ф)Г/Л] —(1/Г) \x[nT/k — z]d*.
о
В частности, при линейно возрастающем входном сигнале
x=Vt, установившееся значение погрешности при я+е-—ф^О
имеет вид
т
бу[/г, e] = V(n + e-y)T[k-(l/T) §V(nT/k — *)*"=
о
(VT/2 + VeT/k при ф = 0;
^\VT(s — l/2)/k при Ф = £/2+ 1/2;
максимальная оценка погрешности
/УТ (1/2+1/*) при Ф=,0;
тах " (КГ/2* п?и ф - m + 1/2.
Следовательно, бтах уменьшается с ростом числа каналов.
Однако при работе параллельного преобразования в режиме,
когда погрешность от запаздывания не может быть исключена
(ф=0), использование числа каналов более двух или трех
мало эффективно, так как погрешность преобразования
уменьшается достаточно медленно.
При случайном входном сигнале, заданном корреляционной
функцией Rxx(t), и восстанавливающем операторе-экстраполя-
торе нулевого порядка по Лагранжу относительная дисперсия
погрешности преобразования
р^]ог-1--НЧ<--'>тН*+
о
+ rafl*"(*-" >*■** <7-22)
О О
292 •

Оценка помехоустойчивости преобразования при ЭНП по
Лагранжу определяется третьим слагаемым формулы (7.22)
после замены Rxx{^\—Т2) на корреляционную функцию помехи
#u(ti—Т2).
В частности, если случайный сигнал имеет постоянную
спектральную плотность мощности в полосе частот от 0 до соо,
т. е. /?^(r)=a2A:sina)oT/(a)ot), то, воспользовавшись (6.15)
с учетом, что шаг временной дискретизации равен T/k, получим
8» [О, «Н JJ-
(2/ + 1)!(2/ + 1)
1=1
xj-^K—Ф + *)"+,-(—f^T + T^}. (7-23)
Усредненная дисперсия погрешности преобразования
(-1)'(<о<Л2/ ( 2 Г 1
.) l ' U (2/ + l)!(2/+l) \ fe2/4i[s
2/+2
l=l ' ' ' '
X
Х1(1-<р + ^)2^2-(^-ф)2'+2-(1—р)2'+2 + <ргГ+2] + 7^7]}.
(7.24)
Для анализа влияния числа каналов на погрешность
преобразования воспользуемся первым членом ряда (7.24):
f (*V02 / 2 I 3 , 3 \ nrx„ m _ п.
18
(соо Л2
18
\ k*
1
2£2
As
v;
ирп у — w,
* ! 1
при ф ■= — -+- —.
2 2
Следовательно, увеличение числа параллельных каналов
приводит к уменьшению дисперсии погрешности
преобразования.
Помехоустойчивость преобразования при восстановлении
экстраполятором нулевого порядка не зависит от числа
параллельных каналов. Это следует из того, что величина k не
входит в третье слагаемое выражения (7.22).
Используя рассмотренную методику, можно получить
расчетные формулы при других восстанавливающих операторах.
293

Глава 8
ОСОБЕННОСТИ РАСЧЕТА ОЦЕНОК
ПОГРЕШНОСТЕЙ ЦИФРОВЫХ
ТЕЛЕИЗМЕРИТЕЛЬНЫХ СИСТЕМ
8.1. ПРИНЦИПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ ВРЕМЕННОЙ ДИСКРЕТИЗАЦИИ В ЦИФРОВЫХ
ТЕЛЕИЗМЕРИТЕЛЬНЫХ СИСТЕМАХ
В современных телемеханических системах передача
цифровой телеизмерительной информации осуществляется, как
правило, по тракту телесигнализации. Пусть, например,
кодовая серия состоит (рис. 8.1,а) из k\ разрядов
телесигнализации, 2&2 разрядов для передачи информации двух телеизмеряе-
мых параметров, k$ служебных разрядов (в частности,
проверочных разрядов систематического избыточного кода, кодового
г , т '
Рис. 8.1. Временная дискретизация аналого-цифровым преобразователем
с АИМ при передаче телеизмерительной информации по тракту ТИ—ТС
префикса поцикловой синхронизации). Если т — длительность
передачи^ элементарного символа, то В=1/т— скорость мани-
294

пуляции и Т= (&1+2&2+£з) /В — время передачи кодовой
серии. Пусть At— сумма времен запаздывания в канале связи и
декодирования кодовой информации приемным
полукомплектом телесигнализации — телеизмерения (ТС —ТИ).
Рассмотрим вначале случай применения АЦП с АИМ,
когда временем аналого-цифрового преобразования можно
пренебречь. Тогда цифровой эквивалент при пренебрежении
погрешности квантования по уровню равен x\(t2), X\(U)••• по
первому каналу ТИ, x2{t2) и *2(^) • •. — по второму каналу
(рис. 8.1,6 и в). Приемник получает информацию после приема
и декодирования кодовой серии соответственно в моменты /з+
+Д*, t6+At,... (рис. 8.1,г и д). Отсюда следует, что тракт
временной дискретизации в случае АЦП с АИМ можно
представить последовательным соединением звена с запаздыванием
Кг(р) = e-/Kfl7\ где у\Т= (2&2+&з) /B+At для первого канала
ТИ, у\Т= (k2-\-ks)/B-\-At для второго канала ТИ и идеального
импульсного элемента с шагом дискретизации Т. Вид
восстанавливающего оператора определяется способом аппроксима-
tni+m,<C
Рис. 8.2. Временная диаграмма работы тракта ТИ—ТС при получении
цифрового эквивалента АЦП с ИАИМ
ции принятого сигнала ТИ в приемном полукомплекте ТС —
ТИ. В частности, если информация ТИ в приемнике
записывается в память и диспетчер получает ее на цифровом дисплее,
то восстанавливающим оператором является экстраполятор
нулевого порядка по Лагранжу. Так как диспетчер, как
правило, использует полученную информацию для управления,
погрешность, вызванная запаздыванием, не исключается. С целью
уменьшения этой погрешности при построении устройств ТС —
ТИ аналого-цифровое преобразование следует осуществлять
как можно ближе к концу кодовой серии, т. е. после передачи
сигналов ТС (рис. 8.1,а).
Таким образом, математическая модель тракта временной
дискретизации и восстановления в системах телемеханики при
использовании АЦП с АИМ совпадает с рассмотренными
моделями в гл. 5. Специфика систем ТИ учитывается только
видом звена Ki{p).
Рассмотрим далее случай использования АЦП с ИАИМ.
Пусть цифровой эквивалент на каждом цикле передачи опре-
295

деляется средним значением функции X\(t) за время от tHi-\-h
цо tni+mry где /<т<£ь / н/ — момент начала t-ro цикла, и
средним значением функции x2(t) за время от tHi+l\x до tHi-\-
+m\i, где ^i^/i<m1^1+A2 (рис. 8.2). Приемник, так же как
и в предыдущем случае, получает информацию после приема и
декодирования кодовой серии при /=Лн+(&1+2&2+^з) /Д+At.
Отсюда следует, что тракт временной дискретизации можно
представить как последовательное соединение линейного звена
К\(р) и идеального импульсного элемента с шагом
дискретизации Т. Для первой телеизмеряемой величины линейное звено
реализует оператор
t-(T+At-m-c)
*iW = 75=7F 1 хг№; (8.1)
t—(T + At-lx)
*i(rt = : — е -е ]. (8.2)
(т —/)хр
Аналогичный оператор имеет место для второй
телеизмеряемой величины, получаемой заменой т на ть / на /i, X\(t)
на x2(t).
Таким образом, математическая модель тракта временной
дискретизации в системах телемеханики при использовании
АЦП с ИАИМ совпадает с рассмотренными моделями в гл. 5.
Специфика систем ТИ учитывается только видом звена К\(р)-
Рассмотренные случаи иллюстрируют принципы построения
математических моделей временной дискретизации в цифровых
телеизмерительных системах.
8.2. РАСЧЕТ ОЦЕНОК ПОГРЕШНОСТЕЙ
В ТЕЛЕИЗМЕРИТЕЛЬНЫХ СИСТЕМАХ
Если вероятность отказа от декодирования при наличии
обнаруживаемых приемником ошибок пренебрежимо мала и
трансформацией кодовой серии можно пренебречь, то шаг
временной дискретизации в телемеханических системах с
инерционной и циклической синхронизацией постоянен [45]. В этом
случае методика расчета оценок погрешностей, вызванных
временной дискретизацией, совпадает с изложенной в гл. 5 и 6.
Использование этой методики для АЦП с АИМ и для случая
передачи кодовой серии, приведенного на рис. 8.1, рассмотрим
на примере.
Пример 8.1. Корреляционная функция гауссовского стационарного
центрированного сигнала x1(t) задана выражением Rx x (x)=ax2sino)0^/(o)ox), сигнала
х2 (t) —выражением RXiXu(v) = a*2 cos |3т. Диспетчер получает информацию
на цифровом дисплее (т. е. восстанавливающий оператор ЭНП по Лагранжу)
296

и использует ее для управления технологическим процессом (т. е. погрешность
от запаздывания не может быть исключена). Заданы: £ —скорость передачи
информации, k\ — число разрядов ТС, k2 — число разрядов по каждому
каналу ТИ, кг — число служебных разрядов.
Диапазон изменения телеизмеряемых величин с вероятностью 0,997
равен ±3а*. Шаг квантования по уровню q = 6o*/(2ft2 — l); k2=S (при этом
o2jc><72). Требуется определить усредненную среднеквадратическую
погрешность преобразования по каждому из каналов.
Дисперсия погрешности преобразования в случае гауссовского
стационарного центрированного сигнала при o2x>q2 равна сумме дисперсий
погрешностей, вызванных временной дискретизацией и квантованием по уровню.
Отсюда
dl = ? + q<2/l2a2x=d2 + 3/(2ki-\)2.
В соответствии с данными табл. 5.4 текущее значение относительной
дисперсии погрешности при восстановлении экстраполятором нулевого
порядка и ф=0 (погрешность от запаздывания не исключается) определяется
выражением
вт[0, е]-2{1—/?хх[(Н-ф1)П/Яхх(0)}, (8.3)
откуда
1
гя= ^[О, e]de.
6
Для первого канала ТИ (piT=(2k2-\-kz)/B-]-At1 для второго — (k2-{-
+k3)/B-\-M.
Относительная усредненная дисперсия погрешности для первого канала
s\nu0\e(kl+2k2 + k3)/B+(2k2 + k3)/B + M]) ф
<о0[е (b1 + 2k2+k3)/B+(2k2 + k3)/B+At) У
(2й»—1)1
Xde+. tJ ; (8.4)
для второго канала
Ю5-Ц
2{\-cos$[t(k1 + 2k!t+k3)lB + (k2 + k3)/B +
о
3 |'/2
'-I)2)
+ ^]}^+(2>1. „Л • (8-5)
Как правило, А/<т=1/£ и этой величиной можно пренебречь.
Приведенная к диапазону ТИ усредненная оценка погрешности в
случае гауссовских сигналов в х^б раз меньше Y~Y*.
297

Неравномерность шага временной дискретизации в
телемеханических системах может быть вызвана отказом от
декодирования приемником при обнаружении ошибок,
использованием пошаговой синхронизации с временным импульсным
признаком [46], адаптивными алгоритмами при передаче
телеизмерительной информации, наличием приоритетных прерываний
в сложной сети большой телемеханической системы. Исходной
информацией, необходимой для расчета погрешностей и
помехоустойчивости телеизмерительного тракта в случае
использования среднеквадратических отклонений погрешностей,
являются законы распределения, описывающие случайные
интервалы дискретизации, минимальный и максимальный шаги
дискретизации для определения верхних и нижних оценок СКО.
Методика расчета этих погрешностей изложена в гл. 5.
С целью иллюстрации ее использования рассмотрим расчет
оценок погрешностей тракта телеизмерений при неравномерной
временной дискретизации, вызванной подавлением кодовой
серий при отказе приемника от декодирования для случая
использования АЦП с АИМ.
При равновероятности всех конфигураций ошибок t-й
кратности вероятность подавления кодовой серии [47]
где P'i — вероятность ошибки i-й кратности в кодовой серии
при отсутствии рассинхронизации распределителей временной
системы телемеханики; Ррас — вероятность рассинхронизации,
обнаруженной приемником; В^обн — число ошибок t-й кратности,
обнаруживаемых (но не исправляемых) приемником; Wi=
= Сп{ — число ошибок t-й кратности.
В этом случае при статистической независимости
подавления кодовых серий вероятность подавления п подряд кодовых
серий определяется выражением (см. § 4.6)
Р[п] = {1-Ртл)Р&- (8-6)
Математическое ожидание числа подряд подавленных
кодовых серий
й=1/(1-Р„0д). (8.7)
Если Т= (&1+2£2+&з)/В — длительность кодовой серии, то
математическое ожидание времени, в течение которого
происходило подавление, Т=пТ.
При отказе приемника от декодирования теряется
информация о значении телеизмеряемых параметров, что равносильно
рассмотрению неравномерного шага временной дискретизации.
Поток отсчетов из-за независимости подавления кодовых серий
является рекуррен-Гным. Закон распределения шага временной
298

дискретизации Гд, кратного Г, с учетом (8.6) имеет вид
оо
РТ (Гд) - J 8 (Гд _ лгГ) (1 - Рпод) Я*"1, (8.8)
где б(...) — б-функция соответствующего аргумента.
В этом случае усредненная среднеквадратическая оценка
погрешности при интерполяционной процедуре восстановления
(напомним, что погрешность от запаздывания от интерполяции
должна быть исключена) определяется выражением (5.151).
Учитывая статистическую независимость шагов временной
дискретизации (рекуррентность потока) и подставляя (8.8)
в (5.151), получаем
V* =--{2 ... 2 VK71, пгТ,..., nM.T)(l-Pm)
— м х
м—\л 1 *х * под; А
K = l «Af-l=1
п —\ п—\ пМ-\~~1)1/2
X •'под •'под ••• 'под / (^•^z
Усредненная оценка погрешности с учетом случайного
момента сравнения при интерполяционной процедуре
восстановления получается после подстановки (8.8) в (5.157) с
учетом (8.7):
(ОО 00
2 ••• 2 V(«.7\ ^.....Лм-.ПХ
"°=1 "m-i=i
X ("о + Пг + ... + пм_,)М{1 -Pmf+l /%д ' - Я^-1 '}'/2 • (8.10)
При экстраполяционной . процедуре восстановления,
воспользовавшись общими выражениями (5.169) и (5.174),
находим
V& = \f,... 2 & ("от, nj,..., пм т) х
.«„=1 «м=1
Х(1-^под)М+1^д1...Рп;д_1}1/2; (8.11)
Vk= | 2 ••• 2 «5,(«/, «хГ,..., пмг)х
м
X (1 -Л„д)м+2 /%д !... рПпо^пм}Ш ■ (8.12)
299

Рассмотрим далее используемый достаточно широко
частный способ восстановления— экстраполяцию нулевого порядка.
При этом М=0 и
/^= U 8~2 ("Л (1 - />под) Р^д1} ' ;
Так как шаг временной дискретизации кратен Г, то удобней
использовать формулы б2, полученные при равномерной
дискретизации, заменив в них Т на пТ (см. гл. 5 и 6), а у\Т — на
величину длительности временного интервала от момента
отсчета до конца кодовой серии плюс Д£ (см. § 8.1). В частности,
для первого канала ТИ (см. рис. 8.1) при ЭНП,
воспользовавшись данными табл. 5.5, получаем
8~2{пТ) = "я^оГ [1 - JRxx{mT + *lT)ds\ =
L 0 J
=^k!1-l/?"K+(2*-+s-)T+A']*}-
4 0
Таким образом, методика определения погрешностей
цифровых измерительных систем базируется на общих моделях
тракта аналого-цифрового преобразования и восстановления
как при равномерной, так и при неравномерной временной
дискретизации.

СПИСОК ЛИТЕРАТУРЫ
1. Пугачев В. С. Теория случайных функций и ее применение к задачам
автоматического управления. М.: Физматгиз, 1962.
2. Вентцель Е. С. Теория вероятностей. М.: Наука, 1962.
3. Свешников А'. А. Прикладные методы теории случайных функций. М.:
Наука, 1968.
4. Баранов Л. А., Бакеев Е. Е. Аналого-цифровые преобразователи
устройств автоматики и телемеханики электрифицированных железных дорог.
М.: Транспорт, 1979.
5. Баранов Л. А., Костырев В. Ф. Оценки вероятности контроля
нормированных параметров при наличии систематических и случайных погрешностей//
Тр. Омкс. ин-та инж. ж.-д. трансп. 1976. Т. 176. С. 22—26.
6. Гитис Э. И., Пискунов Е. А. Аналого-цифровые преобразователи. М.:
Энергоиздат, 1981.
7. Заволокин А. К. Последовательные преобразователи непрерывных ве
личин в числовые эквиваленты. М.—Л.: Госэнергоиздат, 1962.
8. Новицкий П. В., Кноринг В. Г., Гутников В. С. Цифровые приборы
с частотными датчиками. Л.: Энергия, 1970.
9. А. с. 302667 СССР. Индукционный импульсный датчик скорости
электромашинного типа/ Н. И. Куренков, Е. В. Ерофеев, А. С. Егнус// Открытия.
Изобретения. 1971. № 15.
10. Домрачев В. Г., Матвеевский В. Р., Смирнов Ю. С. Схемотехника
цифровых преобразователей перемещений. М.: Энергоатомиздат, 1987.
11. Борзов М. И. Индуктивные преобразователи угла в код. М.: Энергия,
1970.
12. Клебанский Р. Б. Преобразователи кода в напряжение. М: Энергия,
1973.
13. Универсальные электронные преобразователи информации/ В. Б.
Смолов, Е. А. Чернявский, Т. И. Полянская, Б. А. Кудриков. Л.: Машиностроение,
1971.
14. Ефимов В. М. Квантование по времени при измерении и контроле. М.:
Энергия, 1969.
15. Левин Б. Р. Теоретические основы статистической радиотехники.
Кн. I. M.: Советское радио, 1969.
16. Кавалеров Г. И., Мандельштам С. М. Введение в информационную
теорию измерений. М: Энергия, 1974.
17. Лившиц 3. А., Рабинович В. И., Савенко М. В. Численные методы
решения задач оптимального квантования// Автометрия. 1970. № 3. С. 3—13.
18. Стратонович Р. Л., Гришанин Б. А. Ценность информации при
невозможности прямого наблюдения оцениваемой величины// Изв. АН СССР
Техническая кибернетика. 1966. № 3. С. 3—15.
19. Баранов Л. А. Статические погрешности преобразования частоты и
временных интервалов в код// Метрология. 1974. № 7. С. 29—37.
20. Шастова Г. А. Кодирование и помехоустойчивость передачи
телемеханической информации. М.—Л.: Энергия, 1974.
196321' ЦыПКИН Л 3 Те°Рия линейных импульсных систем. М: Физматгиз,
Физматг^зЖУ1963Э* Импульсные системы автоматического регулирования. М.:
301

23. Баранов Л. А. Динамические погрешности аналого-цифровых
преобразователей при случайном входном сигнале// Автоматика и телемеханика. 1974.
№ 1. С. 145—152.
24. Котельников В. А. О пропускной способности «эфира» и проволоки
в электросвязи// Материалы к 1-му Всесоюзному съезду реконструкции дела
связи и развития слаботочной промышленности. Изд-во ред. упр. связи РККА,
1933.
25. Баранов Л. А. Математические модели аналого-цифровых
преобразователей с восстанавливающими устройствами// Автоматика и телемеханика.
1976. № 12. С. 130—135.
26. Березин И. С, Жидков И. П. Методы вычислений. М.: Физматгиз,
1959.
27. Баранов Л. А. Временная дискретизация случайных сигналов с
восстановлением по методу наименьших квадратов/ Моск. ин-т инж. ж.-д. трансп.
М., 1987. Деп. в ВИНИТИ. № 4481—В87.
28. Милн В. Э. Численный анализ. М.: ИЛ, 1951.
29. Горелов Г. В. Нерегулярная дискретизация сигналов. М.: Радио и
связь, 1982.
30. Артомонов Г. Г., Тюрин В. Д. Анализ информационно управляющих
систем со случайным интервалом квантования сигнала по времени. М.:
Энергия, 1977.
31. Кокс Д., Льюис П. Статический анализ последовательности событий.
М.: Мир, 1969.
32. Вентцель Е. С. Исследование операций. М.: Советское радио, 1972.
33. Анго А. Математика для электро- и радиоинженеров. М.: Наука, 1964.
34. Темников Ф. Е., Афонин В. А., Дмитриев В. И. Теоретические основы
информационной техники. М.: Энергия, 1979.
35. Баранов Л. А. Оценки погрешности восстановления сигналов при
нерегулярной дискретизации// Радиотехника. 1983. № 8. С. 41—43.
36. Карпелевич Ф. И. Элементы теорий марковских цепей и массового
обслуживания, их применение в решении транспортных задач. Методическое
пособие. М., МИИТ. 1981. Ч. И.
37. Новоселов О. Н„ Фомин А. Ф. Основы теории и расчета
информационно-измерительных систем. М.: Машиностроение, 1980.
38. Аршинов М. Н., Баранов Л. А. Расчет оценок погрешностей и
помехоустойчивости при временной дискретизации случайных сигналов с
восстановлением по методу наименьших квадратов/ Моск. ин-т инж. ж.-д. трансп.
М., 1987. Деп. в ВИНИТИ. № 6824—В87.
39. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений. М.: Наука, 1971.
40. Баранов Л. А., Лызлов С. С. Анализ точности цифрового измерения
скорости и ускорения поездов// Вестник ВНИИЖТ. 1986. № 6. С. 22—26.
41. Костарев В. Ф., Цыганков В. И. Цифровые измерения в устройствах
железнодорожной автоматики и телемеханики. М.: Транспорт, 1978.
42. Баранов Л. А., Лызлов С. С. Экстраполяционный метод умножения
частоты// Изв. вузов. Приборостроение. 1983. № 4. С. 14—18.
43. А. с. 931515 СССР, МКИ3 В 60 15/30. Устройство для измерения
скорости движения локомотива/ Л. А. Баранов, Я- М. Головичер, С. С. Лызлов,
Д. М. Шмидрик// Открытия. Изобретения. 1982. № 20.
44. .Баранов Л. А. Анализ погрешностей цифровых способов измерения
скорости и ускорения поездов/ Сб. Автоматическое и телемеханическое
управление поездами: Моск. ин-т инж. ж.-д. трансп. М. 1980. Вып. 661. С. 11—40.
45. Тутевич В. Н. Телемеханика. М.: Высшая школа, 1985.
46. Основы автоматики, автоматизация и телеуправление электрических
железных дорог/ И. И. Бенешевич, В. М. Лисицин, В. Я. Овласюк и др.; Под
ред. Н. Д. Сухопрудского. — 2-е изд., доп. и перераб. М.: Транспорт, 1975.
47. Системы автоматического и телемеханического управления
электроподвижным составом/ Л. А. Баранов, Е. В. Ерофеев, В. И. Астрахан и др.;
Под ред. Л. А. Баранова. М.: Транспорт, 1984.

ОГЛАВЛЕНИЕ
Предисловие
Глава 1. Общие сведения о квантовании по уровню и временной
дискретизации аналоговых сигналов 6
1.1. Функции устройств квантования по уровню и временной
дискретизации 6
1.2. Модели сигналов и помех '
1.3. Погрешности при квантовании по уровню и временной
дискретизации И
Глава 2. Принципы построения устройств квантования по уровню
и временной дискретизации 19
2.1. Классификация способов квантования по уровню и временной
дискретизации 19
2.2. Квантование по уровню и временная дискретизация при
промежуточном преобразовании аналогового сигнала во временной
интервал 21
2.3. Квантование по уровню и временная дискретизация при
промежуточном преобразовании аналогового сигнала в частоту . 26
2.4. Квантование по уровню и временная дискретизация в
накопительных аналого-цифровых преобразователях .... 35
'2.5. Квантование по уровню и временная дискретизация в аналого-
цифровых преобразователях считывания 37
2.6. Квантование по уровню и временная дискретизация при
поразрядном кодировании аналогового сигнала 43
Глава 3. Оценки методических погрешностей квантования по уровню 47
3.1. Квазимгновенное квантование по уровню. Оценки методических
погрешностей 47
3.2. Оценки методических погрешностей неравномерного
квантования по уровню 56
3.3. Оценки методических погрешностей квантования по уровню
при промежуточном преобразовании аналогового сигнала в
частоту и временной интервал 59
3.4. Оптимальное неравномерное квантование по уровню ... 69
Глава 4. Временная дискретизация и восстановление непрерывных
сигналов 76
4.1. Модели равномерной временной дискретизации, учитывающие
способ получения цифрового эквивалента 76
4.2. Модели простейших восстанавливающих операторов ... 86
4.3. Восстанавливающие операторы М-го порядка на основе
интерполяционной формулы Лагранжа 93
4.4. Модели восстанавливающих операторов, определенных с
помощью критерия наименьших квадратов 99
303

4.5. Неравномерная временная дискретизация ПО
4.6. Модели потоков отсчетов при неравномерной временной
дискретизации 124
Глава 5. Методические погрешности преобразования сигналов при
временной дискретизации . . 128
5.1. Погрешности преобразования детерминированных сигналов при
равномерной временной дискретизации . . . . . . . . 128
5.2. Погрешности преобразования случайных сигналов, заданных
корреляционными функциями, при равномерной временной
дискретизации 148
5.3. Погрешности преобразования случайных сигналов, заданных
спектральной плотностью, при равномерной временной
дискретизации 169
5.4. Помехоустойчивость преобразования при равномерной
временной дискретизации 174
5.5. Погрешности преобразования случайных сигналов при
неравномерной временной дискретизации 192
5.6. Помехоустойчивость преобразования при неравномерной
временной дискретизации 224
Г л а в а 6. Инженерная методика расчета оценок погрешностей
преобразования случайных сигналов при временной дискретизации и
квантовании по уровню 230
6.1. Расчет оценок погрешностей преобразования случайных
сигналов при временной дискретизации 230
6.2. Расчет оценок помехоустойчивости преобразования сигналов
при временной дискретизации 251
6.3. Расчет оценок погрешностей при равномерной временной
дискретизации случайных сигналов с восстановлением по методу
наименьших квадратов 255
6.4. Математическая модель преобразования аналоговых сигналов
при квантовании по уровню и временной дискретизации. Расчет
погрешностей 270
Глава 7. Методы уменьшения погрешностей преобразования в
системах с частотными датчиками 276
7.1. Методы и модели преобразования частотного сигнала в
цифровой эквивалент 276
7.2. Методы уменьшения статических погрешностей преобразования
при заданном времени преобразования и диапазоне изменения
частоты 279
7.3. Методы умножения частоты 283
7.4. Уменьшение динамических погрешностей преобразования . . 290
Глава 8. Особенности расчета оценок погрешностей цифровых
телеизмерительных систем 294
8.1. Принципы построения математических моделей временной
дискретизации в цифровых телеизмерительных системах . . . 294
8.2. Расчет оценок погрешностей в телеизмерительных системах . . 296
Список литературы 301