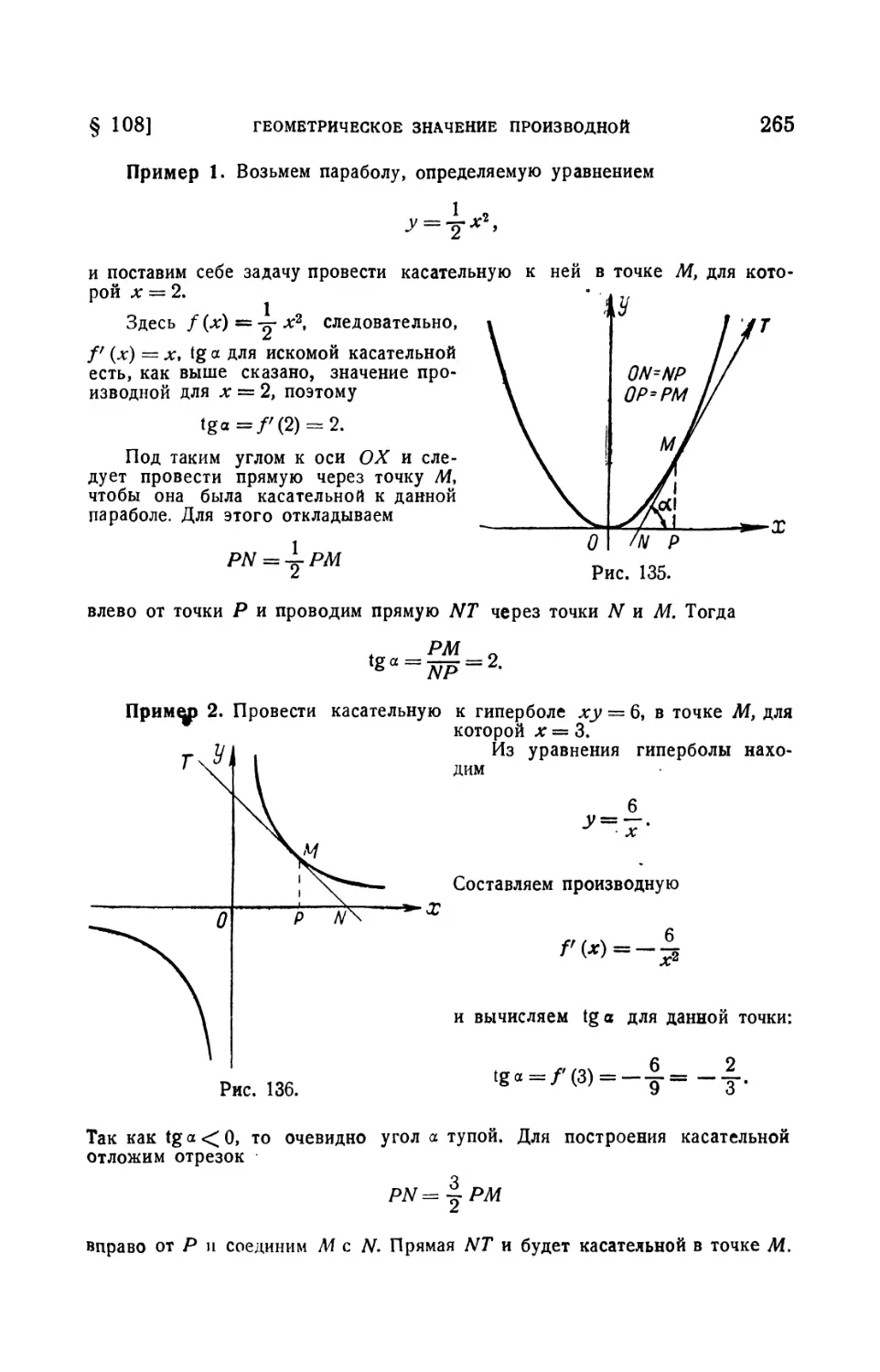
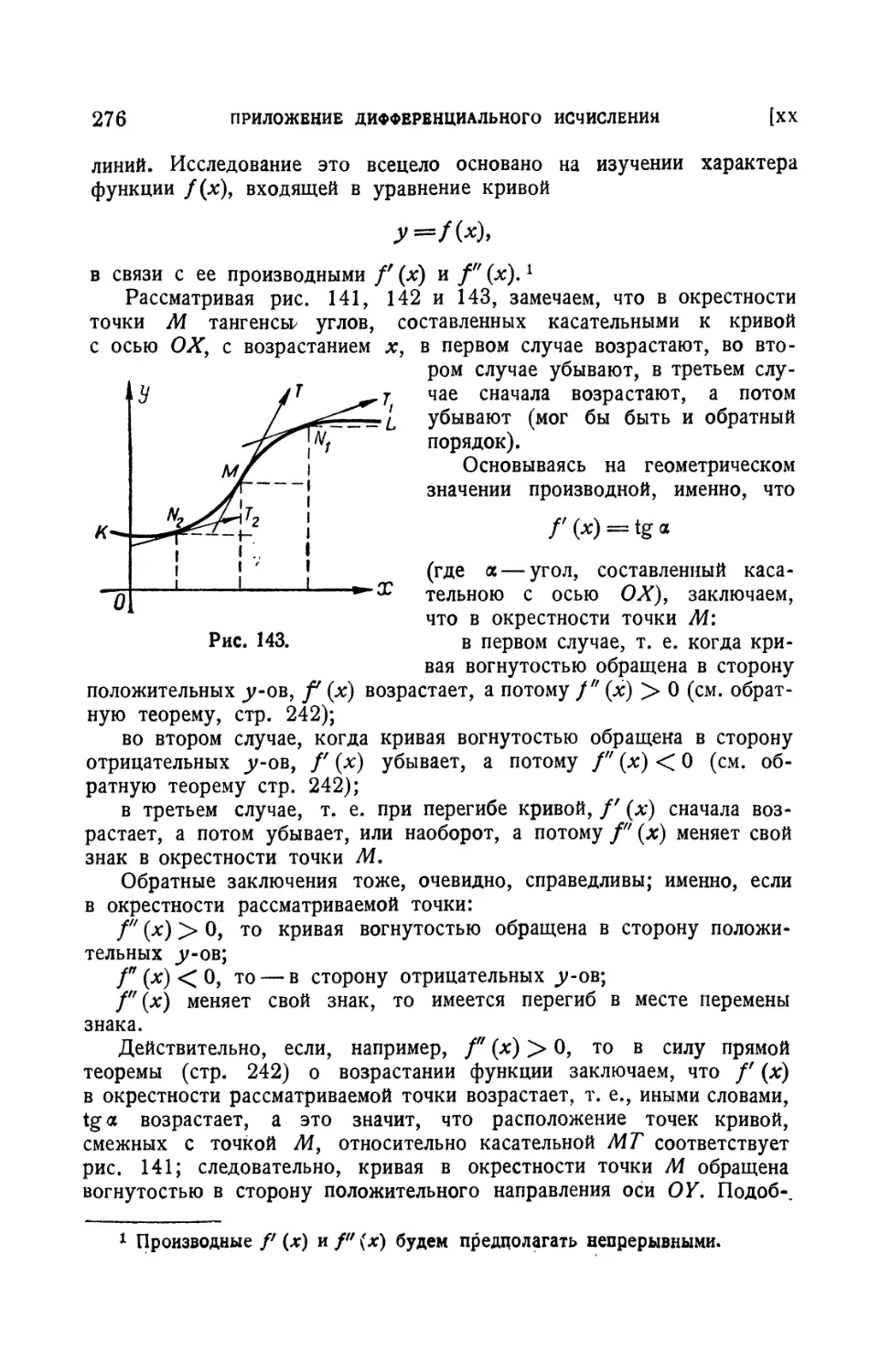
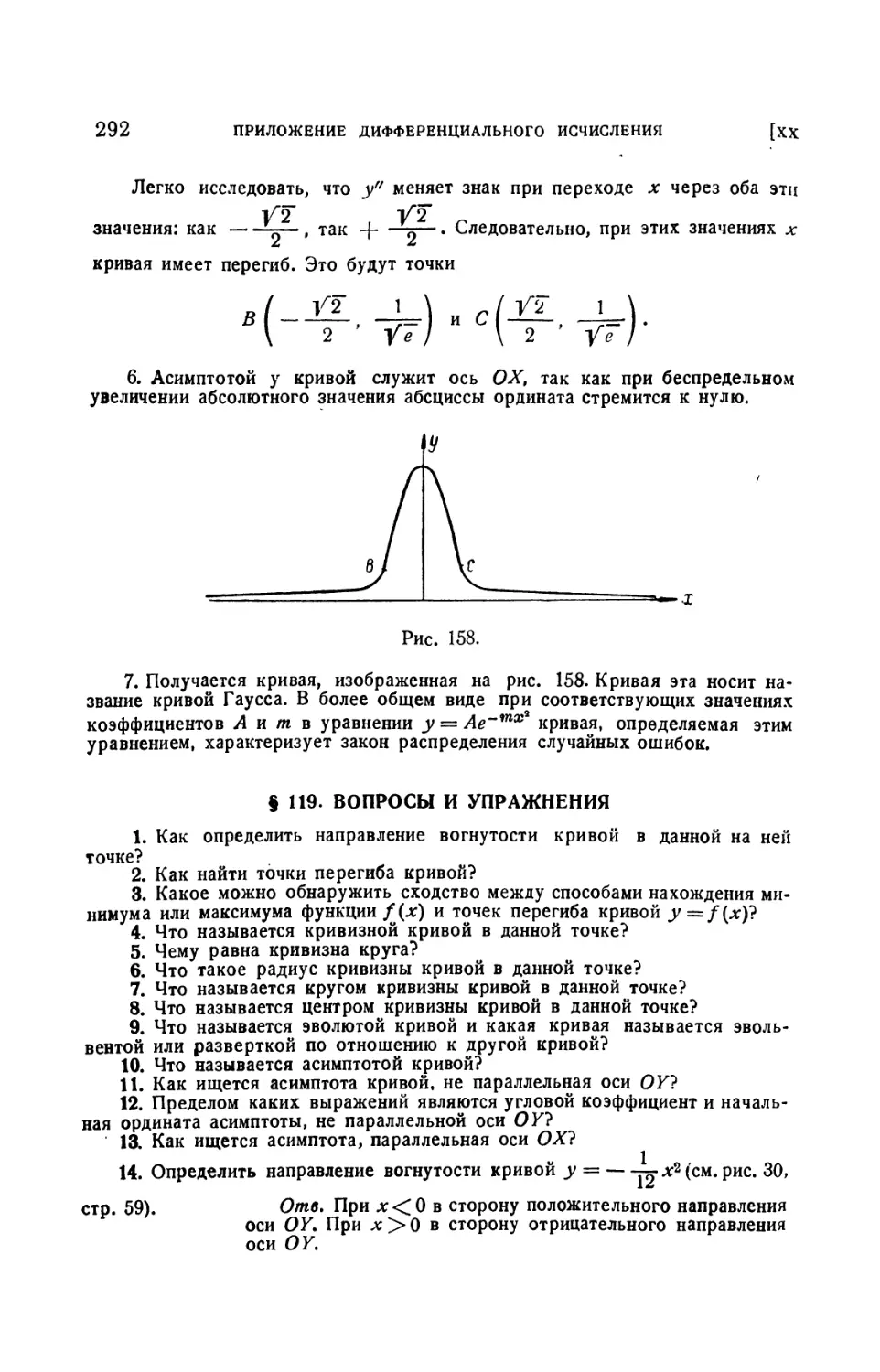
Текст
II. (1. МИХЕЛЬСОН
КРАТКИЙ КУРС
ВЫСШЕЙ
МАТЕМАТИКИ
Допущено Министерством высшего
образования СССР в качестве учебного
(госббир для высших технических
учебных заведений
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1951 ЛЕНИНГРАД
ОГЛАВЛЕНИЕ
Предисловие............................................... * . . 9
Введение ...................................................... П
I. Основы теории определителей
§ 1. Определители 2-го порядка............................ 15
§ 2. Определители 3-го порядка . •........................ 17
§ 3. Разложение определителя по элементам столбца или строки. 19
§ 4. Решение системы трех уравнений 1-й степени с тремя не-
известными ............................................... 22
§ 5. Система однородных уравнений 1-й степени............. 24
§ 6. Вопросы и упражнения................................. 29
II. О проекциях
§ 7. Об отрезках прямых линий......................• • . 31
§ 8. Об углах между прямыми.............................. 32
§ 9. Проекции точки и отрезка на ось..................... 34
§ 10, Теорема о проекции отрезка на ось.................... —
§11. Проекция ломаной линии.............................. 36
§ 12. Проекции точек на плоскость......................... 37
§ 13. Вопросы и упражнения................................ 38
III. О координатах
§ 14. Прямоугольная, или декартова, система координат ...... 40
§ 15. Полярная система координат.......................... 42
§ 16. Основные задачи.................................... 43
§ 17. Вопросы и упражнения................................ 48
IV. Переменные величины и их функции
§ 18. Постоянные и переменные величины ................... 49
§ 19. Общие понятия о функциях . . . •.................... 50
§ 20. Неявные функции..................................... 52
§ 21. Различные типы явных функций........................ 53
§ 22. Круговые функции.................................... 54
§ 23. Вопросы и упражнения................................ 56
V. Графики функций одной переменной и геометрическое значе-
ние уравнения f (х, — 0.
§ 24. График функции =/(х) ............................... 58
§ 25. Геометрическое значение уравнения /(х, J') = 0...... 64
§ 26. Составление уравнений линий по условиям, их определяю-
щим ...................................................... 69
§ 27. Преобразование координат............................ 72
§ 28. Вопросы и упражнения................................ 76
1*
4
ОГЛАВЛЕНИЙ
VI. Прямая линия
§ 29. Первая основная теорема ....***.....................* 78
§ 30. Геометрическое значение коэффициентов а и Ь...........’80
§ 31. Вторая основная теорема (обратная первой)............. 81
§ 32. Примеры на графики линейной функции............... . 82
VII. Задачи на прямую линию
§ 33. Первая группа задач . . •...........................• . 84
§ 34. Вторая группа задач................................... 89
§ 35. Примеры решений задач на прямую линию................. 95
§ 36. Вопросы и упражнения.................................. 98
VIII. Эллипс
§ 37. Уравнение эллипса................................... 100
§ 38. Исследование формы эллипса...............•............102
§ 39. Построение эллипса .................................... —
§ 40. Замечательные точки и линии в эллипсе.................103
§ 41. Диаметры эллипса .....................................105
§ 42. Фокальные радиусы-векторы и директрисы эллипса.......108
§ 43. Уравнение эллипса, отнесенное к вершине...............109
§ 44. Вопросы и упражнения..................................110
IX. Гипербола
§ 45. Уравнение гиперболы...................................112
§ 46. Исследование формы гиперболы......................... 113
§ 47. Построение гиперболы..................................114
§ 48. Замечательные точки и линии в гиперболе...............115
§ 49. Диаметры и радиусы-векторы гиперболы и ее уравнение, от-
несенное к вершине..........................................116
§ 50. Асимптоты гиперболы............................... . 117
§ 51. Свойство асимптот.....................................118
§ 52. Уравнение равнобочной гиперболы, отнесенное к асимпто-
там ................................................... 119
§ 53. Графики гиперболического типа и их приложения ...... 120
§ 54. Вопросы и приложения .................................122
X. Парабола
§ 55. Уравнение параболы...................................124
§ 56. Исследование формы параболы..........................125
§ 57. Построение параболы ................................. —
§ 58. Замечательные точки и линии в параболе...............126
§ 59. Диаметры параболы .................................... —
§ 60. Другие формы уравнений параболы и кривые параболиче-
ского типа................................................ 128
§ 61. Вопросы и упражнения.................................130
XI. Координаты в пространстве
§ 62. Прямоугольные координаты точек.......................132
§ 63. Основные задачи......................................133
§ 64. Вопросы и упражнения................................ 137
XII. Понятие о векторах
§ 65. Основные положения; сумма и разность векторов...........139
§ 66. Произведение вектора на скаляр..........................142
§ 67. Скалярное произведение векторов.........................143
§ 68. Выражение скалярного произведения векторов через их про-
екции на координатные оси.....................................144
§ 69. Вопросы и упражнения....................................146
ОГЛАВЛЕНИЕ
5
XJJL Плоскость и прямая линия в пространстве
§ 70. Уравнение плоскости................................. 147
,§ 71. Уравнения прямой в пространстве.....................153
§ 72. Основные задачи, относящиеся к плоскости и прямой в про-
странстве ................................................ 157
§ 73. Примеры решения задач.............................. 163
§ 74. Вопросы и упражнения.................................167
XIV. Кривые поверхности и линии в пространстве
§ 75. Общая форма уравнений поверхностей и линий в простран-
стве ......................................................169
§ 76. Примеры некоторых поверхностей 2-го порядка.........-170
§ 77. Некоторые типы цилиндрических поверхностей...........176
§ 78. Винтовая линия.......................................177
§ 79. Вопросы и упражнения................................179
XV. Основы теории пределов
§ 80. Предел переменной величины...........................180
§ 81. Основные теоремы о пределе переменной................182
§ 82. Признаки существования предела переменной............187
„ sin х л
§ 83. Предел—-— при х —► 0 и число е........................ —
§ 84. О бесконечно малых величинах.........................191
§ 85. Об эквивалентных бесконечно малых величинах.......... . 194
§ 86. Приращение независимой переменной и функции..........196
§ 87. Непрерывность функции................................197
§ 88. Свойства непрерывных функций.........................199
§ 89. Приближенное вычисление корней алгебраического уравне-
ния .......................................................200
§ 90. Вопросы и упражнения.................................202
XVI. Производная и дифференциал функции
§ 91. Основная задача дифференциального исчисления и опреде-
ление производной........................................ 204
§ 92. Вывод основных формул................................210
§ 93. Дифференциал функции.................................219
§ 94. Вопросы и упражнения.................................224
XVII. Развитие техники дифференцирования функций
§ 95. Производные высших порядков .............................227
§ 96. Дифференциалы высших порядков от функций простого ар-
гумента ...................................................228
§ 97. Дифференцирование неявной функции....................230
§ 98. Параметрическое задание функций......................232
§ 99. Дифференцирование функций, заданных параметрически . . . 234
§ 100. Вопросы и упражнения................................236
XVIII. Свойства функций в связи со свойствами их производных
§ 101. Теорема Ролля.......................................238
§ 102. Формула (теорема) Лагранжа..........................240
§ 103. Возрастание и убывание функций......................242
§ 104. Максимумы и минимумы функции одной переменной .... 244
§ 105. Формула Коши .......................................254
§ 106. Общий метод определения предела отношения двух беско-
нечно малых и бесконечно больших величин...................255
§ 107. Вопросы и упражнения ...............................260
6
ОГЛАВЛЕНИЕ
XIX. О касательных к кривым
§ 108. Геометрическое значение производной...................264
§ 109. Уравнение касательной и нормали к кривой.......... 266
§ 110. Касательная к параболе................................268
§ 111. Касательная к эллипсу.................................269
§ 112. Дифференциал дуги.....................................270
§ 113. Вопросы и упражнения..................................273
свойств кривых линий
§ 114. О направлении вогнутости кривых и о точках перегиба . . . 275
§ 115. О кривизне и радиусе кривизны кривой...............'278*
§ 116. Центр кривизны кривой................................281
§ 117. Асимптоты кривых линий...............................283
118. Исследование формы кривой по ее уравнению............288
§ 119. Вопросы и упражнения.................................292
XXI. Первообразная функция или неопределенный интеграл
§ 120. Основное понятие о неопределенном интеграле..........295
§ 121. Общие приемы интегрирования функций................ 298
§ 122. Интегрирование некоторых типов функций . ............303
§ 123. Вопросы и упражнения.................................314
XXII. Определенный интеграл
§ 124. Задачи, приводящиеся к вычислению предела интегральных
сумм...................................................... 318
§ 125. Понятие об определенном интеграле ................. 321
§ 126. Связь между определенным и неопределенным интегралом 325
§ 127. Свойства определенного интеграла.....................328
§ 128. Вопросы и упражнения-............................... 331
XXIII. Приложение определенных интегралов к геометрии и дру-
гим задачам
§ 129. Вычисление площадей..................................332
§ 130. Вычисление объемов тел............................. 338
§ 131. Вычисление длин дуг..................................342
§ 132. Приложение определенного интеграла к задачам техниче-
ского характера............................................344
§ 133. Понятие о несобственных интегралах...................351
§ 134. Приближенное вычисление определенных интегралов .... 355
§ 135. Вопросы и упражнения.................................362
XXIV. Бесконечные ряды
§ 136. Общие основания.................................. .365
§ 137. Признаки сходимости рядов............................368
§ 138. Признак сходимости знакопеременного ряда.............372
§ 139. Абсолютно и неабсолютно сходящиеся ряды.............373
§ 140. Вопросы и упражнения.................................375
XXV. Формулы Тейлора и Маклорена и их приложение
§ 141. Формула Тейлора для целой рациональной функции......377
§ 142. Формула Тейлора для произвольной функции...........379
§ 143. Разложение в ряд еР..................................383
§ 144. Разложение в ряд sinx................................385
§ 145. Разложение в ряд cosx................................386
§ 146. Формула Эйлера.................................• • . —
§ 147, Разложение в ряд In (1 4-х) , , , ,.................387
ОГЛАВЛЕНИЕ
7
§ 148. Разложение в ряд (I + х)т...........................388
§ 149. Степенные ряды......................................389
§ 150. Гиперболические функции.............................391
§ 151. Вопросы и упражнения ...............................394
XXVI. Дифференцирование функций нескольких переменных
§ 152. Частные производные и полные дифференциалы 1-го по-
рядка функций нескольких независимых переменных .... 395
§ 153. Частные производные и полные дифференциалы высшего
порядка функций нескольких независимых переменных . . . 398
§ 154. Производная и дифференциал функции от нескольких слож-
ных аргументов............................................400
§ 155. Общая формула дифференцирования неявной функции ... 401
§ 156. Нахождение функции по ее полному дифференциалу .... 403
§ 157. Вопросы и упражнения........................' . • . . 407
XXVII. Основы приближенных вычислений
§ 158. Погрешности абсолютные и относительные............409
§ 159. Примеры задач на приближенные вычисления............412
§ 160. Первая группа задач.................................414
§ 161. Вторая группа задач.................................420
§ 162. Вопросы и упражнения.............................. 422
XXVIII. Введение в интегрирование дифференциальных уравне-
ний
§ 163. Понятие о дифференциальном уравнении и его решениях. 424
§ 164. Дифференциальное уравнение 1-го порядка.................427
§ 165. Геометрическое значение дифференциального уравнения 1-го
порядка и его общего интеграла........................... 429
§ 166. Различные формы дифференциальных уравнений 1-го по-
рядка ................................................... 432
§ 167. Уравнения в полных дифференциалах ......................433
§ 168. Уравнения с отделяющимися переменными...............• 434
§ 169. Линейные уравнения..................................... 441
§ 170. Однородные уравнения.............................443
§ 171. Некоторые типы дифференциальных уравнений 2-го порядка. 445
§ 172. Линейные дифференциальные уравнения 2-го порядка .... 451
§ 173. Нахождение частных решений линейного дифференциального
уравнения с постоянными коэффициентами без свободного
члена......................................................453
§ 174. Интегрирование линейного дифференциального уравнения
со свободным членом......................................457
§ 175. Метод вариации произвольных постоянных..................463
§ 176. Вопросы и упражнения................................466
XXIX. Двойные интегралы
§ 177. Двойной интеграл, распространенный на прямоугольник . . . 468
§ 178. Двойной интеграл, распространенный на область, ограни-
ченную криволинейным контуром.......................471
§ 179. Вычисление объемов......................................473
§ 180. Статические моменты, центр тяжести и моменты инерции
плоских фигур............................................476
§ 181. Вопросы и упражнения ...................................478
XXX. Понятие о криволинейном интеграле
§ 182. Криволинейный интеграл как предел суммы ................482
§ 183. Вычисление криволинейного интеграла.....................485
8
ОГЛАВЛЕНИЕ
§ 184. Свойства криволинейного интеграла.....................486
§ 185. Вопросы и упражнения..................................490
XXXI. Задача интерполирования и ее приложения
§ 186. Об интерполировании вообще.........................• 491
§ 187. Формула интерполирования Лагранжа.....................492
§ 188. Линейное интерполирование.............................493
§ 189. Понятие о конечных разностях..........................497
§ 190. Простейшие теоремы о разностях........................498
§ 191. Применение разностей к составлению таблиц значений функ-
ций ..................................................... 500
§ 192. Формула интерполирования Ньютона . • .................503
§ 193. Приложение формулы Ньютона к задаче интерполирования . 505
§ 194. Эмпирические формулы..................................509
§ 195. Вопросы и упражнения............................. . - 510
ПРЕДИСЛОВИЕ
Настоящий краткий курс высшей математики представляет
собой переработку шестого издания моего учебника по общему
курсу высшей математики.
Изменения и дополнения вызваны желанием согласовать мате-
риал руководства с требованиями программы Министерства выс-
шего образования. Однако, имея в виду сохранить прежний характер
руководства, вводящего читателя лишь в самые основы высшего
анализа, я ориентировался на те требования программы, которые
поставлены для втузов с уменьшенным объемом сведений по мате-
матике.
Среди дополнений и изменений, сделанных в новом издании,
отмечу прежде всего включение самых первоначальных сведений
из векторной алгебры. Предпослав изложение их разбору во-
просов о плоскостях и прямых в пространстве, я все же не
нашел возможным обосновать изучение этого отдела на учении
о векторах» Я считал рискованным в столь кратком курсе высшей
математики, каким является настоящее руководство, уклониться от
координатного метода изложения всего комплекса сведений по ана-
литической геометрии. Тем не менее я не мог и оставить элементы
векторной алгебры вовсе без всякого их дальнейшего применения.
Поэтому, продолжая развивать и в геометрии в пространстве преж-
ний координатный метод, я все же счел необходимым приводить и
векторные формы решения отдельных вопросов. Этим я надеялся
избежать резкого и, быть может, на первых порах затруднитель-
ного для учащихся перехода к векторному изложению и вместе
с тем рассчитывал постепенно приучить их к новой форме трак-
товки изученных уже ранее вопросов.
Переработке подвергся отдел об определенном интеграле.
г редпослав этому вопросу три различные задачи, приводящие
к пределу интегральных сумм, я далее веду изложение определен-
ного интеграла как предела такой суммы. Конечно, полной стро-
гости я не мог осуществить в изложении этого вопроса, но пола-
гаю, что отчетливость и целеустремленность основной задачи
интегрального исчисления от такого метода изложения значительно
выигрывают.
10
ПРЕДИСЛОВИЕ
Введены мною также и краткие сведения об определителях
второго и третьего порядка, которые я затем и применил в отделе
аналитической геометрии. Включено в круг вопросов и нахождение
истинных значений некоторого вида функций, а также изложение
основ криволинейных интегралов.
Включены в курс и другие вопросы не столь основного харак-
тера. Должен также отметить, что при изложении вопросов, отно-
сящихся к аналитической геометрии, я несколько усилил роль теории
проекций. Во всем же остальном, в структуре и форме изложения,
я сохранил характер предыдущего издания.
Н. Михельсон
ВВЕДЕНИЕ
В ряду дисциплин, знание которых необходимо всякому работнику,
будь то квалифицированный специалист или просто рядовой работник,
математика занимает исключительное место по значительности охваты-
ваемой ею области применения. Всякое явление, изучаемое с коли-
чественной и ’даже с качественной стороны, неизбежно ведет
к применению математических расчетов, хотя бы самых простых
арифметических.
Чем проще количественные соотношения изучаемых нами явлений,
тем проще и область математической дисциплины, обслуживающей
эти соотношения.
Арифметика и элементарная геометрия, алгебра и тригонометрия
отвечают на огромное количество вопросов, затрагивающих число-
вые соотношения между величинами, но более сложные соотношения
все же не поддаются исследованию при помощи этих элементарных
отделов математики.
Роль высшей математики и заключается в применении ее к ис-
следованию количественных соотношений в тех случаях, когда тре-
буется более совершенный метод и элементарная математика оказы-
вается уже бессильной.
Подобно тому, как в производстве для окончательной выделки
фабриката требуются более совершенные приемы и более чувстви-
тельные приборы, так и во всякой науке, в частности в математике,
Для более глубоких исследований требуются более совершенные
методы и более чувствительный аппарат. Таким методом и является
высшая математика с ее главнейшими аппаратами — аналитической
геометрией, дифференциальным и интегральным исчислениями.
Источником математического анализа вообще является окру-
жающая нас жизнь с ее многообразными явлениями, подчиненными
определенным числовым соотношениям, Непосредственных источников.
12
ВВЕДЕНИЕ
на базе которых создана высшая математика, можно назвать два.
Первый-—это понятие о переменной величине, второй — понятие о ее
пределе. Вне первого не существует второго, вне второго нет высшей
математики.
Казалось бы, что понятие о переменной величине не является
неотъемлемым элементом только высшей математики: алгебра, геоме-
трия и тригонометрия уже знают его; однако в то время как в эле-
ментарных отделах математики переменная появляется лишь в отдель-
ные моменты исследования — в высшей математике она является
основным объектом изучения, составляет главное содержание пред-
мета.
Высшая математика берет свое начало со времени открытия
в XVII веке новых методов математического анализа. Эти методы
были вызваны все нарастающей потребностью разрешить практиче-
ские задачи, которые ставила человечеству окружающая его жизнь—-
прогресс всевозможных форм производства.
Основоположниками этих новых математических методов иссле-
дования, оказавшихся столь могучими, что они позволили легко
разрешать огромное количество нерешенных до того времени на-
сущных задач, были: Декарт (1696—1750), создавший метод ана-
литической геометрии, Ньютон (1642—1727) и Лейбниц (1646—
1716), создавшие метод дифференциального и интегрального исчи-
слений.
С этого времени началось необычайно бурное развитие мате-
матического анализа, направленного как в сторону углубления но-
вых понятий, так и в сторону расширения области применения
новых методов и получения новых достижений. В этой общей работе
значительная, а нередко и первенствующая, роль принадлежит рус-
ским ученым.
Россия включилась в общую работу по развитию новых матема-
тических методов вскоре по возникновении их, с момента основания
в России высшего научного учреждения — Петербургской Академии
Наук (1725 г.). С этого времени Академия Наук являлась и в на-
стоящее время является мировым центром научных достижений, в том
числе и в области математики.
Первое имя, которое необходимо при этом упомянуть, — это имя
Леонарда Эйлера (1707—1783). Еще 19-летним юношей он приехал
в Петербург и принял деятельное участие в научной работе Ака-
демии. С этого времени он полностью связал с нею свое имя,
ВВЕДЕНИЕ
13
Россию сделал Своей второй родиной. Имя этого великого человека
может не быть упомянуто даже в самых кратких курсах высшей
математики. Первенствующая, ведущая роль его в области математики
признавалась всем миром.
F Второй гигант математической мысли — это профессор Казанского
Университета Николай Иванович Лобачевский (1793—1856), смело
порвавший с двухтысячелетней традицией обосновывать геометрию
непременно на постулате Эвклида о параллельных линиях, и со-
здавший новую, логически безукоризненную геометрию на основе
допущения, что через данную точку можно провести, по крайней
мере, две параллельные прямые. Его идея была подхвачена иностран-
ными учеными и вызвала у них продолжение исследований в том же
направлении.
Среди русских математиков того же времени следует отметить
члена Петербургской Академии Наук — Михаила Васильевича Остро-
градского (1801—1862), с именем которого, помимо многочислен-
ных важных его работ, связан известный даже начинающим изу-
чать высшую математику метод интегрирования и знаменитая формула
интегрального исчисления, имеющая огромное приложение не
только в математике, но и в прикладных науках и носящая
его имя.
Россия дала миру и первую выдающуюся своими учеными тру-
дами женщину математика, Софью Васильевну Ковалевскую (1850-т-
1891), научные заслуги которой были признаны Петербургской
Академией Наук, избравшей ее за выдающуюся работу о вращении
твердого тела своим членом-корреспондентом.
Неизгладимый след в истории мировой науки оставил после себя
академик Пафнутий Львович Чебышев (1821—1894), один из вели-
чайших представителей математической мысли, сочетавший свои
огромные достижения с потребностями практической жизни. Напра-
вление его величайших достижений лучше всего характеризуется его
Же собственными словами: „Сближение теории с практикой дает
самые благотворные результаты, и не одна только практика от этого
выигрывает, сами науки развиваются под влиянием ее, она открывает
нм новые предметы для исследования, она предлагает вопросы,
существенно новые для науки, и, таким образом, вызывает на изы-
скание совершенно новых методови.
Чебышев создал вокруг себя целую школу русских математиков
Которые продолжали его работу и также составили славу русской
|4 ВВЕДЕНИЕ
математической науки: А. Н. Коркин, А. А. Марков, А. М. Ляпунов,
А. Н. Крылов и многие другие.
Огромный размах получила математика после Великой
Октябрьской социалистической революции. Впервые были созданы
крупные математические научно-исследовательские институты. Со-
ветская математика заняла ведущее место в мировой науке. Вы-
дающиеся советские математики успешно развивают новые направ-
ления в математике и применяют их в практике социалистического
строительства.
I ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
§ 1. ОПРЕДЕЛИТЕЛИ 2-го ПОРЯДКА
Пусть нам дана система уравнений 1-й степени с двумя неизвест-
ными
а2х -ф- Ь%у — с2. '
Рсп.ая се по известным правилам элементарной алгебры, находим
следующие выражения для неизвестных:
% _ С1^2 — ___ й\С^ — Д2С1 /2)
ахЬ2 — агЬ2 — '
Рассматривая полученные формулы, легко заметить, что структура
знаменателя и числителей у них однообразная. Именно, знаменатель
можно получить следующим образом.
Возьмем произведение
Переставим значки у букв и, изменив при этом знак у произве-
ЛСПИЯ, получим
— а2Ьх.
Сложив эти два результата, мы и найдем знаменатель формул (2).
Числители в формулах (2) составляются подобным же образом
из произведений
cb и ас.
вообще выражение вида А1В2 — Ac>Blt составленное из четырех
чисел
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
ь
А, в.
^2, ^2
называется определителем, составленным из этих чисел^ и обо-
значается следующим образом:
^2? ^2
Таким образом,
= A J^2 А2В1,
Числа, входящие в определитель, называются его элементами.
В установленном условном обозначении, они группируются в строки
и в столбцы.
Определитель, заключающий в себе две строки и два столбца,
носит название определителя 2-го порядка.
В силу установленного, можно сказать, что и в формулах (2)
числители и знаменатели представляют собой определители 2-го по-
рядка; именно:
^1^2 ^2^1 —
#2> ^2
<?i, Ь1
^2? ^2
6Zj^2 ^2^1 —
—
#1, сг
^2’ СЧ
а потому
образом:
решения
системы (1) можно представить следующим
ci, bi
с2*
alf bt
b^
U\t
Co
«b *1
#2> b%
Легко заметить, что знаменателем значений обоих неизвестных
х и у служит определитель, составленный из коэффициентов при
неизвестных в системе (1); он называется определителем системы,
а числителями являются определители, получающиеся из определителя
системы путем замены соответствующих коэффициентов при неиз-
вестных свободными членами.
Пользуясь формулами (4), можно сразу найти решения системы
двух уравнений 1-й степени с двумя неизвестными.
Пример 1. Решить систему уравнений
2х — Зу — 9
5х + 4у = 11.
ОПРЕДЕЛИТЕЛИ 3-ГО ПОРЯДКА
§ 2J
По формулам (4) находим
9, —3 I
_ 11, 4 1_9-4— 11-(— 3)_69_о
” I 2,-3 I “ 2-4 —5-(—3) “23
I 5, 4 I
| 2, 9 |
__ I 5, 11 I _ 2.11-5-9 _ — 23_
" I 2, — 3 1“ 2-4 — 5-(— 3) — 23
15, 4 I
§ 2. ОПРЕДЕЛИТЕЛИ 3-го ПОРЯДКА
Обобщая понятие об определителе на случай большего числа
элементов, возьмем произведение трех чисел
д1^2^8*
Далее, как и в предыдущем случае, составим другие произве-
дения, последовательно переставляя два каких-нибудь значка и меняя
при этом каждый раз знак произведения. Тогда составятся сле-
дующие шесть произведений:
а1^2С3>
--dib^C^
Сумма всех таких шести произведений называется определителем,
составленным из девяти элементов
^1? 1?
&2’ ^2> С2
а& && С3
Сумма эта обозначается следующим образом:
так что
bv Ci
#2’ ^2> ^2
а3> ^3> сз
а& &2> ^2 =
аз, с3
= Й1^3С2 Ч“" a2^1CZ 4“ а$1С2-------^8^2*Te (5)
2 Зак. 2116. Н. С. Михельсон.
1S
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
Этот определитель заключает в себе три строки и три столбца
и соответственно этому называется определителем 3-го порядка.
,(2) Нижеследующее правило дает возмож-
иость легко развернуть в виде многочлена
z zfe? и вычислить определитель 3-го порядка (пра-
вило Саррюса). А именно, выписав элементы
чх ✓ \ / ^/(2? определителя в том порядке, как они распо-
ложены в самом определителе, добавим снизу
/ х /Ах/ чх еще две строки, 1-ю и 2-ю. Затем составим
Z 3й Ч^х 4 • шесть произведений из элементов, располо-
/ / к х х женных по диагоналям, как указано на ри-
®2» V/ сунке (рис. 1).
/ 4 Если первые произведения взять со знаком
рис j ' плюс, а вторые со знаком минус и сложить их,
то и получится развернутое в виде много-
члена выражение определителя.
Пример 2. Вычислить определитель
Выписываем пять строк
1, —2, О
—3, 2, 1,
2, 3, —3
1,-2, О
—3/ 2, 1
2, 3, —3
1, -2, О
—3, 2, 1
и составляем произведения членов, расположенных по диагоналям; тогда
получаем
1,-2, О
-3, 2, 1
2, 3,-3
= 1.2 • (—3) + (—3) • 3 • 0 + 2 • (—2) • 1— 2-2.0— 1 -3-1 —
— (—3) • (—2) • (—3) = — 6 — 4- 3 + 18 = 5.
Пользуясь правилом Саррюса, легко проверить следующие
свойства определителей 3-го порядка. Предоставляем эту проверку
сделать читателям.
1. Определитель не меняет своей величины, если строки сде-
лать столбцами, а столбцы строками, не меняя их номеров.
2. От перестановки двух каких-нибудь столбцов или строк
определитель меняет знак.
3. Определитель равен нулкг.
а) если все члены одного столбца или строки равны нулю*,
$ разложение определителя по элементам столбца или строки 19
ли все члены одного столбца или строки соответственно
°' членам другого столбца или строки}
Рав’ ч если члены одного столбца или строки соответственно
опорциональны членам другого столбца или строки.
пР 4 Определитель не меняет своей величины, если к элементам
какого-либо столбца или строки прибавить соответствующие
элементы другого столбца или строки, умноженные на одно и
то же число.
§ 3. РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПО ЭЛЕМЕНТАМ СТОЛБЦА
ИЛИ СТРОКИ
Группируя попарно шесть членов развернутого выражения (5)
определителя 3-го порядка и вынося при этом общие множители
за скобки, мы приходим к более компактной форме развернутого
определителя. А именно:
«1, *1,
Ь»
аз> ^з?
С2
^3
— ^1^2^3 ^1^3^2 ~4 ^2^8^1 ^2^1^3 4" ^3^1^2 ^8^2^1—
— ^3^2) ^2 (^1С8 ^3С1) 4” а3 (^1С2---^2С1) =
^2? С2
bv сх bx, сх
b с b с
^3> с3 и2’ с2
Последняя формула носит название формулы разложения опре-
делителя по элементам столбца, в данном случае 1-го, так как
множителями при определителях 2-го порядка являются элементы
а1, аъ аз первого столбца.
Группируя члены формулы (5) иначе, можно получить подобные
же разложения определителя по элементам другого столбца. Так,
например, тот же определитель можно преобразовать следующим
образом, вынося за скобки члены 2-го или 3-го столбца.
аъ сх
аЪ ^а,
Й3> ^3, сз
а^, с%
с^
ai> q
6Zg, c^
ax, cx
6Z2> ^2
— cx
^2 Ьх
. Сл -
аз> b$
4~cs
bx
a2>
Подобным же образом, вынося за скобки в выражении (5) члены
-й, 2-й или 3-й строки, получим следующие разложения определителя
2*
20
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
[1
по элементам строк:
«1, ^i,
Яд, ^2’
^3? ^3’
С1
^2> С2
а2’ С2
а3, с3
а2,
а3, Ь2
%
= — «2
ai>
6Zg, ftg
ь1, С1 а1> Cj bt
= а3 1>2, ^2 — &3 ^2> ^2 4~сз а to to
Введя для сокращения письма обозначения:
а1?
а2’ С2
а& ^з> СЪ
^2> C2 bu Cl bi, Cl
^3> C3 — A1} bg, c3 — a2, ^2> C2 — ^3
6Z2> c2 Cj — ^2» Qu, ei = B3 (6)
a& C3 a3, c3 6Z2, ^2
^2? Ь2 ai9 a19
^3 = a3, b3 = ^2» a2, b2 == ^*3?
можно предыдущие разложения по
представить в следующем виде:
Д = а2А2 4“ aQAQ
Д = 4“ Ь2В2 4~ bzB*
= ^1^*1 + ^2^*2 4“ ^3^3
элементам столбцов и строк
Д===: &]Ai —
Д = а2А2 4- Ь2В2 с2С2 (7)
Д = а$А3 4" ^з^з + сз^з
Нетрудно заметить, что каждый из определителей 2-го порядка
в формулах (7) получается из основного определителя 3-го по-
рядка, вычеркиванием из него членов того столбца и строки, на пере-
сечении которых находится элемент определителя, стоящий перед
определителем 2-го порядка в качестве множителя. При этом эти
определители берутся со знаком плюс или минус сообразно тому,
будет ли сумма номеров вычеркиваемого столбца и строки четная
или нечетная. Так, определитель 2-го порядка С2 получается вычер-
киванием 2-й строки и 3-го столбца. Так как сумма номеров вычер-
киваемых строки и столбца равна нечетному числу (24~3 = 5), то
он и берется со знаком минус.
Определитель, получающийся из основного определителя путем
вычеркивания какого-нибудь столбца и строки, называется минором
данного определителя.
§ 3] РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПО ЭЛЕМЕНТАМ СТОЛБЦА ИЛИ СТРОКИ 21
разложение определителя по элементам столбца или строки
ожет служить удобным средством для вычисления определителя,
что иллюстрируется следующим примером.
2,-1, 3
Пример 3. Разложить определитель 1, 2, -1 3, 6, —2 по элементам 2-го
столбца и вычислить этот определитель.
2, —1, 3
1, 2, -1
3, 6, -2
1,
3, -2
= 1
2, 3 1 12, 3
3. -2 Г6, I 1, —1
= (— 2-f-3)-f-2 • (— 4 —9) — 6 • (—2—3) = 5.
Если при этом с помощью четвертого свойства определителя
(см. стр. 19) предварительно преобразовать определитель так,
чтобы в одном из столбцов или строк большинство элементов
обратилось в нуль, то последующее разложение определителя по
элементам этого столбца или строки еще более упростит его
вычисление.
Поясним это на том же примере, а именно: прежде чем разлагать опре-
делитель по элементам столбца или строки, прибавим к элементам 1-го
столбца соответствующие элементы 3-го столбца; тогда, на основании чет-
вертого свойства, найдем, что
КЗ 1 *4 СО — 5,-1, 3
1, 1 ci 0, 2, -1
3, 6, -2 1, 6, -2
Далее, пользуясь тем же свойством, умножим члены 3-го столбца на 2
и прибавим их к членам 2-го столбца; тогда
5, —1, 3
О, 2, —1
1, 6,-2
5, 5, 3
О, 0, -1
1, 2, —2
Последний определитель теперь
тогда два первых члена разложения
разложим по элементам 2-й строки,
обратятся в нуль и мы найдем, что
5, 5, 3
О» 0, — 1 = 1 •
1, 2, —2
5, 5
1, 2
= 10 — 5 = 5.
Для дальнейшего весьма важно отметить, что если в первой из
формул (7) множители а19 а3 заменить элементами другого
какого-нибудь столбца, например Ь19 £3, т. е. составить выра-
жение
4“ ^9^2 ^8^8»
22
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
[1
то такая сумма обращается в нуль. В самом деле, замена чисел
«1, аъ> числами bv &з ведет к тому, что в определителе Д
члены 1-го столбца делаются равными членам второго столбца;
а такой определитель в силу свойства 36 (см. стр. 19) равен нулю.
К такому же результату нетрудно притти и в других случаях
подобной же замены. Таким образом, например, можно притти
к следующим формулам:
4“ ^2^2 4“ ^08 == О’
f 1Л1 4 М2 4“ С3^3 = 9,
4“ а2&2 4“ ^3 = 9»
(8)
и т. п.
§ 4.РЕШЕНИЕ СИСТЕМЫ ТРЕХ УРАВНЕНИЙ 1-й СТЕПЕНИ
С ТРЕМЯ НЕИЗВЕСТНЫМИ
Положим, нам требуется решить следующую систему уравнений:
а1х 4" &1У 4" с1г —
а2Х + М4“С2г = ^2,
«3Х + М4-^ = ^8-
(9)
Как известно из элементарного курса алгебры, решение системы
нескольких уравнений сводится к постепенному исключению сначала
одного, затем другого и т. д. неизвестного, с тем, чтобы наконец
получить уравнение, содержащее одно только неизвестное.
С помощью же определителей такой процесс исключения можно
сделать сразу. А именно, пользуясь указанными выше обозначе-
ниями (6), умножим обе части уравнений соответственно на Ах, А2,
А3 и сложим полученные равенства. Тогда получим
(Ml 4“ М2 4” °3^з) Х 4" (^И1 4" ^2^2 4“ ^з^з)У 4-
4- 4- Ма4~ Ms)г — 4- ^2а2 4- ^з^з» (19)
Но
4" а2&2 4 а8^3 = Д 9 СМ. формулу (7),
4“ ^2^4“ ^3^3 = 9, СМ. формулу (8),
С1А14"М2 + Мз =9, СМ. формулу (8).
(11)
Сумма же, стоящая в правой части уравнения (10), очевидно
представляет тот же определитель Д, только в нем элементы
1-го столбца, т. е. коэффициенты при х, заменены свободными чле-
нами. Обозначим эту сумму знаком Дф; тогда уравнение (10), в силу
равенств (11), примет вид
Д • х — Д .
о?
§ РЕШЕНИЕ СИСТЕМЫ ТРЕХ УРАВНЕНИЙ С ТРЕМЯ НЕИЗВЕСТНЫМИ 23
Подобным же образом, умножая обе части уравнений системы (9)
на В3, а затем на Clf С2, С3 и складывая эти уравнения,
придем еще к двум подобным же уравнениям, и система (9) таким
образом заменится системой новых трех уравнений
Д • х = Дш,
♦ Д • у — Др (12)
Д • z = Д2.
Если Д не равен нулю, то из полученных уравнений находим
значения неизвестных
Подробно эти же формулы представляются так:
х
Ьь ^2» ^2> с2 ^3» ^3> с3 — 1/ . аъ ду ci #2» ^2> с2 а3> ^3> с3 . *7 . 01, bp di #2» ^2» ^2 «3. ^3» &3
^1» С1 #2> ^2» с2 а3> &3’ с3 У «1> bl, «I #2» ^2> ^2 а3> с3 £ — 0Ь by Ci a2t ^2» с2 а3» ^3» с3
Таким образом, подобно тому, как это имеет место для системы
двух уравнений с двумя неизвестными, решения системы трех
уравнений 1-й степени с тремя неизвёстными, при посредстве опре-
делителей, получают значительную простоту и закономерность.
В случае, если определитель системы не равен нулю, значения
неизвестных оказываются вполне определенными и равными частным
от деления двух определителей: делителем у всех их служит опре-
делитель, составленный из коэффициентов при неизвестных; он
называется определителем системы; числителями же являются опреде-
лители, получающиеся из определителя системы путем замены коэф-
фициентов при неизвестных соответственно свободными членами.
В случае, когда определитель системы равен нулю, система
Уравнений может вовсе не иметь решений (уравнения оказываются
несовместными), или же иметь бесчисленное множество решений.1 *
Пример 4. Решить систему уравнений
2х — Зу + г = О,
— Зх + 4у — 22 = 1,
5х у 4z = — 3.
1 Подробное исследование этого вопроса см. в курсе И. И. П р и в а-
порВ а — Аналитическая геометрия, в главе „Определители 2-го и З-го
24
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
Для решения этой системы надо сначала составить и вычислить опреде-
литель системы Д, а затем и определители
2, —3, 1
—3, 4, —2
5, 1, 4
2, 0, 1
-3, -1, —2
5, 10, 4
0, 0, 1
1, —1, -2
—3, 10, 4
= 1.
I 1,-1
1-3, 10
= 7
(при вычислении определителя сначала сумма членов 1-го и 3-го столбцов
сложена с членами 2-го столбца, а затем члены 3-го столбца, умноженные
на —2, прибавлены к членам 1-го столбца)
0, -3, 1 0, 0, 1
1, —2 I
д® — 1, 4,-2 = 1, -2, —2 —• -3, 13 1= ’
-3, 1, 4 -3, 13, 4
2, 0, 1 0, 0, 1
-3, 1, —2 = 1, 1, —2 = 1
5, -3, 4 —3, -3, 4
(члены 1-го и 2-го столбцов оказались равными),
2, —3, 0 2, -3, 0
^Z — —3, 4, 1 = —3, 4, 1 =
5, 1, -3 -4, 13, 0
2, -3
-4, 13
= -(26—12) = -14.
После этого по формулам (10) находим х = 1, у = О, z = — 2.
§ 5. СИСТЕМА ОДНОРОДНЫХ УРАВНЕНИЙ 1-й СТЕПЕНИ
Однородным уравнением 1-й степени называется уравнение без
свободного члена.
Рассмотрим сначала частный случай такой системы уравнений
1-й степени с тремя неизвестными, а именно систему двух одно-
родных уравнений 1-й степени с тремя неизвестными. Случай,
к рассмотрению которого мы переходим, таким образом, предста-
вляет следующая система:
а2х4-<>йу4-с9г = 0. 1 7
Совершенно ясно, что такая система является неопределенной.
Она допускает очевидные решения х = 3/ = г = О и, кроме того,
бесчисленное множество других. Чтобы выяснить характер решений
этой системы, исключим последовательно из уравнений (14) две
неизвестные, например х и у.
Для исключения у умножим первое из этих уравнений на Ь2,
а второе на — и сложим полученные результаты. Получим
(afiz — а2Ь^ х + (b2cx — b^) z = О
или
(/4^2 ^2^1) % — (^1^2-^2^1) (15)
§ 5]
Для
на и
или
СИСТЕМА ОДНОРОДНЫХ УРАВНЕНИЙ 1-Й СТЕПЕНИ 25
исключения х умножим первое уравнение на —а2, а второе
опять сложим их, тогда
— а2^) у -|- (ajC2 — а^) г = О
(«А — а^у — — (а^ — а2с^г. (16)
Легко заметить, что коэффициенты в уравнениях (15) и (16)
оказываются теми определителями, для которых установлены обо-
значения (6). Поэтому, эти уравнения можно переписать так:
C3x = A3z и C3y = B3z. (17)
Из этих уравнений вытекает, что:
I. Если ни один из определителей А3, В3 и С3 не равен нулю,
то из последних уравнений находим
= А
С3
X Z X у Z
/43 С3 Л3 В3 С3 ’
(18)
т. е. что в этом случае все решения системы (14) пропорциональны
определителям Л3, В3 и С3.
Определители эти легко составить следующим образом: выпишем
коэффициенты при неизвестных в порядке их расположения в две
строчки
«1, bu clf
^2*
Тогда нетрудно видеть, что определитель Л3 получается, если,
вычеркнув 1-й столбец, составить определитель из оставшихся ко-
эффициентов; определители В3 и С3 составляются подобным же
образом, если вычеркнуть соответственно 2-й или 3-й столбец; при
этом для получения определителя В3 необходимо ’ определитель,
составленный из оставшихся элементов, взять со знаком минус.
II. Если один из определителей равен нулю, например Л3 = 0,
то, как это видно из уравнений (17), х = 0, a ~- = ~, т. е. одно
#3 ^3
из неизвестных равно нулю, а два других пропорциональны опреде-
лителям В3 и С3.
П1. Если два из определителей равны нулю, например А3 = В3 =
= 0, то из уравнений (17) следует, что x—y = Q, a z произвольно,
т- е. тогда два из неизвестных равны нулю, а третье может иметь
любые значения.
Случай, когда все три определителя равны нулю, А3 = В3 =
=5 С3 = о, приводится к тому, что коэффициенты при неизвестных
одного уравнения соответственно пропорциональны коэффициентам
Другого, = у = так что два уравнения системы (14) сводятся
к одному.
26
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
[I
Пример 1. Решить систему однородных уравнений
Зх + У — 5z = О,
2х + 3у— z = 0.
Составим и вычислим определители Л3, В3, С3.
Для этого, выписав коэффициенты при неизвестных
3, 1, —5
2, 3, — 1
будем вычеркивать последовательно столбцы; тогда
. I1’”5 = И, В3 = -|3'"5 = — 7, С3 = о’<1 = 7-
| 3, — 1 1 2, — 1 2, 3 |
Ни один из этих определителей не равен нулю, следовательно =
у Z
= — > т« е« х> У> z пропорциональны числам 14, —7‘И 7 или, что то
же, 2, — 1, 1. Итак
х = 2&, у = — kt z = k,
где k—коэффициент пропорциональности — произвольное число (включая
и k — 0).
Пример 2. Решить систему однородных уравнений
Зх— 4y4-2z = 0,
Зх + у + 4z = 0.
Вычисляем определители А3, В3 и С3
я — 4, 2 3, 2 I 3, — 4 I
Аа= 1,4 =“18’ Вз = ~ 6, 4 Г0, Сз== 6, 1 Г27’
Определитель В3 = 0,
следовательно у = 0,
х __ z .
а —И8 “27’
т.
пропорциональны числам —18 и 27 или числам —2 и 3. Таким
система имеет следующие решения:
е. х и z
образом,
х = — 2k, z = 3k, у = 0,
где k — коэффициент пропорциональности — произвольное число (включая
£ = 0).
Рассмотрим теперь систему трех однородных уравнений 1-й
степени с тремя неизвестными:
аус + &1У ciz — 0’
а2х Ь2у 4-^ = 0,
а3х + bay 4- caz = 0.
(19)
Система эта отличается от системы (9) лишь тем, что все сво-
бодные члены уравнений — д2 = д3 = 0. В этом случае опреде-
лители
^9 &у
СИСТЕМА ОДНОРОДНЫХ УРАВНЕНИЙ 1-Й СТЕПЕНИ
§ 5]
27
как в этих определителях все члены одного из столбцов равны
* для рассматриваемод системы
Та лю7 Таким образом, уравнения (12)
приводятся к
Д . х — 0, Д - у = 0,
Д . Z = 0.
(20)
Из этих уравнений вытекает, что если Д=£0, то система (19),
кроме очевидного решения х =у = z = 0, не имеет других решений.
Однако, если предложенная система однородных уравнений такова,
что определитель системы равен нулю, то равенства (11) показы-
вают, что х = А19 у = А2, г = Д3 есть решение однородной
системы (19). Точно так же будут решениями и x = В19 у = В2, z = Bg;
х = С19 у = ^, z = C3. Отсюда следует, что если хоть один из
миноров определителя системы отличен от нуля, то система имеет,
кроме очевидного „ нулевого“ решения, еще и другие решения.
Это обстоятельство, как можно показать, сохраняется и тогда, когда
все миноры определителя системы равны нулю; т. е. условие
Д = 0
является условием достаточным для того, чтобы система однородных
уравнений (19) удовлетворялась решениями, не равными нулю одно-
временно.
Таким образом, мы приходим к важному результату, относяще-
муся к системам однородных уравнений 1-й степени:
Для того, чтобы система однородных уравнений 1-й степени
имела решения, неравные нулю одновременно, необходимо и до-
статочно, чтобы определитель системы был равен нулю.
Следует отметить, что в случае, когда Д = 0, одно уравнение
данной системы является следствием двух других, 1 или даже два из
них оказываются следствием одного, т. е. что система трех уравнений
в таком случае приводится к двум или даже к одному уравнению.
Пример 3. Решить систему однородных уравнений
х — 2 у + 3z — 0,
2х — Зу -f- z = О,
х + Зу — 4z = 0.
Система имеет очевидные решения х =у = z = 0.
Посмотрим, не может ли она иметь еще такие решения, которые не все
одновременно равны нулю.
Для этого необходимо вычислить определитель системы
1,-2, 3
2, — 3, 1
1, 3,-4
I, о, 3 1, 0, 0 I, —5 I .
2, 1, 1 = 2, 1, -5 = = 18. 5, —7
1, 5, — 4 1, 5, — 7
1 Доказательство этого заключения |см. И. И. Привалов — Аналити-
ческая геометрия. Глаза ^Определители 2-го и §-го порядка".
28
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
[I
Как видно, Д не равен нулю; следовательно, предложенная система
имеет единственные решения, все равные нулю: х=у = 2 = 0.
Пример 4. Решить систему однородных уравнений
х — Зу — г = О,
х 2у + г = О,
Зх у ~|~ 2 === 0.
Система также имеет очевидные решения х = у = г = 0.
Посмотрим, не может ли она иметь еще такие решения, которые не все
равны нулю одновременно. Для этого вычислим определитель системы
1, -3, —1
1, 2, 1
3, 1, 1
1, -3, -1
1, 2, 1
2, 4, 2
(члены 1-й строки умножены на — 1 и прибавлены к членам 3-й строки).
Определитель системы здесь оказывается равным нулю, а это, как ука-
зано выше, является необходимым и достаточным условием для того, чтобы
нашлись еще решения и притом не все равные нулю одновременно.
Найдем эти решения. Нетрудно заметить, что в предложенной системе
одно уравнение является следствием двух других, и потому система сводится
к двум однородным уравнениям, например к
X — Зу — 2 = 0,
х + 2у -|- 2 = 0.
Решая эту систему, как указано выше (см. стр. 25), находим
X у __ 2
I —3, — 1 “ 1,-1 I 1,-3
I 2, 1 ~ 1, 1 I Ь 2
или
X __ у _ 2
“^2“ 5 ’
т. е. решения пропорциональны числам — 1, — 2, 5, или, что то же, числам
1, 2, —5. Итак, данная система имеет, кроме нулевых решений, еще бесчи-
ленное множество других решений вида
х = k, y = 2k, 2 = -^5k,
где k — произвольное число.
Найденные решения, конечно, должны удовлетворять и третьему из за--
данных уравнений, в чем легко убедиться непосредственно.
Пример 5. Решить систему однородных уравнений
4х — 2y-j-32 = 0>
6х — Зу 4-42 = 0,
2х— у + 2 = 0.
Подсчитаем для этой системы определитель
• Д =
4, - 2, 3
6, —3, 4
2, - I, 1
29
ВОПРОСЫ И УПРАЖНЕНИЯ
§ б]
Так как члены 1-го столбца пропорциональны членам 2-го столбца, то,
числяя определителя, можно на основании основного свойства опреде-
Отелей прямо сказать, что
Д = 0.
Поэтому заключаем, что предложенная система имеет и другие решения,
оме х = у = г = 0. Здесь также одно из трех уравнений данной системы
Ксть следствие двух других. Поэтому, система приводится лишь к двум
каким-либо уравнениям; возьмем первое и второе.
Решая их по известным уже правилам, вычислим определители А3, В3 и С3:
л X у
Отсюда следует, что z = 0, а у = или
х = k, у = 2k, z = 0.
§ 6. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется определителем 2-го порядка?
2. Что называется определителем 3-го порядка?
3. Проверьте на примерах все свойства определителей, перечисленные
в § 2.
4. Что называется минором данного определителя?
5. С какими знаками следует брать миноры определителя при разложе-
нии определителя по элементам столбца или строки?
6. Что называется определителем системы уравнений 1-й степени?
7. Как выражаются через определители решения системы двух уравне-
ний 1-й степени с двумя неизвестными или трех уравнений с тремя неизве-
стными?
8. Что называется однородным уравнением 1-й степени?
9. Какие случаи могут представиться при решении системы двух одно-
родных уравнений с тремя неизвестными?
10. Когда система однородных уравнений 1-й степени с тремя неизве-
стными имеет решения, не все одновременно равные нулю?
И. Вычислить определители:
1, — 2 а, а —- b
5, 3 ’ * b, a + b
в)
sin a, cos al v 2, 1g 2
; r) s
sin 2a, cos 2a | I 4, 1g 4
Ome. a) 13; б) а1 2-}-#2; в) — sin a; r) 0.
12. Вычислить определители:
a)
3, - 2, — 1
5, 1, 3 ;
-2, 3, 4
1, 0, 2 4, з, 4
б) 2, -3, 3 ; в) 3, 2, 3
4, 5, — 1 — 1, — 4, — 1
r)
1,-1, 1
a, —a, b
a2, — a2, b2
Отв. a) 20; 6) 32; в) 0; г) 0.
30
ОСНОВЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
I
13. Вычислить определители:
а)
1, 5, 3 I, 1, 1 0, a, a
2, 3, — 1 ; б) 1,1 + a, 1 ; в) a, 0, a
3, 2, 4 1, 1 1 + ^ a, a, 0
г)
а, Ь, с
Ь, с, а
с, а, b
Отв. а) 0; б) ab; в) 2а3; г) ЗаЬс — а3— Ь3— с3.
14. Решить системы уравнений при помощи определителей:
, Зх —2>+13 = 0, 2х — 10у — 3 = 0, к х-4-ау = Ь,
а> 5х-\-8у — 1=0; °' 4х+ 5_у —1=0; В)х + Ьу = а.
Отв. а) х = — 3, у = 2;
1 1
б) x = 1-,j. = -T;
в) х = а --к Ь, у = — 1.
15. Решить системы уравнений при помощи определителей:
Зх— бу + £—15 = 0; 4х— 3_у-f- 2 = 0; х-\-2у— z— 2 = 0;
a) x + 5_y4-3z+ 9 = 0; б) 2_у+5г —19 = 0; в)Зх + 4г = 0;
2х — y + 4z— 4 = 0; 5х — 7z + 16 = 0; 5х — у + 4z + 1 = 0.
Отв. а) х = 1, у = — 2, z — 0; б) х = 1, у = 2, z = 3;
в) х = 0, у~ 1, z = 0.
16. Решить системы уравнений при помощи определителей:
ч Злг + 4у —6z = 0; б) х + 2у = 0; . х — 4y-|-z = 0;
' * + у — 4z = 0; °' Зх — 5у4-4г = 0; в> 2х — 8у — z = 0;
г) х + 4z = 0;
Зх + 2у + 12г = 0.
Отв. а) х = 10&, у = — б£, z = k; в) х = 4k, у = k, z = 0;
б) х = 8k, у = — 4k, z = — 11k; г) x = — 4k, у = 0, z = k.
YJ. Решить системы уравнений при помощи определителей:
4х — Зу + 5г = 0; х — 4у— 2г = 0; х + 5у —10г = 0;
а) Зх+ у — 2г = 0; б) 2х + у + 3г = 0; в) 2х — 3j> + 6г = 0;
х — 4у —Зг = 0; 9у + 7г = 0; Зх + 2у — 4г = 0;
х — 2у 4- г = 0;
г) 2х + 8у = 0:
4х— y + 2z = 0.
Отв. а) х =у = г = 0; в) х = 0, у = 2k, г = k.
б) х = 10k, y = 7k,z = — 9k; г) х = — 8k, у = 2k, z = 7k.
II. О ПРОЕКЦИЯХ
§ 7. ОБ ОТРЕЗКАХ ПРЯМЫХ ЛИНИЙ
Рассматривая отрезки прямых линий, условимся представлять их
как бы образованными непрерывным движением точки, передвигаю-
щейся от одного конца, называемого началом отрезка, до другого,
называемого концом его. Одновременно
с длиною пройденного при этом пути А ,________________________
будем отмечать и направление движе- 5
ния точки. Это направление будем Рис. 2.
означать самою расстановкой букв,
служащих для обозначения отрезка. Например, отрезок, образован-
ный движением точки от А к В, обозначаем АВ.
Тот же отрезок в случае, если он образован обратным движе-
нием, обозначим В А.
Отрезки, которые рассматриваются не только в отношении их
длины, но и в отношении их направления, называются направлен-
ными отрезками.
Положим теперь, что мы одновременно рассматриваем несколько
направленных отрезков одной и той же прямой LLV
Сообщив прямой LLt определенное направление; например от L
к мы увидим, что некоторые из отрезков этой прямой, как АВ,
ВС, DC и им подобные, по
_____________________________В______________________С своему направлению совпа-
1. дают с направлением прямой
рис з._______________________<LL19 а другие, как BA, CD,
DA и пр., противоположного
с направления. Условимся в первом случае отрезки называть
положительными, а во втором — отрицательными.
Введем далее для удобства изложения термин „величина отрезкаи
в отличие от его длины. Именно, под величиною положительного
Отрезка будем понимать число, измеряющее его длину, а под вели-
чиною отрицательного отрезка — число, измеряющее его длину,
взятое со знаком минус. Например, если длина АВ равна 3, то ве-
личина АВ также равна 3, а величина В А равна —3.
Всякий раз, когда речь будет итти только о длине отрезка, мы
Удем это точно указывать в обозначении прибавлением слова
32
О ПРОЕКЦИЯХ
I"
„длина", например, так: дл. АВ, дл. СВ, дл. ВС и т. д., а под
обозначением АВ, СВ, ВС и т, д. будем всегда подразумевать ве-
личины отрезков.
Из сказанного непосредственно вытекает, что
и следовательно
АВ = — ВА
лв+вд = о.
Длины направленных отрезков всегда выражаются положитель-
ными числами, как бы сами отрезки ни были направлены; а потому
дл. АВ = дл. В А
и следовательно
дл. АВ 4- Дл. В А — 2 дл. АВ — 2 дл. В А,
§ 8. ОБ УГЛАХ МЕЖДУ ПРЯМЫМИ
Из различных углов, образуемых двумя пересекающимися пря-
мыми заданного направления, будем рассматривать и называть углом
между этими прямыми наимень-
ший из углов, составленных
их положительными направле-
ниями.
Например, углом между пря-
мыми АВ и CD будет угол DKB.
Углом между непересекающимися
прямыми заданного направления
называется угол, составленный
прямыми, проведенными из произвольной точки пространства па-
раллельно данным прямым в одинаковом с ними направлении.
Например, угол между АВ и CD есть ^_MON, где ОМ парал-
лельна и одинаково направлена с
АВ, ON параллельна и одинаково
направлена с CD.
Весьма удобно угол между
прямыми АВ и CD обозначать
следующим образом:
(АВ, CD).
Прямые АВ и CD, изобра-
женные на рис. 5, не следует
обязательно представлять себе
Рис. 5.
лежащими в одной плоскости и пересекающимися: в пространстве
они могут оказаться непересекающимися и в то же время непарал-
лельными.
§ «I
ОБ УГЛАХ МЕЖДУ ПРЯМЫМИ
33
Из определения вытекает следующее:
п угол между прямыми не может превзойти т:, т. е. 180s;
о) если прямые параллельны и одинаково направлены, то угол
меЖДУ ними равеН НуЛЮ;
3) если прямые параллельны, но противоположно направлены,
т0 угол между ними равен я;
4) двум данным прямым соответствует один вполне определен-
ный угол.
Установленное таким образом понятие об угле между прямыми, имею-
щими заданное направление, допускает и даже требует расширения.
Дело в том, что задание угла между прямыми еще недостаточно для
определения взаимного положения двух прямых, лежащих хотя бы и
в одной плоскости и образующих данный угол: при определенном
положении одной прямой АВ один и тот же угол может быть
составлен двумя различного направления прямыми CD и C1Dl (рис. 6).
Для определенности положения второй прямой относительно
первой необходимо указывать еще, в которую сторону от линии АВ
надо откладывать угол ш, в сторону по часовой стрелке или в про-
тивоположную. В таких вопросах, следовательно, необходимо ука-
зывать еще направление отсчета углов, подобно тому, как и для
отрезков указывается направление их образования. Согласно этому,
условимся углы, отсчитываемые от основной прямой АВ в сторону
против часовой стрелки, считать положительными и измерять поло-
жительными числами, а углы, отсчитываемые по часовой стрелке, счи-
тать отрицательными и измерять отрицательными числами (рис. 7).
Примечание 1. В случае, если речь идет лишь о размере угла
ежду двумя данными прямыми, понятие о направлении отсчета угла отпа-
томТ; В Этом слУчае нам надо знать лишь абсолютную величину угла, подобно
его КаК И ПрИ РассмотРении отрезка нас может иногда интересовать лишь
поо ^РИмечание2. В некоторых вопросах отсчет углов уславливаются
^роизводить лишь в одну сторону (например, против часовой стрелки или
видмЧаС0В0Й стРелке)> но тогда величина угла может и превзойти я. Оче-
скаж ЧТ0 положение прямой C^Di будет одно определенное, безразлично,
Равнй МЫ’ 1Т° °На С ПРЯМОЙ А& составляет угол равный —« или угол
3 Зак. 2116. Н. С.
34
О ПРОЕКЦИЯХ
I"
§ 9. ПРОЕКЦИИ ТОЧКИ И ОТРЕЗКА НА ОСЬ
Рис. 8.
Представим себе некоторую прямую ОР, направление которой
нам задано, и некоторую точку М в пространстве.
Проекцией точки М на ось ОР называется точка т пересече-
ния с осью ОР плоско-
сти, проведенной через М
перпендикулярно к оси
ОР.
Проекцией отрезка
АВ на ось ОР называется
отрезок ab на оси ОР,
начало которого есть
проекция начала, а ко-
нец — проекция конца
проектируемого отрез-
ка АВ.
Проекция отрезка на
ось по своему направле-
нию, очевидно, может
совпадать с направлением оси или быть противоположной. В первом
случае по общему правилу (см. § 7) величина проекции является
положительной, во втором — отрицательной.
Из определения проекции следует, что прямые Мт, Аа, ВЬ пер-
пендикулярны к ОР.
§ 10. ТЕОРЕМА О ПРОЕКЦИИ ОТРЕЗКА НА ОСЬ
Между длиной отрезка и величиной его проекции на ось
имеется весьма важное соотношение, выражающееся следующей
теоремой.
Теорема. Величина проекции отрезка на ось (или, для сокра-
щения, просто проекция отрезка на ось)1 равна длине самого от-
резка, умноженной на косинус угла, составленного направлением
отрезка и оси проекции.
Пусть АВ — проектируемый отрезок, длина которого I, ab —
его проекция на ось ОР (рис. 9 и 10).
Требуется доказать, что
пр. АВ = 1. соз(ЛВ, OP). (1)
Отрезок АВ с осью проекции ОР может составлять острый,
тупой и прямой угол. Три эти случая рассмотрим отдельно.
1 И в дальнейшем мы часто будем говорить вместо „величина проекции*,
просто „проекция*; из текста всегда будет ясно, идет ли речь о длине
отрезка или его величине.
ТЕОРЕМА О ПРОЕКЦИИ ОТРЕЗКА НА ОСЬ 35
§ Ю|
1 случай: (АВ, OP) < -J (рис. 9).
Проведем через точку А прямую ОГР19 параллельно ОР и одина-
0 с ней направленную, и пусть пр. АВ на ось О1Р1 будет Abv
К° Очевидно, что Abr — ab, т. е. что
пр. АВ на ось OJ^ = пр. АВ на ось ОР,
как отрезки параллельных прямых, заключенные между параллель-
ными плоскостями.
Из прямоугольного треугольника АВЬ1(^£яАЬ1В = следует
дл. Д = дл. ЛВ . cos ДВ/Мр
Так как пр. АВ — ab выражается числом положительным и
равным дл. АЬ19 дл. АВ = 1 и / ВАЬГ = (АВ, ОР) < р то мы и
получаем, что
пр. АВ = I* cos (АВ, ОР).
11 случай: (АВ, ОР)>^ (рис* 10).
Сделав построения, как и в предыдущем случае, из прямоуголь-
ного треугольника АВЬг ( / ВЬХА = находим
дл. АЬХ = дл. АВ • cos / BAbv
Так как теперь пр. АВ = аЬ выражается числом отрицательным
и равным —дл. ЛВр то, желая ввести в предыдущее равенство
величину направленного отрезка Ablf мы должны иметь в виду,
Чт° Abr =±= — дл. АЬг-, кроме того
cos / В Ab, — — cos / ВАР,.
Поэтому имеем
— АВ. == — / • cos / ВАР.
Или 1^-1
АЬ, = I • cos / ВЛРр
пр. АВ = I • cos (АВ, ОР).
3*
36
О ПРОЕКЦИЯХ
In
III случай: (АВ, 0Р) = ^.
В этом случае проекция ЛВ = 0 и cos (Лв, ОР) = 0, так что
равенство
пр. АВ = Z • cos (АВ, ОР)
имеет место и в третьем случае.
Из доказанной теоремы следует, что если проектируемый отре-
зок лежит на прямой, направление которой противоположно напра-
влению отрезка, то величина проекции отрезка на ось равна про-
изведению величины отрезка на косинус угла между направлениями
данной прямой и оси.
§ 11. ПРОЕКЦИЯ ЛОМАНОЙ ЛИНИИ
Рассмотрим теперь ломаную линию ABCDEF, отдельные отрезки
которой последовательно направлены от точки А к В, от В к С и т. д.
от Ё к F. В этом случае отрезки АВ, ВС и т. д. EF называются
составляющими ломаной линии ABCDEF, аотрезок AF, взятый в напра-
влении от начала такой
ломаной линии Л к ее
концу F, называется замы-
кающей ломаной линии.
Теорема. Проекция
на любую ось замыкаю-
щей ломаной линии равна
сумме проекций на ту же
ось отрезков, составляю-
щих ломаную линию.
Пусть ab, be, cd, de, ef—проекции отрезков АВ, ВС, CD, DE,
EF, a af—проекция замыкающей AF на ОР. Тогда
пр. ЛЯ+пр. BC-f-пр. CD-|-np. DE 4- пр. EF = ab-\~bc-[-cd -\~ de-\-ef.
Так как
de — de -J- cf + fe,
то
np. AB пр. BC + np. CD 4- np. DE 4“ np. EF —
= ab 4~ be 4- cd 4- de 4- ef = ab 4- be 4- cd 4- de 4- cf 4“ fe 4“ ef*
Ho
cd 4- de = 0 и fe 4- ef = 0,
поэтому
пр. ЛВ4- np. BC4~ np. “h np. DE nP* EF =
= ab-\-be-{-cf = af = np. AF.
Итак,
np. AB 4~ пр. BC 4- np. CD 4- np. DE4- np. EF — np. AF. (2)
Справедливость этой теоремы, очевидно, не зависит от числа
отрезков ломаной линии и их расположения.
37
ПРОЕКЦИИ ТОЧЕК НА ПЛОСКОСТЬ
§ 12]
§ 12. ПРОЕКЦИИ ТОЧЕК НА ПЛОСКОСТЬ
Представим себе некоторую плоскость Q и точку М в простран-
1 $ Проекцией точки Ж на плоскость Q называется точка т
СТВ&есечения с плоскостью Q перпендикуляра Мт, опущенного из М
ТаПлоскость Q.
Н Ппоекцаей кривой АВ на плоскость Q называется линия ab, все
точки которой суть проекции соответственных точек кривой АВ.
Проекцией некоторой площади S, ограниченной контуром L, на
плоскость Q называется часть плоскости s, ограниченная линией I,
представляющей проекцию контура L на плоскость Q.
Теорема. Площадь проекции треугольника АВС на плоскость Q
равна площади проектируемого треугольника, умноженной на
косинус угла между плос-
костью треугольника АВС и
плоскостью Q.
Рассмотрим сначала тот
случай, когда одна из сторон
треугольника АВ лежит в пло-
скости Q.
Примем АВ за основание
треугольника АВС и его
проекции ABD и пусть СЕ = Н
высота первого, a DE=h
высота второго.
Тогда имеем
ПЛ. АВС = — АВ Н,
пл. ABD — ^AB-h.
Но h = Н- cos а, где а = £_CED есть линейный угол двугран-
ного угла между плоскостями Q и треугольника АВС.
Таким образом найдем, что
пл. ABD — -^ АВ • Н • cos а,
т’ е,
пл. ДвО = пл. ABC. cos
(3)
38
О ПРОЕКЦИЯХ
[II
Пусть теперь треугольник АВС расположен произвольно отно-
сительно плоскости Q. Мы всегда можем предполагать, что пло-
скость Q проходит через одну из вершин треугольника, например Л;
в противном случае мы этого достигли бы, переместив плоскость Q
параллельно самой себе, отчего площадь проекции треугольника не
изменится.
Пусть Д ADE есть проекция треугольника АВС. Продолжим
сторону ВС допересечения ее с плоскостью Q в точке F и со-
Рис. 14.
единим F с А. Тогда обра-
зуются два треугольника,
ABF и ACF, одна сторона
которых лежит в плоско-
сти Q. Проекцией первого
служит A ADF, а проекцией
второго A AEF.
Из чертежа следует:
пл. ADE =
= пл. ADF — пл. AEF.
На основании предыду-
щего случая имеем:
пл. ADF=nj\. ABF • cos а.
пл. Д^ = пл. /ICF-cosa.
Вычитая второе равенство из первого, находим:
пл. ADE = (пл. ABF — пл. ACF) • cos а = пл. ДЗС-cosa,
что и требовалось доказать.
Теорема эта легко обобщается на случай многоугольника, затем
и на любую плоскую фигуру.
§ 13. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Как расширяется понятие об отрезках прямых линий?
2. Какая разница между понятиями: длина направленного отрезка и
величина направленного отрезка?
3. Верны ли равенства дл. АВ = дл. ВА, АВ = — ВА^
4. Как определяется угол между двумя прямыми, пересекающимися п
непересекающимися?
5. Как изменится величина угла между прямыми, если изменить напра-
вление одной из них на противоположное?
6. Изменится ли величина угла между прямыми, если изменить напра-
вление обеих прямых на противоположное?
7. Чему равен угол между двумя параллельными и одинаково напра-
вленными прямыми?
8. Чему равен угол между двумя параллельными и противоположно
направленными прямыми?
9. Как получить проекцию точки на ось?
10. Как получить проекцию отрезка на ось?
И. Что сделается ^проекцией отрезка, если 1) переменить его направление,
2) переменить направление оси?
39
ВОПРОСЫ И УПРАЖНЕНИЯ
§ 131
19 Когда проекция отрезка равна его длине?
13 Когда проекция отрезка равна его длине, взятой с отрицательным
знаком? оверить теореМу 0 проекции отрезка в случае, когда отрезок
параллелен оси проекции.
па*15. Как получить проекцию точки на плоскость?
16* Как проектируются на плоскость: отрезок прямой линии, кривая
ния и площадь, ограниченная кривой линией?
ЛИ 17- Когда площадь проекции плоской фигуры на некоторую плоскость
пявна площади самой фигуры?
F 18. Когда плоская фигура проектируется на плоскость в виде отрезка
прямой линии?
19. В прямоугольном треугольнике АВС угол А = 60°, длина катета
дС = 2. Определить проекции катетов АС и ВС нагипотенузу АВ, (Напра-
вление отрезков и оси проекции определяются расстановкой букв.)
Отв, 1, —3.
20. Отрезки АВ, ВС и АС, имеющие направления, указанные расста-
новкой букв, образуют равносторонний треугольник. Написать формулы для
вычисления проекций каждого из этих отрезков на два другие.
Отв, пр. АВ на ось ВС = — а, пр. АВ на ось АС = ±а,
пр. ВС на ось АВ = — а, пр. ВС на ось АС —— а,
где а — длина стороны треугольника.
21. Определить проекции сторон правильного шестиугольника ABC DEFA
на линию AD, предполагая, что направление всех отрезков указано расста-
новкой .букв и что длина стороны шестиугольника равна единице.
Отв. пр. АВ = пр. CD = -i-, пр. ВС=\, пр. £>Е = пр./7Л = —]-.
пр. EF = — 1.
III. О КООРДИНАТАХ
§ 14. ПРЯМОУГОЛЬНАЯ, ИЛИ ДЕКАРТОВА,
СИСТЕМА КООРДИНАТ
Аналитическая геометрия, как показывает само название этого
предмета, представляет собою ту отрасль математики, которая ставит
себе целью изучение геометрии аналитическим методом. Все • геоме-
трические задачи решаются здесь этим методом, причем более эле-
ментарные— методом алгебраического анализа, а более сложные
также с помошью высшего анализа.
Алгебраический метод применялся в обычном элементарном
курсе геометрии, однако там он не охватывал всей совокупности
геометрических вопросов.
Огромная область вопросов, рассматривающая взаимное положе-
ние точек, линий и других геометрических протяжений, а в связи
с этим изучающая формы линий, поверхностей и их свойства, стоит
в элементарной геометрии в стороне от алгебраического анализа и
почти не затронута им. Охватить анализом и эту весьма важную
совокупность вопросов и составляет цель аналитической геометрии.
Возможность такого охвата, возможность приспособления анализа
к решению всей совокупности задач, входящих в предмет геометрии,
осуществилась лишь благодаря введению в геометрию понятия
о координатах. Действительно, для того, чтоб анализ оказался
способным обслуживать геометрические вопросы, трактующие по-
ложение точек, линий и т. п., необходимо было прежде всего
фиксировать положение простейшего геометрического понятия —
точки при помощи простейшего аналитического элемента — числа
(одного или нескольких), и связав между собой эти простейшие
элементы, через них связать вопросы положения, а затем и другие
вопросы геометрии с анализом.
Таким образом, мы и приходим к мысли рассматривать числа,
могущие характеризовать положение точки в пространстве.
Всякая совокупность чисел, вполне определяющая положение
точки в пространстве, называется ее координатами.
Существуют различные способы определения положения точки
или, иначе, различные координатные системы.
Ограничиваясь сначала изучением геометрии на плоскости, рас-
смотрим два способа, определяющие положение на ней точки, т. е,
§ 141
ПРЯМОУГОЛЬНАЯ, ИЛИ ДЕКАРТОВА, СИСТЕМА КООРДИНАТ
41
системы координат: прямоугольную, или декартову, систему и
^пляоную систему.
Л В прямоугольной системе координат положение точки на пло-
определяется следующим образом.
CKOLi« r v у „ у V_______ „оа
пресекающиеся в точке О и направленные
______точка, данная в плоскости этих пря-
мых.____
Проведем через точку М параллельно
линиям ХхХ и YXY две прямые; они от-
секут на линиях ХхХ и YtY отрезки О А
и О В, начало которых будем всегда счи-
тать в точке О. Величины этих направленных
отрезков, которые условимся обозначать
буквами х и у, и определят положение
точки М. Действительно, всякой точке М
отвечает одна определенная пара чисел х
и у и, обратно, всякой паре чисел х и у
отвечает одна определенная точка плоскости.
Пусть XtX и KjK — две взаимно перпендикулярные прямые,
----------- _ г» .. как указано стрелками,
лл .в
Т----
-—^х
мг[-----
-----Ч
у,
Рис. 15.
Числа эти в силу данного вначале определения и называются
прямоугольными координатами точки М. То, что точка М опре-
деляется координатами х и у, записывают следующим образом:
М
О
Л4 (х, у).
Координата х = О А называется абсциссою точки М, а координата
У == ОВ называется ординатою точки М.
Очевидно, что
для точки /И
для точки М1
для точки ЛГ2
для точки Af3
х > О,
х<0,
х< О,
х > О,
^>0
у>0
у<0
у<0
Прямые ХхХ и KjF называются осями координату первая осью
абсцисс. вторая осью ординат. Точка О пересечения осей называется
началом координат.
Таким образом, чтобы определить координаты какой-нибудь точки
плоскости, надо провести через данную точку прямые, параллельные
°сям координат; тогда величины отрезков, отсекаемых на осях коор-
динат, отсчитанные от начала координат в определенном избранном
Масщтабе, с соблюдением правила знаков, и будут являться прямо-
Уг°льными координатами взятой точки.
Чтобы построить точку, по данным ее координатам, надо отло-
ить от начала координат на осях ХГХ и YXY направленные отрезки,
^личины которых соответственно-равны координатам данной точки;
концов этих отрезков провести прямые, параллельные осям коор-
' пиат; тогда точка пересечения этих прямых и даст искомую точку,
42
О КООРДИНАТАХ
[in
На рис. 16 построена точка М (—2, 3). Указанное построение по-
лезно заменять следующим: на оси ОХ отложить направленный отре-
зок ОА, величина которого равна абсциссе х данной точки как по
абсолютному ее значению, так и по знаку; затем из конца этого
отрезка провести прямую параллельную оси OY, на которой и отло-
жить от точки А отрезок AM, величина которого была бы равна
ординате данной точки как по абсолютному ее значению, так и по
знаку. Конец этого отрезка и будет искомой точкой. На рис. 17
построена та же точка М (— 2, 3).
Весьма полезно заметить, что абсциссы и ординаты любой
точки М можно рассматривать как проекции на оси ОХ и OY
отрезка ОМ, соединяющего начало координат с данною точкой,
так что
х = пр.0А, ОМ,
у = пр.оу ОМ,
так же и для других точек М19 М2, М3 (рис. 15).
§ 15. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
Пусть в плоскости чертежа задана некоторая прямая и на ней
некоторая точка О, и пусть М точка в той же плоскости.
' Соединим точку О с точкой М; тогда
длина отрезка ОМ=р и / MOP—Q,
отсчитываемый от прямой ОР, опре-
делят положение точки на плоскости
координат. Правило знаков при
6 I_____________________I отсчете углов сохраним то, кото-
1 : ►Р рое указано на стр. 33. На рис. 18
Рис. 18. положительное направление от-
счета углов отмечено стрелкой.
Величины р и 6 называются полярными координатами точки Ж;
первая полярным радиусом-вектором, вторая полярным углом
точки М-. ‘ '
43
ОСНОВНЫЕ ЗАДАЧИ
§16]
пиния ОР называется полярной осью, а точка О — полюсом.
Так как полярный радиус-вектор р есть длина отрезка, то, сле-
ельно, р не может иметь отрицательного значения, а всегда
q Чт0 касается полярного угла 0, то он может быть как по ложи-
‘°^ным так и отрицательным, смотря по тому, в которую сторону
^полярной оси отсчитывается угол.
§ 16. ОСНОВНЫЕ ЗАДАЧИ
Как уже известно, положение точки определяется ее координа-
тами. Ввиду этого такие выражения, как, например, „дана точка",
найти точку\ часто употребляемые в аналитической геометрии,
мы будем понимать так: „даны координаты точки", „определить
координаты точки". Самую точку, как сказано раньше, будем обо-
значать соответствующей ей буквой с присоединением к ней в скоб-
ках ее координат. Например,
М(а, Ь)
это значит — рассматривается точка, координаты которой
х = а, у = Ь.
Задача I. Н а й т и величины проекций на координат-
ные оси направленного отрезка,
его крайних точек.
Положим, что нам дан направленный
отрезок MjMq. Точка Л11(х1, уг) пусть
будет началом отрезка, а Ж2(х2, у2) —
концом его.
Для решения задачи соединим на-
чало координат с данными точками и
рассмотрим получающуюся при этом ло-
маную линию и ее замыкающую
^2* По теореме о проекции ломаной
имеем:
зная координаты
пр. OAfj-pnp. ^^2 = пр. ОМ2 (на любую ось).
Принимая за ось проекции сначала CLY, а затем OY и учитывая, что
пр. ОМ1 на ось OX=xv пр. ОМ2 на ось ОХ=х2,
пр. OMi на ось OY = y1, пр. ОМ2 на ось OY=y2
^СМ’ Ф°рмулу (1) § 14), получим
Х1 + =
Л+пр.^Ж^^^
44 о КООРДИНАТАХ [III
Отсюда выводим
ПР-ОХМ1^2 = Х3 — Х1’ (2)
ПР-OF ^1^2 =Л~Л’
Итак, проекция на ось ОХ направленного отрезка равна раз-
поста абсцисс конца и начала отрезка-, проекция на ось OY на-
правленного отрезка равна разности ординат конца и начала
отрезка.
Задача II. Найти расстояние между двумя данными
на плоскости точками (xlf yt) и (х2, у2).
Обозначим искомую длину направленного отрезка чеРез d
и углы, которые он образует с осями координат, через а и (3; тогда,
по теореме о проекции направленного от-
резка (формула (1), § 10) находим
пр.0ХТИ1Л12 = d • cos а.
С другой стороны, на основании най-
денного в предыдущей задаче, имеем:
^•ОХМ1М2 = Х2 — ХГ
Отсюда заключаем, что
Рис. 20. d • cos а = х2—хР
Подобным же образом находим, проектируя на ось OY,
d • cosp=*.y2—
Возвысим оба последние равенства в квадрат и сложим их, тогда
получим
d2 (cos2 а + cos2 Р) = (х2 — Xj)2 + (у2
Но cos2a-]-cos2(3 = cos2аsin9а = 1, поэтому
d2 = (х2—Xj)2 (уя—У1)2,
откуда
d = + V (*2— У1)2-
В частном случае, когда одна из точек совпадает с началом
координат, получаем формулу для расстояния точки М (х, _у) от
начала:
(3)
Пример 1. Найти расстояние между двумя точками Л11 (—2,3) и /И2 (3, —9).
d = /(—2—3)2+ (3 + 9)2 = у25 + 144 = 13.
Задача III. Найти середину отрезка, соединяющего
две данные точки.
§ 161
основные Задачи
45
Пусть точки /MjCxj, и Afa(x2, у2) служат концами отрезка
д/? а точка М — его середина 014 .........
координаты точки М через х и у.
Очевидно, что пр. Af1Al=np./WAf2
так как длины этих
на-
(рис. 21). Обозначим искомые
на любую ось,
отрезков по условию равны и
правлены в одну сторону.
Но
np.ox^4j/W — х — х„
пр. охММ2 = х2 — х.
Следовательно,
Рис. 21.
X-----Л*! = Х2---------X.
Точно так же найдем, что
откуда получаем
У~ У1=У2~ У,
v
х— 2 ’
v =
у 2
Пример 2. Найти координаты середины отрезка AfiAf2, зная координаты
концов (1, —4) и ТИ2(3, 2).
По формулам (4) находим х = = 2, у = —= — 1.
Пример 3. Координаты вершин тре-
угольника АВС суть А (—2, 7), В(3, —3),
С (2, 5); найти длину медианы BD.
Найдем сначала по формулам (4) коор-
динаты точки D
+^0, _у = Щ = 6,
а затем уже расстояние между точками В (3, — 3) и D (0, 6)
BD = + /(3 — О)2 + (-3 — 6)2 = + /9 + 81 = +3/10.
Задача IV. Найти точку, делящую отрезок в дан-
ном отношении.
Пусть (х19 yj и УИ2(х2, у2) две данные точки (рис. 23).
Требуется на прямой МГМ2 найти точку, делящую отрезок ЛТХ/И2
в отношении -2-. Положим для краткости = k. Точку М тре-
буется найти так, чтобы
дл. М'М__.
дл. ЛШ2 —
46
О КООРДИНАТАХ
Проектируя отрезки и ММ2 на ось ОХ, имеем
пр. МгМ = х— xt — дл. МгМ • cos а,
пр. ЛМ42 = х2 — х = дл. ММ2 • cos а.
Деля одно равенство на другое,
находим
х — xj дл. МХМ
х2 — х дл. Л4Л42
Точно так же, проектируя на ось ОУ,
найдем
>2— У
Отсюда, решая эти уравнения
х — xt = kx2 — kx
х (1 As) = x± —{- kx2
x1 + kx2
x~ \ + k
относительно х и у, находим
' У—У1 = кУ2 — ky
У С1 + к) —у! + ky2
_У1 + ^2
у “ 1 +k
(5)
Пример 4. Найти точки, делящие отрезок, заключенный между точ-
ками Afi(—1, б) и Л42 (4, 3), на три равные части.
Для точки М', ближайшей к Мх, имеем
дл. МАМ' = 1
дл. М'М2 2 *
Для другой искомой точки ТИ" имеем
k = 2
дл. __ 2 Рис. 24.
дл. Af"Af2 ““ 1 ‘
Поэтому, по формулам (5) находим
Г ~1+~2’4 _2
Х~ 1+± ~3’
h 2
„_-1+2-4 _ 7
Х ~ 1+2 “ 3 ’
Итак, искомыми точками будут: Mf[
6 + у-З
У' = 5- = 5,
’+т
Х^+^з
В качестве примера на приложение формул (5) решим еще сле-
дующую задачу.
Задача V. Найти центр тяжести системы п мате-
риальных точек: ЛГДх-,, у J, М2(х2,у2), Мп(хп, у^.
Пусть Mlf Жа, Мп система материальных точек, массы ко>
торых пусть будут /п2, тп (рис. 25).
ОСНОВНЫЕ ЗАДАЧИ
47
§ 161
центром тяжести системы материальных точек называется
приложения равнодействующей всех
сил тяжести, приложенных к ма-
териальным точкам.
14з механики известно, что центр
тяжести двух материальных точек
чежит на прямой, их соединяющей,
в расстоянии от каждой из них
обратно пропорциональном массам
этих точек.
Найдем сначала центр тяжести
Ni (х'> У) ДВУХ пеРвых точек и
М2 по формулам (5), имея в виду,
точка
Находим
( т2 .
1+?
ЧТО
А/;
ч •
Рис. 25.
отношение
___ш-lXx + т2х2
пц + т2
(5')
дл. MiNj _ т2
дл. N±M2 тг ’
%
X
, т2
у =-----—-
1+%
Ш1У1 + ЩУ2
Шг + т2
Найдя центр тяжести двух материальных точек М1 и ТИ2, мы можем,
как это следует из закона сложения параллельных сил, заменить
две силы, действующие на массы т1 и /п2, одной, приложенной
к точке N19 и притом такой, как будто обе массы и т2 сосре-
доточены в точке Л/г
Присоединим теперь к точке точку Л43 и найдем центр тяжести
точки с массой т1-}-т2 и 7И3 с массой т%.
По той же формуле (5) имеем
. I ^з
Хг 4* ° • Ха
"__ _ Шу+ т2 3 __ х' (mj + т2) + т$х2
Х 1 । “1“9
' 4" т2
„ _ у + OTi + zna 'Уз __ у' (тг + т2) + т8у3
1 | w3 «1 + «г + «3
Но по предыдущим формулам (5')
х' (mi + ma) = mixi + т^х2 и У' (mi + /йг)= т1-И1 + тъУу
Поэтому
хп ПЦХ! 4~ ^2Х2 + ^3Х3 у// _ + ^2>2 + тзУз t
7^1 4" Ш2 4- пг3 * У nil “Ь ^2 ”Ь ^3
48
О КООРДИНАТАХ
Продолжая таким же образом присоединять дальнейшие мате-
риальные точки, окончательно найдем для координат центра Тяжести
системы материальных точек следующие выражения:
х _ ffliXt + /n2-V2+--hVn _ + m2yt + ... + тпУп
от1 + «2+ •••+«» ’ У /Kj + И2+• • • + «п ’ '
§ 17. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется координатами точек?
2. Как называется каждая из прямоугольных координат точек?
3. Какие знаки имеют прямоугольные координаты точек, находящихся
в отдельности в каждом из четырех координатных углов?
4. Что можно сказать про прямоугольные координаты точек, симметрично
расположенных относительно: 1) оси абсцисс, 2) оси ординат?
5. Что можно сказать про прямоугольные координаты точек, симме-
трично расположенных относительно начала координат?
6. Что можно сказать про ординаты различных точек, расположенных
на прямой, параллельной оси абсцисс?
7. Что можно сказать про координаты различных точек, расположенных
на прямой, параллельной оси ординат?
8. Как называется каждая из полярных координат в отдельности?
9. В каких пределах изменяется значение полярного радиуса-вектора?
10. В каких пределах изменяется значение полярного угла?
11. Что можно сказать про полярный радиус-вектор различных точек,
расположенных на одной и той же окружности с центром в полюсе?
12. Как найти расстояние между двумя данными точками?
13. Как найти середину между двумя данными точками?
14. При делении отрезка на пять равных частей какое значение необхо-
димо дать коэффициенту k в формулах (5), чтобы найти третью точку де-
ления, считая от той, координаты которой не содержат коэффициента k
в этих формулах. Отв 3
15. Координаты вершин треугольника АВС следующие:
Л(- 1,3 — 3/3), В (2, 3), С (-4, 3).
Найти длины сторон, координаты середин сторон и длины медиан.
Отв. Длины сторон = 6, длины медиан = 3
16. Найти точку, равноудаленную от трех точек: А (0,-1); В (—2,2); С (1, 0).
Отв. (-0,7; 0,7).
17. На осях ОХ и OY найти точки, отстоящие от точки (3, —4) на
расстоянии, равном 5. Отв. (0, 0); (6, 0); (0, —8).
18. На биссектрисе координатного угла найти точку, равноудаленную
от точек (—2, —4) и (1, —3). Одав 5_ _ _5)
19. Найти две средние точки, делящие отрезок между точками (—3, 2)
и (0, —1) на пять равных частей.
Отв. (-1,8; 0,8), (—1,2; 0,2).
20. Найти точку пересечения со стороной ВС биссектрисы, проведен-
ной из вершины А треугольника АВС, зная координаты его вершин: А (1, 5),
В (4, 1), С (13, 10).
Отв. (6,5; 3,5).
IV. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ И ИХ ФУНКЦИИ
§ 18. ПОСТОЯННЫЕ И ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
Все величины, встречающиеся при исследовании какого-нибудь
вопроса, делятся на две категории: постоянные и переменные.
Постоянными величинами называются те величины, которые со-
храняют во все время исследования одно и то же определенное
значение, переменными — те, которые могут принимать различные
значения.
Некоторые величины сохраняют свое значение, т. е. оказываются
постоянными при всяких условиях. Таковы, например, отношение
длины любой окружности к своему диаметру, т. е. число тс, отно-
шение длины диагонали любого квадрата к его стороне, равное ]/2,
и т. п. Другие величины таковы, что в одном вопросе они оказы-
ваются постоянными, а в другом — переменными. Условия каждой
в отдельности задачи определяют, какие из величин следует рас-
сматривать как постоянные и какие как переменные.
Обыкновенно для обозначения постоянных величин употребляют
начальные буквы алфавита а, Ь, с, ..., для обозначения же пере-
менных— конечные буквы х, у, z, ...
Во всем дальнейшем мы будем предполагать, что все рассматри-
ваемые значения величин суть числа вещественные. В случае не-
обходимости введения в рассмотрение чисел комплексных будут
Делаться соответствующие оговорки.
Переменные иногда могут принимать любые значения, ничем не
ограниченные; иногда же они ограничиваются какими-нибудь опре-
деленными условиями.
Если все значения переменной х заключены между числами а и Ь,
включая значения а и Ь, тогда говорят, что переменная х изменяется
На отрезке [а, Ь\ и означают это неравенствами
а х^Ь.
Переменная величина при своел^ изменении может по смыслу
аДачи принимать последовательно все без исключения значения,
включенные в данном отрезке [а, £], либо только некоторые,
4 Зак. 2'116. Н. С. Михельсон.
50 ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ И ИХ ФУНКЦИИ '[IV
например, только целые или только рациональные (т. е. целые и
дробные). В первом случае говорят, что переменная изменяется не-
прерывно, или обладает свойством непрерывности, во втором случае
свойством непрерывности она не обладает.
§ 19. ОБЩИЕ ПОНЯТИЯ О ФУНКЦИЯХ
Если переменные х, у, z, ..., и, v таковы, что по смыслу за-
дачи каждой из них можно приписывать частные значения незави-
симо от того, какие значения даны остальным, то такие переменные
называются независимыми переменными.
Если же, задав некоторое частное значение одной переменной,
например х, мы, в силу некоторых обстоятельств, уже не в праве
назначать другой переменной, например у, произвольное значение,
а напротив, если выбранному значению одной переменной соответ-
ствует одно или несколько определенных частных значений другой
переменной, то последняя называется функцией первой, переменная
же независимая — ее аргументом.
Например:
у = х2-]~2х— 4
у = хУх-{-2
<y = lg(X— 1)
Суть различные функции от х.
Рассматривая, например, первую из функций, видим, что
при х — — 4
^ = —1 п х = — 3
У — ~ 4 п х = — 2
у = — 5 п х — — 1
у = — 4 п х = 0
Точно так же объем шара v является функцией его радиуса г
4 я
-и = — кг3
о
или площадь квадрата q — функцией его стороны х
q = x2.
Объем физического тела есть функция его температуры и т. п.
Если мы не знаем точной зависимости у от х или если она нам
и известна, но нам нет надобности выражать ее детально, как
в предыдущих случаях, а мы хотим отметить лишь существование
зависимости у от х, то в таком случае употребляют следующие
обозначения:
.У =/(*), У = _у = ф(х),
Предполагая,
подразУмеваютСЯ
будет записать,
ОБЩИЕ ПОНЯТИЯ О ФУНКЦИЯХ 51
§191
зличные буквы /, F, ф и т. д. означают различные формы
ГДе Р мости у от х, т. е. различные функции от х.
оависи например, что под знаками f(x), F (х) и ф(х)
только что приведенные примеры функций, можно
что
х2+2х —4=/(х),
=F(x),
lg(x—1) =®(x).
Частные значения функции /(х) при частных значениях х—а
или х = £ и т. д. обозначают знаками:
/(a), /(£) и т. д.,
так что, например, f (а) есть частное значение функции / (х) при
х=а-
В случае разобранного выше примера, где
f (х) = х2 + 2х — 4,
числа первого столбца представляют частные значения функции при
соответствующих значениях х, именно:
/(— 4) = 4, /(— 3) = — 1, /(0) = —4 и т. д.
Удобно частные значения независимой переменной и соответствую -
Весьма важно заметить, что не всегда можно найти частные зна-
чения функций; возможны случаи, когда частные значения функций
и не существуют. Пусть, например, имеем функцию /(х) = -^ . Част-
ное значение этой функции при х = 0, т. е. /(0) не существует,
так как деление на нуль невозможно. По той же причине не су-
ществуют значения f(a) и /(—а) для функции
/(х) =
1
•J^X2—д2*
Совокупность значений независимой переменной, для которых
астные значения функции существуют, называют областью суще-
ствования функции.
в Иногда значения одной переменной, например и, определяются
зависимости от нескольких переменных х, у, z.
4*
52 ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ И ИХ ФУНКЦИИ [IV
В этом случае переменная и называется функцией нескольких
переменных х, у, z, что и обозначается так:
н=/(х, у, Z).
Например, и = Зх2у есть функция двух переменных х и у.
Диагональ прямоугольного параллелепипеда d есть функция трех
его измерений: d — ]/ x2-f-y2-]- z2.
Объем прямого кругового конуса v есть функция двух перемен-
ных— радиуса основания и высоты конуса: = утсг2/г.
Частное значение функции f(x, у, z) при х — а, y = b, z = c
обозначается так: /(а, Ь, с).
Например, для /(х, д/, г) = х /(1, 2, —1) = — 2.
§ 20. НЕЯВНЫЕ ФУНКЦИИ
Зависимость между переменными х и у может быть установлена
заданием некоторого уравнения, связывающего у с х.
Так, каждое в отдельности уравнение
у2 — х2 -ф-1 = 0,
ху — х3 4- 2 = 0
устанавливает зависимость между переменными х и у и потому
определяет одну из переменных как функцию от другой, например
у как функцию от х.
Действительно, из этих уравнений следует:
у = ± ]/х2 1,
Пока уравнение, связывающее у и х, не решено относительно у,
функция у считается заданной неявно и называется неявной функ-
цией от х. Уравнение, будучи решено относительно рассматривае-
мой функции, обращает неявную функцию в явную. Не всякое
уравнение, однако, позволяет обратить неявную функцию в явную.
Для задания неявной функции в общем виде устанавливают сле-
дующие обозначения:
/(х, У) — 0 или F(x, д/) = 0 и т. д.
здесь /(х, у) или F(x, у) обозначают левую часть уравнения, свя-
зывающего у с х после переноса в одну сторону всех членов
уравнения. Эта левая часть уравнения, рассматриваемая сама по себе,
РАЗЛИЧНЫЕ ТИПЫ ЯВНЫХ ФУНКЦИЙ
53
§ 211
дставляет функцию двух переменных х и у, почему
ПР требляют вышеуказанное обозначение.
УП°Если уравнения / (х, у) = 0 или F (х, у) == 0 и т.
шить относительно неявной функции, то
ния можно записать так:
для нее и
п.
результат такого
можно
реше-
у = ср (х) или у = Ф (х) и т. п.
Следует отметить, что неявная функция может оказаться много-
значной, т. е. может случиться, что одному значению х соответствует
не одно, а несколько значений у.
§ 21. РАЗЛИЧНЫЕ ТИПЫ ЯВНЫХ ФУНКЦИЙ
Указанные выше общие обозначения не определяют ни точного
вида функций, ни характера их. Но так как нередко приходится
высказывать заключения, распространяющиеся не на всю совокуп-
ность различных функций, а только на отдельные типы, то
очень полезно уметь различать их. Остановимся лишь на явных
функциях.
1) Функция /(х) называется целой рациональной функцией, если
она представляет собой многочлен вида
Po + Pi* + Pa*24-......+Рпхп,
где п — целое и положительное, а коэффициенты р0, рь р2, ... , рп —
какие угодно постоянные числа.
Так, например,
2х3 — 1, У2 — ±х±х*, ах2 + bx с
суть целые рациональные функции от х.
2) Функция / (х) называется дробной рациональной функцией,
если она может быть представлена в виде частного от деления це-
лых рациональных функций. Таковы, например, функции
хЦ-2х2 1 Q4/,2 1
1 — х2 > х —1 ’ х'
Нетрудно заметить, что в целой и дробной рациональной функ-
ции над независимым переменным производятся лишь рациональные
Действия: сложение, вычитание, умножение, деление и возвышение
в Целую степень.
3) Функция / (х) называется иррациональной, если в совокуп-
ность действий, которые необходимо произвести над независимой
переменной для вычисления функции, входит, кроме перечисленных
выще рациональных действий, еще извлечение корня. Таковы:
хЦ- ^27—1 х+ Ух —1
х ’ f^x2^
54
ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ И ИХ ФУНКЦИИ
[IV
Вышеуказанные три типа функций принадлежат к разряду так
называемых алгебраических функций. Функции, не являющиеся алге-
браическими, называются трансцендентными. Из наиболее часто
встречающихся функций этого класса укажем на следующие:
ах — показательная (л > 0),
lgo х — логарифмическая (а > 0),
sin х, cosx, tgx, ctgx, secx, cosec x — тригонометрические,
arc sin x, arc cosx, arctgx, arcctgx, arc sec x, arc cosec x — круговые.
§ 22. КРУГОВЫЕ ФУНКЦИИ
1) arc sin x.
Рассмотрим некоторую окружность с радиусом О А = R и на
ней дугу АС (рис. 26).
Положив
дл. о АС____
R ~
замечаем, что эта величина служит мерою,
выраженной в частях радиуса, дуги АС.
Обозначив далее = х видим, что х
к
есть синус дуги у, т. е.
x = sin>y. (1)
Последнее равенство можно прочитать и так: у — есть дуга, си-
нус которой равен х, что и записывается следующим образом:
у = arc sin х. (2)
Итак, из равенства (1) следует равенство (2). •
Говоря о функции arc sin х, нетрудно заметить, что под этой
функцией скрывается не только дуга АС, но бесчисленное мно-
жество других дуг, как, например/
О АСХ, о А С -{- 2тг,
и т. д.
Действительно, все эти дуги имеют один и тот же синус, как
и дуга у.
Такого рода неопределенность устраняется условием понимать
под arc sin х всегда лишь самую простейшую из всех дуг, именно:
при х>0 дугу в пределах от 0 до ~, на рис. АС,
при х<0 дугу в пределах от 0 до —у, на рис. АС%
„О1 КРУГОВЫЕ ФУНКЦИИ 55
§ 22J
Таким образом, всегда под arc sin х подразумевают дугу, не вы-
ходящую из следующих границ:
ТС _ 7С
— arc sin х .
2) arc cos х.
Сохраняя то же обозначение для дуги, т. е. положив попрежнему
(рис. 27)
дл. о АС
~~Т?
OD OD
назовем через х отношение , так что = х.
Тогда очевидно
x = cosy.
(3)
Отсюда, как и для синуса, заключаем, что у есть дуга, косинус
которой равен х, что и записывается так:
у = arc cos х. (4)
Итак, из равенства (3) вытекает и обратное равенство (4).
Говоря вообще о функции arccosx, нетрудно опять заметить,
что одному и тому же косинусу соответствует не одна только
рассмотренная дуга А С, но и А С\ и еще бесчисленное множество
Рис. 27. Рис. 28.
ДУГ> отличающихся от них на целое число окружностей. Для устра-
нения этой неопределенности уславливаются опять понимать под
arccosx простейшую из всех дуг, именно:
при х>0 дугу в пределах от Одо у, на рис. о АС,
при х<0 дугу в пределах от до тс, на рис. оАС2.
Таким образом, под arccosx понимают дугу в границах
0^ arc cosx^ тс.
56
ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ И ИХ ФУНКЦИИ
[IV
3) arc tg х.
Обозначим (рис. 28)
дл. о АС___________________ АЕ
R ~У’ R
Тогда очевидно х = tgу, откуда обратно: у есть дуга, тангенс
которой равен х, т. е.
у = arc tg х.
Так как одному и тому же тангенсу соответствует также бес-
численное множество дуг: AC, ACt и т. д. (рис. 28), то длячустра-
нения неопределенности aretgx ограничивают неравенствами
Тс _ , _ Тс
—-g-^агс tgx^y.
4) arcctgx.
Функция arcctgx определяется подобным же образом: для нее
устанавливают следующие границы:
О аге сtg х тс.
Приведенная классификация явных функций может быть изобра-
жена следующей схемой:
, f целые
, * J рациональные { Ппп5штр
функции алгебраические | иррациональные 1 ДрОбНые
функции трансцендент-
ные
показательные
логарифмические
тригонометрические
круговые
Схема эта не исчерпывает всего бесконечного разнообразия
функций. Указанные в ней функции составляют совокупность лишь
элементарных функций анализа.
§ 23. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется независимой переменной?
2. В каком случае одна переменная называется функцией другой?
3. Если f (х) есть некоторая функция переменного х, то что означают
символы /(3), /(0), f (а)?
4. Как задается неявная функция?
5. На какие классы делятся все элементарные функции?
6. Для какой цели устанавливаются неравенства, ограничивающие кру-
говые функции?
Q г _ 1 -I
7. /(х) = -°-гч-, найти/(1). Оте./(!)=*
X -ф- о z
ВОПРОСЫ И УПРАЖНЕНИЯ
57
§ 235
8. /(х, J, z) = xey— zex, найти f (0, —1, 2). Отв. —2.
9. /(x) = ^rf. найти/(2),/(2а),/(х+1),/(х)Н-1, /(1), ,
/(№’ 7 1 122
^11 1 X2 х2 9
Отв' 3’ 4й2—1’ х2 + 2х ’ х2—1’ 1—X2’ Х~
1
arc sin 1,
10. Определить следующие частные значения круговых функций:
arc cos 0,
arc tg О,
arc etg ;
. 1 аге sin — аге sin(— /2\ 2 J arc sin (—1),
аге cos — Й’ агс /2 > cos — / Уз\ arc cos g— J
аге tg оо, arc tg 1, arc tg (— /3),
аге etg 0; arc etg (— i); arc etg (— 1^3).
Отв- 2’6’- те те 4 ’ 2 ’ те 2те те 5те 2 ’ 3 * 4 " 6
те те "4’ ‘“'S’ те те Зте 5л: ~3' "2J
V. ГРАФИКИ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
И ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ f(x, j) = 0
§ 24. ГРАФИК ФУНКЦИИ у =f(x)
Введенное раньше понятие о координатах позволяет дать гео-
метрическое изображение функции одной переменной.
Для выяснения этого рассмотрим несколько отдельных примеров.
Пример 1. у = -у х2.
Составим таблицу отдельных значений этой функции.
ординаты точек на плоскости XOY. Тогда на плоскости наметится
ряд точек:
0(0,0), ^(1,1), Ж2(2, 2),
Af3 (3,4-1), Л14 (4, 8), Ж6(-1,1),
Ш-2, 2), Л47(-3, 4-1),
Л48(—4, 8), и т. д.
Абсциссы OAlf ОА2, ОА3 и т. д.
изображают значения независимой
переменной х, а ординаты
А2Л42, А3М3 и т. д. соответствую-
щие значения функции. Чем больше
значений х мы возьмем, тем большее
число точек наметим на чертеже, а
чем ближе будем выбирать значение х одно к другому, тем ближе
будут расположены одна к другой соответствующие точки М.
59
§ 24] ГРАФИК ФУНКЦИИ у =f (х)
ряд этих точек при беспредельном увеличении числа задавае-
„ значений х образует сплошную кривую, изображенную на
мых
чертеже. „
Ординаты каждой точки этой кривой равны значениям функ-
иий у пРи данном х; в этом смысле и говорят, что кривая LtL
служит графиком функции
У = Тх2-
п 1 Ч
Пример 2. у — — у2Х •
Составим опять таблицу некоторых отдельных значений.
х О 1
3 4
и т. д.
О
12
60
ГРАФИКИ ФУНКЦИЙ
[V
Пример 3. у = - j.
Соответственно следующей таблице значений функции
X 1 2 1 2 3 4 5 6 и т. д.
У 12 6 3 2 3 2 6 5 1
X 1 2 — 1 — 2 — 3 — 4 — 5 — 6 и т. д.
У — 12 — 6 — 3 — 2 1 to| СО _ 6_ 5 — 1
намечаем сначала отдельные точки, а затем, увеличивая число зада-
ваемых значений х, и всю кривую (рис. 31). При этом замечаем,
что когда х приближается к нулю, оставаясь положительным, значе-
ния у неограниченно возрастают, тоже оставаясь положительными,
24] график функции j/=/(x) 61
когда х приближается к нулю, оставаясь отрицательным, значе-
а у неограниченно растут по абсолютной величине, оставаясь при
П ом отрицательными. Отсюда вытекает, что график функции состоит
из двух отдельных ветвей ККХ и LLV При х = 0 данная функция
никакого значения не имеет, что и отражается на рисунке перерывом
между ветвями ККХ и LLV
л 2
Пример 4. У = ^—^3‘
Рассуждая по предыдущему и пользуясь нижеследующей табли-
цей значений функции:
X 4 3-1 3 2 4 5 7 '
У 8 4 2 1 1 2
X СО СЧ 4 2 1 0 — 1
У - 8 — 4 — 2 — 1 _2 3 1 2
получим кривую, изображенную на рис. 32, состоящую, как и пре-
дыдущая, из двух разобщенных ветвей. При х = 3 функция не
имеет никакого значения.
Пример 5. У = —2-
Кривая, являющаяся графиком
рис. 33.
Таблица некоторых ее значений
этой функции, изображена на
следующая:
X 1 ±2 ±3 ±=6
У 18 4 2 1 2
С приближением х к нулю со стороны положительных и отри-
цательных значений х значения функции, т. е. ординаты, растут
Непредельно, оставаясь положительными. При х = 0 функция ника-
Кого значения не имеет.
Пример 6. у = 2х.
Рассматриваемая трансцендентная функция есть частный случай
Функции а® (а = 2).
62
ГРАФИКИ ФУНКЦИЙ
[V
Соответственно приведенной таблице значений этой функции
и т. д.
график ее изображен на рис. 34.
Рис. 35*
построим кривую, изображенную на рис* 35*
§ 24]
ГРАФИК ФУНКЦИИ y=f (х)
63
Пример 8. у = sin х.
Графиком функции служит кривая, изображенная на рис. 36,
где О А = тс.
Кривая эта носит название синусоиды.
Пример 9. у = cos х.
Функция изображается такой же кривой, как и предыдущая, но
сдвинутой вдоль оси Ох влево на величину, равную , так как
Кривая
эта носит название косинусоиды.
64
ГРАФИКИ ФУНКЦИЙ
(V
Пример 10. y = tgx.
Функция изображается неограниченным рядом бесконечных вет-
вей, как это изображено на рис. 38, где ОА = к.
Пример 11. у = ctg х.
Функция изображается неограниченным рядом подобных же бес-
конечных ветвей, расположенных как изображено на рис. 39, где
0А = ъ.
§ 25. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ
/(х, у)=0
Для установления геометрического значения уравнения с двумя
сначала несколько примеров отдельных
переменными рассмотрим
уравнений.
Пример 1. х—д/ = 0.
Для того чтобы можно было истол-
ковать уравнение с геометрической
точки зрения, прежде всего сообщим
переменным величинам х и у, входя-
щим в это уравнение, геометрический
смысл, а именно: примем их за коор-
динаты точек плоскости X0Y. Затем
поставим себе следующий вопрос: как
располагаются те точки, координаты
которых удовлетворяют данному ура-
внению? Из уравнения имеем у = х,
т. е. каждому положительному или отрицательному значению х со-
ответствует равное ему положительное или отрицательное значение у.
Это имеет место для всех точек прямой К^К— биссектрисы углов XOY
§ 25] ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ / (х, у) = О 65
И И притом только для точек этой прямой (рис. 40). Таким
образом, между точками прямой К^К, с одной стороны, и уравнением
х—у = ®, с другой стороны, устанавливается тесная связь, состоя-
щая в том, что координаты, всех точек прямой КгК и только точек
этой прямой удовлетворяют данному уравнению. В силу этого,
уравнение х—у = 0 и называют уравнением прямой КгК.
Пример 2. х+у = 0.
Понимая опять под х и у координаты различных точек плоско-
сти XOY, мы можем сказать, что уравнение это определяет пря-
мую L^L, проходящую через начало
координат и делящую пополам вто-
рой и четвертый координатные углы
(рис. 41).
Действительно, из этого уравнения
выводим, что для всех точек рассматри-
ваемого геометрического места у = — х,
т. е. ордината и абсцисса равны между
собою по абсолютной величине, но про-
тивоположны по знаку. А это имеет
место для всех точек биссектрисы уг-
лов Y0Xx и X0Yx и только для этих
точек.
Таким образом, координаты всех
точек прямой LXL и только этих
точек удовлетворяют данному уравнению.
ние х-|-у = 0 называют уравнением прямой LXL.
Рис. 41.
В силу этого, уравне-
Пример 3. х — т = 0, т. е. х = т.
Для решения вопроса, какое геометрическое значение имеет по-
следнее уравнение, достаточно задать себе вопрос: как распола-
у гаются все точки, абсциссы которых рав-
J \j) ны т?
[ Ответ получается сам собой: такие
1 ~д 01 r~~F точки располагаются на прямой DtD^OY
। и отстоящей от оси OY на расстоя-
[ нии 0А = т (рис. 42). Действительно,
------------[_______всех гпочек прямой и только для
0\[Д________________точек этой прямой х — т.
Л Таким образом рассматриваемое уравне-
Рис. 42. ние выражает прямую DXD, т. е. х—т = 0
есть уравнение прямой, параллельной OY.
Пример 4. у — п = Ъ, т. е. у = п.
Рассуждая подобно предыдущему, убеждаемся, что данное урав-
Ние представляет прямую F^F^OX и отстоящую от оси ОХ на
расстоянии ОВ = п (рис. 42).
Зак. 2116. Н. С. Михельсон.
66
ГРАФИКИ ФУНКЦИЙ
fv
Пример 5. л24~^- = ^2*
Предложенное уравнение есть уравнение окружности радиуса а,
с центром в точке О (рис. 43). Действительно, уравнение показы-
вает, что для всякой точки сумма квадратов катетов ОР и РМ есть
величина постоянная, т. е. расстояние ОМ есть величина постоян-
ная и равная а для всех точек, а это последнее имеет место для
всех точек окружности радиуса а,
с центром в начале координат и
только для этих точек.
Пример 6. (х— я)2+СУ — Ь)2 = г2.
Это уравнение есть уравнение окружности, радиус которой
равен г, с центром в точке А (а, Ь), так как только для точек та-
кой окружности квадрат расстояния до точки А будет равен постоян-
ной величине г2 (рис. 44).
Графикам функций, приведенных в примерах 1—И предыдущего
параграфа, также соответствуют свои уравнения. Так, кривая, изобра-
женная на рис. 29, определяется уравнением у — ух2 или 2у—х2= О,
на рис. 30 — уравнением у = — -^х3 или 12j/—х3 = 0, на рис. 31 —
уравнением У=~ или ху — 6’=0 и т. д., на рис. 36 — уравнением
y = sinx, на рис. 37 — уравнением у = cos х.
Кривые могут быть заданы уравнениями и в полярной системе
координат, что поясним на следующих примерах.
Пример 7. Определить геометрическое значение уравнения
р = а,
заданного в полярной системе координат.
Уравнение это отмечает на плоскости координат те точки, у ко-
торых полярный радиус-вектор равен постоянной величине, т. е.,
другими словами, те точки, расстояния которых от полюса равны
одной и той же величине.
§ 25] ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ f (х, у) = О 67
Очевидно, это будут точки окружности, с центром в полюсе,
радиус которой равен а. Следовательно, предложенное уравнение
есть уравнение такой именно окружности в полярной системе коор-
динат.
Пример 8. Определить характер кривой, заданной в полярной
системе координат уравнением
р = аб.
Кривая обладает тем свойством, что полярный радиус-вектор ее
точки возрастает пропорционально полярному углу 0.
При 6 = 0 р — 0 получаем точку О (0, 0)
„ 6=1 радиану р = а „ „ А (а, 1)
„ 0 = 2 радианам р - 2а „ „ В (2а, 2)
„ 0 = 4 радианам р = 3а „ „ С (За, 3)
и т. д.
Кривая делает бесчисленное
множество оборотов около по-
люса. Она называется спиралью
Архимеда (рис. 45).
Рассмотрим теперь общий
случай. Положим, что мы имеем
уравнение вида
F(x, у) = 0. (1)
Как и в вышеприведенных
частных примерах уравнений, со-
общим переменным х и у гео-
метрический смысл, а именно: примем
. Рис. 45.
их за координаты точек
плоскости XOY. Тогда нетрудно будет уяснить, что уравнение (1)
или решенное относительно у уравнение
(2)
вообще говоря, выражает на плоскости некоторую линию.
В * самом деле, пусть для х = ах из уравнения (2) следует зна-
чение у = Приняв ах и Ьх за координаты, наметим точку
Мх(ах, ^).
Дадим теперь х значенйе
х — а^,
^ало отличающееся от тогда, вообще говоря, соответствующее
-У = ^2
68
ГРАФИКИ ФУНКЦИЙ
[V
будет тоже мало отличаться от bv Величины и Ь2 определят
точку Л42, близкую к точке Продолжая давать все новые и новые
значения х, мы получим соответствующие значения у. Точки, по-
строенные таким образом, заполнят, вообще говоря, некоторую
линию, причем координаты всех то-
чек этой линии будут удовлетворять
этом и заключается
В
уравнению
y=f(x),
или, что то же, уравнению
F(x, У) = О-
Ввиду существования столь тес-
ной связи между координатами точек
полученной кривой НН^ (рис. 46) и
уравнением F (х, у) = 0, говорят, что
это уравнение выражает линию HHV
основное положение о геометрическом зна-
чении одного уравнения с двумя переменными.
Это общее положение о геометрическом значении уравнения
f (х. У) — 0 допускает, однако, и исключения.
Чтобы пояснить это, рассмотрим уравнение х24~3'2=0.
Уравнение это не представляет линии, а определяет только одну
точку, именно начало координат. В самом деле, сумма двух квад-
ратов вещественных значений х и у может быть равна нулю лишь
тогда, когда отдельно каждое слагаемое равно нулю. Следовательно,
в данном случае уравнение удовлетворяется только значениями х = О
и у = 0, а эти значения определяют одну только точку и именно
начало координат.
Такое уравнение, как х2 + (.у— 1)24-а2 = 0, где а не равно О,
уже вовсе не определяет никакого геометрического места, так как
не удовлетворяется никакими вещественными значениями х и у.
Действительно, левая часть данного уравнения не может обратиться
в нуль ни при каких вещественных значениях х и у.
Рассмотрим теперь несколько общих задач, относящихся к урав-
нениям линий.
Задача I. Узнать, принадлежит ли точка Af(a, J) ли-
ни и, заданной уравнением y=f (х) или F (х, у) = 0.
Для решения задачи достаточно убедиться, удовлетворяют ко-
ординаты а и b точки М данному уравнению или нет, т. е. про-
верить, будут ли верны равенства
b=f(a) и F(a,b) = 0
или не будут. В первом случае точка принадлежит нашей линии,
во втором нет.
§ 26] СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛИНИЙ 69
Пример 1- Узнать, принадлежат ли точки Afj (1, —1), уИ2 (3, —2) линии
2ху-~>3+1 = °-
Подставляя координаты точек в данные уравнения, находим, что точка
принадлежит данной линии, а М2 не принадлежит этой линии.
Н Пример 2. Проходят ли линии Зх24-у—1 = 0, х2— ху—у2— Зх = О
через начало координат?
Так как координаты начала (0, 0) не удовлетворяют первому уравнению,
а второму удовлетворяют, то, следовательно, первая линия не проходит
через начало координат, а вторая проходит.
Задача II. Найти точку на линии F(x, у) = 0, абсцисса
или ордината которой задана.
Пусть требуется найти ту точку, абсцисса которой равна а.
Подставляя в данное уравнение на место х значение а, получаем
уравнение F(a, у) = 0, из которого и определяем ординатур. Най-
денное значение ординаты вместе со значением х = а, конечно,
будет удовлетворять данному уравнению.
Пример 3. На линии у = 1g х найти точку, в которой данная линия пе-
ресекает ось ОХ.
В точке, где линия пересекает ось ОХ, ордината равна нулю; поэтому
предложенная задача сводится к отысканию такой точки данной линии, в
которой у = 0. Подставляя в данное уравнение это значение, приходим к
уравнению
lgx = 0,
откуда находим, что х = J. Итак, данная линия- пересекает ось OY в точ-
ке (1, 0) (см. рис. 35, стр. 62).
Задача III. Найти точку пересечения линий (х, у) = О
и F2 (х, у) = 0.
Так как точка пересечения двух линий принадлежит обеим ли-
ниям, то ее координаты должны удовлетворять обоим уравнениям
одновременно. Поэтому, для решения задачи необходимо решить
совместно оба уравнения.
Пример 4. Найти точку пересечения линий у2 — х4-2 = 0 и ху2—3=0.
Решим совместно два данных уравнения. Найдя из второго уравне-
ния у2= -- и подставляя это значение в первое, находим:
х2 —2х —3 = 0,
откуда имеем xt = — 1 и х2 = 3.
При х£ = — 1 у = У — 3 мнимое, что не определяет никакой точки.
При х2 = 3 y = ztl, что приводит нас к двум точкам. Итак, линии
пересекаются в двух точках: Afj (3, 1) и М2 (3, —1).
§ 26. СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛИНИЙ ПО УСЛОВИЯМ,
ИХ ОПРЕДЕЛЯЮЩИМ
Определенных правил для составления уравнений различных
линий дать нельзя; тем не менее, все же можно указать некото-
рый общий метод, которым следует руководствоваться для того,
чтобы направить решение в надлежащее русло. Метод этот заклю-
чается в следующем.
70
ГРАФИКИ ФУНКЦИЙ
[V
Прежде всего, надо себе уяснить, какие величины, по условию
задачи, можно считать заданными, т. е. нам известными. Затем не-
обходимо выбрать определенным образом систему координат. За-
дача обыкновенно приобретает наиболее простое решение, если оси
выбрать наиболее рациональным образом, например, если за оси
координат принять прямые, проведенные через определенные точки,
входящие в условие задачи. Установив координатную систему, на-
мечают на плоскости координат некоторую тбчку, которую и пред-
полагают принадлежащей рассматриваемому геометрическому месту.
Затем на основании свойства, которым по условию должна обла-
дать эта точка, составляют уравнение, связывающее координаты
выбранной точки с входящими в задачу данными величинами. При
этом иногда бывает полезно в действительности построить коорди-
наты этой точки и сделать некоторые нужные дополнительные
построения.
Так как намеченная нами точка является одной из точек иско-
мого геометрического места и притом произвольной, то получае-
мое уравнение, связывающее координаты этой точки, будет отно-
ситься ко всем точкам рассматриваемого геометрического места, т. е.
и будет являться его уравнением.
Поясним это на примерах.
Пример 1. Найти уравнение геометрического места точек, из
которых можно провести к двум данным окружностям равные ка-
сательные.
Условие задачи предполагает,
по их взаимному расположению,
Рис. 47.
с координатами х и у является
метрического места, так что
что* окружности нам заданы как
так и в отношении величины их
радиусов. Поэтому мы мо-
жем считать известными
радиусы и г2 окружно-
стей и расстояние d между
их центрами (рис. 47).
Пусть положение окруж^
ностей будет такое, как
указано на чертеже, с цен-
трами в точках и С2.
Соответственно указан-
ному методу примем за
ось ОХ линию, соединяю-
щую центры кругов, а ось
OY проведем через сере-
дину отрезка Затем
предположим, что точка Л1
одной из точек нашего гео-
дл. ЛЬ4: == дл.
(3)
§ 26]
СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛИНИЙ
71
Остается теперь найти уравнение, связывающее координаты
этой точки с данными величинами.
Так как расстояние и радиусы и г2 считаются извест-
ными, то мы можем считать известной и длину DrD2. Пусть
£^£>2 = 20. Соединим центры кругов и С2 с точкою М и с точ-
ками касания. Тогда
= —/-з и МА^С^М2 — г22.
Так как, при выбранной системе координат координаты центров
кругов оказываются следующими:
ci(a~srri> °) и С’а(— а~ гъ> °)>
то
С17И2 = (лг— а — /'i)2+^2 и С2/И2= (х-\-а-\-г^)2-\-у2,
а потому
МА*=(х — а — г^-УУ3 — г2 и МА2 = (х + а + г2)2 «уу2 — г2.
В силу условия (3) имеем
(х — а — и)3 + У — Г1 = (х + а 4- г2)3 -}- /—г}. (4)
Этому-то уравнению и должны удовлетворять координаты
точки М.
Но так как точка М является только одной из точек нашего
геометрического места и притом произвольно нами выбранной, то
тому же уравнению будут удовлетворять и координаты всякой
другой точки геометрического места. Следовательно, уравнение (4)
и является искомым уравнением рассматриваемого геометрического
места точек.
Решение задачи, собственно говоря, закончено; остается лишь
упростить уравнение (4) для того, чтобы выяснить форму этого
геометрического места точек.
Прежде всего замечаем, что из обеих частей уравнения (4) можно
исключить член у2. Далее, раскрывая скобки и упрощая, находим:
х —а —|— г 1 — 2б/х — 2г]Х ~у 2аг 1 — г=
= У -| а3 -У г2 ~у 2ях 2г~>х + 2аг>
(а -у rj х-У (а + г2) х = а — г2)
(2а 4- гх -у г2) х = а (гх — г2)
и наконец
Последнее уравнение показывает, что абсциссы всех точек
Геометрического места есть постоянная величина, т. е. что искомое
72
ГРАФИКИ ФУНКЦИЙ
lv
геометрическое место точек есть прямая, параллельная оси OY или
перпендикулярная к линии центров двух окружностей и отстоящая
от середины отрезка на величину, равную ,
§ 27. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
Мы видели, что при составлении уравнений геометрических мест
весьма большое значение имеет надлежащий выбор координатной
системы; он облегчает самое решение задачи и дает возможность
получить результат в наиболее простой форме.
Но так как выбор системы координат и то или другое распо-
ложение координатных осей не определяется какими-либо общими
правилами, то, естественно, возможны случаи, когда выбранная нами
система не окажется наилучшей для поставленной нами цели, в силу
чего и явится необходимость перейти от выбранной системы к новой.
Таким образом, и возникает задача, носящая название „преобразова-
ние координатОна состоит в следующем.
Зная координаты некоторой точки относительно одной си-
стемы координат, определить координаты той же точки отно-
сительно другой системы.
Задача I. Перенос начала координат без измене-
ния направления осей.
Пусть ОХ и OY—оси прямоугольных координат, относительно
которых положение точки М определяется известными нам коорди-
натами х и у, Пусть далее О1Х1 и — новая система коорди-
натных осей, параллельных и одинаково направленных с первою, но
имеющая начало в точке ОР
Координаты нового начала относительно первой системы должны
быть известны; обозначим их через а и Ь. Искомые координаты
точки М относительно осей ОхХх и OjKj
обозначим через jq и
Итак, задана следующая совокупность
координат точек М и О:
М(х, у), О (а, Ь)
и по ним ищутся новые координаты той
же точки М
М (Xj, ^i).
Рис. 48. Рассмотрим ломаную линию ООГМ
с началом в точке О и концом в М
(рис. 48). Отрезок ОЛ4, взятый в направлении от О к М, служит
ее замыкающею. На основании теоремы о проекции ломаной (§ 11),
имеем:
пр. ОМ = пр. ООг пр. ОГМ.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ
73
§ 271
Принимая в этом равенстве за ось проекции сначала ОЛ, а за-
тем OY, находим на основании формул (1) (стр. 42):
х = а + х1 )
У = b + yv }
Эти формулы и решают задачу.
Пример 1. Точка М имеет координаты 2, —3. Каковы будут координаты
той же точки, если начало координат перенести в точку О± (—1, 4), не
изменяя направления осей.
Здесь х = 2, у — — 3, а = — 1, b = 4; поэтому по формулам (5) имеем
2=-l+xi,
-3=4+^,
откуда и находим новые координаты той же точки.
*1 = 3, У1 = — 7.
Пример 2. В какое уравнение преобразуется уравнение линии
х2 — 4х — 2у + б = О,
если, не изменяя направления осей, перенести начало координат в точку
01(2,1).
По формулам (5) имеем
х = 2 + xlt
у = 1 +У1-
Подставляя эти выражения в уравнение кривой, найдем
(2 + х1)2-4(2 + х1)-2(1+у1) + б = 0,
4 + 4хх + xf — 8 — 4хг — 2 — 2у: + 6 = 0,
Х1 — = О или 3'j ~ у •
Как видно, в новой системе координат уравнение кривой получилось
значительно проще. Сравнивая его с уравнением примера 1 (§ 24), мы видим,
что под уравнением х2—4х—2у +
+ 6 = 0 скрывается кривая, изо-
браженная на рис. 29 (стр. 58).
Задача II. Поворот
°сей без изменения на-
чала.
Пусть ОХ и OY—оси пря-
м°угольных координат, отно-
сительно которых положение
т°чки М определяется изве-
чными нам координатами х
и+• Пусть OXt и OYr — оси
Ио*°й системы координат, по-
ВеРнуТОй относительно первой на угол а. Координаты точки М
относительно этой новой системы обозначим через х1 и yt (рис. 49),
На чертеже
OP = xlf РМ =
74
ГРАФИКИ ФУНКЦИЙ
[V
Рассмотрим ломаную линию ОРМ, для которой замыкающей слу-
жит ОМ. По теореме о проекции ломаной (§11) '
пр. ОМ — пр. ОР -ф- пр. РМ.
Принимая в этом равенстве за ось проекций сначала ОХ, а за-
тем OY и, принимая во внимание формулы (1) (§ 10) и (1) (§ 14),
находим
х = ОР • cos (ОХГ, ОХ) 4- РМ • cos (РМ, ОХ),
у = ОР • cos (OXV OY)-{-PM-cos(РМ, OY).
Но
(ОХи ОХ) = а, (РМ, ОХ) = (ОГр ОХ) = у -J- а,
(ОХ1Г ОУ)=-£ — а, (РМ, OY) = (OYlt ОУ) = а.
Так что
cos (ОХг, ОХ) = cos a, cos (РМ, ОХ) = cos Ц- а) = — sin а,
cos(OAr1, OT) = cos0^ — a) = sina, cos (PM, OY) = cos a.
Поэтому находим
x = Xi cos a — уi sin a 1
. . (6)
у = xt sin a -j-yj cos a. J '
Эти формулы и устанавливают искомую зависимость между перво-
начальными и новыми координатами точки М.
Пример 3. Точка М определяется координатами 2 и —4. Каковы будут
координаты той же точки, если координатные оси повернуть на 90° в сто-
рону против часовой .стрелки? Здесь х = 2, у = — 4 и a = 90°, поэтому
формулы (6) дадут:
2 = xr cos 90° —ух sin 90°
— 4 = Xi sin 90° +yi cos 90°
или
2 = -У1,
— 4 = хр
Таким образом, новые координаты той же точки будут
Д4 (— 4, —2).
Пример 4. В какое уравнение преобразуется уравнение х2—у2 =12,
если оси координат повернуть на 45° в сторону по часовой стрелке?
В данном случае а = —45°, поэтому формулы (6) принимают здесь
такой вид:
х — Xi cos (— 45°) —yj sin (— 45°),
у = Xi sin (— 45°) + ух cos (— 45°).
Но
cos (- 45°) = cos 45° = ,
sin (- 45°) = - sin 45° = —
§ 27]
ПРЕОБРАЗОВАНИЕ КООРДИНАТ
75
Таким образом, имеем _
X = ~ (Х1 + л),
У% , I* ч
3' = -Г2~(— *1+л)-
Подставляя найденные значения в данное уравнение, получим
у (Xt + Л)2 - у (- -VI + -У1)2 = 12,
а после раскрытия скобок и упрощения уравнение приведется к виду
Xj-_Vi = 6.
Это и будет искомое уравнение; оно, как видно, проще начального
и выражает кривую, изображенную на рис. 31 (стр. 60).
Задача III. Преобразование полярной системы ко-
ординат в прямоугольную и обратно.
Пусть ОХ и OY—оси прямоугольной системы координат и
пусть х — ОА, у = AM— прямоугольные координаты некоторой
точки М. Примем ОХ за полярную ось и точку О за полюс и
обозначим полярные координаты точки М
через р и 6.
Из чертежа непосредственно следуют
формулы:
х = pcos6
у — р sin 0 (7)
р= + Ух2-}-у2
tgO = y- (8)
Рис. 50.
Эти формулы и решают поставленную задачу.
Примерб. Полярные координаты некоторой точки р = 2, 0 = у.
Найти прямоугольные координаты той же точки. По формулам (7) находим:
х = 2 cos = 2 • 4" = Ъ
о 2
у = 2 sin = 2- = уз.
о 2
Примере. Прямоугольные координаты точки М: х = 2, у = — 2. Найти
полярные координаты той же точки.
По формулам (8) находим
р = + /4Т4 = + 2/2,
tg6=-y=-l.
Полярный радиус-вектор найден окончательно; что же касается поляр-
°Го угла '' т0 он еще не вполне определен. При tg 0 = — 1 угол 0 может
меть два значения
0 = 135° и 0^ — 45°.
76
ГРАФИКИ ФУНКЦИЙ
[V
Поэтому необходимо еще выяснить, которое значение отвечает действитель-
ности. Прямоугольные координаты точки
(2, -2)
ясно указывают, что точка находится в четвертом координатном угле-
Поэтому из двух значений для угла 6 необходимо в данном случае взять
6 -=-- — 45° = —-г.
4
Итак, полярные координаты рассматриваемой точки будут
Л1(+2Г2,—£).
§ 28. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Как геометрически изображается функция одной переменной?
2. Какое геометрическое значение имеют, вообще говоря, уравнения
вида у =f(x) или F(x, у) = О?
3. Всякому ли уравнению вида F(xf у) = 0 соответствует некоторая
линия на плоскости координат?
4. Как узнать, находится ли данная точка (а, Ь) на линии, уравнение
которой F(x, у) = О?
5. Как найти какую-нибудь точку, принадлежащую линии, заданной урав-
нением вида у = f (х) или F (х, у) = О?
6. Принадлежат ли точки (1, — 2), (2, — 3), (3,10) линии х2—ху + 2у+1=0.
Отв, Да, нет, да.
7. Указать несколько точек (по две) на каждой из линий:
2х — 5у + 8 = 0, у2 — 3х + $у — 4 = 0.
8. На линии х2 — 2у-±-5 = 0 найти точку, ордината которой равна 7.
Отв, (3, 7); (— 3, 7).
9. Построить линии, заданные уравнениями:
а) Зх — 5у + 4 = 0, б) у = 2х + х2,
10. Построить линию, заданную в полярной системе координат уравне-
нием р • 0 = а (гиперболическая спираль).
11. Найти точки пересечения линии ху— 2у—3x-f-6 = 0 с осями коор-
динат.
Отв, Точки (0, 3); (2, 0).
12. Проходят ли линии л3 — ху + у* = 0, 2ху + ех —у = 1, х2 — ху — 1 =
= 0 через начало координат. Qme Да> да нет
13. Найти точку пересечения линий х — 2у — 3 = 0, 2л: -|- Зу + 1[ = 0.
Отв. (1, — 1).
14. Найти точки пересечения линий х2-±-ху — 2 = 0 и х2-±-у2 — 5 = 0,
и Отв. Четыре точки: (2, — 1), (—2, 1).
ЙЧ^М-^-4^)-
15. Составить уравнение геометричс-
ского места точек, равноудаленных от двух
данных точек. Отв. Прямая линия.
, 16. Отрезок АВ перемещается внутри
г прямого угла (см. рис. 51), все время опи-
q_____________________А % раясь своими концами на стороны этого
угла. Найти уравнение линии, которую вы-
Рпс’ 51. черчивает при этом точка М, отстоящая от
концов отрезка на расстояниях а и Ь.
х2 у2
Отв. ^2 ^2 = (За оси координат приняты стороны прямого угла.)
§ 28] вопросы и упражнения 77
17. Два стержня вращаются в одной плоскости вокруг двух данных
точек, оставаясь все время перпендикулярными друг к другу. Составить
уравнение геометрического места точек пересечения стержней.!
Отв. х2 +j/2 = л2, где а — половина расстояния между данными точками.
18. Координаты точки М в прямоугольной системе координат (5, —3).
Определить координаты той же точки, если начало координат перенести
в точку (2, — 1). Оть. ЛГ(3, —2).
19. В какую точку надо перенести начало координат без изменения
направления осей, чтобы прямоугольные координаты точки Л4 (— 1, 4) сдела-
лись равным (2, —4)? Отв. (—3, 8).
20. После перенесения начала координат в точку О± (2, — 3) без измене-
ния направления осей, координаты точки М сделались равными (—3, 1).
Каковы были первоначальные координаты той же точки?
Отв. М (— 1, — 2).
21. Определить прямоугольные координаты точки Л4, полярные коорди-
наты которой равны 4 и — Отв. Л4(2 У 3*, —2).
22. По данным прямоугольным координатам точки М
определить их полярные координаты. Отв. А4 У 2, .
23. Прямоугольные координаты точек удовлетворяют уравнению
у = х2— 4х-|-5. Какому уравнению будут удовлетворять координаты тех же
точек, если начало координат перенести в точку (2, 1), а направление осей
оставить без изменения. Отв. yt = х*.
24. Прямоугольные координаты некоторых точек связаны между собою
уравнением (x2-j-y2)2 = а2 (х2—у2).-Каким уравнением будут связаны поляр-
ные координаты тех же точек. Отв. р2 = a2 cos 20.
VI. ПРЯМАЯ ЛИНИЯ
§ 29. ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА
В § 25 было пояснено, что всякое уравнение вида /(х, j/) = 0
выражает, вообще говоря, некоторую линию. Среди различных
линий, изучаемых аналитической геометрией, наиболее простыми
являются те, которые выражаются алгебраическими уравнениями
первой и второй степени, т. е. уравнениями вида
+ + С = Ах2фВхуфСу*фОхфЕуфЕ = Ь,
где Л, В, С, D, Е и F— некоторые определенные коэффициенты.
Первая из них называется линией 1-го порядка, вторая 2-го
порядка, соответственно степени их уравнений.
Мы начинаем с изучения первой линии.
Теорема. Всякое уравнение вида
АхфВуфС = Ъ (I)
выражает на плоскости координат некоторую прямую.
Для доказательства этой теоремы рассмотрим уравнение (I)
в двух отдельных случаях: в предположении, что коэффициент В = О,
и в предположении, что В ф$. (Одно из этих двух предположений
всегда имеет место.)
I предположение: В = 0.
В этом случае уравнение (I) принимает вид Ах С = 0.
Решая его относительно х, находим
Обозначив для краткости-----= т, получаем уравнение
х = т.
Это уравнение, как мы видели (см. стр. 65), есть уравнение
прямой, параллельной оси 0Y.
Таким образом, уравнение (I) в рассматриваемом случае выра-
жает прямую и притом параллельную оси 0Y.
ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА
79
§ 29]
II предположение: ВфО.
Решая уравнение (I) относительно у, находим
А С
У— ВХ -- в.
Положив для сокращения письма
Д С ,
в~~а’ В ~~Ь’
получаем
у = ax-\-b. (II)
Для исследования геометрического значения уравнения (II) обра-
тим внимание на то, что при х = 0, у = Ь, т. е. что точка 7С(0, Ь)
принадлежит нашей линии.
Отложим на оси OY отрезок
ОК= b (*)
и проведем через точку К прямую /СЛ^, параллельную
оси ОХ
знамена-
Затем перепишем уравнение (II) в виде
у—Ь
--------------------------=а.
х
Теперь представим себе, что точка М (х, у) является
точек, координаты которой удовлетворяют уравнению (1).
твжа следует, что
KP = OQ = x, QM=y, QP = b.
Поэтому из уравнения (1), после замены числителя и
теля соответствующими отрезками, вытекает, что
РМ
КР
Если бы мы взяли другую точку 717 п координаты которой также
Удовлетворяли бы уравнению (1), то подобным же образом нашли
что и
—-—- = а
КР1
(1)
ОДНОЙ из
Из чер-
80
ПРЯМАЯ ЛИНИЯ
[VI
Таким образом, мы обнаруживаем, что для всех точек 7И,
и т. д., координаты которых удовлетворяют уравнению (I) или,
что то же, уравнению (II), имеет место следующее их свойство:
РМ_Р1М1 _ Р2М2 __
КР KPi = КР2
А это, как известно из элементарной геометрии, указывает, что
все такие точки расположены на одной прямой линии. Следовательно,
и во втором предположении, когда В ф 0, уравнение (I) выражает
на плоскости координат прямую линию.
Итак, в обоих случаях, при В = 0 и при В уравнение (I)
всегда выражает некоторую прямую линию.
§ 30. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ КОЭФФИЦИЕНТОВ а и ft.
Коэффициенты а и b уравнения
у = ах b (II)
имеют важное значение в вопросах, относящихся к прямой линии.
А именно, из формулы ОК=Ь предыдущего параграфа видно,
что коэффициент b есть ордината точки пересечения прямой
с осью OY. Коэффициент этот называется начальной ординатой
прямой.
Что касается коэффициента а, то геометрическое его значение
вытекает из формулы (2). Именно: с одной стороны, сдру-
гой £MKP — tg а.
Следовательно
a = tga. (**)
Коэффициент этот называется угловым коэффициентом прямой.
Итак, угловым коэффициентом прямой называется коэф-
фициент при абсциссе х в уравнении прямой, решенном от-
носительно координаты у. Он равен тангенсу угла, составлен-
ного прямой с осью ОХ.
За положительное направление прямой будехм принимать то,
в котором ординаты точек прямой возрастают.
Из формулы (**) следует, что
если а > 0, то а < у,
если а < 0, то а > у,
т. е., что прямая с осью ОХ составляет в первом случае острый
угол, во втором — тупой. Также очевидно, что угол этот будет
тем ближе к прямому, чем больше абсолютная величина углового
коэффициента а.
§ 311
ВТОРАЯ ОСНОВНАЯ ТЕОРЕМА (ОБРАТНАЯ ПЕРВОЙ)
81
Для нахождения углового коэффициента прямой и ее началь-
ной ординаты достаточно решить уравнение прямой относительно у,
тогда коэффициент при х в уравнении, решенном относительно у,
и будет угловым коэффициентом прямой, а свободный член — началь-
ной ординатой прямой.
Так, например, из уравнения прямой Зх — 4 = 0 находим
у х4“2. Следовательно, для этой прямой
а = — -|, Ь=2.
Уравнение, в котором нет члена с у,
ния (П) нельзя. Такая прямая не имеет
углового коэффициента. В этом случае
прямая, как уже известно, параллельна
оси ОУ, угол а = 90°, и так как tga =
= ±оо, то иногда говорят, что угловой
коэффициент такой прямой равен z±zoo.
Угловой коэффициент прямой харак-
теризует скорость изменения у в зави-
симости от изменения х. Именно, не-
трудно видеть, что у изменяется тем
быстрее, чем угол, составляемый пря-
мой у = ах -f- b с осью ОХ, ближе
к прямому, т. е. чем больше абсолютная
величина углового коэффициента. На
привести к виду уравне-
Рис. 53.
рисунке видно, что при одном и том
же изменении х на величину h — PQ ордината прямой LLr изме-
няется на величину
k = FD = h • tg DRQ = h • tg (3,
а ордината прямой KKr лишь на величину
l = EC = h- tg = й - tg а.
§ 31. ВТОРАЯ ОСНОВНАЯ ТЕОРЕМА (ОБРАТНАЯ ПЕРВОЙ)
Теорема, Всякая прямая выражается уравнением 1-й степени.
Пусть ATCi — некоторая прямая, уравнение которой нам тре-
буется найти. Положение ее будет вполне определено, если задать
Длину перпендикуляра ОР и угол, который он образует с осью ОХ.
Пусть дл. ОР = р и {ОР, 0Х) = (л (рис. 54).
Возьмем произвольную точку М на нашей прямой с координа-
ции х = ОХ. у = NM и рассмотрим ломаную линию 0NMP с замы-
кающей ОР.
По известной теореме о проекции замыкающей имеем
пр. CW+ пр. ЛМ4-|-пр. МР = пр. ОР.
6 Зак. 2116. Н. С. Михельсон.
82
ПРЯМАЯ ЛИНИЯ
Принимая за ось проекции линию ОР, получим
пр. ON= ON cost» = х cost»,
пр. NM = NM cos =y sin©,
np. MP = 0,
np. OP — OP = p.
А потому приходим к такому урав-
нению
х cos со -f- у sin © — р. (Ill)
Этому уравнению удовлетворяют
координаты точки М, но так как точка
М выбрана на прямой ККг произвольно,
то тому же уравнению будут удовлетворять координаты всякой
точки прямой КК19 т. е. уравнение (III) является искомым уравне-
нием прямой. Так как оно 1-й степени, то теорема доказана.
Уравнение (III) называется уравнением прямой в нормальном
виде.
§ 32. ПРИМЕРЫ НА ГРАФИКИ ЛИНЕЙНОЙ ФУНКЦИИ
Из доказанного выше следует, что графиком функции у = ах-\-Ь служит
прямая, уравнение которой у = ах + Ь.1
В частном случае, когда b = 0, прямая у = ах проходит через начало
координат и служит графиком прямой пропорциональной зависимости между
у и х. Угловой коэффициент прямой тогда является коэффициентом про-
порциональности, В силу этого, все законы, выражающиеся прямой пропор-
циональной зависимостью между двумя величинами, графически могут быть
изображены различными прямыми, проходящими через начало координат
(рис. 55).
1 По этой именно причине функция 1-й степени ах + b называется
часто линейной функцией. Термин этот распространяется и на функции 1-й
степени со многими переменными, т. е. на функции вида
ах, 4- by cz d
и т. п., которые также называются линейными относительно переменных
X, у, Z и т. д.
§ 32] ПРИМЕРЫ НА ГРАФИКИ ЛИНЕЙНОЙ ФУНКЦИИ 83
Так, законы:
]) масса тела т пропорциональна его объему v:
т = Dv;
2) сила /, действующая на материальную точку, пропорциональна вы-
зываемому ею ускорению w (второй закон Ньютона):
f = mw,
3) относительное растяжение стержня S пропорционально растягиваю-
щей силе р (закон Гука):
р = Е - о
— все иллюстрируются прямыми, если на осях прямолинейных координат
откладывать соответственные величины: в первом случае — объемы и и
массы т, во втором случае — ускорения w и силы /, в третьем случае —
относительные растяжения 5 и растягивающие силы р.
Угловыми коэффициентами этих прямых являются: в первом случае —
плотность данного тела D, во втором случае—масса данной точки т,
в третьем случае — модуль упругости материала Е,
Некоторые другие законы также могут быть истолкованы геометрически
в виде прямых линий.
4) Закон расширения тел от нагревания, выражающийся формулой
V = (1 4- р/) ИЛИ V =
изображается некоторой прямой АВ (рис. 56), если на одной оси отклады-
вать температуры, а на другой — объемы тела. При этом
ОА = — величина объема при t = О,
vop — угловой коэффициент прямой (где р — коэффициент объемного рас-
ширения данного тела).
Чем больше будет величина коэффициента расширения тела, тем прямые,
выражающие этот закон, будут составлять с осью ОХ все больший и боль-
ший угол и тем, следовательно, значительнее будет изменение объема
с изменением температуры тела.
v 5) Закон, дающий зависимость между временем t и пройденным точ-
к°й расстоянием в ее прямолинейном и равномерном движении, выра-
жающийся формулой s = -j- ct, изображается также некоторой прямой ВС,
(Рис. 57), где ОА — s0 есть путь, пройденный точкой к моменту времени
*^0, т. е. к моменту начала отсчета времени, с — угловой коэффициент
прямой и вместе с тем скорость равномерного движения.
Рис. 57 показывает, что s = 0 при t = OD, т. е. что началом отсчета
Пройденного точкой пути является место, в котором точка была в момент
6*
VII. ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ
§ 33. ПЕРВАЯ ГРУППА ЗАДАЧ
Все задачи, относящиеся к прямой, можно разделить на две
группы. В одной из них прямые, одна или несколько, заданы своими
уравнениями, и требуется относительно данных прямых решить не-
которые вопросы. В другой группе уравнения прямых не даны,
а напротив, требуется их найти по данным условиям. Примеры тех
и других задач следуют ниже. Начинаем с задач 1-й группы.1
Задача I. Найти угол а, образованный данной пря-
мой АхфВу С = 0 с осью ОХ.
Если в уравнении В — 0, то прямая параллельна оси OY и потому
И = ~2 '
Если ВфЪ, то, решив уравнение относительно у. находим
угловой коэффициент прямой а. а затем по формуле
я = tg а (3)
и самый угол а.
Пример 1. Определить угол, составленный с осью ОХ прямой
2х —3 = 0.
Прямая, очевидно, параллельна оси OY, а потому а =
Пример 2. Определить угол, составленный с осью ОХ прямой
Зу + 5 = 0.
Прямая, очевидно, параллельна оси ОХ, а потому а = 0.
Пример 3. Определить угол, составленный с осью ОХ прямой
х — Зу -f- 2 = 0.
Решая уравнение относительно у, находим
Угловой коэффициент этой прямой а =
о
\ Под выражениями „дана прямая", „найти прямую** в аналитической гео-
метрии подразумевают: „дано ^равнение прямой", „найти уравнение прямой".
§ 33]
ПЕРВАЯ ГРУППА ЗАДАЧ
85
Пользуясь равенством
== Т,52288, а = 18°26'7".
+ 1
tga = -y, находим по таблицам угол a: Jgtga =
Задача II. Найти угол между двумя данными пря-
мыми: + и 4-Cj =0.
Предположим сначала, что ни одна прямая не параллельна оси ОУ.
Из заданных уравнений определяем сначала угловые коэффициенты
прямых. Пусть они будут а и аР
Обозначив искомый угол между прямыми через а углы, обра-
зуемые прямыми с осью OJV, соответственно через а и f), находим,
что
ш = zb (а — Р)
(z±z в зависимости от того,
из углов больше: а или (3)
tgw = =htg(a — Р) =
t tg a — tg р
— — г+tg a • tg p
Ho tga = a, tgp=a1? i
Эта формула и решает
В случае, если одна из
параллельна оси OY, то
упрощается. В этом случае достаточно определить сначала угол,
составленный другой прямой с осью ОХ, а зная его, определяем и
угол с осью ОУ, т. е. со второй прямой.
Из формулы (4) вытекают два важных следствия:
1) Если а=а17 то tg<o=0, откуда заключаем, что oj==0 и
прямые, следовательно, взаимно параллельны. Обратно, если пря-
мые параллельны, то = 0, tg w = 0, и следовательно а = аг
2) Если 1ДД] = 0, т. е. если а = — ±~, то tg<o = z±rco,
о)=~и прямые взаимно перпендикулярны. Обратно, если пря-
мые перпендикулярны, то = tgw = rtoo, и следовательно
= 0 или а =--------------
‘ 1 а!
Таким образом, условия
а= ах (5)
а = -1 (6)
являются: первое условием параллельности, а второе — перпенди-
кулярности двух прямых.
86 ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ [VU
Пример 1. Найти угол между прямыми 4х4~3 = 0 и 3x-{-2j/— 5 = 0.
Здесь одна из прямых параллельна оси OY, Поэтому определяем угол,
составленный другой прямой с осью ОХ,
3 3
Ее угловой коэффициент а =—т. е. tga =—— .
По таблицам находим а= 180° — 56°I8Z36/Z = 123O41Z24".
Следовательно, искомый угол <о = 123°4lz24" — 90° = 33°41'24".
Пример 2. Найти угол между прямыми 5х — у + 2 = 0 и 2х — Зу + 1 =0.
Данные прямые имеют следующие угловые коффициенты:
е 2
а = 5, = -у.
о
Поэтому по формуле (4) находим
5___
. 3 13 13 1 АЫ
‘8“ = —Ю= 3-3в1’ т’е- “ = 45-
3
Задача III. Найти точку пересечения двух прямых:
Ах By —(— С = 0 и А]Х —р- В^у —|— = 0.
Точка пересечения (если только она существует) есть общая
точка двух прямых. Координаты ее должны, следовательно, удо-
влетворять уравнениям обеих прямых, а потому для отыскания коор-
динат точки пересечения следует решить совместно оба уравнения.
Исключая из данных уравнений сначала одно неизвестное, а затем
другое, находим
(ДВХ — AtB) х 4- (CBt — CjB) = 0,
(ABt — AtB) у + (ACX — ДХС) = 0.
Отсюда следует:
1) Если ABt — то из последних уравнений най-
дется одно значение для х и одно для у, т. е. найдется одна точка
пересечения.
2) Если АВХ — AtB = ^^ но ни одно из выражений CBt — СХВ
и АС\ — ArC ф. 0, то уравнения не удовлетворяются никакими
значениями х и уу т. е. не имеют решения; система несовместна,
точки пересечения нет и, следовательно, прямые параллельны.
А В
В этом случае АВХ = АХВ, т. е. — = —. Таким образом, мы при-
ходим к несколько новой форме условия параллельности прямых.
А именно, прямые параллельны, если коэффициенты при неизве-
стных одного уравнения соответственно пропорциональны таким же
коэффициентам другого уравнения.
Переписав предыдущую пропорцию в форме = убеждаемся,
что новая форма условия параллельности прямых сводится к преж-
ней— к равенству угловых коэффициентов обеих прямых.
§ 33]
ПЕРВАЯ ГРУППА ЗАДАЧ
3) Если АВХ — АГВ = 0 и одно из выражений, например,
СВ — CtB = 0, тогда из этих условий вытекает
А В
A.-Br
£ _ С
т. е. в рассматриваемом случае
^ = £ = -2.
Л1 Bi Ci *
Отсюда следует, что одно из данных уравнений есть следствие
другого, так как все коэффициенты одного соответственно пропор-
циональны коэффициентам другого. Следовательно, в этом третьем
случае рассматриваемые уравнения выражают две совпадающие
прямые.
Пример 1. Найти точку пересечения прямых 2х + 5у — 8 = 0 и
Зх — у 4-5 = 0.
Решая эти два уравнения, находим координаты точки пересечения (—1,2).
Пример 2. Найти точку пересечения прямых: 4х — 12_у 4-5 = 0 и
Зх — 9у — 2 = 0.
Решая эти два уравнения, находим:
12х —36у + 15 = 0
12х —36у — 8 = 0
23 = 0
отсюда ясно, что уравнения эти несовместны. Следовательно, прямые не
пересекаются, т. е. параллельны.
Задача IV. Найти кратчайшее расстояние от начала
координат до прямой Ах-ф-By-J-С = 0.
Пусть прямая, заданная этим уравнением, изображена на рис. 59
прямой RS.
Ищется длина перпендикуляра ОР. 5
Вспомним, что та же прямая мо-
жет быть выражена и уравнением (см. х.
стр. 82) '
х cos ш -j- у sin ш — р = 0,] (III) / х.
где р = ал. ОР, а ® = (ОР, ОХ). 0 /А
Мы имеем, таким образом, гдва
Уравнения для одной и той же пря- рис
хой; а тогда по предыдущему коэффи-
циенты одного уравнения должны быть соответственно пропор-
циональны коэффициентам другого, т. е.
cos со = Ak, sin w = Bk, — р = Ck9
общий коэффициент пропорциональности.
88
ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ
[VII
Из этих уравнений нетрудно определить искомую величину.
Действительно, возвышая первое и второе уравнения в квадрат и
складывая, получаем
(Л2 + В2) Л2 = cos2 ш -|- sin2 ш = 1.
откуда сначала находим k
^2 _ 1 _ £ —______* .
Л2 + В2’ ±Ул2 + в2’
а затем и р
— С
р =-----, - - . (7)
Двойной знак при корне определяется из условия, что р > 0, так
как р есть длина перпендикуляра ОР.
Задача V. Найти кратчай
некие данной прямой представится
шее расстояние отданной
точки до прямой.
Пусть М (х0, уо) данная точка
и Ах + By + С=0 данная прямая.
Мы сумели бы решить эту
задачу по формуле (7), если бы
точка М была началом коорди-
нат. Поэтому преобразуем ко-
ординатную систему, перенеся
начало в точку Л/, не изменяя
направления осей.
Формулы преобразования в
данном случае будут следующие:
поэтому преобразованное урав-
в виде
Л (х0 ATj) + В (yQ 4“Л) 4" с — 0
или
Лх2 4“ ^У1 + (^хо+^о+ О = °-
Роль свободного члена уравнения играет теперь трехчлен Ах0 -L-
4-Ву04~С** Поэтому, применяя формулу (7), находим 6
6 = дл. MQ = ~(^£о±в-Уо+£)
± У Л2 + В2
(8)
Здесь так же, как и в формуле (7), знак z+z надо выбрать так,
чтобы в результате получилось число положительное.
Полезно заметить, что числитель формулы (8) представляет
левую часть уравнения данной прямой, в которую вместо коорди-
ВТОРАЯ ГРУППА ЗАДАЧ
89
§ 34]
нат х и у подставлены координаты данной точки. Это замечание
дает возможность легко запомнить эту формулу.
Пример. Найти кратчайшее расстояние до прямой 5х — 12у 4- 26 = 0 от
начала координат и от точки (5, 1).
Ответ на эти вопросы дают формулы (7) и (8).
По первой из них находим
— 26 26 26 п
±/254-Н4 /169 13
по второй
в = - (5-5-12.14-26) = 39 = 3
± -/25 4-144 13
§ 34. ВТОРАЯ ГРУППА ЗАДАЧ
Задача VI. Найти уравнение прямой, проходящей
через данную точку М (х19 у^.
Задача эта по смыслу вопроса неопределенная: существует бес-
численное множество прямых, проходящих через одну точку —
пучок прямых. Уравнение такого пучка прямых и ищется в этой
задаче. Одна из прямых этого пучка, именно та, которая параллельна
оси OY, будет очевидно иметь уравнение
X = ИЛИ X — хг = 0.
Уравнение всех остальных прямых должно быть вида
у = ах 4- b. (II)
Однако такое уравнение при любых значениях а и b выражает
любую прямую.
Чтобы эта прямая проходила через точку М (х19 у^, координаты
этой точки должны удовлетворять уравнению (И), т. е. должно выпол-
няться условие
Ji = axi + Ь,
которое показывает, каково должно быть Ь, чтобы прямая прошла
через данную точку.
Находя из последнего b и подставляя в (II), получаем урав-
нение искомой прямой. Такое исключение коэффициента b проще
выполнить, вычитая одно равенство из другого. Тогда получим
у— У1 = а(х — *1)- (9)
При различных значениях углового коэффициента а уравне-
ние (9) будет выражать различные прямые, проходящие через за-
данную точку М (х19 у^). Поэтому уравнение (9) принято называть
Уравнением пучка прямых.
Если из этих различных прямых надо выбрать одну определен-
ную, то для этого необходимо включить в задачу какое-нибудь
90 ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ [VII
добавочное условие, по которому и определяется угловой коэф-
фициент а.
Необходимо уяснить себе различный смысл координат х, у и
х19 у! в уравнении (9). Под х19 ух здесь подразумеваются коорди-
наты определенной точки, через которую проходит прямая. Коор-
динаты же х и у являются переменными координатами всех воз-
можных точек прямой. Эти координаты называют текущими коор-
динатами прямой линии.
Пример. Составить уравнение пучка прямых, проходящих через точку
(— 3, 2).
По формуле (9) находим
у — 2 = а (х 4* 3) j
это и будет искомое уравнение пучка прямых, непараллельных оси OY,
и кроме того ответом на задачу служит уравнение
х = — 3, т. е. х 4- 3 = 0,
т. е. уравнение той прямой, которая параллельна оси OY н тоже проходит
через ту же точку.
Задача VII. Найти уравнение прямой, проходящей
через две данные точки M1(xi9 j/J и М2(х2, у2).
По предыдущему, уравнение
у— У1 = а(х — Xt) (9)
есть уравнение пучка прямых, проходящих через точку Из всех
этих прямых мы должны выбрать ту, которая проходит и через
точку Af2. В таком случае коэффициент а не может быть уже про-
извольным, а он должен определяться в данном случае из условия,
что прямая должна пройти через точку Л42.
Условие это выразится следующим равенством:
Уъ— Л = д(л:а — *1)-
Определяя отсюда коэффициент а и подставляя его в уравне-
ние (9), найдем
или
= (10)
У2— У1 *2 — Х1 '
Указанное исключение коэффициента а проще выполнить деле-
нием одного равенства на другое.
Уравнение (10) и есть уравнение искомой прямой.
Пример. Составить уравнение прямой, проходящей через точки Afi (2, — 1)
и Л£>(3, 4).
По формуле (10) пишем искомое уравнение
у 4- 1 _х— 2
44-1“ 3 — 2
«ли после упрощения 5х — у — 11=0.
§ 34]
ВТОРАЯ ГРУППА ЗАДАЧ
91
Уравнение (10) можно представить в виде определителя. Дей-
ствительно, освобождая это уравнение от знаменателей, найдем
У (*2 — Х1) — Х?У1 + Х1У1 = X (у2 — У1) — Х1У2 + Х1У1
или
X (У1 —У2)—У (Х1 — х2) + Xj у2 — Х^У! = 0.
Нетрудно заметить, что левая часть уравнения представляет собой
развернутый по элементам первой строки определитель
х, у, 1
Х1, У1, 1
х2, Л, 1
Поэтому уравнение прямой, проходящей через две данные точки,
можно представить так:
X, у, 1
Х!, У1, 1
х2, У2’ 1
(И)
Легко проверить правильность полученного результата. Дей-
ствительно, последнее уравнение несомненно 1-й степени относи-
тельно х и у, а потому выражает прямую. Прямая эта проходит
через точки ЛЦ и ТИ2, так как подставив вместо х и у координаты
этих точек, мы получим определитель, у которого две строки ока-
зываются равными, а потому (по свойству определителя, см. стр. 18)
он тождественно обратится в нуль.
Уравнение прямой, проходящей через две данные точки, в виде
определителя записывается очень просто, почему этой формой выгодно
пользоваться.
Для предыдущего примера уравнение прямой в форме определителя
будет следующее
X, у, 1
2, -1, 1
3, 4, 1
Раскладывая определитель по элементам первой строки, получаем тот же
результат, что и раньше
— 5х+у + Н=0, 5х —у—11=0.
Задача VIII. Составить уравнение прямой, отсекаю-
ц*ей на оси ОХ отрезок р, а на оси OY отрезок
Искомая прямая, очевидно, проходит через две точки:
М^р, 0) и ЛГ2(0, 0.
92 ЗАДАЧИ НА ПРЯМУЮ линию fvn
Поэтому ее уравнение будет
у — 0__х — р
q — Q 0 — р ’
т* е.
У = х~~р = х । j
q -р р-т-
или
- + ^-=1. (IV)
Р ' я
Это уравнение носит название уравнения прямой в отрезках
на осях и является четвертой формой, в которой записывается урав-
нение прямой.
Когда эти отрезки известны, очень удобно пользоваться этой
формой уравнения при составлении уравнений прямой. Так, напри-
мер. прямая, отсекающая на осях координат отрезки 3 и 2, будет
иметь уравнение
или 2х-4“ 3>у — 6 = 0.
Задача IX. Составить уравнение пучка прямых, про-
ходящих через точку пересечения двух данных пря-
мых
Дх —By —у- С = 0 и —|- Вху —|— С х = 0*
Задачу это можно было бы свести к задаче VI, для этого сле-
довало бы только совместным решением данных уравнений найти
координаты точки пересечения этих прямых. Однако, поставленную
задачу можно решить не только не находя самой точки пересече-
ния, а даже не производя никаких выкладок. Искомым уравнением^
как это сейчас будет объяснено, служит
(Лх + 5д, + С) + Л(Л1х+В^ + б?1) = 0> (12)
где k любое число.
Действительно, уравнение (12) первой степени относительно
координат х и у, следовательно оно выражает прямую линию. Пря-
мая эта несомненно проходит через точку пересечения двух данных
прямых, при любом значении k, так как координаты точки пере-
сечения данных прямых, обращая каждый в отдельности трехчлен
в нуль, обратят и всю левую часть уравнения (12) в нуль, т. е.
будут удовлетворять уравнению (12), что и указывает, что пря-
мая (12) проходит через точку пересечения данных прямых.
Что касается коэффициента k, то он остается неопределенным.
При различных значениях k уравнение (12) будет выражать раз-
личные прямые, проходящие через точку пересечения данных прямых.
ВТОРАЯ ГРУППА ЗАДАЧ
93
§ 34]
Если же из этих прямых надо выбрать одну определенную, то для
этого необходимо включить в задачу какое-нибудь добавочное усло-
вие, которое и даст возможность определить коэффициент k.
Пример. Составить уравнение пучка прямых, проходящих через точку
пересечения прямых Зх — 4у + 2 = О и 2х -f- 5у — 1=0. Искомым уравне-
нием будет
(Зх —4у + 2) + ^(2лг + 5у- 1) = 0.
Если из всех таких прямых мы ^захотели бы выбрать такую, которая
прошла бы и через начало координат, то коэффициент k уже не может
быть произвольным. Он должен быть таким, чтобы координаты начала
О (0, 0) удовлетворяли написанному уравнению.
Подставляя х = 0 и у = 0 в это уравнение, находим 2 — k = 0, следо-
вательно k = 2.
Таково должно быть k, чтобы прямая прошла и через начало. Прини-
мая это в расчет, получаем
Зх — 4у -(- 2 + 2 (2х + 5у — 1) = 0
или
7х + бу = 0.
Задача X. Вычислить площадь треугольника по
координатам его вершин.
Пусть координаты вершин тре-
угольника будут /к
Afifxj, 7^, М2(х2, у2), Ж8(х3, 73). / ! X.
Для вычисления площади Д /И pWaAf3 / I X.
надо знать длину основания Л42Л43 и у__________!________
высоты MtN. 3 Л
По формуле (3) стр. 44 имеем
_______________________________ Рис. 61.
ал. М2МЯ = + V(х2—х3)2 Н- (у2—73)2.
Для нахождения дл. надо воспользоваться формулой (8)
<тр. 88, но для этого необходимо предварительно составить уравнение
прямой М2МЯ.
В форме определителя оно будет
х, у, 1
х2. у2. 1
УА, 1
В этом уравнении коэффициентами А и
будут определители:
(П)
В при переменных х и у
У* 1
Л- 1
= 72—>':!•
Х2, 1
Xg, 1
= — (-*2 — А'в)-
94
ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ
[VII
Поэтому по формуле (8) имеем
дл. MtN
У1, 1
х2, Уз, 1
*з> Уз, 1
± К(№-Л)2+(х2-хз)2
Умножая на дл, М2Л18 и беря половину произведения, получаем
, xi, У1, 1
пл. Д Af1442Af3 = zty
Х2> У29 1
Х3> У& 1
(13)
Знак z±z удерживается тот, при котором площадь будет поло-
жительной.
Задача XI. Найти условие, при котором три данные
точки М19 М29 лежат на одной прямой.
Очевидно, что если три точки лежат на одной прямой, то они
не образуют никакого треугольника или можно сказать, что пло-
щадь образуемого ими треугольника должна равняться нулю. По-
этому условием, чтобы три точки лежали на одной прямой, и будет
пл. Д7И1Л42Л43= 0, т. е.
xi, У1, 1
Х2, Уэ, 1 = °-
Х3, Уз, 1
(14)
Задача XII. Найти условие, при котором три пря-
мые “-J- By —|— С == 0, В}у —1“ —= 0 и А2х -ф- В2х -ф- б?2 = О
прохо дят через одну общую точку.
Чтобы эти три прямые проходили через некоторую точку
Л4 (х0, д/0) необходимо, чтобы ее координаты удовлетворяли всем
трем уравнениям, т. е. чтобы
Лх0+ Вуо+С = °>
^ixo + ^1Уо ~
(15)
^2^0 ^2 — 0.
Составим теперь новую систему трех однородных уравнений
с тремя неизвестными х, у, z\
Ах —|— By -ф- Cz — О,
А^х —В]У “J- C^z = О,
а2х “Ь &?у “Ь с??=
(16)
Сопоставляя последнюю с системой (15), замечаем, что систе-
ма (16) удовлетворяется значениями х = х0, У=У& ^=1, кото-
рые не все одновременно равны нулю. А в таком случае опреде-
литель, составленный из коэффициентов при неизвестных, должен
быть равен нулю (см. § 5, стр. 27). Итак, для того, чтобы три дан-
§ 35]
ПРИМЕРЫ РЕШЕНИЙ ЗАДАЧ НА ПРЯМУЮ ЛИНИЮ
95
ные прямые проходили через одну точку, надо, чтобы определитель
А, В, С
^2> ^*2
= 0.
(17}
равенство это и является
прямых через общую точку.
искомым условием прохождения трех
Пример 1. Проходят ли прямые Зх—у + 1 = 0, 2х4-4у — 3 = 0г
х + 2у + 5 = 0 через одну точку?
Составляем и вычисляем определитель
3,-1, 1
2, 4,-3
1, 2, 5
3, 0, 1
2, 1,-3
1, 7, 5
3, 0, 1
2, 1, — 3
—13, 0, 26
=78 + 13^0.
Ответ — прямые не проходят через одну точку.
Пример 2. Проходят ли прямые Зх — 5у — 9 = 0, 4х «р Чу 29 = 0г
2х — \Чу — 47 = 0 через одну точку?
Составляем и вычисляем определитель
3, —5, —9
4, 7, 29
2, — 17, — 47
3, —5, —9
4, 7, 29
6,— 10,— 18
Так как члены 3-й строки пропорциональны соответствующим членам:
1-й строки, то определитель равен нулю. Следовательно, прямые пересе-
каются в одной точке. Чтобы ее найти, достаточно решить совместно два.
из данных уравнений. Точка эта будет (— 2, — 3).
§ 35. ПРИМЕРЫ РЕШЕНИЙ ЗАДАЧ НА ПРЯМУЮ ЛИНИЮ
Приведем примеры решений задач, объединяющие, изложенные
выше частные задачи.
Пример 1. Провести прямую через точку (2, — 3) параллельно прямой
8х — 2_у 3 = 0.
По формуле (9) пишем общее уравнение прямых, проходящих через,
точку (2, — 3)
у + 3 = л(х-2).
Угловой коэффициент искомой прямой ввиду ее параллельности прямой
8х — 2у 4-3 = 0
Должен быть равен 4 (см. условие (5) параллельности двух прямых, стр. 85)..
Поэтому искомая прямая определяется уравнением
у + 3 = 4(х-2)
Или
4х — у — 11 =0.
Пример 2. Провести прямую через точку (— 1, 4) перпендикулярно,
к прямой х — Зу -|-8 = 0.
96 ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ [УП
Опять по формуле (9) пишем общее уравнение прямых, удовлетворяю-
щих первому условию, т. е. проходящих через точку (— 1, 4)
J'— 4 = а(х+1).
Но ввиду перпендикулярности искомой прямой к данной, угловой коэф-
фициент которой равену, находим по формуле (6), что угловой коэффи-
циент искомой прямой а = —3.
Итак, искомая прямая будет
.У —4 = — З(лг-Ь О
или
Зх+> —1=0.
Пример 3. Провести прямую через точку (2, 0) под углом в 45° к прямой
2х — 5у — 6 = 0.
Так же, как и раньше, сначала пишем уравнение прямой, проходящей
через точку (2, 0):
у = а(х — 2).
Остается найти угловой коэффициент а. Так как угловой коэффициент
данной прямой
2
“ 5 ’
то по формуле (4) (стр. 85) имеем
2
или
5а — 2 __
5+2я “ “ '
откуда и находим два значения для а, соответственно двум возможным
условиям
5а— 2 _ ] 5а— 2 _ 1
5-t-2« “ “ 5 +2а ~ 11
7 3
Из первого a = —t из второго а = —
о I
Итак, существуют две прямые, отвечающие условию задачи
7 3
= —2) и у = — — (х — 2)
ИЛИ
7х —З7—14 = 0 и Зх + 7> —6 = 0.
Пример 4. Через точку пересечения прямых Зх— 2у — 1 = 0 и х Зу 4~
4-4 = 0 провести прямую перпендикулярно ко второй из них. (Задачу ре-
шить, не отыскивая наперед точку пересечения).
Искомая прямая имеет уравнение (см. формулу (12) стр. 92)
Зх — 2у — 1 4- k (х-f- Зу 4- 4) = 0.
Коэффициент k надо определить так, чтобы прямая эта была перпенди-
кулярна к прямой х 4-3_у 4-4 = 0. Для этого, как известно, угловые коэф-
фициенты обеих прямых должны быть обратны по величине и по знаку.
§ 35] ПРИМЕРЫ РЕШЕНИЙ ЗАДАЧ цл ПРЯМУЮ линию 97
Угловой коэффициент данной прямой а=----------угловой коэффи-
о
циент искомой прямой определится, если мы, раскрыв скобки, представим
ее уравнение в форме Ах + By 4- С = 0.
Выполняя эти выкладки, получаем следующее уравнение искомой
прямой
(3 + *)ж + (-2 + ЗА!)> + (-1 + 4й) = 0.
Отсюда вытекает, что искомый угловой коэффициент
3 4-£
ai~ 2 — 3k ‘
Но, в силу перпендикулярности прямых, должно быть ,
поэтому
3 + * о
2 — 3k ~
Из последнего уравнения находим k = 0,3. Подставляя теперь его
в искомое уравнение, получаем
(Зх — 2у — 1) + 0,3 (х + 3> + 4) = 0,
ЗОх — 20> —10 4- Зх + 9у + 12 = 0,
ЗЗх —11_у + 2 = 0.
Пример 5. На прямой Зх + У— 5 = 0 найти точку, которая отстоит на
расстоянии, равном 10, от другой точки той же прямой, абсцисса которой
равна 1.
Для решения задачи ищем сначала ординату той точки прямой
3x4-j — 5 = 0, абсцисса которой равна 1. Из уравнения этой прямой находим
7 = 2. Таким образом, задача состоит в том, что на данной прямой ищется
точка, отстоящая от точки (1, 2) на расстоянии VI6.
Обозначим координаты искомой точки через (х0, 70). Тогда по условию
У(*о-1)2 + (Л-2)2= УН)
или
СГО— 1)* + (.у0 —2Г = 10.
Но необходимо принять еще в расчет то обстоятельство, что искомая
точка должна лежать на данной прямой, а потому се координаты удовле-
творяют уравнению прямой, т. е. должно выполняться равенство
Зху 4" Уь — 5 =0.
Итак, для определения х0, 70 имеем два уравнения, которые и остается
только решить.
Из последнего имеем 7о = 5—Зх0; подставляя 70 в предыдущее уравне-
ние, получаем
(хо-1)?4-(3-Зхо)*=1О
или
1О(хо—1)2=10, Хо—1 = ±1
и следовательно, х^ = 0 и Хо = 2.
Соответственно этим значениям находим 70 = 5 и —1. Итак, имеются
Две точки на прямой, удовлетворяющие условию задачи:
Mi (0, 5) и М2 (2,-1).
7 Зак. 2116. Н. С. Михельсон.
98 ЗАДАЧИ НА ПРЯМУЮ линию [vn
§ 36. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что геометрически выражает уравнение вида Ах-|-By + С = 0?
2. Как пишется уравнение прямой в нормальном виде, уравнение пря-
мой в отрезках на осях?
3. Какой вид имеет уравнение прямой, решенное относительно у?
4. Что выражают переменные х и у в уравнении Ах -]-Ву-\-С = 0?
5. Каковы уравнения прямых: 1) параллельной оси OXt 2) параллельной
оси OY. 3) самих осей ОХ и ОУ, 4) проходящих через начало координат?
6. Что называется угловым коэффициентом прямой и что начальной
ординатой?
7. Какой геометрический смысл имеют угловой коэффициент прямой
и начальная ее ордината?
8. Как определить угловой коэффициент прямой, когда задано ее урав-
нение?
9. Каков угловой коэффициент у прямой, параллельной оси ОХ?
10. Каков угловой коэффициент у прямой, параллельной оси OY?
И. Каков угловой коэффициент у прямой, делящей: 1) первый и третий
координатные углы пополам, 2) второй и четвертый координатные углы
пополам?
12. Как найти угол, образованный прямой с осью ОХ по ее уравнению?
13. Каковы условия параллельности и перпендикулярности прямых?
14. Как найти величины отрезков, которые прямая отсекает на осях
координат от начала?
15. Что означают координаты х^ и ylf х и у в уравнении _у—У1 —
— а (х — х^?
16. Как аналитически выражается прямая пропорциональная зависимость
между двумя величинами?
17. Каков график прямой пропорциональной зависимости?
18. Указать какие-нибудь три точки, лежащие на прямой 2х — 7_у4*
4-3 = 0.
19. Определить угловой коэффициент и начальную ординату прямых
Зх —бу —4 = 0, 5x4-2у 4-8 = 0, З.у —4 = 0, 2x4-1 =0.
20. Построить прямые 2х—у — 4 = 0, х4~3>4~5 = 0 по их угло-
вому коэффициенту и начальной ординате, а также по двум точкам этих
прямых.
21. Провести прямую через точку ( — 4, 2) параллельно прямой 2х — 5у4-
4-3 = 0. Оте. 2х — 5> 4-18 = 0.
22. Провести прямую через точку (0, — 2) перпендикулярно прямой
бх —у 4-2 = 0. Оте. х 4- бу 4- 12 = 0.
23. Провести прямую через две точки (2, — 4), ( — 1, — 6).
Оте. 2х — Зу— 16 = 0.
24. Провести прямую через точку (3, — 2) под углом 30э _к оси ОХ.
Оте. х )3 — Зу — 3()^3 4-2) =0.
25. Провести прямую через точку (—1, 0) перпендикулярно к оси ОХ.
Оте. х 4- 1 = 0.
26. Провести прямую через начало координат под углом 60° к прямой
2х —4у + 9 = 0. Оте. у = (8 + 5/3)х, j = (8—5/3)х.
27. -Найти угол, образуемый прямой Зх4~3_у—2 = 0 с осью ОХ.
Оте. а = 135°.
28. Найти угол, образуемый двумя прямыми 6х — 8_y-f~3 = 0, 12x4-
4-9.у — 5 = 0. Оте. а = 90°.
29. Найти кратчайшее расстояние от точки (3, — 1) до прямой Зх — 4y-f-
4-2 = 0. Оте. & = 3.
30. Найти точку пересечения прямых 2х 4" 7у 4-5 = 0, Зх — 4у — 7 = 0.
Оте. (1,-1).
§ 361
ВОПРОСЫ И УПРАЖНЕНИЯ
99
31. Найти длину отрезка прямой 12х— 5_у + 60 = 0, заключенного между
осями координат. Отв. 13.
32. На прямой Зх — 2у 4~ 9 = 0 найти точки, отстоящие от оси ОХ на
расстоянии, равном 6. Отв. (1, 6), (— 7, — 6).
33. Через точку пересечения двух прямых 2х + 5у— 14 = О и 4х— Зу +
_|_ц = 0 провести прямую, отсекающую на оси ОХ отрезок, равный 4.
Отв. 2х-\-Зу— 8 = 0.
34. В точке прямой 4х— 3_у4~И = 0» абсцисса которой равна 1, восста-
вить к ней перпендикуляр. Отв. Зх + 4у — 23 = 0.
35. Через точку пересечения прямых 2х —6_у + 5 = 0 и 2х — 4у 4- 3 = 0
провести прямую:
а) проходящую через начало координат,
б) проходящую через точку (— 3, 1),
в) параллельную оси OY,
г) составляющую с первой прямой угол в 45°.
Отв. а) 2х —у = 0, б) у — 1=0, в) 2х — 1=0,
г) 2х — у = 0, 2х + 4у — 5 = 0.
36. Через точку, взятую на прямой Зх — 2у + 4 = 0, ордината которой
равна — 1, провести прямую, отсекающую на оси ОХ такой же отрезок,
какой данная прямая отсекает на оси OY. Отв. х — 4у— 2 = 0.
37. Вычислить площадь треугольника, зная уравнения его сторон
х+у — 2 = 0, Зх — 5_у—14 = 0, х — у — 2 = 0. Отв. 4.
38. Лежат ли следующие точки на одной прямой и если лежат, то на
какой:
а) (3,-5); ( — 2, 4); (8,-14); б) (6, —5); ( — 4, 7); (1, 1); в) (3,-4);
(2, 0); (4, -1).
Отв. а) да, 9х + Зу — 2 = 0, б) да, 6х + 5у —11= 0, в) нет.
39. Проходят ли прямые через одну точку и если проходят, то через
какую?
а) Зх — 4j/ + 9 = 0, х + 2у + 4 = 0, 5х — Чу + 6 = 0.
б) 4х — 6> + 15 = 0, 5х + 4у + 13 = 0, х + 12> — 3 = 0.
Отв. а) нет, б) да, через точку
40. Вершинами треугольника служат точки А (1, — 2); В (— 3,4); С (2,-5).
Найти точку пересечения высоты треугольника, проведенной из точки А
с медианой стороны АС.
П Г7 13А
°'"вА"Го’ “T?
41. Зная уравнение гипотенузы у — Зх — 5 прямоугольного треуголь-
ника, его катета х +у—3 = 0 и абсциссу противолежащего ему угла, равную 4,
найти уравнение высоты треугольника, проведенной из вершины прямого
угла. Отв. х 4- Зу — 9 = 0.
42. Дано уравнение катета прямоугольного равнобедренного треуголь-
ника х — 2j/-f-9 = 0 и вершина противолежащего угла (3, —4). Найти урав-
нение и длину высоты, проведенной из вершины прямого угла, и уравнение
гипотенузы.
Отв. Зх— j/4-7 = 0, x + 3j'-— 11 =0, 2/10.
7*
VIII. эллипс
§ 37. УРАВНЕНИЕ ЭЛЛИПСА
Кривых второго порядка, т. е. таких, уравнения которых вто-
рой степени, только три: эллипс, гипербола и парабола. Все эти
кривые, как показывает специальное исследование, вытекают из
одного общего уравнения второй степени вида
А х2 + В ху + Су2 + D х + Еу -f- F = О
при различных, соответствующих каждой кривой, соотношениях
между его коэффициентами. Не вдаваясь в разбор такого общего
исследования, рассмотрим каждую кривую в отдельности в простей-
шей форме ее уравнения.
Эллипсом называется геометрическое место точек, сумма
расстояний которых до двух данных точек есть величина по-
стоянная.
Основываясь на этом определении, нетрудно составить уравне-
ние эллипса. Действительно, пусть Ft и F2— две данные точки,
У
0Ft=0F2
о расстоянии до которых идет речь
в определении, а М — одна из точек
нашего геометрического места. Обо-
значим расстояние между точками Ft
и F2 через 2с, сумму расстояний до
них от точки М через 2а; тогда, сле-
довательно, по определению
дл. FXM Ц-дл. F2M = 2а. (1)
Рис. 62. Для вывода уравнения рассматри-
ваемого геометрического места возь-
мем прямую F2Fx за ось ОХ и, приняв середину расстояния между
Fr и F2 за начало координат, проведем ось OY.
Обозначим координаты точки М через х, у.
Координаты точек Ft и F2 в выбранной нами системе коорди-
нат будут
Л (с, 0)
Г2(-с, 0).
УРАВНЕНИЕ ЭЛЛИПСА
101
§ 37]
По формуле (3) (стр. 44) находим
дл. F^M = У(х — с)2-}-у2, дл. F2M = ]/ (лг —|— с)2 Л-у2, (2)
а потому, по свойству (1) геометрического места, имеем
]/(х-с)2-|-_у2 ]/(х + 42+? = 2а. (3)
Это и есть уравнение рассматриваемого геометрического места.
Остается его упростить, что и достигается нижеследующими пре-
образованиями, имеющими целью освобождение уравнения (3) от
радикалов. Для этого перенесем один из радикалов в правую часть
уравнения и возвысим затем обе части уравнения во вторую сте-
пень, тогда
]/* (х с)2 ~j~y2 = 2а — У(х — с)2 4".У2>
(х 4~ £)2 4“ Д'2 = 4а2— ЬаУ (х — f)24“^2 +(* — с)2 + у2.
По раскрытии скобок и сокращении, получим
сх — а2 — а У(х — с)2 -)-у2-
Далее продолжаем освобождение уравнения от радикала
а ]/ (х— с)2 4~у2 — а2 — сх,
а2 [(* — СУ* 4"-У2] — я4 — 2а2сх 4- с2х2,
а2х2 — 2а2сх 4~ а2с2 4- а2у2 — а^ — 2а2сх 4~ с2х2.
Сокращая опять и собирая члены с переменными х и у в левую
часть, а свободные члены в правую, получаем
(а2 — с2} х2 4- сРу2 — а2 (а2 — с2).
Так как сумма двух сторон треугольника всегда больше тре-
тьей, то
2а > 2с, т. е. а > с,
так что а2— с2 > 0; положив поэтому
а2 — с2 — Ь2, (4)
приходим к уравнению
Ь2х2 а2у2 = а2Ь2.
Разделив все члены последнего уравнения на а2Ь2, находим
окончательно
г 2 А' -
+ (5)
Это уравнение и есть искомое уравнение рассматриваемого
геометрического места точек в упрощенной форме, т, е. уравнение
эллипса в так называемой канонической форме,
102
эллипс
[vin
§ 38. ИССЛЕДОВАНИЕ ФОРМЫ ЭЛЛИПСА
Для исследования формы этой линии решим уравнение (5) от-
носительно у:
у2 _1 х2_____а2 — х2
I2 — 1т2~ ~а2 ’
А2
У2 = -^(«2-*2),
^= — *2- (6)
Уравнение (6) показывает, что:
1) ось ОХ служит осью симметрии кривой, так как одному
значению х соответствуют два равных по абсолютной величине, но
противоположных по знаку значения
и у; точно так же нетрудно убедиться,
решив уравнение (5) относительно
х, что одному значению у соответ-
х'"" ствуют два равных по абсолютной
( q \ д величине, но противоположных по
^_l j знаКу значения х, т. е. что и ось OY
\г У служит осью симметрии;
_______2) для вещественности значений
8,_____у значения абсцисс по абсолютной
величине численно не могут быть
Рис. 63. больше а, т. е.
| х| а;
3) при х = 0 у = ± Ь, т. е. две точки кривой
В(0, Ь) и ^(0, — Ь)
принадлежат эллипсу;
4) с возрастанием абсолютного значения х от 0 до а значения у
по абсолютной величине убывают до 0. Следовательно, точки кривой
приближаются к оси ОХ и
при х — ±а ^ = 0.
Последним намечаются еще две точки:
А (а, 0) и Ах (—я, 0).
Кривая имеет вид, изображенный на рис. 63, где
дл. О А = дл. ОАХ = а, дл. ОВ = дл. ОВг = Ь.
§ 39. ПОСТРОЕНИЕ ЭЛЛИПСА
Более точное суждение о форме эллипса мы можем получить,
построив достаточно большое число его точек. Построение это
может быть выполнено на основании того соображения, что орди-
ната у есть четвертая пропорциональная между
Ь, ]/ а2— х2, а.
§ 40]
ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ И ЛИНИИ В ЭЛЛИПСЕ
103
Это вытекает непосредственно из формулы (6).
Действительно, из уравнения (6) следует
У
ь
Y а2— х2
а
Отсюда и выводим следующее правило построения отдельных
точек эллипса соответственно данной абсциссе:
1) на оси ОХ откладываем ОР = х < а— абсциссу той точки,
которую желаем построить;
2) из точки О, как из центра, опи-
сываем две окружности: одну радиусом
О А = а, а другую радиусом ОВ = Ь;
3) из точки Р восставляем перпен-
дикуляр к оси ОХ до пересечения с
большей окружностью в точке Q;
4) соединяем О с Q прямою и из
точки R пересечения ее с малой окруж-
ностью проводим RM || ОХ,
Точка М и будет искомою точкой
эллипса. Действительно, из подобия
треугольников ORS и OQP следует
Рис. 64.
S/? PQ
Но
OR OQ '
SR = PM, OR = b, PQ — ]fa2 — x2, OQ = a,
так что имеем
РМ Уд2 —х2
Ь а
т. е. что РМ и есть искомая четвертая пропорциональная вели-
чина:
РМ=у.
Указанное построение, как видно, может быть выполнено при
помощи линейки и циркуля.
§ 40. ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ И ЛИНИИ В ЭЛЛИПСЕ
Точки A, Av В, В1 пересечения с эллипсом его осей симмет-
рии называются вершинами эллипса; отрезки О А = а и ОВ = Ь
называются полуосями эллипса, и так как в нашем случае а > b
(см. формулу (4)), то а называется большою полуосью, а b — малою.
Удвоенные такие отрезки, т. е. 2а и 2Ь, называются соответственно
большою и малою осью эллипса.
Точка пересечения осей симметрии — точка О называется
центром эллипса; точка эта является центром симметрии кривой,
так как всякая хорда, проходящая через нее, делится ею пополам.
104 эллипс [viii
Точки и F2 называются фокусами эллипса. Они лежат на
большой оси эллипса. 1 Их расстояние от центра равно с. Из фор-
мулы (4) следует, что
с2 = а2 — Ь2,
т. е.
с~У а2 — b2, (4Z)
и так как с < а, то фокусы лежат внутри эллипса.
Следует отметить еще одну величину, а именно отношение у,
оно называется эксцентриситетом эллипса и обозначается обык-
новенно буквой е. Так как с < а, то для эллипса
Расстояния любой точки эллипса от фокусов называются (фокаль-
ными радиусами-векторами.
В частном случае, когда b = а == г уравнение эллипса обра-
щается в такое
г 2 v2
_= 1
Г2 ' Г2
или
т. е. эллипс обращается в круг радиуса г.
Центр этого круга лежит в начале координат.
Более общее уравнение круга было приведено на стр. 66:
(х — а)2 + (у — Ь)2 = г2.
Центр такого круга уже не в начале координат, а в точке (а, Ь).
Раскрывая скобки в этом уравнении и располагая члены его по
степеням переменных х и у, получим уравнение круга в форме
х2 у2 ^ах 4- 2Ьу а2 + Ь2 — г2 = 0.
Сравнивая его с общим уравнением линии 2-го порядка, приве-
денным на стр. 100, замечаем, что в уравнении круга коэффициенты
при квадратах переменных равны между собой и в данном случае
равны единице, член с произведением координат отсутствует, т. е.
В = 0, коэффициенты при первых степенях переменных D и Е и сво-
бодный член F соответственно равны:
D—2a, E = 2b, F = а24~ Ь2 — г2.
!В случае, если Ъ> а, фокусы оказываются лежащими на оси ОГ,
т, е, попрежнему на большой оси,'
§ 411
ДИАМЕТРЫ ЭЛЛИПСА
105
Таким образом, общее уравнение круга в развернутой форме
может быть представлено в следующем виде:
х2+з'2+^ + Ду + /7 = °-
Обратно, имея уравнение круга в последней форме, нетрудно
привести его к предыдущей и таким, образом определить коорди-
наты центра круга и его радиус. Для этого достаточно лишь до-
полнить двучлены
х2 Dx и у2-\-Еу
полного квадрата, прибавив к обеим частям уравнения соответ-
ствующие величины.
Пример. Найти центр и радиус круга, заданного уравнением
x2+j,2 + 3x-V--^- = 0.
Добавим к-обеим частям уравнения числа — и 4
9 119
x2 + 3x + -J+^-4> + 4--^=^ + 4.
Тогда получим
(Q \2 Q 1 1
*+%) +(J'-2)2 = ^-+j + 4
ИЛИ
/ 3\2
(х+т) + О-2)2 = 9.
Таким образом, радиус круга равен 3, а центр круга лежит в точке
§ 41. ДИАМЕТРЫ ЭЛЛИПСА
Определение диаметра как линии, проходящей через центр, или
как наибольшей из хорд, данное для круга в элементарной геомет-
рии, не может быть использовано для других кривых линий.
Между тем, можно дать такое определение диаметра, чтобы оно
было одновременно пригодно и для круга и для всякой другой
кривой. Для этого стоит лишь вспомнить, что каждый из диамет-
ров круга делит пополам некоторый ряд параллельных между со-
бою хорд. Ввиду этого и установим такое более общее определе-
ние: диаметром кривой называется геометрическое место середин
хорд, параллельных между собою.
На основании этого определения выведем уравнение диаметра
эллипса и посмотрим, какую линию он будет собой представлять>
106
эллипс
[VIII
Для этого наметим ряд каких-нибудь параллельных между собою
хорд: DE, GH, RS и т. д. Их уравнение пусть будет
у = тх~\-п. (7)
динаты точек
У всех этих хорд угловой коэффициент т будет один и тот же,
отличаться же они будут лишь начальной ординатой п.
Прежде чем искать геометрическое место середин всех парал-
лельных хорд, остановимся сначала на одной из них, например DE,
и найдем координаты середины этой хорды, т. е. точки /С.
Координаты этой точки легко найдутся, если мы будем знать коор-
DE с эллипсом, а для этого не-
обходимо решить совместно
уравнение (5) эллипса и
уравнение (7) хорды. Под-
ставляя у, взятое из уравне-
ния (7), в уравнение (5),
получим
х* 2 . т2х2 + 2тпх Ц- л2_______________________________________1
л2 ‘ Ь2 1
или
(Ь2 + а2т2) х2 2тпа2х
^{а2п2 — а2Ь2) = 0. (8)
Решая это последнее
пересечения
хорды
Рис. 65.
/
и найдем абсциссы точек
xt и х2. Подставляя их в
точек:
квадратное уравнение, мы
пересечения D и Е. Обозначим их через
уравнение (7), находим и ординаты этих
уг = тх1 -ф- л,
у2 = тх2 4~ л.
(9)'
Таким образом, задача о пересечении прямой с эллипсом ре-
шена.
Однако, в вопросе о диаметре нас интересуют, как уже сказано,
не сами точки пересечения, т. е. не концы хорды, а ее середина —
точка К- Обозначим координаты этой точки через аир. Так как
точка К есть середина отрезка DE, то
„___ Х1 ~Н х2
2
О _У1 + У2
Р 2 •
Но x1-j-x2 является суммою корней квадратного уравнения (8),
которая, как известно, может быть найдена и без решения квад-
ратного уравнения, именно
г 1 .. __ _ 2а2тп
И ? Ь2^а2т2'
ДИАМЕТРЫ ЭЛЛИПСА
107
§ 4U
Таким образом, не решая квадратного уравнения (8), мы нахо-
дим, что
___ а?тп
а__b^ + aW
Что касается ординаты (3 точки К, то ее проще всего найти из
уравнения (7), так как точка К лежит на хорде DE\ именно
__ а?т?п . _— а?т?п + Ь2п + а-т?п __ Ь2п
г ~~ Ь* + а2тг ‘ П Ь2 + а2т Ь2 + а2т2 ’
Таким образом, координаты середины выбранной нами хорды
найдены.
Разделив найденное значение р на значение а, приходим к урав-
нению
В Ьч
— =------г— или 3 =------о—*
а а/т г а2т ’
связывающему эти координаты между собою.
Последнее уравнение и решает вопрос о диаметре. Именно,
всматриваясь в него, нетрудно заметить, что оно не заключает
в себе коэффициента п. Следовательно, если бы мы взяли какую-
нибудь другую хорду GH, параллельную первой (т. е. с тем же
угловым коэффициентом т), то, повторяя с ней те же рассуждения
и выкладки, пришли бы к подобному же соотношению между ко-
ординатами а! и Pj середины L новой хорды
а2т ’
Отсюда заключаем, что уравнению
У = -^'х (10)
удовлетворяют координаты середины всех хорд, параллельных между
собой и имеющих угловой коэффициент т. Таким образом, урав-
нение (10) и есть уравнение геометрического места середин хорд,
параллельных между собою, т. е. уравнение диаметра эллипса.
Уравнение это первой степени, следовательно, диаметром эллипса
является прямая линия; так как это уравнение не содержит свобод-
ного члена, то диаметр проходит через начало координат и вместе
с тем через центр эллипса. На чертеже диаметр этот изображен
прямой PQ.
Из исследования видно, что всякий диаметр связывается с опре-
деленными хордами, которые он делит пополам. В этом смысле
обыкновенно говорят, что диаметр сопряжен с данными хордами.
Точно так же два диаметра, такие как PQ и RS, из которых один
параллелен хордам, сопряженным с другим диаметром, называются
Сопряженными диаметрами.
108
эллипс
[VIII
Оси симметрии являются также диаметрами эллипса и притом
сопряженными. Подобно тому как это имеет место в круге, они
делят пополам хорды, к ним перпендикулярные. Эти диаметры на-
зываются главными,
§ 42. ФОКАЛЬНЫЕ РАДИУСЫ-ВЕКТОРЫ И ДИРЕКТРИСЫ
ЭЛЛИПСА
В § 37 (стр. 101) мы имели выражения для длин фокальных ра-
диусов-векторов FXM и F2M точек эллипса. Обозначив их соответ-
ственно буквами и г2 по формулам (2) этого параграфа, найдем
П = (х — с)2+/,
Отсюда, вычитая, получим
— г\ = (х + с)3 — (х — с)2, = 4сх
или
(r2’4-ri) (r2 —Г1) = 4сх.
Но по основному свойству эллипса
Г2 4- Г1 = 2а-
Из последних двух равенств простым делением находим
2с
г2 — F = — х,
7 1 а
Присоединяя сюда соотношение
Г2 + Г1 = 2а>
окончательно получаем интересующие нас формулы, по которым
вычисляются длины фокальных радиусов-векторов точек эллипса:
г1=а — ~х=а— ех, (11)
г2 = а -ф- — х = а -ф- ех. (12)
Одновременно с этим рассмотрим две прямые D1E1 и D2E2 (см.
рис. 66), параллельные оси OY, определяемые уравнениями
Прямые эти носят название директрис эллипса.
Расстояния точки М эллипса до этих прямых будут соответ-
ственно равны:
дл, MD< = ——х, дл. — ф-х,
§ 431
УРАВНЕНИЕ ЭЛЛИПСА, ОТНЕСЕННОЕ К ВЕРП1ИНЁ
109
Отсюда легко находим, что
Таким образом, обнаруживается новое свойство точек эллипса,
состоящее в том, что отношение расстояний любой точки эллипса
до фокуса к расстоянию до соответствующей директрисы есть
величина постоянная, равная эксцентриситету эллипса.
§ 43. УРАВНЕНИЕ ЭЛЛИПСА, ОТНЕСЕННОЕ К ВЕРШИНЕ
Уравнение (5) эллипса соответствует такому положению его, когда
начало координат совмещено с центром кривой и оси координат
являются осями эллипса. Посмотрим, какую форму примет уравне-
того же эллипса, если начало
координат переместить в одну из
вершин, например Alf не изменяя
направления осей.
Для получения нового уравне-
ния воспользуемся формулами пре-
образования (5) § 27, которые при-
менительно к рассматриваемому
случаю примут вид
Х =—У=У!.
Подставляя эти значения в уравнение (1), найдем
(— . У2!
а2 ~г ьг —
110
Эллипс
[VH!
Преобразовывая это уравнение, получаем
a2 —Saxj + Xj _
& г Ь* ~ b
Обозначая
Ь2 ь*
а а2
и отбрасывая значки, найдем
у* = 2рх -\-qx2. (13)
Это и есть искомое уравнение эллипса, отнесенное к вершине.
§ 44. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какая кривая называется эллипсом?
2. Как строятся точки эллипса при помощи линейки и циркуля?
3. Назовите замечательные точки и линии в эллипсе.
4. Где лежат фокусы эллипса?
5. Какая точка называется центром эллипса?
6. Какое соотношение имеется в эллипсе между полуосями и расстоя-
нием фокуса от центра?
7. Что такое эксцентриситет эллипса и какова его величина?
8. Что называется диаметром эллипса?
9. Какой вид имеет уравнение диаметра эллипса?
10. Будет ли прямая у = kx диаметром эллипса?
11. Какие диаметры называются сопряженными диаметрами эллипса?
12. Какие диаметры называются главными?
13. Какие формы уравнения эллипса вам известны и как они называются?
14. Найти полуоси эллипсов 4х- + 25v2 = 100, 12х2 + у2 = 3.
Отв. 5 и 2; и 1^3.
15. Расстояние фокусов эллипса (от центра) равно 3, а эксцентриситет -g-.
Найти полуоси эллипса. Отв. 5 и 4.
у~
16. Найти точки пересечения эллипса 7-7 +-777 = 1 с прямой 2х+ 5у +
10 1V
+ 4 = 0.
Отв. (3, -2) и 22).
х- у2
17. Найти уравнение диаметра эллипса — + = 1, сопряженного с хор-
дами параллельными прямой 4х —у + 5 = 0.
Отв. Зх + 16у = 0.
§ 44)
ВОПРОСЫ И УПРАЖНЕНИЯ
111
18. С какими хордами сопряжен диаметр х — 12у = 0 эллипса 2х2 +
Qy2 ~ 1. Отв. т = — 4^
19. Найти длины фокальных радиусов-векторов эллипса 64х2 + 100у2 =
= 6 400 для точки, ордината которой равна 4 УУ.
Отв. 7 и 13.
х2 у2
20. На эллипсе — -|- = 1 найти точку, равноудаленную от центра и
правого фокуса, и определить ее расстояния от этих точек.
21. Найти длину перпендикуляра, восстановленного из фокуса до пере-
сечения его с эллипсом.
Отв.
а
IX. ГИПЕРБОЛА
§ 45. УРАВНЕНИЕ ГИПЕРБОЛЫ
Гиперболой называется геометрическое место точек, разность
расстояний которых до двух данных точек есть величина по-
стоянная.
Пусть и F2 — две данные точки, а М одна из точек нашего
геометрического места. Обозначим расстояние между точками Гг
и F2 через 2с, а разность рас-
стояний до них от точки М че-
рез 2а\ тогда, следовательно, по
qf = r.F м определению
дл. MF* — дл. MFa = 2а.
* Для вывода уравнения рас-
—-----------------------у.---сматриваемого геометрического
^2 места возьмем прямую F2Fr за ось
ОХ и, приняв середину расстоя-
рис. 0g. ния между Ft и F2 за начало
координат, проведем ось OY.
Обозначим координаты точки М через х, у.
Координаты точек Ft и F2 будут
Л(^0), F2(-c, 0).
Тогда
дл. MFt = ]Л(х — с)2 -\~у2,
дл. МР2=У (х-\-с)2-\~у2.
Соответственно свойству изучаемого геометрического места соста-
вляем уравнение
/(x-f-c)2-^^2 — |/(х—с)2+д/2 = 2а.
Это и есть уравнение рассматриваемого геометрического места.
Остается его упростить, что и достигается нижеследующими преобра-
§ 46] ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ ИЗ
зованиями, совершенно аналогичными тем, которые были выполнены
для эллипса:
]/(х-|-с)24-.у2 = 2а-j-У (х — c'-)-j-y2,
(X 4- с)2+У2 = 4а2 + 4д У(х — с)2 +_у2 + (х — c)2-j-y3,
сх — а3 — а У(х — с)2 -f*У2>
с2х2 — 2а2сх а4 = а2х2 — 2а2сх -f- а2с2 + а2у2,
(с2 — а2) х2 — а2у2 = а2 (с2 — а2)<
Из треугольника следует, что
2с > 2а, т. е* с > а,
так что с2 — а2 > 0, поэтому, положив
c2 — a2 = b2, (1)
находим
Ь2х2 — а2у2 = а2Ь2
или окончательно
Это и есть искомое уравнение рассматриваемого геометрического
места точек в упрощенной форме, т. е. уравнение гиперболы в так
называемой канонической форме.
§ 46. ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ
Для исследования формы этой линии решим уравнение (2) отно-
сительно у у3 х3 . х2 — а2. ТГ —1 — а~ ’
отсюда у . V х2 — а2 Ь^~ а ’ у^±^х3-а\ (3)
Из уравнения (3) следует:
1) Ось ОХ служит осью симметрии кривой, так как одному
Значению х соответствуют два равных по абсолютной величине, но
противоположных по знаку значения у,
Точно так же нетрудно убедиться, решив уравнение (2) относи-
тельно х, что одному значению у соответствуют два равных по
абсолютной величине, но противоположных по знаку значения х,
е. что и ось OY является осью симметрии.
8 Зак. 2116. Н. С. Михельсон.
i 14
ГИПЕРБОЛА
2) Для вещественности значений у значения абсцисс по абсолютной
величине не могут быть меньше а,
т. е.
3) При х = а, у = 0; таким
образом находим две точки:
А (а, 0) и At (— а, 0).
На рис. 69 дл. ОА=д.л. OAt =
= а.
4) С возрастанием значения х от а до оо значения у также
растут от 0 до оо, т. е. точки кривой беспредельно удаляются от
осей симметрии.
Кривая имеет вид, изображенный на рис. 69; она состоит из двух
разобщенных ветвей, идущих в бесконечность.
§ 47. ПОСТРОЕНИЕ ГИПЕРБОЛЫ
Более точное суждение о форме гиперболы мы можем получить,
построив достаточно большое число ее точек. Для этого опять, как и
в случае эллипса, обратим внима-
ние на то, что ордината у есть чет-
вертая пропорциональная между
Ь, ]/ х2—а?, а.
Действительно, из уравнения
(3) следует
у _ У —д2
Ь а
Поэтому построение отдель-
ных точек гиперболы соответственно данной абсциссе может быть
следующим:
1) из точки О, как из центра, описываем окружность радиусом
ОР = х (х > а);
2) откладываем отрезки О А = а и ОВ = Ь\
3) из точек А и В восстанавливаем перпендикуляры АС и BD\
4) точку С пересечения первого перпендикуляра с окружностью
соединяем с точкой О;
5) из точки Е проводим прямую параллельно ОХ до пересечения
с прямой РМ, перпендикулярной к ОХ. Точка М и будет искомой
точкой гиперболы, абсцисса которой 0Р = х.
ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ И ЛИНИИ В ГИПЕРБОЛЕ
115
Действительно, из чертежа следует
BE _ АС
ОВ~ ОА 9
Но ВЕ = РМ, ОВ = Ь, АС=Ух2 — а2, ОА = а, так что получаем
РМ У х^—а^
b = а ’
т. е. что РМ и есть искомая четвертая пропорциональная:
РМ=*у.
Указанное построение, как видно, может быть выполнено при
помощи линейки и циркуля.
§ 48. ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ И ЛИНИИ В ГИПЕРБОЛЕ
Точки А и Аг пересечения гиперболы с осью симметрии назы-
ваются вершинами гиперболы.
Величины а и b называются полуосями гиперболы, причем а — ОА
называется вещественною полуосью, а ОВ — мнимою полуосью, мни-
мою потому, что реального значения, подобного значению а — О А,
непосредственно относящегося к рассматриваемой гиперболе, вели-
чина b не имеет.
Точка пересечения осей симметрии — точка О — называется цен-
тром гиперболы; точка эта является центром симметрии кривой,
т. е. всякая хорда, проходящая через нее, делится ею пополам.
Точки Fr и называются фокусами гиперболы; они лежат на
оси симметрии, пересекающей гиперболу, их расстояние от центра
равно с. Из формулы (1) следует, что
С2 = а2_^^2 (1')
или
с = ]/а2^-&2,
и так как с > а, то фокусы лежат за вершинами гиперболы в сто-
рону направления ее ветвей.
Следует отметить еще одну величину, а именно отношение —;
оно называется эксцентриситетом гиперболы и обозначается обыкно-
венно буквою е. Так как для гиперболы с > а, то
$ Расстояния любой точки гиперболы от фокусов называются фокаль-
1ыми радиусами-векторами. ,
В частном случае, когда Ь = аь уравнение гиперболы' будет
х2—у2 = а2. (4)
Такая гипербола называется равнобочной гиперболой.
8*
116
ГИПЕРБОЛА
[1к
§49. ДИАМЕТРЫ, РАДИУСЫ-ВЕКТОРЫ ГИПЕРБОЛЫ И ЕЁ УРАВНЕНИЕ,
ОТНЕСЕННОЕ К ВЕРШИНЕ
Вопросы, поставленные по отношению к эллипсу и разобранные
в §§ 41, 42, 43, можно поставить и по отношению к гиперболе.
Предлагаем читателям самим разобраться в этих вопросах. Здесь же
приведем лишь их окончательные решения с некоторыми добавоч-
ными объяснениями.
1. Определяя диаметр как геометрическое место середин парал-
лельных хорд и рассуждая так же, как в § 41 для эллипса,
метр PQ сопряжен с диаметром /?S.
можно получить следующее
уравнение диаметра гипер-
болы
Ь*
у = -о— х,
а2т ’
(5)
сопряженного с хордами,
угловой коэффициент кото-
рых ;п. Так же, как и в
эллипсе, это будет прямая
линия, проходящая через
центр гиперболы. Каждый
диаметр будет иметь сопря-
женный. На рис. 71 диа-
Один из сопряженных диаметров
не пересекает гиперболу. Оси симметрии являются также сопряжен-
ными диаметрами; они делят пополам перпендикулярные к ним хорды
и называются главными диаметрами.
2. Длины фокальных радиусов-векторов гг и г2 различных
точек гиперболы выражаются через абсциссы точек следующими
формулами:
Для точек левой ветви,
т. е. при х < О
с f
л =---------а
1 а 1
с
Гъ —--------х — а
2 а
Для точек правой ветви,
т. е. при х > О
(6)
В обоих случаях разность радиусов-векторов равна 2а, как и
должно быть для гиперболы.
3. Так же, как и эллипс, гипербола имеет директрисы, которые
лежат между вершинами гиперболы; гипербола так же, как и эллипс,
обладает свойством, что отношение расстояний любой точки гипер-
болы к расстоянию до соответствующей директрисы есть величина
постоянная и равная эксцентриситету.
АСИМПТОТЫ ГИПЕРБОЛЫ
117
§ 50]
Уравнение гиперболы, отнесенное к вершине, принимает форму
У2 = 2рх -J- qx2, (7)
если начало координат перенести в вершину А (а, 0).
Ь2 Ь2
Здесь р = - и 7--,
важного свойства рассмотрим вопрос
(2)
= 1
(9)
§ 50. АСИМПТОТЫ ГИПЕРБОЛЫ
В отличие от других линий второго порядка гипербола обладает
особенным свойством, в силу которого точки ее по мере удаления
их от вершин беспредельно приближаются к некоторым прямым ли-
ниям, называемым асимптотами.
Для выяснения этого весьма
о пересечении гиперболы
х2
а2 Ь2
с прямой, проходящей через начало координат
у = тх. (8)
Как известно, для нахождения координат точек пересечения надо
решить уравнения (2) и (8) совместно.
Подставляя у = тх в уравнение (2), находим
х2 т2х2 1
V lj
b2x2 — а2т2х2 = a2b2,
x2 (b2 — a2m2) = a2b2,
откуда находим x, а по уравнению (8) и у:
ab abm
x =z___________ •, у =------ . .
zt У b2 — a2m2 У b2 — a2m2
Таковы решения системы уравнений (2) и (8).
Формулы (9) показывают, что
если Ь2 — т. е. если т2 < или \т\ < у, то ра-
дикалы, находящиеся в знаменателе формул (9), вещественные и,
следовательно, прямая (8) пересекает гиперболу в двух точках;
если Ь2 — а2т2 < 0, т. е. если т2 > , или I т I > —, то те же
Радикалы оказываются мнимыми и точек пересечения нет.
Рассмотрим теперь случай, когда Ь2— а2т2 = 0, т. е. т2=^,
Другими словами, когда /я = — и /п =-----
а а
118
ГИПЕРБОЛА
[IX
прямые, проходящие через начало
Построим эти прямые.
Для этого, отложив на осях отрезки дл. О А = дл. ОАГ — а и
дл. ОВ = дл. ОВГ = Ь, построим прямоугольник CDEK. Проведя диа-
гонали ЕС и KD и продолжив
их, мы и получим искомые пря-
мые G}G и ННХ.
Действительно,
{^(G^G, ОХ) = tgw = у,
tg(/y/yi( ОХ) = tg(те—ш) = -|.
Эти прямые служат границами
между прямыми, пересекающими
гиперболу, и прямыми, ее не пе-
ресекающими. Очевидно, что все
и лежащие внутри угла HOG,
пересекают гиперболу, ибо для них |/я|<-^-, а все прямые, про-
ходящие через начало и лежащие внутри угла GOHX, не пересекают
гиперболу, так как для них |/я | > —.
Прямые GrG и ННХ называются асимптотами гиперболы.
Уравнения их
Ь
у = — х,
а ’
b
у = ----х.
л а
В случае равнобочной гиперболы уравнения асимптот прини-
мают вид
т. е. асимптоты являются биссектрисами координатных углов и по-
тому взаимно перпендикулярны.
§ 51. СВОЙСТВО АСИМПТОТ
Асимптоты гиперболы обладают тем свойством, что к> ним бес-
предельно приближаются ветви гиперболы по мере удаления ее точек
от вершины.
В самом деле, пусть точка М (х, у) принадлежит гиперболе;
вместе с нею рассмотрим точку AZ на асимптоте (см. рис. 72),
имеющую ту же абсциссу ОР = х, а ординату PN=yr. Так как
точка М лежит на гиперболе, то ордината у найдется из уравнения
гиперболы, т, е,
УРАВНЕНИЕ РАВНОБОЧНОЙ ГИПЕРБОЛЫ
119
§ 52]
а так как М лежит на асимптоте, то ее ордината найдется из уравне-
ния асимптоты, т. е.
Ь
У1 = — X.
-71 а
Возвышая в квадрат и вычитая первое равенство из второго,
находим
У'1~ У9 — &9>
или
(У1 — У) (У1 +^) =
откуди ь2
'и"=л-^ = 7Г+7-
Но так как при беспредельном удалении точки М, а вместе с нею
и точки N, сумма уг 4-Д' беспредельно растет, то дробь ———,
У1 ~гУ
а потому и /ИМ беспредельно уменьшаются, т. е, точки гиперболы
беспредельно приближаются к асимптотам.
§ 52. УРАВНЕНИЕ РАВНОБОЧНОЙ ГИПЕРБОЛЫ, ОТНЕСЕННОЕ
К АСИМПТОТАМ
Посмотрим теперь, какой вид примет уравнение равнобочной
гиперболы х2—у2=а2, если за ось координат принять ее асимп-
тоты. Как уже сказано, асимптоты равнобочной гиперболы взаимно
перпендикулярны и делят коорди-
натные углы пополам, поэтому для
выполнения преобразований доста-
точно повернуть оси координат на
угол в 45° по часовой стрелке или
против нее.
Расположим новые оси коорди-
нат, как указано на рис. 73, т. е.
повернем начальную систему на 45°
по часовой стрелке. Тогда в фор-
мулах преобразования
х = cos а — yt sin а,
у = х1 sin а -J-cos а
следует положить а = — 45°.
Тогда приведенные формулы примут вид
120
ГИПЕРБОЛА
[IX
Подставляя их в уравнение равнобочной гиперболы
ту=к2
Рис. 74,
бочной гиперболы, отнесенное к
или, после упрощений,
а?
xi - Л — -у >
отбрасывая значки и полагая
^2
— = Л2, имеем
ху = /г2. (11)
Это и есть уравнение равно-
асимптотам (рис. 74).
Уравнение это обнаруживает замечательное свойство гиперболы,
состоящее в том, что при таком расположении осей площадь пря-
моугольника, построенного на координатах любой точки гиперболы,
есть величина постоянная:
пл. OPMQ = пл. OP^MiQi = ... = 4г.
§ 53. ГРАФИКИ ГИПЕРБОЛИЧЕСКОГО ТИПА
И ИХ ПРИЛОЖЕНИЯ
Из того же уравнения (11) следует, что равнобочная гипербола,
отнесенная к асимптотам, является графиком обратной пропорцио-
нальной зависимости. Действительно, уравнение (И) показывает, что
во сколько раз увеличивается значение х, во столько же раз умень-
шается значение у и наоборот.
Примером такой зависимости может служить закон Бойля-Ма-
риотта, выражающийся уравнением
pv = С.
График этого закона есть, следовательно, равнобочная гипер-
бола, асимптотами которой служат оси координат; на одной из них
откладываются давления р, на другой — соответствующие объемы
газа v (рис. 75).
Из уравнения (11) следует, что уравнение гиперболы можно
представить и так:
§ 531
ГРАФИКИ ГИПЕРБОЛИЧЕСКОГО ТИПА И ИХ ПРИЛОЖЕНИЯ
121
Вообще кривые, уравнения которых имеют вид
77Z 1 л
У = , где k > О,
(12)
называются кривыми гиперболического типа; эти кривые при Zez£l
относятся к классу кривых высшего порядка.
Закону, выражающемуся уравнением (12), следуют идеальные
газы при так называемом адиабатическом их расширении или сжатии,
т. е. без потери во внешнее пространство или без получения газом
извне тепла.
Как известно из физики, течение
адиабатического процесса описывается
формулой
ъ А С
pvk = const ИЛИ р —
ср
где k = — (отношению теплоемко-
стей при постоянном давлении и при
постоянном объеме).
Примерный график такого про-
цесса изображен на рис. 75.
Постоянная С выражает давление га
полагая v= 1 = ОД, найдем, что
Рис. 75.
при v == 1. В самом деле,
р = С=АВ.
При &==2 уравнение (12) обращается в
С
Кривая эта является графиком зависимости обратно пропор-
циональной квадрату одной из переменных. Ее вид изображен на
рис. 33 (см. стр. 62). Коэффициент С там принят равным 18.
Подобному закону следуют, например:
1) Сила взаимного притяжения двух масс. Сила эта, как известно,
обратно пропорциональна квадрату расстояния между массами
(закон всемирного тяготения Ньютона)
т • т\
2) Освещение, производимое расходящимися лучами, обратно
пропорционально квадрату расстояния освещаемой точки от источ-
ника света
122
ГИПЕРБОЛА
[IX
17.
18.
ваются?
19.
20.
§ 54. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какая кривая называется гиперболой?
2. Как строятся точки гиперболы при помощи линейки и циркуля?
3. Назовите замечательные точки и линии в гиперболе?
4. Где лежат фокусы гиперболы?
5. Какая точка называется центром гиперболы?
6. Какое соотношение имеется между полуосями гиперболы и расстоя»
нисм фокуса от центра?
7. Что такое эксцентриситет гиперболы и какова его величина?
8. Что называется диаметром гиперболы?
9. Какой вид имеет уравнение диаметра гиперболы?
10. Все ли прямые, проходящие через центр гиперболы, ее пересекают?
11. При каком значении углового коэффициента прямая, проходящая
через центр, пересекает гиперболу и при каком не пересекает?
12. Какие прямые называются асимптотами гиперболы?
13. Каковы уравнения асимптот гиперболы?
14. Как по данному уравнению построить асимптоты гиперболы?
15. Как идут ветви гиперболы по отношению к асимптотам?
16. Как аналитически выражается обратно пропорциональная зависимость
между двумя величинами?
Каков график обратной пропорциональной зависимости?
Какие формы уравнений гиперболы вам известны и как они назы-
Найти полуоси гипербол х2 — 2у2 — 2, 4х2 — 9у2 = 1.
Отв. У2 и 1; 4* и Л.
Z о
Написать уравнение гиперболы, зная, что разность между веществен-
ной и мнимой, полуосями равна 1, а эксцентриситет равен .
/п х2 У2 1
Отв- 1б~ тг = 1-
X2 V2
21. Вывести уравнение диаметра гиперболы сопряженного
с хордами, угловой коэффициент которых равен т.
Отв. у = —=— х.
а2т
22. Написать уравнения диаметров гиперболы х2 — 3_у2 = 4, сопряженных
с хордами, соединяющими точки гиперболы, абсциссы которых 2 и —4.
Отв. у -J- х = 0, у — х = 0.
23. Найти точки пересечения гиперболы Зх2—12_у2 = 36 с
j/ — х 5, j/ = дг + 3, у~2х — 1.
Отв. 1) ( — 4, 1), (
\ о
2) (-4, -1).
3) Нет пересечения.
24. Вывести выражения фокальных радиусов-векторов через
точек гиперболы.
Отв. См. § 49.
25. Найти длины фокальных радиусов-векторов для точек гиперболы
X2 V2
—1, абсциссы которых равны ± с.
и*
b2 b2
Qme. — и 2а -4--.
Я я
прямыми
абсциссы
54] ВОПРОСЫ И УПРАЖНЕНИЯ 123
26. Вывести уравнение гиперболы, отнесенное к правой вершине.
Отв. V2= —х + -^-х2.
а а*
27. Написать уравнение асимптот гиперболы 8х2— 3_у2 = 2.
Отв. 2х 1/^2 ± у /3 = 0.
28. Найти угол между двумя асимптотами гиперболы Зх2—J'2= 1.
Отв. ш = 120°.
<^2
29. На гиперболе — &2~ 1 найти точку, равноудаленную от центра
и от правого фокуса. При каком соотношении между полуосями найдется
такая точка? _
Отв. При Ь^аУЗ.
X. ПАРАБОЛА
§ 55. УРАВНЕНИЕ ПАРАБОЛЫ
Параболой называется геометрическое место точек, расстоя-
ния которых до данной точки и данной прямой равны между собою.
Пусть F— данная точка, DDX— данная прямая и М — одна из
точек нашего геометрического места.
Тогда по определению имеем
дл. FM = дл. MD.
Для вывода уравнения параболы
примем за ось ОХ прямую EF,
проходящую через точку F перпен-
дикулярно DXD, а середину отрезка
^*0? FE за начало координат.
Обозначим координаты точки М
через х, у и пусть
дл. FE = p (р > 0).
Тогда расстояние между точками М(х,у) и Отбудет:
дл. FM = (х — +.У2.
Далее из рис. 76 видно, что
дл. MD = дл. AfG-j-дл. GD — x-\--^.
По свойству изучаемого геометрического места точек имеем
Освобождаясь от радикала, получаем
к?—рх+у + у* = х2 4- рх+,
ИССЛЕДОВАНИЕ ФОРМЫ ПАРАВОЛЫ 125
И после упрощения
у2 = 2рх. (1)
Это и есть уравнение искомого геометрического места, т. е.
уравнение параболы в так называемой канонической форме.
§ 56. ИССЛЕДОВАНИЕ ФОРМЫ ПАРАБОЛЫ
Исследуем форму этой линии. Из уравнения (1) имеем
у = — V
а потому:
1) ось ОХ служит осью симметрии кривой, так как одному
значению х соответствуют два равных по
абсолютной величине, но противополож-
ных по знаку значения у\ ось же OY
не является осью симметрии;
2) для вещественности значений у
должно быть
х^О,
т. е. кривая расположена в сторону по-
ложительного направления оси ОХ]
3) при х = 0 у = 0, т. е. точка О
принадлежит линии;
4) с возрастанием х от 0 до оо абсо-
лютное значение^ также растет от 0 до оо,
т. е. точки параболы беспредельно удаляются от осей ОХ и О К
Кривая имеет вид, изображенный на рис. 77; она состоит из одной
ветви, уходящей в бесконечность, и проходит через начало координат.
§ 57. ПОСТРОЕНИЕ ПАРАБОЛЫ
Для более точного суждения о форме параболы следует по-
строить достаточно большое число ее точек. Построение отдельных
откладываем абсциссу
точек может быть выполнено при по-
мощи линейки и циркуля, исходя из
того, что, как видно из уравнения (1),
ордината всякой точки параболы есть
средняя пропорциональная между
2р и х.
Поэтому построение может быть
следующим:
1) откладываем на оси ОХ от-
резок ОК = 2р в отрицательную
сторону оси ОХ]
искомой точки ОР=Х]
126
Парабола
[х
3) строим окружность на КР, как на диаметре;
4) из точки L пересечения окружности с осью OY проводим
прямую LM^OX до пересечения ее с прямой PM | ОХ.
Точка М и будет искомой точкой параболы, абсцисса кото-
рой ОР.
Действительно, по известному свойству перпендикуляра, опущен-
ного из точки окружности на диаметр, отрезок OL, а следовательно,
и РМ будет средним пропорциональным между отрезками диаметра:
ОК = 2р и ОР = х.
§ 58. ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИдИ ЛИНИИ В ПАРАБОЛЕ
Точка О пересечения параболы с ее осью симметрии называется
Веригиной параболы, точка F— ее фокусом.
Фокус параболы находится внутри параболы на оси симметрии
в расстоянии, равном ~ от вершины параболы.
Прямая DDt носит название директрисы параболы (рис. 76).
Величина р называется параметром параболы.
При х = у , у2 = 2р • ~ , т. е. у = ± р.
Отсюда следует, что параметр параболы равен ординате пара-
болы, восставленной из фокуса:
p = FG.
Расстояние FM любой точки параболы от фокуса называется
фокальным радиусом-вектором. Так как дл. FM = дл. MD (см.
рис. 76), то
дл. = (2)
Отношение
ДЛ. РМ _1
дл. AID “ 1?
а так как подобное отношение для эллипса и гиперболы равно
эксцентриситету, то принимают, что эксцентриситет параболы
е = 1.
§ 59. ДИАМЕТРЫ ПАРАБОЛЫ
Так же, как для эллипса и гиперболы, определим диаметр пара-
болы как геометрическое место середин хорд, параллельных между
собою.
Для вывода его уравнения рассмотрим вопрос о пересечении
параболы
у* = 2рх (1)
§ 59]
ДИАМЕТРЫ ПАРАЁОЛЫ
127
с прямой CD, уравнение которой пусть будет
у = тх -f- п.
(3)
Абсциссы и ординаты точек пересечения найдутся из совмест-
ного решения этих уравнений.
Для этого найдем х из уравнения
подставим в уравнение (1), получим
или
ту2 — 2ру 2рп = 0. (4)
Из последнего уравнения мы мо-
жем определить ординаты уг и у2
точек С и D пересечения параболы
с хордой CD, а затем по уравнению
(3) и их абсциссы xt и х2. Однако нам
важно знать координаты не концов
хорды CD, а ее* середины (а, 0). /
что
п___ Х1~^Х2 а_____У1~ЬУ2
«— 2 > р — 2
Но является суммой корней квадратного уравнения (4),
которая, как известно, может быть найдена и без решения уравне-
ния, а именно
,Л+Л = ^.
(3) и найденное его значение
Поэтому ордината точки К, середины хорды CD, оказывается
?=£ и
Всматриваясь в этот результат, мы замечаем, что он не заклю-
чает в себе величины п. Поэтому если бы мы взяли другую хорду,
параллельную первой, и провели то же рассуждение, то для орди-
наты ее середины L получили бы тот же результат.
Отсюда следует, что середины всех хорд, параллельных данной,
Расположены на прямой, параллельной оси ОХ, в расстоянии от нее
Равном , т. е. что диаметром параболы, сопряженным с хордами,
Угловой коэффициент которых т, будет прямая, параллельная оси ОХ.
сравнение его
у^>
т
(6)
128
ПАРАЁОЛА
Итак, обнаруживаете^ что все диаметры параболы параллельны
между собою и вместе с тем параллельны оси параболы. Сопряжен-
ных диаметров парабола не имеет. Ось симметрии является^также
диаметром; она делит пополам хорды к ней перпендикулярные и
называется главным диаметром.
§ 60. ДРУГИЕ ФОРМЫ УРАВНЕНИЙ ПАРАБОЛЫ И КРИВЫЕ
ПАРАБОЛИЧЕСКОГО ТИПА
Если повернуть оси координат на прямой угол в сторону по
часовой стрелке, то уравнение параболы примет вид
Xi = 2pyt,
так как такой поворот равносилен следующему преобразованию:
Х=У1, У = ~х1-
Отбрасывая значки и полагая = k, можно представить урав-
нение параболы в форме
. y=^kx\ (7)
Такая парабола располагается уже вдоль оси OY (рис. 80).
Последняя форма уравнения параболы
встречается во многих приложениях. В этом
виде парабола является графиком зависи-
мости прямо пропорциональной квадратам
величин, откладываемых на оси ОХ.
На рис. 29 (стр. 58) изображена по-
добная парабола, где k принято равным у.
уравнения которых
Вообще кривые,
имеют вид
у = тхп
при и>0,
называются кривыми
параболического типа.
В частном случае, при п = 3 получаем параболическую кривую
у = kxz,
изображение которой для k =—дано на» рис. 30 (стр. 59).
К кривым параболического типа относятся
деляемые уравнением вида
У = РоХп + Р^п -1 + • • • + Рп-1
также кривые, оцре-
п
при п целом и положительном, т. е. такие, для которых у выра-
жается некоторой целой рациональной функцией от х.
§ 60)
ДРУГИЕ ФОРМЫ УРАВНЕНИЙ ПАРАБОЛЫ
129
В частном случае уравнение
у = kx2 -\-lx-\-tn
выражает обыкновенную параболу 2-го порядка, рассмотренную
уже в этой главе, однако, несколько иначе
сительно осей координат. Чтобы выяснить ее
расположение относительно осей ОХ и OY,
преобразуем уравнение (8), перенеся начало
координат в некоторую, пока еще неопре-
деленную точку О1(а, Ь).
По известным формулам имеем
х = а-\- хь y = b-\-yv
Подставляя эти выражения в уравнение (8),
находим
b -Ml = 6 (а + *i)2 +1 (а + -I- т,
(8)
расположенную отпо-
или, раскрывая скобки и собирая члены с одинаковыми степенями
переменной х,
ух = kx\ (2л& 4" О Х14“ (^2 + /я 4“ w — £)•
Выберем теперь а и b так, чтобы
2^4-/= 0 (9)
ka2 4“ la 4“ т — b — 0.
Тогда предыдущее уравнение упрощается и приводится к уравнению
Ух = kx{,
т. е. к обыкновенному уравнению параболы, расположенной отно-
сительно осей и OjKi, как изображено на рис. 81. Относи-
тельно же основных осей ОХ и ОУ она расположена так, что ось
параболы параллельна оси ОУ, но вершина ее смещена: она нахо-
дится не в начале О координат, а в некоторой точке О19 координаты
которой нетрудно найти из уравнений (9).
Так, парабола
у = 2х2 — 4х + 5
имеет вершину, находящуюся в точке Ох (я, Ь), координаты которых найдутся
Из Уравнений (9). Первое из них дает
4я—4 = 0, а — 1.
Из второго находим
b = 2 — 4 + 5 = 3.
9 Зик. 2116. Н. С. Михельсон.
130 нлрлволА lx
Такого рода задачу удобнее решать проще, преобразуя трехчлен, стоя-
щий в правой части уравнения, дополняя первые два члена до полного квад-
рата, а именно предыдущее уравнение можно переписать так:
_у = 2х2 — 4х + 2+3
или
у — 3 = 2(х — If.
Отсюда сразу видно, что координаты вершины будут
а = 1, Ь = 3.
§ 61. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какая кривая называется параболой?
2. Как строятся точки параболы при помощи линейки и циркуля?
3. Назовите замечательные точки и линии параболы?
4. Где лежит фокус параболы?
5. Как выражается через абсциссу расстояние точки параболы до фо-
куса?
6. Как расположены диаметры параболы?
7. Почему у параболы не может быть сопряженных диаметров?
8. Как расположена относительно осей координат парабола, уравнение
которой у = kx2?
9. Графиком какой зависимости оказывается парабола, заданная урав-
нением у = kx27
10. Какую кривую представляет уравнение у — ах2 -\- Ьх с?
И. Какие формы уравнений параболы вам известны?
12. Какое заключение можно вывести из сопоставления канонической
формы уравнения параболы и отнесенных к вершине уравнений эллипса и
гиперболы?
13. Найти параметр парабол: у2 = 4х, у2 = Зх, у = 2х2, Зу = 4xs.
’ 0 3 1 3
Отв. 2, 2 , 4 , 8 .
14. Написать уравнение параболы в канонической форме, проходящей
через точку (2, —4). . Отв. у2 = 8х.
15. Найти координаты фокуса и уравнение директрисы параболы у2 = 20х.
Отв. (5, 0), х + 5 = 0*
16. Найти точки пересечения параболы у2 = 12 х с прямыми у = Зх — 3,
15х — Зу + 1 = 0, у = х + 3.
Отв. (3, 6); , 2^; нет пересечения; одна точка (3, 6).
17. Найти диаметр параболы у2 — Зх = 0, сопряженный с хордой, прохо-
дящей через точки параболы, ординаты которых равны — 1 и 3. *
Отв. у —1=0.
18. Вычислить сумму сторон треугольника, вершинами которого служат
вершина параболы, фокус и точка на параболе ЗУ2 = 16х, ордината которой
Равна-4- Отв. ю|.
О
19. Определить длину хорды параболы у2 = 2рх, проведенной через ее
фокус перпендикулярно к оси симметрии. Отв. 2р.
20. Найти точки пересечения парабол у2 = 4х и у = 2х2.
Отв. (0, 0) и (1, 2).
ПОПРОСИ И УПРАЖНЕНИЯ
131
§ 4311
21. Привести уравнение параболы у = Зх2—12x4-4 к канонической
форме' Отв. у = Зх2.
22. Как расположены параболы, а) у = 4х2, б) у = — 4х2, в) у = 2х2 4“
1 16х*+22, г) у = —2х24"1бх — 22 относительно осей координат?
Отв. а) вершина в начале координат, ось параболы есть
ось OY\
б) вершина в начале координат, осью параболы служит отри-
цательное направление оси OY\
в) вершина (— 4, — 10), ось параллельна и одинаково на-
правлена с осью OY;
г) вершина в точке (4,10), ось параллельна оси OY, но на-
правлена в противоположную сторону.
23. Найти вершину и координаты фокуса параболы у — х2—4x4- 1-
Отв. (2, — 3)(2, — 2~^.
XL КООРДИНАТЫ В ПРОСТРАНСТВЕ
§ 62. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ ТОЧЕК
В пространстве положение точки может быть определено сле-
дующим образом.
Пусть XOY, XOZ, YOZ — три взаимно перпендикулярные пло-
скости, пересекающиеся в одной точке О, и пусть прямые OX, OY,
OZ суть линии их взаимного пересечения. Условимся за положи-
тельные направления этих прямых считать направления OX, OY, OZ,
а противоположные им за отрицательные. Для определения поло-
жения точки М проведем через
нее три плоскости, соответствен-
но перпендикулярные к прямым
OX, OY, OZ. Эти плоскости
отсекут на прямых OX, OY, OZ
(или на их продолжениях в про-
тивоположную сторону) отрезки
ОА, ОВ, ОС, начало которых
всегда будем считать в точке О.
Величины этих отрезков, кото-
рые условимся обозначать соот-
ветственно буквами х, у, z, и
определят положение точки М
в пространстве. Действительно,
всякой точке М отвечает вполне
определенная совокупность чисел х, у, z и всякой совокупности
чисел х, у, z отвечает вполне определенная точка пространства.
Числа х, у, z и называются поэтому координатами точки М.
Для обозначения того, что точка М определяется координатами
х, у, г, пишут
Ж (х, у, г).
Прямые OX, OY, OZ называются координатными осями, точка О на-
чалом координат. Плоскости XOY, XOZ, YOZ называются координат-
ными плоскостями.
Вся система называется прямоугольной системой координат.
§ 63]
ОСНОВНЫЕ ЗАДАЧИ
133
Построение координат точек может быть выполнено и иначе,
чем только что указано. А именно, для построения координат
точки М можно опустить перпендикуляр МР на плоскость XOY,
затем из точки Р его пересечения с плоскостью XOY опустить пер-
пендикуляр на ось ОХ. Тогда отрезки ОА, АР и РМ и будут сов-
падать с координатами точки М как по абсолютному их значению,
так и по знаку. Поэтому и принимают
ОА — х*, АР—у, PM — z.
Весьма полезно заметить, что подобно тому, как и на плоскости
координаты х, у, z точки М можно рассматривать как проекции
на оси OX, OY, OZ отрезка ОМ, соединяющего точку М с началом
координат; так что
х = проекции на ось ОХ отрезка ОМ.
у — проекции на ось OY отрезка ОМ.
z — проекции на ось OZ отрезка ОМ.
Отсюда в силу формулы (1) § 10, имеем
х = ОМ cos (ОМ, ОХ),
у = ОМ cos (ОМ, OY),
z = ОМ cos (ОМ, OZ).
§ 63. ОСНОВНЫЕ ЗАДАЧИ
Задача 1. Определить угол между
ниями в пространстве.
Согласно условию (§ 8) для об-
разования угла (L, Zq) между пря-
мыми L и Zq (рис. 83) проведем из
^ачала координат две прямые ОР и
соответственно параллельные и
прямыми
двумя
z
oplf
одинаково
L и
Тогда
направленные с
(L, Zq) = a).
направле-
В
Рис. 83.
Пусть
то же,
составляют
Zq ИЛИ,
и OPt
направления L и
направления ОР
с осями координат известные нам утлы, значения которых
134
КООРДИНАТЫ В ПРОСТРАНСТВЕ
[XI
даны в следующей таблице:
X Y Z
L. . . . OP (t ₽ у
Ар . . . ОР) Y1
Выберем на прямой ОР произвольную точку
(х, у, г)
и построим ее координаты
ОА — х, АВ=у, BM = z.
Затем рассмотрим ломаную линию О А ВМ с замыкающею ОМ.
По теореме о проекции ломаной имеем:
пр. ОЛ4 = пр. СМ + пр./Ш-}-пр. ВМ.
Проектируя на направление ОРг, находим
ОМ • cos (ОМ, OPJ = О А • cos (О А, OPJ +
+ ЛВ -cos (АВ, ОРХ) + ВМ • cos (ВМ, ОРг),
или
ОМ • cos (Ьг, L) = x* cos (X, Lj) -f-J' • cos (К, LJ -[-z • cos (Z, Lx),
t. e.
OM • cos co = x • cos 04 + У • cos px z • cos
Но известно, что
x == ОМ • cos (ОМ, OX) = ОМ • cos a
у = ОМ • cos (OM, OY) = ОМ • cos p
z = OM • cos (OM, OZ) = OM • cos
§ 63] ОСНОВНЫЕ ЗАДАЧИ 135
Подставляя эти выражения в предыдущую формулу, находим
ОМ • cos = ОМ • cos а • cos 04 4*
4- ОМ • cos р • cos рх 4" ОМ • cos у • cos
или, сокращая на ОМ,
cos со = cos a • cos 04 4-cos P * cos 4- cos у • cos (*)
Таким образом, косинус угла между двумя направлениями
в пространстве равен сумме произведений косинусов углов, соста-
вленных каждым из этих направлений с осями координат.
Из этой весьма важной формулы вытекают также весьма важные
следствия.
Следствие 1. Если направления L и Lx взаимно перпендику-
7t _
лярны, то a)==y, cos со = 0 и, следовательно,
cos a • cos оц 4" cos р • cos pt 4“ cos у • cos = 0;
мы получаем таким образом условие, которому удовлетворяют коси-
нусы углов двух взаимно перпендикулярных направлений.
Следствие 2. Если два направления L и взаимно парал-
лельны, то прямые ОР и ОРг сливаются в одну прямую; тогда
ш = 0, cos ш = 1, углы a = at, Р = рр Т = Ъ
и мы получаем
cos2 a 4- cos2 р -|- cos4 у = 1 (**)
— условие, которому удовлетворяют косинусы углов, составленных
произвольным направлением с осями координат.
Задача И. Н а й т и величину проекций на оси коор-
динат направленного отрезка, зная координаты его
концов.
Положим, нам дан направленный отрезок МгМ2, Точка Mt (xlf yt)
пусть будет его началом, а М2(х2, у2) его концом (см. рис. 84).
Для рещения задачи соединим начало координат с данными точ-
ками и рассмотрим получающуюся при этом ломаную линию ОМ^2
и ее замыкающую ОМ2. По теореме о проекции ломаной имеем:
пр. ОЛ^-ф-пр. М1М2 — пр. ОМ2.
Равенство это является верным при проектировании на любую ось.
136 КООРДИНАТЫ В ПРОСТРАНСТВЕ [XI
Рассчитаем это равенство, принимая за ось проекции ось ОХ,
Так как np.^OAfj = xt и пр.ОхСШ2 = х2, то
Z ^14-пр.0ХЛ11Л4а = х2,
откуда
У ' пр.олЛ11Л12 = х2 —
/ У
/ Точно так же, проектируя на оси
V/ ' OY и OZ, найдем
/ np.oyMjAfg^^—Л
пр.02/И1/И2 = г2 —гР
Рис. 84.
Итак, проекции на оси координат
направленного отрезка равны разности соответствующих коор-
динат конца и начала отрезка.
Мы получили такой же результат, какой был получен и для
отрезка, лежащего в плоскости координат (см. § 10), что, конечно,
и должно было быть.
Задача III. Найти расстояние между двумя данными
в пространстве точками Mt(xlf ylf zj и 7И2(х2, у2, z2).
Для решения задачи проектируем отрезок MrM2 на три коор-
динатные оси.
Проектируя сначала на ось ОХ, имеем
Пр.0Х^1^2 = Х2 — Х1.
С другой стороны, на основании формулы (1) (§ 10)
пр.охЖ= MrM2 cos (МtM2, ОХ) = MtM2 cos а.
Сопоставляя оба эти равенства, получаем
х2 — Х1 = ^1^2 cos а-
Проектируя на другие оси, также найдем
Уч— Л = ^1^2СО8₽
z2 — zx — 1Ж2 cos у.
Возводя последние три равенства в квадрат и складывая, по-
лучим
(х8 — X])2 4- (у^—ухУ 4- (*з — 21)2 — ^1^8 [cos2 а 4" cos9 р 4- cos27j,
ВОПРОСЫ И УПРАЖНЕНИЯ
137
§ 64]
Принимая во внимание формулу (**), находим
= d2 = (х2 — Х,)2 0,з —Л)3 (г2 _ ZJ2,
откуда __________________________________
d= + /(*2 —*i)9+ (Л—-У1)2 + (га—*i)2- (О
Задача IV. Найти точку, делящую отрезок прямой,
заключенный между двумя данными точками, в дан-
ном отношении.
Пусть нам даны точки
Л11 (Хр Ух, и ЛГ2 (х2, у* г.,).
На отрезке 714^2 требуется
найти точку М (х, у, г) такую,
чтобы
дл. Л41Л4__,
дл. ЛШ2 —
Проектируя отрезки МГМ
и ММ2 на ось ОХ, имеем
х — х\ = дл.Л^ТИ cos а,
Рис. 85.
х2— х = дл.Я4Л42соза.
Разделив два последних равенства одно на другое, найдем
х— xi___дл. МГМ___fa
х2 — х дл. ММ2 ’
откуда и определяем
Х1 + kx2
1 + k •
Подобным же образом находим у и z
У1 + ^2 *1+^2
У~ 1+* ’ 1+А? •
При й=1, т. е. при делении отрезка пополам, находим:
v Х1 + х2 _____ У1 + у2 _____ ^1+^2
х ~ 2~ ’ У — ’ Z — 2~ •
(2)
(3)
(4)
§ 64. ВОПРОСЫ И УПРАЖНЕНИЯ
!• Проекциями какого
точек?
отрезка являются прямоугольные координаты
2. Каковы координаты различных точек плоскости ХОУ, плоскости XOZ
и плоскости YOZ7
3» Как выражаются проекции направленного отрезка на оси координат?
138
КООРДИНАТЫ В ПРОСТРАНСТВЕ
[XI
4. Чему равняется косинус угла между двумя направлениями в простран-
стве?
5. Какой формулой выражается расстояние между двумя точками?
6. Какими формулами выражаются координаты точки, делящей отрезок
в данном отношении?
7. Могут ли в пространстве существовать такие направления, которые
с осями координат составляют углы:
а) 120°, 45°, 30°, в) 150°, 90°, 120°,
б) 30°, 60°, 90°, г) 60°, 120°, 135°.
Отв. а) нет, б) да, в) да, г) да.
8. Найти расстояние между точками М1 (1, — 2, 2), М2 (3, 1,-4). Отв. 7.
9. Определить координаты точек, делящих отрезок между точками
Mi(0, —1, 3) и М2(2> 3, —4) на три равные части.
n/2 I 2\ /4 5 5\
0 • (.3 ’ 3 ’ 3)’ \3’ 3 ’ ЗЛ
XII. ПОНЯТИЕ О ВЕКТОРАХ
§ 65. ОСНОВНЫЕ ПОЛОЖЕНИЯ; СУММА И РАЗНОСТЬ
ВЕКТОРОВ
Величины, рассматриваемые в математике, механике, физике и
других дисциплинах, можно разделить на две группы. Одни из них
полностью характеризуются лишь их числовыми значениями (поло-
жительными или отрицательными), другие, напротив, таковы, что
для полной характеристики их недостаточно знать их числовые зна-
чения, а требуется еще указать их направление. Так, например,
такие величины, как масса, температура, плотность, объем и другие
им подобные, определяются лишь их числовыми значениями, а такие,
как сила, скорость, пройденный путь и т. п., требуют для своего
определения знания не только их числового значения, но и их
направления. Первые называются скалярными величинами — скаля-
рами, от латинского слова scalae — лестница, вторые векториаль-
ными— векторами, от слова vector — везущий. *
С каждым вектором можно сопоставить прямолинейный отрезок,
длина которого, в некотором выбранном нами масштабе, равна чис-
ловому значению вектора, и направление которого совпадает
с направлением вектора» Это дает возможность представлять все
векторы некоторыми направленными отрезками и, таким образом,
применить геометрический метод в изучении векторных величин.
Ранее установленное понятие „направленный отрезок" совпадает
с понятием вектора. Так же как и направленный отрезок, вектор
имеет начальную и конечную точку — начало и конец вектора.
Вектор, начало которого в точке Л, а конец в точке В, принято
обозначать двумя буквами со стрелкой наверху или одной буквой
со стрелкой наверху или, наконец, одной буквой, жирным шрифтом,
т- е. так: АВ или а или а. Мы будем придерживаться, как правило,
первых двух способов обозначений. Длины векторов будем обозна-
чать такими же знаками, но без стрелок.
Устанавливая всякое новое понятие, как объект математического
изучения, необходимо установить и основные положения, бтнося-
Щиеся к этому понятию. Ввиду этого установим понятие о равенстве
векторов и о некоторых наиболее элементарных действиях над ними.
140
ПОНЯТИЕ О ВЕКТОРАХ
[XII
Условимся считать векторы равными, если соблюдены следую-
щие три условия: 1) равны их числовые значения, 2) они парал-
лельны, 3) одинаково направлены.
В,----------Так как эти условия не предусматри-
f вают определенного положения начала
/ / вектора, то, следовательно, не нарушая
/ равенства векторов, мы можем перено-
0 сить их параллельно самим себе, а по-
рис тому всегда рассматривать их исходящими
из одной и той же точки.
Заимствуя известные из механики за-
коны сложения сил, скоростей и т. п., назовем суммою двух векто-
ров— диагональ параллелограма, построенного на этих векторах.
Так, ОА-\-ОВ=ОС (рис. 86).
В силу установленного условия равенства векторов
АС=ОВ
имеем также
ОА-\-АС=ОС.
Последнее равенство позволяет упростить построение суммы
двух векторов: для сложения двух векторов строим ломаную линию,
составляющими которой служат данные векторы, тогда замыкающая
этой ломаной и будет являться суммой двух данных векторов:
длАС-дл.ОВ ЭлС1А1^длОВ1
—I———н-------------->— । —» — <----------- । ।—
о в а с - в, о с, А
Рис. 87а. Рис. 876.
Это последнее правило распространяется и на случай, когда
оба вектора расположены на одной прямой. Так, суммой двух век-
—* —>• - > —>• —►
торов О А и ОВ (рис. 87а) будет вектор ОС, где АС=ОВ. так
что
ОА~[-ОВ = ОС.
Суммой двух векторов ОАг и дв\ (рис. 876) будет вектор ОСЬ
так что
ОАг + ов[ = дс[.
Правило нахождения суммы двух векторов, как замыкающей
ломаной линии, распространяется на случай большего числа сла-
1 ь " •> ► ► >
гаемых. Так, суммой векторов ОА, ОВ, ОС и OD будет вектор ОЕ
(рис. 88), если
AF—OB, FG = OC, GE = OD,
§ 65j
ОСНОВНЫЕ ПОЛОЖЕНИЯ; СУММА й РАЗНОСТЬ ВЕКТОРОВ
141
так что
ОД + ОВ + О?+ OD = ОЕ,
Нетрудно показать, что основные законы, переместительный и
сочетательный, относящиеся к сумме числовых слагаемых, сохраняют
силу и по отношению к векторам, 1 т. е.
О А + ОВ — ОВ О А (переместительный закон),
О А 4“ (О В 4~ ОС) = (ОД 4" ОВ) + ОС (сочетательный закон).
Разностью двух векторов называется такой вектор, который,
будучи сложен с вычитаемым вектором, дает уменьшаемый вектор,
дл.ОВ=дл.АС
-4-------) ----- ------->
О В С А
Рис. 90.
т- е. разность О А — ОВ равна такому вектору ОС (рис. 89), что
ос4-ов = 5д.
Нетрудно заметить, что ОС есть замыкающая ломаной ОАС, где
- >• ' ►
вторая составляющая АС равна и параллельна вектору ОВ, но на-
- ►
правлена в противоположную сторону, чем ОВ, Отсюда и вытекает
1 Доказательство см. И. И. П р и в а л о в — Аналитическая геометрия;
**• Е. К о ч и н — Векторное исчисление.
142
Понятие о векторах
[хп
правило: чтобы вычесть вектор, надо прибавить такой же вектор,
но противоположно направленный.
Правило это распространяется и на случай, когда оба вектора
находятся на одной прямой. Так, О А — ОВ = ОС (рис. 90).
§ 66. ПРОИЗВЕДЕНИЕ ВЕКТОРА НА СКАЛЯР
Умножить вектор на целое и положительное число т значит
повторить его слагаемым т раз. В результате полу.чаем вектор,
имеющий то же направление, но
длина которого в т раз больше
-i t । । । длины данного вектора. Так
А1 . 0 А В , г
Рис. 91. 0А ‘ 3 = 0В (рис- 91)-
Указанное правило умножения
вектора на число обычным порядком распространяется на случай
любого положительного значения множителя т.
Произведением вектора на — 1 называется вектор, длина кото-
рого равна длине данного вектора, но направление которого про-
тивоположно данному. Так (рис. 91),
ОД-(— 1) = 5Х. (1)
Отсюда следует, что умножение вектора на любое отрицательное
число сводится к умножению его на такое же положительное число
и перемене направления получаемого вектора.
В случае, если длина вектора равна единице, то такой вектор
—>
носит название единичного вектора. Обозначая через а0 единичный
->
вектор того же направления, как и вектор а, мы в силу предыду-
щего можем написать:
а = т • а0, (2)
где т — число единиц, содержащихся в длине вектора а.
Тут же отметим аналитическую запись параллельности двух век-
торов. Если два вектора а и b параллельны, то
а = b • т, (3)
где т — некоторое число, положительное или отрицательное.
Действительно, умножением одного из параллельных векторов
на некоторый скаляр, положительный или отрицательный, всегда
можно привести его к одной длине и одному направлению с дру-
гим вектором, т. е. сделать его равным другому вектору. Два век-
тора а и та называются колинеарными векторами.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
143
§671 •• ------
§ 67. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Указанные выше правила умножения относится к случаю умно-
жения вектора на скаляр. В приложении векторного исчисления
к задачам механики, физики и другим дисциплинам большое значе-
ние имеют другого характера произведения: произведения вектора
на вектор. Различают два рода таких произведений — скалярное и
векторное, из которых рассмотрим лишь первое.
Скалярным произведением двух векторов называется произве-
дение их длин на косинус угла между ними.
Обозначается скалярное произведение двух векторов ОА и ОВ
или а и b следующим образом:
(ОЛ, О В) или (а, £),
так что
(а, Ь) = а • b cos (а, Ь). (4)
рассмотрение такого произведения объясняется тем,
большое практическое применение. Так, работа, за-
Введение в
что оно имеет
траченная силою F при прямолинейном перемещении точки на про-
тяжении О А = а,
т. е. работа силы
точкой путь:
как известно, выражается следующей формулой:
А = F • а • cos (Л, а),
есть скалярное произведение силы на пройденный
A=(F, а).
Основные законы обыкновенного произведения имеют место и
по отношению к скалярному произведению. 1 Так
(а, Ь) = (#, а) — переместительный закон,
(а Ь, с) = (а, с) -f- (£, с) — распределительный закон,
т • (а, Ь)~(та, Ь)—сочетательный закой.
Весьма важно заметить, что в отличие от обыкновенного произ-
ведения чисел, скалярное произведение двух векторов равно нулю
Не только тогда, когда один из множителей равен нулю, но и тогда,
когда векторы взаимно перпендикулярны, так как тогда cos (а, Ь) —
0. Обратно, если (а, Ь) = 0, но ни один из векторов не равен
нУлю, то векторы взаимно перпендикулярны.
Скалярное произведение двух векторов, как это следует из опре-
деления, есть скаляр.
Зат 1 ^еРвый с очевидностью вытекает из определения (формула (3)). Дока-
тельство второго и третьего см. И. И. Привалов — Аналитическая гео-
етрия; Н. Е. К о ч и н — Векторное исчисление.
144
ЙОЙЯТИЕ о вектора^
[хи
Из формулы (3) следует также, что
(а, Ь) = а • b • cos (а, Ь) — а • пр. Ь,
(а, b) = b • а • cos (а, &) = Ь • np.f а.
В случае, если один из векторов — единичный вектор, то пре-
дыдущие формулы принимают вид
(a, bQ) = а • 1 • cos (a, tft) = пр.^о а, (5)
т. е. скалярное произведение вектора а и единичного вектора bQ
->
равно проекции вектора а на направление единичного вектора.
§ 68. ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
ЧЕРЕЗ ИХ ПРОЕКЦИИ НА КООРДИНАТНЫЕ ОСИ
Представим себе систему прямоугольных координат в простран-
стве и вектор ОМ, начало которого в точке О. Построим коорди-
наты конца этого вектора. Рассма-
тривая ломаную линию ОАРМ и ее
замыкающую ОМ, можно написать на
основе формулы сложения векторов,
что
ОМ = ОА + АР 4- РМ.
Заменяя в этой формуле векторы
х АР и РМ равными им векторами ОВ
>
и ОС, получаем
ОМ = ОА + ОВ + ОС. (6)
Рис. 92. __►. _► __>.
Векторы ОА, О В и ОС называются
- - >
составляющими вектора ОМ на осях координат.
Всякий вектор можно разложить на сумму его трех составляющих.
Очевидно, что составляющие вектора по своему направлению могут
совпадать с направлением осей координат, но могут быть и про-
—>
тивоположно направлены. Кроме составляющих вектора ОМ отло-
жим на каждой из осей координат в положительном направлении
по единичному вектору, которые обозначим через i, j, к и назовем
ортами.
Тогда, обозначая через х, у, z координаты точки М или,
что то же, проекции вектора ОМ на координатные оси, будем
иметь
О А = i • х, OB = j-y, OC=k-z.
§ 68] ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 145
Действительно, как сказано, орты это единичные векторы, кото-
рые всегда направлены в положительную сторону осей координат.
Умножая их на положительные или отрицательные числа — на коорди-
наты х, у, z, т. е. на проекции вектора на координатные оси, полу-
чаем составляющие вектора ОЛ4, направленные соответственно в поло-
жительную или в отрицательную стороны осей координат. Таким
—> >
образом, мы получаем для вектора ОМ — а следующую формулу
ОМ — а = ix 4" jy
дающую его выражение через орты и проекции вектора на коор-
динатные оси.
Формула эта, очевидно, справедлива и не только для вектора,
выходящего из начала координат, но и для вектора, начало кото-
рого находится в любой точке пространства, т. е.
AB — iX-t-jY-^-kZ,
где X, Y и Z — проекции вектора АВ на координатные оси.
Выведем теперь выражение скалярного произведения двух век-
торов через их проекции на координатные оси.
Пусть даны два вектора а и Ь.
По предыдущей формуле имеем
£= i^2+jy2+kz2,
а потому (a, 3)=(i^1+jy1 + kZ1, jX2 +jT2 + kZ2).
Откуда по распределительному закону
(a, b)=(ixv iX2) +(kZv iX2) +
+ j^) + (j^v j^ + CkZp jr2) +
kZ^+or,, kz2)+(kz1; kz2).
Далее по сочетательному закону
= Оад+0, i) lzA + (k, 1)ЗД+
+ 0, ЛВД + О, J) + j)^r2 +
+ (i, к)ад,+о, к)у^2+(к, к)zxzv
Но в силу взаимной перпендикулярности координатных осей,
а следовательно, и ортов, имеем:
(j, i) = 0, (k, i) = 0, (i, j) = 0, (k, j) = 0, (i, k) = 0, (j, k) = 0;
10 Зак. 2116. H. С. Михельсон.
146
ЙОНЯТИЕ О BEKtOPAtf
[xit
с другой стороны
(i, i)=l cos(^^) = l, (j, j) = l, (к, к)=1.
Поэтому
(а, £) = ВД + Y^ + ZtZ2. (7)
Итак, скалярное произведение векторов равно сумме произве-
дений соответствующих проекций их на координатные оси.
§ 69. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется вектором?
2. Как изображаются векторы?
3. Какие обозначения приняты для векторов?
4. Какие векторы называются равными?
5. Как складываются векторы и что является их суммой?
6. Какие основные законы справедливы для суммы векторов и в чем
они заключаются?
7. Как умножается вектор на скаляр?
8. Как аналитически записывается, что два вектора параллельны между
собой?
9. Что называется скалярным произведением двух векторов?
10. Какие основные законы справедливы для скалярного произведения
двух векторов и в чем они заключаются?
11. Что называется единичным вектором?
12. Что называется составляющими вектора на осях координат?
13. Что такое орты?
14. Чему равно скалярное произведение двух различных ортов?
15. Как выражается скалярное произведение двух векторов через их
проекции на координатные оси?
XIII. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 70. УРАВНЕНИЕ ПЛОСКОСТИ
Так же, как и на плоскости, различным геометрическим местам
точек в пространстве могут соответствовать некоторые уравнения,
которым удовлетворяют координаты всех точек данного геометри-
ческого места и только координаты этих точек. Такие уравнения
мы назовем уравнениями данных гео-
метрических мест.
Приведем различные примеры та-
ких уравнений.
I. Составим уравнение плоскости
CD, параллельной плоскости XOY,
т. е. уравнение, которому удовле-
творяли бы координаты всех точек
этой плоскости и только они.
Пусть отрезок ОС — с, тогда
очевидно, что искомым уравнением
будет
z = c. (1)
Действительно, для всех точек Рис. 93.
плоскости CD, и только для точек
Этой плоскости, координата z равна постоянно числу с. (Плоскость CD
следует, конечно, представлять себе неограниченною.)
Рассуждая точно так же, найдем, что
У = Ь
(2)
есть уравнение плоскости BD, параллельной плоскости XOZ (здесь
ОВ = £). Подобным же образом
х = а (3)
есть уравнение плоскости AD, параллельной плоскости YOZ (здесь
О А =» а).
10*
148
ПЛОСКОСТЬ И ПРЯМАЯ» В ПРОСТРАНСТВЕ
[Х111
II. Составим теперь уравнение любой плоскости (рис. 94). Опу-
стим на нее из начала координат перпендикуляр ОР и обозначим:
дл. ОР=р, (ОР, ОУ) = Р
(OP, ОХ) = а, (OP, OZ)=%.
Выберем произвольную точку пло-
скости и построим ее координаты
ОА = х, АК=у, KM = z.
Соединив точку М с Р, мы обра-
за зуем ломаную линию ОАКМР, замы-
кающею которой будет служить ли-
ния ОР.
По известной теореме пишем
пр. О А + пр. ДК+пр. КМ-\-
+ пр. ЖР = пр. ОР.
дикуляр
ОР и приняв во внимание, что
Выбрав за ось проекции перпен-
пр. О А = О А • cos а = х • cos а,
пр. АК= АК • cos {3 = у • cos (3,
пр. КМ = КМ • cos т = z • cos у,
пр. МР = 0, так как MP | ОР,
пр. ОР = ОР =р,
найдем
х cos a -f-y cos р + z cos у = р
или
xcosa-j-^ycos p-f-2cos ?—р = 0. (4)
Такова зависимость между координатами произвольной точки
рассматриваемой плоскости; это и есть, следовательно, уравнение
рассматриваемой плоскости.
Уравнение это 1-й степени относительно х, у, z, откуда и вы-
текает такого рода теорема:
Всякая плоскость выражается уравнением 1-й степени.
III. Докажем теперь обратное положение.
Всякое уравнение 1-й степени вида
Ax-\-By-\-Cz-\-D = Q (5)
выражает в пространстве некоторую плоскость.
Если нам удастся уравнение (5) сделать тождественным с урав-
нением (4), то тем самым1 теорема будет доказана; уравнение (5)
будет тогда выражать то же, что и уравнение (4), т. е. плоскость.
УРАВНЕНИЕ ПЛОСКОСТИ
149
§ 70]
Умножим для этого все члены уравнения (5) на некоторое по-
стоянное число k и подберем его так, чтобы
A& = cosa, B£ = cosp, Ck — cos^ (6)
Dk = — p, (7)
Ta e. чтобы уравнение (5) стало тождественным с уравнением (4).
Для нахождения множителя k возвысим в квадрат уравнения (6)
и сложим
► (А2 -р В2 -f - С2) k2 — cos2 a -J” cos2 ? + cos2 Т-
Но
cos2 а 4" cos2 Р + cos2 Т = 1,
поэтому
№ —------i, k =-------- 1 ---. f еч
Д2 + В24-С2’ ± /Л2+В2_|_ С2
Знак перед корнем определится из равенства (7), когда мы при-
мем в расчет, что р должно быть положительным (так как р » дл. ОР).
Так как
_ —D
Р~ ± уд* + № + С* ’
то знак перед корнем следует всегда брать противоположным знаку
коэффициента D.
При значении А, определяемом формулой (8), уравнение (5) де-
лается тождественным с уравнением (4) и потому выражает плоскость,
что и требовалось доказать.
Формулы (6), соединенные с (8), дают значения косинусов углов
а, Р, у, составленных с осями координат перпендикуляром к пло-
скости:
А о В
cos а =--=====: cos 3 =---------=====.
Zt VA24-B2 + C2 Г ± /А24-В2 + С2 > (IQ)
COS Y =--==£== .
‘ ±z/A2 + B2 + C2
Следствия. Рассмотрим отдельные случаи, когда в уравнении
Ах 4- By 4- Cz 4- D о
некоторые из коэффициентов равны нулю.
1) А = 0.
Уравнение имеет вид: By 4“ Cz 4- D = 0.
В этом случае в силу формул (10) cosa = 0, т. е. а = -^- , по-
этому ОР | ОХ и, следовательно, плоскость параллельна оси ОХ.
2) В = 0.
Уравнение имеет вид: Ах 4“ Cz-\-D = 0.
150
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[XIII
В силу тех же формул здесь cosр = 0, т. е. £ = у, OP | OY
и, следовательно, плоскость параллельна оси OY.
3) С=0.
Уравнение имеет вид: Ax-f~By-}-D = 0.
Рассуждая так же, находим, что плоскость параллельна оси OZ.
4) D = 0.
Уравнение имеет вид: Ах-\-Ву -\-Cz- 0.
Из формулы (9) имеем тогда р = 0, т. е. плоскость проходит
через начало координат.
5) Д=В = 0.
В этом случае плоскость будет параллельна оси ОХ и оси OY,
следовательно, параллельна плоскости XOY.
Уравнение принимает вид:
Cz + D = 0; z = — , или z = с.
6) Д =£) = 0.
Плоскость проходит через начало координат и в то же время
параллельна оси ОХ, следовательно, плоскость проходит через всю
ось ОХ (ось ОХ лежит в данной плоскости).
Подобным образом рассматриваются и другие возможные случаи.
IV. Уравнение плоскости в векторной форме. Установим прежде
всего, как в векторной форме определяется положение точки в про-
странстве. Соединив начало координат с данной точкой М, нетрудно
убедиться, что каждой точке
пространства соответствует один
определенный вектор, такой, как
>
ОЛ4, и, наоборот, каждому дан-
ному вектору ОМ = г соответ-
ствует одна определенная точка
М «—конец вектора.
Отсюда следует, что вектор,
соединяющий начало координат
с данной точкой, вполне опреде-
ляет положение точки в про-
странстве и заменяет собой все
три координаты точки, что и запи-
сывают так: М (г).
Вектор г = ОМ называют ра-
диусом-вектором точки М.
Представим себе некоторую плоскость (рис. 95) и на ней точку М.
Пусть ОР = р — длина перпендикуляра, опущенного из начала коор-
динат на данную плоскость Q.
Длина перпендикуляра и его направление, конечно, вполне опре-
деляют положение плоскости. В предыдущем выводе уравнения цдо-
§ 70]
УРАВНЕНИЕ ПЛОСКОСТИ
151
скости в нормальном виде направление перпендикуляра определялось
углами а, Р и I, составляемыми им с осями координат. Переходя
к векторной форме, это направление можно задать единичным век-
тором п°, направленным, как и сам перпендикуляр, в сторону от
начала координат к плоскости.
Из чертежа видно, что
пр. ОМ на пР = р.
Равенство это выполняется для всякой точки, лежащей на пло-
скости, и потому выражает свойство всех точек данной плоскости.
Введя сокращенное обозначение вектора ОМ через г и вспоми-
ная формулу (5) (стр. 144), мы можем предыдущее равенство записать
так:
(г, п°)=р или (г, п0)—р = 0. (11)
Это и будет уравнение плоскости в векторной форме.
Чтобы перейти от векторной формы уравнения плоскости к ко-
ординатной, достаточно выразить скалярное произведение через проек-
ции векторов на координатные оси по формуле (7) (стр. 146)
= пР-ок Г> = -У>
ПР-0Х = 1 • COS а, Пр.оу п° = 1 • COS Р, пр. oz пР = 1 • COS Т.
Поэтому
(г, п°) = xcosa-^j/cosp Ц-zcos у,
и уравнение (11) принимает известную нам форму
х cos a + j/ cos p z cos -f — p = 0.
V. Уравнение плоскости в отрезках на осях. Предположим,
что в уравнении плоскости
+ + + = 0
коэффициент D отличен от нуля.
Перенесем D в правую часть уравнения и, разделив
Уравнения на — D, представим уравнение (5) в виде
р 1 q 1 г
где буквами р, q, г обозначены для краткости следующие
D D D
Р— А , Я — в , г с.
Полученное уравнение (12) носит название уравнения
в отрезках на осях координат, ввиду ТОГО, что величины р, q, г
(5)
все члены
(12)
величины:
плоскости
152
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[хш
являются отрезками, отсекаемыми плоскостью на осях координат,
Рис. 96.
считая от начала. Действительно, от-
резок ОА на оси ОХ является коорди-
натой х для точки А, т. е. для такой
точки плоскости, у которой
у = 0 и z = 0.
Подставляя эти значения в уравне-
ние (12), найдем:
х = р, т. е. р = О А,
Подобным же образом убедимся, что
q = ОВ и г = ОС.
VI. Уравнение плоскости, проходящей через данную точку.
Общее уравнение всякой плоскости имеет вид:
Ах —|— By Cz D = 0.
Так как плоскость проходит через точку /Ио, то должно иметь
место равенство
Лх0 4“ ДУо 4“ 4" D = °-
Определяя отсюда D и подставляя в предыдущее уравнение или
просто вычитая второе уравнение из первого, находим
А (х — х0) + В (у ~~Уо) 4- C(z — z^ = 0. (13)
Это и будет уравнение искомой плоскости.
Например, уравнение плоскости, проходящей через точку
(1, —2, 3), будет
Л(х-1) + В(^+2) +
4~С(г — 3) = 0.
Коэффициенты А, В, С остают-
ся неопределенными, так как
таких плоскостей — бесчисленное
множество. Для их определения
необходимо задать дополнитель-
ные условия.
В векторной форме уравне-
ние плоскости, проходящей через
данную точку, получается на осно-
вании следующих рассуждений.
Пусть г = ОМ радиус-вектор
a rQ=0MQ радиус-вектор данной
Рис. 97.
переменной точки М плоскости,
точки /Ио.
§ 71]
УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ
153
Соединив точку Мо с точкой Ж, получим вектор /WqAI, который
является разностью между векторами г и г0, т. е.
М^М=г — rQ.
Так как обе точки Мо и М лежат в плоскости перпендикуляр-
ной к вектору п0, то вектор
в каком бы месте данной плоскости ни находилась точка М. Это
свойство можно записать так
(г —г0, "o) = °-
Следовательно, это уравнение и будет искомым уравнением пло-
скости, проходящей через данную точку.
§ 71. УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ
Прямую в пространстве можно рассматривать как пересечение
двух плоскостей
Ах 4- By 4- Cz + D = 0 (плоек. I).
Atx -j- Bty 4* Crz 4- Dt = 0 (плоек. II).
Координаты всех точек прямой должны удовлетворять обоим
этим уравнениям, откуда и заключаем, что прямая в пространстве
определяется системой двух уравнений 1-й степени
Ах 4~ By 4~ Cz 4~ D == о
Агх + 5^4-^4-^ = 0. ( '
Каждое из этих уравнений в отдельности попрежнему пред-
ставляет собой плоскость, а рассматриваемые вместе — прямую
в пространстве.
Преобразовывая эту систему в другую, равносильную ей, мы
можем для одной и той же прямой получить различные виды си-
стем уравнений 1-й степени. Это и понятно, так как одна и та же
прямая может быть рассматриваема как пересечение различных пар
плоскостей.
Так, решая систему (1) относительно х и у, мы придем к другой
форме уравнений прямой линии, а именно к системе
* = «*+?
в которой х и у выражаются через третью координату г.
154
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[ХП1
Каждое в отдельности уравнение системы (2) выражает попрежнему
плоскость: первое параллельную оси OY, второе параллельную оси ОХ.
Уравнения прямой можно вывести и независимо от рассмотре-
ния ее как пересечение двух плоскостей. Действительно, пусть
RS — некоторая прямая, проходящая
через точку
Mq(Xq, Уо> Zq)
и составляющая с осями координат
углы
7-
Возьмем произвольную точку
на этой прямой, координаты которой
обозначим через х, у, z. Положив
для краткости дл. Л4О7И = d, спроек-
тируем вектор MqM на ось ОХ\ имеем
пр. М^М. = AiA = х — х0.
Но с другой стороны
пр. М0М = d • cos а;
поэтому находим х — xQ = d • cos а
или = (3) cos a v '
Проектируя вектор MqM на другие оси, так же найдем
v — у0 = d • cos 8 или -—— d,
s sv г cos р ’
z— z(] = d-cosy или = d.
и 1 cos f
От полученных трех равенств приходим к системе уравнений
x — x^ y—y^^z — z^ ( .
cos a cos р cos у ’ '
которым должны удовлетворять координаты любой точки М на
прямой RS и только точек этой прямой, т. е. получаем систему
уравнений прямой в новой форме.
Эта система заключает в себе два уравнения 1-й степени, т, е,
попрежнему уравнения двух плоскостей.
§ 71] УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ 155
Умножением знаменателей дробей (4) на одно и то же произ-
вольное число k можно систему (4) представить в виде
х — х^ _ у —Уо _ Z—*о /сч
I т п 9 ' '
где
/ = Ajcosa, /n = Ajcos(3, n = kcos*(. (6)
Во многих случаях прямую в пространстве удобнее всего пред-
ставлять именно в форме уравнений (5).
Величины Z, т, п, как видно из уравнений (6), пропорциональны
косинусам углов, составленных прямой с осями координат. Их при-
нято называть угловыми коэффициентами прямой. Пользуясь урав-
нениями (6), можно найти выражения косинусов углов а, 0, 7 через
коэффициенты Z, т, п. Именно, возвышая уравнения (6) в квадрат и
складывая, находим
Z2 /я2 п2 = k2 (cos2 а 4~ cos2 Р "I" cos2 Т) — k2’
откуда
fc = ±//2-|-m2 + n2.
Зная теперь величину k, нетрудно из уравнений (6) найти иско-
мые выражения для cos a, cos0, cos 7:
/ о т
cos а =----г .=., cosр —-------------, =.,
±//24-т2+д2 . //2-|-т2_|_л2
п <7>
C0S^ ± y/2 4-m2_|-rt2‘
По этим формулам можно определить углы а, р и *[, составляе-
мые прямой с осями координат, если эта прямая представлена
в форме уравнений (5).
Наконец, уравнения прямой можно представить еще и в сле-
дующем виде. Обозначив общую величину отношений, входящих
; в уравнения (4), через Z, можно разбить систему (5) на три урав-
нения:
x — Xq = t у —у0 = t Z — = t
I 9 т 9 п '
Тогда прямая представится тремя такими уравнениями:
х — хо +
У=Уо + т(, (8)
z = z0 -|- nt.
Это так называемая параметрическая форма уравнений прямой в про-
странстве, Геометрический смысл входящих в уравнения (8) величин
156 ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ [хш
ясен: х9 у, z переменные координаты различных точек прямой —
текущие координаты прямой; х0, у0, z^— координаты некоторой
определенной точки прямой; /, /п, п — угловые коэффициенты, опре-
деляющие направление прямой; t — вспомогательная переменная, назы-
ваемая параметром. Давая переменной t произвольные значения, най-
дем, всевозможные точки прямой.
Из всех различных форм уравнений прямой более удобной и
употребительной формой является система (5), в которую входят
координаты x0, yQ9 zQ точки, через которую прямая проходит, и
угловые коэффициенты прямой /, т и п.
В случае, если прямая задана уравнениями формы (1), то угловые
коэффициенты ее можно определить следующим образом.
Пусть х0, j/0, Zq координаты некоторой точки нашей прямой.
Так как плоскости (1) проходят через эту точку, то их урав-
нения можно представить в следующем виде:
Л (х — х0) + 5 (у— _у0)Ц-С (z — zo) = O,
A (х — х0) + (у —у0) 4- (z — z0) = 0.
Решая эту систему двух однородных уравнений относительно
трех неизвестных х— х0, у—yQ9 z — zQ, найдем (см. § 5), что зна-
чения этих неизвестных пропорциональны определителям
В, С
в19 с.
А, С А, В
А, ^1 А> вх
т. е. что
* —*0 У—Уо г —*0
в, с Blt Ci — А, С А, * Со
Таким образом мы приходим к форме (5). Сравнивая последние
уравнения с системой (5), обнаруживаем, что
В, С
А,
А, С _ Л, В
А> Сх А19 Bt
(9)
т =
Последние формулы дают возможность легко вычислить угловые
коэффициенты прямой, когда последняя задана уравнениями формы (1).
В случае, если прямая задана или приведена к форме (2), то
приведение ее уравнений к форме (5) производится простым реше-
нием обоих уравнений относительно z и составлением общей про-
порции, как это иллюстрируется на следующем примере.
§ 72]
ОСНОВНЫЕ ЗАДАЧИ
157
Пример. Представить уравнения прямой
х + 2_у — 3z — 4 = 0
Зх — у + 5z + 9 = 0
в различных формах.
Для этого прежде всего решим их относительно х и у,
х + 2_у— 3z — 4 = 0 Зх + 6_у— 9г —12 = 0
6х — 2у+ 10г + 18 = 0 Зх— у + 5г + 9 = 0
7х+ 7*+14 = 0 7_у —14г —21=0
После сокращения всех членов уравнений на 7, приходим к форме (2)
уравнений прямой
х = — z — 2, у = 2г + 3.
В них а = — 1, b = 2, р = — 2, q = 3.
Чтобы привести эти уравнения к форме (5), достаточно свободные члены
перенести в левую часть и затем составить из двух равенств
х + 2 = — z, у — 3 = 2г
пропорцию
x + 2_j/ — 3 z
— 1 “ 2 “ 1 ‘
Сравнивая эти уравнения с уравнениями формы (5), находим
х0 = — 2, у0 = 3, zQ = 0,
I = — 1, т = 2, n = 1.
Наконец, по общему правилу получаем и форму (8), для чего полагаем
'+2_f У—Ъ—f z
— 1 ’ —2 ’ I ’
так что
х = — t — 2
^ = 2/+3
z = t.
Коэффициенты I, т, п можно было бы найти и по формулам (9)
Z:/n:n = 7: —14: —7 = — 1:2:1.
§ 72. ОСНОВНЫЕ ЗАДАЧИ, ОТНОСЯЩИЕСЯ К ПЛОСКОСТИ
И ПРЯМОЙ В ПРОСТРАНСТВЕ
Задача I. Провести плоскость через данную точку
(*о> Уо> zo)-
Ответом на эту задачу служит уравнение
Л (х — х0)-\~В(у — у0)-\-С(г—г0) = О
(см. уравнение (13) стр. 152).
158
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[хщ
Так, плоскость, проходящая через точку (3, —1, 4), будет иметь
уравнение
А (х —3)4- В (у 4-1) + C(z —4) = 0.
Задача II. Провести прямую через данную точку
М Оо, Уо, zo)-
Ответом на эту задачу служат уравнения (5) (стр. 155)
x—XQ__y—yQ_ Z — Zy
I tn П 9
где коэффициенты /, m, n остаются неопределенными, что вполне
соответствует задаче, так как прямых, проходящих через одну точку,
бесчисленное множество.
Например, уравнения прямой, проходящей через точку (2, —3, 4),
будут
х — 2 _У + 3 __ z — 4
I т п '
В векторной форме уравнение прямой, проходящей через дан-
ную точку 7И0(г0), получим на основании следующих рассуждений.
Прямая в пространстве вполне определяется положением точки Л40,
через которую она проходит, и направлением прямой. В векторной
форме она, следовательно, опре-
деляется радиусом-вектором г0
точки Л40 и единичным векто-
ром а0, которому прямая парал-
лельна.
Выберем произвольную точку
прямой М (г), радиус-вектор ко-
торой г. Вектор М0М является
разностью векторов г и г0, т. е.
М^[ =*—\.
С другой стороны, в каком бы месте прямой ни была взята
точка М, вектор
|| а0,
что в векторной форме можно записать так (см. формулу (3), стр. 142):
г — г0 = а0 • t.
Это и будет искомое уравнение прямой в векторной форме.
Задача III. Провести прямую через две данные
точки Mi(xlt ylt zt) и Af2(x2, у2, г2).
§ 72] основные задачи 159
Прямая, проходящая через точку Mlt согласно решению задачи I,
будет иметь уравнения
• У —_ У—У1 = Z —
I т л
Чтобы эта прямая прошла и через точку Л42, необходимо, чтобы
• ^2 —-У! = ^2 — ^
I т п '
Разделяя почленно первый ряд равенств на второй, получим
• у —*1 _ У~У\ = z — Z! ,
• У2 —-У1 Уч — Уг zx >
— уравнения прямой, проходящей через обе точки М1 и М2. Напри-
мер, уравнения прямой, проходящей через точки М{ (2, 0, — 1),
М2(1, 3> — 2)> бУдУт
х — 2_у —0_ z + 1
1—2 —3—О —2 + 1
или
х — 2_ у___z+1
““ з — —1 *
Выведем теперь уравне-
ние в векторной форме
прямой, проходящей через
две данные точки (rj
И ЛГ2Й.
Пусть АВ (рис. 996) пря-
мая, уравнение которой мы рис ggg.
ищем, и М (г) переменная
точка прямой. Из чертежа следует, что в каком бы месте прямой АВ
ни находилась точка М, векторы
MtM = r— г1 и М2М = г— га
параллельны между собой, а это в векторном обозначении записы-
вается так (см. стр. 142, формула (3)):
г—*1 = ^- (*—*я)-
Последнее и является уравнением искомой прямой.
Задача IV. Найти угол между плоскостями Лх -|- By -|“
+ Сг + Д = о и Ахх-\-Вгу -j-C1z-]-D1 = 0.
160
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[XIII
Обозначая через а, р, у углы, составленные с осями координат
перпендикулярОхМ OPt к первой плоскости, а через 04, рь — перпен-
дикуляром ОРа ко второй плоскости, имеем по формулам (10) (стр. 149)
Рис. 100.
± /л24-в2 + с2
о В
cos 8 =--. . - =
г ± /Л3 + В2 + <?2
С
' ±/Л2-|-В2+ С2
А1
cos а. =- ----------
±VAl + Bl+Cj
о
cos В« =--—=^=
±УА1 + В1+С1
С1
COS Yj =-r =
± + Cf
А тогда по формуле (*) (стр. 135) выражение для косинуса угла, со-
ставленного этими перпендикулярами, или, что то же, угла между
данными плоскостями, будет следующее:
cos —• - .
zt У А2 + В2 + С2. у + В2 + С2
(2)
Из последней формулы вытекает условие перпендикулярности
двух плоскостей. Именно для перпендикулярности плоскостей надо,
чтобы cos со = 0, т. е. должно выполняться соотношение
+ «?! = ().
Что касается условия параллельности, то для его получения
заметим, что в случае параллельности плоскостей перпендикуляры
ОР2 и OPi либо совпадают по направлению, либо прямо противо-
положны, а потому должно быть
cos a = ±cosa15 cos р = zt cos cos y = ±cos
т. e.
_____A________ , ____Aj_____
Va2 + b* + c2 ~ ~ Vai+bi + ci 9
В Bt
УА2 + В2 + С2 “ VAl + Bf + Cl9
C Cl
УА* + В* + & ~ VAl + Bl + Cl ’
ОСНОВНЫЕ ЗАДАЧИ
161
§ 72] ----------------
Из этих пропорций вытекает одна общая пропорция
являющаяся условием параллельности плоскостей. Итак,
-j- ВВг 4~ СС1 = 0 —условие перпендикулярности,[плоскостей (3)
Л С
— --- ----------условие параллельности плоскостей. (4)
Л1 £>1
Например, плоскости
2х — 4у 4- 8г — 3 =±= О
Зх —бу 4-12*4-5 = 0
параллельны, так как
2 — 4 _ 8
3 ~ —6 12’
плоскости же
х — 2у 4- 5 = 0
4*4-2у —7г4-1 = 0
взаимно перпендикулярны, так как
ЛЛ14-В^14-СС1 = 1 • 4 —2.2 = 0.
Если плоскости заданы в векторной форме
(r, nJ)—Р1 = О и (г, п^—р2 = о,
го их параллельность означает параллельность единичных век-
торов п® и /zj, перпендикулярных к данным плоскостям. Следо-
вательно, условием параллельности плоскостей будет
± п®.
1 Л
Взаимная перпендикулярность плоскостей означает перпенди-
кулярность единичных векторов nJ и nJ. Следовательно, условием
перпендикулярности плоскостей будет
(nJ, nJ) = O.
Задача V. Найти угол между прямыми — — =
J J r l m
л Zi mr /Zi
11 Зак. 2116. H. С. Михельсон.
162
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[xill
Обозначив через а, [3, а19 — углы, составленные дан-
ными прямыми с осями координат, находим по формулам (7)
(стр. 155)
cos а = 1 cosa2 = _ It
± V/2 + т2 + и2 ’ ± У /?' 4- + n'i
cos |3 = т COS == mt
zt У Р + W2 + п? ’ ± Vl'i + m{ + nl
п cos Yj = nt
cos у = ± y/2H-m2+ я2 ’ ±Vll + ml+nl
а затем, как и в предыдущей задаче, косинус угла <о между прямыми
выразится так:
„ „ III + mmi + nni
COS О) =----......................—.
± V l* + n& + ri>- У+ m* + п\
Аналогичными, как и в предыдущей задаче, рассуждениями
придем к следующим условиям перпендикулярности и параллель-
ности прямых:
11х 4“ тт^ -f- nnr == 0 —условие перпендикулярности прямых (5)
/ т п
~ = — = ------условие параллельности прямых. (6)
Условия параллельности и перпендикулярности прямых
г — r1~aQ1*t и г — г2 = а® . t
в векторной форме будут:
а° = dz aj — условие параллельности (5х)
(аь я2) = 0 — условие перпендикулярности. (6 )
Задача VI. Найти условие перпендикулярности и
параллельности плоскости с прямой.
Пусть прямая LLi и плоскость Q заданы уравнениями
x-£0 = 32z2.o==£zi^ Ax4-By + CzA-D = 0.
I т п i^i ।
Восставим в точке К перпендикуляр КН к плоскости Q. Оче-
видно, что прямая LLX будет параллельна плоскости Q, когда LLX
будет перпендикулярна к КН, и, наоборот, прямая LLi будет
перпендикулярна к плоскости Q, когда она параллельна перпенди-
куляру КН к плоскости.
§ 73|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
163
Направление перпендикуляра КН определяется коэффициентами
А, В, С, а направление прямой LLX коэф-
фициентами /, т, п. Поэтому условия
А —А = £
I ~~~ т п
будут условиями параллельности прямых
и КН, а вместе с тем условиями
перпендикулярности плоскости и прямой.
Напротив, условие
А! —|— Вт —Сп = О
Рис. 101.
будет условием перпендикулярности пря-
мых LLX и КН, а вместе с тем условием параллельности плоскости
и прямой.
Итак,
АВС .
— = — =--------условие перпендикулярности прямой
и плоскости (7)
Л/+ Вт-±Сп = Ъ—условие параллельности прямой и
плоскости. (8)
Условия параллельности и перпендикулярности прямой г—=
= a^-t и плоскости (г, /г°)—р = 0 будут следующие:
aj = zt/z° — условие перпендикулярности прямой и плоскости. (7')
-> ->
(aj, п°) = 0 — условие параллельности прямой и плоскости. (8')
Действительно, первое из них выражает параллельность прямой
и перпендикуляра к плоскости, а второе их перпендикулярность.
§ 73. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Через точку М (0, 2, —1) провести плоскость параллельную
плоскости х — 2у + 5z + 4 = 0.
Уравнение плоскости, проходящей через данную точку, будет
Hx + B(j/-2) + C(z + l)=0.
Для параллельности этой плоскости с данной надо, чтобы
АВС
1 — -2 ~ 5 ’
Т. е. чтобы А — k, В = — 2k, С = 5k.
Подставляя эти значения в уравнение плоскости и сокращая все члены
на k, находим
или
х-2(у/-2) + 5(^ + 1)=0
х — 2у + 5г 4-9 = 0.
i 64 ПЛОСКОСТЬ Й ПРЯМАЯ В ПРОСТРАНСТВЕ [ХП1
Пример 2. Через ось OZ провести плоскость, проходящую через точку
Плоскость, проходящая через ось OZ, имеет уравнение
Ах + By = 0.
Для того чтобы эта плоскость прошла через точку М, координаты этой
точки должны удовлетворять уравнению плоскости, т. е. чтобы 2А 4- 4В = 0
или А = — 2В.
Подставляя значение коэффициента А в уравнение плоскости и сокращая
все члены на В, получим уравнение искомой плоскости:
— 2х -|- у = 0 или у = 2х.
Пример 3. Провести через точку (3, — 1, 0) плоскость перпендикулярно
к двум плоскостям: х — 3z — 2 = 0, 2х + .У — 4z — 1 = 0.
Плоскость, проходящая через данную точку,, будет иметь уравнение
А (х — 3) + В (у + 1) + Cz = 0.
Условия перпендикулярности этой плоскости к двум данным плоскостям
будут таковы:
Л — 36? = 0,
2Л + В — 4С = 0.
Из этих уравнений определяем две какие-нибудь величины через
Третью
А = 36?, В = - 2С
и найденные значения Л и В подставляем в уравнение плоскости; тогда
получим
ЗС (х - 3) — 2С (у + 1) + Cz = 0.
Сокращая члены уравнения на С, найдем
3(х — 3)-2(.y + l) + * = 0
или
Зх — 2y + z —11 =0.
Пример 4. Провести плоскость через три точки
^(2,-1, 4), Л42(-Ь 3, —2), Л43 (0, 2, 3).
Уравнение плоскости, проходящей через первую точку, будет
Л(х-2)+ВСу+1) + С(г--4) = 0.
Эта плоскость должна пройти еще и через точки Л42 и М3, а для этого
надо, чтобы их координаты удовлетворяли тому же уравнению, т. е. чтобы
— ЗЛ + 4В —6С = О,
— 2Л + ЗВ — 6? = 0.
Из этих уравнений находим два коэффициента, выражая их через третий,
как это сделано в предыдущей задаче. Того же самого можно достигнуть,
основываясь на приеме решения системы двух однородных уравнений 1-й
степени с тремя неизвестными, а именно
А В_________С . А _ В =в С
|4, _6| “ _ —3, —61 | — 3,4|’ 14 1’
13, — 11 — 2, — 11 | — 2, 31
т. е* А = 14&, В = 9£, С = - /л
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
165
§ 73]
Подставляя эти значения в уравнение плоскости и сокращая на k, по-
лучим
14(х —2) + 9Су + 1) —(г —4) = 0, или 14х + 9у — г— 15 = 0.
Пример 5. Провести прямую через точку М (4, — 1, 3), Уравнения
искомой прямой сразу пишутся в форме (5) ,или (8) (§ 71):
* j — = - * = -—- или х = 4 + It, у = — 1 + z = 3 + nt.
I т п \ \ ।
В обеих формах угловые коэффициенты прямой I, т, п остаются неопре-
деленными, так как и сама задача неопределенная.
Пример 6. Провести прямую через точку Л4(4, —1, 3) параллельно
м х — 3 z+1
прямой —= у = 3. 5 •
Уравнения искомой прямой, проходящей через точку М, будут
х— 4 j' + l г — 3
/ т п
Чтобы она была притом параллельна данной прямой, надо, чтобы
Z т п
"2
Отсюда I = 2k, т — k, п = —5k. Подставив эти значения в уравнения
искомой прямой и сократив все члены уравнения на А?, окончательно найдем
Пример 7. Через точку М (1, —2, 4) провести прямую перпендикулярно
к плоскости 2х— Зу + z— 4 = 0.
Напишем сначала уравнения прямой, проходящей через данную точку
х — 1 у+ 2 z — 4
I т п ’
Чтобы она была перпендикулярна к данной плоскости, надо, чтобы
I т п
2 ~ -3 = 1 ’
т. е, , т, п должны быть пропорциональны числам 2, —3 и 1, откуда
l=s2k, т = — 3k, п = k.
Подставляя эти значения в уравнения прямой и сокращая все члены
па k, приходим окончательно к уравнениям
х—1 j>4-2 z — 4
2 ~ —3 ~ 1 ’
которые и служат решением задачи.
Пример 8. Провести прямую через точку М (— 1, —4, 3) перпендику-
лярно к двум прямым
2х — 4у + & — 1 = 0 х = 2 + 4Z
л + Зу4-5-0 и _у = — 1 — t
z = — 3 + 2t.
166
ПЛОСКОСТЬ И ПРЯМАЯ в ПРОСТРАНСТВЕ
[хш
Прямая, проходящая через точку ЛГ, имеет уравнения
х + 1 у + 4 - z — 3
I т ~~ п '
Для определения Z, т, п воспользуемся условием перпендикулярности
прямых; предварительно надо лишь найти угловые коэффициенты данных
прямых.
Угловые коэффициенты второй прямой определяются сразу:
/2 = 4, = —1, л2 = 2.
Для нахождения угловых коэффициентов первой прямой применим фор-
мулы (9) (§ 71)
ЧЧ1=-> —|.:»Н ЧИН-
По условию перпендикулярности имеем
— 3Z +/и + Юл = О,
4Z — т + 2л == 0,
откуда Z т п
I ГТоГ-' I — 3, 10 ~ —3, 1’
I — 1, 21 I 4, 2 4,-1
Z т п
ИЛИ 12“ 46-— Г
Поэтому уравнения искомой прямой будут
х + 1 У + 4 2 — 3
12 ~ 46 “ — 1 ’
Пример 9. Провести прямую через точку Af (1, 0, —2) перпендику-
лярно плоскости 4х —у — 5 = 0.
Прямая, проходящая через точку М имеет уравнения
х —-1 __ .У _ 2^2
Z т~~ л
Чтобы она была перпендикулярна данной плоскости, надо, чтобы
4—10
Z т п ’
откуда Z = — 4т и л = 0. Итак, уравнения прямой будут
х —1 у 2 + 2 х— 1 2 + 2
— 4т т 0 — 4 0
или также
х + 4у — 1 =0,
2 + 2 = 0.
Пример 10. Через точку М (3,—3,2) провести прямую параллельно
двум плоскостям х — 4у + 10 = 0, Зх + Зу — z — 4 = 0.
Уравнения прямой, проходящей через точки Л4, будут
х — 3 _ у+ 3 _ z — 2
I ~ т ~~ л
ВОПРОСЫ И УПРАЖНЕНИЯ
167
§ 74]
По условию параллельности прямой с плоскостью имеем
* I— 4т = 0.
3/ -j- 5/м — it = О»
откуда
т п
7“Т = й’
Итак, искомая прямая определяется уравнениями
х — 3 _у + 3 z — 2
4 17 ’
§ 74. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что можно сказать относительно расположения точек, у которых
одна из координат равна нулю?
2. Где в пространстве лежат точки, у которых координаты х=_у = 0
или х = z = 0 или у = z — О?
3. Могут ли быть одновременно равны нулю косинусы трех углов,
образуемых некоторым направлением с осями координат?
4. Что представляет собою в пространстве в отдельности каждое из
следующих уравнений:
х = а, у — Ь, z = с, х = О, у = О, 2 = 0
Hx + By + D = 0, Ax + Cz + D = 0, By + Cz + D=^
Ax + By-\-Cz = 0, Ax + By = 0, Ax + Cz = 0, By + Cz = 0
Ax + D = 0, By + D = 0f Cz + D = 0,
5. Что представляет в пространстве каждая пара следующих уравнений:
{х = 0, Г х = 0, (у= 0, | х = а, (х = а, (у = Ь>
У~0 (2 = 0 (2 = 0 |у = Ь (2 = С I 2 = С,
6. Каковы условия перпендикулярности и параллельности двух плоско-
стей?
7. Каковы условия перпендикулярности и параллельности двух прямых?
8. Каковы условия перпендикулярности и параллельности прямой и
плоскости?
9. На плоскости 2х — y + 5z— 6 = 0 указать какую-нибудь точку, ей
принадлежащую.
10. Найти точки пересечения плоскости Зх — 2y-\-z—12 = 0 с осями
координат. Отв. (4, 0, 0); (0, —6, 0); (0, 0, 12).
И. На прямых, заданных уравнениями
х — 2y~f~3z —1=0 х — 2 __ у __ 2-|-3
2x-f-2y — г + 4 = 0 И 3 1~ТГ2’
Указать какую-нибудь точку, принадлежащую каждой из этих прямых в
отдельности.
ю и » и х — 3 у Ч- 2 2 — 1
1-2. Наити точку пересечения прямой —= -J—- =---------=- с пло-
z о — 2
Гостями координат.
13. Провести плоскость через точку (1, —2, 0).
Отв. А (х — 1) + В (у + 2) + Cz = 0.
168
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
[хш
14. Провести плоскость через три точки:
Afi (0, —1, 2); М2 (1, 2, 2); ЛТ3<(2, 0, —3).
Отв. Зх—y-{-z— 3 = 0.
15. Провести прямую через две точки (2, 3, 1), (0, —3, 2).
„ х —2 у—3 2—1
Отв. —— = -у- = —
16. Провести плоскость через точку (—4, 2, 0) перпендикулярно к прямой
*— 3 __ .у 4- 5 __ z
Г“ ~ 2
Отв. х-{-2у — z — 0.
17. Провести прямую перпендикулярную к плоскости 2х —у 4- 6г — 3 = 0
/1 о 14 х—\у+22—\
через точку (1, —2, 1). Отв. —— — - = —g— .
18. Провести плоскость через начало координат параллельно плоскости
х — 2у 4- Зг — 4 = 0. Отв. х — 2у + Зг = 0.
19. Провести прямую через точку (1, 0, —2) параллельно прямой
х + 3 ~ х — 1 п
—L_ = > = z. Отв. —2—=_у = 2-|-2.
20. В точке пересечения плоскости 2х — Зу 2г -]- 4 = 0 с осью OZ
х у ^ + 2
восставить к плоскости перпендикуляр. Отв. =ч—77—.
z — о 2
21. Провести плоскость через ось OZ и через точку (2, — 1, 5).
Отв. х + 2у = 0.
22. Провести плоскость, параллельную оси ОХ и проходящую через
точки (— 2, 4, — 1) и (1, —3, 2). Отв. 3_у + 7г — 5 = 0.
23. Провести плоскость через точки (3, —1, 0) и (— 2, 4, —3) перпен-
дикулярно к плоскости 4х—у + 3 = 0. Отв. х + 4у + 5z + 1 = 0.
24. Провести прямую через точку (— 3, 2, —5) параллельно плоскостям
х — 4г — 3 = 0 и 2х—у — 5z — 1=0. Отв. Х "Г— = .
25. Провести прямую через точку (0, —4, 2) перпендикулярно к двум
х-f-l У—4 х — у 4-4 = 0
прямым: —2“= —= г и Зх-2>+32 = 0.
2 — 2
26. Найти основание перпендикуляра, опущенного из точки (— 3, — 2, 2)
на плоскость 2х-\-2у— г 4-3 = 0. Отв. (—1, 0, 1).
х I 3
27. Из точки (1, —3, 2) опустить перпендикуляр на прямую —=—- =
__ -V __ г+^
— 3 —1 Отв. 2х — г = 0, у 4- 3 = 0.
28. Найти уравнения следов, оставляемых плоскостью 4х—y-^2z—1=0
на плоскостях координат.
Отв. 4х—у — 1=0, 4x4" 2г—1=0, у — 2г 4-1 = 0,
г = 0; у = 0; х = 0.
29. Найти уравнения проекции прямой Зх — 2у — 4г — 6 = 0; х 4-У —
— 2г 4- 3 = 0 на плоскости координат.
Отв. х — 4у — 12 = 0, 5х — 8г = 0, Зу — 2г 4- 15 = 0,
г = 0; у = 0; х = 0,
XIV. КРИВЫЕ ПОВЕРХНОСТИ и линии
В ПРОСТРАНСТВЕ
§ 75. ОБЩАЯ ФОРМА УРАВНЕНИЙ ПОВЕРХНОСТЕЙ
И ЛИНИЙ В ПРОСТРАНСТВЕ
Мы видели, что уравнение вида
Ах By —|— Cz D = О
выражает плоскость. Покажем теперь, что общее уравнение вида
f{x, у, s) = Q
(1)
выражает, вообще говоря, некоторую поверхность.
В самом деле, представим себе, что, решив уравнение (1) отно-
сительно z, мы нашли
г = ср(х, д/). (2)
Допустим далее, что, задав
ния, например х = а19 у =
Эти три числа alf &19 ct
определяют в пространстве не-
которую точку М1(а1, д19 cj,
координаты которой, очевид-
но, удовлетворяют уравне-
нию (2), а также (1).
Положим, что, задавая
х==а2, у = Ь2, мы найдем
z~c29 т. е. новую точку
М2(я2, ^2, с2)> координаты
которой также удовлетворяют
Уравнению (1).
Продолжая эти рассужде-
ния, т. е. давая х и у все но-
вые и новые значения, мы
переменным х и у некоторые значе-
мы найдем из уравнения (2) z = cv
Рис. 102.
найдем, вообще говоря, бесчисленное множество точек, которые
будут заполнять некоторую поверхность; координаты всех их будут
Удовлетворять уравнению (1),
170 КРИВЫЕ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ [XIV
Из этого мы и можем заключить, что уравнение вида /(х, у, г) = 0
выражает, вообще говоря, некоторую поверхность.
Подобно тому, как два уравнения 1-й степени определяют пря-
мую, система двух уравнений вида
выражает, вообще говоря, некоторую линию в пространстве.
Действительно, эти два уравнения определяют такие точки, кото-
рые лежат и на первой и на второй поверхности, т. е. точки пере-
сечения поверхностей. Совокупность же таких точек представляет,
вообще говоря, некоторую линию. В таком случае система (3) и
будет являться уравнениями этой линии.
§ 76. ПРИМЕРЫ НЕКОТОРЫХ ПОВЕРХНОСТЕЙ 2-го ПОРЯДКА
1. Эллипсоид. Рассмотрим поверхность, определяемую уравне-
нием:
£+£+£=L (4)
Для определения характера этой поверхности рассмотрим форму
сечений этой поверхности некоторыми плоскостями.
Рис. 103.
Рассечем поверхность (4) плоскостью XOY. Уравнение этой пло-
скости
г= 0.
Присоединяя это уравнение к уравнению (4), получим систему
уравнений
г=0 ^ = 0
х21_У2 i_*2 __ 1 или, проще, х2 j у2___1
§ 70] ПРИМЕРЫ НЕКОТОРЫХ ПОВЕРХНОСТЕЙ 2-ГО ПОРЯДКА 171
определяющих, как мы знаем, некоторую линию. Нетрудно понять,
ц-ГО это за линия.
Первое из вышенаписанных уравнений говорит, что мы рассма-
триваем лишь точки плоскости X0Y, а второе в этой плоскости
выражает, как известно, эллипс. Итак, плоскость X0Y пересекает
поверхность по некоторому эллипсу АВА1В1 с полуосями а и Ь.
рассекая поверхность плоскостями X0Z и Y0Z, подобным же
образом найдем, что в сечении получатся эллипсы ACAtQ и ВСВ1С1
с полуосями а, с и Ь, с.
Далее, рассекая поверхность (4) плоскостью z = h параллель-
ною плоскости X0Y, найдем, что линия сечения будет определяться
уравнениями
z = h
т, е. уравнениями
z — h z = h
Последняя система показывает, что линия сечения есть эллипс
в плоскости z = h с полуосями
/ /рТ / 1л
«1 = а / 1 — и 1 - ^2 •
При h — ±c полуоси обращаются в нуль, а эллипс в точку;
при | h | < с полуоси эллипса будут тем больше, чем ближе будет h
к нулю.
При значениях h по абсолютной величине больших с полуоси
Делаются мнимыми, т. е. плоскость не пересекает рассматриваемую
поверхность.
Рассмотренные сечения дают возможность представить форму
изучаемой поверхности, которая называется эллипсоидом. Уравне-
ние (4) называется уравнением эллипсоида.
В частном случае, при а = b = с эллипсоид обращается в шар,
Уравнение которого будет
х2+У2 -|- z2 = а2.
2. Однополостной гиперболоид. Рассмотрим поверхность, опре-
деляемую ^уравнением
Исследование этой
Сечений некоторыми
поверхности проведем также при помощи
плоскостями. Совершенно также, как и
172 КРИВЫЕ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ [XIV
в предыдущем случае, обнаруживается, что плоскость XOY пересе-
кает поверхность по эллипсу АВАхВи с полуосями а и b (рис. 104).
Плоскости же X0Z и YOZ дают в сечении гиперболы CD, C1Dl
и EF, Проверим это для плоскости X0Z\ ее уравнение:
у = 0.
Следовательно, уравнения линии сечения будут в данном случае:
у = 0 или, проще, у = 0
X2 . у2 Z2 __ 1 X2__Z2 _ 1
5? ’ с2-а2
Последняя система определяет гипер-
болу в плоскости XOZ с вещественною
полуосью а и мнимою с (на рис. 104
гипербола СО, Точно так же
сечением плоскостью YOZ получается
гипербола EF, EXFV
Для окончательного суждения о форме
поверхности рассмотрим пересечение по-
верхности плоскостью параллельною плос-
кости XOY.
Пусть ее уравнение будет
Рис. 104. z = h.
Тогда уравнения линии сечения будут
z = h или z — h
а2 "I"^2 С2 — 1> а2 * ‘ с2 ’
или, окончательно,
z = h
Эта система уравнений дает в плоскости сечения эллипс с полу-
осями
, Гл f Л2 , . Гл 1
#1 = и 1/ 1 —]--п и =5= b 1/ 1 -4—».
1 у * 1 у 1 с2 >
С возрастанием абсолютного значения h возрастают и полуоси
этого эллипса.
Рассматриваемая поверхность изображена на рис. 104, Она назы-
вается однополостн.ым гиперболоидом.
6 7(5j ПРИМЕРЫ НЕКОТОРЫХ ПОВЕРХНОСТЕЙ 2-ГО ПОРЯДКА 173
5 Ляпсил.
3. Эллиптический параболоид. Уравнение этой поверхности
следующее:
где р и q одного и того же знака. (Будем предполагать р и q > 0.)
Рассечем поверхность плоскостью XOY.
Уравнения сечения будут
z = 0 или, проще, z = 0
i а
2р “* 2q “ Z 2p'2q~Vt
Последней системе можно удовлетворить единственной совокуп-
ностью значений
х = 0, у = 0, г = 0.
Следовательно, в сечении плоскостью X0Y получаем одну
точку — начало координат (рис. 105).
Рассечем поверхность плоскостью
линию, уравнения которой
у = 0 или, проще, у = О
+ = * ха = 2/^.
Из последней системы обнаружи-
ваем, что в сечении с плоскостью X0Z
имеем параболу ЛОВ, у которой ось OZ
есть ось симметрии.
Точно так же в пересечении с плос-
костью Y OZ получим подобную же
параболу COD.
Наконец, нетрудно показать, что
плоскость z = h, параллельная плос-
кости X0Y при Л > О, пересекает по-
верхность по эллипсу, полуоси кото-
рого возрастают с возрастанием h. Поверхность имеет вид, изо-
браженный на рис. 105. Она называется эллиптическим параболо-
идом.
4. Конус 2-го порядка. Так называется поверхность, уравнение
Которой
fl2 ‘ Z?2 С2
(7)
Исследуем ее при помощи сечений.
КРИВЫЕ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
ixiv
Рассечем поверхность плоскостью XOY. Уравнения сечения будут
или, проще, z = О
х2 у2
а? + 7 " °'
z = Q
X2 у2 22
72 + ^2 72 = 0
Системе таких уравнений
совокупностью значений
х = О,
Следовательно, в сечении
точку — начало координат.
Рассечем поверхность плоскостью X0Z. Тогда
линию, уравнения
Z
можно
У = О,
такой
удовлетворить единственной
z — 0.
плоскостью
получаем одну
чаем
L
4
Рис. 106.
которой
у = 0
X2 у2
в сечении полу-
или
-!=о
^ = 0
X2 Z2
72= °’
или, наконец
_у = 0
о.
Последняя система распадается на две
системы уравнений первой степени
и у = 0
У = 0
— — — = 0
а с
из которых каждая
ходящую через начало координат в плоско-
сти X0Z. Это прямые ATCj и LLi.
Рассекая поверхность плоскостью YOZ, получим подобные же
прямые PPt и уравнения которых будут
выражает прямую, про-
х = 0
и х = 0
У z
т------= °
b с
2
Рассечем теперь поверхность
сти XOY. В сечении получаем кривую, уравнения которой
плоскостью, параллельной плоско-
z — h
х2 у2
или z = h
„ г2
О5 + 62 7 ~ 0
а*-*
С2
t!4
§ 7(П
ПРИМЕРЫ НЕКОТОРЫХ ПОВЕРХНОСТЕЙ 2-ГО ПОРЯДкА
Кривая оказывается эллипсом с полуосями,
ah , bh
а. = — и Ь, = — .
1 с 1 с
На рис. 106 эти эллипсы изображены линиями KL и К^. Их
полуоси будут тем больше, чем больше h.
Наконец, рассечем поверхность какою-нибудь плоскостью, про-
ходящей через ось OZ; ее уравнением будет
Лх-]-Ву = 0, или у = тх, где т =—
В сечении получаем линию, определяемую уравнениями
у = тх
х2 у2 z2
а2 " । № с2
Заменяя во втором из них у через тх,
придем к уравнениям
у = тх
или у = тх
а? с3
1 . m2 1
гДе - + т7 = -
а b а,
или, наконец, разлагая второе из них на множители, приходим к сле-
дующей системе двух уравнений
у = тх
Последняя система распадается на две системы уравнений 1-й
степени
у = тх и у — тх
±-^- = 0 —-J- —= 0
ах с а± 1 с
и, следовательно, выражает две прямые, проходящие через начало
координат. Таким образом, в сечении данной поверхности любой
плоскостью, проходящей через ось OZ, получаем прямые линии,
проходящие через точку О; это убеждает нас в том, что рассма-
триваемая поверхность коническая, с образующими, проходящими
через начало координат, и с направляющей кривой — эллипсом. На
рис. 106 изображены образующие и LLU получающиеся в се-
чении плоскостью ZOX, а также РРХ и RRX, получающиеся в сече-
нии плоскостью YOZ.
176 КРИВЫЕ ПОВЕРХНОСТИ Й ЛИНИИ В ПРОСТРАНСТВЕ [xiV
§ 77. НЕКОТОРЫЕ ТИПЫ ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ
Под цилиндрической поверхностью понимают поверхность, обра-
зуемую движением прямой линии, называемой образующей, которая
перемещается в пространстве, оставаясь параллельной некото-
рому направлению, и пересекает некоторую линию, называемую
направляющей.
Выведем уравнение цилиндрической поверхности, образующие
которой параллельны оси OZ, а направляющей служит некото-
рая линия АВ (рис. 107), лежащая в плоскости XOY и определяемая
уравнениями
z = 0, ф (х, у) = 0. (8)
Выберем какую-нибудь точку поверхности М (х, у, z) на одной
из образующих. Легко видеть, что две координаты х и у этой
точки М имеют те же значения, как
и для точки т, служащей проекцией
точки М на плоскость ХО Y. Поэтому,
координаты х и у точки М удовлетво-
ряют второму из уравнений (8), незави-
симо от того, в каком месте данной
образующей взята точка М9 т. е. неза-
висимо от значения координаты г.
Если взять какую-нибудь другую
точку N, лежащую на другой обра-
зующей той же цилиндрической по-
Рис. 109. верхности, то хотя координаты х и у
этой точки имеют другие значения, чем
координаты точки 2И, но они также независимо от значения z удо-
влетворяют второму из уравнений (8), так как точка W также проекти-
руется на линию АВ.
73] винтовая линия 177
Таким образом, мы видим, что координаты х и у любой точки
поверхности удовлетворяют уравнению <р(х, у) = 0 при произволь-
ном значении координаты г.
Следовательно, уравнение
cp(x, j/) = 0,
определяющее на плоскости XOY некоторую линию, в пространстве
будет служить уравнением рассматриваемой цилиндрической поверх-
ности с образующими параллельными оси OZ.
На этом основании уравнения
' Л2 у2 х2 у2
х2+_У2 = '2, ^2 + 72=1, ^2 — -^=1, у2 — 2рх, y = slnx
и другие, выражающие на плоскости координат XOY кривые: окруж-
ность, эллипс, гиперболу, параболу, синусоиду и др., в пространстве
Дадут цилиндрические поверхности: круговой, эллиптический, гипер-
болический, параболический, синусоидальный цилиндр с образующими
параллельными оси OZ. Они изображены на рис. 108, 109, 110, 111.
§ 78. ВИНТОВАЯ ЛИНИЯ
Представим себе, что плоскость некоторого угла навертывается
на поверхность кругового цилиндра так, что одна сторона QR этого
Угла совмещается с круговым'^основанием цилиндра (рис. 112 и 113).
Тогда другая сторона угла QP расположится на поверхности цилиндра
по кривой, которая называется винтовой линией.
Положим, что при этом точка т стороны QP угла примет поло-
жение точки М на поверхности цилиндра, а точка п стороны QR—
12 Зак. 2116. Н. С. Михельсон.
fxiv
178 КРИВЫЕ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
положение точки В па окружности цилиндра, так что
пт = ВМ
Qn = дл. АВ.
Для вывода уравнения винтовой линии примем основание цилиндра
за плоскость XOY, начало координат совместим с центром круго-
вого основания, тогда ось OZ совпадет
с осью цилиндра; ось ОХ проведем через
точку А — место наложения вершины
угла PQR. Обозначим координаты некото-
рой точки М винтовой линии через х, у, z
и положим = тогда, имея в виду, что ОС = х, СВ=у,
ВМ = z, находим: **
х = г cos/, j> = rsin/, z = nm, (9)
где r=OA = OB — радиус основания цилиндра.
Из треугольника mQn (рис. 112) имеем
пт = Qn • tg а — дл. о АВ • tg а = t • г • tg а.
Поэтому, уравнения (9) принимают вид
х = г • cos/, y = r-sinZ, z=t> г *tga.
Если положить г • tg а = k, то уравнения примут форму
x = r-cos/, y = r-sin t, z = k*t. (10)
Возвышая первые два уравнения во вторую степень и складывая,
находим
х2 у2 — г2.
Из тех же уравнений имеем:
tg£=- т. е. / = arctg —
$ 79] вопросы и упражнения 179
Подставляя найденное значение t в последнее из уравнений (10),
мы вовсе исключаем из системы (10) величину угла t и вместо трех
уравнений (10) получаем два
х2-|-д/2= г2,
г. х У
г = &агс tg—,
геометрически выражающих ту же винтовую линию в форме задания
линий в пространстве двумя уравнениями (см. уравнения (3) § 75).
Однако обыкновенно винтовая линия задается вышеприведенною
системою трех уравнений (10). Это так называемая параметрическая
форма задания винтовой линии. Параметром здесь служит угол /,
через который и выражаются все три координаты точек винтовой
линии.
Расстояние h между двумя последовательными витками винтовой
линии, считая это расстояние по образующей цилиндра, называется
шагом винта и будет, очевидно, равно координате z для той точки
винтовой линии, для которой t = 2тс, так что
h = 2тс& — 2тсг tg а.
§ 79. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что геометрически выражает одно уравнение вида f(x, yf z) = 0?
2. Как определяется линия в пространстве?
3. Что могут определять три независимых и совместных между собой
уравнения вида Л (х, у, z) = 0, z) = 9, /3 (х, у, z) = 0?
4. Как найти точки пересечения поверхности с осями координат?
5. Что выражают в пространстве уравнения:
а) х2 + 4у2=1; б) у = Зх2; в) х2+у2 = 1, г) х2—у2 = 4,
х—у = 0; . 2—2=0?
6. Каково уравнение поверхности шара с центром не в начале координат?
7. Исследовать поверхности второго порядка
х2 у2 z2 х2 у2 z2 х2 у2
+с2 = — 1; 2p~2q = Z'
12*
XV. ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
§ 80. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ
Пусть х—некоторая переменная величина. Положим, что раз-
личные ее значения упорядочены, т. е. между различными значе-
ниями этой переменной установлена некоторая последовательность
так, что мы можем сказать, какие значения переменная принимает
и в каком порядке. В таком случае устанавливается следующее
определение:
Постоянное число а называется пределом переменной х, если
последняя при своем изменении приближается к числу а так,
что абсолютное значение разности х — а становится меньше
сколь угодно малого, наперед заданного положительного числа е
и при дальнейшем изменении остается меньше е.
Таким образом, постоянное число а есть предел переменной х,
если неравенство |х— я|<е1 выполняется для всех значений х,
начиная с некоторого. [
В обозначение этого пишут: (>}
lim х i= а. //1
6'
Пример 1. Пусть переменная х принимает следующий ряд по-
следовательных значений: /
1,1+4» i+4-i“4’ i+4'Ь^’"^^'’• • •
Рассмотрим разности между каждым из них и постоянным числом 2:
2—1 = 1
/ 2-(!+4W
2 — 0 + 22) = т
2 (1 + 2"+22+23)= 8* и т- д>
1 Знак | | обозначает абсолютное значение того выражения, которое
заключено внутри.
§ 80] ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ 181
Мы видим, что разности эти все время убывают и при таком
убывании очевидно могут быть сделаны меньше любого сколь угодно
малого положительного числа е, причем и в дальнейшем останутся
меньше этого в. Поэтому на основании определения заключаем
1йп х = 2.
Пример 2. Пусть переменная х принимает следующий ряд по-
следовательных значений:
1 2 з_ А
2 ’ 3 ’ 4 ’ 5 * * *
Рассматривая разности между единицей и последовательными
значениями переменной
1 4 I
1-_=_И Т. д.,
видим, что на основании определения имеем право написать
1йп х= 1.
Пример 3. Пусть переменная х принимает следующий ряд по-
следовательных значений бесконечной периодической десятичной
дроби:
0,2, 0,22, 0,222, 0,2222...
^2
Рассматривая разности между дробью — и каждым значением
переменной, имеем:
2_Л______________1 \ 2(10 —9)_ 2
9 10“ ioj“~ 90 -“90’
2 22 . о /1 11 \ 2(100 — 99) 2
9 1002 К 9 100j 900 ““900’
2 222 _ п /_1__111 \ __ 2 (1000 - 999) 2
9 1000 Zk9 1000/ 9000 =90и0ИТ‘Д*’
9
а потому заключаем, чъй| lim х = -§•.
Переменная называеКфя бесконечно малой, если предел ее равен
нулю, т. е. если ее значения, начиная с некоторого, делаются и
остаются по абсолютн^р^величине меньше сколь угодно малого
положительного числа.
182
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
Поэтому, например, переменная х, определяемая таким рядом
значений:
будет бесконечно малой.
Точно так же хорда круга по мере ее удаления от центра стре-
мится к пределу, равному нулю, т. е. представляет величину бес-
конечно малую.
Установленное понятие о бесконечно малой величине дает воз-
можность выразить значения переменной через ее предел. Действи-
тельно, если
limx = а,
то, обозначая через а бесконечно малую величину, мы можем зна-
чения переменной представить так:
х — а
(а может быть как положительным, так и отрицательным числом).
Переменная называется бесконечно большой, если ее значения
по абсолютной величине могут превзойти любое положительное
число А, как бы велико оно ни было выбрано, и при дальнейшем из-
менении будут оставаться больше этого числа.
Такая переменная вовсе не имеет предела; однако, для сокра-
щения речи говорят, что пределом такой переменной служит бес-
конечность, и пишут:
limх = ± оо.
Примером такой переменной может служить переменная х, ко-
торая принимает следующий ряд последовательных значений:
а, а2, а3, а4, ... при а > 1.
Переменная величина, значения которой по абсолютной вели-
чине не превосходят некоторого числа, называется ограниченной.
Так, например, sinx и cosx по абсолютной величине не пре-
восходят единицы ни при каких значениях х, поэтому эти перемен-
ные — ограниченные.
Также длина хорды данного круга — переменная ограниченная,
так как не превосходит диаметра.
§ 81. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕЖДЕ ПЕРЕМЕННОЙ
Определение предела переменной, сформулированное в предыду-
щем параграфе, дает возможность проверить, будет ли то или другое
число служить пределом переменной, но не заключает в себе ука-
зания на самый способ отыскания этого числа. Между тем, отыскание
§ 81] ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛЕ ПЕРЕМЕННОЙ 183
предела переменной величины является основной задачей анализа.
Вот почему необходимо ознакомиться с теоремами, могущими слу-
жить существенным пособием при отыскании пределов переменных
величин.
Лемма 1. Алгебраическая сумма конечного числа бесконечно
малых слагаемых есть бесконечно малая величина.
Рассмотрим алгебраическую сумму нескольких (для простоты,
трех) бесконечно малых величин
а+Р+т-
Из определения бесконечно малых величин следует, что а, р, у
по абсолютной величине можно сделать меньше любого положи-
е
тельного числа, например —, т. е.
и
1-гк-Ь
а тогда и + Р + 7 | < е,1 т. е. lim (a -f- р у) = 0, так что сумма
аЧ“?~Ьт— бесконечно малая величина.
Лемма 2. Произведение ограниченной величины на бесконечно
малую есть бесконечно малая величина.
Пусть х — величина ограниченная, а а—бесконечно малая.
Положим, что все значения переменной х по абсолютной вели-
чине не превосходят некоторого положительного числа k. Тогда
очевидно имеем
|Х. а| = |х| • I а I <fe • I «|.
Выбрав а таким, чтобы | а | < у (а это всегда можно сделать, так
как а—бесконечно малая), найдем, что
| х • а | < k • ~ = е, т. е. |х-а|<е,
т. е. что произведение х • а — бесконечно малая величина.
Лемма 3. Произведение конечного числа бесконечно малых
величин есть величина бесконечно малая.
Рассмотрим произведение трех бесконечно малых величин
а • Р • т-
1 Известно, что абсолютное значение суммы не превосходит суммы
абсолютных значений слагаемых, т. е.
И + * + с|=§|а| + |&| + |с |.
Например: | 4 + (— 2) + (— 1) | < 4 + 2+ 1 = 7.
184
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
Каждую из них по абсолютной величине можно сделать меньше
любого числа, например, j/e, т. е.
1«1<’А IPKV*, 1тК3А
а тогда и
I « • Р • 7 I < 8,
т. е. произведение а • [3 • — бесконечно малая величина.
Лемма 4. Частное от деления бесконечно малой величины на
переменную, предел которой не равен нулю, есть бесконечно малая
величина.
Из условия, что переменная х такова, что lim х ф 0, следует,
что всегда можно указать такое положительное число k, что
। । , I 1 I 1
I х I > k, отсюда у < “£,
1 А О
т. е., что-----величина ограниченная. А тогда, на основании леммы 2,
т. е. что —----бесконечно малая величина.
х
Теорема /. Предел алгебраической суммы ограниченного числа
слагаемых равен алгебраической сумме их пределов.
Рассмотрим алгебраическую сумму нескольких (для простоты,
трех) переменных хфу-t-z и пусть
limx = a, = lim z = с.
По сказанному на стр. 182
х = афа, = =
где а, р, т — бесконечно малые величины.
Поэтому
*+.У + г = (Я + ^ + с) + (« + Р + к) •
Но по лемме 1 имеем, что = 8 — бесконечно малая вели-
чина. Из равенства же
х + У = + + + §
непосредственно вытекает, что
lim (х+ z) = a + #4-c = lim х Ц- Итд/ lim z.
§ 81] ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛЕ ПЕРЕМЕННОЙ 185
Теорема 2. Предел произведения конечного числа множителей
равен произведению их пределов.
Сохраняя предыдущие обозначения и ограничиваясь для простоты
случаем двух множителей, имеем
х -у = (а 4“ а) (д4- Р) = ад 4-да + ар + ар.
Но каждое из слагаемых да, ар, ар по лемме 2 и 3 — бесконечно
малые величины, а потому по лемме 1 и их сумма да4"^Р4"аР
есть бесконечно малая величина. Таким образом, имеем ху = ад-]-8.
Из последнего же равенства непосредственно следует, что
lim ху = ab = lim х • limу.
Теорема 3. Предел частного от деления двух переменных
величин равен частному \tx пределов, если предел делителя не
равен нулю.
Сохраняя те же обозначейкЬ^ рассмотрим разность
х а а + а и ab-т-Л — ab — ₽а _ ab — (За
у b~ T+J Т — Ь (Ь + Р) “ b (Ь + Р) •
Но ад — ра — переменная величина бесконечно малая (леммы 1 и 2),
знаменатель же д (д 4- Р) = by — величина переменная, предел кото-
рой д2 по условию не равен нулю.
Поэтому на основании леммы 4 - = 8 бесконечно малая
д (д + р)
величина.
Таким образом, имеем -j = y4“8, откуда и вытекает, что
.. х a lim х
lim — = —= -j----.
у b lim у
Применим изложенные теоремы к примерам.
Пример 1.
lim [(х — 1) sin 2х + х cos х — 2] = lim (х — 1) sin 2х + lim х cos х — 2 = — 2.
«->0 ' а?-» 0 а?->0
Пример 2.
x+Vx—1 lim(x+Vx—1) ,
х— Vx+ 1 Hm (х— ]/х+ 1)
Пример 3.
,, cos 2х lim cos 2х -
lim ----=----------= 1.
tg-f limtg-J
Рассмотренные выше три теоремы о пределе переменных пред-
полагают, как это видно из рассуждений, существование самих
пределов переменных. Если же предела одной или нескольких пере-
менных не существует, или если при рассмотрении предела частного
предел делителя оказывается равен нулю, вышеприведенные теоремы
186
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
применять нельзя. В этих случаях при отыскании предела перемен-
ной иногда бывает полезно применять тождественные преобразования
самой переменной с целью устранить препятствие, мешающее при-
менению теорем. Однако общих правил для этого дать нельзя. Как
мы это увидим впоследствии, общие правила в отдельных и вместе
с тем наиболее важных случаях дает дифференциальное исчисление
(см. § 106).
Следующие примеры иллюстрируют элементарные приемы тех
преобразований, которые полезно применять в случаях, когда непо-
средственное применение приведенных выше теорем невозможно.
г2__ у-_9
Пример 4. Найти lim----=—-—.
а?-> 2 х —
Здесь предел делителя равен нулю и непосредственное применение
теоремы о пределе частного невозможно. Рассматривая делимое, видим, что
и его предел тоже равен нулю.
Если же разложим на множители числитель и знаменатель дроби и со-
кратим ее на общий множитель, то мы устраним препятствие, мешающее
применению теоремы; именно
х2 — х — 2_ (х+1)(х — 2) _ х + 1
х2 —4 (х-|-2)(х —2) - x-f-2 ’
Поэтому
х2 — х — 2 п х + 1 lim(x+l) 3
hm -----5--— = lim —т.
®->2 х^— 4 о?->2 х 4" 2 hm (х-|-2) 4
П Е 1Л ° 1 • х^ 4" ^х 4- 2
Пример 5. Наити hm-----.
X -> 2 х* —
Здесь попрежнему предел делителя равен нулю, но предел делимого
не равен нулю. Таким образом, у нас имеется дробь, знаменатель которой
беспредельно убывает и стремится к нулю, в то время как числитель при-
ближается к 12. Ясно, что в результате такого совместного изменения числи-
теля и знаменателя вся дробь растет беспредельно, что, как сказано, условно
записывается так:
х2 + Зх + 2
lim---------г— = оо.
□?-> 2 х2 —4
Пример 6. Найти lim ь о о——F.
ж->оо 2х2 + Зх + 5
В этом случае ни знаменатель, ни числитель не имеют предела, так как
оба беспредельно возрастают. Здесь полезно провести следующее преобра-
зование, приводящее к результату:
ж^от2х2 + Зх + 5 . Зд. А ~ 2 ’
так как
lim — = 0 и lim А — о,
Я?~»оо X я?->оо х*
§ 82] ПРИЗНАКИ СУЩЕСТВОВАНИЯ ПРЕДЕЛА ПЕРЕМЕННОЙ 187
§ 82. ПРИЗНАКИ СУЩЕСТВОВАНИЯ ПРЕДЕЛА ПЕРЕМЕННОЙ
Применение вышеприведенных теорем и некоторых элементарных
преобразований, вообще говоря, решает в простейших случаях задачу
о нахождении предела переменной, т. е. приводит нас (как это
и показано на примерах) к нахождению предела рассматриваемой
переменной. Однако в анализе нередко встречаются такие перемен-
ные, которые представляют затруднение не только в смысле отыска-
ния их предела, но для которых самое существование предела под-
вергается еще сомнению.
Для таких случаев необходимо установить признаки существова-
ния предела переменной. Имея это в виду, приведем без доказа-
тельства следующие почти очевидные признаки существования пре-
дела переменной.
Признак I. Если значения некоторой переменной z заключены
между двумя другими х и у, имеющими общий предел, то к тому же
пределу стремится и переменная z, т. е. если
x<Zz<Zy и limx = limjz, то \mz = a.
Признак IL Если значения переменной, начиная с некоторого
места, все время возрастают, но все же остаются меньше неко-
торого постоянного числа, то такая переменная имеет предел.
Признак III. Если значения переменной, начиная с некоторого
места, все время убывают, но все же остаются больше некото-
рого постоянного числа, то такая переменная имеет предел.
sin х
§ 83. ПРЕДЕЛ “у" ПРИ X -> О И ЧИСЛО е
Остановимся на двух примерах переменных, имеющих весьма
важное значение в анализе, о существовании предела которых мы
будем судить на основании вышеприведенных признаков.
Пример 1. Существует ли предел переменной—^, когда х стре-
мится к нулю?
Для решения данного вопроса вспомним, что тригонометрия
дает такие неравенства для дуг 1-й четверти:
sin х < x<tgx.
Деля все члены неравенства на sinx, находим
1 .
sin х cos х
Затем деля единицу на каждый член неравенства, другими сло-
вами, перевертывая дроби, находящиеся в неравенствах, получаем
, . sin х .
1 > —-Г > cos X.
188
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
Таким образом, рассматриваемая переменная оказывается заклю-
ченной между двумя величинами. Будем теперь приближать х к нулю.
Так как тогда
lim cosx = 1,
®->о
то на основании признака 1 заключаем, что
.. sin х
lim-----
®->о х
существует и равен 1.
Изменяя х на —хи замечая, что
sin (— х) — sin х sin х
— X —X X ’
заключаем, что и при отрицательном х
.. sinx 1
lim----=1.
®->о х
Пример 2. Существует ли предел переменной когда п
растет беспредельно?
Ограничим сначала наши рассуждения случаем, когда л, воз-
растая беспредельно, принимает только целые и положительные
значения. Тогда, останавливаясь на одном из таких значений пере-
менной (при некотором определенном п), можем по формуле бинома
Ньютона написать:
А ! JLY1— 1 I „ 1 ,| П(п -1) 1 | n (п — 1) (п — 2) 2_ , |
п(п —1)(п —2)...[л —(n —1)] _1_
1 • 2 • 3...и * пп*
Каждый член этого разложения преобразуем по следующему
образцу
/г (п — 1)(п — 2) 1 _ 1 /1(п—l)(/i —2)
1.2- 3 ’ n3 — j.2.3‘ и*
__ 1 п п — 1 и — 2_________ 1 /1 2V1___________—У
Ь2*3*л* п ’ и 1*2-3\ л/\ п)'
тогда находим
Увеличивая п на единицу, мы видим, что при этом возрастает
как число членов правой части предыдущей формулы, так равным
§ 83] предел при х->0 и число е 189
образом растет и каждый в отдельности из членов, начиная с третьего.
Из этого заключаем прежде всего, что переменная с воз-
растанием п все время возрастает.
Далее из формулы (1) следует, что если все двучлены правой
части этой формулы
1 —1 — 1— -,...,1 —
пВ 9 п 9 п9 9 П 9
которые, очевидно, меньше единицы, заменить единицами, то ра-
венство (1) заменится таким неравенством:
О+'га) 1 + 1+П2+bFs + ••• + 1.2-З...Л’
Теперь, если в правой части неравенства (2) заменить все от-
личные от единицы множители, стоящие в знаменателях дробей,
одним и тем же числом 2, то тем более будет справедливо новое не-
равенство
0+4) < 1+1+4+4+4+•••+2^1-
В правой части этого неравенства все члены, начиная со второго,
составляют геометрическую прогрессию. Если теперь эту геометри-
ческую прогрессию мы обратим в бесконечную, приписав к ней
неограниченное количество дальнейших членов, то этим еще более
усилим предыдущее неравенство, поэтому верным является и сле-
дующее неравенство
Просуммируем теперь эту бесконечно убывающую геометрическую
прогрессию. Сумма ее вычисляется по формуле
В данном случае а = 1, q = , поэтому
Таким образом, неравенство (3) приводится к следующему:
/ 1 \п
3.
190 ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ [xv
Итак, переменная (1 с одной стороны, как это доказано
выше, все время возрастает, а с другой стороны, не превосходит
числа 3; следовательно, на основании признака II эта переменная
стремится к некоторому определенному пределу. Предел этот при-
нято обозначать буквой е, так, что
lim 0+i)”=e-
П->ОО \ и /
Впоследствии будет показан способ вычисления числа е. Прибли-
женная его величина такова: е = 2,7182818284 (с точностью до
одной единицы десятого десятичного знака).
/ । 1 у* 7
Предел переменной 11 -f- — J рассмотрен лишь для случая,
когда nf возрастая, проходит целые и положительные значения.
Однако можно доказать, что к тому же пределу рассматриваемая
переменная стремится и в том случае, когда п стремится к беско-
нечности, проходя какие угодно значения, и притом как положи-
тельные, так и отрицательные.
Доказательство этого можно найти в более подробных курсах
анализа.
Число е принято- в высшем анализе за основание системы лога-
рифмов, которые носят название натуральных или гиперболических
логарифмов. Для них установлено обозначение In. В дальнейшем
знак In мы всегда и будем употреблять для обозначения именно
натуральных логарифмов, а прежние десятичные логарифмы будем
обозначать знаком 1g.
Рассмотренный предел переменной может иметь не только чисто
математический интерес. Существуют задачи, где предел этой пере-
менной неизбежно возникает и служит средством их решения.
Рассмотрим, например, следующую задачу.
Пример. Положим, имеется Со грамм-молекул активного вещества. Пред-
полагая, что в единицу времени вступает в реакцию этого вещества,
узнать, какое количество грамм-молекул вступит в реакцию по истечении
времени t.
Так как в единицу времени в реакцию вступает р% вещества, то по
истечении одной единицы времени вступит в реакцию
п ~
грамм-молекул,
1UU
а количество вещества, еще не вступившего в реакцию, будет
Спустя 2 единицы времени количество вещества, не вступившего в ре-
акцию, будет
§ 841
О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ
191
а через t единиц времени оно будет равно
с°(1 — ioo) *
При предыдущем рассуждении мы представляем себе реакцию происхо-
дящей скачками через каждую единицу времени в отдельности. В действи-
тельности же реакция идет непрерывно. Поэтому, для большего приближе-
ния к действительности выгоднее было бы промежуток времени раздробить
на более мелкие части. Произведя тот же расчет через каждую ~ единицу
времени, мы получим количество вещества, не вступившего в реакцию за
промежуток времени t, в следующем виде
С (х_____p_\tn
с°1 ЮОп/
Р
или, полагая = я, в виде
Истинное же количество С остающегося вещества, т. е. не вступившего
в реакцию, выразится пределом предыдущего выражения при увеличении п
№ бесконечности, т. е.
Как видно, для окончательного решения задачи необходимо вычислить
lim (1 —
п -> оо \ Я /
Переменная, предел которой требуется вычислить, отличается несколько
от той, которая рассмотрена на стр. 188 и 189. Постараемся, однако, при-
вести и эту переменную к такой же форме. Для этого положим
k 1
---------------------------= —, т. е. п =— кт.
п т
Тогда
Таким образом, закон, удовлетворяющий условиям поставленной задачи,
выражается в следующем виде:
§ 84. О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ
Как уже было сказано (см. § 80), бесконечно малой величиной
называется такая переменная величина, предел которой равен нулю.
В том же параграфе было изложено, что алгебраическая сумма и
произведение ограниченного числа бесконечно малых величин есть
величина бесконечно малая.
Предложим себе теперь такой вопрос: что представляет собой
частное от деления двух бесконечно малых величин, также ли
192
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
(XV
бесконечно малую величину или какую иную? Другими словами, зай-
мемся задачей о нахождении предела отношения двух бесконечно
малых величин.
Рассмотрим для этого отдельные примеры, в которых перемен-
ную х мы будем считать бесконечно малой.
О? 4- х2
Пример 1. Найти lim х—.
ж->о ”Х ^Х
Здесь, очевидно, числитель и знаменатель — величины бесконечно
малые при бесконечно малом х. Действительно, предел каждого в
отдельности из этих выражений равен нулю.
Так как в данном случае предел знаменателя равен нулю, то
для нахождения предела частного нельзя непосредственно применить
теорему 3 (см. стр. 185).
Но
2х — х2 2 + х
Зх —2x3 =3-2х2 *
Поэтому
.. 2х — х2 1. 2 4- х 2
Зх—2x3 = ^®03 —2x2 — з •
Пример 2. Найти lim 1 cos—.
х -> 0 х
В этом примере опять знаменатель имеет своим пределом нуль,
поэтому опять мы не имеем права непосредственно пользоваться
теоремой о пределе частного.
В рассматриваемом случае находим предел следующим образом:
о . 9 х / . х \
, 2sin2 тг / sin-x- \
.. 1 — cos х .. 2 | 2 . х 1 л
lim -------= lim --------= lim I -------- sin -у 1 = 0.
Я?->0 X ®->0 X Я?->0\ X I
\ 2 /
Пример 3. Найти lim —--T - .
®->o x
Применяя указанный раньше прием, находим
lim
я?->0
Зх + хз
х2 — 2х3
= lim
Ж->0
3 + х2
х — 2х2
= оо.
Приведенные примеры роказывают, что отношение двух убеско-
нечно малых величин может быть и величиной, имеющей конечный,
отличный от нуля предел, и бесконечно малой, и бесконечно большой.
Таким образом, на поставленный в начале параграфа вопрос не
получается определенного ответа. Тем не менее, весьма важно
остановиться еще несколько на этой задаче.
Условимся различать случаи, подобные тем, которые приведены
в трех примерах, следующим образом.
§ 84] О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ 193
Будем говорить, что
1) бесконечно малые величины у и х одного и того же порядка,
если lim — конечен и отличен от нуля\
2) бесконечно малая величина у порядка высшего, чем 'х, если
lim х" = 0;
3) бесконечно малая величина у порядка низшего, чем х, если
lim — = оо.
Приведенные примеры показывают, что при бесконечно малом х
величины 2'х — х2 и Зх — 2х3 суть бесконечно малые одного и того
же порядка;
1—cosx — бесконечно малая порядка высшего, чем х;
Зх-^х3 — бесконечно малая порядка низшего, чем х2— 2х3.
Полезно заметить, что произведение двух бесконечно малых вели-
чин есть бесконечно малая величина порядка высшего, чем каждая
из них. Действительно, пусть х, у — две бесконечно малые величины
X • V
lim —= lim у — 0.
Это и подтверждает высказанное заключение.
Точно так же xw при т > 1 есть бесконечно малая высшего по-
рядка, чем бесконечно малая х.
Такое различение между собою бесконечно малых величин в отно-
шении их порядка имеет за собой вполне реальный смысл и практи-
ческую пользу.
Представим себе две бесконечно малые величины х и х2. Про-
следим их соответственные значения при беспредельном уменьшении х.
X 1 1 2 1 3 1 4 1 5 1 10 1 100 и т. д.
X2 1 1 4 1 '9 1 16 1 25 1 100 1 10000 и т. д.
Совершенно очевидно, что из двух этих переменных вторая
будет стремиться к нулю скорее, чем первая.
С другой стороны, сопоставляя таким же образом значения бес-
конечно малых величин х и 1/х ‘
X 1 1 4 1 9 1 16 1 100 и т. д.
1 1 2 1 3 _1_ ч 1 10 и т. д.
видим, что ]/х стремится к нулю медленнее, чем х.
13 Зак. 2116. Н. С. Михельсон.
194
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
Различение бесконечно малых величин в отношении их порядка
и подчеркивает именно сравнительную скорость стремления к нулю
отдельных бесконечно малых величин. Бесконечно малые одного и
того же порядка стремятся к нулю с одинаковою скоростью, бес-
конечно малая высшего порядка стремится к нулю скорее, а низ-
шего— медленнее, чем основная бесконечно малая, с которой ве-
дется сравнение. В этом и состоит реальный смысл введения поня-
тия о различных порядках бесконечно малых величин.
Польза этого различения заключается в том, что так как зна-
чения бесконечно малых величин высшего порядка могут в продол-
жение своего изменения оказаться значительно меньшими, чем со-
ответствующие значения основной, то в приближенных расчетах
бывает возможно и выгодно отбрасывать бесконечно малые вели-
чины высшего порядка.
При более детальном сравнении двух бесконечно малых величин
уславливаются в следующем: если две бесконечно малые величины
х и у таковы, что lim конечен и нс равен нулю, то величину
у считают бесконечно малой т-го порядка по отношению к
бесконечно малой х.
Так, при бесконечно малом х величина х3 есть бесконечно малая
3-го порядка относительно х, так как
уЗ уЗ уЗ
lim —= 0, lim-^ = 0, a Ит^=1.
х->ох х
Точно так же при бесконечно малом х величина 1—cosx будет
бесконечно малой 2-го порядка относительно х, так как
.. 1 — COS X ..
11Ш ------2---== *im
О5->0 Х 05->(
2 sin2 -g- j sin -g- sin ~
----5—= lim-i-*---------
х х->о
2
_1_
2 •
2
§ 85. ОБ ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ
Обратим внимание еще на один частный случай, и именно на
случай, когда предел отношения двух бесконечно малых величин
равен 1. В этом случае обе бесконечно малые величины называются
эквивалентными.
Так, sinx при бесконечно малом х эквивалентен х, действи-
<. sin х 1 .
тельно lim---= I; tgx эквивалентен х, так как
ж-> о х
.. sinx .. 1
lim-----lim -----= 1,
®->о х x->ocosx
Ит‘85 = Нт^._1_ =
х ж-» о х cos х
195
§ 85] ОБ ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО 'МАЛЫХ ВЕЛИЧИНАХ
х—2х3 эквивалентен х-]-4х2, так как
lim
Ж->0
х — 2х3
х + 4х2
lim
#->о
1—2х2 _
1 +4х
1.
Покажем еще, что In(l-f-x) эквивалентен х.
Действительно
lim --(1 + = lim In (1 -f- xf ‘
0 x ж-> 0
Заменим теперь переменную x, положив x = —, т. e. n — ~ ,
тогда
.. ln(14-x) i- i I l\n i 1
lim —-——— — lim In ( l -|-] = In e = l.
ж->0 X n->oo \ n '
Относительно эквивалентных бесконечно малых величин докажем
следующую теорему, которая во многих случаях облегчает нахож-
дение пределов переменных.
Теорема. При отыскании предела отношения двух бесконечно
малых величин, каждую из них можно заменить ей эквивалент-
ною.
Пусть х и у — две бесконечно малые величины, а х1 и yt — две
другие, соответственно эквивалентные первым. Требуется доказать,
что
lim— = lim —.
X Xi
Дробь можно представить в следующем виде:
х yi'xi х •
Но по условию х эквивалентна х19 а у эквивалентнау19 следо-
вательно,
lim —=1 и lim —=1.
У1 х
Отсюда следует, что
lim — = lim— • — • — = lim — • lim — • lim — = lim — ,
x yt Xi x yr Xi X Xi9
что и требовалось доказать.
Доказанная теорема часто значительно облегчает нахождение
предела отношения двух бесконечно малых величин. На следующих
примерах показано применение этой теоремы.
13*
196
ОСНОВЫ ТЕОРИИ ПРЕДЕЛ В
[XV
Пример 1. Пт а-|ол = Пт — = 3; [sin Зх эквивалентен Зх].
я -> О х гв-> О х
Пример 2. lim 9 ~ = lim — -Т так как In (1—х)
х -> 0 Sin ^Х 35 -> О ^Х
эквивалентен — х, a sin 2х эквивалентен 2х.
S 86. ПРИРАЩЕНИЕ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ И ФУНКЦИИ
Как известно, частное значение функции / (х) при х = а обо-
значается знаком /(а).
Мы будем предполагать, что оно существует.
Так как всякое другое значение независимой переменной можно
обозначить через a-\-h, где h — любое положительное или отри-
цательное число, то и всякое другое значение функции /(х) соот-
ветственно обозначается через
/(« + *).
Будем предполагать, что и оно существует при всех рассматри-
ваемых значениях величины h.
Разность —f(a) покажет тогда, насколько изменяется
функция /(х), когда независимая переменная х изменяет свое зна-
чение а на
Количество А, которое может быть как положительным, так и
отрицательным, принято называть приращением независимой пере-
менной, а разность
приращением функции. Последнее тоже может быть и положи-
тельным и отрицательным.
Весьма часто приращение независимой переменной х обозначается
знаком Дх, а приращение функции знаком А/(х) или просто Д/.
В случае, если функция f (х) обозначена для краткости одной
буквой у, то ее приращение обозначается через Ьу.
Подобное обозначение особенно удобно, когда рассматриваются
одновременно несколько функций одной переменной х
У=/(х), и = <?(х), р = а>(х)
или, если рассматривается одна или несколько функций многих
переменных4
U=F(x, у, г);
тогда такие обозначения, как
Дх, Ду, Дг, Ди, Ati, Д^7,
сразу ясно показывают, о приращении каких величин идет речь.
§ 87] непрерывность функции 197
Рассмотрим примеры вычисления приращений функций.
Пример 1. Положим, что рассматривается функция
- / ч 2х — 1
/(х) = —.
3
Пусть х = 2, тогда / (2) = — = 1,5.
Дадим выбранному нами значению х приращение h равное 0,5, тогда
новое значение функции будет
/(2,5)= 1,6.
Следовательно, приращение функции будет
Д/ = /(2,5) —/(2) = 0,1.
Таким образом, если первоначальное значение х = 2 мы увеличим на 0,5,
то значение функции увеличится при этом на 0,1.
Пример 2. Закон расширения идеального газа в зависимости от измене-
ния его температуры (при постоянном давлении) выражается следующей
формулой:
Здесь t — температура газа в градусах С, Vo— объем газа при 0°,
Vt — объем при температуре t. Объем является функцией температуры.
Представим себе, что первоначальную температуру газа мы увеличили
на 1°С, т. е. AZ= 1, тогда новое значение объема будет
v<+1=
а соответствующее приращение объема
&v=vt+1-vt = ±v0.
Таким образом, при увеличении температуры идеального газа на 1° С
объем его увеличивается па первоначального его объема при 0°.
х/ о
§ 87. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
При рассмотрении приращения функции в связи с приращением
независимой переменной невольно обращает на себя внимание тот
факт, что чем меньшее значение будем давать приращению незави-
симой переменной, тем меньше значение, вообще говоря, полу-
чит и приращение функции. Так как это обстоятельство не всегда
имеет место, то устанавливают следующее определение:
Если бесконечно малому приращению h независимой перемен-
ной соответствует бесконечно малое же приращение
/(«Ч-Л)—/(а)
самой функции^ то говорят^ что /(х) непрерывна при х = а.
198
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
Таким образом, мы называем функцию /(х) непрерывной при
х = я, если при стремлении h к нулю по произвольному закону
lim [/(а-4-ft)— /(а)] = 0,
71 —> о
т. е. если
lim h) =f(a)
-> о
(1)
(2)
или, что то же, если при стремлении х к а по произвольному
закону
lim/(х)=/(а). (3)
х -> а ।
Вышеприведенное определение непрерывности функций впервь^
дано наряду с Коши также Н. И. Лобачевским. Свойство это он
тогда называл „ постепенностью “ и этим термином отмечал то
свойство функции, „когда приращение в ней уменьшается до нуля
вместе с приращением переменной х“.
При решении вопроса, может ли /(х) считаться непрерывной
при х = а, весьма удобно пользоваться именно последним усло-
вием (3). Оно предполагает, конечно, существование lim / (х) и, как
х -> а
уже сказано раньше, частного значения f(a).
Если функция непрерывна при всех значениях х в промежутке
[а, Ь], то она называется непрерывной во всем промежутке. *
Если при х = а функция не обладает свойством непрерывности,
то говорят, что f(x) терпит разрыв непрерывности при х = а.
Рассмотрим теперь несколько примеров для пояснения устано-
вленных понятий о непрерывности и разрывах функций.
Пример 1. f (х) = х3— 2х-{-1 непрерывна при всяком х, так как на
основании теорем о пределе (см. §81) имеем:
lim (х3 — 2x4-1)= lim х3— lim 2x4-1 = л3 — 2а 4-1,
ж-> а х->а х~> а
т. е. lim /(х) =/(а), каково бы ни было а.
а
Пример 2. /(х)
х3—1
х3 4-1
непрерывна при всяком х, так как
х3 — 1 lim (х3—1) а3 — 1
iirn ____= _____- —______ т е
х^а х*4-1 lim(x24-l) а24-1’ ’
lim /(х)=/(а), каково бы ни было а.
х -> а
„ о /-/ ч пг
Пример 3. f (х) = х___- терпит разрыв непрерывности при х = а, так
как ни lim /(х), ни частного значения /(а) не существует.
а
§ 88]
СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
199
При всех других значениях х рассматриваемая функция непрерывна;
так, например,
11 т
lim --------
т
т. с.
lim /(х) =/(*).
Полезно отметить также следующие общие положения:
Если /(х) и ср(х) непрерывны при х — а, то сумма /(х) + ?(х)
непрерывна при х = а, произведение /(х)-ср(х) непрерывно при
/(х)
х = а, частное непрерывно при х = а, если а не корень
функции ?(х).
Действительно,
lim [f (х) <? (х)] = lim / (х) lim © (х) =/(а) + © (а).
lim [/ (х) • <?(х)] =
||тп ^1=
.4.1И
lim /(х) • lim о (х) =/(а) • <р (а).
lim /(х)
т---------у если ° (х) Ф О-
hmT(x) ?(д) ’ х-^а
что и поясняет вы сказан-
§ 88. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
Геометрическое изображение функций дает возможность весьма
просто пояснить некоторые свойства непрерывных функций.
1-е свойство. Если функция
f (х) непрерывна при х = а и
/(а) ф 0, то для значений х, до-
статочно близких к а, функция
f (х) сохраняет один и тот же
знак, и именно знак величины
/(а).
Пусть /(х) изображается кри-
вой KL и пусть абсцисса О А = а
соответствует точке С кривой,
так что AC = f(a).
Из рис. 114 ясно видно, что
ординаты точек, достаточно близ-
ких к точке С, все будут также
положительные, как и сама ордината АС,
ное свойство.
Напротив, если значение функции f (£) = 0, как это имеет место
в точке В, где ОВ = Ь, то значения ординат точек, смежных с точ-
кою В, не будут непременно все одного и того же знака: одни из
них могут быть положительные, другие отрицательные (рис. 114).
200
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
[а, д\ и/ (а) и j(0) разных
У
К
Рис. 115.
2-е свойство. Если функция f (х) непрерывна в промежутке
аков, то в том же промежутке
существует по крайней мере одно
такое число с, что f (f) = 0.
Пусть KL изображает функцию
/(х) и ОА = а, ОВ = Ь.
По условию AD—f(a) и BG —
= f(b) различных знаков. Рис. 115
показывает, что переход от отрица-
тельного значения функции f (я)
к положительному /р) при непре-
рывности функции должен сопро-
вождаться переходом через зна-
чения равные нулю. Именно, при
ОС< — с1, 0С9 = с9, ОС* = с* имеем
/(‘1)=Ж)=Ж) = о.
3-е свойство. Если функция /(х) непрерывна при всех значе-
ниях аргумента в промежутке [а, Ь], то в этом промежутке
данная функция достигает своего наибольшего и наименьшего зна-
чения.
На рис. 115 видно, что функция /(х), изображаемая кривой KL,
принимает на промежутке от О А = а до ОВ = b наибольшее зна-
чение FE при x = OF и наименьшее значение AD при х = ОА.
§ 89. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО
УРАВНЕНИЯ
Второе свойство непрерывных функций может быть применено
для приближенного вычисления вещественных корней алгебраического
уравнения любой степени, т. е. уравнения вида
+Р1х»~1 + р2х”-2 + ... + рп_ хх 4- рп = 0.
Как известно, корнем уравнения называется такое число, кото-
рое обращает уравнение в тождество. В данном случае, следова-
тельно, для решения уравнения требуется найти такое число, кото-
рое бы обратило левую часть уравнения в нуль.
Обозначив левую часть уравнения, через /(х), мы замечаем, что
решение предложенного уравнения равносильно нахождению таких
значений x = clf с2 и т. д., что
/(G) = 0, /(с2) = 0 и т. д.
Так как рассматриваемая функция /(х) непрерывна (как целая
рациональная функция) для всех значений х, то, стало быть, если бы
нам удалось обнаружить, что для двух значений аргумента
х = а и х = b
§ 89] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КОРНЕЙ 201
частные значения функции f (я) и f (Ь) разных знаков, то по свойству
2-му могли бы утверждать, что в промежутке между а и b лежит
корень данного уравнения.
Разделив затем промежуток [а, Ь] на два промежутка, проверяем,
в котором из них заключен корень; последний . промежуток опять
делим на два промежутка и т. д.
Если при этом мы не натолкнемся на точное значение корня,
то, продолжая деление промежутка, мы в состоянии будем подойти
к действительному значению корня как угодно близко. В самом
деле, получаемые промежутки становятся все меньше и меньше,
искомый корень оказывается заключенным все в более и более
тесных границах. Каждая из этих границ может быть принята за
приближенное значение корня. Таким образом и могут быть вы-
числены значения корня и притом с какой угодно степенью точ-
ности. *
Конечно, такого рода способ приближенного вычисления корня
далеко нельзя назвать совершенным. Кроме того, для такого вычисле-
ния необходимо предварительно найти самый промежуток, на гра-
ницах которого рассматриваемая функция принимает значения разного
знака, и, наконец, при этом нельзя еще быть уверенным в том, что
кроме найденного корня уравнение не имеет в данном промежутке
других не обнаруженных нами вещественных корней.
Приведем пример подобного вычисления корня.
Пример. Возьмем уравнение х3— 8х-|-5 = 0.
Обозначив /(х)=х3— 8х-|-5, замечаем, что/(0) = 5, а /(1) = —2
Эти данные показывают, что в промежутке между 0 и 1 имеется корень
предложенного уравнения. Для его вычисления делим этот промежуток по-
полам; вычисляя /(0,5), определяем, в какой части этого промежутка лежит
наш корень. Так как
/(0,5) = 0,125 — 4 + 5 > 0,
то, следовательно, корень лежит между 0,5 и 1.
Для дальнейшего приближения к корню выбираем какое-нибудь число
в промежутке между 0,5 и 1, например 0,7, и вычисляем
/ (0,7) = 0,343 — 5,6 + 5 < 0;
так как
/(0,5)>0, и /(0,7)<0,
то, заключаем, что корень лежит в промежутке между 0,5 и 0,7.
Далее испытываем значение х = 0,6.
Так как
/ (0,6) = 0,216 — 4,8 + 5 > 0,
то корень, следовательно, заключен в промежутке между 0,6 и 0,7.
Таким образом, принимая одно из этих значений за приближенное зна<
ченис искомого корня, видим, что нам удалось вычислить его с точностью
202
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ
[XV
Для дальнейшего повышения точности необходимо продолжить такие
вычисления. При этом для большей наглядности располагают результаты
в такой таблице:
X f(x)
0,60 +
0,65 +
0,66 +
0.67 —
0,70 —
Вычисления удобно вести, пользуясь таблицею степеней. Предыдущая
таблица показывает, что наш корень лежит между 0,66 и 0,67 и, таким обра-
зом, любое из этих чисел есть значение корня с точностью до 0,01.
Продолжая те же рассуждения, находим, что корень лежит между
0,661 и 0,662, что видно из нижеследующей таблицы, которую нетрудно со-
ставить, пользуясь опять таблицею степеней:
X /(*)
0,660 0,661 0 662 • 1 ++
0,665 —
0,670 —
Таким же образом убеждаемся, что один из корней уравнения
х3 — х2 — 10х — 5 = 0
равен —0,546 или —0,547 с точностью до 0,001.
§ 90. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется пределом переменной величины?
2. Какая переменная называется бесконечно малой?
3. Какая переменная называется бесконечно большой?
4. Может ли постоянная величина быть бесконечно большой или беско-
нечно малой?
5. Как можно выразить переменную через ее предел?
6. К какому пределу стремится дробь, когда ее числитель остается огра-
ниченным, а знаменатель растет беспредельно?
7. Что делается с дробью, когда ее числитель остается ограниченным
и =Д0, а знаменатель стремится к нулю?
§ 90]
ВОПРОСЫ И УПРАЖНЕНИЯ
203
8. На каком признаке существования предела переменной основано
sinx _
доказательство того, что lim ---= 1?
о х
9. На каком признаке существования предела переменной строится дока-
/ 1 \п
зательство существования lim 1-1--?
W-> оо \ П)
1Q. Перечислите известные вам эквивалентные бесконечно малые вели-
чины.
И. В каких случаях бесконечно малые величины называются бесконечно
малыми одного порядка, высшего и низшего?
12. Что называется приращением независимой переменной?
13. Что называется приращением функции?
14. В каком случае функция называется непрерывной при х = а>
15. Какими свойствами обладает непрерывная функция?
16. Какие точки кривой, заданной уравнением у = f (х), соответствуют
корням уравнения f (х) = О?
Найти пределы следующих переменных величин:
17. lim (х2 — «-> 0 1) sin 2х Отв. 0. . 2zz -|- 5 22. lim -——- П -> сю 4/2 1 Отв. 1 2 ’
18. lim ^±4 Отв. — А О sin3x 23. lim - _ х -> о sin 2х Отв. 3 2 *
19. lim -9 Отв. Нет. 24. lim - tg 3^ «->o in (i + *) Отв. 3.
20. lim —Х к Х2 л 21. lim - J Х+2 X— 2 Отв. Нет. Отв. 4. .. lh(l-f-3x) 25- 1,m л - а-ю'М! — 2x) Отв. —
XVI. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
§ 91. ОСНОВНАЯ ЗАДАЧА ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
И ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Дифференциальное исчисление обязано своим возникновением
постановке некоторых весьма важных задач геометрического, меха-
нического и чисто аналитического характера. К числу этих задач
относятся, между прочим, задача о проведении касательной к кри-
Рис. 116.
вой в некоторой ее точке, задача
об определении скорости движе-
ния точки в данный момент и
Другие.
Для большей ясности по-
нимания основной идеи диффе-
ренциального исчисления мы и
начнем с рассмотрения этих за-
дач.
Задача I. Провести ка-
сательную к некоторой
кривой в некоторой ее
точке.
Пусть y=f(x) уравнение не-
которой кривой (на рисунке KL) и положим, что требуется прове-
сти касательную к этой кривой в точке М.
Касательной к кривой в данной на ней точке М называется
предельное положение секущей, проходящей через данную точку М
и другую точку кривой, когда последняя точка беспредельно
приближается к данной точке М.
Итак, возьмем на той же кривой другую точку Мг и проведем
секущую MMV Затем, оставляя точку М неподвижной, будем бес-
предельно приближать точку М1 к точке М. При этом секущая,
вращаясь около неподвижной точки М, будет приближаться к неко-
торому предельному положению, т. е. к касательной к кривой
в точке М (на рисунке линия МТ).
Для проведения касательной в точке М, очевидно, нам доста-
точно определить угол а, который должна составлять касательная МТ
с осью ОХ, или, лучше, тангенс этого угла: tga.
§91] ОСНОВНАЯ ЗАДАЧА ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 205
Но угол а можно рассматривать как угол, к которому беспре-
дельно приближается угол со, составленный секущей ММ1 с осью ОХ,
по мере приближения точки к М. Поэтому и tga будет являться
пределом tga), т. е.
tg a = lim tg со
при беспредельном приближении к М.
От возможности вычислить этот предел и зависит, следовательно,
решение задачи.
Пусть координаты точки М будут
ОР = х, PM=y=f(x).
Обозначив = й, найдем, что координаты точки М будут
ОРг = х h, Р1М1 =f (х + й).
Из рисунка следует, что
Поэтому
. ... .. —f(x) /T4
tg a = hm tg cd = hm ——1. (I)
h->o h->o л
Последнее равенство показывает, что для решения задачи о про-
ведении касательной к кривой, уравнение которой у=/(х), не-
обходимо найти
ft-> о h. v ’
Знаменателем этого выражения является приращение независимой
переменной х, числителем же служит соответствующее ему прира-
щение функции.
Таким образом, задача о проведении касательной к кривой сво-
дится к! нахождению предела отношения приращения функции
к приращению независимой переменной, когда последнее стремится
к нулю.
Поясним найденный результат примером.
Пример 1. Положим, что требуется провести касательную к параболе у=х2
в некоторой ее точке М, абсцисса которой х.
Здесь f(x) = х2.
Для вычисления предела (*) дадим х приращение Л.
Новое значение аргумента тогда будет х 4- ht а новое значение функ-
ции f(x + h) = (x-f-Zz)2.
Приращение функции в данном случае примет следующее значение:
/(* + й) —/(V) = (х + Л)2 — х2 = х2 + 2hx + Л2 — х2 = 2йх + й2.
206
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
[XVI
Согласно формуле (I) имеем
,ЕП_1,И №+'<>-/w
h-+0 fl
f. 2hx -I- h2 ,n , tA n
= lim -----I---= lim (2x + Л) = 2x,
h-+o л->о
т. e. что тангенс угла, составленного касательною к данной параболе в раз-
личных ее точках, должен вычисляться
по формуле
tg а = 2х,
так что, например, в точке параболы,
абсцисса которой равна , tg а = 1, и
а = 45°; в точке с абсциссой = 1, tg а = 2
и т. п. и вообще касательную к пара-
боле надо вести под таким углом к оси
ОХ, чтобы тангенс этого угла был ра-
вен удвоенной абсциссе точки касания.
Так, если абсцисса точки М есть ОА,
то, разделив ОА пополам точкой В
и соединив точку М с В, мы и полу-
чим касательную в точке М (рис. 117).
Задача II. Рассмотрим теперь задачу механического характера,
а именно задачу об определении скорости в данный
момент движения некоторой точки.
Для простоты рассмотрим случай прямолинейного движения.
Пусть точка движется по прямой изображенной на рис. 118.
Пройденный точкой путь условимся отсчитывать от некоторой на-
чальной точки А и предположим, что за промежуток времени t
движущаяся точка переместилась из точки
А в точку Ж, так что за этот промежу-
ток времени пройденный ею путь ока-
зался равным длине AM = s. С измене-
нием времени t будет меняться и положе-
4-----------1---Н-
М1
Рис. 118.
ние точки М на прямой, а вместе с тем и пройденный точкою путь s,
отсчитываемый всегда, как мы условились, от точки А. Таким обра-
зом, мы видим, что величину $ можно рассматривать как некоторую
функцию времени t, т. е.
5 =/(/).
Отсюда следует, что если за промежуток времени t точка про-
ходит путь s=f(t), то за промежуток равный пройденный
путь окажется равным
^=/(Н-Д0
(на рис. $1=дл. АМХ), так что приращению времени Д£ соответ-
ствует приращение функции или пройденного пути
Дя =/(;+до—/(/).
Частное от деления Д$ на Д/, т. е.
As
Lt
(1)
§ 91]
ОСНОВНАЯ ЗАДАЧА ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
207
будет тогда являться величиной средней скорости движения точки
за промежуток времени Lt на протяжении пути ММ1.
Чем меньше будет промежуток времени Lt, тем меньше будет
путь ЛМ'Ц, пройденный точкою за этот промежуток, и тем вели-
чина дроби (1) будет точнее характеризовать скорость движения
точки при ее прохождении через точку М, т. е. в момент вре-
мени t. Отсюда следует, что для более точной характеристики
движения нам выгодно промежуток времени выбирать все меньшим
и меньшим, приближая его к нулю.
Скоростью v движения точки в данный момент и называется пре-
дел, /к которому стремится отношение при стремлении Lt
к нулю, т. е.
v= lim
Д£->0
Ls
Lt
(И)
Таким образом, и вторая рассмотренная нами задача сводится
также к нахождению предела отношения приращения функции
к приращению независимой переменной, когда это последнее стре-
мится к нулю.
Поясним и эту задачу примером.
Пример 2. По закону падения тел в пустоте путь, пройденный телом
за промежуток времени Д считая от начала движения, выражается, как
известно, формулой
s- gt2
Здесь, следовательно, f (t) = gt2.
Для нахождения скорости v в любой момент движения требуется найти,
как видно из формулы (II),
Н„ /(' + ^>-/<0 .
Д£->0 Lt
Но /(Z-|- Lt) = g(t-}~ Lt)2. Поэтому
У^^+ДО2--^-^2
1 (г+д/)2—t2
— a. lim -—!------
2 ь д ™0 Ы
= lim (2#4-Д0 = ^.
z Д£-> 0
Итак, исходя из закона движения падающих тел в пустоте, выраженного
вышеприведенной формулой, мы узнали, что скорость такого движения
в любой момент времени может быть вычислена по формуле
Сопоставляя результат (II) решения общей задачи об определе-
нии скорости движения точки с результатом (I) решения задачи
о проведении касательной к кривой, мы замечаем, что обе задачи
208
Производная и дифференциал функции
(xvi
приводят нас к необходимости искать предел отношения прираще-
ния функции к приращению независимой переменной, когда это
последнее стремится к нулю.
Замечательно, что к такому же вопросу приводят нас не только
рассмотренные выше задачи. Нахождение предела (*) является клю-
чом к разрешению весьма большого числа основных задач анализа,
геометрии, механики, а вследствие этого основной причиной необы-
чайного развития за последние два с половиной века математики
вообще и ее приложения к прикладным наукам в частности.
Нахождение этого предела для различных функций и изучение
его свойств в связи со свойствами самих функций и служит основ-
ною задачей одного из важнейших разделов высщей математики,
называемого дифференциальным исчислением.
Как видно из приведенных выше примеров, предел
ИтЛ5+*)-/(*), е)
h+o h ’ v ’
если только он существует, представляет некоторую новую функ-
цию от х. Функцию эту называют производной функции f(x) и
обозначают знаком
/'(*),
так что
f (х) = lim +
Л->0 п
Итак, производной функции f(x) называемся предел отно-
шения приращения функции к приращению независимой пере-
менной, когда это последнее стремится к нулю.
Действие составления производной функции называется диффе-
ренцированием функции.
В случае, если функция обозначена одной буквой, например у,
то ее производная обозначается через у'.
Если для приращения независимой переменной и функции взять
обозначения
h = Дх
/(х 4- h) —/(х) = Д/(х) = Д/= Ду,
то равенство
записать так:
(Л), устанавливающее определение производной, можно
ifl ч .. Д/(х) .. Д/
f (х) = lim 7 — lim ~
J v 7 дж-»о Дт-»од*
или
у' = Пт
Установленное определение производной предполагает, что рас-
сматриваемая функция является непрерывной функцией при выбран-
§ 91] ОСНОВНАЯ ЗАДАЧА ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЙ 209
ном нами значении х, т, е. что
lim /(х)| = 0.
о
Действительно, если бы
Hm [f (х+ А) — /(x)J 4= 0,
то выражение (*) не имело бы предела и, следовательно, функ-
ция /(х) при выбранном значении х не имела бы производной.
Однако, даже в случае непрерывности функции предел отношения (*)
может и не существовать. Если предел выражения (*) существует
и оказывается одним и тем же независимо от того, будет ли величина h
приближаться к нулю со стороны положительных или отрицатель-
ных ее значений, то говорят, что /(х) имеет определенную про-
изводную при рассматриваемом значении аргумента х.
Если функция имеет определенную производную при данном
значении х, то функцию называют дифференцируемой при этом
значении. На это важное различие между непрерывной и дифферен-
цируемой функцией впервые указал Лобачевский,
Общее правило для составления производных от различных
функций состоит из следующих четырех последовательных операций:
1. Приписываем аргументу определенное значение и затем при-
даем ему некоторое приращение Л.
2. Находим соответствующее приращение функции f(x-^h)—/(х).
3. Составляем отношение этих приращений t
4. Ищем предел найденного отношения при стремлении прира-
щения аргумента к нулю.
Для выполнения последнего пункта нельзя указать определенных
правил; в каждом случае поступают сообразно характеру самого
отношения.
Приведем примеры на составление производных.
Пример 3. Найти производную от /(х)=-^-.
Согласно изложенному правилу, приписав независимой переменной х
определенное значение, придаем ему приращение, равное h. Новое значение
этой переменной будет x-f-Л, а новое значение функции /(х4-Л) = х 4- *
Поэтому приращение функции
f(x+h)~/(Х) = -4т — — ---------.
-Г / J X + Л X х(х4-Л)
Тогда
/'«- |1га ЛьЩИ. |1|П Г 1 U__L.
А->о h *(* + ^)J х2
Итак, (_L — — L
\х) х2‘
14 Зак. 2116. Н. С. Михельсон.
210
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИЙ
[xvt
Пример 4. Найти производную от f(x) — Y х.
Приписав независимой переменной х определенное значение, придаем ему
приращение h, тогда f (х + h) = Yx + /г, а потому
и
f (х + Л) -/(х) = ут+т- ут
ft (х) = lim -
Л->о
Yx-\-h— У х
h
Для вычисления предела полученного, выражения умножим числитель и
знаменатель дроби на Yx-^-h Yx, тогда
ч n x + h — х t 1 1
f' (х) = lim -7-7======---= lim ---— = —т=г.
Л->о /г(]Лx4-/z+ Yx) Л->о У * +Л + Yх 2 Ух
Итак,
Задача нахождения для данной функции ее производной есте-
ственно порождает и обратную задачу: нахождение функции по
известной ее производной.
Такая функция по отношению к ее производной называется
первообразной функцией.
Так (см. примеры выше),
2х есть производная от х2
обратно, х2 есть первообразная функция по отношению
1 „ 1_
2
. к
1
К ---------
х .
к 2х
следовательно
и отношение
§ 92. ВЫВОД ОСНОВНЫХ ФОРМУЛ
1) Производная постоянной величины.
Постоянная величина не меняет своего значения,
ее приращение тождественно равно нулю, а поэтому
этого приращения к приращению независимой переменной будет
равно нулю. Потому и предел этого отношения, т. е. производная,
будет тоже равна нулю:
(const)7 = С' = О,
производная от постоянной величины равна нулю,
(1)
§ 921
ВЫВОД ОСНОВНЫХ ФОРМУЛ
211
2) у = хт (где т — целое и > 0).
Для составления производной этой функции дадим х прираще-
ние равное h, тогда и функция получит приращение равное
(х-+-Л)™ — хт.
Поэтому
, .. (x + h)m — х”1
у' = hm У ,Т >------=
л->о п
= lim Ихт 4-тх™-1 h 4- х«»-2. й24~ ... 4_^m_xml —
h->0 " L * J
= lim й-4- ... 4-й’»-11 = mxm-1,
h->oL 1,2 J
так что
(хтУ = mxm~l. (2)
3) y — logx.
Сообщив опять независимой переменной х некоторое определен-
ное значение, придадим ей приращение й, тогда приращение
функции f(x) будет равно
log (х 4- й) — log х = log = log(l 4- -iy
Поэтому
Для вычисления предела положим
h 1
— = —.
X п
Тогда h = Заменяя h этим выражением и замечая, что при
беспредельном уменьшении h до нуля новая переменная п стремится
к бесконечности, имеем
л • log fl 4-t
f к \ п/ 1 v A f 1\п
у = hm------------------ — lim log (14-----) .
П->0О Х Х П-*Х> S\ 1 Л/
1
— вынесено за знак предела, так как предел вычисляется в пред-
положении, что меняется лишь /г; что же касается величины —, то
она сохраняет данное ей значение.
Так как lim fl = e (см. стр. 190), то
T„1inLlog(1+7)” = 710^'
14*
212
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИЙ
[xVI
Итак
(log х)'=4 log е.
(3)
Если логарифм взят при основании е (мы условились обозна-
чать его тогда знаком In), то In е=1, и, следовательно,
(1пх)'=1. (3')
4) у = sin х.
Поступая как и в предыдущих случаях, находим
п . h ( , h\
. z . , 2 Sin 77 . COS x + 77
f .. sin(x + ^ —sin x .. 2 \ ‘ 2j
у = lim —-—!—------------= lim-----------r—------ —
h->0 Л /1->0 л
ош 2 / h \ 2 * ft \
= lim—г----cos (x + -9-) = lim—?— • lim cos (x 4- 77) = cos x,
h^O n \ */ h-yQ ^->0 \ */
2 2
. h
sin T
так как lim —7—=1.
2
Итак
(sinx)' = cosx. (4)
5) ^ = cosx.
о . h . / , h\
Z I £.4 2 Sin-x-«SHI x+-77
f .. cos (x + /z)—cos X .. 2 \ 27
у = hm ——!—f lim----------------------------=
Л Л->0 h h
2 / h \
= — lim —7— • lim sin x 4- 77 = —sin x.
A->0 A h->0 \ 2/
2
Итак
(cosx)' = — sinx.
Таким же способом, основываясь непосредственно на определении
производной, можно было бы продолжать составление производных
других функций. Однако будет проще вывести сначала несколько
общих формул.
6) Производная функции сложного аргумента.
Если у есть некоторая функция от и, где и в свою очередь
некоторая функция от независимой переменной х, т. е. если
у где и = <р(х),
то аргумент называется сложным аргументом, а сама функция у
функцией сложного аргумента.
§ 92] вывод основных формул 213
Большинство функций, с которыми приходится иметь дело в раз-
личных вопросах, можно считать принадлежащими к этому именно
типу. Например
у = sin2 х; здесь у = и2, где и = sin х
у = In cos X') здесь у = In и, где и — cos х.
Задача заключается в нахождении производной функции через
производные функций f (и) и ср(х).1
Дадим переменной х приращение Л, которое для удобства будем
обозначать знаком Дх. Понятно, что такому приращению незави-
симой переменной будет соответствовать некоторое приращение Ди
аргумента и, а вместе с тем и приращение Ду самой функции у.
По определению имеем
, r ^У
y=lim —,
Да?->0^х
но очевидно
Ду Ду Ди
Дх Ди Дх ’
поэтому
f Ду Д/z
у = lim -т—• lim —. (5)
ДИ->0 Д“ Дф->0
Ьу
lim есть производная функции /(zz), считая сложный аргу-
Д и—^0
мент и как бы независимой переменной; ее обозначим через f (zz).
lim 4“ есть производная функции и = ср (х); ее обозначим
д®-»о
через и' или ср' (х).
Таким образом, из соотношения (5) получаем
/=/'(«)•«'. (6)
Итак, для дифференцирования функции сложного аргумента
надо составить производную от этой функции, принимая сложный
аргумент за независимую переменную, и умножить эту производ-
ную на производную сложного аргумента.
Выражение „составить производную от некоторой функции, счи-
тая и или v или другую какую-либо величину за независимую пе-
ременную “ принято заменять выражением „составить производную от
функции по переменной и или по v и т. п.“. Так что в формуле (6)
под знаком /' (zz) подразумевается производная от функции /(zz) по
переменной и, а под и' — производная от и по переменной х.
1 Предполагается, что обе функции имеют производные при рассматри-
ваемых значениях х.
214 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ (XVI
Применим формулу (6) к нижеприведенным примерам функций.
Пример 1. у = sin2x.
Здесь
У(и) = и2, и = sin х
fr [и) = 2и, и' = cos х.
Следовательно,
у' = 2и cos х = 2 sin х cos х = sin 2х.
Пример 2. у = In cos х.
Здесь
f (и) = In и, и = cos X
f'(u) = -i > uf = — sin x.
Следовательно,
7) Производная алгебраической суммы.
Пусть у = и V + w, где и, v, w функции от х.
Дадим переменной х приращение Дх, тогда и, v, w получат
приращения Дм, До, Дю, а у — приращение
Ду — ки Ц- Дv Д'И'.
Ду Дм До Ди/
у = Пт — = lim -т-------Ц lim -т--4 lim «7—,
Да?->0 ^х До?-»0 Да7->0 ^х Дя?->0 ^х
НО
.. Дм , До г Ди/ z
lim — =м, lim -7—== о , lim — = ю.
Дш->0 ^Х Дя?->0 ^х д®->о ^х
Поэтому
(м 4" v= и' 4“ w '• (7)
Следовательно, производная алгебраической суммы нескольких
слагаемых равна алгебраической сумме производных отдельных
слагаемых.
Пример:
(х3 + sin х — 3)' = (х3)' + (sin х)' — (3)' ® Зх2 + со$ х*
8) Производная произведения.
Пусть у = #.о, где м, v — функции от х.
Прологарифмируем произведение (при основании равном числу е)
и от обеих частей полученного равенства возьмем производные
1пу = In и 4-1ПО
ВЫВОД ОСНОВНЫХ ФОРМУЛ
215
§ 92]
Для вычисления этих производных мы должны применить правило
дифференцирования функции сложного аргумента-» Соответственно
ему
(In j)'(1ПИ)' = 1. и', (1п %>)'= 1<
так что
1 г 1 / I 1 ,
— . уг =3 — . и'4----
у и ' V
Умножая все члены равенства на у = и • т/, получаем после сокра-
щения
у' — v . и' и * v',
так что
(г/ . ^)' = . и' 4~ и • тА (8)
" Итак, производная произведения двух множителей равна одному
из множителей, умноженному на производную другого, плюс
другой множитель, умноженный на производную первого.
В случае если в произведение входит три или более множителей,
например, если
у = и • v • w,
то подобным же образом выводим, что
у' == • иг • т/' + WU • w' (8')
и вообще производная произведения нескольких множителей равна
сумме произведений производной каждого из множителей на все
остальные.
В частном случае, когда один из двух множителей — постоян-
ное число, формула (8) упрощается:
(Аи\ = Аи' и • 0 = А • и', (9)
т. е. постоянный множитель при дифференцировании выносится
за знак производной.
Пример 1.
(cos х • sin x)f = cos x (sin x)f 4~ sin x (cos x)' = cos2 x — sin2 x = cos 2x.
Пример 2.
(ax3 4- bx* + ex 4- d)r = (ax3)' 4- (bx*)f 4- (ex)' 4- (rf)' = 3ax2 4- 2bx 4- c.
9) Производная частного (дроби).
Пусть у = — , где и, v — функции от х.
Логарифмируя и составляя производные от каждого члена полу-
чаемого равенства, находим
1пд/ = 1п и — 1пф.
V U V i
216
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
[XVI
w 11
Умножая обе.части последнего равенства над/®—, получим
/ 1 7
у = — . и
z v
и / vur — uv'
V2
Таким образом
vu' — uvf
(10)
т. e. производная дроби равна производной числителя, умноженной
на знаменатель, минус производная знаменателя, умноженная на
числитель, и все деленное на квадрат знаменателя.
Пример*
( *2 Y —(1 — х2)(*2У — *2(1— -Г2)7 _ (1 — х2).2х + х2.2х __ 2х
\1—Х*) (1—X2)2 (1 —X2)2 ~(1—X2)2’
Приведенные в пунктах 6, 7, 8, 9 общие формулы дают возмож-
ность продолжить составление производных, основных функций.
10) у = хт, где т — какое угодно постоянное число.
Логарифмируя, имеем
In у — mln х.
Далее, дифференцируя, находим
1 7 1
— .у = т * —,
у J X ’
откуда
г у mxw 1
у = т • — =-----= тхт-\
хх
Итак,
(хтУ == тх™-1. (2)
Полученная формула показывает, что формула дифференцирования,
выведенная раньше для целой положительной степени, распространяется
на случай какого угодно постоянного показателя. По этой формуле
следует дифференцировать и дроби вида полагая i = x~°,
р_____________________________ р ч_
а также к радикалы вида ]Ух^, полагая У~хч = х? , как это по-
казано в нижеприводимых примерах.
Примеры:
1. (х3)' = 3х2.
2. (х)'4 1^1,
3. (^Y==(x-5)'== —5х-б== —-1.
\хб/ v X6
4. = 8)' = -|х
15 3 у х
§ 92] вывод основных формул 217
11) у — ах. Поступая как в предыдущих случаях, находим
1 У т. е. Iny = xln а, • у’ = In я, у' == у • In а = ах * In а, (ах)' = ах • In а, (11)
В частном случае (ехУ = ех. (11')
12) ^=tgx. Замечая, что , sin х tg X = , ь cos X
находим, применяя формулу дифференцирования частного:
,__/sin х V__cos x (sin x)' — sin x (cos*)'_cos2 x + sin2 x __1_
У \ cos х) Таким образом, COS 2 A? COS2 X COS2X ’ <12>
13) у = ctgx.
z__/cos x\'___sin x (cos x)' — cos x (sin x)'
\ sin х ) sin2 х sin2x Ц- cos2 х 1 sin2x sin2x *
Таким образом, («'- sZ <13)
14) у = arc sin x.
Из этого равенства вытекает, что
х = siny.
Беря от обеих частей последнего равенства производные по
переменной х (т. е. считая х за независимую переменную), найдем
Отсюда
Но
1 = cosy -у'.
1
У cos у
cosy = zt У1 — sin2y = zt У1 — л;2,
218
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
[XVI
и так как у — arc sin х заключаемся в пределах от —у Д° +у
(см. § 22), то cosj/ > 0, поэтому
COSJ7 — + V1 — х2.
Следовательно,
л + /1 — х2 ’
т. е.
(arc sin х)' = -7=L=j-. (14)
у 1 —х2
15) ey = arccosx.
Из этого равенства вытекает, что
x = cos3/.
Дифференцируя это равенство по х, находим
1 = — sin_y «у.
Отсюда
, _____1__
У sin у *
Но ’ _________ _____________
sin у = z±z pl — cos2у = ± У1 — х2,
и так как у = arc cos х заключается в пределах от 0 до к (см.
§ 22), то sin у > 0 и потому
sin_y = ~р V1 — х2.
Следовательно,
, 1
У /Г^Т2 ’
т. е.
(arccosx)'= — y==f. (15)
16) y*= arc tgx.
Отсюда x = cigy.
Дифференцируя, имеем
1 =7^; •/ = (!+fg3>) -У МП-2) -У,
так что
_ 1
У ~ 14-х2’
т, е,
(arctgxj^j-l^. (16)
§ 931
ДИФФЕРЕНЦИАЛ ФУНКЦИИ
219
17) у ==arc ctgx.
Отсюда x = cigy.
Дифференцируя, находим
1 =—= —U + cteV) -У = -(1 +*2) -У,
так что 1
У'—
т. е. J
(arc ctgx)'= —
(17)
§ 93. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Из формулы (А) (стр. 208), служащей определением производной,
непосредственно следует
^.+2^-^ = / (Х) _f_ е, (18)
где е— бесконечно малая величина, обращающаяся в нуль, вместе с А;
отсюда
/(* + А) —/ (х) = h • f' (х) + h • s. (19)
Формула (19) показывает, что приращение функции
/(х-(-А) — /(х)
состоит из двух слагаемых
f (х) • h и е • А.
Первое слагаемое, равное произведению производной на произ-
вольное приращение независимой переменной, является главной
частью всего приращения функции, так как, вообще говоря, это
слагаемое при бесконечно малом А есть бесконечно малая одного
порядка с А; другое же слагаемое высшего порядка, чем А.
Действительно
hm —4т— = f (х), hm -т- = lim е = 0.
7*->0 п 11 h->0
В анализе эта главная часть приращения функции, пропорцио-
начальная приращению независимой переменной, играет не менее
важную роль, чем сама производная f' (х), потому для такого вы-
ражения также устанавливается особое название и обозначение.
Именно, произведение
/'(х) • h
называется дифференциалом функции f (х) и обозначается знаком
rf/(x).
Так чт0 JZZ ч /г \ I. /п\
df(x)=f (х) . А. (В)
Итак, дифференциалом функции f(x) называется произ-
ведение производной f (х) на произвольное приращение h не-
зависимой переменной,
220 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ [XVI
Соответственно ранее приведенным примерам мы можем напи-
сать:
для /(х) = х2, df(x) — 2х • h, т. е. </(х2) = 2х • h
для/(х) = ^-, #(х) = —А, т. е. = —
Положив для краткости в формуле (19) бесконечно малую ве-
личину eh = со, можно переписать эту формулу в следующем виде:
Д/ (х) = df (х) со
или
Ay = dy-j-co. (20)
Обращаем внимание на то, что ввиду произвольности прираще-
ния h, df(x) является, вообще говоря, также произвольным коли-
чеством и что с приближением h к нулю df(x) стремится также
к нулю.
Понятие дифференциал функции имеет большое теоретическое
значение, что и выяснится при дальнейшем изучении курса.
Так же, как и производной, дифференциалу функции можно
дать геометрическое толкование.
Обратимся для этого к рис. 116 на стр. 204.
В нем, как известно,
MQ = h и tg / RMQ = tg а = /' (х).
Поэтому из Л MQR непосредственно получаем
Q/? = AlQ-tga=/,(x).ft,
так что отрезок QR есть дифференциал функции.
С приближением = Л к нулю, отрезок QR = df(x) тоже
будет стремиться к нулю.
Рисунок поясняет также, что дифференциал функции можно
рассматривать как часть приращения функции. Действительно, при-
ращение функции на рисунке изображается отрезком QMt, так
как
QMt =/(х + Л) —/(х) = Д/(х),
а отрезок QR составляет часть этого приращения. Другая его часть
RMt является той бесконечно малой величиной <о высшего порядка,
которая составляет вторую часть приращения функции (см. формулу
(19) этого параграфа).
Обратим внимание на два простейших случая нахождения диф-
ференциала.
1) f(x) = C, т. е. f (х) есть постоянное число,
§ 931
Дифференциал функций
221
Тогда, как известно, /(ж) = 0 и, следовательно,
#(х) = 0.Л = 0
или
Л?=0, (21)
т. е. дифференциал постоянной равен нулю.
2) /(х) = х.
Тогда f (х) = 1 и, следовательно,
df (х) = 1 * h = й,
т. е.
dx = h. (22)
Последнее приводит нас к весьма важному выводу, что диффе-
ренциал независимой переменной означает произвольное прира-
щение независимой переменной и ввиду этой именно произволь-
ности дифференциал независимой переменной не зависит от самой
переменной.
То обстоятельство, что dx = h, позволяет нам везде, где встре-
чается приращение й, заменять его через dx. Ввиду этого формулу
(В) пишут
d/(x)=/'(x) - dx. (В')
Таким образом, дифференциал функции равен произведению
производной на дифференциал независимой переменной.
При сокращенном обозначении та же формула принимает вид:
dy=y'dx. (Bzz)
Из этих формул, как следствие, получается возможность толко-
вать производную как отношение дифференциала функции к диф-
ференциалу независимой переменной, т. е.
= или У=-^. (22)
Из определения дифференциала функции следует, что для его
получения достаточно производную функции помножить на dx.
Таким образом, для нахождения дифференциала по существу нет
надобности в новых формулах. Так, например:
если у — х™, то yf = /nxw“1, a dy = mxm~v dx
если у — ех, то у1 = ех, a dy = exdx.
Однако все же следует отметить некоторые полезные формулы,
относящиеся к дифференциалам функций.
1) dC=O (см. формулу (21)).
2) Пусть j/=/(x), где х = <?(*), т. е. пусть х является здесь
сложным аргументом, зависящим от независимой переменной г,
222 Производная и дифференциал функции [xvi
а у, следовательно, функцией сложного аргумента. Тогда по пра-
вилу дифференцирования функции сложного аргумента (см. фор-
мулу (6), стр. 213), производная от функции jp по независимой пере-
менной z выразится так:
у' —f (*) • х',
где /' (х)— производная от функции /(х) по сложному аргументу
х, а х' — производная сложного аргумента по переменной z. Поэтому
dy — f (х) • х' dz.
Но по определению дифференциала
х' dz = dx,
следовательно
dy = f (x) dx.
Таким образом, мы получаем для дифференциала функции слож-
ного аргумента точно такое же выражение, как и для дифферен-
циала функции простого аргумента. Сопоставляя выписанные ниже
формулы для производных и дифференциалов функции простого
и сложного аргумента:
функция производная дифференциал
х — простой аргумент У = f(x) У =/'(*) dy=f'(x)*dx
х — сложный аргумент y=f(x) y'=f'(x)-x' dy = /' (х) • dx
приходим к заключению, что при составлении производной функции
совершенно необходимо знать, является аргумент, от которого не-
посредственно зависит функция, простым или сложным аргументом;
напротив, при нахождении дифференциала функции это совершенно
несущественно, так как его выражение по форме одно и то же
в обоих случаях.
3) Пусть у = и 4- v w, где и, v, w — функции от х.
Так как
у = я' 4~ г/ 4» <wf,
то
dy = (иг + 4- w') dx = u'dx 4“ v'dx 4- w'rfx = 4"
Итак, дифференциал алгебраической суммы нескольких ела*
гаемых равен алгебраической сумме дифференциалов отдельных
слагаемых:
4) Пусть у = и • где zz, v— функции от х
у = v • и' 4“ я •
§ 931 ДИФФЕРЕНЦИАЛ ФУНКЦИИ 223
следовательно,
d (и • -и) = (ф • и' и • v') dx — v • и’ • dx + и • • dx.
Ho u' -dx = du и ф' • dx = dv, поэтому
d (uv) = vdu-\-udv.
Итак, дифференциал произведения равен одному из множа-
щелей, умноженному на дифференциал другого, плюс другой мно-
житель, умноженный на дифференциал первого.
5) Пусть у = , где и, ф — функции от х
, v • иг — и »vr
у =-------&----’
следовательно,
ifu\ и» и'— u-vr , v-u'dx — u*v’dx vdu — udv
d — =-------------5----dx -----------s--------------—-s-.
\ V / v2 y2 V2
Итак, дифференциал дроби равен знаменателю, умноженному
на дифференциал числителя, минус числитель, умноженный на
дифференциал знаменателя, и все деленное на квадрат знамена-
теля.
Таблица основных формул дифференциального
исчисления
L (ит)' = тит~г - и'.
2. (log и)' = -1 • loge • и'.
3. (In и)' — -i- • и!.
4. (а»)' = аи In а • и'.
5. (еа)' — еа и'.
6. (sin и)' = cos и и'.
7. (cos и)' — — sin и • и’.
9. (ctg«)' = —
to. (arc sin «)'= у==«'-
II. (arc cos и)'—---, * • и'.
’ У1 — «2
12. (arctgz/)'=
13. (arc etg и\ = — 5 • и',
d (ит) = mu"1-1 du.
d(logu) = ^-loge.
Ur
* s du
d(lnu) = —.
d (au) = a" • In a du.
d (e“) = ett du.
d (sin u) — cos и du.
d(cos u) — — sin и du.
d(ctgw) = —
' S ’ Sin2«
d(arc sin «) = .
yi —и2
j / ч du
d (arc cos w) —---r^=—;
' /1 — и-
rf(arctg«) = j-^-2.
d(arcctgz/) = —
224
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИЙ
[XVI
14, (С') = 0, если С постоянн.
15. w)' = u'-^v'-j-w'.
16. (и • v)' = и • v' -f - v • и'.
17. (Л-а)/ = Л»/, если А по-
стоянн.
dC — O.
rf (w-j-p-j-w) = duydv'dw.
d(u v) — udv-[-vdu.
d (Aa) — A du.
18. =
\ v J V2
19. Если у =f(u), где и = <о(х),
то у' —f (и) • и'.
. u\ v du — иdv
d I — =-----=
\ V J V2
dy —f («) du.
§ 94. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется производной функции?
2. Для существования производной должна ли быть функция непрерыв-
ной при рассматриваемых значениях переменной и если да, то почему?
3. Какая геометрическая задача связана с нахождением производной?
4. Какой геометрический смысл имеет производная?
5. Какие вы знаете обозначения для производной?
6. В чем заключается удобство обозначений производных в виде отно-
шения дифференциалов, например так:
dy dz dz
dx* du’ dy
И т. п.
7. Можно ли понимать равенство
lim =
ДЖ->0 Дх dx
так, что будто в пределе &у обращается в dy, а Дх в dx?
8. Как берется производная функции сложного аргумента?
9. Что называется дифференциалом функции?
10. Чему равен дифференциал назависимой переменной?
11. Какая связь имеется между приращением функции и его дифферен-
циалом?
12. Чем отличается приращение функции от ее дифференциала?
13. Какое геометрическое толкование можно дать дифференциалу
функции?
14. Как выражается дифференциал функции?
Примеры для упражнения в дифференцировании функций:
15. _у = 2х3 — Зх2 4~ 4х — 3,
16. у = ЗУх + 2^—1,
1 4 2
17. z= -L_A-4-A + 5)
у2 * У *
18. у = х3In х,
19. z = 2j/sin 3'4-2 COSJZ,
20. и = У~у1пу— Уу^>
у' = 6х2 — 6х 4- 4.
3 4
У 2 /х^ 3^ х'
2'=*-у<(3-8у + 2у2).
У = х2(31пх4-1).
z' = 2у cosy.
u' = —L-(lny + 2-3y).
2 Vy
§ 941
ВОПРОСЫ И УПРАЖНЕНИЯ
225
21. у = z tg z- 1, ь cos г з.— ПА У X 22. _у = з,_ ' 1 — ух 23. у = -— Sin X 4- COS X 25. _р = (х2—1)’" 26. у = In 2х, 27. у = sin (2х — 1), 28. у = х • е4х, 29. у = cos (1 —3z), 30. у = In3 х, 31. у = sinax. y' = —J-п— (z 4- sin z • cos z — sin z^. y COS2 zv 1 7 r 1 y Sy'xsQ —f'x)2- y 1 + sin 2x a, 2(*2+D (zS_i)2- у = 2/nx(x2 —I)”1"1- y' — —~. X yr = 2 cos (2x — 1). yr = e4x (1 +.4x), yr = 3 sin (1 — 3г). r 3 In2 x y x • yr = sin 2x.
32. и = tg4 у, 4tg3j> COS2 J
33. z = arc sin Ух, Лл х 1 34. х = arc tg —, z z' = -1 . 2 У x — x- X>: !_ Ц- г2 ’
35. у = (arc sin x)2, , 2 arc sin x y' = — . /1—X2
36. у = In sin 3x, 37. у = arc tg (In 2x), 38. у = arc sin , 1 —X yf = 3 ctg 3x. y ~ (l + ln22x)-x ' , = 1 У (1—X). -fx(x —2)
39. у = (1 ~ ]/T)2 (1 + У7)3, У =-i^4(l—5z —4 /7). 2 уz
40. у = -Д—, sin3 X л. COS2X 41-J'=sin3x’ 42. у = Л£182£, y arcctg2x , 3 cos x y sin4 X y = _ cosx (2+cos2x) sin4x 4 * , К y (1+4x2)(arcctg2x)2 •
43. у = Vcos4x2, z 4x sin 4x2 y' — ,
44 у _ ^arc sin Ko? t ^arc cos V x 45. v _3tgx-tg3x У 1 — 3tg2x ’ l^cos 4x2 yr = 0 (объяснить, почему?). ' - 3 cos23x *
15 Зак. 2116. Н. С. Михельсон.
226
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
[xvi
«л» (2 1 . I \
Х
47. у = arc sin — .
/1 + х2
Г1____х'2
48. у = arc cos 1/ 7-7—7,
49. у = In (1 + х Ч- У2х + х2),
yz = ------
У 1 + х2
У (1Н-Х2). /1 = Х2'
/ Я + » tg X \
\a — btgx)‘
50. у = аге cos
51. .у = 1п
52. у = (х + k /1 —х2) e*«rcsinx,
2х • У(1 — х) (х2 + х — 1)
, __ ______2аЬ______
— a2 cos2 х — b2 sin2 х'
у = (1Н-£2) ek агс sIn*.
XVII. РАЗВИТИЕ ТЕХНИКИ ДИФФЕРЕНЦИРОВАНИЯ
ФУНКЦИЙ
§ 95. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Мы видели, что производная от некоторой функции /(х) пред-
ставляет, вообще говоря, тоже некоторую функцию от х. От нее
в свою очередь можно искать производную. Такая производная по
отношению к данной функции называется производной второго по-
рядка или, просто, второй производной и обозначается знаком
Г(Х).
Производная от второй производной называется производной
третьего порядка или третьей производной от данной функции
и обозначается
/'"(*)•
Продолжая составлять последовательные производные все дальше
и дальше, будем, вообще говоря, получать все новые функции —
производные высших порядков. Производная /г-го порядка от функ-
ции /(х) обозначается
f^x.
В случае, когда сама функция сокращенно обозначена через у,
ее последовательные производные обозначаются так:
У' f У" 9 Ут9 • • • 9 У^*
Частные значения производных различного порядка от /(х) при
х = а обозначаются знаками:
f (а), Г (а), /"(а), /(*)(а).
Примеры:
1) у = хт.
у' = /ПХ7”-1.
у" = т(т—1)хш-2.
У" = т (т — 1) (т — 2) х™-3
yW — m(m—\). . . (т— n-]-l)xw“n.
Если п\—целое положительное, то
= .... 3-2-1, у™+1) = 0.
15*
228 РАЗВИТИЕ ТЕХНИКИ ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ fxvi!
2) у = In х
3) у = е°°
у' — ех
у" = е30
= (_!)«-»!,2>3—„О* -1)
4) _y = sinx
У = cosx
у" — — sin л;
у'" = — cos х
у1 v = sin х
и т. д.
у(п) = еал
5) у = COS X
у' = — sin х
у" — — cos X
у"' — sin х
У v = cos х
и т. д.
Результаты дифференцирования объединяются следующими об-
щими формулами, в правильности которых легко убедиться проверкой:
(sin х)(») = sin (х + п • у у (cos x)W = cos (х -f- п • 40.
Производные высших порядков других функций не выражаются
так просто. Их мы будем находить последовательно одну за другой.
§ 96. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ ОТ ФУНКЦИЙ
ПРОСТОГО АРГУМЕНТА
Умножив производную на дифференциал независимой переменной
мы, как известно, получаем дифференциал функции
rf/(x)=/'(x)rfx. (1)
Произведение f' (х) dx благодаря присутствию множителя f (х)
само представляет некоторую функцию от х, от которой, в свою
очередь, мы можем искать дифференциал. Таким образом, возникает
понятие о дифференциале от дифференциала данной функции, кото-
рый называется дифференциалом второго порядка (или вторым
дифференциалом данной функции) и обозначается так:
Продолжая рассуждать так далее, получим дифференциал треть-
его, четвертого и вообще л-го порядка:
d8/(x), d4/(x), dnf(x).
§ 96] ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 229
При сокращенном обозначении функции через у дифференциалы
различных порядков обозначаются так:
dy, d2y, d3y, ..., dny.
Формула (1) или, что то же, формула
dy~y'dx (1')
дает выражение дифференциала первого порядка через производ-
ную. Подобные же выражения можно получить и для дифференци-
алов высших порядков, если только у рассматривать как функцию
простого аргумента х. Именно
d2y — d(y' dx) = (у' dx)' • dx =^y" • dx2.
d3y = d(y" • dx2) = (y2 dx2)' • dx=y'" dx3
dny =y(n) . dxn.
При выводе этих формул надо иметь в виду, что dx есть про-
извольная величина, не зависящая от х, и потому при дифференциро-
вании должна приниматься за постоянную; dx2, dx3, ..., dx* раз-
личные степени дифференциала dx.
Из приведенных формул вытекают следующие выражения про-
изводных через дифференциалы функций и независимых переменных:
/ dy
У=-£
У dx"-
d,ly
dxn *
В § 91 мы выяснили геометрический и механический смысл
производной первого порядка. Роль производной второго по-
рядка в вопросах геометрии будет выяснена в дальнейшем изло-
жении курса, что же касается механического значения производной
второго порядка, то его нетрудно установить, зная механический
смысл производной первого порядка.
Положим, что мы рассматриваем прямолинейное движение
точки, совершающееся по некоторому закону, выраженному следую-
щим образом:
‘ S ==/(/),
где, попрежнему, под s подразумеваем пройденный точкою путь
за промежуток времени t.
230
РАЗВИТИЕ ТЕХНИКИ ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ
[XVII
Как уже было выяснено в § 91, скорость движения точки
в данный момент есть значение производной от пути по времени,
т. е.
Как видно из последней формулы, скорость движения, вообще
говоря, является также некоторой функцией от времени. Пусть
Через промежуток времени Д/ скорость изменит свою величину
и будет равна
Приращение скорости за промежуток времени Д/ будет
= — F(t).
Рассчитанное на единицу времени изменение скорости называется
средним ускорением за промежуток времени Д£ и выражается отно-
шением
Av _F(t + dr)-F(f)
М kt
Предел среднего
межутка времени Ы
значив его через w,
ускорения при беспредельном уменьшении про-
называется ускорением в данный момент. Обо-
имеем
хи = lim
Д£ -> 0
lim
Д£->0
Но, в силу того, что v = F(/), получаем
А так как =/'(/) = — , то =
Таким образом, и выясняется механический смысл второй про-
изводной: производная второго порядка от функции, выражаю-
щей зависимость от времени пройденного точкой прямолинейного
пути, равняется ускорению точки в ее прямолинейном движении.
§ 97. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНОЙ ФУНКЦИИ
Как известно из § 20, у называется неявной функцией от х,
если она определяется уравнением, не решенным относительно у,
т. е. уравнением вида
/(х, _у) = 0. (2)
Допустим, что уравнение или вовсе не решается относительно у,
или мы не желаем его решать, но тем не менее мы желаем найти
§ 97]
ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНОЙ ФУНКЦИИ
231
производные от у по х: у', у" и т. д. Для решения этой задачи
рассуждаем следующим образом.
Функция / (х, у) есть функция двух аргументов, из которых
второй сложный аргумент, так как зависит от х в силу уравнения (2).
При этом, если в левую часть уравнения (2) мы подставим на
место у его выражение через х, выведенное из уравнения (2), то
/(х, у) тождественно обратится в нуль, а потому и ее производ-
ная по х тоже обратится в нуль.
Отсюда и вытекает способ нахождения производной у': диф-
ференцируем левую часть уравнения (2) по х, принимая во вни-
мание, что у есть функция от х, результат приравниваем нулю
и из полученного уравнения определяем у'.
Для нахождения у" дифференцируем найденное выражение для
у', помня, что входящее туда у является функцией от х.
Пример 1. Неявная функция у задана уравнением
х2 v2
— А-—-----1 = 0
Д2 £2 1 и’
Дифференцируя левую часть по х, помня, что у есть функция от х
находим:
2х , 2у п
у'=°’
откуда
, Ь2х
У ~~ а2у ’
Для нахождения у" дифференцируем обе части последнего равенства по
х, попрежнему помня, что у есть функция от х:
_______ьг У~~ХУ'
у ~ аУ У ' ’
Заменяя у' его только что найденным выражением, получаем
Ь2 а2у2-\-Ь2х2
а2 '
У
а2у3
Но из основного уравнения вытекает, что а2у2 + д2х2 = а2Ь2, поэтому
и__________________________Ь2 а2Ь2 _ Ь*
У ~ а2 * а2у* ~ •
Пример 2. Неявная функция у задана уравнением у2 = 2рх. Дифферен-
цируя, находим *
2у/ = 2/ъ У = у.
Дифференцируем последнее выражение еще раз, тогда
У/==__р_./=_4.
232
РАЗВИТИЕ ТЕХНИКИ ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ
[XVII
устанавливается при
уравнениями вида
§ 98. ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ФУНКЦИЙ
Функции, которые до сих пор мы рассматривали, задавались
обыкновенно уравнениями, непосредственно связывающими данные
функции и их независимые переменные. Нередко, однако, зависи-
мость функции от независимой переменной 1
помощи новой вспомогательной переменной
х = <? (t)
у = ® (0?
(3)
новую вспомогательную
X
Рис. 119.
в которых каждая из основных переменных х
переменную А Если одно из этих уравне-
ний, например первое, решить относи-
тельно t и найденное значение t подста-
вить во второе, т. е., другими словами,
если из системы (3) исключить перемен-
ную t, то мы и найдем непосредствен-
ную зависимость у через х. Нередко это
последнее уравнение оказывается на-
столько сложнее каждого в отдельности
из системы (3), что исследование зави-
симости у от х удобнее вести, поль-
зуясь системой уравнений (3).
Система уравнений (3) представляет
собой новую форму задания зависимо-
сти у от х (или, наоборот, х от у), называемую параметрической
формой. Вспомогательная переменная t носит название параметра.
Во многих случаях весьма удобно бывает выражать уравнения
различных линий в параметрической форме.
1) Так, параметрическая форма уравнения круга с центром в на-
чале координат и с радиусом, равным а, будет
х = a cos t
y = as\n t.
Действительно, исключая t из этой системы уравнений, полу-
чаем
и у выражена через
(4)
г2
— известное уравнение круга. Геометрический смысл параметра
в системе уравнений (4) непосредственно ясен из рисунка.
2) Параметрическая форма уравнения эллипса с полуосями а и b
будет
х = a cos t
у = b sin t.
(5)
1 Ограничиваемся случаем функции одной независимой переменной.
§ 98] ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ФУНКЦИЙ 233
Действительно, из этих уравнений можно получить сначала
х г
— = COS t
а
У • j.
= Sin t.
b
Возвышая затем оба уравнения в квадрат и складывая, мы исклю»
чаем t и получаем
уравнение эллипса в канонической форме.
3) В § 71 (стр. 155) была приведена параметрическая форма урав-
нений прямой в пространстве (см. уравнение (8)).
4) Параметрическая форма уравнения циклоиды.
Когда какой-нибудь круг катится без скольжения по некоторой
прямой, то каждая точка окружности при таком движении описы-
вает некоторую кривую. Кривая 'эта называется циклоидой. Для
вывода ее уравнения представим себе одно из положений катяще-
гося круга с центром в точке D и точку М на его окружности,
которая вычерчивает циклоиду.
Примем за ось ОХ ту прямую, по которой катится круг, а за
начало координат ту ее точку, с которой соприкасалась точка М
в начальном положении круга. Ось OY направим в сторону круга.
Обозначим координаты точки М через х и у, а радиус круга
через а. Кроме того введем в рассмотрение, в качестве вспомога-
тельной переменной, угол, на который повернулся радиус круга СО,
когда точка, вычерчивающая циклоиду, из начального своего поло-
жения переместилась в положение М. На рис. 120 угол этот ДЛТОЛ;
обозначим его через t.
Построив координаты точки М и проведя прямую МВ парал-
лельно ОХ, находим
х = ОР — ОА — РА
y=PM = AD — BD.
Но
0/1 —дл. kjMA — at, РА = MB— a sin t
AD—a, BD = acost,
234 РАЗВИТИЕ ТЕХНИКИ ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ [XVII
Поэтому получаем
x = a(t— sin /)
у = а(1 —cost). 7
Эти уравнения и являются параметрической формой уравнения
циклоиды. Геометрический смысл параметра t ясен из рассуждения.
Исключив из этих двух уравнений величину /, мы и получим
уравнение, связывающее координаты у и х любой точки рассматри-
ваемой кривой, т. е. уравнение циклоиды. Однако, обыкновенно
этого исключения не производят, так как получающееся уравнение
оказывается сложного вида.
5) В параметрической форме обыкновенно задается и закон движе-
ния в пространстве материальной точки, именно, в виде системы
уравнений
x=f(t)
z = w(t).
Каждое из этих уравнений в отдельности выражает соответствую-
щую координату движущейся точки для каждого данного момента
времени. Исключив из этих уравнений время /, получим два урав-
нения, связывающие переменные, х, у, z между собою, которые и
составляют уравнения траектории движения.
§ 99. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ
ПАРАМЕТРИЧЕСКИ
Задача дифференцирования функции, заданной параметрически
уравнениями
х = ф (t)
У = ® (О»
(7)
заключается в нахождении производных различного порядка от
определяемой этими уравнениями функции. Приняв за функцию
переменную у, а х за независимую переменную, поставим себе за-
дачу найти производные
у', У', у'" и т. д.
или, что то же самое,
dy d2y d3y
dx ’ dx2 ’ dx$
и т. д.
Нахождение этих производных ведется следующим образом.
Найдем дифференциалы dx и dy из системы уравнений (7)
dx = <?' (х) dt (8)
dy = (o' (х) dt (9)
и разделим второе из полученных уравнений на первое; тогда и
§ 99] ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ 235
получаем значение первой производной
, d v io' (f)
У dx «р' (0 ’
Для нахождения у" заметим, что
X = Cy')' = g.
Поэтому находим сначала дифференциал dyr из уравнения (10),
а затем делим полученное выражение на dx, определяемое уравне-
нием (8).
Из уравнения (10), которое для краткости запишем так:
(10)
находим
dy' = F' (/) dt,
а потому
У — '
Тем же путем находим и у'", представив ее так:
У dx ’
(11)
а также и все следующие производные.
отсюда
Пример 1. Найти у' и у" от функции у, заданной параметрически урав-
нениями
х = a cos t
у = a sin t.
Дифференцируя эти уравнения, находим
dx = — a sin t di
dy = a cos t dt,
, dy cost
dx sin t s
Для нахождения производной второго порядка замечаем, как указано выше,
что
У'=^.
dx
(12)
Поэтому определяем сначала из уравнения (12)
dy' =
s sin2t
а затем уже
// dt . . у ..у 1
у" = vr;: (— а sin tdt) -------r-n.
sin21 4 ’ a sin3 Г
236 РАЗВИТИЕ ТЕХНИКИ ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ [XVII
Пример 2. Найти уг и у" из параметрической формы уравнений цик-
лоиды
х = a (t — sin t)
у = а (1 — cos /).
Дифференцируя, получаем
dx = а (1 — cos t) dt
dy = a sin t;
отсюда
Далее ищем производную второго порядка
Уравнение (13) дает
. , (1 — cos t) cos/ — sin2/ cos/—1 1
dy' ®=------77—------------dt = 7=-------X dt = — --------- dt,
J (1 — cos /)2 (1 — COS /)2 1 — cos t
а потому
y a(l —cos/)2’
§ 100. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется производной второго, третьего и т. д. порядка от
функции /(х)?
2. Что называется дифференциалом второго и высшего порядка от функ-
ции /(х)?
3. Как выражаются дифференциалы высшего порядка через производные?
4. Как выражаются производные высшего порядка через дифферен-
циалы?
5. Что означают символы f (a), f" (л), . . . , /^(л) и как их вычи-
слить, если заданы функция /(х) и число а?
6. Как найти производные неявной функции, заданной уравнением
f (*> У) = о?
7. Какое правило дифференцирования лежит в основе приема нахожде-
ния производной неявной функции?
8. В чем заключается параметрическая форма задания функции?
9. Как от параметрической формы перейти к обыкновенной форме
задания функции?
10. Какой геометрический сйысл имеет параметр t в уравнениях круга',
циклоиды?
11. Как ищутся производные от функций, заданных параметрически?
12. у = х5 — Зх2 + 1, найти у"'. 13. у = х sin 2х, найти у". 14. у = е~х\ найти у'". Отв. у'" = Отв, у" = Отв, у'" = : 60x2. 4 cos 2х — 4х sin 2х. 4хе-®’ (3—2%2).
15. у = arc sin —_L_= , найти у". 16. у = tg2 х, найти у". dniR X)” — 2х
Отв, у” = /Эта - (х24-1)2- 2 (14-2 sin2 х) СОЗ* X 1 —2х2
17. у = arctg Ух2 — 1, наитиу". 1 1ft —— _________ плйтп Отв. у" = X2 • У(х2—1)3 e-2a.+e2a>_6
е-х+еЯ!’
§ 100]
ВОПРОСЫ И УПРАЖНЕНИЯ
237
19. f (х) = , найти f" (0). Отв. f" (0) = — 2.
Отв. f" (0) = - 2.
Отв. /"(2) = -^.
Отв. f'" (-U = 4.
20. f (х) = х • е * найти /" (0).
21. /(х) = In (1—х2), найти/" (2).
22. / (ж) = arc tg 2х, найти•
23. Дано уравнение х2 — 2у2 + 1 = 0, найти у' и у”.
Отв.у'=-£~, у"=-±-
2у’ 4у3
24.
25.
26.
Дано уравнение у4 — 4у + х = 0, найти уг и у".
Отв. У = 4 (1 _ , У' = 16 (1
Дано уравнение lnj4-j = x, найти .у' и/.
=41^=(Г^.
3Х2 _J_ у2
Дано уравнение (а — х)_у2 == найти Отв. у1 = ‘^(а — х} у '
27. Исключить параметр t из уравнений х = У — bigt.
X2 V2
28. Исключить параметр t из уравнений х
За/2
“1+/з-
ЗаГ
- 1
Отв. х3 — Зйху+,у3 = 0.
29. Выяснить геометрический смысл параметра t в уравнении эллипса
х = a cos /, у = b sin t. Отв. t= / QOP (см. рис. 64).
30. Найти уг и у" из уравнений х = /2, у = I3.
Отв. у =|о" = А.
31. Найти у' и у" из уравнений х = , у = b tg t.
• Отв. у1 = —, у" = —etg31.
_ a swat J а2
32. Найти уг и уп из уравнений х = а (/-}*- sin t), у = а (1 + cos t).
, sin t ,, 1
тв' ~ 14-cos/,-^“ а (1+ cos Г)2*
33. Гармоническое колебательное движение определяется формулой
s = А • sin 2тс Найти скорость и ускорение движения в момент, равный
1 4Ля2
-^-периода колебания.' Отв. 0,------.
XVIIL СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ
ИХ ПРОИЗВОДНЫХ
Введенное в анализ понятие о производной нередко позволяет
весьма сложные свойства функций обнаруживать при помощи сравни-
тельно несложного исследования ее производных. Таким образом,
открывается путь для приложения дифференциального исчисления
к анализу. Это приложение к анализу основывается на нескольких
фундаментальных теоремах: теореме Ролля и формулах (теоремах)
Лагранжа и Коши.
§ 101. ТЕОРЕМА РОЛЛЯ
Если функция f(x) имеет производную для всех значений х
в промежутке [af Z>] и f (a)=f (b), то внутри того же проме-
жутка найдется, по крайней мере, одно значение х = с такое,
что /' (с) = 0.
Прежде всего заметим, что раз / (х) имеет производную, то / (х)
непрерывна. Это следует из самого определения производной
ч .. f(x + h)—f(x)
/' (х) = lim '—EL-1*
Действительно, числитель f(x-\-h)—f(x) должен быть беско-
нечно малым при бесконечно малом • h, иначе не могло бы суще-
ствовать предела, т. е. производной, а это и означает, что /(х)
непрерывна (см. § 87).
Приняв в соображение, что f (х) непрерывна в промежутке [а,
и что по условию
/(«)=/(*),
можем сделать два заключения:
1) / (х) сохраняет одно и то же значение не только на концах
промежутка, а вообще не меняется на протяжении всего промежутка,
т. е. оказывается постоянной величиной. Тогда f (х) = 0 для всякого
значения х между а и Ь, и теорема доказана: с — любое число
между а и Ь.
I 2) / (х) изменяется на протяжении промежутка [а, Ь]. Так как
на границах значения функции равны между собою, то /(х), не-
§ 1011
1’ЕОРЁМА РОЛЛЯ
239
прерывно изменяясь на протяжении промежутка и возвращаясь
к своему прежнему значению, должна хотя бы однажды достигнуть
где-нибудь в этом промежутке самого большого значения или самого
малого (см. свойство 3-е непрерывных функций). Пусть это будет
при х = с, и именно, предположим, что /(с) наибольшее значение
функции. Тогда составим два отношения:
f(c + h)-f(c) и
------h----- и
(мы будем предполагать, что h > 0).
Оба эти отношения при стремлении h к нулю имеют общий
предел, равный f (с) (по определению производной); при этом первое
отношение, как сейчас ’выясним, не может быть положительным,
а второе не может быть отрицательным.
Действительно, так как / (с) по условию есть наибольшее значение
функции в рассматриваемом промежутке, то
и /(czt*)—/(с)<0.
Таким образом в обоих составленных нами отношениях числи-
тели меньше или равны нулю, и так как их знаменатели разных
знаков, то и заключаем, что пер-
вое отношение не может быть
положительным, а второе отри-
цательным.
Общим же пределом таких
величин может быть только нуль,
так что
/'(*)== О-
Таким образом, теорема до-
казана и во втором предположе-
нии,, т. е. вообще.
Теорема Ролля весьма наглядно поясняется геометрически. В самом
деле, пусть рис. 121 изображает кривую, уравнение которой у =f(x),
и пусть
О A —a AD=f(a)
OB = b BE=f(b).
По условию f (a) (Ь). Рисунок ясно показывает, что между
точками D и Е на кривой существует точка F, в которой касатель-
ная FT параллельна оси ОХ, т. е. такая точка, в которой тангенс
угла, составленного касательной с осью ОХ, равен нулю, а потому
в этой точке производная равна нулю.
Полагая ОС=с, имеем, следовательно, /' (с) = 0.
240 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [XVIII
В случае, если функция для какого-нибудь значения аргумента
в промежутке от а до b не имеет производной, то теорема Ролля
может и не иметь места, как это легко
видно из чертежа (рис. 122).
Действительно, при х = О А — а и
х = ОВ = b значения функции равны
между собой. Тем не менее, на этом
промежутке на кривой нет точки,
в которой касательная была бы парал-
лельна оси ОХ, т. е. нет такого значе-
ния х = с, чтобы /'(с) = 0. Это про-
исходит по той причине, что в этом
промежутке функция / (х) не везде
имеет производную. Действительно,
в точке N касательная NT перпендикулярна к оси ОХ, тангенс угла,
составленного ею с осью ОХ, равен оо, следовательно, и значение
производной в этой точке тоже равно оо, т. е. не существует.
§ 102. ФОРМУЛА (ТЕОРЕМА) ЛАГРАНЖА
Если функция имеет производную для всех значений f (х) в про-
межутке [а, Ь}, то внутри того же промежутка найдется по
крайней мере одно такое число с, что
f(b)-f(a) = (b-a)f'(c). (*)
Теорема, очевидно, будет доказана, если нам удастся показать,
что
Обозначив буквою Р отношение
b — а ’
т. е. положив
=р> (1)
b — а 9 ' 7
рассмотрим новую вспомогательную функцию
<Р (*) =/(*)—/(а) — (X — а) Р.
Функция эта имеет производную
?'(х) =/'(*)-Р (2)
для всех значений х в промежутке [а, 6], так как этим свойством
по условию обладает /(х). Кроме того,
<р (а) = 0,
§ 102] ФОРМУЛА (ТЕОРЕМА) ЛАГРАНЖА 241
что очевидно, и
? (Ь) = о,
так как
р /W-/W
b — а
Таким образом, по отношению к функции ср (х) выполняются все
условия теоремы Ролля, а потому между а и b существует такое
значение х = с, что ср' (f) = 0.
Подставляя х=с в равенство (2), находим
/'(c) —р = 0,
т. е.
/'(С) = Р.
Поэтому равенство (1) обращается в
f(b}b~T
f(J>) —f («) = (£ — «)/' (с),
что и доказывает справедливость формулы. (
•Формулу Лагранжа можно также пояснить геометрически. Пусть
PQ кривая, уравнение которой
y=f(x),
и пусть О А = а и ОВ = Ь, тогда
ЛР=/(а), BQ=f(b)
и
RQ=f(b)—f(a}.
Из чертежа видно, что
b — a •
С другой стороны, из того же
тежа следует, что между точками
Q на кривой можно найти такую
будет ' параллельна хорде PQ. Пусть абсцисса этой точки будет
х = с, тогда
tg*=/'(c).
Р и
точку М, в которой касательная
(3')
Сопоставляя равенства (3) и (3'), приходим к формуле Лагранжа
Таким образом, формула Лагранжа утверждает, что между точками
Р и Q кривой найдется некоторая точка, в которой касательная
параллельна хорде PQ.
Формула (*) называется формулой конечных приращений.
16 Зак. 2116. Н. С. Михельсон.
242 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [xViit
§ 103. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ
Одним из существенных вопросов, возникающих при изучении
какой-нибудь функции, является задача — проследить изменение функ-
ции в связи с изменением независимой переменной, т. е. определить,
растут ли значения функции /(х) с возрастанием независимой пере-
менной х или уменьшаются, а также составить представление (говоря
образно) о скорости * такого изменения. Все эти вопросы находят
разрешение в изучении производных исследуемых функций.
Будем говорить, что функция f(x) возрастает в промежутке
[а, Ь], если каждому большему значению х, взятому в этом про-
межутке, соответствует бблыиее значение функции*, наоборот,
/(х) убывает в промежутке [а, Ь\, если большему значению х
соответствует меньшее значение функции.
Так, sinx возрастает в промежутке [—yj и убывает в про-
Г те Зте 1 х гл
межутке -у ь cosx убывает в промежутке [0, те] и возрастает
в промежутке [те, 2те].
Решение вопроса о том, возрастает или убывает функция в дан-
ном промежутке, основывается на следующих двух теоремах.
Теорема. Если для всех значений х в промежутке [а, Ь]
f (х) > 0, то функция f (х) возрастает в этом промежутке*, если
же f (х) < 0, то f (х) убывает.
Доказательство вытекает из формулы Лагранжа.
Пусть х^ и х2 два какие угодно значения из промежутка [а, Ь],
причем для определенности пусть х2>хх. Тогда по формуле Ла-
гранжа имеем
/ (*2) —/(*1) = (Х2 — *l)f' (С),
где с заключено между xt и х2. •
Рассматривая правую часть этого равенства, замечаем, что ее
первый множитель х2 — хх>0 по условию; что касается второго,
то если:
1) /'(х)>0 для всех значений х в промежутке [а, Ь], то, сле-
довательно, и f (f) > 0 и все произведение
(х2 — Х!)/'(с)>0;
а потому /(х2)—/(*])> 0 или /(х2)>/(х1), т. е. большему зна-
чению х соответствует большее значение функции; следовательно,
/(х) возрастает;
2) если f (х) < 0 для всех значений х в промежутке [а, Ь}, то
/(с)<0 и, стало быть, /(х2)—/(х1) < 0, т. е. f (х) убывает.
Обратная теорема. Если /(х) возрастает в промежутке
[а, Ь], то /'(х)>0 для значений х в этом промежутке*, если
f(x) убывает в промежутке [а, £], то /'(х)<0 для зна-
§ 103]
ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ
243
нений х в этом промежутке (при отдельных значениях х в обоих
случаях /' (х) может быть и равна нулю).
Доказательство следует из определения самой производной:
Л-» о п
Предполагая /г>0, имеем в случае, если / (х) возрастает,
а тогда и все отношение, стоящее под знаком предела, положи-
тельное; поэтому и предел его, вообще говоря, положителен, т. е.
/'(х)>0 (для отдельных значений может случиться /'(х) = 0).
Случай, когда / (х) убывает, доказывается таким же образом.
Обе теоремы находят себе полное отражение при графическом
изображении функции, для чего следует только вспомнить геоме-
трическое значение производ-
ной, а именно, что производ-
ная равна тангенсу угла, со-
ставленного касательной с
осью ОХ.
В самом деле, пусть кривая
KL изображает изменение неко-
торой функции /(х). Рис. 124 "о
ясно показывает, что пока
касательные к кривой состав-
ляют с осью ОХ углы острые,
т. е. пока /' (х) > 0, функция ;
КМ). Но как только производная /' (х) делается отрицательной,
функция из возрастающей делается убывающей (см. часть кривой ML).
Так же ясно рисунок поясняет и обратную теорему. На Промежутке
КМ функция возрастает; вместе с тем во всех точках кривой на
этом промежутке касательные составляют с осью ОХ острые углы,
а поэтому для этих точек /'(х)>0, и только для точки М, в ко-
торой касательная параллельна оси, /' (х) = 0.
Пример. Проследить ход изменения функции f (х) = х2 — 4х-|-3.
Составив производную
/'(х) = 2х- 4 = 2(х — 2),
видим, что
пока х < 2, /' (х) < 0 и, следовательно, / (х) убывает;
пока х > 2, f (х) > 0 и, следовательно, f (х) возрастает.
После этого уже нетрудно для большей наглядности графи-
чески изобразить ход изменения функции
/(х) = х2 — 4х + 3.
16*
244 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [xvill
Действительно, построив сначала точку М (2, —1), мы замечаем,
что в этой именно точке функция f (х) от убывания переходит к воз-
растанию. Поэтому изменение функции сразу уже можно представить
примерно той кривой, которая изображена на чертеже. Для более точ-
ного изображения кривой следовало бы построить еще и другие
точки, но характер изменения функции определенно выясняется и без
построения этих дополнительных точек: точки кривой понижаются
до точки Л4, после чего кривая идет кверху (в сторону возрастания
ординат). Кривая эта, как известно, —
парабола (см. стр. 129). На рис. 125 О А = 2.
Что касается суждения о так назы-
ваемой скорости изменения функции, то
она определяется абсолютным значением
самой производной. Действительно, вели-
чина производной, как известно, опре-
деляет угол наклона касательной к оси
ОХ. Чем она больше по абсолютному
своему значению, тем ближе к прямому
этот угол, и тем быстрее идет измене-
ние функции — ее возрастание или убы-
вание. Следовательно-, по абсолютному
значению производной /' (х) при различных значениях х мы и
можем судить о сравнительной величине скорости изменения функ-
ции /(х).
Так, в приведенном выше примере
f (х) = 2х — 4.
Вычисляя значения производной при х=0 и х=1, находим
f (0) = —4, /' (1) = — 2, т. е. /ДО) по абсолютной величине
больше /' (1). Следовательно, вблизи значения х = 0 функция / (х)
убывает быстрее, чем вблизи значения х=1. И вообще, в проме-
жутке от — оо до 2, т. е. в левой части кривой до точки М,
убывание идет тем медленнее, чем ближе подвигаемся к точке Ж,
а в части кривой вправо от точки М функция /(х) возрастает
и притом тем быстрее, чем дальше отходим от точки М, т. е.
чем больше становится само х.
§ 104. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
Мы видели, что если функция / (х) в некотором промежутке
[а, Ь] все время возрастает, то f' (х) > 0 для значений х, лежащих
в этом промежутке, а если / (х) в промежутке [а, все время
убывает, то /' (х) < 0 для значений х в этом промежутке.
Но может случиться, что / (х) в промежутке [а, сначала
возрастает до некоторого значения х = с, после которого функция
начинает убывать, или, наоборот, сначала убывает, а затем начи-
§ 104] МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 245
нает возрастать. Этот случай указывает нам на возможность суще-
ствования таких значений /(х), которые по сравнению с соседними
значениями той же функции будут наибольшими или наименьшими.
Первые из них называются максимальными значениями функции f (х),
вторые — минимальными. Отыскание таких значений функции во
mhoRix случаях является весьма важным.
Из определения следует, что
f (с) является максимумом функции f(x), если
in. е. если
/(с + А)_/(с)<0
для всякого достаточно малого положительного или отрицатель-
ного значения h\
/(с) является минимумом функции f(x), если
т. е. если
— f(c) >0
для всякого достаточно малого положительного или отрицатель-
ного значения h.
Мы будем сначала рассматривать только такие функции, кото-
рые в изучаемом промежутке [а, &] сами непрерывны и имеют не-
прерывные же производные. Тогда, обращаясь к рисунку, нетрудно
пояснить геометрически понятие макси-
мумов и минимумов функции. Пусть
кривая изображает рассматри-
ваемую функцию f (х) и пусть
ОР1 = С1
ОР2 = с2 P2M2=f(c2)
OP3=Cs P3M3=f(c^
Из рисунка видно, что на пути от К рис 126.
до А41 функция /(х) все время воз-
растает, затем начинает убывать. Это убывание продолжается до
точки Л42, после чего функция становится снова возрастающей.
Следовательно, значение f(c^ есть максимум, а значение /(£2)
минимум функции /(х).
Разыскание максимумов и минимумов функции f (х) основы-
вается на том, что при переходе через максимум функция f (х) из
возрастающей делается убывающей, а при переходе через минимум,
наоборот, из убывающей становится возрастающей. В том и другом
случае производная /' (х) должна непременно менять свой знак.
Таким образом, мы приходим к следующему заключению: для того,
чтобы функция f(x) имела при некотором значении аргумента
х -_- с максимум или минимум. необходимо, чтобы f (х) меняла
246 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [XVIII
свой знак при переходе аргумента через это значение, т. е. чтобы
значения
f'(c — е) И f (с 4-е)
были разных знаков.
Условие это вместе с тем является и достаточным, так как
изменение знака производной указывает на то, что /(х) из возра-
стающей делается убывающей или наоборот, т. е. имеет максимум
или минимум.
Итак, для того, чтобы функция /(х) имела при некотором
значении аргумента х = с максимум или минимум, необходимо
и достаточно, чтобы f'(x) меняла свой знак при переходе аргу-
мента через это значение.
При этом, если изменение знака производной происходит от
-]- к —, то функция /(х) имеет в этом месте максимум, а если от
— к +, то минимум. Но так как изменение знака производной
в случае ее непрерывности (а это мы и предполагаем) возможно
только при тех значениях х, при которых производная обращается
в нуль, то только такие значения в данном случае и могут давать
для функции /(х) максимумы и минимумы.
Отсюда непосредственно вытекает следующее правило для на-
хождения максимумов и минимумов функции /(х).
Составляем производную f (х) и, решая уравнение
/'(*) = О,
находим те значения х, которые обращают производную в нуль.
Пусть эти значения, расположенные в порядке возрастания чисел,
будут
с1> ^2’ ^3» •••> сп\
тогда, определяя знаки производной для значений меньших и боль-
ших каждого из чисел такого ряда, узнаем, меняет ли /' (х) знак
при переходе через эти числа. Если f (х) меняет знак и притом
от + к —, то соответствующее значение х = с дает для функции
максимум, т. е.
f (с) есть максимум функции/(х);
на рис. 126 таким значением аргумента служит х — с1 = ОР^
Если изменение знака происходит от — к +, то f (с) — минимум;
на рис. 126 таким значением аргумента служит х = с2 = ОР2.
Если знак у f' (х) не меняется, то соответствующее значение
х = с не дает ни максимума ни минимума функции /(х); на рис. 126
таким значением является х = с3 = ОР3. В самом деле, хотя в точке М3
так же, как и в точках М1 и ЛТ2, касательная параллельна оси ОХ,
т. е. f (х) = 0 в этой точке, но вблизи от нее f (х) не меняет
знака, / (х) остается возрастающей до и после точки Л!3, т. е.
/(с3) не является ни максимумом ни минимумом функции /(х).
§ 104] МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
247
Пример 1. Найти максимум и минимум
функции
f (х) = х2 — 2х + 3;
составив производную
/,(х) = 2х-2 = 2(х-1),
видим, что
/'W<0,
мы видим сразу, что единственное значение,
обращающее ее в нуль, есть х = 1. Испыты-
ваем это значение, исследуя знак f (х) до и
после значения х = 1. Мы
для значений х < 1
для значений х > 1
меняет знак от
Следовательно, f (х)
к +, а потому заданная функция / (х) имеет
минимум при х = 1.
Этот минимум равен /(1) = 2.
Графически этот минимум представляется
Рассматриваемая кривая — парабола, и точка ее вершина.
на рис. 127 в точке Afj (1, 2).
У
м
1ОаЦ
АМ-2
Рис. 128.
Пример 2. Найти максимум и минимум функции
/(х) = 8x3 — 12x2 + 6*4-1.
Составляем производную от f (х)
/' (х) = 24x2 _ 24х + 6 = 6 (4х2 — 4х + 1) = 6 (2х — 1 )2
/'(*) = 0 при х=у.
При этом, так как f (х) есть точный квадрат, то при
всех других значениях х Р (х) > 0, т. е. не меняет
знака, а потому данная функция не имеет ни макси-
мума, ни минимума.
Ход функции около этой точки изображен на
рис. 128. В точке Aff-i-, 2^ касательная параллельна
оси ОХ, так как j = 0, и в то же время оца пересекает кривую, так
как функция /(х) все время возрастает.
Пример 3. Найти максимум и минимум функции
/(х) = (х-1)2(х + 2)з.
Составляем производную
/'(х) = 2 (х — 1) (х 4~ 2)3 4* 3 (х — I)2 (х 4-2)2 = (х — 1) (х 4~2)2 (5х 4~ !)•
Производная обращается в нуль при трех значениях х;
х=1,'х = — 2, х = —0,2.
Все^эти три значения подлежат исследованию.
248 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [XVIII
Так как функция и се производная непрерывны, то поступаем как ука-
зано, а именно, располагаем исследуемые значения х в возрастающем
порядке и определяем знаки производной для значений х больших и мень-
ших тех, которые подлежат исследованию. Для удобства составим при этом
таблицу:
Значения х -3 —9 — 1 —0,2 0 1 2
Значения /' (х) + 0 + 0 — 0 +
Значения f (х) 0 8,4 0
ни макс, ни мин. макс. мин.
Из таблицы мы видим, что производная /' (х):
1) Вблизи значения аргумента х — —2 знака не меняет, оставаясь поло-
жительной, следовательно /(х) около этого значения все время возрастает и
при х = —2 не имеет ни максимума, ни мини-
мума.
2) Вблизи значения аргумента х = —0,2 ме-
няет знак с положительного на отрицательный,
следовательно f (х) при х = —0,2 имеет максимум,
который и равен /(—0,2) = 8,4;
3) Вблизи значения аргумента х = 1 /' (х)
меняет знак с отрицательного на положитель-
ный, следовательно /(х) при х = 1 имеет мини-
мум, который равен /(1) = 0.
Рис. 129 изображает ход рассмотренной
функции.
Пример 4. Каковы должны быть начальные
концентрации а и b двух веществ, чтобы ско-
рость бимолекулярной реакции была бы наиболь-
шей при условии, что а + b = с = const ?
По закону Вильгельми скорость v реакции
пропорциональна произведению масс нс вступив-
ших в реакцию веществ; так что
v = k (а — tn)(b — tn) = k(a — т) (с — а — т),
где т количество вещества, вступившего в реакцию к моменту времени t.
Для нахождения максимума V, имеем:
dv , , п х
— — k (с — 2а).
da
Производная обращается в нуль при а=-^-, причем при значениях
с dv . м . с dv
а<С~^ з >0, а при значениях я > ту < 9,
2 da ' г 2 da '
§ 104] МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 249
п dv (
Производная — меняет свои знак с + на —, следовательно, при а = b =
с
= -g- скорость реакции будет наибольшей.
Пример 5. В треугольник АВС, основание которого ВС = а и высота
AD = h, вписать прямоугольник наибольшей площади.
Обозначим высоту GH искомого прямоугольника EQHK через х\ тогда
из подобия треугольников АНК и АВС следует
НК __ AL
ВС ~ AD
или
НК h — x
а ~ h 1
откуда
Я/е = й(/г~-х) ;
п
пл. EGHK=aX(h~X}-.
Максимум этой площади и требуется отыскать. Очевидно, максимум ее будет
совпадать с максимумом функции
f(x) = x(h — х),
так как остальные множители — постоянные числа. Поэтому ищем произ-
водную
f (х) = h — 2х.
Затем, решая уравнение h — 2х = 0, находим
< h
Х~ 2 •
Для значений х < /' (х) > 0
Для значений х > fr (х) < 0.
Итак, р (х) меняет знак от плюса к минусу; следовательно f (х) будет
h
иметь максимум при х= -%.
При этом же з-начении х = и площадь прямоугольника, вписанного
в данный треугольник, будет наибольшая. Таким образом, для решения за-
дачи надо провести прямую НК так, чтобы она делила высоту, а следова-
тельно, и стороны АВ и АС, ионолам. Максимум площади
— ah
—=т-
Площадь такого прямоугольника, как видно из последней формулы, со-
ставляет половину площади" треугольника.
Пример 6. При каком соотношении сопротивлений во внешней и вну-
тренней цепи гальванического элемента мощность тока во внешней цепи
будет наибольшей?
250 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [XVIII
Предположим, что мы имеем гальванический элемент с внутренним со-
противлением г.
Предложенная задача заключается в подборе такого сопротивления внеш-
ней цепи, чтобы мощность тока была наибольшей. Известно, что мощность
тока на данном участке цепи выражается произведением падения напряже-
ния и силы тока. Поэтому, обозначив через Р и U соответственно мощность
тока и падение напряжения во внешней цепи, а через I силу тока, имеем
P=UL
Согласно закону Ома для внешней цепи
u = i-r,
так что
P = R*P.
По закону Ома для всей цепи
/ = —____
r + R’
где Е — электродвижущая сила элемента. Поэтому
n R-&
(r+W
Максимум величины Р как функции от аргумента R и требуется найти.
Удобнее, однако, искать минимум обратной величины -—р- (постоянный
Л\
множитель В2 можно отбросить):
d Г (г + Я)21 2/? (г + 7?) — (г-|-7?)2 __ (г +/?) (27? — г —/?) _
dR[ R J- 7?2 “ 7?2
__(/?+ г) (/? —г) •
7?2
Приравнивая производную нулю и решая получаемое таким образом урав-
нение, находим, что
7?= г
(решение R = — г отбрасывается).
Найденная производная меняет свой знак при значениях R смежных с г,
т. е. при значениях R = r — е и 7? == г + е* от минуса к плюсу; следовательно,
при R = r
(r + R)*
-—— имеет минимум,
а потому при R — г мощность тока Р во внешней цепи будет наибольшая.
Другой способ решения задачи на нахождение
максимума и минимума /(х).
Как видно из всего предыдущего, решение задачи на нахождение
максимума и минимума состоит из двух частей:
1) из нахождения тех значений аргумента х, при которых про-
изводная /' (х) обращается в нуль, т, е. решения уравнения
/'W = 0;
§ 104] МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
251
2) из исследования знака производной f (х) для значений аргу-
мента смежных с найденными.
В случае, когда не только сама функция /(х) и ее производ-
ная /'(х) оказываются непрерывными при исследуемых значениях х,
но когда непрерывной оказывается и производная второго по-
рядка f" (х), вторая часть этого решения может быть заменена
определением знака f" (х) непосредственно при тех значениях аргу-
мента, при которых f (х) = 0, что иногда оказывается проще. Этот
прием основан на следующем рассуждении.
Положим, что то значение аргумента, при котором /' (х) = 0,
будет равно с. Тогда:
1) если при этом значении производная второго порядка меньше
нуля, т. е. если f" (с) < 0, то она меньше нуля и вблизи от этого зна-
чения х = с (см. свойство непрерывных функций, § 88), а потому /' (х)
около значения х = с убывает и, переходя через нулевое значение,
она несомненно меняет свой знак с на — ; поэтому функция /(х)
при х = с имеет максимум;
2) если f" (с) > 0, то тем же рассуждением убедимся, что /' (х)
возрастает в окрестности значения х = с, а следовательно, переходя
через нулевое значение, она меняет свой знак с — на т. е. функ-
ция f (х) при х —с имеет минимум;
3) если же f" (с) = 0, то в этом случае вопрос остается еще
открытым; рассмотрение второй производной определенного ответа
нам тогда не дает.
Таким образом мы приходим к следующему новому правилу
решения задачи на максимум и минимум функции при условии не-
прерывности /(х), /'(х) и f" (х):
1) Составляем производную f (х).
2) Ищем те значения х = с, при которых f (х) = 0.
3) Составляем производную второго порядка f" (х).
4) Вычисляем f" (с).
Тогда, если f"(c)<Z®, то f(c)—максимум функции /(х),
если f" (с) > 0, то f (с)—минимум функции /(х),
если fr (с) = 0, вопрос остается нерешенным.
Пример 7. Найти максимум и минимум
/(х) = х3 + Зх2 — 24х — 20.
1. Ищем /' (х) = Зх2 + 6х - 24 = 3 (х2 + 2х — 8).
2. Решаем уравнение x2-f-2x — 8 = 0; х = 2 и х = — 4, т. е. = 2,
с2 = — 4.
3. Составляем /" (х) = 3 (2х 4- 2).
4. Вычисляем f" (2) и f" (—4) (достаточно определить лишь знак):
f" (2) >0, следовательно, /(2) = — 48 (минимум),
/"(—4) < 0, следовательно, f (—4) = 60 (максимум).
Пример 8. Доказать, что закон преломления света при прохождении
луча из одной оптической среды в другую определяет следующее физи-
ческое явление: луч света, выйдя из точки одной среды и преломившись при
252
СВОЙСТВА ФУНКЦИЙ в связи со
СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ
[XVIII
переходе в другую среду, достигает точки В другой среды в кратчайшее
время.
Предположим, что две среды I
от другой линией MN, и пусть луч
Рис. 131.
II, оптически разные, разделены одна
со скоростью vlt а во второй со ско-
ростью v2. Путь АС в первой среде луч
пройдет за время
t
а путь СВ во второй среде — за время
t -св
Всего для прохождения луча света от
точки А до В будет затрачено времени
. J . АС . СВ
t = Л +Ь =---------.
и 1
света распространяется в первой среде
со скоростью vlt а во второй со ско-
ростью v2. Путь АС в первой среде луч
Обозначим дл. ED = I, дл. AD = hx,
дл. BE = /z2- Эти величины можно считать заданными, так как положение точек
А и В задано.
Поставим себе задачу определить, каково должно быть направление
луча АС, чтобы он, выйдя из точки А, достиг точки В в кратчайшее время.
Обозначим для этого дл. CD = х.
Из £\ACD и ВСЕ имеем
дл. АС = Vх2 4- Л2, дл. ВС = V(а — х)3 Л2.
Поэтому
dt
Для нахождения минимума времени t ищем
dt _ 1 х 1 а — х
Но
х jui.CD . а — х дл. п
+ ^-АС ]/(а-х)2+й2 дл'СВ
Поэтому
Приравнивая производную нулю, находим, что должно выполняться
условие;
1 . 1 • G П sin а
— Sill а------Sin? —О пли -=-= = —. (4)
Щ V» Г Sin ₽ Vo v 7
§ 104] МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
253
Нетрудно показать с помощью рассмотрения производной второго по-
рядка, что при этом условии (4) для величины t получается минимум. В са-
мом деле, составляя производную второго порядка, имеем
dx* Щ * х2 + h2
- угг-гуу^. + i—f ,
1 _____________ V (а — -4- hr,
(а—х)-'4-Л^
_ J___________________ j_____________________________
rf-v- “ щ Л*) . /77^ + ’ [(« -.V)- + V(а -х)3+й3 ’
Так как все величины, входящие в последнее выражение, всегда поло-
d4 _ v
жительные, то >0, а потому найденное условие (4) дает минимум для t.
Итак, мы нашли, что при выполнении условия (4) время, затрачиваемое
лучом света при прохождении им пути от точки А до В, оказывается мини-
мумом.
Условие (4) является выражением известного из физики закона пре-
ломления света, что и требовалось установить.
До сих пор мы рассматривали задачу на нахождение максимума
и минимума функции /(х) при условии, что /(х) и f (х), а в по-
следнем случае даже и f" (х), являются непрерывными при рассма-
триваемых значениях аргумента х. При этом было установлено, что
необходимым и достаточным условием для того, чтобы /(с) было
максимумом или минимумом функции /(х), является изменение
знака f (х) в окрестности значения х = с; отсюда и вытекало,
что /'(х) должна обращаться в нуль при х = с. Между тем, пере-
мена знака производной может происходить не только в момент
обращения ее в нуль, но также и при разрыве производной.
Поэтому, для полного решения задачи на максимум и минимум
необходимо подвергнуть исследованию не только те значения
аргумента, при которых f (х) обращается в нуль, но также
и те, при которых она терпит разрыв непрерывности. Таким
образом, ограничение, поставленное раньше, о непрерывности /' (х)
должно отпасть.
Пример 9. Найти максимум и минимум функции
Составляем
/(х) = (2х — 5)Угх2 = 2х3 —5х3.
-1) =
10 (аг— 1)
3 • угх~
/' (*) =
12
3
2В4 ЙВОЙС^вА ФУНКЦИЙ в СВЯЗЙ СО СВОЙСТВАМИ их производных [xvlii
Рассматривая эту производную, мы видим, что она обращается в нуль
при х = 1 и терпит разрыв непрерывности при х = 0. Оба эти значения под-
лежат исследованию в отношении того, меняет ли f (х) знак в окрестности
значений х = 1 и х = 0.
Исследуем значение х = Г, для этого опреде-
лим знак f (х) для значений х, близких к единице.
f (1 — е) < 0, так как числитель < 0, а зна-
менатель >0.
(1+е) >0, так как и числитель и знаме-
натель >0.
Итак fr (х) меняет знак с — на 4" в окрест-
ности значения х= 1, а потому /(1) = — 3 есть
минимум функции f(x).
Исследуем, таким же образом, значение х = 0:
/'(О — е)>0, так как и числитель и знаме-
натель <Р,
fr (0 + е) < 0» так как числитель < 0, а зна-
менатель >0.
Итак fr (х) в окрестности значения х = 0 ме-
няет знак с 4- на —, а потому У(0) = 0 есть
максимум функции/(х/
На рис. 132 представлен график этой функ-
ции. В точке М, для которой fr (х) = 0, касательная параллельна оси ОХ,
в точке О, для которой /' (х) = оо, касательная перпендикулярна к оси ОХ.
§ 105. ФОРМУЛА КОШИ
Если функции f(x) и <р(х) имеют производные при всех зна-
чениях х в промежутке [а, Ь} и ©' (х) не обращается в нуль
ни для одного значения х в этом промежутке, то в том же
промежутке существует значение х = с такое, что
fW)-f(a) = f'(c)
Обозначив буквою Р отношение
?(&) — ? (л) ’
т. е. положив
<? (О — ? (^) ’
рассмотрим новую функцию
F (х) =/(х) —/(а) — [© (х) — <о (а)] • Р.
По отношению к этой функции выполняются все условия теоремы
Ролля. В самом деле, F (х) имеет производную
(*) =/' (*) — W • Р
для всех значений х в промежутке \а, Ь], так как этим свойством
обладают обе функции /(х) и © (х).
(5)
(6)
(7)
§ 106] ОБЩИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПРЕДЕЛЛ О'ГЙОШЁЙЙЙ . . .
С2М
Кроме того F(a) = 0, что сразу видно из равенства (7), и
F(£) = 0, что легко вытекает из того же равенства (7), приняв во
внимание, что Р определяется равенством (6).
Применяя теорему Ролля к функции F(x), заключаем, что F'(х)
обращается в нуль для значения х = с, лежащего между а и Ь,
а потому должно иметь место равенство
/'W —< (f)-P = 0.
Отсюда,
f(c)
(О
разделяя на ср' (г), которое ф 0 по условию, найдем
. Подставляя это значение Р в равенство (6), приходим
к формуле Коши:
Р =
? (О — ? (я) / (О *
§ 106. ОБЩИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ОТНОШЕНИЯ
ДВУХ БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО
БОЛЬШИХ ВЕЛИЧИН
При рассмотрении различных вопросов и при решении задач мы
часто наталкивались на такого рода функции, которые при некото-
ром значении аргумента не имели частного значения, тогда как
предел функций при стремлении аргумента к своему значению
все же существовал. Так, например, такая функция, как
sin х
х
не имеет частного значения при х = 0, так как она при таком зна-
чении аргумента принимает форму -у, тогда как
<. sin х .
lim------= 1.
х
tg*
tg Зх
Точно так же функция
7t
* = -g-, принимая в этом случае
не имеет частного значения при
форму —, тогда как
tgx t. sinx-cos3x .. sinx
lim = lim------------г-5- = lim .-5—
tg Зх я cos x • sin 3x sin 3x
I
2
.. cos Зх
• hm ------—
_ COS X
. ,. cos3x
= — 1 • lim ------
cosx
= — lim
cos3 x — 3 cos x • sinI 2 x
COS X
2
2
= — lim (cos2 x — 3 sin2 x) — 3
256 ' Свойства функций в Связи Со свойствами их производных [xvin
Чтобы лучше уяснить суть вопроса, к изложению которого мы
переходим, рассмотрим детальнее приведенную выше в качестве
, sin х
примера функцию ——.
Вычерчивая ее график, нетрудно убедиться,- что она предста-
вится в виде кривой, изображенной на рис. 133. Кривая распро-
страняется в обе стороны от оси OY бесчисленным множеством
волн; при беспредельном увеличении абсолютного значения х кри-
вая беспредельно приближается к оси ОЛ', а с приближением х
к 0 стремится к единице. Рисунок ясно показывает, что наша
функция непрерывна при всех значениях х, кроме х = 0, и терпит
разрыв непрерывности при х = 0 только потому, что при этом
значении х она не имеет частного значения. Принимая же во вни-
.. sinx ,
мание, что lim -----=1, представляется совершенно естественным
□?-> о х
восполнить недостающее частное значение этой функции при х = 0,
условившись считать это значение равным предельному значению
функции. Этим условием мы устраняем разрыв непрерывности рас-
Схматриваемой функции при х = 0 и делаем ее непрерывной при всех
значениях аргумента.
Такого рода соображение удобно распространить и на другие
подобные случаи. Ввиду этого устанавливают следующее.
В случае, если некоторая функция F (х), не имея частного зна-
чения при некотором значении х = а, в то же время стремится
к определенному пределу с приближением х к а, то за частное
значение функции F (х) при х = а принимают предел, к которому
она стремится при приближении х к а, т. е. полагают
F(a)= lim F(x).
а
Восстановленное таким путем частное значение функции при-
нято называть истинным значением функции при х = а. Задача
определения истинного значения функции при х = а представляет
собой, таким образом, обычную задачу определения предела функции
при стремлении х к а. 1
1 Задачу эту называют еще „раскрытием неопределенности".
§ 106]
ОБЩИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ОТНОШЕНИЯ . . .
257
Мы рассмотрим два случая этой задачи:
1. Когда частное значение функции при х — а принимает
Л- О
форму у.
2. Когда частное значение функции при х = а принимает
. со
форму —.
В этих случаях задача нахождения истинного значения функции
сводится к нахождению предела отношения в первом случае двух
бесконечно малых, а во втором двух бесконечно больших величин.
В отдельных частных случаях подобные задачи решались некото-
рыми специальными приемами, но широкий метод решения этих
задач дает только дифференциальное исчисление. Метод этот изве-
стен под названием правила Лопиталя.
Случай I. Форма
fix}
Положим, нам требуется найти истинное значение дроби
форму q"« Согласно изложенному выше,
принимающей при х = а
требуется найти
lim
х -> а ? (•*)
основывается на применении формулы
/(х) и ср(х) необходимо наложить усло-
когда f (а) == ср (а) = 0.
Решение этой задачи
Коши; поэтому на функции
вия, требуемые этой теоремой. А именно, подразумевая под х не-
которое значение аргумента, близкое к а, положим, что функции
/(х) и ср (х) имеют производные для всех значений аргумента, за-
ключенных между х и а, и что ср' (х) не обращается в нуль ни для
одного из этих значений. Тогда мы имеем право воспользоваться
формулой Коши
/(х)-/(а)
?(*) — ? (я) /(О’
где с лежит между а и х.
Так как по условию / (а) = ср (а) = 0, то предыдущая формула
упрощается и принимает вид:
/(х)
? (*) “ / (О ’
Отсюда следует, что
,imm.
р -> а У ('*’) аз -> а (^)
Но при стремлении х к я, с стремится тоже к а, следовательно
.. f(x) .. f' (с) r f' (х)
hm ^-4 = lim , / = lim z-;.
C^a^(c) Х^ач'(х)
17 Зак. 2116. H. С. Михельсон.
258 СВОЙСТВА 'функций в связи со свойствами ИХ ПРОИЗВОДНЫХ [XVI11
(8)
Итак, мы приходим к следующему результату:
lim 44 = lim Ш
т. е. истинное значение отношения двух функций, принимающего
при х = а форму равно истинному значению отношения их
производных.
Правило Лопиталя распространяется и на случай отыскания
lim 44,
В->«ЛМ’
если /(оо) = <р(оо) = 0.
Действительно, положив в этом случае х = —, имеем
lim 77^1= Ит -
? -> оо ? W у -> о jp
У2
lim-----1----
— Д-.'У
v2 f
— lim —
lim 4/4
?->оо9 (*^)
Пример 1. Найти lim sin х .
Ж->0 х
sinx n cos х 1
hm ----= Urn —:— = I,
что нам было известно и раньше.
хт> — а™
Пример 2. Найти lim —------— .
х-+ахП~аП
xm—am ..
hm —----— = hm
xn__an
x-+a x->c
т ап,_п
ПХ™"1 п
rr о tt о 1, x — sinx
Пример 3. Наити lim --------—
'ft -x П -X
x — sinx 1f 1 — cosx
Um ----5 = lim —x-x—
,-^n -r3 ^-^0 3*2
„ л < О
Последнее отношение при значении х = 0 опять принимает форму -у,
поэтому продолжаем применение правила Лопиталя
.. 1—cos х „ sinx 1
®-»0 3x ®->0 6x 6
I
§ 106] ОБЩИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ОТНОШЕНИЯ . . .
259
Случай II. Форма —.
Требуется найти истинное значение дроби 'ЦЦ, принимающей
? (Л)
при х — а форму —, т. е. требуется найти
когда
и lim . Дока-
v + a't'ix)
/(a) = ср (a) = ею.
Правило Лопиталя, как будет показано, распространяется и на
этот случай.
Положим, что существуют пределы lim
х -> а (А/
жем, что эти пределы равны между собой.
Пусть lim = А и А ф. 0.
(9)
Представим рассматриваемое отношение так:
1
fix) _ 4ix)
<? <х) 1 '
fix)
. О
Форму
Тогда оно при х = а принимает
можно применить правило Лопиталя:
1
lim = lim = lim —f/. .
а;-»о 1 ®->a f ix)
fix) f*(x)
= lim ИтЗЖГ
аг->д/ ? (-^) x-^af La
а потому к нему
4’jx)
Ф8 (*)
В силу условия (9) предыдущее равенство можно представить
так:
A=^J$-AS-
Сокращая на А, что мы имеем право делать, так как по усло-
вию А ф 0, находим:
1 = lim X А или lim = А.
x+af ix) х^аЧЧх)
17*
260 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ (хуш
Следовательно, в случае, если А ф 0,
1- f(x) г f'(x)
lim = lim ~
®-»а?(-У^ а (х)
Правило, однако, остается в силе и для случая, когда
lim == 0.
Для доказательства этого достаточно рассмотреть выражение
/(у) ± j ^/(у)±?(у)
? (х) ~ <Р (у?
/ * /(у)
(знак плюс выбирается в случае, когда при х -> а отношение
остается положительным; знак минус — в противоположном случае);
это выражение попрежнему при х-+а принимает форму —, но пре-
дел его уже не нуль, а единица, так как по предположению
lim = 0.
Поэтому, с одной стороны (по правилу Лопиталя),
f (х)±?(х) )im f'(x)±^r(x) _
a 'e'W
lim ------
v+a ?(*)
= lim
=
х -> а ? О*)
а с другой стороны,
lim /(<>±4(4 = цт [Ш±11= Птф1±1.
ф(-У) a?-»aLcH'v) J аз-»а?(х)
Сравнивая последние два результата, заключаем, что
1- /(у) к /'(у)
hm -7— = lim ;.
В более полных курсах математического анализа доказывается^
что как в этом, так и в предыдущем случаях из существования
второго предела следует существование первого.
Пример 4. Найти lim \П х-.
®->o^gx
1
1ПХ 1} X
lim —----= lim —=-------
®-> о ctS х о *
— sin2x
n sin2x 14 sin х .
= — lim-------= — lim--------lim sin x = 0.
§ 107]
ВОПРОСЫ И УПРАЖНЕНИЯ
261
Пример 5. Найти lim
х ->я
In sin Зх
In sin х
lim = Um _3cos3x.sinx =
In Sin x x->n sin Зх • cos x
n„3cos3x lt sinx o cosx
lim-------- . Um . у = 3 • lim 5-o— =
x -> л cos x g sin Зх x—^ к cos 3x
1.
§ 107. ВОПРОСЫ И УПРАЖНЕНИЯ
1. В чем состоит теорема Ролля?
2. Как пишется формула Лагранжа?
3. В каком случае говорят, что функция возрастает в данном проме-
жутке или что она убывает в данном промежутке?
4. Как по производной функции судят о возрастании или убывании
самой функции?
5. Какое значение функции называется максимумом и какое минимумом?
6. Какое условие является необходимым и достаточным, чтобы функция
имела максимум или минимум при рассматриваемом значении аргумента?
7. Среди каких значений переменной можно искать те, при которых
функция имеет максимум или мунимум?
8. Достаточно ли для существования максимума или минимума функ-
ции /(х), чтобы fr (х) обращалась в нуль или терпела разрыв непрерыв-
ности?
9. Как ищут максимумы и минимумы функции по первой производной?
10. Как ищут максимумы и минимумы с помощью первой и второй
производной?
11. Какой вид имеет кривая вблизи точки /И, если в этой точке произ-
водная обращается в нуль, но знака своего не меняет?
12. Как пишется формула Коши?
13. Что называется истинным значением функции, принимающей при
» v . 0 оо _
частных значениях независимой переменной форму — или — ?
14. В чем состоит правило Лопиталя для нахождения истинных значе-
„ , , 0 оо _
нии функции, принимающих форму или — ?
15. Проверить теорему Ролля на примере функции /(х) = х2—1, поль-
зуясь тем, что для нее /(— 1) = /(1).
16. Проверить теорему Ролля на примере функции /(х) = sin х, поль-
зуясь тем, что для нее /(0) = /(тс).
17. Проверить теорему Ролля на примере функции /(х) = х2— 3x4-5,
пользуясь тем, что для нее /(1) = /(2).
18. Проверить формулу Лагранжа на примере функции /(х)=х2—Зх-|-5,
определив значение х = с, при котором формула оправдывается.
Проследить возрастание и убывание функций:
19. /(х) = 2x2—12x4-5.
Отв. Убывает при х < 3, возрастает при х>3.
20. /(х) = —х3. Отв. Все время возрастает.
21. /(х) = 2х3 — Зх2+ 1 Отв. От —оо до 0 возрастает,
от 0 до 1 убывает,
от 1 до со возрастает.
262 СВОЙСТВА ФУНКЦИЙ В СВЯЗИ СО СВОЙСТВАМИ ИХ ПРОИЗВОДНЫХ [XVIII
22. По закону Бойля-Мариотта, = const, объемы газов убывают с воз-
растанием давления. Согласуется ли это заключение с выводом, получае-
мым на основании рассмотрения производной?
Найти максимумы и минимумы функций:
23. f(x) = 4х3 — Зх2 — 6х + 2. Отв. Минимум при х = 1,
1
максимум при х = — ту.
24. f (х) = 1 — sin х. Отв. Максимум при х = — у + 2£я,
минимум При X=^-\-2kTCt
25. f (х) = х3 — 6x2 + 12х — 8.
Отв. Функция не имеет ни максимума ни минимума.
/ 1 \2
26. f (х) = (Зх — у x2J . Отв. f (0) = 0 минимум,
81
/(3) = — максимум,
f (6) = 0 минимум.
27. f (х) = 24x5 — 15x4 __ 20х3 + 3.
(1 \
—2*) = ^16 (максимУм)»
f (0) = 3 (ни максимум, ни минимум).
28. Какой прямоугольник будет иметь наибольшую площадь при дан-
ном периметре? Отв. Квадрат.
29. Какой из прямоугольных треугольников, имеющих постоянную сумму
катетов, имеет наименьшую гипотенузу? Отв. Равнобедренный.
30. Путь, пройденный материальной точкой, брошенной вертикально
вверх с начальной скоростью t/0, выражается следующей формулой:
S = — +
Определить высоту наибольшего подъема.
„ vo
Отв.
31. Скорость распространения волны, длина которой X, в глубокой воде
пропорциональна
где а постоянная величина. Показать, что скорость достигает минимума
при X = л,
32. Показать, что из всех треугольников данного периметра 2р, кото-
рые можно построить на одном и том же основании, наибольшую площадь
имеет равнобедренный.
33. Из круглого бревна диаметра d надо вырезать для вертикального
столба балку, одинакового по всей длине прямоугольного сечения. Зная, что
сопротивление на сжатие пропорционально площади сечения, определить^
§ 107]
ВОПРОСЫ И УПРАЖНЕНИЯ
263
каковы должны быть стороны прямоугольного сечения, чтобы сопротивление
на сжатие было наибольшим. Отв. Сечение квадратное.
Найти пределы следующих выражений:
34. Hm х3 4-х2 —5x4-3 a,Ti*8-4x24-5x-2> Отв. — 4.
85. „ sin х — х 11m . ® -» о X — tgX In 1 -р— X) 11m ~7~ 7- Отв. 1 2 ’
36. Отв. 0.
:r->T tg(2x — yj
Найти истинные значения следующих выражений:
37 g2a,~1 ’ In (14-х) при х = 0. Отв. 2.
in fl 4- 38. —— arc ctg х ’ при X = оо. Отв. 1.
sin х — х cos х при х = 0. Отв. -j
wln(l—е^) при х = 0. Отв. 0.
ctg х
XIX. О КАСАТЕЛЬНЫХ К КРИВЫМ
§ 108. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ
Мы видели (§ 91), что вопрос о проведении касательной
к кривой, уравнение которой y=f(x), сводится к определению
тангенса угла а, составленного касательной с осью ОХ, и что
. v f(x + h)— f(x)
tg a = lim ——!—£—.
n->o n
Так как вышенаписанный предел и есть производная от функции
f(x), то имеем
tg «=/'(*)•
(1)
Итак, тангенс угла, составленного с осью ОХ касательной в не-
которой точке кривой y=f(x), или, иначе, угловой коэффи-
циент касательной в некоторой
точке кривой, есть значение про-
изводной f (х) для этой точки.
Эта чрезвычайно важная фор-
мула (1) характеризует геометри-
ческое значение производной.
В частных случаях:
1) когда ff (х) = 0 для не-
которого значения х — а, тогда
tg а = 0, а = 0, и касательная в
этой точке параллельна оси ОХ
(на рисунке АТ),
2) когда /'(х) для некоторого
значения х = а перестает суще-
ствовать, обращаясь z±i оо, то тогда а = , и касательная в этой
точке параллельна оси OY (на рисунке ВТ).
3) когда f (х) >0, то tg а > 0 и а < у, т. е.: угол, составляемый
касательною с осью ОХ, острый (на рисунке СТ).
4) когда /(х)<0, то tga<0 и a>j, т. е.: угол, состав-
ляемый касательною с осью ОХ, тупой (на рисунке DT).
§ 108]
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ
265
Пример 1. Возьмем параболу, определяемую уравнением
и поставим себе задачу провести касательную к ней в точке Л4, для кото
рой х = 2.
Здесь / (х) =х2, следовательно,
ff (х) = х, tg а для искомой касательной
есть, как выше сказано, значение про-
изводной для х = 2, поэтому
tga =/'(2) = 2.
Под таким углом к оси ОХ и сле-
дует провести прямую через точку М,
чтобы она была касательной к данной
параболе. Для этого откладываем
PN = у РМ
влево от точки Р и проводим прямую NT через точки N и М Тогда
NP '
tga =
к гиперболе ху = 6, в точке М, для
которой х = 3.
Из уравнения гиперболы нахо-
дим
Составляем производную
и вычисляем tga для данной точки:
tga=/'(3) = —1-= -у-
Так как tga<0, то очевидно угол а тупой. Для построения касательной
отложим отрезок
Q
вправо от Р и соединим М с N. Прямая NT и будет касательной в точке М,
266
О КАСАТЕЛЬНЫХ К КРИВЫМ
[XIX
§ 109. УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ
Пусть д/=/(х) уравнение рассматриваемой кривой. Предложим
себе вывести уравнение касательной к этой кривой в некоторой ее
точке М (х, у).
В этом вопросе под х и у будем подразумевать координаты
только точки касания. Для переменных координат различных точек
касательной МТ возьмем обозначение большими буквами
X и К,
тогда уравнение касательной МТ, как прямой, проходящей через
данную точку М(х, у), будет
Y—у = а(Х— х),
где а — угловой коэффициент касательной. Но согласно формуле (1)
предыдущего параграфа
a = tg а =/'(*)•
Поэтому окончательно уравнение касательной выглядит так:
пишется так:
Y—y—f'(x)(X—x)
или
Y—y—y'(X—x). (2)
Прямая, проведенная через точку
касания М перпендикулярно к каса-
тельной, называется нормалью к кри-
вой в точке М.
Уравнение ее составляется как урав-
нение прямой, проходящей через дан-
ную точку М перпендикулярно к каса-
тельной. Угловой коэффициент нормали
. Таким образом, уравнение нормали на-
Y-y=-jr(X-x).
(3)
Длина отрезка КМ касательной до пересечения его с осью ОХ
называется длиною касательной, его проекция КР на ось ОХ назы-
вается подкасательной.
Длина отрезка ML нормали до пересечения ее с осью ОХ назы-
вается длиною нормали, его проекция PL на ось ОХ—поднормалью.
Величины отрезков подкасательной и поднормали могут быть
найдены весьма просто из треугольников PLM и РКМ. Так как
то
РМ=у и ДЛИ£ = а,
W==J'ctga=^--^? = y-. (4)
PL=ytgv<=yy\ (5)
§ 109] УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ 267
Из тех же треугольников нетрудно вычислить длины касатель-
ной КМ и нормали ML как гипотенузы треугольников, катеты кото-
рых известны:
» = = f VT+7’ (6)
ML = Уу2-\-у2у'2 = у у 1 -1-у'2. (7)
Пример 1. Провести касательную к кривой у = х4— 2х — 1
в точке, абсцисса которой равна 1.
Для решения задачи прежде всего определяем координаты точки
касания. Абсцисса ее дана, поэтому ординату легко находим из
уравнения кривой, полагая в нем х = 1; тогда у = — 2. Итак, точка
касания определена:
Ж(1, — 2).
Далее определяем у' из уравнения кривой
у' = 4х8— 2.
Для рассматриваемой точки касания
у = 2.
Поэтому согласно уравнению (2) находим
F4-2 = 2(X—1)
или, употребляя обычную запись, находим окончательно уравнение
касательной в виде
2х—у — 4 = 0.
2х2__1
Пример 2. Провести касательную к кривой у — —— парал-
лельно прямой х — 4у 4“ 3 = 0.
Угловой коэффициент касательной у' находим из уравнения кри-
вой:
С другой стороны, так как касательная должна быть парал-
лельна прямой х — 4у 3 = 0, то угловой коэффициент ее должен
быть равен . Поэтому для точки касания должно иметь место
равенство
^ = -4 ’
откуда^и находим абсциссу точки касания х = 2.
Далее решение задачи идет по предыдущему. Находим ординату
точки касания
268
О КАСАТЕЛЬНЫХ К КРИВЫМ
[XIX
и так как угловой коэффициент касательной
У=т>
то уравнение касательной получится в виде
7 1
у-Т==7^-2)
или, окончательно,
х— V 4-5 = 0.
§ ПО. КАСАТЕЛЬНАЯ К ПАРАБОЛЕ
Приложим выведенные формулы к параболе
у2 = 2рх.
Для составления касательной к параболе в некоторой ее точке
М (х, у) вычислим ее угловой коэффициент, т. е. у'. Для этого из
уравнения параболы найдем сначала
у = Y 2рх
и затем, дифференцируя, получим
»' = —^= = —L=-P.
2 Y2px Y2px у ‘
Тогда по уравнению (2) уравнение касательной выразится так:
Преобразовывая, найдем
Уу —у2 — рХ—рх
Yy — 2рх = рХ—рх
Yy = р (Х-{-х). (8)
и есть уравнение касатель-
к параболе в любой ее точке
. , У)-
Составим выражения подкасательной и поднормали по формулам (4)
И (5)
У У2 2jox
= —г — — =----------= 2х
У' Р Р
PL = y.y'=y.y = p.
Полученные выражения выясняют интересные свойства параболы
в отношении ее касательной и нормали. Именно: подкасательная
равна удвоенной абсциссе точки касания, а поднормаль к параболе
§ 111]
КАСАТЕЛЬНАЯ К ЭЛЛИПСУ
269
во всех ее точках равна постоянной величине — параметру пара-
болы.
Свойства эти дают возможность легко строить касательные и
нормали к параболе в любой ее точке. Именно, так как дл. КР = 2х,
а ОР = х, то дл. ОК—х. Следовательно, отложив дл. ОК=дл. ОР
и соединив К с Л4, мы и получим касательную к параболе. Для
построения нормали проводим ординату РМ и откладываем в сто-
рону положительного направления оси ОХ отрезок PL = p. Затем
соединяем точку М с L. Линия ML и будет нормалью. Построив
касательную, нормаль можно построить и как перпендикуляр к этой
касательной.
§ 111. КАСАТЕЛЬНАЯ К ЭЛЛИПСУ
Выведем уравнение касательной к эллипсу
— 1
а2 i £2
Для составления производной уг можно было бы, как и в пре-
дыдущей задаче, решить сначала уравнение эллипса относительно д/,
а затем уже искать у'. Однако проще будет найти ту же произ-
водную иначе, путем применения правила дифференцирования неявной
функции. Дифференцируя уравнение эллипса, получаем:
2х . 2у , л
-^г+-#--У = о,
откуда и находим
у=—
а*у
Поэтому уравнение касательной принимает вид:
Преобразовывая, найдем
a?Yy — а2_у2 = — Ь*Хх +
№Хх + a?Yy = д2х2 а?у2.
Разделим все члены уравнения на <z2Z>2:
Хх । Yy х2 , У.
й2 “Г £,2 Я2 “Г J2 >
заменяя правую часть равенства единицей, окончательно получим
4г+-7? = 1- (9)
Составим выражение подкасательной РК по формуле (4)
р» -У_______а2У2 . а2 у2
А У ““ Ь*х х '
270
О касательных к кривым
[XIX
Так как РК есть длина, то для точки М, для которой *>0, сле-
дует знак минус отбросить. Приняв затем в расчет, что
у2 а2 — х2
а? ’
находим
рк= а2~*2-.
Последняя формула показывает,
что для всякого эллипса с одной и
той же полуосью а подкасательные
в точках, имеющих одну и ту же
абсциссу, равны между собою. Сле-
довательно, отрезок РК будет яв-
ляться одновременно и подкасатель-
ной круга радиуса О А = а в точке С.
Отсюда и вытекает способ построения касательной МК к эл-
липсу. Строим круг радиуса а, продолжаем РМ до пересечения
с окружностью в точке С, проводим касательную к кругу в точке С;
этим определим точку К, которую и соединяем с точкой М. По-
следняя прямая и будет касательной к эллипсу.
§ 112. ДИФФЕРЕНЦИАЛ ДУГИ
Рассмотрим некоторую кривую, уравнение которой пусть будет
У =/(*)•
Наметим на этой кривой некоторую определенную точку 7И0, от
которой и будем производить измерение дуг этой кривой (рис. 140).
Выбрав на этой кривой точку
Ж (х, у)
обозначим длину дуги MQM через s.
Совершенно ясно, что длина дуги s
зависит от места точки М на кри-
вой, т. е. зависит от х; следова-
тельно, можно написать
s = F(x).
Если бы сама функция F (х)
была нам известна, то нетрудно
было бы найти от нее производную, а затем и дифференциал. Тем
ds
не менее, как сейчас будет показано, нахождение производной —
и дифференциала ds можно выполнить и не зная вида функции F (х),
руководствуясь лишь определением производной и дифференциала.
§ 112]
ДИФФЕРЕНЦИАЛ ДУГИ
271
Именно, дадим х приращение
bx = PQ,
тогда дуга s получит приращение
As = о MN.
По определению производной
ds «. As
= hm -г— .
^х д®->о
Таким образом, задача сводится к нахождению
Для этого рассмотрим &MNR. В нем
MR = \x, RN=Ny,
хорда MN= ]/Дх24- Ду2.
Как хорда MN, так и дуга MN являются величинами беско-
нечно малыми при бесконечно малом Дх. При этом можно доказать* 1,
что эти величины между собой эквивалентны.
1 Из рис. 140 следует, что
хорда MN < о MN< MS + SN,
хорда MN = V Дх2 + Д.У2,
О MN = As,
MS = V*(A4/?)2 + (/?S)2 = /Дх2 + У2.- Ах2 = f l + У2 • Ах.
SW=a) бесконечно малая высшего порядка, чем Ах (см‘. формулу (21),
§93).
Поэтому вышецаписанные неравенства Дают
УДх2 +Ду2< As< /1 +У2• Дх + ш.
Разделим все члены неравенства на УДх2 + Ду2, тогда получим
I As У 1 4- У'2, • Д-У .____________ш
УДх2 4- AyS у ДХ2 4- Ду у дх2 + Д_у2 ’
Нетрудно доказать, что правая часть этого неравенства стремится к еди-
нице. Действительно,
11™ =
Д£В-> О У Дх2 4- Ду2
пт — - ---
yi+У2
/1 +У2
Нт --------------= 0.
Да?->0 У Дх2 4' Ду2
272
О КАСАТЕЛЬНЫХ К КРИВЫМ
[XIX
Поэтому при нахождении lim т- мы имеем право величину As за-
;____________________ Да? -> о
менить на удха _|_ Ду2. тогда получаем
lim
До? -> О
As
Дх
Um
Да?->0 ^Х
Таким образом, находим
(10)
откуда
ds = /1 -j-y'2 • dx.
(И)
Формула (10) дает искомую производную, а (11) дифференциал
дуги кривой. Последнюю формулу можно написать и в несколько
ином виде, через дифференциалы dx и dy.
ds = 1 * dx = V dx2 + dy2 • (12)
Формула эта дает возможность получить очень простые выра-
жения для косинуса и синуса угла, составленного касательной
с осью ОХ. Действительно, известно, что
(13)
кроме того, известно из тригонометрии, что
Поэтому
cos2 а = 1 .
1 + tg2 а
2 1
cos2 а = -7-j-77
1+У2
. 1
cos а = zt .
/1+У2
Из этого заключаем, что и
As
lim —7=== = 1
До?->0 уДх% -|-
или
дуга МАГ
lim —--------—
да?-> о хорда MN
т. е. бесконечно малая дуга MN и хорда MN величины эквивалентные. (По
поводу более строгого вывода формулы дифференциала дуги см. Смир-
нов В. И. Курс высшей математики, т. I).
tg«=y,
и
273
$ 1131 ВОПРОСЫ И УПРАЖНЕНИЯ
Пользуясь формулой (10), найдем отсюда, что
. dx
cosa = -37
(14)
Для нахождения sin а имеем
, , dy dx , dy
sin a = tg a • cos a==z±z-r---7- = :±-~-.
& dx ds ds
Итак
(15)
§ 113. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какое геометрическое значение имеет производная от данной
функции?
2. Как расположена касательная относительно осей координат, если для
данной точки f' (х) = 0, fr (х) = оо, (х) = 1, f (х) = — 1 ?
3. Как пишется уравнение касательной к кривой в данной точке, и что
означают количества х, у и X, Y, входящие в это уравнение?
4, Как пишется уравнение нормали к кривой в данной на ней точке?
5. Каким свойством обладает парабола в отношении ее касательной?
6. Как построить касательную к параболе в данной на ней точке?
7. Как построить касательную к эллипсу в данной на нем точке?
8. Как найти угловой коэффициент касательной к кривой в данной на
ней точке?
9. Как выражается дифференциал дуги кривой?
10. Известно, что бесконечно малая хорда и приращение дуги, ей со-
ответствующее,— величины эквивалентные. Будут ли эквивалентными та же
хорда и соответствующий ей дифференциал дуги?
11. Как выражается косинус и синус угла, составленного касательной
с осью ОХ?
12. Найти угол, составленный касательной к кривой у = у (см. рис. 31
на стр. 60), в точке, абсцисса которой равна 2. Отв. 122°41,30//.
13. Провести касательную к кривой _у = —-^х3 (см- Рис- 30 на стр. 59)
в точке, абсцисса которой равна —2. Отв. Зх3_у + 4 = 0.
18
14. Провести касательную к кривой у — — (см. рис. 33 на стр. 62)
в точке, ордината которой равна 2.
Отв. 4х-|-3_у—18 = 0 и 4х — 3_у+ 18 = 0.
15. Провести касательные к кривой у = sin х (см. рис. 36 на стр. 63)
тс
в точках, абсциссы которых равны 0, тс.
Отв. у — х = 0, = 1, х = тс.
16. Провести касательную и нормаль к кривой ху — х3—1 = 0 в точке,
абсцисса которой равна 1. Отв. х—j/4-1=0, х-\-у — 3 = 0.
18 Зак. 2116. Н. С. Михельсон.
274
О КАСАТЕЛЬНЫХ К КРИВЫМ
[XIX
17. Найти длины поднормали и подкасательной к кривой _y=cos2x,
в точке, абсцисса которой равна Отв. , -тр
18. Провести касательную к кривой _у = л1пл параллельно прямой
2х— 2j/-|-3 = 0. Отв. у — х + 1 = 0.
19. Провести касательную к кривой у
через начало координат.
х 4- 9
так, чтобы она прошла
Отв. у х = 0, 25у -j- х = 0.
20. Определить угол, под которым пересекаются кривые у2 = 4х и у = 2л2.
(Под углом между кривыми понимают угол между касательными к ним в их
точке пересечения.) Отв.
XX. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ИЗУЧЕНИЮ СВОЙСТВ КРИВЫХ ЛИНИЙ
§ 114. О НАПРАВЛЕНИИ ВОГНУТОСТИ КРИВЫХ
И О ТОЧКАХ ПЕРЕГИБА
Пусть y=f(x) уравнение некоторой кривой KL (рис. 141.
142, 143). Построим в некоторой точке М этой кривой касатель-
ную МТ. При этом кривая в окрестности точки касания М может
иметь три различных положения относительно касательной МТ:
1) Точки кривой, близкие к М, могут быть расположены по ту
сторону от МТ, куда направлена положительная ось jj-ob (рис. 141);
в этом случае говорят, что кривая в точке М обращена вогнутостью
в сторону положительных у-ов.
2) Точки кривой, близкие к М, могут быть расположены от МТ
в сторону отрицательных jj-ob (рис. 142); в этом случае говорят,
что кривая в точке М обращена вогнутостью в сторону отрица-
тельных у-ов.
3) Может случиться, что в точке касания М касательная пере-
секает кривую так, что точки, соседние с точкою М, одни лежат
по одну сторону, другие по другую от касательной (рис. 143), тогда
говорят, что точка М есть точка перегиба кривой.
Исследование направления вогнутости и положения точек пере-
гиба является весьма существенным в изучении природы кривых
18*
276 ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[XX
линий. Исследование это всецело основано на изучении характера
функции /(х), входящей в уравнение кривой
y=f(x),
в связи с ее производными f (х) и f (х).1
Рассматривая рис. 141, 142 и 143, замечаем, что в окрестности
составленных касательными к кривой
точки М тангенсы? углов,
в первом случае возрастают, во вто-
ром случае убывают, в третьем слу-
чае сначала возрастают, а потом
убывают (мог бы быть и обратный
порядок).
Основываясь на геометрическом
значении производной, именно, что
/' (х) = tg«
(где а — угол, составленный каса-
тельною с осью ОХ), заключаем,
что в окрестности точки М:
в первом случае, т. е. когда кри-
с осью ОХ, с возрастанием х,
Рис. 143.
вая вогнутостью обращена в сторону
положительных j/-ob, f (х) возрастает, а потому f" (х) > 0 (см. обрат-
ную теорему, стр. 242);
во втором случае, когда кривая вогнутостью обращена в сторону
отрицательных j/-ob, f (х) убывает, а потому /" (х) < 0 (см. об-
ратную теорему стр. 242);
в третьем случае, т. е. при перегибе кривой, /' (х) сначала воз-
растает, а потом убывает, или наоборот, а потому f" (х) меняет свой
знак в окрестности точки 714.
Обратные заключения тоже, очевидно, справедливы; именно, если
в окрестности рассматриваемой точки:
f" (х) > 0, то кривая вогнутостью обращена в сторону положи-
тельных _у-ов;
f (х) < 0, то — в сторону отрицательных д/-ов;
/" (х) меняет свой знак, то имеется перегиб в месте перемены
знака.
Действительно, если, например, f" (х) > 0, то в силу прямой
теоремы (стр. 242) о возрастании функции заключаем, что /' (х)
в окрестности рассматриваемой точки возрастает, т. е., иными словами,
tga возрастает, а это значит, что расположение точек кривой,
смежных с точкой М, относительно касательной МТ соответствует
рис. 141; следовательно, кривая в окрестности точки М обращена
вогнутостью в сторону положительного направления оси OY. Подоб-,
1 Производные f (х) и f" (х) будем предполагать непрерывными.
§114] О НАПРАВЛЕНИИ ВОГНУТОСТИ КРИВЫХ И О ТОЧКАХ ПЕРЕГИБА
277
ные же рассуждения приводят нас к заключениям, относящимся и
к двум другим случаям.
Итак, направления вогнутости кривой и существование перегиба
определяются рассмотрением /" (х) соответственно только что выска-
занным условиям. •
То обстоятельство, что в точках перегиба /" (х) должна менять
свой знак, а следовательно должна обращаться в нуль, определяет
и метод нахождения точек перегиба. А именно: для нахождения
точек перегиба кривой, уравнение которой y=f(x), следует:
1) Определить вторую производную.
2) Найти корни второй производной, т. е. решить уравнение
/"(х) = 0. «
3) Исследовать эти корни в том отношении, чтобы узнать,
меняет ли f"(x) свой знак в окрестности корня.
Легко заметить, что задача нахождения точек перегиба равно-
сильна задаче нахождения максимума и минимума только не самой
функции /(х), а ее производной /' (х).
Применим выводы к некоторым примерам.
Пример 1. Исследуем направление вогнутости эллипса
£+£=1.
д2 £2
Соответственно выведенному правилу составляем вторую производную
Ь4
у" =—^^-(см. стр. 231, пример 1).
Рассматривая ее, видим, что у"<0 для всех точек эллипса, для кото-
рых у>0, иу">0 для всех точек эллипса, для которых у <0.
Таким образом, подтверждается, что в части, в которой у >0, эллипс
обращен вогнутостью в сторону отрицательного направления оси ОУ, а в части,
в которой у < 0, в сторону положительного направления оси OY.
Пример 2. Исследовать направление вогнутости параболы у* 2 = 2рх.
Опять составляем вторую производную у"
р2
г" = —(см. стр. 231, пример 2).
Отсюда видим, что у" <0 в точках, для которых у >0 и, следовательно,
в этой части парабола вогнутостью обращена в сторону отрицательного напра-
вления оси OY; у">0 в точках, для которых у <0, поэтому в этой части пара-
бола вогнутостью обращена в сторону положительного направления оси OY.
Пример 3. Исследовать направление вогнутости циклоиды
х = a (t — sin/), у = а (1—cost).
1
Вторая производная у" = — -Jcos t)2 < ПРИ всяком значении *
(см. стр. 236); следовательно, циклоида своей вогнутостью во всех точках
обращена в сторону отрицательного направления оси OY.
278
ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[XX
§ 115. О КРИВИЗНЕ И РАДИУСЕ КРИВИЗНЫ КРИВОЙ
Рассмотрим некоторую кривую KL и на ней некоторые две
точки Л/ и Жр В этих точках проведем касательные МТ и
к нашей кривой и назовем угол, составленный этими касательными,
через со. *
Отношение этого угла со к длине дуги ММг называется средней
кривизной дуги MMlf а предел, к которому стремится средняя кри-
визна дугиг когда точка Mt беспредельно приближается к точке М,
называется кривизной кривой в точке М. Таким образом, если кри-
визну кривой в точке М мы обозначим через k, то по определению
мх->мДл.о MrM v 7
Посмотрим, что даст это определение для окружности, радиус ко-
торой будет /?. Выберем на ней точки М и Mt и проведем каса-
тельные МТ и MtTt, а также радиусы ОМ и OMt (рис. 145).
Очевидно, что
а = (МТ, М1Т1) = £М0М1.
Поэтому
дл. о MMt — 7?о),
а кривизна круга.
£ = lim -----Гл л г = Нт -яг = • (2)
дл. oMMi
и»0 #
Итак, кривизна круга во всех его точках есть величина постоянная
и равна единице, деленной на радиус круга.
Отсюда следует, что чем больше радиус круга, тем меньше его
кривизна, и наоборот. С изменением радиуса круга от 0 до оо,
кривизна его меняется от оо до 0, а стало быть, всегда можно
найти круг, имеющий любую наперед заданную кривизну. Ввиду
этого при изучении кривизны другой кривой (не круга) ставят себе
целью подобрать такой круг, кривизна которого равна кривизне
§115] О КРИВИЗНЕ И РАДИУСЕ КРИВИЗНЫ КРИВОЙ 279
кривой в данной точке. Радиус такого круга называется радиусом
кривизны кривой в данной точке и, таким образом, является вели-
чиной обратной кривизне кривой, т. е.
кривой, пользуясь ее уравне-
дуг кривой ведется от точки 7И0.
или
= lim ДЛ. е> мм, .
На основании только что полученной формулы можно вывести
выражение для радиуса кривиз!
нием
J =/(•*)•
Пусть абсцисса точки Л4 Q
146) будет х, а абсцисса точки
х + Дх; углы
(МТ, ОЛ) = а,
(М^, ОЛ) = а-|-Да.
Тогда очевидно, что
о = z±z Да.
Предположим, что измерение
Соответственно этому обозначим
дл. о М$М = s
дл. о М^МХ = $
тогда
дл. о MMt = Д$.
На основании формулы (3) пишем
R = lim м.иМ1==±
ЛГ,->М *° Да->0Да
НО
.. As ds
hm — = —
д«->оДа da
и так как можно написать очевидное равенство
ds ds е da
На dx * dx9
то
Р __ ! ds । (ds л da\
da = \rfx ’ dx) *
280 ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [XX
Остается найти только выражение для
ds da
-г м т,
dx dx
т. е. производные от s по х и от а по х. Первая из этих произ-
водных была выведена в § 112 (см. формулу (10) стр. 272), именно,
Для определения же примем во внимание, что
tga=y'} т. е. a = arctgj/,
и, дифференцируя а как сложную функцию от х, так как у' зави-
сит от х, находим
da_______________________ 1 „
dx~ 1+У2 'У '
Таким образом, получаем
з
П_ _)_(!+ У2)2 (4)
к — — у"
Знак -j- или — надо выбирать так, чтобы R было положительным.
Пример 1. Парабола у2 = 2рх.
Из-уравнения параболы, как известно, получаем (см. стр. 231).
Поэтому
з
(>2+р2)2
В вершине параболы (х=з/ = 0) радиус кривизны оказывается
наименьшим и именно:
кривизна параболы в этой точке наибольшая.
х2 . V2
Пример 2. Эллипс —4-^=1.
Из уравнения имеем (см. стр. 231)
(fly ’ cfiyb
Поэтому
з
Мх2\ 2 а?_у3________ (64х2 + д4_у2)
а4у2/ * &
§ 116]
ЦЕНТР КРИВИЗНЫ КРИВОЙ
281
В вершинах эллипса (±а, 0)
иметь следующие значения:
и (0, zL b) радиусы кривизны будут
в — Ь*
R±a~T
п **
и /?о = у-
Так как мы предполагаем, что а>£, то и Ro > R±a, т. е. что
кривизна в вершинах, лежащих на большей оси, будет больше
кривизны в вершинах, лежащих на меньшей оси.
§ 116. ЦЕНТР КРИВИЗНЫ КРИВОЙ
Мы видели, что всегда можно подобрать такой круг, кривизна
которого равна кривизне кривой в данной на ней точке. Если рас-
положить этот круг так, чтобы он имел в рассматриваемой точке М
кривой общую с ней касательную, притом чтобы центр круга был
помещен со стороны вогнутости кривой, то получим круг, назы-
ваемый кругом кривизны (пунктирная кривая на рис. 147).
Рис. 147.
Центр этого круга называется центром кривизны кривой в дан-
ной на ней точке М, радиус его, как уже сказано, называется
радиусом кривизны кривой в точке М. Для каждой точки кривой
найдется свой центр кривизны. Геометрическое место центров кри-
визны кривой называется эволютой данной кривой (см. кривую GH
на рис. 148), а сама кривая по отношению к ее эволюте называется
эвольвентой или разверткой.
Интересны взаимные свойства этих кривых, которые мы приве-
дем, не останавливаясь на их доказательстве.
1-е свойство. Касательная к эволюте является нормалью к
эвольвенте'(Л4М— касательная к эволюте GH и в то же время нор-
маль к эвольвенте KL и т. д.).
282 ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [хх
2-е свойство. Разность между длинами нормалей двух каких-
нибудь точек эвольвенты равна соответствующей им дуге эволюты,
т. е.
дл. М^— дл. MN = дл. иОр
Выведем теперь формулы, определяющие координаты центра кри-
визны кривой в данной точке, пользуясь уравнением кривой.
Пусть y — f(x) уравнение кривой, и пусть точка С (рис. 149)
центр кривизны этой кривой в точке Л4, так что СМ — R. Обозна-
Рис. 149.
чим через х и у координаты точки М,
а через а, р координаты точки С.
Последние найдутся из следующих
двух условий:
1) точка С лежит На нормали МС
к кривой, проведенной в точке М,
2) точка С находится от точкИ/214
в расстоянии равном радиусу кривизны
R кривой в точке М.
В силу первого условия коорди-
наты аир точки С должны удовле-
творять уравнению нормали
Y-y = -y(X-x).
Следовательно, должно
выполняться равенство
£ —.у = — у (а — х). (5)
В силу второго условия квадрат расстояния между точками М и С
должен быть равен R2. Следовательно,
(« —х)2 + (р— уУ = &.
(6)
Решая уравнения (5) и (6) совместно относительно разностей
а —х и (3—у, находим
а —х = —(Р—>)/ (7)
(P-j)2-y2+(P-j)2=^2
Ф-У2(1 +У2) = Я2-
3
(1 4- у'2) 2
Но , поэтому
§ 117]
АСИМПТОТЫ КРИВЫХ линий
283
Таким образом получаем
₽-Л = ^-
(8)
Прежде чем находить значение для а — х выясним, что в фор-
муле (8) всегда надо брать знак плюс. Действительно, в случае,
изображенном^ на рис. 149, кривая в точке /И обращена вогнутостью
в сторону отрицательного направления оси OY, следовательно
У' < 0.
Но в этом случае и
₽-У < о,
так что в формуле (8) будет знак плюс.
Если бы кривая в точке М своей вогнутостью была обращена
в сторону , положительного направления оси О Y, то мы имели бы
У > о.
Но тогда р будет больше у, т. е. (3 —у > 0, и для установле-
ния соответствия в формуле (8) опять необходимо удержать знак
плюс.
Таким образом, в обоих случаях имеем
Тогда, из формулы (7) находим
так что
(9)
Последние формулы и решают задачу. ’
Пользуясь уравнением кривой, все элементы у, у' и у" фор-
мул (9) можно выразить через х, и тогда те же уравнения можно
рассматривать как параметрическую форму уравнений эволюты кри-
вой. Параметром тогда явится переменная х.
§ 117. АСИМПТОТЫ КРИВЫХ ЛИНИЙ
В отделе аналитической геометрии мы встретились с кривой, назы-
ваемой гиперболой, ветви которой по мере удаления их в беско-
нечность беспредельно приближались к некоторым прямым. Подобные
прямые называются асимптотами, они встречаются и у других линий.
284
ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [XX
Знание того, что некоторая кривая имеет асимптоты, и умение
находить их значительно содействуют уяснению формы кривой.
I. Нахождение асимптоты, не параллельнойоси OY.
Допустим, что некоторая кри-
вая ^£, уравнение которой
Ж ^) = 0, (10)
имеет асимптоту RRV Это значит,
что расстояние МР любой точки М
кривой (рис. 150) до прямой RR19
по мере беспредельного возрастания
х, стремится к нулю, т. е.
lim МР = 0. /
я?->оо
Вместе с перпендикуляром МР
будет одновременно стремиться к
нулю и отрезок NM — разность
между ординатами точек кривой и прямой RP, имеющими одну и
ту же абсциссу О А, т. е.
lim NM = 0.
а?->со
(11)
Действительно, из треугольника NMP следует
....
NM ~~ sin z MNP ’
а потому
lim NM =
®->оо
lim MP
0?->OO
sin z MNP
0.
Заметив это, мы при отыскании асимптот и будем основываться
на условии (11).
Пусть искомое уравнение асимптоты RRr будет
Y = ах-\-Ь,
где Y означает ординату асимптоты, отличную от ординаты соответ-
ствующей точки кривой, имеющей одну и ту же абсциссу х.
Условие (11) аналитически можно записать так:
lim (j/—У) = 0,
®->оо
откуда выводим, что
у— Y — а,
§ 117] асимптоты кривых линий 285
где а — бесконечно малая величина, или
у == ах-\-Ь-\-а. (12)
Итак,, если кривая имеет асимптоту, то ее уравнение при доста-
точно больших значениях х должно принять форму (12), где а —
бесконечно малая величина при бесконечно большом х.
Пример 1. Найти асимптоту кривой
х2у —- 2х3Зх2-J-1 =0.
Решив это уравнение относительно у, находим
J' = 2x-3-l
Оно очевидно имеет форму (12), так как здесь а = — является беско-
нечно малой величиной при бесконечно большом х. Поэтому имеем право
сразу сказать, что прямая
у = 2х — 3
есть асимптота нашей кривой.
Однако такое непосредственное приведение уравнения кривой (10)
к форме (12) не всегда достигается так просто. Поэтому необходимо
дать и другой способ нахождения асимптоты.
Другой способ состоит в определении в отдельности углового
коэффициента а и начальной ординаты b искомой асимптоты.
1) Для нахождения коэффициента а замечаем, что из уравне-
ния (12) следует, что
а = lim —.
я?->оо х
Действительно, из этого уравнения имеем
X * X
1 • Ь "4“ Л Л
и так как lim —!— = 0, то мы и получаем
я»оо х
а = lim —.
Ш->оо Х
Для более легкого нахождения этого предела полагаем
— = t или у = xt
х л
и подставляя y = xt в уравнение кривой, ищем а как lim t\
®->оо
а = lim Л (13).
0?->ОО
Если предела нет, то нет и асимптоты, а если предел найдется,
тр этот предел и будет угловым коэффициентом асимптоты.
286 ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [ХХ
2) Отыскание начальной ординаты основывается на следующем.
Считая угловой коэффициент уже найденным, мы из уравнения
(12) имеем
b= Ит0/ — ах).
а?->оо
Полагая поэтому при известном уже значении а
у — ax = s, т. е. у = ax-^-s,
и подставляя y = ax-j-s в уравнение кривой, ищем b как lim s:
u?->oo
b= lim s. (14)
oo
Из изложенного вытекает следующее правило для нахождения
асимптоты кривой не параллельной оси OY: 1
Для нахождения углового коэффициента полагаем в уравне-
нии кривой y — xt и ищем lim/; при этом a = \\mt.
я?->оо со
Для нахождения начальной ординаты асимптоты полагаем
в уравнении кривой y = ax-\-s (где а предполагается уже найден-
ным) и ищем lim 5; при этом b = lim s.
Я?->ОО Я?->ОО
Пример 2. Найти асимптоту кривой х3— 3kxy-{-y3 = 0. Следуя пра-
вилу, полагаем в уравнении у = xt
x3 — 3kx*t + x3t3 = 0
и ищем lim А
Я?->00
Для этого делим все члены уравнения на х3, получаем уравнение
1_!^ + <з = о,
X 1
которое при х = оо обращается в
/3 + 1 = 0;
из последнего и находим
t = — 1, т. е. а = — 1.
Остается найти только Ь. Для этого делаем в уравнении кривой сле-
дующую подстановку:
у = ах -\-s = — х + s
(найдено, что а = — 1)
х3 — 3kx (— * + $) + ( — .r + s)3 = 0
и ищем lim s.
0?->ОО
Для этого преобразуем полученное уравнение следующим образом:
х3 + З&х2 — 3kxs — х3 + 3x2s — 3xs2 + s3 = 0
Ы 3s2.s3 n
L Js -5 = 0.
X------------------x x3
117] асимптоты кривых линий 287
При х -> оо последнее уравнение обращается в
3k + 3s = О,
откуда
s = — kt т. е. b = — k.
Итак, асимптотою данной кривой служит прямая
у = — х — k.
Пример 3. Найти асимптоту кривой у == е~х~.
Полагаем у = xt, xt = e~x\ откуда
z>-a?3
.
X
е-х^ 1
lim t = lim---- = lim —= 0*
a?->oo a?-> oo % x-^co^^ x
Поэтому a = 0. Ищем начальную ординату &, полагая у = 0 • х + т. е.
у = st и ищем из уравнения кривой lim s или, что то же, lim у:
х->оо ж->оо
lim у = 0, т. е. b = 0.
я;->оо
Итак, асимптотой этой кривой служит ось ОХ.
II. Нахождение асимптот, параллельных оси OY.
Допустим теперь, чти рассматриваемая кривая имеет асимптоту
параллельную оси OY, и пусть OR = m.
Тогда, следовательно, расстояние МР по
мере беспредельного увеличения у должно
стремиться к нулю. А это значит, что из
уравнения кривой должно следовать, что при
стремлении у к ztoo х должно стремиться
к т, т. е.
limx = /n. (15)
2/->ОО
Уравнение (15) определяет т, а следовательно,
и асимптоту
х — т =
(16)
Если lim х не существует, то нет и асимп-
2/->оо
тоты, параллельной оси OY.
Итак, для нахождения асимптоты, параллельной оси OY, следует
из уравнения кривой найти lim х; при этом и определяется т
у-*со
согласно уравнению (15).
288 ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ (ХХ
Пример 4. Найти асимптоту, параллельную оси OY кривой
—1)--2у3 + 1 =0.
Для нахождения lim х делим все члены уравнения кривой на наивысшую
2/-»оо
степень у, т. е. на j8. Тогда получаем
х(1—-)-2 + -i3 = 0.
\ У/ Уа
При стремлении у к оо уравнение дает
lim х = 2.
Следовательно, у данной кривой имеется асимптота
х — 2 = 0.
/
§ 118. ИССЛЕДОВАНИЕ ФОРМЫ КРИВОЙ ПО ЕЕ УРАВНЕНИЮ
Все изложенное в этом отделе и в §§ 104, 108, 109 дает воз-
можность значительно уяснить себе форму линии и примерно
изобразить ее, если известно уравнение линии. Ограничиваемся иссле-
дованием лишь алгебраических ли-
ний, т. е. линий, заданных алге-
браическим уравнением.
Порядок, в котором удобно
вести такое исследование, может
быть следующий:
1. Исследуем, не будет ли ли-
ния симметричной относительно
осей координат. В случае если она
симметрична относительно оси ОХ,
то изучаем только ту ее часть, для
которой у 0; если линия симме-
трична относительно оси OY, то
изучаем ее лишь для значений
х^0. Если линия симметрична относительно обеих осей, то изучаем
лишь часть ее, заключенную в первом координатном угле, т. е. для
х^? 0 и у^ 0.
2. Рассматривая уравнение, определяем, какие значения можно
давать переменной х, т. е. определяем область существования функ-
ции (см. § 19).
3. Определяем максимумы и минимумы ординаты у. Допустим,
что рассматриваемая кривая имеет один максимум и один минимум.
Отмечая эти значения на плоскости координат, мы находим такие,
например, точки, как А и В, вблизи от которых кривая имеет
форму, примерно указанную на рис. 152, — максимум в точке Л, ми-
нимум ,в В.
§ 1181 ИССЛЕДОВАНИЕ ФОРМЫ КРИВОЙ ПО ЕЕ УРАВНЕНИЮ 289
4. Определяем точки, в которых ордината обращается в нуль’
а также и те, в которых абсцисса обращается в нуль.
Этим мы находим точки
пересечения линии с осью ОХ
и ОУ, на рис. 153, например,
точки С, D и Е.
Для решения этой задачи
надо уметь вычислять корни
алгебраических уравнений раз-
личных степеней.
5. Определяем направление
вогнутости в различных частях
кривой и ищем точки перегиба.
Положим, например, что
точки G и Н являются точка-
ми перегиба (рис. 154). Одно-
временно с этим определяем
направление касательных в этих
точках.
Так как в окрестности точ-
ки перегиба кривая по форме
близка к прямой, то направление
касательной в этих точках точ-
нее, чем во многих других, опре-
деляет направление кривой.
6. Ищем асимптоты кривой,
как не параллельные, так и
параллельные оси OY. Допу-
стим, что исследуемая кривая
имеет асимптоту /?5(рис. 155),
параллельную оси OY. Эту
прямую наносим на чертеже.
7. На основании получен-
ных данных строим самую ли-
нию, соединяя намеченные точки
и принимая во внимание, что
линия RS является асимптотой.
Получается кривая, изобра-
женная на рис. 156, состоящая
из двух ветвей.
Для большей точности по-
лезно наметить еще несколько
Рис. 155.
точек кривой, определяемых для’
некоторых значений х, в данном случае в особенности для значе-
ний х, меньших ОС и больших OQ.
19 Зак. 2116. Н. С. Михельсон.
290
ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[XX
Пример 1. Исследовать линию, заданную уравнением
х2(у 4-2) = 4x4-4.
1. Линия эта не симметрична ни относительно оси ОХ, ни ОУ.
. 2. Абсциссе х можно давать любые значения, за исключением х = О,
при котором не существует значения у.
3. Для нахождения максимума и минимума составляем первую произ-
водную у. Из уравнения имеем
= (17)
При х = — 2 имеем минимум; он равен — 3. Отмечаем эту точкуJaa
рисунке: точка А (—2, —3) (рис. 157).
4. Для нахождения точек пересечения с осью ОХ полагаем в уравнении
(16) у = 0и определяем х
х = 1 ± УЗ.
Таким образом, находим две точки пересечения с осью ОХ
Bi(l + /3, 0); В2(1 —/3, 0).
§ 118] ИССЛЕДОВАНИЕ ФОРМЫ КРИВОЙ ПО ЕЕ УРАВНЕНИЮ 291
Точек пересечения с осью OY кривая не имеет.
5. Для определения направления вогнутости и точек перегиба составляем
вторую производную у"
8(* + 3)
З' х4
При — 3 кривая обращена вогнутостью в сторону отрицательного
направления оси OY.
При — Зв сторону положительного направления оси OY.
При х = — 3 кривая имеет перегиб в точке
с(-3’ -24)-
Направление касательной в точке перегиба определяется из уравнения
(18), которое при х = —3 дает:
, 4 4
У = —“27 или ^а = ——.
Таким образом, в точке перегиба касательная составляет с осью ОХ
угол, близкий к л.
6. Для нахождения асимптоты, не параллельной оси OY, переписываем
уравнение (17) в вице
и замечаем, что при стремлении х к ± оо у стремится к —2, поэтому пря-
мая RS, уравнение которой
У------2,
и будет асимптотой нашей кривой. Она параллельна оси ОХ.
Та же кривая имеет еще одну асимптоту, именно, ось OY. Действительно,
при приближении х к нулю у стремится к бесконечности, что подтвер-
ждает высказанное.
7. Принимая во внимание все вышеизложенное, вычерчиваем кривую
(см. рис. 157). Для большей точности наносим еще несколько’точек, напри-
мер: £>(—1, -2). Е(1, 6).
Пример 2. Исследовать линию, определяемую уравнением у = е~х* (кри-
вая вероятности).
1. Линия эта симметрична относительно оси OYt так как от изменения
знака х ордината не меняет своего значения.
2. Абсциссе можно давать любые значения от — оо до + оо.
3. Для нахождения максимума и минимума функции составляем произ-
водную
у' = — 2х£~"®1.
Корень производной лг = О. Это значение дает максимум ординаты. По-
лучаем точку А (0, 1).
4. С осью ОХ пересечения нет, так как ни при каких значениях х ор-
дината у не может равняться нулю.
5. Ищем точки перегиба:
у” = _ 2г-®3 + (2х2 — 1),
1 лГ2
откуда у" = 0 при х = ± —— — ± ——.
><2 2
19*
292
ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[XX
Легко исследовать, что
У2"
значения: как------, так
кривая имеет перегиб. Это будут точки
у" меняет знак при переходе х через оба этц
4---^2—• Следовательно, при этих значениях х
—>2-. ' ) „ c(_£l, 1 V
2 Ve } \ 2 Ye )
6. Асимптотой у кривой служит ось
увеличении абсолютного значения абсциссы
ОХ, так как при беспредельном
ордината стремится к нулю.
7. Получается кривая, изображенная на рис. 158. Кривая эта носит на-
звание кривой Гаусса. В более общем виде при соответствующих значениях
коэффициентов А и т в уравнении у — Ае~тх^ кривая, определяемая этим
уравнением, характеризует закон распределения случайных ошибок.
§ 119. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Как определить направление вогнутости кривой в данной на ней
точке?
2. Как найти точки перегиба кривой?
3. Какое можно обнаружить сходство между способами нахождения ми-
нимума или максимума функции/(х) и точек перегиба кривой j=/(x)?
4. Что называется кривизной кривой в данной точке?
5. Чему равна кривизна круга?
6. Что такое радиус кривизны кривой в данной точке?
7. Что называется кругом кривизны кривой в данной точке?
8. Что называется центром кривизны кривой в данной точке?
9. Что называется эволютой кривой и какая кривая называется эволь-
вентой или разверткой по отношению к другой кривой?
10. Что называется асимптотой кривой?
11. Как ищется асимптота кривой, не параллельная оси ОУ?
12. Пределом каких выражений являются угловой коэффициент и началь-
ная ордината асимптоты, не параллельной оси ОУ?
13. Как ищется асимптота, параллельная оси ОХ?
14. Определить направление вогнутости кривой у ---^х2 (см. рис. 30,
стр. 59). Отв» При х<0в сторону положительного направления
оси ОУ. При х>0 в сторону отрицательного направления
оси ОУ.
Отв-
Отв. 7? = 3.
Отв. у = х 4- 2 и х = 0.
Отв. у = 1 и х = 0.
Отв. х — 1 = 0 и у = 0.
Отв. у — х = 0, у = 0, х = 0.
§ 119] ВОПРОСЫ И УПРАЖНЕНИЯ 293
15. Определить направление вогнутости кривой у = ах (см. стр. 62).
Отв. В сторону положительного направления оси OY.
16. Определить направление вогнутости кривой _y = lgx (см. стр. 62).
Отв. В сторону отрицательного направления оси OY.
17. Определить направление вогнутости и точку перегиба кривой у =
== х3 — Зх2 4- 1 •
Отв. При х<1 в сторону отрицательного направления оси OY.
При х>1 в сторону положительного направления оси OY.
При х = 1 точка перегиба.
18. Определить направление вогнутости кривой, заданной уравнениями
х = a cos31 и у = a sin3t.
Отв. При 0 < в сторону положительного напра-
вления оси OY. При тс < t < 2л в сторону отрицательного на-
правления оси OY.
Найти радиусы кривизны кривых:
19. у = х3 — 2х24- 1 в точке х=1. Отв. /?= /2.
20. у= sinx в точках наибольшего удаления от оси ОХ. Отв. R = 1.
18 * rvr*
21. у = — (см. стр. 62) в точке х = 3.
22. _у3 4- х2у — 8 = 0 в точке х = 0.
Найти асимптоты кривых:
23. х2— ху 4-2x4- 1 = 0.
24. хЦу— 1) = х — 2.
25. ху = 1 4-у.
26. х_у2—j/x24-l = 0.
Исследовать и вычертить кривые, определяемые уравнениями:
27. = х4 — 2х2 4-3.
Отв. Кривая симметрична относительно оси OY; при
х = 0 имеет максимум, при х = ± 1 минимум; при х =
. У'з ,
= zt —3---точки перегиба.
28. у = 12x5 — 45х4 4- 40х3 4- 1.
Отв. При х^= 1 максимум, при х = 2 минимум, при х = 0
9± /17
и х =-----------точки перегиба.
29. = х3 — х2.
Отв. Точка (0, 0) — отдельная точка (уединенная точка);
кривая расположена симметрично относительно оси ОХ, в
сторону положительного направления оси ОХ от точки (1, 0);
/4 4/3\ /4 . 4/Т\ .
точки J и ,----------у— J — точки перегиба.
30. х2у = 4х —у.
Отв. Минимум при_х=_—-1, максимум при х = 1; точки
перегиба: (0, 0), (/3, /3), (— /Т, —/3); асимптота
у = 0.
31. V2(14-x2) —2х = 0.
Отв. Кривая симметрична относительно оси ОХ*, распо-
ложена в той части плоскости координат, для которой х >• 0;
максимум при х = Г, у = 1; минимум при х = 1, у = — 1;
. 54-2/7
точек перегиба две при х = — г; в точке х =у = 0
и
касательной служит ось OY-. ось ОХ служит асимпто-
той.
294 ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [хх
ол 1 —х 32-->"1+х=- Отв. При х = 1 — V? максимум х = 1 -|- У2 минимум При х = — 1 х = 2 — j/TT точки перегиба. х = 2+ /3
33. Найти минимум радиуса кривизны кривой у = In х.
Отв. При х = —у- .
34. Найти максимум кривизны параболы.
Отв. В вершине параболы.
VXI. ПЕРВООБРАЗНАЯ^, ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ
§ 120. ОСНОВНОЕ ПОНЯТИЕ О НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Задача дифференцирования функции дает основание обратной
задаче: по данной производной или дифференциалу некоторой не-
известной функции найти самую функцию, т. е. найти
F(x),
зная, что
И(*)=/М
или что (1)
dF(x)=/(x)dx.
Действие, имеющее целью решить этот вопрос, носит название:
интегрирование функции f(x) и обозначается следующим симво-
лом:
ff(x)dx.
Искомая функция F (х) называется первообразной по отношению
к данной f (х), ее интегралом, или интегралом дифференциала
f(x)dx,
что и обозначают таким образом:
J f(x)dx = F(x).
Итак, первообразной функцией по отношению к данной функции
/(*) называется такая функция F (х), производная которой равна
данной функции /(х), или дифференциал которой равен f(x)dx
(см. равенства (1)).
Пусть, например, F (х) = х3, тогда F' (х) = Зх9, или dF (х)=3х9 dx,
поэтому обратно
j* Зх2 dx = х3.
296 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХ1
Очевидно, что если
J/(x)rfx = F(x),
ТО И
ff(x)dx = F(x) + C, (2)
где С—произвольное постоянное число. Действительно,
[F(x) + C]' = F(x)=/(x).
Таким образом, интеграл всякой функции имеет бесчисленное
множество значений, отличающихся между собой на произвольную
постоянную величину. /
Примеры:
J cos х dx = sin х С
J е2® dx = -|e2® + C
/^-„1п(1 + х) + С.
В правильности написанных результатов убеждаемся путем
дифференцирования. Действительно,
(sin х)' = cos х, (^е2х) = ^е2х *2 = е2х, [In (1
Примером, где подобное, обратное дифференцированию, действие
может понадобиться, могут служить хотя бы следующие две задачи.
Задача 1. Какая линия обладает таким свойством,
что угловой коэффициент касательной в каждой
ее точке равен абсциссе этой точки?
Известно, что если уравнение кривой выражается в виде
У=/(х),
то угловой коэффициент а касательной к ней равен производной от
/(•*), Т. е.
a=f(x)=y'.
По условию задачи в каждой точке искомой кривой
У = х,
такое уравнение устанавливает, следовательно, связь между произ-
водной неизвестной нам функции у и самим х. Задача же требует
нахождения этой неизвестной функции, т. е. нахождения непосред-
ственной зависимости у от х. Это и приводит к интегрированию.
Действительно, если
У = х,
то отсюда находим, что
Г , х2 . п
у = J xdx = -^--\- С,
в справедливости чего убеждаемся простой проверкой.
§ 120J
ОСНОВНОЕ ПОНЯТИЕ О НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
297
изображены пунктиром..
Кривая, определяемая этим уравнением, есть, как известно, пара-
бола, осью которой служит ось OY с параметром, равным единице. Дей-
ствительно, из уравнения получим
х2 = 2у—2С
или
x2 = 2j + CP
На рисунке изображены пара-
болы, обладающие рассматривае-
мым свойством.
Постоянная входящая в урав-
нение кривой, остается неопреде-
ленною, что показывает, что пред-
ложенной задаче отвечает бесчис-
ленное множество парабол, отлича-
ющихся лишь положением вершины.
На рис. 159 сплошной линией
изображена парабола, для кото-
рой = 0, несколько других п:
Задача II. Точка движется по прямой линии со ско-
ростью, возрастающей пропорционально времени.
Определить величину пути, проходимого точкой
в некоторый промежуток времени.
Известно, что если обозначить путь, проходимый точкой, через s,
скорость через 5, а время через t, то скорость движения выра-
жается производной пути по времени, т. е.
По условию задачи
v = kt,
где k — коэффициент пропорциональности.
Поэтому мы имеем такое равенство
Равенство это устанавливает связь между пройденным точкою
путем и временем, однако, связь эта еще не является непосредст-
венным выражением s через t, а только связью между t и производ-
ной от s по /. Зная это, нетрудно получить и искомое выражение s
через £ Именно, переходя от производной к первообразной функции,
т. е. интегрируя, находим
s= J с.
298 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ХХ(
В некоторый момент / = пройденный путь был
В некоторый другой момент t=t^ пройденный путь был
kt\
S2 = — • С-
Следовательно, за промежуток времени /2— пройденный
<5ыл равен
путь
52 — ^2 (h £)•
§ 12Ь ОБЩИЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ’ФУНКЦИЙ
Интегрирование функций, как действие обратное дифференцм-
рованию, черпает свои формулы и приемы из соответствующих
формул и приемов дифференциального исчисления.
Так, всякая формула дифференциального исчисления
dF (х) = /(х) dx
дает соответственную формулу^интегрального исчисления:
J/(x)^x=F(x)4-C.
На этом основании имеем следующую таблицу основных формул:
С Jfm + 1
' ,Г"‘&=-ж+т+с-
/хм+1\
так как d — xmdx (при пф— 1).
2- J^ = lOx+C, так как dIn (последняя формула
дополняет предыдущую для случая, когда ш = — 1);
так как dsinjx = cosxidx;
так как d (— cos х) = sin х dx;
dx
так как dtgx = -j^;
так как rf(— ctgx) =
7. I dx „ _ arc sin x 4- C = — arc cos x -f- C;
'• J /1^ T r-
так как d arc sin|x = d(— arc cos x) = _;
cosxdx = sinx
4. J sin x dx = — cos x C,
» +-c.
« f7Err=-C<g*+C,
§ 121]
ОБЩИЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
299
8‘ J= arcJgх+ С= — arc ctg*+ С,
так как d arc tgx — d(— arcctgx) =
f ax / ax \
9. \ ax dx =т—-4- С, так как d[r—) = axdx;
j in a 1 \in a J ’
10* J ex dx = ex-j-С, так как dex = exdx;
И. j" A-f (x) dx = A f(x)dx, так как d(A • J/(x)rfx)™
= Af(x) dx;
Примеры:
1. = x^dx = 3.^-+C=lx« + C.
5
/*, P 2 y. 3 q. ___
2. I /x2 dx = x 3 dx = —7“ = -f "К*5 4-.C.
J / 0 0
3
о f 2dx f 2x~2 1
3. —— = 2 \x-*dx =---—-4-C =---t + ^-
J x3 J — 2 ’ x2 1 r
fl if 1
4. I — sin x dx = -g- I sin x dx = —j cos x -j- C.
1-й прием интегрирования — разложение на сла-
гаемые.
Прием состоит в том, что подинтегральную функцию предста-
вляют в виде алгебраической суммы отдельных более простых слага-
емых, а затем интегрируют каждое слагаемое отдельно, применяя
формулу
J (jt dx = § udx-\- dx + dx.
В справедливости этой формулы убеждаемся простой проверкой;
действительно:
d [ J и dx У v dx У w dx] = d и dx-\-d vdx-\-d J w dx»
Но на основании определения интеграла
d[ у udx] = и dx, d[§ vdx] = vdx, d[ J w dx] =wdx.
Поэтому
d[ Cudx-^fvdx-^fw dx\ =u dx-^v dx-± w dx=(u -f- v -j- w) dx,
что и требовалось доказать.
300 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [XXI
Примеры:
1. I* (x2+2)2 dx= f (x4 + 4x2 + 4) dx =
' =^+P + 4,
[*Х2 —Х-[-1
dx =
= In х— x~2dx +
14-X2dx-
In x + — —Дт + C.
1 x 2x2
f dx
dX~ J l+x2~
= x — arc tg x + C.
1 — 1 .
—-— dx
2-й прием — интегрирование по частям.
Этот прием заключается в применении нижеследующей формулы
интегрирования по частям
I udtu= uv — С v du.
Она является следствием формулы дифференцирования произведе-
ния и выводится из нее следующим образом:
Так как
d (uv) = и dv-\-v du,
то
uv = J и dv J v du\
откуда и получаем
J* udv= uv — J v du.
Применение этой формулы состоит в том, что дифференциал,
стоящий под знаком интеграла, разбивается на два множителя так,
чтобы один из них можно было принять за дифференциал некото-
рой известной нам функции v\ приняв другой множитель за и и
применяя формулу, мы от интеграла J* udv переходим к j* vdu, ко-
торый может оказаться проще начального.
Примеры:
1. J*x2lnxdx.
Полагаем
In х = и, х2 dx = dv,
так что
С
v = x2dx — -~;
о
тогда
f x2 In xdx = —In X— In x---f X2 rfx=~x3lnx -~-x3+C.
<7 О J О X О и J О V
§ 121] ОБЩИЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ ФУНКЦИЙ 301
2. J х2ех dx.
Полагаем
х2 = и. ех dx = dv,
так что
v = exdx = ех,
тогда
К последнему интегралу, который проще начального, применяем тот же
прием; тогда
л потому
J* х2ех dx = дсМ? — 2хех + 2ех -}- С
3. J* х arc tg х dx. ,
Принимаем
и = arc tg х, xdx = dv,
так что
Jzdx = 4;
Jx2 1 Г X2 X2 11
х arc tg х dx = — arc tg х — — j t = -^arctgx —yx + ^-arctgx +C
(см. пример 3, стр. 300).
3-й прием — введение новой переменной.
Прием этот состоит в том, что в данном интеграле
f(x)dx
вводят новую переменную t вместо х, принимая за t некоторую
функцию от х
t — <n (х),
откуда, обратно,
х = ф (£).
Затем, дифференцируя последнее равенство, находим
dx — ф' (?) dt,
а потому
J f (х) dx = J/ [ад (/)] • <f>' (f) dt.
Если функция <p(/) подобрана так, что получившийся но?ый инте-
грал оказывается проще начального, то цель достигнута.
302 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХТ
Дать общее правило для выбора функции (х) или, что то же,
функции ф(0, нет возможности. Каждый класс функций, а иногда
даже каждый отдельный тип одного и того же класса функций
требуют для их интегрирования своей подстановки. Уменье выби-
рать последнюю и представляет главную трудность задачи.
Примеры:
f dx
J х — а*
Полагаем х — a —t, отсюда dx = dt: (
J^=Pr = 1“'+C=1“<1'-‘» + C-
Выбор такой подстановки хотя и очевиден, но может быть
объяснен еще следующим преобразованием.
Так как dx = d(x — а), то весьма выгодно dx, стоящий под
знаком интеграла, заменить на d(x — а), тогда
f dx Г d(x — а)
J х — а J х — а
После такого преобразования уже становится вполне очевидным,
что если положить х — a = t, то интеграл приведется к табличному
интегралу (формула (2)).
Подобного рода подведение под знак дифференциала некоторых
выражений весьма выгодно применять во многих случаях, для того,
чтобы наметить правильную замену переменной.
2 f xdx
J <14-х2-
Полагаем
1-4-х2 = /,;
дифференцируя, находим
2х dx = dt или xdx dt.
Поэтому
J” =4.(=4 J с=+ с=
= У1 4-х2 + с.
Для того чтобы наметить правильную подстановку, здесь также
было бы выгодно подвести под знак дифференциала некоторое вы-
ражение:4 а именно, умножив числитель и знаменатель на'2, мы за-
мечаем, что
2х dx = d (х2) = d (1 + х2).
$ 122] ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ 303
Таким образом, предложенный интеграл может быть преобразо-
ван так:
f - = 4 Г~*х = ~ f (1 + х2)-М (1 + х2).
J уц-х2 2J У1+Х2 2J v 1 ' v 1 >
Теперь уже ясно видно, что подстановка 1 *2 = / приводит
весь интеграл к табличному (формула (1)).
Применим такой прием еще к нескольким примерам^
3. J tgxdx.
х sin х
Сначала заменяем tgx отношением ™ > а затем применяем прием под-'
ведения под знак дифференциала некоторого выражения
. f sin х . f d cos x t _
tgxdx = -----dx = — ----------= —-lncosx + <?.
J XLOSX J COS X ---—I.-.
4. f S*n dx = f tg2 x • - = f tg2 x d tg x = Jr-tg3x + C.
J cos4x J 6 cos2x. J & * 3 5 1
5. Jx2• /1—4x3dx = _L_ J /1 — 4x3.12x2dx =
= — -jTj-J /1—4x3 d (1—4x3).
Теперь уже очевидно, что следует сделать , подстановку 1—4x3 = f,
тогда
fx2./n^3dx = -^f ё dt = _±t3 +С =
= /^+ С = - ,/(!-4x3)3 + с.
6. I cos3xcfx=-|- cos 3xrf(3x) = 4“SinЗх +С.
J О J О
§ 122. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ
Тип I. J* f(x)dx, где /(х) — целая рациональная функция.
J f (х) dx разбивается тогда на п 1 интегралов на основании
первого приема интегрирования,' именно
J / (х) dx = а0 J x»d
= ао-=ТТ
dx—
‘п-1 2
304 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХ1
т"« "• ЫтУ
Для интегрирования полагаем
ax-\-b — t.
Дифференцируя, находим
adx = dt.
Тогда
т™ J TZTiW-
Полагаем
ах b = t, adx = dt, dx = A dt\
( dx — — f — = A f t~ndt = A . t~n+l \-C =
J (ax-\-b)n a J a J a — n-|-l ‘ c
= a(n—C = — a(n—l)(ax + &)n-i + C-
Тип IV. J ax^-b dX’ где —ЦеЛаЯ Рациональная функция.
Для интегрирования этой функции выделим целую часть из дроби,
стоящей под знаком интеграла. Для этого разделим f(x) на ах-\-Ь.
В частном от этого деления получается некоторая целая функ-
ция ср(х), а в остатке некоторая постоянная А, так что
/(*)
ax-f- b
Данный интеграл разобьется тогда на два известных нам инте-
грала
[ dx = f с? (х) dx + A f —^7-7-
J ах+ b J ‘ v 7 1 J ах 4-6
типа I и II.
Примеры на типы I—IV:
1. J(3X4_-l;c24-5)dx = 3Jx*dx—|-Jx2rfx + 5fdx =
= V*5 —7Г*3 + 5х + С.
О о 1 1
Полагаем 2х — 5 = t, 2dx — dt, dx = dt\
f -2Г=т=i f -г=т1п *+c=4ln (2x _ 5)+c-
§ 122] ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ 305
3 f dx—.
3J (4-х)3 _
Полагаем 4 — х = /, — dx = dt, dx = — dt\
J(4^7jS = “/'73- = = 2"C = c = '2“(4 — Л)2 + C
f x2 —5x + 2 .
4. J x_^ dx.
x2 — 5x 4- 2 I x — 3 x2 — 5x4-2 n 4
r 2 _ Qr ~T 7Г— = X —2 — T
f x2 — 5x4“2, [ . n j A ( dx
------—dx = xdx — 2 dx — 4 ---------- =
J x—-3 J J J x — 3
x2
= -|--2x — 4 In (x—3)4-C.
Тип V. f .
J x2 — a*
Для интегрирования такой функции преобразуем сначала дробь,
стоящую под знаком интеграла, следующим образом:
1 ________1________ 1 . (х + а) — (х — а)
х2 — а2 (х + л) (х — а) 2а (х 4“ а) (х — а) 9
т. е. числитель умножаем на разность двух двучленов, стоящих
в знаменателе, и делаем соответствующее исправление, разделяя
все на 2а. Тогда
Г dx • 1 f (х + а) —(х — а) .______1_ Г х + а
J х2 — а2 2а J (х + а) (х — а) 2а J (х + а) (х — а)
1 f х — а , ________ 1 Г dx_____1 f dx ____
2а J (х + а) (х — а) Х 2а J х — а 2а J х + а
1 fd(x — а) 1 Cd(x + a) 1, z ч 1 . , , ч
= -ст —-------—п- - Л -= о“1п(х — я) — тг I*1 (х 4- а) + С=
2а J х — а 2а J х + а 2а 7 2а 41/1
1 t /х — а\ .
= — 1п —;— + С.
2а \х 4- я J
Тип VI. f
J а2 + х2
Полагаем x — at, dx — a dt\
. ( dx a dt 1 C dt 1 , j 1
J a2 + x2— J a2 + a2^ — J 1 4-12 ~ 7 аГС G —
= —arctg—4-C.
а ь a i
Формулу эту полезно включить в число основных формул и за-
помнить.
20 Зак. 2116. Н. С. Михельсон.
306 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [xxt
(* dx
Тип VII. -•»- , ах , .
J х2 ~\~РХ + Я
Для интегрирования такой функции прежде всего удобно при-
менить преобразование трехчлена, стоящего в знаменателе, при-
ведя его или к сумме или к’разности квадратов, как это известно
из курса элементарной алгебры. А именно
х2 + /?х + ? = х2-|-рх-|-= + ---? )•
Если г корни этого трехчлена вещественные и различные, то
р2 . л р2 о
q — 4 < 0, и полагая q — = — ал, получим
х2+/?х4-? = (^ + уУ— Я2-
п2
Если корни трехчлена мнимые, то q — > 0, и полагая
q — получим
х2 + рх + q = (х + + а2.
п2
Если же корни трехчлена вещественные и равные, то q — = 0,
и трехчлен оказывается полным квадратом
х2 +рх+ q = (х .
Таким образом, предложенный интеграл приводится к одному из
трех видов:
- f dx______f dx
• Jx2+^+7- J +
9 f dx _____ f____dx
J^ + px + ,~J
q f dx _____ f dx
J x^ + px + q ~ J (х+^У
Во всех трех случаях подстановка х-\-^- = t\ приводит инте-
грал к уже известному: в первом случае к типу V, во втором
к типу VI, а в третьем случае к типу III.
В случае вещественности корней трехчлена можно непосред-
ственно применить прием, подобный тому, который был применен
к типу V. А именно, обозначая корни трехчлена через аир, имеем
х2 -|- рх -}- q = (х— а) (х—£).
§ 122]
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ
307
После этого дальнейшее интегрирование ведется следующим
образом:
f dx
dx _ 1__ f (x — g) —(x—-ft) ,
(x-a)(x-₽) — p-а J (x —g)(x —p) aX
1
dx
— In
T"" Vln- J глтгт+7-
Этот интеграл приводится к предыдущему вынесением коэффи-
циента а за скобки в знаменателе. Действительно
а
dx
Т~
а
2
а
dx
Jmx 4- п ,
— ।—dx.
x^+px + q
Интегрирование такой функции начинается с того же преобра-
зования, как и типа VII.
тх -|- п
mx.+ n___dx
P \2 „ X'
±«2
Далее, полагаем х у = t, тогда х = t— и dx = dt, так
что
т
тх + п
п
-dt =
Г tdt I / тр\ Г dt
~mJ Р±аг 2/J P±a*’
Второй из полученных интегралов относится к типу V или VI,
первый же берется следующим образом:
{tdt if 2idt _ j fd(/2±a2) 1
J t2±a2“ 2 J f2±«2— 2 J Z2±«2 — 2 1ПЦ _a
Тип X. J 2 ' - dx, где / (х) — целая рациональная функция
второй или высшей степени.
Для интегрирования этой функции выделяем целую часть из
Дроби, стоящей под знаком интеграла. Для этого делим числитель на
знаменатель. Положим, что от такого деления у нас получилась
20*
308 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХ1
в частном некоторая целая рациональная функция ср(х) и в остатке
тх п\ тогда
___= ф (х\ -1_ тх + п .
х2 + рх 4- q Y v ~ х2 +рх + q
Поэтому данный интеграл разбивается на два интеграла изученного
уже типа:
(см. типы I и IX).
Примеры на типы V—X.
1. f dx
J 3 + х2-
Полагаем х = У~3 • t, dx = УЗ dt;
f dx f V3dt 1 C dt 1 t , , „
J34-X2 J з + зг- уз J i + e- уз
= —7= аГС “7= +
Уз уз
Ответ этот проще было бы сразу написать по формуле типа V, приняв
а2 = 3, т. е. а = Уз.
2. f___________
J X2_|_3X —40-
Знаменатель имеет вещественные корни; найдя их, представим знамена-
тель так:
х2 + Зх — 40 = (х — 5) (х + 8).
f dx f dx __________________________If (x—5) —(x4-8) . _
J X2— 40 J (x — 5)(x-f-8) 13J (x — 5)(x4-8)
1 f dX । 1 f dx 1 , , , O4 , 1 , , еч ,
“ 13J x4-8 +13J x — 5 “ 13 n (x + 8) + i3ln(-v 5) + £-
_ 1 x — 5 „
~ 13 x4-8
O f dx
J 12x2-12x4-7 ' '
Знаменатель имеет мнимые корни, поэтому преобразовываем его так :
12х2-12х4-7= 12(х2-х+^) = 12[(х2-х + 1) + (1-1)] =
Таким образом:
f dx 1 Г dx
12х2—12x4-7 12
1\2 , 1 ’
§ 122] ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ 309
Полагая х — ~2=t> имеем dx = dt и
f dx 1 f dt V3 o , -у, , _
J 12x2— 12x4-7 “12] , 1 “ 12 arctg/3z+c-
Z24--3-
„ f 3x —4 .
4. I 0 j q j r- dx»
J x2 + 2x+-5
Прежде всего преобразуем знаменатель
x2 + 2x + 5 = (x+1)2 + 4
и полагаем
х + 1 = t,
откуда
х = t—1, dx = dt.
f Зх“4 н f 3(^—!) —4 C tdt • f dt __
J x2 + 2x + 5 J /24.4 at~dJ t2 + 4 ZJ /2 + 4
3 C 2tdt _ f di 3f „ 7 o . t ,
— 2 J /2 4 7 J fl 4- 4 — 2 " 4) 2 c tg 2 c‘
Возвращаясь к прежней переменной, имеем
Зх — 4 , 3./9.О |С\ 7 4. х ~h 1 । г”
Х2 + 2x4-5 dX = Т "(Л + 2* + 5)~у arc‘8 + 6-
Произведя деление числителя на знаменатель, найдем
хз—1_ х+1
Х24-1~Х Х2-Н’
Таким образом,
л3 —1 f » f х +1 . х2 С xdx f dx
x2-f-lrfx- J X^X J dx-~2 — J Х24ГТ— J -
= 4 x2 — 4 ln (x2-*- 0 —arctgx-f-C.
Полагаем
x = at, dx==adt\
f dx________f a dt _______ f dt _______
J V^2__ X2 ~ J ya2^a^~ J /T^72-
= arc sin Z-|" = arc sin 4"
Результат этот полезно включить в число основных формул
интегрального исчисления.
310 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХ1
ТИП XII. Г-; ЛХ --
J Yx^ + a?
Интеграл этот берется специальной подстановкой, носящей на-
звание подстановки Эйлера, которая состоит в том, что полагают
/х2±а2 = / — X,
где t новая переменная.
Возвышая обе части равенства в квадрат, находим
х2±а2 = /2— 2/х4~х2
± я2 = /2 — ^tx.
Далее, дифференцируя, имеем
0 = 2tdt— 2tdx — ‘Zxdt,
т. е.
tdx=(t — х) dt.
Отсюда выводим, что
dx dt dx dt
t — x t /x2±a2 t
Поэтому получаем
j “ / 7 “‘ + c=(x + +c'
Формулу эту полезно также включить в число основных формул
интегрального исчисления.
ТИП XIII. f-; dX -
J Y лх2 + Ьх + с
Интеграл этот приводится к одному из типов XI или XII. Для
этого преобразуем подкоренное выражение следующим образом:
ах2 + Ьх4“ с — а |х2-J-х 4“ уj =
Г п . b . Ь* с &2"|
= ДХ2 4---*4-7”54---------Т"9 =
L 1 а 1 4а2 1 a 4а2 J z
Ki b \2 । 4ac — b2~]
x4-q~ 4-------л-о— •
1 2а/ 1 4а2 J
Тогда интеграл принимает вид
Введем теперь новую переменную, положив
х = /, отсюда dx = dt.
§ 122] ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ 311
Кроме того, для сокращения письма примем
4д2 ' = — 4“&2> если 4ас — Ь2 > О,
— &2, если 4ас — Ь2 < 0.
Тогда
Г dx = Г dt
J Уах* + bx + c J V a (Z2±£2)’
При а > 0 приходим к типу XII, так как тогда
Va(P±k*) = Va • V?±k*.
При а < 0 приходим к типу XII или XI, в зависимости от того,
имеем ли мы под корнем сумму или разность. В случае суммы
/а(^а-|-А2) = /а • ]Л84-А:а — тип XII;
имеющаяся мнимость неустранима. В случае разности
/a(Za —А2) = V — a(k2 — P) = ]/“• ]/k2—P — тип XI;
У — а, число вещественное.
Примеры на типы XI—XIII.
1 f
’ J V 4 —х2'
Вводим новую переменную, полагая
х = 2t, dx = 2 dt\
с dx f 2dt f dt . , . „ . x . „
J У4 —x2 J /4 — 4^ J /1— t2 2
2 f
J у л2 —3*
Применяем подстановку Эйлера
Ух2 —3 = Z —х.
х2 — 3 = Z2 — 2tx-\-x2,
отсюда
— 3 = Z2 — 2tx.
Дифференцируем последнее равенство:
0 — 2tdt — 2х dt—2tdx.
Далее преобразуем так:
tdx — (t — х) dt,
dx dt dx dt
„ t — X t Ух2 —3 t
Потому
f-±L_-= f^ = lnf+C = ln(x+V^=3j + C.
J у Xй —— О J t
312
ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [XXI
3 . f -
J /5— 4х— 4х2
Преобразуем подкоренной трехчлен:
5 — 4х — 4х2 = 6 1 — 4х 4х2 = 6 — (1 + 2х)2.
Ввиду этого
_____dx______Г____dx____
/5 —4х —J /б —(1+2хр*
Вводим теперь новую переменную, полагая
1 -|- 2х = Л 2dx — dt, dx = ± dt;
dx
5 — 4x — 4x2
dt
/6^72’
а теперь прямо по формуле (см. тип XI):
Г dx 1 . t . „ 1 . 14- 2х . „
. ----------- — _ arc sin 4- С = — arc sin —- 4- С.
J /5 —4х —4х2 2 /6 2 /6
J* dx
.. -------->.
/ 3x2 —4х— 2
Преобразуем подкоренное выражение:
3x2 — 4х — 2 = v (9x2 _ 12х — 6) =
О
- V (9x2 _ 12х + 4 - 6 — 4) = 4 1(3* — 2)2 — 10];
О о
тогда
Г___________________dx_______ уд- Г______dx______
J /3x2 —4х —2 “ J /(Зх— 2)2-Пб'
Вводим теперь новую переменную, полагая
Зх — 2 = t, 3dx = dt, dx= ~ dt;
о
f. .—_ = XI [—4L= = —in(/+ //2_io)+c=
J /3x2 —4x —2 з J //2—Ю 3
= XIIn (3x — 2 + /9x2—12x —6) + c.
О
Тип XIV. J sinaxdx и J cos2xdx.
Известно, что
. n 1 — cos 2x
sinJx =
2
9 I 4- cos 2x
cos2 X = ——---------
2
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ФУНКЦИЙ
313
§ 122]
Поэтому
f . q 1 fl — COS 2х , if. if n .
sin2 x dx = I------2----dx=^-c) I dx — I cos 2x dx =
= x — J cos 2x d (2x) = x — ~ sin 2x
f cos2 x dx = J —+ ^os 2x dx = L J dx L. J cos 2x dx =
= x + f cos 2x d (2x) = ~ x -J- j sin 2x 4” C.
Тип XV. j sin3xrfx и J cos\xdx.
Эти интегралы берутся разложением их на сумму двух интегра-
лов:
J sin3 х dx = |* sin х • sin2xrfx = J sinx(l—cos2x)rfx =
= J sin x dx — J cos2 x • sin x dx — — cos x -}- J cos2 x d cos x =
= — cos x 4- -j cos3 x 4“ C.
Jcos3xrfx = J cosx(l —sin2x)rfx= J cosxdx— Jsin2xrfsin x =
= sin x — -i- sin3 x 4- C.
Тип XVI. J* ig2xdx и j* ctg2xdx.
Jtg2xrfx= px = tgx-x+C.
Другой интеграл берется таким же способом, принимая во внима-
ние, что
ctg2 х = -Д-----1.
ь sin2 х
Тип XVII. j* tg3x
dx и I ctg3 х dx.
j tg3xrfx = Jtgx • tg2xt/x= J =
tg x , f, , (, j, f sin x j
dx— tgxdx= tgxdtgx— -----------------dx =
COS2 X J ° J & ь J COS X
= i- tg2 x 4“ cos x~\~C-
314 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХ1
Приведенные типы интегралов не исчерпывают, конечно, всех
типов функций, допускающих интегрирование. Большее развитие
этого вопроса можно найти в более подробных курсах. Здесь
только отметим, что для всякой непрерывной функции существует
первообразная, однако не для всякой непрерывной функции ее не-
определенный интеграл может быть выражен через известные нам
элементарные функции анализа (см. стр. 56). Таким образом, хотя
и существует функция, первообразная по отношению к подинте-
гральной, но она может представлять функцию новой природы,
выходящую из круга элементарных функций. В этом случае говорят,
что неопределенный интеграл не берется в конечном виде. Таковы,
например, интегралы
f - Гл----г j f ех , f sin х .
I ху 1 — х6 dx, —dx, I —dx и многие другие.
§ 123. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какая функция называется первообразной по отношению к данной?
2. Какое действие называется интегрированием функций?
3. Почему при интегрировании функций появляется произвольная
постоянная?
4. В чем заключается каждый из трех приемов интегрирования?
Найти следующие интегралы:
5. 1 (лг3 — 2х2 — 3) dx. Отв. 1 — —-=-хЗ—Зх + С.
6. f fr x*dx. Отв. 4- х fr х2 + С. и
7. [dx Jx3- Отв. 4=+с-
8. J (2x2—1)3 dx. Отв. 4 4 О о
§ 123]
ВОПРОСЫ И УПРАЖНЕНИЯ
315
9. 10. J* sin 2х dx. J* е3х dx. Отв. _ .1. cos 2x + C. Отв. 2-еЗх + с. и
11. (ха + 2х) ех dx. Отв. х2ех + С.
12. J* arc tgx dx. Отв. х аге tg х — In (1 + х2) 4- С.
13. f dx Отв. Х1п(2х — 1) + С.
J 2x — 1
14. f x dx Отв. A In (Зх2+ 1) + С.
J 3X2+ j
15. f^x. • Отв. — In3 х 4- С.
J X
16. f dx Отв. iarctg^ + C.
J 4+ *2
17. f dx Отв. аге sin 4"
J /3 —X2
18. f dx ОтВ- 5 lni + 2 +С-
J X2—X — 6*
19. f dx От‘- Дз + С-
J xa4-6x4-9
20. f dx Отв. — аге tg 4- С. 5 5
I x2 + 4x + 29’
21. f 3x + 4 1 x2 + x — 2dx- Отв. A in (х2 + х — 2) +
22. f dx jjXZ2+c-
1 /x2 —3 Г dx Отв. 1п(х4-ТГ*3 — 3 4-С\
23. Отв. In (х 4“ Ух24-4)4-С. 1 1
1 /x2+4
24. Отв. у х 4- 12 s*n 6* + £•
cos23xrfx.
25. /» sin33xdx. Отв. cos3 Зх —cos Зх 4“ С. У о
26. sin x • cos2 x dx. Отв. — ycosSx + C.
27. (^Ldx. 1 sin2x Отв. 1 к С. sin х
28. Г dx Отв. 5 ц. г
1 (Зх — 5)3 • 6(3х — 5)2
29. | Г dx Отв. ! L С. 3(2 —Зх) 1
1 (2 —3x)a ’
316 ПЕРВООБРАЗНАЯ ФУНКЦИЯ, ИЛИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХ1
30. (* dx Отв. In (x + 3+Vx2+6x—16)+C.
J Ух2-±-6х —16
31. f з Отв. 2 In (x2 + 3x + 4) —
J x2+ 3x4-4 18 , 2x + 3 , _
32. J (x2 — 2x) sin x rfx. Отв. (2 + 2x — x2) cos x +
+ (2x — 2) sin x + C.
33. f*3~4x2 + 3rf>. . J * + 2 Otne. — xz — 3x2+ 12x — о
— 21 In (x + 2)+C.
34. Cx2 — 1 . 1 7; dx. „ 4 . x , „
[yflllji -А» — .QI
J x3 + 3 /3 /3
35. f x2 + l . Jx’ll'"- Отв. x+ln^+ j +<?.
36. sin x (1 + 2 sin x) dx. Отв. — cos x + x — у sin 2x +
37. f sin x . —5— dx. J COS3X Ome- 2cos2x +c
38. f X3 —rKdx- J x + 2 Отв. -Lx3— x2+4x—8In(x+2)+ C. О
39. J x2 — 1 dx‘ Отв. In(x+ V- + C.
40. sin x (sin x + cos x) dx. Отв. yx~£' s*n 2* H" "5“ s*n2
41. f cosx . . n dx. J sin2x Отв. -^-In tg^+C.
42. f sin x . . n— dx. J sin 2x Отв. — у lnt£0T "£) +C-
43. f3x + 4 . . , c~ dx. J xa + 5x Г dx 4 11 Отв. In x + In (x + 5) + C- 0 0 /-
44. Отв. ln(x+2+ V"x2 +4x+13)+C.
J /x2 + 4x+13
45. (1 — cos x)3 dx. 5 3 Отв. x — 4 sin x + у sin 2x +
+ 4 sin3 x + C. О
46. J cos x (1 + sin2 x) dx. Отв. sin x + -й- sin3 x 4- C. о
47. f x3 — 2x2 + 4 , J x2 + 2x —3 Отв. — 4x + ~ln(x—!) + 4 1
+ -ln(x+3) + C.
§ 123]
ВОПРОСЫ И УПРАЖНЕНИЯ
317
f гЗ___ I
48. ЧТл -T-Adx'
J х2 + 4л: 4" 4
лл f cos х — sin х ,
49- J —n-з-х - dx-
c dx
50‘ J /8 —2x —x’ '
f dx
«51. I - •- .
Э J y\2_2x
53. J (2x — 3) cos 3x dx,
54. § (х*+1)е-*в dx.
55. | x3e3x dx.
1 9
Отв. Tx2-4x+ ^2 +
+ 12 In (x + 2) + C.
Отв.-----Д----intgA-pC.
sin a: s 2
. x -4" 1
Отв. arc sin —4---p C.
d
Отв. In (x — 1 + /х2 —2x) + C.
Отв. 2 In (x2 4- 3x + 3) —
— 6 /3“arc tg 4. c.
, V3
1 2
Отв. (2x—3) sin ЗхЦ- — cos 3x 4- C.
о У
Отв. — 2-(*2 + x + 4)e“2a’ + C
Отв. -if*3 — -*2 + 4-v — -k-V3®+ c-
о \ О У /
XXII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 124. ЗАДАЧИ, ПРИВОДЯЩИЕСЯ К ВЫЧИСЛЕНИЮ ПРЕДЕЛА
ИНТЕГРАЛЬНЫХ СУММ
Задача I. Положим, нам требуется вычислить площадь, огра-
ниченную некоторой кривой, расположенной со стороны положитель-
ного направления оси ОУ, осью
ОХ и двумя ординатами.
Пусть уравнение кривой
будет
y—f(x)
ОА = а, ОВ = Ь.
Для вычисления этой пло-
•д? щади разобьем отрезок АВ на
п частей, вставив между точ-
ками А и В произвольно ряд
других точек М19 М2,...,
Пусть абсциссы этих точек будут
Хр Х2, АГд, . . . , Хя-р
Отдельные части, на которые разобьется отрезок АВ, обозна-
чим следующим образом:
Xj d = Да?|, Х2 Xt —’ Дх2, . • •, Xj Xj — i — ^Х^, . . ., Ь %n — 1 —
В точках М19 М2, ..., Л4п-1 построим ординаты кривой DC,
тогда вся площадь ABCD разобьется на п полос.
Элементарная математика вообще не дает средств вычислить
ни всю площадь ABCD, ни каждую в отдельности из полос, на
которые разбивается таким образом вся площадь.
Ввиду этого заменим эти полосы соответствующими прямоуголь-
никами, основаниями которых пусть будут служить части отрезка АВ,
а высотами — начальные ординаты каждой полосы у0, у19 ..., у^19
• ••,Уп-19 и составим сумму площадей всех таких прямоугольников:
sn=yo- • Дх9-|- ... +л~1 • д*< + • • • +л>-1 • д*» =
= /(а) • ДХ1+/(*1)д*я+ • • • +/(^-1)Дх< + - • • +/(хп-1)Да:п- 0)
§ 124] ЗАДАЧИ ПЛ ВЫЧИСЛЕНИЕ ПРЕДЕЛА ИНТЕГРАЛЬНЫХ СУММ 319
Чем больше мы будем увеличивать число /г, т. е. чем большее число
прямоугольников мы будем вписывать в рассматриваемую пло-
щадь ABCD, беспредельно уменьшая при этом ширину каждой по-
лосы, тем составленная сумма (1) площадей этих прямоугольников
все точнее и точнее будет представлять вычисляемую нами площадь
ABCD. Таким образом, мы приходим к заключению, что для вы-
числения площади ABCD надо вычислить предел суммы (1), т. е. что
пл. ABCD —
=йИш[/.(а)ДХ14-/(Х1)Дх2+.. •4-/(х1-_1)-Дх<+.. (2)
я->оо
Сумма (1) носит название интегральной суммы.
Задача II. Вычислить работу, совершаемую пере-
менной силой на пути прямолинейного перемещения
материальной точки по направлению действия этой
силы.
Пусть материальная точка М движется по прямой OL от точки А
к точке В, и допустим, что положение движущейся точки М мы
определяем ее расстоянием s от
некоторой определенной точки О t ____________М__________у т L
этой прямой. Положим О А = а, ' д д в
ОВ = Ь. Пусть, наконец, сила,
приложенная к материальной точ- Рис*
ке 7И и действующая по направ-
лению перемещения, выражается некоторой известной нам функцией
от 5 (ее расстояния от точки О)
ю-
Если бы сила на пути перемещения точки была постоянной,
то работа силы на протяжении пути АВ была бы равна произведе-
нию этой силы на длину АВ = Ь — а. Но наша сила меняет свою
величину при перемещении точки и предыдущий расчет был бы не
верен.
Для того, чтобы подсчитать всю работу, совершаемую нашей
переменной силой, разобьем весь путь АВ на п отдельных частей:
— а = Д$п s2 — = Д$2, . .., Si — — .., b — sn-\=^^sn
и допустим на время, что на протяжении каждой части сила не
меняет своей величины, а сохраняет ту величину, которую она имела
в начале каждого промежутка, а именно
‘ /(«), /(Sl)> • • • > • • • >
Тогда работа силы на протяжении каждого в отдельности проме-
жУтка выразится следующим образом:
/(Л)Д^1, f ($j) Д^» ••• ? / (si-1) ••• } f (5п-1)
a вся работа суммой
^п=/(а) Д^-]-/($!) Д^2+ • • • + /С9»-1) ^sn- (3)
320 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХП
Наше допущение о постоянстве силы на протяжении каждого
в отдельности отрезка пути не верно, однако предыдущая сумма
тем точнее выразит действительную работу силы на протяжении всего
пути, чем на большее число частей мы разделим путь АВ, беспре-
дельно уменьшая при этом каждый отрезок пути. Таким образом,
и в этой задаче мы приходим к такому заключению, что для вычи-
сления работы А заданной переменной силы на пути перемещения
материальной точки нам необходимо вычислить предел суммы (3),
т. е. что
Л = lim [/(а) Д51 . +/(«»-1)Д^»Ь (4)
«->оо
Легко заметить, что сумма (3), по существу, ничем не отли-
чается от суммы (1). Сумма (3) та же интегральная сумма, как и
сумма (1).
Задача III. Определить величину пути, пройден-
ного точкой за некоторый промежуток времени в ее
прямолинейном движении, если известен закон, вы-
ражающий скорость дви-
_ । . t_______________t—жения в каждый момент.
' О А в Представим себе числовую
ось ОТ (рис. 162), на которой мы
Рис. 162. будем откладывать от некоторой
начальной точки О время движе-
ния. Пусть О А = а и ОВ = b будут времена начала и конца дви-
жения точки, так что весь промежуток времени движения будет
равен b — а.
Задача предполагает известной величину скорости в каждый
момент движения, т. е.
»=/(/).
Если бы скорость не меняла своей величины во все время дви-
жения, то путь, пройденный точкой за время b — а, был бы равен
v(b— а), но по условию скорость меняется со временем.
Для подсчета пути в наших условиях разобьем промежуток вре-
мени b — а на п промежутков
— CL = /д == • • • > — 1 == • • • > & 1 ===
и предположим, что на протяжении каждого такого промежутка ско-
рость остается постоянной и равной той, которую она имеет в на-
чале каждого промежутка, а именно
/(«),/(/,), , /(^о,... ,
Тогда путь, пройденный точкой за каждый промежуток в отдель-
ности, выразится следующим образом:
/(«Ж /(^9, ... , /(/<_!)М{, ... , /(/„_!)Д/я>
125] ПОНЯТИЕ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 321
а весь путь, пройденный точкой, был бы равен сумме
^/(а) +/&) ^ + • • • + • • • +/ (*„_!) Д<„. (5)
Наше предположение о неизменяемости скорости на протяжении
отдельных промежутков не соответствует действительности; однако,
предыдущая сумма будет тем ближе выражать истинную величину
пути, пройденного точкой за все время, чем на большее число п
промежутков мы разделим промежуток времени b — а, беспредельно
уменьшая при этом каждый отрезок времени.
Таким образом, для вычисления пройденного точкою пути s нам
необходимо вычислить предел суммы (5), так что
s = lim [f (а) Д^+/ (/О Д^+... + / & _ • • • -I- / (Аг-1) Ч] • (6)
Опять мы замечаем, что сумма (5) по существу ничем не отличается
от сумм (3) и (1) предыдущих задач.
Приведенные здесь задачи показывают нам, что все они сводятся
к одной общей задаче — к нахождению предела интегральной суммы,
т. е. к пределу суммы вида (1) таких слагаемых, которое, беспре-
дельно уменьшаясь, стремятся к нулю по мере беспредельного увели-
чения их числа.
Если же принять во внимание, что не только эти три задачи
приводят нас к одной и той же упомянутой задаче, но что к ней
же сводится огромное число других, не менее важных, задач, то
необходимость изучать предел указанной суммы выявляется с пол-
ной очевидностью.
§ 125. ПОНЯТИЕ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Представим себе числовую ось ОХ и на ней отрезок АВ. Пусть
абсциссы точек А и В будут О А = а, ОВ == Ь. Затем положим, что
нам задана некоторая функция /(х) непрерывная при всех значе-
ниях х в промежутке [а, Ь].
Для определенности будем 7
предполагать, что b > a. д 1 1 1 1-1 «' 11
Отметим между точками А
и В ряд других каких-ни- Рис. 163.
будь точек М19 Ж2, ... ,
. .. , Mn_v абсциссы которых пусть будут х1? х2, ... , хй
’ * * ’ %п-1‘
Составим разности абсцисс соседних точек, и пусть
а = Дх1? х2 — хг = Дх2,х^.^Дх^, ..., хп_1 = Дхп.
В каждом из п промежутков, на которые мы разбили отрезок АВ,
Наметим произвольно по одной точке, абсциссы которых обозначим
через
а2> • • • > а*> • ‘ , ап-
21 Зак. 2116. Н. С. Михельсон.
322 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [XXu
Подставим эти значения в выражение заданной нам функции
и вычислим таким образом значения
/(«!>, /(«2)> ••• , /(«,)> ••• , /(а,.)-
Наконец, умножим каждое из этих значений функции на величину
соответствующего промежутка и составим сумму всех таких произ-
ведений, которую обозначим через Sn, так что
Sn = /(«1) Д*1 +/W Д*2 + • • • +/ ^xi +•••+/ («J Д*п- (7)
Таким образом, не относя предыдущие рассуждения к какой-
либо определенной задаче, мы чисто аналитическим путем составили
новую интегральную сумму, подобную интегральным суммам преды-
дущих задач.
Основное и весьма важное положение, относящееся к такой
сумме, заключается в том, что предел такой суммы при беспре-
дельном увеличении числа, п и уменьшении самих промежутков су-
ществует и не зависит ни от способа подразделения промежутка,
ни от выбора промежуточных значений аргумента: а2, .. ., ап.
Для доказательства этого положения составим еще две вспомо-
гательные суммы
£п = М]Дх1+Л12Дл:2+ ... +^4^+ ... +Л4йДхп (8)
оп = т1ДХ1 + 7п2д*2+...+«<Л*;4---------Ь^Дх^ (9)
где Л4Р /И2, . . ., Мп представляют собой наибольшие, а тг; т2, ... тн
наименьшие значения функции / (х) в каждом отдельном проме-
жутке.
Ясно, что
(10)
Далее из всех значений Mlf ТИ2, .. . , Мп выбере^м наибольшее
и обозначим его через М, а из всех значений т}, т2, . .. , тп вы-
берем наименьшее и обозначим его ’через т. Если на место всех
ТИр ТИ2, ... , Мп подставить в сумму (8) одно и то же Л4, а на
место всех т19 т2, ... , тп подставить в сумму (9) одно и то же
т, то очевидно получим
2ге^Л1ДХ1 + Л1Дх2+ ... -|~7ИДхп =
= /И(Дх14-Дх2+ ... 4-Дх.„) = /И(£ — а)
оп тДх^ 4“ тДх2 4~ тЬхп —
= т (Дхх + Дх2 + ... + Дхп) = т (Ь — а).
Таким образом, неравенство (10) полнее представится в виде
——а). (11)
§ 125] ПОНЯТИЕ ОГ» ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 323
Проследим теперь, как будет изменяться сумма при даль-
нейшем подразделении промежутков Дх1? Дх2, . . . , Дхп. Положим,
что промежуток Дх,£ мы разбили на Д'х$ и Д"х^.
Для составления нового значения суммы мы должны будем
теперь каждую часть Д xi и Д"х^ промежутка Ах^ умножить на наи-
большее значение функции /(х) в каждом промежутке в отдель-
ности. Но эти наибольшие значения не могут быть больше
а потому сумма новых двух слагаемых, заменяющих одно, не может
быть больше одного прежнего Mfix^ Итак, от подразделения каж-
дого слагаемого суммы (8), последняя не может возрастать, а сле-
довательно, она йли вовсе не меняется, или убывает. Однако нера-
венство (И) показывает, что если сумма при этом убывает, то
все же остается больше некоторого определенного числа, равного
т(Ь— а). А потому, на основании признака III существования пре-
дела переменной (§ 82) можем утверждать, что при таком подраз-
делении промежутков, когда они все стремятся к нулю, сумма
стремится к определенному пределу, т. е. limv^ существует.
72->оо
Совершенно так же можно доказать, что при подобном же под-
разделении промежутков сумма (9) не убывает, а либо не меняется,
либо возрастает, и так как из неравенства (11) следует, что сумма
эта все же остается при этом меньше М (Ь — а), то опять заклю-
чаем, что при таком подразделении промежутков liman существует
П->оо
Докажем теперь, что
Hm Sn = Hm а„. (12)
П -> оо п -> оо
Для этого рассмотрим разность этих сумм
Sn — <зя = (Mj — mt) Axj + (Ж2 — от2) Дх2 + ... -J- (Мп — mn) Дх„.
Если в правой части этого равенства на место Всех разностей
2И1 — т19 2И2—/п2, ... , Мп — тп поставим одну и ту же, но наи-
большую из них (обозначим ее через Д), то
O^Sn — °»^д (д*1 + д*г + • • • +д^») = д (Ь — а).
При подразделении промежутков сами промежутки беспредельно
убывают, а тогда в силу непрерывности заданной функции каждая
из разностей
Му — Шу, М2 — т2, , Мп— тп 1
стремится к нулю, если Дх1; Дх2, ... , Дхп стремятся к нулю.
Вместе с ними и наибольшая из них тоже стремится к нулю.
А тогда на основании признака I существования предела перемен-
ной (§ 82) р
lim (2„ — о^иО.
П-4оо
21*'
324 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (ХХП
Итак, при подразделении промежутков
Hm Sn= lim
п -> OO п -> OO
Таким образом, мы приходим к заключению, что при увеличении
числа п суммы Sn и ап стремятся к одному и тому же пределу.
Остается теперь только обратиться все к тому же неравенству (10),
чтобы заключить, что и lim Sn существует.
П-> ОО
Действительно неравенства (10) показывают, что переменная Sn
при своем изменении заключается между двумя другими перемен-
ными и ап, стремящимися к одному и тому же пределу. По-
этому на основании признака I существования предела пере-
менной (см. § 82) заключаем, что к тому же пределу стремится и
переменная Sn. Итак,
lim Sn существует и равен lim Sn ~ an«
П->оо n->oo n-> OO
Можно было бы показать, что lim Sn не зависит ни от способа
п -> ОО
подразделения промежутка, ни от выбора чисел ап а2, ..., ап в ка-
ждом промежутке. Интересующиеся доказательством этих последних
положений могут найти их в более подробных руководствах.
Предел интегральной суммы Sn называется определенным
интегралом от функции f(x), взятым в пределах от а до Ь.
Он обозначается знаком
ь
J f{x)dx.
а
Таким образом,
ъ
f/ (х) dx = lim Sn = lim [/(aj +/(a2) A*2+ • • • +/ (“») (*)
n -> OO n -> OO
a
Здесь знак J, растянутое обозначение буквы S, служит напоми-
нанием того, что речь идет не о самой сумме, а о ее пределе: вы-
ражение / (х) dx, стоящее под знаком интеграла, напоминает нам
форму каждого слагаемого, а числа а и Ь, называемые соответ-
ственно нижним и верхним пределами интеграла, указывают на
границы того промежутка, в котором изменяется аргумент функции.
Термин „определенный интеграл“ и самое его обозначение в виде
знака у* напоминает нам ранее введенный нами термин и обозначение
„неопределенного интеграла*, и это не случайно. Далее мы покажем,
что между двумя операциями, ранее установленной — нахождением
первообразной по отношению к данной функции / (х) и новой опе-
рацией— нахождением предела интегральной суммы имеется тес-
§ 126] СВЯЗЬ МЕЖДУ ОПРЕДЕЛЕННЫМ И НЕОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ 325
ная и весьма важная связь, которая нам поможет сложную опера-
цию вычисления предела суммы сводить к отысканию первообраз-
ной функции, т. е. к операции, с которой мы уже познакомились
раньше.
Отметим еще, что по смыслу происхождения определенного
интеграла величина его зависит:
1) от вида подинтегральной функции f (х),
2) от пределов интегрирования а и b
и вовсе не зависит от обозначения аргумента той или другой буквой,
так как значения аргумента, как бы он ни был обозначен, опре-
деляются границами его изменения, т. е. пределами а и Ь. Следо-
вательно, верными являются следующие равенства:
ъ ъ ъ
j* f(x)dx — j* f(f)dt= J f(z)dz и т. п.
d сь а
. Во всех интегралах переменная, как бы она ни была обозначена
через х, t или г, проходит один и тот же непрерывный ряд про-
межуточных значений между а и Ь.
§ 126. СВЯЗЬ МЕЖДУ ОПРЕДЕЛЕННЫМ И НЕОПРЕДЕЛЕННЫМ
ИНТЕГРАЛОМ
Положим, что нам задана некоторая функция / (х), непрерывная
на всем протяжении промежутка [а, Ь], причем для определенности
предположим, что b > cl- Пусть F/(x) является первообразной по
отношению к функции /(х), т. е.
р' (х) =f(x).
Рассмотрим разность двух значений этой функцйи F (х) при х — а
и х = т. е.
F(6)-F(a).
Введя между числами а и b последовательный ряд каких-нибудь
возрастающих чисел
^19 • • • 9
можем написать очевидное равенство:
F (*) — F(a) = [F (xj) - F(a)] + [F (x2) — F (x,)] +
4- [F^J-Fto.,)] + ... + [F(d) -F(x„_x)].
К каждой из разностей применим формулу конечных прираще-
Ний Лагранжа; тогда, например,
P(x<)-F(x<_1) = * F'(^) = ‘
326 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [XXII
Но, так как F' (x)—f (х), то F’ (с») =/ (с<) и потому
F(xj) — F(x,_i) =/ (^) Дх4-.
Следовательно,
Г(й)-Г(а)=/(с1)Дх1+/(с8)Дх2+ ... +
+/(ci)^xt4" ••• +/(fn)^xn, (13)
где с2, сп определенные, требуемые формулой Лагранжа,
числа, каждое в своем промежутке.
Сравним теперь сумму, стоящую в правой части равенства (13),
с интегральной суммой (7) (§ 125)
$„=/(«»)Дх1+/(*2)Дх2+ • •• +Ж)Д*«+ • • • -г/(%)Дхп (7)
и докажем, что при беспредельнохМ увеличении числа п обе суммы
стремятся к одному и тому же пределу. Для этого рассмотрим их
разность:
Sn-\F(b)-F(d)] = [/(«,) —/(*,)] Дхх+ [/(а2)-/(С2)] Дх2 +
+ ••• + [/(«J— №)] ^п- (14)
Обозначим для простоты разности, стоящие в прямых скобках
правой части равенства (14), через
8р е2, . . ., е„,
а через Е и в наибольшую и наименьшую из них; тогда, заменяя все
различные е1? е2, ..., один раз через Е, другой через в, можем
написать такие неравенства:
8(*_a)<S„-[FG>)-F(a)]<E(*-a).
Будем теперь беспредельно увеличивать число п, беспредельно
уменьшая при этом разности Дхь Дх2, ..., Дхп; тогда и числа, за-
ключенные в этих промежутках v
«1 и q, a2 и с2, ..., и сН9
будут беспредельно сближаться друг с другом. В силу непрерыв-
ности функции f (х) разности в2, .. ., еп, а с ними и Е и в будут
стремиться к нулю. Следовательно,
Иш е(Ь — а) = lim Е(£— а) — 0.
П -+ ОО П -> ОО
А тогда по первому признаку существования предела переменной
(см. § 82)
lim (S№-[F(/>) — F(a)]}=0.
§ 126] СВЯЗЬ МЕЖДУ ОПРЕДЕЛЕННЫМ И НЕОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ 327
Отсюда имеем:
lim Sn = F (b) — F (a).
П -> co
b
Ho limSn= \ f(x)dx, а потому мы получаем следующее фунда-
п -> ОО
а
ментальное равенство
ь
$f(x)dx = F(b)-F(a). (**)
а
Определенный интеграл от некоторой функции равен
разности двух частных значений ее первообразной функции,
вычисленных для верхнего и нижнего пределов.
Это чрезвычайно важное положение, найденное Лейбницем и
Ньютоном, сводит вычисление определенного интеграла к нахо-
ждению первообразной функции или интеграла неопределенного, т. е.
заменяет сложную задачу вычисления предела интегральной суммы
задачей более простой и нами уже рассмотренной — интегрирова-
нием функции.
Равенство (**) удобно записывать так:
г
jf(X)dx = [F(x)]a.
а
Надо помнить, что F' (х) =f(x).
г
_ f dx
Пример 1. Вычислить | j .
о
Сначала ищем первообразную функцию по отношению к,данной
Г dx .
.1
1
поэтому
1
1+х2‘
р—^2 = [arc tg = arc tg 1 — arc tg 0 - .
Пример 2. Вычислить J sin х dx.
о
Ищем первообразную функцию:
I sin х dx = — cos х,
поэтому | sin х dx = [ — cos лг]02 = — cos— cos 0) — 1.
b
328 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ХХЦ
§ 127. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Свойство I. Постоянный множитель может быть вынесен за
знак определенного интеграла*,
ь ъ
J Af (х) dx = А f (х) dx.
а а
Свойство- это с очевидностью вытекает из основного предста-
вления определенного интеграла как предела суммы (формула (*),
стр. 324). Постоянный множитель является общим множителем всех
слагаемых интегральной суммы, который и может быть вынесен за
знак суммы.
Свойство II. От перестановки пределов знак интеграла ме-
няется на обратный*.
J f (x)dx — — J / (х) dx.1
а Ъ
Свойство это вытекает с полной очевидностью из следующих
основных равенств:
J f(x)dx=F(b) — F(a), f f (х) dx = F (а) — F (b).
a b f
Свойство III. Каково бы ни было с, определенный интеграл
в пределах от а до b можно разбить на сумму двух интегралов
в предела < от а до с и от с до Ь.
Свойство это проверяется подобно предыдущему: с одной сто-
роны, имеем
ъ
$f(x)dx=F(b)-F(a),
а
с другой стороны,
п Ь
f f(x)dx=>F(c)—F(a) и ff(x)dx = F(b) — F(c).
a c
Складывая последние два равенства, находим
с Ъ
ff (х) dx + J/(х) dx =F(C)— F(a) + F(b)- F (C) = F(b) — F (a),
a c
что и подтверждает справедливость свойства III.
1 /(х) везде предполагается непрерывной в пределах интегрирования.
127] СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 329
На основании этого свойства можно написать, что
Ъ сх с3 Ъ
f/(x)dx=f f (х) dxf (х~) dx... + f f(x)dx.
° ° c> em-i
Свойство IV. Определенный интеграл от алгебраической суммы
шкций равен алгебраической сумме определенных интегралов от
ждого слагаемого*.
ъ ъ ь
J [/(*) + ®(*)]rf*= +J* <o(x)dx.
(L d 0>
Свойство это вытекает из представления определенного Инте-
ла как предела суммы. Каждый элемент интегральной суммы
сбивается на два слагаемых, а потому и вся сумма на две отдель-
е интегральные суммы, и в пределе на два определенных ин-
•рала.
Свойство V. Определенный интеграл равняется разности пре-
го в, умноженной на значение подинтегральной функции для
которого значения аргумента, лежащего между пределами а и Ь\
ъ
f f(x)dx = (b — d)f(c),
а
j с лежит между а и Ь.
Действительно,
f(x)dx = F(t>)—F(a) = (b— &}Ff (с) (по формуле Лагранжа),
Г (х) =/(*),
ютому
ь
f (х) dx— {b — a) f (с).
а
Свойство VI. Если а и f (х) > О для всех значений х в пре-
^ах интегрирования, то и
ъ
J f (х) dx > 0.
а
самом деле, при этих условиях / (с) > 0 и b — а > 0, а поэтому
ь
J/(х) dx = (b — а)/(с) > 0.
330 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [XXlj
Нетрудно видеть, как видоизменится последнее свойство, если бу-
дет b <Z а или / (х) < 0.
Свойство VII. Если Ь>а и /(х)>ср(х) для всех значений х
в пределах интегрирования, то и
ь ь
J* f (х) dx > J <р (х) dx.
а а
Действительно, так как f (х) > ср (х), то / (х) — <р (х) > 0, а тогда
по свойству V и
ъ
J* (/(х) —®(х)|</х>0.
а
Но по свойству IV
ь ъ ь
j* [/(х) — ® (х)] dx = J f(x)dx — J ср (х) dx,
а а а
так что
ъ ъ ъ ъ
j" f (х) dx— J ср (х) й?х > 0, т. е. J / (х) dx > J ср (х) dx.
а а а а
Нетрудно видеть, как видоизменится это свойство, если будет b <Z&
или /(х) < ср (х).
Свойство VIII. Производная определенного интеграла по верх-
нему пределу равна значению подинтегральной функции для этого
предела, а производная по нижнему пределу равна значению под-
интегральной функции для нижнего предела, взятому со знаком
минус.
Известно, что
ь
[f(x) dx = F (b) — F (7z), где Fr (x)=/(x).
a
Если, оставляв нижний предел а неизменным, мы представим
себе, что верхний предел b меняет свое значение, то определенный
интеграл будет функцией от Ь, производная которой по b будет
ъ
-^f(x)dx = F'(fi)=f(b).
а
Подобным же образом найдем, что
ъ
f(x)dx — —f (а).
128]
ВОПРОСЫ И УПРАЖНЕНИЯ
331
1.
2.
3.
ррал^?
5.
§ 128. ВОПРОСЫ И УПРАЖНЕНИЯ
Что такое определенный интеграл?
Какие задачи приводят к вычислению определенного интеграла?
Какую роль играют пределы интегрирования в определенном инте-
От чего зависит значение определенного интеграла?
Зависит ли определенный интеграл от переменной интегрирования?
ъ ь
6. Почему J f (х) dx = J f (z) dz?
a a
7. Как выражается определенный интеграл через первообразную?
8. Какими свойствами обладает определенный интеграл?
Вычислить определенные интегралы:
9. i J x2dx. 0 Отв. 1 3 *
10. n J* cos x dx. Отв. 1.
11. 0 2 f dx Отв. In 2.
12. J x 1 f dx Отв. 7Z
13. J V’l — X2 0 x In x dx. 4 Отв. 21п 2—|
i
1
16. I /О dX7^ • Отв. — }.
J (2х — I)2
о
17. I sin х cos х dx. Отв. 0.
+ *
14. I dx
2,4+л"2’
Отв.
4
1
15. j х arc tg xdx.
о
Отв.-j — •
2
1
1
VT
1
19. I e~?>x dx. Отв
•j &
6
i
20. j xe~x dx. бтв.е .
d
7C
T
21. J tg2xdx. Отв. 1——.
о
4
f n 1
22. xsin2xdx.Ome. — +
re
XXIII. ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
К ГЕОМЕТРИИ И ДРУГИМ ЗАДАЧАМ
§ 129. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
Задача I, рассмотренная в § 124, показывает, что вопрос о вы-
числении площади, ограниченной кривой, расположенной со стороны
положительного направления оси OY, осью ОХ и двумя ординатами,
сводится к вычислению предела интегральной суммы
пл. ABCD = lim [/ (а) Д^ +/(*1) Дх2+ • • • +/(*«-1) Дхп1-
П->ОО
Предел же такой суммы есть определенный интеграл. Таким
образом, мы приходим к следующей формуле для вычисления площади:
ъ
пл. ABCD = £ f (х) dx, (1)
а
где стоящая под интегралом / (х) пред-
ставляет правую часть уравнения кри-
вой, решенного относительно у, а
пределы интеграла являются абсцисса-
ми начальной и конечной точек кри-
вой: О А = а, ОВ = Ь. Они являются
Рис. 164. границами изменения х на протяжении
всей площади.
Формулу (1) пишут еще иначе, в виде
ъ
пл. ABCD = j* у dx.
а
Площади, ограниченные кривой, могут иметь иное расположение
относительно осей координат и иную форму, чем представленную
на рис. 164.
Покажем, как вычислять площадь в таких случаях.
§ 1291
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
333
I. Площадь расположена со
оГо направления оси OY
(рис. 165).
В этом случае все значения функ-
ции / (X) <6, а потому на основании
свойства VI (стр. 329)
ъ
а
стороны отрицатель-
Рис. 165.
Поэтому, чтобы вычислить пло-
щадь в этом случае, необходимо взять
абсолютное значение определенного интеграла;
ъ
пл. ABEF = J f (х) dx
а
лежите той и другой стороны
(рис. 166).
В этом случае
числять каждую
в отдельности; так
с
II. Площадь
У
в
А
£
Рис. 166.
так что
а
Ъ
г
оси
необходимо
часть
что
(2)
ОХ
вы-
площади
(3)
с
где О А — а, ОС = с, ОВ = Ь.
Ш. Площадь ограничена замкнутой кривой
(рис. 167).
Пусть кривая, заданная уравнением ср (х, у) = 0, имеет форму,
изображенную на рис. 167.
В этом случае каждому значе-
нию х должно соответствовать два
значения у, так что уравнение кри-
вой, решенное относительно у,
Должно распадаться на два урав-
нения
Положим, что первое из нихотно- рИс. 167.
сНтся к части кривой CDE, а вто-
Р°е к кривой CFE. Тогда всю площадь CDEFC можно рассматривать
334
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ
I
как разность двух площадей
пл. CDEFC = wi. ACDEB — пл. АСЕЕВ,
поэтому
ъ ъ ъ
пл. CDEEC = | yxdx—j y%dx = | (yr—y2) dx.
a a a
Рассмотрим несколько примеров:
Пример 1. Площадь параболы.
Применим выведенную формулу к вычислению части площади ODB.
Уравнение параболы
_У2 — <2рх
необходимо представить сначала в форме:
Остается вычислить этот определенный интеграл.
Как известно, для вычисления определенного интеграла. надо сначала
найти неопределенный интеграл
( Y2pxdx
или, иначе, первообразную функцию от 1^2/? х
— А
У2рх(1х=У*2р I Ухйх=У2р I х" dx = У*2р • ^-х" = ^х У2рХ-
! I □ о
Найдя неопределенный интеграл, ищем самую площадь:
ов ов
пл. ODB = У^рх dx = х У^рх]^ =
о
= -I- ОВ у/4р- ов= ОВ . BD.
О о
V2p • ОВ = BD — это вытекает из уравнения кривой. Итак
9
пл. ODB = 4 пл. OKDB.
и
§ 129J
' ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
335
Пример 2. Площадь эллипса.
Для вычисления площади эллипса заметим прежде всего, что (рис. 169)
пл. АВА^В^ = 4 пл. ОАВ.
Для вычисления же площади ОАВ применим только что выведенную фор-
мулу 0>-
Величину у, стоящую под знаком интеграла, получим из уравнения
эллипса
- + ^ = 1;
b г_______
Таким образом,
а а
пл. ОАВ = J —| V cfi—x^dx.
о о
Остается вычислить последний определенный интеграл.
Это можно сделать путем непосредственного вычисления сначала не-
определенного интеграла
j V а2— x*dx,
а затем перейти к определенному интегралу. Однако 'значительно проще
сделать это иначе.
Именно, если бы мы стали
вычислять не площадь эллипса,
а круга
X2jryi==a2i
то для одной четверти части пло-
щади круга получили бы подобный
же результат
а
1 Г г________
"4 пл. круга = у я2 — x2dx.
о
Из этого равенства сразу и вытекает величина интересующего нас интеграла
а
| У* Я2------X2 dx 7Ш2.
о
Принимая это в расчет, получаем
пл. ОАВ = -^ai=~
а 4 4 '
4 Вся площадь эллипса
пл. АВА^ = каЬ.
336 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [ХХЩ
Примерз. Площадь, заключенная между равнобочной
гиперболой и ее асимптотой.
Уравнение гиперболы, отнесенной к асимптотам, как известно,
ху = Л2.
Пусть ОА = а, ОВ = Ь, тогда
ъ ь
пл. ABCD = j* ydx = I* Л2^ = ^[1пх]^ —1п«].
а а
Если взять k = 1 и а = 1, то пл. ABCD = In b, т. е. площадь в таком
случае является натуральным ло-
У гарифмом абсциссы конечной
J । точки.
L пример 4. Площадь цик-
лоиды.
Чтобы применить формулу (1)
для вычисления площади одного
звена циклоиды, мы из уравнений
циклоиды
х = a (t — sin t)
у = а (1 — cos t)
----- X находим
U А О dx = а (1 — cos t) dt,
а потому
\ ydx = a2 (1 — cos t)2 dt.
\ Остается взять интеграл от полу-
\ ченного выражения.
И Замечая, что под знаком ин-
р 17q теграла появляется новая пере-
гис. i/и. менная t, мы должны и пределы
интегрирования согласовать с этой
переменной. Пределами интеграла должны теперь служить границы изме-
нения переменной t на протяжении вычисляемой площади.
Полное звено циклоиды опишется тогда, когда круг, чертящий циклоиду
и катящийся по оси ОХ, сделает полный оборот (см. рис. 120, стр. 233),
а тогда t изменится от своего начального значения 0 до конечного 2гс.
Поэтому пределами интеграла должны служить:
начальное значение t для дуги циклоиды 0;
конечное значение t для дуги циклоиды 2л;
21С 2я
пл. АМВ = J* а2 (1 — cos t)2 dt = а2 f (1 — cos t)2 dt.
о , о
По общему правилу вычисляем сначала неопределенный интеграл:
J (1 — cos t)2dt= J (1 —2 cos / + cos2^) dt= '
= J dt—2 j* cos td/+ j* cos2 tdt =
*=t—2 sin t + ’5'^+ -^-sin2/ (см. тип XIV, стр. 312)'
337
$ 129] ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
'Гаким образом, находим
г
Г о 1 "12л
пл. АМВ = a2 I1 — 2 sin —sin 2 Л = а2 • Зк = Зла2.
I2 4 Jo
Итак, площадь одного звена циклоиды равна утроенной площади катящегося
круга, чертящего циклоиду.
Пример б. Площадь секто-
ра, ограниченного кривой и
двумя радиусами -векторами,
проведенными из начала ко-
ординат.
Пусть уравнение кривой KL будет
а абсциссы точек Р и Q: ОА = а,
ОВ = Ь.
Из чертежа видно, что
пл. OPQ— пл. OBQ — пл. О АР — пл. ABQP.
пл. OBQ = ^BQ-OB = ±f(t>).l>,
пл. ОАР = ± АР- 0Л==1/(а) • а,
ъ ъ
пл. ABQP — J f (х) dx — j* у dx.
а а
Так что
ь
пл. OPQ = ±f(t>)-t> — ±-f(a)'a— | f(x)dx.
(I
Но разность
можно рассматривать как результат вычисления определенного инте-
грала; действительно
ь
22 Зак. 2116. Н. С. Михельсон.
33S
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ
|ХХ1ц
а
11оэтому
ь 5 ь ъ
пл. OPQ = 4 J d 1/(х) • Л'1 — I f(x) dx = Y
а а
Ъ Ъ
= 4] (У dxх dy) — | у dx —
а а
Ь Ъ Ь
1 f , . 1 f , f ,
у ydx-}--2 j xdy— | у dx =
и
b
(I
Итак
пл. OPQ =
а
ь
4j (xdy—ydx). (5)
а
Эта формула имеет важное при-
ложение к механике.
Пример 6. Площадь сектора
равнобочной гиперболы.
Приложим найденную формулу к
определению площади сектора О AM равнобочной гиперболы (рис. 172):
х2 —у2 = я2;
пл. 0AM = у | (x dy
a
(x-—T=^=dx—Yx2 — a2dx} =
J \ ( Vx2-a2 /
a
if/ х2 _/—«-----5\ . a2 f dx
= — — у х2 — a2 \dx — -г? =
2 J —Л2 / 2 J /Х2_а2
а а
»^1п(х+ |® = *4п(х_|_ =
а2, х + Ух2 — а2
При а = 1 формула упрощается; именно
пл. ОА М - Y In (х + /д2 — 1).
§ 130. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ
Рассмотрим тело CDEF, ограниченное некоторой боковой по-
верхностью и двумя плоскостями CF и DE* перпендикулярными
к оси ОХ и пересекающими последнюю в точках А и В.
Пусть
OA = a> OB = b.
130]
ВЫЧИСЛЕНИЕ ОЬЪЕМОВ тйл
339
[ля вычисления объема такого тела Разобьем отрезок АВ на п
астей точками, абсциссы которых
-1а рис. 173
•г1> . . . , Xtf, • • • ?
= OQ — Xi.
1ерез все такие точки проведем плоскости, перпендикулярные
тело разобьется на п слоев. Пусть один
с оси ОХ. Ими наше
13 таких слоев будет
На основании
ММГ этого слоя, пло-
щадь которого обозна-
чим через Ui9 построим
прямой цилиндр высотою,
равной толщине слоя
Xi — = ДХ;.
Объем этого цилиндра
будет равен
пл. ММг •PQ=Ui^xi.
Построим подобные же рИСф 173.
цилиндры во всех дру-
гих слоях, составим их сумму и будем беспредельно увеличивать
число п этих слоев. Искомый объем всего тела вычислим как
предел этой суммы, так что
V = lim It/jAx, t7aAx2 + ... + Un&xn\.
Я->00
На основании формулы (*) (стр. 324) найдем, что
ъ
V = § U dx, (6)
а
где U есть площадь различных сечений, перпендикулярных к оси ОХ,
меняющаяся в зависимости от места сечения, т. е. от абсциссы х.
Чтобы можно было воспользоваться формулой (6), необходимо знать
выражение площади U как функции от х.
Пусть
U=F(x),
^гогда окончательно
ъ
V=f F(x)dx.
а
2?*
340 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ |ХХЩ
Объем тела вращения.
Нахождение площади сечения U как функции от х является
первою частью решения задачи на вычисление объема тела. Осо-
бенно легко выполнить эту часть для случая, когда тело образо-
вано вращением некоторой кривой вокруг одной из осей координат.
Рассмотрим случай, когда вычисляется объем тела, получаемого
от вращения вокруг оси ОХ кри-
вой, уравнение которой
J =/(*)•
Сечения такого тела плоскостями,
перпендикулярными к оси ОХ,
х являются кругами, радиусы кото-
рых равны ординатам различных
точек кривой.
Поэтому площадь U любого
такого сечения будет
U = ту2 = Ttf2 (х);
это и будет искомое выражение
от х. Тогда для объема тела
Рис. 174.
площади сечения как функции
вращения получается формула:
ь ъ
V = j* тгу2 dx = ~ J* у2 dx. (7)
а а
Пример 1. Объем эллипсоида.
Применим формулу (6) к вычислению объема эллипсоида.
Проведя некоторое сечение DE перпендикулярно к оси ОХ (см рис. 175)
и обозначив его площадь, как выше» через U, находим
а
V= 2 j* U dx.
О
§ 1301
ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ
341
Остается теперь только найти U как функцию от х. Известно, что уравне-
ние эллипсоида таково:
—= 1
Й8Г&2ТС2 '•
Уравнение кривой сечения, перпендикулярного к оси ОХ, получим, если это
уравнение соединим с уравнением плоскости сечения
х = h, где h = ОР,
Сечение будет эллипсом, уравнение которого в этой плоскости пред-
ставится в виде
J/2 *2 __ ___Л2
£2 + f2 — 1-“H2
или
Полуоси этого эллипса PG и PD будут:
площад^^ке его
а2 ) ’
U = Ttb^Ci = nbc । 1 —
Заменяя теперь h через х, находим искомое выражение площади U как
чаемого от вращения пара- Рис. 176.
болы.
Рассмотрим объем тела, получаемого от вращения части ОВ дуги па-
раболы
>2 = 2рх
вокруг оси ОХ (рис. 176).
Пусть ОР = а.
Тогда искомый объем, согласно формуле (4), будет
а
б
а
342 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [ХХЩ
$ 131. ВЫЧИСЛЕНИЕ ДЛИН ДУГ
Пусть у ==/(х) уравнение некоторой кривой (рис. 177); а и ь
абсциссы концов дуги АВ, длину которой мы желаем вычислить.
Разделим дугу на п частей (хотя бы и неравных) и обозначим
абсциссы этих точек деления
М2, .. . мп^
через
Xj, х2, . .., xif .. . хп_ 1.
Проведя хорды AMlf , /Ип-1в и прини-
мая, что длина дуги есть предел, к
которому стремится периметр
вписанной в дугу ломаной
линии, когда число сторон
этой ломаной увеличивает-
ся беспредельно, имеем
лл.иАВ = s =
— lim [хорды АЛ11-^~
П-> со
+ хорды AfjAf2 -j- ...
<4* хорды -{-...-j-
-["Хорды Мп_1В].
Вычислим длину одной
из этих хорд, например
По формуле (3) § 16, расстояние между этими точками
= /(х.
Но
У1—У1-1 =Ж) — f (хг _ J = (xt — xt _ J f {Ci},
так что
1 +/'2(^) • (X;— x<_1) = / 1+/'2(с«) • Дх<.
Поэтому
5=Лтсо2/ 1-[-//2(^)-дх4-.
В силу же формулы (*) § 125 предел такой суммы может быть заме-
нен определенным интегралом, и мы приходим окончательно к фор-
муле
ъ ъ
S = J /1+/'2(х) dx = | /1+У2 dx. (8)
а а
Это и есть искомое выражение длины дуги. Из нее непосредственно
[вытекает, что
^ = |/ 1 . dx (9J
5 131]
ВЫЧИСЛЕНИЕ ДЛИН ДУГ
343
или _______
ds = |/ + (9')
формула эта была уже раньше выведена (см. § 112).
Пример 1. Дуга астроиды.
Предложим себе вычислить длину ду-
ги кривой, называемой астроидой, имею-
щей форму, изображенную на рис. 178, и
уравнение которой
х 2 3 * -f-y 8 = а 3.
По формуле (5) находим
ол
s = 4^ВА = 4 • J ] ’ 1+У2 dx.
О
Прежде всего определяем ОА\ из уравне-
ния кривой находим, что при у = 0, х = а,
следовательно, О А = а. Затем вычисляем
У и /1 +у2.
Из уравнения кривой выводим
2 2 2
у 3 = а 3 — х3
2 2 _3
у = (а 3 — X 3) 2
£
3 .
2 2_ __2 _2 _2
угъ~(а*—х3)*х 3=я3-х 3— 1;
Поэтому
2,
1+у2 = а8.х 3
У" 1+У2 = а 3 • х 3
1
^11 _____________ go
s = 4* | а3х 3dx = 4as * * х 3dx = 4a3^i—= 6а.
о о 0
входим сначала
Пример 2. Дуга циклоиды.
Из уравнений циклоиды
х == a (t — sin t)
у = а (1 — cos /)
dx = а (1 — cos /) dt
dy ~ sin (dt.
344 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [XXIII
а затем ds
ds2 = dx2 + dy2 = a2 (1 — 2 cos t + cos21 + sin2t) dt2 =
= a2 (2 — 2 cos 0 dt2 = 2a2 (1 — cos t) dt2 = 4a2 sin2 у dt2.
Следовательно,
ds == 2a sin у dt.
Отсюда
f t Г t I2*
5 = 2a sin -x- dt s 2a\ — 2 cos — I =^=
• ' * I ~ L
о
== — 4a (cos к - cos 0) = — 4a (— 1 — 1) = 8a.
§ 132. ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
К ЗАДАЧАМ ТЕХНИЧЕСКОГО ХАРАКТЕРА
Рис. 179.
В § 124 были уже приведены две задачи механического харак-
тера на приложение определенного интеграла: определение работы
силы и пройденного точкой пути. Приведем еще некоторые типы
задач технического характера, решение которых сводится к вы-
числению определенного интеграла.
Задача I. Вы числить массу некоторого
неоднородного тела ABCD, имеющего
форму кругового цилиндра, плотность
Окоторого в каждой точке есть опре-
деленная, известная нам функция от
расстояния этой точки до основания АВ,
именно, пусть
D=/(x).
Если бы тело было однородно, то масса т тела
выразилась бы так:
т= VD,
где V—объем тела.
Но в задаче плотность — величина переменная. Поэтому пред-
ставим себе, что данное тело мы разбили на п слоев толщиной,
равной
Xf -1 — ,
и допустим, что внутри такого слоя плотность не меняется и равна
Ж-i).
Тогда масса такого элементарного слоя Д/п будет
Д^ = ДУ./(х{,1) = №-/(х^|) • Дх0
§ 132] ПРИЛОЖЕНИЕ ИНТЕГРАЛА К ТЕХНИЧЕСКИМ ЗАДАЧАМ 345
где Д1/—объем этого элементарного слоя. Масса же всего тела
выразится тогда
i=n
2 nr9f(xt _1)Дх4-.
<—1
Предположение, что масса не меняется внутри каждого слоя,
неправильно, поэтому и предыдущая формула не выразит искомой
массы тела. Однако, с увеличением числа /г, т. е. числа слоев, на
которые разбивается тело, предыдущая сумма будет все ближе и
ближе подходить к истинной массе тела. Поэтому, увеличивая число
п, мы можем вычислить массу тела как предел написанной выше
суммы
i = n
т = lim 2
п -> оо 1 = 1
А эта формула приводит к определенному интегралу
h
J nr2f(x)dx,
о
где h — высота цилиндра.
Если, например, плотность нижнего слоя равна Do, в дальней-
шем же она увеличивается пропорционально расстоянию от основа-
ния, то
D = Dq —|—
и масса найдется так:
л
т — кг2 (Do kx) dx = тег2 (dqx 4“ ^п)0
о
= (doa+== (d0+%).
Величина О04“у в данных условиях есть, очевидно, плотность
среднего сечения и служит как бы среднею плотностью всего тела,
так что
т = тег2Л£>Средн.
Задача II. Определить работу расширения или сжа-
тия газа, подчиняющегося закону Клапейрона рФ —
~RT (так называемого идеального газа), где р — дав-
ление газа, рассчитанное на единицу площади, ф—
объем, Т — абсолютная температура газа и/? — газо^
В а я постоянная (постоянная Клапейрона),
346
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ
[XXIII
Положим, что газ заключен в цилиндре, площадь сечения кото-
рого Q. Цилиндр закрыт поршнем, который при увеличении или
уменьшении давления передвигается в ту или другую сторону.
Весь процесс расширения или сжатия газа, от положения поршня
в расстоянии s0 от дна цилиндра (рис. 180) до конечного ра-
зобьем на п элементарных этапов, в каждом из которых давление р
мы будем принимать постоянным. Тогда, обозначая элементарное
перемещение поршня через As*, найдем, что элементарная работа
Рис. 180.
газа при таком перемещении
поршня будет
р • Q • Д$ = р • Sv (Q • Ss = Sv).
Вся же работа при этом выра-
зится суммой
V = VX
^pSv.
v = v0
Будем теперь беспредельно
увеличивать число п этапов, на которое мы разобьем весь процесс;
тогда действительная работа расширения газа будет
V = Vv
А = lim ^pdv—fpdv. (10)
п -> ОО V = VQ J
Vj
Предложенную задачу в дальнейшем рассмотрим в двух случаях:
1. При условии, когда процесс расширения или сжатия проис-
ходит при сохранении газом постоянной, первоначальной его темпе-
ратуры, т. е. при полной отдаче во внешнее пространство приобре-
тенного при сжатии тепла, или при получении извне необходимого
количества тепла для поддержания температуры газа, потерянного
им при расширении. Это так называемый изотермический процесс.
2. При условии, когда газ при расширении или сжатии не полу-
чает извне тепла и не теряет его во внешнее пространство. Это так
называемый адиабатический процесс.
1-й случай — процесс изотермический: Т = const. Из уравнения
pv = RT находим
RT
Р=1Г-
Подставляя это выражение для р в формулу (10), находим
«1 «1
А = [ — dv — RT - =
J V J V
Vo v,
RT [In -pp = RT(In vx — in v0) — RTIn —.
Vo
§ 132]
ПРИЛОЖЕНИЕ ИНТЕГРАЛА К ТЕХНИЧЕСКИМ ЗАДАЧАМ
347
Найденное выражение работы можно представить еще иначе, имея
в виду, что в изотермическом процессе объемы газа обратно про-
порциональны давлениям, так что
Vo А’
а поэтому
Д = /?Т1п —.
Р1
Оба найденные выражения работы расширения или сжатия газа
оказываются зависящими от температуры газа и начального и конеч-
ного его объемов или давлений.
2-й случай — процесс адиабатический: Т переменное. При таком
процессе, как показывает термодинамика, величины р и v связаны
соотношением
р • = const = С, (11)
где k есть отношение теплоемкостей газа при постоянном давлении
и при постоянном объеме:
Из соотношения (И) находим
р == С • v~k
и, подставляя это значение р в выражение работы газа (в формулу (10)),
имеем
А = С = С к) =
«0
__ С ( 1 1 \
или
~ 1 Ч-1 vf-V - k-\ Ц v*)'
Последнее выражение можно упростить. Действительно, из фор-
мулы (11) имеем
т. С
ук = —- ,
р
так что
А — Л~Т (тг <г) = ^voPo ~
Но по формуле Клапейрона
pjC,J = flT} и PqVq = RTq,
348 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [ХХШ
Приняв это во внимание, найдем, что
Последнее выражение показывает, что в адиабатическом процессе
работа расширения и сжатия газа зависит лишь от разности началь-
ной и конечной температуры газа и именно пропорциональна этой
разности.
Задача III. Найти среднее значение функции на
протяжении некоторого промежутка ее изменения.
Положим, что для какой-нибудь величины найдены из экспери-
мента или другим путем п ее значений. За среднее значение такой
величины принимают среднее арифметическое всех этих значений,
т. е. величину
Ут + Уг + • •• -4- Уп
п
Представим теперь, что мы имеем не отдельный конечный ряд
значений некоторой величины, а непрерывный ряд значений неко-
торой функции /(х) в промежутке от х = а до х = Ь, и поставим
задачу об определении среднего значения такой функции в рас-
сматриваемом промежутке.
Такого рода вопрос может возникнуть в различных техниче-
ских задачах, как, например, при определении среднего давления
газа в процессе его расширения, среднего значения переменной
силы, в частности электродвижущей силы переменного тока, сред-
него давления воды на плотину, средней скорости молекулы газа
и т. д. Для нахождения среднего значения функции /(х) на про-
межутке значений аргумента от х = а до х = b разделим этот про-
межуток на п частей и, вычислив какое-нибудь значение функции
в каждом из этих промежутков
/(ai)> 7(аа),
составим их среднее арифметическое
/(^)+/(а2)+...+/Ы< (12)
Предел такого выражения при беспредельном увеличении числа п
и называется средним значением функции / (х) на промежутке [а, £].
Покажем, что предел этот существует и приводится к вычислению
определенного интеграла. Для этого умножим и разделим выраже-
ние (12) на b — а. Тогда
п
= 7^- • • • +/(««)]
К ГТ
§ 1321
Приложение интеграла к техническим задачам
349
it b — а *
Положив ---= Дх, найдем, что
п 1
Л = 7^7
Переходя к пределу, имеем
lim М == , _* - lim V / («*) Дх.
аП^оо^
Но, как известно, предел найденной суммы существует и равен
определенному интегралу
lim
П -> ОО
S /(а<)д* = $ f(x)dx.
Поэтому среднее значение функции в промежутке [а, Ь} будет
выражаться формулой
ь
f оредн = ь а j / (х) dX,
а
(13)
Сопоставляя найденное значение с формулой, выражающей свой
ство V определенного инте-
грала (см. стр. 329), находим,
что свойство V по существу
и определяет это среднее значе-
ние, а именно
ь
-^2—j/(x)dx=/(c).
а
Формула эта хорошо ил-
люстрируется геометрически.
Действительно, известно,
что j*/ (x) dx геометрически выражает некоторую
площадь ABCD
а
(рис. 181), где кривая DC определяется уравнением у = /(х), а ОА=а,
О В — Ь, поэтому f(c) оказывается высотою того прямоугольника ABEF
с основанием ДВ, площадь которого равновелика с рассматриваемой
площадью ABCD,
Поясним понятие о среднем значении функции на следующих
примерах:
ь
350
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ
[ХХ1П
Пример к Определить среднее значение давления идеального газа при
его расширении от объема v0 до Vp в условиях изотермического процесса.
Известно, что идеальный газ подчиняется закону Клапейрона
pv — RT.
RT
Отсюда р = , поэтому по формуле (13) имеем
1 f dv _ ln vt
/’оредн. — Vi — V(J J v 11 щ G
= in^=-^a_ln2i.
po—pi pi
Pt Pn
Пример 2. Определить среднее значение электродвижущей силы пере-
менного тока за полупериод от / = 0 до t = ^T, зная, что электродвижу-
щая сила Е выражается следующей функцией от времени:
Г, с . 2к/
£ = £osin-y-.
Тт
^оредн. j J 81П
_2Ей Т / 2itf XT1 _ 2 _ _„
“ Т *2тД C0S Т /0 ~£о-я-0.637 •£(>.
Здесь Ео означает наибольшее значение электродвижущей силы за весь
период; оно приходится на момент t = Т, так как наибольшее значение
. 2п/
sin -уг- соответствует этому значению t.
Рассмотренные выше приложения не исчерпывают всех возмож-
ных приложений определенных интегралов. Формула (*) § 125 дает
возможность вычислить и другие величины, которые можно пред-
ставить как предел суммы бесконечно большого числа бесконечно
малых слагаемых. Полезно заметить, что в зависимости от того, что
конкретно представляет собой это слагаемое, * предел суммы этих
слагаемых, т. е. определенный интеграл, будет выражать соответ-
ствующую им величину. Так, в формулах (1) — (4) подинтегральная
величина (т. е. элемент суммы) представляет собой элемент пло-
щади и сам интеграл — некоторую площадь; в формулах (6) и (7)
величина
Udx
представляет собой элемент объема и весь интеграл — объем неко-
§ 133] ПОНЯТИИ О НЕСОБСТВЕННЫХ ИНТЕГРАЛАХ 351
торого тела, в формуле (8) выражение
Yx^y^dx
является элементом длины и сам интеграл дает длину дуги кривой;
в формуле (10) выражение pdv является элементом работы и сам
интеграл дает величину всей работы и т. п.
Все приложения определенного интеграла к вычислению других
величин основаны на подобных же соображениях.
§ 133. ПОНЯТИЕ О НЕСОБСТВЕННЫХ ИНТЕГРАЛАХ
При установлении понятия об определенном интеграле (см. § 125)
предполагалось, что пределы интеграла числа конечные. Однако это
ограничение может быть иногда устранено, если только расширить
понятие об определенном интеграле. Вопрос этот разберем сначала
на некоторых примерах.
В § 129 среди различных примеров мы рассмотрели площадь ABCD,
ограниченную гиперболой xy — k2 и двумя ординатами AD и ВС
(рис. 182). Мы получили такой
результат: У
ъ
пл. ABCD=^ j -^-dx==
— k2 (In— Ina).
Однако может возникнуть
мысль вычислить площадь гипер- q д g ’ ~
болы, простирающуюся от орди-
наты AD не до ординаты ВС, X
а до более удаленной ординаты \
и, в связи с этим, поставить себе \ ,
задачу: определить предел, к ко- ’
торому будет стремиться пло- Рис. 182.
Щадь, ограниченная гиперболой,
осью ОХ и ординатами AD и ВС, по мере беспредельного удале-
ния второй ординаты от первой, т. е. определить предел инте-
грала при стремлении верхнего предела b к со. Предел такого
интеграла в данном случае не будет существовать, так как
ъ
Г А»2
lim — dx == lim k2 (In b — In a) = oo.
д->ООе/ X Ъ->СО
a
Однако не всегда предел подобной площади не существует, т. е.
Не всегда определенный интеграл не имеет предела, когда верхний
предел его стремится к оо.
352 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ fxxltt
Возьмем, например, площадь ABCD (рис. 183), ограниченную
кривой
k
осью OX и двумя ординатами AD и ВС. Полагая О А = а и ОВ = Ь,
найдем
b
пл. ABCD = —~dx = k — — = k - — -г •
J х2 \ xja \а bj
а
По мере беспредельного удаления ординаты ВС, т. е. при стремле-
нии b к оо, определенный интеграл в этом случае стремится к опре-
деленному пределу:
ь
dx —
а
Таким образом, мы видим, что
ширить понятие об определенном
У
Рис. 183.
иногда возможно и полезно рас-
интеграле, распространив его на
случай, когда верхний предел
стремится к оо.
Принято предел такого ин-
теграла, если он существует,
обозначать так:
f f(x)dx,
так что
со Ъ
(f (х) dx = lim f / (х) dx. (1)
“ &->со J
a a
Точно так же рассматривают
определенный интеграл и в слу-
чае, когда нижний предел стремится к —оо, а именно, если предел
определенного интеграла существует, то полагают
ъ
J f(x)dx =
ь
lim f f(x)dx.
—оо J
а
Пример 1. Найти j* е х dx.
6
f e~xdx =
6
ь
J е~х dx.
о
§ 133] ПОНЯТИЕ О НЕСОБСТВЕННЫХ ИНТЕГРАЛАХ 353
Так как
ь
J* е~х dx = (— е~х)ь = — e~b + eQ = 1 — е~ь,
о
то
оо
f е~хdx= lim (1 —е~ъ) = 1.
О & + оо
I dx
Пример 2. Найти | j •
б
оо Ъ
I’ ттз- = Л”я(,гс 1г ‘ —гс « °> = 7
о о
Понятие об определенном интеграле допускает расширение и
в другом направлении. Дело в том, что до сих пор мы при рассмотре-
нии определенного интеграла всегда ставили условие, чтобы подинте-
гральная функция была непрерывной на всем протяжении проме-
жутка интегрирования, включая и самые пределы интеграла. Однако
от этого требования можно в некоторых случаях отказаться, уста-
новив следующее:
Если функция / (х) обращается в оо при х = £, то под опре-
деленным интегралом
ъ
j* / (х) dx (пусть b > а)
а
понимают
6 —е ’
lim Г f (х) dx,
е->0 J
а
если этот предел существует. Так что в этом случае
Ъ & —е
J / (х) dx = lim J f (x) dx. (2)
a 8->0
Если функция/(x) обращается в оо при х = а, то под инте-
гралом
ъ
^f(x)dx
а
понимают
ъ
lim Г f (х) dx,
23 Зак. 2116. Н. С. Михельсон.
354
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ
|ХХ1П
если этот предел существует. Так что в этом случае
ъ ь
f / (х) dx = lim f f (x) dx. (3)
J 6->0
(L Cb -f” ®
Так, например, в интеграле
ь
f dx
J Vb — x
0
подинтегральная функция обращается в оо при х — Ь. На основа-
нии установленного выше, имеем
Ъ Ъ—в
| — — = lim f dx = lim [— 2 У b — x]Ь =
J Vb —x e-»0 J Vb — X e->0 0
0 0
= lim [— 2/74-2]/^] = 2/£
6->0
И для этого случая расширения понятия определенного инте-
грала можно дать геометрическое
обоснование.
Рассмотрим линию, заданную
уравнением у*(Ь — х) = 1.
Исследуя данную кривую
. 1 .
v = ±— - -, можно убедиться,
yb — х
что она симметрично располо-
жена относительно оси ОХ, со-
стоит из двух ветвей, асимптоти-
чески приближающихся к оси ОХ
и к прямой KL, и имеет форму,
изображенную на рис. 184.
Предел, к которому прибли-
жается площадь ОАВС по мере
приближения ординаты АВ к асим-
птоте KL, и выразится рассмо-
тренным выше интегралом:
lim ОАВС =
ОА-^Ъ
b — е
= lim f —= %Vb.
.-»o J Vb — x
0
Интегралы (1), (2) и (3), рассмотренные в этом параграфе, носят
название несобственных интегралов.
Встречаются и такие случаи, когда подинтегральная функция
обращается в бесконечность в промежутке между пределами.
§ 134] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
355
3
Таков, например, интеграл | —. Его можно рассматри-
J Vx-2
2 3
f dx f dx rT
вать как сумму двух интегралов — и . Послед-
J Yx — 2 J ух— 2
о г 2 г
ние приводятся к предыдущим случаям.
§ 134. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ
ИНТЕГРАЛОВ
Формула (**) (см. § 126), дающая возможность вычислить опре-
деленный интеграл при помощи предварительного нахождения перво-
образной функции, становится бессильной в случае, если оказы-
вается невозможным найти первообразную функцию. В этом случае
приходится обращаться к приближенному вычислению определен-
ного интеграла. Для выяснения метода приближенного вычисления
и получения соответствующих формул обратимся снова к геометри-
ческому представлению определенного интеграла.
Каков бы ни был задан определенный интеграл, его всегда можно
рассматривать как площадь или совокупность площадей, ограничен-
ных некоторой кривой, осью ОХ и двумя ординатами. Приближен-
ное вычисление определенного интеграла, таким образом, может быть
сведено к приближенному вычислению той площади, которую опре-
деленный интеграл собою представляет. Мы рассмотрим два спо-
соба решения поставленной задачи.
1. Способ трапеций. Положим, нам требуется вычислить опре-
деленный интеграл
ъ
J / (х) dx,
а
и допустим, что геометрически он представляет собою площадь,
изображенную на рис. 185. Соединив прямой линией точки D и С,
мы получим трапецию ABCD, площадь которой приближенно можно
принять равной криволинейной площади ABCD и поэтому написать
следующее приближенное равенство:
ъ
J /(х)^хдапл. трап. ABCD.
а
Остается вычислить площадь этой трапеции, чтобы получить
приближенное значение определенного интеграла.
В условиях поставленной задачи мы имеем
ОА = а, ОВ = Ь, АВ — Ь — а.
AD—f(a), BC=f(b).
23*
356 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [XXIII
Поэтому площадь трапеции выразится следующим образом:
пл. трап. ABCD = — • АВ — b \J(a) 4-/(£)] =
= -Ц^-0'о+л),
где для сокращения положено /(я)=.Уо и /(^)=Jr
Таким образом, мы приходим к следующей формуле:
ь
J / (х) dx «(у0+Ji). (1)
а
Полученная таким образом формула, конечно, не может претен-
довать на достаточную точность; зато она отличается чрезвычайной
простотой.
Формулу (1) можно, однако, уточнить, если предварительно
разбить изображаемую определенным интегралом криволинейную
площадь ABCD на п полос (для простоты одинаковой ширины), и
применить формулу (1) к каждой полосе в отдельности (рис/ 186).
Обозначим ширину каждой полосы через
< b — а
и пусть абсциссы точек деления отрезка АВ будут
а, а-|-2Л, ..., я-|"(п—1)^, а-\- nh = Ь.
Соответствующие им ординаты, получаемые из уравнения
у =f (х), пусть будут
№ № У 2, •••> Уп-i, Уп,
тогда
ъ
а
= y(j,o4-i2j,i4_^a+ • • • Ч-2Уп-1 ,
§ 134] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
357
или окончательно
ь
J/(x)dx«^(y0 + 2y1 + 2^+...4-2^_1+Jn). (I)
а
Формула эта известна под названием формулы трапеций. Ошибка,
которую мы делаем, применяя формулу (I), по абсолютной вели-
чине, оказывается, не превышает следующей величины
I (Ь-а)*
I 12д2
м |,
где М наибольшее значение f'(x)9 которое она имеет в промежутке
[а, й].
Пример 1. Рассмотрим интеграл
dx
/Г+*5
Интеграл этот не берется в конечном виде и вычисление его приходится
вести, пользуясь методами приближенного вычисления. Применим способ
трапеций, именно формулу (I), положив в ней п = 5.
Тогда
2п 1А 4
X 1 0 0,2 0,4 0,6 0,8 1,0
1 | 1 1,008 1,064 1,216 1,512 2,000
Vl+хЗ | 1 1,004 1,032 1,103 1,229 1.414
_1 1 0,996 0,969 0,907 0,813 0,707
1<1+хЗ 1
Уо 2Л 2л 2Л 2л Л 1,000 1,992 1,938 1,814 1,626 0,707 (* dx = 0,1 • 9,077 = 0,908. J Vl-h*3 0
9,077
358 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [ХХШ
При сравнении с результатами других более точных вычислений точ-
ность полученного результата оказывается равна 0,001.
Пример 2. Рассмотрим интеграл
f dx
J 1+*2’
о
С одной стороны, известно, что
I dx /«Xi . 1 л
J Г+У2=<аГС{8Х)о = аГС181 = Т-
О
С другой стороны, мы можем к данному интегралу применить только
что выведенную формулу (I) и тем самым вычислить число л.
Полагая в ней п = Ю, а = 0, b = I
и f(x) = 1 v составляем таблицу:
X l+*2 1 1 +*2
0 1 1,0000
0,1 1,01 0,9901
0,2 1,04 0,9615
0,3 1,09 0,9174
0,4 1,16 0,8621
0,5 1,25 0,8000
X 1 + № 1 1+х2
0,6 1,36 0,7353
0,7 1,49 0,6711
0,8 1,64 0,6098
0,9 1,81 0,5525
1,0 2,00 0,5000
По формуле (I)
1
J ГТТа = i[/ (0) +2/(0,1) +2/ (0,2) +2/(0,3) +2/ (0,4) + 2/ (0>5) +
+ 2/(0,6) + 2/(0,7) + 2/(0,8)+2/(0,9)+/(!)]= 0,78498.
Таким образом,
4 = 0.78498 и к = 3,13992.
4 ’
Как видно, я вычислено с ошибкой, меньшей; чем 0,002.
2. Способ парабол. Второй способ вычисления определенного
интеграла состоит в том, что кривая, ограничивающая площадь,
заменяется не прямой, а некоторой кривой, уравнение которой
у = у(х) и которая имеет с данной кривой несколько общих точек.
Рассмотрим тот только случай, когда кривая DGC заменяется
параболой второго порядка KL, имеющей с данной кривой три
общие точки, соответствующие ординатам: начальной AD, конеч-
ной ВС и промежуточной FE, расположенной посередине между
ними (рис. 187).
§ 134] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
359
Пусть ОД = л, OB = b, OF=?-^-, AB = b — a, AF = FB =
Ь — а ,
=—=*•
Положим также /(й)=_у0, /(Д^'*)=.Г1. Так как
функция / (х) нам дана и числа а и Ъ нам известны, то известными
оказываются и количества yQ,
У1 и у2.
Заменяя вычисляемую пло-
щадь ABCGD площадью
ABCHD, мы, следовательно,
полагаем, что
ъ
J f (х) dx пл. ABCHD. (2)
а
Поэтому для решения за-
дачи о приближенном вычи-
слении определенного инте-
грала в рассматриваемом слу-
чае остается лишь вычислить
площадь ABCHD, ограниченную
натами AD и ВС.
Рис. 187.
параболой DHC, осью ОХ и орди
Совершенно ясно, что рассматриваемая площадь не может изме-
нить своей величины, если начало координат мы переместим в точку F.
В предположении, что мы это сделали, представим себе, что
уравнение параболы, так называемой смещенной, в новой системе
координат будет
у = kx*-\-lx~\- т.
Тогда, следовательно,
+ 1ь
пл. ABCHD = j* (kx* Ц- lx ni) dx,
— h
(3)
Что касается коэффициентов k, I, т, входящих в уравнение
параболы, то они найдутся на основании условия, что парабола
имеет три общие точки D, Е и С с кривой DGC, т. е. из условий,
что
kh?—lh~\-ni=y^ 1
k№-\-lh tn = ^2- )
(4)
360 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [XXIII
Решая эти уравнения, мы и найдем коэффициенты k9 I и т.
Будем предполагать, что они нами определены. Тогда
4- h
f /г 2 I , г чл f kX& . Zx2 , \ + Л W . /Д2 .
I (Ах8 + /х4-ти)</х = ^—I—2' + mxJ_h = -3-H—2" +
—п
-\-tnh— (---— tnh\ = -В-k№2mh = 4 (2kh2-\-bm). (5)
\ О / О о
Остается теперь лишь в последнем результате заменить коли-
чества k и т через у0, уг и у2 из уравнений (4).
Для этого, однако, не требуется полностью решать уравнения (4),
как мы это предполагали, а достаточно умножить второе из них
на 4 и все сложить, чтобы получить сразу значение суммы 2kh2 -|-
-f-6/n. Действительно, выполняя указанное, получим
2kh2 + 6m=yQ + 4y1+y^ (6)
Таким образом, на основании равенства (5) имеем
4-л
пл. ABCHD— (kx2-\- lx-\-ni) dx = у (^о + 4Л +^2),
—л
а имея в виду приближенное равенство (2), получаем
&
J / (х) dx « 4 (у 0 + 4У1 +^2)
а
или, окончательно,
ь
| f^dx^^iy. + iy.+y^ (7)
а
Полученную таким образом формулу можно уточнить тем же
путем, как это делается в способе трапеций, а именно: предва-
рительным делением всей площади на п полос (для удобства —
одинаковой ширины) и применением формулы (7) к каждой полосе
в отдельности.
Ширина каждой полосы будет тогда
Ь — а
п *
Обозначим последовательные ординаты, делящие площадь на п
полос, через
-•> У2п-
Кроме этих ординат, мы должны представить себе в каждой по-
лосе промежуточные ординаты, взятые посередине между двумя
последующими. Обозначим их через
У и У з> • • •> .Уап-1*
§ 134] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
361
Применяя теперь формулу (7) к каждой полосе, получим
ь
J f (х) dx яа 6я О0 4- 4yt 4- У2) 4- (Уа 4" 4Уз +л) +
а
+ • • • + —(Уап-а + 4Узп-1 -\~Уап) =
— Qn (Уо + 4У1+ 2у9 4- 4у3 4~ 2у4 4" • • • + 4Уап-14“Уяп)‘
Таким образом, мы приходим к формуле
ь
J / (x)d,Xtt fj'o4“3/2n+4(Л +-Уз+ • • • + ^2п-1) +
а
+ 2 (л + • • • +Лп-2)Ь (Н)
носящей название формулы Симпсона.
Оказывается, что ошибка, которую мы делаем, применяя формулу
Симпсона, по абсолютной величине не превышает следующей вели-
чины:
1/6 —ay М I
К 2 / 90л4| ’
где М — наибольшее значение /IV(x) в промежутке [а, Ь].
Пример 3. Известно, что
2
Если теперь тот же интеграл вычислить, применив формулу интегри-
рования по способу трапеций или парабол, то тем самым мы вычислим,
следовательно, натуральный логарифм двух. Выберем для вычисления фор-
мулу (7). Применительно к данному случаю имеем
г / ч 1 1 L О Д 3
/(.г) = т, а=1, 6 = 2, =
Поэтому находим
I Чг=1(1+4+1)=0,694-
г1 X О \ О Z /
1
Результат этот разнится от истинного значения In 2 на одну единицу
третьего десятичного знака. Как видно, формула (7) при столь простом рас-
чете дает уже порядочную точность.
Попытаемся увеличить точность расчета, разделив промежуток на пять
равных частей и применив формулу Симпсона. Будем иметь
а — 1,0; х2=1,2; = 1,4; лг6 = 1,6; х8— 1,8; 6 = 2,0.
362
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ
[XXIII
Промежуточные значения будут
= 1,1; х3=1,3; хб = 1,5; х7 = 1,7; х9=1,9.
Поэтому по формуле (II)
2
+ 2 (Di + 77 + 775 + 771)1 = I1-5 + 40 • 0,345954 +10 • 0,545635] = 0,693150.
\1л 14 10 1O/J ои
Этим путем мы получаем результат с точностью до трех единиц шестого
десятичного знака. Более точное значение In 2 будет
In 2 = 0,693147.
§ 135. ВОПРОСЫ И УПРАЖНЕНИЯ
ъ
1. Какой формы площадь вычисляется при помощи формулы §ydx?
о
2. Как вычислить площадь, ограниченную осью ОХ, двумя прямыми,
параллельными оси ОУ» и кривой, расположенной со стороны отрицательных
ординат?
3. Какой вид примет формула для площади, ограниченной кривой,
осью ОУ и двумя прямыми, параллельными оси ОХ7
4. Как вычислить длину дуги кривой?
5. Как вычисляются объемы тел?
6. Как вычисляются объемы тел вращения вокруг оси ОХ7
7. Как напишется формула для вычисления объема тела вращения вокруг
оси ОУ7
8. Что представляет геометрически подинтегральнос выражение в фор-
мулах для вычисления:
а) площади,
б) длины дуги,
в) объема,
г) объема тела вращения.
9. В чем заключается приближенное вычисление определенных инте-
гралов по способу трапеций?
10. В чем заключается приближенное вычисление определенных интегра-
лов по формуле Симпсона?
18
И. Вычислить площадь, ограниченную кривой (см. рис. 33 на стр. 62),
осью ОХ и двумя ординатами, соответствующими абсциссам х = 2 и х = 3.
Отв. 3 квадратных единицы.
12. Вычислить площадь, ограниченную осью ОХ и одним звеном кривой
у = sin х (см. рис. 36 на стр. 63). Отв. 2 квадратных единицы.
13. Найти площадь, ограниченну/о кривой у = л4— 2х2-|-3, осью ОХ и
двумя ординатами, соответствующими точкам, в которых кривая имеет ми-
нимум. Отв. 5—.
1 о
14. Вычислить площадь, ограниченную кривой х2у = 4х—у, осью ОХ и
двумя ординатами, соответствующими точкам перегиба. (См. задачу 30, стр.293).
Отв. 8 In 2.
§ 135]
ВОПРОСЫ И УПРАЖНЕНИЯ
363
15. Вычислить длину дуги кривой у — -% In х—заключенной между
3 1
точками, абсциссы которых равны 1 и 2. От в. In 2.
16. Вычислить длину дуги кривой у = In sin х, заключенной между точ-
ками, абсциссы которых равны и ~. Отв, -i- In 3.
z 3 z
17. Вычислить длину дуги параболы j/2 = 4(x —1) от се вершины до
точки, абсцисса которой равна 2. Отв, УТ-1-In (1-|- V2).
18. Вычислить длину дуги кривой, заданной уравнением
у = У—1— arc tg — 1,
от начала координат до точки, для которой х = 1. Отв. е — 1.
х2 у2
19. Найти объем, отсекаемый от эллиптического параболоида ~ + = 2г
плоскостью z = h, Отв, ^.ypq-h2.
20. Убедиться путем применения выведенных формул в справедливости
формулы объема кругового конуса, известной из элементарной геометрии.
21. Вычислить часть объема тела вращения кривой у = х Ух— 1 вокруг
оси ОХ, заключенного между плоскостями х = 1 и х = 2.
„ 17
Отв.
22. От прямого кругового цилиндра радиуса г отсечено клинообразное
тело плоскостью, проходящей через центр основания под углом а к этому
2
основанию. Вычислить объем такого тела. Отв. — г3 tga.
3
23. Материальная точка массы т движется под действием взаимного при-
тяжения, существующего, согласно закону Ньютона, между ней и другой не-
подвижной массой М, Вычислить работу силы при перемещении точки на по-
, Мт
ловину начального расстояния d между точками. Отв. - .
24. Вычислить работу, производимую газом при его расширении в усло-
виях изотермического процесса, если газ следует закону Ван-дер-Вальса
+ ЬУ^Т-
Отв. A = RTln .v.2~b.. + a(-l------
Vi —b \ v2 Vi J
25. Плотность земли в расстоянии х от ее центра выражается формулой
D = 10,6 —0,8 • ) . Вычислить массу столба земли, основание которого
1 см2, на протяжении от центра земли до ее поверхности.
Отв. 4664 тонны.
26. Известно, что скорость v движения тела, вышедшего из состояния
покоя и падающего в пустоте, выражается следующей функцией пройден-
ного им пути s: v = V2gs. Определить среднюю скорость падения тела
на отрезке считая его от начального положения тела.
Отв- %едн = s'»1-
364 ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ К ГЕОМЕТРИИ [XXIII
27. Определить среднее давление воды на плотину прямоугольной формы,
длина которой I и высота погруженной части Л, считая плотность воды D
постоянной на всех уровнях. Отв. -g- lh D.
хч у®
28. Дуга s эллипса Jqj + = на протяжении от х = 0 до х = 8 вы-
ражается следующим интегралом:
8
f,/“ 10000 — 64x2
S-JV 100(100 — Xs)dx;
о
вычислить эту дугу. Отв. Длина дуги с точностью до 0,001 равна 8,502.
29. Вычислить приближенное значение числа тс, применяя формулу тра-
Т
)* dx
— —.
/1—Х2
о
30. Вычислить приближенное значение числа тс, применяя формулу Симп-
1
f dx
сона к интегралу | -у .
6
XXIV. БЕСКОНЕЧНЫЕ РЯДЫ
§ 136. ОБЩИЕ ОСНОВАНИЯ
Выражение вида
и\ + ^2 + из~г • • • + ипА~ • • •, С1)
состоящее из бесконечного множества чисел, следующих одно за
другим по определенному закону, называется бесконечным рядом.
С понятием о бесконечном ряде мы встречаемся еще в элемен-
тарном курсе алгебры, именно при изучении бесконечно убывающей
геометрической прогрессии, которая представляет один из частных
видов бесконечного ряда; например
т+т + 4’ + --• W
Высший анализ идет дальше и рассматривает не только беско-
нечные ряды, составляемые по такому закону, где каждый после-
дующий член ряда получается из предыдущего умножением его на
одно и то же число, но и ряды, члены которых составляются по
другим законам, например,
2^3 4^5
(5)
В общем виде бесконечный ряд представляется в форме (1), где
и2> us> ••• 9 ип, •• • называются членами ряда, причем ип при-
нято называть общим членом ряда, понимая под п любое целое
положительное число.
Так, для ряда (2) *
ип 2^ ’
Для ряда (3)
1
ZZn 32П-1 ’
366 БЕСКОНЕЧНЫЕ РЯДЫ [XXlV
для ряда (4)
1
Un~ 1.2-3...л’
для ряда (5)
Рассматривая сумму п первых членов ряда (1)
5n = zzl + w2+Ms+ • • •
нетрудно заметить, что она является величиной, меняющейся вместе
с числом п. С возрастанием п до бесконечности sn может, как вся-
кая вообще переменная, иметь некоторый определенный предел,
а может и не стремиться ни к какому определенному пределу.
В первом случае, когда предел существует, т. е. когда
lim sn = s,
п ->оо
ряд (1) называется сходящимся, а постоянная величина 5 называется
тогда суммой бесконечного ряда, что и обозначают так:
“h 4“ из 4” • • • =s*
Таким образом, суммой бесконечного ряда называется предел
суммы п первых чисел ряда.
Во втором случае ряд называется расходящимся и такой ряд
суммы не имеет.
Всякая бесконечно убывающая геометрическая прогрессия пред-
ставляет сходящийся ряд. Действительно, сумма п членов такого
ряда, как известно, такова:
а(1 — qn) a aqn
Sn ~ 1 — q
и так как |<?|< 1, то, следовательно, limgn = O, а потому
П->оо
Вычисляя по этой формуле сумму рядов (2) и (3), находим
Ряды (4) и (5) тоже сходящиеся, как это будет показано в даль-
нейшем; сумма первого из них оказывается равною числу е, а сумма
136] ОБЩИЕ ОСНОВАНИЯ 367
второго равна In 2. Так что, согласно установленному, можно на-
писать
е~ 1 l-2-З^- ' ’ •
|п2=1-т+-5-т+---
Приведенные выше результаты вычисления сумм рядов показы-
вают, что бесконечные ряды можно рассматривать как новую форму,
в которой возможно представить различные числа.
Конечно, может показаться сомнительной целесообразность пред-
ставления целого числа 1 или дроби в виде бесконечного ряда
о
(см. выше), однако весьма целесообразным следует признать пред-
ставление в виде бесконечного ряда таких чисел как е или In 2,
так как это дает возможность вычислить числа е и In 2 и притом
с любой степенью точности.
В связи с этим в вопросе о рядах анализ ставит следующую
важную задачу: представить изучаемое число в виде бесконечного
ряда. Разбирая такого рода задачу, можно, например, получить (см.
более полные руководства) такого рода результаты:
4 1 3^5 7^9
1
;sin X 1 1 ! 1
~~х~аХ~~ТЛ~ 3-1 -2-3“Г 5-1-2-3-4-5
о
Однако эта задача анализа — представление данных чисел в виде
бесконечных рядов — не является единственной в вопросе изучения
бесконечных рядов. Дело в том, что сумма некоторого ряда может
оказаться числом, природа которого нам неизвестна или которого
мы вообще не знаем. В таком случае ряд наш явится уже не новой
формой, в которой нам представляется число, а единственной фор-
мой, в которой мы мыслим это число. Тогда бесконечный ряд для
нас уже не вспомогательное средство, а аналитическое выражение,
важное само по себе. Изучение природы такого ряда есть, стало
быть, изучение числа, им изображаемого. Такое изучение и является
второй задачей, которую анализ ставит при рассмотрении беско-
нечных рядов.
Само собою разумеется, что решение этой задачи должно начи-
наться с вопроса о том, будет ли данный ряд сходящимся или расхо-
дящимся, так как в последнем случае ряд вообще не представляет
собою никакого числа. Поэтому прежде всего необходимо устано-
вить признаки, по которым можно было бы судить о сходимости
Или расходимости рядов.
368
БЕСКОНЕЧНЫЕ РЯДЫ
[XXIV
§ 137. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
Необходимым условием сходимости рядов является следующее:
общий член ряда должен стремиться к нулю при беспредельном
возрастании его номера, т. е.
lim ип = 0.
П+оо
В самом деле, если данный ряд
^1 + ^2 + 4" • • • + + + • • •
сходящийся, то
lims„ = s’, а также и =
л+оо п
Тогда
lim (sn — sn_ j) = lim sn — lim sn_ j = 0.
?l + oo n + oo n+oo
Ho
sn sn-l~Un*
Следовательно, для сходимости ряда должно быть
lim ип — О,
71 + 00
что и доказывает высказанное положение.
Следует помнить, что условие это только необходимое, но не
достаточное. Подтверждением этому может служить следующий
ряд, называемый гармоническим:
Общий его член ип = — с беспредельным возрастанием п стремится
к нулю, но ряд этот, как нетрудно показать, расходящийся. В са-
мом деле, сгруппируем его члены следующим образом:
1 +т+(4 + г) + (1 +1+7 + т) +
и рассмотрим каждую группу, заключенную в скобках, в отдель-
ности.
Нетрудно заметить, что:
±4__L>1_l±_£
3 г 4^ 4^4“2
1 +1 +1.1. ± > 1 Ц_ 1 +1 _L ± = 2_
6'6^7+8^8^8^8^82
± । 1 f . 1 I l_i_ . 1 1
9 + 10 “*"••• "г 16 > 16 + 16 + • • • + 16 “ 2
и т. д.
§ 137] ПРИЗНАКИ СХОДИМОСТИ РЯДОВ 3^9
Таким образом, каждая в отдельности такая группа членов
больше , а потому сумма п членов ряда с возрастанием п будет
беспредельно возрастать и может превзойти любое число, т. е.
lim sn не существует, и рассматриваемый ряд, следовательно, рас-
73~>ОО
ХОДЯЩИЙСЯ.
Указанное условие дает возможность некоторые бесконечные
ряды сразу относить к числу расходящихся. Так, ряды
1 —j— 2 -{-• 3 —4 —р ... л —|— . ..
4+4+4+4+.--+„-^г+...
т+4+4+4+---+Ц1+---
будут, очевидно, расходящиеся: первый — так как общий член ряда
растет беспредельно, второй — так как общий член ряда тоже ра-
стет, хотя и не беспредельно, и третий — так как общий член ряда
хотя и убывает, но его предел равен не нулю, а единице.
Изучение признаков сходимости рядов начнем со случая, когда
все члены ряда одного и того же знака, например, положительные.
Кроме того, мы будем предполагать, что условия сходимости вы-
полняются, начиная с первого члена ряда, так как при рассмотре-
нии сходимости или расходимости ряда мы можем не принимать
в расчет любое конечное число начальных членов и считать за
первый тот, с которого наши условия имеют место. Природа ряда,
т. е. его сходимость или расходимость, от этого не изменяется, так
как сумма отбрасываемых начальных членов ряда представляет собой
постоянную величину. Действительно,
П->оо n->oo
= (M1 + M2 +•••+“«) +lim (“i+l + • • • + “»>),
n->OO
откуда видно, что limsn убудет существовать или не существовать
П-»0О
в зависимости от того, будет ли существовать или нет
lim(wi+14-«<+24~ • • • +«п),
П->оо
а сумма начальных членов ряда, как постоянная величина, влияния на
сходимость или расходимость ряда оказывать не будет.
Z-й признак сходимости рядов. Если каждый член ряда
и1 4“ 4" U3 4“ • • • + ип + • • •
Ответственно меньше членов другого заведомо сходящегося ряда
Ц + ^ + ^з+
24 Зак. 2116. Н. С. Михельсон.
370
Бесконечные ряды
Ixxiv
то данный ряд сходящийся} если же каждый член данного ряда
соответственно больше членов другого заведомо расходящегося
ряда, то данный ряд расходящийся.
Повторяем, что члены обоих рядов предполагаются положитель-
ными.
Обозначим через sn и Sn суммы п первых членов ряда первого
и второго и через S — сумму второго ряда, т. е. предположим,
что
lim Sn = S.
Из условия теоремы вытекает, что ’
5л, 5 л. .
П П
Так как члены обоих рядов по предположению положительные,
то обе 'эти суммы с возрастанием п все время возрастают; но
тогда Sn не может превзойти величины S, а значит и sn при своем
возрастании не превзойдет величины 5 и, стало быть, будет иметь
некоторый предел (см. признак II существования предела перемен-
ного— §82), а потому рассматриваемый ряд сходящийся.
Вторая часть признака совершенно очевидна и доказательства
не требует.
Пример 1. Ряд
' 2 22 2<* '
сходящийся, так как он представляет собой бесконечно убывающую геоме-
трическую прогрессию. Новый ряд
1 г J ь * _1_ _ * I
1 ‘ 1.2 ' 2 • 22 * 3 • 23 * ” *
то же сходящийся, так как его члены, начиная с третьего, соответственно
меньше членов первого ряда.
2-й признак сходимости рядов — признак Даламбера.
Если отношение каждого последующего члена ряда к своему пре-
дыдущему, начиная с некоторого места, меньше некоторого по-
стоянного числа а, меньшего единицы, то ряд сходящийся', если же
это отношение больше единицы, то ряд расходящийся.
Будем, согласно сделанному выше соглашению, предполагать,
что условие признака выполняется с первого члена ряда и что
члены ряда
^1 + ^2 + и3+ ... + ип-]- ...
одного и того же знака и именно положительные.
Следовательно,
«2
«1
Ия . Ui '
77 < «, < а и т. д.
«2 «з
§ 137] ПРИЗНАКИ СХОДИМОСТИ РЯДОВ 371
Из этих условий находим, что
#2 <
и3 < аи2 < а2иг
< ои/3 < а3й1
и т. д.
и так как а< 1, то заключаем, что члены нашего ряда, начиная со
второго, соответственно меньше членов бесконечно убывающей гео-
метрической прогрессии
4“ a2^i + а3^! + • • • + + • • •
А так как последний ряд сходящийся, то на основании первого
признака заключаем, что и рассматриваемый ряд тоже сходящийся.
Вторая часть признака — относительно расходимости ряда, в слу-
чае если отношение каждого последующего к своему предыдущему
больше единицы, совершенно очевидна. В самом деле, тогда каждый
последующий член ряда оказывается больше предыдущего, т. е.
члены ряда возрастают, а потому limsn не существует.
П->оо
Следствие: Из доказанного, очевидно, вытекает, что
1) если lim = k < 1, то ряд сходящийся;
п->оо ип
2) если lim ^±1 > 1, то ряд расходящийся;
П-> ОО
3) если lim 2^±^==1, причем отношение приближается к еди-
П->оо ип ип
нице, оставаясь больше ее, то ряд расходящийся; в противном слу-
чае заключения о поведении ряда на основании этого признака сде-
лать нельзя. Это так называемый сомнительный случай.
Пример 2. Ряд 1 + Г2 + ТГКз + 1~2^4 + ’ ’ ’
сходящийся, так как, принимая
1 1
1-2-3- • -(n-l)-n и Un+1~ 1:2.3. • -п(п + 1) ’
имеем
lim Hm —!—= 0<1.
п -> оо Un п -> оо П 1
ПримерЗ. Ряд + +
сходящийся при всяком р.
Действительно, для этого ряда
1 „ _ 1
ttn ~ 2” • п? ’ а”+1 2^+1. (п +1)₽ •
Um _ Um 2^ = lim А. (——Y? = A lim 1 — А
«-*<» ип п->оо2(п+1)р «->°о 2 \«+1/ 2 п^соЛ _|_Ау 2‘
24*
372 БЕСКОНЕЧНЫЕ ^РЯДЫ [XXIV
Указанный признак является наиболее простым из всех других
признаков, определяющих поведение ряда, однако каждый из них
оставляет подобно признаку Даламбера сомнительный случай нере-
шенным. Это объясняется тем, что одни ряды по своей природе
быстро сходятся, а другие медленнее. Выяснить поведение ряда
медленно сходящегося, т. е. такого, члены которого медленно убы-
вают, труднее, чем быстро сходящегося ряда. Для медленно схо-
дящегося ряда необходимо применить более чувствительный при-
знак, способный определить поведение ряда в случаях, когда другие
признаки не решают вопроса. В частности, один из очень чувстви-
тельных признаков дан покойным профессором Киевского Универ-
ситета Ермаковым.
§ 138. ПРИЗНАК СХОДИМОСТИ ЗНАКОПЕРЕМЕННОГО РЯДА
Рассмотрим теперь ряды, последовательные члены которых
поочередно положительные и отрицательные, т. е. ряды вида
и1 —«2+“з —“<+••• (6)
Знакопеременный ряд сходится, если, начиная с некоторого
места, члены ряда по абсолютной величине убывают и притом
так, что lim ип = 0 (признак Лейбница).
П-> ОО
Для доказательства справедливости этого признака рассмотрим
сумму 2я членов этого ряда, представив ее в двух видах:
«2» = («1 — И2> + («8 — "<)+••• + («2» -1 — «2») (7)
52» = И1 (И2 «в) (И4 Ио) • • * (U2n-2~* И2П-1) И2п' (О
Так как члены ряда все время убывают, то все разности, за-
ключенные в скобках, — числа положительные. Поэтому из равен-
ства (7) мы заключаем, что s2n с возрастанием п все время воз-
растает, а равенство (8) свидетельствует, что s2n не превосходит uv
Отсюда следует, что сумма стремится к некоторому опреде-
ленному пределу; назовем его s.
Рассмотрим теперь сумму 2п -|- 1 членов того же ряда. Очевидно
$2п +1 = ^2п+1>
отсюда находим
lim 52п+ 1 = lim 52п + lim W2n+1-
П->оо п->оо П->оо
Но по условию Ншяап+1 = О, поэтому
Я->оо
lims8n+1 = lim s2n = s.
Я->оо П->оо
Итак, сумма четного и нечетного числа членов ряда стремится к
одному и тому же пределу. Следовательно, ряд сходящийся.
§ 139] АБСОЛЮТНО И НЕАБСОЛЮТНО СХОДЯЩИЕСЯ РЯДЫ 373
Пример 1. Знакопеременный ряд (5), приведенный в § 136,
сходящийся, так как его члены удовлетворяют только что приведенному
признаку: члены его убывают по абсолютной величине и стремятся к нулю.
Полезно заметить, что, прерывая знакопеременный ряд на ка-
ком-нибудь члене, мы получаем сумму, которая отличается от
суммы ряда на величину, по абсолютному значению меньшую пер-
вого из отбрасываемых членов ряда.
Действительно, сумму ряда мы можем представить так:
S = —и2-|-и3— ... ±un^un + 1dzun+^ ...
или
5 ~ Sn -4- (Un+1 ^п+2“Ь ип+3 • • •).
Останавливая ряд на члене ип, мы, следовательно, отбрасываем
всю совокупность членов, заключенную в скобках; назовем ее
через гп и рассмотрим ее отдельно, представив следующим обра-
зом:
Гп = Un±i ип+й) (ип+4 ип+&) • • •
Ясно, что гп<яп+1, что и доказывает высказанное замечание.
§ 139. АБСОЛЮТНО И НЕАБСОЛЮТНО СХОДЯЩИЕСЯ РЯДЫ
Теорема. Ряд с членами разных знаков будет сходящимся,
если ряд, составленный из абсолютных значений членов данного
ряда, будет сходящимся.
Положим, мы имеем два ряда
^1 + ^2 + ••• ••• (9)
lwi l + l^l + ••• 4-1 ип I + ••• (Ю)
В первом из них имеются и положительные и отрицательные
члены и пусть s'n и суммы в отдельности положительных и
отрицательных членов, составляющих сумму п первых членов ря-
да (9), так что
s = s' — s”.
п п п
Сумма ап членов ряда (10) тогда представится в виде
% = Sn + ^-
По условию ряд (10) сходящийся, поэтому lim ап = а (суще-
П -> оо
ствует). Суммы s'n и s" возрастают и ограничены. Следовательно,
существуют пределы каждой в отдельности из сумм s' и s" (см. при-
знак II, стр. 187), а тогда будет иметься и предел суммы sn, т. е.
ряд (9) будет сходящимся.
374
БЕСКОНЕЧНЫЕ РЯДЫ
[XXIV
Обратная теорема, однако, не будет верна: ряд с членами раз-
ных знаков может быть сходящимся, а соответствующий ему ряд
абсолютных значений расходящийся.
Так, ряд 1 — 2- + -L —... сходящийся, а ряд 1 4-у + у 4
+ у4" ... расходящийся (гармонический, см. § 137).
Вообще, рассматривая сходящийся ряд, члены которого имеют
различные знаки, и сопоставляя его с рядом, составленным из аб-
солютных значений членов первого ряда, т. е. сопоставляя два ряда
и1Л~и2~]г ••• + ^п + ••• (9)
I ui I +1 1 + ••• -h I ип I + - (19)
в предположении, что ряд (9) сходящийся, можно обнаружить два
случая:
1) Ряд (10) также сходящийся.
2) Ряд (10) расходящийся.
В первом случае сходящийся ряд (9) называется абсолютно
сходящимся, а во втором неабсолютно сходящимся. Таким образом:
Сходящийся ряд называется абсолютно сходящимся, если
ряд, составленный из абсолютных величин членов данного ряда,
также сходящийся.
Сходящийся ряд называется неабсолютно сходящимся, если
ряд, составленный из абсолютных величин членов данного ряда,
расходящийся.
Так, например, сходящийся ряд
1____L+J________,.н-________1____
1-2^1-2-3 1-2-3... п-4-
абсолютно сходится, так как соответствующий ему ряд, составленный
из положительных чисел
1 + 1~г + 1 -2-з + ’ ‘ • + I • 2 - 3 ... /г + • • •>
есть ряд сходящийся (см. пример 2, стр. 371).
Напротив, сходящийся ряд
1-1+±_±+ -4-1-
является неабсолютно сходящимся рядом, так как соответствующий
ему ряд
1-14+4+1+•••+!+•••
является рядом расходящимся (гармонический ряд).
§ 140]
ВОПРОСЫ И УПРАЖНЕНИЯ
375
§ 140. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется бесконечным рядом?
2. Какой бесконечный ряд называется сходящимся, какой расходя-
щимся?
3. Что называется суммой бесконечного сходящегося ряда?
4. Имеется ли сумма у расходящегося ряда?
5. Можно ли бесконечную арифметическую прогрессию причислить
к бесконечному ряду и если да, то будет ли она рядом сходящимся или рас-
ходящимся?
6. Каково условие, необходимое для сходимости каждого ряда?
7. Достаточно ли для сходимости ряда, чтобы предел общего члена
ряда был равен нулю?
8. Каковы признаки сходимости рядов с постоянными знаками?
9. Будет ли знакопеременный ряд сходящимся, если ряд, составлен-
ный из абсолютных величин его членов, есть ряд сходящийся?
10. Каков признак сходимости знакопеременного ряда?
И. Какова ошибка приближенного равенства s^sn в знакоперемен-
ном ряде?
12. Что называется абсолютно и неабсолютно сходящимся рядом?
Найти сумму рядов
9 /2\2 /2\3 / 2 V
,3' Т + ®+(з) +Ы + -" 0“-2'
Й. 0,1 + 0,01 + 0,001 + 0,0001 + ... Отв. -i-.
15‘ Т Оте' 24'
Доказать, что
16, П2 + 2ТЗ + 3^4 + 4Г5+ = 1'
... 111
Указание: ---------=---------• —.
(п — 1) • п п— 1 п
1 «3 *^3«5 ' 5-7^ 2
i8 _Lr_I_ j _L-4- -2
1О- 22—1 ‘32—1 42— 1 ••• - 4 •
Исследовать сходимость рядов:
20 * I * I — -I- - - -
2 ‘2*22 ^3-23 ^4-24
2|4+4+т+4+ -
22-,+т+А+14з-|
i4+ ...
м-т+т+т+т+-
376
БЕСКОНЕЧНЫЕ РЯДЫ
[XXIV
25.1 + 1.2(±y+b2-3(i),+ l-2-3.4.(±)‘+ ...
27-!+у+| + 21+ ...
28' 1 —I -2^ 1-2-3- 1-2-3-4 + "
29. 1-т + А-ГТз+ •••
30 2 3 4- 4 _54-
3°.т- 2 + -3 4 + •••
31 1 2Д-3 -4-
ЗЬ т+5 + •••
XXV. ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА
И ИХ ПРИЛОЖЕНИЕ
§ 141. ФОРМУЛА ТЕЙЛОРА ДЛЯ ЦЕЛОЙ РАЦИОНАЛЬНОЙ
ФУНКЦИИ
Пусть /(х) целая рациональная функция n-ой степени:
/ (х) = «о + aix + а2*2 + • • • + апХп. (1)
Придадим переменной х некоторое определенное значение,
а всякое другое значение переменной обозначим через х -\-h, где h
уже будет играть роль переменной. Значения функции / (х) при
иных, чем х, значениях переменной будут определяться из равенства
/ (х h) = aQ (х 4“ Л) + а2 (х + ^)2 4" • • • 4” ап (х 4” ^)п, (2)
которое после раскрытия скобок в правой его части и распреде-
ления членов по восходящим степеням переменного h примет вид:
f(x -Ь А) = Ао4-AJi + AJfi + . .. + Ап№, (3)
где коэффициенты До, Ап постоянные величины, так как в их
выражения входят только постоянные коэффициенты а0, а19 ..., ап и
выбранное нами определенное значение переменной х.
Значения коэффициентов Ао, А19 ..., Ап определяются непо-
средственно при переходе от равенства (2) к (3). Однако, незави-
симо от этого, определение этих коэффициентов может быть
сделано и более коротким путем. Действительно, равенство (3)
есть тождество, т. е. оно справедливо при всевозможных значе-
ниях переменного h, а потому и последовательные производные
обеих частей равенства (3) по этой переменной h тождественно
равны будут между собою:
/'(х4-А) = Л1 + 2Л2/г4-ЗЛ3й24- ...
Г(х4-Л)=2Л2 + 2.3.Л3/г+ ... 4~(п— 1)пДпй«-2;
/'"(Х_]_А) = 2 • 3 • Д34 2 • 3 • 4 Л4А —2)(л —1)пЛгаА»-8;
А) = 2.3-4... (л — 1) пА„.
378
ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ
[XXV
При последовательном дифференцировании тождества (3) f(x-\-h)
надо рассматривать как сложную функцию от А, именно /(x-j-/?)^
=/ (я), где и = х + h.
Полагая теперь в тождестве (3) и во всех последующих тож-
дествах h= 0, находим
Л0=/(х); A1=f'(x), 2А2 =/"(*), 2-3-4 = Г'(*). • • •
2-3-4 ... (и—1)-/г-Лп=/(«)(х),
откуда находим
Л0=/(х), A2 = ±f"(x), A^^rix), ...
Вследствие этого формула (3) принимает вид:
/(х + А) =/ (х) + hf (х) + (х)+ • • + !. 2.* . ..fW (X). (А)
Это и есть формула Тейлора для целой рациональной функции.
Она часто представляется и в другом виде:
/w =/ («)+<*-«)/' w (»)+•••
• • + Л*1 (»)• w
который мы получим, заменив в формуле (А) х .через а и поло-
жив затем h = x — а.
Последняя формула представляет разложение функции / (х) по
степеням двучлена х — а. Выбор значения а зависит всецело от нас.
Положим, например, мы желаем разложить целую рациональ-
ную функцию
/(х) = х3 —Зх2-|-1
по степеням двучлена х 1. В данном случае а = — 1.
/'(х) = Зх9 — 6х, /"(х) = 6х —6, /'"(х) = 6.
/(-1) = -3, /'(—1) = 9, /"(—1) = —12, Г(-1) = 6.'
Таким образом,
хз_—6(x + 1)2 + (x4-1)3.
Такого рода разложение целой рациональной функции весьма по-
лезно применять, например, при интегрировании рациональной
дроби вида
/(а)
(х—а)т
§ 142] ФОРМУЛА ТЕЙЛОРА ДЛЯ ПРОИЗВОЛЬНОЙ ФУНКЦИИ 379
Поясним это примером. Положим, требуется найти интеграл
разложим функцию, стоящую в числителе дроби, по формуле
Тейлора по степеням двучлена, стоящего в знаменателе. Для этого
примем
/(х) = х3—4x4-5 и а = 2.
Вычисляем производные
f (х) = 3х2 —4
Г(х) = 6х
Г(Х) = 6.
Затем находим
/(2) = 5, /'(2) = 8, (2) = 12, /,,,(2) = 6.
Тогда по формуле Тейлора имеем
х3 _ 4х 5 = 5 8 _ 2) 6 _ 2)2 _|_ _ 2)Зв
Принимая это в расчет, находим
,fx3-4x + 5 f 5 + 8(х —2)4-6(х —2)2+(х —2)3
J (х — 2)< (х —2)4 х~
_ - Г rfx j_of ^х ifif dx if dx ________________
(x —2)* * 6 J (x —2)3 * b J (x —2)2 + J x^2 ~
= —3(x — 2)3 — (x — 2)2~Г^2' + 1п(х + 2) + С-
§ 142. ФОРМУЛА ТЕЙЛОРА ДЛЯ ПРОИЗВОЛЬНОЙ ФУНКЦИИ
Данное нами разложение справедливо только для целой рацио-
нальной функции. Что же касается остальных функций, то мы, не
имея права распространять разложения (А) и (В) на другие функ-
ции, можем, однако, и для них искать форму, подобную найден-
ной нами для целой функции. С этой целью будем искать разложение
произвольной функции в форме:
/(х)=/(а) + (х-а)/'(а) + -4^-Г(а)+ ...4-
4_ (х —д)^-1_____/(п -1) (д) J(x —д)п р
т- 1.2-3 ... (п — I)7 1-2-3 ... /г ’ W
где под Р подразумевается некоторое пока неизвестное нам коли-
чество, отличающееся от fM (а) (иначе правая часть формулы (4)
выразила бы некоторую целую рациональную функцию). Отыска-
ние этой величины и представляет теперь единственную цель
вопроса.
380 ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ [XXV
Мы будем в дальнейшем предполагать, что сама функция /(х)
и ее последовательные производные до (х)* включительно
существуют для всех значений, заключенных между а и выбран-
ным нами значением х.
Для решения вопроса, т. е. для отыскания значения Р, пере-
несем все члены правой части равенства (4) в левую, тогда
г (х) -/(«)- (х - a) f' (а) - f" (а) — ...
------(х —д)”-1---дп _ 1) /а-|_(5.~ р — о (51
1-2-3...(л — 1) 7 w 1-2-3...// ’ W
и рассмотрим, как это мы делали и при выводе формулы Лагранжа,
некоторую новую функцию
Г(г)=/(х)-/(г)-(х-г)/'(г) . • •
_____ fin -1) (?\ ~~ р
1*2-3...(я — \у W W
отличающуюся от левой части равенства (5) только тем, что по-
стоянная величина а в нем заменена переменной г.
Что касается этой функции, то мы можем утверждать прежде
всего, что ее производная существует для всех значений z между а
и х (на основании предположения, сделанного выше относительно /(х)).
Найдем эту производную, при этом /(х) и Р, как независящие
от г, должны рассматриваться как постоянные числа.
F' (z) = —f (z)+f (г) - (х - z)f" (г) + (х- г) f (г) - ...
_|__(х —г)”~2 у(я_!) / х____(х —г)”~* „ ,, . ,
• • • -2.3...(п —2)' 1-2-3...(/г —1)7 ^7^
I (Х-2)П~1
1-2-3...(л—1)
В правой части этого равенства все члены, кроме двух последних,
сокращаются один с другим и мы находим
f' и = - 1.2(Х?. -1) (Ы W + . 2(Х.Х -1) Р- (7)
Кроме того, относительно F(z) можно высказать еще следующее:
F(^) = 0 при z = x, что очевидно,
F (г) = 0 при z = а, что ясно в силу равенства (5).
Таким образом, по отношению к функции F(z) имеются налицо
все условия теоремы Ролля. Применяя ее, заключаем, что между а
и х найдется такое значение z — с, что
Р'(с) = 0,
§ 142] ФОРМУЛА ТЕЙЛОРА ДЛЯ ПРОИЗВОЛЬНОЙ ФУНКЦИИ 381
т. е. что (см. выражение (7))
________________/<п) (с) j__р _ о
1.2-3...(и—1) 7 + 1.2-3...(л— 1) и‘
Сокращая члены последнего равенства на общие множители, полу-
чаем
—/(«)(с) + Р = 0
или
р = /(») (с).
Подставив теперь найденное значение Р в формулу (4), при-
ходим окончательно к формуле Тейлора для произвольной функции
/W =/(.)+(ж-о)/' (О)+-^^Г(«)+ • •
Формула эта отличается от соответствующей формулы для целой
рациональной функции только последним членом
который называется дополнительным членом формулы Тейлора.
В этой форме он был дан Лагранжем.
Числу лежащему между а и х, обычно дают следующую
форму:
<7 = а0 (ат — а), где О<0 < 1.
Эта новая форма при всяком 6, заключенном между 0 и 1, действи-
тельно выражает некоторое число, лежащее между а и х.
При такой форме числа с дополнительный член принимает вид
Rn=т(.х27заГп -Н (* - «)1-
Формула Тейлора пишется и в другой форме:
/(*+*) =/(х) + Л/'(х) + -151-/"(х)+ ...
+ 1.2.3^-1)/("">W + —+ ОТ
которую мы получим из (I), положив сначала x = a-[-h и затем
заменив а буквой х.
Если в этой формуле перенести f(x) в левую часть и при-
нять в расчет, что
/(х + Л)-/(х) = Д/(х), hf(x) = df(x),
= A8/OT(x) = d»/(x) и т. д.,
382
ФОРМУЛЫ ТЕЙЛОРА И МАкЛОРЕНА И ИХ ПРИЛОЖЕНИЕ
[XXV
то формула (II) представится в виде
Д/(х) = df (х) +т^-</2/(х) + r-|^d3/(x)+ . . .
•••+—2.3..~^X+eZt)> <8)
или, положив для сокращения f(x)—y,
АУ = ЧУ + П2 + • • • + Т273"~
Эта формула дает полное выражение приращения функции через
ее дифференциалы и служит развитием формулы (20) на стр. 220.
Если в формуле Тейлора (1) положить а = 0, то придем
к формуле Маклорена
/(х)=/(0) + х/'(0) +^Г(0)+ ...
v-П — 1 vW
+ 1:2^..,^.) (°) + 1.2'.з...„/(п) (“О
Огромное значение выведенных формул выяснится по мере по-
степенного ознакомления с различными вопросами, где имеет место
применение этих формул. Теперь же заметим, что формулы (I)
(II) и (III) дают возможность представить различные функции в форме,
подобной целым рациональным функциям, а потому позволяют вычи-
слять значения функций соответственно различным значениям аргу-
мента. Величина дополнительного члена укажет при этом на ошибку,
которую мы делаем, ограничиваясь начальными членами разложения.
Так, например, полагая
/(*)=/(<*) + (х - a) f (а) + (а) + ...
1 .2-3...(и — 1) 7 W
и отбрасывая, следовательно, дополнительный член, мы делаем ошибку,
равную величине этого члена:
Я» = + 6 (х - а)];
а если М есть наибольшее значение, какое принимает производная
fW [а 6 (х — а)]
при изменении 6 в пределах от 0 до 1, то величина ошибки, кото-
рую мы делаем, не превосходит абсолютного значения величины
Если величина дополнительного члена формулы Тейлора или
Маклорена по абсолютному значению беспредельно убывает и стре-
143] разложение в ряд ех 383
мйТся к нулю по мере увеличения числа п, т. е. числа членов,
которые мы берем для вычисления функции, то можем написать,
/(х) = Jim [/(а) + (х - a)f (а) + + • • •
-I___(•« —Д)П~Х-у(„_ J ) / J.
• ‘ ' 1.2-3...(п—1)У WJ>
/(*) = Пт[/(0) + х/(0)+^Г(0)+-.-
n->ooL 1 z
Это же самое пишут еще проще так:
/ (х) =/(а) + (х - а)Г (о) + («)+•••
/(х) =/(0) -|-х/ (0) + (0) + .. .
В этом случае говорят, что функция / (х) разлагается в беско-
нечный ряд. Знак „многоточие“ указывает на то, что чем больше членов
мы возьмем в этих рядах, тем точнее получим значение функции.
§ 143. РАЗЛОЖЕНИЕ В РЯД ех
Применим формулу Маклорена (III) к функции
f (х) = ех.
Для этого составим последовательно производные от нее и
вычислим их значения при х = 0.
f (х) = ех, f' (х) = ех, ..., /(*0 (х) = ех.
Полагая х = 0 в самой функции и ее производных до (п—1)-ой
производной, находим
/(0) = 1, f (0) = 1, Г(0) = 1,../(»-*)(0) = I.
Производную /(п> (х), появляющуюся в дополнительном члене,
надо вычислить для значения аргумента, равного 9х ф
/(п)(0х) = e0aj.
По формуле (III) тогда находим
**=*+*+те+тет+ • • • +
Где
%п
1.2.з:..п
384 ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ [XXV
Исследуем этот дополнительный член; именно, посмотрим, будет
ли он стремиться к нулю при беспредельном возрастании п.
Мы замечаем, что дополнительный член состоит из двух мно-
жителей:
Что касается второго, то при всяком данном значении х он
представляет величину ограниченную. Остается рассмотреть только
первый.
Каково бы ни было данное значение х (будем предполагать для
определенности, что оно больше нуля), в ряду натуральных чисел
1, 2, 3, 4, .. .
всегда найдутся такие два последовательные целые числа k и
k 1, между которыми заключается х, так что
хп
Заметив это, представим выражение -у-~2 —— так:
X™ XXX XX X X
1 -2-З...П =1*2’з’’’*£в k-\-1 k -|- 2 ’ ’ ’ п '
Произведение первых k множителей обозначим через А, а осталь-
ных п — k множителей — через В. Что касается произведения
д —£
1 2 ’ ’ ’ k ’
то оно при всяком данном х — постоянно. Второе же произ-
ведение с беспредельным возрастанием п, как сейчас увидим,
стремится к нулю. Действительно,
д__ х х х х х х ___( х \n-fc*
75 — Н1*Н2”’ л ’ *4-1 ‘ ” *+1 “U+1/
так что
х / х \п-к
Но утру < 1, а потому k —при беспредельном возрастании //
стремится к нулю; поэтому и
lim В = 0.
П->ОО
Таким образом, приходим к заключению, что
при всяком х>0.
lim
П-> оо
1-2.3...и “
§ 1-14]
РАЗЛОЖЕНИЕ В РЯД sitl X
385
Очевидно, к тому же придем и при х<0. Вместе с этим и
= Нт Ь2Х"= 0. (9)
Итак, мы можем f(x) = e* представить бесконечным рядом:
е — 1 + * + 177 + 1.2.3 + 1 • 2 • 3 • 4 + ’' ’ Р0)
Полагая в этом бесконечном ряде (10) х=1, приходим к беско-
нечному ряду для числа е\
в= 1 +1 +772 + 72^3+ 1 -2.3.4+ • • • •’
который служит для вычисления числа е.
Чем больше членов возьмем в этом ряде, тем точнее получим
значение для е. Взяв десять слагаемых, находим
£ = 2,718279
с точностью до трех единиц последнего десятичного знака.
§ 144. РАЗЛОЖЕНИЕ В РЯД sin X
Применим ряд Маклорена к
f (х) = sin х.
Известно, что
f (х) = cos х, f" (х) = — sin х, f”r (х) — — cos х,
/IV (x) = sinx и т. д.
Подставляя x = 0, находим
/(0) = 0, f' (0) = 1, f" (0) = 0, f" (0) = — 1, fv (0) = 0 и т. д.
Мы видим, * что все четные производные при х = 0 обращаются
& нуль, а все нечетные попеременно в ±1. Поэтому
х3 I л5 . ~
sinx — х 1.2.3+ 1-2-3-4-5
Производную /W(0x), входящую в дополнительный член, мы можем
считать четного порядка, тогда
(6х) = ± sin (6х),
и потому
Rn = — !. 2.3.Т.н Sin
Так как | sin (0х) | sg 1, а
25 Зак. 2116. Н. С. Михельсон.
386 ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ [XXV
как уже доказано выше, то
lim Rn = Q,
П-> оо
и мы получаем разложение sinx в бесконечный ряд в таком виде:
sinx = x 1.2.3+ 1 -2-3.4.5 ” ”
§ 145. РАЗЛОЖЕНИЕ В РЯД COS X
Применяя формулу Маклорена к
/(х) = cos х,
находим
f (х) = — sin х, f" (х) = — cos х, f" (х) = sin х,
/Iv(x) = cosx и т. д.
/(0) = 1, /'(0) = 0, /"(0) = —1, /"'(0) = 0, /IV(0) = l и т. д.,
так что
1 х2 . х4 . п
cosx— 1 1в2+ 1.2.3-4
где
^п = -—2-З...П C0S<9x)-
Но
lim Rn — О,
П ->оо
а потому окончательно получаем ряд для cosx в таком виде:
cos х = 1 -рт2 4"1.2-3-4 ‘ ‘
§ 146. ФОРМУЛЫ ЭЙЛЕРА
До сих пор переменным, рассматриваемым в анализе, мы прида-
вали только вещественные значения. Имея в виду вывести формулы
Эйлера, введем некоторые обобщения. Именно, условимся ряд (10),
выведенный для вещественного значения аргумента, распространять
и на мнимые его значения, т. е. примем, что равенство
I ~2 । *3 I ।
6 ~•1+*+ 1.2-1- 1.2-3^“ 1-2.3.4+..........
справедливо и для мнимых значений. 1 Полагая тогда z — xi, где
i = j/ — 1, находим
exi — 1 ; у; I *2/2 । *3/3 I хЧ4 ।
— 1.2+ 1.2-3*г 1.2.3-4 + • • •'
1 Равенство это служит определением функции ег при z мнимом.
5 147)
РАЗЛОЖЕНИЕ в ряд In (1 -j- х)
387
exi = 1 Д- xi
tfo р = —1, = = — ц р = р»р=19 fl = p.l = i ит. д.,
поэтому
х2 л3 • I , х4 । х6 • i
Ь2“"ГТЗ + 1 «2-3-4 *"1-2-3-4-5 — ’
«*Н1-Й+ ьЙ74----) +
I . ( ~ X2 ! X5 \
+"ЧХ 1-2-3"*“ 1-2-3-4.5 ” J’
В силу же разложений (11) и (12) получаем
e^ = cosx-p isinx. (13)
Заменяя в этой формуле х на — х, найдем
e~xi — cos х — i Sin x. (14)
Складывая и вычитая равенства (13) и (14), получим
exi e-xi = 2 COS X,
exi — e—xi — 2/sinx,
откуда получаются известные формулы Эйлера:
_!_ е - xi
cos х —---*2---,
gXi__ g — xi
sinx =----2/---‘
В одном из дальнейших разделов этого курса формулы Эйлера
найдут себе важное приложение.
§ 147. РАЗЛОЖЕНИЕ В РЯД In (1 4~х)
Применим формулу Маклорена к
/(х) = 1п (1+х).
Для этого составляем последовательные производные и вычи-
сляем их частные значения при х = 0, кроме последней, которую
вычисляем для значения 6х,
/(х) = 1п(1+х) 7(0) = 0
Г(0) = -1
25»
388
ФОРМУЛЫ ТЕЙЛОРА и МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ
Ixxv
Г (*) = (пЛ)-з (о) = i • 2
/1У(*) = -(Тта-4 /IV (0) = — 1 • 2 • 3
/<”>(*) = (- I)’-1 П- •
/(») (вх) = (— I)'1-1
1-2.3...(л—1)
(1 + Ох)”
Применяя формулу Маклорена, получим
у 2 уЗ у 4 у И — 1
Можно показать, что дополнительный член стремится к нулю
только для значений х, заключающихся между —1 и или,
точнее, для значений, удовлетворяющих неравенствам
— 1 <х^1
(на доказательстве этого не будем останавливаться). Поэтому
только для таких значений х мы и можем представить 1п(1-|-х)
в виде бесконечного ряда:
ln(l + x) = x-^ + f-^+---- (15)
Этот ряд служит исходной формулой для вычисления логарифмов
чисел.
§ 148. РАЗЛОЖЕНИЕ В РЯД (1+*)'“
Применим формулу Маклорена к /(х) = (1 х)т, принимая
за т любое постоянное число.
Составляем ряд производных и вычисляем их частные значения
при х = 0; последнюю производную вычисляем при значении аргу-
мента равном Ох
/(х) = (1 + *г /(0) = 1
/'(х) = /n(l-j-x)”1-1 (0) — от
/" (х) = т (т — 1) (1 4- х)’»-2 f (0) = т (т — 1)
(х) — т (т — 1) (/и — 2) (1 4~ х)»»-3 (0) = т. (т — 1) (от — 2)
/(») (х) = от (от — 1) ... (от — п 1) (1 4~ х)*»—»
/(») (6х) = от (от — 1) ... (от — п 4- 1) (1 -р Ох)*»-».
§ 149]
СТЕПЕННЫЕ РЯДЫ
389
Подставляя частные значения функции и производных в фор-
мулу (III) Маклорена, получаем
(1 4- х)” = 1 + /»Х + т {'П ~ ° (/” ~ 2) -L UO
1-2-3
П’
где
1 * 4 - и • > • • Л
Рассматривая полученную формулу, нетрудно заметить, что
при т целом и положительном она обрывается сама собою и об-
ращается в известную из элементарного курса алгебры формулу
бинома Ньютона. При других же значениях т эта формула со-
держит неограниченное число членов.
Исследование дополнительного члена показывает, что с беспре-
дельным возрастанием п величина Rn стремится к нулю для значе-
ний %, по абсолютной величине меньших единицы, т. е. для
— 1 <х< 1.
1-2-3
Таким образом, для этих значений х имеет место формула:
(14-х)'«= 1 + отх + -(^Х2 + Т.у.Т"2) л3+ • • • • 06)
Чем ближе значение х к нулю, тем скорее убывают члены этого
ряда и потому тем меньшую ошибку мы делаем, останавливаясь на
некотором ограниченнохМ числе членов ряда в формуле (16).
При достаточно малом значении х нередко в вычислениях огра-
ничиваются даже только двумя членами ряда, т. е. пользуются сле-
дующими приближенными формулами:
1
1
1
2 Х
2
При х = — ошибку этих приближенных формул можно считать
равною —V.
102а
§ 149. СТЕПЕННЫЕ РЯДЫ
Полученные применением формулы Маклорена бесконечные ряды
относятся к так называемым степенным рядам. Под этим названием
подразумеваются ряды вида
ao + flix + a2x2+ • • • + -•> (17)
1де коэффициенты я0, ах, ап некоторые постоянные числа.
390
ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ
[XXV
Ряды эти имеют огромное значение во многих вопросах анализа
и появляются они не только в результате разложения функции по
формуле Маклорена.
Рассмотренные примеры разложения в ряд различных функций
показывают, что одни из них оказываются сходящимися при всех
значениях аргумента х (таковы ряды для е®, sinx, cosx), другие
сходятся лишь в определенном промежутке значений аргумента.
Положим, что коэффициенты степенного ряда (17) таковы, что
Ит|^±1| = Л,
где А некоторое определенное число. Тогда, применяя признак Да-
ламбера к ряду, составленному из абсолютных значений членов
ряда (17), т. е. к ряду
|«ol + lalxl + la9x9|+ •••+lanx”|+ •••
(18)
имеем
Поэтому:
1) Если А • |х|< 1, то ряд (18) сходящийся, а потому ряд (17)
абсолютно сходящийся. При этом если А = 0, то ряд (17) абсо-
лютно сходящийся при всяком значении х; если Д^О, то ряд (17)
абсолютно сходящийся при значениях |х|<^-, т. е* для значений,
1 I 1 ГТ
лежащих в промежутке от — -д до +^-. Промежуток этот назы-
вается интервалом сходимости. При А = 0 интервал сходимости от
— оо до °°.
2) Если А • |х| > 1, т. е. |х| > то ряды (17) и (18) расхо-
дящиеся, так как тогда последующий член численно больше преды-
дущего, т. е. члены ряда возрастают по абсолютной величине.
Пример 1. Ряд х — -гг + т— ...абсолютно сходящийся для значений
О
|х|<1.
Действительно, здесь
11т 1^1- "т drrIx|=|x|-
n->00 I “П I
Поэтому для значений | х |< 1 ряд будет сходящимся. На основании
признака Лейбница ряд будет сходящимся и для х = + 1.
Приведенный ряд, как известно, выражает In(l-f-x).
х^ х&
Пример 2. Ряд х — -Х- + -С—••• абсолютно сходящийся для значений
о о
|Ж|<1.
§ 150]
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
391
Действительно, здесь
lim I I = lim х2.
П -> CO I Un I П ОО 2/2 4“ 1
Поэтому, для значений | х | < 1 ряд будет сходящимся. На основании
признака Лейбница можно убедиться, что ряд будет сходящимся и для
№± 1.
Приведенный ряд представляет разложение в ряд arc tg х.
§ 150. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Гиперболическими функциями называются следующие функции:
— у(е» + е-®),
имеющие, как видно, непосредственную связь с показательной функ-
цией.
Первая из них называется гиперболическим синусом, вторая—•
косинусом, что и обозначают следующим образом:
sh х = ~(ех — е~х) (19)
ch х = ^(ех-]-е-х). (20)
Подобно тому, как это делается в тригонометрии, вводятся еще
функции:
,, shx ех — е~х /П1Ч
thx = -r—= —т(21)
chx ех-\-е~х v 7
.. chx вх + е~х /опЧ
cthx=-r—=—2--------г?. (22)
shx ех— е~х v 7
Название „ гиперболическиеи дано ввиду того, что, как увидим
ниже, по отношению к ним гипербола играет роль, подобную той,
какую играет круг по отношению к тригонометрическим функциям.
Покажем некоторые свойства гиперболических функций.
Из равенств (19) и (20) вытекают непосредственно следующие
свойства этих функций:
sh 0 = 0 sh (— х) = — sh х,
ch 0=1 ch( — x) = chx
chx4~shx = e® (23)
chx— shx = £-a\ (24)
Отсюда, перемножая равенства (23) и (24), имеем
(chx)9 — (shx)2=l. (25)
392 ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ [XXV
Перемножая равенства (19) и (20), находим
2sh х • chx = -i (е2х— е~2х),
т. е.
sh 2х = 2sh х• ch х. (26)
Возвышая в квадрат равенства (19) и (20) и складывая, получим
(sh х)2 -f- (ch х)2 = у (е2* + e~2*),
т. е.
ch 2х = (ch х)2 -J- (sh х)2. (27)
Кроме вышеприведенных свойств, полезно знать и выражения
производных от гиперболических функций, которые нетрудно выве-
сти из формул (19), (20), (21) и (22), определяющих эти функции:
(sh х)' — (ех — е~х) j = у (с*77 4" е'х) = ch
(ch х)' = (еж4- = Sh
/shx/ chx(shx)'— shx(chx)' (chx)2—(sh x)2 1
(‘h = to) =------- (ch x)2 = (ell X)2 = (Щ2-
Так же выводится и производная от cth х.
Таким образом, получаем следующие формулы:
(sh х)' = ch х, (th хУ = ,
(ch х)' = sh х, (cth х)' = - .
Разложение в ряд гиперболических функций получается непо-
средственно из разложений для
1 х2 j х3 . х4 .
е _l-r-x4-1>24-jT^4-1 2 .. .
< I X2 X3 , X4
е ~ ГТЗ"> 1-2-3-4
На основании этих разложений имеем
sh х = х+1.2.з4" 1.2-3-4-5'4’'' ’
chx= 1 + +1.2.3-4 + • • ’'
Выведенные формулы и другие, которые можно было бы еще
дать, очень напоминают основные соотношения между тригономе-
§ 150]
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
393
трическими функциями. Аналогия между ними обнаруживается еще
большая, если дать геометрическое толкование гиперболическим
функциям.
Обозначим
ch х = X и sh х = Y.
Тогда на основании равен-
ства (25) можем заключить,
что изучаемые функции удовле-
творяют уравнению
X2 — /2=!,
т. е. уравнению равнобочной
гиперболы с вещественной
188), где ОА=1, и выберем
полуосью а = 1.
Изобразим такую гиперболу (рис.
любую на ней точку М с координатами
OP = X и РМ = Г.
Тогда и обнаруживается, что
OP = chx
РМ — sh х.
Таким образом, ch х есть проекция радйуса-вектора гиперболы
на ось OX, a sh х есть проекция его на ОУ, что, как известно,
имеет место и для тригонометриче-
ских функций. Действительно, рассмат-
ривая круг (рис. 189), радиус которо-
го ОА=1, имеем, как известно,
OP = cosx
РМ = sin х.
Что касается аргумента х гипербо-
лических функций, то и в этом отно-
шении обнаруживается аналогия с
тригонометрическими функциями.
В самом деле, основываясь на выведенном раньше выражении
Для площади сектора ОАМ гиперболы
пл. OAW = F = yln(X4- /л2— 1)
(см. стр. 338), находим при наших обозначениях
F = In (ch х -ф- sh х),
394 ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА И ИХ ПРИЛОЖЕНИЕ [XXV
что на основании формулы (23) приводится к равенству
так что
x = 2F.
Совершенно такое же геометрическое значение имеет аргумент х
и в тригонометрических функциях. Действительно, хотя в тригоно-
метрических функциях х является числом, измеряющим в радиусах
дугу AM круга, но при радиусе О А = 1 тем же числом будет
измеряться двойная площадь кругового сектора. В самом деле, площадь
кругового сектора ОАМ = F = ~ ОА - AM, что при ОД=1 дает
F = yX или x=2F.
Таким образом, для тех и других функций х есть удвоенная
площадь сектора или кругового или гиперболического.
§ 151. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Чем отличается формула Тейлора для целой рациональной функции
от той же формулы для остальных функций?
2. Показать, что формула Лагранжа вытекает из формулы Тейлора как
частный случай.
3. В каком случае формулы Тейлора и Маклорена обращаются в бес-
конечные ряды'
4. Для каких значений х справедливы разложения в бесконечные ряды
функций ех, sin х, cos х?
5. Для каких значений х справедливы разложения в бесконечные ряды
функций tn (1 +х) и (1 +
6. Написать разложение в ряд е*х.
7. Написать разложения в ряд sin 2х, cos у х.
8. Вычислить величину пользуясь шестью членами разложения
в ряд. Отв. 1,6487 с точностью до 0,0001.
it
9. Применить разложение в ряд sin х для вычисления sin 30° = sin -g-.
Отв. Три члена ряда дают значение sin ~ = 0,5 с точностью до 0,00001.
10. Как велика погрешность приближенного равенства sin х = х.
Х'^
Отв. Погрешность не превышает -g~ •
11. Применяя формулу бинома Ньютона, вычислить frig’ с точностью
до 0,0001. Отв. 1,0627.
12. Объем тела при 0° вычисляется по формуле V’o= ^ычислить
объем тела при 0°, зная, что его объем при 20° равен 2,145 мл, а коэффи-
циент объемного расширения равен 0,000182.
Отв. Уо = 2,145 — 0,008 = 2,137.
XXVI. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
$ 152. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЕ ДИФФЕРЕНЦИАЛЫ
1-го ПОРЯДКА ФУНКЦИЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
Положим, что нам дана функция / (х, у, z) трех независимых
переменных х, у, z. Дадим одной из них, например х, произволь-
ное приращение Дх, а все остальные оставим без изменения, тогда
и сама функция получит некоторое приращение:
/(х4-Дх, у, z)—f(x, у, z),
и мы можем, как и в случае функции одной независимой перемен-
ной, поставить вопрос об отыскании предела отношения этого при-
ращения функции к приращению независимой переменной, когда
последнее стремится к нулю. Предел этот1 называется частной про-
изводной от f(x, у, г), взятой по xt и обозначается
fx(x, у, Z) или
так что
Пш И(х + Ах> у' г) ~^х’ У’ - df
д®->о L Ьх J &х
Подобным же образом, давая у приращение Ду, а оставляя
теперь х и г без 'изменения, вводится понятие о частной производ-
ной от / (х, у, z) по у и, наконец, по z\ так
lim И^Х| у + г)~Нх> У> ^)] ___ д/
^oL *У J ду
lim
у, г-j-Дг)—/(х, у, z)
Az
Знятгы df df df
онаки следует читать так: частная производная от
Функции / по х, от функции / по у или от функции / по г.
1 Если
он существует.
396
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [XXVI
Самые правила дифференцирования функций нескольких пере-
менных, т. е. правила составления частных производных, остаются
те же, как и для функции одной переменной, только при диффе-
ренцировании по одной из независимых переменных все другие сле-
дует принимать за постоянные, как это ясно следует из самого про-
исхождения частных производных.
Пример 1. /(х, у, z)=y2sinx— 2хе~.
^£=j>2C0SX — 2ezt ^ = 2ysinx, ^- = — 2хе-.
dx ду J dz
Пример 2. Уравнение Клапейрона pv = RT устанавливает зависимость
между величинами pt v и Т.
RT RT pv
1 v ' р ’ R
Соответственно этому найдем:
из первого соотношения
dp RT / 'Г \ др R , .
=— —% (считая Г постоянным) — (считая tr постоянным);
из второго соотношения
dv RT , „ .
— = — (считая Т постоянным)
из третьего
дТ р .
(считая р постоянным)
dv R , ч
(считая р постоянным);
дТ v . ч
(считая и постоянным).
Частные значения производных по х, у и z от функции / (х, у, z)
при х = а, у = д, z = c обозначаются так:
/a, (a, t>, с), fy(a, b, с), f's(a, b, с).
Так что соответственно предыдущему примеру 1:
4(0, 1, 0) = -1, 4(0, 1, 0) = 0; 4(0, 1, 0)^-0.
Умножая каждую из частных производных на соответствующий
дифференциал независимой переменной, получим так называемые
частные дифференциалы функций’.
df . df . df ,
/-dx, /-dy, /-dz.
dx 9 dy ’ dz
Сумма частных дифференциалов функции называется полным диф-
ференциалом и обозначается знаком df
df —~-dx-/^-dy/-~dz.
J dx 1 dy 1 dz
(1)
§ 152]
ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЕ ДИФФЕРЕНЦИАЛЫ
397
Связь между полным дифференциалом функции
и ее полным приращением.
Если одновременно дать приращение всем независимым перемен-
ным, то функция (для простоты письма считаем функцию / (х, у)
зависящей от двух переменных х, у) получит некоторое приращение
Д/=Л*4-Д*, y + ^y)—f(x, у),
которое называется полным приращением функции f(x, у). Пол-
ное приращение А/ можно представить так:
д/=/ (X 4- Дх, у 4- by) —f (X, у) =
= [f(x-fAx, y-fAy)—f(x-]-Ax, у»] 44/(х4-дх, у)— f(x, _у)1-
Каждую из разностей по формуле Лагранжа (сгр. 240) можно
заменить:
первую — на Ду • fy (х Ах, j^),
вторую — на Ах • fx (х^ у),
где под х2 подразумевается число, лежащее между х и x-f-Ax,
под уг— число, лежащее между у и у-\-&у.
Предполагая, кроме того, все частные производные непрерыв-
ными функциями, можем написать, что
4(х+Дх’ Л)=7ИХ, + y)=fx(x, _у)~|-г2,
а
и
к
потому
д/ = [Д (х, у) 4- 8j] by 4- (4 (х, у) 4- е2] Дх =
=Л, (х, у) Дх 4- fy (х, у) Ду 4- г2 Дх 4- 81 Ду.
Положив для краткости
г2 Ax-J-^i &У — а»
замечая, что Ax = dx, ky = dy (см. § 93, стр. 221), приходим
формуле
V = + (2)
Выражение dx + dy, как сказано выше, есть полный дифферен-
циал функции / (х, у). Он является линейным относительно dx и dy.
Что касается величины ш, то она при бесконечно малых dx и dy
оказывается величиной бесконечно малой, высшего чем dx и dy
порядка (ср. формулу. (20) стр. 220).
В силу последнего полный дифференциал
df = %cdx + dlTydy
является главною частью полного приращения функции.
(3)
398 ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [xXVi
§ 153. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЕ ДИФФЕРЕНЦИАЛЫ
ВЫСШЕГО ПОРЯДКА ФУНКЦИЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ
ПЕРЕМЕННЫХ
Частные производные
df df df
дх9 dy9 dz
некоторой функции /(х, у, г) в свою очередь, вообще говоря,
являются некоторыми функциями тех же переменных х, у, z. По-
этому от этих производных можно дальше составлять производные
по разным переменным; они будут называться частными производ-
ными высшего порядка. При этом устанавливают такие обозначения:
W d2f d2f df
, т—, з—з- означают производные от з2- по х, у, z,
dx29 dxdy9 dxdz r dx 9 9
d2f d2f d2f df
a , 3-4, 3—3-----производные от -у- по х, у, z.
dydx9 dy19 dydz F dy 9 9
d2f d2f d2f df
CT’ djdi’ ^-"Роизводные от no x, y, z.
Все эти производные суть частные производные 2-го порядка
функции /(х, у, z).
От этих последних можно составить дальнейшие производные,
для которых устанавливают подобное же обозначение; так
d4f
dx dy2dz
означает частную производную четвертого порядка функции /, взя-
тую раз по х, два раза по у и раз по z.
Никаких новых правил для составления частных производных
высшего порядка не требуется: производные составляются посте-
пенно одна за другой, причем порядок дифференцирования не
играет никакой роли, если получаемые производные непрерывны,
так как тогда результат не зависит от порядка; 1 так
d2f d2f
5—3- = и т. п.
dx dy dy dx
Пример.
/(x, у) = x2y — 2уЗ,
W=2, JV_-2X W 12, н,,
дх* лу’ дх ду ix' ду* 1 у и ‘ д-
1 Доказательство этого положения можно найти в более подробных
курсах дифференциального исчисления.
§ 153J ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШЕГО ПОРЯДКА 399
Вместе с частными производными высших порядков устанавли-
вается понятие и о полных дифференциалах высших порядков от
функций нескольких независимых переменных. Именно, полный
дифференциал от полного дифференциала 1-го порядка называется
полным дифференциалом 2-го порядка и обозначается d2f и т. д.
Рассмотрим, какую форму на основании этого определения
примет выражение полного дифференциала 2-го порядка функции
двух независимых переменных /(х, у). Мы знаем, что дифферен-
циал 1-го порядка выражается так:
<3)
По определению
d?f=d (df).
Следовательно, для составления полного дифференциала 2-го
порядка необходимо составить полный дифференциал от правой
части равенства (3). Согласно правилу надо составить от этого
выражения частные производные по х и по у, каждую из них
умножить на соответствующий дифференциал dx и dy и полученные
выражения сложить.
При составлении частных производных необходимо помнить, что
dx и dy должны рассматриваться как постоянные, так как они
являются произвольными приращениями переменных а* и у, и потому
независящими от самих переменных.
Таким образом, находим
d2/ — f^(dx + ^^-- dy \ dx-]-(^£-
J \dx2 1 dydx J) 1 ydxdy 1 dy2 '
или
Пример.
y) = x\ny.
df , df x
-f- = In y, 4- = —,
дх ду У
d2f = 1 A
dx2 ’ dxdy у 9 dy2 ~~ y2 *
Поэтому
df=lnydx + ydy
d*f=2.Ldxdy-±dy*
400 ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [XXV1
§ 154. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОТ НЕСКОЛЬКИХ
СЛОЖНЫХ АРГУМЕНТОВ
Рассмотрим функцию f(u, v, -w) трех переменных и, v, -w при
условии, что последние в свою очередь являются функциями одной
переменной х. Обозначим эту функцию для сокращения одной
буквой U, так что
U =f(и, v, w).
Такая функция называется сложной функцией от х.
Дадим х некоторое приращение Дх, тогда и, v, w (как функции
этого х) получат приращения Дм, Дея, Aw, а сама функция U при-
ращение
At7 = /(« + Дм, v-J-Av, -w-|-Aw)—f(u, v, te/).
Совершенно так же, как и в § 152 (стр. 397), найдем, что
а„ dU . । dU a . dU A ,
At7 = -5- Дм J- -4— Av -k Ate/ -4- ш,
du 1 dv 1 dw 1 ’
где си — бесконечно малая порядка высшего, чем Ах. Деля затем
обе части равенства на Ах, находим
At/ df &и . df bu _.df Aw . <0
Ax du* bx ' dv* Ax ** dw* Ax Ax *
Переходя к пределу и замечая, что
r At/ dU
Даг-»О &Х
.. Am du
lim — = — = м
дж->од*
.. Av dv 1 ..
hm — — — —v' hm
Да?->()А* dx дж->о
Aw dw f .. co _
— =—=-w, lim — = 0,
Ax dx Л7._^п Ax
находим выражение интересующей нас производной
dU df , . df , , df f
dx du 1 dv 1 dw
Для составления дифференциала dU достаточно, как
производную умножить на rfx, тогда
dU = u'dx 4- v'dx 4- 4“ dx. '
du 1 dv 1 dw
Но
u'dx = du, v'dx=dv, w' dx = dw.
Таким образом, получаем
df . 1 df , 1 df .
dU=^~ du-±--~ dvA--^- dw.
du 1 dv * dw
известно,
(6)
§ 155] общая формула дифференцирования неявной функции 401
Формулы (5) и (6) снова обнаруживают отмеченное на стр. 222
обстоятельство, заключающееся в том, что формула для производной
сложной функции отличается от формулы для производной простой
функции, тогда как формулы для дифференциалов сложной и про-
стой функции по внешнему виду тождественны.
В случае, если и, v, w являются функциями нескольких незави-
симых переменных х, у, г, .. ., то подобно формуле (5) можно
dU dU
составить общие выражения для частных производных и
dU___ df ди i df tdv , df dw
dx du ' fix' dv * dx' dw* dx
dU___df du . df yv , df dw
dy du dy'dv dy'dw dy*
§ 155. ОБЩАЯ ФОРМУЛА ДИФФЕРЕНЦИРОВАНИЯ
НЕЯВНОЙ ФУНКЦИИ
Только что выведенная формула (5) дает возможность получить
общую формулу дифференцирования неявной функции.
Пусть у есть неявная функция от х, заданная уравнением
/(х, у) = 0. (7)
Для решения задачи рассуждаем точно так же, как рассу-
ждали раньше (см. стр. 231). Именно, вообразим, что мы решили
уравнение (7) относительно у и найденное значение у, выраженное
через х, мы подставили в левую часть уравнения (7). Конечно,
левая часть тогда будет тождественно равна нулю, а потому и ее
производная также будет равна нулю. При дифференцировании по
х мы должны, следовательно, у считать функцией от х. Применяя
формулу (5) к левой части уравнения (7), находим
= йГ л .V . /
dx dx ’ dy
и, приравнивая результат дифференцирования, как сказано, нулю,
получаем уравнение
dx 1 dy v 7
откуда и находим
df
/ dx /m
У-—-дГ (9)
d у
Для нахождения общей формулы для производной второго порядка
Неявной функции у пользуемся уравнениехМ (8) так же, как и уравне-
нием (7).
26 Зак. 2116. Н. С. Михельсон.
4о2 ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ХХУ|
Именно, левую его часть рассматриваем как функцию
у, у')
трех переменных х, у, у', из которых две последние являются
функциями от х. Применяя формулу (5) и приравнивая результат
нулю, находим
^=^_L^.y+g,.Z=0.
dx дх'ду^* ду'
Но
дР d2f . d2f ,
дх дх2'дхду 9
дР = d2f /
ду дх ду ду2 У ’
=
ду' ду *
Подставляя эти значения в предыдущее уравнение, находим
уравнение для определения У':
• v'4~ —• v'2-4-—• v" = 0 GO)
дх2 ' ox ду У ду2 У ‘ ду У * ' '
Пример 1. Найти у' и у" из уравнения х3-}-Заху+у3 = 0.
Здесь
f (х» У) = + Заху +У
^ = з,* + з«,. ^_3«Ж+Зз.>
дх2 дх ду ду2 J
По формулам (8) и (9) имеем
г — ~+~ ^аУ — х2^ау
У ~~ Зах-|-3_у2 ах-\-у29
6х + bay' + 6уу2 + (Зах + Зу2)у" = 0.
Из последнего уравнения находим у", причем значение у' заменяем найден-
ным выше. Тогда после упрощения, пользуясь основным уравнением, по-
лучим
„ 2а3 ху
У (ах+У)3*
Метод нахождения производных неявных функций в более сложных
случаях рассмотрим непосредственно на примерах.
д;2 у2 £2
Пример 2. Задано уравнение ^2 + ^2_== связывающее между
собою три переменные х, yf z. Так как уравнение задано одно, то оно опре-
деляет одну из этих переменных через две другие. Следовательно, среди
этих переменных две оказываются переменными независимыми, а третья —
их функцией. Примем за функцию переменную z и предложим себе найти
dz dz
дх ду
§ 156] НАХОЖДЕНИЕ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ
403
Рассуждения для нахождения этих производных будут следующие. Пред-
положим, что уравнение мы решили относительно z и найденное значение
подставили в левую часть того же уравнения. Тогда она обратится тожде-
ственно в нуль, почему и ее производные, взятые в отдельности по х и по
у, будут равны нулю. В этом предположении, т. е. в предположении, что z
является функцией от х и у, дифференцируем левую часть уравнения один
раз по х, принимая у за постоянную, другой раз по у, принимая х за по-
стоянную, и приравниваем результаты нулю, или, как говорят проще, диф-
ференцируем данное уравнение по переменным х или у. Тогда получаем
2х 2z . _п 2У I , dz _ n
а2 с2 дх ’ Ь2 ”** с2 ду
Отсюда
dz __ с2х dz _ с2у
дх a2z ’ ду ~~ b2z *
Производные второго порядка найдутся при дальнейшем дифференци-
ровании только что найденных выражений.
Пример 3. Даны два уравнения
xyz — а* — 0 и х2 -|- у2 — 2az = 0,
связывающие три переменные. Эти два уравнения определяют две перемен-
ные через третью, т. е. определяют две функции через одну независимую
переменную. Примем за независимую переменную х и предложим себе найти
dy dz
производные и не находя явных выражении у и z через х.
Рассуждения при этом будут те же, как и в предыдущем примере. Пред-
положим, что мы решили наши уравнения относительно у и z и найденные
решения подставили в левые части уравнений; тогда последние обратятся
тождественно в нуль. Поэтому, дифференцируя уравнения по единственной
независимой переменной х, получаем
yz + ху XZ = 0 2х + 2Ууг~ — 2а = 0
1 dx dx dx dx
или
dz dy dy dz _
vz4-x_y-T-x2-p- = 0 X -4- у -7^-— a — = 0.
‘ ' dx dx ' 7 dx dx
Решая эти уравнения относительно производных и , находим
dz _ (х2—у2) z dy_ _ (az -[- х2) у
~dx~~ (У2 + «2) ху dx" (у2 + az) х ’
Производные высших порядков получим дальнейшим дифференцирова-
нием найденных выражений.
§ 156. НАХОЖДЕНИЕ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ
ДИФФЕРЕНЦИАЛУ
Нахождение функции по ее дифференциалу для функции одной
переменной является обычным действием интегрирования функций.
Теперь ставится более широкая задача: отыскание функции несколь-
ких переменных по ее полному дифференциалу. Мы разберем этот
вопрос лишь для функции двух переменных.
26*
404 ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [XXVj
Как известно, полный дифференциал такой функции имеет сле-
дующий вид:
Р dx-\-Qdy, (11)
где Р и Q некоторые функции переменных х, у.
Прежде всего поставим себе такой вопрос: всякое ли выраже-
ние вида (11) представляет полный дифференциал некоторой функции
или же функции Р и Q должны быть подчинены некоторому усло-
вию для того, чтобы выражение (11) было полным дифференциалом.
Для этого представим себе некоторую произвольную функцию U
двух переменных х и у. Полный дифференциал ее будет
,тг dU 1 । dU .
dU = -ч— dx~\~^— dy.
дх 1 ду
Чтобы выражение (11) было бы полным дифференциалом этой
функции, необходимо, чтобы имело место тождество
Pdx-\-Qdy = d-^dx^dy. (12)
Ввиду произвольности дифференциалов dx и dy это тождество
необходимо должно распасться на два тождества
~=Р, ^=Q. (13)
дх ’ ду х 7
Действительно, раз равенство (12) должно выполняться при любых
значениях dx и dy, то примем
dx = 1, dy = 0,
тогда придем к первому из тождеств (13). Положив затем
dx = 0, dy = 1,
придем ко второму из них.
Из тождеств (13) дифференцированием получае^м
dW _дР дЮ _JQ
дх ду ду’ ду дх дх’
т. е.
дР_ dQ
ду дх‘ * '
Таким образом, для того, чтобы выражение (И) было полным
дифференциалом некоторой функции, необходимо, чтобы выпол-
нялось условие (*).
Условие это вместе с тем и достаточное. Докажем это, т. е.
докажем, что при выполнении равенства (*) всегда можно найти
функцию U такую, что
dU = Pdx^-Qdy
§ 156] НАХОЖДЕНИЕ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ 405
или (что то же самое), такую функцию U, для которой
dU „ dU
д^=Р И Ty^Q- <13)
Будем искать сначала функцию U, удовлетворяющему, первому из
условий (13).
Общее выражение таких функций, очевидно, будет:
и — J Р dx 4- © (у), (14)
где вместо произвольной постоянной С введена некоторая функция
от у, имея в виду получить самое общее выражение для U по ее
частной производной по х. Однако, искомая функция U должна
удовлетворять еще и второму из равенств (13):
=
ду
Поэтому выражение для U должно быть такое, чтобы
pdx + ?'(.y) = Q- (15)
Для выполнения этого условия надо соответствующим образом по-
добрать пока еще неопределенную и произвольную функцию <?(у).
Посмотрим, можно ли ее подобрать так, чтобы выполнялось
равенство (15), т. е. чтобы
= Pdx. (16)
Замечая, что левая часть равенства (16) есть функция одного у,
мы заключаем, что это равенство тогда только может быть верным,
когда и правая часть его не зависит от х, а это будет, когда
Д f р</х1=о.
дх L ду J J
•Легко проверить, что последнее действительно имеет место при
выполнении условия (*). В самом деле,
Д [q —Д f — Д[Д f Р rfxl =
dx L ду J J дх дх Ldy J |
дх L dx I J
Но
Д f Pdx = P.
дх J
Поэтому
дх [ ду J J дх ду
406
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [XXVl
В случае, если выполняется условие (*), последнее выражение
обращается в нуль, что доказывает, что правая часть равенства (15)
не зависит от х, а следовательно, будет функцией лишь одного у
или даже постоянным числом. В том и в другом случае мы из ра-
венства (16) простым интегрированием найдем функцию ф(у), а затем
и искомую функцию U (см. равенство (14)).
Таким образом, для нахождения функции U такой, чтобы
Р dx + Qdy = dU, достаточно, чтобы выполнялось условие (*).
Итак, необходимым и достаточным условием для того, чтобы
выражение Pdx-\-Qdy было полным дифференциалом некоторой
функции U, служит условие
d^^dQ
ду дх '
Вышеизложенные рассуждения дают нам вместе с тем и способ
нахождения этой функции:
Мы ищем U сначала по формуле (14), причем при вычислении
Р dx переменная у должна считаться постоянной; затем находим
функцию у (у) из уравнения (16) и найденное значение подставляем
в выражение (14).
Пример 1. Дано выражение ydx — xdy\ требуется узнать, будет ли оно
полным дифференциалом некоторой функции или нет?
Здесь
Р = yt Q ^ — х,
df . diQ __ .
ду~ ’ дх~
Условие (*) не выполняется, и, следовательно, предложенное выражение
не есть полный дифференциал.
Пример 2. Рассмотрим выражение (Зх8 + 8ху) dx -ф (4х2 + Зу2) dy.
Здесь
Р = Зх2 + 8ху, Q = 4х2 4- &У2>
дР Q dQ Q
— = 8х, --=8х.
ду дх
Условие (*) выполняется, а потому предложенное выражение есть полный
дифференциал некоторой функции U. Найдем ее.
По формуле (13)
и = J Р dx + ср (у) = J (Зх- + 8ху) dx + <? (у) = хз + 4x3у + ? (у).
Далее подбираем функцию ср (у) так, чтобы = Q, т. е. чтобы
4х2 + '/ Су) = 4x2 + Зу2,
откуда
/ (у) = зл <р (у) = у3 + с.
Таким образом
(/=^3 + 4х\у +У’ + С.
§ 157]
ВОПРОСЫ И УПРАЖНЕНИЯ
407
§ 157. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется частной производной некоторой функции?
2. При дифференцировании по одной переменной какую роль играют
другие переменные?
3. Если дана функция f(x, у), то что означают символы /^(а, Ь)
b)t
4. Что называется полным дифференциалом функции нескольких неза-
висимых переменных?
5. Чем отличается полное приращение функции от ее полного диффе-
ренциала?
6. Сравнить формулу (20) § 93 (стр. 220) с формулой (2) § 152 (стр. 397)
и подметить различие, заключающееся в величинах, обозначенных в этих
формулах знаками df и dy.
7. Каким путем можно составить частную производную второго по-
d2f .
рядка ч—ч— ?
1 дхду
8. Нс представляет ли формула дифференцирования функции несколь-
ких сложных аргументов обобщения формулы дифференцирования сложной
функции одной переменной?
9. Как из уравнения f (х, _у) = 0 определить производную от у по х,
т. е. у'?
10. Каково условие, необходимое и достаточное, чтобы Pdx-j-Qdy
было полным дифференциалом некоторой функции?
11. Дано / (х, у) = х3_у2. Найти f'x (х, у) и f'y (х, у).
Отв. f'x(x, у) = Зх2_у2, f'y (х, у) = 2x»j.
12. Дано /(х, у) — -У х2— у2. Найти и df.
о„1в. д/= х . д/ — Х—^—1 df=xf£-ydy-.
дх у Х2 — J/2 ду у Х2___у2 у х2—У
13. Дано U = х2 sin 2 у + у2 cos 2z. Найти ~.
J дх ду dz
Отв. = 2х sin 2yt = 2х2 cos 2у + 2у cos 2z , = — 2_у2 sin 2z .
14. Дано f(xt у) = 1п(х — у). Найти f'x (0,1) и f'y (1, 2).
О/ив.4(0,1) = -1, 4(1,2) = 1.
15. Дано f(x,y, Найти 4(1,0-1),4(1,0,-1)У'(1,0,-1).
Отв. fx(l, 0,-1)= 1, f’y (1, 0, -1)=-1, (1,0,-1)=|.
16. Дано f (х, у) = х3у — 2х2у2. Найти , & ? , .
J v dxL дхду dy2
Отв» ~ §ХУ ““ 4У2 > t = 3x2 — 8xy, = — 4x2.
dx2 s дхду J ’ dy2
17. Дано z == arc tg^-. Найти d2z.
_ 2xy d2x — 2 (xa — у) dxdy-^2 xy dy2
Ometd (*2+У)2
18. Дано f (x, y) = sin2 x • cos2_y. Найти d2f*
Отв» d2f = cos 2(X cos2 y dx2 — 2 sin 2x cos 2y dx dy — 2 sin2 x cos 2y dy2.
408
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [XXVi
19. Доказать, что для
df . df
ство х + 4~ У = 0.
дх ду-7
20. Доказать, что для
д/ । df
^-х + ±-у = 0.
дх ду-7
функции /(х, _у) = - • arcsill — выполняется тожде-
х у
ху
функции /(х, у) = 2- выполняется тождество
х ~г У
21. Доказать, что для функции f (х, у) = х • е х выполняется тождество
d2f . , Q df । d2f о о
4-4- х2 + 2 -А- -5-- ху + у2 = 0.
дх2 дхду 7 ду27
22. Найти у' из уравнения уех—хеу = 1.
п г еу-уех
0,пв-у=7^^'
23. Найти у' и У' из уравнения xt?y — 1.
°'яв-^=-4’ ^=4-
у" из уравнения 1п (х —у) 4~ х + У = 0.
.у+ 1 .//_ 4(3’ — х)
У — х+1 J {у— х + 1)8
У' из уравнения х2 4- 2ху —у2 = 0.
у 4- х
Отв. у' = , у" = 0. Объяснить, почему у"' = 0.
dz d2z d2z d2z n
— из уравнения ху + yz 4~ xz—а2=0.
у -|- z dz___ _ x_+_z_ d2z __ 2(y-{-z)
у + x ’ ду~~ у 4- x ’ dx2 — (y -f- x)2 '
2z d2z_2(x + z)
(У + х)2' dy2" (y + x)2 “
x2 _|_ = д2 .
x2 — a2 d2z _ xy
z^ ’ дхду ~~ 23
~ и из уравнений xyz — a2 == 0 и x2 + j'2 — 2az = 0.
dy_____у (x2 4- az) dz _ ^(x2—У)
dx x (y2 4- az)f dx x (y2 4~ az)'
Будут ли следующие выражения полным дифференциалом некоторой
функции, и если да, то какой?
a) (3x2j/ — 2ху2) dx 4- (х3 — 2х2у 4- 4у3) dy.
Отв. U — ух3 — у2х2 4-У 4" £•
б) (у — 2x)dx— (x-\-2y)dy. Отв. Нет.
в) (eiy — 2уеЪх) dx + (2хе,г/ — е2х + 2Л) dy.
Отв. U = (х-\-\)ё!у —уе^ + С.
24. Найти у' и
25. Найти у' и
26. Найти
27.
28.
29.
Найти
Найти
dz ________ ______ ____
дх’ dy ’ dx2 ’ дхду ' dy2
dz
Отв. — =
дх
d2z ___
дхду ~
d2z d2z d2z
5—5“ , 3—5 и з—s— из уравнения
дх2 ’ ду2 дхду J
d2z у2 — a2 d2z
Отв. ч-р = -—, -д-х =
дх2 z3 ду2
XXVII. ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИИ
§ 158. ПОГРЕШНОСТИ АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ
Необходимость обратиться к приближенным вычислениям возни-
кает в двух случаях вычисления числового значения аналитического
выражения.
Первый случай это тот, когда данное для вычисления выражение
в силу своего характера приводит при заданных, хотя бы и точных,
значениях входящих в него величин к иррациональным числам, а мы
Желаем заменить этот результат приближенным, но рациональным
числом. Такого рода случай мы встречаем при извлечении корней,
вычислении логарифмов чисел; такого рода случаи дает во мно-
жестве тригонометрия, приближенное решение уравнений и весьма
разнообразные другие операции.
Второй случай когда, независимо даже от формы аналитического
выражения, мы неизбежно должны перейти к приближенным вычи-
слениям, это тот, когда самые числовые значения входящих в фор-
мулу величин задаются нам приближенно. Простейшими примерами
такого рода случаев могут служить выражения
а также всякие формулы, в которых числовые значения входящих
в них величин получаются из опыта, а потому неизбежно заключают
в себе неточность.
Условимся во всем дальнейшем обозначать через
я, Z>, . .., Z (1)
точные значения входящих в формулу величин, через
' <71,^1,..., /1 (2)
заданные их приближенные значения.
Разности
— а, —Ь, .Zt— I
будем называть истинными погрешностями или ошибками прибли-
женных чисел ряда (2).
410 ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ [XXVII
Разности эти могут быть как положительные, так и отрицатель-
ные. В случае если ах— а < 0, т. е. если < а, число аг назы-
вается приближенным значением числа а по недостатку; если же
ах — а>0, т. е. если а^а, то аг называется приближенным зна-
чением по избытку.
Истинные погрешности приближенных значений
«1, Ьь ../j
будем в дальнейшем обозначать через
Да, Д£, ..., Д/. (3)
Как было отмечено, величины эти могут быть как положительными,
так и отрицательными, по их определению имеем:
= л —Да, = b —Д^, • • •, == I*
Приближенные величины соответственно характеру их погреш-
ностей можно разделить на следующие категории:
1. К первой категории мы отнесем те, в которых нам известна
точная величина ошибки и ее знак. Это будет иметь место тогда,
когда вычислителю известны точные значения входящих в формулу
величин, а он, вследствие ли экономии в выкладках или по другим
причинам, отказываясь от точного вычисления, отбрасывает некото-
рое число десятичных знаков в данных числах или даже грубо
округляет их1 и тем самым вводит в выкладки приближенные зна-
чения; при этом точная величина погрешности взятых им чисел, оче-
видно, известна. Так, например, желая получить грубое приближение
для числового значения выражения
А = при а = 9,876; Ь = 6,123; с = 0,18; 0 = 42,071,
мы могли бы заменить
9,876 числом 10
6,123 „ 6
0,180 „ 0,2
42,071 „ 40
и получили бы приближенное значение А = 2. В этом случае нам
известны точные значения погрешностей входящих в формулу ве-
личин и, конечно, нетрудно определить и точную величину погреш-
ности результата.
2. Ко второй категории мы отнесем такие приближенные числа,
в которых нам известен знак погрешности, но не известно ее точ-
ное значение. Например, приняв
z = 3,1415,
---------- •
1 Мы предполагаем, что данные числовые значения величин выражаются
дибо целыми числами, либо десятичной'дробью.
§ 158]
ПОГРЕШНОСТИ АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ
411
мы знаем, что делаем погрешность, про которую можно сказать,
что опа отрицательная и по абсолютной величине не превосходит
0,0001; полагая же
тс = 3,1416,
мы делаем погрешность положительную, по абсолютной величине
не превосходящую 0,0001; или, полагая
/5 = 2,236,
мы делаем ошибку отрицательную, по абсолютной величине мень-
шую 0,001, а полагая
/5 = 2,2361,
ошибка оказывается положительной, по абсолютной величине мень-
шею 0,0001. Так как в рассматриваемом случае нам известен знак
ошибки, то, стало быть, также нам известно, задано ли приближен-
ное значение по недостатку или по избытку.
3. К третьей категории приближенных чисел можно отнести
такие, относительно которых нам неизвестно ни точное значение их
погрешности, ни ее знак. Такого рода приближенные числа могут
появляться в результате эксперимента, когда, например, искомая
величина выводится из целого ряда наблюдений как средняя ариф-
метическая отдельных измерений. В подобных случаях необходимо
знать хотя бы границы погрешностей приближенных чисел.
Под абсолютной погрешностью приближенной величины а мы
будем понимать положительное число, которого не превосходит
абсолютная величина истинной погрешности величины а.
Условимся обозначать пределы абсолютных погрешностей при-
ближенных чисел ряда (2) соответственно знаками
8а, 8£, . .., 8/.
Само собой разумеется, что эта последняя категория приближен-
ных /значений является для вычисления самой неблагоприятной. Тем
не менее, для применимости всех выводимых результатов мы во
всем дальнейшем будем предполагать, что имеем дело с этой именно
категорией величин. В этом предположении будут выведены и все
общие формулы.
В очень многих расчетах полезно вводить еще так называемую
относительную погрешность. Под этим подразумевают отношения
абсолютных 'погрешностей приближенных величин к действитель-
ным значениям этих величин, т. е. отношения
оа ЪЬ
а ' b ’ ’ * ’ ’ /
Мы будем относительные погрешности обозначать буквами
? • ? ?
412 ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ [XXVII
Введение этих величин объясняется тем, что относительные погрещ,
ности ближе характеризуют качество полученного вычислением при,
ближепия или достоинство измерения величины. Так, например, если
в результате измерения двух длин получены следующие величины;
2,21 м с точностью до 0,01 м
и
653,7 м с точностью до 0,1 м,
то второе измерение несомненно относительно более точное, так
как относительные погрешности первого измерения
а второго измерения
~ = °’0002-
4 Duo,/ dUUO
Полезно также иметь в виду, что приближенные значения одних
величин могут быть нам известны с любой степенью точности, тогда
как степень точности других величин может быть ограничена.
Так, например, числа У2, тс, In 3 и т. д. могут быть выражены
рациональными числами с любой степенью точности; значения же
величин, ’ добываемых из опыта, неизбежно имеют определенный
предел точности вследствие несовершенства употребляемых при этом
приборов и ограниченности чувствительности человеческого зрения.
§ 159. ПРИМЕРЫ ЗАДАЧ НА ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
Все задачи приближенного вычисления можно разбить на две
группы. Задачи первой группы можно формулировать так: зная при-
ближенные значения величин, входящих в данную формулу, и их
абсолютные погрешности,, определить предел погрешности резуль-
тата вычисления.
Задачи второй группы можно формулировать так: с какой сте-
пенью точности следует взять входящие в вычисляемую формулу
величины, чтобы получить результат с наперед заданною требуемою
точностью.
В первой группе задач задаются числовые значения величии
с фиксированной степенью точности и по ним определяется степень
точности результата; во второй — наперед задается степень точности
результата и требуется соответственно ему подобрать значения вхо-
дящих в формулу величин с должной для выполнения задачи точ-
ностью.
Та и другая категории задач, кроме решения основного вопроса,
налагают на вычислителя еще одну обязанность: произвести вычи-
сления с наибольшей экономией времени и труда, т. е. вводя в вы-
§ 159] ПРИМЕРЫ ЗАДАЧ НА ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ 413
деление лишь то количество знаков, которое требуется для дости-
жения соответствующей точности результата. Поясним последнее
примерами.
Пример 1. Положим, нам требуется вычислить длину окружности,
зная, что ее радиус, определенный с точностью до 0,1 см, равен
2,3 см. Из формулы c—2itr видно, что так как 2тс > 6, то, в ре-
зультате умножения на 2г приближенного значения радиуса г = 2,3 см,
ошибка этого числа, равная 0,1 см, произведет ошибку результата
по крайней мере в 6 раз большую, и было бы неправильным
с точки зрения экономии вычисления и бесцельным по существу
взять в данном случае за значение к число с большим, чем с одним
десятичным знаком. Таким образом находим
с = 2,3 . 6,2 = 14,26 см
и так как нельзя ручаться в этом результате уже за первый деся-
тичный знак, то в результате имеем
с =14 см с точностью до 1 единицы.
Пример 2. Пусть требуется найти частное , зная, что прибли-
женное значение числа а
= 4,148
задано с точностью до 0,001. Неправильным и бесцельным было бы
в этой задаче вести деление далее четвертого десятичного знака
частного, так как в результате деления данного приближенного
числа на 6 мы должны ожидать ошибку уже в четвертом деся-
тичном знаке. Потому
4,148:6 = 0,6913 (с точностью до 0,0002).
Пример 3. Стороны а и b прямоугольника заданы следующими
приближенными числами:
ах = 5,247 м 1
, г с точностью до 0,001 м.
= 2,894 м J
Требуется вычислить площадь данного прямоугольника с точностью
До 1 м*. Конечно, было бы совершенно бесполезно вести умноже-
ние, сохраняя все десятичные знаки в числах и Ь{. Для вычисле-
ния площади с данной точностью достаточно ограничиться одним
Десятичным знаком в каждом из множителей. Перемножив
5,2 • 2,9= 15,08
отбросив знаки после запятой, мы и найдем, что искомая пло-
щадь равна 15 м1 с точностью до 1 л/2.
Изложенное последнее упрощение вычисления можно оправдать
*°тя бы тем, что, взяв более точные значения сторон прямоуголь-
414 ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ [xXVtl
ника, например, с двумя десятичными знаками, мы получим произ-
ведение:
5,25 - 2,89 = 15,1725,
целая часть которого та же, как и в предыдущем произведении.
§ 160. ПЕРВАЯ ГРУППА ЗАДАЧ
Общая задача. Дана для вычисления функция
f(a, b, с)
(для простоты ограничиваемся тремя переменными). Величины а,
b и с известны лишь приближенно с абсолютными погрешностями,
соответственно равными
8а, ЪЬ, 8с.
Определить абсолютную погрешность результата вычисления
функции f (а, Ь, с) при подстановке вместо а, Ь, с их прибли-
женных значений а1? cv
Предположим, что истинные погрешности приближенных значений
величин а, Ь, с равны Да, &Ь9 Ьс9 тогда
а1==я4-Дя, b1 = b-\-^b9 сх = с-4-Д^.
Подставляя вместо точных значений а, Ь9 с их приближенные, мы
вычисляем вместо функции /(а, Ь9 с) выражение
/(a-f-Да, Ь-\-Ы)9 с + Дс).
Погрешность такого вычисления выразится тогда разностью
f(a-\-La, b-\-kb9 c-j-Дс)—f(a, b9 с).
Но
f (а Да, b kb, с -|- Дс) — f (а, Ь, с) =
= Да +Дс + а>
да 1 дЬ 1 дс 1
(см. формулу (2) стр. 397).
Поэтому, обозначая погрешность вычисления через Д/ и отбра-
сывая малую величину ш, мы можем написать приближенное ра-
венство
Д/Да-I-ДД +Дс,
J да ' дЬ 1 дс 9
где правая часть есть полный дифференциал функции /(а, Ь, с).
Ввиду малости количества ш при малых Да, kb, he мы во всем
дальнейшем примем правую часть вышенаписанного приближенного
равенства за действительную ошибку вычисления и будем писать
Д/ = -^Да-1-^Дд + ^Дс. (4)
J да 1 дЬ 1 дс v 7
§ ИЗО]
ПЕРВАЯ ГРУППА ЗАДАМ
413
Так как самые величины Да, Д£, Дг предполагаются неизвестными,
то, заменяя их соответственно абсолютными погрешностями 8а, 8#,
8г, а частные производные , 4^ их абсолютными величинами,
’ 1 да ’ дЬ ’ дс ’
приходим к искомой нами величине абсолютной погрешности резуль-
тата вычисления функции
8М118“+1<1“+1118е- (5)
П df df df
Ввиду того, что в частные производные входят вели-
чины а, Ь, с, а их точные значения неизвестны, то на практике
абсолютные значения этих частных производных заменяют их наи-
большими абсолютными значениями А, В, С и пишут:
8/==48а + В8£-|-С8г. (6)
Из общей формулы (5) нетрудно вывести все частные формулы,
относящиеся к вычислению погрешностей результатов основных
действий.
1. Определение абсолютной погрешности алге-
браической суммы.
Пусть /(а, б) — а±Ь.
Составляем частные производные от f (а, Ь) и их абсолютные
значения:
<у = 1 ^=+1- т=1 1^1=1
да ’ db — ’ |da| | дЬ |
и по формуле (5) находим
8/=5а4-8£. (I)
По этой формуле (I) и вычисляется предел абсолютной погреш-
ности или просто абсолютная погрешность алгебраической суммы.
Формула эта распространяется на какое угодно число слагаемых.
Итак, абсолютная погрешность алгебраической суммы равна
сумме абсолютных погрешностей слагаемых.
Пример. Вычислить /3—/2 и определить абсолютную погреш-
ность результата, если принять
/3= 1,7320, /2=1,4142.
Данные значения /3 И /2 имеют погрешности, не превосходящие
0,00005, т. е. 8а = ЬЬ = 0,00005. По только что выведенной фор-
муле находим
8 (/З — У 2) = 8а 8Z> = 0,0001
(/3—/2) = 1,7320— 1,4142 = 0,3178.
416
ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
[xxvti
Здесь 0,3178 представляет приближенное значение разности взятых
радикалов с погрешностью, не превосходящей 0,0001, т. е. с абсо-
лютной погрешностью, равной 0,0001. Относительная погрешность
результата не превосходит числа
0,0001
0,3
< 0,0004,
т. е. составляет 0,04°/о вычисляемой величины.
2. Определение абсолютной и относительной
погрешности произведения двух множителей.
Пусть /(я, b}-=a-b (оба множителя можно считать положи-
тельными). Имея в виду применение общей формулы (5), составляем
частные производные
и затем по формуле (5) находим
8/=£8a-|-a8Z>. ' (II)
Это и есть формула для вычисления абсолютной погрешности
произведения двух множителей.
Для нахождения величины относительной погрешности разделим
обе части равенства (II) на ab, тогда
о/ Ъа . ЪЬ
ab а ' b '
Каждый член этой формулы -выражает соответственно величины
относительных погрешностей произведения и каждого из сомножи-
телей. Обозначая их соответственно буквами а, (3, приходим
к очень простому результату
7 = » + ?, (И')
который указывает, что относительная погрешность произведения
равна сумме относительных погрешностей каждого из сомнЬжи-
телей\
Последний результат обобщается на произведение какого угодцо
числа сомножителей.
Примечание. Так как для произведения значительно проще
вычисляется относительная погрешность, то при вычислении абсо-
лютной погрешности произведения удобнее вычислить сначала отно-
сительную, а затем уже по ней и абсолютную погрешность произ-
ведения.
Действительно, зная величину 7 и что = у, находим
8/ =s
§ 160] ПЕРВАЯ ГРУППА ЗАДАЧ 417
Приняв затем за величины сомножителей наибольшие их значения А
и В, найдем величину абсолютной погрешности произведения
= (7)
Пример. Вычислить площадь прямоугольника, стороны которого,
измеренные с погрешностью, не .превосходящей 0,1 см, оказались
равными 42,3 см и 12,8 см. Здесь
f(a, b) = ab.
Приближенные значения сторон
а1=42,3; ^ = 12,8.
Относительные погрешности каждой стороны можно принять не
превосходящими соответственно чисел
® = 0.0025; ЙЗ = 0,008,
т. е. положить
а = 0,0025, (3 = 0,008.
По формуле (!!') имеем
у = 0,0025 + 0,008 = 0,0105 « 0,01.
Величина абсолютной погрешности найдется по формуле (7), в кото-
рой Можно принять
Д = 43 и £=13.
Поэтому имеем
8(л . &) = 43 • 13-0,01 =5,59
или
8 (а • Ь) < 6 см2.
Из приведенного исследования видно, что в результате произведен-
ного измерения сторон прямоугольника мы можем рассчитывать
определить его площадь лишь с точностью до 6 см2. Отсюда и
вытекает характер самого процесса вычисления данной площади,
при котором мы должны стремиться получить лишь целую часть
произведения.
Площадь равна 541 см2 с погрешностью, не превышающей 6 см2.
3. Определение абсолютной и относительной по-
грешности частного.
Пусть /(а, Ь) = у (числа а и b можно считать оба положитель-
ными). Следуя формуле (5), составляем частные производные и их
абсолютные величины:
г да Ъ 9 дЬ = Ь2 9 I да | b 9 | db I Ь2 9
27 Зак. 2116. Н. С. Михельсон.
418
ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
[xxvtt
а затем и абсолютную погрешность частного в виде
8/ = |8а+^8^=6-^±^-6. (III)
Относительная погрешность частного найдется обычным прие-
мом— делением 8/ на величину частного. Из формулы (III) тогда
имеем
cf Ъа ЪЬ
а я. Ь
~Ь
Вводя подобные же обозначения, как и в случае произведения, при-
ходим к формуле
% = «+А (Ш')
Таким образом, относительная погрешность частного равна сумме
относительных погрешностей делимого и делителя (та же формула,
как и для произведения).
Пример. При определении плотности тела по формуле
Z) = —,
v
где т — масса, v— объем тела и D—его плотность, масса была опреде-
лена с точностью до 0,0001 г и оказалась равной 33,5930 г, а объем опре-
делен был с точностью до 0,002 мл и оказался равным 4,574 мл. Определить
плотность тела и абсолютную погрешность такого измерения.
Относительные погрешности массы и объема могут быть приняты рав-
ными соответственно
а =
= 0,000003,
оо
= 0Ж = 0 000222.
4,5 _
Поэтому относительная погрешность результата будет
Y = 0,000225, или у = 0,00023.
Отсюда абсолютная погрешность вычисления плотности будет
W = 0,00023 • 7,5 = 0,0017.
где 7,5 — примерная величина плотности.
Таким образом, в результате измерения мы можем ожидать погреш-
ность в определении плотности, не превышающую 0,0017 или, округляя, 0,002,
что составляет 0,2%.
Из найденного вытекает, что при делении чисел 33,5930 и 4,574 нет
смысла вести деление дальше третьего десятичного знака частного. Итак,
D = 3^0 = 7,344.
4,574
§ 160]
ПЕРВАЯ ГРУППА ЗАДАЧ
418
4. Определение абсолютной и относительной
погрешности степени приближенного числа.
Пусть /(а) = ат (а > 0, т любое число). Тогда = та™~\
и формула (5) сводится только к члену
6/ = тат~^а. (IV)
Это и есть выражение абсолютной погрешности степени.
Для определения относительной погрешности делим обе части
формулы на а™, тогда
bf та^1 * ба
aw ат а ’
т. е.
Р=та. (IV')
Таким образом, относительная погрешность степени равна пока-
зателю степени, умноженному на относительную погрешность
основания.
Формулы (IV) и (IV') относятся к какому угодно значению пока-
зателя, следовательно, имеют место и для извлечения корня любой
г, 1
степени. В частности, при т = -^
? = -Г'
Пример. Определить погрешность результата вычисления приняв
число е равным 2,7183 с точностью до 0,0001.
а) Непосредственное определение абсолютной погрешности.
По формуле имеем1
8 ( /е ) < 0,000034 < 0,00004.
б) Определение абсолютной пргрешности при помощи предварительного
определения относительной погрешности.
Относительная погрешность взятого значения для числа е не превышает
0,00004.
Относительная величина погрешности j/T по формуле (IVх) будет
р =У -0,00004 = 0,00002.
Найдя .величину относительной погрешности Уе, находим абсолютную
погрешность
5 (]/7) = 0,00002 • /?< 0,00002 • У*2ДО = 0,00002 • 1,7 = 0,000034 < 0,00004.
* Число е заменено меньшим числом, и для удобства точным квадратом.
27*
420
ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
[XXVH
Определение абсолютной погрешности в случае задания более
сложной функции ведется так же, как рассмотренные выше простые
случаи, на основании все той же формулы (5) (стр. 415).
Пример. Определить абсолютную погрешность результата вычисления
по формуле
За2 + be
2 V"m
Здесь имеем функцию четырех величин
1 ——
f(a, b, с, т) = у (За2 + М т 2.
Для определения абсолютной погрешности о/ составляем частные произ-
водные от функции f (а, Ь> с, т):
df , -7 df 1
2 а, ~- = —т 2 с>
да дЬ 2
df 1 "~h
I =-7 <3»’+ “>•”*•
Поэтому искомая погрешность будет вычисляться по формуле
1_1 1 _L 1
bf=3m 2а»Ъа-\--^т 2с-ЬЬ-^--^-т 2 b • Ъс— (За2Ьс) т 3Ът.
§ 161. ВТОРАЯ ГРУППА ЗАДАЧ
Задачи второй группы, как сказано раньше, состоят в следую-
щем: с какой степенью точности следует взять входящие в вы-
числяемую формулу величины. чтобы получить результат с на-
перед заданной требуемой точностью.
Положим, требуется вычислить функцию трех величин:
/(а, Ь, с)
с абсолютной погрешностью ш.
Как выведено выше (см, формулу (5)),
Для того чтобы было
8/< <о,
можно 8а, 8£, 8с взять, например, такими, чтобы
|Ж<^, m.8c<“
I да | 3 ’ I db I 3 ’ | de | 3 ’
§ 161] ВТОРАЯ ГРУППА ЗАДАЧ 421
т. е. чтобы
Эти формулы и решают поставленную задачу.
При вычислении 8а, 8£, 8с округляют величины частных произ-
водных, подставляя вместо них их значения по избытку.
Пример 1. С какой степенью точности следует знать величины электро-
движущей силы и сопротивления цепи, чтобы определить силу тока в цепи
с точностью до 0,2 ампера.
Связь между указанными величинами выражается формулой
По формуле (III) имеем 8Z = — or. Чтобы 8Z было меньше 0,2 ампера,
достаточно, чтобы было
1 F
— 8£<0,1 и -48г<0,1,
г Г2
О 1 • г2
т. е. чтобы 8Е<0,1 • г и 8г < ’ .
Положим, что электродвижущая сила около 6 вольт, а сопротивление
около 3 омов, тогда
8£ < 0,1 • 3 = 0,3 вольта.
. ^0,1-9
ог< —— = 0,15 ома.
Таким образом, для поставленной задачи достаточно электродвижущую
силу определить с абсолютной погрешностью в 0,3 вольта, а сопротивление
в 0,15 ома.
Пример 2. С какой степенью точности следует вычислить каждый из
членов разложения в ряд числа е:
_1 1 1 । 1 । 1 । 1 ।
е-*+ 1 +1.2+Ь2.3+1-2.3«4
чтобы получить значение е с точностью до 0,00001.
Прежде всего замечаем на основании таблицы факториалов I •2*3.. .п,
что, начиная с члена ряда
1
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9’
все дальнейшие члены не могут оказать влияния на поставленную точность
определения числа е, так как уже
1.2- 3-4-5-6-7-8-9 < 0’000003’
величина же остальных членов быстро убывает.
Принимая во внимание, что первые три слагаемые—точные числа,
видим, что для достижения требуемой точности каждое из остальных
422
ОСНОВЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
[XXVII
шести слагаемых достаточно определить с точностью, равною —g—, т. е.
с шестью десятичными знаками. Таким образом, находим
1 + 1+П2 = 2’5
Y-4-ъ = 0,166667
П27Г4^-0'"08333
Гатз^та»0'001389
1.2.3. Л. 677^; = 0.000025
2,718279
т. е. е = 2,71828, что и дает действительно значение числа е с требуемою
точностью.
§ 162. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется истинной погрешностью приближенной величины?
2. Что называется приближенным значением величины по недостатку и
по избытку?
3. Всегда ли бывает известна точная величина погрешности?
4. Всегда ли бывает известен знак погрешности?
5. Что называется пределом абсолютной погрешности?
6. Что называется относительной погрешностью?
7. Какие две задачи являются основными в вопросе приближенного
вычисления?
8. Какой формулой выражается величина абсолютной погрешности,
вычисляемой функции?
9. Чему равна абсолютная погрешность алгебраической суммы?
10. Чему равна относительная погрешнос1ъ произведения?
11. Чему равна относительная погрешность частного?
12. Чему равна абсолютная и относительная погрешность степени?
13. Определить абсолютную погрешность, получаемую при определении
плотности D жидкости пикнометрическим способом по формуле
-Pl’
пикнометра пустого;
пикнометра, наполненного водой;
если Pt = 25,36 г + 0,01 г — вес
Р2 = 46,27 г +0,01 г — вес _________________________ v
Р3 = 58,43 г + 0,01 г — вес пикнометра с исследуемой жидкостью.
Отв. 0,003 г/м'з.
14. При определении диаметра капилляра весовым способом по формуле
d = 2
§ 162]
ВОПРОСЫ И УПРАЖНЕНИЯ
423
оказалось, что вес столбика ртути Р = 76 мг + 2 мг, средняя длина его
равна I = 1,75 мм ± 0,005 мм, плотность ртути D ~ 13,55 ± 0,01. Определить
величину относительной и абсолютной ошибки измерения d.
Отв. Относительная погрешность равна 0,017, абсо-
лютная погрешность равна 0,03 мм.
15. Средний коэффициент линейного расширения определяется по фор-
муле
а = -1L___!к.
где t и — температуры наблюдения. Определить абсолютную и относи-
тельную погрешности наблюдения, если известно, что Z = 14,4° С ± 0,05° С,
= 99,Р С zt 0,05° С. Длины стержня lt = 6J,018 см ± 0,001 см, ltl =
= 60,124 см ± 0,001 см, 1ц = 60,002 см ± 0,001 см.
Отв. Относительная погрешность равна 0,03; абсолютная
погрешность равна 0,0000008.
16. Определить, с какой точностью необходимо знать величины, вхо-
дящие в формулу задачи 14, чтобы определить диаметр капилляра с точ-
ностью до 0,01 мм.
Отв. ЪР = 0,2 мг\ оте = 0,01; о/ = 0,005 мм\ о£) = 0,03 г/см\
17. Вычислить с точностью до 0,01 величину выражения
Г те. 9,8765
V 17
Отв.
Г 3,14.9,9
Г 17
1,35.
XXVIII. ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 163. ПОНЯТИЕ О ДИФФЕРЕНЦИАЛЬНОМ УРАВНЕНИИ
И ЕГО РЕШЕНИЯХ
Дифференциальным уравнением называется всякое уравнение,
связывающее независимые переменные с их функциями и произ-
водными этих функций.
В противоположность дифференциальным уравнениям, уравнения,
не содержащие производных, называются конечными.
Дифференциальное уравнение возникает в результате постановки
весьма разнообразного рода задач, аналитических, геометрических,
механических, технических и других.
Задача I. Рассмотрим, например, такую задачу: найти все линии,
обладающие тем свойством, что поднормаль во всякой точке этой
линии есть величина постоянная.
Предполагая, что задача решена, т. е. что мы нашли уравнение
этой кривой, составим для нее выражение поднормали и приравняем
ее постоянной величине. Тогда получаем уравнение
УУ'=Р- (1)
Уравнение это — дифференциальное уравнение, из которого нам
и надо получить выражение искомой функции у через х.
Задача II. Точка движется прямолинейно, причем скорость ее
движения возрастает пропорционально времени. Определить путь,
пройденный точкой за некоторый промежуток времени.
Известно, что скорость прямолинейного движения выражается
„ ds .
производной -ц;, где s — путь, a t—время.
По условию задачи пишем
' ' %-kt. (2)
Полученное уравнение есть опять дифференциальное уравнение,
из которого и требуется найти выражение s как функции времени t.
§ 163] ПОНЯТИЕ О ДИФФЕРЕНЦИАЛЬНОМ УРАВНЕНИИ И ЕГО РЕШЕНИЯХ 425
Задача III. Материальная точка выходит из состояния покоя
под влиянием силы, притягивающей ее к некоторому неподвижному
центру О и изменяющейся пропорционально расстоянию точки до
этого центра. Определить характер движения точки.
Движение, очевидно, будет происходить по прямой, соединяющей
начальное положение точки А с центром притяжения О. Приняв
последнее за начало отсчета пути и зная, что сила выражается
произведением массы на ускорение, приходим к дифференциальному
уравнению
т--ё=—^> (з)
из которого и требуется найти выражение <9 через А
Здесь k — коэффициент пропорциональности, а знак минус по-
ставлен ввиду того, что сила имеет направление, противоположное
отсчету пути <9.
Некоторые дифференциальные QM=S
уравнения содержат лишь одну М
независимую переменную и ее не- 1 д
известные функции с их произ-
водными. Такие уравнения назы- Рис>
ваются обыкновенными дифферен-
циальными уравнениями, например приведенные только что уравне-
ния (1), (2) и (3).
Наоборот, уравнения, содержащие несколько независимых пе-
ременных, их функции и частные производные по различным неза-
висимым переменным, называются уравнениями с частными произ-
водными.
Таковы, например, уравнения
dz dz Л
х -----У з~ = 0 (4)
ду dx v 7
d2z d2z
dx2 dy2
Наивысший порядок производной, входящей в уравнение, при-
нимается за порядок самого уравнения. Из вышеприведенных урав-
нений уравнения (1), (2) и (4)—1-го порядка, (3) и (5) — 2-го
порядка.
Интегрировать дифференциальное уравнение значит определить
неизвестные функции так, чтобы они вместе с их производными
обращали дифференциальное уравнение в тождество.
Найденные таким образом выражения функций называются
решениями дифференциального уравнения.
Так, нетрудно убедиться, что решениями уравнения (1) будут
У = ]/~2рх, у = ]/2р(х—1)
426 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIH
и, вообще,
у = У2р(х — С),
где С—любая постоянная.
Действительно, из последнего находим
(1')
Подставляя
к тождеству.
Точно так
у' =______1P----= P .
z 2 V2p(x —C) V2p (x — C)
теперь выражения у и у' в уравнение (1), приходим
же убедимся, что решениями уравнения
kt* kt* л
S==-2-’ S = — -4
(2)
будут
и, вообще,
(2')
2
постоянная.
где С—любая
Уравнение (3) имеет такие решения:
s = cos at, s = smat, где а = 1/ —
У тп
и, вообще,
s = cos at -J- С2 sin at,
где Сг и С2— произвольные постоянные.
Действительно, из последнего уравнения находим
ds
= — Cta sin at-\- C2a cos at
d*s
(3')
Сга2 cos at— С2а2 sin at,
откуда и видно, что
(с* cos at -j- С9 sin at) = — a2s = — — s,
a/2 41 1 2 7 m 9
т. е. что уравнение (3) обращается в тождество.
Для уравнения (4) и (5) также можно указать решения. Так,
будут удовлетворять уравнению (4).
Действительно, взяв, например, выражение z = х2-]-у2, находим
о dz о
2х, -V— = 2 у
’ ду
дх
§ 164] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-ГО ПОРЯДКА 427
и, подставляя в уравнение (4), приходим к тождеству
2ху — 2ху = 0.
Решениями уравнения (5) будут, например,
z = x~\-y, г = х-у и др.,
что также нетрудно проверить.
В дальнейшем мы совершенно не будем касаться уравнений
с частными производными, а из уравнений обыкновенных рассмотрим
только некоторые типы.
§ 164. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-го ПОРЯДКА
Дифференциальное уравнение 1-го порядка в общем виде можно
представить так:
/(.X, у, у') = 0. (А)
Чтобы уяснить себе характер решений такого уравнения, покажем,
что подобное уравнение может быть аналитически получено из
некоторого конечного уравнения. Пусть
F(x, у, С) = 0 (В)
уравнение между независимой переменной х и ее неявной функцией у,
содержащее, кроме того, некоторую произвольную постоянную
величину С. Это уравнение будем называть конечным уравнением.
Дифференцируя уравнение (В), получим (см. § 155)
Это уравнение, кроме прежних величин, содержит еще новую у',
а потому уравнение (1) можно сокращенно записать так:
Ф (х, л у', Q = 0. (2)
Исключив теперь из уравнений (В) и (2) произвольную постоянную С,
Для чего достаточно решить одно из них относительно С и найден-
ное значение подставить в другое, мы получим некоторое уравнение
вида
/М.УМ, (А)
т- е. обыкновенное дифференциальное уравнение 1-го порядка.
Таким путем, следовательно, мы от конечного уравнения (В)
приходим к дифференциальному уравнению (А). Между этими
Уравнениями, однако, имеется более глубокая связь, чем та, которая
внешне намечается в процессе получения уравнения (А) из (В).
Действительно, из уравнения (В) мы получили сначала урав-
нение (2), принимая в соображение, что у есть та именно функция
428 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
от х, которая определяется уравнением (В). Следовательно, у, удо-
влетворяющая уравнению (В), удовлетворит и уравнению (2). Но
уравнение (А) есть следствие двух уравнений (В) и (2); поэтому
то же значение у удовлетворит и уравнению (А).
Таким образом, конечное уравнение (В) определяет функцию у так,
что ее выражение удовлетворяет дифференциальному уравнению (А),
т. е. служит решением этого дифференциального уравнения.
Уравнение (В) носит название общего интеграла дифференциаль-
ного уравнения (А).
Итак, общим интегралом дифференциального уравнения (Д)
называется такое конечное уравнение (5), содержащее произ-
вольную постоянную^ из которого путем дифференцирования и
исключения произвольной постоянной получается данное диффе-
ренциальное уравнение.
Вместе с тем, как только что выяснено, общий интеграл служит
решением соответствующего дифференциального уравнения. Задавая
произвольной постоянной С различные значения, мы из общего
интеграла, т. е. из общего решения, получим так называемые част-
ные решения дифференциального уравнения.
Поясним сказанное примером. Возьмем конечное уравнение, содер-
жащее произвольную постоянную С
у = С sin х.
Дифференцируя его, получим
У — Ccosx.
В результате исключения С имеем дифференциальное уравнение
y'=yctgx.
По отношению к последнему уравнению конечное уравнение у = С sin х
есть его общий интеграл.
Взятое нами раньше дифференциальное уравнение (1) (стр. 424),
имеет общим интегралом уравнение
у = У2р(х-С), (1')
в чем предлагаем убедиться читателю. __________
Другие решения его, как j/ = |^2px, у = V 2р (х— 1), все за-
ключаются в общем интеграле и вытекают из него при различных
значениях С. Это будут частные решения уравнения.
Точно так же данное выше для уравнения (2) решение (см.
стр. 426)
является общим интегралом уравнения (2), а приведенные там же
другие решения — частными решениями того же уравнения.
§ 165] ГЕОМЕТРИИ. ЗНАЧЕНИЕ ДИФФЕРЕН. УРАВНЕНИЯ 1-ГО ПОРЯДКА 429
По самому своему происхождению общий интеграл обыкновен-
ного дифференциального уравнения 1-го порядка необходимо должен
заключать в себе произвольную постоянную. Эта произвольная
постоянная, сообщающая некоторую общность решению дифферен-
циального уравнения, соответствует общности вопроса, приводящего
к интегрирование дифференциального уравнения.
Задавая произвольную величину С, мы из общего интеграла
получим всевозможные частные решения. Часто, однако, в задачах,
приводящих к интегрированию дифференциальных уравнений, наперед
задаются некоторые условия, определяющие эту постоянную. Напри-
мер, в задаче может заключаться условие — найти не общее выражение
искомой функции у, а то именно, которое при х = а обращалось
бы в величину Ь.
Тогда, следовательно, должно выполняться равенство
F(a, bt С) = 0;
оно и определяет произвольную постоянную С общего интеграла,
соответственно поставленному условию.
Так, например, если к задаче (1) добавить условие: из всех
линий выбрать ту, которая пройдет через начало координат, то
тем самым будет поставлено условие, что при х = 0 должно быть
у = 0.
Вводя это условие в общее решение
у = У2р(х — С),
находим С = 0; поэтому ответом на так поставленную задачу будет
уравнение
у = ]/ 2рх или у2 = 2рх.
§ 165. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ 1-го ПОРЯДКА И ЕГО ОБЩЕГО ИНТЕГРАЛА
Положим, что нам дано дифференциальное уравнение
f(x, у,у') = О (А)
И его общий интеграл
F (х, у, С) = 0. (В)
С геометрической точки зрения последнее уравнение предста-
вляет собою некоторую линию. Ввиду присутствия в нем произ-
вольной постоянной С, которой мы можем давать произвольные
значения, уравнение это представит собой не одну линию, а целую
совокупность линий одного и того же типа или, как говорят,
семейство линий. Само же дифференциальное уравнение, вследствие
присутствия в нем производной, определяющей, как известно, на-
правление касательной, отмечает некоторое определенное свойство
Касательной, принадлежащее семейству кривых (В).
430 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ХХУ1Ц
Кривые эти называются интегральными кривыми.
Рассмотрим отдельные примеры дифференциальных уравнений
и их общих интегралов с геометрической точки зрения.
Пример 1. Уравнение
у = ах Ц- С
является общим интегралом дифференциального уравнения
У = а.
Общий интеграл геометрически выражает семейство прямых
(рис. 191), параллельных между собой, но имеющих различные
Рис. 191.
начальные ординаты С. Диффе-
ренциальное же уравнение отме-
чает основное свойство всех этих
линий во всех их точках в отно-
шении касательных к ним, под-
черкивая, что касательные к этим
линиям (в данном случае они
совпадают с самими прямыми)
имеют один и тот же угловой
коэффициент а.
Пример 2. Нетрудно показать,
что из уравнения у = Сх исклю-
чением постоянной величины С получается дифференциальное урав-
нение у1 = — . Действительно, исключая С из уравнений
у = Сх и у' = С,
находим
у—у'х или У'~~-
Итак, дифференциальное
уравнение
имеет своим общим инте-
гралом уравнение
у = Сх.
Рис. 192.
Последнее представляет семейство прямых (рис. 192), проходящих
через начало координат под различными углами к оси ОХ.
Дифференциальное же уравнение отмечает их свойство, состоя-
щее в том, что угловой коэффициент касательных к ним (в данном
§ 165] ГЕОМЕТРИЧ. ЗНАЧЕНИЕ ДИФФЕРЕН. УРАВНЕНИЯ 1-ГО ПОРЯДКА 431
любой
семей -
в том,
кривых,
случае опять самих прямых) всегда равен отношению ординаты
к абсциссе соответствующих точек.
Пример 3. Уравнение х2—у2=С2 является общим интегралом
уравнения у = у. (Предлагаем убедиться в этом самим читателям).
Уравнение х2—j/2 = C2 представляет собой семейство равно-
бочных гипербол с различными вещественными полуосями (рис. 193).
Дифференциальное же
уравнение отмечает
свойство касательных
в любой точке
из линий этого
ства, состоящее
что tg а = у .
Таким образом, в
точках различных ин-
тегральных
для которых отноше-
ние абсциссы к соот-
ветствующей ординате
сохраняет одну и ту
же величину, т. е. в
точках кривых, распо-
ложенных на одной и той же прямой, проходящей через начало коор-
динат, касательные будут параллельны между собой: 7\ [] Т2|| Т3;
Пример 4. Уравнение у = Сех является общим интегралом диф-
ференциального уравнения у' =у. (Предлагаем убедиться в этом
самим читателям.) Общий
интеграл у — Сех пред-
ставляет собой семейство
кривых (рис. 194) того
типа, который был изо-
бражен уже на рис. 34
(стр. 62).
Дифференциальное же
уравнение выражает свой-
ство касательных во всех
точках каждой такой кри-
вой, состоящее в том, что
во всех точках угловой
коэффициент касательной равен ординате точки касания. Так что, на-
пример, во всех точках различных интегральных кривых, расположен-
ных на прямых, параллельных оси ОХ, касательные параллельны
между собой: ^|]7^||7^; *111Я9||Я8.
432 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
§ 166. РАЗЛИЧНЫЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1-го ПОРЯДКА
Общий вид дифференциального уравнения 1-го порядка, как мы
видели, следующий:
f(x,y,y') = O. (I)
Оно может иногда быть решено относительно у' и представлено
так:
у' = Ф(х,у). (И)
Сама функция Ф (х,у) может быть всегда изображена в виде
частного от деления двух функций от х и у, например, так:
ф (х, у) = —
и потому уравнение (II) можно написать еще следующим образом:
dy Р
dx Q
или
Pdx^Qdy = O, (III)
где Р и Q некоторые функции от х и у.
§ 167. УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ
Рассматривая уравнение в форме (III), полезно прежде всего
задать себе такой вопрос: не будет ли выражение
Р dx Q dy
полным дифференциалом некоторой функции U двух переменных х
и у. Если да, т. е. если
Р dx-\-Qdy = dU,
то тогда предложенное уравнение (III) будет равносильно уравне-
нию dt7=0, и его общим интегралом будет
и=с.
где С—произвольная постоянная.
Таким образом, в этом случае интегрирование дифференциаль-
ного уравнения сводится к нахождению той функции U, полный
дифференциал которой равен левой части дифференциального урав-
нения (III). Задача эта была уже разобрана в § 156.
§ 167]
УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ
433
Пример. Проинтегрировать дифференциальное уравнение
х2уг —у- — (yf — 1) (2ху — 1) = о.
Приведем это уравнение к форме (III); для этого преобразуем его сна-
чала таким образом, чтобы собрать члены, содержащие у',
х2уг — (2ху — 1) уг — у2 + 2ху — 1=0,
У (х2— 2ху + 1)— у2 + 2ху— 1 = 0,
g (хЗ - 2ху + 1) -У + 2ху - 1 = 0,
после чего уравнение приводится к форме (III)
(2ху —у2 — 1) dx + (х2 — 2ху + 1) dy = 0.
Здесь Р = 2ху—у2—1 и Q = х2— 2ху + 1.
дР dQ
Составим частные производные и
^ = 2х — 2у, -— = 2х — 2у.
ду дх
лд др dQ
Мы видим, что , следовательно, левая часть уравнения является
полным дифференциалом некоторой функции. Обозначим се через U и найдем
по правилам, изложенным в § 156:
^- = 2ху — ^2 — 1,
U = J* (2ху —у2— 1) dx = х2у—у2х — х + <р (у),
|у = х2 —2xj> + <f' (>)
должна равняться трехчлену Q, стоящему множителем при dyt т. е.
х2 — 2ху + ср' (j/) = х2 — 2ху + 1.
Отсюда (j) = 1 или ф (.у) =_у + С.
Поэтому искомая функция U такова:
U = х2у —у2х — х +_у + С.
Таким образом, левая часть предложенного уравнения представляет
полный дифференциал найденной функции, поэтому дифференциальное урав-
нение может быть представлено так:
d (х2_у —у2х — х +_у + С) = 0,
откуда
х2у —У* — х + j/ + С = Сх
или, соединяя две произвольные постоянные в одну, приходим окончательно
к общему интегралу данного дифференциального уравнения
х2_у—у2х — х-\~у = С или ху(х—v) — х-\-у — С^
т. е.
(х — у) (ху - 1) = С.
28 Зак. 2116. Н. С. Михельсон.
434 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [xXVlli
§ 168. УРАВНЕНИЯ С ОТДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Как второй случай, когда легко находится общий интеграл диф-
ференциального уравнения, рассмотрим тот, в котором, как принято
говорить, переменные отделяются. Положим, что в уравнении
Р dx + Q dy = О (III)
как Р, так и Q суть произведения функций одного переменного х
на функцию одного у, т. е.
Р =fi (*) • ®i (A Q=fi (*) • ®2 (А
Данное уравнение напишется тогда так:
/10) •<p2(^)rfy = 0. (1)
Разделив уравнение (1) на ср* (j/) -/2(х), получим
dy = 0. (2)
1 ?1СУ) v 7
Так как переменная х здесь заключена в одном только члене,
именно, при dx, а переменная у в другом при dy, то и говорят,
что в уравнении (2) переменные отделены. Очевидно, левая часть
уравнения (2) есть дифференциал суммы двух функций, одной зави-
сящей только от х, другой только от у. Поэтому общий интеграл
уравнения (III) будет следующий:
J fi (X) ~ J <?1 (y) z '
Так как при отделении переменных нам пришлось делить на про-
изведение
<Р1 Су)
то мы могли при этом потерять некоторые решения, заключающиеся
в уравнении
(у) -/aW = o.
Их надо иметь в виду для полного решения вопроса.
Пример 1. Проинтегрировать уравнение
у d х — xdy = 0.
Деля на ху, получаем
X у ~ ’
откуда
In х — In у = In С, т. е. у = С, х = Су,
или, что то же,
у = CiX, где Ci = .
§ 168] УРАВНЕНИЯ С ОТДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ 435
Так как мы делили данное уравнение на произведение ху, то могли
потерять решения
у = 0 и х = 0.
Но, как видно из общего интеграла
х = Су или у = С^х,
решения эти в данном случае заключаются в общем интеграле при
С = 0 и б?! = 0.
Пример 2. Уравнение ууг = р, приведенное на стр. 424, может быть
проинтегрировано следующим образом:
dy
у • = р>
dx г
у dy = р dx (переменные отделены)
^2=рх + Сь
или
у = 2рх + 2С, = 2р (х .
С
Положив для простоты = С, находим общий интеграл уравнения в таком
виде:
_У2 = 2р(х-С).
Кривая, определяемая этим уравнением, есть парабола, ось ее совпадает
с осью ОХ и вершина ее лежит в точке, координаты которой (С, 0). Таким
образом, условию задачи I (см. стр. 424) отвечает целое семейство указанных
парабол с вершинами в произвольной точке оси ОХ.
Пример 3. Найти все кривые, у которых подкасательная в любой ее
точке равна удвоенной абсциссе точки касания. Как известно, выражение
подкасательной таково:
У
Уг'
Поэтому уравнение, отвечающее условию задачи, будет
Выражая производную yf через дифференциалы, получаем уравнение
у dx = 2х dy.
Для отделения переменной делим члены уравнения на ху:
dx 2dy
Интегрируя, находим общий интеграл
ln* + ln 2С = 21пу,
т. е.
In 2Сх = In у2
или
У = 2Сх
обыкновенная парабола с параметром С и с вершиной в начале координат.
28*
436 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [xXVilt
Пример 4. Скорость реакции, т. е. количество вещества, вступающего
в реакцию в единицу времени, пропорционально произведению масс не всту-
пивших еще в реакцию веществ. Определить закон течения реакции, т. е.
зависимость между количеством вещества, вступившего в реакцию, и вре-
менем, истекшим от ее начала, предполагая, что массы двух взаимодей-
ствующих веществ равны.
Пусть А — масса каждого из взаимодействующих веществ, и положим,
что по истечении времени t вступило в реакцию по х грамм-молекул каж-
дого вещества, тогда остаток массы каждого вещества равен А — х. Произве-
дение этих оставшихся масс обратится в
(Л —х)2
и, следовательно,
dx
d-^k(A-x)2,
где скорость течения реакции, a k коэффициент пропорциональности.
В уравнении этом переменные отделяются
dx
Тл = k dt.
(Л — х)2
(4)
Интегрируя, имеем
но
г. rfX--2 = fit + С,
(А — х)2 1
I dx __ 1
J (Л — х)2 ~А — х^
поэтому получаем общий интеграл уравнения в таком виде:
-^—=kt + C.
А — х 1
Условия задачи дают возможность определить и постоянную С.
так как отсчет времени ведется от начала реакции, то при /=0
быть и х = 0.
Принимая это во внимание, находим из уравнения (5)
_1 — с
А
Таким образом, уравнение (5) напишется в виде:
—2_ = й/4- 1
Л — х 1 Л ’
(5)
Именно
должно
или
1
А — х
1
А
kt.
т. е.
А (А — х)
Это и есть известное в химии уравнение, выражающее закон
реакции взаимодействия двух веществ равных масс.
Нетрудно вычертить кривую, определяемую этим уравнением.
(6)
течения
Прежде
всего замечаем, если / = б, тЬ и х = 0; следовательно, кривая проходит
через начало координат.
§ 168]
УРАВНЕНИЯ С ОТДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
437
Затем представив уравнение так:
x = Akt(A — х), (7)
преобразуем его, перенеся начало координат в некоторую точку Оу с коор-
динатами а и 0 (пока еще неопределенными). По формулам преобразования
имеем
/ = а 4
X 5= 0 + Х1.
Подставляя эти значения в уравнение (7), находим
₽+х1 = ЛЛ(а + ^) (Л-p-Xi).
Раскрыв скобки и собрав отдельные члены вместе, получим
Л£*й + (1 + ЛЬ) + Aktx (0 — Л) = ЛЬ (Л — ₽) — ₽.
Подберем неопределенные еще чирла а и 0 так, чтобы
0 —Л = 0
14-ЛЬ = 0.
Из первого находим 0 = Л, из второго а = —При таких значениях а
и 0 уравнение течения реакции принимает вид
ЛЬ1^ = — Л
или
Известно, что это уравнение есть гипербола, отнесенная к асимптотам
и расположенная притом во втором и четвертом координатных углах новых
осей координат.
Таким образом, выяснилось, что закон течения реакции выражается
гиперболой, проходящей через начало координат и асимптоты которой парал-
лельны осям координат. При t = 0 количество вступившего в реакцию веще®
ства х = 0, а с беспредельным увеличением времени это количество прибли-
жается асимптотически к величине Л.
Пример 5. По закону Ньютона скорость охлаждения тела в воздухе
пропорциональна разности температур тела и воздуха. Полагая, что темпе-
ратура воздуха 60, а начальная температура тела 6h определить, через сколько
времени тело охладится до температуры 02.
Выберем некоторый произвольный момент t процесса охлаждения,
в который температура тела равна 6. Скорость охлаждения в этот момент
л „
есть производная от температуры 0 по времени tt т. е. равна . По закону
Ньютона эта скорость пропорциональна разности 6 — 0о (предполагается, что
температура воздуха сохраняется неизменной). На основании этого получаем
дифференциальное уравнение
1'Де k коэффициент пропорциональности, зависящий от природы тела.
Для получения непосредственной зависимости температуры охлаждаю-
щегося тела от времени необходимо интегрировать составленное уравнение.
В этом уравнении переменные отделяются:
438 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
Интегрируя, находим
Отсюда
In (6 — 0о) — kt —|- In С.
6 — 0о = Св^.
Для определения постоянной интегрирования мы имеем дополнительное
условие, а именно, что начальная температура тела была равна 6t. Таким
образом, при t = 0 0 = Поэтому
— % — С.
Подставляя найденное значение С в предыдущее уравнение, приходим
окончательно к следующей зависимости температуры охлаждающегося тела
от времени:
6 — Oq = (0х — Oq) ekt,
откуда
ео . 1 6 — 60
kt = In й----£ или t = -г In х-------£ .
По этой формуле находим, что до температуры 02 тело охладится через
промежуток времени равный
1|п 62~е°
k |П е1_б0
Пример 6. Определить, какую форму следует придать вертикальному
брусу с круговыми поперечными сечениями, чтобы во всех его горизон-
тальных сечениях напряжения сохраняли постоянную величину. (Напряжс-
Рассмотрим площади двух
нием называется сила, рассчитанная на еди-
ницу площади.)
Примером такого стержня может слу-
жить бык моста. Обозначим верхнюю пло-
щадь GH стержня через давление на
нее через Q. Тогда напряжение, испыты-
ваемое этой площадью, будет
По условию задачи то же напряже-
ние должно сохраняться во всех горизон-
тальных сечениях стержня. Так как в дру-
гих сечениях к нагрузке Q прибавляется
еще вес кладки, над ним находящейся, то
для сохранения постоянства величины на-
пряжения во всех сечениях стержень
должен расширяться книзу и поэтому иметь
форму, примерно изображенную на рис. 195.
смежных сечений АВ и CD: F и F + ДЛ
Приращение Д/7, как только что замечено, приходится придавать площади F,
чтобы воспринять добавочное увеличение веса кладки, заключенной между
сечениями АВ и CD.
Принимая этот элементарный слой за цилиндр с основанием F и высо-
тою Дх, найдем, что вес его выразится произведением
D-F-Ьх,
где D плотность кладки. Этот вес и должен быть воспринят площадью Д/7
для сохранения постоянного напряжения а.
§ 168]
УРАВНЕНИЯ С ОТДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
439
Таким образом, мы получаем следующее уравнение
Наше рассуждение основывалось на том предположении, что слой ABCD
является цилиндром. Чем тоньше будет слой, тем точнее последнее равен-
ство будет выражать действительную сущность вопроса. Поэтому, переходя
к пределу, получим следующее дифференциальное уравнение для определения
площадей поперечных сечений
dF^_Р • F
dx а
В этом уравнении переменные отделяются
Отсюда
D
Г) F О ~х
In F= — х-4~ hi С, 1п —= — х и F = Cea ,
а ’ С а
Принимая во внимание начальное условие, а именно, что напряжение на
верхней площади, т. е. при х = 0, должно быть также равно а, находим
значение постоянной С\
F^C,
Итак
в
— X
F=Foe° .
Примем ЕВ=^у, тогда F = kj/?, и, подставляя в предыдущее уравнение, най-
дем, что
Гр-
у^Д/^.е29 .
Г те
В координатной системе XOY с началом в центре верхней площади стержня
и с осью ОХ, направленной по его оси симметрии, последнее уравнение
является уравнением кривой LH вертикального осевого сечения. Боковая
поверхность стержня оказывается поверхностью вращения этой кривой
вокруг оси ОХ, Кривая эта относится к типу кривых
у == аеЪх,
частный случай которых рассмотрен в § 24 (рис. 34).
Пример 7. Определить, какую форму принимает гибкая нерастяжимая
нить, концы которой неподвижно закреплены в двух точках, и которая
свешивается под действием нагрузки, пропорциональной длине горизонталь-
ной проекции отдельной части нити»
440 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
Подобная задача ставится при определении формы, которую принимает
цепь висячего моста, поэтому дальнейшие рассуждения будем вести как бы
для этой последней задачи.
Примем плоскость цепи за плоскость координат XOY. Ось ОХ распо-
ложим в плоскости моста, а ось OY проведем через самую низкую точку
цепи.
Согласно поставленной
Рассмотрим часть АВ цепи
задаче требуется найти уравнение кривой KL.
KL (рис. 197). Она находится в равновесии под
действием трех сил: гори-
зонтального натяжения цепи
И в точке Л, натяжения Г,
направленного по касатель-
ной к кривой в точке В и,
наконец, нагрузки, пропор-
циональной проекции дуги
АВ, т. е. отрезка ОС, (Весом
самой цепи мы пренебре-
гаем ввиду предполагаемой
малости его сравнительно
с нагрузкой.)
Обозначим угол, соста-
вленный касательной ВТ с
осью ОХ, через а и поло-
жим ОС = х.
Согласно условию равновесия отрезка АВ цепи вертикальные и гори-
зонтальные составляющие указанных сил в отдельности должны быть равны:
Вертикальные составляющие
Горизонтальные составляющие
Поэтому имеем:
Силы Н Силы Т Нагрузки
0 Т sin а kx
Н Г cos а 0
Гsin а = kx
Т cos а == Н,
откуда делением находим
tga =
kx
~Н'
Но tga=_/, поэтому мы приходим к следующему дифференциальному ура-
внению искомой кривой:
, kx
Остается проинтегрировать это уравнение, чтобы определить форму кривой.
dy = - х dx
k I k
Xd* + C^~x* + C.
Для определения С примем во внимание, что при х = 0 у = О А = h, так
что
h = С.
§ 169]
ЛИНЕЙНЫЕ УРАВНЕНИЯ
441
Итак, окончательно уравнение кривой будет
ь
y = ^+h.
Кривая оказывается параболой, смещенной вдоль оси ОК на расстояние h.
§ 169. ЛИНЕЙНЫЕ УРАВНЕНИЯ
Дифференциальное уравнение
f{x, у, У) = 0 (I)
называется линейным, если функция f линейная относительно у и у'.
Общий вид линейного дифференциального уравнения поэтому будет
следующий:
Л/ + Оу+Я = о, (1)
где Р, Q, R не содержат ни у ни у', а являются функциями одной
переменной х.
Разделив уравнение (1) на Р(РфО), получим
У + ^ + ^ = о.
Обозначив для сокращения
|=/(х) и J = -F(x),
мы приводим линейное уравнение к виду
X+X(x) = F(x). (2)
Такое уравнение будем называть приготовленным для решения, к
Для интегрирования линейного уравнения введем вместо искомой
функции у две другие: и и V, полагая
у = и • V. (3)
Заметим, что так как функция у должна удовлетворять одному
условию, а именно данному уравнению, а функций мы ввели две,
то одной из них мы можем располагать по произволу.
Дифференцируя равенство (3), получим
dy du . dv
dx ® dx' U dx'
n dy
а подставляя значения у и ее производной в данное уравне-
ние (2), имеем
или
(4)
442 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
Так как одной из функций и или v мы, как сказано, можем
располагать по произволу, то подберем и так, чтобы оно удовле-
творяло уравнению
g-]-«./(x) = 0. (5)
Тогда уравнение (4) обратится в
(6)
Из уравнения (5) нетрудно найти и методом отделения перемен-
ных
In и -р J* f(x)dx — Л,
где А — произвольная постоянная. Так как нам надо найти одно
какое-нибудь значение //, удовлетворяющее уравнению (5), то выби-
раем то, при котором Л = 0, как наипростейшее, т. е.
In и = — J / (x)dx
или
И = = (7)
(Функция ср(х) введена для сокращения письма.)
Найдя и, мы можем подставить ее значение в уравнение (6), из
которого отделением переменных найдем ф. Именно,
? (•*)•£= е(х), т. е. dv=^$dx,
£wrfx+c==“(x)+c’
где ш (х) сокращенно выражает результат интегрирования.
Выражение искомой функции у будет
у — и • v — ср (х) [о(х) С].
Таким образом, линейное уравнение интегрируется до конца.
Окончательное конечное выражение у через х зависит только от
получения в конечном виде значений интервалов, которые встре-
чаются при интегрировании уравнения.
Пример 8. у —_^ = (x4-l)s.
Интегрируя это уравнение вышеуказанным приемом, мы для нахожде-
ния и и v приходим к следующим уравнениям:
rfu 2zz _ dv . ,
A------Г-т=^ ==(x-H)3.
dx x +1 dx 4 * 7
§ 170] ' ОДНОРОДНЫЕ УРАВНЕНИЯ 443
Из первого
1п« = 21п(х+1), м = (х4-1)«
и Л» 1
Подставляя найденное и во второе, имеем:
(х+1)2,й=(х+1)3>
Итак
j = «v=|(x + l)4 + C(x + ir.’
§ 170. ОДНОРОДНЫЕ УРАВНЕНИЯ
Однородными уравнениями называются уравнения, из которых
производная у' может быть выражена в виде функции от отноше-
у
ния —.
х
Всякое однородное дифференциальное уравнение 1-го порядка
можно, следовательно, представить в виде
у=/(й-
Для интегрирования такого уравнения вводят вместо у другую
функцию г, полагая
у
= т. е. у = х • z:
х 9 9
отсюда
Л-U
dx dx »
Подставляя в данное уравнение вместо у и уг их выражения через
z и г', получим
В этом уравнении переменные отделяются; действительно, пре-
образуя, имеем:
xTx=f^~~Z' xdz = [f{z) — z}dx,
и, наконец, dz dx f(z) — z x ’
откуда //(г) — z —lnx InC— ln(c)«
444 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
или, полагая
dz
имеем
1п® = /7(г)
/ x = CeF(z\
Остается в этом результате положить снова г = ^-, тогда и полу-
чим общий интеграл уравнения
Пример 9. Проинтегрировать уравнение
xdy—ydx= У
Легко убедиться, что это уравнение относится к классу однородных
уравнений. В самом деле, разделив все члены уравнения на dx и решив его
« dу
относительно производной , находим
х£-.~ У— Ух2+У2>
или
dx х ’
и окончательно _______
Н+ЛЙ#
rr У
Последнее уравнение показывает, что является функцией отношения
v
~ и, следовательно, предложенное уравнение относится к классу одно-
родных. ♦
После подстановки у = xz, получим
*.g + 2 = 2+
или, сокращая и отделяя переменные,
dz dx
Интегрируя (см. стр. 310), находим общий интеграл
1п(2+ /1 -|-z’) — In х + 1иС
или
z + / Г+г'з = Сх
и окончательно
/ х2+У=Сх2— у.
§ 171] некоторые типы дифферен. уравнений 2-го порядка 445
§ 171. НЕКОТОРЫЕ ТИПЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2-го ПОРЯДКА
Рассмотрим теперь некоторые типы дифференциальных урав-
нений 2-го порядка, интегрирование которых так же, как и рас-
смотренных до сих пор уравнений 1-го порядка, приводится к ква-
дратурам, т. е. к интегрированию функций.
Первый тип. у”
Интегрирование таких уравнений крайне просто: от производ-
ной второго порядка простым интегрированием переходим к про-
изводной 1-го порядка
у = J f(x)dx-j-C},
а затем и к самой функции
у = + J C^dx-YC^.
Выполнив интегрирование, получим
У = «) (х) CjX + С2.
Пример 10. Тело брошено вверх с начальной скоростью ?;0. Определить
для каждого момента времени величину пройденного телом путиь считая
от его положения в начальный момент и предполагая, что оно движется
только под влиянием силы тяжести.
Известно, что под влиянием силы тяжести тело движется с постоянным
ускорением, в данном случае равным — g. С другой стороны, ускорение
выражается производной второго порядка от пути по времени. Поэтому
дифференциальное уравнение движения в данном случае будет
dP ~ ё'
Интегрируя его, получим
й=-^+с‘2
s = - J (^+С1)Л = -^2 + С^+С2.
Постоянные (\ и С2 определяются из имеющихся в данной задаче условий.
1-е условие, состоящее в том, что отсчет пути ведется от начального
момента, определяет С2. Действительно, по этому условию, при Z = 0,
s должно быть также равно нулю, откуда следует, что С2 = 0.
2-е условие, заключающееся в том, что начальная скорость равна
определяет Ср Действительно, условие это требует, чтобы при £=0
ds ~
^ = ^0- Принимая это в расчет, мы из уравнения
получаем
С1 = Го.
Итак, зависимость пройденного телом пути s от времени t в данном
случае окончательно представляется формулой
s = —+
446 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIIl
Второй тип. у" = f (у).
Интегрирование этого типа уравнений ведется следующим об-
разом. Умножим обе части уравнения на 2у'dxi
2у' • у" dx -2f(y)- у' dx.
Левая часть последнего уравнения есть дифференциал от у'2. Пра-
вую же часть можно представить так:
2/ (у) у' dx = 2/ (у) dy.
Таким образом, предложенное уравнение принимает вид
d(y'*) = 2f(y)dx,
откуда выводим, что
/2=2//^)^ + ^
или
у = ± 2 f/Wdy + C^yty, CJ.
В этом последнем уравнении переменные отделяются. Действи-
тельно, его можно переписать так:
Тх = ?(У’ с>)
и затем
откуда и получается общий интеграл
I -Д^Т = Х + С2-
J f (у, с1) — 2
Пример 11. Рассмотрим прямолинейное движение материальной точки
под действием отталкивающей силы, обратно пропорциональной третьей сте-
пени расстояния точки от некоторого не-
М - подвижного центра.
। । д Пусть движение происходит по прямой
О ОД (рис. 198). Точка О — отталкивающий
центр, М—положение материальной точки
Рис. 198. в некоторый момент времени t; ее рас-
стояние ОМ от неподвижного центра обо-
значим через s, а массу точки через т.
Дифференциальное уравнение движения точки будет следующее:
d2s __ k
где k коэффициент пропорциональности.
Составленное уравнение можно переписать так:
,, 9 1 ,, d2s 9 k
s" = а2»-п-, где s" = —и а2 = —.
s3 ’ dt2 т
И, наконец, У* s2 — = ±
§ 171] НЕКОТОРЫЕ ТИПЫ ДИФФЕРЕН. УРАВНЕНИЙ 2-ГО ПОРЯДКА 447
Уравнение это только что рассмотренного типа. Применяя указанный
метод, получим
2s's"dt = , d (s'2) = 2а2 • ^ = а2 • rf f-Ц.
_ „/ 1 , 1 \ a2 s2—Cl
Отсюда S'2 = a2 f - - + -J = _. ——,
, а У s2-C{ ds a V s*—Cx
s _ ’ s ’ dt /С? s
s ds_______ a f s ds _ f a
/ s2—Cl ~ ~ Yci ’ J V s^-Cy ~ “ /Ci
(I /?2
^=a+c2),
Q Ci
Пример 12. Материальной точке, масса которой т и которая в началь-
ный момент находилась на расстоянии а от центра Земли, сообщена на-
чальная скорость v0 в направлении к центру Земли. Чему будет равна ско-
рость этой материальной точки в момент, когда под влиянием силы тяжести
точка пройдет расстояние s (движение предполагается в безвоздушном про-
странстве).
Для составления уравнения, соответствующего условию задачи, необ-
ходимо иметь в виду, что ускорение силы тяжести обратно пропорционально
квадрату расстояния точки от центра Земли. Таким образом, если в началь-
ный момент это расстояние было равно а и за некоторый промежуток вре-
мени t точка прошла путь $, то
g а2
go (a — s)*’
откуда
а2
g~So' (a — s)*'
d2s
Но g = ; таким образом, мы приходим к дифференциальному уравнению
d2s а2 а2
dt2 6U (a — s)2 ’ 60 {a — sy
только что рассмотренного типа.
Умножая обе части уравнения на 2s' dtt получим
д2
2s's" dt = 2gQ • т-гт} • s' dt,
(a — s)2
или
д2
d(s^ = 2g..^—^.ds.
Отсюда находим
J (Д+с=!»-'^+«
И так как
448 введение в интегрирование дифференциальных уравнений [XXVIII
то, следовательно,
®2 = 2№~_ + С.
Для определения постоянной интегрирования вспомним, что по условию за-
дачи в начальный момент, т. е. при t = 0, скорость была равна а 5 = 0.
Таким образом
= 2g-0«2 • + С.
Определяя из последнего уравнения С и подставляя в предыдущее, или,
проще, вычитая последнее уравнение из предыдущего, найдем
Уравнение это и определяет искомую скорость
v=j/’^+v(a4-s-|)-
Третий тип. у" = f (у').
Уравнения этого типа подстановкой yr = z приводятся к диф-
ференциальному уравнению 1-го порядка с отделяющимися пере-
менными. Действительно, тогда у" — zr = , поэтому приходим
к уравнению
откуда
dz . f dz . ~
f(z) —dxw J /(z) —x+Ci.
Найдя и положив I = ср (г), получаем
J T{z) j j iz)
Если последнее решим относительно г, то получим
2 = <o(x + Cj) или = С\).
Отсюда интегрированием находим окончательно общий интеграл
У — J* <*> (•** Q dx 4- С2.
Пример 13. у'=у2.
, dz
Полагаем У = 2, тогда у7 ±= У = -^, а поэтому имеем
* — = ^2
dx
§ 1711 НЕКОТОРЫЕ ТИПЫ ДИФФЕРЕНЦ. УРАВНЕНИЙ 2-ГО ПОРЯДКА
449
Отделяя переменные, получим
Интегрируя, найдем
1
----= х 4- Ci, или z
z * 1
dz
-7 = dx.
Z2
1
1 dy
--------------------------------------- т е —
f- С1 ’ • dx
Интегрируя последнее уравнение, приходим к общему интегралу
у = -1п (x + G) + C2.
Пример 14. Определить, какую форму под действием своей тяжести
принимает однородная гибкая нерастяжимая нить, подвешенная за два ее
конца.
Задача состоит в нахождении уравнения кривой (рис. 199).
л " располагается нить, примем за коор-
[. АВ. Согласно условию равно-
Вертикальную плоскость, в которой
динатную плоскость, причем ось OY
проведем вертикально через самую
низкую точку А кривой, а начало
координат выберем в некотором,
пока еще определенно не намечен-
ном, расстоянии ОА от этой точки.
Так же как и в примере 7 (см. стр. 439),
рассмотрим часть кривой АВ и силы,
под действием которых она нахо-
дится в равновесии. Такими силами
будут: горизонтальное натяжение Н
в точке А, натяжение Г, направлен-
ное по касательной в точке В, и вес
части нити АВ, который пропорциона-
лен длине нити АВ и равен ps, где р
вес единицы длины нити, а $ = дл.
весия, вертикальные и горизонтальные составляющие этих сил должны быть
равны:
Силы Н Силы Т Веса нити
Вертикальные составляющие 0 Т sin а Р$
Горизонтальные составляющие Н Т cos а 0
Поэтому имеем:
Т sin a=ps
Г cos а = Я, .
откуда
< Ps
*а=н-
Но tga=y, поэтому приходим к уравнению
, ps
у=Тг
Для устранения третьей переменной s в этом
по х обе его части, и так как
уравнении, дифференцируем
29 Зак. 2116. Н. С. Михельсон.
4 50 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXV1B
то мы получаем дифференциальное уравнение 2-го порядка, относящееся к
только что рассмотренному типу
= • УГ+7ч
Согласно указанному правилу, полагаем yr = z, тогда у" = zr и полученное
уравнение приведется к уравнению 1-го порядка
Z' = /1 + Z2,
/ р 1 \
в котором переменные отделяются. (Здесь 1 Интегрируя это урав-
нение имеем
dz __ dx
у 1 а ’
откуда
ln(z+ УТ+Т2)=^ + С1 '
(см. тип XII интеграла, стр. 310). Для определения постоянной интегрирования
примем во внимание, что касательная в точке А параллельна оси ОХ, так
что У = z = 0 при х = 0. Принимая это в расчет, находим
In 1 = Cj, т. е. С1 = 0.
Итак, получаем
In (z + /Г+7) = ,
ИЛИ
г+УТ+^ = е~- (1)
Умножением на сопряженный двучлен z— y^l-j-z2 получаем
— 1 = (z— yr+F) ’
откуда
X
z— yi + z2 = —e а • (2)
Складывая равенства (1) и (2) и деля на 2, получаем
z = т. е. у — у (е а — е а J.
Дальнейшее интегрирование приводит нас к результату
а; X
у=т (еа + е а)+с*
Если начало координат выбрать в расстоянии, равном а от точки А, то при
х = 0 у должно быть равно а, а поэтому С2 = 0. При этом уравнение кри-
вой приводится окончательно к виду
XX •
= “)•
Уравнение это носит название уравнения цепной линии*
§ 172] ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА 451
§ 172. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
2-го ПОРЯДКА
Линейным дифференциальным уравнением 2-го порядка назы-
вается уравнение вида
Ау" + =
где А, В, С и D некоторые функции от х.
Так как нельзя предполагать, что А = 0 (иначе уравнение было
бы 1-го порядка), то, деля все члены уравнения на А и для сокра-
щения обозначая
В С D ч
получаем
Уа-\-РУг + яу=/(.х). (1)
Такое уравнение назовем, так же как в случае уравнения 1-го
порядка, приготовленным для решения.
Функция /(х), стоящая в правой его части, называется свобод-
ным членом, р и q — тоже некоторые функции от х.
Интегрирование этого уравнения находится в связи с интегриро-
ванием соответствующего ему уравнения без свободного члена, т. е.
уравнения вида:
и!1 -\-ри' -\-qu = 0 (2)
(здесь и заменяет у).
Интегрированием этого последнего уравнения мы и займемся
сначала. Относительно уравнения (2) можно высказать несколько
теорем.
Теорема /. Если и = их есть решение уравнения (2), то
u = auv где а любая постоянная, также будет решением
Vравнения (2).
Докажем это.
Из и = аиг следует и’= аиу, и" = аи’1, а потому, подставляя
в уравнение (2), имеем
тождественно, так как иг по условию — решение уравнения (2).
Теорема IL Если и = иг и и = и2 два решения уравнения (2),
то и = и}-\- и2 также будет решением уравнения (2).
Действительно, подставляя 1
и = ur и2, и' = и1-\- и^ и" = их -р и’1
в левую часть уравнения (2), находим, что она принимает вид
“1 + мз+Р(Х + из)+?(м1+ из) =
= « + « + рч’-i +
2<У
452 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXV1H
и так как их и zz2 по условию служат решениями уравнения (2),
то в отдельности
<+р«;+?«1=о и <+р<-ни2=о>
а следовательно, и = удовлетворяет уравнению (2), т. е.
является решением уравнения (2), что и доказывает теорему.
Для дальнейшего важно условиться в следующем: решения
и zz2 называются линейно независимыми, если
auj bu2 ф О
ни при каких постоянных значениях чисел а и Ъ, одновременно не
равных нулю.
Теорема III. Если и = их, и = и2 два линейно независимые
частные решения уравнения (2), то общий интеграл уравнения (2)
будет
и = Схи1-\-С2и2, (3)
где С1 и С2 произвольные постоянные числа.
Установим сначала следующее:
Как и для дифференциального уравнения 1-го порядка (см. стр. 428),
под общим интегралом уравнения 2-го порядка будем понимать
конечное уравнение между независимой переменной и ее функцией,
содержащее две произвольные постоянные, и притом такое, что
из него путем двукратного дифференцирования и исключения
произвольных постоянных получается само дифференциальное
уравнение.
Покажем теперь, что этим свойством обладает конечное урав-
нение (3).
Прежде всего заметим, что поставленное в условии теоремы
требование, чтобы решения иг и zz2 были линейно независимыми,
является необходимым условием для того, чтобы в решении (3)
имелись две произвольные постоянные. В самом деле, при условии
аи1 4~ ди2 = О
имеем и2 —----у ui или u2 = kulf где k =----. А тогда
zz = CjZZj4- C2zz2 = С1и14~ C1ku1 = (Сх 4“ ui = Czz1?
т. е. две произвольные постоянные слились в одну.
Остается показать, что из уравнения (3) и двух других, выте-
кающих из него путем дифференцирования, получается само диффе-
ренциальное уравнение (2) исключением постоянных Сг и Са. Дей-
ствительно, дифференцируя два раза уравнение (3), находим
= (4)
«" = с1й;н-сх (5)
§ 173] НАХОЖДЕНИЕ ЧАСТНЫХ РЕШЕНИЙ ЛИНЕЙНОГО УРАВНЕНИЯ 453
Умножая теперь уравнение (3) на <7, (4) на р, (5) на 1 и складывая,
получаем
+ ри' 4- <1и = « 4- 4~ 4- ри'а 4- qu3).
Но так как иг и и2 по условию суть частные решения уравне-
ния (2), то
ui 4- Ри[ 4- = о. “з 4- 4- ?“3 = °-
Поэтому в результате исключения (\ и С9 получаем уравнение
и" -\-ри' —|— = 0.
что и требовалось доказать.
Из теоремы III следует, что для интегрирования уравнения (2)
достаточно найти каким-нибудь образом два линейно независимых
частных решения и, и и2 этого уравнения, чтобы по ним сразу
написать общий интеграл уравнения в виде
и = Саи9.
Поэтому все внимание остается сосредоточить на нахождении
таких частных решений. Этот вопрос полностью разрешается для
линейных дифференциальных уравнений высшего порядка с посто-
янными коэффициентами.
Уравнение и" -]- ри' -\-qu=f (х) называется уравнением с постоян-
ными коэффициентами, если р и q постоянные числа.
§ 173. НАХОЖДЕНИЕ ЧАСТНЫХ РЕШЕНИЙ ЛИНЕЙНОГО ДИФФЕРЕН-
ЦИАЛЬНОГО УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
БЕЗ СВОБОДНОГО ЧЛЕНА
Частные решения такого уравнения находятся -на основании
следующей теоремы.
Теорема IV. Частным решением линейного дифференциального
уравнения
и" ~\-ри' -\-qu = b (2)
с постоянными коэффициентами без свободного члена служит
выражение
где k— корень алгебраического уравнения
*2 + /^ + ? = 0- (*)
Для доказательства этой теоремы поставим себе такой вопрос:
не может ли
и = е^ху
где k постоянное число, служить решением уравнения (2),
454 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXV11I
Чтобы и = екх было решением уравнения (2), надо чтобы оно
вместе со своими производными первого и второго порядка
ur = kekx и и” = йМ®
удовлетворяло уравнению (2).
Если подставить эти значения в левую часть уравнения (2),
го последняя примет следующий вид:
и" -\-qu = екх (й9 + рй -{- <?)•
Чтобы в результате такой подстановки она обратилась тождественно
в нуль, необходимо, чтобы один из множителей
екх или й9 -f- pk + Я
обращался в нуль. Но так как екх ни при каком значении й не
может равняться нулю, то должно быть
ft2+pft_|_9 = 0, (*)
т. е. число й должно быть корнем уравнения (*), чтобы екх было
решением уравнения (2).
Уравнение (*), от решения которого зависит нахождение частных
решений уравнения (2), носит название характеристического урав-
нения по отношению к дифференциальному уравнению (2).
Разберем отдельные случаи, которые могут представиться при
решении, уравнения* (*).
Первый случай. Корни й1 и й2 характеристического уравнения
вещественные и различные.
В этом случае два линейно независимые частные решения урав-
нения (2) будут
= ек& и и2 = е^х9
а потому по теореме III общий интеграл выразится так:
u = C1ek^+C2ek*x.
Пример 1. Проинтегрировать уравнение
и" — и' — 2и = 0.
Составляем характеристическое уравнение
й2 — й — 2 = 0; отсюда йг = 2, й2 = — 1.
Поэтому и\ = Л® и и2» е-® будут частными.решениями уравнения, а общий
интеграл его будет
и = С^2® + С2е~х.
Второй случай. Корни характеристического уравнения — равные:
й1 = й2.
В этом случае из характеристического уравнения мы находим
лишь одно частное решение дифференциального уравнения.
§ 173] НАХОЖДЕНИЕ ЧАСТНЫХ РЕШЕНИЙ ЛИНЕЙНОГО УРАВНЕНИЯ 455
Можно, однако, доказать, что в этом случае другим частным
решением будет служить
и = хек^.
Действительно, тогда
и' = х • ktek^ -J-
и" = х • k}ek&4-26{ек^.
Подставляя эти величины в левую часть уравнения (2), получим
и" -\-ри' -{-qu = x - ек^ -f- pkt + ^) Ч" (2^i + Р)-
По условию
Кроме того, так как в рассматриваемом случае
---q = 0, то kt=—, т. е. 2&14-р = 0-
Поэтому мы видим, что левая часть уравнения (2) обращается в
нуль тождественно; это и доказывает, что хек& служит решением
уравнения (2).
Таким образом, в этом втором случае частными линейно неза-
висимыми решениями дифференциального уравнения служат
и} = ек& и и2 = хек&,
а потому общим интегралом будет
и^С^-^С^хе^
или
и = (С, 4 С2х) ек^.
Пример 2. Проинтегрировать уравнение
и" + 6а' + 9w = 0.
Уравнение Л2 + 6^ + 9 = 0 имеет равные корни = Л2 = — 3.
Поэтому частными решениями предложенного дифференциального урав-
нения будут
• u1 = e-'ix и = х •
а общий интеграл:
и = (С1+С^с)е^х.
Третий случай. Корни kx и k2 характеристического уравнения
комплексные:
kx = а-{- bi, k2 = a— bl.
В этом случае попрежнему
е(а^Ы)х л g(o — bi) х
будут частными решениями дифференциального уравнения.
456 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
Однако эта комплексная форма частных решений может быть
заменена решениями другой формы, свободной от всякой мнимости,
именно решениями
иi = cos Ьх и и2 = еах sin Ьх.
Действительно,
^(а+М) ® — gax . gbxi
e((t-bi)x — gox . Q-bxi'
Но по теореме II сумма и разность этих решений
gax (j>bx4 |_ q - b xi}
qclx (gbxi £ — bxi}
будут также решениями того же дифференциального уравнения. Далее
по теореме I мы можем каждое из них умножить на любое постоянное
число. Умножая первое на , а второе на и вспоминая формулы
Эйлера (см. § 146), получим частные решения вида
gbxi 4- £ - bxi
еах -----—------= еах cos Ьх
2
obxi__р — bxi
е°х-------------- = еах sin Ьх.
Общий же интеграл будет
и = С^о® cos Ьх 4~ С2еах sin Ьх
ИЛИ
и = (С\ cos Ьх -j- С2 sin Ьх).
Пример 3. Проинтегрировать уравнение
и" + Ш 4-13« = 0.
Характеристическое уравнение
+ 4-13 = 0
имеет корни хг 2 = — 2 ±31.
Здесь
а = — 2, 6 = 3,
поэтому частными решениями будут
щ = Cie-*»cos Зх
u2 = sin Зх,
а общим интегралом
и = в’2а? (Ci cos Зх 4- С2 sin Зх).
Пример 4. Проинтегрировать уравнение
d^s
т (см. задачу III, стр. 425).
§ 174] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 457
Для удобства обозначим
тогда предложенное уравнение представится в виде
Соответствующее ему характеристическое уравнение будет
= О,
откуда
k, = zt а V — 1 = al.
Частные решения будут
= cos at, и2 = sin at,
а общий интеграл представится в виде
s = Ci cos at + С2 sin at,
как это и было дано раньше (см. формулу (3'), стр. 426).
§ 174. ИНТЕГРИРОВАНИЕ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ
Все, что до сих пор было рассмотрено, относится к уравне-
нию (2), т. е. к дифференциальному уравнению без свободного
члена. Вопрос об интегрировании дифференциального уравнения (1)
со свободным членом разрешается следующей теоремой.
Теорема V- Общий интеграл уравнения со свободным членом
У'+рУ=/(•*) (О
представляет собой сумму общего интеграла соответствующего
уравнения без свободного члена
и" -\-ри' + qu = Q, (2)
и какого-нибудь частного решения yQ уравнения со свободным
членом.
В теореме требуется доказать, что выражение
У = и У Уо> (6)
где и есть общий интеграл уравнения (2), а у0 есть частное реше-
ние уравнения (1), служит общим интегралом уравнения (1).
Прежде всего замечаем, что уравнение (6) заключает в себе
две произвольные постоянные, содержащиеся в выражении и. Кроме
того, нетрудно проверить, что
^ = «+Jo
458 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIII
удовлетворяет уравнению (4). Действительно, дифференцируя ра-
венство (6) два раза:
У = и'+л
П И I/
у = « 4-л
и подставляя значения у, у' и у" в уравнение (1), приходим к тож-
деству х
(И"+ри' 4- qu.} 4- (Уо -[-рУо -j-qyo) —f(x).
В самом деле, в нем
и 4- ри Ч- Чи = О
ввиду того, что и есть общий интеграл уравнения (2), а
Уо-+-РУо-Ь<7Уо=/(х)
ввиду того, что у0 есть решение уравнения (1).
Итак, выражение (6) содержит две произвольные постоянные и
удовлетворяет уравнению (1). Следовательно, оно является общим
решением, или, иначе, общим интегралом уравнения (1).
В силу доказанной теоремы интегрирование дифференциального
уравнения вида
У" + ру'-\-Ю=/(х) (1)
приводится к решению двух задач:
1) к нахождению общего интеграла соответствующего уравнения
без свободного члена и
2) к нахождению какого-нибудь частного решения уравнения со
свободным членом.
Первая из этих задач рассмотрена и решена полностью выше
для уравнения с постоянными коэффициентами: ее решение приво-
дится к решению характеристического уравнения. Что же касается
второй, то в отдельных частных случаях и она решается очень
просто. Именно, в некоторых случаях по форме свободного члена
/(х) дифференциального уравнения (1) можно предвидеть форму
частного решения этого уравнения, а зная ее, найти и само решение.
Не рассматривая этот вопрос детально, укажем на следующие
случаи:
1. Если свободный член f (х) уравнения (1) будет целой рацио-
нальной функцией n-ой степени, т. е. если
/(*) =Ро+Р1х + Рах2+ • • • +Рпхп,
то и частное решение у$ уравнения (1) будет целой рациональной
функцией, вообще говоря, той же степени, т. е. вида
Уо = Яо 4- Я Iх + Я^ + • • • + ЯпхП-
2. Если
/ (*) = (Го + Р1Х + Г2х2 4- • • • -Г РпхП) е’"х>
I
§ 174] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 459
то, вообще говоря, и у0 будет вида
Уо = (7о 4 <hx 4- 4- • • • 4- <1пхп) е‘‘1х-
3. Если
f (х) = g cos ах + h sin ах,
то, вообще говоря, и yQ будет вида
yQ = k cos ах -]-1 sin ах.
Коэффициенты r/0, qlf ... qn, k, l неизвестны, но их можно
найти по методу, который выясним на примерах и который назы-
вается методом неопределенных коэффициентов.
Пример 1. Проинтегрировать уравнение
У'+У — 6у = х.
I 1аходим сначала общий интеграл уравнения
U" + U'SU = о.*
Для этого решаем характеристическое уравнение:
k* + k — 6 = 0; A?i = 2, /г2 = —3.
Поэтому общий интеграл уравнения без свободного члена будет
Найдем теперь какое-нибудь решение данного уравнения
У'+У~ бу = х.
Ввиду того, что свободный член уравнения равен х, т. е. целой рациональ-
ной функции первой степени, решение у0 будем искать того же вида, как
свободный член уравнения, т. е. в виде функции 1-й степени
yQ = ах + Ь.
Остается определить а и b так, чтобы Уо = ах 4- b действительно было ре-
шением данного уравнения.
Для этого составляем производные
у'й = а> Уо=°
и, подставляя в данное уравнение, приходим к равенству
а — бах — 6Ь = х.
Чтобы это равенство было тождеством, надо, чтобы коэффициенты при оди-
наковых степенях х и свободный член левой части этого равенства были
соответственно равны коэффициентам правой части, т. е. чтобы
— 6а = 1, а — 66 = 0;
1 , 1
отсюда € = --g-, * = -35.
460 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVTH
Итак, частным решением уравнения со свободным членом служит
1 1
” 6 х 36 ’
а общий интеграл будет
у = + Сге-зх _ -1 х _ _L .
О оо
Пример 2. Проинтегрировать уравнение
у" 4- У = 2хМ.
Опять сначала находим общий интеграл уравнения
и" + и' = О,
для чего составляем и решаем характеристическое уравнение
^ + ^ = 0; ^ = 0, = —1.
Поэтому
ц = +
Остается найти частное решение у0 полного уравнения. Ввиду того, что
свободный член равен целой рациональной функции 2-й степени, умножен-
ной на ех> решение ищем вида
у$ г= (ах2 + Ьх + с) ех.
Для отыскания этого решения подбираем коэффициенты а, Ь, с так, чтобы
удовлетворяло данному уравнению. Для этого составляем y'Q и yQ-
у'о = (ах2 + Ьх + с) ех + (2ах + Ь) ех = [ах2 + (2а + Ь) х + (с + &)] ех,
у" = [ах? + (2а + Ь) х + (с 4 &)] е® + [2 а х + (2а + Ь) ] е* =
= [ах* 4- (4а 4- i) х + (с 4- 26 4- 2а)] е*.
Подставляя теперь у0, y’Q и у^ в данное уравнение и сокращая все члены
на ех> получаем
[ах2 + (4д + Ь) х + (с + 2Ъ + 2а)] + [ах2 + (2а +Ь)х+ (с ±Ь)] = 2х2.
Чтобы равенство это было тождеством, необходимо, чтобы коэффициенты
при одинаковых степенях и свободные члены правой и левой частей равен-
ства были равны, т. е. чтобы
2^ = 2, 6а + 2& = 0, 2с + ЗЬ + 2а = 0,
откуда и находим
а = 1, & = —3, с=-^-.
т. е. искомое частное решение будет
>0 = (*2 — Зх4--у^е®,
а общий интеграл уравнения
/ 7 \
У = — Зх Ц-~2~J
$ 174] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 461
Пример 3. Проинтегрировать уравнение
/' — Зу' = sin 2х.
Составляем и решаем характеристическое уравнение
F —ЗА? = 0; ^ = 0, k2 = 3.
Общий интеграл уравнения
и" —Зи' = 0
будет
и = С^ +
Далее ищем частное решение полного уравнения в форме
_у0 = k cos 2х 4» I sin 2х.
Дифференцируя у0 два раза, находим
Vq = — 2k sin 2х -|- 21 cos 2х
у'п = — 4k cos 2х — 41 sin 2х.
Подставляя найденные выражения для у^у^ в данное уравнение, получаем
(— 41 + 6£) sin 2х — (4k + 6/) cos 2х = sin 2х.
Чтобы это равенство было тождеством, необходимо, чтобы
6А> —4/=1; 4£ + 6/ = 0,
откуда и находим
*__L I___________L
26 ’ 13 •
Таким образом, общий интеграл данного уравнения будет
у = С] + С^х -j- cos 2х — -i- sin 2х.
ZO 1О
Необходимо иметь в виду, что при отыскании частных решений
только что рассмотренным методом неопределенных коэффициентов
могут встретиться исключительные случаи, когда ожидаемую форму
частного решения придется несколько изменить.
А именно, при первой форме свободного члена, когда
f(x) =р0+ р1Х +р2х2 4- ... +рпхп,
следует ожидаемую форму частного решения умножить на х, если
нуль является простым корнем характеристического уравнения.
При второй форме последнего члена, когда
/ (*) = (Ро 4- Р1Х + Р2Х* + • • • + РпхП) етя>,
ожидаемую форму частного решения следует умножить на х, если
коэффициент т является простым корнем характеристического урав-
нения, и на л:2, если двойным (кратным) корнем того же уравнения.
При третьей форме свободного члена, когда
/ (x) = g cos ах h sin ах,
462 ВВЕДЕНИЕ в интегрирование дифференциальных уравнений [xxvni
ожидаемую форму частного решения
у0 = k cos ах -|- h sin ах
следует умножить на х, если корень характеристического уравне-
ния равен ~±ai.
Пример 4. Проинтегрировать уравнение
у" — 2уг = 8х — 2,
Находим сначала общий интеграл уравнения
и" — 2и' = О,
для чего составляем и решаем характеристическое уравнение
£2 — 26 = 0; 6(6 —2) =0; 61 = 0, ^ = 2.
Поэтому
и = + С2е*г.
Так как в данном случае как раз нуль есть корень характеристического
уравнения, то частное решение ищем не в форме
у о = ах 4- b, a у0 = ах2 + Ьх.
Дифференцируя, находим
у' = 2ах4-6, у" = 2а.
Подставляя в данное дифференциальное уравнение, получаем
2а — 4ах — 2Ь = 8х 4~ 2,
откуда
а = — 2 и 6 = — 3.
Таким образом, частное решение предложенного уравнения будет
у0 = — 2х2 — Зх,
а его общий интеграл
у = Ci + — 2х2 — Зх.
Пример 5. Проинтегрировать уравнение
у" — 2у' -4- у = ех.
Интегрируя по правилу, найдем, что характеристическое уравнение
б2 —26 4-1 =0
имеет один двойной корень, равный 1, при этом здесь и т = 1. Поэтому,
частное решение ищем вида у0 = Ах2ех.
Дифференцируя, находим
Уо == Ах2ех 4- 2Ахех
у о = Ах2ех + 4Ахех 4- 2Ле^.
Подставляя в уравнение, имеем
Ах2ех 4- 4Ахех 4- 2Аех — 2Ах2ех — 4Ахех 4~ Ах2ех = ех
или 2Аех = ех, откуда А = -у-.
Итак, находим
у = Сугх 4- С^хех 4- -у х2ех.
§ 175] МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ постоянных 463
§ 175. МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ
Приведенные выше приемы нахождения частных решений пол-
ного дифференциального уравнения по виду его свободного члена
не всегда применимы. Существует, однако, другой прием, который
позволяет по найденному общему интегралу уравнения без свобод-
ного члена найти общий интеграл того же уравнения со свободным
членом. Прием этот носит название метода Лагранжа „вариации про-
извольных постоянных * и состоит в следующем.
Пусть нам дано для интегрирования дифференциальное уравне-
ние со свободным членом:
У" + РУ' + <1У=/(х) (1)
и положим, что мы нашли общий интеграл уравнения без свобод-
ного члена
и" -\-ри' -\-qu = Q (2)
в виде
и = ^*1^1 ^2^2* .(3)
Это последнее решение, конечно, не может удовлетворять уравне-
нию (1) ни при каких постоянных значениях Ct и С2. Однако если
отказаться считать и С2 постоянными, то можно поставить себе
задачу — подыскать величины и С2 как функции от х так, чтобы
у = С1и1 4~ (7)
служило решением уравнения (1). В определении этих величин Q
и С2 заключается решение задачи.
Итак у, взятое из уравнения (7) вместе с его производными уг
и у” должно удовлетворять уравнению (1).
Ввиду этого дифференцируем уравнение (7) в предположении,
что С\ и С2 являются уже функциями от х:
Х = С& -j- С2и$ -j- С^и1 -|- C2iz2. (8)
Так как в выражение (7) входят две величины С\ и С2, а оно дол-
жно быть подчинено лишь одному условию — удовлетворять урав-
нению (1), то на Q и С2 можно наложить еще одно какое-нибудь
условие. Именно, подчиним их требованию, чтобы
CittjС3«2 = 0. (9)
Тогда производная у' (см. формулу (8)), примет вид
у = С1«1 + (10)
Дифференцируя ее, находим вторую производную
у" — “Ь С2и2 -j” Ciiii С^и*. (И)
Теперь потребуем,'чтобы величины у, у' и у"\ выражаемые форму-
лами (7), (10) и (11), удовлетворяли уравнению (1) Подставив их
4 (И ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIlt
в это уравнение, получаем
^1и1 4“ ^2и2 4“ €1^1 “И -\~р (CtUi + С24/2) 4“ Q (Схиг 4" =
=f(x).
В последнем уравнении соберем члены, содержащие отдельно С1 и С2,
тогда оно представится в виде
(tti 4“ Ри1 4“ 4ui) 4“ ^2 (и* + Ри2 4” 4“ 4" ^2^2 = f (х) •
Так как иг и и2 являются решениями уравнения без свободного
члена, то
ui 4“Ptti 4“ Чи1 = 0 и н2 4"’/^4"’<7м2 =
а потому последнее уравнение приведется к
<?;«;+c^=f(X). (12)
Таким образом, величины С\ и С2 должны удовлетворять условиям
(9) и (12) для того, чтобы выражение (7) удовлетворяло уравне-
нию (1). Выписав эти условия отдельно
С^и 4“ С2м2 = 0 (9)
С^ + С^;=/(х), (12)
видим, что они представляют систему двух уравнений первой сте-
пени относительно неизвестных Сх и Са. Решив эту систему, най-
дем Ci и С2, как некоторые функции от х:
Q = ?i О)
^2 = ?2 (*)•
По полученным производным путем интегрирования находим и
самые величины Сг и С2:
С1=/ (ж)Н-Л1
С2 = / <?2 (*) dx + ^2 = ш2 (*) + А2>
где и А2— произвольные постоянные. При таких значениях С\ и С2
выражение (7) будет решением уравнения (1). Решение это оконча-
тельно выражается в следующем виде:
У = [ajj (х) 4“ ^11 4" (ш2 (х) 4" ^21 и%
или
^ = л1м14-д24/24-о)1(х) . «J4-M*) • ^2- (13)
Это и будет служить общим интегралом уравнения (1). При
At = Л2 = 0 получается одно из частных решений уравнения (1)
Уо = (й1И‘ «14-^2 (X)- и2.
Таким образом, общий интеграл уравнения (1), как и следовало
ожидать, имеет обычную форму
J = ^l«l + ^2“2+Jo-
§ 175]
МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ постоянных
465
Пример 1. Проинтегрировать уравнение
2 4
У'-^ = -8-т.
Интегрируем сначала уравнение без свободного члена
и" — 4н = о.
Общий его интеграл, как нетрудно видеть, будет
а = С1е2х + С2е~2х.
Применяя теперь метод Лагранжа, будем искать решение предложен-
ного дифференциального уравнения .в виде
y = C1e2:v + C2e-2iVf
считая уже теперь и С2 некоторыми искомыми функциями от х. Диффе-
ренцируя, получаем
у' = 2С1е2х — 2С3е~2х + С' е2х + с'е-2®.
Далее полагаем
С'1е2х + С'е-2х =0,
после чего находим для у" следующее выражение:
у” = 4^?® + 4Сае“2® + 2С'е2® — 2С',е~2х.
После подстановки в дифференциальное уравнение величин у, у' и у” полу-
чим уравнение
2С' е2* — 2С'е~2х = .
1 2 X3 X
Присоединив сюда ранее поставленное условие
+€\е~2х = 0,
определим из этих двух уравнений С[ и С2.
Исключая Сг, находим
4С'е3® —2-____-
461 ~ хз х •
Исключая С,, получим
4С'е— 2х — -___—
4С2е ~х л”
с>=
с’=
отсюда
30 Зак. 2116. Н. С. Михельсон.
466 ВВЕДЕНИЕ В ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [XXVIH
Остается только выполнить интегрирование:
г г ’ e-^dx= г г ^dx.
J \2x3 x J J 2x3 J x
Ко второму из этих интегралов применим интегрирование по частям; тогда
1‘е~2х е~2х Се-2* 1/ е~2х f \
J х dX ~ 2х J 2x2 dx 2х 2 \ 2х J х» dx)~
е~2х е~2х 1 f е~2х
“ 2х + 4x2 + 2 J х» °Х'
Поэтому
Таким же образом берется и второй из интегралов
J (Т " 2x0 dx = e2a,(2x + 4^)-
Поэтому
с1 = е-2а!6?- —C2 = e2a,f-J- + Ан-A-
1 \2х 4x2J 1 11 2 \2х 1 4х2/ 1 2
Общий интеграл дифференциального уравнения будет
у=~ ip+Ae3a>+i+А+А2е~2х-
Итак
у = Aie2x + А2е~2х + .
§ 176. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Какое уравнение называется дифференциальным уравнением?
2. Что значит интегрировать дифференциальное уравнение?
3. Что называется общим интегралом обыкновенного дифференциаль-
ного уравнения?
4. Как получаются из общего интеграла частные решения?
5. Что называется интегральными кривыми?
6. В чем заключается отделение переменных в дифференциальном
уравнении?
7. Какое дифференциальное уравнение 1-го порядка называется линей-
ным и как оно интегрируется?
8. Какое дифференциальное уравнение 1-го порядка называется одно-
родным и как оно интегрируется?
9. Как интегрируются уравнения вида У' = f(x), у" =f(y) и у" = f(y7)?
10. Как составляется характеристическое уравнение для линейного диф-
ференциального уравнения 2-го порядка с постоянными коэффициентами?
11. Как составляется из частных решений общий интеграл линейного
дифференциального уравнения 2-го порядка без свободного члена?
12. Как находится общий интеграл такого же уравнения со свободным
членом?
§ 176]
ВОПРОСЫ И УПРАЖНЕНИЯ
467
Проинтегрировать следующие уравнения:
13. (2х_у — 3_у2) dx + (х2 — 6х_у — 1) dy = 0. Отв. х2у — Зху2 —у = С.
14. еху (ydx-}-x dy) 4- dy = 0. Отв. еху 4-j = С.
15. j/ln xdx + (х In х — х + -у) dy = 0. Отв. ух In х—yx-j-lny = C.
16. х (у + 1) dx—у (х + 1) dy = 0. Отв. = Сех~у.
17. у\пу dx х\п xdy = $. 18. ху' +у = е~~х. Отв. Inx- In у = С. Отв. ху — С — е~х.
19. у' sin х -j-y cos х = sin 2x. 20. (xa-l)y+j=]/ —2д-3; 23. у = 4+^. *(*+?) 24. у" = 6x. 25. У' = -|=. vy Отв. у = sin х 4- -—. 1 sin X Отв. у Ух2 — 1 = С(х4-1) — 1. Отв. 3_у24~2х_у— 2х2 = С. Отв. у3 — бух2 = С. _у_ Отв. (у — х)2 = Сх -е х. Отв. у = х3 + CjX + С2. Отв. 1 у УУ + С1-(2Уу-С1) = = (* + 0>).
26. у" = V1 —У2. 27. у" = cos2 у. Отв. у = С2 — cos (х + Ci). Отв. у = (х + Ci) arc tg (х + Сг) — -.llnri+Cr + C^ + Q.
28. у" — 4у' = 0. 29. у" + 2у = 0. 30. у" — 2у’ +у =0. 31. у"+2у' — 3у = 6х. Отв. у = Ci + С2е4®. Отв. у — Ci cos х + С2 sin х У^Г. Отв. у = Ci&x -f- С2хех. Отв. у = С\вх 4" С2е ^х — 2х —.
32. у" + 4у = 5е®. Отв. у = Ci cos 2х + С2 sin 2х + ех.
33. у" -|- бу' 9у = 10 sin х. Отв. у = СУ?-3® + С2хе~3х+^sinx—
34.У-Х-^+|- 35. У' + у = 2 cos х. 36. у" — 2У = 4(х + 1). 37. У'+У — бу =5е2®. 3 —=-cosx. 5 Отв. у = Ci 4” С2вх — In х. Отв. у = Сг sin х 4- ^2cos х + х sin х- Отв. у = Ci 4~ С2^® — х Зх. Отв. у = Сге2х 4- С2е-3® + хе2®.
30*
XXIX. ДВОЙНЫЕ ИНТЕГРАЛЫ
§ 177. ДВОЙНОЙ ИНТЕГРАЛ, РАСПРОСТРАНЕННЫЙ
НА ПРЯМОУГОЛЬНИК
Пусть задана функция двух независимых переменных /(х, у)9 и
в плоскости XOY некоторый прямоугольник Р, стороны которого
параллельны осям координат ОХ и О Y.
Предположим, что для всех точек этого прямоугольника, т. е.
для всех значений х, у9 соответствующих точкам прямоугольника Р,
функция / (х, у) однозначна и непрерывна.
Продолжим стороны прямоугольника до пересечения с осями
коордицат в точках А, В, С, D и обозначим
ОА = а9 OB=b, ОС = с, OD = d.
Покроем прямоугольник Р сетью прямых, параллельных OY и
отстоящих одна от другой на
некотором расстоянии Дх, а также
сетью прямых, параллельных ОХ и
отстоящих между собой на рас-
стоянии &у. Выделим один из пря-
моугольников, на которые, таким
образом, разбивается весь прямо-
угольник. Площадь его будет равна
Дх • Ду. Отметим на этой элемен-
тарной площадке любую точку М9
ее координаты обозначим через аир.
Составим затем произведение
Ж р) • ДхДу.
Сделаем то же для каждого элементарного прямоугольника, на
которые разбилась вся площадь Р9 и составим сумму выражений,
подобных предыдущему, т. е.
22/(а> ₽) • д*ау,
а)
распространенную на все такие прямоугольники, т. е. на всю пло-
щадь Р. В выражении (1) употреблен двойной знак суммы ввиду
§ 177] ДВОЙНОЙ ИНТЕГРАЛ, РАСПРОСТРАНЕННЫЙ НА ПРЯМОУГОЛЬНИК 469
того, что суммирование необходимо вести двойное — в двух напра-
влениях: вдоль оси ОХ и оси OY.
Будем теперь беспредельно увеличивать число элементарных
прямоугольников, на которые разбита площадь Р, беспредельно
уменьшая при этом Дх и Ьу.
Тогда оказывается, что сумма эта стремится к некоторому опре-
деленному пределу и он не зависит ни от способа разделения пло-
щади Р на элементарные площадки, ни от выбора точек, таких
как М.1 Этот предел называется двойным интегралом, взятым от
функции / (х, у) и распространенным на прямоугольник Р.
Предел такой суммы обозначается следующим образом:
/ f f(x, у) dxdy,
р
так что по определению
J f f(x, у) dx dy = lim ₽) &х &у. (2)
р
Из определения непосредственно вытекает и способ вычисления
двойного интеграла.
Действительно, двойное суммирование можно вести так: сложим
сначала все слагаемые, соответствующие всем прямоугольникам
полосы FH, сумма их будет равна
У = д
&х-
Затем распространим суммирование на все подобные полосы,
т. е. вычислим
а?==Ь У=д
У [Дх- ^/(«. Р)4у]«
х—а у^с
Тогда, следовательно, можно будет написать
Х=Ъ
j* j*/ (х, у) dx dy = lim P) Д-У ]•
p x=a ' y = <'
Суммирование первое распространяется на значения у в преде-
лах от EF=OC = c до EG = OD — d, а суммирование второе
1 Доказательство этого положения можно найти в более подробных
курсах анализа.
470
ДВОЙНЫЕ ИНТЕГРАЛЫ
[XXIX
распространяется на все значения х от О А = а до ОВ = Ь. Вычисле-
ние пределов этих сумм можно заменить соответствующим интегри-
рованием, так что предыдущее равенство приводит к следующему
результату:
ъ д
/ J f(x>y}dxdy~
р
Таким образом, вычисление двойного интеграла, распространенного
на прямоугольник Р, приводится к последовательному вычислению
двух простых интегралов, при этом при интегрировании по одной
переменной другая принимается за постоянную.
f dx[f f(x>y)dA- (з)
Пример. Вычислить интеграл
(х2 + 2ху) dx dy,
распространенный на прямоугольник Р = ОАСВ, где О А = а, ОВ = Ь,
Имеем
Рис. 201.
а Ь
J J(x2 + 2xy) dx dy=Jdx I* (x2-J~2xy) dy,
P об
При интегрировании по у, т. е. при вы-
числении
ь
J (х2 + 2ху) dy,
о
переменную х следует принимать за по-
стоянную, так как такое интегрирование
соответствует суммированию по некоторой полосе, параллельной OY, для
которой х все время сохраняет неизменное значение. Таким образом,
ъ
f (х2 + 2ху) dy = [х2у + ху2] = x2b + xb2,
J о
о
Далее остается вычислить интеграл
° а
/ +xb^x =[^ + ^1 +4а = ^(2в+36).
о Jo
Итак
J / (*а + 2ху) dx dy = у a^b [2а + 3&J.
§ 178]
ДВОЙНОЙ ИНТЕГРАЛ ПО КРИВОЛИНЕЙНОЙ ОБЛАСТИ
471
§ 178. ДВОЙНОЙ ИНТЕГРАЛ, РАСПРОСТРАНЕННЫЙ НА ОБЛАСТЬ,
ОГРАНИЧЕННУЮ КРИВОЛИНЕЙНЫМ КОНТУРОМ
Понятие о двойном интеграле, распространенном на прямоуголь-
ник, обобщается и на случай, когда область интегрирования огра-
ничена криволинейным контуром.
Пусть имеем на плоскости координат замкнутый контур, опре-
деляемый уравнением
<Р (х, У) = 0 (4)
и ограничивающий область Q. Мы сохраним прежнее определение
двойного интеграла. При этом, однако, надо иметь в виду, что неко-
торые из элементарных четырехугольников (примыкающие к грани-
цам области Q) будут криволинейными.
Вычисление двойного интеграла в общем случае производится
аналогично случаю прямоугольника. Пусть требуется вычислить
двойной интеграл •
x,y)dxdy, (5)
Q
распространенный на область Q.
Предположим, что кривая, ограничивающая область Q, такова,
что
чем
прямые, параллельные осям координат, встречают контур не более
в двух точках. Это значит, что из уравне-
ния (4) одному значению х будут соот-
ветствовать, вообще говоря, два значе-
ния у, а одному у — два значения х.
Положим, что, решая уравнение (4) от-
носительно у, мы получили такие два
значения у
У1 = <?1(х) и № = ®2(х). (6)
Приступая к вычислению интеграла (5),
нам необходимо будет вести интегри-
рование сначала по одной из перемен-
ных, считая другую постоянной, а затем Рис. 202.
по другой. Предположим, что мы начинаем
с интегрирования по у, это соответствует суммированию по пло-
щадкам, расположенным на некоторой произвольно выбранной сколь
угодно узкой полосе, например FGHK, а следовательно, интегриро-
ванию в пределах от у = EF до у = EG. Эти значения у, зависящие
от выбранного значения х, будут соответствовать двум значениям у,
выведенным соответственно заданному х из уравнения. (4), т. е.
значениям (6). Таким образом,
472
ДВОЙНЫЕ ИНТЕГРАЛЫ
[XXIX
(7)
координат
так что пределы первого интегрирования по у суть функции пере-
менной X.
Второе интегрирование по х ведется уже в крайних пределах
изменения х, т. е. от х = ОА = а до х = ОВ = Ь. Итак,
Ь Та (®)
[ f(.x> у) dy.
Q a (а?)
Порядок интегрирования можно менять, но тогда изменяются и
. пределы у интегралов.
Пример. Вычислить J* J* xdxdy, где Q — область, ограниченная эллип-
Q
сом, уравнение которого относительно прямоугольных
сколь угодно узкую полосу
для нее у меняется
до у = ЕН. Из уравнения же эллипса
имеем
GH, мы видим, что
от значения у = EG
Выбрав некоторую
Рис. 203.
b_
а
а
У1 =
Эти выражения и будут служить пре-
делами интегрирования по у, интегрирова-
ние же по х следует вести от х = — а до
а, для того, чтобы распространить
интегрирование на всю площадь. Итак,
+ — Va*—&
а
dx
Q
— а
а
Выполняем первое интегрирование:
+ — У а2—х2 ъ -------
а — Уа2—х2
a h ____———
= 2— У а2— х2-х.
ъ ______ а г
-£/^=72
а
--
а
Остается выполнить второе интегрирование для вычисления предложен-
ного в задаче интеграла, и тогда найдем, что
• • 4" я
J I xdxdy = 2~ Уа2 — X2 > х dx ~j* У а2—х2 d (а2—№)=«
9* —а
h г 9 £-.+<»
§ 179]
ВЫЧИСЛЕНИЕ ОБЪЕМОВ
473
§ 179. ВЫЧИСЛЕНИЕ ОБЪЕМОВ
Понятие о двойном интеграле имеет разнообразные приложения.
Одним из самых простых является приложение двойного интеграла
к вычислению объемов тел, ограниченных кривыми поверхностями.
Пусть нам дано вычислить объем V
тела MNPS, ограниченного плос-
костью координат XOY, цилинд-
рическою поверхностью, обра-
зующие которой параллельны оси
OZ, и кривой поверхностью PRST,
уравнение которой z = f(x,y).
Плоскостями, параллельными
плоскостям XOZ и YOZ, разо-
бьем данное тело на элементар-
ные части (столбики), одна из
которых представлена на чертеже
ABCDEFGH. Взамен каждой та-
кой части тела рассмотрим пря-
мую призму, основанием которой
служит тот же прямоугольник
ABCD, а высотою АЕ. Примем АВ = Дх и AD = Ду, тогда объем
призмы
ДУ = пл. ABCD-АЕ = Ьх-by - АЕ.
Если координаты точки А на пл. XOY обозначить через а и 0,
то из уравнения поверхности будет следовать, что
так что
АЕ=/(а, 0),
Д 1/=/(а, 0) • Дх • Ду.
Определив теперь объем V рассматриваемого тела, как предел,
к которому стремится сумма объемов, подобных Д1/, мы и получим
V = lim 0) Дх Ду,
т. с. что
, у) dx dy = J j* z dx
Q Q
Так что V равно двойному интегралу от / (х, y)dxdy, рас-
пространенному на область Q.
Здесь Q, область, лежащая в основании рассматриваемого тела,
является вместе с тем проекцией на пл. XOY поверхности, накры-
вающей данное тело.
474
ДВОЙНЫЕ ИНТЕГРАЛЫ
[XXIX
Конечно, для возможности вычислить V по полученной формуле
необходимо, чтобы было известно как уравнение поверхности
*=/(*, у),
так и уравнение кривой MN\ ограничивающей основание тела.
Рис. 205.
Пример. Вычислить объем шара, радиус которого г.
Для вычисления всего объема шара вычис-
лим сначала 4- его объема, т. е. объем ОАВС.
о
Этот объем ограничен тремя координатными
плоскостями и частью АВС поверхности шара.
По указанному выше, нам необходимо знать
как уравнение поверхности шара, так и уравнение
контура АВ, ограничивающего область АОВ.
Уравнение поверхности шара, центр которого
в начале координат, будет
х2+_у2-кг2 = г2. (9)
Оно выражает свойство шаровой поверх-
ности, по которому все точки одинаково уда-
лены от центра.
Уравнение контура АВ будет уравнением круга
Х2 + J/2 =
Из уравнения (9) определяем
(Ю)
* = / г2 —(х24-У2),
т. е. ту функцию от х и у, которую нужно подставить под знак двойного
интеграла, а уравнением (10) пользуемся для определения пределов интегри-
рования.
Итак, по формуле (8) имеем
объем ОАВС = J* j* У г2—(*2 + _У2) dx dy.
пл. олв
Приступая к вычислению этого двойного интеграла, распространенного на
область ОАВ, мы будем первое интегрирование вести по переменной у.
Для этого мы выбираем некоторое определенное значение х = OD и ведем
интегрирование по сколь угодно узкой полосе DE в пределах изменения у
на протяжении этой полосы, т. е. от у = 0 до у = DE. Значение отрезка
DE найдется из уравнения (10); именно DE будет значением у, выведенным
из этого уравнения (10), т. е. ____________
у = у г2 — x2t
Итак, пределами первого интегрирования по у будут служить
у = 0 и у = Уг2 — х2.
Второе интегрирование будем вести по переменной х в пределах его изме-
нения на протяжении всей области ОАВ, т. е. в пределах от х = 0 до
х = г. Действительно, чтобы охватить всю область интегрирования, необхо-
димо полосу DE передвигать от значения х = 0 до х = г.
Итак,
г Vr-—x-
объем ОАВС = J \dx J j/?2 — № — у2 • dyl.
Q Q
§ 179]
ВЫЧИСЛЕНИЕ ОБЪЕМОВ
475
Остается заняться последовательным вычислением определенных инте-
гралов.
1) Рассмотрим сначала внутренний интеграл
]/Та —
J Уг2—х2—y2dy.
о
Для сокращения письма обозначим временно г2 — x2=k2t тогда
Vr2—ш* к
J* У г2 — х2—у2 dy = J* уk2 — у2 dy.
о о
Определенный интеграл
к
У У&—y2*dy
о
берется сначала интегрированием по частям, а затем разложением на сла-
гаемые
к к к
f V *2—_уа<у = [> • V^—уЦ* _ f -у ;dy = - | А2т{3~3 <o,=
J 0 J У k2—y2 J V k2—y2
о oo
к к
= - f dy + fe2 f .
J J V №—y*
о 0
В правой части равенства появляется снова искомый интеграл. Перенеся его
в левую часть равенства, получим
к к
2 f VW=ytdy = l>? f-7==3,
J J у k2—y2
о 0
а потому
к к к
f У fl—y*dy = — k2 f = — k2 (arc sin = ~k2.
J У 2 J VA2_y 2 \ 4
0 0
Итак
V
j* У r2 — x2^y2 dy = ~ (r2 — %2),
o*
2) Выполним теперь второе интегрирование:
г
| j(f2 — dx.
6
f It . „ 9Ч . ТС Г о А3 |Г ТС/*2
J1-(r2_x2)rfx=T[r2x__j .
О 4
476
ДВОЙНЫЕ ИНТЕГРАЛЫ
[XXIX
Поэтому
объем ОАВС= .
о
Весь же объем шара V будет
8тсг3 4
V= 8 • объем О АВС = = 4 кг3,
о о
§ 180. СТАТИЧЕСКИЕ МОМЕНТЫ, ЦЕНТР ТЯЖЕСТИ
И МОМЕНТЫ ИНЕРЦИИ ПЛОСКИХ ФИГУР
В вопросах, изучаемых в механике и в других технических
дисциплинах, значительную роль играют понятия о моментах и
о центре тяжести линий, площадей и объемов.
Эти понятия в применении к плоским фигурам приводят нас
к вычислению интеграла по соответствующей области и, таким
образом, служат материалом для приложения теории двойных инте-
гралов.
Статическими моментами Мх и Му плоской фигуры относи-
тельно осей координат являются следующие выражения:
Мх = ydxdy, Му = JJ xdxdy, (11)
<2 Q
где Q — рассматриваемая фигура.
Эти статические моменты могут служить для определения коор-
динат центра тяжести фигуры, которые находятся из формул:
Моментами инерции плоской фигуры Q относительно осей коор-
динат являются выражения
Ix = J J у2 dx dy, 1у = у у x2dxdy. (13)
Q Q
Моментом инерции плоской фигуры относительно начала коор-
динат является выражение
А» = J /
(14)
<2
Способ отыскания статических моментов, центров тяжести и
моментов инерции плоских фигур вытекает из самих формул (11),
(12), (13) и (14).
§ 180] СТАТИЧЕСКИЕ МОМЕНТЫ, ЦЕНТР ТЯЖЕСТИ ПЛОСКИХ ФИГУР 477
Пример 1. Найти статические моменты относительно осей координат
и центр тяжести части ОВС сегмента параболы, полагая ОС = а (рис. 206).
По формуле (11) имеем
Mr = J J у dx dy> Му = j* J х dx dy.
овс две
Принимая же в расчет уравнение параболы
У = У2рх
и формулу (7), получаем:
a V2px a V'lpx
Mx=^dxJ ydyt My = fxdxj dy.
0 0 0 0
Для вычисления этих моментов производим сначала внутреннее инте-
грирование
V 2рх ___ V2px
J. fl nl^2PaJ ( , Г yV2pX t/"Q-----
УаУ= 9-J'2 = PX> ^ = [J]O =V2px.
L Jo
0 0
Поэтому искомые моменты выразятся так:
а
Мх = J pxdx=P-^-,
о
Для нахождения координат центра тяжести достаточно найденные вели-
чины моментов разделить на площадь фигуры.
о 9 ___
4ОС- СВ = 4а- V'lpa,
о о
478
ДВОЙНЫЕ ИНТЕГРАЛЫ
[ХХ1Х
то координаты центра тяжести N этой части параболы будут
a2Y%Pa
о
о ______
V2pa
О
У~~2--------
у а У2ра
= -h=4oc.
о о
= 1 У2ра = ^-СВ.
О о
Пример 2. Определить моменты инерции 1Х и 1у части ОВС сегмента
параболы, принимая ОС = а (рис. 207).
По формулам (13) имеем
X
Q
a V2px а ---
Г Г Г Г 1 .
J dx J y^dx = j [jp3]о dx-
0 0 о
а о __ л g _ 5
«if (2,^-^
о о J О о
о о
«= -^Ра2 Vfya-
a V‘2px а
1у= J j x2dxdy = f x2dx j dy = Jx2- Y2pxdx =
QV ooo
a 5
= Y%P |* x 2 dx = Y?P * x3Y* j = у а3 • Y2pa*
§ 181. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется двойным интегралом по прямоугольнику?
2. Как ведется интегрирование при вычислении двойных интегралов?
3. Как определяются пределы интегрирования в случае, если область,
на которую распространяется интегрирование, есть прямоугольник со сторо-
нами, параллельными осям координат?
4. Как определяются пределы интегрирования в случае криволинейного
контура ?
5. Как вычисляются объемы тел при помощи двойного интеграла?
6. Как выражаются через двойные интегралы статические моменты пло-
ской фигуры относительно осей координат?
7. Как находятся координаты центра тяжести плоской фигуры?
8. Как выражаются через двойные интегралы моменты инерции пло-
ской фигуры относительно осей координат и относительно начала коор-
динат?
§ 181]
ВОПРОСЫ И УПРАЖНЕНИЯ
479
9. Вычислить J J ху dx dy, распространенный на прямоугольник
Q
Q = ABCD, где АВ = 2а, AD = 2р (рис. 208). Отв. 0.
10. Вычислить J* j* xydxdy, распространенный на часть ЛОВ сегмента
Q
параболы, при условии, что ОА = АВ (рис. 209).
„ 8 4
Отв. -5- р4.
о
И. Вычислить (x-\-y)dxdy, где Q равнобедренный треугольник
Q
ОАВ (рис. 210).
12. Вычислить J J* (х -|- у) dx dy, где Q равнобедренный треугольник
Q
OCD (рис. 211). k Отв. ---/п3, где т = ОС = CD.
480
ДВОЙНЫЕ ИНТЕГРАЛЫ
[xxtx
13. Вычислить J* j* 2x2ydxdy, где Q полукруг ОАВ радиуса, равного а
ч 8
(рис. 212). Отв. -g-л5.
О
15.
ОАВС,
16.
лоидом
ностью,
С помощью двойного интегрирования доказать, что объем тетраэдра
у которого >ОА = ОВ = ВС = а, равен ~ а3 (рис. 213).
Прямоугольная призма с квадратным основанием накрыта парабо-
х2 + У2 = 2pz. Определить объем призмы, накрытой этой поверх-
пЗ
если сторона основания призмы равна р (рис. 214). Отв.
Рис. 214.
17. Определить центр тяжести плоской фигуры ОАВ, предполагая, что
ОВ дуга параболы у2 = 2рх и что ОА = АВ (рис. 215). Отв. (^Р» ^р)-
§ 181]
ВОПРОСЫ И УПРАЖНЕНИЯ
481
19. Определить центр тяжести кругового сегмента АВ, отсекаемого
стороною вписанного в круг квадрата (рис. 217).
п Г 2г 2г I
Отв' [з(к —2) ’ 3(к —2) ]’
20. Вычислить момент инерции равнобедренного прямоугольного тре-
угольника АВС относительно начала координат (рис. 218).
21. Вычислить момент инерции прямоугольника ОАСВ относительно осей
2 8
координат, полагая О А = 2ОС = 2а (рис. 219). Оте. 1Х = -^ а4, Л = —- а4.
о & о
22. Вычислить момент инерции прямоугольного треугольника относи-
тельно одного из его катетов. Оте. , где а и b катеты треугольника.
23. Вычислить момент инерции круга относительно его центра.
TZr4
Оте. =
31 Зак. 2116. Н. С. Михельсон.
XXX. ПОНЯТИЕ О КРИВОЛИНЕЙНОМ ИНТЕГРАЛЕ
§ 182. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ
СУММЫ
Рассмотренная в § 124 задача II о работе силы предполагала
перемещение точки по прямой. Посмотрим, к чему приводится ре-
шение подобной задачи, если предположить, что движение свобод-
ной точки под действием данной силы происходит по кривой.
Мы будем рассматривать лишь случай движения точки в некоторой
плоскости. Итак, пусть свободная
у ] материальная точка М под дей-
ствием переменной силы F дви-
/ жется в плоскости XOY по кри-
вой KL. Условимся отсчитывать
путь, пройденный точкой по кри-
вой, от некоторой точки С, и обо-
1 с значать его через 5, так что
—-----------------------► X № ДЛ. о СМ.
Рис. 220. Мы предполагаем, что сила, при-
ложенная к материальной точке,—
переменная и зависит от положения точки на кривой. В таком случае
ее можно рассматривать, как функцию координат точек кривой,
т. е. положить, что
F=f(x,y).
Задавая уравнение кривой KL в параметрической форме и по-
лагая, что за параметр принята дуга s, мы можем написать уравне-
ния кривой в виде
* = <?($)
.У = “($)•
Подставляя в выражение F =f (х, у) величины х и у из преды-
дущих уравнений, мы и силу F выразим в виде функции от $, т. е.
Р=Ф($).
§ 182] КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ СУММЫ 483
Для подсчета работы, затраченной силой на пути перемещения
точки М от точки А до точки В, разобьем всю дугу на п частей,
длины которых пусть будут
Asa, ..., Ast-, ..., Д$я.
Работа силы на протяжении элемента пути &sif который мы
принимаем за прямолинейный, выразится следующим произведением
Ф ($<) • д$й
где силу Ф ($<), приложенную к материальной точке, мы считаем
постоянной на протяжении всего элемента пути Ast-. Составим сумму
работ на протяжении каждого в отдельности элемента пути
= Ф (Sj) Asj + Ф (s9) Д$2 + ... + Ф ($„) Д$„.
Эта сумма не выразит нам истинной работы силы на пути пере-
мещения точки по кривой; однако, чем на большее число частей
мы разобьем кривую, тем ближе полученная сумма выразит искомую
работу. Таким образом, для определения работы переменной силы
на пути перемещения материальной точки по кривой необходимо
вычислить предел составленной интегральной суммы Sn. Итак, работа
А = lim Sn.
П-> оо
Нового вида интегральная сумма отличается от рассмотренных
раньше интегральных сумм тем, что элементы Asn Д$2, ..., &sn
являются элементами дуги, а не прямолинейного отрезка.
Предел такой интегральной суммы называется криволинейным
интегралом от функции Ф (s), взятым по дуге АВ, и обозначается
знаком
J Ф (s) ds.
{jAB
Так что
f Ф(у)^= lim [Ф(^1)Д«1 + Ф(5а)Д«2+ ... +Ф($П)Д5„]. (1)
(_>АВ п * °°
Рассмотрим теперь более общий случай той же задачи, когда
переменная сила F, действующая на материальную точку, направлена
в каждый момент не по направлению движения точки, а под неко-
торым углом 7 к этому направлению (рис. 221). Принимая элемент
дуги MN = As за прямолинейный отрезок, положим
Y = (zWF, ЛТД/).
Тогда элементарная работа силы при перемещении точки М на
элемент As будет
bA=f (х, у) cos 7 • As.
31*
484
ПОНЯТИЕ о КРИВОЛИНЕЙНОМ ИНТЕГРАЛЕ
[ххх
письма значки, указывающие номер элемента, отбро-
шены).
Введем в рассмотрение проекции
Дх и Ду элемента Д$ на оси коорди-
нат; тогда
Дх = As cos а
(для
простоты
Ду = As sin а,
где а угол, составленный элементом
As с OX, a — (MN, ОХ).
Точно так же
Р(х, у) и Q(x,
введем проекции
у) силы f (х, у)
на оси координат; тогда
'Р(х, y)=f(x, ,y)cosp
Q(x, j)sinp,
где p угол, составленный направлением силы с
углами cf, р и 7 имеется связь
7 = р —а.
Так что
осью ОХ. Между
cos 7 = cos (р — а) = cos Р • cos а sin 0 • sin а.
Поэтому
AA=f (х, у) cos 7 • As = f (х, у) [cos р • cos а + sin р • sin а] As =
= /(х, у) cos р • As cos а /(х, у) sin 0 • As sin а =
= Р (х, у) Ах Q (х, у) Ду.
Чтобы вычислить всю работу силы при перемещении точки по
кривой от А до В, надо найти предел суммы элементарных работ
при беспредельном увеличении числа частей п, на которые мы раз-
биваем весь путь АВ, так что вся работа
♦ = п
Л= lim 2 [P(x^<)Ax/ + Q(x<.y<)4)'<] (2)
п -> оо г = 1
(снова восстанавливаем значки, указывающие номер элемента).
Предел этой суммы, отдельные элементы которой определяются
заданной кривой, представляет лишь несколько иную форму такого же
криволинейного интеграла, как форма (1).
В этой последней форме (2) чаще всего и представляются криво-
линейные интегралы. 1
1 Функции Р (х, у) и Q (х, у) предполагаются непрерывными и одно-
значными на протяжении пути интегрирования, т. е. во всех точках дуги ЛВ*
§ 183] ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА 485
§ 183. ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
Вычисление криволинейного интеграла ведется следующим образом.
1) Если кривая задана параметрически уравнениями
х = с?(/),
то, подставляя на место х, у и dx, dy их выражения через t и dt,
приходим к обыкновенному интегралу
J Р(х, y)dx-\-Q(x, y)dy =
^jAB
К
= f{P[<? (t), 0) (01 ?' (0 + Q [® (0, <» (01 (0) dt= f Ф (0 dt,
#0 ^0
где /0 и tx значения параметра t для начальной и конечной точек
кривой.
2) Если кривая задана уравнением в обычной форме
У = Г(Х),
то, заменяя у и dy их выражениями через х и dx, также придем
к обыкновенному интегралу
J Р (х, у) dx + Q (х, y)dy = J {Р [х, / (х)] Q [х, / (x)J f (х)} dx,
{jAB xQ
где Xq и xt абсциссы начальной и конечной точек кривой.
Пример 1. Вычислить интеграл ~ J* xdy—у dx, распространенный по
^ав
дуге АВ эллипса (рис. 222).
Уравнения эллипса возьмем в параметрической форме
х = a cos t
у = b sin t.
Тогда
dx — — a sintdt
dy = b cos t dt.
Следовательно,
TC
у J x dy —у dx = (b sin t • a sin t + a cos t • b cos t) dt =
l^jAB 0
it
1 , Г .. nab
^2ab JdZ = —-
о
486 ПОНЯТИЕ О КРИВОЛИНЕЙНОМ ИНТЕГРАЛЕ [XXX
Как известно, предложенный интеграл представляет площадь сектора
(см. формулу (5), стр. 338), что совершенно согласуется и с полученным
результатом. Действительно, известно, что
Пример 2. Вычислить I ху dx + х2 dyt распространенный на дугу ОД
^jOA
параболы ВОД (рис. 223).
Пусть уравнение параболы будет
у = kx2
и абсцисса точки Д равна а.
Тогда
dy = 2kx dx
и
а а
J ху dx + х2 dy = J (kx3 + 2&x3) dx = 3k x3 dx = ka4.
^jOA 6 о
§ 184. СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
Отметим некоторые свойства криволинейного интеграла.
Свойство I. Если линия, по которой берется интеграл, состоит
из отдельных частей, то интеграл по всей линии равен сумме
интегралов, взятых по каждой линии в отдельности в том же
направлении.
Свойство II. При перемене направления пути интегрирования
криволинейный интеграл меняет свой знак на обратный.
Оба свойства являются очевидными.
Свойство III. Если = то величина криволинейного ин-
теграла J Р dx-\-Qdy не зависит от пути интегрирования.
Известно, что если
ду дх 9
то выражение Pdx-\-Qdy есть
полный дифференциал некоторой функции, т. е. Pdx-\- Qdy = dU,
где U (х, у) функция от х, у.
§ 184] СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА 487
Тогда, следовательно,
J Pdx-[-Qdy = f dU (х, у).
{jAB {J AB
Для вычисления последнего интеграла мы должны применить
порядок, указанный в предыдущем параграфе, т. е. выразить под-
ынтегральное выражение через одну переменную.
Для этого, воспользовавшись уравнением кривой у = ср (х), за-
меним у через с?(х). Тогда подинтегральное выражение останется
дифференциалом некоторой функции одной переменной, что сразу же
позволит написать выражение для интеграла в виде разности зна-
чений функции U в начальной и конечной точках дуги. Так что
/точки В
dU(x9y)[U(x9y)] = U (x^y^—U (xQ,y0), (3)
^АВ СМ* Т0ЧКИ А
где х0, у0 и xlf yt означают координаты начальной и конечной то-
чек дуги АВ.
Формула (3), как сейчас увидим, и доказывает высказанное свой-
ство. Действительно, если криволинейный интеграл равняется раз-
ности значений функции U в начальной и конечной точках дуги,
то результат вычисления криволинейного интеграла получится один
и тот же, поведем ли интегрирование по дуге АВ или по какой-
либо другой кривой, соединяющей те же точки (рис. 224).
Пример. Предложим себе вычислить криволинейный интеграл
J 2xydx + x*dy
сначала по дуге круга АВ, радиус которого а, затем по хорде ABt и нако-
нец, по направлению АОВ (рис. 225).
Здесь Р = Чху, Q = x\ = 2х, = 2х.
Следовательно, интеграл не должен зависеть от пути интегрирования.
Для вычисления интеграла по дуге круга возьмем уравнения круга в па-
раметрической форме
х = a cos t
у = a sin t
488
ПОНЯТИЕ О КРИВОЛИНЕЙНОМ ИНТЕГРАЛЕ
[XXX
Тогда
dx = — a sin t dt, dy = a cos t dt.
T
J 2xy dx + x2 dy = j (2a cos t-a sin t •—d sin/4“ a2ws2t-a cos t)dt =
<JAB &
re
1"
= J (— 2a3 sin21 • cos 14- a3 cos81) dt =
Q
re re
= — 2a3[4*sln3^]a + ^3[sin t---i-sin3/]2 = — a34- v a8 = 0.
Ld Jo L 6 Jo 6 d
Вычислим тот же интеграл по хорде АВ.
Уравнение хорды будет х-\-у = а, откуда
у = а — х и dy = — dx.
Поэтому
о
J* 2 ху dx + х2 dy = J* [2х (a — x) — x2] dx =
хорда AB a
= — J* (2 ax — 3xa) dx = — (ax2 — x3)® = 0.
о
Наконец, вычислим тот же интеграл в направлении АОВ.
f 2ху dx + х2 dy = f 2ху dx-}-x2dy-\- f 2xy dx 4- x2dy.
АОВ AO OB
Уравнением линии АО будет у = 0, так что
j* 2ху dx + х2 dy = 0.
АО
Уравнением линии ОВ будет х = 0, так что
J 2ху dx + х2 dy = 0.
ов
Поэтому и
У 2ху dx x2dy = 0.
АОВ
Итак, пример этот полностью подтвердил третье свойство криволиней-
ного интеграла.
§ 184].
СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
489
с- дР &Q
Свойство IV. Если = fno
J Pdx+Qdy
L
по замкнутому контуру равен нулю.
Пусть имеется некоторый замкнутый
тур ABCDA = L (рис. 226), на который
пространяется интеграл
j* Pdx^Qdy.
L
Предложенный интеграл можно разбить
так:
криволинейный интеграл
Pdx + Qdy.
Ь <JABC <JCDA
Но J Pdx-\-Qdy = J Рdx-\-Qdy, так как он не зависит от
kJ CD A kJCBA
дР dQ
пути интегрирования, ведь по условию ; следовательно,
f Pdx-]-Qdy = f Pdx-\-Qdy-\- J Pdx + Qdy =
D UABC ^jCBA
= j* Pdx-\-Qdy— j* Pdx-\-Qdy = 0,
kJABC kJABC
что и требовалось доказать.
В заключение этого вопроса дадим еще один пример конкретной задачи
который приводит нас к криволинейному интегралу.
Из термодинамики известно, что состояние всякого тела определяется
тремя величинами: давлением р, объемом v и абсолютной температурой Т.
Между этими тремя величинами, однако, имеется зависимость, позволяющая
выразить одну из этих величин через две другие. Зависимость эта для газов
определяется формулой Клапейрона
pv — RT = О
или Ван-дер-Ваальса
(р +^)(v-b) = RT,
где R — некоторый тепловой коэффициент и а и b — некоторые постоянные,
различные для разных газов.
Так как из трех величин р; v, Т только две являются независимыми, то,
следовательно, состояние тела определяется двумя из них; пусть это будут
р и 1. С изменением р и v меняется и состояние тела. Приняв количества
р и v за координаты точек, мы можем сказать, что определенным точкам
координатной плоскости соответствует некоторое определенное состояние
тела и, наоборот, каждому состоянию отвечает своя точка плоскости.
Фиксируя на плоскости координат непрерывное изменение состояния
тела, мы чертим на ней некоторую линию, характеризующую процесс, проис-
ходящий в теле.
490 ПОНЯТИЕ О КРИВОЛИНЕЙНОМ ИНТЕГРАЛЕ [ххх
Одной из задач термодинамики и служит расчет количества тепла, погло-
щенного или выделенного телом при переходе из одного состояния в другое.
Для этого разбивают весь процесс на элементарные части, а кривую на
элементарные отрезки и подсчитывают количество тепла, поглощенного и
выделенного на каждом элементарном отрезке.
В термодинамике доказывается, что это элементарное количество тепла
для газов, подчиняющихся формуле Клапейрона, выражается следующей
формулой
dV ^=-^Pdv + ^vdP>
где Ср и cv соответственные теплоемкости при постоянном давлении и
объеме.
Для получения всего количества тепла остается лишь взять интеграл
по кривой, изображающей изменение состояния тела. Итак,
гт С СР J I cv J
U= -^Pdv +-nvdP-
L
Таким образом, расчет количества тепла, поглощенного или выделенного
телом в процессе изменения его состояния, приводится к вычислению криво-
линейного интеграла.
§ 185. ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что называется криволинейным интегралом?
2. В какой форме представляются обыкновенно криволинейные инте-
гралы?
3. Как вычисляются криволинейные интегралы?
4. Какими свойствами обладает криволинейный интеграл?
5. Когда криволинейный интеграл не зависит от пути интегрирования?
6. Вычислить интеграл J* ydx-{- 2х dy, распространенный на четверть
дуги круга радиуса г, заключенной в первом координатном угле в направле-
о ла2
нии против часовой стрелки. Отв,
7. Вычислить тот же интеграл, распространенный на хорду, стягивающую
дугу первой четверти круга в направлении от оси ОХ к OY,
Отв, уЛ
8. Вычислить интеграл j* sin х • cos у dx — cos х • sin у dy> распространен-
ный: 1) на диагональ, проходящую через начало координат квадрата, построен-
л
ного на отрезках, равных -у и отложенных от начала на осях координат
в положительном их направлении; 2) на две стороны того же квадрата,
лежащие на осях координат, считая направления сторон от начала координат.
Отв, 0, 1, — 1.
9. Вычислить интеграл J* sinjy • cos х dx + sin х • cos у dy> распространен-
ный на те же контуры. Отв, 1,0, 0.
XXXI. ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ
§ 186. ОБ ИНТЕРПОЛИРОВАНИИ ВООБЩЕ
Интерполировать какую-нибудь функцию / (х) значит по не-
скольким данным значениям этой функции вычислить любое проме-
жуточное ее значение хотя бы приближенно.
Так формулированная задача заключает в себе еще много не-
определенного и потому допускает весьма разнообразные решения.
Одно из решений заключается в том, что соответственно данным
условиям подбирают некоторую целую рациональную функцию
значения которой совпадали бы со значениями функции /(х) при
некоторых значениях х. Затем, допуская, что для промежуточных
значений х функция /(х) мало отличается от F (х), полагают при-
ближенно
/(x)«F(x) (1)
и, пользуясь этим равенством, вычисляют промежуточные значения
функции /(х). Формулы, подобные (1), носят название формул интер-
полирования.
Суть решения задачи состоит, следовательно, в том, что вы-
числение значений данной функции / (х) заменяется вычислением
значений некоторой целой рациональной функции F (х), что, как
известно, сводится к простым арифметическим действиям.
Такого рода идеей, в сущности, мы уже пользовались при раз-
ложении функций в ряды.
В самом деле, ряды
е =1+ 1+1.2+1.2.3+
____X X3 t X5
sin х — J 1.2-3’ 1-2.3-4-5
и другие в вопросах вычисления самих функций е®, sinx и др.
играют именно роль тех целых функций, которые мы (останавливаясь
на некотором числе членов) полагаем приближенно равными соот-
ветствующим функциям.
492
ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ
[XXXI
Задача интерполирования, однако, не заключается только в раз-
ложении функций в ряды, а, как мы уже сказали, в подборе вообще
некоторой, в простейшем случае целой рациональной функции F (х),
долженствующей заменить при вычислении данную функцию /(х).
§ 187. ФОРМУЛА ИНТЕРПОЛИРОВАНИЯ ЛАГРАНЖА
Положим, что нам известны п -f-1 значений вычисляемой функ-
ции /(х):
/ («о) =Л» /(fli) = У1, • • •/ (ап) = Уп-
Лагранж дал выражение целой рациональной функции Г(х), совпа-
дающей по своим значениям с данной при
х = а0> х = а1, ..., х = ап,
т. е. такой, для которой
F (йо) =Л> F (ai) =У1> •••> F (ап) = уп. (2)
Формула эта имеет следующий вид:
F (х) = (х ~ а'№ ~ ........5х ~ а”}. • у0 +
v (а0 — ai)(a0 — аг)....(аа — ап) лоп
I (х «о) (х gg)........(х ап) ।
(Д1 — «о) («1 — а2).(at-an) W
(х—а0)(х — а1)...(х — ап^)
'(«п-«о)(«п~ «г)...(«п—«п-1) 'Уп'
Простая проверка, именно подстановка на место х значений
а0, а19 ...ап убеждает нас в том, что формула Лагранжа действи-
тельно удовлетворяет условиям (2).
Как видно, функция эта не выше, чем /z-ой степени, если число
заданных значений х равно п 1.
Полагая затем
мы получим формулу интерполирования Лагранжа,
§ 188] ЛИНЕЙНОЕ ИНТЕРПОЛИРОВАНИЕ 493
Равенство это, верное для выбранных п значений а0, а19 ... ап.
является лишь приближенным при других значениях х.1
Замена вычисляемой функции f (х) целой рациональной функцией
F (х) степени имеет наглядный геометрический смысл, именно
замена эта равносильна замене кривой KL, уравнение которой
некоторой параболой /z-ого порядка RS (рис. 227), уравнение которой
и которая с данной кривой KL имеет /г -f- 1 общих точек:
^1, Лд, . . .
§ 188. ЛИНЕЙНОЕ ИНТЕРПОЛИРОВАНИЕ
Обратим особенное внимание на один частный случай. Положим,
что нам требуется вычислить значения функции f (х) в некотором
промежутке, зная только два значения этой функции на его концах:
/(«о)=Л> /(«1)=Л-
Для решения этой задачи подберем целую рациональную функцию
первой степени так, чтобы ее два значения при x = aQ и х = а1
совпадали с соответственными значениями самой функции. Графи-
ком такой функции будет прямая, которая с кривой
У=Цх)
имеет в рассматриваемом промежутке по крайней мере две общие
точки: Л0(а0, _у0), (at, у^.
Это будет, следовательно, секущая, проходящая через точки Ло
и ЛР
Уравнение этой прямой напишется так:
У—Уо = х — ап
У1—Уо Я1 —я0’
Отсюда уже легко получить и саму искомую функцию
У = Р (*) = Уо+£=% (х — ао)-
1*1 с* у
Формула (4) получается непосредственно также и из
Лагранжа (I). Рекомендуем сделать это читателю.
Замена вычисляемой функции f(x) функцией (4) или, что то же,
функцией, удовлетворяющей уравнению (3), геометрически равно-
сильна замене кривой линии ЛОВЛХ прямой ЛОЛР или, другими
1 О величине погрешности такого приближенного равенства см.»
например, Я. С. Безиков ич, .Приближенные вычисления".
(3)
(4)
формулы
494
ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ
[XXXI
°Р’а0
0Q- X QM-y
0R = at RAfy,
Уо
Р
О
Q R
Рис. 228.
словами, равносильна соглашению считать, что на протяжении дуги
приращение функции f (х) пропорционально приращению
переменной х(см. формулу (3)).
Действительно, такая пропорциональность имеет место для всякой
прямой, что непосредственно вытекает как из чертежа, так и из
уравнения прямой (3), в котором разности у—у0 и уг—у0 являются
приращениями функции, а
х— aQ и аг — aQ приращения-
ми переменной х. Конечно, та-
кая пропорциональность для
функции /(х) является только
приближенной; ею пользуются,
вообще говоря, лишь на малых
промежутках [а0, aj и при-
том тогда, когда можно рас-
считывать, что значения функ-
ции / (х) в этом промежутке
достаточно мало отличаются
от значений функций Г(х).
Тем не менее, прием вычи-
сления промежуточных значений функции /(х), основанный на
вышеуказанной пропорциональности, употребляется довольно часто.
Этот прием применяется и в различных таблицах. Вспомним хотя бы
вычисление пятого десятичного знака логарифмов чисел при употребле-
нии пятизначных таблиц.
Интерполирование, основанное на вышеизложенном, т. е. на
замене функции /(х) функцией первой степени (4) и, следовательно,
на применении указанной пропорциональности, носит название ли-
нейного интерполирования.
Приведем несколько примеров такого интерполирования.
Пример 1. Определить плотность D дистиллированной воды при темпе-
ратуре в 18,36° С.
По таблицам плотностей находим
плотность воды при: t= 18,3°.............0,998571
f =18,4°....0,998552.
Принимая, что на промежутке в 0,1° изменение плотности ДР пропор-
ционально изменению температуры ДЛ имеем
при: М = 0,1 °.. .ДР = — 19 единиц шестого знака
Д/ = 0,01°.. .ДР = — 1,9 .
Д/ = 0,06°...ДР = —11,4 „
Таким образом, искомая плотность будет приближенно равна
0,998571
— 11
Р=0,998560.
§ ;188]
ЛИНЕЙНОЕ ИНТЕРПОЛИРОВАНИЕ
495
Пример 2. По данным в пятизначных таблицах логарифмам двух чисел
1g 29360 = 4,46776,
1g 29370 = 4,46790.
найти логарифмы всех промежуточных целых чисел.
Замечая, что при изменении чисел на 10 единиц логарифмы их изменяются
на 14 единиц пятого десятичного знака, и принимая, что на этом промежутке
изменение логарифма пропорционально изменению числа, находим:
lg 29362 = 4,46776
lg 29363 = 4,46776
lg 29364 = 4,46776 + 0,000056
lg 29365 = 4.46776 ----------
lg 29366 = 4,46776
lg 29367 = 4,46776
1g 29360 = 4,46776
1g 29361 = 4,46776 + 0,000014 = 4,46777
‘ ------ 0,000028 = 4,46779
0,000042 = 4,46780
-------- 4,46782
0,000070 = 4,46783
0,000084 = 4,46784
0,000098 = 4,46786
1g 29368 = 4,46776 + 0,000112 = 4,46787
lg 29369 = 4,46776 -f- 0,000126 = 4,46789
1g 29370 = 4,46776 4- 0,000140 = 4,46790
Примечание: Числа третьего столбца входят в столбец так
называемых .partes proportionales*, помещаемых обыкновенно в табли-
цах логарифмов на полях.
Пропорциональность между приращением независимой переменной
и соответствующим приращением функции, которая, по предполо-
жению, в пределах точности вычисления выполняется при линейном
интегрировании, конечно, не всегда имеет место. Поэтому и не всегда
возможно прибегать к такому простейшему приему интерполирова-
ния. В более сложных случаях, когда мы не в праве кривую А^ВАг
заменять прямой или, иначе, функцию / (х) заменять линейной
функцией, приходится вычисляемую функцию f (х) заменять целой
рациональной функцией выше 1-й степени, т. е., говоря геометри-
чески, кривую AqBA^ заменять параболой 2-го, 3-га и т. д. п-го
порядка, в зависимости от того, имеется ли у нас в распоряжении
три, четыре и т. д. л-|-1 данных значений функции/(х). Такой
прием интерполирования носит название параболического интерпо-
лирования и может быть выполнен применением формулы интерпо-
лирования Лагранжа.
Поясним его применение на примере.
Пример 3. Положим, нам требуется по данным значениям некоторой
функции /(х):
/(-1) = 2, /(0) = 1, /(1)=—-2, /(2) = —4
вычислить следующие значения той же функции:
л-4). <})/(»•
Для решения этой задачи составляем по формуле интерполирования
Лагранжа новую функцию F(x), которая при значениях х =—1,0, 1,2
совпадала бы со значениями функции f (х); т. е. такую, чтобы
F( —1) = 2, F(0) = l, F(l) = —2, F(2)= —4.
496 ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ [XXXI
Выписывая эту функцию по формуле (I), находим
— — 2) о , (х + 1)(х — 1)(х — 2)
—Ь —2. —3 1 . _ I . _2
(х+1).х.(х-2) п (х+1).х.(х-1) л
2-1.—1 3-2-1
Произведя выкладки, получаем
F(x) = 1-x3-x2-Ax+1.
Нетрудно проверить, что F(x) действительно удовлетворяет поставлен-
ным ей условиям.
Для приближенного вычисления намеченных промежуточных значений:
/(-4). ,(). /(|),
а также и других промежуточных значений функции f (х), полагаем прибли-
женно
f(x)^F(x),
т. е.
/(Х)«1х3-Х2 -ух+1.
Тогда с некоторым приближением находим, что
<(-4)=>Й. А-
Таким же образом находим и другие промежуточные значения той же
функции f (х) и, конечно, также лишь приближенно.
Примечание. Вычисление значений функции /(х) для значений
х, выходящих из ряда заданных значений аргумента, называется экстра-
полированием. Пользоваться приемом экстраполирования рекомендуется
лишь с особой осторожностью, ввиду возможности сделать при этом
ошибку, оценка которой может оказаться затруднительной.
Уже приведенный пример показывает, что пользоваться формулой
интерполирования Лагранжа не представляет больших удобств, ввиду
сложности самой формулы,, требующей больших выкладок.
Особенным же неудобством этой формулы служит то обстоятель-
ство, что, при желании уточнить расчет введением какого-нибудь
лишнего данного, приходится не исправлять и не дополнять прове-
денные уже выкладки, а всю работу, начиная с составления фор-
мулы Лагранжа, начинать заново. Этого недостатка не имеет фор-
мула интерполирования Ньютона, вывод которой и приводится ниже.
Так как формула Ньютона требует введения нового понятия о ко-
нечных разностях, то к выяснению этого понятия и следует прежде
всего обратиться.
Отмеченный выше недостаток полностью устранен в методе ин-
терполирования по способу наименьших квадратов, данный П. Л. Че-
бышевым. Но, к сожалению, в таком кратком руководстве нет
возможности его касаться.
§ 189| ПОНЯТИЕ О КОНЕЧНЫХ РАЗНОСТЯХ 497
§ 189. ПОНЯТИЕ О КОНЕЧНЫХ РАЗНОСТЯХ
Положим, что мы рассматриваем значения функции / (х) при
х = а, x = a-\~h, х = a-\-2h, . . х = a -f- nh,
т.е. значения
/(а), /(а + й), /(а 4- 2Л), ..., / (а4-nk\
где а и А— известные заданные нам числа.
Разность f(a -\-h)—f(a) мы называли приращением функции
при х = а (см. стр. 196) и обозначали знаком А/ (а). Сохраняя то
же обозначение
/(a^A)—/(а) = Д/(я), (5)
будем теперь называть это приращение конечной разностью, или
просто разностью функции f(x) при х = а, словом „конечной “
подчеркивая; что величину А мы вовсе не предполагаем приближать
к нулю.
Подобно этому установим обозначения
f(a 4- 2А)-f(a + h) = bf(a + А)
f(a-\- 3h)—f(a 4- 2A) = Д/(а 4~ 2A)
.......................................... (6)
f(a 4- nh) —f(a 4- (n — 1) А) = Д/(а 4- (n — 1) A)
и будем называть вышеприведенные разности конечными разностями
функции при
x = a-{-h, x = a + 2h,...........х = а-\-(п—1)А.
Из разностей, имеющихся в равенствах (5) и (6), можно составить
новые разности, которые будем называть конечными разностями 2-го
порядка, или просто разностями 2-го порядка, и обозначать так:
Д/(а4-А) — Д/(а) = Да/(а),
Д/(а4~ 2й) — Д/(а 4~й) = Д2/(а 4~й).
И т. д.
Продолжая те же рассуждения, можно составить разности
третьего, четвертого и т. д. порядков, которые будем обозначать
Д8/ (а), . Д»/ (а 4- А), Д»/(а 4~ 2А). ..
Д</(а), ДУ(а4-А), Д4/(а4-2А)...
И т. д.
Так, например, под Дв/(а-|-ЗА) будем понимать разность
Д5/ {а + 4А) — ДУ (a -j- ЗА).
32 Зак. 2116. Н. С. Михельсон.
498 ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ [ХХХ1
Таблицу таких разностей обыкновенно выписывают в определенном
порядке по следующей, примерно, схеме:
X /(X) Д2/(Х) ДУ(х)
а a-\-h а 2Л f (л) /(а + А) Г(« + 2Л) Д/(а) Д/(а + Л) Д/(а + 2Л) Д2/(а) Д2/(а + й)
а nh f(a + nh) Д/(а + п — 1й) Д2/(а4-л^2й) и т. д.
Пример 4. Рассмотрим пример составления такой таблицы. Возьмем
например, функцию
/(х) = х* — 2*з Зл;— ю
и составим для нее таблицу разностей до третьего порядка включительно
для целых значений х, начиная с х = 0.
X /(X) Д/(х) Д2/(Х) ДУ(х)
0 -10 2 2 24
1 — 8 4 26 48
2 — 4 30 74 72
3 26 104 146 96
4 130 250 242 120
5 380 492 362
6 872 854
7 1726
Таблица эта составляется так: простой подстановкой в нашу функцию
соответствующих значений х вычисляем сначала числа первого столбца,
т. е. значения f (х), затем, вычитая из каждого последующего числа этого
столбца предыдущее число, получаем числа второго столбца, т. е. значе-
ния Д/ (х); подобным образом поступая далее, находим числа третьего и
четвертого столбцов.
§ 190. ПРОСТЕЙШИЕ ТЕОРЕМЫ О РАЗНОСТЯХ
Докажем некоторые основные теоремы о разностях.
Теорема 1. Разности двух функций, отличающихся на по-
стоянную, равны между собою.
Пусть
/(*) = ?(*) 4~£,
тогда
д/ (*) = [? (* + А) + С] -1? (х) + С] = ч» (х + А) - ? (X) = Д? (х).
§ 190] ПРОСТЕЙШИЕ ТЕОРЕМЫ О РАЗНОСТЯХ 499
Из этого видно, что при вычислении разностей постоянное сла-
гаемое можно не принимать во внимание, или, иначе, разность от
постоянного числа равна нулю.
Теорема 2. Постоянный множитель можно вынести за знак
разности.
Пусть
/(х) = С-©(х),
тогда
Д/ (х) = Cep (х -j- h) — Сф (х) = С [ф (х + Л) — ф (х)] = С • Дф (х).
Теорема 3. Разность алгебраической суммы нескольких функ-
ций равна алгебраической сумме разностей этих функций.
Пусть
(*)+%(*),
тогда
Д/ (*) = [®1 (X + Л) 4- ©2 (х + Л)] — [©i (х) 4- ©2 (x)J =
= [®1 (X + Л) — ©1 (х)] 4- [Ф2 (X + й) — ©2 (X)] = Д«1 (х) 4- Д©2 (X)
Теорема 4. Разность п Ц-1 порядка от целой рациональной
функции п-ой степени равна нулю.
Составим сначала разность первого порядка от
/(х)—х’1,
где п — целое и положительное число:
Д (хя) = (х + h)n — х™ = хп nhxn~x 4" 4~---
... 4~ Ая — хя = nhxn~1 4- 1) Л2хя“24~....
Оказывается, что разность от целой и положительной степени
переменной есть целая рациональная функция степени на единицу
ниже, чем данная.
Рассмотрим теперь целую рациональную функцию л-ой степени
общего вида
/(х)=р0^4"Р1^*1+ - --+Рп-1* + Рп-
Применяя теоремы 1, 2 и 3, находим
Д/М=РоА(хП)+Р1Д(хП“1)4“ •“ +Рп-1Д*-
По только что доказанному каждый член этой последней суммы
является целой рациональной функцией степени на единицу ниже
степени, стоящей под знаком разности, а поэтому и вся разность
Д/(х)
представит целую функцию (п—1)-ой степени*
32*
500
ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ
[ХХХ1
Итак, Д/ (х)— многочлен (п—1)-ой степени
ДУ(х) , (л—2)
Д8/(х) , (л-3)
Дл/ (х) — многочлен нулевой степени,
т. е. постоянная.
Дп+1/(х) = 0.
Последнее и требовалось доказать.
§ 191. ПРИМЕНЕНИЕ РАЗНОСТЕЙ К СОСТАВЛЕНИЮ ТАБЛИЦ
ЗНАЧЕНИЙ ФУНКЦИЙ
Обращаясь снова к приведенному на стр. 498 примеру 4, про-
должим таблицу разностей целой функции
/(х) = х4 — 2х34“Зх— 10
до разностей 5-го порядка.
X /(X) Д/(х) Д2/(Х) Д’/(х) ДУ(х) ДБ/(х)
0 — 10 2 2 24 24 0
1 - 8 4 26 48 24 0
2 — 4 30 74 72 24 0
3 26 104 146 96 24 0
4 130 250 242 120 24 0
5 380 492 362
6 872 854
7 1726
Как и следовало ожидать в соответствии с теоремой 4 предыду-
щего параграфа, все разности 5-го порядка равны нулю.
Это обстоятельство сильно упрощает составление разностей для
нашей функции и делает возможным распространение этой таблицы
на другие значения независимой переменной.УГак, для взятой функ-
ции достаточно было бы составить следующую, более сокращенную,
таблицу с пятью значениями функции f (х) в первом столбце,
X /(*) Д/(х) Д*/(Х) ДУ(х) Д</(Х)
0 — 10 2 2 24 24
1 — 8 4 26 48
2 — 4 30 74
3 26 104
4 130
§ 191] ПРИМЕНЕНИЕ РАЗНОСТЕЙ К СОСТАВЛЕНИЮ ТАБЛИЦ 501
чтобы затем, приняв во внимание, что все разности 4-го порядка
равны постоянному числу 24, и предварительно включив их в таб-
лицу, распространить эту таблицу на другие значения х.
При заполнении такой таблицы надо помнить, что, согласно
определению разностей, каждое последующее число какого-нибудь
столбца является суммой предыдущего числа того же столбца и
числа, стоящего рядом с последним (в одной с ним строчке), взя-
того из следующего за ним столбца.
Так, идя вниз, найдем
X /(*) VW Д2/(Х) Д’/(х) ДУ(х)
0 - 10 2 2 24 24
1 2 - 8 — 4 4 30 26 74 48 72 24 24 ду (2) = 48 + 24 = 72
3 26 104 146 96 24 дзу (3) = 72 + 24 = 96 и т. д.
4 130 250 242 120 24
5 380 492 362 144 24
6 7 872 1726 854 1360 506 674 168 Д2/(3) = 744-72 = 146
8 3086 2034 и т. д.
9 ' 5120 1
а идя вверх, соответственно только что сказанному, получим:
X /(•') Д/(х) Д2/(Х) Д3/(х) Д4/(х) дзу 1) = 24-24 = 0
— 5 850 — 448 242 — 96 24 Дз/(—2) = 0 —24 =
— 4 362 — 246 146 — 72 24 = -24
— 3 116 — 100 74 — 48 24
— 2 16 — 26 26 — 24 24 и т. д.
— 1 0 — 10 — 10 0 2 2 2 0 24 24 24 Д2/(—1) = 2 — 0 = 2
и т. д.
Таким образом, для целой рациональной функции 4-й степени
достаточно вычислить лишь пять ее значений, чтобы по ним иметь
возможность простым сложением и вычитанием составить таблицу
значений этой функции через равные промежутки на протяжении
интервала любой величины. Изложенное относится и ко всякой целой
рациональной функции.
Пример 5. Рассмотрим еще один пример составления подобной таб’
лицы. Пусть
/(*) = ig v;
ррим^м
• « = 7650 и h = 1(1
502 ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ [XXXI
и положим, что нам известны вычисленные каким-нибудь способом следую-
щие значения нашей функции с точностью до
1g 7650 = 3,8836614
lg 7660 = 3,8642288
lg 7670 = 3,8847954
lg 7680 = 3,8853612
lg 7690 = 3,8859263
На основании этих данных составляем следующую таблицу раз-
ностей:
X /(*) Д/(х) Д2/(Х) Дз/(х)
7650 7660 7670 7680 7690 3,8836614 3,8842288 3,8847954 3,8853612 3,8859263 0,0005674 0,0005666 0,0<М>5658 0,0005651 —0,0000008 —0.000(4)08 —0,0000007 0,0(4)0000 0,0000001
Хотя мы и не получили разностей, равных нулю, однако раз-
ности 3-го порядка настолько малы, что с некоторою погрешностью
их можно считать равными нулю. Допуская это, мы можем, подобно
предыдущему, распространить эту таблицу на другие значения х,
вычисленные через те же промежутки, равные 10, и получить таким
образом значения логарифмов других чисел. При этом, конечно,
мы не можем претендовать на ту же точность этих результатов,
как и данных чисел.1
Таким образом, мы получаем:
X /(*) Д/(х) Д2/(Х) Д3/(х)
7600 3,8808124 0,0005714 —0.0000008 0
7610 3.8813838 0,0005706 -0,0000008 0
7620 3,8819544 0,<>005698 —O.OOOOJ08 0
7630 3,8825242 0,0005690 —0,0000008 0
7640 3/830932 0.0005682 —0,0000008 0
7650 3,8836614 0,0005674 —0,0000008 0
7660 3 8842288 0,0005666 —0,0000008 0
7670 3,8847954 0.0005658 —0.6000008 0
7680 3,8853612 0,0005650 —0,00и0008 0
7690 3.8859262 0,0005642 —0,1)000008 0
7700 3,8864904 0.0005634 —0.0000008 0
7710 38870538 0,0005626 —0,0О00ио8 0
7720 3,8876164 0,0005618 —0,0060008 0
7730 3.8881782 0.0005610 —0,0000008 0
7740 3,8887392
1 Определение величины погрешностей при таких расчетах см. Я- Cf 0
з и к о в и ч, „Приближенные вычисления0.
§ 192] ФОРМУЛА ИНТЕРПОЛИРОВАНИЯ НЬЮТОНА 503
Найденные значения логарифмов оказываются достаточно точ-
ными: ошибка логарифмов крайних чисел не превышает 2 единиц
шестого десятичного знака. Другие же результаты еще точнее.
Таким образом, мы обнаруживаем, что, зная логарифмы пяти
взятых нами чисел с точностью можно при помощи примене-
ния разностей 1-го — 3-го порядка найти логарифмы ряда других
чисел через каждые 10 единиц и притом с достаточной точностью.
При этом само вычисление требует лишь действий сложения и вы-
читания. Распространение таблицы на значения х вне выбранных
пяти основных является экстраполированием.
Было уже отмечено, что при составлении последней таблицы
разности 3-го порядка были приняты равными нулю. Равенство
нулю всех разностей 3-го порядка возможно лишь для целой ра-
циональной функции 2-й степени. Отсюда следует, что, считая раз-
ности 3-го порядка равными нулю, мы тем самым 1g.г заменили
целой рациональной функцией 2-й степени.
§ 192. ФОРМУЛА ИНТЕРПОЛИРОВАНИЯ НЬЮТОНА
Особое значение в исчислении конечных разностей имеет целая
рациональная функция n-ой степени вида
со(х) = А (х— а) (х— а — Я)(х— а — 2Я) .. .(х — а — п — 1/г), (8)
где А и а некоторые постоянные числа.
В вопросах исчисления конечных разностей функция эта играет
ту же роль, как в анализе бесконечно малых степенная функция хп
с целым и положительным показателем п. Объясняется это просто-
тою составления разностей различных порядков от функции со(х).
Действительно, найдем сначала
Доо(х) = w(x-|-/z)—о>(х).
Для этого составляем
а) (х -f- Я) = А (х + Я — а) (х — а).(х — а — п — 2Я) (9)
и, вычитая из формулы (9) выражение (8), находим
Д оо (х) = А (х — а) (х — а — Я).
....(х — а — п — 2Я) [(хЦ-/г — а) —(х — я —n— 1А)].
Разность, стоящая в прямых скоб/ах, приводится после упроще-
ния к п,Я, поэтому имеем
Дш (х) = АпЯ (х — а) (х — а — Я).....(х — а — п — 2Я). (10)
Таким образом, для составления разности первого порядка от функ-
ции а) (х) надо умножить ее на число множителей, содержащихся
504 ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ [XXXI
в функции, т. е. на степень функции ш (х), и, отбросив последний
множитель, заменить его приращением h.
Полезно заметить, что составление разности от рассматриваемой
функции со(х) напоминает составление дифференциала степени:
d(хп) = лх71-1 • h = пхп~х • dx.
Зная правило составления первой разности от функции со (х),
нетрудно подобным образом составить и разности высших порядков
от функции со (х):
(х) = А (п — 1) n-h2(x — а) (х — а — h).....(х — а — п — 3h)
(х) = Л (л — 2) (л — 1) • nh3 (х — а) (х — a — h)..
.....(х — а — п — 4h)
Д71® (х) = А • 1 • 2 • 3... (л — 1) • nh"
Дп+1(о (х) = Дм (х) = Д71+8® (х) =....= 0.
Пользуясь вышеизложенным свойством функции w (х), поставим
следующий вопрос:
нельзя ли целую рациональную функцию /(х) представить
в форме суммы, расположенной не по степеням переменной х,
а по функциям вида <о(х) различных степеней, т. е. так:
f (х) = Ло -[- Аг (х — а) + А2 (х — а)(х — а — h)-\-
+ А а (х — а)(х — а — h)(x — а — 2Л) 4-...
+ Ап(х — а) (х — а — h)... (х — а — п — 1й). (11)
Поставленная задача разрешится в положительном смысле, если
нам удастся найти определенные значения коэффициентов Ло, Лр . . .
...Лп так, чтобы равенство (11) было бы тождеством.
Для этого составим от обеих частей равенства (Ц) последова-
тельные разности различных порядков до л-ой включительно.
Д/(х) = Л^Ц-Ла2Л(х— я) + Л8ЗЛ (х — а) (х — а — h) + ...
... 4" Annh (х — а) (х — а — h). .. (х — а — п — 2h).
Д2/(х) = Л22/г2 4- Л32 • ЗЛ2 (х — а) 4- Л43 • 4 • h2 (х -а)(х — а — Л)4-
4- ... 4- Лп (л — 1) • nh2 (х — а) (х — а — Л). .. (х — а — л — 3/г).
Д8/(х) = Л3-2.3Л84-Л42.3.4Л8(у —а)4-.. .
... 4- Лп (л — 2) (л*— 1) nh3 (х — а) (х — а — h)...
,.. (х — а — л — 4А),
Дп/(х) = ЛпЬ2.3.?.(л—1).л.^т
§ 193] ПРИЛОЖЕНИЕ ФОРМУЛЫ НЬЮТОНА 505
Так как все вышеприведенные равенства должны быть тожде-
ствами, то, подставляя в них и в тождество (И) х = а, полупим
f(d) = Ло, = Axh, = Л21 -2/z2, Д8/(л) = zl31 - 2 • 3 •
. . . Дп/(а) = лл1.2.3 ... n*hn.
Отсюда и находим коэффициенты
дя=//а) А _W) а - Д2/(а)
^0 J W» 241 \*h ’ 1-2-Л2’
л _ **/(«) л _
8— 1-2-3-ЛЗ ’ ..../1”—1-2-3...n-h*'
Таким образом, поставленная выше задача разрешена в положи-
тельном смысле, и формула (11) представляется в следующем виде:
/(х) = /(я) + Ц(а) + {X~a\{X~h^~-h) Л2/(«) +....
। (х — а) (x—a — h).(x — a — n — lh) f
•••“’ 1-2-3..n-h” a / W-
Это и есть важная в задаче интерполирования формула Ньютона.
§ 193. ПРИЛОЖЕНИЕ ФОРМУЛЫ НЬЮТОНА К ЗАДАЧЕ
ИНТЕРПОЛИРОВАНИЯ
Пока f (х) — целая рациональная функция, формула (II) предста-
вляет собой новую форму той же самой функции, т. е. тождествен-
ное преобразование этой же функции, подобно тому, как формула
Интерполирования (I) Лагранжа представляет также тождественное
преобразование целой рациональной функции F (х).
Предположим теперь, что / (х) не целая рациональна^ функция,
и допустим, что нам известны п частных значений этой функции: (
/(«). /(а + А), /(a-J~2A).. .f(a-\-nh)
при некоторых выбранных нами значениях а и h. По этим значе-
ниям нетрудно вычислить и значения конечных разностей
Д/ (а), Д2/ (а), ДЗ/(а),..., Д(а),
как это было сделано в примерах 4 и 5, и составить формулу (II),
в которой разности различных порядков можно считать известными.
Правая ее часть попрежнему представляет некоторую целую рацио-
нальную функцию, значения которой совпадают с значениями нашей
функции при х равном
6Z, а —[— /г, ci —2/z,. . ., a —nh.
но при других значениях x формула (II) представляет собой лишь
приближенное выражение функции /(х), которым и пользуются для
вычисления функции /(х) при других значениях переменной, В этом
506 ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ [XXXI
смысле формула (II) является формулой интерполирования и назы-
вается формулой интерполирования Ньютона.
Что касается погрешности (х) такого приближенного равенства,
то можно было бы показать, что абсолютное ее значение не пре-
восходит следующей величины:
1Ж*)|
| (х— а) (х— а — h).. .(х ~ а — nh) М \
1 • 2 • 3.. .л (л + 1)
где М представляет наибольшее значение производной
/(”+D (х)
в промежутке от х = а до х = а nh.
По основной идее формула интерполирования Ньютона выпол-
няет то же назначение, как и формула Лагранжа: замену некоторой
функции /(х) целой рациональной функцией л-ой степени, совпадаю-
щей по своим значениям с функцией /(х) при п -|- 1 значениях х.
Геометрически и здесь некоторая кривая, уравнение которой
v=/(x), заменяется параболой n-ой степени, имеющей с кривой
it 4-1 общих точек.
Так как в самую формулу интерполирования Ньютона входят не
задаваемые значения вычисляемой функции /(х), а лишь /(а) и зна-
чения разностей этой функции до л-го порядка при х = л, то при
пользовании этой формулой необходимо, как уже сказано, предва-
рительно по данным значениям
/(а), /(а + й), /(а + 2й),...,/(аЧ-лй)
вычислить разности
Д/(л), Д2/(я), . .., Д”/(а).
Большим преимуществом формулы Ньютона перед формулой
Лагранжа является то обстоятельство, что при увеличении данных
значений функции, которыми мы хотим воспользоваться при интер-
поляции, не приходится перестраивать все формулы, а достаточно
добавить только лишние члены, что вытекает из самой конструкции
формулы Ньютона.
Пример 1. По нижеследующим данным значениям 1g х при основании 10
1g 200 = 2,30103 ,
1g 210 =2,32222
1g 220 = 2,34242
lg 230 = 2,36173
найти логарифмы промежуточных целых чисел.
3 условиях задачи мы имеем
0 = 200, й = Ю, /2 = 3, /(x)=lgx,
§ 193|
ПРИЛОЖЕНИЕ ФОРМУЛЫ НЬЮТОНА
507
Формула Ньютона применительно к данному случаю будет следующей:
,8 „ l8. + . ,8 .+™ Д. 1Е а +
+ (х-гоо)|(,г-2|ОИ,-220)д„ед (,2)
При этом погрешность вычисления по абсолютной величине не пре-
высит
| (х — 200) (х — 210) (х — 220) (х — 230) М |
1-2-3-4
где М — наибольшее значение |/IV (х) | в рассматриваемом промежутке значе-
ний х от 200 до 230.
Для того чтобы знать, с какой точностью мы можем рассчитывать по-
лучить результаты вычислений по формуле Ньютона, займемся сначала вы-
числением предела погрешности.
Так как
? /(•?) = 1g
то
-iv, \ 1*2*3
f (*) =------^4“
За наибольшее абсолютное значение М в данном случае можно принять
д, 1-2-3
М 2U04 ’ °’5'
так как 1g е = 0,43429<0,5, а наименьшее значение х равно 200.
Поэтому
|/? х —200) (х —210) (х—220) (х—230)| 1 *2*3*0,5
1*2*3*4 ’ 2004
Можно было бы показать, что наибольшей величины, по своему абсолют-
ному значению, числитель последней дроби достигает около значения х = 204
и х = 226. Вычисляя эту дробь для значения х = 226, находим
I Я W I < ^716Ю68’4 = = °’00000078- '
Таким образом, пользуясь формулой Ньютона, мы можем ожидать ошибки,
меньшей одной единицы шестого десятичного знака, если только исходные
данные достаточной точности. Так как логарифмы чисел 200, 210, 220 и 230
заданы с точностью до половины единицы шестого десятичного знака, то
рассчитывать можно лишь на ту точность результата, какую при таких усло-
виях может дать формула (12). Исследование ее (см. § 160) показывает, что
в худшем случае ошибка может достичь пяти единиц пятого десятичного
знака. Итак, приступая к вычислению, составляем таблицу разностей:
X 1g х dlgx Д21g х A3lgx
200 210 220 230 2,30103 2,32222 2,34242 2,36173 + 0,02119 + 0,02020 + 0,01931 — 0,00099 - 0,00089 + 0,00010
508
ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ
[XXXI
При Затем ведем расчет по формуле (12). л- = 202
1g 202 = 2,30103 + Л 0,02119 + 2 ' 0,00099 + IО 1 *
+ 2l.283.1J8°-000,°-
lg 202 = 2,30103 1-е слагаемое 0,004238 2-е 0,000079 3-е , . 0,000005 4-е •
2,305352
При х = 204
1g 204 = 2,30103 + — 0,02119 — f • 0,00099 + 1U 1 • Z • 1
+ 4b263.J6 - 0’00010-
1g 204 = 2,30103 . 1-е слагаемое 0,008476 2-е 0,000119 3-е 0,000006 . 4-е
При 2,309631 х — 206
1g206 = 2,30103 + • 0,02119 — Цт"*. .0,00099 +
б . —4 • 14 + 1.2 3-103 •°’00010-
1g 206 = 2,30103 1-с слагаемое 0,012714 2-е 0,000119 3-е 0,000006 4-е
2,313869
При х = 208 1g208 = 2,30103 + • 0,02119 — ,8 а~?3 0,00099 +
+ 81.223.10з12-0’00010-
1g 208 = 2,30103 1-е слагаемое 0,016952 2-е 0,000079 3-е 0,000003 4-е
2,318064
Найденные значения логарифмов, оказывается, отличаются от истинных
не более чем на 0,000002.
Продолжая так далее, можно вычислить логарифмы и других чисел, за-
ключающихся в промежутке от 200 до 230. Для чисел нечетных можно было
бы теперь допустить и линейное интерполирование, воспользовавшись най-
денными уже логарифмами четных чисел; однакр точность полученных ре^
зультатов будет меньшая,
§ 1941
ЭМПИРИЧЕСКИЕ ФОРМУЛЫ
509
Таким образом, получаем:
1g 200 = 2,30103;
1g 201 =2,30319(1);
lg 202 = 2,305352;
lg 203 = 2,30749 (2);
lg 204 = 2.309631;
lg 205 = 2,31175 (0);
Здесь логарифмы нечетных чисе
лированием, почему последние цифры
стоверные.
1g 206 = 2,313869;
1g 207 = 2,31596 (6);
lg 208 = 2,318064;
lg 209 = 2,32014 (2);
lg 210 = 2,32222.
fi получены именно линейным интерпо-
и поставлены в скобках, как мало до-
§ 194. ЭМПИРИЧЕСКИЕ ФОРМУЛЫ
Задаваемые значения функции нередко вытекают из некоторого
эксперимента; они являются тогда частными значениями некоторой,
иногда совершенно неизвестной нам, функции. Нахождение аналити-
ческого выражения такой функции, хотя бы приближенно выражаю-
щей изучаемую экспериментом зависимость, является весьма важной
математической задачей для экспериментатора. Она называется со-
ставлением эмпирических формул. Задача эта, как это вытекает из
всего вышеизложенного, разрешается, между прочим, формулами
интерполирования Лагранжа и Ньютона. В самом деле, положим,
что в результате эксперимента мы нашли следующие значения инте-
ресующей нас величины у при различных значениях х\
при х = а
x = a-\-h
х = а 2Л
У=Уо
У^Уг
У=У2
x = a-\-nh у=уп.
Тогда, принимая значения у за частные значения некоторой функ-
ции f(x), саму функцию можем представить по формуле Лагранжа
так:
f z ч (x — a — h)(x — a — 2h) ... (х—а — nh) .
J[x>~ _h _2h. —3h ...—nh~ -V°
I (x— a)(x — a — 2h) ... (x— a — nh) t (
h. —h- — 3h ... — (я —l)ft -У1 +
। (x— a)(x — a — h) ... (x — a — n — 1Л) 4i
яй • (я — 1) ft (я — 2) л ... 2ft-ft
а по формуле Ньютона так:
/ (*) =-Уо + ~al?2° ~ + ...
I (x —a)(x —a —ft) ... (x —a —n —1ft) л„_,
‘ 1 1-2-3 ... n-hn а У O'
(
510 ЗАДАЧА ИНТЕРПОЛИРОВАНИЯ И ЕЕ ПРИЛОЖЕНИЯ [ХХХ1
где разности Ду0, Дау0 ... Д’% вычисляются общим приемом. Пола-
гая же затем
У=/(х),
получаем искомую эмпирическую формулу.
Однако обе эти формулы могут служить лишь первым шагом
в решении задачи составления эмпирических формул. Помимо всяких
других неудобств, обнаруживающихся при пользовании формулами
Лагранжа и Ньютона в применении их к задаче составления эмпи-
рических формул, неудобство пользоваться этим приемом заклю-
чается в том, что формула, получаемая таким путем, слишком гро-
моздка. В самом деле, для достижения большей точности желательно
пользоваться большим числом данных наблюдений, а увеличение
данных значений изучаемой функции увеличивает степень целой
рациональной функции, составляющей эмпирическую формулу. К тому
же и коэффициенты этой функции нельзя ожидать простыми.
Все это заставляет изменить метод составления эмпирических
формул. Сохраняя основную идею, заключающуюся в задаче интер-
полирования, получение эмпирических формул обычно соединяют
с другой чрезвычайно плодотворной идеей, лежащей в основе
так называемого способа наименьших квадратов. Однако изложение
этого способа не входит в программу настоящего руководства. 1
$ 195. ВОПРОСЫ И УПРАЖНЕНИЯ
1. 6 чем заключается основная задача интерполирования?
2. Какие формулы интерполирования вам известны?
3. Какой степени целую рациональную функцию можно составить ио
ее п частным значениям?
4. Какой геометрический смысл имеет замена вычисляемой функции
целой рациональной функцией л-ой степени?
5. В чем заключается линейное интерполирование с аналитической и
геометрической точек зрения?
6. В чем заключается параболическое интерполирование с аналитиче-
ской и геометрической точек зрения?
7. Какое свойство приписывается приращению функции при линейном
интерполировании?
8. В чем заключается неудобство формулы интерполирования Лагранжа?
Устраняется ли это неудобство в формуле интерполирования Ньютона?
9. Что называется конечной разностью первого и высшего порядка?
10. Чему равны разности л-ого и п + 1-го порядка от целой рациональ-
ной функции л-ой степени?
11. Какие величины в формуле интерполирования Ньютона заменяют
задаваемые значения функции?
12. Когда формулы интерполирования Лагранжа и Ньютона представляют
точное выражение функции и когда приближенное?
13. Можно ли пользоваться формулами Лагранжа и Ньютона для соста-
вления эмпирических формул?
1 См. курсы теории вероятностей, а'также Идельсон, .Уравнитель-
ные вычисления по способу наименьших квадратов*.
$ 195]
Вопросы и упражнение
511
14. Зная, что плотность воздуха при 15° С равна 0,0012256, а при 16° С
0,0012213, определить плотность воздуха при промежуточных значениях
температуры через 0,1° С.
15. Зная., что плотность 10% водного раствора серной кислоты при 15° С
равна 1,06, а 20% раствора при той же температуре равна 1,142, определить
плотность раствора серной кислоты для промежуточных целых процентов.
16. Применяя формулу интерполирования Лагранжа, вычислить значения
3
f(x) при № —, зная, что
/(0) = 1. /(4) = 1.649, /(1) =2,718.
/ 3 \
Отв. f\-£j = 2,117 с точностью до 0,001.
17. Решить предыдущую задачу с помощью формулы интерполирования
Ньютона.
18. Наблюдением установлено, что средние величины атмосферного дав-
ления равны
на уровне моря.............. 760 мм
на высоте 2 км...........• . 597 „
. в 4 в................. 463 .
в . 6 .................. 355 .
Определить средние величины давлений на промежуточных высотах,
выраженных в целых километрах.
Отв. На высоте 1 км — 675 мм.
Редактор Г. П. Акилов
Техн, редактор Я. М. Волчок
Подписано к печати 10Д1 1951 г.
Формат бумаги 60х92/1в. Бум. л. 16.
Печ. л. 32. Уч.-изд. л. 37,93.
47421 тип. зн. в печ. л. Т-01417.
Тираж .15 000 экз. (15 001—30 000).
Цена 13 р. 30 к., переплет 1 р.
Заказ № 2116.
4-я типография им. Евг. Соколовой
Главполиграфиздата
при Совете Министров СССР
Ленинград. Измайловский пр.» 29
Опечатки
Стр. Строка Напечатано Следует читать По чьей вине
71 7 снизу 2дг2 2ага — г* Авт.
107. 6 сверху Ь2 + а2т № + а2т2
151 18 . пр. пр. »
287 ю » 1 1
хе~х2 • хех*
343 1 снизу dy = sin t dy = a sin t Корр.
Зак. 2116.
НС.МИХЕЛЬСОН
КРАТКИЙ КУРС
ВЫСШЕЙ
МАТЕМАТИКИ