Курс высшей математики и математической физики - Ильина В.А., Тихонова А.Н., Свешникова А.Г.

Автор: Ильина В.А. Тихонова А.Н. Свешникова А.Г.

Теги: геометрия топология физика математика алгебра математическая физика высшая математика физматлит

ISBN: 5-02-015234-Х

Год: 1999

Похожие

Курс высшей математики и математической физики. Основы математического анализа Ч.2

Краткий курс высшей математики

Курс высшей математики и математической физики. Выпуск 7. Дифференциальные уравнения

Геометрические методы математической физики

Текст

УДК 514.12 Издание осущктвлено при содействии
ББК 22.151.5 ООО «Фирма "Издательство ACT*
И 46
УЧЕБНИК УДОСТОЕН
ГОСУДАРСТВЕННОЙ ПРЕМИИ СССР ЗА 1980 ГОД
КУРС ВЫСШЕЙ МАТЕМАТИКИ
И МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Под редакцией
А.Н.ТИХОНОВА, В.А.ИЛЬИНА,
А. Г.СВЕШНИКОВА
ВЫПУСК 3
ИЛЬИН В.А., ПОЗНЯК Э.Г. Аналитическая геометрия: Учеб.: Для вузов. —
5-е изд. — М.: Наука. Физматлит, 1999. — 224 с. — (Курс высшей математики
и мат. физики). — ISBN 5-02-015234-Х (Вып. 3)
Один из выпусков «Курса высшей математики и математической физики» под
редакцией А.Н.Тихонова, В.А.Ильина, А.Г.Свешникова. Учебник создан на базе
лекций, читавшихся авторами в течение многих лет иа физическом факультете
Московского государственного университета. Наряду со строгим и полным
изложением программного материала книга содержит разделы, связанные с
практическим применением методов аналитической геометрии, рассмотрены
вопросы обоснования геометрии. Воспроизводится с 4-го изд. A988 г.).
Для студентов высших учебных заведений, обучающихся по специальностям
«Физика» и «Прикладная математика».
Ил. 85.
ТП-98-П-168
ISBN 5-02-015230-7 о ва.ильии. эхлозияк. 1999
ISBN 5-02-015234-Х(Вып.3) О Наука. Фиэматлит, оформление, 1999

ОГЛАВЛЕНИЕ
От редакторов серии 7
Предисловие к пятому изданию 8
Предисловие к четвертому изданию 8
Предисловие к первому изданию 8
Введение 10
Глава 1. Системы координат. Простейшие задачи аналитической гео-
геометрии 12
§ 1. Декартовы координаты на прямой . 12
1. Направленные отрезки на оси A2). 2. Линейные операции над направлен-
направленными отрезками. Основное тождество A3). 3. Декартовы координаты на пря-
прямой A4).
§ 2. Декартовы координаты на плоскости н в пространстве .... 15
1. Декартовы координаты на плоскости A5). 2. Декартовы координаты в про-
пространстве A6).
§ 3. Простейшие задачи аналитической геометрии 16
1. Понятие направленного отрезка в пространстве. Проекция направленного
отрезка на ось A6). 2. Расстояние между двумя точками A7). 3. Деление от-
отрезка в данном отношении A8). 4. Барицентрические координаты B0).
§ 4. Полирные, цилиндрические н сферические координаты .... 21
1. Полярные координаты B1). 2. Цилиндрические координаты B2). 3. Сфериче-
Сферические координаты B3).
Дополнение к главе 1. Определители второго и третьего порядков . . 24
1. Понятие Иатрицы и определителя второго порядка B4). 2. Система двух
линейных уравнений с двумя неизвестными B5). 3. Определители третьего по-
порядка B7). 4. Свойства определителей B9). 5. Алгебраические дополнения и
миноры C0). 6. Система трех линейных уравнений с тремя неизвестными с оп-
определителем, отличным от нуля C3). 7. Однородная система двух лниейиых
уравнений с тремя неизвестными CS). 8. Однородная система трех линейных
уравнений с тремя неизвестными C7). 9. Неоднородная система трех линейных
ураананий с тремя неизвестными с определителем, равным нулю C8).
Глава 2. Векторная алгебра 41
§ 1. Понятие вектора и линейные операции над векторами .... 41
1. Понятие вектора D1). 2. Линейные операция над векторами D2). 3. Поня-
Понятие линейной зависимости векторов D7). 4. Линейные комбинации двух векто-
векторов D8). 5. Линейные комбинации трех векторов D9). в. Линейная зависи-
зависимость четырех векторов E1). 7. Понятие бавеса. Аффинные координаты E3).
8. Проекция вектора на ось и ее свойства E5). 9. Декартова прямоугольная
система координат как частный случай аффинной системы коорднивт E6).
§ 2. Скалярное произведение двух векторов 59
1. Определение скалярного произведении E9). 2. Геоиетряческке свойства ска-
скалярного произведения F0). 3. Алгебраические свойства скалярного произведе-
произведения F1). 4. Выражение скалярного произведения в декартовых координа-
координатах F2).
§ 3. Векторное и смешанное произведения векторов 63
1. Правые и левые тройки векторов и системы координат F3). 2. Определение
векторного произведения двух векторов F4). 3. Геометрические свойства век-
векторного произведения F5). 4. Смешанное произведение трех векторов F6).
5. Алгебраические свойства векторного произведения F8). 6. Выражение век-

4 ОГЛАВЛЕНИЕ
торного произведения в декартовых координатах G2). 7. Выражение смешан-
смешанного произведения в декартовых хоордииатах G3). 8. Двойное векторное про-
произведение G4).
Глава 3. Преобразование декартовых прямоугольных координат на
нлоскости и в пространстве 76
§ 1. Преобразование декартовых прямоугольных координат на пло-
плоскости 76
§ 2. Преобразование декартовых прямоугольных координат в простран-
пространстве 79
1. Общие формулы преобразования G9). 2. Выяснение геометрического смысла.
Углы Эйлера (81).
§ 3. Линейные преобразования . 83
1. Понятие линейных преобразований плоскости (83). 2. Аффинные преобра-
преобразования плоскости (84). 3. Основное свойство аффинных преобразований пло-
плоскости (86). 4. Основной инвариант аффинного преобразования плоскости (88).
5. Аффинные преобразования пространства (89). 6. Ортогональные преобразо-
преобразования (90).
§ 4. Проективные преобразования 92
Глава 4. Уравнение линии иа плоскости. Уравнения поверхности н ли-
линии в пространстве 94
§ 1. Уравнение линии на плоскости 94
1. Понятие об уравнении линии (94). 2. Параметрическое представление ли-
липни (95). 3. Ураеиеиие линии в различных системах координат (97). 4. Два
типа задач, связанных с аналитическим представлением лииии (99). 5. Класси-
Классификация плоских линий (99). 6. О пересечении двух лииий A01).
§ 2. Уравнение поверхности и уравнения лнннн в пространстве . . . 102
1. Понятие об уравнении поверхности A02). 2. Уравнения лиини в простран-
пространстве A03). 3. Цилиндрические и конические поверхности A04). 4. Параметри-
Параметрические уравнения лиини и поверхности в пространстве A06). 5. Классификация
поверхностей A08). 6. О пересечении поверхностей и лииий в пространстве A09).
7. Заключительные замечания A09).
Глава 5. Линейные образы 110
§ 1. Различные виды уравнения прямой на плоскости НО
1. Общее уравнение прямой A10). 2. Неполные уравнения прямой. Уравнение
прямой в отрезках A12). 3. Каноническое уравнение прямой A13). 4. Парамет-
Параметрические уравнения пряной A14). 5. Прямая с угловым коэффициентом A14).
6. Угол между двумя прямыми. Условия параллельности и перпендикуляр-
перпендикулярности двух прямых A16). 7. Нормированное уравнение прямой. Отклонение
точки от прямой A18). 8. Уравиеиие пучка прямых A20).
§ 2. Некоторые задачи на прямую линию на плоскости 122
1. Нахождение нрямой, проходящей через лаииую точку Aft (*i. У\) и соста-
составляющее заданный угол <р с дайной прямой y=kiX + bt A22). 2. Нахождение
биссектрис углов, образованных данными прямыми A23). 3. Условия, при ко
торых данная прямая пересекает данный отрезок АВ A23). 4. Определение
местоположения данной точки М и начала координат О относительно углое,
образованных двумя данными прямыми A24). 5. Условие пересечения трех пря-
прямых в одной точке A24). 6. Нахождение примой, проходящей через точку пе-
пересечения двух данных прямых н удовлетворяющей еще одному условию A25).
§ 3. Различные виды уравнения плоскости 126
1. Общее уравнение плоскости A26). 2. Неполные уравиеиия плоскости. Урав-
Уравиеиие плоскости в отрезках A28). 3. Угол между двумя плоскостями. Условия
параллельности и перпендикулярности плоскостей A29). 4. Уравнение пло-
плоскости, проходящей через три различные точки, не лежащие иа одной пря-
прямой A30). 5. Нормированное уравиеиие плоскости. Отклонение точки от пло-
плоскости A30). 6. Пучки и связки плоскостей A33).
§ 4. Прямая линия в пространстне 134
1. Канонические уравнения прямой в пространстве A34). 2. Уравиеиия прямой,
проходящей через две различные точки М i (Xi, у и г,) и М](Хг. yi. гг> A36).
3. Параметрические уравнения прямой в пространстве A36). 4. Угол между
прямыми в пространстве. Условия параллельности и перпендикулярности пря-
прямых A36). 5. Условие принадлежности двух прямых к одной плоскости A37).
6. Угол между прямой и плоскостью. Условия параллельности а перпеидику-

ОГЛАВЛЕНИЕ 5
ляркости прямой и плоскости A37). 7. Условия принадлежности прямой
*~*' = У~!Л = *~*' K плоскости Ах + Ву + Сг + О=0 A38). 8. Связка
I m n
прямых A38).
§ 5. Некоторые задачи на прямую и плоскость в пространстве . . 139
1. Условие пересечения трех плоскостей в одиой и только в одной точке A39).
2. Нахождение биссектралышх плоскостей двугранного угла, образованного
двумя данными плоскостями A39). 3. Условия, при которых данная плоскость
пересекает данный отрезок АВ (МО). 4. Определение местоположения двух
данных точек Ля В относительно двугранных углов, образованных данными
плоскостями A40). 5. Уравнения прямой, проходящей через данную точку
Mt(x,. t/i.z,) н перпендикулярной данной плоскости Ax + By + Cz + D=0 A40).
6. Уравнение плоскости, проходящей через данную точку Af,(x0. у>, *«) и парал-
параллельной аадаииой плоскости А,х +В,у+ C,z+D,~-0 (МО). 7. Уравнение
плоскости, проходящей через заданную точку Af« (xt, У%. *о) н перпен-
перпендикулярной, заданной прямой т-!-=—J?~^=—JJ""*" (МО). 8- Уравнение
плоскости, проходящей через данную прямую г~^ = *~*1 = Z~Z[. и
* гп п
через заданную не лежащую иа этой прямой точку М„(х0, yt, z0) (Ml). 9. урав-
уравнение плоскости, проходящей через данную прямую —j—"= "' =—^-1-
*i nti п\
и параллельной другой данной прямой —;—-= ———= ¦ * A41). 10. Урав-
неиие плоскости, проходящей через заданную прямую L, и перпендикуляр-
перпендикулярной заданной плоскости л A42). 11. Уравнения перпендикуляра, опущенного из
заданной точки М, иа данную прямую L, A42). 12. Нахождение расстояния от
данной точки Мо до дайной прямой L, A42). 13. Нахождение общего перпен-
перпендикуляра к двум скрещивающимся прямым L, и 1л A42). 14. Нахождение
кратчайшего расстояния между двумя данными скрещивающимися прямыми U
н L, A42).
Глава 6. Линии второго порядка 143
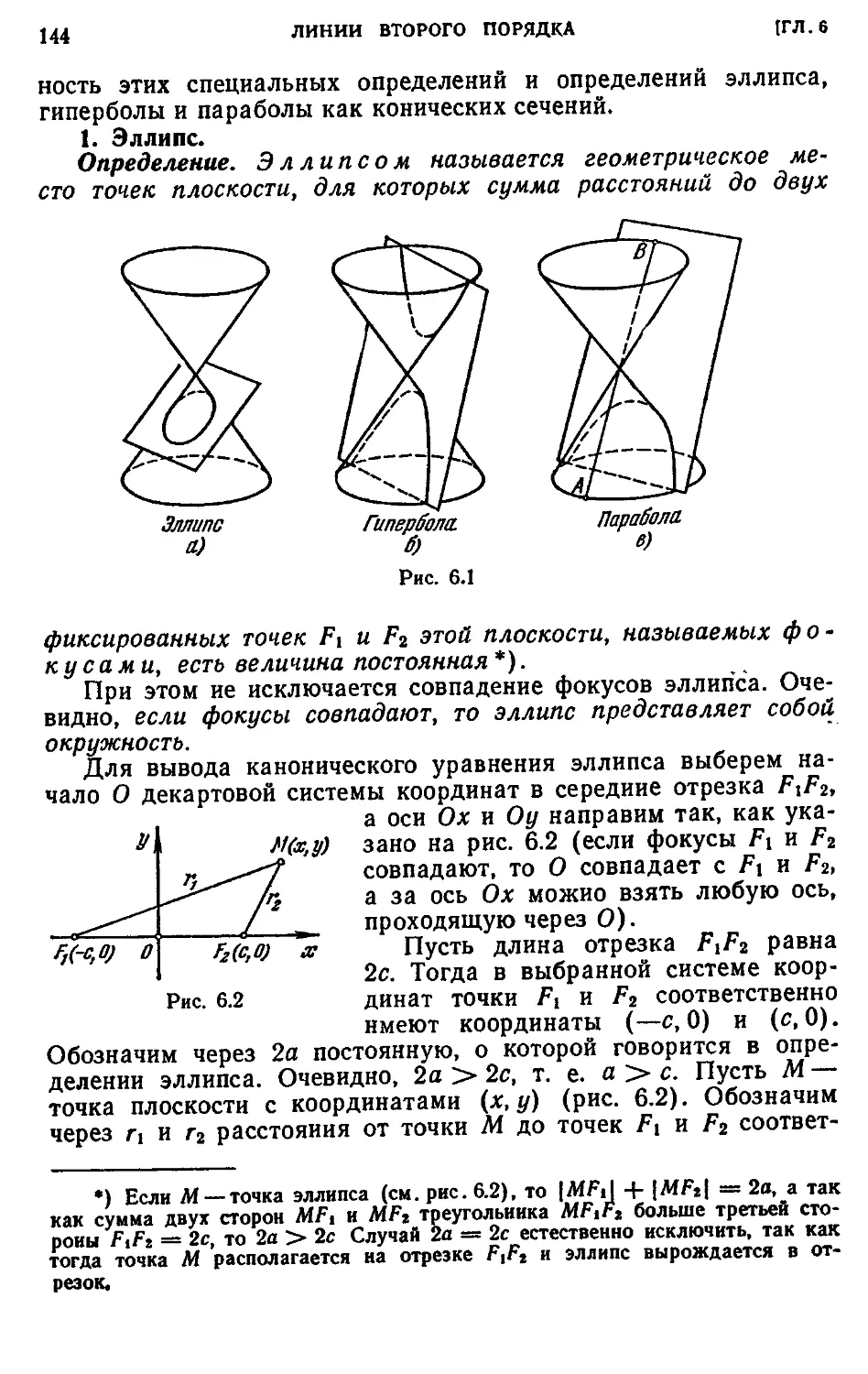
§ 1. Канонические уравнения эллипса, гиперболы и параболы . . . 143
1. Эллипс A44). 2. Гипербола A46). 3. Парабола A47).
§ 2. Исследование формы эллипса, гиперболы и параболы по нх ка-
каноническим уравнениям 149
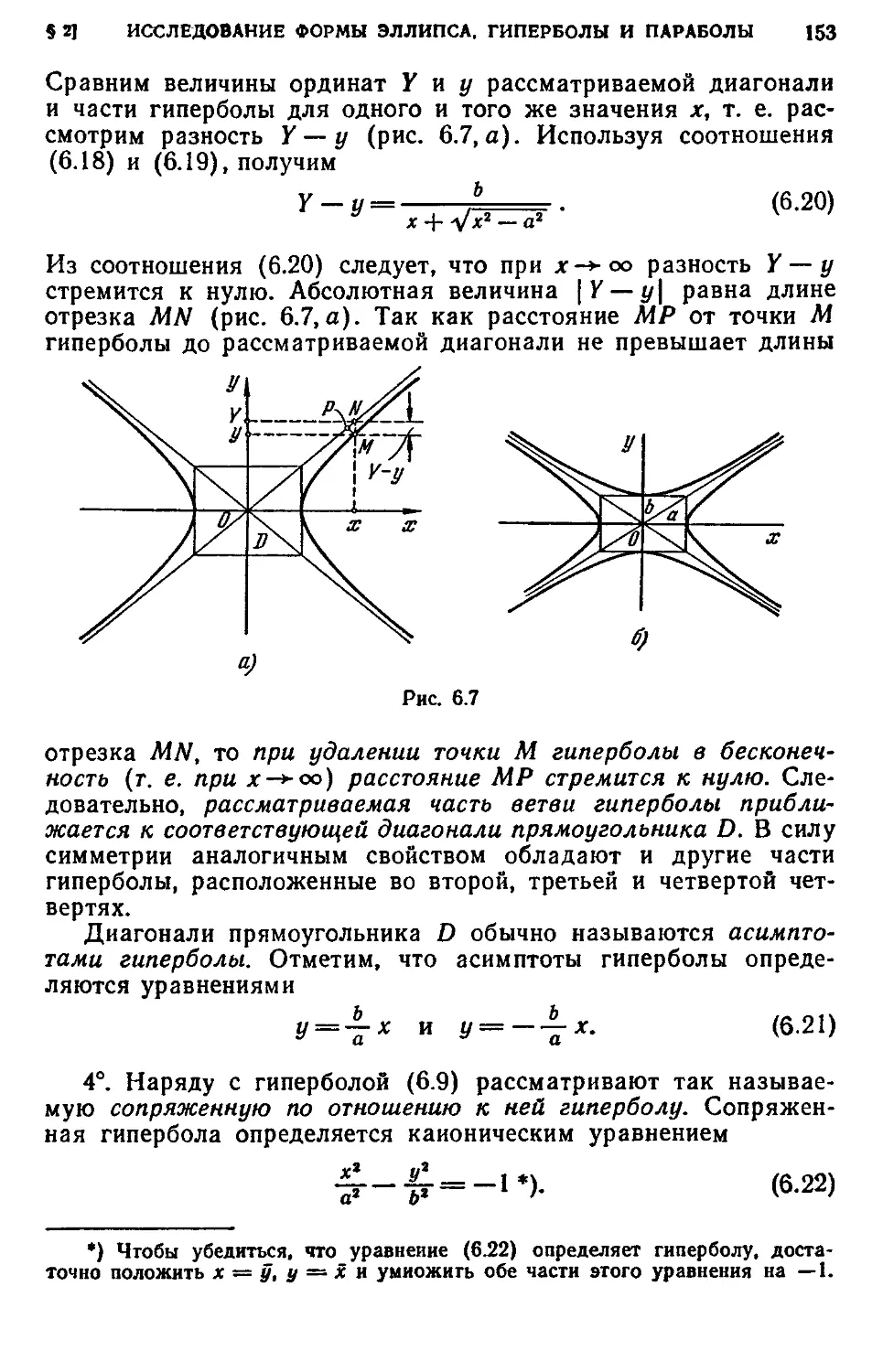
1. Исследование формы эллипса A49). 2. Исследование формы гиперболы A50).
3. Исследование формы параболы A54).
§ 3. Директрисы эллипса, гиперболы и параболы 155
1. Эксцентриситет эллипса и гиперболы A55). 2. Директрисы эллипса и гипер-
гиперболы A56). 3. Определение эллипса и гиперболы, основанное иа их свойстве
по отношению к директрисам A60). 4. Эллипс, гипербола и парабола как ко-
конические сечения A63). 5. Полярные уравнения эллипса, гиперболы и пара-
параболы A64).
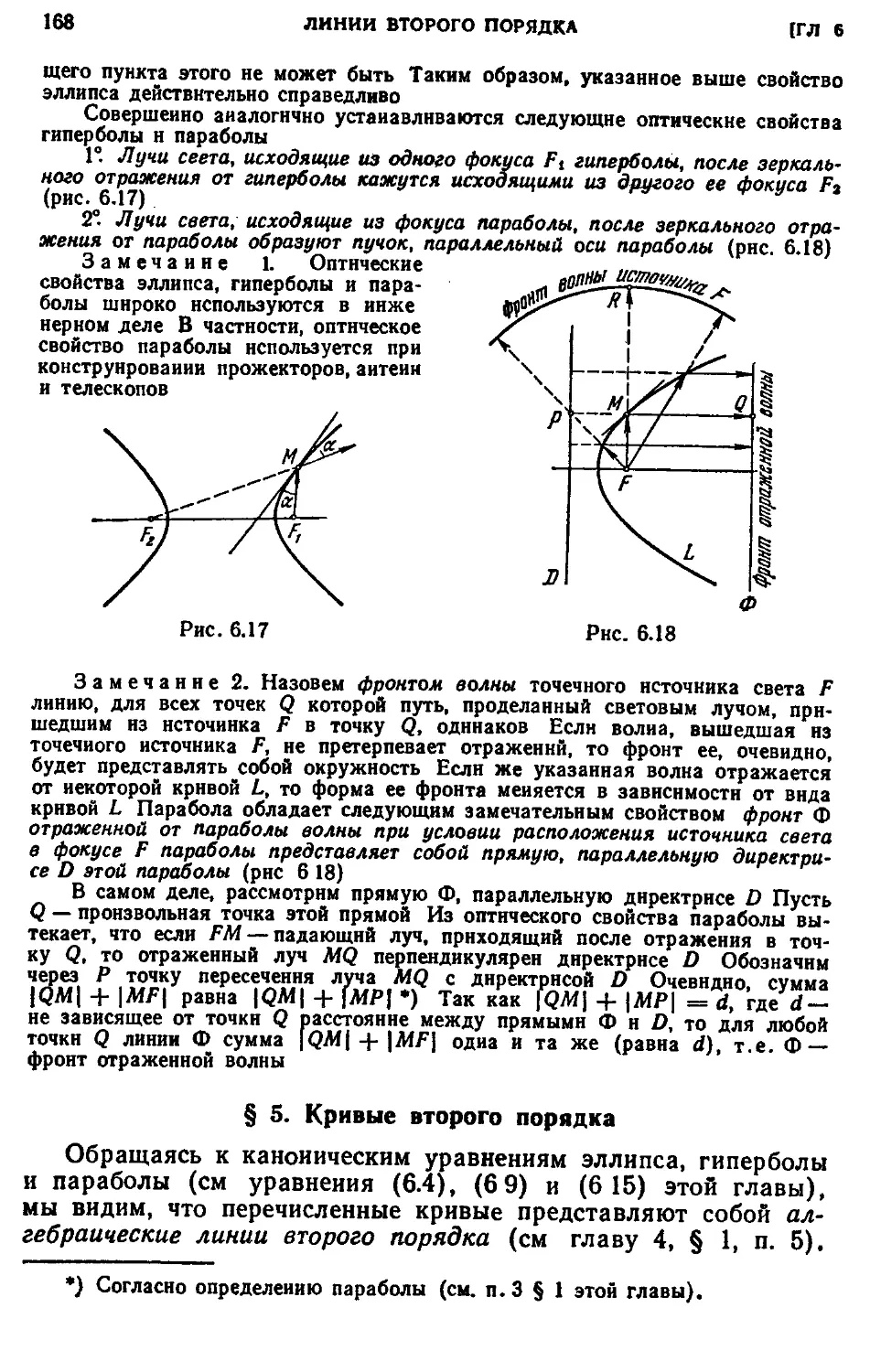
§ 4. Касательные к эллипсу, гиперболе и параболе 166
1. Уравнения касательных к эллипсу, гиперболе и параболе A66). 2. Опти-
Оптические свойства эллипса, гиперболы и параболы A67).
§ 5. Кривые второго порядка 168
1. Преобразование коэффициентов уравнения линии второго порядка при пе-
переходе к новой декартовой системе координат A69). 2. Иивариаиты уравнения
линии второго порядка. Понятие типа линии второго порядка A72). 3. Центр
линии второго порядка A74). 4. Стандартное упрощение любого уравнения ли-
линии второго порядка путем поворота осей A76). 5. Упрощение уравнения цен-
центральной линии второго порядка (/г ф 0). Классификация центральных
линий A76). 6. Упрощение уравнения лниик параболического типа (/з=0). Клас-
Классификация лииий параболического типа A80). 7. Распадающиеся кривые вто-
второго порядка A83).
Глава 7. Поверхности второго порядка 184
§ 1. Понятие поверхности второго порядка 184
1. Преобразование коэффициентов уравнения поверхности второго порядка при
переходе к иовой декартовой системе координат A85). 2. Инварианты уравне-
уравнения поверхности второго порядка A86). 3. Центр поверхности второго по-

6 ОГЛАВЛЕНИЕ
рядка A87). 4. Стандартное упрощение любого уравнения поверхности второго
порцдка путем поворота осев A87).
§ 2. Классификация поверхностей второго порядка 189
1. Классификация центральных поверхностей A89). 2. Классификация нецен-
нецентральных поверхностей второго порядка A92).
§ 3. Исследование формы поверхностей второго порядка по их кано-
каноническим уравнениям 194
1. Эллипсоид A94). 2.' Гиперболоиды A96). 3. Параболоиды A99). 4. Коиус и
цилиндры второго порядка B01). S. Прямолинейные образующие поверхностей
второго иорядка B02).
Приложение. Проблемы оснований геометрии и обоснования метода
координат 205
§ 1. Аксиомы элементарной геометрии 205
1. Аксиомы принадлежности B06). 2. Аксиомы порядка B07). 3. Аксиомы кои-
груэвтыостн B09). 4. Аксиомы непрерывности B11). 5. Обоснование метода ко-
ординат B12). 6. Аксиома параллельности B17).
4 2. Схема доказательства непротиворечивости геометрии Евклида . . 217
§ 3. Схема доказательства непротиворечивости геометрии Лобачевского 221
§ 4. Заключительные замечания о проблемах аксиоматики 223

ОТ РЕДАКТОРОВ СЕРИИ
Данный выпуск серии представляет собой учебник по курсу
аналитической геометрии. Кроме традиционно излагаемого ма-
материала, он содержит изложение некоторых вопросов, находя-
находящих применение в физике и в теоретической механике (понятие
о барицентрических координатах, выяснение роли углов Эйлера
в вопросах преобразования координат, представление произ-
произвольного преобразования в виде трансляции и одного поворота
в пространстве, оптические свойства кривых второго порядка
и т. п.).
Представляет интерес и приложение, содержащее аксиома-
аксиоматику Гильберта, обоснование метода координат и дающее пред-
представление о неевклидовой геометрии.
А. Тихонов, В. Ильин, А. Свешников

ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
Небольшая по объему «Аналитическая геометрия» используется
в качестве основного учебника не только для студентов, обучаю-
обучающихся по специальностям «физика» и «прикладная математика»
университетов, но и на других факультетах университетов, а
также в ряде технических вузов. Вероятно поэтому эта книга
почти отсутствует в библиотеках, хотя общий тираж предыдущих
изданий превышает 270 тысяч экземпляров.
Пятое издание перепечатывается с текста четвертого издания,
в котором исправлено несколько замеченных опечаток.
Июнь 1998 г. В. А. Ильин
ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
Для четвертого издания учебник дополнен материалом,
посвященным линейным и проективным преобразованиям.
Авторы благодарят за помощь при оформлении этого издания
А. В. Ильину.
Март 1987 г. В. Ильин, Э. Позняк
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Эта книга возникла на основе лекций, читавшихся авторами
в течение ряда лет на физическом факультете Московского
государственного университета.
Отметим некоторые особенности изложения. Во-первых, отме-
отметим, что по всей книге идет параллельное рассмотрение случаев
плоскости и пространства.
Весьма подробно излагается векторная алгебра. При ее
изложении сразу же вводится понятие линейной зависимости
векторов, и на его основе устанавливается возможность одно-

ПРЕДИСЛОВИЕ 9
значного разложения вектора по аффинному базису. Отличаются
от общепринятых доказательство распределенного свойства век-
векторного произведения и формулы для двойного векторного
произведения.
В связи с потребностями теоретической механики детально
рассматривается преобразование декартовых прямоугольных ко-
координат. Выясняется роль углов Эйлера и устанавливается, что,
каковы бы ни были два базиса одной ориентации, один из них
может быть преобразован в другой посредством параллельного
переноса и одного поворота вокруг некоторой оси в пространстве.
При описании линейных образов, наряду с изложением
традиционного теоретического материала, рассмотрено большое
число задач идейного характера. Нам кажется, что разбор этих
задач принесет пользу студентам, приступающим к упражнениям.
Не оставлены без внимания и имеющие прикладной характер
вопросы теории образов второго порядка (оптические свойства,
полярные уравнения и т.п.).
Приложение к книге содержит материал, не входящий в
традиционные курсы аналитической геометрии. Здесь дается
представление об аксиоматике Гильберта. Проводится обоснование
метода координат, дается представление о системе развертывания
основных геометрических понятий, об евклидовой и неевклидовой
геометриях и о доказательстве их непротиворечивости.
По программе, действующей в настоящее время, этот материал
не входит ни в один математический курс. Тем не менее этот
материал актуален не только с точки зрения логических
принципов построения геометрии, но и для понимания ряда
разделов современной физики.
При написании этой книги мы широко пользовались советами
и дружеской критикой А. Н. Тихонова и А. Г. Свешникова,
которым приносим свою глубокую благодарность.
Нам хочется также поблагодарить Н. В. Ефимова и А. Ф. Ле-
Леонтьева за прочтение рукописи и сделанные ими замечания.
1968 г. В. Ильин, Э. Лозняк

ВВЕДЕНИЕ
Аналитическая геометрия имеет своей задачей изучение
свойств геометрических объектов при помощи аналитического
метода.
В основе этого метода лежит так называемый метод коор-
координат, впервые систематически примененный Декартом *).
Основные понятия геометрии (точки, прямые линии и пло-
плоскости) относятся к числу так называемых начальных поня-
понятий. Эти понятия можно описать, но всякая попытка дать опре-
определение каждого из этих понятий неизбежно сведется к замене
определяемого понятия ему эквивалентным. С научной точки
зрения логически безупречным методом введения указанных
понятий является аксиоматический метод, в развитии и завер-
завершении которого величайшая заслуга принадлежит Гиль-
Гильберту**).
Аксиоматический метод излагается в Приложении в конце
настоящей книги. Там дается представление о всей системе
аксиом геометрии и о так называемой неевклидовой геометрии,
к которой приводит замена одной из аксиом (так называемой
аксиомы параллельности) утверждением, ее отрицающим.
Там же выясняется вопрос о непротиворечивости как евкли-
евклидовой, так и неевклидовой геометрии и устанавливается, что
конкретной реализацией совокупности объектов, удовлетворяю-
удовлетворяющих аксиомам геометрии, является введение точек как всевоз-
всевозможных упорядоченных троек {х, у, г) вещественных чисел,
прямых —как множества троек (х,у,г), удовлетворяющих си-
системе двух линейных уравнений, и плоскостей — как множества
троек (х,у,г), удовлетворяющих одному линейному уравнению.
Аксиоматический метод закладывает фундамент и для ле-
лежащего в основе аналитической геометрии метода координат.
Ради простоты рассмотрим вопрос о введении координат на
прямой. Возможность введения координат на прямой основы-
основывается на возможности установления взаимно однозначного СО'
1650).
*) Рене Декарт — великий французский математик и философ A596—
Давид Гильберт — великий немецкий математик A862—1943)

ВВЕДЕНИЕ И
ответствия между множеством всех точек прямой и множеством
всех вещественных чисел. Доказательство возможности уста-
установления такого соответствия базируется на аксиомах геомет-
геометрии и на аксиомах (свойствах) множества вещественных чи-
чисел *) и приводится в Приложении к настоящей книге.
Таким образом, в Приложении к настоящей книге читатель
найдет обоснование как системы развертывания основных гео-
геометрических понятий, так и лежащего в основе аналитической
геометрии метода координат.
Метод координат представляет собой глубокий и мощный
аппарат, позволяющий привлекать для исследования геометри-
геометрических объектов методы алгебры и математического анализа.
*) Свойства вещественных чисел в аксиоматический метод введения мно-
множества вещественных чисел излагаются в главе 2 и в Приложении к вы-
выпуску 1 настоящего курса.

ГЛАВА 1
системы координат. простейшие задачи
аналитической геометрии
В этой главе вводятся декартовы координаты *) на прямой,
на плоскости и в пространстве. Рассматриваются простейшие
задачи аналитической геометрии (расстояние между двумя точ-
точками, деление отрезка в данном отношении). Дается понятие
о других системах координат (полярных, цилиндрических и
сферических).
§ 1. Декартовы координаты на прямой
I. Направленные отрезки на оси. Прямую линию **) с ука-
указанным на ней направлением будем называть осью. Отрезок на
оси называется направленным, если указано, какая из его гра-
граничных точек является началом и ка-
* JB Ч% Ч 1_ кая — концом. Будем обозначать на-
Ось правленный отрезок с началом в точ-
Рис. 1.1 ке А и концом в точке В символом АВ
(на рис. 1.1 изображены направлен-
направленные отрезки АВ и CD). Мы будем рассматривать также и так
называемые нулевые направленные отрезки, у которых начало
и конец совпадают.
С каждым направленным отрезком сопоставляется его чис-
числовая характеристика — так называемая величина направлен-
*) Координаты (от латинских слов со — совместно, ordinatus — упоря-
упорядоченный, определенный) — числа, заданием которых определяется положение
точки на прямой, на плоскости или и пространстве (соответственно иа линии
или на поверхности). Заслуга введения метода координат, с помощью кото-
которого задачи геометрии могут быть истолкованы на языке математического
анализа, и, обратно, факты анализа могут приобрести геометрическое толко-
толкование, принадлежит французскому ученому Р. Декарту.
**) В Приложении в конце этой книги рассматривается аксиоматическое
иведение основных геометрических понятий (точек, прямых, плоскостей).
Кроме того, в этом же Приложения устанавливается связь между геометри-
геометрическим понятием прямой линии и понятием числовой оси (см. выпуск 1 «Осно-
«Основы математического анализа»).

S И ДЕКАРТОВЫ КООРДИНАТЫ НА ПРЯМОЙ 13
ного отрезка. Величиной АВ направленного отрезка АВ назы-
называется число, равное длине отрезка АВ, взятой со знаком плюс,
если направление АВ совпадает_с направлением оси, и со зна-
знаком минус, если направление А В противоположно направлению
оси. Величины всех нулевых направленных отрезков считаются
равными нулю.
2. Линейные операции над направленными отрезками. Основ-
Основное тождество. Предварительно определим равенство направлен-
направленных отрезков. Направленные отрезки мы будем перемещать
вдоль оси, на которой они лежат, сохраняя при этом их длину
и направление*).
Два ненулевых направленных отрезка называются равными,
если при совмещении начал этих отрезков совпадают и их
концы. Любые два нулевых направленных отрезка считаются
равными.
Очевидно, необходимым и достаточным условием равенства
двух направленных отрезков на данной оси является равенство
величин этих отрезков.
Линейными операциями над направленными отрезками бу-
будем называть операции сложения таких отрезков и умножения
направленного отрезка на веществен-
вещественное число. с JQ
Перейдем к определению этих one- л в
рацнй.
Для определения^ суммы направ- Рис 1.2
ленных отрезков ЛВ_и CD совместим
начало С отрезка CD с концом В отрезка АВ (рис. 1.2). По-
Полученный при этом направленный отрезок AD называется сум-
суммой направленных отрезков АВ и CD и обозначается символом
AB + CD.
Справедлива следующая основная теорема.
Теорема 1.1. Величина суммы направленных отрезков равна
сумме величин слагаемых отрезков.
^Доказательство. Пусть хотя бы один из отрезков АВ
и CD является нулевым. Если, например, отрезок CD нулевой,
то сумма АВ + CD совпадает с отрезком АВ, и утверждение
теоремы справедливо. Пусть теперь оба_отрезка АВ и CD не-
ненулевые. Совместим начало С отрезка CD с концом В отрезка
АВ. Тогда АВ + CD = AD. Нам нужно доказать справедли-
справедливость равенства АВ + CD = AD. Рассмотрим случай, когда оба
*) Вопрос о возможности перемещения отрезков связан с аксиомами кон-
конгруэнтности (см. Приложение в конце книги и, в частности, сноску на
С 209).

14 СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. 1
отрезка АВ и CD направлены в одну сторону (рис. 1.2). В этом
случае длина отрезка AD равна сумме длин отрезков А~В и CD
и, кроме того, направление отрезка__Ар совпадает с направле-
направлением каждого из отрезков АВ и CD. Поэтому интересующее
нас равенство АВ -\- CD = AD спра-
¦ о . »ff<—*Л—*_ ведливо. Рассмотрим, наконец, еще
А в одии возможный случай, когда отрез-
Рис 1.3 ки АВ и CD направлены в противопо-
противоположные _стороны (рис. 1.3). В этом
случае величины отрезков АВ и CD имеют разные знаки, и по-
поэтому длина отрезка AD равна \АВ -f-CD|. Так как направле-
направление отрезка AD совпадает с направлением наибольшего по
длине из отрезков АВ и CD, то знак величины отрезка AD
совпадает со знаком числа АВ -f- CD, т. е. справедливо равен-
равенство АВ -\- CD = AD. Теорема доказана.
Следствие. При любом расположении точек А, В, С на чис-
числовой оси величины направленных отрезков АВ, ВС и АС удов-
удовлетворяют соотношению
АВ + ВС = АС, A.1)
которое называется основным тождеством.
Операция умножения направленного отрезка на веществен-
вещественное число а определяется следующим образом.
Произведением направленного отрезка АВ
на_число а называется направленный отрезок, обозначаемый
а-АВ, длина которого равна произведению числа \а\ на длину
отрезка АВ и направление которого совпадает с направлением
отрезка АВ при а > 0 и противоположно направлению А В
при а < 0.
Очевидно, величина направленного отрезка а-АВ равна
а-АВ.
3. Декартовы координаты на прямой. Декартовы координаты
на прямой вводятся следующим образом. Выберем иа прямой
1 определенное направление*) и неко-
0 " торую точку О (начало координат)
""""J м *" (рис. 1.4). Кроме того, укажем единн-
р . . цу масштаба. Рассмотрим теперь про-
' ' извольную точку М на прямой. Де-
Декартовой координатой х т о ч к и М будем называть ве-
веШ
личину направленного отрезка
Тот факт, что точка М имеет координату х, символически
обозначают так: М (х).
*) Напомним, что прямая с указанным на ней направлением, называется
осью.

$2] КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 15
Замечание. Введение декартовых координат на прямой
представляет собой одни из способов, с помощью которого лю-
любой точке М прямой ставится в соответствие вполне опреде-
определенное вещественное число х. Вопрос о том, исчерпывается ли
при этом способе все множество вещественных чисел, т. е. бу-
будет ли указанное соответствие взаимно однозначным, положи-
положительно решается в Приложении в конце книги. (См. по этому
поводу также Приложение к выпуску I.)
Пусть Mi(^i) и М2{х2)— две точки на оси. В следующем
утверждении устанавливается выражение величины MiM2 на-
направленного отрезка AfiAl2 через координаты Xi и х2 его начала
и конца.
Теорема 1.2. Величина М^М2 направленного отрезка М\М2
равна Х2 — хи т. е.
М1М2 = х2-х1. A.2)
Доказательство. Рассмотрим на оси три точки О, Ми
М2. Согласно теореме 1.1 справедливо равенство
ОМ! + МХМ2 = ОМг. A.3)
Так как ОМ\ = хи ОМ2 = х2, то из A.3) вытекает нужное нам
соотношение A.2). Теорема доказана.
Следствие. Расстояние p(Mi,M2) между точками М$х$
и Мз {х2) может быть найдено по формуле
l = |*2-*il. A-4)
§ 2. Декартовы координаты на плоскости и в пространстве
1. Декартовы координаты на плоскости. Две перпендикуляр-
перпендикулярные оси иа плоскости с общим началом и одинаковой мас-
масштабной единицей (рис. 1.5) образуют декартову прямоуголь-
прямоугольную систему координат на плоскости. Одну у
из указанных осей называют осью Ох или
осью абсцисс, другую — осью Оу или осью ор-
ординат. Эти оси называют также координатны- ' I
ми осями. Обозначим через Мх и Му соответ- ,
ственно проекции произвольной точки М пло-
плоскости иа оси Ох и Оу.
Декартовыми прямоугольными Рис 1.5
координатами х и у точки М будем на-
зывать соответственно величины направленных отрезков ОМХ
иОМу.
Декартовы координаты х и у точки М называются соответ-
соответственно ее абсциссой и ординатой. Тот факт, что точка М имеет
координаты х и у, символически обозначают так: М(х,у).
Их

16
СИСТЕМЫ КООРДИНАТ ПРОСТЕЙШИЕ ЗАДАЧИ
[ГЛ. !
Координатные оси разбивают плоскость на четыре квад'
ранта, нумерация которых указана на рис. 1.6. На этом же ри-
рисунке указана расстановка знаков координат точек в зависи-
зависимости от их расположения в том или ином квадранте.
2. Декартовы координаты в пространстве. Декартовы коорди-
координаты в пространстве вводятся в полной аналогии с декарто-
декартовыми координатами на плоскости.
У
и
Х<0, у>0
0
т
акО, у<0
I
х>0, у>0
IV
х>0, у<0
х
Рис. 1.6
Рнс. 1.7
Три взаимно перпендикулярные оси в пространстве (коор-
(координатные оси) с общим началом О и одинаковой масштабной
единицей (рис. 1.7) образуют декартову прямоугольную си-
систему координат в пространстве. Одну из указанных осей на-
называют осью Ох или осью абсцисс, другую — осью Оу или осью
ординат, третью — осью Ог или осью аппликат. Пусть Мх, Му
и Мг — проекции произвольной точки М пространства на оси
Оде, Оу и Ог соответственно.
Декартовыми прямоугольными координата-
ми к, у и г точки М будем называть соответственно величины
направленных отрезков ОМХ, ОМУ и ОМг.
Декартовы координаты х, у и г точки М называются соот-
соответственно ее абсциссой, ординатой и аппликатой. Тот факт,
что точка М имеет координаты х, у и г, символически обозна-
обозначают так: М{х,у,г).
Попарно взятые координатные оси располагаются в так на-
называемых координатных плоскостях хОу, уОг и гОх (рис. 1.7).
Эти плоскости разбивают пространство на восемь октантов.
Читатель без труда выяснит расстановку знаков координат то-
точек в зависимости от их расположения в том или ином октанте.
§ 3. Простейшие задачи аналитической геометрии
1. Понятие направленного отрезка в пространстве. Проекция
направленного отрезка на ось. Отрезок в пространстве называет-
называется направленным, если указано, какая из его граничных точек

простейшие задачи аналитической геометрии
17
является началом_и_ какая — концом. Как и в п. 1 § 1 этой
главы символом АВ будем обозначать направленный отрезок
с началом в точке А и концом в точке В.
Рассмотрим в пространстве направленный отрезок MiM2 и
ось Ох (рис 1.8). При этом будем считать, что на оси Ох вве-
введены декартовы координаты
точек.
Проекцией про^А^Мг на-
направленного отрезка М\М2 на
ось Ох называется величина
направленного отрезка MixM2x,
началом М\х которого служит
проекция начала отрезка
М\М2, а концом Mix—-проек-
Mix—-проекция конца отрезка М\М2.
Пусть точки All* и М2х имеют на оси Ох координаты Xi и х*
соответственно. Из определения про* М\М2 н теоремы 1.2 выте-
вытекает справедливость соотношения
Рис. 1.8
про*
= х2 — хх.
A.5)
Установим еще одну формулу для вычисления про* М\М2. Для
этого перенесем направленный отрезок М\М% параллельно са-
самому себе так, чтобы его начало совпало с какой-либо точкой
оси Ох (на рис. 1.8 этой точкой является точка Mix). Обозна-
Обозначим через ф наименьший угол между направлением оси Оде и
направлением отрезка AllJeAf2*, полученного указанным выше па-
параллельным переносом отрезка М\М2 Отметим, что угол <р за-
заключен между 0 и я. При этом очевидно, что угол ф острый,
если направление отрезка М\хМ2х совпадает с направлением Ох,
и тупой, если направление М\хМ2х противоположно направле-
направлению Ох. Используя это, легко убедиться в справедливости сле-
следующей нужной нам формулы:
1 cos ф,
A.6)
в которой |AliM2| обозначает длину отрезка MiM2.
2. Расстояние между двумя точками. В этом пункте мы уста-
установим формулу для вычисления расстояния между двумя точ-
точками по известным координатам этих точек. Эта задача уже
решена для случая точек иа прямой в п. 3 § 1 этой главы
(см формулу A.4)). Ради определенности подробно остано-
остановимся на случае, когда точки расположены в пространстве.
Рассмотрим в пространстве декартову систему координат
Oxyz и точки Mi(xi,</i,zi) и М2{х2, у2, z2) (рис. 1.9). Очевидно,
2 3ак. 168

18
СИСТЕМЫ КООРДИНАТ ПРОСТЕЙШИЕ ЗАДАЧИ
[ГЛ. 1
расстояние p(Mi,M2) между точками Mi и М2, равное длине
направленного отрезка MiM2, равно также длине диагонали
параллелепипеда, грани которого параллельны координатным
плоскостям и проходят через точки
All и М2 (на рис. 1.9 этот паралле-
—-г\ лепипед изображен штриховой ли-
линией). Длина параллельного оси
Ох ребра этого параллелепипеда
''—\-Y' | равна, очевидно, абсолютной вели-
! I \ x чине проекции отрезка MiM2 на ось
У Ох, т. е., согласно формуле A.5),
равна \х2 — Xi\. По аналогичным
s? соображениям длины ребер, парал-
Рнй j 9 лельных осям Оу и Oz, равны со-
соответственно \у2 — У\\ и |г2 — z\\.
Используя теорему Пифагора, получим следующую формулу
для p(Ali,Al2):
0.
р(М„ М2) = У(*2 -
(у2 -
(z2 -
A.7)
Замечание. Формула расстояния между двумя точками
в случае их расположения в плоскости Оху имеет следующий
вид:
3. Деление отрезка в данном отношении. Рассмотрим в про-
пространстве две различные точки All и М2 и прямую, определяе-
определяемую этими точками. Выберем на этой прямой некоторое на-
направление (рис. 1.10). На по-
полученной оси точки М\ и М2
определяют направленный от-
отрезок М\М2.
Пусть М — любая отличная
от М2 точка указанной выше
оси. Число
, Af.Af
ММ,
A.9)
Рис. 1.10
называется отношением, в ко-
тором точка М делит направ-
направленный отрезок MiM2. Таким образом, любая, отличная от ЛГ2
точка М делит отрезок MiM2 в некотором отношении К, где Я.
определяется равенством A.9).
Замечание 1. При изменении направления на прямой,
проходящей через точки Mi и М2, меняют знак величины всех
направленных отрезков. Поэтому отношение ' в правой

$3] ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 19
части формулы A.9) не зависит от выбора направления на
прямой МхМз.
Рассмотрим задачу о вычислении координат точки М, деля-
делящей отрезок М\Мг в отношении К, считая известными коорди-
координаты точек Mi и Мз и число X., где % не равно —1.
Рассмотрим в пространстве декартову прямоугольную си-
систему координат Oxyz, и пусть в этой системе координат точки
iWi, M2 а М имеют соответственно координаты (xi,yi,zi),
(*2,1/2, z2) и {х, у, г). Спроектируем точки АГь Mi и М на коор-
координатные оси (на рис. 1.10 указаны лишь проекции М\х, Mix
и Мх точек All, Mi и М на ось Оде). Очевидно, точка Мх делит
направленный отрезок M\xMiX в отношении %. Поэтому
Согласно теореме 1.2, MixMx = х — jfi, a MxMiX — X2— х. От-
Отсюда и из соотношения A.10) найдем, что х равняется *'t , ?*.
Совершенно аналогично вычисляются координаты у и г точ-
точки ЛГ. Таким образом,
„
* Г+Т y~ 1+я • г Г+1Г- 11Л1)
Формулы A.11) называются формулами деления отрезка в дан-
данном отношении X.
Замечание 2. Очевидно, если Я.= 1, то точка М делит
отрезок AliAl2 пополам. Получающиеся при этом из соотноше-
соотношений A.11) формулы называются формулами деления отрезка
пополам.
Замечание 3. Для положительных значений % точка М
лежит между точками Afi н М2 (в этом случае, как это видно
из A.9), отрезки MiM и ЛШ2 одинаково направлены), а для
отрицательных значений — вие отрезка M\Mi.
Замечание 4. Соотношения A.11) имеют смысл для лю-
любых значений %ф—1. Этим, в частности, н объяснялось ука-
указанное ранее ограничение для значений %.
Пример. Решим задачу о вычислении координат центра
тяжести системы материальных точек.
Используем следующие два допущения, отвечающих извест-
известным физическим предпосылкам:
1) Центр тяжести системы из двух точек Mi н М% с массами
соответственно гп\ и тг находится на отрезке М\Мг н делит
этот отрезок в отношении "К = т^/пц.
2) Центр тяжести системы точек Mi, М2, .... Мп-и Мп
с массами соответственно ть тг, ..., nin-i, тп совпадает с
центром тяжести системы из двух точек, одна из которых яв-

20 СИСТЕМЫ КООРДИНАТ ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. 1
ляется точкой Мп с массой тп, а другая находится в центре
тяжести системы точек Mi, М2 Mn-i (с массами mi, т2, ...
.... гПп-\) и имеет массу т\ -\- т2 -\- ... + тп-\.
Из первого допущения и формул A.11) вытекает, что коор-
координаты х, у и z центра тяжести системы из двух точек
Mi(xi,t/i,zi) и М2(х2, y2tz2) с массами mi и т2 равны соответ-
соответ!±+ +
) ( y) р
ственно ibS!±"!!?l, ""*' + ""*' и т^ + т*\ Поэтому следует
ожидать, что координаты х, у и z центра тяжести системы из
л точек Mi(xi,yi,Zi), 1= 1, 2, .... л, с массами т* могут быть
вычислены по формулам
__ m^i + ... + тпх„
т, + ...+тл
ttl\Z\ + • . • + ttlnZn
т, + ... + т„
В справедливости этих формул можно убедиться по индукции,
если использовать второе допущение. В самом деле, пусть эти
формулы справедливы для системы точек Mi, ..., Мп-\ с мас-
массами т\, .... m«_i. Тогда, например, для абсциссы х рассматри-
рассматриваемой системы точек Mi Мп, согласно второму допущению
и формуле для абсциссы х системы из двух точек, получим вы-
выражение
т» + ...
+тпХп
из которого сразу же вытекает первая формула A.12). Выра-
Выражения для у и z получаются аналогично.
Замечание. Если система точек М« с массами mi распо-
расположена в плоскости Оху, то координаты х и у центра тяжести
этой системы могут быть найдены по первым двум формулам
A.12).
4. Барицентрические координаты. Формулы A.12) используются для вве-
введения так называемых барицентрических координат. Рассмотрим барицентри-
барицентрические координаты иа плоскости. В целях упрощения рассуждений будем счи-
считать, что иа плоскости введены и декартовы координаты Оху. Рассмотрим
какие-либо три различные точки Mi(xi, yt), Мг(хг, уг), Мз(хз, уз), не лежа-
лежащие иа одной прямой, и любую данную точку М(х, у). Выясним, существуют
ли такие три числа mi, mt, m3, удовлетворяющие условию
m, + mt + mt = 1, A.13)
что данная точка М(х, у) будет центром тяжести системы точек Ми Мг, Мз
с массами mlt mt, тз соответственно. Ниже мы убедимся, что прн сформу-
сформулированных требованиях числа mb mi, тз определяются однозначно для
каждой точки М. Оии называются барицентрическими координатами точки М
относительно базисных точек М,, М% и Мг.

§ 4] ПОЛЯРНЫЕ, ЦИЛИНДРИЧЕСКИЕ, СФЕРИЧЕСКИЕ КООРДИНАТЫ
21
Сформулированная задача о существовании чисел ть тг, т3 при условии
A.13) сводится, очевидно, к исследованию вопроса об однозначной разреши-
разрешимости следующей системы трех линейных уравнений *) относительно пц,
пи, ту.
т,ж,
х,
У-
A-14)
Известно, что для однозначной разрешимости квадратной системы линейных
уравнений (система, у которой число уравнений равно числу неизвестных)
необходимо и достаточно, чтобы определитель этой системы был отличен от
нуля (см. Дополнение к этой главе). Для рассматриваемой системы этот
определитель имеет вид
1 1 1
*i x2 Xi
У\ Уг Уз
Этот определитель отличен от нуля, иначе мы получили бы пропорцию
Xi — Xi yt — y\
= - 2— и, обозначив каждое из указанных отношении через
*з — Х\ уз — ух
—X (X Ф—1, ибо точки Mt и Мз различны), пришли бы с точностью до
обозначений к первым двум равенствам A.11). Это означало бы, что точка Mi
делит отрезок М2Мз в отношении X, т. е. означало бы, что точки Мь Мг и М*
лежат иа одной прямой. Таким образом, система A.14) однозначно разре-
разрешима относительно mi, тг, т3. Следовательно, положение любой точки М на
плоскости однозначно определяется относительно базисных точек Mi, Mi, M$
этой плоскости посредством барицентрических координат mi, тг и тг.
Барицентрические координаты в пространстве вводятся совершенно ана-
аналогично. Для этого используются четыре базисные точки, не располагающиеся
в одной плоскости.
My
§ 4. Полярные, цилиндрические и сферические координаты
1. Полярные координаты. Полярные координаты на плоскости
вводятся следующим образом. Выберем на плоскости некото-
некоторую точку О (полюс) и некоторый выходящий из нее луч Оде
(рис. 1.11). Кроме того, укажем едини- у
цу масштаба. Полярными коорди-
координатами точки М называются два чис-
числа р и ф, первое из которых (полярный
радиус р) равно расстоянию точки М
от полюса О, а второе (полярный угол
ф)—угол, на который нужно повернуть
против часовой стрелки луч Ох до сов-
совмещения с лучом ОМ**).
Точку М с полярными координатами р и ф обозначают сим-
символом ЛГ(р, ф).
*) Последние два уравнения этой системы представляют собой следствия
первых двух соотношений A.12) и соотношения A.13).
**) При этом предполагается, что точка М отлична от полюса. Для по-
полюса О полярный радиус р равен нулю, а полярный угол неопределенный,
т. е. ему можно приписать любое значение.
и
Рис. 1.11
М*
а

22
СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ
[ГЛ. 1
Для того чтобы соответствие между отличными от полюса
точками плоскости и парами полярных координат (р, ф) было
взаимно однозначным, обычно считают, что р и q> изменяются
в следующих границах:
0<р<+оо, 0<ф<2я. A.15)
Замечание. В некоторых задачах, связанных с непре-
непрерывным перемещением точки по плоскости, требуется непрерыв-
непрерывное изменение полярных координат этой точки. В таких задачах
удобнее отказаться от ограничений для р и ф, указанных в со-
соотношениях A.15). Если, например, рассматривается враще-
вращение точки по окружности против часовой стрелки (р = const),
то естественно считать, что полярный угол этой точки может
принимать, при большом числе оборотов, значения, большие
2я. Если же рассматривается движение точки по прямой, про-
проходящей через полюс (ф = const), то естественно считать, что
при переходе через полюс ее полярный радиус меняет знак.
Закон изменения величин р и <р выясняется в каждом кон-
конкретном случае.
Установим связь между полярными координатами точки и
ее декартовыми координатами. При этом будем предполагать,
что начало декартовой прямоугольной системы координат на-
находится в полюсе, а положительная полуось абсцисс совпадает
с полярной осью (рис. 1.11). Пусть точка М имеет декартовы
координаты х и у и полярные координаты р и ф. Очевидно,
х = рсозф, y = ps\nq>. A.16)
Полярные координаты р и ф точки М определяются по ее де-
декартовым координатам х и у, очевидно, следующим образом:
р = л/х2-\- у2. Для того чтобы най-
найти величину угла ф, нужно, исполь-
зуя знаки х и у, определить квад-
рант, в котором находится точка М
(см, п. 1 § 2 этой главы и рис. 1.6),
и, кроме того, воспользоваться тем,
что тангенс угла ф равен у/х.
2. Цилиндрические координаты.
Цилиндрические координаты в про-
пространстве вводятся следующим об-
образом. Выберем на фиксированной
плоскости П некоторую точку О и
выходящий из нее луч Ох
(рис. 1.12). Кроме того, рассмотрим ось Oz, проходящую че-
через О перпендикулярно плоскости П. Пусть М — любая точка
пространства, N — проекция этой точки на плоскость П, а
Мг — проекция М на ось Ог. Цилиндрическими ко-
координатами точки М называются три числа р, <р и г,

§4]
ПОЛЯРНЫЕ, ЦИЛИНДРИЧЕСКИЕ. СФЕРИЧЕСКИЕ КООРДИНАТЫ
23
первые два из которых (р и <р) являются полярными коорди-
координатами точки N в плоскости П относительно полюса О и по-
полярной оси Ох, а число г есть величина отрезка OMZ- Точку М
с цилиндрическими координатами р, q> и г обозначают М(р, q>, z).
Наименование «цилиндрические координаты» связано с тем, что
координатная поверхность р = const (т. е. поверхность, все точ-
точки которой имеют одну и ту же координату р) является ци-
цилиндром, прямолинейные образующие которого параллельны
оси Ог (на рис. 1.12 такой цилиндр изображен штриховыми ли-
линиями). Если выбрать оси декартовой прямоугольной системы
координат Охуг так, как указано на рис. 1.12, то декартовы
координаты х, у, г точки М будут связаны с ее цилиндриче-
цилиндрическими координатами р, q>, г соотношениями
A.17)
= pcosq>,
psinq>,
= г.
Замечание. Так как первые две цилиндрические коорди-
координаты риф являются полярными координатами проекции N
точки М на плоскость П, то к этим двум координатам относятся
замечание и выводы, сделанные в предыдущем пункте.
3. Сферические координаты. Для введения сферических коор-
координат в пространстве рассмотрим три взаимно перпендикуляр-
перпендикулярные оси Ох, Оу и Ог с общим началом О (рис. 1.13). Пусть
М — любая, отличная от О точка пространства, N — ее проек-
проекция на плоскость Оху, р — расстояние М от О. Пусть, далее,
в — угол, который образует направленный отрезок ОМ с осью
г, а ф — угол, на который нужно повернуть против часовой
стрелки ось Ох*) до совмещения с
лучом ON. 0 и ф называют широтой
и долготой соответственно.
Сферическими коорди-
координатами точки М называются три
числа р, ф и в **).
Наименование «сферические ко-
координаты» связано с тем, что коор-
координатная поверхность р = const
(т. е. поверхность, все точки кото-
которой имеют одну и ту же координа-
координату р) является сферой (на рис. 1.13
такая сфера изображена штриховой
линией).
Для того чтобы соответствие между точками пространства
и тройками сферических координат (р, ф, 0) было взаимно од-
Рис. 1.13
*) Если при этом смотреть на вращение Ох со стороиы положительного
направления оси Ог.
**) Если точка М совпадает с точкой О, то р = 0. Для точка О коорди-
координаты <р и 6 не имеют определенного значении.

24 СИСТЕМЫ КООРДИНАТ ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ 1
нозначным, обычно считают, что р и q> изменяются в следующих
границах:
4-°°. 0<ф<2я.
Координата в по самому определению заключена между 0 и я.
Отметим, что в задачах, связанных с непрерывным перемеще-
перемещением точки в пространстве, часто отказываются от указанных
ограничений на изменение сферических координат (см. замеча-
замечание в п. 1 этого параграфа).
Если выбрать оси декартовой прямоугольной системы коор-
координат так, как указано на рис. 1.13, то декартовы координаты х,
у, г точки М связаны с ее сферическими координатами р, <р, в
соотношениями
х = р sin в cos ф, # = psinesinq>, z = pcos6. A.18)
ДОПОЛНЕНИЕ К ГЛАВЕ 1
ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ
1. Понятие матрицы и определителя второго порядка. Прямо-
Прямоугольную таблицу из чисел, содержащую произвольное число т
строк и произвольное число л столбцов, называют матрицей.
Для обозначения матрицы используют либо сдвоенные чер-
черточки, либо круглые скобки. Например,
| 2 5 13,111 /25
I 7,2 1 О ИЛИ
1-9 7 6
/25 13.1 N
( 7,2 1 0 ).
\-9 7 6 /
Если число строк матрицы совпадает с числом ее столбцов, то
матрица называется квадратной. Числа, входящие в состав мат-
матрицы, обычно называют ее элементами.
Рассмотрим квадратную матрицу, состоящую из четырех
элементов:
I:: J;l- <ди)
Определителем второго порядка, соответствую-
соответствующим матрице (Д1.1), называется число, равное a\b2 — a2&i и
обозначаемое символом
Итак, по определению
\Z
Элементы, составляющие матрицу данного определителя, обыч-
обычно называются элементами этого определителя.

ДОПОЛНЕНИЕ К ГЛАВЕ I 25
Справедливо следующее утверждение: для того чтобы
определитель второго порядка был равен нулю, необходимо и
достаточно, чтобы элементы его строк (или соответственно его
столбцов) были пропорциональны.
Для доказательства этого утверждения достаточно заметить,
что каждая из пропорций а\/а2 = 61/62 и at/bi = а2/Ь2 экви-
эквивалентна равенству аф2 = аФи а последнее равенство в силу
(Д1.2) эквивалентно обращению в нуль определителя.
2. Система двух линейных уравнений с двумя неизвестными.
Покажем, как применяются определители второго порядка для
исследования и отыскания решения системы двух линейных
уравнений с двумя неизвестными
(коэффициенты а\, Ь\, а2, Ъ2 и свободные члены h\ н п2 счи-
считаются при этом заданными). Напомним, что пара чисел х0, уо
называется решением системы (Д1.3), если подстановка этих
чисел на место х я у ъ систему (Д1.3) обращает оба уравнения
(Д1.3) в тождества.
Умножая первое уравнение системы (Д1.3) на Ь2, а второе —
на —Ь\ и затем складывая полученные при этом равенства, бу-
будем иметь
(аф2 — a2bi) x = 62Aj — bxh2. (Д1.4)
Аналогично путем умножения уравнений системы (Д1.3) на
—а2 и Ci соответственно получим
{а&2 — a2b1)y = a1h2 —
Введем следующие обозначения:
С помощью этих обозначений и выражения для определителя
второго порядка уравнения (Д1.4) и (Д1.5) могут быть пере-
переписаны в виде
Определитель Л, составленный из коэффициентов при неизвест-
неизвестных системы (Д1.3), принято называть определителем этой си-
системы. Заметим, что определители Д* и Дй получаются из опре-
определителя системы Д посредством замены первого или соответ-
соответственно второго столбца свободными членами.
Могут представиться два случая: 1) определитель Д си-
системы отличен от нуля, 2) этот определитель равен нулю.
Рассмотрим сначала случай Д ф 0. В этом случае из урав-
уравнений (Д1.7) мы сразу же получаем формулы для неизвестных,
называемые формулами Крамера:

26 СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. 1
Полученные формулы Крамера (Д1.8) дают решение системы
(Д1.7) и потому доказывают единственность решения исходной
системы (Д1.3). В самом деле, система (Д 1.7) является след-
следствием системы (Д1.3), и поэтому всякое решение системы
(Д1.3) (в случае, если оно существует!) должно являться ре-
решением и системы (Д1.7). Итак, пока доказано, что если у ис-
исходной системы (Д1.3) существует при Д^О решение, то это
решение однозначно определяется формулами Крамера (Д1.8).
Легко убедиться и в существовании решения, т. е. в том,
что при Д ф О два числа х и у, определяемые формулами Кра-
Крамера (Д1.8), будучи подставлены на место неизвестных в урав-
уравнения (Д1.3), обращают эти уравнения в тождества. (Предо-
(Предоставляем читателю самому расписать выражения для опреде-
определителей Д, Ах и Ау и убедиться в справедливости указанных
тождеств.)
Приходим к следующему выводу: если определитель А си-
системы (Д1.3) отличен от нуля, то существует, и притом един-
единственное, решение этой системы, определяемое формулами Кра-
Крамера (Д1.8).
Рассмотрим теперь случай, когда определитель А системы
равен нулю. Могут представиться два подслучая: а) хотя
бы один из определителей Д* или Ау отличен от нуля; б) оба
определителя Д* и Ау равны нулю *).
В подслучае а) оказывается невозможным хотя бы одно из
равенств (Д1.7), т. е. система (Д1.7) не имеет решений, а по-
поэтому не имеет решений и исходная система (Д1.3) (следствием
которой является система (Д1.7)).
В подслучае б) исходная система (Д1.3) имеет бесчислен-
бесчисленное множество решений. В самом деле, из равенств Д = Д* =
= Ау = 0 и из утверждения в конце п. 1 заключаем, что а\/п2=
= 6i/62 = /ii//i2, т. е. заключаем, что второе уравнение системы
(Д1.3) является следствием первого и его можно отбросить.
Но одно уравнение с двумя неизвестными
aix + byy = ft,
имеет бесчисленно много решений (хотя бы один из коэффи-
коэффициентов Ci или Ь\ отличен от нуля, и стоящее при нем неизвест-
неизвестное может быть определено из уравнения (Д1.9) через произ-
произвольно заданное значение другого неизвестного).
Приходим к следующему выводу: если определитель Д си-
системы (Д1.3) равен нулю, то система (Д1.3) либо вовсе не
имеет решений (в случае, если хотя бы один из определителей
*) Из утверждения в конце п. 1 вытекает, что если определитель Д и
один из определителей А, ц Д, равны нулю, то и другой из указанных опре-
определителей равен нулю. В самом деле, пусть, например, Д = 0 и Д* = 0, т. е.
jat = 6|/о2 я />i/n2 — b\lbt. Тогда из этих пропорций получим, что j
hilhi, т. е. Д, = 0.

ДОПОЛНЕНИЕ К ГЛАВЕ t
27
Дж или Ду отличен от нуля), либо имеет бесчисленное множе-
множество решений {в случае, когда Ах = Ау = 0). В последнем слу-
случае два уравнения (Д1.3) можно заменить одним и при реше-
решении его одно неизвестное задавать произвольно.
Замечание. В случае, когда свободные члены h\ и h2
равны нулю, линейная система (Д1.3) называется однородной.
Отметим, что однородная система всегда имеет так называемое
тривиальное решение: х = 0, у = 0 (эти два числа обращают оба
однородных уравнения в тождества).
Если определитель Д системы отличен от нуля, то однород-
однородная система имеет только тривиальное решение. Если же Д=0,
то однородная система имеет бесчисленное множество решений
(поскольку для однородной системы возможность отсутствия
решений исключена). Таким образом, однородная система имеет
нетривиальное решение в том и только в том случае, когда
определитель ее равен нулю.
3. Определители третьего порядка. Рассмотрим квадратную
матрицу, состоящую из девяти элементов:
a\ bi Ci |
а* Ь2 сЛ.
a3 b3 c30
(Д1.10)
Определителем третьего порядка, соответствую-
соответствующим матрице (Д1.10), называется число, равное
аф2с3
и обозначаемое символом
— axc2b3 (ДЫ1)
ui b\ C\
U2 Ьг С2
a3 b3 c3
Итак, по определению
Д =
аг
a3
bx
Ьг
b3
Cy
c3
(Д1Л2)
Как и в случае определителя второго порядка, элементы
матрицы (Д1.10) будем называть элементами самого определи-
определителя. Кроме того, договоримся называть диагональ, образован-
образованную элементами Ci, bt и сз, главной, а диагональ, образованную
элементами сз, Ъ2 и Си — побочной.
Для запоминания конструкции слагаемых, входящих в вы-
выражение для определителя (Д1.11), укажем два правила.
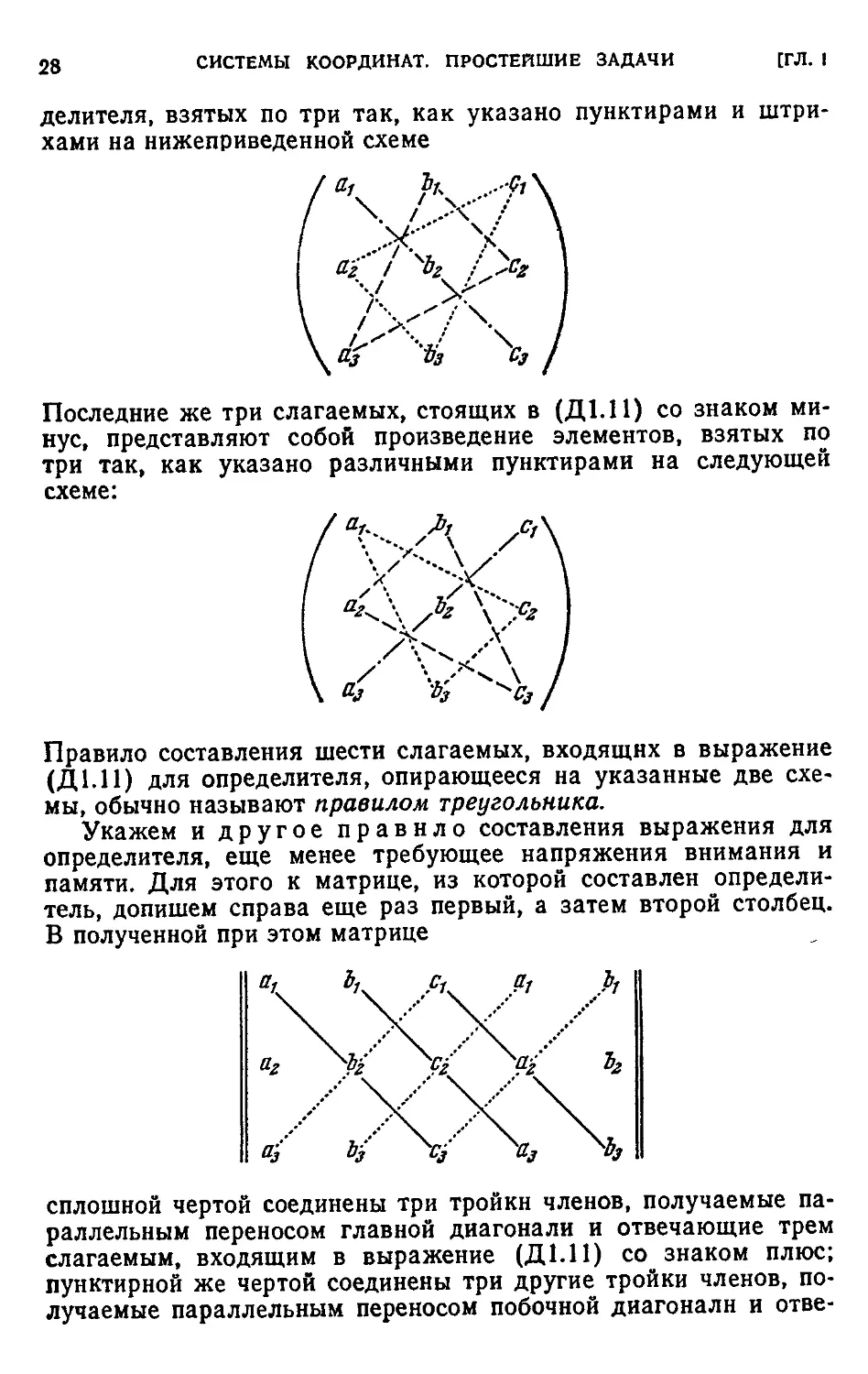
Заметим, что первые три слагаемых, стоящих в (Д1.11) со
знаком плюс, представляют собой произведение элементов опре-

28
СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ
[ГЛ. I
делителя, взятых по три так, как указано пунктирами и штри-
штрихами на нижеприведенной схеме
Последние же три слагаемых, стоящих в (Д1.11) со знаком ми-
минус, представляют собой произведение элементов, взятых по
три так, как указано различными пунктирами на следующей
схеме:
Правило составления шести слагаемых, входящих в выражение
(Д1.11) для определителя, опирающееся на указанные две схе<
мы, обычно называют правилом треугольника.
Укажем и другое правило составления выражения для
определителя, еще менее требующее напряжения внимания и
памяти. Для этого к матрице, из которой составлен определи-
определитель, допишем справа еще раз первый, а затем второй столбец.
В полученной при этом матрице
А
сплошной чертой соединены три тройкн членов, получаемые па-
параллельным переносом главной диагонали и отвечающие трем
слагаемым, входящим в выражение (Д1.11) со знаком плюс;
пунктирной же чертой соединены три другие тройки членов, по-
получаемые параллельным переносом побочной диагонали и отве-

ДОПОЛНЕНИЕ К ГЛАВЕ 1
29
аг
"з
Ьг
Ьг
Ьг
Сг
Сг
Сг
ах с
Ьг Ъ
с, с
2
2 Ьз
2 «3
чающие трем слагаемым, входящим в выражение (Д1.11) со
знаком минус.
4. Свойства определителей. В этом пункте мы установим ряд
свойств определителей. Эти свойства мы будем формулировать
и устанавливать применительно к определителям третьего по-
порядка, хотя, конечно, они справедливы и для определителей
второго порядка и, как выяснится позже (см. выпуск «Линей-
«Линейная алгебра»), эти же свойства справедливы и для определи-
определителей любого порядка п (там же см. понятие определителя по-
порядка п).
Свойство 1. Величина определителя не изменится, если стро-
строки и столбцы этого определителя поменять ролями, т. е.
(Д1.13)
Для доказательства этого свойства достаточно расписать
определители, стоящие в левой и в правой частях (Д 1.13), по
правилу треугольника (или по другому указанному в предыду-
предыдущем пункте правилу) и убедиться в равенстве полученных при
этом членов.
Свойство 1 устанавливает полную равноправность строк и
столбцов. Поэтому все дальнейшие свойства определителя мож-
можно формулировать и для строк, и для столбцов, а доказывать
или только для строк, или только для столбцов.
Свойство 2. Перестановка двух строк (или двух столбцов)
определителя равносильна умножению его на число —1.
Доказательство также получается из правила треугольника
(мы предоставляем его читателю).
Свойство 3. Если определитель имеет две одинаковые строки
(или два одинаковых столбца), то он равен нулю.
В самом деле, при перестановке двух одинаковых строк,
с одной стороны, определитель Д не изменится, а с другой сто-
стороны, в силу свойства 2 он изменит знак на противоположный.
Таким образом, Д = —Д, т. е. 2Д = 0, или Д = 0.
Свойство 4. Умножение всех элементов некоторой строки
(или некоторого столбца) определителя на число К равносильно
умножению определителя на это число X.
Иными словами, общий множитель всех элементов некото-
некоторой строки (или некоторого столбца) определителя можно вы-
выносить за знак этого определителя. Например,
Ал,
а3
Ьг
Ьг
Ас,
С2
Сг
= Л
я,
а2
а3
Ьг
Ь2
Ьг
Сг
Сг
Сг
Для доказательства этого свойства достаточно заметить, что
определитель выражается в виде суммы (Д1.12), каждый член

СИСТЕМЫ КООРДИНАТ ПРОСТЕЙШИЕ ЗАДАЧИ
[ГЛ 1
которой содержит один и только один элемент из каждой стро-
строки и один и только один элемент из каждого столбца.
Свойство 5. Если все элементы некоторой строки (или не-
некоторого столбца) определителя равны нулю, то и сам опреде-
определитель равен нулю.
Это свойство вытекает нз предыдущего (при Х = 0).
Свойство 6. Если, элементы двух строк {или двух столбцов)
определителя пропорциональны, то определитель равен нулю.
В самом деле, в силу свойства 4 множитель пропорциональ-
пропорциональности можно вынести за знак определителя, после чего остается
определитель с двумя одинаковыми строками, равный нулю со-
согласно свойству 3.
Свойство 7. Если каждый элемент п-й строки (или п-го
столбца) определителя представляет собой сумму двух слагае-
слагаемых, то определитель может быть представлен в виде суммы
двух определителей, первый из которых имеет в п-й строке (в
п-м столбце) первые из упомянутых слагаемых и те же эле-
элементы, что и исходный определитель, в остальных строках
(столбцах), а второй определитель имеет в п-й строке (в п-м
столбце) вторые из упомянутых слагаемых и те же элементы,
что и исходный определитель, в остальных строках (столбцах).
Например,
а3
Сз
а1
аз
ь[
Ьг
Ьз
f
С1
сг
Сз
+
ill
а\ ь\ С1
аг Ьг с2
а3 Ь3 с3
Для доказательства этого свойства снова достаточно заметить,
что определитель выражается в виде суммы слагаемых, каждое
из которых содержит один и только один элемент из каждой
строки и один и только один элемент из каждого столбца.
Свойство 8. Если к элементам некоторой строки (или неко-
некоторого столбца) определителя прибавить соответствующие эле-
элементы другой строки (другого столбца), умноженные на произ-
вольный множитель К, то величина определителя не изменится.
В самом деле, полученный в результате указанного прибав-
прибавления определитель можно (в силу свойства 7) разбить иа сум-
сумму двух определителей, первый нз которых совпадает с исход-
исходным, а второй равен нулю вследствие пропорциональности эле-
элементов двух строк (или столбцов) и свойства 6.
Для формулировки еще одного фундаментального свойства
определителя нам понадобятся новые понятия.
5. Алгебраические дополнения и миноры. Соберем в выраже-
выражении (Д1.12) для определителя члены, содержащие какой-нибудь
один элемент этого определителя, и вынесем указанный эле-
элемент за скобки; величина, остающаяся при этом в скобках, на-
называется алгебраическим дополнением указанного элемента.

ДОПОЛНЕНИЕ К ГЛАВЕ t 31
Алгебраическое дополнение данного элемента мы будем обо-
обозначать большой латинской буквой того же наименования, что
и данный элемент, и снабжать тем же номером, который имеет
данный элемент. Например, алгебраическое дополнение эле-
элемента Ь2 бдем обозначать через Вг, алгебраическое дополнение
элемента сз — через Л3 н т. д.
Непосредственно из выражения для определителя (Д1.12)
и из того, что каждое слагаемое в правой части (Д1.12) содер-
содержит один и только один элемент из каждой строки и один и
только один элемент из каждого столбца, вытекают следующие
равенства:
(Д1Л4)
(Д1.15)
Эти равенства выражают следующее свойство определителя:
определитель равен сумме произведений элементов какой-либо
строки (какого-либо столбца) на соответствующие алгебраиче-
алгебраические дополнения элементов этой строки (этого столбца).
Равенства (Д1.14) принято называть разложением опреде-
определителя по элементам соответственно первой, второй или третьей
строки, а равенства (Д1.15) — разложением определителя по
элементам соответственно первого, второго или третьего столбца.
Введем теперь важное понятие минора данного элемента
определителя. Минором данного элемента определителя п-го
порядка*) называется определитель (п—\)-го порядка, полу-
получаемый из данного определителя путем вычеркивания той стро-
строки и того столбца, на пересечении которых стоит данный эле-
элемент.
Например, минор элемента Oj равен ь* СЛ, минором эле-
элемента а2 служит определитель .' ' , и т. д.
Предлагаем читателю самому убедиться в том, что алгебраи-
алгебраические дополнения и миноры связаны между собой по следую-
следующему правилу: алгебраическое дополнение любого элемента
определителя равняется минору этого элемента, взятому со зна-
знаком плюс, если сумма номеров строки и столбца, на пересече-
пересечении которых стоит данный элемент, есть число четное, и со зна-
знаком минус — в противном случае.
Таким образом, соответствующие алгебраическое дополнение
и минор могут отличаться только знаком.
*) В рассматриваемом случае я = 3.

32
СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ
[ГЛ. 1
Следующая таблица дает наглядное представление о том,
каким знаком связаны соответствующие алгебраическое допол-
дополнение и минор
Установленное правило позволяет в формулах (Д1.14) и (Д 1.15)
разложения определителя по элементам строк и столбцов всюду
вместо алгебраических дополнений писать соответствующие ми-
миноры (с нужным знаком)
Так, например, последняя из формул (Д1 14), дающая раз-
разложение определителя по элементам третьей строки, принимает
вид
аг
Ьг
Ь3
Cl
С»
В заключение установим следующее фундаментальное свой-
свойство определителя.
Свойство 9. Сумма произведений элементов какого-либо
столбца определителя на состветствующие алгебраические до-
дополнения элементов этого (другого) столбца равна величине
этого определителя (равна нулю).
Конечно, аналогичное свойство справедливо и применитель-
применительно к строкам определителя. Случай, когда алгебраические до-
дополнения и элементы отвечают одному и тому же столбцу, уже
рассмотрен выше. Остается доказать, что сумма произведений
элементов какого-либо столбца на соответствующие алгебраиче-
алгебраические дополнения элементов другого столбца равна нулю.
Докажем, например, что сумма произведений элементов пер-
первого или второго столбца на соответствующие алгебраические
дополнения элементов третьего столбца равна нулю.
Будем исходить из третьей формулы (Д1.15), дающей раз-
разложение определителя по элементам третьего столбца:
а,
аг
ft.
ft»
Ьг
Сх
Сг
с3
Сз<?з-
(Д1Л7)
Так как алгебраические дополнения Ci, C2 и С3 элементов треть-
третьего столбца не зависят от самих элементов ci, c<i и с3 этого
столбца, то в равенстве (Д1.17) числа с\, сч и с3 можно заме-
заменить произвольными числами h\, кг и Лз, сохраняя при этом в
левой части (Д1.17) первые два столбца определителя, а в пра-
правой части величины С\, Сг и С% алгебраических дополнений.

ДОПОЛНЕНИЕ К ГЛАВЕ 1
33
Таким образом, при любых h\, h2 и А3 справедливо равен-
равенство
л» Ъг Aj
а3 Ъг Лз
= hxCx + А2С2 -f- Л3С3.
(Д1.18)
Беря теперь в равенстве (Д1.18) в качестве hi, А2 и А3 сначала
элементы а\, а2 и аз первого столбца, а затем элементы ftt, ftj
и ft3 второго столбца и учитывая, что определитель с двумя
совпадающими столбцами в силу свойства 3 равен нулю, мы
придем к следующим равенствам:
ахСх + а2С2 + агС3 = 0, ЬХСХ + Ь2С2 + Ь3С3 = 0.
Тем самым доказано, что сумма произведений элементов пер-
первого или второго столбца на соответствующие алгебраические
дополнения элементов третьего столбца равна нулю.
Аналогично доказываются равенства
ахВх + щВ2 + а3В3 = 0, схВх + с2В2 + с3В3 — О,
ft, Ах + Ь2А2 + Ь3А3 == 0, схАх + с2А2 + с3А3 = О
и соответствующие равенства, относящиеся не к столбцам, а к
строкам:
ах А3 + ft,B3 + схС3 = 0, а2А, + Ь2В3 + с2С3 = О,
ах А2 + ft,B2 + схС2 — 0, а3А2 + Ъ3В2 + с3С2 = О,
«2^1 + ftz^i + с2Сх = 0, a3/4i + 63fii + c3C, == 0.
6. Система трех линейных уравнений с тремя неизвестными
с определителем, отличным от нуля. В качестве приложения
изложенной выше теории рассмотрим систему трех линейных
уравнений с тремя неизвестными
l l
<hx + b2y + саг = Аг,
(Д1.19)
(коэффициенты аи а2, а3, Ь\, Ь2, Ъ3, с\, с2, с3 и свободные члены
Ai, А2, Аз считаются заданными). Тройка чисел Хо, у0, 2о назы-
называется решением системы (Д1.19), если подстановка этих чисел
иа место х, у, г в систему (Д1.19) обращает все три уравиения
(Д1.19) в тождества.
Фундаментальную роль в дальнейшем будут играть следую-
следующие четыре определителя:
А=
у ~~~
а,
аг
а8
а,
л,
л3
Ь\ С\
Ьг ct
Ьз с»
h\ С)
А4 сг
Аз Сз
• Ах =
. Аг =
А,
А,
А,
а,
аа
аз
Ьх
Ьг
Ьз
Ьх
Ьг
Ьз
С\
Сг
с%
А,
А3
А,
ЗЗш. 168

34 СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. 1
Определитель Д принято называть определителем системы
(Д 1.19) (он составлен из коэффициентов при неизвестных).
Определители Д*, Аи и Дг получаются из определителя системы
Д посредством замены свободными членами элементов соответ-
соответственно первого, второго и третьего столбцов.
Для исключения из системы (Д1.19) неизвестных у и 2 умно-
умножим уравнения (Д1.19) соответственно на алгебраические до-
дополнения Аи Л2 и Аз элементов первого столбца определителя
Д системы и после этого сложим эти уравнения. В результате
получим
(a^i + а2А2 + а3А3) х + F, Л, + Ь2А2 + Ъ3А3) у +
+ (с,Л, + с2А2 + с3А3) г = hxAx + Ms + Мз- (Д1 -20)
Учитывая, что сумма произведений элементов данного столб-
столбца определителя на соответствующие алгебраические дополне-
дополнения элементов этого (другого) столбца равна определителю
(нулю) (см. свойство 9), получим
alAi+a2A2+a3A3=A, blAl-j-b2A2-\-b3A3=O, CiAi-\-c2A2-\-c3A3=0.
(Д1.21)
Кроме того, посредством разложения определителя Д* по эле-
элементам первого столбца получается формула
Ax«Mi + Mj + M3. (Д1-22)
С помощью формул (Д1.21) и (Д1.22) равенство (Д1.20) пере-
перепишется в следующем (не содержащем неизвестных «/иг) виде:
Д-х = Дх.
Совершенно аналогично выводятся из системы (Д1.19) равен-
равенства Д-1/ = Ау и Д-2 = Д2*).
Таким образом, мы установили, что система уравнений
Д-х = ДХ1 А-у = Аи, Д-2 = Дг (Д1.23)
является следствием исходной системы (Д1.19).
В дальнейшем мы отдельно рассмотрим два случая:
1) когда определитель Д системы отличен от нуля,
2) когда этот определитель равен нулю.
Здесь мы рассмотрим лишь первый случай (рассмотрение
второго случая отложим до п. 9).
Итак, пусть Д ф 0. Тогда из системы (Д1.23) мы сразу по-
получаем формулы для неизвестных, называемые формулами
Крамера:
х = Дх/Д, # = Д^/Д, 2 = Дг/Д. (Д1.24)
*) Для получения этих равенств следует сначала умножить уравнения
(Д1.19) соответственно на алгебраические дополнения элементов второго и
третьего столбцов, а затем сложить полученные равенства.

ДОПОЛНЕНИЕ К ГЛАВЕ 1 35
Полученные нами формулы Крамера дают решение системы
(Д1.23) и потому доказывают единственность решения исход-
исходной системы (Д1.19), ибо система (Д1.23) является следствием
системы (Д1.19), и всякое решение системы (Д1.19) обязано
быть решением и системы (Д1.23).
Итак, мы доказали, что если у исходной системы (Д1.19)
существует при &Ф0 решение, то это решение однозначно
определяется формулами Крамера (Д1.24).
Чтобы доказать, что решение в самом деле существует, мы
должны подставить в исходную систему (Д 1.19) на место х, у
и 2 их значения, определяемые формулами Крамера (Д1.24),
и убедиться в том, что все три уравнения (Д1.19) обращаются
при этом в тождества. Убедимся, например, что первое уравне-
уравнение (Д1.19) обращается в тождество при подстановке значений
х, у и 2, определяемых формулами Крамера (Д1.24). Учитывая,
что А* = ЛИ14-/12-42 + ЛИз, Ду = hiBi + h2B2 + h3B3, Аг =
= hiC\ -}-Л2С2 + Л3С3, будем иметь, подставив в левую часть
первого из уравнений (Д 1.19) значения х, у и г, определяемые
формулами Крамера:
+ Ъху + с,2 = а, ~ + Ьх 4г + с, -?¦ —
= i {в| (А, Л, + Мг + Мз) + Ьх (А,В, + Л2В2 + А3В3) +
+ с, (Л,С, + fhC2 + A3C3)}.
Группируя внутри фигурной скобки члены относительно At, Л2
и Лз, будем иметь
п\Х + Ъху + с,2 =
= •?- {/г, (а, Л, + ft,B, + cfit) + h [аИг + ЬХВ2 + с,С2] +
В силу свойства 9 в последнем равенстве обе квадратные скоб-
скобки равны нулю, а круглая скобка равна определителю Д. Таким
образом, мы получим ахх-{-Ь\у -\-c\Z = hi, и обращение в тож-
тождество первого уравнения системы (Д1.19) установлено. Анало-
Аналогично устанавливается обращение в тождество второго и треть-
третьего уравнений системы (Д1.19).
Мы приходим к следующему выводу: если определитель Д
системы (Д1.19) отличен от нуля, то существует, и притом един-
единственное, решение этой системы, определяемое формулами Кра-
Крамера (Д1.24).
7. Однородная система двух линейных уравнений с тремя не-
неизвестными. В этом и в следующем пунктах мы разовьем аппа-
аппарат, необходимый для рассмотрения неоднородной системы
(Д1.19) с определителем, равным нулю. Сначала рассмотрим

36 СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. 1
однородную систему двух линейных уравнений с тремя неиз-
неизвестными
агХ + Ъа + cfi-O,
azx + Ь2у + с2г = 0.
Если все три определителя второго порядка, которые можно
составить из матрицы
равны нулю, то в силу утверждения из п. 1 коэффициенты пер-
первого из уравнений (Д1.25) пропорциональны соответствующим
коэффициентам второго из этих уравнений. Стало быть, в этом
случае второе уравнение (Д1.25) является следствием первого,
и его можно отбросить. Но одно уравнение с тремя неизвест-
неизвестными а\х-\-Ь\у -\-c\z — О, естественно, имеет бесчисленное мно-
множество решений (двум неизвестным можно предписывать про-
произвольные значения, а третье неизвестное определять из урав-
уравнения) .
Рассмотрим теперь систему (Д1.25) для случая, когда хотя
бы один из определителей второго порядка, составленных из
матрицы (Д1.26), отличен от нуля. Не ограничивая общности,
будем считать, что определитель
Тогда мы можем переписать систему (Д1.25) в виде
а2х -+- Ь2у = — с2г
и утверждать, что для каждого г существует единственное ре-
решение этой системы, определяемое формулами Крамера (см.
п. 2, формулы (Д1.8))
су Ъу\ \ах с,\
Ьг\
а, Ь,
аг Ь2\ \а* bi\
Для дальнейшего удобно ввести в рассмотрение алгебраиче-
алгебраические дополнения Аз, Вз и С$ элементов третьей строки опреде-
определителя
ау
"t
а»
Ьу
b%
Су
Сг
с*
*) Это предположение не снижает общности, ибо порядок следования
неизвестных х, у в г находится в нашем распоряжении.

ДОПОЛНЕНИЕ К ГЛАВЕ 1 37
В силу результатов п. 5 о связи алгебраических дополнений
и миноров можно записать
А — 6| С|
| Сз~~и
U
Основываясь на (Д1.29), мы можем переписать формулы
(Д1.28) в виде
Для того чтобы получить решение в виде, симметричном отно-
относительно всех неизвестных х, у и г, положим t = z/C3 (отме-
(отметим, что в силу (Д1.27) определитель С3 отличен от нуля). По-
Поскольку г может принимать любые значения, то и новая пере-
переменная t может принимать любые значения.
Мы приходим к выводу, что в случае, когда определитель
(Д1.27) отличен от нуля, однородная система (Д1.25) имеет
бесчисленное множество решений, определяемых формулами
x=-Aaf, y = B3t, z = C3t, (Д1.31)
в которых t принимает какие угодно значения, а алгебраиче-
алгебраические дополнения А3, В3 и С3 определяются формулами (Д1.29).
8. Однородная система трех линейных уравнений с тремя
неизвестными. Рассмотрим теперь однородную систему трех
линейных уравнений с тремя неизвестными
щх + Ъху + схг = О,
а2х + Ь2у + c2z = 0, (Д1.32)
агх + Ь3у + c3z = 0.
Очевидно, что эта система всегда имеет так называемое три-
тривиальное решение: х = 0, у = 0, г = 0.
В случае, когда определитель системы Д ф 0, это тривиаль-
тривиальное решение является единственным (в силу п. 6).
Докажем, что в случае, когда определитель А равен нулю,
однородная система (Д1.32) имеет бесчисленное множество ре-
решений.
Если все определители второго порядка, которые можно со-
составить из матрицы
1а, Ь, с, |1
аи h сЛ, (Д1.33)
а3 Ь3 с3 О
равны нулю, то в силу утверждения из п. 1 соответствующие
коэффициенты всех трех уравнений (Д1.32) пропорциональны.
Но тогда второе и третье уравнения (Д1.32) являются след-
следствиями первого и могут быть отброшены, а одно уравнение

38 СИСТЕМЫ КООРДИНАТ. ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. 1
+ biy + ciz = 0, как уже отмечалось в предыдущем пункте,
имеет бесчисленное множество решений.
Остается рассмотреть случай, когда хотя бы один минор ма-
матрицы (Д1.33) отличен от нуля. Так как порядок следования
уравнений и неизвестных находится в нашем распоряжении, то,
не ограничивая общности, мы можем считать, что отличен от
нуля определитель (Д1.27). Но тогда, как установлено в пре-
предыдущем пункте, система первых двух уравнений (Д1.32)
имеет бесчисленное множество решений, определяемых форму-
формулами (Д1.31) (при любом t).
Остается доказать, что х, у и г, определяемые формулами
(Д1.31) (при любом 0> обращают в тождество и третье урав-
уравнение (Д1.32). Подставляя в левую часть третьего уравнения
(Д1.32) х, у и 2, определяемые формулами (Д 1.31), будем
иметь
а3х + Ъ3у + съг = (а3А3 + Ь3В3 + с3С3) t = Д • /.
Мы воспользовались тем, что в силу свойства 9 выражение в
круглых скобках равно определителю Д системы (Д1.32). Но
определитель Д по условию равен нулю, и поэтому при любом t
мы получим а3х + Ь3у + с3г = 0.
Итак, доказано, что однородная система (Д1.32) с определи-
определителем Д, равным нулю, имеет бесчисленное множество решений.
Если отличен от нуля минор (Д1.27), то эти решения опреде-
определяются формулами (Д1.31) при произвольно взятом t.
Полученный результат можно сформулировать еще и так:
однородная система (Д1.32) имеет нетривиальное решение в
том и только в том случае, когда определитель ее равен нулю.
9. Неоднородная система трех линейных уравнений с тремя
неизвестными с определителем, равным нулю. Теперь мы распо-
располагаем аппаратом для рассмотрения неоднородной системы
(Д1.19) с определителем Д, равным нулю. Могут представиться
два случая: а) хотя бы один из определителей Дх, &у или Д2
отличен от нуля; б) все три определителя Ах, &у и Д2 равны
нулю.
В случае а) оказывается невозможным хотя бы одно из ра-
равенств (Д1.23), т. е. система (Д1.23) не имеет решений, а по-
поэтому не имеет решений и исходная система (Д1.19) (след-
(следствием которой является система (Д1.23)).
Переходим к рассмотрению случая б), т. е. случая, когда
все четыре определителя Д, Д*, Д^ и Дг, равны нулю. Начнем
с примера, показывающего, что в этом случае система может
не иметь ни одного решения. Рассмотрим систему
x + y + z = l,
2x + 2y + 2z = 3,
Эх-f Ъу +3г «=а 4.

ДОПОЛНЕНИЕ К ГЛАВЕ I 39
Ясно, что эта система не имеет решений. В самом деле, если
бы решение Хо, уо, г0 существовало, то из первых двух уравне-
уравнений мы получили бы Хо -\- у о + 2о = 1, 2х0 + 2i/o + 2го = 3, а от-
отсюда, умножая первое равенство на 2, получили бы, что 2 = 3.
Далее, очевидно, что все четыре определителя А, А*, Aff и Дг
равны нулю. В самом деле, определитель
1
2
3
1
2
3
1
2
3
имеет три одинаковых столбца, определители A*, Aff и Дг полу-
получаются путем замены одного из этих столбцов свободными чле-
членами и, стало быть, имеют по два одинаковых столбца. В силу
свойства 3 все эти определители равны нулю.
Докажем теперь, что если система (Д1.19) с определителем
А, равным нулю, имеет хотя бы одно решение, то она имеет бес-
бесчисленное множество различных решений.
Предположим, что указанная система имеет решение хо, уо,
г0. Тогда справедливы тождества
= К
+ Ь2у0 -Ь c2z0 = А2, (Д1.34)
Вычитая почленно из уравнений (Д1.19) тождества (Д1.34),
получим систему уравнений
fli {х — х0) + bl(y — y0) + cl{z— z0) = 0,
а2 (х - х0) + Ь2(у- у0) + c2(z — z0) = 0, (Д1.35)
а3 {х — х0) + Ь3(у — у0) + с3 (г — г0) = 0,
эквивалентную системе (Д1.19). Но система (Д1.35) является
однородной системой трех линейных уравнений относительно
трех неизвестных (х — jco), (у — уо) и (г — г0) с определите-
определителем А, равным нулю. Согласно п. 8 последняя система (а стало
быть, и система (Д1.19)) имеет бесчисленное множество реше-
решений. Например, в случае, когда отличен от нуля минор (Д1.27),
мы с помощью формул (Д1.31) получим следующее бесконеч-
бесконечное множество решений системы (Д1.19):
x = xo + A3t, y = yo + B3t, z = zo + C3t
(t принимает любые значения).
Рассматриваемое утверждение доказано, и мы можем сде-
сделать следующее заключение: если А = Ах = Аи = Аг = 0, то
неоднородная система (Д1.19) либо совсем не имеет решений,
либо имеет их бесконечное множество.

40 СИСТЕМЫ КООРДИНАТ ПРОСТЕЙШИЕ ЗАДАЧИ [ГЛ. I
В качестве примеров предлагаем читателю рассмотреть сле-
следующие три системы:
и убедиться в том, что первая система имеет единственное
решение х=\, у—\, z=\ (для нее Д = Д* = А» = Аг = 33),
вторая система не имеет решений (для нее Д = 0, Ау = 1),
а третья система имеет бесчисленное множество решений
(для нее Д = Д* = Ау = Дг = 0), определяемых при произволь-
произвольном t формулами: х = 1, у = t, г = —t.

ГЛАВА 2
ВЕКТОРНАЯ АЛГЕБРА
В этой главе изучаются векторные величины (или просто
векторы), т. е. такие величины, которые, кроме своего числен-
численного значения, характеризуются еще направленностью. Физиче-
Физическими примерами векторных величин могут служить смещение
материальной точки, двигающейся в пространстве, скорость и
ускорение этой точки, а также действующая на нее сила.
В главе изучаются простейшие операции над векторами
(сложение векторов, умножение векторов на число), вводится
понятие линейной зависимости векторов н рассматриваются
основные приложения этого понятия, изучаются различные
типы произведений векторов, актуальные для физических при-
приложений (скалярное и векторное произведение двух векторов,
смешанное и двойное векторное произведение трех векторов).
§ 1. Понятие вектора и линейные операции над векторами
1. Понятие вектора. Абстрагируясь от конкретных свойств,
встречающихся в природе физических векторных величин, мы
приходим к понятию геометрического вектора, или просто
вектора.
Геометрическим вектором (или
просто вектором) будем называть направлен-
направленный отрезок.
Мы будем обозначать вектор либо как на«
правленный отрезок символом АВ, где точки Рис. 2.1
А и В обозначают соответственно начало и
конец данного направленного отрезка (вектора), либо одной
жирной латинской буквой, например а или Ь. На чертеже будем
изображать вектор стрелкой, причем латинскую букву, обозна-
обозначающую этот вектор, будем писать у его конца (рис. 2.1).
Начало вектора называют точкой его приложения. Если
точка А является началом вектора а, то мы будем говорить,
что вектор а приложен в точке А. Для обозначения длины век-
вектора будем пользоваться символом модуля (или абсолютной ве-

42 ВЕКТОРНАЯ АЛГЕБРА (ГЛ 2
личины). Так, \АВ\ и |а| обозначают длины векторов АВ и а
соответственно.
Вектор называется нулевым, если начало и конец его
совпадают. Нулевой вектор не имеет определенного направле-
направления и имеет длину, равную нулю. Это позволяет при записи
отождествлять нулевой вектор с вещественным числом нуль.
Введем важное понятие коллинеарности векторов. Векторы
называются ко л линеарными, если они лежат либо на од-
одной прямой, либо на параллельных прямых.
Теперь можно сформулировать понятие равенства двух
векторов: два вектора называются равными, если они кол-
линеарны, имеют одинаковую длину и
одинаковое направление. Все нулевые
векторы считаются равными.
На рис. 2.2 изображены слева не-
равные, а справа равные векторы а
иЬ.
Из определения равенства векторов
Рис- 2.2 непосредственно вытекает следующее
утверждение: каковы бы ни были век-
вектор а и точка Р, существует, и притом единственный, вектор
PQ с началом в точке Р, равный вектору а *).
Иными словами, точка приложения данного вектора а мо-
может быть выбрана произвольно (мы не различаем двух равных
векторов, имеющих разные точки приложения и получающихся
один из другого параллельным переносом). В соответствии
с этим векторы, изучаемые в геометрии, называют свободными
(они определены с точностью до точки приложения)**).
2. Линейные операции иад векторами. Линейными опера-
операциями принято называть операцию сложения векторов и опе-
операцию умножения векторов на вещественные числа.
Сначала определим операцию сложения двух векторов.
Определение 1. Суммой а + Ь двух векторов а и Ъ назы-
называется вектор, идущий из начала вектора а в конец вектора Ъ
при условии, что вектор Ъ приложен к концу вектора а.
*) В самом деле, существует лишь одна прямая, проходящая через точ-
точку Р и параллельная той прямой, на которой лежит вектор а. На указанной
прямой существует единственная точка Q такая, что отрезок PQ имеет длину,
равную длине вектора а, и направлен в ту же сторону, что и вектор а.
*) В механике и физике, кроме свободных векторов, иногда рассматри-
рассматривают скользящие и связанные векторы. Скользящими называют такие век-
векторы, которые считаются эквивалентными, если они ие только равны, но и
лежат на одной прямой. Примером скользящего вектора может служить сила,
приложенная к абсолютно твердому телу (известно, что две силы, равные н
расположенные на одной прямой, оказывают иа абсолютно твердое тело оди-
одинаковое механическое воздействие). Связанными иазываютси такие векторы,
которые считаются эквивалентными, если они ие только равны, но и имеют
общее начало. Примером связанного вектора может служить сила, приложен-
приложенная к некоторой точке нетвердого (например, упругого) тела.

5 I] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 43
Правило сложения двух векторов, содержащееся в этом
определении, обычно называют правилом треугольника.
Это название объясняется тем, что в соответствии с указан-
указанным правилом слагаемые векторы а и Ь (в случае, если они не
коллинеарны) и их сумма а + Ь образуют тре-
треугольник (рис. 2.3).
Правило сложения векторов обладает теми
же самыми четырьмя свойствами, что и правило
сложения вещественных (или рациональных)
чисел*):
1° а + b=b -f- а (переместительное свойство); р 9 _
2° (а + Ь) + с = а + (Ь + с) {сочетательное
свойство);
3° существует нулевой вектор 0 такой, что а + 0 = а для
любого вектора а (особая роль нулевого вектора);
4° для каждого вектора а существует противоположный ему
вектор ь! такой, что а + а' = 0.
Убедимся в справедливости этих свойств. Свойство 3° непо-
непосредственно вытекает из определения 1. Для доказательства
свойства 4° определим вектор а', противоположный вектору а,
как вектор, коллинеарный вектору а, имею-
имеющий одинаковую с вектором а длину и про-
противоположное направление**). Очевидно,
что взятая согласно определению 1 сумма
вектора а с таким вектором а' дает нуле-
нулевой вектор.
Для доказательства свойства Г прило-
приложим два произвольных вектора а и b к об-
общему началу О (рис. 2.4). Обозначим бук- Рис- 2А
вами Л и В концы векторов а и b соответ-
соответственно и рассмотрим параллелограмму ОВСА. Из определения
равенства векторов следует, что ВС = ОА = л, АС = ОВ =
— Ь.
Из определения 1_и_из рассмотрения треугольника О АС сле-
следует, что диагональ ОС указанного параллелограмма представ-
представляет собой сумму векторов а + Ь, а из рассмотрения треуголь-
треугольника ОВС следует, что та же самая диагональ ОС представ-
представляет собой сумму векторов b + а. Тем самым свойство 1° уста-
установлено.
Остается доказать свойство 2°. Для этого приложим вектор а
к произвольной точке О, вектор Ь к концу вектора а и вектор с
к концу вектора b (рис. 2.5). Обозначим буквами А, В и С
*) См. выпуск 1, главу 2,
**) Для получения А' достаточно поменять ролями начало и конец век-
вектора А.

44
ВЕКТОРНАЯ АЛГЕБРА
[ГЛ. 2
концы векторов a, b и с соответственно. Тогда
(а + Ь) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС,
а + (Ь + с) = ОА + (АВ + ВС) = ОА + АС = ОС,
т. е.свойство 2° доказано.
Замечание 1. При доказательстве свойства 1° обосновано
еще одно правило сложения векторов, называемое правилом
параллелограмма: если векторы а и b
приложены к общему началу и на них
построен параллелограмм, то сумма
а + Ь (или b + а) этих векторов пред-
представляет собой диагональ указанного па-
параллелограмма, идущую из общего на-
начала векторов а и Ъ*).
Доказанные свойства 1°—4° позво-
Рис. 2.5
ляют оперировать с суммой векторов
так же, как с суммой вещественных чисел. В частности, при
сложении трех векторов а, Ь.и с нет необходимости указывать,
как мы понимаем сумму a + b + с (как а + (Ь + с) или как
(а + b)-f-с). Свойства 1°—4° позволяют нам распространить
правило сложения на сумму любого конечного числа век-
векторов. При этом нет необходимости производить сложение по-
последовательно, фиксируя каждый промежуточный результат;
сумма любого числа векторов может быть по-
построена с помощью следующего правила:
если приложить вектор аг к концу вектора зц,
вектор аз к концу вектора &г вектор а„
к концу вектора ап-ь то сумма aj + а2 +
+ а3 + • • • + ал будет представлять собой
вектор, идущий из начала вектора &\ в конец
вектора а„.
Сформулированное правило сложения,
проиллюстрированное на рис. 2.6, естественно
назвать правилом замыкания ломаной до мно-
многоугольника (на рис. 2.6 ломаная ОА\А2А3_11. Ап замыкается
до многоугольника путем добавления звена ОАп).
Наконец, свойства Г—4° позволяют исчерпывающим обра-
образом решить вопрос о вычитании векторов.
Определение 2. Разностью а — b вектора а и вектора Ъ
называется такой вектор с, который в сумме с вектором Ъ дает
вектор а.
Рис. 2.6
•) Следует особо оговорить случай, когда векторы а и b коллинеарны.
В этом случае параллелограмм, построенный на векторах а и Ь, вырождается
в отрезок, понятие его диагонали теряет смысл, а сумма векторов а и Ь
может быть получена из определения 1,

§ 1] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 45
С помощью свойств Г—4° элементарно доказывается, что
существует, и притом единственный, вектор с, представляющий
собой разность а — Ь, причем этот вектор равен с = а + Ь', где
Ь'—вектор, противоположный Ъ.
В самом деле, если с = а + Ь', то на основании свойств
Г —4°
т. е. вектор с представляет собой разность а — Ь.
Убедимся теперь в однозначности разности а — Ь. Предпо-
Предположим, что, кроме вектора с = а + Ь', существует еще один век-
вектор d такой, что d + b = a. Тогда, с одной стороны, (d + b) +
+ b' = а + Ь' = с, с другой стороны, (d + Ь) + b' = d + (b +
+ b') = d + 0 = d, т. е. с = d.
Непосредственно из определения 2 и из правила треуголь-
треугольника сложения векторов вытекает следующее правило по-
построения разности а —Ь: разность
а — Ь приведенных к общему началу векторов
aub представляет собой вектор, идущий из
конца вычитаемого вектора b в конец умень-
уменьшаемого вектора а.
Это правило иллюстрируется на рис. 2.7.
Перейдем, наконец, к рассмотрению one- рис 27
рации умножения вектора на вещественное
число.
Определение 3. Произведением оса (или аа) век-
вектора а на вещественное число а называется вектор Ь,
коллинеарный вектору а, имеющий длину, равную |а|-|а|, и
имеющий направление, совпадающее с направлением вектора а
в случае а > 0 и противоположное направлению вектора а в
случае а < 0.
Замечание 2. В случае, когда а = 0 или a = 0, произве-
произведение аа представляет собой нулевой вектор, направление ко-
которого неопределенно.
Геометрический смысл операции умножения вектора на чис-
число можно выразить так: при умножении вектора а «а число а
вектор а «растягивается» в а «раз».
Конечно, надо тут же оговорить условность термина «рас-
«растягивается», ибо действительное растяжение происходит лишь
при а > 1; при 0 < а < 1 происходит не растяжение, а сжатие,
а при отрицательном а, кроме растяжения (при |сс|> 1) или
сжатия (при |а|< 1), происходит еще изменение направления
вектора на противоположное.
Операция умножения вектора на число обладает следую-
следующими тремя свойствами:
5° a(a + b)= aa + ab [распределительное свойство число-
числового сомножителя относительно суммы векторов);

46 ВЕКТОРНАЯ АЛГЕБРА [ГЛ 2
6° (а + р)а = аа + ра (распределительное свойство вектор-
векторного сомножителя относительно суммы чисел);
7° а(Ра) = (a(i)a (сочетательное свойство числовых сомно-
сомножителей).
Для доказательства свойства 5° приложим векторы а и b
к общему началу О и построим на них параллелограмм, диаго-
диагональ которого будет представлять собой сумму а + Ь (рис. 2.8).
При «растяжении»*) сторон этого па-
аа/ ^-d7 Раллелограмма в а раз в силу свойств
подобия диагональ также «растяги-
«растягивается» в а раз, но это и означает,
что сумма aa + ab равна a(a-t-b).
Свойства 6° и 7° почти очевидны из
наглядных геометрических соображе-
соображений. С учетом оговоренной выше
условности термина «растяжение» свойство 6° означает, что при
«растяжении» вектора а в (а + Р) раз получается такой же век-
вектор, как при сложении вектора а, «растянутого» в а раз, с век-
вектором а, «растянутым» в р раз.
Свойство 7° в тех же терминах означает, что при «растяже-
«растяжении» вектора а сначала в р раз, а потом еще в а раз полу-
получается такой же вектор, как и при «растяжении» вектора а
сразу в ар раз. Итак, мы установили, что линейные операции
над векторами обладают свойствами 1°—7°.
Эти свойства имеют фундаментальное значение, ибо они по-
позволяют производить выкладки в векторной алгебре по тем пра-
правилам, по которым производятся аналогичные выкладки в обыч-
обычной алгебре.
В заключение докажем следующее утверждение.
Теорема 2.1. Если вектор Ъ коллинеарен ненулевому векто-
вектору а, то существует вещественное число i такое, что Ъ = Яа.
Доказательство. Приложим векторы а и b к общему
началу О. Тогда эти векторы расположатся на одной прямой,
на которой мы выберем начало отсчета, мас-
—I ", Д _ штабный отрезок и положительное направле-
0 л в ние. Возможны два случая: 1) векторы а и b
Рис. 2.9 направлены в одну сторону, 2) указанные
векторы направлены в противоположные сто-
стороны**). На рис. 2.9 изображен первый из указанных слу-
случаев.
Обозначим буквами А а В концы векторов а и b соответ-
соответственно и заметим, что, поскольку, вектор а ненулевой, точка А
*) Термин «растяжение> следует понимать в указанном выше условном
смысле. Рис. 2.8 отвечает случаю а > 1.
**) Тривиальный случай, когда вектор Ь нулевой и направление его
неопределенно, можно исключить из рассмотрения, нбо в этом случае равен-
равенство b = Яа реализуется при Я = 0.

§ I] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 47
отлична от О. Но тогда, исключив тривиальный случай совпа-
совпадения точек А и В*), мы (в силу п. 3 § 3 главы 1) можем
утверждать, что точка О делит направленный отрезок ВА в не-
некотором отношении, которое мы обозначим через —К, т. е.
или, что то же самое,
ОВ = Х-ОА**). B.2)
В случае, когда векторы аи b направлены в одну сторону
(как на рис. 2.9), точка О лежит вне отрезка ВА, и потому
отношение B.1) отрицательно, а Я > 0. Если же векторы а и Ь
направлены в противоположные стороны, то точка О лежит
внутри отрезка ВА, и потому отношение B.1) положительно,
аЯ<0.
Докажем, что в обоих случаях b = Я,а, Достаточно доказать,
что два вектора b и Ха 1) коллинеарны, 2) имеют одинаковую
длину, 3) имеют одинаковое направление.
Коллинеарность векторов b и Ха вытекает из коллинеарности
векторов а и b и определения произведения вектора на число.
Равенство длин векторов b и Ял непосредственно следует из
определения произведения вектора на число и соотношения
B.2). Наконец, тот факт, что векторы b и Яа имеют одинаковое
направление, следует из определения произведения вектора на
число и из того, что X > 0, когда а и b одинаково направлены,
и А, < 0, когда а и b противоположно направлены. Теорема до-
доказана.
3. Понятие линейной зависимости векторов. Линейной
комбинацией п векторов яц, &2, ..., а„ будем называть
сумму произведений этих векторов на произвольные веществен-
вещественные числа, т. е. выражение вида
... + а„а„, B.3)
где oi, <Х2, .... ал — какие угодно вещественные числа.
Определение 1. Векторы Ли а2, ..., а„ называются линей-
линейно зависимыми, если найдутся такие вещественные числа
си, иг, .... осп, из которых хотя бы одно отлично от нуля, что
линейная комбинация векторов яц, аг, ..., ап с указанными
числами обращается в нуль, т. е. имеет место равенство
+ ctjaj + ... + aftan = 0.
Векторы at, аг, ..., а„, не являющиеся линейно зависимыми,
будем называть линейно независимыми.
*) В этом случае векторы а и b совпадают и равенство b = Я.а реали-
реализуется при X = 1.
**) Здесь под ОА и ОВ следует понимать величины направленных от-
отрезков.

48 ВЕКТОРНАЯ АЛГЕБРА [ГЛ 2
Дадим другое определение линейно независимых векторов,
основанное на логическом отрицании содержания определе-
определения 1.
Определение 2. Векторы aj, а2, ,.., а„ называются линей-
линейно независимыми, если равенство нулю их линейной ком-
комбинации B.3) возможно лишь в случае, когда все числа ai,
аг ап равны нулю.
Имеют место следующие два утверждения.
Теорема 2.2. Если хотя бы один из векторов &и а2, ..., ал
является нулевым, то эти векторы являются линейно зависи-
зависимыми.
Доказательство. Пусть, ради определенности, вектор
aj является нулевым*), а остальные векторы аг, ..., а„ произ-
произвольны. Тогда обращается в нуль линейная комбинация B.3)
указанных векторов с числами ai = 1, аг = а3 = ... = ап = О,
одно из которых отлично от нуля. Теорема доказана.
Теорема 2.3. Если среди п векторов какие-либо п — 1 век-
векторов линейно зависимы, то и все п векторов линейно зави-
зависимы.
Доказательство. Пусть для определенности векторы
ai, а2, ..,, an_i линейно зависимы, а вектор а„ произволен**).
По определению линейной зависимости найдутся такие веще-
вещественные числа ось аг, .... а„-ь из которых хотя бы одно отлич-
отлично от нуля, что имеет место равенство
• • + an_,aft_, = 0. B.4)
Равенство B.4) сохранится, если мы добавим в левую часть
этого равенства равное нулю слагаемое 0-а„, т. е. справедливо
равенство
а,а, + <Ч*2 + • • • + а„_,ап_, + 0 • aft = 0. B.5)
Так как среди чисел ои, а2, .... а„-ь 0 хотя бы одно отлично от
нуля, то равенство B.5) доказывает линейную зависимость
векторов аь а», ..., а„. Теорема доказана.
Замечание. Конечно, утверждение теоремы 2.3 о линей-
линейной зависимости л векторов останется в силе, если среди этих
векторов линейно зависимыми являются не п—1, а любое
меньшее п число векторов.
4. Линейные комбинации двух векторов.
Теорема 2.4. Необходимым и достаточным условием линей-
линейной зависимости двух векторов является их коллинеарность.
*) Мы всегда можем поменять порядок следования векторов так, чтобы
нулевым оказался первый из векторов.
**) Поменяв порядок следования векторов, мы всегда можем добиться
того, чтобы линейно зависимыми оказались первые я — 1 векторов.

§ I] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 49
Доказательство. 1) Необходимость. Пусть два
вектора а и b линейно зависимы. Докажем коллинеарность этих
векторов.
По определению линейной зависимости найдутся такие ве-
вещественные числа аир, хотя бы одно из которых отлично от
нуля, что справедливо равенство
аа+рЬ = 0. B.6)
Пусть для определенности отлично от нуля число р. Тогда из
равенства B.6) (посредством деления этого равенства на р
и переброски одного члена в правую часть) получим следую-
следующее равенство:
b = —s- a.
р
Вводя обозначение X = —а/р, получим, что b = \&. Таким об-
образом, вектор b равен произведению вектора а на вещественное
число X. По определению произведения вектора на число век-
векторы а и b коллинеарны. Необходимость доказана.
2) Достаточность. Пусть векторы а и b коллинеарны.
Докажем, что эти векторы линейно зависимы. Если хотя бы
один из векторов а и b нулевой, то эти векторы линейно зави-
зависимы в силу теоремы 2.2.
Таким образом, нужно рассмотреть лишь случай, когда век-
векторы а и b ненулевые. Но если вектор а ненулевой, то из кол-
коллинеарности векторов а и b в силу теоремы 2.1 вытекает суще-
существование такого вещественного числа X, что b = Ы, или, что
то же самое,
Ь A)Ь 0. B.7)
Так как из двух чисел X, —1 одно заведомо отлично от нуля,
то равенство B.7) доказывает линейную зависимость векто-
векторов а и Ь. Достаточность доказана.
Следствие 1. Если векторы л и Ъ не коллинеарны, то они
линейно независимы.
Следствие 2. Среди двух неколлинеарных векторов не мо-
может быть нулевого вектора (иначе бы эти векторы оказались
линейно зависимыми).
5. Линейные комбинации трех векторов.
Определение. Векторы называются компланарными,
если они лежат либо в одной плоскости, либо в параллельных
плоскостях.
Теорема 2.5. Необходимым и достаточным условием линей'
ной зависимости трех векторов является их компланарность.
Доказательство. 1) Необходимость. Пусть три
вектора a, b и с линейно зависимы. Докажем компланарность
этих векторов.
4 Зак. 168

50 ВЕКТОРНАЯ АЛГЕБРА [ГЛ. 2
По определению линейной зависимости найдутся такие ве-
вещественные числа о, р и у, хотя бы одно из которых отлично
от нуля, что справедливо равенство
аа + рЬ + ус = 0. B.8)
Пусть для определенности отлично от нуля число у- Тогда из
равенства B.8) (посредством деления этого равенства на у
и переброски двух членов в правую часть) получим следующее
равенство:
Вводя обозначения К = —а/у, ц = —р/у, перепишем послед-
последнее равенство в виде
с = Аа + цЬ. B.9)
Если все три вектора a, b и с приложены к общему началу О,
то из равенства B.9) следует*), что вектор с равен диагонали
параллелограмма, построенного на двух
векторах: на векторе а, «растянутом» в
X раз, и на векторе Ь, «растянутом» **) в
ц раз (рис. 2.10).
Но это означает, что векторы a, b и с
лежат в одной плоскости, т. е. компланар-
компланарны. Необходимость доказана.
2) Достаточность. Пусть векторы
а, Ь и с компланарны. Докажем, что этн
векторы линейно зависимы.
Прежде всего, исключим случай, когда какая-либо пара из
указанных трех векторов коллинеарна. Тогда в силу теоре-
теоремы 2.4 указанная пара векторов линейно зависима, а стало быть
(в силу теоремы 2.3), и все три вектора а, Ь и с линейно зави-
зависимы.
Остается рассмотреть случай, когда в тройке векторов а, Ь,
с ни одна пара векторов не коллинеарна (и, в частности, от-
отсутствуют нулевые векторы***)).
Перенесем три компланарных вектора a, b и с на одну пло-
плоскость и приведем их к общему началу О (рис. 2.10). Прове-
•) В силу правила параллелограмма сложения векторов и определения
произведения вектора на число (см. п. 2). При этом мы исключаем тривиаль-
тривиальный случай, когда векторы а и b коллииеариы. В этом случае компланар-
компланарность векторов a, b и с вытекает из того, что эти три вектора, будучи при-
приведены к общему началу О, лежат на двух проходящих через точку О пря-
прямых: иа одной лежит вектор с, на другой — оба вектора а и Ь.
•*) Термин «растяиутый> следует понимать в указанном в п. 2 условном
смысле.
***) В силу следствия 2 из теоремы 2.4 в паре иеколлинеарных векторов
не могут содержаться нулевые векторы.
В
fib\
¦
а
Рис.
/
2.10
с
А
\
Ла

§ I] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 51
дем через конец С вектора с прямые, параллельные векторам
а и Ь. Обозначим буквой А точку пересечения прямой, парал-
параллельной вектору Ь, с прямой, на которой лежит вектор а, а бук-
буквой В точку пересечения прямой, параллельной вектору а,
с прямой, на которой лежит вектор Ь. (Существование указан-
указанных точек пересечения вытекает из того, что векторы а и b не
коллинеарны.) В силу правила параллелограмма сложения
векторов вектор с равен сумме векторов ОА и OBt т. е.
ОВ. B.10)
Так как вектор ОА коллинеарен ненулевому вектору а (с ко-
которым он лежит на одной прямой), то в силу теоремы 2.1
найдется вещественное число К такое, что
Аа. B.11)
Из аналогичных соображений вытекает существование ве-
вещественного числа \i такого, что
ОВ = цЬ. B.12)
Вставляя B.11) и B.12) в B.10), будем иметь
с = Яа + цЬ. B.13)
Равенство B.13) можно переписать в виде
Так как из трех чисел К, ц, —I одно заведомо отлично от нуля,
то последнее равенство доказывает линейную зависимость век-
векторов a, b и с. Достаточность доказана.
Попутно доказаны следующие утверждения:
Следствие 1. Каковы бы ни были неколлинеарные векторы а
и Ъ для любого вектора с, лежащего в одной плоскости с век-
векторами а и Ь, найдутся такие вещественные числа Яиц, что
справедливо равенство
B.13)
Следствие 2. Если векторы а, Ь и с не компланарны, то они
линейно независимы.
Следствие 3. Среди трех некомпланарных векторов не мо-
может быть двух коллинеарных векторов и не может быть ни
одного нулевого вектора*).
6. Линейная зависимость четырех векторов.
Теорема 2.6. Любые четыре вектора линейно зависимы.
Доказательство. Прежде всего исключим случай, ко-
когда какая-нибудь тройка из указанных четырех векторов ком-
¦) Иначе эти векторы оказались бы лииейио зависимыми.

52
ВЕКТОРНАЯ АЛГЕБРА
[ГЛ.2
планарна. Тогда в силу теоремы 2.5 указанная тройка векторов
линейно зависима, а стало быть (в силу теоремы 2.3), и все
четыре вектора линейно зависимы.
Остается рассмотреть случай, когда среди четырех векто-
векторов а, Ь, с и d никакая тройка векторов не компланарна (и,
стало быть, нет ни одной пары коллинеарных векторов и ни
одного нулевого вектора *)).
Приведем все четыре вектора а, Ь, с и d к общему началу О
и проведем через конец D вектора d плоскости, параллельные
плоскостям, определяемым парами векторов Ьс, ас и ab **)
(рис. 2.11). Точки пересечения указанных плоскостей с пря-
прямыми, на которых лежат векторы а, Ь и с, обозначим соответ-
соответственно буквами А, В п С. (Существование указанных точек
пересечения вытекает из того, что векто-
векторы а, Ь и с не компланарны.)
Убедимся в том, что вектор й—Ш)
равен сумме трех векторов ОА, ОВ и
ОС, т. е.
в
^--
7
7
ОС.
а
Рис. 2.11
B.14)
В самом деле, из правила параллело-
параллелограмма сложения векторов_и_ из паралле-
параллелограмма OCDE (рис. 2.11) вытекает, 4To_d = OC^+ UE, а из
параллелограмма ОВЕА вытекает, что ОЕ = ОА + ОВ. Тем
самым равенство BЛ4) установлено.
Так как вектор ОА коллинеарен ненулевому вектору а (с ко-
которым он лежит иа одной прямой), то в силу теоремы 2.1 най-
найдется вещественное число Я, такое, что
Ьа. B.15)
Из аналогичных соображений вытекает существование веще-
вещественных чисел ji и v таких, что
ОВ = цЬ, <xT=vc. B.16)
Вставляя B.15) и B.16) в B.14), будем иметь
d = ba + nb + vc. B.17)
Равенство B.17) можно переписать в виде
O. B.18)
*) Согласно следствию 3 из теоремы 2.5 в тройке некомпланарных век-
векторов ие может содержаться ии одной пары коллннеарных векторов и ни
одного нулевого вектора.
*•) Векторы, входящие в каждую из указанных трех пар, не коллннеарны,
а поэтому каждая из указанных трех пар определяет некоторую плоскость.

S I] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 53
Так как из четырех чисел X, ц, v, —1 одно заведомо отлично
от нуля, то равенство B.18) доказывает линейную зависимость
векторов а, Ь, с и d. Теорема доказана.
Попутно доказано следующее утверждение:
Следствие 1. Каковы бы ни были некомпланарные векторы
а, Ь и с, для любого вектора d найдутся такие вещественные
числа К, \i и v, что справедливо равенство
d = *a + nb + vc. B.17)
7. Понятие базиса. Аффинные координаты.
Определение 1. Говорят, что три линейно независимых век-
вектора a, b и с образуют в пространстве базис, если любой век-
вектор d может быть представлен в виде некоторой линейной
комбинации векторов a, b и с, т. е. если для любого вектора d
найдутся такие вещественные числа %, ц и v, что справедливо
равенство B.17).
Аналогично определяется базис на некоторой плоскости п.
Определение 2. Говорят, что два лежащих в плоскости я
линейно независимых вектора а и Ъ образуют на этой плоскости
базис, если любой лежащий в плоскости п вектор с может
быть представлен в виде некоторой линейной комбинации век-
векторов а и Ь, т. е. если для любого лежащего в плоскости я
вектора с найдутся такие вещественные числа Я, и ц, что спра-
справедливо равенство B.13).
Справедливы следующие фундаментальные утвер-
утверждения:
1) любая тройка некомпланарных векторов a, b и с образует
базис в пространстве;
2) любая пара лежащих в данной плоскости неколлинеар-
ных векторов а и b образует базис на этой плоскости.
Для доказательства первого из этих утверждений доста-
достаточно заметить, что, каковы бы ни были три некомпланарных
вектора a, b и с, они линейно независимы (в силу следствия 2
из теоремы 2.5), и для любого вектора d найдутся веществен-
вещественные числа %, ц и v такие, что справедливо равенство B.17)
(в силу следствия из теоремы 2.6). Утверждение 2) доказы-
доказывается аналогично (с помощью следствия 1 из теоремы 2.4
и следствия 1 из теоремы 2.5).
В дальнейшем для определенности будем рассматривать
базис в пространстве. Итак, пусть а, Ь, с — произвольный базис
в пространстве, т. е. произвольная тройка некомпланарных век-
векторов. Тогда (по определению базиса) для любого вектора d
найдутся такие вещественные числа %, ц и v, что будет спра-
справедливо равенство
d = %& + цЬ + vc. B.17)

54 ВЕКТОРНАЯ АЛГЕБРА [ГЛ 2
Принято называть равенство B.17) разложением вектора d no
базису а, Ь, с, а числа Я, ц и v — координатами вектора d от-
относительно базиса а, Ь, с.
Докажем, что каждый вектор d может быть единствен-
единственным способом разложен по базису а, Ь, с, или (что то же
самое) координаты каждого вектора d относительно базиса а,
Ь, с определяются однозначно.
Допустим, что для некоторого вектора d, наряду с разложе-
разложением B.17), справедливо еще и другое разложение по тому же
самому базису
d = ra+n'b + v'c. B.19)
Почленное вычитание равенств B.17) и B.19) приводит к со-
соотношению *)
(Я - Я') а + (ц - ц') Ь -f (v - v') с = 0. B.20)
В силу линейной независимости базисных векторов а, Ь, с со-
соотношение B.20) приводит к равенствам
Я, - Я' = 0, ц — ц' = 0, v - v' = 0,
или Я = Я', ц = ц', v = v'. Единственность разложения по ба-
базису доказана.
Основное значение базиса состоит в том, что линейные опе-
операции над векторами при задании базиса становятся обычными
линейными операциями над числами — координатами этих век-
векторов. Именно справедливо следующее утверждение.
Теорема 2.7. При сложении двух векторов di и &?, их коор-
координаты (относительно любого базиса а, Ь, с) складываются.
При умножении вектора di на любое число а все его коорди-
координаты умножаются на это число.
Доказательство. Пусть di = A,ia + (iib + vtc, дг = Яга -f
+ ЦгЬ + v2c. Тогда в силу свойств Г—7° линейных операций
(см. п. 2)
di + d2 = ft, + Я2) а + (ц, + Ц2)Ь + (v, + v2)c,
ad, = (аЯ,) а + (ац,) Ь + (av,) с.
В силу единственности разложения по базису теорема до-
доказана.
Перейдем теперь к определению так называемых аффин-
аффинных**) координат точки.
*) Возможность почленного вычитаиня равенств B.17) и B.19) н произ-
производимой группировки членов вытекают из свойств лииейиых операций над
векторами (см. п. 2).
**) Термин «аффинный» происходит от латинского слова affinis, что
означает смежный, или соседний.

§ 11 ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 55
Аффинные координаты в пространстве определяются зада-
заданием базиса а, Ь, с и некоторой точки О, называемой началом
координат.
Аффинными координатами любой точки М на-
называются координаты вектора ОМ (относительно базиса
а, Ь, с).
Так как каждый вектор ОМ может быть, и притом един-
единственным способом, разложен по базису а, Ь, с, то каждой точке
пространства М однозначно соответствует тройка аффинных
координат Я, ц, v.
Разумеется, декартовы прямоугольные координаты являются
частным случаем аффинных координат, соответствующим трой-
тройке взаимно ортогональных и единичных базисных векторов.
Более подробно этот важный частный случай рассматривается
в п. 9 настоящего параграфа.
В заключение заметим, что свойства базиса и понятие аф-
аффинных координат на плоскости вполне аналогичны случаю
пространства.
8. Проекция вектора на ось и ее свойства. Прежде всего оп-
определим проекцию вектора а = АВ на произвольную ось ы.
Обозначим буквами А' и В' основания пер-
перпендикуляров, опущенных на ось и из то-
точек А п В соответственно (рис. 2.12).
Проекцией вектора а=АВ на
ось и называется величина А'В' направ-
направленного отрезка А'В' оси и.
Договоримся обозначать проекцию век-
вектора а на ось и символом прц а. Построе-
Построение проекции вектора а = ЛВ на ось и ил- Рис 2.12
люстрируется на рис. 2.12, где символом
аир обозначены две проектирующие плоскости (т. е. плоско-
плоскости, перпендикулярные оси и и проходящие через концы А и В
вектора а = АВ).
Для дальнейшего нам понадобится понятие угла накло-
наклона вектора а = А~В к оси и. Этот угол может быть опреде-
определен как угол <р между двумя выходящими из произвольной
точки М лучами, один из которых имеет направление, совпа-
совпадающее с направлением вектора & — АВ, а другой — направ-
направление, совпадающее с направлением оси и (рис. 2.12).
Очевидно, на величину угла наклона вектора а к оси и не
влияют выбор точки М выхода указанных выше лучей и за-
замена оси и любой другой осью v, имеющей то же направление,
что и ось и.
Докажем следующее утверждение.

56 ВЕКТОРНАЯ АЛГЕБРА 1ГЛ.2
Теорема 2.8. Проекция вектора а на ось и равна длине век-
вектора а, умноженной на косинус <р угла наклона вектора а
к оси и.
Доказательство. Обозначим через v ось, проходящую
через начало А вектора а и имеющую то же направление, что
и ось и (рис. 2.12), и пусть С — проекция_В на ось v. Тогда
ZBAC равен углу <р наклона вектора & = АВ к любой из осей
и или v, причем точка С заведомо лежит в указанной иа
рис. 2.12 проектирующей плоскости 0 (т. е. в плоскости, пер-
перпендикулярной оси и и проходящей через точку В).
Далее, можно утверждать, что А'В'— АС*), ибо оси и и о
параллельны и одинаково направлены и отрезки этих осей, за-
заключенные между параллельными плоскостями аир, равны.
Так как по определению пр„ а = А'В', то мы приходим к ра-
равенству
приа = ЛС. B.21)
Но величина АС представляет собой проекцию направленного
отрезка АВ на ось v, которая (в силу п. 1 § 3 главы 1) равна
/lC = |/lB|Cos<p = |a|cos<p. B.22)
Из сопоставления равенств B.21) и B.22) вытекает равенство
пр„ а = | а | cos ф. B.23)
Теорема доказана.
Основные свойства проекции вектора на ось заклю-
заключаются в том, что линейные операции над векторами приводят
к соответствующим линейным операциям над проекциями этих
векторов (на произвольную ось).
Именно справедливо следующее утверждение:
При сложении двух векторов di и Йг их проекции на произ-
произвольную ось и складываются. При умножении вектора di на лю-
любое число а проекция этого вектора на произвольную ось и
также умножается на число а.
Доказательство этого утверждения отложим до п. 9. Опи-
Описанные свойства проекции вектора на ось естественно назвать
линейными свойствами.
9. Декартова прямоугольная система координат как частный
случай аффинной системы координат. Как уже отмечалось выше,
декартова прямоугольная система координат является частным
случаем аффинной системы, отвечающей тройке взаимно орто-
ортогональных и единичных базисных векторов.
*) Здесь под А'В' следует понимать величину направленного отрезка А'В'
оси и, а под АС — величину направленного отрезка АС оси и.

S I] ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 57
—В случае декартовой прямоугольной системы базисные век-
векторы принято обозначать не буквами а, Ь, с, а буквами i, j, k.
Итак, каждый из векторов i, j, k имеет длину, равную единице,
причем эти три вектора взаимно ортогональны (обычно направ-
направления векторов i, j, k берут совпадающими с направлениями
декартовых осей Ох, Оу и Ог соответственно).
В силу основных результатов п. 7 каждый вектор d может
быть, и притом единственным способом, разложен по декар-
тову прямоугольному базису i, j, k, т. е. для каждого вектора d
найдется, и притом единственная, тройка чисел X, У и Z*) та-
такая, что справедливо равенство
d = Xi + Y\ + Zk. B.24)
Числа X, Y, Z называются декартовыми прямоугольными
координатами вектора d. Если М — любая точка пространства,
то определенные в главе 1 декартовы прямоугольные коорди-
координаты этой точки совпадают с декартовыми прямоугольными ко-
координатами вектора ОМ.
Если вектор d имеет декартовы прямоугольные координаты
X, У, Z, то мы будем использовать следующую символику:
(у v 7\
Геометрический смысл декартовых прямоугольных коорди-
координат вектора выясняет следующее утверждение.
Теорема 2.9. Декартовы прямоугольные координаты X, Y
и Z вектора d равны проекциям этого вектора на оси Ох, Оу
и Ог соответственно.
Доказательство. В полной аналогии с рассуждениями,
проведенными при доказательстве теоремы 2.6 (п. 6), приложим
вектор d к началу О декартовой системы
и проведем через конец D этого вектора
три плоскости, параллельные координатным
плоскостям Оуг, Охг и Оху (рис. 2.13).
Точки пересечения указанных плоскостей
с осями Ох, Оу и Ог соответственно обо-
обозначим буквами А, В и С. *А
Как и при доказательстве теоремы 2.6, о^т-
получим, что 1
Рнс. 2.13
/
Дальнейшие рассуждения упомянутой теоремы (с учетом из-
изменившихся обозначений) приводят нас к равенствам
= Zk. B.25)
*) В случае декартовой прямоугольной системы для координат вектора d
вместо Я, ц, у мы будем использовать обозначения X, Y, Z.

58 ВЕКТОРНАЯ АЛГЕБРА [ГЛ 2
В рассматриваемом случае декартовой прямоугольной систе-
системы параллелепипед, построенный на базисных векторах i, j, k
и имеющий вектор d своей диагональю, является прямоуголь-
прямоугольным. Поэтому проекции вектора d на оси Ох, Оу и Oz соответ-
соответственно равны величинам О А, ОВ и ОС. Для доказательства
теоремы иам остается убедиться в том, что О А — X, ОВ = У,
OC — Z.
Убедимся, например, в равенстве ОА — Х. В силу B.25)
ОА = Х\. Отсюда и из того, что i — единичный вектор, выте-
вытекает, что |ОЛ| —|Х|. Но_и_знаки чисел О А и X совпадают, ибо
в случае, когда векторы О А и i направлены в одну сторону, оба
числа ОА и X положительны, а в случае, когда векторы ОА и i
направлены в противоположные стороны, оба числа ОА и X от-
отрицательны. Итак, ОА = X. Аналогично доказываются равен-
равенства ОВ = У и ОС = Z. Теорема доказана.
Обозначим буквами а, 0 и у углы наклона вектора d к осям
Ох, Оу и Oz соответственно.
Три числа cos a, cosp и cosy принято называть направляю-
направляющими косинусами вектора d.
Из теорем 2.9 и 2.8 (см. формулу B.23)) вытекают следую-
следующие формулы для координат X, У и Z вектора d:
X = |d|cosa, y = |d|cosp, Z == | d | cos Y. B.26)
Так как квадрат диагонали прямоугольного параллелепи-
параллелепипеда равен сумме квадратов его сторон, то из равенств ОА = X,
ОВ = У и ОС = Z мы получим следующее выражение для дли-
длины вектора d через его координаты:
| d | = */X2 + Y* + Z2. B.27)
Из формул B.26) и B.27) вытекают следующие выражения для
направляющих косинусов вектора d через координаты этого
вектора:
2
COS V = —j .
r Ух* + у2 + z*
Возводя в квадрат и складывая равенства B.28), получим, что
cos2 a + cos2 p + cos2 v = 1»
т. е. сумма квадратов направляющих косинусов любого вектора
равна единице.
Так как вектор d однозначно определяется заданием трех
его координат, то из формул B.26) ясно, что вектор d одно-
однозначно определяется заданием его длины и трех направляющих
косинусов.

§ Я СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 59
В заключение докажем сформулированные в конце преды-
предыдущего пункта линейные свойства проекции вектора на ось,
т. е. докажем, что при сложении двух векторов di и d2 их про-
проекции на произвольную ось и складываются, а при умножении
вектора di на любое число а его проекция на произвольную ось
и умножается на число а.
Пусть дана произвольная ось и и любые векторы di и d2.
Введем декартовы прямоугольные координаты так, чтобы ось и
совпала с осью Ох. Пусть
d, = Х,1 + KJ + Z,k, d2 = X2i + YJ + Z2k.
Тогда в силу теоремы 2.7
d, + d2 = (J, + Х2)\ + (К, + Г2) j + (Z, + Z2)k,
Но в силу теоремы 2.9 и того, что ось и совпадает с осью Ох,
можно утверждать, что
X1 = npud1, X2 = npud2, Xi + Х2 = пр„ (d, + d2),
a#i = пр„ (adj.
Таким образом, прц (di + d2) = пр„ d, + прц d2, пр„ (ad() = а прц dlf
и сформулированное утверждение доказано.
§ 2. Скалярное произведение двух векторов
1. Определение скалярного произведения.
Определение 1. Скалярным произведением двух
векторов называется число, равное произведению длин этих век-
векторов на косинус угла между ними.
Скалярное произведение векторов а и Ь будем обозначать
символом аЬ. Если угол между векторами а и Ь равен <р, то
по определению скалярное произведение этих двух векторов
выражается формулой
ab = |a||b|cosqp. B.29)
Сформулируем другое определение скалярного про-
произведения двух векторов, эквивалентное определению 1. Для
этого воспользуемся понятием проекции вектора Ь на ось, опре-
определяемую вектором а. В соответствии с обозначениями п. 8 § 1
будем обозначать проекцию вектора Ь на ось, определяемую
вектором а, символом пр„ Ь. На основании теоремы 2.8 получим
npeb = |b|cos<p. B.30)
Сопоставление равенств B.29) и B.30) приводит нас к сле-
следующему выражению для скалярного произведения:
ab = |a|npeb. B.31)

60 ВЕКТОРНАЯ АЛГЕБРА [ГЛ. 2
Конечно, в проведенных рассуждениях можно было бы поме-
поменять ролями векторы а и Ь. При этом мы пришли бы к следую-
следующему выражению для скалярного произведения:
аЬ = | Ь | прг, а. B.32)
Выражения B.31) и B.32) приводят нас к следующему
определению скалярного произведения (эквивалентному опре-
определению 1).
Определение 2. Скалярным произведением двух
векторов называется число, равное произведению длины одного
из этих векторов на проекцию другого вектора на ось, опреде-
определяемую первым из указанных векторов.
Понятие скалярного произведения векторов родилось в ме-
механике. Если вектор а изображает силу, точка приложения ко-
которой перемещается из начала в конец вектора Ь, то работа w
указанной силы определяется равенством
w = \ а || Ь |cos<p,
т. е. равна скалярному произведению векторов а и Ь.
2. Геометрические свойства скалярного произведения.
Теорема 2.10. Необходимым и достаточным условием орто-
ортогональности двух векторов является равенство нулю их скаляр-
скалярного произведения.
Доказательство. 1) Необходимость. Пусть век-
векторы а и Ь ортогональны, <р — угол между ними. Тогда cos<p=0
и в силу формулы B.29) скалярное произведение аЬ равно
нулю.
2) Достаточность. Пусть скалярное произведение аЬ
равно нулю. Докажем, что векторы а и Ь ортогональны. Прежде
всего исключим тривиальный случай, когда хотя бы один из
векторов а или b является нулевым (нулевой вектор имеет не-
неопределенное направление, и его можно считать
ортогональным любому вектору). Если же оба
вектора а и Ь ненулевые, то |а|>0 и |Ь|>0,
и поэтому из равенства аЬ = 0 и из формулы
B.29) вытекает, что cos <р = 0, т. е. векторы а
и Ь ортогональны.
Теорема доказана.
Прежде чем сформулировать следующее ут-
Рис. 2.14 верждение, уточним понятие угла <р между век-
векторами а и Ь. Приведем произвольные векто-
векторы а и Ь к общему началу О (рис. 2.14). Тогда в качестве
угла ф между векторами а и Ь можно взять любой из двух
указанных на рис. 2.14 углов <pi и <рг. В самом деле,
сумма углов <pi и <р2 равна 2я, и поэтому cos <pi = cos <p2> а в
определение скалярного произведения входит только косинус
угла между векторами. Из двух углов <pi и <рг один заведомо

§ 2] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 61
не превосходит п (на рис. 2.14 не превосходит л угол q>i). До-
Договоримся в дальнейшем под углом между двумя векторами
подразумевать тот угол, который не превосходит п.
Тогда справедливо следующее утверждение.
Теорема 2.11. Два ненулевых вектора а и Ь составляют
острый (тупой) угол тогда и только тогда, когда их скалярное
произведение положительно (отрицательно).
Доказательство. Так как векторы а и Ь ненулевые,
то в силу формулы B.29) знак скалярного произведения совпа-
совпадает со знаком cos <р. Но если угол <р не превосходит я, то cos <p
положителен тогда и только тогда, когда <р — острый угол, и
отрицателен тогда и только тогда, когда <р — тупой угол. Тео-
Теорема доказана.
3. Алгебраические свойства скалярного произведения. Ска-
Скалярное произведение векторов обладает следующими четырьмя
свойствами:
Г ab = Ьа (переместительное свойство);
2° (аа)Ь = а(аЬ) (сочетательное относительно числового
множителя свойство);
3° (а-f Ь)с— ас + Ьс (распределительное относительно сум-
суммы векторов свойство);
4° аа > 0, если а — ненулевой вектор, и аа = 0, если а —
нулевой вектор*).
Убедимся в справедливости этих свойств. Свойство Г непо-
непосредственно вытекает из формулы B.29).
Для доказательства свойства 2° воспользуемся определе-
определением 2 скалярного произведения, т. е. формулой B.32). Учи-
Учитывая, что проекция вектора на ось обладает линейным свой-
свойством пр&(аа) =» апраа (см. конец п. 8 и конец п. 9 § 1), по-
получим
(аа) b = | b | • пр4 (аа) = a | b | • пр4 а = a • (ab).
Тем самым свойство 2° доказано.
*) Отметим, что в курсе линейной алгебры вместо множества векторов
рассматривают множество элементов а, Ь, ... любой природы. Если для эле-
элементов этого множества определены операция сложения н операция умноже-
умножения на вещественное число и для этих операций справедливы те же самые
свойства Г — 7°, которые установлены нами для линейных операций над
векторами (см. п. 2 § 1), то указаииое множество элементов называется ли-
линейным пространством.
Произвольное линейное пространство называется евклидовым простран-
пространством, если: 1) известно правило, посредством которого любым двум элемен-
элементам а и Ь этого пространства ставится в соответствие число, называемое
скалярным произведением этих элементов и обозначаемое символом ab; 2) ука-
указанное правило таково, что для скалярного произведения справедливы только
что сформулированные свойства 1°—44.
Таким образом, пространство всех геометрических векторов с определен-
определенными нами линейными операциями н скалярным произведением представляет
собой один из примеров линейного евклидова пространства.

62 ВЕКТОРНАЯ АЛГЕБРА [ГЛ 2
Для доказательства свойства 3° снова воспользуемся фор-
формулой B.32) и линейным свойством проекции вектора на ось
пре (a -f b) sas пре а + пре b (см. п. 8 § 1). Получим
(а + Ь)с = | с | ¦ прс(а + Ь) — | с | • (прс а + пре Ь) =
=г | с | прс а +1 с | • пре b = ас -f be.
Нам остается доказать свойство 4°. Для этого заметим, что
непосредственно из формулы B.29) вытекает, что аа = |а|2,
т. е. скалярный квадрат вектора равен квадрату длины этого
вектора. Отсюда, в частности, вытекает, что скалярный квад-
квадрат аа положителен, когда вектор а ненулевой, и равен нулю,
когда вектор а нулевой.
Доказанные свойства имеют фундаментальное значение. Они
позволяют при скалярном перемножении векторных многочле-
многочленов выполнять действия почленно, не заботясь при этом о по-
порядке векторных множителей и сочетая числовые множители.
Указанная возможность будет существенно использована в сле-
следующем пункте.
4. Выражение скалярного произведения в декартовых коор-
координатах.
Теорема 2.12. Если два вектора а и b определены своими
декартовыми прямоугольными координатами
а = №, Yit ZJ, Ъ = {Х2, У2, Z2),
то скалярное произведение этих векторов равно сумме попар-
попарных произведений их соответствующих координат, т. е.
ab = J, Хг + У,Г2 + ZXZ2. B.33)
Доказательство. Составим из тройки базисных векто-
векторов i, j и к все возможные пары и для каждой из пар подсчи-
подсчитаем скалярное произведение. Учитывая, что базисные векторы
являются попарно ортогональными и имеют единичную длину,
получим
ij = l, ji = 0, kl-0,
ij = 0, jj = l, kJ-O, B.34)
ik = 0, jk = O, kk=l.
Далее, учитывая, что а = XA -f Kij -f Z,k, b = X2i + Y2j + Z2k,
и опираясь иа установленную в предыдущем пункте возмож-
возможность почленного скалярного перемножения векторных много-
многочленов, получим
ab = ВДН + Х,У2Ц + X,Z2ik + y,X2ji + YJM + У^к +
+ Z,X2ki + Z,y2kj + Z,Z2kk.
Из последнего равенства и соотношений B.34) вытекает фор-
формула B.33), Теорема доказана.

§ 31 ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 63
Следствие 1. Необходимым и достаточным условием орто-
ортогональности векторов
&={XuY1,Zl} и b={X2,Y2,Z2}
является равенство
XlX2 + Y1Y2 + Z1Z2 = 0.
Это следствие непосредственно вытекает из теоремы 2.10
и формулы B.34).
Следствие 2. Угол tp между векторами
а = {Xi, Yx, Z,} и b = {Х2, Y2, Z2)
определяется по формуле
coscp = — x,xt + YtYt + z,z, B35)
Jx\ + y\ + z\ ]x\ + y\ + z\
~ ab
В самом деле, cosq> = -j—гтуг. и нам остается воспользо-
воспользоваться формулой B.33) для скалярного произведения и фор-
формулой B.27) для длины вектора.
§ 3. Векторное и смешанное произведения векторов
1. Правые и левые тройки векторов и системы координат.
Определение 1. Три вектора называются упорядочен-
упорядоченной тройкой {или просто тройкой), если указано, какой
из этих векторов является первым, какой — вторым и какой —
третьим.
При записи тройки векторов мы всегда будем располагать
эти векторы в порядке их следования. Так, запись Ьас означает,
что первым элементом тройки является вектор Ь, вторым — век-
вектор а и третьим — вектор с.
Определение 2. Тройка не компланарных векторов abc назы-
называется правой (левой), если выполнено одно из следующих
трех условий:
1° если, будучи приведены к общему началу, эти векторы
располагаются так, как могут быть расположены соответствен-
соответственно большой, несогнутый указательный и средний пальцы пра-
правой (левой) руки;
2° если после приведения к общему началу вектор с распо-
располагается по ту сторону от плоскости, определяемой векторами
а и Ь, откуда кратчайший поворот от а к Ь кажется совершаю-
совершающимся против часовой стрелки (по часовой стрелке);
3° если, находясь внутри телесного угла, образованного при-
приведенными к общему началу векторами а, Ь, с, мы видим пово-
поворот от а к Ь и от него к с совершающимся против часовой
стрелки (по часовой стрелке).

64 ВЕКТОРНАЯ АЛГЕБРА [ГЛ. 2
Легко проверить, что условия Г, 2° и 3° эквивалентны между
собой. Предоставляем читателю с помощью каждого из условий
Г, 2° и 3° убедиться в том, что тройка abc, изображенная на
рис. 2.15, является правой, а тройка abc, изображенная на
рис. 2.16, является левой.
Замечание. Понятие правой и левой тройки теряет смысл
для компланарных векторов.
Если две тройки векторов либо обе являются правыми, либо
обе являются левыми, то говорят, что эти тройки одной ориен-
ориентации. В противном случае говорят, что
рассматриваемые две тройки противопо-
противоположной ориентации.
Всего из трех векторов a, b и с мож-
можно составить следующие шесть троек:
Т abc, bca, cab, B.36)
Рис. 2.15 Рис. 2.16 bac, acb, cba. B.37)
С помощью условия 3° определения 2 легко проверить, что
все три тройки B.36) той же ориентации, что и тройка abc,
а все три тройки B.37) имеют ориентацию, противополож-
противоположную abc.
Определение 3. Аффинная или декартова система коорди-
координат называется правой (левой), если три базисных век-
вектора образуют правую (левую) тройку.
Ради определенности договоримся в дальнейшем рассмат-
рассматривать только правые системы координат.
2. Определение векторного произведения двух векторов.
Определение. Векторным произведением, вектора а
на вектор b называется вектор с, обозначаемый символом с =
= [ab] и удовлетворяющий следующим трем требованиям:
1) длина вектора с равна произведению длин векторов а и b
на синус угла ф между ними *), т. е.
| с I = | [ab] | = | а 11Ы sin Ф; B.38)
2) вектор с ортогонален к каждому из векторов а и Ь;
3) вектор с направлен так, что тройка векторов abc является
правой **).
*) В соответствии с договоренностью, принятой в п. 2 § 2, в качестве
угла между векторами берем тот угол ф, который не превосходит п. Прн
этом всегда sin ф ^ О и величина B 38) неотрицательна. Из формулы B 38)
следует также, что в случае коллинеарных векторов аи b определяемый век-
вектор с = [ab] является нулевым.
**) Требования 1) и 2) определяют вектор с с точностью до двух взаим-
взаимно противоположных направлений. Требование 3) отбирает одно из этих двух
направлений. В случае, когда а и b коллннеарны, тройка abc является ком-
компланарной, но в этом случае уже из требования 1) вытекает, что с = 0.

§3} ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 65
Понятие векторного произведения также родилось в меха-
механике. Если вектор b изображает приложенную в некоторой
точке М силу, а вектор а идет из некоторой точки О в точку М,
то вектор с = [ab] представляет собой момент силы b относи-
относительно точки О.
3. Геометрические свойства векторного произведения.
Теорема 2.13. Необходимым и достаточным условием кол-
коллинеарности двух векторов является равенство нулю их вектор-
векторного произведения.
Доказательство. 1) Необходимость вытекает из самого
определения векторного произведения: для коллинеарных век-
векторов а и b векторное произведение по определению равно нулю
(см. формулу B.38) и сноску*) на с. 64).
2) Достаточность. Пусть векторное произведение [ab]
равно нулю. Докажем, что векторы а и b коллинеарны.
Прежде всего исключим тривиальный случай, когда хотя
бы один из векторов а или b является нулевым (нулевой вектор
имеет неопределенное направление, и его можно считать кол-
лииеарным любому вектору). Если же оба вектора а и b нену-
ненулевые, то |а|>0 и |Ь|>0, и поэтому из равенства [ab] = О
и из формулы B.38) вытекает, что sin q> = 0, т. е. векторы а и b
коллинеарны.
Теорема доказана.
Теорема 2.14. Длина (или модуль) векторного произведения
[ab] равняется площади S параллелограмма, построенного на
приведенных к общему началу векторах а и Ь.
Доказательство. Так как площадь параллелограмма
равна произведению смежных сторон этого параллелограмма
на синус угла между ними, то теорема непосредственно выте-
вытекает из формулы B.38).
Чтобы получить следствие из теоремы 2.14, введем поня-
понятие орта.
Определение. Ортом произвольного ненулевого вектора с
назовем единичный вектор, коллинеарный с и имеющий одина-
одинаковое с с направление.
Следствие из теоремы 2.14. Если е — орт векторного про-
произведения [ab], a S — площадь параллелограмма, построен-
построенного на приведенных к общему началу векторах а и Ь, то для
векторного произведения [ab] справедлива следующая фор-
формула:
Se *). B.39)
*) Если векторы а и Ь коллинеарны (и, в частности, если хотя бы один
из векторов а и Ь нулевой), формула B.39) остается справедливой, ибо в
этом случае равны нулю как векторное произведение [ab], так и площадь S
построенного на векторах а и Ь параллелограмма.
5 Зак. 168

66 ВЕКТОРНАЯ АЛГЕБРА [ГЛ.2
Замечание. Из определений орта и векторного произве-
произведения вытекает, что тройка abe является правой (ибо тройка
ab[ab] является правой).
Следующее свойство устанавливает важную для дальней-
дальнейшего формулу.
Теорема 2.15. Если с — какой-нибудь вектор, я— любая со-
содержащая его плоскость, е — единичный вектор, лежащий в
плоскости я и ортогональный к с, g— единичный вектор, орто-
ортогональный к плоскости я и направленный так, что тройка ecg
является правой, то для любого лежащего в плоскости п век-
вектора а справедлива формула
[ac] = nPea-|c|g. B.40)
Доказательство. Достаточно доказать, что векторы,
стоящие в левой и правой частях B.40): 1) имеют одинаковую
длину, 2) коллинеарны, 3) имеют одинаковое направление.
В силу теоремы 2.14 | [ас] | = S, где S — площадь построен-
построенного на приведенных к общему началу векторах а и с паралле-
параллелограмма. Длина вектора, стоящего в правой части B.40), рав-
равна |с| |преа|, т. е. тоже равна S, ибо если за основание указан-
указанного параллелограмма принять вектор
с, то высота его h будет равна |преа|,
(рис. 2.17).
Коллинеарность векторов, стоящих
в левой и правой частях B.40), выте-
вытекает из того, что оба эти вектора орто-
Рис. 2.17 гональны к плоскости я (вектор [ас]
в силу определения векторного произ-
произведения, а вектор преа•|с | g в силу того, что вектор g по усло-
условию ортогонален к плоскости я).
Остается проверить, что векторы, стоящие в левой и правой
частях B.40), одинаково направлены.
Для этого достаточно заметить, что векторы [ас] и g одина-
одинаково направлены (противоположно направлены), когда тройка
acg является правой (левой), т. е. когда векторы а и е лежат
по одну сторону от с (по разные стороны от с*)) и проекция
прва является положительной (отрицательной), но это и озна-
означает, что векторы [ас] н npea-|c|g всегда одинаково направ-
направлены.
Теорема доказана.
4. Смешанное произведение трех векторов. Пусть даны три
произвольных вектора a, b и с. Если вектор а векторно умно-
умножается на вектор Ь, а затем получившийся при этом вектор
*) При этом мы исключаем тривиальный случай, когда вектор а колли-
неарен вектору с. В этом тривиальном случае [ас] = 0 и пр« а = 0, так что
равенство B.40) очевидно.

§ 3] ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 67
[ab] скалярно умножается на вектор с, то в результате полу-
получается число lab]с, называемое смешанным произведе-
произведением векторов a, b u с.
Геометрический смысл смешанного произведения вскрывает
следующая теорема.
Теорема 2.16. Смешанное произведение [ab]c равно объ-
объему параллелепипеда, построенного на приведенных к общему
началу векторах a, b и с, взятому со знаком плюс, если тройка
abc правая, и со знаком минус, если тройка аЬс левая. Если
же векторы a, b и с компланарны, то [ab]c равно нулю.
Доказательство. Прежде всего, исключим тривиаль-
тривиальный случай, когда векторы а и b коллинеарны. В этом случае
векторы a, b и с компланарны*), и нам требуется доказать,
что смешанное произведение [ab]c равно нулю. Но последнее
очевидно, ибо векторное произведение [ab] двух коллинеарных
векторов а и b равно нулю.
Остается рассмотреть случай, когда векторы а и Ь не кол-
коллинеарны. Обозначим через S площадь параллелограмма, по-
построенного на приведенных к общему началу векторах а и Ь,
а через е — орт векторного произведения [ab].
Тогда, как доказано в предыдущем пункте, справедлива
формула B.39). С помощью этой формулы и формулы B.31)
для скалярного произведения получим
[ab]c = (Se)c = S(ec) = S|e|npec=S-npec. B.41)
Сначала предположим, что векторы a, b и с не компланарны.
Тогда пр„с с точностью до знака равна высоте h параллелепи-
параллелепипеда, построенного на приведенных к
общему началу векторах a, b и с, при
условии, что основанием служит па-
параллелограмм, построенный на векто-
векторах а и b (рис. 2.18).
Таким образом, с точностью до
знака правая часть B.41) равна обь-
ему V построенного на векторах а, Ь
и с параллелепипеда. Остается уточ- ' рИс. 2.18
нить знак.
Очевидно, что пре с = -\-h, если векторы е и с лежат по
одну сторону от плоскости, определяемой векторами а и Ь, и
пре с = —hf если векторы е и с лежат по разные стороны от
указанной плоскости. Но это означает, что пр, с = +А, если
тройки abc и abe одной ориентации, и пре с = —А, если указан-
указанные тройки противоположной ориентации. Так как по опреде-
*) Ибо среди трех иекомплаиарных векторов не может быть двух кол-
лииеариых векторов (см. следствие 3 из теоремы 2.5).

68 ВЕКТОРНАЯ АЛГЕБРА [ГЛ. 2
лению векторного произведения тройка abe является правой
(см. конец предыдущего пункта), то
( -f-A, если abc —правая тройка,
\ — А, если abc — левая тройка.
Для завершения доказательства теоремы достаточно вставить
это значение пр«с в правую часть B.41).
В случае, когда векторы a, b и с компланарны, вектор с ле-
лежит в плоскости, определяемой векторами а и Ь, откуда сле-
следует, что пр«с = 0, и по формуле B.41) [ab]c = 0. Теорема
полиостью доказана.
Следствие 1. Справедливо равенство [ab] с = a [be].
В самом деле, из переместительного свойства скалярного
произведения вытекает, что a [be] = [be] а, и достаточно дока-
доказать, что [ab] с = [be] а. С точностью до знака, последнее ра-
равенство очевидно, ибо как правая, так и левая его части с точ-
точностью до знака равны объему параллелепипеда, построенного
на векторах a, b и с. Но и знаки правой и левой частей послед-
последнего равенства совпадают, ибо обе тройки abc и Ьса относятся
к группе троек B.36) и имеют одинаковую ориентацию
(см. п. 1).
Доказанное равенство [ab] с = a [be] позволяет записывать
смешанное произведение трех векторов a, b и с просто в виде
abc, не указывая при этом, какие именно два вектора (первые
два или последние два) перемножаются векторно.
Следствие 2. Необходимым и достаточным условием ком-
компланарности трех векторов является равенство нулю их сме-
смешанного произведения.
В самом деле, компланарность векторов в силу теоремы 2.16
влечет равенство нулю их смешанного произведения. Обратное
вытекает из того, что для некомпланарных векторов смешан-
смешанное произведение (в силу той же теоремы) равно отличному от
нуля объему параллелепипеда.
Следствие 3. Смешанное произведение трех векторов, два
из которых совпадают, равно нулю.
В самом деле, такие три вектора заведомо компланарны.
5. Алгебраические свойства векторного произведения. Вектор-
Векторное произведение векторов обладает следующими четырьмя
свойствами:
Г [ab] = — [Ьа] (свойство антиперестановочности сомножи-
сомножителей) ;
2° [(oa)b] = o[ab] (сочетательное относительно числового
множителя свойство);
3° [ (а -f- Ь) с] = [ас] + [be] (распределительное относительно
суммы векторов свойство);
4° [аа] = 0 для любого вектора а.

§ 3] ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 69
Убедимся в справедливости этих свойств.
Для доказательства свойства Г положим c = [ab], d =
= [ba]. Если векторы а и b коллинеарны, то в силу теоре-
теоремы 2.13 c = d = O, и свойство Г доказано. Если же а и b не
коллинеарны, то векторы с и А, во-первых, имеют одинаковую
длину (в силу формулы B.38) для длины векторного произве-
произведения) и, во-вторых, коллинеарны (в силу того, что оба вектора
end ортогональны к плоскости, определяемой векторами а и Ь).
Но тогда либо с = d, либо с = —d. Если бы имела место пер-
первая возможность, то по определению векторного произведения
обе тройки abc и Ьас оказались бы правыми, но это невозможно,
ибо в силу п. 1 эти тройки противоположной ориентации*).
Итак, с = —d, и свойство Г полностью доказано.
Для доказательства свойства 2° положим с = [(аа)Ь],
d = a [abj и прежде всего исключим тривиальные случаи, когда
вектор а коллинеарен b или когда а = 0. В этих случаях
(в силу теоремы 2.13 и определения произведения вектора иа
число) мы получим, что с = d = 0, и свойство 2° доказано.
Пусть теперь векторы а и Ь не коллинеарны и а Ф 0. Дока-
Докажем, что и в этом случае векторы си d равны. Обозначим бук-
буквой ф угол между векторами а и Ь, а буквой t|> угол между
векторами аа и Ь. По определению длины векториого произве-
произведения и произведения вектора на число можно утверждать, что
|c| = |a||a||b|sin4>, |d|»|a||a||b|sinq>. B.42)
Учтем теперь, что могут представиться два случая: 1) Ф=ф
(когда а > 0 и векторы а и аа направлены в одну сторону;
рис. 2.19); 2) \|>=я —ф (когда а < 0 и векторы а и аа на-
направлены в противополож-
противоположные стороны; рис. 2.20).
В обоих случаях sin ф =
= sin ф и в силу формул
B.42) |с| —|d|, т. е. векто-
векторы с и d имеют одинаковую „
Я л ни и "
Д
ни и
Далее, очевидно, что век- (a>0J
торы cud коллинеарны, Рис. 2.19 Рис. 2.20
ибо ортогональность к пло-
плоскости, определяемой векторами аа и Ь, означает ортогональ-
ортогональность и к плоскости, определяемой векторами а и Ь.
Для доказательства равенства векторов end остается про-
проверить, что эти векторы имеют одинаковое направление. Пусть
а > 0 (а < 0) *, тогда векторы а и аа одинаково направлены
(противоположно направлены), и, стало быть, векторы [ab]
B.3
*) Одна нз этих троек входит в группу B.36), а другая —в группу
17).

70 ВЕКТОРНАЯ АЛГЕБРА [ГЛ. 2
и [(aa)bj также одинаково направлены (противоположно на-
направлены), а это означает, что векторы d = o[ab] и с =
= [(оа)Ь] всегда одинаково направлены. Свойство 2° дока-
доказано.
Переходим к доказательству свойства 3°. Рассмотрим от-
отдельно два случая: 1) случай, когда векторы a, b и с ком-
компланарны; 2) случай, когда эти векторы не компланарны.
В первом случае векторы a, b и с, будучи приведены к об-
общему началу, располагаются в одной плоскости, которую мы
обозначим буквой п. Пусть е — единичный вектор, принадлежа-
принадлежащий плоскости п и ортогональный к вектору с, a g — единичный
вектор, ортогональный к плоскости я и такой, что тройка ecg
является правой.
Согласно теореме 2.15
npeb-|c|g, [(a + b)c] =
Свойство 3" непосредственно вытекает из последних трех
формул н из линейного свойства проекции пре а •+¦ пр« b =
— пр.(а + Ь) (п. 8§ 1).
Пусть теперь векторы a, b и с не компланарны. Так как три
вектора [(а-|-Ь)с], [ас] и [be] ортогональны к вектору с, то
эти три вектора компланарны, а стало быть (в силу теоремы
2.5), линейно зависимы. Но это означает, что найдутся такие
числа Я, ц и v, хотя бы одно из которых не нуль, что справед-
справедливо равенство
Я, [(а Н- Ь) с] = ц [ас] -f v [be]. B.43)
Остается доказать, что Я, — ц и k = v*). Докажем, например,
что Я = ц. Для этого, пользуясь уже доказанным (в п. 3 § 2)
распределительным свойством 3° скалярного произведения,
умножим равенство B.43) скалярно на вектор b и учтем, что
смешанное произведение [bc]b равно нулю (в силу следствия 3
из теоремы 2.16). В результате получим
Поскольку векторы a, b и с ие компланарны, смешанное произ-
произведение [ас]Ь не равно нулю, и для доказательства равенства
Я, = ц достаточно доказать равенство смешанных произведе-
произведений [(a + b)c]b и [ас]Ь. Равенство абсолютных величин ука-
указанных смешанных произведений вытекает из того, что (в силу
теоремы 2.16) эти абсолютные величины равны объемам двух
*) Так как по условию хотя бы одно из указанных чисел отлично от
нуля, го, доказав, что X = ц = v, мы можем поделить равенство B.43) иа
число X = ц = v, в результате чего получим свойство 3°.

§ 3J ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 71
параллелепипедов с равновеликими основаниями*) (на рис. 2.21
эти равновеликие основания заштрихованы штрихами разных
наклонов) и с общей высотой h, опущенной из конца вектора с
(рис. 2.21).
Равенство знаков указанных смешанных произведений вы-
вытекает из определения правой (левой) тройки с помощью
условия 3° (см. п. 1), ибо из
этого условия **) очевидно, что
тройки acb и (a-f-b)cb одной ори-
ориентации. Равенство Я,=ц доказано.
Аналогично (посредством умно-
умножения B.43) скалярно на вектор
а) доказывается равенство Я, = v.
Свойство 3° полностью доказано.
Остается доказать с в о й ст в о
4°, утверждающее, что векторный
квадрат любого вектора равен ну- Рис. 2.21
лю, но это свойство непосредствен-
непосредственно вытекает из теоремы 2.13 и из того, что любой вектор а
коллинеарен сам с собой.
Замечание. Оба свойства 2° и 3е формулируются при-
применительно к первому сомножителю векторного произведе-
произведения. (Свойство 2° утверждает возможность сочетания числового
множителя о с первым множителем векторного произведе-
произведения, а свойство 3° утверждает возможность распределения от-
относительно суммы векторов первого сомножителя вектор-
векторного произведения.)
Естественно возникает вопрос, справедливы ли аналогичные
свойства применительно ко второму сомножителю вектор-
векторного произведения, т. е. можно ли утверждать, что
[a (ab)] = a [ab] и [а (Ь + с)] = [ab] + [ас]. B.44)
Оказывается, свойства B.44) уже являются следствия-
м и свойств 2° и 3° и свойства антиперестановочности Г. В са-
самом деле, из свойств 1°, 2° и 3° вытекает, что
[a (ab)] = - [(ab) а] = - а [Ьа] = a [ab]
н аналогично
[а (Ь + с)] [(Ь + с) а] — - {[Ьа] -+• [са]} — [ab] + [ас].
*) Основанием одного параллелепипеда служит параллелограмм, по-
построенный на векторах а и Ь, а другого — параллелограмм, построенный на
векторах а + Ь и Ь. Равиовеликость указанных параллелограммов вытекает
из того, что они имеют общее основание, совпадающее с вектором Ь, и об-
общую высоту, опушенную из конца вектора а + b на вектор Ь.
**) А также из того, что вектор а + Ь лежит в одной плоскости с век-
векторами а и Ь, причем «между ними».

72 ВЕКТОРНАЯ АЛГЕБРА [ГЛ. 2
В заключение отметим, что доказанные свойства имеют фун-
фундаментальное значение. Они позволяют при векторном пере-
перемножении векторных многочленов выполнять действия почленно
и производить сочетание числовых множителей (но при этом
необходимо либо сохранять порядок векторных множителей,
либо при изменении этого порядка менять знак на противопо-
противоположный]).
В следующем пункте мы будем существенно использовать
эти свойства.
6. Выражение векторного произведения в декартовых коор-
координатах.
Теорема 2.17. Если два вектора а и Ъ определены своими
декартовыми прямоугольными координатами
a={Xj, Y\, ZJ, Ь = {Х2, *2> ^2)>
то векторное произведение этих векторов имеет вид
[ab] = {YlZ2-Y2Zi, ZiX2-Z2Xl, Х,У2-Х2У,}. B.45)
Для запоминания формулы B.45) удобно использовать сим-
символ определителя *) и переписать эту формулу в виде
[ab] =
i J k
xt r, z,
X2 Y2 Zt
B.450
Раскрывая определитель, стоящий в правой части B.45'), по
элементам первой строки, мы получим разложение вектора [ab]
по базису i, j, k, эквивалентное B.45).
Доказательство теоремы 2.17. Составим из тройки
базисных векторов i, j и к все возможные пары и для каждой
из пар подсчитаем векторное произведение. Учитывая, что ба-
базисные векторы взаимно ортогональны, образуют правую трой-
тройку и имеют единичную длину, получим **)
НЧ-о, [ji] = -k,
[ij] = к, Ш] = 0, [kj] = -i, B46)
[ik] = — j, [jk] = i, [kk] = O.
Далее, принимая во внимание, что а = Х\\ + У\\ + Zik, b =
= Х2\ + ^aj + Zik, и опираясь на установленную в предыду-
предыдущем пункте возможность почленного векторного перемножения
*) Теория определителей второго и третьего порядков изложена в До-
Дополнении к главе 1.
**) При этом мы учитываем также, что векторный квадрат вектора ра-
равен нулю (свойство 4° из п. 5), и принимаем во внимание, что, поскольку
тройка ijk является правой, обе тройки Jkl и klj являются правыми, а все
три тройки jik, ikj и kji — левыми (см. п. 1, формулы B.36) и B.37)).

§3] ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 73
векторных многочленов, получим
[ab] = ВД [И] + X,Y2 [ij] + XXZ2 [ik] + YXX2 [ji] + YXY2 [jj] +
+ r,z2 [jk] + z a [ki] + ад [kj] + zxz2 [kk].
Из последнего равенства и соотношений B.46) вытекает раз-
разложение
[ab] = (Y,Z, - KjZ,) I + (Z A - Z2*,) j + № - *,У,) k,
эквивалентное равенству B.45). Теорема доказана.
Следствие. Если два вектора а = {Xi, Y\,Z\} и b={X2,Y2,Z2}
коллинеарны, то координаты их пропорциональны, т. е.
т2'='71==т;-
Заметим, что в знаменателях последних равенств могут стоять
нули. Чтобы обойти эту трудность, мы раз и навсегда догово-
договоримся всякую пропорцию а/Ь = c/d понимать в смысле равен-
равенства ad = be.
Для доказательства следствия достаточно заметить, что из
равенства нулю векторного произведения и из формулы B.45)
вытекают равенства
которые в силу сделанного выше замечания эквивалентны до-
доказываемым пропорциям.
7. Выражение смешанного произведения в декартовых коор-
координатах.
Теорема 2.18. Если три вектора a, b и с определены своими
декартовыми прямоугольными координатами
а= {Хи Yb Z,}, b = {Х2, Y2, Z2), с = {Х3, Y3, Z3),
то смешанное произведение abc равняется определителю, строки
которого соответственно равны координатам перемножаемых
векторов, т. е.
abc=
Y2 Z2
B.47)
z Yz Z»
Доказательство. Так как смешанное произведение abc
равно скалярному произведению векторов [ab] и с и поскольку
координаты вектора [ab] определяются формулой B.45), а ко-
координаты с равны {Х3, Y%,Zz), то в силу выражения B.33) для
скалярного произведения векторов в координатах получим
abc = X3 (YiZ2 - Y2Zi) + Y3 (ВД - ВД) + Z3 (Х,У2 - X2Y{).
Если воспользоваться выражением для определителя вто-
второго порядка и символом такого определителя, то последнее

74 ВЕКТОРНАЯ АЛГЕБРА 1ГЛ. 2
выражение можно переписать в виде
abc =
3 У 2 + Z3 У„ у. • (^-4о)
| Aj Zj | I Ла Г 2 |
Формулы B.47) и B.48) эвивалентны, ибо при разложении
определителя, стоящего в правой части B.47), по третьей стро-
строке получается выражение, стоящее в правой части B.48)*).
Теорема доказана.
Следствие. Необходимым и достаточным условием компла-
компланарности трех векторов а = {Х\, Y\,Z\}, b = {Х2, Y2,Z2) и с =
= №> Y3, Z3) является равенство нулю определителя, строка-
строками которого служат координаты этих векторов, т. е. равенство
X: Г, Z,
V V ? С\
л2 ii z2 =0.
Аз мъ &Ъ
В самом деле, достаточно привлечь следствие 2 из теоре-
теоремы 2.16 и воспользоваться формулой B.47).
8. Двойное векторное произведение. Пусть даны три произ-
произвольных вектора a, b и с. Если вектор b векторно умножается
на вектор с, а вектор а также векторно умножается на вектор-
векторное произведение [be], то получающийся при этом вектор
[a[be]] называется двойным векторным произведе-
произведением.
Теорема 2.19. Для любых векторов a, b и с справедлива
формула **)
[a [be] ] = b (ас) - с (ab). B.49)
Доказательство. Рассмотрим отдельно два случая:
1) векторы b и с коллинеарны; 2) векторы b и с не колли'
неарны.
В первом случае обозначим через со орт вектора с и учтем,
что с = |с| -со, b = ±|b| -co, где знак плюс берется для случая,
когда векторы b и с одинаково направлены, а знак минус — для
случая, когда b и с противоположно направлены. С помощью
этих формул для с и b получим, что b(ac) —c(ab) = 0***), т. е.
правая часть B.49) равна нулю. Но и левая часть B.49) равна
нулю, ибо векторное произведение [be] двух коллинеарных век-
векторов равно нулю. Для первого случая теорема доказана.
*) См. формулу (Д1.16) из п. 5 Дополнения к главе 1.
••) Для запоминания этой формулы удобно следующее правило:
двойное векторное произведение равно среднему вектору, умноженному на
скалярное произведение двух остальных, минус другой вектор внутреннего
произведения, умноженный на скалярное произведение двух остальных. Это
правило годится и для случая, когда внутреннее векторное произведение от-
относится к первым двум векторам: с его помощью получается следующая
формула Г[аЬ]с] = Ь(ас) —а (Ьс), являющаяся следствием B.49).
***) В самом деле, элементарный подсчет показывает, что как Ь(ас), так
и c(ab) равно ±|Ь|-|с|-(асо) со.

§3] ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 75
Переходим к доказательству теоремы для случая, когда век-
векторы b и сне коллинеарны. Так как вектор [a[be]] ортогонален
вектору [be], а последний ортогонален плоскости, определяе-
определяемой векторами b и с, то векторы [a[be]], b и с компланарны,
а поэтому (в силу следствия 1 из теоремы 2.5) вектор [a[be]]
можно разложить по двум неколлинеарным векторам b и с как
по базису, т. е. найдутся вещественные числа аир такие, что
[a[bc]] = ab + pc. B.50)
Остается доказать, что a = ас, р = —аЬ. Докажем, например,
что a = ас. Воспользуемся теоремой 2.15. Для этого обозначим
буквой я плоскость, определяемую векторами b и с, буквой е —
единичный вектор, лежащий в я и ортогональный к с, буквой
g — единичный вектор, ортогональный плоскости я и такой, что
тройка ecg является правой. По теореме 2.15
[bc] = nPeb-|c|-g. B.51)
Если со — орт вектора с, то правая тройка ecog образует де-
декартов прямоугольный базис. Разложим вектор а по этому ба-
базису, учитывая, что координаты равны проекциям вектора а на
базисные векторы:
а = е-преа + <V npca + g • npga. B.52)
Умножая векторно B.52) на B.51) и учитывая, что [eg] = —со,
[cog] = е, [gg] = 0 (сравните с формулами B.46)), получим
[a [be] ] = — Cq • пре а • пре b • | с | + е • прс а • пре b • | с |. B.53)
Сравнивая формулы B.50) и B.53), будем иметь
ab + рс = — Cq • прв а • пре b • | с | + е • прс а • прв b • | с |. B.54)
Остается умножить обе части B.54) скалярно на е и учесть,
что be = npeb, сое = 0, ее = 1. Окончательно получим
а • преЬ = прса • npeb • |с| или а = |с| • npca = ac.
Для доказательства равенства р = —ab следует в проведен-
проведенных рассуждениях поменять ролями векторы с и b и учесть, что
[а [со] = —[a [be] ]. Теорема доказана.
Замечание. Дадим другое доказательство теоремы 2.19, основанное
на специальном выборе декартовой прямоугольной системы и на непосред-
непосредственном просчете в координатах всех выражений, участвующих в форму-
формуле B.49). Направим ось Ог вдоль вектора с, а ось Оу возьмем в плоскости
векторов b и с. Тогда векторы а, Ь и с будут иметь следующие координаты:
а = {X, Y, Z), Ь = {0, Г, Z'}, с = {0, 0. Z").
Применяя формулу для векторного произведевня B.45), будем иметь [be] =
== {Y'Z", 0, 0}, а отсюда по той же формуле B.45)
[a [be]] «= {0, ZY'Z", - YY'Z'% B.55)
Далее, очевидно, что (ас) = ZZ", (ab) = YY' + ZZ', а поэтому
b (ас) — {0, Y'ZZ", Z'ZZ"), B.56)
с (ab) = {0, 0, YY'Z" + ZZ'Z"). B.57)
Из сопоставления равенств B.55), B.56) и B.57) вытекает формула B.49).

ГЛАВА 3
ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ
КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
В этой главе устанавливаются формулы, по которым преоб-
преобразуются координаты произвольной точки плоскости (или соот-
соответственно пространства) при переходе от одной декартовой
прямоугольной системы к произвольной другой декартовой
прямоугольной системе.
Мы доказываем, что координаты произвольной точки отно-
относительно первой системы являются линейными функциями ко-
координат той же точки М относительно второй системы.
Попутно мы устанавливаем, что если две дерактовы прямо-
прямоугольные системы на плоскости я (в пространстве) образованы
парами (тройками) одной ориентации, то одна из этих систем
может быть совмещена с другой посредством параллельного
переноса и последующего поворота на некоторый угол <р в пло-
плоскости п (вокруг некоторой оси в пространстве).
§ 1. Преобразование декартовых
прямоугольных координат на плоскости
Пусть на плоскости п заданы две произвольные декартовы
прямоугольные системы координат: первая, определяемая
началом О и базисными векторами i и j,
и вторая, определяемая началом О'
и базисными векторами i' и V
(рис. 3.1).
Поставим перед собой цель — выразить
координаты х и у произвольной точки М
?_ ^_ плоскости я относительно первой систе-
0 i г мы координат через координаты xf и у'
pHt з j этой же точки М относительно второй
системы координат.
Заметим, что координаты хну совпадают с координатами
вектора ОМ в разложении его по базису_[), а координаты х'
и у' совпадают с координатами вектора О'М в разложении его
.

§ 1] ПРЕОБРАЗОВАНИЕ КООРДИНАТ НА ПЛОСКОСТИ 77
по базису i'j', т. е.
C.1)
C.2)
Если обозначить через а и Ъ координаты начала О' второй
системы относительно первой системы, то
Oa = ai+b]. C.3)
Так как любой вектор на плоскости я можно разложить по
базису ij, то найдутся числа ац, сиг, «21 и агг такие, что
i' = aul + a12j, Г = 02,1 + 022]. C.4)
В силу правила треугольника сложения векторов (см. рис. 3.1)
Ш=~бб' +1УМ. C.5)
Вставляя в правую часть C.2) значения V и j', определяемые
формулами C.4), и после этого подставляя в C.5) значения
(Ш, (УМ и 7ЮГ, определяемые формулами C.1), C.2) и C.3),
и группируя слагаемые относительно i и j, получим *)
+ (b + 0,2*' + 022/) j. C.6)
В силу единственности разложения вектора по базису из ра-
равенства C.6) получим искомые формулы преобразования ко-
координат
Мы приходим к следующему замечательному выводу: ка-
каковы бы ни были две произвольные декартовы системы на
плоскости я, координаты любой точки плоскости я относительно
первой системы являются линейными функциями коор-
координат той же точки относительно второй системы.
Установив этот фундаментальный алгебраический факт, пе-
перейдем к геометрической интерпретации полученных формул.
Для этого договоримся обозначать символом cos(ab) косинус
угла между векторами а и Ь. Помножая каждое из равенств
C.4) скалярно сначала на i, а затем на j и учитывая, что И = 1,
jj = 1, ij = 0, получим **)
a12 = cos (i'j), 021 = cos (j'i), a22
C.8)
*) Возможность сгруппировать слагаемые относительно 1 и J вытекает
из свойств линейных операций иад векторами (см. п. 2 § 1 главы 2).
**) Учитываем также, что скалярное произведение двух единичных век-
векторов равно косинусу угла между ними.

78 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ [ГЛ. Э
Будем существенно различать следующие два случая: 1) слу-
случай, когда базисные векторы направлены так, что оба кратчай-
кратчайших поворота от i к j и от V к j' совершаются в одном направ-
направлении (либо оба по часовой стрелке, либо оба против часовой
стрелки); 2) случай, когда базисные векторы направлены так,
что кратчайшие повороты от i к j и от V к ]' совершаются в
противоположных направлениях.
В обоих случаях обозначим через ф угол между базисными
векторами i и V, отсчитываемый в направлении, отвечающем
кратчайшему повороту от i к j. Тогда е*ц = соэф.
В первом случае угол между базисными векторами j и j'
также равен ф, и поэтому первая система координат может быть
совмещена со второй посредством параллельного переноса
вдоль вектора ТЮ' и последующего поворота в плоскости я
вокруг начала на угол ф (этот случай изо-
изображен на рис. 3.1).
Во втором случае угол между базис-
базисными векторами j и j' равен я — ф и пер-
первую систему координат невозможно совме-
совмеJ
о
стить со второй посредством параллельного
-^ переноса и поворота, не выводящего из
плоскости я (нужно еще изменить направ-
направление оси ординат на противоположное
или, что то же самое, взять изображение
Рнс. 3.2 плоскости я в плоском зеркале. Второй
случай изображен на рис. 3.2).
Пользуясь формулами C.8), подсчитаем для обоих случаев
коэффициенты аи, an, <X2i и агг *).
В первом случае получим: ац = созф, а22 = созф, а12 =
= cos (-j— ф) = sin ф, ct2i = cos (-|r + фJ = —• sin ф.
Во втором случае получим: аи = coscp, агг = соэ(я— ф) =
е= — COS ф, а12 = COS (-у — ф) = Sin ф, Ct2i = COS (-| ф)=ЗШф.
Таким образом, в первом случае формулы преобразова-
преобразования координат C.7) принимают вид
х = а + xr cos ф — \f sin ф, у = Ь + xf sin ф + \f cos ф. C.9)
Во втором случае соответствующие формулы преобразо-
преобразования принимают вид
у = Ь + х' sin ф — \f cos ф. C.10)
Если мы примем договоренность рассматривать только такие
системы координат, у которых кратчайший поворот от первого
*) Все углы отсчнтывэются в направлении, отвечающем кратчайшему,
повороту от 1 к j.

§2] ПРЕОБРАЗОВАНИЕ КООРДИНАТ В ПРОСТРАНСТВЕ 79
базисного вектора ко второму происходит против часовой стрел-
стрелки (будем называть такие системы правыми), то второй слу-
случай будет исключен и любое преобразование координат будет
определяться формулами C.9).
Приходим к выводу, что, каковы бы ни были две правые
системы координат Оху и О'х'у', первая из них может быть со-
совмещена со второй посредством параллельного переноса вдоль
вектора 00' и последующего поворота вокруг начала на не-
некоторый угол ф.
Разрешая уравнения C.9) относительно хг и у', получим
обратные формулы, выражающие координаты х' и у1 любой
точки М относительно второй системы через координаты ее
относительно первой системы*):
x' = (x-a)cosq> + (y — &)sinq>, j
yf = — (x — a) sin ф + (У ~ b) cos <f. ) \ • )
Общее преобразование координат C.9) распадается на сум-
сумму двух преобразований, одно из которых отвечает только па-
параллельному переносу системы, а другое — только повороту
системы вокруг начала на угол q>.
В самом деле, полагая в формулах C.9) угол поворота ф
равным нулю, получим формулы преобразования координат
при параллельном переносе системы вдоль вектора 00' =
= {а,Ь}:
х = а + х', у = Ь + у'- C.12)
Полагая в тех же формулах C.9) координаты а и Ъ век-
вектора 00' равными нулю, получим формулы преобразования ко-
координат при повороте системы вокруг начала на угол ф (в на-
направлении против часовой стрелки)
х = х' cos ф — у' sin ф, у = х* sin ф + у' cos ф. C.13)
§ 2. Преобразование декартовых прямоугольных координат
в пространстве
1. Общие формулы преобразования. Пусть в пространстве
заданы две произвольные декартовы прямоугольные системы
координат: первая, определяемая началом О и базисными
векторами ijk, и вторая, определяемая началом О' и базис-
базисными векторами i'j'k'.
Поставим перед собой цель — выразить координаты х, у и г
произвольной точки М относительно первой системы через ко-
координаты ж', «/'иг' этой же точки М относительно второй си-
системы.
*) Так как определитель системы C.9) равен единице, то эту систему
можно разрешить относительно х' и у'.

80 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ [ГЛ. 3
Заметим, что координаты х, у, г совпадают с координатами
вектора ОМ в разложении его по базису ijk, и координаты х',
у', г' совпадают с координатами вектора О'М в разложении
его по базису i'j'k', т. е.
ОМ = xi 4- у] 4- гк, C.14)
ОМ = х'\' 4- у'У 4- г'к'. C.15)
Если обозначить через а, Ь и с координаты начала О' второй
системы относительно первой системы, то
00' = а\ + Ь\ + ск. C.16)
Так как любой вектор можно разложить по базису ijk, то най-
найдутся девять чисел аш (/ = 1, 2, 3; m = 1, 2, 3) таких, что
i' = a,,i + a12j + aI3k, j' = a2ii + a22j + a23k, k' = c^l + a32j + a33k.
C.17)
В силу правила треугольника сложения векторов
ОМ^Од' + СГМ. C.18)
Вставляя в правую часть C.15) значения V, У и к', опреде-
определяемые формулами^ C.17)^ и после этого подставляя в C.18)
значения ОМ, О'М и 00', определяемые формулами C.14),
C.15) и C.16), и группируя слагаемые относительно i, j и к,
получим
xl + у\ + гк = (а + а,,*' + о*,/ + 03,2') i +
+ Ф + а12^ + аи/ + аз2г') j + (с + а13ж' + <%/ + <%«/') к. C.19)
В силу единственности разложения вектора по базису из
равенства C.19) получим искомые формулы преобразования ко-
координат;
х = а + а,,*' + <X2i/ + a3Iz',
у = Ь + а12х' + 022/4-0322', C.20)
z = с 4-
Итак, доказано следующее фундаментальное утвержде-
утверждение: каковы бы ни были две произвольные декартовы прямо-
прямоугольные системы координат, координаты х, у и г любой точки
пространства относительно первой системы являются линей-
линейными функциями координат х", у' и z/ той же точки относи-
относительно второй системы.
Умножая каждое из равенств C.17) скалярно сначала на 1,
а затем на j и на к, получим следующие выражения для

§2] ПРЕОБРАЗОВАНИЕ КООРДИНАТ .^ПРОСТРАНСТВЕ 81
чисел aim'. ^
T, a12 = cos(i'j), a,3 = cos(rk),
, a22 = cosC/'j), 033 = cos (j'k),
a31 = cos (Pi), a32 = cos (k^j), a33 = cos (Pk).
2. Выяснение геометрического смысла. Углы Эйлера. Уясним
геометрический смысл формул преобразования C.20). Для вы-
вычисления чисел aim и их геометрического значения предполо-
предположим, что первая и вторая системы имеют общее начало (т. е.
а = Ь = с = 0).
Ради определенности будем считать, что обе системы Oxyz
и Ох'у'г' являются правыми.
Введем в рассмотрение три угла, полностью характери-
характеризующие расположение осей второй системы относительно пер-
первой. Обозначим через и ось, совпадающую
с линией пересечения координатной пло-
плоскости Оху первой системы с координатной
плоскостью Ох'у' второй системы и на-
направленную так, что три направления Ог,
Oz' и и образуют правую тройку
(рис. 3.3).
Пусть теперь а|> — угол между осями Ох
и и, отсчитываемый в плоскости Оху от
оси Ох в направлении кратчайшего пово-
поворота от Ох к Оу, в — не превосходящий я Рнс- 33
угол между осями Oz и Ozf и, наконец, <р —
угол между осями и и Ох', отсчитываемый в плоскости Ох'у' от
оси и в направлении кратчайшего поворота от Ох' к Оу'.
Три угла ф, of и 0 называются углами Эйлера *). Очевидно,
по трем углам Эйлера и по направлениям осей Ох, Оу и Ог
однозначно определяются направления осей Ох', Оу' и Oz'.
Если заданы три угла Эйлера, то преобразование первой
системы Oxyz во вторую систему Ох'у'г можно представить
в виде последовательного проведения следующих трех поворо-
поворотов:
1) поворота системы Oxyz на угол rj? вокруг оси Ог, пере-
переводящего эту систему в систему Ox\y\Z\ (рис. 3.4);
2) поворота системы Ох\у&\ на угол 0 вокруг оси Ох\, пе-
переводящего эту систему в систему Ох2у2г2 (рис. 3.5);
3) поворота системы Ох^у-яг на угол <р вокруг оси Огч =
= Ог', переводящего эту систему в систему Ох'у'г' (рис. 3.6).
Каждый из указанных трех поворотов производится в одной
из координатных плоскостей соответствующей системы. Поэто-
•) Леонард Эйлер A707—1783)—великий математик, член Петербург-
Петербургской Академии наук, ббльшую часть жизни провел в России, по происхожде-
происхождению швейцарец.
6 Зак. 168

82 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ГГЛ.З
му для соответствующих координат при каждом таком повороте
будут справедливы формулы вида C.13) (см. § 1).
Рис. 3.S
Рис. 3.6
Это позволяет написать следующие формулы:
1) для первого поворота
х — jc, cos ф — у{ sin ф, у = хх sin ф + ух cos ф, г = г1; C.21)
2) для второго поворота
Х\=*х2, ух = у2cos6 — z2sin6, г, = у2sin6 + z2cos6; C.22)
3) для третьего поворота
х2 = х' cos ф — tf sin ф, i/2 = л' sin ф + у' cos ф, г2 = 2'. C.23)
Внося C.23) в C.22), а затем C.22) в C.21), получим
х = (л' cos ф — yr sin ф) cos ф —
— [(#' sin ф + tf cos ф) cos 6 — г' sin 6] sin ф,
i/ = (xr cos ф — tf sin ф) sin ф + C.24)
+ [(*' sin ф + y' cos ф) cos 6 — z' sin 6] cos ф,
z = (xf sin ф + i/' cos ф) sin 6 + У cos 6.
Сравнивая формулы C.24) с формулами C.20) (прн а =
е= & = с = 0), окончательно получим выражения для чисел am
через углы Эйлера:
Оц = cos ф cos ф — sin ф cos 6 sin ф,
а12 = sin ф cos ф + cos ф cos 6 sin ф,
aI3 = sin 8 sin ф,
O2i = — cos ф sin ф — sin ф cosS cosф,
et22 = — sin ф sin ф + cos ф cos 9 cos ф, C.25)
Огз = sin в cos ф,
аз] = sin i|> sin 9,
032 = — cos ф sin 8,
азз = cos 9.
Для вывода формул C.25) мы использовали допущение, что
обе системы имеют общее начало. Разумеется, отказ от этого
допущения не изменит вида формул C.25), ибо ни направление

§3] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ 63
осей координат, ни величина углов Эйлера не зависит от того,
где выбрано начало первой и второй систем.
Самое общее преобразование координат представляет собой
суперпозицию (последовательное проведение) параллельного
переноса и трех производимых в соответствующих координат-
координатных плоскостях поворотов и определяется формулами C.20),
в которых (при условии, что обе системы являются правыми)
числа аш выражаются через углы. Эйлера по формулам C.25).
Формулы, аналогичные C.25), могут быть получены и для
случая, когда системы Охуг и О'х'у'г" либо обе являются ле-
левыми, либо имеют разную ориентацию.
Замечание. Если Охуг и O'x'y'zf — две произвольные
правые декартовы прямоугольные системы в пространстве, то
первая из них может быть совмещена со второй посредством
параллельного переноса, совмещающего их начала, и одного
поворота вокруг некоторой оси в пространстве.
Для нахождения указанной оси, во-первых, учтем, что она
проходит через общее начало О' совмещенных посредством па-
параллельного переноса систем (ибо это начало остается непо-
неподвижным при повороте), и, во-вторых, заметим, что если О'М' —
произвольный вектор, лежащий на искомой оси вращения, то
координаты точки М' не изменяются при повороте.
Отсюда вытекает, что для нахождения координат xf, у' и z1
точки М' в системе O'x'y'z' следует в системе C.20) (взятой
прн а = Ъ = с = 0) положить х = х/, у=у", z = z\ Это при-
приведет нас к следующей однородной системе трех уравнений
с тремя неизвестными:
(а„ — 1) х' + oj,/ + аз,2' = 0,
аи*' + («22 - 1) / + озг*' = 0, C.26)
ЩзХ' + аяУ' + (Озз — 1) г* = 0.
С помощью формул C.25) можно показать, что определитель
этой системы равен нулю. Стало быть, в силу п. 8 Дополнения
к главе 1 система C.26) имеет нетривиальные решения, кото-
которые определяют совокупность коллннеарных векторов ОМ', ле-
лежащих на оси вращения.
Одним из таких векторов будет вектор О'М'0 = {xf, t/, I},
координаты х' и у' которого определяются из первых двух
уравнений C.26) при z' = 1.
§ 3. Линейные преобразования
1. Понятие линейных преобразований плоскости. Линейным
преобразованием плоскости я называется преобразование, при
котором каждая точка М^х, у\ этой плоскости переходит в

84 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ [ГЛ. Э
точку М', координаты х', у* которой определяются формулами
х = апх + al2y + Oi3t „ ._.
, . . C.27)
tf = а21х + а^у + 023.
Обычно говорят, что соотношения C.27) задают линейное пре-
преобразование плоскости. Определитель
Д=Ь' "" C.28)
I а21 2 N '
называется определителем линейного преобразования C.27).
В случае А ф 0 преобразование C.27) называется невырож-
невырожденным, а в случае А = 0 — вырожденным. Мы в дальнейшем
будем рассматривать невырожденные линейные преобразова-
преобразования, т. е. будем считать АфО*). Такие линейные преобразова-
преобразования называются аффинными.
Замечание. Наименование линейное преобразование объ-
объясняется тем, что координаты xf, у1 точек М' — образов точек
М(х, у) (сами эти точки называются прообразами точек М')
являются линейными функциями координат х, у. Отметим, что
определение линейных преобразований инвариантно относи-
относительно выбора декартовой системы координат, поскольку коор-
координаты точки в одной декартовой системе координат выра-
выражаются линейно через ее координаты в любой другой декарто-
декартовой системе координат.
2. Аффинные преобразования плоскости. В предыдущем
пункте мы отметили, что аффинные преобразования плоско-
плоскости — это линейные преобразования C.27), для которых А ф 0.
Перечислим некоторые свойства таких преобразованнй.
1°. Последовательное выполнение двух аффинных преобразо-
преобразований является аффинным преобразованием.
Это свойство проверяется непосредственно.
2°. Тождественное преобразование х' = х, у' = у также яв-
является аффинным.
Действительно, для этого преобразования
3°. Преобразование, обратное данному аффинному (т. е. пре-
преобразование плоскости я, переводящее точки М'(х',у') в точки
М (х, у)), также является аффинным.
*) Если Д = 0, то с помощью преобразования C.27) все точки М(х, у)
плоскости п преобразуются в точки М'(х', у'), расположенные на некоторой
прямой. Действительно, если Л = 0, то аи = faizi, аи «= Алгг- Поэтому, если
мы умножим иа —А, второе из соотношений C.27) и сложим с первым, то
получим х' — Ху' = аи — Хагз. Мы видим, что координаты х', у' точек М'
удовлетворяют линейному уравнению, т.е. все точки М' лежат иа прямой.

§31 ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ 85
Докажем это свойство. Обратное преобразование может
быть получено следующим образом. Найдем х н у из соотно-
соотношений C.27). Для этого перепишем их следующим образом:
ai2y = x' — а13,
а2Хх + а^у = у' — а23.
Решение этой системы имеет такой внд:
ж/Д, г/ = Д„/А, C.29)
где
|ап au\-j-(\ а |*'~fli3 21 д \ац *'— а\г\
~U |^и *~\ л» ~ \а„ у'-ап\
(см. Дополнение к главе 1, формулы (Д1.8) н (Д1.6)). Рас-
Раскроем выражения для А* и Aj, по формуле (Д1.2) и подставим
полученные значения в C.29). Получим следующие выражения
для обратного преобразования:
„ 2 ^ «12 ,/ 1 |
Видим, что обратное преобразование является линейным. Чтобы
убедиться, что оно является аффинным, остается доказать, что
его определитель А' ф 0. В самом деле,
А'-
Д22 Д12
Д Д
~~д~ ~д~
Д||О22— <»12Д21
Д*
Итак, доказано, что преобразование, обратное данному аф-
аффинному, также является аффинным.
4°. Аффинное преобразование представляет собой взаимно
однозначное преобразование плоскости.
Это означает, что каждая точка М'(х',у') есть образ един-
единственной точки М(х, у) н в свою очередь каждая точка М(х,у)
представляет собой прообраз лишь одной точки ЛГ(лг'.у').
Докажем это свойство. Предположим, что две точки М (х, у)
и М(х, у) преобразуются с помощью C.27) в одну точку
M'(xf,t/).'Тогда путем вычитания из соотношений C.27) ана-
аналогичных соотношений для координат х, у точки Л? получим
следующую систему линейных уравнений для разностей х — х,
У — У-

86 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ [ГЛ. 3
Эта система имеет нулевое решение х — ? = 0, у —17 = 0, а так
как ее определитель А = г" ?"\фО, то это нулевое решение
единственно. Итак, х = х, у = у, т. 'в. точки М и М совпадают.
Таким образом, каждая точка М'(х', у') есть образ единствен-
единственной точки М(х,у). Обращаясь к формулам C.30), путем ана-
аналогичных рассуждений мы убедимся, что каждая точка М(х, у)
представляет собой прообраз лишь одной точки М'(х',у').
3. Основное- свойство аффинных преобразований плоскости.
Докажем следующее утверждение:
Теорема 3.1. При аффинном преобразовании плоскости каж-
каждая прямая переходит в прямую и параллельные прямые пере-
переходят в параллельные прямые.
Доказательство. Рассмотрим на плоскости я прямую
L, определяемую уравнением
= 0. C.31)
Чтобы выяснить, что представляет собой совокупность точек
M'(xf,yf) — образов точек М(х,у), расположенных на прямой
L, — подставим в уравнение C.31) вместо х и у их выражения
через *', у* по формулам C.30). В результате получим соотно-
соотношение вида
' ' = Ъ. C.32)
Мы видим, что х' и у1 удовлетворяют линейному уравнению
C.32), т. е. точки М'(х', у") расположены на прямой L', опре-
определяемой уравнением C.32).
Итак, доказано, что все точки прямой L при аффинном пре-
преобразовании C.27) переходят в точки прямой U. Так как при
обратном аффинном преобразовании C.30) все точки прямой
U перейдут в точки прямой L, то в силу взаимной однознач-
однозначности аффинного преобразования (см. п. 2, свойство 4°), пря-
прямая L переходит в прямую U. Итак, при аффинном преобразо-
преобразовании прямая переходит в прямую.
Перейдем к доказательству второй части теоремы. Пусть L\
и L2 — параллельные прямые, a L, и L'2— их образы при аф-
аффинном преобразовании C.27) плоскости я. Допустим, что пря-
прямые L\ и L'2 имеют общую точку М'. Так как аффинное преоб-
преобразование взаимно однозначно, то М' — образ только одной
точки М, причем М должна принадлежать и L\ и L2, что не-
невозможно, поскольку Lj и L2 параллельны. Следовательно,
L[ и Lj не имеют общих точек, т. е. параллельны. Теорема до-
доказана.
Естественно поставить вопрос о геометрическом способе за-
задания аффинного преобразования плоскости. Определенный от-
ответ на этот вопрос дает следующее утверждение:

§31 ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ 87
Теорема 3.2. Аффинное преобразование плоскости опреде-
определено однозначно, если заданы образы трех точек, не лежащих
на одной прямой и эти образы также не располагаются на од-
одной прямой.
Доказательство. Пусть точки Mi(xi,tji), М2(х2,у2),
Мз(хз,уз) плоскости я не лежат на одной прямой и точки
М\ (х/1, у\), М'2 (х'2, у'2), М'3 (х3, у'3) этой плоскости также не ле-
лежат на одной прямой. Убедимся, что существует единственное
аффинное преобразование плоскости я, переводящее точки Mi,
М2, М3 в точки Щ, ЬА'г, М3 соответственно.
Пусть искомое аффинное преобразование задается соотно-
соотношениями C.27) с неизвестными коэффициентами аи, а\2, а:з,
а2\, а22, а23. Докажем, что при наших предположениях эти ко-
коэффициенты определяются однозначно и, кроме того, определи-
определитель А, вычисленный по формуле C.28), отличен от нуля. Этим,
очевидно, и будет завершено доказательство теоремы.
С помощью первой из формул C.27) получим соотношения
C.33)
которые можно рассматривать как систему трех линейных урав-
уравнений относительно неизвестных аи, а\2, an. Определитель этой
системы
Xi «I 1
г — *i У г — У\\ /о ол\
,-*. у3-У1\ <3-34)
отличен от нуля, так как по абсолютной величине равен пло-
площади параллелограмма, построенного на неколлинеарных век-
векторах МХМ2 и MtM3 *)• Поэтому система C.33) однозначно раз-
разрешима относительно аи, а]2 и аи. Обращаясь ко второй из
формул C.27), с помощью аналогичных рассуждений убедимся,
что и величины a2i, a22 и а23 определяются однозначно. Таким
образом, однозначно определяется линейное преобразование
C.27), переводящее точки М\, М2 и Мг соответственно в точки
М\, М2 н М3. Остается доказать, что определитель А (см. C.28))
полученного преобразования отличен от нуля. Обратимся к
хг
Хг
У\
Уг
Уз
1
1
1
_*) Так как точки Mi, M» в М» ве лежат ва одной прямой, то векторы
М,М2 и М\М» не коллииеариы. В системе координат Охуг (ось Ог перпенди-
перпендикулярна плоскости п) эти векторы соответственно имеют координаты {х* — xi,
У» — У и 0} и (дгз —xi, у» —у и 0). Поэтому модуль векторного произведения
этих векторов равен модулю определителя C.34) и, как известно, равен пло-
площади параллелограмма, построенного на данных векторах.

88 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ (ГЛ. 3
определителю
/ / г г
v __ «*. it __ II.
C.35)
/ / г г
х2-х{ у2-у1
г г г г
*
Этот определитель отличен от нуля, так как по абсолютной ве-
величине равен площади параллелограмма, построенного на не-
коллннеарных векторах М[М2 и М[М'3 *). С помощью первой из
формул C.27) получим для элемента х'2 — х\ определителя
C.35) следующее выражение:
Аналогичные выражения получим с помощью формул C.27) и
для остальных элементов определителя C.35). Подставляя най-
найденные выражения для x2 — x'v у12 — у[, хг — х[ и t/a — у[ь C.35),
после несложных преобразованнй получим
C.36)
н-
реде
Г 1
н у2-
*i Уз-
лителн
х'2-х\
г г
г
У\
У\
«21
г г
У2~У\
Уз —У
г
I
1
«12
а22
*2~*|
х3 — хх
1 Х2 — *х Уг~
—
Хх Уз-
Уг —
Уз —
Ух\
Ух 1
Ух
Ух
отличны от нуля, то из C.36) следует, что иД = г" a'J|
I 1 2 I
Теорема доказана.
Замечание. Аффинное преобразование, для которого
д_ a,i в|2 _ | называется эквиаффинным, т. е. сохраняющим
I Й21 2 | Г
площади. Для таких преобразований соотношение C.36) озна-
означает равенство площадей параллелограммов, построенных на
векторах М,М2 и MlMs и на векторах М\М2 и М\М'3.
4. Основной инвариант аффинного преобразования плоскости.
Простым отношением трех точек А, В и С на прямой L назы-
называется число
/ Л р>Г\ _ "" /О Г>1\
\ЛиО) ryp t \О.О/)
которое, очевидно, равно отношению, в котором точка В делит
направленный отрезок АС.
Докажем следующее утверждение:
Теорема 3.3. Простое отношение трех точек на прямой яв-
является инвариантом аффинного преобразования.
*) Эти векторы иеколлииеарны, так как точки М\, М2 и м'3 ие лежат
на одной прямой. См. предыдущую сноску.

6 31 линейные преобразования 89
Иными словами, простое отношение трех точек на прямой
не меняется при аффинных преобразованиях.
Доказательство. Рассмотрим три точки А(хи у{),
В(х2,у2) и С(х3)у3) на прямой L. Из формул A.11) главы 1 для
координат точки, делящей отрезок АС в отношении Я, = АВ/ВС,
получаем для рассматриваемого случая следующее выражение
для К:
Пусть Af(xfl, ^), В'{хг2, у2) н С(х'3, у'3) — образы точек А, В и
С соответственно прн аффинном преобразовании C.27). Точка
В' делит отрезок А'С в отношении А/, причем
C.39)
Из C.27) получаем
4 - х\ = ап (*2 -
Из соотношений C.38) получим, что х2 — х\ = Х(хз — х2) и
Уг — У1 = к(уз — у2)- Подставляя найденные значения х2 — xi
и У2 — У1 в первую из формул C.40), получим
К - х\ = Л [ап (хз - х2) + «м (^з - Уг)]-
Подставим теперь в числитель правой части C.39) найденное
выражение для х'2 -*[,ав знаменатель — выражение длял^—х'2
(см. вторую формулу C.40)). После сокращения на ац(*з —
— Х2)-\-п12{уз — Уг) получим Я, = А/. Так как Я, = АВ/ВС =
= (ЛВС) иА,' = Л'В7В'С/ = (Л'В/С) (см. C.37)), то (АВС) =
= (А'В'С'), т. е. при аффинном преобразовании простое отноше-
отношение трех точек не меняется. Теорема доказана.
Замечание. Простое отношение трех точек называется
основным инвариантом аффинного преобразования, так как че-
через него могут быть выражены все другие инварианты аффин-
аффинного преобразования.
5. Аффинные преобразования пространства. Аффинным пре-
преобразованием пространства называется преобразование, при
котором каждая точка М(х, у, z) пространства переходит в точ-
точку ЛГ, координаты л', у", г! которой определяются формулами
х' = аих + al2y + al
yr = a2ix + a22y + a23^ + a2i, C.41)
г' = а31х + Оз2у + a^z + а31,

90 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ [ГЛ. 3
причем определитель
Д =
Oil О|2 Д|3
Дц агг а23
вл вза "зз
считается отличным от нуля: Д ф 0.
В полной аналогии со случаем плоскости доказываются сле-
следующие свойства аффинных преобразований пространства:
1°. Последовательное выполнение аффинных преобразований
пространства является аффинным преобразованием простран-
пространства.
2°. Тождественное преобразование является аффинным.
3°. Преобразование, обратное данному аффинному, также
является аффинным.
4°. Аффинное преобразование пространства взаимно одно-
однозначно.
Основное свойство аффинного преобразования пространства
формулируется следующим образом: при аффинном преобразо-
преобразовании пространства плоскости переходят в плоскости, прямые
в прямые, параллельные плоскости и прямые переходят в па-
параллельные плоскости и прямые.
Геометрический способ задания аффинных преобразований
пространства основан на следующем утверждении: аффинное
преобразование пространства определено однозначно, если за-
заданы образы четырех точек, не лежащих на одной плоскости,
и эти образы также не лежат на одной плоскости.
Как н в случае плоскости, основным инвариантом аффинного
преобразования пространства служит простое отношение трех
точек.
6. Ортогональные преобразования. Линейное преобразование
на плоскости
х' = ацх + а12у + а13
называется ортогональным, если выполняются соотношения
au+ali=1> ^2 + <&=l, auai2 + a2ia22 = 0- C.43)
Из соотношений C.43) следует, что
Поэтому ортогональное преобразование всегда является аф-
аффинным. Докажем основное свойство ортогональных преобра-
преобразований.
Теорема 3.4. При ортогональных преобразованиях сохра-
сохраняются расстояния между точками.

§3] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ 91
Доказательство. Пусть точки М\{х\,у{) и M2(*2,fte)
посредством ортогонального преобразования C.42) переводятся
соответственно в точки М\ (*{, t/Л и М2 (х^ t/2). Требуется дока-
доказать, что отрезки МХМ2 и М[М2 имеют равные длины. С по-
помощью формул C.42) н C.43) получаем
= К (х2 - х{) + al2(y2 - У1)]2 + fo, (хг - Xl) + а^ (у2 — yt)]2 =
- К+4д (*» - *,J+К+О (у2 - у гJ +
+ 2 (а, ^12 + 021^22) (х2 — *,) (у2 — ух) =
= (х2 - xtf + (у2 - yxf = I М,М212.
Итак, | iWjAf21 = | Al^Ala |. Теорема доказана.
Замечание. Так как прн ортогональных преобразованиях
расстояния сохраняются, то любая фигура на плоскости пре-
преобразуется в равную ей фигуру*). Иными словами, ортого-
ортогональное преобразование на плоскости можно рассматривать
как движение этой плоскости. При движении ортогональная
система координат переходит в ортогональную систему коор-
координат. Этим можно объяснить термин ортогональное преобра-
преобразование.
Ортогональные преобразования обладают следующими свой-
свойствами **):
Г. Последовательное выполнение двух ортогональных пре-
преобразований есть ортогональное преобразование.
2°. Тождественное преобразование хг = х, у1 = у является
ортогональным преобразованием (для этого преобразования со-
соотношения C.43), очевидно, выполняются).
3°. Преобразование, обратное ортогональному, также яв-
является ортогональным.
Линейное преобразование в пространстве
х1 = апх + апу + а13г + а1Ь
у' = а21х + а22у + а2аг + а2ь C.44)
г' = а31х + а32у + аззг + ам
называется ортогональным, если выполняются соотношения
°. C-45)
зз
— *. а:зап
*) Например, любой треугольник преобразуется в равный треугольник
(равенство по трем сторонам).
**) Эти свойства становятся особенно наглядными, если рассматривать
ортогональное преобразование как движение.

92 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ [ГЛ 3
Ортогональное преобразование является" аффинным. Справед-
Справедливо следующее основное свойство ортогональных преобразова-
преобразований: при таких преобразованиях сохраняются расстояния между
точками. Доказательство может быть проведено в полной ана-
аналогии с доказательством теоремы 3.4.
Ортогональные преобразования в пространстве обладают
следующими свойствами.
1°. Последовательное выполнение ортогональных преобразо-
ваний является ортогональным преобразованием.
2°. Тождественное преобразование х' = х, у' = у, г' = г —
ортогональное преобразование.
3°. Преобразование, обратное ортогональному, также орто-
ортогональное.
§ 4. Проективные преобразования
Проективными преобразованиями на плоскости называются
преобразования вида
/ __ Дц* *Ь Дцу -\- Дц / Дя* Ч* Д2»У * Д»з
~~ а31* + Дз»У + Дзз ' ^ ~ Дз!* + Дз«У + Дзз '
коэффициенты ац которых удовлетворяют условию *)
Дц Д12 Д]
Д31 Дз» Дэ
При проективном преобразовании C.46) плоскости особую роль
играет прямая L, определяемая уравнением
а31х + а32у + азз = 0.
Для точек этой прямой знаменатели в выражениях для х' и у'
(см. C.46)) обращаются в нуль, и поэтому преобразование
C.46) не определено для точек этой прямой.
Отметим, что проективное преобразование инвариантно от-
относительно выбора декартовой системы координат, так как фор-
формулы перехода от одной декартовой системы координат к дру-
другой линейны и поэтому прн переходе к новой системе коорди-
координат вид преобразований C.46) ие меняется. Непосредственной
проверкой можно убедиться, что последовательное проведение
двух проективных преобразований является проективным пре-
преобразованием, тождественное преобразование и преобразование,
обратное проективному, — также проективные преобразования.
При проективных преобразованиях точки, лежащие на прямой,
переходят в точки, также лежащие на прямой.
*) Геометрически это условие означает, что три прямые ц+»у+1з
5== 0, O2i« + any + дм = 0 и a»tx + а^у + д» = 0 ие пересекаются в одной
точке (см. п. 5 § 2 главы 3).

§ *] ПРОЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ 93
Основным инвариантом проективного преобразования яв-
является так называемое сложное (ангармоническое) отношение
(ABCD) любых четырех точек А, В, С и D на прямой, которое
определяется как частное двух простых отношений:
(ABCD) = (ACB):(ADB).
Инвариантность сложного отношения (ABCD) четырех точек
прямой может быть обоснована так же, как и инвариантность
простого отношения при аффинных преобразованиях.
Проективными преобразованиями в пространстве называют-
называются преобразования вида
/ ^_ Дп* + анУ + Дцг + а14
, __
" а4,х
а4,х + аиу + а43г + аи
__ аюх + ацу
для которых четыре плоскости
апх + а12у + ах& + а,4 = О,
ОцХ + аггУ + а&г + а24 = О,
+ азйУ + азз« + Яз4 = О»
^ = О
не пересекаются в одной точке.
Отметим, что проективное преобразование в пространстве не
определено для точек плоскости, определяемой уравнением
а1Хх + аА2у + О4з2 + аи = 0.
Непосредственной проверкой можно убедиться, что последо-
последовательное проведение двух проективных преобразований, тож-
тождественное преобразование и преобразование, обратное проек-
проективному,— также проективные преобразования. При проектив-
проективных преобразованиях точки, лежащие в одной плоскости, пере-
переходят в точки, также лежащие в одной плоскости, а точки, ле-
лежащие на прямой, переходят в точки, лежащие на прямой.
Основным инвариантом проективного преобразования в про-
пространстве является сложное отношение (ABCD) = (ACB):(ADB)
любых четырех точек А, В, С и D на прямой.

ГЛАВА 4
УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ. УРАВНЕНИЯ
ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
В этой главе рассматривается один из важнейших вопросов
аналитической геометрии — вопрос об аналитическом представ-
представлении линии на плоскости и поверхности и линии в простран-
пространстве при помощи уравнений, связывающих их координаты*).
Обсуждаются простейшие задачи, связанные с таким аналити-
аналитическим представлением, и приводится классификация плоских
линий и поверхностей. Доказывается, что порядок алгебраиче-
алгебраической линии (и соответственно поверхности) не зависит от вы-
выбора декартовой прямоугольной снстемы.
§ 1. Уравнение линии на плоскости
1. Понятие об уравнении линии. Предположим, что на пло-
плоскости я иам заданы: 1) декартова прямоугольная система ко-
ордннат Оху и 2) некоторая линия L. Рассмотрим некоторое
уравнение, связывающее две переменные величнны хну**)
ф(х,у) = 0. D.1)
Определение. Уравнение D.1) называется уравнением
линии L (относительно заданной системы координат), если
атому уравнению удовлетворяют координаты х и у любой точ-
точки, лежащей на линии L, и не удовлетворяют координаты х и у
ни одной точки, не лежащей на линии L.
С точки зрения этого определения сама линия L представ-
представляет собой (в заданной системе координат) геометрическое
место точек, координаты которых удовлетворяют уравнению
D-1).
*) По поводу самого понятия линии (или соответственно поверхности)
отсылаем читателя к главе 11 выпуска 1 настоящего курса.
**) Равенство Ф(д:, у) = 0, где Ф(х, у) —заданная функция двух пере-
переменных хну, называется уравнением, если это равенство справедливо ие для
всех пар вещественных чисел х, у. Равенство Ф(х, у) = О, справедливое для
всех пар вещественных чисел х, у, называется тождеством.

S П УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ 95
Если (в заданной системе координат) рассматриваемое урав-
уравнение вида D.1) является уравнением линии L, то мы будем
говорить, что это уравнение определяет линию L.
Замечание. Нетрудно указать такое уравнение вида D.1),
которое либо определяет геометрический образ, отличный от
того, что мы привыкли понимать под термином «линия», либо
вообще не определяет никакого геометрического образа. Так,
уравнение х2 + У2 = 0 определяет на плоскости Оху лишь одну
точку @,0), а уравнение х2-\- у2-\-1 = 0 вообще не определяет
никакого геометрического образа. Для того чтобы уравнение
вида D.1) определяло геометрический образ, отвечающий на-
нашему привычному представлению о линии, следует, вообще го-
говоря, подчинить функцию Ф(х, у) некоторым ограничениям (на-
(например требованию однозначной разрешимости функциональ-
функционального уравнения D.1) относительно одной из переменных). Эти
ограничения выясняются в курсе математического анализа (см.
выпуск 1, главу 15, § 2, п. 3).
Пример. Убедимся в том, что уравнение
(x-aJ + (y-bJ = r2 D.2)
является уравнением окружности радиуса г > 0 с центром в
точке Мо(а,Ь). В самом деле, точка М(х, у) лежит на указан-
указанной окружности тогда н только тогда, когда расстояние между
точками М(х, у) и Мо(а, Ь) равно г, т. е. тогда и только тогда,
когда квадрат расстояния между указанными точками
(х — аJ-\-(у — ЬJ равен г2. Таким образом, координаты любой
точки М(х,у), лежащей на указанной окружности, удовлетво-
удовлетворяют уравнению D.2), а координаты любой точки, не лежащей
на указанной окружности, не удовлетворяют уравнению D.2).
Уравнение окружности радиуса г > 0 с центром в начале
координат имеет более простой вид, а именно
= г2. D.3)
2. Параметрическое представление линии. Для аналитиче-
аналитического представления линии L часто бывает удобно выражать
переменные координаты х и у точек этой линии прн помощи
третьей вспомогательной переменной (или параметра) t:
D.4)
где функции ф@ и я|>@ предполагаются непрерывными по па-
параметру t (в некоторой области {/} изменения этого параметра).
Исключение из двух уравнений D.4) параметра * приводит
к рассмотренному выше уравнению вида D.1)*).
*) Такое исключение заведомо возможно, если хотя бы одна из функций
х = ф(<) или у = >|>@ имеет обратную (достаточные условия для этого см.
в п. 4 § 2 главы 15 выпуска 1).

96
УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ
[ГЛ. 4
Параметрическое представление линии на плоскости есте-
естественно возникает, если эту линию рассматривать как путь,
пройденный материальной точкой, непрерывно движущейся по
определенному закону. В самом деле, если переменная t пред-
представляет собой время, отсчитываемое от некоторого начального
момента, то задание закона двнжения н представляет собой за-
задание координат хну движущейся точки как некоторых не-
непрерывных функций х = ф@ и у = i|>(/) времени t.
Примеры. 1) Установим параметрические уравнения
окружности радиуса г > 0 с центром в начале координат. Пусть
У
х
Рис. 4.1
Рис. 4.2
М(х,у) — любая точка этой окружности, а / — угол между ра-
радиусом-вектором ОМ и осью Ох, отсчитываемый против часо-
часовой стрелки (рис. 4.1). Очевидно, что
х = г cos t, у —г sin t. D.5)
Уравнения D.5) и представляют собой параметрические урав-
уравнения рассматриваемой окружности. Параметр t может прини-
принимать любые значения, но для того, чтобы точка М(х, у) одни
раз обошла окружность, следует ограничить область изменения
параметра полусегментом 0 ^ t < 2я. Заметим, что для исклю-
исключения параметра / из уравнений D.5) достаточно возвести в
квадрат и сложить эти уравнения; мы получим при этом урав-
уравнение D.3) предыдущего пункта.
2) Установим параметрические уравнения так называемой
циклоиды, которая определяется как путь, описываемый одной
из точек М окружности, катящейся без скольжения по непо-
неподвижной прямой. Примем за ось Ох декартовой прямоугольной
системы ту прямую, по которой катится окружность, за начало
координат — одну из точек, в которых точка М катящейся
окружности выходит на указанную прямую, и направим ось Оу
так, чтобы ее положительная полуось лежала по ту же сторону
от Ох, что н катящаяся окружность (рис. 4.2).
Фиксируем произвольное положение катящейся окружности
и обозначим для этого положения буквой С — центр, а буквой
А—точку касания с осью Ох. Примем за параметр / угол, на

S 1] УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ 97
который повернулась катящаяся окружность при перемещении
из положения с точкой касания в начале координат О в поло-
положение с данной точкой касания А. Так как качение происходит
без скольжения, то О А = Rt, где R — радиус окружности.
В силу того, что декартовы прямоугольные координаты х и у
точки М равны проекциям вектора ОМ на оси координат (см.
п. 9 § 1 гл. 2), и в силу линейного свойства проекции вектора
на ось (см. п. 8 и 9 § 1 главы 2) получим
х = прх ОМ = пр* О А + пр* АС + прх СМ,
——— —^ —— , j4 о)
у = npj, ОМ = пру О А + пру АС + пру СМ.
Учитывая, что угол АСМ, отсчитываемый от вектора СЛ в на-
направлении по часовой стрелке (рис. 4.2), может отличаться от
угла t лишь на величину, кратную 2я, будем иметь
пр* O~A = Rt, пр,ЛС = 0, пр* СМ = — /? sin /,
npj,O^ = 0, пру AC = R, пр„ CM = — Rcos t.
Вставляя эти значения в формулы D.6), окончательно по-
получим параметрические уравнения циклоиды
х ==/?(/— sin 0, y = R(l—cost). D.7)
Параметр / в уравнениях D.7) может принимать какие угодно
значения.
Замечание. Часто линию L определяют не уравнением
D.1), а разрешенным (например, относительно у) уравнением
D.8)
Подчеркнем, что определение линии разрешенным уравнением
D.8) представляет собой частный случай параметрического
определения этой линии (при х = /, у = /(/))•
3. Уравнение линии в различных системах координат. Вид
уравнения линии L зависит не только от вида самой линии L,
но и от выбора системы координат. Уравнение линии меняется
как при переходе от одной декартовой системы координат
к другой, так н прн переходе от декартовых к каким-нибудь
другим координатам.
Если D 1) представляет собой уравнение линии L относи-
относительно декартовой прямоугольной системы координат Оху, то,
чтобы получить уравнение той же линии L относительно любой
другой системы координат, достаточно подставить в D.1) на
место х и у их выражения через новые координаты.
Так, например, линия L, определяемая в декартовой системе
Оху уравнением D.1), в полярной системе*) будет опреде-
*) Конечно, прн этом предполагается, что полюс совмещен с началом
декартовых координат, а полярная ось — с осью Ох.
7 Зак. 168

98 УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ
ляться уравнением
[гл.4
где введено обозначение Ф1 (р, ф) = Ф(р cos <p, p sin q>) (см. фор-
формулы перехода от декартовых координат к полярным; гла-
глава 1,§4).
Использование для определения некоторых линий недекар-
недекартовых систем координат объясняется тем, что уравнение линии
имеет при этом более простой вид.
Пример. Предположим, что ось и вращается (против ча-
часовой стрелки) вокруг неподвижной точки О и по этой вра-
щающейся оси движется точка М так, что длина р вектора ОМ
пропорциональна углу ф поворота оси и, отсчитываемому от
некоторой неподвижной оси Ох (рис. 4.3).
Линия, описываемая точкой М, называ-
называется спиралью Архимеда.
Если ввести полярную систему координат,
поместив полюс в точку О и направив поляр-
полярную ось вдоль оси Ох, то по самому опреде-
определению спиралн Архимеда ее уравнение имеет
вид
р = аф, D.9)
где р —полярный радиус, ф —полярный угол, а — коэффициент
пропорциональности, который будем считать отличным от нуля.
На рис. 4.3 сплошной линией изображена часть спиралн Архи-
Архимеда для случая а > О, а штриховой линией — часть спирали
Архимеда для случая а < О *).
Уравнение D 9) спиралн Архимеда в полярной системе координат отли-
отличается чрезвычайной простотой. Для того чтобы читатель убедился, насколько
сложно выглядит уравнение той же спирали Архимеда в декартовой прямо-
прямоугольной системе, приведем это уравиение для случая а > 0. Имея в виду,
что
Рис. 4.3
arctg— + 2яп
arctg — -f- я + 2яп
-5- sgn у + 2яп
при
при
при
X
X
X
>о,
<о,
= 0,
где я = 0, ±1, ±2, .... мы получим, что для случая а > 0 спираль Архи-
Архимеда определяется следующей бесконечной системой уравнений (номер я
*) Конечно, при неограниченном изменении угла ф (в случае а > 0 в
положительную, а в случае а < 0 в отрицательную сторону) как сплошная,
так и штриховая спнрали будут иметь бесчисленно много завитков, не изо-
изображенных на рис. 4.3.

§ Ц УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ 99
принимает значения 0, ±1, ±2. ...):
У** + У2 = а( arctg — + 2яп ) при х > О,
V** + У* — а Г arcig — + я + 2яп } при ж < О,
11/1 а а f-*- sgn у -f 2яп J при ж = О.
4. Два типа задач, связанных с аналитическим представле-
представлением линии. В связи с аналитическим представлением линии воз-
возникают задачи двух типов. Задачи первого типа заключают-
заключаются в изучении свойств линии при помощи заранее данного
уравнения этой линии. Такое изучение проводится средствами
математического анализа и выходит за рамки аналитической
геометрии. В самом деле, уравнение линии устанавливает функ-
функциональную зависимость между координатами точек этой линии
и задача первого типа, по существу, представляет собой гео-
геометрическое исследование графика функции (см. главу 9 вы-
выпуска 1).
Задачи второго типа заключаются в выводе уравнения ли-
линии, заранее заданной геометрически (например, линии, задан-
заданной как геометрическое место точек, удовлетворяющих некото-
некоторым условиям).
Примерами задач второго типа могут служить все рассмот-
рассмотренные в пп. 1—3 задачи (вывод уравнения окружности, цик-
циклоиды и спирали Архимеда).
5. Классификация плоских линий. Исходя из аналитического
представления линий относительно декартовых прямоугольных
систем координат, устанавливают следующую классификацию
плоских лиинй.
Определение 1. Линия называется алгебраической,
если в некоторой декартовой прямоугольной системе координат
она определяется уравнением
Ф(*, </) = 0, D.1)
в котором функция Ф(х, у) представляет собой алгебраический
полином *).
Определение 2. Всякая неалгебраическая линия называется
трансцендентной.
Определение 3. Алгебраическая линия называется линией
порядка п, если в некоторой декартовой прямоугольной си-
системе координат эта линия определяется уравнением D.1), в
котором функция Ф(х, у) представляет собой алгебраический
полином п-й степени.
*) То есть сумму конечного числа слагаемых вида а«*У, где k я / —
целые неотрицательные числа, а*< — некоторые постоянные.

100 УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ [ГЛ.4
Иными словами, линией п-го порядка называется линия,
определяемая в некоторой декартовой прямоугольной системе
алгебраическим уравнением степени п с двумя неизвестными.
Для установления корректности определений 1, 2 и 3 необхо-
необходимо доказать следующее утверждение.
Теорема 4.1. Если линия в некоторой декартовой прямо-
прямоугольной системе координат определяется алгебраическим урав-
уравнением степени п, то эта линия и в любой другой декартовой
прямоугольной системе координат определяется алгебраиче-
алгебраическим уравнением той же степени п.
Доказательство. Предположим, что линия L в некото-
некоторой декартовой прямоугольной системе координат определяется
уравнением
Ф(х, у) = 0, D.1)
левая часть которого представляет собой алгебраический поли-
иом степени л, т. е. сумму слагаемых вида
где k и / — целые неотрицательные числа, причем наибольшее
значение суммы k + / равно л, aki — некоторые постоянные, при-
причем хотя бы для одной пары Аи/, составляющих в сумме п, по-
постоянная аи отлична от нуля.
Возьмем на той же плоскости любую новую декартову пря-
прямоугольную систему координат О'х'у'. Тогда, как доказано в
§ 1 главы 3, для координат любой точки в старой и новой си-
системах справедливы формулы преобразования C.7). Чтобы по-
получить уравнение линии L в новой системе О'х'у', достаточно
подставить в левую часть D.1) на место х н у их значения,
определяемые формулами C.7). Мы получим при этом сумму
слагаемых вида
ак, (а + апх' + ацу')к (Ь
Отсюда ясно, что уравнение линии L в новой системе О'х'у'
будет представлять собой алгебраическое уравнение степени не
выше, чем п.
Если в проведенных рассуждениях поменять ролями системы
Оху н О'х'у', то мы убедимся в том, что указанное алгебраи-
алгебраическое уравнение (в системе О'х'у') имеет степень не ниже чем
п (иначе переход от О'х'у' к Оху повысил бы степень уравне-
уравнения). Таким образом, линия L определяется в новой системе
О'х'у' алгебраическим уравнением степени, равной п. Теоре-
Теорема 4.1 доказана.
Примером алгебраической линии второго порядка мо-
может служить окружность (уравнение D.3) которой в некоторой

УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ
101
декартовой прямоугольной системе является алгебраическим
уравнением второй степени). Примером трансцендентной
линии может служить спираль Архимеда, уравнение которой
в декартовой прямоугольной системе не является алгебраиче-
алгебраическим (см. п. 3).
Замечание. Будем называть алгебраическую линию L распадающейся,
если алгебраический полином Ф (х, у) степени п ^ 2, стоящий в левой части
уравнения этой линии, распадается на произведение Ф|(*, у)Фг(х, у) двух
алгебраических полиномов Ф|(х, у) и Фг(х, у) степеней fe> 1 и я — 4> 1
соответственно.
Из равенства Ф(х, у) = Фх(х, у)-Фг(х, у) очевидно, что координаты х
и у точки М удовлетворяют уравнению Ф(дг, у) = 0 тогда и только тогда,
когда эти координаты удовлетворяют хотя бы одному из уравнений
ф,(л, у) = о или Фг(х, у) = 0. Это означает, что лниия L, определяемая
уравнением Ф(х, у) = 0, распадается иа две линии: лниию L,, определяемую
уравнением <Di (х, у) = 0, и линию L%, определяемую уравнением Фг (х, у) = 0.
Так, линия четвертого порядка, определяемая уравнением
х* + у* + 2х*уг - Ъх2 -
(х* + у
2 —
(хг + у2 - 4) = 0,
распадается иа две окружности, определяемые уравнениями х1 + уг — 1 = 0 и
хг + уг _4 _ о.
Линия четвертого порядка, определяемая уравнением
х* + у*
- 2х* - 2«/2 + 1 = (х2 + у2 - II = 0,
распадается иа две «слившиеся» окружности, определяемые уравнением вто-
второго порядка х% + у% — 1 = 0. В отношении этой последней линии следует
договориться, какое из чисел 2 или 4 мы будем понимать под ее порядком.
в. О пересечении двух линии. Важную роль в аналитической
геометрии играет задача о нахождении точек пересечения двух
произвольных линий L\ и Li, определяемых уравнениями
<Di(jc, у) = 0 и ФгОс, #) = 0 соответственно. Так как искомые
точки пересечения в случае, если они существуют, должны од-
одновременно лежать как иа линии L\, так н на линии Li, то
координаты этих точек должны удовле-
удовлетворять каждому из уравнений Фх(х, у) =
= 0 н Ф2(х,у) = 0.
Такнм образом, для нахождения коор-
координат всех точек пересечения следует ре-
решить систему уравнений
Ф, (х, у) = 0, Ф2 (х, у) = 0. D.10) Мг(Ц-Т)
Каждое решение системы D.10) опре-
определяет точку пересечения линий L\ и L2. Рис- 4А
Если система D.10) не имеет решений, то линии L\ и L2 ие пере-
пересекаются.
Так, для нахождения точек пересечения двух окружностей,
определяемых уравнениями х2 + у2 = 1 и (х — IJ + у2 = 2,

102 УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ ?ГЛ. 4
решаем систему уравнений
х2 + у2-1=0, {х-1J + у2-2 = 0. D.11)
Вычитая из первого уравнения D.11) второе, получим 2х=0,
откуда х = 0. Вставляя это значение х в первое уравнение, най-
найдем, что у == ± 1. Получаем две точки пересечения Mi(Q, 1) и
М2@,— 1) (рис. 4.4).
Можно доказать, что если L\ и Ц — две нераспадающиеся алгебраиче-
алгебраические линии порядков тип соответственно и если одна из этих линий не
содержится целиком в другой, то эти линии имеют не более чем т-п то-
точек пересечении (см. любой курс высшей алгебры).
§ 2. Уравнение поверхности и уравнения линии
в пространстве
1. Понятие об уравнении поверхности. Предположим, что нам
заданы: 1) декартова прямоугольная система координат Охуг
в пространстве и 2) некоторая поверхность S. Рассмотрим не-
некоторое уравнение, связывающее трн переменные величины
х, у и г:
Ф(х,у,г) = 0. D.12)
Определение. Уравнение D.12) называется уравнением
поверхности S (относительно заданной системы коорди-
координат), если этому уравнению удовлетворяют координаты х, у и z
любой точки, лежащей на поверхности S, и не удовлетворяют
координаты х, у и г ни одной точки, не лежащей на поверх-
поверхности S.
С точки зрения этого определения сама поверхность S пред-
представляет собой (в заданной системе координат) геометрическое
место точек, координаты которых удовлетворяют уравнению
D.12).
Если (в заданной системе координат) рассматриваемое урав-
уравнение D.12) является уравнением поверхности S, то мы будем
говорить, что это уравнение определяет поверхность S.
Конечно, не всякое уравнение с тремя переменными вида
D.12) определяет геометрический образ, отвечающий нашему
привычному представлению о поверхности (и вообще опреде-
определяет реальный геометрический образ: рассмотрите уравнение
х2 + у2 -+- z2 + I = 0)- Чтобы уравнение вида D.12) определя-
определяло геометрический образ, отвечающий нашему представлению
о поверхности, следует, вообще говоря, подчинить функцию
Ф (х, у, г) некоторым ограничениям (например, требованию од-
однозначной разрешимости функционального уравнения D.12) от-
относительно одной из переменных). Этн ограничения выясняются
в курсе математического анализа (см. выпуск 1, главу 15, § 2).

9 2] УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ ЮЗ
Аналогично определяется уравнение поверхности S в любой
другой (не обязательно декартовой прямоугольной) системе ко-
координат. Если D.12) представляет собой уравнение поверхности
S в декартовой прямоугольной системе кординат Oxyz, то, что-
чтобы получить уравнение той же поверхности S относительно
любой другой системы координат, достаточно подставить в
D.12) на место х, у и г их выражение через новые координаты.
Использование для определения некоторых поверхностей не-
недекартовых систем координат объясняется тем, что уравнение
поверхности имеет прн этом более простой вид.
Легко убедиться в том, что в декартовой прямоугольной
системе Oxyz уравнение сферы радиуса R > 0 с центром в точке
Мо(а, Ь, с) имеет вид *)
(x-aJ + (y-bJ + (z-cJ = R\ D.13)
В самом деле, точка М(х, у, г) лежит на указанной сфере
тогда н только тогда, когда квадрат расстояния между точками
М(х, у, г) и М0(а, Ь, с)
равен R2. В случае, когда центром Мо сферы служит начало
координат (т. е. а = 0, 6 = 0, с = 0), уравнение D.13) прини-
принимает более простой вид:
x2 + y2 + z2 = R\ D.14)
Если ввести сферические координаты г, 8, q>, связанные с де-
декартовыми координатами так, как указано в п. 3 § 4 главы 1,
то уравнение сферы радиуса R с центром в начале координат
принимает вид г = R.
Это последнее уравнение, сразу вытекающее нз геометри-
геометрического определения сферы, может быть получено н посред-
посредством подстановки в D.14) на место х, у и z их выражений че-
через сферические координаты.
2. Уравнения линии в пространстве. Линию в пространстве
естественно рассматривать как пересечение двух поверхностей,
т. е. как геометрическое место точек, находящихся одновременно
на двух поверхностях.
Если Ф\ (х, y,z) = Q и Ф2 {х, y,z) = 0 суть уравнения двух
поверхностей, пересечением которых является данная линия L,
то: 1) координаты любой точки, лежащей на линии L, удовле-
удовлетворяют обоим указанным уравнениям; 2) обоим указанным
уравнениям не удовлетворяют координаты ни одной точки, не
лежащей на линии L.
*) Эта сфера определяется как геометрическое место точек М{х, у, г),
расстояние каждой из которых от точки М0(а, Ь, с) равно R.

104 УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ [ГЛ.4
Таким образом, два уравнения
®i (х, у, г) = 0, Ф2 (х, y,z) = 0 D.15)
совместно определяют линию L, т. е. являются уравнениями этой
линии.
Разумеется, данную линию L можно представить двумя
уравнениями бесчисленным множеством способов: вместо дан-
данных двух поверхностей можно взять любую пару поверхностей,
пересекающихся по той же линии L. Аналитически это означает,
что вместо системы D.15) можно взять любую эквивалентную
систему.
Например, уравнения двух сфер
совместно определяют лежащую в плоскости Оху окружность
радиуса единица с центром в начале координат. Ту же самую
окружность можно определить и двумя уравнениями
во втором из которых в качестве R можно взять любое веще-
вещественное число, превосходящее единицу.
3. Цилиндрические и конические поверхности. Предположим,
что в пространстве задана декартова прямоугольная система
координат Oxyz.
Определение 1. Поверхность S называется цилиндриче-
цилиндрической поверхностью с образующей, параллельной оси Oz,
если она обладает следующим свойством: какова бы ни была
лежащая на этой поверхности точка Мо(хо,уо,го), прямая ли-
ния, проходящая через эту точку и параллельная оси Oz, цели'
ком лежит на поверхности S.
Любую целиком лежащую на цилиндрической поверхности
S прямую называют образующей этой поверхности.
Совершенно аналогично определяются цилиндрические по-
поверхности с образующими, параллельными осям Ох или Оу.
Определение 2. Поверхность S называется конической
с вершиной в начале координат О, если она обладает следую-
щим свойством: какова бы ни была лежащая на этой поверх-
поверхности и отличная от начала координат точка Мо(хо, уо, Zo), пря-
прямая линия, проходящая через точку Мо и через начало коорди-
координат О, целиком лежит на поверхности S.
Постараемся выяснить, какими уравнениями определяются
цилиндрические и конические поверхности.
Ради определенности будем рассматривать цилиндрическую
поверхность с образующей, параллельной оси Oz.
Докажем, что всякое уравнение вида
Р(х,у)=*0, D.16)

f 2] УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ 105
связывающее две переменные х и у и не содержащее г, опреде-
определяет цилиндрическую поверхность с образующей, параллель-
параллельной оси Oz.
Пусть /Ио (хо, Уо, г0) — любая точка, лежащая на поверхности
S, определяемой уравнением D.16). Тогда координаты этой
точки должны удовлетворять уравнению D,16), т. е. справед-
справедливо равенство
F(x0, yo) = O. D.17)
Достаточно* доказать, что любая точка М прямой, проходя-
проходящей через Мо и параллельной осн Oz, также лежит на поверх-
поверхности S, т. е. имеет координаты, удовлетворяющие уравнению
D.16).
Какова бы ни была точка М прямой, проходящей через
Мо(хо, уо, г0) и параллельной оси Oz, ее абсцисса н ордината те
же, что н у точки Мо, т. е. равны соответственно х0 и уо, а ап-
аппликата z имеет какое угодно значение. Но в уравнение D.16)
входят только абсцисса и ордината, а они в силу равенства
D.17) удовлетворяют этому уравнению.
Тем самым доказано, что 5 — цилиндрическая поверхность
с образующей, параллельной оси Oz.
Заметим, что на координатной плоскости Оху уравнение
D.16) определяет плоскую линию, которую обычно называют
направляющей рассматриваемой цилиндрической поверхности.
В пространстве эта линия определяется двумя уравнениями:
F(x, y) = 0, 2 = 0,
первое из которых определяет рассматриваемую цилиндриче-
цилиндрическую поверхность, а второе — координатную плоскость Оху*).
В качестве примера приведем уравнение х2 + у2 = г2, опре-
определяющее круглый цилиндр с образующей, параллельной оси
Oz, и с направляющей, представляющей собой лежащую в пло-
плоскости Оху окружность единичного радиуса с центром в начале
координат.
Перейдем к выяснению вида уравнения конической поверх-
поверхности.
Напомним, что определенная для любых значений аргумен-
аргументов функция F(x,y,z) называется однородной функцией (сте-
(степени п), если, каково бы ни было вещественное число k, спра-
справедливо равенство
F (kx, ky, kz) = knF (x, у, z). D.18)
Докажем, что уравнение
F(x, у, z) = 0, D.19)
*) Ибо уравнению z = 0 удовлетворяют координаты любой точки, лежа-
шей иа плоскости Оху, и не удовлетворяют координаты ни одной точки, ие
лежащей иа этой плоскости.

100 УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ [ГЛ.4
в котором F(x,y,z) является однородной функцией любой сте-
степени п, определяет коническую поверхность.
Пусть Mo(xo,yo,zo)— любая отличная от начала координат
точка, лежащая на поверхности S, определяемой уравнением
D.19). Тогда справедливо равенство
F (х0, у0, Zo) = O. D.20)
Достаточно доказать, что, какова бы ни была точка M(x,y,z),
лежащая на прямой, проходящей через точку Мо(хо, у0, г0) и
через начало координат О, координаты х, у и г этой точки удо-
удовлетворяют уравнению D.19).
Так как векторы ОМ н ОМр коллинеарны (как лежащие на
одной прямой) и вектор ОМо является ненулевым, найдется
(в силу_ теоремы 2.1) вещественное число k такое, что ОМ =
= If ОМо. На основании линейных свойств координат вектора
(см. п. 8 § 1 главы 2) можно утверждать, что координаты век-
вектора ОМ равны соответствующим координатам вектора ОМ0,
умноженным на число k, т. е.
Из последних равенств и нз того, что F(xty,z) (как однород-
однородная функция некоторой степени п) удовлетворяет соотношению
D.18), получим
F(x, у, z) = F(kx0, ky0, kzo) = knF(xo, у0, z0),
а отсюда в силу равенства D.20) окончательно будем иметь
F(x, у, z) = 0.
Доказательство того, что поверхность 5, определяемая уравне-
уравнением D.19) с однородной функцией F(x,у,г), является кониче-
конической, завершено.
Заметим, что прямые, целиком лежащие на конической по-
поверхности, называются ее образующими и что все образующие
(как это видно из проведенного доказательства) проходят через
начало координат О.
Простейшим примером конической поверхности может слу-
служить круглый конус, определяемый уравнением х2-\-у*— z2=0.
Эта поверхность исследуется в п. 4 § 3 главы 7. Функция
F(x,y,z) — х2 + у2— z2, задающая ее уравнение, является од-
однородной функцией второго порядка.
4. Параметрические уравнения линии и поверхности в про-
пространстве. В п. 2 мы рассматривали линию в пространстве как
пересечение двух поверхностей. Возможен и очень естествен
с кинематической точки зрения и другой подход к понятию ли-
линии в пространстве, основанный на рассмотрении этой линии
как пути, пройденного материальной точкой, непрерывно дви-
движущейся по определенному закону.

§ 2] УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ 107
Как и для случая плоской линии (см. п. 2 § 1), этот подход
приводит к параметрическому представлению линии в простран-
пространстве, заключающемуся в том, что координаты х, у и г любой
точки данной линии задаются как непрерывные функции неко-
некоторого параметра t (преставляющего собой время). Итак, при
таком подходе координаты х, у, г любой точки линии L за-
задаются как три функции
определенные и непрерывные в некотором промежутке измене-
изменения параметра t.
Конечно, этот способ определения линии в пространстве
эквивалентен определению ее в виде пересечения двух поверх-
поверхностей. Чтобы убедиться в этом, предположим, что хотя бы одна
(например, третья) из функций D.21) допускает обратную.
В таком случае из третьего равенства D.21) получим, что t =
— X (z)» и» подставляя это значение t в первые два равенства
D.21), получим уравнения двух поверхностей
пересечением которых служит данная линия.
В качестве примера приведем параметрические уравнения
окружности радиуса г > 0, лежащей в координатной плоскости
Оху и имеющей центр в начале координат. В декартовой пря-
прямоугольной системе на плоскости Оху такая окружность опре-
определяется одним уравнением х2-\-у2=г2 (см. п. 1 § 1), в про-
пространстве же эта окружность определяется двумя уравнениями:
r2, z==0,
первое из которых определяет цилиндрическую поверхность, на-
направляющей которой служит рассматриваемая окружность и
образующая которой параллельна оси Ог, а второе уравнение
определяет координатную плоскость Оху.
Из п. 2 § 1 мы уже знаем, что на плоскости Оху параметри-
параметрические уравнения окружности х2 + у2 = г2 имеют вид *=rcos?,
у = г sin t, где 0 <: t < 2я.
Очевидно, та же окружность в пространстве задается тремя
уравнениями:
х = г cos /, у = г sin /, г = 0,
причем параметр t пробегает полусегмент 0 ^ t <. 2л.
Для параметрического задания поверхности координаты лю-
любой точки этой поверхности должны быть заданы как функции
не одного, а двух параметров р и q. Убедимся в том, что три
уравнения
* = ф(Р, q), y = $(p,q), z = x(P, Я) D.22)
определяют в пространстве некоторую поверхность.

108 УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ [ГЛ.4
Для этого предположим, что хотя бы одна пара из трех
уравнений D.22) может быть разрешена относительно парамет-
параметров р и q. Допустим, например, что из первых двух уравнений
D.22) р и q могут быть выражены как функции х и у: р =
= Ф\(х,у), q = <3>2(x,y).
Вставляя эти значения р н q в третье уравнение D.22), мы
получим уравнение с тремя переменными
г - % [<Di (х, у), Ф2 (х, у)] = 0,
определяющее, как нам известно, некоторую поверхность*).
В качестве примера приведем параметрические уравнения
сферы радиуса г > 0 с центром в начале координат:
х = г cos0 sin Ф, J/ = r sin 0 sin ф, г =
Здесь параметры 0 и ф представляют собой угловые сфериче-
сферические координаты (долготу и широту) точек поверхности сферы
(см. § 4 главы 1). Для того чтобы все точки сферы обходились
один раз, следует ограничить область изменения параметров
промежутками 0 ^ 0 < 2я, 0 ^ <р <: я.
5. Классификация поверхностей. В полной аналогии с клас-
классификацией плоских кривых устанавливают следующую класси-
классификацию поверхностей.
Определение 1. Поверхность называется алгебраической,
если в некоторой декартовой прямоугольной системе координат
она определяется алгебраическим уравнением с тремя перемен-
переменными.
Определение 2. Всякая не алгебраическая поверхность назы-
называется трансцендентной.
Определение 3. Алгебраическая поверхность называется по-
поверхностью порядка п, если в некоторой декартовой
прямоугольной системе координат она определяется алгебраи-
алгебраическим уравнением степени п с тремя переменными.
Для установления корректности этих определений необхо-
необходимо доказать следующее утверждение.
Теорема 4.2. Если поверхность в некоторой декартовой пря-
прямоугольной системе координат определяется алгебраическим
уравнением степени п, то эта поверхность и в любой другой де-
декартовой прямоугольной системе координат определяется ал-
алгебраическим уравнением той же степени п.
Доказательство теоремы 4.2 вполне аналогично доказатель-
доказательству теоремы 4.1 и опирается на доказанное в § 2 главы 3
утверждение: каковы бы ни были две произвольные де-
декартовы прямоугольные системы координат, координаты х, у
и г любой точки пространства относительно первой системы яв-
являются линейными функциями координат х', у' и г' той же
*) Конечно, при этом требуются некоторые ограничения.

5 2] УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ 109
точки относительно второй системы. С помощью этого утверж-
утверждения и рассуждений, полностью аналогичных тем, которые
проводятся при доказательстве теоремы 4.1, мы получим, что
если поверхность S в некоторой декартовой прямоугольной си-
системе Oxyz определяется алгебраическим уравнением степени п,
то эта поверхность в любой другой декартовой прямоугольной
системе О'х'у'г' определяется алгебраическим уравнением сте-
степени не выше п. Поменяв ролями системы Oxyz и О'х'у'г,
мы завершим доказательство теоремы 4.2.
Замечание 1. Так же как и в случае плоской линии, вво-
вводится понятие распадающейся алгебраической поверхности.
Замечание 2. Пространственная линия называется ал-
алгебраической, если она может быть определена как пересечение
двух алгебраических поверхностей.
Всякая не алгебраическая линия называется трансцендентной.
6. О пересечении поверхностей и линий в пространстве. Для
отыскания точек пересечения поверхностей или линий (или по-
поверхностей и линий) следует рассмотреть совместно уравнения,
определяющие указанные геометрические объекты. Решение
полученной при этом системы и определит нам координаты всех
точек пересечения. Если полученная система не имеет решений,
то точек пересечения нет.
Так, например, если заданы две линии, первая из которых
определяется уравнениями Ф\ (х, у, г) = 0 и Фг(л:, у, z) = 0, а
вторая — уравнениями Фз(х,у,г)=0 и <&i(x,y,z)—Q, то коор-
координаты точек пересечения этих двух линий (в случае, если точки
пересечения существуют) обязаны быть решением системы че-
четырех уравнений с тремя неизвестными:
Ф1 (х, у, z) = 0, Ф2 (х, у, г) = 0,
Фз (*, У, г) = 0, Ф4 (х, у, г) = 0.
Так как число неизвестных меньше числа уравнений, то послед-
последняя система, вообще говоря, не имеет решений, т. е. две линии
в пространстве, вообще говоря, не пересекаются.
7. Заключительные замечания. Линии и поверхности выше
второго порядка не входят в учебные курсы аналитической гео-
геометрии (им посвящены специальные сочинения). В нашем курсе
мы ограничимся изучением плоских линий и поверхностей пер-
первого и второго порядков.
В главе 5 будут рассмотрены линии и поверхности первого
порядка (их называют также линейными образами*)). В гла-
главе 6 изучаются плоские линии второго порядка, в главе 7 —
поверхности второго порядка.
*) Термин «линейный» объясняется тем, что в левой части уравнения
первого порядка стонт линейная функция.

ГЛАВА 5
ЛИНЕЙНЫЕ ОБРАЗЫ
Эта глава посвящена всестороннему изучению прямых линий
на плоскости н плоскостей и прямых линий в пространстве.
Убедившись в том, что этими объектами исчерпываются все
линейные образы (т. е. геометрические объекты, определяемые
линейными уравнениями), мы вводим в рассмотрение различные
виды уравнений прямой и плоскости и останавливаемся на их
использовании для решения важнейших задач.
§ 1. Различные виды уравнения прямой на плоскости
1. Общее уравнение прямой. Докажем сначала, что если на
плоскости я задана произвольная прямая линия L и фиксиро-
фиксирована произвольная декартова прямоугольная система Оху, то
прямая L определяется в этой системе уравнением первой сте-
степени.
Достаточно доказать, что прямая L определяется уравнением
первой степени при каком-то одном специальном выборе декар-
декартовой прямоугольной системы на плоскости я, ибо тогда она
будет определяться уравнением первой степени и при любом
выборе декартовой прямоугольной системы на плоскости я (в
силу теоремы 4.1). Направим ось Ох вдоль прямой L, а ось Оу
перпендикулярно к ней. Тогда уравнением прямой будет урав-
уравнение первой степени у = 0. В самом деле, этому уравнению
будут удовлетворять координаты любой точки, лежащей иа
прямой L, и не будут удовлетворять координаты ни одной точки,
не лежащей на прямой L.
Утверждение доказано.
Докажем теперь, что если на плоскости я фиксирована про-
произвольная декартова прямоугольная система Оху, то всякое
уравнение первой степени с двумя переменными х и у опреде-
определяет относительно этой системы прямую линию.
В самом деле, пусть фиксирована произвольная декартова
прямоугольная система Оху и задано уравнение первой степени
Ах + Ву + С = 0, E.1)

S tj РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ Щ
в котором А, В и С — какие угодно постоянные, причем из по-
постоянных А и В хотя бы одна отлична от нуля. Уравнение E.1)
заведомо имеет хотя бы одно решение Хо, уо*), т. е. существует
хотя бы одна точка Мо{хо,уо), координаты которой удовлетво-
удовлетворяют уравнению E.1):
+ С = О. E.2)
Вычитая из уравнения E.1) тождество E.2), мы получим урав-
уравнение
(у-уо) = О, E.3)
эквивалентное уравнению E.1). Достаточно доказать, что урав-
уравнение E.3) определяет относительно системы Оху некоторую
прямую. Мы докажем, что уравнение E.3) (а стало быть, и
E.1)) определяет прямую L, проходящую через точку Мо(хо,уо)
и перпендикулярную вектору п = {А, В) (так как А и В одно-
одновременно не равны нулю, то вектор п ненулевой).
В самом деле, если точка М(х, у) лежит на указанной пря-
прямой L, то ее координаты удовлетворяют уравнению E.3), ибо
в этом случае векторы п = {А, В} и МоМ = {х — Хо, у — у0}
ортогональны и их скалярное произведение
А(х-хо + В(у-уо) E.4)
равно нулю. Если же точка М{х, у) не лежит на указанной пря-
прямой L, то ее координаты не удовлетворяют уравнению E.3),
ибо в этом случае векторы п и МоМ не ортогональны, и поэтому
их скалярное произведение E.4) не равно нулю. Утверждение
доказано.
Уравнение E.1) с произвольными коэффициентами А, В и С
такими, что А и В не равны нулю одновременно, называется
общим уравнением прямой. Мы доказали, что прямая,
определяемая общим уравнением E.1), ортогональна к вектору
п = {А, В). Этот последний вектор мы будем называть нор-
нормальным вектором прямой E.1).
Заметим, что если два общих уравнения Ах + By + С = О
и А\х-\-В\у-\- С\ = 0 определяют одну и ту же прямую, то най-
найдется такое число t, что справедливы равенства
Al = At, Bi = Bt, С, =а, E.5)
г. е. коэффициенты А\, В\, С\ второго уравнения равны соответ-
соответствующим коэффициентам А, В и С первого уравнения, умно-
умноженным на некоторое число t.
В самом деле, А и В одновременно не равны нулю. Пусть, например.
Тогда, взяв произвольное дго, мы получим из уравнения E.1) Уо =
А С

112 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ.5
В самом деле, по условию прямые, определяемые уравне-
уравнениями Ах -\- By -}- С = 0 и А\Х -\- Вху -\- Ci =0, сливаются. Ста-
Стало быть, нормальные векторы п = {Л,В} и ni — {A\,Bi} кол-
линеарны. Так как, кроме того, вектор п ненулевой, найдется
(в силу теоремы 2.1) число / такое, что tii = nt, а отсюда и из
линейного свойства координат вектора вытекают первые два из
равенств E.5). Докажем справедливость и последнего равен-
равенства E.5). Слившиеся прямые имеют общую точку Мо(хо,уо),
гак что Ах0-\-Ву0-\-С — 0 и А\хо-\- BiyQ-\- С\ = 0. Умножая
первое из этих равенств на / и вычитая из него второе равен-
равенство, будем иметь (At — А{)х0 +(Bl — Bi)yo + (Ct — Ci) = 0.
Отсюда в силу первых двух равенств E.5) Ct— С\ — 0, т. е.
С, = Ct.
2. Неполные уравнения прямой. Уравнение прямой в отрезках.
Общее уравнение прямой E.1) называется полным, если все
его коэффициенты А, В и С отличны от нуля. Если хотя бы
один из указанных коэффициентов равен нулю, уравнение на-
называется неполным.
Рассмотрим все возможные виды неполных уравнений.
1) С = 0, уравнение Ах-\- By — 0 определяет прямую, про-
проходящую через начало координат (поскольку координаты на-
начала удовлетворяют этому уравнению).
2) В = 0, уравнение Ах + С — 0 определяет прямую, парал-
параллельную оси Оу (поскольку нормальный вектор этой прямой
п = {Л,0} ортогонален оси Оу).
3) А = 0, уравнение By + С = 0 определяет прямую, парал-
параллельную оси Ох (поскольку нормальный вектор этой прямой
п = {0, В} ортогонален оси Ох).
4) В = 0 и С = 0, уравнение Ах = 0 определяет ось Оу (в
самом деле, эта прямая параллельна оси Оу и проходит через
начало координат).
5) А = 0, С = 0, уравнение By = 0 определяет ось Ох (ибо
эта прямая параллельна оси Ох и проходит через начало коор-
координат) .
Рассмотрим теперь полное уравнение прямой E.1) и пока-
покажем, что оно может быть приведено к следующему виду:
4-+4—1. E.6)
о
называемому уравнением прямой в отрезках.
В самом деле, так как все коэффициенты А, В и С отличны
от нуля, мы можем переписать уравнение E.1) в виде
х . у ,
- С/А -*" - С/В ~
и затем положить а = —С/А, Ь = —С/В.

S 1] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ ИЗ
Заметим, что в уравнении «в отрезках» E.6) числа а и b
имеют простой геометрический смысл они равны величинам
отрезков, которые отсекает прямая на осях Ох и Оу соответ-
соответственно (отрезки отсчитываются от начала координат, см
рис 5 1) Чтобы убедиться в этом, достаточно найти точки пе-
пересечения прямой определяемой уравнением
E 6), с осями координат Например, точка
пересечения с осью Ох определяется из со-
совместного рассмотрения уравнения прямой
E.6) с уравнением у —О оси О* Мы полу-
получим координаты точки пересечения х = а,
у = 0 Аналогично устанавливается, что коор-
координаты точки пересечения прямой E.6) с Рис.5.1
осью Оу имеют вид х = 0, у = b
Уравнение прямой в форме «в отрезках» удобно использо-
использовать для построения этой прямой на чертеже
3 Каноническое *) уравнение прямой. Любой ненулевой век-
вектор, параллельный данной прямой, будем называть направ-
направляющим вектором этой прямой
Поставим перед собой задачу найти уравнение прямой, про-
проходящей через данную точку M$x\,yi) и имеющей заданный
направляющий вектор q = {/, пг}
Очевидно, точка М(х, у) лежит на указанной прямой тогда
и только тогда, когда векторы М\М = {х — Х\, у — у$ и q =
= {/, пг} коллинеарны, т е тогда и только тогда, когда коор-
координаты этих векторов пропорциональны (см. следствие из тео-
теоремы 2.17)
!L=r-=1J~ EJ)
Уравнение E.7) и есть искомое уравнение прямой Это уравне-
уравнение называют обычно каноническим уравнением прямой
Заметим, что в каноническом уравнении E.7) один из зна-
знаменателей / или пг может оказаться равным нулю (оба числа
/ и пг равняться нулю не могут, ибо вектор q = {/, пг) ненуле-
ненулевой) Так как всякую пропорцию a/b = c/d мы договорились
понимать как равенство ad = be, обращение в нуль одного из
знаменателей в E 7) означает обращение в нуль и соответ-
соответствующего числителя В самом деле, если, например, / = 0, то,
поскольку пгфО, из равенства 1(у — yi)=m(x — *i) заклю-
заключаем, что х — *i = 0
В заключение запишем уравнение прямой, проходящей че-
через две данные точки M\(xi,yi) и М2(*2.У*) (конечно, эти точки
считаются отличными друг от друга). Так как за направляю-
*) Термин «канонический» (от греческого xavoiv — правило, предписание,
образец) понимается здесь как «типовой» «традиционный».
S Зак. I6S

114 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ. 5
щий вектор такой прямой можно взять вектор q = М\М2 =
= {х2 — xit t/2 — у\} и прямая проходит через точку Mi(x\,y\),
то из канонического уравнения E.6) получим уравнение иско-
искомой прямой в виде
4. Параметрические уравнения прямой. Параметрические
уравнения прямой элементарно получаются из канонического
уравнения этой прямой. Примем за параметр i величину, стоя-
стоящую в левой и в правой частях E.7). Так как один из знаме-
знаменателей E.7) отличен от нуля, а соответствующий числитель
может принимать какие угодно значения, то областью измене-
изменения параметра t является вся вещественная ось: —оо < t <
< оо.
Мы получим х — xi = //, у — yi = mi или окончательно
x = xi + lt, y = yi + mt. E.9)
Уравнения E.9) и есть искомые параметрические уравнения
прямой. Уравнения E.9) допускают наглядную механическую
интерпретацию. Если считать, что параметр / — это время, от-
отсчитываемое от некоторого начального момента, то пара-
параметрические уравнения E.9) определяют закон движения мате-
материальной точки по прямой линии с постоянной скоростью v =
= л/Р+ пг2 (такое движение происходит по инерции).
5. Прямая с угловым коэффициентом. Рассмотрим любую
прямую, не параллельную оси Ох. Введем понятие угла на-
наклона этой прямой к оси Ох. Предполо-
Предположим, что рассматриваемая прямая пересекает
ось Ох в точке А (рис. 5.2). Возьмем на оси
Ох произвольную точку М, лежащую по ту
сторону от точки А, куда направлена ось Ох,
а на рассматриваемой прямой произвольную
~7a "%-*? точку N, лежащую по ту сторону от точки А,
' куда направлена ось Оу. Угол а = Z.NAM
Рис. 5.2 назовем углом наклона данной прямой к
оси Ох.
Если прямая параллельна оси Ох нли совпадает с ней, то
угол наклона этой прямой к оси Ох мы будем считать равным
нулю.
Тангенс угла наклона прямой к оси Ох назовем угловым
коэффициентом этой прямой. Если обозначить буквой
k угловой коэффициент данной прямой, а буквой а угол на-
наклона этой прямой к оси Ох, то по определению можно запи-
записать k = tg a.
Заметим, что для прямой, параллельной оси Ох, угловой ко-
коэффициент равен нулю, а для прямой, перпендикулярной оси

§1]
РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
115
Ох, угловой коэффициент не существует (в последнем случае
иногда формально говорят, что угловой коэффнциент «обра-
«обращается в бесконечность»).
Выведем уравнение прямой, проходящей через данную точку
Mi(x\,y\) и имеющей данный угловой коэффнциент k.
Для этого докажем сначала следующее утверждение:
если прямая не параллельна оси Оу и имеет направляющий
вектор q == {l,m}, то угловой коэффициент этой прямой k ра-
равен k = m/l.
Пусть а — угол наклона прямой к оси Ох, а 0 — угол на-
наклона направляющего вектора q = {/, m) к оси Ох. Так как
прямая может быть наклонена к оси
Ох под острым или под тупым углом
и ее направляющий вектор q может
иметь два противоположных направ-
направления, то возможны четыре случая,
изображенных на рис. 5.3. В случаях
1) н 3) 0 = а и для проекций на оси
вектора q справедливы формулы
1)
V
/ = | q | cos 0,
= |q|cos(-f--e) = |
х
г)
О
Рис. 5.3
В случаях 2) и4H = я — аи для проекций вектора q спра-
справедливы формулы / == | q | cos в, m = —| q J sin в.
Таким образом, в случаях 1) и 3) tg0 = tga и m// = tg0
а в случаях 2) и 4) tg8 = — tga и m// = — tg0.
Стало быть, во всех четырех случаях tg a = m/l, н утверж-
утверждение доказано.
Для того чтобы вывести уравнение прямой, проходящей че-
через заданную точку M\(xi,yi) и имеющей заданный угловой
коэффициент k, умножим обе части канонического уравнения
E.7) на m и учтем, что m/l = k.
Получим искомое уравнение в виде
E.10)
= yi — kxu то
E.П)
Если теперь обозначить через Ь постоянную
уравнение E.10) примет вид
k + b
Уравнение E.11) называется уравнением прямой с угловым
коэффициентом. В этом уравнении k обозначает угловой коэф-
коэффициент данной прямой, а Ь представляет собой величину от-
отрезка, отсекаемого данной прямой на оси Оу, начиная от на-
начала координат. Чтобы убедиться в этом, достаточно рассмот-
рассмотреть совместно уравнение E.11) и уравнение х = 0 оси Оу и

116 ЛИНЕЙНЫЕ ОБРАЗЫ (ГЛ. 5
найти координаты точки пересечения оси Оу и прямой E.11):
х = О, у = b (рис. 5.4).
6. Угол между двумя прямыми. Условия параллельности к
перпендикулярности двух прямых.
а) Пусть сначала две прямые Ц и L2 заданы общими урав-
уравнениями
п^л -f- D\y ~г* i-»i U И /12A -j~ D2y iT »-»2 ^*
Так как нормальным вектором прямой L\ является вектор п =
= {Ль Bi}, а нормальным вектором прямой
L2 является вектор п2—{А2,В2}, то задача
об определении угла между прямыми L\ и L2
А сводится к определению угла <р между векто-
/_ рами ni и пг*).
о\ ^ Из определения скалярного произведения
Рис. 5.4 niti2 = | ni 11 п21 cos ф и из выражения в коор-
координатах длин векторов ni и п2 и их ска-
скалярного произведения получим
E.12)
Итак, угол <р между прямыми L\ и L2 определяется с помощью
формулы E.12).
Условие параллельности прямых L\ и L2, эквива-
эквивалентное условию коллинеарности векторов tii и п2, заключается
в пропорциональности координат этих векторов, т. е. имеет
вид **)
4т=ъ- <5ЛЗ>
Условие перпендикулярности прямых L\ и L2
может быть извлечено из формулы E.12) (при cosq> —0) или
выражено равенством нулю скалярного произведения ni-n2.
Оно имеет вид
Л,Л2 + В,В2 = 0. E.14)
б) Пусть теперь две прямые L\ и L2 заданы каноническими
уравнениями
н х — xt _у — у%
Так как направляющими векторами прямых L\ и L2 служат
векторы qi = {/i, mi} и <\z = {/2, m?}, то в полной аналогии со
случаем а) мы получим:
*) Любые две пересекающиеся прямые образуют два угла, в сумме рав-
равных я Нам достаточно определить один из них.
**) При этом, как и выше, мы понимаем пропорцию alb = cjd в смысле
равенства ad = be.

§ I] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ \\J
1) формулу для угла <р между прямыми L\ и L2:
E.120
f + ml V'2 + m2
2) условие параллельности прямых L\ и L2.
4^ = — , E.130
3) условие перпендикулярности прямых L\ и L2:
0. E.140
в) Пусть, наконец, две прямые L\ и L2 заданы уравнениями
с угловым коэффициентом
Если ai и a2 — углы наклона прямых L\ и L2 к оси Оде,
а ф — один из углов между этими прямыми, то из элементар-
элементарных соображений (рис, 5.5) вытекает, что „
Ф = a2 — cti.
Таким образом,
Рис. 5.5
Мы получаем следующую формулу для определения угла <р:
Tfi-r <512">
Если в этой формуле поменять ролями k\ и k2 (от чего факти-
фактически лишь изменится знак на противоположный), то эта фор-
формула определит нам другой угол между прямыми, смежный по
отношению к прежнему углу (эти два угла в сумме составляют я
и тангенсы их отличаются лишь знаком).
Прямые параллельны, когда тангенс угла между ними ра-
равен нулю, т. е. условие параллельности имеет вид
kx = k2 E.13")
(при этом числитель в E.12") равен нулю, а знаменатель строго
положителен).
Условие перпендикулярности прямых L\ и L2 также можно
получить из E.12"). Оно отвечает случаю, когда тангенс углаф
не существует, т. е. случаю обращения знаменателя формулы
E.12") в нуль: kik2+ 1 =0.
Итак, условие перпендикулярности прямых L\ и L2 имеет
вид
к2 = ~Щх. E.14")

118 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ.5
7. Нормированное уравнение прямой. Отклонение точки от
прямой. Рассмотрим какую угодно прямую L. Проведем через
начало координат О прямую п, перпендикулярную L, и обозна-
обозначим буквой Р точку пересечения указанных прямых (рис. 5.6).
На прямой п возьмем единичный век-
тор п, направление которого совпадает
с направлением отрезка ОР (в случае
совпадения точек О и Р направление п
выберем произвольно).
Поставим перед собой цель — выра-
L д
р
^ * зить уравнение прямой L через два па-
Рис. 5.6 раметра: 1) длину р отрезка ОР, 2) угол 0
между вектором п и осью Ох.
Так как п — единичный вектор, то его координаты, соответ-
соответственно равные его проекциям на оси координат, имеют вид*)
n = {cose, sine}. E.15)
Очевидно, точка М(х,у) лежит на рассматриваемой пря'
мой L тогда и только тогда, когда проекция вектора ОМ на
ось, определяемую вектором п, равна р, т. е. при условии
пр„ОЛ?=р. E.16)
Так как п —единичный вектор, то в силу определения 2 ска-
скалярного произведения (см. п. 1 § 2 главы 2)
пр„ОМ = п-ОЖ E.17)
Имея в виду, что ОМ = {х,у}, а. вектор п определяется равен-
равенством E.15), мы получим следующее выражение для скаляр-
скалярного произведения этих векторов:
n-OM = jtcose-r-t/sme. E.18)
Из сопоставления E.16), E.17) н E.18) вытекает, что точка
М(х,у) лежит на прямой L тогда и только тогда, когда коор-
координаты этой точки удовлетворяют уравнению
р = 0; E.19)
E.19) и есть искомое уравнение прямой L (выраженное через
два параметра: вир). Это уравнение называется нормирован-
нормированным уравнением прямой.
Введем теперь фундаментальное понятие отклонения произ-
произвольной точки М от данной прямой L. Пусть число d обозначает
расстояние от точки М до прямой L. Назовем отклонением
б точки М от прямой L число -\-d в случае, когда точка М
*) В силу того, что проекция вектора иа любую ось равна модулю этого
вектора, уыиожеииоыу иа косинус угла наклона к оси (см. п. 8 § 1 главы 2).

SI] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ 119
и начало координат О лежат по разные стороны от прямой L,
и число —й в случае, когда М и О лежат по одну сторону от L.
Если же начало координат О лежит на прямой L, мы поло-
положим отклонение равным -\-d в случае, когда М лежит по ту
сторону от L, куда направлен вектор п, и равным —d в про-
противном случае.
Выясним геометрический смысл левой части уравнения
E.19) при любых хну.
Теорема 5.1. Левая часть нормированного уравнения пря-
прямой E.19) равна отклонению точки М с координатами х, у от
прямой L, определяемой уравнением E.19).
Доказательство. Спроектируем ,
точку М на ось, определяемую вектором п.
Пусть Q — проекция точки М. Отклонение б
точки М от прямой L равно PQ, где PQ
обозначает величину направленного отрез-
отрезка PQ оси, определяемой вектором п. Да- ~q
лее, из основного тождества (см. главу 1)
очевидно (рис. 5.7), что Ряс. 5.7
-р. E.20)
Но OQ = npnOM, а последняя проекция в силу формул E.17) н
E.18) равна х cos 9 + у sin 0. Итак,
E.20')
Сопоставляя формулы E.20') и E.20), получим
6=*cos9 + ysin8 — p E.21)
Теорема доказана.
Теорема 5.1 приводит нас к следующему правилу: для
нахождения отклонения б точки М (х0, уо) от прямой L следует
в левую часть нормированного уравнения прямой L подставить
на место х и у координаты х0 и у0 точки М.
Разумеется, это правило позволяет отыскивать н расстояние
от точки М до прямой L, ибо расстояние равно модулю откло-
отклонения.
В заключение укажем алгоритм приведения общего уравне-
уравнения прямой Ах + Ву-\-С = 0 к нормированному виду E.19).
Так как указанное общее уравнение и уравнение E.19)
должны определять одну и ту же прямую, то (в силу замечания
в конце п. 1) найдется число t такое, что
M = cos9, IB = sin 9, Ю = — р. E.22)
Возвышая в квадрат первые два равенства и затем складывая
их, получим Р{А2 + В2)= 1, откуда
'^ <5-23>

120 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ.5
Остается уточнить, какой из знаков ± следует взять в формуле
E.23). Так как по смыслу расстояние р всегда неотрицательно,
то из третьего равенства E.22) заключаем, что знак t противо-
противоположен знаку С.
Итак, для приведения общего уравнения прямой Ах -+- By -+-
-f- С = 0 к нормированному виду E.19) следует умножить его на
нормирующий множитель E.23), знак которого противоположен
знаку С.
8. Уравнение пучка прямых. Совокупность лежащих на дан-
данной плоскости я прямых, проходящих через некоторую точку 5
этой плоскости, принято называть пучком прямых с центром в S.
Центр 5 пучка прямых полностью определяется заданием
двух различных прямых этого пучка. Зная центр пучка S(x\,yi),
легко написать уравнение любой прямой этого пучка: для этого
можно, например, использовать уравнение E.10) прямой, про-
проходящей через точку S(x\,yi) и имеющей заданный угловой ко-
коэффициент k. Однако при решении задач представляется удоб-
удобным уметь писать уравнение любой прямой, проходящей через
точку пересечения двух данных прямых, ие вычисляя координат
этой точки пересечения.
В этом пункте и решается задача о нахождении уравнения
пучка прямых, центром которого служит точка пересечения двух
данных прямых, определяемых уравнениями
Alx + B1y + Ci = 0 и А2х + В2у + С2 = 0.
Докажем следующую основную теорему.
Теорема 5.2. Если А\Х+ В\у -f С\ = 0 и Аъх+ Вгу + С2 — 0
суть уравнения двух различных прямых, пересекающихся в неко-
некоторой точке S, а а и р— какие угодно не равные одновременно
нулю числа, то
а (Л,лг + В{у + С,) + р (А2х + В2у + С2) = 0 E.24)
есть уравнение прямой, проходящей через точку S. Более того,
какова бы ни была наперед заданная проходящая через точку S
прямая, она определяется уравнением E.24) при некоторых
аир.
Доказательство. Прежде всего установим, что при лю-
любых а и р, не равных одновременно нулю, равенство E.24) пред-
представляет собой уравнение первого порядка (т. е. в этом равен-
равенстве хотя бы один из коэффициентов при х или при у не равен
нулю). Собирая в равенстве E.24) коэффициенты при х и у,
перепишем это равенство в виде
(аА, + Р А2) х + (ofl, + РВ2) у + («С, + рС2) = 0. E.240
Если бы имели место равенства аА\ -f- рЛ2 = 0 и аВ\ + рВ2 = 0,
то из этих равенств, предполагая, например, что а=й=0*), мы
*) По условию одно из чисел а и {$ отлично от нуля.

1 1] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ 121
получили бы
AJA2 = - р/а, BJB2 = - р/а, т. е. АХ1А2 = Вх/В2.
Последнее равенство (см. п. 6) есть условие параллельности пря-
прямых, определяемых уравнениями А\х + В^у -\- С\ = 0 и Л2д; -f-
-f- В2у-\- С2 = 0, и противоречит предположению о том, что эти
прямые пересекаются и не совпадают.
Итак, E.24) при любых а и р, не равных одновременно нулю,
представляет собой уравнение первой степени, определяющее
(в силу результатов п. 1) некоторую прямую.
Эта прямая заведомо проходит через точку S(Xo, t/0) пересе-
пересечения двух прямых, определяемых уравнениями
^O и
В самом деле, так как S{x0, yo) принадлежит каждой из двух
указанных прямых, то справедливы равенства
Cl = 0 и
из которых вытекает, что при любых аир
а (Л.д^о + В{у0 + С,) + р (А2х0 + В2у0 -f C2) = 0,
т. е. координаты х0 и у0 точки 5 удовлетворяют уравнению
E.24).
Остается доказать, что, какова бы ни была наперед за-
заданная проходящая через точку S прямая, она определяется
уравнением E.24) при некоторых аир. Наперед заданная про-
проходящая через точку S(xo,yo) прямая однозначно определяется
заданием еще одной отличной от S точки М*(х*, у*), ей принад-
принадлежащей. Таким образом, достаточно доказать, что не равные
одновременно нулю аир можно выбрать так, что координаты
х*, у* наперед заданной точки М* будут удовлетворять уравне-
уравнению E.24) при этих аир. Подставляя в E.24) на место х и у
координаты х* и у* точки М*, получим равенство
a (AlX' + Bly* + С,) + р (А2х* + В2у' + С2) = 0. E.25)
Прежде всего заметим, что E.25) представляет собой уравнение
относительно а и р. В самом деле, оба выражения в круглых
скобках, являющиеся коэффициентами при аир, обратиться
в нуль не могут, ибо это означало бы, что две прямые, опреде-
определяемые уравнениями Aix + В\у + С\ =0 и А2х + В2у + С2 = 0,
проходят через точку М*. (Последнее невозможно в силу того,
что эти прямые ие совпадают и проходят через точку S, отлич-
отличную от М*.) Итак, хотя бы одна из круглых скобок в E.25)
отлична от нуля. Пусть, например, А\Х* + Biy* + Ci Ф0. Тогда,
задав произвольно р ф 0, мы определим из уравнения E.25)

122 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ. S
коэффициент а:
При указанных аир прямая, определяемая уравнением E.24),
проходит через точку М* (х*, у*). Случай, когда отлична от нуля
вторая из круглых скобок в E.25), рассматривается аналогично.
Теорема доказана.
Замечание. Так как в уравнении пучка E.24) хотя бы
одно из чисел аир отлично от нуля, то можно записывать
уравнение пучка не с двумя коэффициентами а и р, а с одним
коэффициентом %, равным их отношению. Так, если отлично от
нуля а, то, поделив E.24) на а и положив % = р/а, мы полу-
получим уравнение пучка в виде
(А* + В1У + С,) + А. (А2х + В2у + CJ = 0. E.26)
Следует, однако, отметить, что уравнение E.26) содержит все
прямые, проходящие через точку пересечения прямых, опреде-
определяемых уравнениями Aix + В{у + С\ = 0 и Ачх + В2у + d = 0,
за исключением одной прямой — прямой, определяемой уравне-
уравнением А2х + В2у + С* = 0 (она не получится из E.26) ни при
каком %).
§ 2. Некоторые задачи на прямую линию на плоскости
Выше уже был рассмотрен ряд задач иа прямую линию на
плоскости (нахождение угла между двумя прямыми, установле-
установление условий параллельности и перпендикулярности двух пря-
прямых, вычисление отклонения и расстояния точки от прямой, на-
нахождение уравнения прямой, проходящей через точку пересече-
пересечения двух данных прямых).
В этом параграфе мы рассмотрим ряд задач, развивающих
и углубляющих материал предыдущего параграфа.
1. Нахождение прямой, проходящей через данную точку
Mi(*i, Jfi) и составляющей заданный угол <р с данной прямой
у = k\X + b\. Будем искать уравнение прямой, проходящей через
точку Mi(xb^i) и составляющей заданный угол <р с прямой,
определяемой уравнением y = klx-\-bi, в форме E.10):
Прямая E.10) проходит через точку Mi(xi,#i), н нам остается
выбрать ее угловой коэффициент k так, чтобы она составляла
угол ф с прямой y = kix-\-bi. Заметим, что, взяв уравнение
искомой прямой в виде E.10), мы исключаем из рассмотрения
прямую х = х\, проходящую через точку М$х\,у$ и перпенди-
перпендикулярную оси Ох. Так как искомая прямая у = kx + (У\ — kx\)

§ 2] НЕКОТОРЫЕ ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ НА ПЛОСКОСТИ 123
и прямая у — k\x -\- bi составляют угол <р, то в силу формулы
E.12")
k~kl
Из последнего уравнения определяем угловой коэффициент k
искомой прямой: k — kx = ±tg<p ± kkx tg<p, и, стало быть, при
A ± k\ tg ф) ф 0 получим
В случае, если знаменатель в формуле E.27) обращается в нуль,
угловой коэффициент ие существует, и искомую прямую, оче-
очевидно, следует определить уравнением х = х%.
Итак, окончательно, получаем уравнения двух искомых пря-
прямых в виде
1>*-и--ёЙ*г<*-*.> й *-*
при кх\%<$Ф ± 1;
2) y~yi = kl +2tgФ (*-xt) и х = ж, при
3) JC = X, И У — У\= *'~2еФ-(х — ДС() При
2. Нахождение биссектрис углов, образованных данными
прямыми. Запишем уравнения двух прямых в нормированном
виде. Пусть это будут
*cos8-j- t/ sin в — р = 0 н х cos в, + у sin 8, — р, = 0.
Левые части этих уравнений равны отклонениям 6i и 62 точки
М (х, у) соответственно от первой и от второй прямых. На одной
из биссектрис (отвечающей тому углу, в котором лежит начало
координат) эти отклонения равны и по модулю, и по знаку, иа
другой биссектрисе отклонения 6i и бг равны по модулю и про-
противоположны по знаку. Таким образом, уравнения искомых бис-
биссектрис имеют вид
(дс cos 8 + у sin 8 — р) — (х cos 8, -f у sin 8, — р,) = 0,
(х cos 8 -f- у sin 8 — р) + (х cos 8, + у sin 8, — р,) = 0.
3. Условия, при которых данная прямая пересекает данный
отрезок АВ. Запишем уравнение прямой в нормированном виде
х cos 8 + у sin 8 — р = 0 и, подставив в левую часть последнего
уравнения сначала координаты точки А, а затем координаты
точки В, найдем отклонения бл и бв соответственно точек Л и В
от данной прямой. Для того чтобы данная прямая пересекала
отрезок АВ, необходимо и достаточно, чтобы точки А н В ле-
лежали по разные стороны от этой прямой, т. е. необходимо и до-
достаточно, чтобы отклонения Ьа и бв имели разные знаки.

124 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ. 6
4. Определение местоположения данной точки М и начала
координат О относительно углов, образованных двумя данными
прямыми. Пусть заданы две пересекающиеся прямые и требуется
определить, в одном, в смежных или в вертикальных углах, об-
образованных этими прямыми, лежат данная точка М и начало
координат О. Запишем уравнения данных прямых в нормирован-
нормированном виде и, подставив в левые части указанных уравнений коор-
координаты точки М, вычислим отклонения 6i и б2 точки М от пер-
первой и второй прямых соответственно. По определению отклоне-
отклонения точка М и начало координат О лежат в одном углу, если
оба отклонения 6i и бг отрицательны, в вертикальных углах,
если отклонения 6i и бг оба положительны, и в смежных углах,
если 6i и бг имеют разные знаки.
5. Условие пересечения трех прямых в одной точке. Найдем
условие, необходимое и достаточное для того, чтобы три прямые,
определяемые уравнениями
А{х + Вху + С, = 0, А2х + В2у + С2 = 0 и А3х + В3у + С3 = О,
пересекались в одной и только в одной точке.
Так как мы ищем условия, при которых точка пересечения
только одна, то необходимо предполагать, что из трех дан-
данных прямых какие-нибудь две прямые пересекаются в одной
точке (ибо в противном случае у трех прямых либо вовсе не бу-
дет точек пересечения, либо будет их бесконечно много). Таким
образом, необходимо требовать, чтобы из трех определителей
второго порядка
А, В, I \А, В, I | Аг Вг I „ R
Л ft I * \ A Р I I Л О! \ )
Л» "I | I "I "> I I Л5 °3 I
хотя бы один был отличен от нуля.
Ради определенности предположим, что первые две из ука-
указанных трех прямых пересекаются в одной точке (т. е. предпо-
предположим, что отличен от нуля первый из определителей E.28)).
Тогда, для того чтобы три прямые пересекались в одной точке,
необходимо и достаточно, чтобы третья прямая А3х -\- Вгу -f-
-\-Сз = 0 принадлежала пучку, образованному первыми двумя
прямыми
а (Л,х + В,у + С,) + р (Л2х + В2у + С2) = 0.
В силу замечания в конце п. 1 § 1 найдется некоторое число
(обозначим его —у) такое, что все коэффициенты последнего
уравнения равны соответствующим коэффициентам уравнения
А + В3у + Сз = 0, умноженным на это число, т. е.
аЛ, + рЛ2 = — y4j, aAl-\-^A2 + yA3 = 0,
аВ, + рВ2 == — УВ3, или аВ, + рВ2 + \В3 = 0,

At
В,
с,
At
в2
С,
Аз
вэ
с3
=
А,
А2
А3
В,
В2
в3
с,
С2
с3
§ 2] НЕКОТОРЫЕ ЗАДАЧИ НА ПРЯМУЮ ЛИНИЮ НА ПЛОСКОСТИ 125
Последние равенства представляют собой однородную систему
трех уравнений относительно трех неизвестных а, р и у. Так как
образующие пучок коэффициенты а и р" не равны нулю одновре-
одновременно, то указанная система обязана иметь нетривиальное ре-
решение, для чего необходимо и достаточно (см. Дополнение к
главе 1, п. 8), чтобы определитель этой системы
E.29)
С, С, С3 А3 В3 С3
был равен нулю.
Итак, для того чтобы три прямые, определяемые уравнениями
Aix + В>у + С, = О, А2х + В3у + С2 = 0 и Агх + В3у + С3 = О,
пересекались в одной и только в одной точке, необходимо и до-
достаточно, чтобы обращался в нуль определитель E.29) и был
отличен от нуля хотя бы один из определителей E.28).
Мы пришли к этому утверждению, предположив, что первые
две из указанных трех прямых пересекаются в одной точке.
К этому же результату приводит и предположение о том, что
пересекаются в одной точке любые другие две из указанных
трех прямых (впрочем, последнее ясно из соображений сим-
симметрии).
6. Нахождение прямой, проходящей через точку пересечения
двух данных прямых и удовлетворяющей еще одному условию.
Пусть требуется найти уравнение прямой, проходящей через
точку пересечения двух неколлинеарных*) прямых, определяе-
определяемых уравнениями Aix -J- В\у -\- Cj =0 и А2х -f- В2у -J- Сг = 0, и,
кроме того, удовлетворяющей одному из следующих трех усло-
условий: а) отсекающей на осях отрезки равной длины; б) парал-
параллельной заданной прямой А3х + В3у + Сз = 0; в) перпендику-
перпендикулярной заданной прямой А3х -f- Вгу -\- С3 = 0.
Искомая прямая принадлежит пучку
а (Л,х + Bty + С,) + р (А2х + В2у + С,) = 0. E.30)
Для определения постоянных а и р (а точнее, их отношения)
будем использовать дополнительное условие.
В случае а) мы должны собрать в E.30) коэффициенты при
х и у и приравнять друг другу модули этих коэффициентов
(мы приравниваем друг друг не сами коэффициенты при х и у,
а их модули, так как требуется, чтобы отсекаемые на осях от-
отрезки имели равную длину, а не величину). В результате полу-
получим уравнение |aAi + рЛ2| = |рВ2 + aBi| или a(Ai:=F Bi) =
= —р(Л2ч=В2). Заметим, что обе круглые скобки обратиться
в нуль не могут (так как прямые Atx + В\у-\- С\ = 0 и А2х -f-
+ В2у + Сг = 0 ие коллинеариы), и, стало быть, из последнего
*) Прямые называются неколлинеарными, если онн не параллельны н не
совпадают.

126 ЛИНЕЙНЫЕ ОБРАЗЫ (ГЛ. 5
равенства, задавая произвольно один из коэффициентов аир,
мы найдем другой из этих коэффициентов.
В случае б) учтем, что у двух параллельных прямых коэф-
коэффициенты при х и у пропорциональны (см. § 1, п. 6, условие
E.13)).
Таким образом, мы получим
. == 5 или a {AiB3 — BiA3) = р (В2А3 — А2В3).
Заметим, что в последнем равенстве обе круглые скобки не мо-
могут обратиться в нуль (иначе бы прямые А\х-\- В\у -\- С\ = 0 и
Агх + В2у + Сг = 0 оказались коллинеарными), и поэтому из
последнего равенства, задавая произвольно один из коэффициен-
коэффициентов а и р, мы найдем другой из этих коэффициентов.
В случае в) используем для прямой E.30) и прямой Аъх +
+ В3у + С3 = 0 условие перпендикулярности E.14) (см. § 1, п. 6).
В результате получим (аЛ, + §А2)А3 -\-(аВ\ + рВ2)В3 — 0
или а{А\А3-\-BiB3) = —Р(А2А3 + В2В3). Заметим, что обраще-
обращение в нуль обеих круглых скобок последнего равенства невоз-
невозможно (иначе мы получили бы, 4TO-gL=-gi- и прямые v4i* +
+ В\у + С\ = 0 и А2х + В2у + Сг = 0 коллинеарны). Таким об-
образом, задавая в указанном равенстве произвольно один из
коэффициентов а и р, мы определим нз него другой из этих
коэффициентов.
§ 3. Различные виды уравнения плоскости
1. Общее уравнение плоскости. Содержание этого пункта
полностью аналогично содержанию п. 1 § 1. Мы докажем два
утверждения.
Г. Если в пространстве задана произвольная плоскость п и
фиксирована произвольная декартова прямоугольная система
Охуг, то плоскость я определяется в этой системе уравнением
первой степени.
2°. Если в пространстве фиксирована произвольная декар-
декартова прямоугольная система Охуг, то всякое уравнение первой
степени с тремя переменными х, у и г определяет относительно
этой системы плоскость.
Для доказательства первого утверждения достаточно уста-
установить, что плоскость я определяется уравнением первой сте-
степени при каком-то одном специальном выборе декартовой пря-
прямоугольной системы, ибо тогда она определяется уравнением
первой степени и при любом другом выборе декартовой прямо-
прямоугольной системы (в силу теоремы 4.2). Расположим оси Ох и
Оу в плоскости я, а ось Ог направим перпендикулярно этой пло-
плоскости. Тогда уравнением плоскости я будет уравнение первой

§ 31 РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПЛОСКОСТИ 127
степени г = 0. В самом деле, этому уравнению будут удовлетво-
удовлетворять координаты любой точки, лежащей на плоскости я, и не
будут удовлетворять координаты ии одной точки, не лежащей
на плоскости я. Утверждение 1° доказано.
Для доказательства утверждения 2° фиксируем произволь-
произвольную декартову прямоугольную систему Oxyz и рассмотрим про-
произвольное уравнение первой степени
Ax + By + Cz + D*=0, E.31)
в котором А, В, С к D — какие угодно постоянные, причем из
постоянных А, В и С хотя бы одна отлична от нуля. Уравнение
E.31) заведомо имеет хотя бы одно решение хо, уо, Zo*), т. е.
существует хотя бы одна точка Мо(хо,уо,zo), координаты кото-
которой удовлетворяют уравнению E.31):
Лх0 + Ву0 + Cz0 + D = 0. E.32)
Вычитая из уравнения E.31) тождество E.32), получим урав-
уравнение
А(х-ха) + В(у~ уо) + С (г - z0) = 0, E.33)
эквивалентное уравнению E.31). Достаточно доказать, что урав-
уравнение E.33) определяет относительно системы Oxyz некоторую
плоскость. Мы докажем, что уравнение E.33) (а стало быть,
и уравнение E.31)) определяет плоскость я, проходящую через
точку Mo(xo,yo,zo) и перпендикулярную вектору п = {А, В, С)
(так как хотя бы одна из постоянных Л, В и С не равна нулю,
то вектор п ненулевой).
В самом деле, если точка М (х, у, г) лежит на указанной
плоскости я, то ее координаты удовлетворяют уравнению E.33),
ибо в этом случае векторы п={А,В, С} и МоМ—{х— хо,
у — у0, z — z0} ортогональны и их скалярное произведение
А(х-хо) + В(у-уо) + С(г-гй) E.34)
равно нулю. Если же точка М (х, у, г) не лежит на указанной
плоскости я, то ее координаты не удовлетворяют уравнению
E.33), ибо в этом случае векторы п и М0М не ортогональны и
поэтому их скалярное произведение E.34) не равно нулю.
Утверждение 2° доказано.
Уравнение E.31) с произвольными коэффициентами А, В, С
и D такими, что из коэффициентов А, В и С хотя бы. один отли-
отличен от нуля, называется общим уравнением плоскости.
*) В самом деле, хотя бы одна из постоянных А, В, С отлична от нуля.
Пусть, например, С Ф 0. Тогда, взяв произвольные х0 и у<>, получим из урав-
уравнения E.31) 20 = — -Q-х„ — -?-уо-

128 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ.5
Мы доказали, что плоскость, определяемая общим уравне-
уравнением E.31), ортогональна к вектору п={А, В, С}. Этот послед-
последний вектор мы будем называть нормальным вектором плоскости
E.31).
Заметим, что если два общих уравнения
Ax + By + Cz + D = Q, Atx + В{у + С,г + ?>, = О
определяют одну и ту же плоскость, то найдется такое число t,
что справедливы равенства
At = At, В, = В/, Cx = Ct, Dx=Dt,
т. е. коэффициенты A\, Bu Ci и D\ второго уравнения равны
соответсвующим коэффициентам А, В, С и D первого уравнения,
умноженным на некоторое число t.
Доказательство этого утверждения вполне аналогично дока-
доказательству утверждения, содержащегося в замечании в конце
п. 1 § 1. Мы предоставляем читателю провести его самому.
2. Неполные уравнения плоскости. Уравнение плоскости в от-
отрезках. Общее уравнение плоскости E.31) называется пол-
полным, если все его коэффициенты А, В, С и D отличны от нуля.
Если хотя бы один из указанных коэффициентов равен нулю,
уравнение называется неполным.
Рассмотрим все возможные виды неполных уравнений:
1) D = О, уравнение Ах + By + Cz = 0 определяет пло-
плоскость, проходящую через начало координат (поскольку коорди-
координаты начала удовлетворяют этому уравнению).
2) А = 0, уравнение By + Cz -J- D = 0 определяет плоскость,
параллельную оси Ох (поскольку нормальный вектор этой пло-
плоскости п ={0, В, С) перпендикулярен оси Ох).
3) В = 0, уравнение Ах ¦+¦ Cz -\- D = 0 определяет плоскость,
параллельную оси Оу (ибо этой оси перпендикулярен нормаль-
нормальный вектор п ={А, 0, С}).
4) С = 0, уравнение Ах -\-By-\-D = 0 определяет плоскость,
параллельную оси Oz (ибо этой оси перпендикулярен нормаль-
нормальный вектор п ={А, В, 0}).
5) А = 0, В = 0, уравнение Cz + D = 0 определяет плоскость,
параллельную координатной плоскости Оху (ибо эта плоскость
параллельна осям Ох и Оу).
6) А==0, С = 0, уравнение Ву-\- D = 0 определяет пло-
плоскость, параллельную координатной плоскости Oxz (ибо эта пло-
плоскость параллельна осям Ох и Oz).
7) В=0, С = 0, уравнение Ах-\- D =0 определяет пло-
плоскость, параллельную координатной плоскости Oyz (ибо эта
плоскость параллельна осям Оу и Oz).
8) А—0, В = 0, D = 0, уравнение Cz = 0 определяет коор-
координатную плоскость Оху (ибо плоскость параллельна Оху и про-
проходит через начало координат).

§ 3] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПЛОСКОСТИ 129
9) Л=0, С = 0, D=0, уравнение Ву = 0 определяет коор-
координатную плоскость Oxz (ибо плоскость параллельна Oxz и про-
проходит через начало координат).
10) В = 0, С = 0, D = 0, уравнение Л* = 0 определяет коор-
координатную плоскость Oyz (ибо плоскость параллельна Оуг и про-
проходит через начало координат).
Рассмотрим теперь полное уравнение плоскости E.31) и по-
покажем, что оно может быть приведено к следующему виду:
Т + Т + Т^1' <5-35)
называемому уравнением плоскости в отрезках.
В самом деле, так как все коэффициенты А, В, С и D от-
отличны от нуля, мы можем переписать уравнение E.31) в виде
= 1
и затем положить а = —D/A, Ь = —D/B, с==—D/C.
Заметим, что в уравнении «в отрезках» E.35) числа а, Ь и с
имеют простой геометрический смысл: они равны величинам
отрезков, которые отсекает плоскость на
осях Ох, Оу и Oz соответственно (отрезки
отсчитываются от начала координат, см.
рис. 5.8). Чтобы убедиться в этом, доста-
достаточно найти точки пересечения плоскости,
определяемой уравнением E.35), с осями
координат. Например, точка пересечения с
осью Ох определится из совместного рас-
рассмотрения уравнения плоскости E.35) с Рис. 5.8
уравнениями у = 0 и z = 0 оси Ох. Мы по-
получим координаты точки пересечения х = а, у = 0, z = 0. Ана-
Аналогично устанавливается, что координаты точки пересечения
плоскости E.35) с осью Оу равны х = 0, у = Ь, г = 0ис осью
Oz равны х = 0, у — 0, z = с.
3. Угол между двумя плоскостями. Условия параллельности
и перпендикулярности плоскостей. Пусть две плоскости п\ и яг
заданы общими уравнениями А\х + В\у + C\Z + Dy = 0 и А2х -f-
+ Вгу + dz + Di = 0. Очевидно, вопрос об определении угла
между указанными плоскостями сводится к определению угла <р
между их нормальными векторами ni = {Ль Ви С\} и nj =
= {ф,В2,С2}*).
Из определения скалярного произведения П]П2 —|ni| |n2|cos<p
и из выражения в координатах длин векторов ni и п2 и их
*) Любые две пересекающиеся плоскости образуют два угла, в сумме
равных я. Нам достаточно определить один из этих углов.
9 Зак. 168

130 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ. 5
скалярного произведения, получим
cos ф
J A\+ B\+ C\*J А\ +
Итак, угол <р между плоскостями щ и я2 определяется с по-
помощью формулы E.36).
Условие параллельности плоскостей щ и пг, эквивалентное
условию коллинеарности векторов щ и п2, заключается в про-
пропорциональности координат этих векторов, т. е. имеет вид*)
Условие перпендикулярности плоскостей п% и яг может быть
извлечено из формулы E.36) (при cos<p=0) или выражено
равенством нулю скалярного произведения векторов ni и п2. Оно
имеет вид
Л, А2 + В,В2 + Cfi2 = 0. E.38)
4. Уравнение плоскости, проходящей через три различные
точки, не лежащие на одной прямой. Поставим перед собой
цель — вывести уравнение плоскости, проходящей через три раз-
различные точки Mi(xuyi,zi), M2(x2,y2,z2) и Мз(х3, Уз, z3), не ле-
лежащие на одной прямой. Так как указанные три точки не лежат
на одной прямой, векторы MtM2 = {x2 — х\, у2 — y\,z2 — z\) и
М\Мъ = {хз — х1г уз — уь^з — Zi} не коллинеарны, а поэтому
точка M(x,y,z) лежит в одной плоскости с точками Mi, M2 и М3
тогда и только тогда, когда векторы MiM2, М1М3 и MiM =
= {х — х\,у — уи z — Zi} компланарны, т.е. тогда и только тогда,
когда смешанное произведение этих трех векторов равно нулю
(см. главу 2, § 3, п. 4).
Используя выражение смешанного произведения в координа-
координатах, мы получим необходимое и достаточное условие принад-
принадлежности М(х, у, z) к указанной плоскости в виде (см. главу 2,
§ 3, п. 7)
¦х, У — У\ г-г,
х, уг — У1
хх у3 — ух г3 — г,
= 0. E.39)
Уравнение первой степени E.39) и является уравнением иско-
искомой плоскости.
5. Нормированное уравнение плоскости. Отклонение точки
от плоскости. Рассмотрим какую угодно плоскость я. Проведем
через начало координат О прямую п, перпендикулярную пло-
плоскости я, и обозначим буквой Р точку пересечения прямой п и
*) При этом, как и всюду выше, мы понимаем всякую пропорцию
а/Ь •= c/d в смысле равенства ad = be.

§ 3] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПЛОСКОСТИ 131
плоскости я (рис. 5.9). На прямой п возьмем единичный вектор
п, направление которого совпадает с направлением отрезка ОР
(в случае совпадения точек О к Р направление п выберем про-
произвольно).
Поставим перед собой цель — выразить уравнение плоскости
я через следующие параметры: 1) длину р отрезка ОР, 2) углы
а, р и y наклона вектора п к осям Ох, Оу и г
Ог соответственно.
Так как п — единичный вектор, то его ко-
координаты, соответственно равные его проек-
проекциям на оси координат, имеют вид*)
п = {cosa, cosP, cosy). E.40)
Очевидно, точка M(x,y,z) лежит на рас-
рассматриваемой плоскости я тогда и_только то- Рнс. 5.9
еда, когда проекция вектора ОМ на ось,
определяемую вектором п, равна р, т. е. при условии
пр„ОМ = р. E.41)
Так как п — единичный вектор, то в силу определения 2 ска-
скалярного произведения (см. п. 1 § 2 главы 2)
прп0~М = п-0М. E.42)
Имея в виду, что 0М = {х, у, г), а вектор п определяется ра-
равенством E.40), мы получим следующее выражение для ска-
скалярного произведения этих векторов:
п • ОМ = х cos а + у соз р + г cos у. E.43)
Из сопоставления E.41), E.42) и E.43) вытекает, что точ-
точка М (х, у, г) лежит на плоскости я тогда и только тогда, когда
координаты этой точки удовлетворяют уравнению
х cos а + у cos р + г cos \ — р = 0. E.44)
E.44) и есть искомое уравнение плоскости я, выраженное через
параметры р, а, р и у. Это уравнение называется нормирован-
нормированным уравнением плоскости.
Введем теперь фундаментальное понятие отклонения произ-
произвольной точки М от данной плоскости я. Пусть число d обозна-
обозначает расстояние от точки М до плоскости я.
Назовем отклонением б точки М от плоскости я число
-\-d в случае, когда точка М и начало координат О лежат по
*) В силу того, что проекция вектора иа любую ось равна модулю этого
вектора, умноженному на косниус угла наклона к оси (см. п. 8 § 1 главы 2).

132 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ. б
разные стороны от плоскости я, и число —d в случае, когда М
и О лежат по одну сторону от я.
Если же начало координат О лежит на плоскости я, поло-
положим отклонение равным -\-d в случае, когда М лежит по ту сто-
сторону от я, куда направлен вектор п, и равным —d в противном
случае.
Имеет место следующее важное утверждение.
Теорема 5.3. Левая часть нормированного уравнения пло-
плоскости E.44) равна отклонению точки М с координатами х, у,
г от плоскости я, определяемой уравнением E.44).
Доказательство. Спроектируем точку М на ось, опре-
определяемую вектором п. Пусть Q—проекция точки М (рис. 5.9).
Отклонение б точки М от плоскости я равно PQ, где PQ обо-
обозначает величину направленного отрезка PQ оси, определяемой
вектором п. Далее, из основного тождества (см. главу 1) оче-
очевидно (см. рис. 5.9), что
6 = PQ = OQ-OP = OQ-p. E.45)
Но OQ = прп0М, а последняя проекция в силу формул E.42) и
E.43) равна х cos а + У cos р ¦+- г cos у. Итак,
OQ = х cos a + У cos p -f- z cos у. E.46)
Сопоставляя формулы E.45) и E.46), получим 6=jccosa +
4- У cos Р + 2 cos у — р. Теорема доказана.
Теорема 5.3 приводит нас к следующему правилу: для на-
нахождения отклонения б точки Мо(хо, Уо, го) от плоскости я сле-
следует в левую часть нормированного уравнения плоскости я под-
подставить на место х, у и z координаты х0, уо и Zo точки Мо.
Разумеется, это правило позволяет отыскивать и расстояние
от точки М до плоскости я, ибо расстояние равно модулю от-
отклонения.
В заключение укажем алгоритм приведения общего уравне-
уравнения плоскости E.31) к нормированному виду E.44). Так как
указанное общее уравнение и уравнение E.44) должны опреде-
определять одну и ту же плоскость, то (в силу замечания в конце
п. 1 этого параграфа) найдется число t такое, что
M = cosa, /B = cosp, /С = созу, tD— — p. E.47)
Возвышая в квадрат первые три равенства E.47), складывая
их и учитывая, что сумма квадратов направляющих косинусов
равна единице (см. п. 9 § 1 главы 2), получим t2(A2-{-В2-{-
+ С2)— 1, откуда
/ = ч ' —. E 48)
Остается уточнить, какой из знаков ± следует взять в фор-
формуле E.48). Так как по смыслу расстояние р всегда неотрица-

§ 3] РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПЛОСКОСТИ 133
тельно, то из последнего равенства E.47) заключаем, что знак
t противоположен знаку D.
Итак, для приведения общего уравнения плоскости Ах -f-
-\- By -\- Cz -\- D = О к нормированному виду E.44) следует
умножить его на нормирующий множитель E.48), знак которого
противоположен знаку D.
6. Пучки и связки плоскостей. Совокупность всех плоскостей,
проходящих через одну и ту же прямую L, называется пуч-
пучком плоскостей (с центром в L).
В полной аналогии с теоремой 5.2, относящейся к пучку
прямых, доказывается следующее утверждение:
Если AiX + Bly+C1z + Di = O и А2х + В2у + C2z + D2 = 0
суть уравнения двух различных и не параллельных плоскостей,
пересечением которых служит некоторая прямая L, а а и р—
какие угодно не равные одновременно нулю числа, то
а (Л,* + Вху + Cxz + D,) + р (А2х + В$ + C2z + D2) = 0 E.49)
есть уравнение плоскости, проходящей через прямую L. Более
того, какова бы ни была наперед заданная проходящая через
прямую L плоскость, она определяется уравнением E.49) при
некоторых а и р.
Доказательство этого утверждения (не содержащее по
сравнению с доказательством теоремы 5.2 никаких новых идей)
представляем читателю.
Сформулированное утверждение позволяет задавать пря-
прямую L, являющуюся линией пересечения двух ие совпадающих
и не параллельных плоскостей АуХ-{- В\у-{- C\z + D\ = 0 и
Ат.х -f- B2y -f- C2z -f- Dn = 0, не только двумя уравнениями этих
плоскостей, но и любыми двумя различными уравнениями пучка
E.49) (полученными при каких угодно аир).
Совокупность всех плоскостей, проходящих через данную
точку Мо(хо,уо,2о) называется связкой плоскостей (с
центром в Мо) ¦
Легко убедиться в том, что уравнение связки с центром
в Мо(хо, уо, Zo) имеет вид
A(x~xo) + B(y-yo) + C(z-zo)=O, E.50)
где А, В к С — какие угодно числа, не равные одновременно
нулю.
В самом деле, всякая плоскость, определяемая уравнением
E.50), проходит через точку Мо(хо,уо,Zo). С другой стороны,
если я — наперед заданная плоскость, проходящая через точ-
точку Мо (хо, уо, %о). то эта плоскость однозначно определяется за-
заданием, кроме точки Мо(хо, уо, Zo), еще нормального вектора
п = {А, В, С} и потому определяется уравнением E.33) (см.
п. 1 этого параграфа), совпадающим с уравнением E.50).

134 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ. 5
§ 4. Прямая линия в пространстве
1. Канонические уравнения прямой в пространстве. Выше
(см. п. 6 предыдущего параграфа) уже отмечалось, что прямую
линию в пространстве, являющуюся линией пересечения двух
различных и не параллельных плоскостей, определяемых урав-
уравнениями AiX + Biy + CiZ + Di = 0 н А2х + Вгу + C2z -f D2 =
= 0*), можно задавать либо двумя уравнениями этих плоско-
плоскостей, либо двумя любыми различными уравнениями пучка
а (Л,* + Вху + C,z + Di) + р (Агх + В^у + C2z + D2) = 0
(отвечающими произвольно взятым числам аир).
При решении многих задач более удобным является спе-
специальный вид уравнений прямой в пространстве, к выводу ко-
которого мы и переходим.
Договоримся называть любой ненулевой вектор, параллель-
параллельный данной прямой, направляющим вектором этой прямой.
Выведем уравнения прямой, проходящей через данную точ-
точку пространства Mi(x\,yi,Zi) и имеющей заданный направляю-
направляющий вектор q = {/, m, n}. Для этого заметим, что точка
М(х, у, г) лежит на указанной прямой тогда и только тогда,
когда векторы MiM = {х— xlt у — у\, г — z{) и q = {/, гп, п}
коллинеарны, т. е. тогда и только тогда, когда координаты этих
векторов пропорциональны (см. следствие из теоремы 2.17)
*?>-*=*¦-!=*¦. E.51)
Уравнения E.51) суть искомые уравнения прямой, проходящей
через точку М\(х\,у\,г{) и коллинеарной вектору q= {/,m,n}.
Эти уравнения принято называть каноническими уравнениями
прямой.
Заметим, что в канонических уравнениях E.51) одно или
два нз чисел /, m н п могут оказаться равными нулю (все три
числа /, m и п равняться нулю не могут, так как вектор q =
= {/,m,n) ненулевой). Так как всякую пропорцию a/b = c/d
мы договорились понимать как равенство ad = be, обращение
в нуль одного из знаменателей в E.51) означает обращение в
нуль и соответствующего числителя. В самом деле, пусть, на-
например, I = 0, а п Ф 0 (хотя бы одно из трех чисел I, m и п
не равно нулю). Тогда из пропорции **' =—^-^-, эквива-
эквивалентной равенству (дг — xi)n = (z — z{)l, заключаем, что х —
О
•) Из п. 3 § 3 следует, что для того, чтобы плоскости, определяемые
уравнениями Atx + Btf + CiZ + Di = 0 и A& + Вгу + Сгг + Dt — 0, ие сон-
падали и не былн параллельны, необходимо и достаточно, чтобы нарушалась
хотя бы одна из пропорций AJAi = BJBi = C,/Ci.

i 4] ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ 135
В заключение покажем, как прямую, заданную уравнениями
двух различных и не параллельных плоскостей
lZ + Dx = О,
привести к каноническому виду E.51). Достаточно найти:
1) хотя бы одну точку M\(xi,yuzi), через которую проходит
прямая E.52); 2) направляющий вектор q = {/, пг, п} прямой
E.52).
Начнем с нахождения координат х\, у и z\ точки Afi, через
которую проходит прямая E.52). Так как плоскости, опреде-
определяемые уравнениями E.52), не параллельны и не сливаются, то
А В С
нарушается хотя бы одна из пропорций —г- — -&-=-тг-- Это оз-
начает, чтохотя ^5ы один из трех определителей второго по-
порядка
Ах В
А2 в.
в /-' • \ л п \ отличен от нуля (см. Допол-
нение к главе 1, п. 1). Пусть ради определенности отличен от
нуля определитель ,' „' . Тогда, взяв вместо г произвольное
число Z\ и подставив его в уравнения E.52), определим из си-
системы E.52) соответствующие этому zt значения Xi и у\\
г В, (С2г, + Dt) - В2 (С,г, + Р>)
А,В2 — А2В,
+D,)-A, (С2г, +D2)
»»~ А1В2-А2В1
В частности, можно взять Z\ = 0. Тогда, воспользовавшись фор-
формулами E.53), мы получим, что прямая E.52) проходит через
точку М (Bib-Wi AtDi-AiD* Q\
точку Ml\<AlBt_AiBt > л,в2-Л2В,' "J'
Для нахождения координат /, т, п направленного вектора q
прямой E.52) заметим, что вектор q ортогонален каждому из
нормальных векторов п\ = {А\, BitCi} и пг = {/42, В2, С2} пло-
плоскостей E.52), так что можно положить вектор q = {/, пг, п)
равным векторному произведению [nin2]. Пользуясь выраже-
выражением векторного произведения в координатах (см. п. 6 § 3
главы 2), мы получим: 1 = В\С2 — В2Си т—С\А2 — С2А\,
п = А \В2 — AiB\.
Таким образом, для случая, когда отличен от нуля опреде-
определитель \А1 J , канонические уравнения прямой E.52) имеют
вид
В,Р2 — В2РХ А2РУ — а,р2
А,В2 — А2В, А,В2 — А2ВХ г

136 ЛИНЕЙНЫЕ ОБРАЗЫ (ГЛ. 5
Аналогично записываются канонические уравнения прямой
E.52) для случая, когда отличен от нуля определитель
В> Ч или И1 С'1
2 *-*2 I I -**2 ^2 I
2. Уравнения прямой, проходящей через две различные точки
JMi(*i»yi.Z\) и Af2(*2,У2,г2). Эти уравнения имеют вид
Х — Хх __ V—у, __ Z — Zy
хг — х, у г —Ух z2 — z,
Для получения их достаточно заметить, что прямая проходит
через точку M$x\,yi,Z$ и имеет направляющий вектор q =
= М1М2 = {*г — *ь Уъ— У\, 22 — Zi}, и воспользоваться кано-
каноническими уравнениями E.51).
3. Параметрические уравнения прямой в пространстве. Па-
Параметрические уравнения прямой в пространстве элементарно
получаются из канонических уравнений E.51) этой прямой.
Примем за параметр t каждое из отношений E.51). Так как
один из знаменателей E.51) отличен от нуля, а соответствую-
соответствующий числитель может принимать какие угодно значения, то
областью изменения параметра t является вся вещественная
ось: —оо</<+оо. Мы получим х — X\ = lt, y — y\ = mt,
z — Z\ = nt, или окончательно
x = xl + lt, y = yl + mi, z = zl + nt. E.54)
Уравнения E.54) и есть искомые параметрические уравнения
прямой. Если принять параметр t за время, отсчитываемое от
некоторого начального момента, то параметрические уравнения
E.54) определяют закон движения материальной точки по пря-
прямой линии с постоянной скоростью v = -y/l2 -f- tn2 + tiz (такое
движение происходит по инерции).
4. Угол между прямыми в пространстве. Условия параллель-
параллельности и перпендикулярности прямых. Пусть две прямые в про-
пространстве L\ и Li заданы своими каноническими уравнениями
-?ZL?i = i^li. = ^lLH ?^L = JL^?L = ?nfL. тогда за-
1\ Ш\ fli 12 ftl2 П-2
дача определения угла между этими прямыми сводится к опре-
определению угла ф между их направляющими векторами:
q, = {/„ т,, п,} и Я2 = {/г. "*2> "гЬ
Пользуясь определением скалярного произведения qiq2 =
= Iflil |q2|cosq) и выражением в координатах указанного ска-
скалярного произведения и длин векторов qi и q2, мы получим
для определения угла ф следующую формулу:
// f f /1- ee\

§ 4] ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ 137
Условие параллельности прямых L\ и L2, эквивалентное
условию коллинеарности векторов qi и q2, заключается в про-
пропорциональности координат этих векторов, т. е. имеет вид *)
/1//2 = m1/m2 = rt1/rt2. E.56)
Условие перпендикулярности прямых L\ и L2 может быть
извлечено из формулы E.55) (при cos ф = 0) или выражено
равенством нулю скалярного произведения qiq2. Оно имеет вид
/,/2 + ЩЩ + п\п2 = 0- E.57)
5. Условие принадлежности двух прямых к одной плоскости.
Две прямые в пространстве L\ и L2 могут: 1) пересекаться,
2) быть параллельными, 3) скрещиваться. В первых двух слу-
случаях прямые L\ и L2 лежат в одной плоскости.
Установим условие принадлежности одной плоскости двух
прямых, заданных каноническими уравнениями
х — х, _ у — у, _ г — г, и х — х2 __ у — уг __ г — г2
• I tTt\ It \ l% Tt\% t%2
Очевидно, что для принадлежности двух указанных прямых
одной плоскости необходимо н достаточно, чтобы три вектора
= {1г, m2, пг} были компланарны, для чего в свою очередь не-
необходимо н достаточно, чтобы смешанное произведение указан-
указанных трех векторов равнялось нулю. Записывая смешанное про-
произведение указанных трех векторов в координатах (см. п. 7
§ 3 гл. 2), приходим к следующему необходимому и достаточ-
достаточному условию принадлежности двух прямых L\ и L2 одной пло-
плоскости
= 0. E.58)
Если прямые L\ и L2 удовлетворяют условию E.58), то они
либо пересекаются, либо параллельны. Так как условие па-
параллельности прямых L\ и L2 имеет вид E.56), то для пересе-
пересечения прямых L\ и Li необходимо и достаточно, чтобы они
удовлетворяли условию E.58) и чтобы нарушалась хотя бы
одна из пропорций h/k = mi/m2 = ni/n2.
6. Угол между прямой и плоскостью. Условия параллельно-
параллельности н перпендикулярности прямой и плоскости. Рассмотрим пло-
плоскость я, заданную общим уравнением Ах -f- By -f- Cz -f- D = 0,
*) Как и всюду выше, любую пропорцию a/b = cjd понимаем в смысле
равенства ad = be.

138 ЛИНЕЙНЫЕ ОБРАЗЫ (ГЛ. S
и прямую L, заданную каноническими уравнениями * ~*! =
__У — У\ _ z — zx
т п
Поскольку угол ф между прямой L и плоскостью я является
дополнительным к углу ty между направляющим вектором пря-
прямой q = {/, т, п} и нормальным вектором плоскости п =
= {А,В,С} (рис. 5.10), то из определения
скалярного произведения qn= |q| |n|cost|? и
нз равенства cos г|) = sin ср мы получим для
определения угла <р между прямой L и пло-
плоскостью я следующую формулу:
Al + Bm + Cn
sin ф =
ф
У Л*
Условие параллельности прямой L и пло-
Рнс. 5.10 скости я (включающее в себя принадлеж-
принадлежность L к я) эквивалентно условию перпен-
перпендикулярности векторов п и q и выражается равенством нулю
скалярного произведения этих векторов:
п = 0. E.59)
Условие перпендикулярности прямой L и плоскости я экви-
эквивалентно условию параллельности векторов п и q и выражается
пропорциональностью координат этих векторов *):
7. Условия принадлежности прямой j
к плоскости Ах + Ву + Cz + D = 0. Эти условия выражаются
двумя равенствами:
xl + Byl+Czl + D = 0
E'6О)
первое из которых означает, что точка Mi(jci,^i,Zi), через ко-
которую проходит прямая, принадлежит плоскости, а второе есть
условие параллельности прямой и плоскости E.59).
8. Связка прямых. Совокупность всех прямых, проходящих
через данную точку М$х\,у\,г$, называется связкой пря-
прямых (с центром в точке М\). Легко убедиться в том, что
уравнения связки прямых с центром в точке
M{) имеют вид
E.61)
*) Как всегда, всякую пропорцию a/b = c/d понимаем в смысле равен-
равенства ad = be.

§5] ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ 139
где /, m и п — какие угодно числа, ие равные одновременно
нулю.
В самом деле, всякая прямая, определяемая уравнениями
E.61), проходит через точку M$xuyuz$. С другой стороны,
если L — наперед заданная прямая, проходящая через точку
M$xi,y\,Z$, то эта прямая однозначно определяется заданием,
кроме точки M$xi,yuz$, еще направляющего вектора q =
= {/, т, п} и потому определяется каноническими уравнениями
E.51), совпадающими с уравнениями E.61).
§ 5. Некоторые задачи иа прямую и плоскость в пространстве
1. Условие пересечения трех плоскостей в одной и только в
одной точке. Для того чтобы три плоскости, соответственно оп-
определяемые уравнениями
Л,* + В,*/+ C,z+ ?>, = (),
B2y + C2z + D2 = 0, E.62)
+ Взу + Сз2 + Ц, = О,
пересекались в одной и только в одной точке, необходимо и до-
достаточно, чтобы был отличен от нуля определитель
At Bt С,
Аг Вг Сг . E.63)
А3 ?>з Сз
В самом деле, в этом и только в этом случае система E.62)
имеет единственное решение (см. Дополнение к главе 1).
2. Нахождение биссектральных плоскостей двугранного угла,
образованного двумя данными плоскостями. Запишем уравне-
уравнения двух данных плоскостей в нормированном виде. Пусть это бу-
будут: х cos ai + у cos Pi -f- z cos yi — Pi = 0 и x cos аг ¦+• У cos P2 -+-
-f- z cos Y2 — p2 = 0.
Левые части этих уравнений соответственно равны отклоне-
отклонениям 6i и б2 точки М(х,у, г) от первой и от второй плоскостей.
На одной из биссектральных плоскостей (отвечающей тому
двугранному углу, в котором лежит начало координат) эти от-
отклонения равны и по модулю, и по знаку, иа другой биссек-
тральной плоскости отклонения 6i и 62 равны по модулю и про-
противоположны по знаку.
Таким образом, уравнения искомых биссектральных плоско-
плоскостей имеют вид
(х cos a, + у cos p, -f z cos Yi — Pi) —
— (х cos а2 + у cos p2 + z cos Y2 ~ P2) = 0>
(x cos а, + у cos p, + z cos Yi — Pi) +
+ (x cos 02 + у cos p2 + z cos Y2 — P2) = 0.

140 ЛИНЕЙНЫЕ ОБРАЗЫ (ГЛ. 5
3. Условия, при которых данная плоскость пересекает дан-
данный отрезок АВ. Записав уравнение данной плоскости в нор-
нормированном виде и подставив в левую часть последнего
уравнения сначала координаты точки А, а затем координаты
точки В, найдем отклонения бл и бв точек А и В соответственно
от данной плоскости.
Для того чтобы данная плоскость пересекала отрезок АВ,
необходимо и достаточно, чтобы точки А и В лежали по разные
стороны от плоскости, т. е. необходимо и достаточно, чтобы от-
отклонения бл и бв имели разные знаки.
4. Определение местоположения двух данных точек А и В
относительно двугранных углов, образованных данными плоско-
плоскостями. Пусть заданы две пересекающиеся плоскости и требуется
определить, в одном, в смежных или в вертикальных углах,
образованных двумя данными плоскостями, лежат две данные
точки А и В.
Записав уравнения данных плоскостей в нормированном
виде, вычислим отклонения б(д" и бд* точки А от первой и вто-
второй плоскостей н отклонения бв° и бв' точки В от первой н
второй плоскостей. По знакам этих четырех отклонений заклю-
заключаем, по одну нли по разные стороны от каждой нз плоскостей
лежит каждая из точек А и В. Очевидно, если точки А к В ле-
лежат по одну сторону от первой плоскости и по одну сторону от
второй плоскости, то эти точки лежат в одном углу, обра-
образованном данными плоскостями. Если точки А и В лежат по
одну сторону от одной плоскости и по разные стороны от дру-
другой плоскости, то эти точки лежат в смежных углах. Если,
наконец, точки А н В лежат по разные стороны и от той, и от
другой плоскости, то эти точки лежат в вертикальных
углах.
5. Уравнения прямой, проходящей через данную точку
M\(xi, уи z,) и перпендикулярной данной плоскости Ах-{-By +
-\-Сг + D=0. Эти уравнения имеют вид * ~А *' = у ~ у'= г ~^ г',
ибо направляющим вектором искомой прямой служит нормаль-
нормальный вектор плоскости п = {А, В, С}.
6. Уравнение плоскости, проходящей через данную точку
Мо(хо, у о, zQ) и параллельной заданной плоскости Atx-\- В,у +
+ CiZ+Di=0. Это уравнение имеет внд At(x—xo) + Bi(y—yo) +
+ Ci(z — Zo) = O. В самом деле, искомая плоскость принадле-
принадлежит связке плоскостей E.50) и имеет тот же нормальный век-
вектор п = {A\,BU Ci), что и данная плоскость.
7. Уравнение плоскости, проходящей через заданную точку
X — Xi
Мо(хо, Уо, z0) и перпендикулярной заданной прямой -. =
= — = —. Это уравнение имеет внд 1(х — хо) +

§ 5] ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ 141
+ т(у— Уо)-\-п(г — 20) = 0. В самом деле, искомая плоскость
принадлежит связке плоскостей E.50) и имеет в качестве нор-
нормального вектора направляющий вектор заданной прямой q =
= {/, т, п).
8. Уравнение плоскости, проходящей через данную прямую
х — ж, у — yt г — z,
—j— = = и через заданную не лежащую на
этой прямой точку Мо(Хо, tfo, z0). Искомая плоскость принад-
принадлежит связке плоскостей E.50), т. е. определяется уравнением
А (х — х0) + В (у — уо) + C(z — zo) = 0. Используя условия E.60)
принадлежности данной прямой к искомой плоскости, получим
следующие равенства:
+ B(yl-y0) + C(zl-z0) = 0,
Сп = 0. E'64)
Точка Мо (х0, уо, Но) по условию не лежит на дайной прямой.
Это означает, что нарушается хотя бы одна из пропорций
*. - *о = у. - Уо = г, - г0 ^ и поэтому из системы E.64) два
нз коэффициентов А, В, С можно определить через третий. Вы-
Выбрав затем произвольно этот третий коэффициент (например,
положив его равным единице), мы получим уравнение искомой
плоскости.
9. Уравнение плоскости, проходящей через данную прямую
=и параллельной другой данной прямой
уравнение искомой плоскости. Используя условия E.60) при-
принадлежности данной прямой к искомой плоскости, получим
Axx+Byi + Czi +D = 0, All + Bmi + Cnl = 0. Кроме того,
используя условие E.59) параллельности искомой плоскости и
второй данной прямой, получим А12 + Вт2 + Сп2 = 0. В ре-
результате получим систему трех уравнений
Alt + В/п, + Сп, = 0,
из которой три из коэффициентов А, В, С, D могут быть выраже-
выражены через четвертый (в силу того, что две данные прямые не па-
параллельны и нарушается хотя бы одна из пропорций 1\/12 =
= т\/т? = П1/П2, получим, что хотя бы одни из определителей
*) Предполагается, что две данные прямые не параллельны.

142 ЛИНЕЙНЫЕ ОБРАЗЫ [ГЛ.5
третьего порядка матрицы
1*1 У\ 2, 111
f, m, «i 0
h m2 п2 О Ц
отличен от нуля, и поэтому какие-то три из коэффициентов А,
В, С, D можно выразить через четвертый). Положив указанный
четвертый коэффициент равным единице, мы получим уравне-
уравнение искомой плоскости.
10. Уравнение плоскости, проходящей через заданную пря-
прямую L\ и перпендикулярной заданной плоскости я. Эта задача
сводится к предыдущей. Чтобы убедиться в этом, мы сначала
через точку .Mi прямой L\ проведем прямую L2, перпендикуляр-
перпендикулярную плоскости л (такая задача решена в п. 5), и затем через
прямую L\ проведем плоскость, параллельную прямой L2.
11. Уравнения перпендикуляра, опущенного из заданной
точки Afo на данную прямую L,. Искомый перпендикуляр пред-
представляет собой линию пересечения двух плоскостей: 1) плоско-
плоскости, проходящей через точку Afo и прямую L\ (такая плоскость
найдена в п. 8), 2) плоскости, проходящей через точку Afo и
перпендикулярной к прямой L\ (такая плоскость найдена в
п. 7).
12. Нахождение расстояния от данной точки Мо до данной
прямой Lx. В предыдущем пункте найдены уравнения перпенди-
перпендикуляра Lz, опущенного из точки Afo на прямую L\. Решая сов-
совместно уравнения прямых L\ и Z,2, мы найдем точку Afi осно-
основания указанного перпендикуляра, а затем и искомое расстоя-
расстояние, равное длине отрезка AfoAfi.
13. Нахождение общего перпендикуляра к двум скрещиваю-
скрещивающимся прямым L\ и L2. Проведем через прямую Lx плоскость по.
параллельную прямой L% (эта задача решена в п. 9). После
этого проведем две плоскости п\ и яг, перпендикулярные пло-
плоскости по и проходящие через прямые L\ и L% соответственно
(см. п. 10). Искомый перпендикуляр представляет собой линию
пересечения плоскостей ш и пг.
14. Нахождение кратчайшего расстояния между двумя дан-
данными скрещивающимися прямыми L\ н L2. Для решения этой
задачи достаточно построить плоскость по, указанную в преды-
предыдущем пункте, и найти расстояния от любой точки прямой Ьг
до плоскости яо.

ГЛАВА 6
ЛИНИИ ВТОРОГО ПОРЯДКА
В этой главе изучаются геометрические свойства эллипса,
гиперболы и параболы, представляющих собой линии пересе-
пересечения кругового конуса с плоскостями, не проходящими через
его вершины. Эти линии часто встречаются в различных вопро-
вопросах естествознания. Например, движение материальной точки
под воздействием центрального поля силы тяжести происходит
по одиой из этих линий. В главе также исследуются кривые
второго порядка, т. е. линии, определяемые в декартовых коор-
координатах, алгебраическими уравнениями второй степени. В част-
частности, выясняется, что эллипс, гипербола и парабола являются
такими линиями и что этими тремя линиями и изученными в
предыдущей главе линейными образами исчерпываются все
линии, определяемые алгебраическими уравнениями второй
степени.
§ 1. Канонические уравнения эллипса, гиперболы и параболы
В начале этой главы мы говорили о том, что эллипс, гипер-
гипербола и парабола представляют собой линии пересечения круго-
кругового конуса с плоскостями, не проходящими через его вершину.
Именно, если секущая плоскость пересекает все прямолиней-
прямолинейные образующие одиой полости конуса, то в сечении получится
линия, называемая эллипсом (рис. 6.1,а). Если секущая пло-
плоскость пересекает образующие обеих полостей конуса, то в се-
сечении получится линия, называемая гиперболой (рис. 6.1,6).
И, наконец, если секущая плоскость параллельна одной из об-
образующих конуса (на 6.1, в — это образующая АВ), то в сече-
сечении получится линия, называемая параболой. Рис. 6.1 дает чи-
читателю наглядное представление о форме рассматриваемых
линий.
В этом параграфе даются специальные определения эллип-
эллипса, гиперболы и параболы, основанные на их фокальных свой-
свойствах, и выводятся так называемые канонические уравнения
этих кривых. Ниже, в п. 4 § 3, будет установлена равносиль-

144
ЛИНИИ ВТОРОГО ПОРЯДКА
[ГЛ.6
ность этих специальных определений и определений эллипса,
гиперболы и параболы как конических сечений.
1. Эллипс.
Определение. Эллипсом называется геометрическое ме-
место точек плоскости, для которых сумма расстояний до двух
Эллипс
а)
Гипербола.
6)
Рис. 6.1
Парабола,
е)
фиксированных точек Fi и F2 этой плоскости, называемых фо-
фокусами, есть величина постоянная *).
При этом ие исключается совпадение фокусов эллипса. Оче-
Очевидно, если фокусы совпадают, то эллипс представляет собой
окружность.
Для вывода канонического уравнения эллипса выберем на-
начало О декартовой системы координат в середиие отрезка FiF2,
а оси Ох и Оу направим так, как ука-
указано на рис. 6.2 (если фокусы F\ и F2
совпадают, то О совпадает с F\ и F2,
а за ось Ох можно взять любую ось,
проходящую через О).
Пусть длина отрезка FtF2 равна
2с. Тогда в выбранной системе коор-
координат точки Л и F2 соответственно
имеют координаты (—с, 0) и (с, 0).
Обозначим через 2а постоянную, о которой говорится в опре-
определении эллипса. Очевидно, 2а > 2с, т. е. а > с. Пусть М —
точка плоскости с координатами (х, у) (рис. 6.2). Обозначим
через т\ и г2 расстояния от точки М до точек Fi и Fz соответ-
F,(-C,0) О
F2(c,O)
Рис. 6.2
*) Если М — точка эллипса (см. рис. 6.2), то \MFi\ + \MFt\ = 2а, а так
как сумма двух сторон MFt и MFt треугольника MFiF» больше третьей сто-
стороны FiFt = 2с, то 2а > 2с Случай 2а = 2с естественно исключить, так как
тогда точка М располагается на отрезке FtFt и эллипс вырождается в от-
отрезок.

fcl] КАНОНИЧЕСКИЕ УРАВНЕНИЯ 145
ственно. Согласно определению эллипса равенство
г, + г2 = 2а F.1)
является необходимым и достаточным условием расположения
точки М(х,у) на данном эллипсе.
Используя формулу расстояния между двумя точками (см.
формулу A.8) п. 2, § 3 главы 1), получим
F.2)
Из F.1) и F.2) вытекает, что соотношение
/ / = 2а F.3)
представляет собой необходимое и достаточное условие распо-
расположения точки М с координатами х и у на данном эллипсе.
Поэтому соотношение F.3) можно рассматривать как уравне-
уравнение эллипса. Путем стандартного приема «уничтожения радика-
радикалов» это уравнение приводится к виду
где
Ь2 = а2-с2*). F.5)
Так как уравнение F.4) представляет собой алгебраическое
дледствие уравнения эллипса F.3), то координаты хну любой
точки М эллипса будут удовлетворять и уравнению F.4). По-
Поскольку при алгебраических преобразованиях, связанных с из-
избавлением от радикалов, могли появиться «лишние корни», мы
должны убедиться в том, что любая точка М, координаты ко-
которой удовлетворяют уравнению F.4), располагается на данном
эллипсе. Для этого, очевидно, достаточно доказать, что вели-
величины г\ и гг для каждой точки удовлетворяют соотношению
F.1). Итак, пусть координаты х и у точки М удовлетворяют
уравнению F.4). Подставляя значение у2 из F.4) в правую
часть выражения F.2) для гь после несложных преобразова-
преобразований найдем.что г, = д/(а + •?•*)• Так как а+ •?-* > 0**), то
/"! = а + -?• х. Совершенно аналогично найдем, что г2=а —с- х.
Таким образом, для рассматриваемой точки М
г, = а+ -?-*, г2 = а-±х, F.6)
*) Напомним, что о > с, н поэтому аг — сг > 0.
•*) Поскольку |*| sg а н с/о < 1. Заметим, что неравенство
непосредственно вытекает из уравнения F.4), нз которого ясно, что .
10 Зак. 16S

146 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ. в
т. е. г\ + гг = 2а, и поэтому точка М располагается на эллипсе.
Уравнение F.4) называется каноническим уравнением эллипса.
Величины а и b называются соответственно большой и малой
полуосями эллипса (наименование «большая» и «малая» объ-
объясняется тем, что а > Ь).
Замечание. Если полуоси эллипса а и b равны, то эл-
эллипс представляет собой окружность, радиус которой равен
R = а = Ь, а центр совпадает с началом координат.
2. Гипербола.
Определение. Гиперболой называется геометрическое
место точек плоскости, для которой абсолютная величина раз-
разности расстояний до двух фиксированных точек Fi и Fz этой
плоскости, называемых фокусами, есть величина постоянная*).
Для вывода канонического уравнения гиперболы выберем
начало координат в середине отрезка F\Fz, а оси Ох и Оу на-
направим так, как указано на рис. 6.2. Пусть длина отрезка FiF2
равна 2с. Тогда в выбранной системе координат точки Fi и F2
соответственно имеют координаты (—с, 0) и (с, 0). Обозначим
через 2а постоянную, о которой говорится в определении ги-
гиперболы. Очевидно, 2а < 2с, т. е. а < с **).
Пусть М — точка плоскости с координатами (х, у) (рис. 6.2).
Обозначим через г\ и г2 расстояния MFi и MF2. Согласно опре-
определению гиперболы равенство
|г,-г2| = 2а F.7)
является необходимым и достаточным условием расположения
точки М на данной гиперболе.
Используя выражения F.2) для гх и г2 и соотношение F.7),
получим следующее необходимое и достаточное условие распо-
расположения точки М с координатами х и у на данной гиперболе:
I У (* + cf + у*- У(* - сJ + у* | = 2а. F.8)
Используя стандартный прием «уничтожения радикалов», при-
приведем уравнение F.8) к виду
*) Фокусы Fi и Ft гиперболы естественно считать различными, нбо если
указанная в определении гиперболы постоянная не равна нулю, то нет ни
одной точки плоскости при совпадении Ft и Ft. которая бы удовлетворяла
требованиям определения гиперболы. Если же эта постоянная равна нулю и
Л совпадает с Ft, то любая точка плоскости удовлетворяет требованиям
определения гиперболы.
**) Если М — точка гиперболы, то |AfFi| — \MFt\ — 2а, а так как раз-
разность двух сторон MFi и Мгг треугольника MFiFt меньше третьей стороны
FiFt — 2с, то 2о > 2с. Случай 2о = 2с естественно исключить, так как
тогда точка М располагается иа прямой F%F2 вне отрезка F\F» и гипербола
вырождается в два луча.

§ 1] КАНОНИЧЕСКИЕ УРАВНЕНИЯ 147
где
Мы должны убедиться в том, что уравнение F.9), получен-
полученное путем алгебраических преобразований уравнения F.8), ие
приобрело новых корней. Для этого достаточно доказать, что
для каждой точки М, координаты хну которой удовлетворяют
уравнению F.9), величины гх и г% удовлетворяют соотношению
F.7). Проводя рассуждения, аналогичные тем, которые были
сделаны при выводе формул F.6), найдем для интересующих
нас величин г\ и п следующие выражения *):
•4*ПРИ*>0' f -a + -x при х>0,
— а — ~х при * < О, (^ а~—-х при дс<0.
F.11)
Таким образом, для рассматриваемой точки М имеем \г\—г%\ =
= 2а, и поэтому она располагается на гиперболе.
Уравнение F.9) называется каноническим уравнением ги-
гиперболы. Величины а и Ъ называются соответственно действи-
действительной и мнимой полуосями гиперболы.
3. Парабола.
Определение. П араболой называется геометрическое
место точек плоскости, для которых расстояние до некоторой
фиксированной точки F этой плоскости равно расстоянию до
некоторой фиксированной прямой, также расположенной в рас-
рассматриваемой плоскости.
Указанная в определении точка F называется фокусом па-
параболы, а фиксированная прямая — директрисой**) параболы.
Для вывода канонического уравнения параболы выберем
начало О декартовой системы координат в середине отрезка
FD, представляющего собой перпендикуляр, опущенный из фо-
фокуса F на директрису***), а оси Ох и Оу направим так, как
указано на рис. 6.3. Пусть длина отрезка FD равна р. Тогда
в выбранной системе координат точка F имеет координаты
(р/2,0). Пусть М — точка плоскости с координатами (х,у).
Обозначим через г расстояние от М до F, а через d— расстоя-
*) При этом мы должны учесть, что \х\ ^ а и с/а > 1, Заметим, что
неравенство \х\ ^ а непосредственно вытекает из уравнения F.9).
**) Слово директриса означает направляющая.
***) Естественно считать, что фокус F ие лежит на директрисе, ибо в
противном случае точки плоскости, для которых были бы выполнены условия
определения параболы, располагались иа прямой, проходящей через F пер-
перпендикулярно директрисе, т.е. парабола выродилась бы в прямую.

148 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ 6
ние от М до директрисы (рис. 6.3). Согласно определению па-
параболы равенство
r = d F.12)
является необходимым и достаточным условием расположения
точки М на данной параболе. Так как
у2, d =-§- + **), F.13)
то, согласно F.12), соотношение
-f-1/2 =4+* FЛ4)
представляет собой необходимое и достаточное условие распо-
расположения точки М с координатами х и у на данной параболе.
Поэтому соотношение F.14) можно
рассматривать как уравнение па-
-fM(x,y) раболы. Путем стандартного при-
приема «уничтожения радикалов» это
уравнение приводится к виду
у2 = 2рх. F.15)
р *- Убедимся в том, что уравнение F.15),
F(j>0) & полученное путем алгебраических
преобразований уравнения F.14),
не приобрело новых корней. Для
Рис 6.3 этого достаточно доказать, что для
каждой точки М, координаты хну
которой удовлетворяют уравнению F.15), величины г и d равны
(выполнено соотношение F.12)).
Из соотношения F.15) вытекает, что абсциссы х рассматри-
рассматриваемых точек неотрицательны, т. е. х ^ 0. Для точек с неотри-
неотрицательными абсциссами d = •?- + х. Найдем теперь выражение
для расстояния г от точки М до F. Подставляя у2 из выраже-
выражения F.15) в правую часть выражения для г F.13) и учитывая,
что х ^ 0, найдем, что г = 4- + я.Таким образом, для рассмат-
рассматриваемых точек г = d, т. е. они располагаются иа параболе.
Уравнение F.15) называется каноническим уравнением па-
параболы. Величина р называется параметром параболы.
*) Эта формула верна лишь для точек с неотрицательными абсцисса-
абсциссами х. Для точек с отрицательными абсциссами, как легко видеть, выполняется
соотношение т> й, и поэтому такие точки можно исключить из рассмотрения.

ИССЛЕДОВАНИЕ ФОРМЫ ЭЛЛИПСА, ГИПЕРБОЛЫ И ПАРАБОЛЫ
149
§ 2. Исследование формы эллипса, гиперболы
и параболы по их каноническим уравнениям
Мы уже имеем наглядное представление о форме эллипса,
гиперболы и параболы (рис. 6.1). Исследование канонических
уравнений этих линий позволяет выяснить свойства, более точно
характеризующие их форму.
1. Исследование формы эллипса. Для удобства запишем еще
раз каноническое уравнение эллипса F.4):
1.
F.4)
При этом будем считать а> Ь.
Г. Эллипс имеет две взаимно перпендикулярные оси сим-
симметрии {главные оси эллипса) и центр симметрии (центр эл-
эллипса)*). Действительно, в уравнении F.4) величины х и у
фигурируют в четных степенях. Следовательно, если коорди-
координаты х и у точки М удовлетворяют уравнению F.4) (т. е.
точка М располагается на эллип-
эллипсе), то этому уравнению удовле-
удовлетворяют координаты (—х, у) и
(х, —у) симметричных ей точек
относительно осей координат и
координаты (—х, —у) точки, сим- у&
метричной М относительно на- 'уу/\
чала координат (рис. 6.4). УУ/
Таким образом, если эллипс
задан своим каноническим урав-
нением F.4), то главными осями
этого эллипса являются оси ко-
координат, а центром эллипса —
начало координат. Точки пересечения эллипса с главными ося-
осями называются вершинами эллипса. Точки А, В, С, D на
рис. 6.4 — вершины эллипса. Очевидно, эти вершины имеют со-
соответственно координаты (—а,0), @,6), (а,0), @,—Ь).
Замечание 1. Очевидно, длины отрезков, образованных
пересечением эллипса с главными осями, равны 2а и 26. Так
как 2а > 26, то главная ось, образующая в пересечении с эл-
эллипсом отрезок 2а, называется большой осью эллипса. Другая
главная ось иазывается малой осью эллипса.
Если эллипс задан уравнением F.4), то при а> b большой
осью будет ось Ох, а малой — ось Оу. При Ь> а большой
осью будет ось Оу, а малой — Ох.
Рнс. 6.4
*) Если эллипс представляет собой окружность, то любая прямая, прохо-
проходящая через центр окружности, является осью симметрии. Отметим, что цен-
центром эллипса является точка пересечения главных осей.

150
ЛИНИИ ВТОРОГО ПОРЯДКА
[ГЛ. 6
Замечание 2. Очевидно, фокусы эллипса располагаются
на его большой оси.
2°. Весь эллипс содержится внутри прямоугольника \х\^ а,
\у\^*Ь (на рис. 6.4 этот прямоугольник не заштрихован).
В самом деле, из канонического уравнения F.4) вытекает, что
х2/а2 ^ 1 и у2/Ь2^1. Эти неравен-
неравенства, очевидно, эквивалентны неравен-
неравенствам |*|^ а и |у|^6.
3°. Эллипс может быть получен
посредством равномерного сжатия
окружности. Рассмотрим окружность
(рис. 6.5), заданную уравнением
7+^=1. F.16)
Произведем теперь равномерное
сжатие плоскости к оси Ох, т. е. та-
такое преобразование, при котором точ-
точка с координатами (х, у) перейдет в
точку с координатами (х,у), причем
х = х, а у — — у. Очевидно, при этом преобразовании окруж-
окружность _(_6.16) перейдет в кривую, определяемую уравнением
, т. е. в эллипс.
2. Исследование формы гиперболы. Обратимся к канониче-
каноническому уравнению гиперболы F.9)
Рис. 6.5
У* _ 1
—г?— 1.
Г. Гипербола имеет две оси симметрии (главные оси гипер-
гиперболы) и центр симметрии (центр гиперболы). При этом одна
из этих осей пересекается с гиперболой в двух точках, которые
называются вершинами гиперболы. Эта ось называется действи-
действительной осью гиперболы.
Другая ось ие имеет общих точек с гиперболой и поэтому
называется мнимой осью гиперболы.
Таким образом, мнимая ось гиперболы разделяет плоскость
иа правую и левую полуплоскости, в которых расположены
симметричные относительно этой оси правая и левая ветви ги-
гиперболы.
Справедливость указанного свойства симметрии гиперболы
вытекает из того, что в уравнении F.9) величины х и у фигу-
фигурируют в четных степенях. Следовательно, если координаты х
и у точки М удовлетворяют уравнению F.9) (т. е. точка М
располагается на гиперболе), то этому уравнению удовлетво-
удовлетворяют координаты (—х,у) и (х,—у) симметричных ей точек

S2]
ИССЛЕДОВАНИЕ ФОРМЫ ЭЛЛИПСА, ГИПЕРВОЛЫ И ПАРАБОЛЫ
151
У
Рис. 6 6
относительно осей координат и координаты (—х, —у) точки,
симметричной М относительно начала координат (рис. 6.6).
Таким образом, если гипербола задана своим каноническим
уравнением F.9), то главными осями этой гиперболы являются
оси координат, а центром гиперболы — начало координат.
Убедимся теперь, что ось Ох является действительной осью
гиперболы, точки А(—а,0) и В(а,0)— вершинами гиперболы
и ось Оу является мнимой
осью гиперболы. Для этого до-
достаточно доказать, что ось Ох
пересекает гиперболу в точ-
точках Л и В, а ось Оу не имеет
общих точек с гиперболой.
Так как ординаты точек оси
Ох равны нулю, то для выяс-
выяснения величины абсцисс то-
точек пересечения этой оси с ги-
гиперболой нужно в уравнении
F.9) положить у = 0. После
этого мы получим уравнение
х2/а2 = I, из которого нахо-
находятся абсциссы точек пересе-
пересечения оси Ох с гиперболой. Полученное уравнение имеет
решения х = —а и х = а. Следовательно, ось Ох пересекает
гиперболу (т. е. является ее действительной осью) в точках
А(—а, 0) и В(а,0) (т. е. эти точки и есть вершины гиперболы).
Поскольку абсциссы точек оси Оу равны нулю, то для ординат
точек пересечения этой оси с гиперболой получаем из F.9)
уравнение —у2/Ь2 = 1, которое не имеет действительных реше-
решений. Следовательно, ось Оу является мнимой осью гиперболы.
Замечание. Фокусы гиперболы располагаются на ее дей-
действительной оси.
2°. Рассмотрим область G, которая получена объединением
прямоугольника D, координаты хну точек которого удовлетво-
удовлетворяют неравенствам |*|<а, |у|<6, и тех двух углов, образо-
образованных диагоналями этого прямоугольника, в которых распола-
располагается мнимая ось гиперболы (на рис. 6.6 эта область заштри-
заштрихована). Убедимся, что в области G нет точек гиперболы.
Разобьем область G иа две части G\ и О2, где G\ представ-
представляет собой полосу, абсциссы х точек которой удовлетворяют
неравенству |*|< a, a d — остальная часть области G*). Оче-
Очевидно, в полосе Gi нет точек гиперболы, так как абсциссы х
*) Область О] представляет собой, очевидно, полосу, заключенную между
безгранично продолженными вертикальными сторонами прямоугольника ?>.
Область <?2 состоит из четырех частей, каждая из которых располагается
в одном из координатных углов.

152 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ 6
точек, расположенных на гиперболе, удовлетворяют неравенству
\x\^sa*). Обратимся теперь к точкам области G2. Заметим,
что каждая точка Gz либо лежит на диагонали прямоугольника
D, либо за его диагональю**). Поскольку диагонали D опре-
ь ъ
деляются уравнениями у = —* и у = — —х, то координаты х
и у точек Gt в силу их расположения удовлетворяют неравен-
неравенству b/а ^\у\/\х\ ***). Из этого неравенства вытекает нера-
неравенство |*|/а г?1 \у\/Ь, из которого в свою очередь следуют не-
равенства —j-—р-^0<1, а так как для точек гиперболы
х2 и2
—j |j-= 1, то в области Gi нет точек гиперболы.
3°. Установим важное свойство гиперболы, связанное с ее
расположением относительно диагоналей прямоугольника D, о
котором говорилось выше.
В общих чертах это свойство заключается в том, что ветви
гиперболы приближаются к диагоналям прямоугольника D.
В силу симметрии гиперболы это свойство достаточно выяс-
выяснить для части гиперболы, расположенной в первой четверти.
Координаты х и у точек гиперболы, расположенных в первой
четверти, удовлетворяют условиям х ^ а, у ^ 0 ****). Обра-
Обращаясь к уравнению F.9), мы видим, что при указанных условиях
это уравнение эквивалентно соотношению
Иными словами, рассматриваемая часть гиперболы представ-
представляет собой график функции F.17)*****). Легко убедиться, что
эта функция может быть представлена в следующей форме:
У = -х- ^ Д -. F.18)
а х + V*2 — а2
Обратимся теперь к диагонали прямоугольника D, располо-
расположенной в первой четверти. Она определяется уравнением
Y = \x. F.19)
X2 V2
*) Из канонического уравнения гиперболы вытекает, что —у = 1 + -|j-,
т.е. хг1аг ^ 1. Последнее неравенство эквивалентно неравенству |*| ^ а
**) Будем говорить, что точка М плоскости лежит за диагональю пря-
прямоугольника D, если перпендикуляр, опущенный из М на ось Ох, пересекает
эту диагональ
***) Абсциссы х точек G2 не равны нулю
, В силу свойства 2° гиперболы F 9) абсциссы ее точек удовлетво-
удовлетворяют условию \х\ ^ а Для точек первой четверти это условие может быть
записано в виде х ^ а
*****) По поводу понятия график функции см выпуск 1, главу 1, § 2, п. 4.

ИССЛЕДОВАНИЕ ФОРМЫ ЭЛЛИПСА. ГИПЕРБОЛЫ И ПАРАБОЛЫ
153
Сравним величины ординат У к у рассматриваемой диагонали
и части гиперболы для одного и того же значения х, т. е. рас-
рассмотрим разность У — у (рис. 6.7,а). Используя соотношения
F.18) и F.19), получим
ь F.20)
У-у =
х + V*2 -«
Из соотношения F.20) следует, что при лг~>-оо разность У — у
стремится к нулю. Абсолютная величина \У — у\ равна длине
отрезка MN (рис. 6.7,а). Так как расстояние МР от точки М
гиперболы до рассматриваемой диагонали не превышает длины
Рис. 6.7
отрезка MN, то при удалении точки М гиперболы в бесконеч-
бесконечность (г. е. при ж->-оо) расстояние МР стремится к нулю. Сле-
Следовательно, рассматриваемая часть ветви гиперболы прибли-
приближается к соответствующей диагонали прямоугольника D. В силу
симметрии аналогичным свойством обладают и другие части
гиперболы, расположенные во второй, третьей и четвертой чет-
четвертях.
Диагонали прямоугольника D обычно называются асимпто-
асимптотами гиперболы. Отметим, что асимптоты гиперболы опреде-
определяются уравнениями
у = ±х и у = - — х. F.21)
4°. Наряду с гиперболой F.9) рассматривают так называе-
называемую сопряженную по отношению к ней гиперболу. Сопряжен-
Сопряженная гипербола определяется каноническим уравнением
F.22)
точно
*) Чтобы убедиться, что уравнение F.22) определяет гиперболу, доста-
ю положить х = у, у — х и умножить обе части этого уравнения на — 1.

154
ЛИНИИ ВТОРОГО ПОРЯДКА
[ГЛ. 6
На рис. 6.7, б изображены гипербола F.9) и сопряженная ей
гипербола F.22). Очевидно, что сопряженная гипербола имеет
те же асимптоты, что и данная. Иными словами, асимптоты со-
сопряженной гиперболы определяются уравнениями F.21). Заме-
Заметим, что гипербола F.9) в свою очередь является сопряженной
по отношению к гиперболе F.22).
3. Исследование формы параболы. Обратимся к канониче-
каноническому уравнению параболы F.15):
уг = 2рх. F.15)
1°. Парабола имеет ось симметрии (ось параболы). Точка
пересечения параболы с осью называется вершиной параболы.
Действительно, в уравнении F.15) ве-
fM(x,y) личина у фигурирует в четной степени.
Следовательно, если координаты хну
точки М удовлетворяют уравнению F.15)
(т. е. точка М располагается на парабо-
параболе), то этому уравнению удовлетворяют
координаты (х, —у) симметричной ей
точки относительно оси Ох (рис. 6.8).
Таким образом, если парабола задана
своим каноническим уравнением F.15),
то осью этой параболы является ось Ох.
Очевидно, вершиной параболы является
начало координат.
2°. Вся парабола расположена в пра~
вой полуплоскости плоскости Оху. В са-
самом деле, так как р>0, то уравнению F.15) удовлетворяют
координаты точек лишь с неотрицательными абсциссами. Та-
Такие точки располагаются в правой полуплоскости.
3°. Из рассуждений п. 3 § 1 этой главы вытекает, что ди-
директриса параболы, определяемой каноническим уравнением
F.15), имеет уравнение
у = — /7/2. F.23)
4°. Любые две параболы подобны друг другу. Пусть у2 =
— 2рх и у2 = 2р*х — канонические уравнения этих парабол
в декартовой системе Оху, y = kx — уравнение произвольной
прямой, проходящей через О, а (х, у) и (х*,у*)—координаты
точек пересечения этой прямой с параболами. Используя кано-
канонические уравнения, получим х = 2p/k2, у — ±2p/k, х* = 2p*/k2,
у* = ±2p*/k. Из последних формул вытекает, что -р- =р/р*,
-Уг = р1рт.Но эти равенства означают подобие рассматриваемых
парабол относительно точки О.
Рнс. 6.8

§3] ДИРЕКТРИСЫ ЭЛЛИПСА, ГИПЕРБОЛЫ И ПАРАБОЛЫ 155
5°. Отметим, что кривая у2 = 2рх при р < 0 также является
параболой, которая целиком располагается в левой полупло-
полуплоскости плоскости Оху. Чтобы убедиться в этом, достаточно за-
заменить х на —х и —р на р,
§ 3. Директрисы эллипса, гиперболы и параболы
Определение параболы, данное в п. 3 § 1 этой главы, бази-
базировалось на свойстве этой кривой, которое связано с ее фоку-
сом и директрисой. Это свойство можно сформулировать также
и следующим образом: парабола есть геометрическое место то-
точек плоскости, для которых отношение расстояния до фокуса
к расстоянию до отвечающей этому фокусу директрисы есть
величина постоянная, равная единице.
Оказывается, отличный от окружности эллипс и гипербола
обладают аналогичным свойством: для каждого фокуса*) эл-
эллипса или гиперболы можно указать такую прямую, называе-
называемую директрисой, что отношение расстояния от точек этих
кривых до фокуса к расстоянию до отвечающей этому фокусу
директрисы есть величина постоянная.
Данный параграф посвящен выяснению этого свойства эл-
эллипса и гиперболы.
1. Эксцентриситет эллипса и гиперболы. Обратимся к эллип-
эллипсу (гиперболе). Пусть с — половина расстояния между фоку-
фокусами эллипса**) ^гиперболы), а — большая полуось эллипса
(действительная полуось гиперболы).
Определение. Эксцентриситетом эллипса (гиперболы)
называется величина е, равная с/а:
е = с/а. F.24)
Замечание 1. Учитывая связь величины с с длинами а
и Ь большой и малой полуосей эллипса (с длинами действи-
действительной и мнимой полуосей гиперболы) (см. формулы F.5) и
F.10)), легко получить следующие выражения для эксцентри-
эксцентриситета е:
для эллипса е=д/1 —-г, F.25)
для гиперболы е= л/\ +-jr • F.250
Из формул F.25) и F.25') вытекает, что эксцентриситет эл-
липса меньше единицы, а эксцентриситет гиперболы больше
единицы***).
*) Напомним, что отличный от окружности эллипс и гипербола имеют
по два фокуса.
**) Если эллипс представляет собой окружность, то с = 0.
**•) Напомним, что величина Ь как для эллипса, так и для гиперболы
не равна нулю,

156
ЛИНИИ ВТОРОГО ПОРЯДКА
[ГЛ б
Отметим, что эксцентриситет окружности равен нулю (для
окружности Ь = а).
Замечание 2. Два эллипса (две гиперболы), имеющих
одинаковый эксцентриситет, подобны В самом деле, из фор-
формулы F.25) для эксцентриситета эллипса (из формулы F.25')
для эксцентриситета гиперболы) вытекает, что эллипсы с оди-
одинаковым эксцентриситетом имеют одинаковое отношение Ь/а
малой и большой полуосей (гипербо-
е=д лы с одинаковым эксцентриситетом
имеют одинаковое отношение Ь/а мни-
мнимой и действительной полуосей). Та-
Такие эллипсы (гиперболы) подобны*).
Замечание 3. Эксцентриситет
эллипса можно рассматривать как
меру его «вытянутости»: чем больше
эксцентриситет е (см. формулу F.25)),
тем меньше отношение Ь/а малой по-
полуоси эллипса Ъ к его большой полу-
полуоси а. На рис. 6.9 изображены эллип-
эллипсы с разными эксцентриситетами, но
с одинаковой большой полуосью а.
Замечание 4. Эксцентриситет
гиперболы можно рассматривать как
числовую характеристику величины раствора угла между ее
асимптотами. В самом деле, отношение Ь/а равно тангенсу
половины угла между асимптота-
асимптотами гиперболы.
2. Директрисы эллипса и ги-
гиперболы.
Г. Директрисы эллипса. Мы
выяснили, что любой, отличный
от окружности эллипс имеет
большую и малую оси и центр —
точку пересечения этих осей (см.
Рнс. 6.10 п. 1 § 2 этой главы). Обозначим
через с половину расстояния
между фокусами F\ и F% эллипса, через а его большую полу-
полуось и через О его центр (рис. 6.10).
Пусть е — эксцентриситет этого эллипса (так как эллипс от-
отличен от окружности, то е ф 0) и я — плоскость, в которой рас-
расположен эллипс. Малая ось эллипса разбивает эту плоскость
Рнс. 6.9
*) Чтобы убедиться в этом, достаточно расположить эти эллипсы (соот-
(соответственно гиперболы) так, чтобы их центры и одноименные главные оси
совпадали Тогда из канонических уравнений легко следует подобие кривых
с равными отношениями Ь(а.

§3] ДИРЕКТРИСЫ ЭЛЛИПСА, ГИПЕРБОЛЫ И ПАРАБОЛЫ 157
на две полуплоскости. Обозначим через щ (i — 1, 2) ту из этих
полуплоскостей, в которой лежит фокус Ft (i = 1, 2).
Определение. Директрисой Di (» = 1, 2) эллипса, отве-
отвечающей фокусу F, (i = 1,2), называется прямая, расположен-
расположенная в полуплоскости Я| (i = 1, 2) перпендикулярно большой оси
эллипса на расстоянии а/е от его центра.
Замечание 1. Выберем начало декартовой прямоугольной
системы координат в середине отрезка F1F2, а оси Ох и Оу на-
направим так, как указано на рис. 6.10. Тогда, очевидно, уравне-
уравнения директрис Di (i = 1, 2) эллипса можно записать следую-
следующим образом:
уравнение директрисы ?>,: х = — а/е,
уравнение директрисы D2: х — а/е.
Замечание 2. Директрисы эллипса расположены вне эл-
эллипса. Действительно, эллипс расположен в прямоугольнике
|лг|^а, |(/|^& (см. п. 1 § 2 этой главы и рис. 6.4), стороны
которого перпендикулярны большой и малой осям эллипса.
Из определения директрис вытекает, что они параллельны
двум перпендикулярным большой оси эллипса сторонам этого
прямоугольника. Поскольку упомянутые стороны отстоят от
центра эллипса на расстоянии а, а директрисы — на расстоянии
а/е > а @<е<1), то директрисы расположены вне пря-
прямоугольника, а следовательно, и вне эллипса.
Замечание 3. Мы только что выяснили, что директрисы
расположены вне эллипса. Отсюда вытекает, что точки эллипса
и его центр расположены по одну сторону от каждой из его
директрис.
Замечание 4. Обозначим через р расстояние от фокуса
эллипса до соответствующей этому фокусу директрисы. По-
Поскольку расстояние от центра эллипса до директрисы равно
а/е, а расстояние от центра эллипса до фокуса равно с, то р
равно — — с *). Так как с = ае, то для р получаем следующее
выражение:
(J)a.±=^-. F.27)
Докажем теорему, выясняющую важное свойство отличного
от окружности эллипса и его директрис.
Теорема 6.1. Отношение расстояния ri от точки М эллипса
до фокуса Fi к расстоянию dt от этой точки до отвечающей
*) Напомним, что центр эллипса и его фокусы расположены на большой
оси, которая перпендикулярна директрисам Поэтому с учетом расположения
центра, фокуса и отвечающей ему директрисы (рис. 6.10) р равно а/е — с.

158
ЛИНИИ ВТОРОГО ПОРЯДКА
[ГЛ 6
этому фокусу директрисы Di равно эксцентриситету е этого эл-
эллипса.
Доказательство. Пусть F\ и Р2—фокусы эллипса*).
Выберем декартову прямоугольную систему координат так, как
это указано в замечании 1 этого пункта (рис. 6.10). В п. 1 § 1
этой главы мы выяснили, что при таком выборе системы коор-
координат расстояния Г\ и н от точки М(х, у) эллипса до фокусов
F\ и F2 определяются формулами F.6). Так как отношение с/а
равно эксцентриситету е этого эллипса, то для г\ и г2 мы полу-
получим выражения
тх = а + ex, r2 = a — ex. F.28)
Найдем теперь расстояния di от точки М эллипса до директрис
Dt. Используя уравнения директрис Di (см. формулы F.26)),
легко убедиться в том, что нормированные уравнения дирек-
директрис имеют вид (см. п. 7 § 1 главы 5):
нормированное уравнение директрисы Dx: —х — т===0,
нормированное уравнение директрисы D2: x — — — §.
Так как точка М(х, у) эллипса и начало координат находятся
по одну сторону от каждой из директрис (см. замечание 3 этого
пункта), то расстояние di и d2 от точки М(х,у) до директрис
Di и D2 равны соответствующим от-
отклонениям М(х,у) от D\ и D2, взя-
взятым со знаком минус, и мы полу-
получим (в силу F.29) и теоремы 5.1):
ex
а — ех
F.30)
Используя формулы F.28) и F.30),
найдем, что
e, t = l, 2.
Теорема доказана.
Рис 6 и 2°. Директрисы гиперболы. Обо-
Обозначим через с половину расстоя-
расстояния между фокусами F\ и F2 гиперболы, через а ее дей-
действительную полуось и через О ее центр (рис. 6.11). Пусть
е — эксцентриситет этой гиперболы и я — плоскость, в которой
расположена гипербола. Мнимая ось гиперболы разбивает эту
плоскость на две полуплоскости. Обозначим через щ (i = 1, 2)
ту из этих полуплоскостей, в которой лежит фокус Fi (i = 1, 2).
*) Так как эллипс отличен от окружности, то его фокусы ие совпадают.

§3] ДИРЕКТРИСЫ ЭЛЛИПСА. ГИПЕРБОЛЫ И ПАРАБОЛЫ 159
Определение. Директрисой Di (i=l, 2) гиперболы, от-
отвечающей фокусу Ft (» = 1, 2), называется прямая, располо-
расположенная в полуплоскости щ (i = 1, 2) перпендикулярно действи-
действительной оси гиперболы на расстоянии а/е от ее центра.
Замечание 5. Выберем' начало декартовой прямоуголь-
прямоугольной системы координат в середине отрезка FiF2, а оси Ох и Оу
направим так, как указано на рис. 6.11. Тогда, очевидно, урав-
уравнения директрис Di (/ = 1, 2) гиперболы можно записать сле-
следующим образом:
уравнение директрисы Д: х— — а/е,
_ . F.о1)
уравнение директрисы D2' х — а/е.
Замечание 6. Директрисы гиперболы целиком располо-
расположены в области G, не содержащей точек гиперболы (см. 2° п. 2
§ 2 этой главы и рис. 6.6). В самом деле, в 2° п. 2 § 2 этой
главы мы убедились, что полоса Gb определяемая в выбранной
в замечании 5 системе координат Оху неравенством |дс|<а,
содержится в области G. Но эта полоса содержит директрисы
гиперболы, так как, согласно F.31), для точек директрис
\x\ = -j <а, ибо для гиперболы е > 1. Расположение дирек-
директрис гиперболы указано на рис. 6.11.
Замечание 7. Только что сделанное замечание позволяет
обосновать расположение директрис гиперболы, указанное на
рис. 6.11. Именно, очевидно, что точки левой (правой) ветви
гиперболы и ее центр О расположены по разные стороны от
директрисы D\ (Дг)> а точки правой (левой) ветви гиперболы
и ее центр О расположены по одну сторону от директрисы
Dx (Dt).
Замечание 8. Обозначим через р расстояние от фокуса
гиперболы до соответствующей этому фокусу директрисы. По-
Поскольку расстояние от центра гиперболы до директрисы равно
а/е, а расстояние от центра гиперболы до фокуса равно с, то
р — с—- *). Так как с = ае, то для р получаем формулу
п?=±.. F.32)
Докажем теорему, выясняющую важное свойство гиперболы и
ее директрис.
Теорема 6.2. Отношение расстояния п от точки М гиперболы
до фокуса Fi к расстоянию di от этой точки до отвечающей
*) Напомним, что центр гиперболы и ее фокусы расположены на дей-
действительной оси, которая перпендикулярна директрисам. Поэтому с учетом
расположения центра, фокуса н отвечающей ему директрисы (см. рис. 6.11)
р равно с .

160 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ б
этому фокусу директрисы Di равно эксцентриситету е этой ги-
гиперболы.
Доказательство. Для доказательства этой теоремы нуж-
нужно рассмотреть следующие четыре случая: 1) точка М находит-
находится на левой ветви гиперболы, исследуется фокус F\ и дирек-
директриса D\\ 2) точка М находится на правой ветви гиперболы, ис-
исследуется фокус F\ и директриса D\\ 3) точка М на левой ветви,
фокус F2, директриса D2; 4) точка М на правой ветви, фокус F2,
директриса D2. Так как рассуждения для каждого из случаев
однотипны, то мы ограничимся лишь первым случаем.
Расположим систему координат так, как это указано в за-
замечании 5 этого пункта. Так как абсцисса х любой точки
М(*• У) левой ветви гиперболы отрицательна, то расстояние Г\
от этой точки до фокуса F\, согласно формулам F.11), равно
— а — •?- х. Так как с/а = е, то для г\ получим выражение
г,= a —ex. F.33)
Директриса D\ определяется первым из уравнений F.31). Со-
Согласно п. 7 § 1 главы 5 нормированное уравнение этой дирек-
директрисы имеет вид
-х-± = 0. F.34)
Так как точка М левой ветви гиперболы и начало координат
находятся по разные стороны от директрисы D\ (см. замеча-
замечание 7 этого пункта), то расстояние d\ от точки М до директри-
директрисы D\ равно отклонению М от D\, и мы получим (в силу F.34)
и теоремы 5.1)
dt=-a-ex . F.35)
Используя формулы F.33) и F.35), найдем, что r\/di = e.
Для первого случая теорема доказана. Остальные случаи рас-
рассматриваются аналогично.
3. Определение эллипса и гиперболы, основанное на их свой-
свойстве по отношению к директрисам. Теоремы 6.1 и 6.2, доказан-
доказанные в предыдущем пункте, выясняют свойство отличного от
окружности эллипса и гиперболы, связанное с директрисами
этих кривых. Убедимся в том, что это свойство эллипса и ги-
гиперболы может быть принято в качестве их определения. Рас-
Рассмотрим в плоскости я точку F и прямую D (рис. 6.12). Будем
предполагать, что точка F не лежит на прямой D. Докажем
следующее утверждение.
Теорема 6.3. Геометрическое место {М} точек М плоскости
п, для которых отношение е расстояния г до точки F к расстоя-
расстоянию d до прямой D есть величина постоянная, представляет со~
бой эллипс (при е ¦< 1) или гиперболу (при е > 1).

S3]
ДИРЕКТРИСЫ ЭЛЛИПСА. ГИПЕРБОЛЫ И ПАРАБОЛЫ
161
При этом точка F называется фокусом, а прямая D —
директрисой рассматриваемого геометрического места.
Доказательство. Убедимся, что в некоторой, специаль-
специально выбранной системе координат геометрическое место точек,
удовлетворяющее требованиям сформулированной теоремы,
определяется при е < 1 уравнением -^- + -j^ = 1 (т. е. является
Хг и2
эллипсом), а при е>1—уравнением—;—-|j-=l (т. е. яв-
является гиперболой) *). Пусть R — точка пересечения прямой D
и прямой А, проходящей через F перпендикулярно D (рис. 6.12).
На прямой А выберем положительное
направление от F к R при е <. 1 и
от R к F при е> 1 (на рис. 6.12 по-
показан случай е<1). Так как даль-
дальнейшие рассуждения для случая е>1
и «<1 идентичны, мы проведем их
подробно для е < 1, т. е. для случая,
определяющего эллипс. Обозначим че-
через р расстояние между точками F
и R. Вспоминая расположение дирек-
директрисы эллипса относительно его цен-
центра (см. п. 2 этого параграфа), есте-
естественно выбрать начало О координат
на прямой А слева от точки R на расстоянии а/е. При задан-
заданных е и р величина а/е может быть определена при помощи
формулы F.27) (см. также замечание 4 п. 2 этого параграфа).
Иными словами, естественно положить
F.36)
Будем теперь считать прямую А с выбранным началом О
и направлением от F к R1 осью абсцисс. Ось ординат направим
так, как указано на рис. 6.12. В выбранной системе координат
фокус F имеет координаты (с, 0), где
У
0
А
М(х,у) d
X р
F(c,O)
а
е **
D
R х
Рис. 6.12
С — Р х_ег ).
а директриса D определяется уравнением
F.37)
F.38)
*) Эти уравнения, как было выяснено в § 1 этой главы, являются урав-
уравнениями эллипса и гиперболы.
**) Формула F.37) вытекает из формулы с = RO—RF и формул RF «• р
ПЗак. 168

F2 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ 6
Перейдем теперь к выводу уравнения рассматриваемого гео-
геометрического места точек. Пусть М — точка плоскости с коор-
координатами (х, у) (рис. 6.12). Обозначим через г расстояние от
точки М до фокуса F и через d расстояние от точки М до ди-
директрисы D. Соотношение
r/d = e F.39)
является необходимым и достаточным условием расположения
точки М на геометрическом месте {М}.
Используя формулу расстояния между двумя точками М и
F (см. формулу A.8) п. 2 § 3 главы 1) и формулу для расстоя-
расстояния от точки М до прямой D (см. п. 7 § 1 главы 5), получим
F.40)
d = ±-x*). F.41)
Из F.39), F.40) и F.41) вытекает, что соотношение
F.42)
представляет собой необходимое и достаточное условие распо-
расположения точки М с координатами х и у на геометрическом ме-
месте {М}. Поэтому соотношение F.42) является уравнением гео-
геометрического места {М}. Путем стандартного приема «уничто-
«уничтожения радикалов», а также используя формулы F.36) и F.37),
это уравнение легко привести к виду
?+•?-1. <6-43)
где б2 = а2 — с2.
Для завершения доказательства иам нужно убедиться в том,
что в процессе преобразования уравнения F.42) в уравнение
F.43) ие появились «лишние корни».
Рассуждая, как и в п. 1 § 1 этой главы, мы убедимся в том,
что расстояние г от точки М, координаты х и у которой удов-
удовлетворяют уравнению F.43), до точки F(c, 0), может быть вы-
вычислено по формуле г = а — ^х. Используя соотношение F.37)
и формулу а = 1 ^е2 , получим для г следующее выражение:
г = а — ех. F.44)
Так как точка М, координаты хну которой удовлетворяют
F.43), расположена слева от прямой D (для таких точек
*) Формула F.41) верна лишь для точек М(х, у), расположенных слева
от прямой D. Однако точки, расположенные справа от прямой D, равно как
и точки прямой D, можно исключить из рассмотрения, так как для этих то-
чек r/d ^s 1, а мы рассматриваем точки, для которых r/d = е < 1.

S3]
ДИРЕКТРИСЫ ЭЛЛИПСА. ГИПЕРБОЛЫ И ПАРАБОЛЫ
163
х ^ а, а для точек прямой D: х = а/е, где е < 1), то для рас-
расстояния d от М до D справедлива формула F.41). Отсюда и
из формулы F.44) вытекает, что для рассматриваемых точек М
выполняется соотношение r/d = е, т. е. уравнение F.43) яв-
является уравнением геометрического места {М}. Аналогично
рассматривается случай е > 1.
Замечание. Используя доказанную теорему и определе-
определение параболы, мы можем сформулировать следующее определе-
определение отличного от окружности эллипса, гиперболы и параболы.
Определение. Геометрическое место {М} точек М плоскости
я, для которых отношение е расстояния г до точки F этой пло-
плоскости к расстоянию d до прямой D, расположенной в плоско-
сти я, есть величина постоянная, представляет собой либо эл-
эллипс (при О < е < 1), либо параболу (при е = I), либо гипер-
гиперболу (при е>\). Точка F называется фокусом, прямая
D — директрисой, а е — экс-
эксцентриситетом геометриче-
геометрического места {М}.
4. Эллипс, гипербола и парабола как
конические сечения. В начале этой гла-
главы указывалось, что эллипс, гипербола
и парабола представляют собой линии
пересечения кругового конуса с плоско-
плоскостями, не проходящими через его верши-
вершину. В этом пункте мы докажем теорему,
обосновывающую справедливость этого
утверждения.
Теорема 6.4. Пусть L — кривая,
являющаяся эллипсом *), гиперболой или
параболой. Можно указать такой круго-
круговой конус К и такую плоскость п, что
линия пересечения плоскости я с кону-
конусом К представляет собой кривую L.
Прежде чем перейти к доказатель-
доказательству этой теоремы, сделаем следующее
замечание.
Замечание. Пусть L* — лнння
пересечения конуса К с некоторой пло-
плоскостью л*, не проходящей через верши-
вершину конуса, a L — лнння, подобная L*.
Найдется плоскость л, линией пересече-
пересечения которой с К будет ляння L.
Существование такой плоскости оче-
очевидно, ибо параллельные плоскости пе-
пересекают конус К по подобным линиям, коэффициент подобия которых равен
отношению расстояннй от вершнны конуса до этнх плоскостей.
Доказательство теоремы 6.4. Очевидно, лнння пересечения конуса К
с плоскостью, перпендикулярной его осн и не проходящей через его вершнну,
представляет собой окружность, т. е. эллипс, эксцентриситет е которого равен
нулю.
Рассмотрим плоскость л*, не перпендикулярную оси АВ конуса К и не
проходящую через его вершину О (рис. 6.13). Пусть L* — линия пересечения
*) При этой эллипс может представлять собой окружность.

164 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ 6
этой плоскости и конуса Впишем в конус сферу S, касающуюся плоскости я*
в точке F. Пусть *> — плоскость окружности R, по которой сфера S касается
конуса К, и D — прямая, по которой пересекаются плоскости я* и *> Убе-
Убедимся, что L* удовлетворяет требованиям определения, сформулированного
в предыдущем пункте, т е является либо отличным от окружности эллипсом,
либо параболой, либо гиперболой В процессе рассуждений выясним, что
в зависимости от наклона плоскости л* и от величины угла, который со-
составляют образующие конуса с его осью, кривая L* может иметь любой
положительный эксцентриситет е Этим, очевидно, н будет завершено доказа-
доказательство теоремы, тек как любые две кривые второго порядка *) с одинако-
одинаковым эксцентриситетом подобны (см. пп. 3 и 4 § 2 этой главы и замечание 2
п 1 § 3 этой главы), а согласно сделанному перед доказательством теоремы
замечанию, любая кривая L, подобная линии L* пересечения конуса К с пло-
плоскостью я*, также представляет собой линию пересечения этого конуса с не-
некоторой плоскостью я
Пусть М— произвольная точка кривой L*, МР — перпендикуляр из этой
точки на плоскость ш, MQ — перпендикуляр из М на прямую D, MF — от-
отрезок, соединяющий точки М и F, MN — отрезок образующей конуса (эта
образующая проходит через точку М, а N — точка пересечения с окруж-
окружностью R) Так как MF и MN — касательные к сфере S нз одной точки М,
то \MF\ = \MN\.
Обозначим через Р угол, который составляет образующая конуса К с его
осью, а через а — угол между плоскостями л* и ш. Очевидно, значения Р
заключены в пределах 0 < р < л/2, а значения а — в пределах 0 < а г?
г? я/2 •¦)
Из рассмотрения треугольников MPN и MPQ, а также из равенства
\MN\ = \MF\ вытекает, что
|MF\ = \MP I/cosp, |AfQ|=|A*P|/sina
Таким образом, для любой точки М кривой L* справедливо равенство
| MF |/| MQ | = sin a/cos P
Поскольку для заданного конуса К и Фиксированной плоскости я* отношение
sin a/cos р не зависит от точки М, то для кривой L* выполнены условия оп-
определения предыдущего пункта, т е эта кривая L* является либо отличным
от окружности эллипсом, либо гиперболой, либо параболой При этом эксцен-
эксцентриситет в кривой L* может быть вычислен по формуле
в = sin a/cos p. F.45)
Докажем, что путем иыбора углов аир можно получить для е любое
положительное значение Выберем, во первых, р так, чтобы величина в cos P
была меньше 1 Такой выбор р возможен, так как р — любое число из интер-
интервала @, л/2) Остается выбрать а так, чтобы выполнялось равенство sin a =
=ecosp (эта формула представляет собой записанную иначе формулу F.45)).
Очевидно, достаточно положить a = arcsin (e cos P) Теорема доказана.
5. Полярные уравнения эллипса, гиперболы и параболы. Об-
Обратимся сначала к окружности радиуса R. Если полюс поляр-
полярной системы поместить в центр окружности, а полярную ось—
произвольно в плоскости окружности, то, очевидно, искомое по-
полярное уравнение будет иметь вид
р=/?. F.46)
То есть эллипс, гипербола или парабола
а ф О, так как плоскость я* ие перпендикулярна оси конуса.

ДИРЕКТРИСЫ ЭЛЛИПСА. ГИПЕРБОЛЫ И ПАРАБОЛЫ
165
Рассмотрим теперь кривую L, представляющую собой отлич-
отличный от окружности эллипс или параболу. Пусть F—фокус кри-
кривой L, D — отвечающая этому фокусу директриса, р— расстоя-
расстояние от F до D и е— эксцентриситет L. Пусть полюс полярной
системы координат совпадает с F, а полярная ось перпендику-
перпендикулярна D и направлена так, как указано
на рис. 6.14. Пусть М — любая точка L.
Согласно определению L (см. п. 3 этого
параграфа)
Так как |FM| = p, a \MP\ = \PN +
+ NM\ — p + pcosq>*), то из F.47) на-
находим следующее выражение для р:
ре
F.48)
к 1 — е cos ф '
Соотношение F.48), представляет со-
собой полярное уравнение отличного от Рис е 14
окружности эллипса или параболы.
Обратимся теперь к гиперболе. Пусть F — один из ее фоку-
фокусов, D — отвечающая этому фокусу директриса, р — расстояние
от F до D, е — эксцентриситет гиперболы. Пусть Wi — ветвь ги-
гиперболы, отвечающая фокусу F,
а №г — другая ветвь гиперболы
(на рис. 6.15 F — правый фокус
гиперболы и W\ — правая ее
ветвь).
Рассуждая, как и в случае
эллипса или параболы, легко
убедиться, что полярное уравне-
уравнение ветви W\ гиперболы имеет
вид F.48). Для ветви №2 поляр- .-,, „
ное уравнение имеет иной вид. '
Заметим, во-первых, что для то-
чек М ветви W2 справедливо соотношение F.47). Выражения
для I^Af | и \МР\ имеют следующий вид:
|FAf| = p, \MP\ = \MN — PN\ = — pcos<p — />**). F.49)
Используя формулы F.49), найдем из F.47) следующее по-
полярное уравнение ветви №2:
г 1 + е cos ф
*) Эта формула верна и в случае, когда А1 находится левее FN, ибо в
этом случае cos ф < 0.
**) Так как для ветви W% угол ф тупой, то cos ф < 0, и поэтому
MN = —р cos ф.

166 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ. 6
Таким образом, полярное уравнение гиперболы имеет вид
для ветви №»•
1 +
Замечанне. Знаменатель в правой части соотношений F.48) и F.50)
ие обращается в нуль. В случае эллипса, когда 0 < е < 1, это очевидно. Для
параболы е = 1, но <р изменяется на интервале @,2л), и поэтому |ecosq>| <
< 1. В случае гиперболы легко убедиться, что для ветви Wi угол <р изме-
изменяется иа интервале Г arccos —, 2я — arccos —J, н поэтому произведение
ecosqp либо ааключено между нулем и единицей, либо отрицательно. Для
ветви Wa угол <р изменяется иа ( агссоз Г J, 2я—arccos Г JJ.
Для этих значений <р выражение е cos <p отрицательно, но больше 1 по аб-
абсолютной величине.
§ 4. Касательные к эллипсу, гиперболе и параболе
1. Уравнения касательных к эллипсу, гиперболе и параболе. Убедимся,
что каждая из кривых L, являющаяся эллипсом, гиперболой или параболой,
представляет собой объединение графиков двух функций. Рассмотрим, на-
например, каноническое уравнение эллипса F.4). Из этого уравнения следует,
что часть эллипса, точки которой имеют неотрицательные ординаты у, есть
график функции
Iх
у=*Ь /\J\--p при — а^х^а, F.51)
а часть эллипса, точки которой имеют неположительные ординаты, есть гра-
график функции
л/1 —^j-
при — а < х < о. F.52)
Обращаясь к каноническому уравнению гиперболы F.9), найдем, что
гипербола представляет собой объединение графиков функций
-X ПРИ *><» и *<-а, F.53)
а из канонического уравнения параболы F.15) вытекает, что эта кривая
есть объединение графиков функций
и y = — <i/2px при х>0. F.54)
Рассмотрим теперь вопрос о касательных к эллипсу, гиперболе н пара-
параболе. Естественно, что касательные к этим кривым будут также касательными
к графикам функций F.51)—F.54). Вопрос о касательных к графикам функ-
функций подробно рассмотрен в выпуске I настоящего курса (см. выпуск I, гла-
главу б, § I, п. 4). Найдем, например, уравнение касательной к эллипсу в его
точке М(х, у), считая при этом уфЬ (пусть ради определенности у>0).
Пусть X, У —текущие координаты точки касательной. Так как ее угловой

5 41 КАСАТЕЛЬНЫЕ К ЭЛЛИПСУ, ГИПЕРБОЛЕ И ПАРАБОЛЕ 167
коэффициент ?=</', где у' =* . — производная функции
а*
F.51), вычисленная в точке х, то уравнение касательной имеет вид*)
Y-y *_ ^ (X - х). F.55)
Учитывая, что точка М(х, у) лежит на эллипсе (т.е. ее координаты х и у
удовлетворяют уравнениям F.51) н F.4)), получим после несложных пре-
преобразований уравнение касательной к эллипсу в следующей форме:
2?+If=l. F.56)
Рассуждая аналогично для случая гиперболы и параболы, получим следую-
следующие уравнения касательных к этим кривым:
, X х Yy , ._ __.
для гиперболы —j р- = 1, F.57)
для, параболы Yy = р (X + дс). F.58)
Замечание 1. В предыдущих рассуждениях был исключен случай
у = 0. В соответствующих точках эллипса, гиперболы и параболы касатель-
касательные вертикальны. Легко убедиться, что
уравнения F.56)—F.58) справедливы и в
этом случае.
Замечание 2. Отметим, что каса-
касательная к эллипсу имеет с иим только одну
общую точку — точку касания. Аналогич-
Аналогичным свойством обладают касательные к ги-
гиперболе и параболе.
2. Оптические свойства эллипса, гипербо-
гиперболы и параболы. Установим следующее оп-
оптическое свойство эллнпса: лучи света, ис-
исходящие из одного фокуса F\ эллипса, р g .«
после зеркального отражения от эллипса "
проходят через второй фокус F2 (рис. 6.16).
Геометрически указанное свойство означает, что отрезки MFt и AfFj образуют
с касательной в точке М эллипса равные углы.
Допустим, что эллипс не обладает указанным свойством, т. е. а^а,
(рис. 6.16). Пусть F" — зеркальное отражение фокуса F{ относительно каса-
касательной К в точке М. Соединим F*x с М н F%. Так как а, Ф av то точка
М* пересечения прямой F*F2 с касательной К не совпадает с точкой М.
Поэтому
\'\ \'\\f\ \-2a F.59)
(о — длина большой полуоси эллнпса). Будем теперь перемещать точку М*
по касательной К от точки М. При таком перемещении сумма \FiM*\ + \F2M*\
неограниченно увеличивается. В начальный момент перемещения эта сумма,
согласно F.59), была меньше 2а. Поэтому в некоторый момент эта сумма
будет равна 2а, а это означает, что на касательной л, кроме точки М, будет
еще одна точка М* эллипса, отличная от М. Согласно замечанию 2 предыду-
*) См. главу 5, уравнение E.10).

168
ЛИНИИ ВТОРОГО ПОРЯДКА
[ГЛ 6
щего пункта этого не может быть Таким образом, указанное выше свойство
эллипса действительно справедливо
Совершенно аналогично устанавливаются следующие оптические свойства
гиперболы и параболы
1°. Лучи сеета, исходящие из одного фокуса Ft гиперболы, после зеркаль-
зеркального отражения от гиперболы кажутся исходящими из другого ее фокуса Рг
(рис. 6.17)
2°. Лучи света, исходящие из фокуса параболы, после зеркального отра-
отражения от параболы образуют пучок, параллельный оси параболы (рис. 6.18)
Замечание 1. Оптические
свойства эллипса, гиперболы и пара-
параболы широко используются в инже
нерном деле В частности, оптическое
свойство параболы используется при
конструировании прожекторов, антенн
и телескопов
Рис. 6.17
Рис. 6.18
Замечание 2. Назовем фронтом волны точечного источника света F
линию, для всех точек Q которой путь, проделанный световым лучом, при-
пришедшим из источника F в точку Q, одинаков Если волна, вышедшая нз
точечного источника F, не претерпевает отражений, то фронт ее, очевидно,
будет представлять собой окружность Если же указанная волна отражается
от некоторой кривой L, то форма ее фронта меняется в зависимости от вида
кривой L Парабола обладает следующим замечательным свойством фронт Ф
отраженной от параболы волны при условии расположения источника света
в фокусе F параболы представляет собой прямую, параллельную директри-
директрисе D этой параболы (рис 6 18)
В самом деле, рассмотрим прямую Ф, параллельную директрисе D Пусть
Q — произвольная точка этой прямой Из оптического свойства параболы вы-
вытекает, что если FM — падающий луч, приходящий после отражения в точ-
точку Q, то отраженный луч MQ перпендикулярен директрисе D Обозначим
через Р точку пересечения луча MQ с директрисой D Очевидно, сумма
\QM\ + \MF\ равна \QM\ + \МР\ •) Так как \QM\ + \МР\ = d, где d —
не зависящее от точки Q расстояние между прямыми Ф н D, то для любой
точки Q линии Ф сумма [QAf| + \MF\ одна и та же (равна d), т.е. Ф —
фронт отраженной волны
§ 5. Кривые второго порядка
Обращаясь к каноническим уравнениям эллипса, гиперболы
и параболы (см уравнения F.4), F 9) и F 15) этой главы),
мы видим, что перечисленные кривые представляют собой ал-
алгебраические линии второго порядка (см главу 4, § 1, п. 5).
*) Согласно определению параболы (см. п. 3 § 1 этой главы).

9 5] ХРИВЫЕ ВТОРОГО ПОРЯДКА 169
Естественно поставить вопрос о том, какие еще линии являются
алгебраическими линиями второго порядка. Этот вопрос и рас-
рассматривается в настоящем параграфе.
Рассмотрим общее алгебраическое уравнение второго по-
порядка
а„дс2 + 2а12ху + аюу2 + 2а13х + 2а^у + Язэ = 0. F.60)
Линия L, определяемая этим уравнением (т. е. алгебраиче-
алгебраическая линия второго порядка), рассматриваемая как геометри-
геометрический объект*), не меняется, если от данной декартовой пря-
прямоугольной системы координат перейти к другой декартовой си-
системе координат.
Отметим, что исходное уравнение F.60) и уравнение, полу-
полученное после преобразования координат, алгебраически эквива-
эквивалентны (см п. 5 § 1 главы 4). Можно ожидать, что при спе-
специальном выборе декартовой системы координат уравнение
F.60) примет настолько простой вид, что геометрическая ха-
характеристика линии L не будет представлять затруднений.
Этим методом мы воспользуемся для выяснения всех типов
линий второго порядка В процессе рассуждений мы укажем
правила, с помощью которых выбирается система координат, в
которой уравнение линии L выглядит наиболее просто. Мы
сформулируем также признаки, позволяющие узнать тип линии
второго порядка по ее исходному уравнению.
1. Преобразование коэффициентов уравнения линии второго
порядка при переходе к новой декартовой системе координат.
Так как переход от одной декартовой прямоугольной системы
координат на плоскости к другой декартовой прямоугольной си-
системе координат может быть осуществлен путем некоторого па-
параллельного переноса системы координат и последующего по-
поворота (включая в поворот и зеркальное отражение (см. § 1
главы 3)), мы рассмотрим отдельно вопрос о преобразовании
коэффициентов уравнения F.60) при параллельном переносе
и при повороте. При этом, конечно, будем считать, что в урав-
уравнении F.60) по крайней мере один из коэффициентов ац, а и
или Д22 отличен от нуля.
Условимся о следующей терминологии: группу слагаемых
а\\хг-{-2ai2xy + аюу' левой части F.60) будем называть груп-
группой старших членов этого уравнения, а группу слагаемых
2fli3JC + 2а2з«/+ Дзз будем называть линейной частью уравнения
F.60). При этом коэффициенты ац, ац, а2г будем называть
*) Может оказаться, что уравнение F.60) не определяет линнн этому
уравнению могут удовлетворять координаты лишь одной точки или не нан-
дется нн одной точки, координаты которой удовлетворяют F.60) Однако н
в этом случае мы будем говорить о геометрических объектах, определяемых
уравнением F.60), называя эти объекты вырожденными или мнимыми По-
Подробнее об этих вопросах см. в главе 4.

170 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ. в
коэффициентами группы старших членов, а коэффициенты аи,
«2з и Дзз — коэффициентами линейной части F.60). Коэффи-
Коэффициент а3з обычно называется свободным членом уравнения
F.60).
1°. Преобразование коэффициентов при параллельном пере-
переносе. Пусть декартова прямоугольная система координат О'х'у'
получена параллельным переносом системы Оху вдоль вектора
00'. Как известно, старые и новые координаты точки связаны
соотношениями
' 0, F.61)
где дсо, Уо — координаты начала О' в системе Оху (см. главу 3,
§ 1, формулы C.12)). Подставляя выражения F.61) для х и у
в левую часть F.60), мы получим уравнение L в системе О'х'у'.
Очевидно, это уравнение имеет вид
а
п
где
х'2 + 2а18хУ + аи«/'2 + 2а'13х' + 2</ + «зз = °. F-62)
«13 = «11*0+ «12%+ «13-
«23 = «12*0 + «22% + «23' F-63)
«33 = «11*0 + 2а12*о1/о + «22%* + 2«13*0 + 2«23% + «33-
Обращаясь к уравнению F.62), мы можем сделать следую-
следующий важный вывод: при параллельном переносе системы ко-
ординат коэффициенты группы старших членов не изменяются,
а коэффициенты группы линейных членов преобразуются по
формулам F.63).
Замечание 1. Используя первую и вторую из формул
F.63), можно, очевидно, выражению для а'зз придать следую-
следующий вид:
<з = («13 + «1з) *о + («23 + «2з) У* + «зз- F-64)
2°. Преобразование коэффициентов при повороте. Пусть де-
декартова прямоугольная система координат Охгу/ получена по-
поворотом системы Оху на угол <р (при этом ие исключается по-
поворот на угол ф, равный нулю). Как известно, старые и новые
координаты точки связаны соотношениями
* = jic'cos<p — #'sin<p, y — xf sin<p+«/'cos<p F.65)
(см. главу 3, § 1, формулы C.13)). Подставляя выражения
F.65) для х и у в левую часть F.60) и группируя коэффи-
коэффициенты при различных степенях х' и у', мы получим уравнение

§ SJ КРИВЫЕ ВТОРОГО ПОРЯДКА 171
L в системе Ох'у*. Очевидно, это уравнение имеет вид
а'^х'2 + 2a'12xY + c?/2 + 2a[jf + 2a'^f + a^— 0, F.66)
где')
a'n = a12 sin 2Ф +1 (an - аю) cos 2Ф + 4 (ou + аи).
<2 = — -i- («u - «22) sin 2Ф + fli2cos 2Ф.
«22 «12sin 2Ф - T («ii - «и) cos 2Ф + T (an + аи). F-67)
Мы можем сделать следующий важный вывод:
При повороте системы координат коэффициенты а'и, а'и, а^
группы старших членов уравнения F.66) выражаются лишь че-
через угол ф поворота и через коэффициенты аи, аи, агг группы
старших членов уравнения F.60); коэффициенты а'13 и а'^ урав-
уравнения F.60) выражаются лишь черев угол ф и коэффициенты
an и д2з уравнения F.60); свободный член не изменяется (т. е.
Замечание 2. Обозначим через А, В к С соответственно
величины
а у(ц
Введем, далее, угол а, считая cos a = -jp-, sin a = ^
при А ф 0 и a = 0 при A = 0, и угол р, считая cos (J — агз/С,
sin p = au/C при С =й= 0 и р = 0 при С = 0 **). Тогда, очевид-
очевидно, выражения F.67) для коэффициентов а'и можно переписать
*) При выводе этих формул использовались равенства 2 sin <p cos <p =
, , 1 — cos 2ш , 1 + cos 2ф
= sin 2ф, sin2 Ф = g——, cos» ф = j—*-.
**) Известно, что, каковы бы нн были величины Р и Q, удовлетворяющие
условию Р* + Q3?= 0, можно найти такой угол Y. что cos у = д . и
sin Y ^

172 ЛИНИИ ВТОРОГО ПОРЯДКА
в следующей форме:
а'п = A sin Bф + а) + В,
а\г = A cos Bф + а),
[ГЛ 6
F.68)
Отметим, что величины А, В и С и углы а и р не зависят от q>.
2. Инварианты уравнения линии второго порядка. Понятие
типа линии второго порядка. Назовем инвариантом уравнения
F.60) линии второго порядка относительно преобразований де-
декартовой системы координат такую функцию f(au, an азз)
от коэффициентов ац этого уравнения, значения которой не ме-
меняются прн переходе к новой декартовой прямоугольной си-
системе координат. Таким образом, если f(au, 012. .... азз) —
инвариант н artj — коэффициенты уравнения линии второго по-
порядка в новой системе декартовых координат, то
f(fln. ai2 азз) = ^(аи. a'i2 ai>)-
Докажем следующую теорему.
Теорема 6.5. Величины
= a
а,г
«IX
/з==
«II «|> «13
«и "и а2з
°IS "j3 O33
F.69)
являются инвариантами уравнения F.60) линии второго по-
порядка относительно преобразований декартовой системы коор-
координат.
Доказательство. Очевидно, инвариантность величин 1и
h, h достаточно доказать отдельно для параллельного переноса
системы координат и для поворота.
Рассмотрим сначала параллельный перенос системы коор-
координат. Мы установили в 1° предыдущего пункта, что при этом
преобразовании координат коэффнцненты группы старших чле-
членов не изменяются. Поэтому не изменяются и величины 1\ н /2.
Займемся величиной h- В новой системе координат OWy' ве-
величина /з равна
" '12
«12
/
°13
«22
г
«23
«23
°33

КРИВЫЕ ВТОРОГО ПОРЯДКА
173
Вычитая из последней строки этого определителя первую стро-
строку, умноженную на х0, н вторую, умноженную на у0 (*о н у0—
координаты нового начала СУ), и используя прн этом выраже-
выражения для а\3 и а'23 нз формул F.63) и выражение F.64) для а'33,
найдем, что этот определитель равен *)
«11 «12
2 2
3
3
- о23уо + «зз
Если теперь вычесть из последнего столбца полученного опреде-
определителя первый столбец, умноженный на хо, и второй, умножен-
умноженный на уо, и использовать при этом выражения для а'13 и а'гг нз
формул F.63), то в результате получится определитель, стоя-
стоящий в правой части выражения для h в формулах F.69). Итак,
инвариантность /3 при параллельном переносе системы коорди-
координат доказана.
Рассмотрим теперь поворот декартовой системы координат.
В 2° предыдущего пункта мы нашли, что прн этом преобразо-
преобразовании коэффициенты а'ц уравнения линии L в новой системе
связаны с коэффициентами ац уравнения этой линии в старой
системе с помощью формул F.68) (см. замечание 2 предыду-
предыдущего пункта). Докажем теперь инвариантность Л, h и /3.
Имеем, согласно F.68),
1\ = а'п + а'п = 25 = а„ + а22,
П = «и<4 ~ < = В*-А* = апа„ - а?2.
Таким образом, инвариантность 1\ и h доказана. Обратимся
теперь к
1
1
2
3
г
«12
г
«22
«13
«13
«4
«33
Разлагая этот определитель по элементам последнего столбца,
учитывая только что доказанную инвариантность /2> т. е. ра-
равенство
1
f
2
«22
1
«12
2
«22
¦) Напомним, что при указанных преобразованиях значение определителя
ие меняется (см. Дополнение к главе 1).

174
и равенство
лучим
ЛИНИИ ВТОРОГО ПОРЯДКА
[гл е
'з = <
(см. последнюю из формул F.67)), по-
+ азз12. F.70)
0,2 а,
22
«13 а23
«12
«13 «23
Согласно формулам F.68) первое слагаемое в правой части
F.70) может быть преобразовано следующим образом:
*13
»13 «23
— С sin
— С Sin
(ф + р)
- A sin Bq> + а) + В
Ccos(q>+P)
= С2 sin (ф + Р) {Л cos (ф + а - 0) - В sin (Ф + р)}. F.71)
Совершенно аналогично получается равенство
*23
г
«И
г
«13
/
«12
г
3
Из соотношений F.70) —F.72) получаем
1'3 = AC2 sin BР — а) — ВС2 + а^г
F.72)
F.73)
Так как величины А, В, С, углы а, {5 и /а не зависят от угла <р
(это вытекает из инвариантности h н замечания 2 предыдущего
пункта), то из F.73) следует, что 1'ъ также не зависит от угла
Ф, т. е. при любом значеннн ф имеет одно н то же значение.
Но а'ц = ац, при ф = 0, и поэтому /д = /3. Таким образом, ин-
инвариантность /3 также установлена. Теорема доказана.
Геометрические характеристики линий второго порядка и их
расположение вполне определяются значениями инвариантов 1\,
h и /з- В зависимости от знака инварианта 1% эти линии раз-
разделяют на следующие три типа:
эллиптический тип, если I* > 0,
гиперболический тип, если 1г < 0,
параболический тип, если h = 0.
Очевидно, тип линии не меняется при изменении декартовой си-
системы координат. Ниже мы дадим полную классификацию ка-
каждого из указанных типов линий.
3. Центр линии второго порядка. В предыдущем пункте мы
установили, что при параллельном переносе декартовой систе-
системы изменяются лишь коэффициенты группы линейных членов
уравнения линии второго порядка.
Попытаемся найти такую декартову систему координат
O'tfyf (полученную параллельным переносом системы Оху), в
которой уравнение F.62) данной линии L второго порядка не
содержало бы слагаемых 2а'13х/ н 2а'&у', т. е. коэффициенты

5 S] КРИВЫЕ ВТОРОГО ПОРЯДКА 17S
ai3 и ам былн бы Равиы нулю. Пусть х0 и уй — координаты
начала О' искомой системы. Обращаясь к формулам F.63),
найдем, что величины х<>, уо представляют собой решение сле-
следующей системы линейных уравнений:
а23 = 0. F.74)
Уравнения F.74) называются уравнениями центра линии вто-
второго порядка, а точка О' с координатами (х0, у0), где х0 а у0 —
решения системы F.74), называется центром этой линии.
Поясним смысл наименования «центр» линии. Пусть начало
координат перенесено в центр О'. Тогда уравнение линии L
примет вид
а^2 + 2акгх'у' + апу'2 + а^ = 0. F.75)
Пусть точка М(х/,у/) расположена на L. Это означает, что ее
координаты х' и у' удовлетворяют уравнению F.75). Очевидно,
точка М*(—Xе,—у'), симметричная с М относительно О', также
расположена на L, ибо ее координаты также удовлетворяют
уравнению F.75). Таким образом, если у линии L существует
центр (У, то относительно центра точки L располагаются сим-
симметрично парами, т. е. центр линии L является ее центром
симметрии.
Замечание 3. Если линия L второго порядка имеет центр,
то инварианты !2, /з и свободный член а^ в уравнении F.75)
связаны соотношением
/з = /2азз- F-76)
В самом деле, в силу инвариантности /3 получим в системе
координат О'х'у?
«п а„ О
/3= «12 О22 О
О 0 а'х
Из последней формулы и вытекает соотношение F.76).
Наличие центра у линии второго порядка связано с разре-
разрешимостью уравнений центра F.74). Если уравнения центра
имеют единственное решение, то линию L второго порядка бу-
будем называть центральной*). Так как определитель систе-
системы F.74) равен 12, а необходимым и достаточным условием
существования единственного решения этой системы является
неравенство нулю ее определителя, то мы можем сделать сле-
следующий важный вывод: линии эллиптического типа (fa > 0) и
гиперболического типа G2 < 0) и только эти линии являются
центральными.
*) Таким образом, центральная линия имеет единственный центр.

176 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ в
Замечание 4. Если начало координат перенесено в центр
О' центральной линии L второго порядка, то уравнение этой
линии будет иметь вид
апх'2 + 2а12хУ + а^2 + ? = 0. F.77)
Действительно, после переноса начала в центр уравнение линии
примет вид F.75). Так как для центральной линии /гт^О, то
из формулы F.76) найдем, что агзз = 1з/12- Подставляя это вы-
выражение для йде в формулу F.75), мы получим уравнение
F.77).
4. Стандартное упрощение любого уравнения линии второго
порядка путем поворота осей. Докажем, что любое уравнение
F.60) линии L второго порядка путем специального поворота
координатной системы может быть приведено к уравнению, в
котором не будет содержаться слагаемое 2arnx't/, т. е. ко-
коэффициент а'2 будет равен нулю. Такое упрощение уравнения
второго порядка мы будем называть стандартным.
Естественно, мы будем предполагать, что в исходном урав-
уравнении F.60) коэффициент an не равен нулю, ибо в случае
ai2 = 0 поставленный вопрос является решенным.
Пусть ф — угол поворота искомой повернутой системы ко-
ордннат. Обращаясь ко второй из формул F.67), найдем, что
искомый угол ф является решением следующего тригонометри-
тригонометрического уравнения:
— у (аи — а») sin 2ф + Щг cos 2ф = 0. F.78)
в котором, по предположению, ацфО. При этом предположе-
предположении очевидно, что F.78) имеет следующее решение:
ctg 2ф = (а„ - аъI2а1г. F.79)
Итак, если мы повернем систему координат на угол <р, опреде-
определенный нз равенства F.79), то в повернутой системе координат
уравнение линии L не будет содержать слагаемого 2а[3хгу/ и,
кроме того, согласно формулам F.67), азз—азз- Иными слова-
словами, это уравнение будет иметь следующий внд:
а'пх'2 + а'^'2 + 2а'13х' + 2а'^у' + ам = 0. F.80)
5. Упрощение уравнения центральной линии второго порядка
(lt =ф 0). Классификация центральных линий. Выводы, сделан-
сделанные в предыдущих двух пунктах, позволяют решить вопрос о
классификации всех центральных линий второго порядка. Ре-

$ 61 ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ^ПРОСТРАНСТВЕ 177
шенне этого вопроса мы проведем по следующей схеме. Во-пер-
Во-первых, путем переноса начала координат в центр линии F.60) мы
приведем ее уравнение к виду F.77). После этого произведем
стандартное упрощение уравнения F.77):
1) если ai2=0, то оставим систему координат О'х'у' неиз-
неизменной и изменим лишь обозначение х' на х", у1 на у", ац
на а",;
2) если ацфО, то перейдем к повернутой системе коорди-
координат О'х"у", вычисляя угол поворота <р по формуле F.79) и нс-
пользуя при этом формулы F.67) (с заменой a'lf на а";) н фор-
формулу F.80). В обоих указанных случаях найдем, что уравнение
любой центральной линии L в системе координат О'х"у"
имеет вид
а>+<«,"'+ ?=<>. F.81)
Дальнейшая классификация линий основывается на анали-
анализе уравнения F.81). При этом используется связь коэффициен-
коэффициентов а"х и а^ с инвариантами /i и /2.
Рассмотрим отдельно лнннн эллиптического типа н линии
гиперболического типа.
1°. Линии эллиптического типа (/2>0). Обратимся к ис-
исходному уравнению F.60) линии L эллиптического типа. Так
как /2 = a, fix — аг12 > 0, то апа22>0, т. е. коэффициенты ац н
с22 оба отличны от нуля н имеют одинаковый знак, совпадаю-
совпадающий со знаком /ь поскольку /i = an + 022. Без ущерба для
общности можно считать оба эти коэффициента положитель-
положительными (этого всегда можно добиться нормировкой исходного
уравнения F.60), т. е. умножением его на —1 (при такой нор-
нормировке знак инварианта 1\ станет положительным, знак ин-
инварианта /2 не меняется).
Справедливо следующее утверждение.
Теорема 6.6. Пусть уравнение F.60) линии L эллиптического
типа (/г > 0) нормировано так, что /j > 0. Тогда при /3 < 0
это уравнение представляет собой эллипс. При /3 = 0 уравне-
уравнению F.60) удовлетворяют координаты лишь одной точки. При
h > 0 уравнению F.60) не удовлетворяют координаты никакой
точки плоскости.
Прн /3 — 0 уравнение F.60) называется уравнением выро-
вырожденного эллипса. При /з > 0 F.60) называется уравнением
мнимого эллипса.
Доказательство. Так как для уравнения F.81) It =
= а"у -f a?, а /2 = а^а'^, то из условия /i > 0 и h > 0 вы-
вытекает положительность а"х и а?. Поэтому уравнение F.81)
12 3ак. 168

178 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ. 6
линии L может быть записано следующим образом:
„р„/з<о my*, fay-1' {6-82)
прн /3 = 0
прн/3>0 ^L_ + gL-,=-l. F.84)
Очевидно, уравнение F.82), отвечающее случаю /3 < 0, пред-
представляет^ собой каноническое уравнение эллипса с полуосями
и л/т^г. Уравнению F.83), отвечающему случаю
V V22
/3 = 0, удовлетворяют координаты лишь одной точки х" = 0,
у" — 0. Уравнению F.84) не удовлетворяют координаты ника-
никакой точки плоскости, ибо левая часть этого уравнения не от-
отрицательна, а правая отрицательна. Для завершения доказа-
доказательства теоремы достаточно заметить, что каждое из уравне-
уравнений F.82), F.83), F.84) эквивалентно исходному уравнению
F.60) соответственно для случаев /з < 0, /3 = 0, /3 "> 0, и по-
поэтому сделанные выше геометрические выводы для уравнений
F.82), F.83) и F.84) справедливы и для уравнения F.60).
Теорема доказана.
Замечание 5. Остановимся подробнее на случае, когда
уравнение F.60) эллиптического типа определяет эллипс. При
этом мы будем считать, что это уравнение нормировано так,
что Л > 0. Координаты (хо, уа) центра этого эллипса представ-
представляют собой решение системы F.74). Так как новая ось О'х"
является одной нз главных осей эллипса (это вытекает нз того,
что в системе O'xf'y" уравнение эллипса имеет канонический
внд, и поэтому оси координат О'х" и О'у" совпадают с глав-
главными осями эллипса (см. п. 1 § 2 этой главы)), то угол наклона
Ф этой оси со старой осью Ох может быть найден по формуле
F.79). Наконец, нз уравнения F.82) вытекает, что полуоси эл-
лнпса равны л /~ ,? и •* / ~ >/ , причем коэффициенты
V Vn V Va
фф
V V
аи н а22 выражаются через коэффициенты пц исходного урав-
уравнения F.60) (см. первую и третью формулы F.67); при этом
нужно положить Оц sbs а\х ио^ = а^).

S 5J ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ 179
Итак, зная инварианты н формулы преобразования коорди-
координат, можно вычислить полуоси эллипса и выяснить его распо-
расположение относительно исходной системы координат Оху.
2°. Линии гиперболического типа (/г < 0), Справедливо
следующее утверждение.
Теорема 6.7. Уравнение F.60) линии L гиперболического
типа при 1з?*0 представляет собой гиперболу, а при /з = 0 —
пару пересекающихся прямых.
Доказательство. Так как для уравнения F.81) /2 =
= а"ха'^, то из условия /2 < 0 вытекает, что а^ и а'? имеют
разные знаки. Для определенности будем считать а'[{ > 0,
а < 0 (случай а," < 0, а* > 0 рассматривается аналогично).
Тогда уравнение F.81) может быть записано следующим об-
образом:
при /3<0
при /3 = 0 *"* -— f =0, F.86)
при /3>0 ?—г-.2 --? , У , ч2 =1. F.87)
Г ~ I I —ml*— i
\ V ^2°11 / \ V ^(~"а22) /
Очевидно, уравнение F.85), отвечающее случаю /3 < 0, пред-
представляет собой каноническое уравнение гиперболы, для кото-
которой ось Оу является действительной осью, а ось Ох — мнимой
осью, причем мнимая и действительная полуоси этой гнперболы
соответственно равны л I *„¦ н ,»/ / 3 „. . Уравнение
V 2°11 V 2\—а22/
F.87), отвечающее случаю /з > 0, также представляет собой
каноническое уравнение гиперболы, для которой ось Ох яв-
является действительной осью, а ось Оу — мнимой осью, причем
мнимая и действительная полуоси этой гиперболы соответствен-
соответственно равны
Уравнение F.86), отвечающее случаю /з = 0, можно запи-
записать в виде

180 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ. 6
Этому последнему уравнению удовлетворяют лишь координаты
точек, расположенных на прямых
Для завершения доказательства теоремы достаточно заметить,
что каждое нз уравнений F.85) — F.87) эквивалентно исход-
исходному уравнению F.60) соответственно для случаев /3 < 0,
/з = 0, /з > 0, и поэтому сделанные выше геометрические вы-
выводы для уравнений F.85) — F.87) справедливы и для уравне-
уравнения F.60). Теорема доказана.
Замечание 6. Остановимся подробнее на случае, когда
уравнение F.60) гиперболического типа определяет гиперболу,
т. е. когда 1$фЬ.
Координаты (хо, уо) центра этой гиперболы представляют
собой решение системы F.74). Угол наклона <р осн О*' (яв-
(являющейся либо действительной, либо мнимой осью гиперболы)
со старой осью Ох может быть найден по формуле F.79). На-
Наконец, в процессе доказательства теоремы были указаны вели-
величины действительной и мнимой полуосей гиперболы. Их значе-
значения вычисляются через /2, /3, а"х и а%г. Коэффициенты а"х и а&
выражаются через коэффициенты ац исходного уравнения
F.60) (см. первую и третью формулы F.67); прн этом нужно
положить а"{ = а'и и а'^^а'^). Уравнения асимптот гиперболы
без труда могут быть найдены по ее каноническим уравнениям
F.85) или F.87).
Итак, зная инварианты н формулы преобразования коорди-
координат, можно вычислить действительную и мнимую полуоси ги-
гиперболы и выяснить ее расположение относительно исходной
системы координат Оху.
6. Упрощение уравнения линии параболического типа (/2=0).
Классификация линий параболического типа. Заметим, во-пер-
во-первых, что для уравнения F.60) параболического типа инвариант
1\ отличен от нуля. В самом деле, если Л = ац + а2г = 0, то
2 2
'? = аи + аи + 2апа22 = 0> т- е. аиа^==—~Т--Т- Так как
/2 = ацая~ 0,2 = 0, то, используя только что полученное выра-
2 2
женне для апап, найдем что ?• jf-==ai2> откуда следует,
что аи = 022 = ai2 = 0. Но, по предположению, по крайней
мере один из коэффициентов аи, агг, аи отличен от нуля. Итак,
/ФО.
Произведем стандартное упрощение уравнения F.60):
1) если аи = 0, то оставим систему координат Оху неизменной

§ 51 ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ 181
и изменим лишь обозначение х на х", у на у', ещ на a'lf, 2) если
«12 Ф 0, то перейдем к повернутой системе координат Ох'у',
вычисляя угол поворота по формуле F.79) н используя при
этом формулы F.67). В обоих указанных случаях уравнение
F.60) примет вид F.80). Так как для уравнения F.80) 1Х =
= а'и + а'^, 12 = а'иа'2, то из условия 1\фЬ, /2 = 0 вытекает, что
один нз коэффициентов а'п и а'2г равен нулю, а другой не равен
нулю.
Для определенности будем считать а'п=0, а'^ФО (случай
а'п ф 0, а22 = 0 рассматривается аналогично). При этом пред-
предположении /, = а'п, так как I ^ = &\\Л-а'?? Итак, уравнение ли-
линии F.60) параболического типа после стандартного упроще-
упрощения может быть записано в следующей форме*):
hy/2 + 2a'13xf + 2a'i3y' + ai3 = Q. F.88)
Дальнейшее упрощение уравнения F.88) может быть достиг-
достигнуто путем специального параллельного переноса системы ко-
координат Ох'у'. Предварительно перепншем F.88) в следующей
форме:
( 4J + 2<3*' + «и—?-°- F-89)
Вид уравнения F.89) подсказывает, как выбрать специальный
параллельный перенос системы координат Oxfy1. Нам нужно,
( , <4V
чтобы первое слагаемое /t \\f + -j—J в левой части F.89)
имело вид 1\у\ а остальные слагаемые сохранили свой внд.
Поэтому следует положить у" равным у'+ —« а х" Равным х'.
Итак, перейдем теперь к новой системе координат, полученной
путем следующего параллельного переноса:
/
им
F.90)
Введем обозначения
/*
иг п °23
' I
В силу соотношений F.89), F.90) и F.91) уравнение линии L
параболического типа в новой системе координат О"х"у"
*) Если аиФ0, A22 = 0, то /t = an и вместо уравнения F.88) мы полу-
полу' ' '
e*'
чим уравнение /j*'2 + 2ej3*' + а^у' + а33 = 0, которое путем изменения обо-
обозначений х на у', у на /, а[3 на а^ н а'а на а[3 переходит в уравнение F.88).

182 ЛИНИИ ВТОРОГО ПОРЯДКА [ГЛ. 6
примет вид
Iitl* + 2tf*" + i& = 0. F.92)
Докажем теперь следующее утверждение.
Теорема 6.8. Уравнение F.60) линии L параболического
типа при 1зФ0 представляет собой параболу, а при /3=0 —
либо пару параллельных действительных прямых (которые мо-
могут быть слившимися), либо пару мнимых параллельных пря-
прямых*).
Доказательство. Выясним вопрос о связи между ве-
величинами а и /3. Для уравнения F.92) имеем
0
о /, о
13
= -/,<;. F.93)
а,ч О а,,
1*3 ОД
Так как h Ф0, то при 1зФ0 и аФ О, если же h = О, то и
а — 0. Используя этот вывод, мы можем записать уравнение
F.92) следующим образом:
F.94)
при /3 = 0 (т. е. при а = 0) 1{у + а'^ = 0. F.95)
Очевидно, уравнение F.94), отвечающее случаю 1зФ0, пред-
представляет собой параболу. Чтобы убедиться в этом, совершим
следующий параллельный перенос системы координат:
Х = х" + -?Щ-, Y = y", F.96)
и введем обозначение
р = |а;/3//,|. F.97)
Тогда вместо F.94) мы получим уравнение У2 = 2рХ или У2 =
= —2рХ, которое является каноническим уравнением пара-
параболы.
Уравнение F.95), отвечающее случаю /з = 0, может быть за-
записано так:
У «?//,. F.98)
Если — а?//, > 0, то уравнение F.98) представляет собой пару
параллельных прямых у'/==л/—а^7 и У" — ~~V~азз/71'»
*) Термин «мнимые параллельные прямые» будет разъяснен в процессе
доказательства.

§ 5] ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ 183
если — а^//, = 0, то F.98) представляет собой ось Ох",
уравнение которой у" = 0 (это уравнение можно рассматривать
как предельный случай при а^->0, т. е. как пару слившихся
прямых). Если, наконец, — а^//, < О, то уравнению F.98) не
удовлетворяют координаты никакой точки плоскости, т. е. гео-
геометрический образ является мнимым. Обычно говорят, что в
последнем случае уравнение F.98) определяет пару мнимых
параллельных прямых. Теорема доказана.
Замечание 7. Для случая /з^О, когда уравнение F.60)
параболического типа определяет параболу, читатель без труда
найдет параметр р этой параболы и ее расположение относи-
относительно исходной координатной системы Оху. Для этого нужно
использовать переход от уравнений F.60) к уравнению F.88),
описанный в начале этого пункта, н формулы F.90), F.91),
F.96), F.97).
7. Распадающиеся кривые второго порядка. Лииню L нторого порядка,
определяемую уравнением F.60), будем называть распадающейся, если левая
часть этого уравнения может быть представлена в виде произведения двух
многочленов первой степени. Очевидно, если в данной декартовой прямо-
прямоугольной системе координат линия L является распадающейся, то она будет
распадающейся в любой другой декартовой прямоугольной системе координат:
при преобразовании координат многочлен первой степени остается многочле-
многочленом первой степени и каждый многочлен-сомножитель преобразуется незави-
независимо от других сомножителей. Это свойство многочленов позволяет сформу-
сформулировать необходимое н достаточное условие распадения кривой второго по-
порядка.
Теорема 6.9. Для того чтобы линия L второго порядка была распа-
распадающейся, необходимо и достаточно обращение в нуль инварианта /з.
Доказательство. Мы доказали (см. теоремы 6.6—6.8), что уравне-
уравнение любой линии L второго порядка может быть приведено к одному нз
видов F.82)—F.87), F.94) и F.95).
Распадающимися среди этих лнннй являются лишь те, для которых
/э = 0 н, наоборот, если h — 0, то уравнение линии приводится к виду, из
которого, очевидно, следует свойстно распадения. Теорема доказана.

ГЛАВА 7
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
В этой главе мы познакомимся с понятием и основными ти-
типами поверхностей второго порядка. Кроме того, будут указаны
способы исследования таких поверхностей.
§ 1. Понятие поверхности второго порядка
В силу определений 1 иЗизп. 5§2гл. А поверхностью
S второго порядка будем называть геометрическое место
точек, декартовы прямоугольные координаты которых удовле-
удовлетворяют уравнению вида
апх2 + пцу2 + a^z2 + 2al2xy + 2anyz + 2al3xz + 2анх +
+ 2пну + 2a3Az + aAi = 0, G.1)
в котором по крайней мере один нз коэффициентов аи, а22, а3з.
я 12. 023, о 1з огличен от нуля.
Уравнение G.1) будем называть общим уравнением поверх-
поверхности второго порядка.
Очевидно, поверхность второго порядка, рассматриваемая
как геометрический объект *), не меняется, если от данной де-
декартовой прямоугольной системы координат перейти к другой
декзртовой системе координат. Отметим, что исходное уравне-
уравнение G.1) и уравнение, полученное после преобразования коор-
координат, алгебраически эквивалентны.
Ниже мы убедимся, что для каждого уравнения G.1) можно
указать такую специальную систему координат, в которой урав-
уравнение G.1) примет столь простой вид, что геометрическая ха-
характеристика поверхности S не будет представлять затруднений.
Используя этот метод, мы дадим полное описание всех типов
поверхностей второго порядка.
*) Может оказаться, чго уравнение G.1) не определяет поверхности:
этому уравнению могут удовлетворять лишь координаты точек, расположен-
расположенных яа прямой линии, или координаты лишь одной точки, или не найдется
нн одной точки, координаты которой удовлетворяют G.1). Однако в в этих
случаях мы будем говорить о геометрических объектах, называя нх соответ-
соответственно вырожденными или мнимыми.

§П ПОНЯТИЕ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 185
1. Преобразование коэффициентов уравнения поверхности
второго порядка при переходе к новой декартовой системе коор-
координат. Рассмотрим отдельно параллельный перенос и поворот
координатных осей.
Условимся о следующей терминологии: группу слагаемых
+ аюг2 + 2al2xy + 2a^yz + 2al3xz
левой части G.1) будем называть группой старших членов
этого уравнения, а группу слагаемых
2а1Ах + 2аиу + 2а^ + аи
будем называть линейной частью уравнения G.1). При этом
коэффициенты flu, а22, азз, аи, а23, ач будем называть коэф-
коэффициентами группы старших членов, а коэффициенты аи, а24,
аи, я« — коэффициентами линейной части G.1). Коэффициент
fl44 обычно называется свободным членом уравнения G.1).
Рассмотрим сначала параллельный перенос декарто-
декартовой системы координат. Как известно, старые и новые коор-
координаты точки связаны соотношениями
х = х' + х0, У = у' + Уа, z = z' + zQ, G.2)
где дго, Уо, %й — координаты нового начала О' в старой системе
Охуг (см. главу 3, формулы C.20)). Подставляя выражения
G.2) для х, у, z в левую часть G.1), получим уравнение 5
в новой системе O'xfy'zf. Это уравнение имеет вид
апх'2 + апу'2 + Оззг'2 + 2а12*У + 2a23yV + 2al3*V +
+ 2а;/ + 2a'2iy' + 2a'3iz' + а'„ = 0, G.3)
где
+ fl23Z0 + aM>
аи = апхо
+ 2aay0z0 -f 2al3xozo + 2а^хй + 2a2iyQ + 2a3iz0 -f au.
Обращаясь к уравнению G.3), мы можем сделать следующий
важный вывод: при параллельном переносе системы координат
коэффициенты группы старших членов не изменяются, а коэф-
коэффициенты группы линейных членов преобразуются по форму-
формулам G.4).
Рассмотрим теперь поворот декартовой системы коор-
координат-

186
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
[ГЛ. 7
Как известно, старые и новые координаты точки связаны
соотношениями (см. главу 3, формулы C.20))
т12/ + тхз/,
х =
у
г
т21х' + т^у' +
G.5)
где тц = тц суть косинусы углов, которые составляют друг с
другом старые и новые координатные оси. Подставляя выраже-
выражения G.5) для х, у и z в левую часть G.1) и группируя коэффи-
коэффициенты при различных степенях xf, у' и У, мы получим уравне-
уравнение S в системе Ojc'j/V.
Это уравнение имеет вид
V +
a44 = 0. G.6)
Легко убедиться в справедливости следующего важного вывода
о структуре коэффициентов а'ц: при повороте системы коорди-
координат коэффициенты группы старших членов уравнения G.6) вы-
выражаются лишь через величины тц, фигурирующие в соотно-
соотношениях G.5), и через коэффициенты группы старших членов
уравнения G-1); коэффициенты a\v a'w a'M уравнения G.6) вы-
выражаются лишь через величины тц и коэффициенты аи, аи, а3*
уравнения G.1); свободный член не изменяется (т. е. а'и = аиу
При этом, если в исходном уравнении все коэффициенты аи,
аи, аз4 были равны нулю, то все коэффициенты au, a'u, a'3i так-
также будут равны нулю. Из выводов этого пункта следует, что
путем параллельных переносов можно упрощать группу линей-
линейных членов уравнения G.1), не меняя при этом коэффициентов
группы старших членов, а путем поворотов системы можно
упрощать группу старших членов этого уравнения.
2. Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение:
Величины
/а —
«11
аи
а»
0,2
«22
«23
«13
023
«33
«12
«22
«12
«22
«23
«24
I
'
«13
«13
«33
«34
«22
«23
«14
«24
«34
«44
«23
«33
|+|в33
I ^ I «13
«11
«11
«12
аи
«13
«м
являются инвариантами уравнения G.1) поверхности второго
порядка относительно преобразований декартовой системы ко-
координат.
Доказательство этого утверждения приведено в выпуске
«Линейная алгебра» настоящего курса.

§ 1] ПОНЯТИЕ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 187
3. Центр поверхности второго порядка. Попытаемся найти
такую декартову систему координат O'x'y'z' (полученную па-
параллельным переносом системы Oxyz), в которой уравнение G.3)
данной поверхности S второго порядка не содержало бы слагае-
слагаемых 2а'нх', 2a'2iy' и 2a'3iz', т. е. коэффициенты а'и, a'n и a'3t
были бы равны нулю. Пусть х0, уа и z0 — координаты начала О'
искомой системы. Обращаясь к формулам G.4), найдем, что
величины jc0, ya, zq представляют собой решение следующей си-
системы линейных уравнений:
ацХо + ai2y0 + ааг0 + а14 = О,
al2xQ + ОяУо + a-aZo + а24 = 0, G.7)
а13х0 + аау0 + a&zo + а^ — 0.
Уравнения G.7) называются уравнениями центра поверхно-
поверхности второго порядка, а точка О' с координатами (x0,yQ,zo), где
х0, у0 и zQ — решения системы G.7), называется центром этой
поверхности.
Допустим, что поверхность S второго порядка имеет центр
О' (т. е. система G.7) имеет решение (ха, уо, z0)). Перенесем
начало координат в центр О'. Так как при параллельном пере-
переносе коэффициенты группы старших членов не изменяются и
начало координат переносится в центр, то уравнение поверх-
поверхности 5 в системе O'x'y'z' примет вид
апх'2 + апул Л- а^2 + 2а'12хУ + 2a'23y'z/ + 2a'l3x'yf + а'ы = 0.
G.70
Очевидно, если точка M(x/,yr,zf) расположена на поверхности
S (т. е. ее координаты х', у*, г' удовлетворяют уравнению
G.77)), то и точка М* (—х', — у', — г'), симметричная с М отно-
относительно О', также расположена на S. Таким образом, если
у поверхности S существует центр О', то относительно центра
точки S располагаются симметричными парами, т. е. центр по-
поверхности является ее центром симметрии.
Наличие центра у поверхности второго порядка связано с
разрешимостью уравнений центра G.7). Если уравнения центра
имеют единственное решение, то поверхность S второго порядка
будем называть центральной*).
Отметим, что центральными поверхностями являются лишь
те, для которых инвариант h отличен от нуля, ибо этот инва-
инвариант равен определителю системы G.7) уравнений центра.
4. Стандартное упрощение любого уравнения поверхности
второго порядка путем поворота осей. Докажем, что в некоторой
декартовой прямоугольной системе координат уравнение данной
*) Таким образом, центральная поверхность имеет единственный центр.

188 ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ.7
поверхности S второго порядка не содержит слагаемых
2a'l2x'y', 2a'2?/z' и 2a\jc'zf, т. е. в уравнении поверхности S ко-
коэффициенты a\v a'n и а\г равны нулю.
Обозначим через F группу старших членов уравнения G.1)
F = ацх2 + ппУ2 + аза*2 + 2а12ху + 2aayz + 2ai3xz G.8)
и рассмотрим значения F в точках сферы я радиуса 1 с цент-
центром в начале координат. Иными словами, рассмотрим значения
F(x,y,z) для всех тех значений х, у и г, которые связаны со-
соотношением *)
? f Pl. G.9)
Пусть Р — та точка сферы я, в которой значение F{x,y,z) яв-
является максимальным**). Направим новую ось Ozr из начала
координат в точку Р, а оси Ох' и Oyf перпендикулярно оси Oz/.
Очевидно, в системе координат Ox't/z' точка Р имеет координа-
координаты @,0,1).
Так как в новой системе координат Ох'у'г! выражение для
F имеет вид***)
F = а'пхЛ + а'пУГ* + <&г'2 + Ча'^'у' + 2a'23yV + 2<3*V, G.10)
а сфера я определяется уравнением
*'2 + /Ч2/2=1, G.11)
то значения F в точках я могут быть получены с помощью
G.10) для всех тех значений (x',y/,z/), которые связаны соот-
соотношением G.11). В частности, максимальное значение F будет
в точке @,0,1).
Убедимся, что в выражении G.10) группы старших членов
в системе Ox'y'z' коэффициенты а'а и а'13 равны нулю. Дока-
Докажем, например, что а'13 — 0 (доказательство равенства а'23 = 0
проводится аналогично). Для этой цели рассмотрим значения F
в точках окружности L, являющейся линией пересечения сферы
G.11) с плоскостью у' = 0, т. е. с плоскостью Ox'zf. Пусть в —
угол, который образует радиус-вектор точки М на окружности
L с осью Oz/. Координаты х', у*, zr точки М, очевидно, равны
х' = sin в, / = 0, z' = cose. G.12)
*) Соотношение G.9) представляет собой уравнение сферы радиуса 1
с центром в начале координат.
**) Сфера я является замкнутым ограниченным множеством и служит
областью задания непрерывной функции F трех переменных х, у и г. Отсюда
следув! существование на сфере л такой точки Р, в которой F имеет макси-
максимальное значение (см. выпуск 1 курса, главу 14, теорему 14.7).
**•) Напомним, что при повороте коэффициенты группы старших членов
выражаются лишь через величины mih фигурирующие в соотношениях G.5),
и через коэффициенты группы старших членов в выражении G.8) (см. п. 1
этого параграфа).

§2] КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА 189
Подставляя эти значения х', у' и г' в G.10), получим следую-
следующее выражение для F в точках L:
F — а'п sin2 9 + <4 cos2 9 + 2a'l3 sin 9 cos 9 =
— °U о*3 + м 0°" cos20 + o^,sin20. G.13)
Таким образом, значения F в точках L могут быть представле-
представлены в виде функции G.13) угла в. Эта функция имеет при 9 = 0
максимальное значение (из формул G.12) следует, что значе-
значению 0 = 0 отвечает точка с координатами @,0,1), в которой
значение F максимально). Отсюда вытекает, что производная
функции G.13) равна нулю в точке в = 0. Дифференцируя
G.13) по 8 и полагая в полученном выражении 9=0, получим
равенство 2а{3 = 0, из которого вытекает равенство нулю коэф-
коэффициента а[3. Для доказательства равенства а'23 = 0 нужно рас-
рассмотреть значения F на окружности N, являющейся линией пе-
пересечения сферы G.11) с плоскостью д/ = 0, и повторить про-
проведенные выше рассуждения. Итак, в системе координат Ox'y'sf
группа F старших членов уравнения поверхности S второго по-
порядка имеет вид
2 2* G.14)
причем на выбор осей Ох' и О у' не накладывалось никаких
требований, кроме требований перпендикулярности осн Ог'.
Иными словами, при повороте системы Ox'y'z' вокруг оси Ог7
на любой угол группа F старших членов будет иметь вид G.14).
При этом координаты х' и у' преобразуются по формулам по-
поворота системы координат на плоскости, а координата z7 не
меняется. Поэтому можно выбрать такую систему координат,
в которой коэффициент а\2 при произведении xfy' будет равен
нулю.
Итак, мы убедились в том, что существует такая система
прямоугольных декартовых координат Ох'у'2, в которой урав-
уравнение поверхности S имеет вид
+ а'и = 0. G.15)
Приведение уравнения G.1) поверхности S к виду G.15) мы
будем называть стандартным упрощением уравнения поверх-
поверхности.
§ 2. Классификация поверхностей второго порядка
1. Классификация центральных поверхностей. Пусть S —
центральная поверхность второго порядка. Перенесем начало
координат в центр этой поверхности, а затем произведем стан-

190 ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. 7
дартное упрощение уравнения этой поверхности. Используя вы-
выводы пп. 1, 3 н 4 § 1 этой главы, легко убедиться, что в резуль-
результате указанных операций уравнение поверхности примет вид *)
a4i = 0. G.16)
Так как инвариант h Для центральной поверхности отличен от
нуля и его значение, вычисленное для уравнения G.16), равно
ап-пп-пзз, то коэффициенты ац, агг и а3з удовлетворяют
условию
аиФО, а^фО, аззт^О. G.17)
Возможны следующие случаи.
Г. Коэффициенты аи, а22, Дзз одного знака, а коэффициент
а« отличен от нуля. В этом случае поверхность S называется
эллипсоидом.
Если коэффициенты ац, ai2, взз. ац одного знака, то левая
часть G.16) ни при каких значениях х, у, г не обращается в
нуль, т. е. уравнению поверхности 5 не удовлетворяют коорди-
координаты никакой точки. В этом случае поверхность S называется
мнимым эллипсоидом.
Если знак коэффициентов ац, а», азз противоположен знаку
коэффициента ац, то поверхность 5 называется вещественным
эллипсоидом. В дальнейшем термином «эллипсоид» будем на-
называть лишь вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической
форме. Очевидно, числа —ац/ац, —пц/пю, —пц/пц положи-
положительны **). Обозначим эти числа соответственно а2, Ь2, с2. После
несложных преобразований уравнение эллипсоида G.16) мож-
можно записать в следующей форме:
¦?+¦{!¦+7F-1. G.18)
Уравнение G.18) называется каноническим уравнением эллип-
эллипсоида.
Если эллипсоид задан своим каноническим уравнением
G.18), то оси Ох, Оу и Oz называются его главными осями.
2°. Из четырех коэффициентов аи, Я22, азз, аи два одного
знака, а два других — противоположного. В этом случае поверх-
поверхность 5 называется однополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают
в канонической форме. Пусть, ради определенности, ац > 0,
> 0, а3з < 0, а« < 0. Тогда числа —а«/аи, —сщ/a-n,
/ положительны. Обозначим эти числа соответственно а2,
•) Прн этом окончательную систему координат мы обозначим Охуг.
*•) Согласно G.17) и определению эллипсоида коэффициенты ац, аа, вм,
044 не равны нулю и знак аи противоположен знаку аи, ац, а3з.

в Я КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА 191
Ь2, с2. После несложных преобразований уравнение G.16) одно-
полостного гиперболоида можно записать в следующей форме:
Уравнение G.19) называется каноническим уравнением одно-
полостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим
уравнением G.19), то оси Ох, Оу и Oz называются его глав-
главными осями.
Замечание 1. Если знаки коэффициентов аи, а22, азз, а44
распределены иначе, чем в рассмотренном случае, то канониче-
каноническое уравнение G.19) легко может быть получено путем пере-
переименования осей координат.
3°. Знак одного из первых трех коэффициентов ац, а&, а3з,
пц противоположен знаку остальных коэффициентов. В этом
случае поверхность 5 называется двуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канони-
канонической форме. Пусть ради определенности а и < 0, а2г < О»
а3з > 0, ац < 0. Тогда ац/ац > 0, аи/а^ > 0, —аи/азэ > 0-
Обозначим этн числа соответственно через а2, Ь2, с2. После не-
несложных преобразований уравнение G.16) двуполостного ги-
гиперболоида можно записать в следующей форме:
г2 ,л -г
^ ffr=-l. G.20)
Уравнение G.20) называется каноническим уравнением двупо-
двуполостного гиперболоида.
Если двуполостный гиперболоид задан своим каноническим
уравнением, то оси Ох, Оу и Oz называются его главными
осями.
Замечание 2. Если знаки коэффициентов ац, а22, азз, ац
распределены иначе, чем в рассмотренном случае, то канони-
каноническое уравнение G.20) легко может быть получено путем пе-
переименования осей координат.
4°. Коэффициент ац равен нулю. В этом случае поверхность
S называется конусом второго порядка.
Если коэффициенты аи, а-щ, а3з одного знака, то левая часть
G.16) обращается в нуль (ац = 0) лишь для x = y = z = 0,
т. е. уравнению поверхности 5 удовлетворяют координаты
только одной точки. В этом случае поверхность S называется
мнимым конусом второго порядка. Если коэффициенты аи, а-а,
а3з имеют разные знаки, то поверхность 5 является веществен-
вещественным конусом второго порядка.
Обычно уравнение вещественного конуса второго порядка за-
записывают в канонической форме. Пусть ради определенности
вц>0, а22 > 0, а3з<0. Обозначим 1/вц, l/а-а, — 1/а3з со-

192 ПОВГРХНОСТИ ВТОРОГО ПОРЯДКА (ГЛ. 7
ответственно через а2, Ь2, с2. Тогда уравнение G.16) можно за-
записать в виде
•5Г+|г-7г = 0. G.21)
Уравнение G.21) называется каноническим уравнением веще-
вещественного конуса второго порядка.
Замечание 3. Если знаки коэффициентов ац, а22, а3з рас-
распределены иначе, чем в рассмотренном случае, то каноническое
уравнение G.21) легко может быть получено путем переимено-
переименования осей координат.
Замечание 4. В следующем параграфе мы докажем, что
вещественный конус второго порядка образован прямыми ли-
линиями, проходящими через фиксированную точку.
2. Классификация иецеитральных поверхностей второго по-
порядка. Пусть 5 — нецентральная поверхность второго порядка,
т. е. поверхность, для которой инвариант /3 равен нулю (см.
п. 3 § 1 этой главы). Произведем стандартное упрощение урав-
уравнения этой поверхности. В результате уравнение поверхности
примет вид G.15). Так как инвариант /3 = 0 и его значение,
вычисленное для уравнения G.15), равно ап*Ди'азз. то °Дин
или два нз коэффициентов а'и, а'п, а33 равны нулю*). В соот-
соответствии с этим рассмотрим следующие возможные случаи.
Г. Один из коэффициентов а'и, а^, а3% равен нулю. Ради
определенности будем считать, что а'33 = 0 (если равен нулю
какой-либо другой из указанных коэффициентов, то можно пе-
перейти к рассматриваемому случаю путем переименования осей
координат). Перейдем от координат х', у', г' к новым коорди-
координатам х, у, г по формулам
G.22)
2
Подставляя х', у' и г', найденные из G.22), в левую часть G.15)
н заменяя затем а'п на а,,, а^ на а22, а'ЗА на р и а'<4 на q,
получим следующее уравнение поверхности S в новой системе
координат Охуг;
«и*2 + атзУг + 2pz + q = 0. G.23)
A) Пусть р — 0, q=0. Поверхность S распадается на пару
плоскостей
х ± V— <W°u У — О-
*) Все перечисленные коэффициенты не могут быть равны нулю, так как
при преобразовании координат порядок уравнения ие изменяется (см. гла-
главу 4).

§2] КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА 193
При этом, очевидно, эти плоскости будут мнимыми, если знаки
а и и an одинаковы, и вещественными, если знаки ац и а&
различны.
B) Пусть р =¦ 0, q^O. Уравнение G.23) принимает вид
аих2 -\-йпУ* + <7 = 0. G.24)
Известно (см. п. 3 § 2 главы 4), что уравнение G.24) является
уравнением цилиндра с образующими, параллельными оси Ог.
При этом, если аи, ац и q имеют одинаковый знак, то левая
часть G.24) отлична от нуля для любых х и у, т. е. цилиндр
будет мнимым. Если же среди коэффициентов ац, a2j и q
имеются коэффициенты разных знаков, то цилиндр будет веще-
вещественным. Отметим, что в случае, когда аи и а22 имеют оди-
одинаковые знаки, а q — противоположный, то величины —q/an
и —q/a2i положительны. Обозначая их соответственно через а2
и Ь2, мы приведем уравнение G.24) к виду
¦? + ¦?-1. G-25)
Таким образом, в отмеченном случае мы имеем эллиптический
цилиндр. В случае, когда ац и а22 имеют различные знаки, по-
получим гиперболический цилиндр. Легко убедиться, что уравне-
уравнение гиперболического цилиндра может быть приведено к виду
"Si"—fr=1- G-26)
C) Пусть рфО. Произведем параллельный перенос систе-
системы координат, выбирая новое начало в точке с координатами
Го, 0, —у")- ПРИ этом оставим старые обозначения координат
х, у, г. Очевидно, для того чтобы получить уравнение поверх-
поверхности 5 в новой системе координат, достаточно заменить в урав-
уравнении G.23) 2 на Z — -3-. Получим следующее уравнение:
ацХ2 -J- пяУг -j- 2рг = 0. G.27)
Уравнение G.27) определяет так называемые параболоиды.
Причем, если ац и а2г имеют одинаковый знак, то параболоид
называется эллиптическим. Обычно уравнение эллиптического
параболоида записывают в канонической форме:
2 = ||-+J?. G.28)
Уравнение G.28) легко получается из G.27). Если ац и an
имеют разные знаки, то параболоид называется гиперболиче-
гиперболическим. Каноническое уравнение гиперболического параболоида
13 3ак. 168

194 ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ГГЛ. 7
имеет вид
а »
Это уравнение также легко может быть получено из G.27).
2. Два из коэффициентов а'п, а'^, а'33 равны нулю. Ради
определенности будем считать, что а'п = 0 и 0^ = 0 (если рав-
равны нулю какие-либо другие два из указанных коэффициентов,
то можно перейти к рассматриваемому случаю путем переиме-
переименования осей координат). Перейдем от xf, у', г7 к новым коор-
координатам х, у, г по формулам
G.30)
азз
Подставляя ^,/и/, найденные из G.30) в левую часть G.15)
и заменяя затем а'гз на а33, а'14 на р, аи на q и а'ы на г, по-
получим следующее уравнение поверхности S в новой системе ко-
координат Охуг:
a!az' + 2px + 2qy + r = 0. G.31)
A) Пусть р = 0, q = 0. Поверхность S распадается на пару
параллельных плоскостей
г = ± -V—r/азз. G.32)
При этом, очевидно, этн плоскости будут мнимыми, если знаки
азз и г одинаковы, и вещественными, если знаки а33 и г различ-
различны, причем при г = 0 эти плоскости сливаются в одну.
B) Хотя бы один из коэффициентов р или q отличен от нуля.
В этом случае повернем систему координат вокруг оси Ог так,
чтобы новая ось абсцисс стала параллельной плоскости 2рх -f-
-f- 2qy -f- r = 0. Легко убедиться, что при таком выборе системы
координат, при условии сохранения обозначения х, у и г для
новых координат точек, уравнение G.31) примет вид
= 0, G.33)
которое является уравнением параболического цилиндра с об-
образующими, параллельными новой оси Ох.
§ 3. Исследование формы поверхностей
второго порядка по их каноническим уравнениям
1. Эллипсоид. Для исследования формы эллипсоида обра-
обратимся к его каноническому уравнению G.18) (см. п. 1 преды-
предыдущего параграфа)
? ? ?«1. GЛ8)

6 3] ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА 195
Из уравнения G.18) вытекает, что координатные плоскости яв~
ляются плоскостями симметрии эллипсоида, а начало коорди-
координат— центром симметрии. Числа а, Ь, с называются полуосями
эллипсоида и представляют собой длины отрезков, от начала
координат до точек пересечения эллипсоида с осями координат.
Эллипсоид представляет собой ограниченную поверхность, за-
заключенную, как это видно из G.18), в параллелепипеде |x|=Sj a,
\у\^Ь, \г\^ с. Чтобы более наглядно представить себе форму
эллипсоида, выясним форму линий пересечения его плоскостя-
плоскостями, параллельными какой-либо из координатных плоскостей.
Ради определенности рассмотрим линии Lh пересечения эл-
эллипсоида с плоскостями
г = А, G.34)
параллельными плоскости Оху. Уравнение проекции Lh линии
Lh на плоскости Оху получается из уравнения G.18), если по-
положить в нем z = А. Таким образом, уравнение этой проекции
имеет вид
¦? + ?-!-?. G.35)
Если положить
i—^r. G.36)
то уравнение G.35) можно записать в виде
хг и1
~^г "Ь ~уг ~ *» G.37)
т. е. Lh представляет собой эллипс с полуосями а* и V, кото-
которые могут быть вычислены по формулам G.36). Так как Lh
получается «подъемом» L\ иа высоту А по оси О г (см. G.34)),
то и Lh представляет собой эллипс.
Представление об эллипсоиде можно получить следующим
образом. Рассмотрим на плоскости Оху семейство эллипсов
G.37) (рис. 7.1), полуоси а* и Ь* которых зависят от А (см.
G.36)), и каждый такой эллипс снабдим отметкой А, указываю-
указывающей, на какую высоту по оси Ог должен быть «поднят» этот
эллипс. Мы получим своего рода «карту» эллипсоида. Исполь-
Используя эту «карту», легко представить себе пространственный вид
эллипсоида. На рис. 7.2 изображен эллипсоид.
Эллипсоид может быть получен равномерным сжатием сфе-
сферы относительно двух перпендикулярных плоскостей. Именно,
если а — наибольшая полуось эллипсоида, то он может быть
получен из сферы *)
*) Очевидно, сфера представляет собой эллипсоид с равными полуосями.

196
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
П"Л,7
равномерным сжатием ее сначала относительно плоскости Оху
с коэффициентом сжатия Ь/а, а затем относительно плоскости
Охг с коэффициентом сжатия с/а.
В заключение отметим, что линии пересечения эллипсоида
с плоскостями представляют со-
бой эллипсы.
В самом деле, такая линия
представляет собой ограничен-
ограниченную линию второго порядка *)
(ограниченность линии вытекает
V
Рис. 7.1
Рис. 7.2
из ограниченности эллипсоида), единственной же ограниченной
линией второго порядка является эллипс.
2. Гиперболоиды.
1°. Однополостный гиперболоид. Обратимся к каноническо-
каноническому уравнению G.19) однополостного гиперболоида
1.
G.19)
Из уравнения G.19) вытекает, что координатные плоскости яв-
являются плоскостями симметрии, а начало координат — центром
симметрии однополостного гиперболоида.
Рассмотрим линии Lh пересечения одиополостного гипербо-
гиперболоида плоскостями г = А. Уравнение проекции L\ такой линии
на плоскость Оху получается из уравнения G.19), если поло-
положить в нем 2 = А. Полагая
G.38)
*) Преобразуем систему координат так, чтобы в новой системе коорди-
координат Ох'у'г' секущая плоскость определялась уравнением г' = 0. После та-
такого преобразования эллипсоид будет определяться уравнением второго по-
порядка. Полагая в этом уравнении г* == 0, мы получим уравнение второго
порядка лвяии пересечения эллипсоида и плоскости г' — 0.

3] ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕН ВТОРОГО ПОРЯДКА
197
найдем, что уравнение этой проекции имеет вид
L
-•2
G.39)
т. е. La представляет собой эллипс с полуосями а* и Ь*
Рассмотрим «карту» расположенной над плоскостью Оху
части однополостного гиперболоида*), т. е. семейство эллип-
эллипсов G.39), каждый из которых снабжен отметкой А, указываю-
указывающей, на какую высоту по оси Ог
должен быть поднят этот эллипс
(рис. 7.3). Обращаясь к карте одно-
полостиого гиперболоида, мы видим,
что наименьший из рассматривае-
рассматриваемых эллипсов G.39) получается для
А = 0 (см. также формулы G.38)).
Горловой эллипс
Рис. 7.3
Ряс. 7.4
Этот эллипс называется горловым.. С увеличением А размеры
эллипса G.39) неограниченно увеличиваются. Таким образом,
однополостиый гиперболоид представляет собой поверхность,
состоящую из одной полости и подобную трубке, неограниченно
расширяющейся в положительном и отрицательном направле-
направлении по оси Ог (рис. 7.4). Отметим, что сечения однополостного
гиперболоида плоскости Оуг и Охг представляют собой гипер-
гиперболы, определяемые соответственно уравнениями
с'
"Г
1.
Эти гиперболы изображены на рис. 7.4.
2°. Двуполостный гиперболоид. Из канонического уравнения
G.20)
4+?~? —1 G.20)
*) Расположенная под плоскостью Оху часть однополостного гипербо-
гиперболоида симметрична рассматриваемой части относительно этой плоскости.

198
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
[ГЛ. Г
двуполостного гиперболоида вытекает, что координатные пло-
плоскости являются его плоскостями симметрии, а начало коорди-
координат— его центром симметрии.
Линии Lh пересечения двуполостного гиперболоида плоско-
плоскостями 2 = h представляют собой эллипсы, уравнения проекций
которых на плоскость Оху имеют вид
а*2 т Ь*
где
G.40)
G.41)
Из формул G.41) вытекает, что секущая плоскость z = h на-
начинает пересекать двуполостиый гиперболоид лишь при |А|^
^ с*). Иными словами, в слое между
плоскостями г = —с и г = с не со-
содержится точек рассматриваемой по-
поверхности; в силу симметрии относи-
относительно плоскости Оху она состоит из
двух полостей, расположенных вне
указанного выше слоя.
На рис. 7.5 изображена «карта»
верхней полости двуполостного гипер-
гиперболоида. Из формул G.41) следует,
что при увеличении А эллипсы G.40)
неограниченно увеличиваются, так что
полости двуполостного гиперболоида
Рис. 7.5
Рис. 7.6
представляют собой бесконечные чаши. На рнс. 7.6 изображен
двуполостиый гиперболоид. Отметим, что сечеиия двуполостно-
двуполостного гиперболоида плоскостями Оуг и Охг представляют собой
гиперболы (см. рис. 7.6).
*) При |А| < с подкоренное выражение в формулах G.41) отрицательно.

§31
ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
199
3. Параболоиды.
1°. Эллиптический параболоид. Обращаясь к каноническому
уравнеиию G.28) эллиптического параболоида
G.28)
мы видим, что для него Охг и Оуг являются плоскостями сим-
симметрии. Ось Ог, представляющая линию пересечения этих пло-
плоскостей, называется осью эллиптического параболоида. Из
уравнения G.28) вытекает, что эллиптический параболоид рас-
расположен в полупространстве г^О. Линии Lh пересечения эл-
эллиптического параболоида плоскостями г = А, А > 0, представ-
представляют собой эллипсы, проекции b'h кото-
которых на плоскости Оху определяются урав-
уравнением
*2 , Л ,
где
G.42)
G.43)
Из формулы G.43) следует, что при уве-
увеличении А эллипсы G.42) неограниченно
увеличиваются, так что эллиптический па-
параболоид представляет собой бесконечную
чашу. На рис. 7.7 изображен эллиптический Рис. 7.7
параболоид.
Обратимся к сечениям эллиптического параболоида плоско-
плоскостями у = А и х = А, параллельными соответственно коорди-
координатным плоскостям Охг и Оуг.
Плоскость х = А, например, пересекает эллиптический пара-
параболоид по параболе
г — -
¦h.
G.44)
Очевидно, парабола G.44) получается таким параллельным
переносом параболы
* = 0, G.45)
представляющей собой сечение эллиптического параболоида
плоскостью х =¦ 0, при котором ее вершина, имеющая коорди-
координаты @, 0, 0), переходит в точку с координатами (x = h,
у = 0, г —И?/а2). Иными словами,, эллиптический параболоид
образуется путем параллельного перемещения параболы G.45),
когда ее вершина движется вдоль параболы, г = х2/а2, у = 0,
представляющей собой сечение эллиптического параболоида
плоскостью у — 0.

200
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
(ГЛ.7
Совершенно аналогично можно убедиться в том, что эллип-
эллиптический параболоид может быть получен путем параллельного
перемещения параболы, представляющей собой сечение пара-
параболоида плоскостью у = 0 вдоль сечения плоскостью х = 0.
2°. Гиперболический параболоид. Из канонического уравне-
уравнения G.29)
2==-?-? <7-29>
гиперболического параболоида вытекает, что плоскости Охг и
Оуг являются плоскостями сим-
симметрии. Ось Oz называется осью z
гиперболического параболоида.
Ь=о
Рис. 7.8
Рис. 7.9
Линии г = h пересечения гиперболического параболоида
с плоскостями г = А представляют собой при А > 0 гиперболы
G.46)
х*
„•2
1
с полуосями
G.47)
а при А < 0 — сопряженные гиперболы для гипербол G.46)
4т—^ 1 G-48)
а о
С полуосями
а'==ал/— A, b' — b-yf—h. G.49)
Используя формулы G.46)—G.49), легко построить «карту»
гиперболического параболоида (рис. 7.8). Отметим еще, что
плоскость 2 = 0 пересекает гиперболический параболоид по
двум прямым
У=±^х. G.50)
Из формул G.47) и G.49) вытекает, что прямые G.50) яв-
являются асимптотами гипербол G.46) и G.48).

§31
ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
201
Карта гиперболического параболоида дает представление
о его пространственной форме (рис. 7.9). Как и в случае эл-
эллиптического параболоида, можно убедиться в том, что гипер-
гиперболический параболоид может быть получен путем параллель-
параллельного перемещения параболы, представляющей собой сечение
плоскостью Охг {Oyz), когда ее вершина движется вдоль пара-
параболы, являющейся сечением параболоида плоскостью Oyz
(Охг).
4. Конус и цилиндры второго порядка.
Г. Конус второго порядка. В предыдущем параграфе мы
назвали вещественным конусом второго порядка поверхность S,
определяемую уравнением G.21):
Убедимся, что вещественный конус S образован прямыми ли-
линиями, проходящими через начало О координат. Естественно
называть точку О вершиной конуса.
Для доказательства сформулирован-
сформулированного утверждения, очевидно, достаточно
установить, что прямая L, соединяющая
произвольную, отличную от начала ко-
координат точку Мо(хо,уо, 2о) конуса G.21)
и начало координат О (рис. 7.10), цели-
целиком располагается на конусе, т. е. коор-
координаты (х, у, г) любой точки М прямой
L удовлетворяют уравнению G.21).
Так как точка Afo(*o, Уо, z0) лежит на
конусе G.21), то
fi
Jt
zo
G.51)
Координаты (х, у, г) любой точки М пря-
прямой L равны соответственно txo, tyo, tzo, Рис. 7.10
где t — некоторое число. Подставляя эти
значения для х, у и г в левую часть G.21), вынося /2 за скоб-
скобки и учитывая G.51), мы убедимся в том, что М лежит на
конусе. Таким образом, утверждение доказано. Представление
о форме конуса может быть получено методом сечений. Легко
убедиться, что сечения конуса плоскостями z = А представляют
собой эллипсы с полуосями a' = ^r h, b' = — A.
С С
2°. Цилиндры второго порядка. В процессе классификации
поверхностей второго порядка нам встретились эллиптический,
гиперболический н параболический цилиндры. Уравнения этих

202 ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
поверхностей соответственно имеют вид
Рис. 7.11 дает представление о форме этих цилиндров.
1ГЛ. Г
G.52)
Рис. 7.11
Заметим, что цилиндры G.52) состоят из прямых линий, па-
параллельных оси Ог.
5. Прямолинейные образующие поверхностей второго по-
порядка. Кроме конуса и цилиндров, поверхностями второго по-
порядка, состоящими из прямолинейных образующих, являются
однополостный гиперболоид и гиперболический параболоид.
Более точно, справедливо следующее утверждение.
Через каоюдую точку однополостного гиперболоида и гипер-
гиперболического параболоида проходят две различные прямые ли-
линии, целиком располагающиеся на указанных поверхностях.
Таким образом, однополостный гиперболоид и гиперболиче-
гиперболический параболоид покрыты двумя различными семействами пря-
прямолинейных образующих. На рис. 7.12 и 7.13 показано распо-
расположение прямолинейных образующих соответственно на одно-
полостиом гиперболоиде и гиперболическом параболоиде.
Рассмотрим сначала однополостный гиперболоид, заданный
своим каноническим уравнением
1.
G.19)
Очевидно, любая прямая Г*, определяемая как линия пересе-
пересечения плоскостей
*) Уравнение параболического цилиндра уг = 2рх легко получается из
уравнения G.33) путем переименования осей коорданат н простых арифмети-
арифметических операций.

I 3) ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
203
при любом отличном от нуля значении к целиком располагается
на гиперболоиде G.19), ибо уравнение G.19) представляет
собой алгебраическое следствие уравнений G.53) (уравнение
G.19) получается из уравнений G.53) путем их перемножения).
Прямая Гм: 1 — -т- = 0, Y~b~~F = ® соответствует уравнениям
Рис. 7.12
Рис. 7.13
G.53) при X = оо. Точно так же легко убедиться, что любая
прямая Г\, определяемая как линия пересечения плоскостей
x_
a
куда включается прямая П»: 1+-|- = 0, i + yeO, соответ-
соответствующая Я, = оо, при любом значении X располагается на ги-
гиперболоиде G.19).
Нетрудно заметить, что прямые Г* н Г\ различны. Таким
образом, на однополостиом гиперболоиде имеются два различ-
различных семейства прямых Г* и Г*. Для завершения доказатель-
доказательства утверждения достаточно убедиться, что через любую точку
гиперболоида проходит иекоторая прямая семейства Г* и иеко-
иекоторая прямая семейства Г?. Мы ограничимся доказательством
этого лишь для семейства Г*, ибо для семейства П, доказа-
доказательство аналогично.
Пусть точка Мо{хо,уо,г<>) находится иа гиперболоиде G.20),
так что
G.54)

204 ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГД,7
Если точка Мо лежит на прямой Г» или Го, то утверждение
очевидно. В противном случае выберем такое значение Л, чтобы
числа хо, уа, 2о удовлетворяли первому из уравнений G.53), и
обозначим его через Л<>. Таким образом,
^) G-55)
Убедимся, что при выбранном значении Л = к0 числа х0, уо, г0
удовлетворяют и второму из уравнений G.53), что означает,
что точка М0(хо,уо,го), принадлежащая гиперболоиду, принад-
принадлежит также и прямой G.53). Допустим, что это не так. Тогда
1+-Т- <7-56)
Перемножая G.55) и G.56), получим неравенство
4 *о . , Уо
которое противоречит соотношению G.54). Таким образом, пря-
прямая Гл, располагается на гиперболоиде и проходит через за-
заданную его точку Мо(хо,Уо, г0).
Совершенно аналогично рассуждая, можно убедиться, что
гиперболический параболоид г = -^т — -^Г покрыт двумя семей-
семействами прямых Щ и Пл, которые соответственно задаются урав-
уравнениями
(-ee, ее).

ПРИЛОЖЕНИЕ
ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
И ОБОСНОВАНИЯ МЕТОДА КООРДИНАТ
§ 1. Аксиомы элементарной геометрии
Будем рассматривать три множества объектов лю-
любой природы: объекты первого множества будем именовать
точками и обозначать большими латинскими буквами А, В,
С, ..., объекты второго множества будем именовать прямыми
и обозначать малыми латинскими буквами а, Ь, с, ..., объекты
третьего множества будем именовать плоскостями и обозна-
обозначать греческими буквами а, Э, у,...
Будем считать, что в рассматриваемых множествах каким-
либо способом определены соотношения между объектами,
выражаемые тремя терминами: принадлежит, лежит между и
конгруэнтен*). Например, точка А принадлежит прямой а или
плоскости а; точка В, принадлежащая прямой а, лежит между
принадлежащими той же прямой точками А я С; отрезок пря-
прямой а, ограниченный принадлежащими этой прямой точками А
и В,- конгруэнтен отрезку прямой Ь, ограниченному принадле-
принадлежащими этой прямой точками С и D.
Будем требовать, чтобы указанные соотношения удовлетво-
удовлетворяли формулируемым ниже двадцати аксиомам**).
Все аксиомы разделяются на пять групп.
Группа I содержит восемь аксиом принадлежности.
Группа II содержит четыре аксиомы порядка.
Группа III содержит пять аксиом конгруэнтности.
Группа IV содержит две аксиомы непрерывности.
Группа V содержит одну аксиому параллельности.
Переходим к формулировке аксиом по группам. Одновре-
Одновременно будем указывать некоторые утверждения, вытекающие
из формулируемых аксиом. Это поможет нам выяснить основ-
*) То есть «равен».
**) Во всем остальном как природа сайта объектов, так и способ зада-
задания соотношений между этими объектами являются произвольными.

206 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИЙ ГЕОМЕТРИИ
ные принципы логического развертывания геометрии и обосно-
обосновать возможность установления взаимно однозначного соответ-
соответствия между множеством всех точек прямой и множеством всех
вещественных чисел, т. е. обосновать метод координат.
1. Аксиомы принадлежности.
1.1. Каковы бы ни были две точки А и В, существует пря-
прямая а, которой принадлежат обе эти точки.
1.2. Каковы бы ни были две различные точки А и В, суще-
существует не более одной прямой, которой принадлежат эти точки.
1.3. Каждой прямой а принадлежат по крайней мере две
точки. Существуют по крайней мере три точки, не принадлежа-
принадлежащие одной прямой.
Указанные три аксиомы исчерпывают список аксиом принад-
принадлежности планиметрии. Следующие пять аксиом вместе с ука-
указанными тремя аксиомами завершают список аксиом принад-
принадлежности стереометрии.
1.4. Каковы бы ни были три точки А, В и С, не принадле-
принадлежащие одной прямой, существует плоскость а, которой принад-
принадлежат эти три точки. Каждой плоскости принадлежит хотя бы
одна точка.
1.5. Каковы бы ни были три точки А, В и С, не принадле-
принадлежащие одной прямой, существует не более одной плоскости, ко-
которой принадлежат эти точки.
1.6. Если две принадлежащие прямой а различные точки А
и В принадлежат некоторой плоскости а, то каждая принадле-
принадлежащая прямой а точка принадлежит указанной плоскости.
1.7. Если существует одна точка А, принадлежащая двум
плоскостям а и р, то существует по крайней мере еще одна
точка В, принадлежащая этим плоскостям.
1.8. Существуют по крайней мере четыре точки, не принад-
принадлежащие одной плоскости.
С целью использования привычной для нас геометрической
терминологии договоримся отождествлять между собой следую-
следующие выражения: 1) «точка А принадлежит прямой а (плоскости
а)»; 2) «прямая а (плоскость а) проходит через точки А»,
3) «точка А лежит на прямой а (на плоскости а)»; 4) «точка А
является точкой прямой а (плоскости а)» и т. п.
С помощью указанных аксиом уже могут быть доказаны
некоторые теоремы. Так, из аксиомы 1,2 непосредственно выте-
вытекает следующее утверждение.
Теорема 1. Две различные прямые не могут иметь больше
одной общей точки.
Предоставляем читателю доказательство следующих утвер-
утверждений, вытекающих из аксиом 1,1—8*).
*) В случае возникновения затруднений отсылаем читателя к книге
Н. В. Ефниова «Высшая геометрия», — М.: Наука, 1978.

e u аксиомы элементарной геометрии 207
Теорема 2. Две плоскости либо совсем не имеют общих то-
точек, либо имеют общую прямую, на которой лежат все их об-
общие точки.
Теорема 3. Плоскость и не лежащая на ней прямая не могут
иметь больше одной общей точки.
Теорема 4. Через прямую и не лежащую на ней точку или
через две различные прямые с общей точкой проходит одна и
только одна плоскость.
Теорема 5. Каждая плоскость содержит по крайней мере
три точки.
2. Аксиомы порядка.
11.1. Если точка В прямой а лежит между точками А и С
той же прямой, то А, В и С — различные точки указанной пря-
прямой, причем В лежит также и между С и А.
11.2. Каковы бы ни были две различные точки А и С, на
определяемой ими прямой существует по крайней мере одна
точка В такая, что С лежит между А и В.
11.3. Среди любых трех различных точек одной прямой
существует не более одной точки, лежащей между двумя дру-
другими.
Сформулированные три аксиомы относятся к расположению
геометрических объектов на прямой и поэтому называются ли-
линейными аксиомами порядка. Формулируемая ниже последняя
аксиома порядка относится к расположению геометрических
объектов на плоскости. Для того чтобы сформулировать
эту аксиому, введем понятие отрезка.
Пару различных точек А и В назовем отрезком и будем
обозначать символом АВ или ВА. Точки А я В будем называть
концами отрезка АВ. Точки прямой, определяемой А и В, лежа-
лежащие между А и В, будем называть внутренними точками или
просто точками отрезка АВ. Остальные точки указанной прямой
будем называть внешними точками отрезка АВ.
11.4. (аксиома Паша). Если А, В и С — три точки, не лежа-
лежащие на одной прямой, и а — некоторая прямая в плоскости,
определяемой этими точками, не содержащая ни одной из ука-
указанных точек и проходящая через некоторую точку отрезка АВ,
то эта прямая проходит также либо через некоторую точку от-
отрезка АС, либо через некоторую точку отрезка ВС.
Подчеркнем, что из одних аксиом порядка II, 1—4 еще не
вытекает, что любой отрезок имеет внутренние точки. Однако,
привлекая еще аксиомы принадлежности 1,1—3, можно дока-
доказать следующее утверждение.
Теорема 6. Каковы бы ни были две различные точки А
и В, на прямой, ими определяемой, существует по крайней мере
одна точка С, лежащая между А и В,

208 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
Предлагаем читателю, опираясь на аксиомы 1,1—8 принад-
принадлежности и аксиомы II, 1—4 порядка, последовательно доказать
следующие утверждения *).
Теорема 7. Среди любых трех различных точек одной пря-
прямой всегда существует одна точка, лежащая между двумя
другими.
Теорема 8. Если точки А, В и С не принадлежат одной пря-
прямой и если некоторая прямая а пересекает**) какие-либо два
из отрезков АВ, ВС и АС, то эта прямая не пересекает третий
из указанных отрезков.
Теорема 9. Если В лежит на отрезке АС и С — на отрезке
BD, то В и С лежат на отрезке AD.
Теорема 10. Если С лежит на отрезке AD, а В —на отрезке
АС, то В лежит также на отрезке AD, а С — на отрезке BD.
Теорема 11. Между любыми двумя различными точками
прямой существует бесконечно много других ее точек.
Теорема 12. Пусть каждая из точек С и D лежит между
точками А и В. Тогда если М лежит между С и D, то М лежит
и между А и В.
Теорема 13. Если точки С и D лежат между точками А и В,
то все точки отрезка CD принадлежат отрезку АВ (в этом слу-
случае мы будем говорить, что отрезок CD лежит внутри отрез-
отрезка АВ).
Теорема 14. Если точка С лежит между точками А и В, то:
1) никакая точка отрезка АС не может быть точкой отрезка СВ.
2) каждая отличная от С точка отрезка АВ принадлежит либо
отрезку АС, либо отрезку СВ.
Указанные утверждения позволяют упорядочить множество
точек любой прямой и выбрать иа этой прямой направление.
Будем говорить, что две различные точки А я В прямой а
лежат по разные стороны (по одну сторону) от третьей точки О
той же прямой, если точка О лежит (не лежит) между А я В.
Из указанных выше утверждений вытекает следующая теорема.
Теорема 15. Произвольная точка О каждой прямой а раз-
разбивает все остальные точки этой прямой на два непустых класса
так, что любые две точки прямой а, принадлежащие одному
и тому же классу, лежат по одну сторону от О, а любые две
точки, принадлежащие разным классам, лежат по разные сто-
стороны от О.
Таким образом, задание иа любой прямой двух различных
точек О я Е определяет иа этой прямой луч или полупрямую
ОЕ, обладающую тем свойством, что любая ее точка и точка Е
лежат по одну сторону от О.
*) Впрочем, доказательство всех приводимых ниже утверждений можно
найти в книге Н. В. Ефимова «Высшая геометрия» (цит. иа с. 206).
**) Под термином «прямая пересекает отрезок» мы подразумеваем, что
указанная прямая содержит некоторую внутреннюю точку этого отрезка.

S IJ АКСИОМЫ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ 209
Выбрав на прямой а две различные точки О и Е, мы можем
теперь определить порядок следования точек на прямой по
следующему правилу: 1) если А и В — любые точки луча ОЕ,
то будем говорить, что А предшествует В, если А лежит между
О и В; 2) будем говорить, что точка О предшествует любой
точке луча ОЕ; 3) будем говорить, что любая точка, не принад-
принадлежащая лучу ОЕ, предшествует как точке О, так и любой
точке, принадлежащей лучу ОЕ; 4) если А и В —любые точки,
не принадлежащие лучу ОЕ, то мы будем говорить, что А пред-
предшествует В, если В лежит между А и О.
Легко проверить, что для выбранного порядка следования
точек прямой а справедливо свойство транзитивно-
транзитивности: если А предшествует В, а В предшествует С, то А пред-
предшествует С.
Аксиомы, приведенные выше, позволяют упорядочить и точки,
принадлежащие произвольной плоскости а. Предлагаем чита-
читателю доказать следующее утверждение*).
Теорема 16. Каждая прямая а, принадлежащая плоскости а,
разделяет не лежащие на ней точки этой плоскости на два не-
непустых класса так, что любые две точки А и В из разных клас-
классов определяют отрезок АВ, содержащий точку прямой а, а лю-
любые две точки А и А' из одного класса определяют отрезок АА',
внутри которого не лежит ни одна точка прямой а.
В соответствии с утверждением этой теоремы мы будем го-
говорить, что точки А к А' (одного класса) лежат в плоскости а
по одну сторону от прямой а, а точки А и В (разных классов)
лежат в плоскости а по разные стороны от прямой а.
3. Аксиомы конгруэнтности.
111,1. Если А и В — две точки на прямой а, А' — точка на
той же прямой или на другой прямой а', то по данную от точ-
точки А' сторону прямой а' найдется, и притом только одна, точ-
точка В' такая, что отрезок А'В' конгруэнтен отрезку АВ. Каждый
отрезок АВ конгруэнтен отрезку В А **).
Ill, 2. Если отрезки А'В' и А"В" конгруэнтны одному и тому
же отрезку АВ, то они конгруэнтны и между собой.
111,3. Пусть АВ и ВС — два отрезка прямой а, не имеющие
общих внутренних точек, А'В' и В'С — два отрезка той же пря-
прямой или другой прямой а', также не имеющие общих внутрен-
*) В случае затруднений см. книгу Н. В. Ефимова «Высшая геомет-
рия> (цит. на с. 206).
**) Из этой аксиомы вытекает возможность перемещения отрезка АВ
вдоль прямой, иа которой он лежит (с сохранением его длины и направле-
направления). Будем говорить, что направленный отрезок CD получен в результате
перемещения направленного отрезка АВ, если отрезок CD конгруэнтен от-
отрезку АВ и если либо отрезок AD лежит внутри отрезка ВС, либо отрезок ВС
лежит виутрн отрезка AD.

210 ПРИЛОЖЕНИЕ ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
них точек. Тогда, если отрезок А В конгруэнтен отрезку А'В',
а отрезок ВС конгруэнтен отрезку В'С, то отрезок АС конгруэн-
конгруэнтен отрезку А'С.
Сформулированные три аксиомы относятся к конгруэнтности
отрезков. Для формулировки двух следующих аксиом нам по-
понадобится понятие угла и его внутренних точек.
Пара полупрямых h и k, выходящих из одной и той же точ-
точки О и не лежащих на одной прямой, называется углом и обо-
обозначается символом Z (Л, k) или Z (k, Л).
Если полупрямые Л и & задаются двумя своими точками
О А и ОВ, то мы будем обозначать угол символом ZAOB или
ZBOA.
В силу теоремы 4 любые два луча Л и k, составляющие угол
Z. (Л, k), определяют, и притом единственную, плоскость а.
Внутренними точками Z (Л, k) будем называть те точки пло-
плоскости а, которые, во-первых, лежат по ту сторону от прямой,
содержащей луч Л, что и любая точка луча k, и, во-вторых,
лежат по ту сторону от прямой, содержащей луч k, что и любая
точка луча Л.
111.4. Пусть даны Z(h,k) на плоскости а, прямая а' на этой
же или на какой-либо другой плоскости а' и задана определен-
определенная сторона плоскости а' относительно прямой а'. Пусть п' —
луч прямой а', исходящий из некоторой точки О'. Тогда на
плоскости а' существует один и только один луч k' такой, что
Z (Л, k) конгруэнтен Z. (Л', k'), и при этом все внутренние точки
Z (A', k') лежат по заданную сторону от прямой а'. Каждый
угол конгруэнтен самому себе.
111.5. Пусть А, В и С — три точки, не лежащие на одной пря-
прямой, А', В' и С — другие три точки, также не лежащие на
одной прямой. Тогда, если отрезок А В конгруэнтен отрезку
А'В', отрезок АС когруэнтен отрезку А'С и ZBAC конгруэнтен
ZB'A'C, то ZABC конгруэнтен ZA'B'C и Z.ACB конгруэнтен
ZA'C'B'.
Договоримся теперь о сравнении неконгруэнтных отрезков
и углов.
Будем говорить, что отрезок А В больше отрезка А'В', если
на прямой, определяемой точками А и В, найдется лежащая
между этими точками точка С такая, что отрезок АС конгруэн-
конгруэнтен отрезку А'В'. Будем говорить, что отрезок АВ меньше от-
отрезка А'В', если отрезок А'В' больше отрезка АВ.
Символически тот факт, что отрезок АВ меньше отрезка
А'В' (конгруэнтен отрезку А'В'), будем записывать так:
АВ<А'В' (АВ = А'ВГ).
Будем говорить, что ZAOB больше ZA'&B', если в пло-
плоскости, определяемой ZAOB, найдется луч ОС, все точки ко-

§ II АКСИОМЫ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ 211
торого являются внутренними точками Z.AOB, такой, что Z.AOC
конгруэнтен Z.A'0'В'. Будем говорить, что Z.AOB меньше
ZA'O'B', если ZA'O'B' больше ZAOB.
С помощью аксиом принадлежности, порядка и конгруэнт-
конгруэнтности можно доказать целый ряд классических теорем элемен-
элементарной геометрии. Сюда относятся: 1) три широко известные
теоремы о конгруэнтности (равенстве) двух треугольников;
2) теорема о конгруэнтности вертикальных углов; 3) теорема
о конгруэнтности всех прямых углов; 4) теорема о единствен-
единственности перпендикуляра, опущенного из точки на прямую; 5) тео-
теорема о единственности перпендикуляра, восстановленного из
данной точки прямой; 6) теорема о внешнем угле треугольника;
7) теорема о сравнении перпендикуляра и наклонной.
Предлагаем читателю самому последовательно доказать
только что перечисленные теоремы.
4. Аксиомы непрерывности. С помощью аксиом принадлеж-
принадлежности, порядка и конгруэнтности мы произвели сравнение отрез-
отрезков, позволяющее заключить, каким из трех знаков <С, = или
> связаны данные два отрезка.
Указанных аксиом, однако, недостаточно: 1) для обоснова-
обоснования возможности измерения отрезков, позволяющего поставить
в соответствие каждому отрезку определенное вещественное
число; 2) для обоснования того, что указанное соответствие яв-
является взаимно однозначным.
Для проведения такого обоснования следует присоединить
к аксиомам I, II, III две аксиомы непрерывности.
IV, 1 (аксиома Архимеда). Пусть АВ и CD — произвольные
отрезки. Тогда на прямой, определяемой точками А и В, суще-
существует конечное число точек А\, А2, ..., АП, располоокенных так,
что точка А\ лежит между А и А2, точка А2 лежит между Ai
и Аг, ..., точка Ап-\ лежит между А„-2 и Ап, причем отрезки
ААи А\А2 Ап-\А„ конгруэнтны отрезку CD и точка В ле-
лежит между А и Ап.
IV, 2 (аксиома линейной полноты). Совокупность всех точек
произвольной прямой а нельзя пополнить новыми объектами
(точками) так, чтобы: 1) на пополненной прямой были опреде-
определены соотношения «лежит между» и «конгруэнтен», определен
порядок следования точек и справедливы аксиомы конгруэнт-
конгруэнтности III, 1—3 и аксиома Архимеда IV, 1; 2) по отношению
к прежним точкам прямой определенные на пополненной прямой
соотношения *лежит между* и «конгруэнтен» сохраняли ста-
старый смысл.
Мы сейчас докажем, что присоединение к аксиомам I, I—3,
II и III, 1—3 аксиомы Архимеда IV, 1 позволяет поставить в со-
соответствие каждой точке произвольной прямой а определенное
вещественное число х, называемое координатой этой точки,
а присоединение еще и аксиомы линейной полноты IV, 2 позво-

212 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
ляет утверждать, что координаты всех точек прямой а исчер-
исчерпывают множество всех вещественных чисел.
5. Обоснование метода координат. Прервем на время изло-
изложение аксиом геометрии, чтобы на основании уже изложенных
аксиом дать обоснование метода координат на прямой.
Сначала докажем следующее утверждение.
Первая основная теорема. Аксиомы I, 1—3, II, III, 1—3 и
аксиома IV, 1 Архимеда позволяет ввести на любой прямой а
координаты так, что выполнены следующие требования:
1°. Каждой точке М прямой а соответствует определенное
вещественное число х, называемое ее координатой.
2°. Разным точкам соответствуют разные координаты, при-
причем точка Mz лежит между М\ и М3 тогда и только тогда, когда
либо Xi<.x2<Zx3, либо Xi'>x2'>Xz (здесь Х\, х2 и х3 — коор-
координаты точек Mi, М2 и М% соответственно).
3°. Отрезки М\Мг и М[М'г конгруэнтны тогда и только тогда,
когда х2 — х\ = х'2 — х[ (здесь хи х2, х[ и х'г — координаты точек
М\, М2, М[ и М'2 соответственно).
4°. Если вещественные числа х\ и х2 представляют собой ко-
координаты некоторых точек, то и вещественное число х\ ± х2
представляет собой координату некоторой точки.
Доказательство. Выберем на прямой а произвольную
точку О в качестве начала координат и произвольную отличную
от О точку Е в качестве точки с координатой единица. Пусть
М — произвольная точка прямой а. Ради определенности пред-
предположим, что М лежит с той же стороны от О, что и Е (аксио-
(аксиомы 1,1—3, II и III, 1—3 обеспечивают возможность установле-
установления порядка следования точек на прямой а). Каковы бы ни
были целое положительное число п и целое неотрицательное
число пг, мы можем, откладывая отрезок ОМ в одном и том же
направлении последовательно п раз, построить отрезок п-ОМ
и аналогично построить отрезок пг-ОЕ (возможность отклады-
откладывать конгруэнтный отрезок в любом направлении и брать сумму
конгруэнтных отрезков, не имеющих общих внутренних точек,
вытекает из аксиом 1,1—3, II и III, 1—3).
В силу только что упомянутых аксиом любые два отрезка
мы можем сравнивать. Стало быть, и отрезки п-ОМ и пг-ОЕ
при различных пит будут связаны либо знаком <С, либо
знаком ^.
Рассмотрим все возможные рациональные числа /л/л. Их
можно разбить на два класса, относя к верхнему классу те из
них, для которых
п-0М<ш-ОЕ, (П.1)
и к нижнему классу те, для которых
п-ОМ^ш-ОЕ. (П.2)

§ 11 АКСИОМЫ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ 213
Убедимся в том, что эти два класса однозначно определяют
вещественное число х, которое мы и поставим в соответствие
точке М и назовем ее координатой.
Сначала убедимся в том, что любое рациональное число из
верхнего класса больше любого рационального числа из ниж-
нижнего класса. Приводя любые два рациональных числа из раз-
разных классов к общему знаменателю и обозначая последний че-
через п, мы из (П.1) н (П > получим, что числитель числа из
верхнего класса больше числителя числа из нижнего класса.
Отсюда и вытекает, что число из верхнего класса больше числа
нз нижнего класса.
Далее заметим, что оба класса не являются пустыми: ниж-
нижнему классу заведомо принадлежит рациональное число нуль,
а для установления непустоты верхнего класса достаточно по-
положить л=1 и заметить, что аксиома Архимеда IV, 1 гаран-
гарантирует существование такого натурального числа пг, что при
п= 1 справеливо неравенство (П.1).
В силу теоремы о точных гранях непустого ограниченного
сверху (снизу) множества *) существует точная верхняя грань
х рациональных чисел нижнего класса и точная нижняя грань
х рациональных чисел верхнего класса.
Убедимся в том, что эти грани х и х заключены между как
угодно близкими рациональными числами и поэтому совпа-
совпадают**). Достаточно доказать, что существуют как угодно
близкие числа разных классов, а это вытекает из того, что для
как угодно большого номера п найдется номер m такой, что ра-
рациональное число (ш + \)/п приналежит верхнему классу, а ра-
рациональное число т/п принадлежит нижнему классу***).
Положим теперь х = х = х и поставим вещественное число х
в соответствие точке М, назвав его координатой этой точки. Тре-
Требование Г обосновано.
Пусть теперь Mi и М*— какие угодно две точки, лежащие
по ту же сторону от О, что и Е, и такие, что Mi лежит между О
и М2, т. е. OMz > OMi. Докажем, что если xi и х% — координаты
точек Mi и Mi соответственно, то Х2 > xi.
Выберем номер п настолько большим, чтобы разность отрез-
отрезков ОМ2 и 0М\, повторенная п раз, превзошла отрезок ОЕ (это
можно сделать в силу все той же аксиомы Архимеда IV, 1).
Тогда, обозначая через m наибольшее целое число, для кото-
которого
п • OMi > ш ¦ ОЕ,
*) См. выпуск 1, теорему 2.1.
**) См. выпуск 1, лемму на с.48.
***) Тот факт, что для любого номера я найдется указанный номер m
(такой, что справедливо (П1)), снова вытекает нз аксиомы Архимеда IV, I.

214 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
мы получим, что
п • ОМ1 < (т + 1) • ОЕ, (П.З)
и в силу сделанного выше выбора номера п
п • ОМ2 >{т + 1) • ОЕ. (П.4)
Из (П.З) заключаем, что рациональное число (т-\-\)/п отно-
относится к верхнему классу по отношению к точке М\, т. е. (т +
4-l)/n ^ *i, а из (П.4) заключаем, что то же самое рацио-
рациональное число (т-\- \)/п относится к нижнему классу по отно-
отношению к точке М2, и поэтому х2~>(т-\-\)/п. Тем самым не-
неравенство Х2 > xi доказано.
Если теперь мы имеем на прямой а какое угодно число то-
точек, идущих в порядке О, Mi, М2 Мп (в сторону ?*)),
то из только что доказанного утверждения для координат этих
точек получим О < х\ <. х2 < ... < хп.
Тем самым для случая расположения точек по ту же сторону
от О, что и Е, требование 2° доказано. Для точек М, лежащих
на прямой а по другую сторону от О, совершенно аналогично
вводятся отрицательные координаты и повторением тех же рас-
рассуждений мы устанавливаем требования 1° и 2° в общем виде.
Для установления требований ° и 4° мы сначала докажем,
что если на прямой а в положительную сторону от О взяты
точки Mi, М2 и М, причем Mt лежит между О и М и отрезки
МХМ и ОМ2 конгруэнтны, то x = xt + x2 (здесь х, xi и х2 —
координаты точек М, М\ и М2 соответственно).
Возьмем из нижних классов, отвечающих координатам х\
и х2, два произвольных рациональных числа, обозначив их (пос-
(после приведения к общему знаменателю п) соответственно через
т\/п и гп2/п. Тогда
п • 0Мх >т, • ОЕ, n-OM^nuf ОЕ.
Складывая последние два неравенства, получим
га • ОМ>(т, + т2) • ОЕ. (П.5)
Точнее говоря, в левой части (П.5) мы получим сумму п раз
отложенного отрезка ОМ\ и п раз отложенного отрезка OAfj,
но после перегруппировки слагаемых мы н получим п раз по-
повторенную сумму отрезков 0М\ и ОМ2, т. е. п-ОМ **).
*) В дальнейшем эта сторона именуется положительной.
**) То, что в геометрической сумме отрезков мы можем, не меняя суммы,
переставлять слагаемые, вытекает из следующих соображений. Достаточно
убедиться в возможности перестановки для двух слагаемых, а это непосред-
непосредственно вытекает из аксиомы III, 3, в формулировке которой ничего не ска-
сказано о порядке, в котором «приставляются» друг к другу слагаемые отрезки
А'В' и В'С. При любом нх порядке сумма кС конгруэнтна отрезку АС.

§ 1] АКСИОМЫ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ 215
Из неравенства (П.5) заключаем, что рациональное число
?h- _|_ J0*. принадлежит нижнему классу, отвечающему ко-
координате х.
Совершенно аналогично, взяв любые рациональные числа
Ш\/п и тг/я из верхних классов, отвечающих координатам Jti
_, ttl\ ¦ /По
и х2, мы убедимся в том, что рациональное число — + —
принадлежит верхнему классу, отвечающему координате х.
Но тогда из определения суммы вещественных чисел и из
того, что рациональные числа как из верхнего, так н из ниж-
нижнего классов как угодно точно приближают соответствующую
координату, мы получим, что вещественное число х равно сум-
сумме х\ + хг.
Тем самым нами доказано, что отложить от точки Му с ко-
координатой х\ (в положительную сторону) отрезок ОМ2 — это
все равно, что построить точку М с координатой х, удовлетво-
удовлетворяющей условию х = Х\ + Хг, где хз ~> 0 — координата точки Мъ.
Это утверждение мы доказали для случая Х\ > 0, но легко
распространить его н на общий случай (предоставляем это чи-
читателю). Из доказанного утверждения сразу же вытекает тре-
требование 4°, а для доказательства утверждения 3° достаточно
заметить, что откладывание данного отрезка равносильно до-
добавлению к координате точки постоянного слагаемого. Первая
основная теорема полностью доказана*).
Замечание. Особо подчеркнем, что в первой основной тео-
теореме не утверждается, что каждому вещественному числу х со-
соответствует определенная точка на прямой (т. е. не утверждает-
утверждается, что соответствие между точками прямой и вещественными
числами является взаимно однозначным).
Мы сейчас увидим, что это невозможно доказать, опираясь
только на аксиомы I, 1—3, II, III, 1—2 и IV, 1 и не привлекая
аксиому линейной полноты IV, 2.
Вторая основная теорема. Пусть справедливы аксиома I,
1—3, II, III, 1—3, IV, 1 и на прямой а введены координаты.
Тогда, для того чтобы каждому вещественному числу х отвечала
некоторая точка прямой а, т. е. для того, чтобы между всеми
точками прямой а и всеми вещественными числами существо-
существовало взаимно однозначное соответствие, необходимо и достаточ-
достаточно, чтобы была справедлива аксиома линейной полноты IV, 2.
Доказательство. 1) Достаточность. Докажем, что
если существуют вещественные числа х, которым не отвечает
никакая точка прямой а, то аксиома IV, 2 заведомо несправед-
несправедлива.
*) Подчеркнем, что при доказательстве пераой основной теоремы аксио-
аксиомы I, 1—3 и II использовались лишь для установления порядка следования
точек на прямой.

216 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
Пусть существуют указанные вещественные числа х. Каж-
Каждое из иих мы назовем новой точкой и присоединим все новые
точки к совокупности прежних точек прямой а.
На пополненной прямой (назовем ее а) уже каждому ве-
вещественному числу отвечает точка, и обратно.
Определим на а соотношения «лежит между» и «конгруэн-
«конгруэнтен». Будем говорить, что точка М2 прямой а лежит между Mi
и Мз, если либо х\ < х2 <Z *з. либо х\ > Xi > хз, где под х\,
х2 и х3 нужно понимать координату соответствующей точки Ми
М2 и М3, если эта точка прежняя, и самую эту точку, если она
новая. Очевидно, что в применении к прежним точкам опреде-
определенное на а соотношение «лежит между» сохраняет старый
смысл.
Будем говорить, что отрезок М\М2 прямой а конгруэнтен
отрезку той же прямой М\М'2, если х2 — хх = х'2 — х[, где под
xv x2, х\ и х'2 нужно понимать координату соответствующей
точки Ми М2, М\ и М'2, если эта точка прежняя, и самую эту
точку, если она новая. Снова очевидно, что в применении к
прежним точкам определенное на а соотношение «конгруэнтен»
сохраняет старый смысл.
Очевидно также, что для точек пополненной прямой а опре-
определен порядок следования и справедливы аксиомы конгруэнт-
конгруэнтности III, 1—3 и аксиома Архимеда IV, 1.
Тем самым мы установили возможность пополнения прямой,
противоречащую аксиоме линейной полноты IV, 2.
Достаточность доказана.
2. Необходимость. Докажем, что если аксиома линей-
линейной полноты IV, 2 не имеет места, то координаты всех точек
прямой а не исчерпывают всех вещественных чисел.
Если аксиома VI, 2 не имеет места, то существует пополнен-
пополненная новыми точками прямая а, для всех точек которой опреде-
определены соотношения «лежит между» и «конгруэнтен», определен
порядок следования и справедливы аксиомы конгруэнтности
111,1—3 и аксиома Архимеда IV, 1. В силу первой основной
теоремы на пополненной прямой а можно ввести координаты
(в этой теореме аксиомы 1,1—3 и II использовались лишь в
форме возможности установления на данной прямой порядка
следования точек).
Мы получим, что каждой точке пополненной прямой а отве-
отвечает определенное вещественное число, причем разным точкам
отвечают различные вещественные числа. Но отсюда следует,
что те вещественные числа, которые отвечают точкам, произво-
производящим пополнение, не будут соответствовать ни одной точке
исходной прямой а. Необлходимость доказана. Вторая основная
теорема полностью доказана.

§2] НЕПРОТИВОРЕЧИВОСТЬ'ГЕОМЕТРИИ ЕВКЛИДА 217
6. Аксиома параллельности. Самая последняя аксиома
играет в геометрии фундаментальную роль, определяя разделе-
разделение геометрии на две логически непротиворечивые и взаимно
исключающие друг друга системы: евклидову и неевклидову
геометрии.
В геометрии Евклида эта аксиома формулируется так:
V. Пусть а—произвольная-прямая и А— точка, лежащая
вне прямой а, тогда в плоскости а, определяемой точкой А и
прямой а, существует не более одной прямой, проходящей че-
через А и не пересекающей а.
Долгое время геометры выясняли вопрос о том, не является
ли аксиома параллельности V следствием всех остальных
аксиом I, II, III, IV. Этот вопрос был решен Лобачевским*),
который доказал, что аксиома V не является следствием аксиом
I—IV.
По-другому результат Лобачевского можно сформулировать
так: если к аксиомам I—IV присоединить утверждение, отри-
отрицающее справедливость аксиомы V, то следствия всех этих по-
положений будут составлять логически непротиворечивую систему
(неевклидову геометрию Лобачевского).
Схема доказательства непротиворечивости геометрии Лоба-
Лобачевского излагается в § 3 настоящего Приложения.
Здесь же мы отметим, что систему следствий, вытекающих
из одних только аксиом I—IV, обычно называют абсолютной
геометрией. Абсолютная геометрия является общей частью как
евклидовой, так и неевклидовой геометрий, ибо все предложе-
предложения, которые могут быть доказаны только с помощью аксиом
I—IV, верны как в геометрии Евклида, так и в геометрии Ло-
Лобачевского (примеры таких предложений читатель найдет в
предыдущих пунктах).
§ 2. Схема доказательства непротиворечивости
геометрии Евклида
Наметим схему доказательства непротиворечивости всех пяти
групп аксиом геометрии Евклида.
Ради простоты ограничимся доказательством, непротиво-
непротиворечивости планиметрии Евклида, т. е. установим не-
непротиворечивость системы аксиом I, 1—3, II—V.
Для доказательства достаточно построить какую-нибудь кон-
конкретную реализацию совокупности объектов, удовлетворяющих
всем указанным аксиомам.
Мы построим так называемую декартову или арифметиче-
арифметическую реализацию совокупности объектов, удовлетворяющих
*) Николай Иванович Лобачевский — великий русский математик A793—
1856).

218 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
аксиомам планиметрии. Тем самым вопрос о непротиворечиво-
непротиворечивости планиметрии Евклида будет сведен к вопросу о непротиво-
непротиворечивости арифметики.
Назовем точкой любую упорядоченную пару вещественных
чисел (х, у), а прямой — отношение трех вещественных чисел
(w.v'.w) при условии, что и2 + v2 Ф 0 *).
Будем говорить, что точка (х, у) принадлежит прямой
(и : v : w), если справедливо равенство
их + vy + w = 0. (П.6)
Докажем справедливость аксиом I, 1—3.
Каковы бы ни были две различные точки (х\,у\) и (х2, {/г)>
прямая **) (г/i — у2: хг — х\ : х\у2 — *2«/i), как легко убедиться,
содержит эти точки (аксиома 1,1).
Далее из уравнений
ых, + Щ\ + w — 0, их2 + vy2 + w = 0
вытекает, что u:v:w=(yi—y2):(x2 — xl):(x1y2 — x2yi), так
что точками (хи у{) и (х2, у%) определяется только одна пря-
прямая (u:v:w) (аксиома 1,2).
Наконец, справедливость аксиомы 1,3 вытекает из того, что
уравнение (П.6) с двумя неизвестными хну всегда имеет бес-
бесчисленное множество решений и не всякая пара х и у есть ре-
решение уравнения (П.6).
Теперь определим соотношение «лежит между». Так как
и2 + v2 Ф 0, то либо и ф 0, либо v ф 0.
Если v Ф 0, то будем говорить, что точка (х2, у2) лежит ме-
между (хи yi) и (х3, уз), если либо xt < х2 < х3, либо Х\ > Хг >
> хз. Если же и=0 (при этом заведомо иФО), то будем го-
говорить, что точка (х2,уз) лежит между (хь yi) и (х3, у3), если
либо г/i < г/2 < Уз, либо ух > у2 > у3.
Справедливость аксиом II, 1—3 проверяется тривиально.
Несколько кропотливую проверку аксиомы Паша II, 4 мы опу-
опустим.
Обратимся теперь к определению соотношения «конгруэн-
«конгруэнтен». С этой целью рассмотрим так называемое ортогональное
преобразование. Преобразование
х' = аух + Ь& + си у'=*а2х + Ь2у + с2, (П.7)
*) Отношением (и; v: w) называется совокупность трех вещественных
чисел и, v, w прн условии, что прн любом X ф 0 совокупности и, о, w и
\и, Xv, \w рассматриваются как тождественные.
••) Так как точки (*i, y\) и (хг, уг) различны, то (*i— *г)Ч-(У1—9г)гФ
Ф0

§ 21 НЕПРОТИВОРЕЧИВОСТЬ ГЕОМЕТРИИ ЕВКЛИДА 219
переводящее произвольную точку (х, у) в определенную точку
С*'»*/')» называется ортогональным, если выполнены соотно-
соотношения
а? + *?«1, а\ + Щ=\, од + бД-О. (П.8)
Легко доказать, что всякое ортогональное преобразование
(П.7), (П.8) можно представить в одной из следующих форм:
либо в виде
х' = ах — р«/ + сь г/' = р* + ш/ + с2, (п.9)
либо в виде
х'*=ах + $у + си yf = рх - ay + с2, (П.10)
причем в обоих случаях а2+р2 = 1. Преобразования (П.9) и
(П.10) обычно называют ортогональными преобразованиями со-
соответственно первого и второго рода.
Пусть даны произвольная прямая (и :v:w) и на ней неко-
некоторая точка (хо, у0), так что их0 + vy0 + w = 0.
Легко убедиться в том, что совокупность точек (х,у), где
принадлежит прямой (и :v : w) для любого вещественного чис-
числа /. Далее ясно, что при t > 0 все указанные точки (х, у) ле-
лежат по одну сторону от точки (хо, г/о), а при / < 0 эти точки
лежат по другую сторону от (х0, уо).
Иными словами, уравнения (П.11) при всевозможных поло-
положительных / определяют все точки полупрямой, исходящей из
точки (хо, уо) и лежащей на прямой (u:v:w). Эту полупрямую
мы будем обозначать символом (хо, yQ, v, —и).
Оказывается, всякое ортогональное преобразование (как
первого, так и второго рода) переводит любую полупрямую
снова в полупрямую. Более точно, справедливо следующее
утверждение: ортогональное преобразование (П.9) или (П.10)
переводит полупрямую (х0, уа, v, —и) в полупрямую
(*о« Уо* v> —"')' где для случая преобразования (П.9)
xfQ = ax0— р«/0 + с,: Уо=$хо
ы' = —
и для случая преобразования (П.10)
х'0 = ах°+ РУо + с,; y'Q = р*0 - ау0 + с2;
о' = av — ри; и' = — ро — аи.
Теперь назовем отрезок АВ конгруэнтным отрезку А'В', если
существует ортогональное преобразование, которое переводит

220
ПРИЛОЖЕНИЕ ПРОБЛЕМЫ ОСНОВАНИИ ГЕОМЕТРИИ
точку А в точку А', а точку В в точку В'. Угол /L{h,k) назо-
назовем конгруэнтным Z.(A', k'), если существует ортогональное
преобразование, переводящее полупрямую h в полупрямую h'
и полупрямую k в полупрямую k'.
Далее нужно перейти к проверке аксиом III, 1—5. Аксиома
111,2 вытекает из групповых свойств ортогонального преобра-
преобразования, в силу которых как последовательное проведение двух
ортогональных преобразований, так и преобразование, обрат-
обратное к ортогональному, снова являются ортогональными преоб-
преобразованиями. Проверка остальных аксиом группы III требует
кропотливой техники и использования указанного выше утвер-
утверждения, и мы ее опустим.
Что же касается аксиом непрерывности, то аксиома Архи-
Архимеда IV, 1 проверяется непосредственно, а справедливость
аксиомы полноты IV, 2 вытекает из того, что между всеми точ-
точками любой прямой и всеми вещественными числами можно
установить взаимно однозначное соответствие (см. вторую
основную теорему из п. 5 § 1).
Нам остается еще проверить справедливость аксиомы па-
параллельности V. Пусть (и : v : w)—произвольная прямая и
(*о, Уо) — точка вне ее, так что их0 + 0«/о + w ф 0.
Пусть {и! : v': w') — прямая, проходящая через точку
(*о> Уо). т. е. удовлетворяющая условию
u'xo + v'yQ + w' = Q. (П. 12)
Поскольку эта прямая не пересекает прямую (u:v:w), долж-
должна быть несовместна система уравнений
Из несовместности системы (П.13) заключаем, что и': и =
= о': v, или, что то же самое, и' = Хи, v' = %v, где Я — неко-
некоторое число. Но тогда из (П.12) получим w' = — А,(ых0 + vy0),
т. е. и': v': w' = и : v : — (ихо + vy0) ¦ Итак, отношения и': v': w'
однозначно определены, т. е. существует единственная прямая
(и': v': w'), проходящая через (х0, уо) и не пересекающая пря-
прямой (и : v : w).
Тем самым доказательство непротиворечивости планиметрии
Евклида завершено.
Замечание. Аналогично доказывается непротиворе-
непротиворечивость стереометрии Евклида. Для этого мы назы-
называем точкой любую упорядоченную тройку вещественных чисел
(x,y,z), прямой — совокупность всех троек (х, у, г), элементы
х, у, z которых связаны системой двух линейных уравнений,
плоскостью — совокупность всех троек (х, у, г), элементы х, у, г
которых удовлетворяют одному линейному уравнению.

5 3J НЕПРОТИВОРЕЧИВОСТЬ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО 221
§ 3. Схема доказательства непротиворечивости
геометрии Лобачевского
Для простоты ограничимся доказательством непро-
непротиворечивости планиметрии Лобачевского, т. е.
построим конкретную реализацию совокупности объектов, удов-
удовлетворяющих аксиомам I, 1—3, II—IV и аксиоме, отрицающей
справедливость V. Для построения указанной реализации мы
будем опираться на уже установленную нами непротиворечи-
непротиворечивость планиметрии Евклида, т. е. сведем вопрос о непротиворе-
непротиворечивости планиметрии Лобачевского к вопросу о непротиворечи-
непротиворечивости планиметрии Евклида. Излагаемая в этом параграфе мо-
модель принадлежит А. Пуанкаре*).
Рассмотрим на евклидовой плоскости горизонтальную пря-
прямую х и опирающуюся на нее верхнюю полуплоскость.
Все точки этой верхней полуплоскости мы назовем неевкли-
неевклидовыми точками, а все лежащие в верхней полуплоскости полу-
полуокружности с центром на прямой х и все вертикальные полу-
полупрямые, исходящие из точек прямой х, назовем неевклидовыми
прямыми (кстати, указанные полупрямые удобно рассматривать
как полуокружности бесконечно большого радиуса).
Мы определим между неевклидовыми точками и неевклидо-
неевклидовыми прямыми соотношения «принадлежит», «лежит между» и
«конгруэнтен» и убедимся в справедливости всех аксиом
абсолютной геометрии (т. е. аксиом 1,1—3, II—IV).
После этого мы покажем, что в построенной модели справед-
справедлива аксиома параллельности Лобачевского (т. е. отрицание
аксиомы V Евклида).
Мы будем говорить, что неевклидова точка А принадлежит
неевклидовой прямой а, если точка верхней полуплоскости А
лежит на полуокружности а.
Справедливость аксиом I,1—3 устанавливается тривиально.
Так, аксиомы I, 1 и 1,2 эквивалентны утверждению, что через
две точки верхней полуплоскости можно провести только одну
окружность, имеющую центр на прямой х. Аксиома 1,3 эквива-
эквивалентна утверждению, что на любой полуокружности имеются по
крайней мере две точки и имеется хотя бы одна точка вне этой
полуокружности.
Перейдем к установлению соотношения «лежит между».
Пусть А, В, С — три точки неевклидовой прямой, изображаемой
полуокружностью а. Будем говорить, что точка В (в неевкли-
неевклидовом смысле) лежит между А и С, если В на полуокружности
а лежит между Л и С (в евклидовом смысле).
При таком определении соотношения «лежит между» легко
устанавливается справедливость аксиом II, 1—3. Впрочем, по-
*) Анри Пуанкаре — французский математик A854—1912).

222 ПРИЛОЖЕНИЕ. ПРОБЛЕМЫ ОСНОВАНИЯ ГЕОМЕТРИИ
рядку следования точек на неевклидовой прямой, изображае-
изображаемой полуокружностью а, можно придать и более наглядный
вид. Выпуская из центра О полуокружности а всевозможные
лучи, мы с помощью этих лучей можем взаимно однозначно
спроектировать все точки полуокружности а на все точки не-
некоторой прямой у, параллельной х и лежащей выше полуокруж-
полуокружности а.
Тогда порядок следования точек неевклидовой прямой а со-
соответствует порядку следования образов этих точек на прямой
у. Попутно докажем, что все точки любой неевклидовой прямой
а находятся во взаимно однозначном соответствии с множеством
всех вещественных чисел.
Нам еще следует проверить аксиому II, 4 Паша, но доказа-
доказательство этой аксиомы является наглядно вполне очевидным,
и мы его опустим.
Теперь мы перейдем к определению соотношения «конгруэн-
«конгруэнтен». В надлежащем его определении и состоит остроумие мо-
модели Пуанкаре. Не вдаваясь в детали, остановимся на основных
идеях определения этого соотношения.
Введем в рассмотрение специальное преобразование евкли-
евклидовой плоскости, известное под названием инверсии. Пусть фик-
фиксирована произвольная окружность радиуса г с центром в точ-
точке А. Инверсией относительно указанной окружности называет-
называется такое преобразование точек плоскости, при котором любая,
отличная от А точка плоскости М переходит в точку ЛГ, лежа-
лежащую на одном с точкой М луче, выходящем из А, и такую, что
выполнено условие AM'-AM = r2.
Назовем неевклидов отрезок АВ конгруэнтным неевклидову
отрезку А В', если существует такая последовательность инвер-
инверсий, что их произведение отображает евклидову круговую дугу
АВ в круговую дугу А'В'.
Неевклидовым углом будем называть совокупность двух не-
неевклидовых полупрямых, исходящих из одной точки.
Назовем неевклидов угол Z.(h',k') конгруэнтным неевкли-
неевклидову углу Z.(h,k), если существует такая последовательность
инверсий, что их произведение отображает стороны первого
угла на стороны второго.
После принятых определений проверка аксиом конгруэнтно-
конгруэнтности III, 1—5 превращается в техническую работу, которую мы
можем опустить.
Проверка аксиомы Архимеда IV, 1 также ие вызывает ни-
никаких трудностей и использует лишь свойства инверсий.
Последняя аксиома абсолютной геометрии — аксиома полно-
полноты IV.2 справедлива вследствие того, что (как это установлено
выше) между всеми точками любой «неевклидовой прямой» и
всеми вещественными числами можно установить взаимно одно-
однозначное соответствие (см. вторую основную теорему из п. 5 § 1).

i 4] ЗАМЕЧАНИЯ О ПРОБЛЕМАХ АКСИОМАТИКИ 223
Итак, для нашей модели справедливы все аксиомы абсолют-
абсолютной геометрии (I, 1—3, II—IV).
Как же обстоит дело с аксиомой параллельности V? Возь-
Возьмем любую «неевклидову прямую», изображаемую полуокруж-
полуокружностью а, и любую точку А, ей не принадлежащую. Легко про-
проверить, что через точку А проходит бесконечно много различ-
различных полуокружностей, имеющих центры на прямой х и не имею-
имеющих общих точек с полуокружностью а.
Это означает, что в рассматриваемой нами модели справед-
справедлива аксиома параллельности Лобачевского.
Тем самым мы завершили доказательство непротиворечиво-
непротиворечивости планиметрии Лобачевского и одновременно показали, что
аксиома параллельности V Евклида не является следствием
аксиом 1,1—3, II—IV абсолютной геометрии.
§ 4. Заключительные замечания о проблемах аксиоматики
При изучении любой системы аксиом естественно возникают
следующие три проблемы: 1) проблема непротиворечивости си-
системы аксиом; 2) проблема минимальности системы аксиом
(выясняющая вопрос о том, не является ли каждая из рассмат-
рассматриваемых аксиом следствием остальных); 3) проблема полноты
системы аксиом (принято систему аксиом называть полной,
если между элементами двух любых ее реализаций можно уста-
установить взаимно однозначное соответствие, сохраняющее уста-
установленные между элементами соотношения).
В § 2 и 3 мы установили непротиворечивость системы аксиом
как геометрии Евклида, так и геометрии Лобачевского.
Проблема минимальности системы аксиом геометрии являет-
является очень трудоемкой и требует обстоятельного исследования.
Примером такого исследования является установленный нами
факт, что аксиома параллельности V не является следствием
остальных аксиом.
Полнота системы аксиом геометрии устанавливается посред-
посредством введения для любой реализации координатной системы и
последующего установления взаимно однозначного соответствия
(с сохранением всех соотношений) между точками, прямыми и
плоскостями данной реализации (в координатной записи) и де-
декартовой реализации, изученной в § 2.

ISBN 5-02-015234-Х
Учебное издание
ИЛЬИН Владимир Александрович,
ЛОЗНЯК Эдуард Генрихович
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Серия «Курс высшей математики и математической физики»
Редактор М М Горячая
Корректоры И Я Кришталь, Н Д Храпко
ЛР№ 020297 от 23.06.97.
Подписано в печать с готовых диапозитивов 20.06.98.
Формат 60x90Vi6. Бумага типографская. Печать офсетная.
Усл. печ. л. 14. Уч.-изд. л. 14,76. Тираж 5000 экз.
Заказ 168. С-025.
Издательская фирма
«Физико-математическая литература «РАН»
117071, Москва В-71, Ленинский проспект, 15.
При участии ООО «Харвест». Лицензия ЛВ № 32 от 27.08.97.
220013, Минск, ул. Я. Коласа, 35 — 305.
Отпечатано с готовых диапозитивов заказчика
в типографии издательства «Белорусский Дом печати».
220013, Минск, пр. Ф. Скорины, 79.