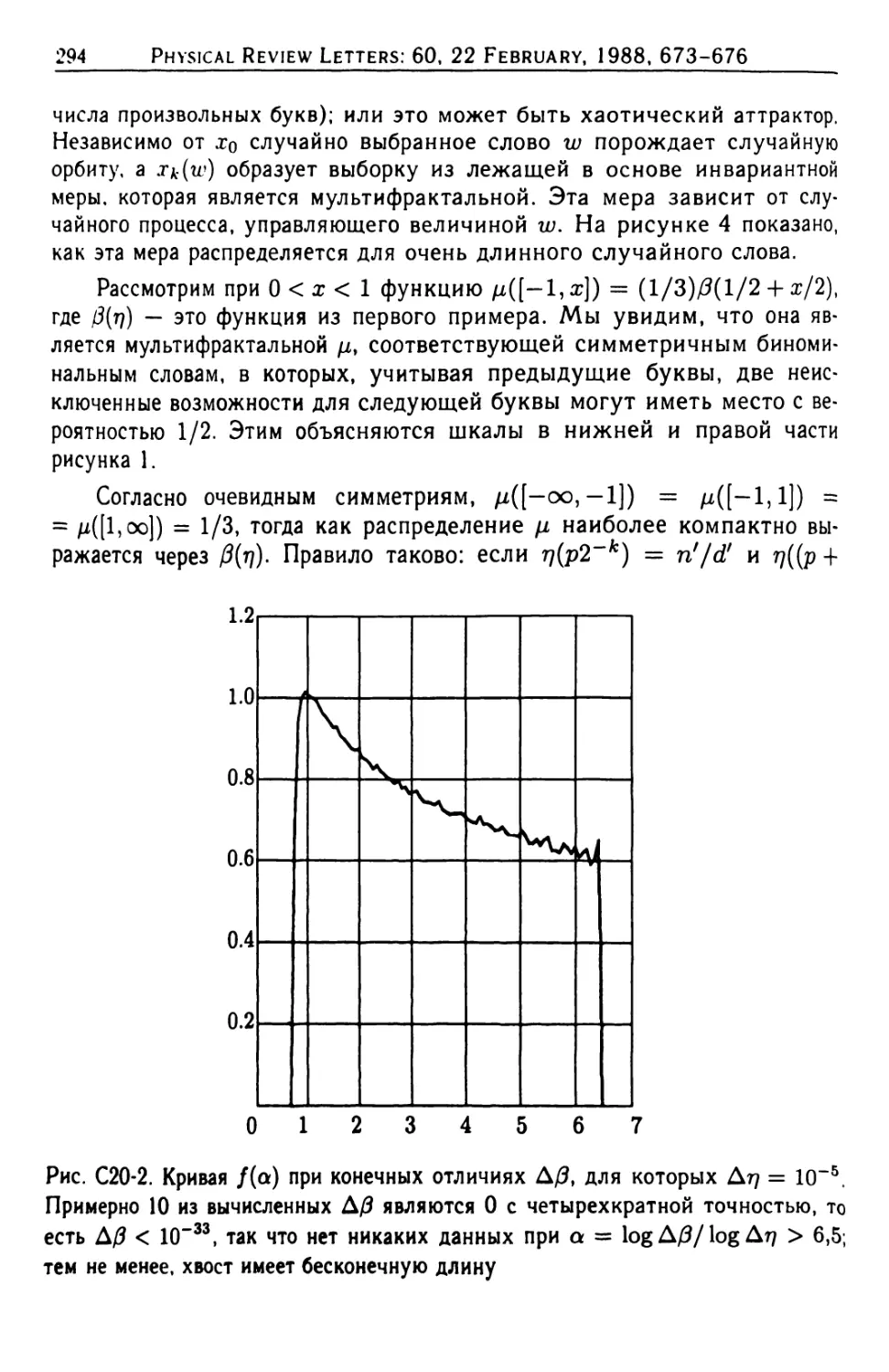
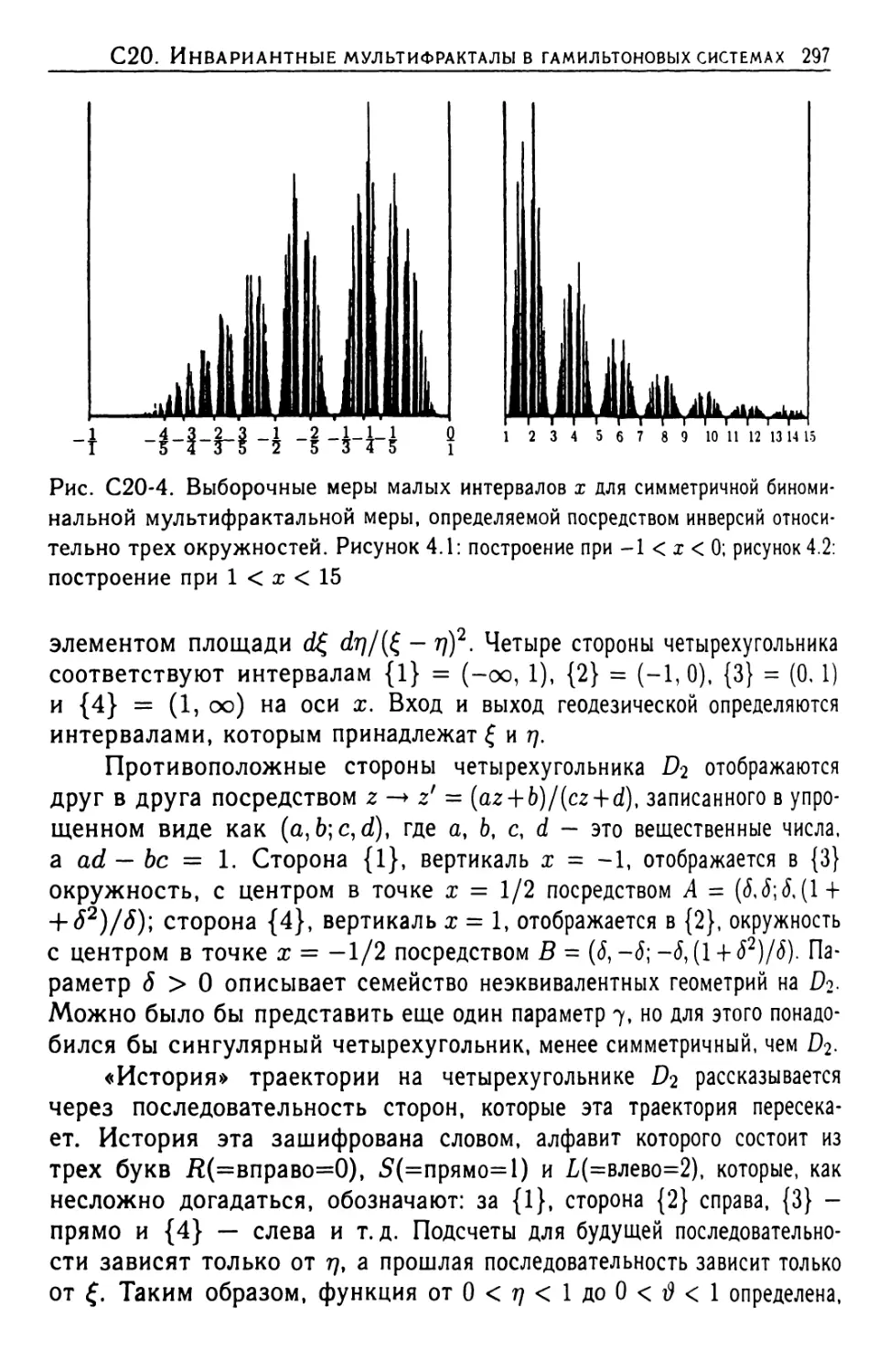
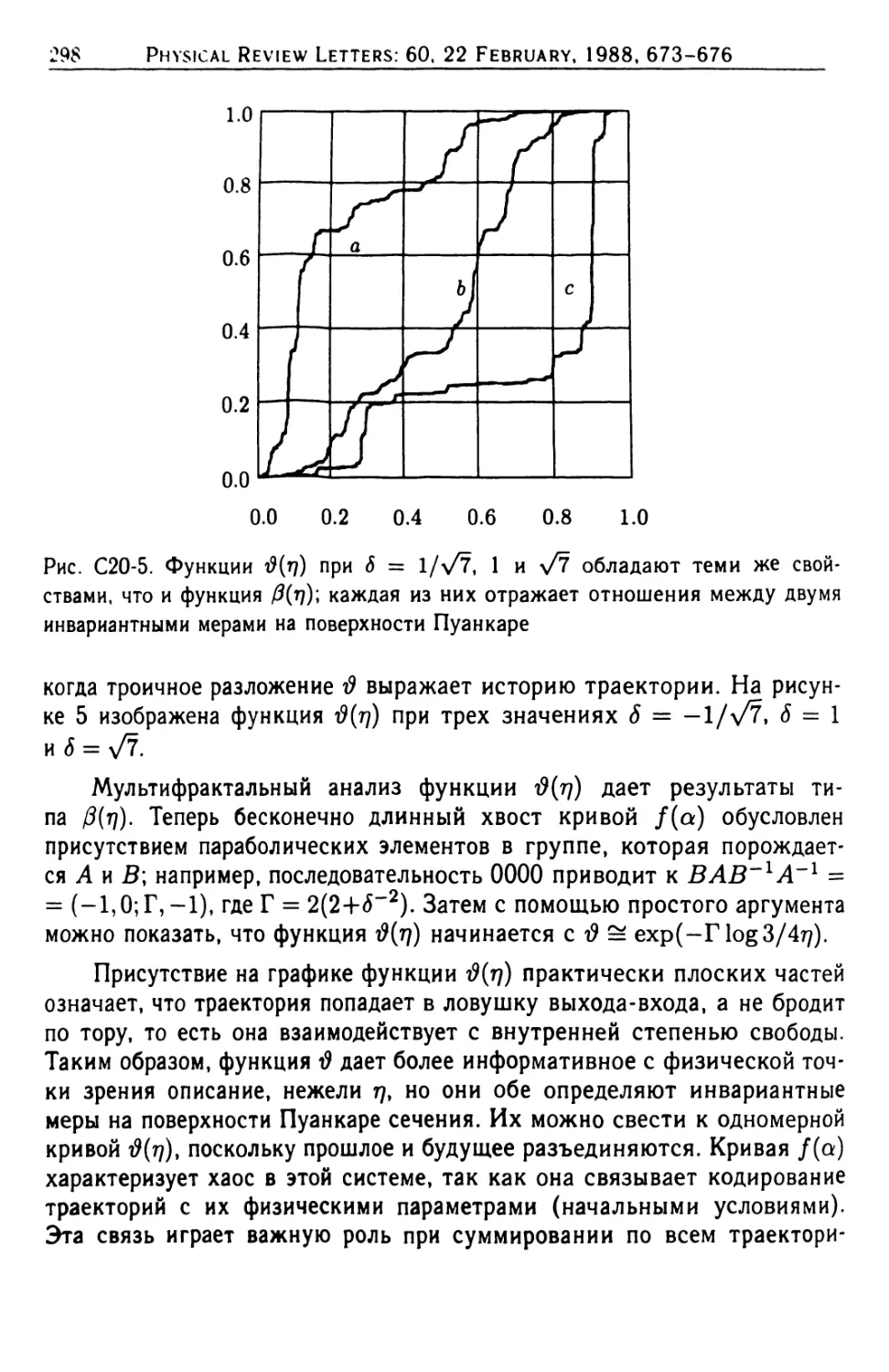
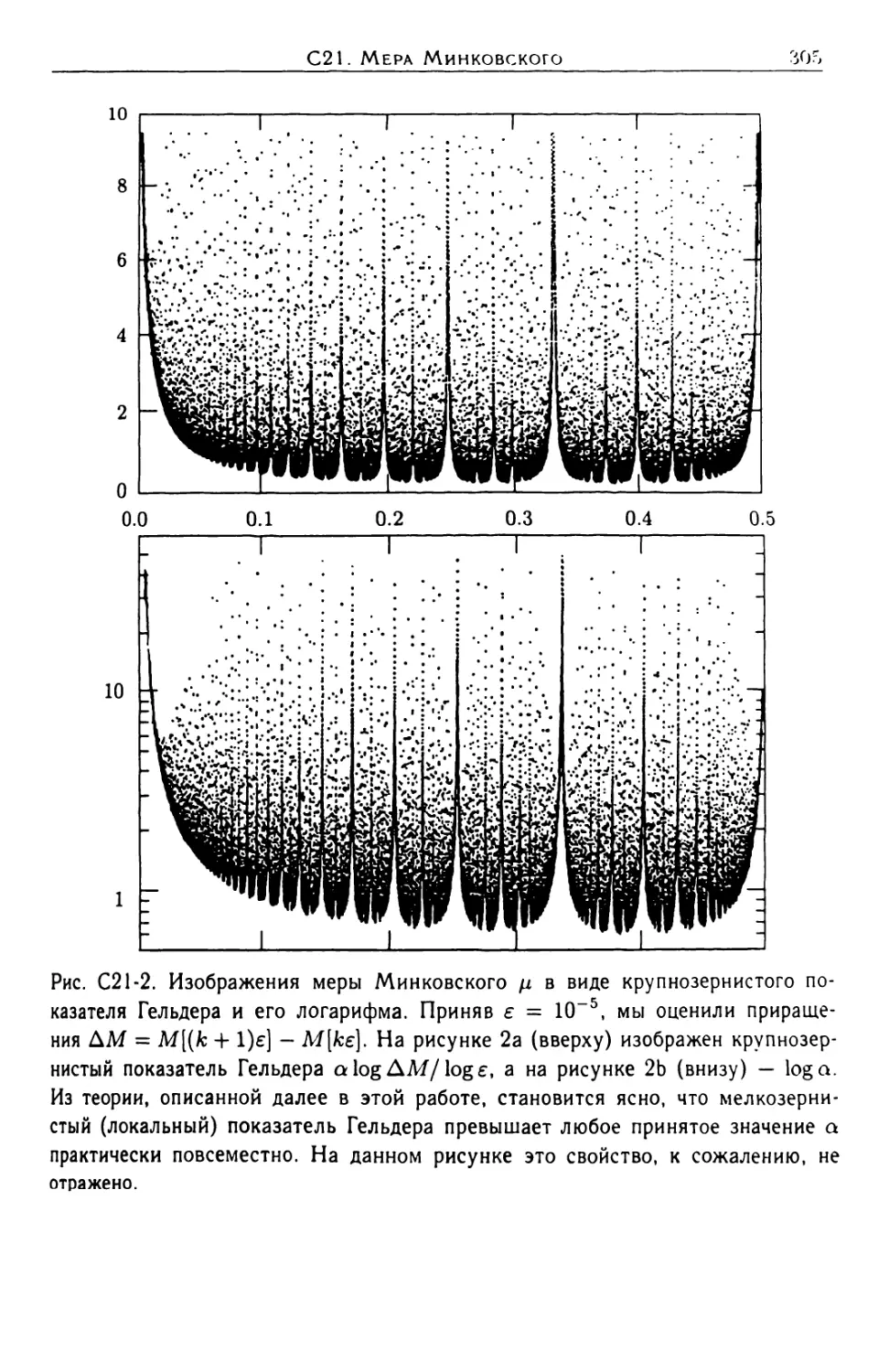
Автор: Мандельброт Б.Б.
Теги: геометрия топология математика фракталы
ISBN: 978-5-93972-772-3
Год: 2009
Текст
Б. Б. Мандельброт
ФРАКТАЛЫ И ХАОС
Множество Мандельброта и другие чудеса
Benoit В. Mandelbrot
Fractals and
Chaos
The Mandelbrot Set
and Beyond
SELECTA VOLUME C
with a foreword by P. W. Jones
and texts co-authored by
CJ.G. Evertsz and M.C. Gutzwiller
Springer
Бенуа Б. Мандельброт
ФРАКТАЛЫ И ХАОС
Множество Мандельброта
и другие чудеса
с предисловием П. У. Джонса
и главами, написанными в соавторстве
с К. Дж. Г. Эверцом и М. К. Гуцвиллером
Перевод с английского Н. А.Зубченко
/?&с
Москва ♦ Ижевск
2009
эн
ББК 22.151
М 231
Интернет-магазин
http://shop.rcd.ru
• физика
• математика
• биология
• нефтегазовые
технологии
Мандельброт Б. Б.
Фракталы и хаос. Множество Мандельброта и другие чудеса. — М.-
Ижевск: НИЦ «Регулярная и хаотическая динамика», 2009. — 392 с.
Немногим более двадцати лет минуло с тех пор, как Бенуа Мандельброт
опубликовал свое знаменитое изображение так называемого множества Ман-
дельброта. Эта картинка кардинально изменила наш взгляд на математическую
и физическую Вселенную! Данная книга рассматривает не тот или иной класс
проблем, а подход к описанию математической и физической Вселенной в це-
лом. Фракталы (термин, придуманный автором) настолько прочно укоренились
в нашем сознании, что сейчас крайне сложно вспомнить тот психологический
шок, который мы испытали в момент их появления. Эта богато иллюстрирован-
ная книга объединяет ранние статьи автора, ставшие сегодня библиографиче-
ской редкостью, с главами, описывающими историю развития фрактальной гео-
метрии. Ключевые темы книги — квадратичная динамика, множества Жюлиа
и Мандельброта, неквадратичная динамика, клейновы предельные множества
и мера Минковского.
ISBN 978-5-93972-772-3 ББК 22.151
© Б. Б. Мандельброт, 2004
© НИЦ «Регулярная и хаотическая динамика», 2009
http://shop.rcd.ru
http://ics.org.ru
Когда-то очень давно мой дядя Шолем Мандельбройт (1899-1983)
раскрыл передо мной мир удовольствий, даруемых итерацией.
Его памяти я посвящаю этот плод моего интеллектуального труда
БЕНУА Б. МАНДЕЛЬБРОТ является профессором математиче-
ских наук Йельского университета и почетным членом исследователь-
ского центра IBM (по физике).
Наиболее известен как основатель фрактальной геометрии, пред-
ставляющей собой первую серьезную попытку количественного исследо-
вания повсеместного понятия неровности.
Автор книг «Les objects fractals», 1975, 1984, 1989 и 1995 (пере-
веденной на баскский, бразильский, болгарский, китайский, чешский,
итальянский, португальский, румынский и испанский языки) и «Фрак-
тальная геометрия природы», 1982 год (переведенной на китайский,
немецкий, японский, корейский, русский и испанский языки). Его мно-
готомный труд «Selecta» начался с работ «Фракталы и масштабирова-
ние в финансах: Прерывность, концентрация, риск» 1997 года, «Frac-
tales, hasard et finance» 1997 года, «Мультифракталы и 1/f шум: Ди-
кая самоаффинность в физике» 1999 года и «Самоаффинность Гаусса
и фракталы» 2002 года. Совместно с М. Л. Фреймом он написал книгу
«Фракталы, графика и математическое образование» 2002 года.
Член американской Академии искусств и наук; член Национальной
Академии наук США; иностранный член Норвежской Академии наук.
Обладатель следующих наград: «Медаль за служение науке»
(«Magna est Veritas»), присужденная Национальной Академией наук
США в 1985 г.; «Медаль Франклина за служение науке» от Института
имени Франклина в Филадельфии в 1986 г.; «Медаль имени Чарльза
Протея Штайнметца», присужденная Институтом инженеров по элек-
тротехнике и радиоэлектронике в 1988 г.; первая премия «Наука для
искусства» от холдинга Луи Виттон-Моэт-Хеннесси в 1988 г.; «Премия
Харви в области науки и технологии» от Израильского технологиче-
ского института в Хайфе в 1989 г.; «Премия Университета Невады»
от 1991 г.; «Премия Вульфа за вклад в физику» от 1993 г.; «Премия
концерна Хонда» от 1994 г.; «Медаль Вермей города Парижа» от 1996 г.;
«Награда имени Джона Скотта» от 1999 г.; «Награда имени Льюиса
Фрая Ричардсона», присужденная Европейским геофизическим обще-
ством в 2000 г.; «Премия имени Уильяма Проктера» от общества «Сиг-
ма Кси» в 2002 г. и «Премия Японии в области науки и технологии»
в 2003 г.
Он также получил «Награду за выдающиеся достижения» от
Калифорнийского технологического института и «Премию имени Гум-
больдта», учрежденную Фондом Александра фон Гумбольдта.
Выпускник Парижской Политехнической школы; магистр и бака-
лавр аэронавтики Калифорнийского технологического института; док-
тор математических наук Парижского университета. Почетный профес-
сор: университета Сиракуз, университета Лаврентия (Канада), Бостон-
ского университета, университета штата Нью-Йорк, университета Гель-
фа (Канада), университета Далласа, Юнион-колледжа, университета
Буэнос-Айреса (Аргентина), Открытого университета Великобритании,
Афинского университета экономики и бизнеса, университета Св. Эндрю
(Шотландия), университета Эмори, Бременского университета (Герма-
ния), университета Пейс и Тель-Авивского университета (Израиль).
До сотрудничества с IBM работал в Национальном центре научных
исследований в Париже, в компании «Филипс Электронике», в Масса-
чусетском технологическом институте, в Принстонском Институте до-
полнительного образования, в Женевском университете, в университете
Лилля и в Политехнической школе. Читает лекции в Массачусетском
технологическом институте. Приглашенный профессор экономики, затем
прикладной математики, математики и практической математики в Гар-
варде; машиностроения в Йельском университете; физиологии в Меди-
цинском колледже имени Альберта Эйнштейна. Профессор Академии
наук Политехнической школы в Париже. Преподавал в Кембридже (Ве-
ликобритания) в ранге приглашенного специалиста в колледже Гонвил-
ля и Кейуса, читает лекции в лаборатории имени Кавендиша и является
членом Института математических наук имени Исаака Ньютона.
Формально Мандельброт был самоучкой, но в его ранних работах
чувствуется сильное влияние Поля Леви, Норберта Винера и Джона фон
Неймана. Проповедуя «единство знаний и чувств», он ищет меру поряд-
ка в физических, математических или социальных явлениях, характе-
ризующихся обширными данными вкупе с невероятной изменчивостью
моделей.
Содержание
Главы, помеченные звездочкой (*) и датированные 2003 го-
дом, публикуются впервые. Главы, снабженные пометкой вида
(М 1985g), публиковались ранее; первоисточник (помеченный анало-
гичным образом) можно найти в библиографии. Тексты, вошедшие
в настоящее издание, и те, что были опубликованы в томах Е,
N и Н серии «Selects», помечены в библиографии звездочкой и бук-
венно-цифровым обозначением соответствующей главы (или про-
сто буквенным обозначением тома).
★Предисловие Питера У. Джонса (2003)........................ 11
★Введение (2003)............................................ 16
ЧАСТЬ I. КВАДРАТИЧНЫЕ МНОЖЕСТВА ЖЮЛИА И МАН-
ДЕЛЬБРОТА .............................................. 27
*С1. Квадратичная динамика: от наблюдения к открытию (2003) 29
*С2. Выражение признательности, или Люди, благодаря кото-
рым я пришел к квадратичной динамике (2003).......... 50
СЗ. Фрактальные аспекты итерации отображения z —* Az(l — z)
при комплексных А и г ............................... 63
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 81
С5. Комплексное квадратичное отображение и его множество М106
С6. Точки бифуркации, приближение «п в квадрате» и гипоте-
за (на основании результатов, полученных М. Л. Фреймом
и К. Митчеллом)..................................... 132
С7. «Нормированный радикал» множества М............... 136
С8. Размерность границы множества М равна 2 146
09. Множества Жюлиа, содержащие гладкие компоненты ... 151
Содержание
9
СЮ. Последовательности множеств Жюлиа, заполняющие плос-
кую область, и интуитивное обоснование возникновения
дисков Зигеля................................155
СИ. Непрерывная интерполяция квадратичного отображения и
покрытие внутренних областей множеств Жюлиа 164
ЧАСТЬ II. НЕКВАДРАТИЧНАЯ РАЦИОНАЛЬНАЯ ДИНА-
МИКА .............................................177
*С12. Хаос в неквадратичной динамике: рациональные функции
из формул удвоения (2003).....................179
С13. Отображение z —» A(z + 1/z) и переход от линейного хаоса
к хаосу плоскостному (компьютерное подражание Хокусаю) 188
С14. Два неквадратичных рациональных отображения из фор-
мул удвоения Вейерштрасса....................200
ЧАСТЬ III. СИСТЕМЫ ИТЕРИРОВАННЫХ НЕЛИНЕЙНЫХ
ФУНКЦИЙ И ФРАКТАЛЬНЫЕ ПРЕДЕЛЬНЫЕ МНОЖЕ-
СТВА КЛЕЙНОВЫХ ГРУПП.............................215
*05. Клейновы группы, их фрактальные предельные множества
и СИФ: история, воспоминания и имена..........217
С16. Самоинверсные фракталы, аполлониевы сети и мыло . . . 225
С17. Симметрии: увеличение/уменьшение, фракталы и непра-
вильность форм ..............................243
08. Самоинверсные фракталы, соприкасающиеся сигма-диски
и предельные множества инверсных («клейновых») групп 257
ЧАСТЬ IV. МУЛЬТИФРАКТАЛЬНЫЕ ИНВАРИАНТНЫЕ МЕ-
РЫ ..............................................277
* С19. Меры, которые экспоненциально убывают почти везде:
ОДА и Минковский...................................279
С20. Инвариантные мультифрактальные меры в хаотических га-
мильтоновых системах и аналогичных структурах (Gutz-
willer & М 1988).............................. 290
10
Содержание
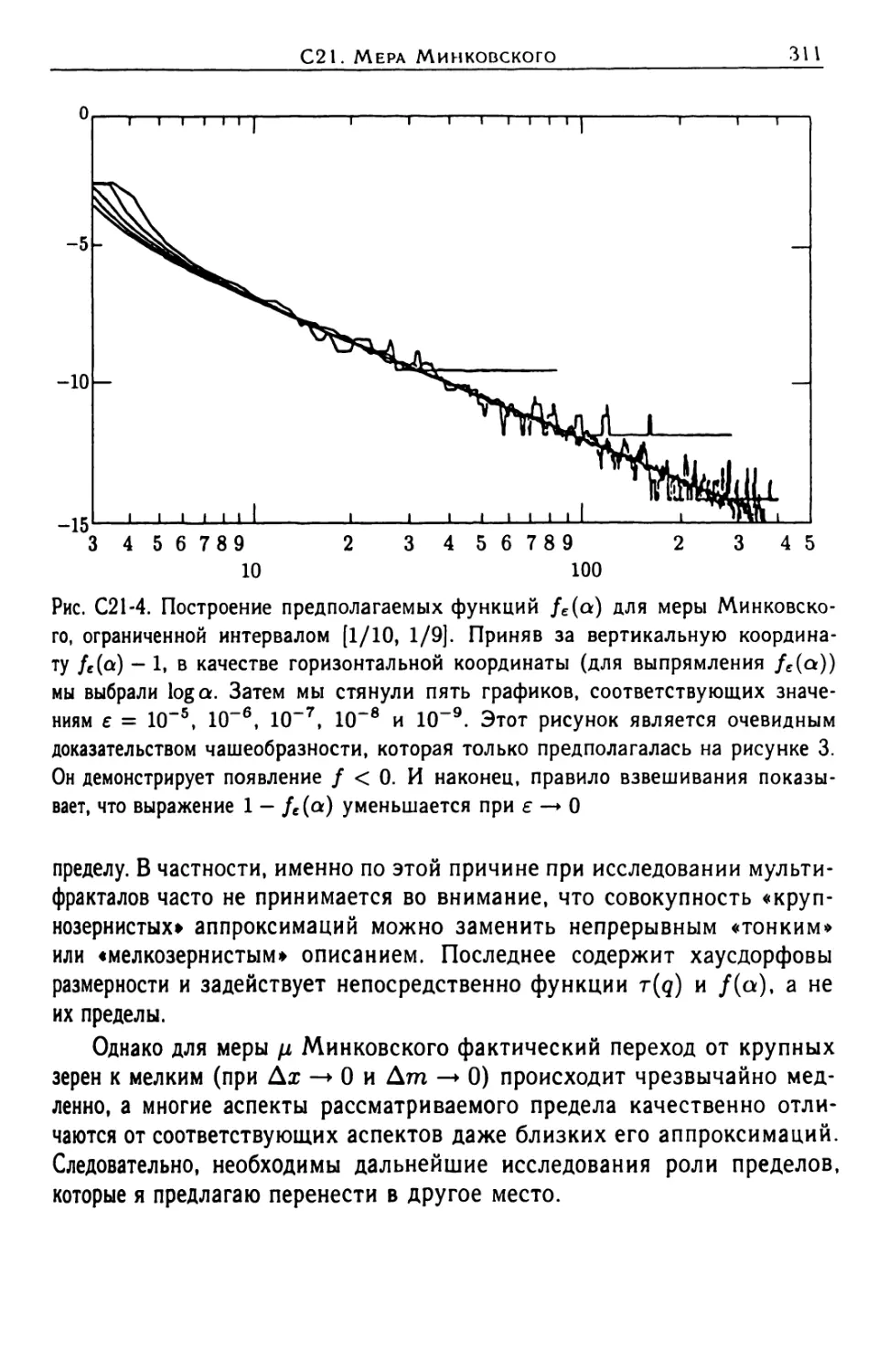
С21. Мера Минковского и мультифрактальные аномалии в ин-
вариантных мерах параболических динамических систем . 300
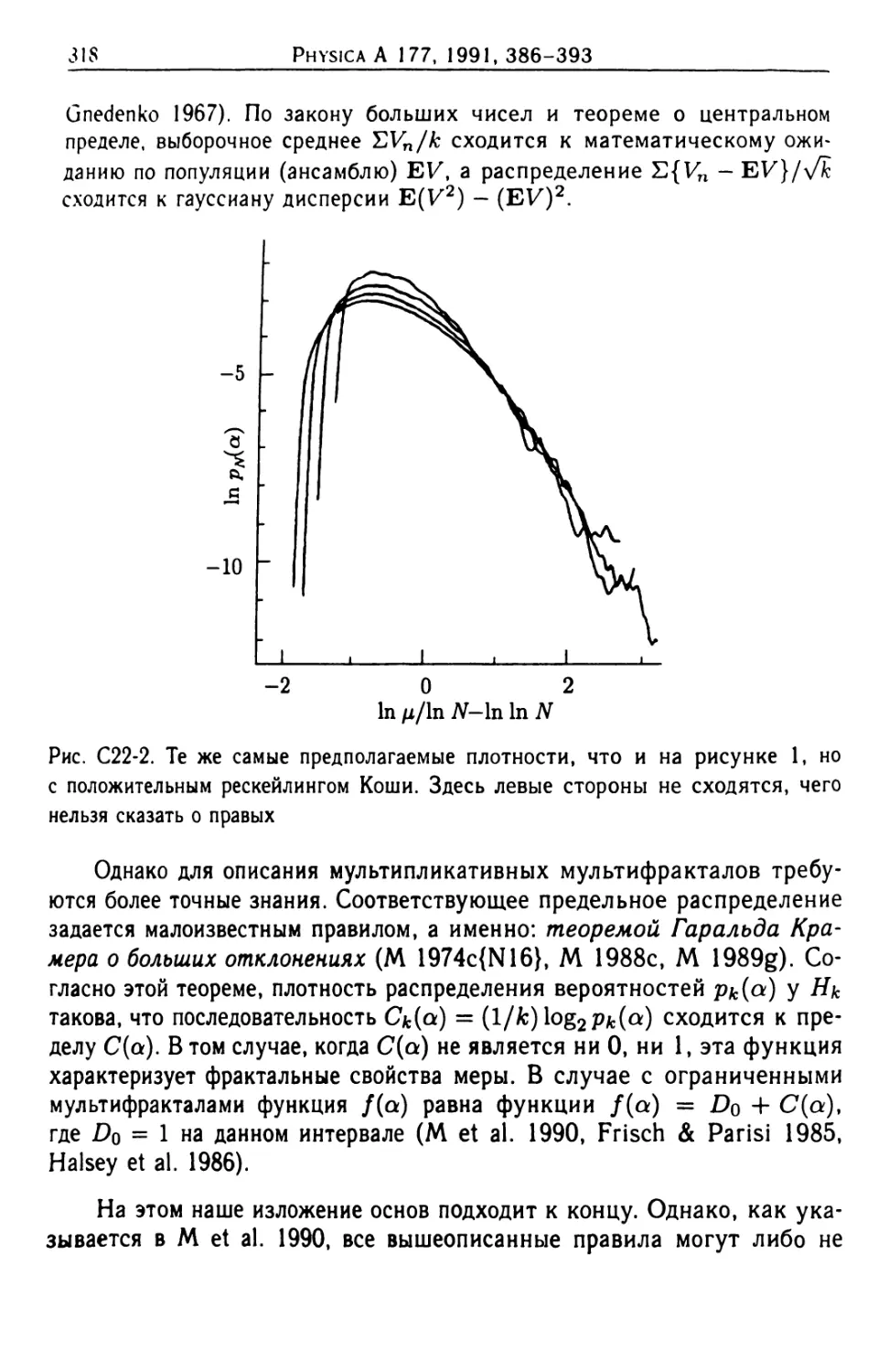
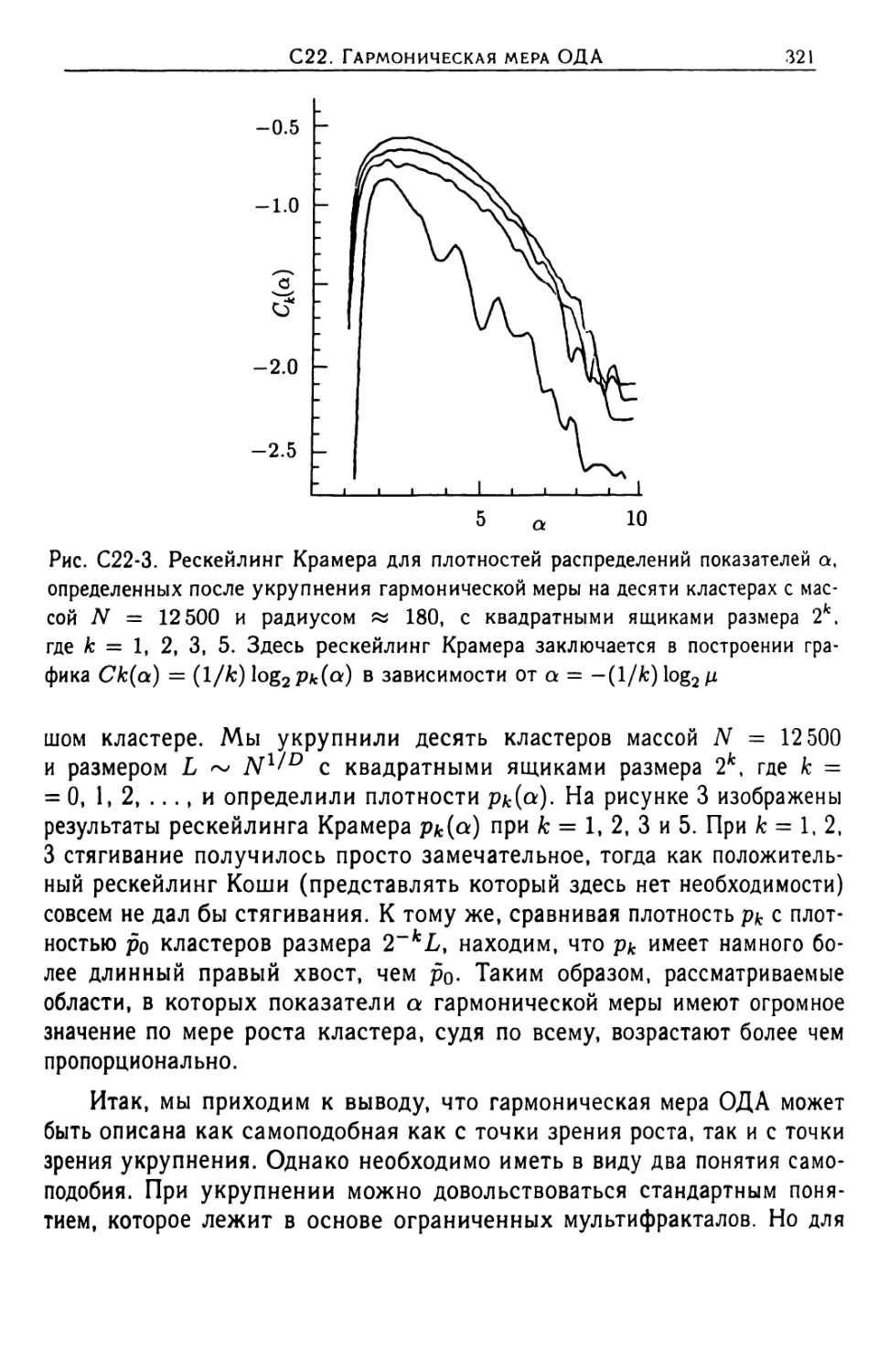
С22. Гармоническая мера ОДА и расширенное понятие о само-
подобии (М & Evertsz 1991) ......................313
ЧАСТЬ V. СИНОПСИС И ИСТОРИЧЕСКИЕ ОЧЕРКИ ... 323
* С23. Неисчерпаемая функция z2 + с.................325
* С24. Фату и Жюлиа.................................335
* С25. Математический анализ: пребывание во мраке...345
Общая библиография, включая указания на авторские права 352
Предметный указатель..................................380
Предисловие Питера У. Джонса
(Йельский университет)
Двадцать три года назад Бенуа Мандельброт впервые представил
научной общественности знаменитое изображение множества, известно-
го ныне как множество Мандельброта. Доступные в то время графиче-
ские средства выглядят сегодня крайне примитивными, в оригинальных
же черновиках Мандельброта разобрать что-либо почти невозможно,
однако эта нехитрая картинка самым что ни на есть кардинальным об-
разом изменила наши представления о математической и физической
вселенной. За прошедшее время фракталы (имя им также дал Ман-
дельброт) успели настолько прочно укорениться в научном обиходе, что
теперь уже довольно сложно вспомнить то потрясение, какое они тогда
вызвали. В двадцать первом веке исследователь, приступая к рассмот-
рению той или иной задачи, без лишних раздумий прибегает к ком-
пьютерному моделированию — использовать настольный компьютер для
изучения новых феноменов или отыскания путей решения самых разных
задач стало сегодня рутинной процедурой. В 1980 году все было иначе.
Когда в науке происходит смена парадигмы, проводниками этой сме-
ны редко выступают ученые, принадлежащие к старой гвардии. Требу-
ются совершенно новые методы, а привычная ортодоксальная система
часто переворачивается с ног на голову.
Тридцать лет назад, несмотря на появление первых признаков гря-
дущих перемен, в математическом сообществе бытовало мнение, суть
которого сводилась к тому, что картинкам доверять не следует — какую
бы информацию они в себе не несли, полагаться на нее опасно. Физи-
ки уже включили компьютерное моделирование в свои университетские
программы, а математики все еще предпочитали работать по старин-
ке. Возможно, такое их отношение объясняется отчасти тем, что мощ-
12 Предисловие Питера У, Джонса (Йельский университет)
ность тогдашних компьютеров оставляла желать лучшего, однако лишь
отчасти; были и другие причины. В математике, как считали многие,
необходимо прежде всего руководствоваться общностью и абстрактно-
стью. Такой интеллектуальный фундамент оказался весьма непрочным,
и в последующие двадцать лет мы могли наблюдать, как один за другим
рушатся опиравшиеся на него предрассудки.
В моей собственной области математического анализа в 50-60-е го-
ды прошлого века преобладали аналогичные настроения — все с нетер-
пением ожидали, что вот-вот будут разработаны некие чудесные аб-
страктные методы для решения широкого класса вполне конкретных
задач. Еще немного, и мы сформулируем корректные аксиомы и хит-
роумные теоремы для банаховых пространств и алгебр, и тогда побе-
да будет за нами. В конце 60-х группами математиков во Франции,
Швеции и США (Чикагская школа) были разработаны абсолютно но-
вые методы, которые не только позволяли доказать некоторые старые
гипотезы, но и открывали заманчивые новые горизонты, — оставаясь
при этом как нельзя более конкретными по своей природе. С надеждой
на абстрактное спасение — по крайней мере, в наиболее экстремаль-
ных его формах — пришлось расстаться как с наивным заблуждением.
Особенно нуждались в разработке конкретного инструментария задачи
статистического характера. (Следует отметить, что в других областях
математики абстрактные методы оказывались порой потрясающе успеш-
ными, даже при решении весьма конкретных задач. Как это обстоятель-
ство повлияет в будущем на развитие этих областей, остается только
предполагать.)
Сегодня мы с интересом оглядываемся на тот период и видим оди-
нокую фигуру Бенуа Мандельброта. Он рассматривает картинки, при-
ходит на основании увиденного к каким-то выводам (причем выводы
эти имеют отношение не только к математике), а окружающие его лю-
ди, по большей части, не обращают на него ни малейшего внимания.
Трудно представить себе человека, более чуждого какой бы то ни было
ортодоксальности.
Для того чтобы оценить вклад Мандельброта в науку, необходи-
мо прежде всего отказаться от стремления запихнуть каждого ученого
в персональный картотечный ящик. Как вы назовете человека, который
одновременно занимается математикой, физикой, экономикой, гидроло-
гией, геологией, лингвистикой, и это еще не весь перечень? И что вы
скажете о человеке, чей метод освоения новой области знаний часто
состоит в отыскании загадочных закономерностей, паттернов, картинок
и статистических данных? Первого никак нельзя назвать ученым, а вто-
Предисловие Питера У. Джонса (Йельский университет)
13
рое никак не может быть наукой! Вот только Бенуа Мандельброт имен-
но так и поступает, его метод (по крайней мере, на начальном этапе
изучения проблемы) очень прост: он разглядывает картинки, а они рас-
сказывают ему свои истории.
В середине XVI века Галилей смотрел на небо в телескоп и видел
там удивительные фигуры, недоступные прежде человеческому глазу.
Очень похожим образом Мандельброт берет самые современные ком-
пьютеры, исследует с их помощью феномены, недостаточно хорошо опи-
сываемые существующими жесткими формулами, и — ап! — получает
в результате странные и неожиданные картины. Более того, он подо-
зревает, что картины, наблюдаемые в математической задаче, вполне
могут объяснить, например, «всплески» в финансовой отчетности или
наблюдаемые аномальные свойства той или иной физической системы.
Возможно, эти редкие всплески или другие аналогичные события ока-
жутся в конечном счете не такими уж и редкими; возможно, они даже
являются проявлением некоего неотъемлемого свойства изучаемой си-
стемы!
Едва заступив за порог математики, Мандельброт начинает следую-
щую фазу исследования: он строит математический аппарат и уточняет
полученные результаты. Попробуйте-ка сегодня втолковать подкованно-
му в математике ученику средней школы, что изящные фрактальные
изображения на компьютерном мониторе сами по себе интереса не пред-
ставляют, что никакой достоверной информации они в себе не несут;
а еще попробуйте убедить его в том, что похожие фракталы в различ-
ных задачах похожи благодаря чистой случайности.
Даже если предположить, что недоверие к картинкам успело к то-
му времени несколько поблекнуть, остается все же неясным, почему
ранние работы Мандельброта о фракталах (знаменитая «Фрактальная
геометрия природы», например) завоевали столь громкую популярность
среди научного сообщества в целом. Страницы этих работ отнюдь не бы-
ли посвящены исключительно методологии доказательства теорем, как
подобало бы «настоящему» математическому трактату. Скажем так: при
желании найти во «Фрактальной геометрии природы» и теоремы, и стро-
гие их доказательства несложно, сложнее отыскать (особенно с точки
зрения математика) какую ни на есть связь между рассматриваемыми
в книге феноменами (и сопутствующими картинками) — четко сформу-
лированных теорем на все возможные случаи автор книги не предлагает.
Сколь жалкой была бы наша жизнь, если бы при изучении все-
ленной мы вынуждены были использовать лишь дозволенные методы!
Представьте себе незавидное положение практикующего биолога — ни
14
П редисловие Пите ра У. Джонса (Йельский университет)
одного «чистого» набора данных и никакой возможности установить
хоть какие-нибудь причинно-следственные связи. Потребуем, чтобы он
сформулировал теорему? Следует ли геологу, изучающему пласты гор-
ных пород, искать прежде всего подходящую теорему, когда он способен
достичь большего, применив формализм мультифрактальных мер? Тра-
диционный научный подход предполагает, что сначала мы должны по-
пытаться составить описание рассматриваемой системы; эта, на первый
взгляд, простая задача зачастую оказывается более сложной, чем при-
нято считать. Вряд ли Кеплер смог бы сформулировать свои знаменитые
законы, не перевороши он прежде горы данных в поисках закономерно-
стей.
Не исключено, впрочем, что картинки, которые изучал Мандель-
брот, имеют абсолютно случайную природу, а любое их отношение к ка-
ким-либо интересным научным результатам — всего лишь совпадение.
В качестве поучительного примера можно привести все то же множество
Мандельброта М. Несмотря на двадцатилетние интенсивные его иссле-
дования лучшими аналитиками мира, мы до сих пор не знаем, является
ли множество М локально связным (так называемая гипотеза MLC);
любые попытки продвинуться в этом направлении непременно заходят в
тупик. На сегодняшней день эта задача считается одной из центральных
в комплексной динамике; решение ее, возможно, приведет к потрясению
основ. Нам известно лишь, что геометрия множества At дьявольски
сложна, а размерность его границы, как доказал М.Сисикура, равна
двум.
♦Словарь Салливена» предлагает множество аналогий между ите-
рациями рациональных функций и теорией клейновых групп, однако
многое еще остается неясным. Мы не знаем, например, может ли мно-
жество Жюлиа или предельное множество (клейновой группы) иметь
положительную площадь в общем случае (а не только в случае полной
сферы). Если все множества Жюлиа квадратичного полинома имеют ну-
левую площадь, то гипотезу Фату о плотности гиперболических систем
можно для квадратичных полиномов считать доказанной. Отметим еще,
что из MLC следует как гипотеза Фату для квадратичных полиномов,
так и несуществование некоторых (но не всех) множеств Жюлиа с по-
ложительной площадью.
Еще один пример — граница броуновской оболочки, представлен-
ной на с. 243 ♦Фрактальной геометрии природы». Компьютерное моде-
лирование и рассуждение по аналогии привели Мандельброта к пред-
положению, что броуновская граница имеет размерность 4/3 и может
служить моделью (непрерывного) случайного блуждания без самопе-
Предисловие Питера У. Джонса (Йельский университет)
15
ресечений (СББС). Не так давно справедливость этого предположения
была доказана Г.Лоулером, О. Шраммом и В. Вернером. Представлен-
ное ими впечатляющее доказательство опирается в значительной степе-
ни на новые процессы, предложенные Шраммом и получившие название
SLE1. Иначе говоря, границу броуновской оболочки можно представить
с помощью процесса SLE (размерность 8/3). Тем самым подтвержда-
ется и другое предсказание Мандельброта: области по разные стороны
броуновской границы «статистически подобны и независимы». Доказа-
тельство существования СББС — и возможности его отождествления
с процессом SLE (8/3) — является одной из важнейших задач, стоящих
перед теорией вероятностей.
Ведущую роль сыграл Мандельброт и в изучении мультифракталов.
Хотя кое-где в анализе Фурье и теории конформных отображений муль-
типликативные меры с сингулярным носителем известны относительно
давно, их тонкую структуру никто не рассматривал, и при решении
физических задач они до Мандельброта практически не применялись.
Кроме того, именно Мандельброт первым записал распределение /(а)
в виде нормированных логарифмов больших вероятностей отклонения.
И пусть многие задачи пока не решены, дивные картины, которые
сегодня по силам воспроизвести и упомянутому выше школьнику, все
так же удивляют и завораживают нас. Мандельброт немало сделал для
того, чтобы изменить наш взгляд на мир, и книга, которую вы держите
в руках, позволяет несколько лучше понять, как ему это удалось. В ней
не просто рассказывается о некотором классе задач — она предлагает
вполне конкретный подход к исследованию математической и физиче-
ской вселенной. Подход, который не потеряет со временем своей ак-
туальности, а, напротив, непременно займет должное место в рабочей
доктрине грядущей математической революции, какую бы форму эта
доктрина в конечном итоге ни приняла.
Нью-Хейвен, Коннектикут, Питер У. Джонс,
1 октября 2003 года профессор математики,
Йельский университет *
’От англ. Schramm - Loewner evolution — эволюция Шрамма - Лувнера. — Прим, перев.
Введение
Взаимосвязи между фракталами и хаотическими динамическими
системами многочисленны и разнообразны. Однако эта книга не являет-
ся ни монографией по таким взаимосвязям, ни учебником.
Основную ее часть составляют репринты специальных статей, на-
писанных в восьмидесятые годы прошлого века и ставших моим непо-
средственным вкладом в четыре великие и вечные раздела математики:
(А) итерация Фату-Жюлиа квадратичного отображения z2 + c, (В) ите-
рация Фату-Жюлиа других рациональных отображений, (С) «клейно-
вы» предельные множества Пуанкаре и (D) соответствующие сингуляр-
ные меры. В полном объеме эти работы невозможно сегодня найти ни
в одной отдельно взятой библиотеке. Их немного, но некоторые приобре-
ли немалый вес в математических кругах, а прочие, думаю, цитируются
реже, чем они того заслуживают.
Для того чтобы гладко соединить упомянутые разделы под одной
обложкой, я написал новые главы, а некоторые репринты снабдил для
большей ясности новыми предисловиями и аннотациями. Широко рас-
пространено довольно странное убеждение, будто бы наука есть занятие
предельно скучное и бесстрастное. Представленные в книге историче-
ские и биографические очерки убедительно доказывают обратное.
Богатая событиями история и ранее не публиковавшиеся иллюстра-
ции могут привлечь к книге внимание читателей, не интересующихся
математикой per se2. В помощь этим читателям в разных главах кни-
ги помещены пояснительные материалы, сравнительно более «легкие»
для усвоения (особенно рекомендую обратить внимание на главу С23
и первую половину главы С17).
Содержание четырех основных разделов
Часть 1. Итерация квадратичного отображения и множество
Мандельброта. Получаемый итерацией Фату-Жюлиа объект, обозна-
чаемый сегодня буквой М и называемый «множеством Мандельброта»,
2Самой по себе (лат.). — Прим, перев.
Введение
17
открыл в свое время новые широкие горизонты. В случае квадратичного
отображения, я определил множество Л4 на плоскости комплексной пе-
ременной с посредством следующего условия: последовательность с, <?+
4-с, (с2 + с)2 + с, ... не должна расходиться. Впоследствии мы убедим-
ся, что такое определение, каким бы произвольным оно ни казалось на
первый взгляд, имеет под собой глубокое обоснование. По контрасту
с крайней простотой определения сложность и красота множества Л4
производят неизгладимое впечатление.
В 1980 году я внимательно пригляделся к построенным компью-
тером картинкам, что привело меня к нескольким поразительным на-
блюдениям, которые (одни сразу же, другие — некоторое время спустя)
переросли в математические гипотезы касательно природы квадратич-
ного множества Мандельброта. Несмотря на простоту формулировки,
доказать эти гипотезы оказалось весьма нелегким делом. Более того,
самая важная из них — утверждающая, что множество Мандельброта
является локально связным, и скандально известная под аббревиатурой
MLC — не доказана до сих пор.
Эти наблюдения и составили в совокупности открытие множе-
ства — фундаментальный контраст между просто созерцанием кар-
тинки и открытием мы обсудим в главе С1.
Фракталы и множество Мандельброта в школе. У множества
Мандельброта, равно как и у всей фрактальной геометрии в целом, есть
одно поразительное и очень важное универсальное свойство: неизведан-
ные территории здесь начинаются сразу за порогом привычных и эле-
ментарных вещей, которым сегодня учат во многих средних школах. Тот
факт, что граница с неизведанным всегда рядом, какую изученную об-
ласть ни возьми, весьма способствует успешному преподаванию. В биб-
лиографии упомянуты представители двух «волн» обучающих матери-
алов по фракталам. Вдохновителем первой стал Хайнц-Отто Пайтген.
Над другой работает Майкл J1. Фрейм в соавторстве со мной (сюда вхо-
дят и цикл лекций Фрейма, доступный в мировой паутине и на DVD).
Часть II. Неквадратичные итерации. Готовя материалы для этой
книги, я наткнулся на один весьма приятный сюрприз. В старых архивах
(1977-1979), сохраненных моим помощником-программистом Марком
Р. Лаффом, неожиданно обнаружились нигде не публиковавшиеся ил-
люстрации (аккуратно датированные), относящиеся к неквадратичным
рациональным отображениям. Эти иллюстрации ясно показывают, что
моим открытиям 1980 года предшествовал довольно продолжительный
начальный период проб и ошибок, период бурной деятельности и смут-
Введение
18
ных догадок. Я полагал, что все документальные свидетельства из того
периода безвозвратно утрачены, поэтому редко упоминал о нем. Глядя
с высоты сегодняшних знаний, всякий с легкостью различит на рисун-
ках в главе С14 общую форму и характерные признаки тех квадратич-
ных множеств Жюлиа и Мандельброта, что рассматриваются в части I
этой книги. Впрочем, неквадратичный «фон» на моих первых картинках
оказался столь сложным, что тогда, в 1979 году, я с ними практически
ничего поделать не мог.
Никакого нового света на то, что произошло в 1980 году, эта наход-
ка. конечно же, не проливает, однако в сочетании события 1979 и 1980
дают весьма интересный случай научного поиска и открытия, чему и по-
священы несколько глав, написанных специально для этой книги.
Часть III. Предельные множества клейновых групп. Здесь мо-
ей заслугой является быстро сходящийся алгоритм, который заполнил
давнишний пробел в старой теории. Этот алгоритм позволяет путем по-
следовательных приближений построить множество, самоинверсное от-
носительно заданного набора окружностей.
Часть IV. Экспоненциально убывающие мультифрактальные ме-
ры. Глава С20 была написана после того, как мы с Мартином Гут-
цвиллером, моим коллегой по IBM, внезапно осознали, что, работая
в совершенно различных областях физики, мы оба исследуем одну и ту
же весьма странную сингулярную меру. Мы без труда объединили на-
ши результаты в одной статье. В конечном итоге выяснилось, что эту
загадочную меру давным-давно определил Г. Минковский, однако она
вполне заслуживала дополнительного исследования.
Мотивация и рабочие инструменты
Сильная устойчивая мотивация. В большой степени — я и сам
порой удивляюсь, насколько в большой — мое мышление было под-
стегнуто тем обстоятельством, что я был тогда достаточно молод и от-
важен, чтобы овладеть искусством обращения с компьютером, и в то
же время, достаточно стар и осторожен, чтобы не пытаться отринуть
некоторые древние математические традиции. Традиции эти зародились
всего лишь в начале двадцатого века, однако к семидесятым его годам
они уже успели закостенеть и стать совершенно немодными. Эти же
традиции и побудили меня заняться изучением итераций на сложных
рациональных отображениях, описанным во второй части книги.
Введение
19
Мои занятия не имели практически никакого отношения к «теории
хаоса», возвестившей возрождение интереса к нелинейности в 70-х. Да,
вещественное отображение х2 + с играет в теории хаоса не последнюю
роль, однако, как уже было сказано, до комплексного аналога этого
отображения я добирался слишком долго и неохотно.
Об относительной роли изображений (грубых или детальных)
и человеческого глаза. Среди людей, занимавшихся в 70-80-е годы
чистой математикой, почти безраздельно царила убежденность в том,
что картинки могут привести только к другим картинкам, но никак
не к новым математическим идеям. Прошло совсем немного времени,
и от убежденности этой не осталось и следа, причем немалую роль
сыграло в этом мое «поразительное изобретение» — в своих работах
я в значительной степени опирался на точные, детальные изображения
в ущерб схематическим диаграммам. Кстати сказать, картинка в этом
смысле подобна показанию какого-либо измерительного прибора. Одно-
го показания, как правило, недостаточно. Недостаточно и одной кар-
тинки.
Если точнее, то мои математические гипотезы в большей степени
опирались на качество визуального анализа, нежели на качество изобра-
жения. В самом деле, как мы вскоре убедимся, высококачественная гра-
фика не была ни необходимым (глава С1), ни достаточным (глава С12)
условием для открытия множества Мандельброта.
В общем и целом получается, что главным результатом научных
трудов всей моей жизни стало возвращение глаголу «видеть» его искон-
ного смысла, порядком подзабытого как в общепринятом употреблении,
так и в лексике «твердой» (количественной) науки: видеть — значит,
воспринимать глазами.
Одни фрактальные изображения предельно реалистичны и легко
«сходят» за настоящие фотографии гор, облаков, деревьев или звездных
скоплений. Другие абсолютно абстрактны (как, например, изображения
множества Мандельброта). Некоторые из этих изображений (как среди
первых, так и среди вторых) обладают в нашем восприятии самостоя-
тельной эстетической ценностью. Огромное количество людей помещает
изображения фракталов в Интернете. Думаю, что такой участи заслу-
живают и мои старые файлы — несмотря на архаичную черно-белую
графику, они по-прежнему актуальны. Если найдется подходящая «пло-
щадка», то я был бы не прочь выставить свое небольшое собрание ри-
сунков, отдельные экземпляры из которого представлены в этой книге,
на «постоянную экспозицию» в мировой паутине.
20
Введение
Фрактальная геометрия и разработка количественной
теории шероховатости
Разнообразие проявлений фрактальной геометрии продолжает удив-
лять как специалистов, так и людей, далеких от науки. Мы и сегодня не
можем уверенно определить ее в какие-либо рамки, классифицировать,
сопоставить с существующими научными дисциплинами.
Лично я склонен (так сказать, постфактум) видеть во фрактальной
геометрии фундамент для создания науки о шероховатости, о нерегу-
лярности формы — аналогичным образом (но все же иначе) развились
в свое время самостоятельные науки из исследований яркости/цвета,
громкости/высоты звука, теплоты, веса. К исследованию шероховатости
мы подступились позднее, нежели к изучению прочих своих ощущений,
так как предмет здесь оказался существенно сложнее. Для количествен-
ного измерения шероховатости необходимы показатели Гёльдера и раз-
мерность Хаусдорфа, а эти концепции появились в нашем распоряжении
значительно позже, чем, скажем, понятие о периодических колебаниях;
фрактальная же геометрии просто первой признала, что эти величины
действительно описывают нечто «реальное».
Используемый математический инструментарий и характер реша-
емых задач ставят фрактальную геометрию в довольно тесные рамки,
и все же, несмотря ни на что, она умудряется сохранять свое разнооб-
разие — качество редкое, крайне интересное и, я уверен, очень важное.
Фрактальная геометрия уже пережила свои детские болезни, преодоле-
ла прочие кризисы, без которых не обходится ни одна интеллектуаль-
ная инициатива с претензиями на синтетичность, и заняла свое место
во взрослой жизни. Сегодня мы говорим, что фрактальная геометрия
изменила наши представления о природе вещей, причем «мы» — это
не только большинство математиков, физиков, инженеров, художников
и прочих профессионалов своего дела, но и вообще все без исключения
люди.
Открытая математика и математика-крепость. Со времен
древних греков (Архимед и Платон) и по сей день взгляды на сущ-
ность математики мечутся между двумя крайностями. Я называю эти
крайности открытая математика и математика-крепость. Первую
можно представить в виде множества самых разных, расставленных где
придется зданий, которые постоянно строятся и перестраиваются, снаб-
жены множеством дверей и окон, сквозь которые видны разнообразные
живописные пейзажи. Наивысшим же устремлением математики-кре-
Введение
21
пости является высокая, полностью отгораживающая ее от мира стена
с одной-единственной узенькой калиткой. Обитатели крепости полага-
ют, что благодаря такому устройству ничто не нарушит мерного ритма
их трудов, а без людей, оставшихся за стеной, они прекрасно обойдутся.
Я и сам убежден, что математика и наука вообще относятся к ве-
личайшим достижениям человечества, однако все имеющиеся в нашем
распоряжении свидетельства говорят о том, что история науки и исто-
рия человеческой цивилизации неразрывно переплетены между собой.
Те, кто полагает математику-крепость независимой от общества, про-
сто-напросто принимают желаемое за действительное, само же предпо-
ложение о возможности такой независимости не выдерживает никакой
критики.
Фракталы и чистая математика
«Фрактальная геометрия природы» (M1982F) стала первым томом
моей серии «Selecta»3, за ней последовали М1997Е, M1999N и М2002Н;
последний том (том С, или М2004С) вы держите в руках. Буквенно-циф-
ровые обозначения поясняются на первой странице библиографии. Пре-
небрежение в мнемоническом коде книг «Selecta» алфавитным порядком
намекает на то, что книги эти можно читать в любой последователь-
ности.
Три предшествующих тома целиком посвящены «состоянию» слу-
чайности и изменчивости, которое я назвал «диким». Том С, вообще
говоря, никак с упомянутыми тремя не связан за одним существен-
ным исключением. Главы С20 и С21 не только затрагивают одну из
тем M1999N (мультифрактальность), но и были написаны по резуль-
татам исследований в области статистической физики, к которым меня
привела ограниченная диффузией агрегация. Именно поэтому на место
главы С22 я поместил статью М & Evertsz 1991.
Прежние планы включали в себя выпуск еще нескольких томов «Se-
lecta». Однако с тех пор, благодаря пришествию Интернета, мир успел
основательно измениться, и последующие тома «Selecta» я буду разме-
щать на своем сайте в виде так называемых «веб-книг». Каждая такая
книга будет состоять из титульной страницы, предисловия и перечня
глав со ссылками на статьи из моего архива. Учитывая разнообразие
тем, над которыми я работал и работаю, предоставляемая мировой пау-
тиной гибкость оказывается весьма ценным качеством.
3Избранные [труды] (лат). — Прим, перев.
Введение
Глава «Общий обзор» тома М2002Н (глава НО в моей системе обо-
значений) содержит не совсем полный, но наиболее свежий «отчет о со-
стоянии» фрактальной геометрии, в котором я попытался определить
суммарное воздействие фрактальной геометрии на математику. Когда
фрактальная геометрия еще только начиналась, мне часто доводилось
слышать возмутительные своей несправедливостью замечания в том ду-
хе. что «фракталы не решили еще ни одной математической задачи».
Это уже давно неправда — впрочем, и тогда большого смысла в этих за-
мечаниях не было. С меня достаточно того, что я принес в математику
множество новых задач и гипотез. Каждая такая задача или гипотеза
открывала перед математиками новое необъятное поле для исследова-
ния, а меня увлекали за собой другие интересы. В этой книге я собрал
примеры, получившие наиболее широкую известность, однако хотя бы
краткого упоминания заслуживают и некоторые другие.
Например, в M1982F я предложил, а в М2002Н более подробно
исследовал концепции броуновского кластера и броуновской границы,
кульминацией чего явилось предположение о том, что хаусдорфова раз-
мерность такой границы должна быть равна 4/3. В сочетании с размер-
ностями перколяции и кластеров Изинга (предположенными аналогич-
ным образом) постоянное всплывание числа 4/3 в самых разных фе-
номенах принесло аналитикам немало головной боли; в 1998 году за
проблему взялись всерьез, что привело к появлению блестящих доказа-
тельств за авторством Дюплантье, Лоулера, Шрамма, Вернера и Смир-
нова. А еще раньше было показано, что все те же 4/3 дают и некоторые
формальные гипотезы (общим числом примерно дюжина), относящиеся
к различным областям анализа. На сегодняшний день доказано, что все
они являются следствиями одной общей гипотезы; с соответствующей
математикой, правда, пока еще не все ясно.
В томе M1999N собрано много ранних статей, в которых я вво-
дил и исследовал случайные мультипликативные сингулярные меры, на-
зываемые сегодня «мультифрактальными»; пример такой меры описан
и в этой книге, в части IV. Причем целью их введения было отнюдь
не умножение эзотерических сущностей — я искал модель для турбу-
лентности и некоторых процессов в экономике. Из моих предположений
выросла активная и весьма успешная подобласть математики, с их помо-
щью были сведены в систему некоторые особенности ОДА (как уже упо-
миналось), и кроме того, они лежат в основе применяемых сегодня прин-
ципов статистического моделирования изменений рыночных цен. Чем
дальше я ослаблял ограничения, накладываемые на мультифракталь-
ные сомножители, тем интереснее становились получаемые В рСЗуЛЬТЗТС
Введение
23
структуры. В статьях, вошедших в M1999N, я начал с микроканониче-
ских сомножителей и добрался до канонических. В недавних работах,
написанных в соавторстве с Ж. Барралем, рассматриваются уже произ-
ведения импульсов и другие функции.
Публикация красноречивых изображений всем давно известных
«экспонатов» — кривых Коха и Пеано, а также канторовой пыли — вы-
звала еще более широкую и фундаментальную «смену ракурса». Когда-
то эти множества считались «патологическими» и даже «чудовищными».
Я же показал их с другой стороны — как грубые, но неоспоримые мо-
дели («карикатуры») реальности, той самой реальности, к которой на-
ука прежде боялась даже подступиться, реальности, характеризуемой
упорным фактом: подавляющее большинство объектов окружающей нас
вселенной отнюдь не являются гладкими, напротив, порой они отлича-
ются весьма высокой шероховатостью. Для примера я интерпретировал
«кривые» Пеано как траектории движения объекта, перемещающегося
по заполняющей плоскость сети рек.
Норберт Винер однажды назвал своим главным вкладом в науку
сведение вместе двух диаметральных противоположностей: математиче-
ской тонкости лебегова интегрирования и напористой физики Гиббса
и Перрена. Кроме того, Винер (как и Пуанкаре) очень активно (и небез-
успешно) способствовал широкой популяризации ведущихся на перед-
нем крае науки исследований. По обоим пунктам теорию фракталов
можно, вероятно, определить как бурный второй расцвет винеровской
модели броуновского движения.
Общие благодарности
Позвольте мне здесь добавить несколько слов к тем благодарностям,
которыми заканчиваются вошедшие в книгу работы (и которые я оста-
вил там, где им полагается быть), и к тем, что можно найти во вводных
главах к каждой части. Прежде всего, хочу от всего сердца поблагода-
рить соавторов совместных статей за разрешение на публикацию этих
статей здесь.
Вот уже более тридцати пяти лет Исследовательский Центр име-
ни Томаса Дж. Уотсона при корпорации International Business Machines
(Йорктаун-Хайтс, шт. Нью-Йорк) предоставляет единственное в своем
роде убежище всевозможным «белым воронам» от науки и поддержива-
ет их исследования, крайне необходимые как той же науке, так и все-
му обществу в целом, но не находящие в высокоакадемических кругах
24
Введение
и финансирующих их организациях ни доброго слова, ни материальной
поддержки.
В той тихой гавани и были написаны оригиналы старых статей,
вошедших в этот сборник. Бесценную помощь с компьютерной графи-
кой и программированием мне оказали Марк Р. Лафф, В. Алан Нортон,
Дж. А. Гивен (в IBM) и Питер Молдейв (в Гарварде, в 1980 году). При-
ведение исходных текстов в приличный вид и подготовку этой книги
к печати (изрядно мною затянутую) выполнили мои постоянные секре-
тари: X. Кэтрин Дитрих (1933-2003), Дженис Ризничок, Лесли Васта,
Премла Кумар, Кимберли Тетро, Кэтрин Маккарти и Барбара Уайт. По-
сле ухода из IBM я остался в Йорктауне в качестве внештатного по-
четного консультанта все той же IBM — в основном, для того, чтобы
иметь возможность работать над книгами «Selecta». В этой работе мне
помогали очень многие люди; я не могу их всех здесь перечислить, но
это не означает, что я не испытываю к ним благодарности. Неуклюжий
английский некоторых моих старых работ был тщательно отредактиро-
ван Хелен Мюллер-Ландау, Ноем Эйзенкрафтом и другими (разумеется,
смысл остался тем же, что и раньше). Оригиналы доступны в библиоте-
ках, и кроме того, я постепенно выкладываю их на своем сайте.
Никто и не предполагал, что разработанный в IBM новаторский
язык для обработки текста Script для платформы VM проживет (без
какой-либо поддержки) целых десять лет. Прожил. Однако часы неумо-
лимо тикают, и, возможно, эта книга станет последним большим проек-
том, созданным с помощью Script'^.
Вообще, Йорктаун в дни своего расцвета в качестве «кузницы науч-
ных кадров» занимает в моей жизни особое место. Это название прочно
ассоциируется у меня с именами таких давних друзей и коллег, как Ри-
хард Ф. Фосс, Мартин Гутцвиллер, Рольф Ландауэр (1927-1999) и Фи-
лип Э. Зайден (1934-2002). Что касается «управленческой верхушки»
IBM, то в те годы, когда писались первые из помещенных в этом сбор-
нике статей (бред и авантюра, по общему мнению), мою работу горя-
чо поддержал Ральф Э. Гомори, мой неизменный начальник на протя-
жении всего его продвижения по карьерной лестнице — сначала ру-
ководитель группы, затем управляющий отделом, и наконец старший
вице-президент IBM и директор по исследовательской работе. В напи-
санном для М1997Е Предисловии Гомори вспоминает о «старых добрых
временах».
Следует упомянуть и еще одну гавань, которая также немало по-
способствовала привнесению в мою жизнь желанного равновесия между
академизмом и более практическими соображениями. Я говорю о Йель-
Введение
25
ском университете, где я читал курс лекций на кафедре математики
еще будучи сотрудником IBM. Впоследствии я еще раз удостоился че-
сти быть приглашенным на должность профессора в Йеле — в основ-
ном благодаря усилиям Р. Р. Койфмана и Питера У. Джонса, за что я им
очень признателен. Среди моих йельских постдоков — Карл Й. Г. Эверте,
в соавторстве с которым мы написали статью, вошедшую в этот сборник
в виде главы С22.
И последнее (по порядку, но не по значимости): эту книгу я посвя-
щаю не только дяде Шолему. Я посвящаю ее еще и моей жене, Алиетте.
Если бы не ее постоянное и чрезвычайно деятельное участие, если бы
не ее неизменно доброжелательная поддержка, я не только не смог бы
собрать под одной обложкой все эти статьи, я бы их даже не написал.
Декоративное изображение. Все права защищены. Бенуа Б. Мандельброт. 2004
Часть I
КВАДРАТИЧНЫЕ
МНОЖЕСТВА ЖЮЛИА
И МАНДЕЛЬБРОТА
Первая публикация
С1
Квадратичная динамика:
от наблюдения к открытию
В этой главе описываются обстоятельства, при которых мне по-
счастливилось открыть в 1980 году множество, составляющее главный
предмет этой книги. Вообще говоря, впервые я увидел это множество
еще в 1979 (в главах С12 и С14 вся эта история подробно задокументи-
рована), однако еще с год мялся и топтался на месте.
В М1980п{СЗ} я «вывел в свет» современную теорию комплексной
динамики — точнее, теорию квадратичной динамики отображений z2 + c
и Az(l — z). Затем вышла «Фрактальная геометрия природы» (M1982F),
круг читателей которой оказался значительно шире. В короткие сроки
множеством Мандельброта заинтересовались очень многие, причем ин-
терес этот приобрел невиданную интенсивность. Многие выдающиеся
математики немедленно занялись изучением нового объекта и достигли
в этом начинании поразительных результатов, спровоцировавших исто-
рически значимую и в общем благотворную перемену во взглядах мате-
матического сообщества в целом. Еще вчера балом правила «общность
любой ценой». Сегодня мы с гораздо большей готовностью признаем
интересными задачи «частные».
Мои собственные интересы между тем сместились в иные обла-
сти — поэтому я мало что знаю о последних достижениях квадратичной
динамики и, соответственно, не смогу подробно о них здесь рассказать
(из последних обзоров порекомендую статью Urbanski 2003).
Следует упомянуть и о повсеместной «страстной увлеченности»
множеством Мандельброта. Этот социальный феномен до сих пор на-
блюдается, что приводит всех в изумление, а меня, разумеется, в полный
восторг. Феномен имеет спонтанный характер, никаких комитетов и об-
щественных организаций тут, уверяю вас, не замешано. Можно пред-
положить, что интерес к математике — явление среди людей не такое
30
Cl Квадратичная динамика: от наблюдения к открытию
уж редкое, но только при условии, что связи этой самой математики
с природой, с видимым невооруженным глазом миром, не подавляют-
ся активно, а напротив, выносятся на всеобщее обозрение и всячески
приветствуются.
Этот интерес, быть может, привлечет к настоящей книге и чи-
тателей, принадлежащих к так называемой «широкой публике». Ради
них я во вводных главах несколько расширил значение термина «ис-
торическая справка» и добавил описание фактов, давно и хорошо из-
вестных профессиональным математикам. Ранние мои тексты (напри-
мер. М1986р) были в этом отношении прискорбно неполны.
В первом разделе главы я дам краткий обзор, в разделах 2 и 3
остановлюсь на некоторых моментах подробнее, выражению же призна-
тельности отведу следующую главу.
На страницах всей книги размещено множество «красивых» карти-
нок, в этой же главе для подкрепления основной мысли мне придется
«обратиться к истокам». Рисунки CI-1, Cl-2, Cl-3, С1-4 и С1-5 воспро-
изводят в уменьшенном виде те самые грубые изображения, что привели
меня во время весеннего семестра в Гарварде в 1980 году к открытию
множества Мандельброта (многие из этих картинок публикуются впер-
вые). Особое внимание следует обратить на их количество и разнообра-
зие (о котором к тому времени, как они вновь попали ко мне в руки,
я успел позабыть). Компьютер не проставлял дату создания автоматиче-
ски, но я расположил их приблизительно в хронологическом порядке.
Для публикации этих старых картинок мне пришлось прибегнуть
к многократному ксерокопированию. Поскольку изображенные на них
объекты сегодня широко известны, а качество самих картинок оставляет
желать лучшего, я рискнул некоторые из них уменьшить.
I. Путь от визуального наблюдения к открытию
1.1. Определение и ключевая цитата из Адриена Дуади
Сегодня всем известно (у меня, по крайней мере, создалось такое
впечатление), что множество Л4 определяется на плоскости комплекс-
ной переменной с при условии, что последовательность с, с2 4- с, (с2 +
+ с)2 + с, ... не является расходящейся. Термин «множество Мандель-
брота А4» предложил Адриен Дуади, «потому что первым изображения
этого множества получил с помощью компьютера Бенуа Мандельброт,
и он же первым описал некоторые его свойства».
Cl. Квадратичная динамика: от наблюдения к открытию
31
Verba volant, scripta manent4. Процитированные выше слова за-
нимают вторую и третью строчки (считая снизу) страницы 161 в ста-
тье Douady 1986, к которой я в этой главе еще вернусь.
Для нас важны как сами эти слова, так и год публикации статьи.
Несмотря на краткость, утверждение Дуади делится на две четко раз-
граниченные части, одна из которых не столь существенна, зато вторая
универсальна и в историческом смысле весьма значима. То, что изоб-
ражения множества Мандельброта первым получил именно я и именно
в 1979 году, конечно, замечательно, однако с точки зрения математи-
ка хвалиться тут особо нечем. В разделе 2 я покажу, что сам по себе
вопрос о «первом изображении» вовсе не так важен, как его пытаются
представить. А из раздела 3 читатель узнает, что собственно откры-
тие было сделано позднее, в 1980, и заключалось оно именно в первом
описании многих фундаментальных свойств множества М. Вот откры-
тие уже важно, так как все последующие судьбоносные для математики
события без него просто не произошли бы.
Прежде всего, конечно же, привлекает внимание чрезвычайно силь-
ный контраст между неотразимой простотой определения множества АЛ
и его визуальной математической сложностью — контраст, наиболее точ-
но отражающий суть одного из важнейших открытий конца двадцатого
века.
Основное содержание этой книги составляют репринты статей, в ко-
торых я впервые представил наиболее значительные свои наблюдения
в виде математических задач и/или гипотез.
1.2. Причины исследования множества Мандельброта и обзор
ключевых наблюдений
1.2.1. Орбиты, их предельные точки (или циклы) и «заполнен-
ные» множества Жюлиа. Рациональная функция комплексной пере-
менной z есть отношение двух полиномов от z. Обозначим через /(г, с)
рациональную функцию от z, зависящую также от комплексного пара-
метра с, одномерного или многомерного. При неизменном с орбита на-
чальной точки го определяется как бесконечная последовательность го.
zi(z0, с) = /(z0, с). г2(г0, с) = /(zi, с) и т.д. — в общем виде гк(г0, с) =
= /[zfc_i(z0, с), с].
Начиная с конца девятнадцатого века, такие последовательности
используются для описания идеализированных динамических систем
4Слова улетают, написанное остается (лат.). — Прим, перев.
Cl. Квадратичная динамика: от наблюдения к открытию
с дискретным временем к. В таком контексте представляется важным
составить классификацию точек го и с в зависимости от предельного
поведения соответствующих орбит. При каких значениях орбита пере-
стает сходиться и становится «хаотической»? При каких значениях она
сходится к одной из нескольких неподвижных точек (или конечных цик-
лов) и может быть названа «упорядоченной»?
Квадратичная динамика занимается случаями, когда функция f
представляет собой полином второго порядка. Изменяя переменную г,
функцию / можно свести либо к г2 + с, либо к Аг(1 — г). И в том,
и в другом случае имеется один комплексный параметр: с или А. Если
начальная точка го орбиты находится на достаточном удалении от на-
чала координат, то при любом с существует некоторая бесконечно уда-
ленная неподвижная точка, к которой эта орбита сходится. Существу-
ют, однако, и такие точки го, начинаясь в которых орбита не сходится
в бесконечности. Все эти точки в совокупности составляют «заполнен-
ное множество Жюлиа», соответствующее данному параметру с.
1.2.2. А4° и Л4. При некоторых значениях с орбиты некоторых
точек г0 сходятся не к точке в бесконечности, но к конечному устойчи-
вому циклу размера N > 1. В 1979 году я заинтересовался (в уже упоми-
навшемся контексте динамических систем) построением множества Л4°
таких значений с и классификацией этих значений в зависимости от N.
Аналитическое исследование множества Л4° во всех представляю-
щих хоть какой-то интерес случаях невозможно. Поэтому я попробовал
численный подход. Однако задача оказалась чрезвычайно трудоемкой
в смысле вычислений, и полученная в итоге аппроксимация Л4° пред-
ставляла собой набор неясных пятен. Отнюдь не упростил задачу и тот
факт, что тогда, в 1979, я решил начать не с квадратичных, а с гораздо
более сложных функций /(г, с) — подробный отчет см. в С14. Здесь же
я возобновлю рассказ с того момента, когда я вернулся к /(z) = z2 + с.
Мне пришло в голову, что коль скоро существуют предельные мно-
жества, должны существовать и области сходимости, разделенные кри-
выми. Следовательно, искомое мною множество А4° должно быть под-
множеством множества тех точек с, при которых множество Жюлиа
является не пылевидным, но связным. Благодаря Фату и Жюлиа, у ме-
ня имелся замечательный критерий, недвусмысленный и очень просто
программируемый для случая квадратичного отображения: точка с при-
надлежит множеству М тогда и только тогда, когда орбита с начальной
точкой г,, = 0 (так называемой «критической точкой») не сходится в бес-
конечно Такое множество значений с полностью идентично множе-
ству Л4. определенному выше.
Cl. Квадратичная динамика: от наблюдения к открытию
33
Я предположил, что множество Л4 является замыканием множе-
ства Л4°, да и в любом случае исследовать М несколько проще, а зна-
чит, на него стоит обратить более пристальное внимание. Это мое пред-
положение сегодня чаще всего формулируют иначе; говорят, что мно-
жество Мандельброта локально связно (гипотеза MLC). Несмотря на
героические усилия, ни истинность, ни ложность его пока не доказаны.
Какое счастье, что сам я решил тогда не связываться с доказательством!
1.2.3. Структура, составленная из «атомов», объединенных
в «молекулу». Продолжая описание моих первых ключевых наблю-
дений множества А4, Дуади говорит (Douady 1986, с. 162): «Когда
смотришь на множество Мандельброта, первой привлекает внимание
область, ограниченная кардиоидой с «перегибом» в точке 0,25 и круг-
лой вершиной в точке —0,75. Затем — касательный к кардиоиде диск
с центром в точке -1 и радиусом 0,25. Приглядевшись, различаешь мно-
жество меньших дискообразных элементов, также касательных к кар-
диоиде и по большей части чрезвычайно мелких. К каждому из этих
элементов примыкает огромное количество еще меньших дискообраз-
ных элементов, к каждому из которых примыкает огромное количество
еще меньших дискообразных элементов... и так далее и так далее.»
Здесь с вашего позволения я прерву монолог Дуади и расскажу
об обстоятельствах, сопутствовавших открытию этих самых «дискооб-
разных элементов» при исследовании квадратичного отображения в его
альтернативной форме z —> Az(l - z). После нескольких итераций на
крупной сетке мы увидели, что в множестве М обозначились очень
грубые очертания дисков |Л| < 1 и |А — 2| < 1. Две строчки алгеб-
раических формул подтвердили, что появления этих дисков следовало
ожидать. Кроме того, на вещественной оси справа и слева от упомяну-
тых дисков мы обнаружили очертания дискообразных «атомов». Причем
нам показалось, что они «отпочковываются» на тех самых интервалах,
что теория бифуркаций дает для вещественного отображения х2 4- с
(см. Myrberg 1962). Последующие вычисления позволили получить бо-
лее четкую картинку, и — не без помощи воображения — я увидел,
что атомы выстраиваются в строгую иерархию, где на каждом атоме
«сидит» множество более мелких атомов. Точки, в которых к большим
дискообразным атомам примыкали атомы меньшего диаметра, оказались
именно там, где им следовало находиться теоретически. Иначе говоря,
мы получили геометрические воплощения не только для всем известной
последовательности Мирберга двойных бифуркаций, но и для любой
последовательности бифуркаций произвольного порядка.
34
Cl. Квадратичная динамика: от наблюдения к открытию
♦*
Рис. С1-1. [Гарвард, начало 1980 г.] К сожалению, отыскать самое первое по-
лученное мною изображение всего множества нам так и не удалось (первая
картинка, сделанная в IBM в 1980 году, помещена в одной из последующих
глав). Здесь, вверху, вы видите увеличенное изображение одного из наиболее
♦замусоренных» уголков Л4 неподалеку от бифуркации третьего порядка. В се-
редине и внизу — самые старые из сохранившихся изображений двух крупней-
ших »островов» (тоже увеличенные); первый перекочевал целиком с верхней
картинки, а от второго видна лишь половина, срезанная по вещественной оси
(другую половину мы не обсчитывали, экономии ради).
Cl. Квадратичная динамика: от наблюдения к открытию
35
1.2.4. «Спутники» или «прибрежные острова». А также жем-
чуг в грязи. Однако вернемся к Дуади (Douady 1986). «Но это еще
не все! Оставим большую кардиоиду ... и двинемся ... к точке Мир-
берга-Фейгенбаума (координата —1,401) ... Отрезок от этой точки до
точки —2 принадлежит множеству Л4, и на этом интервале мы видим
маленький кардиоидообразный элемент с перегибом в точке -1,75, окру-
женный целым семейством дискообразных спутников — в точности так
же, как и большая кардиоида. Вообще говоря, таких кардиоидообразных
элементов, ... как показал Б. Мандельброт, здесь бесконечно много.
И не только на вещественной оси.»
Как же были открыты эти «прибрежные острова»? Как можно убе-
диться, взглянув на рис. С1-1, первые полученные нами изображения
выглядели страшновато — дело осложнялось еще и тем, что наш прин-
тер «Versatic» имел скверную привычку в изобилии усеивать проходя-
щие через него бумаги разнокалиберными пятнами. Впрочем, тот ква-
лифицированный, дотошный и неутомимый наблюдатель, каким я был
тогда, усмотрел во всем этом графическом безобразии не лишний повод
посетовать, но призыв удвоить бдительность. Желая убедиться, что в по-
явлении пятен повинна не только никуда не годная гарвардская аппара-
тура (о которой я еще расскажу ниже), я поехал в Йорктаун, где провел
день, который никогда не забуду. На мэйнфрейме в IBM мы и получи-
ли то самое изображение, которое сегодня выступает в роли символа
фрактальной геометрии и не нуждается в том, чтобы я помещал его еще
и здесь. Впоследствии оно стало рисунком 1 в статье М1980п{СЗ}, а по-
том попало в M1982F (глава 19, с. 189, верхний рисунок; эта глава — со
всеми картинками и под номером С4 — вошла и в настоящий сборник).
На новом изображении упомянутое безобразие исчезать отказалось,
более того, некоторые пятна расположились относительно друг друга
с крайне подозрительной симметричностью. Поскольку «натуральным»
пятнам симметричность обычно не свойственна, и те, и другие про-
сто напрашивались на увеличение и более пристальное изучение. После
увеличения многие мелкие пятна таки исчезли. Другие же не только
остались на прежних местах, но и продемонстрировали сложную «мо-
лекулярную» структуру, оказавшись миниатюрными версиями будущего
множества Мандельброта для отображения z -» г2 + с.
Никак не могу отделаться от мысли: не будь тот памятный день
в Йорктауне таким суматошным, организуй я все должным образом,
мы, возможно, ограничились бы верхней половиной картинки. И ника-
кой симметрии просто не увидели бы — со всеми вытекающими отсюда
последствиями.
36
01. Квадратичная динамика: от наблюдения К открытию
Далее мы сосредоточились на ответвлениях, соответствующих би-
фуркациям различного порядка, и сравнили получающиеся в каж-
дом случае прибрежные острова. Оказалось, острова эти располагают-
ся в точности на пересечениях, образуемых «лучами» звездообразных
структур и логарифмическими спиралями!
Обнаружив в грязи столь прекрасные жемчужины, я с новой стра-
стью погрузился в исследование, результатом которого стала моя первая
статья о множестве Мандельброта (М1980п{СЗ}); некоторые из вошед-
ших в нее иллюстраций были подготовлены уже после моего возвраще-
ния в IBM из Гарварда. Очень скоро статью опубликовали в «Анналах
Нью-Йоркской Академии наук», среди материалов крупной конференции
по проблемам нелинейности — иначе говоря, аудитория была обеспечена
самая широкая. Уже по названию статьи («Фрактальные аспекты итера-
ции отображения z —> Az(l - z) при комплексных А и z») можно видеть,
что я ставил перед собой цель способствовать возрождению эксперимен-
тальной математики — для объяснения результатов моих наблюдений
старая математика не годилась, требовалась новая.
1.2.5. Ажурные структуры, объединяющие острова в связное
множество At. Далее в работе 1986 года Дуади пишет: «И это еще
не конец... Все эти компоненты в форме кардиоиды связаны с глав-
ной кардиоидой нитями, к которым прилегают маленькие компоненты
в форме кардиоиды, каждый из которых находится в окружении своего
набора спутников. Эти нити образуют очень изощренную сеть».
И снова позволю себе дополнить. Параллельно с увеличением от-
дельных участков множества At мы строили также множества Жюлиа,
выбирая в качестве параметра с значения, лежащие внутри островных
молекул (примеры таких множеств даны на рис. С1-4). Это, очевидно,
и был тот пресловутый момент «эврика», к которому меня подготовили
предшествующие десятилетия работы в математике. Полученные фигу-
ры тоже расщеплялись на множественные острова, каждый из которых
представлял собой уменьшенную копию множества Жюлиа, соответ-
ствующего аналогичному значению с из континентальной молекулы мно-
жества At. При этом мы осознавали, что где-то здесь наверняка кроет-
ся подвох. Понятно, что внутренние области островов перекрываться не
могут, однако согласно критерию Жюлиа (подкрепленному увеличенны-
ми изображениями отдельных участков), промежутки между островами
должны быть частично заполнены геометрическими структурами весьма
хитроумной формы. Лучше всего, на мой взгляд, эту форму иллюстри-
рует следующая аналогия: представьте себе широкую реку НЗСТОЛЬКО
широкую, что перепрыгнуть с одного берега на flnvrnft 2 «
н d на другой способны толь-
Cl. Квадратичная динамика: от наблюдения к открытию
37
Рис. С1-2. [Гарвард, начало 1980 г.] Более четкие изображения участка мно-
жества Мандельброта вблизи бифуркации порядка 11. На этот раз я намере-
вался выяснить, является ли множество М связным. Соответственно, я постро-
ил и несколько других изображений, начиная квадратичные итерации с иных,
нежели критическая г0 = 5, начальных точек. Плохое качество картинок не поз-
волило мне тогда сделать какие-либо решительные выводы. Более убедительные
косвенные свидетельства в пользу связности я получил посредством других по-
строений (см. пояснение к рис. С1-4).
ко очень большие звери. Для того чтобы перебраться на другой берег
смогли звери меньшего размера, необходимо поставить посреди реки ка-
мень. Для еще меньших зверей нужно добавить еще по камню на каж-
ci. квадратичная динамика: от наблюдения к открытию
Рис. С1-3. [Гарвард, начало 1980 г.] Различные множества Жюлиа при значе-
ниях комплексного параметра в пределах главной континентальной молекулы
множества Мандельброта.
дый проток. А теперь представьте, что нам предстоит переправить на
ту сторону зверя настолько дьявольски крохотного, что процесс добав-
ления камней придется повторять до бесконечности. В конечном итоге
Cl. Квадратичная динамика: от наблюдения к открытию
39
Рис. С1-4. [Гарвард, начало 1980 г.] Различные множества Жюлиа при значени-
ях комплексного параметра, приходящихся на «островные молекулы» множества
Мандельброта. Согласно теореме, доказанной Жюлиа и Фату, эти множества
Жюлиа связны. То есть их «разрозненный» вид есть исключительно следствие
дискретности используемых в вычислениях переменных. Эти построения сыг-
рали важную роль в моих размышлениях, поскольку достаточно убедительно
показали, что из аналогичной разрозненности множества М на первых изобра-
жениях совершенно не следует, что оно не может быть связным.
40
Cl. Квадратичная динамика: от наблюдения к открытию
Рис. С1-5. [Гарвард, начало 1980 г.] Один из ранних этапов: я представил себе
поверхность, определяемую в каждой точке А некоторой функцией Я(А), зна-
чение которой равно количеству итераций, необходимых для получения нера-
венства |/„(1/2)| > 2. Множество М при таком подходе определяется значени-
ем Н = оо. В M1982F, на с. 189, имеется помимо прочего иллюстрация, изоб-
ражающая поверхности уровня Я(А) в оттенках серого (здесь эта иллюстрация
тоже есть, см. главу С4). В 1986 году Пайтген и Рихтер (Peitgen & Richter 1986)
научили нас изображать изолинии и разные ракурсы поверхности Я(А) в ярких
красках. Однако в начале 1980 мне были доступны для изучения лишь вер-
тикальные сечения этой поверхности, соответствующие прямым в плоскости А.
На этом рисунке я совместил на одном графике три в оригинале различных
сечения, соответствующие прямым А = t + 0,00001г, А = t + 0,0001г и А =
= t + 0,001г (t — абсцисса, Н 300). Диапазон t (на оригинальных графиках
не указанный), очевидно, соответствует малым островам на вещественной оси
плоскости А. Для удобства и наглядности первое и второе сечение на рисун-
ке приподняты — на 100 и на 50 шагов итерации, соответственно. Получен-
ный результат подтвердил предположения, сделанные на основе вещественных
(в противоположность комплексным) итераций.
Cl. Квадратичная динамика: от наблюдения к открытию
41
каменные «острова» соприкоснутся своими «береговыми линиями», об-
разовав «дьявольский» полимер, «звенья» которого нам невидимы, так
как любые реальные вычисления неминуемо ограничены сеткой.
Возвращаясь к множеству Л4, отметим, что крайне важную роль
сыграл в нашей истории тот факт, что у нас уже имелась, благодаря
Мирбергу, теория итераций вещественного отображения х2 + с. Теория
вполне допускала предположение, что цепь островов множества А4, на-
низанных на вещественную ось, связна, что береговые линии этих ост-
ровов соприкасаются на вышеописанный «дьявольский» манер. А это,
в свою очередь, позволяло предположить, что все множество М пред-
ставляет собой связный дьявольский полимер.
Я, впрочем, подошел к делу с той степенью осторожности, какая
вообще-то мне не свойственна — возможно, это было вызвано тем, что
предыдущий год мне пришлось провести в обществе почти исключи-
тельно «чистых» математиков. Я представил связность множества М
не как гипотезу, которую придется подтверждать, а как вопрос, на ко-
торый предстоит найти ответ. Различие больше по форме, нежели по
сути, однако оно вынудило меня в М1980п{СЗ} изобретать для мно-
жества М некий неуклюжий суррогат, свойства которого можно бы-
ло описать математически более «строго». К 1982 году я покончил
с неуверенностью в себе и в M1982F расставил все по местам. Вопрос
тем временем приобрел чисто академический характер: в том же 1982
А. Дуади и Дж. X. Хаббард представили доказательство связности мно-
жества Л4 и углубились в детальное исследование этого удивительного
объекта.
1.2.6. «Звездообразные структуры» и таинственная схожесть
множеств Жюлиа и «соответствующих» углов множества Мандель-
брота. В процессе непрерывных «метаний» от множества М к отдель-
ным множествам Жюлиа я пришел к другому потрясающему открытию.
Я увидел, что множество М не только содержит информацию о числе
точек в предельных циклах, но и имеет таинственный «иероглифиче-
ский» характер. В само множество М входит целый искаженный набор
уменьшенных версий всех множеств Жюлиа.
Среди других моих ранних наблюдений значились «звездообразные
структуры», свойственные множеству Жюлиа с параметром с и окрест-
ности параметра с во множестве Мандельброта.
1.2.7. Гипотеза о том, что размерность Хаусдорфа-Безиковича
границы М равна 2. Эта гипотеза постепенно совершенствовалась
и в конечном ее виде она представлена в главе С8.
42
Cl Квадратичная динамика: от наблюдения к открытию
2. Подробное изучение несущественного вопроса:
Какими были «первые изображения» множества
Мандельброта?
Повторюсь: несмотря на свою краткость, фраза Дуади, приведен-
ная в разделе 1.1, затрагивает два совершенно разных вопроса, которые
в этом и следующем разделах мы обсудим по отдельности и во всех
подробностях.
2.1. Для математики интерес представляет не сам рисунок,
а основанные на нем описания и исследования
Дуади говорит, что я был «первым создавшим рисунки» М. Это на
самом деле так. Более того, он точно использует слово «рисунки» во
множественном числе, что имеет большое значение. Однако это утвер-
ждение требует подробного пояснения. Предположим, что какой-то ис-
торик из будущего обнаруживает, что Жюлиа и/или Фату где-то мимо-
ходом заметили следующее: при |с| > 2 множество Жюлиа квадратич-
ного отображения вполне несвязно. Такой гипотетический, но вполне
понятный результат привел бы к «приблизительному изображению» М
в форме круга. Из этого предположения невозможно сделать никаких
выводов, поэтому его никак нельзя называть первым.
Вместо рассмотрения гипотетических результатов обратим внима-
ние на два документально подтвержденных изображения, касающихся
другого объекта, а именно: ограниченных диффузией агрегаций (ОДА),
которые будут рассматриваться в главе С22. После открытия ОДА в ра-
боте Уиттена и Сандера (Witten & Sander 1981) в процессе изучения
соответствующей литературы было найдено множество старых изобра-
жений природных объектов, по форме напоминающих ОДА. Однако эти
рисунки не привели ни к каким открытиям, поскольку подходящие ин-
струменты появились только с развитием фрактальной геометрии. Фрак-
талы были необходимым условием блестящего и очень важного описа-
ния, которое предоставили Уиттен и Сандер. Именно эти авторы откры-
ли ОДА, а более ранние рисунки не заслуживают внимания.
Аналогичным образом, рисунок 2 главы С19 помог обнаружить в ра-
боте М & Evertsz 1991 некоторые очень интересные особенности потен-
циала Лапласа вблизи ОДА. Кто-то из ученых потом указал на похожее
изображение, сделанное ранее. Но то изображение было создано с един-
ственной целью — проиллюстрировать какую-то методику вычислений,
и к нему не было сделано никаких комментариев. Возможно, оно было
«первым», но его забыли — как оно, впрочем, того и заслуживало.
Cl. Квадратичная динамика: от наблюдения к открытию
43
2.2. Гарвардские расчеты 1980 г.
В 1980 году «мозги» программистов и минимальную компьютерную
мощность, необходимые для создания простейших изображений, мог за-
получить любой попросивший. В отношении научных исследований все
сидели в одной лодке. Всего несколькими годами ранее при подготовке
работы М 19750 я протестировал свою фрактальную модель береговых
линий, накладывая буквы О, X, М и W и раскрашивая острова флома-
стером.
Более того, я открыл множество Мандельброта в 1980 году, рабо-
тая в Гарварде, оборудованном на тот момент одними из самых слабых
в научной среде компьютеров. В подвале Научного центра стоял первый
«еще необъезженный» компьютер D.E.C. Vax 50, рисунки рассматри-
вались на катодно-лучевой трубке Tektronix (очень старой и бледной),
а копии делались на принтере Versatec, которым никто не умел поль-
зоваться. Работать мы могли только по ночам, когда у нас был всего
один конкурент по работе с компьютером — химик Мартин Карплюс.
Мы поочередно использовали практически все рабочее время компью-
тера.
Все это достаточно ярко показывает, что моя постоянная работа
в Исследовательском центре имени Томаса Дж. Уотсона в IBM и каче-
ство их компьютеров не были решающим фактором тех ранних откры-
тий. И хотя очень многие придерживаются противоположного мнения,
оно противоречит фактам.
В 1979 году (об этом говорится в главе С14) качество компьюте-
ров в IBM позволило мне лишь увидеть множество Мандельброта, но
не исследовать его. В любом случае, IBM абсолютно не предусматри-
вало работу с изображениями. У меня не было отдельной лаборатории
с подходящим современным оборудованием, а только хорошие друзья,
которые создали пригодную машину, которая стала родоначальником
искусства передачи изображения. Ставшие теперь классикой рисунки
в работах М 1977F и М 1982F потребовали героических усилий и таких
вложений в очень редкие умения и оборудование, которые до открытия
представлялись неоправданными.
2.3. Как главный рисунок из М 1980п{СЗ} оказался в центре
внимания
Грязь на моих ранних рисунках замечали все. Принимая во внима-
ние, что прибрежные «острова» было сложно отличить от точек грязи,
я постоянно предупреждал своих ассистентов по работе с принтером.
44
Cl. Квадратичная динамика, и.
что точки на моем рисунке, датированном 27/3/80, не надо «чистить».
Однако в главе СХХ подтверждается, что они все-таки «чистили» тот
рисунок, к большой радости тех, кто читал мои работы или слушал мои
доклады по ним. Позже в процессе подготовки этой книги в моих ар-
хивах был обнаружен рисунок более высокого качества, датированный
10/12/81. На нем значится то же самое предупреждение: «Не пытайтесь
счистить частицы пыли. Они настоящие». Еще позднее на этой надписи
появилась другая — на французском языке: «IMPRIMEUR: N'EFACEZ
PAS СЕ QUI SEMBLE N'ETRE QUE DE PETITES SALETES SUR CE
CLICHE ELLES SONT TOUTES REELLES ET IMPORTANTES».
Mfr
Ua/, Jit Utb
и ы/Асёг ce
fj'irju Out №*<
Itrnn mwtik juz и
Все тщетно! Более того, в процессе подготовке той книги мне на ум
пришла ужасная мысль: а как же рисунки множества М, помещенные
в такой популярной работе как M1982F? С момента первой публикации
множество М полиномов z2 + с подверглось обновлению, чтобы пока-
зать знаменитые «волоски» или «полимерные структуры». В моих ран-
них работах это множество носило название ^-отображения, потому
что у физиков было принято обозначать константу с как — р, а следова-
тельно, рассматриваемое отображение записывалось как z —► z2 — р.
Однако оригинальное изображение множества М полиномов Az(l -
- z) (первоначально именуемое Х-отображением) претерпело измене-
ния, коих не должно было быть. О ужас! На нем более не было то-
чек! Я незамедлительно ринулся проверять свои архивные копии первой
распечатки. Точки там были. Совершенно ясно, что невежды печатно-
го дела воспользовались процессом обновления и снова провернули это
злодеяние.
В заключение хочется сказать, что мое послание было услышано
многими несмотря на качество рисунка, а не благодаря ему. Открытие
множества М состоялось только после того, как рисунки вдохновили
мае на создание их ОПИСЗНИЙ.
Cl. Квадратичная динамика: от наблюдения к открытию
45
3. Открытие множества Мандельброта и возрождение
экспериментальной математики
Памятуя о постоянных сбоях в функционировании якобы «прекрас-
ных графических устройств IBM», невольно задаешься вопросом: поче-
му множество Мандельброта не открыл какой-нибудь другой ученый,
у которого был доступ к лучшим технологиям, чем у меня в 1980 году?
Отчасти ответ на этот вопрос кроется в загадке научного открытия. От-
крытие имеет место быть когда инструментами (как интеллектуальны-
ми, так и физическими) располагает человек, обладающий, помимо всего
прочего, мотивацией, сообразительностью и желанием их использовать.
А у меня был мотив — разобраться в ответвлениях тех точек грязи.
Именно мои гипотезы о тех участках пыли (а вовсе не беспрерыв-
ный доступ к компьютерам) пробудили интерес во многих математиках,
что позже заставило всех поверить в доказательную способность на-
блюдений. На церемонии открытия Йельского университета в 1962 году
Джон Ф. Кеннеди сказал: «Великим врагом истины очень часто ока-
зывается не ложь намеренная, хитрая и бесчестная, а миф — давний,
убедительный и реалистичный». Это и был миф — слишком давний,
убедительный и чересчур реалистичный — о том, что эксперименты
в математике стали бесполезны.
3.1. Ключевой факт, который постоянно неверно понимают
и толкуют: в процессе развития многих наук (особенно давно
сложившихся) наступает период, когда опытный глаз мастера
оказывается крайне важным
Сейчас не помешает вспомнить некоторые примечательные примеры
того, какую важную роль сыграло правильное толкование зрительных
образов. Телескоп был изобретен, сконструирован и выпущен в Голлан-
дии как игрушка. По крайней мере один человек, Томас Хэрриот (1560-
1621), известный в свое время астроном и математик, догадался навести
его на Луну и сделать зарисовки увиденного. Его рисунки сохранились,
но содержат лишь бесструктурные кляксы.
Галилео Галилей (1564-1642) стал использовать телескоп далеко не
первым, но именно он превратил его из игрушки в необходимый прибор.
Он был опытным художником, но, надо сказать, не очень хорошим по
сравнению с гениями эпохи тосканского Ренессанса. Однако его умений
как раз хватило для новой работы с изображениями, полученными с по-
мощью телескопа. Хэрриот, получив направление к структурам, которые
46
Cl. Квадратичная динамика: ОТ НАБЛЮДЕНИЯ К ОТКРЫТИЮ
не смог открыть сам. незамедлительно подтвердил их существование.
Он вполне мог бы присоединиться к Т.Х. Хаксли, который, прочитав
труд Дарвина ^Происхождение видов», воскликнул: «Какой же я дурак,
что не додумался до этого!»
Вообще, Галилей (намного) обошел своих современников, изобрел
физику и стал первым ее представителем по одной весьма веской при-
чине. Он вылепил современную науку, руководствуясь мнением, что ис-
тина заключена не в древних книгах, написанных людьми, а в «великой
книге Природы», открытой человеческому взору. В сущности, Галилей
выступил против утверждения Нового Завета, что «в начале было сло-
во». Если бы он осмелился поспорить с Библией — что маловероятно,
поскольку он (в отличие от меня) боялся идти на конфликт с Церко-
вью, — он мог бы воскликнуть: «В начале были картинка и глаз». А еще
лучше: «В начале слово присоединилось к картинке и глазу».
Но продолжим. Микроскоп и фотографическая камера уже исполь-
зовались во времена Сантьяго Рамон-и-Кахаля (1852-1934), но их су-
ществования было недостаточно для того, чтобы исследовать сложную
(нет. не «сложную», а «в высшей степени запутанную») нервную систе-
му человека. И опять-таки «судьба» выбрала для этого дела Рамон-и-
Кахаля потому, что такая задача выходила за рамки «обыденного», а он
(возможно, единственный в свое время) был отлично подготовлен для ее
решения. Обладая достаточным опытом, бесконечным терпением и та-
лантом художника, он — вопреки чудовищной неточности имевшегося
в его распоряжении микроскопа — увидел настоящие чудеса и изобра-
зил увиденное на ставших классическими рисунках, которые в течение
долгого времени оставались непревзойденными. В 1950 году мои дру-
зья-неврологи все еще пользовались рисунками, впервые опубликован-
ными в практически средневековой Испании в 1890-х годах. И я считаю
постыдным, что Кахаль так и не вкусил славы, которой достоин.
Стоит упомянуть еще одного ученого, обладавшего «особым» зрени-
ем — метеоролога и геофизика Альфреда Вегенера (1880-1930). Долж-
но быть, люди и раньше замечали, что юго-западное побережье Африки
практически совпадает с северо-восточным побережьем Южной Аме-
рики. Но только Вегенер нашел в себе смелость сделать следующий
шаг — от наблюдения к открытию. Он сравнил ископаемые, разделен-
ные Атлантическим океаном, и предположил, что некогда существовал
первичный континент, в котором произошел разлом, и его части отдели-
лись друг от друга.
Галилей и Кахаль занимают высокие позиции в моем личном пан-
теоне великих ученых. В некотором роде (безо всяких претензий на
Cl. Квадратичная динамика: от наблюдения к открытию 47
такую же значимость) мой опыт был похож на то, что сделали они.
Я думал о Кахале, когда открывал множество М, и о Галилее, когда
открывал размерность границы броуновской оболочки, равную 4/3.
Основные различия очевидны: Галилей был основателем практи-
чески всего, Рамон-и-Кахаль углубил уже ведущиеся исследования,
а я способствовал возрождению после долгого перерыва. «Судьба», ко-
торая помогла мне оживить теорию итераций, сначала выбрала меня
для определения новой роли зрительного восприятия в такой области,
в математике, где оно наряду с точными подсчетами практически бы-
ло предано анафеме и нежелательно настолько, насколько это только
возможно.
3.2. Математическая культура в 1960-е и 1970-е годы
В рамках существовавшей тогда культуры открытие множества
Мандельброта было бы невозможно, поэтому оно ознаменовало собой
исторический переход. Сегодня (но не в то время) лишь немногие ма-
тематики согласились бы с утверждением того, кто не открывал это
множество: изучение множества М отражает «довольно инфантильное
и в некоторой степени недоразвитое понимание математики» (Brooks
1989).
Традиции, в которых воспитывались математики еще совсем недав-
но, описал Станислав Улам (1909-1984). Можно было бы ожидать, что
он выскажется в поддержку правильности и полезности рисунков, со-
зданных его соратниками. Однако в 1974 году Улам написал (Ulam,
1974, стр. 378 и 490): «Математика на самом деле не нуждается ни в на-
блюдениях, ни даже в экспериментах. И все же... компьютерные вычис-
ления. .. помогли установить некоторые любопытные факты... Ферми
выразил... мнение, что стоило бы прибегнуть к использованию в ма-
тематике. .. нелинейных систем. Результаты (описанные в знаменитом
докладе Ферми, Паста и Улама и приведенные в работе Ulam, 1974]...
заинтересовали и удивили Ферми».
Вынужденное признание Уламом пользы компьютерных исследова-
ний укрепило среди чистых математиков неприятие к ним, которое было
очевидно до самого 1979 года. К примеру, выдающихся молодых ма-
тематиков не раз приглашали посетить Исследовательский центр IBM
с лекциями на различные темы в некоей надежде на то, что перспекти-
вы использования компьютеров способны вызвать интерес. Провал был
полным и абсолютным. И только много позднее некоторые сообщества,
хотя и без особого энтузиазма, приняли мои «неправильные» методы.
48
Cl. Квадратичная динамика: от наблюдения к открытию
Ну что можно сказать серьезным ученым, которые не желают ви-
деть разницу между наблюдением и открытием? Некоторые из них до
сих пор пытаются найти «рисунки множества Л/», относящиеся к более
ранним годам, чем какое-нибудь изображение из моей коллекции, или
тот единственный экземпляр, обнаруженный в работе Brooks & Metelski
1981 и столь часто упоминаемый после 1988 года. Тот единственный
рисунок был настолько нечетким, что не мог привести (да и не привел)
к какому-либо открытию.
Для того чтобы показать, насколько непродуктивными могут стать
эти поиски «первопроходца», позвольте мне перейти от итерации к са-
мим фракталам. Кто собрал первую обширную коллекцию рисунков,
в которых четко узнаются фракталы? Возможно, это был великолеп-
ный Хокусай Кацусика (1760-1849), которому я с удовольствием отдаю
должное, публикуя рисунок С16 в работе M1982F и в главе С13. На его
незабываемых, сделанных от руки рисунках из «Ста видов горы Фуд-
зияма» потрясающе изображены облака и деревья. Все, кто способен
видеть и кто знаком с фрактальной геометрией, признают, что Хокусай
обладал идеальным «чутьем на фракталы».
Но ни он, ни другие пейзажисты не пытались перенести фракталы
в математику или науку в целом. Этим мы обязаны современникам Кан-
тора и Пеано, а также вашему покорному слуге. Тем не менее, Хокусаю
отведена главная роль в представлении фракталов (в моем сегодняшнем
понимании) как феномена, в той или иной форме известного человече-
ству с незапамятных времен.
Весьма и весьма долгая предыстория фракталов заслуживает от-
дельного обсуждения, но она поднимает проблему, которую я оставляю
на рассмотрение специалистов. Во времена Кантора, Пеано и прочих
в мире царило увлечение Японией, так что непосредственное влияние
Хокусая на искусство Западной Европы не вызывает никаких сомнений.
Распространилось ли это влияние с художников на математиков (без
объявления должной благодарности)?
3.3. Смена курса а математике?
В работе Bourguignon 1999 возникает совершенно другой мир. При-
веду вольный перевод одной из цитат: «На мой взгляд, необходимо раз-
личать будущее математики и будущее тех, кто называет себя матема-
тиками. Будущее математики полно надежд и задач, ждущих решения-
Но, боюсь, что математики его испортят страшась перемен и не осме-
ливаясь открыться навстречу новому, а также из-за склонности сооб-
Cl. Квадратичная динамика: от наблюдения к открытию
49
щества, в которое они объединились, исключать (следовало бы сказать
«отлучать», поскольку здесь явно присутствуют религиозные нотки) из
своей науки целые области знания. Математики должны распахнуть ок-
но в мир не боясь простудиться от порыва свежего ветра». Я читал этот
текст, испытывая смешанное чувство удовольствия и удивления.
4. Заключение
Вчитайтесь в мудрое высказывание Уайтхеда (Whitehead 1974,
стр. 127): «Подойти вплотную к истинной теории и постичь ее точное
применение — две очень разные вещи. Этому нас учит история нау-
ки. Все важное уже было сказано кем-то, кто не сумел этого открыть».
В этой фразе можно заменить слово «сказано» на «увидено», и ее смысл
от этого утрачен не будет.
Вклад в математику и/или науку в целом сводится не к рисунку,
а скорее к рисунку вкупе с описанием. Без слов и формул рисунок
можно отметить только за его художественное исполнение. Рисунки не
могут играть никакой роли, если у людей нет интереса к ним и другим
аспектам «реальности».
Эта мысль будет раскрыта подробнее в следующей главе, которая
повествует о некоторых ученых и учебных заведениях. Все они повлияли
на меня в процессе поиска своего места в мире.
Первая публикация
С2
Выражение признательности, или Люди,
благодаря которым я пришел к квадратичной
динамике
Сначала эта глава состояла из одной страницы, на которой я выра-
зил свою благодарность трем людям: Мандельбройту, Дуади и Хаббарду.
Однако очень скоро этого мне показалось мало, и, по мере увеличения
числа страниц, в тексте стали проскакивать неизбежные автобиографи-
ческие нотки. Затем я невольно расширил смысл слова «благодарность»,
вкратце упомянув о Бурбаки, ставшем для меня воплощением Неме-
зиды.
При первом упоминании имена главных действующих лиц выделя-
ются жирным прямым шрифтом или жирным курсивом. Читатель,
незнакомый с историей математики, а особенно, французской матема-
тики середины двадцатого века, найдет здесь некоторые любопытные
факты. Более подробная историческая справка приводится в главе 25.
1. Шолем Мандельбройт (1899-1983)
Прежде всего, мне хотелось бы еще раз упомянуть о человеке, ко-
торому я посвятил эту книгу. Я бесконечно благодарен своему дяде
Шолему, именитому математику, попавшему в Коллеж де Франс, луч-
шее учебное заведение страны, в возрасте тридцати восьми лет; мне в ту
пору было тринадцать. Так что я всегда знал, что наука — это не толь-
ко собрание пыльных томов, но и весьма интересное занятие; поэтому
я, сколько себя помню, был вовсе не чужд того, чтобы стать ученым.
Умный, дерзкий и амбициозный, Мандельбройт уехал из родной
Польши во Францию в двадцать лет в статусе «идеологического» бежен-
ца, отвергнутого чрезмерно абстрактной «польской математикой», разви-
тием которой на тот момент занимался Вацлав Серпински (1882-1969).
Шолема же влекла математическая школа, правившая бал в Париже
в 1920-е годы; она ассоциировалась с именем Анри Пуанкаре (1854-
1912). Шолем сблизился с Жаком Адамаром (1865-1963) и Вито
С2. Выражение признательности
51
Вольтерра (1860-1940) — самыми влиятельными математиками того
времени в Париже и Риме, соответственно. Позже к Шолему во Фран-
ции присоединился мой отец, сбежавший от польской экономической
депрессии и политического застоя. Стычки между Серпинским и моим
дядей по вопросам математики и не только (!) спасли нам жизнь.
Мы с дядей любили друг друга, но имели совершенно разные науч-
ные пристрастия и проводили время в бесконечных спорах, особенно на
тему выбора наилучшего способа посвятить свою жизнь умственному
труду. Каждый из нас с непоколебимой преданностью следовал за своей
путеводной звездой. Я критично относился к его выбору, хотя хорошо
понимал всю ценность проделанной им работы; он же так никогда и не
понял выбор, сделанный мной. Как бы то ни было, в целом и в частно-
стях, он был моим первым и главным наставником, а его общее влияние
на меня можно определить как очевидное, обширное и в высшей сте-
пени позитивное. В конце концов, я взял у него подробное интервью
и разместил работу Mandelbrojt 1985 на своем веб-сайте.
2. Первая встреча с Николя Бурбаки
В феврале 1945 года я сдал вступительный экзамен в престижную
Высшую нормальную школу. Я мог бы считаться лучшим в физико-
математическом классе, который насчитывал всего пятнадцать студен-
тов (со всей Франции)! Это был воистину «акробатический трюк», по-
скольку из-за войны я готовился к этому экзамену не два года, а всего
несколько недель. Думаю, что своим успехом я обязан, главным обра-
зом, природным способностям к геометрии.
В тот момент дядя сказал мне, что, судя по всему, наша Школа вот-
вот попадет под влияние утопического движения, направленного в сто-
рону математической абстракции, «чистоты» и изоляции, которые вкупе
именовались Николя Бурбаки. Мой дядя был самым старым представи-
телем этой группы в ее первоначальном составе. По окончании Второй
мировой войны он решил «досрочно уйти на пенсию», но не прекратил
общаться со старыми друзьями. Его размышления можно найти в рабо-
тах Mandelbrojt 1982, 1985 и в главе 25.
Членов группы Бурбаки чрезвычайно волновало политическое влия-
ние в рамках разных возрастных групп и дисциплин. Они получили воз-
можность учить детей (хотя и не признавали французскую математику,
которая еще вчера была «новой»), распространять правильное мышле-
ние среди молодежи, попрекать стариков, изолировать рьяных еретиков
и навязывать свои стандарты строгости и свои предпочтения повсюду,
52
С2. Выражение признательности
даже там, где они были совершенно неуместны. Что и говорить, они
причинили науке несказанный вред.
Члены Бурбаки создали вокруг своего кружка атмосферу «тайного
общества», которая сохранилась и после того, как они захватили власть.
Многие бывшие члены этого сообщества практически ничего не говорят
о нем. Этот кружок, претендующий на то, чтобы считаться образцом
«благоразумия», до сих пор оказывает влияние на историю, а потому
отнюдь не лишним будет рассказать об отношении Бурбаки к науке
и геометрии.
Андре Вейль (1906-1998) сначала считался лишь одним из пер-
вых среди равных членов-основателей Бурбаки, но после смерти его
официально признали главным идейным лидером. Защитив докторскую
диссертацию, он провел год в Геттингенском университете у Давида
Гильберта (1862-1925) — там, где в одном здании соседствовали теоре-
тическая физика, численные методы и еще более эзотерические области
математики. Это случилось благодаря желанию Гильберта и идее Фе-
ликса Клейна (1849-1943), которую развил Рихард Курант (1888-1972).
Всеобщее внимание было сосредоточено на рождении квантовой меха-
ники, коим мы обязаны физикам Максу Борну (1882-1970) и Вернеру
Гейзенбергу (1901-1976). Однако для Вейля существовал один рай на
земле — абстракция; он сам его создал и взрастил сначала в Париже,
а затем и в США. В его раю математики воспитывались в атмосфе-
ре, незапятнанной каким-либо нечистым контактом. Вместе с тем, его
взгляды на мир были крайне предвзятыми, а его собственная жизнь,
описанная в работе Weil 1992, имела прискорбно мало общего с офи-
циальной историей, равно как и влияние, которое он так стремился
оказывать на других.
Другой отец-основатель, Жан Дьедонне (1906-1992), часто опи-
сывал Бурбаки как реакцию нескольких неординарных индивидов на
различные аспекты развития Франции после Первой мировой войны.
К тому же, во Франции 1940-х и 1950-х годов царила идеология все-
общего потребления, которая заставила самых выдающихся моих совре-
менников служить одному из нескольких всепожирающих дел. Как бы
то ни было, Дьедонне было на руку считать, что «некоторые математи-
ческие объекты, например, кривая Пеано, совершенно неинтуитивны.. •
они — экстравагантны». В главе 7 работы М 1982F это мнение оспа-
ривается с точностью до наоборот; там дается приблизительный образ,
одномоментно изменивший нашу «интуицию»: оказывается, очертания
дыхательных путей представляют собой почти заполняющую простран-
ство поверхность.
С2. Выражение признательности
53
Представитель более позднего поколения членов Бурбаки, Лоран
Шварц (1915-2002), проявил некоторый интерес к физике. Однако в ра-
боте Schwartz 1997 говорится (с. 58): «Контраст между моей любовью
к геометрии и почти полным отсутствием у меня геометрического ви-
дения не может не озадачивать. Мои воспоминания начисто лишены
образов. .. Грубо говоря, я люблю не наглядную геометрию, а ту гео-
метрию, которая близка к алгебре или математическому анализу. Из-за
отсутствия пространственного воображения я так и не научился водить
машину. Я могу доказать теорему Паппуса, но мне не под силу предста-
вить соответствующий рисунок».
До сего момента речь шла о французах, добившихся успеха в той
среде, против которой я выступил в 1945 году. Однако работа кипела
и у американцев. В труде Stone 1962 года Маршалл Стоун (1903—
1989) возвестил о «перевороте в математике», обусловленном «открыти-
ем полной независимости математики от физического мира... Если мы
сравним современную математику с математикой конца девятнадцато-
го века, мы, возможно, немало удивимся тому, как быстро увеличился
объем и возросла сложность наших математических познаний; однако
при этом мы не должны забывать, насколько тесно это развитие связано
с переходом к абстракции, а также со все возрастающим интересом к по-
лучению и анализу общих математических моделей. Действительно, при
подробном рассмотрении мы видим, что именно этот новый курс, воз-
никший исключительно благодаря отрыву математики от се прикладных
отраслей, стал источником ее удивительной живучести и невероятного
развития в текущем веке».
Еще раз скажу, что упоминание этих людей и их взглядов необы-
чайно расширило значение слова «благодарность» в данном контексте
Да, они оказали на меня колоссальное влияние, ведь те усилия, кото-
рые я прилагал, сначала стремясь держаться от них как можно дальше,
а впоследствии приложив руку к свержению продвигаемой ими идеоло-
гии, стали важной частью моей жизни и, конечно же, работы, описанной
в этой книге.
3. Два дня в Высшей нормальной школе и что из этого вышло
Цитата из работы М. Стоуна в разделе 2 напоминает мне об одной
симпатичной и весьма познавательной автобиографии. В работе Hewitt
1990 автор пишет: «Стоуна и прочие гарвардские математики преподали
мне крайне важные уроки о нашем замечательном предмете:
• Правило № 1. Уважай свою профессию.
• Правило №2. Если сомневаешься, смотри Правило № 1».
54
С2. Выражение признательности
Мой дядя тоже глубоко уважал свою профессию. Его личное мне-
ние о Бурбаки никоим образом не затрагивало Высшую нормальную
школу. Он страстно желал, чтобы я учился именно там. Я поступил
туда, но уже на следующий день бросил учебу. Он был чрезвычайно
разочарован, постоянно волновался за мое будущее и только перед са-
мой своей смертью перестал спрашивать меня: «Но почему?».
Да, просто потому, что война, в которой мне посчастливилось вы-
жить, и успешная сдача экзаменов вскружили мне голову настолько, что
престиж и авторитет не особо меня волновали. Это учебное заведение
с жесткими рамками абсолютно не подходило для человека с сильным
характером, мечтавшего внести свою лепту в дело восстановления по-
рядка в природном хаосе. Для меня зрительное восприятие и геометрия
были не только способом набрать сногсшибательный балл на вступитель-
ных экзаменах. Я благоговел перед ними и потому отказался от золотой
возможности «перерасти» их и стать «настоящим математиком». Вместо
этого (по крайней мере, так кажется мне) я продолжал готовить себя
к разглядыванию пыли на некачественных компьютерных рисунках.
В Париже мой переход из Высшей нормальной школы в Политех-
ническую вызвал целую бурю эмоций, которая долго не могла утихнуть.
Не поступай я туда, это, наверное, во многом упростило бы мою жизнь.
С другой стороны, на мой семидесятилетний юбилей в Кюрасао прие-
хали Директор Высшей нормальной школы и еще один ее выпускник.
Шутки ради они «присудили» мне звание «почетного вечного первокурс-
ника».
В 1945 году я удивительно четко представлял, чему хочу посвятить
свою жизнь, хотя для других это было непостижимо. Поэтому теперь,
когда мне почти восемьдесят, я с глубокой радостью отмечаю следую-
щее. Я ничуть не сожалею о том, что не доказал ни одну из сложных
теорем, потому что я достиг практически всего, на что надеялся. Кро-
ме того, в последние годы я принимаю некоторые попытки преподавать
математику. Мы прилагаем массу усилий, чтобы устранить последствия
слепоты Андре Вейля в науке и Лорана Шварца — в рисунках, и к своей
большой радости выясняем, что среднестатистическому человеку мате-
матика все-таки небезразлична.
И напоследок: Бурбаки воцарился в Высшей нормальной школе дву-
мя годами позже, чем ожидал мой дядя. Мало того, что это место со-
вершенно для меня не подходило; мне было бы там еще и скучно. Felix
culpa?.
^«Счастливая вина» — грех, который привел к еще большей добродетели, чем до его
свершения — Прим, перев.
С2. Выражение признательности
55
4. Первая встреча с теорией Фату-Жюлиа
Через несколько лет после 1945 года я понял, что четко знаю, чего
хочу. В тот момент мой дядя предпринял еще одну попытку спасти меня
для чистой математики — для математики, которой он занимался и кото-
рую любил; ее краткое описание дано в главе С25. Одна из его любимей-
ших тем, созданная Пьером Фату (1878-1929) и Гастоном Жюлиа
(1893-1978), получила свое развитие приблизительно в 1917 году и ка-
салась итерации рациональных функций. Личные отношения моего дяди
с Жюлиа были не самыми дружескими; однако дядя был целиком и пол-
ностью согласен с утверждением, обратным тому, о чем говорил Плутарх
в «Перикле», 2.1: «Если произведение доставляет удовольствие, из этого
еще не следует, чтобы автор его заслуживал подражания».
Пережив ранний расцвет и не зная, куда двигаться дальше, ма-
тематическая теория итераций «впала в спячку». Нет, работы по дан-
ной теме время от времени, конечно, появлялись, и, кроме того, был
еще Поль Монтель (1876-1975), который изредка подбрасывал дров
в огонь. В своей работе Фату и Жюлиа весьма и весьма полагались на
теорию Монтеля о «компактном семействе функций» и, возможно, доба-
вили к ней самое изящное приложение. Несколько лет спустя Монтель
стал научным руководителем моего дяди в работе над кандидатской
диссертацией и посвятил теории итераций несколько курсов, но про-
двигаемые им идеи не произвели особого впечатления и благополучно
канули в лету. Та же участь постигла главу VII {«Itdration des fonctions
rationnelles») из работы Montel 1927 и главы XXIII, XI и XII {«Recur-
rences du premier ordre», «Itdration» и «Iteration des fonctions d cercle
fondamental», соответственно) из Montel 1957. Видимо, больше никому
не было дела до этих работ.
Жюлиа (мой преподаватель дифференциальной геометрии в Поли-
технической школе) был настолько «не в моде», насколько это возможно.
В центре внимания была абстракция, а «капитаном» в области матема-
тического анализа во Франции (как показано в главе С25) был мой
дядя; однако во всем остальном мире это направление не пользовалось
особым успехом.
Абсолютно уверенный в моих способностях, дядя представил меня
Монтелю и предложил «теорему Фату-Жюлиа» в качестве темы для
кандидатской диссертации. Он полагал, что, если мне удастся найти но-
вый «ракурс» для возрождения теории итераций, которая к тому времени
уже на протяжении тридцати лет находилась в застое, то передо мной
откроется возможность сделать блестящую карьеру. Он даже одолжил
мне очень ценные оригиналы статей, переданные ему их авторами.
56
С2. Выражение признательном и
Я бросил все свои силы на изучение этой темы, но, увы, безре-
зультатно. Мой дядя, безусловно, ожидал, что искомый новый ракурс,
который будет направлять меня подобно путеводной звезде, должен по-
явиться в рамках самой математики. Именно так все и случилось, прав-
да, тридцать лет спустя и в процессе внимательного изучения огромного
количества графических изображений, генерированных с помощью ком-
пьютера.
Тем не менее, в 1952 году я защитил диссертацию, хотя ее те-
ма не имела ничего общего с теорией Фату и Жюлиа. Однако, как ни
странно, косвенно она все же была связана с моим дядей. К этой работе
меня подтолкнула бумага, которую он достал из своей мусорной корзины
и дал прочитать мне. Моя диссертация породила геометрию фракталов
и мультифракталов в том виде, как их понимали в середине семидесятых
годов. Создавая эту геометрию, я приобретал опыт использования изоб-
ражений, которым не обладал больше никто: изучая рисунки, я хотел
открыть математические факты, поразмыслить над ними и, возможно,
даже доказать. А когда пришло время, я вернулся к теореме Фату-
Жюлиа.
5. Как Адамар (уже перешедший в мир иной) стимулировал мое
возвращение к теории итераций
Я не собирался возвращаться к различным формам итерации, одна-
ко сейчас, оглядываясь назад, мне представляется, что это возвращение
было неизбежно. Роль спускового крючка сыграл необычный панегирик
Пуанкаре, приведенный в работе Hadamard 1912. Этот исключительный
исторический документ попал мне на глаза в промежутке между ра-
ботами М 19750 и М 1977F. Он напомнил мне о неприязни, которую
участники Бурбаки испытывали по отношению к Пуанкаре, а также
о щекотливой ситуации, сложившейся вокруг празднования в 1954 го-
ду столетия со дня его рождения. В результате, работа Hadamard 1912
сподвигла меня на переход от изучения линейных фракталов к иссле-
дованию нелинейных. Наставник и герой моего дяди также во многом
повлиял и на меня.
В работе М 1982F (с. 415) и главе С15 рассказывается, как ме-
ня поразила потрясающая история Адамара о практически одновремен-
ном появлении протофрактальной пыли сразу в двух контекстах. До
того момента наиболее распространенным контекстом был ПОИСК таких
контрпримеров, которые привели Кантора к объектам, позднее исполь-
зованным мною в качестве «изобоажйиий^ „„„ '
р ии» природы и культуры. Однако
С2. Выражение признательности
о/
Пуанкаре совершенно независимым образом открыл малоизвестный вто-
рой источник, который Адамар счел более восхитительным, с чем я то-
же не могу не согласиться. То были предельные множества некоторых
групп Клейна, о чем я подробно расскажу в части III данной книги. Все
это напомнило мне о том, что частным мотивом для своего исследова-
ния рациональных итераций Жюлиа полагал динамические аргументы,
представленные еще Пуанкаре.
В процессе изучения работы Адамара я осознал, что все изучаемые
мной фракталы инвариантны относительно линейных преобразований.
Каждый из них можно было бы описать с помощью емкого понятия:
«линейный фрактал». Линейные модели поверхности Земли или беспо-
рядочного движения невероятно эффективны, но феномены, лежащие
в их основе, носят нелинейный характер. Благодаря Адамару, теперь
мои модели казались мне (в зависимости от настроения) либо чудесны-
ми, либо подозрительными.
Поскольку я некоторое время изучал аэронавтику в Калифорний-
ском технологическом институте, я успел привыкнуть к наводящим ужас
уравнениям Навье-Стокса и прочитал работу фон Кармана «Инженер-
ные решения нелинейных проблем» 1940 года (Karman 1940). Поэтому
с нелинейными системами как таковыми я познакомился много раньше,
чем возникла теория хаоса.
6. Возрождение и новый расцвет теории Жюлиа - Фату
Сходив «налево» и завязав отношения с группами Фукса и Клейна,
описанными в главе С15, я воссоединился со своей научной невестой,
которую выбрал для меня дядя. На этот раз я «искал путем наблюде-
ний».
В течение некоторого времени поиски мои шли ни шатко ни вал-
ко, о чем, как уже говорилось, я подробно написал в главе С12. Все
сошлось в одну точку в 1979-1980-х годах, когда меня пригласили про-
читать цикл лекций на математическом факультете в Гарварде. Я бла-
годарен Барри Мазуру за это приглашение, ведь оно стало подоплекой
самых плодотворных лет моей жизни, и Хейсуке Хиронака за его го-
степриимство и дружескую поддержку. Я читал лекции по фракталам
студентам-первокурсникам и, кроме того, вместе со своими коллегами
работал над вышедшей в тот же год статьей Gefen, М, & Aharony 1980.
С позиций дня сегодняшнего мне кажется более важным, что
я имел возможность продолжить работу над теорией итераций с по-
мощью замечательного программиста Питера Молдейва, закончившего
58
С2. Выражение признательности
Гарвардский университет в 1980 году. В 1979 году, когда я только при-
был в Гарвард, мои новые коллеги не восприняли рисунки всерьез, но
мало-помалу их отношение заметно изменилось. Не успев остыть после
распечатки на принтере, свойства формирующегося будущего множе-
ства Мандельброта ежедневно представлялись вниманию коллег перед
дверью деканата математического факультета. В конце весны 1980 года
я объединил весь накопленный материал в единый цикл лекций, ока-
завшийся весьма популярным, и провел несколько семинаров в городе.
Я также описал свой курс в частной беседе Жану Лере (1906-1998),
когда тот приезжал в Массачусетский технологический институт. Было
время, когда я представлял его в качестве моего возможного научного
руководителя в работе над кандидатской диссертацией. Он вспомнил ра-
боту Жюлиа, удивился тому, что ее оказалось возможно реанимировать,
и заметил, что «видимо, пришло время».
В некоторых ранних работах исследуемое мной множество называ-
лось «множеством-разделителем». В других трудах оно именовалось
р-отображением, потому что раньше физики обозначали квадратичное
отображение как z -* z2 - р. В тех же работах место положения экви-
валентного отображения z —> Az(l — г) называлось Х-отображением.
Следующим шагом была поездка в Институт высших научных ис-
следований (ИВНИ), расположенный под Парижем, в городе Бюр-сюр-
Иветт. За приглашение туда я безмерно благодарен Давиду Рюэлю. Как
уже говорилось, поскольку слова улетают, написанное остается, моя
лекция в ИВНИ от 13 ноября 1980 года практически не отличалась
от работы М 1980n {СЗ}, и я раздавал слушателям фотокопии гранок.
Но при этом я также представил и новые иллюстрации: как плачевные
оригиналы из Гарварда, так и более приличные варианты, полученные
позднее в IBM.
Вся аудитория прониклась восторгом. Я «кожей» чувствовал, что
это — самый незабываемый момент моей жизни. В тот момент произо-
шло «официальное» возрождение теории Фату-Жюлиа.
7. Первые встречи с Адриеном Дуади и Джоном X. Хаббардом
Я благодарен Дуади и Хаббарду по трем причинам:
• За энтузиазм, который они проявили по отношению к моей работе
сразу после лекций в ИВНИ в 1980 году. На этот счет в работе
Douady 1986 сказано: «Должен признаться, что в 1980 году, когда
я говорил своим друзьям, что мы с Дж. X. Хаббардом приступаем
С2. Выражение признательности
59
к изучению z —+ z2 + с, все они удивленно смотрели на меня и за-
давали один и тот же вопрос: «Вы надеетесь обнаружить что-то
новое?».
• За то, что множество, открытое и описанное мною, они назвали
множеством Мандельброта — термином, который они придумали
специально для этой цели. Цитата из работы Douady 1986 приведе-
на в самом начале предыдущей главы.
• За то, что они «продвигали» этот термин в математическом сообще-
стве.
Имя Дуади было давно знакомо не только мне, но и всем матема-
тикам. Однако встретились мы только в Университете Пари-Сюд (Орсе)
после моей лекции по алгоритму «Клейна», описанному в части III. Это
было то ли 10, то ли 12 ноября 1982 года. Не могу сказать точно, но
11 ноября исключается, поскольку во Франции это праздничный день.
Цитата из работы Douady 1986 приобретает дополнительный смысл, ко-
гда узнаешь, что ее автор входил в состав Бурбаки и был в то время
официальным лидером кружка. Из-за внезапной (и необратимой) сме-
ны его интересов образ Бурбаки потускнел как для его участников, так
и для окружающих, что произвело настоящий фурор в научном сообще-
стве.
День 15 ноября 1980 года обозначен в моей старой записной книж-
ке особым образом, и я помню его в мельчайших подробностях. Дуади
и члены его семьи пригласили нас с женой в гости и после ужина
собрались вокруг меня. Я подробно описал им некоторые из своих от-
крытий, а они засыпали меня вопросами, на которые я незамедлительно
отвечал. Короче говоря, я рассказывал о том, как в течение пятнадца-
ти лет копил знания для создания фрактальной геометрии, а особенно
для написания работ М1975О и M1977F. Еще раз повторю: в основе
этих знаний лежало внимательное и продуктивное изучение различных
рисунков. В поиске нового понимания я многократно смотрю и пересмат-
риваю множество рисунков; я играю с ними. (И одного рисунка всегда
мало!)
Неудивительно, что Дуади, как и другие выдающиеся «чистые» ма-
тематики, никогда не изучал рисунки с этой точки зрения. Я предложил
ему целую кипу наблюдений в виде гипотез, многие из которых уже име-
ли полное описание. Он «был обращен в мою веру» быстро и навсегда.
Я уже слышал о Хаббарде раньше, поэтому и пригласил его прочи-
тать лекции в Исследовательском центре IBM в 1979 году. Он приехал
60
С2. Выражение признательности
и рассказал об изображении множества Жюлиа в ньютоновском методе
нахождения корней уравнения г3 — 1 = 0, которое издавна полюбилось
Э. Шредеру, А. Кэли и Фату с Жюлиа. Программисты из Университета
Пари-Сюд (Орсе) подготовили это изображение для иллюстрации курса
лекций, которые он читал там по приглашению. Хаббард принес четы-
ре распечатки формата А4 с обгоревшими краями. Я склеил их вместе
и дал ему чистую уменьшенную копию, которую он мог показывать во
время своих лекций.
В следующий раз я увидел Хаббарда в 1980 году, когда он ненадол-
го приехал в Гарвард, где услышал отголоски вышеупомянутого семи-
нара. Я подготовил краткое описание результатов своих исследований
и обсудил с ним мой грядущий приезд в ИВНИ.
После лекции, которую я прочитал в ноябре 1980 года в ИВНИ, Ду-
ади и Хаббард начали изучать мои гипотезы и первыми в очень короткие
сроки превратили их в систематизированную математику. Им (а также
Нессиму Сайбони, который не публиковал этот результат своей работы)
удалось доказать, что множество Мандельброта М является связным.
Они провели семинар на эту тему и один раз любезно пригласили меня
выступить в качестве лектора.
Их еще более серьезная гипотеза относительно локальной связно-
сти множества М («MLC») по-новому формулирует его предполагае-
мое отношение к множеству А/0, которое первоначально сподвигло меня
на изучение множества М. Эта гипотеза пока не доказана, но даже
частичные результаты заслуживают всяческих похвал и уже принесли
Ж.-К. Йоккозу и К. Макмаллену медали Филдса.
Дальнейшие исследования
Очень быстро весь Париж узнал о моей работе и о термине, при-
думанном Дуади и Хаббардом для ее обозначения. Вернувшись в IBM
в полном неведении относительно всех этих событий, я завершил работу
над «Фрактальной геометрией природы», М 1982F. Она увидела свет
в середине 1982 года, и глава 18 в ней посвящалась итерации. Созда-
ние изумительных рисунков стало возможно благодаря моим знаниям
о том, что для этого требуется, и программному обеспечению, которое
было разработано Ричардом Ф. Фоссом и В. Аланом Нортоном и спо-
собствовало огромной популярности М 1982F. Эти люди заслуживают
повторной похвалы.
Огромная «популярность» множества М, как уже отмечалось, по
большей части была спонтанной, но в самом начале ей нужен был некий
С2. Выражение признательности
61
толчок для разгона. Все научное сообщество находится в неоплатном
долгу перед Хайнцем-Отто Пайтгеном и Петером X. Рихтером,
чьи прекрасные цветные картинки были объединены в работу Peitgen
& Richter 1986, а перед этим представлены в работе Dewdney 1985
в журнале «Scientific American». На их фоне все мои усилия выгля-
дели невзрачными. Я немедленно принял решение не конкурировать,
а сотрудничать, и эти блестящие ученики стали моими близкими дру-
зьями.
В сентябре 1987 года Национальный научный фонд организовал
недельную региональную конференцию по фракталам в университете
города Цинциннати. Я благодарен Джону У. Милнору за его поддержку
и прочитанные им лекции.
8. Смена настроения и «большой скандал»
К 1988 году множество Мандельброта из экзотической новинки пре-
вратилось в тему многих выступлений на праздновании столетней годов-
щины Американского математического общества. К сожалению, к тому
времени некоторые люди повели себя не вполне корректно. Упоминания
о том, как все начиналось, мало-помалу сошли на нет, а люди, кото-
рые всего этого не видели и даже не потрудились проверить имеющиеся
документы, занялись распространением всевозможных глупых сплетен.
Конечно, никому не хотелось быть «без вины виноватым», но пересу-
ды постепенно утихли, когда все претензии сошли на нет, на поверку
оказавшись противоречащими самим себе или бездоказательными. Бла-
годаря этому, вопрос, нередко остающийся невыясненным до последнего,
на этот раз прояснился на самом раннем этапе. У меня не осталось ни
одного «конкурента», который мог бы документально подтвердить свое
право на открытие первых и наиболее важных свойств множества М:
существование атомов и островов, связность этого множества и размер-
ность его границы, равную 2. Исторический аспект всего вышесказан-
ного более подробно раскрыт в следующих вводных главах.
9. Послесловие
За последние двадцать лет в математике произошли такие пере-
мены, что события, описанные в данной главе, юным читателям могут
показаться невероятными. Они, конечно, удивятся тому, что с 1920-х по
1980-е годы теория Фату-Жюлиа пережила всего один значительный
шаг вперед. Да, знаменитый Карл Людвиг Зигель (1896-1981) испра-
вил техническую ошибку в работе Жюлиа и открыл «диски Зигеля».
62
С2. Выражение признательности
Его работа (попытки определения мотивов которой предпринимаются
в M1985g{C10}) оказала серьезное влияние на математический анализ
в целом, но не стала новым толчком к развитию теоремы Фату-Жюлиа.
Кроме того, в работу над теорией итераций включились некоторые уче-
ные из Скандинавских стран.
Основная причина, по которой теория итераций функций, создан-
ная Фату и Жюлиа, была предана забвению, неоднократно упоминается
и подробно описывается в главе С25: эта теория принадлежит к об-
ласти математического анализа, остававшегося крайне «немодным» на
протяжении многих десятилетий. Поэтому интерес, который многие за-
мечательные математики проявили к моим наблюдениям/гипотезам ка-
сательно множества Мандельброта, ознаменовал собой историческую
перемену и отказ от сугубо идеологического отношения к своему ре-
меслу. Жаль, конечно, что этот путь не был гладким, но мне приятно
осознавать пользу от выполненной мною работы.
Annals of the New York Academy of Sciences, 1980
C3
Фрактальные аспекты итерации отображения
z —► Az(l — z) при комплексных Л и z
Глава-предисловие о рисунках, в частности, об «отсутствующих
пятнах» на рисунке 1 (2003)
Как уже говорилось в главе С1, эта работа, изобилующая множе-
ством «новинок», способствовала возрождению теории итераций. Она
также содержит много новых наблюдений касательно множества на
//-плоскости, для которого А. Дуади и Дж. X. Хаббард быстро приду-
мали название «множество Мандельброта». Каждое наблюдение было
сформулировано в виде математической гипотезы или подтолкнуло к со-
зданию таковой. Таким образом, рисунки, приведенные в этой работе,
сыграли фундаментальную роль в истории.
Тем не менее, из-за событий, описанных в главе С1, рисунок I из
оригинального текста был чрезвычайно плохого качества и явно про-
тиворечил комментарию к нему. Последний включает в себя подробное
описание обнаруженных мною явных «грязных пятен» как «островов».
Однако в последнюю минуту «корректор» почему-то приказал эти пятна
стереть.
Исключительно жесткая необходимость вынуждала меня добавлять
к своему рисунку несколько пятен каждый раз, когда я хотел его пока-
зать. Это стало отличным поводом для шуток, но факт остается фактом
(хотя многие и по сей день полагают, что мои рисунки всегда были
безупречны).
Поскольку испорченный оригинал сохранился, его, наконец-то,
можно выставить на всеобщее обозрение, сделав рисунок 1 составным.
Основная его часть — это моя первоначальная иллюстрация, а рядом
с ней находится часть очищенного от «грязи» рисунка, «улучшенного»
в процессе распечатки.
Не стоит и говорить, что в оригинале не видно «волосков», кото-
рые (по терминологии главы С1) связывают острова в «полимер». Алго-
ритм, благодаря которому их можно увидеть, был открыт намного позже
У. П. Терстоном.
Ы Awals oi the New York Academy of Sciences, 357, 1980
Большое историческое значение другого рода имеет рисунок 4, ко-
торый впоследствии стал рисунком 198 в работе М 1982F{FGAQ. На-
сколько мне известно, он является первым опубликованным приме-
ром модели, созданной с помощью «системы итерированных функций»
(СИФ), которая обсуждается в части X. Асимптотически, СИФ обрат-
ной динамики квадратичного отображения повторяет основную кривую
Жюлиа, состоящую из множества петель. Однако, с предасимптотиче-
ской точки зрения, эта кривая имеет очень нечеткие очертания. В неко-
торых точках она выражена слишком явно, тогда как в других — прак-
тически не видна. Эта нерегулярная экспозиция, наблюдающаяся также
в СИФ клейновых групп, служит признаком мультифрактальности.
В этом репринте разделы были пронумерованы. •
Предположим, что нам дано отображение z —» f(z, Л), где f — это
рациональная функция комплексных чисел z и А. Требуется рассмотреть
итерации отображения zn = /(/(.../(zo))) начальной точки zq- Кэли,
Фату и Жюлиа полагали, что для того чтобы получить общее пред-
ставление о поведении этих итераций, нужно, чтобы переменные А и zq,
а следовательно, и zn были комплексными. Однако, последние обширные
исследования отображения z —* Az(l - z), как, например, рассмотрен-
ные в работах Giirel & Rossler 1979 и Helleman 1980, ограничиваются,
в основном, действительными значениями переменной А, принадлежа-
щими к промежутку А € (1,4], и действительными значениями пере-
менной z € [0, 1]. Таким образом, несмотря на всю их значимость, они
остаются ограниченными и неполными. Масштабное изучение неогра-
ниченных комплексных переменных А и z проливает новый свет на ре-
зультаты этих ограниченных исследований и позволяет выявить важные
новые факты.
В этом свете перенос акцента на изучение еще более общих отоб-
ражений {г -• f(x, у, А); у -» д(х, у, А)} кажется преждевременным.
1. Введение
В настоящей работе особо выделяется роль неограниченного изу-
чения рациональных отображений с помощью различных фракталь-
ных множеств, в том числе А-фракталов на A-плоскости и z-фракталов
на z-плоскости. Некоторые из этих отображений представляют собой
фрактальные кривые (с топологической размерностью 1), а другие —
«пыль» (с топологической размерностью 0). Особый интерес вызывают
.--фракталы, так как они могут считаться фрактальными аттрактора-
СЗ. Фрактальные аспекты итерации отображения z->Az(1-z)
65
ми соответствующим образом определенных (обобщенных) дискретных
динамических систем, в основе которых лежат обратные отображения.
Намеки на это даны в работах Fatou 1906, 1919-1920 и Julia 1918 (и да-
же в еще более раннем труде А. Пуанкаре по близкой теме клейновых
групп (P.S. 2003. См. М 1983m {С18})). Однако явное и систематическое
описание фракталов появилось только в работах М 19750 и М 1977F,
где впервые было сформулировано само понятие, дано его определение
и даже название: «Фрактальное множество — это множество, для кото-
рого фрактальная размерность (Хаусдорфа-Безиковича) всегда превы-
шает топологическую размерность». В этой работе представлены свежие
иллюстрации, которые лучше, чем когда-либо, демонстрируют интуитив-
ную основу данного определения. Текст представляет собой выдержки
из работы М 1982F{F‘GAQ.
В разделе 5 этой статьи рассказывается о «странных» аттракторах.
2. А-фрактал Q
Буквой Q мы обозначаем множество значений переменной А, об-
ладающее следующим свойством: начальные точки zq, для которых
| limn_oo zn\ < оо, образуют замкнутую область (то есть множество
с внутренними точками). Ни для кого не секрет, что, когда начальной
точкой является «критическая» точка zq = 0,5, достаточно, чтобы имело
место неравенство | limn_oo zn| < оо. Та часть Q, для которой Re(A) > 1,
изображена на рисунке 1, тогда как остальная часть Q симметрична это-
му рисунку относительно прямой Re(A) = 1.
Здесь обнаруживается поразительный (и, на мой взгляд, новый)
факт: рисунок 1 составлен из нескольких несвязанных частей.
2.1. Область связности £ и ее фрактальная граница
Самая очевидная особенность рисунка 1 — это большая связная об-
ласть £, окружающая А = 2. Эта область £ делится на ряд подобластей,
которые можно описать по очереди.
Первая подобласть £о состоит из точки А = 1 и открытого диска |А-
- 2| < 1. Этот диск на рисунке 1 не окрашен для того, чтобы пояснить
структуру остальной части. Если А € £о> то существует конечная устой-
чивая неподвижная точка. [Доказательство: при Rc(A) > 1 устойчивая
предельная точка, если таковая существует, находится в 1 — 1/А; тогда
условие /|( 1 - 1/А) lor It 1 сводится к |А2| < 1].
66
Annals of the New York Academy of Sciences, 357, 1980
Остальная и крайне интересная часть области С, на рисунке 1 за-
крашена черным. «Малые размеры» этой черной области означают, что,
по большей части, ничего необычного в отображении z —» Az(l — z) нет.
Однако при этом в маленьких, но не обращающихся в нуль областях А
имеют место многие интересные и странные явления (некоторые из них
остаются загадкой до сих пор, тогда как другие полагают связанными
с гораздо более сложными преобразованиями).
Каждая подобласть £ второго шага обозначена одним или несколь-
кими рациональными числами а//?. Подобласть £(а/0) является откры-
той, если не считать введенную в нее предельную точку, в которой она
прицепляется к £0 как «отросток», — это точка А —2 = — схр[-2тгга//3].
При А € £(о//3) последовательность zn характеризуется устойчивым
предельным циклом периода (3. Этот цикл можно получить с помо-
щью одной /3-кратной бифуркации путем непрерывного изменения зна-
чений А, начиная с произвольно выбранной устойчивой неподвижной
точки, например, с устойчивой неподвижной точки zq = 0 5, соответ-
ствующей Ао = 2.
Каждая подобласть £ третьего шага обозначена двумя рациональ-
ными числами: £(cti//3i, ог/^г)- Эта подобласть является открытой,
не считая точки, в которой она прицепляется (опять-таки как «отро-
сток») к £(ai//3i). При А е £(ai//3i, аг/^г) последовательность zn
характеризуется устойчивым предельным циклом периода [З1/З2, полу-
чившимся в результате двух последовательных бифуркаций: /^-кратной
и /32-кратной, соответственно, — начиная с устойчивой неподвижной
точки в £0.
Следующие серии подобластей обозначены аналогичным образом
с помощью все большего количества рациональных чисел ai/3i... а^ЦЗ».
Область £ объединяет все значения А, что приводит либо к устойчивым
предельным точкам последовательности zn, либо к устойчивым предель-
ным циклам, которые можно свести к устойчивым предельным точкам
с помощью процесса, обратного бифуркации. Я предлагаю для этого про-
цесса термин «слияние», вследствие чего называю область £ «областью
слияния».
Области £(а//3) и т.д. имеют форму, близкую, но не стопроцент-
но совпадающую с формой диска. Короче говоря, граница каждого от-
ростка является почти точной уменьшенной копией границы всей обла-
сти £. Если вспомнить классическое строение снежинки (М 1977F), то
не останется никаких сомнений в том, что граница области £ является
фрактальной кривой.
СЗ. Фрактальные аспекты итерации отображения z-^Az(\-z)
67
Рис. СЗ-1. Отображение A-области Q на комплексной плоскости. Вещественная
ось направлена вверх и начинается в точке Л = 1. Центр окружностей находится
в точке Л = 2, а вершина — в точке А = 4. {P.S. 2003: см. введение к этой главе}
68 Annals of the New York Academy of Sciences, 357, 1980
2.2. Преобразование области M с помощью часто используемой
преобразованной переменной ш = (2z — 1)А/2
Это преобразование переводит отображение z —> Az(l — z) в отоб-
ражение и.’ —* р -о?2, где ц = Л2/4 — А/2. В результате А-множество £
заменяется p-множеством М. Копией дисков |А — 2| < 1(= £о) и |А| 1
(= область, симметричная £о относительно Re(A) = 1) служит фор-
ма Но, ограниченная кривой четвертого порядка, описываемой уравне-
нием /I = е2'7/4.е'7/2. Вот тут-то и возникает срочная необходимость
во множествах М и Mq. Поэтому известная нерешительность ученых
в вопросе выбора между обозначениями, содержащими А или fi, в этом
случае не получает разрешения: форма области £q намного проще фор-
мы Мо. но область М при этом полезнее области £.
2.3. Области неслившихся, или К-слившихся, устойчивых циклов
Помимо С область Q состоит из множества маленьких подобластей.
Вообще, я обнаружил, что, по крайней мере, некоторые из видимых пя-
тен грязи или чернил на рисунке 1, на самом деле, не имеют никакого
отношения ни к грязи, ни к чернилам: более подробные отображения
выявляют четкие «острова», своей формой напоминающие область М,
если закрыть глаза на нелинейную деформацию масштаба один к одно-
му. В свою очередь, каждый остров находится в окружении подостровов
и так — до бесконечности.
Когда А принадлежит островной деформированной копии Со, тогда
последовательность zn характеризуется устойчивым предельным циклом
периода и> > 1. Когда же А лежит в островной деформированной ко-
пии £(oi3i •••ов/^в), последовательность zn обладает устойчивым пре-
дельным циклом периода ш/31.,.08- И вновь у нас может появиться
желание свести эти циклы путем последовательных слияний, обуслов-
ленных непрерывными изменениями А, в неподвижную точку Ао = 2.
Однако это невозможно. Ни один из этих постоянных циклов не вырож-
дается в неподвижную точку.
Некоторые острова области С, пересекающие вещественную ось,
образуют интервалы, которые определяли и активно исследовали ранее.
Все понимали, что цикл с А в таком интервале не вырождается в точ-
ку А = 2 при вещественных значениях А. Мы также видим, что он не
вырождается и при комплексных значениях As.
2.4. Радиальные модели в распределении областей неслияния
Острова, которые пересекают вещественную ось, можно назвать
«подчиненными» значению А = Ч кло ________
л оо9, которое, как известно, указы-
СЗ. Фрактальные аспекты итерации отображения z-*Xz(1-z)
69
вает на самую правую точку области Со и соответствует бесконечной
последовательности следующей 2-бифуркации. Другими словами, я счи-
таю, что каждый остров подчиняется некоторому значению Л, соответ-
ствующему бесконечной последовательности следующих друг за другом
бифуркаций. Когда первая из этих бифуркаций является бифуркацией
высокого порядка, а именно, при 01/2тг = ai//3i и большом значении /31,
возникает потрясающая подчиненность (которая отлично просматрива-
ется на подробном A-отображении). Однако эта подчиненность очевидна
уже на рисунке 1 для самой дальней точки «отростка», соединенного
с областью Со в точке 01/2тг = 1/3. К тому же, острова выстроены вдоль
направлений /Зв, лучеобразно расходящихся из некоторой «прибрежной
точки». В частности, если А соответствует нескольким последователь-
ным бифуркациям, другая /31 не влияет на количество лучей. Более
подробное описание дано в работе М 1982F{FGN}.
3. 2-фрактал ^(А)
Теперь переходим к семейству фракталов z-плоскости, связанных с
отображением z —> Az(l - z).
3.1. Определение
Во-первых, вспомним, что z = оо при любых А является устойчивой
неподвижной точкой. {Доказательство: при и = 1/z, отображение име-
ет вид и —> д(и) = и2/Х{и — 1), в силу чего д = 0 It 1}. Для каждого зна-
чения А, z-фрактал ТДА) определяется как (закрытое) множество таких
точек zoi. что | limn_oo Zn| 0 оо, а именно: точек, итерации которых не
сходятся к оо. Это множество ТДА) никогда не бывает пустым: оно вклю-
чает zq = 0 (которая является неустойчивой неподвижной точкой, все
итерации которой также удовлетворяют zn = 0), а также все конечные
прообразы zq и их предельные точки. Более того, фрактал Д(Х) всегда
ограничен: несложно увидеть, что он располагается (весьма свободно!)
в круге |z — 0,5| = 2,5. Граница фрактала ^(А) обозначается 7 * (А).
На рисунке 2 приведен пример 7-кратной бифуркации.
3.2. Исключительные значения А, для которых фрактал ^(А)
имеет стандартную форму
Эти значения А сводятся кА = 4, А = 2иА = оо.
70
Annals of the New York Academy of Sciences, 357, 1980
Если Л = oo, то Л*(оо) сводится к точкам 0 и 1. Очевидно, что zn 5
= ос за понятным исключением z0 / 0 и zo = 1: эти значения дают
неопределенное выражение zi = Ооо. Неопределенность исчезает, если
отметить, что при обратном преобразовании эти точки остаются неиз-
менными. Важность обратного преобразования тут же станет очевидной.
Если Л = 4, то У ♦ (4) и, соответственно, 7^(4) сведутся к интер-
валу [0.1]. Действительно, введение новой переменной ш = — (2st - 1)
превращает отображение z —> z(l - z) в отображение ш —> 2си2 - 1,
а еще одна новая переменная и = cos-1 си дает и —► 2и, откуда ип =
= 2пи. При Im(u) 0, |Im(ttn)| -+ оо и \zn\ —> оо. Таким образом,
представление 7"(4) через координату и является вещественной осью,
откуда следует, что ш е [-1, 1] и z е [О, 1].
При А = 2 та же самая новая переменная w превращает отображе-
ние z -» 2z(l - г) в отображение а> —> си2, а это значит, что 7 ♦ (2)
представляет собой круг |cu| = 1, т. е. \z — 0,5| = 0,5 и замкнутый диск,
ограниченный этим кругом. Ясно, что cun —> 0, откуда zn —► 0,5 только
при zq G J"(2) - Т ♦ (2), и cun —> оо, откуда zn —► оо (только при С, обо-
значающем комплексную плоскость), zq € С — /"(2). Если zq & У * (2),
так что zq = ехр(2тггу), то последовательность zn является эргодической
на 7’*(2), только при иррациональном значении у/2тг; если у/2тг = а/Д
тогда последовательность zn проходит неустойчивый цикл периода (3.
Из предыдущих примеров видно, что множество ^(А) может иметь
топологическую размерность 0 (отдельные точки или пыли), 1 (кривые)
или 2 (области). При всех других значениях А, ^(А) представляет со-
бой нестандартное множество, именуемое фракталом, однако в процессе
работы постоянно встречаются примеры всех топологических размерно-
стей. В целях экономии места в этой книге описаны лишь некоторые из
них (см. работу М 1982F{FG/V})-
3.3. Форма фрактала J’(A) при А 6 £
При некоторому удалении А от А = 2 окружность Т * (2) места-
ми «мнется» и мало-помалу возникают все более выраженные складки.
Пока А 6 £о. граница множества Т * (А) с топологической точки зре-
ния остается окружностью. Когда же А достигает точки (3 — кратной
бифуркации, топология границы Т * (А) изменяется: на ней появляют-
ся множественные «защипы», к каждому из которых сходятся /3 точки
границы 7 * (А).
Например, поскольку А перемещается по вещественной оси вправо
и А -♦ 3, фрактал Т’(А) сводится к характеристической форме, изоб-
СЗ. Фрактальные аспекты итерации отображения z^Az(l-z)
71
Рис. СЗ-2. Отображение фрактала ^(А) для Л вблизи 7-кратной бифуркации.
{P.S. 2003: в М1980п представлено заполненное множество Жюлиа, нарисован-
ное в IBM (на этой странице вверху слева). Оно заменило первоначальный
бледный оригинал (внизу справа), нарисованный ранее в Гарварде в то же самое
время, что и заполненные множества Жюлиа, изображенные на рисунке С 1.3.}
Annals of the New York Academy of Sciences, 357, 1980
Рис. C3-3. Суперпозиция множества J"(A) для нескольких вещественных значе-
ний А: Л = 1 (бледно-серое), А = 1,5 (серое), А = 2,5 (темно-серое), А = 2,9
(черное). Форма при А = 3 названа в этой книге «формой Сан Марко». Все
четыре изображения имеют две общие точки: z = 0 и z = 1 {P.S. 2003: См.
также рисунок С4.4.)
СЗ. Фрактальные аспекты итерации отображения г->Аг(1-х)
73
раженной на рисунке 3. (Я назвал ее «формой Сан Марко* в честь
очертаний веницианской базилики на фоне неба вместе с ее отражени-
ем в затопленной пьяцце ... и бесконечной экстраполяции.)
Когда за /31-кратной бифуркацией следует /Зг-кратная бифуркация,
/31-складка и защипы в /Зг-складке обычно приходятся на разные точки.
Как бы то ни было, множество ^(А) остается связным, пока А находится
в области связности С.
3.4. Форма фрактала /Г(А) при A G Q — С
Я обнаружил, что когда А лежит в области несвязности, множе-
ство ^"(А) чаще всего имеет совершенно другую форму.
(А) Внутренняя часть множества J’(A) прерывается.
(Б) Компоненты внутренней части множества ^(А) обладают оди-
наковой формой, за исключением деформаций, создаваемых самим отоб-
ражением z —> Az(l — г).
(В) Эта одинаковая форма схожа с формой (связной) внутренней
части множества ^(А*), где А* является точкой, отображенной на А
при одновременном нелинейном отображении области связности £ на
рассматриваемый остров.
(Г) Существует убедительное свидетельство связности самого мно-
жества ^(А), так как, помимо компонентов своей внутренней части и их
границ, оно включает целую сеть фрактальных нитей.
3.5. Форма фрактала /F(A), когда (А) является иррациональной
пограничной точкой области £
Иррациональной пограничной точкой области £ называется погра-
ничная точка этой области, отличная от рациональных точек, в которых
«отросток» соединяется с областью £о или другим «отростком». Когда А
стремится от внутренней точки области £ к иррациональной погранич-
ной точке, возникает либо бесконечная последовательность бифуркаций
конечной кратности, либо (как при А —» ехр(27ггу с иррациональным у)
прямая оо-кратная бифуркация, либо конечная последовательность би-
фуркаций конечной кратности, приводящая к оо-кратной бифуркации.
Я предполагаю, что фрактал ^(А) при любом раскладе стремится
принять форму разветвленной кривой (множество без внутренних то-
чек). То же самое можно сказать и о границе этого фрактала F * (А).
В случае с вещественными иррациональными точками, лежащими на
интервале А = [3,569, 4], это предположение является верным, посколь-
ку фрактал J’(A) представляет собой подмножество вещественной оси.
74
Annals of the New York ACADEMY of outiNCtd, 001, 1У611
Мы знаем, что связность ДА) (или ее отсутствие) зависит от значе-
ния А. Возникает интересная задача, которая пока что ждет своего
решения: соотнести связность множества ДА) со свойствами невеще-
ственных значений А.
3.6. Форма фрактала ДА) при Л Q
В самой первой публикации на тему общих свойствах итерации
(Fatou, 191) говорится, что при вещественном А > 4, фрактал ДА) очень
близок ко множеству Кантора. Оперируя языком новой терминологии,
принятой в М 1977F, это линейная фрактальная пыль.
Чтобы пояснить этот результат, отклонимся от темы и вспом-
ним, что классическое троичное множество Кантора является Т7-мно-
жеством, соответствующим особому отображению-«навесу», определен-
ному как z -» 1,5 - 3|z - 0,5|. Действительно, при таком отображении
все точки в открытой средней трети z G [1/3, 2/3] дают z\ > 0, отку-
да limzn -ос. Все точки в открытых средних третях боковых третей,
z € [1/9. 2/9] или z G [7/9, 8/9], дают zi > 0, но z? < 0, откуда опять-та-
ки zn — -х. И так далее. В совокупности эти средние трети состав-
ляют множество ДА). Его /с-е троичные точки, называемые конечными
точками средних третей fc-ro шага, при п к дают zn = 0, и поэтому
сходятся к неустойчивой предельной точке. Некоторые из нетроичных
точек множества ДА) сходятся к неустойчивому циклу периода > 1,
тогда как другие являются эргодическими.
Согласно терминологии М 1977F, это множество ДА), будучи пре-
рывистым на всей своей протяженности, называется фрактальной пы-
лью; его топологическая размерность Dr = 0. С другой стороны, его
фрактальная размерность D = -Iog2/log3 > 0. Так как D > Dr, это
множество является фракталом.
4. z-фрактал ДА) как фрактальный аттрактор
Сегодня отображение типа z —» Az(l — 1) традиционно считает-
ся динамической системой. И в его аттракторе (это может быть одна-
единственная точка или конечное число точек) нет ничего интересного.
Тем не менее, поскольку для z —► Az(l - z) множество ДА) является
множеством-репеллером, по тому же принципу для обратного отображе-
ния z -> 1/2 + е(1/4 - z/A)1/2 с е = ±1 оно является множеством-ат-
трактором.
Точнее говоря, последнее утверждение справедливо только в случае
соответствующего расширения понятия «динамической системы». Это
СЗ. Фрактальные аспекты итерации отображения z—>Xz(1-z)
75
расширение необходимо, поскольку вышеуказанное обратное отображе-
ние не является уникальным, а зависит от некоторого параметра е, на-
зываемого «ярлыком»; поэтому оно является отображением 1 на 2, а к-е
итерация является отображением 1 на 2к. Рассмотрев всю совокупность
этих итераций, в работе Julia 1918 ее автор показал, что они плотны
на всей протяженности Т7 * (А). Но этот результат нас не удовлетворяет,
поскольку интуитивное определение динамических систем требует отоб-
ражения с единственным значением. Для этого я предлагаю основать
дискретную динамическую систему в области пересечения комплекс-
ной плоскости множеством-ярлыком, состоящим из двух точек: + и
Последовательность еп составляется по своим собственным правилам,
независимо от последовательности zn, тогда как последовательность гп
регулируется последовательностью еп. Например, последовательность еп
может представлять собой процесс Бернулли независимой случайной по-
следовательности подбрасывания монетки или более общую случайную
эргодическую последовательность. Вывод, кажется, напрашивается сам
собой (хотя, признаюсь, детали я не проверял): любая эргодическая по-
следовательность еп порождает траекторию, проекция которой на ком-
плексную плоскость является плотной на границе Г * (А).
При А = 2, когда граница Т7 * (А) представляет собой окружность,
инвариантная мера, как известно, является равномерной. При А = 4, ко-
гда J7 * (А) — [0, 1], инвариантная мера, естественно, является проекцией
вещественной оси равномерной меры на окружность, откуда следует,
что она обладает плотностью «арккосинуса» 7г-1[х(1 -т)]-1/2. Прове-
денные опыты показали, что обе выше обозначенные меры легко ап-
проксимируются динамическими траекториями случайных выборок. То
же самое справедливо и для формы Сан Марко, изображенной на рисун-
ке 4. С другой стороны, в самых интересных случаях, как на рисунке 2,
граница Т * (А) отличается крайней извилистостью; здесь-то и возника-
ют сложности. Конечная (инвариантная) мера на границе 7“*(А) крайне
неровная. Для описания верхушек глубоких «фьордов» требуется ис-
пользование узко специальных последовательностей еп, а потому они
описываются очень редко по сравнению с областями вблизи внешних
границ рисунка.
5. Отступление в область «странных аттракторов»
Термин «аттрактор» стал очень часто ассоциироваться с прилага-
тельным «странный», и у читателя есть все основания поинтересовать-
76
Annals of the New York Academy of Sciences, dt>/, iy«O
ся, есть ли хоть что-то общее у странных и фрактальных аттракторов.
А ведь и правда, есть.
5.1. Во-первых
Для многих странных аттракторов была определена фрактальная
размерность (Хаусдорфа -Безиковича) D, и оказалось, что она всегда
строго больше их топологической размерности. Поэтому эти аттракторы
(и, вероятно, другие, а, возможно, даже все странные аттракторы) явля-
ются фрактальными множествами. Для аттрактора Смейла фрактальная
размерность D определена в М 19776. Аттрактор Зальцмана-Лоренца
с г = 40, а = 16 и b = 4 имеет фрактальную размерность D ~ 2,06; этот
результат независимо друг от друга получили М. Г. Веларде и Я. Г. Си-
най, которые рассказывали об этом в частных беседах, но, насколько
мне известно, полученные результаты не опубликовал ни один из них.
[Совсем недавно выяснилось: препринт работы X. Мори и X. Фуджиса-
ка подтверждает определенное мной значение D для аттрактора Смей-
ла и значение Веларде-Синая D для аттрактора Зальцмана - Лоренца.
Для отображения Хенона с а = 1,4 и b = 0,3 в этой работе опреде-
лено D = 1.26.] Тот факт, что значение D ~ 2,06 очень близко к 2,
но определенно больше 2, означает, что аттрактор Зальцмана - Лоренца
несомненно не является стандартной поверхностью, но при этом отли-
чается от таковой не очень сильно.
Уместность упоминания фрактальной размерности D в этом контек-
сте может озадачить тех, кому этот параметр знаком только как мера
нерегулярности непрерывных кривых, поэтому, с позволения читателя,
замечу, что в этом примере D является не мерой нерегулярности, а ме-
рой того, как гладкие поверхности наслаиваются друг на друга — своего
рода разновидность определения фрагментации, которая также рассмат-
ривается в работах М 19750 и M1977F.
Кроме того, из работ М 19750 и M1977F следует, что размерность
Хаусдорфа - Безиковича была не единственным кандидатом на роль
фрактальной размерности, но выбрали именно ее, поскольку: (а) она
лучше всего изучена, (б) она важна для теории, и (в) в большинстве
случаев выбор не имеет значения, поскольку различные приемлемые
альтернативные размерности имеют тождественные значения.
В результате дальнейших исследований, проведенных в этом на-
правлении, недавно была выдвинута и опытным путем подтверждена
гипотеза о наличии связи между фрактальной размерностью странного
аттрактора и его числами Ляпунова (препринты X. Мори и X. Фуджиса-
ка; Д. А.Рассела, Дж. Д.Хэнсона и Е.Отта).
СЗ. Фрактальные аспекты итерации отображения z-+Xz(\-z)
77
5.2. Во-вторых
Обратный вопрос: являются ли изучаемые мной фрактальные
аттракторы «странными»? Ответ зависит от того, какое значение вклады-
вается в последнее слово. Согласно старомодному значению, являюще-
муся мягким синонимом слов «чудовищные», «патологические» и анало-
гичных эпитетов, которые когда-то применялись по отношению к фрак-
талам, — ответом будет «да, но зачем стараться возрождать термин,
обоснование для которого исчезло с выходом работ М 19750 и M1977F,
где было доказано, что странности во фракталах не больше, чем в очер-
таниях береговой линии или горной гряды».
Рис. СЗ-4. 64000 первых положений динамической системы, «притянутой» к
фрактальной форме Сан Марко
К сожалению, с тех пор термин «странный» приобрел технический
смысл, настолько особенный, что аттрактор Зальцмана-Лоренца дол-
жен называться «странным-странным». В этом смысле, многие фрак-
тальные аттракторы моих динамических систем странными никак не
назовешь. На самом деле, понятие «странности» отражает нестандарт-
ные топологические свойства, тогда как нестандартные фрактальные
свойства, о которых говорилось в разделе 5.1, как говорится, «идут при-
78
Annals of the New York Academy of Sciences, 357, 1980
цепом». В таком смысле, (а) топологическая окружность (интуитивно
понимаемая как замкнутая кривая без двойных точек) является стран-
ной, какой бы «помятой» она ни была; соответственно, (б) фрактальные
аттракторы (А) при |А-2| < 1 совершенно точно странными не будут.
Однако фрактальные аттракторы, связанные с другими рациональ-
ными отображениями, которые я изучал в М 1982F{/:'G/V}, действи-
тельно имеют некоторые топологические особенности. Таким образом,
ответ на наш вопрос неоднозначен. Но сам вопрос не имеет особого зна-
чения. На мой взгляд, применительно к аттракторам термин «странные»
исчерпал свою пользу, а потому от него стоит отказаться.
Обсуждение (опущенное в печатном издании)
Д-р Г. Д. Грейбер. Не могли бы Вы описать, каким образом фрак-
талы связаны с изучением физических систем, состоящих из множества
взаимодействующих частиц?
Д-р Мандельброт. Напрямую в моей книге «Фракталы» эта про-
блема не освещалась, но она непременно будет рассмотрена в {P.S. 2003,
M1982F}. Основная проблема состоит в том, что число существующих
областей применения постоянно растет, а потому трудно поддается ор-
ганизации.
(А) Во многих областях физики и астрономии (причем создается
впечатление, что новые области появляются почти каждый месяц) ана-
литические отношения между наблюдаемыми объектами выражаются
с помощью законов масштабной инвариантности. Я считаю, что ана-
логичные законы должны действовать и в отношении геометрических
форм, имеющих место во всех подобных случаях. В обычной евкли-
довой геометрии свойством масштабной инвариантности могут похва-
статься только прямые, но при масштабировании физических явлений
встречаются какие угодно формы и все они значительно отличаются от
прямых. Фрактальная геометрия позволяет совместить масштабирование
с предельной неровностью форм. Она доказывала свою эффективность
всякий раз, когда я обращался к ней в своих экспериментах, а потому
я готов взять на себя смелость рекомендовать ее каждому. В любом
случае, между аналитическими феноменологиями масштабирования, со-
зданными другими учеными, и моей геометрической феноменологией
масштабирования существует определенное сходство, при этом у послед-
ней больше разнообразия, но нет аналога для групп перенормировки.
(Б) Что касается дробных размерностей в физике (например, в ап-
проксимациях типа 4-е), исключительно полезных, но совершенно непо-
СЗ. Фрактальные аспекты итерации отображения z—Az(l-z)
79
нятных с точки зрения математики, возникает следующий вопрос. Мож-
но ли объяснить их в рамках фрактальной геометрии? Ответ на этот
вопрос пока не известен. {P.S. 1980. В работе Gefen, М, & Aharony 1980
рассматривается модель Изинга на различных фрактальных решетках
одинаковой фрактальной размерности. Мы устанавливаем, что критиче-
ская температура удовлетворяет условию Тс > 0 для одних решеток,
тогда как для других Тс > 0 в зависимости от тонких топологиче-
ских свойств разветвления. P.S. 2003. См. также работу Gefen, Meir,
М, & Aharony 1983.}
(В) Если заглянуть глубже, можно увидеть, что успешное использо-
вание масштабно-инвариантных фракталов для моделирования природ-
ных объектов, по сути своей, парадоксально. Такие фракталы не изме-
няются при линейных преобразованиях, тогда как соответствующие им
природные модели, как правило, отличаются высокой степенью нелиней-
ности. Такое несоответствие заставило меня заняться изучением фрак-
талов, полученных путем нелинейных преобразований. Как уже дока-
зано, многие аналитические формулы, выражающие законы масштабной
инвариантности, являются линейными аппроксимациями вблизи непо-
движных точек в группах перенормировки, поэтому нельзя исключать
тот факт, что подобную параллель можно будет провести и для мас-
штабно-инвариантных фракталов.
(Г) Пока идет поиск возможного мотива для постепенного совер-
шенствования фрактальных моделей с точки зрения физики, этот про-
цесс оправдывается, главным образом, тем, что на сегодняшний день
данные модели обеспечивают простейший способ представления фак-
тической информации. Обратимся к созданным мной последовательным
моделям распределения галактик. Первая модель сводит не имеющую
решения задачу N тел к бесконечной совокупности задач двух тел,
при этом аппроксимация необоснованна, но дает теоретические двух-
и трехточечные корреляции, тождественные тем, которые в независи-
мом исследовании методом простого подбора получили Джим Пиблс
и его коллеги. Позже Пиблс обнаружил, что найденная им ранняя эм-
пирическая трехточечная корреляция плохо совпадает с данными, а по-
лученная мной четырехточечная теоретическая корреляция не совпадает
с данными вообще. В результате, в работе М 1975и рассмотрена следу-
ющая простейшая модель, которая обладает тождественными фракталь-
ными свойствами, но отличается от первой по нескольким позициям, не
связанным с фракталами. Новая модель подтверждает подходящие че-
тырехточечные корреляции Пиблса и предсказывает существование тео-
ретической трехточечной корреляции, которая совпадает с данными по
80
Annals of the New York Academy of Sciences, 357, 1980
всем параметрам! Однако эта корреляция не соответствует наблюдаемой
♦лакунарности» данных. К счастью, всем вышеизложенным требовани-
ям удовлетворяет третья простейшая модель (М 1979и). Я весьма оза-
дачен тем успехом, который имеют математические модели, выбранные,
в основном, благодаря своей формальной простоте и свойствам инвари-
антности.
(Д) Разумеется, в большинстве случаев необходимо множество па-
раметров. Благодаря счастливой случайности, (чего я опять не понимаю,
но за что мы должны быть благодарны) по мере совершенствования мо-
делей нашему вниманию один за другим открываются новые параметры.
(Е) Основным параметром всегда остается фрактальная размер-
ность. Во многих случаях она определена очень точно, например, D =
= 1,23 для галактик, D = 1,89 для критических перколяционных кла-
стеров и D = 2,06 для аттрактора Зальцмана - Лоренца. Эти значения —
не порядки величин, а точно определенные постоянные. Из всего выше-
сказанного следует, что со временем важность фракталов будет только
возрастать.
Фрактальная геометрия природы, 1982
С4
Канторова пыль и пыль Фату.
Самоквадрируемые драконы
Предисловие (2003 г.)
Эта глава повторяет главу 19 работы М 1982F с небольшими допол-
нениями, а именно: с рисунком С5 из работы М 1982F (он расположен
еще и на обложке той книги), а также с отрывком и несколькими ил-
люстрациями из работы М 1985g, наиболее уместными именно в этой
главе.
Используемый в некоторых частях оригинала 1982 года (и более ни
в одной другой книге) термин «сепаратор» обозначает объект, который
Дуади (без моего ведома) уже назвал «множеством Мандельброта» (см.
главу 1). Во избежание путаницы и устаревшего употребления данного
мною названия в этом издании используются либо термины, характер-
ные для труда 1982 года, «//-отображение» и «A-отображение», либо,
если невозможно сказать по-другому, универсальный термин «множе-
ство М».
В большинстве глав книги М 1982F рисунки сопровождались длин-
ными комментариями и были собраны в конце основного текста — имен-
но такой формат я счел компромиссным. Новые удивительные иллю-
страции должны быть настолько большими, насколько это возможно,
но крупные картинки прерывают текст. Сегодня эти изображения из-
вестны всем, поэтому я ничего не потеряю, если помещу в этой книге
их уменьшенные копии, тогда как полноразмерные версии можно будет
увидеть на моем веб-сайте.
Глава 19 работы М 1982F выстроена достаточно сложным образом.
Замыслена она была, как минимум, весьма искусно и, возможно, не ме-
нее эффективно (хотя об этом можно поспорить), однако в этом издании
такое ее построение сохранить не удалось. Еще более кардинальные из-
менения пришлось внести в главу С16 — бывшую главу 18 книги М
1982F. Несколько чрезмерно длинных комментариев к рисункам были
вставлены в текст, однако комментарии на страницах со 188 по 191
очень тесно связаны друг с другом и с текстом на страницах 183-184,
Процесс перестройки этого «многомерного» материала в «линейное» по-
вествование был похож на операцию по разделению нескольких сиам-
ских близнецов за один раз. Некоторые части были продублированы,
другим не нашлось места, и их пришлось отбросить, а несколько неболь-
ших отрывков, как уже сказано, были «позаимствованы» из публикаций
того же года с четким указанием источников.
Если бы я знал, насколько сложной окажется эта линеаризация,
я бы не взялся за ее осуществление. В поисках абсолютной исторической
точности вы можете обратиться к оригиналу 1982 года, достать который
не составит труда.
В какой-то момент я почувствовал настоятельную необходимость
признать, что глава 19 из М 1982F является плодом «заднего ума»,
поэтому я не мог переписывать ее сто раз. Также я не мог добавить
и несколько страниц для того, чтобы «вдохнуть жизнь» в последний
вариант, так как уже были готовы предметный указатель и содержание
этой книги и т.д., и т. п.
Однако первоначально данная глава была настолько трудно чита-
ема, что ее необходимо было изменить даже ценой задержки выпуска
книги. Наконец-то, свою роль в полной мере сыграли рисунки (приоб-
ретшие. в сущности, культовый статус), да и текст сократился с неве-
роятной быстротой, поскольку для подавляющего большинства «читате-
лей» он не имел практически никакого значения.
Удивительно другое: судьба главы 18 книги М 1982F, воспроизве-
денной далее в виде главы С16, сложилась совершенно иначе. У текста
и рисунков не было очевидных недостатков, но прошла целая вечность
прежде, чем предельные множества Клейна привлекли к себе внимание,
которого они давно заслуживали.
Многочисленные переиздания работы М 1982F повлекли за собой
некоторые изменения. В оригинальном издании рисунок 185 был взят
из работы М 1980п(СЗ), поэтому в данной книге он не приводится во
избежание повторения. Вместо этого, на рисунке 2 представлен видоиз-
мененный рисунок 185, полученный между 1983 и 1985 годами.
В этой главе мы рассмотрим два семейства очень простых нелиней-
ных преобразований и исследуем несколько таких фрактальных мно-
жеств, которые при этих преобразованиях остаются инвариантными
и для которых они могут служить генераторами.
Во-первых, дробно-линейное преобразование вещественной линии
поможет нам лучше понять нашу старую знакомую — канторову пыль.
В свою очередь, это более глубокое понимание поможет оценить ре'
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 83
Рис. С4-1. [Рисунок 192 из книги М 1982 FJ. Самоквадрируемые пылевидные
множества Фату на интервале [0, 1] (объяснение см. в тексте)
зультаты вещественных и комплексных квадратичных преобразований
вида х —> /(я) = х2 — р, где х и р вещественны, и z —> /(z) = х2 - р,
где z = х + iy и р — комплексные числа.
Элементарный случай р = 0 довольно скучен с геометрической точ-
ки зрения, однако другие значения р ведут к потрясающим фрактальным
красотам, многие из которых были впервые продемонстрированы в рабо-
те М 1980п{СЗ}.
Удобнее всего получать упомянутые инвариантные формы с помо-
щью итераций (т. е. многократных применений) одного из вышеуказан-
ных преобразований. Исходные значения мы будем обозначать через хо
или zq, а результаты fc-й итерации функции f или f — через или Zk-
Хронологически изучение итераций можно разделить на три эта-
па. Первый, связанный с комплексной переменной z, прошел под зна-
менами Пьера Фату (1878-1929) и Гастона Жюлиа (1893-1978). Их
публикации являются шедеврами классического комплексного анализа;
ими восхищаются математики, однако на их фундаменте чрезвычайно
сложно что-либо построить. В своей работе, о которой данная глава
дает лишь весьма сжатое представление, я стараюсь придать большую
ч
ф|'и 1 Vlhll VI I I < IMI I ГНЧ 111 ’111 •< »/l Ы , I Л I 0
jmaihun> ц\ основным открыт иям, объединяя аналн т с <|>ii iiiiuh’i и но
дробными иллюстрациями, в результате чего обнаруживается великое
множество неизвестных ранее фактов.
Рис. С4-2. (Рисунок 185 из работы М 1982F]. Примеры заполненных множеств
Жюлиа при некоторых важных вещественных значениях Л: Справа: А = 1, 1,5,
2.0, 2.5 и 3.0. А = 1 - двустворчатая раковина. А = 2 — диск. А = 3 — своего
рода безудержная математическая экстраполяция очертаний венецианской бази-
лики на фоне неба вместе с ее отражением в затопленной пьяцце (я окрестил
эту кривую ^драконом Сан Марко*). Вверху: А = 3,3260680. Эта А и А 2
являются ядерными параметрами (описанными в тексте) соответствуют веще-
ственным предельным циклам с периодами 2 и 1.
Последовавшее за этими открытиями возрождение помогло устано-
вить тесную связь свойств итераций с теорией фракталов. Из того фак-
та, что находки Фату и Жюлиа оказались недостаточно проработаны
для того, чтобы стать основой теории фракталов, мы можем сделать
вывод, что даже классический анализ нуждается иногда в наглядности
и интуитивной понятности, причем компьютерное моделирование может
оказать ему в этом смысле серьезную помощь.
Канторова пыль и пыль Фату. Самоквадрируемые драконы 85
Рис. С4-3. [Рисунок 187 из работы М 1982 F[. Обобщение самоквадрирУеМЬЙ
фрактальных кривых Жюлиа при вещественных X, изменяющихся в HHTePBaJli
от 1 (основание) до 4 (вершина). Альтернативное изображение представлено
странице 176
96
Фрактальная геометрия пнигущя,
Следующий промежуточный этап включает в себя исследования
П. Дж.Мирбергом итераций вещественных квадратичных отображе-
ний R (см., например, Myrberg 1962, Stein & Ulam 1964 и Brolin 1965).
На текущем этапе исследователи, по большей части, игнорируют
прошлое и сосредотачивают свои усилия на отображениях интерва-
ла [0,1] в себя (за подробностями рекомендую обратиться к обзорам
Gurel & Rossler 1979, Helleman 1980, Collet & Eckman 1980, Feigenbaum
1981 и Hofstadter 1981). В последнем разделе главы рассматривается по-
казатель 6 по работам Grossmann & Thomae 1977 и Feigenbaum 1978:
доказывается, что существование 6 следует из более явного свойства
итераций в комплексной плоскости (т. е. их фрактальности).
Возможность получения канторовой пыли посредством
нелинейного преобразования
Из главы 8 работы М 1982F нам известно, что троичная канто-
рова пыль I инвариантна при преобразованиях подобия, если коэффи-
циент подобия имеет вид 3_fc. Это самоподобие является, безусловно,
очень важным свойством, однако его недостаточно для определения I.
Напротив, мы можем полностью определить множество I как наиболь-
шее ограниченное множество, инвариантное при следующем нелинейном
преобразовании («перевернутое V»):
х -»/(х) = {1/2 - |х - 1/2|}/г, где г = 1/3.
Точнее, мы многократно повторяем это самоотображение веще-
ственной оси, при этом исходное значение xq «размазано» по оси х,
а окончательные значения сводятся к точке х = —оо и канторовой пы-
ли L Неподвижные точки х = 0их = 3/4 принадлежат I.
Набросок доказательства инвариантности множества С. По-
скольку /(х) = 3 при I < 0, итерации всех точек хо < 0 сходятся
к -ос прямо, то есть всегда справедливо неравенство хп < 0. Для
точек хо > 1 прямой сходимости предшествует один предваритель-
ный этап, так как х* < 0 для всех к 1. Для точек в пустой обла-
сти 1/3 < ю < 2/3 предварительных этапов будет два, так как xi > О,
но Хк < 0 для всех к > 2. Для точек в пустых областях 1/9 < хо < 2/9
или 7/9 < хо < 8/9 предварительных этапов будет уже три. В более об-
щем виде это выглядит так: если интервал ограничен пустой областью,
которая отправляется в -оо после к предварительных этапов, то сред-
няя треть (открытая) этого интервала отправится прямо в —оо после
к + 1-го этапа. Однако ни одна точка множества (. не уходит в — оо-
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 87
Рис. С4-4. [Рисунок 188 (внизу) из работы М 1982 F], ^-отображение представ-
лено значениями // внутри замкнутой черной области. Его пересечение с веще-
ственной осью представляет собой горизонтальный отрезок от большой точки
заострения (// = —1/4) до вершины = 2).
Конечность внешнего порога
Для того, чтобы распространить эти выводы на обобщенную кан-
торову пыль с N = 2 и г в интервале от 0 до 1/2 достаточно вставить
желаемое значение г в выражение /(гт) = {1/2|т - 1/2|}/г. Если вы хо-
тите получить какую-либо другую пыль, вам нужно лишь проследить,
чтобы график функции f(x) имел соответствующую зигзагообразную
форму.
Однако аналогичного метода для экстраполяции канторовой пыли
на всю вещественную ось не существует. Это — частное проявление
одного очень общего свойства: нелинейная функция /(д-), как правило,
заключает в себе некоторый конечный внешний предел 17. Для ли-
нейных же преобразований (подобий и аффинностей), как нам хорошо
Ри< С4-5 [Рисунки 1 и 2 из работы М 1985g]. Построение //-отображе-
ния г — f»tc. - р как предела монотонно убывающих аппроксимаций,
каждая из которых представляет собой лемнискату уравнения \fk * (0. //)| =
- 2 Эти кривые служат границами областей, окрашенных в различные оттенки
серого Верхняя половина: к = 1, 2, 3. 4 и 5. Нижняя половина: А’ = 7, 9 и 14.
известно, характерен порог Q = zv; при возникновении необходимости
ь конечном пороге его приходится вводить искусственно.
Анатомия канторовой пыли
Из главы 7 работы М 1982F нам известно, что множество / явля-
ется очень «разреженным», и все же поведение итераций /(т) приводит
к лучшему пониманию тонких различий между его точками.
Вряд ли кто при первом знакомстве с канторовым множеством смог
избежать искушения предположить, что оно в конечном итоге сходит-
ся к концевым точкам открытых пустых областей. Тем не менее, такое
предположение весьма далеко от истины, поскольку множество t содер-
жит. по определению, все пределы последовательностей концевых точек
пустот
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 89
Рис. С4-6. [Рисунок 189 (вверху справа) из работы М 1982F и рисунок 4 из М
1985g]. Черная фигура представляет собой близкую аппроксимацию А-отображе-
ния для z —► Az(l — z) в виде лемнискаты |Д 1/2, д| = const при очень большом
значении к. На маленькой диаграмме изображены оси координат и абсциссы
основных значений А.
Этот факт не считается интуитивно очевидным. В работе М 19S2F
Ганс Хан привел массу аргументов в пользу того, что у так называемой
«интуиции» совершенно отсутствует геометрическое содержание. .Много
лет назад я (равно как и мои соратники и единомышленники) вполне
понял бы, если бы он внес эти предельные точки в свой список концеп-
ций, существование которых может оправдать лишь холодная логика
Однако из настоящего обсуждения мы с вами вынесем интуитивное
доказательство того, что упомянутые предельные точки обладают силь-
ными и отличными от других индивидуальностями.
Например, точка т = 3/4, которую функция /\д) оставляет неиз-
менной, не принадлежит ни какому-либо из интервалов средней трети
ни границе какого-либо из этих интервалов. Итерации точек вида г =
90
Фрактальная геометрия природы, гл. 19
Рис. С4-7. (Рисунок 189 (вверху) из работы М 1982FJ. «Корона» Д-отображения.
Полное A-отображение на Рисунке 6 симметрично относительно прямой А =
= 1 + i0. Половина A-отображения при А 1 состоит из значений А внутри
замкнутой черной области, изображенной на этом рисунке, и диска |А — 2| 1.
Когда же А принадлежит короне, то даже многократно повторенное преобра-
зование z -» Az(l - z) не переводит точку zo = 1/2 ни в одну предельную
точку, будь та конечной или расположенной в бесконечности. Оси координат
представлены на маленькой диаграмме на рисунке 6.
= (1/4)/3* сходятся к точке х = 3/4.. Кроме того, существует беско-
нечное множество предельных циклов, каждый из которых состоит из
конечного числа точек. Множество £ содержит также точки, преобразо-
вания которых бесконечно перемещаются вокруг него самого.
Генератор квадратов
Производящая функция f(x) преобразования «перевернутое V», ис-
пользуемая в предыдущих разделах, была выбрана из-за того, что она
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 91
Рис. С4-8. [Рисунок 189 (внизу слева) из работы М 1982F]. Подробная картина
A-отображения вблизи точки А = 2 — ехр(—2тгг/3). Множество М представляет
собой предел областей вида |/n(l/2)| < R. Несколько таких областей показаны
в совмещении друг с другом. При больших п эти области, равно как и само
A-отображение, выглядят несвязными; в действительности, они связны, но вне
сетки, использованной при вычислениях.
дает знакомый нам результат. Однако полученная с ее помощью канто-
рова пыль выглядит несколько надуманной. Заменим ее функцией
х —» /(х) = Ах(1 - х),
неожиданное богатство свойств которой было впервые замечено Фату
(Fatou 1906). Сдвинув точку начала координат, изменив масштаб оси х
и положив // = А2/4 — А/2, можно записать эту функцию в следующем
виде ~
х —> fix') = х2 — р.
Исходя из соображений удобства, мы будем использовать то А и /(д),
то д и /(ж).
Мне представляется уместным назвать функцию f(x) (или /(i))
генератором квадратов. Возведение в квадрат является, безусловно,
алгебраической операцией, однако здесь оно получает геометрическую
интерпретацию, поэтому множества, которые оно оставляет инвариант-
ными, можно называть самоквадрируемыми. Строго говоря, возведение
в квадрат заменяет точку абсциссы с координатой х точкой абсциссы
с координатой т2. Таким образом, самоквадрируемых точек на оси всего
три: т = х, т = 0 и т = 1. Может показаться, что добавление -р едва
ли способно что-либо в этом изменить, однако на самом деле оно от-
крывает множество самых неожиданных возможностей, рассмотрением
которых мы и займемся ниже.
Вещественные самоквадрируемые пылевидные множества Фату
История уже знакомой всем канторовой пыли значительно облегчи-
ла нам задачу по изложению сути удивительного открытия Пьера Фату.
Работа Fatou 1906 представляет собой истинный шедевр в рамках того
странного литературного жанра, который называется «заметки в «От-
четах» Парижской Академии наук». Задача пишущего в этом жанре
часто сводится к тому, чтобы раскрыть по возможности меньше, но при
этом создать впечатление, что автор учел все, что только можно было
учесть.
Среди прочих восхитительных откровений, которые лучше всего
понимаешь только после тщательного самостоятельного изучения, в ра-
боте Fatou 1906 отмечается следующее наблюдение, проще всего вы-
ражающееся через X. Когда число А вещественно и либо А > 4, ли-
бо А < -2, наибольшее ограниченное множество, остающееся инвари-
антным при преобразовании х -» /(ж) = Az(l — х), представляет собой
пыль, заключенную в интервале [0,1]. Это множество, которое являет-
ся близким родственником канторовой пыли, я называю вещественной
пылью Фату.
На рисунке 1 эти пылевидные множества представлены при изме-
нении вертикальной координаты -4/А в интервале от —1 до 0. Черные
интервалы отмечают концевые точки трем порядка от 1 до 5. Концевые
точки Xi и Х2 средней тремы являются решениями уравнения Ах(1 -
- х) = Г, на рисунке они образуют параболу. Тремы второго порядка
оканчиваются в точках ц,2, 11,2, ®2,i и 2:2,2 — таких, что Ахт1П(1 -
= ИТ.Д.
Мне думается, что эта замечательная связь между пылевидны-
ми множествами, подобными канторовым, и одной из элементарнейших
функций заслуживает самой широкой известности, не ограниченной уз-
ким кругом специалистов.
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 93
Рис. С4-9. [Рисунок 189 (внизу справа) из работы М 1982FJ. Подробная кар-
тина A-отображения вблизи точки А = 2 - ехр(-2тг/100). У этого стократно
ветвящегося дерева и у z-отображения на рис. 13 имеется несколько весьма
удивительных общих свойств.
При вышеуказанных значениях А вещественная пыль Фату также
остается наибольшим ограниченным самоквадрируемым множеством в
комплексной плоскости.
94
Фрактальная геометрия природы, гл. 19
Самоквадрируемые кривые Жюлиа на плоскости (М 1980п {СЗ})
Положив А = 2 и р = 0, получаем простейшую самоквадрируе-
мую кривую — окружность |z| = 1. При преобразовнии z —* z2 кольцо,
однократно опоясывающее окружность, растягивается в кольцо, опо-
ясывающее эту же окружность дважды, причем «пряжка» при z = 1
остается неподвижной. Соответствующая наибольшая ограниченная са-
моквадрируемая область — диск |z| 1.
Однако введение вещественного р / 0 или любого комплексно-
го р открывает один за другим целый ряд настоящих ящиков Пандоры,
доверху набитых бесчисленными возможностями, которые радуют глаз
в той же степени, в какой дают пищу для ума. Заполненное множество
Жюлиа определяется (для каждого А) как максимальная ограниченная
область при отображении z -» Az(l - z), то есть как множество z, кото-
рое при квадратичном отображении не уходит в бесконечность. Таким
образом, множество Жюлиа определяется как граница заполненного
множества Жюлиа.
Множества Жюлиа при вещественных значениях параметров А
или р
Нижняя часть рисунка 2 не вызывает вопросов, тогда как его
верхняя часть представляет собой компактное комбинированное изоб-
ражение — привлекательное, но в то же время несколько загадочное.
Представьте себе пять заполненных множеств Жюлиа, напечатанных на
кальке матовыми чернилами: белыми для А = 1,5 и 2,5 и черными —
для А = 1, 2 и 3. Последующее наслоение этих рисунков друг на друга
в порядке увеличения значения А дает наблюдаемую фигуру.
Чтобы не портить красивую картинку, мы отказались от нанесе-
ния координат. Горизонтальной линией симметрии служит вещественная
ось, пересекающая эти множества Жюлиа в точках х = 0 и х = 1.
Рис. С4-10. [Рисунок 188 (вверху) из работы М 1982F]. Вид А-отображения
(за исключением двух единичных дисков) после инверсии относительно точ-
ки А = 1. Оно напоминает горизонтальную полосу, подтверждающую наличие
окружностей, изображенных на рисунке 9. Правильность других кажущихся
окружностей подтверждается с помощью других инверсий.
С4. Канторовл пыль и пыль Фату. Самоквадрируемые драконы 95
Рис. С4-11. [Обложка книги и рисунок С5 из работы М 1982F; цветной негатив
оригинала представлен разными оттенками серого]. Дракон Жюлиа при п =
= п' = 5. Обложка книги М 1982F с цветным оригиналом этого рисунка име-
ется на личном сайте автора
Рисунок 3 служит своего рода интерполяцией между частным при-
мером, представленным на рисунке 2, и объединением всех значений А,
изменяющихся в интервале от 1 до 4 по вертикальной оси. Каждое
горизонтальное сечение этого сегмента представляет собой множество
Жюлиа. При помощи сложной графики эта «драпировка» была построе-
на в памяти компьютера с помощью процесса, который сводится к отсе-
чению от исходного куба всех точек, итерации которых при отображе-
нии z -♦ Az(l - z) уходят в бесконечность.
Рис. С4-12. [Рисунок 190 (вверху) из работы М 1982F], Поджарый дракон
Жюлиа атлетического сложения при п = 11 (вверху) и истощенный дракон,
испытавший на себе большое число бифуркаций (внизу)
«Поясом» нашей задрапированной фигуры является множество
Жюлиа при А = 2. При всех остальных значениях А множества Жюлиа
являются фрактальными кривыми. Можно различить замечательные
«складки», расположение которых изменяется в зависимости от А; ниже
пояса они «вдавлены» внутрь, а выше пояса они выступают наружу.
Особый интерес представляют наросты на стене, с которой свиса-
ет драпировка. К сожалению, данная иллюстрация не может показать
сложную структуру верхней части модели во всей ее красе. Однако
с учетом вышесказанного теория Мирберга-Файгенбаума об итерации
вещественного отображения х —» Ai(l - х) предстает в более общем
виде.
(А) Для каждого значения А, драпировка включает в себя (в ка-
честве своего рода «опоры») фрактальное дерево, составленное из ите-
рированных прообразов точек вещественного интервала [О, 1]. При всех
малых и некоторых больших значениях А < 3, ветви этого дерева об-
ладают по всей своей длине некоторой толщиной. Однако при других
больших значениях А от дерева остается лишь голый остов, полностью
С4 КЛНТ()|‘О1Ь\ ПЫЛЬ И пыльфм >’ < ,VA< >FB' ТРИР «НАВН V’’> >' 'V?
Рис. С4-ГЗ. |Рисунок 191 (внизу справа) из работы N\ 1982F^ ГАноюр>^
дракон Жюлиа, для которого значении парамсчра близко к значению \
или /т — -1/4, характерному для базовой формы двустворчатой раковины
Фрактальная геометрия природы, гл. 19
лишенный толщины. На рисунке мы можем видеть ветви вдоль пря-
мых .г = 1 2 или у = 0, остальные же при данном графическом процессе
неизбежно оказываются потеряны.
(Б) Некоторые горизонтальные участки стены за драпировкой пол-
ностью покрыты крохотными «холмами» или «складками», однако мы
можем увидеть лишь немногие, самые выдающиеся из них. В теории
вещественных итераций эти холмы и складки относятся к нехаотичным
интервалам параметра, о которых рассказано в работе Myrberg 1962.
Если говорить о множестве М, к которому мы сейчас переходим, они
относятся к «молекулам-островам», пересекающим вещественную ось.
Рис. С4-14. [Рисунок 190 (внизу) из работы М 1982F]. «Тело дракона» или
«6-дракон» (исчислимо бесконечное множество драконов, имеющих одинаковую
форму), полученный при параметре, лежащем на молекуле-острове вблизи Л - 1
и д = -1/4, что явствует из рисунка 9.
Множества Жюлиа при комплексных значениях параметров р,
или А и множество М
При переходе от вещественных значений /х и А к комплексным,
нарисованные мной множества Жюлиа продемонстрировали потрясаю*
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 99
щее разнообразие форм «самоквадрируемого дракона», которые можно
оценить, заглянув на несколько рисунков вперед. Каждая самоквадри-
руемая кривая привлекательна по-своему. Я, например, нахожу самыми
привлекательными «драконов», изображенных на рисунках И, 12, 13
и 14. Чтобы упорядочить их очевидное и невероятное разнообразие, мы
попросту должны были ввести какой-нибудь организующий принцип.
Подходящим критерием, который через некоторое время выявился сам.
стала связность заполненного множества Жюлиа. Критерий связности
зависит от того, уводит или нет многократное преобразование z -* г2 -
— р точку zo = 0 в бесконечность. Этот критерий определяет множество,
которое я открыл и которое в общем случае будет называться множе-
ством М.
Короче говоря, параметр р дает «//-отображение» — черную фигуру,
изображенную на рисунке 4. В теории это — некая «предельная лем-
ниската», т. е. предел при п —» оо алгебраических кривых, называемых
«лемнискатами» и определяемых выражением |/n(0)| = R, где R есть
некоторое большое число. Если принять т = шахп до момента п -
= т, мы получим приблизительные //-отображения, представленные на
рисунках 4 и 5. При увеличении т аппроксимация становится более
точной.
Таким же образом параметр А дает «A-отображение», изображенное
на рисунке 6 и более подробно на рисунках 7, 8, 9 и 10.
Тонкая структура множества М: А- или //-атомы
и А- или д-молекулы, континент и острова
Прежде чем представить различные фигуры множеств Жюлиа при
невещественных А или //, мне хотелось бы сказать несколько слов о тон-
кой структуре параметрического отображения. В зависимости от кон-
кретного случая, ради простоты описания, в качестве параметра мы бу-
дем использовать либо А, либо р.
Атомы и молекулы. Максимальное открытое множество внут-
ри множества М разбивается на бесчисленное множество максимально
связных открытых областей, которые я предлагаю называть «атомами».
Границы двух атомов либо совсем не пересекаются, либо имеют одну об-
щую точку (назовем ее «связью»), которая принадлежит множеству М.
Точка заострения затравки связью не бывает никогда.
Бесконечное множество атомов, связанных как непосредственно,
так и через атомы-посредники, образуют «молекулу».
..^пабоажение с центральной кардиоидой и Х-отображение
С двумя дисками |А - 2| = 1 и |А| = 1 без точки А = 0. В этих
областях А имеет такие значения, что итерации точки zq = 1/2 схо-
дятся к некоторой предельной точке, а не уходят в бесконечность. На
рисунке 7 эти диски оставлены пустыми, чтобы подчеркнуть, что форма
остальной части образует «корону», внешняя граница которой является
фрактальной кривой.
Отростки. Корона разбивается на «отростки», «корнями» которых
являются «принимающие связи», расположенные на окружностях |А| =
= 1 или [А — 21 = 1. А корня имеет вид А = ехр(2тг?т/п) или А = 2 -
- exp(2irim/n), где т/п — неприводимое рациональное число, мень-
шее 1.
Инверсия Х-отображения относительно окружности с цен-
тром в точке А = 1. Если внимательно рассмотреть отростки в ко-
роне на A-отображении, представленном на рисунке 7, может сложить-
ся впечатление, что «соответствующие точки» лежат на «описанной»
окружности, проходящей через точку А = 1 и с центром справа от точ-
ки А = 2. Рисунок 10 подтверждает истинность этого впечатления, по-
скольку перевернутое отображение содержит горизонтальную верхнюю
«огибающую». Правильность других кажущихся окружностей подтвер-
ждается с помощью других инверсий.
{P.S. 2003. Это наблюдение положило начало целому ряду важных
исследований, в том числе «п-квадрируемой» гипотезе и «нормирован-
ному» множеству М, описанным ниже в главах С6 и С7.}
Молекулы-острова. Многие «пятна», возникающие при вышеопи-
санных отображениях, представляют собой истинные «молекулы-остро-
ва», о которых впервые сообщается в работе М 1980п{СЗ}. Форма такой
молекулы идентична форме всего д-отображения целиком, если не учи-
тывать нелинейного искажения.
Периоды. Каждому атому сопоставлено некоторое целое число w,
его «период». Когда точка д лежит внутри атома периода w, итера-
ции /п(г) уходят в бесконечность или образуют устойчивый предельный
цикл, состоящий из w точек. _
Внутри атома периода w справедливо неравенство |/w(-zM)| < 1.
где - любая точка предельного цикла, соответствующего данному д.
На границе атома |/«(zM)| = 1, причем равенство fw(zu) = 1 описывает
точку заострения, или «корневую» точку.
Основания и деревья. Обозначив период атома через ш, определим
его основание как кривую, на которой значение \
значение вещественно.
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 101
Основания, лежащие на вещественной оси, известны в теории са-
моотображений как интервал [0, 1], а их замыкание — как интер-
вал [—2, 4].
Ядра. Каждый атом содержит точку (назовем ее «ядром»), в кото-
рой выполняются неравенства /^(гд) = 0 и /ш(0) = 0.
Ядра, расположенные на вещественной оси, впервые были описа-
ны в работе Myrberg 1962; после этого они всплыли лишь в статье
Metropolis, Stein, & Stein 1973. Соответствующие отображения часто
называют «сверхустойчивыми» (Collet & Eckman 1980).
Если рассматривать равенство |/w(0)| =0 как алгебраическое урав-
нение относительно р, то его порядок равен 2W-1. Следовательно, может
существовать не более 2Ш-1 атомов периода w; в действительности их
меньше, за исключением случая w = 1. При w = 2 уравнение /г(0) = О
имеет два корня, однако один из них уже является ядром «предыдуще-
го» атома периода 1. В более общем виде все корни уравнения /т(0) = О
являются также корнями уравнения Ат(0) = 0, где к — целое число,
большее 1.
Заметим далее, что каждая рациональная граничная точка, рас-
положенная на границе атома периода w и удовлетворяющая усло-
вию = схр(2тггт/п), где т/п — неприводимое рациональное
число, меньшее 1, заключает в себе «принимающую связь», готовую
присоединить атом периода nw. Как следствие, некоторые новые атомы
соединяются с существующими принимающими связями.
Однако в этот процесс оказываются вовлечены не все новые атомы,
и оставшимся не остается ничего иного, как послужить затравкой для
новых молекул. Таким образом, число молекул бесконечно.
Бифуркация и слияние. Когда значение р непрерывно изменяет-
ся внутри молекулы, каждое направленное наружу прохождение связи
ведет к бифуркации; w умножается на п. Пример, увеличение веще-
ственного р приводит к мирбергову удвоению периода. Инверсия би-
фуркации, которую я рассматриваю в работе М 1980п{СЗ} и называю
слиянием, должна прекратиться по достижении периода затравки моле-
кулы. Молекула-континент является областью слияния в с = 1. Каждая
молекула-остров является областью слияния не в с = 1, а в ядре мо-
лекулы-острова. Форма дракона или субдракона регулируется значения-
ми /№) и м/с.
Множество М как фрактал; показатель Фейгенбаума 8 как
следствие. Я предполагаю, исходя из «перенормировочных» соображе-
102
Фрактальная геометрия природы, гл. 19
ний, что чем дальше находятся атомы от затравки своей молекулы, тем
более идентичными становятся их формы.
Следствие: граница каждой молекулы локально самоподобна. Так
как она не является гладкой в малом масштабе, мы можем считать ее
фрактальной кривой.
Это локальное самоподобие позволяет обобщить одно свойство би-
фуркации Мирберга, о котором сообщают Гроссман и Томэ, а также
Фейгенбаум. Длины отрезков, отсекаемых все уменьшающимися отрост-
ками на вещественной оси А и /х, образуют убывающую геометрическую
прогрессию с коэффициентом 6 = 4,66920... (Collet & Eckman 1980).
Первоначально считалось, что существование коэффициента 6 обуслов-
лено особенностями аналитического метода. Рассмотренный в новом
свете показатель 6 оказывается связан с более широким свойством фрак-
тального скейлинга.
Каждая бифуркация из т > 2 ветвей вводит дополнительный ба-
зисный коэффициент.
Топологическая размерность. Когда точка лежит вне множе-
ства М, наибольшим ограниченным самоквадрируемым множеством яв-
ляется пыль (пыль Фату). Если же р находится внутри множества М
или является связью, то таким наибольшим множеством будет об-
ласть, ограниченная некоторой самоквадрируемой кривой. Из принад-
лежащих М точек р по крайней мере несколько дают древовидную
кривую. Если множество не расходится в бесконечность, его тополо-
гическая размерность равна 0 (для пылевидных множеств Фату), 1 (для
недоедающих драконов) и 2 (для всех остальных драконов).
Ветвление. Когда А находится внутри одного из открытых пустых
дисков, изображенных на рис. 189 (вверху), самоквадрируемая кривая
будет простой замкнутой кривой (петлей без ветвления), как на рисун-
ках 2 и 3.
Когда А принадлежит окружностям |А| = 1 или |А—2| = 1 или лежит
в окружающей их открытой связной области, самоквадрируемая кривая
имеет вид разветвленной сети с тремами, ограниченными фрактальными
петлями, как драконы на рисунке 13.
Когда же А лежит внутри молекул-островов, которые, как мы вскоре
покажем, являются областями нестремления к точке 1, самоквадри-
руемая кривая представляет собой либо <5-петлю, либо <5-дракона, как на
рисунке 14. Новой петли 6 не вводит.
Словом, я обнаружил, что замыкание других атомных оснований
разбивается на совокупность деревьев, каждое из которых укореняет-
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 103
ся на принимающей связи. В каждой точке такого дерева мы имеем
несколько степеней ветвления — степень ветвления для концов ветвей
плюс порядки бифуркации, ведущей к корню дерева. Кроме того, когда
корень дерева приходится на атом-остров, сюда следует добавить по-
рядки бифуркации, ведущей от дисков |А - 2| С 1 или |А| С 1 к этому
атому.
Выборка «драконов» множества Жюлиа, для которых значения ц
и А не являются вещественными
Если верить слухам, то фрактальность множеств Жюлиа при g/0
была полностью доказана Деннисом Салливеном и для некоторых дру-
гих случаев, и я ничуть не сомневаюсь, что такое доказательство осу-
ществимо для всех случаев без исключения. Если не ограничиваться
только вещественными значениями д и А, появляется большое разнооб-
разие великолепных множеств Жюлиа.
Последовательные бифуркации и «истощенный дракон». В от-
ростке, который соответствует значению 0/2тг = т/п, где п и т —
целые числа, порядок бифуркации и, соответственно, число драконьих
голов (или хвостов, если хотите) вокруг каждой точки сочленения ра-
вен п. Вторая бифуркация порядка т'/п' разбивает каждую из этих
областей на п1 «сосискообразных» связей и еще более утончает их.
Самый известный из всех драконов изображен на рисунке 11, взя-
том с обложки и рисунка С5 работы М 1982F. Такой дракон получается
при п = п' = 5. Верхняя половина рисунка 12 соответствует п = 11.
Нижняя же половина свидетельствует о том, что дракон, испытавший
на себе множество бифуркаций, теряет всю свою плоть и ссыхается
в скелетообразную разветвленную кривую.
Драконья линька. Дракон, возводящий сам себя в квадрат, пред-
ставляет собой совершенно бесподобное зрелище! Чудовищная «линька»
отделяет бесчисленные складки от кожи на брюхе и спине дракона.
Затем она растягивает шкуру на брюхе и спине так, что ее длина —
которая, разумеется, и без того бесконечна — увеличивается вдвое! За-
тем шкура вновь складывается вдоль спины и брюха. И наконец, на
последнем этапе, все складки аккуратно водворяются на новые места.
Особый предел А = 1. Драконы Пеано. Чтобы получить умерен-
но упитанного дракона — ни чрезмерно тучного, ни слишком костля-
вого — следует поместить точку А внутри отростка на некотором рас-
стоянии от его корня при 0 = 2тг/п. Красиво перекрученные драконы
104
Фрактальная геометрия природы, гл. 19
получаются, когда точка А лежит около одного из двух суботростков,
соответствующих порядку бифуркации от 4 до 10: один из суботрост-
ков дает изгиб влево, другой - вправо. При п —> оо величина 0 -+ 0;
следовательно, А стремится к 1. Форма соответствующего дракона неиз-
бежно должна устремиться к форме двустворчатой раковины (окружа-
ющей верхнюю часть рисунка 2 и образующей основание задрапиро-
ванной фигуры на рисунке 3). Однако между п = оо и п очень боль-
шим, но конечным, имеется все же качественное различие, а потому
этот предел относится к разряду «особых». Во-первых, рассмотрим, чем
двустворчатая раковина отличается от фигуры на рисунке 13, соответ-
ствующей п = 100. По мере того, как п —► оо, растет число конечностей
дракона, его шкура сминается, а ее фрактальная размерность при этом
возрастает. Вся конструкция представляется этаким «драконом-отшель-
ником», пытающимся забиться внутрь двустворчатой раковины А = 1
и способным заполнить всю ее внутреннюю область без остатка, т.е,
размерность дракона стремится к D = 2. Что же получается? Самок-
вадрируемая кривая Пеано? Безусловно, однако, как нам известно из
главы 7 работы М 1982F, кривые Пеано вовсе не являются кривыми.
Так происходит и здесь: по достижении размерности D = 2 наш дра-
кон прекращает свое существование в виде кривой и перевоплощается
в область плоскости.
«Области дракона* или «6-драконы», полученные при выборе А
в «молекуле-острове*. Множество Жюлиа попадает в одну из трех
общих категорий в зависимости от положения параметра относитель-
но множества М. Параметры, лежащие вне множества М, соответству-
ют обобщенным пылевидным множествам Фату. Параметры, принадле-
жащие молекуле-континенту, соответствуют «драконам». Последний же
случай (когда параметр лежит внутри молекулы-острова) представлен
на рисунке 14.
{P.S. 2003. Эту иллюстрацию необходимо пояснить. При создании
рисунков 13 и 14 я намеренно использовал значения параметра, близкие
к р = 1/4 (или А = 1), при которых возникает множество Жюлиа,
имеющее форму двустворчатой раковины, представленную на рисунке 2.
Благодаря этой уловке, я получил возможность выделить два раз-
ных аспекта. С одной стороны, если говорить о «форме вообще», то
множество Жюлиа нельзя назвать крайне чувствительным к точному
значению параметра: «общую огибающую», близкую по форме к дву-
створчатой раковине, мы наблюдаем не только на рисунке 13, но и на
С4. Канторова пыль и пыль Фату. Самоквадрируемые драконы 105
С другой стороны, детальная структура области, ограниченной этой
огибающей, крайне чувствительна к значению обозначенного выше па-
раметра. Так, рисунок 14 состоит из бесконечного множества отдель-
ных драконов. Все они имеют одинаковую форму, определяемую сугубо
локальными условиями, а именно: положением параметра внутри «мо-
лекулы-острова», к которой он принадлежит. Если выбрать в качестве
параметра ядро этой молекулы, мы получим дискообразных отдельных
драконов. Если же параметром будет точка заострения молекулы-остро-
ва, то образуется бесконечное множество двустворчатых раковин. А из
рисунка 14 видно, что параметр не тянется по всей длине основания,
а заключен в атоме, полученном в результате единственной бифуркации
четвертого порядка.
Термин «отросток» никогда не использовался после выхода в свет
работы М 1982F. А вот заимствования из химической терминологии
не ограничились только «атомами» и «молекулами», и в работе М 1985g
появились новые термины, вполне заслуживающие хотя бы упоминания.
Это так называемые структуры дьявольской плотины, полимера и клея.
Из факта связности множества М следует связность всех молекул друг
с другом. Однако связи между молекулами множества М разительно от-
личаются от связей между его атомами. Возьмем ядра двух молекул А
и В и соединим их внутри множества М непрерывной кривой с пара-
метром и 6 [0, 1] так, что значения и, содержащиеся внутри молекулы,
образуют открытый интервал. Два таких интервала никогда не соприка-
саются друг с другом, а дополнением к их объединению будет фракталь-
ная пыль. Проведя аналогию с распространенным термином «чертова
лестница», о молекулах, пересекающихся между А и В, стали говорить,
что они образуют «чертову гать», а множество М имеет структуру «дья-
вольского полимера». В случае квадратичного отображения его ветвями
являются незамкнутые петли. Полностью закрытое множество М отли-
чается от полуоткрытого наличием рассеянных точек, «склеивающих»
молекулы. Эти точки образуют фрактальную пыль.}
Physica D. 7. 1983. 22-1-239
Комплексное квадратичное отображение
и его множество М
Предисловие к главе (2003). В этой главе, по умолчанию, пред-
полагается, что множество Л/ представляет собой замыкание множе-
ства Л/о- включающего такие значения параметра, что квадратичная
динамика, помимо точки в бесконечности, характеризуется конечным
устойчивым предельным циклом. Вообще-то, гипотеза о существовании
такого математического свойства была выдвинута еще в 1983 году, но,
несмотря на все приложенные усилия, она не доказана до сих пор. Это
эквивалент «гипотезы MLC» о локальной связности множества М. Изна-
чально название звучало так: «О квадратичном отображении z —> z2 - д
при комплексных р и г, фрактальная структура множества М и мас-
штабная инвариантность». Подразделы оригинала были пронумерованы.
Аннотшцш. Для каждого комплексного значения ц обозначим
наибольшее ограниченное множество в комплексной плоскости, оста-
ющееся инвариантным при отображении z -» /(z) = z2 — д, через ^(д).
В работах М 1980п{СЗ} и М 1982F{FGN}, а также в главе 19 {С4}
сообщалось о различных замечательных свойствах множества Мо (мно-
жества тех значений комплексной переменной д, для которых ^(д) со-
держит области) и о замыкании М множества Mo (P.S. 2003: см. раздел
•Предисловие к главе»}. Цели этой работы таковы:
(А) Заново сформулировать некоторые ранее описанные свойства
множеств 7(g), Mq и М и рассказать о новых наблюдениях.
(Б) Вывести некоторые известные свойства отображения f при ве-
щественных значениях д и г, когда д € —] — 1/4, 2[, a z g] — 1/2 -
- 1/2>/1 + 4д, 1/2 + 1/2уТ+1д]. При изучении свойств квадратичного
отображения во многих отношениях гораздо удобнее использовать не
интервал, а комплексную плоскость. (Этот факт наглядно доказывает
истинность выражения: «Чтобы упростить теорию, следует усложнить
переменные». {P.S. 2003. Так любил говаривать Гастон Жюлиа, который
в 1945 году обучал меня дифференциальной геометрии}).
С5. Комплексное квадратичное отображение и его множество М 107
(В) Представить некоторые последние работы из области чистой
математики, появившиеся благодаря М 1980п{СЗ). Автор настоятельно
рекомендует продолжать активные исследования в этой области.
В центре этой работы лежат иллюстрации, поэтому текст пред-
ставляет собой расширенные комментарии к ним. Дополнительные ри-
сунки представлены в работах М 1980п{СЗ) и главе 19 работы М
1982F{FG/V}{C4}.
1. Обсуждение рисунков от 1А до 1Е.
Иллюстрация действия отображения z —» f(z, ц) = z2 — ц на
большой комплексный круг.
Последовательности алгебраических кривых, приближающие
множества-репеллеры (Жюлиа) Т * (pi)
Преобразование изучать намного проще при наличии конкретного
визуального представления производимого им действия. Известно, что
при отображении z —* f(z, ц) точка в бесконечности является устойчи-
вой неподвижной точкой /, в силу чего она является притягивающей
точкой. Чтобы круг достаточно большого радиуса г с центром в точ-
ке 0 попал в область притяжения оо, достаточно удовлетворить усло-
вию г > г\у = 1/2 + (1/2)-^/1 + 4|д|. Круг радиуса rw с центром в точ-
ке 0 обозначается через W0 и называется «кругом-воронкой»; тогда ра-
диус rw будет называться «радиусом воронки», так как орбиты всех
точек, не принадлежащих Ж0, «уносятся» от нулевой точки.
С другой стороны, некоторые комплексные значения z не при-
тягиваются к оо. К ним относятся ограниченные неподвижные точ-
ки 1/2 + (1/2)yi + 4/i и их последовательные прообразы. Обозначим че-
рез Д/i) максимальное ограниченное множество, инвариантное при пре-
образовании /(z, д). По определению кругов-воронок, множество Дд)
содержится в Ж0. Кроме того, при каждом значении к множество Дд)
принадлежит k-у прообразу Ж0 при /(z), т. е. прообразу Ж при Д(;).
Последнее множество определяется уравнением |/к(г, д)| = rw и обо-
значается W~k. Это алгебраическая кривая, называемая «лемнискатой»
(Walsh 1956). Лемнискаты, соответствующие растущим значениям к. не
перекрываются и образуют монотонную последовательность. Их можно
назвать «параллельными» при f(z, ц). Множество Др) является преде-
лом этих кривых вкупе с их внутренними областями.
Обозначим через границу множества Т7. Множество Т7* явля-
ется пределом множества W~k при к —► оо, представляет собой множе-
ство-репеллер /(z, д) и также называется множеством Жюлиа.
История: самые ранние базовые понятия, связанные с глобаль-
ной итерацией, были описаны еще в работе Fatou 1906; основная же
часть оригинальной теории появилась практически одновременно в тру-
дах Julia 1918 и Fatou 1919. Поскольку термин «множество Жюлиа» уже
был занят, я решил почтить память Фату, обозначив это множество 7*.
А теперь обратим внимание на содержательные иллюстрации. При
четырех выбранных значениях д изображения a-d на рисунке 1 демон-
стрируют внутренние области множества Н’о. а также некоторые кривые
множества в суперпозиции. Этим мне хотелось предоставить на-
глядный пример того, что топология У множества Жюлиа Т7* весьма
зависит от значения д. В частности, граница множества может быть
(а) кривой без петель («простой»), ограничивающей некоторую область,
(Ь) кривой с многочисленными точками, ограничивающей бесчисленное
количество областей, (с) деревом («разветвленной кривой без петель»,
♦дендритом»), которое вообще не окружает области, (d) вполне несвяз-
ной пылью.
На рисунке 2 приведен пример аттрактора Л*.
2. Обсуждение рисунков от 2А до 2F. Классификация значений р
с помощью топологии множества ^(д). Множества Мо и М0М.
Последовательности алгебраических кривых,
приближающих MqM. Континент, острова, звездообразные
структуры, дьявольские плотины
На этой серии рисунков подробно изображается множество тех зна-
чений д, при которых Дд) остается связным множеством. Мы обозна-
чим его через М, а множество значений д, при которых ^(д) имеет
внутренние точки, т.е. содержит области, — через Мо. На рисунке (на-
пример, на рисунке За) множества Мо и Л/ визуально неотличимы друг
от друга, и все же они имеют весьма различные структуры.
2.1. Построение множеств Мо и М. Метод, использованный
при создании рисунков la-id, весьма громоздок и ненадежен, но мы
можем про него забыть, благодаря следующему принципу, сформулиро-
ванному Гастоном Жюлиа. Множество /(//) несвязно тогда и только
тогда, когда последовательность итераций z = 0, начиная с — р, р2 — р
и (д2 - д)'2 - д2 - д, сходится в бесконечности.
Это обеспечивается выполнением следующего необходимого и до-
статочного условия: значение |А(0, д)| должно превосходить (при неко-
тором значении к) радиус воронки rw = 1/2+1/20 + 4|д|, полученный
в раздед£ 1. Когда |д| > 2, это условие выполняется при к = 1. Таким
С5. Комплексное квадратичное отображение и его множество М 109
Рис. C5-I. Действие отображения z —♦ z2 - /1 на серый круг (частично усечен-
ный): (а) множество Жюлиа является замкнутой фрактальной кривой без пе-
тель, (Ь) множество Жюлиа является замкнутой фрактальной кривой с петлями.
(с) множество Жюлиа является фрактальным деревом, (d) множество Жюлиа
является фрактальной пылью («канторово множество»).
по
Physica D, 7, 1983,224-239
образом, множества Afo и А1 целиком лежат внутри замкнутого дис-
ка |д| 2. Более того, программа в целом упростится (хотя прогоны
несколько удлинятся), если гц- заменить единым порогом, равным 2. Из
раздела 1 следует, что тождество |Д(0, д)| = 2 определяет в [/-плоско-
сти некоторую алгебраическую кривую (так называемую «лемнискату»).
Все лемнискаты содержат точку ц = 2, но более они нигде не пере-
секаются и образуют монотонную последовательность. Множество М
является пределом этих кривых вкупе с их внутренними областями.
Как известно, величина д называется сверхустойчивой минималь-
ного периода к, если Д(0,д) = 0. Однако //,(0, д) / 0 при любом h<k.
Следовательно, /„*-(0,/л) = 0 при любом целом п, так что все свер-
хустойчивые д не повторяются до бесконечности и, таким образом, при-
надлежат множеству М. В работе Walsh 1956 говорится, что лемниска-
та не может иметь петлю внутри петли: она всегда представляет собой
либо единичную петлю, либо определенное количество петель, внутрен-
ние области которых не совпадают. В настоящем случае получается, что
лемнискаты являются простыми петлями при всех значениях к, а значит,
М является связным множеством. Но сначала необходимо остановиться
на других свойствах множества Л/.
2.2. Континентальное подмножество Mq. По причинам, с ко-
торыми читатель ознакомится совсем скоро, структура, изображенная
на рисунке 2а, становится понятной благодаря размещению сетки значе-
ний р таким образом, что вещественные значения д остаются непрове-
ренными. С первого взгляда видно, что основная масса черных точек ле-
жит на большом «континенте» с сильно развитой структурой. Структура
эта просто поразительна и напоминает «кактусовое дерево»; я описал ее
как «молекулу», составленную из бесчисленного множества «атомов».
В центре находится «атом-затравка» в форме кардиоиды; он включает
все значения д, при которых f(z,p) имеет, помимо оо, одну устойчивую
предельную точку. Атому четкой круглой формы справа от кардиоиды
принадлежат все значения д, при которых имеет устойчивый
цикл периода 2; тогда как почти круглым атомам справа от него соот-
ветствуют устойчивые циклы периодов 4, 8 и т. д. Точками соединения
этих атомов служат значения д, соответствующие бифуркациям базово-
го вещественного параметра д. Другие почти круглые атомы, которые
касаются кардиоиды, соответствуют циклам порядка к :• 2.
2.3. Форма множества М вблизи значения Доо в правой око-
нечности континентального подмножества. Масштабная инвари-
антность е плоскости и ее использование для повторного выведе-
С5. Комплексное квадратичное отображение и его множг/ гр,о М 111
Рис. С5-2. Внутренняя область множества Жюлиа (множества-репеллера) отоб-
ражения z —> z2 — ц после двух последовательных шестикратных бифуркаций
ния (в качестве следствия) известного свойства масштабной инва-
риантности бифуркаций на вещественной прямой. Рассмотрим по-
следовательность атомов, которая сходится к оконечности континента.
Кажется, что все атомы, в сущности, очень похожи и касаются двух по-
лупрямых, симметричных относительно вещественной оси и сходящихся
к Доо> называемому точкой накопления бифуркаций. Это геометрическое
свойство масштабной инвариантности, а точнее, асимптотической мас-
штабной инвариантности.
Рис С5-3 la; Общий вил множества Л/<, отображения z z~ - //. (b)
мент острова ЛЬ, «пятно- в правой части рисунка За. (с) Элемент острова Л/»'
•пятно- в нижней ча<-1И рисунка За
С5. Комплексное квадратичное отображение и его множество М 113
Отсюда следует вывод: отрезки, отсекаемые на горизонтальной оси
этими атомами, с геометрической точки зрения, уменьшаются при каж-
дой бифуркации. Безусловно, истинность этого вывода ни у кого не вы-
зывает сомнений, поскольку сделали его Гроссман, Томэ и Фейгенбаум.
Чтобы подтвердить идентичность формы атомов с помощью более
строгого эксперимента, мы заново нарисовали множество Л/, заменив
параметр /л на v = log(/i — //оо)- В результате, атом-затравка, имеющий
форму кардиоиды, значительно уменьшается; почти идентичными ему
становятся и другие атомы.
2.4. Большой остров справа от континента. Другие острова.
Помимо континента множество Mq включает несколько разбросанных
пятен. Я питаю надежду, что эти пятна не попались в поле зрения зор-
ких редакторов и корректоров настоящего издания. Беспокойство мое не
беспричинно: дело в том, что корректоры, работавшие над М 1980п{СЗ},
стерли несколько таких пятен по причине своей твердой убежденности
в том, что это обычная грязь!
На самом же деле, эти пятна никакого отношения к грязи не имеют,
поэтому, я думаю, будет нелишним посвятить несколько строк рассказу
о том, как я их открыл. Исследуя свой первый приблизительный рисунок
множества М, я тоже решил, что большинство из них — грязь. Однако
самое большое пятно, расположенное справа от континента, выглядело
слишком большим, чтобы счесть его фикцией. Не составило никакого
труда проверить, что оно пересекает ось вещественных значений р на
интервале, открытом Мирбергом и Метрополисом, Штайном и Штайном
(см. работу Collet & Eckmann 1980), для которого характеризу-
ется устойчивым циклом периода 3. Я увеличил это пятно (рисунок 2Ь)
и выяснил, что оно, в сущности, представляет собой точную уменьшен-
ную копию континента. При этом увеличении также выяснилось, что
другие интервалы Мирберга пересекают очень маленькие копии конти-
нента.
Таким образом, самая правая оконечность континента тянется вдоль
вещественной оси по весьма необычной дороге. По аналогии с чертовой
лестницей (М 1982F{/?OA/}, стр. 83) я назвал ее «чертовой гатью». Эта
метафора родилась следующим образом: сначала в реку, которую нуж-
но перейти, помещаются большие камни для обычных сверхвеликанов,
затем камни поменьше — для обычных великанов, маленьких велика-
нов, суперменов и так далее до чертовски крохотных тварей. В конце
концов, между камнями не остается ровным счетом никакого положи-
тельного расстояния, пусть даже сколь угодно малого. Вещественная
Ill
Physica D, 7, 1983. 224-239
ось проходит по центру этой дороги таким образом, который хорошо
известен людям, знакомым с вещественным преобразованием
И вот тут мне удалось связать сразу несколько непонятных резуль-
татов с одним и тем же источником. Во-первых, оказалось, что для
периодов 1, 2 и 3 каждое сверхустойчивое значение ц является «ядром»
атома, явно принадлежащего континенту или острову, расположенному
за пределами вещественной оси. Однако два сверхустойчивых д пери-
ода 4 остались «неприсоединенными», и чем больше становился пери-
од, тем больше сверхустойчивых д оставалось «неприсоединенными».
Кто-то может сказать, что некоторые атомы содержат ядра с множе-
ственными корнями или несколько одиночных ядер, но эти атомы вы-
глядели бы иначе, чем атомы наименьшего периода 1, 2 или 3, тогда
как, в действительности, все атомы могут иметь только одну из двух
форм: кардиоиду, присущую затравке, или круг, расположенный справа
от нее.
Во-вторых, за исключением точки Доо. оконечности континента не
выказывали никаких признаков того, что за ними последует чертова
гать. О третьем наблюдении мы уже говорили ранее: множество Mq,
с невысокой точностью вычерченное на решетке средней плотности, ка-
залось окруженным разрозненными грязными пятнами.
Увеличение большого пятна грязи справа от М (рисунок Зс) од-
ним махом разрешило все три загадки: большинство пятен не исчезли,
а оказались островами, по своей топологии и общей форме идентичны-
ми континенту. Очень скоро выяснилось, что эти острова не разбросаны
беспорядочно, а образуют «звездообразные» массивы (более подробно
это описано в работах М 1980n{C3}, М 1982F{FG2V}).
Массив, близкий к точке бифуркации порядка 11, представлен на
рисунке 4. В процессе дальнейшего увеличения между крупными остро-
вами, расположившимися вдоль каждого «луча», открывались все новые
и новые постоянно уменьшающиеся островки. Эта картина напомнила
о вышеописанном факте «пронзания» постоянно уменьшающихся остро-
вов вещественной осью. Теперь, когда аналогия с вещественной осью
становилась все более очевидной, можно было предположить, что ост-
рова в каждом луче соединяются друг с другом кривыми, которые пред-
ставляют собой копии вещественной кривой, но увидеть их невозможно,
поскольку кривые (не являющиеся осью) практически всегда попада-
ют между точками решетки, используемой в компьютерном моделирова-
нии. Все вышесказанное подразумевает, что звездообразная структура
отраж^т бмовую структуру дерева и что множество М связно. Не
оуле^ымть. что для аппроксимации множества М использовалась
С5. Комплексное квадратичное отображение и его множество М И5
некоторая последовательность лемнискат, способных (согласно общим
результатам) распадаться на отдельные петли. Сам факт связности М
свидетельствует о том, что аппроксимирующие лемнискаты являются
отдельными петлями. Истинность этого факта подтвердилась вплоть до
прообразов высших порядков окружности \р] = 2, части которой начали
«проваливаться» между точками решетки.
Рис. С5-4. Подробное изображение сети Мо за пределами континента, представ-
ленного на рисунке За
Нет нужды говорить, что выводы, основанные на компьютерных ис-
следованиях, не равносильны настоящим доказательствам. (Также не
,Ц
I X.
s— . "^чые доказательства обеспечивают стрсгу-»
t , у вис '•«омимачия ; В любом случае, математи 'уку
гтп*.ж ио*» ».о*"ьг-'^№» выводов по множеству М оказалось тл,-
*-*&>** v «змт*ы*. о чем говорится в работе Douady &
, /дцх бы кевбзмо*но без этих выводов.
2^ Инверсия би^/риции: понятие слияния. В литера*уре --.
'z- нико'да не упоминается обратный г.у>л".'.
*-**" ***'' :к2АЛ*- когда д начинается с некоторого значеиг?
t row* ** 1 за'равкл) и постоянно меняется, не покидая остроаа
чжа ** х*т*" завами В работе М 1980п этот обратный бифурка-
у,, "УлИ« назван •слияние*» Такое название обусловлено тем. что
-рдажл*? ccj^cjH область стремления к некоторой устой-
предельной *г/чкс тогда как каждый остров является областью
гхм**** г **т«/горому периодическому циклу, но не к предельней
’ОЧГЛ
2Ж Вн^мреммие координаты атомов и островов. Гомологиче-
ское мочал. Рассмотрим атом минимального периода к и зададим zM
t дг/юй W устойчивого цикла. соответствующего значению парамет-
ра д Нам известно, что комплексное число !’к(г^,ц) по модулю мс-нь-
вм I Еч действительные и мнимые части служат вещественными коор-
динатами точки р внутри атома, которому она принадлежит. Две точки
с одинаковыми внутренними координатами можно назвать гомологиче-
скими внутри соответствующих им атомов. Множество значений р, для
ылорыт число является вещественным, будет называться «ос-
иоваиием» атома, био простирается от точки, в которой fk(zn^) - 1
(а случае затравки это будет точка заострения), до точки бифуркации
порядка 2. где с -1
К тому же, положение каждого атома в его острове можно обозна-
чить с помошыо так называемого «адреса», а именно: некоторой после-
довательности целых чисел, определяющих последовательность бифур-
каций. которые приводят к атому атому, начиная с затравки в форме
кардиоиды На самом деле каждая бифуркация отмечена рациональным
числом яц/m*. тле mt г 2 и 0 > щ > mt. Таким образом, достаточ-
но перечислить эти щ и пц через запятую. Полагаю, никто не станет
спорить, что адрес затравки-кардиоиды — 0 (да и другие адреса могут
начинаться с 0, хотя это вовсе не обязательно).
Совокупность адреса атома и значения числа и образует
виутреииюю координату точки р в пределах острова, которому /х при-
надлежит. Две точки с одинаковыми внутренними координатами можно
назвать «гомологическими» в пределах соответствующих островов.
С5 Комплексное квадратичное отображение и его множество М 117
В основании острова соединяются основание затравки-кардиоиды
и основания атомов, соответствующих бифуркации т, = 2. Концевая
точка основания каждого острова гомологична оконечности конти-
нентального подмножества множества А/.
2.7. Аргумент об «универсальности класса*, объясняющий схо-
жесть островов. Предположим, что д является сверхустойчивым зна-
чением д минимального периода к. Мы хотим определить форму атома,
ядром которого является д*.
Члены низших порядков в разложении fk(z,p) в окрестности z = О
и д = д* можно записать как 4- А^(д — да). А теперь определим
и проверим строгую версию аргумента об «универсальности класса»,
а затем — его более слабую версию.
Строгая версия гласит, что форма атома с ядром да зависит только
от членов низших порядков в разложении fk(z,p) в окрестности z = О
н д = да. Если бы это было так. то да образовала бы ядро затравки
в форме кардиоиды. Этот атом и молекула, выращенная на нем, были
бы похожи на континент; вот только размер сократился бы в отноше-
нии 1/0к^к- Согласно более мягкой версии, мы можем учесть несколько
членов более высокого порядка в окрестности z = 0 и д = да, но мы
по-прежнему не рассматриваем поведение fk(z,p) вдали от z = 0 и д =
= да. Такой аргумент предполагает наличие нижеследующих свойств.
(А) Атом с ядром в да является затравкой молекулы, а его форма напо-
минает континентальную кардиоиду, за исключением некоторой слабой
нелинейной деформации. (Б) Другие атомы, полученные путем бифур-
кации, располагаются вокруг этой затравки, как на континенте, опять
же не считая слабой деформации.
При изучении реального множества Mq обнаруживается, что ис-
тинность предположения (А) влечет за собой истинность предположе-
ния (Б). Более того, (А) не выполняется, только когда (А) и (Б) заменя-
ются следующими свойствами. (А') Атом не является затравкой и имеет
практически круглую форму. (Б') Другие атомы, полученные путем би-
фуркации, располагаются вокруг атома с ядром в дЛ/а так же, как их
копии располагаются вокруг континента, если не считать преобразова-
ния, выпрямляющего точку заострения.
При п — 2 сверхустойчивыми значениями, удовлетворяющими ра-
венству д2 - д = О, являются да = 0 или 1. В окрестности да = 1
имеем Д(г, д) = (z2 — д)2 - д = г4 - 2дг2 4- д2 - д ~ —2г2 + (д - 1),
что предполагает существование атома, идентичного базовой кардиоиде,
уменьшенной в 1/2 раза и перенесенной вправо на 1. Однако в действи-
118
Physica D. 7, 1983. 224-239
тельностн размеры атома в каждом направлении больше, а его формой
служит правильный диск.
Вполне оправданно ожидать, что условием истинности предсказа-
ний об универсальности класса (А) и (Б) в их более слабой версии
является большое значение
Другой аргумент об универсальности класса (еще недостаточно хо-
рошо разработанный) предполагает, что атомы, по мере удаления от
затравки своих островов, принимают все более универсальную форму.
2.8. Объяснение формы множества F ♦ (д) при р*, лежащем
на острове, с помощью аргумента об «универсальности класса».
В рамках строгой версии аргумента об универсальности класса также
высказывается предположение относительно множества ^*(д): (В) Мно-
жество Жюлиа У ♦ (д) (назовем его «маленьким драконом») получает
путем сокращения в коэффициенте & множество Жюлиа, которое пред-
сказывается полным множеством Л * (z, р) для точки, располагающейся
на континенте и гомологичной точке р, а именно: р' = 0k^k(p - д*).
Более слабая версия аргумента об универсальности класса выдвигает
предположение (В'). Часть множества Жюлиа Т * (д) получает (путем
сокращения в коэффициенте Д) множество Жюлиа, наличие которо-
го предсказывает полное множество F(z,p) для точки, находящейся на
континенте и гомологичной точке р.
В результате исследования реальных множеств Т * (д) выясняет-
ся, что часть множества У ♦ (д) в окрестности точки z = 0 действи-
тельно является маленьким драконом, предсказанным более слабой вер-
сией (В'). Однако более строгое предсказание (В) содержит довольно
неверное и нечеткое представление о структуре множества У * (д) в це-
лом. Это множество не сводится к маленькому дракону в окрестности
точки z = 0, а составлено из бесконечного числа слегка деформирован-
ных копий этого маленького дракона.
Эти копии составляют чертову гать с той же структурой, которую
мы уже встречали в форме множества М. (Рисунок 5 относится к слу-
чаю, когда д располагается очень близко к ядру кардиоиды на рисун-
ке Зс.) Таким образом, эти копии размещаются вдоль дерева. Сама же
форма этого дерева привносит нечто совершенно чуждое аргументу уни-
версальности. Она, фактически, определяется величиной р, а никак не
точкой на континенте, гомологичной д. Эта форма очень медленно из-
меняется вместе с д и приблизительно определяется д*.
Чтобы получить еще более грубую, но полезную аппроксимацию,
для начала введем значение параметра р", соответствующее оконеч-
ности острова, содержащего д*. Эта точка гомологична классической
С5. Комплексное квадратичное отображение и его множество 'J ]\Ч
Рис. С5-5. Внутренняя часть множества Жюлиа при расположенной вблизи
ядра прибрежного «острова» Л/о
вещественной точке расположенной на оконечности континента.
В следующем разделе исследования множеств Жюлиа У мы увидим,
что величина является одним из значений ;z, при которых множе-
ство F * (/i) сводится к дереву: в роли его основания выступает ве-
щественный интервал, имеются также ветви, но нет плоти. Когда
является оконечностью острова (но не континента), множество
также представляет собой дерево, хотя и не содержит прямых интерва-
лов. Возвращаясь к множеству Т7 * (/z), отметим, что копии драконов,
принадлежащие этому множеству, располагаются вдоль дерева, прибли-
жением которого служит множество У * (//).
Рис. С5-6. Часть множества Л1о отображения z —>> Az(l — z) после инверсии
и сжатия.
g,. Приблизительные подсчеты копий коэффициента <5
^VW>«aqufi порядка > 2. Для целей этого подраздела разумно
= 1 ±РИ/Г~~т^Овые координаты, заменив параметр р, на параметр А
Vi +4ц, что соответствует отображению z —>• f * (z, Л) =
С5. Комплексное квадратичное отображение и его множество М 121
— г). Соответствующее преобразование множества Мп представлено на
странице 250 работы М 1982F{FG/V}. Форма континента теперь отли-
чается от формы островов, так как затравкой для него теперь служит
не кардиоида, а два диска. Однако у этой измененной формы есть свои
плюсы. Первое преимущество, установленное с помощью пера и бумаги,
заключается в том, что бифуркация от устойчивой неподвижной точ-
ки к циклу периода т повторяется в точках, где Л или 2 - А имеет
вид ехр(2тггп/т), причем целое число п меньше, чем т.
Второе преимущество обнаружилось только после получения и ис-
следования множества Мо- Выяснилось, что оконечности «главных» от-
ростков, расположенных вокруг окружности |А - 2| = 1 и определенных
как отростки, укоренившиеся в точках ехр(2тгг/т), судя по всему, раз-
мещаются вдоль круга большего размера, диаметр которого начинается
в точке А = 1 и заканчивается где-то за точкой А = 3. Поэтому при
инверсии множества Мо относительно А = 1 с неподвижной точкой А =
= 3 должны получаться отростки, расположенные между параллельны-
ми прямыми. К тому же, преобразование корня m-го главного отростка
должно находиться от А = 3 на расстоянии, равном 2tg(l/7r/2-7r/m) =
= 2ctg(7r/m) по вертикали. Для больших значений т это дает 2т/л,
то есть ряд точек, разделенных равными промежутками.
Перевернутое множество Мо, изображенное на рисунке 6, построе-
но при использовании на двух осях очень разных единиц, в силу чего
рисунок остается понятным, отражая многие значения т. Вышеупомя-
нутый факт подтвержден для всех значений, кроме т = 2 и 3, то есть
в результате экстраполяции от отростков с более высоким значением т
получается меньший отросток для т = 2. Обозначим через Л высоту
перевернутых отростков для больших значений т. Для круглых атомов
эти свойства инверсии приводят к тому, что относительный линейный
размер отростка порядка т составляет Лвш2(тг/т)[2 - Лзт2(7г/т)]-1.
Грубо говоря, это — коэффициент последовательных абсолютных изме-
нений ц между бифуркациями порядка т, то есть т-я копия коэффи-
циента 1/6 из работ Гроссмана и Томэ, а также Фейгенбаума. На самом
деле, этот коэффициент близок к т~2 для всех т.
3. Обсуждение рисунков 7-10. Пучок-репеллер при
вещественном д и комплексном z. Примеры влияния значения ц
на форму и топологию множества-репеллера (Жюлиа) ^*(р)
На рисунках 7-10 горизонтальные координаты х и у выражают
действительную и мнимую части величины z, а вертикальная коорди-
122
PHYSICA D, 7, 1983, 224-23У
ната соответствует /г. На этих рисунках изображен пучок множеств
Жюлиа 7»(д) от -1/4 до 2. Мы ставили своей целью показать, что
форма множества 5»(д) изменяется непрерывно, тогда как его тополо-
гия подвергается прерывистым перемещениям. Пучок рассекли парал-
лельно плоскости тОр, и две его половины отделили друг от друга...
3.1. Компьютерное моделирование пучка. В теории множе-
ства 7 ♦ (д) существуют два построения «доказательства существо-
вания». Первое использовано в рисунках la-Id. Второе заключается
в создании прообразов неустойчивой неподвижной точки z' = 1/2 4-
+1/20 + 4д. Это второе построение эффективно только при значени-
ях д, близких к 0, когда множество F * (д) представляет собой неслож-
ную петлю. Вообще, какое бы построение мы ни рассматривали, для
получения приемлемой аппроксимации необходимо провести невероятно
длинные компьютерные расчеты. В целях эффективности компьютерно-
го моделирования лучше всего создать несколько альтернативных по-
строений и использовать их сочетания. Лишь постфактум выяснилось,
что эти программы весьма полезны для понимания имеющихся фактов.
На рисунке 7 изображены несколько «вуалей» и «оболочка», на рисун-
ке 8 - только вуали (для ясности некоторые этапы были пропущены),
а на рисунках 9 и 10 — только оболочка.
3.2. Ребра и вуали. Для любого значения р «хребтом» гори-
зонтального сечения пучка служит интервал вещественных значений
из ]-?./[. Ребрами же являются прообразы интервала ]—z', z'[ при /(z);
они представлены на рис. 8 вплоть до восьмого порядка. Хорошо извест-
но, что при f(z) интервал ]-/, z'[ не сходится в бесконечности, а значит,
хребет и ребра принадлежат множеству 7"(р), и, так сказать, образуют
его «скелет». Ребра, соответствующие различным значениям р, сливают-
ся воедино, образуя несколько «вуалей», в том числе квадратную стену
в плоскости у = 0 и округлую стену в плоскости х = 0. Переход че-
рез сверхустойчивое значение д переводит вуали из состояния, когда
они свисают с округлой стены, в состояние, когда они свисают с квад-
ратной стены; другими словами, от свисания вуали высокого порядка
к свисанию вуали более низкого порядка. Прообразы неустойчивой непо-
движной точки z' являются кончиками ребер. Точное отношение между
замыканием ребер и множеством 5"(д) зависит от значения р.
3.3. Сверхустойчивые значения р. При сверхустойчивых значе-
ниях р замыкание ребер представляет собой область, тождественную
множеству ^(д). Поэтому, следуя той же анатомической аналогии, мож-
но сказать, что множество 7(р) являет собой «кожу да кости». Очевид-
С5. Комплексное квадратичное отображение и его множество М 123
ный пример — /1 = 0, когда F(jn) представляет собой диск единичного
радиуса, а ребра /с-го порядка — отрезки, соединяющие 0 с точками ви-
да ехр(2_Ас7гг/п), где п является таким целым числом, что 0< п < 2*+1.
• Рисунок 11 • Рисунок 12
3.4. Хаотические значения ц. При хаотических значениях д, за-
мыкание ребер представляет собой дерево, которое опять-таки тожде-
ственно множеству ^(/z). Очевидным (хотя и вырожденным) примером
служит /1 = 2. Вообще-то, множество Д2) и его ребра сводятся к хреб-
ту [-2, 2]. Очевидно, что для получения Д2) проще всего нарисовать
хребет, а не использовать построение доказательства существования,
которое заполняет Д2) густыми прообразами z = 2.
Рис. С5-7. Перспектива верхней части пучка-репеллера множеств Жюлиа при
вещественных /z (по вертикали) и комплексных z (по горизонтали)
Когда значение /z близко к сверхустойчивому или хаотическому,
максимальное инвариантное множество Д^) легко аппроксимировать
с помощью нескольких уровней ребер. Поскольку множество ДО) яв-
ляется просто диском, а все остальные сверхустойчивые или хаотиче-
124
PHYSICA D, 7. 1983, 224-239
ские значения fi попадают в интервал ]1, 2[, то проще всего нарисовать
несколько уровней ребер для каждого значения д, принадлежащего ин-
тервалу ]1.2[. Легче провести «лишнее» компьютерное моделирование,
чем выяснять, стоит ли его проводить.
3.5. Устойчивые, но не сверхустойчивые значения р. Остальные
вещественные значения д е] - 1/4,2[ — это р, для которых существует
устойчивая неподвижная точка или конечный период, не являющийся
при этом сверхустойчивым. При этих значениях р множество ребер не
отличается высокой плотностью в области и не остается деревом даже
в предельном случае. Для описания результирующей структуры мно-
жества У * (д) смешаем предыдущую анатомическую метафору с био-
логической: можно сказать, что при этих значениях р ветви деревьев
асимптотически соединяются, образуя «крону». Ясно, что голое иссле-
дование прообразов неустойчивой неподвижной точки z' не позволило
отделить те случаи, когда кончики ветвей несвязны и образуют пыль,
от тех случаев, когда они связны.
3.6. Оболочка. Как уже говорилось, построение доказательства
существования множества Т * (д) через прообразы z' эффективно, ко-
гда 7*(д) представляет собой несложную петлю, то есть при р, близких
к д = 0. Когда же множество ^*(д) отличается хотя бы умеренной «кур-
чавостью», петли в форме точки заострения остаются незаполненными
даже после того, как другие части множества У * (д) переживут мно-
гократное покрытие. (Замечание для знатоков: это объясняется тем, что
данный метод воспроизводит на множестве Жюлиа инвариантную меру,
которая может быть чрезвычайно неровной.)
Эффективным графическим методом считается метод, затрачиваю-
щий приблизительно равное количество времени на обработку каждой
части множества 7♦ (д). Оболочка на рисунке 1 была нарисована с по-
мощью следующего генератора оболочек (Norton, 1982). На каждую го-
ризонтальную плоскость накладывали квадратную решетку, причем по-
ложение точки решетки заносилось в память компьютера, когда (а) ее
k-я итерация попадала в круг радиуса 2 и (б) k-я итерация по край-
ней мере одного из ее соседей выходила за пределы этого круга. Эти
точки определялись с помощью метода поиска, который берет за начало
неустойчивую неподвижную точку а/ и является очень эффективным,
так как число утерянных точек (проверенных, но не сохраненных) на-
много меньше количества сохраненных Точек.
множество содержит очень много петель
1^Вгенер,торов(ИИИ1П|>впускает
много точек,
С5. Комплексное квадратичное отображение и его множество М 125
Рис. С5-8. Увеличение верхней части «вуалей» рисунка 7
принадлежащих множеству J’ * (g). Он пропускает «A-части», которые
(по определению) настолько малы, что просачиваются между точками
решетки, и «В-части», которые (по определению) велики, но связаны
с неустойчивой неподвижной точкой z' через А-части.
При исследовании оболочки изнутри (рисунок 4) эти А- и В-части,
расположенные вверху, не играют никакой роли, поскольку они, так или
иначе, будут спрятаны. Обсуждаемое ниже свидетельство можно было
бы скрыть включением ребер. Когда же оболочка исследуется снаружи,
как на рисунках 7, 8 и 9, А- и В-части, напротив, имеют значение. К сча-
стью, многие точки, пропущенные генератором оболочки, «подбирает»
генератор ребер, и сочетание первого со вторым приводит к довольно
точному представлению о внешней форме пучка.
Я не собирался раскрывать этот рисунок, и вид изнутри был вычис-
лен ненамеренно. Felix culpa.
I ?t'
Рис. C5-9. Перспектива пучка-репеллера в
отсутствие сети: вид снаружи.
• • Основные выводы. По мере увеличения /г множество-репел-
лер непрерывно меняется, а его топологические характеристики демон-
ное м *°Т ИЗМенения колебательного характера. Наибольшее инвариант-
множество постоянно меняется в пределах каждого интервала Мир-
С5. Комплексное квадратичное отображение и его множество V 127
Рис. С5-10. Перспектива пучка-репеллера: внутренний срез, на котором видны
бифуркации
берга, к которому принадлежит величина /т. Предположим однако, что ...
уменьшаясь, проходит значение —1/4 или значение, гомологичное -1 4.
внутри острова. Тогда непрерывная крона начинает разрываться, в ре-
Physica D, 7. 1983, 224-239
l,i II I I I • I I III. • I‘l
I , • I . i . I I I . w . I . I 4 • i • • • ' •
Рис. C5-11. Элемент верхней части рисунка 9: срез по плоскости у = 10 3 при
использовании х и у в качестве координат.
зультате чего образуется пыль и ♦испаряется» плоть, С противополо»
ных сторон хаотического значения у кончики дерева образуют разны(
кроны.
В окрестности точки у. = 0 оболочка отличается чрезвычайной гл а:
костью. Вообще, по мере удаления у от у, = 0 количество складок ш
С5. Комплексное квадратичное отображение и ею множество л/ 129
Рис. С5-12. Еще более четкое изображение элемента верхней части рисунка 12
после рассечения по плоскости у = 10-зи при использовании .г и у в качестве
координат
множестве Т7*^) увеличивается очень медленно и постепенно, поэтому
я предположил, что фрактальная размерность множества У * (р) пред-
ставляет собой очень регулярную функцию от р — бесконечно диффе-
ренцируемую и, возможно, аналитическую. Истинность этого предполо-
жения получила подтверждение в работе Ruelle 1982.
3.8. Интерпретация нижней части внутреннего вида оболочки.
Бифуркации. Помимо четко различимого круга при р = 0, самой пора-
зительной особенностью этого вида служат выступы, накладывающиеся
рядами на ряды. Самый нижний ряд расположен на высоте р = 3/4.
При вещественных р меньше 3/4 отображение /(г) (как при веществен-
ной, так и при комплексной г) имеет устойчивую предельную точку.
При р = 3/4 этот устойчивый предел в процессе бифуркации переходит
в устойчивый предельный цикл периода 2. В то же время, мы видим,
что множество * (р) превращается из простой петли в петлю с беско-
нечным количеством узлов. (Выступы можно сосчитать, они имеют две
130
Physica D, 7, 1983, 224-2.39
предельные точки, неустойчивую неподвижную точку z' и -г'.) Следу-
ющий самый высокий ряд выступов отмечает вторую бифуркацию и так
далее.
Безусловно, читателю знакома диаграмма дерева, описанная в ра-
боте Мау 1976. Она отображает изменение, которое претерпевают д
значений ,т для всех точек в соответствующем устойчивом цикле. Если
это дерево наложить на рисунок 4, то его корни окажутся на заострен-
ном кончике в нижней левой части, а точка каждой ветви прикрепится
к соответствующему выступу. Диаграмму Мэя можно продолжить, что-
бы получилось отображение изменения с р «вещественной предорбиты
цикла», определенной как множество вещественных z, которые в конце
концов попадают точно в цикл. Получившаяся в результате диаграм-
ма отображения предорбиты будет состоять из многих деревьев, ветви
которых цепляются за каждый выступ рисунка 4.
3.9. Интерпретация нижних частей внутреннего и наружно-
го видов оболочки. Интервалы Мирберга для значений р. Верхняя
часть пучка представляет собой практически белую стену, которая из-
вестна нам из построения генератора вуали. Однако эта стена прерыва-
ется висячими «узлами», образующими горизонтальные полосы. Каждая
такая полоса соответствует интервалу Мирберга для р.
3.10. Интерпретация некоторых горизонтальных и вертикаль-
ных сечений пучка. Когда р принадлежит интервалу Мирберга, гори-
зонтальным сечением пучка является дерево, образованное «чертовой
гатью». Поскольку эта гать непрерывно изменяется вместе с р, те опо-
ры, которые пересекают плоскость х = 0, образуют что-то вроде черто-
вой бревенчатой мостовой.
Теперь перейдем к вертикальным сечениям. Сечение у = 0 всего
пучка ограничено полупараболой р = х2 + 2х при х < 1/2 и отрезками
от (д = -1/2) до (д = -1/4, х = 1/2) и от (д = 2, х = —1) до (д = 2,
х = 2). Нижняя часть этой вазообразной фигуры плотно заполнена, а ее
верхняя часть увенчана полосами Мирберга.
Рассмотрим аналогичные вертикальные сечения верхней части обо-
лочки при у = 10-3 (рисунок И) и элемента при у = 1О-10 (рисунок 12).
Здесь мы видим много черных фигур, каждая из которых является ис-
каженной копией всего вазообразного пучка. При таком значении д, ко-
гда итерации f(z,p) не являются хаотическими, пересечение множест-
ва .F * (д) со стеной у = 0 является счетным множеством. Оно насчи-
тывает две точки накопления, когда д принадлежит континенту, причем
эти точки можно сосчитать, когда они лежат на острове. При хаоти-
С5. Комплексное квадратичное отображение и его множество А/—13£
ческих значениях g пересечением множества Т * (ц) со стеной служит
отрезок.
Благодарность. Компьютерными программами для создания изоб
ражений использованных в этой статье (многие из них отличаются вы
сокой сложностью), я обязан своему коллеге В. А. Нортону.
Хаос фракталы и динамические системы
Под редакцией У. Смита и П. Фишера. 1985
С6
Точки бифуркации, приближение
«п в квадрате» и гипотеза (на основании
результатов, полученных М. Л. Фреймом
и К. Митчеллом)
Предисловие к этой главе и добавленный рисунок (2003)
Гипотеза о п2, и «учению которой посвящен второй раздел этой гла-
вы, была впервые доказана в работе Guckenheimer & McGehee 1984.
Я и еще два автора приняли участие в так называемом году итерации,
который в 1983-84 годах организовали в Институте Миттаг-Леффлера
в Дьюрсхольме (Швеция) Леннарт Карлесон и Питер. У. Джонс. Во вре-
мя моего семинара два слушателя неожиданно перестали слушать и на-
чали быстро что-то записывать. После семинара они поспешили пред-
ставить доказательства, которые оказались похожими и вылились в на-
писание общего доклада. Они объяснили феномен п2 через нормальные
формы резонансных бифуркаций с множителем ехр(2тгг/п). В резуль-
тате более подробных исследований выяснилось, что после повторного
масштабирования эти области устойчивости приобретают предельную
форму. Таковы выводы теории аналитических нормальных форм для па-
раболических точек. См., например, работу Shishikura 2000.
В разделе 1 приводится «грубое приближение п в квадрате», кото-
рое автоматически определяет отклонения от этого приближения. Чис-
ленно эти отклонения были изучены Майклом Л. Фреймом и Керри
Митчеллом. Полученные ими результаты представлены на рисунке 1.
Это - исключение из правила, так как остальные части книги ограни-
чиваются моими первоначальными наблюдениями и их прямыми след-
ствиями.
Для каждого «атома», укоренившегося на круге |А| = 1 множества
Мандельброта отображения z Az(l - z), Фрейм и Митчелл рассмат-
ривают вектор от корня до центра, определенного f = 0. На верхнем
рисунке изображено отклонение произведения п2 (длины этого векто-
С6. Приближение *п в е вал вл те*
ра) от его грубого приближения, равного 1. На нижнем рие.нж- -o^aia-
угол между этим вектором и вектором, соединяющим корень а’ома , на-
чальной точкой А = 0.
Обоим рисункам присуща поразительная "фра/.та > э-и
очень похожи на мультифракталы с рис. С21.2, родственные меое
ковского.
Рис. С6-1. Отклонения от приближения «п в квадрате», о которых рассказыва-
ется в предисловии к этой главе.
Аннотация. Предполагается, что при определенных значениях :
и А производные функции /(г, А) в точности удовлетворяют некоторо-
му свойству, именуемому правилом п2. Численные подсчеты полностью
134
.Хаос, фракталы и динамические системы, 1985
подтверждают это правило, однако математическое доказательство пока
отсутствует.
1. Эмпирические заключения о радикалах М\
Множество Мх. родственное отображению z —► Аз(1 — z), содержит
круг, окруженный скоплениями атомов, имеющими форму отростков (со-
гласно моей химической терминологии, называемыми «М-радикалами»).
Корнями этих атомов являются точки вида Ао = схр(2тггт/п). «Откры-
тый» атом, корень которого уходит в связь Ао, является геометрическим
местом точек, удовлетворяющих условию А)| < 1, где гд — од-
но из значений в устойчивом периодическом цикле из п точек, соот-
ветствующих А. Расстояние между Ао и ядром атома будет называться
♦радиусом» атома и обозначаться через гт,и.
Первое заключение. Радикалы практически идентичны по фор-
ме половине самого множества М\. Значит, такую же форму имеют
и подрадикалы любого порядка, а половина множества М\ практи-
чески самоподобна.
Второе заключение. Если принять т/п за несократимую дробь,
то радиус rm,n практически не зависит от т.
Третье заключение в грубом приближении (Mandelbrot
1983р{С5}). Радиус гт,п практически равен п~2.
Вывод. Сравним радикалы, корни которых получены в результа-
те различных последовательностей бифуркации, а порядки имеют одно
и то же произведение п?,пь Если объединить все вышеизло-
женные заключения, получается, что эти отростки имеют практически
одинаковые радиусы.
Третье заключение в более точном приближении. Величи-
на п~2 служит точным, приближением расстояния от связи Ао до
проекции ядра на полупрямую от 0 до Ао.
2. Математическая гипотеза, истинность которой
объясняет вышеизложенные заключениям
В предыдущем разделе термины «практически идентичны», «прак-
тически не зависит» и «практически равен» отражают важное свойство
изменчивости, которое еще предстоит исследовать в будущем. Тем не
С6. Приближение «п в квадрате
135
менее, вышеприведенные заключения вылились в следующее точное ма-
тематическое утверждение, подтвержденное численно для многих значе-
ний 7п/п, хотя и не имеющее общего доказательства.
«Частная гипотеза о п2». Рассмотрим полупрямую от точ-
ки X = 0 до связи X = схр(2тггт/п), соответствующей бифуркации
от 1 до 71. Возьмем производную функции fn(zX,X) по этой полупря-
мой. В точке Ао эта производная равна —п2.
Обобщение. Функция . Частная гипотеза о п2 рассматрива-
ет производные по прямой, ортогональной границам атомов, связанным
с точкой Ло. Более того, если |А| 1, то функция \f'(z\, А)| тождествен-
на |А|; значит, ее производная по тому же радиальному направлению
равна 1.
Определим функцию д(Х) при А на полуоткрытом множестве М как
равную А), гДе п ~~ эт0 период предельного цикла, соответству-
ющего A, a z\ — точка в этом предельном цикле. Ясно, что |<?(А)| = 1,
если А является связью. При выражении через д(Х) частная гипотеза
о п2 гласит, что, когда А пересекает некоторые особые точки бифурка-
ции в п, градиент |<?(А)| умножается на -п2.
Понятно, что эта новая формулировка инвариантна, т. е. она не
изменяется при замене параметра А параметром р или любой функ-
цией (коих существует великое множество) от А, достаточно гладкой
в окрестности точки Ао и сохраняющей ортогональность. К тому же,
инвариантная форма легко встраивается в следующее обобщение.
«Общая гипотеза о п2». Обозначим через Ао связь между двумя
атомами, соответствующую бифуркации от порядка по до порядка
поп, и рассмотрим (дХ) вдоль кривой, пересекающей Ао в направле-
нии, ортогональном границам связанных атомов. Отношение произ-
водных |j(A)| справа и слева от точки Ао равно -п2.
Комментарий. Все заключения были бы верными, будь А)
линейной функцией от А внутри каждого атома и подтвердись гипотеза
о п2. Действительно, в таком случае каждый атом на континенте мно-
жества М\ был бы диском, а функция /„(гд,А) обращалась бы в ноль
в ядре и по модулю равнялась бы единице вдоль круговой границы
диска. Радиус атома был бы обратным производной функции /^(сд,А)
в корне этого атома, а потому не зависел бы от т и равнялся п~2.
Благодарности. Я благодарен В. Алану Нортону и Джеймсу А. Ги-
вену за множество полезных дискуссий. Компьютерные программы для
вычисления радиусов rm>n написал Дж. А. Г. под руководством В.А. Н.
Также ценную помощь оказали Линда Солофф и Дженис X. Кук.
Хаос, фракталы и динамические системы
Под редакцией У. Смита и П. Фишера, 1985
С7
«Нормированный радикал» множества М
Предисловие к этой главе (2003 год)
Оригинальная аннотация была расширена. Так ли уж прост «нор-
мированный радикал» или он все-таки представляет какой-то интерес?
К моему сожалению, впоследствии этот вопрос так и не привлек особого
внимания.
Отрывок. «Нормированный радикал» множества М определя-
ется как фигура, в точности удовлетворяющая всем свойствам самопо-
добия, приблизительно справедливым для всех молекул множества М
квадратичного отображения. Из явных построений следует, что допол-
нением R служит (т-луночка, а множество не перекрывает само себя.
Кроме того, показано, что фрактальная размерность D границы радика-
ла R удовлетворяет равенству Е2°ф(п)п-2£> = 1, где ф(п) — это теоре-
тико-числовая функция Эйлера.
Грубым первым приближением служит решение D = 1,239375 урав-
ОС
нения £n1-2D = C(2D — 1) - 1 = тг1 2/6, где £ — это дзета-функция
2
Римана. Менее изящное, но несомненно более точное второе прибли-
жение: D = 1,234802. Это же значение D применимо к множествам М
других отображений в том же классе универсальности.
Кроме того, вводятся интересные законы распределения вероятно-
стей «ранг-размер».
1. Введение
Множество М, будучи замечательным множеством в комплексной
плоскости, играет центральную роль в динамике, неявно присутствую-
щей в процессе итерации полиномов, рациональных функций и других
аналитических отображений. В этой работе основное внимание сосредо-
точено на квадратичном отображении, которое имеет вид z —♦ /(г, А) =
С7. «Нормированный радикал» множества М
137
= Az(l — z), где z и А являются комплексными числами. Молекулы
соответствующего множества М приблизительно самоподобны. В разде-
ле 2 «нормированный радикал» определяется как фигура, для которой
точно выполняются эти правила самоподобия. Кроме того, там же утвер-
ждается, что И не перекрывает сам себя. В разделе 3 отсутствие пере-
крытия радикалом TZ самого себя доказывается через явное построение
дополнения к TZ. Раздел 4 являет собой отступление в сторону основ
теории чисел, которая пригодится в разделе 5. В разделе 5 определя-
ется фрактальная размерность границы ft, а в разделе 6 представлены
некоторые интересные законы распределения вероятностей.
2. Нормированный радикал 'R,. Определение,
отсутствие перекрытия самого себя
Определение И. как ст-диска. Из рисунка 1 видно, что нормиро-
ванный радикал 1Z множества М представляет собой ст-диск, то есть
счетную совокупность замкнутых дискообразных атомов, и строится
рекурсивно следующим образом. Атомом нулевого поколения являет-
ся единичный диск, тогда как атомы первого поколения представляют
собой диски, касающиеся этого единичного диска, причем точки каса-
ния («связи») имеют вид А = ехр(2тггт/п), а радиусы равны п-2. Для
каждого атома k-го поколения с радиусом п~2 задаются такие внутрен-
ние координаты, что его центр имеет координату 0, а связь с диском
(к - 1)-го поколения — координату п~1. Затем этот атом fc-ro поколения
«украшается» атомами (А:+1)-го поколения, внутренние координаты свя-
зей которых имеют вид п~2 ехр(2тггт/у), а их радиусы равны n~xv~2.
Неограниченный вариант радикала. Вариант данного построе-
ния изменяет этапы экстраполяции интерполяции. Этот процесс очень
утомительно описывать, но он дает, в сущности, такой же результат,
что и предел простой интерполяции (как описано выше), увеличен-
ной в 400 раза при неподвижной правой точке. «Кусочек» этой экс-
траполяции присутствует на рисунке 1 в виде частично заполненного
диска.
Определение термина, «луночка». Если взять круг С и круг С",
который касается С' и по-другому содержится в С, то множество точек
внутри С и снаружи С" называется открытой луночкой.
Дополнение к радикалу И, представленное в виде а-луночки.
Дополнение к радикалу 11 покрыто cr-луночкой, а именно: счетной
\ \ •; । • । м hi и ни и mh'ii < 1111 и< 11 мы. 1 ‘MS
Pm '.7-1 По определению, нормированный радикал 7Z множества М являет-
ся /7-диском На данном рисунке дается его приближение в виде объединения
достаточно большой группы замкнутых дисков.
бесконечной совокупностью открытых луночек. Это построение вы-
полнено на основе различных свойств радикала 7£, описанных в леммах
раздела 3. Один из последующих этапов построения приводится на ри-
сунке 2. Данное построение настолько эффективно, что рисунок 2 не
производит должного впечатления. Поэтому на рисунке 3 представлена
другая иллюстрация, где каждая луночка изображена в виде веера из
линий, и мы четко видим, как перекрывают друг друга разные веера.
(Как ни удивительно, но изначально этот красивый и емкий рисунок
получился в результате ошибки в компьютерной программе.)
С7. «Нормированный радикал* множества М
139
Следствие. Отсутствие перекрытия самого себя. Замкнутые
диски, построенные согласно вышеизложенному определению 71, не пе-
рекрывают друг друга нигде, за исключением связей.
Рис. С7-2. Дополнение к нормированному радикалу 7Z, как говорится в этой ста-
тье, представляет собой cr-луночку. Здесь представлено его приближение в виде
объединения не слишком большого числа луночек. По определению, подради-
калы являются уменьшенными версиями самого радикала. Поэтому в процессе
изучения подрадикалов растущего размера мы узнаем, каким образом возраста-
ющее число луночек определяет дополнение к 7Z: сначала — как диск, а затем —
но всех подробностях.
Отображение z —* h(zrf), такой комплексный параметр, что
ео множество М состоит из нормированных радикалов R мно-
жества сингулярная зависимость т/ от р. Обозначим через г?
комплексную переменную в плоскости, содержащей радикал 7?. Внут-
ренние части 71 и континентальной молекулы М отображения, записан-
юго в виде f * (z,p) = z2 — р, можно поставить в дважды непрерывное
140
Хаос, фракталы и динамические системы, 1985
взаимно-однозначное соответствие p(rf) таким образом, что при /i(z,r/) =
- f ♦ [г.//(г/)] функция «?(А) (М 1985g{C6), раздел 6) является ку-
сочно-линейной внутри каждого атома множества М. Таким образом,
молекула множества Л/ отображения /?(z,7/) и есть сам радикал 11.
Вспомним, однако, что «универсальность» Фейгенбаума в применении
к отображению /*, ограниченному вещественной осью, подсказывает,
что отношение диаметров последовательных атомов, пересеченных ве-
щественной осью, принимает значение 4,66920 для обширного класса
отображений. Для отображения //(2,77) его значение равно 4, поэтому
данное отображение не принадлежит к тому же классу универсально-
сти, что и f * (z,//).
Для примера рассмотрим окрестность предельных точек //оо и т^,
соответствующих бесконечной последовательности бифуркаций второго
порядка. В этой окрестности (//оо — //) ос (т/оо — ^)bg4,66/iog4 Аналогич-
но, копии А для ряда n-кратных бифуркаций с п > 2 были рассчитаны
в работе Cvitanovic & Myrheim 1982, они также близки к п“2, хотя
и отличаются от этого значения. Таким образом, соответствующее зна-
чение //(т/) сингулярно на границе радикала 7£.
«Сдутый» вид И. На рисунке 4 изображено, что произошло бы
с И. если бы каждый диск периметра 2тт~2 стал плоским «дублетом»:
отрезком длины im~2, покрытым сначала в одном направлении, а за-
тем в противоположном. Правая сторона параметризуется величиной 6,
принадлежащей интервалу [0,7г], а левая — величиной 0 из интерва-
ла [тг,27г]. Два атома, касающиеся друг друга при 0 = д, заменяются
дублетами, коллинеарными инициаторам, а все остальные ортогональ-
ные атомы заменяются дублетами, ортогональными исходному.
3. Окружности, оскулирующие радикал 7?.,
и доказательство того, что дополнение к 72.
может быть покрыто сг-луночкой
Комментарий. Леммы, рассматриваемые в этом разделе, имеют
явные приблизительные эквиваленты в реальном множестве М отобра-
жения z -♦ Az(l - z).
Лемма А. Бесконечная последовательность бифуркаций приво-
дит к точке [-5/3, 0]. Доказательство. Диаметры дисков в этой бес-
конечной последовательности равны 2, 2(1/4), 2(1/4)2 и т. д. Сумма этих
диаметров составляет 8/3.
С7. «Нормированный радикал* множества М
141
Рис. С7-3. Изображение тождественно рисунку 2, за исключением ошибки в про
грамме. Каждая луночка должны была быть нарисована как объединение запол
венных четырехугольников; здесь же показано объединение контуров этих четы-
рехугольников. Этот рисунок лучше объясняет алгоритм получения <т-луночек,
кроме того, он обладает еще одним немаловажным достоинством — красотой.
Лемма В. Радикал 1Z содержится в замкнутом диске с цен-
зом 0 и радиусом 5/3. Доказательство. Согласно лемме А, в этом
диске находятся все связи, полученные благодаря конечной последо-
мгельности бифуркаций порядка 2. Вполне достаточно будет рассмот-
реть такую последовательность бифуркаций, чтобы не все порядки ,
nj...., ng были равны 2, и показать, что она всегда ведет к образованию
связи, содержащейся в пределах описанного выше диска. В самом деле,
усмотрим ломаную от 0 до связи, получившейся в результате первой
^фуркации, затем — до центра соответствующего атома, потом — до
И.' Хаос, фракталы И димл,.,.,
связи, возникшей в результате следующей бифуркации, и т. д.... Мак-
симальное значение каждого вектора в этой ломаной по модулю равня-
ется вектору прямой, соответствующей пд = 2, и, по крайней мере, один
из этих векторов по модулю будет меньше. Следовательно, сумма этих
векторов меньше 5/3.
Лемма С. Вблизи корня радикала 1Z в точке ехр(2тг?0) при 9 = О
окружность кривизны (обратный радиус), равная p~l = 1 — 4/Зтг2,
локально оскулирует радикал 11. Доказательство. Применим лемму
В к каждому подрадикалу Н. Подрадикал, координатами связи которо-
го являются ехр(г0) = ехр(2тгтг/п), находится внутри диска с радиу-
сом (5/3)п-2 и центром, расположенным на расстоянии 1 + п~2 от 0.
Более того, он лежит в диске с радиусом (5/3)(m/n)2 и центром, от-
стоящим от нуля на расстоянии 1 4- (т/п)2. Эти увеличенные ограни-
чивающие диски почти полностью перекрывают друг друга, но внешняя
граница их объединения представляет собой гладкую кривую. Вблизи
точки 0 = 0 эта граница является кривой, выражаемой уравнением i =
= —у2/2 + (8/3)(j//2tt)2 = -у2[1/2 - 2/Зтг2] = у2/2р. Следовательно,
ее локальная кривизна равна р - 1 = 1 — 4/Зтг2, а это означает, что
оскулирующая окружность имеет радиус р ~ 1,1562.
Лемма D. Радикал 11 содержится в диске с центром в точ-
ке -1/3 и радиусом 4/3. Доказательство. При 0/2л = и расстояние
от точки -1/3 до точки, которая является увеличенным ограничиваю-
щим диском, составляет самое большее l/3{5it2 + \/[1 4- 9(1 + и2)2 +
+ 6(1+ u2)cos(17tu)]}. Несложно увидеть, что эта величина равна 4/3
при u = -1,0 или 1, и меньше 4/3 при всех остальных и, принадлежа-
щих интервалу (-1,1].
Лемма Е. Вблизи точки связи ехр(2тт/п) разделим 1Ъ на
подрадикал, большой атом которого является окружностью ради-
уса п~2, и некоторый остаток. Окружность кривизны п2(1 — 4/3-тг2)
локально оскулирует подрадикал, а окружность кривизны 4п2/Зтг2-1
локально оскулирует остаток.
Следствие леммы Е. Оскулирующие луночки. Подрадикал
и остаток не перекрываются локально; более того, они локально
разделены *оскулирующей луночкой», существующей между оскули-
рующими окружностями.
Комментарий к лемме Е. В глобальном смысле каждая оскули-
рующая луночка пересекает радикал 11. Следовательно, для покрытия
дополнения к И нужны луночки меньшего размера, чем оскулирующие
Лемма F. Комплементарные луночка. К каждому подрадика-
лу радикала 1Z, большой атом которого является диском радиу-
са г, присоединим комплементарную луночку, имеющуюся между
двумя следующими окружностями-, описанной вокруг атома окруж-
ностью радиуса (4/3)г и окружностью радиуса (6,6)(4/3)г, касатель-
ной к описанной окружности в точке связи подрадикала. Такая лу-
ночка называется комплементарной, поскольку она находится за
пределами радикала 1Z. Пересечение внешней части 7Z с окружностью,
описанной вокруг всего радикала, покрывается сг-луночкой, определяе-
мой как объединение комплементарных луночек подрадикалов.
Комментарий к лемме F. Одна из окружностей, включающая та-
кую луночку, очевидна, так как луночка находится за пределами ради-
кала TZ тогда и только тогда, когда одна из ограничивающих окружно-
стей описана вокруг атома. Численный коэффициент 6,6 был получен
методом проб и ошибок. Однако несложно доказать, что внешнюю часть
радикала 11 можно покрыть немного более причастными множествами.
Как показано на рисунке 3, структура внешней части К четко очер-
чена небольшим числом луночек. Эта же структура хорошо просмат-
ривается и на одной половине множества М, что, собственно, и под-
толкнуло меня к данному исследованию, в ходе которого было получено
настоящее объяснение.
4. Теоретико-числовая функция Эйлера ф(п) и род
Теоретико-числовой функцией Эйлера ф(п) называется число несо-
кратимых дробей знаменателя п. Определим </>*(n) = S^=1</>(u). По тео-
реме Мертенса, ~ (3/7r2)2+0(nlogn) при п —> оо (Hardy & Wright
1960, Теорема 330), что в грубом приближении дает ф(п) ~ (6/тг2)п ~
-0,6079271гг.
Рис. С7-4. Граница радикала 1Z после того, как каждый из его дисков «сдул-
ся» до двух наложенных друг на друга отрезков. Отрезки, соответствующие
бифуркациям второго порядка, расположены на одной линии, тогда как те, что
соответствуют бифуркациям более высокого порядка — ортогональны.
144
Хаос, фракталы и динамические системы, 1985
В результате подробного исследования было получено более точное
представление ф* = (3/тг2){п24-7?[Ц-/?(7?)] + а}. Эта формула определяет
некоторое число о и некоторую функцию /3(п). Эта /3 очень похожа на
неизменную случайную функцию п, которая колеблется в ограниченном
интервале с центром в точке 0, а представление тг[1 + /3(тг)] «случай-
ного члена» имеет порядок величины квадратного корня «дрейфующего
члена» 7j2 + n. Функция (3(п) обладает очень интересными свойствами,
которые во всех подробностях будут описаны в другой работе. Заметим,
что конечная разность вышеуказанной ф * (п) при /3(п) равной нулю
составляет (6/тг2)тг.
5. Значение фрактальной размерности D границы
радикала ft
Согласно свойству самоподобия 11, D является решением уравне-
ОС
ния £ Ф(п)п~21> = 1, генерирующего D. Численное решение, получен-
п=2
ное с помощью ньютонова метода, составляет D = 1,239375. Используя
старший член формулы Мертенса для ф(п), получаем простую прибли-
ОО
женную функцию, генерирующую D, а именно: (6/тг2) 52nl-2D = 1, то
2
есть ((2£>-1) = 1 + 7г2/6. Численное решение составляет D = 1,245947.
Малость этого значения D объясняет «костлявость» рисунка 4.
6. Законы распределения вероятностей «ранг-размер»,
полученные с помощью подрадикалов ft
Классифицируем подрадикалы, непосредственно примыкающие к 11,
с помощью возрастающих значений п и, для каждого п, с помощью
возрастающих значений тп. Ранг подрадикала в этом списке обозна-
чим через р. Число подрадикалов, радиус базовой окружности которых
п
равен п-1, равно функции ф(п) Эйлера (раздел 3), откуда 52 0(и) =
П = 1
= ф ♦ (тг) — это такое число р, при котором радиус базовой окружно-
сти п2. В приближении Мертенса ф* (п) ~ (3/тг2)п2; следовательно,
мы получаем два правила: 1) «линейный размер подрадикала ~ 1/ранг»
и 2) «площадь подрадикала ~ 1/(ранг)2».
Это примеры так называемого статистического правила «ранг-раз-
мер», которое наблюдается у многих природных явлений; некоторые из
них перечислены в М 1982{FGM} (например, глава 38) {P.S. 2001. См.
С7. «Нормированный радикал» множества М
145
также работу М 1997Е, Глава Е7}. К сожалению, примеры, в которых
это правило получено с помощью теоретического аргумента, встреча-
ются сравнительно редко, что значительно повышает ценность примера
настоящего. Так как S(l/n) = оо, линейный размер невозможно взве-
сить, чтобы получить вероятность, однако эту операцию можно про-
делать с площадью: достаточно разделить ее на сумму всех площадей
подрадикалов.
Существует ли такая экспонента D, при которой N~D является ве-
роятностью подрадикала и никакой взвешенный префактор не нужен
вовсе? Такая D должна удовлетворять уравнению ^2 Ф(п)тГ2[) = 1,
п=2
поэтому она представляет собой фрактальную размерность границы 11.
По аналогии с другими неслучайными фракталами получается, что ха-
усдорфова мера границы 1Z положительна, конечна и может быть при-
нята равной 1. В таком случае n"2D является (безо всякого префакто-
ра) хаусдорфовой мерой границы подрадикала, укоренившегося в точке
ехр(2тггт/п). Эта мера наделяет математическим смыслом интуитивное
понятие точки, равномерно распределенной по границе 11.
7. Теоретико-числовая функция м(п)
Обозначим через i/(n) число окружностей радиуса п~2, содер-
жащихся в 71. Известно, что размерность многих фрактальных кривых,
дополнение к которым построено в виде объединения открытых «пу-
стот» (например, Аполлониева салфетка; М \982{FGN}, стр. 170{С16}),
равна такому значению D, которое управляет распределением линей-
ных размеров этих пустот. То есть F является численным префактором,
и р(п) ~ F(n~2)~D = Fn2D. Разумно предположить (хотя это еще нуж-
но доказать), что это отношение также справедливо и для 71. Согласно
этой гипотезе, i/(n)oon2D.
У функции v(k) есть прямое арифметическое толкование. Это число
отдельных произведений таких несократимых дробей, что знаменателем
произведения является п при условии, что каждая перестановка отдель-
ного множителя считается отдельно. Это определение выглядело бы на-
думанным, если бы в его основе не лежало конкретное применение.
Безусловно, неизбежен вопрос, играет ли эта i/(n) еще какую-нибудь
роль в «неабелевой» арифметике.
Благодарность. Я благодарен В. Алану Нортону, Джеймсу А. Гиве-
ну и Дженис X. Кук за множество полезных дискуссий. Компьютерные
программы для создания рисунков 1, 2 и 3 и вычисления D были напи-
саны Дж. X. К.
Хаос, фракталы и динамические системы
Под редакцией У. Смита и П. Фишера, 1985
С8
Размерность границы множества М равна 2
Предисловие к главе (2003). К большому счастью (хотя и несколь-
ко запоздало), гипотеза, высказанная в этой статье, в конце концов, по-
лучила подтверждение в работе Shishikura 1984. Очевидно, далее право-
мерен вопрос о хаусдорфовой мере этой границы с размерностью 2. До
сих пор не известно, равна ли эта мера нулю или имеет положительное
значение.
Аннотация. Предполагается, что фрактальная размерность Хау-
сдорфа -Безиковича границы множества М комплексного отображения
равна 2.
В этой статье предпринята попытка описания структуры «дьяволь-
ского полимера», связывающей молекулы множества М. Это может быть
разветвленный полимер (дерево), как в случае отображения z —» Az(l -
- z), когда дополнение связно, или сеть, дополнение к которой пред-
ставлено совокупностью открытых множеств, а еще сеть, структура
дополнения которой еще не до конца изучена, как в случае отобра-
жения z -> X(z + 1/z). В данной статье рассматривается отображе-
ние z -» Az(l - z), но гипотеза, описываемая в процессе его изучения,
несомненно может применяться для самых разнообразных случаев.
Гипотеза. Граница множества М представляет собой кривую
с фрактальной размерностью, равной 2.
История вопроса. Рисунок 1 (негатив рис. 164 из работы М
№2{FGN}) был получен в результате рекурсивного создания (белых)
ветвей. Отношение длин ветки до и после каждой ее точки медлен-
но увеличивается до >/2/2 по мере приближения к кончикам ветвей,
а отношение ширины к длине снижается до нуля. На левой половине
рисунка этот коэффициент, выражающий отношение ширины к длины,
уменьшается даже быстрее, чем на правой. При увеличении общая фор-
ма изображения не меняется, но относительная толщина аналогично
расположенных ветвей снижается до нуля. Это, как и предполагалось,
означает, что оба рисунка не являются самоподобными. И вот почему:
И 7
С8. Рл JMEF’HOC.r Ь 1РАНИНЫ МНОЖЬ'ЛИА Л/ РАНИЛ 2
Рис. С8-1. Построение двух кривых с фрактальной размерностью D -2, из
работы M1982F{FGN}, рис. 164
фрактальная размерность сторон и кончиков ветвей равна 2. (Значение
при котором отношение ширина/длина уменьшается до нуля, не влияет
на значение D).
Доказательство. На рисунках 2 и 3 изображена локальная струк-
тура границы множества М при «увеличении» окрестности типичной
точки границы континентальной молекулы. В частности, если через л
обозначить «золотое отношение» а = (\/5 - 1 )/2, то на рисунках 2
и 3 будет в увеличенном виде представлен небольшой элемент мно-
жества М вблизи точки А = ехр(2тп7т) и еще меньший подэлемент
Центр каждого элемента приблизительно совпадает со значением па-
раметра вида Хт = ехр(2тг/гтш), где ат — отношение т-го и ir> -
+ 1)-го чисел Фибоначчи. Эти ат представляют собой последовательные
приближения к золотому отношению <т. Кроме того, в размер каждого
элемента входит радикал, укоренившийся в точке \„(, и звездообраз-
ная структура из лучей и островных молекул за пределами его оконеч-
ности.
Поразительное общее сходство рисунков 2 и 3 с рисунком 1 сл\ •к-^
явным доказательством вышеизложенной гипотезы.
\ V .
х к I х . i •! 11 Hill x МИЧИ Kill UK и мы, 1985
Рис C8-2. Элемент множества М отображения z —» Az(l — z) в пространстве
параметров при величине — log А/2тгг, принадлежащей окрестности золотого от-
ношения । Vo - 1 )/2. В правом верхнем углу просматривается диск |А| < 1
Обсуждение. Что обуславливает поведение, представленное на ри-
сунках 2 и 3? Для того чтобы это выяснить, сравним звездообразные
структуры лучей и островных молекул, расположенные за пределами
хода земного радикала в множестве М. Порядки разветвления этих
структур суть порядки бифуркации последовательности, ведущей к рас-
сматриваемому кончику. Если радикал большой, произведение порядков
бифуркации, как показано в работе III, будет маленьким; следователь-
но. и самый большой из них также будет маленьким. Поэтому звез-
дообразные структуры больших радикалов напоминают редкие «дере-
вья» Например, кончик, соответствующий бесконечности бифуркаций
второго порядка, увенчан копьем без ветвей. Точно также, в работе М
1982Fx{/?GN} на стр. 189 изображен кончик, соответствующий одной
бифуркации третьего порядка и бесконечному множеству бифуркаций
второго порядка, с небольшим ветвлением. Однако на той же стр. 189
С8. Размерность н’днииы множества М равна 2
И9
Рис. С8-3. Увеличенный элемент рисунка 2 в пространстве параметров, в об-
ласти верхнего правого угла. И вновь справа вверху виден диск tA| < 1. Этот
рисунок очень похож на рисунок 2, но с более узкими белыми полосками. Этот
признак указывает на D = 2
в М 1982{/7G7V} показано, что одна бифуркация сотого порядка с после-
дующей бесконечностью бифуркаций второго порядка дает гораздо бо-
лее плотную структуру. По мере уменьшения размера радикалов быстро
возрастает вероятность возникновения бифуркаций очень высокого по-
рядка, в результате чего их звездообразные структуры превращаются во
все более густые «кусты».
Очевидно, что локальная форма границы множества М определя-
ется бесконечным множеством бесконечно маленьких и «кустистых»
структур. Они теснят друг друга, в результате чего возникает выше-
упомянутая гипотеза.
Комментарий. Рисунок 1 был получен за 7 лет до рисунков 2-3.
На последних маленькие веточки изображены полностью, тогда как на
150 Хаос, фракталы и динамические системы, 1985
рисунке I они появляются только при разделении несколько более кп
ных ветвей. Рисунок 1 представляет собой разновидность Фрактальной
модели легкого. Более подходящим фоном для этой аналогии могла бы
послужить фрактальная модель кровеносной системы!
Благодарность. Рисунок 1 подготовил Зигмунд В. Хандельман.
Рисунки 2 и 3 получил Джеймс А. Гивен, используя программы, на-
писанные В. Аланом Нортоном.
Хаос, фракталы и динамические системы
Под редакцией У. Смита и П. Фишера, 1985
С9
Множества Жюлиа, содержащие гладкие
компоненты
Множество Жюлиа F* отображения z —» /(z) = z1 — ц может
быть границей атома, молекулы или «дьявольского полимера» в плос-
кости z. Обозначим границу одного из атомов множества F* через Н.
Когда g / 0 является ядром атома-кардиоиды множества М, фракталь-
ная размерность D границы Н предполагается равной 1. Таким образом,
Н может быть как спрямляемой кривой (точно определенной длины),
так и только пограничной фрактальной кривой (с логарифмически рас-
ходящейся длиной). В этой статье рассматривается более четкая версия
рисунка 5 из М19831{С5) и дается более подробный анализ замечания,
в неявном виде сделанного в том труде.
Отображение z —► /(z) =z2 - ди его множества Жюлиа F
В случае квадратичного отображения множество Жюлиа F явля-
ется границей множества F точек, которые не повторяются до беско-
нечности при /. При ц = 0 множество F является единичным кругом,
а при fj, = 2 — интервалом. При всех остальных значениях р множе-
ство F является негладким множеством.
Особый интерес представляют такие д, при которых множество F
содержит внутренние точки, а именно: точки, располагающиеся внут-
ри множества М, плюс связи между атомами множества М. Структура
множества F зависит от /х, и мы рассмотрим некоторые возможные ва-
рианты.
Когда р. находится в большом атоме континентальной молекулы
множества М, множество F является атомом, то есть множество F
представляет собой жорданову кривую (простую петлю).
Когда /х расположена в континентальной молекуле множества М,
но не в ее большом атоме, F представляет собой молекулу, объединение
(неисчислимо бесконечного) количества связанных атомов.
152 Хаос, ФРАКТАЛЫ И дпплгн. ----------* wu
Когда // находится в островной молекуле множества Л/, множе-
ство F обладает структурой «дьявольского полимера».
Во втором и третьем случаях, описанных выше, дополнение к мно-
жеству F включает неисчислимо бесконечное количество максимально
открытых компонентов, в которые не входит бесконечно удаленная точ-
ка. Назовем границу одного из этих компонентов Н. Тогда другие ком-
поненты будут прообразами Н при f(z). Поскольку множество и его
прообразы являются гладкими образами друг друга, они имеют оди-
наковую «частную» фрактальную размерность D, которая равна, самое
большее, размерности границы F. Когда фрактальное множество пред-
ставляет собой объединение кривых, по отдельности более гладких, чем
в совокупности, тогда (М 1982F, стр. 119) обшая фрактальная размер-
ность характеризует не иррегулярность целого, а его фрагментацию.
В работе Fatou 1919 было показано, что в общем случае подмноже-
ство множества F не может быть изолированной аналитической дугой.
Если же условия расширить, то множество F может включать неизоли-
рованные аналитические дуги.
Знаменитый пример
При вещественном значении р, и хаотическом отображении /(z)
множество F содержит вещественный интервал и его прообразы, пред-
ставляющие собой гладкие алгебраические кривые. В этом случае «раз-
ветвленный полимер» F обладает особенно простой структурой. В самом
деле, вещественный интервал [-zz, z'], где z = 1/2 +1/2(1 + 4/z)1/2, вхо-
дит в множество F и даже, можно сказать, образует его «основание»
в том смысле, что граница Н и совокупность ее прообразов напоминают
«бусины», нанизанные на интервал [-z', z']. Прообразы [—z', zz] также
являются гладкими кривыми в составе множества F и формируют его
«ребра», на которые подобно «бусинам» нанизаны другие прообразы Н.
В начальной точке О и в каждом ее прообразе бесчисленные ребра пе-
ресекаются, а вблизи начальной точки эти ребра являются практически
прямыми и расходятся от нее лучами.
Выводы о множествах Жюлиа, когда ц является ядром большого
атома-кардиоиды множества М и ц / О
В этом случае границу Н можно определить как границу области
непосредственного притяжения z = 0. Начальной точкой можно счи-
Рис. С9-1. Множество Жюлиа, состоящее из практически круглых молекул с од-
ним атомом. Отображение имеет вид z —» z2 — g, где д — ядро самого большого
атома самого большого острова за пределами радикала, соответствующего би-
фуркации пятого порядка. Порядок данного цикла равен 6.
тать ядро множества Н, а ядрами прообразов Н будут соответствую-
щие прообразы О. При у, = 0 множество Н идентично множеству F
и является кругом. При д / 0 можно сделать вывод о том, что форма
множества Н очень близка к диску, поэтому F является объединением
множеств практически круглой формы. Они выглядят настолько гладки-
ми, что может показаться, будто у них есть касательные, в силу чего их
154 Хаос, фракталы и динамические системы, 1985______________________
южно спрямить. Уже упоминался тот факт, что, соединяясь, они образу-
ют «разветвленный дьявольский полимер», пример которого представлен
на рисунке 1.
Благодарность. Рисунок 1, представляющий собой усовершен-
твованную версию рисунка 5 из М19831{С5}, был создан Джеймсом
I Гивеном с помощью программ, написанных В. Аланом Нортоном.
Хаос, фракталы и динамические системы
Под редакцией У. Смита и П. Фишера, 1985
сю
Последовательности множеств Жюлиа,
заполняющие плоскую область,
и интуитивное обоснование
возникновения дисков Зигеля
Предисловие к главе (2003). В данной статье не делается абсо-
лютно никаких попыток доказать тот факт, что диски Зигеля относятся
к квадратичной динамике. Мы лишь ставим перед собой цель сделать
их появление «естественным» и даже «очевидным».
Аннотация. Внутри множества М отображения z —» Axz(l-
- z) рассмотрим последовательность точек Хт, где предельной точкой
является А. Обозначим соответствующие множества F* через Т * (Ат)
и F*(A). В общем случае lim77*(Am) = 77*(limAm), но существует од-
но очень важное исключение. В некоторых случаях множества F * (Ат)
сходятся не ко кривой или к пыли, а к области A-плоскости, часть кото-
рой называется диском Зигеля J, тогда как остальная ее часть состоит
из прообразов J. В таких случаях множество Т7 * (lim Am) является не
множеством Т7 * Ат, а только его границей. Интуитивное обоснование
такого поведения изучается и иллюстрируется на примере так называ-
емых кривых Пеано, а в отношении нерациональной и незигелевой А
ставится математический вопрос.
1. Введение
Особые случаи математических теорий (которые во всех осталь-
ных отношениях можно считать интуитивными) зачастую демонстриру-
ют поведение, на первый взгляд «резко отклоняющееся от нормального»
и требующее очень сложного, с технической точки зрения, подхода. Так,
физикам трудно поверить, что функции F, для которых limF(A'n) пол-
ностью отличается от F(limA’n), могут иметь вполне определенное зна-
чение. Именно таким особым случаем теории итераций рациональных
156
Хаос, фракталы и динамические системы. 1985
функций (и других аналитических функций) служат диски, существо-
вание которых доказано в работе Siegel 1942. Доказательство и рисун-
ки. представленные в данной работе, относят «диски Зигеля» к кривым
Пеано, значит вполне правомерно заключить, что поведение диска Зиге-
ля в действительности полностью объяснимо. Можно даже сказать, что
такого поведения «следовало ожидать по физическим причинам».
Мы рассматриваем динамику некоторых крайне нелинейных отоб-
ражений : —» f(i) комплексной плоскости на саму себя и в начальной
точке отделяем линейные члены от нелинейных, записывая отображение
в виде z —<• Xz + g(z), где g(z) удовлетворяет условию д(0) = д'(0) = 0.
Во избежание ненужных затруднений мы остановимся на квадратичном
отображении g(z) = —Xz2.
2. История вопроса: кривые Пеано
Ключ к доказательству следует искать в концепции «заполняю-
щей плоскость кривой» Пеано, которую фрактальная геометрия приро-
ды нашла средн чудовищных множеств, продемонстрировав ее огромное
и совершенно определенное значение. «Заполняющая плоскость кривая»
на самом деле представляет собой последовательность обычных кри-
вых, Сп. имеющих неожиданный предел. Для данного примера нам по-
дойдет достаточно простой вариант: предположим, что кривые tn явля-
ются петлями без кратных точек (жордановы кривые). Критерий пове-
дения Пеано заключается в существовании такой плоской области V,
что каждая точка Р области Р может быть записана в виде Р =
= linin^oc Рп, где Рп принадлежит tn- Таким образом, предел кривой tn
является совсем не кривой, а целой областью Р. Тем не менее, что-
бы получить в пределе кривую, можно предположить, что пределом 1п
является граница области Р, которая представляет собой кривую, обо-
значаемую I. В классических примерах Пеано, Гильберта и Серп и некого
L является квадратом. Но в некоторых построениях, выполненных недав-
но, Р является очень нерегулярной фрактальной кривой. Так, в работе
М 1982F{FGAr} на страницах 68-69 представлен мой собственный при-
мер, в котором границей t кривой Пеано является кривая «снежинки
Коха».
В данной статье говорится о том, что для ряда последовательностей
множеств Жюлиа характерно именно такое «пеаново» поведение. При
этом совершенно неважно, что tn — жордановы кривые. Нам еще пред-
стоит столкнуться с последовательностями кривых Пеано, обладающих
бесконечным множеством кратных точек.
СЮ. Круги Зигеля
157
3. Диски Зигеля
Говорят, что отображение —► f(z) имеет диски Зигеля, когда су-
ществует ограниченная область плоскости (открытая и связная), внутри
которой отображение z —> Xz 4- p(z), в сущности, сводится к его ли-
нейному члену, то есть отображение эквивалентно повороту угла в. Это
означает, что подходящая деформация z (голоморфной функции, полу-
ченной в результате решения уравнения Шредера) порождает некоторую
величину о;, при выражении через которую рассматриваемое отображе-
ние принимает вид (си—а>о) —► (lu—сио)е*2тгг0. Круги с центром в точке
преобразуются во вложенные жордановы кривые, объединение которых
покрывает внутреннюю часть диска Зигеля.
Когда диск Зигеля существует, А имеет вид А = ехр(2тп0), где 0 —
«число Зигеля», т. е. иррациональное число, удовлетворяющее опреде-
ленным условиям, довольно сложным, но достаточно мягким для того,
чтобы эти числа обладали единичной мерой на интервале [0. 1]. При-
близительно эта мысль выражается так: зигелево число в невозможно
точно приблизить с помощью последовательности рациональных чисел.
Поскольку угол поворота z —► Xz иррационален, все итерации являются
эргодическими.
Как можно назвать динамику, соответствующую /(z), когда в явля-
ется числом Зигеля? Выбирайте, что вам ближе: высокоорганизованная
или высокодезорганизованная.
Ключевым шагом к пониманию этого поведения, на мой взгляд, яв-
ляется изучение отображения Зигеля f = Xz — Xz2 как предела соответ-
ствующей последовательности квадратичных отображений mf. Итера-
ция ставит в соответствие каждому отображению ш/ некоторое множе-
ство Жюлиа границу области, которая в процессе итерации не ухо-
дит в бесконечность. Множество Жюлиа предельного отображения /,
в общем случае, представляет собой предел множеств Жюлиа отображе-
ний т/. Но когда предел f является отображением Зигеля, множество
Жюлиа предельного отображения f полностью отличается от предела
множества Жюлиа аппроксимирующих отображений mf. Вообще, мно-
жество Жюлиа данного предела является кривой. Но предел множеств
Жюлиа — не кривая, а ограниченная область 7) комплексной плоскости.
Эта область Р включает некоторую компоненту диска Зигеля и пред-
ставляет собой объединение диска Зигеля с его прообразами при /.
Множество Жюлиа, Т7*, предела f отображения mf является границей
области 7?.
\ : \ iii " л;. \ ‘.mi'ij < мн < Hi I f мы, 1 985
Рис CIO-1 Множества Жюлиа отображения z Az(l - z) в пространстве
переменной z. нарисованные при четырех значениях параметра А. Чтобы про
демонстрировать характер сходимости к диску Зигеля, за log Алгг/2тгг приняты
равиональные числа 2/3, 8/13, 34/55 и 144/233. Они принадлежат последова-
тельности Фибоначчи, которая сходится к золотому отношению >/5 — 1)/2. КаК
известно, количество «лепестков» в этих «цветах» является знаменателем вь1'
ражения log АГ1Ч/2тгг. К сожалению, на данном рисунке эти лепестки видны не
очень четко Метол выделения лепестков представлен на следующих рисунках
СЮ. Круги Зигеля
159
Рис. С1О-2. Чтобы разделить лепестки в пространстве переменной z. ко-
рень Ат = ехр[2тгг(55/89)], показатель которого принадлежит последователь-
ности Фибоначчи, заменили ядром радикала с корнем в точке Ат. На этом
рисунке изображен общий вид соответствующего множества Жюлиа. Белые,
черные и серые зоны представляют, соответственно, значения го, сходящиеся
к бесконечности, к циклу или не сходящиеся до момента остановки вычислений.
Каждый лепесток простирается до неустойчивой неподвижной точки в середине
серой зоны
4. Приближение золотого параметра Л = ехр(2тгг<т)
с помощью последовательности «связей» или значений Л,
при которых бифуркация конечна
В работе Siegel 1942 говорится о том, что в число членов Зиге-
ля входит золотое отношение а, которое лучше всего определить как
непрерывную дробь, составленную исключительно из единиц, а имен-
но: о — 1/(1 + 1/(1 + 1/(1 + 1/...))). Очевидно, что о удовлетворяет
уравнению <т2 +<7-1, корень которого (меньше 1) равен 1/2(—l + v'5) =
= 0,6180339.
Чтобы интуитивно прочувствовать действие отображения z —►
-»e2’ri<7z(l- z), это действие было получено в виде предела действий двух
аппроксимирующих последовательностей отображений z—»Amz(l - д).
160
\VV. ФРАКТАЛЫ II ДИНАМИЧЕСКИЕ СИСТЕМЫ, 1985
Рис. С10-3. Рисунки 3 и 4 представляют собой детальное изображение окрест-
ности начальной точки рисунка 2 и аналогичной фигуры для следующего от-
ношения из ряда Фибоначчи logA/27n = 89/144. При переходе от рисунка 3
к рисунку 4 достигается приближение к золотому отношению, лепестки утонча-
ются, а их контур сходится к внутренней части плоской области
При первом исследовании Ат удовлетворяло равенству |Ат| = Ь
но вместо отображения z —► е27ГЙттг(1 - z) была использована аппрок-
симация z —> e27rH7z(l - z), где ат — рациональное число, разложе-
ние непрерывной дроби которого состоит из т повторений 1. Это ^“е
число Фибоначчи. Согласно общей теории М-множества М\ отобра-
жения z — Az(l - z), каждое параметрическое значение Am = e2^ffT71
является точкой бифуркации: точкой соприкосновения атома |Д| < *
СЮ. Круги Зигеля
161
с меньшим атомом, причем порядок бифуркации n(m) равен знаменате-
лю &т.
На рисунках 1.1-1.4 изображена одна половина внутренней части
аппроксимирующих множеств Жюлиа для избранных значений тп. (Вто-
рая половина полностью ей симметрична). Очень скоро начинают появ-
ляться многочисленные фигуры, имеющие форму цветка, причем число
их лепестков принадлежит последовательности Фибоначчи. В то же вре-
мя множество Жюлиа в некоторых других точках начинает сужаться.
5. Приближение золотого параметра А = ехр(2тгг<т)
с помощью последовательности сверхустойчивых А
Проблема предыдущей аппроксимирующей последовательности со-
стоит в том, что визуально лепестки неотделимы друг от друга; что-
бы их разделить, нужно применить альтернативную аппроксимирующую
последовательность. Она приближает отображение z —► e^az(i-z) сооб-
ражением Z ► * z(l — z), где Am* обозначает «ядро» атома перио-
да п(тп) с корнем в точке ехр(2тгг<т). Эта Ат* является сверхустойчивым
значением, т.е. п(т)-я итерация отображения mf удовлетворяет усло-
вию »n/n(m)(0) = тД(то)(0) = 0. На рисунках 2-4 изображены те же
самые лепестки: прижатые друг к другу в предыдущем случае, здесь
они разделились.
6. Математический вопрос
Иррациональные числа 0 делятся на два класса: числа Зигеля, со-
ставляющие подавляющее большинство, и все остальные числа. Пред-
положим, что 0т сходится к незигелеву числу и попробуем предста-
вить поведение множеств Жюлиа 5т* в этом случае. Для простоты
сконцентрируем внимание на множестве Qm, которое определяется как
пересечение множества Fm* с подходящим кругом. В случае числа Зи-
геля факт сходимости множества Fm* к заполняющей область кривой
означает, что множество Qm сходится к целому кругу. Когда множе-
ство Лп* не является заполняющей область последовательностью (так
как 0 сходится к рациональному числу), qTn сходится к канторовой пы-
ли, имеющей нулевую меру.
Вышеперечисленные наблюдения приводят к следующему вопросу:
каким будет поведение Qm, когда число 0 не является ни рациональ-
ным числом, ни числом Зигеля? Будет ли оно сходиться к канторовой
пыли с размерностью 1 или даже с положительной линейной мерой?
1ОС XАОС. ФРАКТАЛЫ И ДИНАМИЧЕСКИЕ СИСТЕМЫ. 1985
Рис. С10-4. См. комментарий к рисунку 3
В последнем случае множество Т* обладало бы положительной плоском
мерой.
7. Диски Зигеля как предел фрактальных пылевидных множеств
В разделе 4 (соотв. 5) значение Л на границе множества М отобра-
жения /(z) приближается значениями Хт, лежащими на границе множе-
ства М (соотв., внутри него). А теперь выберем приблизительные зна-
чения за пределами множества М. Соответствующие множества Жюлиа
являются пылевидными. Когда аппроксимирующие функции сходятся
СЮ. Круги Зигеля
163
к рациональному значению Л = схр(2тггт/п), эти пылевидные множе-
ства сливаются в кривые. Тем не менее, в результате схождения Ат
к числу Зигеля Л получается пыль, сливающаяся в область.
8. История
Впервые «диски Зигеля» были описаны в работе Julia 1918 (см. Julia
1968 I, с. 311-317). Затем Жюлиа обещал предоставить доказательство
того, что они не могут существовать (Julia 1968, с. 321); позже он при-
знал, что его доказательства ошибочны и, в конце концов, прекратил
изучение этого вопроса (Julia 1968 I, начиная со стр. 21 внизу). В рабо-
те Siegel 1942 существование этих дисков было доказано для некоторого
множества иррациональных значений в с мерой, равной 1. С тех пор это
множество было расширено.
Благодарность. Я благодарен Грегори и Давиду Чудновски за
интересные комментарии о дисках Зигеля, а также В. Алану Нортону
и Джеймсу А. Гивену за множество полезных дискуссий и за написание
компьютерных программ для создания иллюстраций к этой статье.
Physica Scnpta, T9, 1985
Cll
Непрерывная интерполяция квадратичного
отображения и покрытие внутренних
областей множеств Жюлиа
Предисловие к главе (2003). Учитывая ту мгновенную и потряса-
ющую популярность, которую завоевала итерация квадратичного отоб-
ражения, не перестает удивлять почти полное отсутствие интереса к до-
полнительной теме этой статьи. Значительное влияние на такое поло-
жение дел оказало «малое количество работ на эту тему» в сборнике
научных трудов, появившемся в неподходящем для этого журнале. Бы-
ло бы неплохо переиздать этот труд с дополнениями и великолепными
цветными иллюстрациями.
Как бы там ни было, поднял ли кто-либо эту идею вновь и развивал
ли ее независимо? Этот вопрос, как и многие другие, касающиеся итера-
ции, должен изучать нейтральный наблюдатель с помощью тщательного
социологического анализа.
Первоначально заголовок звучал так: «Непрерывная интерполяция
комплексного дискретного отображения z —•• Az(l — z) и родственные во-
просы. О динамике итерированных отображений, IX». Получено 5 сен-
тября 1984 года, принято 9 сентября 1984 года.
Аннотация. В этой работе представлено несколько выводов по ди-
намике непрерывной интерполяции (прямой и обратной) квадратичного
отображения комплексной плоскости. Как известно, в сложном предель-
ном случае |А| = 1 динамика демонстрирует сложные структуры, кото-
рые зависят от того, является ли argA/2?r рациональным числом или
числом Зигеля. В данной работе устанавливается, что эти структуры
(являющиеся копией для |А| < 1) представляют собой покрытие внут-
ренних областей множества 1, регулирующее интерполяцию Шредера
прогрессивной динамики, ее внутреннюю инверсную функцию и пери-
одические или хаотические предельные свойства внутренней инверсной
функции
С. 11 Непрерывная интерполяция квадратичного отображения 165
Потрясающая особенность упорядоченности хаоса заключается
в том, что многими его геометрическими аспектами управляют фракталы
а многие его физические аспекты подчиняются фрактальной геометрии.
Введение
В геометрии динамики итерированных отображений важную роль
играют два фрактальных множества: множество Т (Julia 1928, Fatou
1919) в плоскости z и граница множества М в пространстве параметров.
Множество Т отображения представляет собой замыкание неустойчи-
вых неподвижных точек и постоянных циклов, тогда как М — это мно-
жество значений параметров, для которых 1 является связным множе-
ством. В работе Blanchard 1984 для упрощения утверждений и призна-
ния труда Фату дополнение множества Z было названо «множеством 5*».
В нашей работе максимальные открытые компоненты множества 7 бу-
дут называться «компонентами Т7».
В данной статье речь идет о неистощимом квадратичном отобра-
жении, записанном в виде z —► /(г) = Az — Az2 или z —* f * (z) =
= z2 - д. Компоненты T7 определяются для значений параметров в под-
множестве множества М, а именно: в множестве MQ таких значений
параметров, при которых отображение /(z) имеет конечный предельный
цикл (и обычную предельную точку в бесконечности). Преимущество
вида /(z) заключается в том, что диск |А| < 1 принадлежит А/0 и что
для |А| < 1 предельной точкой является z = 0, а множителем в предель-
ной точке — сама А.
В статье также рассказывается о новых структурах, которые появ-
ляются при |А| < 1 и управляются аргументом в = arg А. Не секрет, что
при |А| = 1 арифметические свойства 0/2/z определяют такие структуры,
как бифуркация-«лепесток» (Blanchard 1984, с. 101) и диски Зигеля.
В данной главе говорится о том, что обобщения к вышеупомянутым
структурам присутствуют уже при |А| < 1.
Эти структуры наблюдались благодаря интуиции, обретенной в рам-
ках фрактальной геометрии при демонстрации (явно, самой первой) по-
ведения решений уравнения Шредера и выведения покрытия внутренних
областей компонентов 7.
Главным выводом является «универсальность»: топологическая
структура покрытия внутренних областей зависит исключительно от 6,
а не от |А|. Такое заключение можно сделать непосредственно из вида
структуры бифуркации/лепестка или диска Зигеля, который соответ-
ствует тому же самому значению 0 в предельном случае |А| = 1.
166
Physica Scripta, T9, 1985
Вследствие всего вышесказанного, фрактальная размерность мно-
жества I плавно изменяется по мере того, как |А| —» 1, причем О остается
неизменной. Именно этим обстоятельством может объясняться создание
некоторых теорем, над которыми, как я слышал, работал Н.Сибони.
Эти и другие подобные наблюдения касаются темы, которая дол-
гое время не вызывала особого интереса и присутствует в заголовке по
причине своей привлекательности. Итерации zq, z\ = /(го), .... =
= /(гд- - 1) = Л-(го). образующие последовательность с целочисленным
индексом к. могут быть приведены к последовательности z( = /((zq)
(где t является вещественным) путем решения «уравнения Шредера».
Более того, когда zo принадлежит фундаментальному покрытию внут-
ренних областей, непрерывное время может быть инвертировано, так
что zt = будет определяться для положительных и отрицатель-
ных вещественных чисел. Движение вперед при |Л| < 1 не отличается
сложностью по причине существования устойчивой точки аттрактора, но
арифметические свойства 0/2тг важны для динамики движения назад.
Нельзя исключать вероятность того, что некоторые высказанные
здесь наблюдения известны, хоть и не в явном виде.
2. Функция Шрёдера
Общие значения А € М° будут рассматриваться в разделе 8;
в остальном же тексте для простоты мы предположим, что А / О,
но |А| < 1. В таком случае множество Т представляет собой жорда-
нову кривую, множеством внутренних точек которой являются ограни-
ченная компонента 7 и область притяжения zj = 0. К каждой точке
в этой внутренней области в работе Schroder 1870 приписана функ-
ция cr(z) = limk-,00 A_fc/jt(z), удовлетворяющая функциональному урав-
нению Шредера a[/(z)] = Acr(z).
Для различных значений А на рисунках представлены аппроксими-
рующие отображения функции cr(z) в форме веера из кривых посто-
янного аргумента, а также в некоторых случаях из кривых постоян-
ного модуля. Чтобы их построить, нужно нарезать кусочки «пирога»,
расходящиеся веером от з/, раскрашенные в черный и белый цвета
попеременно и разделенные равноудаленными полупрямыми. Затем на-
рисуем вокруг zj =0 кольцо, внешним радиусом которого служит неко-
торое малое р* > 0. Когда /k(zo) впервые окажется в пределах дис-
ка |Д(зо)| < Р*> проверим, попадает ли A_fc/fc(zo) на черную или на
белую точку и окрасим zo соответственно. Это приводит к появлению
черных полос, границы которых приближают изолинии аргумента 0(z).
С.11 Непрерывная интерполяция квадратичного отображения 167
Рис. СП-1. Покрытие внутренних областей при вещественных А на интерва-
ле ]0,1[
Чтобы разрезать эти черные полосы белыми кусочками кривых, которые
очерчивают приблизительные изолинии |а(д)|, не будем окрашивать до-
вели первая А(до) модуля > р* имеет модуль > р*(1-е) при достаточно
малой е > 0. При р* —> 0 аппроксимация улучшается, и мнимый паттерн
вблизи z — 0 исчезает.
3. Покрытие внутренних областей
Как ясно видно из рисунков, функция Шредера определяет покры-
тие внутренней области ограниченной компоненты F. Границы элемен-
тов покрытия представляют собой гладкие кривые, за исключением счет-
ного числа изгибов на 90 градусов. Элемент покрытия, содержащий г/,
назовем основным, тогда как все прочие элементы будут его прообразами.
Нельзя не отметить сходство с гиперболическим покрытием, ко-
торое разработали Анри Пуанкаре и Феликс Клейн для клейновых
групп отображений комплексной плоскости фрактального линейного ви-
да z -+ (az + Ь)/(cz + d).
4. Интерполяция Шредера z2 — р к непрерывному времени
в фундаментальном покрытии
При выражении через функцию Шредера <т(г) интерполяция /(д')
в фундаментальном покрытии просто приравнивается к использованию
168
Physica Scripta, T9, 1985
Рис. Cl 1-2. Покрытие внутренних областей при некоторой Л вблизи интерва-
ла ;0.1[. Небольшое изменение А (по сравнению с рисунком 1) значительно
изменяет покрытие
логарифмической спирали для интерполяции последовательности точек,
которые, как известно, располагаются вдоль этой спирали. В отноше-
нии а эта внутренняя интерполяция является непрерывной и обратимой,
как в прямом направлении, между zo и передним аттрактором Zf = О,
так и в обратном направлении, между zq и обратным аттрактором В,
который представляет собой подмножество множества Т, рассматривае-
мого в разделе 6. Тем не менее, при выражении через z интерполяция
не является непрерывной, за исключением случаев вещественного и по-
ложительного значения А. И наоборот, эта интерполяция будет непре-
рывной в диске вблизи zf = 0, где листья фундаментальной области
присоединены друг к другу.
(Помимо «фундаментальной» интерполяции можно выделить еще
♦гармоническую» и «субгармоническую» интерполяции. Если известен
интеграл h, гармоническая интерполяция представляет собой отображе-
ние кривой a(zf) = (A1/h)ta(zo), а субгармоническая интерполяция -
это отображение кривой o{zj) = (Х,1)1<т(го). Гармоника включает все
точки o(zf) = Xka(zo), а субгармоника — нет).
(Интерполяция в терминах «функции Пуанкаре» впервые была
представлена в работе S. Lattes в 1917 году; две вышеобозначенные ин-
терполяции сравниваются в работе Dubuc 1982.)
С.11 Непрерывная интерполяция квалратичного огоьраж?ния 1G9
Рис. С11-3. Покрытие внутренних областей при вещественных знамени-
ях Л €) - 1, 0[
5. Зависимость покрытия внутренних областей от X
Топология покрытия внутренних областей зависит только от 0 =
= arg А, а не от | А| и представляет собой остро разрывную функцию 0
(рисунки 1 и 2). Это замечание важно, поскольку множество I, которое
окружает покрытие, непрерывным образом изменяется вместе с |А| и 6*.
пока А е MQ.
Получаются интересные следствия в отношении внутренней интер-
поляции /(z) как функции времени и функции А. Движение вперед от
данной г() имеет разрывы в точках 0 и |А|. Движение назад непрерыв-
но в |А|. Его зависимость от 0 становится разрывной после достаточно
долгого времени, но для короткого промежутка времени она может быть
непрерывной.
6. Обратный аттрактор В, пересечение множества I с границей
фундаментального покрытия и листья фундаментального
покрытия
Ясно, что множество В инвариантно, но неустойчиво при дей-
ствии /(z). Оно будет называться фундаментальным инвариантным мно-
жеством I.
1'0
Physica Scripta. T9. 1985
Рис. Cl 1-4. Покрытие внутренних областей при argA/2?r = т/п, где п - 5,
а |А| намного меньше 1
Рациональный случай. Если 0/2тг = т/п, то множество В со-
держит п точек, каждая из которых является инвариантной при дей-
ствии fn(z). У прямого отображения /(z) аттрактором является непо-
движная точка, вследствие чего цикл равен 1. Однако, внутреннее
определение многозначного обратного отображения f(z), находящегося
внутри фундаментального покрытия, имеет предельный цикл размера п,
а именно: В.
Каждой точке В соответствует интервал значений arg[cr(z)] шири-
ной 2тг/п, который сокращается до интервала значений argz вблизи z =
= 0. Каждый интервал определяет «лист» в фундаментальном покры-
тии. Листья присоединены друг к другу в окрестности zj = {0,0}, но
расщепляются при удалении от г/ и в окрестности множества I они
разделены. Каждый лист следует рассматривать как состоящий из двух
полулистьев, разделенных «ребром», которое рассекает лист пополам че-
рез arg[<r(z)].
Известно, что множество Т можно внутренним образом отобра-
зить на круг; следовательно, каждой точке множества Т можно при-
С.11 Непрерывная интерполяция квадратичного отображения 171
>ис. С11-5. Покрытие внутренних областей при том же arg Л, что и на рисунке 4,
при |Л|, приближающейся к 1. Листья расщепляются в общем радиальном
вправлении. {P.S. Вращение минимизировало редукцию}
воить внутренний аргумент ф. Каждая точка множества В имеет ар-
умент ф и интервал аргументов arg[cr(z)]. Действие /(с) заменяет <?
ia 20, a arg[cr(z)] на arg[cr(z)] + arg Л. Несовпадение двух этих операций
объясняет, почему изучение итерации невозможно без фракталов.
Physica Scripta, T9, 1985
Вывод, ^-аргументы точек множества В тождественны 0-аргумен-
там точки '( = 0 в предельном случае, когда Л заменяется парамет-
ром \' = Л/ |А| и происходит бифуркация. Другими словами, 0-аргумен-
ты п точек В зависят только от Л через значение 0.
Рис. СИ-6. Покрытие внутренних областей при argA/17r — золотой середине
(число Зигеля) и |Л| меньше 1
На круге, когда точка аргумента ф остается инвариантной при
отображении 9 —> 2к9, отношение ф1/2тг представлено последовательно-
стью двоичных знаков, которые периодичны с периодом 2к. Существуют
2к/к циклов, причем многие из них могут сводиться друг к другу. Есть
правило для определения особого инвариантного неустойчивого множе-
ства, которое отображается на В.
Нерациональный случай. При нерациональном 0/2п множество $
является множеством Кантора (фрактальной пылью). Для доказатель'
ства существования этой инвариантной пыли Кантора достаточно вЫ'
С. 11 Непрерывная интерполяция квадратичного отображения 173
Рис. С11-7. Покрытие внутренних областей при том же arg Л, что и на рисунке 6,
и при |Л|, приближающейся к 1. Листья не расщепляются, а скорее стремятся
слиться в диск Зигеля. {P.S. 2003: Вращение минимизировало редукцию}
брать в круге точку, для которой 0/2тг представляет собой бесконеч-
ную последовательность таких двоичных чисел, что за нулем никогда
не следует нуль. Очевидно, что этим свойством обладают также и точки
вида 20, a D удовлетворяет условию 2° = 1,618.
Когда множество В является канторовой пылью, каждый полулист
связан с тремой В (открытым интервалом в дополнении к I). Тем не
менее, листья фундаментального элемента покрытия больше не распада-
174
Physica Scripta, T9, 1985
ются на два полулиста. Напротив, один полулист вырождается, а ребро
идет вдоль стороны листа, которая не направлена к средней точке тремы.
7. Выводы относительно предела |А| —► 1 при радиальном
приближении
Жюлиа и Зигель показали, что в пределе |А| = 1 важно, является
ли число 0/2тг (а) рациональным, или (б) иррациональным и числом Зи-
геля, или (в) иррациональным, но не числом Зигеля. В рациональных
случаях 0/2тг = т/п соответствует Л 6 М°. Если это так, то топо-
логия множества Т определяется в основном значением п. Когда |А| =
= 1, а в/2тг является «числом Зигеля», множество Т состоит из границы
«диска Зигеля» и его прообразов при f(z). В настоящей статье пред-
ставлены новые факты, а именно: арифметическая природа 0/2тг важна
уже при |А| = 1 для радиальной связи свойств относительно |А| = 1
и |А| —> 1, т. е. с инвариантной в. Множество Т получает двойные точки,
когда точки множества В движутся либо к Zf = 0, либо вокруг нее.
Когда 0/2тг является рациональным т/п, (рисунки 4 и 5) все точ-
ки п в множестве В сходятся к Z/ = 0. Каждый лист расщепляет-
ся вдоль своего ребра на две половины. Таким образом, каждый эле-
мент покрытия делится на п кусочков, каждый из которых представ-
ляет собой два полулиста и имеет одинаковую ширину при выражении
через arg[<j(z)]. Фундаментальный элемент покрытия отождествляется
с лепестком (Blanchard 1984, с. 101).
Когда 0/2ir является иррациональным числом Зигеля (рисунки 6
и 7), конечные точки каждой тремы в множестве В сходятся по окруж-
ности к одной и той же точке, которая зависит от тремы. В результате
элементы покрытия сохраняют свою идентичность при |А| —► 1. Фунда-
ментальная область все больше отделяется от остальной части внутрен-
ней области множества I. В пределе |А| = 1, она образует диск Зигеля,
ограниченный фрактальной жордановой кривой, подмножеством множе-
ства I.
Не секрет, что случай, когда 0/2тг является иррациональным незиге-
левым числом, представляет определенную сложность. Предполагается,
что в этом случае каждая точка множества В вновь сходится к и/ = О,
а фундаментальная область расщепляется на счетную бесконечность ли-
стьев (= полулистьев) разной ширины при выражении через arg[<r(z)].
Таким образом, условие |А| = 1 на покрытии внутренних областей
и оболочке его множества I достигается по-разному. Покрытие внутрен-
них областей не имеет непрерывной зависимости от в ни при |А| < 1-
C.l I НЕПРЕРЫВНАЯ ИНТЕРПОЛЯЦИЯ КВАДРАТИЧНОГО ОТОБРАЖЕНИЯ 175
ни при |Л| = 1. Зависимость оболочки от 0 непрерывна при |Л| < 1, но
разрывна при |А| = 1.
Поскольку форма множества Т плавно меняется при радикаль-
ном |А| —> 1, фрактальная размерность £>(А) множества I гладко
сходится к некоторому пределу. Но при |А| = 1, форма J прерывисто
меняется вместе с 0. Следовательно, радиальный предел О(А), судя по
всему, является крайне негладкой функцией 0.
8, Случай, когда А 6 Л/°, но |А| > 1 и |А — 2| > 1
Для таких А существует предельный цикл размера N(A), а мно-
жителем служит некоторая функция Л(А), удовлетворяющая усло-
вию |Л| < 1. С каждой А при |Л| / 0 можно связать значение пара-
метра А, которое находится в том же самом атоме М° и удовлетворяет
условиям |А(А')| = 1 и arg[A(A')] = arg[A(A)]. Арифметические свой-
ства arg[A(A')]l/27r определяют структуру покрытия для значения пара-
метра А и предельное поведение внутренней обратной функции fe^z).
9. Сверхустойчивый случай
При А = 0 аргумент 0 не определен, он является сверхустойчи-
вым значением параметра, ядром атома в множестве М. В этом случае
уравнение Шредера заменяется уравнением Бётчера, а каждая компо-
нента Т, в том числе и внешняя область множества Т, является отдель-
ным элементом покрытия. К подробному обсуждению этого вопроса мы
вернемся позже.
Благодарность. Иллюстрации подготовлены Эрико Хиронакой
с помощью компьютерных программ, разработанных ею специально для
этих целей.
Альтернативное изображение нижней части рисунка С4.3 при выражении
<ерез д. Оно составлено из самоквадрируемых фрактальных кривых Жюлиа
иля вещественной д, изменяющейся от —1/4 (внизу) и выше. Источник:
клан Нортон «Обобщение и изображение геометрических фракталов в трех-
керном пространстве». Компьютерная графика: 16(3) (1982) 61-67. Я бла-
годарен доктору Нортону за разрешение воспроизвести это произведение ис-
кусства. а также за создание рисунка С4.3.
Доктор Нортон значительно расширил итерацию квадратичного отображе-
ния от комплексных чисел до кватернионов, что подтверждает упомянутый
выше труд, а также его статья «Множества Жюлиа в кватернионах», Ком-
пьютеры и графика: 13(2) (1989) 267-278. Такими примерами изобилует
книга М I982F.
Часть II
НЕКВАДРАТИЧНАЯ
РАЦИОНАЛЬНАЯ
ДИНАМИКА
Первая публикация
С12
Хаос в неквадратичной динамике:
рациональные функции из формул удвоения
Путь научного исследования, завершающийся научным открытием,
не всегда поддается логике, о чем история неустанно напоминает как
любителям, так и профессионалам. Во многих отношениях комплекс-
ное квадратичное отображение, которое можно свести к z —> z2 + с,
z -♦ A(z2 - 2) или z —> Az(l — z), является простейшим нелинейным
отображением. Именно поэтому первые подробные исследования в ра-
боте Fatou 1906 касались его глобального действия. Позже в 1960-х
и 70-х годах тщательно изучалось ограничение z2 — р до вещественного
квадратичного отображения х2 — р-, тогда же все четко осознали, что
зависимость орбит этого вещественного отображения от параметра р
несет в себе определенные сложности: для нее характерны последова-
тельность бифуркаций Мирберга, дерево Мея и число Фейгенбаума.
Вскоре после этого публикация моих работ, представленных в части I.
привела к популяризации комплексного квадратичного отображения.
Из-за непреодолимого желания провести «интерполяцию» извест-
ных событий многие люди, не являвшиеся их свидетелями, полагают
само собой разумеющимся, что я как начал свои компьютерные иссле-
дования итерации с квадратичного отображения, так и закончил им же.
На самом деле, моя работа выглядела совершенно иначе. И до, и после
судьбоносной зимы 1980 года, описанной в главе С1, я изучал многие
отображения, гораздо более сложные, нежели квадратичное, но опуб-
ликовал лишь одну работу (М1984k{C 13}), краткое изложение которой
уже было представлено в M1982F, на странице 465 второго издания
этой книги от 1983 года. В целом, огромную работу, которая так и не
была опубликована, можно разделить на три части.
Многие мои наблюдения, сделанные после 1980 года, весьма смут-
ны, и уже были тщательно зафиксированы другими людьми. Дабы из-
180
С. 12 Неквадратичная динамика из формул удвоения
бежать любого намека на то, что я хочу отнести эти результаты на свой
счет, я оставляю свои труды в прежнем состоянии: неопубликованными.
Но, вероятно, стоит отметить финальную работу, которая весьма укра-
шает M1982f, но полностью лишена каких бы то ни было объяснений.
Эти «бабочки» появились, когда я пытался применить метод Ньютона
к экспоненциальной функции. Хотя эта задача меня пугала, здравый
смысл подсказывал мне, что я должен двигаться дальше.
Вторая часть моей работы понятна и не упоминается в названии
этой главы. Зимой 1980 года я также изучал отображения z —> Az(l -
- ;*) при многих целых к > 1. Результаты этого труда многократно
воспроизводились не только профессионалами, но и любителями. В ка-
честве дополнения к основной истории, краткий раздел 1 иллюстрирует
вышеизложенные выводы с помощью героически необработанных под-
линных древностей.
Третью же часть стоит запечатлеть на бумаге, по крайней мере, по
следующим причинам: чтобы отдать должное истории и чтобы способ-
ствовать возможному будущему возрождению этой темы и осуществ-
лению вечной мечты педагогов: развитии у студентов, остановивших
свой выбор на теории итераций и освоившихся с квадратичным отоб-
ражением, желания исследовать также прилегающие аспекты. Анализ
неквадратичных отображений весьма способствует пониманию процесса
перехода от порядка к хаосу, а разнообразие оных в буквальном смысле
поражает.
1. Примеры отображений вида z —► Az(l — zk)
Почему бы после z2 - р и/или Az(l — z) не рассмотреть zk - р
и/или Xz(l-zk), где к — целое число больше 2? Рисунки множества М,
которые я сделал для Az(l-zfc), имеют лишь одно достоинство (которое
хорошо просматривается на простом рисунке 1): они были нарисованы
очень давно.
2. Три хаотических отображения, исследованные Латте
и основанные на функциях, для которых формула удвоения
является рациональной функцией
2.1. История вопроса
В самом начале я недооценивал комплексное квадратичное отобра-
жение и считал, что оно слишком «невзрачное» для изучения. Одна-
ко опыт, полученный мной в области экспериментальной математики,
С. 12 Неквадратичная динамика из формул удвоения
181
заставил меня мало-помалу продолжать исследования. Дядя рассказал
мне об одном французе, современнике Фату и Жюлиа, — Самуэле Лат-
те (1873-1918), выделившем несколько отображений, которые сегодня
называют хаотическими. Свои поиски ограничивающего руководящего
принципа я начал с семейств, для которых хаотические примеры Латте
являются особыми случаями. Некоторые результаты, полученные мной
при анализе этих отображений, представлены в настоящей части.
Затем мои приоритеты сдвинулись в сторону написания М 1982F,
так что я не занимался изучением теории итерации всерьез. Тем не
менее, из-за невероятной популярности квадратичного отображения его
исследования продолжались. К тому же, неквадратичные отображения
были кратко упомянуты в широкодоступной работе М 1986р и часто
встречались в моих «выступлениях со слайдами». Казалось очевидным,
что к ним должны проявить интерес не только многие ученые, но и бо-
лее широкая публика. К моему удивлению, этого не случилось. Поэтому
своего рода тестом может служить моя чрезвычайно запоздавшая пер-
вая публикация подмножества выполненных мною рисунков в главе С14.
Надеюсь, что некоторые читатели обратят на них особое внимание, про-
должат работу, которую я бросил практически двадцать пять лет назад,
и перейдут на принципиально новый этап развития этой темы.
Такие предсказания — дело тонкое. Должен признаться, что я ожи-
дал прилив внимания к кватернионным множествам Жюлиа, несколь-
ко примеров которых имеются в труде М 1982F. Однако невнимание
к кватернионным итерациям можно объяснить нежеланием связываться
с неровными поверхностями, которые сложны для передачи, да и сами
кватернионы могут казаться недоступными.
2.1. Латте
Как было известно Фату и Жюлиа, комплексное квадратичное отоб-
ражение z -» z2—/z при // = 2 можно записать в виде (z/2) —► 2(z/2)‘2-l.
При замене переменной г/2 = cos# отображение z —► z2 - 2 преобразу-
ется в отображение удвоения в 20. Не секрет, что это отображение
хаотично на интервале [0, 2тг] величины 0, т. е. на интервале [-2, 2] ве-
личины z.
В работе Lattes 1918 говорится, что два других собрания функций
комплексной переменной обладают одним и тем же свойством: формула
удвоения, порождающая /(2г), является рациональной функцией /(с).
Центр одного из таких собраний находится в точке ctg0; функ-
ции tg0, tg hO и ch0 претерпевают лишь небольшие изменения.
С 12 НГКВАДРАТИЧНАЯ ДИНАМИКА ИЗ ФОРМУЛ УДВОЕНИЯ
Рис. С11-8. Множества Мандельброта для отображений z —» Az(l —zfc), нарисо-
ванные с помощью крайне примитивного графического оборудования в Гарварде
зимой 1980 года. Против часовой стрелки с верхнего левого рисунка: k = 2, 3,
5 и 7
Второе собрание функций включает все эллиптические функции
Вейерштрасса р(с), которые имеют два параметра д2 и дз. Латте изучал
одно множество этих параметров, но я также исследовал и другое.
И снова пример вещественного отображения х2 — р должен был
привести меня непосредственно к А(х2 - 2) и напомнить слова Гастона
Жюлиа, обращенные к студентам Политехнической школы, о том, что
когда в математике возникает трудная ситуация, «зачастую лучший спо-
соб упростить ее — в усложнении». Но наивность и избыточное рвение
сначала увели меня от A(z2 -2). В этой части рассказывается о работе,
на создание которой меня вдохновил труд Латте.
С. 12 Неквадратичная динамика из формул удвоения
183
2.2. Отображение g(z) = (l/2)(z + 1/z)
2.2.1. Мотивация последовать примеру Латте через формулу
удвоения для функции z = ctg0. Элементарное исчисление дает
cos(20) (cos2 0 - sin2 0) i ( 1 \
Ctg 20 = sin(20) ~ 2 cos 0 sin 0 ~ 2 \Ctg ctg 0 ) '
Отсюда, при z = ctg# отображение 0 —► 20 превращается в
Z -> s(z) = j (z + |У
Применим преобразование Мебиуса, определенное с помощью z —
= (u + 1)/(и — 1) или и = (z + l)/(z — 1). В результате, отображе-
ние z —> g(z) превращается в отображение и —» и2. Таким образом, все
начальные точки zq в полуплоскости Rc(z) > 0 повторяются к z =
= 1. Другими словами, все начальные точки uq (то есть принадлежащие
диску |u| > 1) повторяются к и = оо. Все начальные точки в полуплос-
кости Re(z) < 0 (то есть принадлежащие диску |u| < 1) повторяются
к z = —1 (то есть и = 0). В результате, репеллер, а именно: множе-
ство Жюлиа, — является мнимой осью Re(z) = 0, соответствующей
кругу |и| = 1.
Как и все рациональные отображения, отображение z —► g(z) =
= (l/2)(z + 1/z) является хаотическим на своем множестве Жюлиа,
которое представляет собой линию. И наоборот, его упорядоченность на
плоскости практически идеальна. Мы уже показали, что это же заме-
чание справедливо и для отображения z —» z2 - 2, если его выразить
через в.
2.2.2. Первоначальная мотивация отображения p(z), следую-
щая примеру Кэли через решение уравнения z2 — 1 = 0 методом
Ньютона - Рафсона. Исторически сложилось так, что изучение общих
свойств итерации началось, когда Кэли в своей работе от 1879 года для
решения уравнения /(z) = z2 —1 =0 воспользовался методом Ньютона -
Рафсона. Этот метод заключается в многократном повторении отображе-
ния z -> z - /(z)//'(z), в силу которого при z2 — 1 он приводит к ите-
рации рациональной функции g(z) = (z2 - l)/2z = X(z -I- 1/z). Как уже
упоминалось, репеллер представляет собой мнимую ось Re(z) = 0. В ре-
зультате, применение метода Ньютона к решению уравнения г2 - 1 = 0
выливается в очень упорядоченное поведение.
184
С. 12 Неквадратичная динамика из формул удвоения
Еще о решении уравнения z3 + 1 = О методом Ньютона-Раф-
сона. Сэр Артур Кэли пытался повторить успех, достигнутый при ре-
шении уравнения ;2-1 = О, взявшись за уравнение z3 — 1 =0, но потер-
пел неудачу. Его исследования застопорились, когда он раскопал «серые
зоны» значений zo, в отношении которых ему не удалось доказать, что
результат метода Ньютона не имеет сложной зависимости от началь-
ных условий. Желание разобраться в причинах неудачи Кэли подвигло
Гастона Жюлиа на создание его общей теории комплексной итерации
и (по завершении долгого периода полного пренебрежения) привлекло
внимание Джона X. Хаббарда, который плотно занялся исследованиями
в этой области.
2.3. Формула удвоения для эллиптической функции
Вейерштрасса p(z) и получающиеся рациональные отображения
2.3.1. Отображение Wi(z) = (1/4)(1 + z2)2/[z(z2 — 1)] и ис-
ходный хаос Латте на плоскости. Жюлиа неоднократно упоминал,
что именно Латте выделил рациональное отображение
, и _1_ ~2\2
^и/,(2) = f .
4 z(zz - 1)
Как и во всех остальных случаях, это отображение является хао-
тическим на своем множестве Жюлиа. Особенность этого отображения
заключается в том, что его множество Жюлиа представляет собой це-
лую комплексную плоскость.
2.3.2. Эллиптические функции Вейерштрасса p(z) и их фор-
мула удвоения. Латте открыл отображение Wi(z), заметив, что оно
получается из элементарного отображения 0 —» 26 при замене перемен-
ной z = р(0), где р(0) является особым случаем эллиптической функции
Вейерштрасса. По поводу этих функций я ссылался на следующие (воз-
можно, устаревшие) источники: работа Tannery & Molk 1898 и Whit-
taker & Watson 1902-1927. В двух словах, отправной точкой служит
уравнение эллиптической функции:
\dz) = 4у “521/-РЗ-
Третий параметр gi был заранее устранен с помощью добавления
к у подходящей константы для сокращения слагаемого с у2. Решение
z
С
С. 12 Неквадратичная динамика из формул удвоения
185
Рис. С11-9. [Рисунок viii из М 1982F.] В дополнение к главе 13, в черный
цвет окрашена область притяжения одного из двух предельных циклов отоб-
ражения z —► A(z + 1/z) при тщательно подобранной Л. Область притяжения
другого предельного цикла симметрична черной области относительно центра
этого рисунка. Здесь она распадается на разные оттенки серого, причем каждый
соответствует одной точке в этом другом цикле. Черные и нечерные области
напоминают квадратичную итерацию. Они переплетаются замысловатым обра-
зом. Невероятный пример переплетения представлен в главе С13 для другого
неквадратичного отображения
дает z как функцию z(C), а функция Вейерштрасса представляет собой
обратную функцию z(C).
Из всей чрезвычайно обширной теории эллиптических функций нам
понадобится только формула удвоения
р(2и) =
[p2(u) - g2/4]2 + 2g3p(u)
4p3u - ^2р(«) - <7з
186
С. 12 Неквадратичная динамика из формул удвоения
В работе Whittaker & Watson 1927 мне не удалось найти этой фор-
мулы в явном виде, но в труде Tannery & Molk 1898 достаточно было
поместить уравнение эллиптической функции в формулу CIII7 на стра-
нице 93.
Использование параметров д2 = 4 и дз = 0 сильно упрощает фор-
мулу удвоения; видимо, именно поэтому Латте остановил на них свой
выбор, и это привело его к получению Wi(z).
2.3.3. Непостоянное хаотическое отображение. Как следует из
раздела 4, сначала я изучал нехаотические «обобщения» хаотического
отображения Латте. Затем, выбрав следующие очевидные упрощающие
параметры (д2 = 0 и д3 = 4), я исследовал «обобщения» непостоянного
хаотического отображения
г _ W2(z) =
1 z(z3 + 8)
4 z3 — 1
Помимо простоты, отображение Латте и его вариант, соответству-
ющий 52 = 0 или д3 = 0, демонстрируют различные виды симметрии,
которые будут описаны и проиллюстрированы в главе С14.
3. Коэффициент А создает однопараметрические семейства
отображений Xg(z), AWi(z) и АИ^С^), каждое из которых
включает хаотическое отображение как особый случай
Теперь вернемся к моим поискам (до 1980 года) стоящих однопа-
раметрических семейств отображений, пригодных для изучения. Я счел
необходимым ограничить свой поиск семействами, включающими в ка-
честве особого случая некоторую точку хаоса, которая уже хорошо изу-
чена, но может спровоцировать новые исследования.
Поскольку я полагал, что самые богатые структуры могут возник-
нуть только благодаря самым сложным отображениям, и знал об отоб-
ражении, которое анализировал Латте, в 1979 году я начал с изучения
итерации для отображений z —> AWi(z), а затем перешел к z —♦ АИ'г(.г).
В частности, я рассчитывал, что их поведение при А близких к 1 помо-
жет продемонстрировать сущность подхода к плоскостному хаосу. Ри-
сунки, которые я сделал в 1979 году, сейчас открыты заново и впервые
опубликованы в главе С14.
Позже я занялся изучением отображения 5(2, А) = A(z 4- 1/z).
В М 1983к{С13} изложены результаты тех исследований; со страни-
цы 465 (второго издания) и рисунка VIII работы М 1982F речь идет
С. 12 Неквадратичная динамика из формул удвоения
187
именно об этом изображении. Рисунок 2 в этой книге представляет тот
аспект, который вызывает меньше всего возражений. Рисунок X из М
1982F воспроизведен в М 1983к{С 13}.
Распираемый желанием поделиться своей радостью, я рассказал об
этой работе Адриену Дуади, когда вез его из Нью-Йорка в международ-
ный аэропорт имени Джона Кеннеди. Мы продолжили разговор в ко-
фейне в аэропорту, и Дуади сразу начал называть его «отображением
Кеннеди-Мандельброта». Подыскивая симпатичные названия для дру-
гих комплексных отображений, я задумался: не назвать ли их в честь
«Ла Гардии» или «Ньюарка»?
Как бы то ни было, Дуади продолжил работу и описал переплете-
ние, характеризующее рисунок 2 как «замужество». Выбрав другую А,
он скрестил «кролика» и «собор» (последний относится к дракону Сан-
Марко, пример которого представлен на рисунке 3 в М 1980п{СЗ} и во
многих других работах). «Собор», кстати, — это неверное название, так
как Церковь (так же, как и я) называет Сан-Марко базиликой.
Хаос и статистическая механика.
Под редакцией И. Курамото, 1984
С13
Отображение z —> Л (z -f- l/z) и переход от
линейного хаоса к хаосу плоскостному
(компьютерное подражание Хокусаю)
Предисловие к главе (2003 год). Причины для выбора отображе-
ния, описываемого в этой главе, указаны в главе С12.
Подражание Хокусаю Кацусике (1760-1849) заключается в приве-
дении на этой странице его рисунка и детальной его трактовке на сле-
дующей странице.
с 13. Переход от ЛИНЕЙНОГО хаоса а
Это подражание — не просто жест в адрес гостеприимных японцев,
оно имеет под собой веские основания, которые заслуживают самого
подробного изложения. Безусловно, Хокусай был знаменитым японским
художником, но, на мой взгляд, он заслуживает еще большей славы
за свое потрясающее «чутье на фракталы». Художник Тернер «обла-
дал чутьем на» свет, льющийся сквозь туман. А художники-«кубисты»
1900-х лет «отлично разбирались» в простых формах, которые были пол-
ностью формализованы задолго до них. Скорее всего, эти художники
предпочитали виды, радующие их глаз. Хокусай проявил намного боль-
ше смелости, поскольку направил свой взор на формы, которые были
формализованы лишь спустя много лет после его смерти.
В частности, изображение, приведенное на предыдущей странице,
взято из альбома черно-белых рисунков «Сто видов горы Фудзияма»
(Хокусай 18..). Очень похожий цветной вариант «ukiyo-е» можно найти
в его книге «Тридцать шесть видов горы Фудзияма». Она намного более
известна, и в 1983 году была единственной, которую я знал и рисунок
из которой воспроизвел в работе М 1982F под номером С16. Но, в ка-
честве примера темы «искусство, опережающее математику и науку»,
настоящая версия не только лучше в черно-белом варианте, но она так-
же вызывает намного больший интерес. Вероятно, творчество Хокусая
является лучшим доказательством того, что фрактальные структуры бы-
ли известны человечеству с незапамятных времен, но описывались они
только посредством искусства. Математика присоединилась к нему в де-
вятнадцатом веке, а естественные науки — приблизительно в 1960 году.
Учитывая мою хроническую привычку публиковать лишь часть сво-
ей работы, я закончил данный труд только потому, что готовился к од-
ной очень интересной встрече в Киото. Большой интерес тогда вызывало
одно свойство динамических систем, а именно тот факт, что бассейны
притяжения аттрактора часто имеют фрактальные границы. При напи-
сании этой статьи я поставил перед собой цель продемонстрировать сей
факт в контексте, для которого не нужны узко специальные математи-
ческие исследования.
Будучи на тот момент понятием новым, фрактальная размерность
вызывала немало сомнений и многие полагали (хотя и не высказывали
это во всеуслышание), что она представляет собой единственную зна-
чимую особенность границы. Возможно, формированию такого мнения
у ряда читателей поспособствовал труд M1982F. Но этого не должно
было быть, поскольку в этой книге также вводилось новое понятие «ла-
кунарности», Дальнейшее развитие оно получило в работах М 1993п,
М 1995z и М 1998е. Тем не менее, нельзя отрицать, что как в 1993 го-
190
Хаос и статистическая механика, 1984
ду, так и в наши дни лакунарность остается недостаточно изученным
понятием.
Аннотация. Термины «хаос» и «порядок в хаосе» оказались очень
ценными, но до сих пор не желают поддаваться четкому определению.
До сих пор важно выделять случаи, когда переход к плоскостному ха-
осу можно проследить подробным и объективным образом. В данной
статье сделана попытка показать, что отличным примером вышесказан-
ного служат итерации отображения, для которого комплексными чис-
лами являются как z, так и А. Тема этого отображения поднимается
в М 1982F{/?GA/}, но только на странице 465, которая была добавлена
в 1983 году при втором издании, поэтому данную статью можно считать
самодостаточной, ф
Отображение z —»g(z) = A(z+l/z) было выбрано для исследований,
поскольку оно обладает несколькими ценными свойствами. (А) В пре-
делах обширной области А существуют два различных предельных цик-
ла, симметричные друг другу относительно z = 0. (Б) Соответствую-
щие изменения А приводят к одновременной бифуркации обоих циклов
в циклы, большие в п > 2 раз. (В) Хаос, преобладающий при опре-
деленной А, распространяется на всю плоскость z. Свойства (А), (Б)
и (В) абсолютно не характерны для комплексного квадратичного отоб-
ражения z —» f(z) = z2 — р. На самом деле, при каждом р один из
предельных циклов / сводится к точке в бесконечности, которая ни-
когда не разветвляется. Хаос же, когда он имеет место, заключается
в движении по малому подмножеству плоскости z.
1. Резюме. Относительность понятия хаоса
Львиную долю этой статьи составляют пояснения к нескольким ри-
сункам, на которых при различных А представлена форма множества
Жюлиа Т’*, то есть границы открытых областей притяжения устойчи-
вых предельных точек и циклов. Различные последовательности рисун-
ков соответствуют разным «сценариям» изменения А и порождают отоб-
ражения, которые постепенно переходят из области линейного хаоса
и плоскостного порядка в область сомнительного или бесспорного плос-
костного хаоса.
Чтобы представить эти изображения в перспективе, статья содер-
жит сравнения с полиномиальными отображениями. Для начала отме-
тим, что специальное отображение z —► z2 — 2, ограниченное веществен-
ным интервалом [-2, 2], называется «совершенно хаотическим». Однако
с 13. Переход от линейною лл>л.
то же самое отображение, обобщенное на комплексную плоскость, сле-
дует назвать практически полностью упорядоченным, поскольку все zf)
(кроме принадлежащих вещественному интервалу [-2, 2]) повторяются
к оо. Как известно (Collet & Eckmann 1980), существует много других р,
при которых отображения z —► z2 — р на соответствующем вещественном
интервале являются хаотическим. При этом те же самые отображения
демонстрируют минимальную хаотичность на плоскости в том смысле,
что область исключительных zo, которые не повторяются к ос, меньше
для хаотических ро, чем для любых нехаотических р, которые можно
обнаружить произвольно близко к ро.
Таким образом, нам совершенно необходима объективная мера пе-
рехода к хаосу. Наиболее очевидным кандидатом на измерение упорядо-
ченности является фрактальная размерность D множества Жюлиа Т7*.
В данной работе установлено, что D действительно вполне подходит
для ряда случаев, но при этом создает очень интересные сложности для
других сценариев, когда множество Т7* включает более одной формы,
а значит имеет более одной размерности.
Самый известный сценарий был впервые выдвинут Дж.Мирбергом
и очень подробно изучается во многих работах (Collet & Eckmann 1980).
Согласно этому сценарию, переход от линейного хаоса к плоскостно-
му происходит посредством бесконечной последовательности конечных
бифуркаций произвольного порядка. Когда этот сценарий применяется
к g(z), как в разделе 5, множество остается фрактальной кривой,
размерность D которой возрастает от 1 до 2, в силу чего ее соразмер-
ность 2-D действительно является приемлемой мерой упорядоченности.
По альтернативному сценарию, которым мы обязаны работе Siegel
1942, фрактальная размерность D также постоянно изменяется от 1 до 2.
но интуиция подсказывает нам, что на плоскости этот предел будет
не вполне хаотическим. Ключ к разгадке этого парадокса в том, что
соответствующее множество имеет две различные формы, а значит,
и две разные размерности.
Согласно третьему сценарию, который мы сейчас рассмотрим, пе-
реход к плоскостному хаосу осуществляется в отсутствие бифуркации,
а фрактальная размерность D стремится к 2.
2. При вещественной А и |А| > 1 итерация упорядочена везде,
кроме множества Т*
При А = 0, все точки, кроме 0 и оо, за один шаг переходят к О,
после чего их движение перестает быть определенным. При |А| > 1,
192
Хаос и статистическая механика, 1984
в ос существует неподвижная точка-аттрактор, которая противоречит
нашему условию (А).
При вещественной А > 0 отображение g(z) сохраняет знак Re(z),
а при вещественной А 0 0 итерированное отображение <72(2) сохраня-
ет Re(z). В более общем смысле, множество Жюлиа является мнимой
осью для всех вещественных А / 0.
3. Невещественные А, удовлетворяющие неравенству |А| < 1
При таких А множество Жюлиа Т7* представляет собой либо целую
комплексную плоскость, либо фрактальную кривую. В последнем случае
7* обладает следующими свойствами.
7* (очевидно) симметрично относительно z = 0 и самоинверсно
относительно окружности |z| = 1.
Т7* включает z = 0 и является неограниченным. Это очевидно, ко-
гда неподвижные точки z = ±\/1 — А устойчивы: если z0 итерирует
в одну из неподвижных точек, то — zq итерирует в другую неподвижную
точку, поэтому окружность с радиусом mod (z0) должна пересекать
множество 5*. (Необходимо также добавить начальную точку z = О,
так как является закрытым множеством).
При z -> оо множество 7* асимптотически самоподобно. В самом
деле, если |z| < 1, a zq итерирует в некоторый цикл, то A(z + 1/z) ~ Az
в тот же самый цикл. Будучи самоинверсным, множество 7* при z -»О
также асимптотически самоподобно. Когда топологически множество 7*
является линией, то при z —> 00 и z —> 0 эта линия закручивается по
логарифмической спирали. Обе спирали закручиваются в одном и том
же направлении, но не создают общей линии, поскольку вблизи |z| = 1
исчезает масштабная инвариантность.
Начнем с вещественной А, для которой множество Т7* является
прямой, а затем изменим А и проследим как Т7*, меняется от прямой
до все более замысловатой кривой. Для этого нарисуем полуоткрытый
вариант «множества Мандельброта», определенного в М 1980п{СЗ).
Полуоткрытое множество М представляет собой максимальное мно-
жество таких А, что итерация этого отображения обладает конечным
предельным циклом. Его замыканием является обычное множество М.
Полуоткрытое множество М отображения z —> A(z + 1/z) представлено
на рисунке 1. (За исключением поворота на 90°, рисунок 1 повторяет
рисунок X из второго и последующих изданий работы M1982F.)
При ближайшем рассмотрении оказывается, что полуоткрытое мно-
жество М состоит из молекул М, в свою очередь состоящих из ато-
Cl3. Переход от линейного хаоса к хаосу плоскостному
193
мов М, причем обе эти формы совершенно типичны для отображе-
ний A(z + 1/z) и
В настоящем исследовании рассматриваются три различных сцена-
рия, которые начинаются с абсолютного порядка, существующего при А,
принадлежащих вещественному интервалу [0, 1] (по этой причине мно-
жество Жюлиа отождествляется с мнимой осью), и завершаются плос-
костным хаосом. Мы сосредоточим свое внимание на молекуле М, ко-
торая содержит дискообразный атом М 11/2| < 1/2. Несложно заметить,
что этот атом объединяет все А, для которых итерация /(г) имеет две
предельные точки: г = ±\/А/\/1 - А.
4. От штиля до Великой Волны: компьютерное подражание
Кацусике Хокусаю (1760-1849) (рисунок 2)
При любых А, принадлежащих диску |А — 1/2| < 1/2, топологически
множество Жюлиа 5* представляет собой прямую, которая закручива-
ется при z —> 0 или z —> оо по логарифмическим спиралям, симмет-
ричным друг другу относительно 0. Наиболее привлекательны и позна-
вательны эти спирали в том случае, когда они не слишком растянуты
и не слишком сжаты. По этой причине рассмотрим несколько различных
значений параметра: в недрах атома М |А — 1/2| < 1/2, между А = 1/2
и окрестностью 1/2 4- г/2. Для упрощения сложностей, которые возни-
кают вблизи |г| = 1 и никак не связаны со спиралями, выберем окно
(демонстрируемая часть комплексной плоскости) шириной 200 единиц,
а множества J7* будут вращаться, чтобы их легче было сравнивать.
Множества J* показаны в виде границ между черной «водой» и «бе-
лым» воздухом, которые являются областями притяжения двух предель-
ных точек. Как и задумывалось, на первой части рисунка 2 возникает
абсолютно спокойное черное море, то есть плоскостной порядок. На ри-
сунках, сменяющих друг друга против часовой стрелки, видны все более
угрожающие черные волны.
Одновременно с этим возрастает фрактальная размерность D мно-
жества 5*. В данном контексте D показывает, сколько десятичных раз-
рядов го в счетной базе Ь нужно знать, чтобы определить, притягивает-
ся zq к Jx/y/l - А или к -х/А/%/1 — А. Чтобы установить этот факт,
нарисуем в нашем окне ряд ящиков с относительной длиной сторо-
ны и = 1/Ь. Грубо говоря, множество Т7* пересечет bD этих ящиков.
Запишем ji = bD~2 и произвольно выберем = хо + iyo в ящике. С веро-
ятностью 1—/?, первых b десятичных разрядов т0 и уо будет достаточно,
чтобы определить, куда притягивается zq. В общем, первых к b десятич-
ных разрядов zq и уо достаточно с вероятностью (1 - ^^“^^(Р-г)
194
Хаос и статистическая механика, 1У«4
В среднем, количество b десятичных разрядов, необходимых для
определения предела, составляет 1/(1 — /?). При малой соразмерно-
сти 2 - D ожидаемое число е «десятичных разрядов» базы, необходимых
для определения предела, равно loge /6(1 — /?) ~ 1/(2 — D).
5. Первый путь за пределы Великой Волны.
Сценарий бифуркаций Мирберга
На рисунке 3 представлены множества Т7* при двух значениях А.
На верхнем изображении А лежит после бифуркации в 4 и близко ко
второй бифуркации в 3 (но не доходя до нее). На нижнем рисунке А
достигается с помощью двух последовательных бифуркаций в 4, за ко-
торыми следует бифуркация в 3. Таким образом, первая А смещена от
центра атома за пределами атома |А — 1/2| < 1/2. Вторая А расположена
вблизи ядра малого атома М за пределами малого атома М, присоеди-
ненного к нижней части |А — 1/2| > 1/2. Четвертая Л представлена на
странице VIII второго и последующих изданий M1982F {PS2003} и вос-
производится в главе С12 на рисунке 2.
При первой бифуркации образуется «белая вода», так как толща
воды и толща воздуха разбиваются на крупные капли, причем некоторые
из них действительно огромны. Последующие бифуркации разбивают
эти капли на более мелкие и так далее до бесконечности. Очевидно, что
мы наблюдаем постепенное движение к полной замене отдельной черной
воды и белого воздуха на нечто, не являющееся ни водой, ни воздухом.
Тут нельзя не вспомнить о критической температуре из физики.
При приближении плоскостного хаоса фрактальная размерность D
множества Т7* стремится к 2, а коэффициент /3 — к 1.
6. Второй путь за пределы Великой Волны.
Спираль, ведущая к хаосу (рисунок 4)
Выберем теперь значение А, принадлежащее атому |А — 1/2| < 1/2,
но чрезвычайно близкое к А = 1. Соответствующее множество Т7* пред-
ставлено на рисунке 4. Совершенно ясно, что если А -+ 1, то /? —► 1
и приближение к хаосу происходит в отсутствие бифуркации. Воз-
можно, данную ситуацию проще визуализировать с помощью парамет-
ра р = 1/А и переменной и = 1/z. Эта замена переменной никак не
влияет на множество J7*. Что касается дисков, представим, что эти из-
ломы сходятся и соединяются. Следовательно, вода (и, симметрично ей,
воздух) разделяются на диски, связанные друг с другом исключительно
Рис. С13-1. Самые большие молекулы М в верхней правой четверти полуоткры-
того множества М отображения z —» A(z -I- 1/z). Ради ясности, атомы |А| < 1
и |А —1/2| > 1/2 не закрашены в черный цвет, а изображены пустыми, в виде
двух белых окружностей
точечным образом. Два диска содержат точки ± + х/1 — А и называются
дисками Зигеля; назовем оставшиеся диски продисками Зигеля. В каж-
дой междисковой связи воздух пересекается с водой, но на протяжении
большей части плоскости они четко отделены друг от друга множе-
ством 7*. Не удивительно, что фрактальная размерность Т7* принима-
ет значение Ds, которое бесспорно меньше 2. В среднем, необходимо
порядка 1/(2 - Ds) десятичных разрядов, чтобы определить, является
ли zq черной или белой точкой. К тому же, здесь нет никакого предель-
ного цикла. Итерация zq изображена белым (черным) цветом, продиски
Зигеля в конечном итоге оказываются в белом (черном) диске Зигеля.
В масштабе окна шириной в 200 единиц, выбранного для рисунка 3,
диски Зигеля настолько малы, что режим Зигеля весьма напоминает
схождение.
Теперь, чтобы получить представление о том, как выглядит множе-
ство 7* при Л, расположенных практически рядом с Ах, необходимо
знать, что диски Зигеля возникают, когда топологически кривая Т7*
X.AOi II i 1 Al 111 1ИЧЕСКЛЯ МЕХАНИКА, 1984
Рис. С13-2. От центра против часовой стрелки: множества Жюлиа отображе-
ния z — X(z + 1/z) при нескольких А «от штиля до Великой Волны». Подража-
ние К. Хокусаю
представляет собой прямую, сворачивается и заполняет область или
плоскость, как описано и проиллюстрировано в работе М 1985g{C10).
Когда А расположена практически рядом с Xs, изломы, о которых гово-
рится в предыдущем абзаце, не сходятся и не соединяются. Наоборот,
внутренняя часть каждого черного диска частично расщепляется на мно-
жество (в данном случае на 157) очень узких «фьордов», проникающих
вглубь белых областей, не соприкасаясь с центром фиктивного белого
пятна, но максимально к нему приближаясь. Аналогичным образом, сле-
дует представить симметричные черные фьорды, вонзающиеся в белую
область.
Поскольку границы белых и черных фьордов принадлежат множе-
ству кривая Т7* очень близка к тому, чтобы заполнить всю плос-
кость. Поскольку ее размерность приближается к 2, нам так и хочется
предположить, что соответствующее отображение r/(z) является абсо-
лютно хаотическим. Но это не так. На самом деле, в сценарии Зи-
геля раскрывается одна важная тонкость: необходимо повнимательнее
С13. Переход от линейного хаоса к хаосу плоскостном/
197
Рис. С13-3. Множества Жюлиа при двух А, порождающих практически полно-
стью хаотические отображения g(z) в случае повторных бифуркаций по сцена-
рию Мирберга
1 9S
X\OC II СТАТИСТИЧЕСКАЯ МЕХАНИКА, 1984
Рис. CI3-4. Множество Жюлиа при X, порождающей практически полностью ха-
отическое отображение д(г) и получающейся по совершенно другому сценарию.
Топологически эта кривая является прямой линией
рассмотреть коэффициент /3. При очень крошечных значениях стороны
клетки мы получаем 0oorl~D. Тем не менее, когда г к < £, где £ -
это функция 2 - D, оказывается, что 0=1. Таким образом, небольшая
величина 2 - D означает, что каждую клетку со стороной < £ будет
пересекать 7*. Но это ничего не говорит об относительных пропорциях
черного и белого в клетках < £. В настоящем случае фьорды настолько
узки, что клетка < £ окрашена, в основном, либо в черный цвет, либо
в белый в зависимости от того, находится ли она в области, которая
на рисунке 5 полностью закрашена черным или белым цветом. Ожидае-
мое количество десятичных разрядов базы Ь определяется тем, хотим ли
мы узнать цвет го точно или с высокой вероятностью. Для абсолютной
точности нужно 1/[1 - 6D-2] десятичных разрядов, а для достижения
высокой вероятности — всего 1/[1 - bD^\.
Другими словами, общий вид, который получается в результате
компьютерных ограничений на рисунке 5, не так уж обманчив. На самом
деле, он помогает раскрыть основную истину. Когда А находится очень
близко к Xs. форма 7* определяется двумя отдельными размерностями:
размерностью самого множества и размерностью 7*, соответствующей
ближайшему зигелеву значению X.
С13. Переход от линейного хаоса к хаосу плоскостном /
199
Рис. С13-5. Множество Жюлиа при Л, порождающей бесспорно хаотическое
отображение g(z) и получающейся в сценарии Зигеля
Нужно признать, что для создания практически полного плоскост-
ного хаоса необходимо, чтобы все маленькие клетки (а) пересекали Т7*
и (б) были примерно наполовину черными и наполовину белыми. При
этих условиях для достижения полного хаоса недостаточно множе-
ства 5*, практически целиком заполняющего пространство, с размер-
ностью, близкой к 2. Разговор о других результатах изучения этой темы
отложим до более подходящего случая.
Благодарность. Рисунки подготовил Джеймс А. Гивен с помощью
компьютерных программ, написанных В. Аланом Нортоном.
Первая публикация; рисунки датированы 1974 годом
С14
Два неквадратичных рациональных
отображения из формул удвоения
Вейерштрасса
Эта глава извлечена из запасника давно «потерянных» изображе-
ний, созданных в 1979 году с помощью Марка Р. Лаффа. В данной
книге они, наконец-то, публикуются впервые в сопровождении объясне-
ний и комментариев, представляя документально зафиксированные по-
дробности истории, рассказанной в главе С12. Некоторые рисунки весь-
ма привлекательны и в большинстве своем отражают базовое различие
между созерцанием и открытием, описанное в главе С1.
На примере простейших графических изображений, полученных
в Гарварде в 1980 году, главой С1 доказано, что высокое качество ри-
сунков не является необходимым условием открытия множества Ман-
дельброта. Более того, нужен даже не цвет, необходимы знания уче-
ного. В настоящей же главе устанавливается противоположный факт:
высокого качества рисунков, которыми я располагал в 1979 году, также
оказалось недостаточно.
Чтобы убедиться в вышесказанном, просмотрите великолепные ри-
сунки, представленные в данной главе. В любом из них множество М
обнаруживается только апостериори. Также, совершенно «очевидно»,
что многие из моих ранних множеств Жюлиа представляют собой слож-
ные «композиты» или «сплавы», созданные из «элементов», которые я от-
крыл в 1980 году в процессе изучения квадратичной итерации. Я видел
эти элементы в 1979 году, но не смог систематизировать и описать их.
Как следствие, открытия не последовало. Могло ли открытие пойти дру-
гим путем, если бы из композитов 1979 года я сумел получить элементы
1980 года? Однако думать о том, что могло бы случиться, — лишь на-
прасно время терять.
В момент своего появления эти рисунки были вполне современны,
затем отсутствие цвета превратило их в побывавшую в употреблении
мебель, сегодня же они представляют собой ценный антиквариат. Время
им. ДВА неквадратичных РАЦИОНАЛЬНЫл .
от времени я собирался дополнительно поработать над теоретическим
обоснованием этих рисунков, прежде чем публиковать их, но сейчас
я уже не планирую к ним возвращаться. Поскольку значимость этих
рисунков существенно зависит от их возраста, для каждого из них ука-
зывается дата, которая автоматически печаталась на оригинале.
1. Функция Латте Wi(z) и отображение z —+ AWi(z)
В главе С12 отображение удвоения Латте Wi(z) записывается как
4 Z(Z2 — 1).
Этот рассказ об отображении z —> AWi(z) начинается с множеств
Жюлиа, за коими следует описание менее изученных, но, возможно,
более значимых ранних результатов, касающихся множества Мандель-
брота для этого отображения.
1.1. Множества Жюлиа с вещественным параметром А,
«элементами» которых являются «драконы Сан-Марко»
На рисунках 1 и 2 представлена часть плоскости z. Значение А та-
ково, что отображение z —> AIVi(z) имеет два цикла, каждый из которых
порядка 2. В целом, отображение z —> AVKi[AWi(z)] обладает четырьмя
предельными точками, поэтому нарисованы четыре изображения. Под-
разумевалось, что они будут использоваться как прямые разделители
цветов на задуманной четырехцветной экспозиции.
На рисунке 1 черные точки являются начальными точками z0 ор-
бит, которые сходятся к одному из циклов, а белые точки представляют
собой начальные точки орбит, сходящихся к другому циклу.
Оглядываясь назад, можно сказать, что каждый из черных или бе-
лых элементов покрытия (если не обращать внимания на размер) явля-
ется нелинейно деформированным драконом Сан-Марко, описание кото-
рого дается в работе М 1980п{СЗ}. Таким образом, указанная мною А
соответствует квадратичному отображению z —+ 2z(l — z), характеризу-
ющему первую бифуркацию z —> Az(l - z). К сожалению, у меня нет
никаких записей насчет того, осознавал ли я, что именно делаю.
На рисунке 2 каждый из черных элементов покрытия с рисунка 1
разделяется на несколько черных и белых элементов, в совокупности
напоминающих «шиш-кебаб». Теперь цвет зависит от положения орбиты
202 С14 Два неквадратичных рациональных отображения
после определенного количества шагов, то есть от предельной точки
квадратичного отображения z —> AWi [AWi (z)].
1Л. Эвовепт множества Жюлиа, ограниченный «жордановыми
кривыми» без самопересечений
Как подсказывает нам форма элементов на рисунках 3 и 4, основ-
ные значения А соответствуют двум значениям А < 2 в квадратичном
случае. В каждом случае достаточно использовать два цвета, так как
предельное множество состоит из двух предельных точек, не подверг-
шихся бифуркации.
1Л. Множества Жюлиа при вещественных значениях Л, близких
ж хаотическому значению А = 1
Значение А = 1 возвращает нас к отображению Латте, для которо-
го «множество Жюлиа» заполняет всю комплексную плоскость. Я хотел
понять, как осуществляется приближение к этому «хаосу» при значени-
ях А. стремящихся к единице. Для вещественного квадратичного отоб-
ражения х —► х1 + с этот подход имел четкую аналитическую основу.
Но, как всегда, когда речь заходит о фрактальной пыли на прямой, по-
лучить визуальное представление оной оказалось не так-то просто. Яв-
ления, которые имеют место на плоскости, сложнее изучать, но проще
представлять визуально.
Изучение z —» АИ^з) при А —» 1 показало, что каждый из циклов
второго периода на рисунках 1 и 2 подвергается ряду последователь-
ных бифуркаций, с которыми мы хорошо знакомы благодаря веществен-
ному квадратичному отображению. Вскоре предельных точек в цикле
становится настолько много, что одного цветового разделения на одну
предельную точку будет уже недостаточно. Вместе этого белым (и, со-
ответственно, черным) цветом покрасили все точки, полученные путем
бифуркации из белого (соответственно, черного) цикла на рисунке 1.
Безусловно, Латте предвидел, что выбор значения А слишком близ-
кого к единице привел бы к полной бессмыслице. Рисунки 5 и 6 полу-
чились в результате обработки нескольких значений А. На протяжении
всего этого процесса меня не покидало чувство, будто я пытаюсь сфото-
графировать чеширского кота из «Алисы в Стране Чудес* в тот самый
момент, когда он вот-вот исчезнет. Если бы я потерпел неудачу и это ис-
следование не к чему бы ни привело, полученный результат отправился
бы в корзину для мусора.
циклов. КВ/К2ЫИ из которых составлен из двух точе?:. дл = : т~ стаже-
ь<аг-^И'/г, ’
14. *Предвестники» будущего множества ^Мандельброта
За рисунками 1-4 последовало множество вариантов, которые л:л
чались при других значениях А. Путаница все росла и росла, и я реши:,
ся на следующий шаг. Я попытался определить множество комплек
иых А. при которых множество Жюлиа отображения с —* АН ; с име<
конечное число конечных предельных циклов. Другими словами, я
копию будущего множества Д/° квадратичного отображения. К
гда А принадлежит этому множеству, положение орбиты посче бопьш^’
количества итераций сводится к множеству S конечного размера’.'
204
014 Два неквадратичны.х рациональных отображения
05/09/79
Рис. С14-2. [05.09.1979]. Разложение одной из областей притяжения Ai ИД (г) на
рисунке 1. Эта область разбивается на области притяжения двух из предельных
точек отображения z —> AilVi[AHzi(z)]
Каждое раннее исследование должно составляться с расчетом на
скорость его проведения, поэтому я начал с того, что срезал путь. Я рас-
суждал так: если существуют предельные циклы, значит, они находятся
недалеко от z = 0. Действительно, сначала надо было рассмотреть по-
лучившиеся в результате множества А, а строгое обоснование вполне
могло подождать своего часа.
Иллюстрация от 1979 года, на которой изображены «остро-
ва множества М». Располагая знаниями о квадратичном случае, мы
Рис. С14-3. [04.16.1979]. То же самое, что и на рисунке 1, но при значении
параметра А2 / Ai
не нуждаемся в истолковании того, что видим на рисунке 7.1. На чер-
ном фоне все немедленно узнают несколько маленьких версий будущего
квадратичного множества Л/°.
Обратясь к уже имеющимся у нас знаниям еще раз, мы поймем, что
эти маленькие «штучки» соответствуют островным молекулам квадра-
тичного множества Мандельброта. Вспомним, что в квадратичном слу-
чае эти острова имеют относительно малые размеры. Именно по этой
причинена ранних рисунках, представленных в главе С1, они похожи
на пятна грязи. Здесь их копии имеют относительно большой размер,
так что с грязью их уже не спутаешь. На других комплексных отобра-
жениях, которые я изучал в последние годы, эти острова еще заметнее.
I I I [l> \ 111 Kb \ 'ir\l ll'IHbIX I’XHIIOH АЛЫ I HIX ОЮЬРЛЖ! НИЯ
M’WII 16 )Q'9
Рис. C14-4. [04.16.1979]. To же самое, что и на рисунке 1, но при значении
параметра А3 Д2 Ai
Если постараться еще сильнее, можно вспомнить, что квадратичное
множество Л/° строится с помощью последовательных аппроксимаций
границы М изнутри. Каждый дискообразный атом М° приближается
с помощью последовательности более мелких дисков, и только в пределе
у атомов появляется общая касательная в точке их связи. Соответству-
юший эффект отлично просматривается на рисунке 7.1.
Большое значение имеет дата создания рисунка 7.1. Физически
я уже был в Гарварде, но рисунки продолжали (медленно) создаваться
04/25/79
Рис. С14-5. [04.25.1979]. То же самое, что и на рисунке 1, но при значении
параметра А4, близком к значению А = 1, которое соответствует хаосу Латте
в IBM. Я не буду сейчас строить предположения насчет того, могло ли
смутное воспоминание о рисунке 7.1 несколько месяцев спустя навести
меня на мысль увеличить маленькие пятна грязи на грубых рисунках
1980 года, воспроизведенных в главах С1 и СЗ.
Еще более глубокое погружение в воспоминания о былом позволило
сделать вывод, что само множество Мандельброта и свойственную ему
универсальность я открыл практически одновременно.
Однако ретроспектива — это напрасная трата времени. В общем
и целом, малый размер этих объектов и то немногое, что я помню о ме-
208 С14. Два неквадратичпо.л г^..~.ыит
05/07/79
Рис. С14-6. [05.07.1979]. То же самое, что и на рисунке 5, но при значении
параметра >5. которое еще ближе к значению Л = 1, соответствующему хаосу
Латте
тоде их создания, приводят к мысли, что рисунок 7.1, в момент его
появления, был предварительным изображением, которое не стоило пуб-
ликовать, но над которым стоило потрудиться при более благоприятных
условиях.
Более поздняя интерпретация множества Мандельбро-
та XWi(z). Для того, чтобы читатель мог рассмотреть рисунок 7.1
в более широком контексте, на рисунке 7.2 представлена более поздняя
С14. Два неквадратичных рациональных отображения
209
Рис. С14-7. (Вверху справа) на рисунке 7.1 воспроизведена попытка [11.01.1979]
изобразить множество М° отображения z —► Allzi(z). В качестве подтвержде-
ния, на рисунке 7.2 представлена более сложная попытка, предпринятая в IBM
после 1980 года
версия множества Л/° для z —> AlVi(z), полученная после моего воз-
вращения в IBM. Когда это множество А/0 было впервые изображено
в работе М 1986р, оно, насколько мне известно, не привлекло большого
внимания, что опять же меня поражает.
Составное изображение {от 1979 года} атомов множества М
и их взаимоотношений. Нам пришлось нарисовать отдельные части
рисунка 8, поскольку для построения множества А/0 понятие «пре-
дельного множества конечного размера» было разложено на ряд поня-
210
С14. Два неквадратичных наш
иг/\ /ЛИНИЯ
07/26/79
L ; ' 1
Рис. С14-8. Композит из областей множества М° отображения z —* AlVi(z),
порождающего циклы различных размеров
тий «предельных множеств размера к», причем ограничения, связанные
с возможностями компьютера, обусловили конечное значение величи-
ны kmax. Предусмотрительно подумав о цветовом разграничении пред-
лагаемой цветной версии М°, мы, естественно, выводили последова-
тельные значения к по отдельности. Это был чрезвычайно амбициозный
план, а каждое будущее разграничение оказывалось слишком неясным,
чтобы его можно было использовать в преследуемых нами целях. При-
чины этого я не зафиксировал, так что сейчас уже позабыл.
Тем не менее, апостериори все, кто знаком с квадратичным множе-
ством Мандельброта, узнают известную форму его «атомов» и заметят
некоторые характерные особенности их взаимного расположения.
С14. Два неквадратичных рациональных отображения 211
06/02/79
Рис. С14-9. [06.02.1979]. Прообразы квадранта Re(z) > 0, Im(z) > 0, получен-
ного с помощью отображения вида z —» AWi (z)
1.5. Прообраз квадранта {Rez, Imz] при итерациях AWi(z)
Рисунок 9 является одним из самых красивых из огромного портфо-
лио изображений, которые я посвятил различным значениям А в 1979 го-
ду. Здесь все предельные точки, принадлежащие каждому из четырех
квадрантов плоскости, были объединены, а итерация произошла 15 раз.
В результате итераций с меньшим количеством стадий получались са-
мые разнообразные артефакты, всегда сбивающие с толку, но зачастую
необыкновенно прекрасные. Второй квадрант выделен серым цветом.
212 С14. Два неквадратичных рациональных отображения
05/31/79
Рис. С14-10. Области притяжения (белого, серого и черного цвета) трех пре
дельных точек отображения вида z —» AW2(-z)
2. Вариантная функция W2(z) и отображение z —►
В главе С12 вариантное отображение удвоения Вейерштрасса ^2(2)
определено как
1 z(z3 + 8)
2 Ж2(х) = д~2з_1 •
Вообще, отображение z —♦ W2(z) привлекательно тем, что его сим-
метрии обусловлены коэффициентом z3, а следовательно, они отличают-
ся от симметрий отображения z -+ Wi(z).
С14. Два неквадратичных рациональных отображения
213
2.1. Множество Жюлиа при параметре А, не близком
к хаотическому значению А = 1
На рисунке 10 три «цвета» (белый, серый, черный) отмечают зна-
чения z0, которые притягиваются к каждому из 3 предельных циклов.
В целях практичности мы вычислили серую часть, а черную часть —
получили с помощью поворота на 120°.
2.2. «Предвестники» будущего множества Мандельброта
На рисунке 11 видны очертания множества М: довольно четкие
в центральной области и размытые в полутени.
Рис. С14-11. [06.13.1979]. Версия рисунка 8 для отображения z —► AIV2U)
[Обложка книги M1999N, все цвета которой сведены к серым полутонам].
Этот декоративный узор служит иллюстрацией к части III этой книги. Он
называется ^Нагрудником фараона» и заполняет самоинверсный фрактал,
изображенный на рисунке С16.2. В основе алгоритма, описанного в части Ш.
лежат восемь возможных видов «полудрагоценных камней», но в настоящем
версии, по эстетическим соображениям, четыре камня отсутствуют. Програм-
му, генерирующую это изображение, написал К. Дж.Монск.
Часть III
СИСТЕМЫ
ИТЕРИРОВАННЫХ
НЕЛИНЕЙНЫХ ФУНКЦИЙ
И ФРАКТАЛЬНЫЕ
ПРЕДЕЛЬНЫЕ МНОЖЕСТВА
КЛЕЙНОВЫХ ГРУПП
Первая публикация
С15
Клейновы группы, их фрактальные
предельные множества и СИФ: история,
воспоминания и имена
Исторически, клейновы группы предшествовали теории Фату-
Жюлиа, поэтому я изучал эти темы именно в такой последовательно-
сти. Но в данной книге я изменил истории и в первую очередь пред-
ставил тему, в которой наиболее силен или, по меньшей мере, наиболее
известен. В этом введении будет также раскрыта тайна загадочных букв
СИФ. Как и в главе 2, некоторые имена, которые я посчитал нужным
выделить, напечатаны жирным курсивом.
О более позднем моем труде по «клейновым мерам» речь пойдет
в части IV.
1. Начало истории о великом нововведении Пуанкаре, которое он
решил назвать «клейновыми» группами
Вообще, термин «клейновы» в данном случае не свидетельствует
о связи явления с именем его открывателя. Если следовать логике, то
несложно запутаться, поскольку концепция и оригинальное исследова-
ние клейновых групп — это одно из ранних и наиболее выдающих-
ся достижений (совершенное практически в одиночку) Анри Пуанкаре
(1854-1912).
Но, раз первые результаты в этой области принадлежат не Феликсу
Клейну (1849-1925), то почему же для ее названия был выбран имен-
но этот термин? Просто Клейн донимал Пуанкаре, настаивая, что более
специализированные объекты, которые Пуанкаре называл «фуксовыми»,
следует переименовать в «клейновы». Пуанкаре упирался, не желая вы-
полнить эту просьбу, но в конечном итоге сдался и предложил компро-
мисс: пообещал использовать имя Клейна в своем (сделанном Пуанка-
ре!) следующем интересном открытии. И он сдержал свое обещание!!!
Эта история известна из писем, представленных в томе 11 «Собрания
сочинений» Пуанкаре от 1916 года.
218
С15. Клейновы группы
Но при этом Пуанкаре и не думал отказываться от заслуженного
им права на вышеобозначенное открытие. В девятнадцатом веке призна-
ние и название зачастую никак не соотносились друг с другом, как это,
например, имело место в случае гауссова распределения. Аналогично,
автором принципа Дирихле является не Петер Густав Лежен-Дирихле
(1805-1859), а его студент Бернхард Риман (1826-1866). Но вы же зна-
ете сентиментальность историков: они не любят изменять традициям,
и в наше время это открытие многие считают заслугой Клейна. Одна-
ко в главном раннем трактате Frick & Klein 1897 не упоминается ни
сам этот термин, ни спор, порожденный оным в научном сообществе.
(В предисловии Фрикке отмечает, что написал эту книгу самостоятель-
но и благодарит своего уважаемого учителя за то, что он согласился
разделить с ним авторство).
2. Изучение клейновых групп и их предельных множеств
содержит большое количество объектов, впоследствии названных
фракталами; они появились не только как контрпримеры, но
и как «неизбежные следствия теорий аналитических функций
и дифференциальных уравнений»
Согласен, этот факт был абсолютно мне неизвестен, когда я с го-
ловой ушел в написание работы М19750, в которой одновременно вос-
хвалял математиков за создание канторовых множеств и сетовал на то,
что они не применяли свое открытие в конкретных целях. По любым
объективным критериям, мое предположение о наличии связи между
канторовыми множествами и физикой вещественного пространства бы-
ло воспринято как беспрецедентное и абсурдное высказывание.
Согласен, большинство об этом уже не помнят, но в течение го-
да после выхода в свет работы Кантора от 1883 года о данном мно-
жестве (Cantor 1932) и задолго до появления революционных теорий
множеств и функций вещественной переменной, в работах по идеаль-
ной ортодоксальной математике появились упоминания о множествах,
близких к троичному множеству (пыли) и функции Вейерштрасса.
Не соглашусь с тем, что в свое время эти приложения остались без
внимания. Первое встречалось в теории автоморфных функций, просла-
вивших Пуанкаре и Клейна. Их работы развивал Поль Пенлеве (1863-
1933), который добился успехов не только в чистой математике. Он
увлекался машиностроением (и был первым пассажиром Уилбера Рай-
та после катастрофы, в которой погиб Орвилл Райт), а позднее занял-
ся политикой, и во время Первой мировой войны поднялся до поста
премьер-министра Франции.
С15. Клейновы ГРУППЫ
219
Да, невежество мое было абсолютным; оно основывалось на пред-
рассудках и подкреплялось тем, что Кантор, в конце концов, пал жерт-
вой едкого замечания Пуанкаре: «Канторизм [предвещает] радость док-
тора, которого пригласили для изучения роскошного патологического
случая». Однако, когда возникла такая необходимость, Пуанкаре все-та-
ки воспользовался трудами монстров классики в абстрактных матема-
тических моделях физики. И все же следующего этапа (использовать их
для описания окружающей природы) он предвидеть не смог.
Французским студентам моего поколения были знакомы базовые
принципы клейновых групп. Но я не уделял им должного внимания до
одного незабываемого дня: моего знакомства (сначала это было поверх-
ностное прочтение, а затем и страстное увлечение) с невероятным пане-
гириком в честь Пуанкаре, написанным известным математиком и спе-
циалистом в области математической физики, имя которого часто упо-
минается в этой книге, Жаком Адамаром (1865-1963). Мне случилось
прочитать труд Hadamard 1912 в процессе работы над M1997F, поэтому
последняя содержит упоминание о моем новом восприятии трудов Пу-
анкаре, о чем также говорится в М 1982F, но оба случая заслуживают
того, чтобы повторить их в свободном изложении.
Из работы Hadamard 1912. «Пуанкаре фактически предвосхи-
тил появление теории множеств в том смысле, что применил ее еще до
ее возникновения в одном из своих самых потрясающих и по праву са-
мых известных исследований. Ему действительно удалось показать, что
сингулярности автоморфных функций образуют либо полный круг, либо
канторову пыль. Последнюю категорию его предшественники не могли
даже вообразить. Описанное множество является одним из наиважней-
ших достижений теории множеств, но Бендиксон и сам Кантор открыли
его только годы спустя.
Вообще-то, кривые, не имеющие касательных, относят ко классиче-
ским примерам еще со времен Римана и Вейерштрасса. Тем не менее,
каждому понятно, что одно дело, когда некоторый факт устанавливает-
ся в процессе творческого размышления, не имеющего четкой цели или
намерения, кроме желания только лишь доказать существование такой
возможности, такого экспоната в кунсткамере, и совсем другое дело,
когда тот же самый факт возникает в рамках теории, корни которой
уходят в самые обычные и самые существенные проблемы анализа».
Из работы Painlevd 1895. «Я должен подчеркнуть, что между
теорией функций и канторовой пылью существует определенная связь.
Вторая тема была настолько новой, что издателям математической лите-
220 С15. Клейновыгруппы
ратуры пришлось набраться духу, чтобы опубликовать соответствующие
статьи. Многие читатели воспринимали ее не как научные изыскания,
а как философские размышления. Тем не менее, развитие математики
очень скоро показало безосновательность такого мнения. В 1883 году
(который был отмечен двумя памятными для истории математики этого
века событиями) «Acta Mathematical чередовала работы Пуанкаре по
фуксиевым и клейновым функциям с работами Кантора».
Пуанкаре опубликовал основные результаты своей работы в «Соtrip-
les rendus» еще до того, как написанный на немецком языке труд Кан-
тора увидел свет. Одно из его нововведений Пуанкаре принял настолько
быстро, что даже не успел подобрать для него французский эквивалент,
и в своей первой статье, опубликованной в «Acta», обозначил множе-
ства немецким словом Mengen.
3. Алгоритмы построения фрактальных предельных множеств
клейновых групп, а точнее: групп, основанных на инверсиях
Находясь под влиянием слов Адамара о Пуанкаре и еще не столк-
нувшись с «клейновыми» предельными множествами собственной пер-
соной, мне удалось освежить свое понимание, ознакомившись с книгой
Вильгельма Магнуса (1907-1990), который тогда служил профессором
математики в Университете Нью-Йорка. Он прославился своей работой
по теории групп, специальным функциям и математической физике. Ра-
бота Magnus 1974 старомодна в самом прекрасном смысле этого слова.
Она была написана, чтобы привлечь внимание к труду Fricke & Klein
1897, который к тому времени был практически полностью забыт. Со-
ответственно, в ней воспроизводились оригинальные иллюстрации, ко-
торым я уделил немного внимания во время празднования столетия со
дня рождения Пуанкаре в 1954 году.
Возможно ли, что я был единственным человеком достаточно пожи-
лым и старомодным, чтобы иметь основательные знания в традиционной
геометрии, но при этом достаточно молодым и активным, чтобы хорошо
разбираться в компьютерах? Как бы то ни было, Магнус вдохновил ме-
ня на работу. Балуясь с компьютером и рассматривая тысячи рисунков,
я через несколько недель пришел к созданию очень быстрого алгоритма,
который, хоть и с опозданием, но все же был описан в работе М 1982F
{смотрите главу С16) и М 1982т{С18}. На протяжении тех недель мне
помогал отличный программист Питер Оппенгеймер, студент Прин-
стонского университета, который тогда был на каникулах; впоследствии
он сделал карьеру в индустрии СМИ.
С15. Клейновы группы
Чтобы оценить всю простоту моего алгоритма, взгляните на рису-
нок 1 из главы С16, где сравниваются два способа построения предель-
ного множества £ группы, основанной на инверсиях в четырех больших
белых кругах в левой верхней части рисунка. Это предельное клейново
множество представляет собой непрерывную петлю без двойных точек,
то есть жорданову кривую. Метод Пуанкаре (верхняя часть рисунка)
сходится чрезвычайно медленно. Мой метод (средняя часть) сходится
очень быстро; в результате, как общий предел внутренней и внешней ап-
проксимации получается множество £. На нижней части видно, что мой
метод, в сущности, поразительно схож с методом Э.Чезаро (1859-1906)
для классической кривой Коха. В оригинальном контексте (рисунок 43
из работы M1982F) эта нижняя часть сопровождается подробными объ-
яснениями.
4. Неожиданный и, вероятно, значимый перерыв
длиной в 100 лет
На протяжении ста лет многие великие математики, да и, вероят-
но, бесчисленное множество любителей пытались создать быстрый ал-
горитм. Невероятно (а учитывая ту простоту, с которой сей «трофей»
был добыт, даже немного стыдно), но факт: никому из них не удалось
этого добиться. В числе этих искателей был Дэвид Мамфорд, который
сейчас работает в Брауновском университете, а в 1979-1980 годах был
профессором математики в Гарварде, моим коллегой и гостеприимным
хозяином, которому я выражаю огромную признательность.
В декабре 1980 года после того, как я прочитал свою первую лек-
цию по итерации рациональных функций, Мамфорд поинтересовался, не
хочу ли я заняться еще и поисками алгоритма для клейновых предель-
ных множеств. В ответ я показал ему набросок работы М 1982m{C 18}.
Он очень удивился увиденному, а затем заметил, что я использовал
«древние» инструменты, чрезвычайно простые и, без сомнения, близко
знакомые Пуанкаре, Фрикке и Клейну. Он спросил меня, как мне уда-
лось добиться успеха там, где очень многие пытались, но большинство
потерпело крах.
Тогда я в очередной раз вкратце изложил уже не раз рассказан-
ную историю своей научной жизни; историю о том, что, когда я ищу,
я смотрю, смотрю и еще раз смотрю и забавляюсь с рисунками. Од-
на картинка подобна одному прочтению научной работы. Одного раза
никогда не бывает достаточно.
В то время теория клейновых групп находилась в странном поло-
жении. Выдающиеся ученые, как Ларс Альфорс (1907-1996) в Гарварде
С15. Клейновы группы
и Липман Берс (1914-1993) в университете Колумбии, способствовали
весьма ощутимому продвижению этой теории. Однако создавалось впе-
чатление, что их работы слишком сложны для дальнейшего развития,
поэтому мой алгоритм мало кому был интересен. Но однажды, благода-
ря тонким стенам своего рабочего кабинета в Гарварде, я услышал тер-
мин «клейнова группа». Говоривший, коим оказался С. Дж. Паттерсон,
подтвердил, что эта тема практически не вызывает интереса в научном
сообществе. Я убедил его, что нам следует убедиться в недостатке ин-
тереса, и мы организовали семинар. На первую встречу пришло человек
тридцать!
Естественно, одним из них был Мамфорд. Он вызвался помочь мне
в работе, и (за рекордные сроки!) мои ассистенты обучили его компью-
терному программированию. Также я представил его Дэвиду Райту -
именно с ним тогда разговаривал Паттерсон. Он признал, что весьма
силен в программировании, но считает, что выпускники Гарварда не
должны проповедовать эту ересь. Многие (но не все!) увлеклись изуче-
нием возможностей компьютера, и вскоре Мамфорд ушел из алгебраи-
ческой геометрии — области, в которой считался главным авторитетом.
Он проводил компьютерные исследования клейновых групп более слож-
ной структуры, нежели те, которые рассматривал я. Одно из первых
изображений, полученное им во время одного из приездов в IBM, попа-
ло в работу M1982F и представлено там на рисунке 178. В настоящее
время он работает над созданием компьютеризированной теории зрения.
О событиях 1979 года, когда я передал Мамфорду свою преданность
силе наблюдения, написано в замечательной книге (Mumford, Series, &
Wright, 2002). Тут нельзя не задаться вопросом: сможет ли эта книга
произвести тот же эффект, который в свое время произвел труд Peitgen
& Richter 1986? За те двадцать лет, что минули с 1980-х годов, свет
увидели «лавины» книг по итерации, но ни одна из них не касалась
♦Клейна». Этой засухе пора положить конец.
5. Можно ли сказать, что переход от рисунков ради рисунков
к изображениям, открывшим новые математические горизонты,
был предопределен заранее?
Сегодня, спустя много лет после тех событий, может показаться,
что этот переход был предначертан. Однако то, с какими проблемами
нам пришлось столкнуться на своем пути, хорошо видно из следующего
примера. После открытия алгоритма я описал его во время своего приез-
да к Вильгельму Магнусу. Последний был удивлен, потрясен и всячески
С15. Клейновы группы
223
выражал свою поддержку. Затем, незадолго до моего ухода, он передал
мне тяжелую папку с рисунками, изображающими клейновы предель-
ные множества и присланными несколькими преданными почитателями
труда Magnus 1974, имевшими доступ к компьютеру и плоттеру. Те ри-
сунки были более точными, чем изображения, созданные в 1890-х годах,
но они не пробудили ни свежего понимания, ни вдохновения. Сегодня
создание рисунков — это несложный механический процесс, но умение
их «читать» остается большим искусством. Этот приезд к Магнусу, как
показало открытие множества Мандельброта, служит не первым и не
последним подтверждением данного факта.
Кроме того, я показал Л. Берсу исправленную версию рисунка 156
(«разобранного» в М 1982т{С18}) из труда Fricke & Klein 1897. Он
повел себя весьма резко и сказал, что сожалеет о том, что старое изоб-
ражение этого предельного множества оказалось столь дезориентиру-
ющим. Однако интуитивно это изображение было ему ближе, так что
Берс остался верен ему, несмотря ни на что. Был он серьезен или шу-
тил? Вероятнее всего, для него все это не имело значения, поскольку
его интуиция была, скорее, аналитической, нежели визуальной.
6. Понятие СИФ (систем или схем итерированных функций) или
разложимых динамических систем
Когда в 1979 году Мамфорд принимал меня в Гарварде, его уди-
вило, что я всегда начинаю изучение новых клейновых групп с помо-
щью следующего метода. Предположим, что нам дана группа, основан-
ная на преобразованиях Gm. Поставим в соответствие каждому пре-
образованию Gm вероятность рт того, что именно оно будет выбрано
следующим. Для изучения подгрупп положим значения некоторых рт
равными 0. Бесконечная последовательность индексов, m(l), т(2)...
m(/i), ..., определяет «орбиту», которую и следует рассмотреть. На ри-
сунке 4 из М 1980п{СЗ} показано, что я придерживался этого метода,
исследуя полугруппу инверсий z2 + с, а именно: полугруппу, в основе
которой лежит преобразование ±y/z — с.
В конце девятнадцатого века я представлял этот метод в неявном
виде; он не был никем исследован и не имел никакого названия. Впо-
следствии, его стали повсеместно обозначать тремя буквами «СИФ».
Майкл Барнсли назвал его «системами итерированных функций», а Кен-
нет Фальконер — «схемами итерированных функций». На сегодняшний
день известно множество свойств линейных СИФ, которые подтвержде-
ны полными математическими доказательствами.
224 С15. Клейновы группы
Однако, в 1979 году не было предпринято даже попытки математи-
чески доказать клейновы предельные множества. Я понял, что пределы
этих множеств и соответствующей орбиты СИФ вполне могут разли-
чаться. Когда Мамфорд высказал неодобрение подобной бесцеремонно-
сти, я возразил, что лучшего способа «выловить» легкий способ про-
сто не может быть. Кроме того, оба случая, когда эти два множества
действительно различались, заслуживали самого пристального внима-
ния. Для приближения предела СИФ достаточно простого механическо-
го процесса, и именно его следует попробовать в первую очередь. Затем,
нужно изучить достаточное количество вариантов предела СИФ с целью
обнаружения структур, которые видны невооруженным глазом. Затем
наступает период тщательного обдумывания полученной информации.
Безусловно, именно эта стратегия позволила достичь самого известно-
го успеха, коим стало, объявленное чуть позже, открытие множества
Мандельброта.
На самом деле я держал в голове идею «обобщенных СИФ», кото-
рая была выдвинута в главе 20 работы М 1982F, но так и не получила
должного развития. СИФ можно рассматривать как динамическую си-
стему, раскладываемую на ряд операций и «головной процесс», управ-
ляющий последовательностью этих операций. В СИФ головной процесс
представляет собой независимую случайную последовательность т(1),
т(2), ..., 7п(/г), но, в принципе, он может быть любой из «достаточно
смешанных» эргодических динамических систем.
7. Мультифрактальные инвариантные меры клейновых групп
При более подробном исследовании клейновых групп обнаружива-
ются меры, которые анализируются в главе IV этой книги, а особенно
тщательно — в главе С19, служащей вводной к оной.
Фрактальная геометрия природы, 1982, глава 18
С16
Самоинверсные фракталы,
аполлониевы сети и мыло
Предисловие к главе (2003). По сравнению с главой 18 из М
1982F, в этой главе добавлен рисунок из главы 20, имеющий к дан-
ному вопросу самое непосредственное отношение. Поскольку необыч-
ный формат работы M1982F пришлось адаптировать к формату данной
книги, я произвел ряд нелинейных перестановок, которые потребовали
добавления новых комментариев, обеспечивающих логическое изложе-
ние и целостность повествования. На последней странице оригинального
текста был представлен краткий обзор труда М 1983т{С18}; его я ре-
шил исключить. Рисунки были уменьшены, а подписи к ним включены
в основной текст.
Большая часть [М 1982F] посвящена фракталам, которые либо пол-
ностью инвариантны при преобразованиях подобия, либо, по меньшей
мере, «почти» инвариантны. В результате у читателя могло сложиться
впечатление, что понятие фрактала неразрывно связано с самоподоби-
ем. Это решительно не так, однако поскольку мы только начинаем
знакомиться с фрактальной геометрией, мы должны прежде всего рас-
смотреть своего рода фрактальные аналоги прямых линий евклидовой
геометрии... мы можем называть их «линейными фракталами».
В главах 18 и 19 [М 1982F] мы сделаем следующий шаг. В них
вкратце описываются свойства фракталов, которые представляют собой,
соответственно, наименьшие множества, инвариантные при геометриче-
ской инверсии, и границы наибольших ограниченных множеств, инва-
риантных при возведении в квадрат.
Оба этих семейства фундаментально отличаются от самоподобных
фракталов. При должным образом выбранных преобразованиях масшта-
бируемые фракталы остаются инвариантными, однако для их построения
необходимо указать форму генератора и установить ряд других правил.
С другой стороны, одного того, что фрактал «генерируется» каким-либо
нелинейным преобразованием, часто бывает достаточно для определе-
ния, т.е. генерации, его формы. Кроме того, многие нелинейные фрак-
226
Фрактальная геометрия природы, гл. 18
талы ограничены, то есть имеют заранее заданный конечный внешний
порог П < оо. Те, кого по каким-либо причинам не устраивала неогра-
ниченность Q, будут, несомненно, обрадованы этим обстоятельством.
Первые самоинверсные фракталы были представлены на суд публи-
ки в 80-х годах XIX века Анри Пуанкаре и Феликсом Клейном вскоре
после того, как Вейерштрасс построил непрерывную, но недифференци-
руемую функцию — примерно в одно время с множествами Кантора и за-
долго до кривых Пеано и Коха и их масштабно-инвариантных родствен-
ников. Ирония заключается в том, что самоподобные фракталы нашли
себе надежное место под солнцем в качестве материала для всевозмож-
ных контрпримеров и математических игр, а самоинверсные фракталы
образовали узкоспециальный раздел теории автоморфных функций. Тео-
рией этой некоторое время никто не занимался, затем она возродилась,
но в весьма абстрактной форме. Одна из причин того, что самоинверсные
фракталы оказались полузабыты, состоит в том, что их действительная
форма оставалась неисследованной вплоть до настоящей главы, в кото-
рой вашему вниманию будет предложен новый эффективный способ их
построения.
В последнем разделе главы мы рассмотрим одну физическую про-
блему, главным героем которой оказывается простейший самоинверсный
фрактал.
Биологическая форма и «простота»
Как мы вскоре увидим, многие нелинейные фракталы имеют «орга-
нический внешний вид», поэтому данное отступление посвящено биоло-
гической теме. Биологические формы часто чрезвычайно сложны, и мо-
жет показаться, что программы, отвечающие за выращивание таких
форм, должны быть очень громоздкими.
Однако структура упомянутых сложных форм очень часто включа-
ет в себя многочисленные повторы. Вспомните, как в конце главы 6 [из
М 1982F] мы говорили о том, что кривую Коха нельзя считать ни ирре-
гулярной, ни чрезмерно сложной, поскольку она порождается простым
и систематическим правилом. Все дело в том, что правило применяется
снова и снова, последовательными циклами. В главе 17 [из М 1982F]
эти же соображения распространены на кодирование структуры легких.
В главах 18 и 19 [из М 1982F; С4 и С16 в этой книге] мы намерены
пойти гораздо дальше и обнаружить, что одни фракталы, построенные
согласно нелинейным правилам, напоминают то насекомых, то головоно-
гих, тогда как другие похожи на растения. Парадокс исчезает, уступая
место невероятно тяжелому труду воплощения идей в реальность.
С16. Самоинверсные фракталы, аполлониевы сети и мыло
227
{P.S. 2003. Это явное обращение к биологическим формам вдохно-
вило многих авторов на создание работ, в которых некоторые из них
проявляют в развитии данной мысли не вполне обоснованное на данный
момент рвение}.
Стандартная геометрическая инверсия
Следующей по сложности геометрической фигурой после прямой
в евклидовой геометрии является окружность, причем окружность оста-
ется окружностью не только при преобразовании подобия, но и при
инверсии. Многие ученые последний раз слышали об инверсии еще
в школьные годы, поэтому, на мой взгляд, не лишним будет повторить
основные положения. Возьмем окружность С радиуса R с центром в точ-
ке О; инверсия по отношению к окружности С преобразует некоторую
точку Р в точку Р', такую, что Р и Р' лежат на одном луче с началом
в точке О, причем длины отрезков |ОР| и ОР' удовлетворяют равен-
ству |ОР||ОР'| = R2. Окружности, содержащие точку О, инвертируются
в прямые, не содержащие точки О, и наоборот (см. ниже). Окружности,
не содержащие точку О, инвертируются в окружности (см. ниже, тре-
тий рисунок). Окружности, ортогональные С, и прямые, проходящие
через точку О, остаются инвариантными при инверсии относительно С
(четвертый рисунок).
Рассмотрим теперь совокупность трех ок-
ружностей: Ci, Сг и Сз. Обычно — например,
когда открытые ограниченные круги, грани-
цами которых являются окружности Стп, не
пересекаются, — существует окружность Г,
ортогональная каждой из окружностей Ст
(смотрите выше). Если окружность Г суще-
ствует, она совместно самоинверсна относительно Ст.
228
Фрактальная геометрия природы, гл. 18
Эти краткие сведения практически исчерпывают то, что стандартная
геометрия способна нам поведать о самоинверсных множествах. Осталь-
ные самоинверсные множествами фрактальны, и большинство из них
можно назвать какими угодно, но никак не гладкими.
Генератор. Самоинверсные множества. Как обычно, мы начина-
ем с генератора, который в данном случае состоит из некоторого (како-
го угодно) числа hl окружностей Ст. Преобразования, представляющие
собой последовательность инверсий относительно этих окружностей, со-
ставляют то, что алгебраисты назвали бы группой, порождаемой этими
инверсиями; обозначим ее буквой Q. Для обозначения «самоинверсного
множества» имеется и формальный термин: «множество, инвариантное
под действием операций группы Q».
Затравки и кланы. Возьмем любое множество Т (назовем его за-
травкой) и добавим к нему преобразования множества I под действием
всех операций группы Q. Результат, который мы назовем кланом I, яв-
ляется самоинверсным. Хотя, конечно, смотреть тут особо не на что.
Например, если множество Г представляет собой расширенную плос-
кость Rx (т. е. плоскость Rx плюс точка в бесконечности), то клан I
абсолютно идентичен множеству Rx = 1.
Хаотические инверсные группы. Кроме того, может случиться
так, что при некоторой заданной группе Q, основанной на инверсиях,
клан каждой области 1 покрывает всю плоскость целиком. В этом слу-
чае самоинверсное множество также должно представлять собой всю
плоскость целиком. По причинам, которые прояснятся в главе 20 [из М
1982F], я предлагаю называть такие группы хаотическими. Нехаотиче-
скими группами мы обязаны Пуанкаре, однако они носят имя Клейна:
дело в том, что Пуанкаре однажды ошибочно приписал какую-то из
предыдущих работ Клейна Л. Фуксу; Клейн выразил протест, и Пуанка-
ре в знак примирения пообещал, что назовет свое следующее великое
открытие именем Клейна — и ведь назвал!
Придерживаясь пока нехаотических групп, обсудим три самоин-
версных множества, отобранных еще Пуанкаре, затем еще одно мно-
жество неясного происхождения и, наконец, пятое, важность которого
я обнаружил самостоятельно.
Гиперболическая мозаика или тайлинг
Не многим из поклонников творчества Морица Эшера известно,
что этот знаменитый рисовальщик частенько черпал вдохновение непо-
с 16. Самоинверсные фракталы, аполлониевы сети и мыло 229
средственно из трудов «неизвестных» математиков и физиков (Coxeter
1979). Вся его работа часто состояла в простом добавлении украшений
к самоинверсным мозаикам, известным Пуанкаре и представленным на
многочисленных иллюстрациях в работе Fricke & Klein 1897.
Эти множества (обозначим их через J) получаются посредством
объединения кланов самих окружностей
Так как группа Q нехаотична, дополнением объединенных кланов
окружностей Ст является совокупность круговых многоугольников, на-
зываемых «открытыми плитками». Любую открытую плитку (или ее за-
мыкание) можно трансформировать в любую другую открытую (или за-
мкнутую) плитку посредством последовательности инверсий, принад-
лежащих группе <3. Иными словами, клан любой замкнутой плитки
есть Rx. Что более важно, клан любой открытой плитки есть дополне-
ние множества J. A J является, так сказать, «раствором», на кото-
рый укладываются эти плитки. Плоскость Rx самоинверсна. Множе-
ство J и его дополнение также самоинверсны и образуют «гиперболи-
ческое разбиение» или «мозаику» на плоскости Rx. (Английское слово
tessellation, «мозаика», происходит от латинского tessera, «квадрат», ко-
торое, в свою очередь, восходит к греческому слову, обозначающему
«четыре»; однако плитки вовсе не обязательно должны быть четырех-
угольными — подойдет любое число, большее 2.) А на рисунках Эшера
каждая плитка украшена вдобавок причудливой картинкой.
Предельное множество инверсной группы
Самым интересным самоинверсным множеством является самое ма-
ленькое. Оно называется предельным множеством (и обозначается бук-
вой £), поскольку является также множеством предельных точек преоб-
разований любой исходной точки под действием операций группы G. Оно
принадлежит клану любой затравки I. Проясним формальное определе-
ние: множество С состоит из таких предельных точек, которые не могут
быть получены конечным числом инверсий. На интуитивном уровне это
множество можно представить как область скопления бесконечно малых
потомков.
Множество £ можно свести к точке или окружности, однако в об-
щем случае оно является фрагментированным и/или иррегулярным
фрактальным множеством.
Множество £ стоит в мозаике особняком, как «множество беско-
нечно малых плиток». Оно играет по отношению к конечным элементам
мозаики такую же роль, какую играют концы ветвей (см. главу 16) по
230
Фрактальная геометрия природы, гл. 18
отношению к самим ветвям. Однако здесь ситуация проще: подобно £
мозаика J представляет собой самоинверсное множество без остатка.
Аполлониевы сети и салфетки
Множество С называется аполлониевым, если оно состоит из бес-
конечного количества окружностей вместе с их предельными точками.
В данном случае его фрактальность является исключительно следствием
фрагментации. Этот прецедент был изучен и осмыслен (хотя и в несколь-
ко многословной манере) на раннем этапе истории предмета.
Сначала мы построим основной пример,
а затем покажем его самоинверсность. Аполло-
ний Пергский — это древнегреческий мате-
матик, живший в III веке до нашей эры. Он
был представителем александрийской школы
и верным последователем Евклида и изве-
стен, помимо прочего, тем, что составил алго-
ритм построения пяти окружностей, касатель-
ных к трем заданным окружностям. В том слу-
чае, когда заданные окружности взаимно ка-
сательны, число аполлониевых кругов равно
двум. Как мы вскоре убедимся, вполне мож-
но предположить, не потеряв при этом в общности, что две из заданных
окружностей являются внешними по отношению друг к другу, но содер-
жатся внутри третьей, как видно на рисунке справа.
Эти три окружности определяют два круговых треугольника, уг-
лы которых равны 0°. А аполлониевы окружности — это наибольшие
окружности, какие можно вписать в эти треугольники, как показано на
рисунке внизу справа.
Законченное аполлониево построение
включает в себя пять окружностей, три задан-
ных и две аполлониевых, которые вместе
определяют шесть круговых треугольников.
Повторяя вышеописанную процедуру, впишем
в каждый треугольник наибольшую возмож-
ную окружность. Результат бесконечного по-
вторения такой процедуры называется «апол-
лониевой упаковкой». А если добавить к этой
бесконечной совокупности окружностей ее
предельные точки, то получится множество,
С16. Самоинверсные фракталы, аполлониевы сети и мыло
231
которое я назвал «аполлониевой сетью». Область сети, заключенную
внутри кругового треугольника (как показано на рисунке) будем назы-
вать «аполлониевой салфеткой». Если одну из аполлониевых окруж-
ностей первого поколения заменить на любую из заданных внутренних
окружностей, предельное множество никак не изменится. Если указан-
ной аполлониевой окружностью заменить внешнюю заданную окруж-
ность, то построение начинается с трех заданных окружностей, внешних
по отношению друг к другу, и одна из аполлониевых окружностей пер-
вого этапа окажется наименьшей окружностью, описанной вокруг трех
заданных. После такого нетипичного этапа построение продолжается
так же, как описано выше, подтверждая то, что наш рисунок и в самом
деле соответствует наиболее общему случаю.
Упаковка Лейбница. Аполлониева упаковка похожа на конструк-
цию, описанную Лейбницем в письме к де Броссу: «Представьте себе
окружность, а затем впишите в нее еще три окружности наибольшего
возможного радиуса, конгруэнтные друг другу: повторите аналогичную
операцию с каждой из этих окружностей и с каждым промежутком
между ними. А теперь вообразите, что этот процесс продолжен до бес-
конечности. ..».
Аполлониевы
сети самоинверсны
Вернемся к началу построения
аполлониевой сети: трем касатель-
ным окружностям. Добавим сюда
любую из соответствующих апол-
лониевых окружностей и назовем
получившиеся четыре окружности
Г-окружностями. На рисунке спра-
ва все четыре показаны жирными
линиями.
Существует четыре комбина-
ции из трех Г-окружностей (мы
будем называть их триплетами),
и каждой из них соответствует
окружность, ортогональная каж-
дой окружности триплета. Возьмем
эти новые окружности в качестве
генератора и обозначим через Ci,
232
Фрактальная геометрия природы, гл. 18
С2. G и С4 (на рисунке ниже они показаны тонкими линиями). А Г-ок-
ружность, ортогональную окружностям Ci, Cj и Ск, обозначим как Гч*..
Разделавшись с нудным развешиванием ярлыков, получаем заслу-
женную награду. Даже самое поверхностное рассмотрение показывает,
что наименьшее (замкнутое) множество, самоинверсное по отношению
к четырем порождающим окружностям Ст представляет собой аполло-
ниеву сеть, построенную на четырех Г-окружностях. Любопытно, что
об этом наблюдении никто явным образом не сообщает.
При более тщательном изучении мы увидим, что каждая окруж-
ность в сети преобразуется в одну из Г-окружностей, проходя через уни-
кальную последовательность инверсий относительно окружностей С.
Таким образом, принадлежащие аполлониевой сети окружности можно
рассортировать на четыре клана, причем клан, нисходящий от окружно-
сти Tijk, мы будем обозначать как QT^k-
Вязание сетей из одной нити
Аполлониева салфетка и салфетка Серпинского (рис, 205 [из М
I982F]) имеют одно важное общее свойство: дополнение салфетки Сер-
пинского представляет собой объединение треугольников (сг-треуголь-
ник), а дополнение аполлониевой сети или салфетки есть объединение
дисков (ст-диск).
Однако нам также известно, что салфетка Серпинского допускает
альтернативное кохово построение, в котором конечные приближения
являются терагонами (ломаными линиями) без самокасаний, а двойные
точки появляются только в пределе. Это означает, что салфетку Серпин-
ского можно построить, не отрывая карандаша от бумаги; через некото-
рые точки линия пройдет дважды, но она никогда не пройдет дважды
по одному отрезку прямой.
Выражаясь метафорически, салфетку Серпинского можно связать
из одной-единственной нити!
То же верно и для аполлониевой сети.
Несамоподобные каскады и оценка размерности
Круговые треугольники аполлониевой упаковки не подобны друг
другу, следовательно, аполлониев каскад не самоподобен, а аполлоние-
ва сеть не является масштабно-инвариантным множеством. Сейчас сле-
довало бы обратиться к определению Хаусдорфа-Безиковича для раз-
мерности D (как показателя, определяющего меру), которое применимо
С16. Самоинверсные фракталы, аполлониевы сети и мыло
233
к любому множеству, однако получение D таким способом оказывается
удивительно сложным делом. Так, в работе Boyd 1973а,b показано, что
1,300197 < D < 1,314534,
хотя последние (еще не опубликованные) численные эксперименты это-
го же автора дают другой результат: D ~ 1,3058. {P.S. 2003. Точное
значение не известно до сих пор. В труде Thomas & Dhar 1994 предла-
гается D = 1,305686729, а в работе McMullen 1998 — D = 1,305688}.
В любом случае, аполлониевы салфетка и сеть являются фракталь-
ными кривыми. В данном контексте величина D представляет собой
меру фрагментации. Если, например, «удалить» диски, радиус которых
меньше е, то периметр оставшихся промежутков будет пропорциона-
лен e1~D, а площадь — пропорциональна e2~D.
Множество £ в нефуксовых цепях Пуанкаре
Самоинверсные фракталы, получаемые при инверсиях относитель-
но не столь особых конфигураций порождающих окружностей Сгп, ока-
зываются более сложными, чем любая аполлониева сеть. Чуть позже
я познакомлю вас со своей собственной рабочей конструкцией, которая
в большинстве случаев вполне удовлетворительно характеризует мно-
жество С. Она является большим шагом вперед по сравнению с преды-
дущим, предложенным Пуанкаре и Клейном, методом, который весьма
громоздок и очень медленно сходится.
Однако старый метод также сохраняет свою значимость, поэтому
я предлагаю рассмотреть его на примере особого случая. Пусть окруж-
ности Ст образуют конфигурацию, которую можно назвать цепью Пуан-
каре} эта конфигурация представляет собой совокупность М окружно-
стей Ст, расположенных по кругу и соответственно пронумерованных,
так что окружность Ст касательна к Сш_1 и Cm+i (по модулю М) и не
пересекает никаких других окружностей цепи. В этом случае множе-
ство £ представляет собой кривую, которая разделяет плоскость на две
области — внешнюю и внутреннюю. (Воздавая должное Камилю Жор-
дану, который первым обнаружил неочевидность того, что плоскость
можно таким образом разделить одной-единственной петлей, такие пет-
ли называются с тех пор кривыми Жордана).
В случае когда все окружности Ст ортогональны одной окружно-
сти Г, множество £ совпадает с Г. Этот случай, называемый фуксовым,
в настоящей главе не рассматривается.
234
Фрактальная геометрия природы, гл. 18
Построение Пуанкаре для множества С
Ниже приводится полное описание общепринятого построения мно-
жества С и моего альтернативного варианта для случая особой цепи
с М = 4, показанной на следующем рисунке.
Для получения £ Пуанкаре и Клейн (см. Poincare, Fricke & Klein
1897) поэтапно заменяют исходную цепь цепями, составляемыми из все
возрастающего числа все уменьшающихся звеньев. На первом этапе
каждое звено С, заменяется инверсиями остальных звеньев Ст отно-
сительно С,; таким образом, получается, в общей сложности, М(М -
- 1) = 12 меньших звеньев. Они показаны в верхней части рисунка 1
на фоне негативного изображения исходных звеньев. И так далее — на
каждом этапе мы берем полученную на предыдущем этапе цепь и инвер-
тируем ее относительно каждого из исходных звеньев Ст- На рисунке
черным цветом показано несколько последовательных этапов построе-
ния, причем каждый из них наложен на результат предыдущего этапа,
показанный белым цветом на сером фоне. В конце концов цепь истон-
чается в нить, то есть в £.
К сожалению, некоторые звенья и после достаточно большого коли-
чества этапов остаются довольно крупными, и даже сильно продвинутые
аппроксимации предельной цепи дают довольно слабое представление
о множестве £. Это неприятное сбойство прекрасно проиллюстрировано
в работе М 1983пт{С18}.
Понятие о фрактальной оскуляции
Мой способ построения множества £ основан на новом для нас по-
нятии фрактальной оскуляции, которое расширяет рамки ее очевидного
воплощения в аполлониевом случае.
Стандартная оскуляция. Это понятие непосредственно связа-
но с концепцией кривизны. Первым приближением стандартной кривой
в окрестности регулярной точки Р является касательная прямая. Вто-
рым приближением является окружность, касательная к которой в этой
точке совпадает с упомянутой прямой, а кривизна — с кривизной кри-
вой. Такая окружность называется оскулирующей.
Для различения окружностей, касательных к данной кривой в точ-
ке Р, очень удобно использовать параметр (обозначим его буквой и),
который представляет собой инверсию (произвольно ориентированного)
интервала, соединяющего точку Р с центром окружности. Обозначим
индекс оскулирующей окружности через ио- Если и < uq, то небольшой
С16. Самоинверсные фракталы, аполлониевы сети и мыло
235
Рис. С16-1. [Рисунок объединяет изображения со страницы 173 и рисунки 177
и 43 из М 1982F]. Два построения предельного множества. На верхней части
представлен классический метод (Пуанкаре), на средней — предложенный мной
альтернативный способ, напоминающий построение Чезаро снежинки Коха, при-
веденное в нижней части
участок кривой с центром в точке Р целиком лежит с одной стороны
касательной окружности, если же и < и0, то — с другой.
Величина ио есть то, что физики называют критическим значе-
нием, а математики — разрезом. Кроме того, значение |ио| определяет
локальную «кривизну».
Глобальная фрактальная оскуляция. В случае аполлониевой се-
ти попытка определить оскуляцию через кривизну лишена смысла. Од-
236
Фрактальная геометрия природы, гл. 18
нако в любой точке сети, где касательны две принадлежащие упаков-
ке окружности, они, очевидно, «охватывают» остаток множества £, за-
ключенный между ними. Возникает искушение назвать обе окружности
оскулирующими.
Для того, чтобы распространить это понятие на неаполлониевы мно-
жества £, выберем точку, в которой С, имеет касательную, и возьмем
в качестве отправной точки определение обыкновенной оскуляции, осно-
ванное на понятии критичности (или разреза). Новизна же заключается
в том, что при -оо < и < 4-оо мы заменим одно критическое значе-
ние ио двумя различными значениями, и' и и" > и', которые определим
следующим образом: при любом и < и' множество С целиком лежит
с одной стороны нашей окружности, при любом и > и" — с другой,
а при и' < и < и" части С находятся и с той, и с другой стороны
окружности. Что же касается окружностей с индексами, равными и'
и и", я предлагаю обе эти окружности считать фрактально оскулирую-
щими.
Любая окружность ограничивает два открытых диска (один из них
содержит центр этой окружности, другой — точку в бесконечности). От-
крытые диски, ограниченные оскулирующими окружностями и не при-
надлежащие множеству £, мы будем называть оскулирующими дисками.
Случается и так, что одна или обе оскулирующие окружности вы-
рождаются в точку.
Локальное и глобальное. Возвращаясь к стандартной оскуляции,
заметим, что эта концепция является локальной, так как ее определение
никак не зависит от формы кривой на каком-либо удалении от точки Р.
Иными словами, кривая, касательная к ней и оскулирующая окружность
могут иметь сколько угодно точек пересечения кроме Р. Напротив, при-
веденное выше определение фрактальной оскуляции глобально, хотя это
различие и не принципиально. Фрактальную оскуляцию можно опреде-
лить и локально, причем с соответствующим расщеплением «кривизны»
на два числа. Как бы то ни было, в нашей теперешней задаче глобальная
и локальная оскуляции совпадают.
Оскулирующие треугольники. С аналогом глобальной фракталь-
ной оскуляции мы, если помните, уже встречались. Для того, чтобы
определить внутреннюю область нашей старой знакомой снежинки Ко-
ха (кривой К) как <т-треугольник, достаточно увеличивать треугольни-
ки, выкладываемые на каждом следующем этапе построения фигуры,
изображенной на рисунке 70 [из М 1982FJ, настолько, насколько это
возможно без пересечения их со снежинкой.
С16. Самоинверсные фракталы, аполлониевы сети и мыло
237
ст-диски, оскулирующие множество С
Оскулирующие диски и сг-диски являются ключевыми фигурами
в моем новом, свободном от недостатков [свойственных методу Пуан-
каре], способе построения множества £. Этот способ демонстрируется
в полном виде впервые (хотя о нем уже упоминалось в 1981 году в «Ма-
тематическом календаре»6). Суть его в том, что следует инвертировать
не сами окружности Ст, а некоторые из окружностей которые
(согласно определению на странице 244 [из М 1982F]) ортогональны
триплетам Ci, Cj и Ск- Здесь мы опять полагаем, что не все окружно-
сти совпадают с одиночной окружностью Г.
Ограничение М = 4. Если ограничить число исходных окружно-
стей М четырьмя, то мы сможем быть уверены в том, что для любого
триплета г, j, к один из двух открытых дисков, ограниченных окруж-
ностью (т. е. либо внутренний, либо наружный), не содержит ни
одной из точек 7mn, определенных ранее. Обозначим этот свободный от
точек 7 диск через Aijk-
Основой моего способа построения £, представленного в средней
горизонтальной части рисунка 1, послужили следующие наблюдения:
все свободные от 7 диски Д^ оскулируют £; таким же свойством обла-
дают их инверсии и повторные инверсии относительно окружностей Ст,
а кланы, построенные с применением дисков Д1дк в качестве затравок,
заполняют всю плоскость за исключением кривой £.
Цепь Пуанкаре, изображенная в более крупном масштабе
Как и в большинстве случаев, первый этап построения обрисовыва-
ет кривую £ довольно точно. Последующие стадии весьма «эффективно»
добавляют все более мелкие детали, и после нескольких этапов мы уже
вполне можем мысленно интерполировать кривую £, не отвлекаясь на
ошибки, от которых, к сожалению, не свободен подход Пуанкаре.
Левая фигура средней полосы рисунка 1. В цепях Пуанкаре
с М = 4 по крайней мере один из дисков Д^ (назовем его Д123)
всегда не ограничен и пересекается с диском Дз41- (На данном рисун-
ке диск Д341 также не ограничен, однако в других случаях это не так.)
Объединение дисков Д]2з и Д341 (показанное на рисунке серым цветом)
дает первое приближение области, внешней к кривой £. Оно аналогично
приближению области, внешней к кривой Коха /С, с помощью правиль-
ного выпуклого шестиугольника, изображенного на нижней полосе.
6The 1981 Springer Mathematical Calendar. — Прим, перев.
238
Фрактальная геометрия природы, гл. 18
Диски Д034 и Д412 также пересекаются, и их объединение (пока-
занное на рисунке черным цветом) дает первое приближение внутренней
области С. Оно аналогично приближению внутренней области кривой К.
с помощью двух треугольников, образующих правильную шестиконеч-
ную звезду, изображенную в нижней полосе слева.
Средняя фигура средней полосы рисунка 1. Второе приближение
области, внешней к кривой £, достигается добавлением к дискам Д123
и Д341 их инверсий относительно окружностей С4 и Сг, соответственно.
Результат (серая область) аналогичен второму приближению области,
внешней к кривой /С, в нижней полосе.
Соответствующее второе приближение внутренней области £. до-
стигается добавлением к дискам Д234 и Д412 их инверсий относительно
окружностей Ci и Сз, соответственно. Результат (черная область) ана-
логичен второму приближению внутренней области кривой /С в левой
части нижней полосы рисунка.
Правая фигура средней полосы рисунка 1. Внешняя область £
(серый цвет) является объединением кланов Д123 и Дз41- Внутренняя
же (черный цвет) — объединением кланов Д234 и Д412- Черная и се-
рая открытые области вместе покрывают всю плоскость (за вычетом
кривой £). Тонкая структура внутренней области £ для другой цепи
Пуанкаре представлена в М 1983ш{С18).
Обобщения
Цепи из пяти и более звеньев. В случае, когда число исходных
звеньев в цепи Пуанкаре превышает четыре, мой новый способ построе-
ния множества £ включает в себя дополнительный шаг: сначала следует
разделить окружности Г на две группы. Дело в том, что некоторые из
окружностей Г в этом случае таковы, что каждый из ограниченных ими
открытых дисков содержит, по меньшей мере, одну точку утп, в резуль-
тате чего диск Д^к оказывается не определен. Такие окружности Г не
оскулируют кривую £, а пересекают ее. Однако для построения кри-
вой £ они нам не нужны.
Остальные окружности Гук определяют оскулирующие диски Дук,
которые, в свою очередь, также делятся на два класса. При добавле-
нии к диску Дук первого класса его кланов мы получим внутреннюю
область кривой £; проделав же такую операцию с диском, принадлежа-
щим ко второму классу, получим внешнюю область £.
Это верно для многих (но не для всех) случаев, когда окружно-
сти Ст не образуют цепь Пуанкаре.
С16. Самоинверсные фракталы, аполлониевы сети и мыло
239
Перекрывающиеся и/или разорванные цепи. В случае, когда
окружности Ст и Сп имеют две точки пересечения 7^п и 7^п, эти точ-
ки совместно заменяют точку 7. Если же окружности Ст и Сп не имеют
ни одной точки пересечения, 7 заменяется двумя взаимно инверсными
точками 7^п и 7^п. Критерий идентификации становится при этом
довольно громоздким, однако основная идея остается неизменной.
Разветвленные самоинверсные фракталы. Кривая С может со-
единять в себе характерные особенности как смятой петли (кривой Жор-
дана), так и аполлониевой сети, в результате чего мы получаем фрак-
тально разветвленную кривую, близкую к тем, что мы рассматривали
в главе 14 [из М 1982F], но часто гораздо более причудливого вида, как
на рисунке С7.
Самоинверсные пыли. Множество С может также оказаться фрак-
тальной пылью.
{P.S. 2003. Пример предельного множества как аттрактора СИФ
или «разложимой динамической системы»
Основная часть данной главы повторяет главу 18 из М 1982F, од-
нако рисунок 283 главы 20 воспроизводит нагрудник фараона, который
тесно связан с этой темой. В этой книге он изображен на рисунке 2.
На обложке книги M1999N это изображение приводится в цвете и со-
провождается пояснительной диаграммой, также представленной на ри-
сунке 2. Шесть его окружностей расположены таким образом, чтобы
предельное множество представляло собой совокупность окружностей.
Выбирая эти окружности с предопределенной вероятностью мы получа-
ем то, что в главе 20 из М 1982F названо «разложимой динамической
системой», а теперь именуется СИФ.}
Аполлониева модель смектической структуры
В этом разделе мы ознакомимся с ролью, которую понятия аполло-
ниевой упаковки и фрактальной размерности играют в описании клас-
са веществ, известных под названием «жидкие кристаллы». В процессе
этого ознакомления нам предстоит обратиться к одной из наиболее ак-
тивных областей современной физики — теории критических точек.
Примером критической точки может служить «точка» на диаграмме
температура-давление, описывающая физические условия, при которых
в пределах одной физической системы могут сосуществовать в равно-
весии твердая, жидкая и газообразная фазы. Аналитические характери-
240
Фрактальная геометрия природы, гл. 18
стики физической системы в окрестности критической точки масштабно-
инвариантны, следовательно, подчиняются степенным законам с некими
конкретными критическими показателями (см. главу 36 [из М 1982F]).
Многие из этих показателей оказываются фрактальными размерностя-
ми. и вот перед вами первый пример.
Рис. С16-2. Рисунок С16-2. [Рисунок 283 из М 1982F и более детальный вариант
рисунка со страницы 129 из M1999N]. Изображающая «генератор» часть рисун-
ка состоит из шести серых кругов. Инверсии относительно этих кругов, совме-
щенные с предварительно заданными вероятностями, определяют «разложимую
динамическую систему», или СИФ. График из 64000 точек служит орбитой
этой системы (несколько первых точек на рисунке опущены). Эта орбита обра-
зует самоинверсный фрактал, но области в окрестностях точек его заострения
заполняются чрезвычайно медленно. (В части V эта медленность в упрощен-
ном виде анализируется для меры Минковского.) Новый алгоритм, описанный
в данной главе, опирается на оставшиеся восемь окружностей, изображенных на
рисунке жирными линиями. На разрисованном нагруднике фараона, представ-
ленном на странице 214, четыре окружности из восьми и их последовательные
инверсии представлены четырьмя видами «полудрагоценных камней».
Для описания жидких кристаллов я обращусь к работе Bragg 1934.
Эти прекрасные и таинственные субстанции подвижны, как жидкости,
однако с оптической точки зрения ведут себя подобно кристаллам. Их
длинные цепеобразные молекулы имеют довольно сложную структуру.
Некоторые жидкокристаллические фазы называются смектическими (от
С16. Самоинверсные фракталы, аполлониевы сети и мыло
241
греческого «ст/1777/1»», что означает «мыло»), так как они моделируют
мылообразные органические системы. Молекулы смектического жидко-
го кристалла расположены в слое вертикально и параллельно друг дру-
гу, как колосья на поле, при этом толщина слоя равна длине молеку-
лы. В результате получаются очень гибкие и прочные слои или листы,
которые, будучи деформированными, стремятся вернуть себе прежнюю
форму. При низких температурах слои располагаются один на другом,
точно листы в книге, образуя при этом твердый кристалл. Однако при
повышении температуры становится возможным легко сдвигать слои от-
носительно друг друга. Каждый слой представляет собой двумерную
жидкость.
Эта почти заполняющая плоскость фигура представляет собой пре-
дельное множество £ для группы гомографий. Дэвид Мамфорд постро-
ил его в 1982 году в ходе исследований, стимулом для которых послу-
жили новые результаты, о которых говорится в данной главе, а затем
любезно разрешил опубликовать свое построение в этой книге.
Особый интерес представляют фокальные конические структуры.
Жидкокристаллический блок разделяется на два набора пирамид, при-
чем основания половины из них располагаются на одной из двух проти-
воположных граней, а вершины — на другой. Жидкокристаллические
слои внутри каждой пирамиды оказываются свернутыми и образуют
множество очень заостренных конусов. Все конусы имеют общую вер-
шину и приблизительно перпендикулярны плоскости основания пира-
миды. В результате основанием каждого конуса является диск, ограни-
ченный окружностью. Минимальный радиус е такой окружности равен
толщине слоя жидкого кристалла. Когда конусы заключены внутри про-
странственной области — в данном случае, пирамиды с квадратным ос-
нованием, — диски, образующие основания конусов, распределяются по
основанию этой области (пирамиды). Для получения равномерного рас-
пределения следует начать с размещения на основании диска наиболь-
шего радиуса. Затем поместим диски наибольшего возможного радиуса
в каждый из остающихся углов и так далее. Если такое размещение про-
должать до бесконечности, в результате получится точная аполлониева
упаковка.
Физические свойства такой модели мыла зависят от общих площа-
ди и периметра пустых промежутков, которые связаны с фрактальной
размерностью £>, своего рода фотографического «негатива», то есть сал-
фетки, сквозь отверстия которой не проходят молекулы мыла. Физиче-
ские подробности этого явления можно найти в работе Bidaux, Воссага,
Sarma, Seze, de Gennes, & Parodi 1973.
242
Фрактальная геометрия природы, гл. 18
Рис. С16-3. [Рисунок 254 из M1982F]. Самогомографический фрактал, открытый
Дэвидом Мамфордом. Группы, основанные на инверсиях, интересуют математи-
ков прежде всего потому, что они связаны с определенными группами томогра-
фий. Гомография (называемая также гомографией Мебиуса или дробно-линей-
ным преобразованием) отображает z-плоскость по закону z —* {az + 6)/(cz + с!),
где ad-bc = 1. В наиболее общем виде эта гомография может быть представлена
как результат инверсии, симметрии относительно линии (что есть вырожденная
инверсия) и вращения. Вот почему при отсутствии вращения исследователь то-
мографий может почерпнуть много интересного из изучения групп, основанных
на инверсиях. Очевидно, однако, что введение вращений открывает новые бога-
тые возможности.
Симметрия
Под редакцией И.Харгиттаи и Т. Лорена, 2002
С17
Симметрии:
увеличение/уменьшение, фракталы
и неправильность форм
Предисловие к главе (2003). Этот текст нетехнического характе-
ра преследует две цели.
Во второй его половине с помощью СИФ иллюстрируется прибли-
зительная самоподобность в случае клейновых предельных множеств,
причем она относится, скорее, к мерам, нежели к множествам.
Первая же половина представляет собой краткое введение во фрак-
талы, которое должно оказаться полезным, по крайней мере, некоторым
читателям. Ее можно было бы разбить и, «объединив» с главой С23,
определить в последнюю часть этой книги. Но к чему лишние хло-
поты?
Характеристика фракталов
Грубо говоря, фракталы — это формы, которые имеют одинаковый
вид как при близком, так и при дальнем рассмотрении. Фрактальная
геометрия известна (или печально известна, в зависимости от точки
зрения) числом и явным разнообразием областей ее применения: от ма-
тематики, финансов и естественных наук до искусства.
Такое разнообразие всегда удивляет, но в этой главе мы попыта-
емся доказать, что оно совершенно естественно. Вообще, универсаль-
ность фракталов самым непосредственным образом связана с тем, что
они неотделимы от свойства, которое само по себе встречается повсюду.
Этим свойством является неправильность формы. Она долго не подда-
валась анализу, и фракталы сыграли роль первого широко применимого
ключа, позволившего хоть в какой-то степени подчинить себе хотя бы
некоторые из ее загадок.
244
Симметрия (Стокгольм), 2002
Кратко определение «имеют одинаковый вид как при близком,
так и при дальнем рассмотрении» можно выразить термином «самопо-
добный», который не требует объяснений. Безусловно, самоподобность
свойственна также прямой и плоскости. Эти известные формы служат
важной начальной точкой для многих наук, которые в совершенстве
овладели гладкостью. Дело в том, что способность «иметь одинаковый
вид как при близком, так и при дальнем рассмотрении» выходит за
пределы понятий прямой и плоскости. Она также характерна для раз-
личных форм, называемых фракталами. Я дал этим объектам имя, ввел
их в базовые модели неправильности форм и способствовал их размно-
жению.
Научное определение фракталов звучит так: «формы, инвариантные
при увеличении или уменьшении». На профессиональном жаргоне неко-
торых очень развитых областей науки такие инвариантности называются
симметриями. Это в достаточной мере объясняет, почему данная работа
была включена в эту книгу. Однако, на то есть еще одна, более важная
причина: очень скоро мы покажем, что подходящие комбинации весьма
обычных на первый взгляд симметрий таят в себе много сюрпризов для
их внимательного исследователя. Они спонтанно воспроизводят самопо-
добность, т.е. порождают фракталы.
Данная тема была вынесена в название статьи, и каждое слово из
названия уже было упомянуто (по крайней мере, вскользь) и даже вы-
делено курсивом. Тем не менее, следует рассказать об этимологии двух
из этих слов. В древнегреческом языке слово «summetria» простира-
лось много дальше простого обозначения своего собственного отраже-
ния в зеркале. Его близким синонимом было выражение «в точной про-
порции», которое чаще всего использовалось для описания произведения
искусства или музыкального произведения как «гармоничного». Со вре-
менем значения большинства слов становятся более многочисленными
и разнообразными. В развитых науках группы инвариантностей-симмет-
рий довольно абстрактны и малопонятны. В основе же теории фракта-
лов, напротив, лежат понятные и в высшей степени наглядные значения
этих слов. В данной работе мы покажем, что наиболее типичные из них
тесно связаны с простейшей зеркальной симметрией.
Что касается слова фрактал, то я придумал его в один памятный
вечер, зимой 1975 года, взяв за основу очень конкретное латинское при-
лагательное *fractus», обозначающее форму камня после очень сильного
удара. Из-за своей относительной молодости у слова «фрактал» не бы-
ло времени на развитие, поэтому его значение редко выходит за рамки
понятия неправильности формы.
Cl7. Симметрии
245
Земные вопросы, старые и новые, и повсеместность
неправильности формы в природе или культуре
Пуанкаре как-то заметил, что существуют вопросы, которые нам хо-
чется задать, и вопросы, которые возникают сами. Сейчас я перечислю
некоторое количество последних, причем нарочито бессистемным обра-
зом. Первые несколько вопросов касаются Природы и показывают, что
вопрос, который давно требовал ответа, видимо, оставлен детям.
• Как измерить и сравнить неправильность формы самых обычных
объектов типа щебня, металла, стекла или куска ржавого железа?
• Какова длина береговой линии Великобритании?
• Какую форму имеет Земля, а точнее: гора, береговая линия, течение
реки или водораздел двух рек? Иными словами, может ли термин
«геометрия» передать то, что обещает, но на самом деле даже не
рассматривает?
• Как определить скорость ветра во время бури?
• Какую форму имеет облако, пламя или сварной шов?
• Какова плотность галактик во Вселенной?
Недавно ряд вопросов к этому списку добавила культура:
• Как отличить настоящую музыку (старую или новую, хорошую или
плохую) от обычной какофонии?
• Как измерить изменение потока сообщений в сети Интернет?
• Как измерить неустойчивость цен на финансовых рынках?
Конкретная и конструктивная математика добавляет другие вопро-
сы, от которых пресловутый «среднестатистический человек» довольно
далек.
• Как охарактеризовать границу между двумя областями притяжения
в хаотической динамической системе?
• Как охарактеризовать границу плоскостного случайного блужда-
ния?
246
Симметрия (Стокгольм/, zuuz
• Как охарактеризовать случайное блуждание без самопересечений?
• Как охарактеризовать критические кластеры перколяции?
В одном примечательном примере изучения природы фрактальная
геометрия стала инструментом выбора после того, как с ее помощью
было сделано открытие.
• Как характеризовать ограниченные диффузией агрегаты (ОДА)?
Существует достаточное основание рассматривать все эти вопросы
совместно. Объекты последней группы построены «искусственно», по-
средством алгоритмов, которые полностью описаны, и, на самом деле,
чрезвычайно просты. С другой стороны, эти объекты невероятно слож-
ны. Любая нить, ведущая к их пониманию, непременно приведет также
к пониманию объектов, которые созданы Природой или являются непод-
властными нам аспектами культуры.
Выражение «неправильной формы» появляется только в одном из
вышеперечисленных вопросов, но понятие, на котором оно основано,
просматривается в каждом из них. (Слово «иррегулярный» было бы
более изящным, но выражение «неправильной формы» лучше передает
смысл). На все эти вопросы геометрия ответить не могла вплоть до появ-
ления фрактальной и мультифрактальной геометрии, в рамках которой
зародился полезный прикладной подход, основывающийся на удивитель-
ном факте: и в природе, и в культуре неправильность формы очень часто
является фрактальной.
Сначала в одной области, потом в следующей и так далее, фракталь-
ная геометрия стала первым инструментом, обеспечившим возможность
появления теории неправильности формы. Для примера рассмотрим пер-
вый из вышеуказанных вопросов. Первое свидетельство о фрактально-
сти изломов металла появилось в работе М. Passoja & Paullay 1984; до
этого же данное свойство демонстрировалось на втором и последующих
рисунках из М19871. С тех пор мы получили множество доказательств
данного факта и сумели показать, что он имеет место как для очень ма-
леньких размеров, так и для размеров в 100000 раз больше. Колебания
цен представляют собой мультифрактальные функции. Первое свиде-
тельство, описанное в М 1997Е, впоследствии получило многочислен-
ные подтверждения.
Для контраста рассмотрим обратный вопрос.
• Разумным приближением каких природных или рукотворных форм
служат простейшие гладкие формы евклидовой геометрии?
С17. Симметрии
247
Для первобытного человека Природа уготовила всего несколько
гладких форм: траектория движения камня, падающего вертикально
вниз; полная луна или солнце, окутанные дымкой; небольшие озера,
поверхность которых не возмущает ни течение, ни ветер. Напротив,
homo faber беспрестанно накапливает все новые и новые примеры, коим
несть числа. Так, человек изо всех сил старается избавиться от непра-
вильности формы автомобильных поршней, плоских стен и столешниц,
романо-китайско-американских уличных сетей, а также (последнее по
порядку, но не по значимости!) большинства разделов математики (что
только способствует дальнейшему распространению и так уже нередкого
убеждения, будто геометрия — наука «холодная и сухая»).
Но, если забыть об этом последнем вопросе, то оставшиеся вполне
складываются в некоторую систему, которую можно расширять до бес-
конечности. Причина проста и заключается она в том, что неправиль-
ность формы распространена в Природе повсеместно. В творениях рук
человеческих ей, возможно, не слишком рады, но при этом ее не все-
гда устраняют, а иногда это в принципе невозможно сделать. Примеры
этого встречаются в некоторых разделах математики, где они в свое
время описывались как «патологические» или «чудовищные», а также
опять-таки в приведенном выше списке вопросов.
Без лишних слов ясно, что каждый из этих вопросов принадле-
жит какой-то определенной области науки или машиностроения. Также
понятно, что с практической точки зрения лучше не тратить время на
изучение неправильности формы, а попытаться от нее избавиться. Фрак-
тальная геометрия, напротив, приняла неправильность формы во всех ее
проявлениях и изучает ее ради своих собственных интересов.
Неправильность формы освоена наукой намного хуже других
чувств, например, звука
Принято считать, что число органов чувств у человека равно пяти.
Вполне возможно, что это правда, но истинное количество различных
сообщений, передаваемых этими органами чувств, значительно больше.
Возьмем, к примеру, звук. Даже сегодня акустика в концертных за-
лах далека от совершенства; запись речи или песни проходит успешно
для гласных, но не для согласных, а барабаны, вообще, полны зага-
док. Учитывая все аспекты, можно сказать, что наука о звуке остается
неполной, но при этом она все же достигла многого.
Давайте же будем учиться на ее успехах. Наука эта добилась мно-
гого, используя здоровый оппортунизм, что, в общем-то, вполне типич-
248
Симметрия (ciukiujidm;, zuuz
но для науки вообще. Отложив в сторону трудные вопросы, она сна-
чала выбрала идеализированный звук струнных инструментов и труб
в качестве «образца», который достаточно реалистичен и в то же вре-
мя подчиняется математическим законам, поэтому его даже можно на-
звать простым. Акустика лишь классифицирует факты, которым не да-
ет характеристику или объяснение. Она строится на «гармоническом
анализе» маятниковых движений и функциях синуса/косинуса. Она
определяет одну фундаментальную гармонику и несколько второстепен-
ных, после чего, в свое время, строит полный ряд Фурье. Последне-
му свойственна периодичность, т. е. переходная инвариантность, кото-
рая в широком смысле характерна для симметрии. Примером такого же
рода служит открытый Ньютоном спектральный анализ света, хотя со-
став некогерентного белого света оставался неясным вплоть до 1930-х
годов.
Говоря в общем, гармонии, которые Кеплер увидел в движениях
планет, долгое время игнорировали, и тем не менее, зачастую началь-
ной точкой любой науки является именно выделение гармонии из хаоса
сырых фактов.
Масштабная инвариантность для неправильности формы — все
равно, что гармоничный звук для акустики
В отличие от акустики, изучая неправильность форм, мы до недав-
него времени не обращались даже к тем элементарным вопросам, кото-
рые были перечислены выше. Можно сказать, что в основе моего вклада
в науку лежит тот факт, что, как и акустика, изучение неправильности
форм не может превратиться в серьезную науку, пока не сделан следу-
ющий шаг: пока не определена базовая инвариантность/симметрия, то
есть богатый источник гармонии, присущей многим структурам, форму
которых можно назвать неправильной.
Еще буквально позавчера понятия неправильности формы и гар-
монии считались антитетичными. В классификации глубоких человече-
ских забот, от возвышенных до низменных, эти понятия оказались бы
на противоположных концах шкалы. Однако перемены способны стереть
любые границы такого рода. В качестве кандидатов на роль представи-
телей гармоничной неправильности форм я предложил объекты, непра-
вильность форм которых остается инвариантной при увеличении/умень-
шении.
По самой удивительной иронии в моей научной жизни этот первый
в истории систематический подход к неправильности форм возник из аб-
С17. Симметрии
249
солютно неожиданного источника, окутанного крайней математической
таинственностью. Видимо, именно этим объясняется, почему неправиль-
ность форм так долго не поддавалась науке.
Простые симметрии
В известном всем виде концепция симметрии вызывает либо лю-
бовь, либо ненависть. Мои собственные ощущения зависят от контек-
ста. Мне не нравятся симметричные лица и комнаты, но я посвятил всю
свою научную жизнь изучению фракталов. Сейчас мы шаг за шагом,
окольными путями, будем приближаться к примерам фракталов.
Среди симметрий наиболее известный и понятный образец — это
связь некоторого объекта с его отражением в идеально гладком зеркале.
Для получения объекта, который при отражении остается инвариантным
(неизменным), достаточно «симметрировать» абсолютно произвольный
объект, объединив его с его отражением в зеркале. Получается, что
таких объектов может быть бесконечно много.
Примером симметрии относительно вертикальной оси служит кару-
сель в парке аттракционов. Симметрия относительно точки ненамного
сложнее.
Теперь заменим симметрию относительно одного зеркала симметри-
ями относительно двух параллельных зеркал. Можно получить «дина-
мическую» симметрию любого объекта, отразив его в первом зеркале,
затем — во втором, потом — снова в первом, после этого — во втором
и так далее. Предмет бесконечно разрастается, а его предел дважды ин-
вариантен посредством зеркальной симметрии. К тому же, он не изме-
няется и при параллельном перемещении в любом направлении, размер
которого кратен двойному расстоянию между плоскостями. Как и для
одиночного зеркала, определяющее условие предполагает бесконечное
множество таких объектов.
Симметрия относительно круга немного сложнее, но она же и чрез-
вычайно важна. Начнем с рассмотрения предмета, симметричного от-
носительно прямой. Затем преобразуем всю плоскость посредством опе-
рации, которая называется геометрической инверсией и представляет
собой очень естественное обобщение преобразования х в его алгебраи-
ческую инверсию 1/х. Получается, что геометрическая инверсия преоб-
разует (почти) любую прямую в круг. После такой инверсии плоскости
объект, который раньше был симметричен относительно исходной пря-
мой, становится симметричен относительно инверсии этой прямой, то
250
Симметрия (Стокгольм), 2002
От простых симметрий к диким и к самоподобности
Пока все идет нормально. В элементарной французской школьной
геометрии было полно таких примеров. Через несколько курсов все ста-
ло усложняться, но очень постепенно. Специальные профессиональные
издания пытались всех убедить, что ученые работают на бесконечной
границе науки, но всем было ясно, что эта старая геометрия себя изжи-
ла и превратилась в мертвую науку.
Тут же многие поспешили заявить, что умерла вся более или менее
наглядная геометрия. На самом же деле, еще с 1880-х (!) годов в работах
Анри Пуанкаре присутствовали зачатки совсем других, но очень нагляд-
ных разработок. Однако они оставались незамеченными вплоть до появ-
ления компьютерной графики и моей работы, примером которой служит
нижеизложенное. Благодаря фрактальной геометрии, сегодня идея Пуан-
каре получила широкое распространение, и с ее помощью мы совершим
плавный переход от простейшей симметрии к самоподобной неправиль-
ности форм. В следующем разделе понятие неправильности форм будет
немного расширено, а еще через один раздел вы поймете, что оно вполне
естественно. Рисунки 1 • Рисунки 2 • Рисунки 3
Самоподобная «трижды инвариантная пыль Т>» с генератором
симметрии, состоящим из трех частей
Техническое значение термина «пыль» прояснится по мере дальней-
шего повествования. Рассмотрим плоскую диаграмму, которую назовем
«генератором», состоящим из трех частей: двух параллельных прямых
и окружности, расположенной посредине между ними, как показано на
рисунке 1 слева. Может ли геометрическая фигура быть симметричной
относительно каждой из трех частей этого генератора одновременно?
Если это справедливо для более, чем одной фигуры, можно ли опреде-
лить наименьшую из них (назовем ее Р)? Уже набившая всем оскоми-
ну «интуиция» привела к тому, что великие мыслители решили, будто
сложность любого понятия следует измерять длиной кратчайшей опре-
деляющей его формулы или сентенции. Такая точка зрения подразуме-
вает, что с удвоением длины определяющей формулы, соответствующее
исследование усложняется в два раза.
При подобном рассмотрении создается ощущение, что наш генера-
тор содержит лишь небольшое отклонение за пределы отдельных со-
ставляющих, что выглядит вполне безобидно. К счастью для нас, но,
к сожалению для этого ошибочного определения сложности, эта очень
С17. Симметрии
251
простая комбинация инверсий тут же преподносит большой сюрприз.
Оказывается, она сопряжена со скачком через гигантскую пропасть, от-
деляющую изучение элементарной геометрической симметрии от боль-
шой сложности, присущей фракталам.
И для тех, кто (пока) еще мало знает о фракталах, и для тех,
кто знает о них достаточно, самый простой путь к их пониманию —
компьютерная графика, благодаря которой все это стало возможным.
Рис. С17-1. На рисунках 2 и 3 изображены два моста между простейшими сим-
метриями (относительно прямой или окружности, причем последняя является
геометрической инверсией), с одной стороны, и самоподобностью, то есть фрак-
тальностью, с другой. Оба рисунка построены по точкам с помощью орбиты,
которая представляет собой бесконечную случайную последовательность нико-
гда не повторяющихся симметрий.
Генератор пыли Р на рисунке 2, изображенный слева, состоит из двух па-
раллельных прямых и окружности радиуса г, расположенной между ними.
Для 1-г мы приняли положительное значение, что предполагает существо-
вание между точками истинных пустот. Следовательно, Р представляет собой
«вполне несвязное множество», каковое я назвал пылью. На рисунке 2 значе-
ние 1 - г очень мало, но ради ясности на изображении слева я его увеличил.
Генератор кривой I на рисунке 3, изображенный справа, состоит из двух па-
раллельных прямых и двух окружностей. Поскольку эти окружности и прямые
(как показано на рисунке) касаются друг друга, то орбита, хотя и очень мед-
ленно, но вливается в непрерывную кривую.
Выражение «минимальная трижды инвариантная», вынесенное в на-
звание раздела, может вызвать опасения, что пыль V подобна пресло-
вутой иголке в стоге сена, но дело обстоит с точностью до наоборот.
Тактика поиска V не более сложна, чем та «динамика», которой мы
252 Симметрия (Стокгольм), 2002
ilui
личений». Эта пыль Р (верхнее изображение) полностью размещена в пределах
горизонтальной оси. Подчеркнутая часть верхнего изображения увеличивается
на втором рисунке и так далее.
Для наглядного представления пыли лучше всего нарисовать «гистограмму»:
разделить ось на небольшие «отсеки», а число точек в каждом отсеке предста-
вить с помощью вертикального столбика (это фрактальный аналог плотности).
Смысл в том, что (если не принимать во внимание небольшие деформации)
увеличенные гистограммы такого построения имеют очень похожий вид. Точнее
говоря, каждая часть (сверху вниз) наглядно представляет орбиту, длина ко-
торой (а следовательно, и «плотность») возрастает. Чтобы продемонстрировать
все подробности полной диаграммы, ее раскладывают по горизонтали, а отсеки
сужают, чтобы их количество оставалось постоянным.
С17. Симметрии
253
пользовались для создания множества зеркальных симметрий: мы берем
произвольно выбранный объект, добавляем его зеркальное отражение
и так далее, бесконечное число раз. Однако есть два отличия: динами-
ку, которая находится в поиске симметричной пыли 7?, непреодолимо
«влечет» к своей добыче, а добыча ее в высшей степени специфична
и невероятно сложна.
Процесс генерации 7? как предельного множества, возникший около
века назад, сейчас называется «игрой хаоса». Чтобы понять подробно-
сти этого процесса, затратив минимальные усилия на создание систе-
мы условных обозначений и написания компьютерных программ, важ-
но знать, что множество V полностью содержится в «горизонтальной»
оси, которая определяется как прямая, пересекающая центр генерирую-
щей окружности с абсциссой 0 и перпендикулярная двум генерирующим
прямым с абсциссами — 1 и 1. Следовательно, учитывая, что радиус ге-
нерирующей окружности обозначается через г < 1, инверсия попросту
преобразует х в г2/х.
В совокупности, точки, симметричные х относительно генерирую-
щих прямых и окружности, имеют абсциссы -х - 2, -х + 2 и т2/х,
соответственно. С простотой этих формул трудно поспорить, однако вы-
ращенный из столь простой затравки объект очень скоро предстанет
перед нами как чрезвычайно сложный.
Вспомним симметризацию объекта относительно одного или двух
параллельных зеркал. Поскольку при зеркальной симметрии размер объ-
екта сохраняется, результат зависит от объекта, который мы начали
симметрировать. Таким образом, этот вид симметризации «отражает»
(игра слов получилась ненароком) первоначальные условия. Однако со-
всем иначе ситуация складывается с отражением во внутреннюю об-
ласть окружности: объект при этом уменьшается. В результате, процесс
поиска нашего минимального трижды симметричного множества 7? мо-
жет оказаться совсем другим. Начальная точка с абсциссой го и по-
следовательность случайных ходов, вне всякого сомнения, оказывают
влияние на первые точки орбиты. Однако можно доказать, что эти про-
извольно выбранные исходные данные не имеют никакого ощутимого
влияния на предел орбиты. На практике получается, что этот предел
отождествляется с орбитой, из которой было удалено несколько первых
точек.
Алгоритм становится проще, если xq выбрать за пределами окруж-
ности и на самом первом этапе заменить хо на -х - 2 или на -х + 2.
Второй и последующий этапы лучше защищены от возврата, поэтому
для того, чтобы определиться с предпочтением одной из двух возмож-
254
Симметрия (Стокгольм), 2002
Рис. С17-3. Три варианта самоинверсной кривой €. В отличие от пыли Т>, изоб-
раженной на рисунке 2, эти три варианта кривой I изгибаются вверх, вниз и по
окружности. «Плотность» пришлось бы рисовать вдоль оси, ортогональной плос-
кости, поэтому мы ее опустили. Пустоты Т> настоящие, а пустоты в (. ложны; на
более длинной орбите их длины уменьшаются до нуля
ностей (но не повторения), достаточно будет подбросить монетку (или
предоставить компьютеру произвольно выбрать 0 или 1).
Увидеть значит поверить. Чтобы убедиться воочию, построение ор-
биты этого процесса лучше всего проследить на экране компьютера.
К сожалению, точечно-растровое изображение на экране не позволя-
ет увидеть, что орбита не сливается, а остается пылью. Поэтому на
рисунке 2 нам пришлось представить пыль с помощью гистограммы;
ниже мы увеличили небольшую ее часть, а еще ниже увеличили еще
более мелкие части. Поразительно, но факт: эти увеличенные изобра-
жения практически идентичны, то есть очень маленькие части нашего
предельного множества I практически тождественны (за исключением
С17. Симметрии
255
размера) его просто маленьким частям. Таким образом, это предельное
множество инвариантно при уменьшении. Учитывая его самоподобность,
заключаем, что это фрактал.
Самоподобная «четырежды инвариантная кривая £» с генератором
симметрии, состоящим из четырех частей
Чтобы перейти от пылевых множеств к собственным неправильным
кривым, достаточно просто выбрать в той же самой концептуальной
«окрестности» другую тропинку. Сохранив две параллельные прямые
из прошлого построения, добавим к ним не одну, а две окружности
одинакового радиуса, причем каждая из них касается другой окружно-
сти и одной из двух прямых, как показано на рисунке 1 справа. Что-
бы и впредь не использовать в рамках данной статьи формулы, оста-
вим удовольствие от рисования предельного множества тем, кто уме-
ет программировать геометрическую инверсию относительно плоскости,
в противоположность инверсии относительно прямой. В отличие от ри-
сунка 2, рисунок 3 не содержится в прямой и не является пылевым
множеством, состоящим из точек, разделенных пустотами. Теперь точ-
ки сливаются, хотя и медленно, в непрерывную кривую, у которой ни
в одной точке нет касательных. У кривой нет и петель, поэтому она так-
же называется «односвязной», т. е. две указанные точки она соединяет
одним-единственным способом.
Как и трижды симметричная пыль 2?, этот четырежды симметрич-
ный объект практически самоподобен во многих смыслах. Это особенно
очевидно относительно «средней точки», в которой кривая «оскулирова-
на» (т. е. очерчена) двумя окружностями, пересекающимися под некото-
рым углом.
В заключение
Путь от простой симметрии до самоподобности, проделанный в этой
статье, практически неисхожен, но весьма привлекателен и достоин
большего внимания, которое мы сейчас как раз и пытаемся привлечь.
Для этого необходимо упомянуть о двух альтернативах.
На сегодняшний день многим известен пример, аналогичный пы-
ли Р и полностью (линейно) самоподобный. Речь идет о «каскадном»
построении, описанном Георгом Кантором. Это простое построение се-
годня известно многим, но ведь это абсолютно искусственный объект.
Также многим знаком и аналог £, тоже полностью (линейно) самоподоб-
256
Симметрия (Стокгольм). 2002
ный, — это каскадное построение, созданное Г. фон Кохом. Это постро-
ение тоже не блещет сложностью, оно также известно многим, но и оно
являет собой абсолютно искусственный объект.
Анализируя рисунок 3, понимаешь, что кривую t можно постро-
ить по аналогии с кривой Коха. Для этого необходимо последовательно
заменить короткие дуги большой окружности более длинными дугами
окружности меньших размеров, причем длина дуги измеряется в граду-
сах. Это построение отвечает на вопрос Пуанкаре. Как ни странно, этот
вопрос оставался без ответа вплоть до появления М 1982, 1983.
Открыв объект, связанный с £, Пуанкаре назвал его кривой (однако
в сноске добавил: «если это можно назвать кривой»). Правомерность та-
кого названия не была очевидной до тех пор, пока £ относили к разряду
♦математических патологий». Однако фрактальная геометрия определя-
ет такие формы как природные модели, так что теперь никто уже не
посмеет сомневаться в том, что они являются кривыми.
Благодарность. Программы для создания рисунков написал Аарон
Бененав.
Mathematical Intelligencer 5, 9-17, 1983
C18
Самоинверсные фракталы,
соприкасающиеся сигма-диски
и предельные множества
инверсных («клейновых») групп
Предисловие к главе (2003). Оригинальная работа содержала
«окрашенные» рисунки. После долгих обсуждений весьма либерально
настроенный редактор журнала «Intelligencer» Джон X. Эвин согласил-
ся опубликовать эти рисунки на передней и задней обложках журнала,
которые прежде всегда были черно-белыми. Их наложили на более тем-
ный вариант традиционной желтой обложки книг издательства «Шприн-
гер-Верлаг». Чтобы удовлетворить требованиям используемой на IBM
программы обработки текста Script (некогда одна из первых программ
такого рода, сегодня она уже доживает свой век), мне пришлось заново
пронумеровать рисунки и вставить комментарии к ним. Последний рису-
нок представляет собой черно-белую репродукцию оригинальной задней
обложки.
Редактор также добавил к моему тексту ряд основных фактов ка-
сательно инверсии относительно окружности р, которую французские
студенты в тридцатые годы (подобно мне) впитали с молоком матери,
но для большинства читателей эта тема оставались покрытой мраком
неизвестности.
За невзрачным фасадом сложного математического анализа в стиле
1900-х гг. скрывается геометрия невероятной видимой красоты и способ-
ности к внушению. Намек на нее присутствовал уже в великом старом
трактате Fricke & Klein 1897 «Lectures on Automorhic Functions»7, но
полное развитие она получила лишь в работе М 1982F{/?GW}. Рисунки
из труда Фрикке и Клейна заслуживают включения в разряд наиболее
известных математических иллюстраций, поскольку содержат мозаики
гиперболической плоскости, авторство которых миллионы далеких от
7Лекиии по автоморфным функциям. — Прим, перев.
258
Mathematical Intelligencer, 5, 9-17, 1983
математики людей сейчас приписывают Морицу К. Эшеру. В данной ра-
боте более подробно исследуется небольшой кусочек этой вселенной —
геометрии предельного множества особой группы, основанной на ин-
версиях, представленных в работе Фрикке и Клейна. Это предельное
множество, по терминологии М 1982F{F'CLV}, является фрактальной кри-
вой. Оно было принято на веру и воспроизведено в некоторых известных
книгах, благодаря чему свое представление о нем смогли сформировать
многие поколения математиков.
К несчастью, рисунки, тщательно разработанные на компьютере,
раскрыли богатую структуру, что доказывает неточность и обманчивость
иллюстрации Фрикке и Клейна. Традиционный алгоритм Пуанкаре для
построения предельного множества (смотрите работы Poincare 1914+)
отличается запутанностью и низкой эффективностью.
К счастью, благодаря, в том числе, и точной компьютерной графи-
ке, я смог создать новый алгоритм, порождающий предельное множе-
ство С для многих групп Q, основанных на инверсиях. Этот алгоритм
был в общих чертах описан в 1981 году (в Mathematical Calendar, из-
даваемом «Шпрингер-Верлаг») и подробно изложен в главе 18 труда М
1982F{FGN} (в данной книге это глава С16). Он не является универ-
сальным для всех случаев, а разбивает группы, основанные на инвер-
сиях, на обладающие и не обладающие свойством «прямой оскуляции».
(При этом предельное множество может приобрести такое свойство по-
сле изменения базиса).
Но в данной работе мы не станем подробно останавливаться на этих
новых различиях. Нашей единственной целью является демонстрация
этого алгоритма и его эффективности путем досконального описания
его применения к наиболее удивительным примерам Фрикке и Клейна.
Интересно будет определить множества, а особенно, самые малень-
кие из оных, которые остаются инвариантными под действием груп-
пы геометрических преобразований. Подобный вопрос впервые поднял
Лейбниц, предположивший, что единственные фигуры, инвариантные
при любых преобразованиях подобия на плоскости, — это прямые и са-
ма плоскость (смотрите М 1982F{FG/V}, стр. 570). В рамках допущения
гладкости он, безусловно, прав: это единственные связные и гладкие ин-
варианты, называемые самоподобными множествами. Но, отказавшись
от стандартных условий гладкости и ограничив подобия, можно обнару-
жить много других самоподобных множеств, которые являются не фи-
гурами стандартной геометрии, а фрактальными множествами, как-то,
например: множества Кантора (вполне несвязные множества, то есть
♦пылевые множества» по терминологии М 1982F{/ГG^}), границы сне-
С18. Предельные множества клейновых групп
259
жинок Коха (негладкие кривые) и траектория броуновского движения
(самая известная самоподобная случайная кривая).
Данная работа, написанная в том же духе, посвящена группе нели-
нейных преобразований. Имея М > 3 окружностей Cm(l С тп. М) на
плоскости, которые мы будем называть генерирующими, мы рассмотрим
группу Q, порожденную инверсиями относительно этих окружностей.
Если за начальную точку выбрать центр окружности С радиуса Я, то
инверсия относительно С будет описываться в полярных координатах
как отображение (г, 0) —> (Л2/г, в). В нижеследующем рассуждении са-
мым главным, что можно сказать об инверсиях, будет их свойство отоб-
ражать окружности в окружности, причем прямая становится окружно-
стью через точку в бесконечности.
Множества, инвариантные под действием этой группы, можно назы-
вать самоинверсными множествами под действием Q. Замкнутая плос-
кость, включая ее точку в бесконечности, самоинверсна под действием
каждой группы. А для многих групп она представляет собой единствен-
ное стандартное решение. Однако существует одно важное исключение
(называемое фуксовым) — когда все окружности Ст ортогональны об-
щей окружности Г. В этом случае (включающем большинство примеров
при М = 3) окружность Г самоинверсна под действием группы Q, по-
скольку любая окружность, ортогональная окружности С, инвариантна
под действием инверсии в С.
Также будет любопытно исследовать случай, исключенный выше-
изложенным определением. Когда М = 2 и конечные диски, ограни-
ченные окружностями Ci и Сг, не пересекаются, две точки являются
взаимно инверсными относительно как окружности Ci, так и окруж-
ности Сг. (Если Г представляет собой диск, ограниченный окружно-
стью Ci и точкой 721 в конечном диске, ограниченном окружностью С\.
и точкой 712 в конечной окружности, ортогональной окружностям С\
и Сг, тогда точки 712 и 721 принадлежат окружности Г). Следовательно,
множество {712,721} самоинверсно. Некоторые очень особенные фуксо-
вы группы также имеют самоинверсное множество, которое сводится
к двум точкам.
С другой стороны, первый ученый, коснувшийся этой темы — Пу-
анкаре — еще сто лет назад заметил, что в результате отказа от стан-
дартных условий гладкости получаются странные подмножества плос-
кости — замкнутые самоинверсные множества. Незадолго до того (!),
как Кантор в 1884 году представил свое множество, и задолго до того,
как в 1904 году Кох описал свою недифференцируемую кривую, явля-
ющуюся границей снежинки, Пуанкаре заметил, что в типичных кон-
260
Mathematical Intelligencer, 5, 9-17, 1983
фигурациях генераторов Cm самоинверсное множество £ может быть
либо вполне несвязным множеством («пылью»), либо недифференцируе-
мой кривой (без касательной или с касательной, но без кривизны). (Он
также отметил, что здесь следует сделать оговорку, «если это можно
назвать кривой»... Более поздние исследования понятия кривой пока-
зали, что не только можно, но и нужно).
Предельное множество
Как получить самоинверсное множество? Ответ прост: можно на-
чать с любого множества S и увеличить его как раз настолько, чтобы
сделать самоинверсным. Для любого множества S объединением всех
преобразований g(S) при g е Q, по определению, является клан QS.
Обычно это называется орбитой множества S, но мне больше по ду-
ше термин «клан». Естественно, замыкание QS представляет собой за-
мкнутое самоинверсное множество. Это справедливо и для подмноже-
ства (QS)', состоящего из всех предельных точек клана QS. Вспомним,
что точка Р является предельной точкой множества, если каждая проко-
лотая окрестность Р (то есть окрестность без самой точки Р) пересекает
это множество; а множество предельных точек называется производным
множеством.
В частности, можно начать с любой произвольной точки Ро, затем
образовать клан QPq и получить производное множество (GPo)'. Удиви-
тельно, но факт: при свободных условиях производное множество (а) не
зависит от точки Ро, поэтому его можно обозначить £; и (б) имеет ну-
левую площадь (что эквивалентно плоской мере Лебега). Производное
множество £ обладает несколькими очень важными характеристически-
ми свойствами. Это множество не только самоинверсно, оно еще и ми-
нимально. Оно (по построению) является предельным множеством Q.
Более того, на этом множестве группа G непрерывна, а за его преде-
лами она перестает быть таковой. И последнее полезное свойство: со-
вершенно очевидно, что группа G в дополнение к своей базе включает
бесконечное количество инверсий и что множество £ является произ-
водным множеством центров этих инверсий. Насколько мне известно,
последнее утверждение в такой формулировке в литературе не встреча-
ется, но его эквивалентность построению Пуанкаре множества £ видна
невооруженным глазом.
Какую форму имеет множество £? Наши познания о множествах
Кантора и Коха расширяются благодаря существованию разнообразных
прямых и прозрачных построений. Форма же минимального самоинверс-
С18. Предельные множества клейновых групп
261
ного множества £, напротив, оставалась малоизученной. Чтобы запол-
нить этот пробел, я изобрел новое построение, которое включает само-
инверсные открытые множества, полученные как кланы открытых дис-
ков. Я называю их «сигма-дисками» или «<т-дисками», причем буква а
не требует разъяснений, т. к. указывает на то, что <т-диск представляет
собой счетное объединение дисков. Дополнение самоинверсного ст-дис-
ка также является самоинверсным множеством, а минимальное само-
инверсное множество £ обычно может быть представлено как допол-
нение конечного объединения <т-дисков. Можно сказать, что каждый
из этих сг-дисков оскулирует множество С. Это построение оскулиру-
ющего er-диска можно сделать рекурсивным: с каждым новым шагом
рекурсии множество £ очерчивается очень быстро — намного быстрее,
чем при классическом построении Пуанкаре.
Фуксовы группы при М = 3, для которых множество £ является
окружностью Г
Уже отмечалось, что когда д является фуксовой группой, окруж-
ность Г самоинверсна. Случай, когда окружность Г представляет со-
бой минимальное самоинверсное множество, имеет место, когда М = 3,
а каждая из трех окружностей Ci, Ci и Сз касается двух других (рису-
нок 1.1). Инвертируя плоскость относительно точки касания 712 окруж-
ностей Ci и Ci, получаем ситуацию, изображенную на рисунке 1.2,
где окружности Ci и Сг представляют собой параллельные прямые,
а окружность Сз касается их обеих. Также преобразуется и группа:
теперь ее порождают отражения в окружностях С\ и Сг и инверсия
в окружности Сз. Нетрудно увидеть, что множество £ является окруж-
ностью Г. Группа, изображенная на рисунке 1.2, представляет собой
особую «модулярную» подгруппу.
Небольшое отступление. Примем центр окружности Сз за на-
чальную точку, а ее радиус равным 1. Тогда каждое вещественное зна-
чение Xi можно записать единственным образом: как ц + рь где ii
является четным целым числом со знаком, a piE принадлежит открыто-
му интервалу ] - 1,1[. Точно так же, 1/pi = ii+pi- При рациональных
значениях a?i все значения pk также рациональны. По мере возраста-
ния к знаменатели величины рк уменьшаются, и, в конечном итоге,
при к = К мы получаем рк = 0 или 1. Назовем К глубиной jp Для
иррациональных чисел К = оо, для целых чисел К = 0. Не составляет
труда доказать, что каждое рациональное значение ti при рк = 0 явля-
ется преобразованием хК = 0 посредством группы д, тогда как каждое
262 Mathematical Intelligencer, 5, 9-17, 1983
Рис. C18-1. Иллюстрация некоторых аспектов инверсии в окружностях
рациональное значение xi при рк = 1 представляет собой преобразо-
вание хк = 1 при целом ik/4 и хк = -1 во всех остальных случаях.
К тому же, очевидно, что каждое значение ц при рк = 0 является
предельной точкой х\з при рк + 1 = 1. Заключение: если абсцисса Ро
рациональна, множество QPo является плотным в окружности Г.
Некоторые фуксовы группы при М = 3, для которых
множество £ является фрактальной пылью; оскулирующие
сг-интервалы
На рисунке 1.3 приведен весьма показательный случай, когда М —
= 3 и группа является фуксовой, а множество £ представляет собой
очень маленькое подмножество окружности Г. Допустим, что Г явля-
ется ортогональной окружностью и что конечные диски, ограниченные
окружностями Ci, С2 и Сз, не пересекаются. Мы уже отмечали, что
на окружности Г существуют точки 712 и 721, которые являются взаим-
но инверсными относительно как окружности Ci, так и окружности С2.
Теперь, если нашу плоскость инвертировать относительно точки 712, по-
лучится рисунок 1.4. Поскольку 712 уходит в бесконечность, то окруж-
ность Г превращается в прямую линию; а С\ и С2 превращаются в две
окружности с общим центром 721. Нетрудно заметить, что та полови-
на Г, которая не содержит точки 713 и 731, а также точки 723 и 732, не
принадлежат множеству £. С помощью этой полупрямой мы определяем
открытый интервал ]7i2, 721 [•
Таким образом, самоинверсное множество ^712, 721 [, которое пред-
ставляет собой <т-интервал (объединение непересекающихся открытых
интервалов), полностью находится в дополнении множества £. Это спра-
ведливо и для <т-интервалов £]71з, 7зх [ и £]723, 7з2[- Дополнением этих
трех a-интервалов также является множество £, что уже не так оче-
видно, как в предыдущем случае. Это фрактальная пыль нулевой длины
(линейная мера Лебега), представляющая собой самоинверсный вариант
обычного самоподобного множества Кантора.
Форму множества £ можно очертить с быстро возрастающей точ-
ностью, вставляя интервалы дополнения £ в порядке убывания длины.
Также можно использовать порядок возрастания длины самых коротких
слов в I, с помощью которых эти открытые интервалы получаются из
ОДНОГО ИЗ hij, 7ji[.
Хотя мне самому сложно поверить в новизну вышеизложенного ал-
горитма, я не помню, чтобы где-нибудь встречал его описание. {P.S.
2003 г. Более ранних ссылок обнаружено не было}.
Фрикке и Клейн: запутались сами и запутали других
Предельное множество не сложно найти для группы, порожденной
инверсиями относительно трех окружностей, но как насчет более круп-
ных конфигураций? Для решения этой задачи был создан новый алго-
264
Mathematical Intelligencer, 5, 9-17, 1983
ритм построения множества £. Он тоже настолько элементарен, что его
могли бы открыть (но не открыли!) в 1880-х годах, когда Анри Пуанкаре
и Феликс Клейн впервые затронули эту тему. Поэтому данный алгоритм
лучше всего изучать на классических рисунках предельных множеств £
некоторых особых инверсных групп, представленных в работе Fricke &
Klein 1897.
Основное противоречие заключается не в том, что истинные множе-
ства С включают такие элементы, которые никто не будет даже пытаться
нарисовать от руки. Даже если эти элементы исключить (проще всего
это сделать, остановив новый алгоритм после прохождения небольшого
числа шагов), «старое множество £» выглядит более грубо: оно лишено
структуры и системы.
Наверное, чтобы проиллюстрировать мое построение, лучше всего
подробно рассмотреть хотя бы один пример. Нашей отправной точкой
будет рисунок 2.1, на котором изображены пять окружностей, представ-
ленных на рисунке 156 работы Фрикке и Клейна. На рисунке 2.2 воспро-
изводится соответствующее «старое множество £», как его описывали
Фрикке и Клейн. Оно состоит из замысловатой кривой и совокупно-
сти окружностей, изображенных весьма схематично. «Истинное множе-
ство £» предстает в разных вариациях на многих последующих рисунках
в этой статье. На рисунке 3 истинное множество £ изображено в виде
границы черного фона. Рисунок 4
Сейчас кажется очевидным, что бедолага-чертежник при подготов-
ке рисунка 2.2 (согласно легенде он был студентом из группы будущих
инженеров, в которой преподавал Фрикке) точно определил несколько
точек множества £, а затем нарисовал «какую-то чрезвычайно замыс-
ловатую и сложную кривую», проходящую через эти точки. Поскольку
Фрикке не знал, чего ожидать, чертежник не получил никаких четких
указаний.
Замечу, что черная область на рисунке 2.1, рассматриваемая как от-
крытая (не включающая генерирующие окружности), разделяется на три
отдельные максимальные открытые области, которые мы будем обозна-
чать черезРз (треугольник), (четырехугольник) и Р5 (пятиугольник,
содержащий точку в бесконечности). Из этого следует, что исследова-
ние множества £ можно начать с анализа предельных множеств двух
подгрупп группы Q'. первой — фуксовой подгруппы порожденной ин-
версиями относительно трех окружностей, ограничивающих область Рз,
и второй — подгруппы Qi, порожденной инверсиями относительно че-
тырех окружностей, ограничивающих область Р4. В конце концов, пре-
дельное множество подгрупп входит в предельное множество группы.
С18. Предельные множества клейновых групп
265
Рис. С18-2. Согласно работе Fricke & Klein 1897, на рисунке 2.2 представлено
предельное множество при инверсиях относительно пяти окружностей, изобра-
женных на рисунке 2.1
Фуксова подгруппа <7з
Как старое, так и истинное множество С схожи в одном: оба вклю-
чают одну большую окружность, которую мы будем обозначать через £з,
и более мелкие окружности. Окружность £з ортогональна трем генери-
рующим окружностям Сг, Сз и С$, которые ограничивают область Т>3.
Из предыдущего обсуждения нам также известно, что эта окружность
является предельным множеством подгруппы Q3.
Предположим теперь, что мы приняли С = (QPoY, где Ро — про-
извольная точка окружности £3. Более того, у нас есть представле-
Рис. С18-3. Граница между черным и белым представляет собой правильную
форму инвариантной кривой, (неверно) представленной на рисунке 2.2
ние £ - (££3)', которое чрезвычайно избыточно, но все же весьма
полезно для описания предельного множества. Приблизительное изоб-
ражение множества £, основанное на этом представлении, представлено
на рисунке 4. Оно ограничивает само себя элементами группы Q, по-
лучающимися в результате инверсий, число которых меньше некоторого
большого числа К.
Большие окружности представлены тонкими кривыми, а окружно-
сти, радиус которых меньше толщины больших окружностей, представ-
лены точками. Если бы этот алгоритм продолжился дальше, то все эти
точки слились бы в бесконечно разветвленную кривую. Воздержись мы
Рис. С18-4. Быстро сходящаяся аппроксимация инвариантной кривой, представ-
ленной на рисунке 3, образами окружности под действием некоторой последова-
тельности инверсий
от изображения больших окружностей, результат существенно бы не
изменился, поскольку каждую точку на каждой окружности можно по-
лучить другим способом, а именно: как предел точек, принадлежащих
более мелким окружностям, т. е. точек, которые символизируют малень-
кие окружности.
Множество £ можно представить с помощью одной формулы £ =
= (£7£зУ. вот только она достаточно громоздка. Последователь-
ность Qk^3, где Qk представляет собой совокупность результатов, са-
мое большее, К инверсий, сходится к С быстрее, чем последователь-
268
Mathematical Intelligencer, 5, 9-17, 1983
ность $кР(ь связанная с любой одиночной точкой P0- Тем не менее, она
сходится очень медленно — без удивительных компьютерных программ,
примененных для рисунка 3, этот алгоритм привел бы только к очень
приблизительному представлению о множестве £.
Основанная на цепочке подгруппа G4
Самое поразительное несоответствие между старым множеством £
и истинным множеством £ связано с предельным множеством £4, со-
ответствующим подгруппе ^4, основанной на четырех окружностях С\,
С2. Сз, и Ci, которые касаются области Р4. Согласно терминологии М
1982F{FG7V}, эти окружности образуют связную «цепочку Пуанкаре»,
в которой каждое звено касается двух своих соседей. (В результате, пре-
дельное множество £4 представляет собой жорданову кривую.) Старое
множество £4, отделенное от остальной части рисунка 2.2, изображено
на рисунке 5.1, а истинное множество £4, построенное по моему новому
алгоритму, представлено на рисунках 6 и 7.
Для определения множества £4 нам (опять-таки) нужно опреде-
лить, что не входит в £4.
Для начала отметим, что для любых трех окружностей Ci, Cj, С к
существует общая ортогональная окружность I\jk, которая проходит че-
рез точки касания G, Cj и Сц- В этом случае окружности Гук отделены
друг от друга, то есть группа Q4 не является фуксовой.
Каждая окружность Гук делит плоскость на два диска: ограничен-
ный и неограниченный. Один из этих двух открытых дисков не содержит
точек касания четырех окружностей; обозначим его через Дук. Что-
бы убедиться в этом, достаточно инвертировать плоскость относительно
окружности с центром в точке касания 7у. Окружности выстраивают-
ся, как показано на рисунке 5.2, а Гук превращается в горизонтальную
прямую: преобразование Aijk представляет собой полуплоскость выше
или ниже преобразования Гук.
Теперь вполне очевидно, что инверсия относительно одной из четы-
рех окружностей не может перенести точку касания внутрь Дук- Следо-
вательно, ни одно из преобразований Дук не содержит преобразования
точки касания. Если использовать точку касания четырех дисков, то
диск Дук должен оказаться в дополнении. С другой стороны, грани-
ца Дук (окружность Гук) включает предельное множество фуксовой
подгруппы, порожденной инверсиями относительно окружностей Ci, Cj
и Ск. Следовательно, любой открытый диск, содержащий Дук, должен
пересекаться с множеством £.
С18. Предельные множества клейновых групп
269
Рис. С18-5. Рисунок 5.1 получен из рисунка 2.2. Рисунок 5.2 получается при
инверсии четырех окружностей в цепочке Пуанкаре
Рассмотрим теперь четыре открытых диска Дг_,к и их кланы по от-
дельности. Один из «инициаторов», а именно: диск Дш. — является
неограниченным и пересекается с диском Дгз4- (В данной конфигура-
ции диск Д234 также не ограничен — на самом деле, Г234 представляет
собой практически прямую линию, однако в других конфигурациях че-
тырехзвенных цепочек Пуанкаре диски Д234 могут быть ограничены).
В совокупности, диски Д124 и Д234. легко узнаваемые на рисунке 8,
служат первым приближением внешней области множества £4.
Эта и последующие приближения аналогичны приближениям кри-
вой снежинки Коха К,, представленной на рисунке 70 в работе М
1982F{FG^}.
Другие диски-инициаторы Д^к, а именно: диски Д123 и Диз, —
ограниченны и пересекают друг друга. Они хорошо просматриваются
на рисунке 7. В совокупности они представляют первое приближение
внутренней области множества £4.
Второе приближение внешней области множества £4, также легко
различимое на рисунке 8, достигается посредством добавления к дис-
кам Д124 и Д234 их инверсий относительно окружностей Сз и С\, соот-
ветственно. Соответствующее второе приближение внутренней области
множества £4 получается путем добавления к дискам Д123 и Д143 их
инверсий относительно окружностей С4 и С2, соответственно.
Mathematical Intelligencer. 5, 9-17. 1983
Рис. Cl8-6. Новый быстрый алгоритм для построения внешней области исправ-
ленного рисунка 5.1
Дополнение <т-диска (счетного объединения дисков), состоящее из
четырех кланов Q^ijk, сжимается до кривой £4. Объединение четы-
рех «дисков-инициаторов» само по себе служит полезным приближени-
ем дополнения множества £4. Приближения, в которых используется
результат К или меньшего количества инверсий, быстро сходятся ко
кривой £4.
Рисунок 8, который воспроизводит заднюю обложку оригинала,
обобщает построение рисунка 7 до целой группы Q.
С18. Предельные множества клейновых групп
271
Фрактальная оскуляция; оскулирующие диски
Поскольку множество £4 не пересекается ни с одним из четырех от-
крытых дисков, индексы которых с ним связаны, но пересекается более,
чем в одной точке с окружностью, ограничивающей каждый диск Д^,
множество £4 и диск Д^ можно назвать оскулирующими.
В стандартном контексте дифференциальной геометрии понятие ос-
куляции существует в связи с концепцией кривизны. Для любой стан-
дартной кривой вблизи обычной точки Р приближением первого порядка
служит касательная. Приближением второго порядка является окруж-
ность, называемая «оскулирующей» и имеющая ту же касательную и ту
же кривизну.
Рис. С18-7. Новый быстрый алгоритм для построения внутренней области ис-
правленного рисунка 5.1
Рис. С18-8. [Задняя обложка работы М1983т, цвета которой изменены на раз-
ные оттенки серого]. Новый быстрый алгоритм для построения внутренней обла-
сти правильной инвариантной кривой, (неверно) представленной на рисунке 2.2
Окружности, касающиеся кривой в точке Р, можно обозначить с по-
мощью индекса и, который представляет собой величину, обратную рас-
стоянию от точки Р до центра нашей окружности. Индекс оскулирукэ-
щей окружности будем записывать как uq. При и < и0 небольшая часть
кривой с центром в точке Р целиком расположена по одну сторону ка-
сательного круга, за исключением самой точки Р. А при и > и0 она, за
исключением все той же точки Р, полностью лежит по другую сторону-
Мы называем критическим значением или разрезом.
С18. Предельные множества клейновых групп
273
Для фракталов определение оскуляции через кривизну не имеет
смысла. Однако, существует бесконечное количество точек, в которых
предельное множество £ любой цепочки Пуанкаре помещается между
двумя дисками, касающимися друг друга. Например, точка касания ге-
нерирующих окружностей Ci и Cj принадлежит множеству £, причем £
умещается между двумя дисками и Д;7ь Оба этих диска так и хо-
чется назвать оскулирующими.
Для точного определения этого понятия возьмем точку Р, в кото-
рой множество £ имеет касательную, и для начала определим обычную
оскуляцию, основанную на критичности (=разрезе). Отличие в том, что,
по мере изменения параметра и, единственная критическая величина uq
заменяется двумя разными значениями, и' и и" > и', которые мы опре-
деляем следующим образом: при любых и < и1 множество £ полностью
располагается по одну сторону нашей окружности, исключая точку Р.
При любых и > и" множество £ полностью лежит по другую сторону,
а при и' < и < и" части множества £ находятся по обе стороны окруж-
ности. Я предлагаю назвать обе окружности с параметрами и1 и и"
фрактально оскулирующими множество £. Открытые диски, ограни-
ченные оскулирующими окружностями и не пересекающие множество £,
будут называться оскулирующими дисками. Вполне возможна ситуация,
когда один или два оскулирующих диска вырождаются в точку.
Как известно, стандартная оскуляция — понятие локальное, по-
скольку его определение не зависит от формы кривой, удаленной от
точки Р. Я же, напротив, определил фрактальную оскуляцию глобаль-
но, так как в этом случае требовался именно такой подход. При таком
раскладе определить локальную версию будет совсем несложно.
Группа Q; классификация окружностей как оскулирующих
или пересекающих множество £
Мы нашли, что для подгруппы £4 каждая из 4!/3!1! = 4 окруж-
ностей Vijk, определенных как ортогональные к трем из генерирующих
окружностей Ст, оскулирует множество £4. При других конфигурациях
генерирующих окружностей Ст, включая конфигурацию, представлен-
ную на рисунке 5, и цепочки Пуанкаре при М > 4, ситуация услож-
няется.
Для примера рассмотрим дополнение предельного множества £.
Нам уже известно, что для порождения внутренней области множе-
ства £3 необходим клан Д235 под действием подгруппы Q3, а для порож-
дения внутренней области множества £4 необходимы кланы Дщ и Д234
под действием подгруппы £4. Таким образом, ясно, что для порождения
274
Mathematical Intelligencer, 5, 9-17, 1983
внутренней области множества С (рисунок 6) нужны кланы Д235. Д123
и Дгзз под действием группы Q. Аналогично, для порождения внешней
области множества С (рисунок 7) необходимы кланы Д345, Д145 и Д125
под действием группы Q.
Однако, с окружностями, основанными на триплетах 234 и 135, де-
ло обстоит совершенно иначе. В любом из этих случаев некоторые из
оставшихся окружностей Ст располагаются во внутреннем диске
и во внешнем диске £Гг7ъ соответственно. Два открытых диска, а имен-
но: £Г1?к и его инверсия относительно окружности, расположенной
внутри диска ЗГу*. покрывают всю плоскость. То же самое справед-
ливо и в отношении диска Более того, оба клана QJTijk и в£Гук
тождественны целой плоскости. Следовательно, при ijk = 234 или 135
ни внутренняя, ни внешняя области не могут служить диском-ини-
циатором оскулирующего ст-диска. Однако, дополнением множества С
по-прежнему является сг-диск, и его можно получить как объединение
кланов вида б^к-
Кроме того, когда диск определить возможно, тогда он нужен
для построения, в противном случае можно обойтись и без него. (Тем
не менее, когда окружности Ci, Cj и Ск образуют фуксову подгруп-
пу, предельным множеством которой является полная окружность Г^к,
построение множества £ происходит гораздо быстрее при включении
диска ^rijfc.)
Общее правило. Для того чтобы в случае с группой Q нам по-
надобился триплет г, j, к, должны выполняться следующие условия:
(А) Существует однозначно определяемая окружность, ортогональная
окружностям Ci, Cj и Ck', (Б) Либо внутренняя, либо внешняя об-
ласть окружности Гук не содержит никаких точек касания двух любых
окружностей Ст и Сп.
Более общие нефуксовы группы
Последнее правило применимо к более общим группам Q, основан-
ным на инверсиях. Во-первых, заменим точки касания, когда окружно-
сти Ст и Сп не являются касательными. Как уже ранее отмечалось
в этой работе, когда окружности Ст и Сп не пересекаются, существуют
две точки (-утп, принадлежащая Ст, и упт, принадлежащая Сп), кото-
рые являются взаимно обратными относительно как Ст, так и Сп. Когда
окружности Ст и Сп пересекаются, обозначим точки их пересечения че-
рез и 7*т. Теперь условие (Б), приведенное в конце предыдущего
раздела, можно обобщить следующим образом: окружность Г^к являет-
С18. Предельные множества клейновых групп
275
ся оскулирующей, если при любых тип либо ее внутренняя, либо ее
внешняя область не включают точку 7mn, а включают или точку 7^п,
или точку 7пт» но никак не обе.
Фуксовы группы и оскулирующие интервалы
Если существует окружность Г, ортогональная всем окружно-
стям Ст, мой алгоритм всегда приводит к созданию Г, однако мно-
жество £ может являться либо Г, либо фрактальным пылевым подмно-
жеством Г.
Кроме того, группа может быть непрерывной на всем своем про-
тяжении (я называю этот случай хаотическим и не рассматриваю его
в этой работе). В таком случае множество С представляет собой це-
лую плоскость. Для построения множества £, когда оно не является
плоскостью, используются оскулирующие интервалы.
Когда оба интервала, ограниченные точками 7^ и 77ь не содержат
других точек 7mn, все множество £ сводится к точкам 7;7 и 7^. Этот
случай играет для фуксовых групп ту же вырожденную роль, которую
сами фуксовы группы играют для других групп, основанных на инвер-
сиях.
Благодарность. Иллюстрации к этой работе были выполнены
с помощью компьютерных программ, написанных доктором В. А. Нор-
тоном.
Часть IV
МУЛЬТИФРАКТАЛЬНЫЕ
ИНВАРИАНТНЫЕ МЕРЫ
Первая публикация
С19
Меры, которые экспоненциально убывают
почти везде: ОДА и Минковский
Когда происходит оценка нового математического достижения,
некоторые пуристы допускают использование компьютера, но оскорб-
ляются присутствием сильного физического мотива. Данная часть пред-
ставляет собой новую возможность обсудить пример такой ситуации.
1. Случай постоянного (двустороннего) взаимодействия
математической эзотерики с физикой
В предыдущих частях этой книги физика играла, главным образом,
косвенную роль, поскольку при введении каждой темы внутренняя логи-
ка существующей математики развивалась не без участия компьютера.
Тот факт, что эта математика произошла из физики, был благополучно
забыт. И хотя она возродилась в виде теории хаоса, я неоднократно по-
вторял, что моя мотивация родом из математики приблизительно 1900-х
годов.
В этой части, как показывает данное введение, представлен иной
подход, и кое-кто может усомниться в уместности главы С22 в теку-
щей работе, но, по размышлении, любые подобные сомнения исчезают.
Труд Gutzwiller & М 1988 {С20} возник как вполне естественный итог
деятельности авторов, которые, занимаясь изучением двух областей фи-
зики, несвязанных ни друг с другом, ни с клейновыми группами, ока-
зались на одном пути, далеком от традиционной «прикладной матема-
тики». Говоря языком предфрактальной науки, мы исследовали «пример
неслучайной сингулярной меры на единичном интервале, который явля-
ется аномальным, поскольку практически повсеместно экспоненциально
обращается в нуль». Язык сломаешь.
Ну разве это не подходящий для эзотерики объект? На самом де-
ле, как сообщил нам Юваль Перес, эту же математическую структуру
много лет назад рассмотрел Герман Минковский (1864-1909), который
дал ей определение и на этом поставил точку. Много позже упоминание
о ней из уст Ж. Адамара услышал Арно Данжуа (1883-1974), который
заинтересовался ею и пришел к выводу, что мера Минковского инва-
280 С19. Экспоненциально убывающие мультифрактальные меры
риантна под действием некоторых очень особенных клейновых групп.
Результаты этих математиков, а также их отдельных немногочисленных
последователей упомянуты в работе M1999s{C21}.
Поскольку Минковский относится к числу тех ученых, на которых
я равняюсь, я с удовольствием использую термин «мера Минковско-
го» и также ничего не возразил бы против «Минковского-Данжуа».
Но эзотерика есть эзотерика, и эта мера так и не получила широкой
известности. Если бы мы с Гутцвиллером не отличались обширностью
интересов, мы бы продолжили свою работу в блаженном неведении от-
носительно того, что было.
Гутцвиллер пришел к мере Минковского прямо от гамильтоновых
систем, я же пробирался к ней окольными путями. Сначала я заинтере-
совался изучением ОДА, загадочных агрегаций, ограниченных диффу-
зией, которые были открыты в работе Witten & Sander 1981 и относятся
к вычислительной физике конденсированного состояния. В разделе 4
представлена информация для тех, кто не знаком с этой темой: рису-
нок 1 — это, по сути, большая модель плоскости ОДА, а на рисунке 2
показана часть цилиндрической ОДА из работы М & Evertsz 1991. Ее
небольшой размер не позволяет четко увидеть «фьорды», которые обра-
зуют деревья с ветвями, становящимися чрезвычайно тонкими.
На рисунке 2 также представлены изолинии потенциала Лапласа,
которые уменьшаются до невероятно мизерных размеров в нижней части
самых тонких фьордов. Такое же поведение отмечается и у гармониче-
ской меры, определенной как градиент потенциала вдоль границы. Сог-
ласно моей терминологии, я стремился представить гармоническую меру
Лапласа на ОДА — пример случайной мультифрактальной меры при под-
держке случайной фрактальной кривой. Чтобы хоть в какой-то степени
♦подтолкнуть» решение этого чрезвычайно сложного вопроса, я рассмот-
рел грубое приближение, отказавшись от случайности и приняв линей-
ную опору. Мера Минковского возникла в виде очень приблизительной
♦карикатуры», на которой резко выделялись самые маленькие значения
гармонической меры. Неуловимая связь клейновых пределов (раздел 3)
с ОДА (раздел 4) проходит через все мультифракталы (раздел 2).
2. Спектр мультифракталов/Гельдера: при малых и больших
значениях а; нули и экспоненциальные нули
2.1. Краткий обзор мультифракталов (М 1969b, M1972J и M1974f)
Рассмотрим неубывающую функцию F(t). Ее дифференциал dF на
интервале dt является мерой. В мультифракталах показатель, который
С19. Экспоненциально убывающие мультифрактальные меры 281
мы обозначаем через а, вводится посредством отношения вида
мера на интервале длиной dt —» (dt)a.
Я знал, что показатель Гельдера-Липшица функции /(t) вошла
в математическую эзотерику около 1870 года как минимальное значе-
ние amin > 0 на интервале. С физической точки зрения, сингулярную ме-
ру необходимо было описать куда более точно, рассматривая значение а
для каждого значения t. В частности, для решения проблемы периодиче-
ской турбулентности из раздела механики жидкостей я разработал поня-
тие, впоследствии названное «мультифрактальностью» и технику, пере-
росшую в «мультифрактальный формализм», который мне больше нра-
вится называть «анализом Гельдера». В его основе лежит функция /(о),
которая, в сущности, представляет собой подходящее распределение ве-
роятностей для а. Собранием этих ранних работ с комментариями слу-
жит труд M1999N.
Мультифракталы получили широкую известность благодаря работе
Halsey et al. 1986, которую один из ее соавторов, Л. П. Каданофф, мет-
ко назвал (смотрите страницу 73 из M1999N) изложением моих идей.
К сожалению, педагогическое превосходство эвристического подхода,
использованного в Halsey et al., привело к тому, что у большинства
читателей сложилось ошибочное представление, будто график функ-
ции /(а) всегда имеет форму математического символа Р, растянутого
между amin > 0 и атах < оо.
2.2. «Аномалия» при атах = 00
В рамках мультифрактального формализма в применении к мере
Минковского сейчас можно сказать, что вплоть до 1990 года матема-
тическая эзотерика рассматривала только две величины: amin и а = 1.
Точно также, ранние исследования ОДА касались других небольших
значений а вблизи amin > 0. Однако значение атах < оо также являет-
ся важной описательной характеристикой меры. Поэтому всевозможные
попытки оценить атах предпринимались неоднократно. Однако все эти
усилия не дали никаких результатов для ОДА. В работе Gutzwiller & М
1988{С20} говорится о сложностях с нахождением значения атах для
меры Минковского. Для обратной же меры Минковского было найде-
но значение amjn = 0. И только в процессе создания М 1993s{C21}
я впервые осознал, что ат;п = 0 для обратной меры Минковского озна-
чает Отах = оо для самой меры Минковского, и тогда стало понятно, по-
чему значение аШах никак не удавалось найти. Это объяснение привело
к тому, что глава С20 утратила свою актуальность, однако она остается
полезным предостережением от опасностей, которые, подобно раннему
282 С19. Экспоненциально убывающие мультифрактальные меры
этапу исследования ОДА, таит в себе бездумное использование мульти-
фрактального формализма. В работе М & Evertsz 1991{С22} содержится
вывод о том, что сложность определения отах тесно связана с «ано-
малиями», соответствующими впадинам глубоких «фьордов», которые
ясно просматриваются на рисунках 1 и 2. Это наблюдение подтолкнуло
авторов к проверке возможности того, что гармоническая мера меньше
любого выражения «степенного закона» вида —* dtQ с конечной а.
2.3. Меры с экспоненциальными нулями, встречающимися
практически повсеместно: определение
Анализ ОДА и «карикатуры» ее меры Минковского помог мне вы-
вести гипотезу о том, что атах = оо подразумевает меру, которая экспо-
ненциально убывает на множестве t меры 1. Дадим полное определение
этого понятия.
Когда + попадает в открытый интервал, такой как fi([t,t +
+ <#]) = 0, показатель Гельдера обычно не определяется. Но стоит за-
метить, что автоматическое применение его определения дает a(i) = оо.
Если говорить в общем: когда на каждом интервале, произвольно близ-
ком к t, существует положительная мера, как в случае с мерой Минков-
ского д, существуют и такие точки, в которых а(£) = оо.
Эти возможности предполагают, что понятия «нуля» и «экспоненци-
ального нуля» необходимо обобщить от функций до сингулярных мер.
Точнее говоря, tn является правым нулем меры ц при ат?(£) = оо, a tn
представляет собой правый экспоненциальный ноль, когда (если с' и с"
являются постоянными больше 0) мы имеем д([£, Z-4-cZ£]) < с' схр(-с"/dt)
при достаточно малом значении dt > 0.
Определения, касающиеся а^, подобны только что описанному. Ко-
гда t представляет собой одновременно левый и правый нуль или экспо-
ненциальный нуль, он будет называться нулем, или экспоненциальным,
нулем.
В результате небольшого расширения аргументов глав 20 и 21 по-
лучаем, что для меры Минковского у практически каждое значение t
является экспоненциальным нулем.
3. Место меры Минковского среди прочих мультифрактальных
инвариантных мер, порожденных некоторыми особыми
клейновыми группами
Возможность того, что значение аШах = оо считается «критиче-
ским» в более широком контексте при атах < оо. Понятие СИФ бы-
ло описано в главе С15. Создание последовательных положений СИФ
фактически приравнивается к приданию каждой ранее невесомой точке
С19. Экспоненциально убывающие мультифрактальные меры 283
теоретически бесконечно малой массы или меры. Теперь же мы перей-
дем от клейновых предельных множеств к инвариантным мерам на этих
множествах. Для этого обсуждения подойдет оригинальное построение
Пуанкаре (называемое «жемчужинами Индры»). Низкая скорость его
схождения была немалым недостатком в части III. Но здесь она помо-
гает разъяснить смысл очень больших значений показателя Гельдера а,
которые, в свою очередь, дают объяснение ей самой.
3.1. Базовое построение: три равные и равноудаленные
окружности
Рассмотрим три окружности Ci, С2 и Сз, которые не пересекаются
и имеют одинаковый радиус р. Нарисуем окружность С, которая орто-
гональна всем трем и радиус которой мы будем использовать в качестве
единицы измерения длины. Также предположим, что эта модель инва-
риантна при повороте на 2тг/3, и распределим единичную массу вдоль
окружности С с постоянной плотностью. Каждая часть окружности С
внутри Ci, С2 и Сз будет переносить массу 1/3.
Во время первого этапа построения жемчужин Индры окруж-
ность Ci инвертируется относительно С2 и С3. Допустим, что эта ин-
версия преобразует массу 1/6 относительно каждой из двух жемчужин.
Всего на первом этапе порождаются шесть жемчужин, масса каждой
из которых равна 1/6. В результате к-й итерации создается ожерелье
fc-ro порядка, состоящее из 2к жемчужин, каждая из которых имеет
равнораспределенную массу (1/3)2“\
Внутри каждой жемчужины грубая плотность вдоль окружности С
определяется как общая масса, поделенная на длину пересечения жем-
чужины окружностью С. Числителем для каждой жемчужины явля-
ется (1/3)2“к, а постоянного знаменателя нет. Следовательно, грубая
плотность в маленьких жемчужинах является большой (маленькая а),
а в больших жемчужинах — маленькой (большая а). По мере возраста-
ния fc, как размер жемчужин, так и грубая плотность становятся очень
разнородными. Можно подумать, что жемчужины все более малого раз-
мера состоят из все более ценного «материала», который использует-
ся все более экономично, чтобы обеспечить одинаковую ценность всех
жемчужин.
3.2. Некритические случаи; мультифрактальность инвариантной
меры и анализ Гельдера
При р —► 0 инверсия относительно окружности становится прак-
тически линейной. Несложно проверить, что первоначально однородная
284 С19. Экспоненциально убывающие мультифрактальные меры
масса сужается до фрактальной пыли очень малой размерности, крайне
близкой к канторовой пыли с равномерной мерой на ней. Неравенство
противопоставляет группу жемчужин Индры, которые приблизительно
равны друг другу, и пустые области окружности С.
В сверхкритическом случае, когда р > рсгц = \/3, окружности С\,
С2 и Сз пересекаются друг с другом, что порождает особые проблемы.
В субкритическом случае, когда р находится между 0 и у/3, степень
неравенства напоминает ситуацию с канторовой пылью.
На рисунке 2 главы С17 изображен случай, когда, по эстетическим
соображениям, значение р немного меньше х/3, но инверсия не позволя-
ет определить р прямо с рисунка.
3.3 «Критический случай», когда общий радиус р
окружностей Ci, С2 и Сз принимает значение pCrit = л/З
В главах С20 и С21 рассматривается критический случай, когда р =
= у/3. При этом значении каждая окружность касается двух своих со-
седей. После инверсии относительно точки соприкосновения окружно-
стей С2 и Сз обе окружности, касающиеся друг друга, превращают-
ся в параллельные прямые. Этот случай порождает мер)’ Минковского
и поэтому представляет огромный интерес для данной части.
4. Заметки об ограниченных диффузией агрегациях
4.1. Построение ОДА
Кластер ОДА возникает, когда «атом» совершает броуновское дви-
жение до тех пор, пока не врежется в исходную «затравку». На рисун-
ке 1 эта затравка также является атомом, а на рисунке 2 она пред-
ставляет собой (открытое) дно полуцилиндра. При столкновении атома
с затравкой они «сплавляются», и новый броуновский атом стартует
в направлении более крупной цели. Согласно классическому результа-
ту, описанному в работе Kakutani 1944, распределение точек попадания
подчиняется «гармонической мере», родственной потенциалу Лапласа.
В рамках альтернативной модели пробоя диэлектрика (МПД) правила
роста ОДА основываются именно на этой мере (Niemeyer et al. 1984).
С помощью компьютерного моделирования получено огромное ко-
личество подтверждений того, что прибытие многих атомов преобразует
затравку в кластер, которому присуща примерно одинаковая степень
сложности на всех масштабах наблюдения. Следовательно, любое мате-
матическое определение понятия фрактала должно содержать ОДА.
С19. Экспоненциально убывающие мультифрактальные меры 2В5
Рис. С19-1. Очень крупный образец плоскостной ОДА, которая называется «кру-
говой», поскольку вырастает из затравки, сокращенной до одного атома
Простота правил роста ОДА и базовая роль, которую они играют
в понимании многих физических явлений, стали толчком для обширных
количественных исследований (Pietronero & Tosatti 1986; Feder 1988;
Meakin et al. 1988; Vicsek 1989; Aharony & Feder 1989). Однако полной
теории нет до сих пор. По-прежнему отсутствует и даже более про-
стое объяснение получающейся в результате комплексной структуры.
По моему давнему убеждению одна из причин этого кроется в наличии
определенных отклонений от строгой самоподобности.
Сначала считалось, что эти отклонения мало чем отличаются от
отклонений, вызванных критическими явлениями. В отношении послед-
286 С19 Экспоненциально убывающие мультифрактальные меры
Рис. С19-2. Уменьшенная модель плоскостной ОДА, которая называется «цилин-
дрической», поскольку вырастает из дна полуцилиндра (открытого). Эта ОДА
достаточно мала, чтобы вычислить потенциал Лапласа и нарисовать его изоли-
нии. Последние являют собой не только средство графического представления
задачи, но и важнейший инструмент исследования. Таким образом, возникает
любопытное визуальное сходство между ОДА и множеством Мандельброта. Из
двух этих явлений ОДА сложнее поддается анализу
них уже существует обширная теория, и специалисты надеялись, что
теория ОДА может быть создана даже в отсутствие точного и полного
описания. Эта оптимистичная точка зрения в настоящее время утрати-
С19. Экспоненциально убывающие мультифрактальные меры 287
ла свою популярность, так что точным описанием мы более не можем
пренебречь.
4.2. Ирония судьбы: принятие некоторых «аномалий»
в гармонической мере вблизи ОДА за «реальные» стимулировало
поиск аналогичных аномалий в математических структурах
и привело к обычной игрушке Минковского
В работе Halsey et al. 1986 также было высказано предположение,
что гармоническая мера является мультифрактальной и что в качестве
необходимого инструмента анализа можно использовать мультифракта-
лы, которые первоначально были описаны в M1974L Обсуждение ОДА
планировалось разделить на две части: при больших и малых значени-
ях а.
Основное внимание уделялось кончикам, в которых растет кластер.
В этой области гармоническая мера имеет наибольшее значение, а со-
гласно общей теореме из труда Makarov 1997, кончики образуют пыль
с размерностью 1. Другой крайностью является значение Qmax, которое
должно было помочь количественно определить «степень недоступно-
сти» самых глубоких точек внутри «фьордов» ОДА. По этой причине
начались активные поиски значения атах- К сожалению, разные ученые
(а часто один и тот же специалист при разных попытках) постоянно
приходили к противоположным выводам.
Из работы Carleson & Jones 1992 я заключил, что свойство са-
моподобности предполагает, что атах < оо. Самоподобность является
геометрическим свойством, которое нельзя проверить напрямую, а толь-
ко с помощью количественных признаков. В результате у меня родилась
дикая мысль, что, на самом деле, атах может быть бесконечной величи-
ной, а это означает, что гармоническая мера является экспоненциально
пренебрежимой с вероятностью единица. Этот вывод вкупе с тем, что
для ОДА не характерна строгая самоподобность, мог бы стать очень
важным результатом, будь у меня достаточно времени и помощников
для дальнейшего исследования ОДА.
4.3. Физическая обоснованность мотива, обусловленного ОДА,
поставлена под сомнение
Читатель-математик, который даже не взглянет на главу С, может
с радостью ознакомиться с «преждевремнным эпилогом» уже в данной
главе.
288 С19. Экспоненциально убывающие мультифрактальные меры
Исследования, описанные в работе М & Evertsz 1991, предполага-
ют, что отах = оо. Это означает, что гармоническая мера, судя по всему,
экспоненциально убывает практически повсеместно вдоль границы кла-
стера. Это особенно справедливо в отношении самых кончиков очень
тонких «ветвей фьорда».
Но не спешите вопрошать: «Почему все происходит именно так?»
Данная возможность настолько исключительна, что для подтверждения
или опровержения этих результатов необходимы дальнейшие исследова-
ния. На самом деле, в последнее время ходят разговоры о еще более
невероятной возможности. В глубине фьордов гармоническая мера мо-
жет быть еще меньше экспоненциально пренебрежимой. Она может во-
обще обратиться в нуль. В таком случае верхняя граница графика f(x)
будет проходить ниже единицы в бесконечности.
Эта последовательность взаимовлияний и мнений является приме-
ром особенных сложностей и рисков, связанных с проведением физиче-
ского анализа на мрачной границе двух наук. Когда тот или иной вопрос
переходит из ранга науки как таковой в математику, многовековой опыт
показывает, что его изучение продолжается само по себе: успех одной
идеи в определенной области не гарантирует ее успеха в другой сфере,
но и не мешает ему.
Как бы то ни было, мой первоначальный интерес к ОДА позволил
расширить наши знания о мере Минковского, вот только расширение
это ограничилось добавлением ряда новых проблем к уже имеющимся.
4.4. ОДА — очень сложная, но захватывающая тема
Точная оценка гармонической меры требует колоссального объема
компьютерных исследований и немалого опыта. Говоря в общем, моя ра-
бота по структуре ОДА только подтвердила чрезвычайную запутанность
данной темы. Но, к моему великому сожалению, ту же самую работу
слишком часто принимают как доказательство того, что изучение это-
го вопроса является рискованным и бесперспективным делом. Читатель,
интересующийся данной темой, может расширить рамки главы 22, обра-
тив внимание на другие мои работы, указанные в библиографии, а так-
же на труды, которые в них процитированы. Как бы то ни было, я до
сих пор считаю ОДА и ее отклонение от самоподобности удивитель-
ным явлением, которое заслуживает дальнейшего исследования. Однако
недостаток времени и ресурсов привел к тому, что в последних сво-
их работах я отдавал предпочтение подходу, не основанному на атах-
Вместо этого я изучал распределение пустот, ограниченных пересечени-
С19. Экспоненциально убывающие мультифрактальные меры 289
ем ветвей кластера с большой окружностью, центром которой является
затравка кластера.
В настоящее время мы имеем весьма смутное представление об
ОДА. Как правило, в исследованиях не учитывается тот факт, что са-
моподобность доминирует не только в предельном случае, но и при раз-
мерах, которые невозможно проанализировать на практике. Таким об-
разом, получается, что значение а1Пах будет расти до тех пор, пока не
перестанет расти — в настоящий момент это предположение нельзя ни
подтвердить, ни опровергнуть экспериментальным путем.
Подтверждение, что для ОДА необходимо условие атах = оо, толь-
ко укрепит мнение об ОДА как о действительно очень сложном явле-
нии.
Physical Review Letters: 60, 22 February, 1988, 673-676
C20
Инвариантные мультифрактальные меры
в хаотических гамильтоновых системах
и аналогичных структурах
(Gutzwiller & М 1988)
Аннотация. Кодирование хаотических траекторий в гамильтоно-
вых системах и стохастическое отображение точек на окружностях слу-
жат примером нового вида мультифрактальной меры, показатель Гель-
дера которой варьируется от 0 до оо.
1. Введение
В этом письме представлены и проанализированы некоторые
необычные мультифрактальные меры на вещественной оси, которые
мы обнаружили в независимых исследованиях в несколько иных кон-
текстах. Их отличительной чертой является тот факт, что omin = О
и/или Отах = оо. где о (по определению М 1982{FGAf}, стр. 540, ко-
торое в настоящее время принято повсеместно) является показателем
Гельдера. Эти мультифрактальные меры имеют одно и то же геометри-
ческое происхождение, и мы полагаем, что они являются простейшими
представителями большого класса. Гутцвиллер взял свои примеры из
классических гамильтоновых систем, демонстрирующих «жесткий ха-
ос». Мандельброт же взял примеры из стохастических отображений то-
чек на трех или более окружностях, которые могут быть циклически
касательными. Наш первый (еще более простой) пример связан с эле-
ментарной арифметикой. Изначально он возник в процессе изучения
третьего примера и оказался эквивалентным второму. Мы представим
свои мультифракталы и их свойства и объясним физику и геометриче-
скую мотивацию, на которых оные основаны, а также смешаем механику
и геометрию с арифметикой и математическим анализом. За границей
новых примеров мультифрактальной меры математический анализ поз-
воляет добиться лучшего понимания структуры фазового пространства
в гамильтоновых системах с жестким хаосом.
С20. Инвариантные мультифракталы в гамильтоновых системах 291
2. Первый пример: простая проблема из арифметики
Представим вещественное число г) посредством его непрерывной
дроби
1
п0 Ч---------- •
пг + 7Г~-Z—
Предположим, что 0 < г) < 1, то есть по = 0 и при к > 0. Тогда
последовательность пк связывает с г/ вещественное двоичное число 0
(где 0 < (3 < 1), состоящее из произведения ni - 1 и 0, за которым
следует произведение пг и 1, за ним произведение пз и 0 и так далее.
Функции 0(т)) и t](J3) являются непрерывными и монотонно возрас-
тающими. Поскольку /3(1 — г?) = 1 — 0(ji), достаточно представить /3(ту)
при 0^ (3 0,5 (рисунок 1) (Шкалы х и р, объясняются во втором
примере.)
Однако график /3(т?) представляет собой не чертову гать, опреде-
ленную как интеграл меры, присущей канторовой пыли. На самом де-
ле, 0(т/) является сингулярной функцией, а ее производная обращается
в нуль не на полных интервалах, а в повсеместно плотном множестве.
В нижней части кривой это свойство просматривается достаточно четко:
маленькие значения т] дают ni 1/т], поэтому
13 = exp(-ni log 2) “ exp[-(log2)/?y].
То же самое происходит каждый раз, когда т] приближается к рацио-
нальному числу, поскольку тогда в его непрерывной дроби присутствует
большое целое число щ.
Однако кривая /?(ту) не является и интегралом классической бино-
минальной мультифрактальной меры (М 1982{FGN}, стр. 387), относя-
щейся к множеству точек, для которых знаки 0 и 1 в бинарном пред-
ставлении имеют некоторые особые предельные частоты q и l-q. Тем не
менее, приращения функции /3(ту) определяют мультифрактальную меру.
Для каждого интервала (ту, туЧ-Дту) мы определяем показатель Гель-
дера а
а = log[(/3(?7 4- Дту)) - /?(»у)]/ log Дту = log ДД/ log Дту.
При произвольном выборе интервала первой описательной характе-
ристикой мультифрактала является распределение плотности вероятно-
сти показателя а. В труде Frisch & Parisi 1985 (M1999N, стр. 94-96)
было сделано важное наблюдение, согласно которому логарифм этой
292
Physical Review Letters: 60, 22 February, 1988, 673-676
плотности является фрактальной размерностью. В последних работах
по применению мультифракталов, начиная с труда Halsey et al. 1986,
этот логарифм плотности обозначается через /(а).
Мы оценили /(а) непосредственно из числа появления различ-
ных ДЗ = (Дг/)а, соответствующих некоторому заранее выбранному
значению Дту. Как выяснилось, наибольшее значение Д/3 для заданно-
го Лг] возрастает, когда z? является золотой серединой 7, а [3 = 2/3. Та-
ким образом, amin = log2/ log(l/72) — 0,7202, что подтверждено числен-
но. Графическое изображение /(а) имеет чрезвычайно длинный хвост
(см. рис. 2). На самом деле, около 10 данных не изображены, посколь-
ку значения Д/З приближены 0 с четырехкратной точностью (точность
112 бит < IO"33). При рациональных значениях ту получаем
log А/З (log 2)/Ат/
а = hm -—т— = —;------------= сю.
Ajj—O log Д77 log Д77
{P.S. 2003. Если продолжить анализ этого аргумента, выясняется,
что d/З имеет экспоненциальные нули}.
Обратная кривая ту(^) имеет очень крутые участки; ее /(а) характе-
ризуется комплиментарной формой: длинной «головой», в которой /(а)
очень близка к а (заметим, что а всегда является верхней границей
для /(а)), и обычным коротким хвостом С Ctmax = log(l/72)/log 2 =
= 1,3884, как подтверждается численно. Были также обсчитаны и го-
раздо более крупные модели, но в данном случае вполне достаточно
двойной точности (8 байтов). На рисунке 3 представлены все значе-
ния Дт/.
3. Второй пример, обусловленный фуксовыми группами
В простейшем виде этот пример включает три отображения веще-
ственной оси на саму себя: х —► /о(®) = 1/х, х —> fii(x) = 2 - х
и х /ь(х) = -2-х. Квадрат каждого из этих отображений является
единичным отображением. Группа, основанная на этих трех отображе-
ниях, связывает с каждым словом w, то есть с каждой троичной после-
довательностью букв 0, R и L, результат последовательности отображе-
ний /о. /д и Д. Эта группа являет собой сведение к вещественной оси
скелета «фуксовой группы», фундаментальной областью которой явля-
ется сингулярный треугольник, ограниченный окружностью единичного
радиуса с центром в точке 0 и вертикальными прямыми х = 1 и х = -1-
Необходимые знания о фуксовых группах сводятся к двум фактам.
С20. Инвариантные мультифракталы в гамильтоновых системах 293
Рис. С20-1. «Скользкая чертова лестница». У этого рисунка есть два толко-
вания. Шкалы т] и /3 относятся к функции из первого примера, вычисленной
при 0 < г) < 1/2. Абсциссы вертикальных прямых образуют первые уровни
рядов Фарея. Шкалы х и р, касаются функции /z([—1, х]) из второго примера.
На этом графике изображено появление очень маленьких значений показателя
Гельдера а
А) Когда существующая группа распространяется на комплексную
плоскость посредством замены х на z, ее предельным множеством стано-
вится вся вещественная ось. То есть, если даны орбиты z0 под действием
всех слов w, то множеством предельных точек этих орбит является вся
вещественная ось при любом значении zq-
Б) Группа, распространенная на комплексную плоскость, непрерыв-
на на вещественной оси и дискретна на остальных участках. Орбита Хк
вещественного значения хо под действием слова w может вернуться про-
извольно близко к хо, не возвращаясь непосредственно к xq.
Теперь отойдем от рассмотрения фуксовых групп. Ограничим наши
слова таким образом, чтобы две последовательные буквы отличались
друг от друга, причем первая буква — не 0, если х € [-1. 1], не L,
если х < — 1, и не R, если х > 1. Тогда каждое применение /о на
интервале сжимается, а применение /д и Д сохраняет исходную дли-
ну. Следовательно, существует аттрактор, который не зависит от х0,
а, значит, зависит от слова w. Это может быть любая из точек х = 1.
I = -1 или х ± оо; также это может быть цикл периода 3 (если
какое-то слово является периодическим и повторяется после конечного
294
Physical Review Letters: 60, 22 February, 1988, 673-676
числа произвольных букв); или это может быть хаотический аттрактор.
Независимо от хо случайно выбранное слово w порождает случайную
орбиту, a Xk(w) образует выборку из лежащей в основе инвариантной
меры, которая является мультифрактальной. Эта мера зависит от слу-
чайного процесса, управляющего величиной w. На рисунке 4 показано,
как эта мера распределяется для очень длинного случайного слова.
Рассмотрим при 0 < х < 1 функцию ^([—1, х]) = (1/3)Х?( 1/2 + х/2),
где 13(т)] — это функция из первого примера. Мы увидим, что она яв-
ляется мультифрактальной р, соответствующей симметричным биноми-
нальным словам, в которых, учитывая предыдущие буквы, две неис-
ключенные возможности для следующей буквы могут иметь место с ве-
роятностью 1/2. Этим объясняются шкалы в нижней и правой части
рисунка 1.
Согласно очевидным симметриям, /г([—оо, —1]) = ^([—1,1]) =
= д([1, оо]) = 1/3, тогда как распределение р наиболее компактно вы-
ражается через Правило таково: если rj(p2~k) — п'/d! и т/((р +
Рис. С20-2. Кривая /(а) при конечных отличиях Д/3, для которых Дт? = 10~5.
Примерно 10 из вычисленных Д/3 являются 0 с четырехкратной точностью, то
есть Д/3 < 10-33, так что нет никаких данных при а = log Д/3/ log Дт? > 6,5;
тем не менее, хвост имеет бесконечную длину
С20. Инвариантные мультифракталы в гамильтоновых системах 295
4- 1)2—к) = п"/d", где р, к, п', п", d! и d" являются целыми числа-
ми > 0, то р((р -И 1/2)2-Ас) = (п' 4- n")/(d' 4- d"}. 3iq подразделение
Фарея.
Не составляет труда перейти к асимметричным биноминальным сло-
вам и последовательностям букв, управляемых процессом Маркова или
другим процессом без долговременной памяти.
Рис. С20-3. Кривая /(а) при конечных отличиях Дту для постоянных значе-
ний А/? = 2“26. Представлены все данные; кривая начинается линейно с еди-
ничным наклоном, что свидетельствует об очень маленьких значениях а. Эта
линейная зависимость при а < 1 не совсем очевидна, поскольку для малых зна-
чений а данных пока недостаточно. Наибольшие скачки р наблюдаются при 3 =
= 0 и 1, где Др = 1/26, так что а = log Др/log Д/3 log 26/26 log 2 = 0,1786,
как и наблюдается в действительности.
4. Третий пример, обусловленный гамильтоновой системой
Рассмотрение этого примера начинается с анализа сингулярного че-
тырехугольника в верхней плоскости (х,у\ границами которой яв-
ляются окружности с радиусом 1/2 и центром в точках х = -1/2 и т =
= +1/2 и вертикальные прямые х = -1 и х = +1. Если отождествить
296
Physical Review Letters: 60, 22 February, 1988, 673-676
противоположные стороны, этот четырехугольник превратится в тор.
Однако, этот тор обладает одной исключительной точкой, поскольку
вершина четырехугольника располагается бесконечно далеко в гипер-
болической метрике ds2 = (dx2 4- dy2)/y2. (Тор можно сравнить с за-
крытым ящиком, а исключительную точку — с узким отверстием для
входа и выхода частиц, словно оные рассеиваются от какой-то молекулы
с внутренней степенью свободы, Gutzwiller 1983).
На следующий шаг нас вдохновили труды Series 1985, 1986. Она
рассматривает сингулярный треугольник Di — правую половину D2, ко-
торая ограничена окружностью радиуса 1/2 с центром в точке х = 1/2
и вертикальными прямыми х = 0 и х = 1. Геодезическая представлена
евклидовой окружностью с центром на оси х, которая тянется от х = £
(прошлое) к х = т? (будущее). Рассмотрим особый случай £ < 0 < т?. Гео-
дезическая входит в треугольник Di через вертикальную сторону х =
= 0. При 0 < г) < 1 геодезическая выходит из треугольника Di через
окружность и возвращается в треугольник D\ посредством преобразова-
ния z' = z/(l-z). При 1 < т] < оо геодезическая выходит из треугольни-
ка Pi через вертикаль х = 1 и возвращается в Z>i посредством z' — z—l.
В первом случае говорят, что геодезическая поворачивает направо, а во
втором — налево.
Если продолжать в том же духе, будущее геодезической связано
с последовательностью букв R и L или (что то же самое) с последо-
вательностью целых чисел (no, ni, п2 ...), которая означает по, умно-
женное на L, за которым идет ni, умноженное на R, за ним — п2,
умноженное на L, и так далее. Буквенную последовательность лучше
всего представить с помощью вещественной /3 с тем же двоичным раз-
ложением, тогда как
т? = по 4------—-------,
ni 4-------—
712 + “777
и это, действительно здорово. Следовательно, функции /3(rf) и т?(/3) в на-
чале этой Буквы связывают интуитивное описание геодезической 0 с ее
координатами в системе сингулярного треугольника т].
В сингулярном четырехугольнике D2 появляются функции с та-
кими же необычными характеристиками; их можно интерпретировать
как физические свойства хаотических гамильтоновых систем. Началь-
ную точку £ и конечную точку т] геодезической можно использовать
в качестве координат на поверхности Пуанкаре сечения с инвариантным
С20. Инвариантные мультифракталы в гамильтоновых системах 297
Рис. С20-4. Выборочные меры малых интервалов х для симметричной биноми-
нальной мультифрактальной меры, определяемой посредством инверсий относи-
тельно трех окружностей. Рисунок 4.1: построение при -1 < х < 0; рисунок 4.2:
построение при 1 < х < 15
элементом площади d£ dr//(£ - rf)2. Четыре стороны четырехугольника
соответствуют интервалам {1} = (-оо, 1), {2} = (-1, 0), {3} = (0.1)
и {4} = (1, оо) на оси х. Вход и выход геодезической определяются
интервалами, которым принадлежат £ и г/.
Противоположные стороны четырехугольника D2 отображаются
друг в друга посредством z z' = (az + b)/(cz+d), записанного в упро-
щенном виде как (a, b;c, d), где а, b, с, d — это вещественные числа,
a ad — be = 1. Сторона {1}, вертикаль х = -1, отображается в {3}
окружность, с центром в точке х = 1/2 посредством А = (1 +
+ j2)/J); сторона {4}, вертикаль х = 1, отображается в {2}, окружность
с центром в точке х = —1/2 посредством В = (5,(1 + <52)/<5). Па-
раметр <5 > 0 описывает семейство неэквивалентных геометрий на О?.
Можно было бы представить еще один параметр 7, но для этого понадо-
бился бы сингулярный четырехугольник, менее симметричный, чем £>2-
«История» траектории на четырехугольнике D? рассказывается
через последовательность сторон, которые эта траектория пересека-
ет. История эта зашифрована словом, алфавит которого состоит из
трех букв Я(=вправо=0), 5(=прямо=1) и £(=влево=2), которые, как
несложно догадаться, обозначают: за {1}, сторона {2} справа, {3} -
прямо и {4} — слева и т. д. Подсчеты для будущей последовательно-
сти зависят только от т), а прошлая последовательность зависит только
от £. Таким образом, функция от0<т;<1до0<$<1 определена,
298
Physical Review Letters: 60, 22 February, 1988, 673-676
Рис. C20-5. Функции i?(n) при <5 = I/a/7, 1 и \/7 обладают теми же свой-
ствами, что и функция /?(п); каждая из них отражает отношения между двумя
инвариантными мерами на поверхности Пуанкаре
когда троичное разложение & выражает историю траектории. На рисун-
ке 5 изображена функция при трех значениях 6 = —1/\/7, <5 = 1
и <5 = х/1.
Мультифрактальный анализ функции т9(т?) дает результаты ти-
па Теперь бесконечно длинный хвост кривой /(а) обусловлен
присутствием параболических элементов в группе, которая порождает-
ся А и В; например, последовательность 0000 приводит к ВАВ-1А-1 =
= (-1,0; Г,-1), где Г = 2(2+<5-2). Затем с помощью простого аргумента
можно показать, что функция начинается с О = exp(-riog3/47j).
Присутствие на графике функции ^(г?) практически плоских частей
означает, что траектория попадает в ловушку выхода-входа, а не бродит
по тору, то есть она взаимодействует с внутренней степенью свободы.
Таким образом, функция 1? дает более информативное с физической точ-
ки зрения описание, нежели ту, но они обе определяют инвариантные
меры на поверхности Пуанкаре сечения. Их можно свести к одномерной
кривой т?(?7), поскольку прошлое и будущее разъединяются. Кривая /(а)
характеризует хаос в этой системе, так как она связывает кодирование
траекторий с их физическими параметрами (начальными условиями).
Эта связь играет важную роль при суммировании по всем траектори-
С20. Инвариантные мультифракталы в гамильтоновых систем »у. 299
ям (классическое приближение к путевому интегралу Фейнман
по всем периодическим орбитам, как в формуле следа сРПкА " '
показано в работе Gutzwiller 1980 в отношении анизотоопнпй Та КаК
Кеплера, где используется бинарное кодирование такие cv роблемы
вычисляться непосредственно как суммы по кодовым словам “ М°ГУ’1
Некоторые рисунки были подготовлены Режанпм Го„
(Получено 27 октября 1987 года) анье-
Хаос в Австралии
Под редакцией Дж. Брауна и А.Опие, 1993
С21
Мера Минковского и мультифрактальные
аномалии в инвариантных мерах
параболических динамических систем
Предисловие к главе (2003). Этот репринт объединяет работу
Ml993s с более ранним репринтом (Ml995s), в который были внесе-
ны некоторые изменения.
Аннотация. Автор недавно доказал, что важная сингулярная
неслучайная мера, определенная в 1900 году Германом Минковским,
является мультифрактальной и обладает практически наверняка беско-
нечным показателем а. Следовательно, атах — оо, а ее распределе-
ние /(а) не имеет уменьшающейся правой стороны, соответствующей
уменьшающейся функции /(а). Факт ее левосторонности создает мно-
жество очень интересных затруднений. В 1932 году Данжуа заметил,
что эта мера Минковского представляет собой ограничение до [0, 1] ме-
ры аттрактора для динамической системы на прямой, основанной на
отображениях х —> 1/2 + 1/4(х - 1/2), х —» —х и х —» 2 — х. В данной
работе говорится, что из замечания Данжуа следует, что новые «мульти-
фрактальные аномалии» из-за левосторонности /(а) распространяются
на инвариантные меры некоторых динамических систем.
Первоначальный подход автора к мультифракталам, основанный на
распределении грубого значения показателя Гельдера а, также вводит
приблизительные меры pe(dt), которые были «огрублены» в процессе
замены непрерывной t кратными е > 0. Таким образом, эта теория
строится вокруг последовательности наблюдаемых аппроксимирующих
функций графики которых не являются левосторонними.
Основной целью этой краткой статьи является описание моего жиз-
ненного опыта и предостережение, которое мне хотелось бы донести
до специалистов, намеревающихся заняться изучением мультифракта-
лов. Существует распространенное мнение, что распределение f (a) для
каждой мультифрактальной меры р удовлетворяет условию / > 0, а его
график напоминает математический символ О. Согласно классическим
результатам 1930-40-х годов (полученным Безиковичем, Эгглестоном
и др.), это мнение вполне обоснованно, когда р является биноминальной
или практически биноминальной мерой.
Но для многих мер (одни из которых — теоретические, а другие
получены из самой природы) подобное ожидание оказывается непра-
вомерным, в той или иной степени. И это порождает множество так
называемых «аномалий». Некоторые аномалии родственны мерам в ве-
щественном пространстве. К подобным примерам относятся распределе-
ния турбулентного рассеяния (понятие мультифрактала впервые возник-
ло именно в таком контексте) и гармонической меры вблизи кластера
ОДА. В настоящее время эти аномалии начинают получать признание;
в частности, по ссылкам видно, что я посвятил их изучению несколько
работ.
Полагаю, что многие из тех же самых аномалий также встретятся
и для мультифрактальных мер, существующих в динамических систе-
мах. Целью данной работы является рассказать студентам, изучающим
меры на аттракторах, о предыдущих результатах, достигнутых в этой
области. Для этого я буду рассматривать меру Минковского д, которая
является самой привлекательной, но и чрезвычайно аномальной.
В применении к данной мере мой подход к мультифракталам (на-
зовем его «методом распределений»), как вскоре станет ясно, обяза-
тельно будет касаться двух отдельных аспектов функции /(а). Во-пер-
вых, существует теоретическая «популяционная» функция /(а). Для ме-
ры Минковского р форма этой функции не П; напротив, она является
левосторонней, то есть монотонно возрастает в направлении максиму-
ма /(оо) = 1 и не имеет правой (уменьшающейся) стороны. Но пред-
положим, что р — это крупнозернистая мера на интервалах длиной е,
благодаря чему ее можно наблюдать. В таком случае метод распределе-
ний позволяет определить эмпирическую «выборку» f£(a) для каждого
значения е. Эту выборку можно видеть, и для меры Минковского ее
форма совершенно отлична от формы /(а).
При е —» 0 мы имеем /(а) —> /е(а), а это значит, что в основе
метода распределения лежит логически согласованная теория. Однако
схождение происходит мучительно медленно, и чрезвычайно сингуляр-
но. Экстраполяция формы функции /(а) из формы f£(a) требует боль-
шой аккуратности.
Эти результаты свидетельствуют об ограниченности «термодинами-
ческой» теории, на которой основывается функция f(a). В некоторых
случаях функция /(а) очень грубо приближается с помощью предтер-
модинамических результатов, полученных при е > 0, сколь бы малым ни
было значение е. В отличие от изученных левосторонних мультифрак-
302
Хаос в Австралии, 1993
талов, меру Минковского невозможно получить с помощью мультипли-
кативного каскада. Тем не менее, некоторые свойства р мы впервые
предположили на основании приближения р с помощью мультиплика-
тивного мультифрактала, и правильность полученных результатов была
впоследствии доказана.
При изучении мер аттракторов лучше сначала проанализировать
меры, поддерживаемые странными аттракторами. Однако в литературе
по мультифракталам до сих пор наблюдается полная неразбериха. Это
свидетельствует о том, что данная тема намного сложнее, чем многие
привыкли считать, поэтому лучше всего изучать каждый вопрос после
исключения всех ненужных сложностей.
1. Мера Минковского на интервале [0,1]
Мера Минковского р, а также обратная мера Минковского легко
поддаются описанию и не создают проблем при работе, при этом они
отличаются очень интересными и совершенно неожиданными особенно-
стями. Они являются дифференциалами двух возрастающих сингуляр-
ных функций: М(х) и обратной ей Х(т), соответственно.
Проще всего начать с определения обратной функции Минковско-
го Х(т), построение которой происходит пошагово, согласно следующе-
му принципу. На первом этапе мы задаем Х(0) = 0 и Х( 1/2) = 1/2. На
втором этапе происходит интерполяция: значение Х(1/4) принимается
за среднее Фарея для Х(0) и Х(1/2), где среднее Фарея для двух несо-
кратимых отношений (а/с) и (b/d) определяется как (a + b)/(c + d). Во-
обще, k-й шаг начинается с определения функции Х(т) для т = р2~к,
где р представляет собой четное целое число, и использует средние Фа-
рея для интерполяции к т = р2~к, где р является нечетным целым
числом. В конечном итоге, Х(т) распространяется на интервал [1/2,1]
посредством принятия равенства Х(1 - т) = 1 — Х(т). Получающаяся
в результате функция Х(т) является непрерывной и сингулярной, она
возрастает на каждом интервале, то есть не имеет конечной производ-
ной ни в одной точке. Она имеет обратную функцию М(х) с такими
же свойствами, которые проиллюстрированы «скользящей лестницей»
на рисунке 1.
Дифференциалы д и р функций Х(т) и М(х) представляют со-
бой сингулярные меры. На двух частях рисунка 2 изображена мера р,
оцененная для интервалов длиной 10-5.
В работе Minkowski 1911 (том 2, стр. 50-51) М(х) названа «?(з;)
функцией». Вообще, «функция» — это термин, который в ряде случаев
С21. Мера Минковского
303
2 - х.
является для математика истинным спасением. До труда Denjoy 1932
о мере д написано было мало (если вообще было). В той работе ей
приписывалось следующее свойство: она является ограничением до [0. 1]
меры аттрактора для динамической системы на прямой, основанной на
отображениях
х —> — Ч---------, х —► —х и
2^4(а; — 1/2)’
Стандартным методом превращения такого набора функций в ди-
намическую систему, безусловно, является случайный выбор следующе-
го действия. Этот метод был использован на рисунках 282 и 283 из
M1982F, а в настоящее (и в последнее) время он называется СИФ: си-
стемой итерированных функций.
Такое толкование позволяет доказать, что корни функции М(х)
уходят глубоко в теорию чисел (модулярных функций) и в фуксовы
или клейновы группы. Однако, с точки зрения данной работы, основное
достоинство вышеуказанной динамической системы заключается в ее
чрезвычайной простоте. Я предполагаю, что любая сложность или за-
труднение на пути исследования инвариантных мер непременно появят-
ся в более сложных системах, основанных на физических явлениях.
Более того, нельзя забывать, что у работы Gutzwiller & М1988{С20}
было две задачи. Я анализировал вышеописанные отображения, а мой
соавтор занимался изучением важной гамильтоновой системы, в кото-
рой х является мерой Луивилля, а т — второй инвариантной мерой,
предоставляющей не менее интересную информацию об индивидуаль-
ных траекториях.
2. Функции /(а) и /£(а) меры Минковского
2.1. Теоретическая функция f(oc). Для выведения функций /(а)
меры Минковского д и обратной меры Минковского д мы вынуждены
отправить читателя к другим источникам (пока что не опубликован-
ным). Первое и самое главное, что следует отметить — это факт су-
ществования для этих мер теоретической функции /(а): функция f (а)
является хаусдорфовой размерностью множества таких точек х, для ко-
торых показатель Гельдера Н(х) принимает значение а. В случае с ме-
рой д график функции /(а) обладает следующими свойствами:
• функция /(а) определяется для а amin = — 1/log2 72 ~ 0,7202 ...,
где 7 является золотой серединой ~ 0,6180... (полученной в работе
Salem 1943 и - независимо — в труде Gutzwiller & М 1988)
304
Хаос в Австралии, 1993
Рис. С21-1. График функции Минковского М(х) при 0 < х < 1/2. В отличие от
знаменитой чертовой лестницы Кантора (M1982F, рисунок 125), график функ-
ции М(х) не имеет настоящих ступенек, а лишь приближение к оным, поэтому
в работе Gutzwiller & М1988{С20} эта лестница называется «скользящей»
• Qi = [2 Jq log2(l + i)dM(a:)]_1 = 0,874... (получено в работе Kinney
1960)
• f(a) —» 1 при а —» оо. Это свойство функции /(а) сильно влияет
на природу множества точек х при Я(х) > а: мера этого множества
равна единице.
2.2. Проблема выведения формы функции f(a) из имеющих-
ся данных. После аналитического определения функции /(а) мы не
можем не продолжить исследования. Теперь логично будет задаться во-
просом, можно ли вывести эту функцию и тогда, когда механизм нашей
динамической системы не известен и мы располагаем лишь некоторы-
ми «эмпирическими данными». В таком контексте понятие «данных»
может означать одно из двух: либо «грубую» (либо крупнозернистую,
или квантованную) форму функции М(х), эффективно вычисленной для
значений х, ограниченных кратными некоторого кванта Да: = е. Слово
«данные» также может относиться к длинной орбите вышеописанной
динамической системы, то есть к длинному ряду последовательных зна-
С21. Мера Минковского
Рис. С21-2. Изображения меры Минковского /л в виде крупнозернистого по-
казателя Гельдера и его логарифма. Приняв е = 10-5, мы оценили прираще-
ния ДМ = М[(к + 1)е] - М[/се]. На рисунке 2а (вверху) изображен крупнозер-
нистый показатель Гельдера a log ДМ/log е, а на рисунке 2Ь (внизу) — logo.
Из теории, описанной далее в этой работе, становится ясно, что мелкозерни-
стый (локальный) показатель Гельдера превышает любое принятое значение а
практически повсеместно. На данном рисунке это свойство, к сожалению, не
отражено.
306
Хаос в Австралии, 1993
чений J-. Их также необходимо записать в крупнозернистом формате.
Многим физическим величинам в вещественном пространстве свойство
♦ крупнозернистое™» присуще изначально, то есть они определяются не
на непрерывной шкале, а лишь на интервалах, длина которых кратна
некоторому кванту Ат = е, что объясняется существованием атомов
или квантов. У других физических величин существуют внутренние
пределы полезной интерполяции; так, турбулентный поток, например,
является локально гладким. В данном случае крупнозернистость — это
результат необходимой конечности фактических вычислений и наблюда-
емых орбит.
Принимая во внимание приблизительный характер имеющихся дан-
ных, можно сказать, что существует, по крайней мере, два способа по-
иска получения или оценки функции f(a).
2.4. Метод моментов в приложении к распределению Мин-
ковского. Наиболее известный метод оценки функции /(a) (Frisch &
Parisi 1985 и Halsey et al., 1986) по праву носит название «метода мо-
ментов». Он начинается с крупнозернистых мер р£(х), содержащихся
в последовательных интервалах длиной е, и продолжается согласно сле-
дующему сценарию: а) нахождение совокупности моментов, входящих
в «статистическую сумму», определенную как х(с, q) = б) оцен-
ка значения r(q) посредством «подгонки» прямой к данным logx(£, <?)
в сравнении с loge и в) получение функции /(а) как преобразования
Лежандра т(д).
Если метод моментов применить к мере Минковского р механиче-
ски, это либо не даст никаких результатов вообще, либо получится пол-
ная ерунда. В частности, более тщательные механические реализации
данного метода не соответствуют наклону r(q), при этом мы не прове-
ряем прямолинейность исходных данных (это можно увидеть и невоору-
женным взглядом). Но данные Минковского при q < 0 вовсе не прямые.
Таким образом, разумно заключить, что «никакой r(q) не существует».
Поскольку при q > 0 такой сложности не возникает, подобные выво-
ды часто сопровождаются утверждением, будто имеющиеся данные «не
вполне» мультифрактальны. Менее аккуратные механические реализа-
ции метода моментов попросту подгоняют данные под т(д). В зависимо-
сти от набора правил, используемых для подгонки, и деталей процесса
квантования, эти методы могут выдать предполагаемую т(<?), которая не
будет выпуклой. Получающееся в результате «преобразование Лежанд-
ра» — не однозначная функция, a f(a) — вообще загадка. При исполь-
зовании других механических методов сложность оценки т(<?) сначала
С21. Мера Минковского
307
устраняется с помощью «стабилизации» этой оценки, производимой тем
или иным способом. В результате может появиться некоторая функ-
ция /(а), но при этом мы вряд ли сможем определить, что она означает
и для чего предназначена.
Сейчас самое время упомянуть об основной характеристике метода
моментов. При оценке значения r(q) из имеющихся данных применяется
предельный процесс е —> 0. Но предасимптотические данные, соответ-
ствующие е > 0, не определяют приблизительную функцию fe(a).
2.5. Метод распределений. Вторым способом оценки функ-
ции /(а) служит метод распределений, который используется во
всех моих работах, перечисленных в библиографии. Я пользовался им
с 1974 года, и с каждым разом я все больше убеждаюсь в его полез-
ности. Ключ прост. В методе моментов практически сразу вычисляются
моменты меры ре(х), входящие в статистическую сумму x(c,q), тогда
как в методе распределений для каждого значения е рассматривается
полное распределение частот меры m£(i). Эти распределения образуют
графики, которые статистики называют «гистограммами*.
Сначала весь диапазон исследуемых величин о подразделяется на
равные «секции», причем мы фиксируем количество данных в каждой из
них. Если число секций слишком мало, информация теряется, но если
секций слишком много, основная их часть останется пустой. В случае
с мерой р Минковского, существует много значений а, расположенных
чуть выше «min, а несколько значений этой величины поднимаются до
очень высокого уровня.
Обозначим через Nb количество данных в секции Ь. При большом
значении Nb для оценки плотности распределения вероятности показате-
ля а служит отношение Nb/Aa. Если М, = 1, а соседние секции пусту-
ют, оценить вероятности можно путем усреднения достаточно большого
числа соседних секций; вероятности эти очень малы.
Оценив плотность распределения вероятности ре(т), получаем
, / х _ log Ре (о)
loge
Таким образом, метод распределений создает последовательность
функций Л(а). Поскольку f£(a) представляет собой нормированный ло-
гарифм меры, каждая f£(a) — это ни что иное, как гистограмма, заново
построенная в дважды логарифмических координатах и должным обра-
зом взвешенная. Эти гистограммы нужно оценить для ряда значений г.
Когда рассматриваемая мера является мультифрактальной, последова-
тельность /е(а) сходится к пределу /(а), т. е. функция /(а) входит
308
Хаос в Австралии. 1993
в теорию в виде
/(«) = Ji™/И^-
Обычной реакцией на гистограмму является фраза: «А к чему такие
хлопоты? Все мы знаем, что информацию, которую они содержат, также
можно найти (к тому же, в более организованной форме) в моментах.
Кроме того, моменты более знакомы, и с ними намного проще работать,
чем с гистограммами». К сожалению, в этой фразе не учитывается вся
сложность фракталов и мультифракталов.
При изучении фракталов обычные распределения вероятностей ре-
гулируются степенным законом, а моменты теоретического распределе-
ния высокого порядка бесконечны. Соответствующие выборочные мо-
менты (а иногда даже и выборочное среднее значение) демонстрируют
совершенно неустойчивое поведение. Они не дают никакой полезной ин-
формации и могут привести к ошибочным результатам.
Теперь переходим к мультифракталам. Когда, при f > 0, функ-
ция /(а) действительно имеет форму Г), моменты не вызывают никаких
проблем, метод моментов отлично работает, а метод распределений ме-
нее эффективен в плане получения /(а). Но во всех непростых случаях
выборочные моменты, входящие в статистическую сумму, доставляют
много хлопот. Единственным выходом в таком случае служит метод
распределений.
2.6. Метод распределений, в приложении к мере Минковского.
В работе Gutzwiller & М1988 использовались гистограммы, причем на
рисунке 2 (здесь — это рисунок 3) представлена полученная нами эм-
пирическая последовательность /е(аг). Для получения этого графика мы
укрупнили х, а затем (в сущности) укрупнили и М. «Квант» М был кро-
хотным, поскольку он попросту представлял собой наименьшее М(х +
+ е) - М(х), которое можно было получить на нашем компьютере при
четырехкратной точности. Таким образом, значения, которые компьютер
не мог отличить от 0 (10% от общего числа), просто не использовались.
Получившаяся в результате кривая, основанная на имеющихся дан-
ных, совершенно не похожа на теоретическую левостороннюю кри-
вую /(а). Она, как обычно, начинается с левой стороны в форме
бесспорно выпуклой «шапки». Средняя часть удовлетворяет неравен-
ству А(п) > 1, что не может быть истинно для f(a), но это ожидаемый
результат и один из неизбежных недостатков метода распределений, ко-
торый можно исправить. И, наконец, существует правая сторона в форме
вогнутой «чаши», что явилось полной неожиданностью, поскольку тео-
ретически функция /(а) должна иметь форму выпуклой «шапки» на
всей своей протяженности.
С21. Мера Минковского
309
Рис. С21-3. Раннее построение предполагаемой функции fe(a) для меры Мин-
ковского. Взято из работы Gutzwiller & М1988{С20}
Мы отказались от попыток найти более удачный способ исследова-
ния этой вогнутости-выпуклости. Мы даже не приблизились к анализу
моего следующего предположения насчет того, что предполагаемая по-
следовательность /£(а) (если ее достаточно расширить) при достаточно
больших значениях а становится < 0. Мы показали, что при q < О
момент х(?,£) не является функцией степенного закона е. Однако, к на-
шему разочарованию, нам не удалось определить функцию /(а) анали-
тическими методами. Мы действительно предсказали правильную фак-
тическую форму функции /(а) (но не записали ее) и переключились на
функции felfii) и /(а), которые отличаются настолько сильно.
310
Хаос в Австралии, 1993
Недавно я вернулся к изучению этой проблемы. Рисунок 4 был
подготовлен с помощью метода, который вычисляет значение выраже-
ния .Щг + dr) — М(х) напрямую, а не через М{х). Это можно сде-
лать с произвольной относительной точностью, поэтому мы можем до-
стигнуть огромных значений показателя а. На рисунке 4 представлены
убедительные подтверждения более ранних предположений относитель-
но существования у эмпирической функции /(о) правой чашеобразной
стороны и отрицательного хвоста.
Это явное несовпадение между теорией и даже самыми лучшими
экспериментами подтолкнуло меня к тщательному выведению теорети-
ческой функции /(а) и предсказанной функции Форма функ-
ции /(а) уже упоминалась. В отношении же fe(a) достаточно сказать,
что при больших значениях е
~ 1 — (const) log а/ log е.
Рисунок 4 подтверждает эту зависимость от данных.
2.7. Является ли функция /(а) полезным понятием в случае
с мерой р Минковского? Отмечу еще раз, что наши последние оцен-
ки последовательности f£(a) даже не приблизились к воспроизведению
истинной формы графика функции /(а), несмотря на то, что они бы-
ли выполнены с точностью, выходящей за пределы любого вообразимо-
го физического измерения. Даже более ранние оценки, представленные
в работе Gutzwiller & М 1988{С20} были далеко за пределами возмож-
ностей физики.
С учетом описанных сложностей можно ли заключить что в слу-
чае меры Минковского функция /(а) является бесполезным понятием?
Несомненно, эта мера подтверждает то, что я неустанно повторял на про-
тяжении многих лет: /(а) — это невероятно тонкий инструмент. Самым
подходящим для нее контекстом служат распределения, то есть теория
вероятностей. Более того, она не касается наиболее известных и «тру-
доемких» частей этой теории, а именно: тех, что связаны с законом
больших чисел и теоремой о центральном пределе. Она полностью со-
средоточена в теории вероятностей больших отклонений, которая и сама
является довольно непростой темой.
3. Замечания
3.1. О непрерывных моделях как аппроксимациях и о «термо-
динамике». Почему физики изучают недостижимые пределы? Просто
потому, что зачастую проще описать предел, чем некоторую конечную
структуру, которую можно рассматривать как аппроксимацию к этому
С21. Мера Минковского
311
Рис. С21-4. Построение предполагаемых функций /е(а) для меры Минковско-
го, ограниченной интервалом [1/10, 1/9]. Приняв за вертикальную координа-
ту Л(а) - 1. в качестве горизонтальной координаты (для выпрямления /е(а))
мы выбрали logo. Затем мы стянули пять графиков, соответствующих значе-
ниям е = 10~5, 10-6, 10“7, Ю-8 и 10-9. Этот рисунок является очевидным
доказательством чашеобразности, которая только предполагалась на рисунке 3.
Он демонстрирует появление f < 0. И наконец, правило взвешивания показы-
вает, что выражение 1 — Л (а) уменьшается при е —♦ 0
пределу. В частности, именно по этой причине при исследовании мульти-
фракталов часто не принимается во внимание, что совокупность «круп-
нозернистых* аппроксимаций можно заменить непрерывным «тонким»
или «мелкозернистым» описанием. Последнее содержит хаусдорфовы
размерности и задействует непосредственно функции т(д) и /(а), а не
их пределы.
Однако для меры д Минковского фактический переход от крупных
зерен к мелким (при Дгг —» 0 и Дтп —» 0) происходит чрезвычайно мед-
ленно, а многие аспекты рассматриваемого предела качественно отли-
чаются от соответствующих аспектов даже близких его аппроксимаций.
Следовательно, необходимы дальнейшие исследования роли пределов,
которые я предлагаю перенести в другое место.
312
Хаос в Австралии, 1993
Как уже было описано, непрерывная предельная аппроксимация
подчиняется «термодинамическому» описанию. Таким образом, медлен-
ная и сингулярная сходимость в случае меры /2 Минковского свидетель-
ствует о фундаментальном практическом ограничении термодинамиче-
ского описания.
3.2. Параболические и гиперболические динамические системы.
Для выделения важнейшей составляющей нашей специальной динами-
ческой системы необходимо рассмотреть, как изменятся ее свойства при
изменении самой системы. Если мы хотим, чтобы функция /(а) приняла
форму П, достаточно заменить первое из трех наших отображений на
х_л + .
2 + х — 1/2’
где р < 1/4. При р —► 1/4 правая сторона графика /(а) удлиняется
и отодвигается к бесконечности, а аномалии исчезают асимптотиче-
ски. Формально гиперболическая система превращается в параболиче-
скую. Следовательно, рассмотренные нами аномалии обусловлены пара-
болическим характером системы. Что касается предела функции /(а),
различия между параболическими и гиперболическими случаями уси-
ливаются при р —► 1/4. Однако фактические наблюдения проводятся
в предасимптотическом диапазоне, и для большинства значений е по-
следовательность /е(а) будет, в сущности, одинаковой как для р = 1/4,
так и для р, близкого к 1/4.
3.3. Вместо заключения. Кажущаяся «странность» фактов, опи-
санных в данной работе, не должна пугать читателя, обладающего прак-
тическим складом ума. Если вновь применить типичную для фракталь-
ной геометрии модель, оказывается, что все эти «странности» вовсе не
такие уж странные и им можно только порадоваться.
4. Благодарности
Работа, приведшая к написанию данной статьи, началась в 1987 го-
ду. Прошедшие с того времени годы ознаменовались бесценными дис-
куссиями с М. К. Гутцвиллером, К. Дж.Эверцом, Т. Бедфордом и И. Пе-
ресом. Рисунки 1, 2 и 4 подготовил Дж. Кленк. Перес, написавший кан-
дидатскую диссертацию по этой теме, сообщил нам, что приведенное
нами определение предвосхитили Минковский и Данжуа. Таким об-
разом, мы с Гутцвиллером независимо друг от друга заново открыли
меру д еще до того, как объединили свои усилия, а вот функция /(а)
от д не исследовалась до написания нашей совместной работы (хотя
и неполной).
Physica A 177, 1991, 386-393
C22
Гармоническая мера ОДА и расширенное
понятие о самоподобии (М & Evertsz 1991)
Предисловие к главе (2003). Поскольку уместность данной главы
многим может показаться неочевидной, она объясняется в главе С19.
Аннотация. ОДА почти самоподобна, но отклонения от простой
самоподобности не подлежат сомнению, а измерение их статистической
природы показало себя непростым делом. Мы продемонстрируем, что
ОДА следует удивительному новому правилу масштабной инвариантно-
сти. Оно заключается в том, что изучаемая область, содержащая кро-
хотную гармоническую меру, по мере роста кластера возрастает более
чем пропорционально. Это правило масштабной инвариантности также
косвенным образом свидетельствует о том, что гармоническая мера ре-
шетки ОДА подчиняется гиперболическому распределению вероятности
экспоненты, равной 1. Согласно этому распределению, выборочные мо-
менты демонстрируют неустойчивое поведение, что объясняет, почему
к ОДА не применим обычный ограниченный мультифрактальный фор-
мализм.
В данной работе описываются два новых масштабно-инвариантных
свойства гармонической меры р на плоской ОДА. Необходимость по-
лучения двух отдельных методов скейлинга подразумевает, что понятие
самоподобия в действительности распадается на несколько отдельных
подпонятий. Наше более важное новое масштабно-инвариантное свой-
ство меры р необычно, т. к. оно предполагает, что ОДА удовлетворяет
не традиционно постулируемой форме самоподобия, а его «расширен-
ной форме». Мы сравниваем маленькие кластеры ОДА с уменьшен-
ными и крупнозернистыми кластерами и обнаруживаем между ними
неожиданные систематические различия. Грубо говоря, «исследуемая»
область, обладающая крошечной гармонической мерой, по мере увели-
чения кластера возрастает более чем пропорционально. В одно время
ученые надеялись, что гармоническую меру можно представить в рам-
ках ограниченной формы понятия мульт и фрактал a (Frisch & Parisi 1985,
Halsey et al. 1986). Это означало бы, что мера р самоподобна в крайнем
смысле этого понятия. Учитывая локальные иррегулярности р, харак-
314
PHYSICA A 1//, 1331, оои~озо
тернзуемые классическим показателем Гельдера а, структуру сильного
самоподобия можно охарактеризовать либо функцией r(q), определен-
ной для всех значений —оо < q < +оо, либо функцией /(а), график
которой имеет асимметричную форму символа А. К сожалению, за ис-
ключением, возможно, областей с наибольшей вероятностью роста, этот
мультифрактальный анализ ОДА давал противоречивые или неприем-
лемые по какой-либо другой причине результаты. Как и многие другие
авторы, мы считаем эти сложности очевидным доказательством того, что
к ОДА не применимы масштабно-инвариантные отношения степенного
закона, характеризующие ограниченные мультифракталы. Эти наблюда-
емые «аномалии» тесно связаны с поведением малых гармонических мер.
Однако недавно мы с помощью наглядных примеров показали, что
несуществование функции r(q) для всех q может и не означать, что
мера не является самоподобной. Меры, описанные в М et al. 1990, от-
носятся к более общей теории мультипликативных мультифракталов (М
1974f{N15), М 1988с, М 1989g); тем не менее, правая сторона кри-
вой /(а) полностью отсутствует, поэтому меру р, можно назвать «лево-
сторонним мультифракталом». Однако главная тема данной работы вы-
ходит далеко за пределы определения функции /(а). Мы утверждаем,
что односторонняя кривая /(а) неадекватно описывает распределение
левосторонней меры ц. Помимо масштабной инвариантности, необхо-
димой для описания /(а), для характеристики других важных аспек-
тов меры ц необходимы дополнительные масштабно-инвариантные отно-
шения.
В данной работе предпринята попытка решения проблемы распреде-
ления гармонической меры /х с использованием прямого вероятностного
метода (М 1974f{N15), М 1988с, М 1989g). Основная причина выбора
этого метода заключается в том, что попытки рассмотреть гармониче-
скую меру ОДА в рамках ограниченного мультифрактального формализ-
ма. судя по всему, не увенчались успехом, потому что для малых зна-
чений ц характерно высокое статистическое рассеяние. Одним из след-
ствий этого является сложность вывода из малых измеренных д. Таким
образом, экспоненциальное убывание минимальной вероятности (посту-
лированное в работе Blumenfeld & Aharony 1989) было бы сложно как
подтвердить прямыми методами, так и опровергнуть, представив иные
альтернативы. Другое следствие заключается в том, что статистические
методы (например, определение статистической суммы) становятся, как
минимум, ненадежными.
Мы провели численный расчет как для круговой, так и для цилин-
дрической ОДА. Наши рисунки относятся к геометрии тел вращения,
С22. Гармоническая мера ода
5 1 □
но подобные результаты получаются и в рамках цилиндрической геомет-
рии. Мы вырастили десять кластеров из N — 50 000 частиц по алгорит-
му случайного блуждания Й. Хаякава, с помощью которого выращивают
более привычную местную версию ОДА. Потенциал подсчитывался по-
средством решения дискретного уравнения Лапласа итеративно на квад-
ратной решетке, лежащей в основе роста, с граничными условиями 0 на
кластере и 1 на окружности с радиусом, равным 3/2 от общего размера
кластеров. Местная гармоническая мера д на границе кластера теорети-
чески пропорциональна градиенту потенциала, но мы аппроксимировали
ее с помощью потенциала в ближайшей окрестности кластера, а затем
нормализовали (Niemeyer et al. 1984). Для каждого кластера мера р
определялась на последовательных стадиях роста N — 781, 3125, 12 500,
50000; то есть для Nk = 4kNo при Nq = 781 и к = 0, 1, 2, 3. На каждой
стадии, к, мы оценивали плотность распределения вероятности р/Да)
показателя Гельдера а = logд/logпосредством определения выбо-
рочной частоты а для каждого кластера и последующего осреднения по
более чем десяти кластерам.
Если бы гармоническая мера ОДА была ограниченным муль-
тифракталом, можно было бы ожидать, что величины Сдг(а) =
= (1/logAT) logp/v(a) будут сходиться к более известным величи-
нам f(a)/Do — 1 при N —► оо (М et al. 1990, М 1974f). Тогда гра-
фики функции Cjv(a) служили бы аппроксимацией функции /(а). (Эти
правила рескейлинга обычно выражаются через размер L кластера, но
в этом случае L ~ .) Также отметим, что фактическая сходимость
к /(а) может быть чрезвычайно медленной, а аппроксимация /(а) с по-
мощью Cn(q) далека от точности. Тем не менее, на рисунке 1 изоб-
ражен верхний уровень группирования при низких значениях а. Одна-
ко на правых сторонах не наблюдается никаких признаков схождения
при N -► оо. Сложности, возникающие при определении функции /(а)
по методу Лежандра, начинающемуся с т(д), вероятно, проистекают ис-
ключительно из этих хвостов.
На рисунке 2 представлены те же самые данные, только обрабо-
танные по нестандартному для физики сценарию, который мы назы-
ваем положительным рескейлингом Коши. За абсциссу принимает-
ся log д/log TV-log log/V, а за ординату — сам без перенормиров-
ки. Теперь именно правые стороны получающихся в результате графиков
стягиваются в один-единственный.
Странный (на первый взгляд) метод рескейлинга, использованный
для получения рисунка 2, был выбран намеренно, а не в результате ряда
проб и ошибок. На его создание нас вдохновила малоизвестная в физи-
316
Physica A 177, 1991, 386-393
ке теорема о пределе; в ней предел представляет собой асимметричную
или положительную случайную переменную Коши. Эта теорема отно-
сится к теории мультипликативных мультифракталов (М 1974f{N15}).
Прежде чем заново излагать основные идеи этой теории, отметим, что
в случае с ОДА все последовательные стадии, которые мы будем опи-
сывать, являются лишь гипотетическими.
Рассмотрим правильную сетку с базой 2 на единичном интерва-
ле [0.1] и обозначим через Z(/?lt /?2, • • •, 0k) интервал [/, t + е], где е =
= 2~к, t = 0, 0k (в двоичном представлении), a 0i равно 0
или 1. Структура мультипликативного мультифрактала определяется
с помощью случайной переменной М, математическое ожидание кото-
рой удовлетворяет ЕМ = 1/2 (для обеспечения сохранности) и другим
условиям (М, 1989g, Stanley & Ostrowsky 1988). Первая стадия муль-
типликативного каскада начинается с массы, равной 1 на [0, 1], и ее пе-
рераспределения путем передачи подинтервалу Z(/?i) массы M(0i). На
второй стадии интервалу 1(01, /32) передается масса M{0\)M(0i, /?2).
После к стадий интервал Z(/3i, /?2, ..., 0k) содержит массу
Mt(e) = М{0Х)М{0^02) - - • 02, .... 0к).
Каждая реализация каскада (то есть каждая затравка «случайного» ге-
нератора) порождает новую «выборку». Правила мультипликации оста-
ются статистически неизменными на каждой стадии измельчения в том
смысле, что, если задано t, множители М(0\), М(02) и т. д. являются
независимыми и тождественно распределенными (н.т.р.). Следователь-
но, меры, получающиеся из этих бесконечных каскадов, статистиче-
ски самоподобны и мультифрактальны в более общем смысле (М et al.
1990, М 1989g, Stanley & Ostrowsky 1988, M 1974).
Теперь для удобства введем новую случайную переменную V =
= -log2M, плотность распределения вероятности которой (р(у)) полу-
чается из плотности вероятности М, и запишем
Нк = logg(e)/loge =
к
= 1(V(01) + V(01,02) + + rn, • -, 0k)) = (1/fc) £ Vn.
к n=l
Эта H является случайной переменной, выборочное значение кото-
рой, обозначаемое через а, попросту являет собой показатель Гельдера
(«прочность сингулярности»). В данном контексте показатель — это вы-
борочная средняя величина к н.о.р. случайных переменных Ц, ..., Vjt
С22. Гармоническая мера ОДА
317
с плотностью распределения вероятности p(v). Суммы таких перемен-
ных неоднократно исследовались в теории вероятностей (Gnedenko &
Kolmogorov 1954-1968).
Рис. С22-1. Рескейлинг Крамера плотностей распределений значений а, опре-
деленных из десяти кластеров масс N = 781, N — 3125, N = 12500 и W =
= 50000. При этом рескейлинге строятся ордината Cw(а) — (l/logAT)lnpjv(a)
и абсцисса а = — In/x/lnN. Для ограниченного мультифрактала предел Cjv(a)
при N —» оо должен был бы иметь вид /(a)-1. Здесь же, наоборот, правые
хвосты распределений не сходятся
По построению, вышеупомянутые мультипликативные каскады по-
рождают статистически самоподобные меры. Следовательно, можно
надеяться, что плотности распределения вероятностей рк(а)Нк, соот-
ветствующие последовательным предфрактальным уровням к, можно ре-
нормализовать (или стянуть) таким образом, что подходящая ренорма-
лизованная версия плотности рк будет сходиться к пределу, отличному
от 0 или оо. Если предел существует, он характеризует фрактальные
свойства мультифрактальной меры.
Во-первых, предположим, что существуют, как первый, так и вто-
рой моменты распределения р(и). Это кажется почти очевидным, но
оказывается особым случаем. Затем допустим, что действуют два зна-
комых нам правила теории вероятностей (Gnedenko & Kolmogorov 1968,
318
Physica A 177, 1991, 386-393
Gnedenko 1967). По закону больших чисел и теореме о центральном
пределе, выборочное среднее ^Vn/k сходится к математическому ожи-
данию по популяции (ансамблю) EV, а распределение S{Vn — EV}/\/fc
сходится к гауссиану дисперсии E(V2) — (EV)2.
In д/ln N— In In N
Рис. C22-2. Те же самые предполагаемые плотности, что и на рисунке 1, но
с положительным рескейлингом Коши. Здесь левые стороны не сходятся, чего
нельзя сказать о правых
Однако для описания мультипликативных мультифракталов требу-
ются более точные знания. Соответствующее предельное распределение
задается малоизвестным правилом, а именно: теоремой Гарольда. Кра-
мера о больших отклонениях (М 1974c{N 16), М 1988с, М 1989g). Со-
гласно этой теореме, плотность распределения вероятностей pt(a) у Нк
такова, что последовательность Cfc(a) = (l/fc)log2pfc(a) сходится к пре-
делу С(а). В том случае, когда С(а) не является ни 0, ни 1, эта функция
характеризует фрактальные свойства меры. В случае с ограниченными
мультифракталами функция /(а) равна функции /(а) = Do + С(а),
где Do = 1 на данном интервале (М et al. 1990, Frisch & Parisi 1985,
Halsey et al. 1986).
На этом наше изложение основ подходит к концу. Однако, как ука-
зывается в М et al. 1990, все вышеописанные правила могут либо не
С22. Гармоническая мера ОДА
319
действовать, либо приводить к тривиальным результатам. В качестве
важной предварительной иллюстрации предположим, что случайные пе-
ременные Vn подчиняются распределению Коши, то есть обладают плот-
ностью распределения вероятности «лоренциана» pi(v) = 1/[тг(1 + v2)].
Специалистам по теории вероятностей известен следующий факт, кото-
рый несложно проверить: в случае Коши сумма Y,Vn/k имеет то же рас-
пределение, что и каждое из ее слагаемых Vn, то есть pkta) = pi(a).
С другой стороны, EV = оо и Е(У2) = оо, поэтому выражения, вхо-
дящие в закон больших чисел и гауссов центральный предел, теряют
смысл. Что касается последовательности Cfc(a) = (1/А:) logpk(a), она
принимает вид Ск(а) = —(1/А:) log[7r(l + а2)]. Таким образом, С'(а) =
= Пт^-юо Ск(а) = 0, поэтому /(а) = Dq. Другими словами, в данном
случае не подходят не только обычные (гауссовы) масштабно-инвари-
антные свойства, но даже рескейлинг Крамера приводит к полному вы-
рождению.
Во всех таких случаях человек всегда возлагает надежды на но-
вую схему ренормализации и альтернативу функциям С(а) или /(а).
Кроме того, для более полной характеристики фрактальных свойств ме-
ры ц может понадобиться не одна нормализация. Это справедливо для
левосторонней фрактальной меры (М et al. 1990) и, согласно результа-
там данной работы, для ОДА. В отношении ОДА нормализация /(а),
предложенная Крамером, порождает стягивание при низких значениях а
(рисунок 3), тогда как положительный рескейлинг Коши создает стяги-
вание при высоких значениях этой величины, как показано на рисунке 2.
Для значений V, подчиняющихся распределению Коши, факт неза-
висимости распределения Нк от к сам по себе является неожиданным
альтернативным свойством масштабной инвариантности. Сей факт озна-
чает, что для различных уровней крупнозернистости изображения плот-
ностей Pfc(a) автоматически стягиваются к распределению Коши. Это
очень сильное свойство, поскольку, как известно, именно оно уникаль-
ным образом характеризует распределение Коши среди всех возможных
пределов сумм н.о.р. случайных переменных.
Однако в нашем контексте величины Vn невозможно представить
с помощью распределения Коши, поскольку условие М < 1 означа-
ет, что V = — log А/ > 0. Но предположим, что, как в случае Ко-
ши, Pr{V > v} ~ v-1. В такой ситуации переменная V находит-
ся в области притяжения положительного закона Коши (Gnedenko &
Kolmogorov 1968), который, и мы можем это доказать, сложным обра-
зом связан со случаем А = 1 мультифракталов, рассмотренных в труде
М et al. 1990. Основным следствием является тот факт, что плотно-
320
Physica A 177, 1991, 386-393
сти Hk можно стянуть посредством выведения величины, пропорцио-
нальной log к. Следовательно, в наших кластерах к — logN мы вновь
получаем рескейлингЁа-loglogTV, использованный на рисунке 2. И на-
оборот, если известно, что распределение является пределом при про-
цедуре рескейлинга, в результате которого возникает рисунок 1, такое
распределение считается идеально определенным. К тому же, можно
показать, что хвост функции /(а) при а —» оо ведет себя, как в слу-
чае А = 1 в работе М et al. 1990. Таким образом, /(а) = — сехр(—с'а),
причем с и с' являются положительными постоянными.
Индивидуальные ошибки в выборке случайной переменной Коши
имеют тот же порядок величины, что и средняя ошибка во многих
выборках. Примерно также дело обстоит и с положительным случаем
Коши. По этой причине выборочные моменты для гармонической меры
ОДА демонстрируют неустойчивое поведение и тем самым объясняют,
почему метод моментов не подходит для определения функции /(а).
Как известно, exp(-L2) является абсолютной нижней границей по-
ведения наименьшей вероятности роста в решетке ОДА (Evertsz et al.
1991, Lee et al. 1989). Предположим, как подсказывают вышеописанные
результаты, что Hk находится в области притяжения положительного
случая Коши. Тогда Рг{Я^ > а} ~ а-1. Наибольшее значение атах(А)
в выборке N таких случайных переменных, по идее, должно удовле-
творять Рг{Нк > атах(АГ)} « 1/АГ, то есть атах(Я) ~ N. В кластере
N мест ожидается, что поведение, подобное оному у ехр(—LD), будет
демонстрировать наименьшая вероятность, где D — фрактальная раз-
мерность кластера. Именно такое поведение было принято для ОДА
в труде Blumenfeld & Aharony 1989.
Когда распределение невозможно описать с помощью моментов, ста-
тистики обращаются к «квантилям». Хвостовой квантиль Пг порядка г
у Hk (где 0 < г < 1) определяется с помощью Рг{Я*; > Qr} = г.
В положительном случае Коши все Qr ведут себя как log к. Следова-
тельно, представим, что рассматриваемые д проверяются систематиче-
ски, путем стирания более низких значений до размера г. Тогда цензу-
рированный минимум Дтт(Н УДОВЛвТВОрЯЛ бы УСЛОВИЮ log(/imin(r)) ~
~ -logLloglogL. При несистематическом цензурировании можно ожи-
дать, что «Мпйп» окажется где-то между распадом квантиля и распадом
абсолютного минимума.
Вышеописанное предельное распределение было получено посред-
ством изменения размера кластера. Существует также возможность изу-
чения предельного поведения плотности распределения вероятностей,
полученных через укрупнение гармонической меры на отдельном боль-
С22. Гармоническая мера ОДА
321
Рис. С22-3. Рескейлинг Крамера для плотностей распределений показателей а.
определенных после укрупнения гармонической меры на десяти кластерах с мас-
сой N = 12500 и радиусом « 180, с квадратными ящиками размера 2к,
где к = 1, 2, 3, 5. Здесь рескейлинг Крамера заключается в построении гра-
фика Ск(а) = (1/А:) log2Рк(а) в зависимости от а = -(!/£) log2 д
шом кластере. Мы укрупнили десять кластеров массой N - 12 500
и размером L ~ N1'0 с квадратными ящиками размера 2fc, где к =
= О, I, 2, .... и определили плотности Рк(а). На рисунке 3 изображены
результаты рескейлинга Крамера pt(a) при к = 1, 2, 3 и 5. При к = 1, 2,
3 стягивание получилось просто замечательное, тогда как положитель-
ный рескейлинг Коши (представлять который здесь нет необходимости)
совсем не дал бы стягивания. К тому же, сравнивая плотность pk с плот-
ностью ро кластеров размера 2~kL, находим, что рк имеет намного бо-
лее длинный правый хвост, чем ро- Таким образом, рассматриваемые
области, в которых показатели а гармонической меры имеют огромное
значение по мере роста кластера, судя по всему, возрастают более чем
пропорционально.
Итак, мы приходим к выводу, что гармоническая мера ОДА может
быть описана как самоподобная как с точки зрения роста, так и с точки
зрения укрупнения. Однако необходимо иметь в виду два понятия само-
подобия. При укрупнении можно довольствоваться стандартным поня-
тием, которое лежит в основе ограниченных мультифракталов. Но для
322
Physica A 177, 1991, 386-393
описания роста необходимо альтернативное правило рескейлинга, а так-
же расширенное понятие самоподобия.
Безусловно, наше экспериментальное открытие того, что ОДА удо-
влетворяет расширенному понятию самоподобия, не зависит от теорети-
ческого аргумента, который привел нас к проверке возможности поло-
жительного рескейлинга Коши. В данной работе поднимается сложный
вопрос о применимости к ОДА теории случайных мультипликативных
процессов, но ответа на него не дается. Мы уже отмечали, что каскад,
предложенный этой теорией, до сих пор остается в ранге гипотетиче-
ского. так какова же причина такой эффективности этой теории? Этот
же вопрос возникает и в контексте турбулентности, где ограниченных
мультифракталов также недостаточно.
Данный текст воспроизводит доклад R-16595 об исследовании, про-
веденном в IBM, от августа 1990 года с небольшими редакторскими
поправками. К настоящему моменту этот же эксперимент был повторен
с вне-вне решеткой (off-off lattice) ОДА. Получающиеся в результате
графики практически невозможно отличить от рисунков, представлен-
ных в данной работе.
Часть V
синопсис
И ИСТОРИЧЕСКИЕ ОЧЕРКИ
Некоторые главы из этой части имеют вводный характер
и созданы с целью помочь даже непрофессионалам извлечь
для себя что-то полезное из данной книги-, в таком же клю-
че написана и первая половина главы С_. В остальных гла-
вах представлена самая разная информация.
Черновик написан приблизительно в 1982 году, первая публикация
С23
Неисчерпаемая функция z2 + с
Предисловие к главе (2003). «Шум», который поднялся после вы-
хода в свет M1982F, был таким сильным, что редакционный совет еже-
месячного журнала Scientific American начал подумывать о том, чтобы
посвятить этому труду основную статью очередного номера. Они по-
обещали предоставить место для цветных рисунков, которые уже на-
чинали пылиться в моих разбухших книжных шкафах. Короче говоря,
статья эта так и не была написана, поскольку ее предвосхитила публи-
кация Dewdney 1985 в колонке «Математические игры» этого же жур-
нала предварительного образца изображения, представленного в труде
Peitgen & Richter 1986. Рисунок с обложки назывался «Изучением мно-
жества Мандельброта», а в названии статьи присутствовало словосоче-
тание «самый сложный математический объект». Я не использования ни
одного из этих терминов, но жаловаться мне было не на что.
Как бы то ни было, я подготовил некоторые записи для того, что-
бы редакторы журнала напечатали под моим именем статью, которая
так никогда не вышла в свет. Мне вернули этот текст, когда появилась
работа Дьюдни, и здесь в качестве неформального введения в тему пред-
ставлен его сокращенный вариант для тех читателей, которые хотели бы
с ним познакомиться.
Аннотация. Предположим, что очень элементарное преобразова-
ние — из z в z2 + c — повторяется бесконечно. В процессе этого появля-
ются геометрические фигуры — фрактальные аттракторы, фрактальные
репеллеры и прочие фрактальные множества — они поражают своим
количеством, разнообразием и красотой.
Кажется, наше общество считает, что любому человеку просто
необходимо знать, что 2 х 2 = 4, и полезно знать, что площадь квадрата
со стороной х равняется х х х = х2. Поэтому выражение х2 произно-
сится как «х в квадрате», а возведение в квадрат, сплошь и рядом, счи-
тается элементарной операцией. Более того, уравнение параболы имеет
вид у = ах2 + с, где у — высота, измеренная от горизонтальной оси
до некоторой точки, ах — расстояние, измеренное по горизонтали. Это
326
С23. Неисчерпаемая функция z2 + с
уравнение имеет практическое значение, поскольку оно описывает тра-
екторию движения камня, падающего в пустом пространстве, будучи
брошенным в горизонтальном направлении. После получения такого ре-
зультата нематематику может показаться, что возможности операции
возведения в квадрат полностью себя исчерпали.
Но это совсем не так. На самом деле, для того, чтобы вдохнуть
в нее новую жизнь и превзойти любые ожидания, достаточно совсем
небольшого, на первый взгляд, изменения. Для объяснения этого изме-
нения заметим, что для получения параболы достаточно однократного
проведения операции по возведению в квадрат: х —> х2 + с, после чего
полученный результат используется уже независимо от самой операции.
Но давайте подвергнем результат операции по возведению в квадрат той
же самой операции, а затем повторим все вновь и вновь.
Такое повторение произвольной операции называется «итерацией»,
и в данном случае его достаточно для превращения мнимой скуки в без-
граничный восторг. Побуждение к итерации и многие из ее наиболее
важных свойств проистекают непосредственно из физики. Физики рас-
сматривают итерацию как упрощенное представление «состояния» дина-
мической системы и ее развития во времени. По определению, динами-
ческая система представляет собой преобразование, с помощью которого
ее сегодняшнее состояние получается из ее вчерашнего состояния, а ее
завтрашнее состояние — из состояния сегодняшнего. Следовательно,
для получения завтрашнего состояния системы из ее вчерашнего состоя-
ния можно применить базовое преобразование дважды: одно за другим.
Но можно также применить итерированное преобразование один раз.
В общем, сейчас физики полностью разделяют точку зрения, кото-
рую великий Анри Пуанкаре первым высказал в 1880-е годы, заявив, что
эволюция динамической системы подчиняется итерациям повседневного
преобразования. Именно по этой причине поведение итераций заслужи-
вает обсуждения. В некоторых случаях, как ожидали физики со времен
Ньютона, итерации демонстрируют очень гладкое поведение. Но в дру-
гих случаях их поведение довольно неожиданно оказывается сложным,
и этот факт имеет чрезвычайно большое значение.
Для того чтобы полностью оценить вторую возможность, уместно
вспомнить, что еще Галилей, Ньютон, Лаплас и иже с ними обнаружили,
что простые динамические системы ведут себя идеально гладко и пред-
сказуемо. Это открытие оказало огромное влияние на западное миро-
воззрение как таковое. С незапамятных времен считалось, что большин-
ство аспектов природы и человеческой натуры невозможно предсказать
и проконтролировать. Однако механика являлась в этом плане большим
С23. Неисчерпаемая функция z -t- с
исключением, и многие люди, включая любителей, философов и уче-
ных, пришли к выводу, что механика является единственной идеальной
моделью, к которой должна стремиться вся прочая интеллектуальная
деятельность. Безусловно, мыслящие люди признавали, что большин-
ство областей знания очень далеки от предсказуемости и абсолютной
управляемости. Тем не менее, обе эти характеристики люди продолжа-
ли рассматривать как отдаленные, но непоколебимые идеалы.
На самом деле, как это часто случается, зерно будущего разруше-
ния этого идеала зародилось уже в момент его наивысшего триумфа, то
есть в конце девятнадцатого века.
Первый симптом. Движение жидкостей, без сомнения, является
прототипичной проблемой механики; тем не менее, турбулентное дви-
жение нельзя назвать предсказуемым или управляемым. Над этим во-
просом бились специалисты по рациональной механике девятнадцатого
века, например, сэр Гораций Лэмб, а ближе к нашему времени такие
великие умы как Энрико Ферми.
Второй симптом. Динамика Пуанкаре была сосредоточена вокруг
поиска доказательства устойчивости Солнечной системы. Однако Пуан-
каре не только не смог найти реального доказательства этого, но и про-
явил недюжинный дар предвидения, поняв, что в общей картине упу-
щен какой-то важный аспект. Чистая математика нередко разочаровыва-
ет физиков, поскольку зачастую ограничивается лишь одобрением того,
что и так казалось «очевидным». Но Пуанкаре заметил, что в случае
с планетарными системами многие возможности очень неустойчивого
поведения нельзя исключать заранее.
Однако Пуанкаре не стал развивать эту мысль, и у нее нашлось
мало последователей в самодовольной научной среде того и даже бли-
жайшего к оному времени. Ученые располагали избытком «более симпа-
тичных» проблем, с которыми надо было разобраться в первую очередь;
к тому же, определенное влияние оказывал и тот факт, что большинство
воспринимало устойчивость как норму.
Тем не менее, в 1970-х годах именно эта работа Пуанкаре ста-
ла очень значимой. В механике произошли кардинальные изменения,
и внезапно ученые практически помешались на хаосе. Следовательно,
по воле случая механика отказалась (по крайней мере, неявным обра-
зом) от своих притязаний служить моделью для менее развитых наук.
Но даже изучение сложности лучше всего начинать с анализа про-
стых преобразований. Поэтому многие ученые независимо друг от друга
пришли к исследованию квадратичного преобразования х —» х2 + с. Два
французских математика 1910-х годов Гастон Жюлиа и Пьер Фату рас-
328
С23. Неисчерпаемая функция z2 + с
ширили горизонты, заменив вещественную переменную х комплексной
переменной г. Вещественное число — это положение некоторой точки
на прямой, а комплексное число, по сути, является точкой на плоскости,
т е. совокупностью координат точки Р. Замена г2 на z2 + c может пока-
заться незначительной, но это невероятно далеко от истины. Напротив,
поведение итераций очень сильно зависит от значения с.
Запоздалая и неожиданная награда пришла, когда в работе Metro-
polis, Stein & Stein, а за ними и в труде Feigenbaum обнаружилось, что
свойства вещественного квадратичного преобразования также наблюда-
ются и у многих других более сложных преобразований. Результаты
были представлены под громким названием «теории универсальности».
С учетом вышеописанных результатов стоит заметить, что данная
книга не стремится к этой форме универсальности, кроме, пожалуй, от-
ступлений, адресованных профессионалам. Самые важные результаты,
которых достиг автор, относятся к расширению теории Фату-Жюлиа.
Ранее даже специалисты рассматривали эту теорию как чрезвычайно
сложную проблему, в изучение которой невозможно привнести ничего
нового. Однако создание точных компьютерных иллюстраций сняло на-
лет тайны и привело нас к поразительным открытиям.
Опишем ключевой момент. Когда х является обычным числом, т. е.
♦ вещественным числом», если говорить на языке математики, то итера-
ция х —» х2 + с касается только геометрических множеств на прямой.
Такие множества важны, но им недостает разнообразия, и единственной
причиной их кажущейся сложности является сложность их визуального
представления. Однако любой, кто читал детективы, может вспомнить
массу случаев, когда последовательность визитов подозреваемого в дом
кажется запутанной, тогда как последовательность его перемещений по
городу подчиняется простым правилам. Поэтому совершенно неудиви-
тельно, что часто для изучения явлений, ограниченных прямой, луч-
ший способ упростить состоит в толковании их как следа, оставленного
на прямой соответствующими явлениями, происходящими на плоскости.
Вновь используя своеобразный лексикон математиков, можно сказать,
что многие математические теории упрощаются, если их «усложнить»,
заменив вещественное число х комплексным числом z.
Одного взгляда на иллюстрации в этой книге достаточно, чтобы
понять, что геометрические следствия итерации в комплексных числах
поистине потрясают. Для многих читателей математика и физика не
представляют особого интереса, но моя работа по итерации оказала вли-
яние на многие области, выходящие за пределы математики и физики.
Оказалось, что оперирование самыми элементарными математическими
С23. Неисчерпаемая функция z2 + с 329
преобразованиями обладает абсолютно неожиданной способностью по-
рождать структуру, являющуюся очень сложной и очень красивой одно-
временно.
Тут появляется новый вид искусства — фрактальное искусство. По-
скольку его можно полностью описать короткими математическими сен-
тенциями, этот вид искусства «минимальнее» любого шедевра, когда-ли-
бо выставлявшегося в художественных галереях. И здесь возникает но-
вый вопрос. Согласно традиционной точке зрения, которая практически
стала клише, математика и наука отличаются от искусства тем, что
в них результатом является открытие, тогда как в искусстве — творе-
ние. Однако в новом фрактальном искусстве результатом лучше всего
считать открытие.
Возможно, читатель засомневается в том, что такие простые уравне-
ния способны породить сложность. На самом деле, в философии класси-
ческой механики (к которой мы уже обращались) долгое время бытовало
противоположное предвзятое мнение, будто «простые» математические
операции должны приводить к простым результатам, а сложных выво-
дов можно добиться только с помощью сложных операций. Необходимо
развеять это мнение, а также подтолкнуть читателя к прочтению самого
текста, не ограничиваясь одним только разглядыванием картинок.
Поэтому позвольте мне сделать небольшое отступление и привести
несколько вольных сравнений. Во-первых, рассмотрим операцию обра-
ботки горячей стали молотом. Ее можно назвать элементарной в том
смысле, что она дает довольно однообразные результаты, но всем из-
вестно, что в руках опытного кузнеца, после многочисленных анало-
гичных ударов, сталь может превратиться в очень красивый меч или
плуг. Вообще-то, это сравнение не вполне отражает суть последующих
открытий. На самом деле, бездумное повторение одного и того же уда-
ра молотом не приведет к интересному результату, и кузнец, который
хочет сделать какую-то сложную вещь, должен менять свои действия
вполне определенным образом, что требует большого опыта. И наоборот,
мы увидим, что даже «абсолютно бездумное» повторение квадратичной
операции, если ее правильно подобрать, породит невероятно сложные
фигуры.
Второе сравнение ближе к третьему и последнему на очереди. Рас-
смотрим револьверный токарный станок, с помощью которого большое
шероховатое бревно превращается в гладкое, конечный радиус которого
равен одной единице длины. Мы не станем принимать в расчет кле-
точную структуру дерева. Поскольку точные резцы работают медленно
и отличаются хрупкостью, нам придется выполнять заданную операцию
330
С23. Неисчерпаемая функция z2 + с
последовательными этапами. Первый резец, который работает быстро,
но грубо, отрезает лишний радиус, оставляя практически круглую, но
неровную фигуру. Затем с помощью другого резца нам удается добить-
ся более маленькой и более гладкой фигуры. Для обеспечения высокой
точности потребуется несколько этапов точения. На последних стадиях
будет удаляться только то количество древесины, какое необходимо для
достижения шероховатости такого порядка, который допускается в ко-
нечном продукте.
Рассмотрим теперь универсальную программу токарной обработки,
которая всегда изменяет радиус 1 + т на более маленький радиус 1 + Vr.
Если первоначальный радиус большой, последовательные этапы сначала
будут происходить быстро, затем медленно. Указание «уменьшить ра-
диус от г до Vr» остается без изменений, поэтому оно выполняет ту
же роль, что и указание «ударить молотом», использованное в первом
сравнении. Но у нового указания также есть исключение: точно тем
же условиям подчиняется и постепенная смена инструментов грубых на
более тонкие.
Для улучшения вышеупомянутых сравнений необходима помощь
компьютера. Даже самое поверхностное знание компьютера определяет
итерацию как очень особый пример логической петли. Поэтому давайте
превратим наш станок в мысленный инструмент, который будет проще
обобщить. Мы описываем каждую последующую стадию токарной обра-
ботки как удаление всех точек Р таким образом, что репрезентативное
комплексное число z, будучи возведенным в квадрат, оказывается за
пределами куска, оставшегося по завершении предыдущей стадии. Это
приводит к обобщению, которое заключается во введении дополнитель-
ного параметра с и удалении всех точек z, так что г2 + с оказывается за
пределами куска, который имелся в момент начала данной стадии.
Изменения, произошедшие в результате введения параметра с, бы-
ло бы невозможно предугадать, но иллюстрации, представленные в этой
книге, показывают, что они могут быть очень значительными. Самым
поразительным фактом является то, что каждая стадия больше не улуч-
шает гладкость после более ранней стадии, а скорее добавляет значи-
тельную деталь, которая не была доступна на предыдущих этапах. Та-
ким образом, предел, к которому сходится наш текущий процесс, вклю-
чает детали всех размеров, вплоть до бесконечно малых.
В это трудно поверить, но Фату и Жюлиа открыли это свойство
предела без каких-либо рисунков. Возможно, именно по этой причине
полученные ими результаты на протяжении шестидесяти лет оставались
в «ничейных» интеллектуальных владениях. Отдельные математики счи-
С23. Неисчерпаемая функция z2 + с
331
тали достижения этих ученых уникальными, но им не удалось развить
эту мысль. Новый инструмент, который я ввел в предположительно «чи-
стую» математику (а именно: компьютерную графику), вдохнул новую
жизнь в эти исследования, а мои выводы привлекли к ним новые умы
по всему миру.
Невероятное геометрическое чутье Жюлиа только подсказывало
ему, что определенные кривые, которые позже назовут множествами
Жюлиа, весьма напоминают фигуру, называемую «снежинкой». И хо-
тя эта кривая включает детали всевозможных размеров, вплоть до бес-
конечно малых, ее можно нарисовать без проблем, и именно поэтому
в 1904 году ее описал швед Хельге фон Кох. На рисунке X в главе С
изображен способ получения кривой Коха. Аналогичные процедуры мо-
гут привести либо к разветвленной кривой, либо к вполне несвязному
множеству точек, называемому «пылью Кантора».
К тому же, вполне очевиден (а потому не требует пояснений) тот
факт, что итеративное удаление может также привести к образованию
прямой, например, посредством стирания всех маленьких квадратов,
кроме тех, которые пересекают главную диагональ. Другими словами,
существует параллелизм между удалением непосредственно определен-
ных треугольников и квадратов и удалением частей, определенных кос-
венно посредством возведения в квадрат.
Единственное отличие состоит в том, что в первом случае необхо-
димы подробно и обстоятельно прописанные правила, а во втором для
определения операции возведения в квадрат достаточно одной корот-
кой формулы. Все это приводит к удивительному заключению: операция
удаления треугольников и квадратов является сложной с точки зрения
алгоритмической. С другой стороны, обычные чертежники не имеют ни
малейшего понятия о возведении в квадрат, но без труда рисуют кривые
Коха, множества Кантора и прочие диаграммы, приведенные на той же
странице. Таким образом, снежинки являются более простыми фигура-
ми с практической точки зрения, поэтому их часто можно встретить на
страницах книг с математическими играми.
Но широкая известность совсем не равноценна большой значимо-
сти. Все эти объекты преследовали лишь одну очень ограниченную цель,
ради которой были созданы: служить контрпримерами.
Поясню чуть подробнее. Раньше физика, механика и математика
считались одной дисциплиной, которая называлась «натурфилософией»,
и внимание динамики к гладкому поведению шло рука об руку со вни-
манием математики к гладким функциями и кривым. В то же самое
время, когда Пуанкаре разрабатывал негладкую динамику, математики
332 С23. Неисчерпаемая функция z2 + с
все больше убеждались в существовании негладких функций и кривых.
Частично из-за желания ответить на обвинения в том, что поиск стро-
гих доказательств — это лишь педантизм и попытка окольным путем
получить то, что и так очевидно, математики искали примеры, в кото-
рых кажущаяся очевидность была, на самом деле, совершенно неверной.
Таким образом, кривые Коха были придуманы с целью продемонстриро-
вать необходимости строгости. С другой стороны, никто не считал, что
они обладают значительным внутренним интересом, и не думал, что у
них есть что-либо общее кроме того, что все они являются «патологи-
ческими» контрпримерами.
Я же, наоборот, открыл, что некоторые из этих (якобы) контрпри-
меров имеют неожиданное общее свойство, называемое самоподобием,
и, кроме того, они очень и очень полезны для непосредственно практи-
ческих целей, например, как модели (или скорее, «рисунки») гор и бе-
реговых линий. Я назвал эти фигуры фракталами и возвел вокруг них
новую фрактальную геометрию природы. Таким образом, снежинка яв-
ляется плотью, кожей которой служит фрактальная кривая; бесконеч-
ное дерево представляет собой фрактальную кривую, не ограничиваю-
щую никакую плоть, тогда как канторово множество — это фрактальная
пыль.
Теперь можно вернуться к преобразованию z —» z2 + с и определить
заполненные множества Жюлиа как состоящие из точек, которые не
уходят в бесконечность при повторяемом квадратичном преобразовании.
При особом значении с = 0 возникает диск (заполненная окружность),
а при особом значении с = 2 — интервал. Все же остальные значения с
порождают фрактальные множества.
Важным выводом (сделанным Пьером Фату и Гастоном Жюлиа) яв-
ляется тот факт, что топология множества Жюлиа сильно зависит от
значения с. Она напоминает кожу, покрывающую плоть, т. е. кривую,
окружающую некоторую область с положительной площадью. Она так-
же может быть кожей без плоти, то есть кривой (в общем случае очень
разветвленной), которая ничто не окружает, или несвязной пылью. Все
эти разнообразные геометрические возможности не нужно было выду-
мывать намеренно, поскольку все они неявно присутствовали в выраже-
нии z2 + с, то есть в простейшей функции, отличной от az + Ь.
Очевидно, что существует необходимость систематизировать зна-
чение с согласно некоторым основным характеристикам множества
Жюлиа. К счастью, Фату и Жюлиа открыли важный критерий для
определения связности множества Жюлиа. Для этого достаточно осу-
ществить преобразования особой точки, называемой «критической».
С23. Неисчерпаемая функция г2 + с
333
В квадратичном случае это точка z = 0. Если эти преобразования про-
должаются до бесконечности, то множество Жюлиа является вполне
несвязной пылью, если же они остаются ограниченными, множество
Жюлиа связно, а множество, которому принадлежит с, называется мно-
жеством Мандельброта М.
Определить это множество не составит труда. Поэтому даже
в 1980 году, в «средние века» компьютерной науки, для изображения
множества М мощной техники не требовалось. (Сегодня нарисовать М
сможет любой ребенок). Но базовое толкование этих рисунков требо-
вало умения и опыта работы в экспериментальной математике. Я со-
здал много изображений М при самых разных значениях с, довольно
подробно отобразив интересные участки плоскости, и пришел к массе
удивительных выводов, приведших к строгой математике, благодаря че-
му данная тема снова стала популярной как у специалистов, так и у не
менее важного среднестатистического человека, будь то мужчина, жен-
щина или ребенок.
Подробная история открытия множества Мандельброта является ос-
новной темой данной книги.
Приложение: Операция z2 — с в комплексных числах
Поскольку данное приложение уже было написано, его включили
в этот сборник, хотя до сих пор не ясно, поможет ли оно хотя бы одному
читателю почерпнуть для себя из этой книги что-то интересное. С помо-
щью комплексного числа очень удобно обозначать положение некоторой
точки Р на плоскости относительно системы, образованной двумя пер-
пендикулярными координатными осями, пересекающимися в точке О,
служащей началом координат. Положение точки Р можно указать с по-
мощью двух отрезков х и у, отложенных по двум ортогональным направ-
лениям. В этом случае хну называются «декартовыми координатами».
Мы записываем z = х 4- iy и называем х вещественной частью, а у —
мнимой частью z. Ясно, что компьютер не имеет ни малейшего понятия
о сложных числах как таковых. Чтобы выполнить преобразование zz -
— с, где с = с' + ic", компьютер меняет исходные числа х на х~ - у- - с',
а у — на 2ху — с". Существует множество программ, при использова-
нии которых пользователю не нужно знать ничего сверх того, что дела-
ет компьютер. Однако некоторое пояснение может оказаться полезным.
Положение точки Р также можно задать с помощью «полярных коор-
динат», которые включают расстояние от начала координат до точки Р
(называемое модулем) и угол 0 между осью х и прямой, соединяющей
334 С23. Неисчерпаемая функция z2 + с
•очку начала координат с точкой Р. В этих координатах наше выра-
жение имеет вид z = ге*в. Для сложения или вычитания комплексных
чисел, то есть для получения z'+z" или z' — z", необходимо сложить или
вычесть по отдельности вещественную и мнимую части z' и z". Преоб-
разование zz заключается либо в замене х на х2 — у2 и у на 2ху, либо
в возведении в квадрат модуля г —♦ г2 и удвоении угла 0 -*20. Когда Р
является точкой с декартовыми координатами 0 и 1, получаем z = i,
откуда г = 1, а 0 = 90°. В этом случае величина z2 (вновь) имеет
модуль 1 и угол 180°; следовательно, z2 = —1. Операцию по ♦извле-
чению квадратного корня из —1» невозможно осуществить с обычными
«вещественными» числами, и первоначально комплексные числа ввели
с целью придания смысла именно этой операции.
Первая публикация
С24
Фату и Жюлиа
Теория итерации рациональных функций восходит к середине де-
вятнадцатого века, а, возможно, даже к Абелю. На протяжении первого
классического периода она неразрывно связала имена Пьера Фату и Га-
стона Жюлиа и породила большие разногласия вкупе с поверхностны-
ми анекдотами и воистину невообразимыми историями. Очень хорошо,
одновременно по-научному и сдержанно, этот период описан в труде
Alexander 1994. Однако его автор основывается на уже опубликованных
работах. Я был ближе к этим людям. Жюлиа, вообще, преподавал мне
дифференциальную геометрию в Политехнической школе. Еще большее
влияние оказали на меня истории, которые о Жюлиа и Фату рассказыва-
ли мой дядя Шолем Мандельбройт (1899—1983), а также другие хорошо
знакомые мне люди. Объединив все услышанное, а также прочитанное
под влиянием услышанного, я рассказываю в данной главе о Фату, за-
тем — о Жюлиа и, наконец, об их совместной работе. В последнем
разделе речь пойдет о последствиях вышесказанного.
1. Пьер Фату (1878-1929)
По прошествии пятидесяти лет после своей смерти Пьер Фату во-
шел в математический Пантеон, но когда-то его считали изгоем, ведь
(строго говоря) он был не настоящим математиком, а всего лишь люби-
телем.
Фату родился 28 февраля 1878 года в городе Луэ (Бретань), а умер
в 1929 году в городе Порнише (Бретань). С 1898 по 1901 годы он учил-
ся в университете (Высшая нормальная школа), где получил «agrege»
(эта ученая степень примерно соответствует степени кандидата педа-
гогических наук по математике). Тогда же он поступил в Парижскую
обсерваторию, где до 1928 года оставался младшим астрономом (*sta-
giaire»=HHTepH, затем ♦а!ёе»=ассистент и позже «аё)о1п1»=младший со-
трудник). Он занимался особыми заданиями, которые часто менялись.
Последнее его задание касалось измерений двойных звезд. Астрономы
почтили память исполнительного сотрудника полными осознания своего
долга некрологами.
336
С24. Фату и Жюлиа
Его имя помнят до сих пор, поскольку он также «подрабатывал»
и математиком. Свою степень доктора наук Фату получил в февра-
ле 1907 года за диссертацию, которую сильно хвалил Поль Пенлеве
(Gispert 1991, стр. 387-388); всю оставшуюся жизнь он занимался во-
просами, которые представляли наибольшую важность для математики
его времени.
В истории есть немало примеров того, как композиторы и поэты за-
рабатывали себе на хлеб способами, никоим образом не связанными с их
профессией. Так, американский композитор Чарльз Ив работал в стра-
ховой компании. Аналогично, французская дипломатия в 1930-х годах
была (к большому несчастью) в руках Алексиса Леже де Сен-Леже.
Попутно он писал стихи под псевдонимом Сен-Жон Перса и в итоге
получил Нобелевскую премию по литературе. Также среди математи-
ков в девятнадцатом веке встречались плененные генералы (Понселе),
полицейские (Фурье) и преподаватели (Вейерштрасс).
Не исключено, что Фату был последним представителем этого пле-
мени. Будучи очень замкнутым человеком, он не рассказывал, почему
старался держаться подальше от основного течения, но Ш. Мандель-
бройт упоминал, что ранее Фату был заклеймен Французской академией
наук как паршивая овца или отступник. Возможно, это случилось, когда
после получения степени кандидата наук он отказался от первой работы
в провинции. В те времена это было практически необходимым условием
для дальнейшего продвижения в Париж. Более того, это не всегда было
обременительно. Например, до того как Мандельбройт в 1929 году по-
лучил назначение в Клермон-Ферранд, из-за недостатка студентов там
не читался курс высшей математики, хотя иных обязанностей у профес-
сора не было.
В результате поиска еще какой-либо информации о личной жизни
Фату выяснилась одна интересная подробность. Анри Картан вспомнил,
что Фату очень любил музыку и особенно восхищался Прокофьевым.
Двадцатилетний Картан со своими друзьями-одногодками встречали со-
рокалетнего Фату (в гордом одиночестве) на недорогих местах в кон-
цертных залах.
О последних годах жизни Фату известны лишь голые факты, ко-
торые довольно трудно проанализировать. В 1927 году он являлся пре-
зидентом Французского математического общества, а в июле 1928 го-
да Обсерватория присудила ему (в возрасте 50 лет!) звание астронома.
В 1929 году он написал «Записки» к своей работе, причем порядка
4/5 этого произведения касалось математики. «Записки* во Француз-
ской академии наук всегда писали и, возможно, по сей день пишут для
337
получения определенной должности, но как раз в его работе об этом ни
сказано ни слова. Он так и не был избран членом Академии наук, даже
в самый низкий ранг «члена-корреспондента», так что, возможно, он
хотел получить это место.
Иногда создается впечатление, что он был близок к тому, чтобы
влиться в основной курс науки, однако есть некоторые факты, явно
свидетельствующие об обратном. Обратите внимание на работу Appell
& Goursat 1929-1930, состоящую из двух томов, каждый из кото-
рых содержит более пятисот страниц. Предисловие к первому изданию
от 1895 года написал Ш. Эрмит. Фату подготовил первый том второго
издания этого труда и получил за это десять процентов рабочей площа-
ди обложки.
Такой же «счет» он получил и за второй том, но здесь дело обстоя-
ло совершенно иначе. Общий охват тем увеличился, Пол Аппель (1855-
1930) скончался, а одностраничное предисловие написал Эдуард Гурса
(1853-1936). В нем есть такие слова: «Когда издатель попросил текст
нашей «Теории алгебраических функций» для переиздания, ... нам по-
казалось нелишним добавить, как минимум, краткую теорию фуксовых
функций. Недавно умерший Фату благодушно согласился выполнить это
задание. Однако вместо нескольких глав, которые мы предполагали уви-
деть, мы получили целый трактат по автоморфным функциям. Мы рады,
что нам удалось поспособствовать изданию такой замечательной книги,
написанию которой вполне могла помешать чрезвычайная скромность
ее автора... Прочтение этого труда лишь усиливает у всех, кто знал
и ценил этого человека, ощущение невосполнимой потери, вызванной
преждевременной кончиной Фату. Он еще многое мог дать науке».
Гурса также упоминает, что «вся рукопись была написана одним
Фату, который закончил ее за несколько месяцев до своей смерти». Без
ответа остались лишь два вопроса. Почему президент Французского ма-
тематического общества взялся за задание, которое мог выполнить куда
менее опытный человек? И почему при издании его работы по авто-
морфным функциям он не был указан как единственный автор? Аппель
ничего не добавил к ней, а Гурса только написал предисловие.
Из под пера Фату также вышла работа по рядам Тейлора. Классиче-
ские аналитики, такие как мой дядя, прилагали огромные усилия, чтобы
продолжить труд Фату. Возможно, еще не настало подходящее время,
но сегодня этот труд известен лишь узкому кругу лиц. Фату писал и об
интеграле Лебега, где ввел одну очень интересную лемму.
Ясно, что лемма — это предположение, которое само по себе не
имеет большого значения, будучи лишь шагом на пути к какой-то бо-
338
С24. Фату и Жюлиа
лее глубокой теореме. Выражение лемма Фату вызывает в памяти та-
кие термины, как лемма Абеля или лемма Шварца. Можно прочитать
огромное множество математических трудов, полагая, что эти великие
ученые не создали никакой значимой глубокой теоремы. Почему? Ве-
роятно, одна из причин кроется в том, что человек никогда не может
по достоинству оценить собственный труд. Кроме того, не исключено,
что эти авторы «приберегали» термин «теорема»для обозначения плода
более тяжелого труда, тогда как более расхожим словом «лемма» они
называли результаты, на получение которых затратили меньше сил, да-
же если эти результаты играют более важную роль. А может, таким
образом потомки иногда чествуют величайших ученых, называя их име-
нами те результаты, которые нашли наиболее широкое применение, даже
несмотря на их максимальную простоту?
2. Гастон Жюлиа (1893-1978)
Историю жизни Жюлиа можно найти в нескольких доступных ис-
точниках. Например, в длинном некрологе Garnier 1978, который по-
явился в Comptes rendus de I’Acaddmie des Sciences (Vie Academique)
286 от 12 июня 1978 года на страницах 126-133.
По этой причине данный раздел будет краток и включит только мои
собственные воспоминания. Гастон Жюлиа родился в феврале 1893 года
в Сиди-бель-Аббесе (Западный Алжир), куда его семья переехала из
Испании. В католической церковной школе быстро заметили недюжин-
ные способности этого ученика. Окончив лицей в Оране, он получил
стипендию для обучения в Париже. В возрасте восемнадцати лет он
был лучшим в своем классе как в Политехнической школе, так и в Выс-
шей нормальной школе. В последней он обучался с 1911 по 1914 годы,
когда началась Первая мировая война. После прохождения ускоренного
курса военной подготовки, 25 января 1915 года его отправили в око-
пы в звании младшего лейтенанта пехоты. Все прочие офицеры из его
роты в тот день погибли, а ему удалось выжить, получив многочислен-
ные ранения, включая глубокую рану на лице. Всю оставшуюся жизнь
он читал лекции в кожаной маске, закрывающей нос и щеку. Также
на протяжении всей жизни ему неоднократно приходилось ложиться на
болезненные операции (многие из которых проводились под местным
наркозом). В 1916 году, лежа на больничной койке, он подготовил свою
кандидатскую диссертацию, за которую получил (престижную) премию
Бордена. Темой следующей его исследовательской работы стала теория
итераций рациональных функций.
С24. Фату и Жюлиа
339
В 1920-х годах Жюлиа был одним из очень немногих молодых и ак-
тивных математиков во Франции. Жизнь в окопах, ранения и многочис-
ленные операций оказали большое влияние на многих ветеранов, но не
на интеллект Жюлиа. Он был необыкновенным человеком и даже на-
циональным символом по нескольким причинам. Немалую роль сыграло
его рождение в принадлежавшем Франции Алжире, при том, что его
родители были испанцами, поскольку Франция гордилась своим звани-
ем «плавильного котла». К тому же, война превратила его в «gueule
cassee», то есть в «разбитое лицо». Он очень быстро продвигался по
академической иерархической лестнице и вскоре стал профессором на
факультете естественных наук в Сорбонне, а в возрасте 41 года его
избрали в Академию наук. Из всех избранных в то время лишь один
член Академии был моложе его — то был один из создателей квантовой
теории с аристократическими корнями: принц Луи де Бройль. Во вре-
мя Второй мировой войны Жюлиа читал лекции в Германии, за что его
позже критиковали. Последние годы своей жизни он провел в старом
Доме инвалидов (рядом с гробницей Наполеона), а его похороны были
проведены с большим официозом в Церкви инвалидов.
Осенью 1945 года я был первокурсником в Политехнической шко-
ле, а Жюлиа — профессором по (базовой дифференциальной) геомет-
рии. Впервые я увидел его с самых задних рядов большой аудитории.
Несколько раз за семестр он вместе с физиком Луи Лепренсом-Ренге
отклонялся от стандартного порядка и приглашал к участию в бесе-
де заинтересованных студентов. Это был самый близкий мне профессор
Политехнической школы, у которого появилось рабочее время. Он также
числился профессором по высшей математике на факультете естествен-
ных наук Парижского университета, где он должен был вести дополни-
тельный курс.
Это был очень энергичный человек с сильным звучным голосом. Его
темпераментное поведение, которое мы называли «средиземноморским»,
резко выделялось на фоне невыразительного преподавателя математи-
ческого анализа, профессора Поля Леви. К сожалению, большую часть
времени Жюлиа зачитывал самые что ни на есть тривиальные лекци-
онные конспекты. В университете они регулярно выдавались в форме
tfeuilles*, то есть больших (формата четвертой доли листа) бланков, ко-
торые в конце года нужно было переплетать, чтоб получить что-то вроде
памятки.
Однако он любил приправлять свои лекции «афоризмами», причем
некоторые из них врезались мне в память: «Те из вас, кто займется
научным исследованием, часто будут понимать, что их обокрали. Если
340
С24. Фату и Жюлиа
человек, которые вас обокрал, не получит славы, невелика потеря. Если
же этот человек добьется славы, вы лишь должны еще больше возгор-
диться своей работой, и в следующий раз вам повезет больше». Также
часто он повторял: «Чтобы упростить, нужно «усложнить». То есть, ес-
ли вы сталкиваетесь с запутанной проблемой и хотите упростить ее,
стоит заменить все вещественные числа комплексными». И без слов по-
нятно, что последнее изречение не выходило у меня из головы в конце
1970-х годов, когда многие мои друзья-физики занимались изучением
вещественной функции х2 + с, а я обратился к теории Фату-Жюлиа об
итерациях комплексной функции z2 + с.
В главе С1 я уже отмечал, что в конце 1940-х годов Поль Монтель
и мой дядя высоко ценили раннюю работу Жюлиа по итерации и дру-
гим областям математического анализа. Но мало кто из математиков
разделял это восхищение. В то время (смотрите главу 25) аналитики
ощущали себя на осадном положении, поскольку тогда правило движе-
ние «Бурбаки». Парадоксальность заключается в том, что члены Бурба-
ки в тридцатые годы «одолжили» семинар Жюлиа, но их привязанность
к громоздким абстрактным структурам максимально отдаляла их от про-
водимого Жюлиа тщательного анализа множества особых и запутанных
примеров.
3. Фату и Жюлиа
Жизнь ученого становится легендой только в том случае, если он
вступает в противоречие с Людьми или с Государством, является цели-
телем или Галилеем, столкнувшимся с Инквизицией, или Оппенгейме-
ром, встретившим Теллера. Театрал никогда не сравнит науку с драмой,
а художник не считает красоту математики приемлемой формой красоты
(здесь необходимо добавить: за возможным исключением фракталов).
В частности, споры о научном приоритете неизбежно воспринима-
ются посторонними как жалкие семейные дрязги. Исключение состав-
лял научный Париж времен моей молодости, в котором часто велись
разговоры о споре за приоритет, возникшем в 1917-1918 годы меж-
ду Пьером Фату и Гастоном Жюлиа. Оба этих ученых сделали одно
из самых ярких математических открытий 1912 года: теорию Монтеля
о «нормальных семействах функций».
Спор Фату-Жюлиа был решен с помощью государственных умов
в середине войны. Был созван суд, судьи приняли решение в пользу
Жюлиа, присудили Фату «утешительный» приз и опубликовали свое
решение. Согласно разделу 2, можно предположить, что существовало
широко распространенное мнение, что эта награда, по крайней мере, от-
С24. Фату и Жюлиа
.341
части предназначалась для того, чтобы облегчить глубокие физические
страдания человека, которого ранее уже отметили как победителя. Но
в разделе 1 также говорится, что проигравшему было знакомо и пора-
жение.
Спор между Фату и Жюлиа будет описан в нескольких документах
в работе, которую составила моя жена Алиетта Мандельброт. Оригина-
лы абсолютно не засекречены и доступны, но известны лишь немногим.
Описанные события, возможно, помогут воспринимать Фату и Жюлиа
как живых людей из плоти и крови, а не как холодные мраморные ста-
туи. И без слов ясно, что, учитывая те ужасные события, я не пытаюсь
найти ни героев, ни виновных.
Для понимания смысла следующей цитаты необходимо знать, что
«запечатанный конверт» представлял собой письмо, которое его автор
мог отправить в Академию наук с просьбой зарегистрировать и открыть
по запросу или по прошествии определенного количества лет. «Запеча-
танный конверт» позволяет отметить ту или иную идею, не открывая
ее возможным конкурентам. Старые «запечатанные конверты» посто-
янно распечатывают, и благодаря некоторым из них в истории науки
появляются новые факты. Работа Julia 1968 представляет собой репринт
большей части труда Жюлиа «Works».
«Замечание о рациональных подстановках», написанное господи-
ном Гастоном Жюлиа, было представлено Академии 24 декабря 1917 го-
да, а позже переиздано в работе Julia 1968 на страницах 105-106. [При-
мечание: Нет никаких указаний на то, что данное Замечание было пред-
ставлено членом Академии.]
«Только что я с интересом прочитал заметку господина Фату, опуб-
ликованную в Proceedings3 заседания от 17 декабря 1917 года. Ее ос-
новные результаты я лично отослал в четырех запечатанных конвертах
в офис Академии 4 июня 1917 года (8401), 27 августа 1917 года (8431),
17 сентября 1917 года (8438) и 10 декабря 1917 года (8466). Распеча-
тав четыре этих конверта, Академия должна убедиться, что результаты,
идентичные выводам Фату (за исключением обозначений и примеров),
представлены там с краткими указаниями относительно методов доказа-
тельства. По любопытному совпадению в одном из моих методов нашли
применение результаты работы господина Монтеля по нормальным се-
мействам аналитических функций, которые также использует господин
Фату. Академия должна принять решение, кому отдать приоритет как
в отношении методов, так и в отношении результатов...
8Труды. - Прим, перев.
342
С24. Фату и Жюлиа
Я решил отправить эти «запечатанные конверты», поскольку в своей
заметке от 21 мая 1917 года господин Фату сообщил Академии о неко-
торых результатах, которых добился и я... ».
Отчет по предыдущей заметке, написанный Джорджем Гумбер-
том. Репринт имеется в работе Julia 1968, I, стр. 107.
«По просьбе Академии я проанализировал содержимое четыре за-
печатанных конвертов господина Жюлиа, которые были открыты на за-
седании 24 декабря, и заметку, в которой тот же автор поднимает во-
прос приоритета... [в отношении] [Заметки от 17 декабря 1917 года]
господина Фату ... В результате сравнения содержимого двух заметок
и четырех запечатанных конвертов выясняется, что утверждение госпо-
дина Жюлиа вполне обоснованно. Этот запечатанный конверт, помимо
всего прочего, содержит результаты, в отношении которых он заявляет
свой приоритет...».
Отчет, составленный Эмилем Пикаром и Джорджем Гумбертом
о присуждении Гран-при в математической науке Гастону Жюлиа. (Про-
токол собрания Академии наук от 2 декабря 1918 года, который не был
представлен в работе Julia 1968.)
♦В процессе принятия решения относительно присуждения данной
награды офис Академии наук получил три труда. Комитет ограничился
работами господина Латте, профессора университета Тулузы, и госпо-
дина Жюлиа, лейтенанта 34 пехотного полка.
... По мере осуществления своего исследования господин Жюлиа
отсылал в Академию запечатанные конверты. После получения послед-
него письма в декабре 1917 года известный геометр господин Фату,
которому теория итераций уже обязана интересными выводами, открыв-
шими новое направление, зафиксировал в наших «Трудах» основную
часть [«la plus grande partie»] тех же самых результатов. Он также
получил их посредством использования свойств нормальных семейств
господина Монтеля. Это не первый случай в истории науки, когда один
или два видных ученых одновременно, двигаясь одним и тем же путем,
приходят к одному открытию...».
Сложно представить, что академики в 1917 году забыли о Яно-
ше Больяи (1802-1860). Когда Больяи открыл свой вид неевклидо-
вой геометрии, его отец Вольфганг настоял на скорейшей публика-
ции результатов, «потому что, судя по всему, многие вещи, когда на-
ступает их время, открываются в нескольких местах одновременно,
подобно тому, как фиалки весной распускаются повсюду». Действи-
тельно, выяснилось, что результаты Яноша Больяи уже были опуб-
ликованы несколькими годами ранее Лобачевским и давно были из-
вестны Гауссу, который предпочел «не распространяться о них, пока
жив».
Стоит пояснить некоторые даты. 24 декабря 1917 года был рож-
дественский сочельник; в том же году произошла битва при Вердене.
Поскольку Первая мировая война завершилась 11 ноября 1918 года,
отчет, опубликованный 2 декабря 1918 года, создавался, когда об окон-
чании войны не было еще и речи, или, возможно, она была еще в самом
разгаре.
Таким образом, в оригинальных документах (помимо всего прочего)
написано, что члены Академии встретились во время войны в рожде-
ственский сочельник для сравнения результатов в уже опубликованных
работах Фату с результатами Жюлиа, которые не были опубликованы,
но были отправлены в запечатанных конвертах. Фату не упоминал о ре-
зультатах Жюлиа 21 мая 1917 года по той причине, что он возобновил
работу, начатую в труде Fatou 1906, а Жюлиа еще не предпринимал
никаких попыток в освоении этого направления. Можно предположить,
что Жюлиа не хотел раскрывать какой-то метод, который желал сохра-
нить еще некоторое время для себя лично.
И, наконец, последнее по порядку, но не по значимости: нужно
ответить еще на пару вопросов. В нашей современной научной культу-
ре как только какая-то математическая проблема становится интерес-
ной, целый рой саранчи, кажется, бросает всякую другую деятельность
и слетается к новой теме, чтобы отхватить приличный кусочек для себя.
Так как же удалось Жюлиа и Фату настолько «вычистить» их общую
тему, что на протяжении такого долгого времени в нее нельзя было
привнести ничего нового? Вообще говоря, в то время научный мир был
далеко не так люден, как сегодня. Если же говорить конкретнее, то
из-за Первой мировой войны произошла практически полная остановка
интеллектуальной деятельности, из-за чего математика осталась в руках
калеки Фату и раненого Жюлиа.
4. Фату и Жюлиа после 1917 года
Одним из вопиющих примеров непризнания является книга «Кто
есть кто в мире науки с античности и до наших дней», опублико-
ванная в 1968 году. Среди французских математиков перечислены вы-
шеупомянутые Аппель и Гурса, а также эфемерный Р. Гарнье, но нет ни
одной ссылки на Фату или Жюлиа.
Жюлиа, который тогда был еще жив, не подходил и для «Словаря
биографий ученных», составленного Джиллиспи в 1970-1976 гг. На
44
С24. Фату и Жюлиа
Фату отвели целых две колонки, а итерация заняла лишь одну строчку
। даже не была включена в библиографию.
Дополнительные свидетельства и мои собственные воспоминания
представлены в главе С25. Как бы то ни было, прекрасной математики
южет быть больше или меньше, в зависимости от веяний моды или
наличия подходящих инструментов, совершенно ясно одно: она будет
жить вечно.
Первая публикация
С25
Математический анализ:
пребывание во мраке
Поскольку данная глава рассчитана на широкий круг читателей, ее
следует начать с очень приблизительной характеристики. Математиче-
ский анализ «подобен исчислению, только намного более продвинуто-
му». Точного определения не существует. Это не удивительно, посколь-
ку по-настоящему важные понятия никогда не получают определения,
даже в математике! Это подтверждается в приложении к предисловию
в работе М 1999N и в обзорной главе труда М 2002Н.
В славные времена правления часто упоминаемого Николя Бурбаки
(с 1950-е по 1970-е годы) у специалистов по математическому анали-
зу были все основания чувствовать себя осажденными. По большин-
ству определений, мой дядя Шолем Мандельбройт считался ведущим
специалистом по математическому анализу. Несмотря на неблагоприят-
ные условия, ему удавалось быть одним из немногих людей, чьи работы
и студенты не позволяли пламени анализа погаснуть.
В данной главе приводятся несколько примеров, которые легко про-
верить и которые позволяют ощутить настроение, царившее в матема-
тике сначала в 1920-х, а потом и в 1950-60-х годах. Последний раздел
представляет собой потрясающий рассказ об экспериментальной мате-
матике.
Работа Адамара от 1934 года как свидетельство о более ран-
нем периоде математики. Имя Адамара упоминалось на протяжении
книги неоднократно. Этот поистине великий человек наконец-то полу-
чил свою научную биографию (Shaposhnikova & Mazya 1995). Он до-
бился признания, доказав теорему о простых числах, на протяжении
практически целого столетия считавшуюся сложной гипотезой, которую
Гаусс выдвинул на основе вычислений в явном виде. Позже Адамар сде-
лал огромный вклад в теорию распространения волн. В частности. он
добился результата, который заслуживает признания и восхищения фи-
зиков, — показал, что волны по-разному распространяются в простран
ствах четной и нечетной размерности вложения. Вообще, большую часть
346
С25. Математический анализ: пребывание во мраке
своей жизни Адамар проработал профессором механики] Эта должность
имеет широкое толкование, поскольку его основная преподавательская
деятельность заключалась лишь в проведении дважды в неделю семина-
ров, на которых приветствовались любые математические аспекты рас-
сматриваемого вопроса.
Тем, кто интересуется историей, я особенно рекомендую прочитать
работу Hadamard 1934. Из этого панегирика Поля Пенлеве (1863-1933),
который по непонятным причинам не был включен в собрание его сочи-
нений «Oeuvres», достаточно привести лишь несколько выдержек.
«В 1880-1890-х годах математики столкнулись с самой серьезной
проблемой со времен изобретения исчисления — интегрированием диф-
ференциальных уравнений. Без этого интегрирования у нас нет язы-
ка для описания изменений. Однако, за исключением некоторых про-
стых и поверхностных примеров, сложность интегрирования оказыва-
ется непреодолимой. И чем больше мы изучаем данный вопрос, тем
больше мы убеждаемся в этом. Всю вторую половину девятнадцатого
века науку вело великое открытие, которое обещало важный прогресс.
То была теория аналитических функций, пролившая свет на понятие
функции, то есть на понятие самого изменения... Точности и гармонии
изучения этих функций невозможно было ожидать при анализе явле-
ний на вещественной прямой... Но в третьей четверти девятнадцатого
века успехи в теории дифференциальных уравнений даже близко не мог-
ли сравниться с удивительным прогрессом, который наблюдался тогда
в изучении функций комплексных переменных...
Но лицо науки менялось. На сцену вышел Пуанкаре и сделал огром-
ный вклад в исследование обоих направлений. По мере появления по-
трясающих открытий ... я часто наблюдал у окружающих восхищение,
в смеси с некоторым беспокойством. Казалось, что большинство этих
результатов не развивается далее. Это действительно было бы серьез-
ным недостатком, если бы дело обстояло именно так. Но теперь мы
понимаем, что после таких значительных прорывов наука должна была,
так сказать, «подкопить силы». Чтобы развить мысль Пуанкаре, прежде
всего разум должен был наполниться его духом».
1950-е и 1960-е годы. Многотомный труд Николя Бурбаки назы-
вается «Элементы математики» (Elements de mathdmatique). Француз-
ское существительное единственного числа «mathdmatique» было непри-
вычным эквивалентом английского слова «mathematik», которое встре-
чается в наименованиях старых кафедр. До 1950-х годов у этого труда
был также подзаголовок, не требующий перевода: «Premiere partie: les
С25. Математический анализ: пребывание во мраке 347
structures fondamentales de Uanalysed. Затем подзаголовок исчез вме-
сте с обещанием написать «Deuxieme partie»}Q, и слово «структура»
осталось само по себе.
Представление о том, как анализ существовал в среде Бурбаки,
можно сложить по следующим цитатам, авторы которых самым непо-
средственным образом повлияли на мою работу.
Kahane and Salem 1962. Жан-Пьер Кахан был учеником моего
дяди, и главная монография, которую он написал совместно с Рафаэлем
Салемом, оказала большое влияние на мою научную жизнь, что подтвер-
ждается в работе Kahane & М 1974{N11}. До выхода той монографии
я считал, что хаусдорфова размерность относится к древней эзотерике
и никак не связана с современностью.
Работу Кахана и Салема открывает цитата из «Одили» Реймона
Кено, выдающейся фигуры литературного мира, который любил мате-
матику (а однажды даже пригласил меня к себе в гости): «Геометрию
и математический анализ надо сравнивать не с архитектурой и не с по-
стройками, а с ботаникой, с географией и даже с физическими науками.
Их задача заключается в описании мира, открытии его, а не в строи-
тельстве или изобретении его, поскольку он существует не внутри, а вне
человеческого разума и совершенно не зависит от оного».
В последующем предисловии эта цитата поясняется подробнее:
«Несколько десятилетий назад этой книге данное предисловие даже не
потребовалось бы, поскольку написано оно для оправдания. Сегодня,
когда большинство (в том числе и лучших) математиков интересуют-
ся главным образом вопросами структуры, эта книга может показаться
устаревшей и в некотором роде не более ценной, чем коллекция сухих
листьев. Поэтому мы должны отметить, что ни в коем случае не ставим
перед собой реакционных целей. Нам знакома красота великих совре-
менных теорем... но мы полагаем, что имеем полное право выказать
свой интерес к этим объектам ради изучения их самих, не пренебрегая
при этом архитектурой, на которой зиждется сама математика как на-
ука. Сколь изолированными ни казались бы эти объекты, в них часто
скрыты свойства, которые вознаградят наше внимание к ним, поставив
невероятно увлекательные проблемы. Некоторые из наших друзей назы-
вают такой подход «рафинированной» математикой, и мы неоднократно
задавались вопросом, что именно они хотят этим выразить: свое восхи-
щение или пренебрежение?»
9Часть первая: фундаментальные аналитические структуры. — Прим, перев.
*°Вторая часть. — Прим, перев.
348
С25. Математический анализ: пребывание во мраке
Magnus 1974. Этот важный учебник уже упоминался мной в гла-
ве С2, когда подчеркивалось его влияние на мою работу по клейновым
группам. Его открывает цитата К. Л. Зигеля: «Математическая вселен-
ная населена не только важными видами, но и интересными особями».
Mandelbrojt 1952. Этот отрывок, возможно, единственное пись-
менное выражение философской позиции моего дяди, был воспроизве-
ден в виде фотографий в приложении к труду Mandelbrojt 1985: «Дол-
жен признаться, что мое сильнейшее желание заниматься математикой
исходит из желания понять внешний мир... в самом высоком смыс-
ле. .. [После того, как кто-нибудь докажет, что существует бесконеч-
ность] простых чисел, разность между которыми равна двум, как-то:
3-5, 11-13 или 17-19, я почувствую такое же удовлетворение, как в тот
момент, когда окончательно пойму расширение Вселенной... Великим
достоинством математики считается обобщение, к частным же случа-
ям нередко относятся весьма пренебрежительно. Но я не могу идеали-
зировать обобщение ... Обобщение прекрасно, когда оно объясняет...
Обобщение должно быть оптимальным... Обобщая только из-за люб-
ви к обобщению или к абстракции, мы рискуем оказаться в мире фор-
мальностей ... Я бы не хотел жить в мире формальной логики, который
представляют себе некоторые мои коллеги... Ни в одном божественном
законе, известном мне, не сказано, что мы должны отречься от бытия,
которое я считаю полным, ради бытия, обладающего теми же преиму-
ществами, но только более сухого и формального. Говорят, что целью
математики является изучение не предметов как таковых, а отношений
между ними. Я согласен с этим, но, на мой взгляд, математик жи-
вет двойной жизнью:... в мире интуитивных представлений и... мире
сложностей, которые приносят столько радости и без которых жизнь
стала бы слишком скучной или слишком простой».
В приведенном тексте ясно чувствуется, хотя и неявная, но жесткая
критика Бурбаки. В личных беседах Шолем был более искренним, и со-
вершенно очевидно, что его взгляды оказали на меня большое влияние.
Lucas 1891. Тема следующих и предыдущих цитат относится не
к математическому анализу, а к экспериментальной математике. Но я за-
хотел включить их в данную книгу, потому что считаю ее самым под-
ходящим для этого местом.
Когда я ознакомился с предисловием к работе Lucas 1891, я понял,
что его необходимо скопировать для будущих нужд. С полным основа-
нием можно сказать, что в то время экспериментальная математика бы-
ла нелюбима и находилась на осадном положении. К счастью, ситуация
С25. Математический анализ: пребывание во мраке
349
изменилась к лучшему. Понимание этого текста не требует глубокого
знания французского языка, поэтому перевод не имеет смысла. Эдуард
Лукас (1842—1981) был профессором «специальных математических на-
ук», и его последним местом работы был лицей Сен-Луи в Париже.
«Сотте toutes les sciences, I’Arithmetique resulte de 1’observation;
elle progresse par l^tude des phenomenes numeriques donnes par des cal-
culs anterieurs, ou fabriqi^s, pour ainsi dire, par Гехрёптеп1а1лоп; mais
elle n’exige aucun laboratoire et possede seule le privilege de convertir
ses inductions en theorems dёductifs. Сотте en Chimie, par exemple, on
prepare les nombres au moyen du calcul; par la diу151ЬПИё, on dёcompo-
se ceux-ci en ё1ётеп15 simples, les facteurs premiers; par la tlforie des
residus potentiels, on dёteгmine leur aspect et, en quelque sorte, leurs fac-
tions mutuelles; enfin par la juxtaposition des nombres tringularies, carrds,
polygonaux, cubiques, etc., la tlforie des formes nurrfriques rappelle Гё1и-
de des systemes cristallins. C’est par 1’observation du dernier chiffre dans
les puissances successives des nombres entiers que Fermat, notre Divus
Arithmeticus, сгёа I’Arithmdtique Эирёпеиге, en donnant Гёпопсё d’un
theoreme fondamental; c’est par la mdthode ехрёптеп1а1е, en recherchant
la ёётоп51гаМоп de cette proposition, que la thdorie des racines primi-
tives fut imaginde par Euler; c’est par 1’emploi imnfdiat de ces racines
primitives que Gauss obtint son сё1ёЬге thdofme sur la division de la cir-
сопГёгепсе en parties ёgales, et celui-ci fut le point de dёpaгt des profondes
recherches d’Abel et de Galois, de MM. Kummer, Hermite et Kronecker,
dans ГА^ёЬге зирёпеиге. ...
La thdorie des suites fcurrentes est une mine indpuisable qui renfer-
me toutes les propridtds des nombres; en calculant les termes successifs
de telles suites, en dёcomposant ceux-ci en facteurs, en recherchant par
Гехрёпте^аПоп les lois de Vapparition et de la reproduction des nombres
premiers, on fera progresser d’une татёге systёmatique letude des pro-
рпё1ё$ des nombres et de leurs applications dans toutes les branches des
Matlfmatiques».11
11 Подобно всем прочим наукам, арифметика проистекает из наблюдения. Она развива-
ется благодаря изучению численных явлений, полученных в результате предшествующих
вычислений или «сфабрикованных», если можно так выразиться, в процессе эксперимен-
тов. При этом она не требует никаких лабораторий и сама по себе обладает привилегией
превращения этих индуктивных выводов в дедуктивные теоремы. Это похоже на то, как,
например, в химии, для вычисления готовят средние числа; чтобы добиться делимости,
сложные объекты раскладывают на простые элементы, простые множители; в теории по-
тенциальных остатков определяют обе стороны и, в некотором роде, их взаимные реак-
ции; наконец, для наложения чисел треугольных, квадратных, многоугольных, кубиче-
ских и т.д. теория численных форм требует изучения кристаллических систем. Именно
350
С25. Математический анализ: пребывание во мраке
Превратности истории. То пагубное влияние, которое Бурбаки
в прошлом оказывали на многие умы, быстро превращается лишь в отда-
ленное воспоминание. Историкам придется проштудировать множество
источников, чтобы понять, что послужило причиной развала этого обще-
ства, и оценить относительный вклад моей работы в этот процесс. Как
бы то ни было, оборонительный оттенок, который ощущается в приве-
денных высказываниях, поражает тех, кто не жил в ту эпоху, но под-
тверждает все сказанное ранее.
В 1950-х и 1960х годах теория Фату-Жюлиа была крайне непо-
пулярной и пребывала во мраке, поскольку включала много частных
примеров и мало «великих современных теорем». Выражения «сухие
листья», «изолированный», «интересная особь» или «частный случай»
идеально ей подошли. Именно по этой причине она выпала из основно-
го математического течения и по многим практическим соображениям
была заброшена. Не забывайте, что для Бурбаки Пуанкаре олицетворял
самого дьявола, который оставил после себя кучу недоказанных утвер-
ждений и открытых вопросов. Они гордились тем, что разгребли эту
кучу. Естественно, идеи Пуанкаре долгое время волновали французских
математиков. В 1880-е годы Эрмит в своих письмах часто жаловался
Митта г-Леффлеру, что молодой Пуанкаре никогда не завершает дока-
зательства. Однако для людей, изучающих хаос и фракталы, Пуанкаре,
без сомнений, является Богом на Земле.
Был ли переход от Пуанкаре к Бурбаки с последующим возвраще-
нием к первому нормальным и предопределенным результатом, вопросом
общего здорового развития? Историю нередко сравнивают с маятником,
который раскачивается вперед и назад, вверх, вниз и снова вверх, от
анархии к тирании и обратно. Такое сравнение помогает разбить ис-
торию математики на небольшие кусочки, вполне подвластные нам, что
резонирует с высказанным лордом Кейнсом мнением, что циклы деловой
благодаря наблюдениям за последней цифрой в последовательных степенях целых чи-
сел. Ферма, наш Divus Arithmeticus, создал высшую арифметику, в рамках которой была
сформулирована фундаментальная теорема. С помощью экспериментального метода уда-
лось продемонстрировать высказанное предположение, о существовании которого теория
п|нхтых корней догадывалась еще со времен Эйлера. Именно благодаря немедленному
И' пользованию этих простых корней, Гаусс получил свою знаменитую теорему о делении
он»\жности на равные части и создал отправную точку для глубоких исследований Абеля
и . <nva. Куммера, Эрмита и Кронекера в высшей математике. ...
!еория рекуррентных рядов — это неисчерпаемый источник, содержащий в себе все
свинства чисел; с ее помощью можно вычислить последовательные члены этих рядов,
риз. «ожить их на множители, экспериментальным путем определить законы появления
и * (Произведения первых чисел, чтобы продолжать систематическим образом изучать
i н«/н. тиа чисел и их применение во всех областях математики (фр.). — Прим, перев.
С25. Математический анализ: пребывание во мраке 351
активности помогают разделить экономическую историю на поддающие-
ся управлению небольшие тома. Мысль эта была высказана не без сар-
казма, поскольку Кейнс считал, что циклы деловой активности не имеют
предсказательной ценности, а я применил его мнение к циклическому
взгляду на развитие математики. Одним из самых лучших результатов
теории хаоса и современного возрождения учения Пуанкаре, возможно,
является то, что сейчас наконец-то настало время, когда мы раз и навсе-
гда можем отказаться от грубой модели представления истории в виде
маятника.
Общая библиография, включая
указания на авторские права
Совпадающие части данной библиографии созданы по различным
мотивам и отличаются по объему.
В более короткой части приводится список репринтов и новых глав.
В оригиналах данных репринтов имелось мало ссылок, большинство из
которых имело весьма общий характер или же устарело. Основной при-
чиной этого было отсутствие достаточного количества литературы.
Вообще, вопросы, которые я рассматривал, сами по себе не были новы-
ми, но их изучение прерывалось надолго. Многочисленные работы по
развитию тех старых трудов появились слишком поздно, чтобы их
можно было упомянуть в библиографии. У меня нет ни обязанности,
ни возможности предлагать продуманный список литературы, кото-
рый я использовал в 2003 году.
В более длинной части в середине данной библиографии перечислено
большинство моих публикаций с ссылками на авторские права в отно-
шении работ, воспроизведенных в этой книге. Такой список был обяза-
тельным в томах «Selected Papers». Возможно, интернет — новая вы-
сокотехнологичная форма самиздата — превратил его в устаревший
симптом Vanitas Vanitarum12. Публикациям, переизданным в одном из
томов ♦Selecta», предшествует аннотация вида *N16, которая отно-
сится к тому N, глава 16. Буквенный код — Е=М1997Е, N=M1999N,
Н=М2002Н, FE=M1997FE.
Источники библиографии в данном списке очень разнообразны,
и некоторые известны лишь немногим читателям, поэтому включены
все имеющиеся варианты. Использованные аббревиатуры: J. — журнал,
Proc. — труды, Тг. — протоколы и Z. — газета.
1. AHARONY, А. & FEDER, J. Eds. 1989. Fractals in Physics. Amsterdam:
North-Holland, Physica: D38, 1-398.
2. Alexander, D. S. A History of Complex Dynamics from Schroder to Fatou and
Julia, Braunschweig/Weisbaden: Vieweg, 1994.
3. APOSTEL, L., MANDELBROT, B. & MORF, A. 1957. Logique, langage et
th^orie de {’information. Paris: Presses Universitaires de France.
|2Суета сует (лат.) — Прим, перев.
Общая библиография, включая указания на авторские права 353
4. APPELL, Р. & GOURSAT, Е. 1895, deuxieme edition, 1929-1930. Th^orie
des fonctions algebriques. Paris: Gauthier-Villars.
5. ASIKAINEN, J., AHARONY, A., RAUSCH, E„ HOVI, J.P. & MANDEL-
BROT, B.B., 2003. Fractal properties of critical Potts clusters. European
Physical Journal'. B34, 479-.
6. BARRAL, J., COPPENS, M-O. & MANDELBROT, B.B., 2003. Multiperio-
dic multifractal martingale measures. Journal des mathematiques pares et
appliquees, in the press.
7. BARRAL, J. & MANDELBROT, В. B., 2002. Multifractal products of
cylindrical pulses. Probability Theory and Related Fields: 124, 409-430.
8. BARRAL, J. & MANDELBROT, B.B., 2004. Multifractal products of
independent random functions: Fractals. Ed. Michael L. Lapidus, Providence,
RI: American Mathematical Society.
9. BARTON, C. & LAPOINTE, P. Eds. 1994. Fractal Geometry and its Use in
the Earth Sciences. New York: Plenum.
10. BARTON, C. & LAPOINTE, P. Eds. 1995. Fractals in Petroleum Geology
and Earth Processes. New York: Plenum.
11. BEARDON, A. 1983. The Geometry of Discrete Groups, New York: Springer-
Verlag.
12. BEDFORD, T.J. 1984. Crinkly Curves, Markov Partitions and Dimension.
Unpublished Ph.D. Thesis, Warwick University, U.K.
13. N6 BERGER, J.M. & MANDELBROT, B.B., 1963. A new model for the
clustering of errors on telephone circuits. IBM Journal of Research and
Development: 7, 224-236.
14. BIDUAX, R., BOCCARA, N., SARMA, G., SEZE, L., DE GENNES, P.G.,
PARODI, O., 1973. Statistical properties of focal conic textures in smectic
liquid crystals. Le J. de Physique, 34, 661-672.
15. BLANCHARD, P. 1984. Complex analytic dynamics on the Riemann sphere.
Bull. American Mathematical Society: 11(1), 85-141.
16. BLUMENFIELD, R. & AHARONY, A., 1989. Breakdown of multifractal
behavior in diffusion-limited aggregates. Physical Review Letters: 62, 2977—
2980.
17. BLUMENFIELD, R. & MANDELBROT, B.B., 1997. Levy dusts, Mittag-
Leffler statistics, mass fractal lacunarity, and perceived dimension. Physical
Review: E56. 112-118.
18. BOURBAKI, N. 1960. Elements d’histoire des mathematiques. Paris:
Hermann.
19. BOURGUIGNON, J. P. 1999. Интервью о «Международном годе Математи-
ки 2000». wmy2000.math.jussieu.fr/wmy_6.html.
20. BOX, G.E. & JENKINS, G.M. 1970. Time Series Analysis, Forecasting and
Control. San Francisco: Holden-Day.
354 Общая библиография, включая указания на авторские права
21. BOYD, D. W. 1973а. The residual set dimension of the Apollonian packing.
Mathematika: 20, 170-174.
22. BOYD, D. W. 1973b. Improved bounds for the disk packing constant.
Aequationes Mathematicae: 9, 99-106.
23. BRAGG, W.H. 1934. Liquid crystals. Nature'. 133, 445-456.
24. BROLIN, H. 1965. Invariant sets under iteration of rational functions. Arkiv
for Mathematik: 6, 103-144.
25. BROOKS, R. 1989. The Mandelbrot set (Letter to the Editor). The Mathema-
tical Intelligencer. 12(1), 3.
26. BROOKS, R. & METELSKI, J. P. 1981. The dynamics of 2-generator
subgroups of PSL (2,0), Riemann Surfaces and Related Topics, Eds. I.Kra
and B. Maskit, Princeton University Press.
27. CALVET, L., FISHER, A., & MANDELBROT, B.B., 1997. Large Deviations
and the Distribution of Price Changes. Cm. Mandelbrot, Calvet & Fisher 1997.
28. CANTOR, G. 1932. Gesammelte Abhandlungen mathematischen und philoso-
phischen Inhalts. Ed. E. Zermelo. Berlin: Teubner. 01ms reprint.
29. CARELSON, L. & JONES, P. W. 1992. On coefficient problems of univalent
functions and conformal dimension, Duke Mathematical J.: 66, 169-206.
30. CARPENTER, L.C., FOURNIER, A., and FUSSEL, D., Display of fractal
curves and surfaces, в печати, Communications of the Association for Com-
puting Machinery.
31. CHOUCHAN, M. 1995. Nicolas Bourbaki: Faits et Idgendres. Argenteuil:
Editions du Choix.
32. C1OCZEK-GEORGES, R. & MANDELBROT, B.B., 1995. A class of
micropulses and antipersistent fractional Brownian motion. Stochastic
Processes and their Applications: 60, 1-18.
33. CIOCZEK-GEORGES, R. & MANDELBROT, B.B., 1996. Alternative
micropulses and fractional Brownian motion (with Renata Cioczek-Georges).
Stochastic Processes and their Applications: 64, 143-152.
34. CIOCZEK-GEORGES, R. & MANDELBROT, В. B., 1996. Stable fractal sums
of pulses: the general case.
35. CIOCZEK-GEORGES, R., MANDELBROT, B. B„ SAMORODN1TSKY, G.
& TAQQU, M.S. 1995. Stable fractal sums of pulses: the cylindrical case.
Bernoulli: 1, 201-216.
36. COLLET, P. and ECKMAN, J.P. 1980. Iterated maps on the Interval as
Dynamical Systems. Boston: Birkhauser.
37. COPPENS, M-O. & MANDELBROT, В. B., 1999. Easy and natural generation
of multifractals; multiplying harmonics of periodic functions. Fractals in
Engineering. Eds. J. L6vy-Vehel, E.Lutton, & C. Tricot. New York. Springer,
113-122.
Общая БИБЛИОГРАФИЯ, ВКЛЮЧАЯ УКАЗАНИЯ на авюнскиь права
38. COXETER, 1979. The non-Euclidean symmetry of Esher’s picture
♦Circle Limit III». Leonardo, 12, 19-25.
39. CVITANOVIC, P. & MYRHEIM, J. 1982. Universal for period n-triplings in
complex mappings, Physics Letters'. 94A, 329-333.
40. *H29 DAMERAU, F.J. & MANDELBROT B.B., 1973. Tests of the degree of
word clustering in samples of written English. Linguistics: 102, 1973, 58-75.
41. DENJOY, A. 1932. Sur quelques points de la theorie des fonctions: Comptes
rendus (Paris): 194, 44-46.
42. DENJOY, A. 1938. Sur une fonction reelle de Minkowski, Journal des
Mathdmatiques Pures et Appliqdes: 62. 105-151.
43. DENJOY, A. 1955. Articles et mdmoires, Paris, Gauthier-Villars, 1955, 2,
925-971.
44. DEVANEY, R. & KEEN, L. Eds. 1989. Chaos and Fractals. The Mathema-
tics Behind the Computer Graphics, Providence, RI: American Mathematical
Society.
45. DEWDNEY, A.K., 1985. A computer microscope zooms in for a look at the
most complex object of mathematics. Scientific American, August, обложка и
стр. 16-21.
46. DIEUDONNE, J. 1975. L’abstraction et 1’intuition mathematique, Dialectica:
29, 39-54.
47. DOUADY, A., 1982. Systems dynamiques holomorphes. Sdminaire Bourbaki.
Astdrisque: 599.
48. DOUADY, A., 1986. Julia sets and the Mandelbrot set, The Beauty of Fractals,
by Heinz-Otto Peitgen & Peter H. Richter, New York: Springer, 161-173.
49. DOUADY, A. and HUBBARD, J., 1982. Iteration des polymones quadratiques
complexes. Comptes rendus (Paris): 294-1, 123-126.
50. DOUADY, A. and HUBBARD, J., 1984. 6tude dynamique des polynomes
complexes. I, II, Publications Mathematiques d’Orsay, Universite de Paris-Sud,
Orsay, France.
51. DOUADY, A. and HUBBARD, J., 1985. On the dynamics of polynomial-like
mappings. Ann. Scientifiques de I’Ecole Normale Supdrieure: 18, 287-343.
52. DUBUC, S. 1982. Theoretical and numerical study of the Dekarlin-McGregor
function. J. Analyse Mathdmatique: 42, 15-37.
53. EVERTSZ, C.J.G., JONES, P.W., & MANDELBROT, B.B., 1991. Behavior
of the harmonic measure at the bottom of fjords. J. Physics: A24, 1889-1901.
54. EVERTSZ, C. J.G. & MANDELBROT, B.B., 199In. Steady state noises in
diffusion limited fractal growth. Europhysics Letters: 15, 245-250.
55. EVERTSZ, C.J.G. & MANDELBROT, B.B., 1992a. Multifractal measures.
Приложение в Chaos and Fractals: New Frontiers in Science, by H.-O. Peit-
gen, H. Jurgens & D. Saupe. New York: Springer, 849-881.
О Б 111 А Я Б И Б Л ИОГРАФИЯ, ВКЛЮЧАЯ УКАЗАНИЯ НА АВТОРСКИЕ ПРАВА
56. EVERTSZ, C.J.G. & MANDELBROT, В. В., 1992b. Self-similarity of the
harmonic measure on DLA. Physica: A185, 77-86.
57. EVERTSZ, C.J.G., MANDELBROT, B.B., & NORMANT, F., I991L Fractal
aggregates, and the current lines of their electrostatic potentials. Physica:
Al77, 589-592.
58. EVERTSZ, C.J.G., MANDELBROT, В. B., & NORMANT, F., 1992t.
Harmonic measure around linearly self-similar trees. J. Physics'. A25, 1781-
1797.
59. EVERTSZ, C.J.G., MANDELBROT, B.B., NORMANT, F., & WOOG, L,
1992. Variability of the form and the harmonic measure for small off-off lattice
diffusion limited aggregates. J. Physics: A45, 5798-5804 & 8985-8986.
60. EVERTSZ, C.J.G., MANDELBROT, B.B., & WOOG, L., 1992. Variability of
the form and the harmonic measure for small off-off lattice diffusion limited
aggregates. Physical Review: A45, 5798-5804
61. FATOU, P. 1906. Sur les solutions uniformes de certaines equations
fonctionnelles. Comptes rendus (Paris): 143, 546-548.
62. FATOU, P. 1919-1920. Sur les solutions equations fonctionnelles. Bull. Soc'tftt
Mathtmatique de France: 47, 161-271; 48, 33-94, & 48, 208-314.
63. FEDER, J., 1988. Fractals. New York: Plenum.
64. FEIGENBAUM, M.J. 1978. Quantitative universality for a class of nonlinear
transformations. J. of Statistical Physics: 19, 25-52.
65. FEIGENBAUM, M.J. 1981. Universal behavior in nonlinear systems. Los
Alamos Science: 1, 4-27.
66. FISHER, A., CALVET, L. & MANDELBROT, B.B. 1997. The Muitifractality
of the Deutshmark / US Dollar Exchange Rates. Cm. Mandelbrot, Calvet &
Fisher 1997.
67. FRAME, M. L., & MANDELBROT, В. B. 2002. Fractals, Graphics, and Ma-
thematics Education, Washington D.C.: Mathematical Association of America
& Cambridge: The University Press.
68. FRAME, M. L, & MANDELBROT, В. B. 2003. Panorama of Fractals and
their Uses. Планируется выпустить книгой. В данный момент находя-
щуюся в работе версию можно найти по следующему интернет-адресу:
http://math.yale.edu/panorama/panorama.htu/.
69. FRICKE, R., & KLEIN, F. 1897. Vorlesungen Uber die Theorie der automor-
phen Functionen. Leipzig: Teubner (Johnson reprint).
70. *N2 FRISCH, U., & PARISI, G. 1985. Fully developed turbulence and
intermittency, in Turbulence and Predictability in Geophysical Fluid
Dynamics. International School of Physics «Enrico Fermi». Course 88, Eds.
M.Ghil et. al. Amsterdam: North-Holland, 84-88.
71. GEFEN. Y., AHARONY, A., & MANDELBROT, В. B. 1983. Phase transitions
on fractals: I. Quasi-linear lattices. J. of Physics: A16, 1267-1278.
Общая библиография, включая указания на авторские права 357
72. GEFEN, Y., AHARONY, А., & MANDELBROT, В. В. 1984. Phase transitions
on Fractals: III. Infinitely ramified lattices. J. of Physics. A17, 1277-1289.
73. GEFEN, Y., AHARONY, A., MANDELBROT, В. B., & K1RKPATRIK, S. 1981.
Solvable fractal family, and its possible relation to the backbone at percolation.
Physical Review Letters: 47, 1771-1774.
74. GEFEN, Y., AHARONY, A., MANDELBROT, B.B., & SHAPIR, Y. 1984.
Phase transitions on fractals: II. Sierpinski gaskets. J. of Physics: A17, 435-
444.
75. GEFEN, Y., MANDELBROT, В. B. & AHARONY, A., 1980. Critical
phenomena on fractals. Physical Review Letters: 45, 855-858.
76. GEFEN, Y., MEIR, Y., MANDELBROT, B.B. & AHARONY, A.,
1983. Geometric implementation of hypercubic lattices with noninteger
dimensionality, using low lacunarity fractal lattices. Physical Review Letters:
50, 145-148.
77. GERNSTEIN, G. L., & MANDELBROT, В. B. 1964. Random walk models for
the spike activity of a single neuron. The Biophysical L: 4, 41-86.
78. GILLESPIE, C.C. (Ed.) 1970-6. Dictionary of Scientific Biography. New
York: Scribner’s.
79. GISPERT, H. 1991. La France Mathematique, 1890-1914. Cahiers d’Histoire
et de Philosophie des Sciences: 34.
80. GIVEN, J.A. & MANDELBROT, B.B. 1983. Diffusion of fractal lattices and
the fractal Einstein relation. J. Physics: A16, L565-L569.
81. GNEDENKO, В. V. 1967. The Theory of Probability. New York: Chelsea.
82. GNEDENKO, В. V. & KOLMOGOROV, A. N. 1968. Limit Distributions for
Sums of Independent Random Variables. Reading, MA: Addison-Wesley.
83. GROSSMAN, S. & THOMAE, S. 1977. Invariant distributions and
stationary correlation functions of one-dimensional discrete processes. Z. fur
Naturforschung: 32A, 1353-1363.
84. GUCKENHEIMER, J. & MCGEHEE, R. 1984. A Proof of the
Mandelbrot N2 Conjecture, http://www.math.umn.edu/~mcgehee
/publications/Mandelbrot N2/Mandelbrot N2.pdf. Cm. Report No. 15,
Djursholm (Sweden): Institut Mittag-Leffler.
85. GUREL, O. & ROSSLER, О. E. Eds., 1979. Bifurcation theory and applications
in scientific disciplines, Annals of the New York Academy of Science: 316, 1-
708.
86. GUTZWILLER, M.C., 1980. Classical quantization of a Hamiltonian with
ergodic behavior. Physical Review Letter: 45, 150-153.
87. GUTZWILLER, M. C., 1983. Stochastic behavior in quantum scattering.
Physica (Amsterdam), 7D, 341-355.
88. *C GUTZWILLER, M.C., & MANDELBROT, B.B. 1988. Invariant
multifractal measures in chaotic Hamiltonian systems, and related structures.
Physical Review Letter: 60, 673-676.
358 Общая библиография, включая указания на авторские права
89. HADAMARD, J. 1912. L’oeuvre mathematique de Poincare. Acta
Mathematical 38, 203-287. Reprints in Poincare 1916-, XI, 152-242, and
Hadamard 1968, 4, 1921-2005.
90. HADAMARD, J. 1934. L’oeuvre scientifique de Paul Painleve. Revue de
Mdtaphysique et de Morale: XLI (3), 289-325.
91. HADAMARD, J. 1968. Oeuvres de Jacques Hadamard. Paris: Editions de
CNRS.
92. HALSEY, T.C., JENSEN, M.H., KADANOFF, L.P., PROCACCIA, I.
& SHRAIMAN, В. I. 1986. Fractal measures and their singularities:
the characterization of strange sets. Physical Review: A33, 1141-1151.
IMPORTANT ERRATA: Physical Review: A34, 1986, 1601.
93. HARDY, G.H. & WRIGHT, E.M. 1960. An introduction to the Theory of
Numbers (4th edition) Oxford: Clarendon Press.
94. HELLEMAN, R. H.G. Ed. 1980. Nonlinear dynamics. Annals of the New York
Academy of Science: 357, 1-507.
95. HERMANN, R. 1991. Fractal Theory. Mathematical Intelligencer: 13, 4.
96. HEWITT, E. 1990. So far, so good: my life up to now. Mathematical
Intelligencer: 12(4), 58-63.
97. HOKUSAI, K. 1834. Fugaku Hyakkei or One Hundred Views of Mt. Fuji.
Оригинал, состоящий из трех небольших томов, представляет собой бес-
ценный библиотечный экспонат. Репринт с комментариями. New York.
George Braziller, 1988.
98. HOFSTADER, D. R. 1981. Strange attractors: mathematical patterns delicately
poised between order and chaos. Scientific American: 254, (ноябрьский вы-
пуск), 16-29.
99. HOVI, J.-P., AHARONY, A., STAUFFER, D., & MANDELBROT, В. B., 1996.
Gap independence and lacunarity in percolation clusters. Physical Review
Letters: 77, 877-890.
100. HUGHES, B. D. 1995-1996. Random walks and random environments.
Oxford: Clarendon Press.
101. HURD, A.J., MANDELBROT, B.B., & WEITZ, D.A. (eds) 1987. Fractal
Aspects of Materials: Disordered Systems. Extended Abstracts of a MRS
Symposium, Boston. Pittsburgh, PA: Materials Research Society.
102. JAFFARD, S. & MANDELBROT, В. B. 1996. Local regularity of nonsmooth
wavelate expansions and application to the Polya function. Advances in
Mathematics: 120, 265-282.
103. JULIA, G. 1918. Memoire sur 1’iteration des fonctions rationnelles. J. de
Mathdmatiques Pures et Appliqudes: 4 47-245. Reprinted (with related texts)
in Julia 1968, 121-319.
104. JULIA, G. 1968. Oeuvres de Gaston Julia, Paris: Gauthier-Villars.
Общая БИБЛИОГРАФИЯ, ВКЛЮЧАЯ УКАЗАНИЯ НА АВТОРСКИЕ ПРАВА 359
105. *N11 KAHANE, J.P. & MANDELBROT, В. В. 1965. Ensembles de
multiplicite aleatoires. Comptes rendus (Paris): 261, 3931-3933.
106. KAHANE, J. P. & SALEM, R. 1963. Ensembles parfaits et series trigonomet-
riques. Paris: Hermann.
107. KAKUTANI, S. 1944. 2-dimensional Brownian motion and harmonic functions.
Proc. Imperial Academy of Sciences (Tokyo): 20, 706-714.
108. KINNEY, J.R. 1960. Note on a singular function of Minkowski. Proc.
American Mathematical Society: 11, 788-794.
109. KRANTZ, S.G. 1989. Fractal Geometry. Mathematical Intelligencer: 11(4),
12-16.
110. KRANTZ, S.G. 1990. Mathematical anecdotes. Mathematical Intelligencer:
12(3), 32-39.
111. KRANTZ, S.G. 1991. Mathematical anecdotes. Mathematical Intelligencer:
13(4), 5.
112. LAIBOWITZ, R.B., MANDELBROT, В. B. & PASSOJA, D.E. Eds. 1985.
Fractal Aspects of Materials. Extended Abstracts of a MRS Symposium,
Boston, Pittsburgh PA: Material Research Society.
113. LAM, С.-H., KAUFMAN, H. & MANDELBROT, В. B. 1994. Orientation of
particle attachment and local isotropy in diffusion limited aggregates (DLA).
J. Physics: A28, L213-217.
114. LATTES, S. 1918a. Sur 1’iteration des substitutions rationnelles et les fonctions
de Poincare. Comptes rendus (Paris): 166, 26-28.
115. LATTfiS, S. 1918b. Sur I’iteration des substitutions rationnelles a deux
variables. Comptes rendus (Paris): 166, 151-153.
116. LATTES, S. 1918c. Sur I’iteration des fractions irrationnelles. Comptes rendus
(Paris): 166, 486-488.
117. LEE, J. & STANLEY, H.E. 1988. Phase transition in the multifractal spectrum
of diffusion-limited aggregates. Physical Review Letters: 61, 2945-2948.
118. LEE, J., ALSTROM, P. & STANLEY, H.E. 1989. Scaling of the minimum
growth probability for the «typical» diffusion-limited aggregation configuration.
Physical Review: A39, 6545-6556; Physical Review Letters Comm.: 62,
3013-3013.
119. LEIBNIZ, G.W. 1894-. Mathematische Schriften. Ed. С. I. Gerhardt. Halle:
H.W. Schmidt (01ms reprint).
120. LEVY, P„ MANDELBROJT, S., MALGRANGE, B. & MALLIAVIN, P. 1967.
La vie et I'oeuvre de J. Hadamard. Geneve: Monographies de 1’Enseignement
Mathematique: 16.
121. LUCAS, E. 1891. Thdorie des nombres. Paris: Gauthier-Villars.
122. MAGNUS, W. 1974. Noneuclidean Tesselations and their Groups. New York:
Academic Press.
360 Общая библиография, включая указания на авторские права
123. MAKAROV, N. G. 1998. Fine structure of harmonic measure. Алгебра и ана-
лиз-. 10, 1-62; перевод в St. Petersburg Mathematical J.: 10(2), 217-268.
124. MANDELBROJT, S. 1952. Pourquoi je fais des mathematiques. Revue de
Mdtaphysique et de Morale: 57(4), 442-429.
125. MANDELBROJT, S. 1985. Souvenirs a batons rompus. Publications du
Sdminaire d'Histoire des Mathdmatiques de I’Universitd de Paris: 6, 1-46.
126. MANDELBROT, В. B. 1951. Adaptation d’un message a la ligne de
transmission, I & II. Comptes rendus (Paris): 232, 1638-1740 & 2003-2005.
127. MANDELBROT, В. B. 1953L An informational theory of the statistical
structure of language, в книге Communication Theory. Ed. W. Jackson.
London: Butterworth, 486-504.
128. MANDELBROT, В. B. 1953t. Contribution a la theorie mathematique des jeux
de communication (кандидатская диссертация). Publications de ITnstitut de
Statistique de I’Uniuersitd de Paris: 2, 1-124.
129. MANDELBROT, В. B. 1954w. Structure formelie des texts et communica-
tion (deux etudes). Word 10, 1-27. Corrections. Word 11, 424. Перевод на
английский, чешский и итальянский языки.
130. MANDELBROT, В. В. 1955b. On recurrent noise limiting coding. Information
Networks, the Brooklyn Polytechnic Institute Symposium, 205-221. Ed.
E. Weber. New York: Interscience. Перевод на русский язык.
131. MANDELBROT, В. В. 1955t. Theorie de la precorrection des erreurs de
transmission. Annales des Tdldcommunications: 10, 112-134.
132. MANDELBROT, В. B. 1956c. La distribution de Willis-Yule, relative au
nombre d’especes dans les genres taxonomiques. Comptes rendus (Paris): 242,
2223-2225.
133. MANDELBROT, В. B. 1956g. Memorandum. University of Geneva:
Mathematics Institute.
134. MANDELBROT, В. B. 1956m. A purely phenomenological theory of statistical
thermodynamics: canonical ensembles. IRE Tr. on Information Theory: 112,
190-203.
135. MANDELBROT, В. B. 1956t. Exhaustivite de I’energie d’un systeme, pour
1’estimation de sa temperature. Comptes rendus (Paris): 243, 1835-1837.
136. MANDELBROT, В. B. 1956w. On the language of taxonomy: an outline of
a thermo-statistical theory of systems of categories, with Willis (natural)
structure. Information Theory, the Third London Symposium. Ed. C. Cherry.
London: Butterworth; New York: Academic, 1956, 135-145.
137. MANDELBROT, В. B. 1957b. Note on-a law of J. Berry and on insistence
stress. Information and Control: 1, 76-81.
138. MANDELBROT, В. В. 1957р. Linguistique statistique macroscopique. In
Apostel, Mandelbrot and Morf, 1-80.
Общая библиография, включая указания на авторские права 361
139. MANDELBROT, B.B. 1957г. Application of Thermodynamical Methods of
Communication Theory and Econometrics. Memorandum of the University of
Lille Mathematics Institute.
140. MANDELBROT, B.B. 1957t. Application of thermodynamical methods of
communication theory and econometrics. Institut Mathematique de 1’Univer-
site de Lille.
141. MANDELBROT, B.B. 1958р. Les lois statistiques macroscopiques du
comportement (role de la loi de Gauss et des lois de Paul Levy). Phychologie
Francaise: 3, 237-249.
142. MANDELBROT, B.B. 1959g. Ensembles grand canoniques de Gibbs; justifi-
cation de leur unicite basee sur la divisibilite infinie de leur dnergie aleatoire.
Comptes rendus (Paris): 249, 1464-1466.
143. *E1O MANDELBROT, B.B. 1959р. Variables et processus stochastiques de
Pareto-Levy et la repartition des revenues, I & II. Comptes rendus (Paris):
249, 613-615 & 2153-2155.
144. MANDELBROT, В. B. 1959s. A note on a class of skew distribution functions.
Analysis and critique of a paper by H. A. Simon. Information and Control-. 2,
90-99.
145. *E10 MANDELBROT, В. B. 1960L The Pareto-Levy law and the distribution
of income. International Economic Review: 1, 79-106.
146. MANDELBROT, В. B. 1961b. On the theory of word frequencies and on related
Markovian models of discourse. Structures of language and its mathematical
aspects. Ed. R. Jakobson. 120-219. New York: American Mathematical
Society.
147. *E11 MANDELBROT, B.B. 1961e. Stable Paretian random functions and the
multiplicative variation of income. Econometrica: 29, 517-543.
148. MANDELBROT, B.B. 1961s. Final note on a class of skew distribution
functions (with a postscript). Information and Control: 4, 198-216 & 300-
304.
149. *E1 EF MANDELBROT, B.B. 1962c. Sur certains prix speculatifs: faits
empiriques et modele base sur les processus stables additives de Paul Levy.
Comptes rendus (Paris): 254, 3968-3970.
150. *E14,15 MANDELBROT, B.B. 1962i. The Variation of Certain Speculative
Prices. IBM External Research Report: NC-87, March, 1962.
151. MANDELBROT, B.B. 1962n. Statistics of natural resources and the law of
Pareto. IBM External Research Report Note: NC-146, June 29, 1962. Cm.
Mandelbrot 1995b.
152. E12 MANDELBROT, B.B. 1962q. Paretian distributions and income
maximization. Quarterly J. of Economics of Harvard University: 76, 57-85.
153. MANDELBROT, B.B. 1962t. The role of sufficiency and estimation in
thermodynamics. The Annals of Mathematical Statistics: 33, 1021-1038.
362 Общая библиография, включая указания на авторские права
154. MANDELBROT, В. В. 1963. Towards a Revival of the Statistical Law of
Pareto. IBM Research Report: NC-227, March, 1963.
155. *E14 MANDELBROT, В. B. 1963b. The variation of certain speculative prices
(Abstract). Econometrica: 31, 757-758.
156. *E14 MANDELBROT, В. B. 1963b. The variation of certain speculative prices.
/. of Business (Chicago): 36, 394-419. Reprinted in Cootner 1964: 297-337.
157. *E3 MANDELBROT, В. B. 1963e. New methods in statistical economics./.
of Political Economy'. 71, 421-440. Reprint in Bulletin of the International
Statistical Institute, Ottawa Session: 40(2), 669-720.
158. *E8 MANDELBROT, В. B. 1963g. A Survey of Growth and Diffusion Models
of the Law of Pareto. IBM External Research Note: NC-253.
159. *E10 MANDELBROT, В. B. 1963i. The stable Paretian income distribution
when the apparent exponent is near two. International Economic Review'. 4,
111-115.
160. MANDELBROT, В. B. 1963j. The Stable Paretian Income Distribution when
the Apparent Exponent is Near Two. Memorandum, appended to a joint reprint
of M 1960i and M 1963L
161. MANDELBROT, В. B. 1963o. Oligopoly. Mergers, and the Paretian Size
Distribution of Firms. IBM External Research Note: NC-246, March 1963.
162. MANDELBROT, В. В. 1964h. Self-Similar Random Processes and the Range,
IBM External Research Note: RC-1163, March 1963.
163. MANDELBROT, В. B. 1964L Self-Similar Random Processes: Extrapolation,
Interpolation and Decay of Perturbations, IBM External Research Note: RC-
1241
164. MANDELBROT, В. B. 1964j. The epistemology of chance in certain newer
sciences. Представлено на The Jerusalem International Congress on Logic,
Methodology and the Philosophy of Science (не опубликовано).
165. *E8 MANDELBROT, В. B. 1964o. Random walks, fire damage amount, and
other Paretian risk phenomena. Operations Research: 12, 582-585.
166. MANDELBROT, В. B. 1964s. Self-similar random processes and the range.
IBM External Research Report: RC-1163, April 1963.
167. MANDELBROT, В. B. 19641 Derivation of statistical thermodynamics from
purely phenomenological principles. J. of Mathematical Physics: 5, 164-171.
168. *N5 MANDELBROT, В. B. 1964w. Self-similar Turbulence and Non-
Wienerian Conditioned Spectra. IBM Research Report: RC-134.
169. *N8 MANDELBROT, В. B. 1965b. Time-varying channels, 1/f noises and the
infrared catastrophe, or: why does the low frequency energy sometimes seem
infinite. IEEE Communication Convention. Boulder, CO.
70. *N7 MANDELBROT, B.B. 1965c. Self-similar error clusters in communica-
tions systems and the concept of conditional stationarity. IEEE Transaction on
Communications Technoogy: 13, 71-90.
Общая библиография, включая указания на авторские права 363
171. *Н9 MANDELBROT, B.B. 1965h. Une classe de processus stochastiques
homothetiques a soi; application a la loi climatogique de H.E. Hurst. Comptes
rendus (Paris): 260, 3274-3277.
172. MANDELBROT, B.B. 1965m. Very long-tailed probability distributions
and the empirical distribution of city sizes. Mathematical Explorations in
Behavioral Science (Cambria Pines CA, 1964). Eds. F. Massarik & P. Ratoosh.
Homewood, III.: R. D. Irwin, 322-332.
173. MANDELBROT, В. B. 1965s. Leo Szilard and unique decipherability. IEEE Tr.
on Information Theory, IT-11, 455-456.
174. *FE MANDELBROT, B.B. 1965z. Information theory and psycholinguis-
tics. Scientific Psychology: Principles and Approaches. Eds. В. B. Wolman &
E.N. Nagel. New York: Basic Books 550-562. Reprint in Language, Selected
Readings. Eds. R.C. Oldfield & J. C. Marshall. London: Penguin. Reprint with
appendices, Readings in Mathematical Social Science. Eds. P. Lazarfeld and
N. Henry. Chicago, III: Science Research Associates (1966: твердая обложка).
Cambridge, MA: M.I.T. Press (1968: мягкая обложка). Перевод на русский
язык.
175. Е19 MANDELBROT, B.B. 1966b. Forecasts of future prices, unbiased
markets, and «martingale» models. J. of Business (Chicago): 39, 242-255.
Важный список опечаток в следующем номере того же журнала.
176. *FE MANDELBROT, B.B. 1966г. Nouveaux modeles de la variation des
prix (cycles lents et changements instantanes). Cahiers de Sdminaire
d'Economdtrie: 9, 1966, 53-66.
177. *N10 MANDELBROT, B.B. 1967b. Sporadic random functions and condi-
tional spectral analysis; self-similar examples and limits. Proc, of the Fifth
Berkeley Symposium on Mathematical Statistics and Probability: 3, 155-179.
Eds. L. LeCam & J. Neyman. Berkeley: University of California Press.
178. *N9 MANDELBROT, B.B. 1967i. Some noises with 1/f spectrum, a bridge
between direct current and white noise. Institute of Electrical and Electronic
Engineers Tr. on Information Theory: 13, 289-298.
179. *E15 MANDELBROT, B.B. 1967j. The variation of some other speculative
prices. J. of Business (Chicago): 40, 393-413.
180. *N12 MANDELBROT, B.B. 1967k. Sporadic turbulence. Proc. Internatio-
nal Symposium on Boundary Layers and Turbulence, including Geophysical
Applications (Kyoto, 1966). Supplement to the Physics of Fluids: 10, Sept.
1967, S302-303.
181. MANDELBROT, B.B. 1967р. Sur lepistemologie du hasard dans les sciences
socliales: invariance des lois et verification des hypotheses, Encyclop^die de
la Pteiade: Logique et Connaissance Scientifique. Ed. J. Piaget. 1097-1113.
Paris: Gallimard.
182. MANDELBROT, B.B. 1967s. How long is the coast of Britain? Statistical
self-similarity and fractional dimension. Science: 155, 636-638.
364 Общая библиография, включая указания на авторские права
183. MANDELBROT, В. В. 1968i. Some aspects of the random walk model of stock
market prices: comment. International Economic Review'. 9, 258.
184. MANDELBROT, В. В. 1968р. Les constants chiffrees du discours. Епсус1орё-
die de la Pldiade: Linguistique, Ed. J. Martinet. Paris: Gallimard, 46-56.
185. *N13 MANDELBROT, В. B. 1969b. On intermittent free turbulence: Abstract,
followed by unpublished draft. Proc, of the Symposium in Turbulence of Fluids
and Plasmas. (Polytechnic Institute of Brooklyn). New York: Interscience.
186. *H30 MANDELBROT, В. B. 1969e. Long-run linearity, locally Gaussian
processes, H-spectra and infinite variances. International Economic Review:
10, 82-111.
187. MANDELBROT, В. B. 1970a. Long-run interdependence in price records and
other economic time series. Econometrica: 38, 122-123.
188. *H30 MANDELBROT, В. B. 1970e. Statistical dependence in prices and inte-
rest rates. Papers of the Second World Congress of the Econometric Society,
Cambridge, England (8-14 Sept. 1970).
189. MANDELBROT, B.B. 1970n. Analysis of long-run dependence in time series:
the R/S technique. Fiftieth Annual Report of the National Bureau of
Economic Research, 107-108.
190. MANDELBROT, B.B. 1970р. On negative temperature for discourse.
Discussion of a paper by Prof. N. F. Ramsey. Critical Review of
Thermodynamics, 230-232. Ed. E.B. Stuart et. al. Baltimore, MD: Mono
Book.
191. MANDELBROT, B.B. 1970y. Statistical Self-Similarity and Non-Laplacian
Chance. Unpublished Trumbull Lectures, Yale University.
192. MANDELBROT, B.B. 1971. Comments on «Application of linear random
models to four annual streamflow series.» Water Resources Research: 7, 1360—
1362.
193. *E20 MANDELBROT, В. В. 1971 e. When can a price be arbitraged efficiently?
A limit to the validity of the random walk and martingale models. Review of
Economics and Statistics: 53, 225-236.
194. *H15 MANDELBROT, B.B. 1971 f. A fast fractional Gaussian noise generator.
Water Resources Research: 7, 543-553.
195. MANDELBROT, B.B. 1971g. The conditional cosmographic principle and the
fractional dimension of the universe. (Статья была отправлена в несколько
периодических изданий, но везде был получен отказ в публикации; впервые
опубликована в работе Mandelbrot 19750.)
196. *Н30 MANDELBROT, B.B. 1971n. Statistical dependence in prices and
interest rates. Fifty-first Annual Report of the National Bureau of Economic
Research: 141-142.
197. MANDELBROT, B.B. 1971q. Analysis of long-run dependence in economics:
the R/S technique. Econometrica: (July Supplement): 68-69.
Общая библиография, включая указания на авторские права 365
198. *Е14 MANDELBROT, В. В. 1972b. Correction of an error in «The variation
of certain speculative prices (1963).» J. of Business-. 40, 542-543.
199. *H30 MANDELBROT, В. B. 1972c. Statistical methodology for nonperiodic
cycles: from the covariance to R/S analysis. Annals of Economic and Social
Measurement: 1, 259-290.
200. MANDELBROT, В. B. 1972d. On Dvoretzky coverings for the circle. Z. fur
Wahrschenlichkeitstheorie: 22, 158-160.
201. *N14 MANDELBROT, В. B. 1972j. Possible refinement of the lognormal
hypothesis concerning the distribution of energy dissipation in intermittent
turbulence. Statistical Models and Turbulence. Eds. M. Rosenblatt & C. Van
Atta. Lecture Notes in Physics: 12, New York: Springer, 333-351.
202. *H16 MANDELBROT, В. B. 1972w. Broken line process derived as an
approximation to fractional noise. Water Resources Research: 8, 1354-1356.
203. MANDELBROT, B.B. 1972z. Renewal sets and random cutouts. Z. fur
Wahrschenlichkeitstheorie: 22, 145-157.
204. *E21 MANDELBROT, В. B. 1973c. Comments on «А subordinated stochastic
process model with finite variance for speculative prices,» by Peter K. Clark.
Econometrica: 41, 157-160.
205. FE MANDELBROT, B.B. 1973L Formes nouvelles du hasard dans les
sciences. Economic Appliqude: 26, 307-319.
206. FE MANDELBROT, В. В. 1973j. Le probleme de la realite des cycles lents, et
le syndrome de Joseph. Economic Appliqude: 26, 349-365.
207. FE MANDELBROT, B.B. 1973v. Le syndrome de la variance infinie, et ses
rapports avec la discontinuite des prix. Economic Appliqude: 26, 321-348.
208. *N16. MANDELBROT, B.B. 1974c. Multiplications aleatoires iterees et
distributions invariantes par moyenne ponderee. Comptes rendus (Paris):
278A, 289-292 & 355-358.
209. *E8 MANDELBROT, В. В. 1974d. A population birth and mutation process, I:
Explicit distributions for the number of mutants in an old culture of bacteria. J.
of Applied Probability: 11, 437-444. (Часть II распространялась в частном
порядке).
210. *N15 MANDELBROT, B.B. 1974L Intermittent turbulence in self-similar
cascades: divergence of high moments and dimension of the carrier. J. of Fluid
Mechanics: 62, 331-358.
211. *H17 MANDELBROT, B.B. 1975b. Fonctions aleatoires pluritemporelles
approximation poissonienne du cas brownien et generalizations. Comptes
rendus (Paris): 28OA, 1075-1078.
212. *H18 MANDELBROT, B.B. 1975f. On the geometry of homogeneous
turbulence, with stress on the fractal dimension of the iso-surfaces of scalars.
Z of Fluid Mechanics: 72, 401-416.
366 Общая библиография, включая указания на авторские права
213. MANDELBROT, B.B. 1975m. Hasards et tourbillons: quatre contes a cles.
Annales des Mines (November): 61-66.
214. MANDELBROT. B.B. 19750, 19840, 19890, 19950. Les objets fractals:
forme, hasard et dimension. Paris: Flammarion.
215. MANDELBROT, B.B. 1975u. Sur un modele decomposable d’univers
hierarchise: deduction des correlations galactiques sur la sphere celeste.
Comptes rendus (Paris): 280A, 1551-1554.
216. *H19 MANDELBROT, B.B. 1975w. Stochastic models for the Earth’s relief,
the shape and the fractal dimension of the coastlines, and the number-area rule
for islands. Proc, of the National Academy of Sciences USA : 72, 3825-3828.
217. *H26 MANDELBROT, B.B. 1975z. Limit theorems on the self-normalized
range for weakly and strong dependent processes. Z. fur Wahrscheinlichkeits-
theorie: 31, 271-285.
218. *N19 MANDELBROT, B.B. 1976c. Geometrie fractale de la turbulence.
Dimension de Hausdorff, dispersion et nature des singularites du mouvement
des fluides. Cxomptes rendus (Paris): 282A, 119-120.
219. *N18 MANDELBROT, B.B. 1976o. Intermittent turbulence and fractal
dimension: kurtosis and the spectral exponent 5/6 4- B. In Turbulence and
Navier Stokes Equations. Ed. R.Temam. (Lecture Notes in Mathematics 565.)
New York: Springer, 121-145.
220. MANDELBROT, B.B. 1977b. Fractals and turbulence: attractors and
dispersion. Turbulence Seminar Berkeley 1976-1977. Eds. P. Bernard & T.Ra-
tiu. Lecture Notes in Mathematics: 615, 83-93. New York: Springer. Перевод
на русский язык.
221. MANDELBROT, B.B. 1977F. Fractals: Form, Chance, and Dimension. San
Francisco: W. H. Freeman.
222. MANDELBROT, B.B. 1977h. Geometric facets of statistical physics: scaling
and fractals. Statistical Physics 13, International IUPAP Conference, 1977.
Eds. D.Cabib et. al. Annals of the Israel Physical Society: 2, 225-233.
223. MANDELBROT, B.B. 19771. Physical objects with fractional dimension:
seacoasts, galaxy clusters, turbulence and soap. The Institute of Mathematics
and its Applications (Great Britain) Bulletin: 13, 189-196. Also in Fluid
Dynamics - les Houches. 1973. Eds. R. Balian & J.L. Peube. New York:
Gordon & Breach, 557-578.
224. MANDELBROT, B.B. 1978b. The fractal geometry of trees and other natural
phenomena. Buffon Bicentenary Symposium on Geometrical Probability, Eds.
R. Miles & J. Serra. Lecture Notes in Biomathematics: 23, 235-249. New
York: Springer.
225. MANDELBROT, B.B. 1978c. Colliers aleatoires et une alternative aux
promenades au hasard sans boucle: les cordonnets discrets et fractals. Comptes
rendus (Paris): 286A, 933-936.
Общая библиография, включая указания на авторские права 367
226. *N5 MANDELBROT, B.B. 1978h. Geometric facets of statistical physics:
scaling and fractals. Annals of the Israel Physical Society'. 2(1). 225-233.
227. MANDELBROT, В. В. 1978г. Les objets fractals. La Recherche'. 9, 1-13.
228. MANDELBROT, B.B. 1979n. Comment on bifurcation theory and fractals.
Bifurcation Theory and Applications, Eds. Gurel & 0. Rossler. Annals of the
New York Academy of Sciences: 316, 463-464.
229. MANDELBROT, В. B. 1979u. Correlations et texture dans un nouveau modele
d’Univers hierarchise, base sur les ensembles tremas. Comptes rendus (Paris):
288A, 81-83.
230. MANDELBROT, B.B. 1980b. Fractals and geometry with many scales of
length. Encyclopedia Britannica 1981 Yearbook of Science and the Future:
168-181.
231. *C3 MANDELBROT, B.B. 1980o. Fractal aspects of the iteration of z —>
Az(l — z) for complex A and z. Non linear Dynamics. Ed. H.G. Helleman.
Annals of the New York Academy of Sciences: 357, 249-259.
232. MANDELBROT, B.B. 1981s. Scalebound or scaling shapes: a useful
distinction in the visual arts and in the natural sciences. Leonardo: 14, 45-47.
233. *E14 MANDELBROT, В. B. 1980c. The variation of certain speculative prices.
Current Contents: 14, 20.
234. MANDELBROT, B.B. 1982F. Comments on computer rendering of frac-
tal stochastic models. Communications of the Association for Computer
Machinery: 25, cover and pp. 581-584.
235. *C4, 16 MANDELBROT, B.B. \982F{FGN}. The Fractal Geometry of
Nature. New York: W. H. Freeman.
236. MANDELBROT, В. B. 1982n. Des monsters de Cantor et Peano a la geometric
fractale de la nature. Penser les mathdmatiques textes reunis pare J.Dieudon-
ne, M. Loi & R. Thom, Paris: Editions du Seuil, 226-251.
237. *C23 MANDELBROT, В. B. 1982s. The inexhaustible function z squared plus
с. Предложено журналом Scientific American, так и не опубликовано там,
но адаптировано в главу С23 данной книги.
238. MANDELBROT, B.B. 1982t. The many faces of scaling: fractals, geometry
of nature and economics. Self-Organization and Derivative Structures. Eds.
W.C.Schieve & P.M. Allen: 91-109.
239. MANDELBROT, В. B. 1983d. Les fractals, les monstres et la beaute. Le Dtbat:
24, 54-72.
240. MANDELBROT, B.B. 1980. In Percolation Structures and Processes. Eds.
G.Deutscher, R. Zallen, & J. Adler. Annals of the Israel Physical Society: 5,
59-80.
241. *C18 MANDELBROT, B.B. 1983m. Self-inverse fractals osculated by sigma
discs, and the limit sets of inversion groups. Mathematical Intelligencer: 5
(Spring), (2), Front and back covers and pp. 9-17.
368 Общая библиография, включая указания на авторские права
242. *С5 MANDELBROT, В. В. 1983р. On the quadratic mapping z -► z2 - p for
complex p and z: the fractal structure of its M set, and scaling. Physica. D7,
224-239.
243. MANDELBROT, B.B. 1984. Some «facts» that evaporate upon examination.
Mathematical Intelligencer-. 11, (осень) 17-19.
244. MANDELBROT, B.B. 1984c. Fractal Sums of Pulses, and New Random
Variables and Functions. (Memorandum superseded by M. 1995n and four
papers coauthored by R. Cioczek-Georges.)
245. MANDELBROT, В. В. 1984d. Profile by Monte Davis. Omni (New York) (фев-
ральский номер) 65.
246. MANDELBROT, B.B. 1984e. Fractals and physics: squig clusters, diffusions,
fractal measures and the unicity of fractal dimensionality. J. of Statistical
Physics: 34, 1984, 895-910.
247. MANDELBROT, B.B. 1984L Squig sheets and some other squig fractal
constructions./, of Statistical Physics: 36, 519-539.
248. MANDELBROT, B.B. 1984j. Fraktal Kikagaku. Traduction japonaise de
Mandelbrot 1982F{FGN}, par H. Hironaka. Tokyo: Nikkei Science.
249. *03 MANDELBROT, B.B. 1984k. On the dynamics of iterated maps, VIII:
The map z —> A(z + 1/z), from linear to planar chaos, and the measurement
of chaos. Chaos and Statistical Mechanics. (Kyoto Summer Institute.) Ed.
Y. Kuramoto, New York: Springer, 32-41.
250. MANDELBROT, B.B. 1984г. Comment on the equivalence between
fraction/spectral dimensionality and the dimensionality of recurrence. J. of
Statistical Physics: 36, 543-545.
251. MANDELBROT, B.B. 1984s. Les images fractales: un art pour 1’amour de la
science et ses applications. Sciences et Techniques: Mai 1984, 16-19, 34-35,
& 65.
252. *N5 MANDELBROT, B.B. 1984w. On fractal geometry and a few of the
mathematical questions it has raised. Proc, of the Twelfth International
Congress of Mathematicians (Warsaw, 1983). Ed. Z. Ciesielski. Warsaw: PWN
& Amsterdam: North-Holland, 1984, 1661-1675.
253. MANDELBROT, B.B. 1985b. Interview by Anthony Barcellos. Mathematical
People. Eds. D. J. Albers and G. L. Alexanderson, Boston: Birkhauser, 205-225.
254. *C6, 7, 8, 9, 10 MANDELBROT, B.B. 1985g. On the dynamics of itera-
ted maps. Paper 111. The individual molecules of the M-set: self-similarity
properties, the N - 2 rule, and the N - 2 conjecture. Paper IV: The notion
of «normalized radical» R, and the fractal dimension of the boundary of R.
Paper V: Conjecture that the boundary of the M-set has a fractal dimension
equal to 2. Paper VI: Conjecture that certain Julia sets include smooth
components. Paper VIE Domain-filling («Peano») sequences of fractal Julia
sets, and an intuitive rationale for the Siegel discs. Chaos, Fractals and
Общая библиография, включая указания на авторские права 369
Dynamical Systems. Eds. Р. Fischer & W. Smith. New York: Marcel Dekker,
213-253.
255. *H21 MANDELBROT, B.B. 19851. Self-affine fractals and fractal dimension.
Physica Scripta: 32, 257-260.
256. *C11 MANDELBROT, B.B. 1985n. Continuous interpolation of the complex
discrete map z —► A(1 — г), and related topics (On the dynamics of iterated
maps, IX.) Ed. N.R. Nilsson, Physica Scripta: T9, 59-63.
257. MANDELBROT, B.B. 1986k. Multifractals and fractals (Letter to the Editor).
Physics today (сентябрьский номер): 11-12.
258. MANDELBROT, B.B. 1986р. Fractals and the rebirth of iteration theory. The
Beauty of Fractals, by Heinz-Otto Peitgen & Peter H. Richter, New York:
Springer, 151-160.
259. MANDELBROT, B.B. 1986г. Comment j’ai decouvert les fractals. (Entretien
avec Marc Lesort) La Recherche (Mars 1986): 420-424.
260. *H22, 23, 24 MANDELBROT, B.B. 1986t. Self-affine fractal sets, I: The
basic fractal dimensions, II: Length and surface measurements, III: Hausdorff
dimension anomalies and their implications. Fractals in Physics (Trieste,
1986). Eds. L. Pietronero & E.Tosatti. Amsterdam: North-Holland, 3-28.
261. MANDELBROT, B.B. 1987c. Propos a batons rompus. Fractals: dimensions
non enti£res et applications, dirigd par G.Cherbit, Paris: Masson, 4-15.
• Перевод на английский язык: Sundry observations. Fractals: Non Integer
Dimensions and Applications. Ed. G.Cherbit Chichester & New York: John
Wiley, 1991, 3-9.
262. MANDELBROT, B.B. 1987d. Die fraktale Geometric der Natur. Перевод на
немецкий язык 1982F{/7G7V}, by R. & U.Zahle. Basel: Birkhauser.
263. MANDELBROT, B.B. 1987e. Fractals. The Encyclopedia of Physical Science
and Technology: 5, 579-593. San Diego, CA: Academic Press.
264. MANDELBROT, B.B. 1987L Gli oggetti frattali. Перевод на итальянский
язык работы Mandelbrot 19750, par R. Pignoni; preface par L. Peliti & A. Vul-
piani. Torino: Giulio Einaudi.
265. MANDELBROT, B.B. 1987m, 1989m. La geometria della natura. Milano:
Montedison. Roma: Edizioni Theoria.
266. MANDELBROT, B.B. 1987г. Towards a second stage of indeterminism in
science (preceded by historical reflections), Interdisciplinary Science Review:
12, 117-127.
267. MANDELBROT, B.B. 1987s. Los objetos fractales. Перевод на испанский
язык М 19750 by J.M. Llosa. Barcelona: Tusquets.
268. MANDELBROT, B.B. 1988c. An introduction to multifractal distribu-
tion functions. Fluctuations and Pattern Formation (Cargese, 1988). Eds.
H.E. Stanley & N. Ostrowsky. Dordrecht-Boston: Kluwer, 345-360.
370 Общая библиография, включая указания на авторские права
269. MANDELBROT, B.B. 1988L Flare: A by-product of the study of a two-
dimensional dynamical system, IEEE Tr. on Circuits and Systems'. 36, 1988,
768-769.
270. MANDELBROT, B.B. 1988m. Naturally creative. Interview by Mike Dibb.
Modern Painters (London), Premier Issue (Spring), 52-53.
271. *H2O MANDELBROT, B.B. 1988р. Fractal landscapes without creases and
with rivers. The Science of Fractal Images. Eds. H.-O. Peitgen & D. Saupe,
New York: Springer, 1988, 243-260.
272. MANDELBROT, B.B. 1988s. People and events behind the science of fractal
images. The Science of Fractal Images. Eds. H.-O. Peitgen & D. Saupe, New
York: Springer, 1988, 1-19.
273. MANDELBROT, B.B. 1989a. The principles of multifractal measures. The
Fractal Approach to Heterogeneous Chemistry. Ed. D. Avnir, New York: Wiley,
45-51.
274. MANDELBROT, B.B. 1989b. An overview of the language of fractals. The
Fractal Approach to Heterogeneous Chemistry. Ed. D. Avnir, New York: Wiley,
3-9.
275. MANDELBROT, B.B. 1989e. A class of multifractal measures with negati-
ve (latent) values for the «dimension» /(a). Fractals' Physical Origin and
Properties (Erice, 1988). Ed. I. Pietronero. New York: Plenum, 3-29.
276. MANDELBROT, B.B. 1989g. Multifractal measures, especially for the
geophysicist. Pure and Applied Geophysics: 131, 5-42. Также Fractals in
Geophysics. Eds. C.H. Scholz & В. B. Mandelbrot. Boston: Birkhauser.
277. MANDELBROT, B.B. 1989h. Lewis Fry Richardson and prematurity in
science. The British Society for the History of Mathematics: 12, October,
2-4.
278. MANDELBROT, B.B. 19891. Survol du langage fractal: Les objets fractals
(3e edition). Paris: Flammarion, 185-240.
279. MANDELBROT, B.B. 1989m. Chaos, Bourbaki and Poincare. Mathematical
Intelligencer: И (лето) 10-12.
280. MANDELBROT, B.B. 1989р. Temperature fluctuations: a well-defined and
unavoidable notion. Physics today. January: 42, 71 & 73.
281. MANDELBROT, B.B. 1989г. Fractal geometry: What is it, and what does it
do? Proc. Royal Society (london): A423, 3-16.
282. MANDELBROT, B.B. 1989s. Fractals: an art for the sake of Science.
Leonardo: 22 (Special SIGGRAPH issue), 21-24.
283. MANDELBROT, B.B. 1989t. The fractal range of the distribution of galaxies:
crossover to homogeneity and multifractals. Large-scale structure and Motions
in the Universe. Eds. F. Mardirossian et al., Dordrecht - Boston: Kluwer, 259-
279.
Общая библиография, включая указания на авторские права 371
284. MANDELBROT, B.B. 1990d. New «anomalous» multiplicative multifractals:
left-sided /(a) and the modeling of DLA. Condensed Matter Physics, in Honor
of Cyril Domb. Physica: A168, 95-111.
285. MANDELBROT, B.B. 1990n. Fractals: a geometry of nature. The New
Scientist: September 15, 1990, cover & pp. 38-43.
286. MANDELBROT, B.B. 1990г. Negative fractal dimensions and multifrac-
tals. Statistical Physics 17, International IUPAP Conference. Ed. C.Tsallis.
Physica: A163, 306-315.
287. MANDELBROT, В. B. 1990t. Limit lognormal multifractal measures.
Frontiers of Physics: Landau Memorial Conference (Tel Aviv, 1988). Eds.
E. A. Gotsman, Y. Ne’eman & A. Voronel. New York: Pergamon, 309-340.
288. MANDELBROT, B.B. 1990w. Two meanings of multifractality, and the no-
tion of negative fractal dimension. Chaos/Xaoc: Soviet-American Perspectives
on Nonlinear Science. Ed. D. K. Campbell. New York: American Institute of
Physics, 79-90.
289. MANDELBROT, B.B. 1991g. The gray and the green. Fractal Forms. Eds.
E. Guyon & H.F. Stanley. Paris: Palais de la Decouverte, 1991.
290. MANDELBROT, B.B. 1991k. Random multifractals: negative dimensions
and the resulting limitations of the thermodynamic formalism. Proc, of the
Royal Society (London): A434, 79-88. Также в Turbulence and Stochastic
Processes: Kolmogorov’s ideas 50 years on. Eds. J.C. R. Hunt, О.M. Phillips
& D. Williams. London: The Royal Society, 1991.
291. MANDELBROT, B.B. 1991n. Fractal craft. (Letter to the Editor.) The New
Scientist: September 14, 1991.
292. *C MANDELBROT, B.B. 1991р. Fractals and the rebirth of experimental
mathematics. Fractals for the Classroom, by H.-O. Peitgen, H.Jurgens, &
D. Saupe, E. M. Matelski, T. Perciante, & L. E.Yunker. New York: Springer,
1991.
293. MANDELBROT, В. B. 1992g. Avant-propos: Physique et structures fractales,
par J.-F. Gouyet. Paris: Masson, 1992.
294. MANDELBROT, В. В. 1992h. Plane DLA is not self-similar, is it a fractal that
becomes increasingly compact as it grows? Physica: A191, 95-107.
295. MANDELBROT, B.B. 1992s. Avant-propos: Dieu joue-t-il aux dis? par 1.
Stewart. Paris: Flammarion, 1992, 7-13.
296. MANDELBROT, B.B. 1993f. Opinions. Fractals: 1, 117-123. Репринт в спе-
циальном выпуске по симметрии: Culture and Science. 4, 1993, 319-328.
297. MANDELBROT, В. В. 1993g. Fractals. Chaos: The New Science. (Gustavus
Adolphus Nobel Conference XXVI.) Ed. J. M. Holte. Lanham MD: University
Press of America, 1993, 1-27.
298. MANDELBROT, В. B. 1993m. A fractal’s lacunarity, and how it can be tuned
and measured. Fractals in Biology and Medicine. Eds. T. F. Nonnenmacher et
al. Basel: Birkhauser, 8-21.
372 ОБЩАЯ БИБЛИОГРАФИЯ, ВКЛЮЧАЯ УКАЗАНИЯ пл по.игспнс НРАВА
299 *С21 MANDELBROT, B.B. 1993s. The Minkowski measure and multifrac-
tal anomalies in invariant measures of parabolic dynamic systems. Chaos
in Australia (Sydney, 1990). Eds. G. Brown & A.Opie. Singapore: World
Publishing, 1993, 83-94. Несколько отредактированный репринт: Fractals
and Disordered Systems. Second Edition. Eds. A. Bunde & S. Havlin. New
York: Springer, 1995.
300. MANDELBROT, B.B. 1994d. Les fractales, I’art algorithmique et le test de
Turing. La science et la mdtamorphose des arts, textes reunis par R. Daudel.
Paris: Presses LJniversitaires de France, 39-52.
301. MANDELBROT, B.B. 1994h. Fractals as a morphology of the amorphous.
Preface of Fractal Landscapes from the Real World, by William Hirst.
Manchester, UK: Cornerhouse Publications, 1994.
302. MANDELBROT, B.B. 1994j. Comment on «Theoretical mathematics... » by
A. Jaffe and F. Quinn, Bulletin of the American Mathematical Society. 1994,
193-196.
303. MANDELBROT, B.B. 1994q. Fractals, the computer, and mathematics
education. Proc, of the International Congress of Mathematics Education,
1CME-7 (Quebec, 1992), Quёbec: Presses de I’Universite Laval, 1994, 77-98.
304. MANDELBROT, B.B. 1995b. Statistics of natural resources and the law of
Pareto. Fractal Geometry and its Uses in the Geosciences and in Petroleum
Geology. Eds. C.C. Barton & P. La Pointe. New York: Plenum, 1-12. Впервые
увидела свет как Mandelbrot 1962n.
305. MANDELBROT, B.B. 1995k. Negative dimensions and Holders, multifractals
and their Holder spectra, and the role of lateral preasymptotics in science.
I. P. Kahane meeting (Paris. 1993). Eds. Aline Bonami & Jacques Peyriere. J.
of Fourier Analysis and its Applications 1995, special issue: 409-432.
306. MANDELBROT, B.B. 19951. The Paul Levy 1 knew. Ldvy flights and Related
Phenomena in Physics (Nice, 1994). Eds. M. F. Schlesinger, G. Zaslawsky, &
U.Frisch (Lecture Notes in Physics). New York: Springer, 1995, ix-xii.
307. MANDELBROT, B.B. 1995n. Introduction to fractal sums of pulses. Ldvy
flights and Related Phenomena in Physics. Eds. M. F. Schlesinger, G. Zaslaw-
sky, & U. Frisch. New York: Springer, 110-123.
308. *C MANDELBROT, B.B. 1995s. The Minkowski measure and multifractal
anomalies in invariant measures of parabolic dynamic systems. Fractals and
Disordered Systems. Second edition. Eds. A. Bundle & S. Havlin. New York:
Springer, 345-353.
309. MANDELBROT, B.B. 1995z. Measures of fractal lacunarity: Minkowski
content and alternatives. Fractal Geometry and Statistics. Eds. C. Bandt,
S.Graf & M. Zahle. Basel & Boston: Birkhauser, 12-38.
3,0 *E mandelbrot, B.B. I997e. Fractals and Scaling in Finance'
D^conunuay, Concentration, Risk. New York: Sprlnger-Verlag.
Общая библиография, включая указания на авторские права 373
3H.*FE MANDELBROT, B.B. 1997FE. Fractales, hasard et finance. Paris.
Flammarion.
312. MANDELBROT, B.B. 1998e. Fractality, lacunarity and the near-isotopic
distribution of galaxies. Current Topics in Astrofundamental Physics. Eds.
N. Sanchez & A. Zichichi. Dordrecht: Kluwer, 585-603.
313. *N MANDELBROT, B.B. 1999N. Multifractals & 1/f Noise: Wild Self-
Affinity in Physics. New York: Springer-Verlag.
314. MANDELBROT, B.B. 1999s. Multifractal walk down Wall Street. Scientific
American: February issue, cover & 70-73.
315. MANDELBROT, B.B. 1999р. Renormalization and fixed points in finance,
since 1962. Statistical Physics 20, International IUPAP Conference (Paris,
1998). Ed. D. lagolnitzer. Physica: A26, 177-187.
316. MANDELBROT, B.B. 2000р. Some mathematical questions arising in fractal
geometry. Development of Mathematics 2000: Ed. J.-P. Pier. Basel: Birkhauser,
795-811.
317. MANDELBROT, B.B. 2001a. Scaling in financial prices: I. Tails and
dependence. Quantitative Finance: 1, 113-123.
318. MANDELBROT, B.B. 2001b. Scaling in financial prices: 11. Multifractals and
the star equation. Quantitative Finance: 1, 124-130.
319. MANDELBROT, B.B. 2001c. Scaling in financial prices: 111. Cartoon
Brownian motions in multifractal time. Quantitative Finance: 1, 427-440.
320. MANDELBROT, B.B. 2001d. Scaling in financial prices: IV. Multifractal
concentration. Quantitative Finance: 1, 641-649.
321. MANDELBROT, B.B. 2001e. Stochastic volatility, power-laws, and long
memory. Quantitative Finance: 1, 588-589.
322. MANDELBROT, В. B. 2001R. Nel mondo dei frattali. Roma: di Renzo.
323. *H MANDELBROT, В. В. 2002H. Gaussian Self-Affinity and Fractals: R/S,
1/f, Globality, Reliefs & Rivers, New York: Springer-Verlag.
324. *C17 MANDELBROT, В. B. 2002w. Symmetry by dilation/reduction, fractals,
and roughness, Symmetry 2000. Eds. I. Hargittai and T. Laurent, I, 133-141.
325. MANDELBROT, В. B. 2003b. Fractal sums of pulses and a practical challenge
to the distinction between local and global dependence. Long range Dependent
Stochastic Processes: Theory and Applications (Bengalore, India, 2002). Eds.
Govindan Rangarajan and Ming Ding. New York: Springer, 118-135.
326. MANDELBROT, В. В. 2003P. Fractals and Multifractals in Finance. Вебк-
нига.
327. MANDELBROT, В. В. 2003L Multifractal power-law distributions, other
«anomalies’», and critical dimensions, explained by a simple example. Journal
of Statistical Physics: 110, 739-777.
328. MANDELBROT, В. В. 2003r. Heavy tails in finance for independent or multi-
fractal price increments. Handbook on Heavy Tailed Distributions in Finance.
374 Общая библиография, включая указания на авторские права
Ed. Svetlozar Т. Rachev (Volume 30 of Handbooks in Finance, Senior Ed.:
William T. Ziemba): 1, 1-34.
329. *C MANDELBROT, В. В. 2004C (Ссылка на саму себя). Fractals and Chaos:
the Mandelbrot Set and Beyond, New York: Springer-Verlag.
330. MANDELBROT. В. B. 2004f (в печати). Fractal sums of pulses: self-affine
global dependence and lateral limit theorems.
331. MANDELBROT, B.B., CALVET, L. & FISCHER, A. 1997. The Multifrac-
tal Model of Asset Returns; Large Deviations and the Distribution of Price
Changes; The Multifractality of the Deutschmark/US Dollar Exchange Rate.
New Haven CT: Cowles Foundation Discussion Papers 1164, 1165 and 1166.
На домашней странице Мандельброта в Интернете.
332. *С19 MANDELBROT, B.B. & EVERTSZ, C.J.G., 1990. The potential
distribution around growing fractal clusters. Nature: 378 (6296), front cover
& pp. 143-145.
333. *C22 MANDELBROT, B.B. & EVERTSZ, C.J.G. 1991. Multifractality of
harmonic measure on fractal aggregates, and extended self-similarity. Physica:
Al 77, 386-393.
334. MANDELBROT, B.B. & EVERTSZ, C.J.G. 199In. Exactly self-similar
multifractals with left-sided /(a). Fractals and Disordered Systems. Eds.
A. Bundle AS. Havlin. 323-346.
335. MANDELBROT, B.B., EVERTSZ, C.J.G. & HAYAKAWA, Y. 1990. Exactly
self-similar «left-sided» multifractal measures. Physical Review: A42, 4528-
4536.
336. MANDELBROT, В. B. & FRAME, M. 1999. The canopy and shortest path in
a self-contacting tree. The Mathematical Intelligencer: 21(#2), 1999, 18-27.
337. MANDELBROT, B.B., GEFEN, Y., AHARONY, A., & PEYRlfcRE, J. 1985.
Fractals, their transfer matrices and their eigen-dimensional sequences. J. of
Physics: A18, 335-354.
338. MANDELBROT, B.B. & GIVEN, J.A. 1984. Physical properties of a new
fractal model of percolation clusters. Physical Review Letters; 52, 1853-1856.
339. MANDELBROT, B.B., KAUFMAN, H., VESPIGNANI, A., YEKUTIELI, I.,
& LAM, C.-H. 1995. Deviations from self-similarity in plane DLA and the
infinite drift scenario. Europhysics Letters: 29, 599-604.
340. MANDELBROT, B.B., KOL, B., & AHARONY, A., 2002. Angular gaps
in radial diffusion-limited aggregation fractal dimensions and non-transient
deviations from linear self-similarity. Physical Review Letters: 88, 055501-
1-4.
341. *H28 MANDELBROT, B.B. & MCCAMY, K. 1970. On the secular pole
motion and the Chandler wobble. Geophysical J.: 21, 217-232.
342. MANDELBROT, В. B. & NORTON, A. Fractal Surfaces Defined by Iteration
of Rational Functions in the Quaternions, в печати.
Общая библиография, включая указания на авторские права 375
343. MANDELBROT, B.B. & PASSOJA, D.E. Eds. 1984. Fractal Aspects of
Materials. Metal and Catalyst Surfaces, Powders and Aggregates. Extended
Abstracts of a MRS Symposium, Boston, Pittsburgh, PA: Material Research
Society.
344. MANDELBROT, В. B., PASSOJA, D., & PAULLAY, A. 1984. The fractal
character of fracture surfaces of metals. Nature: 308, 721-722.
345. MANDELBROT, В. B. & RIEDI, R. H. 1995. Multifractal formalism for infinite
multinomial measures. Advances in Applied Mathematics: 16, 132-150.
346. MANDELBROT, B.B. & STAUFFER, D. 1994. Antipodal correlations and
texture (fractal lacunarity) in critical percolation clusters. /. of Physics: A27,
L237-L242.
347. MANDELBROT, В. B., STAUFFER, D. & AHARONY, A. 1993. Self-similarity
of fractals: a random walk test. Physica: A196, 1-5.
348. *E21 MANDELBROT, B.B. & TAYLOR, H.M. 1967. On the distribution of
stock price differences. Operations Research: 15, 1057-1062.
349. *H11 MANDELBROT, B.B. & VAN NESS, J.W. 1968. Fractional Brownian
motions, fractional noises and applications. SIAM Review: 10, 422-437.
350. MANDELBROT, B.B., VESPIGNANI, A. & KAUFMAN, H., 1995a. Cross-
cut analysis of large radial DLA: departures from self-similarity and lacunarity
effects, Europhysics Letters: 32, 199-204.
351. MANDELBROT, B.B., VESPIGNANI, A. & KAUFMAN, H., 1995b. The
geometry of DLA: different aspects of the departure from self-similarity.
Fractal Aspects of Materials. Eds. F. Family, P. Meakin, B. Sapoval & R.Wool.
Pittsburgh, PA: Materials Research Society, 1995, 73-79.
352. MANDELBROT, B.B. & VICSEK, T. 1989. Directed recursive models for
fractal growth. J. Physics: A22, L377-383.
353. *H1O MANDELBROT, B.B. & WALLIS, J.R. 1968. Noah, Joseph and
operational hydrology. Water Resources Research: 4, 909-918.
354. *H12, 13, 14 MANDELBROT, B.B. & WALLIS, J.R. 1969a. Computer
experiments with fractional Gaussian noises, Part 1, 2 & 3. Water Resources
Research: 5, 228-267.
355. *H27 MANDELBROT, B.B. & WALLIS, J.R. 1969b. Some long-run
properties of geophysical records. Water Resources Research: 5, 321-340.
Reprinted in Barton & La Pointe, 1994, 41-64.
356. *H25 MANDELBROT, B.B. & WALLIS, J.R. 1969c. Robustness of the
rescaled range R/S in the measurement of noncyclic long run statistical
dependence. Water Resources Research: 5, 967-988.
357. *H7 MANDELBROT, B.B. & WALLIS, J.R. 1969d. Operational hydrology
using self-similar processes. Proc, of the Fifth International Conference on
Operations Research. Ed. John Lawrence. London: Tavistock.
376 Общая библиография, включая указания на авторские права
358. MANDELBROT. B.B. & ZARNFALLER, F. 1959. Five-place Tables of
Certain Stable Distributions. IBM Research Technical Report: RC-421.
• ПРИМЕЧАНИЕ: В других работах, соавтором которых являлся Ман-
дельброт, первым указанным автором явлется один из следующих: Apos-
tel, Asikainen, Barral, Berger, Blumenfeld, Calbet, Cioczek-Georges, Coppens,
Damerau, Evertsz, Fischer, Frame, Gefen, Gerstein, Given, Gutzwiller, Hovi,
Hurd, Jaffard, Kahane, Kaufman, Laibowitz, Lovejoy, Musgrave, Riedi, Schae-
fer, Sholz, Shlesinger, Voidman, Wallis, Weitz или Yekutieli.
359. MAY, R. 1976. Simple mathematical models with very complicated dynamics.
Nature: 261, 459-467.
360. McMULLEN, С.Т. 1998. Hausdorff dimension and conformal dynamics, III:
Computation of dimension. American J. Mathematics: 120, 691-721.
361. MEAKIN, P. 1988. The growth of fractal aggregates and their fractal
measures, in: Phase Transitions and Critical Phenomena, Eds. C. Domb and
J.Lebowitz: 12, 335-489.
362. METROPOLIS, N., STEIN, M. L. & STEIN P. R. 1973. On finite limit sets for
transformations of the unit interval. Z of Combinational Theory: A15, 25-44.
363. MINKOWSKI, H. 1911. Gesammelte Abhandlingen, Chelsea reprint.
364. MONTEL, P. 1927. Lemons sur les families normales de fonctions analytiques
et leurs applications, Paris: Gauthier-Villars.
365. MONTEL, P. 1957. Lemons sur les r4currences et leurs applications, Paris:
Gauthier-Villars.
366. MUMFORD, D., SERIES, C., & WRIGHT, D. 2002. Indra's Pearls- The
Vision of Felix Klein. Cambridge: the University Press.
367. MUSGRAVE, F.K. & MANDELBROT, B.B. 1989. Natura ex machina. IEEE
Computer Graphics and its Applications: 9, Jan. Cover & 4-7.
368. MUSGRAVE, F.K. & MANDELBROT, B.B. 1991. The art of fractal
landscapes. IBM J. of Research and Development: 35 1991, front and back
covers & pp. 535-540.
369. MYRBERG, P. J. 1962. Sur I’iteration des polynomes reels quadratiques. Z des
Mathtmatiques pures et appliquts: (9)41, 339-351.
370. NEVAL1NNA, R. 1970. Analytic Functions, New York: Springer.
371. NIEMEYER, 1., P1ETRONERO, L. & WEISMANN, H.J. 1984. Fractal
dimension of dielectric breakdown. Physical Review Letters: 52, 1033-1036.
372. PAINLEVE, P. 1895. Le$on d’ouverture faite en pr£sence de Sa Majestd le
Roi de Sutde et de Norvtge, In Painleve 1972, 1, 100-204.
373. PAINLEVE, P. 1972-. Ouvres de Paul Painlevt. Paris: Editions du CNRS.
374. PEANO, G. 1980. Sur une coube, qui remplit une aire plane. Mathematische
Annalen: 36, 157-160. Перевод в Peano 1973.
375. PEITGEN, H.O. & RICHTER, P. H. 1986. The Beauty of Fractals, New York:
Springer.
Общая библиография, включая указания на авторские права 377
376. PERES, Y. 1994. The self-affine carpets of McMullen and Bedford have infinite
Hausdorff measure. Mathematical Proc, of the Cambridge Philosophical
Society. 116, 513-526.
377. PERES, Y. & KENYON, R. 1996. Hausdorff dimensions of affine-invariant
sets. Israel J. Mathematics: 94, 157-178.
378. PIETRONERO, L. & TOSATTI, E. Eds. 1986. Fractals in Physics, Amster-
dam: North-Holland.
379. POINCARE, H. 1916-. Oeuvres de Henri Poincare, Paris: Gauthier Villars.
380. RIEDI, R. H. & MANDELBROT, В. B., 1997a. Inverse measures, the inversion
formula, and discontinuous multifractals. Advances in Applied Mathematics:
18, 50-58.
381. RIEDI, R.H. & MANDELBROT, B.B., 1997b. Inversion formula for
continuous multifractals. Advances in Applied Mathematics: 19, 332-354.
382. RIEDI, R.H. & MANDELBROT, В.B., 1998. Exceptions to the multifractal
formalism for discontinuous measures. Mathematical Proc, of the Cambridge
Philosophical Society: 123, 133-157.
383. RUELLE, D. 1970. Repellers for real analytic maps. Ergodic Theory and
Dynamic Systems: 2, 99-107.
384. SALEM, R. 1943. Singular monotone functions. Trans. American Mathemati-
cal Society: 53, 427-439.
385. SALEM, R., 1967. Oeuvres Mathdmatiques. Paris: Hermann.
386. SALEM, R. & ZYGMUND, A., 1945. Lacunary power series and Peano
curves. Duke Mathematical J.: 12, 569-578. Также в Salem 1967, pp. 336-
345.
387. SHAFFER, D. W„ LAIBOWITZ, R.B., MANDELBROT, B.B., & LIU, S.H.
Eds. 1986. Fractal Aspects of Materials II. Extended abstracts of a
Symposium, Boston. Pittsburgh PA: Materials Research Society.
388. SCHOLZ, C.H. & MANDELBROT, B.B. Eds. 1989. Fractals in Geophy-
sics. Специальный выпуск Pure and Applied Geophysics: 131(1-2). Также
выпущена в виде книги Basel & Boston: Birkhauser, 2001.
389. SCHWARTZ, L. 1997. Un mathematician aux prises avec le sidcle, Paris:
Odile Jacob. Translation: A Mathematician Grappling with his Century. Basel
& Boston: Birkhauser, 2001.
390. SCHWARZER, S„ LEE, J., BUNDE, A., HAVLIN, S„ ROMAN, H.E. &
STANLEY, H.E., 1990. Minimum growth possibility of diffusion-limited
aggregates. Physical Review Letters: 65, 603-606.
391. SERIES, C. 1985. The modular surface and continued fractions. 1. London
Mathematical Society: (2), 31, 69-80.
392. SERIES, C. 1985. The geometry of Markoff numbers. Геометрическое толко-
вание CM. в Mathematical Intelligencer: 7, 20-29.
378 Общая библиография, включая указания на авторские права
393. SERIES. С. 1986. Geometrical Markov coding of geodesics on surfaces of
constant negative curvature, Ergodic Theory Dynamical Systems'. 6, 601-625.
394. SHLESINGER, M.F., MANDELBROT, B.B., & RUBIN, R.J. Eds. 1984.
Fractals in the Physical Sciences (Gaithersburg, 1983). Специальный выпуск
J. of Statistical Physics: 36, 516.
395. SHISHIKURA, M. M. 1994. The boundary of the Mandelbrot set has Hausdorff
dimension two. Complex analytic methods in dynamical systems: (Rio de
Janeiro, 1992). 222, 389-405.
396. SHISHIKURA, M.M. 1998. The Hausdorff dimension of the boundary of the
Mandelbrot set and Julia sets. Annals of Mathematics: 147, 225-267.
397. SHISHIKURA, M.M. 2000. Bifurcation of parabolic points, в Tan 2000.
398. SEIGEL, C. L., 1942. Iteration of analytic functions. Annals of Mathematics:
43, 607-612.
399. SIERPINSKI, W. 1915. Sur une courbe dont tout points est un point de
ramification. Comptes rendus (Paris): 160, 302. Более подробно в Sierpinski
1974-, II, 99-106.
400. SIERPINSKI, W. 1974. Oeuvres choisies: Ed. S. Hartman et al. Warsaw: Edi-
tions scientifiques.
401. STEIN, P. R. & ULAM, S. 1964. Non-linear transformation studies on
electronic computers. Rozprawy Matematyczne: 39, 1-66. Также в Ulam
1974,401-484.
402. STONE, M. 1961. The revolution in mathematics. American Mathematical
Monthly: 68, 715-734.
403. SULLIVAN, D. 1979. The density at infinity of a discrete group of hy-
perbolic motions. Institut des Hautes Etudes Scientifiques. Publications
Mathematiques: 50.
404. TAN, L. 1984. In Etude dynamique des polynomes complexes Eds. Adrien
Douady & John H. Hubbard, Vol 11, pp. 139-152. Publications Mathematique
d’Orsay, Orsay, France.
405. TAN, L. Ed. 2000. The Mandelbrot Set, Theme and Variations, Lon-
don Mathematical Society Lecture Notes: 274. Cambridge University Press,
Cambridge.
406. TANNERY, J. & MOLK, J. 1898. Elements de la theorie des fonctions
elliptiques. Tome 111, Paris: Gauthier-Villars.
407. THOMAS, P. B. & DHAR, D. 1994. The Hausdorff dimension of the Apollonian
packing of circles. J. of Physics: A27, 2257-2268.
408. URBANSKY, M. 2003. Measures and dimensionalities in conformal dynamics.
Bull. American Mathematical Society: 40, 281-321.
409. VICSEK, T. 1989. Fractal Growth Phenomena. Singapore: World Scientific.
410. *H31 VOLDMAN, J., MANDELBROT, B.B., HOEVEL, L. W., KNIGHT, J.
& ROSNFELD, P. 1983. Fractal nature of software-cache interaction. IBM J.
of Research and Development: 27, 164-170.
Общая библиография, включая указания на авторские права 379
411. V0N KARMAN, Т. 1940. The engineer grapples with nonlinear problems.
Bull. American Mathematical Society: 46, 615-683.
412. WALLIS, J. R. & MANDELBROT, В. B. 1968. 2nd Symposium on the Use of
Analog and Digital Computers in Hydrology, Tucson, AZ, Publication 81 of
the International Association of Scientific Hydrology: 2, 738-755.
413. WALSH, J. L. 1956. The Interpolation and Approximation by Rational
Functions in the Complex Domain, Colloquium Publications: 20. Providen-
ce, RI: American Mathematical Society.
414. WEGENER, A. 1915-1929-1966. The Origins of Continents and Oceans. 1966
год означает, что в этом году Довер перевел немецкое издание 1929 года.
415. WEIERSTRASS, К. 1872. Uber continuirliche Functionen eines reellen
Arguments, die fur keinen Werth des letzteren einen bestimmten Differential-
quotienten besitzen. He публиковалось до Weierstrass 1895-, Mathematische
Werke: II, 71-74.
416. WEIL, A. 1992. A Mathematician Apprenticeship. Basel-Boston: Birkhauser.
417. WEITZ, D. A., SANDER, L.M. & MANDELBROT, B.B. Eds. 1988. Fractal
Aspects of Materials: Disordered Systems. Extended Abstracts of a MRS
Symposium, Boston. Pittsburgh PA: Materials Research Society.
418. WHITTAKER, E.T. & WATSON, G.N. 1902-1927. A course of Modern
Analysis (4th edition). Cambridge: The University Press.
419. WITTEN, T. A. & SANDER, L.M. 1981. Diffusion-limited aggregation, a
kinetic critical phenomenon, Physical Review Letters: 47, 1400-1403.
Предметный указатель
Сл-(а), 316, 317
D, см. Хаусдорфа-Безиковича, раз-
мерность
Н(А), 39
1Г° (окружность круговорота), 107
1Г1(г), 184-186, 201-214
Иг(г), 186,213,214
Х(т) (инверсная функция Минков-
ского), 302-303
Г (окружность), 260-275
а, см. показатель Гельдера
291-298
/3(п), 143
и мультифрактальные инвариант-
ные меры в хаотических гамильто-
новых системах, 291-298
rj: z —* h(zrj) отображение, 139-140
А-фрактал, см. Q (А-фрактал)
А-отображение, 57, 81, 88, 90-92
— инверсное относительно окружно-
сти с центром А = 1, 100
— *корона», 59 (рисунок), 100
— структура множества М и, 98-100
р. (мера), см. меры
Р
— /гатомы и молекулы, 98
— seealso^/i), 1000
— виды множеств Жюлиа и, 151-152
— интервалы Мирберга, 112, 130
— канторова пыль и, 83, 91
— определенная, 67
— отношение кА, 118
— сверхустойчивые значения, 122
топологическая размерность и, 101-
102
— устойчивые, но не сверхустойчивые
значения, 124
— хаотические значения, 111-122
//-отображение, см. также острова и
островные молекулы, неквадратич-
ные рациональные динамики
— z —► Xz(a — zk\ 182
— М (преобразованная область £), 67
— М° для отображения z —► AlVi(z)
и, 209-210
— М-атомы (квадратичные отображе-
ния), 32, 34, 98-101, 104, 112, 151
— М-атомы (неквадратичные отобра-
жения), 192
— М-молекулы, 98, 104, 151
— внутренние координаты, 116
— канторова пыль и, 85, 86
— нормированный радикал множества
М, 136-145
— объяснение универсальностью клас-
са схожести островов, 117
— основания, 116
— отображение z —► A(z -I- 1/z) и, 192,
193
— отображение z —► AWi(z) =
= A(l/4)(1 + z2)2/[z(z2 — 1)], 201-
213
— отображение z —► AWi(z) =
= A(l/4)z(z3 + 8)/(z3-l), 213, 214
— полуоткрытое множество M, z —►
A(z + 1/z) и переход от линейного
хаоса к плоскостному, 192, 193
— построение М° и, 207, 209
— прообраз квадранта {Rez, Imz}
при итерациях AIVi(z), 212, 213
Предметный указатель
381
— слияние и, 116
— структура множества М и, 98-101
— точки бифуркации, приближение п2
и гипотеза, 132-135
— хаотические отображения Латте и,
200-214
^отображение, 57, 81, 98-100
0(п), см. Эйлера, теоретико-числовая
функция ф(п)
бт-диск, 137, 138
— а-дракон, 97, 102-104
— сг-луночка, 138-143
— бт-петля, 102
— бт-треугольник, 232, 237
— a(z), см. функция Шредера
— Аполлониева салфетка и, 232
— Зальцмана-Лоренца аттрактор, 76,
78, 79
— Крамера рескейлинг, 317, 323
— Салем, Рафаэль, 347
— Сан-Марко фрактальная форма, 72,
73, 77, 83, 187, 201
— Сандер, Л. М., 41
— бифуркации и, 112
— гармонические меры на ОДА и рас-
ширенное понятие самоподобия,
313-323
— неправильность форм и, 247-248
— определенный, 260
- оскуляция и, 237, 271-275
— положительный рескейлинг Коши,
316, 319-322
— физические системы и, 78
0(argA), 165-176
/(а)
— Крамера, рескейлинг, 317, 319-320,
323
- и гармонические меры на ОДА,
314-323
— и мера Минковского д и мульти-
фрактальные аномалии в инвари-
антных мерах параболических ди-
намических систем, 300-311
— и мультифрактальные инвариант-
ные меры в хаотических гамильто-
новых системах, 291-298
— метод моментов, 305-307
— метод распределений, 301, 306-309
— положительный рескейлинг Коши,
316, 319-322
— «термодинамическая» теория для,
301, 309-310
/£(а), 301-311
rw (радиус водоворота), 107, 109
и(п), 145
z-фрактал, см. J'(A) (г-фрактал)
^компонент, 165-166
^(А) (г-фрактал), 69-76
— как фрактальный аттрактор, 75-76
— определенные, 69-70
— отображения, 36, 71
— размерность, 70, 75
— связность и, 73
— форма, 70-75
— фрактальная пыль и, 75
Ям). Ю6-130
— связность и, 109
— форма пучка репеллеров и тополо-
гия, 121-130
Т7* (м)
— аргумент об универсальности клас-
са и маленькие драконы, 117-118
— определенные/описанный, 107-109
£ (минимально самоинверсное множе-
ство), 259-275
£ (область слияния), 65-69
Q (А-фрактал), 65-69
— звездообразные модели распределе-
ния областей неслияния, 69
— области несливающихся устойчи-
вых циклов, 67-69
— область слияния £ и ее фракталь-
ная граница, 65, 67
— определенный, 65
— отображение, 66
— преобразованная область М, 67
Автоморфные функции, см. самоин-
версные фракталы
Агрегации ограниченные диффузией
(ОДА), 313-323
— первые изображения, 41-43
Адамар, Жак, 50, 56-57, 219, 345-346
Акустика. 247-248
Альфорс, Ларс, 221
Аполлониево множество, 229-240
— Аполлониева упаковка, 231
— жидкие кристаллы и, 239-240
— множества и салфетки, 229-233
— несамоподобный каскад, 232
— нефуксовы цепи Пуанкаре, 233
— построения, 233-237
— самоинверсное свойство, 231-232
— сеть, сплетенная из одной нити, 232
— фрактальная размерность, 232-233
Аполлоний Пергский, 229
Аппель, Поль, 337
♦Атомы», см. М-атомы (неквадратич-
ные отображения); М-атомы (квад-
ратичное отображение)
Аттрактор обратный, 170-175
Ахарони, А., 78-79
Барнсли, Майкл, 223
Бедфорд, Т., 311
Бененав, Аарон, 255
Берс, Липман, 221-222
Вечера уравнение, 176
Биноминальная мультифрактальная
мера, 291, 296
Биологическая форма, нелинейные
фракталы и, 226
Бифуркация
— и предел бесконечной последова-
тельности, 141
— масштабно-инвариантные свойства
на вещественной прямой, 112
— обратная, см. слияние
— последовательные бифуркации и
♦истощенный дракон», 102-103
— приближение п2 и гипотеза, 132-
135
— структура множества М и, 101
— сценарий Мирберга бифуркацией
для бифуркаций отображения z —►
X(z+ 1/z), 193-194
— число Фейгенбаума 6 и, 101, 118-
119
Больяи, Янош, 342
Брэгг, В. X., 239
Бурбаки, Николя, 51-52, 55, 346, 349
Вегенер, Альфред, 46
Вейерштрасса формулы удвоения,
200-214
Вейерштрасса эллиптическая функ-
ция, 184-186
Вейль, Андре, 51-52
Веларде, М. Г., 76
Высшая нормальная школа, 53-55
Вычисление
— возрождение экспериментальной
математики, 45-48
— вычислительные возможности в
Гарварде (1980), 43
Галактик распределение, 79
Галилей, Галилео, 45-46
Гамильтоновы системы, 290-298
Ганье, Режан, 298
Гельдера показатель а
— и гармонические меры на ОДА,
314-323
— и мера Минковского д и мульти-
фрактальные аномалии в инвари-
антных мерах параболических ди-
намических систем, 300-311
— и мультифрактальные инвариант-
ные меры в хаотических гамильто-
новых системах, 290-298
Генератор квадратов, 90-91
Генерирующие функции
— генератор квадратов для канторовой
пыли, 90-91
Предметный указатель
383
— нелинейные преобразования и кан-
торова пыль, 85-86
— самоинверсные множества и, 227,
257-275
— самоподобная кривая с генератором
симметрии, состоящим из четырех
частей, 254-255
— самоподобная фрактальная пыль с
генератором симметрии, состоящим
их трех частей, 248-254
Геодезическая, 296-298
Геометрическая инверсия, 226-227
Гефен, М„ 78-79
Гивен, Джеймс, А., 135, 145, 149, 153,
198
Гильберт, Дэвид, 52
Гиперболические динамических систе-
мы, 311
Гистограммы, 306
Гнеденко, Б. В., 319
Гомографическое преобразование, 241
Гроссманн, С., 101
Гукенхаймер, Дж., 132
Гумберт, Джорджес, 342
Гурса, Эдуард, 337
Гутцвиллер, М. К., 290-298, 303, 307,
309,311
Дар, Д., 232
Денжуа, А., 300, 302
Динамические системы разложимые,
см. итерированных функций систе-
мы
Дирихле принцип, название, проис-
хождение, 218
Драконы
- а-дракон, 97, 102-104
- Жюлиа драконы, 94-96, 102-103
- Пеано драконы, 103
— аргумент об универсальности клас-
са и маленькие драконы, 117-118
— «истощенные драконы», 102-103
- «область дракона», 97, 103
Дробно-линейное преобразование, 241
Дуади, Адриен, 30-31, 59-60, 187
— описание множества Мандельброта,
32-39
Дьедонне, Жан, 52
Дьюдни, А. К., 325
Жидкие кристаллы, 239-240
Жидкостей динамика, 327
Жордан, Камилль, 233
Жорданова кривая
— Жюлиа, Гастон, 55-56, 83. 328, 332
— афоризмы, 340
— биографические заметки, 338-340
— исторические заметки о научном
прецеденте, 340-343
— клейново предельное множество и,
220, 267
— кривая Пеано и, 156
— отображение z —* z2 - р и, 151
— отображение z —► А(1/4)(1 +
+ z2)2/{z(z2 - 1)] и, 201
— функция Шредера и, 166
Жюлиа заполненное множество, 31-
32, 83
— определенное, 94, 332
Жюлиа множества для квадратичного
отображения, 37, 38, НО, 119, 165
— аргумент об универсальности клас-
са и маленькие драконы, 117-118
- виды, 108, 109, 151-152, 332
— гладкие компоненты, 186-188
— диски Зигеля и, 155-162, 174-176
— драконы Жюлиа, 94-96, 102-103
— заполняющие область последова-
тельности, 155
— кривые Пеано и, 155-162
— критическая точка, 32, 332
— множество М и, 40-41, 97-104
— непрерывная интерполяция квад-
ратичного отображения и покры-
тие внутренних областей множеств
Жюлиа, 164-176
384
Предметный указатель
— определенные/описанные, 107-109,
330-332
— при вещественной А или д, 83, 84,
94-97
— при комплексной р или Л, 98, 102-
104
— самоквадрируемые кривые Жюлиа
на плоскости, 92-94
— самоквадрируемые фрактальные
кривые Жюлиа, 84
— связность и, 38-40, 332
— «снежинка» Коха и, 330-331
— форма и топология пучка репелле-
ра, 121-130
Жюлиа множества для неквадратич-
ных отображений, 201-213
— z —► A(z -F 1/z) и огрубление хаоса,
188-198
— отображение z —> A(l/2)(z + 1/z),
183
— отображение z —► A(l/4)(1 +
+ z2)2/[z(z2 - 1)], 184-186
— отображение z —► A(l/4)z(z3 +
+ 8)/(z3-l), 201-213
— отображение z —► A(z + 1/z), 213,
214
Заполняющие плоскость кривые, 156
Затравки и кланы, инверсия и, 227
Зигель, Карл Людвиг, 61, 191
Зигеля диск, 155-162
— как предел фрактальной пыли, 162
— определенный, 156-157
— отображение и, 195-198
— покрытие внутренних областей мно-
жеств Жюлиа для квадратичного
отображения, 174-176
Зигеля число, 157, 160-161, 172-176
Золотое сечение, 148, 160, 172-174,
292
Изинга модель, 78-79
Инверсия
— Аполлониево множество, 229-240
— гиперболическая мозаика или тай-
линг, 228
— томографические преобразования,
231
— инверсия в окружностях, 257—275
— «кланы» и, 227, 259-260
— предельное множество инверсной
группы, 228-229, 257-275
— самоинверсные множества, 227
— самоинверсные фракталы, 225-241
— стандартная геометрическая, 226-
227
— хаотические инверсные группы, 228
Инверсные группы, см. клейновы груп-
пы
Интерполяция: непрерывная интер-
поляция квадратичного отображе-
ния покрытие внутренних областей
множеств Жюлиа, 164-176
«Истощенные драконы», 102-103
Итерация
— введение в, 326-332
— исторические заметки о, 55-61,
328-330, 340-343
Итерированных функций системы
(разложимые динамические систе-
мы), 222-223, 239
Кантор, Г., 255
Канторова пыль, 75, 81-104, 108, 331
— анатомия, 89-90
— генератор квадратов, 90-91
— инвариантность и, 86-88
— исторические заметки о канторовом
множестве, 218-219
— конечность внешней границы, 88-
89
— обратный аттрактор В и, 175
— порождение, 83-88
— предельные точки, 90
Каскад
— Аполлониев каскад, 232
Предметный указатель
385
- ОДА и, 317-319
Кахан, Жан-Пьер, 347
Кацусика, Хокусай, 47-48
Квадратичная динамика, введение в
— seealsoMHo>KecTBo М для квадра-
тичного отображения; множества
Жюлиа для квадратичного отобра-
жения, 1000
Квадратичная динамика, введение в,
259-267; , 29-48
Кланы, инверсия и, 227, 259-260
Клейн, Феликс, 52, 167, 218-219, 226,
228, 233, 257-258, 263-264
Клейновы группы
— исторические заметки о, 218-223
— итерированных функций системы
(разложимые динамические систе-
мы), 222-223
— фрактальная оскуляция и, 271-275
— фрактальные предельные множе-
ства, 220, 257—275
Кленк, Дж., 311
Колле, П., 100, 101
Колмогоров, А. Н., 319
Комплексные числа, 328-329, 333
— афоризм Жюлиа о, 340
Координаты декартовы, определенные,
332
«Корень», 100
Кох, Хельге фон, 255, 330
Коха кривая «снежинка», 156, 226,
234, 237, 255, 330-331
Коши распределение, 320
Коши рескейлинг, положительный,
316, 319-322
Крамера рескейлинг, 317, 319-320, 323
Крамера теорема о больших отклоне-
ниях, 319-320
Кривизна, оскуляция и, 235-237
Кук, Дженис X., 135, 145
Курант, Рихард, 52
Кьюнью, Реймонд, 347
Кэли, Артур, 63-79, 183
Латте хаотические отображения, 181 —
186, 200-214
Латте, Самуэль, 181
Лафф, Марк Р., 200
Лебега мера, 259, 263
Лежен-Дирихле, Петер-Густав, 218
Лейбниц, Г. В., 258
Лейбница упаковка, 231
Лемнискаты, 98, 107, 109-110, 113-
115
Лерей, Жан, 57
Лукас, Эдуард, 349-350
Луночка
— сг-луночка, 138-143
— комплементарная луночка, 143
— определенная, 138
— оскулирующая луночка, 142
Мёбиуса преобразование, 183, 241
Мазур, Барри К., 57
Макгихи, Р., 132
Макмюллен, К.Т., 232
Мамфорд, Дэвид, 221-223, 240
Математика
— возрождение экспериментальной
математики, 45-48
— исторические заметки о математи-
ческом анализе, 345-350
— исторические заметки о научном
приоритете в, 340-343
Мера Минковского обратная, 302-303
Мертенса приближение, 143
Меры
гармонические меры на ОДА и рас-
ширенное понятие о самоподобии,
313-323
мера Минковского и мультифрак-
тальные аномалии в инвариантных
мерах параболических динамиче-
ских систем, 300-311
мультифрактальные инвариантные
меры в хаотических гамильтоновых
системах, 290-300
386
Предметный указатель
Метод распределений. 301, 306-309
Метрополис, Н., 100, 112, 328
Милнор, Джон У., 61
Минковский, Герман, 300
Минковского мера, 300-311
- /(а) и fe(a\ 303-309
— изображение Д(а), 308, 310
— мера Минковского в виде крупно-
зернистой а и ее логарифм, 304
— мера Минковского и инверсная ме-
ра Минковского, 302-303
— метод моментов, 305-307
— метод распределений, 301, 306-309
Минковского функция, 302-303
Мирберг, П.Дж., 85, 100, 112, 191
Мирберга интервалы, 112, 130
Мирберга сценарий бифуркаций для
отображения z —► A(z 4- 1/z), 193-
195
Мирхайм, Дж., 141
Митчелл, К., 132-135
Множество М для квадратичного
отображения, 33, 36, 106-130, см.
также A-отображение; //-отобра-
жение
— М° в сравнении с М, 32, 165
— атомы и молекулы, см. М-атомы
(квадратичное отображение); М-
молекулы
— бифуркация и, 101
— введение в проблему, 325-333
— вещественное х в сравнении с ком-
плексным z, 328-329
— исторические заметки о, 45-48,
258-332
— множества Жюлиа и, 40-41, 97-
104, 165,330-332
— нормированный радикал И, 136-
145
— описание Дуади, 32-41
— определенное, 30-31
— открытие, 30-41
— первые изображения, 41-44, 63
— построение, 109-110
— построение М°, 109-110, 207, 209
— приближение п2 и гипотеза, 132-
135
— размерность Хаусдорфа - Безикови-
ча границы, 41, 146-149
— связность и, 38-40, 98, 332
— слияние и, 101
— тонкая структура, 98-101
— топологическая размерность и, 101—
102
— фрактальная природа, 101
— фрактальные аспекты z —► Az(l-z)
при комплексных А и z, 63-79
Множество Mq для квадратичного
отображения, 32, 111, 115, 120, 165
— Магнус, Вильгельм, 220, 347
— Мандельбройт, Шолем, 50-51, 347-
349
— Мандельброт, Алиетт, 341
— Мандельброта множество, см. мно-
жество М для неквадратичных
отображений; множество М для
квадратичного отображения
— континентальное подмножество,
110-112
— острова, 111-116
— построение, 109-110, 207, 209
Множество Т
— обратный аттрактор и, 170-175
— определенное, 165
— пересечение с границей базовых
элементов, 170-175
— фрактальная размерность, 165, 176
Множество-репеллер, ^(А) (z-
фрактал) и, 75
Мозаика, гиперболическая, 228
Молдейв, Питер, 57
Молк, Дж., 184, 186
Моментов метод (распределение Мин-
ковского), 305-307
Монтель, Поль, 55
Мори, X., 76
Предметный указатель
387
Мультифракталы, гармонические меры
на ОДА и расширенное понятие о
самоподобии, 313-323
Мультифрактальная мера
— в хаотических гамильтоновых си-
стемах, 290-298, 313-323
— мера Минковского ц и мультифрак-
тальные аномалии в инвариантных
мерах параболических динамиче-
ских систем, 300-311
— мультифрактальные аномалии, и
мера Минковского, 300-311
Мыло, 239-240
Наймайер, И., 316
Неправильность формы, 243-248
— акустика и, 247-248
— вездесущность в вопросах о приро-
де, 244-245
— масштабная инвариантность и, 247-
248
— позднее появление в качестве пред-
мета изучения, 246-247
Нефуксовы группы, 212, 275, см. так-
же неквадратичная рациональная
динамика цепи Пуанкаре
- z-(l/2)(z + l/z), 183-184
- Z -+ (1/4)(1 + z2)2/[z(z2 - 1)], 184-
186
- z - (l/4)z(z3 + 8)/(z3 - 1), 186
- z -> Az(a - zk), 182
- z A(1/4)(1+z2)2/[z(z2- 1)]. 201-
213
- z - A(l/4)z(z3 + 8)/(z3 - 1), 213,
214
- z-*A(z + l/z), 185-198
— введение в, 175-187
— хаотические отображения Латте,
181-186, 200-214
Нормированный радикал 11, 136-145
— дополнение как ст-луночка, 138-143
— неограниченный вариант, 137
— несамопересекающиеся, 139
— окружности, которые оскулируют
7г, 141-143
— определенный, 136, 137
— отображение z —► h,(zrf), 139-140
— сдутая форма, 141, 142
— теоретико-числовая функция v(n),
145
— теоретико-числовая функция Эйле-
ра ф(п), 143-144
— термин «луночка», 138
— фрактальная размерность границы,
136, 144
Нортон, В. Алан, 60, 130, 135, 145,
149, 153, 198, 275
Ньютона-Рафсона метод, 183-184
ОДА, см. агрегации, ограниченные
диффузией
«Область дракона», 97, 103
Окружности
— Аполлониево множество, 229—240
— гиперболическая мозаика или тай-
линг, 228
— жидкие кристаллы и, 239-240
— инверсия и, 226-227, 257—275
— минимально самоинверсное множе-
ство как окружность Г, 260-261
— мультифрактальные инвариантные
меры в хаотических гамильтоновых
системах, 290-298
— симметрия относительно, 248-254
— упаковка Лейбница, 231
— фрактальная оскуляция и, 235-237,
271-275
— цепи Пуанкаре и, 233, 267-270
Оппенгеймер, Питер, 220
Оскуляция
— Аполлониево множество и, 235-237
— оскулирующая лунка, 142
— самоинверсные фракталы, оскули-
рующие сг-диски, 271-275
— самоподобная кривая с генератором
симметрии, состоящим их четырех
частей, 255
388
Предметный указатель
♦Основания», 100-116
Острова и островные молекулы, 33-38,
100-101
— (Т-драконы и. 103-104
- внутренние координаты, 116
— квадратичный и неквадратичный
случаи, 207
— множество A/о и, 111-116
— объяснение универсальностью клас-
са схожести островов, 117
— основания, 116
— структура чертового полимера и,
151
♦Отростки», 100-102, 104
Пайтген, Хайнц-Отто, 39, 60, 325
Параболические динамические систе-
мы, 300-311
Паризи, Г., 291, 313, 320
Паттерсон, С. Дж., 221
Пеано драконы, 103
Пеано кривые, 155-162
Пенлеве, Поль, 219-220, 346
Перес, Й., 311
Перколяционные кластеры, фракталь-
ная размерность, 79
Пиблз, Джим, 79
Пикар, Эмиль, 342
Положительный рескейлинг Коши,
316,319
Полярные координаты, определенные,
333
Правило места-размера, 144
Приближение п2 и гипотеза, 132-135
♦Прибрежные» острова, множество
Мандельброта и, 33-39, см. также
острова и островные молекулы
Принимающие связи, 100, 101
Пуанкаре цепь, 233-234, 237-238,
267-270
Пуанкаре, Анри, 50, 56, 167, 218-220,
226, 259, 263, 326-327, 350
Пучок-репеллер, форма и топология,
121-130
Разветвление, 102, 238-239
Размерность, см. также Хаусдорфа-
Безиковича размерность
Размерность, , 70, 75, 101-102
Райт, Д., 222
Рамон и Кайал, Сантьяго, 46
Распределений, метод (мера Минков-
ского), 301, 306-309
Риман, Бернхард, 218
Рихтер, Петер X., 39, 60, 325
Рюэль, Дэвид, 57
СИФ, см. системы итерированных
функций (разложимые динамиче-
ские системы)
Самогомографический фрактал, 240
Самоинверсная кривая, 251, 253
Самоинверсные фракталы, 225-241
— Аполлониево множество, 229-240
— генератор, 227
— гиперболическая мозаика или тай-
линг, 228
— жидкие кристаллы и, 239-240
— затравки и кланы, 227
— оскулирующие сг-окружности, 257—
275
— предельное множество инверсной
группы, 228-229
— разветвление, 238-239
— стандартная геометрическая инвер-
сия, 226-227
— фрактальная оскуляция, 235-237
— хаотические инверсные группы, 228
— цепь Пуанкаре, 233-234, 237-238
Самоквадрируемые множества
— кривые Жюлиа на плоскости, 92-94
— определенные, 91
— пылевые множества Фату на веще-
ственной прямой, 92
— топологическая размерность и, 101 —
102
Предметный указатель
389
Самоподобие
— гармонические меры на ОДА и
расширенное понятие самоподобия,
313-323
— канторова пыль Кантора, 85-86
— локальное самоподобие границ мо-
лекул, 101
— самоподобная кривая с генератором
симметрии, состоящим их четырех
частей, 254-255
— самоподобная фрактальная пыль
с генератором симметрии, состоя-
щим их трех частей, 248-254
— самоподобные фракталы, отличаю-
щиеся от самоинверсных и линей-
ных фракталов, 225
— симметрия и, 243-244
Связность, 38-40, 73, 98, 109, 332
— вполне несвязные множества, см.
фрактальная пыль
Сепаратор, 57, 81
Сериес, П.Р., 222, 296
Серпинского салфетка, 232
Сибони, Нессим, 60, 165
Синай, Я. Г., 76
Системы частиц, 78-79
Скользкая чертова гать, 292, 303
Слияние, 65-69, 101
— определенное, 67, 116
Смейла аттрактор, 76
Солнечная система, 327
Солофф, Линда, 135
Соразмерность как мера упорядоченно-
сти, 191
Статистическое правило места-
размера, 144
Сто видов горы Фудзияма (Хокусай),
189
Стоун, Маршалл, 52-53
Странные аттракторы
— виды, 247-248
— окружности и, 248, 254
— самоподобие и, 243-244
— симметрия, 243-255
— «странности», 77-78
— фрактальная размерность и, 76-77
Тайлинг
— гиперболическая мозаика (окруж-
ности), 228
— покрытие внутренних областей мно-
жеств Жюлиа для квадратичного
отображения, 164-176
Таннери, Дж., 184, 186
Теория о критической точке для жид-
ких кристаллов, 239-240
«Термодинамическая» теория для /(а),
301, 309-310
Терстон, У. П., 63
Томае, С., 101
Томас, П. Б., 232
Тор, 296
Тридцать шесть видов горы Фудзияма
(Хокусай), 189
Уиттен, Т. А., 41
Уиттэкер, Э. Т., 184, 186
Улам, Станислас, 47
Универсальности класса, аргументы
об, 117-118, 140
Универсальности теория, 328
Уолш, Дж. Л., 107, 109
Уотсон, Г.Н., 184, 186
Фальконер, Кеннет, 223
Фараона нагрудник, 239
Фату пыль, 81 — 104
— М-множество и, 101-102
— топологическая размерность и, 101-
102
Фату, Пьер, 55-56, 83, 328, 332
— биографические заметки, 335-337
— исторические заметки о научном
приоритете, 340-343
Фату-Жюлиа, теория итерации, исто-
рические заметки, 55-61, 328-330,
340-343
390
Предметный указатель
Фейгенбаума число J, 101, 118—119
Фейри ряды, 292, 295
Физические системы, фракталы и, 78-
79
Формула удвоения, 181-186, 200-214
Фосс. Рихард Ф., 60
Фрагментация
- Аполлониево множество и, 229, 233
— фрактальная размерность и, 77, 233
Фрактальная оскуляция, 235-237
Фрактальная пыль
- 7(A) и, 75
— диски Зигеля как предел фракталь-
ных пылевых множеств, 162
— и различие между замкнутым мно-
жеством М и полуоткрытым множе-
ством М, 104
— минимально самоинверсное множе-
ство как, 263
— множества Жюлиа и, 108, 109, 162,
331,332
— обратный аттрактор и, 175
— самоподобная фрактальная пыль с
генератором симметрии, состоящим
из трех частей, 248-254
Фрактальная размерность, см. размер-
ность Хаусдорфа - Бези ковича
Фрактальное искусство, 329-330
Фрактальное множество, см. также
7(A) (z-фрактал); множество М
для неквадратичных отображений;
множество М для квадратичного
отображения; Q (А-фрактал)
— неправильность форм и, 243-248
— определенное, 64
— самоподобие и симметрия, 243-244,
248-254
— самоподобные фракталы, отличаю-
щиеся от самоинверсных и линей-
ных фракталов, 225
Фрейм, М.Л., 132-135
Фрикке, Р., 218, 228, 233, 257-258
263-264
Фриш, У., 265, 313, 320
Фуджисака, X., 76
Фуксовы группы, 260-266, 275, 293,
295
Хаббард, Джон X., 40, 59-60, 184
Хан, Ганц, 90
Хандельман, Зигмунд У., 149
Хаос, 327
— меры, 190-193
— мультифрактальные инвариантные
меры в хаотических гамильтоновых
системах, 290-298
— отображение z —► A(z + l/z) и пере-
ход от линейного хаоса к плоскост-
ному, 188-198
— хаотические инверсионные группы,
228
— хаотические отображения Латте,
181-186, 200-214
Хаусдорфа - Безиковича размерность
— для 7(A) (z-фрактала), 75
— для Аполлониева множества, 232-
233
— для аттрактора Зальцмана-Лорен-
ца, 79
— для границы М (квадратичного
отображения), 41, 146-149
— для границы нормированного ради-
кала 7£, 136, 144
— для множества Т (квадратичного
отображения), 165, 176
— для распределения галактик, 79
— и меры упорядоченности для
неквадратичных систем, 190-193
— и мультифрактальные инвариант-
ные меры в хаотических гамильто-
новых системах, 290-298
— и определение фрактального множе-
ства, 64
— как мера фрагментации, 233
— странные аттракторы и, 76-77
Хаякава, Й., 314
Предметный указатель
391
Келси, Т.К., 313, 320, 389
Хиронака, Хейсуке, 57
Хиронака, Эрико, 176
Хокусай, К„ 188, 189, 192, 193
Хэрриот, Томас, 45
Цвитанович, Р., 141
Чезаро, Е., 220, 234
Чертов полимер, 40, 104, 146-151
Чертова гать, 113, 118, 130
Чертова лестница (скользкая), 292,
303
Шварц, Лоран, 52
Шишикура, М.М., 146
Шредер, Е., 38
Шредера функция, 165-169
Штайн, М., 100, 112, 328
Штайн, П.Р., 100, 112, 204
Эвертц, К. Ж. Дж., 311
Эвинг, Джон X., 257
Эйлера теоретико-числовая функция
ф(п), 136, 143-144
Экман, Дж.П., 100, 101
Эшер, Мориц, 228
«Ядра», 100, ИЗ
Интересующие Вас книги нашего издательства можно заказать почтой или
электронной почтой:
subscribe@rcd.ru
Внимание: дешевле и быстрее всего книги можно приобрести через наш
Интернет-магазин:
http://shop.rcd.ru
Книги также можно приобрести:
1. Москва, ИМАШ, ул. Бардина, д. 4, корп. 3, к. 414, тел. (499) 135-
54-37
2. МГУ им. Ломоносова (ГЗ, 1 этаж)
3. Магазины:
Москва: «Дом научно-технической книги» (Ленинский пр., 40)
«Московский дом книги» (ул. Новый Арбат, 8)
Книжный магазин «ФИЗМАТКНИГА» (г. Долгопрудный,
Новый корпус МФТИ, 1 этаж, тел. 409-93-28)
С.-Пб.: «С.-Пб. дом книги» (Невский пр., 28)
Бенуа Б. Мандельброт
Фракталы и хаос
Множество Мандельброта и другие чудеса
Дизайнер Л. Н. Загуменова
Технический редактор А. В. Широбоков
Компьютерная верстка Д. В. Панкратов, С. В. Высоцкий
Корректор Г. Г. Тетерина
Подписано в печать 22.10.2009. Формат 60 х 841/16.
Печать офсетная. Усл.печ.л. 22,79. Уч. изд. л. 23,87.
Гарнитура Таймс. Бумага офсетная №1. Заказ №56.
Научно-издательский центр «Регулярная и хаотическая динамика»
426034, г. Ижевск, ул. Университетская, 1.
http://shop.rcd.ru E-mail: mail@rcd.ru Тел./факс: (-1-73412) 500-295