Б. Мандельброт
ФРАКТАЛЫ,
СЛУЧАЙ И ФИНАНСЫ
‘DtfttatnicA
Издание осуществлено в рамках
программы "Пушкин” при
поддержке Министерства
иностранных дел Франции
и посольства Франции в России.
Ouvrager#alis€ dans le cadre du
programme daided lapublication
Poucbkine auec le soutien du Ministere
des Affaires EtrangjbresJran^ais et de
FAmbassade de France enRussie.
BENOIT MANDELBROT
FRACTALES, HASARD
ET FINANCE
(1959-1997)
FLAMMARION
БЕНУА МАНДЕЛЬБРОТ
ФРАКТАЛЫ, СЛУЧАЙ
И ФИНАНСЫ
(1959-1997)
Перевод с французского В. В. Шуликовской
Под редакцией А. Р. Логунова
/?&с
Москва ♦ Ижевск
2004
УДК 516.15, 519.21
Интернет-магазин
http://shop.rcd.ru
•	физика
•	математика
•	биология
•	нефтегазовые
технологии
Мандельброт Б.
Фракталы, случай и финансы. — Москва-Ижевск: НИЦ «Ре-
гулярная и хаотическая динамика», 2004, 256 стр.
Книга известного американского математика Бенуа Ман-
дельброта посвящена фрактальной геометрии и фундаменталь-
ным вопросам случайности. Судя по всему, фрактальную геомет-
рию Мандельброт придумал, когда писал труды по финансам в
шестидесятые годы. Данное произведение содержит, среди про-
чих, эти труды, которые ранее не издавались, а также фундамен-
тальные представления о случайности.
Для экономистов, философов, физиков и математиков.
ISBN 5-93972-341-1
© Editions Flammarion
© НИЦ «Регулярная и хаотическая динамика», 2003
http://rcd.ru
http://ics.org.ru
Оглавление
Введение............................... 10
Предисловие............................ 22
ЧАСТЬ ПЕРВАЯ: ФРАКТАЛЫ................. 47
Глава 1.1. Признанный и принесший плоды «меза-
льянс» .............................. 49
О неизбежных вопросах (49). Метод: фрактальная
геометрия (50). Средства: важность непосредствен-
ного наблюдения (51). Средства: «принцип масшта-
бирования» (52). Значение инвариантностей (54).
Фракталы и хаотическая динамика (55).
Глава 1.2. Самоподобие и самоаффинность ...	58
Концепция линейного самоподобия (58). «Снежин-
ки» и «прохождения» (59). Концепция линейной са-
моаффинности (61). Диагональные самоаффинно-
сти (64). Самоаффинное моделирование в финан-
сах (66).
Глава 1.3. Принципы масштабирования, масшта-
бируемые распределения, фрактальные размер-
ности и показатель Н........................ 69
Самоподобие и фрактальная размерность (70). Са-
моаффинность и показатель Н (71). Связь между
размерностью и фракгальностью (72).
ЧАСТЬ ВТОРАЯ: МНОЖЕСТВЕННОСТЬ «СОСТО-
ЯНИИ» СЛУЧАЯ................................ 75
Глава 2.1. От случая ручного к случаю стихийному 77
Теория вероятностей (78). Закономерности случая и
ограничения в их применении (80). На лезвии но-
жа (81). От ручного к стихийному (82). Берег Брета-
ни (84). Концепция множественности «состояний»
6
Оглавление
случая в ее количественном выражении (86). Слу-
чай «ручной», «стихийный» и «медленный» (88).
«Изобретательность» стихийного случая (91). Вы-
воды: науки и случай (92).
Глава 2.2. Философские притчи и финансовые «пу-
зыри» ........................................... 94
Кладбище юных поэтов (94). Мираж в Туманах (95).
Парадокс вероятного значения (97). Мартингалы и
рациональные «пузыри» (99).
Глава 2.3. Белый гауссовский шум и несколько дос-
таточно понятных примеров стихийного случая 102
Белый гауссовский шум (102). Причинные связи и
ручной шум (104). Обычная центральная предельная
теорема, ее мощность и ее ограниченность (105).
Теорема — это еще не безусловная истина (106).
«Контрпримеры» Коши: переменная, блуждание и
белый шум (108). Лучник с завязанными глаза-
ми (109). Противоречия, связанные с шумом Ко-
ши (110). Коши против Бьенеме (ПО). Гарольд
Джеффрис (1891-1989) (114). Концентрация воз-
вращений к исходной точке при игре в «орлян-
ку» (115). Хольцмарк: ньютоново притяжение и кон-
центрация (116). Виллис-Юл-Лурия-Дельбрюк:
концентрация в мутациях (121).
Глава 2.4. L-устойчивые распределения..........124
Устойчивость гауссовского распределения (124).
Распределение Коши и его обобщения (125). Асим-
птотическое поведение (127). Билогарифмические
графики некоторых симметричных L-устойчивых
распределений (127).
Глава 2.5. Ной, Иосиф и несколько примеров сти-
хийного случая, малопонятных, но неизбежных 130
Случайность в Библии (130). Флуктуации Ноя и
Иосифа (131). Гауссовский 1//-шум (132). Беско-
нечная память — как такое возможно? (134). Тур-
булентность, проблема Изинга и критические фено-
мены (135). Стихийный случай, которого можно из-
бежать (136). Инвариантность при редукции как на-
учный принцип (136). Попытки избежать стихийно-
Оглавление
7
го случая (138). Переходные эффекты и медленный
случай (138). Изменение масштаба измерения (140).
Обращение к различным смесям (141). Кредо в за-
вершение главы (142).
ЧАСТЬ ТРЕТЬЯ: СЛУЧАЙНОЕ НА БИРЖЕ ... 145
Глава 3.1. Разрывность и концентрация («модель
[М1963]»).................................... 146
Биржи (147). Статистическое описание экономи-
ки (149). Броуновская модель и ее предысто-
рия (150). Недостатки броуновской модели (151).
Стационарность и интуиция, часть 1 (154). Негаус-
совость в финансах (156). Симптом разрывно-
сти (159). «Фильтры» С. С. Александера (160). Мо-
менты и другие типичные величины (163). Кор-
ректировка гистограмм. Старые и новые крите-
рии (167). Понятие L-устойчивости (168). Роль мас-
штабируемых асимптот (171). Стационарность и
интуиция, часть 2 (173).
Глава 3.2. Псевдопериодичности
(«модель [М1965]») .......................... 175
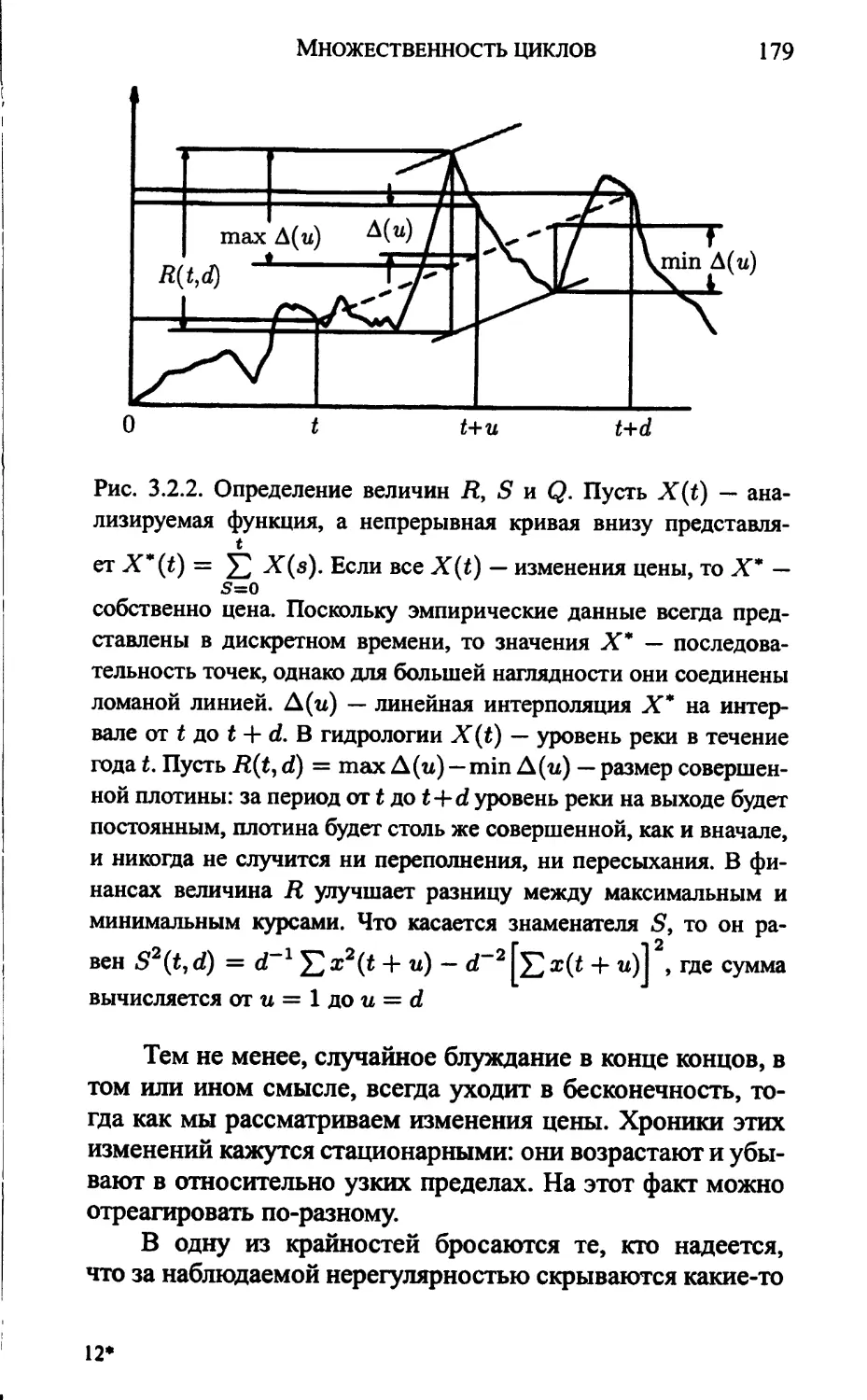
Описание и управление (175). Множественность
циклов (177). Реальны ли медленные циклы? (180).
Интерпретация спектров (181). Феномен Херс-
та (183). Самоаффинность в гауссовском случае и
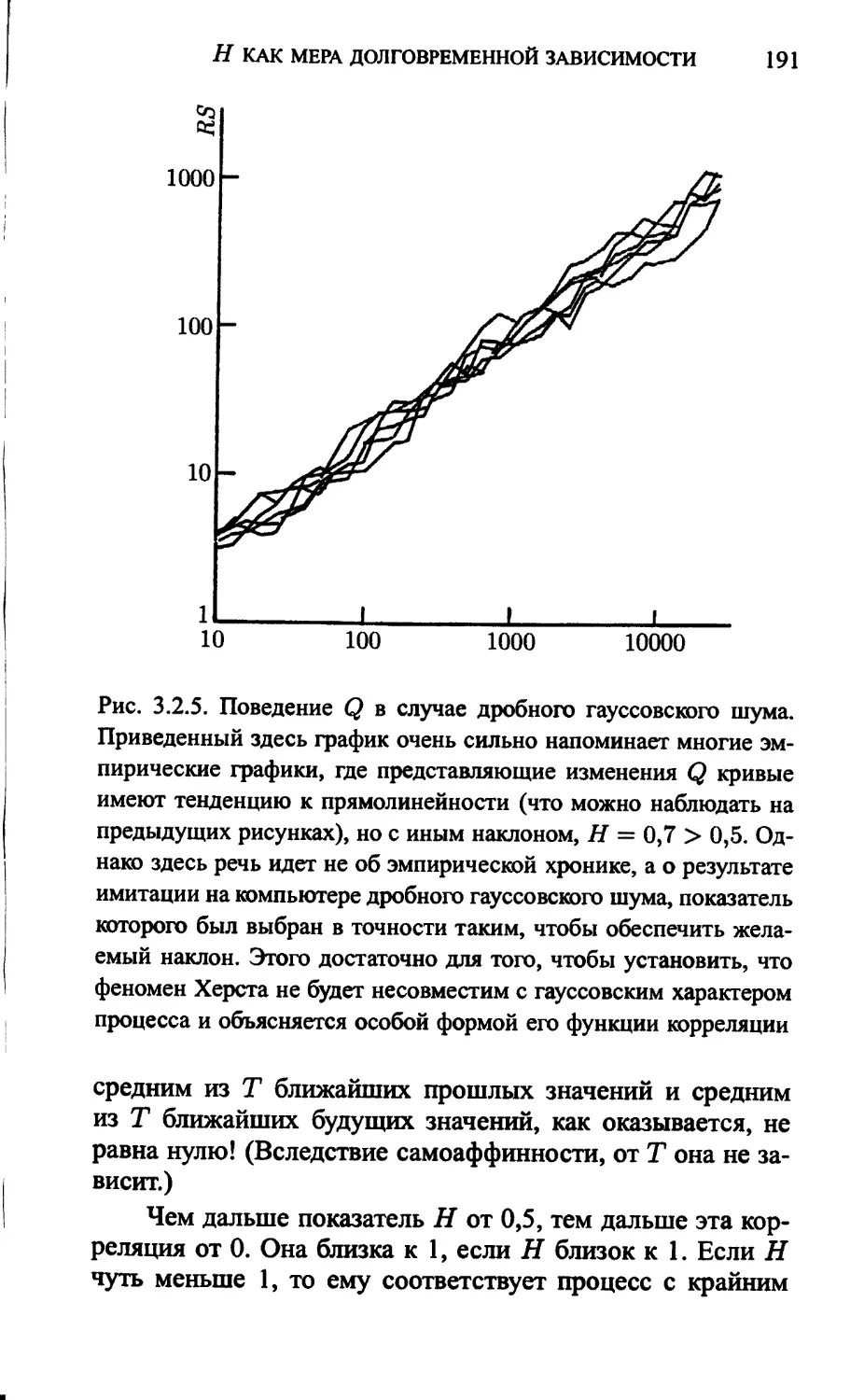
дробные шумы (190). Показатель Н как мера дол-
говременной зависимости и демонстрируемая цик-
лами тенденция (190). Показатель Н в гидрологии
и финансах (192). Заключение (193).
Глава 3.3. Заключение (1997): броуновская дроб-
ность в мультифрактальном биржевом времени
(«модель [М1963]») .......................... 195
Унифрактальность и мультифрактальность (196).
Понятие «биржевого времени» (197). Этап на пути к
модели «третьего поколения»: фрактальное бирже-
вое время (198). Мультифрактальное биржевое вре-
мя (199). Набросок модели (200). И снова мульти-
фрактальное биржевое время (201). Нерекурсивные
модели (202).
8	Оглавление
ЧАСТЬ ЧЕТВЕРТАЯ: СЛУЧАЙНОЕ В РАЗГОВОР-
НОЙ РЕЧИ ....................................203
Предисловие: 1951 год (206). 5. Итак, линия опре-
деляет рп, а также (209). Введение (210). Первая
аппроксимация: закон Ципфа (214). Вторая аппрок-
симация: так называемый «закон Ципфа-Мандель-
брота» (214). Объяснение закона Ципфа-Мандель-
брота (219). Количество информации (220). Первый
вывод закона о частоте слов (222). Второй вывод:
оптимальные частоты (225). Температура дискурса,
«отрицательные температуры» (227).
Библиография.................................229
Марии-Терезе Троншон-Конше,
профессору французского языка в Тулле в
1940-1941 годах
Памяти Марселя-Поля Шютценбергера,
друга всей жизни
Введение
На обложке книги изображен «золотой куст» или «зо-
лотая ветвь»; это реально существующий материальный
объект, им можно полюбоваться в Минералогической кол-
лекции Национального музея естественной истории в Па-
риже (экспонат предоставлен фондом «Эльф»). Этот со-
зданный природой шедевр искусства является символом
данной книги, поскольку он объединяет в себе три темы,
фигурирующие в ее заглавии.
Форма «золотого куста» — фрактал (свойствам фрак-
талов посвящена первая часть книги). Фрактальность выра-
жается в наличии отверстий или иных характерных струк-
тур, диапазон величин которых очень широк, — в качестве
таких структур можно рассматривать, например, экономи-
ческие и финансовые «циклы». Выделим одну важную осо-
бенность: упомянутые экономические характеристики име-
ют верхнюю и нижнюю границу, что вообще свойственно
всякому естественному фрактальному образованию (в про-
тивоположность математическим конструкциям).
«Золотой куст» представляет собой полисинтетиче-
ский агрегат, порожденный бесчисленными и малоизучен-
ными силами природы. В нашем распоряжении есть лишь
один инструмент, позволяющий представить себе резуль-
тат деятельности таких сил. Этот инструмент — случай, и
о нем мы поговорим во второй части данной книги. Вы-
ступая же в защиту своей личной и все еще новой точки
зрения, я заявляю, что случай может проявляться во множе-
стве различных «состояний», и что одно из его состояний,
связанное с финансами, заслуживает того, чтобы быть от-
несенным к разряду стихийных. Речь идет не о математи-
ческом изяществе (математическое изложение будет, скорее
всего, весьма кратким), но об общих идеях.
Введение
И
Наконец, я думаю, что читатель сочтет символичным
тот факт, что изображенный на обложке куст состоит из
практически чистого золота, более чем наполовину вы-
свободившегося из белой кварцевой «подушки», в которой
его не так давно и нашли в Калифорнии. Эта символика
подводит нас к теме третьей части книги, где представле-
ны различные модели, предложенные мной для описания
поведения спекулятивных цен.
В течение тридцати лет эти работы почти не находи-
ли применения, зачастую их критиковали вдоль и поперек.
Однако время оказалось милосердным к ним: они пережи-
ли критику и сегодня вызывают большой интерес. Сначала
мы представим эти работы в их исходном, историческом,
виде, а также рассмотрим мои нынешние идеи, касающие-
ся данной области.
Что касается четвертой части, несколько загадочной,
поскольку на ее содержание в заглавии книги никаких на-
меков нет, то она слегка, но не полностью, выпадает из
основного русла изложения; дабы не прерывать ход наших
мыслей, мы не будем говорить о ней сейчас, лучше мы
посвятим ей отдельное введение.
Перейдем от предмета изложения к манере изложения.
Ни в коем случае не следует считать эту книгу исчерпыва-
ющей, а приведенные в ней ссылки вовсе не претендуют
на полноту. Важно отметить также, что книга не являет-
ся строго математической, имеются в ней рассуждения и
иного рода, пусть и в небольшом количестве.
В книге используется множество математических ин-
струментов, как традиционных, так и новых, предложен-
ных мной для изучения финансовых процессов. Вкратце об
этих инструментах рассказано в предисловии, кроме того,
они рассмотрены в главах 1.2, 1.3, 2.4 и 3.3. За дальней-
шими сведениями можно обратиться к работам [М1997Е],
[М, Fisher &Calvet 1997], [Calvet, Fisher &М 1997] и [Fisher,
Calvet & M 1997]. Обозначения, использованные при оформ-
лении ссылок, объясняются в начале списка литературы.
Таким образом, книга эта по большей части оказыва-
ется очень разной. Она преднамеренно содержит мало фор-
12
Введение
мул и адресована скорее тем читателям (причем вовсе не
обязательно экономистам), которые формальному анализу
предпочитают так называемое «интуитивное» понимание,
объяснение «на пальцах». Не меньший интерес книга мо-
жет представлять и для философов — как знамение новой
эпохи, наступающей с введением стихийной случайности
в теорию вероятностей и теорию статистического вывода.
Теперь о том, что касается дат, вынесенных в под-
заголовок книги. Именно в 1959 году начался мой путь
экономиста, путь долгий и чрезвычайно извилистый. Мо-
ей первой публикацией была короткая записка в двух ча-
стях, помещенная в «Comptes rendus»; полный текст этой
и последующих записок по рассматриваемой теме можно
найти в предисловии. Вторая дата, 1997 год, отражает мое
теперешнее положение все на том же пути (которое, несо-
мненно, окажется не менее преходящим). Предваритель-
ный набросок этого положения приведен в главе 1.2, более
же подробному описанию посвящена глава 3.3, полностью
новая. Все, что на настоящий момент можно считать наи-
более завершенным в моих моделях, представлено там.
Предмет главы 3.3 составляет необходимость одновре-
менного учета двух особенностей, характерных для наблю-
даемых явлений; они противоречат известной упрощенной
модели, в рамках которой постулируется, что цены изменя-
ются случайным образом или, иначе говоря, по типу бро-
уновского движения. Эта «модель столкновений» представ-
лена на рис. 1.1. С другой стороны, очень хорошо известно,
что цены имеют тенденцию к разрывности, или, по мень-
шей мере, их изменения стремятся к «концентрации». Это
одно из многочисленных проявлений явной зависимости от
времени.
В качестве замены броуновскому движению я и сегод-
ня предлагаю свою «модель [М 1972]», более точно опреде-
ляемую в научных терминах — ниже я их подробно объяс-
ню — как «регулярное броуновское движение в мультифрак-
тальном времени» или «мультифрактальная модель возвра-
та активов» (multifractal model of asset returns, MMAR). Пре-
дыдущие мои модели датируются 1963-1965 годами и
Введение
13
Рис. 1.1. Случайные изменения, аппроксимация броуновского дви-
жения (вверху); последовательность его приращений (внизу)
вкратце описаны в предисловии. Мы будем называть их
«модель [М 1963]» и «модель [М 1965]». Эти модели огра-
ничиваются, соответственно, первой и второй из упомя-
нутых выше характерных особенностей и представлены в
главах 3.1 и 3.2 в пересмотренном варианте 1973 года.
Следует сразу обозначить цель этой работы. Она мо-
жет показаться чересчур амбициозной, однако вполне соот-
ветствует идеалу, сформулированному когда-то Эйнштей-
ном: «конечная цель любой науки — охватить наибольшее
число эмпирических фактов, выведя их логически из как
можно меньшего количества гипотез или аксиом». Именно
так я и действовал в своем стремлении постичь эти весьма
простые математические формулы; надеюсь, впрочем, что
вытекающие из них синтетические хроники нелегко будет
14
Введение
отличить от реальных исторических хроник Биржи. Упомя-
нутому принципу, который мы будем называть «принципом
лестницы», можно придавать разный смысл, с каждым ра-
зом все более общий. Я же делаю все возможное и невоз-
можное, чтобы избежать ослабления этого принципа. Было
бы весьма заманчиво и совсем несложно присоединить к
нему этакое «мановение руки», якобы совершенствующее
этот принцип с целью наилучшего представления фактов, в
действительности же разрушающее его. Однако я к таким
мановениям руки прибегать не намерен.
Какими бы амбициозными ни представлялись цели
моих работ, они, тем не менее, остаются вполне земными.
На рис. 1.2 показаны изменения цен акций, а рис. 1.3 пред-
ставляет численную имитацию некоторой математической
модели. Сравним эти рисунки друг с другом и с рис. 1.1,
который, напомним еще раз, иллюстрирует броуновскую
модель. Особое внимание следует обратить на повседнев-
ные различия (внизу), которые «говорят» гораздо громче,
чем собственно хроники (вверху). Одного взгляда достаточ-
но, чтобы понять, что броуновская модель в данном случае
неприемлема, тогда как между правильно подобранными
фактами и «имитациями» может обнаруживаться удиви-
тельное сходство. В главе 3.3 мы увидим, что примеры
таких имитаций можно получить с помощью конструкций
настолько простых, что никто и не ожидал от них ничего
подобного, читатель же, несомненно, удивится (вместе со
мной), что для понимания этого факта надо было ждать до
сегодняшнего дня.
Уточним роль этих изображений. Я убежден, что спо-
собность к имитации представляет собой не что иное, как
разновидность понимания. Однако я всегда говорил, и да-
же охотно «признавал», что зрительные образы непремен-
но следует сопровождать объективными статистическими
комментариями. Так мы и будем поступать во всех случаях.
И все же, подразумеваемый в моих моделях принцип
никоим образом не претендует на объяснение поведения
цен. Как и все остальные, я сожалею об этом, но поде-
Введение
15
Рис. 1.2. Изменение курса акций IBM в логарифмических коорди-
натах (вверху) и их относительные ежедневные изменения (внизу)
лать ничего не могу. Как бы то ни было, я твердо верю
в мудрость одного совета, о котором, как я слышал, мож-
но прочесть в одной старой (1687 года) книге, в «Истории
оракулов» Фонтенеля (1657-1757).
«Прежде чем искать причину какого-либо факта,
необходимо как следует убедиться в том, что та-
16
Введение
Рис. 1.3. Образец случайного процесса в соответствии с «моде-
лью [М 1972]» изменения цен. Построение выполняется согласно
графику вверху слева, подробное объяснение см. в главах 1.3 и 3.3
Введение
17
кой факт действительно имеет место. Правда, этот
метод оказывается слишком медленным для боль-
шинства людей, которые по своей естественной
склонности ищут причины, пренебрегая истин-
ностью факта; он, однако, позволяет в конечном
счете избежать обычной нелепицы: открытия при-
чины того, чего вовсе не существует.»
Применимо к нашему случаю: прежде чем занимать-
ся финансовой инженерией и ее «производными продукта-
ми», необходимо «как следует убедиться в том, что такой
факт действительно имеет место». Мне нравится объяс-
нять, и я слишком хорошо знаю, что (особенно это каса-
ется физиков) удовлетворение, которое могло бы вызвать
открытие фрактальности в стольких разнообразных обла-
стях, во многих случаях оказалось ослаблено из-за мед-
лительности в объяснении обнаруженных феноменов. Это
разочарование распространяется и на область финансов, и
мне довелось испытать его в полной мере. Но у инженера
нет свободного времени, чтобы брать на себя еще и горе-
сти ученого. В финансах, как и во всех других областях,
необходимо в первую очередь «как следует убедиться» в
наличии факта, а потом уже действовать.
Описанные соображения в равной мере учитывались и
при подготовке книги [М1997Е]. Это первый том, недавно
опубликованный издательством Springer в английской се-
рии моих «Selecta»1; эта серия по оформлению несколько
отличается от французской. Название книги («Fractals and
Scaling in Finance: Discontinuity, Concentration, Risk»1 2), как
мне думается, в переводе не нуждается, а текст в равных
пропорциях содержит как новые результаты, так и реприн-
ты статей шестидесятых годов. Чтобы не повторяться в
дальнейшем, расскажем об этой работе подробнее прямо
здесь. Будучи втрое или вчетверо больше настоящей фран-
цузской книги, вышеупомянутое английское издание может
1 «Избранные произведения» (лат.). — Прим. пер.
2«Фракталы и скейлинг в финансах: разрывность, концентрация, риск»
(англ.). — Прим. пер.
2 Б. Мандельброт
18
Введение
служить справочником со всех точек зрения: математиче-
ской точности, разнообразия приложений и других более
тонких материй.
Напомним: вместо «модель, описанная — или заявлен-
ная — в [М 1963b {Е14}]» мы будем использовать сокра-
щение «модель [М 1963]». Так же поступим и с моделя-
ми [М1965] и [М1972].
Упомянем об одном факте, о котором много говорит-
ся в М 1997FS: я работал поочередно во многих областях,
на первый взгляд, весьма различных. Поэтому хотелось бы
точнее обозначить то место, которое занимают предлагае-
мые здесь идеи и умозаключения в общем процессе раз-
вития моих представлений и в последовательности моих
работ. Не составляя заранее никаких планов и, быть мо-
жет, не придерживаясь даже сколько-нибудь заметного со
стороны распорядка, я посвятил всю свою жизнь изучению
фракталов, и результатом тысячи всевозможных перипетий
явилось движение, напоминающее ход маятника — движе-
ние от случайного к неслучайному (вехами на этом пути
стали «основание» фрактальной геометрии и, в частности,
открытие и описание структуры, которую вскоре стали на-
зывать «множеством Мандельброта») и назад, снова к слу-
чайному.
В этой зигзагообразной «карьере» имеются два пери-
ода, посвященных случайному, как раз к ним и относятся
мои работы о финансах. Основные идеи этих работ вскоре
получили дальнейшее развитие в обзорах на французском
языке (а именно, в [М 1966г], [М 1973v] и [М 1973j]), по-
явившихся в очень специализированных технических жур-
налах — таких, как «Economic Appliquee»3 (в то время
его возглавлял Франсуа Перру) и «Cahiers d’Econometrie»4
(возглавляемый Рене Руа). Кроме того, отметим в каче-
стве небольшой исторической справки, что работа, из ко-
торой впоследствии выросла книга [М19750] («Фракталь-
ные объекты: форма, случай и размерность», издательство
3 «Прикладная экономика» (фр.). — Прим. пер.
4«Журнал эконометрики» (фр.). — Прим. пер.
Введение
19
Flammarion), по изначальному замыслу должна была вклю-
чать в себя и упомянутые выше обзоры, которым там отво-
дилось почетное место. Этому, однако, помешали извест-
ные технические причины, в результате чего мне пришлось
отложить публикацию этих обзоров более чем на двадцать
лет.
Вернемся к двум составляющим этой книги, обращен-
ным в прошлое и в будущее. Мои годы подталкивают меня
к подведению итогов, к «назначению срока». Исходя из
этих соображений, я и затеял публикацию лучших своих
работ в упомянутом выше виде, то есть в составе собрания
«Selecta», в которое, разумеется, должны войти и новые ра-
боты: та часть, что появится в первую очередь, состоит из
данной книги, [М 1997Е], а также других книг, которые еще
должны выйти, как на французском, так и на английском
языках.
Прежде всего, в главах 3.1 и 3.2 я возвращаюсь к
[М 1973v] и [М1973j], детально их пересматриваю и вклю-
чаю сюда же некоторые разделы из [М 1966г]. Что ка-
сается главы 2.1, то ее первые наброски появились еще
в [M1973f], полному же тексту пришлось ждать вплоть
до [М1996р]. Глава 2.2 представляет собой выдержку из
[М 1975т].
Вот собственно и все, подчеркну лишь, что смысл этой
книги заключается вовсе не в воспоминаниях о прошлом.
Она дает прекрасную возможность оценить произошедшие
со временем перемены к лучшему, как с точки зрения каче-
ства моделей (о чем свидетельствуют главы 1.3 и 3.3), так и
с философской точки зрения (см. обсуждение «случайных
состояний» во второй части книги).
В вышеописанном нелегком процессе рождения идей
нередки были повторы; сейчас они представляются мне
скорее полезными, чем вредными, поэтому я не стал их
исключать, разве что частично.
Теперь пару слов о методологии. Детальный учет
крайне запутанных и сложных финансовых данных — зада-
ча, требующая слишком многих усилий, чтобы наука могла
2*
20
Введение
подступиться к ее решению непосредственно, минуя про-
межуточные этапы. Да и в любом случае наука никогда не
обращается к частному, она ищет скрытое общее. Как раз
поэтому наука даже и не помышляет о точном воспроиз-
ведении зигзагов рис. 1.2.
В данном случае полезную метафору нам предоставля-
ет живопись: в намерения художника-портретиста не вхо-
дит «клонирование» природы, он лишь стремится передать
некоторые существенные ее аспекты. Эта метафора, разу-
меется, неполна, однако она весьма точно определяет место
и роль математических моделей реальности.
Любопытно, что в живописи под моделью понимается
не портрет, но субъект, изображаемый на портрете. То есть
укоренившееся в науке употребление термина «модель» и
его художественное использование противоположны друг
другу. Когда модель воспроизводится нарочито упрощенно,
получается эскиз, (Это справедливо как для живописи, так
и, например, для вышивки.)
Впрочем, вернемся к Фонтенелю. Я принадлежу не к
тем ученым, кто стремится во что бы то ни стало выстроить
законченную «теорию всего», но к тем, кто довольствуется
получением длинной последовательности эскизов, с каж-
дым разом все более и более реалистичных. Что же каса-
ется данной книги, я ни в коем случае не претендую на
то, что мои новейшие работы станут последним словом в
решении задачи о представлении финансовой реальности.
Наконец, я рад случаю выразить признательность лю-
дям, во многом благодаря которым эта книга появилась на
свет. Я долго обсуждал ее с Марселем-Полем Шютценбер-
гером (1922-1996) и имел возможность оценить его советы,
всегда беспощадные, глубокие и уместные.
Само по себе то обстоятельство, что я решил написать
книгу на французском языке, внезапно оказало на меня
очень благоприятное воздействие: оно воскресило в мо-
ей памяти уроки и советы Марии-Терезы Конше, всегда
бывшей для меня примером любви как к родине, так и к
родному языку.
Введение
21
Наконец, как и все, написанное мною прежде, эта кни-
га обязана Алиетте Мандельброт большим, чем я когда-ли-
бо смогу выразить.
Предисловие:
работы 1959-1965 гг.
Как указано в подзаголовке, основная часть этой кни-
ги (по главу 3.3 включительно) завершается 1997 годом —
неопубликованной моделью самоаффинной изменяемости и
указанием на ее применимость к изменению курсов валю-
ты. Из соображений симметрии и исторической последо-
вательности, а также желая соответствовать принципу
«Selecta», я решил начать эту книгу с репринтов самых
первых моих работ, связанных с экономическими вопроса-
ми.
Первым из этих документов по времени публикации
стала работа [М1959р] (в двух частях с одинаковыми за-
главиями, что часто приводит к путанице). В этой работе
впервые предпринята попытка использовать в эксперимен-
тальной науке L-устойчивые распределения*, в свое время
эта идея привлекла внимание Мориса Фреше, его замеча-
ния учтены в ответах, из которых состоит вторая часть
[М1959р]. В совокупности эти два очень коротких текста
и сейчас представляют собой превосходное резюме для по-
следующих более детальных статей ([М 1960i], [М1961 е],
[М1962е]), воспроизведенных в [М1997Е]. Впрочем, сам
по себе предмет работы [М1959р] совершенно не связан
с темой настоящей книги.
Иначе обстоит дело с [М 1962с]. Эта работа стала
моей первой публикацией по финансам и до сих пор остает-
ся прекрасным резюме для «модели [М1963]», послужив-
шей отправной точкой для моих исследований в области
динамики цен. В тексте главы 3.1 приведены два рисунка
оттуда.
Предисловие
23
Настоящее предисловие следует рассматривать как
заблаговременное и весьма уверенное заявление о том, что
моя работа в области финансов состояла не только в раз-
витии, улучшении, защите и продвижении идей, лежащих
в основе [М 1962с] и модели [М 1963]. Моя работа выхо-
дит далеко за эти рамки — прежде всего, в силу понимания
неизбежного противоречия между фактами и всевозмож-
ными упрощенными идеями — такими, например, как мо-
дель случайного движения.
В качестве иллюстрации позвольте привести исто-
рию одной аномалии, которая присутствует в [М 1962с]
и заслуживает того, чтобы рассказать о ней не откла-
дывая. Представленные ниже кривые 1а и 2а описывались
мною как кривые, основанные на ежедневных данных за пе-
риод с 1900 по 1905 годы. Эти данные мне предоставило
Министерство сельского хозяйства США. Следовательно,
отличие этих кривых от кривых 16 и 2Ь заставляет пред-
положить, что между 1900 и 1950 годами распределение
изменений log Z(£+l)—log Z(t) оставалось неизменным по
форме, однако его масштаб значительно уменьшился. То
есть перед нами очевидное проявление нестационарности\
это предположение не лишено оснований и было без осо-
бых сомнений принято моими коллегами, но у меня вызвало
смутные подозрения.
Более того, свойства распределения logZ(t + 1) —
—log Z(t), казалось, обнаруживают очень сильную тенден-
цию к взаимной компенсации: большие изменения в каком-
то одном смысле тут же компенсировались — частично,
но достаточно систематически — изменениями в проти-
воположном смысле.
Мне приятно упомянуть о том, что еще в [М 1963b]
{El4} я потрудился сообщить обо всех этих отклонени-
ях от заявленной в [М 1962с] модели. Несколькими года-
ми позднее, то есть в [М 1972b] {Е14}, было указано на
ошибку, допущенную при чтении данных за 1900-1905 го-
ды. Соответствующим образом исправленные кривые 1а*
и 2а* стали практически неотличимы от кривых 1Ь и 2Ь.
24
Предисловие
Нестационарность оказалась слабее, чем можно было по-
думать.
Данное обстоятельство, впрочем, ни в коей мере не
меняет того факта, что преобразование, переводящее 1а
в 1с и 2а в 2с, предполагает, по-видимому, количество
дней в месяце, меньшее, чем в действительности. Это —
неопровержимый признак статистической зависимости,
тема, которая всегда находилась в центре моих последую-
щих исследований, начиная с [М 1962с] и [М 1963b] {El4}
и заканчивая настоящей книгой, где упомянутая тема за-
нимает отнюдь не последнее место.
Последний представленный в предисловии документ,
[М1965Ь], послужил источником «модели [М1965]», рас-
сматриваемой в главе 3.2. По стечению обстоятельств
этот текст был написан в терминах гидрологии, впрочем,
его очевидное обобщение на случай финансов не замедлило
воспоследовать: см., например, [М 1972с].
Отметим, что в [М 1965h] я ссылаюсь на Херста не
совсем точно. Вместо величины R/S, смысл которой бу-
дет объяснен в главе 3.2, я начинаю с рассмотрения более
простого варианта, величины R. Похоже, эту ошибку до-
пускают все читатели Херста. Публикации других — весь-
ма, кстати, уважаемых — авторов, страдают тем же в
большей или меньшей степени. К счастью, эта ошибка на
[М1965h] никак не повлияла. Впрочем, я очень скоро обна-
ружил ее и немало выиграл при ее исправлении, поскольку
рассмотрение величины R/S привело меня к новой, очень
интересной статистической технике.
Многие ссылки на источники в [М1965h] носят непол-
ный или временный характер. Ссылки из записки (2) в окон-
чательном виде можно найти в [М 1997Е], ссылки из за-
писки (3) — в [М1997N], а из записки (4) — в [М1997Н].
В заключение, несколько слов о терминологии. Как это
часто бывает, особенно в тех случаях, когда работа не
находит немедленного принятия, не все из использованных
в этих старых записках терминов пережили свое время.
В [М упоминается о законе, или распределении, Па-
рето-Леви (PL) вместо устойчивого распределения. Мой
Предисловие
25
термин принят не был, и я смирился с L-устойчивостью,
которая, по-видимому, «прижилась». В [M1965h] гово-
рится о внутренней гомотетии (self-similarity5 в записке).
В употребление вошел термин, который я однажды пред-
ложил Жозефу Кампе де Ферье, самоаффинность, и при
подготовке к публикации я был вынужден смириться —
увы! — ис этим.
5 Самоподобие (англ.) — Прим, перев.
26
Предисловие
Теория вероятностей и экономика. — Переменные и
стохастические процессы Парето-Леви и
распределение доходов. Записка (*) г-на Бенуа
Мандельброта. Передана г-ном Жозефом Кампе де
Ферье.
1.	Переменные Парето-Леви. Предлагается (х)
представить распределение доходов (или некоторых их ка-
тегорий) с помощью устойчивого вероятностного распре-
деления Парето-Леви, полностью асимметричного и с ко-
нечным средним значением, т. е. когда показатель а удовле-
творяет неравенству 1 < а < 2. В контексте данной задачи
это распределение будет называться «законом Парето-Ле-
ви» (PL).
2.	Форма плотности вероятности Парето-Леви.
Плотность этого распределения р(и) определяется форму-
лой (см. (2))
log<p(z) = -i'Mz-c|z|“|l -
где
oo
<p(z) = / exp(izu)p(u)du.
—oo
В окрестности среднего значения (М) выражение
для р(и) можно получить непосредственным вычислением;
оказывается, что р(и) сильно асимметрично (и напоминает
логнормальное распределение). При и —> —оо, р(и) очень
быстро возрастает. Леви показал, что при и —> оо
р(и) ~ ск(а)и~^1}.
Оказывается, что при а, близких к 3/2, это правило
применимо и к очень малым значениям и (если за начало
координат принять такое и, для которого М = 0). Иначе
говоря, плотность р(и) очень быстро начинает удовлетво-
рять слабой форме закона распределения В. Парето (отку-
да и наша терминология).
Предисловие
27
Итак, распределение PL представляется хорошим пер-
вым приближением на всей области изменения и. Однако
те случаи, когда доход подчиняется слабому закону распре-
деления Парето с а > 2, требуют другой теории.
3.	Обоснование выбора закона PL. Устойчивые
распределения таковы, что при X' = a'U + b' и X" =
= a"U + b" сумма X' + X" также имеет вид aU + b (где а
и b зависят от а', а", Ь' и Ь"). Однако одним из наибо-
лее удивительных свойств распределения доходов является
именно его «нечувствительность» к точному определению
слова «доход»: по-видимому, один и тот же закон приме-
ним и к полному доходу, и к различным его составляющим,
взятым по отдельности. Понятое буквально, это свойство
может иметь место только в том случае, когда и части, и
целое подчиняются некоторому устойчивому закону рас-
пределения. Ряд других наблюдений позволяет нам исклю-
чить закон Гаусса (который устойчив), более того, можно
потребовать, чтобы E(U) < оо, а р(—и) быстро убывало
при и —> оо.
Второе обоснование. Устойчивые переменные — это
единственные возможные пределы нормированных сумм
п
А(п) 52 Ui — В(п), состоящих из п переменных Ui9 незави-
г=1
симых и одинаково распределенных (с точностью до выбо-
ра масштаба и начала координат). Предпринимались мно-
гочисленные попытки объяснить распределение доходов,
постулируя, что это распределение «следует» из большо-
го числа «составляющих»: мы надеялись, что можно бу-
дет применить какую-нибудь предельную теорему из тео-
рии вероятностей с тем, чтобы прийти к каким-то выво-
дам о форме «результата», почти ничего не зная о «со-
ставляющих». Между тем, единственным допустимым в
данном случае пределом сумм является закон Гаусса, од-
нако для представления дохода U он практически неприго-
ден, поэтому мы попытались использовать для этого пред-
ставления функцию log U (то есть предположили, что рас-
сматриваемые нами «составляющие» мультипликативны);
28
Предисловие
к сожалению, «логнормальное» распределение не годит-
ся для больших (или отрицательных!) и. Мы заметили,
что негауссовские устойчивые распределения позволяют
предохранить аргумент от аддитивности, не меняя мас-
штаб доходов. Из других наблюдений следует еще и необ-
ходимость E(U) < оо и очень быстрого убывания р(—и)
при и —> оо.
4.	Свойства закона PL. Леви показал, насколько
негауссовские устойчивые законы отличаются от закона
Гаусса; можно заметить, что их свойства превосходно адап-
тируются к экономической действительности. Напомним,
что если U — сумма N переменных вида PL, a 17г распре-
делены одинаково, то имеется вероятность, что значение и
суммы U по большей части состоит из самого большого
среди значений щ'9 если и очень велико, то оно будет мало
отличаться от самого большого из щ.
Точно так же, если U = U' 4- U” (где 17', U" и U —
негауссовские и устойчивые), а и очень велико, то с очень
большой вероятностью или значение и', или и" оказывает-
ся пренебрежимо малым по сравнению с и (однако которое
именно, a priori неизвестно).
5.	Стохастические процессы PL. Будем говорить,
что процесс U(t) имеет вид PL, если любое распределе-
ние I7(ti), [7(t2), • • •, I7(tn) представляет собой п-мерное
устойчивое распределение с 1 < а < 2, а распределе-
ние U (t) подчиняется одномерному закону PL. Для этого
функция Ф(5) на с. 214 (2) должна изменяться только в
том гиперквадранте, когда щ 0 для всех г. Если же эта
функция вырождается в конечное количество J скачков Ф7-
по направлениям Vj9 то вектор U с координатами U(ti)
будет равен сумме J векторов Wj9 где Wj по направлению
совпадает с Vj9 а его длина задана переменной, подчиня-
ющейся закону PL, не зависящей от длин других Wj и
имеющей коэффициент с, равный Ф^.
Обоснование выбора этих n-мерных устойчивых рас-
пределений можно также связать либо с критерием инва-
Предисловие
29
риантности, либо с критерием сложения процессов, разви-
вающихся независимо друг от друга.
6.	Марковские последовательности типа PL; слу-
чай больших значений и. Если некоторая последова-
тельность типа PL (то есть процесс с дискретным време-
нем) является марковской, то она определяется единствен-
ной двумерной переменной {U(£), I7(t + 1)]\
Если имеется только два направления Vj9 одно из ко-
торых — длина оси U(t + 1), то получаем обобщение бро-
уновского движения Орнштейна-Уленбека, рассмотренное
Дж. Л. Дубом.	_
Если все направления Vj отличаются от осей коорди-
нат, то можно показать, что в той области, где u(t) по-преж-
нему велико, функция log U(t) осуществляет «случайное
движение», т. е. что U(t + есть случайная перемен-
ная, не зависящая от Если U (t) — ежегодный доход, то
получаем свойство, которое выдвигал в качестве постулата
Чемпернаун в своей модели закона Парето (3). В насто-
ящей модели это мультипликативное поведение U можно
вывести при куда менее сильных предположениях.
7.	Поведение марковских последовательностей ти-
па PL при и, близких к М. Если u(t) известно, то U(t +
+ 1) можно построить следующим образом. Запишем u(t)
J
как u(t) ~ 22	(0> гДе переменные Uj(t) независимы (мы
не учитываем того, что значение u(t) фиксировано!) и име-
ют тип PL с коэффициентами с, равными, соответствен-
но, (cos )Q (где Qj — угол между Vj и осью U(£)). Затем
J
можно представить U(t + 1) как 22 (tg0j)uj(t). Деление
j=i
на Uj(t) осуществляется заново каждый год. Эта конструк-
ция легко интерпретируется в экономических терминах.
8.	Последовательности, образованные методом не-
постоянных средних. Другая важная категория последо-
вательностей типа PL получается при составлении, с ис-
пользованием вспомогательной последовательности неза-
30
Предисловие
висимых переменных R(t), выражения вида U(t) =
= K(T)R(t — Г), где ядро К (Г) таково, что U (t) схо-
т=о
дится. Конструкция из § 7 остается в силе, но все Uj(t + 1)
существенно зависят от Uj(t),
9.	Заключение. Переменными и процессами типа PL
легко управлять (даже если они представляются очень
«странными» неискушенному взгляду, привычному к гаус-
совским переменным и процессам). Следовательно, они
представляют собой (как минимум) первую удобную ста-
дию в последовательном приближении к реалистической
теории распределения доходов.
(*) Заседание 27 июля 1959.
(х) Это предположение содержится в наших докладах о
работе в C.N.R. S., начиная с 1955 года. См. также замеча-
ния в нашей статье из сборника Information Theory (Butterworth
ed., London, 1956) и в нашей же статье из обзора Psychologic
Frangaise, 4, 1958, р. 237. Формулировку теории в ее первом
достаточно разработанном виде можно найти в двух стереотип-
ных отчетах (январь 1956 и ноябрь 1957 года); кроме того, она
была представлена весной 1958 года на семинаре (Seminaire de
Recherche operationelle, M. G. Th. Guilbaud) в Институте Анри Пу-
анкаре. Более подробно теория изложена в нашей статье, кото-
рая должна появиться в Revue International d’Economique (ян-
варь 1960), и кроме того, готовится к изданию книга Modeles
macrostatistiques.
(2) P.Levy, Addition des variables aleatoires, Paris, 1937.
(3) G. Champemowne, Economic Journal, 63, 1953, p. 318.
Протоколы заседаний Академии наук от 3 августа 1959 года.
(Comptes rendus des seances de Г Academic des Sciences, t. 249,
p. 613-615.)
Предисловие
31
Теория вероятностей и экономика. — Переменные и
стохастические процессы Парето-Леви и
распределение доходов. Записка (*) г-на Бенуа
Мандельброта. Представлена г-ном Морисом Фреше.
Сообщение господина Фреше (г) предоставляет нам случай
упомянуть о третьем обосновании выбора случайных переменных
типа PL и уточнить некоторые детали теории, намеченной в нашей
предыдущей заметке (2) (см. также (3)).
1. Об отрицательных доходах. Как и многие дру-
гие, г-н Фреше отмечает, что, по-видимому, неудобно ин-
терполировать закон распределения доходов с помощью
плотности р(и)9 которая при всех и < 0 остается поло-
жительной. Уточним, что при и —> —оо плотность р(и)
убывает гораздо быстрее, нежели любая показательная
функция ехр(—s|u|), где s > 0. Этот неклассический ре-
зультат получается при замене характеристической функ-
ции 0(£) двусторонней обобщенной функцией G(s) =
= J ехр(—su)p(u)du9 причем можно показать (4), что для
—оо
случайной переменной типа PL упомянутая обобщенная
функция сходится при s > 0:
G(s) = exp [Ms + csQ] при всех s > 0.
В общем виде теория PL представляет собой один
из тех редких случаев, когда G(s) использовать удобнее,
чем 0(C), пусть даже р(и) > 0 при всех и.
Итак, неудобство, связанное с применением закона PL,
a priori вызывает не больше сложностей, нежели их воз-
никает при интерполяции некоторых положительных вели-
чин — таких, например, как рост призывников — с помощью
нормального распределения. (Можно пойти еще дальше и
сказать, что преимущество заключается лишь в том, что од-
на и та же формула (т. е. одна и та же теория) одновременно
охватывает высокие положительные доходы и убытки (то-
гда как средние доходы подчиняются другим механизмам,
не похожим на механизмы, действующие в случае экстре-
мальных величин). Во всяком случае, мы не настаиваем
32
Предисловие
на этом, так как по-прежнему используем закон PL при
рассмотрении других феноменов, где отрицательные вели-
чины не имеют смысла.)
2. О предположении, согласно которому log U есть
переменная, столь же «естественная», как и сама U.
Г-н Фреше указывает, что это предположение позволяет
объяснить закон Парето самым элементарным образом, и
приводит соответствующий пример. В некотором смысле
можно сказать, что модель Чемпернауна (1953), на которую
мы ссылались в (2), представляет собой обоснование фор-
мулы, предложенной Фреше в 1939 году. Кривая Фреше
задает угол при и = mediane(tZ); Чемпернаун же скруг-
ляет этот угол лишь благодаря тому, что вводит большое
количество параметров, практически не поддающихся на-
блюдению.
Использование log С7 представляется достаточно ра-
зумным в рамках теории распределения заработной пла-
ты, т.е. в очень строгой иерархии (3). Однако в общем
случае большое значение и a priori представляет собой
типическую сумму многих составляющих. Следовательно,
отправная точка данной теории неизбежно будет связана
с аддитивным уровнем переменной U. С другой сторо-
ны, использование log 17, даже недостаточно обоснованное,
плодотворно — а значит, желательно — в тех случаях, ко-
гда результатом теоретического рассмотрения должно стать
некоторое приближение. Нам кажется, что наша теория,
основанная на законе PL, кардинально отличается от всех
методов, основанных на log U — отличается тем, что со-
четает оба эти требования. Именно это ее свойство —
в частности, последний абзац из шестого раздела в рабо-
те (2) — образует центральную теорему нашей теории.
3. О знаке разности а — 2 и о зависимости между
аддитивными составляющими U. Очень многих бес-
покоит тот факт, что наша теория ограничивается случа-
ем а < 2. Между тем, нам представляется, что лучше по-
лучить многое, исходя из теории, основанной пусть и на
слабых предположениях, но без гипотезы о независимости
Предисловие
33
различных частей U, Впрочем, независимость и впрямь ка-
жется более разумным предположением для слаборазвитых
обществ и для древних форм развитых обществ, поскольку
для них а < 2. Напротив, в случае современных запад-
ных обществ, где значение а близко к 2 или превосходит 2,
предположение о независимости становится абсурдным.
Принимая во внимание вышесказанное (включая § 2),
можно предложить метод, позволяющий ввести зависи-
мость между составляющими дохода. Мы исходим их то-
го, что марковская последовательность типа PL, т.е. 17 (t),
где U(t) — сумма независимых составляющих Uj(t)9 ве-
дет себя при больших и так же, как и случайное блужда-
ние log U(£) ((2), см. также примечание (3)). Далее предпо-
лагается, что наша зависимость никак не затрагивает того
факта, что log U(t) играет здесь существенную роль, но из-
меняет вероятность того, что значение log U (t) будет расти
при осуществлении этого случайного блуждания величины
дохода. Так можно получить все значения а.
4. О третьем обосновании выбора закона PL. Ре-
грессия в марковской последовательности типа PL и
обобщенная задача Рагнара Фриша. Из построения,
проведенного в § 7 работы (2) следует, что
E{£7(t+l)/u(t)} = Q'u(t) и E{I7(£)/u(t+l)} = Q'-u(£+l);
более того, можно показать, что для стационарного процес-
са Q 1 и Q' 1.	___
Этот результат по-прежнему верен, если векторы Vj
направлены вдоль осей координат. (Однако случайное дви-
жение из § 6 работы (2) и из рассмотренного выше § 2 воз-
можно лишь тогда, когда векторов Vj9 направленных вдоль
упомянутых осей, не существует.)
Эта линейная регрессия тесно связана со следующей
задачей, которую поставил Р. Фриш, а разрешили К. Р. Рао и
Э. Фикс (6). Положим X = aZ + А и Y = bZ + В, где Л, В
и Z — независимые случайные переменные, а а и b — числа.
Требуется найти условия, при которых регрессия Y на X
линейна, в предположении, что первые моменты случай-
ных переменных конечны и даже равны нулю, если это не
3 Б. Мандельброт
34
Предисловие
меняет хода рассуждений. Как выясняется, для этого необ-
ходимо и достаточно, чтобы Z, А и В были устойчивыми
переменными с конечным вероятным значением, то есть
либо гауссовскими, либо разностями переменных типа PL,
произвольным образом взвешенными. Если к тому же потре-
бовать, чтобы р(и) при и —» —оо очень быстро убывало,
то эти переменные должны быть либо гауссовскими, либо
типа PL.
Построение, проведенное в §7 работы (2), обобщает
выражения Р. Фриша, так как при условии наличия векто-
ров Vj, направленных вдоль осей, можно записать:
Х(= U(t)) = Y^Zj+A и Y(= tf(t+l)) = Ybizj+B-
Оказывается, необходимое и достаточное условия
остается тем же самым.
Теперь предположим, что линейная регрессия — это
экспериментальный факт или желаемая аппроксимация
некоторого эксперимента. Допустим также, что построе-
ние из § 7 работы (2) можно интерпретировать каким-либо
внутренним образом — например, вводя флуктуации курсов
валюты при различном ее размещении. Эта курсы зависят
от aj и bj, а их регрессия должна оставаться линейной
независимо от их значений. Допустим, наконец, что плот-
ность р(и) не может быть гауссовской и очень быстро убы-
вает при и —оо.
Тогда последовательность годовых доходов должна
быть последовательностью типа PL, а годовой доход —
переменной типа PL. Таково третье обоснование нашего
фундаментального предположения.
(г) M.Frechet, Comptes rendus, 249, 1959, р. 1837.
(2)	В. Mandelbrot, Comptes rendus, 249, 1959, р. 613.
(3)	Воспользуемся случаем, чтобы указать на две опечатки
в (2): а) во второй строке § 3 вместо ОК следует читать X =;
Ь) во второй строке с. 615 вместо U(t + 1) — u(t) следует чи-
тать U(t + l)/w(t) или, что точнее, [U(t + 1) - M]/[u(t) - М].
Сделаем также небольшое замечание относительно терми-
нологии: в терминологии П.Леви закон PL не квалифицируется
Предисловие
35
как «устойчивый», кроме случая М = 0; иначе говоря, его сле-
дует считать «квазиустойчивым». Однако Гнеденко и Колмогоров
используют слово «устойчивый» в двух случаях (см. их «Предель-
ные распределения сумм независимых случайных переменных»,
в английском переводе «Limit distributions for sums of independent
random variables», 1954). Это дает нам право считать два обосно-
вания из третьего параграфа (2) абсолютно эквивалентными.
(4)	См., например, теорему IV, с. 7 из Paley and Wiener,
Fourier Transforms in the Complex domain, 1934.
(5)	H. F. Lydall, Econometrica, 27,1959, p. 110. Формально эта
теория идентична теории частоты повторения слов в разговоре
(закон Эсту-Ципфа), которую мы предложили в Comptes rendus,
232, 1951, р. 1638 и существенно развили позже. Мы думали о
модели такого же типа, как у Лайделла, но не опубликовали ее,
поскольку использование log U не показалось нам оправданным.
(6)	C.R.Rao, Econometrica, 15, 1947, р. 245-249 (erratum
17, 1949, р. 212); E.Fix, Berkeley symp. On Math. Statistics and
Probability, 1949, p. 79-91. См. также R.G. Laha, Annals of Math.
Statistics, 27, 1956, p. 187-1195. Эта задача Фриша очень тесно
связана с «характеристическим свойством нормального закона ве-
роятностей», исследованным Ж. Дармуа (см. G. Darmois, Comptes
rendus, 232, 1951, р. 1999).
Протоколы заседаний Академии наук от 23 ноября 1959 года.
(Comptes rendus des seances de Г Academic des Sciences, t. 249,
p. 2153-155.)
3*
36
Предисловие
Теория вероятностей и статистическая экономика. —
О некоторых спекулятивных ценах: эмпирические
факты и модель, основанная на аддитивных
устойчивых негауссовских процессах Поля Леви.
Записка (*) г-на Бенуа Мандельброта. Представлена
г-ном Жозефом Кампе де Ферье.
1.	Новое эмпирическое наблюдение. Для начала рас-
смотрим, как меняются во времени некоторые спекулятив-
ные цены. Кривые 1 и 2 на рис. 1 относятся к це-
нам на хлопок на различных американских рынках при
условии немедленной доставки товара; однако очень по-
хожие результаты верны и для других видов сырья,
а также для некоторых промышленных продуктов. Ес-
ли Z(t) — цена при закрытии биржи в день t, то
L(t,T)=lnZ(t+T) — InZ(t). Кривыми la и 2а пред-
ставлены зависимости Fr[L(t, 1) > и] и Fr[L(t, 1) < —и]
за 1900-1904 годы; кривыми 1Ь и 2Ь — зависимости
Fr[L(t, 1) > и] и Fr[L(t, 1)<—и] за 1944-1958 годы; кри-
выми 1с и 2с — зависимости Fr[L(t, один месяц)>и] и
Fr [Z(i, один месяц) <—и] за 1880-1940 годы. Мы исполь-
зовали билогарифмические координаты (удивительно, что
до сих пор — по крайней мере, насколько нам известно —
никто не попытался представить изменения цен подобным
образом). Под Fr здесь понимается относительная частота.
Очевидно, что все эти кривые, пусть и различные,
очень быстро превращаются в прямые с одинаковым уг-
лом наклона, близким к а = 1,7. Итак, можно записать,
что
log{Fr[L(t,Т) > и]} ~ —alogu + logC'(F),
log{Fr[£(t,T) < -u]} - -alogu + logC"(T).
Таким образом, два «хвоста» асимптотически удовле-
творяют закону Парето; С' / С", следовательно, имеется
легкая асимметрия; среднее значение Z(t, Т) практически
равно нулю.
Поскольку кривые 1а и 1b параллельны, распределе-
ние L(t, 1) за все время войны претерпело измене-
ния только в масштабе. Мы убедились, что за период
Предисловие
37
шкала абсцисс рисунков 2а, 2Ь и 2с
u=0,01 u = 0,l	и=1,0
шкала абсцисс рисунков la, 1b и 1с
Рис. 1. Кривые la, 1b, 1с, 2а, 2Ь и 2с: см. объяснения в тексте
с 1816 по 1940 годы распределение L(t, 1) изменилось
очень мало. Итак, параллельность кривых 1а и 1с (рав-
но как и кривых 2а и 2с) показывает, что распределение
один месяц) отличается от распределения L(t, 1) толь-
ко масштабом: можно сказать, что закон распределения
L(t,T) «устойчив относительно изменения Г». Заметим
также, что при а < 2 распределение L(t, 1) содержит толь-
ко первый момент (рис. 2); иными словами, большая часть
статистических «рецептов» оказывается неприменимой.
2.	Аддитивная модель изменений цен. Видоизме-
нив классическую гипотезу Башелье, предположим, что
последовательные изменения logZ(t) независимы. В этом
случае устойчивость, рассмотренная в §1, сливается с
устойчивостью в смысле Поля Леви, а характеристическая
функция для L(t, Г) неизбежно принимает вид
НС) = exp{iMC - СТ|£|“ [1 - tg(jcwr)]},
38
Предисловие
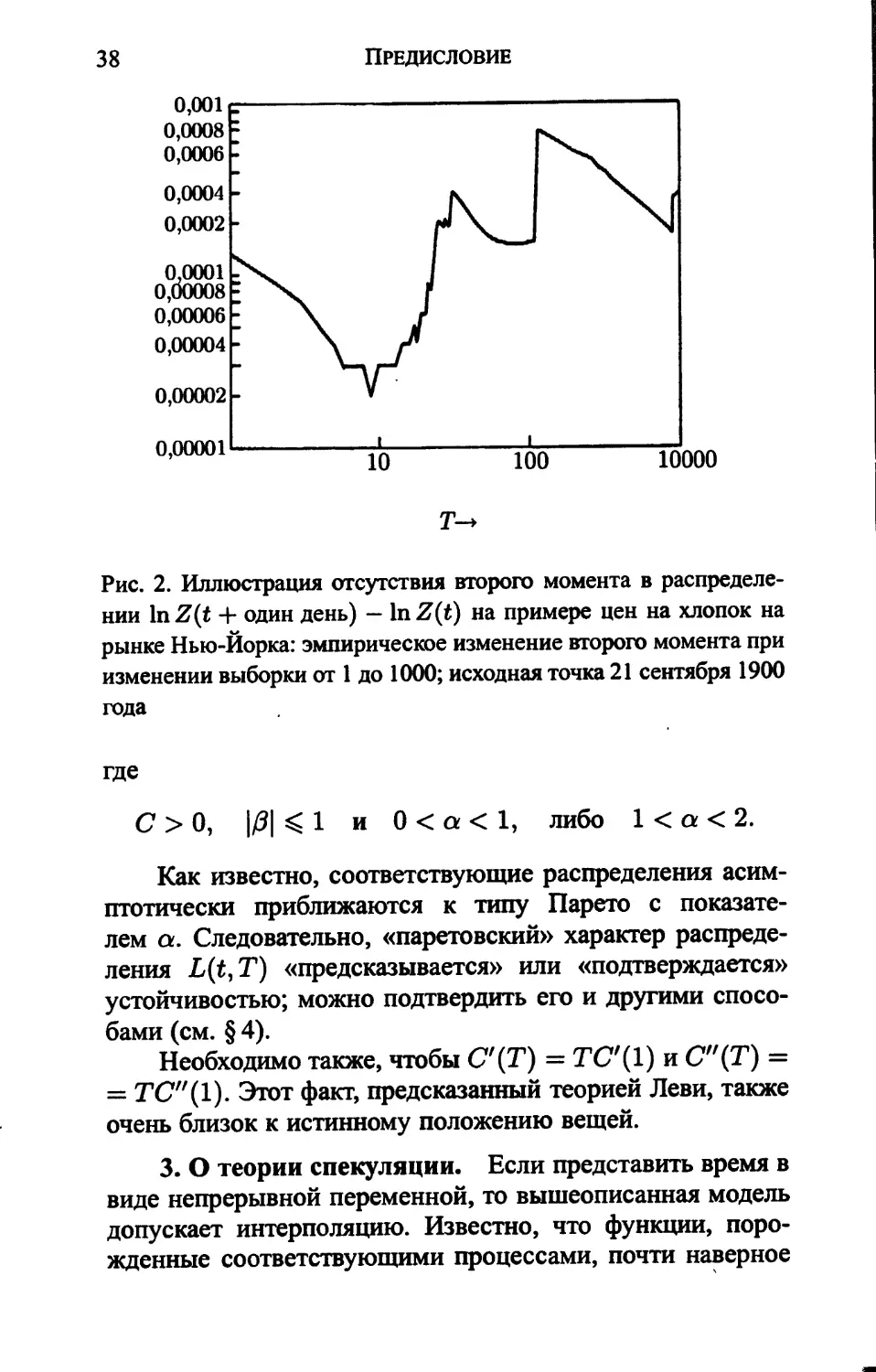
Рис. 2. Иллюстрация отсутствия второго момента в распределе-
нии lnZ(t + один день) — InZ(t) на примере цен на хлопок на
рынке Нью-Йорка: эмпирическое изменение второго момента при
изменении выборки от 1 до 1000; исходная точка 21 сентября 1900
года
где
С > 0, \0\	1 и 0 < а < 1, либо 1 < а < 2.
Как известно, соответствующие распределения асим-
птотически приближаются к типу Парето с показате-
лем а. Следовательно, «паретовский» характер распреде-
ления L(t,T) «предсказывается» или «подтверждается»
устойчивостью; можно подтвердить его и другими спосо-
бами (см. § 4).
Необходимо также, чтобы С'(Т) = ТС"(1) и С"(Т) =
= ТС"(1). Этот факт, предсказанный теорией Леви, также
очень близок к истинному положению вещей.
3.	О теории спекуляции. Если представить время в
виде непрерывной переменной, то вышеописанная модель
допускает интерполяцию. Известно, что функции, поро-
жденные соответствующими процессами, почти наверное
Предисловие
39
и почти всюду разрывны. Отсюда вытекают весьма значи-
тельные с точки зрения теории спекуляции следствия. Ве-
роятность разорения равна нулю только тогда, когда маржа
составляет 100%.
4.	Более подробно с только что представленными
результатами можно ознакомиться в докладе NC-87 Ис-
следовательского центра компании IBM, расположенного
в Йорктаун-Хайтс (штат Нью-Йорк, С. Ш. А.). Наша тео-
рия спекулятивных цен обнаруживает теснейшую связь с
нашей же теорией доходов, изложенной ранее (г).
(*) Заседание 21 мая 1962 года.
(г) International Economic Review, 1,1960, р. 79-106 и 3,1962
(готовится к печати); Econometrica, 29, 1961, р. 517-543; Quarterly
Journal of Economics, 76, 1962, p. 57-85.
Протоколы заседаний Академии наук от 4 июня 1962 года.
(Comptes rendus des seances de Г Academic des Sciences, t. 254,
p. 3968-3970.)
40
Предисловие
Теория вероятностей и статистическая
климатология. — Класс стохастических процессов,
гомотетичных самим себе; их приложение к
климатологическому закону Г. Э. Херста. Записка (*)
г-на Бенуа Мандельброта. Передана г-ном Жозефом
Кампе де Ферье.
1. Последовательная кумулятивная область и эм-
пирический закон Херста. Пусть X(t) есть некоторая
непрерывная действительная функция времени t; запишем
max[X(t)-X(t0)]- пйп [X(t)-X(t0)].
Эта функция M (назовем ее «последовательной кумулятив-
ной областью» функции X) играет важную роль в инже-
нерном деле. Например, некоторые методы расчета плотин
основываются исключительно на значении функции М, где
под X(t) —X(t°) понимается количество воды, протекаю-
щей сквозь сечение реки за время от t° до t, и, в мень-
шей степени, на вероятном значении этого количества. От-
сюда — очень тщательное изучение эмпирических значе-
ний М, осуществленное Гарольдом Эдвином Херстом (х).
Херст установил и гораздо более общий факт, состоящий в
том, что к множеству хроник, связанных с метеорологией —
таких, как изменение уровня воды, температуры, давления,
толщины слоев и т. д. — применимы следующие законы:
1) значение M(t°, Г) пропорционально величине Тн,
где Н — некоторая константа;
2) значение Н находится в промежутке между 1/2 и 1,
чаще всего вблизи 3/4.
Известно, что Н = 1/2 в случае, когда X — «бро-
уновское движение» Башелье, Винера и Леви, и что зна-
чение М асимптотически пропорционально Г1/2 для всех
остальных рассмотренных ранее стохастических процессов
с конечными вторыми моментами (2). Таким образом, от-
крытие Херста имеет столь же теоретическое, сколь и прак-
Предисловие
41
тическое значение. Из него обычно делают вывод, что ме-
теорологические последовательности нестационарны даже
в первом приближении, а изменение М отражает измене-
ния климата, пока еще не доступные для вероятностного
анализа. Я надеюсь показать, что это не всегда так.
2.	Случайные функции, гомотетичные самим себе.
В дальнейшем этим термином мы будем обозначать новый
класс функций X (t), определяемых следующим свойством.
Процесс, порождающий X, таков, что существует кон-
станта Я, для которой приведенная функция T~HX(Th)
(где 0 < h < 1) подчиняется не зависящему от Т закону
распределения (равномерно гомотетична самой себе) или,
по меньшей мере, асимптотически не зависит от Т (асим-
птотически гомотетична самой себе).
Броуновское движение гомотетично самому себе с
константой Н = 1/2; обобщим его на значения Н в диапа-
зоне от 1/2 до 1 (3).
Если функция X гомотетична самой себе, то среднее
значение последовательной кумулятивной области должно
удовлетворять эмпирическому закону Херста. Точно так же
и средние значения других мер отклонения функции X (t)
(например, среднеквадратичное отклонение) должны быть
пропорциональны Тн,
3.	Пример. Пусть время дискретно, а
X'(t) = X(t)-X(t-l);
предположим, что E[X'(t)X'(t 4- г/)] есть функция С(у),
зависящая только от и (иначе говоря, Хг является стаци-
онарной функцией второго порядка). Предположим также,
что
1йп С(й(г//1/°)2”2Я = 1 или -1 < 2Я-2 < 0 и р° > 0.
Р—>оо
В этом случае дисперсия разности X (tQ 4- Т) — X(t°) зада-
ется формулой
ТС(0) + 2££ОД
Г=1 3=1
42
Предисловие
и ведет себя асимптотически, как Т2Н. То есть можно по-
строить приведенную функцию T~H[X(t9 + Th) — X(t0)]
и действительно показать, что эта функция по распределе-
нию стремится к некоторому пределу при Т —> оо. Отсюда
следует, что разность X(t) — X(t°) асимптотически гомо-
тетична самой себе.
Сформулированное выше условие относительно С(у)
выполняется, если
X'(t)= £ K(t — s)Y'(s),
s=—оо
где переменные Y'(t) ортогональны, а К есть ядро, огра-
ниченное так, чтобы значение К(з)з”я+3/2 стремилось
при $ —> оо к некоторому конечному пределу. Такая функ-
ция X(t) образует «подвижное среднее», для которого по-
следствия старых «причин» убывают до нуля гораздо мед-
леннее, чем в случае К = ехр(—Ьз), характерном для мар-
ковских процессов.
4.	Процессы, равномерно гомотетичные самим се-
бе. Для равномерной гомотетии необходимо, чтобы вре-
мя было непрерывным, функция X гауссовской, а ее про-
изводная Хг должна для всех и иметь ковариацию, рав-
ную {у/у^)2Н~2. Следовательно, для и = 0 эта ковариа-
ция бесконечна или, иначе говоря, допустима только в том
случае, когда мы обобщаем теорию случайных функций,
допуская белый шум (то есть такие ковариации, при кото-
1
рых / C(s)ds < оо).
о
Ковариация С(у) = (у/у^)2Н~~2 соответствует по-
движному среднему некоторого белого шума, взвешенного
с помощью ядра, пропорционального зя”3/2. То есть речь
в данном случае идет о дробном интеграле белого шума в
смысле Римана и Лиувилля.
Равномерно гомотетичные самим себе процессы по-
лучаются как пределы при б = 0 процессов, определенных
Предисловие
43
для t, кратного €, с помощью ковариации
[1/2Н-2(1/+£)2Я+(1/+2£)2Я>-2(1/°)-2Я(2Я)-1(2Я-1)-1.
Интерполяция и экстраполяция. Если известно, что
Х(0) = О, Х(Т) и Е(Х) = 0, то вероятное значение при
условии X (t) оказывается таким, что непрерывную и диф-
ференцируемую нелинейную функцию
E[x(t)|x(T)]/x(T) = |[|t/r|2H +1 - |i - г/т|2Я]
можно при t —> оо продолжить с помощью экстраполяции,
пропорциональной (f/T)2#”1. Тот же результат применим
и в случае асимптотической гомотетии, если Т очень вели-
ко.
5.	Абсолютно непрерывные спектры, бесконечные
в начале координат, и разложение X(t) на направ-
ляющую и колеблющуюся части. Закон Херста экви-
валентен предположению о том, что спектральная плот-
ность 5(и>) производной X'(t) при малых ведет себя
как £>и>1-2Я. В этом случае плотность 5(0) бесконечна,
но спектр не содержит «полосы» в точке и) = 0. Со ста-
тистической точки зрения при данной выборке конечной
длины Т° эмпирический спектр нельзя отличить от сум-
мы, состоящей из функции Дирака в начале координат и
функции, равной S(u>) при ш > 1/Tq и вырождающейся
в	в противном случае. Это равносильно раз-
делению каждой выборки на две составляющих: колеблю-
щуюся и другую, которую можно интерпретировать как
направляющую или как выражение «климата». Таким об-
разом мы, по-видимому, реабилитируем предположение о
конечной плотности 5(0), что эквивалентно абсолютной
интегрируемости С и приводит нас к заключению, что и от-
клонения, и последовательная область X пропорциональ-
ны Т1/2. Действительно, по мере увеличения Т° направля-
ющую приходится вновь интерпретировать как проявление
некоторого все возрастающего числа «медленных циклов».
Иначе говоря, мое объяснение закона Херста равнозначно
44
Предисловие
использованию одного и того же механизма как для мед-
ленных изменений климата, так и для быстрых изменений
уровня осадков (4).
6.	Практическое использование процессов, гомоте-
тичных самим себе. Статистическое исследование про-
цессов, гомотетичных самим себе, еще только начинается.
Необходимо определить законы распределения различных
мер отклонения X(t) — для того, чтобы мы могли осо-
знанно оценивать величину Н на основании малых выбо-
рок (выборки Херста чрезвычайно длинны, так что оценка
представляет некоторую сложность).
Есть опасение, что такое статистическое исследование
окажется слишком сложным и вынудит нас прибегнуть в
конечном счете к численным методам — таким, например,
как метод Монте-Карло. Так, при расчете плотин можно
будет вычислить вероятность того, что плотина данной вы-
соты приведет к высыханию реки прежде, чем пройдет Т
лет. К счастью, нет необходимости проводить отдельные
вычисления для каждого значения высоты и Т. Действи-
тельно, свойство «самогомотетичности» позволяет исполь-
зовать классический метод анализа размерностей: проведя
вычисления для Т = 100 и всего диапазона высот, можно
без труда получить вероятности, относящиеся к любому
другому значению Т. (*)
(*) Заседание от 22 февраля 1965 года.
(г) Н.Е. Hurst, Trans. Amer. Soc. Civil Eng., 116, 1951,
p. 770-808; Proc. Inst. Civil Eng., 1, 5, 1956, p. 519-590. Крат-
кий обзор этих работ и ссылки на теоретические работы, предше-
ствовавшие моей, можно найти в книге Р. А. Р. Moran, The theory
of storage, J. Wiley, 1959, p. 65.
(2) Эта гипотеза приемлема во многих случаях, однако она
вовсе не очевидна, и в ряде климатологических последователь-
ностей нам даже приходится от нее отказаться. Отказавшись же,
можно обратиться к теории «устойчивых» случайных перемен-
ных Поля Леви, видоизменив при этом некоторые мои результаты,
относящиеся к изменению цен. См. мою работу The variation of
certain speculative prices (J. Business, 36, 1963, p. 394-419), опуб-
Предисловие
45
ликована также в антологии Пола Кутнера The random character
of stock market prices, ed. by Paul H. Cootner), MIT Press, 1964.
(3). Концепцию «самогомотетичности» можно так же обоб-
щить на значения Н, меньшие 1/2, но для этого надо сна-
чала ввести новые концепции условной случайной функции и
условной стационарности. См. мою статью Self-similar error
clusters in communication systems and the concept of conditional
stationarity (I.E.E.E. Trans. Communication Technology, COM-12,
1964, p. 155-174), а также мой доклад Self-similar turbulence and
non-Wienerian conditional spectra.
(4) О дальнейшем исследовании этих проблем сообщается
в моих докладах Self-similar random processes and the range, и
Self-similar random processes: extrapolation, interpolation and decay
ofperturbations.
(P. O. Box 218, Yorktown Heights,
New-York, U. S.A.)
C. R. Acad. Sc. Paris, t. 260, p. 3274-3277 (22 марта 1965 года).
ЧАСТЬ ПЕРВАЯ
ФРАКТАЛЫ
В названии этой книги перед двумя старыми и хоро-
шо известными (если не сказать «интуитивно понятны-
ми») терминами стоит термин относительно новый и все
еще немного загадочный. В приведенных выше работах о
фракталах не упоминается, однако идея фрактальности
там все же присутствует, пусть и в скрытом виде; впро-
чем, сам о том не подозревая, я использовал эту идею еще
в своей докторской диссертации, защищенной в Париже
в 1952 году. Таким образом, на понятии фрактала стоит
остановиться подробнее.
Глава 1.1 представляет собой общее введение, в ней
поднимается ряд очень старых и весьма настоятельных
вопросов, остававшихся долгое время без ответа.
Глава 1.2 состоит из двух частей. Она начинается
с очень краткого описания некоторых классических то-
чек зрения на самоподобие. Заканчивается глава 1.2 са-
моаффинностью — темой, центральной для моих работ,
посвященных финансам. Вопросы, о которых идет речь,
стоят в повестке дня, это предмет очень активных иссле-
дований, им посвящены мои работы из «Selecta», начиная
с [М1997N] и [М1997Н].
В главе 1.3 вкратце изложены концепции, позволя-
ющие осуществить количественное исследование фрак-
тальности — если предположить, что числами вообще
можно измерить «шероховатость» в широком семействе
объектов, включая финансовые графы. Здесь же мы позна-
комимся с поразительным числом, называемым фракталь-
ной размерностью, и выясним, почему при рассмотрении
48
ЧАСТЬ ПЕРВАЯ
интересующих нас вопросов удобнее воспользоваться по-
казателем Гёлъдера-Херста Н.
Эта книга не является введением в теорию фрак-
талов. Кроме [М19750] (Les objets fractals, forme, hasard
et dimension) на французском языке опубликовано мно-
жество других простых обзоров — например, [М 1982п],
[М1997FS], [Gouyet 1992], [Sapoval 1996].
Глава 1.1
Признанный и принесший
плоды «мезальянс»
Почему унаследованная от Евклида геометрия так ча-
сто удостаивается определения «холодной» и «сухой»? От-
части потому, что она неспособна описать форму финансо-
вой хроники, облака, горы, морского берега или дерева. Фи-
нансовые хроники — это не периодические колебания, не
восходящие или нисходящие прямые, изображающие «тен-
денции»; облака — не сферы, горы — не конусы, берега
островов — не окружности, кора дерева отлична от поверх-
ности цилиндра, а молния ударяет отнюдь не по прямой.
Лишь художники всегда это понимали, а Эжен Дела-
круа (1798-1863) однажды, говоря об архитектуре, очень
удачно заметил: «Человек все идеализирует. Прямая ли-
ния — его изобретение, в природе прямых нет».
О неизбежных вопросах
Эта несостоятельность геометрии привела к тому,
что научная литература оказывается неспособной (ничуть,
впрочем, этим не огорчаясь) дать сколько-нибудь вразуми-
тельный ответ на некоторые неизбежно возникающие во-
просы, в чем несложно убедиться на приведенных ниже
примерах.
«Как измерить изменчивость биржевых хроник — хотя
бы для того, чтобы иметь возможность реалистично оце-
нивать финансовый риск?»
«Как измерить длину берега Бретани?»
4 Б. Мандельброт
50
Глава 1.1
«Как можно охарактеризовать форму речного берега,
линии водораздела или границы области притяжения, при-
чем не с гидравлической, но с динамической точки зре-
ния?»
«Как измерить и сравнить шероховатость самых обык-
новенных объектов — таких, например, как расколотый ка-
мень, склон горы или кусок ржавого железа?»
«Какова форма облака, языка пламени, сварного шва?»
«Какова плотность распределения галактик во Вселен-
ной?»
Говоря в целом, я еще в самом начале своей научной
карьеры пришел к выводу, что многочисленные реально
существующие формы настолько нерегулярны или изло-
маны, что сложность Природы не только количественно,
но и качественно превосходит все то, что допускает гео-
метрия Евклида. Для того, чтобы охарактеризовать отрезок
или окружность, достаточно некоторого небольшого коли-
чества отдельных измерений, в природе же это число столь
велико, что его можно считать практически бесконечным.
Существование вышеупомянутых объектов бросает
нам вызов: сможем ли мы описать форму того, что гео-
метрия объявила «бесформенным» или «аморфным». До
сих пор этот вызов оставался без ответа.
Метод: фрактальная геометрия
Решившись принять упомянутый вызов, я задумал и
разработал новую геометрию природы, а затем использо-
вал ее во множестве различных областей. Я не говорю
«применил», поскольку развитие фрактальной геометрии
происходило исключительно в связи с этими различными
способами ее использования.
Фракталы — это объекты (математические, природные
или созданные человеком), которые мы называем непра-
вильными, шероховатыми, пористыми или раздробленны-
ми, причем указанными свойствами фракталы обладают в
одинаковой степени в любом масштабе. Можно сказать, что
Средства: важность непосредственного наблюдения 51
форма этих объектов не изменяется от того, рассматри-
ваем мы их вблизи или издалека. В финансовом смысле, как
мы скоро увидим, фрактальность означает изменчивость,
одинаковую на всех уровнях.
Изучение таких объектов составляет задачу фракталь-
ной геометрии. Она тесно соприкасается с соседними обла-
стями человеческой деятельности, в результате чего можно
говорить о существовании, например, геометрии стихий-
ного случая и геометрии хаотического детерминизма.
Речь, по сути, идет не о новой теории и, тем более,
не о новой дисциплине, но о новом методе. Его изначаль-
ная цель совпадает с целью любой науки: искать элементы
порядка, способные прояснить хаос тех посланий, которые
Человек получает от своих органов чувств. Успешнее всего
мой метод проявляет себя при разрешении старых и новых
вопросов без ответов, а также старых и новых ответов без
вопросов (ниже я поясню, что это такое).
Библиография четвертого издания моей книги
[М19750] включает в себя сотни специальных книг, по-
священных фракталам, показывая тем самым, что мой эн-
тузиазм оказался заразительным, а область применимости
фракталов вышла далеко за рамки моих работ по финансам
и других моих первоначальных замыслов. И все же имен-
но я первым осознал и во всеуслышание объявил о том,
что фракталы — не панацея; я вовсе не рекомендую фрак-
тальные методы всем подряд, и уж тем более никогда не
пытался навязывать их кому бы то ни было.
Средства: важность непосредственного
наблюдения
Поставленные в начале этой главы конкретные вопро-
сы оставались без ответа исключительно ввиду отсутствия
подходящих средств наблюдения. Для решения этих вопро-
сов не годилось ни одно из имеющихся в нашем арсенале
средств, однако продолжительные усилия, начинавшиеся с
всевозможных заимствований, из областей приземленных
4*
52
Глава 1.1
и возвышенных, мало-помалу позволили нам составить но-
вый арсенал, пригодный для реализации фрактального ме-
тода.
Прежде всего я позаимствовал у так называемых «чи-
стых» наук главный инструмент естественной истории
прошлых эпох. Речь идет о непосредственном наблюде-
нии, простом взгляде, на помощь которому, что вполне
естественно, приходит впоследствии все, что только мож-
но вообразить, — так натуралист помогает своему глазу,
используя лупу или микроскоп.
Экономист, желающий получить объективную коли-
чественную картину происходящего на рынке, с легко-
стью пренебрегает мелкими деталями журнальных графи-
ков, представляющих изменения цен. Зачастую он спешит
эти графики «пригладить», чтобы разглядеть скрытую под
внешней оболочкой реальность, которую он полагает наи-
более существенной. Философы, как правило, любят пого-
ворить о противоречии между «внешним видом» и «су-
тью вещей»; известно, что великий математик Лагранж
(1736—1813) настаивал на том, чтобы изгнать из механи-
ки все рисунки и чертежи, причем он не был ни первым,
ни последним математиком-иконоборцем.
Я же, напротив, испытываю глубокое почтение ко все-
му, что можно обнаружить при «поверхностном» наблюде-
нии — при условии, разумеется, что это наблюдение доста-
точно продолжительно и беспристрастно.
Средства: «принцип масштабирования»
Очень часто «внешний вид» позволяет осуществить
лишь качественное наблюдение, что приводит порой к си-
туациям анекдотичным или даже достойным отнесения к
фольклору. Разумеется, всем известно, что как анекдоты,
так и фольклор правдивы далеко не всегда — а значит, слиш-
ком доверять им не надо, однако и отвергать без разбору
не следует.
Именно поэтому я вполне буквально воспринимаю тот
анекдот, где некто, изучая зигзаги в биржевой хронике, взя-
Средства: «принцип масштабирования»
53
той из какого-то журнала и не зная ее масштаба, не смог
сообразить, что представляют собой эти колебания: часо-
вые, дневные или месячные изменения цен. Точно так же,
разглядывая карту, на которой не указан масштаб, мы не
сможем догадаться о размерах неизвестного архипелага.
Так, принимая некоторые анекдоты всерьез, я нашел и
определил средства, позволяющие придать им точное вы-
ражение, равно как и подвергнуть строгой проверке, сперва
экспериментальной, потом (в зависимости от случая) тео-
ретической или математической.
Первый набор инструментов, позволяющих заняться
изучением этих разнообразных и очень будничных про-
блем, я нашел в работах моего учителя и великого специа-
листа в теории вероятностей Поля Леви (1886-1971).
Второй набор я разыскал среди тех монструозных —
иначе говоря, патологических — образований, первые при-
меры которых датируются 1838 годом и которые доста-
вили столько радости математикам-иконоборцам в период
с 1875 по 1925 год. Математики очень быстро отказались
от этих монстров, заявив, что им недостает общности, а
может быть, потому что эти примеры были слишком спе-
цифичны, чтобы стать действительно знаменитыми. На тот
момент, когда они привлекли мое внимание, никаких осо-
бых применений им так и не нашлось.
Эти объекты можно было бы назвать «ответами без
вопросов», по меньшей мере, без качественных вопросов.
Среди трех небольших книг на французском языке, кото-
рые, по моим расчетам, должны появиться почти одновре-
менно, есть и «Полеты над фракталами», [М 1997FS], эта
книга возвращает нас к задаче детального описания приро-
ды этих претенциозных «монстров» и рассказывает о том,
как фрактальной геометрии удается сорвать с них покров
таинственности. Сначала эта геометрия приняла некоторых
из них в свои ряды, а затем — и это главное — помогла им
умножиться в удивительном количестве.
Есть ли среди всех этих заимствований со всех сторон
и переплетений всевозможных далеких друг от друга дис-
циплин какая-нибудь связующая нить, объединяющая их в
54
Глава 1.1
рамках одного метода? Этой связующей нитью, определя-
ющей понятие фрактала, стала идея о том, что некоторые
феномены нашего мира имеют одинаковую структуру при
рассматривании их вблизи или издалека (т. е. в любом мас-
штабе) — когда мы увеличиваем картинку, желая разгля-
деть что-либо получше, изменяются лишь незначительные
детали. Так, каждый малый участок фрактала представляет
собой ключ к целой конструкции.
Мы будем обозначать эту идею как «принцип мас-
штабирования», ему соответствует английское выражение
«principle of scaling». Он проявляется и при слиянии эле-
ментов, далеких друг от друга по внешнему виду. Я увидел
самоподобие не только в фольклоре, о котором я говорил
выше, но и в структуре тех математических монстров, ко-
торые были открыты с 1875 по 1925 годы! В последнем
случае самоподобие не вызвало заметного интереса и бы-
ло поэтому так же отброшено, когда эти объекты подверг-
лись обобщению для нужд математиков. Никто не работал с
самоподобием систематически, не существовало даже тер-
мина для его обозначения, такой термин появился лишь на
поздней стадии моих работ.
К самоподобию очень близко более общее понятие са-
моаффинности, в главе 1.2 будет показано, что в рассужде-
ниях о финансах оно оказывается более приемлемым.
Значение инвариантностей
В более общих словах, фрактальная геометрия посто-
янно обращается к различным понятиям инвариантностей.
Это последнее слово очень важно: если бы мой подход из-
начально не зависел от подходов других математиков и от
физики моего времени (так же, впрочем, как и от эконо-
мической науки), то фрактальная геометрия разделила бы
судьбу той стержневой идеи, которую высказал еще Феликс
Клейн (1849-1925): важные научные идеи охотнее всего ор-
ганизуются вокруг инвариантностей и структур.
Общее понятие инвариантности, свойственной фрак-
талам, характеризуется английским прилагательным «sea-
Фракталы и хаотическая динамика	55
ling». Ввиду отсутствия эквивалента, это слово можно
использовать и во французском языке. Предпочитая ему
французский неологизм, не слишком отличающийся от
него по произношению, я вернулся к английской паре
scalar-scaling, ведущей свое происхождение от латинско-
го слова scalax. Латинское scala уже дало во французском
языке слово «scalaire»1 2, поэтому я предлагаю использовать
и второе слово из вышеприведенной английской пары в
форме «sealant»3.
Фракталы и хаотическая динамика
Изначально, особенно в моих работах, посвященных
финансам, фрактальная геометрия была прежде всего об-
ращена к статистике. Таким образом, в книге [М19750]
(«Фрактальные объекты») предлагалось не просто описы-
вать горы, облака, деревья, скопления галактик и следы
биржевого курса, но описывать их достаточно совершен-
ным образом, позволяющим имитировать эти реальные
объекты и создавать их дубликаты с помощью математиче-
ских формул (весьма, надо сказать, простых). Тот факт, что
эти дубликаты или имитации были основаны на статисти-
ческих моделях, вызывал законное удивление. Потому что
никто не ожидал, что в объяснении происходящего окажет-
ся столько случайного.
Написанный мною для проводившегося в 1964 году
Международного конгресса обзор (вышел в свет этот текст
гораздо позднее [М 1987г]) привел меня к противопостав-
лению двух стадий неопределенности, которые я в главе 2.1
называю случайностью «ручной» и случайностью «стихий-
ной», или даже «дикой». В главе XIII «Фрактальных объ-
ектов» я говорю о том, как долго в своих трудах я колебал-
1 Которое можно перевести, помимо прочего, как «шкала» или «мас-
штаб». — Прим, перев.
2Скалярный, скаляр (франц.). — Прим, перев.
3По-русски получается что-то вроде «масштабируемый». — Прим, пе-
рев.
56
Глава 1.1
ся относительно других терминов, которые не столь легко
сходили с языка.
Более того, только закончив «Фрактальные объекты», я
понял, что формальные фракталы можно столь же успешно
использовать в динамике. В моей первой английской кни-
ге, [М 1977F], об этом упоминается на с. 255-9, там же я
цитирую Адамара и Пуанкаре.
Однако теория детерминистского хаоса как раз тогда
находилась в стадии образования. Очень хорошо читает-
ся книга, написанная на эту тему Глейком [Gleick 1986].
Фундаментальный факт состоит в том, что динамическая
система может быть абсолютно детерминистской, но не
обнаруживать правильного и ручного поведения, а имен-
но этим поведением ограничиваются все известные мне
курсы механики. Она может обнаруживать так называемые
хаотические формы поведения. Они неслучайны, но рас-
сматривать их как нечто, возникающее не результате сти-
хийного случая, стоит большого труда.
Изучение детерминистского хаоса порождает бесчис-
ленное количество очень сложных геометрических форм.
Обычная геометрия полностью непригодна для их изуче-
ния, тогда как фрактальная геометрия изначально представ-
ляла собой средство, в высшей степени подходящее для их
изучения. Например, мои работы 1974-76 годов развивали
(тогда еще никак не называя его) мультифрактальный ме-
тод для изучения геометрических форм, создаваемых тур-
булентностью в обычном пространстве. Но тот же самый
метод можно без особых усилий распространить и на ча-
стоты возвращения динамической системы, рассматривае-
мой в «фазовом пространстве» — вообще говоря, для этого
метода можно найти новое и очень широкое поле прило-
жений. Таким образом, фракталы заняли самую что ни на
есть центральное место в самом сердце динамики. В част-
ности, часто повторяемое утверждение о том, что фракталь-
ная геометрия носит исключительно статический характер,
лишено всяких оснований.
Термин «хаос», прежде чем ему приписали только что
обсуждавшийся формальный смысл, часто использовался
Фракталы и хаотическая динамика	57
для описания поведения биржи. Отсюда только один шаг
отделяет нас от постановки вопроса о том, можно или
нельзя объяснить данное поведение в вышеупомянутом
формальном смысле. Более того! В механике хаос вызывает
удивление, поскольку там действуют неоспоримые детер-
министские законы. При изучении же финансов действия
сколько-нибудь похожих законов мы не наблюдаем.
В главе 2.1 предполагается существование так называ-
емого «медленного» случая, располагающегося где-то меж-
ду случаем ручным и случаем стихийным. Хотя мы и не
склонны преувеличивать полезность сравнений и метафор,
все же возникает искушение спросить, нет ли и у такого
случая своей противоположности в механике.
Глава 1.2
Самоподобие и
самоаффинность
Многие из тех структур, которые когда-то считались
чудовищными или патологи ческими и которые фракталь-
ная геометрия превратила в полезные орудия науки, за-
служивают того, чтобы оценивать их как протофракта-
лы. Здесь приставка «прото» имеет такой же смысл, как в
термине «протолатинский», то есть «относящийся к языку,
который предшествовал латыни».
Особого интереса заслуживают две категории протоф-
ракталов — самоподобные и самоаффинные протофракта-
лы. В этой главе приведены некоторые примеров, представ-
ляющие эти две категории. Глава очень коротка и отлича-
ется чрезвычайной простотой. Для начала мы вспомним о
вещах, широко известных во фрактальной геометрии, а в
конце приведем рассуждения, совсем недавно обнаружив-
шие поразительную созидательную мощь.
Концепция линейного самоподобия
Некоторый объект называется самоподобным, если его
«целое» (то есть сам объект, взятый целиком) можно раз-
делить на «части», каждая из которых получается из цело-
го посредством преобразования подобия, то есть редукции
или линейного сжатия. Такая редукция может распадать-
ся на гомотетию, которая иногда сопровождается перено-
сом, отражением или вращением. Последняя составляющая
приобретает решающее значение, когда мы переходим от
«Снежинки» и «прохождения»	59
самоподобия к самоаффинности. Говорят, что такой объ-
ект «инвариантен по отношению к семейству редукций».
(Редукции не могут быть произвольными, они должны об-
разовывать «полугруппу»).
С математической точки зрения процесс редукции
можно повторять произвольное число раз. Отсюда сразу
следует, что самоподобный математический объект состо-
ит из бесконечно малых деталей.
Аналогичным образом «самоподобие» может озна-
чать, что всякая часть объекта, подходящим образом «уве-
личенная», может быть наложена на большую его часть.
Повторяя этот процесс неопределенное число раз, мы ви-
дим, что такой объект, который называется «инвариантным
относительно увеличения», обязательно имеет бесконечно
большой размер.
Между тем реально существующие фракталы ограни-
чены и лишены бесконечно малых деталей.
«Снежинки» и «прохождения»
Есть два замечательных объекта, которые я называю
здесь «огибающим» и «заполняющим», каждый из них
представляет собой фрактал.
Огибающая кривая: кривая Коха или «снежинка». Этот
объект придумал в 1904 году математик Хельге фон Кох с
чисто педагогической целью: помочь другим математикам
выбраться из наезженной колеи и расширить хоть немного
свой кругозор.
Ему хотелось убедить скептиков не только в том, что
можно построить непрерывную кривую, не имеющую ка-
сательной ни в одной точке, но и в том, что это свойство
получается очень простым образом. Один пример такой
кривой был в то время хорошо известен, но настолько сло-
жен, что еще в 1904 году некоторые ученые с надеждой
полагали, что создатель упомянутой кривой, великий ма-
тематик Карл Вейерштрасс (1815—1897), допустил в этом
случае — с кем не бывает? — какую-то ошибку!
60
Глава 1.2
Для того, чтобы построить внутреннюю область тре-
ти снежинки, надо предпринять шаги, показанные на
рис. 1.2.1. Начинаем с отрезка единичной длины, который
делится на три части. К средней из этих частей прила-
гаются два других отрезка так, чтобы получился равно-
сторонний треугольник. Точно так же поступаем затем с
отрезками длины 1/3, 1/9, 1/27 ит.д.
Рис. 1.2.1. Построение кривой Коха («снежинки»). Последова-
тельные аппроксимации кривой представлены границей между
черным и белым
Концепция линейной самоаффинности 61
Через п поколений равносторонних треугольников по-
лучаем ломаную линию, которая и будет границей объекта,
изображенного на рис. 1.2.1. Ее длина равна 4/3 в степе-
ни п. Поскольку множитель 4/3 больше единицы, эта дли-
на бесконечно возрастает вместе с п. Граница стремится к
пределу бесконечной длины.
Заполняющее движение. Это аппроксимация объекта,
который обычно называют «кривой, заполняющей плоскую
область». Этот термин делает ее загадочнее, чем нужно, по-
скольку никакое разумное определение не позволяет нам
охарактеризовать такой объект как «кривую». Я уже давно
решил — в подражание термину «броуновское движение»
и в ознаменование заслуг Джузеппе Пеано (1858—1931) —
назвать этот объект «движением Пеано». Это движение, ко-
торое в конце концов проходит через каждую точку плоско-
сти. В силу некоторых весьма глубоких причин, некоторые
точки плоскости посещаются несколько раз, однако само-
пересечений такое движение не имеет.
В 1977 году мне пришел в голову новый объект — дви-
жение Пеано, проходящее через всю внутреннюю область
кривой Коха и «заполняющее» «снежинку» целиком.
На рис. 1.2.2 и 1.2.3 показано построение моего движе-
ния Пеано до скругления углов и после него. Аппроксими-
рующая кривая ЗВ на рис. 1.2.3 состоит из 13 дуг окружно-
сти. На аппроксимирующей кривой ЗС каждая из этих дуг
заменяется уменьшенной копией всей кривой. Эти копии
выполнены в черном и белом цвете и представляют собой
«позитив» на выпуклых дугах (как в верхней части ЗВ) и
«негатив» на вогнутых. Таким образом, аппроксимирую-
щая кривая ЗС состоит из 132 дуг? с каждой из которых
мы проделываем ту же процедуру, и т. д.
Концепция линейной самоаффинности
Подчеркнем, что в самоподобии непременно участвует
концепция вращения, а также изменения длины отрезка, в
частности, можно говорить об операции уменьшения этой
62
Глава 1.2
Рис. 1.2.2. Построение заполняющей кривой. На этом рисунке,
взятом из [М 1982F] («Fractal Geometry of Nature»1), с. 69, пока-
зан лишь принцип построения, который заключается в примене-
нии к единичному отрезку генератора, состоящего из тринадцати
отрезков (слева). Для того, чтобы у аппроксимирующих кривых
не было двойных точек, уменьшенные копии генератора долж-
ны размещаться весьма специфическим образом, как показано на
рисунке справа. Каждую уменьшенную часть можно заменить на
симметричную ей относительно некоторой прямой; в данном слу-
чае положения частей выбраны, исходя из эстетических соображе-
ний, с тем, чтобы сделать рис. 1.2.3 по возможности гармоничнее,
более похожим по очертаниям на волну
длины в некотором соотношении г. Такие операции обык-
новенно представляются совершенно невинными, однако
они перестают быть таковыми в тех областях, которые за-
трагивает эта книга.
Рассмотрим в этой связи хронику ценовых изменений,
т. е. график, задающий цену Р как функцию от времени t.
Когда отрезок проекции, равной At и ДР, параллелен оси
времени или оси цен, то его длина определена в терми-
нах единиц времени или цен. А если отрезки наклонные?
Возникает искушение действовать как обычно, пользуясь
теоремой Пифагора. Для этого следует прежде всего при-
дать какой-то смысл сумме квадратов At и ДР. Однако
1 «Фрактальная геометрия природы» (англ.) — Прим, перев.
Концепция линейной самоаффинности
63
Рис. 1.2.3. Построение заполняющей кривой, где каждый отрезок
прямой заменен на дугу величиной в шестую часть окружности
этого мы сделать не можем — по той простой причине, что
единицы времени и цен выбирались независимо друг от
друга! Точно так же единственные двугранники, которые
мы можем определить, имеют углы, равные 90° или 180° и
стороны, параллельные осям координат.
Из всего этого не следует, что мы должны отказаться
от идеи построить график фрактальной функции — надо
лишь прежде обобщить представление о «форме, одина-
ковой вблизи и издалека». Эта задача решается посред-
ством редукции, которая уже не является подобием, но
представляет собой более общее линейное преобразование.
64
ГЛАВА 1.2
Такие преобразования называют странным термином «аф-
финные» — старинный и, к сожалению, неприкосновенный
термин, введенный великим математиком Леонардом Эй-
лером (1707-1783).
Изучение самоаффинности исключает вращение, од-
нако ее операции распадаются на перенос и редукцию,
подверженную куда меньшему числу ограничений, чем в
случае самоподобия. Формальное нововведение: необходи-
мо обобщение, допускающее необратимую редукцию. Но
при всем этом теория самоаффинности неизбежно сложнее
и запутаннее, чем в случае самоподобия. Без решения оста-
ются множество очень простых математических вопросов.
Диагональные самоаффинности
К счастью, можно достичь замечательного компромис-
са между простотой и мощностью, используя аффинно-
сти, которые я называю диагональными, так как у их мат-
рицы есть только диагональные элементы, принимающие,
впрочем, значения, не равные между собой. Такая аффин-
ность — это преобразование, сжимающее графики в двух
разных отношениях: в отношении rt по времени и в ка-
ком-либо другом отношении гр по цене. (Именно это могут
делать новые машины для лазерного копирования.)
Мы будем говорить, что некоторая хроника обладает
диагональной самоаффинностью, если ее редуцированная
форма полностью идентична, точно или только статисти-
чески, любой ее части, менее протяженной во времени.
Термины «редуцированный» и «точный» расплывча-
ты, их можно определить многими разными способами.
Но в рамках данной книги мы можем избежать связанных
с этим осложнений. На рис. 1.2.4 показано, как строит-
ся самоаффинная кривая, соединяющая точки X (0) = 0
и X (1) = 1 внутри единичного квадрата. В качестве «ини-
циатора» берется диагональ с единичным наклоном, а в
качестве «генератора» — ломаная линия, т.е. кривая, со-
ставленная из конечного числа отрезков прямой таким об-
Диагональные самоаффинности
65

г-
Рис. 1.2.4. Два диагональных самоаффинных построения. Если
осуществить построение, показанное в верхней части рисунка,
то результат будет похож на броуновское движение, тогда как
построение в нижней части напоминает хронику изменения цен
5 Б. Мандельброт
66
Глава 1.2
разом, чтобы проходить из левого нижнего угла в правый
верхний (см. маленький график вверху слева). На следу-
ющем этапе каждый отрезок генератора заменяется своей
аффинной копией, уменьшенной и перенесенной так, что-
бы две ее крайние точки совпадали с концами исходного
отрезка (второй маленький график). Далее показаны 3-й
и 4-й этапы, а также некоторый значительно более поздний
этап.
Самоаффинное моделирование в финансах
Можно ли извлечь хоть что-нибудь интересное из этих
столь наивных построений? A priori стоило бы проявить
скептицизм, однако такое отношение будет в корне невер-
ным — в этом, собственно, и заключается самая важная
мысль, которую я хочу сообщить вам своей книгой.
Прежде всего, снежинка фон Коха и в самом деле
очень быстро «упала» в разряд математических игрушек.
А в качестве одного из своих первых жестов, фрактальная
геометрия с успехом продемонстрировала, что с этой кри-
вой можно играть и в весьма серьезные игры. Используя
термины, заявленные во Введении, можно сказать, что в
работе [М19750] показано, что кривая Коха представляет
собой в действительности не модель берегов некоего остро-
ва, но их математический эскиз. Аналогичным образом в
главе 3.3 настоящей книги предложена идея, согласно ко-
торой самоаффинные кривые описанного выше вида суть
эскизы финансовой реальности!
Каждый этап построения приводит к созданию более
совершенной «предфрактальной» аппроксимации в виде
ломаной кривой, составленной из все меньших и мень-
ших отрезков. Попутно заметим, что эти отрезки посте-
пенно оказываются все ближе к вертикальным. При такой
аппроксимации предфрактал на каждом этапе построения
вытягивается в фиксированном отношении, большем еди-
ницы, точно так же, как на каждом этапе построения сне-
жинка вытягивается в отношении 4/3.
Самоаффинное моделирование в финансах 67
Асимптотически длина этой кривой стремится к беско-
нечности. Выражаясь математически, пределом будет гра-
фик объекта, который называют «функция с неограничен-
ной вариацией». Свойство, обозначаемое этим термином,
похоже, не только является абстрактным, но и не допускает
никакой интерпретации. Более того, в применении к графи-
ку, представляющему изменение цен, неограниченная ва-
риация означает следующее: если бы мы могли неограни-
ченно долго покупать дешевле и перепродавать дороже,
используя преимущества малейшего зигзага (и без посред-
ников, которым надо платить), то наш доход стал бы бес-
конечным.
Генератор легко «рандомизировать», попросту изме-
няя случайным образом порядок его отрезков еще до его
редукции посредством аффинного преобразования. Сло-
во «рандомизировать» я произвел от устаревшего соче-
тания «а randon»2, достаточно пригодного для выраже-
ния идеи «случайности»; в английский язык оно пере-
шло в форме «at random»3. Если рандомизировать мо-
дель берега на манер фон Коха, то мы сильно рискуем
получить недопустимые для береговой линии самопересе-
чения. Следовательно, в реальности самоаффинные кон-
струкции имеют явное преимущество перед самоподобны-
ми.
Как бы то ни было, заранее представить себе все то,
что может нам дать рандомизированная самоаффинность,
невозможно, хотя некоторую помощь в этом может ока-
зать вычислительная техника. Вернемся к рис. 1.2 и 1.3 и
вновь сравним их. Во введении было сказано (правда, без
должных объяснений), что предложенная на рис. 1.3 мо-
дель получается в результате невероятно простого процес-
са. Теперь мы в состоянии уточнить, что речь здесь идет
о самоаффинной функции, построенной так же, как и на
рис. 1.2.4.
2Это сочетание можно приблизительно перевести как «куца глаза гля-
дят», «наугад». — Прим, перев.
3Почти то же самое — «наугад», «наобум», «куда глаза глядят». — Прим,
перев.
5*
68
Глава 1.2
Если мы хотим изменить результат (для придания ему
большей или меньшей изменчивости), то вполне достаточ-
но изменить генератор. Обобщая все, что сказано в главе Е6
книги [М 1997Е], я очерчу в главе 3.3 правила, позволяю-
щие описать эту зависимость и управлять ею. Более то-
го, в последнем разделе упомянутой главы описан менее
искусственный (поскольку нерекурсивный) порождающий
процесс. Помешать читателю заглянуть в указанный раздел
прямо сейчас автор, разумеется, не в силах.
За время своего развития фрактальная теория цен ста-
ла как более мощной, так и более простой. В некотором
смысле мы уже достигли цели, которую я ставлю в этой
книге, не потерявшись во всех теоретических хитроспле-
тениях. Однако я еще ничего не объяснил, посему прошу
читателя не слишком торопиться.
Глава 1.3
Принципы масштабирования,
масштабируемые
распределения, фрактальные
размерности и показатель Н
В главе 1.1 я уже ссылался на «принцип масштабиро-
вания», хотя и не очень настойчиво. Между тем именно он
и лежит в основе фрактальной геометрии, поэтому на нем
необходимо остановиться подробнее.
Говорят, что две измеримые величины X и Y связаны
законом масштабирования, когда существует такой пока-
затель €, ЧТО
X = Ye,
или, иначе говоря, когда
logX
logV
= const.
Особое значение имеет тот случай, когда X — случай-
ная переменная, а У = Pr {X > х}. Тогда масштабируемое
распределение определяется соотношением
Pr {X > х} = х а.
Традиционно в качестве показателя выбирается бук-
ва а, так как именно ее ввел Парето в свой закон распре-
деления личных доходов.
70
Глава 1.3
В действительности он утверждал лишь, что масшта-
бируемое распределение применимо в области больших до-
ходов. Итак, следует сразу провести различие между одно-
родными законами масштабирования, которые выполняют-
ся при всех значениях X и Y со знаком =, и асимптоти-
ческими законами масштабирования, когда знак равенства
заменяется на знак К асимптотическим законам предъ-
является меньше требований, поэтому они встречаются ча-
ще.
Будем говорить, что некоторый феномен удовлетворя-
ет принципу масштабирования, если все относящиеся к
этому феномену величины связаны друг с другом законом
масштабирования.
Все эти понятия имеют аналитический характер, а по-
нятия самоподобия и самоаффинности имеют совершенно
очевидные геометрические прообразы.
Самоподобие и фрактальная размерность
Для характеристики самоподобия используется гео-
метрический показатель, заслуживающий особого внима-
ния, это размерность подобия, частный случай фракталь-
ных размерностей, которые выглядят тем удивительней,
что их значения могут быть дробными.
Вернемся к построению кривой, составляющей сне-
жинку. Генератор состоит из N = 4 отрезков, каждый из
которых имеет длину г = 1/3. Со многих точек зрения
важны не столько взятые по отдельности величины N и г,
сколько их отношение
Jog7y_
log(l/r) ’
которое и определяет размерность подобия.
Как это можно увидеть в [М19750], [M1977F]
и [М1982F], да и во многих других источниках, понятие
размерности можно с равным успехом определить и мно-
гими другими способами. Для самоподобных множеств это
Самоаффинность и показатель Н	71
разнообразие, в общем, не имеет большого значения: все
определения в конце концов приводят к одной и той же
величине.
Самоаффинность и показатель Н
В случае самоаффинности все оказывается гораздо
сложнее. Прежде всего, утрачивает свой смысл понятие
размерности подобия, а фрактальную размерность здесь
можно определить только посредством различных обобще-
ний, куда менее естественных, чем уникальная размерность
самоподобных объектов.
Здесь и сейчас нас интересует (весьма важный, впро-
чем, и со многих других точек зрения) случай самоаф-
финности в применении к кривой, получаемой как график
функции, — например, график цены Р в зависимости от
времени t. Тогда наиболее важным показателем будет по-
казатель, позволяющий записать
P(t + At) - P(t) ~ (4t)"(t)
или, иначе,
Этот показатель я получил в результате нового прочте-
ния работ математика Гёльдера (1859-1937), исследовавше-
го только бесконечно малыми значениями At, и гидролога
Херста (1880-1978) — человека, достаточно далекого от ка-
ких бы то ни было математических тонкостей.
Вернемся к финансам. В моих моделях цена P(t) — это
недифференцируемая функция времени t, что на практике
означает, что угол наклона отношения &Р/Ы очень сильно
зависит от At (и от случая), так что он бесполезен при
оценке уровня изменчивости. Напротив, показатель H(t)
изменяется мало, поэтому может быть очень полезен, при
условии, что мы привыкнем рассуждать в терминах этого
показателя.
72
Глава 1.3
Более того, поведение Н составляет основу одно-
го существенного различия: модели [М1963] (глава 3.1)
и [М1965] (глава 3.2) характеризуются не зависящим от t
показателем Я; именно поэтому они называются «уни-
фрактальными», тогда как модель [М1972] (глава 3.3) ха-
рактеризуется переменным показателем Н и поэтому на-
зывается «мультифрактальной».
Связь между размерностью и
фрактал ыюстью
Этот последний раздел представляет собой отступле-
ние, в котором вводятся несколько концепций, раздража-
ющих меня своим формалистским характером, но мы не
должны совершенно забывать о них.
Возвращаясь к концепции размерности, заметим, что
числовой характеристикой всего множества является чис-
ло Рнв, называемое размерностью Хаусдорфа-Безикови-
ча. В моей книге «Фрактальные объекты» размерность £>нв
используется в качестве квазисинонима «фрактальной раз-
мерности», причем всякий раз подчеркивается, что это
некоторое упрощение. Тогда я полагал, что значения дру-
гих математических определений могут отличаться от 7?нв
только в очень редких случаях. Дальнейшее развитие фрак-
тальной геометрии привело к тому, что количество опреде-
лений растет, и конца этому процессу не видно. Понятие
фрактальной размерности стало своего рода общим поня-
тием, а определение Хаусдорфа-Безиковича сохранилось
лишь в качестве частного примера, кстати, зачастую не
очень удобного. Придавать ему особый статус «первого
среди равных» (prima inter pares) представляется теперь
уже не совсем уместным.
Вдохновившись бритвой Вильяма Оккама, я даже го-
тов был приложить усилия к тому, чтобы помешать размер-
ностям умножаться сверх необходимости, однако необхо-
димость и сама оказалась вынужденной умножаться, при-
чем довольно быстро. Из самоаффинности следует множе-
Связь МЕЖДУ РАЗМЕРНОСТЬЮ И ФРАКТАЛЬНОСТЬЮ 73
ственностъ фрактальных размерностей, а из мультифрак-
тальности следует (глава 3.3), что их должно быть беско-
нечно много.
Последний неизбежный вопрос: можно ли определить
фракталы математически? Ничуть не лучше, чем это мож-
но сделать в таких устоявшихся дисциплинах, как теория
вероятностей и топология. Да, в [М1977F] и [М1982F] я
опрометчиво предложил «наглядное» или «тактическое»
определение для концепции фрактала. Однако его суще-
ственные недостатки, ставшие вскоре явными, заставили
меня отказаться во втором издании [М1982F] от этого опре-
деления. Тем не менее его продолжают цитировать, а оно
продолжает сбивать всех с толку.
Я говорил, что множество Е фрактально, если два чис-
ла Dhb и Dt, которые можно сопоставить любому множе-
ству, удовлетворяют неравенству
Dhb > Dt*
Величина Dt представляет собой топологическую
размерность; всем известная концепция, согласно которой
точка, прямая, квадрат и куб имеют размерность Dt =
= 0,1,2иЗ.
Итак, вышеуказанное неравенство потеряло свое зна-
чение. Однако его достоинство заключается в том, что оно
по-прежнему символизирует один важный факт. Мы очень
часто упускаем из виду, что «изучение математики форм»
имеет много нетопологических составляющих. Одна такая
нетопологическая составляющая, к которой принадлежат
понятия самоподобия и самоаффинности, оставалась за-
бытой и безымянной; развив ее, я назвал ее фрактальной.
Эта книга, не затрагивая проблем размерности, использует
фрактальные построения в экономической статистике.
ЧАСТЬ ВТОРАЯ
МНОЖЕСТВЕННОСТЬ
«СОСТОЯНИЙ» СЛУЧАЯ
Так почему же мы настолько хуже разбираемся в фи-
нансах и метеорологии, нежели в физике? По очень распро-
страненному мнению это исключительно вопрос возраста:
математика и физические науки созревали куда дольше,
чем экономические и метеорологические исследования. Но
я считаю, что истинная причина в другом: физические
науки систематически отбирали свои объекты среди наи-
более легких из имеющихся. Я задержусь на этой теме, по-
скольку она представляется мне очень важной для объяс-
нения причин, по которым я считаю, что вышеупомянутая
разница в простоте носит не только «количественный»
характер, — иначе говоря, это не только вопрос степени,
ступени, которую, как мы надеемся, шаг за шагом можно
будет преодолеть. Эта разница, скорее, «качественная» —
она требует новых методов и даже нового философского
отношения.
Вот хорошая метафора, которая вскоре сослужит
нам немалую службу, — речь в данном случае идет не о
предметах, которые более или менее горячи, но о предме-
тах, у которых есть несколько возможных «состояний»,
настолько же отличающихся одно от другого, как газооб-
разное, твердое и жидкое.
Финансовые данные, заставившие меня обратиться
к понятию различных «состояний случая», будут обсу-
ждаться в третьей части книги. Вторая же часть но-
сит более общий характер. Глава 2.1 представляет собой
неформальное введение. В главе 2.2 предлагается отступ-
76
ЧАСТЬ ВТОРАЯ
ление, которое приведет нас к одному важному факту
В главе 2.3 описан стихийный случай, который можно объ-
яснить и точно, и просто. В главе 2.5 мы займемся малоиз-
вестными, но неизбежными разновидностями стихийного
случая.
Глава 2.1
От случая ручного к случаю
стихийному
Разнообразие природных и социальных феноменов
бесконечно, гораздо меньше существует разновидностей
математических методов, способных укротить их; случа-
ется также, что не имеющие, на первый взгляд, ничего
общего феномены обнаруживают одну и ту же математи-
ческую структуру. Вот уже 30 лет, как я умом признаю
справедливость этой философской констатации. Мои рабо-
ты, посвященные бирже, постепенно продвигались вперед,
а в работах о шумах и турбулентности я предвидел обна-
ружение аналогичных математических структур. Во всех
этих случаях речь шла о первых стадиях построения фрак-
тальной геометрии.
Именно поэтому цель данной главы состоит в том,
чтобы показать, что понятие «случай» выступает в науке
в самых разных формах и что мы только выиграем, если
предположим, что случай может находиться в нескольких
различных «состояниях». Легче всего справиться с состо-
янием, которое я, по должном размышлении, предлагаю
называть живым и выразительным термином «ручное», —
это состояние случая уже тысячу раз доказало нам свою
полезность, но его недостаточно для описания процессов,
происходящих на бирже, или многие другие природные или
социальные феномены. Для того, чтобы понять нерегуляр-
ность этих феноменов, необходимо обратиться к другому
состоянию случая, для которого я воспользуюсь другим
живым и выразительным термином — «стихийное». Кроме
78
Глава 2.1
того, необходимо допустить наличие третьего состояния,
которое я буду называть «медленным».
Невозможно не провести здесь аналогии с физикой
(аналогии, которую я считаю весьма полезной), т. е. отож-
дествить ручной случай с газообразным состоянием веще-
ства, стихийный — с твердым, а медленный — с жидким.
Итак, в чем же заключалась центральная мысль моих
работ в области финансов? Общепринятое, судя по все-
му, предположение следовало за физикой и успокаивалось
на броуновском движении. Допускалось, что цены — это
непрерывные функции от времени, а их флуктуации не бо-
лее значительны, чем флуктуации, описываемые уже клас-
сическим распределением Гаусса. Но изучение фактов по-
казало обратное: функции разрывны, а их флуктуации до-
стигают огромных значений. И если броуновский случай
очень легко квалифицировать как ручной, то для описания
биржи необходима какая-то совершенно другая форма слу-
чая. Технические аспекты моего подхода будут описаны
позже, а эта глава посвящена лишь некоторым естественно
возникающим философским вопросам.
Теория вероятностей
Для человека непосвященного или для философа по-
нятие «случая» едино. Его математическое единство выра-
жается абстрактным и очень обобщенным образом. Даже
слишком обобщенным, как мы вскоре увидим, поскольку
это единство затемняет некоторые фундаментальные раз-
личия. Более того, в аксиоматике растворяется специфич-
ность теории вероятностей, так что в конце концов эта
теория становится всего лишь еще одним, мало чем выде-
ляющимся разделом теории меры.
В третьей четверти нашего века в научных исследо-
ваниях преобладали исследования единого, абстрактного
и общего. Математики охотнее проявляли интерес уже не
к «вычурным деталям» анализа или геометрии, но к их
«фундаментальным» структурам. Точно так же физики на-
Теория вероятностей
79
ходили удовлетворение в исследовании «фундаментальных
частиц».
Конечно, наука не может не изучать общее, и я сам
ощущаю очень сильное притяжение этих структур. Более
того, моя долгая научная карьера оказалась отмечена обна-
ружением и изучением некоей новой общей структуры, ко-
торая неявно присутствует во множестве внешне разнород-
ных феноменов и пронизывает как математику, так и физи-
ческие, биологические и социальные науки. Эта структура
связана с инвариантностью при редукции и при растяже-
нии, а объекты, которые она изучает, называются фракта-
лами.
Однако (возможно, в этом кроется некий парадокс)
именно создание фрактальной геометрии заставило меня
вскоре предположить (и найти тому многочисленные под-
тверждения), что единство мира случайных моделей, и да-
же единство самой теории вероятностей обманчиво. С ин-
тересовавшей меня точки зрения теория вероятностей об-
наруживала все более и более тревожные аналогии с тео-
рией вещества.
Как известно, применяя одни и те же общие законы
материи в различных ситуациях, мы обнаруживаем суще-
ствование нескольких очень разных «состояний» вещества.
Два таких состояния были известны всегда, для их обо-
значения используются слова латинского происхождения
«solid» (твердое) и «liquid» (жидкое), а слово «газ» было
образовано в XVII веке из греческого «хаос». Иначе говоря,
физика едина и многообразна одновременно. Ее единство
отражено в том, что все эти состояния (и другие, новые, ко-
торые мы все продолжаем открывать) выводятся из одних и
тех же принципов и используют одни и те же концепции —
например, такие, как температура и давление. Многообра-
зие же физики проявляется в том, что состояния вещества
очень заметно отличаются друг от друга.
Мне довелось пережить аналогичную «дифференциа-
цию» в случае с теорией вероятностей. Сейчас я вижу слу-
чай как нечто единое, но при этом способное проявляться в
нескольких формах, столь же отличных друг от друга, как
80
Глава 2.1
газ от твердого тела. Я настаиваю на следующем: если вве-
сти в математику различия между состояниями случая, то
это лишь дополнит математику, не изменив ее. Зато в корне
перевернет интерпретацию этих самых состояний. Чтобы
лучше понять все это, обратимся к истории.
Закономерности случая и ограничения в их
применении
Для начала обдумаем одно утверждение, которое мож-
но найти на первой странице знаменитого трактата, одним
из соавторов которого является Андрей Николаевич Кол-
могоров (1903-1987), известный математик, введший в те-
орию вероятностей аксиоматику и придавший теории веро-
ятностей законченный вид, превратив ее в область, доступ-
ную для изучения методами «чистой» математики. Итак, в
предисловии к книге [Gnedenko & Kolmogorov 1954] чита-
ем: «любая эпистемологическая величина в теории веро-
ятностей основана на том, что случайные феномены, рас-
сматриваемые в их коллективном действии в большом мас-
штабе, создают неслучайную закономерность».
Я уверен, что если провести среди математиков и спе-
циалистов в области эмпирических наук соответствующий
опрос, то он покажет, что они согласны с этим утверждени-
ем Гнеденко и Колмогорова. К сожалению, вышеуказанный
тезис несколько двусмыслен, и я считаю, что его всеобщее
одобрение зачастую отражает недопонимание, последствия
которого проявляются ежедневно и носят очень серьезный
характер.
Уточним: скрупулезный математик интерпретирует
этот тезис как утверждение о том, что всякое коллектив-
ное действие имеет хотя бы один аспект, который окажет-
ся ограниченным, регулярным и неслучайным. В любом
случае, это ограничение в смысле не может удовлетворить
ни ученого, ни инженера; оба они нуждаются в уверенно-
сти, что такая коллективная и неслучайная регулярность
затрагивает и интересующие их феномены. Более того, ес-
На лезвии ножа
81
ли регулярность таки имеется, то они хотели бы убедиться,
что она устанавливается достаточно быстро и асимптоти-
ческие значения отражают структуру конечной системы,
потому что только такие системы и встречаются в природе.
На лезвии ножа
Сделаем еще несколько уточнений. Классическая фор-
ма случая — это последовательность чисел, полученных
при бросании игральной кости: после десяти бросков доля
«двоек» может быть очень разной (случайный феномен), но
если бросать кость очень много раз (в большом масштабе),
то эта доля будет очень близка к одной шестой (неслучай-
ная закономерность). Иначе говоря, когда количество на-
блюдений заметно увеличивается или когда точность ана-
лиза становится достаточно малой, случайные флуктуации
нейтрализуются. Очень быстро их относительное значение
становится несущественным.
Широкое распространение получил пример, связан-
ный с тем представлением, которое мы себе составляем
о лезвии хорошо заточенного ножа. (Я настаиваю на том,
что речь идет именно о том представлении, которое мы себе
составляем: действительность может быть самоаффинной,
то есть куда более сложной!) Если рассматривать вышеупо-
мянутое лезвие в микроскоп, то оно покажется необычайно
неправильным, однако для невооруженного глаза оно пред-
ставляется абсолютно прямым. И мы смело можем про-
должить задаваемое этим лезвием направление, исходя из
одного его отрезка, большего, чем любые неправильности
этого лезвия, но меньшего, чем лезвие в целом.
Рассмотрим также электрический ток в проводнике,
например, в медном проводе: если сильно увеличить этот
ток и подать его на клеммы громкоговорителя, то мы отчет-
ливо услышим так называемый «термический шум». Одна-
ко обычный амперметр показывает вполне определенную
силу тока, и не требуется много времени, чтобы измерить
ее точно. Причина заключается в том, что проводник при-
6 Б. Мандельброт
82
Глава 2.1
ходит в состояние совершенного равновесия с точки зрения
термодинамики.
Два этих случая порадовали бы Декарта, поскольку
предполагают возможность разложения сложной проблемы
на составляющие: сначала мы изучаем тенденцию (здесь
она прямолинейна), а потом накладываем на нее флуктуа-
ции.
При изучении термического шума часто используются
два выражения: гауссовское распределение и броуновское
движение. В общем, нам надо дать качественное определе-
ние понятию случая, «недалеко ушедшего от броуновского
движения».
Когда я говорю, что мои друзья-статистики ограничи-
ваются изучением случая, который я взял на себя смелость
назвать ручным, это вовсе не означает, что я над ними по-
тешаюсь: при столкновении с такой формой случая неиз-
бежно возникают различные затруднения, однако диапазон
этих затруднений ограничен, и напряженная работа позво-
ляет статистикам и физикам их преодолевать. Более того
физики, как известно, долгое время полагали, что они во-
обще подчинили себе случай. На мой взгляд, причина их
уверенности была в том, что им посчастливилось начать с
тех задач, в которых случай можно было одолеть — имен-
но потому, что это был ручной случай. Во всякой науке,
где случай носит ручной характер, утверждение Гнеденко
и Колмогорова приобретает очень сильный смысл, и такая
наука может стать точной.
От ручного к стихийному
Тем не менее всем известно, что существуют области
знаний, издавна признанные и разграниченные, но не под-
дающиеся количественным оценкам. Ниже мы опишем три
области такого рода: первая имеет отношение к географии,
самая очевидная связана с финансами, а третья располага-
ется в рамках физики — предметом изучения здесь явля-
ются, например, турбулентность в жидкостях и различные
От ручного К СТИХИЙНОМУ	83
виды электронного шума, о которых мы мало что знаем,
отчего и называем их «аномальными».
Когда я только начинал свои изыскания, я был с этими
разделами науки совершенно незнаком, так что я обратился
за помощью к ученым из числа своих знакомых. Каждый
из них в изобилии располагал всевозможными данными и
долго пытался описать их и интерпретировать с помощью
общепринятых методов. Конечно, за неимением альтерна-
тивы все они применяли методы ручного случая. Однако
даже невероятная изворотливость моих знакомых не спа-
сла их от сокрушительного поражения.
Таким образом, именно внутренняя логика моего под-
хода (которую я сейчас объясню) заставила меня изменить
направление моих работ и от «социальной науки» перейти
к науке физической. Эталоном для этих работ послужи-
ла точность, присущая классической статистической физи-
ке, — следует, впрочем, признать, что этому эталону при-
шлось пережить, по меньшей мере, весьма нелегкие вре-
мена (к этому мы еще вернемся несколько позднее).
В 1964 году, во время подготовки к выступлению на
«Международном конгрессе по логике и философии в нау-
ке» (Иерусалим) я столкнулся с необходимостью провести,
наконец, различие между ручным случаем и случаем, кото-
рый таковым не является.
Оказалось, что ручной случай статистической меха-
ники представляет собой не более чем «первую стадию»
неопределенности в науке. Таким образом, неизбежным
оказывается переход к некоей «второй стадии». Мало-по-
малу я начал рассматривать эти последовательные стадии
как два «состояния» с внутренне различными свойства-
ми.
При этом ни о каком изменении теории вероятностей
речь вовсе не идет! Стихийный случай также обладает ка-
чествами, которые прекрасно удовлетворяют закономерно-
стям Гнеденко и Колмогорова. Однако эти качества не име-
ют решающего значения, тогда как существенные характе-
ристики подвержены флуктуациям, которые ручными уже
не являются.
6*
84
Глава 2.1
Есть и другие задачи, в которых имеются важные ха-
рактеристики, сходящиеся к каким-то неслучайным законо-
мерностям, но чрезвычайно медленно, приводя нас к необ-
ходимости признать наличие третьего, промежуточного со-
стояния случая.
Теперь уточним эти слишком общие рассуждения на
примерах.
Берег Бретани
Сначала представим себе берег Бретани — таким, ка-
ким он выглядит с борта низко летящего самолета. При-
нимая во внимание то, что говорилось выше о хорошо за-
точенном лезвии, мы будем рассматривать форму берего-
вой линии на некотором очень малом участке как результат
нерегулярностей, наложившихся на «общую тенденцию»,
представленную прямолинейным отрезком. Нам, возмож-
но, захотелось бы продолжить это направление, прочертив
бесконечную линию, но все мы знаем, что такая экстра-
поляция ничего не означает. Если изучать берег с борта
самолета, летящего несколько выше, то «локальные» нере-
гулярности становятся невидимыми и, как следствие, пре-
небрежимыми. Напротив, мы заметим новые нерегуляр-
ности — скажем, «районные». Если взлететь еще выше,
то и они скроются за другими нерегулярностями, которые
можно назвать «областными», и так далее. Даже если рас-
сматривать всю Бретань целиком, то никому и в голову не
придет определять «общее направление» береговой линии
посредством прямолинейной экстраполяции. «Картезиан-
ское» расчленение на тенденцию и флуктуации становится
невозможным.
Второй пример «дикого» случая в географии настоль-
ко же стар, насколько и всем известен: это хроника еже-
годных разливов Нила. Образ рассуждения, сформировав-
шийся при исследовании ручных флуктуаций, молчаливо
предполагает, что средние уровни ежегодных разливов, из-
меренные за несколько последовательных и не слишком
Берег Бретани
85
кратких периодов времени, должны быть примерно равны
между собой.
Совсем наоборот, библейская притча о Иосифе, сыне
Иакова — притча о «тучных и тощих коровах» — предпо-
лагает, что два последовательных средних, взятые за семь
лет, могут (по крайней мере, иногда) оказаться очень раз-
ными. Согласно более новым и поэтому более доступным
для проверки данным, средние уровни, измеренные за 17 и
за 70 лет одинаково расходятся друг с другом.
Обратимся к флуктуациям в финансах. Где же здесь
то экономическое равновесие, предположительный экви-
валент «нормального» термодинамического равновесия?
Очень рано у меня возникло ощущение, что понятие эко-
номического равновесия лишено всякого содержания и что
для описания изменений цен недостаточно лишь слегка из-
менить ручной случай, включив в него какие-то мелкие но-
вовведения.
В математическом смысле идея стихийного случая
восходит к очень давним временам, еще к 1853 году. В са-
мом деле, вызванная им тревога проявляется уже во вре-
мя жесткой дискуссии между Коши и Бьенеме, о которой
рассказывается в главе 2.3. Если перефразировать завер-
шившее эту дискуссию восклицание, то «неизвестно, как
бы мы назвали ремесленника, создавшего инструмент, ко-
торый измеряет со стихийными ошибками». Итак, возмож-
ность такого поведения уже тогда рассматривалась как па-
тология, и никто не ожидал столкнуться с ним в действи-
тельно существующих феноменах.
Другой важный пример, известный менее, чем он того
заслуживает: флуктуации силы электрического тока, прохо-
дящего через тонкие металлические пластинки, угольные
микрофоны, контакты, полупроводники и прочие радио-
электронные элементы. Если сильно увеличить этот ток,
то окажется, что он подвергается возмущениям в виде так
называемого 1//-шума. Иначе говоря, мощность сигнала
на любой частоте обратно пропорциональна этой самой
частоте; если точнее, то эта пропорциональность дает мощ-
ность В в окрестности единицы.
86
Глава 2.1
Если изобразить этот шум и хронику разливов Нила на
графиках аналогичных размеров, то окажется, что эти гра-
фики на удивление похожи внешне. Этот факт подчеркива-
ет то, что контраст между ручным и стихийным затрагивает
не масштабы, но структуру.
Сразу заметим, что разница между «белым» и «чер-
ным» имеет досадное обыкновение допускать множество
промежуточных уровней «серого». Таким образом, между
ручным и стихийным немедленно обнаруживается проме-
жуточная зона, некое «третье состояние». Например, су-
ществуют ситуации, расположенные где-то между лезвием
ножа и берегом Бретани, — например, западное побережье
Америки, когда за всеми флуктуациями достаточно хорошо
прослеживается общее направление.
Математическим примером такой медленной сходимо-
сти будет логнормальное распределение — на мой взгляд,
типичный волк в овечьей шкуре. Такая чрезвычайно медли-
тельная случайность и определяет в полной мере состояние
медленного случая. Неизбежная необходимость в выделе-
нии трех состояний случая возникла тогда, когда постав-
ленные Природой задачи заставили меня преобразовать те-
орию вероятностей от общего безразличного абстрактного
к очень структурированному конкретному.
Концепция множественности «состояний»
случая в ее количественном выражении
Для получения этого выражения рассмотрим вкратце
историю предельных теорем теории вероятностей. Изна-
чально (по ходу рассказа я позволю себе вносить некото-
рые уточнения и дополнения) речь шла о некотором коли-
честве J бросков монеты, в результате которых с одина-
ковой вероятностью выпадает орел, приносящий выигрыш
Полю, и решка, приносящая выигрыш Франциску. (Мне
хотелось, чтобы инициалы наших игроков совпадали с на-
чальными буквами слов «орел» и «решка»1). Ниже пока-
1 Pile ou face (фр.) — «орел или решка». — Прим, перев.
Концепция множественности «состояний» случая 87
зано, как упрощается распределение выигрышей Поля при
увеличении J.
Относительная частота случаев, когда монета падает
орлом вверх, приближается к 1/2. Это самый простой слу-
чай «закона больших чисел». Взвешенная разность между
этой частотой и 1/2 подчиняется распределению, которое
все приближается к «нормальному» распределению Гаусса.
Это наиболее простой вариант «центральной предельной
теоремы». Со временем эти результаты распространились
и на другие случаи. Отсюда происходит видение присущей
Природе неопределенности, опирающейся, подобно храму
Бодлера, на три «живые колонны»2.
А.	«Закон больших чисел» (часто называемый «эргодиче-
ской теоремой»). Этот закон утверждает, что когда вре-
мя Т стремится к бесконечности, эмпирическое сред-
нее
t=l
т
стремится к неслучайному пределу, который, в за-
висимости от дисциплины, обозначается EX, MX
или {X).
Следующие две колонны образуют «классическую
форму центральной предельной теоремы» (уточним, что
речь идет о «классической форме», потому что, как мы
увидим в дальнейшем, существуют и другие формы этой
теоремы, применимые к стихийному случаю).
В.	Можно определить такую функцию А(Т), что выра-
жение
£[X(t)-EX]
t=l
Л(Г)
2Имеются в виду строки из сонета Бодлера «Соответствия»: «Приро-
да — некий храм, где от живых колонн Обрывки смутных фраз исходят
временами.». — Прим. пер.
88
Глава 2.1
будет стремиться к гауссовскому пределу.
С.	Взвешивающий множитель А(Т) равен
А(Т) = VT.
Тот же результат можно выразить и в другой, мате-
матически эквивалентной форме, которую часто опуска-
ют, полагая ее очевидной. Даже если «броски обобщенных
игральных костей» не являются независимыми, все равно
принято считать, что достаточно отдаленные друг от дру-
га «будущее» и «прошлое» практически независимы. Так
происходит часто, но не всегда.
Случай «ручной», «стихийный» и
«медленный»
Все, что будет сказано в дальнейшем, связано так или
иначе с истинностью вышеупомянутых теорем. Необходи-
мо различать три варианта случая.
Ручной случай. Мы можем придать точный смысл
словам о том, что эти теоремы «применимы и примени-
мы быстро». Если дело обстоит именно так, то флуктуация
будет называться «ручной». Вообще, отсюда следует, что
наиболее интересные структуры не являются статистиче-
скими.
Ручные флуктуации уже описаны математиками: мно-
гие из них получили у ученых свое объяснение, а инженеры
неплохо научились управлять ими с целью сделать их более
терпимыми.
Медленный случай. Может случиться так, что «кол-
лективное действие» подчиняется теоремам А, В и С, но
пределы достигаются настолько медленно, что они почти
ничего не могут сообщить нам о том, с чем мы можем
столкнуться при решении конкретных научных задач. И да-
же если мы располагаем успокоительными сведениями о
Случай «ручной», «стихийный» и «медленный» 89
применимости в данном случае теорем А, В и С, сле-
дует помнить, что теоремы эти — не более чем мираж,
поскольку реально существующий мир конечен. Опира-
ясь на совершенно иные (однако в чем-то параллельные
нашим) рассуждения, великий экономист Джон Мейнард
Кейнс (1883-1946) напоминал своим коллегам, что «через
долгий промежуток времени мы все умрем».
В чем же тогда состоит практическая применимость
предельных теорем? Выборки, изучаемые в макроскопи-
ческой физике, настолько огромны (число Авогадро имеет
порядок 1023), что здесь никаких сложностей не возника-
ет. Но рассмотрим логнормальную переменную, представ-
ляющую собой попросту показатель в экспоненциальном
представлении некоторой гауссовской переменной. За дол-
гий период времени ее случайные свойства подавляются,
поскольку она имеет конечные моменты (среднее, диспер-
сию и т.д.), причем эти моменты можно получить с по-
мощью простых формул; итак, логнормальная переменная
кажется ручной. Но если рассматривать короткий или сред-
ний промежуток времени, то все куда-то пропадает, и ее
поведение представляется стихийным. С этой переменной
обращаются так, словно она ручная, однако на самом деле
это прекрасный (и опасный) хамелеон.
Стихийный случай. Имеется два симптома, которые
знаменуют собой полный провал ручной сходимости флук-
туаций. Эти симптомы могут действовать поодиночке или
в комбинации: (а) случайное появление отклонений, очень
больших по сравнению с тем, что хотелось бы считать
«нормой» и (Ь) случайное появление слишком длинных по-
следовательностей таких величин, что каждая из них, взя-
тая по отдельности, мало уклоняется от нормы, однако эти
уклонения в одном и том же направлении настолько «на-
стойчивы», что среднее значение достигается либо очень
медленно, либо не достигается вовсе.
Воспользовавшись сюжетами двух широко известных
библейских историй, о которых мы поговорим в главе 2.5,
я предлагаю называть примеры, связанные с этими дву-
90
Глава 2.1
мя симптомами «флуктуацией Ноя» и «флуктуацией Иоси-
фа», соответственно. Отдельные примеры флуктуаций то-
го и другого рода известны уже давно, но каждый раз их
рассматривали по отдельности, так что их существование
оставалось своего рода секретом. В своих работах я заяв-
ляю об их значимости и об их единстве; стихийный случай
заслуживает того, чтобы рассматривать его как объект са-
мостоятельного изучения.
Можно спросить себя, почему до сих пор его не при-
знавали в таком качестве. Объяснением этого факта явля-
ется непонимание, то есть цитировавшаяся уже идея, суть
которой заключается в том, что случайное, взятое в боль-
шом масштабе, всегда создает некоторую неслучайную за-
кономерность. Как уже было сказано, дело обстоит не со-
всем так, и специалисты в области теории вероятностей
это знали. И если прочие ученые не обращали внимания
на стихийный случай, то это только потому, что «вероят-
ностники», в зависимости от обстоятельств, либо преуве-
личивали, либо преуменьшали вышеуказанную «стихий-
ность».
Преувеличивали те, кто хотел изобразить стихийность
«исключительной», «патологической», не имеющей ника-
кого применения. Ее преуменьшали или прятали от глаз
ученых в духе того поиска всеобщности, который 30 лет
назад был характерен для всех наук. Никому не хотелось
говорить о том, что та или иная теорема, эргодическая или
центральная предельная, не выполняется; вместо этого мы
говорили, что ее можно «обобщить», даже не изменяя ее
названия.
«Обобщение» — это мощная и основополагающая кон-
цепция. Но на некоторой «количественной» стадии содер-
жимое центральных предельных теорем изменяется «ка-
чественным» образом, теряя тот интуитивно понятный
смысл, которым мы до тех пор пользовались. В то же
время «обобщение» вызывает одну лишь досаду, если
из-за него возникает впечатление, что общность получа-
ется за счет каких-то малых затрат, без настоящих измене-
ний.
«Изобретательность» стихийного случая
91
«Изобретательность» стихийного случая
На мои работы всегда оказывал сильное влияние тот
факт, что мое мышление тесно связано со зрительными
образами. По-видимому, это обстоятельство получило ши-
рокую известность в связи с «множеством Мандельброта».
Но то же можно сказать и о моих исследованиях случайно-
го, и эта моя особенность позволила мне прийти к одному
важному выводу.
Для того, чтобы сформулировать этот вывод, сравним
разные виды электрического шума и «шумы» на финансо-
вых рынках, соответствующие изменениям цен. Тепловой
шум (как уже было сказано, ручной) является монотонным,
без особенностей, т. е. его, очевидно, достаточно легко ис-
ключить («отфильтровать»). Совсем иначе ведут себя бир-
жевые тенденции, 1//-шумы или любые другие стихийные
шумы — они, по-видимому, беспрестанно изменяют свой
характер. У них в изобилии имеются свойства, о которых
можно сказать, что каждое из них обусловлено чем-то, что
нельзя считать результатом чистого случая. Так обстоит де-
ло, если ограничиваться обычным, то есть ручным случаем.
Я же обнаружил — и это наблюдение сначала просто
ошеломило меня, — что упомянутые выше свойства можно
«очень легко» получить как результаты стихийного слу-
чая. Таким образом, волнующий и замечательный феномен
чистого случая можно наделить свойством, которое кро-
ме как «изобретательностью» и не назовешь. Я несколько
отвлекусь от нашей темы, чтобы тут же сказать, что имен-
но такая изобретательность позволила мне десятью годами
позже получить фрактальные земные псевдорельефы, став-
шие теперь классическими, так что их повсюду повторяют
и имитируют.
Принимая во внимание все вышесказанное легко заме-
тить, что ручной и дикий случай отличаются друг от дру-
га настолько же, насколько рассеянный газ отличается от
жидкости. Что совместимость и чрезвычайная обобщен-
ность правил, описывающих эти виды случая на наиболее
абстрактном уровне ничуть не мешают этим двум случа-
92
Глава 2.1
ям ставить перед нами очень разные вопросы. Здесь, по
аналогии с медициной, надо смириться с тем, что процесс
«лечения» может принимать самые разные формы.
Надо сказать, что термин «стихийный» — новый. Сна-
чала я назвал такую случайность «злокачественной»; слово
это, если вдуматься, можно понимать двояко, хотя ни одно
из его значений не подразумевает ничего демонического.
В своем медицинском смысле оно подразумевает самые
разные проблемы, для которых в само понятие лечения
и ухода вкладывается совершенно иной смысл, нежели в
противоположных, «ручных», случаях.
Выводы: науки и случай
Стихийные (или неручные) флуктуации встречаются
во всех науках. Повсеместную распространенность неруч-
ного случая я прежде всего обнаружил, скажем так, в «не
совсем точных» науках; моим гидом здесь был Джордж
Кингсли Ципф — человек восторженный, пусть и не все-
гда свободный от ошибок. В «точных» же науках, напро-
тив, стало, пожалуй, правилом отыскивать неручное пове-
дение лишь в некоторых изолированных примерах. Так,
фундаментальные шумы в физике — это тепловые шумы, а
они, как ни крути, ручные\ стихийные феномены считались
«особыми случаями», не имеющими, как хотелось верить,
особого значения.
Если мы хотим доказать, что та или иная наука пе-
решла в разряд точных, то самыми существенными будут
в таком доказательстве аргументы, демонстрирующие руч-
ной характер наиболее важных из имеющихся в данной
науке флуктуаций. И наоборот, науки, в которых основ-
ными видами шума управляет стихийный случай, рискуют
долгое время оставаться среди «не совсем точных».
Широко распространено и противоположное мнение:
единственное преимущество точных наук состоит в том,
что у них было больше времени для развития — мне, впро-
чем, кажется, что эта точка зрения противоречит урокам
Выводы: НАУКИ И СЛУЧАЙ	93
истории. Даже если ограничиться теми феноменами, кото-
рые наш разум называет физическими, то задача о пред-
сказании разливов рек и задача о предсказании положения
планет были поставлены приблизительно в одно и то же
время, однако первая из них надолго осталась в области
суеверий, тогда как вторая развивалась самым блестящим
образом — результатом этого развития, собственно, и ста-
ла физика, «как она есть». Просто «так случилось», что
флуктуации в последней задаче малы и в пределе прене-
брежимы.
Итак, может оказаться, что одни науки внутренне
сложнее других. Можно опасаться, что «степень точности»
произвольной науки не во всех случаях имеет некоторый
более или менее большой предел. Переходя от более точ-
ных наук ко все менее и менее точным, мы увидим, как
убывает в них доля интересных свойств, представляющих
собой упорядоченное коллективное действие, равно как
и доля потенциально интересных свойств, допускающих
упорядочивание.
Глава 2.2
Философские притчи и
финансовые «пузыри»
Случайности, которые предлагает нам Природа, при-
водят нас к парадоксу с чудесной и обескураживающей
легкостью. Мы покажем это в начале главы с помощью
двух историй, касающихся парадокса вероятного значе-
ния, иначе говоря, ловушек, предполагающих неизвестное
и непредвиденное там, где распределение вероятности мас-
штабируемо. Затем наш тон становится куда серьезнее, и,
используя те же самые идеи, мы покажем, что целиком
и полностью рациональная Биржа запросто может стать
предметом некоторых «дутых» теорий.
Этимологическая деталь: если бы мы с вами жили
в XVIII веке, в заголовке главы стояло бы «притчи с на-
меком».
Кладбище юных поэтов
На кладбище, где покоятся ученые, мыслители и по-
эты, умершие молодыми, каждый памятник воплощает со-
бой символ разлома: наполовину обрушенная колонна, рас-
щепленное посередине перо, разодранная пополам книга,
или отбитое донышко реторты. Старый кладбищенский
сторож, сам поэт и очень ученый человек, охотно объяс-
няет этот символизм.
«Знаете ли Вы, — говорит он, — что на каждого смерт-
ного, написавшего за свою жизнь два стихотворения, при-
ходится четверо других, написавших только по одному, а
Мираж в Туманах
95
на каждого, кто написал N стихотворений, приходится N в
квадрате таких, у кого все творчество свелось к их первой
работе. С точки зрения математики отсюда следует, — про-
должает он, — что если ученый написал N работ, то можно
надеяться, что в будущем он напишет еще в среднем столь-
ко же, конечно, если этому не помешают тяготы старости,
как это, к сожалению, произошло со мной.
Математическое ожидание этих будущих работ опре-
деляется очень малым числом творцов, сравнимых с Вик-
тором Гюго, и множеством прочих, которые, скорее всего,
далеко не пойдут. Но поэт завершает свой путь здесь лишь
в том случае, если он умер молодым, к критикам наше ми-
лосердие глухо. Мы считаем, что похитившая его Смерть
остановила его в точности посередине карьеры, которая
обещала продлиться еще долго, если она уже была плодо-
творна, или недолго, если право найти себе вечный покой
здесь дала ему его единственная работа.»
Мираж в Туманах
Есть такая местность, которая называется Край Деся-
ти Тысяч Озер; названием каждого озера служит его поряд-
ковый номер в ряду озер, расположенных по уменьшению
ширины.
Действительно, самое большое из этих озер представ-
ляет собой целое море, можно было бы даже назвать его
Океаном; ширина его составляет по меньшей мере 1600 ки-
лометров. Озеро с номером г имеет ширину 100/у/f кило-
метров, а ширина десятитысячного озера равна приблизи-
тельно 1 километру (там есть еще много других озер, но
мы будем полагать, что они слишком малы, чтобы стоило
принимать их в расчет).
Сразу за этой местностью начинаются Туманы. Край
этот получил свое название потому, что там можно видеть
только на расстоянии до 1 километра. Царство Умозаклю-
чений и Вероятных Значений, нанеся на карту Край Озер,
направило своих исследователей на завоевание Туманов.
96
Глава 2.2
Солдатам Царства было известно, что ширина озер в
неведомой стране подчиняется тому же распределению, что
и в соседнем Крае Озер.
Ввиду того, что в расчет необходимо было принимать
только те озера, которые нельзя полностью окинуть взгля-
дом с одной из точек на берегу, и из-за непроницаемо-
сти Туманов, потребовалось прибегнуть к Статистической
Оценке Расстояния.
Вооруженные верой в Вероятное Значение, они всякий
раз подсчитывали и пересчитывали, исходя из уже прой-
денного расстояния, математическое ожидание той части
задачи, которую еще оставалось выполнить.
Итак, любой исследователь, готовый взяться за весла
и пуститься в плавание по озеру, другого берега которого
он не видит, знал, что расстояние, которое ему предсто-
ит преодолеть, составляет не менее одного километра, в
среднем же оно равно 5 километрам. Если, проплыв на
лодке несколько километров, он еще не достигал проти-
воположного берега, то это означало, что ему оставалось
покрыть расстояние, еще в 5 раз большее. А затем, со-
вершенно неожиданно, из Туманов выступали деревья, и
путешествие подходило к концу.
«Да обрушатся на голову этого предсказателя все
несчастья мира!» Он над нами издевается или все же ошиб-
ся в расчетах? Первый путешественник вначале еще верил
в результаты этих расчетов (а как же иначе?), однако ему
вскоре пришлось сдаться перед лицом математической оче-
видности. Забавный факт: путешественник приближается
к завершению своего труда (который заключается в изме-
рении ширины озера), а вероятное значение этой самой
ширины тем временем все продолжает расти.
Люди шумят, люди поражены, а ветераны терпеливо
объясняют, что этого никак не избежать, что другой берег
озера непременно окажется миражом. Тем не менее он су-
ществует, а фантастические призраки Туманов не только
всегда в конце концов рассеиваются, но в общем случае
рассеиваются довольно быстро. Во всяком случае сам факт
того, что мы преодолели несколько километров, ничего не
Парадокс вероятного значения
97
встретив на пути, должен заставить умолкнуть всякую на-
дежду на то, что нам попалось небольшое озеро, и увели-
чить уверенность в том, что озеро это имеет средние или
большие размеры, увеличивается также и страшная опас-
ность того, что мы, ни о чем не ведая, попали прямиком в
Океан.
То, что кажется миражом, в конце концов всегда бу-
дет достигнуто, если проявить достаточное упорство. Надо
грести вперед, кроме того весьма благоразумно будет время
от времени возвращаться назад и пополнять запасы прови-
зии — тише едешь, дальше будешь.
Другой берег всякий раз появляется именно тогда, ко-
гда с точки зрения здравого смысла он кажется как никогда
далеким.
Итак, здесь можно самым буквальным образом приме-
нять всякого рода речевые штампы. Не сдавайся в послед-
нюю минуту. Туман не может вечно скрывать деревья. Надо
смириться и не принимать всерьез никакие заверений о за-
ранее предвиденных расходах на путешествие, ведь всякий
перерасход непременно подразумевает еще большие пере-
расходы. В конце концов мы увидим свет в конце тоннеля,
но последний этап («последняя минута») тяжелее всего; с
этой точки зрения никакая местность не будет сложнее, чем
Край Десяти Тысяч Озер.
Парадокс вероятного значения
Нет никакого сомнения в том, что с точки зрения ста-
тистики поэты ничем не отличаются от химиков, а именно
для химиков А. Лотка открыл свой закон обратной зависи-
мости от квадрата N. Точно так же нет оснований прово-
дить различия между поэтами и актерами телевидения, о
которых на Бродвее говорят (если верить слухам), что их
будущие достижения в любой момент времени (в среднем)
совпадают с достижениями прошлыми. Закон Лотки имеет
чисто эмпирический характер, и я не знаю ни одного хоть
сколько-нибудь достоверного объяснения этого закона.
7 Б. Мандельброт
98
Глава 2.2
Что касается второй притчи, то статистика наших де-
сяти тысяч озер идентична той статистике, которая, как
отмечает Я. Корчак, правит всей остальной Землей (доста-
точно обратиться к «Альманаху», чтобы убедиться в ис-
тинности этих утверждений). Я посвятил этим озерам мно-
жество страниц своих «Фрактальных объектов». Надеюсь,
мне удалось показать, что эта статистика очень неплохо
согласуется с тем, что берега океанов имеют бесконечно
большую длину и фрактальную размерность, превосходя-
щую единицу.
Эти две притчи основаны на парадоксальном, на пер-
вый взгляд, выражении, которое определяет вероятное зна-
чение, зависящее от масштабируемой случайной перемен-
ной. Будем рассуждать так: пусть у нас есть случайная
переменная U, заданная неравенством U h, где вели-
чина h называется порогом. В притчах постулируется, что
соответствующее вероятное значение пропорционально h
(например, равно Ah, где А — некоторая константа).
Однако вышеупомянутая пропорциональность следует
из того, что распределение вероятностей предполагается
масштабируемым, то есть
Рг{С7 > и} = u”Q, где а = А/(А — 1).
Доказательство: если все, что мы знаем о такой пере-
менной U, — это то, что U h, где h известно, то получаем
условную вероятность
Рг{[7 > и | U > h} = (U/h)~a.
Отсюда следует, что вероятное значение U — h рав-
но h/(a - 1) (CQFD1).
Иначе говоря, масштабируемое распределение не име-
ет собственного масштаба, но всегда заимствует масштаб
наблюдателя; в первой притче постулируется, что а = 2;
во второй, что а = 1,25.
!Се qu’il faut demontrer (фр.) — Что и требовалось доказать. — Прим,
перев.
Мартингалы и рациональные «пузыри» 99
Мартингалы и рациональные «пузыри»
В работах [М 19750] и [М1997FS] можно видеть, что
масштабируемое распределение управляет очень многими
случайными процессами в геоморфологии и общественной
жизни человечества. Теперь несколько нарушим логиче-
ский порядок и перейдем к некоторым следствиям, кото-
рые могут возникнуть из парадокса вероятного значения в
другой ситуации — когда величина математического ожи-
дания совершенно не совпадает с реальной, так как на нее
сильно влияют малочисленные экстремальные случаи.
Как уже неоднократно (и более или менее детально)
повторялось в этой книге, самые простые финансовые мо-
дели включают в себя гипотезу о том, что последователь-
ные изменения логарифма цены стационарны и незави-
симы. Эта модель называется «случайным блужданием».
В некоторых случаях, изученных в главе 3.1, и эта первая
аппроксимация уже довольно хороша, но она всегда оста-
ется всего лишь аппроксимацией; как можно будет вско-
ре убедиться, к числу абсолютных защитников случайного
блуждания я не принадлежу.
Причина, по которой имеет смысл говорить о нем в
этой главе, состоит в том, что придумавший «случайное
блуждание» Луи Башелье предложил его только потому,
что это наиболее простой пример процесса, удовлетворяю-
щего более общему, нежели затрагивается здесь, принци-
пу ([Bachelier 1914], р. 180):
«Принцип математического ожидания, — Операции
на Бирже подчиняются закону спроса и предложения, кро-
ме того, каждый из маклеров волен предпринять как ту
или иную биржевую операцию, так и противоположную ей;
не следует полагать, что какая-то из спекулятивных опера-
ций a priori благоприятна или неблагоприятна для одного
из контрагентов... Именно этот факт выражен в правиле:
математическое ожидание любой операции равно нулю...
Этот принцип... применим... к любой операции, какова
бы ни была ее сложность, при условии, что эта операция
основана на последних изменениях курса.»
7*
100
Глава 2.2
Эта цитата практически определяет то, что математики
называют «мартингалом».
Продолжим объяснение того, почему эта концепция
оказывается столь успешной в данной главе. Многие ав-
торы (начиная с Башелье, хотя, быть может, я невнима-
тельно его читал) создают впечатление, что мартингалы —
это не процессы с обязательно независимыми прираще-
ниями, но процессы с почти независимыми приращения-
ми. Однако это заведомо неправильно. В чем мы сейчас
и убедимся, построив небольшую экономическую систему,
в которой цены образуют мартингал, очень непохожий на
случайное блуждание. Технические детали можно найти в
работе [М 1966b {Е14}].
Исходная точка: изучая случайные переменные U (как
физические, так и экономические), играющие в экономи-
ческой системе роль экзогенных переменных, я устано-
вил, что многие из них имеют масштабируемое распре-
деление.
Предположим теперь, что цена некоторого продукта
должна меняться как QU, где Q — некоторая константа.
Допустим, что мы знаем об U только то, что ее значение
превосходит h > 0. Если мы хотим предсказать и при-
нять в расчет вероятное значение переменной С7, то при
известном h изменение цены принимает вид Qha/(а — 1).
Этот множитель образует нечто среднее между наиболее
вероятным случаем, когда значение разности U — h мало,
и не столь вероятным случаем, когда U — h очень вели-
ко. Этот множитель неявно предполагает, что некая Биржа
ценностей использует одну и ту же валюту и для измерения
реально существующих вещей, и для измерения ожиданий.
В качестве заключения: в масштабируемом случае це-
на будет следовать за этими изменениями, усиливая их.
Следовательно, рано или поздно мы наконец узнаем в точ-
ности, чему равно U; к этому моменту в цену будут внесе-
ны грубые поправки, равные вербализовавшимся предска-
заниям. В результате ценам приходится регулярно подни-
маться без видимых признаков остановки, поэтому когда
они таки где-то останавливаются, это всегда неожиданно —
Мартингалы и рациональные «пузыри»
101
данное правило справедливо до тех пор, пока не случается
какого-либо чудовищного разрывного обвала цен.
А в той Вселенной, где случайное не является мас-
штабируемым, все вышеописанное происходило бы почти
непрерывно, или, по крайней мере, так казалось бы наблю-
дателю, находящемуся на некотором удалении.
Никто не станет утверждать, что такая модель оправ-
дывает все резкие скачки на Бирже, поскольку они являют-
ся неизбежными последствиями похвального подчинения
принципу вероятного значения. Тем не менее интересно,
что какая-нибудь хроника может содержать поразительные
«конфигурации», будучи при этом мартингальной, то есть
такой, что любое знание о ее прошлом бесполезно для
предвидения среднего ее значения в будущем.
Скептики никогда не перестанут спрашивать себя, ка-
ким образом, имея перед глазами столь странные проявле-
ния Здравого Смысла, можно распознать тревожные сигна-
лы Безумия или же фальсифицирующих манипуляций.
Глава 2.3
Белый гауссовский шум
и несколько достаточно
понятных примеров
стихийного случая
В этой главе, как и в главе 2.5, воспроизведены неиз-
данные заметки, написанные мною в разное время в педа-
гогических целях. Данная глава начинается с примера наи-
более прирученного случая, далее следуют примеры сти-
хийного случая, допускающие полное объяснение. Приме-
ры (в основном, старые, кроме одного, за моим авторством)
весьма разнообразны. Они не связаны напрямую с финан-
сами, но должны подготовить читателя к встрече с главны-
ми вопросами этой книги.
Белый гауссовский шум
Смешанный термин «белый гауссовский шум» образо-
ван из слов, позаимствованных соответственно из акусти-
ки, романтического периода истории теории вероятностей
и из оптики. Вкратце, в настоящий момент он означает
последовательность независимых (отсюда «белый») слу-
чайных переменных (собственно «шум»), подчиняющихся
закону распределения, который принято называть «гауссов-
ским».
Сразу подчеркнем очень важный факт: шум может
быть белым, не будучи гауссовским. Действительно, одним
Белый гауссовский шум
103
из отличительных качеств моей модели [М1972], касаю-
щейся спекулятивных цен, было то, что белый шум в ней
мог быть негауссовским, причем весьма явным и грубым
образом.
Плотность гауссовского распределения имеет хорошо
известный вид
ах/2тг '	2(т2 /
Этой функции соответствует кривая, которую приня-
то называть «огивой Гальтона». Говорят, что эта кривая
центрирована относительно среднего р, а ее типичное от-
клонение равно а. Она симметрична, и ее «хвосты» очень
быстро убывают. Медиана — это такая величина, что веро-
ятность превзойти ее равна 1/2; здесь медиана совпадает
со средним р\ четверти — это такие величины, что вероят-
ности превзойти их равны 1/4 и 3/4.
В главе 3.1 мы подробно рассмотрим обычную мо-
дель изменения цены, где постулируется, что логарифм
цены logZ(t) ведет себя как броуновское движение B(t).
Полезно вспомнить, что это движение определяется как
случайный процесс, причем для любых интервалов (ti,
и (£3,^4), где t3 > ^2, приращения £(£2) - B(ti) и В(^) —
— В(£з) являются независимыми и гауссовскими. Отсюда
следует, что при всех t разность B(t) — В(0) оказывается
гауссовской с дисперсией, равной t.
Если ожидание этого приращения равно нулю, то по-
лучаем следующий закон масштабирования: распределение
величины
B(t + d) - B(t)
у/d
не зависит ни от t, ни от d.
Отклонение, равное 10а, заслуживает того, что бы счи-
тать его огромным. Его вероятность близка к 10”23; это
число обратно знаменитому «числу Авогадро», которым
измеряется количество молекул в одном моле вещества. Од-
нако относительно часто встречаются случаи, когда можно
104
Глава 2.3
утверждать, что биржевые колебания образуют белый гаус-
совский шум, а отклонения при этом превосходят 10а. Это-
го достаточно, чтобы полностью отказаться от гауссовской
модели Биржи.
Первая иллюстрация гауссовского шума была приве-
дена на рис. 1.1, другую иллюстрацию можно найти в гла-
ве 3.1. Если рассматривать различные выборки такого шу-
ма с достаточно близкого расстояния, то кажется, что они
очень отличаются друг от друга — как и должно быть по са-
мому определению случая. И наоборот, издалека они очень
похожи друг на друга и кажутся очень «монотонными». На-
пример, в общем случае они дают оценки, очень близкие
к значениям двух определяющих процесс параметров, то
есть к его среднему д и его дисперсии а2.
Причинные связи и ручной шум
Предположим, что между величинами, на числовые
характеристики которых влияет белый гауссовский шум,
существует какая-то причинная связь. Если вышеуказан-
ные характеристики имеются в изобилии, то мы нисколько
не должны бояться, что шум помешает нам открыть пред-
полагаемую взаимосвязь.
Возьмем, например, медную проволоку. Шум, влия-
ющий на электрический ток, можно считать практически
белым и гауссовским, и нам достаточно найти среднее за
какой-то относительно короткий период, чтобы полностью
исключить случай и получить величину, которая определя-
ет равновесную силу тока. Несомненно, этого достаточно,
чтобы понять, что этот шум не помешает открытию закона
Ома, каковой закон в силу причинно-следственных связей
определяет вышеуказанную силу тока как отношение меж-
ду напряжением и сопротивлением, причем обе величины
ведут себя весьма «шумно».
Что касается интенсивности теплового шума, то она
пропорциональна произведению температуры на коэффи-
циент, который принято называть «спектральная полоса
Обычная центральная предельная теорема 105
пропускания». Этот результат содержится в законе Найкви-
ста, о котором я могу с уверенностью сказать, что если бы
теория запоздала, то его можно было бы легко установить
эмпирически.
Обычная центральная предельная теорема,
ее мощность и ее ограниченность
Как бы то ни было, а в исторической действитель-
ности закон Найквиста, как мне кажется, был изначально
выведен теоретически, исходя из статистической механики,
с помощью рассуждений, которые заслуживают того, что-
бы описать их подробнее, так как они представляют собой
превосходный образец статистического рассуждения:
А) Случайный фактор возникает хотя бы вследствие того,
что электрический ток представляет собой результат
суммарного вклада, образуемого воздействием боль-
шого количества электронов; в принципе мы, может
быть, и могли бы отдельно проследить за движени-
ем каждого электрона (так как законы этого движения
хорошо известны), но на практике это, строго говоря,
невозможно.
В)	Электрон, который, как выясняется впоследствии,
внес самый большой вклад, оказывает пренебрежимо
малое воздействие по сравнению с суммарным воздей-
ствием всех других электронов.
С)	Если шум «белый» (независимый), то все возможные
частоты вносят одинаковый вклад; это следствие тео-
ремы о равном распределении энергии, сама эта тео-
рема основывается на «эргодических» аргументах.
D)	Если шум гауссовский, то он «обязан» этим централь-
ной предельной теореме, в уникальность которой стре-
мятся поверить очень многие.
106
Глава 2.3
Этапы приведенной выше аргументации характерны
для статистической механики. Их красота и их сила про-
исходят из простоты их предсказаний: здесь уместно вспо-
мнить уже цитированные в главе 2.1 слова из работы Гне-
денко и Колмогорова [Gnedenko & Kolmogorov 1954] о том,
что «коллективное действие» регуляризует все что угодно;
более того, такая коллективная упорядоченность во всех
случаях принимает одну и ту же форму.
Физики говорят об «универсальности». Они умеют по-
казать, что нет ничего страшного в том, чтобы неправильно
сформулировать основные предположения, как это быва-
ет из-за незнания деталей, например, межатомных взаи-
модействий или по каким-то другим причинам. Благодаря
«универсальности» и упорядоченности все это «простит-
ся», окончательный результат всегда будет одинаков.
Теорема — это еще не безусловная истина
Идеи предыдущего раздела получили такое распро-
странение и имели такой успех, что может показаться свя-
тотатством напоминание о двух фундаментальных истинах.
Во-первых, «математическая теорема» — это утвер-
ждение, у которого есть тысяча достоинств, но это совсем
не то же самое, что «закон природы». Какой бы мощной она
ни была, всякая математическая теорема подразумевает ряд
гипотез, которые, конечно же, могут оказаться чрезвычай-
но общими, но тем не менее неприменимыми именно в том
случае, который нас интересует.
Далее, произвольная предельная теорема очень ред-
ко имеет непосредственный практический смысл; в общем
случае нас интересует поведение, которое можно охаракте-
ризовать как «предпредельное». Однако оно зачастую име-
ет слишком сложный характер, не позволяющий удобно им
управлять, тогда как соответствующие числовые значения
неотличимы от значений, полученных с помощью асимпто-
тического распределения, которым управлять легко.
Отсюда следует, что теорема о сходимости имеет прак-
тическое значение только тогда, когда эта сходимость яв-
Теорема — это еще не безусловная истина
107
ляется достаточно быстрой. Следовательно, в принципе,
прежде чем применять какую-нибудь теорему, необходимо
ответить на два вопроса: 1) выполняется ли эта теорема
асимптотически? и 2) применима ли она?
Эти вопросы чрезвычайно сложны, и среди уче-
ных-практиков принято констатировать, что зачастую «слу-
чается» так, что выводы теорем остаются верными, даже
если соответствующие гипотезы неверны. Более того, ма-
тематики (чтобы иметь возможность заявлять о результа-
тах, обладающих большой общностью) вынуждены изу-
чать сходимость в наиболее неблагоприятном случае, а от-
сюда вытекает, что величины, подчиняющиеся предельным
теоремам, «имеют привычку» сходиться быстрее, чем пред-
виделось. Вывод: не стоило и беспокоиться.
В течение долгого времени такое поведение приво-
дило к полезным теориям, но я считаю, что скоро мы до-
стигнем пределов его применимости. Вспомним старую ба-
нальность эпохи 1900-х годов: тогда говорилось, что физи-
ки пользуются гауссовским распределением для «ошибок»,
потому что они полагают, что необходимость этого дока-
зана математиками, тогда как математики изучают только
гауссовское распределение, так как верят, что универсаль-
ность его применимости установлена физиками.
Специалисты в области теории вероятностей гордятся
тем, что они далеко ушли от этого состояния; однако никто
бы так не сказал, если бы прочел большую часть учебни-
ков, позволяющих нам судить о прогрессе теории вероятно-
стей снаружи. Словарь следует за модой; из-за стремления
к строгости предварительные математические данные раз-
бухают и усложняются, что отодвигает границу области,
внутри которой, как было показано, действует распределе-
ние Гаусса.
Что касается происходящего за пределами этой обла-
сти, то в общем случае курсы и учебники довольствуются
тем, что приводят единственный контрпример, который хо-
тя бы из-за своей единственности кажется каким-то абсур-
дом. Этим контрпримером является процесс Коши. Сейчас
мы подробно его рассмотрим, прежде чем перейти к другим
108
Глава 23
примерам, ставящим перед нами аналогичные проблемы.
В главе 2.4 будут сделаны выводы, а в главе 2.5 мы пой-
дем дальше того, что уже хорошо известно, и прежде чем
поставить более общие задачи, поговорим об 1//-шуме.
«Контрпримеры» Коши: переменная,
блуждание и белый шум
Случайная переменная, носящая имя великого фран-
цузского математика Огюстена Коши (1789-1857), опреде-
ляется как переменная с нормированной плотностью веро-
ятностей, равной
1
7Г(1 + X2)
Это преобразование Фурье для характеристической функ-
ции exp(-|z|).
Огива Коши, представляющая вышеуказанную плот-
ность, отличается от огивы Гальтона более заостренной
вершиной и более длинными хвостами. На первый взгляд
обе кривые кажутся очень похожими, однако думать так
было бы серьезной ошибкой!
Процесс Коши, или, точнее, «белый шум Коши», —
это процесс с независимыми величинами типа Коши. Он
обладает таким свойством: его среднее,
гад
т 1
тоже представляет собой нормированную переменную ти-
па Коши. Говорят, что она идентична переменным X(t) по
распределению. Усреднение не оказывает никакого влияния
на изменчивость, и закон больших чисел здесь неприме-
ним. Говорят также, что белый шум Коши «неэргодичен».
Блуждание Коши — это функция C(t), приращениями
которой C(t + d) — C(t) являются независимые случайные
Лучник с завязанными глазами
109
переменные типа Коши. Отсюда следует, что распределе-
ние
C(t + d) - C(t)
d
не зависит ни от t, ни от d.
Бесконечные ожидание и дисперсия. Сделаем еще од-
но замечание, которое окажется очень важным в дальней-
шем: ожидание и дисперсия переменной типа Коши заданы
интегралами

* J 1 + ?
—оо
X [ x2dx
* J 1 + Z
Однако оба эти интеграла расходятся. Точно так же обстоит
дело и с другими моментами порядка q > 1. Отсюда сле-
дует, что выражение, входящее в центральную предельную
теорему, не имеет смысла, а саму теорему можно приме-
нить разве что в «обобщенном» виде, который полностью
меняет ее смысл. Обычные теоремы в данном случае успе-
ха не имеют, потому что здесь часто присутствуют экстре-
мально большие величины — флуктуации, которые я буду
называть «флуктуациями Ноя».
Феномен концентрации. Если рассматривать сумму
независимых переменных типа Коши, то слагаемым с наи-
большей абсолютной величиной не только нельзя прене-
бречь, но может оказаться, что оно близко ко всей сумме
по относительной величине. Это очень важный факт.
Лучник с завязанными глазами
Остановимся на минуту и приведем пример явления,
имеющего распределение Коши. Это совершенно искус-
ственный пример, в точности перенесенный из одного
школьного упражнения, но как раз своей простотой он и
сослужит нам службу. Этот пример следует из равенства
Pr{X > х} = ± arcctgx.
по
Глава 2.3
Пусть стрелок из лука располагается непосредственно
перед мишенью, нарисованной на стене. Глаза его завяза-
ны, так что он может стрелять только наугад. С вероятно-
стью 1/2 он вообще не попадет в стену, но мы не будем
учитывать этот случай; с вероятностью 1/2 он заденет ее, а
его ошибка при стрельбе будет, как выясняется, случайной
переменной с распределением Коши.
Потребуем от него минимизировать среднее его оши-
бок при стрельбе. Наш стрелок ничего не выиграет от своей
настойчивости. Во всех случаях его средняя ошибка будет
зависеть от тех редких случаев, когда он стреляет почти па-
раллельно стене, и стрела касается ее лишь очень и очень
далеко от мишени. С таким же успехом он мог бы закон-
чить стрельбу и после первого выстрела.
Противоречия, связанные с шумом Коши
Шум Коши инвариантен относительно своего сред-
него — признание важности этого факта и выработка со-
ответствующей реакции на него последовали незамедли-
тельно. Чтобы убедиться в этом, достаточно взглянуть на
протокол заседания Академии Наук от 29 августа 1853 го-
да в «Comptes rendus de Г Academic des Sciences»1. Здесь
мы найдем дискуссию между Коши и Иренеем Бьенеме
(1796-1878) (подробнее об этом интересном человеке мож-
но прочесть в [Heyde & Seneta 1977]). Дискуссия эта забав-
на, актуальна, и легко читается (во всяком случае, с точки
зрения человека моего возраста). Если читатель придер-
живается много мнения, то последующие два раздела он
может с легкостью пропустить.
Коши против Бьенеме
В течение всего августа 1853 года Коши вел с Бье-
неме дискуссию о средних или наиболее вероятных ре-
зультатах, а также о «методе наименьших квадратов». Этот
1 «Отчеты Академии Наук» (фр.). — Прим, перев.
Коши ПРОТИВ Бьенеме
111
метод состоит в том, чтобы оценить (располагая неким на-
бором экспериментальных данных) «истинное» значение,
минимизируя сумму квадратов ошибок, получаемых при
коррекции. Разумно ли поступать таким образом во всех
случаях? Коши в этом усомнился, Бьенеме же возразил в
следующих выражениях:
«Во время заседания 8 августа 1853 года господин Ко-
ши отрицал точность замечательного результата, открыто-
го и доказанного Лапласом; суть этого результата состоит в
том, что метод наименьших квадратов применим к данным
наблюдений, каково бы ни было распределение вероятно-
стей ошибок.»
Далее смесь возвышенного и вульгарного:
«На первый взгляд кажется, что существует некая за-
гадочная связь между вероятностями и этим интегралом,
который обнаружил господин Гаусс в самом начале его
исследований. Равным образом многие ученые полагали,
что более глубокое понимание теории вероятностей долж-
но привести к осознанию того, что распределение вероят-
ностей ошибок выражается функцией Гаусса. Но именно
здесь кроется одно из тех неточных мнений, которые при-
водят к ошибочным последствиям: и таких последствий
возникает очень много, как с точки зрения теории, так и в
практических результатах. Здесь достаточно будет сказать
следующее: 1) не существует необходимой связи между
этой экспонентой и распределением вероятностей; 2) это
не более чем очень удобное средство аппроксимации, ко-
торое можно было бы заменить другими формулами; 3) мы
беспрестанно возвращаемся к ней, потому что она очень
подходит для представления функции в окрестности мак-
симума, впрочем эта экспонента представляет функцию
лишь приблизительно; и 4) даже в тех вопросах, где экс-
понента предлагает нам наиболее легкий способ аппрок-
симации, она зачастую дает результаты, ошибочность ко-
торых становится очевидной, как только мы хотим при-
менить их для хоть сколько-нибудь сложных рассуждений,
вместо того, чтобы принимать ее за то, чем она являет-
ся в действительности — то есть за чисто арифметиче-
112
Глава 2.3
ский механизм, подходящий для непосредственных расче-
тов.»
Затем тема развивается, причем можно подумать, что
эти строки написаны совсем недавно:
«Но вышесказанное неприменимо к среднему значе-
нию квадратов разностей между ошибками и их средним.
Оно не является произвольным элементом аппроксимации;
не является оно и, как полагал Гаусс, некоей произвольной
мерой точности, которую можно заменить любым другим
средним четных степеней. Напротив, в среднем квадрати-
ческом содержится фундаментальное условие разложения
вероятностей по мере увеличения количества наблюдений;
и хотя и нельзя сказать a priori, что мы не можем найти ка-
кую-нибудь более удобную для нас функцию (отличную от
средних в четной степени), можно во всяком случае утвер-
ждать, что даже в предположении подобного открытия та-
кую функцию можно будет заменить на среднее квадрати-
ческое, если воспользоваться им подходящим образом.»
Наконец, мы сталкиваемся со странным рассуждени-
ем, когда, выступая в защиту результата Лапласа, Бьенеме
в конце концов отрицает его точность (и, следовательно,
присоединяется к мнению Коши). Продолжим чтение:
«Кроме того, предположим на мгновение... что сред-
нее квадратическое вообще не имеет конечного значения.
Сами результаты наблюдения предупреждают об этом да-
же наиболее невнимательного наблюдателя. Поскольку бу-
дет необходимо, чтобы большие значения ошибок имели
заметную вероятность, а тогда они будут присутствовать
если и не так же часто, как другие, то по крайней мере
в достаточно большой пропорции. Таким образом мы по-
лучим результаты наблюдений, пугающие своей несогла-
сованностью; эти результаты, несомненно, будут отброше-
ны, а инструменты или процессы наблюдения подвергнутся
основательной корректировке.
Возьмем в качестве примера функцию вероятно-
стей ..., на которую указывает господин Коши... Можно
сразу понять, что инструмент, подверженный влиянию по-
добного вероятностного закона, обычный ремесленник да-
Коши ПРОТИВ Бьенеме
113
же не пустит в продажу. Неизвестно, как можно назвать то
здание, которое он построил бы таким инструментом...
Какую бы меру мы ни захотели взять в качестве еди-
ницы ошибки, можно будет с легкостью найти в окрест-
ности этой единицы ошибку, в шесть раз большую или в
шесть раз меньшую. Следовательно, очень большие ошиб-
ки проявятся очень быстро. Простой подсчет, основанный
на функции
Рг{Х < х} = (2/7r)arctgx,
показывает нам, что можно ставить 2 против 1 на то, что мы
найдем ее в десяти наблюдениях, и более чем 7 против 1,
если этих наблюдений будет хотя бы двадцать.
Относиться к подобному инструменту настороженно
призывает самая обыкновенная внимательность.
Скажу больше, это очень странный инструмент. Он
настолько же надежен в одном единственном наблюдении,
насколько и в среднем из 10, из 20, из 1000 или из какого
угодно количества наблюдений — или, скорее, он настолько
же опасен в среднем из 1000 наблюдений, как и в одном-
единственном. Действительно, очень легко убедиться, что
распределение вероятностей... среднего... из п наблю-
дений в точности равно... каким бы большим или ма-
лым ни было число п, распределению одной-единственной
ошибки. В данном случае в нашем распоряжении оказыва-
ется инструмент, с помощью которого можно осуществить
лишь одно-единственное наблюдение.
Следует признать, что подобный пример никоим обра-
зом не противоречит открытию Лапласа. Конечно, под сло-
вами «какая угодно функция» можно подразумевать только
функцию, способную давать результаты если и не слишком
точные, то, по меньшей мере, тем более точные, чем боль-
ше труда затратит наблюдатель, умножая количества своих
сложных операций.
Так же и господин Пуассон — первым упомянувший
о функции «арктангенс», — разве он из-за этого с мень-
шим доверием отнесся к методу наименьших квадратов?
8 Б. Мандельброт
114
Глава 2.3
Он ограничился лишь уверением, что на практике, несо-
мненно, мы с такой гипотезой не встретимся.»
Иначе говоря, и Пуассон, и Бьенеме рассуждали в тех
же выражениях, что и многие экономисты вчерашнего дня,
которые, даже не говоря об этом, полагали, что примеры,
для которых метод наименьших квадратов не применим,
«на практике, несомненно, не встречаются».
Гарольд Джеффрис (1891-1989)
Чтобы сменить тон, но сохранить при этом общую
идею, почитаем Джеффриса ([Jeffreys 1948], с. 244):
«Можно заметить, что многие физики полностью от-
казались от обычной (то есть гауссовской) теории ошибок,
поскольку систематические ошибки присутствуют всегда
и количество их отнюдь не уменьшается от того, что мы
берем среднее по большому числу наблюдений. Этим фи-
зикам хотелось бы верить... [что] среднее не обязательно
лучше отдельного наблюдения, а единственная цель повто-
рения наблюдений — защититься от грубых ошибок; мож-
но отказаться от такой позиции под тем предлогом, что
она противоречит теории вероятностей, однако этот отказ
неразрывно связан с верой в то, что нормальное распреде-
ление есть единственно возможное распределение. В самом
деле, поведение старомодного физика оказывается полно-
стью формализуемым. Если каждое наблюдение подчиня-
ется распределению Коши, а среднее подчиняется в точно-
сти тому же самому распределению... Впрочем, детальное
изучение допущенных во время наблюдения ошибок, в об-
щем случае, показывает, что они далеки от распределения
Коши и гораздо ближе к нормальному распределению...
Следовательно, точка зрения старомодного физика не столь
уж абсурдна. Ее можно разделить на две части... первая
из которых ошибочна, а вторая допускает переоценку...»
Этот текст чрезвычайно показателен даже в своей дву-
смысленности. Джеффрис-физик смог вызвать беспокой-
ство у Джеффриса-статистика в связи с применимостью
Концентрация возвращений к исходной точке 115
ручного случая, но это беспокойство недостаточно вели-
ко, чтобы отказаться от такого случая совсем. Немного
предвосхитим события: случай, на который ссылается и на
который надеется Джеффрис, случай, промежуточный меж-
ду случаем Гаусса и Коши, стал известен уже в 1949 году.
Вскоре мы встретимся с ним в главе 2.4 в виде L-устойчи-
вых распределений.
Концентрация возвращений к исходной точке
при игре в «орлянку»
Пьер и Франциск — два «порождения мысли» Бернул-
ли, неутомимые и бесконечно богатые, с которыми мы уже
встречались ранее. Начиная с 1700 года, они безостановоч-
но играют в орлянку, используя одну и ту же монету.
В каждый момент времени t, когда выпадает решка
(это событие обозначается буквой Р, от слова «pile» —
«решка»), Пьер выигрывает один бальский денье и X (t) =
= 1; после каждого орла (F, от «face» — «решка») один
бальский денье выигрывает уже Франциск и X(t) = — 1.
Выразительнее всего эту игру описывает последова-
тельность X (t) и их средних. Мы получаем непосредствен-
ный прототип ручной флуктуации. Впрочем, у этой игры
есть и другие аспекты, бесконечно менее ручные, и они не
перестают беспокоить нашу «интуицию».
Определим, например, «прерывание» — интервал вре-
мени U между последовательными моментами, в которые
запас денег у Пьера и Франциска возвращается к состо-
янию, наличествовавшему в некий предыдущий момент
времени, выбранный в качестве начального. По опреде-
лению эти прерывания статистически независимы, и мы
знаем, что (по крайней мере, если верить Огюстену Кур-
но) при и 1, вероятность Рг{17 > и} пропорциональ-
на и"-1/2.
В частности, математическое ожидание U бесконеч-
но! Эта особенность возникает из-за того, что как толь-
ко мы признаем, что U велико, мы должны ожидать, что
8*
116
Глава 2.3
оно окажется чрезвычайно велико. Действительно, боль-
шое прерывание наблюдается тогда, когда Пьер или Поль
обретают большое преимущество перед своим давнишним
соперником; чем больше это преимущество, тем дальше мы
находимся от точки возвращения. И вот результат: среднее
из п последовательных прерываний вовсе не сходится к
чему бы то ни было, его распределение еще более рассе-
яно, чем распределение каждого входящего в его состав
прерывания, взятого отдельно.
Для того чтобы получить сходящуюся величину, мы
должны разделить вышеуказанную сумму из п прерываний,
но не на само число п (как в законе больших чисел), а на
его квадрат, который растет гораздо быстрее. Полученная
таким образом сумма сходится к некоторому пределу, но
этот предел вовсе не является гауссовским.
Более того, если сумма п прерываний очень велика,
то это, несомненно, происходит от того, что одно из сла-
гаемых в ней преобладает. В этом смысле перед нами все
симптомы крайне сильного и перманентного эффекта Ноя.
С другой точки зрения мы получаем здесь пример эффекта
Иосифа. Действительно, пусть функция Ж(^) по опреде-
лению положительна тогда, когда выигрывает Франциск, и
отрицательна, когда выигрывает Поль. Эта функция W(t)
никогда не будет велика, но она чрезвычайно «настойчи-
ва».
Хольцмарк: ньютоново притяжение и
концентрация
В 1920-е годы норвежский физик Ян Хольцмарк
(1894-1975) изучал утолщение спектральных полос. Сама
по себе эта задача давно забыта, но осталось ее решение,
переведенное на язык ньютоновой гравитации.
Пусть бесконечно много точечных звезд единичной
массы случайно распределены в трехмерном пространстве,
независимо друг от друга и с единичной плотностью. Наша
цель — изучить полное ньютоново притяжение Q, которое
ХОЛЬЦМАРК: НЬЮТОНОВО ПРИТЯЖЕНИЕ И КОНЦЕНТРАЦИЯ 117
все они оказывают на одну из них; мы будем называть эту
звезду Астер.
В общих чертах, решение начинается с изучения звезд,
находящихся от звезды Астер на расстоянии, превосходя-
щем некий очень большой радиус R. Можно легко пред-
ставить себе, что их суммарное воздействие пренебрежимо
мало, потому что взаимно противоположные звезды ней-
трализуют друг друга. Отсюда следует, что притяжение Q
очень близко к суммарному притяжению звезд, содержа-
щихся в нашей сфере радиуса R. Известно, что количе-
ство этих звезд есть переменная Пуассона, ее вероятное
значение равно (4/3)тгЯ3. Если R велико, то их коли-
чество практически неслучайно. Следовательно, с точки
зрения ручного случая, надо ожидать, что полное притя-
жение представляет собой трехмерный гауссовский век-
тор, каждая координата которого, независимо от двух дру-
гих, подчиняется одномерному закону распределения Гаус-
са.
Если это рассуждение верно, то вклад звезды с наи-
большей силой притяжения будет почти обязательно пре-
небрежимо мал по сравнению с полным притяжением. Ес-
ли мы обманемся в этих ожиданиях и окажется, что вклад
такой звезды относительно велик, и если мы покажем эти
данные статистику, то у него возникнет искушение объяс-
нить вышеуказанную величину «аберрацией» (или, на ан-
глийский манер, «outlien>2), он посоветует нам не прини-
мать ее в расчет.
Однако эти мнимые аберрации в действительности
представляют собой преобладающее свойство нашей за-
дачи, доказывая тем самым, что она выходит за пределы
ручного случая. Это можно показать с помощью любого из
приведенных здесь отдельных аргументов.
• Случайно выбранная звезда вносит в притяжение Q
составляющую с бесконечной дисперсией. Выберем
единицы измерения так, чтобы гравитационная посто-
2Нечто, находящееся снаружи, отделенное от целого (англ.). — Прим,
перев.
118
Глава 2.3
явная равнялась единице и чтобы сила притяжения
была обратна квадрату расстояния. Договорившись об
этом, выясним, какие условия необходимы для того,
чтобы сумма Q была гауссовской.
Попытаемся найти дисперсию случайной величины U.
Притяжение произвольной звезды (U) превосходит и,
если расстояние от этой звезды до Астера (г) меньше,
чем 1/^/ц. Следовательно, вероятность Pr{U>u} рав-
на отношению объемов двух сфер с радиусами 1/\/й
и R соответственно, то есть u~3/2R~3. Соответствую-
щая дисперсия равна интегралу
R
| J и~5^2и2 du R~3.
о
Однако этот интеграл бесконечно велик, следователь-
но, сумма частичных притяжений не может быть гаус-
совской.
• Противоречие, обусловленное той ролью, которую в
доказательстве Хольцмарка играет бесконечная дис-
персия. Представляется очевидным, что в приведен-
ном выше рассуждении что-то не ладится, ведь физи-
ческая величина может быть только конечной. В конце
концов, как заметил Макс Борн, радиусы звезд не рав-
ны нулю, и поэтому сила притяжения, с которой каж-
дая из них воздействует на Астер, обязательно ограни-
чена, следовательно, имеет конечную дисперсию — та-
ким образом, выполняется условие, существенное для
того, чтобы центральная предельная теорема остава-
лась в силе.
Но этот аргумент малоубедителен, поскольку, с дру-
гой стороны, количество звезд имеет конечную грани-
цу (соответствующую точному заполнению простран-
ства), следовательно, предельный переход невозмо-
жен.
ХОЛЬЦМАРК: НЬЮТОНОВО ПРИТЯЖЕНИЕ И КОНЦЕНТРАЦИЯ 119
Итак, для устранения всяческих парадоксов следова-
ло бы рассматривать предельное поведение (точечные
звезды и бесконечно малая плотность) как простую
аналитическую аппроксимацию, удобную для «пред-
предельного» поведения, поскольку реализуется имен-
но оно. Как странно, что нас так утешает конечный
характер физической величины, пусть даже точное ее
значение очень велико и не оказывает на нас сколько-
нибудь заметного эффекта! Едва ли необходимо ука-
зывать на то, что и экономисты все время прибегают
к тому же утешительному средству, не имеющему под
собой никаких реальных оснований.
Распределение силы притяжения для точечных звезд
в зависимости от их средней плотности. Вообразим
себе, что каждая звезда с одинаковой вероятностью
может быть «зеленой» или «голубой», и запишем Q =
= V + В, где V и В обозначают тот вклад, который
вносят звезды этих двух типов в общую силу притя-
жения. Чтобы изучить, как подействует на распреде-
ление Q удвоение плотности звезд 5, достаточно, как
мы видим, сравнить распределение Q с распределени-
ями V или В.
Для этого, учитывая, что вкладом тех звезд, расстоя-
ние от которых до звезды Астер превышает 7?, мож-
но пренебречь, увеличим в 21/3 раза расстояние от
Астера до всех звезд в сфере радиуса R. Их плот-
ность будет идентична плотности зеленых звезд, пол-
ное притяжение будет равно V, а притяжение, с кото-
рым каждая звезда действует на Астер, уменьшится в
отношении 2“2/3. Для полного притяжения получаем
следующий результат:
сумма V + В подчиняется
тому же закону распределения, что и 2W.
В более общем случае, когда кроме зеленого есть еще
три цвета, распределение Q совпало бы с распределе-
нием 42/3У.
120
Глава 2.3
В терминах плотности 6 притяжение Хольцмарка про-
порционально плотности звезд в степени 2/3. То есть Q
принимает следующий вид:
52/3 х (притяжение,
соответствующее плотности 5 = 1).
В главе 2.4 мы вернемся к этому условию идентич-
ности в распределении — речь идет о L-устойчивости
или «устойчивости в смысле Поля Леви». По срав-
нению с характеристическим свойством инвариантно-
сти распределения Коши, новизна здесь заключается
в том, что количество отдельных вкладов N нужно
возводить не в степень 1/2, но в степень 2/3.
Если обозначить этот показатель через 1/а, то в случае
Хольцмарка требуется а = 3/2, в случае Коши а = 1,
а в классическом случае Гаусса а = 2.
•	Распределение вклада, вносимого самой близкой звез-
дой. Предыдущие рассуждения показывают, что это
притяжение по форме равно
52/3 х (притяжение,
соответствующее плотности 5 = 1).
•	Феномен концентрации. Притяжение наиболее близ-
кой звезды имеет тот же порядок величины, что и
полное притяжение. Этот неизбежный результат нахо-
дится в полном противоречии с нашими привычками.
Ручной случай предполагает, что самый большой из
частичных вкладов пренебрежимо мал по сравнению
с целым.
•	Выводы. Повторим еще раз, что о задаче Хольцмар-
ка вспомнили лишь постольку, поскольку ей посчаст-
ливилось быть упомянутой в качестве контрпримера
у Чандрасекхара [Chandrasekhar 1943]. Она вернулась
на сцену в [М1960i {ЕЮ}] в качестве иллюстрации к
рассуждениям о распределении доходов. Тот, кто чи-
тал [М19750], знает, что это как раз в духе фракталь-
ной геометрии: превращать интуитивные контрприме-
Концентрация в мутациях
121
ры в орудия науки! Отныне феномен концентрации
занимает свое место среди тех различий, которые я
обнаруживаю между ручным и стихийным случаем;
в частности, он находится в центре математического
анализа финансов.
Виллис - Юл - Лурия -Дельбрюк:
концентрация в мутациях
Задача Хольцмарка имеет свой аналог в биологии — в
задаче о количестве мутаций в старой колонии бактерий;
первыми эту задачу рассмотрели биологи Сальвадор Лурия
(1912-1991) и Макс Дельбрюк (1906-1981).
Частичное решение упомянутой задачи, приведенное
в [Luria & Delbriickl943], составило одну из основ моле-
кулярной биологии, но сама по себе эта задача оказалась
очень сложной и на данный момент почти забыта (в даль-
нейшем мы изучим некоторые возможные причины этого
забвения). В конце концов, отвечая на прямой вызов Дель-
брюка, я все же ее решил (см. [М 1974d {Е8}]). Там же я
и отметил, что она похожа на еще одну забытую задачу,
поставленную в 1920-х годах ботаником Дж. К. Виллисом
и решенную некоторое время спустя английским статисти-
ком Джорджем Одни Юлом (1871-1951), столпом англий-
ской школы во время ее Золотого века.
По Лурия и Дельбрюку бактерии размножаются де-
лением и являются объектом мутаций, каждая из которых
создает некоторый клон. Вероятность подвергнуться мута-
ции за промежуток времени dt равна т dt9 она одинакова
для любой бактерии в любой момент времени. Точно так же
обстоит дело с вероятностью деления, dt для нормальных
бактерий и gdt для мутантов.
Обозначив возраст культуры через t, мы приходим к
задаче о нахождении распределения количества мутантов в
клоне и в культуре. Нас интересует случай, когда t велико,
т. е. культура «старая».
Время от времени Лурия и Дельбрюк наблюдали в
своих культурах очень большие клоны, по величине на
122
Глава 2.3
несколько порядков превосходящие любое «типичное зна-
чение», например, медиану (напомним, что медиана опре-
делялась как величина, превосходимая в половине всех слу-
чаев). Сравнивая различные культуры, они нашли такие, в
которых размер самого большого клона был гораздо боль-
ше суммы размеров всех остальных.
Этими случаями можно было бы пренебречь, сочтя их
отклонениями. Однако биологи отметили их значимость и
предложили следующее объяснение.
Прежде чем «родится» следующий клон, перворо-
жденный среди клонов получает время для заметного уве-
личения своих размеров. Общее количество мутантов M(t)
будет велико тогда и только тогда, когда мутация в ходе экс-
перимента происходит очень рано, что почти всегда случа-
ется благодаря вкладу одного-единственного клона, самого
старого и, как следствие, самого крупного.
Приведенного выше краткого объяснения оказалось
достаточно для зарождения молекулярной биологии. Очень
странно, но исследование точного распределения количе-
ства мутантов продвигалось вначале весьма вяло, если не
считать работы Ли и Коулсона [Lea & Coulson 1949]. Мно-
го усилий было затрачено на вычисление вероятного значе-
ния после конечного времени £, дисперсии этого значения и
других моментов. Так, было установлено, что эти моменты
расходятся при t —> сю, однако их значений недостаточ-
но для определения искомого распределения. Чтобы дать
общее понятие об этих рассуждениях, можно сказать, что
они похожи на вычисление моментов притяжения у Хольц-
марка, в случае звезд с ненулевым радиусом. Асимптоти-
ческое расхождение моментов выглядело парадоксальным
и совершенно невыносимым.
Вернемся на двадцать лет назад. В 1920-х годах Юл,
вдохновленный идеями ботаника Дж. К. Виллиса, посту-
лировал таксономическую дифференциацию, которая дей-
ствует следующим образом: виды размножаются точно так
же, как и наши бактерии, а эволюция время от времени при-
водит к появлению новых родов, так появляются мутанты у
наших бактерий. Юл нашел распределение количества ви-
Концентрация в мутациях	123
дов в одном роде для конечного t и его предел при t оо.
Он также расценивал расхождение моментов при f —> оо
как нечто возмутительное, избегая его с завидной интел-
лектуальной акробатикой, из-за которой его работы тяжело
читать.
Однако Юл все же получил, с точностью до истол-
кования, распределение количества мутантов в некотором
клоне. Вывести отсюда точное распределение в одной куль-
туре было делом техники, не представлявшим концептуаль-
ных трудностей ни для конечного t, ни для t —> оо.
В этом пределе распределение Лурия-Дельбрюка, в
точности как распределения Коши и Хольцмарка, обладает
свойством инвариантности, которое определяет L-устойчи-
вость и будет рассмотрено в главе 2.4. Все зависит от пока-
зателя а, который представляет собой функцию от различ-
ных скоростей размножения и формирования мутантов; в
общем случае этот показатель близок к 1.
При а = 1 показатель имеет то же значение, что и
в распределении Коши; однако количество мутантов М (t)
всегда положительно, следовательно, их распределение не
совпадает с распределением Коши, но является одной из
его вариаций, обладающей одной его характерной чертой.
Оставляя в стороне сложности, на которых мы здесь оста-
навливаться не будем, можно сказать, что это распределе-
ние обладает тем же свойством инвариантности: среднее
двух независимых измерений M(t) (не считая поправочно-
го члена) имеет то же распределение, что и единственное
измерение.
Глава 2.4
L-устойчивые распределения
Все примеры, обсуждавшиеся в главе 2.3, начиная с
процесса Коши и заканчивая задачей Лурия-Дельбрюка,
имеют одну существенную общую черту: распределения,
которым они подчиняются, являются «L-устойчивыми».
Данная глава представляет собой обобщение, где эта кон-
цепция рассматривается более подробно и с некоторыми
преднамеренными повторениями.
Устойчивость гауссовского распределения
Нормированная случайная гауссовская переменная X
обладает следующим существенным свойством. Пусть G'
и G" — две независимые гауссовские переменные, при-
чем EG' = О, EG" = О, EG'2 = а'2 и EG"2 = а"2.
Известно, что сумма G = G' + G" тоже является гауссов-
ской, EG = 0, a EG2 = а'2 + а"2. Это означает, что нор-
мированная гауссовская переменная X является решением
следующего функционального уравнения:
s'X' + s"X" = sX,	(S)
где коэффициент s зависит от s' и s" и задается вспомога-
тельным соотношением
52 = 3'2 + 3"2.	(А2)
Уравнение (S) определяет L-устойчивость или, точнее,
«устойчивость по Леви».
Распределение Коши и его обобщения
125
Следует подчеркнуть, что с точки зрения (S) и (А2)
коэффициенты s' и s" представляют собой всего лишь мас-
штабирующие множители. В гауссовском случае оказыва-
ется, что они пропорциональны сгг и а", в других случаях
их приходится определять из других соображений.
Противоположное рассуждение. Пусть нам дана сум-
ма п переменных Хт, независимых и одинаково распре-
деленных, причем мы требуем, чтобы существовал такой
вес А(п), при котором величина
^Хп’
имела бы то же распределение, что и каждая из перемен-
ных X. В более общем виде, мы ищем такие две функции А
и В, чтобы разность
имела бы такое же распределение, что и каждая из пе-
ременных X. В классическом случае именно так и будет,
если все переменные X — гауссовские, a A(N) = АГ1/2
и B(N) = EX.
Распределение Коши и его обобщения
Само по себе распределение Коши удовлетворяет со-
отношению (S) вместе с дополнительным соотношением
s = s' + s".	(Ai)
Великое открытие Коши. Существуют другие симмет-
ричные распределения, удовлетворяющие функционально-
му уравнению (S). Введем один-единственный параметр
(например, а), тогда вспомогательное соотношение (А2)
примет вид
sa = 5'a + s"a.	(Aq)
126
Глава 2.4
Коши полагал, что а может быть любым положительным
действительным числом, однако Леви показал, что необхо-
димо и достаточно, чтобы
О < а 2.
Соответствующая плотность вероятностей имеет вид
а
i j ехр(—иа) cos(ux)du.
о
Преобразование Фурье, которое принято называть характе-
ристической функцией, записывается следующим образом:
ехр(—|z|a).
За исключением случаев а = 2 (Гаусс) и а = 1 (Коши)
решения в аналитическом виде не существует. Более того,
если а<2, то момент ЕХд конечен только тогда, когда q<a.
Добавим к X неслучайный множитель 5. Если ЕХ <оо,
для чего требуется а > 1, то можно принять 6 = ЕХ. Ха-
рактеристическая функция принимает вид
ехр(—i5z — 7|z|q),
где 71у/<* > 0 — масштабирующий параметр. В общем слу-
чае его уже нельзя определить через посредство моментов,
но можно использовать расстояние между медианой X и
ее квартилями.
В 1920-х годах к этой задаче обратился Поль Леви.
Именно в его терминологии описанная выше инвариант-
ность называется «устойчивостью»; термин этот весьма
неудачен, что стало причиной многих недоразумений, одна-
ко отбрасывать его совсем тоже нельзя. Поэтому я ограни-
чился «L-устойчивостью» или «устойчивостью по Леви».
Леви показал также, что существуют несимметричные
устойчивые распределения, и нашел их общий вид в инте-
гральной форме. Выражение через элементарные функции
допускает лишь один асимметричный случай — распреде-
ление, возникающее при возвращении к положению равно-
весия при игре в орлянку.
АСИМПТОТИЧЕСКОЕ ПОВЕДЕНИЕ
127
Асимптотическое поведение
В общем случае (то есть, не учитывая гауссовский слу-
чай а = 2) об L-устойчивых распределениях можно сказать
лишь то, что их асимптотическое поведение вычислимо
приблизительно, а именно:
Рг{Х > х} - Сх~а,
где С — некоторая константа, именуемая «предмножитель».
В билогарифмических координатах log я и logPr наибо-
лее удивительной чертой всех таких кривых будет то, что
они заканчиваются прямолинейным участком, задаваемым
уравнением
logPr{X > х} = log С — a log я.
Более того, отношение
Рг{х > 4
Pr{X < -х}
при х —> оо имеет предел, который определяет отноше-
ние интенсивности двух хвостов. Если предел равен нулю,
то больше плотность отрицательной части, а положитель-
ной можно пренебречь. Если предел бесконечно велик, то
все наоборот. Если предел равен 1, то обе части равны.
Если предел принимает какое-то значение между нулем и
бесконечностью, то они не равны, но имеют сравнимые
плотности.
Билогарифмические графики некоторых
симметричных L-устойчивых распределений
На рис. 2.4.1 показаны (в вышеприведенных обозна-
чениях) случаи, когда <5 = 0, 7 = 1,/3 = 0, а значения а
изменяются от 1 (Коши) до 2 (Гаусс). По горизонтали от-
кладываем log и; по вертикали —
logPr{C7 < —и} = logPr{C7 < и}.
128
Глава 2.4
Эти графики взяты из [М 1963b {Е14}], они основаны на
неопубликованных таблицах, просчитанных в 1962 году по
моей просьбе в Исследовательском Центре Томаса Дж. Уот-
сона (Thomas J. Watson Research Center) корпорации IBM.
Прямолинейная асимптота, отмеченная пунктиром, со-
ответствует «закону Парето». Отсюда первый тест на
L-устойчивый характер U: убедиться, что этот хвост дей-
ствительно прямолинеен. Для а, близких к 1, каждый хвост
содержит в себе вероятность, примерно равную 1/10; сле-
довательно, вышеуказанный тест можно реализовать с по-
мощью выборок средних размеров. Но если а растет от 1
до 2, то эта вероятность убывает. Для а = 1,99 она умень-
шается примерно до 1/10000, и для вышеописанного теста
требуются очень большие выборки.
Перед асимптотой графики, соответствующие различ-
ным значениям а, искривляются и в конце концов становят-
ся практически неотличимыми. В частности, очень сбли-
жаются их интерквартили. Фама и Ролл [Fama & Roll 1968]
определяют «радикальный» интерпроцентиль как рассто-
яние между процентилями, соответствующими вероятно-
стям 0,28 и 0,72. Этот множитель удобен для непосред-
ственной приближенной оценки величины 1,6471/Q — мас-
штабирующего параметра. Те же авторы приводят и та-
блицы, в которых показано, как можно основать оценку а
на отношении между более высокой процентилью (напри-
мер, 0,05) и процентилью 0,28.
После 1963 и 1968 годов в вычислении L-устойчивых
плотностей и в оценке а был достигнут огромный про-
гресс, но мы не будем задерживаться на его описании ни
в этой книге, ни в [М1997Е]. Интересующихся отсылаю
к [McCullough 1996] и к главе 18 из [М 1997Е].
Билогарифмические графики распределений
129
Рис. 2.4.1. Некоторые симметричные L-устойчивые распределе-
ния. Объяснения даны в тексте
9 Б. Мандельброт
Глава 2.5
Ной, Иосиф и несколько
примеров стихийного случая,
малопонятных, но неизбежных
После прочтения глав 2.3 и 2.4 можно прийти к вы-
воду, что примеры стихийного случая очень показательны,
но малоинтересны: они либо сфабрикованы искусственно
для услады влюбленных в «патологию» математиков, ли-
бо представляют собой исключения, запрятанные в темных
уголках различных областей науки, основу которых состав-
ляет случай ручной.
Эта глава предназначена для того, чтобы показать, что
подобное впечатление неверно настолько, насколько это во-
обще возможно. Как только мы принимаем во внимание
стихийный случай, мы тут же начинаем повсюду видеть
его примеры, включая сюда и ситуации чрезвычайной зна-
чимости. Можем мы их объяснить или нет, но эти примеры
неизбежны. Большую роль в их изучении играют различ-
ные законы масштабной инвариантности: некоторые из них
напоминают инвариантность распределений Гаусса и Ко-
ши относительно сложения, другие намного богаче. Эти
инвариантности нельзя вывести из каких-то базовых прин-
ципов, но они удобны, экономичны и учитывают реальные
факты.
Случайность в Библии
Откроем Библию:
Флуктуации Ноя и Иосифа	1 з 1
«... разверзлись все источники великой бездны, и окна
небесные отворились. И лился на землю дождь сорок дней
и сорок ночей.» Бытие, VII.
«... вот наступает семь лет великого изобилия во всей
земле Египетской; после них настанут семь лет голода.»
Бытие, XLI.
В Библии эти события происходят по воле Бога. Но
те простые смертные, кого такое объяснение не удовлетво-
ряет, могут представить себе эти события только одним
образом: как следствия двух разных видов случайности,
способной на стихийные эксцессы.
Флуктуации Ноя и Иосифа
Позволим себе поэтическую вольность и интерпрети-
руем эти слова из Библии так, словно они описывают не
события, являющиеся проявлением чего-то странного или
патологического, а, напротив, две характерные особенно-
сти тамошнего климата.
Эти физические явления настолько значимы, что даже
входят в тройку первых феноменов, потребовавших осмыс-
ления человеком. Третье явление — регулярность движения
небесных тел; нет нужды напоминать о том, что астроно-
мия была первой среди наук, а ее методы и идеи оказали
чрезвычайное влияние на развитие других наук.
Когда случай носит «дикий» характер и отсутствие
сходимости возникает из-за необычайно сильного роста
некоторых величин (как в белом шуме Коши), мы говорим
о проявлении «эффекта Ноя».
Этот эффект не зависит от существования внутрен-
ней упорядоченности в данных — например, от времен-
ной упорядоченности в хрониках разливов Нила. Так, в
демографии эффект Ноя возможен при любой классифи-
кации индивидуумов, производится ли она по алфавиту,
по возрасту или в виде матрикулярных списков. Если же
отсутствие сходимости при стихийном случае возникает
из-за статистической взаимозависимости («псевдопериоди-
9*
132
Глава 2.5
ческого» характера), то мы говорим о проявлении «эффекта
Иосифа».
В третьей части будет показано, насколько существен-
ное значение имеют эффект Ноя и эффект Иосифа в обла-
сти финансов. А в этой главе мы приведем несколько очень
разных примеров, иллюстрирующих эти эффекты.
Гауссовский 1//-шум
Оказывается, помимо процесса Коши существует и
другой процесс, который можно подобрать таким образом,
чтобы его средние сходились сколь угодно медленно. Ни
закон больших чисел, ни центральная предельная теоре-
ма в данном случае неприменимы, и ручным этот процесс
не будет. Его называют «1//-шумом», поскольку его спек-
тральная плотность обратно пропорциональна частоте /.
Точнее, она пропорциональна f~B, где В — показатель, не
имеющий универсального характера, но, как оказывается,
зачастую близкий к 1.
Этот шум до сих пор очень мало известен, несмотря на
свое значение как для практики, так и для теории. По-мо-
ему, он заслуживает того, чтобы однажды стать таким же
классическим, как и шум Коши. 1 //-Шум может быть гаус-
совским или вообще не быть таковым. Если он гауссовский,
то он не обнаруживает ни одного из тех свойств, которые,
как мы знаем, не позволяют сходиться средним у Коши.
У нашего шума имеется другой источник несходимости:
дело в том, что очень средние по размеру значения могут
быть чрезвычайно стойкими, то есть имеются очень долгие
и очень медленные «циклы».
Два первых открытия, связанные с 1//-шумом, каса-
лись флуктуаций электрического тока, протекающего че-
рез тонкие металлические пленки (Ж. Бернамонт) и через
угольные микрофоны (X. А. Фредерик, К. Й. Христенсен и
Г. Л. Пирсон). Если усилить эти флуктуации и сделать их
слышимыми, то мы услышим «треск, выстрелы, шкворча-
ние». Если передать их на катодный экран, то мы увидим,
что уровень, который мы принимали за интенсивность тока
Гауссовский 1 //-шум
133
в состоянии равновесия, в действительности обнаруживает
чрезвычайную изменчивость.
Впоследствии были найдены и другие примеры такого
шума: при протекании электрического тока через несовер-
шенный контакт между металлическими проводниками, то
есть, как следствие, в любом наблюдаемом электрическом
токе низкой частоты, при прохождении сигнала через мем-
браны нейронов и, возможно, даже при вековом движении
географического полюса.
Особого упоминания заслуживает еще один пример.
Речь идет об ошибках, обнаруженных в официальном эта-
лоне времени; в США таким эталоном являются атомные
часы, установленные в Национальном Институте Стандар-
тов и Технологии в Боулдере (штат Колорадо). В действи-
тельности таких часов двое, причем они сконструированы
так, чтобы быть по возможности идентичными друг дру-
гу; вторые часы служат образцом для сравнения. Разница
между показаниями двух часов позволяет оценить порядок
величины ошибки в первых часах; в течение нескольких
лет за этой разницей очень тщательно следили.
В соответствии с довольно давно установленным соот-
ношением, ошибка при измерении одной секунды состав-
ляет приблизительно 10“12 секунды, ошибка при измере-
нии одной минуты — около 10“12 минуты, ошибка при
измерении одного часа — около 10“12 часа и т. д.
Иначе говоря, есть вероятность, что большая часть
ошибок на промежутке времени порядка 60 секунд, со-
ставляющих одну минуту, в основном, компенсируют друг
друга, однако помимо этого существуют и другие источ-
ники ошибок, очень малых, пока мы остаемся в пределах
нескольких секунд, но настолько «стойких», что они накап-
ливаются, и, когда мы переходим к минутам, в конце кон-
цов оказывается, что интенсивности этих ошибок вполне
достаточно, чтобы точно уравновесить предвиденный вы-
игрыш в точности. То же самое происходит и на более
высоких уровнях: как только у относительно «быстрых»
флуктуаций появляется время для того, чтобы уравнове-
сить друг друга, вмешивается новая «медленная» флуктуа-
134
Глава 2.5
ция, опровергая наши оптимистичные ожидания. Читатель
наверняка вспоминает сейчас берег Бретани, о котором мы
говорили в главе 2.1. Но там речь шла о самоподобии, здесь
же — о самоаффинности.
Бесконечная память — как такое возможно?
Использованное выше определение «1//-» связано с
формой спектральной плотности процесса — это понятие
мы очень скоро обсудим. Если бы упомянутая форма дей-
ствительно оставалась применимой вплоть до нулевой ча-
стоты, то спектральная плотность в точке отсчета была бы
бесконечна. У нас были бы веские основания сделать от-
сюда вывод, что и сама память процесса (какое бы опреде-
ление ни принять для этого несистематизированного тер-
мина) бесконечна.
Мы кричим и негодуем. Бесконечная память подра-
зумевает, как нам кажется, возможность своего рода воз-
действия на расстоянии, а эту концепцию наука не может
принять с чистой совестью. Конечно, ньютоновское грави-
тационное притяжение скрывает-таки в себе определенное
воздействие на расстоянии. Эту идею приняли, однако пол-
ностью от проблем избавиться так и не удалось. За неиме-
нием альтернативы физики страдали и ждали Эйнштейна.
Здесь можно вспомнить и о квантовых воздействиях на
расстоянии, о которых пишут в газетах.
К нашему великому облегчению, парадокс бесконеч-
ной памяти в интересующем нас случае очень легко ис-
ключить. Достаточно заметить, что каждая 1//-флуктуация
отражает единственный, так сказать, «скалярный», аспект
некоторого феномена, который, но если взять этот феномен
целиком, то его сложность будет такова, что ее с полным
правом можно считать бесконечной.
Итак, мы рассматриваем только одну координату неко-
торой «векторной» системы, имеющей бесконечно много
других координат. Достаточно разумно предположить, что
вышеуказанная система имеет конечную или даже нулевую
память. Однако нет никакого повода делать отсюда вывод,
Турбулентность, проблема Изинга
135
что именно так должно обстоять дело и с каждой из коорди-
нат! Иначе говоря, изначально ничто не говорит нам о том,
что полагать память бесконечной, а спектре 1//-образным
абсурдно. Следовательно, мы не можем отвергать экспе-
риментальные результаты, которые так часто и настойчиво
наводят нас на эту мысль.
Турбулентность, проблема Изинга и
критические феномены
На этом этапе необходимо принять трудное решение.
Было бы уместно рассмотреть стихийный случай в том
виде, в каком он проявляется в физике, на примере двух
очень непохожих друг на друга феноменов: речь идет о
турбулентности и критических феноменах.
Первый из них изучается уже очень давно, и, применив
к этой задаче понятие «подобия», предложенное Ричардсо-
ном и Колмогоровым, я вполне осознанно сформулировал
для себя следующее представление: с одной стороны, все
виды случая здесь стихийны; с другой стороны, многие из
них, если можно так выразиться, вынуждены обладать ин-
вариантностями. К сожалению, стихийным случаем в тур-
булентности сложно управлять.
Что же касается критических феноменов, то хотя они
и известны с давних пор, их активное изучение началось
только тридцать лет назад. Прогресс оказался настолько
быстрым, что сегодня многие их аспекты уже вполне по-
нятны. Я ничего не знал об этой теории до 1970-х годов?
и она никак не повлияла на мои работы, посвященные фи-
нансам.
Ее прототипом может служить модель Изинга, в рам-
ках которой магнит представляется в виде совокупности
«стрелок», ориентированных в двух возможных направле-
ниях (вверх и вниз) и размещенных вдоль некоторой кри-
вой, прямой или на плоскости в точках с целыми коорди-
натами.
Не желая прерывать повествование, я не стану задер-
живаться на том сходстве, которое обнаруживается меж-
136
Глава 2.5
ду упомянутыми разделами физики и приведенными ранее
примерами, как, впрочем, и поведением в экономике. Во
всех случаях речь идет о свойствах систем, состоящих из
большого количества элементов, и наша цель — найти зако-
ны, управляющие всей совокупностью, исходя из законов,
управляющих ее элементами.
Стихийный случай, которого можно избежать
Стихийный случай вызывает страх, мы стремимся лю-
бой ценой его избежать. Действительно, есть ситуации,
когда это можно сделать без больших усилий. Например,
переменная Коши получается как отношение двух неза-
висимых гауссовских переменных, а это означает, что мы
рискуем рано или поздно обнаружить, что статистический
алгоритм был выбран неразумно и от стихийного случая
можно избавиться, всего лишь изменив этот самый алго-
ритм.
Точно так же (см. главу 2.4) начало всей молекуляр-
ной биологии было положено опытом Лурия и Дельбрюка,
но та же молекулярная биология вполне могла пренебречь
результатами этого опыта и обратиться к иным, более удоб-
ным в обращении «инструментам». Тем не менее, как выяс-
няется, во многих случаях (вспомним о приведенной в гла-
ве 2.3 цитате из книги Гнеденко и Колмогорова [Gnedenko
& Kolmogorov 1954]) снабдивший нас вышеупомянутыми
инструментами Создатель просто не оставил нам никаких
средств, способных их заменить.
Теперь мы готовы сначала детально изучить метод,
позволяющий иметь дело со стихийным случаем, а затем
его антитезу, причем я объясню, почему я считаю ее непри-
емлемой.
Инвариантность при редукции как научный
принцип
Я придаю большое значение следующему наблюде-
нию: есть примеры стихийных флуктуаций, для которых
Инвариантность при редукции как научный принцип 137
инвариантность была доказана аналитически, и другие
примеры, где она выводилась (с большим трудом) из непо-
средственных подсчетов, наконец, есть примеры, где ин-
вариантность постулировалась для удобства и обнаружи-
валось, что это позволяет получить приемлемое описание
действительности.
Уже упоминалось о том, что в математике (как и
в любой науке) инвариантности играют совершенно осо-
бую роль, и их высокий статус вполне оправдан. Разли-
чие состоит в том, что в физике инвариантности — это
фундаментальные законы или же их можно к таким зако-
нам свести, тогда как инвариантности, которые я посту-
лирую в экономике или гидрологии, полностью «бесплот-
ны».
Разумно ли, полезно ли будет предоставить таким ин-
вариантностям гражданские права в науке? Ответ должен
быть осторожным, потому что каждая наука, как известно,
беспрестанно развоплощается, становясь все более отвле-
ченной. Термодинамика, например, начинала с изучения
механизмов, но потом оказалась формализована в виде ве-
ликих «Начал», которые запрещают какие бы то ни было
формы вечного двигателя и допускают проверку лишь по-
средством очень дальних следствий из них. Если верить
Ю. Вигнеру, то и сами эти начала можно свести к симмет-
рии и к другим, весьма глубоким и не менее абстрактным
утверждениям.
При такой исторической перспективе турбулентность —
в том виде, в каком она была описана как в работах Кол-
могорова, так и в моих работах — остается какой-то ано-
малией. Что делать, что думать, если идеал абстракции,
получаемый в других науках лишь посредством медлен-
ной дистилляции, оказался достигнут сразу же? К сожале-
нию, бритву Оккама («Entia non sunt multiplicanda praeter
necessitatem»1) можно с тем же успехом применить и к
инвариантностям — преумножать их число сверх необхо-
димости также не следует.
’Не следует преумножать число сущностей сверх необходимого
(лат.). — Прим, перев.
138
Глава 2.5
Конечно, настанет день, когда инвариантности в эко-
номике и гидрологии получат свое объяснение, то есть бу-
дут сведены к другим инвариантностям, полагаемым бо-
лее фундаментальными. Но что делать, пока этого еще не
произошло? Ответ на этот вопрос мы и попробуем сейчас
найти.
Попытки избежать стихийного случая
Собранные выше примеры показывают, что о суще-
ствовании стихийных флуктуаций люди подозревали уже
давно. Тем не менее, как мы видели, они не только не
осознавали этот факт в явном виде (что перекликается со
словами Фонтенеля, процитированными во введении), но
и вся история наук представляет собой перечень попыток
избежать встречи со стихийным случаем «лицом к лицу».
Я убежден, что именно поэтому и сами авторы, и редакто-
ры журналов отправляли в корзину многочисленные сооб-
щения о проявлении эффектов Ноя и Иосифа, а действи-
тельное количество подобных случаев серьезно недооце-
нивалось. Очевидно, мою убежденность, в силу самой ее
природы, никаким примером подкрепить нельзя.
Переходные эффекты и медленный случай
Зачастую в поисках опоры мы хватаемся за утвержде-
ние о том, что эффекты Ноя и Иосифа могут быть только
переходными. Отсюда — поразительные и дорогостоящие
попытки построить процессы, которые я рассматриваю как
имитацию этих эффектов при среднем количестве данных,
асимптотически всегда ручных.
Один из примеров связан с теоретической задачей
Хольцмарка. Еще один — 1//-шум. Поскольку средние этих
флуктуаций не сходятся, заинтересованные лица быстро
поняли, что их нельзя рассматривать как ручные. Тут же
возник вопрос о том, будет ли память «действительно бес-
конечной» или она «попросту» очень велика, и будет ли
Переходные эффекты и медленный случай
139
она, в частности, больше интервалов времени, образующих
обычную длину выборки.
Дискуссия вокруг этих тем предоставляет нам очеред-
ной пример могущества догмы, которое мы уже наблюдали
в действии в главе 2.3, в споре между Коши и Бьенеме. По-
лучила распространение мысль о том, что если бы у нас
была возможность достаточно долго изучать 1//-шум, что
позволило бы получить действительно низкие частоты, то
в конце концов мы достигли бы некоего «поворотного мо-
мента» (и преодолели бы его), после чего все пришло бы
в порядок. Иначе говоря, в итоге оказалось бы, что наблю-
даемые ошибки являются ручными — на чем, впрочем, и
настаивают все теоретические исследования.
Таким образом, поощрялось эмпирическое исследова-
ние подобных поворотных моментов, однако очень скоро
обнаружилось, что это пустая затея (например, ошибки в
эталоне времени не сходятся даже через пять и более лет).
Можно было даже наблюдать, как экспериментаторы пыта-
ются установить рекорд самого долгого эксперимента, не
достигающего стадии «поворотного момента». Иначе го-
воря, стало ясно, что обоснование догмы, утверждавшей,
что ошибки не могут не быть ручными, отодвигается за
непрерывно удаляющийся горизонт. Можем ли мы, долж-
ны ли мы в таких обстоятельствах по-прежнему принимать
ее всерьез?
Другой поразительный пример — распределение лич-
ных доходов. Формула, предложенная Парето в 1896 году,
имеет, как мы увидим, одну особенность — ее дисперсия
бесконечно велика. Это и есть проявление эффекта Ноя;
если он постоянен, возможность применения центральной
предельной теоремы исключается.
Многим авторам эта последняя возможность казалась
попросту немыслимой; ее следовало избежать любой це-
ной. Некоторые предлагали урезать аналитическое выраже-
ние Парето, учитывая тот факт, что никакой личный доход
не превосходит, допустим, триллиона франков. Конечно,
это позволяло спасти желанный вывод, то есть «приру-
ченность» асимптотического поведения; нужный результат
140
Глава 2.5
получается за счет отодвигания вышеупомянутой асимпто-
тики в будущее, не представляющее для нас никакого ин-
тереса.
Ряд других авторов (начиная с самого Парето) предла-
гали добавить к вычисляемому распределению экспонен-
циальный член, который будет играть свою роль только
в асимптотике. Многие авторы настаивали на том, что-
бы заменить это распределение на логнормальное, которое
опять-таки не окажет особого воздействия на данные обыч-
ной величины, но взамен предложит нам ручную асимпто-
тику.
Изменение масштаба измерения
При невозможности изменить орудие исследования
можно прибегнуть к другому средству: преобразовать на-
блюдаемую величину нелинейным образом.
Если в примере со слепым лучником вести счет ошиб-
кам по углу, а не по расстоянию между точкой попада-
ния и мишенью, то, по-видимому, он будет распределен
«ручным» образом. Для того же, чтобы перейти от одного
способа счета к другому, достаточно применить функцию
арктангенса.
Та же самая функция, примененная к изменениям спе-
кулятивных цен, «срезала» бы большие изменения и при-
вела бы к вполне ручному поведению распределения. Но
преобразованная величина не имеет никакого конкретного
смысла, а поведение ее сумм (по отношению к которому
и определяется ручной характер) не представляет никакого
интереса. Складывая пять ежедневных последовательных
изменений цены, мы получаем изменение цены за неделю,
тогда как складывая арктангенсы этих величин (цен), мы
не получим ничего интересного.
Точно так же нет ничего конкретного в логарифме на-
селения некоторого города. Это не означает, что преобразо-
вание, лишенное конкретного содержания, не может быть
удобным: например, сила землетрясений и «звездотрясе-
ний» определяется как логарифм участвующей в процессе
Обращение к различным смесям	141
энергии, поскольку величина собственно энергии в обра-
щении неудобна; в таких действиях нет ничего ужасного,
коль скоро мы не позволяем себе вместо значений энергии
складывать эти величины.
Обращение к различным смесям
Вынужденные сталкиваться со стихийными флуктуа-
циями, многие авторы, невольно или преднамеренно, обра-
щаются к смешиванию разнородных данных. Достаточно
будет дать этой смеси отстояться, рассуждают они, и мы
вернемся к ручному случаю.
В применении к экономике и гидрологии это мнимое
картезианство a priori предполагает — так как доказатель-
ства здесь, якобы, и не требуется, — что большие измене-
ния цены качественно отличаются от малых и ими нужно
оперировать отдельно под тем предлогом, что первые ин-
тересны для экономики, а вторые — только для изучения
спекуляций. Утверждают также, что непериодические цик-
лы, в большом количестве встречающиеся в экономике и в
гидрологии, относятся к различным предметам в зависимо-
сти от того, являются они «медленными» или «быстрыми».
Примеры Хольцмарка и Лурия-Дельбрюка показыва-
ют, что эта точка зрения не всегда оправданна. В самом
деле, из нее следует совершенно абсурдный факт — звезда
Астер и обычные клоны качественно отличаются от звез-
ды Астер, имеющей очень близкого соседа, и от больших
клонов.
Таким образом, мы возвращаемся к бритве Оккама,
но на сей раз в применении к научным дисциплинам. Я
считаю, что эти дисциплины, как и всякие другие сущно-
сти, не следует преумножать сверх необходимого. Когда
различие между дисциплинами само по себе основано на
одних лишь критериях интенсивности эффектов, это вызы-
вает недоверие.
Эту мысль можно уточнить с помощью одного заведо-
мо комичного примера. Никто же не утверждает, что лужи,
142
Глава 2.5
пруды, озера, моря и океаны составляют различные объек-
ты исследования единственно из-за своих названий. Хотя
это различие было бы очень удобным со статистической
точки зрения, поскольку внутри каждой из этих категорий
флуктуации площади носили бы умеренный характер, то-
гда как смешивание этих категорий приводит к колоссаль-
ной изменчивости. Этот случай позволяет нам увидеть, что
повседневный язык может привести к классификации, ко-
торая окажется полезной, но не обязательно будет носить
внутренний характер.
Рассмотрим аналогичным образом величину звезд.
Предположение о том, что звезды каждой отдельной ве-
личины образуют отдельный объект изучения, — гипотеза
a priori вполне постижимая, но ее законность следует под-
тверждать, опираясь на критерии, не сводящиеся к одному
лишь «размеру».
Кредо в завершение главы
Крайняя реакция на стихийные флуктуации — уверен-
ность в том, что их можно свести если не к детерминизму,
то хотя бы к ручному случаю, в точности так, как это де-
лается в задачах Хольцмарка и Лурия-Дельбрюка. Конеч-
но, я разделяю эту надежду, но всему должно быть свое
место и свое время. Несмотря на гигантские усилия, мы
далеки от того, чтобы в принципе свести турбулентность к
другим феноменам, полагаемым более фундаментальными.
Очевидно, было бы смешно ждать такого упрощения в ее
технических приложениях.
Но я считаю, что точно так же смешно было бы ожи-
дать этого и в ее научном описании. Чтобы объяснить
свою позицию, хочу сослаться на великий спор, потряс-
ший квантовую физику в связи со «скрытыми переменны-
ми». Вопрос состоял в том, чтобы выяснить, непреодолима
ли квантовая неопределенность или же ее можно объяс-
нить с помощью каких-либо скрытых переменных. Неко-
торых физиков этот вопрос очень увлек, но большинство
Кредо в завершение главы	143
полагало, что ответ на него ничего не дал бы для реше-
ния действительно существующих проблем, и к тому же
формальная красота и предсказательная мощь квантовой
теории и без того служат для нее вполне достаточными
доказательствами.
Конечно же, я вовсе не утверждаю, что стихийный
случай столь же фундаментален, что и случай квантовый.
Но мне кажется, что во многих реальных ситуациях будет
мудро поступать так, словно так оно и есть.
ЧАСТЬ ТРЕТЬЯ
СЛУЧАЙНОЕ НА БИРЖЕ
В этой части изучается биржа в свете эффекта Ноя
(глава 3.1), эффекта Иосифа (глава 3.2) и их комбинации
(глава 3.3).
Сначала напомним суть эффекта Ноя, уже обсуждав-
шегося во второй части: цена акции или облигации — равно
как и ставка процента или обменный курс — могут изме-
ниться мгновенно, если к этому вынуждают обстоятель-
ства.
Теперь эффект Иосифа: большие изменения цены
нельзя распределить во времени более или менее регуляр-
ным образом, они сосредотачиваются на коротких под-
периодах, а данные имеют непериодическое, но очевидно
циклическое поведение, включая и очень медленные циклы.
В этой части новые сведения сосредоточены в гла-
ве 3.3, которая имеет совершенно особое предназначение.
Цель этой главы — дать обзор моих самых последних ра-
бот, в которых фигурируют эффект Ноя и эффект Иоси-
фа.
В главах ЗА и 3.2 пересматриваются модели [М 1973v]
и [М 1973j] соответственно. Кроме того, в текст включе-
ны фрагменты из [М 1966г], а длинноты заменены ссыл-
ками на вторую часть настоящей книги. Для удобства, а
также ради соответствия духу «Selecta», редакция этих
фрагментов оставлена достаточно близкой к редакции
старых текстов. При этом, даже если мы терпимо от-
носимся к повторам, возникают некоторые проблемы. Тон
этих работ, естественный и уместный в 1973 году, когда
я говорил о новых вещах, вызывавших некоторое сопро-
тивление, сегодня, скорее всего, показаться анахроничным.
Но, думаю, я все же рискну.
10 Б. Мандельброт
Глава 3.1
Разрывность и концентрация
(«модель [М1963]»)
В этой главе мы представим (не вдаваясь в из-
лишние технические подробности) основные идеи «моде-
ли [М 1963]». Это была первая модель, разработанная мной
для реалистичного описания изменения цен, действовав-
ших на некоторых фондовых и товарных биржах. Мой ин-
терес к бирже возник прежде всего из желания исследовать
хроники экономического происхождения, долговременные
и изобилующие интересными событиями, определение ко-
торых не допускает статистических манипуляций, затруд-
няющих их интерпретацию. На рис. 1.2 показан действу-
ющий курс акций на одной весьма активной бирже; из-
менение собственно цены сочетается здесь с изменением
ее ежедневных скачков. Взгляните также на рис. 3.1.1. На
рисунке 1.2 отчетливо видно, что изменения цены никогда
не образуют независимой гауссовской последовательности.
Настоящая глава посвящена тому случаю, когда в первом
приближении зависимостью можно пренебречь, т. е. когда
негауссовость доминирует над изменчивостью.
Математики, возможно, найдут ключ к этой главе в
следующей фразе: в модели [М1963] постулируется, что
изменения цены L-устойчивы и независимы. Здесь эта идея
развивается и мотивируется, возможно, даже чересчур по-
дробно. В связи с чем опять повторюсь: я не особо старался
избежать повторов уже сказанного в предыдущих главах.
Биржи
147
Рис. 3.1.1. Хроника изменения цены. Здесь представлен опублико-
ванный в «New York Times» индекс цен на акции анонимных ком-
паний, допущенных на Нью-йоркскую фондовую биржу. Следует
особо отметить наличие частых разрывных скачков, хотя пред-
ставленный период имел репутацию относительно «спокойного».
Еще интереснее исследовать изменение цен на сырье и товары:
здесь перед нами тот исключительный случай, когда данные не
только чрезвычайно изобильны (и достоверны), но и имеют, поми-
мо прочего, большое практическое значение и вызывают большой
теоретический интерес
Биржи
Перечислим аргументы в пользу изучения бирж.
Изобилие данных: если связать воедино сырье, акции
и облигации, проценты и курсы валюты, даже не учитывая
при этом биржи, не слишком активные или слишком за-
висимые от действий их участников или капризов властей,
то мы получаем в распоряжение необыкновенно богатые
эмпирические данные, включая сюда подробные данные о
ценах и прочих экономических величинах. Некоторые то-
варные биржи имеют вековую историю, и известны тем,
что обнародуют без какой бы то ни было дополнительной
обработки именно те цены, которые действительно имели
место на их торгах. Сегодня мы располагаем также дан-
10*
148
Глава 3.1
ными «высокой частоты»; они используются в тестах, о
которых будет рассказано в главе 3.3.
Практическое значение: мы не будем говорить о вли-
янии конкретных данных на благосостояние биржевых иг-
роков, и я согласен с тем, что биржевые хроники суть «ка-
рикатуры» на фундаментальные экономические хроники —
одни черты оригинала в них преувеличены, а другие, на-
против, приглушены. Это, впрочем, не означает, что иска-
женным оказывается все. Не следует пренебрегать тем вли-
янием, которое оказывает на экономику, скажем, Ганы курс
цен на какао, а на экономику Новой Зеландии — цены на
шерсть. Причем влияют не только долговременные тенден-
ции изменения, но и внезапные кратковременные скачки.
Теоретическое значение: некоторые экономические
переменные, такие как количество рабочих или объем про-
изводимой ими продукции, жестко связывают экономику
с физикой и с демографией, причем каждая дисциплина
вводит некую свойственную ей инерцию. Другие перемен-
ные — в первую очередь, цены — имеют чисто экономиче-
ский характер.
Побудительная сила: изучение биржи подвигло меня
на изучение некоторых физических флуктуаций, масштаб
которых далеко превосходит все то, что мы наблюдаем в
так называемой макроскопической физике.
Часть из них влияет на экономику непосредственно,
в виде экзогенных переменных. То, что гидрологические
флуктуации напоминают биржевые, забавным образом под-
тверждает поговорку, согласно которой биржа и погода оди-
наково непредсказуемы. Важнее вот что: по крайней мере
некоторые из существенных экономических хроник обу-
словлены теми экзогенными флуктуациями, о которых я
только что говорил.
Перейдем от мотивировок к инструментам, которы-
ми мы будем пользоваться; инструменты эти несколько
необычны, так как математические характеристики эконо-
мики в основе своей отличны от характеристик класси-
ческой физики. Любой инструмент, будь он старый или
новый, нельзя выбирать только из-за его удобства, необхо-
Статистическое описание экономики 149
димо добиваться последовательных компромиссов между
удобством и применимостью.
Принятый нами решительно эмпирический метод на-
зывается у физиков «феноменологическим»: мы не стре-
мимся «объяснить» факты, сведя их к более фундаменталь-
ным теориям, мы просто представляем положение вещей
по возможности наиболее простым, экономичным, точным
и упорядоченным образом.
В этой главе учтены некоторые результаты, описан-
ные в [М 1963b {Е14}] и [М1967j {Е14}]. Ту же точку зре-
ния разделяют и многие мои ученики, первым из них по
времени был Э. Ф. Фама. В библиографию включены мно-
гочисленные более поздние работы (в частности, труды
Д. Зайденвебера и К. Вальтера).
Статистическое описание экономики
Самой простой (и, как следствие, наиболее привлека-
тельной) моделью случайной флуктуации является «бро-
уновское движение»; в такой модели постулируется непре-
рывность цен и то, что их последовательные изменения
суть независимые гауссовские случайные величины. Ре-
альные финансовые хроники в рамки этой модели не
укладываются. Модели, разработанные мною ей на сме-
ну, сразу и очень решительно демонстрируют совсем дру-
гие характеристики. В одном из критических комментари-
ев, сопровождавших переиздание [М 1963b {Е14}], Кутнер
[Cootner 1964] назвал мой подход «революционным».
Воспользовавшись медицинской терминологией, мож-
но сказать, что новизна проявляет себя в виде многочис-
ленных «симптомов», внешне очень различных, но состав-
ляющих, в сущности, один большой «синдром».
В этой главе рассматривается обнаруженный мною
еще в 1960-х «синдром бесконечной дисперсии», характер-
ный для многочисленных естественных флуктуаций. В пре-
дисловии упомянуто, что изначально такие флуктуации
применялись в решении задачи о распределении доходов,
150
Глава 3.1
однако в полной мере их значимость проявилась именно в
контексте цен.
На первом этапе я изучал отдельные хроники. На вто-
ром (о чем уже говорилось в конце главы 2.2) — взаимодей-
ствие двух хроник, одна из которых относилась к финан-
сам, а другая представляла собой некую фундаментальную
экономическую хронику. Предназначение этих моделей бы-
ло достаточно скромным, что позволяло со всей строгостью
подходить к качеству представления ими действительно-
сти.
Броуновская модель и ее предыстория
Читатель уже знает: всякий, кто рискнет заняться изу-
чением какой-нибудь реальной биржевой хроники, сначала
непременно столкнется с призраком Башелье. Луи Баше-
лье (1870-1940) стал самым настоящим предтечей, даже
знакомство с его биографией заслуживает того, чтобы по-
тратить на него время. В 1900 году теория вероятностей
сводилась, по большей части, к собранию простых комби-
наторных примеров, статистика еще не появилась на свет, а
Парето был практически единственным математиком-эко-
номистом. Именно в 1900 году Башелье получил звание
доктора математических наук, защитив диссертацию на те-
му «Математическая теория спекуляций».
Пусть Z(t) — цена данного количества некоторого про-
дукта в момент времени t. Башелье постулирует, что Z(t +
+ Т) — Z(t) есть гауссовская случайная величина, среднее
значение которой равно нулю, а дисперсия зависит от t
и Т. Рассматривается поправка, согласно которой гауссов-
ской случайной величиной будет, скорее, выражение
L(t, Г) = log Z(t + Т) - log Z(t).
Тем самым устраняется единица цены и исключается воз-
можность (присутствующая в исходной модели) того, что
цена Z окажется отрицательной.
Анри Пуанкаре, рецензент этой докторской диссерта-
ции, полагал, что «ее тема ... несколько далека от тех тем,
Недостатки броуновской модели	151
которые обычно изучают наши кандидаты». Диссертация
была принята — без особого, впрочем, энтузиазма, удо-
стоившись всего лишь «похвального отзыва». Случилось
так, что именно Башелье сменил впоследствии Пуанкаре
в его трудах по исследованию основ теории вероятностей.
До 1914 года он опубликовал несколько других работ, в
одной из которых представлены комбинаторные вычисле-
ния — тривиальные, но весьма запутанные (если верить
Кейнсу), однако при жизни Башелье так и не «открыли»,
должность профессора в университете Безансона он полу-
чил только в 1935 году, незадолго до ухода на пенсию.
Поль Леви, с которым я был хорошо знаком, расска-
зывал мне, что он в свое время начал читать эту диссер-
тацию, но вскоре прекратил, встретив одно явно неверное
утверждение. Если бы он продолжил чтение, то увидел бы,
что последовательность рассуждений была все же совер-
шенно правильной. В системе взглядов, характерных для
эпохи Пуанкаре, она даже обладала математической стро-
гостью. Во всяком случае, в ней строгости было больше,
чем в выступлениях таких физиков, как Эйнштейн, Ланже-
вен, Фоккер и Планк, вскоре после этого независимо пере-
открывший процесс Башелье в виде модели броуновского
движения. Большей строгости не существовало в природе
вплоть до 1923 года и трудов Норберта Винера, а новые
результаты появились лишь в 1930-е годы, благодаря Полю
Леви.
В современных терминах утверждение Башелье мож-
но сформулировать так: в первом приближении цена ве-
дет себя как броуновское движение, или как «винеровский
процесс», или как «процесс Винера-Леви». В свое время
мы расскажем об основных свойствах этих процессов. См.
также рис. 1.1, 3.1.2 и 3.1.3.
Недостатки броуновской модели
К сожалению, несмотря на то, что история ее прекрас-
на, печальна и достойна того, чтобы ее рассказать, уро-
152
Глава 3.1
/д
2000
500
р л\

"*" ’	'7Д*
V.
"' I	—1
4000	5000
3000
1000
Рис. 3.1.2. Броуновское движение. Этот рисунок, являющийся,
несомненно, самым знаменитым изображением случайного дви-
жения, взят из книги Феллера [Feller 1950], том 1. Он иллюстри-
рует результаты игры в орлянку: по оси абсцисс отложено коли-
чество бросков монеты, по оси ординат — мой выигрыш после t
бросков монеты, исходя из допущения, что я выигрываю один
денье при выпадении «орла», а ты выигрываешь один денье при
выпадении «решки». По-видимому, Башелье этого рисунка нико-
гда не видел; моделирование этого процесса стала повсеместно
доступной лишь благодаря компьютеру. Вверху: 1 t 500;
посередине: 1 t 5000; внизу: 1 t 10000
вень аппроксимации «броуновской» модели не оправдыва-
ет возлагаемых на нее ожиданий. Скептицизм, выражен-
Недостатки броуновской модели
153
Рис. 3.1.3. Новая выборка белого гауссовского шума. Эта выборка
смоделирована на компьютере, то есть в действительности она
«псевдослучайна». Попросту говоря, она подобна графику, изоб-
раженному в нижней части рис. 1.1, а здесь у нас появляется
удобный повод сделать несколько общих замечаний. То, что ко-
роткой выборки оказывается достаточно для того, чтобы питать
наше интуитивной представление о белом гауссовском шуме, объ-
ясняется просто: хотя ни одна его деталь не воспроизводится в
точности, кажется, что шум повторяется, при этом никакая его
часть ничем особенным не выделяется. Этот пример дает нам
лишь интуитивное представление о стационарности, математиче-
ское определение несравнимо глубже. При использовании других
стационарных случайных процессов с короткой памятью (напри-
мер, так называемых процессов ARMA или GARCH) нам нужно
будет лишь добавить вариации за короткий период времени. Ре-
зультат оказывается весьма далек от того, чтобы позволить нам
понять все богатство структуры таких, например, графиков, как
тот, что представлен на рис. 1.2. Процессы же с долгой памятью
способны порождать самые разнообразные интересные конфигу-
рации, включая и представленные на рис. 1.2. Это, в свою очередь,
позволяет ожидать, что естественный феномен, отображающий
все разновидности интересных конфигураций, можно смоделиро-
вать с помощью стационарного случайного процесса достаточной
общности
ный Пуанкаре (в рецензии на диссертацию) в отношении
эмпирических «доказательств» Башелье, равным образом
уместен и в отношении современных доказательств. В са-
мом деле, построим гистограммы, зафиксировав Т и поз-
154
Глава 3.1
водив t принимать все значения, кратные Т. Как показали
Уэсли Митчелл, Морис Оливье и Фредерик Миллс (в пе-
риод между 1910 и 1925 годами), хвосты таких гистограмм
настолько длинны, что бессмысленно предполагать, буд-
то они происходят из гауссовской популяции. Существует
множество способов представления изменения цены.
А) Специалисты в области «технического анализа» на-
мерены научиться предсказывать будущее на основе изме-
нений прошлого. Их методы весьма изящны, но их описа-
ние редко бывает точным настолько, чтобы сделать возмож-
ной их проверку. В исключительных допускающих провер-
ку случаях полученные с их помощью результаты оказы-
ваются необоснованными. Мы убедимся в это на примере
«фильтров», предложенных С. С. Александером.
В) Самые разные авторы искренне полагают, что изме-
нения цен непредсказуемы, но не подчиняются тому виду
случая, который определен в теории вероятностей. Такие
изменения можно назвать «неожиданными».
С) Башелье сам ослабил свои высказанные в 1900 году
идеи, допустив, что дисперсия случайной величины L(t, Т)
зависит от t. Более того, он отметил, что смесь гауссовских
распределений с разными дисперсиями дает распределе-
ние с очень длинными краями. И добавил, что некоторые
большие изменения цены происходят вследствие так на-
зываемых «угроз взрыва», так что их нельзя рассматривать
вместе с малыми случайными изменениями. Эти два допол-
нения, которые Башелье внес в свою модель, существенно
ограничивают ее значимость.
Стационарность и интуиция, часть 1
Очень многие авторы полагают, что изменения цены
подчиняются постоянно изменяющимся вероятностным за-
конам. Иначе говоря, нестационарным законам. Эта точка
зрения заслуживает того, чтобы обсудить ее более основа-
тельно.
Если изменение дисперсии случайной величины L(t, Т)
происходит вследствие статистической нестационарности,
Стационарность и интуиция, часть 1	155
то возникает вопрос, можно ли применить теорию вероят-
ностей к исследованию цены Z(t).
Во всяком случае, из рассуждений Башелье (пункт С)
мы можем непосредственно заключить, что по сравнению с
изменчивостью непредсказуемой экономики изменчивость
любого случайного процесса оказывается недостаточной.
Однако это будет не более чем априорный предрассудок.
Похоже, имеются две концепции стационарности: матема-
тическая стационарность доказывает, что она никоим обра-
зом не интуитивна, а ее мощь, по-видимому, крайне недо-
оценивается, интуитивная же стационарность, как выясня-
ется, накладывает очень много ограничений. Это скорее
ошибка анализа, нежели отождествление двух разных по-
нятий, то есть стационарного случая и случая, названного
в главе 2.1 «ручным».
В частности, принято полагать, что стационарность
исключает возможность какого-либо значительного изме-
нения и какой-либо нетривиальной конфигурации. Но ни-
что не ограничивает теорию вероятностей рассмотрением
малых флуктуаций вокруг некоторой вероятной величины.
Когда мы говорим, что изменение цены находится в компе-
тенции вероятностного анализа, это вовсе не означает, что
оно мало, оно попросту непредсказуемо при современном
состоянии этого анализа.
С этой точки зрения я предлагаю перевернуть обыч-
ные рассуждения: вместо того, чтобы говорить, что неко-
торые изменения велики, поскольку они имеют причину,
я буду говорить, что, наблюдая большое изменение цены,
мы приходим к выводу о необходимости отыскать (вооб-
ще говоря, a posteriori) причины, спровоцировавшие это
изменение; малые изменения такого особого внимания не
заслуживают.
Итак, стационарность нельзя исключать a priori', но
не в меньшей степени ее необходимо подтверждать, что
постепенно и будет сделано. Самое сильное подтверждение
уже было приведено в конце главы 2.2.
В заключение отметим, что аргументы Башелье, пы-
тавшегося избежать недостатков броуновской модели, —
156
Глава 3.1
это всего лишь другой способ уклониться от вызова, кото-
рый бросает нам неизвестное. Лично я считаю, что вполне
возможно сохранить некоторые основные идеи, изменив
при этом броуновское движение сверху донизу.
Негауссовость в финансах
Построим гистограмму изменений цены, подобную
той, что представлена на рис. 1.2. Можно констатировать,
что зачастую она почти симметрична, при этом, как пра-
вило, отчетливо заметно, что нормальной она не являет-
ся. Иначе говоря, она очевидно отлична от «огивы Галь-
тона», соответствующей гауссовскому распределению. См.
рис. 3.1.4 и 3.1.5.
Оптимальная гауссовская аппроксимация, показанная
на рис. 3.1.4, одинаково плоха на всех участках. Что ка-
сается гауссовской аппроксимации над «куполом» (то есть
для всех величин, кроме 2% крайних справа и 2% край-
них слева), то она плоха только на двух хвостах. Если же
описать ее так, чтобы она покрывала 96% случаев, то гаус-
совская аппроксимация уже не будет казаться такой плохой.
Иначе говоря, возникает искушение поступить с длинными
хвостами так, чтобы вовсе о них не думать: либо отрезать
их, либо спрятать. Отрезать означает поступить как физик,
который, повторяя одно и то же измерение, получает мно-
го очень тесно сгруппированных величин, а кроме них —
одну-две другие, с остальными не согласующиеся. Он от-
брасывает эти последние, поскольку они якобы обуслов-
лены «аберрацией», не представляющей интереса, или же
«загрязнением».
Спрятать длинные хвосты — операция более тонкая.
Гауссовость — самый верный друг статистика; общеизвест-
но, что при необходимости обработать данные, очевидно
не являющиеся нормальными (например, непосредствен-
ные баллы, набранные на экзамене или на психологиче-
ском тесте), статистик эти данные «нормализует». В США
студенты называют эту процедуру «записывать под кри-
Негауссовость в финансах
157
Рис. 3.1.4. Первая иллюстрация того факта, что в типичных случа-
ях распределения изменения цены заведомо являются негауссов-
скими. Две представленные гистограммы [Tintner 1940] соответ-
ствуют пятым и десятым разностям в месячных ценах на шерсть.
Непрерывные кривые в виде купола представляют собой попыт-
ку гауссовской «интерполяции» данных. По сравнению с гауссов-
ской кривой средние величины слишком малочисленны, малых
величин слишком много, а большие — слишком велики. От них
можно избавиться, если счесть их «аберрацией», но это удалось
бы, если бы они очевидно отделялись от других, чего, однако, не
происходит ни здесь, ни на рис. 3.1.5, ни на последующих ри-
сунках. Впрочем, если бы эти данные мы получили на магнитной
ленте, без построения графика, то даже такая очевидная неудача
гауссовской аппроксимации могла бы остаться незамеченной
вую». В качестве общей оценки затем представляется сред-
нее частных оценок, нормализованных таким образом. Мне
158
Глава 3.1
Рис. 3.1.5. Негауссовский характер и проверка L-устойчивости.
Прежде всего этот график свидетельствует о заведомо негауссов-
ском характере изменения цен на зерно в Чикаго с 1883 по 1934
годы [Working 1934а]. Абсцисса линейна, а ордината — гауссов-
ская. Гауссовские данные должны были бы образовать «прямые
Генри». Для проверки на L-устойчивость мы объединяем в этом
графике изменения за неделю (•), за «месяц» из четырех недель
(х) и за год (4-). Деления на оси абсцисс от —0,3 до 0,3 от-
носятся к графикам «их, деления от —0,6 до 0,6 относятся к
графикам 4-. Поскольку а близко к 2, при таком изменении мас-
штаба изменения цен за месяц должны совпасть с еженедельными
изменениями цен. Так в этом случае и происходит
совершенно серьезно предлагали точно так же нормали-
зовать изменения цены (не уточняя, впрочем, законно ли,
единожды нормализовав цены, находить их среднее!). Я же,
напротив, считаю, что длинные хвосты гистограмм изме-
Симптом РАЗРЫВНОСТИ
159
нения цены скрывают значительную информацию, и есть
много веских оснований вплотную ими заняться.
Симптом разрывности
Если кривые, постулируемые броуновским движени-
ем, непрерывны, то кривые, которые встречаются в дей-
ствительности, таковыми не являются. При этом каждый
раз, когда цена терпит сильный разрыв, к хвостам распре-
деления изменений цены добавляется новая точка. Впро-
чем, верно и обратное: если гистограммы далеки от гаус-
совских, а изменения цены независимы, то колебания цен
должны быть разрывны. (Математическое доказательство
имеет чисто технический характер, и приводить его здесь,
думаю, не стоит.)
Итак, симптом «длинных хвостов» тесно связан с
симптомом «разрывности в цене».
Вопрос о разрывности — насущный, но очень непро-
стой вопрос. Среди тех, кто полагал, что этот вопрос раз-
решен, — Альфред Маршалл, поместивший на титульный
лист своего знаменитого труда «Экономикс» фразу: «Natura
non facit saltus»!1 Во всяком случае, в экономике время
нельзя делить на части, меньшие (допустим) одной секун-
ды, а в дискретном времени, как известно, математиче-
ское понятие непрерывности теряет смысл. Итак, возникает
вопрос исключительно прагматического порядка: которая
из двух аппроксимаций (постулирующих, соответственно,
непрерывность и разрывность) будет проще и понятнее?
Поразмышляем о величинах, которые пришли в эконо-
мику из физики. Способность к производству терпит раз-
рыв в каждый момент времени, когда открывается новый
завод, однако мы полагаем разумным обращаться с ней так,
словно эта величина непрерывна в математическом смыс-
ле, даже дифференцируема, и подчиняется дифференци-
альным уравнениям. Думаю, что имея дело с ценой надо, *
Природа не совершает скачков (лат.) — Прим. пер.
160
Глава 3.1
наоборот, быть готовыми встретить скачки, которые сохра-
няют свое значение (в относительных единицах измерения)
даже с долговременной точки зрения.
Вот априорное теоретическое обоснование этого утвер-
ждения: и спрос, и предложение, определяющие цену, опре-
деляются как объективными факторами, так и предчувстви-
ями. И даже если мы согласимся с непрерывной аппрокси-
мацией первых, то вторые могут совершенно измениться
в результате физического «сигнала», продолжительность и
энергия которого пренебрежимо малы, как вошедший в по-
говорку «росчерк пера». А заодно очень рискует совершить
«дестабилизирующие» скачки и рациональность в опреде-
лении цены.
«Фильтры» С. С. Александера
Теперь приведем экспериментальное доказательство.
Обычно надеются на то, что описанные выше разрывно-
сти имеют чисто локальный эффект. Если рассматривать
разрывности издалека, то они объединяются, что позволя-
ет ими пренебречь. Существуют теоретические соображе-
ния, доказывающие, что это не так [М 1966b {Е19}]; но еще
сильнее убеждает в этом одна правдивая история — исто-
рия рождения, падения и забвения «метода» спекуляции,
основанного на «фильтрах».
В 1961 году Александер определил р%-й фильтр как
«черный ящик», который следит за изменениями цены, от-
мечая все ее локальные максимумы и минимумы. Фильтр
принимает решение о покупке в первый (после включения)
момент времени, когда цена достигает локального миниму-
ма плюс в точности р%. Решение о продаже он принимает
в первый (после покупки) момент времени, когда цена до-
стигает локального максимума минус в точности р%. И так
далее, чередуя покупки и продажи.
Оставалось убедиться в правильности этого принци-
па, располагая только хрониками, содержащими максимум
и минимум цены за каждый день. Итак, Александер посту-
«Фильтры» С. С. Александера
161
лировал, что в течение дня, когда максимум цены впервые
превосходит предыдущий минимум хотя бы на р%, най-
дется момент времени, в точности совпадающий с преды-
дущим минимумом плюс р%. То же самое происходит в
случае убывания цены.
В этих рассуждениях используется свойство непре-
рывных функций. Если непрерывная функция f(t) рав-
на f(t') в момент времени t' и f(t") в момент времени t"9
причем /(f) < у <	то между t' и f' существует хотя
бы один момент времени ty> когда у = f(ty).
Итак, Александер, ничтоже сумняшеся, предположил,
что в действительности цена представляет собой непре-
рывную функцию от времени, и пришел в результате своих
вычислений к выводу, что метод фильтров сулит гораздо
больше преимуществ, чем метод, заключающийся в покуп-
ке и удержании портфеля.
Этот результат был обнародован как раз в то время,
когда я работал над [М 1963b {Е14}]. Изначально предпо-
лагавшаяся непрерывность показалась мне обманчивой, и
я отметил ([М 1963b], с. 417), что сигнал о покупке «по
Александеру» вполне может попасть на день очень силь-
ного повышения цены. Более того, упомянутое сильное по-
вышение цены может произойти ночью или в воскресенье,
или же тогда, когда биржа открыта, но все операции по ка-
ким бы то ни было ценным бумагам приостановлены, что
на Нью-йоркской бирже происходит куда чаще, чем можно
было бы предположить.
В каждом из этих случаев сигнал о покупке «по Алек-
сандеру» невозможно выполнить. Если покупать сразу, как
только появляются продавцы, то почти всегда приходится
платить больше, чем ожидалось. Александер полагал, что
этим источником ошибок можно пренебречь, но я не наме-
рен был с ним соглашаться.
Необходимо подчеркнуть еще одну вещь. Цену, по ко-
торой совершаются сделки, нельзя задать каким-либо без-
личным алгоритмом. Она определяется агентом по обме-
ну, так называемым «специалистом», который основывает
свой выбор на записях, где он отмечает предложения о по-
11 Б. Мандельброт
162
Глава 3.1
купке и продаже. Однако Комиссия по ценным бумагам и
биржам (Security Exchange Commission, SEC) — федераль-
ный орган Соединенных Штатов Америки, — в обязанности
которой входит надзор за биржей, предписывает специа-
листу «обеспечивать непрерывность купли-продажи». Лю-
бое вмешательство в операции должно получить одобрение
SEC. Нередко специалист может этого избежать, если будет
вести себя как продавец или покупатель малых, принадле-
жащих лично ему, пакетов акций. Таким образом, скачок
цены перестает быть неизбежным, поскольку его можно
«разбить» за счет разумно размещенных промежуточных
цен.
Вот почему изменения цены при нормальных последо-
вательных сделках никогда не бывают велики (их распреде-
ление близко к гауссовскому). Но мы знаем, что изменения
цены на интервале заранее оговоренной продолжительно-
сти имеют распределение с очень длинными хвостами. По-
лучить право на покупку по такой промежуточной цене,
разумеется, прекрасно, но в этом случае покупатель во-
все не следует совету Александера, что бы он (покупатель)
при этом ни думал. В общем случае, такому покупателю
следует дождаться очередного вздувания цен. И он опять
заплатит больше, чем предполагал Александер.
Я взял на себя смелость предсказать, что те поправ-
ки, которые Александер счел пренебрежимо малыми, мо-
гут уничтожить все явное преимущество, ожидавшееся от
метода фильтров. Когда в 1964 году Александер переделал
свои тесты, исключив этот источник ошибок, мое предска-
зание сбылось, и метод фильтров потерпел крах. В 1966 го-
ду Фама и Блюм похоронили его окончательно, выполнив
новые вычисления, в которых индексы цен были заменены
собственно ценами.
Обнаружение того, что какой-либо «метод» не облада-
ет той «надежностью», на которую он претендовал, вообще
говоря, не заслуживает ни славы, ни удивления. И не сле-
дует обвинять автора, чья основная ошибка состояла в том,
что он был достаточно ясным, чтобы быть спорным. Тем
не менее, описанный выше эпизод сохраняет свою значи-
МОМЕНТЫ И ДРУГИЕ ТИПИЧНЫЕ ВЕЛИЧИНЫ 163
мость: в нем подчеркивается то, что даже в масштабе декад
и даже после мощного объединения скачков посредством
подсчета индексов, значение этих скачков остается очень
заметным.
Моменты и другие типичные величины.
Конкретные результаты бесконечной
дисперсии
Теперь оставим в стороне синдром разрывности и зай-
мемся поочередно двумя уровнями статистики.
Из них более элементарным является уровень «опи-
сательной статистики», определяемый как использование
«типичных значений» при обработке таблиц частотности.
Обычные типичные значения — среднее эмпирическое (ме-
ра локализации), квадратичный эмпирический скачок (мера
рассеяния) и индексы асимметрии и эксцесса.
Среднее эмпирическое. Особых проблем в случае из-
менений цены это значение не причиняет — в том смысле,
что средние, соответствующие выборкам, возрастающим
по размеру, достаточно быстро стабилизируются вблизи
некоторой величины, которую можно принять за аналог
асимптотического предела. При более точном анализе про-
блемы все-таки появляются, но лучше будет обсудить их
ниже, привязав к синдрому Иосифа, который будет рас-
смотрен в главе 3.2.
Среднее квадратическое, Дря некоторых цен оно ведет
себя весьма ненадежным образом.
а)	Эти значения, соответствующие различным выборкам
одной и той же длины, могут относиться друг к другу
даже как 1 к 100, то есть различаться на два порядка
величины (рис. 3.1.6).
Ь)	Для выборок с последовательно возрастающей дли-
ной эти значения, по-видимому, не стабилизируются.
Таким образом, не существует величины, которую хо-
телось бы принять в качестве аналога предельной ве-
личины (рис. 3.1.7).
11*
164
Глава 3.1
Рис. 3.1.6. Первый пример, демонстрирующий неустойчивый ха-
рактер второго эмпирического момента. Здесь рассматриваются
величины logZ(t 4- один день) — logZ(t), где Z(t) — цена на
хлопок (spotprice2) на Нью-йоркской хлопковой бирже. 1500 пер-
вых значений, соответствующих периоду 1900—1905 годов («годы
урожая» считаются с осени), разделены на 30 последовательных
выборок длиной в 50 значений каждая. В гауссовской перспекти-
ве все ординаты имели бы одинаковый порядок величины, между
тем шкала ординат имеет логарифмический характер. Наиболь-
шая ордината и в самом деле превосходит наименьшую на два
порядка
с)	Вклады различных значений в среднее квадратиче-
ское очень отличаются. Наибольшим индивидуальным
вкладом нельзя пренебречь, даже когда выборка очень
велика.
d)	Грубо говоря, среднее квадратическое возрастает вме-
сте с длиной выборки.
Такое поведение наводит на мысль о гетерогенности
данных (например, нестационарности) или о том, что дан-
165
Моменты и другие типичные величины
Рис. 3.1.7. Вторая иллюстрация неустойчивого характера вто-
рого эмпирического момента. Здесь рассматривается раз-
ность log Z(t 4- одна неделя) — log Z(t), где Z(t) — цена на зерно,
как на рис. 3.1.5. Выборка возрастает от 1 до 1000, каждый раз
включая в себя предыдущую выборку. Если бы ожидание квад-
рата переменной было конечным и не очень большим, то кривая
должна была бы стремиться к некоторому пределу. В данном слу-
чае это не так
ные статистически гомогенны, но выборка слишком мала,
чтобы судить об их достоверности.
И если неизбежно первое объяснение, то, как уже от-
мечалось, статистик мало что может здесь сделать.
Если неизбежно второе объяснение, то ожидание (те-
оретическое среднее) квадратов уже не будет образовывать
интересное для нас «типичное значение», и его величина
будет играть в теории не более чем вспомогательную роль.
Более того, статистику придется все время сталкиваться с
проблемами, возникающими из-за малости выборок, а эта
перспектива ни у кого энтузиазма не вызывает.
166
Глава 3.1
Тем не менее существует и третья, менее тривиаль-
ная, возможность; поначалу она шокирует, но в конце кон-
цов оказывается (удивительная вещь), что в этом случае
все упрощается. Почему бы не рассмотреть теоретическую
возможность бесконечной дисперсии?
Может несколько испугать то, что бесконечная диспер-
сия не может не повлечь за собой необходимости и для са-
мой переменной становиться иногда бесконечно большой.
Но переменная Коши конечна почти наверное, тогда как
ее дисперсия бесконечно велика. Желая показать, что бес-
конечная теоретическая дисперсия необычайно упрощает
развитие математической стороны дела, проведем анало-
гию с повседневной жизнью: известно, что жизнь фотогра-
фа очень упростилась бы, если бы он мог удалиться от объ-
екта съемки на бесконечно большое расстояние; в общем-
то, в действительности приблизительно так и получается,
когда объект находится пусть на конечном, но достаточ-
но большом расстоянии. Достаточно, чтобы это расстояние
превышало некоторый порог, который зависит, в частности,
от качества объектива и установленной диафрагмы.
Тем не менее, бесконечность беспокоит. Даже если
бесконечная дисперсия соответствует фактам, может ока-
заться, что очень большая, но конечная дисперсия так же
хороша. Например, можно было бы обрезать с краю хвосты
распределения Коши, предпочитая таким образом прибли-
жать бесконечное с помощью очень большого конечного.
Но многократно подтвержденный опыт теоретиков подска-
зывает скорее обратную процедуру. Например, распреде-
ление Бернулли высокого порядка содержится в конечной
области, но обычно его предпочитают заменять на гауссов-
скую аппроксимацию, даже когда конкретные величины,
о которых идет речь, положительны. Нас очень мало бес-
покоит то, что в гауссовском распределении утверждается,
будто рост новобранцев или балл на психологическом тесте
может оказаться меньше нуля!
В том же смысле часто бывает полезно приближать
дискретное непрерывным. Некоторые полагают, что уделом
общественных наук — среди них и науки экономические —
Корректировка гистограмм. Старые и новые критерии 167
навсегда останется дискретная и конечная математика и
комбинаторика и что лишь физические науки имеют право
на непрерывность и математический анализ. Не вижу ни-
каких реальных оснований для того, чтобы соглашаться с
правильностью такого разделения.
Корректировка гистограмм. Старые и новые
критерии
Другой уровень элементарной статистики, более тон-
кий, нежели метод типичных значений, — это метод анали-
тической корректировки. Речь идет о приближенном пред-
ставлении гистограмм с помощью функций, входящих в
список допустимых. В случае, когда имеются основания
сократить этот список до гауссовского распределения, кор-
ректировка почти не оспаривается. Но если этот список
велик и разнообразен, то «механическая корректировка»
приобретает очень дурную репутацию.
Возникающие вокруг нее противоречия даже неизбеж-
ны, поскольку всякая аппроксимация — это обязательно
компромисс между противоречащими друг другу требо-
ваниями. Даже понятие «расстояния» между функцией и
эмпирической гистограммой можно определить многими,
различными и противоречивыми, способами. Например,
можно не приписывать никакого веса качеству аппрокси-
мации на хвостах; тогда получится аппроксимация, которая
прячет хвосты, обрезая их.
Что касается концепции «простоты», то с приходом
компьютера она сильно изменилась: сегодня многие фор-
мулы, требующие большого объема вычислений, но про-
стые в написании, заслуживают рассмотрения в качестве
простых. Возьмем выражение, определенное как преоб-
разование Фурье некоторой очень элементарной функции.
При отсутствии элементарного аналитического выражения
это выражение неразрешимо вручную, компьютер же со-
чтет его очень простым.
Отсюда новая сложность, ведь в случае изменений це-
ны мы одновременно имеем дело с многими эмпирически-
168
Глава 3.1
ми кривыми: гистограммы изменения цены за один день,
за неделю, за месяц, а также за один час и за год.
Если корректировать эти кривые по отдельности, то
нет никаких оснований ожидать, что результаты корректи-
ровки будут совместимы. Предположим, например, что це-
на подчиняется законам «случайного блуждания». Откор-
ректировав наилучшим образом распределение ежеднев-
ных изменений, мы получим распределение еженедельных
изменений цены с помощью формулы свертки, применен-
ной к сумме случайных величин.
При этом мы рискуем обнаружить, что результат
непригоден для аналитического применения, а это вступа-
ет в противоречие с вышеупомянутым критерием простоты
функции. Итак, необходимо выбирать между а) раздель-
ной корректировкой различных участвующих в деле вели-
чин и Ь) глобальной корректировкой, основанной на орга-
низованном семействе распределений и минимизирующей
функцию ошибок, определенную как компромисс между
ошибками, относящимися к каждой из этих величин.
Такой компромисс часто встречается в науке. Если
Кеплер в поисках представления траекторий планет по-
думал об эллипсах, то прежде всего потому, что он рас-
сматривал эти кривые как взаимно совместимые (и близ-
кие к совершенству!). Для каждой планеты эллипс — всего
лишь приближение, причем комбинации Птолемея, состав-
ленные из эпициклов, которые наматываются на цикл, сам
по себе эксцентричный, дают лучшее приближение.
Этим критерием компромисса часто оправдывают
гауссовскую корректировку. Хотя распределения ежеднев-
ных, еженедельных и ежемесячных изменений цены не яв-
ляются гауссовскими, с ними поступают так, словно они
таковыми являются.
Понятие L-устойчивости
Последний аргумент следует рассмотреть подробнее.
Он основан на известном факте, значение которого часто
Понятие L-устойчивости
169
даже недооценивают: распределение Гаусса остается инва-
риантным относительно сложения независимых перемен-
ных. Поль Леви предложил обозначать это свойство терми-
ном «устойчивость». Неудачный выбор, потому что немно-
гие из общеупотребительных терминов несут в себе так
много различных научных значений. Желая избежать дву-
смысленности, мы употребляем здесь более благоразумный
термин «L-устойчивость». О ней мы говорили в главе 2.4.
Даже не задаваясь этим вопросом, ученые ведут се-
бя так, как будто L-устойчивость характерна только для
распределения Гаусса. Между тем это верно лишь для тех
величин, которые имеют конечную дисперсию. Например,
еще в главе 2.4 упоминалось, что распределение Коши так-
же устойчиво, причем это оказалось возможным именно
благодаря его бесконечной дисперсии.
Коши также показал, что существуют и другие сим-
метричные устойчивые распределения, зависящие от па-
раметра а (о чем говорится все в той же главе 2.4). Ес-
ли 1 < а < 2, то они занимают промежуточное положение
между распределением Коши (а = 1) и распределением
Гаусса (а = 2).
Наконец, Поль Леви показал (и это очень важно), что
а не может превосходить 2, и дополнил семейство устой-
чивых распределений несимметричными членами. Эти по-
следние используются в экономике двояко: слабая асиммет-
рия встречается у некоторых цен, которые чаще имеют тен-
денцию к росту, чем к падению (при всем том падают они,
как правило, сильнее, чем возрастают). Наибольшая асим-
метрия встречается при распределении доходов, для кото-
рого, как мне, по-видимому, удалось показать, L-устойчи-
вое распределение оказывается предпочтительнее, нежели
распределение Парето. Читатель может обратиться к статье
[М1959р], воспроизведенной в предисловии, а также к ра-
ботам [М 1960i {Е14}], [М1961 е {Е14}] и [М 1962е {Е14}].
Чтобы проверить, принадлежат ли распределения из-
менений цены к числу L-устойчивых хотя бы в первом при-
ближении, я сравнил распределения ежедневных измене-
ний цены и ежемесячных изменений, разделенных на под-
170
Глава 3.1
ходящий коэффициент изменения масштаба. Два из этих
тестов показаны на рис. 3.1.5 и 1.
На рис. 3.1.5 важно то, что кривые, соединяющие знач-
ки • и х, накладываются друг на друга (чтобы обеспечить
этот эффект, при построении кривых использованы разные
масштабы).
На рис. 1 существенно то, что в пределах двух серий,
составленных из трех соединяющих точки кривых (слева
и справа на рисунке), три кривые отличаются только боко-
вым переносом (шкала для этих трех кривых одна и та же,
а изменение масштаба осуществляется именно при пере-
носе).
Рисунки 3.1.5 и 1, а также тысяча других, которые мы
не можем включить в эту книгу из-за недостатка места,
показывают нам, что можно постулировать «принцип», о
котором уже заявлялось во введении к данной главе.
«Исходя из соображений, которые еще предстоит опре-
делить, распределения изменений некоторых цен, по-види-
мому, имеют бесконечную дисперсию и являются L-устой-
чивыми».
Поскольку четыре параметра — это слишком много,
начнем с гистограмм, симметричных относительно начала
координат. Вспомним, что их плотность зависит только от
двух параметров (а и 7) и имеет вид
оо
Ра(и) = i j exp(-T7s“)cos(s|u|)ds.
о
Параметр а, определяющий меру изменчивости хро-
ник, всегда находится между 0 и 2. Значение а = 1 со-
ответствует распределению Коши, а максимальное значе-
ние а = 2 соответствует гауссовской плотности. Таким об-
разом, настоящая модель включает в себя модель Башелье.
А в случае а = 2 параметр 7 пропорционален дисперсии
случайной величины U. При а < 2 дисперсия бесконечно
велика, но 7 по-прежнему можно принять в качестве меры
«рассеяния случайной величины U».
РОЛЬ МАСШТАБИРУЕМЫХ АСИМПТОТ
171
Опишем тест, который был реализован в компании
«Bell Telephone Laboratories». Поскольку величина 2 — а
представляет собой меру разрывности движения, тест ими-
тировал различные движения, показатели которых а были
равны (насколько мне известно) 1,5; 1,6; 1,7; 1,8; 1,9. Сме-
шав эти кривые с броуновским движением (а = 2), их
показали агенту по обмену валюты, заявив, что они со-
ответствуют различным имитационным моделям, и только
одна из них иллюстрирует поведение биржи; именно эту
кривую ему и предложили определить.
Эксперт сразу исключил броуновское движение а =
= 2, а также кривую с а = 1,9, поскольку они обнару-
живали слишком много закономерностей в своих деталях.
Затем он исключил кривую с а = 1,5 как слишком непра-
вильную. Степень нерегулярности при а = 1,7 показалась
ему ближе всего к разумной. Оказалось (рис. 1), что имен-
но это значение получается при непосредственной оценке
показателя а во многих экономических хрониках.
Таким образом, теоретическая дисперсия совершает
разрывный скачок, когда а стремится к своему предельно-
му значению 2, но для конечных выборок контраст между
случаями «а чуть меньше 2» и «а = 2» не настолько силен,
как между черным и белым. Правильнее будет сказать, что
при убывании а от 2 до 0 мы получаем «серое» все более
и более темного цвета. Пусть, например, V°(a,7V,g) обо-
значает величину, которая с вероятностью q оказывается
меньше, чем эмпирическая дисперсия выборки длины 7V.
При заданных N nq величина V0 непрерывно изменяется,
точнее, монотонно убывает вместе с а. Более того, V0 мало
изменяется даже в том случае, когда теоретическая диспер-
сия чрезвычайно велика, вплоть до бесконечно большой.
Роль масштабируемых асимптот
Самый непосредственный и по-прежнему наиболее
важный тест на применимость L-устойчивых распределе-
ний основан на асимптотической форме их плотностей.
172
Глава 3.1
В главе 2.4 было указано, что для L-устойчивой величи-
ны U предел
lim Pr{U и}иа
и—>оо
существует, а его значение конечно и положительно.
С практической точки зрения остается определить, начи-
ная с какого момента вероятность Рг{С7 > и}иа сливается
со своим пределом.
Если а очень близко к 2, то предел достигается очень
поздно, и L-устойчивая плотность отличается от гауссов-
ской только с точки зрения очень больших выборок. Если а
меньше 1,8, то предел достигается достаточно быстро, что
позволяет проверить, подчиняются ли хвосты эмпириче-
ского распределения данному масштабируемому распреде-
лению.
В билогарифмических координатах мы должны полу-
чить прямую линию. Отсюда новый тест на устойчивость:
проверить, будут ли хвосты эмпирических распределений
в билогарифмических координатах приближаться к прямо-
линейным. Если это выполняется, то тест пройден.
Затем мы оценим L-устойчивую плотность с помощью
численного интегрирования и выясним, до каких пор мож-
но применять прямолинейную асимптоту. Тогда можно бу-
дет проверить, совпадают ли в теории и в действитель-
ности точки расхождения относительно этой асимптоты.
Все эти — и другие — тесты действительно выполнялись,
и их результаты оказывались одинаково положительными.
Таким образом, можно сказать, что принцип устойчивости
получил удовлетворительное подтверждение.
О тестах на устойчивость можно узнать в [М 1963b
{Е14}], [М 1967j {Е15}], [Fama 1965], [Roll 1970], [Blume
1970] и в других работах. Что касается работ, которые были
представлены как критические, но в конце концов привели
к моделям, неотличимым от моей, смотрите [Clark 1973] и
дискуссию в [М 1973с {Е21}].
Теперь вспомним, что масштабируемые асимптоты ха-
рактеризуют эмпирический закон Парето для распределе-
ния личных доходов. На Неофициальной Бирже Научных
Стационарность и интуиция, часть 2	173
Репутаций флуктуации закона Парето испытывали голово-
кружительные взлеты: в свое время и в своем месте этот
закон возносился до небес, но теперь он обречен на осме-
яние и зачастую вызывает некую неловкость. Не пытаясь
анализировать исторические причины этой неловкости, хо-
чу указать на одну очень важную логическую причину. Бес-
конечная дисперсия изолировала этот закон в контексте эле-
ментарной вероятности и статистики.
Мы своими глазами видим, как преобразуется беско-
нечная дисперсия, превращаясь из неудобной и даже, по
слухам, невыносимой характеристики в фундаментальное
орудие объяснения [М 1963е {ЕЗ}].
Стационарность и интуиция, часть 2:
кратковременные и долговременные
соотношения
На рис. 1 особенно интересно сравнить кривые, соот-
ветствующие 1900 и 1950 годам. После коррекции ошибки
(описанной в пояснении) эти кривые становятся практиче-
ски неразличимыми, что и постулировалось в нашей ги-
потезе стационарности. Как было заявлено в начале этой
работы, мы увидим, что концепция стационарности, в силу
отдельных нюансов, разделяется. С одной стороны, у нас
есть интуитивная стационарность, выражающая тот факт,
что хотя различные части некоторого процесса очень отли-
чаются друг от друга, у них есть общие фундаментальные
черты. С другой стороны, у нас есть математическая стаци-
онарность. Без нее нет теории, но она, по всей видимости,
неспособна учесть нерегулярности, наблюдаемые в эконо-
мическом поведении.
Чтобы быть более точными, займемся фундаменталь-
ным вопросом: существует ли разрыв между спекулятив-
ными изменениями цены за короткий промежуток времени
и такими же долговременными изменениями, которые и
интересны для экономики? Чтобы ответить на этот вопрос,
рассмотрим кривые 1с и 2с на рис. 1. Они представля-
174
Глава 3.1
ют собой два хвоста распределения месячных изменений
цены на хлопок за период 1880—1940 годов. Размах этих из-
менений настолько широк, что они оказывают влияние не
только на биржи, но и на все секторы национальной эко-
номики: каждая из экстремальных точек на кривых 1с и 2с
соответствует некоторому событию — например, серьезно-
му экономическому кризису, — оставившему глубокий след
в исторических хрониках.
Следовательно, необходимо подчеркнуть, что в пер-
вом приближении амплитуду этих событий можно полу-
чить, оценивая L(t,T =один месяц) как сумму измене-
ний L(t,T =один день), взятую по всем дням, входящим
в рассматриваемый месяц. При втором приближении воз-
никают затруднения, которые являются симптомами зави-
симости.
Более того, линии 1с и 2с имеют очень регулярный
вид, наша совокупность данных за месяц совершенно не
похожа на смесь малых случайных изменений и больших
изменений, причинных по своей природе. Иначе говоря,
при рассмотрении этих кривых сложно провести границу
между спекуляцией и экономикой.
Честно говоря, это результат оказался весьма неожи-
данным и своей интерпретации еще не получил. Я не могу
обсуждать его здесь, но надеюсь, что он послужит приме-
ром к утверждению, помещенному в начале этой главы:
экономист не должен пренебрегать той помощью, кото-
рую оказывает ему изучение биржи при описании фактов,
неоспоримо принадлежащих к области экономики.
Глава 3.2
Псевдопериодичности
(«модель [М1965]»)
В этой главе параллельно обсуждаются роль очень
долгого периода в поведении экономических хроник — не
ограничиваясь одними лишь хрониками цен — и в поведе-
нии некоторых физических хроник.
Эти последние представляют двойной интерес, как в
смысле их собственного значения, так и в смысле непо-
средственного воздействия на экономику. Для сельскохо-
зяйственной продукции количество продукта, а следова-
тельно, и его цена, непосредственно зависят от полного
количества осадков, регистрируемых в течение сезона со-
зревания. Так, в Библии описан эпизод с тучными и тощими
коровами — помимо прочего упоминается и потребовавше-
еся для урегулирования флуктуации вмешательство фара-
она и его правительства (которым руководил Иосиф, сын
Иакова). Колебания цен и разливов Нила похожи друг на
друга, поэтому описывать их следует параллельно, равно
как и оценивать, контролировать и регулировать риски.
Для простоты долговременный период изучается в
гауссовских рамках. Долговременность и негауссовость бу-
дут объединены в главе 3.3.
Описание и управление
Для кратковременного управления уровнем воды в Ни-
ле используется невысокая плотина, для долговременно-
го — высокая. Повсеместно допускается, что кратковре-
менного управления недостаточно, между тем сейчас мы
176
Глава 3.2
понимаем, что глобальное управление изобилует непред-
виденными трудностями.
Аналогичным образом проблема управления встает и
в экономике, где все гораздо сложнее. Управление нельзя
осуществить посредством одной-единственной плотины,
оно осуществляется на многих уровнях, которые могут
быть относительно независимыми и даже действовать в
противоположных смыслах. В главе 3.1 было указано на
результат из [М 1963b {Е19}]: спекулятивный рынок, кото-
рый рациональным образом предваряет события с точки
зрения интересов своих участников, может автоматически
прийти к тому, чтобы ввести в цены разрывность; имеют-
ся и другие последствия, которые могут вызвать в обще-
стве желание противодействовать им как «дестабилизиру-
ющим». Аналогичные трудности мы рискуем обнаружить,
если вместо мгновенных разрывностей, представляющих
собой кратковременный феномен, будем рассматривать гло-
бальные эффекты.
Для осуществления наиболее эффективного управле-
ния требуется хорошее описание, и мы будем искать его
в долговременном контексте. Мы будем заведомо прагма-
тичными, ограничившись тем, что физики называют фено-
менологией, то есть таким описанием, которое объясняет
множество фактов в рамках единой математической моде-
ли.
Конечно, свести эту модель к изначальным причи-
нам будет сложно. Традиционно большинство экономистов
ищут чисто экономическое объяснение — полностью беря
за образец теорию термодинамических флуктуаций. Точно
так же большая часть гидрологов ищет объяснение чисто
климатическое. В обоих случаях находилось также и неко-
торое количество энтузиастов, веривших в пятна на солнце.
Сегодняшний экономист начнет, пожалуй, с предположе-
ния о возможности отделить экономические механизмы от
феноменов, обусловленных физическими фактами, оказы-
вающими реальное влияние на экономику. Впрочем, все
это весьма сложно, и лучше всего будет начать с описа-
ния.
Множественность циклов
177
Множественность циклов
Если сравнивать экономические хроники с хрониками
разливов Нила, то первое их сходство состоит в характер-
ном для обоих непериодическом циклическом поведении.
Итак, все последующие рассуждения будут, в первую оче-
редь, связаны с так называемой проблемой реальности цик-
лов и, в частности, долгих циклов.
Рассматривая циклические феномены, мы поражаем-
ся тому, насколько много длительностей имеют различные
циклы, равно как и слабости критериев их определения и
дифференциации (см. рис. 3.2.1). Например, хроника, охва-
тывающая целый век, год за годом, не имеет ежегодной
сезонности, но обнаруживает короткие циклы продолжи-
тельностью от 5 до 10 лет, а также долгие циклы с про-
должительностью от 20 до 40 лет. То, что в близкой пер-
спективе казалось тенденцией к росту, в действительности
оказывается началом цикла, который тут же заканчивается
изменением направления. Некоторые наблюдатели увидят
в той же самой хронике и средние циклы, но им будет слож-
но провести различие между «укороченными» средними и
«удлиненными» короткими циклами (или же между «удли-
ненными» средними и «укороченными» длинными).
Еще большее изобилие данных возникает в случае
биржевых хроник, составлявшихся изо дня в день. В гидро-
логии и климатологии мы располагаем хрониками разливов
Нила, хрониками изменений климата в Аризоне (о кото-
рых можно узнать по изменению толщины годовых колец
произрастающих там особого вида сосен, имеющих чрез-
вычайно большую продолжительность жизни, — большую
даже, чем у секвойи) и хрониками изменений климата неко-
торых регионов Канады и Швеции (по изменению толщи-
ны слоев в пластах засохшего ила на дне ископаемых озер).
В этих хрониках, содержащих сотни или даже тысячи дан-
ных, обнаруживаются весьма долгие циклы, столетние и
тысячелетние.
Здесь мы подходим к очень существенному различию.
Все, что мы говорили о множественности циклов, можно
12 Б. Мандельброт
178
Глава 3.2
„1Ы1jhltdjuljllbkjl
Рис. 3.2.1. Две хроники, характеризующие чрезвычайное много-
образие непериодических циклов. Исходные данные были уте-
ряны, поэтому мне известно лишь то, что представленные здесь
кривые описывают два из трех очень разных процессов, а именно:
а) хроника разливов реки; Ь) имитация дробного гауссовского шу-
ма; с) экономическая хроника. Эта неопределенность оказывается
весьма кстати: она подчеркивает поразительное сходство выше-
упомянутых процессов. Низкие частоты (долгий период) проявля-
ются во всех этих случаях в виде всевозможных «конфигураций».
В частности, эти две кривые содержат практически три очень
медленных цикла. Иначе говоря, кажется, что длина волны этих
циклов пропорциональна длине выборки. Однако из механизма,
порождающего дробный шум, не следует никакого «истинного
цикла»; то, что мы так ясно здесь видим, — не более, чем «ар-
тефакты». За отсутствием доказательства противоположного, тот
же вывод возможен и для экономических и геологических хроник
дословно применить и к случайным блужданиям, пример
которых приведен на рис. 3.2.2.
Таким образом, источником непериодического цикли-
ческого поведения является, возможно, накопление непред-
виденных и чисто случайных изменений. Честь откры-
тия такой возможности, несомненно, принадлежит Уоркин-
гу [Working 1934b].
Множественность циклов
179
Рис. 3.2.2. Определение величин R, S и Q. Пусть X(t) — ана-
лизируемая функция, а непрерывная кривая внизу представля-
t
ет X*(t) = 22 ^(s)- Если все X(t) — изменения цены, то X* —
s=o
собственно цена. Поскольку эмпирические данные всегда пред-
ставлены в дискретном времени, то значения X* — последова-
тельность точек, однако для большей наглядности они соединены
ломаной линией. Д(ц) — линейная интерполяция X* на интер-
вале от t до t 4- d. В гидрологии X(t) — уровень реки в течение
года t. Пусть R(t, d) = max Д (и) — min Д (и) — размер совершен-
ной плотины: за период от t до t+d уровень реки на выходе будет
постоянным, плотина будет столь же совершенной, как и вначале,
и никогда не случится ни переполнения, ни пересыхания. В фи-
нансах величина R улучшает разницу между максимальным и
минимальным курсами. Что касается знаменателя S, то он ра-
вен S2(t, d) = d"1 22 x2(t + «) ~	[Z2 x(t + w)] > гДе сумма
вычисляется от u = 1 дои = d
Тем не менее, случайное блуждание в конце концов, в
том или ином смысле, всегда уходит в бесконечность, то-
гда как мы рассматриваем изменения цены. Хроники этих
изменений кажутся стационарными: они возрастают и убы-
вают в относительно узких пределах. На этот факт можно
отреагировать по-разному.
В одну из крайностей бросаются те, кто надеется,
что за наблюдаемой нерегулярностью скрываются какие-то
12*
180
Глава 3.2
механизмы, каждый из которых соответствует некоторому
вполне определенному периоду или, скажем так, аппрокси-
мативному периоду, так называемой «константе времени»;
различия между разными периодами вполне отчетливы и
позволяют надеяться, что эти самые периоды можно иден-
тифицировать и отделить друг от друга. Эта надежда и
привела в 1900—1920 годах к так называемому «методу пе-
риодограмм».
Когда в 1925 году в Оксфорде Уильям Беверидж при-
менил этот метод к курсу цен на пшеницу, то сначала
всем показалось, что периодограмма позволяет обнаружить
очень отчетливые циклы. Однако вскоре возникли подозре-
ния, связанные с большим количеством различных циклов,
и в конце концов выяснилось, что статистический метод
Бевериджа была неверна. Основательно преобразованная
инженерами-электриками, она однажды привела к «спек-
тральному анализу», о котором мы еще поговорим. Резуль-
таты применения этого метода были очень обманчивы, как
в экономических науках, так и в гидрологии. Адельман
[Adelman 1965] и Грейнджер [Granger 1966] показали, что,
по всей видимости, никакая периодичность не имеет ста-
тистического значения. Таковы «артефакты».
Реальны ли медленные циклы?
Все это вдохновляет нас на рассмотрение другого,
экстремального с точки зрения экономических механиз-
мов, поведения: допустим, что количество этих механиз-
мов очень велико, а их временные константы перекрыва-
ют друг друга и не поддаются разделению. Говорят, что
они образуют не «полосатый», но, скорее, «непрерывный»
спектр. На этом этапе вернемся немного назад, чтобы рас-
смотреть с самого начала циклический характер случайно-
го блуждания. Определившись с подходящей концепцией
спектра, констатируем, что спектральная плотность про-
порциональна /~2, где f — частота. Иначе говоря, в про-
тивоположность множеству тонких полос, которые ожидал
Интерпретация спектров	181
увидеть Беверидж, этот спектр обнаруживает одну, широ-
кую и размытую, полосу в окрестности источника частот.
Отсюда и следует то, в чем мы уже убедились: все
периодичности суть «артефакты», не характеристика про-
цесса, но, скорее, совокупный результат зависящий от соб-
ственно процесса, длины выборки и суждения экономиста
или гидролога. Первый из упомянутых факторов является
внешним по отношению к наблюдателю, второй (в зависи-
мости от конкретного случая) может предполагаться зара-
нее или выбираться произвольно, а третий субъективен во
всех случаях, то есть представляет собой продукт челове-
ческого восприятия и предмет разногласий. (Впрочем, эти
разногласия зачастую касаются только деталей, что может
представлять интерес с точки зрения теории восприятия.)
Случайное блуждание — хорошая иллюстрация, но
(повторим еще раз) нестационарная. Возвращаясь к ста-
ционарным процессам, можно ожидать, что в их спектре
обнаружится широкая полоса, размытая по направлению к
источнику частот, и останется только определить ее точную
форму.
Интерпретация спектров
В «спектральном анализе» предполагается, что слу-
чайная функция U(t) такова, что выражение
С(Т) = E[U(t)U(t+ Т)]
является конечным для любой пары моментов времени t
nt + Tn принимает значения, не зависящие от Т. В этом
случае С(Т) определяет ковариацию U (£). Отсюда следу-
ет, что спектральный анализ должен оказаться совершен-
но бессмысленным для экономических хроник, у которых
дисперсия бесконечна. Ничего не остается, как усомниться
в том факте, что дисперсия по большей части состоит из
вкладов, образованных отклоняющимися значениями. Ес-
ли С(Т) определено корректно, а время дискретно, то спек-
182
Глава 3.2
тральная плотность [7, в свою очередь, определяется как
5(5) = 2С(0) + 4	С(Т) cos(2ttT).
Т=1
Известно, что если logZ(t) — броуновское движение,
а переменная «время» принимает лишь целые значения,
то L(t, 1) представляет собой «белый» процесс, то есть
спектральная плотность 5(5) не зависит от частоты. Ес-
ли же, напротив, Z(t) есть последовательность цикличе-
ских флуктуаций, не являющихся гармоническими в стро-
гом смысле этого слова, то 5(5) содержит пики для каждой
из частот, соответствующих какому-либо циклу.
Мы уже говорили, что пикам эмпирической спектраль-
ной частоты в действительности ничего не соответствует,
за одним исключением, когда частота примерно соответ-
ствует длине волны, равной длине выборки. В термино-
логии, принятой в спектральном анализе и созданной под
влиянием ньютоновского оптического спектра, можно ска-
зать, что типичные экономические спектры чрезвычайно
«красны».
Следует отметить, что большая часть точных разделов
спектрального анализа не удовольствуется постулировани-
ем существования ковариации и спектра. Если ковариация
не является почти периодичной, то многие спектральные
техники требуют более сильного условия
§C(s) < оо,
3=1
которое можно записать в виде
5(0) = 20(0) + Jc(s) < оо.
3=1
Многие выдающиеся авторы предполагали, что вели-
чину 5(0) можно принять в качестве меры «памяти» про-
цесса. Но на практике измерение этой величины наталкива-
ется на те же самые трудности, что и эффективное измере-
ние дисперсии некоторого процесса. Когда 5(5) монотонно
Феномен Херста
183
и быстро возрастает при 6 —> 0, как оценить 5(0) с какой
бы то ни было точностью? Повторим еще раз — никто не
может со всей уверенностью утверждать, что 5(0) = оо,
но, конечно же, ее значение очень велико, а возникающие
при его оценке трудности представляют собой одно из про-
явлений того факта, что это значение никак не влияет на
интересующие нас в данный момент величины.
Наконец, иногда можно действовать так, словно вели-
чина 5(0) бесконечна. Например, можно считать, что 5(5)=
= 5“в, где 0 < В < 1. Я изучал некоторые особенности
этого процесса в [М1965 {Н}], [М & van Ness 1968 {Н}] и
в других статьях, собранных в [М1997Н]. Терминология
в этих статьях далека от экономической, но читатель мо-
жет легко перевести их на язык экономики. Так что здесь
я удовольствуюсь тем, что сделаю два вывода.
Вывод практический: если наблюдаемые спектры за-
даны в виде, предложенном Адельманом и Грейнджером,
то детально обсуждать положение максимума преждевре-
менно: действительно, в существующих статистических те-
стах предполагается, что 5(0) конечно, так что здесь они
неприменимы.
Теоретический вывод имеет более общее значение.
В природе процессы со спектром, имеющим вид 5~в, по-
рождают траектории., соответствующие по внешнему виду
медленным циклам. С исторической точки зрения эти цик-
лы очень реальны, но с точки зрения предсказаний они
таковыми не являются, поскольку длина их волны меняет-
ся в широких пределах при переходе от одной выборки к
другой.
Для упрощения нашей работы оставим в стороне спек-
тральные рассуждения и рассмотрим совсем другую техни-
ку, более чувствительную к искомым эффектам.
Феномен Херста
Гарольд Эдвин Херст (1880-1978) — английский фи-
зик, ставший великим «нилологом» и заслуживший про-
184
Глава 3.2
звище Абу Нил, «отец Нила». Наука обязана ему одним
замечательным статистическим изобретением и одним за-
мечательным эмпирическим открытием, которые оказыва-
ются предпочтительнее спектрального анализа, когда речь
идет о том, чтобы измерить, с какой интенсивностью неко-
торая хроника стремится быть циклической, но не пери-
одической, — поведение, представляющее собой один из
аспектов долговременной статистической зависимости.
Херст, не отдавая себе в этом отчета, ввел но-
вую статистическую технику, основанную на выраже-
нии 7?(t,d)/S(t,d), где t называется точкой отправления,
ad- замедлением. Определение R/S дано в пояснении
к рис. 3.2.2. С помощью метода R/S, Т значений функ-
ции X (t) преобразуются в диаграмму из нескольких линий,
каждая из которых соответствует фиксированному значе-
нию t и одному из возрастающих значений d.
В качестве примера и отправной точки для сравнения
нам послужит рис. 3.2.3, на котором представлено пове-
дение (R/S)/Vd в случае, когда значения функции X(t)
независимы, стационарны и имеют гауссовский тип. Мы
видим, как тесно переплетаются кривые вдоль некоторой
горизонтальной прямой. Таким образом, R/S пропорцио-
нально Vd.
Эмпирическое открытие Херста состоит в том, что
диаграммы R/S, относящиеся к эмпирическим хроникам, в
общем случае состоят из кривых, тесно обвивающих неко-
торую прямую, но угол наклона Н этой прямой изменяется
от случая к случаю.
Иногда он равен 0,5 (с небольшими отклонениями),
иногда принимает такие значения, как 0,7 и даже 0,85.
Неравенство Н > 0,5 исключает гипотезу о том, что все
величины X являются независимыми и гауссовскими.
Итак, возникают два вопроса. Как объяснить тот факт,
что Н > 0,5? И каков практический смысл разницы, на-
блюдаемой в значениях Н?
Феллер [Feller 1951] так писал об этом открытии: «оно
ставит перед нами проблему, интересную сразу с двух точек
зрения, статистической и математической». Процитируем
Феномен Херста
185
(R/S)d~™
-----------1__________I__________L_
10	100	1000	10,000
Рис. 3.2.3. Поведение Q/\/d в случае независимых гауссовских
величин. По оси абсцисс отложены логарифмы замедления d, а по
оси ординат — логарифмы величины Q/Vd, где Q = R/S, Каж-
дая из кривых соответствует четырем искусственным выборкам
из 30000 сгенерированных на компьютере значений некоторой
псевдослучайной независимой гауссовской функции. Как пред-
сказывает теория, эти кривые переплетаются вблизи некоторой
прямой с углом наклона 0. Таким образом, кривые, соответству-
ющие Q, будут иметь угол наклона 0,5. Эмпирические графики
легко различить, поскольку вместо отдельных выборок мы рас-
полагаем последовательными порциями одной и той же выборки
с равномерно распределенными точками отправления t Отсю-
да следует, что соответствующие кривые имеют разную длину и
не будут независимыми. Однако их графики пройдут практиче-
ски так же, как показано выше. Феномен Херста, выраженный
с помощью первого из представленных выше графиков, состоит
в следующем: различные кривые ведут себя очень по-разному,
они располагаются вблизи некоторой прямой, угол наклона кото-
рой, Н, зачастую превосходит 0,5 настолько нарочито, что этот
факт невозможно объяснить простой статистической флуктуацией
также Ллойда [Lloyd 1967]: «Таким образом, мы оказыва-
емся в одной из тех ситуаций, столь полезных для теорети-
ков, когда эмпирические открытия упорно не согласуются
с теорией. Все описанные [в цитируемой статье] исследо-
вания единодушно предсказывали, что R(t, d) должно воз-
растать пропорционально y/d, тогда как Херст делает эмпи-
рическое (и весьма хорошо документированное) открытие,
186
Глава 3.2
что R(t,d) возрастает пропорционально d в степени Я,
где Я находится вблизи 0,7. Итак, мы вынуждены прий-
ти к выводу, что либо теоретики дают своим собственным
работам неверную интерпретацию, либо их теории имеют
ложное обоснование; возможно, верны оба вывода.»
Перейдем теперь к обзору тех объяснений, которые
давались феномену Херста: а) «несомненно, все дело в
маргинальности распределения b) «несомненно, это
характерно для некоторой переходной зоны» или с) «несо-
мненно, это возникает из-за очень необычной структуры
корреляций».
В качестве теста для первого из этих объяснений вы-
берем совершенно негауссовский процесс с независимыми,
тем не менее, значениями и построим соответствующую
диаграмму R(t, d)/S(t, d). На рис. 3.2.4 показано, что даже
если распределение этого процесса подчиняется закону Ко-
ши, — каковое распределение обладает чрезвычайно «тол-
стыми» хвостами — или логнормальному распределению, —
для которого характерна очень большая асимметрия, — ве-
личина R(t, d)/S(t, d) все равно изменяется как \/d.
Итак, по всей видимости, первое из возможных объ-
яснений эффекта Херста не годится. Здесь следует особо
отметить, что поведение самой R(t, d) зависит от распре-
деления. То есть именно деление на S(t,d) избавляет по-
ведение частного R(t,d)/S(t,d) от всякой зависимости от
маргинального распределения. С этой точки зрения необхо-
димо подчеркнуть, что в процитированных выше отрывках
и Феллер, и Ллойд говорят о R(t, d), а не о R(t, d)/S(t, d).
Они были плохо знакомы с собственно открытием или
плохо читали Херста. Я хорошо знаю Уильяма Феллера,
который рассказывал мне, как к нему приехал за советом
посланец от Херста. Опасаясь, что слишком сложный рас-
сказ не привлечет внимание великого человека, он пред-
ставил ему упрощенную версию, которая, как он полагал,
была хорошей первой аппроксимацией.
К сожалению, такие ошибки при общении между экс-
периментаторами и математиками случаются очень часто.
Иногда в результате таких ошибок мы получаем чистую
Феномен Херста
187
(R/S)d'Oi
Рис. 3.2.4. Поведение Q в двух независимых, но негауссовских
случаях. Принцип построения тот же, что и на предыдущем ри-
сунке; все X по-прежнему независимы. В верхней части рисун-
ка X обладает логнормальным распределением exp(G), где G —
гауссовская величина; внизу X обладает распределением Коши.
Оба этих распределения являются в высшей степени негауссов-
скими. Однако у кривых наблюдается та же тенденция к гори-
зонтальному среднему, что и в гауссовском случае. Этого вполне
достаточно, чтобы заключить, что феномен Херста не следует из
распределения X
математику, занятую лишь самой собой, иногда (и да-
же, пожалуй, слишком часто) — математику вроде бы
прикладную, но совершенно бесплодную. Если не счи-
тать случая с гауссовской переменной X, путаница меж-
ду Я и R/S имеет очень серьезные последствия. Напри-
мер, Моран [Moran 1959] отмечает, что если распределе-
ние X L-устойчиво с показателем а, то Н = 1/а (см.
главу 3.1). Но феномен Херста относится к R/S. Можно
сделать Морану комплимент: он, по-видимому, почувство-
188
Глава 3.2
вал, что феномен Херста есть проявление самоаффинности
(как мы вскоре увидим). Но для уточнения модели одной
самоаффинности недостаточно.
Можно пойти и дальше. В примере Морана факт «ро-
ста пропорционально d в степени Н» касается только ти-
пичного возрастания. В действительности возрастание бу-
дет объектом огромных статистических флуктуаций. Итак,
следует ожидать, что наблюдаемые R будут настолько нере-
гулярными, что сложно представить, как из их поведения
можно вывести какой-либо закон.
Второе объяснение, подразумевающее переходные фе-
номены, связано со следующим фактом: если X — марков-
ская случайная функция с положительной при всех d кор-
реляцией C(d), то диаграмма Херста оказывается сложнее,
чем в случае независимой X. Здесь диаграмма заканчива-
ется в зоне, содержащей прямую с углом наклона 0,5, но
начинается она в переходной зоне, где вполне можно на-
блюдать и больший наклон. Если корреляция слаба, то пе-
реходный период короток; сильная корреляция может при-
вести к сколь угодно долгому переходному периоду. Про-
должая объяснение, связанное с переходом, предположим,
что, располагая более длинными хрониками, мы могли бы
продолжить диаграмму Херста и увидеть, что эта диаграм-
ма меняется и приобретает в конце концов наклон, рав-
ный 0,5. То, что изначально она располагалась в зоне с
наклоном 0,7, никакого глубинного смысла (с этой точки
зрения) не имеет.
У этих рассуждений есть два недостатка. С одной сто-
роны, корреляцию, соответствующую d = 1, можно из-
мерить непосредственно, причем полученные значения бу-
дут слишком малы, чтобы объяснить переходный характер.
С другой стороны, необходимо привести примеры, когда
мы можем наблюдать конец переходного периода, сопрово-
ждающийся конечным наклоном, равным 0,5. Однако таких
примеров у нас нет.
Более того, согласно данным Де Геера, предполагае-
мый переходный период в случае датируемых плейстоце-
ном слоев ила должен был бы длиться, по меньшей мере,
Феномен Херста
189
шесть тысяч лет. По данным Шульмана, переходный пери-
од в случае годовых колец сосен в Аризоне должен был
бы длиться, по меньшей мере, две тысячи лет. По данным
принца Омара Тусуна, переходный период в случае раз-
ливов Нила должен был бы составить, по меньшей мере,
тысячу лет. Настолько длительное временное состояние —
при полной, к тому же, невозможности определить, к ка-
кому пределу оно стремится, — очевидно, уже не стоит
рассматривать как переходное!
Переходное состояние может возникать и из распре-
деления X — причем ничуть не хуже, чем из марковской
зависимости. В 1964 году Моран предположил, что пере-
менная X подчиняется гамма-распределению с очень боль-
шой асимметрией, и показал, что результирующая R сна-
чала возрастает как d, а затем, асимптотически, — как Vd.
Однако эта модель не имеет никакого отношения к задаче
Херста, поскольку в задаче Херста мы имеем дело с вели-
чиной R/S,& S также претерпевает значительные флукту-
ации.
Итак, мы приходим к третьему объяснению. Вернем-
ся к Ллойду [Lloyd 1967]: «Херст выдвинул идею, согласно
которой его феномен обусловлен структурой корреляций
рассматриваемых хроник». На это Г.А.Барнар возразил,
что здесь не подошла бы никакая функция с простой кор-
реляцией. Что касается Морана, то он утверждал, что нера-
венство Н > 0/5 не должно было бы выполняться, разве
что в тех случаях, когда корреляция принимает «совсем уж
необычный и малоправдоподобный» вид — какой именно
вид, он, впрочем, не уточнил.
Мне, между тем, удалось воздать Херсту должное,
построив класс гауссовских процессов, которые я окре-
стил «дробными шумами» и которые позволяют показа-
телю Н принимать произвольные значения между 0 и 1.
Корреляции этих процессов не будут «простыми», как и
предвидел Барнар, но это еще не основание от них от-
казываться. Совсем наоборот, вполне естественно, когда
необычное эмпирически требует необычного математиче-
ски!
190
Глава 3.2
Самоаффинность в гауссовском случае и
дробные шумы
Не будем забывать, что в данной главе мы ограничи-
ваемся гауссовским случаем, когда S, по сути своей, — не
имеющая особого значения константа. Размышления над
феноменом Херста привели меня к тому, что я связал этот
феномен с тем фактом, что величина
X*(t) = £x(s)
3=1
обладает свойством инвариантности, которое в главе 1.2 мы
назвали «самоаффинностью». В случае, когда эти величи-
ны — гауссовские, я предполагаю называть их «дробными
броуновскими движениями».
Соответствующие изменения X, которые я называю
«дробными гауссовскими шумами», — стационарные про-
цессы. Кроме ожидания и дисперсии, у них есть только
один параметр. Этот параметр в точности совпадет с по-
казателем Я, и мы можем оценить его на графиках R/S.
Параметр Н может меняться от 0 до 1, наиболее интерес-
ная область расположена между 0,5 и 1. Точка Н = 0,5
соответствует белому шуму. Пример поведения R/S в этих
случаях показан на рис. 3.2.5.
Показатель Н как мера долговременной
зависимости и демонстрируемая циклами
тенденция
Самое поразительное свойство дробных шумов связа-
но с зависимостью между прошлым и будущим. Обычная
интуиция в области стационарных процессов подсказывает,
что достаточно отдаленные друг от друга будущее и про-
шлое должны становиться асимптотически независимыми.
Именно так оно и есть для белого шума. Но в случае дроб-
ных шумов, у которых Н не равен 0,5, корреляция между
Н КАК МЕРА ДОЛГОВРЕМЕННОЙ ЗАВИСИМОСТИ
191
Рис. 3.2.5. Поведение Q в случае дробного гауссовского шума.
Приведенный здесь график очень сильно напоминает многие эм-
пирические графики, где представляющие изменения Q кривые
имеют тенденцию к прямолинейности (что можно наблюдать на
предыдущих рисунках), но с иным наклоном, Н = 0,7 > 0,5. Од-
нако здесь речь идет не об эмпирической хронике, а о результате
имитации на компьютере дробного гауссовского шума, показатель
которого был выбран в точности таким, чтобы обеспечить жела-
емый наклон. Этого достаточно для того, чтобы установить, что
феномен Херста не будет несовместим с гауссовским характером
процесса и объясняется особой формой его функции корреляции
средним из Т ближайших прошлых значений и средним
из Т ближайших будущих значений, как оказывается, не
равна нулю! (Вследствие самоаффинности, от Т она не за-
висит.)
Чем дальше показатель Н от 0,5, тем дальше эта кор-
реляция от 0. Она близка к 1, если Н близок к 1. Если Н
чуть меньше 1, то ему соответствует процесс с крайним
192
Глава 3.2
пределом стационарности, который можно рассматривать
как нечто среднее между белым шумом, полностью сво-
бодным от зависимости, и броуновским движением, для
которого зависимость очень сильна, но чисто кумулятивна
и которое не является стационарным. Когда Н возрастает
от 0,5 до 1, устойчивость процесса становится все замет-
нее. С практической точки зрения это выражается в том,
что возникающие разнородные «циклы» — не имеющие, не
забываем, никакого периодического характера — различа-
ются все яснее. В частности, большую важность становятся
медленные циклы.
Вернемся ненадолго к неубывающей корреляции меж-
ду прошлым и будущим. Можно назвать это поведение
странным и даже отклоняющимся, но, оказывается, оно
столь же характерно, сколь и неизбежно; если его исклю-
чить, то у нас не останется никакого способа объяснить
феномен Херста. Постоянная корреляция между средними
значениями X свидетельствует о том, что функция ковари-
ации X убывает очень медленно, а ряд, составленный из
ковариаций, является расходящимся. Как было показано в
предшествующем изложении, другие точки зрения, по-ви-
димому, требуют, чтобы расходилась дисперсия, что тоже
может показаться отклонением.
Показатель Н в гидрологии и финансах
В гидрологии показатель Н практически всегда пре-
восходит 0,5. Одним из исключений является Рейн — ре-
ка, которая, как выясняется, бедна историями, подобны-
ми истории Иосифа. Нил, в этом смысле, представляет со-
бой один из самых крайних случаев. Наблюдаемые значе-
ния Н достаточно хорошо подтверждают интуицию «лите-
ратурных географов»: у рек с репутацией «неправильных»
(нестационарных) — таких, как Луара — значения Н боль-
ше, чем у рек «без истории».
В экономических хрониках, связанных с величинами,
отличными от цен, показатель Н с равной частотой при-
Заключение
193
нимает самые различные значения, которые вновь согла-
суются (в общих чертах) с классификацией этих хроник в
зависимости от интенсивности их стремления к циклично-
сти.
Изменения спекулятивных цен, наоборот, ведут себя
очень интересно и относительно просто. Экономическая
теория утверждает, что на спекулятивном рынке, доста-
точно активном, чтобы быть близким к «совершенному»,
или хотя бы к «эффективному», любая цена должна вести
себя как процесс того типа, который математики называ-
ют «мартингалом»; см. конец главы 3.1, [М 1966b {Е19}]
и [М1971 {Е20}]. Эффективность связана с действиями
людей, занимающихся арбитражными операциями, то есть
людей, которые, например, покупают и продают в различ-
ное время.
Обычно ожидают, что изменения цен в арбитражных
операциях дадут Н = 0,5. Действительно, так и происхо-
дит с некоторыми продуктами, с действиями некоторых,
очень больших, обществ и с некоторыми облигациями.
С другого края располагаются цены на продукты, для кото-
рых никакой арбитраж невозможен. Здесь уместно приве-
сти пример процентных ставок, которые платят при арбит-
раже (в Нью-Йорке их называют «call money»1), для них по-
казатель Н очень высок. Между этими двумя крайностями
размещается целая гамма промежуточных возможностей,
перечислять их здесь было бы слишком утомительно. До-
статочно сказать, что величина Н — 0,5 представляет собой
меру несовершенства такого рынка.
Заключение
После такого долгого статистического экскурса непло-
хо было бы вернуться к проблеме «реальности экономи-
ческих циклов». Анализ R/S подтверждает и значительно
усиливает спектральный анализ: общее правило гласит, что
экономические циклы настолько далеки от периодичности
1 Займы до востребования (англ.). — Прим, перев.
13 Б. Мандельброт
194
Глава 3.2
и настолько зависят как от длины имеющейся в нашем рас-
поряжении выборки, так и от предпочтений наблюдателя,
что вплоть до новых распоряжений их следует рассмат-
ривать как артефакты. Если верить Кейнсу [Keynes 1940],
ценность таких циклов заключается прежде всего в том,
что с их помощью очень удобно разбивать на главы учеб-
ники по истории экономики.
Глава 3.3
Заключение (1997):
броуновская дробность в
мультифрактальном биржевом
времени («модель [М1963]»)
Эта очень краткая заключительная глава, составленная
исключительно из неопубликованных материалов и снаб-
женная загадочным заголовком, который нужно поскорее
объяснить, завершает данную часть книги наброском са-
мой последней из моих фрактальных моделей в области
финансов. Если читатель желает получить еще более ком-
пактное резюме, то я посоветую ему еще раз изучить (если
он до сих пор этого не сделал) рис. 1.2 и 1.3 во введении.
Если читателя интересуют подробности, то он найдет их в
английском издании [М1997Е].
Напомним, что в главах 3.1 и 3.2 подробно обоснованы
работы, содержание которых датируется 1963 и 1965 года-
ми, а форма — не считая некоторых особенностей стиля —
1966 и 1973 годами. Как и должно быть с началами любой
теории, в этих старых текстах все очень сильно упрощено,
причем преднамеренно: в рамках модели [М1963] рассмат-
ривались исключительно разрывности (эффект Ноя), тогда
как в модели [М1965] — исключительно псевдоциклы (эф-
фект Иосифа). Однако следовало предвидеть, что авторы,
пожелавшие убедиться в применимости выводов глав 3.1
и 3.2, непременно столкнутся с многочисленными примера-
ми, когда эти два эффекта неразделимы, то есть непримени-
мыми оказываются и модель [М1963], и модель [М1965].
13*
196
Глава 3.3
Например, скачки на рис. 1.2, показывающие наличие эф-
фекта Ноя, концентрируются, что говорит об одновремен-
ном наличии эффекта Иосифа.
Бесполезно говорить, что построение модели, сочета-
ющей в себе оба эффекта, представляет собой серьезный
вызов. Эта задача всегда занимала и по-прежнему занимает
меня. Постепенно она становилась все сложнее, а сегодня
вдруг дошла до той стадии, когда одна, появившаяся у ме-
ня еще в 1972 году, идея поразительно все упростила. Цель
этой краткой главы — сделать набросок модели [М 1972],
которая сейчас представляет собой мой ответ — лучший и в
то же время самый простой — на вышеупомянутый вызов.
Речь пойдет о результате, который стал вторым большим
новшеством после броуновской модели Башелье.
Унифракталыгость и мультифрактальность
Рассмотрим изменение цены dP9 соответствующее ин-
тервалу времени dt, и вернемся к главе 3.1, дабы поза-
имствовать оттуда определение показателя Гельдера-Хер-
ста Н. Напомним, что с точки зрения самоаффинных кри-
вых, которые являются графиками функций, этот показа-
тель играет ту же роль, какую играет фрактальная размер-
ность с точки зрения самоподобных множеств.
•	В модели Башелье [В 1900] предполагалось, что
dP ~ (dt)1/2.
Показатель не изменяется со временем и равен 1/2.
•	В моделях [М1963] и [М1965] предполагалось, хотя и
по совершенно разным причинам, что результат имеет
вид
dP ~ (dt)".
Показатель Н по-прежнему не зависит от времени, но
отличен от 1/2.
Понятие «биржевого времени»
197
Можно сказать, что вплоть до настоящего времени сте-
пень, в которую возводилось dt, принимала одно и то
же значение для всех t. Из этих соображений моде-
ли [В 1900], [М 1963] и [М 1965] можно охарактеризо-
вать как унифрактальные.
•	Из модели [М1972], напротив, следует, что
Здесь показатель H(t) непрерывно изменяется со вре-
менем и принимает множество значений. Из этих со-
ображений данная модель характеризуется как мулъ-
тифрактальная.
Понятие «биржевого времени»
Что следует из изменчивости показателя H(t), и какая
терминология подходит для рассуждений о нем?
Поскольку речь идет о малых dt, то большое значе-
ние H(t) означает медленное изменение P(t), Пусть, на-
пример, k < H(t) < к -I-1, где к — некоторое целое чис-
ло, большее 1. Отсюда следует, что в момент времени t у
функции P(t) есть к производных, причем все они равны 0.
(Если учитывать еще и производные нецелого порядка, по-
лучившие широкое применение для фракталов, то они об-
ращаются в нуль вплоть до порядка Я(£).)
Напротив, малое значение H(t) означает быстрое из-
менение P(t). Например, если 0 < H(t) < 1, то в момент
времени t у P(t) есть бесконечно много производных.
Теперь мы подходим к ключевой идее. Мы больше не
будем выражать изменчивость цены с помощью перемен-
ного показателя, основанного на обычном времени, которое
показывают часы. С таким же успехом можно поменять их
ролями и представить себе изменчивость с постоянным по-
казателем, но в «биржевом времени», которое течет в очень
неправильном ритме.
198
Глава 3.3
Эта концепция совершенно законна, поскольку, как и
большая часть человеческой деятельности, биржа не под-
чиняется времени, которое измеряют физические часы;
совсем наоборот, ее активность постоянно то ускоряется
(«разогревается»), то замедляется («охлаждается»). Могут
возникнуть опасения, что в такой модели будет в большой
степени присутствовать произвол, но это не так, и наиболее
простое решение имеет очень понятное определение.
Этап на пути к модели «третьего поколения»:
фрактальное биржевое время
Я ненадолго остановлюсь на некоторых исторических
подробностях, которые читатель может с легкостью про-
пустить. Как я уже говорил, однажды факты бросили нам
вызов и потребовалось объединить эффекты Ноя и Иоси-
фа. По иронии судьбы, в [М1972j] содержался ключ к хо-
рошему ответу на вышеупомянутый вызов, но у меня не
было времени, чтобы развить эту идею. Однако, когда я
в 1973 году писал начальные варианты глав 3.1 и 3.2, где-то
в глубине души я остро почувствовал, что эти тексты — во
всяком случае, потенциально — уже совершенно устарели.
Это чувство несколько озадачило меня, но не поколебало
моей убежденности в том, что написанное мной в любом
случае ближе к истинному положению вещей, чем чисто
броуновский консенсус, которому я стремился противосто-
ять.
Промежуточный этап был обозначен уже в [М & Taylor
1967 {Е21}]. Вот его источник. В модели [М 1963] акцент
был сделан на разрывностях, относящихся к тому време-
ни, которое измеряют часы. Некоторые же критики, на-
против, старались привлечь внимание к противоположным
вещам, к существованию периодов, которые располагают-
ся между разрывностями, заведомо превосходящими мини-
мум, установленный для изменений цены. Такие периоды
действительно существуют, что в модели [М1963] отрица-
лось. В этом случае обнаруживается, что изменения цены
Мультифрактальное биржевое время
199
между последовательными сделками имеют почти гауссов-
ское распределение. Во всяком случае, у их распределения
нет длинных хвостов, которые в реальных процессах и в
модели [М1963] обнаруживаются у изменений цены за по-
следовательные интервалы времени с заранее предписан-
ной длительностью. Таким образом, получалось, что мы
столкнулись с вопиющим противоречием.
Это и стало предметом обсуждения в [М & Taylor 1967]:
необходимо было показать, что всякое противоречие исче-
зает, если допустить, что за очень короткий интервал вре-
мени может произойти неограниченное количество сделок.
Это означает, что сделки совершаются в биржевом време-
ни, а биржевое время может совершать скачки по отноше-
нию ко времени, которое измеряется часами.
Мультифрактальное биржевое время
Как было сказано выше, ключ, позволяющий вый-
ти за пределы фрактального времени, находился в кон-
це [М1972j {N14}]. Эта работа посвящена исследованию
«прерывистого» характера турбулентного движения жид-
костей, она стал моей первой полной статьей на очень важ-
ную тему «мультифракталов». Приведем здесь небольшого
параграф, завершавший [М1972j].
«Взаимодействие... между множащимися возмуще-
ниями и логнормальными распределениями и [вычисли-
мость] имеет следствия в других областях науки, где встре-
чаются очень асимметричные распределения, а именно, в
экономике. Упомянув об этом факте, более подробную ра-
боту над ним я оставляю до более удобного случая.»
Я собирался очень скоро сдержать неявное обеща-
ние, подразумеваемое этими словами, но на это у меня
ушло двадцать пять лет. Хотя вспоминал я о нем часто.
Однако, насколько мне известно, эта идея так и ждала
своей реализации вплоть до почти одновременного вы-
хода этой книги, [М1997Е], [М, Fisher & Calvetl997],
[Calvet, Fisher & M 1997] и [Fisher, Calvet & M1997].
200
Глава 3.3
Большая часть требуемых инструментов находилась у
меня в руках еще в 1972 году, этим и объясняется термин
«модель [М1972]».
Набросок модели
Практическая полезность различия между унифрак-
талъным и мультифрактальным состоит в том, что теперь
принцип масштабирования можно обобщить, позволив по-
казателю Н быть переменным. Что же касается диагональ-
ных самоаффинных конструкций, которыми заканчивалась
глава 1.3, достаточно будет сказать, что ко всем этим кон-
струкциям вышеуказанный принцип применим.
Напомним, что у них имеется генератор, образован-
ный из конечного числа интервалов Im (1 т М).
Обозначим через хт и ут проекции этих интервалов, и
пусть Нт - logym/\ogxm.
И вот мы почти у цели. В общих чертах, термином уни-
фракталъность обозначают те случаи, когда все Нт иден-
тичны, а термином мулыпифрактальностъ — противопо-
ложные случаи. Имеется также мезофрактальный случай,
описанный в [М & Taylor 1967 {Е21}], то есть в рамках мо-
дели [М1963]. В данной книге нам придется обойти этот
случай стороной; подробное его описание можно найти в
разделе Е6.4 книги [М 1997Е].
В только что намеченном контексте унифрактально сть
и мезофрактальность имеют то фундаментальное преиму-
щество, что они представляют собой (соответственно) про-
стой и достаточно простой случаи; фундаментальный же
их недостаток заключается в том, что эти случаи являют-
ся чрезвычайно частными. Если самоаффинная (в смысле,
описанном в главе 1.2) конструкция, выбирается «случай-
но», то очень много шансов за то, что вероятность не ока-
заться мультифрактальной равна для нее нулю, тогда как
унифрактальные и мезофракгальные случаи могут стать
хорошими аппроксимациями.
Концептуальные рамки этих размышлений подтвер-
ждают тот факт, что не только модель [В 1900], но и мо-
И СНОВА МУЛЬТИФРАКТАЛЬНОЕ БИРЖЕВОЕ ВРЕМЯ 201
дели [М1963] и [М1965] носят чрезвычайно частный ха-
рактер, тогда как введение мультифрактальности позволяет
очень сильно увеличить общность. Конечно, процитиро-
ванные выше работы затрагивали эти новые возможности,
выделяя особо изучение курсов обмена валюты, так как им
соответствуют самые изобильные и самые надежные дан-
ные. Мы пока что очень далеки от того, чтобы полагать их
в полной мере исследованными.
Первая задача состояла в том, чтобы организовать
большое число рядов и классифицировать их в соответ-
ствии с характеристиками некоторой определенной функ-
ции /(а). В [М 1974с] я ввел эту функцию с помо-
щью распределений ДР; некоторые предпочитают назы-
вать ее спектром сингулярностей. Частный случай был
изучен в [Calvet, Fisher & М1997]. Необходимо предосте-
речь читателя от формального применения функции /(а);
список надежных источников информации можно найти
в [Evertsz & М 1992].
И снова мультифрактальное биржевое время
Наконец, мы подходим к характеристике (фундамен-
тальной и еще не опубликованной) наброска моделей, обра-
зованных самоаффинными рекурсивными конструкциями.
Используя интервалы, проекции которых равны хт и ут,
можно всегда определить величину DT как положитель-
ный корень следующего фундаментального порождающего
уравнения:
£1^ = 1.
Тогда рисунок, образованный интервалами хт и ут, дол-
жен будет ассоциироваться с другим, скажем так, «упоря-
доченным» рисунком, который образован интервалами ут
и
< = |Ут|°Г.
По самому своему построению эта модель будет унифрак-
тальной с показателем
Ят* = l/Dy.
202
Глава 3.3
Время, на которое она ссылается, будет биржевым време-
нем, оно изменяется пропорционально х*т, тогда как обык-
новенное время (время, которое показывают часы), изме-
няется пропорционально хт. Выполнив рекурсивную ин-
терполяцию, получаем, что биржевое время, если отсчиты-
вать его в единицах обыкновенного времени, представляет
собой функцию не только возрастающую (само собой ра-
зумеется), но и мультифрактальную.
Вывод: осциллирующие мультифрактальные модели,
определенные в предыдущем разделе, могут быть пред-
ставлены в виде унифрактальных моделей, изменяющихся
в мультифрактальном биржевом времени.
Нерекурсивные модели
Вернемся к знакомой нам теме фрактальной геомет-
рии. Как уже говорилось в главе 1.2, самоподобная кривая
Коха («снежинка») вовсе не заслуживает того, чтобы рас-
сматривать ее только как модель некоего побережья. Лучше
всего сказать, что она представляет собой всего лишь «на-
бросок модели». Чтобы «подняться» выше — на уровень
модели, — необходимо сделать два шага.
Нужно разрушить ограничения рекурсивное™, в со-
ответствии с которой накапливаются равносторонние тре-
угольники со сторонами, равными 3_fc. Их следует рандо-
мизировать (т. е. сделать случайными).
Мы уже говорили, что в случае самоподобных рекур-
сивных построений такая рандомизация приводит к про-
блемам (например, к образованию петель), тогда как в са-
моаффинном рекурсивном случае никаких сложностей не
возникает. Что касается рекурсивное™, то есть средства ее
избежать, они описаны в главе Е6 книги [М1997Е].
Наибольшая простота достигается следующим обра-
зом. Биржевое время нерекурсивно и мультифрактально;
что же касается процесса, за которым мы следим в бирже-
вом времени, то он представляет собой не что иное, как
броуновское движение — обыкновенное или дробное.
ЧАСТЬ ЧЕТВЕРТАЯ
СЛУЧАЙНОЕ В
РАЗГОВОРНОЙ РЕЧИ
Закончить эту книгу о финансах исследованием ста-
тистики разговорной речи — темой, которая вовсе не упо-
мянута в заглавии и, на первый взгляд, никак с финансами
не связана — меня побудили три очень разных соображе-
ния.
Прежде всего, надо признать, мной двигали сенти-
ментальные соображения, поскольку мой первый научный
успех неожиданно оказался связан именно с этой темой.
Подобно «Selecta» и предисловию, эта часть начинается
с воспроизведения статьи [М 1951], ставшей моей первой
«настоящей» публикацией. Заметим, что «сигнал» — это
слово, которое первым пришло мне в голову в качестве
обозначения «белого в словах».
Кроме того, были и прагматические соображения,
тоже весьма в духе «Selecta»: среди моих бумаг обнару-
жился текст, который вполне можно было включить в
эту книгу, а именно, статья [М 1968w].
Но главным было внутреннее, очень серьезное, сооб-
ражение. Напомним, что главную тему моих работ, по-
священных финансам, составляли масштабируемые (гла-
ва 1.3) и L-устойчивые (глава 2.4) распределения. Если бы
я нашел время на то, чтобы написать более подробную
книгу, то я сказал бы о том, что масштабируемому рас-
пределению подчиняется масса других важных феноменов,
рассмотренных в [М1977Е]. Например, распределение до-
ходов, которое все-таки было упомянуто в этой книге. Или
распределения городского населения и численности людей,
занятых в промышленных предприятиях. Но оказывает-
204
ЧАСТЬ ЧЕТВЕРТАЯ
ся, что самым элементарным — иначе говоря, наиболее
фундаментальным — примером масштабируемого распре-
деления является закон Ципфа для распределения слов в
человеческой речи.
Будет полезно, особенно тем, кто уже прочел рань-
ше эту часть или хотя бы ее первые страницы, то есть
статью [М1951], задержаться здесь и ознакомиться с
некоторыми комментариями к ней. Важно здесь то, что
закон Ципфа по сути сводится к следующему', «что-то»
есть величина, обратная «чему-то еще».
Это означает, что закон Ципфа имеет масштабиру-
емый характер в смысле? предложенном в главе 1.1. Од-
нако из заключения к статье [М 1951] видно, что «мо-
дель [М1951]» неизбежно приводит к выражению ви-
да {г + v)~B. В этом выражении сочетаются вычислимая
зона и «купюра» для малых значений г, а множитель V
учитывает сжатие данных. Как выяснилось, приступая к
этой работе, я не имел ни малейшего понятия о вышеука-
занном сжатии, так что V никоим образом не следует
из мгновенного преобразования какого-то теоретическо-
го результата, оно представляет собой неизбежное след-
ствие модели [М1951].
Полезно также отметить, что существование ха-
рактерных купюр типично для «естественных» или спон-
танных масштабируемых феноменов. В некоторых случа-
ях можно учитывать эти купюры с помощью некоторого
множителя, вроде вышеописанного V. Однако в других слу-
чаях это невозможно, так как купюра затрагивает боль-
шие значения в ряду г. Все это составило предмет главы 7
книги [М1997Е].
Тонкостью этих вопросов отчасти объясняется, по-
чему закон Ципфа выглядит как «чудо морское». Мы за-
бываем, что он существует и вполне объясним. А затем,
время от времени кто-нибудь воскрешает его с обновлен-
ными надеждами. Когда же надежды рушатся, закон воз-
вращается к своему мертвому состоянию.
Конечно, более предпочтительным представляется
несколько более монотонное существование. Как бы то ни
СЛУЧАЙНОЕ В РАЗГОВОРНОЙ РЕЧИ 205
было, находящийся в моем распоряжении текст занимает
здесь место какого-нибудь другого, лучшего, текста, ведь
у меня нет времени на то, чтобы переписать его заново
или перевести, воспользовавшись [М1997Е].
206
ЧАСТЬ ЧЕТВЕРТАЯ
Предисловие: 1951 год
Статистическая механика и теория информации. —
Адаптация сообщения к линии передач: I. Кванты
информации. Статья Бенуа Мандельброта,
представлена г-ном Жаком Адамаром.
Слова (в обычном смысле) подчиняются привилегированной
статистике вида рп ~ А(п 4- по)“в, они естественным образом
осуществляют квантование информации.
1. Кодирование по Шеннону (г). Для передачи со-
общения необходимо сгруппировать буквы равными пор-
циями, квантами. Статистика этих квантов при их удлине-
нии стремится к статистике Лапласа, среднее количество
сигналов, посылаемых при сообщении, стремится к мини-
муму, пропорциональному Н = — 52 Рп log рп — величине,
определяющей количество информации. Приблизительные
кодировки, предложенные Шенноном, являются чисто те-
оретическими и бесполезны на практике, они не требуют
специальных сигналов, отмечающих конец кванта.
2. Ординальное кодирование. Реалистичным пред-
ставляется предположение, что кванты определены a priori,
а их цифровые коды, разделенные сигналами, заметно обо-
гащают теорию. Наша кодировка, называемая ординальной,
должна будет соответствовать классификации квантов по
убыванию рп и классификации кодировок по возрастанию
затрат (времени, энтропии или другой критической суб-
станции). Эта кодировка зависит только от линии, и за-
кодированное таким образом сообщение будет наименее
дорогостоящим при данных рп.
Но, в общем случае, оно не будет наименее дорогосто-
ящим при данной величине Н, и это не случайная после-
довательность символов. Отсюда возникают две последо-
вательные задачи адаптации подлежащего кодировке сооб-
щения к линии.
Мы покажем, что линия полностью определяет опти-
мальное сообщение. Следует заметить, что все экспери-
ментальные статистики слов (в обычном смысле) в пись-
Предисловие: 1951 год	207
менных языках, собранные Дж. К. Ципфом (2), имеют опти-
мальный тип, определенный этими двумя задачами. Следо-
вательно, слова представляют собой естественные кванты
информации.
Пусть q +1 — количество состояний Ед, состояние Eq
зарезервировано для сигналов, обозначающих конец слова
(то есть q > 2). Предположим, что q мало по сравнению с
количеством слов Я. Пусть Сд — стоимость Ед, — ко-
личество последовательностей символов (цифр) общей сто-
имостью j, N(j) — количество последовательностей стои-
Q
мостью J. Тогда М (J) = 52	~ С’р), откуда асимпто-
1
тически M(j) ~ АР, где М — наибольший корень урав-
<7	J
нения	= 1, a N(j) = 52Л/(г) ~ -п0 + AP“JO,
1	о
если jn - jo ~	+ по), где М — корень уравне-
9	9
ния $2 = 0 (а не = 0), a j — соответствующие затраты,
о	1
Частный случай. Если Ci = 1, М = q9 M(j) = ЛР в
точности, а
W(j) = М(М -	- 1),
то величина
Ь = -1 + 'Hogg"^ + [1оМп + 9(9 - I)-1}]
есть стоимость n-го члена по порядку возрастания за-
трат (3 * * * * * *).
3. Рассмотрение с точки зрения затрат. Адапта-
ция рп к Н и к линии (то есть к способу кодирования).
Стоимость передачи при ординальном кодировании равна
в среднем С + Со = 52Pnjn + Со за слово. По Шеннону
она будет пропорциональна Н = — 52 Рп logрп. При дан-
ной Н превышение затрат (то есть избыточность) мини-
мально, когда рп = АМ~в^п, где В 0 зависит от линии
208
ЧАСТЬ ЧЕТВЕРТАЯ
и (прежде всего) от Н. Пусть 0 = 1/В — кибернетическая
температура сообщения.
н = pnBjn log М + log	),
= -(log2	JnPn) ]•
Согласно неравенству Шварца, выражение в квадрат-
ных скобках больше нуля, поэтому dH/dB < 0, dH/dQ > 0.
Когда 0 изменяется от 0 до +оо, Н непрерывно возрастает
от 0 до log Я. Таким образом, Н определяет 0 при дан-
ном R. Следовательно, наш критерий связан с обращением
в нуль свободной вариации величины А = С — QH (то
есть превышения затрат, если затраты на символ по Шен-
нону равны 1 /0). Если понимать С как энергию,’ а Н как
энтропию, то величина А, соответствующая используемой
энергии Гельмгольца, равна свободной рассеиваемой энер-
гии. Таким образом, представляется вполне справедливым
рассматривать R как объем, а Я и 0 как переменные со-
стояния.
Если В > 1, то объем R может быть бесконечно велик.
Это удобно (поскольку сложно сосчитать редкие слова) и
не приводит к абсурду, потому что, с одной стороны, слова
очень высокого ранга в данном случае очень мало добавля-
ют к Я или к С, а с другой стороны, в реальном тексте доля
слов, превосходящих некоторую известную длину, всегда
пренебрежимо мала. Энтропия Н возрастает от 0 до ос, в
то время как О изменяется от 0 до 4-1.
4. Структурная точка зрения. Адаптация рп и Н
к линии (то есть к способу кодирования). Требуется,
чтобы закодированное сообщение представляло собой ста-
ционарную случайную последовательность состояний Ед.
Пусть rfg = Рг(Яр). Тогда для кодирования n-го члена тре-
буется 1 сигнал плюс / символов:
Pn = (1 - r'0)f 1r'o JJ =	° , IJ Гд,
1 'О х 'О
Предисловие: 1951 год	209
где рп должно зависеть только от общей стоимости, т. е.
суммы затрат для символов, поскольку это единствен-
ная величина, имеющая физический смысл; отсюда г'д =
q
=	где М', определяемое из равенства У^М,Са =
о
= 1, то же, что и во втором параграфе. Тогда рп =
= AM~Bin — закон того же типа, что и в парагра-
фе 3, причем А = Fq(1 - Гд)-1, а В = logMM' =
= log Mr/ log M 1.
5. Итак, линия определяет рП9 а также
с + Со = - 22 Pn logM- Р„ + [- logM, (1 - rf>)]
(что при Гд —> оо позволяет обнаружить свойство абсолют-
ного минимума в выражении Я).
Поведение рп. Поскольку jn ~ jo 4- logM(n + ng), по-
лучаем рп ~ А'(п + пд)“в, что поразительно точно согла-
суется с результатами Ципфа (2).
При j 1, рп ~ А'пВ (ординальный закон), что со-
ответствует статистике Больцмана. Именно к этому закону
и привел бы нас соответствующий способ кодирования.
Для меньших j (когда В — 1	1) рп ~ А'(п + пд)"1:
здесь нет скрытых расхождений с ординальным законом,
в том же смысле, что и в статистике Ферми-Дирака, и по
тем же причинам — из-за квантования затрат и исключения.
(г) Bell System Technical Journal, 27, 1948.
(2) Human Behavior and the Principle of Least Effort,
Addison-Wesley Press, 1949.
(3) [log#] = 1+ целая часть logx.
Протоколы заседаний Академии наук от 30 апреля 1951 года.
(Comptes rendus des seances de Г Academic des Sciences, t. 254,
p. 3968-3970.)
14 Б. Мандельброт
210
ЧАСТЬ ЧЕТВЕРТАЯ
Введение
В этой части книги рассматривается краткая встреча двух
великих порождений человеческой мысли: теории информации и
психолингвистики — и дается представление о теории частоты
слов, явившейся результатом их взаимодействия. В дальнейшем
каждый из «родителей» последовал своим путем, и теперь можно
описать «дитя», так сказать, «объективно», не вспоминая, отку-
да оно взялось. Однако с исторической точки зрения это было
бы несправедливо, а с точки зрения философии случая — просто
ошибочно. Эта часть носит, в основном, неформальный характер,
все математические манипуляции отнесены в конец.
Итак, занавес поднят — представим актеров. Основной от-
личительной особенностью теории информации (появившейся на
свет уже взрослой и во всеоружии в 1948 году, через посред-
ство двух знаменитых статей Клода Шеннона) является прису-
щая ей оригинальная манера сочетания двух идей из числа наи-
более древних и фундаментальных в науке: алгоритма и случая.
Конечно, они никогда не были чрезмерно далеки друг от дру-
га — достаточно вспомнить азартные игры XVII и XVIII веков,
статистическую механику 1900 года и, наконец, квантовую тео-
рию 1925 года. Поэтому теория Шеннона никоим образом не стала
в науке переломной, более того, с течением времени она все бо-
лее и более естественным образом входит в теорию вероятностей.
Между тем, вплоть до 1948 года было предпринято лишь несколь-
ко отдельных попыток решить задачу о формализации того факта,
что человеческая речь в высшей степени структурирована и в то
же время в не меньшей степени непредсказуема.
Шеннон показал, что некоторые аспекты вышеупомянутой
структуры можно описать с помощью алгоритмов кодирования,
а их непредсказуемый характер передается посредством система-
тического использования той же статистической модели, какую
в 1913 году предложил Марков для описания некоторых аспектов
романа Пушкина Евгений Онегин,
Шеннон также показал, что степень структуры некоторой
системы сигналов допускает описание через меру степени беспо-
рядка, именуемую «количеством информации» (подобно тому, как
степень структуры некоторой молекулярной системы допускает
описание (a contrariox) через меру степени беспорядка, имену-
емую «энтропией»). Упомянутое «количество», если правильно
1От противного (лат.) — Прим, перев.
Введение
211
его понимать, никогда не претендовало на учет всего того, что
скрывается под вербальным понятием «информация». Теория же
информации стремится охватить не только лингвистический дис-
курс, но и все остальные формы коммуникации, хотя действитель-
ный успех был достигнут лишь в отношении форм, восходящих
именно к дискурсу.
Важность работы Шеннона была оценена очень быстро. Бо-
лее того, через двадцать пять лет после публикации этой работы
мне сложно восстановить в памяти силу моей собственной реак-
ции и реакции моих друзей на это событие. Нам показалось, что
открылся какой-то новый мир — тогда мы не понимали, что изоби-
лие новых работ в период между 1945 и 1948 годами есть отча-
сти всего лишь отражение почти полного отсутствия публикаций
между 1940 и 1945 годами. Еще не высохли чернила, а энтузиасты
уже пустились в путь, обещая в качестве немедленной награды
способ применения теории информации к какой угодно проблеме.
Консерваторы, правда, полагали, что это слишком хорошо, чтобы
оказаться правдой, кое-кто добавлял, что нельзя ожидать слишком
многого от очередного претендента на роль математической па-
нацеи; профессиональные математики также смотрели на новую
теорию с подозрением. Сегодня все эти споры в прошлом, все
предсказания оказались ложными. Выяснилось, что теория ин-
формации весьма сложна в применении, и много профессиональ-
ных математиков искупили свои первичные колебания работой,
проводившейся с тем большим энтузиазмом. Теория информации
обуржуазилась до мозга костей.
Перейдем к другому действующему лицу нашей истории.
Термин «психолингвистика» (или просто «лингвистика») очень
хорошо подходит для описания одного статистического закона,
вызвавшего в свое время немалое удивление, доходящее до сту-
пора, — речь идет о законе, связанном с именем Джорджа Кингсли
Ципфа. Ципфу и его закону и посвящен остаток этой части книги.
Начнем с вопроса о терминологии и продолжим наше вве-
дение экскурсом в древнюю историю. Несколько отклоняясь от
классической терминологии Фердинанда де Соссюра, мы будем
различать язык (систему правил) и дискурс (последовательность
письменных или разговорных знаков). (Для обозначения послед-
него понятия Соссюр использовал термин «речь», весьма, на мой
взгляд, неоднозначный.)
Среди технических проблем, связанных с дискурсом, наи-
более древними, бесспорно, являются проблемы криптографии
14*
212
ЧАСТЬ ЧЕТВЕРТАЯ
(kryptos «тайный, скрытый»), стенографии (stenos «сжатый») и
телеграфии (telos «далекий»). Эти проблемы находят решение в
рамках теории информации, однако я хотел бы показать, почему
их также следует рассматривать как часть лингвистики.
Все эти техники (tekhne «искусство»; любопытно, как порой
меняют свое значение некоторые слова!) стремятся преобразо-
вать на свой лад фонетические (ркдпё «голос») и графические
(graphos «письмо») знаки дискурса — знаки, которые, разумеется,
«произвольны» в смысле де Соссюра. Криптограф ищет код, по
возможности лишенный структуры, поскольку любая структура
может помочь противнику разгадать его секрет. Стенографист и
телеграфист ищут, каждый по своему, код, по возможности наи-
более короткий.
Рассмотрим все это более детально, оставляя тем не менее
в стороне некоторые технические сложности: допустим, что ко-
дирующие и декодирующие машины могут быть сколь угодно
сложными, а память «человеческого звена» бесконечна. Очевид-
но, что в этих идеальных обстоятельствах всякое усовершенство-
вание нашего понимания структуры языка и дискурса способ-
ствует увеличению эффективности криптографии и стенографии.
В идеале знание грамматики позволяет идентифицировать ту или
иную фразу как неправильную; если предположить, что работо-
датель стенографиста всегда говорит грамматически правильно,
то стенографист сможет экономить знаки, сопоставляя их уже
встречавшимся фразам.
В общем случае, знание статистики дискурса указывает, ка-
ким образом заменять часто встречающиеся речевые клише еди-
ными более короткими знаками. В результате получаются более
короткие стенограммы и — поскольку клише помогают разгадать
секрет — более «устойчивые» криптограммы. (Вскоре мы увидим,
что экономия и секретность приводят в конце концов к одной и
той же цели.) Таким образом, совершенные криптограф и сте-
нографист полностью используют всю лингвистическую инфор-
мацию. Можно ли ожидать, что наиболее интересная для этих
инженеров языка информация совпадет с информацией, наиболее
интересной для грамматиста? Рассчитывать на это было бы наив-
но! Совсем наоборот, следует опасаться, что, доведя свой труд до
совершенства, эти две группы (каждая со своей стороны) получат
в конечном итоге абсолютно несовместимые модели. Именно так
и произошло. Странно, что возможность одновременного суще-
ствования таких противоречащих друг другу моделей беспокоит
Введение
213
лингвистов сильнее, чем противоположность этих моделей бес-
покоит физиков!
Для языкового инженера самым многообещающим матери-
алом является не граматика, но статистические свойства языка.
Больше всего здесь поражает различие в простоте между двумя
самыми важными «звеньями» дискурса, а именно, фонемой (или
буквой) и словом. Частота букв, равно как и частота «n-грамм»
(последовательностей из п букв), использовалась криптографами
и телеграфистами с самого первого дня. За несколько десятиле-
тий до Шеннона Самюэль Морзе осознал, что было бы неплохо
сопоставить самые короткие комбинации точек и тире наиболее
часто встречающимся буквам, криптографы же веками использу-
ют в своем деле приблизительные оценки вышеуказанных частот.
Однако в этом смысле мы очень быстро достигаем непреодолимо-
го предела, поскольку отдельные буквы представляются слишком
малыми, чтобы вызывать какой-то собственный интерес; знание
частоты их употребления почти ничего не говорит нам о частоте
употребления их больших по размеру объединений. Что касает-
ся n-грамм, то они более полезны, но слишком искусственны с
лингвистической точки зрения.
Слова представляются гораздо более перспективными, исхо-
дя из двух соображений: a priori, поскольку они являются неотъ-
емлемой частью дискурса, и a posteriori (как мы вскоре убедимся),
потому что игра соединения букв в слова приводит к грандиозно-
му и глобальному упрощению. Определение слова как последова-
тельности букв между двумя соседними пробелами ставит много
проблем, однако есть основания полагать, что при восприятии
дискурса мы используем «отрывки» близлежащих слов. Поэто-
му статистическое изучение слов началось очень рано. Впрочем,
первые попытки в этом направлении были краткими и изолиро-
ванными, если сравнивать их со всей жизнью, которую посвятил
этому вопросу Джордж Кингсли Ципф (1902-1950), автор много-
численных книг, чрезвычайно тесно сочетающих в себе уважение
к фактам и игру воображения.
Прежде чем мы приступим к описанию его результатов, нам
понадобится одно определение. Возьмем длинную выборку, со-
ставленную из к слов, взятых из разных текстов одного автора, и
упорядочим все фигурирующие там слова по убыванию их частот.
Слово, которое встречается чаще всего, получает ранг 1; в общем
случае2 это определенный артикль «1е», иногда — местоимение
2Для французского языка. — Прим, перев.
214
ЧАСТЬ ЧЕТВЕРТАЯ
«je»3. Слово ранга 2 — это следующее по частоте употребления
слово. Обозначим через VK(r) слово, которое в данной классифи-
кации имеет ранг г. Продолжаем эту процедуру до тех пор, пока
не закончится текст, при этом слово И7 (г) встретится нам г(т, к)
раз. Для часто повторяющихся слов такая классификация будет
однозначной; для слов, встречающихся 3, 2 или 1 раз, имеется
возрастающая неоднозначность, но с нашей точки зрения она не
важна. Итак, частота употребления слова И7 (г) равна г(т, к)/к.
Первая аппроксимация: закон Ципфа
Как выясняется, в первом приближении вышеупомянутая ча-
стота обратно пропорциональна рангу г, умноженному на десять,
то есть
= 1 = j_i
к Юг 10 г 
Число 10 в данном случае не имеет никакого отношения к деся-
тичной системе счисления; несмотря на свою простоту, множи-
тель 10 носит чисто эмпирический характер.
Необходимо подчеркнуть следующий факт: определение
ранга предполагает, что частота г(т, к)/к изменяется в направле-
нии, обратном увеличению г, однако из этого определения никоим
образом не следовало, что она будет изменяться обратно пропор-
ционально г, — это чисто эмпирическое открытие. Общепринятый
метод для установления и подтверждения этих соотношений за-
ключается в переходе к билогарифмическим координатам, где по
горизонтали откладывается логарифм ранга г, а по вертикали —
логарифм частоты г(т, к)/к. Вышеприведенная первая аппрокси-
мация позволяет предположить, что полученная таким образом
диаграмма будет представлять собой прямую с наклоном п — 1,
то есть параллельную второй биссектрисе координатных осей
(непрерывная линия на рис. 4.1).
Вторая аппроксимация: так называемый
«закон Ципфа-Мандельброта»
Помимо прочего, из первой аппроксимации следует, что за-
кон о частоте слов был бы одинаков для всех авторов, независимо
3Я (фр.). — Прим, перев.
Вторая аппроксимация
215
Рис. 4.1. Два теоретических закона распределения частоты слов
от используемого языка. В этом проявляется просто необычайная
«универсальность» (как говорят физики, см. [Sapoval 1997]) язы-
ка! В действительности же оказывается, что для большей части
данных график «ранг-частота» отличается от прямой с накло-
ном — 1, причем отличается по-разному.
Прежде всего, несколько наиболее частых слов (малые зна-
чения г), по-видимому, не подчиняются никакому точному закону,
но — в общем и целом — попадают ниже, чем это было бы верно
по закону первого приближения. Более того, в таких языках, как
французский, многие слова из числа наиболее употребительных
также определены наименее корректно. Распределение изменяет-
ся в зависимости от того, считаем ли мы «1е» и «Г»4 одним словом
или разными.
Во-вторых, если опустить наиболее частые слова, то график
«ранг-частота» остается прямым, но в общем случае неверно,
что эта прямая параллельна второй биссектрисе координатных
4Краткая форма определенного артикля «1е». — Прим. пер.
216
ЧАСТЬ ЧЕТВЕРТАЯ
осей; чаще всего ее наклон больше 1 и тем ближе к 1, чем «более
богатым» оказывается словарь.
Комбинируя два вышеприведенных замечания, приходим к
следующей формуле — той, что соответствует пунктирной линии
на рис. 4.1:
i(r,k) = Pk(r + V)~B.
Заглавными буквами Р, V и В обозначены параметры. В выше-
описанном первом приближении они сводятся к Р = 1/10, V = 0
и В = 1. Параметр В — это наклон кривой «ранг-частота». Для
каждого субъекта эти параметры фиксированы, однако у разных
субъектов они могут быть различными. Они не характеризуют
какой-то определенный язык, хотя возможно, что их «типичные
значения» стремятся к систематической зависимости от исполь-
зуемого языка и что случаи В < 1 (как мы увидим в конце этой
части) характерны, в основном, для очень нетипичных языков.
Эмпирические данные представлены на рис. 4.2 и 4.3.
Заметим между прочим, что в приведенных выше рассужде-
ниях улучшенный закон для г (г, k) вводился за счет так называе-
мой «грубой подгонки под график», однако этот способ не соот-
ветствует исторической правде, поскольку первоначально данный
закон был выведен с помощью теории, очень подробно представ-
ленной в [М 1955b]. Если мы и отмечаем этот момент, то лишь
потому, что есть люди, которые полагают любую корректировку
графика занятием сугубо недостойным. На мой взгляд, представ-
ленные рассуждения не заслуживают такого пренебрежительного
отношения; возможно, здесь уместно рассказать, как именно все
происходило. Пытаясь разными способами объяснить первую ап-
проксимацию Ципфа — с которой меня самого познакомили без
каких бы то ни было графиков, — я неизменно приходил к вы-
шеупомянутому закону. Я уже готов был оставить эту тему, когда
в конце концов мне в руки попала работа, содержащая данные,
из которых я понял, что моя аппроксимация лучше аппроксима-
ции Ципфа, и во всех мои последующих усилиях нет никакой
необходимости.
При нынешнем состоянии статистики в общественных нау-
ках закон P(r + V)~B можно без особого преувеличения считать
самым обоснованным из всех имеющихся. Тем не менее, некото-
рые сомневаются, что в данном контексте вообще может выпол-
няться какой бы то ни было закон. Поэтому, прежде чем этот закон
объяснять, неплохо будет показать, что он ни в коем случае не аб-
сурден, что не возникает никакого конфликта между ним и двумя
Вторая аппроксимация
217
Рис. 4.2. Эмпирические данные, относящиеся к различным немец-
ким (А, В, С, D) и одному норвежскому (N) авторам
интуитивными представлениями, возникающими у нас в отноше-
нии дискурса, — в зависимости от того, рассматриваем ли мы его
с точки зрения «говорящего» или «слушающего». Говорящий мо-
жет претендовать на то, что используемые им слова более или
менее однозначно определены теми мыслями, которые он желает
выразить. Если он достаточно педантичен, то он будет даже пре-
тендовать на то, что эта определенность в выборе слов управля-
ется неким фиксированным алгоритмом. Слушающий, напротив,
осознает iy роль, которую играет в рассматриваемом процессе
лингвистическая произвольность: существует бессчетное количе-
ство способов выразить одну и ту же мысль. Если он достаточно
скептичен, то он будет даже утверждать, что последовательность
воспринимаемых им слов почти полностью случайна.
218
ЧАСТЬ ЧЕТВЕРТАЯ
Рис. 4.3. Эмпирические данные, относящиеся к выборкам с убы-
вающей длиной (от I до VIII) из текстов одного английского авто-
ра. Видно, что кривая смещается без изменения формы. Ее асим-
птотический наклон В характерен для данного субъекта. Как вы-
яснилось, он страдает шизофренией, поэтому с семантической
точки зрения его речь очень бедна. Этот факт ослабляет ограни-
чения, которые могли бы осложнить статистику, и представляет
собой поразительный пример «нормы», составляющей закон Цип-
фа - Мандельброта
Вообще говоря, нет ничего странного в том, что случай игра-
ет здесь некоторую роль. Чтобы согласовать точки зрения говоря-
щего и слушающего, можно представить себе, что в распоряжении
первого имеется систематический набор орудий, а неопределен-
ность в выборе орудия, которым он воспользуется, достаточна для
Объяснение закона Ципфа - Мандельброта	219
того, чтобы убедиться, что частота их использования, в общем,
вполне определена. Здесь предполагается, что говорящий упоря-
дочивает слова в зависимости от частоты использования, а поря-
док этот, в свою очередь, определяет вышеупомянутую частоту.
Если для Пьера ранг слова КАФЕ равен 177, а для Франциска 315,
то в речи Пьера это слово появляется с частотой, равной пример-
но 1/1770, а в речи Франциска — 1/3150.
Объяснение закона Ципфа-Мандельброта
Наконец мы переходим к проблеме объяснений. Я выдвигал
много разных объяснений, обладающих свойством математиче-
ской эквивалентности, но, как оказалось, они взывают к интуитив-
ным представлениям настолько различным, что наиболее горячие
защитники одних методов порой оказываются самыми холодными
критиками других. Были и попытки дать объяснения, несводимые
к моим, но они или очень туманны — начиная с объяснения самого
Ципфа — или некорректны математически. Некоторые авторы до
сих пор упорствуют в несбыточной надежде получить диффузию,
исходя из уравнения в частных производных первого порядка.
Два основных варианта моей модели интерпретируются, со-
ответственно, в терминах упомянутых выше задач криптографии
и телеграфии. В теории информации считается классическим тот
факт, что если вооружить криптографа и телеграфиста одним ал-
фавитом и усадить кодировать слово за словом (разделяя слова
пробелами), то оптимальные решения окажутся у обоих одинако-
выми. (Точнее, каждый получит множество эквивалентных опти-
мальных решений, и эти два множества будут идентичными.)
Известно также, что для системы, произвольной по частоте
слов, требование разделять коды пробелами в общем случае ста-
новится источником либо структур, которые могут помочь про-
тивнику в расшифровке, либо неэффективности в использовании
букв. Однако я сумел показать, что существует особая система ча-
стоты слов, для которой это неверно — система, которую можно
называть «оптимально адаптированной к пословному кодирова-
нию». Как оказалось, эта система удовлетворяет вышеописан-
ной второй аппроксимации. Иначе говоря, как мы сейчас увидим,
частота употребления слов — это, в общем, единственное, что
нужно адаптировать к разделению слов посредством пробелов.
Использование экстремальных критериев, когда требуется,
чтобы та или иная величина была сколько угодно большой или
220
ЧАСТЬ ЧЕТВЕРТАЯ
сколько угодно малой, широко известно в физике: например,
«принцип наименьшего действия», «принцип максимума энтро-
пии», «принцип производства минимума энтропии». Эти крите-
рии ведут свое происхождение из XVIII века и основаны на созна-
тельном переносе различных интроспективных «принципов» наи-
меньшего усилия, которые, как предполагалось, свойственны че-
ловеческому поведению. Затем они объявились и в общественных
науках, хотя и в совершенно математизированной форме, заслу-
жив тем самым определенную репутацию — например, в рамках
формализма, который его авторы не побоялись назвать «матема-
тической экономикой» (хотя и в очень туманном и, как следствие,
несколько нелепом виде). К этой категории и относится «принцип
наименьшего усилия», название которого послужило заголовком
одной из работ Ципфа. Более того, именно исходя из этого заго-
ловка (не будучи знакомым с самой работой), я и придумал первое
объяснение закона
P(r + V)~B.
Как мы увидим далее, при заданном количестве информации
по Шеннону этот закон соответствует «наименьшему количеству
букв». Между тем, как вскоре выяснилось, многие читатели сде-
лали отсюда вывод, будто я формализовал и, следовательно, об-
основал всю «теорию Ципфа». Я никогда не претендовал на та-
кое и не собираюсь этого делать впредь. Сейчас, во избежание
недоразумений, мне представляется «политически» более пред-
почтительным сделать упор на оптимальности статистики слов
по отношению к задаче криптографии: эту область человеческой
деятельности не так легко ассоциировать с мыслью о глубинном
совершенстве человека.
Краткого упоминания заслуживает и третий вариант. С те-
чением времени становится ясно, что желания «говорящего» из-
меняются, а вместе с ними должна меняться и структура частоты
слов. Согласно некоторым, не слишком неразумным, гипотезам
(вторая аппроксимация), оказывается, что закон о частоте — и
только он — остается без изменений, а все прочие законы сходят-
ся к нему как к общему пределу.
Количество информации
Этот параграф преследует две разные цели: для неискушен-
ного в предмете читателя — представить наше изложение так же
Количество информации
221
независимо, как это делается в учебнике; для информированного
читателя — объединить некоторые предостережения.
Дискретное распределение вероятностей — это множество,
составленное из положительных чисел рп, где = 1. Здесь
индекс п пробегает значения от 1 до АГ, причем N может быть
бесконечно большим. Тогда количество информации по Шеннону
определяется как сумма
н = -^PnlogaPn.
Это определение можно обосновать по меньшей мере тремя
способами; но сначала следует провести различие между словом
«лексическим» (когда говорят «количество разных слов») и сло-
вом «текстовым» (когда говорят «полное количество слов»). При-
ведем пример выражения, в котором сочетаются оба этих смысла:
«частота лексического слова КАФЕ в данном тексте, состоящем
из 1500 текстовых слов, равна 1/1775». Некоторые выражения —
например, «частота текстового слова» — оказываются попросту
бессмысленными и никогда не употребляются. Поэтому, для упро-
щения изложения вместо, например, выражения «частота лекси-
ческого слова» мы будем говорить просто «частота слова». Ниже
приведены три мотивировки определения количества Н (по воз-
растанию содержания и уязвимости).
1)	В теореме Шеннона величина Н вводится как нижний пре-
дел количества бинарных знаков (0 или 1), необходимых в
среднем для передачи сообщения, текстовые слова которо-
го независимы, а лексические слова имеют вероятности рп.
Когда некоторое аналитическое выражение играет настоль-
ко важную роль, полезно присвоить ему какое-нибудь легко
запоминающееся имя, даже если (как это сделано в неко-
торых доказательствах теоремы Шеннона) вышеуказанное
выражение вводится чисто формальным образом.
2)	Другие доказательства теоремы Шеннона настаивают на
двух промежуточных этапах. Прежде всего, если лексика
включает в себя два равновероятных слова, то Н = 1; ес-
ли имеется N равновероятных слов, то Н = log2 N. Таким
образом, на первом этапе количество информации Н равно
(с точностью до преобразования) количеству лексических
слов. Это позволяет интерпретировать Н как меру богатства
словаря.
222
ЧАСТЬ ЧЕТВЕРТАЯ
Затем допустим, что числа рп различны. Когда к достаточно
велико, можно показать, что тексты, составленные из к тек-
стовых слов, разделяются на два класса: количество слов в
текстах первого класса почти равно 2кн, причем каждое из
них имеет вероятность, очень близкую к 2~кН, тогда как в
текстах второго класса слова чрезвычайно многочисленны,
но их общая вероятность очень мала, так что при первом
приближении ими можно пренебречь. Отсюда следует (это
и есть наш второй этап), что длинный текст ведет себя прак-
тически так, как если бы он состоял из 2кН равновероятных
лексических слов. Величина Н и здесь выступает как мера
богатства словаря.
3)	Наконец, многие авторы ставят во главу угла термин «инфор-
мация», трактуя его аксиоматически. Они приходят к выво-
ду о неизбежности того, чтобы связать этот термин с Н и
только с Н, потому что это выражение не только удовлетво-
ряет некоторым аксиомам, характеристическим для данной
концепции, но и является единственным выражением, обла-
дающим этим свойством.
По-моему, от такого аксиоматического подхода больше вре-
да, чем пользы. В нем предполагается некоторое единство в
концепции информации, что, конечно же, неправильно, по-
скольку другие авторы (начиная с Р. А. Фишера) исходят из
других аксиом, столь же убедительных внешне, а заканчи-
вают выражениями, совсем иными как концептуально, так и
численно. Нравится нам это или нет, но аксиоматика больше
подходит для украшения надгробных памятников, чем для
растущей и меняющейся науки.
Перечисленные выше замечания находят свое отражение в
различных методах, с помощью которых в статистической термо-
динамике вводится концепция энтропии. Некоторые авторы пред-
почитают показывать, конструктивно и a posteriori, что энтропия
задается выражением, формально идентичным выражению, опре-
деляющему меру информации. Интересы других сосредоточены
на том, чтобы показать a priori, что никакое другое выражение
здесь не годится. Я предпочитаю первый метод.
Первый вывод закона о частоте слов
Обезьяны за печатной машинкой и случайные последова-
телъности букв и пробелов. Мы начнем с закона о частоте слов в
Первый вывод закона о частоте слов
223
дискурсе, который представляет собой независимую случайную
последовательность символов, то есть букв и пробелов, отмечаю-
щих конец слова.
В первом приближении представим себе, воспользовавшись
одним старым клише, что этот дискурс составлен обезьяной, ко-
торая случайным образом печатает символы с фиксированной ве-
роятностью для каждой клавиши. Пусть ро — вероятность набрать
пробел, а Л/ — количество букв в алфавите, причем каждой бук-
ве соответствует одинаковая вероятность. Если некоторое слово
содержит т букв, то его вероятность равна произведению веро-
ятностей его составляющих; точнее,
ро[(1 ~Ро)/М]т = poexp{-mlog[M/(l - ро)]}.
Это выражение можно переписать в виде ро ехр{—0т}. Здесь /3 =
= log[Af/(l — ро)] — положительная величина, зависящая от М
иро.
Следующий этап состоит в установлении соответствия меж-
ду т и рангом слова по убыванию частоты. Прежде всего, имеется
одно-единственное лексическое «слово», составленное из нулево-
го количества речевых букв, ему мы приписываем ранг 1; затем
имеется М лексических слов, составленных из одной речевой
буквы, им мы приписываем ранги от 2 до М 4- 1 (выбранный
порядок не имеет значения), и так далее. Имеется М лексических
слов из т речевых букв, причем ранги этих слов имеют верхний
предел,
г^1 + Л/ + М2+...+Мт = (Л/”1"1 - 1)/(Л/ - 1),
откуда следует, что
тп —1 4- log[(M — 1)г 4-1]/ log М.
У рангов есть также и нижний предел
г > 1 + м + м2 + ... + ЛГ"-1 = (Мт - 1)/(М - 1),
откуда следует, что
т < log[(Af — 1)г 4-1]/ log М.
Таким образом, связь между рангом и вероятностью задается сту-
пенчатой кривой, которая остается постоянной, пока г изменяется
224
ЧАСТЬ ЧЕТВЕРТАЯ
в пределах между (Mm — 1)/(М — 1) и выражением того же само-
го вида, в котором т заменено на т + 1. Приблизительно можно
записать, что
т та log[(M — 1)г]/ log М.
Отсюда следует, что вероятность ро ехр{—/Зт} одного слова из т
речевых букв можно переписать следующим образом:
р(г) = ро ехр{-/3/ log М log[(М — 1)т]} =
= ро(М - 1)-вг-в = Рг"в,
где В мы определили как В = р/ log М, а Р = ро(Л/ — 1)~в.
Полученное таким образом соотношение со всей очевидно-
стью идентично описанной выше второй аппроксимации. Его осо-
бенность состоит в том, что здесь полное количество лексических
слов бесконечно; вторая особенность, связанная с предыдущей, —
мы всегда получаем В > 1, причем эксцесс В—1 тем меньше, чем
больше М или чем меньше ро. В то же время, в общем случае Р
отличается от 1/10.
Если говорить в общем, то полученный выше результат де-
лает закон Ципфа удивительным по своей очевидности, настолько
просты те гипотезы, из которых мы только что его вывели.
А если конкретно, то более глубокого изучения заслуживают
три момента. Во-первых, в рамках рассмотренной модели коли-
чество различных лексических слов бесконечно. Во-вторых, на
параметр В накладывается ограничение: В > 1. В-третьих, дей-
ствительная связь между г и р задается ступенчатой функцией.
Для некоторых наборов данных эти черты вполне приемлемы,
в других случаях это не так, и совершенно необходима вторая
аппроксимация. Покажем, как можно ее получить. Но сначала
необходимо сделать небольшое отступлении.
Отступление. В описанной выше модели единственным раз-
личием между буквами и пробелом является то, что пробел выпол-
няет функцию разделения слов. Следовательно, эту модель можно
с таким же успехом применить и к «псевдословам», определяе-
мым повторением какой-нибудь буквы, — скажем, «е». Именно
в этом хотели убедиться Дж. Ф. Миллер и Э. Ньюмен. Результат
оказался отчасти ожидаемым — закон Рг“в таки применим, — а
отчасти поразительным — условие В > 1 оказалось заменено на
прямо противоположное В < 1.
Какими бы преходящими ни были эти результаты, они, са-
мое малое, предполагают, что обычный пробел выполняет некую
Второй вывод: оптимальные частоты 225
особую роль. Этот факт согласуется и с духом психологических
экспериментов, которые показывают, что слова воспринимаются
не как последовательности отдельных букв, но как блоки. Един-
ственным общим элементом в двух кодировках слов, в мозге и
посредством букв, является пробел.
Второй вывод: оптимальные частоты
Частоты называются оптимальными, если, при заданной ме-
ре информации Шеннона, они требуют наименьшего среднего ко-
личества букв на слово.
Зафиксируем для начала полное количество слов в слова-
ре, R, который может быть конечным или бесконечным.
Первый этап оптимизации. Если придать каждому слову
некоторую вероятность, то становится ясно, что для минимиза-
ции среднего количества букв требуется использовать R наибо-
лее коротких комбинаций букв, причем существует взаимно одно-
значное соответствие между классификацией слов по убыванию
вероятности и по возрастающему количеству букв.
Второй этап оптимизации. Система вероятностей должна
естественным образом удовлетворять двум ограничениям.
Прежде всего,
52 = 1-
Более того, мы полагаем известной меру информации Шен-
нона, что выражается равенством
-52p(r)log2p(r)= н-
Вышеупомянутую Н можно выбрать произвольно в интервале
от 0 до log2 R.
Минимизировать следует среднее количество букв на лекси-
ческое слово, а именно:
ЕМ = У>(г)тп(г).
Для этого воспользуемся классическим методом множителей
Лагранжа.
1)	Запишем линейную комбинацию трех вышеупомянутых ве-
личин, две из которых выбраны и фиксированы, а третью
мы хотим минимизировать, то есть
- 52 р(г)log р<г)_ 19 52 р(г)т(г)+а 52•
15 Б. Мандельброт
226
ЧАСТЬ ЧЕТВЕРТАЯ
Затем минимизируем последнее выражение, предполагая,
что его производные по всем переменным р(г) обращаются
в нуль. Это приводит к R соотношениям:
— 1 — logp(r) — /Зт(г) + а = О,
что дает
р(г) = ехр(а — 1)ехр[—/Зтп(т)].
Пока ничего не изменилось бы, пожелай мы зафиксиро-
вать ЕМ и максимизировать Н.
2)	Следующий этап состоит в выборе а и /3 так, чтобы они удо-
влетворяли двум вышеупомянутым ограничениям. Из усло-
вия Р(г) — 1 следует, что
ехр(1 — а) = ехр[—/Зтп($)],
то есть
р(г) = ехр[—$m(r)]/(exp[—/Зт(з)]).
Чтобы теперь найти /3, нужно воспользоваться либо услови-
ем
- 52 р(г) log2 Р(Г) = Н>
если фиксирована мера Я, либо условием
У^р(г)тп(г) = ЕМ,
если фиксирована величина ЕМ.
Формально только что установленное соотношение между г
и р(г) в точности совпадает с соотношением, полученным в пер-
вой части этого раздела. Впрочем, появляется новый параметр R:
если значение R конечно, то параметр В может быть меньше 1.
Обобщение. Вместо того, чтобы просто считать буквы, пред-
положим, что они могут иметь разную стоимость (передачи), при-
чем стоимость некоторой речевой буквы может зависеть от стои-
мости предыдущей буквы. Вычислительные подробности услож-
няются, но результат в общих чертах остается тем же самым.
Важное различие состоит в том, что наблюдавшиеся до сих пор
траектории функции т(г) могут при малых значениях г исчез-
нуть или, по меньшей мере, стать короче. Следовательно, улуч-
шается представление функции тп(г) по ее среднему поведению.
Температура дискурса, «отрицательные температуры» 227
Температура дискурса, «отрицательные
температуры»
Следует обратить внимание на две аналогии между, с од-
ной стороны, моделями из второй части предыдущего раздела и,
с другой стороны, физикой, которую мы сначала рассмотрим с
одной широко известной точки зрения, а затем — с другой точки
зрения, весьма малоизвестной, хотя и очень захватывающей.
Прежде всего, теория оптимизации, с помощью которой мы
получили соотношение между р(г) и тп(г), позаимствована непо-
средственно из статистической термодинамики. Тот факт, что экс-
тремальное распределение можно с тем же успехом охарактери-
зовать как полностью случайное, известен и в термодинамике. В
последней в качестве доказательства можно использовать отож-
дествление 1/0 с произведением физической температуры Т на
некий фиксированный множитель к (который физики называют
постоянной Больцмана).
Таким образом возникает искушение точно так же посту-
пить и здесь — по крайней мере, в смысле терминологии — назвав
параметр 1/0 «температурой дискурса». Ее точка отсчета и еди-
ница измерения имеют внутренний характер. Мы видим, что с
точки зрения возможных значений R важно знать, попадает ли
значение 1/0 левее или правее 1. При «низких температурах»,
соответствующих 0 > 1, параметр R может быть как бесконеч-
ным, так и конечным, тогда как при «высоких температурах»,
соответствующих 0 < 1, R и тп(г) должны быть обязательно
ограниченными.
У этого последнего свойства имеется любопытный аналог в
физике. Там также существует разрывное значение 1/0, которое,
как выясняется, равно скорее 0, чем 1. Случаи, когда возможно
это разрывное значение превзойти, были найдены физиком Нор-,
маном Рамсеем — разумеется, совершенно независимо, но по-
чти в то же время, когда мне удалось объяснить тог факт, что
температура дискурса может превосходить значение 0 = 1. Фи-
зическая температура мала, когда велико значение 1/0 (точнее,
когда 1/0 > 0); температура высока, когда мало значение 1/0
(точнее, когда 1/0 < 0).
Отсюда следующий парадокс: в зависимости от физической
структуры исследуемой системы температура Т может вести себя
очень по-разному. Если эквивалент нашей тп(г) — т. е. энергия —
неограничена, то Т может изменяться от 0 до бесконечности —
15*
228	ЧАСТЬ ЧЕТВЕРТАЯ
разумеется, не включительно. С другой стороны, существуют фи-
зические системы, — представляющие собой, в действительности,
относительное отклонение от нормы,— для которых эквивалент R
ограничен. При увеличении в такой системе температуры Т она
сначала принимает положительные значения и возрастает, а за-
тем, перейдя через разрыв в бесконечности, совершает скачок от
чрезвычайно большой положительной величины до отрицатель-
ной величины с очень большим абсолютным значением и снова
начинает расти. Шкала температур начинается и заканчивается на
абсолютном нуле Т — 0, одинаково недостижимом как с положи-
тельных, так и с отрицательных исходных значений.
Библиография
Ниже приводится список работ, на которые я ссылаюсь
в тексте книги, где они обозначены согласно следующему пра-
вилу: одна или несколько фамилий, далее год публикации и, если
необходимо, идентифицирующая буква а, Ь, с, ...
Есть, впрочем, и исключения: свою фамилию я сокращаю
до буквы М, работы же идентифицируются не по случайным
буквам, но в соответствии с мнемоническим правилом (статьи —
строчными буквами, книги — прописными), которым я пользуюсь
во всех списках своих работ.
Более того, к обозначению работ, вошедших в различные
тома «Selecta», добавляется окончание — например, {Е14}, что
означает главу 14 в [М 1997Е], том Е в собрании «Selecta».
Напомним: вместо «модель, описанная — или заявлен-
ная — в [М 1963b {Е14}]» в книге используется сокращение «мо-
дель [М 1963]». Так же обстоит дело и с моделями [М1965]
и [М 1972].
Следует отметить, что этот список представляет собой
не просто перечень цитируемых работ. Из-за недостатка време-
ни в сочетании (один раз не считается) с желанием сделать как
можно лучше, я сократил и дополнил уже существующий список.
Это библиография из [М 1997Е], книги на английском языке, в ко-
торой развиты те же идеи, что и здесь, но с гораздо большими
математическими подробностями. Понятно, что в результате
список получился весьма несовершенным: он не претендует на
полноту и перегружен случайными работами. Тем не менее, я
надеюсь, что он окажется полезным.
230
Библиография
•	ADELMAN, I. 1958. A stochastic process analysis of the
size distribution of firms. Journal of the American Statistical
Association: 58, 893-994.
•	ADELMAN, I. 1965. Long cycles: fact or artifact? American
Economic Review: 60, 444-463.
•	ADLER, R., FELDMAN, R. & TAQQU, M. (eds) 1997. A
Practical Guide to Heavy Tails: Statistical Techniques for
Analysing Heavy Tailed Distributions. Boston: Birkhauser.
•	AITCHISON, J. & BROWN, J.A.C. 1957. The Lognormal
Distribution. Cambridge: Cambridge University Press.
•	ALEXANDER, S. S. 1961. Price movements in speculative
markets: trends or random walks. Industrial Management Review
ofM. I. T: 2, Part 2,7-26. Reprinted in [Cootner 1964]: 199-218.
•	ALEXANDER, S. S. 1964. Price movements in speculative
markets: No. 2. Industrial Management Review of M.I. T: 4,
Part 2, 25-46. Reprinted in [Cootner 1964]: 338-372.
•	AROV, D.Z. & BOBROV, A. A. 1960. The extreme members
of samples and their role in the sum of independent variables.
Theory of Probability and Its Applications: 5, 415-435 of the
Russian original (377-396 in the English translation.)
•	ARMITAGE, P. 1952. The statistical theory of bacterial
populations subject to mutation. Journal of the Royal Statistical
Society: В 14, 1-40.
•	ARMITAGE, P. 1953. Statistical concepts in the theory of
bacterial mutation. Journal of Hygiene: 51, 162-184.
•	AUERBACH, F. 1913. Das Gesetz der Bevolkerungskonzentra-
tion. Petermans Mitteilungen: 59, 74-76.
•	AYRES, H. 1963. Risk aversion in the warrant markets.
Industrial Management Review: 5, 45-54. Reprinted in [Cootner
1964]: 497-505.
•	BACHELIER, L. 1900. Theorie de la speculation. (These de
doctorat es Sciences Mathematiques, Faculte des Sciences de
Paris, soutenue le 29 Mars, 1900). Annales Scientifiques de
Г Ecole Normale Superieure: III-17,21-86. Reimpression, Paris:
Gabay, 1995. Traduction anglaise dans [Cootner 1964]: 17-78.
Библиография
231
BACHELIER, L. 1914. Le Jeu, la chance et le hasard.
Flammarion.
BAILLIE, R.T. 1996. Long-memory processes and fractional
integration in econometrics. Journal of Economics: 73, 5-59.
BARNDORFF-NIELSEN, O. & BLAESILD, P. 1983. Hyperbo-
lic distributions. Encyclopedia of Statistical Sciences: New York:
Wiley, 3, 700-707.
BARNEY, W. 1964. An Investigation of Parametric Variation in
a Moving Average Investment Rule. Unpublished S. M. Thesis,
M. LT.
BARTLETT, M. S. 1966. An Introduction to Stochastic Processes
(Second edition). Cambridge: Cambridge University Press.
BARTON, C.C. & LAPOINTE, P.R. (eds) 1995. Fractal
Geometry and its Uses in the Geosciences and Petroleum
Geology. New York: Plenum.
BATEMAN H. 1954. Tables of Integral Transforms: 2. New
York: McGraw-Hill.
BAUER, J. 1964. A Diffusion Index as Applied to Price
Movement in the Stock Market. Unpublished S.M. Thesis,
M. LT.
BEALE, R.E. 1966. Review of [Cootner 1964]. Journal of
Political Economy: 74, 219.
BENCKERT, L.-G. & STERNBERG, I. 1957. An attempt
to find an expression for the distribution of fire damage
amount. Transactions 15th International Congress of Actuaries:
2, 288-294. New York.
BERAN, J. 1994. Statistics for long-memory processes. London:
Chapman & Hall.
*N5 BERGER, J.M. & MANDELBROT, B.B. 1963. A new
model for the clustering of errors on telephone circuits. IBM
Journal of Research and Development: 7, 224-236.
BIENAYME, J. 1853. Considerations a 1’appui de la decouverte
de Laplace sur la loi de probabilite dans la methode des moindres
canes. Comptes Rendus (Paris): 37, 309-329.
232
Библиография
•	BILLINGSLEY,?. 1968. Convergence of Probability Measures.
New York: Wiley.
•	BLANCHARD, O. J. & WATSON M. W. 1982. Bubbles, rational
expectations, and financial markets. Crises in the Economic and
Financial Structure. P. Wachtel (Ed.). Lexington, MA: Lexington
Books.
•	BLATTBERG, R. & GONEDES. N. 1974. A comparison of
Student’s and stable distributions as statistical models of stock
prices. Journal of Business: 47, 244-280.
BLUME, M. 1968. The Assessment of Portfolio Performan-
ce: An Application of Portfolio Theory. University of Chicago
Dissertation.
•	BLUMENTHAL, R.M., GETOOR, R.V. & RAY, D. On the
distribution of first hits for the symmetric stable process.
Translation of the American Mathematics Society: 99, 540-554.
•	BONESS, A. J. 1962. A Theory and Measurement of Stock
Option Value. Ph. D. Dissertation, University of Chicago.
•	BONESS, A. J. 1962. Some evidence on the profitability of
trading in put and call options. [Cootner 1964]: 475-498.
•	BOWLEY, A.L. 1933. The action of economic forces in
producing frequency distribution of income prices and other
phenomena: suggestion for a study. Econometrica: 1, 358-372.
•	BRADA, J., ERNST, H. & VAN TASSEL, J. 1966. The
distribution of stock price differences: Gaussian after all?
Operations Research: 14, 334-340.
•	BRAS, R. F. & RODRIGUEZ-ITURBE. 1993. Random Functions
and Hydrology. New York: Dover.
•	CALVET, L., FISHER, A. & MANDELBROT, В. B. 1997. Large
deviations and the distribution of price changes (to appear).
•	CANTELLI, F. P. 1921. Sulla deduzione delle leggi de frequenza
da considerazioni di probabilita. Metron: 1, 83-91.
•	CASTELLANI, M. 1951. On multinomial distributions with
limited freedom: a stochastic genesis of Pareto’s and Pearson’s
curves. Annals of Mathematical Statistics: 21, 289-293.
Библиография
233
CAUCHY, А. 1853. Sur les resultats les plus probables. Comptes
Rendus (Paris): 37, 198-206.
CHAMPERNOWNE, G. 1953. A model of income distribution.
Economic Journal: 63, 318-351. Reprinted as Appendix 6
to Champemowne, G. The Distribution of Income Between
Persons. Cambridge, U.K.: Cambridge University Press, 1973,
245-283.
CHANDRASEKHAR, S. 1943. Stochastic problems in physics
and astronomy. Reviews of Modem Physics: 15, 1-89. Reprinted
in [Wax 1954].
CIOCZEK-GEORGES, R. & MANDELBROT, B.B. 1995. A
class of micropulses and antipersistent fractional Brownian
motion. Stochastic Processes and their Applications: 60, 1-18.
CIOCZEK-GEORGES, R. & MANDELBROT, B.B. 1996.
Alternative micropulses and fractional Brownian motion (with
Renata Cioczek-Georges). Stochastic Processes and their Appli-
cations.
CIOCZEK-GEORGES, R. & MANDELBROT, B.B. 1996.
Stable fractal sums of pulses: the general case.
CIOCZEK-GEORGES, R., MANDELBROT, B.B., G., &
TAQQU, M.S. 1995. Stable fractal sums of pulses: the
cylindrical case. Bernoulli: 1, 201-216.
CLARK, P.K. 1973. A subordinated stochastic process model
with finite variance for speculative prices. Econometrica: 41,
135-155.
COOTNER, P.H. 1960. Returns to speculators: Telser vs.
Keynes. Journal of Political Economy: 68, 396-404, and
Rejoinder, ibid, 415-418.
COOTNER, P.H. 1962. Stock prices: Random walks vs. finite
Markov chains. Industrial Management Reviews of M. I. T: 3,
24-45. Reprinted in [Cootner 1964]: 231-252.
COOTNER, P.H. (Ed.) 1964. The Random Character of Stock
Market Prices. Cambridge, MA: M. I. T. Press.
COWLES, A. 1933. Can stock market forecasters forecast?
Econometrica: 1, 309-324.
234
Библиография
•	COWLES, А. 1938. Common Stock Indexes 1871-1937. Bloo-
mington, IN: Principia Press, 499.
•	COWLES, A. 1960. A revision of previous conclusions
regarding stock price behavior. Econometrica: 28, 909-915.
Reprinted in [Cootner 1964]: 132-138.
•	COWLES, A. & JONES, H. E. 1937. Some a posteriori
probabilities in stock market action. Econometrica: 5, 280-294.
•	DARLING, D. A. 1952. The influence of the maximum term in
the addition of independent random variables. Transactions of
the American Mathematical Society: 73, 95-107.
•	DARLING, D. A. 1956. The maximum of sums of stable random
variables. Transactions of the American Mathematical Society:
XX, 114-169.
•	DAVIS, L.E. 1960. The New England textile mills and the
capital market: a study of industrial borrowing 1840-1860.
Journal of Economic History: 20, 1-30.
•	DAVIS, L.E. & HUGHES, J.R.T. 1960. A dollar-sterling
exchange 1803-1895. Journal of Economic History Review: 13,
52-78.
•	DEFRANCE, G. 1948. Distribution et Dispersion des Prix
et Salaires en Belgique, These de 1’Institute de Statistique,
Universite de Paris.
•	DOOB, J.L. 1942. The Brownian movement and stochastic
equations. Annals of Mathematics: 43, 351-369. Reprinted
in [Wax 1954].
•	DOOB, J.L. 1953. Stochastic Processes. New York: Wiley.
•	EINSTEIN, A. 1956. The Theory of Brownian Motion, New
York: Dover (reprint).
•	ELLIOTT, R. N. 1994. R. N. Elliotts Masterworks: the Definitive
Collection. Gainesville, GA: New Classics Library.
•	EVERTSZ, C. J. G. 1995. Fractal geometry of financial time
series. Fractals: 3, 609-616.
•	EVERTSZ, C.J.G., PEITGEN, H.O. & VOSS, R.F. 1996.
Fractal Geometry and Analysis: The Mandelbrot Festschrift,
Curasao 1995. Singapore: World Scientific.
Библиография
235
FAMA, E.F. 1963a. The Distribution of Daily Differences of
Stock Prices', a Test of Mandelbrot's Stable Paretian Hypothesis.
Doctoral dissertation. Graduate School of Business, University
of Chicago. Published as [Fama 1965].
*E16 FAMA, E.F. 1963b. Mandelbrot and the stable Paretian
hypothesis. Journal of Business (Chicago): 36, 420-429.
Reprinted in [Cootner 1964]: 297-306.
FAMA, E. F. 1965. The behavior of stock-market prices. Journal
of Business (Chicago): 38, 34-105.
FAMA, E.F. 1970. Efficient capital markets: a review of theory
and empirical work. Journal of Finance: 25, 383-417. Also
in Frontiers of quantitative economics. (Ed.) M. D. Intrilligator.
Amsterdam: North Holland, 1971, 309-36.
FAMA, E.F. & BLUME, M. 1966. Filter rules and stock-market
trading. Journal of Business (Chicago): 39, 226-241.
FAMILY, F. & VICSEK, T. (eds) 1991. Dynamics of Fractal
Surfaces. Singapore: World Scientific.
FEDER, J. 1988. Fractals. New York: Plenum.
FELLER, W. 1936. Zur theorie der stochastischen prozesse.
Mathematische Annalen: 113, 119-160.
FELLER, W. 1940. On the integro-differential equations of
purely discontinuous Markoff processes. Transactions of the
American Mathematical Society: 48, 488-515.
FELLER, W. 1950. An Introduction to Probability Theory and
its Applications. New York: Wiley.
• ПРИМЕЧАНИЕ. Этот классический двухтомный труд вы-
держал несколько изданий. Том 1 (первое издание) вышел
в 1950 году. Оба тома мы обозначаем здесь как [Feller 1950],
при необходимости указывая дополнительную информацию.
FELLER, W. 1951. The asymptotic distribution of the range of
sums of independent random variables. Annals of Mathematical
Statistics: 22, 427.
FERMI, E. 1949. On the origin of the cosmic radiation. Physical
Review: 75, 1169-1174.
236
Библиография
•	FIELITZ, B.D. & ROZELLE, J.P. 1983. Stable distributions
and the mixtures of distributions hypotheses for common stock
returns. Journal of the American Statistical Association: 78,
28-36.
•	FISHER, A., CALVET, L. & MANDELBROT, B.B. 1997. The
multifractality of the Deutshmark I US Dollar exchange rates (to
appear).
•	FRECHET, M. 1927. Sur la loi de probabilite de 1’ecart
maximum. Annales de la Societe Polonaise de Mathematiques
(Cracovie): 6, 93.
•	FRECHET, M. 1941. Sur la loi de repartition de certaines
grandeurs geographiques. Journal de la Societe de Statistique
de Paris: 82, 114-122.
•	FRECHET, M. 1959. Sur la repartition des revenus. Comptes
Rendus (Paris): 249, 837-9.
•	FRIEDMAN, J.B. 1974. The architect’s compass in creation
miniatures of the later middle ages. Tradition, Studies in Ancient
and Medieval History, Thought, and Religion: 419-429.
•	GIBRAT, R. 1932. Les inegalites economiques. Paris: Sirey.
•	GLEICK, J. 1986. La theorie du chaos. Vers une nouvelle
science. Paris: Flammarion.
•	GNEDENKO, B.V. & KOLMOGOROV, A.N. 1954. Limit
Distributions for Sums of Independent Random Variables.
English translation by K.L. Chung. Reading, MA: Addison
Wesley. [Оригинальное издание: ГНЕДЕНКО Б. В., КОЛМО-
ГОРОВ А. Н. Предельные распределения для сумм незави-
симых случайных величин. — М.-Л.: ГИТТЛ, 1949, 264 с.]
•	GODFREY, M.D., GRANGER, С. W. J., & MORGENSTERN,
О. 1964. The random walk hypothesis of stock market behavior.
Kyklos: 17, 1-30.
•	GOUYET, J.F. 1992. Physique et structures fractales. Paris:
Masson.
•	GRANGER, C. W.J. 1966. The typical spectral shape of an
economic variable. Econometrica: 34, 150-61.
•	GRANGER, C.W.J. 1968. Some aspects of the random walk
Библиография
237
model of stock market prices. International Economic Review:
9, 253-257.
GRANGER, C.W.J. & MORGENSTERN, O. 1963. Spectal
analysis of New York Stock Exchange prices. Kyklos: 16, 1-27.
Reprinted in [Cootner 1964]: 162-188.
GRANVILLE, J. E. 1960. A Strategy of Daily Stock Market
Timing for Maximum Profit. Englewood Cliffs, NJ: Prentice-Hall.
GREENE, M. T. & FIELITZ, B. D. 1979. The effect of long-term
dependence on risk-return models of common stocks. Operations
Research: 27, 944-951.
GRENANDER, U. & ROSENBLATT, M. 1957. Statistical
Analysis of Stationary Time Series. New York: Wiley.
GUMBEL, E.J. 1958. Statistics of Extremes. New York:
Columbia University Press.
HAGSTROEM, K.-G. 1960. Remarks on Pareto distributions.
Skandinavisk Aktuarietidskrift: 33, 51-71.
HADAMARD, J. 1898. Les surfaces a courbures opposees et
leurs lignes geodesiques. Journal de Mathematiques pures et
appliquees: 5 IV, 27-73.
HADAMARD, J. 1945. The Psychology of Invention in the
Mathematical Field. Princeton University Press. (Reprint, New
York: Dover, 1954.)
HALBFASS, W. 1922. Die Seen der Erde. Erganzungsheft Nr.
185 zu Petermanns Mitteilungen, Gotha: Justus Perthes.
HALL, P. 1981. A comedy of errors: the canonical form
for a stable characteristic function. Bulletin of the London
Mathematical Society: 13, 23-27.
HANNA, F.A., PECKHAM, J. A. & LERNER, S.M. 1948.
Analysis of Wisconsin Income: 9, Studies in Income and Wealth.
New York: National Bureau of Economic Research.
HANNAN, E.J. 1960. Time Series Analysis. London: Methuen
& New York: Wiley.
HART, P.E. 1902. The size and growth of firms. Economica:
New series, 29, 29-39.
238
Библиография
•	HART, Р.Е. & PRAIS, S. 1956. The analysis of the business
concentration: a statistical approach. Journal of the Royal
Statistical Society: A 119, 150-181.
•	HELPERN, S. R. 1962. An Analysis of Stock Price Movements
Using Stop Orders. Unpublished S. B. Thesis, M. I. T.
•	HEYDE, C.C. & SENETA, E. 1977. I.JBienayme: Statistical
Theory Anticipated. New York: Springer.
•	HOLT, D.R. & CROW, E.L. 1973. Tables and graphs of the
stable probability density functions. Journal of Research of the
National Bureau of Standards (Mathematical Sciences): 77B,
143-198.
•	HOLTSMARK, J. 1919. Uber die Verbreiterung von Spektralli-
nien. Annalen der Physik: 58, 577-630.
•	HOUTHAKER, H. S. 1959. Education and income. Review of
Economics and Statistics: 41, 24-27.
•	HOUTHAKKER H.S. 1959. The scope and limits of future
trading. Allocation of Economic Resources, Essays in honor of
Bernard Haley. M. Abramovitz (Ed.): 134-159.
•	HOUTHAKKER, H.S. 1961. Systematic and random elements
in short-term price movements. American Economic Review: 51,
164-172.
•	HURST, H.E. 1951. Long-term storage capacity of reservoirs.
Transaction of the American Society of Civil Engineers: 116,
770-808.
•	HURST, H.E. 1955. Methods of using long-term storage in
reservoirs. Proceedings of the Institution of Civil Engineers.
Part 1, 519-577.
•	HURST, H.E., BLACK, R.P., and S1MA1KA, Y.M. 1965.
Long-Term Storage, an Experimental Study. London: Constable.
•	JANICKI, A. & WERON, A. 1994. Simulation and Chaotic
Behavior of Stable Stochastic Processes. New York: Marcel
Dekker.
•	JEFFREYS, H. 1948. Theory of Probability. Oxford: The
University Press.
Библиография
239
JOHNSOH N. L., KOTZ, S. & BALAKRISHNAN, N. 1994-5.
Continuous Univariate Distributions (2nd ed.) New York: Wiley.
KATZ, R. 1963. The profitability of put and call option writing.
Industrial Management Review: 5, 56-69.
KENDALL, D. G. 1952. Les processus stochastiques de crois-
sance en biologie. Annales de [Institute Henri Poincare: 13,
43-108.
KENDALL, M. 1953. The analysis of economic time-series.
Part I. Journal of the Royal Statistical Society: A 116, 11-25.
Reprinted in [Cootner 1964]: 85-99.
KEYNES, J.M. 1939. Professor Tinbergen’s method. Economic
Journal: 49, 558-568.
KEYNES, J.M. 1970. On the method of statistical business
research. Economic Journal: 50, 145-156.
KOLMOGOROV, A. N. 1933. Foundation of Probability Theory.
Berlin: Springer.
KOLMOGOROV, A.N. 1941. The local structure of turbulence
in incompressible viscose fluid for very large Reynolds numbers.
Doklady Akademii Nauk SSSR: 30, 301-305. Reprinted in [Fri-
edlander & Topper 1961], 159-161.
KOLMOGOROV, A.N. 1962. A refinement of previous hy-
potheses concerning the local structure of turbulence in a
viscous incompressible fluid at high Reynolds number. Journal
of Fluid Mechanics: 13, 82-85. Original Russian text and
French translation in Mecanique de la Turbulence, (Colloque
International de Marseille, 1961), Paris: Editions du CNRS.
447-458.
KORCAK, J. 1938. Deux types fondamentaux de distribution
statistique. Bulletin de I Institut Intenwtional de Statistique: 3,
295-299.
KRIGE, G. D. 1960. On the departure of ore value distributions
from the lognormal model in South African Gold Mines.
Journal of the South African Institute of Mining and Metallurgy:
231-244.
KRUIZENGA, R. J. 1956. Put and Call Options: a Theoretical
and Market Analysis, Ph. D. Dissertation, M. I. T.
240
Библиография
•	KRUIZENGA, R.J. 1964. Introduction to the option contract.
In [Cootner 1964]: 377-391.
•	KRUIZENGA, R.J. 1964. Profit returns from purchasing puts
and calls. In [Cootner 1964]: 392-411.
•	LAMPERTI, J. 1966. Probability : a Survey of the Mathematical
Theory. Reading, MA: W. A. Benjamin.
•	LANGE, 0.1932. Die Preisdispersion als Mittel zur Statistischen
Messung. Wirtschaftlicher Gleichgewichtsstorungen, Leipzig.
•	LARSON, A. 1960. Measurement of a random process in future
prices. Food Research Institute Studies: 1, 313-324. Reprinted
in [Cootner 1964]: 219-230.
•	LAURENT, A.G. 1957. A stochastic model for the behavior
of a set of price index-numbers and its application. Operations
Research: 5, 600.
•	LAURENT, A.G. 1959. Comments on Brownian motion in the
stock market. Operations Research: 7, 806-807.
•	LEA, D.E. & COULSON, C.A. 1949. The distribution of the
number of mutants in bacterial populations. Journal of Genetics:
49, 264-285.
•	LEVINE, S. 1962. Heuristic Determination of Optimum Filters
for Use in a Rule for Speculative Market Action, S. M. Thesis,
M. LT.
•	LEVY, P. 1925. Calcul des probability. Paris: Gauthier-Villars.
•	LEVY, P. 1937-54. Theorie de I ’addition des variables aleatoires.
Paris: Gauthier-Villars. (Deuxieme edition, 1954).
•	LEVY, P. 1948-1965. Processus stochastiques et mouvement
brownien. Paris: Gauthier-Villars.
•	LEVY, P. 1970. Quelques aspects de lapensee d’un mathemati-
cian. Paris: Blanchard.
•	LEVY-VEHEL, J. & WALTER, C. 1997. Les marches fractals:
efficience, ruptures et tendances sur les marchesfinanciers. Paris:
Presses Universitaires de France. (Collection «Finance».)
•	LOEVE, M. 1955. Probability Theory. New York: Van Nostrand.
(Recent editions published by Springer.)
Библиография
241
•	LOTKA, A. J. 1925. Elements of Physical Biology. Baltimore,
MD: Williams & Wilkins Reprinted as Elements of Mathematical
Biology. New York: Dover, 1956.
•	LOVEJOY, A.D. 1936. The Great Chain of Being. Cambridge,
MA: Harvard University Press.
•	LOVEJOY, S. & MANDELBROT, В. B. 1985. Fractal properties
of rain, and a fractal model. Tellus A: 37, 209-232.
•	LURIA, S.E. & DELBRUCK, M. 1943. Mutations of bacteria
from virus sensitivity to virus resistance. Genetics: 28,491-511.
•	LYDALL, H. F. 1959. The distribution of employment income.
Econometrica: 27, 110-115.
•	MACAULAY, F. R. 1922. Pareto’s laws and the general problem
of mathematically describing the frequency of income. Income
in the United States, Its Amount and Distribution, 1909-1919:
2. New York: National Bureau of Economic Research.
•	MACAULAY, F.R. 1932. The Smoothing of Economic Time
Series. New York: National Bureau of Economic Research.
•	MACAULAY, F. R. 1936. Some Theoretical Problems Suggested
by the Movements of Interest Rates, Bond Yields, and Stock
Prices in the United States since 1856. New York: National
Bureau of Economic Research.
•	MACHLUP, F. 1960. The supply of inventors and inventions.
Welwirtschafliches Archiv: 85, 210-254.
•	MALKIEL, B.G. 1973. Random Walk Down the Street. New
York: W.W. Norton. (Sixth edition, 1996).
•	FE4 MANDELBROT, B.B. 1951. Adaptation d’un message a
la ligne de transmission, I & II. Comptes Rendus (Paris): 232,
1638-1740 & 2003-2005.
•	MANDELBROT, B.B. 1953L An informational theory of the
statistical structure of language, in Communication Theory, (Ed.)
W. Jackson. London: Butterworth, 486-504.
•	MANDELBROT, B.B. 1955b. On recurrent noise limiting
coding. Information Networks, E. Weber (Ed.). New York:
Interscience: 205-221.
16 Б. Мандельброт
242
Библиография
•	MANDELBROT, B.B. 1956g. Memorandum. University of
Geneva Mathematical Institute.
•	MANDELBROT, B.B. 1956m. A purely phenomenological
theory of statistical thermodynamics: canonical ensembles. IRE
Transactions on Information Theory'. 112, 190-203.
•	MANDELBROT, B.B. 1957р. Linguistique statistique macro-
scopique. Dans: Logique, Langage et Theorie de ITnformation,
par L.Apostel, В. B. Mandelbrot & R.Morf. Paris: Presses
Universitaires de France, 1-80.
•	MANDELBROT, B.B. 1957r. Application of Thermodynami-
cal Methods in Communication Theory and Econometrics.
Memorandum of the University of Lille Mathematics Institute.
•	MANDELBROT, B.B. 1958р. Les lois statistiques macroscopi-
ques du comportement (role de la lot de Gauss et des lois de
Paul Levy). Psychologic Frangaise: 3, 237-249.
•	*FEP MANDELBROT, B.B. 1959р. Variables et processus
stochastiques de Pareto-Levy et la repartition des revenus, I
& II. Comptes Rendus (Paris): 249, 613-615 & 2153-2155.
•	MANDELBROT, B.B. 1959s. A note on a class of skew
distribution functions. Analysis and critique of a paper by
H. A. Simon: Information and Control: 2, 90-99.
•	*E10 MANDELBROT, B.B. 19601. The Pareto-Levy law and
the distribution of income. International Economic Review: 1,
79-106.
•	MANDELBROT, B.B. 1961s. Final note on a class of skew
distribution functions (with a postscript). Information and
Control: 4, 198-216 & 300-304.
•	MANDELBROT, В. В. 1961 b. On the theory of word frequencies
and on related Markovian models of discourse. Structures of
language and its mathematical aspects. R. Jakobson (Ed.). New
York: American Mathematical Society: 120-219.
• *E11 MANDELBROT, B.B. 1961e. Stable Paretian random
functions and the multiplicative variation of income. Economet-
rics: 29, 517-543.
• *E12 MANDELBROT, B.B. 1962q. Paretian distributions and
Библиография
243
income maximization. Quarterly Journal of Economics: 76,
57-85.
•	*E14 & 15 MANDELBROT, B.B. 1962i. The Variation of
Certain Speculative Prices. IBM Research Report NC-87,
March, 1962.
•	*FEP MANDELBROT, B.B. 1962c. Sur certains prix speculatifs:
faits empiriques et modele base sur les processus stables additifs
de Paul Levy. Comptes Rendus (Paris): 254, 3968-3970.
•	*E14 MANDELBROT, B.B. 1963a. Abstract: Econometrica:
31, 757-758.
•	*E14 MANDELBROT, B.B. 1963b. The variation of certain
speculative prices. Journal of Business: 36, 394-419. Reprinted
in [Cootner 1964]: 297-337.
•	*E3 MANDELBROT, B.B. 1963e. New methods in statistical
economics. Journal of Political Economy: 71,421-440. Reprinted
in Bulletin of the International Statistical Institute, Ottawa
Session: 40 (2), 669-720.
•	*E8 MANDELBROT, B.B. 1963g. A Survey of Growth and
Diffusion Models of the Law of Pareto. IBM External Research
Note NC-253.
•	*E10 MANDELBROT, В. В. 1963i. The stable Paretian income
distribution when the apparent exponent is near two. International
Economic Review: 4, 111-115.
•	*E10 MANDELBROT, B.B. 1963j. The Stable Paretian
Income Distribution, when the Apparent Exponent is Near
Two. Memorandum appended to a joint reprint of [M 1960i]
and [M1963i].
•	*E13 MANDELBROT, B.B. 1963o. Oligopoly, Mergers, and
the Paretian Size Distribution of Firms. IBM Research Note
NC-246, March 1963.
•	*E8 MANDELBROT, В. B. 1964o. Random walks, fire damage
and related risk phenomena. Operations Research: 12, 1964,
582-585.
•	MANDELBROT, B.B. 1964t. Derivation of statistical thermo-
dynamics from purely phenomenological principles. Journal of
Mathematical Physics: 5, 164-171.
16*
244
Библиография
•	MANDELBROT, B.B. 1965b. On recurrent noise limiting
coding. Information Networks, the Brooklyn Polytechnic Institute
Symposium, 205-221. New York: Interscience.
•	*H MANDELBROT, B.B. 1965h. Une classe de processus
stochastiques homothetiques a soi; application a la loi clima-
tologique de H. E. Hurst. Comptes Rendus (Paris): 260, 3274-7.
•	*E8 MANDELBROT, В. B. 1965m. Very long-tailed probability
distributions and the empirical distribution of city sizes.
Mathematical Explanations in Behavioral Science. F.Massarik
& P. Ratoosh (Eds.). Homewood: Richard D. Irwin, 322-332.
•	*E19 MANDELBROT, B.B. 1966b. Forecasts of future prices,
unbiased markets, and «martingale» models. Journal of Business:
39, 242-255. Important errata in a subsequent issue of the same
Journal.
•	*FE3.1 & 3.2E MANDELBROT, B.B. 1966r. Nouveaux
modeles de la variation des prix (cycles lents et changements
instantanes). Cahiers du Seminaire d‘econometric: 9, 1966,
53-66.
•	MANDELBROT, B.B. 1967b. Sporadic random functions and
conditional spectral analysis; self-similar examples and limits.
Proceedings of the Fifth Berkeley Symposium on Mathematical
Statistics and Probability: 3, 155-179.
•	*E15 MANDELBROT, В. В. 1967j. The variation of some other
speculative prices. Journal of Business: 40, 393-413.
•	*E21 MANDELBROT, В. В. 1968i. Some aspects of the random
walk model of Stock Market prices: comment. International
Economic Review: 9, 258.
•	*FE4 MANDELBROT, B.B. 1968w. Information theory and
psycholinguistics: a theory of word frequencies. Readings in
Mathematical Social Science. P.Lazarfeld & N. Henry (Eds.),
Cambridge, MA, MIT Press. 350-368.
• MANDELBROT, B.B. 1969e. Long-run linearity, locally Ga-
ussian process, H-spectra and infinite variances. International
Economic Review: 10, 82-111.
• MANDELBROT, B.B. 1970a. Long-run interdependence in
Библиография
245
price records and other economic time series. Econometrica:
38, 122-123.
MANDELBROT, B.B. 1970e. Statistical dependence in prices
and interest rates. Papers of the Second World Congress of the
Econometric Society, Cambridge, England.
MANDELBROT, B.B. 1970n. Analysis of long-run dependence
in time series: the R/S technique. Fiftieth Annual Report of the
National Bureau of Economic Research, 107-108.
MANDELBROT, B.B. 1970y. Statistical Self-Similarity and
Non Laplacian Chance. 1970 Trumbull Lectures, Yale University.
*E20 MANDELBROT, B.B. 1971e. When can price be
arbitraged efficiently? A limit to the validity of the random walk
and martingale model. Review of Economics and Statistics: 53,
225-236.
MANDELBROT, B.B. 197In. Statistical dependence in prices
and interest rates. Fifty-first Annual Report of the National
Bureau of Economic Research, 141-142.
MANDELBROT, B.B. 1971q. Analysis of long-run dependence
in economics: the R/S: ef. technique. Econometrica: 39 (July
Supplement), 68-69.
*E14 MANDELBROT, B.B. 1972b. Correction of an error in
«The variation of certain speculative prices» (M 1963b). Journal
of Business: 40, 542-543.
MANDELBROT, B.B. 1972c. Statistical methodology for
nonperiodic cycles: from the covariance to the R/S analysis.
Annals of Economic and Social Measurement: 1, 259-290.
*N14 MANDELBROT, B.B. 1972j. Possible refinement of
the lognormal hypothesis concerning the distribution of energy
dissipation in intermittent turbulence. Statistical models and
turbulence. M. Rosenblatt & C. Van Atta (Eds.). Lecture Notes
in Physics 12, New York: Springer, 333-351.
*E21 MANDELBROT, B.B. 1973c. Comments on «А subor-
dinated stochastic process with finite variance for speculative
prices», by Peter K. Clark. Econometrica: 41, 157-160.
*FE2.1 MANDELBROT, B.B. 1973f. Formes nouvelles du
hasard dans les sciences. Economic Appliquee: 26, 307-319.
246
Библиография
•	*FE3.2 MANDELBROT, В. В. 1973j. Le probleme de la realite
des cycles lents, et le syndrome de Joseph. Economic Appliquee:
26, 349-365.
•	*FE3.1 MANDELBROT, B.B. 1973v. Le syndrome de la
variance infinie et ses rapports avec la discontinuite des prix.
Economic Appliquee: 26, 321-348.
•	*E8 MANDELBROT, B.B. 1974d. A population birth and
mutation process, I: Explicit distributions for the number of
mutants in an old culture of bacteria. Journal of Applied
Probability: 11, 437-444. (Part II was distributed privately.)
•	*N16 MANDELBROT, B.B. 1974c. Multiplications aleatoires
iterees, et distributions invariantes par moyenne ponderee.
Comptes Rendus (Paris): 278A, 289-292 & 355-358.
•	*N15 MANDELBROT, B.B. 1974f. Intermittent turbulence
in self-similar cascades: divergence of high moments and
dimension of the carrier. Journal of Fluid Mechanics: 62,
331-358.
•	MANDELBROT, B.B. 1975h. Limit theorems on the self-nor-
malized range for weakly and strongly dependent processes.
Zeitschrift fur Wahrscheinlichkeitstheorie: 31, 271-285.
•	*FE2.1 MANDELBROT, B.B. 1975m. Hasards et tourbillons:
quatre contes a clef Annales de Mines (Novembre) 1-6.
•	MANDELBROT, B.B. 19750. Les objets fractals: forme,
hasard et dimension, Paris: Flammarion.
•	*E14 MANDELBROT, B.B. 1982c. The variation of certain
speculative prices. Current Contents: 14, 20.
•	MANDELBROT, В. B. 1982F. The Fractal Geometry of Nature.
New York: Freeman.
•	MANDELBROT, B.B. 1982t. The many faces of scaling:
fractals, geometry of nature and economics. Self Organization
and Dissipative Structures. W. C. Schieve & P. M. Alien: 91-109
(Eds.).
• MANDELBROT, B.B. 19861. Self-afiine fractals and fractal
dimension. Physica Scripta: 32, 257-260.
• MANDELBROT, B.B. 1986t. Self-affine fractal sets, I: The
Библиография
247
basic fractal dimensions, II: Length and area measurements, III:
Hausdorff dimension anomalies and their implications. Fractals
in Physics (Trieste, 1985). Ed. L.Pietronero and E.Tosatti.
Amsterdam: North-Holland, 3-28.
MANDELBROT, B.B. 1987r. Toward a second stage of
indeterminism in science (preceded by historical reflections),
Interdisciplinary Science Reviews: 12, 117-127.
MANDELBROT, B.B. 1995b. Statistics of natural resources
and the law of Pareto. Fractal Geometry and its Uses in the
Geosciences and in Petroleum Geology. Edited by С. C. Barton
& P. La Pointe. New York: Plenum, 1-12. First appeared as IBM
Research Note: NC-146, June 29, 1962.
MANDELBROT, B.B. 1995f. Measures of fractal lacunari-
ty: Minkowski content and alternatives. Fractal Geometry and
Stochastics. C.Bandt, S.Graf & M. Zahle (Eds.). Basel and
Boston: Birkhauser: 12-38.
MANDELBROT, B.B. 19951. The Paul Levy I knew. Levy
Flights and Related Phenomena in Physics (Nice, 1994).
M. F. Schlesinger, G.Zaslawsky & U. Frisch (Eds.) (Lecture
Notes in Physics). New York: Springer, 1995, ix-xii. First
appeared as IBM Research Note: NC-146, June 29, 1962.
MANDELBROT, B.B. 1995n. Introduction to fractal sums and
pulses. Levy Flights and Related Phenomena in Physics. Edited
by G. Zaslawsky, M. F. Shlesinger & U. Frisch (Lecture notes in
Physics). New York: Springer, 110-123.
*	FE2.1 MANDELBROT, B.B. 1996р. Du hasard benin au
hasard sauvage. Le hasard (Cahier special de Pour la Science):
12-17.
*	E MANDELBROT, B.B. 1997E. Fractals and Scaling in Fi-
nance: Discontinuity, Concentration, Risk. New York: Springer-
Verlag.
*	H MANDELBROT, B.B. 1997H. Fractals & Self-Affinity:
R/S, 1/ f, Global Dependence, Relief & Rivers. New York:
Springer-Verlag.
*	N MANDELBROT, B.B. 1997N. Multifractals & 1/f Noise.
New York: Springer-Verlag.
248
Библиография
•	*FE MANDELBROT, B.B. 1997FE. Fractales, hasard et
finance. Paris: Flammarion.
•	*FS MANDELBROT, B.B. 1997FS. Survols des Fractales.
Paris, Flammarion.
•	MANDELBROT, B.B., FISHER, A. & CALVET, L. 1997. The
multifractal model of asset returns (to appear).
•	*E21 MANDELBROT, B.B. & TAYLOR, H.M. 1967. On the
distribution of stock price differences. Operations Research: 15,
1057-1062.
•	*H MANDELBROT, В. B. & VAN NESS, J. W. 1968. Fractional
Brownian motions, fractional noises and applications. SIAM
Review: 10, 422-437.
•	*H MANDELBROT, B.B. & WALLIS, J.R. 1968. Noah,
Joseph and operational hydrology. Water Resources Research:
4, 909-918.
•	*H MANDELBROT, B.B. & WALLIS, J.R. 1969a. Computer
experiments with fractional Gaussian noises, Part 1,2 & 3. Water
Resources Research: 5, 228-267.
•	*H MANDELBROT, B.B. & WALLIS, J.R. 1969b. Some
long-run properties of geophysical records. Water Resources
Research: 5, 321-340.
•	*H MANDELBROT, В. B. & WALLIS, J. R. 1969c. Robustness
of the rescaled range R/S in the measurement of noncyclic
long-run statistical dependence. Water Resources Research: 5,
967-988.
•	MANDELBROT, B.B. & ZARNFALLER, F. 1959. Five-place
Tables of Certain Stable Distributions. IBM. Research Technical
Report RC-421.
•	ПРИМЕЧАНИЕ: См. также другие мои работы, в соавтор-
стве с Berger, Calvet, Cioczek-Georges, Fisher и Lovejoy.
• MANSFIELD, E. 1962. Entry, Gibrat’s law, innovation, and the
growth of firms. American Economic Review: 52, 1023-1051.
• MARSHALL, A. 1890. Principles of Economics. New York:
Macmillan. The ninth (variorum) edition, with a second volume
of annotations by C. W. Guillebaud, appeared in 1961.
Библиография
249
MATHERON, G. 1962. Traite de geostatistique appliquee. 1,
Paris: Technip.
MCCULLOCH, J.H. 1996. Financial applications of stable
distributions. Statistical Methods in Finance. G. S. Maddala &
C.R. Rao (Eds.). (Handbook of Statistics: 14). Amsterdam:
Elsevier: 393-425.
MCKIE, J. W. 1960. Market structure and uncertainty in oil and
gas exploration. Quarterly J. of Economics: 74, 543-571.
ME1DELL, B. 1912. Zur Theorie des Maximums (resumes
detailles en anglais et fran^ais). Comptes-Rendus du Septieme
Congres d’Actuaires, Amsterdam: 1, 85-99.
MEIDELL, B. 1937. Zur Theorie und Praxis des Maximums
in Lebensversicherung. Comptes-Rendus du Onzieme Congres
d'Aduaires, Paris, 1, 469.
MILLER, H. P. 1955. The Income of the American People. New
York: Wiley.
MILLS, F. C. 1927. The Behavior of Prices. New York: National
Bureau of Economic Research.
MIROWSKI, P. 1990. From Mandelbrot to chaos in economic
theory. Southern Economics Journal, 57, 289-307.
MIROWSKI, P. 1996. Mandelbrot’s economics after a quarter
century. Fractals, 3, 581-196. Reprinted in Evertsz & al 1996:
177-196.
MITCHELL, W.C. 1915. The making and using of index
numbers. Introduction to Index Numbers and Wholesale Prices in
the United States and Foreign Countries. U.S. Bureau of Labor
Statistics Bulletin 173. Reprinted in 1921 as Bulletin 284.
MOORE, A. 1962. A Statistical Analysis of Common Stock
Prices. Unpublished Ph.D. dissertation. Graduate School of
Business, University of Chicago.
MOORE, H. L. 1911. The Laws of Wages. New York: Macmillan.
MORRIS, W. S. 1962. Towards a Workable Theory of Markets.
New York: W. S. Morris & Co.
MORLAT, G., BILLIET & BERNIER. 1956. Les crues de la
Haute Durance. Symposia Darcy, Dijon.
250
Библиография
•	NIEDERHOFFER, V. 1959. Clustering of stock prices. Opera-
tions Research: 13, 258-265.
•	NOLAN, J.P. 1996a. Numerical calculation of stable densities.
Preprint.
•	OFFICER, R. R. 1972. The distribution of stock returns. Journal
of the American Statistical Association: 67, 807-812.
•	THE OIL AND GAS JOURNAL. 1958. Journal survey of proved
reserves: Where the nation’s oil is stored. The Oil and Gas J.,
January 27, 1958: 163-168.
•	OLIVIER, M. 1927. Les nombres indices de la variation des
prix. Paris.
•	OLSEN 1996. Это общее обозначение отсылает читателя к
большому собранию препринтов и редких статей, состав-
ленному компанией «Olsen & Associates» из Цюриха. Ниже
в алфавитном порядке перечислены авторы представленных
в собрании работ: В. Chopard, М. М. Dacarogna, R.D.Dave,
С. G. de Vries, С. L. Gauvreau, D. M. Guillaume, C. Jost, C. Mor-
genegg, U. A. Muller, R.J.Nagler, M. Oudsaidene, O.V Pictet,
R. Schirru, M. Schwarz, M.Tomassini, J.E. von Weizsacker,
J. R. Ward. (Статьи можно распечатать прямо из «сети».)
•	OSBORNE, M.F.M. 1959. Brownian motion in the stock
market. Operations Research: 1, 145-173. Reprinted in Cootner
1964: 100-128. Reply to Comments. Operations Research: 7,
807-811.
•	OSBORNE, M.F.M. 1962. Periodic structure in the Brownian
motion of stock prices. Operations Research: 10, 345-379.
Reprinted in [Cootner 1964]: 262-296.
•	PARETO, V. 1896 (1965). Cours d‘economic politique. The
second date refers to the reprint in Pareto: Oeuvres completes.
Geneva: Droz.
•	PARIKH, C. 1991. The unreal lift of Oscar Zariski. New York:
Academic Press.
•	PARZEN, E. 1960. Modern Probability Theory and its Applica-
tions. New York: Wiley.
•	QUETELET, A. 1835. Sur I’homme et le developpement de ses
facultes: Essai de physique sociale. Paris: Bachelier.
Библиография
251
RACHEV, S. T. 1996. Modeling Financial Assets with Alternative
Stable Models. New York: Wiley.
RACHEV, S.T. & MITTNIK, S. 1997. Stable Modelling
in Finance. Special Issue of the journal Mathematical and
Computer Modelling.
RAY, D. 1958. Stable processes with an absorbing barrier.
Transactions of the American Mathematical Society: 89, 16-24.
REMERY, R. 1946. Distribution et dispersion des prix fran^ais
depuis 1929. These de 1’Institut de Statistique, Universite de
Paris, Bulletin de la Statistique Generale de la France.
RICHARDSON, L.F. 1922. Weather prediction by numerical
process. Cambridge University Press. The Dover reprint contains
a biography as part of the introduction by J. Chapman.
RICHARDSON, L.F. 1960. Statistics of deadly quarrels. A
chapter of Arms and Insecurity. Chicago: Quadrangle Books.
ROBERTS, H.V. 1959. Stock market «patterns» and financial
analysis: methodological suggestions. Journal of Finance: 14,
1—10. Reprinted in [Cootner 1964]: 7-16.
ROLL, R. 1970. Behavior of Interest Rates: the Application of
the Efficient Market Model to U. S. Treasury Bills. New York:
Basic Books.
ROY, A. D. 1951. Some thoughts on the distribution of earnings.
Oxford Economic Papers: 3, 135-146.
ROZELLE, J. & FIELITZ, B. 1980. Skewness in common stock
returns. Financial Review: 15, 1-23.
RUTHERFORD, R. S.G. 1955. Income distributions: a new
model. Econometrica: 23, 277-294.
RVACEVA, E.L. 1954. On the domain of attraction of
multidimensional distributions. Ucenye Zapiski Lvovskogo Go-
sudarstvennogo Universiteta, Ser. Mekh. Mat.: 6, 5-44.
SAMORODNITSKY, G. & TAQQU, M. S. 1994. Stable Non-Ga-
ussian Random Processes. New York: Chapman & Hall.
SAMUELSON, P.A. 1957. Intertemporal price equilibrium:
A prologue to the theory of speculation. Weltwirtschaftliches
Archiv, 79, 181-221.
252
Библиография
•	SAMUELSOH Р. А. 1965. Proof that properly anticipated prices
fluctuate randomly. Industrial Management Review: 6, 41-49.
•	SAMUELSON, P. A. 1967. Efficient portfolio selection for
Pareto-Levy investments. Journal of Financial and Quantitative
Analysis: 2, 107-122.
•	SAPOVAL, B. 1997. Universalites etfractales: jeu d’enfants ou
delit d’inities? Paris: Flammarion.
•	SHOHAT, J. A. & TAMARKIN, J.D. 1943. The Problem of
Moments. Providence, RI: American Mathematical Society.
•	SICHEL, H. S. 1952. New methods in the statistical evaluation
of mine sampling data. Transactions of the Institute of Mining
and Metallurgy: 61, 261-288.
•	SIMON, H. A. 1955. On a class of skew distribution functions.
Biometrika: 42, 425-440.
•	SIMON, H. A. & BONINI, C. 1958. The size distribution of
business firms. American Economic Review: 48, 607-617.
•	SKOROHOD, A. V. 1954. Asymptotic formulas for stable Pare-
tian laws. Doklady Akademii Nauk SSSR: 731-35. Or: Selected
Translations in Mathematics Statistics and Probability (American
Mathematical Society): 1961, 157-161.
•	STEIGER, W. 1964. A test of nonrandomness in stock price
changes. In [Cootner 1964]: 98, 254-61.
•	STENT, G. 1972. Prematurity and uniqueness in scientific
discovery. Scientific American: 227 (December) 84-93. Also see
his book, Paradoxes of progress, New York: W. H. Freeman.
•	TAQQU, M. 1970. Note on evaluations of R/S for fractional
noises and geophysical records. Water Resources Research: 6,
349-50.
•	TAKANO, K. 1954. On some limit theorems of probability
distributions. Annals of Statistical Mathematics: 6, 37-113.
•	TAKANO, K. 1955. Central convergence criterion in the
multidimensional case. Annals of the Institute of Statistical
Mathematics: 7.
•	TELSER, L. 1958. Future and the storage of cotton and wheat.
Journal of Political Economy: 65, 233-255.
Библиография
253
TELSER, L. 1960. Reply, Journal of Political Economy: 68,
404-415.
THEBAUT, J. Y. 1961. Distribution lognormale de certains
caracteres de quelques phenomenes geologiques et ses appli-
cations. Revue de Statistique Appliquee: 9, 37-87.
THURSTONE, L. L. 1947. Multiple-factor Analysis. Chicago:
University of Chicago Press.
TINBERGEN, J. 1956. On the theory of income distribution.
Welwirtschaftliches Archiv: 77, 155-175. Also in TINBERGEN,
J. 1959, Selected Papers. Amsterdam: North-Holland, 243-263.
TINTNER, G. 1940. The Variate-Difference Method. Blooming-
ton, IN: Principia Press.
VON SAVITSCH & BENKTANDER, G. 1953. On the variation
of the risk premium with the dimension of the house within fire
insurance. Skandinavisk Aktuarietidskrift: 26, 203-214.
VOSS, R.F. 1992. 1// noise and fractals in economic time
series. Fractal Geometry and Computer Graphics. J. L. Encar-
nacao, H.-O. Peitgen, G. Sakas & G. Englert (Eds.). New York:
Springer, 45-52.
WALSH, J. 1949. Review of Zipf 1949. Scientific American.
WALTER, C. 1994. Les structures des hasard en economic:
efficience des marches, lois stables, et processus fractals. (Ph.D.
Thesis in Economics, Institut d’Etudes Politiques).
WALTER, C. 1995. Levy-stability-under-addition and fractal
structure of markets: implications for the actuaries and emphasi-
zed examination of MATIF national contract. Proceedings of the
5th AFIR Colloquium (Bruxelles): 3, 1285-1330. To be reprinted
in [Rachev & Mittnik 1997].
WALTER C. 1996. Une histoire du concept d’efficience sur
les marches financiers. Annales: Histoire, Sciences Sociales, 4,
873-905.
WALTER C. 1996. Chronique dans la revue Pour la Science.
WAX, N. (Ed.) 1954. Noise and Stochastic Processes. New York:
Dover, 1954.
254
Библиография
•	WEISS, Н.К. 1963. Stochastic model for the duration and
magnitude of a deadly quarrel. Operations Research: 11,
101-121.
•	WESTERGAARD, H. L. & NYBOELLE, H. C. 1928. Grundzdge
der Theorie der Statistik, Jena: G. Fischer.
•	WILLIS, J.C. 1922. Age and Area. Cambridge: Cambridge
University Press.
•	WOLD, H. 1938. A Study in Stationary Time Series. Stockholm:
Almqvist & Wicksell. (Second edition, 1954.)
•	WOLD, H. & WHITTLE, P. 1957. A model explaining the Pareto
distribution of wealth. Econometrica: 25, 591-595.
•	WORKING, H. 1933. Price relations between July and September
wheat futures at Chicago since 1885. Wheat Studies: 9, 187-238.
•	WORKING, H. 1934. A random-difference series for use in
the analysis of time series. Journal of the American Statistical
Association: 29, 11-24.
•	WORKING, H. 1934. Prices of cash wheat and futures at
Chicago since 1883. Wheat Studies of the Stanford Food
Institute: 2, 75-124.
•	WORKING, H. 1948. Theory of the inverse carrying charge in
future markets. Journal of Farm Economics: 30, 1-28.
•	WORKING, H. 1960. Note on the correlation of first differences
of averages in a random chain. Econometrica: 28, 916-918.
Reprinted in [Cootner 1964]: 129-131.
•	YOUNG, M. S. & GRAFF, R. A. 1995. Real estate is not normal:
a fresh look at real estate return distribution. Journal of Real
Estate Finance and Economics: 10, 225-259.
•	YOUNG. 1969. Winter meeting of the Econometric Society, New
York, 1969.
•	YOUNG, W.E. 1971. Random walk of stock prices; a test of the
variance time function. Econometrica: 34, 797-812.
•	YULE, G.U. 1924. A mathematical theory of evolution, based
on the conclusions of Dr. J.C.Willis, F.R.S. Philosophical
Traditions of the Royal Society (London): 213B, 21-87.
Библиография
255
ZAJDENWEBER, D. 1976. Hasard et prevision (These pour le
Doctoral es Sciences Economiques, Faculte de Droit de Paris,
December 1972). Paris: Economica.
ZAJDENWEBER, D. 1994. Self-similarite de 1’index CAC 40.
Revue d’Economie Politique: 104, 407-434.
ZAJDENWEBER, D. 1995a. Business interruption insurance,
a risky business. A study on some paretian risk phenomena.
Fractals: 3, 601-608.
ZAJDENWEBER, D. 1995b. Extreme values in business
interruption insurance, The Journal of Risk and Insurance: 63,
95-110.
ZIPF, G.K. 1941. National Unity and Disunity. Bloomington,
IN: Principia Press.
ZIPF, G.K. 1949. Human Behavior and the Principle of
Least-effort. Cambridge, MA: Addison-Wesley. Reprint, New
York: Hefner.
ZOLOTAREV, V. 1985. Stability Problems for Stochastic
Models: Proceedings Uzhgorod, 1984. Lecture Notes in Ma-
thematics: 1155. New York: Springer.
ZOLOTAREV, V. 1986. One-Dimensional Stable Distributions.
Providence, RI: American Mathematical Society.
Интересующие Вас книги нашего издательства можно заказать почтой или
электронной почтой:
subscribe@rcd.ru
Внимание: дешевле и быстрее всего книги можно приобрести через наш
Интернет-магазин:
http ://shop.rcd.ru
Книги также можно приобрести:
1.	Москва, ФТИАН, Нахимовский проспект, д. 36/1, к. 307,
тел.: 332-48-92 (почтовый адрес: Нахимовский проспект, д. 34).
2.	Москва, ИМАШ, ул. Бардина, д. 4, корп. 3, к. 414, тел. 135-54-37.
3.	МГУ им. Ломоносова (ГЗ, 1 этаж).
4.	Магазины:
Москва: «Дом научно-технической книги» (Ленинский пр., 40)
«Московский дом книги» (ул. Новый Арбат, 8)
«Библиоглобус» (м. Лубянка, ул. Мясницкая, 6)
Книжный магазин «ФИЗМАТКНИГА» (г. Долгопрудный,
Новый корпус МФТИ, 1 этаж, тел. 409-93-28)
С.-Пб.: «С.-Пб. дом книги» (Невский пр., 28)
Бенуа Мандельброт
Фракталы, случай и финансы
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Компьютерная верстка С. В. Высоцкий
Корректор 0.3. Логунова
Подписано в печать 01.06.2003. Формат 80 х lOO1^.
Печать офсетная. Усл. печ.л. 11,84. Уч. изд. л. 14,32.
Гарнитура Таймс. Бумага офсетная №1.
Доп. тираж 2000 экз. Заказ № 2360.
Научно-издательский центр «Регулярная и хаотическая динамика»
426034, г. Ижевск, ул. Университетская, 1.
Лицензия на издательскую деятельность ЛУ №084 от 03.04.00.
http://rcd.ru E-mail: borisov@rcd.ru
Отпечатано в полном соответствии с качеством
предоставленных диапозитивов в ОАО «Дом печати — ВЯТКА».
610033, г. Киров, ул. Московская, 122.