Фракталы и мультифракталы - Божокин С.В., Паршин Д.А.

Автор: Божокин С.В. Паршин Д.А.

Теги: физика фракталы

ISBN: 5-93972-060-9

Год: 2001

Похожие

Фракталы на Солнце

Фракталы в физике

Фракталы в радиофизике и радиотехнике. Топология выборки

Фракталы, случай и финансы

Текст

С. В. Божокин
Д. А. Паршин
R&C

С. В. Божокин, Д. А. Паршин
ФРАКТАЛЫ
И МУЛЬТИФРАКТАЛЫ
Учебное пособие
R&G
Москва ¦ Ижевск
2001

УДК 530.1
Интернет-магазин
http://shop.rcd.ru
Интересующие Вас книги, выпускаемые нашим издательством, дешевле и быстрее всего
приобрести через интернет-магазин. Регистрация в магазине позволит Вам
• приобретать книги по наиболее низким ценам;
• подписаться на регулярную рассылку сообщений о новых книгах;
• самое быстрое приобретение новых книг до поступления их в магазины.
Божокин СВ., Паршин Д. А.
Фракталы и мультифракталы. — Ижевск: НИЦ «Регулярная и хао-
хаотическая динамика», 2001, 128 с.
Учебное пособие посвящено изложению основных идей фрактальной и мультифрак-
тальной геометрии. Примеры различных фрактальных структур можно встретить
во многих явлениях природы. Фрактальные образы с успехом используются при опи-
описании хаотического поведения нелинейных динамических и диссипативных систем,
турбулентного течения жидкости, неоднородного распределения материи во Вселен-
Вселенной, при исследовании трещин и дислокационных скоплений в твердых телах, при
изучении электрического пробоя, диффузии и агрегации частиц, роста кристаллов
и т. д. Много интересных идей фрактальной геометрии нашли свое применение в эко-
экономике при анализе колебаний курса валют, в биологии для объяснения морфологи-
морфологического строения различных биологических объектов, в физике твердого тела для
описания перехода Андерсона металл-диэлектрик и других свойств неупорядоченных
систем.
Пособие написано по материалам курсов лекций, прочитанных авторами в разное
время на физико-механическом факультете Санкт-Петербургского государственного
технического университета для студентов 4-5 курсов, обучающихся на специальнос-
специальностях "Биофизика", "Физика металлов" и "Спектроскопия твердого тела".
Пособие будет полезно аспирантам и студентам физических специальностей, ин-
интересующихся современными проблемами физики.
ISBN 5-93972-060-9
© Божокин СВ., Паршин Д.А., 2001
© НИЦ «Регулярная и хаотическая динамика», 2001
http:// rcd.ru

СОДЕРЖАНИЕ
Введение 5
1 ФРАКТАЛЫ 12
1.1 Регулярные фракталы 12
1.1.1 Понятие фрактала 12
1.1.2 Длина береговой линии 13
1.1.3 Фрактальная размерность множества 15
1.1.4 Канторовское множество 17
1.1.5 Снежинка Коха 18
1.1.6 Салфетка и ковер Серпинского 20
1.1.7 Губка Менгера 24
1.1.8 Кривые Пеано 25
1.1.9 Вселенная Фурнье 30
1.2 Итерации линейных систем 32
1.2.1 Системы итерируемых функций 32
1.2.2 Метод случайных итераций, или игра в хаос . . 37
1.2.3 Игры с поворотами 42
1.2.4 Сжимающие аффинные преобразования 49
1.2.5 Лист папоротника 54
1.3 Нелинейные комплексные отображения 63
1.3.1 Квадратичные отображения 63
1.3.2 Неподвижные точки. Циклы 64
1.3.3 Множество Жюлиа 66
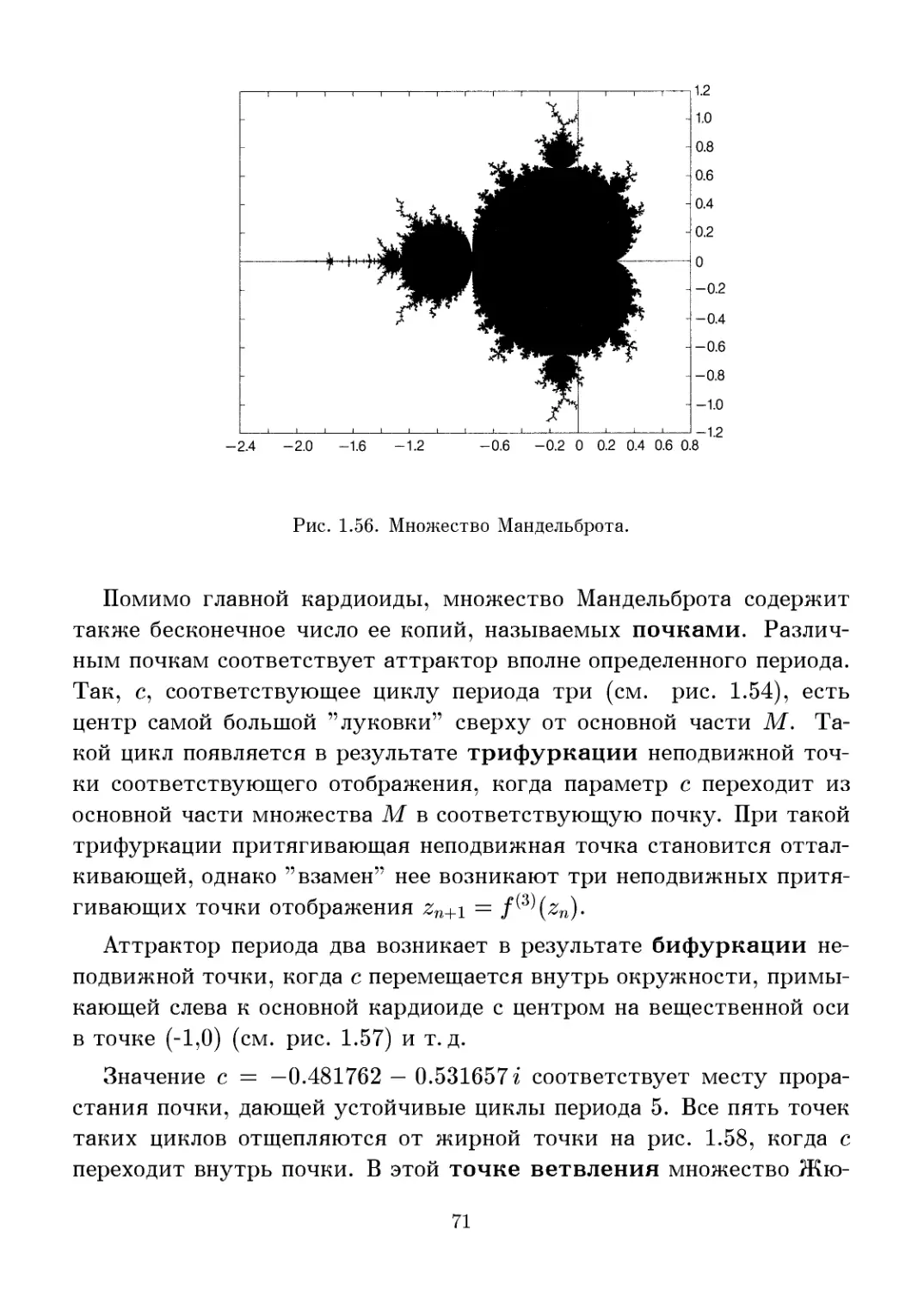
1.3.4 Множество Мандельброта и классификация мно-
множеств Жюлиа 70
1.3.5 Построение множества Мандельброта 76
1.3.6 Комплексные Ньютоновы границы 78
2 МУЛЬТИФРАКТАЛЫ 83
2.1 Геометрическое описание мультифракталов 83
2.1.1 Что такое мультифрактал? 83
2.1.2 Обобщенные фрактальные размерности Dq . . . 86
2.1.3 Фрактальная размерность Dq и информационная
размерность D\ 89
2.1.4 Корреляционная размерность D<i 92
3

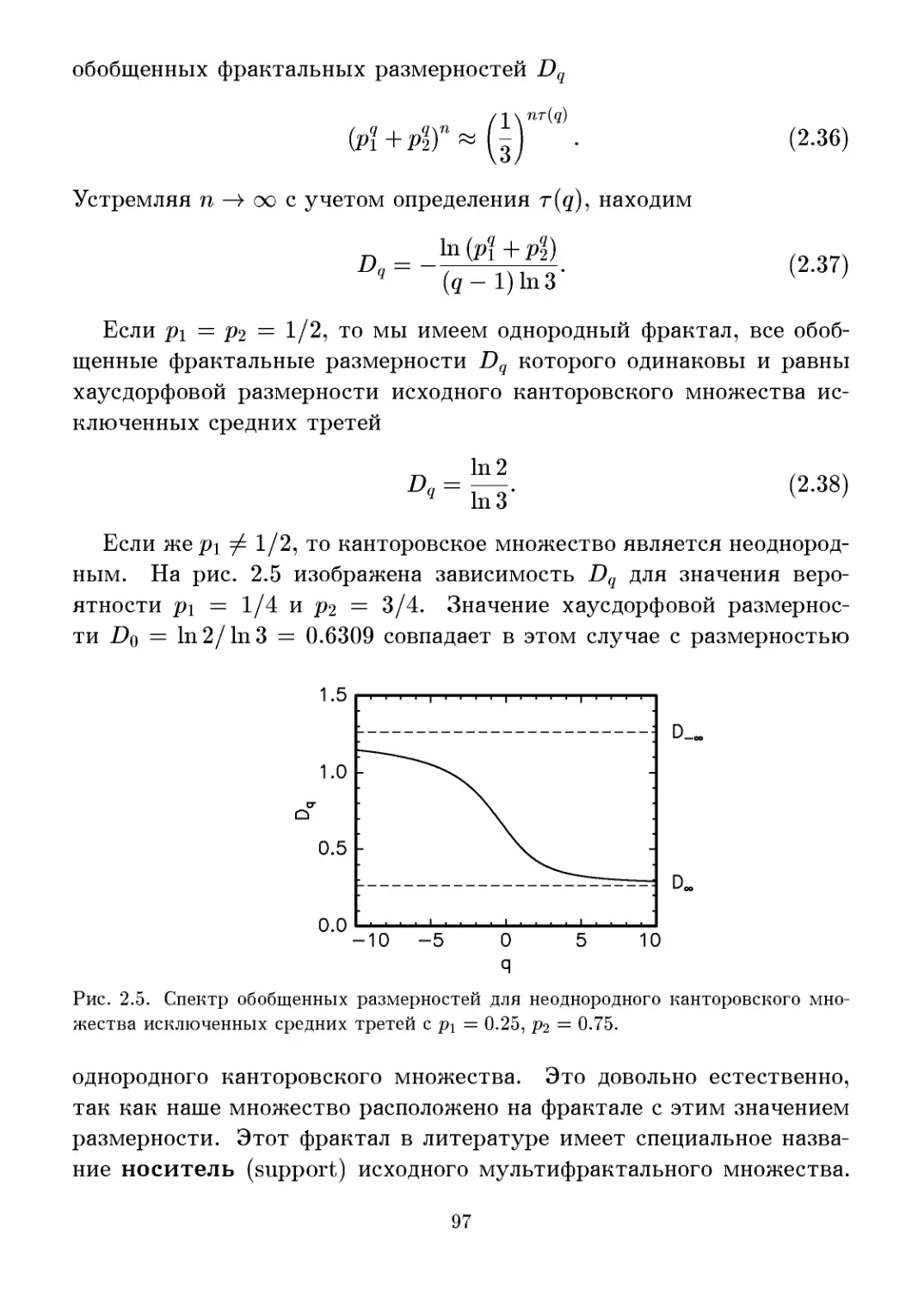
2.1.5 Свойства функции Dq 95
2.1.6 Неоднородное канторовское множество 95
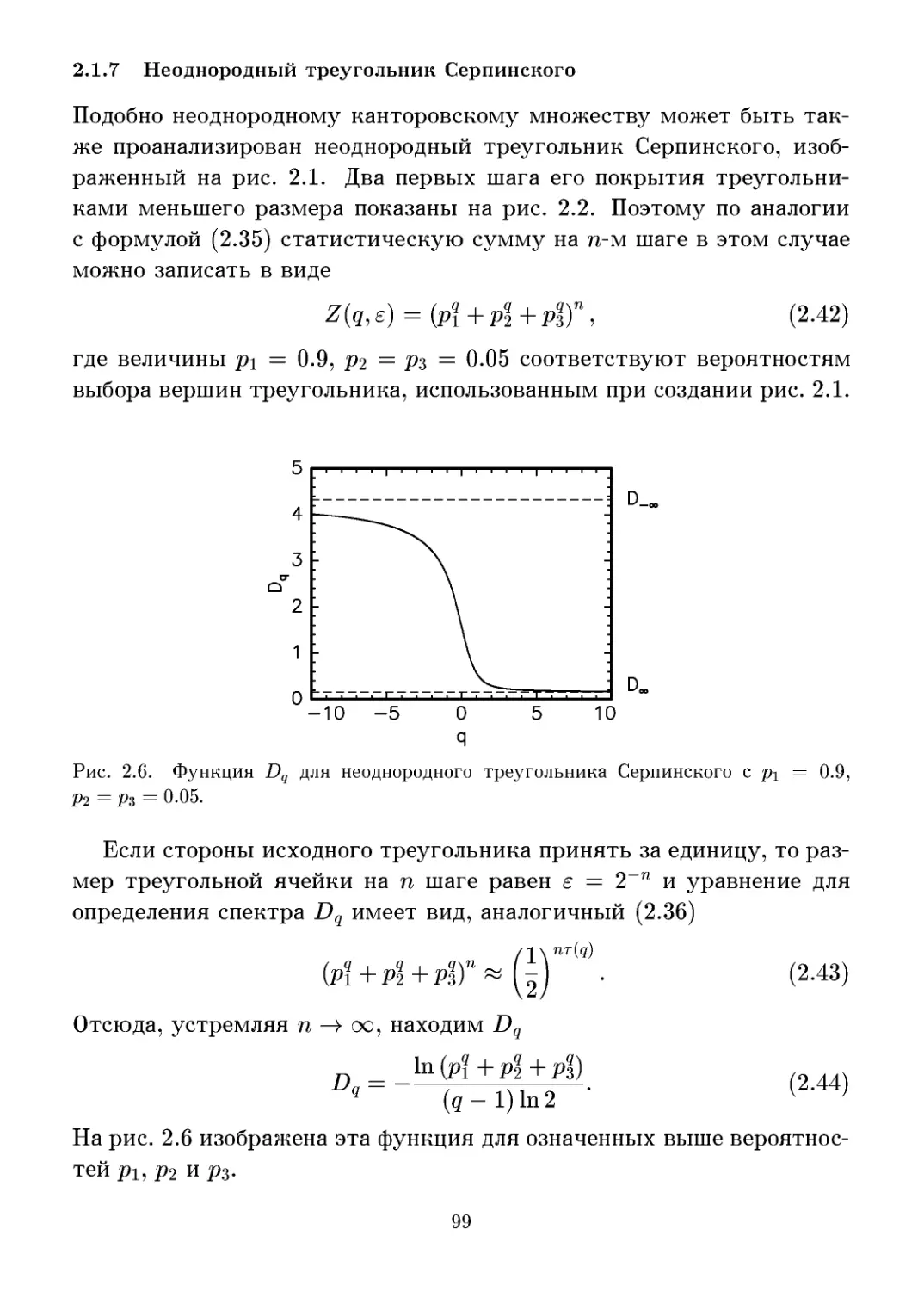
2.1.7 Неоднородный треугольник Серпинского .... 99
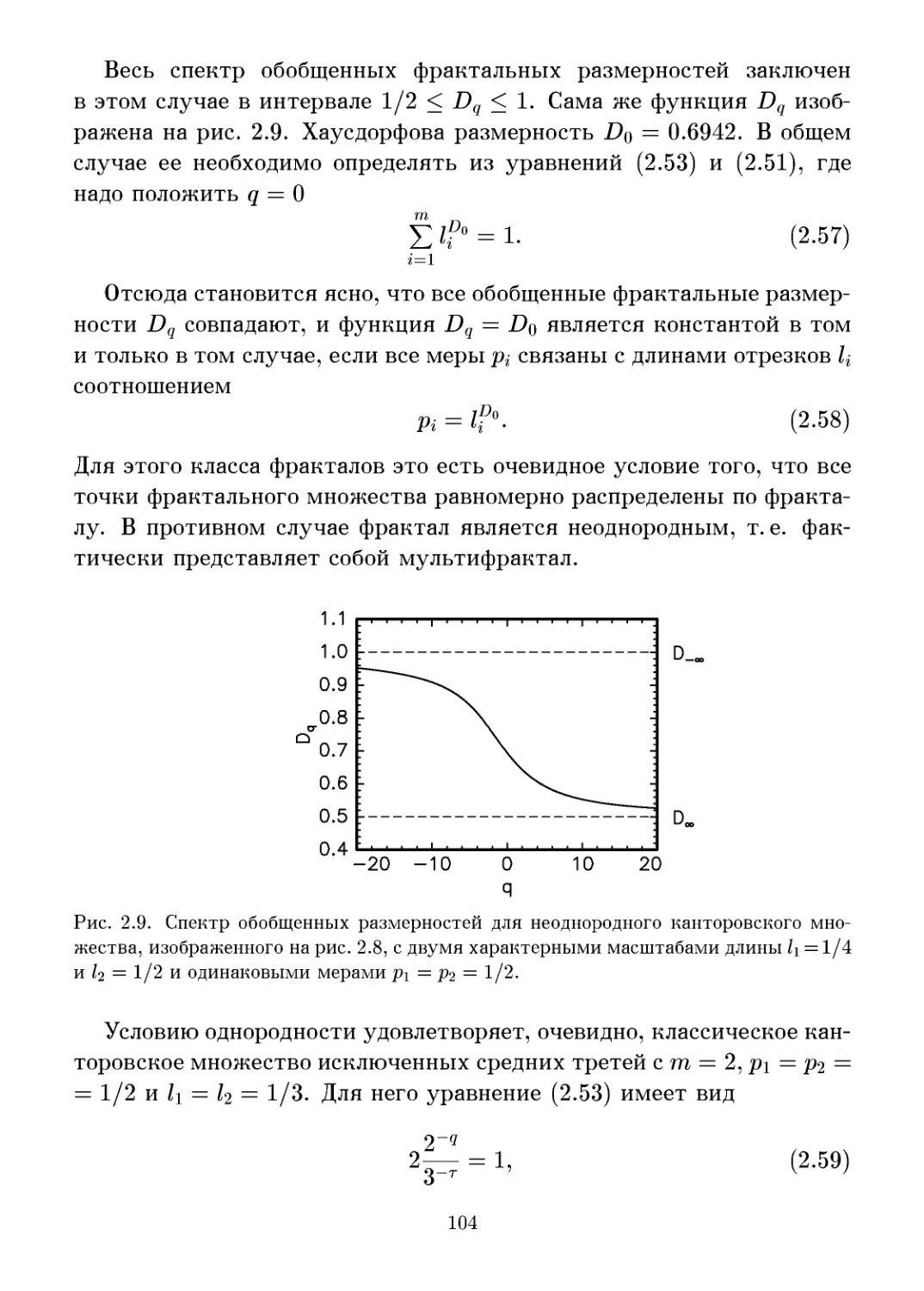
2.1.8 Канторовское множество с двумя характерными
масштабами длины 101
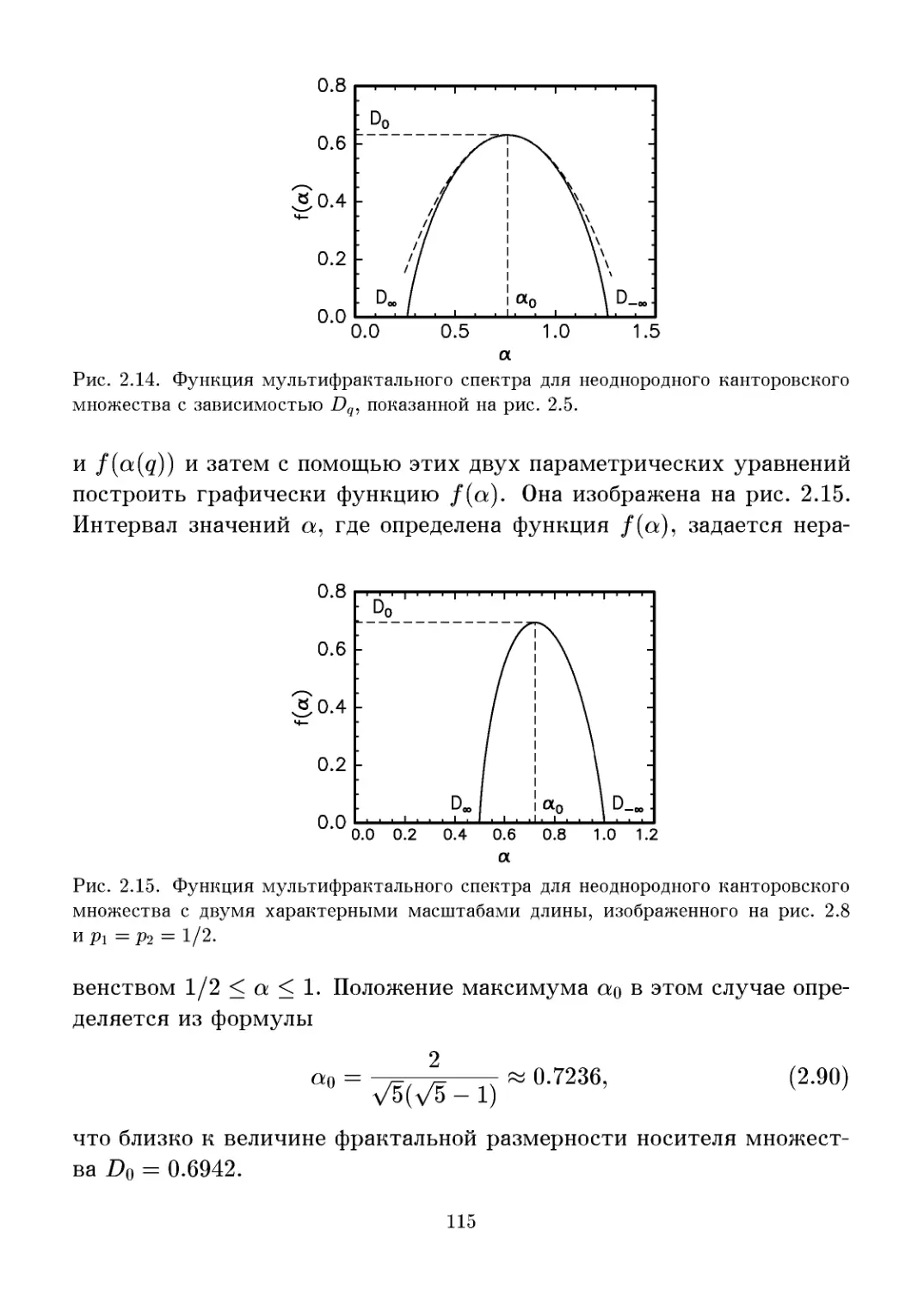
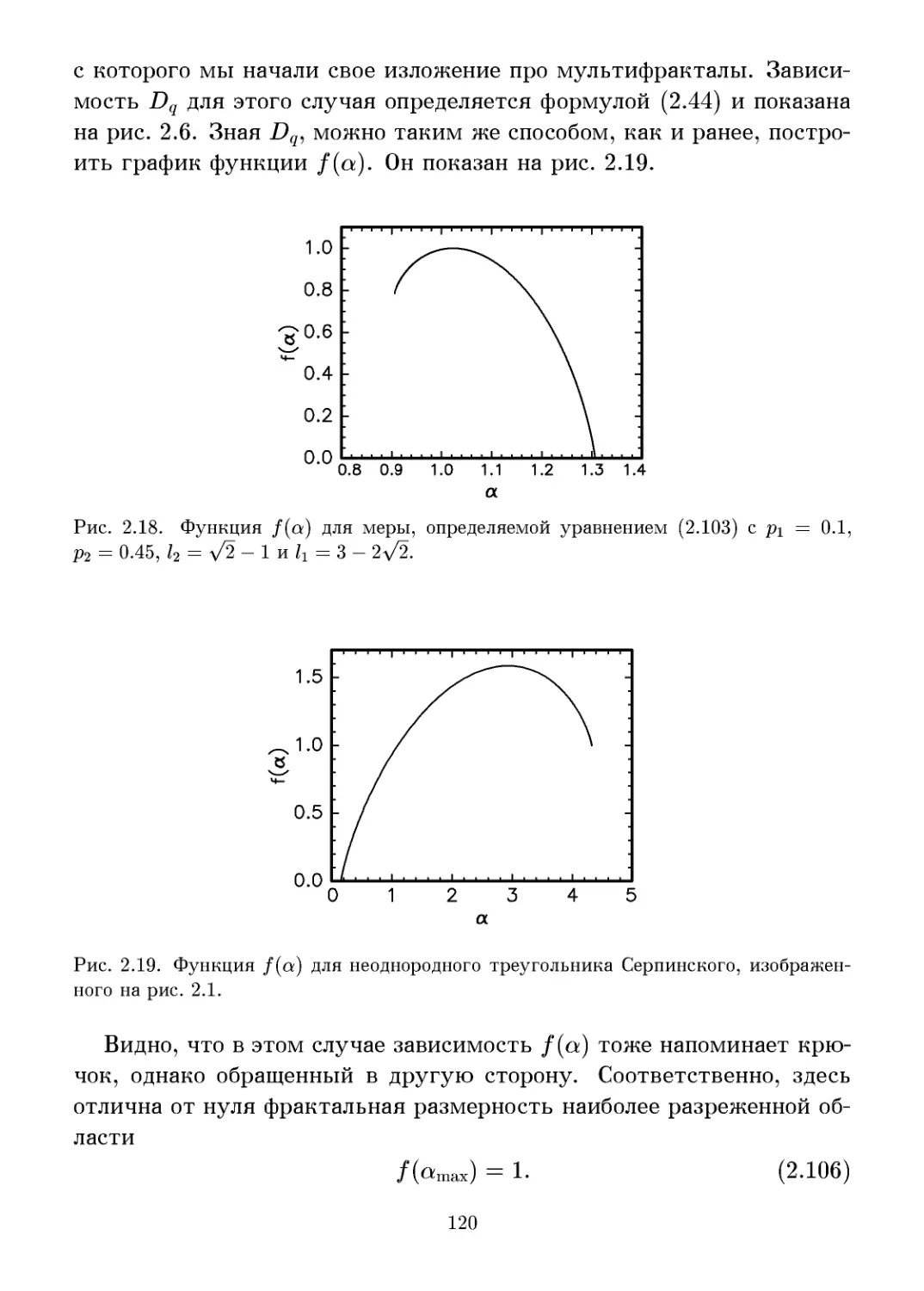
2.2 Функция мультифрактального спектра f(a) 105
2.2.1 Спектр фрактальных размерностей 105
2.2.2 Преобразование Лежандра 109
2.2.3 Свойства функции f(a) Ill
2.2.4 Примеры функций f(a) 114
2.3 Применение теории мультифракталов в физике 121
2.3.1 Переход Андерсона 121
Литература 131

Введение
Язык науки стремительно меняется в современном мире. История
развития физики насчитывает уже не одно столетие. За это время из-
изучено огромное количество разнообразных явлений природы, откры-
открыты фундаментальные законы физики, объясняющие различные экс-
экспериментальные факты. Каждый раз, сталкиваясь с новыми природ-
природными объектами, ученые вводят в язык науки новые категории, тер-
термины и понятия. Математики, и особенно физики, при описании
всего богатства и удивительной красоты окружающего нас мира под-
подчас мыслят образами, используя эстетические категории в качестве
критерия, если не истины, то по крайней мере художественной завер-
завершенности. Великий ученый Галилео Галилей, рассуждая о научном
познании окружающего мира, в 1623 году писал:
"Вся наука записана в этой великой книге, — я имею в виду
Вселенную, — которая всегда открыта для нас, но которую
нельзя понять, не научившись понимать язык, на котором
она написана. А написана она на языке математики, и ее
буквами являются треугольники, окружности и другие гео-
геометрические фигуры, без которых человеку невозможно ра-
разобрать ни одного ее слова; без них он подобен блуждаещему
во тьме."
До недавнего времени геометрические модели различных природ-
природных конструкций традиционно строились на основе сравнительно
простых геометрических фигур: прямых, многоугольников, окруж-
окружностей, многогранников, сфер. Однако очевидно, что этот классичес-
классический набор, вполне достаточный для описания элементарных струк-
структур, становится плохо применимым для характеристики таких слож-
сложных объектов, как очертание береговых линий материков, поле ско-
скоростей в турбулентном потоке жидкости, разряд молнии в воздухе,
пористые материалы, форма облаков, снежинки, пламя костра, кон-
контуры дерева, кровеносно-сосудистая система человека, поверхность
клеточной мембраны и др. В последние 15-20 лет для описания этих
и им подобных образований ученые все чаще используют новые гео-
геометрические понятия.

Одним из таких понятий, изменившим многие традиционные пред-
представления о геометрии, явилось понятие фрактала. Оно было введе-
введено в обращение замечательным французским математиком польского
происхождения Бенуа Мандельбротом в 1975 году. И хотя в мате-
математике похожие конструкции в той или иной форме появились уже
много десятков лет назад, в физике ценность подобных идей была
осознана лишь в 70-е годы нашего столетия. Важную роль в широком
распространении идей фрактальной геометрии сыграла замечатель-
замечательная книга Б. Мандельброта "Фрактальная геометрия природы" [1].
Фрактальные объекты, согласно своему начальному определению, об-
обладают размерностью, строго превышающей топологическую размер-
размерность элементов, из которых они построены. Характеризуя новые
идеи, Мандельброт писал:
"Почему геометрию часто называют холодной и сухой? Од-
Одна из причин заключается в ее неспособности описать фор-
форму облака, горы, дерева или берега моря. Облака — это не
сферы, горы — это не конусы, линии берега — это не окруж-
окружности, и кора не является гладкой, и молния не распростра-
распространяется по прямой... Природа демонстрирует нам не просто
более высокую степень, а совсем другой уровень сложнос-
сложности. Число различных масштабов длин в структурах всегда
бесконечно".
Основой новой геометрии является идея самоподобия. Она выра-
выражает собой тот факт, что иерархический принцип организации фрак-
фрактальных структур не претерпевает значительных изменений при рас-
рассмотрении их через микроскоп с различным увеличением. В резуль-
результате эти структуры на малых масштабах выглядят в среднем также,
как и на больших. Здесь следует провести разницу между геометрией
Евклида, имеющей дело исключительно с гладкими кривыми, и бес-
бесконечно изрезанными самоподобными фрактальными кривыми. Эле-
Элементы кривых у Евклида всегда самоподобны, но тривиальным об-
образом: все кривые являются локально прямыми, а прямая всегда
самоподобна. Фрактальная же кривая, в идеале, на любых, даже са-
самых маленьких масштабах не сводится к прямой и является в общем
случае геометрически нерегулярной, хаотичной. Для нее, в частнос-
частности, не существует и понятия касательной в точке, так как функции,
6

описывающие эти кривые, являются в общем случае недифферен-
цируемыми.
Возможно, что наиболее убедительным аргументом в пользу из-
изучения фракталов является их бросающаяся в глаза красота. Фрак-
Фрактальные объекты удивительным образом перекинули мост между ло-
логическим подходом к познанию природных явлений, который присущ
научному мышлению, и интуитивным подходом, когда человек пыта-
пытается воссоздать окружающий мир с помощью богатства эстетических
форм и звуков. Оказывается, что при анализе многих фракталов,
построенных на основе точных математических алгоритмов, более
уместны эстетические категории и ассоциации. В подтверждение
этого приведем слова выдающегося немецкого математика Германа
Вейля A885-1955 гг.):
"В своей работе я всегда пытался объединить истину с кра-
красотой, а когда мне приходилось выбирать между ними, я
обычно выбирал красоту".
Многие крупные достижения науки о фракталах стали возмож-
возможны только с использованием методов вычислительной математики,
которая в настоящее время немыслима без применения современ-
современных компьютеров. "Компьютерные эксперименты" позволили полу-
получить достаточно полное представление о разнообразных фрактальных
структурах и причинах их возникновения. Часто теоретическое мо-
моделирование этих структур подчас даже опережало эксперименталь-
экспериментальные методы изучения реальных природных объектов сложной формы.
Любопытно отметить, что с появлением фракталов вычислитель-
вычислительная математика стала сама непосредственно участвовать в создании
истинных эстетических ценностей. Главным образом это относится
к компьютерной графике, которая переживает сегодня период интен-
интенсивного развития. Она оказалась способна воссоздать на экране мони-
монитора бесконечное разнообразие фрактальных форм и пейзажей, погру-
погружая зрителя в удивительное виртуальное пространство, существую-
существующее в "воображении" компьютера. В настоящее время при помощи
сравнительно простых алгоритмов появилась возможность создавать
трехмерные изображения фантастических ландшафтов и форм, ко-
которые способны преобразовываться во времени в еще более захваты-
захватывающие картины. С другой стороны, часто искусственные изображе-
7

ния фракталов столь схожи с естественными, природными формами,
что их невозможно отличить друг от друга. Стремительное втор-
вторжение компьютеров в мир искусства во многом изменило понятие
красоты и гармонии, живописной выразительности и точности вос-
воссоздания окружающего мира.
Конечно, до сих пор не утихают споры — может ли вычисли-
вычислительная машина создавать произведения искусства. И хотя, на наш
взгляд, становится постепенно ясно, что ответ на этот вопрос скорее
является положительным, давайте оставим предмет этого спора буду-
будущим искусствоведам и философам и перейдем к непосредственному
изучению этого нового раздела естествознания.
Несколько слов об истории развития идей фрактальной геометрии.
Она тесно связана с именами таких известных математиков, как
Вейерштрасс, Кантор, Пеано, Хаусдорф, Безикович, Кох, Серпинский
и др. Так Вейерштрасс впервые ввел в обращение непрерывную, но
нигде не дифференцируемую функцию. Хаусдорф в 1919 г. ввел по-
понятие о дробной размерности множеств и привел первые примеры
таких множеств. Среди них были канторовское множество, кривая
Коха и другие экзотические объекты, мало в то время известные за
пределами чистой математики. Оригинальные идеи Хаусдорфа впо-
впоследствии были существенно развиты Безиковичем.
Большой вклад в будущую фрактальную геометрию внесли также
знаменитые работы французских математиков Г. Жулиа и П. Фату,
которые в начале 20 века занимались теорией рациональных отобра-
отображений в комплексной плоскости. Практически полностью забытая,
их деятельность получила неожиданное развитие в начале восьмиде-
восьмидесятых годов, когда с помощью компьютеров математикам удалось по-
получить прекрасные картины, показывающие примеры таких отобра-
отображений. Это уже была эра фрактальной геометрии, поскольку неза-
незадолго до этого, в середине 70-х годов, в науке появился совершенно
новый термин "фрактал", характеризующий нерегулярный, но само-
самоподобный объект, который удобно было характеризовать нецелочис-
нецелочисленной размерностью.
Для многих стало очевидно, что старые, добрые формы евклидо-
евклидовой геометрии сильно проигрывают большинству природных объек-
объектов из-за отсутствия в них некоторой нерегулярности, беспорядка

и непредсказуемости. Может быть, в будущем новые идеи фрак-
фрактальной геометрии помогут нам изучить многие загадочные явления
окружающей природы. В настоящее время фракталы и мультифрак-
талы стремительно вторгаются во многие области физики, биологии,
медицины, социологии, экономики. Методы обработки изображений
и распознавания образов, использующие новые понятия, дают воз-
возможность исследователям применить этот математический аппарат
для количественного описания огромного количества природных объ-
объектов и структур.
Язык фрактальной геометрии необходим, например, при изуче-
изучении поглощения или рассеяния излучения в пористых средах, для
характеристики сильно развитой турбулентности, при моделирова-
моделировании свойств поверхности твердых тел, для описания диэлектричес-
диэлектрического пробоя и молнии, при анализе процессов усталостного разруше-
разрушения материалов, при исследовании различных стадий роста вещества
за счет диффузии и последующей агрегации, в квантовой механике
при описании геометрической структуры волновых функций в точке
перехода Андерсона металл-диэлектрик. Удивительно то, что сходные
геометрические формы встречаются в совершенно различных облас-
областях науки: в астрофизике при описании процессов кластеризации га-
галактик во Вселенной, в картографии при изучении форм береговых
линий и разветвленной сети речных русел и, например, в биологии,
при анализе строения кровеносной системы или рассмотрении слож-
сложных поверхностей клеточных мембран.
Данное пособие представляет собой введение в физику и геометрию
фракталов и мультифракталов. Оно состоит из двух частей. В пер-
первой части излагаются ставшие уже классическими различные при-
примеры фрактальных структур. Основной количественной характерис-
характеристикой фрактала здесь является его фрактальная размерность. Вна-
Вначале подробно разбираются математические модели идеально само-
самоподобных (регулярных) фракталов: однородного канторовского мно-
множества, кривой Коха, салфетки и ковра Серпинского, губки Менгера
и Вселенной Фурье. Для большинства из них фрактальная размер-
размерность может быть вычислена аналитически. Даются также примеры
кривых Пеано, которые плотно заполняют некоторые области на плос-
плоскости (часто имеющие фрактальную границу) и имеют целочислен-
целочисленную фрактальную размерность, равную двум.
9

Далее в пособии рассматриваются системы линейных отображе-
отображений на плоскости, аттракторами для которых являются введенные
выше регулярные фракталы, а также многие другие. Подробно ана-
анализируется, например, класс сжимающих аффинных преобразований,
которые позволяют воссоздать на экране компьютера изображение
листа папоротника, которое очень трудно отличить от реально су-
существующего в природе.
В заключении первой части рассматриваются нелинейные комп-
комплексные отображения, главным из которых безусловно является прос-
простейшее квадратичное. Особенностью этих отображений является то,
что границы их областей притяжения имеют, как правило, фракталь-
фрактальную структуру. Это так называемые множества Жюлиа и связанное
с ними множество Мандельброта. Сходной задачей является итера-
итерационный процесс нахождения корней кубического уравнения zs = 1
на комплексной плоскости с помощью так называемого алгоритма
Ньютона. Оказывается, что области притяжения для корней этого
простого уравнения тоже имеют сложную фрактальную границу.
Во второй части пособия рассматриваются основные идеи коли-
количественного описания мультифракталов. Для их полной харак-
характеристики требуется уже не одна, а целый спектр фрактальных раз-
размерностей, число которых в общем случае бесконечно. Важность этой
науки заключается в том, что большинство природных фракталов
на самом деле являются мультифракталами. Говоря кратко, муль-
тифрактал — это неоднородный фрактал. В настоящее время теория
мультифракталов представляет собой бурно развивающуюся область
науки, и основные ее концепции активно используются для объясне-
объяснения многих явлений в самых различных областях естествознания.
Мультифрактальный анализ с успехом применяется при описании
структурного распределения неоднородных звездных скоплений в ас-
астрофизике, при исследовании агрегационных свойств клеточных эле-
элементов крови в биологии, для характеристики основных этапов эво-
эволюции ансамбля дислокаций и усталостного разрушения материа-
материалов в физике металлов. Мультифрактальные концепции широко ис-
используются в теории развитой гидродинамической турбулентности,
при изучении несоразмерных структур и квазикристаллов в физике
твердого тела, в теории спиновых стекол и неупорядоченных систем,
в квантовой механике и физике элементарных частиц.
10

В настоящее время теме фракталов и мультифракталов посвящено
много книг и обзоров (в основном на английском языке), огромное
число страниц в Интернете и большое количество научных статей,
опубликованных в ведущих научных журналах мира по математи-
математике, физике, химии, биологии, астрономии, экономике и языкознанию
и др. Если бы мы захотели привести полную библиографию этих
работ, то для ее опубликования потребовалась бы, как минимум, от-
отдельная книга. Мы ограничились лишь некоторыми основными до-
доступными, а также, на наш взгляд, ключевыми работами, приведен-
приведенными в списке используемой литературы. Читатели этих трудов
смогут найти в них фамилии ученых, внесших свои оригинальные
идеи в современную науку о фракталах. Приведен также сравни-
сравнительно большой, хотя и далеко не полный перечень "фрактальных"
страниц в Интернете. На них обсуждаются многие затронутые проб-
проблемы и содержится огромная коллекция рисунков самых различных
фракталов и фрактальных структур, а также доступных компьютер-
компьютерных программ, используемых для их построения.
Авторы надеются, что данное учебное пособие поможет студентам
и аспирантам в их первом знакомстве с удивительным миром фракта-
фракталов и будет способствовать дальнейшему более глубокому изучению
этого интереснейшего раздела современной физики.
11

1 ФРАКТАЛЫ
1.1 Регулярные фракталы
1.1.1 Понятие фрактала
Сравнительно давно в математике возник образ объекта, более объем-
объемистого, но тем не менее сходного с линией. Некоторым ученым было
трудно примириться с понятием линии, не имеющей ширины, поэто-
поэтому постепенно ими стали изучаться геометрические формы и струк-
структуры, имеющие дробную пространственную размерность. На сме-
смену непрерывным кривым, обладающим всеми своими производными,
пришли ломаные или очень изрезанные кривые. Ярким примером та-
такой кривой является траектория броуновской частицы. Так в науке
возникло понятие фрактала [1].
Фракталами называются геометрические объекты: линии, по-
поверхности, пространственные тела, имеющие сильно изрезанную фор-
форму и обладающие свойством самоподобия. Слово фрактал произошло
от латинского слова fractus и переводится как дробный, ломаный. Са-
Самоподобие как основная характеристика фрактала означает, что он
более или менее единообразно устроен в широком диапазоне масшта-
масштабов. Так, при увеличении маленькие фрагменты фрактала получают-
получаются очень похожими на большие. В идеальном случае такое самоподо-
самоподобие приводит к тому, что фрактальный объект оказывается инвари-
инвариантным относительно растяжений, т. е. ему, как говорят, присуща
дилатационная симметрия. Она предполагает неизменность основных
геометрических особенностей фрактала при изменении масштаба.
Конечно, для реального природного фрактала существует некото-
некоторый минимальный масштаб длины /тш, такой, что на расстояни-
расстояниях / « /min его основное свойство — самоподобие — пропадает. Кро-
Кроме того, на достаточно больших масштабах длин I > /max, где /тах —
характерный геометрический размер объектов, это свойство самопо-
самоподобия также нарушается. Поэтому свойства природных фракталов
рассматриваются лишь на масштабах /, удовлетворяющих соотноше-
соотношению /min <C I <C /max- Такие ограничения являются довольно естест-
естественными, потому что, когда мы приводим в качестве примера фрак-
12

тала — изломанную, негладкую траекторию броуновской частицы, то
мы понимаем, что этот образ является очевидной идеализацией. Дело
в том, что на маленьких масштабах сказывается конечность массы и
размеров броуновской частицы, а также конечность времени соударе-
соударения. При учете этих обстоятельств траектория броуновской частицы
становится плавной кривой.
Отметим, что свойство точного самоподобия характерно лишь для
регулярных фракталов. Если вместо детерминированного спосо-
способа построения включить в алгоритм их создания некоторый элемент
случайности (как это бывает, например, во многих процессах диф-
диффузионного роста кластеров, электрическом пробое и т.д.), то возни-
возникают так называемые случайные фракталы. Основное их отличие
от регулярных состоит в том, что свойства самоподобия справедли-
справедливы только после соответствующего усреднения по всем статистичес-
статистически независимым реализациям объекта. При этом увеличенная часть
фрактала не точно идентична исходному фрагменту, однако их ста-
статистические характеристики совпадают.
1.1.2 Длина береговой линии
Первоначально понятие фрактала в физике возникло в связи с зада-
задачей об определении длины береговой линии. При ее измерении по
имеющейся карте местности выяснилась любопытная деталь — чем
более крупномасштабная берется карта, тем более длинной оказыва-
Рис. 1.1. Определение длины береговой линии между точками А и В.
ется эта береговая линия. Пусть, например, расстояние по прямой
между расположенными на береговой линии точками А и В равно R
13

(см. рис. 1.1). Тогда, чтобы измерить длину береговой линии между
этими точками, мы расставим по берегу жестко связанные друг с
другом вешки так, что расстояние между соседними вешками равня-
равнялось бы, например, / = 10 км. Длину береговой линии в километрах
между точками А и В мы примем тогда равной числу вешек минус
одна, помноженному на 10. Следующее измерение этой длины мы
произведем подобным же образом, но расстояние между соседними
вешками сделаем уже равным / = 1 км.
Оказывается, что результат этих измерений будет различным. При
уменьшении масштаба / мы будем получать все большие и большие
значения длины. В отличие от гладкой кривой, линия морского по-
побережья оказывается зачастую настолько изрезанной (вплоть до са-
самых маленьких масштабов), что с уменьшением длины звена I ве-
величина L — длина береговой линии — не стремится к конечному
пределу, а увеличивается по степенному закону
L « / (— ) , A.1)
V / /
где D > 1 — некоторый показатель степени, который называется
фрактальной размерностью береговой линии. Чем больше вели-
величина D, тем более изрезанной является эта береговая линия. Проис-
Происхождение зависимости A.1) интуитивно понятно: чем меньший мас-
масштаб мы используем, тем меньшие детали побережья будут учтены
и дадут вклад в измеряемую длину. Наоборот, увеличивая масштаб,
мы "спрямляем" побережье, уменьшая длину L.
Таким образом, мы видим, что для определения длины береговой
линии L с помощью жесткого масштаба / (например, с помощью цир-
циркуля с фиксированным раствором), необходимо сделать N = L/1 ша-
шагов, причем величина L меняется с I так, что N зависит от / по закону
N « (R/l)D. В результате с уменьшением масштаба длина береговой
линии неограниченно возрастает. Это обстоятельство резко отличает
фрактальную кривую от обычной гладкой кривой (типа окружности,
эллипса), для которой предел длины аппроксимирующей ломаной L
при стремлении к нулю длины ее звена / конечен. В результате для
гладкой кривой ее фрактальная размерность D = 1, т. е. совпадает с
топологической.
Приведем величины фрактальных размерностей D для различных
14

береговых линий. Например, для Британских островов D « 1.3, а для
Норвегии D « 1.5. Фрактальная размерность побережья Австралии
D « 1.1. Близкими к единице оказываются и фрактальные размер-
размерности других побережий.
1.1.3 Фрактальная размерность множества
Выше мы ввели понятие о фрактальной размерности береговой ли-
линии. Дадим теперь общее определение этой величины. Пусть d —
обычная Евклидова размерность пространства, в котором находится
наш фрактальный объект (d = 1 — линия, d = 2 — плоскость, d = 3
— обычное трехмерное пространство). Покроем теперь этот объект
целиком ^-мерными "шарами" радиуса I. Предположим, что нам по-
потребовалось для этого не менее, чем NA) шаров. Тогда, если при
достаточно малых I величина NA) меняется с / по степенному закону
NA) ~ ^ A.2)
то D — называется хаусдорфовой или фрактальной размернос-
размерностью этого объекта. Очевидно, что эта формула эквивалентна соот-
соотношению N « (R/l)D, использованному нами выше для определения
длины береговой линии.
Формулу A.2) можно переписать также в виде
1-ю In/
Это и служит общим определением фрактальной размерности D. В
соответствии с ним величина D является локальной характеристи-
характеристикой данного объекта.
Давайте покажем, что это определение дает привычные нам це-
целочисленные значения размерности для обычных хорошо известных
множеств. Так, для множества, состоящего из конечного числа изо-
изолированных точек, JV, минимальное число d-мерных "шаров" х, с по-
помощью которых мы можем покрыть это множество, при достаточно
малом размере шаров совпадает, очевидно, с количеством точек, т. е.
NA) = N и не зависит от диаметра этих шаров L Следовательно,
1 Под "шаром" в зависимости от задачи мы будем понимать также и куб, и квадрат,
и просто отрезок прямой.
15

согласно формуле A.3), фрактальная размерность этого множества
D = 0. Она совпадает с обычной Евклидовой размерностью изолиро-
изолированной точки d = 0 (точка — нульмерный объект).
Для отрезка прямой линии длиной L (состоящего из бесконечно-
бесконечного числа точек) минимальное число NA) одномерных отрезков раз-
размера I, с помощью которых можно покрыть данный отрезок целиком,
равно, очевидно, NA) = L/1. В этом случае, согласно формуле A.3)
(или A.2)), фрактальная размерность D = 1, т.е. совпадает с Евкли-
Евклидовой размерностью отрезка прямой d = 1. Для области площадью S
гладкой двумерной поверхности число необходимых для ее покрытия
квадратиков NA) = S/12 (при достаточно малых I), поэтому фрак-
фрактальная размерность гладкой поверхности D = 2. И наконец, для
покрытия некоторого конечного объема V необходимо NA) = V/73
кубиков с ребром L Следовательно, фрактальная размерность этого
множества D = 3.
Разберем теперь некоторые классические примеры регулярных
фракталов, которые обладают свойством идеального самоподобия. Их
покрытие можно осуществлять элементами, из которых состоит дан-
данный фрактал. В этом случае имеет место упрощенный вариант фор-
формулы A.3) для определения фрактальной размерности. Пусть на не-
некотором этапе покрытия фрактала нам пришлось использовать, как
минимум, NA) таких элементов характерного размера /, а на дру-
другом N(lr) элементов размера V. Тогда величина фрактальной раз-
размерности D может быть вычислена по формуле
Очевидно, эту формулу можно переписать в виде
(
что является следствием выражения A.2). Начнем наше рассмотре-
рассмотрение ниже с однородного канторовского множества.
16

1.1.4 Канторовское множество
Рецепт его построения заключается в следующем (см. рис. 1.2). Пер-
Первоначально берется отрезок прямой единичной длины. Затем он де-
делится на три равные части, и вынимается отрезок в середине, на-
находящийся между точками 1/3 и 2/3. Это первый шаг итерацион-
итерационной процедуры. На втором шаге подобной же процедуре деления на
три равные части и последующего удаления середины подвергается
каждый из двух оставшихся отрезков. Так продолжается до беско-
бесконечности. Нетрудно видеть, что суммарная длина получившихся в
пределе отрезков равна нулю, так как мы исключили в результате
длину, равную 1:
124 1/24 \ 1 1
= 1.
A.6)
Следовательно, возникшее множество представляет собой бесконеч-
бесконечное число изолированных точек, которое и получило название кан-
торовского множества 2.
1/3
1/3
1/9 1/9
1/9 1/9
N=1
N=2
N=4
ОО
Рис. 1.2. Канторовское множество.
Вычислим теперь фрактальную размерность этого множества. Вос-
Воспользуемся для этого, например, формулой A.3). Очевидно, что на
п-м шаге нашего построения мы имеем 2п отрезков длиной 1/Зп каж-
каждый. Поэтому в качестве NA) на этом шаге мы можем взять величи-
величину 2П, а в качестве / — величину 1/Зп. Предел I —>¦ 0 соответствует
2 Часто так называют любое несвязное фрактальное множество точек с отличной
от нуля нецелочисленной фрактальной размерностью D.
17

пределу п —>¦ оо. Поэтому фрактальная размерность равна
In2n In 2
D = - lim
In3
= 0.6309 .
A.7)
Она оказалась меньше Евклидовой размерности пространства (d = 1),
в котором располагается это множество (т.е. его длина равна нулю),
но все-таки отлична от нуля, т. е. больше топологической размер-
размерности элементов (точек) этого множества. По математической тер-
терминологии данный объект представляет собой несчетное множество
точек, обладающее мощностью континуума.
1.1.5 Снежинка Коха
Для построения снежинки Коха выполним следующие операции (см.
рис. 1.3). Рассмотрим в качестве нулевой итерации равносторонний
Рис. 1.3. Снежинка Коха.
треугольник. Затем каждую из сторон этого треугольника разделим
на три равные части, уберем среднюю часть и в середине достро-
достроим равносторонний треугольник так, как изображено на рис. 1.3. На
следующем шаге такой же процедуре деления на три равные части
и достраивания равностороннего треугольника подвергается каждая
18

из сторон новой фигуры, и так до бесконечности. В результате воз-
возникает симметричная, похожая на снежинку, бесконечно изломанная
кривая 3, которая представляет собой самоподобное множество, назы-
называемое снежинкой Коха. Она была так названа в честь шведского
математика Helge von Koch, который впервые описал ее в 1904. Отли-
Отличительной ее особенностью является то, что она, будучи замкнутой,
тем не менее нигде себя не пересекает, поскольку достраиваемые тре-
треугольники каждый раз достаточно малы и никогда не "сталкиваются"
друг с другом.
Подсчитаем ее фрактальную размерность. Возьмем в качестве
длины стороны исходного треугольника 1 = 1, тогда число отрезков
такой длины, которые покрывают снежинку Коха на этом (нулевом)
шаге, равно NA) = 3. Затем при переходе к следующему шагу (сред-
(средний фрагмент в верхнем ряду на рис. 1.3) мы имеем Г = 1/3, а число
отрезков N(lr) = 12. Поэтому фрактальная размерность снежинки
Коха (в соответствии с A.4)) равна
v J
lnC) In3
Эта величина больше единицы (топологической размерности ли-
линии), но меньше Евклидовой размерности плоскости, d = 2, на ко-
которой расположена кривая. Таким образом, снежинка Коха представ-
представляет собой линию бесконечной длины, ограничивающую конечную
площадь 4. На п-м шаге ее длина L = 3 • D/3)п. Если в качестве мас-
масштаба измерения взять величину I = A/3)п, то формулу для L можно
представить в виде, аналогичном формуле A.1) для длины береговой
линии
L = z(^\ =l(j) , где R = 31/D и 2.39, A.9)
a D определяется выражением A.8). При этом вычисленное выше
значение фрактальной размерности может, очевидно, быть получено
из общей формулы A.4) при рассмотрении любых двух итераций с
номерами п и п + т. Это является следствием идеального самоподо-
самоподобия.
3 Т.е. она не имеет производной ни в одной точке.
4 Нетрудно убедиться, что она никогда не выходит за пределы окружности, опи-
описанной около исходного треугольника.
19

1.1.6 Салфетка и ковер Серпинского
Регулярный фрактал, называемый салфеткой Серпинского (Sier-
pinski gasket) 5, получается последовательным вырезанием централь-
центральных равносторонних треугольников так, как показано на рис. 1.4.
Рис. 1.4. Построение салфетки Серпинского.
В результате получается "дырявая" фигура (см. рис. 1.5), состоя-
состоящая из бесконечного числа изолированных точек. Фрактальная раз-
размерность салфетки Серпинского подсчитывается по формуле A.4)
= 1.5849 . A.10)
Здесь на нулевом шаге мы имеем один равносторонний треугольник
с длиной стороны / = 1, а на следующем — три равносторонних тре-
треугольника со сторонами /' = 1/2. Поэтому / = 1, NA) = 1, а /' = 1/2,
N(l') = 3. Салфетка имеет нулевую площадь, поскольку нетрудно
проверить, что в процессе ее построения была исключена площадь,
в точности равная площади исходного треугольника. Об этом же го-
говорит и значение фрактальной размерности D < 2, которая меньше
размерности плоскости, на которой находится этот объект.
Подсчитаем теперь периметр исключенных областей. Если сторона
исходного треугольника была равна 1, то на первом шаге построения
периметр центрального треугольника равен 3/2. На втором шаге к
нему добавляются три новых треугольника с общим периметром, рав-
равным 9/4 и т.д. Очевидно, что на п-м шаге периметр V определяется
5 Его называют также треугольником Серпинского.
20

Рис. 1.5. Салфетка Серпинского.
суммой геометрической прогрессии
g) =з
fc=l
1)"
•©'
A.11)
С другой стороны, масштаб длины на п-м шаге равен / = 1/2п. По-
Поэтому формула для периметра, выраженного через этот масштаб,
приобретает вид, схожий с формулой A.1) для длины береговой линии
A.12)
где D определяется формулой A.10).
Рис. 1.6. Инициирующий элемент и генератор для кривой Серпинского.
Можно построить непрерывную линию, обладающую таким значе-
значением фрактальной размерности и геометрически эквивалентную сал-
21

фетке Серпинского. Инициирующим элементом для такого построе-
построения берется отрезок единичной длины, который потом заменяется на
конструкцию, называемую генератором, состоящую из трех отрез-
отрезков длиной 1/2, расположенных под углом 120° друг к другу (см.
рис. 1.6). Затем каждый из этих трех отрезков заменяется, в свою
очередь, на генератор в два раза меньшего размера так, как показано
на рис. 1.7 слева. Правая часть того же рисунка изображает следую-
следующий шаг этой процедуры. Контуры будущей салфетки Серпинского
Рис. 1.7. Второй и третий шаги в построении кривой Серпинского.
отчетливо проступают на следующих двух этапах (см. рис. 1.8). Эта
процедура повторяется до бесконечности. Легко видеть, что каждое
следующее изображение может быть получено из предыдущего путем
склеивания трех уменьшенных в два раза его копий, две из которых
повернуты на угол в 120° и —120° относительно оригинала.
Рис. 1.8. Следующие два шага в построении кривой Серпинского.
Аналогично салфетке Серпинского можно построить квадратный
ковер Серпинского (triadic Sierpinski carpet), который является
двумерным аналогом канторовского множества исключенных сред-
22

Рис. 1.9. Построение квадратного ковра Серпинского.
них третей. Рецепт его создания состоит в следующем. Вначале
берется квадрат с длиной стороны, равной единице. Затем каждая
из сторон квадрата делится на три равные части, а весь квадрат,
соответственно, на девять одинаковых квадратиков со стороной, рав-
равной 1/3. Из полученной фигуры вырезается центральный квадрат.
Затем такой же процедуре подвергается каждый из 8 оставшихся
квадратиков и т. д (см. рис. 1.9).
Рис. 1.10. Квадратный ковер Серпинского.
В результате получается дырявый квадратный ковер Серпинского
со значением фрактальной размерности
= 1.8928 .
A.13)
23

Он также представляет собой пример идеального самоподобного фрак-
фрактала. Его фрактальная размерность, однако, больше, чем у салфетки
Серпинского, т. е. он является в каком-то смысле менее дырявым.
1.1.7 Губка Менгера
Рецепт создания пространственного аналога квадратного ковра Сер-
Серпинского, называемого губкой Менгера (Menger sponge), состоит в
следующем. Каждая грань куба, имеющая единичную длину, делится
на 9 равных квадратиков так же, как и при построении квадратного
ковра Серпинского. В результате исходный куб разбивается на 27
одинаковых кубиков с длиной ребра, равной 1/3. Затем, удаляя 7
кубиков (один центральный и 6 из центра каждой из граней), проти-
противоположные грани исходного куба соединяются сквозным централь-
центральным отверстием квадратной формы. В результате из 27 остается 20
маленьких кубиков.
Рис. 1.11. Губка Менгера.
24

Такая итерационная процедура с вырезанием сквозных отверстий
и последующего превращения каждого оставшегося кубика в 20 еще
более мелких кубиков с размером в три раза меньше исходного про-
продолжается до бесконечности. В результате этих операций образуется
идеально самоподобный объект, называемый губкой Менгера. Каж-
Каждая грань исходного куба выглядит при этом так же, как квадратный
ковер Серпинского (см. рис. 1.11).
Фрактальная размерность губки Менгера равна
D = ^ = 2.7268 . A.14)
1П
Поскольку 2 < D < 3, то это говорит о том, что губка имеет нулевой
объем, но обладает бесконечной площадью поверхности своих пор.
Из вышеизложенного легко заметить, что для фигур, обладающих
свойством идеального самоподобия, правило A.4), позволяющее опре-
определить размерность D, можно переформулировать иным образом.
Так, если множество, состоящее из одинаковых элементов, строится с
помощью самоподобного процесса, причем на любом шаге каждый из
элементов с линейными размерами / заменяется р подобными элемен-
элементами, размерами l/q (с q > 1) каждый, то фрактальная размерность
такого объекта очевидно равна
D = ^. A.15)
Ing
Например, для кривой Коха р = 4, q = 3, поэтому величина D =
= 1п4/1пЗ (см. формулу A.8)).
Заметим, что для всех рассмотренных выше регулярных фракта-
фракталов фрактальная размерность D оказалась меньше, чем размерность
того пространства d, в котором находится данный фрактальный объ-
объект. Неравенство D < d отражает факт некомпактности фрактала,
причем чем больше различаются величины d и D, тем более рыхлым
является фрактал.
1.1.8 Кривые Пеано
Существуют, однако, фракталы, которые плотно заполняют простран-
пространство, в котором они находятся, так что их фрактальная размер-
25

ность D = d. Одним из примеров такого рода являются кривые Пе-
ано (Peano curves). Первая из них была найдена Пеано в 1890 г.
Начальным (инициирующим) элементом здесь можно выбрать еди-
единичный квадрат, каждая из сторон которого на следующем шаге за-
заменяется генератором, показанным на рис. 1.12 (справа). Он состоит
Рис. 1.12. Генератор для кривой Пеано.
из 9 отрезков длины 1/3, соединенных под прямым углом друг к
другу. Цифры показывают способ обхода данной кривой. При такой
геометрии неизбежны две точки самоконтакта 2-6 и 5-9. В резуль-
результате исходный квадрат преобразуется так, как показано на рис. 1.13.
Рис. 1.13. Построение кривой Пеано.
Затем каждый из отрезков образовавшейся фигуры длиной в 1/3
преобразуется подобным же образом, и так до бесконечности. В ре-
результате возникает самоподобная непрерывная кривая, плотно запол-
заполняющая квадратную область с площадью, равной 2. Ее фрактальная
26

размерность
D = -
Существуют, однако, и кривые Пеано, в которых, в отличие от пре-
предыдущего случая, отсутствуют точки самоконтакта (так называемые
само-избегающие кривые). Одним из примеров такого рода являет-
является кривая Госпера (Gosper curve). Инициатором для нее является
отрезок единичной длины, а генератор показан на рис. 1.14 справа.
Он состоит из 7 отрезков длиной 1/л/7 каждый (поэтому фракталь-
Рис. 1.14. Инициатор и генератор для кривой Госпера.
ная размерность этой кривой тоже равна 2). Пунктиром показана
треугольная решетка, служащая своеобразной образующей для этого
генератора. Следующие три шага процесса построения показаны на
рис. 1.15.
vrZy л го л'-Wi /1) л /I) д("^К(^
\ /\_Л
/) ) '
Рис. 1.15. Следующие 3 шага в построении кривой Госпера.
Интересной отличительной особенностью кривой Госпера является
то, что граница области, называемой "островом Госпера", которую
27

она заполняет в пределе бесконечного числа шагов, сама является
фрактальной с нецелочисленной размерностью D = 1пЗ/1п\/7 =
= 1.1291. Такие острова можно использовать для непрерывного по-
Рис. 1.16. Фрактальная граница острова Госпера.
крытия плоскости, так как можно показать, что они идеально стыку-
стыкуются друг с другом. Более того, семь таких островов, состыкованных
вместе (один в центре и шесть вокруг него), образуют снова остров
Госпера в три раза большего размера. Заметим, что подобным свой-
свойством из правильных многоугольников обладает только квадрат.
Рис. 1.17. Алгоритм построение дракона Хартера-Хейтуэя.
И наконец, приведем пример кривой Пеано, для которой область,
которую она заполняет на плоскости, имеет весьма причудливую
форму. Это так называемый дракон Хартера-Хейтуэя (Harter-
Heightway dragon). Первые 4 шага его построения изображены на
рис. 1.17. Как следует из рисунка, каждый из отрезков прямой на
28

следующем шаге заменяется на два отрезка, образующих боковые
стороны равнобедренного прямоугольного треугольника, для которо-
которого исходный отрезок являлся бы гипотенузой. В результате отрезок
как бы прогибается под прямым углом. Направление прогиба чере-
чередуется. Первый отрезок прогибается вправо (по ходу движения сле-
слева направо), второй — влево, третий — опять вправо и т.д. Для
удобства восприятия на каждом рисунке пунктиром показана кон-
конфигурация предыдущего шага. Таким образом, после каждого шага
число имеющихся отрезков удваивается, а длина каждого соответ-
соответственно уменьшается в л/2 раз. Поэтому фрактальная размерность
образующейся в результате (после бесконечного числа шагов) кривой
равна 2, т.е. кривая заметает собой конечную площадь. О форме
образующейся необычной фигуры можно получить представление из
рис. 1.18, где изображены 12-е и 16-е "поколения" дракона. Дракон
представляет собой своеобразную гирлянду в форме двухсторонней
правой спирали, состоящую из подобных друг другу спиралевидных
звеньев, непрерывно уменьшающихся в размерах от центра к пери-
периферии.
Рис. 1.18. 12-е и 16-е поколения дракона Хартера-Хейтуэя.
Вызывает лишь изумление, как такой достаточно примитивный
алгоритм приводит к столь необычной геометрической конструкции.
Биологический подтекст, фигурирующий в названии кривой, застав-
заставляет задуматься, а не закодирована ли в генах каким-нибудь схожим
простым образом информация о форме и размерах существующих в
природе живых организмов? Рассмотренная выше кривая представ-
представляет собой лишь один из многих примеров так называемых Л-систем
(L-system), изобретенных Аристидом Линденмаером (Aristid Linden-
29

mayer) в 1968 г. для моделирования биологического роста. Он по-
показал, что предельная геометрия даже очень простых систем может
быть необычайно фрактальной.
1.1.9 Вселенная Фурнье
В попытке понять устройство Вселенной мы неизбежно сталкива-
сталкиваемся с понятием фрактала. Так, предположим, что нам захотелось
узнать, с какой средней плотностью распределены звезды (или га-
галактики) в видимой части Вселенной. Представим себе сферу доста-
достаточно большого радиуса R, внутри которой находится очень много
N ^> 1 звезд. Тогда по определению средняя концентрация звезд
п = N/V(R), где V(R) = 4тгЛ3/3 — объем сферы. Можно предпо-
предположить, что если радиус сферы достаточно велик, то концентрация
звезд не будет зависеть от этого радиуса, и мы получим ответ на
интересующий нас вопрос.
Опытные данные, однако, говорят об обратном. С ростом R ве-
величина п непрерывно уменьшается. И, что интересно, уменьшение
происходит примерно по степенному закону п ос RD~3, где D « 1.23,
т. е. намного меньше 3. Это соответствует тому, что число звезд в
сфере радиуса R растет как
N ос RD = Я1'23, A.17)
т. е. гораздо медленнее, чем было бы в случае их однородного распре-
распределения в пространстве. Таким образом, распределение звезд и галак-
галактик во Вселенной сильно неоднородно. Количественной мерой этой
неоднородности может служить отличие показателя степени D от 3.
Саму же величину D можно отождествить с фрактальной размернос-
размерностью распределения материи во Вселенной. Это последнее утвержде-
утверждение нуждается в пояснении.
Действительно, при определении, например, фрактальной размер-
размерности D береговой линии, мы исходили из соотношения N « (R/l)D,
где величина R была расстоянием между парой точек А и В на бере-
береговой линии по прямой, длина / <С R была нашим масштабом измере-
измерения, а число N показывало, сколько раз этот масштаб укладывал-
укладывался вдоль береговой линии между точками А и В. В соответствии с
30

этой формулой фрактальную размерность D можно трактовать дво-
двояко. С одной стороны, в полном согласии с определением A.2) она
показывает, как с уменьшением масштаба / растет число элементов,
с помощью которых можно покрыть некоторую выделенную область
на данном фрактале. С другой стороны, она показывает, как то же са-
самое число растет с увеличением R — размера этой области. Причина
такой двойственности, очевидно, кроется в том, что у фрактала нет
своего собственного масштаба длины, а поскольку число N должно
быть безразмерным, то показатель степени D оказывается одним и
тем же как для зависимости N ос RD, так и для зависимости N ос l~D.
Как можно себе наглядно представить распределение звезд в трех-
трехмерном пространстве, имеющее фрактальную размерность D, близ-
близкую к единице? Разумеется, ответ на этот вопрос сильно неоднозна-
неоднозначен. Существует бесконечное количество различных конструкций,
имеющих одно и то же значение фрактальной размерности. Одним
из классических примеров, который мы сейчас рассмотрим, являет-
является вселенная Фурнье (Fournier universe), названная так по имени
американского журналиста и изобретателя, который предложил ее
в 1907 г. Она показана на рис. 1.19.
Р '"*
R2
R3
Рис. 1.19. Вселенная Фурнье.
Каждая точка на этом рисунке представляет собой одну галакти-
галактику. Они объединены в скопления радиуса R\ по 7 галактик в каждом
31

скоплении. На рисунке видны только пять из них: недостающие две
расположены симметрично над и под плоскостью рисунка, на пря-
прямой, проходящей через центр скопления6. В свою очередь, семь та-
таких скоплений аналогичным образом объединены в одно суперскоп-
суперскопление радиуса Лг- Затем по такому же принципу из семи супер-
суперскоплений строится одно суперсуперскопление радиуса R^, причем
R3/R2 = R2/R1 и т. д. В результате многократного повторения тако-
такого процесса возникает самоподобная фрактальная структура.
Ее фрактальную размерность легко определить, заметив, что, как
следует из рисунка, в сфере радиуса i?2 содержится в семь раз больше
галактик, чем в сфере радиуса Ri, т.е. iV(i?2) = 7N(Ri). Решением
этого уравнения является степенная функция N ос RD, где
- (L18)
У Фурнье Л 2 = 7i?i, поэтому размерность такой вселенной равняет-
равняется 1. Как видно, она для этого вовсе не обязательно должна быть
прямой или какой-нибудь другой плавной кривой. Более того, она
даже не должна быть связной. Меняя отношение R2/R1, легко постро-
построить фрактальные вселенные с другими размерностями D, близкими
к единице.
1.2 Итерации линейных систем
1.2.1 Системы итерируемых функций
Как мы уже убедились, многие регулярные фракталы строятся пу-
путем бесконечного повторения нескольких простых операций, скажем,
замены одного элемента некоторой комбинацией других, ему подоб-
подобных. Так, например, салфетка Серпинского получается при замене
исходного большого треугольника тремя треугольниками в два ра-
раза меньшего размера, расположенных друг относительно друга так,
как показано на рис. 1.4 в центре. Затем эта же операция повторя-
повторяется с каждым из этих трех маленьких треугольников, и так далее
6 Скопления имеют форму правильного восьмигранника — октаэдра (гранями ко-
которого являются 8 равносторонних треугольников), в 6 вершинах и в центре которого
расположены 7 галактик.
32

до бесконечности. Возникает естественный вопрос, а нельзя ли эту
"процедуру замены" перевести на язык математических формул.
Так или примерно так в середине 80-х годов появился метод Сис-
Систем Итерируемых Функций — СИФ (Iterated Function System —
IFS) как простое средство получения фрактальных структур. Он
был придуман американским математиком М. Барнсли (М. Barnsley),
работавшим тогда в технологическом институте штата Джорджия.
Сущность этого метода на примере уже упомянутой выше салфетки
Серпинского заключается в следующем.
A/2, л/3/2)
A/2,л/3/2)
@,0)
A,0)
@,0)
Рис. 1.20. Преобразование t\. В скобках даны декартовы координаты вершин.
Поместим исходный равносторонний треугольник с длиной сто-
стороны, для определенности равной единице, на комплексную плос-
плоскость [z] так, как показано на рис. 1.20 слева. Теперь зададимся
вопросом, каким линейным преобразованием t\ на комплексной плос-
плоскости он переводится в равносторонний треугольник в два раза мень-
меньшего размера, показанный на рис. 1.20 справа? Ответ достаточно
прост. Поскольку левое основание обоих треугольников лежит в нача-
начале координат z = 0, то функция fi(z), осуществляющая это преобра-
преобразование, определяется выражением
h : fi(z) = -z.
A.19)
Если теперь сместить этот маленький треугольник по горизонта-
горизонтали вправо на величину, равную 1/2, то получим преобразование ^
переводящее исходный треугольник в треугольник, изображенный
на рис. 1.21 справа. Соответствующая этому преобразованию функ-
33

Рис. 1.21. Преобразование t2.
ция /2B), очевидно, равна
-
-
A.20)
Наконец, последний, третий, маленький треугольник получается с
помощью преобразования t^, показанного на рис. 1.22. Отвечающая
Рис. 1.22. Преобразование Ц.
ему функция fz(z) получается из fi(z) трансляцией на комплексный
вектор 1/4 + г\/3/4
A.21)
_ 1 1 .л/3
~ 2^ + 4+ZX"
В итоге три вышеназванные линейные функции fi(z), /2B) и
осуществляют искомое преобразование исходного треугольника в три
треугольника в два раза меньшего размера. Возникает вопрос, а что
будет, если теперь каждый из этих трех маленьких треугольников в
34

свою очередь подвергнуть этим трем преобразованиям. Тогда воз-
возникнет уже 9 треугольников с размером в 4 раза меньше исходного.
Непосредственной проверкой можно убедиться, что это приводит к
картинке, изображенной на рис. 1.4 справа.
L. \
L. \
Рис. 1.23. Преобразование
Например, выполняя сначала преобразование ts, а затем преобра-
преобразование t2, мы в итоге получаем треугольник со стороной 1/4, пока-
показанный на рис. 1.23 справа, и т.д.. Общий случай показан на рис. 1.24
справа, где изображены все эти треугольники с обозначением резуль-
результирующего преобразования — генеалогического кода, при помощи
которого они были получены из исходного треугольника. Слева пока-
показан первый шаг итерационной процедуры. Большой треугольник, в
который "вписаны" подобным образом три маленьких треугольника
в два раза меньшего размера, мы будем ниже называть ячейкой.
Рис. 1.24. Два первых поколения итераций системы из трех линейных отображений.
Комбинация tjti, стоящая в каждом из девяти маленьких треуголь-
треугольников, означает, что этот треугольник был получен из исходного сна-
35

чала применением преобразования t{, а затем к полученному тре-
треугольнику было применено преобразование tj. Правило построения
этой последовательности легко угадывается. На первом месте спра-
справа стоит первое преобразование. Оно соответствует позиции дан-
данного треугольника в его ячейке в соответствии с обозначениями на
рис. 1.24 (слева). На втором месте стоит второе по счету преобразова-
преобразование, которое соответствует позиции уже этого большого треугольни-
треугольника в его ячейке и т. д. Отметим очевидную некоммутативность двух
(разных) преобразований, т.е. генеалогические коды {t\t2) и (^l)
соответствуют разным треугольникам.
Ниже на рис. 1.25 приведено 4-е поколение итераций, состоящее
из З4 = 81 треугольника, и показан генеалогический код двух из
них. Ясно, что, действуя подобным образом, мы в точности воспро-
воспроизводим алгоритм построения салфетки Серпинского. Поэтому после
бесконечного числа шагов мы придем в конце концов к множеству
точек, образующих этот фрактал.
(t3t1t2t2)
Рис. 1.25. 4-е поколение итераций.
Сам по себе этот факт безусловно интересен. Но, с другой стороны,
что мы при этом узнали нового? Несколько другим способом получен
уже известный фрактал, и все? Оказывается, что далеко не только
36

это. Принципиально новое заключается в том, что для получения
точно такого же предельного результата мы могли бы стартовать с
любой фигуры, необязательно имеющей форму равностороннего тре-
треугольника. Это, например, мог быть круг или квадрат или любая
другая замысловатая (и даже несвязная) фигура, произвольным об-
образом расположенная на плоскости. На каждом шаге уменьшаясь в
размерах в два раза и утраиваясь в количестве, эти фигуры в конце
концов превратились бы в неразличимые глазом бесформенные точ-
точки, образующие фрактал — салфетку Серпинского.
Причина такого поведения предельно проста. Она заключается в
том, что салфетка является своеобразным аттрактором для этой
системы из трех линейных преобразований fi(z), /2B) и /з(^), на-
называемых в литературе Системой Итерируемых Функций или сокра-
сокращенно СИФ. Поскольку салфетка — аттрактор, то, как мы увидим
ниже, процесс его построения можно было начать даже с одной един-
единственной точки!
1.2.2 Метод случайных итераций, или игра в хаос
Рассмотрим следующую незамысловатую игру, которую М. Барнсли
назвал игрой в хаос (chaos game). Возьмем уже знакомый нам рав-
равносторонний треугольник с вершинами в точках А, В и С. Выберем
внутри этого треугольника произвольным образом начальную точку.
Бросим теперь игральную кость, представляющую собой кубик, на 6
гранях которого проставлены буквы А, В и С. Пусть каждая буква
присутствует на двух из них, тогда вероятность выпадания любой
буквы одинакова и равна 1/3.
Допустим, что в результате первого броска выпала буква А. Со-
Соединим мысленно нашу начальную точку с вершиной треугольника
А отрезком прямой и на его середине поставим точку (см. рис. 1.26).
Пусть теперь она будет играть роль начальной. После чего повторим
вышеописанную процедуру с бросанием кубика и проставлением точ-
точки в середине соответствующего отрезка. Допустим, на втором шаге
выпала буква С, потом В, затем опять С и т. д. В результате на каж-
каждом шаге мы будем получать все новые и новые точки. Спрашивается,
как распределятся внутри треугольника эти точки после достаточно
большого числа шагов?
37

в
А С
Рис. 1.26. Игра в хаос. Первые 4 шага.
Ниже, на рис. 1.27 (слева направо), показаны результаты этой игры
соответственно с 5000, 10 000 и 50 000 точек. Невероятно, но факт —
по мере увеличения числа точек все явственнее проступает струк-
структура треугольника Серпинского. Видно, что, хотя каждый раз выбор
вершины треугольника происходит чисто случайным образом, возни-
возникающее множество точек на плоскости отнюдь не случайно и обладает
ярко выраженной фрактальной структурой.
Рис. 1.27. Игра в хаос. Результат.
Связь этой простой игры в хаос с системой итерируемых функ-
функций, рассмотренной в предыдущем параграфе, легко прослеживает-
прослеживается. Действительно, можно заметить, что по сути на каждом шаге
к начальной точке z применялось (случайным образом выбранное)
одно из трех вышеописанных линейных преобразований fi(z), /2B)
или fz{z). Если обозначить координаты вершин треугольника А, В,
С на комплексной плоскости через za, Zb и zc соответственно, то по-
38

скольку za = 0, Zb = 1/2 + гл/3/2 и zc = 1, видно, что
/2W =
z + za
2
2
Z + Zb
2
1
= 2*'
= 2^
2~ '
1
2'
1 .
4
4
A.22)
Таким образом, треугольник Серпинского, являясь аттрактором
для этой системы итерируемых функций, возникает и при чисто слу-
случайном выборе последовательности преобразований tjtjtk Можно
показать, что изображающая точка в результате бесконечной цепоч-
цепочки случайных итераций сколь угодно близко подойдет к каждой точке
этого фрактального множества. Рис. 1.28 поясняет эту мысль.
Рис. 1.28. Как появляется аттрактор.
Возьмем, например, начальную точку в центре самого большого
исключенного треугольника. На следующем шаге изображающая точ-
точка оказывается в центре одного из трех треугольников поменьше.
Эти треугольники представляют собой геометрическое место точек,
которые находятся на половине расстояния до соответствующих вер-
вершин от точек большого центрального треугольника. При следующей
39

итерации точка попадает в центр еще меньшего исключенного тре-
треугольника и т. д. В конце концов уже после небольшого числа итера-
итераций точка попадет в исключенный треугольник столь малого размера,
что его можно для всех практических целей считать точечным 7.
Разумеется, для этой игры было совершенно несущественно, что
исходный треугольник являлся равносторонним. С равным успехом
ее можно было провести в треугольнике любой формы (см. рис. 1.29).
Рис. 1.29. Скошенный треугольник Серпинского.
А что будет, если мы теперь несколько изменим правила игры?
Например, будем проставлять точку не на середине отрезка, а на
расстоянии в 1/3 от соответствующей вершины. Результат показан
на рис. 1.30. Получившееся множество точек можно назвать дву-
двумерным аналогом канторовского множества исключенных средних
третей. Нетрудно подсчитать, что фрактальная размерность соот-
соответствующего аттрактора равна единице.
В качестве исходной фигуры можно выбрать и любой другой мно-
многоугольник. Например, квадрат. Однако в случае квадрата нас ожи-
ожидает сюрприз. Если проводить игру по тем же правилам, что и для
треугольника Серпинского (т. е. ставить новую точку на середине
отрезка), то точки равномерно заполнят весь квадрат (подумайте,
почему?). Но если, например, взять правильный шестиугольник и
7 После 10 итераций размер этого маленького треугольника составляет 2 10 ~
10~3 от размера исходного треугольника, а после примерно 30 итераций становится
сравнимым с размером атома!
40

Рис. 1.30. Фрактальная пыль, D = 1.
ставить точку не в середине отрезка, а на расстоянии в 1/3 от со-
соответствующей вершины, то эти точки в процессе итераций образу-
образуют множество, которое условно можно назвать шестиугольником
Серпинского. Он показан на рис. 1.31.
Рис. 1.31. Шестиугольник Серпинского.
Как видно, он состоит из 6 одинаковых частей, каждая из которых
подобна целому, но имеет размер в три раза меньше исходного. По-
Поэтому его фрактальная размерность D = In 6/In 3 = 1.6309. Кстати,
именно в этом случае игра в хаос будет настоящей игрой в кости,
так как теперь на шести гранях игрального кубика можно поставить
цифры от одного до шести, соответствующие каждой из вершин шес-
шестиугольника. Заметьте также, что внутренняя граница этой фигуры
представляет собой нам уже известный фрактал — снежинку Коха
(см. рис. 1.3).
Систему итерируемых функций для этой и ей подобных задач лег-
легко написать в общем виде, пользуясь заданными алгоритмами игры.
41

Так, для произвольного n-угольника в случае, когда следующая точка
ставится на расстоянии в 1/т от соответствующей вершины, где / —
расстояние до нее начальной точки, а т — некоторое (не обязательно
целое) число, превышающее единицу, эта система имеет вид
fi(z) = —z + —-г{1 в = 1,2,..., п. A.23)
т т
Здесь Zi — комплексные координаты вершин многоугольника. На-
Например, для п = 2 {z\ = 0,Z2 = 1) и т = 3 получаем СИФ для уже
известного канторовского множества исключенных средних третей
(см. рис. 1.2).
1.2.3 Игры с поворотами
Как видно во всех рассмотренных выше случаях, каждое линейное
преобразование включало в себя сжатие в т раз (одинаковое для обо-
обоих осей X и Y) и параллельный перенос на некоторый комплексный
вектор. Наши возможности существенно расширятся, если в систему
преобразований мы включим еще и повороты. В качестве примера
найдем СИФ для кривой Коха.
1/2 + г
О 1/3 2/3 1
Рис. 1.32. Генератор для кривой Коха.
Инициатором для кривой Коха является отрезок единичной дли-
длины, который на следующем шаге преобразуется в генератор, изоб-
изображенный на рис. 1.32. Числа показывают координаты соответствую-
соответствующих вершин на комплексной плоскости. Система итерируемых функ-
функций, осуществляющих данное преобразование, выглядит следующим
42

образом
h(z) = \z, h(z) = \e^z + 1,
h(z) = \е-"'Ч + 2iM /() \ \
Первое преобразование ti, осуществляемое функцией fi(z), есть прос-
просто сжатие в 3 раза исходного отрезка @,1). Второе преобразование t^
включает в себя такое же сжатие, поворот против часовой стрелки
вокруг начала координат на угол в 60° и последующий сдвиг по гори-
горизонтали вправо на 1/3. Третье преобразование t% сжимает в три раза
исходный отрезок, поворочивает его на угол 60° по часовой стрел-
стрелке и затем смещает параллельно самому себе на комплексный век-
вектор 1/2 + гл/3/6. Наконец, четвертое преобразование сжимает отре-
отрезок в 3 раза и смещает его по горизонтали вправо на 2/3. Заметим,
что порядок выполняемых операций здесь важен.
Если теперь этим четырем преобразованиям подвергнуть сам ге-
генератор, то получим конструкцию, изображенную на рис. 1.33. Она
состоит из 16 отрезков длиной 1/9, и для каждого из них показана
последовательность операций, с помощью которых он был получен из
исходного единичного отрезка К.
-4L3
ч
Чг Ч4 Чг t4t4
Рис. 1.33. Положения элементов
Саму кривую Коха можно получить, повторяя этот процесс до бес-
бесконечности. Для этого удобно, как и ранее, воспользоваться мето-
методом случайных итераций (игрой в хаос). Каждому из 4 преобразова-
преобразований A.24) припишем одинаковую вероятность р^ = 0.25. После этого,
начав с некоторой точки zq в комплексной плоскости и выбирая слу-
случайным образом последовательность преобразований, будем получать
все новые и новые точки — z\ = fi(zo), z<i = fj(zi), z^ = fk{z2) и т.д.
43

В итоге после примерно 150000 итераций придем к множеству точек,
изображенно]
Рис. 1.34. Кривая Коха, полученная методом случайных итераций системы функ-
функций A.24).
Рассмотрим еще одну игру с поворотами. Пусть на плоскости у
нас имеются всего две точки А и В. Выберем случайным образом
начальную точку zq и одну из этих двух точек. Пусть, например,
на первом шаге "выпала" точка А. Мысленно соединяем ее с началь-
начальной отрезком прямой линии, длина которого пусть будет равна I, и
перемещаемся вдоль этого отрезка в точку, отстоящую от А на рас-
расстоянии 1/л/2. Поворачиваемся затем вокруг А по часовой стрелке
на угол в 45° и ставим в этом месте новую точку, которая теперь
будет играть роль начальной. После чего опять случайным образом
выбираем одну из точек А или В и повторяем весь процесс сначала.
Результат этой игры для 5 • 104 и 106 точек показан на рис. 1.35.
Рис. 1.35. Двойной дракон Хартера-Хейтуэя с 5 • 104 и 106 точек.
Видно, что точки в процессе итераций плотно заполняют на плос-
плоскости некоторую область с весьма причудливыми очертаниями. Что-
то подобное мы уже видели! Действительно, это изображение очень
44

похоже на дракон Хартера-Хейтуэя (см. рис. 1.18). Отсутствуют
только характерные "осиные талии" — перемычки, соединяющие раз-
разные части дракона. Может быть наш дракон немного потолстел?
Оказывается, причина вовсе не в этом, а в том, что здесь изобра-
изображен не один, а два совершенно одинаковых дракона Хартера-Хейтуэя,
один из которых повернут на 180° относительно другого. Они рас-
располагаются один над другим так, что выпуклости одного в точности
попадают во впадины другого. Их стыковка настолько идеальна, что
между ними не существует никаких пробелов. Поэтому эту фигуру
и называют двойным драконом (twindragon). Одним из интерес-
интересных геометрических свойств двойного дракона является то, что его
можно покрыть четырьмя уменьшенными копиями его самого.
Систему итерируемых функций, соответствующую двойному дра-
дракону, можно легко написать. Пусть координаты точек А и В на комп-
комплексной плоскости соответственно равны: z\ = г — 1 и z2 = г + 1. Тогда
h(z) = ± ±
-±=(Z - zJeW + Zl =-±=ге/ - 1,
^ -^ + z2 = ^ze-^4 + i. A.25)
Поскольку точки в процессе итераций с этими двумя функциями
плотно заполняют на плоскости некоторую область, фрактальная раз-
размерность соответствующего аттрактора равна двум. Это естествен-
естественно, так как совпадает с фрактальной размерностью кривой Пеано для
одинарного дракона. Однако граница этой области фрактальна и име-
имеет дробную размерность. Можно показать, что генератором для та-
такой границы может служить следующая конструкция (см. рис. 1.36).
0
Рис. 1.36. Генератор контура двойного дракона.
45

Она образована из одного большого отрезка длиной 1\ = 1/\/2 и
двух маленьких с длинами h = h = 1/2\/2 = if, расположенных
параллельно друг другу и перпендикулярно большому. Поскольку в
нашем распоряжении имеется два масштаба, то фрактальная размер-
размерность контура D определяется при этом из уравнения (см. B.57))
/f + 2Zf = l. A.26)
Оно эквивалентно кубическому уравнению для величины х = 2DI2
ж3-ж2-2 = 0, A.27)
которое имеет один вещественный корень хо « 1.69562. Отсюда на-
находим, что D « 1.5236.
Рис. 1.37. Контур двойного дракона.
Система итерируемых функций, осуществляющая преобразование
единичного отрезка @,1) в вышеобозначенный генератор, выглядит
следующим образом
4+ V
+4 \'
Если теперь в методе случайных итераций выбирать эти преобра-
преобразования с одинаковой вероятностью (равной 1/3), то результирующее
множество точек будет неоднородным вдоль границы (см. рис. 2.10)
46

и, как мы увидим в Части 2, будет представлять собой по сути муль-
тифрактал. Однако однородность распределения будет гарантирована
в случае выбора вероятностей в соответствии с алгоритмом B.58)
D
0.59, р2 = Р2, = Щ и 0.201.
A.29)
Заметим, что согласно формуле A.26) сумма этих вероятностей будет
равна единице. Тогда мы получим рис. 1.37.
Найдем теперь систему итерируемых функций для самого дракона
Хартера-Хейтуэя. На рис. 1.38 изображен принцип построения драко-
дракона. Равнобедренный прямоугольный треугольник ABC (изображен-
(изображенный на рисунке пунктиром) заменяется на следующем шаге на два
ему подобных треугольника ADB и ВЕС. Зная координаты концов
этих отрезков (они показаны в круглых скобках), можно вычислить
коэффициенты двух линейных преобразований, которые осуществля-
осуществляют эту замену.
А (-1,1)
\
\
\
\
\
\
\
\
С A,1)
В @,0)
Рис. 1.38. Генератор для построения СИФ дракона Хартера-Хейтуэя.
Первое преобразование переводит треугольник ABC в треуголь-
треугольник ADB, причем вершины треугольников переходят друг в друга
по правилу А —>• А, В ч D и С ч В. Оно соответствует поворо-
повороту треугольника ABC вокруг начала координат (т.е. точки В) по
часовой стрелке на угол 45°, сжатию вдоль осей X и Y в л/2 раз и
трансляции на единицу влево:
h(z) = l=ze-^ - 1. A.30)
47

Рис. 1.39. Дракон Хартера-Хейтуэя, построенный методом случайных итераций. Сле-
Слева — 3 • 104 итераций, справа — 106.
Второе преобразование переводит треугольник ABC в СЕВ, при-
причем вершины треугольников переходят друг в друга по прави-
правилу А -+ С, В -+ Е и С -+ В:
hi. A.31)
л/2
Оно соответствует повороту треугольника ABC вокруг точки В на
угол в 135° по часовой стрелке, сжатию вдоль осей X и Y в л/2 раз и
трансляции на единицу вверх в положительном направлении оси Y.
Рис. 1.40. Гирлянда "волков", полученная с помощью функций A.30) и A.32).
Эти два линейных комплексных преобразования и составляют сис-
систему итерируемых функций, аттрактором для которой является дра-
дракон Хартера-Хейтуэя. В этом нетрудно убедиться с помощью метода
случайных итераций. Выбирая эти два преобразования случайным
образом, с одинаковой вероятностью 50%, получим для 3 • 104 и 106
итераций множества точек, изображенные на рис. 1.39.
48

Интересная модификация возникает, если мы второе преобразо-
преобразование выберем так, чтобы переход треугольника ABC в треуголь-
треугольник ВЕС происходил по правилу А —^ В, В 4 Е и С ч С. Это
соответствует функции
^*ei^ + i A.32)
вместо A.31). Здесь звездочка означает операцию комплексного со-
сопряжения. Казалось бы, невинная затея, и результат не должен от
этого измениться. Рис. 1.40, однако, свидетельствует об обратном.
1.2.4 Сжимающие аффинные преобразования
Рассмотренные выше линейные преобразования на комплексной плос-
плоскости являются частными случаями более общего аффинного пре-
преобразования плоскости
xn+i = ахп + Ъуп + е,
уп+1 = схп + dyn + /. A.33)
Его можно представить в матричной форме
уп+1 ) \с d ) \уп
Так, например, согласно уравнению A.21) преобразование t^ мож-
можно записать в виде
хп+1 W 1/2 0 W хп \ ( 1/4 \
уп+1 ) ~ [ 0 1/2 ) [у,,) + [ V3/4 ) ¦ AМ>
Видно, что оно сводится к двухкратному сжатию вдоль осей X и Y,
и сопровождается трансляцией на некоторый вектор.
Преобразование, соответствующее функции A.30), можно записать
таким образом
хп+1 W 1/2 1/2 W хп \ ( -1
уп+1 ) ~ { -1/2 1/2 ) [у„ ) + [ 0
Оно сводится к сжатию в \[2 раз по обоим осям, повороту на 45° и к
трансляции.
49

Наконец, преобразование, задаваемое функцией A.32), соответству-
соответствует такому же сжатию, отражению в горизонтальной плоскости, по-
повороту на угол в 45° и трансляции
хп+1 \ = ( 1/2 1/2
уп+1 J I 1/2 -1/2
Уг
о
1
A.37)
В общем же случае аффинное преобразование на плоскости зада-
задается шестью независимыми действительными числами. Два числа е
и / описывают обычную трансляцию, а четыре числа а, 6, с, d задают
произвольное линейное преобразование при неизменном положении
В
В
С
В
1 D
A
D
D
Рис. 1.41. Действие аффинного преобразования на единичный квадрат ABCD при
е = / = 0.
начала координат @,0). Если при аффинном преобразовании не ме-
меняется направление обхода произвольного контура, то его, согласно
рис. 1.41, можно представить себе как произведение 3 преобразова-
преобразований
/ „ Z. \ _ _ _
= Т2,-Т2-Т1. A.38)
Первое переводит единичный квадрат в произвольный прямоуголь-
прямоугольник со сторонами г\ и г2 и описывается диагональной матрицей
Ъ =
Г1 0
0 г2
A.39)
Это соответствует простому масштабированию двух координатных
осей.
50

Второе преобразование описывает скос этого прямоугольника в
горизонтальном направлении на угол а и превращение его в парал-
параллелограмм со сторонами ri, v^j cos а и углом тг/2 — а между ними
И наконец, третье преобразование есть простой поворот получив-
получившегося параллелограмма на угол C вокруг начала координат
/cos/* -sin/3\
у sm/5 cosp J
Поскольку определитель произведения матриц равен произведе-
произведению определителей, то нетрудно видеть, что det^ = г\г<х и положи-
положителен. Это является признаком того, что преобразование не меняет
направления обхода контура. Действительно, во всех четырех случа-
случаях направление обхода параллелограмма ABCD все время происходит
по часовой стрелке.
Рис. 1.42. Отражение в вертикальной плоскости меняет направление обхода.
Если же определитель аффинного преобразования отрицателен, то
это значит, что преобразование включает в себя еще и операцию отра-
отражения в вертикальной (Tv) или в горизонтальной плоскости
A.42)
В этом случае, как видно из рис. 1.42, направление обхода конту-
контура ABCD меняется на противоположное.
51

Таким образом, в зависимости от знака det А четыре коэффициен-
коэффициента аффинного преобразования a,b,c,d можно всегда выразить через
два масштабных фактора г\,Г2 и два угла а и /9. Они характеризуют
форму, размеры, ориентацию и направление обхода получившегося
параллелограмма. Фактически аффинное преобразование описывает
переход от прямоугольной декартовой к произвольной косоугольной
(правой или левой) системе координат.
Неподвижной точкой аффинного преобразования называется
точка, которая остается на месте под воздействием данного преобра-
преобразования. Она называется притягивающей, если, начав с произволь-
произвольной точки на плоскости, мы в процессе итераций будем все время к
ней приближаться.
Если длина произвольного отрезка при аффинном преобразовании
уменьшается, то оно называется сжимающим. Сжимающие аффин-
аффинные преобразования играют ключевую роль в системах итерируемых
функций. Можно показать, что именно в этом случае они имеют сво-
своим аттрактором фрактальное множество.
В применении же к одному аффинному преобразованию это озна-
означает, что неподвижная точка отображения A.33) является притяги-
притягивающей. Действительно, применяя последовательно шаг за шагом это
преобразование к произвольному отрезку конечной длины, мы путем
последовательных сжатий в конце концов придем к отрезку сколь
угодно малой длины, и в пределе бесконечного числа шагов этот отре-
отрезок выродится в точку. Эта точка, очевидно, и будет неподвижной
точкой (аттрактором) нашего отбражения.
Неподвижные точки каждого отображения, входящего в систему
итерируемых функций, очевидно, принадлежат фрактальному мно-
множеству. Нетрудно убедиться, что в случае треугольника Серпинского
этими точками являются вершины треугольника.
Выясним, в каком случае аффинное преобразование является сжи-
сжимающим. Пусть (хо, уо) — притягивающая неподвижная точка отобра-
отображения A.33). Иными словами, имеет место равенство
хо = ахо + Ьуо + е,
у о = схо + dyo + /. A-43)
52

Непосредственной подстановкой можно убедиться тогда в том, что
хп+1 -хо = а(хп -хо) + Ь(уп -уо),
A44)
уп+1 - уо = с(хп - х0) + d{yn - уо)
Поскольку неподвижная точка (хо,уо) по условию является притя-
притягивающей, это означает, что расстояние до нее при каждой итерации
сокращается, т. е.
(хп+1 - х0J + (уп+1 - уоJ < (хп - хоJ + (уп - уоJ- A-45)
Воспользовавшись A.44), получаем, что для этого должно выполнять-
выполняться условие
F(u, v) = (аи + bvJ + (си + dvJ < 1 A.46)
при любых и и v таких, что и2 + v2 = 1. Здесь под и и v понимаются
величины
ц- Хп~Хо v- Уп-уо A.47)
\f(xn-x0J + (Уп-УоJ' \J{xn - хоJ + (Уп - УоJ
Физический смысл функции F(u,v) заключается в том, что она
описывает относительное уменьшение квадрата длины расстояния до
неподвижной точки после каждой итерации. Можно показать, что
точно так же при каждой итерации меняется и квадрат длины произ-
произвольного отрезка. Поэтому ^F(u,v) есть не что иное, как коэффи-
коэффициент сжатия аффинного преобразования для отрезка заданной ори-
ориентации (характеризуемой единичным вектором с компонентами и
и v).
Очевидно, что функция F(u,v), будучи по определению величиной
сугубо положительной, на единичной окружности в плоскости (it, i;)
меняется в ограниченных пределах. Следовательно, она достигает
там своего минимального и максимального значений. Аффинное пре-
преобразование будет сжимающим, если максимальное значение этой
функции окажется меньше единицы.
Нахождение этих значений является задачей на условный экстре-
экстремум функции двух переменных. С помощью метода неопределенных
множителей Лагранжа она сводится к нахождению безусловного экс-
экстремума функции
F(u,v) + \(l-u2-v2), A.48)
где А — множитель Лагранжа.
53

Приравнивая нулю частные производные по и и v от этой функции,
приходим к системе уравнений
(а2 + с2)и + (ab + cd)v — Хи = О,
(ab + cd)u + (b2 + d2)v - \v = 0. A.49)
Ее можно записать в матричной форме
v \oa\ca\v \ v
где Ат — транспонированная матрица.
Таким образом, для обеспечения экстремума функции F(u,v) на
единичной окружности вектор должен быть собственным век-
тором матрицы АТА, а соответственно величина Л — ее собственным
значением. Поскольку характеристическое уравнение квадратное, то
в общем случае имеется два таких значения.
Умножая первое из уравнений A.49) на и, а второе на г? и затем
складывая, получим, что экстремальное значение функции F(u, v) = Л.
Максимуму, очевидно, соответствует максимальное собственное зна-
значение — Атах, а минимуму — минимальное, Amin. Длина произволь-
произвольного отрезка L после применения аффинного преобразования A.34)
оказывается заключенной в интервале
A.51)
Поэтому преобразование будет сжимающим при условии Лтах < 1.
Коэффициент сжатия при этом обычно определяется наибольшей ве-
величиной, л/Атах.
1.2.5 Лист папоротника
Одним из наиболее ярких примеров среди различных систем итери-
итерируемых функций, несомненно, является открытая М. Барнсли систе-
система из четырех сжимающих аффинных преобразований, аттрактором
для которой является множество точек, поразительно напоминающее
по форме изображение листа папоротника. Ее можно представить
54

в виде следующей таблицы
а
0
0.85
0.2
-0.15
b
0
0.04
-0.26
0.28
с
0
-0.04
0.23
0.26
d
0.16
0.85
0.22
0.24
е
0
0
0
0
f
0
1.6
1.6
0.44
Р
0.01
0.85
0.07
0.07
A.52)
Каждая строчка этой таблицы соответствует одному аффинному пре-
преобразованию с коэффициентами а, 6, с, d, е, / в соответствии с выраже-
выражением A.34). В последнем столбце таблицы приведены вероятности р,
в соответствии с которыми в методе случайных итераций выбирается
то или иное преобразование.
Результат действия этой системы функций на некоторую началь-
начальную точку для разного числа итераций приведен на рис. 1.43. Видно,
,¦><
Рис. 1.43. Лист папоротника. Слева направо показано 2000, 4000, 10 000, 50 000
и 200 000 итераций.
как с ростом числа итераций действительно возникает все более и
более четкое изображение листа папоротника, удивительным обра-
образом напоминающее существующее в природе растение.
Это множество точек бесконечно самоподобно, как и полагается
всякому фракталу. Как следует из рис. 1.44, увеличенные малые
фрагменты изображения подобны целому. Для разрешения этих фраг-
фрагментов необходимо только, чтобы число итераций было достаточно
велико.
Таким образом, чем больше используемое разрешение, тем больше
точек требуется внести в память компьютера для того, чтобы постро-
построить соответствующее изображение. С другой стороны, запоминать
55

координаты этих точек вовсе не требуется, так как они каждый раз
могут быть заново получены с использованием системы функций, за-
заданных таблицей A.52).
Рис. 1.44. Увеличенный фрагмент листа папоротника.
В результате всего 28 чисел содержат всю необходимую информа-
информацию об этом нетривиальном рисунке! Возникает мысль, а нельзя ли
подобным образом "кодировать" и другие изображения. Эта идея,
будучи реализованной на практике, позволила бы сжимать изображе-
изображения в десятки или даже в сотни раз. И действительно в 1988 г. она
была успешно воплощена Барнсли и Слоаном в созданной ими совмест-
совместно компании по кодированию и сжатию графической информации с
помощью соответствующим образом подобранной системы функций.
Давайте разберем более подробно этот замечательный пример и
дадим по возможности наглядную геометрическую интерпретацию
числам, приведенным в таблице A.52). Для этой цели на рис. 1.45
показано действие этой системы функций на квадрат ABCD (изобра-
(изображенный на рисунке пунктиром), повернутый на 45° так, что одна из
его диагоналей совпадает с вертикальной осью у, а другая параллель-
параллельна горизонтальной оси х (на рисунке, чтобы избежать громоздкости,
сами оси не показаны 8). Начало координат при этом совпадает с
точкой А.
Первое преобразование соответствует сжатию этого квадрата в
вертикальный отрезок прямой, длина которого составляет 16% от
диагонали квадрата. Он обозначен на рисунке цифрой 1. Как мы
убедимся ниже, это будущий "стебель" всех листьев папоротника.
8 По этой же причине не показаны также вершины А$ всех возникающих
параллелограммов.
56

с,
в
Рис. 1.45. Действие системы функций A.52) на квадрат ABCD.
Второе преобразование превращает квадрат ABCD в квад-
квадрат A2B2C2D2, который имеет размер в 85% от оригинала, повернут
по часовой стрелке относительно вершины А на угол в 2.7° и смещен
по вертикали вверх на расстояние в 1.6 см. 9
Третье аффинное преобразование переводит квадрат ABCD в па-
параллелограмм A3B3C3D3. Для этого сторона квадрата АВ сжимается
в 3.07 раза и поворачивается вокруг точки А на угол в 46.25° против
часовой стрелки. Сторона же квадрата AD этим преобразованием
сжимается примерно в 3.12 раза и поворачивается в том же направ-
направлении на угол в 52.6°. После чего образовавшийся (близкий к ромбу)
параллелограмм сдвигается вертикально вверх на 1.6 см.
Наконец, четвертое преобразование трансформирует исходный
квадрат в параллелограмм A4B4C4D4. Для этого сторона АВ сжи-
сжимается в 3.29 раза и поворачивается по часовой стрелке вокруг на-
начала координат на угол примерно в 137.7°. Сторона же AD сжима-
сжимается в 2.74 раза и поворачивается на угол в 30.4°, но против часовой
стрелки! Затем получившийся параллелограмм смещается на 0.44 см
по вертикали вверх.
Сантиметр здесь несколько условная единица длины.
57

Заметим, что в результате четвертого преобразования направле-
направление обхода вершин параллелограмма A4B4C4D4 меняется на проти-
противоположное по сравнению с исходным квадратом ABCD. Другими
словами, четвертое преобразование содержит в себе операцию отра-
отражения (например, в вертикальной плоскости) и переводит в итоге
правую систему координат в левую. Смысл этого действия для по-
получения правильного изображения листа папоротника мы выясним
несколько позже.
Давайте теперь исключим первое преобразование из нашей систе-
системы функций. В результате получим СИФ вида
A.53)
всего с тремя функциями и исправленными вероятностями (которые
в сумме всегда должны давать единицу). Изображение, полученное
итерациями этой СИФ, показано ниже на рис. 1.46 (слева).
а
0.85
0.2
-0.15
b
0.04
-0.26
0.28
-0
0
0
с
.04
23
26
0
0
0
d
.85
.22
.24
е
0
0
0
f
1.6
1.6
0.44
0
0
0
Р
.86
.07
.07
Рис. 1.46. Лист без стебля (слева) и стебель без листьев (справа).
Как видно, в нем отсутствует стебель. Это и понятно. Ведь за фор-
формирование стебля как раз и ответственно первое и второе аффинные
преобразования. Действительно, если мы теперь оставим только их
A.54)
0
а
0
.85
0
b
0
.04
с
0
-0.04
0
0
d
.16
.85
е
0
0
f
0
1.6
0
0
Р
.05
.95
то получим стебель, изображенный на рис. 1.46 справа.
58

Довольно очевидно, что за слабый изгиб листа папоротника впра-
вправо ответственен поворот на угол в 2.7°, фигурирующий во втором
преобразовании. Если мы теперь исключим этот поворот, то полу-
получим систему функций вида
A.55)
Соответствующее этой системе изображение аттрактора приведе-
приведено на рис. 1.47 слева. Как и следовало ожидать, в нем уже нет из-
а
0
0.85
0.2
-0.15
b
0
0
-0.26
0.28
с
0
0
0.23
0.26
d
0.16
0.85
0.22
0.24
е
0
0
0
0
f
0
1.6
1.6
0.44
Р
0.01
0.85
0.07
0.07
Рис. 1.47. Прямой лист папоротника. Слева — A-55), справа — A.56).
гиба, лист папоротника получился прямой. Если теперь трансляцию
в четвертом преобразовании сделать такой же, как и в третьем, т. е.
использовать систему функций
A.56)
то получим изображение, приведенное на рис. 1.47 справа. Таким
образом, трансляция в третьем и четвертом преобразовании зада-
задает относительное положение листьев папоротника по обе стороны от
стебля.
а
0
0.85
0.2
-0.15
b
0
0
-0.26
0.28
с
0
0
0.23
0.26
d
0.16
0.85
0.22
0.24
е
0
0
0
0
f
0
1.6
1.6
1.6
Р
0.01
0.85
0.07
0.07
59

Кажется, теперь мы начинаем понимать, как работает система
функций A.52). Первые два преобразования формируют стебель,
второе и третье формируют листья с одной стороны, а второе и чет-
четвертое — с другой стороны стебля (см. рис. 1.48). Относительное
положение листьев определяется трансляцией.
'У/
к/
Рис. 1.48. Аттрактор второго и третьего (слева) и второго и четвертого (справа)
преобразований системы функций A.52).
Нам осталось разобраться, зачем нужно отражение в четвертом
преобразовании. Для этого воспользуемся упрощенной версией сис-
системы функций A.52). А именно, для третьего и четвертого преобра-
преобразований используем матрицы Л.3,4 соответственно:
X _ 1 I cos 60° - sin 60° \ л _ I ( ~ cos 60° sin 60°
3 ~ 3 I sin 60° cos 60° ) ' 4 ~ 3 \ sin 60° cos 60°
A.57)
Первая из них соответствует сжатию в 3 раза по обеим осям и
повороту против часовой стрелки на угол 60°. Вторая в дополнение
к первой содержит еще и операцию отражения в вертикальной плос-
плоскости, т.е. замену х —>¦ —х. В итоге вместо A.52) мы приходим к
системе функций
A.58)
Результат действия этой системы функций показан на рис. 1.49 слева.
а
0
0.85
0.1667
-0.1667
b
0
0.04
-0.2887
0.2887
с
0
-0.04
0.2887
0.2887
d
0.16
0.85
0.1667
0.1667
е
0
0
0
0
f
0
1.6
1.6
0.44
Р
0.01
0.85
0.07
0.07
60

Если же теперь для четвертого преобразования мы вместо поворо-
поворота на +60° и последующего отражения в вертикальной плоскости ис-
используем поворот на —60° (т.е. по часовой стрелке), то получим сис-
систему функций
A.59)
а
0
0.85
0.1667
0.1667
b
0
0.04
-0.2887
0.2887
с
0
-0.04
0.2887
-0.2887
d
0.16
0.85
0.1667
0.1667
е
0
0
0
0
f
0
1.6
1.6
0.44
Р
0.01
0.85
0.07
0.07
Результат ее итераций показан на рис. 1.49 справа.
Рис. 1.49. Лист папоротника с правильным изгибом (слева) и с неправильным (спра-
(справа).
Сравнивая два изображения, мы понимаем, что отражение приво-
приводит к правильному изгибу тех листьев, которые расположены с пра-
правой стороны от стебля. Если бы во втором преобразовании не содер-
содержалось этого изгиба, то лист папоротника был бы прямой и результат
действия обоих преобразований A.58) и A.59) тогда, очевидно, был
бы одинаков.
Меняя параметры аффинных преобразований, входящих в систему
функций A.52), можно получить различные модификации листа папо-
папоротника (см. рис. 1.50). Часто они оказываются совсем не похожими
на своего "родителя".
И в завершение этого параграфа приведем СИФ для растения, ко-
которое особенно популярно в канун нового года. Это, безусловно, елка,
61

Рис. 1.50. Представители "семейства папоротниковых".
и построить ее можно по образу и подобию листа папоротника, надо
только, чтобы ее ветки смотрели не вверх, как листья у папоротни-
папоротника, а вниз (см. рис. 1.51). Левая елка получена с помощью системы
Рис. 1.51. Елки.
функций A.60), где в качестве третьего и четвертого преобразований
использованы соответственно повороты на +120° и —120° со сжатием
в 3 раза по обоим осям
а
0.1
0.85
-0.1667
-0.1667
-0
0.
b
0
0
.2887
2887
0.
-0
с
0
0
2887
.2887
0
0
-0.
-0.
d
.16
.85
1667
1667
е
0
0
0
0
f
0
1.6
1.6
1.6
Р
0.01
0.85
0.07
0.07
A.60)
62

Правая елка получена с помощью системы функций A.61)
а
0.1
0.85
-0.2357
-0.2357
-0
0.
b
0
0
.2357
2357
0.
-0
с
0
0
2357
.2357
0
0
-0.
-0.
d
.16
.85
2357
2357
е
0
0
0
0
f
0
1.6
1.6
1.6
Р
0.01
0.73
0.13
0.13
A.61)
где, в отличие от предыдущего случая, поворот в двух последних
преобразованиях произведен на угол ±Зтг/4. Использованы также
несколько другие значения вероятностей. Кроме того, для большей
правдоподобности изображения в обоих случаях мы несколько утол-
утолщили "ствол" (подумайте, за счет чего?).
1.3 Нелинейные комплексные отображения
1.3.1 Квадратичные отображения
Еще одним изящным алгоритмом создания фрактальных объектов на
плоскости является использование комплексных отображений, со-
сопоставляющих одному комплексному числу zn = xn+iyn другое комп-
комплексное число zn+i=xn+i+iyn+i по итерационному правилу zn+i=f(zn),
где f(z) — некоторая нелинейная функция z, n — номер итерации.
Из наиболее известных примеров такого рода рассмотрим простей-
простейшее квадратичное отображение
zn+1 = f (zn) = z2n + с
A.62)
где с = $Rc + i^sc — некоторая комплексная константа с веществен-
вещественной -ftc и мнимой Sc частью. Естественно, что это отображение всегда
может быть представлено в виде двух вещественных отображений
хп+1 = х2п-у
yn+i = 2хпуп
A.63)
в соответствии с которыми точка на комплексной плоскости с коор-
координатами (хп, уп) переходит в точку с координатами (xn+i, yn+i)- Ка-
Кажущаяся простота этого алгоритма никак не сопоставима с потряса-
потрясающей красотой и разнообразием тех фрактальных структур, которые
при этом возникают.
63

1.3.2 Неподвижные точки. Циклы
Однако, прежде чем приступить к их геометрическому построению,
введем необходимые термины и понятия. Неподвижной точкой z
отображения zn+i = f(zn) мы будем называть корень уравнения f(z) =
= z (его также называют неподвижной точкой функции f(z)). Оче-
Очевидно, что, начав процесс итераций в этой точке, мы никогда ее не
покинем. Можно сказать, что это есть своеобразное состояние рав-
равновесия. Однако, как известно, равновесие может быть трех типов:
устойчивым, неустойчивым и безразличным. В полной аналогии с
этим неподвижная точка отображения тоже может быть трех типов:
притягивающей, отталкивающей и нейтральной .
Если, стартовав в непосредственной близости от неподвижной точ-
точки, мы будем в процессе итераций к ней неограниченно приближать-
приближаться, то такая неподвижная точка называется притягивающей. Соот-
Соответственно, стартовав в непосредственной близости от отталкиваю-
отталкивающей неподвижной точки, мы будем от нее удаляться. Нейтральная
неподвижная точка характеризуется тем, что, стартовав в достаточно
малой ее окрестности, мы будем все время находиться в этой окрест-
окрестности, не приближаясь и не удаляясь от нее.
Чтобы определить характер неподвижной точки z отображе-
отображения f(z), надо вычислить производную f'(z). Если |/'(z)| < 1, то
точка z является притягивающей, если |/'(z)| > 1, то отталкива-
отталкивающей, и наконец, если |/'(z)| = 1, то неподвижная точка является
нейтральной. Эти утверждения станут понятными, если разложить
функцию f(z) в ряд Тейлора вблизи точки z:
f(z) = f(z) + (z-z)f'(z). A.64)
Тогда, принимая во внимание, что f(z) = z, отображение zn+\ = f(zn)
можно представить в виде
zn+1-z = (zn-z)f'(z). A.65)
Отсюда видно, что расстояние до неподвижной точки \zn — z\ в процес-
процессе итераций растет, если |/'(z)| > 1? уменьшается, если |/'(z)| < 1, и
остается постоянным (в линейном приближении), если |/'(z)| = 1.
10 В первых двух случаях ее также называют устойчивой и неустойчивой
соответственно.
64

При анализе отображений наряду с неподвижными точками важ-
важную роль также играют так называемые периодические точки и
циклы, состоящие из этих периодических точек. Так, например,
цикл периода два состоит из двух точек (j и ^ таких, что
/(Ci) = 6 и /fe) = Ci. A-66)
Очевидно, что начав процесс итераций в одной из точек цикла, мы его
никогда не покинем и будем по очереди переходить из одной точки
цикла в другую.
Нетрудно убедиться в том, что точки цикла (д и ($ являются не-
неподвижными точками отображения
zn+1 = f(f(zn)) = fW(zn). A.67)
Действительно, применив, например, операцию / к равенству /(Ci) =
= B и воспользовавшись тем, что /(Сг) = Съ получим:
= №) = Ci- A-68)
Аналогичным образом показывается, что /(/(Сг)) = Сг-
Помимо цикла периода 2 у рациональных отображений существу-
существуют циклы и всех высших порядков с п = 3,4, Если (о — периоди-
периодическая точка периода п, то она является неподвижной точкой функ-
функции f<yn\z) = /(... (f(f(z)))...). Очевидно также, что точка z, непо-
неподвижная для f(z), является неподвижной и для f^n\z).
Для того чтобы охарактеризовать устойчивость периодической точ-
точки ?, надо вычислить производные /^ (?). Пользуясь правилом диф-
дифференцирования сложной функции, легко показать, что эта произ-
производная — одна и та же для всех точек цикла. Например, для цикла
периода два
/B)/(Ci) = /'(/(Ci))/'(Ci) = /'&)/'(&) = /B)/(С2). A.69)
Если эта производная по модулю меньше единицы, то цикл называ-
называется притягивающим.
Аттрактором на комплексной плоскости мы будем называть точ-
точку (или точки), к которой сходится процесс итераций zn+\ = f(zn)
при п —У оо. В качестве такого аттрактора может выступать притя-
притягивающая неподвижная точка или притягивающий цикл определен-
определенного периода. Иногда таких аттракторов может быть несколько, они
65

также могут состоять из бесчисленного количества точек и представ-
представлять собой непрерывную линию или какое-нибудь другое (например,
канторовское) множество. Если же в процессе итераций изображаю-
изображающая их точка уходит на бесконечность, то аттрактором такого про-
процесса считается бесконечно удаленная точка.
1.3.3 Множество Жюлиа
Вернемся теперь к нашему квадратичному отображению и рассмот-
рассмотрим для начала простейший пример, когда значение комплекной кон-
константы с = 0. В этом случае отображение имеет две неподвижные
точки z\ = 0 и 2?2 = 1. Первая из них является притягивающей, так
как f'{z\) = 0, а вторая — отталкивающей (/'(^) = 2).
Пусть начальная точка будет равна некоторому комплексному чис-
числу zq. В этом случае при каждой итерации вычисляется точный
квадрат предыдущего числа: zq —>¦ z\ —>¦ z\ —>¦ z\ —>¦.... Для этой
последовательности в зависимости от zq имеется три возможности:
1. Начальная точка zq такова, что \zo\ < 1. Тогда в процессе итера-
итераций числа по модулю получаются все меньше и меньше, и их
последовательность неуклонно приближается к нулю. То есть
ноль является аттрактором для такого процесса (и притягиваю-
притягивающей неподвижной точкой этого отображения).
2. Начальное значение zq по модулю больше единицы, \zq\ > 1. Тог-
Тогда последовательные числа zn по модулю становятся все больше
и больше, стремясь в итоге к бесконечности. В этом случае ат-
аттрактором является бесконечно удаленная точка.
3. Начальная точка лежит на окружности единичного радиуса, т. е.
Zq\ = 1. В этом случае, очевидно, и все точки нашей последова-
последовательности продолжают оставаться на этой единичной окружнос-
окружности.
Таким образом, в рассмотренном примере на комплексной плоскос-
плоскости z имеется две области притяжения. Одна лежит внутри окруж-
окружности единичного радиуса, и принадлежащие ей точки имеют своим
аттрактором ноль — притягивающую неподвижную точку. Другая
66

расположена снаружи от этой окружности и имеет аттрактором бес-
бесконечно удаленную точку. Границей между этими двумя областями
притяжения является окружность единичного радиуса. На ней лежит
вторая (отталкивающая) неподвижная точка квадратичного отобра-
отображения z<i = 1 (а также отталкивающие неподвижные точки отобра-
отображений всех высших порядков f^n\z)).
Казалось бы, ситуация предельно проста, и нет смысла ждать ка-
какого-либо "подвоха" в том случае, если величина с в формуле A.62)
отлична от нуля. Граница, по-видимому, останется гладкой и будет
иметь форму каким-то образом деформированной окружности, а при-
притягивающая точка переместится из начала координат в другое место.
Рис. 1.52. Бассейн притягивающей неподвижной точки, с = —0.12375 + 0.56508 г.
Однако не все так просто! Давайте, например, возьмем в качестве
с ненулевое значение с = —0.12375 + 0.56508 г. Здесь для последо-
последовательности zq —У Z\ —У Z2 —У ... также имеется три возможности
типа перечисленных выше. Отличие, однако, заключается в том, что
внутренний аттрактор уже не является нулем, и самое главное —
граница не является гладкой. На рис. 1.52 показана эта граница и
внутренняя точка, к которой сходится процесс итераций. Видно, что
граница сильно изломана. Можно убедиться, что под лупой любого
увеличения эта граница будет столь же изломанной, как и без нее
(см. рис. 1.53).
67

Рис. 1.53. Фрактальная структура границы.
Мандельброт назвал это фрактальной структурой такой гра-
границы. Она напоминает извилистую линию морского берега, которая
становится тем длиннее, чем более мелкий масштаб используется для
ее измерения. Одной из характерных особенностей этой границы яв-
является ее самоподобие. Если взглянуть на любой из ее фрагментов,
то можно убедиться, что одна и та же форма встречается в разных
местах и имеет разные размеры.
Рис. 1.54. Бассейн притягивающего цикла периода 3, с = —0.12 + 0.74 г.
В математике такие границы областей притяжения называют мно-
множествами Жюлиа. Во время первой мировой войны французские
математики Гастон Жюлиа и Пьер Фату изучали их свойства для бо-
более общего случая рациональных отображений в комплексной плос-
плоскости. Их увлекательная деятельность оставалась в основном не-
неизвестной даже большинству математиков, поскольку в отсутствие
68

современной компьютерной графики было почти невозможно пере-
передать их тонкие идеи. Например, Жюлиа и Фату было хорошо извест-
известно о самоподобии, они доказали, что всю границу можно восстано-
восстановить по любой произвольно малой ее части путем конечного числа
итераций формулы z —> z2 + с.
Если выбрать теперь другое значение с, например, с = —0.12+
+0.74г, то получим рис. 1.54. Теперь множество Жюлиа представля-
представляет собой не одну "деформированную окружность", а состоит из беско-
бесконечного числа деформированных окружностей, образующих, однако,
связное множество. Внутренние точки этого множества притя-
притягиваются уже не одной неподвижной точкой, а циклом из трех то-
точек (j, B, Сз? отмеченных на рисунке более крупно. В итоге, стар-
стартовав внутри одной из таких деформированных окружностей, после
достаточно большого числа итераций, изображающая точка по очере-
очереди будет переходить между этими тремя точками. Математически
это означает, что
C2 = /(Ci), Сз = /(С2) и С1 = /(Сз), A-70)
где f(z) = z2 + с. Иными словами, эти три точки являются корнями
алгебраического уравнения шестой степени z = f^(z), т.е. непо-
неподвижными точками отображения zn+\ = f(f{f{zn))). В этом легко
убедиться, если применить к любому из трех написанных соотноше-
соотношений два раза операцию /(...) и воспользоваться двумя другими.
Рис. 1.55. Пыль Фату, с = 0.11031 - 0.67037 г.
69

Таким образом, для каждого значения комплексного параметра с
имеется свое множество Жюлиа, ограничивающее те области комп-
комплексных чисел zo, которые в процессе итераций не уходят на беско-
бесконечность. С изменением с, очевидно, меняется и геометрия границ
областей притяжения, т. е. множеств Жюлиа. Может случиться так,
что области притяжения исчезнут вовсе и связная граница превра-
превратится в облако изолированных точек, называемое пылью Фату (см.
рис. 1.55). Часто эти точки группируются весьма причудливым об-
образом вокруг определенных мест, и разрешение рисунка становит-
становится явно недостаточным, чтобы в ограниченной области комплексной
плоскости показать бесконечное число точек.
Если мы в качестве начальной выберем наугад одну из этих то-
точек, то последовательные итерации отображения z —У z2 + с будут
переводить нас из одной точки этого множества в другую довольно
хаотичным образом. Если же в качестве начальной будет взята лю-
любая другая точка (не из множества Жюлиа), то в процессе итераций
мы уйдем в конце концов на бесконечность.
1.3.4 Множество Мандельброта и классификация множеств Жюлиа
Существует правило, позволяющее определить, какой вид будет иметь
множество Жюлиа при том или ином значении с. Это правило приво-
приводит нас к множеству Мандельброта. Оно показано на рис. 1.56 как
закрашенная черным цветом часть комплексной плоскости. Видно,
что оно имеет необычайно сложную структуру. Каждое комплекс-
комплексное число с либо принадлежит черной структуре М, либо нет. Из
произвольной точки множества М можно попасть в любую другую,
не покидая множества М, т. е. множество Мандельброта является
связным.
Соответствующие множества Жюлиа процесса z —У z2 + с сущест-
существенно различаются. Они представляют из себя связные структуры,
когда с лежит внутри М, и рассыпаются на бесконечное число изо-
изолированных точек (пыль Фату), когда с лежит снаружи. Например,
самая большая кардиоида в центре содержит те значения с, при ко-
которых множество Жюлиа будет более или менее деформированной
окружностью, охватывающей область притяжения устойчивой непо-
неподвижной точки (см. рис. 1.52).
70

-2.4 -2.0 -1.6 -1.2
-0.2 0 0.2 0.4 0.6 0.8
-1.2
Рис. 1.56. Множество Мандельброта.
Помимо главной кардиоиды, множество Мандельброта содержит
также бесконечное число ее копий, называемых почками. Различ-
Различным почкам соответствует аттрактор вполне определенного периода.
Так, с, соответствующее циклу периода три (см. рис. 1.54), есть
центр самой большой "луковки" сверху от основной части М. Та-
Такой цикл появляется в результате трифуркации неподвижной точ-
точки соответствующего отображения, когда параметр с переходит из
основной части множества М в соответствующую почку. При такой
трифуркации притягивающая неподвижная точка становится оттал-
отталкивающей, однако "взамен" нее возникают три неподвижных притя-
притягивающих точки отображения zn+\ = f^(zn).
Аттрактор периода два возникает в результате бифуркации не-
неподвижной точки, когда с перемещается внутрь окружности, примы-
примыкающей слева к основной кардиоиде с центром на вещественной оси
в точке (-1,0) (см. рис. 1.57) и т.д.
Значение с = —0.481762 — 0.531657 г соответствует месту прора-
прорастания почки, дающей устойчивые циклы периода 5. Все пять точек
таких циклов отщепляются от жирной точки на рис. 1.58, когда с
переходит внутрь почки. В этой точке ветвления множество Жю-
71

Рис. 1.57. Притягивающий цикл периода 2, с = —1.
Рис. 1.58. Параболический бассейн около неподвижной точки.
лиа стягивает теперь уже маргинально устойчивый аттрактор,
являющийся переходным между аттрактором с одной устойчивой не-
неподвижной точкой и аттрактором, в качестве которого выступает
устойчивый цикл периода 5. Это называется параболическим слу-
случаем динамики. На рис. 1.59 показаны еще два примера множеств
Жюлиа подобного вида.
Помимо точек, где прорастают почки, основное тело множества
Мандельброта обладает граничными точками совершенно иных ти-
типов. Так, например, для с = —0.3904 — 0.58679 г получим рис. 1.60; в
этом случае неподвижная точка тоже будет маргинально устойчивой
и по нашей классификации относится к типу нейтральных. Отли-
72

б)
Рис. 1.59. Параболический случай, а) с = —1.25; с > —1.25: притягивающий цикл
периода 2; с < —1.25: притягивающий цикл периода 4; б) при подходящем произволь-
произвольно малом изменении с маргинально устойчивая неподвижная точка превращается в
притягивающий цикл периода 20.
чие от параболического случая заключается в том, что граница не
подходит к неподвижной точке. Не достигают ее и другие точки
при своем движении. Линии, напоминающие окружности, изобра-
Рис. 1.60. Диск Зигеля около неподвижной точки и его прообразы.
женные на рисунке, являются инвариантными. Это означает, что
выбрав начальную точку на какой-нибудь из этих "окружностей",
мы ее уже никогда не покинем в процессе итераций. Внутри облас-
области, ограниченной множеством Жюлиа, процесс протекает следующим
образом: сначала точки перескакивают из меньших, переферийных,
73

деформированных окружностей в большие до тех пор, пока не по-
попадут внутрь диска, содержащего неподвижную точку. Этот диск
называется диском Зигеля в честь немецкого математика Карла
Людвига Зигеля. После того как точки попадают туда, они начина-
начинают "вращаться" вокруг неподвижной точки по своим инвариантным
" окружностям".
Рис. 1.61. Дендрит, с = %.
Приведенные примеры иллюстрируют типичные случаи, когда
множество Жюлиа является связным и охватывает некоторую об-
область с внутренними точками. Однако эти примеры не описывают
всех возможных структур множеств Жюлиа. Как видно из рис. 1.56,
множество Мандельброта окружено иглоподобными более или менее
разветвленными и изогнутыми антеннами. Если поместить с на са-
самый конец одной из таких антенн, то мы получим и множества Жю-
Жюлиа подобной формы. На рис. 1.61 показан пример с = г. Такие
дендриты не имеют внутренности, т. е. они не ограничивают собой
никакой области притяжения на комплексной плоскости. Стартовав
с любой точки на этом дендрите, мы будем продолжать оставаться
на нем бесконечно долго, совершая хаотические блуждания. Если же
начальная точка с ним не совпадает, то мы уйдем в конце концов на
бесконечность.
При более пристальном рассмотрении оказывается, что на каждую
антенну множества М нанизано множество маленьких копий боль-
большого множества М, число которых бесконечно (см. рис. 1.62). Если
значение с находится в одной из этих миниатюрных копий М, то
74

Рис. 1.62. Маленькие копии большого множества М.
соответствующее множество Жюлиа является некоторой комбинаци-
комбинацией дендрита и множества Жюлиа, полученного для соответствующего
значения с из основной части М. При этом последнее копируется бес-
бесконечное число раз и насаживается на дендрит. На рис. 1.63 показан
один из примеров такого рода.
Рис. 1.63. Дендрит с бусами. Множество Жюлиа из вторичного множества Ман-
дельброта.
Если взять значение с снаружи М, то единственным аттрактором,
как и в случае чисто дендритовой структуры, будет бесконечность.
Множество Жюлиа тогда распадается в облако точек, называемое
пылью Фату. Эта пыль становится все мельче и мельче по мере
удаления с от М. Если с находится вблизи границы М, то пыль
75

образует завораживающие фигуры, один пример которых был пока-
показан на рис. 1.55, а другой изображен на рис. 1.64. Эти фигуры всегда
фрактальны, самоподобны и несут в себе хаотическую динамику.
Рис. 1.64. Множество Жюлиа при некотором значении с из долины морских коньков.
1.3.5 Построение множества Мандельброта
Для того чтобы построить множество Мандельброта, надо опреде-
определить, является ли связным множество Жюлиа для соответствующе-
соответствующего значения с. Это, вообще говоря, является довольно сложной за-
задачей. Однако существует важная теорема, доказанная независимо
Жюлиа и Фату, что множество Жюлиа связно тогда и только тогда,
когда, стартовав из начала координат (zq = 0), последовательность
итераций zn не уходит на бесконечность. Это служит эффективным
критерием определения того, принадлежит ли данное значение с мно-
множеству Мандельброта или нет, и фактически является способом его
построения.
Так, выбрав на комплексной плоскости некоторое значение с и взяв
в качестве начальной точку zq = 0, мы имеем в соответствии с ал-
алгоритмом A.62) такую последовательность чисел: z\ = с, z<i = с2 + с,
^з = (с2 + сJ + с и т. д. Если эта последовательность не имеет своим
пределом бесконечно удаленную точку, то данное значение с принад-
принадлежит множеству Мандельброта. Очевидно, начальной точкой этой
последовательности может служить и само значение с.
Разумеется, реально продолжать до бесконечности процесс ите-
итераций невозможно, и на практике ограничиваются неким конечным,
76

но достаточно большим числом итераций N. Однако, чем ближе (с
наружной стороны) мы находимся к границе множества М, тем боль-
большее значение N мы должны взять и тем точнее должны быть наши
расчеты. Подытожив, мы приходим к следующим трем правилам:
• Если точка с находится далеко от множества Мандельброта, то
последовательность итераций zn+\ = z\ + с, стартующая в точ-
точке zq = 0, быстро уходит на бесконечность.
• Если с расположена поблизости от множества Мандельброта, то
последовательность итераций уходит на бесконечность медленно.
Тем медленнее, чем ближе к границе М мы находимся.
• Если с лежит внутри множества Мандельброта, то последователь-
последовательность итераций никогда не уходит на бесконечность.
Другой важной технической деталью является легко доказываемое
утверждение, что если \с\ < 2 и изображающая точка вышла в процес-
процессе итераций за границы круга радиуса 2, то затем она уже достаточно
быстро уходит на бесконечность.
Этим правилам соответствуют алгоритмы раскраски цветных ри-
рисунков с изображением множества Мандельброта. Само множество
при этом окрашивается, например, в черный цвет. Точки, лежащие
снаружи М, окрашиваются в различные цвета в зависимости от чис-
числа итераций, требуемых, чтобы пересечь границы круга радиуса 2.
Один и тот же цвет соответствует одному и тому же числу итера-
итераций N.
Глядя на рисунки, изображающие различные части множества Ман-
Мандельброта или на соответствующие им множества Жюлиа, поража-
поражаешься огромному количеству информации, которое в них содержит-
содержится. Это бесконечное разнообразие форм и конструкций, которое от-
открывается нашему взгляду, никак не сопоставимо с банальной прос-
простотой формулы, их породившей: zn+\ —> z\ + с. Можно считать, что
итерационный процесс, определяемый этой формулой, — это необы-
необычайно эффективный способ расшифровки информации, содержащейся
в исходных данных (значении комплексного параметра с и положении
начальной точки zq), которые являются своеобразным ключом.
Подобное явление наблюдается и в биологии, где вся генетичес-
генетическая информация о будущем организме заложена в структуре малень-
77

кой молекулы ДНК. Это, конечно, не означает, что множество Ман-
дельброта может служить моделью какого-либо биологического явле-
явления. Оно лишь, как и рассмотренные нами ранее простейшие Л-сис-
темы, представляет собой пример того, как достаточно простая ди-
динамическая система может развить, казалось бы, незначительную
информацию, содержащуюся в ключе, и породить разнообразные вы-
высокоорганизованные структуры.
1.3.6 Комплексные Ньютоновы границы
Еще одним примером появления фрактальных границ областей при-
притяжения является алгоритм Ньютона для приближенного нахождения
корней уравнения f(z) = 0 в комплексной плоскости. Для функции
действительной переменной его также часто называют методом ка-
касательных. В этом случае он сводится к следующему.
Пусть нам задана функция /(ж), для которой известно приближен-
приближенное значение ее корня х\, а также значение функции в этой точ-
точке f{x\) и ее первой производной f'(x\). Тогда, проводя касательную
к графику функции /(ж) в этой точке и определяя ее пересечение
с осью ж, мы получим уточненное положение корня, равное x<i (см.
рис. 1.65).
Af(x)
Рис. 1.65. Метод касательных.
Поскольку уравнение касательной к графику функции /(ж) в точ-
точке х\ выглядит следующим образом
у = f'(xi)(x-xi) + f(xi),
A.71)
78

то, приравнивая у нулю, получаем, что уточненное значение корня x<i
связано с предыдущим значением х\ соотношением
- = - (L72)
Беря теперь значение Х2 в качестве приближенного и повторяя этот
алгоритм, находим следующее значение а?з и т. д. Этот процесс быстро
сходится к истинному значению корня. Грубо говоря, число верных
десятичных знаков удваивается на каждом шаге. Этот метод не ме-
менее эффективен и для комплексных чисел.
Это значит, что, стартовав в непосредственной близости от зна-
значения корня уравнения f{z) = 0, мы, используя итерационный ал-
алгоритм
T\Zn) (л 7QN
zn+i = zn- , l-L-'^j
/ \zn)
получим последовательность комплексных чисел, быстро сходящую-
сходящуюся к этому корню. Возникает правомерный вопрос, а что будет, если
начальная точка zq выбрана в плоскости комплексных чисел не вблизи
от корня, а произвольным образом?
Этот вопрос в 1977 г. был задан молодому американскому мате-
математику Джону Хаббарду (John Hubbard) его студентами-первокурс-
студентами-первокурсниками, когда он преподавал им математику в Парижском универ-
университете Орсэй. Хаббард довольно быстро доказал, что для уравнения
второй степени данная последовательность всегда будет сходиться к
ближайшему корню. Исключение составляют случаи, когда началь-
начальная точка zq равноудалена от обоих корней, т. е. лежит на прямой,
проведенной через середину отрезка, соединяющего два корня, пер-
перпендикулярно ему. В этом случае последовательность итераций все
время остается на этой прямой, совершая хаотическое движение.
Однако уже для уравнения 3-й степени такой же простой ответ ему
найти не удалось. В этой неудаче он был неодинок. Оказывается, еще
в конце XIX века с этой же проблемой безуспешно сражался и Артур
Кэли (Arthur Cayley). Он также нашел ответ для уравнения 2-й степе-
степени и анонсировал случай многочленов более высокой степени как бу-
будущую публикацию, но ей так и не суждено было появиться. Однако
у Хаббарда было существенное преимущество — в его распоряжении
79

был компьютер! К концу семестра он вместе со своими студентами
уже получил несколько важных экспериментальных результатов.
Z2
Z2,
Рис. 1.66. "Пирог Ньютона", zx = 1, z2 = -1/2 + гд/3/2, z3 = -1/2 - гд/3/2.
Они начали с простейшего уравнения третьей степени z3 — 1 = 0.
Это уравнение, как известно, имеет 3 корня — один расположен-
расположенный на действительной оси и равный 1 и два комплексно- сопряжен-
сопряженных: — 1/2 + iy/3/2 и —l/2—i-\/3/2. Нанесенные на комплексную плос-
плоскость, они образуют равносторонний треугольник, так что если ци-
циферблат часов принять за единичную окружность, то один корень
соответствует 3 часам, другой 7 и третий 11. Легко показать, что
эти корни действительно являются притягивающими неподвижными
точками (аттракторами) отображения A.73) с f(z) = z3 — 1
^. A.74)
Стартовав в непосредственной окрестности каждого из корней, ме-
метод Ньютона быстро сходился к этому корню. В самом грубом при-
приближении комплексную плоскость можно было, как пирог, разделить
на три равные части, каждая из которых являлась областью притя-
притяжения соответствующего корня (см. рис. 1.66). Эта была именно та
картинка, которую первоначально представлял себе Хаббард (и мно-
многие другие до него). Однако более скрупулезное компьютерное иссле-
исследование выявило, что геометрия границ областей притяжения имеет
гораздо более сложную форму.
Так, если раскрашивать разные области притяжения разным цве-
цветом, то на экране монитора возникала картинка, изображенная на
80

рис. 1.67. Из этого рисунка видно, что граница областей притяже-
притяжения состоит из сильно переплетенных самоподобных (фрактальных)
структур. Оказалось, что на границе между любыми двумя цвета-
цветами всегда расположена гирлянда островков третьего цвета. Границы
этих островков, в свою очередь, состоят из гирлянд островков мень-
меньшего размера соответствующего дополнительного цвета и т.д (см.
рис. 1.68). Непрерывно уменьшаясь в размерах, детали границы по-
постоянно воспроизводят самих себя. В результате оказывается, как
неправдоподобно это не звучит, что каждая точка такой фрактальной
границы соседствует сразу с тремя областями притяжения!
Рис. 1.67. Структура границ областей притяжения трех корней уравнения гъ = 1.
Если теперь взять произвольное уравнение третьей степени, то
в некоторых случаях, наряду с областями притяжения к одному из
трех корней, на комплексной плоскости можно обнаружить области
начальных значений, стартуя из которых точка притягивается к цик-
циклу, который не связан ни с одним из корней. Интересно, что форма
этих областей удивительно напоминает множества Жюлиа для много-
многочленов второй степени. Можно сказать, что существуют "хорошие"
(по отношению к методу Ньютона) уравнения, для которых почти
все начальные точки ведут к какому-либо корню, и "плохие", для ко-
81

торых метод Ньютона иногда приводит к появлению притягивающего
цикла.
Рис. 1.68. Увеличенный участок границы.
Таким образом, если коэффициенты нашего уравнения зависят от
некоторого комплексного параметра с, то, меняя значения этого пара-
параметра, мы будем получать либо хорошие, либо плохие уравнения. Ес-
Если теперь на комплексной плоскости [с] окрашивать, скажем, в чер-
черный цвет те области, которые соответствуют плохим уравнениям, то
при сильном увеличении этих областей можно увидеть разбросанные
повсюду маленькие черные копии множества Мандельброта.
82

2 МУЛЬТИФРАКТАЛЫ
2.1 Геометрическое описание мультифракталов
2.1.1 Что такое мультифрактал?
В этой части мы изложим основы теории мультифракталов — неод-
неоднородных фрактальных объектов, для полного описания которых,
в отличие от регулярных фракталов, недостаточно введения всего
лишь одной величины, его фрактальной размерности D, а необходим
целый спектр таких размерностей, число которых, вообще говоря,
бесконечно. Причина этого заключается в том, что наряду с чисто
геометрическими характеристиками, определяемыми величиной D,
такие фракталы обладают и некоторыми статистическими свойства-
свойствами.
В
E ^k?l?l;,:, &.?. ?. „ г
A
A
ii, ?.
Д, A /^, /'
D
A2.t\ ?',...'
i,?r._ ?.,.... L,.l. .
C
Рис. 2.1. Игра в хаос с неравными вероятностями. Показано 107 итераций.
Проще всего пояснить, что понимается под "неоднородным фрак-
фракталом" на примере треугольника Серпинского, полученного с помо-
помощью метода случайных итераций, который мы рассмотрели в первой
части. Мы показали, что система итерируемых функций для этого
фрактала состоит из трех линейных преобразований на комплексной
плоскости A.22), каждое из которых выбиралось с одинаковой веро-
вероятностью, равной 1/3. В результате мы получили рис. 1.27.
83

Допустим, однако, что в методе случайных итераций мы теперь по
какой-то причине отдали предпочтение одной из вершин треугольни-
треугольника, например, вершине А, и стали выбирать ее с вероятностью 90%.
Две же остальные вершины В и С для нас по-прежнему равноценны,
но на их долю теперь приходится всего лишь по 5%. Результат такой
"несимметричной игры" изображен ниже на рис. 2.1.
Видно, что точки внутри треугольника ABC распределены теперь
крайне неравномерно. Большая их часть находится у вершины А и ее
прообразов. В то же время у вершин В и С (и их прообразов) их име-
имеется крайне мало. Тем не менее по обычной терминологии данное
множество точек (при стремлении числа итераций к бесконечности)
является фракталом, так как сохранилось основное свойство фракта-
фрактала — самоподобие. Действительно, треугольник DFC, хотя в нем в 20
раз меньше точек, по своим статистическим и геометрическим свой-
свойствам полностью подобен большому треугольнику ABC. Так же, как
и в большом треугольнике, точки в нем концентрируются в основном
вблизи вершины D — аналоге вершины А.
Рис. 2.2. Распределение точек по треугольнику Серпинского, изображенного на
рис. 2.1.
На рис. 2.2 более детально показано результирующее распределе-
распределение точек по треугольнику Серпинского. Цифры в каждом из ма-
маленьких треугольников показывают его относительную заселенность
точками множества.
Однако, несмотря на неравномерность распределения точек по фрак-
фракталу, его фрактальная размерность осталась при этом преж-
84

ней, D = In 3/In 2. Покрытие этого множества все более и более мел-
мелкими треугольниками можно осуществить по тому же алгоритму,
что и ранее. Такое совпадение заставляет нас заняться поиском иных
количественных характеристик, которые могли бы отличить нерав-
неравномерное распределение точек от равномерного.
Другой, более сложный пример неоднородного фрактала, который
мы бы хотели еще привести, показан на рис. 2.3. Здесь слева показан
большой квадрат со стороной, равной единице, который на этом (ну-
(нулевом) этапе полностью покрывает собой некоторое фрактальное мно-
множество точек Л4. На следующем (первом) этапе, в центре рисунка,
показано, как то же самое множество можно покрыть тремя меньши-
меньшими квадратами со сторонами 1\ = 1/2, /2 = ^3 = 5/16, в которых, соот-
соответственно, содержится доля р\ = 1/2, р2 = 1/3 и рз = 1/6 всех точек.
1/9 1/18 1/18 1/36
1/3
1/6
1/2
1/6
1/12
1/6
1/12
.1/4
Рис. 2.3. Пример мультифрактала, подчиняющегося ренормализационной схеме.
Здесь h = 1/2, h = h = 5/16, Pl = 1/2, р2 = 1/3, р3 = 1/6.
Следующий этап покрытия (изображенный на рисунке справа) со-
содержит уже 9 квадратиков со сторонами 1\ = 1/4, 1\12 = hh — 5/32
(в нижнем правом углу) и 121\ = 5/32, \\ = ^з — 25/256 (вверху
справа и слева). Относительная заселенность этих квадратиков точ-
точками множества показана на рисунке. Она соответствует произведе-
произведению факторов заселенностей (вероятностей): р\ = 1/4, р\Рч = 1/6,
Р\Р2, = 1/12 — для нижней правой группы, р2р\ = 1/6, р\ = 1/9,
ViVz = 1/18 — для верхней левой и р^рх = 1/12, р^р2 = 1/18, р\ = 1/36 —
для верхней правой группы. Отметим, что имеется строгое соответ-
соответствие между заселенностью квадратика pjPi и его размерами ^7г.
85

Дальнейший процесс разбиения и покрытия множества Л4 осу-
осуществляется в соответствии с этой ренормализационной схемой. Каж-
Каждый квадратик, имеющий на п-м шаге размер / и заселенность р, за-
заменяется на п + 1 шаге на три квадратика с размерами ll\, Ifo, //3
и заселенностями ppi, pp2, ррз соответственно, расположенными та-
таким же образом относительно друг друга, как показано на рис. 2.3
в центре п.
Два рассмотренных выше случая представляют собой примеры не-
неоднородных фракталов. Под словом "неоднородный" мы здесь по-
понимаем неравномерное распределение точек множества по фракта-
фракталу. Причина неоднородности в обоих случаях одна и та же — раз-
разные вероятности заполнения геометрически одинаковых элементов
фрактала, или в общем случае несоответствие вероятностей запол-
заполнения геометрическим размерам соответствующих областей. Такие
неоднородные фрактальные объекты в литературе называются муль-
тифракталами, и их изучением мы и займемся в дальнейшем.
2.1.2 Обобщенные фрактальные размерности Dq
Дадим общее определение мультифрактала. Рассмотрим фракталь-
фрактальный объект, занимающий некую ограниченную область С размера L
в Евклидовом пространстве с размерностью d. Пусть на каком-то
этапе его построения он представляет собой множество из N ^> 1 то-
точек, как-то распределенных в этой области. Мы будем предполагать,
что в конце концов N —>¦ сю. Примером такого множества может
служить треугольник Серпинского, построенный методом случайных
итераций. Каждый шаг итерационной процедуры добавляет к этому
множеству одну новую точку.
Разобьем всю область С на кубические ячейки со стороной е <С L
и объемом ed. Далее нас будут интересовать только занятые ячей-
ячейки, в которых содержится хотя бы одна точка. Пусть номер занятых
ячеек i изменяется в пределах i = 1, 2,... N(e), где N(e) — суммар-
суммарное количество занятых ячеек, которое, конечно, зависит от размера
ячейки е.
11 Очевидно, что предыдущий пример построен по схожему алгоритму с 1\ = 12 =
= h = 0.5 и pi = 0.9, р2 = Рз = 0.05.
86

Пусть П{{г) представляет собой количество точек в ячейке с но-
номером г, тогда величина
jH{e) = Вт Ц^ B.1)
представляет собой вероятность того, что наугад взятая точка из на-
нашего множества находится в ячейке %. Другими словами, вероятнос-
вероятности pi характеризуют относительную заселенность ячеек. Из условия
нормировки вероятности следует, что
Щв)
Е Pi(e) = 1- B-2)
г=1
Введем теперь в рассмотрение обобщенную статистическую
сумму Z(q,e), характеризуемую показателем степени q, который
может принимать любые значения в интервале —оо < q < +оо
Щв)
Z(q,e)= ?р?(е). B-3)
г=1
Спектр обобщенных фрактальных размерностей Dq, харак-
характеризующих данное распределение точек в области С, определяется
с помощью соотношения
D, = 1^, B.4)
где функция r(q) имеет вид
. ч ,. \nZ(q,e) ,
r(g) = lim—-^-Л B.5)
У J e^O ]ne V '
Как мы покажем ниже, если Dq = D = const, т. е. не зависит
от q, то данное множество точек представляет собой обычный, регу-
регулярный фрактал, который характеризуется всего лишь одной вели-
величиной — фрактальной размерностью D. Напротив, если функция Dq
как-то меняется с q, то рассматриваемое множество точек является
мультифракталом.
Таким образом, мультифрактал в общем случае характеризуется
некоторой нелинейной функцией r(q), определяющей поведение ста-
статистической суммы Z(q,s) при е —>¦ О
N(e)
Z(q,e)= E #) « eT(e). B-6)
г=1
87

Следует иметь в виду, что в реальной ситуации мы всегда имеем
конечное, хотя и очень большое число дискретных точек N, поэтому
при компьютерном анализе конкретного множества предельный пере-
переход е —>¦ 0 надо выполнять с осторожностью, помня, что ему всегда
предшествует предел N —>¦ сю.
Покажем теперь, как ведет себя обобщенная статистическая сумма
в случае обычного регулярного фрактала с фрактальной размернос-
размерностью D. В этом случае во всех занятых ячейках содержится одинако-
одинаковое количество точек
^ B.7)
то есть фрактал является однородным. Тогда очевидно, что отно-
относительные населенности всех ячеек, Pi(s) = 1/N(e), тоже одинаковы,
и обобщенная статистическая сумма принимает вид
Z{q,e)=Nl-'\e). B.8)
Учтем теперь, что, согласно определению фрактальной размернос-
размерности D, число занятых ячеек при достаточно малом е ведет себя следу-
следующим образом
N(e) и ?~D. B.9)
Подставляя это в формулу B.8) и сравнивая с B.6), мы приходим
к выводу, что в случае обычного фрактала функция
r(q) = (q- 1)D, B.10)
т. е. является линейной. Тогда все Dq = D и действительно не зави-
зависят от q. Для фрактала, все обобщенные фрактальные размерности Dq
которого совпадают, часто используется термин монофрактал.
Если распределение точек по ячейкам неодинаково, то фрактал
является неоднородным, т. е. представляет из себя мультифрактал,
и для его характеристики необходим целый спектр обобщенных фрак-
фрактальных размерностей Dq, число которых, в общем случае, бесконеч-
бесконечно.
Так, например, при q —>¦ +оо основной вклад в обобщенную статис-
статистическую сумму B.3) вносят ячейки, содержащие наибольшее число
частиц щ в них и, следовательно, характеризующиеся наибольшей
вероятностью их заполнения рг-. Наоборот, при q —>¦ —сю основной

вклад в сумму B.3) дают самые разреженные ячейки с малыми значе-
значениями чисел заполнения р(. Таким образом, функция Dq показывает,
насколько неоднородным является исследуемое множество точек С.
В дальнейшем для характеристики распределения точек необходи-
необходимо знать не только функцию r(q), но и ее производную, непосредст-
непосредственно вычисляемую из выражений B.5) и B.3)
Ще)
do
Эта призводная, как мы увидим, имеет важный физический смысл.
Здесь же повторим, что если она не остается постоянной и меняется
с q, то это означает, что мы имеем дело с мультифракталом.
2.1.3 Фрактальная размерность Do и информационная размерность D\
Выясним теперь, какой физический смысл имеют обобщенные фрак-
фрактальные размерности Dq для некоторых конкретных значений q. Так,
при q = 0 из выражения B.3) следует, что
B.12)
С другой стороны, согласно формулам B.6) и B.4),
{0) Do. B.13)
Сопоставляя эти два равенства, мы приходим к соотноше-
соотношению N(e) « e~D°. Это означает, что величина Dq представляет со-
собой обычную хаусдорфову размерность множества С. Она является
наиболее грубой характеристикой мультифрактала и не несет инфор-
информации о его статистических свойствах.
Выясним теперь смысл величины D\. Поскольку при q = 1, в силу
условия нормировки вероятности B.2), статистическая сумма равна
Z(l,e) = l, B.14)
то тA) = 0. Таким образом, мы имеем неопределенность в выраже-
выражении B.4) для D\. Раскроем эту неопределенность с помощью очевид-
89

ного равенства
Ще) Ще)
Z(q, г) = Y, р\ = Y, Pi exp [{q - 1) ]nPi]. B.15)
г=1 i=l
Теперь, устремляя q —>¦ 1, раскладывая экспоненту и учитывая усло-
условие нормировки B.2), получаем
Ще) Ще)
Z(q -+ 1, г) и S fe + (q - l)Pi \nPi] = 1 + (q - 1) ? Pi lnp,-. B.16)
г=1 г=1
В результате мы приходим к следующему выражению
= lim ^ . B.17)
С точностью до знака числитель в этой формуле представляет со-
собой энтропию фрактального множества S(e):
Ще)
S(e) = - E Pilnpi. B.18)
г=1
Такое определение энтропии множества полностью идентично исполь-
используемому в термодинамике, где под pi понимается вероятность об-
обнаружить систему в квантовом состоянии i. В результате величина
обобщенной фрактальной размерности D\ связана с энтропией S{e)
соотношением
^ B.19)
Прежде чем далее характеризовать эту величину, напомним, что
в термодинамике энтропия есть мера беспорядка в системе. Простой
пример, где молекулы газа, помещенные вначале в одну половину
сосуда, заполняют весь сосуд, когда убирается перегородка, пока-
показывает, что в этом процессе беспорядок, а следовательно, энтропия
возрастает. Этот рост беспорядка связан с ростом нашего незнания
о состоянии системы, поскольку до удаления перегородки мы знали
больше о расположении молекул.
Основываясь на подобных соображениях, Клод Шенон обобщил по-
понятие энтропии 5, известное в термодинамике, на абстрактные зада-
90

чи теории передачи и обработки информации. Для этих задач энтро-
энтропия стала мерой количества информации, необходимой для определе-
определения системы в некотором положении г. Другими словами, она явля-
является мерой нашего незнания о системе.
Поясним эти соображения на простом примере. Допустим, имеет-
имеется ящик с двумя отделениями, в одном из которых находится точка.
Однако мы не знаем, в каком. Спрашивается, сколько вопросов с от-
ответом да или нет нужно задать, чтобы определить местоположение
точки? Ответ очевиден — один вопрос. Эту информацию принимают
за единицу и называют ее бит.
Для обнаружения точки в ящике с четырьмя возможными состо-
состояниями требуется уже два вопроса, и, соответственно, мера нашего
незнания о системе равна двум битам. Эту информацию можно запи-
записать как логарифм по основанию два от числа возможных состояний
системы
7 = log24. B.20)
Теперь становится понятно, что справедливо логарифмическое соот-
соотношение между максимальным количеством информации / и числом
состояний М
7 = log2M. B.21)
Так, например, чтобы определить положение точки на шахматной
доске с 64 = 26 клетками, требуется 6 вопросов.
В предыдущем случае ящика с двумя состояниями количество ин-
информации в один бит можно выразить также следующим образом
/=-glog4 + Jl°g2|). B.22)
Учитывая, что 1/2 = Р\ = Р2 — есть вероятность обнаружить систе-
систему в одном из ящиков, эту формулу можно переписать так
/ = -EP.-log2Pi- B-23)
i
В таком виде она справедлива и в случае ящика с М = 2й состоя-
состояниями, где все вероятности pi = 1/М одинаковы. Более того (и это
как раз и составляет результат, полученный Шеноном), эта формула
остается справедливой и в случае неравных вероятностей р^, однако
91

ее нужно тогда понимать в смысле среднего значения по большому
числу испытаний. Отсюда уже остается всего один шаг до соотноше-
соотношения между энтропией S(s) и количеством информации /.
Возвращаясь к исходной задаче о распределении точек на фрак-
фрактальном множестве С, можно сказать, что поскольку, как следует
из B.19),
S(e) и ?~D\ B.24)
то величина D\ характеризует информацию, необходимую для оп-
определения местоположения точки в некоторой ячейке. В связи с этим
обобщенную фрактальную размерность D\ часто называют инфор-
информационной размерностью. Она показывает, как информация, не-
необходимая для определения местоположения точки, возрастает при
стремлении размера ячейки в к нулю.
2.1.4 Корреляционная размерность D2
Рассмотрим еще один частный случай, q = 2, и покажем, какой физи-
физический смысл имеет обобщенная фрактальная размерность D<i- Для
нее справедливо следующее выражение
N(e)
B.25)
Определим парный корреляционный интеграл
I(e)= Hm ±?6>(?-|rn-rm|), B.26)
где суммирование проводится по всем парам точек нашего фракталь-
фрактального множества с радиус-векторами гп и rm; 0(х) — ступенчатая
функция Хевисайда, 9{х) = 1, если х > 0 и 0(х) = 0, если х < 0.
Сумма в выражении B.26) определяет число пар точек п, т, для ко-
которых расстояние между ними меньше, чем в. Поэтому, поделенная
на N2, она определяет вероятность того, что две наугад взятые точки
разделены расстоянием меньшим, чем в 12.
12 На самом деле надо делить на число пар, равное N(N — l)/2, но мы здесь не
интересуемся численными коэффициентами, а только зависимостью от е.
92

Эту же вероятность можно определить и по-другому. Величина pi,
согласно своему определению B.1), представляет собой вероятность
попадания точки в i-ю ячейку с размером е. Следовательно, величи-
величина р\ представляет собой вероятность попадания в эту ячейку двух
точек. Суммируя р\ по всем занятым ячейкам, мы получаем веро-
вероятность того, что две произвольно выбранные точки из множества С
лежат внутри одной ячейки с размером е. Следовательно, расстояние
между этими точками будет меньше или порядка е. Таким образом,
с точностью до численных коэффициентов, принимая во внимание
равенство B.25), получаем
N(e)
J(e)« ? P2i~eD2. B.27)
г=1
Мы приходим к выводу, что обобщенная размерность D<i определя-
определяет зависимость корреляционного интеграла 1{е) от ? в пределе е —>¦ 0.
По этой причине величину D<i в литературе называют корреляци-
корреляционной размерностью.
Установим теперь ее связь с парной корреляционной функцией.
Для этого введем плотность вероятности р(г)
р(г) = ^?*(г-гО. B.28)
По своему физическому смыслу p(r)ddr — есть вероятность обнару-
обнаружить точку фрактального множества в объеме ddr вокруг точки г.
Она, очевидно, удовлетворяет условию нормировки
I p{r)ddr = 1. B.29)
с
Парная корреляционная функция связана с р(г) следующим обра-
образом
С(г) = / ^(г')р(г' + г) А'. B.30)
с
Она представляет собой плотность вероятности двум произвольным
точкам множества находиться на расстоянии г друг относительно
друга. Под интегралом в этом выражении стоит плотность условной
вероятности иметь одной точке координату г' + г, если другая точка
имеет координату г'.
93

В силу отсутствия характерного масштаба длины, для введенной
таким образом корреляционной функции С (г) характерно степенное
поведение с расстоянием г, т. е. C(r) « l/W3, где C — некоторый
показатель степени. Легко показать, что он связан с корреляционной
размерностью D<i соотношением
0 = d-D2, B.31)
где d — обычная евклидова размерность пространства.
Действительно, в силу своего определения плотности условной ве-
вероятности величина С (г), будучи проинтегрирована по ^-мерной сфе-
сфере радиуса е, определяет вероятность того, что две наугад взятые
точки из множества С окажутся внутри этой сферы. Иными словами,
это есть не что иное, как введенный нами выше корреляционный
интеграл 1{е)
е
1(е) и / drrd~xC{r) и ed~0. B.32)
о
Сравнивая это с выражением B.27), мы приходим к соотноше-
соотношению B.31).
Далее мы покажем, что в случае мультифрактала с фрактальной
размерностью D$ < d справедливо также неравенство D<i < d. Поэто-
Поэтому показатель степени /9 > 0 и корреляционная функция С(г) убывает
с расстоянием г. Причину этого убывания можно пояснить так. Рас-
Рассмотрим для простоты однородный фрактал с размерностью D < d.
Тогда для него D<i = D. Количество точек в каждой ячейке размера е
в этом случае одинаково и пропорционально щ{г) ос еп'. Если мы
теперь разделим эту величину на объем ячейки ed, то получим плот-
плотность точек р(е), которая будет уменьшаться с увеличеним размеров
ячейки р{г) ос l/ed~D = 1/е@. Это уменьшение плотности р с ростом
размеров ячейки и является физической причиной спада корреляци-
корреляционной функции С (г).
Можно также легко доказать, что если корреляционная функция
мультифрактала убывает с расстоянием по степенному закону C(r) ~
l/rd~D2, то ее фурье компонента С (к) в зависимости от волнового
вектора к тоже меняется по степенному закону С (к) ~ 1/к°2.
94

2.1.5 Свойства функции Dq
Как мы уже говорили, мультифрактал характеризуется неоднород-
неоднородным распределением точек по ячейкам. Как известно из термодина-
термодинамики, энтропия неоднородного распределения молекул газа в сосуде
всегда меньше энтропии их однородного распределения (в том же со-
сосуде), когда газ везде обладает одной и той же плотностью. Соот-
Соответственно, если бы точки, составляющие мультифрактал, были бы
распределены по нему равномерно по всем N(s) ячейкам с вероят-
вероятностью р^ = 1/N(e), энтропия такого распределения была бы макси-
максимальна и равна
Ще)
SmaX(?) = - ? Pi In Pi = \nN(e) и -D0\ne. B.33)
г=1
Другими словами, она была бы больше фактической величины энтро-
энтропии мультифрактала, рассчитанной для реального неоднородного рас-
распределения точек, S(s) = —Dilne. Отсюда следует важный вывод,
что информационная размерность мультифрактала D\ всегда меньше
или равна его хаусдорфовой размерности Dq.
Это неравенство можно обобщить для произвольного показателя
степени q и доказать, что обобщенная фрактальная размерность Dq
всегда монотонно убывает (или в крайнем случае остается постоян-
постоянной) с ростом q
Dq > Dq> при q' > q. B.34)
Знак равенства имеет место, например, для однородного фрактала.
Максимального значения Dmax = .D-oc величина Dq достигает при
q —>¦ —сю, а минимального Dm\n = Д^ при q —>¦ оо.
2.1.6 Неоднородное канторовское множество
Рассмотрим ниже простой пример, который позволит нам вычис-
вычислить спектр обобщенных фрактальных размерностей Dq аналитичес-
аналитически и продемонстрировать основные свойства функции Dq. Возьмем
уже знакомое нам канторовское множество исключенных средних
третей. Пусть в начале процедуры (нулевой шаг) у нас имеется еди-
единичный отрезок, по которому как-то распределены N точек нашего
фрактального множества. На первом шаге мы уже имеем 2 отрезка по
95

краям первоначального единичного интервала, каждый из них дли-
длиной 1/3. Пусть наши исходные N точек распределены по ним теперь
следующим образом. Левый отрезок заселен с вероятностью р\ и име-
имеет p\N точек, а правый с вероятностью рч = 1 — pi, и на нем, соот-
соответственно, находится P2N точек. Затем с каждым из этих отрезков
мы поступаем аналогичным образом. В результате на втором шаге
у нас уже имеется 4 отрезка длиной 1/9, заселенных с вероятностью
(слева направо) р\, Р1Р2, РчРх-, р\ (см- Рис- 2.4) и т.д.
Р=1
Pi P1P2 Р2Р1 Р2
Рис. 2.4. Неоднородное канторовское множество.
Повторяя эту процедуру некоторое число раз, мы приходим к сле-
следующей картине распределения точек. На шаге п наше множество
состоит из 2й отрезков длиной 1/Зи, заселенных с вероятностями р™,
Pi~1P2, Pi~2p\i • • • 1Р2 (не в порядке их расположения!). Нетрудно со-
сообразить, что число отрезков, характеризуемых вероятнос-
вероятностью pi~mp2n, равно С™, т.е. числу сочетаний из п элементов по т.
В результате при п —>¦ оо и р\ ф 1/2 мы в конце концов приходим
к неоднородному фрактальному множеству.
На п шаге нашей процедуры обобщенная статистическая сум-
сумма B.3) для нашего мультифрактала имеет вид обычного бинома Нью-
Ньютона
Z(q, е)=± С™ (РГтР?У = (Pi + PIT • B.35)
т=0
Поскольку на этом шаге размер ячейки е = 3~и, то мы на основании
соотношения B.6) приходим к следующему уравнению для спектра
96

обобщенных фрактальных размерностей Dq
B.36)
Устремляя п —>¦ оо с учетом определения r(q), находим
q~
B.37)
Если р\ = p2 = 1/2, то мы имеем однородный фрактал, все обоб-
обобщенные фрактальные размерности Dq которого одинаковы и равны
хаусдорфовой размерности исходного канторовского множества ис-
исключенных средних третей
B.38)
Если же р\ ф 1/2, то канторовское множество является неоднород-
неоднородным. На рис. 2.5 изображена зависимость Dq для значения веро-
вероятности р\ = 1/4 и рч = 3/4. Значение хаусдорфовой размернос-
размерности Dq = In 2/ In 3 = 0.6309 совпадает в этом случае с размерностью
Рис. 2.5. Спектр обобщенных размерностей для неоднородного канторовского мно-
множества исключенных средних третей с р\ = 0.25, рг = 0.75.
однородного канторовского множества. Это довольно естественно,
так как наше множество расположено на фрактале с этим значением
размерности. Этот фрактал в литературе имеет специальное назва-
название носитель (support) исходного мультифрактального множества.
97

По этой причине величину Dq часто называют размерностью носите-
носителя мультифрактала.
Раскрывая неопределенность в формуле B.37), находим инфор-
информационную размерность
йЬй+йЬй B 39)
Di
Она, как и следовало ожидать, меньше размерности Do, а корреля-
корреляционная размерность D<i = 0.4278, в свою очередь, меньше, чем D\.
Таким образом, мы видим, что действительно в этом случае Dq яв-
является монотонно убывающей функцией q.
Предельных значений эта функция достигает, как мы говорили,
при q = ±00. Эти значения Dm[n = D^ и -Dmax = -D-oo равны
D°° = "In? = °618 И ^-оо =-^у = 1-2618. B.40)
Носитель мультифрактального множества может сам по себе и не
являться фракталом. Например, если мы исходный единичный отре-
отрезок в предыдущем примере разделим на первом шаге на 2 равные
части с длиной 1/2. Первой части припишем вероятность (меру) pi,
а второй рч- Далее с каждым из двух образовавшихся отрезков по-
поступим аналогичным образом и т. д. Нетрудно тогда сообразить, что
спектр обобщенных фрактальных размерностей будет определятся из
выражения, аналогичного B.37)
In
В этом случае размерность Dq = 1, так как теперь носителем наше-
нашего мультифрактала является весь единичный отрезок целиком, т. е.
объект с пространственной размерностью d, равной единице. Все
остальные обобщенные фрактальные размерности заключены в ин-
интервале между
Дзс = — 1п?>2/1п2 и D-oo =—\npi/ln2
(pi < Р2). График функции Dq в этом случае выглядит качественно
так же, как показано на рис. 2.5.
98

2.1.7 Неоднородный треугольник Серпинского
Подобно неоднородному канторовскому множеству может быть так-
также проанализирован неоднородный треугольник Серпинского, изоб-
изображенный на рис. 2.1. Два первых шага его покрытия треугольни-
треугольниками меньшего размера показаны на рис. 2.2. Поэтому по аналогии
с формулой B.35) статистическую сумму на п-м шаге в этом случае
можно записать в виде
Z(q,s) = {р\ -\-р\ + Рз)п ? B.42)
где величины р\ = 0.9, рч — Ръ — 0.05 соответствуют вероятностям
выбора вершин треугольника, использованным при создании рис. 2.1.
Рис. 2.6. Функция Dq для неоднородного треугольника Серпинского с pi = 0.9,
Р2 = Рз = 0.05.
Если стороны исходного треугольника принять за единицу, то раз-
размер треугольной ячейки на п шаге равен е = 2~п и уравнение для
определения спектра Dq имеет вид, аналогичный B.36)
B.43)
B.44)
Отсюда, устремляя п —>¦ сю, находим Dq
q~
[q - 1) In 2
На рис. 2.6 изображена эта функция для означенных выше вероятнос-
вероятностей pi, р2 и р3.
99

A
Рис. 2.7. Заселенность множества на разных расстояниях от вершины А.
Размерность носителя мультифрактала Dq = In 3/In 2 = 1.5849
и совпадает с фрактальной размерностью салфетки Серпинского. Ин-
Информационная размерность
L +P2lnp2 +P3
D =
1 ~
Pi
In 2
= о 569
B.45)
и корреляционная D<i = 0.2951 оказываются в этом случае существен-
существенно меньше величины Dq. Это, разумеется, связано с сильным разбро-
разбросом значений вероятностей р\ = 0.9 и р2 = Рз — 0.05. Минимальное
и максимальное значения D±oo равны
= 0.152 и
= 4.3219.
In 2 ~" 1п2
Этим предельным значениям можно придать следующий физичес-
физический смысл. Рассмотрим, например, величину Д^ = Dm[n. Опишем
вокруг треугольника ABC окружность радиуса R с центром в вер-
вершине А. Спрашивается, как будет зависеть от R относительная доля
всех точек ра фрактального множества, расположенных внутри этой
окружности? Как следует из рис. 2.7, для окружности радиуса R =
= 1/2" эта доля равна ра = р\. Действительно, внутри первой окруж-
окружности, радиус которой равен единице (п = 0), расположены все точки
100

множества, т.е. ра = 1. Внутри второй окружности радиуса R =
= 1/2 доля всех точек ра = р\ (см. рис. 2.2). Внутри третьей окруж-
окружности радиуса R = 1/4 доля точек ра = р\ и т.д.
Исключая из этих соотношений величину п, находим
Pa=Pi= pilnR/ln2 = iTln^/ln2 = RD^. B.47)
Аналогичным образом для доли всех точек внутри окружностей с
центром в вершинах треугольника В или С получим
pb=Pc = RD™*. B.48)
Качественно эти степенные зависимости легко понять. Основная
масса всех точек расположена вблизи вершины треугольника А, по-
поэтому при малых Д < 1 доля точек pa{R) растет с R сравнитель-
сравнительно быстро. И наоборот, вблизи вершин В или С расположена лишь
сравнительно небольшая часть всех точек множества. Поэтому вбли-
вблизи нуля с увеличением радиуса функции p^c(R) растут значительно
медленнее.
2.1.8 Канторовское множество с двумя характерными масштабами дли-
длины
Приведем еще один пример неоднородного канторовского множества,
где причиной неоднородности, однако, является наличие нескольких
пространственных масштабов при том, что все меры (т. е. вероятнос-
вероятности) pj совпадают. Как и раньше, стартуем с отрезка единичной дли-
длины. На первом шаге заменим его двумя отрезками с длинами 1\ = 0.25
и 12 = 0.5, примыкающими соответственно к его левому и правому
концам. Обоим отрезкам припишем одинаковую меру р = 1/2. За-
Затем повторим ту же процедуру с каждым из этих двух отрезков.
В результате получится уже 4 отрезка с длинами l\, I1I2, hh и l\
и одинаковыми мерами, равными 1/4. Продолжая этот процесс до
бесконечности, мы получим в конце концов неоднородное канторов-
канторовское множество, т. е. мультифрактал. Первые шаги этого процесса
изображены ниже на рис. 2.8.
Чтобы определить спектр обобщенных фрактальных размерностей
в этом случае, нам надо видоизменить соотношение B.6), определя-
определяющее функцию r(q), так как теперь в нашем распоряжении имеется
101

M=1
M=2
oo
Рис. 2.8. Неоднородное канторовское множество с двумя характерными масштабами
длины li = 1/4, 12 = 1/2 и pi = р2 = 1/2.
не один характерный масштаб г, а много. Итак, рассмотрим какое-
то фрактальное множество, расположенное в ограниченной области
d-мерного Евклидового пространства. Предположим, что на неко-
некотором этапе его разбиения мы разделили его на некоторое количест-
количество М достаточно малых непересекающихся кусочков, Si, S2, • • •, Sm-,
так что каждый из этих кусочков имеет меру рг- и лежит внутри
сферы радиуса U. При этом все U ограничены сверху условием U < I.
Определим теперь обобщенную статистическую сумму следующим
образом
^- B-49)
г=1 Ч
Основное наше утверждение заключается в том, что при достаточ-
достаточно большом М величина Г будет порядка единицы, лишь только если
будет выполнено условие
г = r(q) = (q- l)Dq. B.50)
Мы оставим здесь эту теорему без доказательства, обратив лишь вни-
внимание на то, что соотношение B.6) является ее частным случаем,
когда все ^ одинаковы и равны е.
Применим теперь эту теорему к одному частному случаю, когда
к нашему множеству применима так называемая рекурсионная про-
процедура разбиения 13. Она заключается в следующем. Пусть вначале
мы имеем множество с мерой 1 и размером 1 (например, отрезок еди-
единичной длины). Разделим это множество на куски Si (г = 1, 2,..., т)
13 Частный случай такой процедуры изображен на рис. 2.3.
102

с мерами pi и размерами U < 1. На этом первом шаге мы можем
записать функцию Г в виде
На втором шаге каждый из этих т кусков, в свою очередь, делится
на т кусочков с мерами, уменьшенными на множители pj, и размера-
размерами, уменьшенными на множители lj (j = 1,2, ...,m). В результате
мы получим уже т2 кусочков. Функция Г на этом шаге, очевидно,
равна
T2(q,T) = [T1(q,r)}2. B.52)
На п шаге по индукции получаем тп кусочков и
В пределе достаточно большого числа п таких последовательных раз-
разбиений наша статистическая сумма будет стремиться либо к нулю,
либо к бесконечности. И лишь в одном случае она будет порядка
единицы. Это произойдет, если
ri(<z,r) = l. B.53)
Это и есть уравнение для функции r(q), а функция Ti(q,r) называет-
называется генератором для такого мультипликативного процесса разбиения
множества.
В нашем конкретном примере канторовского множества, изобра-
изображенного на рис. 2.8, величина т = 2, и генератор равен
Т1(Я,г) = § + §. B.54)
Подставляя сюда рг = р2 = 1/2, 1\ = 1/4 и 12 = 1/2, получаем уравне-
уравнение для г
2Т + 4Т = 2'7. B.55)
Решая это квадратное уравнение, находим функцию r(q)
In (л/1 + 2<?+2 - 1)
= -М2 - L
103

Весь спектр обобщенных фрактальных размерностей заключен
в этом случае в интервале 1/2 < Dq < 1. Сама же функция Dq изоб-
изображена на рис. 2.9. Хаусдорфова размерность Dq = 0.6942. В общем
случае ее необходимо определять из уравнений B.53) и B.51), где
надо положить q = 0
т
Е 1?° = 1- B-57)
Отсюда становится ясно, что все обобщенные фрактальные размер-
размерности Dq совпадают, и функция Dq = Dq является константой в том
и только в том случае, если все меры рг- связаны с длинами отрезков U
соотношением
Pi = if0. B.58)
Для этого класса фракталов это есть очевидное условие того, что все
точки фрактального множества равномерно распределены по фракта-
фракталу. В противном случае фрактал является неоднородным, т. е. фак-
фактически представляет собой мультифрактал.
~ D.
-20
Рис. 2.9. Спектр обобщенных размерностей для неоднородного канторовского мно-
множества, изображенного на рис. 2.8, с двумя характерными масштабами длины Zi = l/4
и I2 = 1/2 и одинаковыми мерами р\ = р2 = 1/2.
Условию однородности удовлетворяет, очевидно, классическое кан-
торовское множество исключенных средних третей с т = 2, р\ = р2 =
= 1/2 и 1\ = ^2 = 1/3. Для него уравнение B.53) имеет вид
B.59)
104

которое дает
In 2 In 2
или Dq = Do = bsm B-60)
В этом случае 1/2 = A/3Iп2/1п3, т.е. действительно pi = 1г °.
Рис. 2.10. Неоднородный контур двойного дракона с р\ = р2 = Рз = 1/3.
Теперь становится понятным, почему в первой части пособия для
получения контура двойного дракона (см. рис. 1.37) мы выбрали в ме-
методе случайных итераций вероятности рг- A.29) в соответствии с фор-
формулой B.58). Так, если бы наш выбор каждого из трех преобразова-
преобразований A.28) был бы равновероятен, то мы пришли бы к рис. 2.10. Видно,
что точки вдоль контура распределены теперь крайне неравномерно
по сравнению с рис. 1.37, и этот контур фактически представляет
собой мультифрактал.
2.2 Функция мультифрактального спектра f(a)
2.2.1 Спектр фрактальных размерностей
В предыдущей главе мы сформулировали понятие мультифрактала —
объекта, представляющего собой неоднородный фрактал. Для его опи-
описания мы ввели набор обобщенных фрактальных размерностей Dq,
где q принимает любые значения в интервале —оо < q < oo. Однако
величины Dq не являются, строго говоря, фрактальными размернос-
размерностями в общепринятом понимании этого слова 14.
14 По этой причине они и называются обобщенными размерностями.
105

Поэтому часто наряду с ними для характеристики мультифрак-
тального множества используют так называемую функцию муль-
тифрактального спектра f(a) (спектр сингулярностей мульти-
фрактала), к которой, как мы увидим в дальнейшем, больше под-
подходит термин фрактальная размерность. Мы покажем, что величи-
величина f(a) фактически равна хаусдорфовой размерности некоего одно-
однородного фрактального подмножества из исходного множества С, ко-
которое дает доминирующий вклад в статистическую сумму при за-
заданной величине q.
Одной из основных характеристик мультифрактала является набор
вероятностей р^, показывающих относительную заселенность ячеек е,
которыми мы покрываем это множество. Чем меньше размер ячейки,
тем меньше величина ее заселенности. Для самоподобных множеств
зависимость р^ от размера ячейки е имеет степенной характер
Pi{e) « ?ai, B.61)
где оц представляет собой некоторый показатель степени (разный,
вообще говоря, для разных ячеек г). Известно, что для регулярного
(однородного) фрактала все показатели степени щ одинаковы и равны
фрактальной размерности D
Pi = 1/N(e) и eD. B.62)
В этом случае статистическая сумма B.3) имеет вид
N(e)
Z(q, е) = ? Р?(г) = Ще)^ « eD^l\ B.63)
г=1
Поэтому r(q) = D(q — 1) и все обобщенные фрактальные размернос-
размерности Dq = D в этом случае совпадают и не зависят от q.
Однако для такого более сложного объекта, как мультифрактал,
вследствие его неоднородности, вероятности заполнения ячеек р-ь в об-
общем случае неодинаковы, и показатель степени оц для разных ячеек
может принимать различные значения. Как мы увидим ниже, доста-
достаточно типичной является ситуация, когда эти значения непрерывно
заполняют некоторый закрытый интервал (amin?«maxM причем
Pmin ~ ? ? а Ртах
106

Установим сперва связь этих предельных значений а со значени-
значениями производной от функции r(q). А именно, рассмотрим преде-
пределы этой производной при q —>• ±00. Так, если мы возьмем значе-
значение q —>• 00, то при выполнении суммирования по г в выражении B.11)
будет существенен вклад только наиболее заселенных ячеек, каждая
из которых характеризуется максимальной вероятностью заполне-
заполнения ртах. Оставив в сумме только такие ячейки (численностью iVmax),
МЫ ВИДИМ, ЧТО ЧИСЛИТеЛЬ Выражения B.11) равен ^VmaxPmax lnPmax5
а знаменатель iVmaxp-^ax In г. В результате, учитывая, чтортах « ?amin,
искомый предел производной оказывается равным amin. Аналогич-
Аналогичным образом, если q —>• —00, то при суммировании в выражении B.11)
необходимо учитывать только наименее заселенные ячейки, харак-
характеризующиеся вероятностью рш\п. В этом случае очевидно, что про-
производная dr/dq стремится к значению атах.
Величину этой же производной при достаточно больших по модулю
значениях q можно вычислить и по-другому. Для этого заметим, что
в том случае, когда функция Dq имеет конечные пределы при q —>• ±00
(равные D±oo), функция r(q) может быть аппроксимирована следую-
следующим образом: r(q —>• ±00) и qD±oo. Таким образом, мы приходим
к важному выводу, что
dr
dq
'ОС
= а
dr
dq
= D-ov = amax. B.65)
>—00
Т.е. интервал возможных значений а определяется предельными зна-
значениями (при q —>• ±00) обобщенных фрактальных размерностей Dq.
Перейдем теперь к вопросу о распределении вероятностей различ-
различных значений щ. Пусть n(a)da есть вероятность того, что скг- нахо-
находится в интервале от а до а + da. Другими словами, n(a)da пред-
представляет собой относительное число ячеек г, обладающих одной и той
же мерой pi с скг-, лежащими в этом интервале. В случае монофрак-
монофрактала, для которого все оц одинаковы (и равны фрактальной размер-
размерности D), это число, очевидно, пропорционально полному количеству
ячеек N(e) « s~D, степенным образом зависящим от размера ячей-
ячейки е. Показатель степени в этом соотношении определяется фрак-
фрактальной размерностью множества D.
Для мультифрактала, однако, это не так, и разные значения оц
встречаются с вероятностью, характеризуемой не одной и той же
107

величиной D, а разными (в зависимости от а) значениями показателя
степени /(а),
п(а) и e~f{a). B.66)
Таким образом, физический смысл функции f(a) заключается
в том, что она представляет собой хаусдорфову размерность некоего
однородного фрактального подмножества Са из исходного множест-
множества С, характеризуемого одинаковыми вероятностями заполнения яче-
ячеек pi « ea. Поскольку фрактальная размерность подмножества оче-
очевидно всегда меньше или равна фрактальной размерности исходного
множества Dq, имеет место важное неравенство для функции f(a)
/(а) < А)- B.67)
В результате мы пришли к выводу, что набор различных значений
функции f{a) (при разных а) представляют собой спектр фрак-
фрактальных размерностей однородных подмножеств Са, на которые
можно разбить исходное множество С. Отсюда становится понятным
термин мультифрактал. Его можно понимать как некое объедине-
объединение различных однородных фрактальных подмножеств Са исходного
множества С, каждое из которых имеет свое собственное значение
фрактальной размерности f(a).
Поскольку любому подмножеству принадлежит лишь часть от об-
общего числа ячеек N(s), на которые мы разбили исходное множест-
множество С, условие нормировки вероятностей B.2), очевидно, не выпол-
выполняется при суммировании только по этому подмножеству. Сумма
этих вероятностей оказывается меньше единицы. Поэтому и сами
вероятности рг- с одним и тем же значением оц очевидно меньше (или
в крайнем случае одного порядка), чем величина s^ai\ которая обрат-
обратно пропорциональна числу имеющихся ячеек, покрывающих данное
подмножество (напомним, что в случае монофрактала рг- « 1/N(s)).
В результате мы приходим к следующему важному неравенству для
функции f(a). А именно, при всех значениях а
/(а) < а. B.68)
Знак равенства имеет место, например, для полностью однородного
фрактала, где f{a) = а = D. Впоследствии мы увидим, что это
свойство тесно связано со свойством B.34) функции Dq, которая либо
монотонно убывает, либо остается постоянной при увеличении q.
108

2.2.2 Преобразование Лежандра
Установим теперь связь функции f(a) с введенной нами ранее функ-
функцией r(q). Вычислим для этого статистическую сумму Z(q,e). Под-
Подставляя в выражение B.3) вероятности рг- « sai и переходя от сум-
суммирования по г к интегрированию по а с плотностью вероятнос-
вероятности B.66), мы получим
N(e)
Z{q,s) = ? Pi{e) ~ I dan{a)eqa и j daeqa~f{a). B.69)
i=l
Так как величина е очень мала, то основной вклад в этот интеграл
дадут те значения a(q), при которых показатель степени qa — f{a)
оказывается минимальным (а соответственно, подынтегральная функ-
функция — максимальной). Этот вклад, очевидно, будет пропорционален
значению подинтегральной функции в точке максимума. Само же
значение a(q) определяется при этом из условия
?[qa -
= 0. B.70)
a=a(q)
Очевидно также, что из условия минимума мы имеем
d2
[qa - f(a)]
аа a=a(q)
> 0. B.71)
В результате получаем, что зависимость a(q) неявным образом
определяется из уравнения
Я = ^ B.72)
аа
и что функция f(a) является всюду выпуклой
f"(a) > 0. B.73)
Подставляя это значение a(q) в интеграл B.69), получаем выраже-
выражение для статсуммы
Z{q,s) ^eqa{q)-f{a{q)). B.74)
Это означает, что величина f(a(q)) действительно определяет фрак-
фрактальную размерность того подмножества ?a(g), которое дает доми-
доминирующий вклад в статистическую сумму B.69) при заданной вели-
величине показателя степени q.
109

Сравнивая выражение B.74) с выражением B.6), приходим к вы-
выводу, что
r(q)=qa(q)-f(a(q)). B.75)
Отсюда с помощью уравнения B.4) можно найти функцию Dq
^ B.76)
Таким образом, если мы знаем функцию мультифрактального
спектра f(a), то с помощью соотношений B.72) и B.76) мы можем
найти функцию Dq. Наоборот, зная Dq, мы можем найти зависи-
зависимость a(q) с помощью уравнения
«Ы = ^ К? " !) AJ B-?7)
и после этого найти из B.76) зависимость f(a(q)). Эти два уравнения
и определяют (в параметрическом виде) функцию /(а).
Для доказательства соотношения B.77) продифференцируем вы-
выражение B.75) по а
dr dq dq df ,
^"/= « + «/-/¦ 2-78
dq da da da
Принимая во внимание, что q = df /da, и сокращая это равенство
на dq/da, приходим к соотношению
^ B.79)
dq
эквивалентному выражению B.77).
Выражения B.75) и B.79) задают преобразования Лежандра от
переменных {q,r(q)} к переменным {a,f(a)}
dr
а = —,
aq B.80)
Обратное преобразование Лежандра определяется формулами B.72)
и B.75)
B.81)
da -*'
110

Подобные рассуждения позволяют с помощью соотношений B.79)
и B.72) связать вторые производные этих функций
B.82)
da2
dq2
Как известно, для однородного фрактала Dq = D = const. Поэто-
Поэтому а = dr/dq = D и f(a) = qa — r(q) = qD — D(q — 1) = D. В этом
случае "график" функции f{a) на плоскости (а,/(а)) состоит всего
из одной точки (D,D). Обратимся теперь к более интересным слу-
случаям, когда график функции f(a) состоит не из дискретных точек,
а представляет собой некоторую непрерывную линию. Каковы тогда
общие свойства этой функции?
2.2.3 Свойства функции /(а)
Проанализируем теперь поведение функции f(a) для различных зна-
значений а. Поскольку, согласно B.72), f'(a) = q, то при q = 0 произ-
производная функции f{a) обращается в ноль. Это значит, что в некоторой
точке «о — ск(О) функция f(a) имеет максимум (напомним, что функ-
функция f(a) является всюду выпуклой).
lmin
а
Рис. 2.11. Максимум функции /(а) равен фрактальной размерности Dq.
Значение функции в максимуме легко определить, если восполь-
воспользоваться выражением B.76). Положив в нем q = 0, мы получим,
что /(«о) = Dq, т.е. максимальное значение f(a) равно хаусдорфо-
вой размерности мультифрактала Dq, т.е. фрактальной размерности
111

носителя меры. Качественно эта ситуация отражена на рис. 2.11.
Там же показаны границы интервала (ат[п, amax) 5 в котором задана
функция f(a). Заметим, что обращение функции f(a) в ноль на этих
границах (как показано на рисунке) вовсе не обязательно, и в ря-
ряде случаев f{a) в одной из этих точек (или в обоих) может быть
и отлична от нуля. Обязательным условием, однако, является обра-
обращение в бесконечность производной f'(a) в этих двух точках. Это
является прямым следствием соотношения B.72) и того факта, что
точки amm,max соответствуют значениям q —>• ±00.
Функция f(a) вблизи своего максимума может быть аппрокси-
аппроксимирована параболой. Кривизна параболы определяется значением
второй производной от этой функции в точке а0- Пользуясь соот-
соотношением B.82), получаем, что /"(а0) = Vr"@)- Дифференцируя
теперь формулу r(q) = (q — l)Dq дважды и принимая во внимание,
что т'@) = «о? мы приходим к выражению
т"@) = 2(Д) - а0) - D'qU- B.83)
Отсюда следует искомая аппроксимация
f(a) я Do - г / (а~а°) B.84)
JK ) 2[2(ао-А))+А/4о]
Из условия выпуклости функции f(a) очевидно, что величина, сто-
стоящая в квадратных скобках в этом выражении, должна быть всегда
положительна. Часто последнее слагаемое, D^Lq, в этих скобках чис-
численно мало, и им можно пренебречь.
Рассмотрим теперь случай q = 1. Поскольку тA) = 0, то из B.75)
следует, что аA) = /(аA)). С другой стороны, согласно B.72), про-
производная от функции f(a) в этой точке равна 1: f'(a(l)) = 1. Диф-
Дифференцируя соотношение r(q) = (q — l)Dq no q с учетом B.79)
^ q B.85)
и полагая в нем q = 1, мы получаем, что скA) = D\. Таким образом,
мы имеем
Di = аA) = /Ml)), B.86)
112

т.е. информационная размерность D\ лежит на кривой f(a) в точке,
где а = f{ot) и f'(a) = 1. Это дает нам графический способ опреде-
определения информационной размерности по кривой f(a) (см. рис. 2.12 ).
f(ct)
D,
а
D,
Рис. 2.12. Нахождение информационной размерности Di: D\ = a = f(a).
То, что графики функций а и f{a) касаются друг друга имен-
именно в точке (Di,Di), вовсе не случайно. Напомним, что /(аA)) —
это значение фрактальной размерности того подмножества из С, ко-
которое дает наибольший вклад в статистическую сумму при q = 1. Но
при q = 1 статистическая сумма в силу условия нормировки равна 1
и не зависит от размера ячейки е. Следовательно, этот наибольший
вклад должен быть также порядка единицы. Поэтому в этом (и только
в этом) случае вероятности заполнения ячеек р^ « еа обратно пропор-
пропорциональны числу имеющихся ячеек п(а) ~ г~^а\ т.е. f(a) = a.
Рассмотрим теперь случай q = 2. Пользуясь формулой B.76), по-
получаем
D2 = 2а{2) - /(аB)) B.87)
или /(аB)) = 2скB) — D2, что соответствует геометрическому пос-
построению на рис. 2.13 .
Как мы уже отмечали, неравенство B.68), а > f(a), выведенное
нами выше из качественных соображений, эквивалентно утвержде-
утверждению, что производная D'q < 0. Докажем здесь это. Для этого про-
продифференцируем выражение Dq = r(q)/(q — 1) по q. Принимая во
113

2a-D,
Рис. 2.13. Геометрическое определение корреляционной размерности D2.
внимание соотношения B.79) и B.75), получим
dDf.
а - /(а)
B.88)
dq (q - IJ '
Отсюда при а > f{a) и следует вышеприведенное неравенство D'q < 0.
2.2.4 Примеры функций f(a)
Рассмотрим теперь на конкретных численных примерах вид функции
мультифрактального спектра f(a). Начнем со случая неоднородного
канторовского множества, зависимость Dq для которого дается фор-
формулой B.37) и изображена на рис. 2.5. Пользуясь вышеприведенны-
вышеприведенными формулами, находим сначала зависимость a(q) = dr/dq, а затем
и величину f(a(q)) = qa(q) —r(q). Полученные зависимости и опреде-
определяют в параметрическом виде функцию f(a). Она для этого случая
изображена на рис. 2.14. Пунктирная парабола показывает квадра-
квадратичную аппроксимацию с использованием формулы B.84). Положе-
Положение максимума «о определяется выражением
dT b^+lnf» -—- B.89)
dq
21n3
0.7618.
Следующий пример, который мы рассмотрим, — это неоднород-
неоднородное канторовское множество с двумя характерными масштабами дли-
длины, изображенное на рис. 2.8. Спектр обобщенных размерностей Dq
для этого случая показан на рис. 2.9. Аналогичным образом с помо-
помощью формулы B.56) для r(q) мы можем определить функции a(q)
114

0.5 1.0 1.5
a
Рис. 2.14. Функция мультифрактального спектра для неоднородного канторовского
множества с зависимостью Dq, показанной на рис. 2.5.
и f(a(q)) и затем с помощью этих двух параметрических уравнений
построить графически функцию f(a). Она изображена на рис. 2.15.
Интервал значений а, где определена функция /(а), задается нера-
0.0 0.2 0.4 0.6 0.8 1.0 1.2
Рис. 2.15. Функция мультифрактального спектра для неоднородного канторовского
множества с двумя характерными масштабами длины, изображенного на рис. 2.8
и Pi = Vi = 1/2.
венством 1/2 < а < 1. Положение максимума «о в этом случае опре-
определяется из формулы
2
0.7236,
B.90)
что близко к величине фрактальной размерности носителя множест-
множества Д) = 0.6942.
115

Давайте теперь посмотрим, как в этом конкретном примере, непо-
непосредственно анализируя статистическую сумму, можно прийти к кон-
концепции мультифрактального спектра f(a). Этот анализ является до-
достаточно поучительным и поможет нам лучше понять основные идеи,
изложенные выше. Рассмотрим здесь случай произвольных значе-
значений ръ р2, h, h-
На п шаге разбиения нашего множества статистическая сумма
имеет вид
Г„(?,т)= (у + у) =1- B-91)
Раскроем бином в средней части этой формулы
i-nKQ^) — z^ ип Pi Pi \li h ) — L- l/.yz;
т=0
Мы ожидаем, что в пределе п —>• оо величину этой суммы будет опре-
определять ее наибольший член. Чтобы его найти, необходимо решить
уравнение
^ [m) ()"] = 0. B.93)
Воспользовавшись формулой Стирлинга
lnn! = nlnn-n, B.94)
мы находим после несложных преобразований, что уравнение B.93)
эквивалентно следующему
_ ln(n/ml)+gln(pi/p2) @ o-v
т ~ Hhjh) • ( 95)
Так как мы ожидаем, что максимальное слагаемое в B.92) опреде-
определяет значение суммы, мы имеем (в пределе п —>• оо) второе уравнение
imrnq(n-m)q
mq (n
Pi Pi
min-m
Ylfl
= 1. B.96)
Подставляя уравнение B.95) в уравнение B.96), мы после некоторых
алгебраических преобразований находим:
In (—) In (l-f) - In (— - l) ]nh = q (lnpi In l2 - lnp2 In h). B.97)
\m/ \h/ \m )
116

Таким образом, мы видим, что для каждого значения q сущест-
существует величина п/т, которая является решением уравнения B.97)
и, в свою очередь, определяет значение г с помощью формулы B.95).
Максимальный член суммы, который определяет величину т, для
заданного значения q происходит из подмножества Ст, состоящего
из N(m) = С™ отрезков, каждый из которых имеет одну и ту же
длину /j"i2~m- Поэтому фрактальная размерность / этого подмножес-
подмножества по определению должна быть найдена из уравнения
ИЛИ
= (п/т - 1) Ы(п/т - 1) - (п/т) Ы(п/т)
+ (n/m-l)lnl2
Мера (т.е. вероятность), сопоставляемая каждому из этих от-
отрезков, равна p'i'P2~rn. Поэтому условие для определения показателя
степени а, характеризующего вероятность заполнения ячеек в под-
подмножестве Ст, выглядит следующим образом
ртрп-т= (irnq-my^ B.100)
ИЛИ
(
= ]пр1 + (п/т1)]пр2 Г2
Ink + (п/т-l)\nl2' [
В результате, для любого заданного значения q мы имеем набор
из N(m) отрезков, характеризуемых величиной a(q) и обладающих
фрактальной размерностью f(q), которые дают доминирующий вклад
в статистическую сумму. По мере изменения q различные подмно-
подмножества Ст из нашего фрактального множества определяют величи-
величины r(q) и Dq. Можно показать, что уравнения B.95), B.97), B.99)
и B.101) приводят нас снова к хорошо известному соотношению
r=(q-l)Dq = qa(q)-f(q). B.102)
Рассмотрим теперь поучительный пример, в котором функция
мультифрактального спектра f(a) не обращается в ноль на одной из
границ своего интервала (o;min,amax). Он является обобщением кан-
торовского множества с двумя характерными масштабами длины, по-
показанного на рис. 2.8. Однако в этом случае мы разделим единичный
117

отрезок на три отрезка с длинами l^ h и \ч так, что два отрезка
с длиной, равной 1^ расположены по краям единичного интервала,
а отрезок длины 1\ расположен точно посередине между ними (см.
рис. 2.16). В сумме они по-прежнему составляют единичный отре-
1
Р2 Pi P2
12
Рис. 2.16. Канторовское множество с тремя характерными масштабами длины.
зок, т.е. 1\ + 2^2 = 1. Двум крайним отрезкам припишем меру р2,
а среднему меру р\. Очевидно, что р\ + 2р2 = 1- Мы также будем
предполагать, что l<i > li и что P2/I2 > Pi/h-
На следующем этапе каждый из этих трех интервалов подразде-
подразделяется на три более мелких интервала подобным же образом и т. д.
В результате мы получим некоторое мультифрактальное множест-
множество. Поскольку оно расположено на исходном единичном отрезке, его
фрактальная размерность Dq, очевидно, равна 1. Кроме того, наи-
наиболее заселенные ячейки в нем стягиваются не к одной точке (как
это было в предыдущих примерах), а к множеству точек с некоторой
отличной от нуля фрактальной размерностью. Поэтому мы ожида-
ожидаем, что в этом примере наименьшее значение ат[п, т. е. D^, будет
соответствовать величине /, отличной от нуля. Так как отрезки
с наименьшей плотностью по-прежнему стягиваются в одну точку,
мы ожидаем, что сктах = -D-oo будет соответствовать величине / = 0.
Генератор нашего мультипликативного процесса определяется фор-
формулой B.51) ст = 3. Поэтому уравнение для r(q) выглядит следую-
следующим образом (см. B.53))
т) = § + 2§ = 1. B.103)
118

Для численного анализа этой формулы рассмотрим частный слу-
случай, когда 1\ = Х\. Совместно с условием /i+2/2 = 1 это дает /2 = л/2 —1
и 1\ = 3 — 2л/2- В качестве вероятностей возьмем значения р\ = 0.1
и Р2 = 0.45. Тогда уравнение B.103) превращается в квадратное для
величины х = Х^т и его неотрицательное решение дает нам величи-
величину г
q ln(pi/p2) + In (/L + (pi/p2)g - 1)
^. B.104)
Отсюда естественным образом получаем спектр обобщенных фрак-
фрактальных размерностей Dq. Он показан на рис. 2.17. Предельные зна-
значения Dq определяются формулами
0.9059,
.^ = amax =
1.306. B.105)
ь2 ^ П1 ь2
Функция мультифрактального спектра f{a) для этого множества
показана на рис. 2.18. Как и предсказывалось выше, ее максимальное
значение соответствует величине Dq = 1, а
In 2
/Кпп) = -—~ 0.7864 /0,
так что левая часть этой кривой напоминает крючок.
10 20
Рис. 2.17. Спектр обобщенных фрактальных размерностей для неоднородного кан-
торовского множества, определяемого уравнением B.103), с р\ = 0.1, р2 = 0.45,
Аналогичную форму принимает функция мультифрактального
спектра для неоднородного треугольника Серпинского (см. рис. 2.1),
119

с которого мы начали свое изложение про мультифракталы. Зависи-
Зависимость Dq для этого случая определяется формулой B.44) и показана
на рис. 2.6. Зная Dq, можно таким же способом, как и ранее, постро-
построить график функции f(a). Он показан на рис. 2.19.
1.0
0.8
0.6
0.4
0.2
п п
-
-
-
х"" 0.8 0.9
1.0 1.1 1.2 1.3 1.4
а
Рис. 2.18. Функция f(a) для меры, определяемой уравнением B.103) с
р2 = 0.45, /2 = л/2-1и/1=3- 2д/2.
= 0.1,
1.5
1.0
0.5
0.0
0 1 2 3 4 5
а
Рис. 2.19. Функция /(а) для неоднородного треугольника Серпинского, изображен-
изображенного на рис. 2.1.
Видно, что в этом случае зависимость f(a) тоже напоминает крю-
крючок, однако обращенный в другую сторону. Соответственно, здесь
отлична от нуля фрактальная размерность наиболее разреженной об-
области
/(«шах) = 1. B.Ю6)
120

Как нетрудно видеть, эта область расположена на стороне треуголь-
треугольника ВС и ее прообразах.
2.3 Применение теории мультифракталов в физике
2.3.1 Переход Андерсона
Концепции мультифрактального анализа широко применяются в на-
настоящее время в физике неупорядоченных систем при изучении так
называемого перехода Андерсона 15. При этом решается квантово-
механическая задача о движении одной частицы массы т в случай-
случайном потенциале V(r). Уравнение Шредингера для волновой функции
ф(г) имеет стандартный вид
- — Аф(г) + У(т)ф(т) = Еф(т). B.107)
ZTYb
В зависимости от энергии Е и степени беспорядка все возмож-
возможные состояния частицы Фе{г) делятся на два класса: локализованные
и делокализованные. Локализованные состояния обладают волновой
функцией, экспоненциально спадающей с расстоянием
№(г)|~ехр(-|г-го|/?), B.108)
где ? — радиус локализации, зависящий от энергии Е. Делокализо-
Делокализованные состояния, напротив, распределены по всему объему образца.
Одним из простейших примеров делокализованного состояния в кван-
квантовой механике является плоская волна, характеризующая движение
частицы с заданным импульсом fik
ф(г) ~ exp(ikr). B.109)
Энергия Ес, отделяющая локализованные состояния от делокализо-
ванных, называется порогом подвижности. Ее положение зависит
от массы частицы и степени беспорядка в системе. Примечательно,
что радиус локализации ? на пороге подвижности обращается в бес-
бесконечность
Показатель степени v в этой формуле называется критическим ин
дексом радиуса локализации.
15 Часто его также называют переходом металл-диэлектрик.
121

Переход от локализованных состояний к делокализованным при из-
изменении какого-то параметра в системе (энергии, силы беспорядка)
и называется переходом Андерсона. Величина ? существует и по дру-
другую сторону перехода, на его металлической стороне. Только здесь
она имеет физический смысл длины корреляции, которая также об-
обращается в бесконечность в точке перехода. По этой причине иногда
в литературе переход Андерсона именуют квантовым фазовым пере-
переходом.
Интенсивные численные исследования последних лет показали, что
в точке перехода Андерсона (т. е. точно при энергии Ес) волновые
функции являются делокализованными и имеют сложную самоподоб-
самоподобную фрактальную (а точнее, мультифрактальную) структуру. Энер-
Энергия Ес (а соответственно, и точка перехода) определена, строго го-
говоря, для бесконечного образца. Если же образец имеет конечные (но
достаточно большие) размеры L, то переход является "размытым"
и осуществляется в узкой полосе энергий вблизи энергии Ес такой,
что выполняется условие
?>?, т.е. \Е - Ес\ < Ь~11\ B.111)
Для формулировки условия локализации существуют разные при-
приемы. Один из них — это подсчет так называемого обратного числа
заполнения (inverse participation number). Оно характеризует обрат-
обратную величину объема, занимаемого волновой функцией в простран-
пространстве, и совпадает со вторым моментом плотности вероятности об-
обнаружения частицы в той или иной точке образца
М2 = j &т\ф(т)\А. B.112)
Интеграл в этой формуле берется по всему объему образца. Величина
d определяет размерность пространства, в котором задана волновая
функция. Первый момент, очевидно, всегда равен 1, так как соответ-
соответствует вероятности обнаружения частицы во всем образце
Mi = |Л|^(г)|2 = 1 B.113)
и отражает собой известное правило нормировки волновых функций.
Для локализованного состояния с учетом условия нормиров-
нормировки B.113) огибающая волновой функции может быть записана в виде
B.114)
122

Поэтому для него щ ^ ^ B и5)
и не завистит от размера образца L.
Напротив, для делокализованного состояния типа плоской волны
^(г) и L~d/2 exp(ikr) B.116)
величина М2 зависит от размера образца L степенным образом
М2 и L~d. B.117)
В этом случае волновая функция равномерно заполняет весь объем
образца.
Если же делокализованное состояние имеет фрактальную струк-
структуру, то для него естественно ожидать следующей зависимости второ-
второго момента М2 от размера L:
М2 ~ L~D\ 0<D2<d. B.118)
Показатель степени D2 в этой формуле называется корреляционной
размерностью данной волновой функции. Неравенство D2 < d озна-
означает, что объем, который занимает эта волновая функция, составляет
при L —> оо бесконечно малую часть полного объема образца Ld.
Именно такое поведение второго момента для волновых функций
в точке перехода Андерсона и было обнаружено в численных экспери-
экспериментах. Они показали, что квадрат модуля волновой функции со-
состоит из редких всплесков в пространстве с амплитудой, намного
превышающей средний уровень. Всплески большой амплитуды окру-
окружены всплесками с меньшей амплитудой и т. д., формируя тем самым
некую самоподобную фрактальную структуру.
Аналогичным образом можно проанализировать и более высокие
моменты квадрата модуля волновой функции. Оказалось, что и они
в точке перехода степенным образом зависят от размера образца
Mq = jddr^(r)\2q - ?-(«-№. B.119)
Величины Dq называются обобщенными фрактальными размернос-
размерностями волновой функции. Очевидно, что величина Dq = d, поскольку
нулевой момент Mq в этом случае попросту совпадает с объемом об-
образца Ld. Все же остальные обобщенные фрактальные размерности
подчиняются неравенствам
d = Dq > Dx > D2 > ?>3 > ... > D^ ф 0. B.120)
123

Эти неравенства означают, что волновая функция в точке перехо-
перехода Андерсона фактически представляет собой мультифрактал. Но-
Носителем этого мультифрактала является все d-мерное пространст-
пространство, поскольку волновая функция во всех точках образца (за исклю-
исключением множества меры нуль) отлична от нуля. Поэтому размер-
размерность Dq = d. Величина D\ называется информационной размернос-
размерностью волновой функции. Она определяется формулой
B.121)
In Li
Мы видим, что имеет место определенная аналогия задачи о гео-
геометрии волновой функции в точке перехода Андерсона с тем, что мы
уже рассматривали в предыдущих параграфах, изучая мультифрак-
талы. Эта аналогия становится еще более очевидной, если мы отож-
отождествим вероятность р,, входящую в формулу B.3) для статсум-
мы Z(q,e), со значением квадрата модуля волновой функции |-г/?(гг-) |2
в некоторой точке г^. Величине е в этом случае соответствует малый
параметр 1/L. Суммирование по i в формуле B.3) надо при этом
заменить на интегрирование по г.
Более строго эту процедуру можно выполнить следующим обра-
образом. Для этого надо весь объем образца V = Ld разбить на малые
ячейки fti размером е <С L. Число этих ячеек N(e), очевидно, рав-
равно [L/e)d. После этого величину pi надо отождествить с вероятностью
обнаружения частицы в ячейке с номером г
f. B.122)
Далее величина статсуммы Z(q,e) определяется обычным образом,
как в B.3), в виде суммы по этим ячейкам.
Мультифрактальная геометрия волновой функции означает, что
при L —>¦ оо и е —> 0 (порядок этих операций важен!) имеет место
скейлинг
N(e) /х (q-l)Dg
Такой подход позволяет определить спектр обобщенных фрактальных
размерностей Dq для одной конкретной волновой функции. При этом
124

анализируется, как при заданном значении L и реализации беспоряд-
беспорядка в системе статсумма Z(q,e) изменяется с размером ячейки е. Из
физических соображений следует, что размер ячейки, будучи малым,
должен тем не менее превышать характерное межатомное расстояние.
Найденная таким образом зависимость Dq для волновой функции
в точке Андерсоновского перехода имеет вид, аналогичный тому, что
мы уже видели на примерах неоднородного канторовского множества
на рис. 2.5 и рис. 2.9. Однако, поскольку эта волновая функция задана
в d-мерном пространстве, всегда выполняется равенство Dq = d.
Зная функцию r(q) = (q — l)Dq, можно определить распределе-
распределение сингулярностей мультифрактала, т.е. функцию f(a). Численные
расчеты показывают, что она тоже имеет вид кривой с максимумом,
подобный тому, что изображен на рис. 2.14 и рис. 2.15. Максимум
этой функции, т.е. значение /(«о), всегда равно d.
Функция f(a) играет в теории перехода Андерсона весьма важную
роль. С одной стороны, она представляет собой спектр фракталь-
фрактальных размерностей мультифрактала, каковым является критическая
волновая функция. С другой стороны, эта же величина определяет
статистику значений волновой функции в неупорядоченной системе.
Действительно, примем для простоты размер ячейки е = 1. Тогда
вероятность нахождения частицы в ячейке с номером % определяется
формулой а.
Pi ~ [j) , B.124)
где L — размер образца в единицах е. Эту же формулу можно пере-
переписать и по-другому ,
Щ « -=^. B.125)
Вероятность заполнения ячейки р^ представляет собой случайную
величину. Такой же случайной величиной является, очевидно, и по-
показатель степени щ. Однако распределение значений а для муль-
мультифрактала известно. Оно определяется формулой B.66)
п(а) и (j) = exp [f(a) lnL]. B.126)
Как мы знаем, вблизи своего максимума при некотором значе-
значении а0 функция f(a) может быть аппроксимирована параболой
f(a)=d-rj(a-a{)J, B.127)
125

где г\ = f"(ao)/2. Поэтому при больших L распределение п(а) при-
принимает вид
n(a) ~exp[-77lnL(a-a0) ]. B.128)
Учитывая, что а = — lnp/lnL, получаем отсюда функцию распреде-
распределения вероятностей р;
V{p) ~ exp
B.129)
Это есть так называемое лог-нормальное распределение. По-
Поскольку вероятности р-ь характеризуют величину |-0(гг-)|2, мы прихо-
приходим к результату, что квадрат модуля критической волновой функ-
функции распределен лог-нормально по объему образца. Этот важный
в практическом отношении вывод является очевидным следствием
мультифрактальной структуры волновой функции в точке перехода.
Закону лог-нормального распределения подчиняются и другие фи-
физические величины, как, например, проводимость. Они вблизи от
перехода Андерсона и в самой точке перехода (в отличие от ситуации
вдали от перехода в хорошем металле) сильно флуктуируют от об-
образца к образцу. Эти флуктуации носят название мезоскопических
и интенсивно изучаются в последние годы в физике неупорядоченных
систем.
Концепция мультифракталов оказалась довольно плодотворной
и в других областях физики. Например, при изучении сильно раз-
развитой турбулентности, неоднородных звездных скоплений, диффу-
диффузионно-ограниченной агрегации, процессов разрушения вещества,
строении крови и т. д. Ее польза со временем становится все более
несомненной и, может быть, именно на этом пути нас ждут новые
и интересные открытия в будущем.
Литература
[1] Mandelbrot В. В., The fractal geometry of nature, San Francisco, Freeman, 1982.
[2] Пайтген Х.-О., Рихтер П. X., Красота фракталов, М.: Мир, 1993.
[3] Шустер Г, Детерминированный хаос, М.: Мир, 1988.
[4] Мун Ф., Хаотические колебания, М.: Мир, 1990.
[5] Gleick J., Chaos: Making a New Science, Viking Penguin, 1987.
[6] Barnsley M., Fractals Everywhere, Academic Press, Boston, 1988.
[7] Фракталы в физике, М.: Мир, 1988.
126

[8] Федер Е., Фракталы, М.: Мир, 1991.
[9] Смирнов Б. М., Физика фрактальных кластеров, М.: Наука, 1991.
[10] Карпов В. Г., Субашиев А. В., Что такое фракталы? ЛПИ, 1989.
[11] Зельдович Я. Б., Соколов Д. Д., Фрактали, подобие, промежуточная асимптотика, Успе-
Успехи физических наук, т. 146, вып. 3, с. 493, 1985.
[12] Соколов И. М., Размерности и другие геометрические критические показатели в
теории протекания, Успехи физических наук, т. 150, вып. 2, с. 221, 1986.
[13] Олемской А. И., Флат А. Я., Использование концепции фрактала в физике конденсиро-
конденсированной среды, Успехи физических наук, т. 163, № 12, с. 1, 1993.
[14] Зосимов В. В., Лямшев Л. М., Фракталы в волновых процессах, Успехи физических на-
наук, т. 165, №4, с. 361, 1995.
[15] Жиков В. В., Фракталы, Соросовский образовательный журнал, №12, с. 109, 1996.
[16] Вишик М. И., Фрактальная размерность множеств, Соросовский образовательный жур-
журнал, №1, с. 122, 1998.
Страницы в Интернете
1. http://home.ural.ru/~shabun/fractals/index.htm
2. http://chat.ru/~fractals/index.htm
3. http://www.visti.net/cplusp/alL96/6n96y/6n96yla.htm
4. http://www.iph.ras.ru/~mifs/rus/danilov.htm
5. http://www.geocities.com/CapeCanaveral/2854/
6. http://archives.math.utk.edu/topics/fractals.html
7. http://www.cosy.sbg.ac.at/rec/ifs/f-faq.html
8. http://www.cosy.sbg.ac.at/rec/ifs/index.htm
9. http://www2.vo.lu/homepages/phahn/fractals/barnsley.htm
10. http://www.swin.edu.au/astronomy/pbourke/fractals/randomifs/
11. http://www.swin.edu.au/astronomy/pbourke/fractals/leaiifs/
12. http://www.swin.edu.au/astronomy/pbourke/fractals/fern/
13. http://www.swin.edu.au/astronomy/pbourke/fractals/gasket/
14. http://www.swin.edu.au/astronomy/pbourke/fractals/ roger_bagula/roger5.html
15. http://www.ealnet.com/ealsoft/fracted.htm
16. http://climate.gsfc.nasa.gov/~cahalan/FractalClouds/ PractalClouds.html
17. http://polymer.bu.edu/
18. http://polymer.bu.edu:80/doc/HS.html
19. http://polymer.bu.edu:80/doc/Ter.html
20. http://polymer.bu.edu:80/doc/Ero.html
21. http://polymer.bu.edu:80/doc/ECD.html
22. http://polymer.bu.edu:80/doc/Lic.html
23. http://math.bu.edu/DYSYS/dysys.html
24. http://math.bu.edu/DYSYS/arcadia/index.html
25. http://math.bu.edu/DYSYS/chaos-game/chaos-game.html
26. http://math.bu.edu/DYSYS/FRACGEOM/index.html
27. http://math.bu.edu/INDIVIDUAL/bob/books.html
28. http://www2.unican.es/~gutierjm/linksfractals.html
29. ftp://spanky.triumf.ca/fractals/
30. http://spanky.triumf.ca/www/spanky.html
31. http://spanky.triumf.ca/www/fractint/fractint.html
127

32. http://spanky.triumf.ca/www/fractint/lsys/tutor.html
33. http://www-chaos.umd.edu/nonlinear_sites.html
34. http://sprott.physics.wisc.edu/
35. http://sprott.physics.wisc.edu/chaos.htm
36. http://sprott.physics.wisc.edu/chaos/henongp.htm
37. http://sprott.physics.wisc.edu/fractals.htm
38. http://sprott.physics.wisc.edu/phys505/
39. http://sprott.physics.wisc.edu/pubs/paper210.htm
40. http://www-syntim.inria.fr/fractales/
41. http://acacia.ens.fr:8080/home/massimin/quat/f_gal.ang.html
42. http://www.cnam.fr/fractals.html
43. http://www.anu.edu.au/ITA/ACAT/contours/catalogue.html
44. http://www.cstp.umkc.edu/personal/bhugh/home.html
45. ftp://rtfm.mit.edu/pub/usenet/news.answers/fractal-faq
46. http://www.cis.ohio-state.edu/hypertext/faq/usenet/fractal-faq/ faq.html
47. http://homepage.seas.upenn.edu/~lau/fractal.html
48. http://homepage.seas.upenn.edu/~rajiyer/math480.html
49. http://www.math.okstate.edu/mathdept/dynamics/lecnotes/ nodel.html
50. http://www.math.okstate.edu/mathdept/dynamics/lecnotes/ node41.html
51. http://www.mathcs.sjsu.edu/faculty/rucker/chaos.htm
52. http://www.625-net.com/archive/0497/worldbuilder.htm
53. http://www.fractalus.com/gumbycat/lesson3.html
54. http://nis-www.lanl.gov/~mgh/mand.shtml
55. http://life.csu.edu.au/complex/tutorials/tutorial3.html
56. http://www.mostang.com/mw/iss06/fractl.html
57. http://cogsci.ucsd.edu/~arobert/ifs.html
58. http://cogsci.ucsd.edu/~arobert/ifstech.html
59. http://library.advanced.org/12740/netscape/discover/page9.html
60. http://www.home.aone.net.au/byzantium/ferns/fractal.html
Сергей Валентинович Божокин, Дмитрий Алексеевич Паршин
Фракталы и мультифракталы
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Корректор М. А. Ложкина
Подписано в печать 05.09.01. Формат 60 х 841/16. Усл. печ. л. 7,44. Уч. изд. л. 7,55.
Печать офсетная. Гарнитура Computer Modern Roman. Бумага офсетная № 1.
Тираж 1000 экз. Заказ №
Научно-издательский центр «Регулярная и хаотическая динамика»
426057, г. Ижевск, ул. Пастухова, 13.
Лицензия на издательскую деятельность ЛУ №084 от 03.04.00.
http://rcd.ru E-mail: borisov@rcd.ru
Отпечатано в полном соответствии с качеством
предоставленных диапозитивов в ФГУП «Полиграф-ресурсы».
101429, г. Москва, ул. Петровка, 26.
128