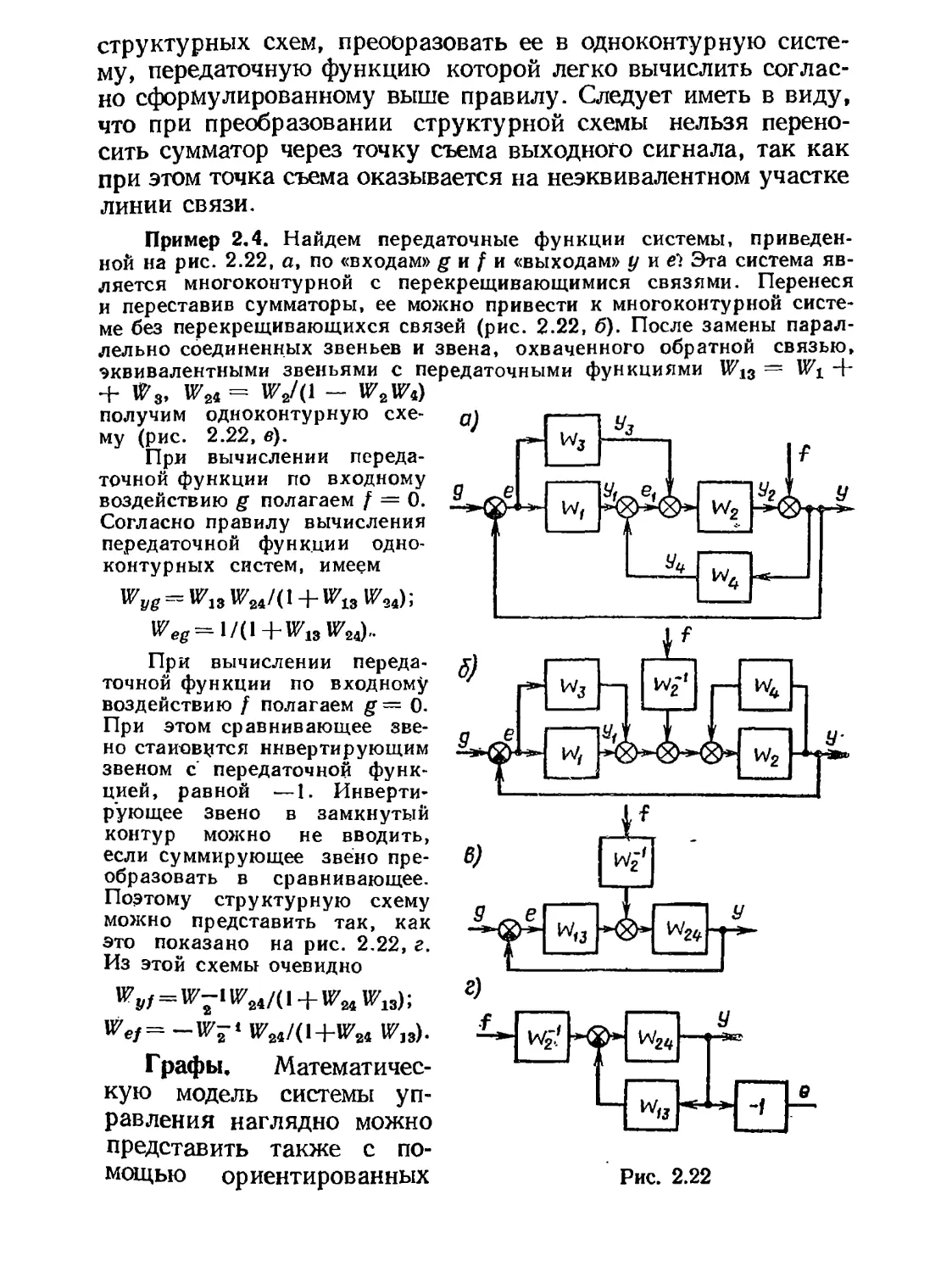
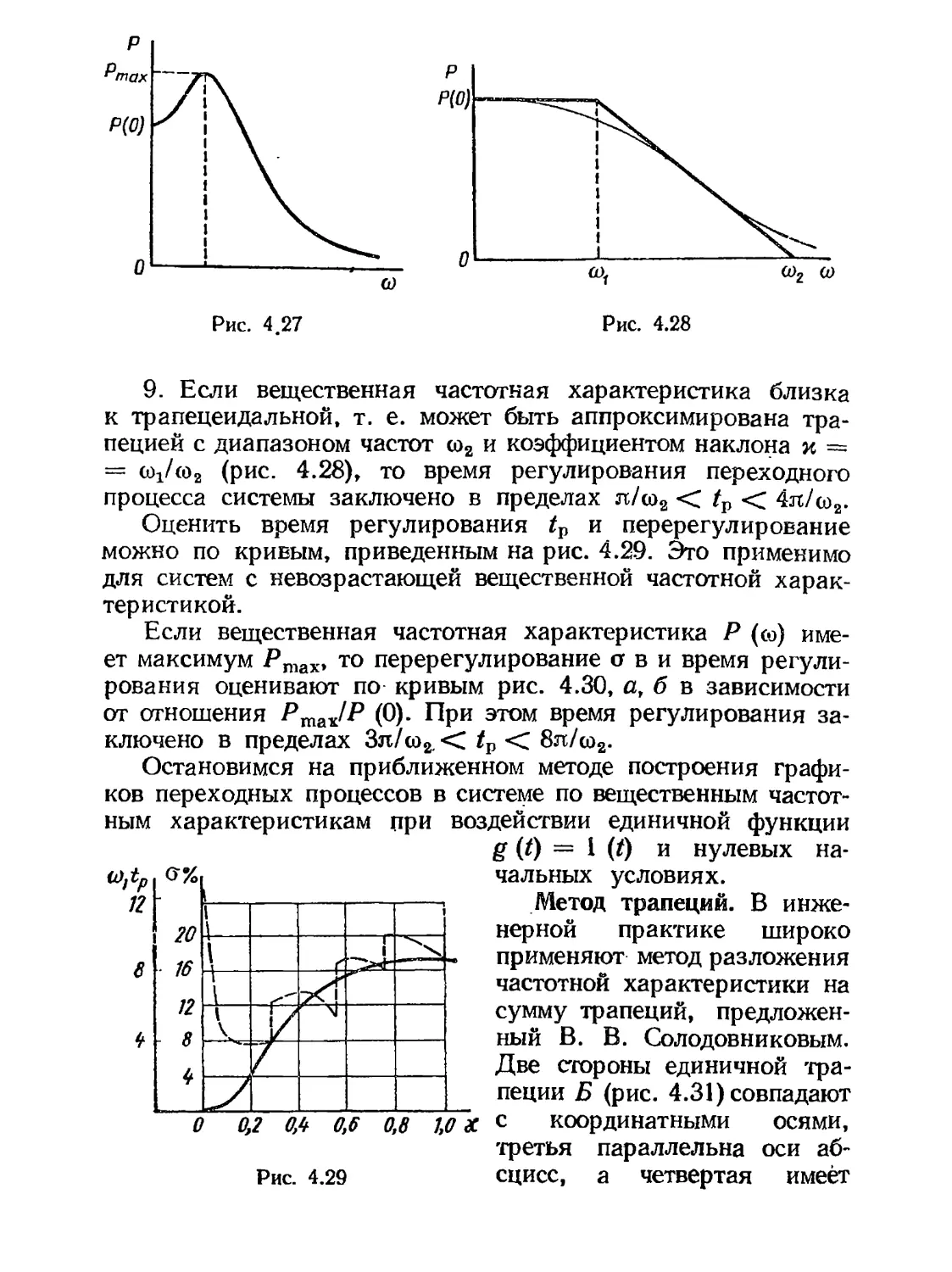
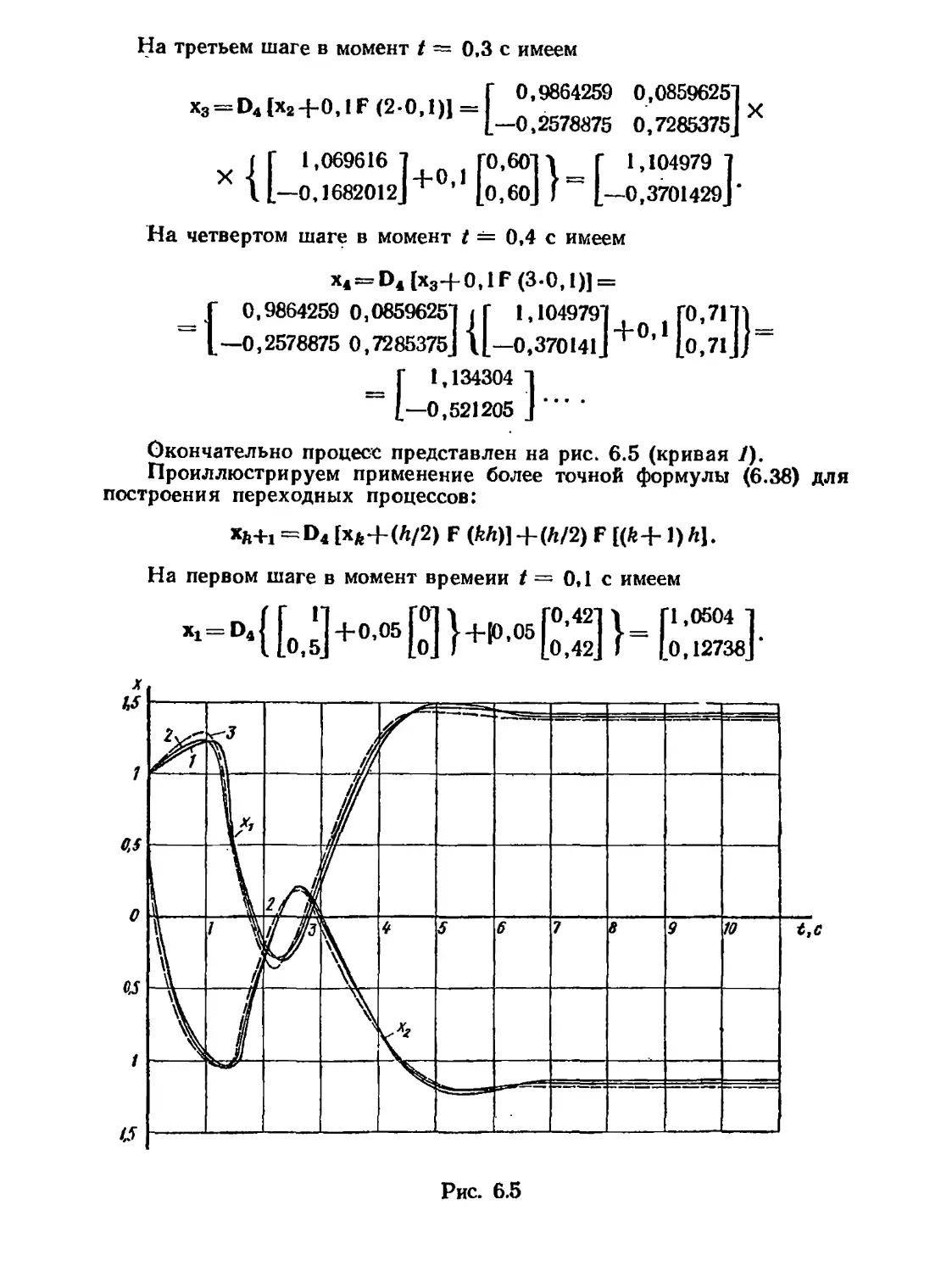
Теория автоматического управления. Часть 1. Теория линейных систем автоматического управления - Воронов А.А.

Автор: Воронов А.А.
Теги: инженерное дело техника в целом автоматика математика теория автоматического управления
Год: 1986
Похожие
Теория автоматического управления. Часть 2. Теория нелинейных и специальных систем автоматического управления
Теория линейных систем автоматического регулирования и управления.
Теория систем автоматического управления
Теория автоматического управления
Текст
                    ТЕОРИЯ
автоматического
УПРАВЛЕНИЯ
В двух частях
Под редакцией академика А. А. Воронова
Издание второе,
переработанное и дополненное
Часть первая
ТЕОРИЯ ЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Жопущеио Мшщстерстбом высшего
II срсОнего a\eii\ta.tbHozo образования СССР
€ качестве учебника 0.1.9 студешпов вузов,
обучающихся по специа.лыюсти
^Абто.иатика и телемеханика"
МОСКВА
«ВЫСШАЯ ШКОЛА"
1986

ББК 32.965
тзз
УДК 62—52
Н. А. Бабаков, А. А. Воронов, А. А. Воронова,
Г. А. Дидук, Н. Д. Дмитриева, Д. П. Ким,
Б. М. Меиский, П. Н. Попович
Рецензенты:
кафедра Московского высшего
технического училища им. Н. Э. Баумана
(зав. кафедрой — акад! АН СССР Е. П. Попов);
чл.-кор. АН СССР С. В. Емельянов
(Всесоюзный научно исследовательский институт
системных исследований)
Теория автоматического управления: Учеб. для
ТЗЗ вузов по спец. «Автоматика и телемеханика». В 2-х ч.
Ч. I. Теория линейных систем автоматического
управления / Н. А. Бабаков, А. А. Воронов, А, А.
Воронова и др.; Под ред. А, А. Воронова.—2-е изд., перераб.
и доп. — М.; Высш. шк., 1986. — 367 с, ил.
в книге изложены основные понятия и принципы управления,
математическое описание, аналитические и машинные методы исследования
устойчивости и качества линейных непрерывных систем. Наряду со
стационарными системами рассмотрены нестационарные системы н системы
с чистым запаздыванием. По сравнению с 1-м изданием (1977 г.) 2-е
издание переработанб^ и дополнено. Заново написана гл. 6, переработаны
гл. 4, 5» внесены .изменения в другие главы.
2404000000—267;^ ББК 32.965
001(0.1)>>86 ^^^^^^ 6Ф6.5
© Издательство «Высшая школа», 1977
© Издательство «Высшая школа», 1986, с изменениями

ОГЛАВЛЕНИЕ
Предисловие 3
Введение . . 5
Глава 1. Основные понятия и определения 13
§ I. Сущность проблемы автоматического управления . 13
§ 1.2. Фундаментальные принципы управления 16
§ 1.3. Основные виды автоматического управления .... 22
§ 1.4. Об основных законах регулирования 31 >
Г лава 2. Математическое описание автоматических систем
управления . 33
§ 2.1. Уравнения динамики и статики. Линеаризация . . 33
§ 2.2. Основные свойства преобразования Лапласа .... 37
§ 2.3. Формы записи линейных дифференциальных
уравнений. Передаточные функции i . . . . 40
§ 2.4. Частотные характеристики . ... 44
§ 2.5. Временные характеристики 49
§ 2.6. Элементарные звенья и их характеристики .... 52
§ 2.7. Структурные схемы, графы, уравнения и
частотные характеристики стационарных линейных систем 64
§ 2.8. Многомерные стационарные линейные системы . . 81
§ 2.9. Нестационарные линейные системы . ....... 94
§ 210. САР напряжения генератора постоянного тока.
Математическое описание 105
Глава 3. Устойчивость линейных систем автоматического управ-
#лення 114
Понятие устойчивости 114
Общая постановка задачи устойчивости по A.M.
Ляпунову 117
§-3^вг-^еор.е*га А. М. Ляпунова об устойчивости движения
по первому приближению 121
§^^3J/ Условия устойчивости линейных систем
автоматического управления 123
§ З.&л Алгебраические критерии устойчивости 128
§'3.6.. Частотные критерии устойчивости 137
§ 3.7. Анализ устойчивости по логарифмическим частотиым
характеристикам . . . .-^ . 153
§ 3.8. Построение областей устойчивости в плоскости
параметров системы 155
§ З.Э. Устойчивость систем с запаздыванием и систем с
иррациональными звеньями . 167
§ 3.10. Устойчивость нестационарных систем 175
Глава 4, Методы оценки качества регулирования линейных
систем 179

§ 4.1. Общие положения 179
§ 4,2. Оценка качества регулирования в установившемся
режиме (коэффициенты ошибок) 180
§ 4.3. Оценка качества переходного процесса при
воздействии ступенчатой функции 185
§ 4.4. Оценка качества регулирования при гармонических
воздействиях 187
§ 4.5. Корневые методы оценки качества регулирования 189
§ 4.6. Корневые годографы 194
§ 4.7. Интегральные оценки качества переходных
процессов . , . 204
§ 4.8. Частотные методы оценки качества регулирования 214
§ 4.9. Чувствительность систем автоматического
управления i 231
Глава 5. Обеспечение устойчивости, повышение качества регу=
лироваиня и синтез линейных автоматических
систем .236
§ 5.1. Общие положения 236
§ 5.2. Корректирующие устройства . 237
§ 5.3. Преобразовательные элементы 244
§ 5.4. Повышение точности в установившихся режимах 250
§ 5.5. Обеспечение устойчивости и повышение запаса
устойчивости 260
§ 5.6. Выбор параметров и синтез корректирующих
устройств по корневым годографам! 264
§ 5.7. Синтез корректирующих устройств по
логарифмическим амплитудно-частотным характеристикам 268
Гкаеа 6. Машинная реализация методов теории автоматического
управления ........ 283
§ 6.1. Математические модели автоматических систем и
особенности реализации их на ЭВМ 283
§ 6.2. Анализ устойчивости по уравнениям переменных
состояния и по характеристическому уравнению 293
§ 6.3. Функционально-преобразованные матрицы и их
применение. Критерий В. И. Зубова ......... 298
§ 6.4. Матричный критерий устойчивости, не связанный
с обращением матрицы 307
§ 6.5. Векторные методы построения переходных
процессов в линейных системах 315
§ 6.6. Векторный способ построения переходных процессов
в нелинейных системах 324
§ 6.7. Стандартные численные методы интегрирования . 328
§ 6.8. Машинная реализация частотных методов . ... 333
§ 6.9. Построение областей устойчивости и динамического
качества как задача параметрического синтеза . . 339
§ 6.10. Модифицированный метод D-разбиения.
Применение полиномов Чебышева 341
§ 6.11. Универсальные методы построения областей ус-
\ тойчивости и динамического качества 353
Список литературы 362

ПРЕДИСЛОВИЕ
Учебник «Теория автоматического
управления» издается в двух частях.
Настоящая книга является первой частью
учебника и состоит из введения и шести
глав.
Во введении дан краткий
исторический очерк основных этапов развития
теории автоматического управления.
Глава 1 содержит основные понятия и
определения и знакомит с
фундаментальными принципами управления,
различными алгоритмами функционирования
автоматических систем управления.
Глава 2 посвящена математическому
описанию с помощью дифференциальных
уравнений, передаточных функций,
временных и частотных характеристик,
структурных схем и графов одномерных
и многомерных, стационарных и
нестационарных систем автоматического
управления. Глава 3 знакомит с различными
критериями устойчивости
(алгебраическими и частотными)» понятием
D-разбиения. Наряду с обыкновенными
линейными стационарными системами
рассматриваются вопросы устойчивости
линейных нестационарных систем, а также
систем с запаздыванием. В главе 4
рассмотрены оценки качества по
временным и частотным характеристикам, кор^
невым годографам и интегральным
показателям. Глава 5 знакомит с
различными методами синтеза параметров и
корректирующих цепей Линейных систем
управления с целью обеспечения
устойчивости и повышения качества, а также со
средствами коррекции. В главе 6 описа-

ны различные численные способы решения алгебраических
и дифференциальных уравнений, алгоритмы оценки
устойчивости и качества систем автоматического управления, удобных
для реализации на ЦВМ.
Второе издание существенно переработано и дополнено.
Заново написана глава 6 и дополнена глава 2, Значительно
переработаны главы 4 и 5. Изменения претерпели и остальные
главы.
В написании учебника принимали участие Н. А. Бабаков
(гл. 2), А. А. Воронов (введение, гл. I, 5), А. А. Воронова (гл.6),
Г. А. Дидук (гл. 6), Н. Д. Дмитриева (гл. 4), Д. П.
Ким (гл. 2), Б. М. Менский (гл. 5), П. Н. Попович (гл. 3).
Авторы выражают глубокую благодарность рецензентам—
академику С. В. Емельянову и коллективу кафедры
Московского высшего технического училища им. Н. Э.
Баумана, руководимой чл.-кор. АН СССР Е. П. Поповым, за ценные
замечания, способствовавшие улучшению книги, а также
сотрудникам кафедры «Проблемы управления» Московского
института радиотехники, электроники и автоматики за помощь
при подготовке рукописи к печати.
Все замечания и пожелания по книге можно направлять по
адресу: 101480, Москва, ГСП'4, Неглинная ул., д, 29(14,
издательство «Высшая школау>. Авторы с благодарностью
примут их и используют в дальнейшей работе над учебником.
Авторы

ВВЕДЕНИЕ
В число научных дисциплин,
образующих науку об управлении,
входит теория автоматического управления
и регулирования. Вначале она
создавалась для изучения статики и динамики
процессов автоматического управления
техническими объектами —
производственными, энергетическими,
транспортными и т.п. Основное ее значение
сохранилось и в наше время,хотя в последние
годы ее выводами и результатами
начинают пользоваться и для изучения
динамических свойств системы управления
не только технического характера, но
и экономического, организационного,
биологического и т. д.
Для осуществления автоматического
управления техническим процессом
создается система, состоящая из
управляемого объекта и связанного с ним
управляющего устройства. Как и всякое
техническое сооружение, система
должна обладать конструктивной жесткостью
и динамической прочностью. Эти чисто
механические термины в данном случае
несколько условны. Они означают, что
система должна выполнять заданные ей
функции с требуемой точностью,
несмотря на инерционные свойства и на
неизбежные помехи. Пока объект
обладает достаточной жесткостью и динамичес-
кой прочностью, потребности в
автоматическом регулировании не возникают.
С необходимостью построения
регуляторов первыми, по-видимому,
столкнулись создатели высокоточных
механизмов, в ПeDBVЮ OUPnAITf, иаоло Hovm^^

очень небольшие; но действующие непрерывно помехи,
накапливаясь, приводили в конечном итоге к отклонениям от
нормального хода, недопустимым по условиям точности.
Противодействовать им чисто конструктивными средствами,
например улучшая точность и чистоту обработки деталей, повышая
их массу или увеличивая полезные усилия, не всегда
удавалось, и для повышения точности в состав часов стали
вводить регуляторы. На рубеже нашей эры арабы снабдили
поплавковым регулятором уровня водяные часы. В 1675 г.
X. Гюйгенс встроил в часы маятниковый регулятор хода.
Другой причиной, побуждавшей строить регуляторы, была
необходимость управлять процессами, подверженными столь
сильным помехам, что при этом утрачивалась не только
точность, но зачастую и работоспособность системы вообще.
Предшественниками регуляторов для подобных условий можно
считать применявшиеся еще в средние века центробежные
маятниковые уравнители скорости хода водяных мукомольных
мельниц. Но хотя отдельные автоматические регуляторы
появлялись в давние времена, они оставались любопытными в
истории эпизодами и серьезного влияния на формирование
техники и теории автоматического управления не оказали.
Бурное развитие этих направлений началось лишь в XVUI и
XIX столетиях, в эпоху промышленного переворота в Европе.
Первыми промышленными регуляторами этого периода
являются автоматический поплавковый регулятор питания котла
паровой машины, построенный в 1765 г. И.И. Ползу новым в
Барнауле; центробежный регулятор скорости паровой
машины, на который в 1784 г. получил патент английский, механик
Дж. Уатт; первое программное устройство управления ткацким
станком от перфокарты (для воспроизведения узоров на
коврах), построенное в 1808 г. Ж- Жаккаром. Эти регуляторы как
бы открыли путь потоку изобретений принципов
регулирования и регуляторов, продолжавшемуся вплоть до середины
XX в. В этот период появились регуляторы с воздействием по
производной (братьев Сйменсов), по нагрузке (инж. Ж- Пон-
селе), сервомоторы с жесткой обратной связью (инж. Л. Фар-
ко), регуляторы с гибкой обратной связью (изодромные),
импульсные регуляторы «на отсечку пара».
Паровая машина не случайно стала первым объектом для
применения техники и теории регулирования, так как она не
обладала способностью устойчиво работать сама по себе, не
имела «самовыравнивания». Ее неблагоприятные динамичес-

кие свойства часто приводили к тому, что подключенный к ней
регулятор действовал не так, как ожидал конструктор,
«раскачивал» машину или вообще оказывался неспособным
управлять ею. Все это, естественно, побуждало к проведению
теоретических исследований. Однако до конца 60-х годов прошлого
века теоретические исследования регулирования отличались
тем, что мы называем сегодня «отсутствие системного подхода».
Исследователи еще не сознавали, что в технике рождается
новое направление. Они считали, что регуляторы были лишь
вспомогательным придатком к машине, приборной
разновидностью «модераторов», «уравнителей хода», дублировавшей
функции маховиков, Во многих работах рассматривались
идеальные безынерционные регуляторы. Шагом вперед были
работы, учитывавшие динамику регулятора, но и в них
регулятор рассматривался отдельно от машины. Авторы обычно
добивались хорошего успокоения колебаний самого регулятора,
считая, что этого достаточно и для его спокойной работы на
машине. При таких подходах теоретические исследования не
могли стать основой для новой науки и. были лишь
дополнительными частными проработками в рамках прикладной мех-аники,
придатком к ее разделу о паровых машинах.
Коренное изменение в подходе к проблеме и в методологии
исследований внесли три фундаментальные работы,
содержащие, по существу, изложение начал новой науки: работы Дж.
Максвелла «О регуляторах» (1866) и И. А. Вышнеградского
«Об общей теории регуляторов» (1876). и «О регуляторах
прямого действия» (1877). Дж. Максвелл и И. А. Вышнеградский
осуществили системный подход к проблеме, рассмотрев
регулятор и машину как единую динамическую систему, перейдя к
исследованию малых колебаний и линеаризовав сложные
дифференциальные уравнения системы, что позволило дать
общий методологический подход к исследованию самых
разнородных по принципам действия и конструкции систем,
заложить основы теории устойчивости и установить ряд важных
общих закономерностей регулирования по принципу обратной
связи. Особо важную роль в то время сыграла работа И. А.
Вышнеградского, отличавшаяся глубоким инженерным
подходом, рассмотревием самых важных для техники тех лет
объектов и содержавшая кроме ценных практических рекомендаций
истоки ряда современных методов исследования качества
регулирования (диаграммы устойчивости и распределения
корней, выделение областей устойчивости и монотонности и Др.)-
Поэтому современники И. А. Вышнеградского считали

его основоположником теории автоматического
регулирования.
Работа Дж. Максвелла осталась в то время почти незаме-*
ченной, так как она рассматривала малоинтересный для
широкого круга инженеров объект (механизм ведения телескопа),
явно полезных практических выводов не делала и даже по
умозрительным выводам рекомендовала астатические регуляторы,
практически непригодные для промышленных машин того
времени. Ее роль была оценена значительно позднее, когда теория
автоматического регулирования сформировалась в
самостоятельную общую научную дисциплину.
Уже в ранние годы теория регулирования стала
стимулировать разработки математического плана. По рекомендации
Дж. Максвелла был разработан Раусом алгоритм для оценки
расположения корней характеристического уравнения и
устойчивости. По просьбе А. Стодолы А. Гурвицем'был выведен де-
термлнантный критерий устойчивости. Работы словацкого
инженера и ученого А. Стодолы занимают видное место в теор-
рии устойчивости регулирования паровых и гидравлических
турбин, в учете влияния на процесс регулирования длинного
трубопровода.
Крупный вклад в теорию внесен Н. Е. Жуковским, автором
труда «О прочности движения» и первого русского учебника
«Теория регулирования хода машин» (1909). Н. Е. Жуковский
дал математическое описание процессов в длинных
трубопроводах, рассмотрел влияние сухого трения в регуляторах,
исследовал некоторые процессы импульсного регулирования
посредством уравнений в конечных разностях.
К началу XX в. и в первые его десятилетия теория
автоматического регулирования формируется как общая дисциплина
с рядом прикладных разделов, таких, как регулирование
электрических машин и систем — X. Тома (1914), Р. Жюиль-
яр (1933), В. С. Кулебакин (1926), С. А. Лебедев и П. С.
Жданов (1932), Н. М. Крылов и Н. Н. Боголюбов (1932);
регулирование двигателей — М. Толле (1905), У. Тринкс (1919);
тепловых и паросиловых установок — Т. Штейн (1926),
Г. Вюнш (1930), Ю. Г. Корнилов и В. Д. Пивень (30-е годы),
паровых турбин — А. В. Щегляев (1933), различных
производственных процессов — В. Оппельт (1939) и др. Особенно
четко мысль о теории регулирования как дисциплине
общетехнического характера проводится в работах И. Н.
Вознесенского (1922—1949) — руководителя одной из крупных
советских школ в этой области.

Усложнение систем, связанное с повышением
интенсивности Процессов, скоростей, требований к точности и качеству,
приводит к необходимости создания более эффективных
методов исследования. Мысль исследователей обращается к час-
тотным методам, позволяющим сочетать аналитические и
наглядные графические приемы, теоретические и
экспериментальные методы исследования. Появляются работы: X. Найквиста
(1932), в которой рассматривается критерий устойчивости
радиотехнических усилителей с обратной связью, основанный
на свойствах частотной характеристики разомкнутой системы,
и А. В. Михайлова «Гармонический метод в теории
регулирования» (1938), в которой обосновывалась целесообразность
применения частотных методов в теории регулирования и
предлагается новый критерий (критерий Михайлова), не требующий
предварительного размыкания цепи регулирования. Методы
Найквиста и Михайлова вошли в практику в послевоенные
годы. В 1946 г, Г. Боде и Л. Мак-Кол ввели логарифмические
частотные характеристики. Флойддля исследования качества
предложил аппроксимировать вещественную частотную
характеристику суммой трапеций. Г. Браун, А. Холл, Д, Кемп-
белл, Г. Честнат, В. В. Солодовников завершили разработку
частотных методов синтеза и расчета систем, придав им
форму, удобную Для инженерных расчетов.
В 40—50-е годы разрабатываются основы теории
нелинейных систем. Задача существенно затруднялась из-за отсутст-
вия единого общего математического аппарата для нелинейных
задач. Продвинуться в этом-направлении удалось тогда, когда
из всего множества частных видов нелинейных систем были
отобраны для исследования суженные классы, имеющие
вместе с тем достаточно широкое распространение в практике, т. е.
системы, в которых можно выделить две части: линейную
динамическую и нелинейную статическую. Наиболее детально
были исследованы кусочно-линейные аппроксимации
нелинейных статических характеристик.
Одно из важных направлений исследования устойчивости
нелинейных систем с аналитическими характеристиками
нелинейной части, основывающееся на работах А. А, Ляпунова
(1896), развивалось в СССР в работах А. И. Лурье (1944—
—1951), А.М. Летова (1955) и др. Завершающим этапом этого
направления можно считать разработку теории абсолютной
устойчивости. Проблема была выдвинута А. И. Лурье и В. И.
Постниковым (1944), более детально сформулирована М. А. Ай-
зерманом (1949, 1963) и доведена до изящного решения

румынским ученым В. дМ. Поповым (1959), который
использовал частотные представления, что позволило в дальнейшем
применить эти методы для синтеза нелинейных систем.
Большое значение для качественного исследования
нелинейных систем имеют методы, базирующиеся на
представлении переходных процессов траекториями в фазовых
плоскостях и пространстве. Основы направления заложены
А. А. Андроновым и его школой в 1930—1940 гг. Метод
фазовой плоскости, обладая большой наглядностью и всеобщим
охватом совокупности возможных движений, несмотря на
ограниченность уравнениями второго (иногда третьего) порядка,
позволил вскрыть ряд характерных особенностей процессов в
нелинейных системах: предельные циклы, скользящие режимы,
захватывание и т. п. Сочетание фазовых
представлений с аналитическими методами исследования многомерных
фазовых пространств дало возможность предложить и
исследовать новый важный класс систем с переменной структурой,
сохраняющих высокое качество работы в условиях
значительных изменений параметров объекта (С. В. Емельянов и др.,
60-е годы). Работа удостоена Ленинской премии в 1971 г.
Я. 3. Цыпкиным разработаны основы теории релейных
(1955) и импульсных (60-е годы) систем с различными
видами модуляции. Цикл этих работ удостоен Ленинской премии
в 1960 г.
Для определения параметров автоколебаний и условий их
возникновения приближенными методами И. fA. Крыловым и
Н. И. Боголюбовым (1934) был разработан метод
гармонического баланса. Л. С. Гольдфарб дал графоаналитический
метод нахождения в первом приближении частоты и амплитуды
основной гармоники автоколебаний с помощью частотных
характеристик. Дальнейшее развитие этот метод получил в
работах Е. П. Попова и др.
Развитие теории автоматического регулирования в
послевоенные годы было исключительно плодотворным и
многогранным и невозможно, хотя бы бегло, даже упомянуть о всех
основных направлениях и авторах. Ограничимся коротким
упоминанием об основных новых разделах теории, посвященных
разработкам новых фундаментальных принципов управления,
выполненных советскими авторами.
Трудами Г. В. Щипаноэа, В. С. Кулебакина, Б. И.
Петрова и других разработаны теория автоматического
регулирования по возмущению, теория компенсации возмущений и
инвариантности.

в. в. Казакевичем, А. А. Фельдбаумом, А. А. Красовским
и другими разработаны принципы экстремального управления
и теория поиска экстремума (дуального управления). Л. С.
Понтрягин, А. М. Летов, Н. Н. Красовский и другие создали
основы теории оптимального управления, обеспечивающего
выражаемое обычно функционалом максимальное значение
показателя технико-экономической эффективности
процесса в динамике. Разработка теории экстремальных
(самонастраивающихся) оптимальных систем дала основание расширить
название курса «Теория автоматического управления и
регулирования», поскольку рассматриваемые в нем виды
управления не ограничиваются только регулированием.
Значение теории автоматического управления в настоящее
время переросло рамки только технических систем.
Динамические управляемые процессы имеют место в живых
организмах, экономических и организационных человеко-машинных
системах. В таких системах функции управления не могут быть
полностью переложены на автоматические устройства.
Принятие наиболее ответственных решений остается за человеком.
Системы, в которых автоматизируется часть операций, а
другая часть выполняется человеком, получили название
«Автоматизированные системы управления» (АСУ). АСУ создаются
на нескольких уровнях: технологических процессов (АСУТП)
и предприятия (АСУП), отрасли и т. д. В АСУ широко
используется вычислительная техника. Изучейие принципов
построения АСУ составляет предмет специального учебного курса.
Соотношение между числом автоматизированных и
неавтоматизированных операций в АСУ различных уровней
неодинаково. На низшем уровне (АСУТП) роль автоматических
устройств и роль динамики превалируют. На высших уровнях
учет динамики становится существенно труднее как
вследствие усложнения структуры системы и возрастания числа
управляемых переменных, так и вследствие увеличения числа и
возрастания роли не поддающихся формализации на
математическом языке факторов. В настоящее время интенсивно
развиваются новые разделы динамики управления: «Динамика
сложных систем», изучающая системы высокой размерности со
сложной структурой, описание которых может быть
выполнено на математическом языке, и «Системная динамика»,
изучающая поведение сложных систем при наличии как
формализуемых, так и неформализуемых факторов. Одним из основных
методов исследования в системной динамике является
имитационное моделирование. В настоящее время изучение динамики

сложных систем и системной динамики выходит за рамки
излагаемого в данной книге курса обнов теории автоматического
управления.
Законы динамики в сложных системах обычно не являются
основными и определяющими само управление, как это
свойственно техническим системам, но тем не менее их влияние
зачастую существенно и отказ от их учета приводит к крупным
потерям В автоматизированных системах управления (АСУ)
технологическими процессами роль динамики бесспорна и
превалирует, но она становится все более ясной и в других типах
АСУ по мере расширения, их не только информационных, но
и управляющих функций.
В утвержденных на XXVII съезде КПСС Основных
направлениях экономического и социального развития СССР
на 1986—1990 годы и иа период до 2000 года
предусмотрено внедрять автоматизированные системы в различные
сферы хозяйственной деятельности, и в первую очередь
в проектирование, управление оборудованием и
технологическими процессами. В решении этих задач исследования
и разработки в области теории автоматического
управления играют исключительно важную роль.

Глава 1
УО
ОСНОВНЫЕ понятия
[И ОПРЕДЕЛЕНИЯ
§ 1.1, Сущность проблемы
автоматического управления
Целенаправленные процессы,
выполняемые человеком для удовлетворения
различных потребностей, представляют
собой организованную совокупность
действий — операций, которые делят на
два класса: рабочие операции и
операции правления. К рабочим операциям
относят действия, непосредственно
необходимые для выполнения процесса
в соответствии с. теми природными
законами, которыми определяется ход
процесса, например снятие стружки при
обработке детали на станке, вращение
вала двигателя и т, п. Замену труда
человека в рабочих операциях назьгоа-
ют механизацией, цель которой —
освобождение человека от тяжелых
операций, требующих больших затрат
физической энергии (земляные работы, подъем
грузов); во вредных операциях
(химические, радиоактивные процессы); в
однообразных, утомительных для нервной
системы операциях (завинчивание
однотипных винтов при сборке, заполнение
большого количества типовых
документов, выполнение большого объема
стандартных вычислений и т. п.).
Для правильного и
высококачественного выполнения рабочих операций их
необходимо направлять действиями
другого рода — операциями управления,
которые обеспечивают в нужные моменты
времени начало, порядок следования и

прекращение отдельных операций, обеспечивают вьщеление
необходимых для их выполнения ресурсов, задают нужные
параметры самому процессу: направление, скорость, ускорение
рабочего инструмента, температуру, концентрацию в химическом
процессе и т. д. Совокупность управляющих операций
образует процесс управления.
Операции управления также частично или полностью
могут выполнять технические устройства. Замену труда человека
в операциях управления называют автоматизацией, а
технические устройства, выполняющие операции управления,—
— автоматическими устройствами. Совокупность
технических средств — машин, орудий труда, средств механизации,
выполняющих данный процесс, — с точки зрения управления,
-является объектом управления. Совокупность средств
управления и объекта образует систему управления. Систему, в
которой все рабочие и управляющие операции выполняют
автоматические устройства, ^ называют автоматической системой.
Систему, в которой автоматизирована только часть операций,
другая же их часть (обычно наиболее ответственная)
сохраняется за людьми, назьгоают автоматизированной (частично
автоматической) системой.
Объектами и операциями управления охватываются
технические процессы и агрегаты, группы агрегатов, цехи,
предприятия, людские коллективы и организации и т. д.
Всякий технический процесс характеризуется
совокупностью физических величин, называемых показателями,
координатами, а иногда параметрами процесса. Будем избегать
термина «параметр» в этом смысле, так как им обычно
обозначают физические константы самих устройств. Для
осуществления управления и-построения управляемых систем нужны
знания двоякого вида: во-первых, конкретные знания данного
процесса, его технологии и, во-вторых, знание принципов и
методов управления, общих для самых разнообразных объектов и
процессов. Конкретные, специальные знания дают возможность
установить, что и как следует изменять в системе, чтобы
получить требуемый результат. Будем считать, что все это
задано технологами, и будем изучать, абстрагируясь от
частных свойств, только общие законы и методы управления и
способы их реализации.
При автоматизации возникает необходимость в различных
видах операций управления. К одному из видов относятся
операции начала (включения), прекращения (отключения)
данной операции и перехода от одной операции к другой (пере-

о) ^
ш
УО
д)
в)
.X, и
УО
Рис. 1.1
ключения). Различные аспекты этих видов операций
рассматриваются в теории переключающих устройств и отчасти в
теории расписаний, составляющих предмет других курсов.
Другая группа операций связана с контролем за
координатами с целыо установления, не вышли ли они за допустимые
границы. Эта группа операций состоит в измерении значений
координат и выдаче результатов измерение & удобной для. чела-
века-оператора форме. Операции этой группы
рассматриваются в теории автоматического контроля.
Для правильного и высококачественного ведения процесса
нексторые из его координат — управляемые координаты —
должны поддерживаться в определенных границах или
изменяться по определенному закону. Поэтому третью группу
операций управления — операции по поддерживанию
заданного закона изменения координат — изучают в теории
автоматического управления, которой посвящена эта книга.
Необходимость в управлении значениями координат
возникает в том случае, когда нормальный ход процесса
нарушается из-за различного рода возмущений, т. е. колебаний
нагрузки, воздействий внешней среды или внутренних помех.
Пусть X = {лгх, ^2, x„} — совокупность управляемых
координат процесса. В схеме, изображенной на рис. 1.1, а,
б, объект представлен прямоугольником, а управляемые
координаты, или, как их часто назьщают, выходные величины
объекта, — одиночными стрелками, если они Скалярные
величины Хх, лгз,..., или двойными при изображении вектора х.
На схеме показаны также возмущающие воздействия z = {z^^
z^, Zi) и управляющие воздействия и = а^у Um),
прикладываемые к управляющему органу объекта УО, с
помощью которого можно изменять координаты х. Величины х, и и
Z в зависимости от природы объекта связаны различными
математическими зависимостями. В общем случае
x-A(z,u), (М)
где А — оператор, определяющий вид зависимости.

в простейшем случае, когда это обычная функциональная
зависимость
x=F(z,u), (1.2)
объект назывгютстатическим или безынерционным, а
зависимость (1.2) или ее графическое тображент — статической
характеристикой объекта (рис. 1.1, в).
Если объект обладает инерцией, то изменения координат
под воздействием возмуш^ений z или управлений и происходят
не мгновенно и в этом случае объект назывелот динамическим.
Величины X, U и Z в динамических объектах связаны
дифференциальными, интегральными или разностными уравнениями.
Изменения координат в нормальном требуемом ходе
процесса определяются совокупностью правил, предписаний или
математических зависимостей, называемой алгоритмом фун-
цианирования системы. Алгоритм функционирования
составляется на основании технологических, экономических и других
требований без учета динамических искажений. В теории
автоматического регулирования алгоритм функционирования
считают заданным.
Алгоритм управления будет зависеть как от алгоритма
функционирования, так и от динамических свойств системы.
§ 1.2. Фундаментальные принципы управления
Зная статические и динамические свойства управления
системы, можно построить математическую модель системы и
найти такой алгоритм управления, который обеспечивает
заданный алгоритм функционирования при известных, заданных
воздействиях. Однако модель всегда приближенно выражает
свойства оригинала, а возмущающие воздействия могут
изменяться не известным заранее образом, поэтому и при найденном
алгоритме управления фактическое поведение системы будет
отличаться от желаемого, определяемого алгоритмом
функционирования.
Чтобы приблизить поведение к требуемому, алгоритм
управления нужно увязать не только со свойствами системы и
алгоритмом функционирования, но и с фактическим
функционированием системы.
В основе построения системы автоматического управления
лежат некоторые общие фундаментальные^ принципы управле-

Рис. 1.2
ния, определяющие, каким образом осуществляется увязка
алгоритмов функционирования и управления с фактическим
функционированием или причинами, вызывающими
отклонение функционирования от заданного. В настоящее время в
технике известны и используют три фундаментальных принципа:
разомкнутого управления, компенсации и обратной связи.
Принцип разомкнутого управления. Сущность принципа
состоит в том, что алгоритм управления вырабатьгоается
только на основе заданного алгоритма функционирования и не
контролируется другими факторами — возмущениями или
выходными координатами процесса. Общая функциональная схема
системы показана на рис. 1.2, а. Задание (t) алгоритма
функционирования может вырабатываться как специальным
техническим устройством — задатчиком программы /, так и
выполняться заранее при проектировании системы и затем
непосредственно использоваться при конструировании
управляющего устройства 2. В последнем случае блок / на схеме
отсутствует. В обоих случаях схема имеет вид разомкнутой
цепочки, в которой основное воздействие передается от входного
элемента к выходному элементу 5, как показано стрелками. Это и
дало основание названию принципа. Близость л: и лго в
разомкнутых системах обеспечивается только конструкцией и
подбором физических закономерностей, действующих во всех
элементах .
Несмотря на очевидные недостатки, этот принцип
используют очень широко. Элементы, представляемые разомкнутой
цепью, входят в состав любой системы, поэтому принцип пред-
ставля£1сяла£:т МШГ' WI^m, что его не всегда выделяют как

один из фундаментальных принципов. Этому способствует и
то, что общих правил построения разомкнутых цепей можно
выделить не много. Основные правила, полезные
конструктору, существенно зависят от частных свойств конкретных
устройств и изучаются в специальных прикладных курсах по
приборостроению и машиностроению.
Упоминавшиеся вьппе операции включения, отключения и
переключения часто выполняют с помощью различных
логических элементов и их наборов (выключателями, реле,
элементами И, НЕ, ИЛИ и др.), каждый из которых может
представлять собой элемент с управлением по разомкнутой цепи.
Другим типом этих элементов могут бьггь датчики
программы, состоящей из устройства запуска программного элемента
и самого программного элемента (например, устройство пуска
и барабан музыкальной шкатулки, магнитофон,
профилированный кулачковый механизм, приводимый в движение
двигателем и осуществляющий перемещение рабочего инструмента по
заданному контуру, и т. п.).
Следующим типом элементов являются линейные
преобразователи. Один вид таких преобразователей осуществляет
пропорциональное преобразование одной физической величины в
другую, более удобную для использования, другой их вид —
усилители — имеют на входе и выходе одну и ту же
физическую величину, но с различными значениями ее количественньпс
показателей. Используются также нелинейные
функциональные преобразователи.
К элементам разомкнутого типа можно отнести и многие
счетно-решающие элементы, выполняющие операции
дифференцирования, интегрирования и формирования разных
дифференциально-интегральных операторов.
Принцип компенсации (управление по возмущению). Если
возмущающие воздействия настолько велики, что
разомкнутая цепь не обеспечивает требуемой точности выполнения
алгоритма функционирования, то для повышения точности иногда
возможно, измерив возмущение, ввести по результатам
измерения коррективы в алгоритм управления, которые
компенсировали бы вызываемые возмущениями отклонения алгоритма
функционирования.
Так как отклонение регулируемой величины зависит не
только от управляющего U, но и от возмущающего z
воздействия, т. е. X = Fi (Ui, z), то в принципе можно подобрать
управление U == Fj (z) таким образом, чтобы в установившемся
режиме отклонение отсутствовало, т. е. Ах = — (ux, z) ^. 0.

Так, в простейшем линейном случае, если
характеристика объекта в статике Xq = k^u — k;^ z, то, выбирая и =
== Xq/Kq + ^/^0» получим X = л'о = const.
функциональная схема регулирования по возмущению
показана на рис. 1.2, б. Примерами систем компенсации могут
служить; известная из физики биметаллическая система
стержней с разными коэффициентами теплового расширения в
маятнике хронометра, обеспечивающая постоянство длины
маятника при колебаниях температуры; схема компаундирования
генератора постоянного тока, обеспечивающая неизменность
напряжения при колебаниях тока нагрузки (рис. 1.3). Если
э. д. с. генератора = ЛФв линейно зависит от его потока
возбуждения Ф в. а уменьшение напряжения вызвано только
активным сопротивлением якоря, т. е. пропорционально току
нагрузки, то для поддержания постоянства заданного
напряжения надо изменять э. д. с. генератора в функции тока
нагрузки по закону £г = + ^го- Такое изменение
осуществляют с помощью дополнительной компаундной обмотки /СО,
по которой проходит ток /„, равный или пропорциональный
току якоря /. с помощью компаундирования, выбирая
коэффициент пропорциональности при /, можно уменьшить ста-
тизм характеристики б, сделать его равным нулю или
изменить знак статизма, получив возрастание напряжения при
росте нагрузки (перекомпенсация). Следует подчеркнуть, что
компенсация достигается только по измеряемым возмущениям.
Так, в приведенном примере не компенсируются колебания
температуры, скорости приводного двигателя и ряд других
факторов, вследствие чего ошибку нельзя свести к нулю даже
при идеальном компаундировании.
Принцип регулирования паровой машины по моменту
сопротивления на ее валу был предложен в 1830 г.
французским инженером Ж- Понселе, однако реализовать свое
предложение на практике ему не удалось, потому что
динамические свойства машины (астатизм) не
допускали непосредственного использования
принципа компенсации. В 1940 г. Г. В. Щипа-
нов предложил принцип достижения
независимости управляемой величины от
возмущений — так называемый принцип
инвариантности. Г. В. Щипанов пытался получить
компенсацию путем соответствующего
подбора связей в регуляторе, не измеряя
непосредственно возмущение. Он получил матема- Рис. 1.3

тические условия для такого подбора, но попытки
реализовать эти условия наталкивались на физическую
нереализуемость. Это вызвало в свое время острую длительную
дискуссию, в которой крупные специалисты вообще ставили под
сомнение возможность самого принципа инвариантности. В. С.
Кулебакин в 1948 г. и Б. Н. Петров в 1955 г, показали, как
следует строить системы, чтобы в них можно было реализовать
принцип инвариантности.
Принцип обратной связи. Регулирование по отклонению.
Систему можно построить и так, чтобы точность выполнения
алгоритма функционирования обеспечивалась и без измерения
возмущений. На рис. 1.2, в показана схема, в которой
коррективы в алгоритм управления вносятся по фактическому
значению координат в системе. Для этой цели в конструкцию
системы вводят дополнительную связью, в которую могут входить
элементы для измерения х и для выработки корректирующих
воздействий на управляющее устройство. Схема имеет вид
замкнутой цепи, что дало основание назвать осуществляемый в
ней принцип принципом управления по замкнутому контуру.
Введенную дополнительную цепь называют цепью обратной
связи, так как направление передачи воздействий в
дополнительной связи обратно направлению передачи основного
воздействия на объект.
Схема, изображенная на рис. 1.2, в, представляет собой
наиболее общий вид замкнутых систем. По такой схеме строят,
например, многие преобразовательные и счетно-решающие
элементы. В управлении же наиболее широко распространен
частный вид замкнутых систем, в которых коррекцию
алгоритма управления осуществляют не непосредственно по
значениям координат X, а по их отклонениям от значений,
определяемым алгоритмом функционирования Xq, г, е. Ах = Xq — х.
Схема, реализующая эту разновидность управления с
обратной связью, показана на рис. 1.2, г, в которой: элемент 1
задает алгоритм функционирования, а элемент сравнения —
сумматор 2 — осуществляет вычитание х из х^, т. е.
вырабатывает величину Ах, называемую отклонением или ошибкой
управления. Часто оказывается целесообразным
вырабатывать управляющее воздействие в функции не только Лл;, но
также его производных и интегралов по времени:
w= /( Длг.Дл:,..., J Ajcd/,... ^Ах==-Хо—х. (1.3)

Рис. 1 4
Функция / должна быть
неубывающей функцией Ахи
одного с ней знака. Относительно
других аргументов ее знак
определяется из анализа.
Управление в функции
отклонения при упомянутых
требованиях к функции / называют
регулированием. Управляющее
устройство в этом случае
называют автоматическим
регулятором. Объект 3 и регулятор 2 (см. рис. 1.2, г) образуют
замкнутую систему, называемую системой автоматического
регулирования (САР), Регулятор, вырабатывающий
управляющее воздействие и в соответствии с алгоритмом
управления (1.3), образует по отношению к выходу объекта
отрицательную связь, поскольку знак А:^, как следует из (1.3), обра-
тен знаку х. Обратную связь, образуемую регулятором,
называют главной обратной связью. Кроме нее внутри регулятора
могут быть и другие местные обратные связи.
Если регулируется несколько величин лтд, х^ посредством
нескольких управлений «i, W2>---> т. е. если х и и — векторы,
соответствующие стрелки изображают двойными линиями
(см. рис. 1.1, б). .
Пример системы автоматического регулирования
напряжения генератора постоянного тока показан на рис. 1.4. С
делителя напряжения ДН снимается напряжение kut,
пропорциональное регулируемому напряжению Оно
сравнивается с напряжением щ эталонной батареи. Разность Ал: = и^—
— KUv подается на вход усилителя У, к выходу которого
подключен якорь двигателя постоянного тока Д. Двигатель
приводит в движение регулирующий орган — реостат,
включенный в цепь обмотки возбуждения ОВ генератора. При
увеличении «г сверх заданного значения двигатель переместит
ползунок реостата так, чтобы сопротивление реостата увеличилось и
напряжение, подводимое к ОВ, уменьшилось. Следствием будет
уменьшение регулируемого напряжения.
В данной схеме мощности сигнала Ал: оказывается
недостаточно для непосредственного управления током возбуждения,
поэтому и использован усилитель У. Такие системы называют
системами непрямого регулирования. В маломощных системах
иногда можно применить прямое регулирование, управляя
исполнительным органом непосредственно от сигнала ошибки.

принцип обратной связи широко распространен не только
в технике, но и в процессах управления, осуществляемых в
^ивых организмах (системы регуляции различных функций—
температуры, ритма кровообращения и др.). В управлении
общественными организациями этот принцип реализуется в
виде проверки исполнения принятых решений и распоряжений,
играющих роль управляющих воздействий.
В ряде случаев эффективно применение комбинированного
регулирования по возмущению и отклонению (см. рис. 1.2, 5),
например компаундирование с коррекцией мощных
синхронных генераторов. Комбинированные регуляторы объединяют
достоинства обоих принципов — быстроту реакции на
изменение возмущений и точное регулирование независимо от того,
какая причина вызвала отклонение.
§ L3. Основные виды автоматического
управления
На первом этапе развития техники управления
использовался практически лишь один вид автоматического управления
— поддержание заданного постоянного значения
регулируемой величины. Долгое время под системами автоматического
регулирования понимался именно этот вид. Впоследствии
число видов увеличивалось, и вполне вероятно, что
упоминаемые ниже шесть основных их видов не исчерпывают не
только возможные виды в будущем, но и существующие сегодня.
Стабилизация. Системы поддержания постоянства
управляемой величины называют также системами стабилизации.
Желаемый закон в них имеет вид {t) = const.
Пример системы автоматической стабилизации напряжения
генератора постоянного тока был рассмотрен в § 1.2 (рис. 1.4).
Если в этой схеме изъять цепочку ДН — эталонная батарея
— У — Д, то получим систему стабилизации, действующую
по разомкнутому контуру. В ряде установок местного значения,
где не требуется высокой точности стабилизации, такие
разомкнутые схемы используют и в наши дни.
Известна важная особенность систем регулирования по
отклонению: если в них использовать регуляторы, состоящие
только из элементов, осуществляющих обычные аналитические
преобразования, т. е. обладающих аналитическими статичес-

кими характеристиками, то регулирование по отклонению
может уменьшить, но не устранить ошибку.
Рассмотрим схему с простейшими линейными
преобразовательными звеньями. Уравнения статики для такой схемы
^м. рис. 1.2, г) будут
x kf^u^ k^z; « = k^Ax = Лр (xq — jc), (1.4)
где ko, kpUkg — постоянные коэффициенты, называемые
соответственно коэффициентами передачи объекта, регулятора и
нагрузки.
Из (1.4) получаем
ко k
о
кг
I + Ajo^p " l+^o^p
т. е. значение регулируемой величины х зависит от
нагрузки 2, уменьшаясь с ее ростом.
Регулирование, в котором установившаяся ошибка при
постоянном заданном значении х^ зависит от нагрузки, назьгоа-
ют статическим. Установившаяся статическая ошибка
1
1 + ^0 ' 1 + kok-p ^ ^
Выражение это громоздко, и для оценки степени зависимости
статической ошибки от нагрузки г переходят к уравнениям,
связывающим относительные безразмерные отклонения Ф = Ад^/лгщш! ^= А^'^^ном»
где абсолютные значения Ах = х — Xmin и Дг = г — гном отнесены
к базовым значениям, соответствующим номинальной нагрузке ^ном
(рис. 1.5). Вообще статизм 6 равен относительной крутизне
регулировочной характеристики х = F (z) [илк ф = Ф (Я)1, т. е.
д=^^д(р/дК. (1.6)
Если характеристика прямолинейна, то
Афтах (Xmax-^^mln)/Xmin (-^тах—^тпш) ^
^Кпах (^ном—0)/%ом -^mln
6 =
Статический регулятор поддерживает постоянное значение
регулируемой величины с ошибкой. Статизм — это
величина относительной статической
ошибки при изменении
нагрузки от холостого хода до
номинальной. В некоторых системах
статическая ошибка
нежелательна. Тогда переходят к
регулированию, в котором она в силу
структуры системы равна нулю, рис. 1.5

т. е. к астатическому регулировав
ШШШШШШШШ^ Регулировочная характеристика
идеального астатического регулирск
z^Qf^ вания представляет собой прямую
линию, параллельную оси нагрузки
Рис. 1.6 (рис. 1.6). Вследствие неточности
регулятора регулируемая величина
может принимать любое значение внутри некоторой зоны (на
рисунке заштрихована), но ошибка при этом не будет зависеть
от нагрузки. Для получения астатического регулирования в
регуляторе нужно устранить жесткую зависимость между
положением регулирующего органа и значением регулируемой
величины, с тем чтобы одно и то же значение регулируемой
величины можно было поддерживать при любой нагрузке. Для
этого в цепь регулирования вводят астатическое звено.
Примером астатического звена является интегрирующее звено,опи-
i
сываемое уравнением и = k I Ах dt или du/dt = k Ал;.
Регулятор при этом будет находиться в равновесии только в
том случае, когда duldt == Ал: = О, т. е. когда
регулируемая величина будет равна заданному значению.
Электрический двигатель является примером астатического звена.
В схеме, изображенной на рис. 1.4, двигатель, перемещающий
ползунок реостата возбуждения, — астатическое звено, а
изображенная система есть система астатического
регулирования.
Программное управление. При программном управлении
алгоритм функционирования задан и можно построить
специальное устройство — датчик программы, — вырабатывающее
Хо (О- Таким образом, все схемы, показанные на рис. 1.2,
в которых Хо (О есть заданная функция, а звенья /
представляют собой датчики программы, вырабатывающие эту
функцию, относятся к классу систем программного управления.
Программное управление можно осуществить по любому из
фундаментальных принципов или с помощью их комбинации.
В практике используют два вида систем программного
управления: системы с временной программой и системы с
пространственной программой. В системах первого вида датчик
программы вырабатывает непосредственно функцию х^ (0-
Примерами могут служить устройства, в которых движение
часового механизма или двигателя с равномерным ходом
преобразуется с помощью функциональных преобразователей (про-

филированных кулачков, реостатов и т. п.) в движение
Хо (О- к таким устройствам относят устройства программы для
изменения температуры закалочных печей, заводные игрушки,
магнитофоны, проигрыватели и т. д. Системы второго вида
используют в программном управлении
металлообрабатывающими станками. В них движение исполнительного органа
(инструмента) осуществляется по заданной в пространстве траектории,
закон же движения по траектории во времени мало существен
и в широких пределах может быть произвольным.
Используются два способа пространственного
программного управления. Первый состоит в том, что движение по
каждой из координатных пространственных осей выполняется
отдельным приводом, движение по одной из осей задается
произвольно (обычно равномерным), а остальные движения
увязываются с первым так, чтобы инструмент двигался по
заданной траектории. Примером может служить
копировальный Т1алец Я, скользящий по шаблону 3 в системе
управления / копировальным станком 2 (рис. 1.7). Одно движение —
подача по оси х двигателем — происходит равномерно,
второе — движение по оси у — задается профилем кулачка
(шаблона 3). При обработке изделия 4 инструмент Ф станка
2 повторяет движение пальца П. Второй способ состоит в том,
что заданн ая траектория описывается с помощью системы
параметрических уравнений, в которых параметром является
время, а затем строится решающее устройство, задающее
движение приводам по отдельным осям в соответствии с
этими параметрическими уравнениями.
Системы программного управления по своей структуре
также могут быть статическими и астатическими, однако,
поскольку величины Xq (t) и z в них непостоянны, стати^1еская
ошибка не устраняется, так как возникают установившиеся
ошибки, зависящие от скорости и высших производных. Для
устранения этих составляющих
ошибки можно вводить в систему
дополнительные астатические звенья
(повышать порядок астатизма). Этот
вопрос рассматривается более
детально в § 5.2.
Следящие системы. В следящих
системах алгоритм
функционирования заранее не известен. Обычно
регулируемая величина в таких системах
должна воспроизводить изменение не- Рис. 1.7

которого внешнего фактора, следить за ним. Так,
автоматически управляемые зенитное орудие должно поворачиваться,
следя за полетом цели. Следящая система может быть
выполнена в соответствии с любым фундаментальным принципом
управления и будет отличаться от соответствующей системы
программного управления тем, что вместо датчика программы
в ней будет помещено устройство слежения за изменениями
внешнего фактора.
В качестве примера следящей системы на рис. 1.8 приведена
упрощенная схема отработки угла. Регулируемой величиной является
угол поворота Ggbix управляемого объекта 2. Приводной Двигатель 3
питается от электрбмашннного усилителя /. Входное воздействие
подается на сельсии-датчик 5 в виде угла поворота 9вх его ротора.
Соединенные по трансформаторной схеме сельсин-датчик и
сельсин-приемник 4, механически связанный с нагрузкой, вырабатывают
напряжение, пропорциональное рассогласованию 8 — бвх — ^вых между
входным и выходным валами следящей системы. Напряжение ошибки
усиливается усилителями Ух и " электромашинным усилителем У и цо-
ступает на якорь исполнительного двигателя 5, вращающего
одновременно объект (нагрузку) 2 и ротор сельсина-приемника до тех пор, пока
рассогласование не станет равным нулю.
Системы с поиском экстремума показателя качества. В
ряде процессов показатель качества или эффективности процесса
может быть выражен в каждый момент времени функцией
текущих координат системы, и управление можно считать
оптимальным, если оно обеспечивает поддержание этого
показателя в точке максимума, например настройку радиоприемника
на частоту передающей станции по наибольшей громкости
приема или по наибольшей яркости свечения индикаторной
лампы. Такое управление обладает одной нежелательной
особенностью: когда точка настройки под воздействием различных
возмущений окажется
смещенной от экстремума,
неизвестно, в каком направлении
следует воздействовать на
регулирующий орган, чтобы
вернуть ее к экстремуму.
Поэтому экстремальное
управление начинают с поиска:
сначала выполняют
небольшие пробные движения в
каком-то выбранном
направлении, затем анализируют ре-
Рис. 1.8 акцию системы на эти пробы
^2
7
J.

и,
РО
ВУ
Т
У1У
г
тэ
Рис. 1.9
и после этого по
результатам анализа вырабатывают
управляющее воздействие
в виде импульса,
приближающего систему к
экстремуму.
Первые упоминания в
литературе об
экстремальных регуляторах
содержатся, по-видимому, в
статье М. Леблана (1922),
где описан регулятор для колебательного контура
электропоезда, и в 1926 г, в книге Т. Штейна, где высказывалась идея
регулирования топки парового котла по минимуму потерь в
дымовой трубе. Далее предложения экстремальных
регуляторов давались и исследовались Ю. С. Хлебце^ичем (1940) и
В. В. Казакевичем (1943). Широкую же известность в
мировой литературе принцип экстремального регулирования
приобретает в 50-х ходах после ъыхода в свет статей Дрейпера, Ли
и других и книги Цян Сюэсеня (1954).
На рис. 1.9 приведена функциональная схема
экстремального регулирования с поиском.
Измерительно-преобразующий элемент ИПЭ, измеряющий координаты процесса и
вычисляющий показатель качества J = Fi {х^, х^,,,., Хп),
подключен к выходу объекта О. Устройство пробных воздействий
У ив генерирует пробные воздействия v^, и^,..., на систему
регулирующих органов РО. Логическое устройство ЛУ,
получая информацию как о введенных пробных воздействиях,
так и об изменении J под их влиянием, анализирует
полученные данные и результат сообщает вычислительному
устройству ВУ, которое вырабатывает управляющие воздействия Uu
«2,....
Для поиска экстремума необходим чувствительный элемент,
обнаруживающий экстремум. Один из способов обнаружения
экстремума функции одной переменной у = f (х) состоит в
измерении производной dyldXi, Необходимые и достаточные
условия экстремума выражены соотношениями:
dyldx = 0; d^y/dx^ < О для максимума;
dy/dx = 0; d^y/dx^ > О для минимума.
Для измерения dy/dx используют или измерения в
достаточно близких смежных точках разностей Дл: = л:^ — х^ и ==
^ У2 ~ Ух и вычисления их отношения Kylt^x » dyldXy
или же другие методы, например известный из радиотехники

метод синхронного детектирования. Ьместо трудно
реализуемого технического измерения второй производной чаще всего
делают проверку знака величины Ау в окрестности
предполагаемого экстремума: у должно быть положительным в
окрестности минимума и отрицательным в окрестности
максимума. Однако одиночной проверкой можно пользоваться лишь в
том случае, если известно, что экстремум существует, что он
единственный и что в рабочей области нет точек перегиба
функции. Если одно из этих условий не выполняется, поиск
усложняется. Так, если отсутствие точек перегиба не
гарантировано, то в случае функции одной переменной надо проверить
значения по обе стороны предполагаемого экстремума. В
случае функции многих переменных используют
вычислительные устройства поиска, основывающиеся на математических
итерационных методах решения экстремальных задач:
Гаусса—Зайделя, градиента, наискорейшего спуска и т. п.
Прямой метод измерения dyldx часто трудно реализуем,
поэтому используют и другие методы обнаружения экстремума:
релейные и шаговые схемы с логическими элементами для
анализа знаков, способы «запоминания экстремума», точнее—
наибольшего (или наименьшего) из ряда наблюдений в
процессе поиска значений, и с ним сравниваются последующие.
Подробнее экстремальные (самонастраивающиеся) системы
рассмотрены в гл. 10.
Если в рабочей области системы существует несколько
локальных экстремумов, то упомянутые методы позволяют
обнаружить лишь один из локальных экстремумов, именно тот,
в окрестности которого оказалась исходная точка поиска. Для
нахождения глобального экстремума, если априорной
информации об его окрестности нет, приходится просматривать
всю рабочую область, выявляя все локальные экстремумы и
сравнивая их между собой. Поскольку в системах
экстремального управления измеряется значение управляемой величины,
они относятся к классу систем управления по замкнутому
контуру.
Оптимальное управление. Оптимальное управление в
последние годы начали применять как в технических системах
для повышения эффективности производственных процессов,
так и в системах организационного управления для
совершенствования деятельности предприятий, организаций,
отраслей народного хозяйства.
В организационных системах обычно интересуются
конечным, установившимся результатом команды, не исследуя эф-

ВМ
'Ах to
фективность во время переходного
процесса между отдачей команды и
получением окончательного результата.
Объясняется это тем, что обычно в таких
системах потери в переходном процессе
достаточно малы и влияют несуществен-
йо на общую величину выигрыша в
установившемся режиме, поскольку сам
установившийся режим значительно более "
длителен, чем переходный процесс. Но
иногда динамика не исследуется из-за математических
трудностей. Методам оптимизации конечных состояний в
организационных и экономических системах посвящены курсы
методов. оптимизации и исследования операций.
В управлении динамическими техническими системами
оптимизация часто существенна именно для переходных
процессов, в которых показатель эффективности зависит не
только от текущих значений координат (как в экстремальном
управлении), но и от характера изменения в прошлом, настоящем
и будущем, и выражается некоторым функционалом от
координат, их производных и, может быть, времени.
В качестве примера можно привести управление бегом
спортсмена на дистанции. Так как его запас энергии ограничен
физиологическими факторами, а расходование запаса зависит от характера бега,
спортсмен уже ие может в каждый момент отдавать максимум
возможной мощности, чтобы не израсходовать запас энергии преждевременно
н ие выдохнуться иа дистанции, а должен искать оптимальный для
своих особенностей режим бега.
Нахождение оптимального управления в подобных
динамических задачах требует решения в процессе управления
достаточно сложной математической задачи методами
вариационного исчисления или математического программирования в
зависимости от вида математического описания
(математической модели) системы. Таким образом, органической
составной частью системы оптимального управления становится
счетно-решающее устройство или вычислительная машина.
Принцип поясняется на рис. 1.10. На вход вычислительного
устройства (машины) ВМ поступает информация о текущих
значениях координат х с выхода объекта О, об управлениях и
с его входа, о внешних воздействиях z на объект, а также
задание извне различных условий: значение критерия
оптимальности граничных условий х (0), х (оо ), информация о
допустимых значениях лг^ХимСиит. п. Вычислительное

устройство по заложенной в него программе вычисляет
оптимальное управление и. Оптимальные системы могут быть как
разомкнутыми, так и замкнутыми.
Адаптивные системы. В реальных условиях внешние
возмущения иногда приводят к изменению не только координат,
но и параметров системы (коэффициентов уравнений), причем
в таких системах, как баллистические ракеты, изменения
параметров существенны. Изменения параметров, вышедшие
за определенные границы, приводят не только к
количественным ошибкам или к ухудшению других показателей качества
системы, но зачастую и к полной потере ее работоспособности.
Эти потери качества часто невозможно устранить, находясь
в рамках первоначально принятого фундаментального
принципа управления, это можно сделать лишь путем изменения
параметров (а иногда и структуры) системы так, чтобы приблизить
математическое описание претерпевшей изменения системы к
ее исходной модели настолько, чтобы сохранить
работоспособность первоначально принятого фундаментального
принципа управления.
Системы, автоматически изменяющие значение своих
параметров или структур при непредвиденных изменениях
внешних условий на основании анализа состояния или поведения
системы так, чтобы сохранялось заданное качество ее работы,
называют адаптивными системами (от лат. adaptio —
приспособление). Термин заимствован из биологии, где
адаптацией называют приспособление организма к изменяющейся среде
с целью сохранения жизнедеятельности. Но в теории
управления (так как любая автоматическая система в каком-то смысле
приспосабливается к изменениям среды) понятие адаптации
умышленно сужено: к ней относят лишь такие виды
приспособления, которые осуществляются путем изменения
управляющим устройством параметров или структуры системы
по данным анализа ее работы.
Адаптивные системы с изменением значений параметров
иногда называют самонастраивающимися, а системы с
изменением структуры и алгоритма управления —
самоорганизующимися.
Обычно адаптивная система содержит в качестве «ядра»
схему, реализующую один из фундаментальных принципов
управления, а контур адаптации пристраивают к ней как
вторичный, осуществляющий коррекцию параметров. Контур
адаптации, обычно состоящий из устройства измерения ИУ,
вычисления ВУ и управления УУ, может быть разомкнут

а)
ИУ
ВУ
УУ
6НП
и
-0-
б)
ИУ
ВУ
УУ
бНП
V
(рис. 1.11, (2). если
на его вход подается
только входное
воздействие, ' или
замкнут (рис. 1.11, б),
если он реагирует
также и на выход
системы. Контур
самонастройки
воздействует на блок
настройки параметров
БНП, который может
быть включен не
только
последовательно, как
показано на рисунке, но
и любым другим способом, например в цепь обратной связи.
Вычисление воздействий для коррекции параметров —
весьма сложная математическая задача, поэтому в составе
адаптивных систем используют различные моделирующие,
счетно-решающие устройства и даже вычислительные машины.
Способы адаптации и соответствующие им схемы различаются
главным образом алгоритмами и реализующими их
программами ЭВМ, Более детальное описание адаптивных систем
приводится в гл. 10.
Рис. 1.11
§ 1.4. Об основных законах регулирования
Законом регулирования называют математическую
зависимость, в соответствии с которой управляющее воздействие на
объект вырабатывалось бы безынерционным управляющим
устройством.
В технике используют довольно много различных законов
регулирования, которые тесно связаны с конструкцией
управляющего устройства, и одним из распространенных видов
классификации регуляторов является классификация по законам
управления.
Многие из законов регулирования, реализуемых
различными регуляторами релейного, импульсного действия,
экстремальными ит. п., рассматриваются далее в процессе
изложения теории. Здесь ограничимся упоминанием о наиболее рас-

пространенных законах, реализуемых линейными
регуляторами по отклонению непрерывного действия. В этих
простейших законах управляющее воздействие линейно зависит от
отклонения, его интеграла и первой производной по
времени. При описании законов наиболее удобно использовать
безразмерные относительные переменные е = ^х/х^. [i — u/uq,
где Xq и Ufj — базовые значения (например, соответствующие
номинальному режиму объекта).
Пропорциональный закон (обозначаемый П): (х = k^e.
Регулятор, осуществляющий этот закон, называют
пропорциональным. Постоянную fep называют коэффициентом
передачи (усиления) регулятора, обратную величину — статизмом
регулятора. С возрастанием статизма регулятора возрастает и
статизм регулирования. Интегральный закон (И):
[Х-: — fed/ или dp,/d/ = 6/r.
о
Постоянная Т имеет размерность времени, и ее называют
постоянной времени интегрирования. Интегральный
регулятор — астатический, и именно с его помощью осуществляется
рассмотренная выше простейшая схема астатического регу-
-лирования. Пропорционально-интегральный закон (ПИ):
11 =
Иногда его называют пропорциональным законом с
интегральной коррекцией. Регулятор ПИ также обеспечивает
астатическое регулирование. В этом можно убедиться, представив
уравнение в виде d\i/dt = kp (de/dt + е/Г).
В состоянии равновесия при постоянных воздействиях
должно быть d[i/dt = (); de/dt == О, откуда равновесие может
иметь место лишь при е = 0. Пропорционально-интегрально-
дифференциальный закон (ПИД):
Постоянные и Тд соответственно называют
постоянными времени интегрирования и дифференцирования. Регулятор
ПИД так же обеспечивает астатическое регулирование.
Производную dddt вводят в закон регулирования для повышения
качества процесса регулирования.

^1 у
МАТЕМАТИЧЕСКОЕ
ОПИСАНИЕ
АВТОМАТИЧЕСКИХ
СИСТЕМ УПРАВЛЕНИЯ
§ 2.1. Уравнения динамики и статики.
Линеаризация
На определенном этапе разработки
и исследования автоматической
системы управления получают ее
математическое описание — описание процессов,
проистекающих в системе, на языке
математики. Математическое описание
может быть аналитическим (с помощью
уравнений), графическим (с помощью
графиков, структурных схем и графов) и
табличным (с помощью таблиц).
Для получения математического
описания системы обычно составляют
описание ее отдельных элементов. В
частности, для получения уравнений систе-
мы составляют уравнения для каждого
входящего в нее элемента. Совокупность
всех уравнений элементов и дает
уравнения системы.
Уравнения (а также структурные
схемы) автоматической системы
управления называют ее математической
моделью. Такое название обусловлено тем,
что при математическом описании
(составлении уравнений) физических
процессов всегда делают какие-либо
допущения и приближения. Математическая
модель одной и той же системы в
зависимости от цели исследования может
быть разной. Более того, инсн^да
полезно при решении одной и той же задачи
на разных этапах принимать разную
математическую модель: начать
исследование с простейшей модели, а затем ее по-

и
у
степенно усложнять, с тем чтобы учесть
дополнительные явления и связи,
которые на начальном этапе были отброшены
как несущественные. Сказанное
обусловливается тем, что к математической
модели предъявляются противоречивые тре-
Рис. 2.1 бования: она должна, с одной стороны,
как можно полнее отражать свойства
оригинала, а с другой стороны, быть по возможности простой,
чтобы не усложнять исследование.
Система управления и любой ее элемент производят
преобразование входного сигнала х (t) в выходной сигнал у (t).
С математической точки зрения они осуществляют отображение
у (О - Ах (О,
согласно которому каждому эле]у1енту х (/) из множества X
входных сигналов (х (/) g X) ставится в соответствие
единственный, вполне определенный элемент у {t) из множества Y
выходных сигналов [у {t) g Yl. В приведенном соотношении А
называется оператором. Оператор, определяющий
соответствие между входным и выходным сигналами системы
управления (элемента), называется оператором этой системы
(элемента). Задать оператор системы — это значит задать правило
определения выходного сигнала этой системы по ее входному
сигналу.
Рассмотрим математическое описание непрерывных систем
управления с помощью дифференциальных уравнений. В
большинстве случаев звенья и системы описываются нелинейными
дифференциальными уравнениями произвольного порядка.
Здесь под звеном понимается математическая модель
элемента. Для примера рассмотрим звено (рис. 2.1), которое можно
описать дифференциальным уравнением второго порядка
F(i/,i/,i/'.w,ei) + /-0, (2.1)
где у — выходная величина; « и / — входные величины; у
и и — первые производные по времени; у — вторая
производная по времени.
Уравнение (2.1), описывающее процессы в звене при
произвольных входных воздействиях, называют уравнением
динамики. Пусть при постоянных входных величинах и ^ и^
и / = /® процесс в звене с течением времени установится:

выходная величина примет постоянное значение у У^.
Тогда (2.1) примет вид
F - 0,0. и\ 0) + Р - 0. (2.2)
Это уравнение описывает статический или установившийся
режим и его называют уравнением статики.
Статический режим можно описать графически с помощью
статических характеристик. Статической характеристикой
звена или элемента (а также системы) называют зависимость
выходной величины от входной в статическом режиме.
Статическую характеристику можно построить экспериментально,
подавая на вход Элемента постоянное воздействие и измеряя
выходную величину после окончания переходного процесса,
или расчетным путем, используя уравнение статики.
Если звено имеет несколько входов, то оно описывается с
помощью семейства или семейств статических характеристик.
Например, звено, характеризукщееся в статическом режиме
уравнением (2.2), можно описать графически с помощью
семейства статических характеристик, представляющих собой
кривые зависимости выходной величины у от одной входной
величины и (или /) при различных фиксированных значениях
другой — / (или и).
Линеаризация. Обычно автоматические системы
описывают нелинейными дифференциальными уравнениями. Но во
многих случаях можно их линеаризовать, т. е. заменить
исходные нелинейные уравнения линейными, приближенно
описывающими процессы в системе. Процесс преобразования
нелинейных уравнении в линейные называют линеаризацией.
В атоматических системах должен поддерживаться
некоторый заданный режим. При этом режиме входные и выходные
величины звеньев системы изменяются по определенному
закону. В частности, в системах стабилизации они принимают
определенные постоянньш значения. Но из-за различных
возмущающих факторов фактический режим отличается от
требуемого (заданного), поэтому текущие значения входных и
выходных величин не равны значениям, соответствукмдим
заданному режиму. В нормально функционирукндей автоматической
системе фактический режим немного отличается от требуемого
режима и отклонения входных и выходных величин входящих
в нее звеньев от требуемых значений малы. Это позволяет
произвести линеаризацию, разлагая нелинейные функции,
входящие в уравнения, в ряд Тейлора. Линеаризацию можно
производить по звеньям.

Пример 2.1. Проиллюстрируем изложенное на примере звена,
описываемого уравнением (2.1). Пусть заданному режиму
соответствуют
и^и*\ « = «*; у^у*; у = у*\ у=у*. (2.3)
Обозначим отклонения реальных значений и, f к у от требуемых
через Ли, А/ и Аг/, т. е. Аи = и — и*, = f ^ f*^ ^ у ^ у*.
Тогда и и* + Аи; li ~ и* + Аи; / = /* + А/; «/ = i/* + Ai/; у =
= у* + J\y; у = у* + ^'у- Подставим эти выражения в (2.1) и,
рассматривая F как функцию от независимых переменных и, и, у, у и у\
разложим ее в ряд Тейлора в точке (2.3) и отбросим малые члены
более высокого порядка, чем отклонения. Тогда (2Л) примет вид
F* + (dFldyr Ai/+ {dFldgr ^y+ldF/ду)* AiJ^ (dF/ди)* ^u +
-\-(dF/du)* Аи+/* + А/ = 0. (2.4)
Здесь звездочка сверху обозначает, что соответствующие
функции и производные вычисляются при значениях аргумента,
определяемых соотношениями (2.3). Когда в системе устанавливается заданный
режим, уравнение (2.1) принимает вид + /* = 0. Вычтя это ураВ'
ние из (2.4), получим искомое уравнение звена в отклонениях:
Оо A^'+fli ^y-\-a2 tsxj—bQ tiu--b^ ^u-^Cq A/ = 0, (2.5)
тде ao=(dF/dy)*; a^ = {dF/dy)*\ a^^^idF/dy)*]
bo= —(dF/du)*\ 6i= — (af/au)*; Co-=—I.
Если время / явно не входит в исходное уравнение (2.1) и, кроме
того, заданный режим является статическим— величины у* ^ и* и /*
ие зависят от времени, то коэффициенты линеаризованного уравнения
(2.5) являются постоянными.
Звенья и системы, которые описываются линейными
уравнениями, называют соответственно линейными звеньями и
линейными системами.
Уравнение (2.5) было получено при следующих
предположениях: 1) отклонения выходной Ау и входной Аи величин
достаточно малы; 2) функция F обладает непрерывными
частными производными по всем своим аргументам в окрестности
точек, соответствующих заданному режиму. Если хотя бы одно
из этих условий не выполняется, то линеаризацию
производить нельзя. По поводу первого условия необходимо отметить
следующее: нельзя раз и навсегда установить, какие
отклонения считать малыми. Это зависит от вида нелинейности.
Часто нелинейную зависимость между отдельными
переменными, входящими в уравнение звена, задают в виде
кривой. В этих случаях линеаризацию можно произвести
графически.

Рис. 2.2
Геометрически линеаризация
нелинейной зависимости между
двумя переменными (рис. 2.2)
означает замену исходной кривой АВ
отрезком ее касательной А'В' в
точке 0\ соответствующей
заданному режиму, и параллельный
перенос начала координат в эту
точку.
В зависимости от того,
входит или нет время явно в
уравнение, системы разделяют на
стационарные и нестационарные.
Автоматические системы управления (звенья) называют
стационарными, если они при постоянных внешних
воздействиях описываются уравнениями, не зависящими явно от
времени. Это означает, что свойства системы со временем не
изменяются. В противном случае система называется
нестационарной. Для линейных систем можно дать также следующее
определение: стационарными линейными системами (звеньями)
называют системы (звенья), которые описываются линейными
уравнениями с постоянными коэффициентами;
нестационарными линейными системами (звеньями) или системами с
переменными параметрами — системы (звейья), которые
описываются линейными уравнениями с переменными
коэффициентами.
§ 2.2. Основные свойства преобразования Лапласа
В этом параграфе даны основные сведения о
преобразовании Лапласа, которые будут использованы при рассмотрении
систем, описываемых линейными дифференциальными
уравнениями.
Преобразованием Лапласа называют соотношение
I
ставящее функции х {t) вещественного переменного в
соответствие функцию X (s) комплексного переменного s (s == а-Ь
+/0)). При этом X (О называют оригиналом,, а X (s) — изобра-

жением или изображением по Лапласу, То, что л: (t) имеет
своим изображением X (s) или оригиналом X (s) является х (О,
записывается так:
х{1)ФХ (s) или X{s)= X (ty
Иногда также пользуются символической записью
X{s)^L{x (0},
где L — оператор Лапласа.
Предполагается, что функция х (/), которая подвергается
преобразованию Лапласа, обладает следующими свойствами:
X (О определена и кусочно-дифференцируема на всей
положительной числовой полуоси [о, оо]; х {t) =0 при / < 0;
существуют такие положительные числа VW и с, что \х {t)\ ^ Же^'
при О ^ -< оо. Функции, обладающис указанными тремя
свойствами, часто называют функциями-оригиналами.
Соотношение
Cq—JOO
определяющее по известному изображению его оригинал (в
точках непрерывности последнего), называют обратным
преобразованием Лапласа, В нем интеграл берется вдоль любой
прямой Res ~ Gq> с. Символически обратное преобразование
Лапласа можно записать так:
x(t)^L-^ {X(s)},
где символ — обратный оператор Лапласа.
Остановимся на основных свойствах преобразования
Лапласа.
1. Свойство линейности. Для любых постоянных аир
L {ахх (t) + (0} = ccL {Хх т + PL {х^ (t)}.
2. Дифференцирование оригинала. Если производная х (t)
является функцией-оригиналом, т. е. обладает указанными
выше тремя свойствами, то L {х (t)} == sX (s) — л: (0), где
in)
X{s) = L {x (t)}, x(0) = lim x (t). Если п-я производная x (i)
является функцией-оригиналом, то
(in) \ , (n-l)
L\x{t)]^s'^Xis) —s^-> X(0) —s^-^x(0)—...—x (0),
(ft) (ft)
где x{0) ^limx (/). Л = 0,1,...,п —1.

Если начальные условия нулевые, т. е. л: (0) = л: (0)
, . . = х (0) = О, то последняя формула принимает
вид L {х (t)} = 5" X (s). Таким образом, при нулевых
начальных условиях дифференцированию оригинала
соответствует умножение изображения на s.
3. Интегрирование оригинала. Интегрирование оригинала
сводится к делению изображения на s:
о )
4. Теорема запаздывания. Для любого положительного
числа т
L {х (t—x)} = е-«^ L {х (/)} ^ е-^Х (S).
5. Теорема о свертке (теорема умножения изображений).
Если Хх (t) и Xz (t) — оригиналы, а (s) и Х^ (s) — их
изображения, то
f t
Xi(s)• Ха(s) =i= ^ Xi(i:)x2{t—r)dT== ^ x^ir) Xi{t—x) dr.
Интеграл правой части равенства называют сверткой
функций Xi (t) и Xz (t) и обозначают х^ (t) * (t):
t i
xx (0 * Xz (t) = j (t) x^ (t -T) dx... J xz (t) x^ {t -x)dx.
6. Теоремы о предельных значениях. Если х (t) —
оригинал, а X (s) — его изображение, то х (0) = lim sX (s) и при
существовании предела л: (оо) = Ит х (t)
л: (со) lim sX(s),
^' 1. Теорема разложения. Если функция X (s) = Л (s)/5 (s)
дробно-рациональна, причем степень полинома числителя
меньше степени полинома знаменателя, то ее оригиналом
является умноженная на 1 {t) функция
("к-1)1 s-'ftds"ft-'

где — корни уравнения В (s) = О, а п^^ — их кратности
и / — число различных корней. Если все корни уравнения про-
ешб, то эта формула разложения принимает вид
где п — степень полинома B(s), В' (s^ = ~ .
CiS я
Пример 2.2. Пусть изображение
X (s) = 4 (s -Ь \)/ls (S + 2П
Согласно принятому обозначению,
А (s) = 4 ($ Ч- 1); В (s) = s (s + 2)2; В' (s) 3s« + 8s + 4.
Функция X is) имеет полюсы (корни уравнения В {$) = о] =
= О, «2 = —2. Полюс sj является простым, а полюс sg — кратным, имея
кратность Л2 = 2. Простому полюсу % соответстнует слагаемое
кратному полюсу — слагаемое
' », "т -77-7l^(»)(«-«8)"'e"J='
(па—1)1 e^s, ds'**~'
= lltn 4-
s^_2 as
Поэтому x (<) = 1 + (2<— 1) e
-2/
= (2^-l)e--2<
§ 2.3. Формы записи линейных диффенциальных
уравнений. Передаточные функции
При описании автоматических систем управления широко
используют символическую форму записи линейных
дифференциальных уравнений. Рассмотрим ее на примере уравнения
(2.5). Перепишем его, опустив для сокращения записи знак
Д и оставив в левой части только члены, содержащие
выходную переменную и ее производные:
Uo'y + ai'y + a^y^bou + b^u + Cof. (2,6)

Введем для операции дифференцирования обозначение
т. е.
dldt^p\ d4dt'=p^.
Используя его, уравнение (2.6) можно записать в виде
+ ОгРУ + а^У = Ьфи + Ь^и + cj. (2.7)
При записи и преобразовании дифференциальных уравне
НИИ оператор (операцию дифференцирования) р можно
рассматривать как алгебраический сомножитель, а выражение
ру^ как произведение, не обладающее свойством
коммутативности: нельзя вместо ру писать ур. Учитывая это замечание,
перепишем (2.7), вынеся у ииза скобки:
{аор^ + агр + а^)у = фоР + bj) и + cj. (2.8)
Введем обозначения Q (р) = а^р^ + + Cg, Ri (р)
=feoP + ^2 (р) ^0- С помощью 0ТИХ обозначений
уравнение (2.8) можно записать в более компактной форме: •
Q{p)y = Ri{p)u + R,ip)f. (2.9)
В уравнении (2.9) Q (р) (дифференциальный оператор при
выходной величине) называют собственным оператором^ а
Riip) и /?2 (р) (дифференциальные операторы при
входных величинах) — опера/порами воздействия.
Передаточные функции. Отношение оператора
воздействия к собственному оператору называют передаточной
функцией или передаточной функцией в операторной форме.
Звено, описываемое уравнением (2.6) или, что то же самое,
уравнениями (2.7) — (2.9), можно характеризовать двумя
передаточными функциями: передаточной функцией Wi (р) по
входной величине и, т. е.
tt^i (Р) = Ri (pVQ (р) = {Кр + ^i)/(t3^o/+
+ «iP + «2). (2.10)
и передаточной функцией 1^2 (р) по входной величине /, т.е.
«^2 (Р) = R2 iPVQ (р) = Со/{а,р^ + а,р + а^). (2.П)
Используя передаточные функции, уравнение (2.6)
записывают в виде
y-W^{p)u + W,{p)f. (2.12)
Это уравнение представляет собой условную,более
компактную форму записи исходного уравнения (2.6). Уравнения (2.8),

(2.9) и (2.12) называют уравнениями в символической или
операторной форме записи.
Наряду с передаточной функцией в операторной форме
широко используют передаточную функцию в форме
изображений Лапласа.
Передаточной функцией или передаточной функцией в
форме изображений Лапласа называют отношение изображения
выходной величины к изображению входной величины при
нулевых начальных условиях. Если звено (система) имеет
несколько входов, то при определении передаточной функции
относительно какой-либо одной входной величины
остальные величины полагают равными нулю.
Пример 2.3. Найдем передаточные функции в форме изображений
Лапласа для звена, описываемого уравнением (2.6).
Перейдем в обеих частях этого уравнения к изображениям Лапласа:
Используя свойства линейности и дифференцирования оригинала
(Ье и 2-е свойства преобразования Лапласа), при нулевых начальных
условиях получим
(aos2 + ajs + а^) Y (s) = {b^s + b^) V (s) -f- c^F (5), (2.13)
где К (s) - L[y (0}; V (s) ^ L [u (/)}; F (s) = L {/ (0).
Полагая последователь ног f (s) = О и t/ (s) = О и определяя
каждый раз отношение выходной величины к входной, получим
»r.(s,=-|i^=.-—-. (2.14)
r (S) GoS +aiS+02
Сравнивая выражения (2.10), (2.11) и (2.14), нетрудно
заметить, что передаточные функции в форме изображений
Лапласа и в операторной форме с точностью до обозначений
совпадают.
Передаточную функцию в форме изображения Лапласа
можно получить из передаточной функции в операторной
форме, если в последней сделать подстановку р = s. В общем
случае это следует из того, что дифференцированию оригинала—
символическому умножению оригинала на р — при
нулевых начальных условиях соответствует умножение
изображения на комплексное число s.
Сходство между передаточными функциями в форме
изображения Лапласа и в операторной форме чисто внешнее. Оно
имеет место только в случае стационарных звеньев (систем).

Если звено является нестационарным, т. е. коэдхрициенты в
(2.6) зависят от времени, формула (2.14) неверна.
Используя передаточные функции (2.14), уравнение (2.13)
в изображениях Лапласа можно записать
Y (s) = Wx (s) и (s) + (s) F{s). (2.15)
Это уравнение, как и уравнение (2.13), адекватно исходному
дифференциальному уравнению (2.6) только при нулевых
начальных условиях. Если начальные условия не равны нулю,
то уравнениями (2.13) и (2.15) как математическими
описаниями исходного звена пользоваться нельзя.
Передаточные функции системы наряду с
дифференциальными уравнениями широко используются для описания систем
автоматического управления (САУ). Но при ненулевых
начальных условиях они не всегда являются их
исчерпывающими характеристиками. Если собственный оператор и оператор
воздействия системы имеют общие множители (нули)^ то они
при вычислении передаточной функции сокращаются. И в этом
случае по передаточной функции системы нельзя
восстановить ее дифференциальное уравнение и получить описание
процессов в ней при произвольных начальных условиях.
Рассмотрим для примера системы, которые описываются
уравнениями X — X = g ^ g\ X + X = g. Им соответствует передаточная функ
ции U7 (р) = + 1). Их решениями при g — i являются
соответственно X (t) = Cie-' + С^ё + t — I; х (t) =^ Се-' + ^ — 1- Эти
решения совпадают только при нулевых начальных условиях. При других
начальных условиях они не совпадают и передаточная функции
W (р) — 1/{р 4-1) не может служить описанием системы,
определяемой первым из приведенных дифференциальных уравнений.
Стандартная форма записи линейных дифференциальных
уравнений. Обычно линейные дифференциальные уравнения
с постоянными коэффициентами не выше второго порядка
записывают в стандартной форме. При этом члены, содержащие
выходную величину и ее производные, записывают в левой
части уравнения, а все остальные члены — в правой;
коэффициент при выходной величине делают равным единице. Если в
правой части содержатся производные, то члены, содержащие
какую-либо одну входную величину и ее производные,
объединяют в одну группу и коэффицент при соответствующей
входной величине выносят за скобки.
Уравнение (2.6) в стандартной форме принимает вид
Т1У + ТгУ+у==кг(Т^й+и) + к2!. (2.16)

где Tl = а^/а^; = а^/а^; К = hla<^, = bjb^,
В уравнении (2.16) постоянные и имеют
размерность времени и их называют постоянными времени, а
коэффициенты А, и ^2 — передаточными коэффициентами. Если
исходное уравнение (2.6) не содержит у («2 = 0), то в
стандартной форме коэффици^ент при производной у должен быть равен
единице: обе части уравнения делят на коэффициент с^.
В символической форме уравнение (2.16) принимает вид
(Пр^+Т^Р+\)у ^kAT^P +\) u + k^l
Напомним, что это уравнение представляет собой
условную запись уравнения (2.16).
§ 2.4. Частотные характеристики
Важное значение при описании линейных стационарных
систем (звеньев) имеют частотные характеристики. Они
получаются при рассмотрении вынужденных движений системы
(звена) при подаче на ее вход гармонического воздействия.
Для линейных систем справедлив принцип суперпозиции,
который можно сформулировать следукмцим образом:
реакция системы на несколько одновременно действующих входных
воздействий равна сумме реакций на каждое воздействие в
отдельности. Это позволяет ограничиться изучением систем
только с одним входом. В общем случае уравнение линейной
стационарной системы с одним входом можно записать так: .
+ ...+6m)". (2.17)
Ее передаточная функция по определению
г = + . (2.18)
Функцию W 0"й)). которую получают из передаточной
функции (2.18) при подстановке в нее р = /ю:
W (/ю) = <^<^)'"+^1 (/«Д)"*"' + • ■ • +<'т ^ ^2.19)

называют частотной перебаточной функцией, частотная
передаточная функция является комплекснозначной функцией от
действительной переменной о, которая называется частотной.
Функцию W можно представить в виде
W (т) = {/ (о) + jV И = А (о)) e/v«^), (2.20)
где
А (О)) - Vy^H + V^((o\
<p(o)) = argir(/o)).
Если \HTgW(j(o)\^n/2, то
(2.21)
(2.22)
На комплексной плоскости (рис. 2.3) частотная
передаточная функция W (/о) определяет вектор ОС, длина которого
равна А (о), а аргумент (угол, образованный этим вектором с
действительной положительной полуосью) — ф (со). Кривую,
которую описывает конец этого вектора при изменении
частоты от О до оо (иногда от — оо до оо), называют амплитудно-
фазовой частотной характеристикой (АФЧХ).
Частотную передаточную функцию будем называть также
амплитудно-фазовой частотной функцией. Ее действительную
часть и (fi)) = Re И?" (/со) и мнимую часть V (со) = lmW (/со)
будем называть соответственно вещественной и мнимой
частотной функцией. График вещественной частотной функции
[кривая зависимости U = U (со)] называют вещественной
частотной характеристикой, а график мнимой частотной функции—
мнимой частотной
характеристикой.
Модуль А (со) = \W (/со) I
называют амплитудной
частотной функцией, ее
график — амплитудной
частотной характеристикой.
Аргумент ф (co)==arg W (/со)
называют фазовой частотной
функцией, ее график —
фазовой частотной
характеристикой.
Кроме перечисленных
частотных характеристик ис- Рис. 2.3
JV

пользуют еще логарифмические частотные характеристики
(ЛЧХ) — логарифмические амплитудные частотные
характеристики (ЛАЧХ) и логарифмические фазовые частотные
характеристики (ЛФЧХ). Назовем функцию
L (о>) = 20 Ig Л (о) = 20 lg\W
логарифмической амплитудной частотной функцией. График
зависимости логарифмической амплитудной частотной функции
L ((о) от логарифма частоты (Igfo) называют логарифмической
амплитудной частотной характеристикой (ЛАЧХ). При
построении ЛАЧХ по оси абсцисс откладывают частоту в
логарифмическом масштабе: на отметке, соответствующей значению
Igco, пишут само значение со, а не значение Igo, а по оси
ординат — L (о). Логарифмической фазовой частотной характе-
ристикой (ЛФЧХ) называют график зависимости фазовой
частотной функции ф (о) от логарифма частоты Ig При его
построении по оси абсцисс, как и при построении ЛАЧХ, на
отметке, соответствующей значению Igo, пишут значение
Единицей L (о)) является децибел, а единицей логарифма
частоты в ЛЧХ—декада. Декадой назьгоают интервал, на
котором частота изменяется в 10 раз. При изменении частоты
в 10 раз говорят, что она изменилась на одну декаду.
Ось ординат при построении ЛЧХ проводят через
произвольную точку, а не через точку ю == 0. Частоте ел = О
соответствует бесконечно удаленная точка: Ig (а-^ — оо при ю ->0.
Рассмотрим, какой физический смысл имеют частотные
характеристики и как можно построить их экспериментально.
Найдем математическое описание вынужденного движения
системы при подаче на ее вход гармонического воздействия,
например
W = cos (ot. (2.23)
Для этого решим уравнение (2.17), подставив в правую
часть выражение (2.23). Общее решение имеет вид
У it) =yc(t) + yAf)^ (2-24)
где у^ — общее решение однородного уравнения, sl Ув —
частное решение неоднородного уравнения.
Составляющая Ус {t) определяет свободные движения
(переходный процесс). В устойчивых системах она со временем
запухает: ус (t) ->-0 при t -^оо. Вынужденное движение
описывается частным решением Ув (О- Чтобы найти его, предста-

вим входное воздействие (2.23) с помощью формулы Эйлера в
виде суммы:
где
= !f2i e/^^ «2 — е-'"'. (2.25)
2 2
Используя принцип суперпозиции, решение уравнения (2.17)
можно также представить в виде суммы у = Уг + Уг. где Ух —
решение при и === щ, гу<^ — решение йри и- = и^- Иайдем
отдельно каждое из этих решений. Подставим выражение для
Ui в правую часть уравнения (2.17) вместо и. Так как
pux = ^ ре/^' = ^ (/<о) е/*^' = (/со) Wj,
2 2
(2.26)
F^Ui = P {pui) = р (/юы,) = (/©)« Ml,...,
Р"" «1 =(/»)'" «1.
уравнение (2.17) примет вид
(flo P" + aiP^^-^+... + 0„) й + I^'O (/со)'» + Ь, (/ш)'"-' +
+ ... + 6J«i. (2.27)
Частное решение последнего уравнения будем искать'
в виде
1/1 = Л1Ы1 = л!^е/«^', (2.28)
где А не зависит от времени. При подстановке этого
выражения в (2.27) получим
Iflo (/«)" + fli (/«)"-' + ... + а„1 «1 = [Ьо (/о))'" +
+ 6l(/(0)'»-' + ... + 6„ltti,
откуда
^ _ fco (/«>)'" +^1 (/«>)'""' + .. ■ +frm
* со (/<в)"+в1 (/«»)"-' + • "+01. "
Очевидно, это выражение совпадает с частотной
передаточной функцией (2.19) рассматриваемой системы:

Подставив это выражение в формулу (2.28), получим
^/1^Л(а))^еЛ'^'+''<'»)1. (2.29)
Теперь найдем частное решение исходного уравнения,
подставив вместо и выражение для «а из (2.25). Так как
Р«2 = ^ ре-'«« = (-/<») ^ е-/*>' = ( - /to) «2.
«2 = Р (Р«2) = ( —/«>)" «8 «2 = ( —/©)'" «8.
ТО (2.17) в этом случае
(flo/'"+OiP"-4-...+fln)f/2 = lbo(-^to)'" +
^-6l(-^«))"-•+...+bJ«2.
Частное решение этого уравнения будем искать в виде
Проделав те же выкладки,-что и при нахождении частного
решения f/i, получим
= (—/О)) = Л (со) е-/Ф(^^) Л (о) е-Ясо*+Ф(со)1^ (2.30)
Сложив (2.29) и (2.30) для у^ и у^у найдем математическое
описание вынужденного движения:
4^ = f/l + f/з = >1 Wm cos (0)f + ф(С1))1. (2.31)
Таким образом, при гармоническом воздействии в устойчи-
шх системах после окончания переходного процесса, выходная
величина также изменяется по гармоническому закону, но с
другими амплитудой и фазой. При этом отношение амплитуд
выходной и входной величин равно модулю, а сдвиг фазы —
аргументу частотной передаточной функции. И, следовательно,
амплитудная частотная характеристика показывает
изменение отношения амплитуд, а фазовая частотная
характеристика—сдвиг фазы выходной величины относительно
входной в зависимости от частоты входного гармонического
воздействия.
Из приведенной физической интерпретации частотных
характеристик ясно, как строить их экспериментальным путем.
Для экспериментального построения частотных характерис-

тик имеется специальная аппаратура, в состав которой
входят генератор гермонических колебаний с регулируемой
частотой и устройства для измерения амплитуды и фазы
колебаний.
Частотные характеристики используют для описания как
устойчивых, так и неустойчивых систем. Но в последнем
случае они не имеют такого ясного физического смысла.
§ 2.5. Временные характеристики
Другой важной характеристикой автоматических систем
(звеньев) являются переходные и импульсные переходные
функции и их графики — временные характеристики. Их
используют при описании линейных систем, как стационарных,
так и нестационарных.
Переходной функцией системы (звена) называют функцию,
описывакхцую изменение выходной величины системы
(звена), когда на ее вход подается единичное ступенчатое
воздействие при нулевых начальных условиях. Переходную функцию
обычно обозначают h (/). Иначе: переходная функция h {t) есть
функция, описьюающая реакцию системы (звена) на
единичное ступенчатое воздействие при нулевых начальных
условиях.
Аналитически единичное ступенчатое воздействие можно
описать единичной функцией
1 при ^>0;
О при /<0.
График переходной функции — кривая зависимости
функции h {t) от времени t — называют переходной или разгонной
характеристикой.
Импульсной переходной или весовой функцией (функцией
веса) системы (звена) называют функцию, описьгоающую
реакцию системы (звена) на единичное импульсное воздействие при
нулевых начальных условиях; обозначают эту функцию w (/).
График импульсной переходной функции назьгоают
импульсной переходной характеристикой.
Переходную и импульсную переходную характеристики
называют временными характеристиками.
При определении весовой^ функции было использовано
понятие единичного импульса. Физически единичный импульс
1(0-

можно представить как очень узкий импульс, ограничивающий
единичную площадь. Математически он описьшается функцией
6 которую называют дельта-функцией; дельта-функция
является обобщенной функцией. Теория обобщенных
функций — сравнительно новый раздел функционального анализа,
и здесь она не будет рассматриваться. Отметим только, что в
рамках теории обобщенных функций любые встречающиеся в
приложении функции обладают производными любого
порядка. В частности, существует производная от единичной
функции — она равна дельта-функции: 1 (^) = б (/). Обладает
производными любого порядка и дельта-функция.
Перейдем к определению дельта-функции и ее
производных. При этом воспользуемся тем обстоятельством, что при
решении практических задач, как правило, дельта-функция и ее
производные встречаются только на промежуточных этапах.
В окончательном результате они или отсутствуют, или
фигурируют под знаком интеграла в произведении с какой-либо
«обычной» функцией. Поэтому нет прямой необходимости
отвечать на вопрос, что такое дельта-функция, а достаточно
ответить на вопрос, что означает интеграл от произведения
дельта-функции или какой-либо ее производной и обычной
функции. Руководствуясь приведенными соображениями, дельта-
функцию можно определить так: дельта-функция есть
функция, которая обладает следующими свойствами:
J 6(0d/= |б(0г«^-1; (2.32)
— оо —8
|°6(0ф(0^<= |б(0(р«)<^<-ф(0)- (2.33)
— оо —8
Производные от дельта-функции можно определить по
следующим соотношениям:
J б (О ф (О dt=^ J б (О Ф (О = (0); (2.34)
— оо —8
^ (т) S(m) (m)
J б(Оф(0й^= |б(/)ф(0Л-(-1)'"ф(О), (2.35)
— оо —8
где 8 — произвольное положительное число; ф (/) — обычная
функция, обладающая т-й производной; б {t) — m-я
производная по времени от дельта-функции.

Найдем изображение по Лапласу от дельта-функции и ее про-^
изводных. При этом преобразование Лапласа будем
трактовать как предельное соотношение
— Б
Используя соогношения (2.32)~(2.35), нетрудно получить
(т)
L (б (/)} - 1. L {б (0} = S, L { б (0} - (2.36)
Рассмотрим линейное дифференциальное уравнение с
постоянными коэффициентами в общем виде:
(«о + «1 + + «n) y^iboP'^ +b^P'^-' +
+ ... + 6m)«. (2.37)
В изображениях по Лапласу это уравнение принимает вид
Y {s)^W (s) и {si (2.38)
где W (s) = {boS ^ + Ьф '«-^ + ... + 6 m)/(«oS" + a^s
...Ч- Or) есть передаточная функция.
Как легко проверить, используя (2.36), уравнение (2.38)
справедливо и в тех случаях, когда w = 1 (/) или w = б (/).
В соответствии с определением весовой функции при и =
= б {t) переменная у (t) = w (t). И так как L{6 (t)} =1,
то при этом (2.38) можно записать
L (wit)l = Г (S). (2.39)
Таким образом, передаточная функция равна изображению
по Лапласу от весовой функции и соответственно
W (/) = L-^ {W (s)}. (2.40)
Последнюю формулу можно использовать для вычисления
весовой функции.
Установим связь между весовой и переходной функциями..
Так как L{\ (t)} 1/s, то уравнение (2.38) при w = 1 (/)
принимает вид
L{h(t)} = Wis)±.
S
сравнив эту формулу с (2.39), нетрудно заметить, что sL{h{t)}=
= L {w (t)}. Так как при нулевых начальных условиях умно-

жению изображения на s соответствует дифференцирование
оригинала, то из последнего равенства w (t) = h (t). Весовая
и переходная функции, как и передаточная функция, являются
исчерпывающими характеристиками системы (звена) при
нулевых начальных условиях. По ним можно однозначно
определить выходную величину при произвольном входном
воздействии. Действительно, исходя из уравнения (2.38), с помощью
теоремы о свертке (свойство 5 преобразования Лапласа) можем
записать
t t
X (t) = (t—т) и (т) dx (т) и (t —х) dx.
Эта формула, как и уравнение (2.38), справедлива только при
нулевых начальных условиях.
§ 2.6. Элементарные звенья и их характеристики
Выше звено было определено как математическая модель
элемента. Вообще же звеном называют математическую модель
элемента, соединения элементов или любой части системы.
Звенья, как и системы, могут описываться
дифференциальными уравнениями довольно высокого порядка, и в общем
случае их передаточные функции могут быть записаны в виде
W (S) - (6о s'" + 6i s'"+ 6 J/(ao +a^s^-' +
4-... + aJ. (2.41)
Ho всегда их можно представить как соединения типовых
или элементарных звеньев, порядок дифференциальных
уравнений которых не выше второго.
Из курса алгебры известно, что полином произвольного
порядка можно разложить на простые множители — множители
вида
k^s, {d^s + da), (diS^ + d^s + d^), (2.42)
поэтому передаточную функцию (2.41) можно представить как
произведение простых множителей вида (2.42) и простых
дробей вида
k/s. k/{d,s + d^h k/id.s' + d^s + d,). (2.43)

Звенья, передаточные функции которых имеют вид простых
множителей (2.42) или простых дробей (2.43), назьшают
типовыми или элементарными звеньями.
Прежде чем переходить к изучению элементарных
звеньев, вспомним формулы для модуля и аргумента комплексного
числа. Пусть комплексное число представлено в виде
отношения двух произведений комплексных чисел.
= П
Так как Zi = |2i |е' *г. \= |е' то для модуля и
аргумента комплексного числа имеем
П \ч\
Л- 1
Таким образом, справедливо следующее правило модулей
и аргументов комплексных чисел: модуль комплексного числа,
представленного в виде отношения двух произведений
комплексных чисел, равен отношению произведения модулей
сомножителей числителя к произведению модулей сомножителей
знаменателя, а его аргумент — разности суммы аргументов
сомножителей числителя и суммы аргументов сомножителей
знаменателя.
Пропорциональное звено. Пропорциональным называкэт
звено, которое описывается уравнением у (f) ku (О, или, что
то же, передаточной функцией W (s) = k.
Частотные и временнйе функции этого типового звена
имеют следующий вид:
W ijid) = k\ V(03) V (со) = 0; A (со) = k;
ф (a>) = 0; L (со) = 201g k; h (t) =fel(0; w {t) Ь (t).
Ha рис. 2.4 представлены некоторые из характеристик
пропорционального звена: амплитудно-фазовая частотная
характеристика (рис. 2.4, а) есть точка на действительной оси;
фазовая частотная характеристика (и ЛФЧХ) совпадает с
положительной полуосью частот; логарифмическая амплитудная
частотная характеристика (рис. 2.4, б) параллельна оси частот и

а)
б)
L(w)
201дИ
в)
hit)
lg(0))
Рис. 2.4
Проходит на уровне L (о) = 20 Ig fe. Переходная
характеристика (рис. 2.4, в) параллельна оси времени и проходит на
уровне А = Л.
Интегрирующее звено. Интегрирующим называют звено,
которое описывается уравнением ру = ku или передаточной
функцией W (s) = k/s.
Частотная передаточная функция W (/о) = fe// о =
= — jk/со. Остальные частотные и временные функции имеют
следующий вид;
и{(й) = 0; I/(о) = — fe/w; Л (со) = Л/ш; Ф (со) =
= — л/2; L (со) = 20 Ig fe —20 Igco; А (t) - kt; w (t) = k.
Амплитудно-фазовая частотная характеристика (рис. 2.5, а)
интегрирующего звена совпадает с отрицательной мнимой
полуосью. ЛФЧХ (рис. 2.5, б) параллельна оси частот и
проходит на уровне ф = — л/2; сдвиг фазы не зависит от частоты и
равен — л/2. ЛАЧХ (рис. 2.5, б) — наклонная прямая,
проходящая через точку с координатами со= 1 и L (со) = 20 Ig*.
Как видно из уравнения L (со) = 20 Igfe— 20 Ig со, при увеличении
частоты на одну декаду ордината L (со) уменьшается на 20 дБ.
Поэтому наклон ЛАЧХ равен — 20 дБ/дек (читается: минус
двадцать децибел на декаду). Переходная характеристика
и
♦
Рис. 2,5

представляет собой
прямую, проходящую через
начало координат с
угловым коэффициентом
наклона, равным k (рис.
2.5, в).
Дифференцирующее
звено. ^
Дифференцирующим называют звено,
которое описывается
уравнением у = kpu или
Частотные и
а)
д)
20lgh
9М
Ж/2
IgW
Рис. 2.6
передаточной функцией W (s) = ks.
временные функции имеют следукаций вид:
W (у©) = /Асо; и (со) = 0; V (а) = kco; А (со) = ftw;
Ф (со) = эт/2; L (со) = 20 Ig ft + 20 Ig со; ft (/) = 6 (t); w (0=
= 6 (0.
Амплитудно-фазовая частотная характеристика (рис. 2.6,«)
совпадает с положительной мнимой полуосью. ЛФЧХ
(рис. 2.6,6) параллельна оси частот и проходит на уровне
<р = я/2; сдвиг фазы не зависит от частоты и равен п/2.
ЛАЧХ есть прямая, проходящая через точку с
координатами о)= 1 и L(ce) =?= 20 Ig ft и имеющая наклон 20 дБ/дек
(читается: плюс двадцать децибел на декаду); L (ш)
увеличивается на 20 дБ при увеличении частоты на одну декаду.
Апериодическое звено. Апериодическим звеном первого
порядка называют звено, которое описывается уравнением
(Тр +l)y^ku (2.44)
или передаточной функцией
W (S) = k/{Ts + 1).
Это звено также называют инерционным звеном или
инерционным звеном первого порядка. Апериодическое звено в отличие
от вышерассмотренных звеньев характеризуется двумя
параметрами: постоянной времени Т к передаточным
коэффициентом к.
Частотная передаточная функция
W (/о) - к/{Т}(д + 1). (2.45)
Умножив числитель и знаменатель на
комплексно-сопряженное знаменателю число, получим
и (со) = k/[{Tio)^ + 11; V (<д) - йТб>/1(Гсо)^ + П. (2.46)

Амплитудную и фазовую частотные функции можно
определить, воспользовавшись правилом модулей и аргументов.
Так как модуль числителя частотной передаточной функ-
ции (2.45) равен ft, а модуль знаменателя 1^(7 со)^ + 1, то
/1(со)=й/У(То)2+1.
(2.47)
Аргумент числителя W ij(o) равен нулю, а аргумент
знаменателя arctg (оГ, поэтому ф (о)) = arg W (jo>) = — arctg оГ.
Из (2.47).
L (ш) 20 Ig Л (й)) = 20 Ig ft ^20 lgK(ro>)2 + l • (2.48)
Решив дифференциальное уравнение (2.44) при « == 1 (/) и
нулевом начальном условии (л: (0) = 0), получим А (t) ==
= ft (1 — е -'/^). Весовая функция
tt;(/)=A(0 = (ft/r)e~'/^.
АФЧХ апериодического звена (рис. 2.7, а) есть
полуокружность, в чем нетрудно убедиться, исключив из
параметрических уравнений (2.46) АФЧХ частоту.
Логарифмическая амплитудно-частотная характеристика
представлена на рис. 2.7, б. На практике обычно
ограничиваются построением так называемой асимптотической ЛАЧХ
(ломаная линия на том же рис. 2.7, б). Только в критических
случаях, когда небольшая погрешность может повлиять на
выводы, рассматривают точную ЛАЧХ. Впрочем, точную ЛАЧХ
можно легко построить по асимптотической ЛАЧХ если вос-
ZDlgK
4J
Н и
\w-0
-7С/2
г)
0.6 1
2 и Б W t520 spuO 5068 70 ВО 85 67 68 83 Ш if (u)) град
W ВЛ2 т Ш 0,2 ОЛ 0,71 г и е W W во wo ГО)
Рис. 2.7

пользоваться следующей зависимостью (AL — разность
между асимптотической и точной ЛАЧХ):
Г© . . .0,10 0.25 0,40 0.50 1,0 "2,0 2,5 4,0 Ю,0
AL . . . 0,04 0,25 0.62 0,96 3,0 0,96 0,62 0,25 0,04
Частоту (Oi = l/T, при которой пересекаются асимптоты,
называют сопрягающей. Точная и асимптотическая ЛАЧХ
наиболее сильно отличаются при сопрягающей, частоте;
отклонение при этой частоте примерно равно 3 дБ.
Уравнение асимптотической ЛАЧХ имеет вид
201gfe при cixccoi;
20 Ig/fe —20 Ig Т(о при со ^ (Oi.
Оно получается из уравнения (2.48), если в нем под корнем при
<о < coj пренебречь первым слагаемым, а при со ^ coi — вторым
слагаемым. Согласно полученному уравнению,
асимптотическую ЛАЧХ можно строить следующим образом: на уровне
L (со) = 20 \g k до частоты со = coj провести прямую,
параллельно оси частот, а далее через точку с координатами со =
= coj м L (со) = 20 Ig ft — прямую под наклоном — 20 дБ/дек-
По АФЧХ или ЛАЧХ легко определить параметры Тик
апериодического звена (рис. 2.7).
Логарифмическая фазовая частотная характеристика
изображена на рис. 2.7, б. Эта характеристика асимптотически
стремится к нулю при со О и к—я/2 при со оо. При со = со^
фазовая частотная функция принимает значение — я/4, т. е.
ip (coi) = — л/4. ЛФЧХ всех апериодических звеньев имеют
одинаковую форму и могут быть получены по какой-либо
одной характеристике параллельным сдвигом вдоль оси частот
влево или вправо в зависимости от постоянной времени Т.
Поэтому для построения ЛФЧХ апериодического звена можно
воспользоваться шаблоном или номограммой (рис. 2.7, г).
Переходная характеристика апериодического звена
(рис. 2.7, в) представляет собой экспоненциальную кривую.
По ней можно определить параметры: передаточный
коэффициент, равный установившемуся значению Л (оо); постоянную
времени, равную значению /, соответствующему точке
пересечения касательной к характеристике в начале координат с ее
асимптотой (рис. 2.7, в).
Форсирующее звено. Форсирующим звеном, или форсирую-
щим звеном первого порядка называют звено, которое
описывайся уравнением
у^к(Тр + \)и

или, что то же, передаточной функцией
W (s) = k (Ts + 1).
Это звено, как и апериодическое, характеризуется двумя
параметрами: постоянной времени Т и передаточным
коэффициентом к.
Частотная передаточная функция
W - k (Tjoi + 1).
Остальные частотные и временные функции имеют следующий
вид:
(УИ-Л; К(со)-№ /1(со)=А;К(Гсо)2+1;
ф (со) - arctg Г со; L (со) - 20 Ig + 2D lgV(T(o)^ + 1;
Л (О = k [ТЬ (t) + 1 (01; w it) k iTb (t) + 6 (/)].
АФЧХ (рис. 2.8, a) есть прямая, параллельная мнимой оси и
пересекающая действительную ось в точке U = k. ЛАЧХ
изображена на рис. 2.8, б. Как и в случае апериодического звена, на
практике ограничиваются построением асимптотической
ЛАЧХ (ломаная линия). Частоту coi = соответствующую
точке излома этой характеристики, называют сопрягающей
частотой.
Уравнение асимптотической ЛАЧХ форсирующего звена
L(co);
20lgft при со<со,;
201g^ + 201gTco при co>coi.
Асимптотическая ЛАЧХ при со < со j параллельна оси
частот и проходит на уровне L =^ 20 Igfe, а при со ^ имеет
наклон 20 дБ/дек.
ЛФЧХ форсирующего звена можно получить зеркальным
отражением относительно оси частот ЛФЧХ апериодического
звена и для ее построе;
S)
<Р(0))
НО))
ZDlgk
Рис. 2.8
НИЯ можно
воспользоваться тем же
шаблоном и номограммой (см.
рис. 2.7, г), которыми
пользуются для
построения последней.
Колебательное, кон-
^/=/г сдо) сервативиое и
апериодическое второго порядка

звенья. Звено, которое можно описать уравнением
или в другой форме
(Гу + 21Тр + \)у = Ли. (2.49)
где Г = 7^01 5 = Тх/(2Т), или передаточной функцией
W (s) - fe/(rV + 2grs + 1), (2.50)
называют колебательным, если О < g < I, консервативным^
если g == О (Г1 i= 0), и апериодическим звеном второго порядка»
если S ^ 1. Коэффициент g называют коэффициентом
демпфирования.
Колебательное звено. (О < g < 1). Частотная
передаточная функция
W 0*0) = k/li\ — rW)+/2grol.
Умножив числитель и знаменатель на
комплексно-сопряженное знаменателю выражение, получим вещественную и
мнимую частотные функции:
Фазовая частотная функция, как это видно из АФЧХ
(рис. 2.9, а), изменяется монотонно от О до — л и выражается
формулой
ф((0) =
-arctg jBTS-. при со
у _^-arctgj^^^ прио>1/Т.
Логарифмическая фазовая частотная характеристика (рис.
2.9, б) при со -> О асимптотически стремится к оси частот, а
при о оо — к прямой ф = — л. Ее можно построить с
помощью шаблона. Но для этого необходимо иметь набор
шаблонов, соответствующих различным значениям коэффициента
демпфирования.
Амплитудная частотная функция
А (о) = к/ V"(l~T2wy + (2gra))2,
логарифмическая амплитудная функция
L (со) - 20 Ig ft-20 lgK(l-7^'<^T + (2grco)^ (2.51)

Уравнение асимптотической ЛАЧХ имеет вид
20 Ig k при со < соь
20 Ig ft —40 Ig Гсо при со > coi,
где coi = \1Т является сопрягающей частотой. Оно
получается из уравнения (2.51), если под корнем при со <: coi оставить
только единицу, а при со > со^ — слагаемое Г*со*.
Асимптотическая ЛАЧХ (рис. 2.9, б) при со <: «1 параллельна оси
частот, а при со ^ coi имеет наклон — 40 дБ/дек.
Следует иметь в виду, что асимптотическая ЛАЧХ (рис.
2.9, б) при малых значениях коэффициента демпфирования
довольно сильно отличается от точной ЛАЧХ. Точную ЛАЧХ
можно построить по асимптотической ЛАЧХ,
воспользовавшись кривыми отклонений точных ЛАЧХ от асимптотических
(рис. 2.9, г).
Решив дифференциальное уравнение (2.49) колебательного
звена при м == 1 (О и нулевых начальных условиях [у (0) =^
= ^ (0) = 01, найдем переходную функцию:
Р
л (o = ft =
1—
е-«' 81п(р^ + Фо)
где a = g/r; p = Kl
Весовая функция
w(t)==h{t)^
Р
sinp/.
По переходной характеристике (рис. 2.9, е) можно
определить параметры колебательного звена следующим образом.
6) LM
Рис. 2.9

Рис. 2.10
Передаточный коэффициент k определяют по
установившемуся значению h (оо) переходной функции. Постоянную вре-
мении Т и коэффициент демпфирования можно найти из
уравнений
или
где Гк — период колебаний; w — амплитуды двух
соседних колебаний относительно установившегося значения
(рис. 2.9. е).
Консервативное звено (| = 0). Передаточная функция
W (s) = ft/(rs^ + 1).
Частотная передаточная функция
W (/со) = kl{\ — Гсо^).
Фазовая частотная функция, как это следует из АФЧХ
(рис. 2.10, а),
О при со< 1/Г;
—л при со > 1/Т
ф(со)-
Это выражение можно получить из фазовой частотной
функции колебательного звена предельным переходом при ^ 0.
Нетрудно выписать выражения для остальных частотных
функций; ЛЧХ приведены на рис. 2.10, б.
Переходная функция
А (/) = А: (1 ^ cos coi t); со^ = 1/Т

Переходная характеристика (рис. 2. Ю, в) представляет
собой график гармонических колебаний.
Апериодическое звено второго порядка Ц ^ 1).
Передаточную функцию (2.50) при i ^ 1 можно преобразовать к виду
{T,s+\){T^s+\)'
где
Апериодическое звено второго порядка можно представить
как последовательное соединение двух апериодических
звеньев первого порядка. Оно не относится к числу элементарных
звеньев.
Форсирующее звено второго порядка. Так называют
звено, которое описывается уравнением
y^k (-Гр^ + 21Тр +1)и
или, что то же, передаточной функцией
W (s)^ k (TV + 2lTs + 1) (2.52)
при условии, что о ^ g < 1.
Не представляет трудности получить выражения для
частотных и BpeMCHHt^ix функций и построить соответствующие
характеристики.
На рассмотрении этих вопросов останавливаться не будем,
Заметим только, что при частотах, превышающих сопрягают
щую частоту, ЛАЧХ имеет нак.лон 40 дБ/дек и ЛФЧХ по.луча-
ется зеркальным отражением относительно оси частот ЛФЧХ
соответствующего колебательного или консервативного звена.
Если g > I, то звено с передаточной функцией (2.52) не
относится к числу элементарных; его можно представить как
последовательное соединение двух форсирующих звеньев
первого порядка.
Неминимально-фазовые звенья. Звено назьшают
минимально-фазовым, если все нули и полюсы его передаточной
функции имеют отрицательные или равные нулю
вещественные части. Звено назьшают неминимально-фазовым, если хотя
бы один нуль или полюс его передаточной функции имеет
положительную вещественную часть.
Напомним, что нулями передаточной функции W (s) =
= R {s)/Q (s), где R (s) и Q (s) — полиномы от s, называют кор-

Рис. 2.11
ни уравнения R (s) = О, т. е. такие значения s, при которых
передаточная функция обращается в нуль, а полюсами —
корни уравнения Q (s) = 0, т. е. такие значения s, при которых
передаточная функция обращается в бесконечность..
Все рассмотренные выше элементарные звенья относятся
к минимально-фазовым. Примерами неминимально-фазовых
элементарных звеньев являются звенья с передаточными
функциями:
W (s) = k/(Ts — 1); W {s) = k (Ts — I); W (s) - ft/(rV—
—2lTs + 1); W (s) = k (TV — 2lTs + 1)
и др. Для неминима.льно-фазового звена характерно, что
у него сдвиг фазы по модулю больше, чем у
минимально-фазового звена, имекщего одинаковую с неминимально-фазовым
звеном АЧХ.
На рис. 2.И приведены ЛЧХ неминимально-фазовых
звеньев с передаточными функциями W (s) = l/(Ts —- 1) (рнс.
2.11, a)uW (s)=-k (Ts— 1) (рис. 2.П, б). ЛАЧХ этих
звеньев совпадают с ЛАЧХ апериодического (см. рис. 2.7, б) и фор-
сирукядего (см. рис. 2.8, б) звеньев. Сдвиг фазы у последних
меньше: фазовые частотные функции апериодического и
форсирующего звеньев по абсолютной величине не превышают
значения я/2, а фазовые частотные функции соответствующих
неминимально-фазовых звеньев достигают по абсолютной
величине значения я. К неминимально-фазовым звеньям относят
также звено чистого запаздывания с передаточной функцией
W (S) = fte-^^
Частотная передаточная функция
W (/со) fee -Z^** = k (cos сот — / sin сот).

Рис. 2.12
Для остальных частотных и временных функций имеем:
и {(6) = k cos (от; V ((о) = — А sin от; А (о) = k\
чр (ш) = — (от; L (ш) = 20 Ig k; h (t) = kl {t — т); w (t) =
= kb {t — x).
Амплитудно-фазовая частотная характеристика (рис. 2Л 2,
а) — окружность с центром в начале координат и радиусом k.
Каждой точке этой характеристики соответствует
бесконечное множество значений частот. ЛАЧХ (рис. 2.12, б)
совпадает с ЛАЧХ пропорционального звена с передаточной функцией
А, ЛФЧХ (рис. 2.12, б) — с графиком функции f/ = — т10^
{у = Ц(о); X = lg(o). Переходная характеристика приведена
на рис. 2.12, в.
§ 2.7. Структурные схемы^ графы, уравнения
и частотные характеристики стационарных
линейных систем
Структурной схемой в теории автоматического управления
называют графическое изображение математической модели
автоматической системы управления в виде соединений
звеньев. Звено на структурной схеме условно обозначают в виде
прямоугольника с указанием входных и выходных величин,
а также передаточной функции внутри него. Иногда вместо
передаточной функции указывают уравнение или
характеристику. Звенья могут быть пронумерованы и их передаточные
функции, уравнения или характеристики представлены вне
структурной схемы.

Ьходные и выходные величины записывают в виде
изображений, если передаточные функции задают в форме
изображений. Если же передаточные функции задают в операторной
форме или звенья описывают дифференциальными уравнения-
Ц]л, то входные и выходные переменные записывают в виде
оригинала.
Сравнивающие (рис. 2,13, а, б) и суммирующие (рис. 2.13,в)
звенья изображают в виде круга, разделенного на секторы.
В сравнивающем звене сектор, на который подается «вычитае-
^мoe», затемняют (рис. 2.13, б) или перед соответствующим
входом ставят знак минус (рис. 2.13, а).
Структурную схему широко используют на практике при
исследовании и проектировании автоматических систем упраз-
ления, так как она дает наглядное представление о связях
между звеньями, о прохождении и преобразовании сигналов в
системе.
При математическом описании автоматическую систему
обычно изображают в виде блок-схемы и для каждого «блока»
(элемента) записывают уравнения, исходя из физических
законов, которым подчиняются процессы в нем. Структурную
схему можно составить на основании этой блок-схемы и
полученных уравнений или только на основании последних. И
дальнейшие преобразования, необходимые для получения
уравнений и передаточных функций системы, проще и нагляднее
производить по структурной схеме.
Звено на структурной схеме не обязательно изображает
модель какого-либо отдельного элемента. Оно может быть
моделью элемента, соединения элементов или вообще любой
части системы.
Основные правила лреобразования структурных схем.
1. Последовательное соединение звеньев (рис. 2.14, а). При
последовательном соединении выходная величина каждого
предшествующего звена является входным воздействием
последующего звена. При преобразовании структурных схем
цепочку из последовательно соединенных звеньев можно
заменить одним звеном (рис.
2.14, б) с передаточной ^t) 5) в)
функцией W (s), равной а^^^/ОчУ^УгУ^ ^1/ОчД-У2 ^jl/Оч^=У|^Уа
произведению
передаточных функций отдельных
п
звеньев: W (s)=n Wi (s).
i=i Рис. 2.13

Ms. ^
Рис.
2.14
Запишем уравнения звеньев Ух = Wir/o» У2 = ^^гУ!»-.-» Уп =
Исключив из этой системы переменные Уи f/a* Уп-ь
получим
^ W^W^,.., W^y,,
откуда
П Wi.
2. Параллельное соединение звеньев (рис. 2.15, а). При
параллельном соединении на вход всех звеньев подается один и
тот же сигнал, а выходные величины складываются. Цепь из
параллельно соединенных звеньев можно заменить одним
звеном (рис. 2.15, б) с передаточной функцией W (s), равной
сумме передаточных функций входящих в нее звеньев: W (s)^
п
S (5)- Д-^я вывода этой форму.ш составим уравнения
для каждых звеньев:
Сложив эти уравнения и учитывая, что у = ^ Уг, получим
i ~ 1
искомую формулу.
3. Звено, охваченное об ратной связью (рис. 2.16, а).
Принято считать, что звено охвачено обратной связью, если его
выходной сигнал через какое-либо другое звено подается на
вход. При этом если сигнал Ух обратной связи вычитается
из входного воздействия т. е. е^ == Уо— у^, то обратную
связь называют отрицательтй. Если сигнал Ух обратной
связи складывается с входным воздействием у^, т. е. е^ = Уо +
+ f/i, то обратную связь называют положительной.
Разомкнем обратную связь перед сравнивающим звеном
(рис. 2.16, а). Тогда получим цепь из двух последовательно
соединенных звеньев. Поэтому передаточная функция W разом-

кнутой цепи (рис. 2.16, а) равна произведению передаточной
функции прямой цепи и передаточной функции ^
обратной связи: W = W^oc (рис. 2.16, б).
Передаточная функция замкнутой цепи с отрицатель-
ной обратной связью — звена, охваченного отрицательной
обратной связью, — равна передаточной функции прямой цепи,
деленной на единицу плюс передаточная функция
разомкнутой цепи:
И^з W^n/(1 + W^).
Для вывода этой формулы выпишем уравнения для каждого
звена:
В этой системе последнее уравнение — уравнение
сравнивающего звена — называют уравнением замыкания.
Исключив переменные е^ и у^ из приведенной системы,
получим уравнение У ^ (Уо — W^,cy) или (1 + W^,c)y=
= U^n^o'Отсюда
Если обратная связь положительна, то аналогично
получим = w^/(i — wy
Передаточная функция замкнутой цепи с положительной
обратной связью равна передаточной функции прямой цепи,
а)
а)
Уг
Wn
1^
(■*■)
5;
5)
в)
'ас
Ус
у,
W
W
Рис. 2.15
Рсс. 2.16

деленной на единицу минус передаточная функция
разомкнутой цепи. Если передаточная функция W^o.c = 1, то обратная
связь называется единичной и структурная схема
изображается так, как показано на рис. 2.16, в. Передаточная функция
при этом принимает вид = ^rvH\ + ^п) при
отрицательной обратной связи и IP^g = WJ(\ — Wji при
положительной обратной связи. ^
При преобразовании структурных схем возникает
необходимость переноса и перестановки сумматоров и узлов.
Рассмотрим, какие изменения в схеме при этом нужно произвести.
4. Перенос сумматора (рис. 2.17). Легко показать, что при
переносе сумматора по ходу сигнала необходимо добавить
звено с передаточной функцией, равной передаточной функции
звена, через которое переносится сумматор (рис. 2.17, а). Если
сумматор переносится против хода сигнала, то необходимо
добавить звено с передаточной функцией, равной обратной
передаточной функции звена, через которое переносится сумматор
(рис. 2.17, б).
При переносе сумматора возникают неэквивалентные
участки линии связи. Эти участки на рис. 2.17 заштрихованы.
5. Перенос узла (рис. 2Л8, а). При переносе узла также
необходимо добавить звено. Если узел переносится по ходу
сигнала, то добавляется звено с передаточной функцией, равной
обратной передаточной функции звена, через которое
переносится узел (рис. 2.18, б). Если узел переносится против хода
сигнала, то добавляется звено с передаточной функцией,
равной передаточной функции звена, через которое переносится
узел (рис. 2.18, в).
а)
У,
1
W2
Уг Ус
Рис. 2.17

а)
в)
У/
Уг
W2
Рис. 2.18
6. иерестановш узлов и сумматоров (рис. 2.19). Узлы
можно переставлять местами (рис. 2,19, а). Точно так же можно
переставлять сумматоры, не добавляя звена (рис. 2.19, б).
При перестановке узла и сумматора (перенос узла через
сумматор) необходимо добавить звено — суммирующее или
сравнивающее (рис. 2.19, в, г).
При переносе узла через сумматор, а также при
перестановке сумматоров возникают неэквивалентные участки линии
связи. Эти участки на рисунке заштрихованы.
Вычисление передаточной функции одноконтурной
системы. Замкнутую систему (структурную схему) называют одно-
контурнойу если при ее размыкании в какой-либо точке
получается цепочка из последовательно соединенных звеньев и.ди
цепь, не содержащая параллельных и обратных связей.
Рассмотрим одноконтурную систему, приведенную на
рис. 2.20, а. Найдем передаточную функцию по входу g и
выходу у. Участок по ходу сигнала от точки приложения
входного воздействия до точки съема выходного сигнала назовем
прямей Цепью (рис. 2.20, а), а цепь из последовательно соединенных
звеньев, входящих в замкнутый контур (рис. 2.20, б), —
разомкнутой цепью. Как легко проверить, справедливо следующее
правило: передаточная функция одноконтурной системы

о)
9 ^
Прямая цепь
Wo
S)
Разомннутая цепь
С отрицательной
(положительной) обратной связью
равна передаточной
функции прямой цепи,
деленной на единицу плюс
[минус) передаточная функция
разомкнутой цепи:
W2
Рис.
2.20
W
ид'
Ц^о
1 ± W, W,
1 ± W
где — передаточная функция прямой цепи; W —
передаточная функция разомкнутой цепи.
Сформулированное правило справедливо для любой
одноконтурной системы.
Вычисление передаточной функции многоконтурной
системы. Замкнутую систему (структурную схему) называют
многоконтурной, если при ее размыкании получается цепь,
содержащая параллельные или обратные связи, или, иначе,
замкнутую систему называют многоконтурнойу если она
помимо главной обратной связи содержит местные обратные или
параллельные связи. Говорят, что многоконтурная система
имеет перекрещиваюи{иеся связи, если контур обратной или
параллельной связи охватывает участок цепи, содержащий
только начало или конец другой цепи обратной или
параллельной связи (рис, 2.21, а, б).
Для вычисления передаточной функции многоконтурной
системы необходимо прежде всего перестановкой и переносом
узлов и сумматоров освободиться от перекрещивающихся
связей. Затем, используя первые три правила преобразования
о)
6)
Рис. 2.21

структурных схем, преооразовать ее в одноконтурную
систему, передаточную функцию которой легко вычислить
согласно сформулированному выше правилу. Следует иметь в виду,
что при преобразовании структурной схемы нельзя
переносить сумматор через точку съема выходного сигнала, так как
при этом точка съема оказывается на неэквивалентном участке
линии связи.
Пример 2,4. Найдем передаточные функции системы,
приведенной на рис. 2.22, а. по «входам» gn f и «выходам» у п e'i Эта система
является многоконтурной с перекрещивающимися связями. Перенеся
и переставив сумматоры, ее можно привести к многоконтурной
системе без перекрещивающихся связей (рис. 2.22, б). После замены
параллельно соединенных звеньев и звена, охваченного обратной связью»
эквивалентными звеньями с передаточными функциями 1^13 = +
получим одноконтурную схе- q\
му (рис. 2.22, в).
При вычислении
передаточной функции по входному
воздействию g полагаем f = 0.
Согласно правилу вычисления
передаточной функции
одноконтурных систем, имеем
l^eg== 1/(1+1^13 W^24)"
При вычислении
передаточной функции по входному
воздействию / полагаем g~ 0.
При этом сравнивающее
звено стаиов1([тся инвертирующим
звеном с передаточной
функцией, равной —1.
Инвертирующее звено в замкнутый
контур можно не вводить,
если суммирующее звено
преобразовать в сравнивающее.
Поэтому структурную схему
можно представить так, как
это показано на рис. 2.22, г.
Из этой схемы очевидно
Графы,
Математическую модель системы
управления наглядно можно
представить также с по-
модью ор иентиров анных
Рис. 2.22

графов. Графом называется [1] совокупность множества V
точек, называемых вершинами^ и множества R простых (т. е.
само непересекающихся) кривых, называемых ребрами,
удовлетворяющих следующим условиям: 1) каждое незамкнутое
ребро содержит ровно две точки множества У, которые
являются граничными точками ребра; 2) каждое замкнутое ребро
содержит только одну точку из V (граничные точки
совпадают); 3) ребра (кривые из множества R) не имеют общих точек,
за исключением точек из множества V.
На рисунке вершина изображается точкой или
окружностью. Граф обозначают одной буквой G или парой букв (1/, /?),
где V — множество вершин, R — множество ребер графа.
Если множества V и R состоят из конечного числа элементов,
то граф (1/, R) называется конечным. Граф Gi = {Vi, Ri),
который состоит из части вершин {Vi с= V) и части ребер
(Ri CZ R) графа G = (V, /?), называется подграфом G. При
этом G называется подграфом G^. Если вершины и,, и
являются граничными точками ребра г, то говорят, что г
инцидентно каждой из вершин и и, обратно, каждая из вершин
и Vi инцидентна г. Граничные точки ребра г, очевидно,
можно определить как вершины, т. е. точки из множества У,
инцидентные г. Если ребро замкнуто, т. е. оно имеет только
одну граничную точку, то ребро называется петлей.
Если ребра ориентированы, т. е. на каждом ребре задано
направление, то граф называется ориентированным графом,
или орграфом. Ориентированные ребра называются дугами.
Поэтому ориентированный граф, или орграф, можно
определить как совокупность множества V вершин и множества
D дуг, удовлетворяющих перечисленным выше трем
условиям. Вершина, являющаяся начальной граничной точкой
дуги du называется ее начальной вершиной, а вершина,
являющаяся конечной граничной точкой дуги — ее конечной
вершиной.
Последовательность дуг^!,..., (не обязательно разных),
для которой конечная вершина Vi дуги di является
начальной вершиной дуги d^^i, г = 1, « 1, называется
ориентированным маршрутом (ормаршрутом). Ориентированный
маршрут называется замкнутым, если конечная вершина
Дуг^и dn совпадает с начальной вершиной t^o дуги di. В
противном случае ормаршрут называется незамкнутым. Ормаршрут,
в котором нет повторяющихся дуг (все дуги разные),
называется путем от вершины к вершине если он незамкнут, и
контуром (ориентированным циклом), если он замкнут. Если

а)
Рис. 2.23
все вершины Vq, t^i,..., Vj^ различны, то путь или контур
называется простым (в случае контура и совпадают).
Вершины и будем называть соответственно начальной и
конечной вершинами пути, а остальные вершины —
промежуточными. Дуги di и ^2 называются параллельными или строго
параллельными, если они имеют общие начальную и конечную
вершины.
Гра^ системы управления представляет собой
ориентированный граф, который обладает следующими свойствами 13J :
1. Каждая дуга (ребро со стрелкой, указывающей
направление распространения сигнала) изображает звено и
характеризуется оператором изображаемого ею звена. Поэтому можно
говорить о передаточной функции, дифференциальном
уравнении, частотных и временш^хх функциях дуги.
2. Каждой вершине ставится в соответствие одна из
переменных. Если к вершине подходит (входит в нее) только одна
дуга, то соответствующая ей переменная равна выходной
величине дуги (выходной величине изображаемого ею звена).
Если к вершине подходят несколько дуг, то соответствующая
ей переменная равна сумме выходных величин этих дуг.
Входная величина дуги (входная величина изображаемого ею
звена) равна переменной вершины, из которой эта дуга исходит.
Если из вершины исходят несколько дуг, то входная
величина всех этих дуг одна и та же.
Граф системы управления легко построить по ее
структурной схеме. И наоборот, по графу системы управления
нетрудно построить структурную схему. При построении графа
системы управления по ее структурной схеме нужно исходную
схему (рис. 2.23, а) представить так, чтобы в сумматорах все
переменные складывались с положительным знаком (рис. 2.23,
б). Затем по последней схеме построить граф (рис. 2.23, в),
руководствуясь следующими правилами: 1) каждый сумматор
заменяется вершиной, которой ставится в соответствие
выходная переменная заменяемого сумматора; 2) каждое звено (пря-

моугольник на
структурной схеме) заменяется
дугой с оператором, равным
оператору замен яемого
звена; 3) каждой
переменной (в том числе перемен-
Рис. 2.24 ной, обозначающей внеш-
ш нее воздействие)
соответствует своя вершина. Если нужно изобразить выход одной
из дуг (например, дуги с передаточной функцией на
рис. 2.24, а), входящих в общую вершину, то следует ввести
дополнительную, конечную для этой дуги вершину и
соединить эту вершину с исходной вершиной дугой с единичным
оператором (рис. 2.24, б).
На графе системы управления, как правило, для
обозначения дуги и ее оператора, точно так же как и для обозначения
вершины и соответствующей ей переменной, будет
использоваться одна и та же переменная. И поэтому выражения «дуга
с оператором W» и «дуга W»y а также выражения «вершиина,
соответствующая переменной х» и «вершина х» будут иметь
одинаковый смысл.
Формула Мейсона. Как нетрудно показать, параллельные
дуги (рис. 2.25, а) можно заменить одной дугой с передаточной
функцией, равной сумме передаточных функций исходных
дуг (рис. 2.25, б). Простой путь, если нет не принадлежащих
ему дуг, инцидентных его промежуточным вершинам, можно
заменить дугой с передаточной, функцией, равной
произведению передаточных функций дуг этого пути. Так, например,
п
простой путь на рис. 2.25, в можно заменить дугой W = П Wi
t=r 1
(рис. 2.25. г). Простой путь на рис. 2.25, д заменить дугой
нельзя, так как имеются не принадлежащие этому пути дуги
и U7^, инцидентные его промежуточным вершинам.
Для упрощения графа и вычисления передаточной функции
системы управления по ее графу можно также
воспользоваться формулой Мейсона
т
Здесь Wi — передаточная функция /-го простого пути от
вершины g к вершине х, равная произведению передаточных функ-

ций дуг, входящих в этот путь; т — общее число таких путей;
д — определитель графа;
Д 1-S »^о,- + 2 Woj ^0.- 2 ^oj Wot -ь....
/./г i,k,l
где в первой сумме W^j—передаточная функция /-го простого
контура, равная произведению передаточных функций
входящих в этот контур дуг, и суммирование производится по всем
простым контурам; во второй сумме WojWqj, — произведение
передаточных функций /-го и k-ro контуров и суммирование
производится по всем несоприкасающимся парам
контуров; в третьей сумме W^j Wq^ ^oi— произведение
передаточных функций /-го,/г-го и/-го контуров и суммирование
производится повеем несоприкасающимся тройкам контуров и т. д.;
Л,. — определитель подграфа, получающегося из исходного
графа при удалении дуг и вершин 1-го простого пути, а также
всех дуг, инцидентных этим вершинам.
Два контура (пара контуров) называются
несоприкасающимися, если они не имеют общих дуг и (или) общих вершин.
Тройка (четверка и т. д.) контуров называется
несоприкасающейся, если любая пара контуров из этой тройки (четверки и
т. д.) является несоприкасающейся.
Подграф, получающийся при удалении дуг и вершин
какого-либо простого пути, а также всех дуг, инцидентных
удаляемым вершинам, будем называть подграфом,
соответствующим этому простому пути.
Рис. 2.25

Граф на рис. 2.26, а имеет два простых пути от вершины
g к вершине х (пунктирные линии с точками). Передаточные
функции этих путей = WuWi2^is\ = W^^W^^.
Он содержит пять простых контуров (см. замкнутые
пунктирные линии) с передаточными функциями
= W^, Го, =
u/^x w,^ w.^ w,, w,,- = w^, w,, U73«;
и три несоприкасающиеся пары контуров с передаточными
функциями 1^01 и W7o3, IFoi и И7о4. W^oi и U^os-
Этот граф не содержит несоприкасающихся троек и
большего числа контуров, поэтому определитель
Л = 1 - (W^oi + W^oa + W^o3 + W^o. + W^os) + (W^oiX
Подграф, соответствующий первому простому пути (рис. 2,26,
б), имеет один контур, а подграф, соответствующий второму
простому пути (рис. 2.26, в), — два контура. ОпределитСсаи
этих подграфов - 1 — W^^\ Л2 = 1 — (W^oi + W^os) +
Согласно формуле Мейсона. передаточная функция
= (U7iiU7„u-i3Ai + w^rW^^^oУ^.
пример 2,5. Вычислим передаточные функции системы
управления, рассмотренной в гфимере 2.4 (см. рис. 2.22, а). Граф этой системы
Рис. 2 26

Рис. 2.27
управления приведен на
рис. 2.27. Найдем
передаточные функции Wyg, Wyf и Weg.
От вершины g к вершине
у имеется два простых пути
с передаточными функциями
u?^; = Wo Щ ^ ^1 «^2;
Имеется три контура с
передаточными функциями l^J^oi^^
. Несоприкасающихся пар и большего числа контуров граф не
содержит. Поэтому его'определитель
Л = I + Wo-, + -^l+W.W^-W^W. + W^W:,.
Подграфы» соответствуюшие простым путям от вершины g к
вершине у, замкнутых контуров не содержат, и их определители Aj = 1,
1.
По формуле Мейсона,
От вершины f к вершине у ведет один простой путь — дуга Wq,
Соответствующий этому пути подграф не имеет замкнутых контуров,
и его определитель I. Следовательно,
Wyf = l^e/А = I / (i + 1^2 - 4- ^2 Ws).
От вершины g к вершине ^ ведет также один простой путь — дуга
Wo- Соответствующий этому пути подграф имеет один контур с
передаточной функцией U^'oi = WoWa, и его определитель Ai — 1 — Wni =
- 1 - W^W^.
Передаточная функция
Weg = 1^0 А^/Л = (I -И^а + V^2~«^2 + ^2 ^з).
Дифференциальные уравнения. Зная передаточные
функции системы, нетрудно записать ее дифференциальные
уравнения. Если система имеет одну управляемую величину, то для
ее полного описания достаточно иметь одно дифференциальное
уравнение, выражающее зависимость между выходной и
входной величинами.
Автоматические системы с одной управляемой величиной
называют одномерными. В общем виде дифференциальное
уравнение одномерной системы с двумя входными величинами,
например задающим воздействием g и возмущающим
воздействием /, можно записать как
<л) <rt-l) (т) (m~l)
aoy + aiy + ... + any=^bQg + big + .. + bmg +
it) (/-1)
+ cJ + cJ + ... + c,f.

Получим дифференциальное уравнение системы,
рассмотренной в примере 2.4 (рис. 2.22, а). Для нее
У = Wy,g + W,ff. (2.53)
Это дифференциальное уравнение в символической форме,
связывающее выходную величину у с входными величинами.
Аналогично можно записать дифференциальное уравнение
относительно любой другой «выходной» величины. Исходя из
определения передаточной функции нетрудно перейти от урав
нения (2.53) к обычной «несимволической» форме записи.
Допустим, например, что = ki; Wi = kol{p + 1);
W^ = kjp\ W^=^k^, Тогда
где k = l/(koks); -1/^ 7^2 = (1 + Ma - W l{k^k^)\
Поэтому на основании (2.53)
П'у^Т.у \~y'-=T,g^g + k(f + f).
Частотные характеристики. При исследовании и
проектировании автоматических систем обычно используют
амплитудно-фазовые и логарифмические частотные характеристики
разомкнутых систем. Передаточные функции W (s)
разомкнутых одноконтурных, а иногда и многоконтурных систем
можно преобразовать к виду
W(s)^ П WAS), (2.54)
где Wi (s) — передаточные функции элементарных звеньев.
В этом случае модули и аргументы 4acT0tHbix
передаточных функций системы и звеньев Л (о) \W (/(о)|;
(03)-|U7, (/(0)1; ф (О)) argU7 (/(о); ф, (со) = arg Wtijio)
в соответствии с правилом модулей и аргументов комплекс
ных чисел связаны между собой соотношениями
АМ^ П Л,(со); (2.55)

Веи^ественные и мнимые частотные функции системы
определяются равенствами
и (о) ^ А (со) cos ф (со);
1/(со) = Л (со) sin ф ((О).
(2.57)
, , Пользуясь полученными соотношениями (2.55)—(2.57),
можно построить АФЧХ. Из (2.55) очевидно
(2.58)
1
где L (со) =^ 20 Ig Л (со) и U (со) = 20 Ig (со) —
логарифмические амплитудные частотные функции.
Из (2.56) и (2.58) вытекает следующее правило построения
ЛЧХ (ЛАЧХ и ЛФЧХ) систем, передаточные функции
которых преобразованы к виду (2.54): строят ЛЧХ отдельных
звеньев и затем их графически складывают.
На основании (2.58) можно также сформулировать
несколько иной, более простой порядок построения ЛАЧХ.
Проиллюстрируем это сначала на
конкретном примере.
Пусть W (s)=100 (s4-l)/k^ X
X (10s + 1) (0,01 5^ +0,1 s+1)],
Логар ифмическа я ам пл итуд-
ная частотная функция
L(co)==40—v20 Igco-^
-20lgK(10co)^+l +
+201gl/V-+l-
-20 Ig V(\ -^0,01o>Y+ (0,Ico)^
Асимптотическая ЛАЧХ
рассматриваемой системы состоит
из четырех асимптот (рис. 2.28,
а, б, в) и строится следующим
образом. Вычислим
сопрягающие частоты:
щ = 1/10-0,1; со2== 1;
Здесь
соз - 1/ai - 10.
coj, и o>3—
сопрягающие частоты апериодического,
форсирующего и колебательного
звеньев соответственно.
Рис. 2.28

Напомним, что при построении асимптотической ЛАЧХ
элементарных звеньев при частотах, меньших сопрягающей
частоты, под корнем оставляют только единицу (остальными
членами пренебрегают), а при частотах, больших сопрягающей
частоты, —члены с наивысшей степенью со. Поэтому в
рассматриваемом примере при (о < со^
L (со) « 40 — v201gco.
Это уравнение первой асимптоты. Согласно этому
уравнению, первую асимптоту проводят через точку с
координатами о ==1 и L = 20 Ig ^ с наклоном — v20 дБ/дек. Она
кончается на первой сопрягающей частоте.
При o)i ^ О) <: «2 аналогично имеем
L (о) « 40 ^ v201g со — 201g Юсо - 20 v 20 Igco —
— 20 Igco.
Это- уравнение второй асимптоты. Ее наклон изменяется
на — 20 дБ/дек и обусловливается апериодическим звеном.
Вторую асимптоту проводят от конца первой асимптоты до
второй сопрягающей частоты согласно ее уравнению с наклоном
(_ V 20—20) дБ/дек.
При С02 ^ со < СОз
L (со) » 20 — v201gco 20lgco -f- 201gco - 20 — vx
X20 Igco.
Это уравнение третьей асимптоты. Ее наклон изменяется
на 20 дБ/дек и обусловливается форсирующим звеном. Третью
асимптоту проводят от конца второй асимптоты до третьей
сопрягающей частоты с наклоном — v-20 дБ/дек.
При со ^ СОз .
L (со) = 20 — v.20lgco — 40 Ig O.lco = 60 — v20lgco —
— 401g CO.
Это уравнение последней, четвертой, асимптоты. Ее наклон
изменяется по отношению к третьей асимптоты на —40 дБ/дек
и обусловливается колебательным звеном.
Теперь нетрудно сформулировать общее правило
построения асимптотической ЛАЧХ системы с передаточной
функцией вида
U7(s)= П Wiis),
1=1
где Wi (s) — передаточные функции элементарных звеньев.

Правило построения асимптотической ЛАЧХ.
1. Вычисляют сопрягающие частоты и значение 201gfe,
где k — передаточный коэффициент системы, равный произ-
п
ведению передаточных коэффициентов звеньев (& = Ylki).
f = i .
2. Строят первую асимптоту, которую проводят До первой
сопрягающей частоты через точку с координатами о = 1 и
L = 201gfe с наклоном — v-20 дБ/дек. Здесь v равно разности
между числами интегрирующих и дифференцирующих
звеньев.
3. Проводят вторую асимптоту от конца первой асимптоты
до второй сопрягающей частоты. Ее наклон изменяется на
20,—20, 40 или — 40 дБ/дек в зависимости от того, является
ли 0)1 сопрягающей частотой форсирующего,
апериодического, форсирующего второго порядка или колебательного
звена соответственно.
4. Строят каждую последующую асимптоту аналогично
второй. Изменение наклона (1 + 1)-й асимптоты зависит
от того, сопрягающей частотой какого элементарного звена
является щ.
Если какая-либо сопрягающая частота является кратной
и ее кратность равна /, т. е. имеется / одинаковых
элементарных звеньев,'то изменение наклона при этой частоте в / раз
больше, чем при соответствующей простой частоте.
Для колебательных звеньев с малым коэффициентом
демпфирования <: 0,4) асимптотическая ЛАЧХ должна быть
скорректирована в окрестности сопрягающей частоты по
точным формулам или с помощью кривых поправок (см. рис. 2.9, г).
§ 2.8. Многомерные стационарные линейные
системы
Многомерными системами или системами многосвязного уп-
равления называют автоматические системы управления, в
которых имеется несколько (больше одной) управляемых
величин. Соответственно объекты, имеющие несколько
управляемых величин, называют многомерными объектами или
объектами многосвязного управления. ^
Примерами многомерных объектов могут быть: самолет,
у которого управляемыми величинами являются курс, углы

тангажа и крена, высота, скорость; паровой котел, в котором
регулируется температура, давление пара и другие величины.
Обычно управляемые величины называют выходами или
выходными величинами. И поэтому многомерные системы еще
определяют как автоматические системы с многомерным
(векторным) выходом.
Многомерные системы и объекты называют линейными и
стационарными, если они описываются системой линейных
дифференциальных уравнений с постоянными
коэффициентами.
Уравнения многомерных стационарных линейных систем
и объектов. Пусть Ух, ур обозначают выходные величины,
"if Wm —параметры управления или задающие
воздействия и Д, fi — возмущающие воздействия. Уравнения
многомерных стационарных линейных систем и объектов в
общем случае можно записать в виде следующей системы:
%1 {Р)У1 + ..-+ «1р {р)Ур = ^11 + +bim {Р) Wm+
+ ... (р)/.
I (Р) i^l + ... + ^РР (Р) f/p = Ьр 1 (Р) «1 + ... + Ьрт (Р) «т +
+ ^р1 {p)fi + ^.. + Cpiip)fi,
или в более компактной форме
р т I
S ciu(p)yj-= 2 f'ij(P)^J+ 2 ^ij(P)fj^ ^ = 1,...,?. (2.59)
/=1 /=1 /-1
Здесь atj (р), btj (р), Ctj (р) обозначают стационарные
линейные операторы, т. е. полиномы от оператора
дифференцирования с постоянными коэффициентами.
Переходя в обоих частях (2.59) к изображениям Лапласа,
при нулевых начальных условиях получим систему
алгебраических уравнений:
У (S) (s) = 2 (^) + 2 (^)'
y-l /=1 /=1
/-l....,p, (2.60)
где
(s) = L{ys (<)}, Uj (s) = (<)}. Fj is) ^ L {fj (t)).

Для многомерных систем удобна матричная форма записи
уравнений.
Введем в рассмотрение матрицы
У =
У1
1Уо:
аМ ... aipip)
_ api(p) ...opoip)
u --.
Cll(P):.Cu{p)
lCpiip)...Cptip)
'biiip)... bi^ip)'
ГЛ1
B(p) =
; f =
•
; c(p) =
b(,l{p)...bpm(p) _
с их помощью (2.59) в матричной форме будет
A(p)y = B(p)u + C(p)f.
(2.61
Точно так же можно записать (2.61) в изображениях
Лапласа в матричной форме:
А (s) Y (s) = В (s) и (s) + С (S) F (s). (2.62)
Здесь
4i(s)-aip(s)
A(s) =
Яр, (s)...app(s).
; Y(.s) =
y'pis).
B(s) =
(•«)••• ^lm(s)
.6pl (S)...6pm (s).
U(s) =
; c(s)=^
Cn(s)... Cii(s)
"fi(s)*
Cp,(s)...Cp,(s) .
В (2.61), после умножения и сложения матриц, в правой и
левой частях получатся матрицы-столбцы. Приравняв их
соответственные элементы, получим систему уравнений (2.59).
Аналогично, выполнив указанные операции над матрицами
и приравняв соответственные элементы матриц левой и правой
Частей матричного уравнения (2.62), получим систему (2.60).
Пример 2.6. Пусть исходная система дифференциальных
уравнений имеет вид
(По Р + Ol) ^1 + 02 У2 ^0 Р«1 + biu^\
«3 У1 Н- («4 P + ^si У2 ^ ^2 «2-

в матричной форме, как нетрудно проверить, эта система записывается
в виде
А у = В {р) U,
где
аз а^р + аъ
ВЫ-
О А
Передаточная матрица. Для описания многомерных систем
и объектов, как и в случае одномерных систем, можно
использовать передаточные функции. Передаточной функцией
U7« (s) (в изображениях Лапласа) по /-му параметру
управления и i-му выходу называют отношение изображения Лапласа
выходной величины yi к изображению входной величины Uj при
нулевых начальных условиях. По определению,
W4,(s)==Yi{s)/Uj(s). (2.63)
Эту передаточную функцию можно вычислить следующим
образом. В системе (2.60) приравниваем нулю изображения всех
возмущающих воздействий и параметров управления, кроме
Uj (s). Из полученной системы алгебраических уравнений
находим решение Yi (s), а затем, разделив его на Uj (s), получим
искомую передаточную функцию.
Аналогично определяют передаточную функцию wlf (s)
по /-му возмущающему воздействию и i-му выходу:
(2.64)
В случае многомерных систем (объектов) для ее полного
описания необходимо иметь р-т передаточных функций по
управлению а tJ-l передаточных функций по возмущению. Эти
передаточные функции записывают в виде матриц:
W«(.s) =
Wf(.s) =
(2.65)
(2.66)
Матрицы (2.65) и (2.66) называют матрицами
передаточных функций или передаточными матрицами: матрица (2.65)—
по управлению., а матрица (2.66) — по возмущению.

Передаточные матрицы дают полное описание многомерных
систем (объектов) при нулевых начальных условиях. С их
помощью уравнения (2.60) или (2.62) многомерной системы в
изображениях Лапласа можно записать в следующем виде:
Y (s) = W'^ (s) и (s) + W (s) F (s). (2.67)
Действительно, согласно определению (2.63), когда
изображения всех возмущающих воздействий и параметров
управления, кроме и J (s), равны нулю, имеем
Yi{s)=^Wb{s)Uj{s), i=^\ р; / = U...,m.
Аналогично, из (2.64)
Yi{s)==Wl;{s)Fj{sl р; /^1 /.
В общем случае, когда все параметры управления и
возмущающие воздействия отличны от нуля, используя принцип
суперпозиции, можем записать
yi{s)=- 2 S K(s)F,{sl / = 1 р. (2.68)
Очевидно, (2.67) является матричной формой записи
полученной системы (2.68).
Рассмотрим способы вычисления передаточных матриц.
Первый способ, указанный выше, основан на использовании
определений (2.63) и (2.64). Второй способ основан на
соотношениях
W« (s) - (s) В (s); Wf (s) - Д-^ (s) С (s). (2.69)
Эти соотношения получают следующим образом. Умножим
слева обе части матричного уравнения (2.62)
A(s)Y(.s)=^B(.s)U(s) + C(.s)F(s)
на обратную матрицу (s). Тогда получим
Y {$) = А-1 (S) В (S) и (S) 4- А-1 (s) С (s) F (s).
Приравнивая правую часть полученного уравнения к правой
части равносильного ему уравнения (2.67), получим
соотношения (2.69).
Как известно из курса высшей алгебры, обратная матрица
4i(s)...^ip(s)"''^
|A(s)f
^^pi(s)... Лрр(5)^

Здесь Aij (s) — алгебраическое дополнение элемента (s).
Знак Т обозначает операцию транспонирования.
Пример 2.7. Пусть система (объект) описывается уравнениями
£/i-h£/i + £/2 = «i-f Л; i/i-h£/i+{/2 = W2 + /2'
Перейдем к изображениям Лапласа (при нулевых начальных условиях)
(s2 + S) Y, (S) + Kg (s) = и, (s) + F, (s);
(s + 1) Y, (s) + sY, {s) = (s) + f, (s).
В Матричной форме эта система записывается так:
A(s) Y(s)-B(s)U(s) + C(s)F{s).
где
A(s) =
S2 + S
1 О
О 1
Найдем обратную матрицу A-i(s):
|A(s)| = (s+l)(s2_l); Аг,=8; Л2=
21--1;
• + s\ A-i(s)-
1
1
s -(s+1)
(s+l)(s2-l) L -1 s^ + s
—1
s2 + s
Так как В (s) и С (s) являются единичными матрицами, то
W" (s)-W^ (s)-A-i (s).
Весовые или импульсные переходные матрицы. Пусть
управляющий параметр Uj = б (t), а остальные управляющие
параметры и возмущающие воздействия равны нулю. При этом
решение (2.59) многомерной системы при нулевых начальных
условиях обозначим ш"; (О, (О.---- ^р/ (О- Эти функции
называют весовыми или импульсными переходными
функциями. Функция oyj/ (t) описывает реакцию системы на i-u
выходе при действии в точке приложения у-го параметра
управления единичного импульса и называется импульсной переходной
или весовой функцией по /-му параметру управления и t-му
выходу. Матрицу
w«(/) =
составленную из весовых функций по управлению, называют
импульсной переходной или весовой матрицей по управлению.

Аналогично определяют импульсную перехо;^ную или весовую
матрицу по возмущению:
Здесь w\j (t), wlj (t) — решение (2.59) многомерной
системы, когда /i = б (t), а все остальные возмущающие
воздействия и параметры управления равны нулю.
Весовые матрицы, как и передаточные матрицы, дают
полное описание многомерной системы (объекта).
Установим связь меаду весовыми и передаточными
матрицами.
Согласно определению (2.63) передаточной функции Wij (s),
Y^{s) = W^,f(s)Uj{sl r^l....,p. (2.70)
Так как Uj (s) = L{6 (0} = 1 и уг (t) == w4f (t) при Uj =
= 6 (^) и остальных входных воздействиях, равных нулю, то
из уравнения (2.70)
n(.s) = L{<(Ol-=j wb{t)e-^^dt, (2.71)
f = 1,.-..р; /= 1,..., rn.
Аналогично можно показать, что
W[f{s)^L[w{f{t)\==Jw[i{t)e-'^dt, /=1 р, /-=!,...,/.
о
(2.72)
Таким образом, передаточные функции (элементы
передаточных матриц) равны изображению Лапласа от весовых функций
(элементов весовых матриц).
В матричной форме (2.71) и (2.72) принимают вид
с»
W (s) = L (w (0> = J w (0 e-'' dt;
CO

По определению, интеграл от матрицы равен матрице
интегралов от ее элементов.
Запишем формулу для определения выходных величин по
весовым матрицам при произвольных входных воздействиях.
Учитывая, что оригиналами от передаточных функций
являются весовые функции, и используя теорему о свертке, из
(2.68)
т I .
УЛ^)=- 2 S H/(5)F,(s).
переходя к оригиналам, получим
т оо
ydt)^ S f wti{t^T)U^(T)dT +
/ оо
4-
-t J wyt-T)U(T)dT, t-l,....,p.
Эта система в матричной форме записывается как
у (О f w« (^ ^ т) u (т) йт + J (/ -т) f (т) dT.
Таким образом, связь между выходными и входнЫхМи
величинами с помощью весовых матриц записывается так же, как и в
одномерном случае.
Запись дифференциальных уравнений в нормальной форме
Коши. При рассмотрении многих вопросов удобно, если
уравнения одномерных и многомерных систем записаны в виде
нормальной системы. Нормальной системой или системой в
нормальной форме Коши называют систему дифференциальных
уравнений первого порядка, разрешенных относительно
производных. В частности, нормальной системой линейных
дифференциальных уравнений называют систему
Xi- i aax^'r % i=I,....n. (2.73)
/=1 /=1 /-1
В матричной форме она записывается как
x = Ax + Bu + Cf, (2.74)

где
'^11- "in'
...
...
; А =
....
; u=
...
B =
••• ''iro
/Г
■c„...
Cli'
Матрицы-столбцы x, u и f также называют векторами. Вектор
X называют фазовым вектором или вектором состояния, а его
координаты Хг, — фазовыми координатами. Вектор и
называют вектором управления или просто управлением, а его
координаты «1, ... Um — параметрами управления: Вектор
f называют вектором возмущения или просто возмущением, а
его /-Я координата — /-м возмущением или /-м возмущающим
воздействием.
Наряду с неоднородным уравнением (2.74) рассмотрим
однородное уравнение
х = Ах. (2.75)
Пусть х<^) = (х<1) кО^У, х<2) = (х<2> ,...,jc<2))7',...,
= (x<y), х<^>)^ образует п линейно независимых решений
этого уравнения. Любую такую систему называют
фундаментальной системой решений уравнения (2.75). Составим
матрицу, полагая в качестве ее i-ro столбца t-e решение из
фундаментальной системы:
Ф(ty
xV^{t),.,x[^Ut)
L х<«>(0...хГ(0 .
Эту матрицу называют фундаментальной матрицей
уравнений (2,73) — (2.75). Если при ^ = /о фундаментальная
матрица обращается в единичную, то она называется
нормированной. Используя произвольную фундаментальную матрицу
Ф (О, нормированную (обозначим ее X {t, Q) можно
представить в виде
X (/, /о) = Ф (О Ф-* (д; X (/„ g = Е. (2.76)

с помощью нормированной фундаментальной матрицы
решение неоднородного уравнения (2.74) при всех ^ и х (^о)
= х*^ можно представить в виде соотношения
X (О = X (Л to) + X (/. т) [Ви (т) + С/.(т)1 dx, (2.77)
и
которое называется формулой Kouiu, В справедливости этой
формулы легко убедиться непосредственной подстановкой в
уравнение (2.74), воспользовавшись при этом матричным
уравнением
Х(^д=^АХ(/,/о); Х(^о, д-=Е,
которое справедливо во всех t. Это уравнение следует из того,
что каждый столбец фундаментальной матрицы является
решением (2.75).
Отметим ряд основных свойств нормированной
фундаментальной матрицы. Воспользовавшись (2.76), для любых t, t'
и to легко получить следующие равенства:
X (t, X (/:, /о)—X (Л /о); х-1 (/, g X(/о, 0.
Если матрица А постоянна, то фундаментальная матрица
X (ty to) зависит только от разности t — to и имеет вид X (t~
— /о) ^ A^f-^o;. Матричная функция е а(^~^о; называется
экспоненциальной матрицей или матричным экспоненциалом
и определяется суммой ряда
еА(^-^о) ^ Е+ А (t-t^) + ^ А^(t-to)' +... +
-hJ-A-(^-g- + .... (2.78)
п\
Рассмотрим уравнение, сопряженное (2,75): z = — A^z.
Если Z (t, to) -V- нормированная фундаментальная
матрица этого уравнения, т. е.
= - Z (t, to); z (/о. g - Е.
at
то формулу Коши можно представить в виде
X (О - (to. t) X (g + j (to. t) [Bu (T) + Cf (T)l dT. (2.79)

Действительно, дифференцируя тождество X (t, Q /,
Х-Ч^ ^о) = Е. получаем
или
AX g x-1 g + ^ (^ ^ -o.
Из последнего уравнения
= ~Х-1(/, gA.
или после транспонирования
dt
Сравнивая это уравнение с уравнением для Z (t, g, получаем
2(лд^[Х-1(л toW
или
z^g о-=>^-Чд о-х(^ д.
При подстановке этого выражения в (2.77) получается (2.79).
пример 2.8. Пусть система описывается уравнениями
или в матричной форме уравнением
X = Ах 4- В«,
где
Найдем нормированную фундаментальную матрицу, пользуясь
(2.78). Так как
А =
0 г
0
; в-=
0 0.
.1
'0
1
"0
0'
А" =
0
0"
0
0.
0
0
.0
0.
Х(^-/о) = еА<^-^°>
1 0
0 г
т t~t^-
+
.0 0
0 1.
0 0.

Согласно формуле Коши, решение неоднородного уравнения при
X (/о) = х*^ имеет вид
х(0 =
t
. (•
I t~x
0
xo-l-j
.0 1
.0 1
Ц.
откуда прн скалярной записи получим
t i
л^ЛО—-л:? + (/-~/о)^?+J (t-x)u(x)dx\ x^(t)=--x%+l^u{x)dx.
Преобразование дифференциальных уравнений к
нормальной системе. Дифференциальные уравнения, разрешимые
относительно старшей производной, всегда можно привести к
нормальной системе. Рассмотрим, как преобразуются
уравнения одномерной стационарной линейной системы управления.
Пусть система управления описывается уравнением
(rt) (п-П
с^оУ+агУ +...+а„^ = 6о"- (2.80)
Введем новые переменные
Xi = y\ Х2г=хз;...; х„_,=^х„. (2.81)
Из (2.81) и (2.80)
7-- - (^1 + + ... + йп Xi) + и. (2.82)
«о «о
Объединяя (2.81) и (2.82), получим нормальную систему
1, 2,..., п—1;
х,,^ ^-(«iXnH-a2X„_i + ... + a„Xi) + —
(2.83)
эквивалентную исходному уравнению (2.80). Используя
обозначения (2.81), легко определить решение системы (2.83),
имея решение уравнения (2.80), и, наоборот, определить
решение уравнения (2.80), имея решение системы (2.83).
Рассмотрим более общий случай, когда система
управления описывается уравнением
(п) (n-l) (m) (m-1)
аоУ + сцУ +.^^+any^boU + bxU т<п, (2.84)
или в символической форме

Учитывая, что в этом уравнении дифференциальные
операторы при выходной и входной величинах и обратные им
операторы коммутативны, запишем его в виде [3]
(b^p^ + b,p^~' + ... + bJ-^y^
= К р'^ + Gi -» + ... + а J-^« = Xi
или
у = Фо Р"^ + Ьг + bj X,; (2.85)
^ = К+ «1 р'^-» 4-... 4- Xi. (2.86)
Введем обозначения
Xi = Х2\ = Xgj...; =^Хп. (2.87)
Учитывая их, из уравнения (2.86) получаем
Хп = '-(^i-^n 4-a2^n-i+ + Xi) + — w.
Объединяя это уравнение с уравнениями (2.87), получаем
нормальную систему
= t=: 1.2,..., п —1;
Хп^ - {ai Хп^+ ^2 4 ... х^) 4 — i^,
Оо Со
эквивалентную исходному уравнению (2.84). Выходная
переменная системы управления и новые переменные связаны
соотношением [см. (2.85)1
у &о Wi + biX^ + ,,, + ft,^ xi.
Рассмотрим, наконец, как преобразуется к нормальной
системе общее уравнение одномерной стационарной линейной
системы управления с двумя внешними воздействиями,
которое запишем в виде
(п) (п—1) (п) (п—1)
У + агУ +... f a„i/ = bn« + bn-i W +...4^« +
in)
+ Cnf + Cn^if 4-... + ^о/- (2.88)
Здесь для удобства коэффициенты в правой части
пронумерованы в обратном порядке. Кроме того, в уравнение (2.88) вклю-
чены'производные входные величин и и / до п-го порядка
включительно. Но такая запись не нарушает общности, так как

если в действительности порядки старших производных
входных величин меньше п и равны m и / соответственно, то это
значит, что в уравнении (2.88) коэффициенты Ь„ = bn-i = ...
= bm+i = О и = - Cf^i = 0. Уравнение (2.88)
может быть преобразовано в нормальную систему вида
(2.89)
n— 1
где коэффициенты и pj определяют из следующих
соотношений:
1,..., п -1; а„-6о— 2 ^n-k^hl
Po^^ni К j=^Cj~ 2 «n-ft-;Pft,
(2.90)
Выходная величина у связана с фазовыми координатами
равенством
= + ао«+Р(/. (2.91)
Доказательство эквивалентности уравнения (2.88) и системы
(2.89) при условии (2.90) и (2.91) имеется, например, в [81.
§ 2,9, Нестационарные линейные системы
Нестационарными линейными системами или линейными
системами с переменными параметрами называют системы,
которые описываются линейными дифференциальными
уравнениями с переменными коэффициентами. Для их Описания по-

мимо дифференциальных уравнений могут быть использованы
передаточные функции, переходные и весовые (импульсные
переходные) функции, частотные функции и их
характеристики. Кроме того, для графического представления
нестационарных систем могут быть использованы структурные схемы и
графы. Однако методы, основанные на графических
представлениях, не так эффективны, как в случае стационарных систем.
Правила преобразования структурных схем и графов,
установленные при изучении стационарных систем, в случае
нестационарных систем несправедливы.
Рассмотрим некоторые способы описания одномерных
нестационарных систем. Они могут быть обобщены на
многомерные системы так, как это было сделано при описании
стационарных линейных систем.
Так как для линейных систем (как стационарных, так и
нестационарных) справедлив принцип суперпозиции, то'для
простоты можем ограничиться рассмотрением систем с одним
входом.
Уравнение одномерной нестационарной системы (объекта)
с одним входом в общем случае можно записать в виде
(п) (пг-1) (т) (т—1)
^b^,{t)u (2.92)
или, в символической (операторной) форме
Q(p.t)y-R (р. t) и, (2.93)
где нестационарные линейные дифференциальные операторы
Q (Р, t) ^ а, (О р- ^ а, (О ^ + ... а, (t);
R{р. О - ь,(t)p'^ + b,(t)P'--' + ...-['bm(0.
Весовые функции. Как уже было определено, весовой
функцией называют решение уравнения (2.92) при и (t) 6 (t — т)
и нулевых «начальных» условиях, т. е. функцию, которая
описывает реакцию на единичный импульс системы, находящейся
в момент приложения импульса в исходном состоянии. Здесь
т обозначает момент приложения импульса и в определении
под начальными условиями понимают значения выходной
величины и ее производных в момент т. При рассмотрении
стационарных систем обычно в качестве начала отсчета времени при-

нимают момент приложения входного сигнала и
поэтому в этих случаях полагают т = 0. В данном случае
этого де.лать нельзя. Реакция нестационарной системы
зависит не только от времени / — т, отсчитываемого от момента
приложения импульса, но и от самого значения т. Поэтому
весовая функция нестационарной системы — обозначим её
W {t—т, т)—являются функцией от двух переменных* от
текущего времени t и момента т приложения импульса.
Реакция — процесс на выходе системы — не может
возникнуть до приложения входного сигнала: следствие не может
предшествовать причине. Поэтому
w{t—x, т) = О при /< т. (2.94)
Это условие называют условием физической осуществимости
или условием физической реализуемости, В случае
стационарной системы условие физической осуществимости имеет вид
W (О = о при ^< 0.
Получим формулы, определяющие связь между выходной
и входной величинами нестационарной линейной системы
управления через ее весовую функцию. Так как, по
определению. W (t — т, т) есть решение уравнения (2.93) при и {t) =
6 {t — т), то можем записать
Q (я, t)w{t-x, т) - /? (р, t)b{t- т). (2.95)
Умножим обе части на « (т) dx и проинтегрируем по т от —сю
до С50. а затем, вынеся коэффициенты уравнения за знак
интеграла (это возможно, так как они не зависят от т) и поменяв
местами операции интегрирования и дифференцирования,
получим
оо оо
Q{p,t) j w(t—T,x)u{-z)dx=R{p,t) J и{\)Ь(1-х)Лх. (2.96)
— GO — ОО
Из определения дельта-функции
оо
J u{T)b(t—x)dT=u{t),
— оо
поэтому (2.96) можно переписать в виде
оо
Q{pJ) j w{t—x,x)u{x)dx = R{p,t)u{t).

Из последнего равенства, которое выполняется тождественно,
вытекает, что функция
оо
^/(0= j w{t—T,x)u{i)dT (2.97)
— оо
является решением уравнения (2.93) при произвольном
заданном и (t). Нижний предел интегрирования х = — оо в (2.97)
совпадает с моментом подачи входного воздействия. Поэтому
(2.97) является искомой формулой, определяющей связь
между выходной и входной величинами нестационарной линейной
системы в «установившемся» режиме. Учитывая условие
физической осуществимости (2.94), формулу (2.97) можно
записать также в виде
t
y{t)= J w(t — x,x)u{x)dx. (2.98)
— оо
Аналогично, умножив обе части равенства (2.95) на и (т) dx
и проинтегрировав их от О до оо, получим формулу
оо
i/(/)=-J w{t-x,x)u{x)dx.
определяющую выходную величину нестационарной линейной
системы, когда на ее вход подается воздействие и (i) в момент
/ = 0. С учетом условия физической осуществимости ее также
можно записать в виде
^(/) = |ш(/~-т, х)и{х)dx.
Если зафиксировать переменную т, то весовая функция
W (t — т, т) будет функцией от одной переменной t, зависящей
от параметра т, и называться нормальной весовой функцией.
Нормальная весовая функция определяет изменение выходной
величины системы в течением времени при подаче на ее вход
единичного импульса в заданный момент т.
Если зафиксировать переменную t — рассматривать ее как
параметрI — то весовая функция w (t — х, х) будет функцией
от одной переменной х и называться сопряженной весовой
функцией. Сопряженная функция определяет зависимость реак-

ции системы в фиксированный момент / от моменту т
приложения единичного импульса.
Передаточные функции. Передаточная функция W (/?, О
нестационарной системы в операторной форме определяется
также, как и передаточная функция стационарной сисгемы
(в операторной форме) и равна отношению оператора R (р, t)
воздействия к собственному оператору Q (р, /):
W'Cp, 0-=«(а 0/Q(p,0.
Понятие передаточной функции W (s, t) в изображениях
Лапласа требует уточнения. Его нельзя определять как
отношение изображений выходной и входной величин, так как при
этом не ясно, как вычислять W (s, i) по заданному
дифференциальному уравнению системы. Кстати, между передаточными
функциями W (р, t)\iW (s, /) нет такой простой связи, как это
было между передаточными функциями W {р) (s)
стационарных систем.
Перейдем к определению передаточной функции W (s, t).
Для этого воспользуемся физическим свойством частотных
передаточных функций.
Как известно, частотная передаточная функция W(j(o)
стационарной системы имеет следующий физический смысл: ее
модуль равен отношению амплитуд гармонических колебаний
на выходе и входе системы, а ее аргумент—сдвигу фазы.
Частотная передаточная функция W (/со) стационарной системы
связана с ее передаточной функцией W (s) соотношением
Аналогичная связь должна существовать между частотной
передаточной функцией W (/со, t) нестационарной системы и ее
передаточной функцией W (s, t). Поэтому, определив
частотную передаточную функцию W (/со, /), автоматически получим
определение передаточной функции W (s, t).
Как будет показано дальше, при подаче на вход
нестационарной линейной системы гармонического сигнала на ее
выходе устанавливается «гармонический» сигнал той же частоты,
но с переменной амплитудой. И частотную передаточную
функцию W (/со, t) определим как такую, зависящую от параметра
t комплекснозначную функцию от частоты, у которой модуль
равен отношению амплитуд «гармонических» колебаний на
выходе и входе нестационарной системы, а аргумент — сдвигу
фазы.

Для системы с весовой функцией w (t — т, т) таким
свойством обладает функция
оо
W (/со, о j ш (0, ? —G) е-^'^в dd. (2.99)
о
Это соотношение примем за определение частотной
передаточной функции нестационарной линейной сисгемы с весовой
функцией W (t — т, т). Для ее передаточной функции W (s, f)
из (2.99) получаем
оо
W(s,t)^^w(6, t~в) е~«вdo. (2.100)
о
Передаточные функции W (/со, t) и W (s, /) называют
параметрическими,
Итак, параметрической частотной передаточной функцией
нестационарной линейной системы (с весовой функцией (w (t —
— г)) называют функцию (/со, t), определяемую
соотношением (2.99). Параметрической передаточной функцией
нестационарной линейной системы (с весовой функцией w (t — т,т))
называют функцию W (s, t), определяемую соотношением
(2.100).
Докажем, что функция W (/со, /), определяемая
соотношением (2.99), действительно обладает свойствами частотной
передаточной функции.
Пусть на вход нестационарной линейной системы с весовой
функцией W {t — т, т) подается гармонический сигнал и =
= cos соЛ Представим его в виде сухМмы
и^^иг + Щ^-^ е/^' + ^
2 2
Используя (2.98)
t
y(t)== J w(t-T,r)u(x)dr
— оо
при u=ui=-^ получим
i

Сделаем замену переменной t — т = G. Тогда
оо
yAt)=-!^\^w(G, t—Q)d<^(t-^) de =
оо
= ^ ^i<^t J (G, / —6) e-/^e rfo.
Введем обозначение lF(/(o, 0=-" [ ьу(в, ^ —e)e-/<^^dG.
При этом последнее выражение для {t) принимает вид
у^ (О W (/О), t) ^ d<^t (2.101)
Аналогично, при и e~f*^^ получим
Г/ПО-(-/со, 0'Y^e-/<o^ (2.102)
где
оо
Щ .^/0), /) = j (6, / ---ё) е/^в do.
о
Решения (2.101) и (2.102) можно переписать в виде
Ух (О = А (О), О еЯ<о<+ф«^. 01;
(t) ^ А (о), О ^ е-Я<о/+Ф«о. оJ,
где
А (О), О .11^' (/со, 01; Ф (со, t) = arg (/со, О-
Пользуясь принципом суперпозиции, для выходной
величины у при и = Um COS (Ot ПОЛуЧИМ ^ = + f/z = (сО, О X
X Um COS [Ш/ + ф (со, 01.
Таким образом, действительно модуль функции W (/(о, t),
определяемой (2.99), равен отношению амплитуд выходного и
входного гармонических сигналов, а ее аргумент — сдвигу
фаз.
Установим зависимость между изображениями (Лапласа)
выходной и входной величинами.

Перепишем (2.98) у (t) = \ w {t— т, т) и (т) dx, используя
—оо
замену переменной / — т = 9, в следующем виде:
оо
y{t)^{ w{e,t—Q)u{t-Q)dd, (2.103)
о
Представим входную величину с помощью обратного
преобразования Лапласа:
u{t)=— f t/(s)e'Ms,
2л/ J
(To—/оо
где и (s) ^ L {и (0), и подставим ее в (2.103):
Наменяв порядок интегрирования, получим
у{1)^Л^ J «7(s)e^« J ш(е, ^—e)e-e«deUs.
Очевидно, внутренний интеграл равен параметрической
передаточной функции W (5, /). Поэтому можем записать
(Уо-Ь/«)
(То —/оо
Этот интеграл совпадает с обратным преобразованием Лата-
са. Поэтому, обозначив Y (s, t) изображение выходной
величины у (t), получим
Г (S, t) = Г (s, /) и (s). (2.104)
Из этого уравнения следует, что параметрическая
передаточная функция равна отношению изображений выходной н
входной величин.
Если известна параметрическая передаточная функция и
изображение входной величины, то ho (2.104) можно
определить изображение выходной величины, а затем, пользуясь
таблицами или каким-либо другим способом, найти и саму
выходную величину.

Параметрическую передаточную функцию можно отыскать,
пользуясь ее определением (2.100), если известна весовая
функция. Но проще ее можно определить по
дифференциальному уравнению.
Пусть нестационарная линейная система описывается
дифференциальным уравнением
Qip.t)y it). - R ip, t) и (О,
где
Q(P. t) (0 + «1 (0P"-» -f-... + an (0.
R {p. t) = b, (0 + bx (t) p-^-y +... + 6,Л0.
Тогда ее параметрическая передаточная функция
подчиняется дифференциальному уравнению
+ -!-^^=R(M). (2.105)
«I df
где
Q-Q(s,/)-ao(/)5- + aj(Os"-^+...+«n(0; 1 (2 106)
/?(5.0-fco(0s'" + bi(0s'«-^ -Ь...-f \
Дифференциальное уравнение (2.105) для параметрической
передаточной функции имеет такой же порядок, что и
дифференциальное уравнение системы. Него решение так же сложно,
как и решение исходного уравнения. Поэтому рассмотрим один
из приближенных методов решения уравнения (2.105).
Перепишем его в следующем виде:
Q (S, /) W (S, t)^ R (S, t) + N {W (s, t)), (2.107)
где
ds dt 2! ds^ dt^
1 d^'Q d^'W
(2.108)
Решение будем искать в виде ряда
W{s, /), - Wois, t)+ Wxis. t)+ ...
В качестве нулевого приближения примем
Wois, t)=^ R (s, t)/Q(s, /). (2.109)

Это будет передаточной функцией системы с «замороженными»
коэффициентами. Для вычисления первой поправки (s, О
подставим в правую часть уравнения (2.107) полученное
нулевое приближение, а в левую часть — сумму нулевого
приближения и первой поправки. Тогда для {s, t) получим
Wx (s, t)^-N {Wo (s, t)}/Q (5, t). (2.110)
Аналогично для f-й поправки получим
W, (s, t) - N {Wt,, (s, t)}/Q (s, 0. (2.111)
Пример 2.9. Найдем параметрическую передаточную функцию
нестационарной системы, которая описывается уравнением
В данном случае
Q (S. /) = aos 4- fli + at\ R (s. bo;
Уравнение (2.107) принимает вид
(aoS + аг + at) W (s, t)^ 6o + iV ( Г (s.
где N [W (s. 0} == aodW/dt.
Для нулевого приближения и первой поправки на основании
(2.109) и (2.110) можем записать
Wo (s. О ^ V(oos -Ь fli + at); (s, t) сшо V(aos + «1 + aQ^.
Пользуясь (2.111), можно вычислить последующие поправки. Но если
а мало, то можно ограничиться только первой поправкой и тогда
W(s,t)^W,(s, t)+W, is. f) = ^o(a.s+.+cc/)^ + aao6o .
(aos + ai + at)^
Квазистациоиарные системы. Если коэффициенты
уравнения (2.92) нестационарной системы изменяются медленно, то
такую систему называют квазистационарной. При описании
квазистационарных систем широко используют метод
замороженных коэффициентов. Этот метод является приближенным,
и основан он на «замораживании» коэффициентов; в
уравнении нестационарной системы переменные коэффиценты аДО
и bi {t) заменяются постоянными коэффициентами at {t') и
bi {t')y равными значениями исходных коэффициентов в какой-
либо фиксированный момент времени Передаточная
функция системы с замороженными коэффициентами равна
нулевому приближению (2,109) передаточной функции
нестационарной системы при фиксированном времени t = t\

Принимается что коэффициенты уравнения
нестационарной системы изменяются медленно (система квазистационарна),
если за время переходного процесса они изменяются
незначительно. Здесь под временем переходного процесса
понимается минимальное время; по истечении которого (с момента
приложения единичного импульса) абсолютные значения весовой
функции системы с замороженными коэффициентами не
превышают некоторой заданной достаточно малой положительной
величины.
Если промежуток времени, на котором рассматривают
процесс квазистационарной системы, является большим, то
изменения коэффициентов ее уравнения могут быть значительными.
Тогда при использовании метода замороженных коэффицен-
тов весь промежуток времени разбивают на несколько
интервалов и на каждом интервале систему описывают
уравнениями с постоянными коэффициентами, равными значениям
переменных коэффициентов в какой-либо момент времени из
рассматривает мого интервала.
Формула Коши. В нормальной форме Коши уравнения
одномерной или многомерной нестационарной линейной системы
в обш.ем случаеимеют вид
= S ctij{t)xj+ ^bi,{t)ui + 2 cu{t)fi^ t = n,
j=\ i=\
(2.112)
или в матричной записи
X - А (/) X + В (/)'U + С (О f. (2.113)
Здесь X обозначает фазовый вектор, и — вектор управления
или задающего воздействия, f — вектор возмущающих
воздействий.
Пусть Ф (О обозначает фундаментальную матрицу
уравнения
х«А(Ох, (2.114)
т. е. матрицу, столбцы которой образуют п линейно
независимых решений уравнения (2.114). Тогда матрица
Х(^ д=Ф(ОФ~мд
является нормированной фундаментальной матрицей. Если
известна фундаментальная матрица Х(^, д, решение (2.113)

при начальном условии х (/q) = определяется формулой
Коши
оо
х(0=Х(^ to)x^+ ^X{t, T)[B(T)u(T) + C(T)f(T)]dT.
о
Эта формула позволяет определить решение неоднородного
уравнения (2.113), если известна какая-либо система из п
линейно независимых решений однородного уравнения (2.114).
§ 2.10. САР напряжения генератора постоянного
тока. Математическое описание
Рассмотрим в качестве примера вывод дифференциальных
уравнений и передаточных функций системы
автоматического регулирования (САР) напряжения генератора постоянного
тока, блок-схема которой приведена на рис. 2.29. Она состоит
из электронного усилителя У, двигателя постоянного тока с
независимым возбуждением Д, являющегося исполнительным
элементом, генератора Г (объекта регулирования) и делителя
напряжения ДН, выходное напряжение которого в
сравнивающем устройстве вычитается из заданного Uq. Определим
сначала дифференциальные уравнения и передаточные функции
отдельных элементов, входящих в рассматриваемую систему.
Начнем с объекта регулирования.
Генератор. Управление генератора производится путем
изменения переменного сопротивления включенного в цепь
возбуждения (рис. 2.30, а). Обозначив через R^,^ его
номинальное значение, т. е. значение R^, при котором ток в цепи
возбуждения принимает номинальное значение е^.ц, можно
записать
Отклонение Д/? переменного сопротивления
пропорционально углу ф поворота вала двигателя:
ДТ? = — С1ф. (2.115)
Здесь Ci — положительная постоянная, знак минус указьгоа-
ет, что при повороте вала двигателя в положительном
направлении сопротивление R^^ уменьшается, в отрицательном —
увеличивается. Таким образом, входной (управляющей)
величиной генератора является угол ф, а выходной — падение

ud
ДН
Рис 2.29
^г2
9
f<ri
'6
напряжения Ur на
нагрузке.
Составим уравнение
динамики генератора
без учета влияния
гистерезиса, вихревых
токов и т. п. На рис. 2.30, б
приведена
эквивалентная электрическая схема
генератора. На ней и
— активное и
индуктивное сопротивления
обмотки возбуждения,
бг — э. д. с. генератора,
г„ — активное
сопротивление обмотки якоря
(его индуктивным
сопротивлением
пренебрегаем), —
сопротивление нагрузки
(нагрузка предполагается
активной). Э. д. с.
генератора связана с током
возбужден и я
нелинейной зависимостью
er=F{hl (2.116)
Рис. 2.30
примерный график
которой приведен на рис.
2.30, е. Дополнительное сопротивление выбирается таким,
что током через него по сравнению с током нагрузки можно
пренебречь. С учетом сказанного можно записать:
для цепи возбуждения
Us-{r. + Rn.u + ^R)i. + Lsdijdt; (2.117)
для якорной цепи
e, = {rn + Rn)i^; u,^R,in. (2.118)
В статическом режиме при номинальных значениях токов
возбуждений /р.н и якоря tj,.!. эти уравнения принимают вид
"в.н=(^ + /?п.н)/в.н; (2.119)
^г.н=(^я+/?н.н)^я
н.н *я.н-
- (2.120)

Произведем линеаризацию в рабочей точке,
соответствующей номинальным значениям токов возбуждения и якоря.
Подставим в (2Л17) Ib = ^*b.h + А/в и выражение (2Л15).
Отбрасывая малый член CiAtB<p более высокого порядка, чем Дг'в
и ф, и учитывая (2Л19), получим
или в символической форме
(T^p+l) - Й1ф, (2.121)
где
Произведя линеаризацию (2.116), получим
^г^^г.н + ^гД^в, (2.122)
где
OF
Со
ди
^в = 'в.н
Используя это выражение для и уравнение статики (2Л20),
уравнения (2.118) можно преобразовать к виду
с,М,= (-^+ 1 )Au,--^AR„i„. (2.123)
\ Ан.н / 'хн.н
Исключив ИЗ (2.121) и (2,123) Д/в. окончательно получим одно
уравнение, связывающее входную (управляющую) ф и
выходную Д^г величины и возмущение jF = ^rj„ генератора;
(Г^р ^l)Au, = k,xip + k,^(T^p + l)h (2.124)
где
В изображениях Лапласа это уравнение принимает вид
{T,s+l)U, (S) = k,, Ф (s) + k^{T,s + l)F (s),
где Ur (s) = L{Au^}; Ф (s) = L (ф); F (s) = L {/}. К
генератору приложены два внешних воздействия (ф и /), и он
описывается двумя передаточными функциями: передаточной
функцией Н^ф по управляющему воздействию и передаточной
функцией по возмущению. Для них имеем:
в операторной форме
Гф (р) = к,АТьР + 1); Wf ip) = Аг2.

или
(Т,р+1)Г^ + ^рц> ^-±^ (2Л26>
где Т„ = LJr'n — электрическая постоянная времени цепи
якоря.
На основе законов механики можно записать уравнение
для моментов
или
^р'<Р = Мер-Ме. (2,127>
где / — момент инерции вала двигателя (с учетом нагрузки);
Л1вр — вращающий момент; — момент сопротивления.
Вращающий момент пропорционален току якоря:
M«p-C4t^. (2.128)
Значение постоянной с^, как и Cg, зависит от тока
возбуждения и конструкции двигателя.
Исключив из (2.126), (2.127) и (2.128) момент М^^ и
ток /я, получим
Это уравнение можно преобразовать к виду
(Гя Т^ш Р^ + Гем Р + 1) РФ = "у -Ад2 (Гя Р + 1) Me, (2.1 29)
где Т^эм = Jt^'Jc^^ — электромеханическая постоянная
времени; = Сз и йдз = Гя/сяС4 — передаточные
коэффициенты.
В изображениях Лапласа уравнение двигателя принимает
вид:
(Т^я Т^.м?' + Гам5+ 1) 5Ф (S) = k^U^is) - Ад, (r^S + 1) Me(s),
(2 130)
где t/y (s) =1 {Ыу}; (s) = L {М}е.
Передаточные функции двигателя имеют вид:
по управляющему воздействию
iXn Твм 7\.м Р+1) Р '

по возмущению (моменту сопротивления М^)
Ц7 (р) = ^пг{ТяР+1)
W^is)^ .
Структурная схема приведена на рис. 2.31, в, откуда видно,
что математическая модель двигателя может быть
представлена: по возмущению — в виде последовательного
соединения форсирующего, колебательного (или двух
апериодических, если Т^^ < 2VT^ Тэм) и интегрирующего звеньев, а по
управляющему воздействию — колебательного (или двух
апериодических, если Т.^^ < 2VTJ\^) и интегрирующего
звеньев.
Усилитель, сравнивающее звено, делитель напряжения.
Эти элементы описываются уравнениями
Uy^kyBi 8 = ^0—ид, u^=^kj^u^, (2.131)
где ky — коэффициент усиления усилителя; йд —
«коэффициент деления» делителя.
Линеаризованное уравнение генератора связывает
отклонение с внешними воздействиями ф и /. Поэтому небходи-
мо преобразовать систему уравнений (2.131), так, чтобы она
зависела от отклонения Awj, (а не от w^).
Запишем последние два уравнения системы (2.131) следу-
щим образом:
Е= WoH + Auo—(ид.н + А^д); «д.^-1-А^д = йд(«,.н+Аи,), (2.132)
где "д.н — номинальные значения задающего воздействия
и напряжения делителя, определяемые равенствами
«д.н = К "г.ш t^OH = Ид.„. (2,133)
Уравнения (2.132) с учетом (2.133) можно записать так:
АИд = Аи^; е = Awo — Д«д-
В изображениях Лапласа уравнения усилителя,
сравнивающего устройства и делителя напряжения принимают
следующий вид:
Uy{s)^k^E(s); £(s)=t/o(s)-t/«(5); Uj,{s)^k^UAsh
где £(s)=L{6}; U,{s)^L{Au,}; [/д (s) - L {А«д}.

Рис. 2.32
Передаточные функции усилителя Wy и делителя В^д имеют
вид
Эти звенья являются пропорциональными. Сравнивающее
звено имеет два входа и описывается двумя передаточными
функциями: передаточной функцией по входу, куда
подается уменьшаемое,
и передаточной функцией по входу, куда подается
вычитаемое.
Уравнение и передаточные функции системы. На рис. 2.32
приведена структурная схема САР напряжения генератора,
составленная по полученным уравнениям и передаточным
функциям отдельных элементов. Используя правило нахождения
передаточной функции одноконтурных систем, определим ее
передаточные функции.
Передаточная функция разомкнутой системы
и7 *
где k = ЛуЛдг^гх^д — передаточный коэффициент
разомкнутой системы.
Передаточные функции прямой цепи:
по задающему воздействию Auq П^'ц.^ = И^/Лд," по моменту
сопротивления Мс
по возмущению / W^f = ^^2-

Для передаточных функций замкнутой системы (относительно
выхода Д^г) имеем: по задающему воздействию Aw©
^ W^J{\ 4 W) = \ —,
по моменту сопротивления
где &о ^riT^H*. = *д2 ^ii; по возмущению /
Уравнение системы в символической форме имеет вид
или
(йо s" + + og + Оз S + Oj) = Л„ Ано —
— фо S + fci) + (Оо s^ + aiS^ + chS^i- Оз S) Л
Об обозначениях передаточных функций. Выше
использовались два обозначения для передаточных функций: W (р)
и W (s). Первое указывает на то, что передаточная функция
рассматривается как некоторый оператор, осуществляющий
преобразования входной величины и (t) в выходную х (t). Это
записывается в виде соотношения
x = W{p)u. (2.134)
Для вычисления х по заданным и и W (р) требуется решать
дифференциальное уравнение, т. е. достаточно простой
расшифровки W (р), позволяющей перевести W (р) на язык
алгоритмов, нет, и (2.134) следует рассматривать скорее как
символическую запись дифференциального уравнения. Второе
обозначение W (s), полученное из изображений Лапласа X (s) и
и (s) для переменных х (t) ни (/), указывает на то, что W (s)
рассматривается как обычная функция комплексной
переменной S. В этом случае можно записать
X{s) = W{s)U{s) (2.135)

с оговоркой, что это соотношение справедливо для нулевых
начальных условий. В этом случае W (s) используется,
например, для вычисления частотных характеристик W (/со).
Двойственность происхождения функций W^(s) и УХ/ (р)
привела в литературе и к двойственности в обозначениях у
разных авторов. Мы в дальнейшем будем использовать, как
правило, обозначение W (s) для передаточных функций или
(s) = О для характеристических уравнений, сохраняя
обозначения W (р) для тех случаев, когда W(p) явно
рассматривается как оператор, а не как комплексная алгебраическая
функция, а также тогда, когда W (s) не совпадает с W (р),
например для систем с переменными параметрами. В последнем
случае часто в число аргументов функции W будет наряду с
оператором р вводиться и параметр, от которого она зависит,
например W (р, /).

Глава 3
jV(w)
УСТОЙЧИВОСТЬ
ЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
§ 3.1. Понятие устойчивости
На любую автоматическую систему
всегда действуют различные внешние
возмущения, которые могут нарушить ее
нормальную работу. Правильно
спроектированная система должна
устойчиво работать при всех внешних
возмущениях.
В простейшем случае понятие
устойчивости системы связано со
способностью ее возвращаться (с определенной
точностью) в состояние равновесия
после исчезновения внешних сил,
которые вывели ее из этого состояния. Если
система неустойчива, то она не
возвращается в состояние равновесия, из
которого ее вывели, а либо удаляется от
него, либо совершает вокруг него
недопустимо большие колебания.
Наблюдения показывают, что
некоторые положения равновесия системы
устойчивы к небольшим возмущениям, а
другие принципиально возможные
равновесные положения практически не
могут быть реализованы.
Наглядно устойчивость равновесия
представлена на рис. 3.1, где изображен
шар, расположенный в некотором
углублении (рис. 3.1, а), на некоторой
выпуклой поверхности (рис. 3.1, б), на
плоскости (рис. 3.1, в).
Положение равновесия шара
характеризуется точкой i4 о- В случае,
изображенном на рис. 3.1, а, при всяком откло-

нении шара от положения равновесия, например в точку Лх,
он будет стремиться снова возвратиться к положению
равновесия — в точку А о (при отсутствии сил трения) или к
некоторой конечной области, окружающей положение
равновесия, например в точку Л 2 (при наличии сил трения).
Такое положение равновесия устойчиво. Случай,
изображенный на рис. 3.1, б, соответствует неустойчивому положению
равновесия. Рис. 3.1, в соответствует безразличному
равновесию. На рис. 3.1, г состояние равновесия устойчиво лишь
до тех пор, пока отклонение не вышло за некоторую
границу, определяемую, например, точкой В. Выйдя за эту
границу, шар уже не вернется в точку Л о, а будет двигаться
вправо от точки В либо все время удаляясь, либо до нового
состояния равновесия в зависимости отформы поверхности, т, е.
в конечном счете в зависимости от уравнений движения шара.
Поэтому в общем случае, рассматривая нелинейные
системы, вводят понятие устойчивости «в малом», «в большом» «в
целом». Система устойчива «в малом»,
если констатируют лишь факт
наличия области устойчивости, но не
определяют каким-либо образом ее
границы. Систему называют устойчивой
«в большом», когда определены
границы области устойчивости, т. е.
определены границы области начальных
отклонений, при которых система
возвращается в исходное состояние,
и выяснено, что реальные начальные
отклонения принадлежат этой
области. В том случае, когда система
возвращается в исходное состояние при
любых начальных отклонениях,
систему называют устойчивой «в целом».
Устойчивость «в целом» для
определенного класса нелинейностей
называют «абсолютной» устойчивостью.
Так, например, случай,
изображенный на рис. 3.1, а, соответствует
устойчивости «в целом», а случай,
изображенный на рис. 3.1, г, может
соответствовать. либо устойчивости
«в большом», либо устойчивости «в
малом». Очевидно, что система, устойчи- p^c 3.I

вая «в целом», будет устойчива «в большом» и «в малом»;
система, устойчивая «в большом», будет устойчива и «в малом».
На рис. ЗА, д изображено еще одно принципиально
возможное для нелинейных систем состояние равновесия, которое
называют полу устойчивым.
Для того чтобы дать определение устойчивости равновесия,
вводят понятие о невозмущенном состоянии равновесия, соо-^-
ветствующем состоянию покоя в точке Aq на рис. 3.1, а, и
возмущенном состоянии, соответствующем, например, точке
i4i, в которую внешняя сила привела шар и затем прекратила
свое действие. Система будет устойчивой, если из возмущенного
состояния она перейдет в некоторую заданную область,
окружающую невозмущенное состояние равновесия.
В рассмотренном выше примере с шаром вопрос об
устойчивости решается довольно просто. Однако следует заметить,
что в общем случае далеко не всегда ясно, при каких
условиях равновесное положение системы будет устойчивым.
Понятие устойчивости можно распространить и на более
общий случай, когда в качестве невозмущенного состояния
рассматривают не положение равновесия системы, а ее движение,
например движения системы по некоторой наперед заданной
траектории.
Допустим, что заданное движение системы при отсутствии
возмущений должно определяться некоторым законом
изменения независимых координат у\ У2 (О» •••» Уп (О- По
аналогии со случаем равновесия положения, заданное движение
называют невозмущенным движением. Внешние возмущения,
действующие на систему, вызовут отклонение действительного
движения системы от заданного. Действительное движение
системы называют возмущенным движением. Пусть
действительное движение системы определяется независимыми
координатами Ух (О, У2 (О» Уп (О- В общем случае у^ (t) фу\ (t),
y2{t)^y2{ty yn{t)^yl(ty
Заданное^евозмущенное движение будет устойчивым, ее-
ли после приложения внешнихшл (возмущений), которые
затем снимают, мозмутенное движение по истечении
некоторого времени войдет в заданную область Ху^ (f) — yl (01 ^ е^,
где Ei = const — заданные величины, I = 1,2,..., п.
Чтобы проиллюстрировать сказанное, предположим, что
невозмущенное движение происходит по траектории А, а
возмущенное движение происходит по траектории Б (рис. 3.2, а).
Возьмем на этих траекториях две произвольные точки и
N^, отвечающие одному и тому же моменту времени /. При

Рис. 3.2
устойчивом движении траектория Б должна быть близка к
траектории А.
Следует заметить, однако, что близость траекторий А и Б
является необходимым условием устойчивости движения, но
недостаточным. Действительно, расстояние между точками
}\JA л 1\/Б^ отвечающими одному и тому же моменту времени,
может возрастать не только для расходящихся, но и для
близких траекторий (рис. 3.2, б).
§ 3.2. Общая постановка задачи устойчивости
по А. М. Ляпунову
Впервые строгое определение устойчивости было дано
русским ученым А. М. Ляпуновым в 1892 г. в работе «Общая
задача об устойчивости движения». Отсутствие такого определения
часто приводило к недоразумениям, так как движение,
устойчивое в одном смысле, может оказаться неустойчивым при другом
понимании этих слов, и наоборот. Определение
устойчивости А. М. Ляпунова оказалось настолько удачным и
наилучшим образом удовлетворяющим многим техническим задачам,
что оно в настоящее время принято как основное.
Пусть движение системы автоматического управления
описывается дифференциальными уравнениями, которые могут
быть приведены к виду
(3.1)
где У1-- вещественные переменные, характеризующие
состояние системы управления (обобщенные координаты); — из-
вестные функции переменных ^/i, у^*^--, Уп^ времени удовлет-

воряющие условиям существования и единственности
решения.
" Исходное состояние системы при t = однозначно
определяется начальными значениями переменных tji, которые
обозначим //ю. i/2o» ^no-
Каждой совокупности начальных значений ^/ю, г/го.---»
Упо соответствует единственное решение (3.1) для всех t > to
Уь = yiWio, У20 Упо^ 0. (3.2)
Решение (3.2) описывает какое-либо движение системы,
определяемое исходным состоянием.
Некоторое вполне определенное движение системы, подле-
ошщее исследованию на устойчивость, называют невозмуи^ен-
ным двиэюением»
Заметим, что выбор невозмущенного движения является
произвольным. Это может быть любое возможное движение
системы, как установившееся, так и неустановившееся.
Допустим, что в качестве невозмущенного движения выбрано
такое, которое описывается заданными функциями времени
Уг^У\{()\ У^.-=уШ --'^yn-ynit), (3.3)
Предположим, что функции ^/^* (t) являются частным
решением дифференциальных уравнений (3.1), т. е.
dyt (t)ldt ^ Y, (у\, yh yt i). (3.4)
удовлетворяющим начальным условиям при t ^
Ух-У\{и)\ У2-У2((о)\ Уп--Уп{(^У (3.5)
В частном случае, когда параметры системы не
изменяются со временем и функции не зависят явно от t, движения
(3.3) являются установившимися. Им отвечают решения
у] = const, (3.6)
служащие корнями уравнений
Yiitj^, у^, Уп)-0. (3.7)
Изменим условия (3.5), дав начальным значениям
переменных у^, ^2» ••■» Уп небольшие по модулю приращения е^, eg,...,
бп, т. е. пусть при t ~ to
Ух ^- У\ (to) -1- еь У2 = У1 {to) + 62; ; Уп - Уп (to) f (3.8)
Движение системы, отвечающее измененным начальным
условиям ^(3.8), называют возмущенным движением. Другими ело-

вами, возмущенным овижением системы называют всякое
иное движение системы, отличное от нево^муи^енного.
Введем новые переменные
^i^yi{()-yHt), (3.9)
равные разности переменных yi в возмущенном и
невозмущенном движении. Переменные Xi называют отклонениями или
вариациями величин yi. Если все отклонения равны нулю
хг = 0; Х2 = 0; Хп = О, (3.10)
то возмущенное движение yi (/) будет совпадать с
невозмущенным движением yi (/), т. е. невозмущенному движению
отвечают нулевые значения переменных х^.
Пусть при / = /о переменные Xi принимают какие-либо
начальные значения Xto, из которых по крайней мере одно не
равно нулю:
Xi = Xio = е^. (3.11)
Начальные значения отклонений (3.11) называют
возмущениями.
А. М. Ляпуновым было дано следующее определение
устойчивости: невозмущенное движение называют устойчивым по
отношению к переменным х^, если при всяком произвольно
заданном положительном числе е, как бы мало оно ни было, можно
выбрать другое такое положительное число 6 (г), что при
всяких возмущениях х^, удовлетворяющих условию
2 xfo^b, (3.12)
i== 1
и при любом t > to будет выполняться неравенство
i хН/)<8, (3.13)
1^ I
в противном случае движение неустойчиво.
Определению устойчивости А. М. Ляпунова можно дать следующую
геометрическую интерпретацию- Совокупность отклонений х^, jcg,
.... в л-мерном пространстве переменных х^, х^, Хп определяет
точку М (ее называют изображающей точкой). В возмущенном
движении при изменении величин х^^ х^ Хп изображающая точка будет
описывать некоторую траекторию. Невозмущецному движению д^^ — О
отвечает неподвижная точка — начало координат.
Рассматривая, например, случай, когда i = 3, построим в трех-
3
мерном пространстве координат Xi две сферы; сферу е = 1L ^х^ о. ра-

диусом "l/fi и сферу 6^2 xfo с радиусом 1/6. Выберем радиус
сферы е произвольно малым. Если невозмущенное движение устойчиво,
то для этой сферы должна найтись другая сфера 6, обладающая
следующим свойством; изображающая точка УИ, начав свое движение из
любой точки Мо, лежащей внутри или иа поверхности сферы 6, при своем
дальнейшем движении остается всегда внутри сферы е, никогда не
достигая ее поверхности (рис. 3.3).
Если же невозмущениое движение неустойчиво, то траектория
изображающей точки М с течением времени пересечет сферу е изнутри
наружу (или попадет на ее поверхность) при сколь угодно близком
положении точки Мо к началу координат.
Заметим, что при г > 3 надо рассматривать движение
изображающей точки в многомерном пространстве относительно
гиперповерхностей (гиперсфер) и рассмотрение теряет наглядность.
Практически устойчивость данного невозмущенного
движения означает, что при достаточно малых начальных
возмущениях возмущенное движение будет сколь угодно мало
отличаться от невозмущенного движения. Если невозмущенное
движение неустойчиво, то возмущенное движение будет
отходить от него, как бы малы ни были начальные возмущения.
Если невозмущенное движение устойчиво и при этом любое
возмущенное движение при достаточно малых начальных
возмущениях стремится к невозмущенному движению, т. е.
limxi(t)^0, (3.14)
то невозмущенное движение называют асимптотически
устойчивым.
При асимптотической устойчивости изображающая точка
с течением времени должна неограниченно стремиться к
началу координат, не выходя из сферы е.
Отметим некоторые особенности определения устойчивости
по А. М. Ляпунову. Во-первых, предполагают, что
возмущения налагаются только на начальные условия, иначе говоря,
возмущенное движение происходит
при тех же силах (источниках
энергии), что и невозмущенное движение.
Во-вторых, устойчивость
рассматривают на бесконечно большом
промежутке времени. В-третьих, возмущения
предполагаются малыми. Несмотря на
эти ограничения, определение А. М.
Ляпунова устойчивости движения
является эффективным и плодотвор-
Рис. 3.3 ным в приложениях.

_§ 3.3. Теорема А. М. «Ляпунова об устойчивости
движения по первому приближению
Когда известно общее решение дифференциальных
уравнений движения (3.1), можно непосредственно определить
значения переменных t/i (t) в возмущенном движении, составить
вариации Xi = yi (t) — y7it) и, исследуя их, решить вопрос об
устойчивости невозмущенного движения yj (t). Однако, как
правило, исследование устойчивости • движения производят
не путем анализа общего решения, а методами, основанными
на качественном анализе дифференциальных уравнений
возмущенного движения, которьш удовлетворяют отклонения
(вариации) л:^.
Чтобы вывести уравнения возмущенного движения, найдем
из (3.9) переменные yi (t) = yl {t) + Xi{t) и подставим эти
значения yt (t) в дифференциальные уравнения движения (3.1).
Тогда
dynt)/dt+dXi(t)idt = Y,{y]+Xx, yl + x.,, i/A + x^, t). (3.15)
Если правые части уравнений (3.15) допускают разложение в
степенные ряды Тейлора, то после этого разложения по
степеням Xi получим
^ + ^^глуь у1 .... Уп, 0+(-р-) + •
dt dt \ dxi Jo
- + ('^)/n+Ri{Xu .V2, X,), (3.16)
где Ri (лг;, Xg,..., Xn) совокупность членов, зависящих от
отклонений Xi в степени выше первой.
Учитывая (3.4), будем иметь
dXi(t)/dt=:aixXx + ai.^x^ + ,.,+ainXn + Ri(xx, х^, Хп). (3.17)
В уравнениях (3.17) коэффициенты
^.•.==(^1 (3.18)
в общем случае являются функциями времени t, в частности,
они могут быть постоянными. В дальнейшем, если не будет
оговорено особо, будем считать коэффициенты а,-;^ постоянными.
Уравнения (3.17) называют дифференциальными
уравнениями возмишенного движения.

Если отклонения Xt достаточно малы, то, пренебрегая
^£(•^1. -^2. Хп), получим линеаризованные уравнения
aXi/dt==aiiXi + ai2X2 + ..,+ainXn, / = 1, 2, п, (3.19)
называемые уравнениями первого приближения.
Во многих случаях устойчивость движения исследуют по
уравнениям первого приближения. Это объясняется не только
простотой этого метода, но также и тем, что знания процессов,
происходящих в реальных системах, позволяют надежно
определять только первые линейные члены. Однако на
основании уравнений первого приближения можно дать иногда
неверное заключение об устойчивости движения. Поэтому,
естественно, возникает вопрос об определении условий, при
выполнении которых по уравнениям первого приближения можно
дать правильные ответы об устойчивости движения. Эту
исключительно важную и принципиальную для теории
автоматического управления задачу впервые поставил и решил
А, М. Ляпунов.
Системе уравнений (3.19) соответствует
характеристическое уравнение, которое можно записать следующим образом:
Un—s ai2 ■-. fliu
^21 ... Ozn
= 0. (3.20)
Из (3.20) можно найти его корни s,-, где = 1, 2, п,
которые в общем случае имеют вид 5^ = а£ Ч= /сог, гдеа^- и о)^ —
вещественные и мнимые части корней соответственно.
Для исследования устойчивости систем по их
линеаризованным уравнениям принципиально важны следующие
теоремы А. М. Ляпунова, которые приведем без доказательства.
Теорема 1. Если вещественные части всех корней Si
характеристического уравнения (3.20) первого приближения
отрицательны, то невозмущенное движение асимптотически
устойчиво.
Теорема 2. Если среди корней Si характеристического
уравнения (3.20) первого приближения имеется хотя бы один
корень с положительной веш^ественной частью, то
невозмущенное движение неустойчиво.
Если среди корней характеристического уравнения
имеется один или несколько нулевых корней, а вещественные
части остальных корней отрицательны, то этот случай называют

критическим. .Как показал Ляпунов, в критическом случае
устойчивость (неустойчивость) невозмущенного движения не
может быть оценена по уравнениям первого приближения, так
как она зависит от вида нелинейной функции Ri (xi, Xg,....
Хп)^ и поэтому в этом случае требуется рассмотрение
дифференциальных уравнений возмущенного движения (3.17) в их
исходном виде.
Теоремы Ляпунова имеют весьма важное значение, так как
они позволяют судить об устойчивости нелинейных систем по
их линеаризованным уравнениям (уравнениям первого при-
ближения).
§ 3.4. Условия устойчивости линейных систем
автоматического управления
Покажем, как на основе изложенного выше определения
устойчивости А. М. Ляпунова можно найти условия
устойчивости линейных (линеаризованных) систем автоматического
управления.
Дифференциальное уравнение линейной системы
автоматического управления, записанное для регулируемой
выходной величины X (/) при наличии управляющего воздействия
g (t), имеет вид
(Со + аф^-» + ...+ fl^) X (О -
= (bop-^ + Wp^-' +...+bJg(0, (3.21)
где flo» о,п и Ьо> — постоянные коэффициенты,
а р = didt — оператор дифференцирования.
Изменение регулируемой величины х (t) при произвольном
внешнем воздействии g (t) представляет собой решение
уравнения (3.21):
X (t) = (О + (ty (3.22)
в (3.22) первое слагаемое (t) — вынужденная
составляющая, имеющая тот же характер, что и правая часть уравнения
(3.21). Она определяется как частное решение неоднородного
дифференциального уравнения (3.21) с правой частью:
(ао ;t7« + + + а^) х^ (t) =
= {ЬоР^ + ЬгР^--'+^..+6т) е (О- (3.23)

Второе слагаемое jc^b (О — свободная (переходная)
составляющая, которая определяется общим решением однородного
дифференциального уравнения (3.21) без правой части:
(«оР" + агР^-' + ... + aj (t) = 0. (3.24)
Обычно в теории автоматического управления
интересуются устойчивостью вынужденной составляющей х^ (t)
переходного процесса. Поэтому за невозмущенное движение системы
необходимо принять вынужденную составляющую
переходного процесса л:в (t). Тогда возмущенным движением будет любое
возможное в системе изменение регулируемой величины х (t),
а отклонением или вариацией — свободная составляющая
Xcnit) = X (1)^x^(1). -
Возмущениями, по А. М. Ляпунову, являются начальные
значения Хсв, которые возникли в мoмeнI,^^^JoJПoд
действием внезапно подействовавших дополнительных внешних сил,
т. е. начальные значения лГсво- Дифференциальными
уравнениями возмущенного движения первого приближения в
данном случае будут уравнения (3.24).
В соответствии с определением устойчивости по А. М.
Ляпунову система будет асимптотически устойчивой, если с
течением времени при < оо свободная составляющая будет
стремиться к нулю, т. е. лгсв (О 0. Чтобы найти эту
составляющую, необходимо решить дифференциальное уравнение (3.24):
^»-^дв(0 +...+а„Хе.(0=-0. (3.25)
Решение уравнения (3.25) находят как лгсв (О = С'е*^.
Дифференцируя это выражение п рази подставляя в (3.25),
после сокращения на общий множитель Се^* получаем
ао s'* + ах -» +... = 0. (3.26)
Полученное алгебраическое уравнение (3.26) называют
характеристическим уравнением. Его корни s^, Sg, Sn
будут определять характер переходного процесса в системе.
Нетрудно заметить, что по своему виду левая часть уравнения
(3.26) совпадает с дифференциальным оператором при
выходной величине в уравнении (3.21), поэтому
характеристическое уравнение получают обычно, приравнивая к нулю
дифференциальный оператор при выходной величине в исходном
дифференциальном уравнении (3.21), т. е.
а,р^ + агр--' + ... + ап^О. (3.27)

Jw
-^52
1 -JiOi
Isj
Рис 3.4
Следует заметить,
однако, что в
характеристическом уравнении (3.27),
р г= S означает уже не
символ дифференцирования,
а некоторое комплексное
число.
Решецие
характеристического уравнения степени
п содержит п корней.
Корни характеристического
уравнения обыкновенного
линейного
дифференциального уравнения с
постоянными коэффициентами могут быть вещественными,
комплексными попарно сопряженными, мнимыми попарно
сопряженными, нулевыми. В общем случае
Si = «£ + /(Of. (3.28)
На рис. 3.4 показаны возможные положения корней в
комплексной плоскости корней s при
Si = «1; S2 = tta + /0)2; S3 = а2 — /(Og; = 0; S5 =
= — «5 ; Sq = —aQ + ]щ; 5^ = — — /we-
Если все корни разные, то их называют простыми. Если
среди корней есть одинаковые, то их называют кратными.
Обычно корни с отрицательными вещественными частями
принято называть левыми, поскольку они в комплексной
плоскости корней расположены слева от мнимой оси, а корни с
положительными вещественными частями — правыми корнями.
Условие устойчивости линейной системы формулируется
следущим образом: для того чтобы линейная система была
асимптотически устойчива, необходимо и достаточно,
чтобы все корни ее характеристического уравнения (3.27) были
левыми.
Указанное условие устойчивости легко пояснить, рассматривая
решение однородного уравнения (3.25), которое при отсутствии
кратных корней имеет вид
1=1
(3.29)
где Si — корни характеристического уравнения (3.27); Ct —
постоянные интегрирования, определяемые из начальных условий.

Заметим» что корни характеристического уравнения si зависят
только от вида левой части дифференциального уравнения (3.21)
линейной системы. Постоянные интегрирования Ci зависят и от вида
правой ее части, поэтому быстота затухания и форма переходного
процесса определяются как левой, так и правой частями исходного
дифференциального уравнения (3.21). Однако, поскольку в понятие
устойчивости входит только факт наличия или отсутствия затухания
переходного процесса, устойчивость линейной системы не зависит от вида
правой части дифференциального уравнения (3.21) и определяется только
характеристическим уравнением (3.27).
Прн составлении (3.21) предполагалось, что внешние
возмущающие воздействия отсутствуют. Если записать дифференциальные
уравнения движения системы относительно возмущающего воздействия, то
в этом случае левая часть (3.21) остается без изменения, а правая будет
иметь другой вид. Так как характер переходного процесса в линейной
системе определяют только по виду левой части дифференциального
уравнения (3.21), то для определения качественной картины
переходных процессов лрактйчески безразлично, записать ли исходное
дифференциальное уравнение для управляющего или возмущающего
воздействия.
Вещественным корням характеристического уравнения st = at
в (3.29) соответствуют слагаемые, представляющие собой экспоненты
Очевидно, что отрицательным (левым) корням < О
соответствуют затухающие экспоненты (рис. 3.5, а), положительным (правым)
корням aj > О — возрастающие экспоненты (рис. 3.5, б) и при
нулевых корнях щ = О слагаемые представляют собой прямые,
параллельные оси времени (рис. 3.5, в). ^
Комплексные корни характеристического уравнения всегда
бывают попарно сопряженными: st = af + /сй£ и si^i = OLg — /q^.
Слагаемые, определяемые этими корнями в (3.29), могут быть при
использовании ' известной формулы Эйлера е*'^^^ = cos о)^ t±:
±/sino)i/ представлены в виде de^^^'^'^^^^ + Q+i €^^*~'*^«^'=
= i4e^' sin {<di ^ + ярг), где и "^i — новые постоянные.
В этом случае прн сс^ < О получаются затухающие колебания
(рис. 3.5, г), при > О ~ расходящие колебания (рис. 3.5, д) и прн
сс£ = О — незатухающие колебания (рис. 3.5, е). Для устойчивости
и в этом случае необходимо выполнение условия < 0. В самом
общем случае среди корней характеристического уравнения (3.27) могут
быть кратные корни. Если имеется г кратных корней s^, то в (3.29)
появятся слагаемые вида
(Ci, г-1 t'-^ + t+Ci^) eV.
Если корень Sj at ± /(^i имеет отрицательную вещественную
часть ai < О, то множитель е*'* будет с течением времени убывать.
Множитель в скобках неограниченно растет, поэтому мы имеем
неопределенность ор-О. Однако известно, что ебыстрее стремится к
нулю, чем выражение Q,r-i поэтому при ai < О эта группа
слагаемых с течением времени также стремится к нулю.

б)
в)
г)
е)
Система i/mouQuda
Um Хс§ (i) =0 у
di£-0
Система неустойяиба
Рис. 3.5
Система нейтралит
Таким образом, видно, что в самом общем случае для устойчивости
линейной системы необходимо и достаточно, чтобы все корни
характеристического уравнения (3.27) были левыми.
Вычисление корней просто лишь для характеристического
уравнения первой и второй степеней. Существуют общие
выражения для корней уравнений третьей и четвертой степеней,
но эти выражения громсйдки и практически малопригодны.
Общие выражения для корней уравнений более высоких
степеней вообще невозможно написать через коэффициенты
характеристического уравнения. Поэтому важное значение
приобретают правила, которые позволяют определять
устойчивость системы без вычисления корней. Эт правила называют
критериями устойчивости, С помощью критериев
устойчивости можно не только установить, устойчива система или нет,
но и выяснить, как влияют на устойчивость те или иные
параметры и структурные изменения в системе.
Критерии устойчивости могут быть разделены на
алгебраические и частотные, С математической точки зрения все Крите-

рии устойчивости эквивалентны, однако целесообразный вы-
^ор того или иного критерия устойчивости при решении
конкретных задач позволяет провести исследование устойчивости
наиболее простым путем.
§ 3.5. Алгебраические критерии устойчивости
Алгебраические критерии устойчивости позволяют судить
об устойчивости системы по коэффициентам
характеристического уравнения
D (s) -ао s« + «1 s«-1 + ... + = 0. (3.30)
Из алгебраических критериев устойчивости наиболее
широкое распространение получили критерии устойчивости
Рауса и Гурвица.
Прежде чем познакомиться с ними, заметим, что
необходимым условием устойчивости системы любого порядка является
положительность всех коэффициентов характеристического
уравнения (3.30):
flo > 0; > 0; Un > 0. (3,31)
Действительно, в соответствии с теоремой Безу уравнение
<3.30) можно представить в виде произведения множителей,
содержащих корни s^, Sj. .... s^^:
«о is — Si)(s — ... (s — sj = 0. (3.32)
Если все корни характеристического уравнения будут
отрицательны, то все множители выражения (3.32) будут иметь
вид
fio is +. |ai|)(s + К I)... (s + К I) = 0. (3.33)
где = — |а^| — значения корней.
Производя перемножение в (3.33), получим (3.30), в
котором все коэффициенты будут определяться положительными
членами [a^l выражения (3.33), т. е. будут положительны.
/Если характеристическое уравнение (3.30) имеет комплекс-
ribie корни с отрицательными вещественными частями, то оно
может быть представлено в виде
До is + К|) is + Hal — /^2) is + КI + /(U2)... is +
+ Ы = О

или
ao(s + Ml(s + \cc2\r + ii^l] ... (s + lan|)=0. (3.34)
Уравнение (3.34) также приводится к виду уравнения
(3.30) с положительными коэффициентами.
Для систем первого и второго порядков необходимое условие
устойчивости является и достаточным условием
устойчивости^ поскольку в этом случае при положительных
коэффициентах характеристического уравнения все его корни
являются левыми. Однако для систем третьего и высших порядков
положительность коэффициентов характеристического
уравнения является необходимым условием устойчивости, но не
достаточным. В этом случае все вещественные корни
характеристического уравнения (если они есть)'левые, комплексные
же корни могут быть и правыми.
Критерии устойчивости Рауса и Гурвица позволяют по
коэффициентам характеристического уравнения (3.30) без
вычисления его корней сделать вывод об устойчивости системы.
Критерий устгойчивости Рауса. Этот критерий
устойчивости был в 1877 г. предложен английским математиком Э.
Раусом в виде некоторого правила (алгоритма), которое наиболее
просто поясняется табл. 3.1.
В первой строке табл. 3.1 записывают в порядке
возрастания индексов коэффициенты характеристического уравнения
(3.30), имеющие четный индекс: йо, Cg, G4. «в» во второй
строке — коэффициенты (3.30) с нечетным индексом: а^, «з,
CTg, ... .
Любой из остальных коэффициентов таблицы определяют
как
Ch,i^i-z-^^i Cfe+i. £-1» (3.35)
где
Г1^Сг,1^г1сг,г^г^ (3.36)
В (3.35) и (3.36) k — индекс, означающий номер столбца
табл. 3.1; / — индекс, означающий номер строки табл. 3.1.
Заметим, что число строк таблиц Рауса равно степени ха"^
рактеристического уравнения плюс единица («> + 1).
После того как таблица Рауса заполнена, по ней можно
судить об устойчивости системы. Условие ^ устойчивости Рауса
формулируется так: для того чтобы система автоматического
управления была устойчива, необходимо и достаточно, чтобы

Таблица 3.1
Коэффициент г.
Строка
(/)
Столбец
1
2
3
4
—
1
«2 = ^21
—
2
«1—^12
08 = ^22
...
Г8=ао/а1
3
C2S=Cf4-~''3C5
^33 = ^:6—''з ^7
...
Г4 = С1/Сз5
4
^14 = Оз —^4^23
^24 = 06—^4^33
^34—с?—^4^43
...
5
^1Б = С2з —ГбС24
^25 = ^33 —ГбСз4
^ЗБ = С4з—Гб С44
...
/
^2,1 = ^3, г-2 —^£ ^3. г-х
^3.£=С4,г-2—''£^4,£-1
...
...
...
...
...

коэффициенты первого столбца таблицы Рауса имели один и
тот же знак, т. е. при ао >0 были положительными:
Cii=^o>0; с^-=С1г>0; с^^>0\ ...; Ci, >0. (3.37)
Если не все коэффициенты первого столбца положительны,
то система неустойчива, а число правых корней
характеристического уравнения равно числу перемен знака в первом
столбце таблицы Рауса.
Критерий Рауса особенно удобен, когда заданы числовые
значения коэффициентов характеристического уравнения
(3.30). 1В этом случае определение устойчивости можно
выполнить довольно быстро даже при характеристических
уравнениях высокого порядка.
Форма алгоритма, с помощью которого составляют таблицу
Рауса, очень удобна для программирования ЭВМ, поэтому
критерий Рауса нашел широкое применение при
исследовании влияния на устойчивость либо коэффициентов
характеристического уравнения, либо отдельных параметров системы, не
очень сложным образом входящих в эти коэффициенты, с
помощью быстродействующих ЭВМ.
Пример 3.1. Пусть характеристическое уравнение системы £> (s) =
+ 6s^ + 21s* + 44s» + 62s2 + 52s + 100 = 0.
Для определения устойчивости системы по коэффициентам этого
уравнения составим таблицу Рауса (табл. 3.2),
Имеется две перемены знака коэффициентов первого столбца:
следовательно, система неустойчива, а характеристическое уравнение
имеет два правых корня.
Критерий устойчивости Гурвица. В Ш95 г. немецким
математиком А. Гурвицем был разработан алгебраический
критерий устойчивости в форме определителей, составляемых из
коэффициентов характеристического уравнения системы.
Из коэффициентов характеристического уравнения (3,30)
строят сначала главный определитель Гурвица
«5
Oi} аз
О ai Аз
«7
а.
О ао «2 ^4
0 0 0 0
О
О
О
а„
(3.38)

Таблица 3.2
Коэффициент
Строка
Столбец (Л)
1
2
3
4
1
ао=1
СГ2=21
С4 = 62
Сб=100
—
2
Cl =6
сз=44
Сб = 52
С7 = 0
Гз = со/с1- 1/6--0,167
3
ci3 = 21—0.167.44= 13,65
С2з=-62—0,167.52 =
Сзз= 100—0,167.0 =
0
= 53,3
= 100
'"4 == /Ci3 = 6/13,65 =^
4
Ci4 = 44—0,44.53,3 = 20,6
С24 = 52—0,44.100 =
С34 = 0—0,44.0=0
0
= 0,44
= 8
r5 = Cl3/Cl4 =
5
Ci5 = 53,3—0,66.8 = 48
С25= 100-0.66-0 с=
0
0
= 13,65/20.6-0,66
= 100
Гб=-с,д/с,5 = 20,6/48 =
6
= 8-^0.43.100= -35
С26 = 0—0,43-0 = 0
0
0
-0,43
r:=Ci5/Ci6 = 48/---35 =
7
Cj7--=l00-(-1.37).0 =
0
0
0
= —1,37
= 100

по следующему правилу: по главной диагонали
определителя слева направо выписывают все коэффициенты
характеристического уравнения от до в порядке возрас1ания
индексов. Столбцы вверх от главной диагонали Aonojiiisuor коэффи-
циентами характеристического уравнения с последовательно
возрастающими индексами, а столбцы вниз — кoэq}фициeнгa-
ми с последовательно убывающими индексами. На место
коэффициентов с индексами больше п {п — порядок
характеристического уравнения) и меньше нуля проставляют нули.
Отчеркивая в главном определителе Гурвица, как показано
пунктиром, диагональные миноры, получаем определители
Гурвица низшего порядка:
fll (h
Wo «2
«1 «3 «5
UQ ^4
^3
0 at
A. =
% fifs 0^5
Go «2 «4
0 fll flg
(3.39)
Номер определителя Гурвица определяется номером
коэффициента по диагонали, для которого составляют данный
определитель. Критерий устойчивости Гурвица формулируется
следующим образом: для того чтобы система
автоматического управления была устойчива, необходимо и достаточно, чтобы
все определители Гурвица имели з^шки, одинаковые со
знаком первого коэффициента характеристического уравнения
Cq, m. е. при flo > О были положительными.
Таким образом, при а^>0 для устойчивости системы не-
обходимо и достаточно выполнения следующих условий:
Аз
«о ^2
>0; Дз==
(h «3
flo «2 «4
flj fl3
О
>0;
fll flg flg
«О ^2 «4
О fll flg
ООО
... о
... о
... о
... fln
>о.
(3.40)

Раскрывая, например, определители Гурвица для
характеристических уравнений первого, второго, третьего и
четвертого порядков, можно получить следующие условия
устойчивости:
1) для уравнения первого порядка (п = !), т. е. ао s +
+ ai =0, условия устойчивости
^0 > 0; Oi > 0; (3.41)
2) для уравнения второго порядка (п = 2), т. е. floS^+
+aj^s + «2 = 0, условия устойчивости
ао > 0; > 0; а^ >0; (3.42)
3) для уравнения третьего порядка (п ^ 3), т. е. ао^ +
+ ajS^ + a2S + а^ = О, условия устойчивости
ао > 0; а, > 0; а^> 0; а^> 0; (3.43)
«1^2 -«о^з>0; (3.44)
4) для уравнения четвертого порядка (п=^4), т . е. a^s^ +
+aiS^ + a^s^^ + .а^8 + а^^ О, условия устойчивости
flo>0; fli>0; аа>0; а^>0; а^>0-, (3.45)
Оз (fli fl2 —fl^o йз) —^1 «4 > 0. (3.46)
Таким образом, необходимым и достаточным условием
устойчивости для систем первого и второго порядков является
положительность коэффициентов характеристического
уравнения. Для уравнения третьего и четвертого порядков кроме
положительности коэффициентов необходимо соблюдение
дополнительных неравенств (3.44) и (3.46).
При м ^ 5 число подобных дополнительных неравенств
возрастает, процесс раскрытия определителей становится
довольно трудоемким и громоздким. Поэтому критерий
устойчивости Гурвица обычно применяют при м ^ 4. При м ^ 5
целесообразно применять формулируемый ниже критерий
устойчивости Льенара — Шипара либо при использовании
критерия устойчивости Гурвица переходить к численным методам с
использованием ЭВМ.
В последнем столбце главного определителя Гурвица (3.38)
отличен от нуля только один коэффициент а„, поэтому
^n=ar.^г-г• (3.47)

Из (3.47), видно, что при > U для проверки устойчивости
системы достаточно найти только определители Гурвица от
до An-i- Если все определители Гурвица низшего порядка
положительны, то система находится на границе
устойчивости, когда главный определитель равен нулю:
Д,,=-а„Д^_,. (3.48)
Последнее равенство возможно в двух случаях: = О или
A,,_j = 0. В первом случае система находится на границе
апериодической устойчивости (один из корней
характеристического уравцения равен нулю); во втором случае — на гга-
нице колебательной устойчивости (два
комплексно-сопряженных корня характеристического уравнения находятся на
мнимой оси).
Используя критерий Гурвица, можно при заданных
параметрах системы принять за неизвестный какой-либо один
параметр (например, коэффициент усиления, постоянную
времени и т. д.) и определить его предельное (критическое)
значение, при котором система будет находиться на границе
устойчивости.
Следует заметить, что критерий Гурвица можно получить
из критерия Рауса, поэтому иногда критерий Гурвица
называют критерием Рауса — Гурвица.
Критерий устойчивости Льенара — Шипара. Для
исследования устойчивости систем автоматического управления,
имеющих порядок характеристического уравнения п ^ 3,
удобно применять одну из модификаций алгебраического
критерия устойчивости Гурвица, предложенную в 1914 г. П. Лье-
наром и Р. Шипаром.
Доказано, что в том случае, когда все коэффициенты
характеристического уравнения (3.30) положительны (а^ > О, ai >
><), ад > 0), из того факта, что положительны все
определители Ai, Ag, Ag,... с нечетными индексами, следует и
положительность определителей А. Гурвица Дд, Д4, Дв.
с четными индексами, и наоборот.
Поэтому в тех случаях, когда выполнены необходимые уело-
еия устойчивости, т. е. ао>0, ai>0,..., an >0, необходимые и
достаточные условия устойчивости сводятся к тому, чтобы
среди определителей Гурвица Дх, Ag, Д« были
положительны все определители с четными (или же все определители с
нечетными) индексами.

Таким образом, для того чтобы система автоматического
управления была устойчива, необходимо и достаточно, чтобы
выполнялись следующие неравенства:
Ai>0, Аз>0, А5>0,
или
А2>0, А4>0, Ле>0, ....
(3.49)
(3,50)
Последняя формулировка критерия устойчивости,
называемая критерием устойчивости Льенара — Шипара, требует
раскрытия меньшего числа определителей, чем обычный
критерий Гурвица, а поэтому особенно удобна при исследовании
устойчивости систем автоматического управления высокого
порядка.
Пример 3.2, Пусть характеристическое уравнение системы D (s) ==
= 12s* -f 2s2 + 4s + 50 = 0. Система неустойчива, так как
коэффициент ci = 0.
Пример 3.3. Характеристическое уравнение системы D (s) — 3s^ +
+ IDs* + 5s^ — 7s2 -|- s + 100 = 0. Система неустойчива, так как
«3 ^ —7 < 0.
Пример 3.4. Характеристическое уравнение системы D (s) =
= 2ss + 6^ + 10s + 15—0. Все коэффициенты этого
характеристического уравнения положительны, и определитель Гурвица Ag с четным
индексом равен
Со Сг
«1 ^2--Со сз = 6-10 —2.15 = 30>0.
Следовательно, система устойчива.
Пример 3.5. Характеристическое уравнение системы
D (S) = (1 + T^s) (1 + Тф) (1 + Т^) + К = О,
где К — коэффициент усиления разомкнутой системы; Т^* Т'г» —
постоянные времени отдельных динамических звеньев системы. Найдем,-
пользуясь критерием Гурвица, предельнее значение коэффициента
усиления разомкнутой системы К^^\ функцию постоянных времени
Тг. 5^2. 7^3-
Перепишем характеристическое уравнение в виде
D (S) = Т^Т^Т^ -f (Т^Т^ + ПГз + Г^Т^з) + (5^1 П + Т^) s+
-Ь 1 + = Gos^ + cis" + + аз = О, .
где ^ - Г1Г2Г3; «1 = Т^Т^ -V ПТ^ + T^Ts; а,=^ Тг+ Т^;
«3=1+^-

Согласно критерию устойчивости Гурвица, система третьего
порядка будет устойчива, если выполняются следующие неравенства:
> 0; fli > О, > О, сз > О, fliflg — со^з > 0.
В данном случае все коэффициенты характеристического
уравнения положительны, поэтому система будет устойчива, если
(ПТ^ + ПТ^ + Т^Т^) (П + -h Гз) > ^1^27^3 (1 +
Последнее неравенство можно переписать в виде
Ж (1 + Та + Тз) (1 + 1/т2 + 1/тз) ~ 1,
где
Предельное (критическое) значение коэффициента усиления, при
котором система будет находиться на границе устойчивости, равно
К^р = (I + -^2 + ts) (1 + 1/^2 + IZ-^s) - 1.
Из последнего выражения следует, что предельный коэффициент
усиления системы определяется ие абсолютными значениями постоянных
времени динамических звеньев, а их относительными значениями. Чем
более резко отличаются постоянные времени друг от друга, тем больше
Ккр- В частном случае, когда = Тд = 1, т. е. Ti = = Т^,
значение /Скр минимально и равно всего лишь Ккр ~ 8.
§ 3.6. Частотные критерии устойчивости
Частотные критерии устойчивости позволяют судать об
устойчивости систем автоматического управления по виду их
частотных характеристик. Эти критерии являются
графоаналитическими и получили широкое распространение, так как
позволяют сравнительно легко исследовать устойчивость
систем высокого порядка, а также имеют простую
геометрическую интерпретацию и наглядность.
Принцип аргумента. В основе частотных критериев
устойчивости лежит следствие из известного в теории функций
комплексного переменного принципа аргумента, который кратко
излагается ниже.
Пусть дан некоторый полином /г-й степени D (s) = aoS'^+
-^a^s^~^ + ... + Этот полином в соответствии с теоремой
Безу можно представить в виде D (s) = (s — Si) (s — Sg)...
... (s — Sn)y где Si = + /coj — корни уравнения D (s) = 0.
Ha комплексной плоскости s каждый корень геометрически
может быть изображен вектором, проведенным из начала
координат к точке Si (рис. 3.6, а). Длина этого вектора равна
модулю комплексного числа Sj, т. е. \Sil а угол, образован-

ный вектором с положительным направлением
действительной оси, — аргументу или фазе комплексного числа s^, т. е.
Arg
Величины (s — Si) геометрически изображаются векторами,
проведенными из точки к произвольной точке s (рис. 3.6, б).
В частном случае при s = /ш получим
D (/to) = «о (/со — Si) (/со — s3), (/со — Sn). (3.51)
Концы элементарных векторов (/со — Sj) будут находиться
на мнимой оси в точке s = /со (рис. 3.6, в).
В выражении (3.51) D (/со) представляет собой вектор,
равный произведению элементарных векторов (/со — s^) и
действительного числа «о-
Модуль этого вектора равен произведению модулей
элементарных векторов и «о*
|D (/со) I = flol/co — Sill /со — S2I...I /со — Sal (3.52)
а аргумент или фаза его равна сумме аргументов элементарных
векторов:
Arg D (/со) - Arg (/со — Si) + Arg (/со — S2)+...+
+ Arg (/со — s,,)- (3.53)
Условимся считать вращение против часовой стрелки
положительным. Тогда при изменении со от — оо до со каждый
элементарный вектор повернется на угол я, если его начало,
т. е. корень s^, расположено слева от мнимой оси, и на угол
— я, если корень расположен справа от мнимой оси (рис. 3.7).
Предположим, что полином D (s) имеет т правых корней и
п — т левых.
V
0 к ■ 0 (X
в) .,.
Рис. 3.6

претацйёй принципа аргумента и пшволяет судить об
устойчивости системы на основании рассмотрения некоторой
кривой., называемой кривой Михайлова.
Пусть дано характеристическое уравнение системы (3.30).
Левую часть характеристического уравнения называют
характеристическим полиномом
D is) - «о + «1 ^ + ... + (3.56)
Если подставить в этот полином чисто мнимое значение
S = /со, то получим комплексный полином
D (/со) = ао (/со)« + а, (/со)« -1 + ... + а^ - X (со) + / У (о) =
-D((o)e/^(^), (3.57)
где
Х(со) = ап—а„-2Со2 + «п-4^^—..., 1 щ
Г((о) -о)(ап-.1 -ап-з<«>Нап--б«*^...)1
называют соответственно вещественной и мнимой функциями
Михайлова; функции D (со) и -ф (со) представляют собой
модуль и. фазу (аргумент) вектора D (/со).
При изменении частоты w вектор D (jio), изменяясь по
величине и направлению, будет описывать своим концом в
комплексной плоскости некоторую кривую, называемую кривой
(годографом) Михайлова.
В соответствии с (3.55) угол поворота вектора D (/со)
вокруг начала ксюрдинат при изменении частоты со от О до сх>
равен
4 Arg D (/со) \tzV-^-f 0^ -2m).
Отсюда определяем число правых корней полинома D (s),
т. е.
Из (3.59) видно, что число правых корней т будет равно нулю
при одном-единственном условии
А Arg D (/ш) \%^^ - я/г/2. (3.60)
Условие (3.60) является необходимым, но не достаточным
условием устойчивости. Для устойчивости системы
необходимо и достаточно, чтобы все п корней характеристического урав-

нения были левыми; иначе говоря, среди них не должно быть
корней, лежащих на мнимой оси и обращающих в нуль
комплексный прлином D (/о)), т. е. должно выполняться еще одно
условие
D (/со) :^0. (3,61)
Формулы (3.60) и (3.61) представляют математическое
выражение критерия устойчивосги Михайлова: для того чтобы
система автоматического управления была устойчива,
необходимо и достаточно, чтобы вектор кривой Михайлова D (/со)
при изменении а> от О до оо повернулся, нигде не обращаясь в
нуль, вокруг начала координат против часовой стрелки на
угол пп/2, где п — порядок характеристического уравнения.
Заметим, что для усгойчивых систем кривая Михайлова
начинается при О) = О на вещественной положительной полуоси,
поскольку при > О все коэффициенты харакгерисгического
уравнения положительны и D{0) = > 0. Кроме того, для
устойчивых систем, описываемых обыкнЪвенными
дифференциальными уравнениями с постоянными коэффициентами,
фаза (аргумент) яр (со) с ростом частоты со должна возрастать
монотонно, т. е вектор Z)(/co) должен поворачиваться только
против часовой стрелки, поскольку с росгом частагы монагон-
но возрасгают имеющие одинаковые (положительные) знаки
фазы элементарных векторов (/со — s^), являющиеся
слагаемыми фазы вектора £>(/со) (см. (3.53)).
Учитывая сказанное выше, критерий устойчивости
Михайлова можно сформулировать так: для того чтобы система
автоматического управления была устойчива, необходимо и
достаточно, чтобы кривая (годограф) Михайлова при изменении
частоты со от О до оо, начинаясь при со = О на вещественной
положительной полуоси, обходила только против часовой
стрелки последовательно п квадрантов координатной
плоскости, где п — порядок характеристического уравнения.
Кривая Михайлова для усгойчивых систем всегда имеет
плавную спиралевидную форму, причем конец ее уходит в
бесконечность в том квадранте координатной плоскости,
номер которого равен степени характеристического уравнения.
На рис. 3.9 показаны типичные кривые Михайлова для
усгойчивых систем, описываемых уравнениями, начиная от
первого (л == 1) и кончая пятым (л = 5) порядком. Для
удобства сравнения коэффициенты во всех случаях приняты
одинаковыми.

Признаком неустойчивосш систегды является нарушение
числа и последовательности пройденных кривой Михайлова
квадрантов координатной плоскости, вследствие чего угол
поворота вектора D (/со) оказывается меньше, ч&л пп/2. Число
правых корней неустойчивой системы можно определить по
(3.59).
На рис. 3.10 показаны кривые Михайлова для
неустойчивых и нейтральных систем. Рис. 3.10, а — при со = О кривая
Михайлова начинается на отрицательной вещесгвенной
полуоси; система неустойчива. Рис. 3.10, б — порядок уравнения
п = 5, а кривая Михайлова находится вся в одном
квадранте (этому соответствует характеристическое уравнение D (s)==
== a^s^ + a^s^ + «2 = 0); сисгема неустойчива. Рис. 3.10, в —
нарушена последовательность прохождения квадрантов;
система неустойчива. Рис. 3.10, г—кривая Михайлова начинаег-
ся в начале координат, т. е. в характеристическом
уравнении имеется по крайней мере один нулевой корень; система
находится на границе апериодической устойчивосги;
небольшая дефоррлация кривой Михайлова (прерывистая линия)
делает систему устойчивой. Рис. Я. 10, д— кривая Михайлова
п^роходит при некотором значении частоты сок через начало
координат, т. е. в характерисгическом уравнении имеются
чисто мнимые корни =Ь /со^; система находится на границе
колебательной устойчивости; небольшая деформация кривой
Михайлова делает систему устойчивой (прерывистая линия).
Рис. 3.10, е — кривая Михайлова проходит через начало ко«
ординат, но небольшой деформацией кривой Михайлова
удовлетворить условиям устойчивосги нельзя; систеш
неустойчива.
Посгроение кривой Михайлова практически производится
либо методом контрольных точек, либо методом
вспомогательных годографов. Первый метод
сводится к определению ряда
точек кривой Михайлова, соагвет-
с1гвующих фиксированным
значениям часташ со^ включая
(обязательно) часготы точек пересечения
кривой с осями координат,
которые находятся как корни
уравнений (3.62) и (3.63). При втором
методе предварительно определяют
годографы отдельных звеньев си-
Рис. 3.9 стемы и по ним строят искомую
f7=2
ii 1
1
/ 1
ii 1 \ V

Рис. 3.10
кривую Михайлова, применяя правила умножения и
сложения векторов.
Анализируя годографы Михайлова, можно установить
следующее следствие из критерия устойчивости Михайлова. При
последовательном прохождении кривой Михайлова
квадрантов координатной плоскосги вещественная и мнимая оси
пересекаются ею поочередно. В точках пересечения кривой
Михайлова с вещесгвенной осью обращается в нуль мнимая функ-
тя Михайлова Y (со), а в точках пересечения кривой с
мнимой осью обращается в нуль вещественная функция X (со).
Пштому - значения частаг, при которых происходит
пересечение кривой с вещественной или мнимой осью, должны
являться корнями уравнений
X (со) = 0; (3.62)
К (со) = 0.
(3.63)
Вещественную X (о) и мнимую Y (со) функции Михайлова
можно представить графически в виде кривых (рис. З.П).
Точки пересечения этих кривых с осью абсцисс дают значения
корней уравнений (3.62) и (3.63). Если значения coq, cog,
СО4, ... есгь корни уравнения (3.63), а о)1,;о)з,;а)5—•
уравнения (3.62), причем соо < со2< o}4<...,o)i < соз< 0)5...,

Рис. 3.11
TO для устойчивой системы обязательно соблюдение
неравенства
0)о< COi< (02< 0>з< со4 < (оЬ< ... . (3.64)
В связи с указанным следсгвием можно привести другую
формулировку критерия устойчивости Михайлова: система,
автомшшческого управления будет устойчива тогда и только
тогда, когда вещественная X (со) и мнимая Y (со) функции
Михайлова, приравненные нулю, имеют все действип^ельные
и перемежающиеся корни, причем общее число этих корней
равно порядку харакшристического уравнения п, и при со = О
удовлегпворяю/пся условия
X (0) > О, Г' (0) > 0.
На рис. 3.11, а приведен прршер графиков X (со) и F (со)
для устойчивой системы, а на рис. 3.11, б — для неустойчивой
системы.
Для уравнений до шестого по{)ядка включительно условие
перемежаемости корней дает возможносгь легко провести
аналитическое исследование устойчивости, не вычерчивая кривую
Михайлова. При этом обычно определяюг только корни
уравнения У (со) = 0. Перемежаемскть корней уравнений X (о))=0
и F (со) О можно проверить подстановкой в X (со)
найденных корней уравнения У (со) = 0. Как видно из рис. 3.11 ,а,
знаки X (со) при подстановке возрастающих по абсолюгной
величине корней должны чередоваться.
Пример 3.6. Определить устойчивость системы,
характеристическое уравнение которой
D (S) = + 6s5 + 15s* + 20s3 + 15s2 -f 6s -Ь 1 = 0.

Подставляем s = /to к находим вещественную и мнимую функции
Михайлова:
X (О)) = —о)« + 15а>* ~ 15й)2 +1 = 0;
К (со) = 6) (бсо^ — 200)2 + 6) = 0.
Находим корни уравнений Y (о)) = О, т. е. щ = 0; 0)4 — З.ЗЗо)^ +
+1=0. откуда
<«)|.4= 1.67 гЬ 1/2.78-^1; w|=0.36; (о|=2,96.
Если перемежаются корни, то перемножаются и их квадраты,
поэтому нахождение (Og и со^ не обязательно.
Проверим, чередуются ли знаки X (со) при подстановке о)| и й>|.
X fco^) = -0,363 + 15.0,36» - 15.0,36 + I = -~2,51;
X (coj = -2,96» + 15-2,962 — 15-2,96 + 1 > 0.
Так как все корни Y (со) вещественны и знаки ординат X (со),
соответствующие этим корням, чередуются, то система устойчива.
Критерий устойчивости Найквиста. Этот частотный
критерий устойчивости, разработанный в 1932 т, американским
ученым Г. Найквистом, позволяет судить об устойчивсхгги
замкнутой системы по виду амплитудно-фазовой характеристики
разомкнутой сисгемы.
Пусгь передаточная функция разомкнутой сисгемы
+ . т<„. (3.65)
Подставляя в (3.65) s = /со, получаем частотную
передаточную функцию разомкнутой системы:
Г (/о) = ^ ^'"'^ ^ + ' + •••+
Q (/«) Со (/«)"+с, (/«)«- ^ + ...+Сп
= £/(<») + /Т((в) = Л(<о)е/*<'*), (3.66)
где {/ ((о) и К ((о) — действительная и мнимая части
частотной передаточной функции соответственно; модуль А (<о) и
фаза If (сй) частотной передаточной функции равны А (<») =
- VUH<o) + V^{<oy, ^ («) = Arctg Щ.
Если изменять частоту со от — с» до <х>, то вектор W (/со)
будет меняться по величине и фазе. Кривую, описываемую
концом этого вектора в комплексной плоскости, называют ампли-

тудно-фазовой xapaKtmpucmu-
кой разомкнутой системы
(рис. 3.12).
Амплитудно-фазовая
характеристика симметрична агноси-
тельно вещественной оси,
поэтому обычно вычерчивают только
ту часть ее, которая
соответствует положительным частотам
со^О (сплошная линия на рис.
3.12), а ветвь этой характерисш-
ки, соответствующая
отрицательным часютам со < О
(пунктирная линия на рис. 3.12), может быть найдена как
зеркальное отражение ветви, соответсгвующей положительным
частотам, относительно вещественной оси.
Рассмсугрим вспомогательную функцию
^{s)=\ + W(s)=\+R {s)/Q (s) = IQ (s) + R (s)]/
IQ (s), = D is)/Q (s), (3.67)
Рис. 3.12
Q(s)-
полином
где D (s) =Q (s) + R (s) = «о + a^s^'^ + ..
характеристический полином. замкнутой систерды;
= CqS"^ + CiS"~* + ... + Cn — характеристический
разомкнутой системы; R (s) = bo, s'"+ b^s^-^ + ...
— полином степени m.
Заметим, что так как в реальных системах сгепень
полинома R (s) не выше сгепени полинома Q (s), т. е. m ^ п, то
степени числителя и знаменателя дроби (3.67) одинаковы и
равны л.
Подставляя в (3.67) s = /со, получим
Ф (/со) = 1 -f И7 (/со) = [Q (/o))-f /?(/o))]/Q(/co)=:D (/co)/Q (/со).
(3.68)
Пусть характеристическое уравнение замкнутой системы
D (s) = О имеет т правых корней и п—т левых корней, а
характеристическое уравнение разомкнутой системы Q (s) = О
имеет / правых и /г — I левых корней.
При изменении частоты о) от — оо до оо изменение угла
поворота вектора ф (joy) на основе принципа аргумента будет
ДА rg ц (/со) IS^lco = А Arg D (j(o) -А ArgQ (/со) =
= п [(п —т) —т] —п 1(п —1)—1] = 2п (I —т). (3.69)

Для устойчивости замкнутой системы необходимо и
достаточно, чтобы все корни ее характеристического уравнения
были левым]и, т. е« т=^0. Отсюда суммарный поворот
вектора ф (/со) устойчивой системы вокруг начала координат
должен быть равен
А Arg ф (/со) \%ZZ,^ ^ 2nh (3.70)
где / — число правых корней характеристического уравнения
разомкнутой систерлы.
Обычно рассматривают только положительные частоты
О) > О, в этом случае угол поворота вектора ф(/со) будет вдвое
меньше, т. е.
А Argф(/со) |[о=~ --я/ -2я//2. (3.71)
Таким образом, если разомкнутая система является
неустойчивой и имеет / правых корней, то замкнутая система будет
устойчива тогда и только тогда, когда амплитудно-фазовая
характеристика вспомогательной функции ф (/о) при изменении
частоты со от О до оо охватывает начало координат в
положительном направлении 1/2 раз.
Легко заметить, чго число оборо^гов вектора ф (/о) вокруг
начала координат равно числу оборотов вектора W (/со)
вокруг точки (—1, /0).
На основании сказанного вьттекает следующая
формулировка критерия устойчивосги Найквиста: если разомкнутая
система автоматического управления неустойчива^ то, для того
чтобы замкнутая система автоматического управления была
устойчива, необходимо и достаточно, чтобы
амплитудно-фазовая характеристика разомкнутой системы W (/со) при
изменении частоты кх) от О до оо охватывала точку (—1, / 0)
в положительном направлении 112 раз, где I — число правых
корней характеристического уравнения разомкнутой системы.
На рис. 3.13, а показана амплитудно-фазовая
характеристика ф (/со), а на рис. 3.13, б — амплитудно-фазовая
характеристика W (/со), соответствующие усгойчивой замкнутой
системе, которая в разомкнутом состоянии была неустойчива и
имела число правых корней / = 2. Обычно в реальных сисге-
мах W (/со)|(о== оо = О, и поэтому ф (/со) |^^_ „ = 1.
При сложной форме характеристики W могут
возникнуть затруднения при определении числа ее оборотов
вокруг критической точки (—1, /0). В этом случае для суждения
об усгойчивосги удобно применять «правило переходов»,
предложенное Я. 3. Цыпкиным.

Назовем переход характерисгики W (/о>) через отрезок ве-
щественной оси слева от точки (—1, /0), т. е. через отрезок
(—оо, —1), при возрастании со положительным, если он
происходит сверху вниз, и отрицательным, если он происходит
снизу вверх. Если характеристика W (/со) начинается на
отрезке (— оо, —1) при со == О или заканчивается на нем при со =
= оо, то в этих случаях считают, что она совершает полпере-
хода.
Тогда критерий Найквиста можно сформулировать так:
если разомкнутая система автоматического управления
неустойчива, то, для того чтобы замкнутая система
автоматического управления была устойчива, необходимо и достаточно,
чтобы разность между числом положительных и
отрицательных переходов амплитудно-фазовой характеристики
разомкнутой системы W (/со) через отрезок вещественной оси (— со,
—1) при изменении частоты (д от О до оо была равна 1/2, где
I — число правых корней характеристического уравнения
разомкнутой системы.
Если сисгема автоматического управления в разомкнутом
состоянии устойчива, т. е. / = О, то приращение аргумента
вектора ср (/со) равно нулю:
AArg(p(/co)|S=-oc=2n/=-0.
(3.72)
Это означает, что для устойчивости замкнутой системы
необходимо, чтобы амплитудно-фазовая характерисгика <р (/со)
не охватывала начало координат (рис. 3.14, а), а амплитудно-
фазовая характеристика W (/со) не охватывала точку с
координатами (—1, /0), (рис. ЗЛ4, б).
Таким образом, для этого наиболее часто встречающегося
на практике случая получаем следую!дую формулировку
критерия Найквисга: если разомкнутая система
автоматического управления устойчива, то замкнутая система автоматичес-
Рис. 3.13

a)<Q
o)>0
Рис. 344
кого управления будет устойчива, если амплитудно-фазовая
характеристика разомкнутой системы W (/со) не охватывает
точку (—1, /0).
Амплитудно-фазовые характерисггики разомкнутых сгати-
ческих сисгем автоматического управления при изменении час-
гагы О) от—со до оо образуют замкнутый контур. У
астатических разомкнутых систем, которые содержат интегрирующие
звенья , амплитудно-фазовые характеристики не образуют
замкнутого контура. Для таких систем характеристическое
уравнение разомкнутой системы имеет корни, равные нулю, и
может быть записано в виде
Q(s)-svQ, (s) = 0, (3.73)
где V — порядок астатизма; Qi (s) — полином, не имеклдий
корней, равных нулю.
Частотная передаточная функция разомкнутой
астатической системы, содержащей интегрирующие звенья,
W (/О)) = W (S) |s= /со = Qi (S) [s^yco -
=-R{M/l(jWQi(i^)l (3.74)
При (0= О частотная передаточная функция астатической
сисгемы обращается в оо, а ее амплитудно-фазовая характе-
рисгика прегерпевает разрыв. Поэтому в этом случае трудно
решить вопрос об устойчивости замкнутой системы, так как
неясно, охватывает ли амплитудно-фазовая характеристика
W Ц<х}) точку (—1, /0).
Векторы /О) при изменении частоты о от — с» до оо
изменяют при переходе через начало ксюрдинат фазовый угол
скачком с — д/2 до д/2, но в каком направлении происходит
их поворот в момент перехода через начало ксюрдинат, сказать
невозможно. Чтобы сх:вободиться от этой неопределеннсх:ти.

идя по мнимой оси при изменении частоты со от—оо до оо,
обходят начало координат в плоскости корней справа по
полуокружности бесконечно малого радиуса г (рис. 3.15), т. е.
считают не S = О, а S = ге'"'^ (г -4- О, — зх/2 ^у^п12).
Тогда все нулевые корни дадут точно такой же угол
поворота, как левые корни, т. е. каждый из векторов повернется на
ir, и формулы (3.54) и (3.55) сохраняют свою силу.
Обходу начала координат по малой дуге г е^'^ в плоскости
корней соответствует передаточная функция разомкнутой си-
стерды
1
(3.75)
где и — свободные члены полиномов R (s) и Qi (s).
При г О модуль R-> оо/а аргумент if меняется ат vjt/2
до — v3t/2 при изменении v от — я/2 до л:/2. Таким образом,
во время движения по полуокружности бесконечно малого
радиуса в плоскости корней частотная передаточная функция
разомкнутой системы W (/(о) может быть представлена в виде
вектора бесконечно большой длины, поворачивающегося на
комплексной плоскости по часовой стрелке на угол, равный—
— vn (от vn/2 до —vn/2).
При изменении со ат О до оо, т. е. при r О и О < у ^зх/2,
частотная передаточная функция W (/ю) будет изменяться по
дуге бесконечно большого радиуса, описывая угол от О до
— vn/2. На рис. 3.16 показана амплитудно-фазовая характе-
Рис. 3.15
Рис. 3.16

Рис. 3.17
/и (CD}
Рис. 3.18
ристика разомкнутой аста-
тР1ческой системы с аста-
тизмом первого порядка
V = 1.
На основе сказанного
выше для определения ус-
тойчивости систем с аста-
тизмом любого порядка v
достаточно построить
одну ветвь
амплитудно-фазовой характеристики
разомкнутой системы,
соответствующую
положительным частотам, дополнить
ее дугой — vn/2
окружности бесконечно большого
радиуса и затем
применить критерий
устойчивости Найквиста.
Например, если
разомкнутая астатическая
система неустойчива, то
замкнутая система будет устойчива, если при изменении
частоты (О от О до сю амплитудно-фазовая
характеристика разомкнутой астатической системы W (/со), дополненная
дугой — vn/2 бесконечно большого радиуса, охватит точку
(—1, /0) в положительном направлении 1/2, раз, где / — число
правых корней характеристического уравнения разомкнутой
системы.
На рис. 3.17 приведена амплитудно-фазовая характеристика
разомкнутой системы с астатизмом второго порядка v = 2.
Замкнутая система в этом случае будет неустойчива, так как
амплитудно-фазовая характеристика W (/со), дополненная
дугой — vn/2 == — п бесконечно большого радиуса, всегда
охватывает точку (—1, /0) в отрицательном направлении (по
часовой стрелке).
На рис. 3.18 приведена амплк[тудно-фазовая
характеристика разомкаутой системы с астатизмом второго порядка,
которая после дополнения ее дугой — vn/2 = — п бесконечно
большого радиуса не охватывает точку (—1, /0) (число
положительных и отрицательных переходов через отрезок (— оо, —1)
равно нулю). Следовательно, замкнутая система будет
устойчива.

Однрш из достоинств критерия.Найквиста является то, что
он может быть применен и в тех практически важных случаях,
когда неизвестны уравнения некоторых звеньев системы либо
даже неизвестно уравнение всей разомкнутой системы в целом,
но амплитудно-фазовая характеррютика разомкнутой системы
может быть получена экспериментально. Кроме того,
критерий Найквиста позволяет, как это будет показано ниже,
довольно просто исследовать устойчивость систем с
запаздыванием.
Так как параметры системы определяют обычно
приближенно и в процессе работы они могут изменять свое значение,
то важна оценка удаления амплитудно-фазовой
характеристики разомкнутой системы W (/со) от точки (—1, /0). Это
удаление определяет запас устойчивости, который
характеризуется двумя величинами: запасом устойчивости по фазе и
запасом устойчивости по ам-
плитуде.
, Запас устойчивости по
^"^^^ фазе определяют как
величину угла ф = п (сос)|
для частоты сОс, при
которой \W (со)с| \\ по
амплитуде — как величину
отрезка оси абсцисс ft,
заключенного между
критической точкой (—1, / 0) и ам-
плк[тудно-фазовой
характеристикой (рис. 3.19).
С ростом коэффициента
усиления разомкнутой
системы модуль амплитудно-
фазовой характеристики
также растет и при
некотором значении
коэффициента уср1ления К = /Скр,
называемого критическим
коэффициентом усиления,
амплитудно-фазовая
характеристика пройдет через
точку (—1, /0), т. е.
система будет на границе
устойчивости. При К > Kvp
система будет неустойчива.
Рис. 3.19
JVfco)
N
\
0 j 1 U{co)
w>0
Рис. 3.20

Однако встречаются системы (с внутренними обратными
связями), в которых потеря устойчивости может произойти не
только при увеличении коэффициента усиления, но также и
при его уменьшении. Этим случаям могут соответствовать так
называемые клювообразные амплитудно-фазовые
характеристики (рис. 3.20). В этих случаях запас устойчивости по
амплитуде определяется величинами двух отрезков h оси абсцисс,
заключенных между критической точкой (—1, /0) и
амплитудно-фазовой характеристикой.
Чтобы система обладала требуемым запасом устойчивости
при заданных величинах h и ф, около критической точки (—1,
/0) вычерчивается некоторая запретная область в виде
сектора, ограниченного величинами ±11 и Ч=ф, в которую амплк[туд-
но-фазовая характеристика W (/со) не должна входить
(рис. 3.20).
§ 3.7. Анализ устойчивости по логарифмическим
частотным характеристикам
В инженерной практике широкое применение получил ана -
лиз устойчивости систем автоматического управления,
основанный на применении логарк[фмических частотных
характеристик разомкнутой системы. Это обусловлено прежде всего
тем, что построение логарифмических частотных
характеристик разомкнутых систем, особенно имптотических
логарифмических частотных характеристик, значительно проще, чем
построение годографа амплитудно-фазовых характеристик.
Покажем, каким требованиям должны удовлетворять ло-
гарк[фмическая амплк[туднО"Частотная характеристика (ЛАХ) и
логарифмическая фазочастотная характеристика (ЛФХ)
разомкнутой системы, при которых обеспечивалась бы устойчи-
всхггь системы в замкнутом состоянии.
Как было показано выше, устойчивость связана с числом
переходов амплитудно-фазовой характеристики W (/со)
отрезка (—ex., —I)'отрицательной вещественной полуоси. Когда
амплк[тудно-фазовая характеристика W (jco) пересекает
отрицательную вещественную полуось, ЛФХ пересекает одну из
линий ± п (2/ + 1), где i = О, 1,2, 3, ... (рис. 3.21). Переходы
через эти линии не опасны с точки зрения устойчивости, если
они совершаются справа от точки (— 1, / 0), т. е. если при этом
модуль амплитудно-фазовой характеристики меньше единицы

|й^(/(о)|<1 и, следовательно, если ординаты ЛАХ
отрицательны, т. е. Lm Л (со) -= 20 lg\W (/со)|< 0. Поэтому область
отрицательных ЛАХ при исследовании устойчивости
интереса не представляет.
Положительному переходу (сверху вниз) через отрезок
(—оо, —1) характеристики W (/со) соответствует пересеченр1е
ЛФХ при Lm А (со) > О прямых + jx (2/ + 1) CHPisy вверх
(точка 2 на рис. 3.21), а отрицательному переходу — сверху
вниз (точка / на рис. 3.21).
Критерий устойчивости Найквиста применительно к
логарифмическим частотным характеристикам может быть
сформулирован следующим образом: для того чтобы система
автоматического управления была устойчива, необходимо и
достаточно, чтобы разность между числом положительных и
отрицательных переходов логарифмической фазочастотной
характеристикой прямых ± (2i + 1), i = 0,1, 2,..., во всех
областях, где логарифмическая амплитудно-частотная
характеристика положительна hmA (со) > О, была равна 112 {1 — число
правых корней характеристического уравнения разомкнутой
системы).
На рис. 3.21 приведены для примера амплР1тудно-фазовая
характеристика разомкнутой системы W (/со) и
соответствующие ей ЛАХ и ЛФХ. Из анализа этих ЛАХ и ЛФХ видно, что
разность между числом положительных и отрицательных
переходов ЛФХ прямых — п при Lm А (со) > О равна нулю.
Таким образом, если разомкнутая система была устойчива
(/ = 0), то и замкнутая система будет устойчива, при этом
запасы устойчивости по амплитуде равны hi и Лг» а запас
устойчивости по фазе равен ф.
i
Рис. 3.21

§ 3.8. Построение областей устойчивости в плоскости
параметров системы
При исследовании устойчивости большое практическое
значение имеет построение областей устойчивости в плоскости
одного или каких-либо двух параметров, влияние которых на
устойчивость исследуют, а также построение семейства
областей устойчивости в плоскости двух параметров при различных
фиксированных значениях третьего параметра.
Уравнение границ областей устойчивости можно находить,
пользуясь любым критерием устойчивости. Однако чаще всего
на практике применяют наиболее общий метод построения
областей устойчивости, который был предложен Ю. И. Ней-
марком. и назван им методом О-разбиения,
Понятие о D-разбиении. Рассмотрим характеристическое
уравнение замкнутой системы п-го порядка, которое делением
на коэффициент при переменном s с наивысшей степенью
всегда может быть приведено к виду
D(s)==s" + fliS"~4-...+a^-0, a^^l. (3.76)
Представим себе /г-мерное пространство, по координатным
осям которого отложены коэффициенты уравнения (3.76).
Это пространство называют пространством коэффициентов.
Каждой точке пространства коэффициентов соответствуют
конкретные числовые значения коэффициентов уравнения (3.76)
и соответствующий им полином п-го порядка. Уравнение
(3.76) имеет п корней, расположение которых на комплексной
плоскости корней s зависит от числовых значений
коэффициентов Ui.
Если изменять коэффициенты at уравнения (3.76), то его
корни в силу их непрерывной зависимости от коэффициентов
будут перемещаться в комплексной плоскости корней,
описывая корневые годографы.
Чтобы представить сказанное выше геометрически,
рассмотрим характеристическое уравнение третьего порядка {п = 3)
D (s) = + ais'+ аф + = 0. (3.77)
Если взять три взаимно перпендикулярные оси и
откладывать по ним значения коэффициентов аа, ^з, то получим
трехмерное пространство коэффициентов, каждой точке
которого соответствуют вполне определенный полином третьей сте-

пени и вполне определенные три корня в комплексной
плоскости корней S (рис. 3.22).
Например, точке УИ, имеющей координаты а^м и а^м,
соответствует полином Dm{s) =^ ^ -\- а^мй? + a,^ms + а^^м.
имеющий три корня s^Mj s^m и s^m в плоскости корней (рис.
3.22, а). Другой точке, например имеющей координаты а^^л^э
«2^v и a^Ny соответствует полином Dn (р) = ^ + Uins^ +
+ cIzns + a^N, корни которого SiN, s^N и и. т. д.
При некотором значении коэффициентов уравнения (3.77)
один из корней попадает в начало координат или пара корней
попадает на мнимую ось, т. е. корни его будут иметь вид О или
zb i(Ok и, следовательно, соответствующая точка в
пространстве параметров будет удовлетворять уравнению
D (/со,) = а^^Г+а,итГ + Цщ) +а,^0. (3.78)
Этому уравнению при — оо < со < оо соответствует
некоторая поверхность S, часть которой показана на рис. 3.22,
б.
При изменении коэффициентов корни
характеристического уравнения также изменяются и попадают на ттшую ось
тогда, когда точка в пространстве коэффициентов попадет на
поверхность S. При пересечении такой поверхности S корни
переходят из одной полуплоскости корней в другую.
Следовательно, поверхность S разделяет пространство
коэффициентов на области, каждой точке которых соответствует
определенное одинаковое число правых и левых корней. Эти области
обозначают D (т), где т — число правых корней
характеристического уравнения. Разбиение пространства коэффициентов
на области с одинаковым числом правых корней внутри
каждой области и выделение среди полученных областей области
устойчивости называют методом £)-разбиения.
6}
02
0.
t3
м
9i'
Рис. 3.22

Для характеррютаческого
уравнения третьего порядка J4~—---^^^ а -con ь
в пространстве коэффициен- ^ ^ ^" ^
тов можно наметить четыре
области: D (3), D (2), D (1),
D (0). Последняя область
D (0) будет областью
устойчивости.
Если изменяются не все ко- Рис. 3.23
эффициенты, а часть из них,
например два—и при ^ const, то вместо поверхности
получим линию, которая является сечением поверхности
S плоскостью ^3 = const. Эта линия разделит плоскость
коэффициентов Ui — «2 на области с одинаковым числом правых
корней (рис. 3.23).
Для уравнений более высокого порядка (п > 3) вместо
обычного трехмерного пространства получаются многомерное
пространство и гиперповерхности, разбивающею это
пространство на области, что сильно усложняет задачу, а рассмотрение
теряет наглядность.
Так как переход через границу D-разбиения в
пространстве коэффициентов соответствует переходу корней
характеристического уравнения через мнимую ось, то уравнение границы
D-разбиения в общем случае
\ DOVo) -(/o>)« + ai(/(o)«~J + ... + -0. (3.79)
Из (3.79) видно, что уравнение границы D-разбиения
может быть получено из характеристического уравнения систе-
(Мы заменой s = /со. Границу D-разбиения можно строить не
только в пространстве коэффициентов at характеристического
уравнения, но и в пространстве параметров срютемы
(постоянных времени, коэффициентов усиления и Тс д.), от которых
зависят коэффициенты характеристртеского уравнения.
/?-разбкение по одному (комплексному) параметру.
Предположим, что требуется выяснить влияние на устойчивость како-
го-лР1бо параметра v, линейно входящего в
характеристическое уравнение. Для этого сначала характеристическое
уравнение приводят к виду
D (S) = S (S) + vN is) = О, (3.80)
где S (s) — полином, не зависящий от v; N (s) — полином,
содержащий умножк[телем.

граница В-разбтиия определяется уравненрюм
D (/(о) = 5 (/со) + vN (/со) - О, (3.81)
откуда
V = —S (/co)/yV (/со) X (со) + jY (со). (3.82)
Так как изменяемый параметр v в лршейных системах
является не комплексным, а вещественным числом (коэффициент
усиления, постоянная времени и т. д.), то (3.82) стедовало бы
дополнить условием Y (со) = 0. Однако при первоначальном
построении не будем делать этого ограничения и будем
временно считать изменяемый параметр комплексной величиной v,
отмечая это чертой сверху, чтобы отличить ее от вещественного
значения v.
Давая со значения от—оо до оо, можно по (3.82) вычислк[ть
X (со) и Y (со) и построить на комплексной плоскости v границу
D-разбиения.
При построении границы D-разбтиия достаточно
построить ее для положительных значений со и затем дополнить
зеркальным отображением построенного участка относительно
действительной оси (рис. 3.24, б).
Если при изменении со от — оо до оо в плоскости корней
двигаться по мнршой оси и штриховать ее слева (ppic. 3.24,а),
то такому движению в плоскости v соответствует движение по
границе /)-разбР1ения, которую также дггрр1хуют слева по
обходу при изменении со от — оо до оо (рис. 3.24, б).
Если в плоскости V пересекать границу D-разбиения по
направлению штриховки (стрелка /), то в плоскости корней
один из корней переходит из правой полуплоскости в левую.
Если же в плоскости v пересекать границу/)-разбиения против
штриховки (стрелка 2), то в плоскости корней, один из корней
переходит из левой полуплоскости в правую.
Если штриховка двойная (например, в точке пересечения
кривых), то мнимую ось пересекают два корня.
о)
6)
1 ^
\0 +
Рис. 3.24

Для определения области D {т), и в частности области ус"
тойчивости D (0), достаточно знать распределение корней (т.е.
число правых и левых корней) при каком-лР1бо одном
произвольном значении параметра v = Vq. Переходя в плоскости v от
этого пара]\4етра к любому другому, по числу пересечений
границы D-разбиения, направлению и числу штриховок можно
определить значению D (т) в любой другой точке.
Претендентом на область устойчивости является область,
внутрь которой направлена штриховка и которая поэтому
соответствует области с наибольшим числом чевых корней.
Чтобы установить, является ли эта область действР1тельно
областью устойчивости, необходимо задаться какрш-либо значе-
HPieM Vo, лежащим в этой области. Подставрш Vq в'характерис-
тическое уравнение, нужно, используя любой критерий
устойчивости, установить, все ли корни характеристического
уравнения будут при этом левыми. Если при этом не все корни
будут левыми, то области устойчивости нет, т. е. измененрюм
только параметра v нельзя сделать систему устойчивой.
Так как изменяемый параметр является вещественным
числом; то из полученной области устойчивости выделяют только
отрезок устойчивостЫу т. е. отрезок вещественной оси,
лежащий в области устойчивости, например отрезок Л £ на рис.
3.24, б,
/^-разбиение по двум параметрам. На практике часто
требуется выяснить влияние на устойчивость не одного параметра,
а двух, которые линейно входят в характеристическое
уравнение замкнутой системы так, что характеристическое
уравнение можно привести к виду
D (s) = vN (s) + \х M(s) + L(s) = О, (3.83)
где (s), М (s), L (s) — полиномы от s; v и [i — изменяемые
параметры, влиянием на устойчивость которых интересуются.
Подставляя в (3.83) s = /о, получим выражение для
границы D-разбиения в плоскости параметров:
D (/(О) = vN (/о) + [iM (/О)) + L (/(О) = 0. (3.84)
Введем обозначения
M(/co) = Mi((o) + /M2(co);
L(/<o) = Li((o) + /L2(a))
(3.85)

и разобьем (3.84) на два уравнения, приравняв отдельно
вещественную и мнимую части нулю:
vTVi (0)) + jiMi (о) + Li {(о) = 0; (3.86)
vN^ (о>) + liM^ (©) + La (0)) = 0. (3.87)
Решение сисгемы уравнений (3.86) и (3.87) относительно
V и (Д.
V = Дх/А; (3.88)
(i = Дг/А, (3.89)
где Д =
A^i((o)Mi(co)
Л^2(со)Мг(со)
Д,=
Д.=
главный определитель системы;
(3.90>
(3.91)
—Li (со) Ml (со)
— ^2(С0)/И2 (со)
Л^1(со) -Li(co)
ЛА2(^) -/^2(0>)
(3.92)
— частные определители системы..
Так как (со), (со) и La (со)—нечетные функции со,
то А, Ai и Ag тайже нечетные функции со, а v и {х — четные
функции со.
Задавая различные значения со от — оо до сю, для каждого
со по параметрическрш уравнениям (3.88) и (3.89) определяем
величинь! V и [х и строрш границу D-разбиения в плоскости
этих параметров.
При этом возможны следующие три случая:
1. При заданной частоте со;^ определитель А, а также
определители Ai и Ag не равны нулю одновременно. Тогда (3.86)
и (3.87) совместны, а (3.88) и (3.89) определяют для заданного
значения со;, точку в плоскости параметров v и |л. При
фиксированном со^ (3.86) и (3.87) представляет собой в этом
случае в плоскости v и [д, пересекающиеся прямые 1 и 2,
показанные на рис. 3.25, а.
2. При некотором значении со^ определитель А
обращается в нуль, а определители А^ и не равны нулю. Тогда (3.86)
и (3.87) несовместимы и не имеют конечных решений. Прямые
1 и 2 параллельны и не пересекаются, как это показано на
рис. 3.25, б.

а)
Ai to
AztO
5)
в)
Рис. 3.25
3. При некотором значении % определитель Д и оба
определителя Ai и Да равны нулю одновременно. Тогда v и fi
становятся неопределенными. В этом случае, как известно, одно
из уравнений (3.86) и (3.87) становится следствием другого,
отличаясь от него на некоторый постоянный множитель.
Прямые 1 и2 (рис. 3.25, в) сливаются друг с другом и, таким
образом, в плоскости V и fi для заданного щ получается не точка,
атак называемая особая прямая, уравнение которой Vi Ni (%)+
+ liiMi ((0^) + Ьг (щ) = 0.
Особая прямая не относится к кривой £)-разбиения, так
как всем точкам этой прямой соответствует одно и то же
значение частоты О) = и направление движения по прямой при
изменении о) установить невозможно.
В большинстве практических задач особые прямые
получаются при значениях (о==0 йсо^оо.В этом случае хотя бы
один из коэффициентов v и входит в коэффициенты,
соответствующие свободному aQ и старшему а^ членам
характеристического уравнения. Особая прямая при о>==0 получается
приравниванием нулю коэффициента tt^, особая прямая при со =оо
получается приравниванием нулю коэффициента а^. Если ад и
an не зависят от v и (г, то эти особые прямые отсутствуют.
После того как граница D-разбиения и особые прямые ло-
строены, их необходимо заштриховать, пользуясь следующим
правилом: при возрастании ю от — со до оо граница О-разби-
ения штрихуется слева, если А > О, и справа, если Д <; 0.
Поскольку, как было отмечено выше, v и (г являются
четными функциями CO., граница D-разбиения при положительных
и отрицательных значениях частоты совпадает. При
изменении со от — оо до ой мы обходим кривую D-разбиения ^два
раза и поэтому она штрихуется всегда двойной штриховкой.
Штриховка особых прямьрс, как правило, одинарная и
производится так, чтобы вблизи точки сопряжения особой прямой

и кривой С-разбиения заштрихованные и незаштрихованные
стороны прямой и кривой были направлены друг к другу
(рис. 3.26, а, б). В тех, сравнительно редких, случаях, когда
особая прямая имеет место при некотором конечном значении
частоты (о = (о^^ Ф О и при этом А проходит через нуль и
меняет знак, особая прямая штрихуется по приведенному вьаие
правилу, но двойной штриховкой (рис. 3.26, в). Если ofce особая
прямая имеет место при о = ^о^^Ф^ и при этом А, проходя
через нуль, не меняет знака, то особая прямая не
штрихуется и исключается из рассмотрения (рис. 3.26, г).
Следует обратить внимание на то, что знак определителя
А, определяемого (3.90), зависит от порядка расположения
членов в (3.86) и (3.87). Чтобы не допустить грубых ошибок при
нанесении штриховки, необходимо в (3.86) и (3.87) сначала
написать члены, содержащие параметр, откладываемый по оси
абсцисс, т. е. v, а затем члены, содержащие параметр,
откладываемый по оси ординат, т. е. ji.
После нанесения штриховки определяют область, претен-
дующую на область устойчивости, т. е. область, внутрь которой
направлена штриховка. Затем, выбирая любые значения v =
= и (ш = jLifl, лежащие в этой области, и подставляя их в
характеристическое уравнение, нужно с помощью любого из
рассмотренных ранее критериев устойчивости определить, все
ли корни характеристического уравнения будут при этом
левыми. Если при этом не все корни будут левыми, то в плоско-
при а)к
0
0
Рис. 3.26

сти параметров v и ооласти устойчивости нет, т. е.
изменением только V и JLi сделатд> систему усгойчивой нельзя. Если же
при этом все корни окажутся левыми, то рассматриваемая
область действительно является областью устойчивости D (0).
После этого можно разметить области D (т) в любой другой
точке плоскости параметров v и [л, имея в виду, что
пересечение границы D-разбиения (или особой прямой с двойной
штриховкой) из заштрихованной зоны в незаштрихованную
соответствует переходу двух комплексно-сопряженных корней из ле-
эой полуплоскости корней в правую и наоборот. Пересечение
особой прямой с одной штриховкой соответствует переходу
одного корня.
Пример 3.7. Пусть характеристическое уравнение замкнутой
системы автоматического управления
D(s) (1 + T^s)(l + T^s)(l + T^s) + К =0.
где К — коэффициент усиления разомкнутой системы; Ти Tz, —
постоянные времени отдельных динамических звеньев.
Требуется построить границу D-разбиення в плоскости
коэффициента усиления разомкнутой системы К.
Запишем характеристическое уравнение в виде D (s) = S (s) +
+ vyV (s) = 0. где S (s) = (1 + ^s) (1 + T^s) (1 + T^s); N (s) - 1;
V = K, Подставляя в характеристическое уравнение s = /со,
получаем выражение для границы D-разбиения:
D (/со) - (1 + т (1 + /соГ^) (I +/Гз) +К = 5 (/со) + vN (/со) ===0,
откуда
V = К = -5 (M/N (/со) = --(1 +/С0Г1) (1 -f/соГ^,) (I +/соГз) =
(со)+/К (w),
где
X (со) - (Г, Т, Гз + Г, Гд) -1;
У (со) = со [Т^ Г, со^-(Г1 + Г, +Тз)1.
Задаваясь различными значениями частоты со > О, определяем
X (со) н К (со) и строим на комплексной плоскости кривую
D-разбиения, соответствующую положительным частотам (сплошная линия на
рис. 3.27). Ветвь кривой D-разбиения, соответствующую
отрицательным частотам со < О, находим как зеркальное отображение
относительной вещественной оси построенного участка для со > О (пунктирная
линия на рис, 3.27). Затем кривую D-разбиения штрихуем слева по
обходу при изменении частоты со,от —оо до оо.
Кривая D-разбиення делит плоскость на три области: /, // и
///. Претендентом на область устойчивости является область /, так
как к ией направлена штриховка. Чтобы проверить, действительно ли
эта^)бласть является областью устойчивости, задаемся значением
V = Vo = О» лежащим в этой области, подставляем его в характернсти-

E
Рис. 3.27
ческое уравнение и
определяем корни
получающегося при этом
характеристического уравие-
ння D (s) = (1 + ris)X
Х(1 + Г25)(1+Гз5) =
= О, все Корин которого
и Sg = l/T'g ЯВЛЯЮТСЯ
левыми; следовательно,
область / является
областью устойчивости
i>(0).
Так как
Коэффициент усиления К не
является комплексной величиной, то нас будет интересовать только
отрезок устойчивости АБ, совпадающий с действительной осью,
находящейся в области устойчивости.
Система будет устойчива, если значение К изменяется в пределах
—1 < /С < ^Скр. Отрицательным значениям К соответствует
положительная обратная связь. Для нахождения /Скр следует определить
сначала значение со, при котором Y (со) — 0. Если корень этого уравнения
со = cDo, то Ккр = X (соо). Производя вычисления, получаем
о>? = (7^1 + 7^2 + 7'з)/(7^1 7^27^3);
Ккр=Х(Шо) = (1+^2+Тз)(1 + 1/Т2+1/Тз)-1,
где Та = Tjr^\ Тз = Г3/Г1.
На рис. 3.27 показаны области D (0), D (1) и D (2). Область D{3)
в данном случае отсутствует. Это означает, что при положительных
значениях Т^, 7^2 и Т'з и любом значении К невозможно, чтобы все три
корня характеристического уравнения одновременно были правыми.
Пример 3,8, Рассмотрим теперь ту же систему, но будем
интересоваться влиянием постоянной времени иа устойчивость.
Запишем характеристическое уравнение в виде
£) (S) = [(1 +Га S) {1 +ГзS) +/(1 + [S (1 s) (1 +Г3s)] =
=S(s)+vW(s),
где 5(5) = (Н-Г25)(1Ч-7'8«)+Л:; Л^(8)=5(1+Гг5)(1+Гз«):
Подставляя в характеристическое уравнение s = /ш, получаем
выражение для границы D-разбиення:
D (М =S (/0))+(/ю) = (1 (1 Н-/о)Г,) +
+К+П 1(0 (1 +7wrj) (1 + /соГ,) =0,
откуда
v = r,= -[(1 +/о>7'2) (1 +/соГз) + К1/1/со (1 +/юГ,) (1 +/юГз)] =
==X(«)) + /V(ft)).

Задаваясь различными зиачеииями частоты со, можно вычислить X (со)
и К (to), а затем построить границу D-разбиення, которая показана на
рис. 3.28. Эта кривая также штрихуется слева по обходу при
изменении частоты со от —оо до оо.
Кривая разбивает плоскость иа четыре области: /, //, /// и IV.
Претендентами на область устойчивости являются области I и П.
Проверим, является ли область / действительно областью устойчивости.
При Ti = О характеристическое уравнение D (s) = (T^s + 1) {T^s +
_jl 1) /С = 0 является уравнением второго порядка с
положительными коэффициентами; следовательно, оно имеет все левые корни.
Строго говоря, область / соответствует ТгфО и при этом
характеристическое уравнение имеет третью степень. При уменьшении одни
из корней характеристического уравнения перемещается в плоскости
корней влево и при = О становится отрицательным бесконечно
большим. Исходя из теоремы о непрерывной зависимости корней от
коэффициентов уравнения можно утверждать, что система будет
оставаться устойчивой ие только при = О, но и в некоторой области
малых значений Ti, Следовательно, область / является областью
устойчивости D (0).
Далее, пересекая кривую D-разбиения по числу штриховок и их
направлению, размечаем области D (1) и D (2). Заметим, что в данном
случае имеются две области устойчивости D (0).
Система будет устойчива при О < T^i < 7"? и при T^i > Т^.
Система будет неустойчива при < T^i < Гб.
Пример 3.9. Рассмотрим ту же самую систему, что и в примере
3.8, но будем считать, что два параметра системы — коэффициент
усиления разомкизтой системы К и постоянная времени 7\ — могут
варьироваться одновременно.
Для определения влияния изменения этих параметров на
устойчивость построим границу D-разбиения в плоскости двух параметров:
Ti и К.
Перепишем характеристическое уравнение в виде
D (S) = V [Г,Тз5» + (Т, + Ts)^ + s] + ix r^rgs^ + (Г, +
+ Гз) S + 1 = О,
где v= Тг; и -К.
Подставляя в характеристическое уравнение s=/o), получаем
выражение для границы D-разбиения D (/о) ^- vN (т) + аМ (fw) -~
+ l (/со)-0. где yV(/cD) = [Г2Г3 (/о))з +(Г2+Г3) {j^)^ + M;M{j<d)-.
со=*
^ X(<o)=ReTi
Рис. 3.28

Приравняв нулю действительную и мнимую части, получим
следующую систему двух уравнений:
—V (Га Гз соз ^ю) +0и + (7^2 + Т'з)« = 0.
Решаем эти уравнения относительно v и fi;
V = (Г2 -Ь Гз) /(Г^ Гз со2 ^ 1); - Г., Гз 0)3 -1 +
Главный определитель системы
-(7^2 + 7^3) 0)^ 1
— (ГаГзюЗ—со) О
= (7^2 Гз 0)2-1)0).
Кривую D-разбиення можно построить, задаваясь значениями ча-
<:тоты О) от О до оо и вычисляя v н fi для фиксированных значений
частоты. Однако на практике для облегчения построения сначала строят
кривую D-разбиення качественно. Для этого качественно строят
зависимость V и от О) (или со^), а затем, пользуясь ими и исключая со,
строят качественную границу D-разбнеиия. Качественное построение v =^
= / (со) и [i = f (о)), а также граница D-разбиения показаны на
рис. 3.29.
Особые прямые находим, приравнивая нулю свободный член н
коэффициент при старшей степени s характеристического уравнения.
Особую прямую, соответствующую о) == оо, находят из выражении
Щ == TiT^Ts = 'vT^Tq = О, откуда уравнение особой прямой v = 0.
Особую прямую, соответствующую ю — О, находят из выражения
гг71=1+/С=1+И = 0, откуда уравнение особой прямой [л = — 1.
Кривую D-разбнення штрихуют двойной штриховкой при
изменении частоты со от О до оо слева по обходу, если главный определитель
А > О, и справа по обходу, если главный определитель А < О. Особые
О
т
0
CP" г
1
Рис. 3.29

прямые в данном случае штрихуют одннариои штриховкой, причем
заштрихованные стороны прямых и кривой D-разбнення направлены
друг к другу.
Итак, главный определитель А < О при О < со < yViT^Ts)
Д > О при со > yUiT^Ts).
Кривая D-разбиення и особые прямые делят плоскость (v, р,) на
шесть областей: /, //, V и VI. Претендентами на область
устойчивости являются области I vl IV. Рассмотрим точки,
принадлежащие полупрямой [х = iFC == О при v Г1 > О, т. е. положительную
часть оси абсцисс.
При /С = О и любом 7^1 > О характеристическое уравнение
D (S) = (1 + Тг8) (1 + Тф) (1 + Гд5) == 0;
следовательно, все три корня характеристического уравнения при
этом будут левыми, т. е. = -^ит^; Sa =^ —1/7^2 и s3 ^ —1/7^з-
Таким образом, положительная часть оси абсцисс принадлежит
области устойчивости D (0), а пбэтому и вся область / являетси
областью устойчивости.Переходя из этой области в другие через границу
D-разбиения или особую прямую, размечаем остальные об^хасти D (1)
и D (2). Заметим, что в данном случае имеются две области
устойчивости D (0), однако нас будет интересовать только область устойчивости
D (0), соответствующая физически осуществимым положительным
значениям постоянной времени T^i > О.
Построение границы D-разбиення в плоскости двух параметров
дает полную картину влияния этих параметров на устойчивость
системы. При малых значениях коэффициента усиления К система
устойчива прн любых значениях Тг. При больших значениях К система
устойчива лишь при достаточно малых либо достаточно больших значениях
Tit что совпадает с результатами, полученными в примере 3.8.
§ 3.9. Устойчивость систем с запаздыванием
и систем с иррациональными звеньями
Системы автоматического управления могут содержать
звенья, и которых зависимость между входной и (t) и
выходной у (t) величинами имеет вид
y(t)^u{t-rl (3.93)
где т — постоянная величина, называемая временем
запаздывания. Такие звенья называют запаздывающими, так как они
воспроизводят изменения входной величины без искажения,
но с некоторым постоянным запаздыванием т.
Передаточная функция запаздывающего звена (см. § 2.6)
W^.an(5)=--e-^^ (3.94)

а)
X
5)
Рис. 3.30
VJ(p)
^зап(Р}
Звенья с чистым запаздыванием часто встречаются в
различных технологических процессах, когда материал
перемещается из одной точки в другую с помощью ленточных
транспортеров; в системах регулирования толщины листа при
прокатке; в системах магнитной записи и воспроизведения и т. д.
Системы автоматического управления, содержащие хотя
бы одно запаздывающее звено, называют системами с
запаздыванием. Процессы в системах с запаздыванием описываются
дифференциально-разностными уравнениями.
Во многих тепловых процессах, а также при передаче сигналов
на расстошле по длинным электрическим, гидравлическим и другим
линиям наблюдается запаздывание, распределенное по всей длине
линии, которое в отличие от чистого запаздывания приводит к искажению
передаваемых сигналов. Системы, содержащие звенья с распределен-
иым запаздыванием, требуют для своего описания дифференциальных
уравнений в частных производных. Во многих случаях в результате
решения указанных уравнений в частных производных с учетом
граничных условий после некоторых упрощающих предположений для
системы автоматического управления в целом получают
дифференциально-разностные уравнения такого же типа, как и для систем с чистым
запаздыванием.
На практике широко применяют аппроксимацию передаточных
функций сложных систем с распределением параметрами с помощью
передаточных функций систем с сосредоточенными параметрами и
эквивалентных постоянных времени чистого запаздывания. Иногда
сложные системы высокого порядка с сосредоточенными параметрами,
содержащие большое количество инерционных звеньев, также
можно заменить для приближенного исследования более простой системой
низкого порядка, но содержащей звенья с чистым запаздыванием.
В дальнейшем будем рассматривать только системы с чистым
запаздыванием.
Структурная схема одноконтурной системы
автоматического управления, содержащей одно запаздывающее звено, может
быть представлена либо так, как показано на рис. 3.30, а,
если запаздывающее звено находится в прямой цепи, либо так,
как показано на рис. 3.30, б, если запаздываюп^ее звено
находится в цепи обратной связи.

Передаточная функция разомкнутой системы с
запаздыванием равна
Wr is) W^san W (s) ^ e-^ (3.95)
где W (s) R {s)/Q (s) — передаточная функция разомкнутой
системы без учета запаздывания, представляющая собой
дробно-рациональную функцию оператора s.
Заметим, что если в одноконтурной системе имеется
несколько последовательно соединенных запаздывающих
звеньев, то они могут быть заменены одним запаздывающим звеном
с эквивалентной постоянной времени запаздывания, равной
сумме всех постоянных времен запаздывания.
Если запаздывающее звено находится в прямой цепи, то
передаточная функция замкнутой системы
(Р) -StT ^ -= ^-(^)/^- (^)- (3.96а)
\+W^(s) Q(s)+R{s)e-'''
Если же запаздывающее звено находится в цепи обратной
связи, то передаточная функция замкнутой системы
U7,,(s).-^^_- Ш (3.966)
Из (3.96а) и (3-966) видно, что независимо от места
включения запаздывающего звена характеристическое уравнение
системы с запаздыванием HiyteeT вид
Dr (s) =Q(s) + R (s) е- - 0. (3.97)
Это характеристическое уравнение из-за наличия
множителя е"^^ является не полиномом, а трансцевдентной функцией
оператора s и в отличие от обыкновенного алгебраического
уравнения имеет бесконечное множество корней. Так как
то (3.97) можно рассматривать как уравнение «бесконечной
степени».
Для того чтобы линейная система с постоянным
запаздыванием была устойчива, необходимо и достаточно, чтобы все
корни уравнения (3.97) были левыми. Нахождение корней
уравнения (3.97) затруднительно, поэтому для исследования

устойчивости систем с запаздыванием используют критерии
устойчивости.
Следует иметь в виду, что алгебраические критерии
устойчивости Рауса и Гурвица в их обычной форме для исследования
систем с запаздыванием непригодны, причем для устойчивости
линейных систем первого и второго порядков с запаздыванием
только положительности коэффициентов
характеристического уравнения уже становится недостаточно. Существуют
различные алгебраические критерии устойчивости для систем
с запаздыванием, которые являются аналогами
критериев Рауса и Гурвица, однако в инженерной практике они
широкого применения не нашли из-за их относительной
сложности.
Для исследования устойчивости систем с запаздыванием
можно применять основанные на принципе аргумента
частотные критерии устойчивости Михайлова и Найквиста либо
метод Л-разбиения>
Уравнение кривой (годографа) Михайлова системы с
запаздыванием получают после подстановки s = /со в
характеристическое уравнение (3.97), т. е.
(/(О, е/"^) = Q (/со) + R (/со) е-= 0. (3.98)
Наличие в (3.98) множителя е--'*"^ делает очертания
кривой Михайлова достаточно сложными, и формулировка этого
критерия для систем с запаздыванием становится не такой
простой, как для обычных систем. Как показал Я- 3. Цыпкин, для
исследования устойчивости систем с запаздыванием очень
удобно применять критерий устойчивости Найквиста.
Заключение об устойчивости замкнутой системы с
запаздыванием делается на основании исследования поведения
амплитудно-фазовой характеристики Wt (/со) разомкнутой системы
с запаздыванием относительно точки (—1, /0). Формулировка
критерия устойчивости Найквиста для систем с
запаздыванием в этом случае аналогична формулировке дяя обычных
систем, имеющих дробно-рациональные передаточные функции.
Частотную передаточную функцию Wx (/(о) разомкнутой
системы с запаздыванием находят, подставляя s = /со в (3.95):
Wr (jio) = W (/со) е-/^-^ = А (со) е/^(«> е-/*'»*^ -
-Л(со)е'^^^<"\ (3.99)
где W (/со) = 6/ (со) -Ь jV (со) — амплитудно-фазовая
характеристика разомкнутой системы без учета запаздывания;

л (со) = \W (/со)| =^--Уи^ И + 1/"^ И
—амплитудно-частотная характеристика; i|) (о) = Arctg — фазочастотная
характеристика разомкнутой системы без учета запаздывания;
я|)^(со) - ФИ — шт (3.100)
фазочастотная характеристика разомкнутой системы с
запаздыванием.
Из (3.99) и (3.100) видно, что наличие запаздывающего
звена не меняет модуля Л (со) амплитудно-фазовой
характеристики разомкнутой системы W (/со), а вносит лишь
дополнительный отрицательный фазовый сдвиг 0)т, пропорциональный
частоте, причем коэффициентом пропорциональности
является время запаздывания т.
Зная амплитудно-фазовую характеристику W (/со)
разомкнутой системы без запаздывания, легко" построить
амплитудно-фазовую характеристику Wxijai) разомкнутой системы с
запаздыванием. Для этого каждый модуль Л (ш^-) вектора
амплитудно-фазовой характеристики W (/(о) нужно повернуть на
угол (o,-T по часовой стрелке. С ростом частоты со угол сот
будет быстро расти, а модуль Л (со) обычно уменьшается,
поэтому амплитудно-фазовая характеристика Wx{j(o)
разомкнутой системы с запаздыванием -имеет вид спирали,
закручивающейся вокруг начала координат (рис. 3.31). «Закручивание»
амплитудно-фазовой характеристики из-за наличия
дополнительного фазового сдвига сот, вообще говоря, ухудшает
условие устойчивости, так как вся амплитудно-фазовая
характеристика приближается к критической точке (—1, /0). Однако
иногда при сложной форме амплитудно-фазовой
характеристики W (/со) введение постоянного запаздывания может
улучшить условия устойчивости.
Изменяя время запаздьша-
ния т в широких пределах,
можно найти такое его
значение, при котором
замкнутая система будет
находиться на границе устойчивости,
В ^ этом случае хэрактери- ^^''^
стика Wx (/со) будет
проходить через точку (—1,/0).
Время запаздывания т^р и
соответствующее ему
значение частоты Шкр, при кото- p„c. 3.31

рых \Fr (/со) проходит через точку (—1,/0), называют
критическими.
Для критического случая справедливо следующее условие:
= W (;Чф) е-''"нр V = А (а),,р) е' f^Kp)""kp^kpI =
-----1. (3.101)
Условие (3.101) можно записать раздельно для амплитуд
и фаз вектора; (/^кр)- -
Л(^кр) = 1«^х(/а)нр)| = 1; (3.102)
(о)«р) = ^ Кр) -«^р т„р =^ -я (2t + 1). (3.103)
где / = О, 1, 2. 3, ...
Из (3.102) можно найти сначала ш„р, а затем из (3.103)
найти т„р, То е.
<Ji>Kp ^кр ^кр
Для систем автоматического управления с запаздьшанием
основное значение имеет минимальное критическое время
запаздывания (при i = 0), которое является в то же время и
граничным
Arctg i^biPL
^ _ л + ^?(€Окр) ^ (^Окр) _ Ф (tOKp) (3.105)
СОкр «кр СОкр
где ф (сокр) = л; + Arc tg iii^^ — запас устойчивости по фа-
^кр
зе.
Пример 3.10. Передаточная функция разомкнутой системы с
запаздыванием
Определить критическое время запаздывания т^р.
Частотная передаточная функция разомкнутой системы с
запаздыванием
(/«)-/(e~'"V(l+/«r).
Следовательно, условие (3.102) в" данном случае
I (/^кр) I = I [^^/(1 +/«кр Л1 l^^V^+Kp'^ = 1 •
Из последнего выражения находим критическую частоту:
сокр = 1/^~/7'. К>1.

Рис. 3.32
Фазовый сдвиг на критической частоте
^(coKp)=-ArctgcoKpr= -Arctg V/<'' —1-
-По (3.105) находим критическое время запаздывания:
jt—Arctg Ук^—\ _ у, jt —Arctg — I
со,
При сложном выражении для частотной передаточной
функции W (jcd) разомкнутой системы определение критического
времени запаздывания просто выполнить графически. Условие
А (сйкр) = |W (/«кр)! = 1 определяется пересечением
годографа W (/со) с окружностью единичного радиуса с центром
в начале координат (рис. 3.32). Точка пересечения определяет
одновременно сокр и угол ф (о)„р), который, будучи разделен на
(Окр. даст значение критического времени запаздывания.
Если имеется несколько точек пересечения годографа
W (/со) с окружностью единичного радиуса, например при
<«>1кр1 <»2«р н созкр (рис. 3.33), то система будет иметь
несколько критических граничных времен запаздывания:
'^1кр = ф(С01кр)/0)1кр; Т^2кр=^фКкр)/^2кр; Ч^3кр=ф(«3кр)/«3кр.
причем минимальное время запаздывания равно т^р jrdn =
= Ti„p. Система будет устойчива при т < т^^р, а также при
1^2кр < 'Г < Тдкр. Система будет* неустойчива при т^кр < т <
< т^2кр. а также при т > Тз^р. Наблюдаемое в этом случае
чередование участков устойчивости и неустойчивости системы

при непрерывном изменении х (а также других параметров
системы) является характерной особенностью многих систем с
постоянным запаздыванием.
Обычно для повышения быстродействия и точности
системы время запаздывания т стремятся уменьшить, поэтому
критерий устойчивости формулируется лишь для минимального
времени запаздывания.
Система автоматического управления будет устойчива,
если время запаздЬшания т меньше минимального
критического времени запаздывания: т < т^р jnin-
Критическое время запаздывания легко определяют и в
том случае, когда для исследования системы с запаздыванием
применяют логарифмические амплитудно-частотные (ЛАХ)
й фазочастотные (ЛФХ) характеристики. В этом случае
окружность единичного радиуса представляют осью абцисс. ЛАХ
системы с запаздыванием совпадает с ЛАХ исходной системы
без запаздывания. Дополнительный фазовый сдвиг, который
надо учесть при построении ЛФХ системы с запаздыванием,
определяют из (3.100). Точки пересечения ЛАХ с осью абсцисс
определяют критические частоты со^ф, а запасы по фазе
(с учетом кратности), отнесенные к соответствующим
критическим частотам, определяют критические времена запаздывания
Звенья с распределенными параметрами, описываемые
уравнениями в частных производных, имеют иногда
передаточные функции вида
W{s)^KlV^. (3.106)
W{s) = Kl{\+VsT); (3.107)
W{s)^e-'^'^, (3.108)
где К — коэффициент усиления звена.
Выражения (3.106) и (3.107) отличаются от передаточных
функций интегрирующего и инерционного звеньев (см. § 2.6)
только квадратным корнем. По аналогии с интегрирующими
и инерционными звеньями такие звенья называют
полуинтегрирующими и полуинерционными. Звенья, имеющие
передаточные функции вида (3.106), (3.107), (3.108), называют
иррациональными звеньями. Выражение (3.108) не только
иррационально, но и трансцендентно. С иррациональными
звеньями приходится встречаться, рассматривая различные диффу-

зионные и тепловые объекты, линии связи с потерями, с
распределенными сопротивлениями и емкостями и т. п.
Устойчивость замкнутых систем автоматического
управления, содержащих иррациональные звенья, может быть
исследована с помощью критерия устойчивости Найквиста.
Формулировка критерия устойчивости Найквиста в этом случае
аналогична формулировке для обычных систем автоматического
управления, содержащих звенья с дробно-рациональными
передаточными функциями.
§ 3.10. Устойчивость нестационарных систем
Линейными системами с переменными параметрами или
нестационарными системами (см. § 2.9) называют системы,
процессы в которых описыва^отся линейными дифференциаль-
пъши уравнениями с переменными во времени
коэффициентами
[а, {t)p- + ai(t)pn-' + ...+ar, (01 х (t) ^
- [Ьо (О + fci (О Р"^- * + fern (01 g (0. (3.109)
где X (t) и g (t) — выходная и входная величины системы
соответственно; Ui (О, bi (О — переменные коэффициенты,
являющиеся известными функциями времени и задаваемые либо
графически, либо аналитически; р = d/dt символ
дифференцирования.
Для нестационарных систем понятие устойчивости имеет
некот9рую специфику. Действительно, если предположить, что
входная величина системы g (t) == go =^ const и к моменту
времени переходные процессы в системе закончились, т. е.
если принять р = d!dt ^ О, то из (3.109) для ^> имеем
^(0 = ^^о. (3.110)
Из (3.110) видно, что в зависимости от характера
изменения коэффициентов Un (t) и (t) в нестационарной системе
даже при постоянной входной величине выходная величина
может изменяться неограниченно долго. Так как время работы
реальных систем ограничено, что установившегося значения

в нестационарной системе за время ее работы не наблюдается
и поэтому понятие асимптотической устойчивости (см. § 3.2)
практически теряет свой смысл.
Существуют точные методы исследования устойчивости
нестационарных систем, но они довольно сложны и на
практике, обычно пользуются приближенными методами.
' Наиболее простым приближенным методом исследования
устойчивости нестационарных систем является метод
замораживания коэффициентов. Он может применяться в тех слу-
"чаях, когда нестационарная система работает в течение
ограниченного интервала времени 7", а коэффициенты уравнения
(3.109) за время протекания переходного процесса в системе
изменяются относительно мало. В соответствии с этим методом
для некоторого фиксированного значения времени t =
определяют соответствующие ему значения Ci (4) и 6| (4)
коэффициентов дифференциального уравнения (3.109),
заменяют исходную нестационарную систему некоторой
фиктивной стационарной системой и исследуют устойчивость
последней, применяя один из рассмотренных выше критериев
устойчивости. Если полученная таким образом стационарная
система устойчива, то считают, что исследуемая нестационарная
система тоже устойчива в рассматриваемый момент времени.
Затем проводят аналогичное исследование устойчивости для
других фиксированных моментов времени, лежащих в
интервале О < f ^ Т, где 7* — время работы системы.
—" Если во всем рабочем интервале времени Т условия
устойчивости стационарной системы, получаемой методом
замораживания коэффициентов, выполняются, то исходную
нестационарную систему^ на этом интервале считают устойчивой.
Следует заметить, что результаты, получаемые при
исследовании устойчивости нестационарных систем методом
замораживания коэффициентов, не являются вполне достоверньши,
поскольку сам этот метод не имеет какого-либо
математического обоснования. Степень достоверности будет тем выше,
чем меньше изменяются коэффициенты за время протекания
переходного процесса.
Эффективность рассматриваемого метода может зависеть от
правильного выбора фиксированных моментов времени, для
которых замораживаются коэффициенты.. Необходимо так
выбирать эти моменты, чтобы .охватить все юзможные
варианты значений коэффициентов, обратив особое внимание на
«опасные» точки, в которых происходит значительное изменение
коэффициента, смена его знака и т. п.

пример 3.11. Система автоматического управления описывается
дифференциальным уравнением
1ао P^+aj Р^+Й2 it) Р+а^]х (/) = bog (/),
(3.111)
где Со = 0. 1 at = 4,2 с^; {t) (72 ~ 0,10с; = 400; 6о ^ 400.
Оценить приближенно устойчивость системы, если время работы
ее Г = 100 с.
Рассмотрим систему с замороженными коэффициентами при ^ = О
и / = Г= 100 с.
В этих случаях характеристическое уравнение, соответствующее
исходному дифференциальному уравнению (3.111), будет
ОАр^ + 4.2р2 + 72р + 400 = 0;
0.1рЗ + 4,2р2 + 62р + 400 = 0.
(3.112)
(3.113)
Для. (3.112) находим кории: = —10 c-i; рд^з = (—16 ± /12) с-*.
Степень устойчивости (см. § 4.5) *i == Ipil = 10 c-i. Время
переходного процесса < Зт)-1 == 0,33 с. Для (3.113) корни pi = —25 c-i;
= (—6,8 rh /8,7) c-i. Степень устойчивости ij = 8,8 c-i. Время
переходного процесса < 3tj-i =5 0,34 с.
За время переходного процесса коэффициент «а (О изменяется иа
величину ^ 0,1-0,34 = 0,034, что составляет приблизительно
0,05 %. Следовательно, система может рассматриваться как квазиста-
циоиариая. Оценка устойчивости может быть сделана методом
замораживания коэффициентов^ характериотического уравнения. Применяя
критерий устойчивости Гурвица, имеем Qiuz (О > «оСз*
Подстановка числовых значений дает 4,2 (72 — 0,10 > 40. Последнее
неравенство выполняется в диапазоне времени О ^ f ^ Г. Следовательно,
исходная нестационарная система устойчива.
В общем случае, когда коэффициенты уравнения (3.109)
изменяются значительно, при исследовании устойчивости
нестационарных систем пользуются понятиш технической
устойчивости, или устойчивости на конечном интервале времени.
Систему считают технически устойчивой (устойчивой на
данном интервале времени работы системы Г), если
выходная величина х (f) не превосходит некоторой заданной
величины Хдоп при O^t^T.
Допустимое значение
величины Хдод выбирается в
каждом конкретном случае
из технических
соображений.
На рис. 3.34
показаны возможные графики
изменения х (t) для
нестационарных систем. Крише
' и 2 соответствуют тех- Рис. 3.34

нически устойчивой системе, а кривые 3 и4 — технически
неустойчивой системе. Из рис. 3.34 видно, что система может
быть одновременно устойчива технически и неустойчива
асимптотически (кривая /) и, наоборот, неустойчива
технически и устойчива асимптотически (кривая 3). Так как в
нестационарной системе изменение х (t) зависит от момента подачи
входного сигнала g (f), то на техническую устойчивость будут
оказывать влияние и начальные условия, и характер
входного сигнала.
В насто5пцее время не существует достаточно простых и
достаточно общих критериев технической устойчивости. По
существу, единственный способ проверки устойчивости
нестационарных систем заключается в нахождении кривой
выходной величины X (t) при заданном входном воздействии g (t)
(внешнем возмущении). Определение х (f) производят обычно
либо с помощью различных приближенных аналитических
методов, либо методами математического моделирования на
аналоговых или цифровых вычислительных машинах.

Глава 4
МЕТОДЫ ОЦЕНКИ
КАЧЕСТВА
РЕГУЛИРОВАНИЯ
ЛИНЕЙНЫХ СИСТЕМ
§ 4.1. Общие положения
При исследовании систем
автоматического регулирования приходится
решать задачу обеспечения требуемых
показателей качества переходного
процесса: быстродействия, колебательности,
перерегулирования, характеризующих
точность и плавность протекания
процесса. Будем, .как и в предьщущих
главах, предполагать, что система
автоматического регулирования описывается
системой линейных дифференциальных
уравнений с* постоянными
коэффициентами. При изменении воздействия g (t)
на входе системы (рис. 4.1) выходную
величину X (t) можно записать так:
^it)^x^^it)+x^{t), (4.1)
где X (О — решение дифференциального
уравнения, описывающего систему;
•^св (О — свободная составляющая
переходного процесса, соответствующая
общему решению однородного
дифференциального уравнения.
Если последнее не имеет кратных
корней, то
(4.2)
где С| — постоянная интегрирования,
значение которой определяют
параметры системы и начальные условия; —
корни характеристического уравнения
замкнутой системы D (s) = 0; х^ (/) —

3(ti /Qygf*)
X (f.) вынужденная составляющая
переходного процесса,
обусловленная законом
изменения g(t).
Из (4.1) видно, что каче-
р 4 J сгво переходного процесса
можно оценить по его-
составляющим АГсв (t) и Хъ (О»
в этом смысле различают две группы показателей: первая
группа—показатели качества переходного процесса Хс^ (/);
вторая — показатели, характеризующие вьгаужденную
(установившуюся) составляющую х^ (t), по которой определяют
точность системы.
Показатели качества, определяемые непосредственно по
кривой переходного процесса, называют прямыми оценками
качества. Кривая переходного процесса может быть получена
теоретически или экспериментально.
В тех случаях, когда расчет переходного процесса связан с
большими трудностями, используют косвенные оценки
качества. Например, к косвенным оценкам качества можно
отнести запасы устойчивости по фазе и по амплитуде,
рассмотренные в гл. 3.
§ 4.2. Оценка качества регулирования
в установившемся режиме
(коэффициенты ошибок)
Рассмотрим показатели качества, характеризующие
вынужденную составляющую ошибки (t) системы. Если на входе
системы (рис. 4.1) действует сигнал g (t), то установившаяся
ошибка регулирования системы (t) — g" (О —-^в (0> где
(t) — вынужденная составлякщая регулируемой величины
(4.1).
Если g (f) дифференцируема во всем интервале О < ^ ^ оо,
то ошибка системы ев (t) мо^ет быть представлена в виде
ряда:
fв (О = Соg(О + Q dg{i)ldt + ^C^a'g(t)ldt^ +... +
m!
Crr,d^g{t)/dt% (4.3)

где коэффициенты Со,
^1» ^2» Принято называть коэффициент
тами ошибоКо Формула (4.3) получена следующим образом.
Передаточная функция замкнутой системы относительно
ошибки (рис. 4.1)
Wge (s) = l/П + W (s)l = £e (s)/G (s). (4.4)
Из (4.4) можно найти выражение для изображения
ошибке (s) = G (s)/U + W(s)l (4.5)
кй:
Разложим передаточную функцию по ошибке Wge (s) в
ряд по возрастающим степеням s в окрестности точки 5 = 0,
что соответствует большим значениям времени {t->- оо), т. е.
значению установившейся ошибки при заданном управляющем
воздействии.
В соответствии с (4.5) можно записать
ml
G{s).
(4,6)
Если передаточная функция Wg^ (s) является
дробно-рациональной функцией
TO разложение в ряд Wg^ (s) можно осуществить делением
числителя на знаменатель, располагая члены полинома в
порядке возрастания степеней. Переходя в (4.6) от изображений к
оригиналам, можно получить для (t) выражение (4.3).
Коэффициенты ошибок С©» Ci, Cg, ... определяют по
формулам разложения функции Wge (s) в ряд Тейлора:
гам
(s)
ds Js= o'
Js=0
. s=0
(4.7)

Если ^ (/) = 1 (t), то все производные dg {t)/dt
: d^g {t)ldf = ... = d'-^g {t)ldt^ = 0, тогда
ml rf/m
В данном случае Co = Wgz (0) — значение установившейся
ошибки в замкнутой системе.
Если g{t) = U то dg{t)/dt=:l, а d^ g(i)/dt^^...
rf*" g (t)ldt^ = 0; коэффициенты Q = U^ge (0);
ds
. a Q[£Pfir(0/d/2] _... = C^[d'"g(0/rf/'«]=0
s=0
И Т. д.
Коэффициент Со называют коэффициентом статической или
позиционной ошибки; коэффициент — коэффициентом
скоростной ошибки, Са — коэффициентом ошибки от ускорения.
В статических системах коэффициент Со отличен от нуля.
В системах с астатизмом первого порядка Cq = 0, С^Ф 0.
В системах с астатизмом второго порядка Со = Ci = 0;
Cg Ф 0. Увеличение числа интегрирующих звеньев приводит
к повышению порядка астатизма системы, т. е. к нулевым
значениям нескольких коэффициентов ошибок, но при этом
усложняется обеспечение устойчивости системы. Если на
систему помимо задающего воздействия g (О действует и
возмущение f (t) (рис. 4.Й), то астатизм системы относительно g (t)
и f (t) зависит от места включения интегрирующего звена.
Пусть воздействия на САУ являются постоянными
величинами и равны g (t) = go; / (О = /о- Рассмотрим несколько
случаев.
1. В системе отсутствуют интегрирующие звенья.
Элементы У и 2 системы (рис. 4.2) являются инерционными звеньями
f^^j и соответственно
равны
хП)
Рис. 4.2
^1 (S) =К /(1 + «Л);
(4.8)

Тогда на основании метода суперпозиции установившаяся
ошибка САУ
е (О = Bg (О + 8^ (0. (4.9)
где eg (/) — ошибка отработки системой задающего
воздействия:
I
WiwX
go
a (/) ^ ошибка, вызванная действием помехи:
в данном случае САУ является статической относительно
обоих воздействий, так как (t) фО и (/) Ф 0.
2. Допустим, что в элемент 2 рассматриваемой системы
(рис. 4.2) включено интегрирукщее звено, а элемент /
является инерционным звеном, как и в случае 1. При этом передаточ-
най функция элемента 2
(s) - k^/is (1 + sT^)l
Тогда составляющие (t) и 8/ (t) ошибки системы (4.9)
s=o— lfe,A2+s(l+s7',)(l+sra)Js=o
go=0;
Li+ri(5)w^2(s)
.ftifta+sCl+sTiXI+sT-s)]
/«--=
fo
S=0 ^1^2
¥=0.
Следовательно, САУ является астатической относительно
задающего воздействия g (t) и статической относительно
возмущения / (/).
3. Пусть интегрирующее звено включено в элемент /,
передаточная функция его при этом равна
Wx (s) - Ms (1 + sT^)].
Второе звено является инерционным звеном, а передаточная
функция его та же, что и в случае 1.

Рассчитаем составляющие ошибки eg (t) и (t):
1
sH + sTi){l+sT,)
hki+s{l+sTi){\+sT^)
i=0
Ife,fe2+s(l+sr,)(l+sr2).
Поскольку и (/) и (/) = 0, система является
астатической и относительно воздействия g (/), и относительно
возмущения / (О.
Нужно отметить, что метод коэффициентов ошибок
применяется при сравнительно медленно меняющихся воздействиях.
Пример 4.1, Для системы (рис. 4.1) определить значение
установившейся jomndKH системы. Передаточная функция системы в
разомкнутом состоянии
«7(s)-Ms(l +sri)(l +57-2)1,
где k = \0 tr-i; Ti = 0,2 с; = 0,02 с.
Выходной сигнал меняется по закону ^(0 = 5+ 20/ + 20^.
Найдем передаточную функцию замкнутой системы относительно
ошибки:
G(s)
s(l+sT{i(\+sT,)
s(\+sTj)(l+sT^) + k'
!^ПТг+!?(Тг+Т^)+8+к
Коэффициенты ошибок Ci и (Со = О, так как система астати*
ческая) определяют по (4.7) или разложением в ряд по возрастающим
степеням s функции W^^ (s) делением числителя на знаменатель:
«^ge (s) =CiS+C, ... =s/ft+s^ (Ti + T^-l/k)/k^... .
Коэффициенты Cg, ... вычислять не имеет смысла, так как функция
g (О имеет только две производные, не равные нулю.
Определим первую и вторую производные входного воздействия
g(0:
g(0=20 +40<; g(0=40.
Тогда ев (О = С, g (О + g (О = 2.48+4/.

§ 4.3. Оценка качества переходного процесса
при воздействии ступенчатой функции
Переходный процесс в системе зависит не только от свойств
САУ, но и от характера внешнего воздействия, которое в
общем случае может быть сложной функцией времени.
Поведение системы рассматривают при следующих типовых
воздействиях: единичной ступенчатой функции 1 (/), импульсной б (t)
и гармонической функций. Прямые оценки качества получают
по кривой переходной характеристики h (О, т. е. при
воздействии единичной ступенчатой функции
I о при /<0
и йулевых начальных условиях.
Эту характеристику можно построить для выходной
величины или для отклонения 8св (О (Р^^с. 4.3, а, б). К прямым
оценкам качества относят:'
1. Время регулирования — минимальное время, по
истечении которого регулируемая величина будет оставаться
близкой к установившемуся значению с заданной точностью
|есв(01<0 при i^t^
(4.10)
или
где Д — постоянная величина, значение которой нужно
оговаривать (задается величина А в процентах от
установившегося значения выходной величины йуст)-
^)

2. Перерегулирование о — максимальное отклонение
переходной характеристики от установившегося значения
выходной величины, вьфаженное в относительных единицах или
процентах:
где Лтах1 — значение первого максимума, или
^ I ^св (о Imaxi JQQ _ I Сев (о Imaxi Jqq
hycT " |есв(0)|
Допустимое значение перерегулирования в каждом
конкретном случае будет подсказано опытом эксплуатации
системы, обычно о — 10 -т- 30 %, но в некоторых случаях
допускается и до 70 %. Иногда перерегулирование недопустимо
совсем.
3. Частоту колебаний со = 2л/7, где Т — период
колебаний для колебательных переходных характеристик.
4. Число колебаний п, которое имеет переходная
характеристика А (t) или 8св (t) за время регулирования (/р).
При проектировании систем чаще всего допускают п =
= 1 4- 2, а иногда и до 3—4, но в некоторых случаях
колебания в системе недопустимы.
5. Время достижения первого максимума ^^ах-
6. Время нарастания переходного процесса —
абсциссу первой точки пересечения кривой переходной
характеристики h (t) с уровнем установившегося значения Л^^т или
кривой отклонения e^B (/) с осью абсцисс.
8. Декремент затухания к, равный отношению модулей
двух смежных перерегулирований:
^ ^ I ^maxl —hy^^ |/| Ajnax2 '^уст !•
Перечисленные показатели качества могут быть
дополнены другими, но это обусловлено спецификой конкретной
системьг.
Определение приведенных выше прямьгх оценок качества
переходного процесса проиллюстрировано на рис. 4.3, а, б.
Переходные процессы, возникающие в системах при
скачкообразных воздействиях, принято делить на три группы:
монотонные, апериодические и колебательные. У монотонных
процессов первая производная выходной величины х (/) не
меняет знак (кривая а на рис. 4.4), у апериодических знак про-

изводной X (О меняется не
более одного раза (кривая б на
рис. 4.4), а у колебательных —
первая производная х (t)
меняет свой знак периодически
(теоретически бесконечное число
раз) (кривая в на рис. 4.4).
Нужно отметить, что в
настоящее время при бурном
развитии вычислительной техники Р"^- ^-^
трудности, связанные с
расчетом переходных процессов и выбором возможных вариаций
параметров системы, существенно уменьшаются, поэтому роль
прямых оценок качества при проектировании САУ возрастает
§ 4.4. Оценка качества регулирования
при гармонических воздействиях
При гармонических воздействиях качество системы
принято оценивать по амплитудно-фазовой, амплитудно-частотной,
фазочастдгной и логарифмическим частотньп^
характеристикам. Для оценки качества переходного процесса используются
следующие величины: показатель колебательности М,
резонансная (собственная) частота сор, полоса пропускания
системы соо, частота среза соср» запасы устойчивости по модулю
и по фазе.
Показатель колебательности М — это отношение
максимального значения амплитудно-частотной характеристики
^зтах(^) замкнутой систсмы К сс значснию при со = о
(рис. 4.5):
М = ЛзшахИМз(0). (4.11)
при Лз(0) = 1 показатель колебательности М = ^зшахС^)-
Показатель колебательности характеризует склонность
системы к колебаниям. Чем вьпие М, тем менее качественна
система при прочих равных условиях. Считается допустимым,
если 1,1 <М < 1,5.
Частоту сор, при которой амплитудно-частотная
характеристика замкнутей САУ имеет максимум, называют
резонансной частотой системы (рис. 4.5); на этой частоте гармони-

Аз(0)^1
Рис. 4,5
Рис. 4.6
ческие колебания проходят через систему с наибольшим
усилением.
Полоса пропускания системы (рис. 4.6) — это интервал
частот от со О до coq, при котором выполняется условие
^8К)<0,707Лз(0)
(4.12)
или при (0) == 1 величина Лд (щ) ^0,707. Полоса
пропускания не должна быть слишком широкой, иначе система
будет воспроизводить высокочастотные помехи.
Частота среза о)ср — частота, при которой амплитудно-
частотная характеристика системы принимает значение,
равное 1, т. е. Лз (оср) — 1. Эта частота косвенно характеризует
длительность переходного процесса. Время регулирования
обратно пропорционально частоте среза:
^р^(1 ~2)2л/ц
(4.13)
Если переходный процесс имеет одно-два колебания, то время
достижения переходной характеристикой первого максимума
(4.14)
Склонность системы к колебаниям характеризуется
величинами ее запасов устойчивости по модулю и по фазе,
определение которых дано в предыдущей главе. В хорошо
демпфированных системах запас устойчивости по амплитуде
колеблется в пределах от 6 до 20 дБ, а запас по фазе — от 30 до 60°.
Так как рассмотренные выше показатели косвенно
определяют быстродействие, перерегулирование и т. п., то их
используют и для расчета систем, находящихся под воздействием
непериодических возмущений.

§ 4.5. Корневые методы оценки качества
регулирования
Известно, что характер переходного процесса в системе
определяют по ее реакции на единичное ступенчатое
воздействие. Переходная характеристика h (t) системы может быть
вычислена с помощью обратного преобразования Лапласа
(по формулам разложения Хевисайда):
— tt^gx(s)l=L~*-^•
s ^*^^J sD(s)
Если D (s) не имеет кратных корней, то
h{t)=L-^
Л(0 = ^
D{0)
+2
i=l
SiD' (Si)
(4.15)
где Si — корни характеристического полинома замкнутой
системы D (s) = 0; D' (Si) ^ dD {s)/ds\s^s^ — первая
производная характеристического полинома D (s) по s при s = s^.
Из (4.15) видно, что на характер переходного процесса
влияют и числитель и знаменатель передаточной функции
замкнутой системы (s). Если числитель W^^ (s) не имеет
нулей, т. е. представляет собой постоянную причину, то
характер переходных процессов можно оценить по ее полюсам, т. е.
корням характеристического уравнения замкнутой САУ
D (S) = 0.
Для приближенной оценки качества переходного процесса
в системе нужно на плоскости корней s выделить область, в
которой располагаются корни ее
характеристического уравнейия. Чаще всего
эту область представлякуг трапецией
(рис. 4.7). Корни характеристического
уравнения располагаются внутри этой
трапеции ABCD^ на ее сторонах и
основаниях хотя бы по одному корню, а
вне ее—ни одного. Для выделения этой
области на плоскости корней вычисляют
параметры: степень устойчивости rj,
колебательность \1 и значение |
вещественной части максимально удаленного
корня от мнимой оси. Рис 4.7

Понятие степени устойчивости rj введено Я. 3. Цыпкиным
и П. В. Бромбергом. Степенью устойчивости rj называют
расстояние от мнимой оси до ближайшего корня или ближайшей
пары сопряженных комплексных корней. Степень
устойчивости г\ определяет ближайшее к мнимой оси основание, трапеции
AD (рис. 4.7).
Пусть общее решение дифференциального уравнения
системы
^(0- VCee'*', (4.16)
где Si — корни характеристического уравнения D (s) = 0.
Составляющая этого решения, определяемая степенью
устойчивости, запиш^ся в виде
^п(0=^пе-^^ (4.17)
для случая вещественных корней или
;c„(0=C^e-^^sinp/ (4.18)
для случая, когда среди корней есть пара
комплексно-сопряженных.
В большинстве случаев переходный процесс можно
считать закончившимся тогда, когда затухнет составляющая
переходного процесса, определяемая степенью устойчивости^ т. е.
порядок величины времени затухания процесса можно грубо
оценить по наиболее медленно затухающей составляющей
хг] (t) [см. (4.17), (4.18)1. В случае, когда ближайшим к мнимой
оси является вещественный корень, из (4.17) можно получить
следующую зависимость: ^ -^1п^ . Если принять,
например, Д 0,05, то время переходного процесса = ^ х
X in ^ ^ 3/г\. В том случае, когда ближайшей к мнимой
оси является пара комплексных корней, из (4.18) можно найти
верхнюю границу времени переходного процесса: ^ .
Можно поставить две задачи:
1. По заданным параметрам- системы — коэффициентам
D (s) — определить степень устойчивости системы (задача
анализа степени устойчивости).
2. По заданной степени устойчивости определить
значение варьируемых параметров системы (задача синтеза САУ
по заданной степени устойчивости).

Воспользуемся методом, изложенным в 112J.
Предлагается сместить мнимую ось влево на величину rj, тогда один
корень окажется на мнимой оси, а система — на границе
устойчивости. Это соответствует обращению в нуль старшего
определителя Гурвица: А» = ^п-A^_i == 0. Это условие дает
уравнение, по которому, задаваясь коэффициентами, можно
определить Г] или решить обратную задачу.
Пусть характеристическое уравнение системы
Dis)=^aoS" +aiS"-\ + ,..+an^iS + an = 0.
Введем новую переменную г = s + г]. Подставив значение
S == Z — Г) в уравнение D (s) = О, получим новое смещенное
уравнение:
/1о г« + /!i z'^-' + ... + Л 2г + = О, (4 Л 9)
где
(4.20)
Если в смещенном уравнении окажется i4rt = О, то
ближайшим к мнимой оси окажется нулевой корень, а если АпфО,
то пара сопряженных комплексных корней.
Условие границы устойчивости для системы, описанной
уравнением (4.19), по критерию Гурвица A„_i==0 при
соблюдении всех остальных условий устойчивости Гурвица.
Колебательностью системы |х называют тангенс угла,
образованного отрицательной вещественной полуосью и лучом из
начала координат к корию, у которого отношение мнимой
части к действительной максимально (рис. 4.7):
= tgф = (p/a)^„ (4.21)
где Р — значение мнимой части корней D (s);
а—действительная часть.
При известных параметрах системы можно определять
значение колебательности \к (задача анализа колебательности)
или решать обратную задачу — задачу синтеза САУ по
заданной колебательности. Для этого в характеристическое
уравнение системы вводится замена s = }ze~'^^, равноценная
повороту мнимой оси на угол (ах/2 — {рм), при этом пара
сопряженных комплексных корней окажется на мнимой оси, а
фиктивная система — на границе устойчивости. Колебательность
IX является оценкой переходкого процесса сверху, при
увеличении ц возрастает число колебаний п за время регулирова-

w и fZt
Рис. 4 8
ния И возрастает перерегулирование. Реальный переходный
процесс может иметь значительно лучшее качество.
Запишем смещенное характеристическое уравнение:
Во + Bi » +... + г + В„ = О, (4.22)
где
B,-f-^ е-'^"^**>^л^а,. (4.23)
В (4.22) часть коэффициентов — комплексные числа.
Так как фиктивная система находится на границе
устойчивости, то (4.22) имеет пару сопряженных мнимых корней
St = ±/р£ = ±!щ.
Если в (4.22) подставить /<о вместо г й разделить
смещенный характеристический полином на мнимую и
действительную части, то их можно поочередно приравнять нулю, получив
при этом систему двух уравнений
и (фл1, щ) = 0; и (фл|, о)|) = 0.
Исключив из этой системы «£, получим искомое значение
q>M и 11 = tg4>M [111.
Эту задачу можно решать, используя свойства корней
алгебраических уравнений по формулам Виета.
Впервые анализ распределения корней в области
устойчивости на примере САУ третьего порядка выполнил И. А. Выш-
неградский.

Оценка прямых показателей качества переходного
процесса — времени регулирования /р и перерегулирования о
(см. § 4.3) — по известным г], ^ и [л для любого распределения
корней и любых начальных условий пока не найдена. Но для
определенных классов распределения корней и начальных
условий можно построить две кривые: мажоранту и
миноранту, которые ограничивают кривую переходного процесса
сверху и снизу:
u(t)^x{t)^v{f), (4.24)
где и (t) — миноранта, а v {t) — мажоранта.
Методы построения мажорант и минорант разработа-'ы
С. А. Чаплыгиным, Н. Н. Лузиным, А. А. Фельдбаумом [И]
и уточнены А. М. Рубинчиком [8].
Приведем некоторые формулы для расчета мажорант и
минорант без доказательства. Для случая вещественных
корней и нулевых начальных условий х (0) = О, д:' (0) = ... =
=г д<"-1) (0) = О мажоранта и миноранта описываются
соответственно уравнениями
t>(/)=:=e-^'
w(0 = e-^'.
(72-1)!
(4.25)
(4.26)
-Перерегулирование для этого класса корней отсутствует.
На рис. 4.8 показаны кривые и {x)uv (т) для разных степеней
уравнения, причем т = г]^ — относительное время. Чем выше
л, тем грубее оценка. Если
учесть величину ^, то можно
сблизить миноранту и
мажоранту [2, 111.
Для систем, имеющих
среди корней пару
комплексно-сопряженных, при тех же
начальных условиях
мажоранта описывается
уравнением (4.25), а миноранта
u{t) = ~v (t). (4.27)
При этом перерегулирование
о^е-"/^ (4.28)
Если X {0)=Хо, то о^Хое~^/^
что проиллюстрировано на
рис. 4.9.
Рис. 4.9

Используя мажоранту и миноранту, можно оценить
время регулирования переходного процесса:
где — время регулирования по миноранте; t^^ — время
регулирования по мажоранте.
§ 4.6. Корневые годографы
Траектории, описываемые на комплексной плоскости
корнями характеристического уравнения замкнутой системы при
плавном изменении одного из ее параметров от О до со,
называют корневым годографом. Располагая корневым годографом,
можно выбрать необходимое значение варьируемого
параметра, соответствующее наиболее выгодному расположению
корней с точки зрения требований к качеству конкретной
системы. В СССР основополагающими работами в этом
направлении были работы К. Ф. Теодорчика, развитые Г. А. Бендрико-
вым и С. П. Стрелковым в 1948—1949 гг., в США — работы
В. Ивенса в 1950 г.
Используя метод корневого годографа, можно решать
следующие задачи [91: построение годографов полюсов
передаточной функции замкнутой системы при изменении одного из ее
параметров; оценки влияния параметров системы,
появляющихся при ее усложнении; качественной и количественной
оценки реакции системы на типовой сигнал при изменении
значения параметра системы; синтеза корректирующих
элементов системы.
Для непрерывных линейных систем существует несколько
методов построения корневых годографов, в частности
методы Ивенса, Теодорчика—Бендрикова и Удермана.
Наиболее трудоемким является метод Ивенса. Используя этот
метод, можно оценить несколько вариантов с точностью 3—5 %,
что удобно на первом этапе проектирования. Метод
Теодорчика—Бендрикова позволяет проводить более детальные
расчеты с использованием ЭВМ.
Рассмотрим метод Ивенса. Передаточная функция
замкнутой системы (рис. 4.10)
W,^ (s) = Wx {s)/l\ + Wx (s) (s)l, (4.29)
где is) (s) = W (s) (4.30)
— передаточная функция разомкнутой системы.

Mi)
Рис. 4Л0
или
Характеристическое уравнение замкнутой системы
Z) (S) - 1 + (S) Г, (5) ^ О (4.31)
Г (s) - -1. (4.32)
Надо отметить, что излагаемый метод наиболее пригоден
для выбора общего коэффициента k передаточной функции
разомкнутой системы (s), которая содержит его как
множитель.
Уравнение (4.32) можно записать в виде системы
уравнений относительно модулей и фаз:
\W{s)\ - \Wr(s) r,(s)l = 1; (4.33)
arg W (s) ±(2/ + 1) (4.34)
где / - 0, 1. 2, ...
Уравнение корневых годографов (4.34) является основой
для их построения.
Пусть известны нули и полюсы передаточной функции
разомкнутой системы: Si, s^, Sn — полюсы,\, «2. —
нули. Тогда передаточная функция разомкнутой системы
(S-S1)(S-~S2)
(4.35)
где а — множитель, появляющийся при разложении
числителя и знаменателя W (s) на множители; к — общий коэффи-.
циент усиления; т ^п.
Сомножители (двучлены) числителя (s — lj) и
знаменателя {S — Si) функции (4.35) на плоскости корней
изображаются векторами (s — sj) и (^ — s,), которые образуют с
вещественной осью углы BjiQi) (рис. 4.11). Тогда аргумент W (s)

можно записать как разность аргументов числителя и знаме-
т п
нателя arg W (s) = ^ 6/ — 2 ^/ " уравнение (4.34) при-
/=1 1=1
мет вид
^ е/ - 2 е, = ± (2v -f 1) л, (4.36)
где V = О, 1, 2, ...
Уравнение (4.33) удобнее представить как
или
причем
|Г (s)| ^akl - К
k = 1/(с/), (4.37)
i =-hljl и (4.38)
где Ij ~~ длина соответствующих векторов (s — Sj), / =^ 1,
.... т; li — длина векторов (s — s^), 1= 1, п.
Корневые годографы строят по (4.36), куда к не входит.
Для уже найденных корней по (4.37) определяют к. В.
Ивенсом предложено специальное устройство «Spirul» для
ускорения построения корневых годографов. Оно состоит из
прозрачного транспортира для сложения углов (6) и
логарифмической спирали для перемножения длин векторов (/), по
которым определяют величину /г. Описание этого устройства
приведено в [2] и работах В. Ивенса.
Построение корневых годографов требует знания их
свойств, которые приведем ниже без доказательств.
1. Комплексные части корневых годографов попарно
сопряжены, и ветви годографа симметричны относительно
вещественной оси.
2. Число ветвей корневого годографа равно порядку
уравнения D (s) = О, т. е. числу полюсов передаточной функции
замкнутой системы W^^^ (s).
3. Ветви корневого годографа начинаются при k = О
в полюсах передаточной функции разомкнутой системы W (s).
4. При /г оо m ветвей корневого годографа стремятся
к т нулям передаточной функции разомкнутой системы, а
остальные п — т ветвей уходят в бесконечность.
5. п — т ветвей корневого годографа, уходящие в
бесконечность, имеют асимптоты, число которых равно разности

порядков числителя и знаменателя передаточной функции
разомкнутой системы W (s), т. е. п — т. Асимптоты выходят
из одной точки на вещественной отрицательной полуоси с
абсциссой
под углами
е„ - (2/ + 1) л/(п — ml
(4.39)
(4.40)
где / -= О, I, 2, п — т — 1.
6. Точки пересечения корневого годографа с мнимой
осью могут быть найдены с использованием одного из
критериев устойчивости. Если /г ^ то эти расчеты не вызовут
трудностей, а для систем более высокого порядка эта часть
построения годографа наиболее трудоемка. В этом случае
можно рекомендовать алгоритм Рауса, чрезвычайно удобный
для реализации на ЦВМ, или метод проб по уравнению фаз
(4.36).
7. Точки на действительной оси, из которых одна ветвь
корневого годографа уходит в верхнюю полуплоскость, а
сопряженная ей ветвь — в нижнюю или, наоборот, приходят в
эти кратные точки (кратные корни на действительной оси),
можно найти из условия нулевого приращения суммы арг\
ментов в (4.36) при переходе от этой точки к близкой ей, нг
лежащей на действительной оси. При этом нужно учитыват»
знаки приращения углов AG.
Проиллюстрируем примером определение точек пересе
чения с действительной осью. На рис. 4.12 показано
расположение полюсов передаточной функции разомкнутой системы,
S = —а — двукратный нуль. Определим величину а. При
увеличении k на Ak двукратный нуль превратится в два комплек-

сно-сопряженных: S4 к В уравнении (4.36) ввиду малости
Д6 заменим их тангенсами, тогда получим
(о/а — «/(|s2| — а) — «/(|«з1 — а) = О, а > 0.
Сокращая «, определим величину а.
8. Ветви корневого годографа, совпадающие с отрезками
действительной оси, располагаются в тех ее частях, справа от
которых находится нечетное число действительных нулей и
полюсов разомкнутой системы. Это свойство является
следствием уравнения (4.36).
9. При (п — т) > 2 часть ветвей корневого годографа аг-
клоняется влево от мнимой оси, а другие — вправо. В [9]
показано, что при оценке переходных процессов можно
учитывать лишь те ветви годографа, которые отклоняются вправо.
Те из них, кспюрые располагаются ближе к мнимой оси,
называются доминирующими. Иначе говоря, система п-го порядка
в динамике будет вести себя как эквивалентная система более
низкого порядка, нули и полюсы которой совпадают с группой
нулей и полюсов, наиболее близких к мнимой оси и началу
координат плоскости s.
10. Углы выхода из комплексного полюса и углы входа в
комплексный нуль определяют из уравнения фаз (4.36),
записанного для этого полюса или нуля, т. е.
е^, = db(2v + 1) 180° - (4.41)
Рассмотрим пример построения корневого годографа с
использованием перечисленных выше свойств.
Пример 4.2. Пусть известна передаточная функция разомкнутой
системы
W (S) ^ [Л (S + 3)l/[s {S -f- 4) (s2 -f 2s + 2)J.
Характеристическое уравнение залп<нутой системы
D (s) = s« H- 6s3 >f- 10s2 4- (8 + Л) s -I- ЗЛ = 0.
Передаточная функция разомкнутой системы имеет нули: — —-3
и полюсы; Si =0, «2 == —4, 53,4 = — 1 ± /1-
Расположение нулей и полюсов на плоскости s показано на
рис. 4.13. Число ветвей корневого годографа равно 4 (свойство 2).
Согласно этому свойству, при k = О ветви начинаются в полюсах Sj,
«2» ^3» ^4 и при k оо (свойство 4) одна ветвь стремится из полюса
Si ^ О в нуль71 ~ —3, а из полюса Sg == —4 стремится в бесконечность
по действительной оси (рис. 4.14).

Рис. 4.13
От
/J
2 Re
-4 -J -2 -/
{? Re
Рис. 4.14
Определим число асимптот: n — m=4 — 1=3 (свойство 5).
Определим координату пересечения асимптоты с действительной осью,
OA-^{i^st-^sj^ 1{п-т) =
= [0^4—1 —3)1/(4—1)^—I
и углы асимптот:
где t=r О, 1. 2; . = 18073 = 60!; 6^2= (2 -г I) 18073 =г |80";
©аз --^ (4 4- I) 18073 = 300°- —60° (рис. 4.15).
Определим точки пересечения с мнимой осью (свойство 6). По
критерию Гурвица, для уравнения
D (s) = aos^ ■+ ai^ +- a^s^ ■+ AjS + а^-
+ ЗЛ=0,
уравнение границы устойчивости
Аз = GiCaflta — Cocl — а\а^ — 0.
Отсюда /?гр = 6, а граничная частота
«йо = ±Усз/«1 Vl4/6 ^ ±1,53 (рис.
4.16).
Определим углы выхода годографа
из полюсов Sg и S4 (свойство 10):
в;-(61 + 62 + 63+64) = 180°.
Углы Oi, 62, 63, 64 указаны на
рис. 4.13: 61 ==-- 26.5°; 61 135°; во =
= 18,2°; 64 - 90°; 63 = -^(180° + 61 +
+ 62 + 64) ~ 6i - — 36,7°.
«*+ б5« + lOs^ + (8 f
дт
/
4
-3 -2 -/ЛЛ
0 Re
-во'
W >.
Рис. 4.15

Чтобы определить при k — Л^р = 6 полюсы на вещественной
отрицательной полуоси (чисто мнимые уже определены: 53,4 —
= -1>уо)о = ±1 »53/), воспользуемся свойством корней (свойство
Виета).
п
1. П S/=:( —О'^Дп/Ло; SlS2S3S4 = 3/jrp/l.
Так как 5354=0?, то Si S2 = ЗЛгp/(og-
/i
2- 2 «1/^0; Sj-i-S2 + S3+54^-=—6.
1=1
Так как «3+54= О, то 8^ + s^— —6.
Решаем систему уравнений:
S1S2-=3.6/1,532;
^i-f —в
5i='-l,8; 52 =-4,2.
Если необходимо повысить точность расчетов, то нужно
использовать уравнение (4.36).
Рассмотрим еще один метод построения корневых
годографов, предложенный Э. Г. Удерманом [6, 91. В предлагаемом
методе для построения корневого годографа используется
кривая D-разбиения в плоскости варьируемого параметра с
помощью годографа затухания.
Выделим в характеристическом уравнении замкнутой
системы D (s) варьируемый параметр А. Тогда
характеристическое уравнение S (s) +
+ AR (s) = 0.
Уравнение кривой
D-разбиения в
плоскости параметра А
A=^-S (/co)/i? (/О)).
(4.42)
Уравнение (4.42)
позволяет в комплексной
плоскости А выделить
область устойчивости
\| Л системы, т. е. ту область,
(Чр=В) где корни уравнения
\'h53j'-ju)f,t) (s) = О имеют
отрицательную вещественную
Рис. 4.16 часть.

Рис. 4.17
Удерманом введено пл/i
понятие годографа
затухания [91.
Годографы
затухания — линии
постоянной частоты со = const
и переменного затуха- {(у=о)
кия а = var в
плоскости варьируемого
параметра Л, т. е, годографы
затухания — это
отображения линий,
перпендикулярных мнимой оси
в плоскости корней s,
а так как кривая D-разбиения является конформным
отображением мнимой оси на плоскости параметра 4f то
годографы затухания ортогональны кривой D-разбиения (рис. 4.17).
Л^гр, ^2rp — это отрезок устойчивости.
Из точек Cl, Cs и Cg (на кривой D-разбиения) проведены
три годографа затухания до пересечения с отрезком
устойчивости в точках Di, D2 и Dg. В точке характеристическое
уравнение имеет в числе прочих пару комплексно-сопряженных
корней Si,2 = — cti ± /^1 ^Ри Л =^ В точке при А =
= А^ корни Si,2 = — «2 ± /0)2- В точке Dg при А А^
корни Si,2 =^ —0^3 гЬ /^3- Таким образом, можно построить
доминирующие ветви корневого годографа при изменении
значения параметра Л.
В [91 показано, что для определения величины а в точках
пересечения годографа затухания с отрезком устойчивости
нужно оценить отрезок кривой D-разбиения CiE^ = C^D^ в
единицах частоты. Тогда Oi оз^ — и>|. Аналогично
поступают для точек D2, Dg и т. д.
Для построения корневого годографа нужно в (4.42)
заменить S на (—а + /о)):
Л (—а + /(й) = —S (—а + /О))//? {—а + /Ъ). (4.43)
Используя разложение в ряд Тейлора для полиномов
S (—а + /О)) и R {—а + /о)), (^АЗ) можно представить [91
как
Л(—а + /(й) =
Б(а)-^Б''(а)+^Б(4)(а) + ...

0)4
-В'(а)+^В(3)(а)-...
2!
4!
3!
-1
. (4.44)
где Б (а) = S (—а); С (а) - 7? (—а); В' (а) =^ dB (a)/da;
C{a)^dC{a)lda\ В''(а)== d"" В {u)/da^; С (а) ^ d^ С (а)/ da^
Чтобы определить действительные корни
характеристического уравнения D (s) = О, нужно использовать (4.44) при
ct> = 0.
Пример 4.3. Дана передаточная функция разомкнутой системы
W (S) = /г/[(1 + зТг) (1 + sT^) (1 + sTs)h
где Г, = 0,1 с; = 0,2 с; = 0,3 с.
Варьируемый параметр в данном случае к. Характеристическое
уравнение замкнутой системы
D (S) = (1 -f- 8Тг) (1 + sT^) (1 + sTs) + k = 0.
Уравнение кривой D-разбиения (рис. 4.18) в плоскости k
+ 1'<^Тг) (I + /а)Г2) (1 + /а)Гз).
В соответствии с (4.44) запишем выражение для k {—а + /со):
-fi' {С6) + —fi^3> (a)
где ao-ri Га Гз = 0.008; - (Л Г^ + Га Tg-f Г3) =0,14;
«2 = 7^1 + 7^2-Ь7'з=0,7; a.,-I, fi(a)=:^(-^a)=aoa3-.aia2_^g;
В' (a) = 3ooa2-"2a, a + aa; В" (a) =6ao a—2ai; B"' {a)=-6a.
Тогда
+ /co
0)^
'бас
[0,008аЗ—0.14a2_j_o,7a —
--1+0)2 (0.024a —0,14)]+ /a)[ — 0.024a2-1-0,28a~-0.7+0,0080)2].
Если принять a = 0. то получим уравнение кривой D-разбиения
Проведем из точки Cj, соответствующей частоте о) = 4, годограф
затухания до пересечения с отрезком устойчивости (—I -г- 11,25).
В точке D, определим значение k — 1,8; «1 = 5,5 — 4 = 1.5.
Аналогично, для годографа затухания из точки ~ 7,5;
«2 = 8»6 — 8 = 0,6 и т. д. (рис. 4.18, а).

Лл5
Рис. 4.18
Вычислим значения k\ принимая а == 1,5 и о = 4 (точка DJ;
06 = 0,7 и о) = 8 (точка Dg). При этом получим значения ki и k^,
близкие к рассчитанным выше.
Чтобы определить корни характеристического уравнения D (s) = 0,
подставим в выражение для k (—а + /ш) значение (а = 0.
По полученным данным можно построить доминирующие ветви
корневого годографа (рис. 4.18, б).
Можно отметить, сравнивая рассмотренные методы, что
метод Ивенса требует меньше времени для вычислений, чем
метод Удермана, не требующий поиска. Существуют и другие
методы построения корневых годографов, например с
использованием логарифмических частотных характеристик.
Аналитические методы построения требуют использования
вычислительных машин для расчетов, но дают высокую точность.
Построение корневого годографа — это только первый этап
анализа или синтеза автоматического регулирования. Как
было упомянуто в начала параграфа, по корневому
годографу можно судить о качестве регулирования (о реакции
системы на типовое воздействие) и о выборе необходимых
корректирующих устройств.
Задаваясь значением варьируемого параметра системы,
можно вычислить ее переходную характеристку h (/), используя
формулы разложения Хевисайда.
Для случая простых (некратных) корней переходную
характеристику вычисляют по формуле (4.15), которую можно
записать в более удобной для вычисления форме 19]. Запишем
характеристический полином системы D (s) (4,15) в виде
произведения двучленов: D (s) = (s — 5i) (5 — Sg) ... (5 — s„), где

Si, s2. Sn — его корни. Определим производную D' (s) =
= dD {s)/ds, принимая для простоты п = 3:
dD (s)/ds = (S — s2) (S — s3) + (S — Si) (S — s3) + (s — Si) X
X (s — s2).
Подставляя в это выражение s = s^, обратим в нуль все
слагаемые, кроме первого, при s = Sg — все, кроме второго,
при S = Sg — все, кроме третьего. Таким образ(ш, значение
производной D' (s) при s = Si будет равно произведению
п — 1 сомножителей
D'isd- П {Si-s^l
Заменяя в (4.15) D' (Sf) полученным выражением, можно
написать следующую формулу для вычисления характеристики:
h(t)=-^+ У ■ (4.45)
D(0) « ^ '
ft = i
Этим выражением удобно пользоваться, располагая
построенными корневыми годографами, определяя значения
длин и аргументов векторов (s^ — s^) по чертежу годографа.
Подробнее с упомянутыми вопросами можно ознакомиться
в [9].
§ 4.7. Интегральные оценки качества
переходных процессов
Интегральные оценки качества являются интегралами по
времени от некоторых функций переходного процесса
свободной составляющей выходной величины Хсв (t) или ошибки
8св (О- Цель использования таких критериев состоит в том,
чтобы получить общую оценку быстродействия и отклонения
регулируемой величины от установившегося значения. Широко
используются линейные и квадратичные интегральные оценки.
Линейные оценки вычисляются по формуле
Jo = Je-«^/«ee,. (4.46)

Рис, 4.19
Рис. 4.20
Однако чаще используют моменты /-го порядка, т. е, оценки
вида
о
(4.47)
(4.48)
оо
V"
(4.49)
Простейшей из этих оценок является Joo (4.47), Если
система устойчива, то lim (О = О, интеграл Jqq стремится
к конечному значению, равному площади под кривой Ссв (О
(рис. 4.19). Чем выше быстродействие системы, тем меньше
величина /оо» поэтому параметры системы следует выбирать
так, чтобы Jqq стремился к минимуму, т. е. djQQ/dA = О,
где А — варьируемый параметр системы. Недостатком этой
оценки является то, что она применима к монотонным или
апериодическим процессам. При колебательном процессе
(рис. 4.20) площади, ограниченные {t), складьюают
алгебраически и минимуму Jqq может соответствовать процесс с
большим числом колебаний п, т. е., с малым быстродействием
и даже с незатухающими колебаниями.
Для 8св (s) изображение по Лапласу

Сравнивая это выражение с (4.47) для /оо» можно записать
со
^о = |ееЛО^^ = £ов(0).. (4.50)
Разложим е-"' в ряд по степеням st:
e-" = \—st + 0,bs'f.... (4.51)
Подставим (4.51) в выражение для определения £св (s), т. е.
оо оо оо
^св (S) е,, (О dt = J бе, (О dt-S j tB,, (t) dt +
0 0 0
оо
+ 0,5s^ f ^''еез(0^' —- =^0- s/oi4-0,5sVo2—... . (4.52)
0
Если разложить Е^в (s) по степеням s в ряд:
£св(«)=^св(0) +(-^2^) s-o,5(il^) S- + ...,
\ ds Js = 0 \ ds^ Js=0
(4.53)
ТО, сопоставляя (4.52) и (4.53), можно сделать следующее
заключение, приравнивая выражения при равных степенях s:
V as js = 0
s=0
as"
s= 0
(4.54)
(4.55)
(4.56)
Если сравнить результаты (4.50), (4.54)—<4.56) с
коэффициентами ошибок, приведенными в § 4.2, то /оо = ^оэ J'oi =
= (—1) Сг; Jon = (-1)" Сп. где Со, Ci, —
коэффициенты ошибок.
Квадратичные интегральные оценки
вычисляются по формулам
(4.57)

/2i = f [е|в(0+т!ее\(0]й<;
(4.58)
f [е?в (О -!- Tf 8с% (О + ... + е[«)2 (01 dt, (4.59)
о
где Ti, Tg, т^ — постоянные величины.
Оценки /21,J^n называют обобщенными квадратичными
оценками.
Геометрический смысл интегральной квадратичной оценки
пояснен на рис. 4.21. Выбирая параметры системы по
минимуму квадратичной интегральной оценки J^q, приближаем
кривую (О к осям и t.
Методы вычисления этих оценок предложены А. И.
Мандельштамом й Н. Д. Папалекси в 1909 г. В 1937 г. акад. А. А.
Харкевич применил эту оценку для исследования режимов
работы усилителей, в 1948 г. А. А. Красовский и А. А. Фельд-
баум использовали ее для исследования качества линейных
систем автоматического регулирования.
Рассмотрим методы вычисления квадратичных
интегральных оценок (t) = h^c^ — h(t). По определению,
/.{А(0)-Я(5) = —U7^,(s).
S
По теореме о предельных переходах,
Аует = lim h (t) = lim sH (s) Wg^ (0);
следовательно.
Поскольку Wgfj, (s) — дробно- ^
рациональная функция, то и
Я (s) можно записать в виде ^2
дробно-рациональной функции:
_Ьо s'"+bi s'"-^+ ... 4-6m-i H-fcm
CoS«+a, sn-i+ ... +an-i s+a„'
(4.60)
Рис. 4.21

при m < n оценку /20 (4.57) можно вычислить, используя
коэффициенты fco» н «о» (4.60), по формулам,
приведенным ниже без вывода [4]:
/20 —
оо
(В„ Д„ + в, +... + д^_, +
+ Д^_1 + В^ Д^) - .^2^.
(4.61)
где Д — определитель Гурвица, составленный из
коэффициентов:
«п
—«п
0
On
0
—an
0
0
0
0
О
О
О
О
О
(4.62)
в котором все коэффициенты с меньшим индексом О и большим
п заменяют нулями. Определители До, Д^ получают из
(4.62) заменой столбца (v + 1) столбцом а^О, О, а
V = О, 1, т.
Коэффициенты Во» ^m-i» определяют как
i5v --Ь%г-^~ 2bm-v+i Ьт-^^ 1 "Ь ... + 2 (-^1)^ bm^2v\ (^-бЗ)
Интегральную квадратичную оценку /20 можно вычислять
по заданной частотной характеристике замкнутой системы.
Пусть Е (/со) — изображение Фурье для функции есв (0.
на основании теоремы свертки в комплексной области для
L {бсв (О бсв (0} можно записать [71 при s == О
оо оо
Ло = J(О = с I ^св (/to) Г(4.64)
есв it) Луот- h (О = £со (Н = ~- (0) - Г ,h (/(0)],
(4.65)

где (/€o) — комплексный коэффициент усиления
замкнутой системы.
Таким образом, по (4.64) и (4.65) можно вычислить /20.
Выражение (4.64) есть формула Рэлея*.
Существуют таблицы расчета интеграла /20 в функции
коэффициентов bo, brr. и Ло, изображения по Лапласу
сигнала ошибки £св (s) для m = п — 1 и до п = 10. В табл. 4.1
приведены формулы для /30 при п = 1 >^ 5.
Таблица 4.1
/20 = ^8/(2aoai).
n = 2. /20 = (^f ao + 6g 02) /(2ao Ci Oa).
« , аз Д^а + (^1 —26o 62) аз ao +^2 Qi До
«="5. /20= --; ; •
2ao«3 («1 «2—Oo аз)
hi (—a| «1 + cf4 аз a^) + (6| —2^2 60) ai a^ ao +
J _ —2^3 ^1) Gacti ao + 6j (—азeg +Q2 ai Qq)
2^4 ao (—a* af —a§ ao + Oi ag «3)
-^20=^ ^?то + (бг-2б2бо)т,4-6|~-26зб1 +
где
то = — (ог '^i —а* ^гО /^3= — (озm^—ai т^);
ао а&
mi = —«Б 02 4-04 аз; т^ = — {gq mz);
аъ
tn^ — —0500 + 0401; ^ъ~аь (04 m4 — 02 ^з + оо ^2)-
При выборе параметров системы по минимуму оценки /20
часто получают нежелательную колебательность процесса,
так как приближение процесса h (f) к идеальному скачку
вызывает резкое увеличение начальной скорости, что, в свою
очередь, может вызвать высокое перерегулирование, умень-
* Эта формула была получена и Парсевалем, поэтому в
литературе ее также называют и формулой Парсеваля.

шив при этом запас устойчивости. В обобщенных
квадратичных оценках /gu •••» ^гп накладывают ограничение не только
на величину отклонения е (t), но и на скорость отклонения
е (t) в /21» а также и на производные второго, третьего и
высших порядков в /22» Jznj что означает приближение кривой
не к ступенчатой функций, а к экспоненте в случае /31 и к
более плавной, но сложной кривой в случае использования
^22» •••» /гп'-При выборе параметров САУ по минимуму /21.
/гп существен выбор постоянных т^, ...» т„,
определяющих вес производных в обобщенных квадратичных оценках
(4.58), (4.59). Значительное увеличение т^, т„ приводит к
отсутствию перерегулирования, но увеличивает время
регулирования. При малых Ti, Тп уменьшение колебательности
будет незначительным. Выбор т^, т„ осуществляется с
учетом постоянной времени экстремали, к которой
целесообразно приближать процесс.
Остановимся на методике расчета системы по минимуму
обобщенной квадратичной оценки:
/2i = |[Bc%(0 + Tf ес\(0]Л.
Этот интеграл можно представить в виде суммы двух
интегралов:
/21 = I [есв (О + Ti ёев (01' dt^ J (i) (О dt =
= I l^cB (О + Ti (01" dt ^2Ti J (0 ^^ев (0-
Если система устойчива, то lim Есв (t) = О, тогда
1 еев (О ^8ев (О = е?в (О J = е?в (0).
о о
Кроме того, интеграл J^i будет иметь минимально
возможное значение
Л1п,1п=%ее^(0) (4.66)
при
ееЛО+тхёеЛО^О. (4.67)

Если
TO решение дифференциального уравнения (4.68)
есв(0=ее«(0)е-^/-^
(4.68)
(4.69)
является оптимальным по минимуму (экстремальным)
переходным процессом (где — постоянная времени этого
процесса).
При выборе параметров системы по минимуму J^i обычно
имеет место агклонение /2imin от наименьшего значения
•/^211111^ ^- *^2lmln — J^Lmln = б > 0.
А. А. Фельдбаумом [101 было показано, что переходный
процесс будет отличаться от экстремального на величину,
меньшую Кб/Ti, т. е.
(4.70)
По величине б можно оценить отклонение истинного
переходного процесса е^в (О от экстремального (рис. 4.22). При
увеличении порядка системы увеличивается и ширина зоны
dzY^/T^u при этом уменьшается точность оценки качества
системы (приближения переходного процесса к экстремали);
во избежание этого используют оценки вида (4.59).
Величину задают по требуемому времени регулирования ^р, т. е.
^р/6 < Ti < /р/3.
Следует заметить, что задача выбора параметров по
минимуму /20 или /21 решается аналитически лишь в несложных
случаях для САУ
невысокого порядка. В про- ^св
тивном случае расчеты
существенно
усложняются и задачу следует
решать численно на
ЦВМ.
Рассмотрим примеры
выбора оптимального
значения какого-либо
лараметра системы по
минимуму /20 и /21-
Пример 4.4. Вычислить
значение коэффициента
усиления системы, миии- Рис. 4.22

мизирующее квадратичную интегральную оценку Узо- Известна
передаточная, функция разомкнутой системы
W (S) = k/ls (1 + sT,) (I + sT,)h
где Tl = 0,01 с; Т^ = 0.03 с.
Входной сигнал — единичная функция g {i) ~ Л (о-
Изображение отклонения (о по Лапласу
' S S 1 + u^(s) S s(\+sTi)(\+sT^)^k
s^T,T^-{^s'(Ti + T^)-]^s + k Cos3 + Ois2 + e?2S + e?3 '
где bQ==:ao^TiT^=^3-\0-*\ = a, = Ti + Га = 4-10-2; 62 = 02==!;
ая = *
Воспользуемся формулами для вычисления /до» приведенными
в табл. 4.1 для п = 3:
J ^1 Qq Qi + (^1 — 2feo ^a) Qq Q3 + Q2 Q3
_ Qq Qi—^Cq of — 1_^ k (Ci~Co) + Qi
Определим частную производную:
dJ2o _ 1 fe(af-Qo)(%-feQo)~[feK-flo) + fli](Qi-2^^ofe)
Определим /г из dJ2o/dk=0, т.е. ft^ (q2 ^2ao «i ^ — «1 =0.
Подставляя числовые значения коэффициентов, получим
+ л 61,5 - 4м02 = о,
откуда ^опт — 37.
Пример 4.5. Определить оптимальное значение коэффициента
усиления /?, соответствующее минимуму обобщенной квадратичной оценки
21*
Передаточная функция разомкнутой системы W (s) = k/ls (1 +
+ sT)]; Г 0.1 с; т = 0,5 с.
Входной сигнал — единичная функция ^ (/) = 1 (/). Можно
представить В виде суммы;
оо оо оо
О 0 0

Изображение отклонения tea (О по Лапласу
2_ 1 i 1 s(l+sr)
5 ^ge<^)~ 5 { + W(s) ^ s s(l+sr)+r
sT + \ 6oS+^i
где bo oo - T^'^ bi = ai-- I; flg =
Воспользуемся данными табл. 4.1 и определим значение J^q
для п = 2:
J20 (Ь1 flo-ЬЬ8 fl2)/(2co «1 «2) - (7^-Ь ft)/(2ГЛ) = (1 + kT)/(2k).
Определим изображение производной (О свойства
преобразований Лапласа:
ёсв (0==s^cB (s)^ecB (0).
По теореме о предельном переходе,
еев(0)=11т есв (О - Ит s£cB(s)-lim - I.
t-^O S->oo S-voo Qo S^-f'fll S-rGt2
Тогда L lecB (01 (^o s^+bi s)/(flo + Oi 02) - I -
- -fe/(s* r + s+ fe)- (60 s+fri)/(flo s' + fli
где 6o 0; bi = —ft; Gq = t'i «1 = I; ^ k.
Теперь можно определить интеграл
оо
о
пользуясь формулой для /.^0 из табл. 4.1 для п ^ 2:
Итак. = (I -f- kT)/(2k) + tW.
Определим /гопт из dJ^Jdk — О, т. е.
(— 2 + 2А;2 T'^)/(4ft2) =---(— 1 + ft'^ т2)/(2Л;2) _ о.
откуда т2 - -1; аопт = У 17^2 = 1 /т - 2с-1.
Оптимальный переходный процесс описывается в соответствии с
формулой (4.69) выражением
ес«(0-все(0)е-^/^е-''-» /21 ш1п^- "^^^+ *Y^ = 0.55.
Так как есв(0) = 1, то по (4.66) наименьшее значение оценки /Ji =
^^''^i^cB Следовательно 6 = Jaimm^'^8imtn=Q»t)5.
Согласно (4.70) Десв(0= ±Уб/т= Vo,05/0,5 ^ ±0,33 (рис. 4.2).
Интегральные оценки качесгва широко используются при
синтезе оптимальных САУ в качестве критерия оптимальности.

§ 4.8. Частотные методы оценки качества
регулирования
Частотные методы исследования систем управления широко
используют в инженерной практике. Они основаны на
привычном для инженеров графическом изображении динамических
характеристик системы, поэтому нашли применение при
расчетах систем автоматического управления и позволили
разработать ряд удобных инженерных методов анализа и сиетеза
систем автоматического регулирования. В СССР большую роль
в пропаганде и развитии частотных методов сыграли работы
В. В. Солодовникова. В них приведены метод оценки качества
по вещественным частотным характеристикам, метод
построения переходных процессов по вещественным трапецеидальным
характеристикам при ступенчатых воздействиях, а также
метод синтеза корректирующих устройств. В рабагах была
доказана возможность применения частотных методов к
различным системам с распределенными параметрами и с
запаздыванием. Применение этих методов позволяет определить
такие важные показатели качества, как быстродействие,
перерегулирование, колебательность процесса. Эти вопросы хорошо
освещены в литературе, и имеется большое количество
вспомогательных таблиц и графиков, что в значительной степени
упростило инженерные расчеты.
Прежде всего остановимся на аналитической зависимости
между переходной характеристикой и частотными
характеристиками системы. Если на линейную систему воздействует
гармонический сигнал, то и установившееся значение
выходной величины будет гармоническим:
Х(/со)- ir^x(/co)G(/co), (4.71)
где X (/(о) — изображение выходной величины х (t) по Фурье;
G (/со) — изображение входной величины g (О по Фурье;
(/^) — комплексный коэффициент усиления замкнутой
системы.
При воздействии на систему единичной ступенчатой
функции g (t) = i (t) выходная величина, являющаяся переходной
характеристикой системы h (t), определяется через
вещественную частотную или мнимую частотную характеристику
замкнутой системы:

оо
x(t)=h(t)^—{sinо>Ш. (4.72)
о
где Р (о) — вещественная частотная характеристика
замкнутой САУ;
оо
X (О - ft (А - — Г cos (оШ + Р (0). (4.73)
П J О)
о
где Q (со) — мнимая частотная характеристика замкнутой
системы.
Определение переходной характеристики по (4.72), (4.73)
возможно лишь численными методами с применением ЦВМ.
Но возможен и другой путь, связанный с аппроксимацией
вещественной и мнимой частотных характеристик
линейно-кусочными функцями. Это позволяет получить достаточно
удобные выражения для приближенного построения переходной
характеристики.
Если на систему действует произвольное возмущение, то
переходный процесс определяется по обобщенным веш^ествен-
ной и мнимой характеристикам:
P,,(co)Re[\r^,(/co)G(/co)l;
Q,,(<o)=Im[U^^,(/o>)G(/(o)],
(4.74)
где G (j(o) =^ J (О е-^'^' di — изображение входного воздей-
0
ствия g (t) по Фурье. При этом необходимо, чтобы полюсы
функции W (s) G (s) располагались слева от мнимой оси.
Рассмотрим основные свойства вещественных частотных
характеристик и соответствующих им переходных процессов.
Из (4.72) следуют основные свойства Р (со) и ft (О- Приведем
их без доказательств.
1. Свойство линейности; если вещественную частотную
характеристику можно представить суммой
sin (utdv>.
(4.75)

то и переходный процесс h (t) может быть представлен суммой
составляющих:
A(0-i/b(0- (4.76)
2. Соответствие масштабов по оси ординат для Р (со) и
h (/). Если умножить Р (со) на постоянный множитель а, то
соответствующие значения h (t) тоже умножаются на этот
множитель а.
3. Соответствие масштабов по оси абсцисс для Р (со) и
h {t). Если аргумент со в соответствующем выражении
частотной характеристики умножить на постоянное число (рис.
4.23, а), то аргумент и в соответствующем выражении
переходного процесса будет делиться на это число (рис. 4.23, б), т. е.
оо
h (t/a) = — f sin соШ. (4.77)
Jt J О)
о
4. Начальное значение вещественной частотной
характеристики равно конечному значению переходкой
характеристики:
Ит Р (со) = lim х (О = h {t),
0)-»>0 t'-hoo t~>oo
Начальное значение мнимой частотной характеристики
Q (0) = 0.
5. Конечное значение вещественной частотной
характеристики равно начальному значению оригинала переходной ха-
рактеристики:
^ ^^^^t-^"^' lim Р (со; = lim x{t) ^-lim ft (О-
Представляют интерес
разрывы непрерывности и
пики в вещественной
частотной характеристике.
Предположим, что при со = COi
вещественная частотная
характеристика имеет разрыв
непрерывносги Р (щ) = оо,
при этом характеристическое
уравнение системы будет
Рис. 4.23 иметь мнимый корень s,- =

i
J
r
Рис. 4.24
Рис. 4.25
= =b/coi, т. е. в системе устанавливаются незатухающие
гармонические колебания, если остальные корни левые.
Характеристика для этого случая показана на рис. 4.24, а.
По-видимому, высокий и острый пик частотной характеристики, за
которым Р (со) переходит через нуль, при частоте, близкой к
о>1, соответствует медленно затухающим колебаниям
(рис. 4.24,6).
6. Чтобы переходная характеристика системы имела
перерегулирование, не превышающее 18 % (о < 18 %), веш.ест-
венная частотная характеристика должна быть
положительной невозрастающей функцией частоты (рис. 4.25), т. е.
Р (со) > о, dP ((o)/d(o < 0.
7. Условия монотонного протекания переходного
процесса. Чтобы переходный процесс имел монотонный характер,
достаточно^ чтобы соответствующая
ему вещественная частотная
характеристика Р (со) была положительной,
непрерывкой функцией частоты с
отрицательной, убывающей по
абсолютному значению производной (рис.
4.26, а, б), т. е.
Р (со) > О, \dP (co)/dcol < 0.
8. Определение наибольшего
значения перерегулирования о^^х "^Р^"
ходного процесса по максимуму
вещественной частотной
характеристики Р (со) (рис. 4:27):
Crnax 11,18Яшах(0)1/Р (0), (4.78)
где Pjng^x — максимальное значение
Р (со); Р (0) — начальное значение
Р (со = 0). Рис. 4.26

Рис. 4 27
Рис. 4.28
9. Если вещественная частотная характеристика близка
к трапецеидальной, т. е. может быть аппроксимирована
трапецией с диапазоном частот cog и коэффициентом наклона >с =
= coi/wg (рис. 4.28), то время регулирования переходного
процесса системы заключено в пределах n/cog < < 4п/(02.
Оценить время регулирования ^р и перерегулирование
можно по кривым, приведенным на рис, 4.29. Это применимо
для систем с невозрастающей вещественной частотной
характеристикой.
Если вещественная частотная характеристика Р (со)
имеет максимум Ртах. ТО псререгулирование а в и время
регулирования оценивают по кривым рис. 4.30, fl, б в зависимости
от отношения PmaJP Ф)' При ЭТОМ время регулирования
заключено в пределах Зя/соа. < /р < вя/сог-
Остановимся на приближенном методе построения
графиков переходных процессов в системе по вещественным
частотным характеристикам при воздействии единичной функции
g (О = 1 (О и нулевых
начальных условиях.
Метод трапеций. В
инженерной практике широко
применяют метод разложения
частотной характеристики на
сумму трапеций,
предложенный В. В. Солодовниковым.
Две сюроны единичной
трапеции Б (рис. 4.31) совпадают
с координатными осями,
третья параллельна оси
абсцисс, а четвертая имеет
12
20
16
п
8
4
\
1
1
\
А
\^
У
V
у
О 0,2 ОЛ 0,6 0,8 hO Х
Рис. 4.29

а)
а%
30
20
Ю
О
/
/ /,/ U2 и 1Л ^(0)
V 12 h3 1Л Р(0}
Рис. 4.30
наклон у. cOi/coa. Функция, соответствующая частотной
характеристике Б (рис. 4.31), записывается так:
1 при 0<со<х;
Р(со)= 1-_((о--х)/(1—х)-(1—(0)/(1-~х) при х<со<1;
О при со < О и со > 1.
Если принять такую единичную трапецию за некоторую
вещественную частотную характеристику, то соответствующая
ей переходная /i-функция определяется интегралом:
/К 1
- U ^ J (1-Х) со I
1
!
Si(T) -~xSi(xT)
cos Т —COS XT
(4.79)
где Si (т) = ( do>—интегральный синус.
J (X)
Значения /i-функций
даны в табл. 4.2. р
Для трапеции с другой
высотой Pft, основанием cog
и точкой излома COi = KCOg f
(характеристика а на
рис. 4.31) получим (по
свойсгвам 2 и 3 об
изменении масштабов) q
hn (О = Pnh (т/coj, (4.80)
где / = т/соо.

Обычно поступают так:
сначала характеристику Р (о)
приблизительно разбивают на
прямолинейные отрезки, при этом
в окресгности экстремумов
прямолинейные отрезки
располагаются параллельно оси <о
(рис. 4.32, а). Далее из точек
изломов проводят линии так, чю
характеристика оказывается
разбитой на несколько трапеций,
частично наложенных одна на
другую. Затем эти трапеции
вычерчиваются на другом
чертеже таким образом, чтобы
основание каждой из них легло на
ось со (рис. 4.32, б).
Для всех трапеций
определяют hi (тО, по (4.80) —
соответствующие им hi (t); вычерчи-
вакуг кривые на одном графике;
их знаки должны совпадать со
знаками ординат
соответствующих трапеций. Суммируя
графически вычисленные процессы
(рис. 4.32, в), получим h (t) =
= ^hi it).
Можно также
характеристику Р (со) представить
линейными отрезками, но
распределить их с лучшим
приближением к кривой и тогда
пользоваться методом треугольников,
предложенным А. А.
Вороновым [2]. Полученные при
пересчете значения ti из т^ по (4.80)
могут не совпадать для отдельных трапеций, поэтому
при.использовании метода трапеций возникает необходимость
графического суммирования составляющих кривых hi (О» что
ухудшает точность результатов. От этого недостатка
свободен метод треугольников.
Представим характеристику Р (со) линейными отрезками
(рис. 4.33), обеспечив возможно лучшее приближение к кри-
hz(t)
Рис. 4.32

вой; отрезки продолжаем до пересечения с осью ординат, при
этом площадь под кривой будет разбита на пять треугольников:
АОВ, BCD, DEF, FGH, GHK. Затем каждый из треугольников
заменим другим с основанием, равным проекции основания
данного треугольника на ось со, с высотой, равной стороне,
лежащей на оси Р, На рис. 4.34, а, б показана замена /\рВС
.]^а A^i^i^i так, чтобы О^А^ = OA и О^В^ = BD.
,.: Из (4.79) при к - О
Л(г)=А(51т-1=^) (4.81)
определяют значения Л-функции для единичного треуголь-
«ика ((Oi = //i = 1).
Соответствующие значения ft-функции даны в табл. 4.3.
Заметим, что переходный процесс для, треугольной частотной
характеристики
описывается монотонной функцией р
времени. Для того чтобы
показать это,
продифференцируем (4.81):
dh
dx
— 2 / sint
sin т
cos
(i-cosx). (4.82)
Из полученного
выражения видно, что
производная h' (т) положительна
и обращается в нуль при
значениях т = 2kn, где
ft==0, 1, 2, ...
Переходный процесс
для треугольников,
замещающих Р ((о),
определяют из следующей
зависимости: Хи {t)^Phh (т/(о„),
где Ph — высота; <о^ —
основание замещающего
треугольника.
Ркс. 4.33

0.0
0. 05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
О, 45
OvO
0,5
1,0
1.5
2,0
2,5
3,0
3.5
4,0
4,5
5,0
5,5
6,0
6,5
7,0
7,5
8.0
8,5
9,0
9,5
10,0
10,5
il.O
11,5
12,0
12,5
13,0
13,5
14,0
14,5
15,0
15,5
16,0
16,5
17,0
17,5
18.0
18,5
19.0
Ю,5
20,0
20,5
21,0
21,5
0.000
0,138
о.зю
0.449
0,572
0,674
0,755
0,783
0,857
0.883
0.896
0,900
0,904
0,904
0,904
0.907
0,910
0,918
0,924
0.932
0,939
0,946
0,947
0,949
0,950
0,950
0,950
0,950
0,952
0,954
0,956
0.959
0.961
0,964
0,965
0,966
0,966
0.966
0.967
0.967
0,967
0.968
0,968
0.969
0,000
0.165
0.326
0.469
0,597
0.705
0.790
0,853
0,896
0,923
0,936
0.940
0,943
0,942
0,944
0,94Ь
0.951
0,956
0,965
0.972
0.978
0,985
0.988
0,988
0,988
0,989
0,989
0.990
0,989
0.990
0,993
0,995
0,997
0,999
1.001
1,002
1.002
1,001
1.000
1.000
1,000
1.002
1,002
1.002
0,000
0,176
0,340
0.494-
0,628
0,797
0,828
0,892
0,938
0,960
0,978
0.986
0,982
0.980
0,979
0,980
0,985
0,989
0,997
1,004
1,009
1,013
1,015
1,016
1,015
1.013
1,012
1,011
1,011
1,012
1 ,012
1,014
1,015
1.016
1,016
1.015
1,015
1.015
1,015
1.014
1,013
1,012
1,011
1,011
0,000
0.184
0,356
0,516
0.655
0.833
0.863
0.928
0,974
0.997
0,012
1,С19
1.013
1.009
1,006
1,006
1,008
1,010
1,016
1,022
1,025
1.028
1,029
1.027
1.025
1.022
1,019
1,017
1.016
1.015
1.014
1.014
1.014
1.014
1.013
1.012
1.011
1.009
1,008
1.006
1.005
1.004
1,003
1,003
192 О
0.000
0.
0,371
0.538
0,683
0.867
0,896
0,963
1,008
1.029
1,042
1,046
1,037
1,030
1,024
1,019
1,020
1,021
1.02О
1,029
1,031
1.033
1,031
1,028
1,024
1,019
1.015
1,011
1,009
1.008
1,007
1.006
1,006
1.005
1,005
1.003
1,
1.001
0,998
0,996
0,995
0,994
0.994
0,99b
002 О
0.000
.199
0.386
0,560
0.709
0.833
0.928
0,994
1,039
1.057
1,067
1,067
1,054
1,043
1,035
1,02Ь
1.024
1,022
1,025
1,027
1,027
1,028
1.025
1.021
1.015
1.010
,005
1.000
0,997
0.996
0,995
0.995
0.995
0,995
0,995
0,995
.995
0,994
0.992
0,991
0.991
0.991
0.992
0.992
,594 0,603 0
О
О
О
I
1
1
1
0,000
0,207
0,401
0.
0,681
0.839
0,958
1.024
1,0б0
1,080
1,087
1,083
1,065
1,050
1,037
1,025
1.021
1,018
1,018
1.019
1.019
1.017
1,014
1,010
1,
0,999
О,
0,990
0,988
0,987
О,
0,989
О,
0,993
0,994
0,994
0.995
0,995
0.995
0,995
0.995
0.996
0.997
0.999
004 О
994 О
988 О
991 О
,000 О
.223 О
.432 О
.000 0,
.2150.
0,4170.
.617
.7610.786
.891 0,938
,987 1.013
,050 1,074
,090 1,107
,100 1,115
,103 1,112
1,093 \ ,095
1,070 1,068
1,049 1.043
,033 1,023
,017 1,
1,012 0,995
1,007 0,992
,006 0,992
1.006 0,
1,006 0,
1,005 0.
1.002 0.
0,999 0.991
.994 0,988
0.990 0.
,986 0.
0,983 0.
0.983 0.
0,985 0,
,987 0,991
0,988 0,996
,992 0,998
0.905 1,002
0,997 1,005
0.998 1.006
,005 О
,993 О
,993 О
.993 О
,993 О
.986 О
.985 О
.984 О
985 О
988 О
1,001
1.001
1,001
1.001
1.001
1.002
1,004
1,008
1.007
1,006
1.005
1.005
1,004
1,003 1.004
1.004
,000
.231
.447
0,646
0,810
0,943
1,038
1,095
1,124
1,129
1,117
1,197
1 .062
1,033
1.009
.989
0,98]
0,977
0,978
,982
,987
,991
,991
0,989
0,987
.986
.987
,988
,991
.996
1,000
1,004
1,007
1,009
1,010
1,010
1,010
1,009
1,006
1,004
1.002
1.001
1.001
1.001

Таблица 4.2
0.50
0,55
0.60
0,65
0,70
0.75
0,80
0,85
0,90
0,95
1 ,00
,000 0,000
,240 0,248
,4610,476
,6650,685
,833 0,856
0,967 0,985
,061 1,082
,1151,132
,1421,152
.138 1,134
,118 1,115
,092 1,083
,051 1,037
1,018 1,001
0,993 0,975 0,957
0,974 0,958
0,966 0,951
0,966 0,949
0,970 0,960 0,961
0,000
0,255
0,490
0,706
0,878
1,010
1.100
1,145
1,158
1,134
1.107
1,070
1,021
0,982
0,944
0,941
0,944
0,975 0,972
0,982 0,985
0,987 0,996
0,993 1,002
0,997 1,006
0,997 1,006
0,997 1,006
0,997 1,006
0,998 1,006
1,000 1,006
1.002 1,006
1.005 1,007
1,008 1,007
1,011 1,008
1,011 1,008
,012 1,007
1.0091,005 0,997
1,008 1.002
1,006 0,999
1,0010,995
0,998 0,992
0,996 0,991
0,995 0,991
0.995 0,993 0,997
0,996 0,995 1,000
0,980
0.993
1,007
1,014
1,017
1,019
1,018
1,014
1,010
1,008
K005
0,002
1.001
1,000
1.001
0,999
0,997
0.995
0,993
0.992
0,992
0,994
0,000
0,259
0,505
0,722
0,899
1,031
1,117
1,158
1,159
1,138
1,098
1,050
1,003
0,946
0,941
0,926
0,935
0,948
0,966
0,987
1,006
1,017
1,027
1,029
1,026
1,019
1,012
1,005
0,999
0,994
0,993
0,993
0.994
0,996
0,997
0,998
0,998
0,998
0,997
0,996
0,995
0,996
0,996
0.995
0,000
0.267
0,519
0,740
0,919
1,042
1,130
1,161
1,160
1,132
1,084
1,032
0,984
0.948
0.927
0,922
0,932
0.951
0,976
1.000
1,020
1,033
1,039
1,037
1.027
1,017
1.005
0,995
0,987
0,983
0,983
0,985
0,990
0,995
0,999
1,002
1,004
1,003
1.004
1,003
1,003
1,001
0,999
0,998
0,000
0,275
0,534
0,758
0,938
1,060
0,142
,166
1,161
1,127
1,069
1,016
0,956
0,936
0,917
0.911
0.936
0.958
0,990
1,015
1.036
1.046
1,047
1,043
1,025
1,010
0,993
0,982
0.974
0,970
0,976
0,984
0,983
1,001
1,008
1,012
1,014
1,012
1,009
1.005
1,001
0,996
0,993
0.992
0,000
0,282
0,547
0,776
0,956
1,078
1,154
1 ,171
1,156
ЫИ
1,053
0.994
0,949
0,920
0,911
0.920
0,944
0,974
1,006
1.033
1.049
1.054
1.048
,034
.015
0.995
0.980
0,968
0,96o
0.969
0.978
0.991
1.003
1.014
1.020
1.023
1,020
1,014
1,006
0,998
0.991
0,986
0,983
0.986
0.000
0.290
0,562
0.794
0,974
1,098
1,164
1Л74
1.149
1.099
1.037
0,979
0,934
0,910
0,908
0,927
0,955
0,990
1,023
1.048
1,059
1,058
1,044
1.024
1,000
0,979
0,964
0,9Sa
0,961
0,971
0,987
1,003
1,018
1,027
1,030
1.027
1,018
1,007
1,007
0.985
0,979
0,976
0.975
0,988
0,000
0,297
0,575
0,813
0,986
1,113
1,172
1,175
1,141
1.085
1,019
0,962
0,922
0,903
0,909
0,934
0,970
1,006
1,039
1.059
1,063
1,055
1,034
1,010
0,984
0.965
0,955
0,954
0,965
0.981
1,001
1,019
1.031
1.036
1,032
1,023
1,038
0,993
0.981
0,973
0,972
0,974
0.981
0.997
0,000
0,304
0,593
0,832
1,003
1,125
1.176
1,175
1.131
1,071
1,001
0.951
0,920
0,903
0,915
0,946
0,986
1,023
1,053
1,066
1.062
1.048
1,021
0.994
0,969
0,954
0,950
0,958
0,976
0.997
1,017
1,032
1,039
1,038
1,027
1,013
0.993
0,978
0,969
0,967
0,974
0.990
!,002
1,013
0,000
0,314
0,603
0,844
1,020
1,133
1,178
1,175
1,118
1.053
0,986
0,932
0,906
0,905
0.925
0,958
1,004
1,041
1,06.1
1,066
1,056
1,033
1,005
0,977
0,958
0,949
0,955
0,970
0,990
1,010
1,030
1.040
1,039
1.028
1.012
0,988
0,979
0,969
0,956
0,973
0.985
1,001
1,016
1,024

22,0
22,5
23,0
23,5
24,0
24,5
25,0
25,5
26,0
0.0
0,971
0,973
0,974
0,975
0,975
0.975
0,975
0,975
0,975
0,05
1,002
1,002
1,005
1,005
1,005
1,005
1,005
1,005
1,005
0,10
1,011
1,011
1.011
1,010
1,010
1,009
1.008
1.008
1.007
0.15
1,002
1,002
1,002
1.002
1,001
1,000
1,000
0,999
0,999
0,20
0,995
0,996
0,996
0,996
0,996
0,996
0,995
0,995
0,995
0.25
0.993
0,995
0,997
0,998
0,999
0,999
0.999
0,999
0.999
0.30
1,000
1,002
1,004
1,004
1,005
1,005
1,005
1,004
1.004
0.35
1.005
1,006
1,007
I,
1,007
I.
1,004
1,
1,002
0030
0,40
1,004
1,004
1,003
1,003
1,002
1,001
1.000
,998
0,997
0,45
1.000
0.999
0.999
0,998
0.997
0,997
0,996
0.996
0.996
Рассмотрим несколько случаев нахождения ординат
вещественной частотной характеристики по другим
характеристикам системы: амплитудно-фазовой, логарифмическим
частотным характеристикам, кривым D-разбиения в плоскости
одного параметра системы.
Остановимся на определении Р (<о) по амплитудно-фазовой
характеристике системы.
Передаточная функция замкнутой системы (см. рис. 4.1).
U/,,(/o>)-=.
^ (/со)
1 +
(4.83)
Определим Р (со):
Р (ш) = Re Г,, (/<о) = cos (а - fi). (4.84)
где а — аргумент вектора
W (/со); р — аргумент вектора
[1 + W (/со)1.
Соответствующее построение
приведено на рис. 4.35.
В. В. Солодовниковым
разработан метод построения
круговой диаграммы для нахожде
ния линий равного значения
Р (со) = const и Q (со) = const,
т. е. если W (/со) = м (со) +
+ V (со), то из (4.83) имеем

Продолжение табл. 4.2
0.50
0.55
0.60
0,65
0.70
0.75
0,80
0.85
0.90
0.95
1.00
0.
0,997
0.
О,
,996 0
.9981
,999 1
,000 1
1,000
1, "
и
000 1
ООО I
1,0001
,996
1,000
,001
.002
,002
1,002
,002
,002
,002
1,000
1,004
1,006
1,007
1,008
1,006
1.004
1,002
1.000
0,997
1,000
1,001
1,002
1,003
1,003
1,003
1,002
1,001
0,997
0,996
0,997
0,998
0,999
1,000
1,001
1,002
1,002
0,991
0,992
0,994
0,997
1,000
1,002
1,003
1.004
1,004
0,991
0,998
1,002
1.007
1,008
1,008
1,005
1.004
1,002
0.997
1.008
1,015
1,017
1,017
1,014
1,008
1,001
0,987
1,012
1,022
1,025
1,023
1,015
1,005
0,991
0,986
0,984
1,024
1,028
1,027
1,023
1,012
0,995
0,985
0,978
0,977
1,029
1,026
1,016
1,002
0.998
0,979
0,975
0,977
0,983
u + jv
\+u + iv
jl+u^jv) (u + jv)
0 + u)^+v^
V
(l+u)2+c;^
или
(P — 1) m2 + (2P — 1) « + (P — 1) ir* + P = 0; (4.85)
Qu" + 2Q« + Qt^^ — о + 0. (4.86)
Кривая (4.85) является окружностью, центр которой Р =
i= const лежит на оси абсцисс, так как уравнение не содержит
v\ окружности имеют общую точку и = О, « = 1, w =
= —Р(1 — Р). Радиус окружности
/? = 0,5|1-Р|. (4.87)
Соответствующие кривые показаны на рис. 4.36 с указанием
значений Р, для которых эти окружности построены.
Аналогично находят все
окружности Q = const
(рис. 4.36). Радиус
окружности
R = 1/12 IQ)]. (4.88)
На круговую
диаграмму накладывают
кривую W (/со),
выполненную в том же
масштабе, и считывают
значения Р (oj), которые
\NU0))
От W(ja))
6
О Re W(ju))
Рис. 4.35

Таблица 4.3
1 П
1
1 ^
1 ^
1 "
1 ^
1 ^
0,00
0,00000
1
0,50
0,158
1,0
0,310
7,0
0,904
01
0,00318
51
0,161
1
0,339
2
0,904
02
0,00637
52
0,164
0,367
4
0,906
03
0,00955
53
0,167
3
0,395
6
0,907
04
0,0127
54
0,171
4
0,422
8
0,909
0,05
0,0159
0,55
0,174
1.5
0,449
8,0
0,911
06
0.0191
56
0.177
0.475
2
0.913
07
0,0223
57
0,180
7
0,500
4
0.916
08
0,0254
58
0,183
0.525
6
0,919
09
0,0286
59
1,186
0.548
8
0,922
0,10
0,0318
0,60
0,189
2.0
0,571
9,0
0.925
11
0,0350 !
61
0,192
1
0.593
2
0.928
12
0,0382
62
0,195
2
0,615
4
0,931
13
0,0415
63
0,198
3
0,635
6
0,934
14
0,0446
64
0,201
4
0,655
8
0,936
0,15
0,0477
0,65
0.204
2,5
0,674
10,0
0,939
16
0,0509 1
66
0.208 1
0,691
2
0,941
17
0,0541
67
0,2П
7
0,709
4
0,943
18
0,0573
68
0,214
8
0,725
6
0,945
19
0,0604
69
0,217
9
0.740
8
0,946
0,20
0,0637
0.70
0,220
3,0
0,755
11,0
0,947
21
0.0668
71
0,223
1
0,768
11,5
0,949
22
0,0700
1 72
0,226
2
0,781
12,0
0,950
23
0,0731
73
0,229
3
0,793
12,5
0,950
24
0,0763 1
74
0,232
4
0,«04
13,0
0,950
0,25
0,0794 ,
0,75
0,235
3,5
0,815
13,5
0,950
26
0,0826
76
0.238
6
0,824
14,0
0,951
27
0,0856
77
0,241
7
0,833
14,5
0,954
28
0,0889
0,0921
78
0,244
0,247
8
0,842
15,0
0,956
29
79
9
0,849
15,5
0,959
0,30
0,0952-
0,80
0,250
4,0
0,856
16,0
0,961
31
0,0984
81
0,253
1
0,862
16,5
0,963
32
0,100
82
0,256
2
0,868
17,0-
0,965
33
0,105
83
0.259
3
0,873
17,5
0,966
34
0,108
84
0,262
4
0,878
18,0
0,966
0,35
0,111
0,85
0,265
4,5
0,882
18,5
0,966
36
0,114
86
0,268
6
0,885
19,0
0,966
37
0,117
87
0,271
7
0.888
19,5
0,967
38
0,121
88
0,274
8
0,891
20,0
0,967
0,124
89
0,90
0,277
9
0,894
21,0
0,968
0,40
0,127
0,280
5.0
0,895
22
0,971
41
0,130
91
0,283
2
0,899
23
0,973
42
0,133
92
0,286
4
0,901
24
0,975
43
0,136
93
0,289
6
0,902
25
0,975
44
0,139
94
0,292
8
0,903
30
0,980
0,45
0,142
0,95
0,295
6,0
0,903
40
0,984
46
0,146
96
0,298
2
0,903
50
0.987
47
0.149
97
0,301
4
0,903
100
0,994
48
0,152
98
0,304
6
0,903
120
0,995
49
0.155 1
1 99
0,307
8
0,903

соответствуют индексам окружностей сегки. пересекающей
^пивую W и<а) в точках, соответствующих частотам coj.
'^Вещественную частотную характеристику определяют по
логарифмическим частотным характеристикам. Передаточную
фуН1Л^шо разомкнутой системы можно записать через
амплитуду и фазу:
W (/<о) г= А («) e'f«'» = А (со) [cos ф (ю) + /sin ф . (4.89)
Если (4.89) подставить в (4.83) и разделить вещественные и
мнимые части, то ^ д.,,,^д^,^,озф«о) . ^4.90)
Л« (CD) +2А (о) cos ф (О)) + I '
orco-i^ >4«o)sm(p(<o) (4 91)
^ Л2 (о>)+2Л (о>) cos q> (о>)+1
0/п W(Ju))
Рис 4.36

По этим формулам построены номограммы для
определения Р (со) и О (со) по логарифмическим частотным
характеристикам. Эти номограммы построены на плоскости, по оси
абсцисс которой отложены значения ф, а по оси ординат —
20 Ig А (стороны квадрата). На эту плоскость накладывают
ЛАФЧХ разомкнутой системы с указанием частоты. Значения
вещественной частотной (или мнимой) характеристики
определяют по точкам пересечения нанесенной кривой ЛАФЧХ
с кривыми номограммы. Эти номограммы представлены на
рис. 4.37.
Lm, дБ <ру грод
~o2Q -300 -2д0 -260 ~2^^0 -220 -200 ЧдО 460 -т 420-iOO -80 -ВО -/^0 Ьт,дБ
-320 -300 "280 -260 -2^0 -220 -200 -160 -160 -"UW -120 -100 -80 -60 -❖^
(fy град
Рис. 4.37

Оценка качества
по показателю
колебательности.
Определение показателя
колебательности М
приведено в § 4.4. Если
АЧХ системы при
нулевой частоте
равна 1 (Лз (0) - 1), то
показатель
колебательности
М = Лз max И =
М=0,£7
л А ]
fj 2 и
Ж.
Чтобы определить
показатель колеба- Рис. 4.38
тельности системы,
можно воспользоваться амплитудно-фазовой частотной
характеристикой разомкнутой системы W (/со) = w (со) + jv (со), где
u^ReW (/со), V (со) 1т W (/со).
Показатель колебательности можно вычислить так:
М-
У[1+и(0))]2+Г/2(0))
1+И(С0) + Р(0))
Возведя в квадрат обе части равенства, получим
{[1 + и (со)Р + (со)} = (со) + i;^ (со).
Hocvie алгебраических преобразований можно записать
[и (со) + MV{M^- l)f +1;2 (со) = ЖV(M^ ~ 1)^ (4.92)
Выражение (4.92) является уравнением окружности с
радиусом R = М/{М^ — 1) и с центром, смещенным от начала
координат влево на величину С = М^/{М^ — I). Задаваясь
различными значениями М от О до оо, можно построить
семейство таких окружностей (рис. 4.38). При М = 1 окружность
вырождается в прямую {R оо, С-^ оо), параллельную
мнимой оси и проходящую через точку (—О, 5, /0):
l\m(C-R) - Um [MV{M^-l)-М/{М^^ 1)1 =^0,5.

Рис. 4.39
При О <i М <. I
окружности располагаются справа
от линии, соответствующей
М = 1, а при Л1 > 1 —
слева от нее. Если оо, то
окружность вьгрождается в
точку с координатами [—1,
/01. Номограммы можно
использовать для построения
амплитудно-частотной
характеристики замкнутой системы
Л 3 (<о). Для этого на
номограмму наносят
амплитудно-фазовую характеристику
разомкнутой системы W (/(о), далее по точкам пересечения
последней с окружностями определяют значения А^(о)).
Когда нужно оценить значение показателя колебательности М, то
строить амплитудно-фазовую характеристику не нужно, а
необходимо только оценить, какой наименьшей окружности
она коснется; значение М = const, соответствующее этой
окружности, и будет показателем колебательности.
При проектировании системы может быть поставлено
условие, чтобы показатель колебательности М не превышал
заданного значения. Это значение определяет ту запретную
область, куда не должна заходить амплитудно-фазовая
характеристика разомкнутой системы W (/со) (рис. 4.39). В том
случае, когда Л1 = 1, систему автоматического регулирования
можно рассматривать как колебательное звено. При этом
передаточная функция замкнутой системы
W^.^s)-l/(l+2|rs-|-7^s^).
во
бй
W
20
С
0,25 0.5
Рис. 4.40
W Ь25 U5 U7S 2,0 М
Рис. 4.41

Для этой передаточной функции люжно найти зависимости
между перерегулированием а, показателем колебательности
Му запасом устойчивости по фазе Дгр и параметром затухания
g. Эти кривые приведены на рис. 4.40. Для той же
передаточной функции можно определоть зависимость между
перерегулированием а и показателем колебательности (рис. 4.41).
§ 4.9. Чувствительность систем автоматического
управления
Параметры системы автоматического управления в
процессе работы не остаются равными расчетным значениям.
Это объясняется изменением внешних условий, неточностью
изготовления отдельных устройств системы, старением
элементов и т. п. Изменение параметров САУ, т. е. изменение
коэффициентов уравнений системы, вызывает изменение
статических и динамических свойств системы.
Зависимость характеристик системы от изменения каких-
либо ее параметров оценивают чувствительностью. Под
чувствительностью понимают свойство системы изменять режим
работы вследствие отклонения каких-либо параметров от
номинальных значений. Для числовой оценки чувствительности
используют функции чувствительности, определяемые как
частные производные от координат .системы или показателей
качества процессов управления по вариациям параметров:
Uij^(dXi/dajf, (4.93)
где Xi — координаты системы; — параметр системы.
Индекс О означает, что функция Utj вычисляется при
номинальных значениях параметров.
Система, значения параметров которой равны
номинальным и не имеют вариаций, называется исходной системой, а
движение в ней — основным движением. Система, в которой
имеют место вариации параметров, называются
варьированной системой, а движение в ней — варьированным движением.
Разность между варьированным и основным движениями
называют дополнительным движением.
Допустим, что исходная система описывается системой
нелинейных дифференциалььп>1Х уравнений
dXi/dt^fi(Xu Хгг'у «1, «т). (4-94)

Пусть в некоторый момент времени в системе произошли
вариации параметров Да^-, где / == 1, 2, т; тогда
параметры станут равными + Да^-. Если вариации параметров
не вызывают изменения порядка уравнения, то варьированное
движение описывается новой системой п уравнений первого
порядка
Sci/dt=fi{xu Хп, а^ + Да1, а^+Да^, i = 2, п.
(4.95)
Разность решений уравнений (4.94) и (4.95) определяет
дополнительное движение:
Дх,(0--^ИО-^£(0. (4.96)
Если Xi и Xi дифференцируемы по aj (/ = 1, m), то
дополнительное движение (4.96) можно разложить в ряд Тейлора
по степеням Да^. При малых вариациях параметров
ограничимся в разложении лишь линейными членами. Нужно отметить,
что в случае конечных вариаций такое приближение
недопустимо. Итак, можно записать уравнения первого
приближения для дополнительного движения:
AXi (t, Даь Да J = ^ ^^i"
Учитывая формулу (4.93), можно записать
т
AXiiU Да,, Да^= ^ "^i^^^
/=1
Следовательно, располагая функциями чувствительности
и задаваясь вариациями параметров, можно определить
первое приближение для дополнительного движения.
Продифференцируем уравнения исходной системы (4.94)
по af
д I dxi \ d ( dxi \ duij ^
( dxj \ ^ d 1 dxj \ dug ^ у Jll^ ^
\ dt I dt \ daj ) dt dxn
+ ^, t 1, 2, /г, 1, 2, m. (4.99)
Полученные линейные дифференциальные уравнения (4.99)
называются уравнениями чувствительности. Решение их
дает функции чувствительности u^j. Следует заметить, что в си-

A'r
-1
л у сложности
уравнений (4.99) их решение
весьма затруднительно. (SA_J/^^jj_^^
М. Л. Быховскйм пред-
ложен структурный ме- д ^
тод построения модели
для определения функ- Рис. 4.42
ций чувствительности
[131.
Для определения функций чувствительности можно
использовать уравнения системы или ее передаточные функции.
Пусть САУ описывается уравнением
D{p)x(t) = K{p)g(th (4.100)
где D (р) =^ р""\- аг (ai, а^) р'^"^ + ... + (ai, а^)
— собственный оператор системы;
л: (Р) - + frl («1 ^р) А?'"-^ + ... + &т («1 Otft) —
оператор воздействия g (t)\ р = dldt\ п'^т.
Запишем уравнения чувствительности,
продифференцировав (4.100) по ар:
D (р) Up = Lp (р) g-Mu (р) X (4.101)
при ^ = 0;
p^Uf^^O; Lj,{p)=dK{p)/dap; Мр{р) ^dD(p)/dap.
По уравнению (4.101) можно представить структурную
схему модели чувствительности для определения функции
(рис. 4.42). Эту схему можно упростить.
Пусть общей частью операторов (р), Lp (р)
является оператор Lq ip), а операторов (/?), уи^ (р) —
оператор Мо (р). Тогда можно записать
Lp{p)^Lq(p)LI{p); (4.102)
Мр (р) - Мо (р) Ml (р). (4.103)
Подставляя выражения (4.102) и (4.103) в (4Л01), можно
переписать уравнение чувствительности так:
О (р) Up - Lo (р) Ц (р) g -Mq (р) Ml ip) X, (4.104)
Структурная схема модели чувствительности в
соответствии с (4.104) показана на рис. 4.43. В этой модели выделена

г
d(S)
Рис. 4.43
общая часть для определения всех функций (/)-
Дополнительные блоки модели (рис. 4.43) реализуют операторы
L% (р) и Ml (р), с общей частью они соединены
переключателем П, Как видно из схемы рис. 4.43, функция
чувствительности координаты x определяется последовательно во времени
по всем параметрам. Для одновременного определения всех
функций чувствительности по параметрам используем
передаточные функции системы [13].
Выходная координата системы х (t) связана с задающим
воздействием g (t) зависимостью
X(s)= Г (5)G(s), (4.105)
где W (s) = К {s)/D (s) — передаточная функция системы;
X (s) и G (s) — изображение по Лапласу выходной и входной
величин.
Определим изображение функции чувствительности Uk (s),
дифференцируя (4.105) по а^:
Hb(S)
H,(s)
■и,
^ т (S) X (S) ^ а In г (S)
dak ^ (S) dWk (S)
X
(4.106)
Рис. 4.44
где Wk (s) — передаточная
функция элемента,
параметром которого является а^.

Обозначим общую часть ^g^^^ly через Яр (s), тогда
а для функции чувствительности можно записать
С/,(5) = Х(5)Я„(«)Я,(8)-^
dak
или
1/,(5)=^Х(5)Яо(5)ЯИ5), где ЯИ5)-Я,(5)^^А(^.
На рис. 4.44 показана схема модели для одновременного
определения функций чувствительности по параметрам Oj,
ttfe. Рассмотренный метод позволяет упростить модель
чувствительности за счет упрощения общей части модели, в
частности общая часть может быть представлена
пропорциональным звеном. Подобное упрощение модели используется в
беспоисковых системах оптимизаций.

Глава 5
ОБЕСПЕЧЕНИЕ УСТОЙЧИВОСТИ.
ПОВЬШЕНИЕ КАЧЕСТВА
РЕГУЛИРОВАНИЯ
И СИНТЕЗ ЛИНЕЙНЫХ
АВТОМАТИЧЕСКИХ СИСТЕМ
§ 5.1. Общие положения
\
Первой проблемой, которая решалась
теорией автоматического
регулирования, было обеспечение устойчивости
автоматических систем. Позднее
центральной задачей стало достижение
необходимого качества регулирования.
Систематизация и обобщение накопленных
знаний привели к созданию методов
научного проектирования (синтеза) систем
с заданными показателями точности
регулирования и быстродействия.
В настоящей главе излагаются
основные сведения о способах и средствах
улучшения свойств линейных систем
автоматического регулирования. Затем
рассматриваются наиболее
употребительные методы их синтеза.
Проблема обеспечения требуемых
свойств линейных автоматических
систем весьма сложна. В ней могут быть
выделены прежде всего следующие
частные задачи: обеспечение устойчивости
(стабилизация); повышение запаса
устойчивости (демпфирование); повышение
точности регулирования в
установившихся режимах (уменьшение или устранение
статической ошибки воспроизведения
задающего воздействия, уменьшение или
устранение влияния постоянных
возмущений); улучшение переходных
процессов (увеличение быстродействия,
максимальное уменьшение динамических
ошибок воспроизведения воздействия и от
возмущений).

Иногда несколько частных задач могут быть решены
совместно, в других случаях они оказываются противоречивыми.
В зависимости от назначения системы и предъявляемых к ней
требований одни задачи становятся основными, а другие
отодвигаются на второй план или снимаются.
Всякая система автоматического регулирования должна
быть устойчивой. Однако запас устойчивости в системе
стабилизации (с постоянным или редко изменяемым задающим
воздействием) может быть значительно меньше, чем в следящей
системе (с непрерывно или часто изменяющимся задающим
воздействием). Если параметры регулируемого объекта
определены приближенно или могут изменяться в процессе
эксплуатации системы, то необходим больший запас устойчивости,
чем при точно установленных и неизменных параметрах.
В системах стабилизации обеспечивается максимально
возможное или хотя бы необходимое уменьшение влияния
возмущений. В следящих системах, кроме того, обеспечивается
максимально возможное или необходимое быстродействие и
уменьшение как статических, так и динамических ошибок
воспроизведения задающего воздействия.
Требования в отношении быстродействия должны
соответствовать мощности исполнительного элемента регулятора.
Использование элементов для нужных преобразований сигнала
управления не должно приводить к существенному повышению
УЕРвня помех, присутствующих в задающем воздействии.
Когда устойчивость и необходимое качество не могут бьггь
достигнуты простым изменением параметров системы
(коэффициентов передачи, постоянных времени отдельных звеньев),
тогда эта задача решается введением в систему
дополнительных устройств, называемых корректирующими.
§ 5.2. Корректирующие устройства
Корректирующее устройство включают в систему
автоматического регулирования по-разному. Возможно
последовательное включение корректирующего устройства в прямую
цепь системы (рис. 5.1, а), в этом случае оно называется
последовательным корректирующим устройством. Его
передаточная функция на рис. 5.1, а обозначена
Последовательное корректирующее устройство включают
непосредственно после датчика рассогласования или же пос-

ле предварительного усилителя. Второй вариант включения
используют чаще. Дело в том. что уровень сигнала
рассогласования обычно весьма мал и корректирующее устройство
снижает чаще всего уровень сигнала, поэтому при первом
варианте включения последовательного корректирующего
устройства потребуется иметь предварительный усилитель
значительно более высокой чувствительности, чем при втором варианте.
Применение последовательных корректирующих устройств
наиболее удобно в системах, у которых сигнал управления
представляет собой напряжение постоянного тока. В этих
случаях корректирующее устройство выполняюг обычно из
пассивных электрических четырехполюсников, обеспечивающих
разнообразное преобразование сигнала. Еще большие
возможности дают активные электрические четырехполюсники
постоянного тока.
В системах, у которых сигналом управления является
модулированное напряжение переменного тока,
последовательные корректирующие устройства менее удобны по той причине,
что электрические четырехполюсники переменного тока имеют
существенные недостатки (см. § 5.3) и применяются редко, для
использования же пассивных четырехполюсников
постоянного тока оказываются необходимыми дополнительные элементы
(рис. 5.2). Модулированный сигнал переменного тока сначала
выпрямляется фазочувствительным демодулятором ФД и
затем фильтром Ф at-
фильт ровываются
высшие гармоники-
Только после этого
осуществляется
соответствующее
преобразование сигнала
четырехполюсн и к о м
постоянного тока.
Преобразованный
сигнал постоянного
тока вновь
превращается модулятором М
в модулированный
сигнал переменного
тока, если это
необходимо для действия
послед)тощих
элементов системы.
ч
'кг
В)
н
Рис 5.1

Параллельно-вст р е ч- ^Ц'^Л-^-Г?^^^
ное корректирующее ' ' ' »
шъ^^р-^ trj-- '
устройство показано на
рис. 5.1.6. В данном Рис 5.2
случае корректирующее
устройство является
обратной связью, чаще всего отрицательной, которая
охватывает один из элементов прямой цепи системы. Этим
элементом обычно является исполнительный элемент или выходной
каскад усилителя (усилитель мощности). Такое
корректирующее устройство называют параллельным. Его передаточную
функцию будем обозначать Т^кг-
Передаточная функция участка цепи с параллельным
корректирующим устройством
W2 = W^/(\ + W,W^^), (5 Л)
Обычно в достаточно широком и существенном для
качества системы диапазоне частот справедливо неравенство
\W2(HW^iJa^\^\. (5.2)
Тогда в этом диапазоне частот
\^2(/«)«1/Г„2(/«). (5.3)
Таким образом, при удовлетворении неравенства (5.2)
свойства участка цепи с параллельным корректирующим
устройством определяются только лишь свойствами этого
корректирующего устройства.
Указанное обстоятельство является большим достоинством
параллельного корректирующего устройства. При
удовлетворении неравенства (5.2) свойства участка прямой цепи,
охваченного параллельным корректирующим устройством, и их
изменения в процессе действия системы це влияют на ее
свойства. Несущественные нелинейности этого участка и изменения
его параметров (коэффициентов передаточной функции W<^)
не сказываются на динамических свойствах системы. Это
справедливо только при неизменных параметрах самого
параллельного корректирующего устройства.
Достоинство данного корректирующего устройства также
в том, что его вход подключен к выходу исполнительного
элемента или усилителя мощности, т. е. к выходу мощного
элемента с высоким уровнем сигнала. Поэтому в качестве
параллельных корректирующих устройств могут быть
использованы даже достаточно мощные элементы. Но широко используют

и пассивные четырехполюсники постоянного тока, и тогда
весьма просто обеспечить сложное преобразование сигнала
участком цепи с параллельным корректирующим устройством.
Следует заметить, что влияние местных обратных связей,
реализующих параллельные корректирующие устройства,
весьма разнообразно. Корректирующие обратные связи делятся
на жесткие и гибкие. Жесткая обратная связь действует на
систему как в переходном, так и в установившемся режиме,
т. е. ll^jKoc (0) =7^ О, и реализуется она безынерционным или
инерционным звеном. Гибкая обратная связь действует лишь
в переходных режимах, реализуется она или чисто
дифференцирующим с передаточной функцией
или инерционно-дифференцирующим звеном
W^iaj'-^k^s/iT^s+l),
Предположим, что звено с передаточной функцией W
охвачено отрицательной обратной связью с передаточной
функцией Wq, Тогда эквивалентная передаточная функция этого
участка цепи IF, = W/{1 + WW^).
Наиболее характерны следующие случаи. Пусть
апериодическое звено охвачено жесткой обратной связью, т. е.
W = k/{Ts + 1) и IFo = fto- В этом случае
Гз = k/(Ts + I + kkoi =^ kJ(T^ s + 1), (5.4)
где k^ = k/{l+kkQ) и 7з-7/(1ч-Л^о).
Таким образом, жесткая отрицательная обратная связь не
изменяет структуру апериодического звена, но уменьшает его
инерционность, т. е. уменьшает постоянную времени.
Одновременно уменьшается передаточный коэффициент звена.
Если обратная связь гибкая, т. е. Wq = ftoS, то
W, = k/(Ts + 1 + kko s) = k/{T, s + 1), (5.5)
где T^ = T + kkQ.
Следовательно, гибкая отрицательная обратная связь не
изменяет структуру и не влияет на передаточный коэффициент
апериодического звена. Она лишь увеличивает его
инерционность — его постоянную времени.

Пусть интегрирующее звено охвачено жесткой обратной
связью W ^ kis w Wo = ko» В этом случае
W, ^ k/{s + kko) = kJ{T, s + 1), (5.6)
где k^^l/ko и T^^l/(kkoh
Таким образом, жесткая отрицательная обратная связь
превращает интегрирующее звено в апериодическое.
Если обратная связь гибкая, т. е. Wq = ^о^. то
W^~-=k/is-\ kkoS)^kJs, (5.7)
где k^^kliX +kkoh
Гибкая обратная связь не изменяет структуру
интегрирующего звена, но уменьшает его передаточный коэффициент
(увеличивает постоянную времени интегрирования = 1/к^)>
Предположим, что колебательное звено охвачено жесткой
обратной связью, т. е. W == k/(T^s^ + 2lTs + I) и Wo ^ ко*
При этом
= Й/(Я ^ + 21TS + 1 + kko) =
= МП5^ + 2|зГз5+1), (5.8)
где k,^k/(l+kko); T,=^T/V\+kko; l,^l/Vl+kko.
Жесткая отрицательная обратная связь не изменяет
структуру колебательного звена, но уменьшает постоянную времени
и коэффициент демпфирования. Уменьшается также
передаточный коэффициент звена.
При гибкой обратной связи возможны два варианта. Если
Ао<2Г (1-|)/А, (5.9)
то
= к/[Т^ ^ + 21TS 4-1 + kko S] = k/[T^ s2 + Ts + 11, (5.10)
где 1з = S + kko/{2n
Слабая отрицательная гибкая связь не изменяет
структуру колебательного звена и лишь увеличивает его коэффициент
демпфирования.
Если же
ft,>2r(l-i)/fe, (5.11)
Гз = kll{T,s + 1) {T,s + 1)1, (5.12)
где Ti-0,5(r i-Yr^~4T^); П = 0,Ъ{г ^VF^^);
г-2|Г + Л^

Сильная отрицательная гибкая связь превращает
колебательное звено в последовательное соединение двух
апериодических звеньев.
Еще один случай: идеальное усилительное звено охвачено
инерционной обратной связью, т. е. W = k и Wq =^ ККТф +
+ 1). Тогда
W, = k{T^s+ тт, S + 1 + ААо) = (7^0 5 + 1), (5.13)
где K^k{{\+kk,)\ T,^TJ{\+kk,),
Таким образом, инерционная отрицательная обратная связь
превращает идеальное усилительное звено в реальное
форсирующее звено, создающее производные от входного сигнала.
Из рассмотренных примеров можно заключить, что даже
простейшие отрицательные обратные связи могут существенно
изменить свойства типовых динамических звеньев. Еще
больший эффект дают сложные отрицательные и положительные
обратные связи. В [1, 31 подробно изложено влияние
сложных обратных связей на свойства типовых динамических
звеньев и их соединений. Следовательно, если основные элементы
регулятора по своей физической природе позволяют создать
обратные связи, то динамические свойства этих элементов
зачастую могут быть изменены в нужном направлении.
Параллельное корректирующее устройство — это третий
вариант включения устройства в САУ (см. рис. 5.1, в).
Включенное таким образом корректирующее устройство будем
называть прямым параллельным и его передаточную функцию
будем обозначать W^s-
Иногда прямое параллельное корректирующее устройство
оказывается весьма удобным, так как при меньшей сложности
обеспечивает нужное преобразование сигнала управления.
Пусть, например, = И^кз = —kiJ(Ts + 1).
Тогда передаточная функция данного участка цепи
= W^3 + W,^ =ks{T3S+l )/(Ts + 1)
где кз = ks —*кзэ ^3 =^ К ^/(^3
Следовательно, при малой разности (ftg — k^^ получается
реальное форсирующее звено с большой постоянной времени
дифференцирования. Уменьшение передаточного коэффициента
этого участка прямой цепи должно быть скомпенсировано
соответствующим увеличением передаточного коэффициента
усилителя.

Синтезируют корректирующее устройство на основании
некоторого комплекса требований к свойствам системы (см. § 5.1).
Сначала определяют требуемое значение передаточной функции
Wi,i последовательного корректирующего устройства. Затем
выясняют, при каких значениях передаточных функций W^^z
параллельного корректирующего устройства и Wi,^ прямого
параллельного корректирующего устройства будет получен
тот же эффект, после чего уже можно решать, какое
корректирующее устройство целесообразнее создавать. Составим
формулы для такого расчета.
По каждой из структурных схем (см. рис. 5.1) составим
передаточные функций разомкнутой цепи и приравняем эти
выражения друг другу. Получаем
WW,a ^ W/{1 + W^,) ^ W (I + W,s/W,), (5.14)
где W W^W^W.,, ^
Из (5.14) определяют формулы перехода от одного вида
корректирующего устройства к другому:
=== 1/(1 + W^^) ^ 1 + W^JW,'
(5.15)
Если значение передаточной функции W^^ оказывается
отрицательным, то параллельное корректирующее устройство
должно включаться в виде положительной обратной связи.
При отрицательном значении передаточной функции И^^з
выходной сигнал прямого параллельного корректирующего
устройства должен вычитаться из выходного сигнала участка
В настоящее время корректирующие устройства
являются основным способом повышения качества линейных
непрерывных систем регулирования по отклонению. Иногда в
системе одновременно используют два корректирующих
устройства: последовательное и параллельное или параллельное
и прямое параллельное. Таким образом, функции, которые
должны выполнять корректирующее устройство,
распределяются между двумя корректирующими устройствами. Они
могут быть выполнены из более простых элементов.
Составим формулы для замены последовательного
корректирующего устройства двумя: последовательным и
параллельным; такой вариант наиболее вероятен.

-0т
ил
Рис. 5,3
Итак, пусть определена передаточная функция
Wпоследовательного корректирующего устройства (рис. 5.1, а),
при которой система будет иметь необходимые динамические
свойства. Однако из-за сложности W^^i решено создать в
системе два корректирующих устройства: последовательное и
параллельное (рис. 5.3). Определяем передаточные функции
разомкнутой цепи каждой из этих систем и приравниваем их
Друг другу:
rW^«, = WW[al{\ + W^2 W^k2). (5Л6)
Из этого равенства следует, что
«^Hi = ir«i(l + W^2U^k2); W^k2=(W'ki-V1^hJ/(M^2W^hi). (5.17)
Можно выбрать передаточную функцию
параллельного корректирующего устройства и по первому из равенств
(5.17) определить необходимое значение W'y,\ передаточной
функции последовательного корректирующего устройства или
же выбрать передаточную функцию Wi\ последовательного
корректирующего устройства и тогда второе из равенств
(5.17) определит необходимое значение Wl^ передаточной
функции параллельного корректирующего устройства.
Аналогично можно составить формулы для замены
последовательного корректирующего устройства последовательным и
прямым параллельным или же параллельным и прямым
параллельным.
§ 5.3. Преобразовательные элементы
Корректирующие устройства систем регулирования
осуществляют преобразование сигнала управления. С этой целью
их составляют из элементов, которые удобно называть
преобразовательными. Используются электрические (наиболее ши-

роко), механические, гидравлические, пневматические и иные
преобразовательные элементы. Рассмотрим основные из них.
Пассивные четырехполюсники постоянного тока. Это
электрические цепи из резисторов, конденсаторов и индуктивностей.
Общая схема пассивного четырехполюсника показана на
рис. 5.4. Входное и выходное напряжения постоянного тока
обозначены соответственно через Ui и Wg; Zi (s) = i?i + 1/
/(Cis) + LiS и (s) = /?2 + 1/(^25) + l2s — операторы
сопротивлений четырехполюсника; С^, Li — соответственно
активные сопротивления, емкости и индуктивности; —
полное сопротивление нагрузки.
Если напряжение приложено к нагрузке с бесконечно
большим полным сопротивлением z^, то передаточная функция
пассивного четырехполюсника
Wu (s) = Z2 (sVlzi (s) + Z2 (5.18)
Варьируя вид операторов сопротивлений Zi (s) и (s) и
значения Rt, Ci, L^, можно получить большое количество
четырехполюсников, описываемых различными
передаточными функциями W^jj. Стоимость пассивных четырехполюсников
низкая, а стабильность параметров достаточно высокая.
Этими достоинствами объясняется широкое использование их
в системах автоматического регулирования, у которых
сигналом управления является напряжение постоянного тока.
Основной недостаток пассивных четырехполюсников
заключается в том, что они ослабляют сигнал; кроме того, при
конечном значении полного сопротивления нагрузки
преобразование сигнала отклоняется от желаемого,
соответствующего виду передаточной функции Н^^, составленной по (5.18).
Наиболее характерные схемы пассивных четырехполюсии-
ков постоянного тока показаны в табл. 5.1. Там же
приведены их передаточные функции и логарифмические частотные
характеристики.
Принято разделять четырехполюсники на
дифференцирующие, интегрирующие и интегродифференцирующие.
Дифференцирующие четырехполюсники
(схемы 1 и 2 в табл. 5.1) в опре- ^ ^
деленном диапазоне частот диффе- '
ренцируют сигнал и создают по-
ложительный сдвиг по фазе.
Интегрирующие четырехполюсники
(схемы 3, 4 в табл. 5.1) в некотором о—
диапазоне частот обеспечивают рис. 5.4

Тоолица 5.Z
Электрическая
схема
Логарифмические час -
тошные характерисгики
Передаточная функции
где T^-P^Cf; Т2 = Я^С^,
причем
Г
о
90
Wg = -(T2S*I)/(T,S),
где Tf-RiC^; Т^^Я^Сг,
причем
а) Т,>Т,>Т,>Т^
VT, i/Тг Щ
1 >ytt
где к = Rj/^t
Ti = (R,^-R2)C,;T2=R2(r,;
b=(R3*Ri,)C2; T^=R^C2,
причем
L,= 20lgk;
ЛОВ на входе. Все это весьма существенные достоинства
активных четырехполюсников. Однако они значительно сложнее
и дороже пассивных четырехполюсников.
В табл. 5.2 приведены простейшие схемы активных
четырехполюсников, их передаточные функции и частотные
характеристики. Схема / является дифференцирующей, при /?i = О
ее передаточная функция принимает вид = —T^s, Схема
2 ~ интегрирующая, при i^g = О передаточная функция
:= —l/(ris). Схема 3 — интегродифференцирующая.
Варьируя операторы сопротивлений (s) и (s) и
параметры их элементов, можно получить активные четырехпо-

o-c
люсники с более
сложными передаточными
функциями.
Дифференцирую щ и й
трансформатор.
Распространенным
преобразовательным элементом 5 7
является трансформатор,
обеспечивающий
дифференцирование сигнала постоянного тока. Его схема и
приведены на рис. 5.7, а передаточная функция
W^=ak^ 7\s/(Ts+}),
ЛАЧХ
равна
(5.22)
где а = RJir^ + Rid'y К = Щ^Щ — коэффициент
трансформации; Тг = Li/{ri + ^i) и Гг = ^2,/(г2, + R2) — постоянные
времени первичной и вторичной обмоток; Т ^ Т^Л- Т^.
Дифференцирующий трансформатор позволяет избежать
гальванической связи между цепями входного и выходного
сигналов, что иногда совершенно необходимо. Его часто ис-
пол]ьзуют в виде параллельного корректирующего устройства.
При этом в цепь вторичной обмотки может быть включен
необходимый пассивный четырехполюсник.
Пассивные четырехполюсники переменного тока. Такие
четырехполюсники преобразуют сигнал, являющийся
модулированным напряжением переменного тока. Выполняются они
из резисторов и конденсаторов и обеспечивают приближенное
дифференцирование сигнала (огибающей модулированного
напряжения) в некотором диапазоне частот. При этом частота о
изменения сигнала должна быть значительно ( по крайней
мере на порядок) меньше несущей частоты о^, т. е. частоты
переменного тока. Недостаток этих четырехполюсников еще и в
том, что изменение
несущей частоты*
заметно влияет на их ff,
динамические
свойства.
На рис. 5.8
приведены схема и
приближенная
эквивалентная ЛАХЧ одного из
пассивных
четырехполюсников перемен- Рис. 6.8

Horo тока. Его приближенная эквивалентная передаточная
функция
<^-='>
где Т = 2RjC^C2 (Q + Cg); а ^ (Q + CMiC^ + i?2 X
X (QH- C2)]< 1.
Недостатки пассивных четырехполюсников переменного
тока и однообразие их свойств ведут к использованию в цепях
с модулированным сигналом пассивных четырехполюсников
постоянного тока. Этот вопрос рассматривался в §5.2.
Кроме рассмотренных электрических преобразовательных
элементов используются еще тахогенераторы и тахометриче-
ские мосты постоянного и переменного тока, дроссельные и
емкостные дифференциаторы переменного тока [7], а также
более сложные элементы.
§ 5.4. Повышение точности в установившихся
режимах
В системе регулирования по отклонению установившаяся
ошибка имеет три составляющие:
^ст==«^-Ье/+^'ч.э. (5.24)
где Eg — ошибка воспроизведения задающего воздействия
£^ — ошибка, вызываемая действием возмущений; £^.3 — ошиб
ка чувствительного элемента, измеряющего рассогласование.
Составляющая e^^g зависит от физической природы и
конструкции чувствительного элемента. Она может быть
уменьшена лишь использованием высокоточного элемента. При этом
может потребоваться снижение уровня сравниваемых
сигналов и, следовательно, увеличение передаточных
коэффициентов остальных элементов регулятора.
Как было показано в гл. 4, установившаяся ошибка может
быть представлена в виде ряда (4.3). При этом коэффициенты
ошибок воспроизведения С©, Ci, вычисляют по
передаточной функции Wg^ (s) замкнутой системы для ошибки
воспроизведения, а коэффициенты ошибки от возмущения Со/,
Cift . С^/— по передаточной функции Wfe{s) замкнутой
системы для ошибки относительно возмущения по формулам
(4.7).

Нужно заметить, что в статической системе
Со-1/(1+Л); Co/ = V(l+%
(5.25)
где k — передаточный коэффициент разомкнутой системы;
kf — передаточный коэффициент прямой цепи от возмущения
/ до выходной координаты у.
Следовательно, уменьшение установившейся ошибки при
постоянных значениях задающего воздействия и возмущения
достигается увеличением передаточного коэффициента
разомкнутой системы. Однако с увеличением статической точности
в большинстве случаев уменьшаются запасы устойчивости и
при значительном увеличении k система становится
неустойчивой.
Противоречие между статической точностью и
устойчивостью проиллюстрировано на рис. 5.9, где сплошными линиями
показаны логарифмические частотные характеристики
разомкнутой системы с передаточной функцией
W = k/l(T,s + I) (Т^ + I) (Т^ + 1)1
(5.26)
при k = 20, = 0,5 с. Га = 0,025 с, = 0,01 с. Если
передаточный коэффициент увеличить до k == 60, то ЛАЧХ
принимает положение, показанное пунктиром. Чйстотд среза
увеличилась и запас устойчивости по фазе уменьшился с у = 26*"
до Yl = 3"". Столь малый запас по фазе совершенно недопустим.
При повышении статической точности путем увеличения
передаточного коэффициента k разомкнутой системы
необходимы мероприятия для обеспечения достаточного запаса
устойчивости. Они будут рассмотрены в следующем параграфе.
Возможно, вообще говоря, создание такбй структуры системы,
которая допускает неограниченное увеличение передаточного
коэффициента k разом- ^
кнутой цепи [21. '^^
Другой путь
повышения статической
точности — обеспечение ас-
татизма. В астатической
системе младшие
коэффициенты ошибки имеют
следующие значения:
Со=0; Q = l/fe,;
О), с
Рис. 5.9

Рис. 5.10
где — передаточный
коэффициент разомкнутой
системы, называемый в
данном случае
добротностью системы по скорости
(или коэффициентом
добротности по скорости).
Таким образом, в астатической системе отсутствует
установившаяся ошибка от постоянного задающего воздействия и
постоянных возмущений.
Как было показано в гл. 4, астатизм достигается введением
интегрирующего звена в прямую цепь системы . Для
астатизма относительно возмущения интегрирующее звено должно
быть введено до точки, в которой приложено возмущение
(рис. 5.10).
Влияние интегрирующего звена на динамические свойства
системы приведено на рис. 5.11, где сплошными линиями
показаны логарифмические частотные характеристики системы с
передаточной функцией (5.26). При введении в разомкнутую цепь
этой системы интегрирующего звена характеристики
принимают положение, показанное пунктиром. Фазочастотная
характеристика переместилась вниз на —^90°, а
амплитудно-частотная характеристика повернулась вокруг точки а по
направлению часовой стрелки . В результате запас устойчивости по
фазе уменьшился с v == 26° до недопустимо малого значения
Vi = 6°. Система остается устойчивой, но переходный процесс
будет сильно колебательным. Кроме того, уменьшилась
частота среза и переходные процессы будут более
продолжительными.
Однако в других ситуациях введение интегрирующего
звена может не только не ухудшить, а даже улучшить
динамические свойства системы.
Пусть, например,
постоянные времени системы
с передаточной
функцией (5.26) имеют
следующие значения: =
-0,05 с, 7^- 0,0025
с и = 0,001 с.
Логарифмические частотные
характеристики
разомкнутой системы показаны
Рис. 5.11 рис. 5.12 сплошными
20
ЧбО'
9

ct) , . ^) ^ усилительного звена
rn
у
И/
: с передаточным
коэффициентом т на
входе. В установив-
атемся режиме
Р"^- 5-*^ y=mg^kl{\-\-k), (5.28)
где k — передаточный коэффициент разомкнутой системы.
При т = \ + Mk получаем у = g^n сис1^ема является
астатической относительно, задающего воздействия.
Недостаток этих способов в том, что а статизм
обеспечивается только при сохранении указанных соотношений между
передаточными коэффициентами. Неточное определение
передаточного коэффициента какого-либо элемента системы и его
изменение в процессе эксплуатации ведут к появлению
статической ошибки. Астатизм, достигнутый введением
интегрирующего или изодромного звена, сохраняется и при изменении
параметров системы. Однако нужно иметь в виду, что введение
двух интегрирующих звеньев в систему, состоящую из
усилительных, апериодических и колебательных звеньев, сделает ее
структурно-неустойчивой. Возможно обеспечение астатизма и
более высокого порядка. При этом из-за введения большого
числа интегрирующих или изодромных звеньев и мероприятий,
обеспечивающих требуемые динамические свойства, структура
САУ значительно усложняется.
Компенсация внешнего воздействЕ^я (обеспечение Е'«нварЕ'«-
антности). Рассмотренные выше способы улучшения,
статических и динамических свойств системы связаны лишь с
изменениями параметров элементов САУ и структуры ее отдельных
участков, но при этом не затрагивают принципа действия
системы.
Помимо принципа регулирования по отклонению
существует принцип регулирования по внешнему воздействию
(см. гл. I). Значительный эффект дает их одновременное
использование. В этом случае системы называются
комбинированными. Кроме замкнутого контура они имеют
дополнительную цепь влияния внешнего воздействия — возмущения или
задающего.
Система комбинированного регулирования.
Комбинированное регулирование используют в системах для уменьшения
влияния сильного возмущения. Это возможно в том случае,
если возмущение доступно измерению. При этом в системе со-

здается дополнитель- f
ная цепь воздействия .—Г^-«—VV^-*—
основного возмуще- д —i i j—» i—» Xr i—t U
НИЯ. Ha рис. 5.14 no- ^^Н8Н^@-^^
казана структурная 1
структурная
схема такой системы.
Здесь W^, W^. и
— передаточные ^-^^
функции
регулируемого объекта, исполнительного элемента и двух каскадов
усилителя; и — передаточные функции измерительного и
преобразовательного элементов дополнительной цепи
воздействия возмущения /. Эта дополнительная цепь должна
компенсировать влияние возмущения / на регулируемую координату
у, поэтому ее следует называть компенсирующей.
Компенсирующую цепь обычно включают в прямую цепь системы между
каскадами усилителя или на вход последовательного
корректирующего устройства (если таковое имеется).
Составим передаточную функцию замкнутой системы
(рис. 5.14) относительно возмущения:
V^fy - (Г„.^ W, W,^-1)/(1 + Г), (5.29)
где и^^.ц = W^Wq — передаточная функция компенсирующей
цепи; W= ttJ^iU^gl^s^e — передаточная функция
разомкнутого контура.
Если
W2W,W,,^^\, (5.30)
то передаточная функция системы относительно возмущения
/ равна нулю и возмущение / не влияет на регулируемую
координату. В этом случае говорят, что регулируемая
координата у инвариантна (независима) от возмущения /.
Один из разделов теории автоматического управления
изучает принципы построения САУ, реализующие полную или
частичную инвариантность от внешних возмущений. 3iot
принцип носит название принципа инвариантности. Большое
значение в развитии теории инвариантности и ее практическом
приложении имели работы В. С. Кулебакина, Н. Н. Лузина,
Б. Н. Петрова и др.
Равенс1Во (5.30) является условием полной
инвариантности от /. Полной (с точностью до переходной составляющей)
инвариантностью называют независимость регулируемой
координаты у от изменений возмущения / — независимость

функций у (t) от вида функции / (/). Однако начальные
значения возмущения и его производных создают переходную
составляющую регулируемой координаты. Если же и начальные
значения возмущения и его производных не влияют на
регулируемую координату, то имеет место абсолютная
инвариантность, для достижения которой необходимо удовлетворение
дополнительных условий. Так, в рассматриваемой системе
абсолютная инвариантность будет иметь место только при
безынерционных элементов W^, U^g, и Wq.
Удовлетворение условия полной инвариантности (5.30)
чаще всего сопряжено со значительными трудностями из-за
инерционности основных элементов. Пусть, например,
= V(l + T^s); = KI{Tls^ + 21T^ + 1); =
= kj{\ + T^); = k^.
Подставив эти выражения в (5.30), получаем условие
инвариантности:
«^к.ц 1 /(W^ W,) ^ (T,s^i){ns^ + 2lT,s+l)^
= /^н.ц [Ts П s-^ + (П + 217, П) ^ + (Тг + 217^) s + 11,
где ^к.ц = (^2*з)~*.
В данном случае для полной инвариатности
преобразовательный элемент компенсирующей цепи должен создавать
первую, вторую и третью производные сигнала измерительного
элемента. Практически ограничиваются созданием
производных не выше второй, так как многократное
дифференцирование сигнала сложно, неточно и ведет к сильному повышению
уровня помех.
Предположим, что компенсирующая цепь вьтолняется с
передаточной функцией
W,.^ = k^,^l(T, + 2^s + ll
т. е. ее преобразовательный элемент создает только первую
производную от входного сигнала. Тогда из (5.29) получаем
\у/ -kATlT^s^{Tl^2lT,T,)sn
При выбранной компенсирующей цепи возмущение и его
первая производная не будут влиять на регулируемую
координату. Однако старшие производные возмущения, начиная
со второй, будут оказывать влияние на регулируемую коорди-

нату так же, как и при отсутствии компенсирующей цепи. В
данном случае будет достигнута частичная (до первой
производной включительно) инвариантность у от /. Чем глаже
функция / {t), тем эффективнее ее компенсация. При частичной
инвариантности начальные значения возмущения и всех его
производных будут создавать переходную составляющую у так
же, как и при полной инвариантности.
Однако выбранная передаточная функция компенсирующей
цепи не может быть реализована. Физически реализуема лишь
такая передаточная функция, у которой степень числителя не
выше степени знаменателя. Следовательно, в рассматриваемом
примере компенсирующая цепь может быть выполнена лишь
с передаточной функцией
й^к.ц = ^н.ц [(7^3 + 2Е7^2) S + 1 ]/(ts + I),
где т — достаточно малая постоянная времени.
Указанное обстоятельство препятствует точному
удовлетворению условия инвариантности. Такую же роль играют
неточности в определении параметров реальных элементов и
погрешности при выполнении элементов по выбранной
передаточной функции (хотя она принципиально и может быть
реализована). В результате передаточная функция системы
относительно возмущения даже в лучшем случае (когда
компенсирующей цепью создается нужное количество производных)
оказывается не равной нулю, но с достаточно малыми
коэффициентами числителя. Тогда и влияние возмущения на
регулируемую координату оказывается весьма малым. Принято
говорить, что достигается инвариантность с точностью до малой
величины е.
Несмотря. на указанные трудности и даже, чаще всего,
невозможность достижения полной и тем более абсолютной
инвариантности, комбинированное регулирование имеет большие
достоинства. Компенсирующая цепь практически устраняет
или хотя бы существенно уменьшает влияние основного
возмущения. Вследствие этого снижаются требования к
замкнутому контуру регулирования. В системе стабилизации он
может иметь меньший передаточный коэффициент разомкнутой
цепи и уменьшаются трудности обеспечения его устойчивости
и достаточного запаса устойчивости. При наличии
компенсирующей цепи по возмущению замкнутый контур менее сложен.
Следует заметить, что компенсирующая цепь не влияет на
устойчивость замкнутого контура. Однако сама
компенсирующая цепь должна быть устойчивой.

Иногда вызывает
Hl''/^ [—I затруднения измере-
у ние возмущения. Тог-
LllJl
и/;
Рис. 5.16
" да используют
некоторые приемы,
позволяющие-
приближаться к инвариантности
регулируемой
координаты от возмущения
без непосредственного измерения последнего 15]. В частности,
создается компаундирующая связь, т. е. дополнительная связь
внутри замкнутого контура регулирования по одной из его
промежуточных координат, зависящих от возмущения
(несущих информацию о возмущении).
Комбинкр01занная следящая ск^астема. Основной целью
следящих систем является возможно более точное
воспроизведение регулируемой координатой изменяющегося
задающего воздействия. Этому способствует дополнительная цепь по
задающему воздействию. Следящую систему в этом случае
называют комбинированной следящей системой, ее типичная
структурная схема показана на рис. 5.15. Здесь замкнутый
контур такой же, как и на рис. 5.14, а — передаточная
функция дополнительной цепи.
Эта цепь улучшает воспроизведение регулируемой
координатой задающего воздействия, так как форсирует
переходные процессы при изменении g^, и ее следует называть
форсирующей цепью. Она чаще всего состоит только из
преобразовательного элемента. Включается форсирующая цепь в замкнутый
контур так же, как и компенсирующая, т. е. обычно между
каскадами усилителя.
В комбинированной следящей системе воспроизведение
задающего воздействия обеспечивается главным образом
форсирующей цепью. Замкнутый контур играет в этом отношении
второстепенную роль. Его основная задача — уменьшение
влияния возмущений.
По структурной схеме комбинированной следящей
системы (рис. 5.15) определяем передаточные функции
относительно задающего воздействия:
Wg=^W(\ + W^IW^I{\ + W) (5.31)
и для ошибки слежения:
= (1 — WW^IW^W + (5.32)
где W =

= WJW - \I{W^W^W^). (5.33)
TO передаточная функция относительно задающего
воздействия обращается в единицу, а передаточная функция для
ошибки слежения — в нуль. Следовательно, (5.33) — это условие
инвариантности ошибки слежения е от задающего
воздействия, или условие идеального воспроизведения выходной ко-
Ьрдинатой у задающего воздействия g.
Выполнение (5.33) связано с большими трудностями,
нежели выполнение (5.30). Причина в том, что сигнал
форсирующей цепи должен преодолеть не только инерционность
исполнительного элемента регулятора, но и регулируемого
объекта.
Ранее указывалось на практическую невозможность
создания производных выше второго порядка, поэтому в
комбинированных следящих системах достигается лишь частичная
инвариантность ошибки е от задающего воздействия g до нулевой,
первой или второй производной включительно. Это означает
соответственно астатизм первого, второго и третьего
порядков относительно задающего воздействия.
Неизбежная (хотя и незначительная) инерционность
дифференцирующих элементов, а также неточности в
определении параме1ров и изготовлении элементов регулятора ведут к
тому, что и частичная инвариантность обеспечивается лишь
с точностью до малой величины 6.
Несмотря на это, комбинированное регулирование
значительно увеличивает точность слежения и находит широкое
применение. Чем медленнее изменяется задающее воздействие
g, тем больший эффект дает частичная инвариантность е
от g.
При наличии форсирующей цепи роль замкнутого контура
следящей системы уменьшается и он может быть выполнен из
более простых элементов. Форсирующая цепь не влияе!^ на
устойчивос1Ь замкнутого контура, но сама эта цепь должна
быть устойчивой.
Если в комбинированной следящей системе имеется
сильное возмущение, то точность слежения может быть
увеличена еще более созданием компенсирующей связи по этому
возмущению. Преобразовательные элементы обеих цепей частично
могут быть объединены, и может оказаться, что для создания
компенсирующей цепи потребуется только элемент,
измеряющий возмущение.

§ 5.5. ОбеспеченЕ^е устОЕ^чивости и повышение
запаса устойчивости
Способы придания системам автоматического
регулирования устойчивости и достаточного запаса устойчивости
(способы стабилизации и демпфирования) разнообразны. В § 5.2
рассматривалась возможность решения этой задачи выбором
основных элементов регулятора и изменением их
динамических свойств с ломощью местных обратных связей. Выясним,
как влияет на устойчивость изменение наиболее
характерного параметра — постоянной времени апериодического звена.
На рис. 5.16 сплошными линиями изображены
логарифмические частотные характеристики разомкнутой системы с
передаточной функцией (5.26). При увеличении с 0,5 до 1 с
характеристики принимают положение, показанное
пунктирными линиями. Увеличение постоянной времени приводЕ^ят
к увеличению запаса устойчивости по фазе с у = 26° до yi =
= 60°. Заметим, что сопрягающая частота coi = l/Ti
расположена левее частоты среза Шср-
Если же сопрягающая частота апериодического звена
расположена правее частоты среза Шср» то увеличение
постоянной времени этого звена уменьшит запас устойчивости.
Очевидно, что изменение постоянной времени колебательного
звена влияет на запас устойчивости аналогичным образом.
Влияние постоянной времени форсирующего звена [звена с
передаточной функцией Wф = k {Ts + 1)] противоположно.
Итак, если сопрягающая частота апериодического или
колебательного звена расположена левее частоты среза
логарифмической ампли1удно-частотной характеристики разомкнутой
системы, а сопрягающая
^01
Рис. 5.16
частота форсирующего
звена расположена
правее частоты среза, то
увеличение постоянной
времени каждого из этих
звеньев ведет к
увеличению запаса устойчивостЕ^я
[4]. Указанная
зависимость справедлива лишь
при условии, что
сопрягающая частота распо-

изображенные на рис. 5.18 сплошными линиями,
свидетельствуют о неустойчивости замкнутой системы, так как фаза
достигает —180° при частоте, меньшей частоты среза.
Введем в прямую цепь системы дополнительное звено с
передаточной функцией В/р 1/(Гд5 + 1), где Тд - 8 с.
Тогда характеристики системы принимают положение,
показанное на рис. 5.18 пунктирными линиями, и на основании их
можно видеть, что замкнутая система становится устойчивой.
Запас по фазе составляет Yi = SI""- Увеличением постоянной
времени дополнительного звена запас устойчивости по
фазе можно увеличить.
Устойчивость достигнута введением апериодического
звена, постоянная времени которого значительно больше
постоянных времени имеющихся апериодических звеньев. При этом
высокочастотная часть логарифмической
амплитудно-частотной характеристики сместилась вниз. Так же изменилась и
логарифмическая фазочастотная характеристика. Такой
прием обеспечения устойчивости или повышения запаса
устойчивости называют демпфированием с подавлением высоких ча^
стот (демпфированием с внесением отрицательных фазовых
сдвигов).
Апериодическое звено с большой постоянной времени
представляет собой фильтр низких частот и подавляет
высокочастотные помехи. В этом достоинство данного вида
демпфирования. Значительное уменьшение частоты среза и,
следовательно, быстродействия системы является весьма существенным
недостатком.
Если ось абсцисс пересекается асимптотой ЛАЧХ,
имеющей наклон —20дБ/дек, и слева от частоты среза Оср только
одна сопрягающая частота, то система остается устойчивой и
запас устойчивости не изменяется при увеличении передаточ-
Рис. 5.18

L,dB
20 .
0
0-
-20'
-wo"
9
Lfu})
Lj(u})
0,1
100
-
-
Рис, 5Л9
НОГО коэффициента к разомкнутой системы. Нужно только
одновременно с увеличением к пропорционально увеличивать
постоянную времени апериодического звена. Предположим
далее, что в рассматриваемую систему введено
дополнительно идеальное форсирующее звено с передаточной функцией
= T^s + и гле Tj^ = 0,01 с. На рис. 5.19 изображены
логарифмические частотные характеристики разомкнутой
цепи исходной сис1^емы (сплошные линии) и системы с
дополнительным звеном (пунктирные линии). В замкнутом состоянии
система с дополнительным звеном будет устойчивой, запас по
фазе составляет Vi = ^З"".
Теперь устойчивость достигнута введением не
апериодического, а форсирующего звена. В результате высокочастотная
часть ЛАЧХ сместилась вверх. Такое же изменение и у ЛФЧХ,
поэтому данный прием называют демпфированием с подняти-
ш высоких частот (демпфированием с внесением
положительного фазового сдвига).
Введением форсирующего звена могут быть обеспечены
устойчивость и необходимый запас устойчивости при любой
переда-ючной функции исходной системы (если она становится
структурно устойчивой). Одновременно увеличивается и
быстродействие. Однако существенно увеличивается и влияние
высокочастотных помех. Последнее обстоятельство является
серьезным недостатком данного вида демпфирования и
ограничивает его применение.
Предположим еще, что в рассматриваемую систему введено
дополнительно сложное звено с передаточной функцией
«^д (7^2д S + 1) (Гзд S + 1)/[Т,д S + 1) (Г,д S + 1)],
где 0,1 с; Т,^ = Т^^ = 0,01 с и = 0,001 с.

Рис. 5,20
На рис. 5.20 показаны логарифмические частотные
характеристики разомкнутой цепи исходной системы (сплошные
линии) и системы с дополнительным звеном (пунктирные линии).
В замкнутом состоянии система с дополнительным звеном ус*
тойчива, запас устойчивости по фазе = 49°.
Устойчивость достигнута смещением вниз среднечастоткой
части ЛАЧХ, и данный прием называют демпфированием с
подавлением средних частот. Этот вид демпфирования
промежуточный между двумя первыми, и применяют его наиболее
часто.
Рассмотренные приемы стабилизации и демпфирования
систем автоматического регулирования являются основными, но
далеко не исчерпывают всех возможностей.
§ 5.6. Выбор параметров и синтез корректирующих
устройств по корневым годографам
Наглядность и простота исследования влияния отдельных
параметров системы на ее динамические свойства составляют
несомненные достоинства метода корневых годографов и
обусловливают его применение как для выбора параметров, так
и для синтеза корректирующих устройств.
Пусть требуется выбрать какой-то параметр а
(передаточный коэффициент элемента, постоянную времени, коэффициент
демпфирования). Тогда при постоянных значениях всех
остальных параметров нужно задавать различные значения а i,
... внутри возможных пределов изменения этого параметра

в данной системе и построить траектории корней (корневой
годограф). Затем можно выбрать такое значение а, при
котором имеет место наиболее благоприятное расположение нулей
и полюсов. Корни следует вычислять наиболее простым
численным методом, так как большой точности не требуется из-за
приближенности корневой оценки качества.
Для выбора значения передаточного коэффициента k
разомкнутой системы необходимо построить корневой годограф
при изменении ft. Способ построения такого корневого
годографа разработан весьма детально (см. § 4.6).
При синтезе корректирующего устройства используют
различные исходные положения. В простейшем случае полагают,
что переходный процесс зависит от ближайшего к мнимой оси
вещественного полюса. Вместе с тем пользуются и
предположением, что наилучшие динаглические свойства система имеет,
когда ближайшей к мнимой оси будет пара
комплексно-сопряженных полюсов. Однако добавление третьего ближайшего к
мнимой оси вещественного полюса обычно улучшает качество
переходного процесса.
Необходимо также учитывать влияние нулей
передаточной функции, поэтому для определения качества
переходного процесса наиболее правильно рассматривать три
ближайших полюса и один нуль передаточной функции замкнутой
системы.
Порядок синтеза также может быть различным. Пусть
требуется выбратё последовательное корректирующее
устройство по заданным показателям качества переходной
характеристики и при заданном значении передаточного коэффициента
k разомкнутой системы. Тогда можно поступать следующим
образом [11: выяснить влияние k на показатели качества;
построить корневой годограф нескорректированной системы при
изменении k и отыскать на нем точки, соответствующие
заданным показателям качества; добиться прохождения
траекторий корней при заданном значении k вблизи выбранных
точек, вводя дополнительные нули и полюсы; составить
передаточную функцию последовательного корректирующего
устройства по дополнительно введенным нулям и полюсам.
Следует иметь в виду, что при введении диполя, т. е.
полюса и нуля, близко расположенных друг к другу, показатели
качества почти не изменяются, но передаточный коэффициент
может быть увеличен.
Пример расчета по изложенной схеме приведен в 11].

Предположим, что динамика системы определяется парой
комплексно-сопряженных полюсов:
%.о2=—о^о±/Ч- (5.34)
Тогда передаточная функция замкнутой системы
(s) kgHn + 2Го 5os + 1). (5.35)
Ha основании переходной характеристики,
соответствующей этой передаточной функции, определяют зависимость
и о)о от времени регулирования /р и относительно перерегули-
рования G [31, т. е.
«о^З/^р; а-е-««оЛоо. (5.36)
Теперь синтез последовательного корректирующего
устройства по заданным значениям k, и а будет слагаться из
следующих этапов:
I. Намечают положение определяющей пары полюсов Sqi
и So2, т. е, пары полюсов передаточной функции (5.35),
которая приблизительно эквивалентна передаточной функции
скорректированной системы на основаниц^аданных показателей
качества /р и а. При этом используют соотношения (5.36).
На диаграмме достаточно отметить только один полюс Sqi-
2. Наносят на диаграмму полюсы и нули неизменяемой
части системы.
3. Вводят дополнительные нули и полюсы так, чтобы
траектория корней скорректированной системы при изменении
k проходила вблизи полюса .Желательно скомпенсировать
нулями ближайшие к мнимой оси полюсы неизменяемой
части системы, с тем чтобы влияние полюсов и Sq^ на
динамику системы было действительно определяющим. Точка Sqi
будет принадлежать траектории корней скорректированной
системы, если удовлетворяется уравнение фаз (4.36).
4. Вводят диполь так, чтобы передаточный коэффициент
k имел необходимое значение. При этом" для вычисления k
используют (4.37).
5. Составляют передаточную функцию последовательного
корректирующего устройства по введенным полюсам и нулям.
6. Для проверки выполнения требований строят
переходную характеристику скорректированной системы.
Пример 5.1. Передаточная функция неизменяемой части системы
Wo (s) = k/ls (0,ls+ I) (0,05s + I)].
Требуется выбрать последовательное корректирующее устройство,
обеспечивающее при > 10 следующие показатели качества: 0,5 с <

'Л
ct
Рис. 5.2!
< /р < 0,7 с; 20% < о <
<30%.
Подставляя в (5.36) /р =
= 0,5 и а = 0,2, получаем
а,:=6; е-» Wo ^0,2;
соо=И,2.
Наносим на комплексную
плоскость (рис. 5-21)
определяющий полюс Soi = — 6 +
+ /11,2 и полюсы
неизменяемой части системы Si =^ 0; $2= — Ю; Sg — — 20. Вводим
дополнительный нуль ^1 = — 10, который скомпенсирует ближайший к
мнимой оси полюс «2 неизменяемой части системы.
Введем еще дополнительный полюс так, чтобы полюс Soi
находился на траектории корней скорректированной системы. Для этого
по уравнению фаз определяем угол 8^ наклона вектора 4, т. е.
64= 180° —(е1 + ез) = 180^—(118° + 39°)=23°.
Подсчитаем, какому значению передаточного коэффициента k
соответствует точка Soi траектории корней скорректированной системы
(4.37):
k - /г/з//(5з54) = 12,6.17,8.28,55/(20.26.4) = 12.
Значение k удовлетворяет требованиям; следовательно, вводить
диполь не требуется.
По значению нуля h и полюса S4 определяем передаточную
функцию последовательного корректирующего устройства:
W,,{s) =Лк(0,15-Ц)/(0,0425+1).
При этом передаточная функция скорректированной системы
Wg (S) = 12/ls (0.05s Ч- 1) (0,O42s4-1) + 12] =
= l/(0,000175s3 + 0,00767 + 0,08335+ 1) =^ l/[(O,029x
Xs + 1) (0,0061 Is« + 0,54s + l)] = 5650/i(s + 34,5) (s« + 9s+ 164)].
Переходная
характеристика системы
Л (О = 1—0,157 6
-34.6^
+ 1.14е--^'5'х
X sin (12^—2,ЗП
изображена на рис. 5.22.
Она имеет следующие
показатели качества:
== 0,635 с и 0=27 %
Итак, при
выбранном последовательном
корректирующем устрой-

стве система удовлетворяет требованиям. Однако следует заметить, что
показатели качества скорректированной системы заметно отличаются
ОТ тех значений (^р = 0.5 с; а = 20 %). по которым производится
расчет. Зто объясняется недостаточным удалением полюсов S3 и S4 (см.
ркс. 5.21) от определяющей пары комплексно-сопряженных полюсов.
В результате полюсы скорректированной системы имеют следующие
значения: s^^^ = — 4,5 ± /12; = ~ 34,5 т. е. пара комплексно-
сопряженных' полюсов отличается от выбранной (определяющей) и на
динамику системы' оказывает влияние полюс Sg.
§ 5.7. Синтез корректирующих устройств
по логарифмическим амплитудно-частотным
характеристикам
Рассмотрим еще один метод синтеза корректирующих
устройств, весьма детально разработанный и нашедший широкое
применение.
Пусть передаточная функция неизменяемой части системы
W,{s)=^k,R,{s)/[s-oQ^(s)l
где /?о (s); Qo (s) — полиномы от s со свободным членом,
равным единице; ко, — постоянные величины.
Потребуем, чтобы система была астатической v-ro порядка,
имела добротность ft, перерегулирование не более а и время
регулирования не более /р. Такой комплекс требований
весьма часто предъявляют к следящим системам. Значения
порядка астатизма v и добротности k выбирают, исходя из
необходимой точности регулирования в установившихся
режимах. Выбором показателей качества переходной
характеристики — перерегулирования а и времени регулирования —-
гарантируются необходимые быстродействие и динамическая
точность системы.
В некоторых случаях необходимо, чтобы при начальном
рассогласовании ускорение регулируемой координаты ке
превышало некоторого допустимого значения w. Такое
ограничение необходимо, например, в механических системах,
когда регулируемой координатой является перемещение.
Предупреждается появление в регулируемом объекте и в
исполнительном элементе недопустимых перегрузок (механических,
электрических и т. п.).
Легко установить, что если порядок астатизма Vq
неизменяемой части системы меньше v, то в усилитёльно-преобразо-

нательном элементе необходимо иметь (v — v^) интегрирующих
звеньев. Так же легко определяется необходимое значение
передаточного коэффициента
преобразовательно-усилительного элемента, равное к/ко-
Задача сводится, следовательно, к синтезу
корректирующего устройства, обеспечивающего необходимые
динамические свойства системы. При этом будем полагать, что
передаточная функция неизменяемой части системы
W^Q(s) = kRQ{s)/ls^QQ{s)l (5.37)
так как уже выяснено. Какой передаточный коэффициент
должен иметь усилительно-преобразовательный элемент и
нужны ли в нем интегрирующие звенья.
Метод синтеза корректирующих устройств, разработанный
В. В. Солодовниковым [81, основывается на соответствии
между логарифмическими частотными характеристиками
разомкнутой системы и ее статическими и динамическими
свойствами в замкнутом состоянии. Метод используется для систем
минимально-фазового типа, и поэтому достаточно
рассматривать лишь логарифмическую амплитудно-частотную
характеристику разомкнутой системы.
Построение ЛАЧХ неизменяемой части системы.
Асимптотическую ЛАЧХ Lo (со) нужно строить по передаточной
функции Wo (s), определяемой (5.37). Предварительно каждый из
полиномов Ro (s) и Qo (s) передаточной функции Wo (s) следует
разложить на множители вида (Tts + 1) и (77s^ + 2Tjls + 1),
где|<1.
Разложение это удобно осуществлять итерационным
методом, предложенным О. М. Крыжановским. Изложение метода
с примерами его применения дано в [91.
Пусть имеется полином третьей степени
С (S) = + «is2 + a^s + I = ао + c^s^ + c^s + с^),
где Cl = ai/ooi = а^/ао и 1/ло.
Вычисляем: «1 = с^/с^; == — Oi); а^ = c^/ic^ — Pi); Pa^
=«2 (i^i — a^); «3 = ^3/(^2 — P2); Рз = «3 ~ «3) и т. д.
Если процесс сходящийся, т. е, с увеличением i значения щ м pi
стремятся соответственно к некоторым пределам а и р, то
G (5) = is/a + 1) (aaos^ + Р^о 5 + 1).
Процесс вычисления щ и Р^- может оказаться расходящимся. Тог*
да нужно делать такие вычисления:
а, ==Гй/с1—; аг = C2/{i?i—«а)—Сз/(С1—«1)2;
«3 — cj(ci — tta) — cjict — «2) ^ и т. д.

Рис. 5.23
Построение желаемой ЛАЧХ. Желаемой называют
асимптотическую ЛАЧХ (со) разомкнутой системы, имеющей^же-
лаемые (требуемые) статические и динамические свойства.
Желаемая ЛАЧХ (рис. 5.23) состоит из трех основных
асимптот: низкочастотной, среднечастотной и высокочастотной.
Кроме того, могут быть сопрягакщие асимптоты, которые
соединяют основные.
Строится желаемая ЛАЧХ на основании требований к
системе. Ранее было выяснено, что низкочасгготная асимптота
ЛАЧХ разомкнутой системы определяет статические
свойства. Если передаточная функция (5.37) разомкнутой- системы
имеет передаточный коэффициент k и порядок астатизма v,
удовлетворяющие требованиям, то низкочастотной
асимптотой желаемой ЛАЧХ (со) является низкочастотная
асимптота ЛАЧХ Lo (со) неизменяемой части системы. На рис. 5.23
показан именно такой случай.
Среднечасгготная асимптота ЛАЧХ разомкнутой системы
и ее сопряжение с низкочастотной определяют динамические
свойства системы — устойчивость и показатели качества
переходной характеристики.
Построение среднечастотной асимптоты желаемой ЛАЧХ
начинают с выбора частоты среза (Оср. Для этого
используется номограмма (рис. 5.24), составленная В. В. Солодовнико-
вым. Она определяет зависимость перерегулирования о и
времени регулирования ^р от максимума Р^ах вещественной
частотной характеристики замкнутой сисггемы, причем время
регулирования /р дано в виде функции частоты среза (Оср.
Номограмма используется следукяцим образом. По
заданному значению перерегулирования о определяют значение

^niax- Затем по Р
гоах
<дср, Т. е.
max определяют соотношение между и
(5.38)
На рис. 5.24 показано, как по значению о = 30%
определено р^^^ = 1,27 и затем = 3.5зх/(Оср.
Из (5.38) вычисляют частоту среза o)cpi, при которой
время регулирования не превысит заданного значения. Если
при начальном рассогласовании ускорение регулируемой
координаты ограничивается значением w, то частота среза не
должна быть больше Осрг, т. е.
f^cp2 = K2£7i^. (5.39)
Частота среза (Осрг соответствует оптимальному переходному
процессу при допусггимом ускорении w.
Таким образом, частота среза должна быть выбрана по
одному из следующих условий:
со.
CP
'СО,
•ср1 или С0^р1<С0ср<С0^р2.
(5.40)
Чем больше Оср, тем меньше время регулирования.
Однако если cDcp2<Ccocpi, то ©ср не должна быть больше сосра-
В этом случае требование в отношении времени
регулирования, возможно, не будет удовлетворено.
Среднечастотная асимптота желаемой ЛАЧХ проводится
через точку (Оср с наклоном —20 дБ/дек. При большем наклоне
трудно обеспечить необхо-
2il
<0г
50
3D
20
W
—
—
-"7
7
А
А
-У
т
/
г
.-■к-.
1
♦
"Х-
S
/.f иг а р,
max
Рис. 5.24
димый запас устойчивосгги
и допустимое
перерегулирование.
Протяженность средне-
частотной асимптоты
устанавливается исходя из
необходимого запаса
устойчивости. Из этих же
соображений выбирают ее
сопряженнее низкочасуготной
асимптотой. Кроме того,
сопр ягакхцу ю асимптоту
следует выбирать так,
чтобы характеристика (о))
возможно меньше
отличалась от Lq (со) и коррек*

60
50
^0
го
to
-30
-25
-15
20 - W
- 5
0^- О
1
Si
-V
ч т
ч ■
_4__
-t-
г-
1,1 U2 1,3 bit U5
Рис. 5.25
тирующее устройство -^^грод 1^^,дБ
было возможно бО"
лее простым.
Для указанного
выбора по ранее
найденному значению
Р^^х с помощью
кривых, показанных на
рис. 5.25, определяют
избыток фазы Y и
предельные значения
логарифмических
амплитуд. Избыток
фазы у должен быть
обеспечен на том
участке характеристики
(со), для которого
справедливо
(5.41)
Этот участок охватывает среднечастотную асимптоту и,
возможно, часггь сопрягакхцей асимптоты.
Сначала нужно провести прямую с ординатой L„ (пунктир
на рис. 5.23). Затем нанести сопрягающую асимптоту. Если
наклон низкочастотной асимптоты О или —20 дБ/дек, то
наклон сопрягающей асимптоты выбирается равным —40 или
—60 дБ/дек. Начинать ее можно из точки среднечастотной
асимптоты с ординатой L^. После этого проверяют избыток
фазы Ya при частоте со^, где ордината (со) равна L^.
Значение Ya подсчитывается по формуле
у^ = я —уп12 — \knl2 — 21 со^/о)^ j +
-f ^lnl2 — 0)^/0)^J, (5.42)
где V — порядок астатизма; cof — сопрягающие частоты
меньше соа, при которых наклон (со) увеличивается на 20 дБ/
/дек; k — число сопрягающих частот со^; (О; — сопрягающие
частоты, меньшие со^, при которых наклон (со)
уменьшается на 20 дБ/дек; / — число сопрягающих частот со^.

Если фаза ср определяется каким-либо другим способом,
то избыток фазы определякуг как
Та = 180^ + Ф, (5.43)
где ф < 0. ^ /
Если избыток фазы оказывается меньше необходимого,
то сопрягающую асимптоту следует переместить влево. В
противном случае (при слишком большом избытке фазы)
сопрягающая асимптота перемещается вправо. Чем. больший
диапазон часггот занимает низкочастотная асимптота, тем лучше
система воспроизводит низкочастотные изменения задающего
воздействия.
Высокочастотная асимптота желаемой ЛАЧХ мало влияет
на свойства сисггемы, поэтому ее следует выбирать так, чтобы
корректирующее устройство было возможно более простым.
Это достигается при совмещении высокочастотных асимптот
характеристик L^{(o) и Lq (о>). Если совмещение не удается,
то высокочастотная асимптота L^^ (о) должна иметь тот же
наклон, что и высокочастотная асимптота L© (о).
После выбора высокочастотной асимптоты желаемой ЛАЧХ
и сопряжения ее со среднечастотной асимптотой проверяют
избыток фазы yQ при частоте о^, где ордината характеристики
L^(u)) равна —L^, т. е.
у^ = п — ^ со^/со,, (5.44)
где Qcp — относительный наклон среднечастотной
асимптоты (при наклоне —20 дБ/дек ^ср = 1); ^ — сопрягающие
частоты, большие частоты среза Оср; т — число частот со^.
Если у^ меньше требуемого значения, то высокочастотную
асимптоту желаемой ЛАЧХ нужно переместить вправо.
Для более точного подсчета фазы при частотах Оа и соб
используют номограмму (рис. 5.26). Номограмма должна быть расположена
так, чтобы ее ось относительных частот &/щ была параллельна оси час*
тот'характеристики JL« (to). Стрелка номограммы должна быть
совмещена с той частотой со,-, для которой подсчитывается фаза ф,-.
Затем для каждой асимптоты характеристики (to) по номограм*
ме определяется AS, т. е. приращение S иа данном участке частот, и
Л5 умножается на наклон асимптоты в дБ/дек (с учетом знака
наклона). Сумма этих произведений есть значение фазы ф,- в градусах.
Поимео подсчета фазы с помощью номограммы показан на рис.
5.27. В данном случае ш = О (2.25-1.5)^40 (1,5-0) - 20 (1.3 ^0)+
+ 20(2,25—1,3) = — 67^
Выбор корректирующих устройств. Передаточная функция
разомкнутой системы с посждовательным корректирующим

ttmS=
2A
T'
s
S
Й
п5
2^2
Z.2
'..9П-
■c,u -
- ^ Я -
UQ -
■ i с ^
Л
7,0-
. .1 С
ho -
/
ив
. -f л -
10-
у
r
1,4-
- -4 О
\
/
4 П
uo -
n о
\
/
П О
0,6 -
■ -п с ^
, /
и,в
■ -П Р
/
Utb
. .я /|—
- Л 9
■ 0,^-
f
0,1
Рис. 5.26
/О
100
устройством (см. рис. 5.1, а) г = «^o«^«i, где = W^W^W^,
и для ЛАЧХ справедливо соотношение L (©) = Lo (w) +
+ i-Ki (со). Желаемая ЛАЧХ ((о) есть ЛАЧХ разомкнутой
системы, которая должна быть получена введением
последовательного корректирующего усп-ройсггва. Следовательно,
((D) ^ Lo (со) + L«i (со); L«i (со) = (со)-L^ (со), (5.45)
т. е. для определения ЛАЧХ последовательного
корректирующего устройства из желаемой ЛАЧХ нужно вычесть ЛАЧХ
неизменяемой части си-
20
стемы. Вычитание
ординат достаточно сделать
на всез^ сопрягающих
часгготах этих
характеристик. Затем
полученные точки соединить
прямыми (см. рис. 5.23).
По ЛАЧХ L«i (со)
корректирующего
устройства можно
определить полиномы (s)
и Qki (s) его функции
«^Kl = i?Kl (s)/Qki (s).
Каждой сопрягакяцей
частоте со^, при кото-
Рис. 5.27

рой наклон ЛАЧХ увеличивается на 20 дБ/дек,
соответствует множитель (s/<Oj + 1) в полиноме Qki (s).
Сопрягающей частоте (Oj, при которой наклон ЛАЧХ уменьшается на
20 дБ/дек, соответствует множитель (s/(Oj + 1) в полиноме
(s). Если при какой-то частоте или ©j наклон ЛАЧХ
изменяется на 40 дБ/дек, то ей соответствует квадрат
указанного множителя.
Затем, пользуясь формулами (5.15), следует определить
передаточные функции W^z и W^s соответственно
параллельного и прямого параллельного корректирующих устройств,
эквивалентных требуемому последовательному
корректирующему устройству. Если передаточная функция W^i сложная,
то по формулам (5.17) целесообразно выяснить, при каких
передаточных функциях Wki и Wk2 требуемое
последовательное корректирующее устройство может быть заменено
двумя корректирующими устройствами: последовательным и
параллельным.
На основании полученных результатов и физических свойств
элементов неизменяемой части системы можно выбрать один
из вариантов включения корректирующего устройства. При
отсутствии очевидных и веских преимуществ одного или двух
из возможных вариантов следует рассматривать все варианты.
По виду передаточной функции корректирующего
устройства может быть выбрана схема пассивното четырехполюсника
для реализации этой передаточной функции. Краткие
сведения о пассивных четырехполюсниках даны в § 5.3. Более
обширные сведения можно, например, получить в [7, 81.
Легко реализукутся передаточные функции с полиномами
/?„ (s) и Q„ (s) первой и второй степеней. При более высокой
степени этих полиномов следует использовать два пассивных
четырехполюсника, соединенных последовательно. Основные
соображения о такой возможности изложены в § 5.3.
После выбора электрической схемы необходимо вычислить
требуемые значения емкостей и сопротивлений и убедиться в
возможности физического выполнения этой схемы с
необходимыми параметрами ее передаточной функции. В частности,
не следует предусматривать пассивный четырехполюсник с
очень малым (менее 0,1—0,05) передаточным коэффициентом
или с весьма большими емкостями. Не следует также иметь в
одной схеме емкости (или сопротивления), значительно, на
2—3 порядка, отличающиеся друг от друга по величине.
Обычно требуемые значения параметров передаточной
функции пассивного четырехполюсника можно иметь при несколь-

ких вариантах значений его элементов. В корректирующих
устройствах используют и активные четырехполюсники
(см. § 5.3).
Следует указать на одно обстоятельство. Предположим, что
параллельное корректирующее устройство (см. рис. 5.1, ё)
охватывает участок цепи с астатизмом v-ro порядка, т. е.
где /?2 (s); Q2 {s) — полиномы от s с равным единице
свободным членом.
Корректирующее устройство не изменит порядок
астатизма этого участка цепи, если его передаточная функция
W^K2 - /?к2 (s) sVlQn2 (4U (5Ла)
где /?к2 (s); Qk2 (s) — полиномы от s с равным единице
свободным членом.
Действительно, при таком корректирующем устройстве
передаточная функция рассматриваемого участка цепи
^ i + W^ й7«2 IQ2 is) Qb2 is) + k., /?2 (5) /?Ь2 (S) I '
T. e. астатизм участка остался прежним.
Заключительные этапы синтеза. При построении желаемой
ЛАЧХ предполагалось что неизменяемая часть системы с
усилителем имеет необходимый передаточный коэффициент.
После выбора корректирующего устройства передаточный
коэффициент разомкнутой системы, как правило, изменяется.
И теперь нужно окон«1ательно определить необходимое
значение передаточного коэффициента усилителя. На этом
синтез системы закончен.
Однако построение желаемой ЛАЧХ основано на
определенных допущениях. Кроме того, могла иметь место
приближенная реализация требуемой ЛАЧХ корректирующего
устройства. Поэтому совершенно необходима проверка
качества синтезированной системы. С этой целью строится
переходная характеристика замкнутой системы и определяются
показатели ее качества. Если система третьего порядка, то
переходную характеристику удобнее строить операционным
методом. Методика определения корней данного полинома
изложена в начале данного параграфа. При более высоком
порядке системы нужно пользоваться методом вещественных
частотных характеристик (трапецеидальных или треугольных).
При аппроксимации вещественной частотной характеристики
отрезками прямых необходимо учитывать следующее: аппрок-

симацию начинать из начальной точки характеристики; при
не слишком сложной форме характеристики достаточно
заменить ее четырьмя-пятью трапециями (или треугольниками);
ч<хвост» характеристики, т. е. ее конечный участок с
ординатами менее О, 1 от начальной, можно отбросить.
При существенном невыполнении требований к системе —
при перерегулировании и времени регулирования больше
допустимых значений — необходимо выяснить и усггранить
причины неудачного решения.
Кроме ошибок в расчете могут быть неточной
реализация требуемой передаточной функции коррректирук>щего
устройства и недостаточным избыток фазы при контрольных
частотах (о^ и (05.
Возможно также значительное отличие вещественной
частотной характеристики синтезированной системы от типовой,
для которой справедливы номограммы (см. рис. 5.24 и 5.25),
положенные в основу расчета. В этом по(У1еднем случае рас-
счет следует повторить, задавшись значениями о и tp меньше
требуемых.
Пример 5.2, Регулируемый объект и исполнительный элемент при*
Горной следящей системы описываются передаточной функцией
Wo (s) = k/ls (0,005s + 1) (0,01 s + 1)].
Требуется выбрать последовательное корректирующее устройство,
обеспечивающее при k ^ 200 с-* и v = 1 следующие показатели
качества: о < 30% и < 0,5 с. Допустимое ускорение регулируемой
координаты W = SO рад/с^ при начальном рассогласовании =0,1 рад.
Прежде чем начать расчет, заметим, что при k = 200 система без
корректирующего устройства неустойчива. Действительно, в этом
случае ее характеристическое уравнение
0.0005s3 + 0^06 52 s2 200 = О
и определитель Гурвица
Glfla — <^<^з ~ 0,06 —
—0,1 = — 0,04 < 0.
Расчет начинаем с
построения ЛАЧХ
неизменяемой части
системы. При со == I
вычисляем ординату 20 Ig ^ =
- 20 ig 200 = 46 дБ;
сопрягающие частоты
coi - 1/0,05 = 20 с-*;
Юа = 1/0,01 = ЮОс-^
ЛАЧХ неизменяемой
части системы Lo (со)
состоит из трех асимптот
Рис. 5.28 и построена на рис. 5.28.
-1

Переходим к построению желаемой ЛАЧХ. ЛАЧХ неизменяемой
части имеет требуемый порядок астатизма и передаточный
коэффициент, поэтому низкочастотная асимптота желаемой ЛАЧХ совпадает с
низкочастотной асимптотой ЛАЧХ неизменяемой части системы.
Для заданного значения о — 30% по номограмме (см. рис, 5.24)
определяем
''тах=^27 и ^р-= 3,5д/(0ср.
Вычисляем нижний предел частоты среза желаемой ЛАЧХ:
cocpi 3, 5я/^р = 3, 5я/0.5 = 22с-1.
По (5.39) находим верхний предел частоты среза:
ttep2 = == VSOTOTT = 22.4 с-1.
Выбираем сос = 22 с^* и через эту точку проводим среднечастотную
асимптоту желаемой ЛАЧХ с рекомендованным ранее наклоном
— 20 дБ/дек (рис. 5.28). Далее по кривым (см. рнс. 5.25) для Ртах —
= 1,27 определяем, что необходим избыток фазы у = 40° при
ординатах L^K (w), лежащих в пределах ±Lm = 14 дБ. Проводим прямую с
ординатой + 14 дБ и из точки пересечения ее со среднечастотной
асимптотой желаемой ЛАЧХ строим пробную сопрягающую асимптоту с
наклоном — 40 дБ/дек.
Пусть высокочастотной асимптотой желаемой ЛАЧХ будет
высокочастотная асимптота ЛАЧХ неизменяемой части системы.
Сопряжение среднечастотной асимптоты желаемой ЛАЧХ с высокочастотной
начинаем при частоте cOg.
Теперь нужно проверить избыток фазы при контрольных частотах
(Оа и 0)6- Воспользуемся номограммой для подсчета фазы по
асимптотической ЛАЧХ, изображенной на рис. 5.26.
Подсчитываем фазу при частоте (Оа:
<ра = —20 (2,25 —2,04) — 40 (2.04^0) - 20 (2,16-0) —
— 40(2,2—2.16) — 60 (2,25 — 2.2) - — 133,6°.
Следовательно, избыток фазы
Ya = 180—133,6 = 46.4°.
Подсчитываем фазу при частоте cog:
^ _20 (2.25—2,22)— (40 (2,22—2,16) - 20 (2,16—0,24)—
— 40 (0,24+1,12)—60 (2.25—1.12) - — 163.6^
Избыток фазы при этой частоте
= 180-163,6=16,4°.
При частоте соа избыток фазы превышает требуемое значение на
6°. Допустимо, однако, лишь незначительное перемещение сопрягающей
асимптоты вправо. Оно не расширит сколько-нибудь заметно диапазон
пропускания нижних частот, поэтому останавливаемся ,иа
выполненном сопряжении.
Избыток фазы прн частоте т значительно меньше допустимого.
Для его увеличения высокочастотную асимптоту желаемой АЧХ нуж-

Л{5/С0а+1)
но сместить вправо.
При этом усложнится
корректирующее устрой-
.ство.
Попробуем
проверить качество системы
при составленной
желаемой ЛАЧХ и затем
будем решать вопрюс о
целесообразности ее
изменения.
По
составляем передаточную
функцию разомкнутой
скорректированной системы:
S (в/Шз+ 1) (S/G)2+ 1) <S/W4+ 1)
200(0.24s+l)
где 0)3 = 0,46с
-1
S (2,17s+1) (0.01S+ 1) (0,00574s+1)
coa = 4,2c~i; cOg^lOOc-i; cd4=174c-i.
Передаточная функция замкнутой системы
Wg (s) = WWII + W (s)l = (0.24 s + l)/(6,25 . 10-' s* Ч-
-f 1,74.10-^ s3+0,01 ls2+ 0.245 s+ 1).
Вещественная частотная характеристика, вычисленная по
частотной передаточной функции Wg (усо), представлена на рис. 5.29. Пост-^
роенная по ней переходная характеристика показана на рис. 5.30.
Показатели качества а = 14% и tp = 0,4 с удовлетворяют
требованиям. Перерегулирование даже значительно меньше допустимого,
поэтому составленную желаемую ЛАЧХ можно ие изменять.
Несоответствие показателей качества с их расчетными
значениями объясняется значительным отличием вида вещественной частотной
характеристики скорректированной системы (рис. 5.29) от типовой, по
которой составлены номограммы (см. рис. 5.24 и 5.25).
Вычитая из желаемой ЛАЧХ
{^) ЛАЧХ Lq (о)
неизменяемой части системы, получаем
ЛАЧХ последовательного
корректирующего устройства L„ (ш)
(см. рис. 5.28). По этой ЛАЧХ
составляем полиномы /?к (s) и
W числителя и знаменателя
передаточной функции
корректирующего устройства:
/?к (S) = (s/coa + 1) (s/(Oi + 1)=
= (0,24 s + 1) (0,05 s + 1);
Qk(s)= (s/CO3+ i)(5/«4+ 1) =
Рис. 5.30 (2.17s + 1) (0,0 0574s + 1).

"ex
o-
Рис. 5.31
Желаемую передаточную функцию корректирующего устройства
можно реализовать дифференцирующим и интегрирующим
четырехполюсниками с разделительным усилителем (рис. 5.31).
Передаточная функция дифференцирующего четырехполюсника
l^Ki(s)-V(7\5+l)/(7\s+l),
где П 0,05 RiCi\ - 0,0574 - R^TJiRi + R^.
Значение R^ должно быть выбрано при расчете усилителя. После
этого могут быть определены необходимые значения и Q и
подсчитано значение /гщ.
Передаточная функция интегрирующего четырехполюсника
где Гз 0.24 = /?4 Са; = 2.17 = (R^ + R^) С^.
Выбираем Q Ю мкФ. Тогда R^ = 24 кОм и = 193 кОм.
Усилитель должен иметь коэффициент усиления Ку = /j//Jo^ki» где
ко — передаточный коэффициент регулируемого объекта и
исполнительного элемента.
Приближенные соотношения. Изложенный метод синтеза —
это приближенный метод, поэтому рекомендуется [81 уточнять
желаемую ЛАЧХ с помощью номограмм.
Вместе с этим используют еще большие приближения,
которые значительно упрощают построение желаемой ЛАЧХ
и синтез корректирующего устройства.
На рис. 5.32 показана типовая ЛАЧХ разомкнутой астати-
тической системы. Ей соответствует передаточная функция
siT^s+\)(T^s+\) Til\ s(5 + 0)0(5+0)3) •
где 7^2 > coi< со2< Юд; k~ передаточный
коэффициент разомкнутой системы (добротность по скорости),
равный частоте со', при которой продолжение низкочастотной
асимптоты пересекает ось абсцисс {k — со').
Согласно (41, перерегулирование в системе не превзойдет
20—30%, если удовлетворяются неравенства
СО3/СО2 я:; 10; 2 < (dg/cOcp < 4. (5.48)

Рис. 5.32
При этом время регулирования с достаточной точностью
определяется по частоте среза:
CP-
(5.49)
Следовательно, заданное значение k определяет частоту
со' и затем можно построить прямую, на которой будет лежать
низкочастотная асимптота желаемой ЛАЧХ.
С другой стороны, заданное значение времени
регулирования позволяет определить по (5.49) частоту среза ©ср
желаемой ЛАЧХ. Остается выбрать частоту cOg и cog так, чтобы
удовлетворялись неравенства (5.48).
В результате оказываются известными желаемая ЛАЧХ
и передаточная функция разомкнутой системы. Зная
передаточную функцию неизменяемой части системы, можно
определить необходимую передаточную функцию
последовательного корректирующего устройства.
Неравенства (5.48) определяют частоты cog и со 3 не
однозначно. Поэтому удо1бно сразу же рассматривать несколько
вариантов значений cOg и озд. Затем выбрать тот из них, при
котором система имеет требуемые показатели качества. Для
их определения необходимо, конечно, строить переходные
характеристики замкнутой системы.
Используют и другие приближенные соотношения для
построения желаемой ЛАЧХ. Иногда, особенно при
предварительных расчетах, они оказываются весьма удобными.

Глава 6
МАШИННАЯ РЕАЛИЗАЦИЯ
МЕТОДОВ ТЕОРИИ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
§ 6Л. Математические модели
автоматических систем и особенности
реализации их на ЭВМ
Возможности современной
вычислительной техники позволяют
значительно ускорить сроки
проектирования автоматических систем
управления объектами различного
назначения. Успех в решении задачи в
значительной степени зависит от основных
факторов: математической изученности
управляемого объекта, т. е. от того,
насколько адекватно составлено
математическое описание функционирования
объекта, эффективности прикладных
методов теории автоматического упр_авле-
ния, уровня развития вычислительных
методов, наличия высококачественного
программного обеспечения, от того,
насколько успешно используется
творческий потенциал
исследователя-проектировщика. При этом решающий фактор
остается за человеком, который может
решать многие неформализованные
задачи. Именно этот фактор стимулирует
развитие диалогового проектирования.
Основа автоматизированного
проектирования — математическое описание
функционирования системы. В
настоящее время преобладают и широко
используются три способа
математического описания автоматических систем: 1)
метод передаточных функций и тесно
связанные с ними частотные
характеристики; 2) метод переменных состояния;
3) структурно-топологические методы.

Метод передаточных функций, по существу, представляет
собой применение преобразования Лапласа и частотной теории
для изучения качественного поведения решений обыкновенных
дифференциальных уравнений. Созданные для
проектирования систем с одним входом и одним выходом передаточные
функции и частотная теория до сих пор являются основными
инженерными методами со сложившейся методологией.
Непосредственное изучение исходных дифференциальных уравнений
с заданными начальными условиями заменяется в этих методах
исследованием алгебраических свойств некоторых функций,
порождаемых системой дифференциальных уравнений.
Например, критерий Михайлова и Найквиста основаны на
изучении именно таких функций.
На разработку и усовершенствование ^частотных методов
были затрачены десятилетия; несмотря на «машинный век»,
они не утратили своего значения и не исчерпали всех
возможностей. Многолетние исследования показали, что по глубине
и степе|1и завершенности частотные методы во многих случаях
не имеют вполне эквивалентный замены, а модификация их
применительно к ЭВМ позволяет получать весьма ценную ин-
фюрмацию о проектируемой системе в сжатые сроки. В 70-е
годы Г. Розенброком [19J был создан метод «размытых»
частотных характеристик, предназначенный для
автоматизированного проектирования систем с несколькими входами и выхо"-
дами. Дальнейшее развитие метода было осуществлено
В. В. Солодовниковым и его учениками [131.
В основе метода переменных состояния лежит
представление дифференциальных уравнений в нормальной форме Коши,
которое дополняется алгебраическими уравнениями, связы-
вакяцими выходные переменные с переменными состояния
x-Ax + Bu; I (6 1)
У-=Сх, I
где А, В, С — матрицы коэффициентов размерности п X л,
п X т, г X п соответственно; и — вектор возмущающих
воздействий; т — число входов; г — число выходов.
Математическим аппаратом метода переменных состояния
(МПС) являются матричное исчисление и вычислительные
методы линейной алгебры. Метод переменных состояния
содействовал значительному развитию теории управления. На
языке МПС выполнена большая часть работ по оптимальному
управлению, фильтрГацци, оцениванию. В настоящее время в те-

ории автоматических систем управления наметилось
плодотворное сочетание метода переменных состояния с частотными
методами- Оба способа описания взаимосвязаны и дополняют
друг Друга.
Топологические методы опираются на использование
методов теории графов. Они получают все большее
распространение, однако эффективность их применения во многом зависит
от принципиальных результатов, полученных в теории
графов.
С точки зрения автоматизации проектирования систем
управления с помощью топологических методов представляет
интерес задача формирования передаточных функций по
структурным схемам. Если структура системы выбрана, то, испапь-
зуя передаточные функции динамических звеньев и известные
правила преобразования структурных схем, можно
сравнительно легко составить программу получения передаточной
функции разомкнутой или замкнутой системы при
управляющих или возмущающих воздействиях. Программа нахождения.
передаточной функции сводится к раскрытию скобок,
приведению подобных членов и упорядочиванию коэффициентов по
убывающим степеням полинома. Такая программа часто
является основной при машинных исследованиях (анализ
устойчивости, построение частотных характеристик, построение
областей устойчивости, D-разбиение в плоскости параметров и т. д.).
Автоматизация формирования передаточных функций
позволяет вести параметрический синтез и анализировать различные
структуры. Такие программы успешно применялись для
построения передаточньпс функций сложных систем с
перекрещивающимися обратными связями. Уязвимое место таких
программ — частые случаи переполнения разрядной сетки ввиду
плохой «обусловленности» полинома. Кроме того, существуют
технические трудности при программировании, так как
некоторые алгоритмические языки (АЛГОЛ ФОРТРАН) не
приспособлены для обработки буквенно-символьной информации.
Решение подобных задач стало эффективным на основе
топологических методов. Так, использование методов теории графов
в сочетании со структурными числами дает возможность
получать передаточные функции по любой структуре на языке
ФОРТРАН.
Метод переменных состояния ориентирован на
вычислительные методы теории матриц. Если требуется выполнить
анализ устойчивости по уравнениям переменных состояния
(6.1), то традиционные способы требуют предварительного

приведения матрицы А к характеристическому
уравнению
|A-sE|-(-~l)«(s'' + a,s«-' + ... + a„)=0 (6.2)
с последующим применением критериев устойчивости или
корневых методов. Существующие критерии устойчивости
(Рауса, Гурвица, Льенара—Шипара, Михайлова) могут
применяться только непосредственно к коэффициентам
характеристического уравнения замкнутой системы. Методы локализации
собственных чисел матрицы А (Гершгорина, Островского, Бра-
уэра и др.) дают лишь достаточные условия и малопригодны
для широкого использования.
Получение коэффициентов характеристического уравнения
часто связано с серьезными трудностями вычислительного
характера, несмотря на наличие стандартных программ,
построенных на известных методах. Применительно к задачам
машинного анализа и синтеза сложных автоматических систем
многие методы не вполне подходят из-за чувствительности к
«частным особенностям» матрицы или потери точности из-за
роста погрешности вследствие накопления ошибок
округления.
В последнее время были созданы способы определения всех
собственных чисел матрицы А, не связанные с операцией
вычисления коэффициентов характеристического уравнения. Они
основаны на представлении матрицы А в виде произведения
ортогональной и почти треугольной форм. Наибольшей
универсальностью обладают QR- и QL-алгоритмы. Сущность QRr
алгоритма состоит в представлении исходной матрицы А в
виде произведения двух матриц: ортогональной Q и верхней
треугольной R (нижней треугольной L в случае QL-алгорит-
ма). Предварительно матрица А преобразуется к форме Хассен-
берга Н, а QR-алгоритм всегда предполагает, что такое
приведение выполнено. Матрица Н является верхней
треугольной матрицей, но с наличием субдиагональных элементов.
Например, матрица Хассенберга размерности (4 X 4) имеет вид
* * * *
* * * *
О * * *
0 0**
(6.3)
Процедура метода предусматривает построение матрицы,
подобной матрице А, но имеющей клеточную треугольную
структуру с диагональными блоками IX1 или 2X2 и теми же

собственными числами, что и исходная матрица А.
Приведение исходной матрицы А к матрице Хассенберга Н
осуществляется для сокращения числа операций и экономии
машинного времени. Различные способы (например, метод Хаусхол-
дера и метод Гивенса) приведения к матрице Н
рассматриваются в работах по линейной алгебре.
В теоретическом отношении QR- и QL-алгоритмы мало
различаются. (Э/?-алгоритмы эффективнее испапьзовать, когда
большие элементы матрицы сосредоточены в нижнем правом
углу, а QL-алгоритм — когда большие элементы матрицы
сосредоточены в левом верхнем углу. При правильной
реализации алгоритма на ЭВМ ошибки округления во многих
случаях не оказывают большого влияния на точность нахождения
собственных чисел матрицы А. Описание и особенности
машинной реализации QR- и QL-алгоритмов более подробно
изложены в 14, 5, 14, 151.
Особенности машинных вычислений в задачах
автоматического управления. Успех в решении задач
автоматизированного проектирования автоматических систем во многом
определяется тем, как в действительности осуществляются
действия над числами в ЭВМ. Существенная особенность машинных
вычислений — влияние ошибок округления. Как бы точно ни
осуществлялись операции над числами, для их представления
отводится конечное число знаков и они должны быть
округлены.
В современных цифровых ЭВМ расчеты, как правило,
выполняются в режиме с плавающей запятой. Это связано с
представлением чисел, сильно различающихся по абсолютной
величине. Число разрядов в мантиссе достигает 15 и выше (в
десятичных знаках), и все же встречаются задачи, где такой
точности недостаточно.
Иногда возникает вопрос, почему вообще нужна такая
точность вычислений, как 10^^^ и выше. В большей части
задач науки и техники исходные данные в лучшем случае имеют
точность 10-3—10-^, а часто она не достигает й 10-^ или
бывает еще ниже. На раннем этапе создания цифровых
вычислительных машин Дж. Нейман показал, что для папучения
точности конечного результата, равной 10-^, требуется точность
промежуточных вычислений в арифметических операциях
10-*^. Кроме того, существует эффект усиления ошибок,
образовавшихся от предшествующих операций. Это усиление в
принципе может быстро покрыть любой разрыв. Например,
отношение 10-^ и 10-^^ образуют разрыв 10^. Дж. Нейман

привел пример, когда 425 последовательных операций,
каждая из которых усиливает ошибку только на 5%, заполняют
этот разрыв. Разумеется, приведенный пример лишь
иллюстрирует важность проблемы получения верных результатов
в условиях накопления ошибок округления. В
действительности в реальных машинах результаты округления не столь
неблагоприятны. Все же при решении сложных задач
приходится считаться с ошибками накопления в результате
округления.
В режиме с плавающей запятой почти во всех случаях
происходит округление и в окончательных результатах могут
наблюдаться существенные, искажения. Результаты
округлений, какими бы малыми они ни были, меняют свойства
арифметических операций. Свойства ассоциативности и
дистрибутивности не выполняются на существующих ЭВМ. Произведение
сомножителей, отличных от нуля, может оказаться равным
нулю (это явление известно как «возникновение машинного
нуля при умножении»). Свойство коммутативности
соблюдается лишь в том случае, если имеет место «правильное»
округление [4, 5].
Формирование процесса правильного округления в
современных ЭВМ, работающих в двоичной системе счисления,
затруднительно. В системе счисления с четным основанием
округление реализуется неоднозначно. Считается невозможным
построить процесс округления в «классическом» виде,
основанный лишь на анализе конца мантиссы, таким образом, чтобы
ошибки компенсировали друг друга. Следовательно, на ЭВМ,
по существу, реализуются новые операции, лишь
приближенно изображающие обычные арифметические операции.
Отмеченные особенности не могут быть устранены техническими
средствами, хотя точность может быть значительно
увеличена. Существуют большие возможности увеличения
точности. Они заключаются в применении переменной длины
мантиссы, в использовании сокращенных систем счисления
(например, троичной). -
Распространенным способом анализа точности является
решение задачи с обычной и удвоенной точностью. Совпадение
результатов указывает на отсутствие ошибок округления,
поэтому считается, что остальные вычисления в сходных
задачах можно вести с обычной точностью. Такой подход
распространен и час10 дает удовлетворительные результаты.
Другой подход заключается в использовании специальных
программ, позволяющих записывать числа и выполнять one-

рации над ними с точностью, превосходящей рабочую точность
ЭВМ. Такой способ резко увеличивает объем потребного
машинного времени и загружает память. В'задачах машинного
проектирования систем управления этот способ имеет
ограниченное применение.
Значительный эффект достигается за счет применения
новых вычислительных методов. Изменение вычислительной
схемы или использование нового подхода часто дает возможность
принципиально решить задачу на ЭВМ. Характерна машинная
постановка фильтра Калмана в задачах управления и йавига-
ции. Последовательные вычисления в соответствии с
уравнением Калмана не приводят к
положительно-полуопределенной матрице ошибок. Причина неудачи кроется в операциях с
плохо обусловленными матрицами. Благоприятное изменение
вычислительной схемы позволило применить фильтр
Калмана в космической системе «Аполлон». Сущность применения
вычислительной схемы состояла в использовании метода
«квадратного корня матрицы». Использовался тот факт, что
квадратный корень матрицы имеет разброс элементов в два раза
меньший, чем исходная матрица, и в этом проявляется как бы
эффект «удвоения» разрядной сетки.
Характерно получение передаточных функций по обычным
правилам преобразования структурных схем. В программе
должно быть предусмотрено раскрытие скобок, приведение
подобных членов и вычисление коэффициентов по убывающим
степеням производной. Некоторые коэффициенты
элементарных звеньев малы (как правило, всегда меньше единицы),
поэтому возникает опасность превращения в машинный нуль
старших коэффициентов характеристического уравнения.
При исследовании системы по уравнениям переменных
состояния часто возникает необходимость многократного
построения характеристического уравнения по исходным
матрицам коэффициентов. Задача является частью «полной
проблемы собственных значений» и известна также как проблема
построения векового уравнения. Для того чтобы обойти
многочисленные трудности, в течение десятилетий создавались
различные приемы и методы, подробно изложенные в [15].
В задачах анализа и синтеза автоматических систем
часто имеется определенная специфика, не позволяющая в
полной мере воспользоваться стандартными программами, в
основу которых положены известные методы. Одна группа
методов (А. М. Данилевского, А. Н. Крылова, Хессенберга, Са-
муэльсона и др.) чувствительна к частным особенностям ма-

трицьг, например к «провалам», т. е. к вырождению (в
смысле машинной точности) промежуточных определителей.
Другая (методы, основанные на идее Леверье) не учитывает
быстрый рост погрешности на высоких порядках вследствие
накопления ошибок округления, что ограничивает размерность
решаемых задач.
Прямые корневые методы, базирующиеся на построении
характеристического полинома, также чувствительны к
накоплению ошибок округления. Применение их для
исследования линейных систем порядка показало, что
накопление ошибок округления при построении
характеристического полинома и последующее применение корневых методов
синтеза часто приводили к совершенно неправильным
результатам. Устойчивые системы при определенных сочетаниях
параметров трактовались как неустойчивые и, наоборот,
неустойчивые рассматривались как устойчивые. Многолетние
исследования показали, что при принятой длине разрядных
сеток отечественных ЦВМ граница надежной применимости
метода Ньютона (и его модификаций) составляет п ^ 20.
Если /г> 20, результаты также получаются, но
неопределенность в результатах увеличивается. Они могут быть сильно
искажены ошибками округления.
Особенно значительное накопление ошибки проявляется
при сильной связи корней полинома с его коэффициентами.
Показателен следующий простой пример [И]. Полином
— 4s^ + (6 — 49-10-^) — 4s + I отличается от полинома
(s— 1)* только коэффициентом при s*. Характерно, что это
различие весьма незначительно, всего 49^ 10'^. Однако если
все четыре корня второго полинома равны единице, то у
первого полинома корни таковы: % = 1,02681; Sg = 0,97389;
^3,4 = 0,99965 ± 0,026455. Это значит, что сравнительно
незначительное изменение коэффициентов (всего на 49-10-'^)
приводит к существенному изменению корней (уже на 0,03).
При степенях полинома порядка 20 и выше может наступить
качественное искажение результатов.
Отметим еще одну особенность. Не все традиционные
методы теории автоматического управления одинаково хорошо
приспособлены к машинной реализации. Затруднения
встречаются при реализации D-разбиения, частотных методов,
формировании передаточных функций по структурным схемам.
Ценность С-разбиения как метода построения границ
области состоит в том, что метод не требует какой-либо
направленной процедуры для нахождения первой точки грани-

цы, Т. е. является беспоисковым. Поиск, особенно в виде
полного или частичного перебора точек плоскости параметров»
не всегда является целесообразным из-за затрат машинного
времени и отсутствия уверенности, что точка искомой области
может быть найдена, если область имеет малые размеры.
/)-ра^иение принципиально позволяет сразу найти границы
области устойчивости в плоскости интересующих
проектировщика параметров. Однако свойства метода таковы, что помимо
действительных кривых, являющихся границами искомой
области, появляются «посторонние». «Посторонние» кривые
представляют собой границы областей на плоскости
параметров, соответствующих одинаковому числу корней,
расположенных справа от мнимой оси. Например, одному корню в
правой полуплоскости соответствует определенный диапазон
изменения параметров на плоскости параметров. Два корня
соответствуют другому диапазону изменения параметров, три
корня — третьему и т. д. При больших порядках
характеристического полинома переплетение истинных и «посторонних»
линий может принимать самые причудливые формы и выбор
действительных кривых среди большого количества линий
оказывается весьма трудной задачей при программировании. При
изменении о кривые могут претерпевать бесконечные разрывы
второго рода и ветви могут уходить в бесконечность.
При ручных расчетах для выделения искомой области
служит графическая процедура штриховки по Неймарку. Суть ее
состоит в том, что при движении по кривой в сторону
возрастания 0) штриховку наносят слева, если определитель
положителен, и справа, если он отрицателен. При изменении о от —оо
до +00 получается двойная штриховка, так как при о = О
изменяется знак определителя системы. Если определитель
обращается в нуль,то это приводит к бесконечному разрыву
второго рода. Особенности имеются и при штриховке особых
прямых. Более подробные сведения об этом можно найти в
работах [3, 8].
Штриховка затрудняет полноценную машинную
реализацию метода D-разбиения. Выбор действительной области среди
претендентов, к тому же часто разбросанных во всех
квадрантах, заставляет привлекать алгебраические критерии, методы
непосредственного вычисления корней. Недостатком метода
является также его недостаточная универсальность.
Варьируемые параметры должны входить в коэффициенты
характеристического ур^авнения линейно, возникают трудности при
задании расположения корней внутри трапеции, угла или других

фигур в левой полуплоскости. Все же метод D-разбиения
является единственным беспоисковым методом и может быть с
успехом использован при построении областей устойчивости не
только в автоматических системах, но и в численных методах.
D-разбиение может также использоваться в качестве
параллельного или вспомогательного метода.
Метод D-раэбиения можно существенно видоизменить,
упростить и сделать более универсальным путем введения
полиномов Чебышева. Полиномы Чебышева, обладая свойствами как
гармонических, так и ортогональных функций, являются
уникальными и как будто специально созданы для применения на
ЭВМ. Они, в частности, позволяют вести операции в
вещественной арифметике, что само по себе перспективно с точки зрения
возможной модификации некоторых традиционных методов,
ибо расчеты в комплексной арифметике увеличивают объем
вычислений в четыре раза.
Другой пример — автоматизация построения передаточных
функций в сложных структурных схемах. Наиболее
распространенные алгоритмические языки приспособлены для
операций с числами и не вполне подходят для обработки буквенной
информации. Новые вычислительные методы, создаваемые на
основе графов и структурных чисел, позволяют обойти эти
трудности и значительно уменьшить ошибки округления.
Машинная реализация ЛЧХ имеет ряд особенностей.
Получение амплитудной характеристики не вызывает затруднений.
Трудность кроется в вычислении фазовой характеристики,
которая в общем случае находится не только в первом квадранте,
т. е. является разрывной. Видоизменение метода частотных
характеристик применительно к машинной реализации
приводит к предотвращению ложных скачков фазы и в целом
повышает информационную ценность метода частотных
характеристик. Например, в перспективе оказывается целесообразным
строить новые частотные характеристики — изамплиты
(линии равных запасов устойчивости по амплитуде) и изофазы
(линии равных запасов устойчивости по фазе). Таким образом,
машинная ориентация частотных методов приводит к
появлению новых способов машинного анализа и синтеза.

§ 6.2. Анализ устойчивости по уравнениям
переменных состояния
и по характеристическому уравнению
Пусть процессы в системе описываются уравнением (6.1).
Для того чтобы система (6.1) была асимптотически устойчива,
необходимо и достаточно, чтобы все собственные числа Si
{i = 1, п) матрицы А имели отрицательные действительные
части, т. е. лежали слева от мнимой оси плоскости
комплексного переменного s.
Рассмотрим характеристическое уравнение
(А—sE|=0, (6.4
где Е — единичная матрица.
Корни Si характеристического уравнения (6.4) являются
собственными числами матрицы А. Совокупность всех
собственных чисел образует спектр матрицы А. Сумма элементов,
стоящих на главной диагонали, образует след матрицы А и
обозначается Sp А. След матрицы связан с ее собственными числами
соотношением
Sp А = 2 i ^ = Ь..., п. (6.5)
Раскрывая определитель |А — sE |, получим
характеристическое уравнение
i-lris^ + a^s^-' f ^2S«-' + ...-han)-0, (6.6)
где Oi — сумма всех диагональных миноров первого порядка,
равная следу Sp А; — сумма всех диагональных миноров
второго порядка матрицы А; — определитель матрицы А.
Анализ расположения всех собственных чисел^ матрицы А
относительно мнимой оси осуществляется по коэффициентам
уравнения (6.6) с помощью известных критериев.В системах
высокого порядка получение коэффициентов
характеристического уравнения часто связано с серьезными трудностями
чисто вычислительного характера.
Число диагональных миноров Л-го порядка матрицы А
равно
д.^«(«-1)...(п-й+|)^ Л = 1.2 п.

Таким образом, непосредственное развертывание
характеристического определителя и приведение его к виду (6.6)
эквивалентны вычислению
определителей различных порядков. Для больших значений
п эта задача требует большого объема вычислительной
работы. В связи с этим были разработаны специальные методы
развертывания характеристического определителя минуя
вычисление многочисленных диагональных миноров (методы
Данилевского, Крылова, интерполяции, Леверье—Фаддеева и др-)-
Одним из самых экономичных с точки зрения количества
операций является метод А. М. Данилевского. Сущность его
состоит в приведении определителя
|A-sE| =
an—s «12 ... «in
«21 Cl22—S,..a2n
«nl ... «nn—S
к так нaзывaeIvюмy нормальному виду Фробениуса
«1-5 «2 ... o-n-i а„
1
О
—S ...О
1 О
О
О
О
О 1 ~s
Развертывание определителя, записанного в нормальном
виде Фробениуса, не представляет затруднений. Разлагая
определитель по элементам первой строки, получим
характеристический полином
(— 1)" (S" + «1 s'^-Ч-«ij +... + aj.
Легко убедиться, что элементы первой строки матрицы
Фробениуса суть коэффициенты характеристического полинома.
При вычислении на машине коэффициентов
характеристического полинома целесообразно производить частичную
проверку правильности вычисленных коэффициентов, контролируя
выполнение соотношения
^1 =«H + ^'22+...+«nn=Sp А.
Несмотря на экономичность, метод чувствителен к
вырождению (обращению в нуль) промежуточных определителей.

Метод, предложенный А. Н. Крыловым, заключается в
предварительном преобразовании уравнения
в эквивалентное ему
D(s) =
<}.(s) = |A-sE|
b^—S^ бая... бгп
развертывание которого по степеням s осуществляется
значительно проще, так как определитель можно разлагать по
минорам первого столбца. Метод чувствителен к вырождению
определителей и имеет меньшую точность вычисленных
коэффициентов.
Нечувствителен к вырождению определителей метод Леве-
рье—Фаддеева. Расчетная схема состоит в построении
последовательности
Ai-A; ai-SpAi; Ci = Ai—^lE;
= ACi; a2 = Sp A,J2; C,, = A^ —a^ E;
A„ -= AC^^i; - Sp Ajn\ C„ - A^—E.
Полученные величины а^, a„ представляют собой
коэффициенты характерисгического полинома
A(s) = ( — l)"|A~sE|-s" + ^iS"-»+... + «„.
Отметим, что попутно с вычислением коэффициентов
характеристического полинома может быть построена обратная
матрица А"* = C^-i/a^. Практически метод сводится к п-
кратному перемножению матриц порядка п. Число операций
умножения составляет около (п — 1) п^.
При реализации этого метода на ЦВМ в случае операций
с матрицами высокого порядка может происходить
переполнение разрядной сетки, что вызывает необходимость введения
масштабирования; при вычислении последовательности
матриц Сп происходит накопление ошибки при округлениях,
которое с увеличением порядка матрицы увеличивается, так как

происходит пропадание последних значащих цифр ввиду
вычитания очень близких друг к другу величин. Это приводит к
тому, что при больших порядках матрицы А коэффициенты
характеристического полинома оказываются вычисленными с
пониженной степенью точности. Накопление ошибки
начинается с 7—8-го порядка и в дальнейшем увеличивается с
ростом п. -
Если задана структурная схема системы и имеются
передаточные функции отдельных звеньев, то определение
передаточной функции ведется по обычным правилам структурных
преобразований схем и построение характеристического полинома
не таит в себе принципиальных трудностей. Однако при
ручных расчетах это связано с утомительными выкладками,
которые могут являться источником ошибок. При постановке
задачи на ЦВМ передаточные функции отдельных звеньев
представляются полиномами не выше второго порядка.
Характеристический полином системы может быть записан в виде
P(s)= П (AkSl + B^s + Ckh
Программа должна предусматривать раскрытие скобок и
приведение подобных членов.
Перспективно построение передаточной функции с помощью
топологических методов.
Реализация на ЦВМ этих методов излагается в специальной
литературе.
В настоящее время для оценки расположения корней
характеристического уравнения относительно мнимой оси
существуют критерии Рауса, Гурвица, Льенара—Шипара,
Михайлова, Найквиста, методы непосредственного вычисления
корней (Ньютона, Мюллера, Берстоу). Для анализа
устойчивости импульсных систем используется критерий Шура—
Кона. Все перечисленные критерии опираются на знание
коэффициентов характеристического полинома.
Машинная реализация и сопоставление критериев
показали, что наиболее простой, удобной в реализации и надежной
является вычислительная схема Рауса. Критерий позволяет
исследовать систему с учетом любой заданной степени
устойчивости rj. При этом возникает задача формирования
коэффициентов смещенного характеристического уравнения

Относительно новых коэффициентов уравнение
записывается в виде
- «о+ «1 £«-^ +... + а„ -0.
Коэффициенты UQ, «1,..., On суть
где k — номер коэффициента; С — число сочетаний по — /
из п — 1. ^
Формула для «к может быть представлена так:
Отрицательным значениям величины rj соответствует
смещение прямой S = If] вправо, а положительным — влево.
^ Рассмотрим, например, характеристическое уравнение трет
тьего порядка. Сместим его влево на величину степени устоит
чивости if\. Вычислим коэффициенты «„:
Имеем:
Если характеристическое уравнение записать в виде
+ a^^i S— J + s'^- 2 + ... + ао = 2 - О,
то коэффициенты смещенного уравнения вычисляются по вцдо-.
измененной формуле
«~»-i= i: (-i)'-*a„_,n'-*c^zi
где Сп — число сочетаний из п по m (t = п, л — 1, 0).
Отметим, что в некоторых задачах, например при
направленном выходе в область устойчивости^ критерий Рауса ИС'

пользовать затруднительно, так как он не позволяет ввести
количественную меру. (Это, впрочем, относится и к другим
критериям, в которых используется принцип ДА—НЕТ).
В качестве такой количественной iviepbi, например, может быть
использована вещественная часть ближайшего к мнимой оси
собственного числа Res.^,^^. Величина Re Sj^^x является
непрерывной, хотя и негладкой, функцией параметров. Если
задана область допустимых значений параметров, то
возможно из неустойчивой точки направленно выйти на границу
области устойчивости. Применение критерия Рауса в такой
ситуации приводит к тактике прямого перебора, хотя в силу
экономичности критерия это часто оказывается оправданным
§ 6-3. Функционально-преобразованные матрицы
и их применение. Критерий В. И. Зубова
Рассмотрим систему
x = Ax + F(0, (6.7
где А — матрица коэффициентов размерности п X п; F (t) —
вектор-функция внешних воздействий (п X I).
Пусть на плоскости комплексного переменного s задана
некоторая область D, соответствукщая различным случаям
расположения спектра St исходной матрицы коэффициентов А
системы (6.7). Область D может быть произвольной частью
плоскости S, в том числе левой полуплоскостью или некоторой
заданной частью ее. Обозначим совокупность всех матриц
порядка п, спектр которых находится внутри области D,
через Ag.
С другой стороны, пусть на плоскости комплексного
переменного р задан круг радиуса г с центром в начале координат.
Обозначим через Bp совокупность всех матриц порядка л,
спектр которых находится внутри круга радиуса
|р.|< ^ t - I, п.
Допустим, что существует оператор L, устанавливакхций
взаимно однозначное соответствие двух множеств: А^ и Bp.
Если А е As, то оператор L (А) от матрицы А есть такая
матрица порядка п, что L (А) £ Bp.

Таким образом, оператор L, воздействуя на любую
матрицу А, взятую из множества Ag, переводит ее спектр в
множество точек, содержащихся в множестве Bp. Это значит, что все
собственные числа р,- матрицы В = L (А) будут принадлежать
кругу радиуса г с центром в начале координат.
Эту задачу можно интерпретировать так. Требуется
указать такую аналитическую функцию р = / (s), которая
переводила бы границы множества А^ на границы множества
Bp. Тогда если спектр исходной матрицы А лежит внутри
области D то спектр матрицы В в результате
функционального преобразования будет расположен в круге радиуса г
с центром в начале координат.
Чтобы най^и условия принадлежности спектра матрицы
А области D, требуется указать простые в алгоритмическом
отношении условия нахождения спектра матрицы В в круге.
Если спектр s^- g D, то необходимо и достаточно, чтобы
наибольшее по абсолютной величине собственное число матрицы
В было по модулю меньше величины г. Если г = 1, то
- |р,|< 1
и в этом случае оценка выполняется относительно единичного
круга с центром в на^Шхе координат. Тогда, для того чтобы
Si Q D, необходимо и достаточно, чтобы удовлетворялось
условие
lim [L(A)r^=0,
где О — нулевая матрица.
Аналитическая функция р = f (s) может иметь различную
структуру и отображать ббласть заданного расположения
спектра Si исходной матрицы А не только на единичный круг с
центром в начале координат, но и на области, ограниченные
алгебраическими кривыми высших порядков, вложенными в
единичный круг.
Отображение областей расположения спектра матрицы А
на круг с центром в начале координат или на фигуру,
вложенную в круг , позволяет решить задачу устойчивости линейных
систем по исходной матрице А без определения коэффициентов
характеристического уравнения. Различные отображения
приводят к различным функциональным преобразованиям матриц.
Основы метода функционально-преобразованных матриц были
заложены В. И. Зубовым в 1959 г. [71.

Необходимые и достаточные условия расположения всех
собственных чисел матрицы А в заданной области D
комплексной плоскости % имеют вид
limB^=-0. (6.8)
Л->-оо
где В — один из видов функционально-преобразованных
матриц.
Выполнение условия (6.8) можно проверить по нормам и
модулю следа матрицы В, величине наибольшего по модулю
собственного числа max IpJ, а также другим неравенствам,
известным в высшей алгебре.
Рассмотрим способ анализа устойчивости линейных систем
по уравнениям переменных состояния без построения
характеристического полинома. В теории аналитических функций
широко известно дробно-линейное преобразование
S = (Р + i)/(p - 1). (6.9)
Оно обладает тем свойством, что левая полуплоскость
комплексного переменного s переводится им во внутренность
единичного круга с центром в начале координат плоскости
комплексного переменного р, при этом мнимая ось,
рассматриваемая как окружность бесконечного радиуса, переходит в
единичную окружность. Если комплексная переменная s
перемещается вдоль мнимой оси, то комплексная переменная р
движется вдоль окружности единичного радиуса. Каждой
точке левой полуплоскости соответствует вполне определенная
точка, принадлежащая внутренности единичного круга, и
наоборот, т. е. это соответствие взаимно однозначно: р = (s +
+ 1)/(5-1).
Подставим значение s из (6.9) в характеристическое
уравнение (6.4), тогда
,_jHiLe =0.
р-1
После некоторых преобразований получим
|(_Е_А)-р(Е-А)|=0. (6.10)
Умножим уравнение (6.10) на (Е— А)-^:
j(_E-A){E-A)-»-pE}=0. (6.U)

Матрицу (—Е — А) (Е— А)-^ можно преобразовать:
(_Е_А + Е) (Е—А)-1 - [(Е - А) -^2Е] (Е—А)-^
-Е^2(Е~-А)-\
Характеристическое уравнение относительно новой
переменной р будет иметь вид
|В-<рЕ|-0, где В = Е~2(Е—А)-Ч
Легко видеть, что если все собственные числа Si исходной
матрицы коэффициентов А системы (6.7) лежат в левой
полуплоскости комплексного переменного s, то все собственные
числа Pi построенной матрицы В находятся внутри круга
единичного радиуса с центром в начале координат плоскости
комплексного переменного р. Если хотя бы одно s окажется
в правой полуплоскости, среди р^ найдется такое, для
которого |pil> 1.
Известно, что если собственные числа матрицы В суть
Pi> Рг» Рп. то собственные числа матрицы В'^ равны р},
р2» Рп> т. е. при возведении матрицы В в степень в ту же
степень возводятся и ее собственные числа.
Тогда, если все Si матрицы А системы (6.7) отрицательны,
последовательное возведение матрицы В в степень уменьшает
абсолютную величину собственных чисел pf, ибо все pi
лежат внутри единичного круга с центром в начале координат
и по модулю меньше единицы: \pi\<Z 1-
Критерий формулируется следующим образом: для того
чтобы система (6.7) была асимптотически устойчива^
необходимо и достаточно, чтобы для матрицы
В-Е~2(Е-А)-^ (6.12j
выполнялось условие
В*->0 при fe->oo, (6.13)
где О — нулевая матрица.
Можно доказать, что критерий справедлив во всех
случаях, если матрица Е — А неособая, т. е. когда ее
определитель не вырождается в чу ль. Если |Е — А| = О, то не
существуют (Е — А)~^
Могут быть построены функционально-преобразованные
Матриць! для всех практически важных случаев расположения
спектра матрицы А. Введем, например, степень устойчивости rj ^

Для того чтобы спектр Si матрицы А располагался левее
мнимой оси в области Res<r], необходимо и достаточно,
чтобы удовлетворялось условие
lim В'^ = 0,
где
В=.Е-^2[(1+г1)Е~-А1-Ч
Введем угол 2ф, соответствующий некоторому показателю
колебательности. Для того чтобы спектр матриЩэГ А
располагался внутри угла раствора 2ф с центром в начале координат,
необходимо и достаточно, чтобы соблюдалось требование
lim Вф=:0,
где Бф = Е—2[Е-~/Ае-'Ч)]-1, или B^ = E —2(E + tAe''4^)-\
Матрицы Вф и Вф являются комплексно-сопряженными,
поэтому можно рассматривать лишь одну из них.
Аналогично могут быть сформированы функционально-
преобразованные матрицы В для других случаев
расположения спектра St матрицы А [6, 7].
Выполнимость необходимого и достаточного условия
устойчивости можно установить по факту абсолютного убывания
элементов \Ь%\ матрицы В^. Возведение матрицы в степень
рекомендуется выполнять так, чтобы каждая последующая
матрица являлась квадратом предыдущей, т, е. по закону
ВЛ_В2"-=В2""~'В2'"^'
Тогда ft-я степень матрицы В^ находится через logg k шагов
(128-я степень матрицы В получается через семь, а 1024-я —
через десять возведений матрицы В в степень). В этом случае
в памяти машины не надо постоянно удерживать матрицу В,
так как каждый раз используются лишь полученные из нее
степени.
Изучение степени матрицы В^ {k = 1, 2, 4, 2^^) следует
вести до тех пор, пока не будет соблюдаться неравенство
где Ib^ff I — элементы матрицы В'^ (/, / = 1, п).
Более экономичная оценка возможна на основе
рассмотрения матричных норм и следов. Напомним, что нормой квад-

ратной матрицы В называют действительное число ||В||,
удовлетворяющее условиям:
а) II ВЦ ^ О, причем ЦВЦ = О, тогда и только тогда, когда-
В = 0;
б) ||сВ||==(с|-||В|| (с—число), в частности H-Bi^lj—-ВЦ;
B)||B-fD||^|)B| + |jD|j;
г) IBD[|<|B||.[|D||.
Здесь В и D — матрицы, для которых соответствукщие
операции имеют смысл. В частности, для квадратной матрицы
имеем IIB^JI < IJBjp, где k — натуральное число.
Рассмотрим следующие легко вычисляемые нормы:
IIВ |,-max 2 (6.14)
п
||B||„=^max2|fcu|; (6.15)
/ 1=1
,
l|B|ini-=V ^ЬЪ\ (6.16)
|B:i(iv-=nmax|6,.,.I. (6.17)
Для того чтобы система (6.7) была асимптотически
устойчива и № при ft оо, достаточно, чтобы любая из
норм матрицы В была меньше единицы:
||ВВ<1, (6.18)
т. е. достаточно, чтобы выполнялось условие
min (IВ Вь IIВ Цп, IIВ ||„ь IIВ ||iv) < 1. (6.19)
Если условие (6.19) не соблюдается, то из этого не
следует, что исследуемая точка пространства параметров системы
является неустойчивой. Вопрос об устойчивости должен быть
исследован дополнительно путем рассмотрения степеней
матрицы В*.
Пусть все собственные значения матрицы В лежат внутри
единичного круга с центром в начале координат (|рИ< U
1 = 1,2, п), а все нормы матрицы В больше единицы.
Рассмотрим последовательность степеней
Ъ\ В*, в«,..., в
2^

в силу того что все собственные числа |Рг I < 1, элементы
матрицы начиная с некоторого k убывают, стремясь к
нулю при k-^oo. Тогда на каком-либо шаге HB^^IK 1.
Это условие является необходимым и достаточным при
суждении об устойчивости системы.
Таким образом, оценка устойчивости по нормам
выполняется в такой последовательности.
1. Строится матрица В по исходной матрице
коэффициентов А системы (6.7).
2. Вычисляется какая-либо из норм матрицы В или
контролируется условие (6.19). Если ||В||<1, то исследуемая
точка пространства параметров принадлежит области
устойчивости.
3. Если соотношение (6.19) не выполняется, то матрицу
В следует возводить в степень и рассматривать нормы
последовательных степеней:
ЦВ^У, ||В*1|, 1В«||,...,||В^.
Если при некотором фиксированном k какая-либо из норм
стала меньше единицы 11В*||< I, то условие устойчивости
В'^ О (ft ->> оо) соблюдается.
Рассмотрим иллюстративный пример.
Пример 6.1. Определим, является ли ' система к = Ах + F (t)
асимптотически устойчивой. Матрица А имеет вид
—0.9 3.! -Ч),2-1
А=- -^.4 -2,5 3.2 .
_ 1.1 ^1,5 -3,1.
Функционально-преобразованная матрица В
f—0,21792 —0,82742
В=^Е-2(Е--А)-1 =
->-0,11957 0,49057
L-0,28302 -0,03561
Вычислим нормы матрицы В:
-0.586381
--0,39177
0.49820
п
|(B||j = max 2 |^il=-max[0,21792 + 0,82742 + 0,58638;
* /=|
0.11957-1-0,49057 +0,39177; 0.28302+0,03561 + 0.498201=:-^
= max 11,63172; 1.00191; 0.816831=: 1,63172;
||B||„ = max У I 6j;|-max [0.21792 +0,11957+0,28302;

о, 82742 + 0,49057 + 0,03561; 0,58638 + 0,39177 + 0,49820] =х
= max [0,62051; 1.3536; 1,47635] = 1,47635;
/
== У jO , 217922 + 0,827422 + 0,586382 + 0,11957» + 0,490572 + "
^"•+0,391772+0,283022 + 0,035612 + 0,498202 =:
«=Уо,047489 + 0,6846238+ 0,34384 + 0,0142970 + 0,2406589+"
^■"+0,1534837 + 0,0801003 + 0.001268 + 0,24882032
-1/1,8139639 =!,34683.
При рассмотрении норм достаточное условие устойчивости не
удовлетворяется, т. е.
min(||B|Jj; ||B|lii; IIВ (1,63172; 1,47635; 1,34683)>1.
Возведем матрицу В в степень:
- 0.31238 —0.204712 0,15981-1
В2 0,07828 0,35354 —0,31726 .
--0.07506 0,19896 0.42811.
Норма матрицы \\ В2 || меньше единицы, что указывает на факт
выполнения условия В* О при ft -V оо:
//B^l/j-max [0,676902; 0.74908; 0,69773=^:0,74908< 1.
Рассмотрим возможность оценки собственных чисел
матрицы В по ее следу. Известно, что следы последовательных
степеней матрицы представляют собой суммы всех
собственных чисел р'-, взятых в той же степени, что и матрица В^,
т. е.
SpB'^=pHpH...+p«= ip?.
Если система устойчива и В*^ О, то след Sp также стре^-
мится к нулю при й со.
Если сочетание параметров исследуемой точки
пространства таково, что точка находится достаточно далеко от границы
устойчивости, то матрицу В можно не возводить в степень, а
воспользоваться достаточным критерием неустойчивости
|SpB|>n. (6.20)

Можно показать, что если выполняется условие (6.20), то
среди Pi найдется хотя бы одно, для которого справедливо
условие |Ре1> 1. Это означает, что система является
неустойчивой.
Если соотношение (6,20) не удовлетворяется, никаких
выводов относительно принадлежности исследуемой точки к
области неустойчивости сделать нельзя. В этом случае можно
рассмотреть поведение последовательности следов матрицы
В*, т. е.
ISpB^I; |SpB*|;...;|SpBM.
Программу рекомендуется строить таким образом, чтобы
на каждом шаге возведения матрицы В в степень
контролировать условия устойчивости и неустойчивости.
Устойчивость Неустойчивость
НВ|(<1; |SpB|>n:
II ВЧК 1; |SpB2|>rt;
||ВЧ|<1; |SpBM>n;
m = 1.2.3, ...
Отметим, что функционально-преобразованные матрицы
могут иметь различную структуру. Однако bj ьсех случаях
алгоритм должен строиться так, чтобы однозначно
устанавливалась принадлежность спектра матрицы В кругу радиуса
г = 1 с центром в начале координат или некоторой области,
вложенной в круг.
Возведение матрицы в степень требует операций
умножения и (п — 1) операций сложения. Матричные операции
хорошо поддаются распараллеливанию, и современные
матричные процессоры позволяют значительно сократить время
расчетов. Тем не менее существуют возможности уменьшения
трудоемкости за счет изменения вычислительной схемы.
Например, в некоторых ЭВМ для перемножения матриц
применяется алгоритм Штрассена, в котором число операций
умножения составляет = п^'^^, а число сложений 6/г^'^^ —
— п^. Практически алгоритм Штрассена более эффективен
лишь на высоких порядках матрицы.

§ 6,4. Матричный критерий устойчивости,
не связанный с обращением матрицы
Вычислительные трудности, связанные с нахождением
коэффициентов характеристического полинома по исходной
матрице А уравнений переменных состояний пробудили интерес
к машинно-ориентированным методам анализа устойчивости,
в которых отсутствуют не только операция построения
характеристического полинома, но и операция обращения матрицы.
Операции обращения, где это возможно, желательно избегать.
В матричном критерии (6.13) в
функционально-преобразованную матрицу В входит обратная матрица. Ее появление
связано с использованием дробно-линейного преобразования
(6.9). Рассмотрим подход в общем случае, устраняющий
операцию обращения.
Вообразим себе, что мнимая ось является окружностью
бесконечного радиуса. «Изогнув» ее. получим окружность
конечного радиуса. Таким образом приходим к идее охвата
области расположения спектра Si матрицы А кругом. В
дальнейшем такой круг отображается на единичный круг с центром в
начале координат комплексной плоскости р или на некоторую
область, расположенную внутри этого круга.
Пусть на плоскости s имеется круг радиуса /?, в котором
содержатся все собственные числа Si матрицы А. Центр круга
находится на вещественной отрицательной полуоси в точке
I—/?, 01. Отобразим круг в левой полуплоскости на единичный
круг плоскости р с помощью функции
s = /?(p-i). (6.21)
Подставим значение (6.21) в характеристическое уравнение
(6.7). После несложных преобразований получим
|B-pEl=0, <6 22)
где
B^E + A/R. (6.23)
Тогда если все собственные числа si матрицы А находятся
внутри круга радиуса R в левой полуплоскости комплексного
переменного s, то все собственные числа функционально-
преобразованной матрицы В лежат внутри круга единичного

радиуса с центром в начале координат на плоскости
комплексного переменного р, т. е. IpJ < 1 (i = 1, п).
Имеет место следующее утверждение: для того чтобы все
собственные числа St (i — 1, 2, п) исходной матрицы
коэффициентов А системы (6.7) находились внутри заданного
круга радиуса /?, расположенного в левой полуплоскбсти и
имеющего центр в точке 01, необходимо и достаточно,
чтобы вьтолнялось условие
lim В О,
(6.24)
где В = Е 4 А//?; О — нулевая матрица.
Таким образом, условие принадлежности всех собственных
чисел матрицы А кругу радиуса /?, расположенному в левой
полуплоскости, сводится к возведению
функционально-преобразованной , матрицы В в степень и к изучению
последовательности степеней по нормам и модулю следа. Аналогично
может быть построен критерий с учетом произвольной
степени устойчивости Г).
Пусть задан круг с центром в точке 1—R — т], 01, в котором
находятся все собственные числа матрицы А (рис. 6.1).
Отображая этот круг на единичный круг с центром в начале
координат, можно построить
функционально-преобразованную матрицу.
Для того чтобы все собственные числа Si матрицы А
системы (6.7) лежали в левой полуплоскости внутри круга
радиуса R с центром в точке 1—R —- г), 0J, необходимо и
достаточно, чтобы удовлетворялось
требование
lim В?=0,
k->oo
где
Рис. 6.1
Bi=E + (A--T)E)//?;
О —нулевая матрица.
Первоначальное значение
радиуса может быть выбрано
исходя из свойств конкретной
исследуемой системы, когда
представляется каким-либо образом
косвенно оценить частоту ко-

лебаний в ней, а также по нормам матрицы А или на основе
методов локализации. Слишком большие первоначальные
значения радиуса приводят к аннулированию элементов матрицы
ввиду выхода числа за пределы разрядной сетки машины.
Например, если элементы матрицы А достаточно малы, то
деление на большое значение R еще более уменьшает их, что и
приводит в отдельных случаях к выходу числа за пределы
разрядной сетки. Тот предел, при котором происходит
аннулирование отдельных элементов матрицы А, определяет верхнюю
границу величины радиуса R.
Большие значения радиусов удлинякуг время решения
задачи, так как увеличивают число шагов при исследовании
каждой точки пространства параметров в logs R раз. Так,
увеличение радиуса в 10^ раз требует дополнительно 10 шагов, что
соответствует \0п^ операциям умножения.
Центр круга, охватывающий область расположения всех
собственных чисел матрицы А, отнесен влево на величину
—R — Г), поэтому касательные, проведенные из начала
координат к окружности, приближенно характеризуют
колебательность в системе (рис. 6.1).
Показатель колебательности выражается тангенсом угла
наклона касательной
tg ф - «// = R/V{R + = R/V2Rn + ri\
Выполнив несложные преобразования, показатель
колебательности можно представить как
l/2/?/4-hl
где у = R/k],
Из формулы следует, что показатель колебательности
зависит от отношения двух величин: радиуса круга /?.
охватывающего все собственные числа матрицы А, и степени
устойчивости г\.
В большей части практических расчетов на ЦВМ пределы
изменения показателя колебательности jui составляют от 1 до
5.7.
Кругами подходящего радиуса можно ограничить
интересующую проектировщика область расположения всех
собственных чисел Si и исходной матрицы коэффициентов А в левой
полуплоскости. Однако при возведении матрицы в степень
возможен колебательный характер сходимости. Этот эффект

имеет место тогда, когда какое-либо из собственных чисел
матрицы А достаточно близко расположено от границы круга.
Для устранения этого нетселательного явления можно
использовать функционально-преобразованные матрицы,
соответствующие нелинейному отображению охватывающего
спектр круга.
Рассмотрим матричный степенной ряд
А А2 дз^
R 2! 31 /?з
-4-...+
+
m=0,l,2,..,.
(6.25)
m! R*^
Если для отображения круговой области расположения
всех собственных чисел матрицы А использовать три или
четыре члена ряда (6.25), то явление «колебательности»
подавляется.
При использовании первых трех членов ряда (6.25)
.функционально преобразованная матрица имеет вид
D.-E+- +
/и=-0, 1,2-
(6.26)
В этом случае оценивается принадлежность спектра
матрицы кругу радиуса г = 0,5 с центром в точке 10,5; 01
комплексной плоскости р (рис. 6.2, а).
Для того чтобы спектр матрицы А системы (6.7)
находился внутри круга радиуса R с центром в точке [—R, 01
комплексной плоскости S, необходимо и достаточно, чтобы спектр
матрицы Da располагался внутри круга радиуса г = 0,5,
вложенного в единичный круг с центром в начале координат.
Круг симметричен относительно оси абсцисс и имеет общую
точку [1, 0] с единичным кругом.

при использовании четырех членов ряда (6.25) окружность
радиуса R комплексной плоскости s переходит в
алгебраическую кривую третьего порядка, вложенную в единичный круг
комплексной плоскости р. Эта кривая пересекает оси ОХ в
точках [1/3, 0] и [1, 0] (рис. 6.2, б).
Функционально-преобразованная матрица имеет вид
Оз = Е + -^ + ^Ч-^. /«=.-0.1,2.3. (6.27)
При. использовании пяти членов ряда (6.25)
осуществляется отображение круговой области отображения спектра на
внутренность области, ограниченной алгебраической кривой
четвертого порядка — конхоидой с круговым базисом
(улиткой Паскаля). Эта кривая (рис. 6.2, в) имеет общую точку с
единичным кругом [1, 01 и целиком находится в правой его
половине. Функционально-преобразованная матрица имеет
вид
''•-^+Т+^ + -^ + 1ЙГ' "• = ».'.2.3,4. (6.28)
Функционально-преобразованным матрицам Dg, Dg, D4
может быть поставлен в соответствие скалярный ряд
р^е"^ =l+^+^^ + _f_ + ... + _£L . (6,28а)
При лп = I, т. е. при рассмотрении первых двух членов,
имеет место линейное преобразование. При m = 2, 3, ...
имеет место нелинейное преобразование. Известно, что всякая
квадратная матрица является элементом кольца. Это
позволяет заменить скалярную величину s матрицей А. При такой
замене надо соблюдать Два условия: 1) следить за порядком
следования сомножителей, так как в общем случае кольцо матриц
некоммутативно; 2) следить за операцией деления, так как
не всякая матрица имеет свою обратную. В данном случае
каждая матрица коммутирует caivia с собой и со своей целой
произвольной положительной степенью и эти условия
автоматически соблюдаются.
Можно показать, что функционально-преобразованные
матрицы D^, полученные при круговом охвате и отображении
спектральной области матрицы А, приближают матричную экс-

поненту exp (At), входящую в решение х (/) ехр (А*) Хо
однородной системы х = Ах.
Алгоритм построения процессов с равномерным шагом h
имеет вид
x^-i^DrnXft, Aj=='o, 1,2...., . (6.29)
При использовании матрицы порядок ошибки
составляет — О (h^-^^).
Так, при введении матрицы Dj порядок погрешности О (h^)
соответствует методу Эйлера, при введении матрицы Da
соответствует методу Эйлера—Коши, т. е. —О ф?), при
использовании матрицы d4 — методу Рунге—Кутта четвертого
порядка, т. е. порядок погрешности составляет О (/t^).
При построении процессов в однородной системе с
прогрессивно увеличивающимся шагом алгоритм имеет вид
Xft^D^^Xo, (6.29а)
где Хо — вектор начальных условий.
Таким образом, в матричных критериях, основанных на
построении и исследовании функционально-преобразованных
матриц, заложены возможности не только анализа
устойчивости, но и построения переходных процессов, удовлетворяющих
заданным начальным условиям. В определенной степени
трудоемкость компенсируется увеличением полезной информации.
Алгоритм позволяет анализировать устойчивость
нестационарных систем прямым построением процессов, а также
выявлять временную работоспособность системы на конечном
интервале времени. В нестационарных системах функционально-
преобразованная матрица перестраивается на каждом шаге.
Алгоритм построения процессов в однородной нестационарной
системе имеет вид
где Dm (ft/i) — функционально-преобразованная матрица,
формируемая на каждом шаге А в соответствии с изменением
исходной матрицы А (kh).
Выбор шага h осуществляется по радиусу /? круга, охват
тывающего все собственные числа матрицы А. Величина
А = 1//? является шагом интегрирования, она может
изменяться в широких пределах, при этом основным условием
является нахождение всех собственных чисел матрицы внутри круга
радиуса R. Таким образом, увеличивая длину шага, мы можем
ускоренно строить переходные процессы, при этом вычисли-

тельная устойчивость сохраняется и качественная картина
процессов, несмотря на рост погрешности, не изменяется.
Рассмотрим примеры, иллюстрирующие применение
алгоритмов.
Пример 6.2. Рассмотрим систему
dx^/dt — лг^;
dx^/dt =г 5a:i — 2х^.
Начальные условия х^ (0) == 1; х^ (0) = 0,5. *
Требуется найти решение, которое определяет собственное
движение (устойчивость) снсте1йы. В качестве матрицы выберем
матрицу D4-
Матрица А и вектор начальных условий Xq имеют вид
А-
Круг радиуса /?= с |1 А || , где ЦАЦ — норма матрицы, примем равным
10. Шаг А = I//? = 0,1- Если шаг принять равным h = 0.01 (R =
= 100), то масштаб времени уменьшается и потребуется большее
количество вычислений. При Л = 0,1 матрица имеет вид
0 г
1 '
.—5 —2
0,5
04==Е+АЛ+
0,01
(АЛ2)
+
2!
5 —2
10 —1
(А/2)з (А/1)^
3! 4!
1 0
0 1
—
.0 1.
+0,1
,—5 —2
+
+
0,001
+
0,0001
24
5 12
-^60 —19
10 —1
5 12J
0,97668 0,08988
—0,44941 0,796919 *
Для получения решения можно использовать любую из формул
- Одхл или Xk^tyi Хо.
Решение в момент времени t ^ kh
\ 0,97668 0,08988
Хд = х (0,1)- 0,79691
В момент времени / ~ 0,2
0,99322
—0,49973
0,1 с имеет вид
1
1,02162-
0,5.
--0,05094.
X2=x(0,2)t
и далее
- 0,92514
' 0.82766-
-^0,84461.
; Х4 —
1,00442]'
- 0,59596'
0,34403"
^\ ,2570!.
-1,22888
0,71808
—1.17239
-0,20180*
—0,09570.
Решение системы приведенр на рис. 6.3.

Рис. 6.3
где
Пример 6.3. Рассмотрим однородную нестационарную систему
-5 I '
—1 —10^
А(/) =
Вектор начальных условий
г
Требуется построить решение системы на промежутке [0; 1J
секунд, используя функционально-преобразованную матрицу (ЛЛ).
^ ^ г, , Положим Л = 0,1. При k = I
^to Рис. 6.4 ^
1\
имеем
+
+
+
+
-0,5 0,1
.-0.1 -0,1.
0,12 —0,03 _
0,03 6 . "
_ ' 0,62 0,077
~ —0,07 0.9 ]•
Выполним вычисления в
соответствии с алгоритмом:
Хл+1 = 02(А:Л)хл, ^-0,
I. 2

в моменты времени t = khc значения вектора кк следующие:
х^ = х(0, 1)-02(А;Л)Хо -
Х2=х(0,2) =
хз = х(0,3)
0.62 0.07
0.07 0,9
0,655
0,655
.0,38 J*
Х4=х{0,4) =
0,62 0,065
—0.065 0.8I5jL0,38
0.62 0.061 Г0,4308
-^0,06 0,74] 1о,267125
0,62 0,55 1 Г0,2831235*
—0,055 0,675j [о, 1718245
L0,5J
0,4308
~ 0,267l25j'
0,2831235
PJ718245J*
0,18498691*
.0,10040982]•
Дальнейший ход процессов изображен на рис. 6.4.
§ 6,5, Векторные методы построения переходных
процессов в линейных системах
Анализ устойчивости путем формирования и возведения в
степень функционально-преобразованных матриц, а также с
помощью других эффективных способов аппроксимации
матрицы ехр (А /) таит в себе скрьггые возможности построения
переходных процессов. За счет увеличенного шага можно
получать семейство процессов относительно всех переменных
состояния. Слишком большие значения шага увеличивают
погрешность в решении, однако качественная сторона процессов в
решении сохраняется.
Рассмотрим автоматическую систему, описываемую
уравнением
x = Ax + F(0,
(6.30)
где F (О — вектор внешних возмущений.
Решение системы х {t) при начальных условиях х (0) =
— Хо может быть точно представлено в аналитическом виде:
t
X (О - ехр (АО Хо + J ехр [А (t -т)] F (т) d%. (6.31)
Ставится задача найти аппроксимацию точной записи решения
(6.31) уравнения (6.30),

Положим
ty,^kh\ Xft-x{^ft); ft = 0, 1,2,....
где h — шаг построения процессов.
Из (6.31) получаем
kh
= ехр {khk) Хо + J ехр [А {kh —т)] F (т) dx.
Введем обозначения
kh
= ехр (AAjA)Xo; = J ехр (А (kh -т)1 F (т) dr,
о
тогда
х,,-Ул + г^. (6.32)
Будем вычислять интеграл приближенно по формуле
прямоугольников с шагом h — MR. Используя значения
подынтегральной функции на левых концах частичных промежутков,
получим
kh k-\
J ехр [А {kh -т)] F (т) drЛ 2 ^^РI^ (f^h—ih)\ F (ih) -
1 = 0
fe-i
=А 2 exptAA(fe—01F(t/i).
£ = 0
В качестве ехр (АА) выберем функционально-преобразованную
матрицу Dpi (см. § 6.4). Имеем
y,=-=D^Xo; Zr,=-h'^Dl^'f(ihY
Учитывая (6.32), получим
7iu-^''mX, + h''^0m-^fm. (6.33)
Соотношение (6.33) запишем следующим образом:
х^+1-D^+^o+A S D^+^''F(fA).

Преобразуем правую часть этого равенства:
2'»m-'F(ift)+F(M)
£ = 0
хо + /г 2' F (Ш) + ЛР (АЛ)
£^ О
Сравнение с уравнением (6.33) позволяет алгоритм построения
переходных процессов представить в виде
4+i-D.mlx^ + hFikh)h ft-О, 1, 2, (6.34)
Если использовать точность построения переходных
процессов, соответствующую точности усовершенствованного
метода Эйлера, то формула (6.34) принимает вид
х,+1 = (е + АЛ + [X, + AF {kh)i. (6.35)
Последовательные значения искомого вектора переходных
процессов находятся таким образом:
Xi = (е +АЛ + [Хо + ЛР (0)1;
x2-(e + AA + -^)ixi + AP(/i)];
хз = (е + АЛ + ^)[х2 + ЛР(2А)1; ....
Алгоритм (6.34) может использоваться для построения
переходных процессов в линейных системах при внешних
воздействиях, меняющихся в широком диапазоне. Последние
могут быть достаточно интенсивными, иметь разрывы.
Значения функции F (kh) могут определяться по ходу вычислений
или вводиться таблично.
. Алгоритм (6.34) не накладьгоает каких-либо
принципиальных ограничений на шаг построения процессов, кроме
условия нахождения спектра St матрицы А внутри круга с центром
в точке [—R, 0] в левой полуплоскости. Процесс будет
численно устойчив, если шаг выбрать кратным в<еличине Л. Пусть
вначале вычисления осуществляются с шагом h до точки
h Ih (/ шагов длиной Л), а затем вычисления продолжаются с

шагом в р раз больше, т. е. равньш ph. Рекуррентная формула
для такого способа вычисления имеет вид
X/+p(s+!)-D^{x,+p,4-pftF[(/-t-ps)/i]}; 1,2,.... (6.36)
При р = 1 вычисления ведутся с шагом h и формула (6.36)
переходит в формулу (6.34). Матрица D^, согласованная по
точности с приведенным способом вычисления, имеет вид
Более высокая точность приближения матричной
экспоненты ехр (АО начиная с m = 4 входит в противоречие со способом
аппроксимации интеграла в уравнении (6.31), отражающего
влияние внешнего-воздействия F (t). В этих условиях
требуется повышение точности вычисления интеграла.
Аппроксимируем интеграл
ехр [А {kh -~т)1 F (т) rfx, (6.37)
1
используя правило трапеций. Алгоритм построения
переходных процессов в окончательном виде будет
x,+i=exp(Aft)fx, + (A/2)F(Ajft)] +Л F[(A? + 1)/г]. (6.38)
Вместо ехр (A/i) можно подставить
функционально-преобразованную матрицу (ФП-матрицу) или Dg. Порядок
погрешности при таком способе построения процессов составляет
О ф?). Дальнейшее повышение точности построения
переходных процессов с помощью ФП-матриц Dm может быть
достигнуто с помощью параболической аппроксимации интеграла
(6.37). Построим алгорим для такого способа вычисления
вектора переходных процессов. Имеем
kh
Xft = ехр (Akh) Хо + J ехр [А (М -т)1 F (т) dr. (6.39)
о
Положим, как и прежде, th = k/R = kh. Заменяя в
выражении (6.39) k на 2Л, получим
2/ih
Х2А = ехр {2Ш) Хо + J ехр {А {2kh—%)] F (т) dr.

Далее имеем
т-\-2) h
X2ft+2 - ехр IАА {2k -Ь 2)1 Хо + f ехр (А \{2k + 2) х
Ъ
ХА—Tl}F(T)rfT,
или
Хал + f ехр [А {2kh —х)\ F (т) dx . (6.40)
2ift j
Применим к интегралу в правой части выражения (6.40)
формулу Симпсона. Тогда
f ехр [А {2kh -т)1 F (т) dx = (А/З) {ехр (-2АА) х
2ЛЛ
X F {{2k + 2) А] + F {2kh) 4 4 ехр (- АА) F {{2k + 1) А]).
Выполнив необходимые преобразования, получим
рекуррентную формулу
X2ft+2 = ехр (2АА) [X2ft + (А/3) F {2kh)\ 4- (4/3) А ехр (АА) х
ХЕШ+1)А] + (А/3)Р[(2А>4-2)А], А^О, 1, 2, 3, ....
С учетом функционально-преобразованной матрицы
окончательное выражение алгоритма для построения переходных
процессов имеет вид
Х2,.+2 - [X,, + (А/3) F (2АА)] 4 (4/3) AF [(2А ^ 1) А] 4
4(A/3)F[(2A42)AJ, А = 0, 1, 2, ....
Порядок точности при параболической аппроксимации
интеграла пропорционален О (А*), что соответствует по точности
интегрированию с использованием
функционально-преобразованной матрицы D4
Способ вычисления интеграла вносит систематические опшб-
ки в значение вектора х^. Более подробные способы
исследования точности приводятся в работе 16]. Изложенные алгоритмы
распространяются на построение переходных процессов в
линейных нестационарных системах.

Можно выбрать максимальный шаг построения процессов
по ошибке вычисления вектора на к-ш шаге. Обозначим эту
ошибку через 6^. Тогда величина шага будет равна
I Smax I
где m — число, определяющее структуру
функционально-преобразованной матрицы
= Е + АЛ + +... + k^^h'^lmX
1/2
При т = 1 величина шага h == —s-
l%iaxl
прит-4 h^-f-—^л/
где Ismaxi — наибольшее по модулю собственное число
матрицы А.
Максимальное время, в течение которого ошибка не будет
превосходить заданной величины, равно
bk{m + \)\
tn
Пример 6.4. Проиллюстрируем на простом примере изложенные
способы построения переходных процессов. Все расчеты легко
выполняются на ручных калькуляторах.
Рассмотрим систему дифференциальных уравнений
x = Ax + F(/),
где
О I
~3 -3
. Вектор-функция внешних воздействий F (/) имеет разрывной
характер, причем в точках разрыва она меняет знак. Ее
аналитическое выражение имеет вид
1/2/ —t^ при О < / < I;
^У2Г^ при 1</<2;
/—4 при 2< / < 3;
I при 3 < / < оо.
Вектор начальных условий
п
0,5

Шаг построения процессов выбираем из соотношения h = l//?,
где R — радиус круга, в котором находятся все собственные числа
матрицы А. Величина R может быть приближенно выбрана по норме || А || :
/?>с||А||.
где с — множитель, округляющий значение || А {{ до ближайшего
целого десятка (или сотни). Большие значения R приводят к малому шагу.
Найдем норму:
п
НА||, = тах 2 Ifliyl=-max[l; 6]=?6.
Полагая R = 10, получим Л — 0,1.
Построим переходный процесс по формуле (6.34):
Xfe+i = D;n[Xfe+/iF(fe/i)l, fe=0. I, 2. 3. ...
В качества примем D4:
0.9864259 0.0859625
D4=E+Aft+(AA)V2+(AA)8/6+(Afi)*/24=
—0.2578875 0,7285375
Значения функции F(0 можно вычислить по формулам с любой
точностью. Для иллюстрации примем приближенно:
при ^=0 F(0)=F^^
при /==0.1 F(A) = F(0,l) =
при /=0.2 F(2^)-F(0.2)==
при /=-.0,3 F(3^)=F{0.3) =
при /=0.4 F(4A)=F(0.4) =
0,42
10,42
0.6
0,6
ro.7i
0,71
0,8
Lo,8
На первом шаге в момент времени /=0,1 с получим следующие
"(начения переменных:
Xi=D4[xo+0,lF(0)l =
+0.1
0,9864259 0,08596251 i П
.—0,2578875 0.7285375J I [о.5
На втором шаге в момент времени / = 0,2 с имеем
Ix,+0.IF(0,1)J =
4,029406
0.106382.
1,029406'
+0,1
0,42-
1
• I,069616
.0,106382
0,42
h
—0.1682012

На третьем шаге в момент t = 0,3 с имеем
0,9864259 0,0859625
X3 = D4tX2+0,lF(2.0,l)l:
1,069616
—0J 682012J
+0,1
--0,2578875 0,7285375
1,104979
—0,3701429,
X
0,60] j
0,60
На четвертом шаге в момент ^ = 0,4 с имеем
X4 = D4 [хз+0.IF (3.0.1)1 =
0,9864259 0,0859625
—0,2578875 0,7285375
* 1,134304
.—0,521205 J
I,104979
-0,370141.
+ 0.1
0,71
.0,7IJ
Окончательно процесс представлен на рис. 6.5 (кривая 1),
Проиллюстрируем применение более точной формулы (6.38) для
построения переходных процессов:
Xft+i -1>4 [хл+(Л/2) F (ЛЛ)]+(Л/2) F [(k+ 1)Л1.
На первом шаге в момент времени / = 0,1 с имеем
Xt = D4
1
0.5J
+0.05
1,0504
,0,12738j
Рис. 6.5

На втором шаге в момент времени t = 0,2 с имеем
И далее
1.0504
P,12738j
+0,05
0,42
0.42.
+ 0.05
0.6
P.6j
1.0996
—0,1382
+ 0.05
0,6
.0.6j
1+0.05
0.71
P.71J
1.099617
--0.1382 J*
M404
—0,33464.
Проиллюстрируем построение переходных процессов с помощыо
алгоритма
+ —1Р(2Й + 2)Л].
Матрица D| равна
0.950866 0,147422
--0,442266 0.508598.
На первом шаге в момент времени / ^ 0,2 с имеем
Х2 = D|
Хо+ -J^i^)
+ -^Ш4Р(Л) + -^Р(2Л) =
I
0.5
h
1 4
0,42
0,42
0,6
0,6
1,10428 ■
—0,141877j'
X4-DI
1,10428
—0,141877
+ -J ^^^^(^h)+Y^m=
4
+ Т
0.8
.0.8
0.6-
3 "
0.6
1.178518
—0.4883877
0.71
0,71
+
Далее процесс вычислений идет аналогично вышеизложенному.
Окончательно кривые приведены на рис. 6.5 (кривые 2 и 3).
Отметим, что точность вычислений в последнем методе
соответствует известным методам четвертого порядка. Информация о векторе
переходных процессов выдается только в четных точках X2h+2r в
формуле же используются данные и промежуточных точек.

§ 6.6. Векторный способ построения переходных
процессов в нелинейных системах
Пусть динамика автоматической системы описьгоается
векторным нелинейным дифференциальным уравнением
x=^f(x, /). (6.41)
Представим систему (6.41) в виде линейной и нелинейной
частей:
i=Ax + F(x, 0. (6.42)
Пусть спектр матрицы А системы (6.42) расположен в
левой полуплоскости. Точное решение системы (6.42) можно п^ред-
ставить в аналитическом виде:
x (О = ехр (АО Хо + J ехр [А {i— т)] F [х (т), т] dx, (6.43)
При интегрировании с шагом h получим рекуррентную
формулу
Х;,+1 = ехр (АА) {Xf, j ехр [А (kh — т)] х
XF[x(t), x]dx}, k=0, 1, 2, ....
Вычислим интеграл в правой части рекуррентной формулы.
Используя правило прямоугольников и принимая на левом
конце т = kh, получим
+ л
f ехр (А (kh ~-т)] F [x (т), т] dx = hF (х^, kh).
kh
Таким образом, имеем
х,+1 = ехр {Ah) [x, + hF (х„ kh)l (6.44)
Для повышения точности построения переходных
процессов применим правило прямоугольников не ко всей подьште-
гральной функции, а только к функции F [х (т), т], т. е.
будем считать, что на длине одного шага на промежутке Ikh,
(k + 1) h]
F[x(T). Tl = F(x„ kh).

в этом случае
Xft + F (Xfe, kh) J exp [A {kh-^ x)] dx
x;,+i = exp (АЛ)
Далее,
{k+l)h h
expfA(Aj/i — T)dT] = Jexp( —AT)dT;
1
0
-11
= —A-i [exp (—AA) ~E1 = A-i [E ^ exp (-AA)].
Матричную экспоненту представим в виде
exp(-Aft)=E-Aft+ifl-if)l + ....
Имеем
f exp[A(ftA)-TldT= A-i(AA-i^ ^.J^^... j.
kh
Вынося Ah за скобку и учитывая, что А^^А =^ Е, получим
f explA(M-x)ldT = ft(E—
kh
Итак, имеем следующий алгоритм для построения
переходных процессов:
Хй« = ехр (АЛ) [х, + А (е —^ + _... j F (х,. йд)
(6.45)
Обозначим
Q(AA) = E-^+J^_.... (6.46)
Формулу (6.45) можно записать в виде
Xft+i = ехр (АА) [Xft + AQ (AA) F (x„ kh)\. (6.47)
Более точные формулы для вычисления x^+i можно получить,
используя большое число членов ряда (6.46). В качестве
ехр (АА) можно подставлять функционально-преобразованные,
матрицы Di, D4 или использовать другие способы прибли-

жения. Отметим, что алгоритм с самого начала
предполагает расположение спектра матрицы А слева от мнимой оси.
Выбор шага в изложенном способе построения переходных
процессов легко осуществляется по линейной части системы.
В случае сильного влияния нелинейностей выбор шага
осуществляется другими методами. Подробное их рассмотрение
выходит за рамки данного учебника.
Изложенный векторный способ может быть
распространен на построение переходных процессов в нелинейных
нестационарных системах.
Пример 6.5. Для иллюстрации рассмотрим пример. Пусть
нелинейная система описывается уравнениями
Х2-= —Sxi-~2x2+bxiX2 + 0,5xl-{-xi,
Начальные условия Xi (0) = 1; Xz (0) ~ 0.5. Требуется построить
процессы в системе, удовлетворяющие заданным начальным условиям.
Представим систему в виде линейной и нелинейной частей:
x = Ax+F(x),
где
А =
О 3
-5 ->2
F(x)-
XiXz+XJ
5a:i а'2+0,5Л'2 + ^1. '
Используем функционально-преобразованную матрицу Dg. В
качестве Q выберем матрицу Qg. Шаг примем равным 0,1, что
соответствует выбору его по линейной части. В общем случае такой выбор не
может быть универсальным и зависит от вида нелинейной функции.
Алгоритм построения процессов имеет вид
хл+1= lXk + hQ2 F (хл, kh)].
Построим матрицы Dg и Q^:
(Ah)=
Dg=E+.Ah +
1 0-
0 0.3
1 Г
—
0 I.
+
^0.5 —0.2
+ т.
—0,15 —0.06
0.1 -O.llJ
■ 0.925 0.27
—0,45
0.745,
*
1 0
1
0
0.3
1 -0.15
0 1.
2
—0,5 —0,2.
0,25 1.1
Вектор нелинейной части для каждого шага пересчитываете я. Для
момента времени t = h = 0.1 с вектор F (х^, kh) равен
F(Xo) =
■ Ь0,5
+ 1^
1.5
5.10.5
40.5.12 + 0,52
.3.25

X
Ь5
1
0,5
О
'OA
-/
-2
\
,2 с,
6 0
8 ;
6 ь
4
\
л
\
J
Рис. 6.6
Для момента времени / = 0,1 с имеем
XI = X (0,1) = D2 1хо + (Е -0,5А/1) hf (хо)] =
0,925 0,27
—0,45 0,745
L 0.5 ,
+ 0,1
1 —0,15
[0,25 1,1 .
1,5
3,25
1,255137
10,1711
Для момента времени / — 2Л = 0,2 с вектор нелинейной части
F (X, kh) равен
Г 1,255137.0.1711+ 1,2551372
"J
1,790122"
.1,890728
Решение в момент / = 0,2 с имеет вид
Х2 = X (0,2) = Da [Xi + (Е —0,5АЛ) h? (х^ kh\\ =
0,925 0,27
-_0,45 0,745
,255137
10,1711
+0,1
далее Хз =
I,359254
-1,01481 J*
Х4==
1
0,25
1,414787"
—0,316849.
0,858615-
—I.7938I7J'
-0.15
1.1 J .1.
1,790122
Дальнейший ход вычислений представлен на графике (рис. 6.6).

§ 6.7. Стандартные численные методы
интегрирования
Многие важные задачи анализа и синтеза автоматических
систем решаются нахождением кривых переходных процессов
(выявление интервала устойчивого функционирования
асимптотически неустойчивой системы, оптимальный синтез).
Построить переходный процесс—это значит проинтегрировать
дифференциальное уравнение и получить решение,
удовлетворяющее заданным начальным условиям и возмущающим
воздействиям. Интегрирование может быть осуществлено различными
методами и выполняться с помощью аналоговых или цифровых
ЭВМ. Применение аналоговых ЭВМ позволяет интегрировать
-систему в реальном времени, хотя точность может быть
недостаточной. При использовании цифровых ЭВМ интегрирование
осуществляется стандартными численными методами. К таким
методам относятся методы Эйлера, Рунге—Кутта, Адамса,
Хемминга, Гира.
Рассмотрим скалярное дифференциальное уравнение
Получить точное решение уравнения аналитическими
методами удается весьма редко, поэтому ставится задача
приблизить точное решение с помощью вычислительных (численных)
методов.
Используются два обширных класса вычислительных
методов. К первому относятся одношаговые (одноступенчатые)
методы. В этих методах для нахождения следующей точки х^+х
кривой требуется информация только в одной предыдущей
точке (Xft, tk):
Xk+i=f{Xk. fft).
К этому классу относится решение с помощью разложения в
ряд Тейлора, метод Эйлера, Эйлера—Коши, Рунге—Кутта.
Простейшим является метод Эйлера, основанный на
вычислении точки а:,^+1 посредством прямолинейной экстраполяции
из предыдущей точки лг^. Если х (f) — гладкое решение
уравнения (6.29), то оно имеет разложение в ряд Тейлора. Метод
Эйлера можно рассматривать как приближенное использова-

ние двух членов ряда Тейлора. Наклон решений х {f) в
начальной точке определяется по формуле
Xq =^f{XQ^ /о)«
Приближение Ххкх (ti) находится с помощью двух первых
членов ряда:
X (О ^ Хх-= Хо + hf (Хо, to).
Полагая ^2 = ^ + h, находим х ^ Х2 ^ Xi + hf (лгь t^)
н т. д. Этот процесс можно продолжить по формуле
= + У, fe = 0, 1, 2, ....
Погрешность метода имеет порядок О {h% так как члены
ряда Тейлора, содержащие h во второй и более высоких степенях,
отбрасываются.
Точность метода можно увеличить на порядок, если
использовать среднее значение производной в начале и конце
интервала шага. Геометрически это означает, что наклон касательной
на середине шага меняется. Такой усовершенствованный метод
Эйлера а:^+1 =i х^ + hf (а:^, t^, h) согласуется с разложением
в ряд Тейлора вплоть до членов степени Л^. Порядок ошибки
составляет О (Л^).
Расчетная формула имеет вид
где
Ki^hfix^, h)\ K2=^hf{Xj, + Ki. h+h), 1. k~l.
Таким образом, простой и усовершенствованный методы
Эйлера можно рассматривать как приближение,
использующее два и три члена ряда Тейлора соответственно.
Если использовать большее' число членов ряда Тейлора
x{t + h)==x(t) + hxit) + -^ x(f) + .„,
то можно получить методы более высокого порядка точности.
Использование первых пяти членов ряда Тейлора дает
классический метод Рунге—Кутта четвертого порядка
точности
Х^^г - 4- {Кг + 2К, + 2Ks + К,).
6
где - / (Xft. h); Кг=/ (4 + h/2, % + /С,/2);
К:, = f(fh + Л/2. Xfc + /<2/2); Ki=f{tk+h,Xk + К^).

в методе Рунге—Кутта четвертого порядка не требуется
вычислений производных, функция / вычисляется четыре
раза для продвижения на один шаг вперед. Так как формулы
описывают метод четвертого порядка точности, то порядок
погрешности метода составляет О (h^
быть использована оценка —-
. Для выбора шага может
К _/( 1» которая не должна
превышать нескольких сотых. Имеются модификации формул
Рунге—Кутта. Одна из них, предложенная Мерсоном,
позволяет автоматически выбирать шаг, обеспечивая заданную
точность. Используемые формулы Рунге—Кутта—Мерсона
имеют вид
^fe+i-^^/.+0,5(/Ci + 4/C4 + /C5).
где
/Сз --у А/+ X, + ^ К. + ^/е.);
Погрешность по этому методу оценивается по формуле
где е — заданная точность.
Если правая часть превышает заданную погрешность
более чем в пять раз, шаг h уменьшается в два раза, если правая
часть меньше чем 5/32 заданной погрешности, то шаг
удваивается. Автоматическое изменение шага, по утверждению
Мерсона, на 20% ускоряет процесс по сравнению со стандартной
процедурой Рунге—Кутта с постоянным шагом. Экономия
времени достигается за счет того, что при стандартном методе
шаг выбирается слишком малым и время счета увеличивается.
Можно построить формулы Рунге—Кутта высших степеней,
при этом основная часть расчетов приходится на счет правой
части уравнения. Формула степени точности р требует р-крат-
ного вычисления правой части. Это может привести к значи-

тельному увеличению затрат машинного времени. С другой
стороны, увеличение порядка метода допускает использование
большего шага h. Методы Рунге—Кутта легко
программируются.
Величину шага h можно изменить на любом этапе
вычислений. Метод является «самостартующим», перовые точки
решения вычисляются естественно, как я все остальные.
Перечисленные методы могут быть как явными, так и
неявными. Явными методы назьгоаются по той причине, что
искомое значение лг^^^ на (k + 1)-м шаге выражается явно через
значения л:^ и F^, полученные иа предыдущих шагах.
Например, переходные процессы для явного метода Эйлера
рассчитывают по формуле
Неявные методы — это такие, в которых искомое значение
Xh^i определяется неявно, т. е. через значения jc^+i и F^^^
иа том же шаге. Для неявного метода формула Эйлера имеет
вид
Xu+i=^Xf, + hF{xt,+u h+ih
Важно, что в этом методе можно брать любой шаг, меняя лишь
точность построения процессов. Метод устойчив при любых
значениях h (h> 0).
Вычисление в неявных методах сложнее, чем в явных,
так как приходится решать систему алгебраических
уравнений. Так как неявные методы устойчивы при любом й, то при
интегрировании определенных классов систем общая
трудоемкость может быть меньше.
Ко второму классу относятся многошаговые
(многоступенчатые) методы. Их отличительная черта — использование
информации при вычислении следующей точки (лг^^.!, ^^^.i) ие
только в точке (х^, tk), но и в предыдущих точках.
Многошаговые методы послужили базой для создания методов с
прогнозом и коррекцией. Как следует из названия, вначале
предсказывается значение (прогноз), а затем оно каким-либо
способом исправляется (коррекция). Для корректировки
можно использовать ту же самую формулу. Итерационный процесс
повторяется до тех пор, пока не достигается заданная точность.
Однако, как правило, используются две формулы,
называемые соответственно формулами прогноза и коррекции. Так
как многошаговые методы не обладают «стартовым» свойством,
TP начинать решение надо с помощью одношаговых методов.

Чаще всего для начала решения используется метод Рунге—
Кутта. В настоящее время для интегрирования систем х =
= / {х, t) широко используются методы Адамса—Башфорта и
Хэмминга.
Общая формула прогноза для методов четвертого порядка
точности имеет вид
Ч+1 = ^0 ^fc + Ai Xfe-i + А2 + h (Bo x'k +
+ xU, + xl^ 2 + B3 4-3) + 0 (^J!l^
где t^)\
Aq — 1 •—Ai
Ai == Aiy
Az^Az;
Bo = (55 + 9Ai + 8л2)/24;
B,==(_59+19/l,+32^2)/24;
в2=--(37-^5л1 + 8л2)/24;
Вз = (-9+Л)/24;
£^=(-^251 _19л1—8Л)/6.
Формула прогноза типа Адамса—Башфорта может быть
получена интегрированием обратной интерполяционной
формулы Ньютона [17, 18].
Прогноз по методу Адамса—Башфорта осуществляется
по формуле
24
-9х',^з) +
251
720
Коррекция выполняется по формуле
- ^k + ^-h (9x1,+ , + \9xk ^bxL- , + Xk^ 2) +
+
19
720
ДБ j^(5)
Последние члены в обеих формулах в действительности в
вычислениях не используются и служат для оценки ошибок
дискретизации (усечения).
В распространенном в настоящее время методе Хемминга
используются следующие формулы прогноза и коррекции:
п р о г н о 3'
А 28

коррекция
о 40
Для получения требуемой точности формулы прогноза и
коррекции должны быть одного порядка. Особенность методов
с прогнозом и коррекцией состоит в том, что они позволяют
находить разность между прогнозируемым и
скорректированным значениями и устранять ошибку. Многошаговые методы
более экономичны в смысле затрат машинного времени, так как
используют информацию о ранее вычисленных точках. Однако
при любом изменении величины шага h приходится временно
возвращаться к одношаговым методам. Методы,
разработанные в самое последнее время, позволяют менять порядок
точности и шаг. В качестве корректирующей часто используется
неявная формула, в которую подставляются данные прогноза.
§ 6.8. Машинная реализация частотных методов
Машинная реализация известных, сложившихся в теории
автоматического управления методов состоит в том, чтобы
распространить их иа системы большой размерности, выполнять
исследования не только по одному, но и по нескольким
параметрам, упростить и ускорить процедуру получения
конечных данных, осуществить сервисное представление
результатов (графиков, таблиц, расчетных данных) с помощью
внешних устройств ЭВМ..
Несмотря на наметившуюся тенденцию широкого
внедрения ЦВМ в область анализа и синтеза автоматических систем,
частотные методы применительно к машинной постановке не
утратили своего значения. Наоборот, реализация их на ЦВМ
позволяет в кратчайший срок получать обширную и весьма
ценную информацию о проектируемой системе. По амплитудно-
фазовым частотным характеристикам (АФЧХ) проектировщик
может судить о таких качественных характеристиках, как
запасы устойчивости по амплитуде и по фазе, резонансная
частота и т. д. Исследование реальных объектов с помощью
АФЧХ дает возможность решать задачи анализа
функциональных, структурных и параметрических свойств объекта и
отдельных его частей, идентификации по экспериментально снятым

АФЧХ, синтеза регулятора систем путем подбора
корректирующих контуров.
Рассмотрим возможности вычисления на ЦВМ амплитудно-
фазовых частотных характеристик в логарифмическом
масштабе (ЛАФЧХ) и укажем на особенности и основные трудности,
возникающие при решении этой задачи на машине.
Пусть передаточная функция задана в виде
Q(s) aosn+a,s^-^+...+an ' '
Требуется вычислить U ((d) ^ Re W (/о) и V {ь>)
= Im и/ (/(о), а затем построить
Л(со)-201gK(;Mw) + V'H и
Ф(о) = arctg(V (ш)) + тл, m = 0. ±\, ±2, ...,
где i4 (со) и ф (о)) — амплитудная и фазовая характеристики
исследуемой системы.
Построение частотных характеристик сводится к
многократному вычислению передаточной функции W (s) при
комплексном значении аргумента 8=1 + /о), где р = —1, а о)
принимает значения из некоторого интервала Ы^га* ^тахЬ
и последующему построению графиков модуля и аргумента.
Факт устойчивости или неустойчивости устанавливается по
подсчету точек пересечения фазовой характеристикой линии
Фо = —^ слева от частоты среза Ig {А (о>)} = 0. Машинная
ориентация этого метода оценки устойчивости состоит в
алгоритмизации вычислительной процедуры построения графиков
А (о), ф (о)). Особенность заключается в том, что функция
Ф (со) может находиться не только в первом квадранте, т. е.
может быть разрывной. Это вызывает определенные трудности
при машинной реализации, ибо на ЦВМ легко могут быть
получены только главные значения функции arctg х.
Рассмотрим один из методов построения ЛАФЧХ.
Представим передаточную функцию W (s) в виде комбинации
элементарных функций
(а? + р? + с?)>0.

которые соответствуют передаточным функциям типовых
звеньев системы. Если принять во внимание, запаздывание в
блоках, то их передаточные функции можею записать в виде
Таким образом, можно представить передаточную функцию
любого элементарного звена, полагая соответствующие
коэффициенты а^. Pi, Yi, at, bu Ci равными нулю. Программа
строится для стандартного вида передаточной функции, а
значение полной передаточной функции получается путем
элементарных арифметических действий над комплексными
числами.
При построении ЛАФЧХ иа ось абсцисс, как обычно,
наносятся значения Ig со, меняющиеся в интервале [Ig co^in,
Ig (Oyjjgjj]. На оси ординат откладываются величины 20 Ig А (ш)
и ф (со). Программа вычисления величины 20 Ig Л (со) и ф (со)
состоит из постоянной части, которая содержит стандартную
подпрограмму вычисления элементарной передаточной
функции (6.49), а также стандартной подпрограммы вычисления
функций е^^, sin сот и cos сот и подпрограммы сложения и
умножения пар комплексных чисел. При проектировании
конкретной системы управления достаточно скомбинировать
входы и выходы соответствующих элементарных передаточных
функций и выполнить, где необходимо, замыкание по
известным правилам.
На ЦВМ осуществляется расчет 20 Ig ^£ (со) и ф^ (оо),
i € [1, ^1, по стандартным программам, составленным в
соответствии с выражениями
jiviT^^wm^, ^^^^
Ф, (CD) arctg --arctg ^^^^ + arctg cot, (6.51)
где al -a^/Yi; p/ -^Jyu ^/ -=(^ilCi\ b[ -bjc,.
Используя правила разложения полиномов на множители
ats^ + piS + Yi', CLi^^ + biS + Cl, исходную передаточную
функцию приводят к произведению из звеньев типа (6.49). Тогда
логарифмическая амплитудно-частотная характеристика ра-

зомкнутой передаточной функции W (s), 20 Ig А (со) будет
иметь вид
20Ig^(ca)=-2 201g^a4
а фазовая
N
Такой алгоритм позволяет достаточно компактно
составить программу вычислений ЛАФЧХ. Звод массива
коэффициентов исходных типовых звеньев осуществляется после
их идентификации.
Остановимся на некоторых особенностях построения
ЛАФЧХ по приведенной методике. При реализации формулы
(6.51) для углов значения аргументов в (6.51)
стремятся к оо, что исключает расчет таких точек на ЦВМ. поэтому их
следует заменить на выражения
cp.^arccos ^M^iQco)} ^ arcsini5in^l<ML,
которые не имеют указанных особенностей.
В общем случае при построении характеристики фе ((о)
для звеньев Wi (s) может быть скачок фазы при следующих
сочетаниях коэффициентов bi, pi'.
6,-0; pi#0; bi^O; p,-0; fc,=-p|-=0.
В связи с этим программа вычисления фазы должна
строиться с учетом возможных скачков функции <р (to). Если
Ре =5^ О» bi Ф О, т. е. система демпфирована, то ф (со) —
непрерывная функция и скачка фазы не будет.
В любом из указанных «опасных» сочетаний коэффициентов
следует проверить, попадают ли значения
В интервал изменения частоты (со^, (o^+i). Если (Оц е [ш^,
(o^+iJ, Z ^ I, 2, то функция на этом интервале терпит разрыв
и фаза меняется скачком на величину ±я. Тогда к значению
Ф ((Ofc) на этом интервале следует добавить по формуле
Ф? (со) = фе (ш) ± л.
Для учета скачка фазы можно также использовать
следующий подход. Пусть известно истинное значение фазы ф (со) в

точке О) = (Oft. Выполним вычисления для получения
частотных характеристик в точке (0^+%. Главное значение функции
Ф (^/i+i) ^ точке (О = (Oft+i определяется по формуле (6.51):
Pi о b'f CD
(ci^ - arctg ■ , ^ ~ arctg \ > + arctg от.
Истинное значение ф (o),j^) в случае скачка фазы мо-
щт отлй«йеться-от главного значения ф ((o^+i) слагаемым, рав-
таш дая, уще^:^ ^ ±1. Будем считать, что ш^^.^ = Лса^, где
А —шаг в логарифмическом масштабе. Если шаг h достаточно
мало отличается от единицы, то можно считать, что в случае
скачка фазы разность ф (со^) — ф (co^+i) мало отличается от
/пя. Тогда значение фазовой характеристики в точке co^+i =
== Awft вычисляется по формуле
<p(<0ft4-i) =Ф(со,^.,) + я£ { 1^ (6.52)
где Е (л:) = т.
Если скачка фазы нет, то £ (х) округляется до нуля.
Шаг h построения частотной характеристики должен быть
выбран таким, чтобы колебания фазовой характеристики при
изменении частоты от до со^^.^ не превышали значения л;.
Для определения запаса устойчивости по амплитуде
20 Ig А ((d) необходимо вычислить значение амплитудной
характеристики при том значении о, при котором фазовая
характеристика обращается в —л. Следовательно, нужно найти
корень фазовой характеристики и при этом значении корня
вычислить значение амплитудной характеристики.
Значения (о^^ц, о^, (Og, (о^ах находятся в памяти
машины в виде таблицы. Следовательно, решение задачи сводится
в основном к решению уравнения ф (ш) = —я, левая час^ь
которого задана таблично.
При построении частотного годографа значения (o,i и (о^^^
располагаются достаточно близко, поэтому для эффективного
решения уравнения ф (о)) ~ —л может быть использован
линейный интерполяционный подход. Использование линейной
интерполяции по формуле
«а (Ofc + ф ((Oft) ^^/^^^+^ -
позволяет быстро и достаточно. точно определять значение,
при котором фазовая характеристика Ф (о?) —л. .

в том случае, когда передаточную функцию W (s)
представить в виде звеньев Wi (s) не удается, приходится строить
алгоритм вычисления ЛАФЧХ для общего случая представления
в виде (6.48).
В результате внедрения таких программ
инженеру-проектировщику остается следующая работа: а) написать
выражения для передаточных функций в виде комбинаций
передаточных функций для элементарных звеньев; б) указать, ot
какого входа до какого выхода системы необходимо построить
частотные характеристики.
Использование ЦВМ для получения частотных
характеристик может дать не только существенные выгоды с точки
зрения автоматизации вычислений, но и принципиальные
преимущества по сравнению с обычными «ручными» способами. При
исследовании большого числа точек пространства параметров
целесообразно вьгоодить на печать значения функций А (со)
и ф (со) не при всех (к = 0, 1, 2, ...), а при тех, которые в
наибольшей степени интересуют исследователя. В связи с этим
необходимо выявить те параметры, которые анализирует
исследователь при наличии графика логарифмической
амплитудной характеристики. Обычно это запасы устойчивости по
амплитуде и по фазе, которые могут быть легко получены при
наличии этой характеристики, а также резонансный пик и
частота среза. Такой Подход позволяет не печатать всех значений
>4 (со) и ф (ш) для большого числа со^, а выводить на печать
только действительно интересующие проектировщика
значения запасов устойчивости по амплитуде и по фазе, величины
резонансной частоты и т. д.
Составленные подобным образом программы прошли
достаточную практическую проверку и позволили в полной мере
автоматизировать процесс вычисления логарифмических
амплитудно-фазовых частотных характеристик на ЦВМ.
Частотные методы были реализованы на ЦВМ (в кодах машины) и
применялись В. М. Есиповым еще в начале 60-х годов при
машинном синтезе систем управления.
Можно строить частотные характеристики путем прямого
вычисления вынужденной составляющей уравнения
переменных состояния при подаче на вход гармонического сигнала
А sin со/. Такой способ построения АФЧХ был предложен
Р. И. Сольницевым. Преимущества его состоят в том, что
представляется возможным строить частотные характеристики
непосредственно по уравнениям переменных состояния (ибо
частотная характеристика, по существу, представляет собой ре-

акцию системы при подаче на вход гармонического сигнала^,
устраняются операции с комплексными числами, не нужно
вводить специальных мер для учета неминимально-фазовости,
резонансных свойств. Оказывается возможным упростить и
ускорить получение частотных характеристик системы между
любыми точками ее структуры как для замкнутых, так и для
разомкнутых контуров, а также в определенной степени
распространить такой подход для анализа нелинейных систем.
Особенность применения частотных методов применительно
к машинной постановке заключается в увеличении их
информационной ценности. Можно строить не только сами частотные
годографы, но и выводить на печать данные анализа их, т. е.
строить линии равных значений запасов устойчивости по ам*
плитуде (изамплиты) и линии равных значений запасов по
фазе (изофазы) в зависимости от изменения параметров
системы. Изамплиты и изофазы затем могут быть нанесены на
области заданного качества, в частности на области, построенные
при различных степенях устойчивости и показателях
колебательности. Такое совмещение характеристи-к дает возможность
сразу указать значение запасов устойчивости по амплитуде п
по фазе для любой интересующей проектировщика точки внутри
области устойчивости и, таким образом, существенно
облегчить выбор параметров при синтезе системы автоматического
управления.
§ 6.9. Построение областей устойчивости
и динамического качества как задача
параметрического синтеза
Внедрение ЭВМ в практику проектирования систем
различного назначения расширяет возможности
инженера-проектировщика и позволяет повысить информационную ценность
многих традиционных и новых методов теории управления.
В частности, оказывается возможным поставить задачу
нахождения совокупности параметров, удовлетворяющих заданным
динамическим свойствам. Подобная задача, по существу,
равносильна нахождению области в пространстве параметров,
внутри которой заданный функционал отвечает заранее
поставленным требованиям. Природа области может быть различной
и определяется видом функционала. В наиболее простом
случае это область устойчивости. В дальнейшем в ней может быть

выделена область заданной колебательности, а также области
с другими динамическими свойствами. При определенных
способах введения функционала искомая область является «око-
Лооптимальной»^имржно условно говорить об оптимизации
множеством в пространстве па]раметррв. .
Околооптимальнрё множество трч^к в пространстве пар^-
Метрой представляет практический niffTepec, теоретическая ор-
тимальная точка может находиться внутри такой области. Кри-
цёпций синтеза автоматических систем, основанная на нахрж-
дении и использований областей заданного динамического ка-
чёётва, представляет собой самостоятельную методологич<в-
скую проблему.
Конкретизируем задачу применительно к линейиьщ
автоматическим систШам. Рассмотрим дифференциал систему
•-:--ii:-X = Ax + F-<0.
Пусть элементы матрицы А являются непрерывными
функциями параметров [Хт, изменякщихся в некоторой
ограниченной области П, определяемой неравенствами
где Gi, arrii bu bm — заданные пределы изменения
параметров.
Пусть задан функционал G (jiii, [im), отражающий
качественные характеристики системы. В качестве такого
функционала могут быть использованы ближайшее к мнимой оси
собственное число (степень устойчивости), ограничения чисто
мнимых частей спектра матрицы А или другие показатели,
приближенно характеризующие динамические свойства
переходных процессов. В области допустимых значений Q требуется
найти границы такой подобласти « ci П, внутри которой
введенный функционал отвечает условию
G (fXi, \im) < Л
а вне этой области
G (Их, \im)> и
где / — некоторое заданное число.
Пусть, например, требуется осуществить построение гра-
ницы подмножества б> с: Q так, чтобы спектр матрицы А
располагался внутри заданной области D на плоскости
комплексного переменного s. В частности, если область D есть вся
левая полуплоскость, то задача равносильна построению обыч-^

ной области • устойчивости. Если область D является
полуплоскостью, расположенной левее мнимой оси на расстоянии
щ. от нее, то задача сводится к построению области,
обеспечивающей определенную степень устойчивости. Задавая
различным образом границу области D, можно обеспечить определен-
йые качественные ограничения на переходные процессы. На-
•хоиедение подмножества со с: й (iXh € представляет собой
^бдну из задач параметрического синтеза, так как сводится к
подбору параметров исходя из условий расположения всех
собственных чисел матрицы А в заданной области D левой
полуплоскости.
Методы нахождения искомой области в пространстве
параметров должны быть достаточно эффективны с точки зрения
машинной реализации. Для того чтобы определить границы
области, надо найти надежные и экономичные способы
построения границы на всем ее протяжении, исключая участки,
выходящие за ограничения.
§ 6.10. Модифицированный метод D-разбиения.
Применение полиномов Чебышева
Применяемый в ручных расчетах при построении областей
устойчивости метод D-разбиения в принципе позволяет сразу
определить точные границы, несмотря на наличие
посторонних линий, затрудняющих выи1еление искомой области. D-
разбиение широко применяется для построения областей
устойчивости линейных систем в плоскости двух параметров, если
интересук)щиё проектировщика параметры входят в
коэффициенты характеристического уравнения линейно. D-раЗбие-
ние может быть в значительной степени усовершенствовано и
лучше ориентировано на использование ЭВМ. Метод может
быть эффективно применен для построения областей с
заданным расположением корней характеристического уравнения
в левой полуплоскости (внутри угла, трапеции* и других
фигур), может быть распространен для построения областей
устойчивости в гармонически линеаризованных системах, а
также для областей с заданным расположением корней в
импульсных системах.
: Одним из возможных путей усовершенствования метода
является использование полиномов Чебышева. Полиномы
Чебышева обладают свойствами как ортогональных, так и гар-

монических функций. Все операции выполняются в
вещественной арифметике. На возможность модифицировать D-разбие-
ние применительно к машинной постановке впервые,
по-видимому, обратил внимание Д. Шилак, который создал методы
анализа и синтеза автоматических систем [20]. В дальнейшем
были продолжены исследования по усовершенствованию
метода и расширению его возможностей [61.
Кратко изложим необходимые сведения о полиномах Чебы-
шева. Полиномы Чебышева имеют ряд существенных
преимуществ. Они выражаются через элементарные
тригонометрические функции, обеспечивают наиболее сильную сходимость
при представлении функций, коэффициенты полинома всегда
суть целые числа, что важно с вычислительной точки зрения,
так как целые числа не вносят ошибок округления. Чебышев-
ские многочлены обладают всеми свойствами рядов Фурье.
Их и можно рассматривать как ряды Фурье, замаскированные
с помощью преобразования переменной в = arccos х.
Рассмотрим простое тригонометрическое тождество
cos (п + 1) е + cos (п — 1) 6 = 2 cos е.cos пв (6.53)
и аналогичное ему
sin (п + 1) 6 + sin (п — 1) 6 = 2 cos G-sin пв. (6.53а)
Тождества позволяют вычислить значения cos пв и sin пб
через предыдущие значения cos в и sin в. Если положить
cos в = л: и начать с cos О = 1 И cos в = д:, то формула (6.53)
дает для cos 2в квадратный многочлен от л:, для cos Зв —
кубический многочлен и т. д. Поэтому формулу (6.53) можно
переписать в виде
W = 2;^Г„ {X)(^), п 1, 2, .... (6.54)
В частности.
Го (X) - cos(0) - 1; Гз {х) = ix^ —Зх;
Тг (х) cos X х; (х) = 8x^-^8x^+1;
Т2{х)^^2х^^1;
Полиномы Тп (х) называются полиномами Чебышева 1-го
рода. По рекуррентной формуле (6.54) получаются те же
значения cos пв, но в виде полиномов п-й степени относительно
переменной х = cos в:
cos пв = Тп (х).

Подобный результат имеем для формул (6.53а), если
разделить обе ее части на sin 9. В этом случае исходим из тождеств
sine - sin 29 о п
= 1; — =2 cos в
sine sinG
sin 38
и получаем ^.^ ^ в виде квадратного полинома
относительно X, в виде кубического полинома, и т. д. Полином
п-й степени относительно переменной == cos в мы получаем
через значения +
Sin о
^^^sin(«H-i)e ^5 54^^
sin 6
Рекуррентная формула для Un (х) имеет вид
U,^,(x)=2xUn(x)-U^^,{x); n-l. 2
В частности,
t/oW = -^ =1; С/з(х) = 8х«~4х;
и (х) - ^^^"^'^^^^ ^ и,{х)^\6х^^ 12x^+1;
' Sine
= 2cose=2x;
(/^(Jc)-4х«-Л;
Полиномы Un (х) называются полиномами Чебышева 2-го
рода.
Преобразование х = cos О можно рассматривать как
проекции пересечений полукруга с прямыми, имеющими равные
углы между собой. Неравномерное расположение прямых,
которое сгущается к концам интервала —1 ^ ^ ^ 1,
определяет область задания полиномов Чебышева 1-го и 2-го родов.
Следующая формула связывает полиномы Чебышева 2-го
рода при отрицательных и положительных значейиях
аргумента:
(/п(-^) = (-1)"^пМ.

Полиномы Чебышева 1-го и 2-го родов связаны следующим
образом:
Un W - >:t/„_i {X) + Тп (X), откуда (х) - (У„ (х) -xt/„ _i (х).
Рассмотрим теперь использование полиномов Чебышева для
перестроения D-разбиения. Пусть характеристическое
уравнение имеет вид
GoS'» + aiS'»-^+... + G,= 2 «'."Л^^^О. (6.55)
Корни характеристического уравнения могут быть
различными. Исследуем случаи комплексных, вещественных и чисто
мнимых корней уравнения. Рассмотрим случай комплексных
корней, представив их в тригонометрической форме:
5=0) (cos G + / sin 0). (6.56)
Аргумент 0 изменяется в промежутке [О, л]. Это будет
соответствовать сопряженным корням, расположенным в верхней
и нижней полуплоскостях
Область устойчивости соответствует значениям аргумента
в промежутке [л/2, л1. По формуле Муавра имеем
sfc = О)* (cos А0 + j sin
Подставим выражение (6.56) в характеристическое уравнение
(6.55) и приравняем нулю вещественные и мнимые части.
Получим
2 an-ftO)*cosft0-O: (6.57)
2 an~ftO)ftsinft0=O. (6.58)
Л=1
Отметим, что'в равенстве (6.58) счет начинается сЛ = 1, так
как слагаемые, соответствующие значению ft == О, равны нулю.
Положим cos 6 = Используя полиномы Чебышева, получим
cos Ш^Т^{1)\ sin ftG = sinef/ft^i(g)(sin0=5^0).

Это соответствует случаю определения корней
характеристического уравнения с ненулевой мнимой частью. Равенства
(6.57) и (6.58) запишутся соответственно в ввде
2 с7,_^о)*ГЛЮ=-0; (6.59)
2 ап-п^'ин-^га)=-0. (6.59а)
Сокращая на (о, получим
Искомая область находится в левой полуплоскости, что
соответствует отрицательным значениям аргумента ^ из
промежутка [—1, 0]. Чтобы иметь дело со значениями полиномов
Чебышева от положительного аргумента (что удобно с
вычислительной точки зрения), в равенствах (6.59) и" (6.59а) заменим
переменную I на —|:
2(-1)*а„«,со*Г;,(|)=0; (6.60)
k = 0
2 (-1)^-^ «п-.со^-^ f/,-x(|)=0. (6.61)
в равенствах (6.60) и (6.61) области устойчивости
соответствуют значениям ^ из промежутка 10, S1.
Заметим, что
I = —cos в = cos ф; (6,62)
S = 6) (+ / УГ^^). (6.62а)
Пусть коэффициенты характеристического уравнения
зависят от двух параметров \ii и jig линейно:
ап-п = ocn^fe [ii + P„-ft Ih + Tn-л. (6.63)
Подставляя выражение (6.63) в равенства (6.60) и (6.61),
получим систему относительно параметров jjii и с
коэффициентами, являющимися функциями со и ^:
fi,/lx(o), g) + fi2Bi(o), g) + Q(<o,
М2(^. g) + f^2fi2(0), 5)+С2(С0, 9-0,
(6.64)

где
^1= S {-О*T'ftd);
k=0
(6.65)
ft=0
Решая' систему (6.64) при условии, что
получим
Формулы (6.65) для коэффициентов системы (6.64) можно
упростить, если вместо полиномов Чебышева ввести в
рассмотрение функции
РА<^Л) = {-1)'(^>'Т,а); (6.66)
QJco,S)=:(-l)*co^f/„a). (6.67)
Для этих функций могут быть получены рекуррентные
формулы. Умножая (6.66) на (—1)*+^о)*^Ч получим
(. -1)*+1 со^+1 Т^^^ (g) = (-1 )*+' 2go>^+ ^r, (g) -
_.(_1)*+1со*+>Г,+,(У
или
'^ft+i («. I) - -2©|Pft («, I) -<»2 ((0. I), fe - 1,2
причем
Po («. g> = 7^0 (I) = 1; ''i I) = (g) = - 0)1.

Аналогично, умножая (6.67) на (—1)^+*(о*+\ получим
_(_j)*+ico*+ii;^,,(g)
или
Q*+iK^) = -2g«Q*K£)-o)^Qfc-i(co,g), ft = I,2,.... (6.68)
где Qo I) = t^o (5) = 1; Qi К I) (1) = -2(0^
Таким образом, вместо (6.65) можно применять формулы
Л= i: ссп-л/'л(«. I); Л- S <^n-fcQfc^iK I);
Bi= i Pn-i.Pft(co. ^); B^^ ± Pn-nQft^i(o>. g);
Ci= s Tn-fc/'fcK I); Q= il Tn-fcQi.^i(co,g).
Используя связь между полиномами Чебышева 1-го рода
Tft и 2-го рода l/fc, формулы можно сделать «де проще.
Перейдем от функций Pk к функциям Qui
7^.№) = t/.№)-li^.-.i№).
Умножая на (—1)^со^, получим
1) =Qft (со, S) + т^^г (<о. (6.69)
Подставим теперь выражение (6.69) в формулу для А^.
Получим
Л=«п/'о+ S <^п-лЯлК 2 a^-fcQA(co, g) +
+ |со 2 an--^Q^-i(co, S)
или (так как Qo =^ J)
Аналогично можно получить

Введем обозначения
ft=0
Тогда
A = ^i+g(D^, Bi=B;+ga)B^; С1=:С: + |й)Сг. (6.70)
Подставляя выражения (6.70) в первое уравнение системы
(6.64), получим
или
m^i+mBI+Ci + |(o(fiii42+mfl2 + C3)=0.
Так как последнее слагаемое равно нулю (в скобках стоит
левая часть второго уравнения системы (6.64)), то первое урав-
нение этой системы равносильно уравнению
ViiA\+iJi^B\ + Cl = 0.
Таким образом» в системе (6.64) можно считать, что
Л= 2a„-.ft_,iQft((o.y;
Са- 2V«-ft-lQлK5)•
л=:0
(6.71)

Рассмотрим случай вещественных корней
характеристического уравнения (6.55). Вещественные корни получаются при
g = 1. Тогда S = —О). В этом случае параметры щ и jjig
связаны одним уравнением
А ((о) + JB ((о) + Ь (со) ^ О, (6.72)
где
11-\
С- S Тп-^,.(«); (<й) -(^ 1)*^^
(6.72а)
Для определения G/j+i; (о*) йсполшу^т^я рекуррентная
формула ;i
(to)-. -cbGfti(6)>; ft =0, 1,2^..; .
При этом Go (со) = 1.
В плоскости параметров и {л,2. При каждом значен]ии. (о уравг
ние (6.72) определяет прямую. Это особые прямые.
Если строится область устойчивости,, то определяются две
прямые, соответствующие корню, находящемуся в
бесконечности, и корню, расположенному в начале координат. Если
строится область с заданной степенью устойчивости rj, то
берется корень, расположенный в точке [—rj. 0]. Особые прямые
совпадают с прямыми в традиционном методе D-разбиения и
определяются аналогично.
Найдем область параметров fij и Ца, соответствующую
чисто мнимым корням характеристического уравнения.
Чисто мнимые корни уравнения (6.55) исходя из (6.62а)
получаются при g = 0. При этом s = /со. При ^ = О
рекуррентная формула принимает вид (6.68):
Qfc+iKO) = -co2Q^_i(co,0)
при Qo((o, 0)= 1; (2i(co, 0) = 0.
Отсюда следует, что
(6.73)

и. следовательно, формулы для коэффициентов (6.71),
определяющих систему (6.64), принимают вид
А. ^ Аг (со, 0) = 2 «п-^ал Qtn 0);
Bi=BiKO)= 2 Рп-21с02Л<^.0);
п
Сг = (со. 0) ^ 2i' Qe,. (со. 0);
2
Л-Л(со,0)- 2 an^2A^iQ2;,(a>,0);
ft=0
ft—I
B, = BaKO)=. 2 Pn~2ft-<iQ2jco,0);
(6.74)
Сг = С,(со.О)- 2 Vn-^^-"iQ2ftK0).
функции Q^h (to. 0) вычисляются no рекуррентной (1юрмуле
(6.73) при
QoK 0)= 1.
Параметры (ii и Для каждого значения со, при котором
АгВ2-АВг¥=0,
вычисляются по (|юрмулам
—Q ^2 . i4fl—Cg
(6.75)
Полученные соотношения могут быть применены для псхггрое
кия областей на плосксюти параметров исходя из условия
расположения корней характеристического уравнения внутри
угла, трапеции, полукруга или исходя из заданной степени

7
Рис, 6.7
устойчивости. Например, при построении области изменения
параметров и исходя из расположения корней характери-
ческого уравнения внутри угла 2ф в левой полуплоскости
(рис. 6.7, а) используются формулы (6.65а) и (6.71). При
построении областей изменения параметров с учетом заданной
степени устойчивости (рис. 6.7, б) используются формулы,
полученные для случая вещественных отрицательных корней
характеристического уравнения, т. е. в формулы (6.65а)
подставляются формулы (6.72а).
Пример 6.6. Рассмотрим характеристическое уравнение
замкнутой системы
Со -|-% «3 ^. Д2 ^ S+=^ О.
Коэффициенты характеристического уравнения зависят от двух
параметров III и линейно:
c(i = a|iAi4-piH2H-Yi. i^O, 1,2.3,4.
и имеют вид Со = 0,04 fij; ai = 0,36 jxj -\- 0,04; а2 = 2\ii -\- 0,36;
03=2fii +0.4^1^+2; 04 = 2^l2 + 2.
Необходимо найти значения параметров [ii и fig,, для которых
характеристическое уравнение имеет корни, расположенные слева от
мнимой оси внутри угла ф = 60° (5 = 0,5). Запишем коэффициенты
характеристического уравнения следующим образом:
«о = 0,04; ро = 0; Vo =^ 0; = 0,36; Pi = 0; Yi = 0.04; =2;
р2 ^ 0; Т2 = 0,36; аз = 2; Рз = 0,4; Та =^2; а^^ 0; Р^ =2; = 2.
Определим функции Qj, Qg* Qs Д*"" каждого значения о по
рекуррентной формуле
Qft+i=-2<o|Qfe-ca*Qft^i(Qo-l; <?i=-2ca?).
Для I = 0,5 имеем Qq = Qi = — ^ (п = 4).

Найдем коэффициенты Ai, А^, В^, по формуле (6.71).
Параметры |ii и находятся из решения системы
{:
^1 H+J5iH+C,=0;
откуда икгеем
С^Вх —С| Bj
А^ В^г-А^В^
Ct А^—Сл Ai
А^Д^—А^Вх
при условии, что /iiJBfi А^ВхфО,
Точки |ii и ^£ при различных значениях <о образуют границу
искомой области. Линии, соответствующие вещественным корням,
являются особыми прямыми и определяются из уравнения (6.72),. Искомые
области представлены на рис. 6.8;
Отметим, что каждому вещественному корню на плоскости
параметров соответствует прямая. При практических расчетах
это должно учитываться (как и в обычном методе О^разбие-
ния) с помощью двух особых прямых.
Лрн использовании полиномов Чебышева проблема «лашии-
ной «штриховки по Неймарку» остается нерешенной- В
.случае построения областей устойчивости при различных
степенях устойчивости могут быть использованы любые известные
критерии, например критерий Рауса, а также прямые корне-
tit
о
8
1
0
с
0
0}=
В
4-
W
Фi
со-
7
0
-6
м
.J
h
гЧ
0
-2
с
f1
Рис. 6.8

вые методы. При построении области исходя из расположения
корней характеристического уравнения внутри угла, трапеции
или в других областях слева от мнимой оси корневые методы
являются единственно эффективными.
В заключение отметим, что модифицированный метод D-
разбиения, основанный на применении полиномов
Чебышева, дает возможность вести исследование импульсных, гармо^
нически линелризовайных систем с одной или двумя нелинейг-
ностями.
§ 6.11. Универсальные методы построения
областей устойчивости и динамического качества
; Если каким-либо образом найдена первая то^ка границы
области, можно обойти весь контур, двигаясь вдоЛь границы.
Наиболее простой способ слежения состоит в использовании
принципа взаимно-перпендикулярной ориентации.
Пусть построение границы искомой области происходит в
двумерном пространстве, т. е. на плоскости. Алгоритй
движения вдоль границы состоит в следующем. Направление
изменения параметров на плоскости параметров |Xi и jig
осуществляется в четырех возможных направлениях: вверх, вниз,
влево, вправо, т. е. по сторонам квадрата. В вершинах
квадратов проверяется выполнение условия G (fii, fig) $ /.
Если на данном шаге изменения параметров мы
пересекаем границу^ и попадаем в искомую область, то G {[Хи Иг) < ^•
В этом случае следующий шаг выполняется с поворотом по
часовой стрелке.
Если на очередном шаге изменения параметров мы
пересекаем границу и выходим из искомой области, то G (р-х, p-g) >
> /. В этом случае следующий шаг изменения параметров
выбирается таким образом, чтобы движение происходило с
поворотом против часовой стрелки. Легко видеть, что граница
области находится в точке, где соблюдается условие G (p-i.
Получение более точного положения точки границы
можно осуществить, применяя метод деления интервала, так,
чтобы границы строились по точкам на расстоянии, равном
половине стороны квадрата, или на расстояния, равном одной
трети ее. Алгоритм движения вдоль границы искомой области
иллюстрируется на рис. 6.9. При каждом пересечении границы

печатаются координаты точек, расположенные в вершинах
квадратов внутри (или вне) области:
Для более экономичного слежения по контуру может быть
использован видоизмененный алгоритм. Одно из возможных
изменений заключается в следующем. Если при обходе
контура области по квадратам искомая граница области не
пересекается в течение двух последовательных шагов^ то надо
«окружать» то место; где произошло последнее пересечение, и
впредь до нового пересечения повороты делать после каждого
нечетного шага, причем шаг, на котором было последнее
пересечение, следует считать нулевым. Таким образом, изменение^
на плоскости параметров происходит по квадрату с удвоенной*
ВхоО 6.
Вымд из
..^.)по шодой стреме;
'4-поборот протиб шобой стредш
Рис. 6.9

\
\
1
1
i
■
■
Рис. 6.10
стороной. Повороты, как и прежде, выполняются в
соответствии с правилом: вход в область — поворот по часовой
стрелке; выход из области—поворот против часовой стрелки.
Правило поворотов при пересечении границы искомой области
иллюстрируется на рис. 6.10.
Алгоритм обхода по вершинам прошел достаточную
практическую проверку и, несмотря на усложненную логику,
оказался экономичным. Он легко программируется, при обходе
выполняется относительно небольшое количество лишних
шагов. Замкнутая область сложной конфигурации с перегибами
и крутыми поворотами отслеживается этим алгоритмом без
срывов.
Можно применить более точный способ движения по
границе искомой области («гусеничный)^ метод).
Принцип слежения сводится к повороту и параллельному
переносу координатных осей. Слежение вдоль границы
области состоит в последовательном продвижении вдоль границы с
плмлтью поступательных перемещений и поворотов.

Рйо 6.11
Пусть име1р1^:я да^ точки [х^ yj и [х^, yzh принадлежа-
щре искомой области на плоскости параметров |iii|ii2, и лусть
интересующая нас область лежит справа от прямой, соединяю:
щей точку Ixi, у^] с [х^, i/al. Тогда приближенно можно указать
следующую точку по формулам
х9^2х^ — Хи у^ = 2у^ —
Геометрически это означает, что сделан шаг по прямой,
соединяющей точки U^, yj) и Ix^, y^l, от точки Ixi, Ух] к
точке [-^21 y^h равной расстоянию между этими точками
(рис. 6.П,А, б).
В полученной точке с координатами (лг'', у""] вычисляется
функционал G (д:^, y^h При этом возможны два случая:
I. 0 1Л уЧ~1>0.
Анализируемая точка с координатами [д:^ у^] находится
вне искомой области. Тогда выполняется поворот против
часовой стрелки и производится определение положения новой
точки 1х^, уЦ по формулам
= Ха + 1x9 —Xgl COS —[tf" —sin
У^^У^Л-\х^—х^\ sincto + [f -~^2l cosao.
(676)
где ao — угол поворота.
2. С1Л y^\-l<:0.
Точка находится внутри искомой области. Для выхода на
границу осуществляется поворот по часовой стрелке. Положе-

ние новой точки определяется по формулам
- Х2 + [-^ —Х2] cos а + [f/^ —й1 sin а; j
= [^—^2lsina+[f/>—f/jicosa. J
В полученной точке вновь вычисляется функадонал О 1х^,
и проверяется знак разности G у^\ — /.
Если соблюдается условие G [л:^, — / =^ О, то точка
l/fi, у^] находится точно на границе искомой области.
Если имеет место случай 1, то нахождение следукмдей
точки выполняется по формулам (6.76) в соответствии со
знаком разности G Ы*>, у^^Н — L
Эта процедура продолжается до тех пор, пока случай 1 не
перейдет в случай 2 или наоборот.
Переход сопровождается переменой знака разности
0{х^*^\уЩ^1.
Угол ао делится на два или на три, и процесс
продолжается до тех пор, пока угол щ не станет равным наперед
заданному малшу значению. При практических расчетах величина
«1 ^ l"" отражает достаточную точность. Найденная таким
образом точка границы принимается за новое значение [х^, у^],
причем в качестве точки [xi, уг] берется прежняя точка 1x2,
у2] и процесс повторяется.
Все точки получаются на одинаковом расстоянии от
границы, что не достигается при использовании алгоритма
«блуждания» по вершинам квадратов.
Объем вычислительной работы существенно уменьшается
при использование! малых и фиксированных углов поворота.
Приближенно можно считать sin а jst? а; cos а ^ 1 — а*/2.
При а < 5° ошибка составляет менее 10~*.
Если точка находится внутри области, поворот по часовой
стрелке с учет™ параллельного переноса в точку [xg, у2]
осуществляется по формулам
х^=.Х2 + (х° -Хг) (1 —aV2) + {у^ ^у,) а\
у^ - У2-{^ -Хо) а + (tf> -У2) (I -о? 12).
Если точка находится вне области, поворот против часовой
стрелки с учетом параллельного переноса в точку Ixa, у,]
вьтолняется по формулам
х^^Х2 + {к^ -Х2) (i -aV2) ~{f -у.^ а;

Вычисления в значительной степени упрощаются, если
повороты делать всегда на один и тот же угол. В этом случае для
конкретной задачи величины sin а и cos а вычисляются только
один раз и входят постоянными коэффициентами в формулы.
Например, если взять а = 0,1 рад (5''43'46"), то имеем sin а =
= 0,09983; cos а ^ 0,99500.
Для данного угла имеем формулы:
а) при повороте по часовой стрелке (G < /. точка внутри
области)
х^ = х^ + 0,99500 (Jt« — ха) + 0,09983 (у^ — у^)\
У^ = У2- 0,09983 {х^ - х^) + 0,99500 (t/^ - у^);
б) при повороте против часовой стрелки (G > К точка вне
области)
х* = + 0,99500 {х9 — х^) — 0.09983 — у^)\
У^^У^ + 0,09983 (х« — х^) + 0,99500 — у^).
Точность нахождения границы увеличивается при
использовании малых углов.
Если отслеживаемый контур имеет сложную конфигурацию,
то процедуру построения границы можно разделить на два
этапа: поиск и уточнение границы. В режиме поиска
используются большие углы; в режиме уточнения — малые.
Величина угла ао может быть выбрана из условия окончания
слежения на каждом шаге:
где h — шаг; 6 —заданная точность.
Если заданы точность и шаг, то угол определяется по
формуле ао ^ е/Л.
Движение вдоль участков границы со сложной
конфигурацией может осуществляться с переменным шагом. При введении
переменного шага в формулы вносятся изменения. Пусть
длина шага при переходе из точки Ixi, yi] в точку Ixq, у^] равна /i,
а из точки [х^у yzi в точку [х^ ^1 равна k.
Тогда q = IJh — число, показывающее, во сколько раз
следующий шаг меньше предыдущего.
Координаты новой точки находятся по формулам х\ =
= (9 + I) -^2 — qxx\ У\ ^ {Я+ 1)У2 — ЧУг-
Использование переменного шага и угла приводит к адап-
гивному способу слежения вдоль границы. В зависимости от
условий движения, конфигурации области и других факторов

могут изменяться шаг, углы, выбираться различная точность.
Как в режиме поиска, так и в режиме уточнения может быть
использовано несколько этапов.
Такое дробление на этапы, по-видимому, целесообразно
применять при «увеличении» отдельных участков областей
путем введения в программу надлежащего масштабирования.
Изложенные методы использовались для построения
областей устойчивости и подобластей с заданным расположением
собственных чисел исходной матрицы А системы х = Ах +
+ F (О, а также применялись для автоматизации
отслеживания линий равного уровня. Программа слежения по контуру
без адаптации содержит 337 операторов, с адаптацией — 425
операторов.
Представляет практический интерес использование
симплексного принципа слежения вдоль границы.
Пусть осуществляется движение по прямой по направлению
к границе с некоторым шагом. Выход на границу
определяется тем, что значения функционала G в двух последовательных
а) г
Рис. 6.12

точках Ai и Bi оказываются разных знаков. После
пересечения границы может быть образован равносторонний
треугольник A^B^Ci (рис. 6.12, а—з). Слежение за границей искомой
области будет осуществляться в положительном направлении,
т. е. против хода часовой стрелки. В качестве первой точки *
принимается вершина равностороннего треугольника Di, по- '
строенного на отрезке А^В^ вправо от него, если выход на гра-.';
ницу произошел извне G (А^) > О, G (Bi) < О, и влево, если — '
изнутри G (^i)< О, G (Bi) > 0.
Таким образом, можно продолжить процесс слежения,
«зеркально» отражая ту из вершин, которая находится в
одинаковых условиях с соседней вершиной. Одинаковые условия
означают, что обе вершины «устойчивы» или, наоборот,
«неустойчивы», т. е. значение параметров p,i и р-а соответствуют
устойчивой или соответственно неустойчивой системе.
Координаты точки определяются по координатам точек
Ai и Bi'C помощью формул:
а) при- выходе на границу извне
б) при выходе на границу изнутри .
2
Иг
2
Из построения видно, что та из вершин, которая была
последней, не отражается. В новом треугольнике A^BJ^^ отражается
та вершина, которая находится в одинаковых условиях с
соседней вершиной. В данном случае это вершина Ау, так как
обе вершины «неустойчивы». Процесс последовательного
движения вдоль границы и правила отражения вершин показаны
на рис. 6.12, а~и.
Отметим, что треугольники при таком способе слежения
вдоль границы могут быть и неравносторюнними.

Таким образом, построение границы искомой области
по симплексному методу включает следующую
последовательность действий:
1. Выход в область для пересечений с первой точкой
границы. Выход может быть как направленным, например
с использованием метода конфигураций или градиентных
методов, так и с помощью прямого перебора точек области.
Пересечение границы формирует начало алгоритма
слежения вдоль нее.
2. Пересечение границы образует равносторонний
треугольник с вершинами 1—2—3 (рис. 6.12,а).
3. Далее зеркально «отражается» та из вершин, которая
находится в одинаковых условиях с соседней вершиной
(одинаковые условия означают «устойчивость» или,
наоборот, «неустойчивость», обеих вершин. Не отражается та
вершина, которая была последней. В данном случае
«отражается» вершина 2, так как точки 2 и 5 находятся в
одинаковых условиях (устойчивы), а вершина 3 была последней.
4. Образуется новый равносторонний треугольник, в
данном случае /—3—4.
5. Опять зеркально «отражается» та из вершин, которая
находится в одинаковых условиях с соседней вершиной
(рис. 6.12, б).
6. Далее процесс слежения вдоль границы
осуществляется аналогично вышеизложенному принципу (рис. 6.12,
в—з).

список ЛИТЕРАТУРЫ
К главе I
1. Андронов А, А,, Вознесенский ff.H., Максвелл Д. К.,
Вышнеградский И. А,, Стодола А. Теория автоматического
регулирования (линеаризованные задвчи). М., 1949.
2. Вороное А, А. Современное состояние и проблемы теории
устойчивости. Обзор. — Автоматика и телемеханика. 1982, 5. с. 5-^28.
3. Развитие теории автоматического регулирования в СССР/
Б. Н, Петров, £. Я. Попов, .4. А. Воронов, А. В, Храмой. — В кн.:
Труды Второго всесоюзного совещания по теории автоматического
регулирования. М., 1955, т. 1, с. 13—50.
4. Техническая кибернетика в СССР — В серии: Советская наука
и техника за 50 лет. М., 1978.
К главе 2
1. Басакер Р.» Саати Т, Конечные графы и сети. М., 1974.
2. Бессекерский В. А,, Попов Е. П. Теория систем автоматического
регулирования. М., 1976.
3. Воронов А. А. Основы теории автоматического управления.
Автоматическое регулирование непрерывных линейных систем. М.,
1980.
4. Гельфанд И. М., Шилов Г. £. Обобщенные функции и действия
над ними. Вып. 1. М., 1959.
5. Гноенский Л, С. Каменский Г. Л.. Эльсгольц Л. Э.
Математические основы теории управления систем. М., 1969.
6. Математические основы теории автоматического
регулирования/ Иванов В. Л., Медведев В. С, Чемоданов Б, /(., Ющенко А. С.
М., 1977. т. 1.
7. Понтрягин Л, С. Обыкновенные дифференциальные
уравнения. М., 1965.
8. Теория автоматического управления /Под ред. акад. А. А.
Воронова. Ч. I. Теория линейных систем автоматического управления.
М.. 1977.
К главе 3
1. Айзерман М. А. Теория автоматического регулирования. М..
1966,
2. Бессекерский В. А,, Попов Е. П. Теория автоматического
регулирования. М., 1976.

3. Воронов А. А. Основы теории автоматического управления.
М., 1980.
4. Иващгнко Я. И. Автоматическое регулирование. Теория и
элементы систем. М., 1973. 1978.
5. Ляпунов у4. УИ. Общая задача об устойчивости движения.
М., 1950.
6. Меркин Д. Я. Введение в теорию устойчивости движения. М.,
1971.
7. Техническая кибернетика. Теория автоматического
регулировании/ Под ред. В, В. Солодовникова. Кн. I. М., 1967.
8. Теория автоматического управления/Под ред. А. В. Нетушила.
М., 1976.
9. Сборник задач по теории автоматического регулирования /Под
ред. В, А. Бессекерского М., 1969.
10. А, А. Красовский, Г. С Поспелов. Основы автоматики и
технической кибернетики. М., 1962.
11. Гурецкий X. Анализ и синтез систем управления с
запаздыванием (перевод с польского). М., 1974.
12. Юревич Е. И. Теория автоматического управления. М., 1976.
К главе 4
1. Энциклопедия современной техники. /Гл. ред. А. И. Берг и
Af. И. Трапезников. М., 1962, с. 469, т. 1.
2. Воронов А. А. Основы теории автоматического управления, ч.
I. М., 1965.
3. Джеймс X., НикоАьс Я., Филипс Р, Теория следищих систем.
М.. 1951.
4. Красовский А. А. Интегральные оценки и выбор параметров
систем автоматического регулирования. М., 1954.
5. Курош А. Г. Курс высшей алгебры. М., 1946..
6. Ньютон Дж, К.г ГулдЛ. Л., Кайзер Дж. Ф. Теория линейных
систем. Аналитические методы расчета. М., 1.96].
7. Наумов Б. Н. Теория автоматического регулирования:
Косвенные методы анализа и синтеза качества линейных систем
автоматического управления. М., 1967. (Всесоюзн. заочный
энергетический институт).
8. Рубинчик А. М. Приближенный метод оценки качества
регулирования в линейных системах.— В кн.: Устройства и элементы
теории автоматики и телемеханики. М., 1952.
9. Удерман Э. Г. Метод корневого годографа в теории
автоматических систем. М., 1972.
10. Фельдбаум А. А. Интегральные критерии качества
регулирования.— Автоматика и телемеханика, 1948, т. IX, № 1.
11. Фельдбаум А. А. О рвспределенни корней характериствчес-
кого уравнения систем автоматического регулирования.— Автоматика
и телемеханика, 1948, т. IX, Яг 4.
12. Цыпкин Я. 3., Бромберг П. В. О степени устойчивости
линейных систем.— Известия АН СССР. ОТН, 1945, № 12.
13. Розенвассер Е. Я., Юсупов Р. Af. Чувствительность систем аи.
томатнческого управления. Л., 1969.

к главе 5
1. Воронов Л. i4. Основы теории автоматического управления-
М.. 1965, 4.1.
2. Мееров М. В. Синтез структур систем автоматического регуду-
ррваиия высокой точности. М., 1959.
3. Бессекерский В, Л., Попов Е. П. Теория систем автоматнческр-
го регулирования. М., 1972.
4. Основы автоматического у правления/Под. ред. В, С.
Пугачева. М., 1968.
5. Менский Б. М. Принцип инвариантности в автоматкадском
регулировании и управлении. М., 1972.
6. Макаров И. М„ Менский Б. М. Линейные автоматические
системы. М., 1980.
7. Зайцев Г. Ф. Коррекция систем автоматического управления
постоянного и переменного тока. М., 1969.
8. Техническая кибернетика: Теория автоматического
регулирования/Под. ред. В. В, Солодовникова. М., 1967. Кн. 2.
9. Наумов Б, Н. Переходные процессы в линейных системах
автоматического регулирования. М., 1960.
К главе 6
1. Бахвалов Н. С. Численные методы. М., 1975.
2. Бекдемешев Д. В. Дополнительные главы линейной алгебры.
М., 1983.
3. Воронов А. А. Основы теории автоматического регулирования.
Особые линейные и нелинейные системы. М., 1981.
4. Воеводин В. В. Вычислительные основы линейной алгебры.
М.. 1977.
5. Воеводин В. В., Кузнецов Ю. А. Матрицы и вычисления. М.,
1984.
6. Дидук Г. А. Машинные методы исследования автоматических
систем. Л., 1983.
7. Зубов В. И. Математические методы исследования систем
автоматического регулирования. Л., 1959.
8. Макаров И. М,, Менский Б. М. Линейные автоматические
системы. М., 1977.
9. Мелса Дж.^ Форсайт Дж. Программы в помощь изучающим
теорию линейных систем управления. М., 1981.
10. МаК'Кракен Д., Дорн У. Численные методы и
программирование на ФОРТРАНе. М., 1977.
П. Островский А. М. Решение уравнений и систем уравнений.
М.. 1963.
12. Сольницев Р. И. Машинные методы анализа сложных систем.
Л., 1982.
13. Солодовников В. В., Чулин Н. А. Частотный метод анализа и
синтез многомерных систем автоматического управления. М., 1981.
14. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ.
Линейная алгебра. М.» 1976.

15. Фаддеев Д, /С., Фаддеева В. Н. Вычислительные методы
линейной алгебры. М., i960.
16. Форсайт Дж.^ Малькольм М., Моулер К. Машинные методы
математических вычислений. М., 1960.
17. Хёмминг Р, В. Численные методы. М., 1972.
18. Щуп Т, Решение инженерных задач на ЭВМ. Практическое
]|>УковгодстГв6. М., 1^82.
19. Rosenbrok Н. //. Computer-aided coritrb). system desigh.; tbii-
abh—New York^Sah FfStlcisko: AcadiMliic press, 1974.
20. Shiljak D. Analyses and sinteses of feedback 6t control
systems in the parameters рГапё. —IEEE. Tfahs VV 83. No 7S,. 1904. p.
466 - 472. .