Текст
СОЧ И Н Е НИ Я
ПЕРЕВОД, ВСТУПИТЕЛЬНАЯ
СТАТЬЯ И КОММЕНТАРИИ
И. Н. ВЕСЕЛОВСКОГО
ПЕРЕВОД АРАБСКИХ ТЕКСТОВ
Б. А. РОЗЕНШЕЛЬДА
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1962
ФП
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
В настоящей книге переводчик попытался собрать нее. что уцелело
от произведений Архимеда. Перевод был сделан по тексту сочинений Архи-
Архимеда, изданному Гейбергом B-е издание). Кроме этого, переводчик добавил
в комментариях лее относящиеся к Архимеду тексты, имеющиеся у Паппа
и Гсропа. Наконец, в предлагаемую книгу пошли арабские тексты Архи-
Архимеда, в частности сделанный с любезно предоставленной каирскими уче-
учеными рукописи перевод «Книги о семиугольнике», появляющиеся в печати
впервые. Иеретюд с арабского лыполнен Б. А. Розенфелт.дом.
Есть дна способа переводить дрепних классиков математики: можно
строго держаться характера изложения подлинника, как в случае Архи-
Архимеда сделал бельгийский переводчик Ver Eecke, или же дать его в современ-
современном изложении, как поступил Th. Heath. Подготовляя настоящее издание,
переводчик избрал средний путь: сохранив наложение Архимеда постольку,
поскольку его чтение не затруднит' читателя, он добавил современные алге-
алгебраические формулировки; правильно ли он поступил, об этом пусть судят
читатели.
13 отдельных местах помещены переводы греческих текстов, не при-
принадлежащих Архимеду (позднейшие интерполяции); такие тексты заключены
в квадратные [ ] скобки. В угловых < > скобках стоят добавления
переводчика. Числа в квадратных скобках (например, [2]) представляют
ссылки па комментарий иди на список литературы.
Г5 заключение переводчик должен выразить благодарность Издатель-
Издательству за заботы об улучшении издания книги, Б. А. Розенфельду — за пере-
перевод арабских текстов Архимеда и хлопоты по их разысканию, М. Я. Вы-
Выгодскому и В. П. Зубову — за рецензии, оказавшие помощь переводчику в
его работе над текстом, А. А. Коноплянкину — за подбор иллюстраций
греческих рукописей и Л. Ю. Чернышевой — за ее работу по редакти-
редактированию перевода.
И. Веселовский
Архимед. Один из античных бюстов.
Жизнь Архимеда была описана неким Гераклидом, вероятно, его уче-
учеником (это имя упоминается в сочинениях Архимеда). Биография эта, суще-
существовавшая еще. в шестом веке н. э. (ее читал комментатор Архимеда Ептокий
Аскалоиский), до нас не дошла, так что теперь обстоятельства жизни и дея-
деятельности Архимеда приходится восстанавливать по крайне скудным и отры-
отрывочным упоминаниям у различных авторов.
Если начинать с абсолютно достоверных дат, то мы располагаем лишь
датой смерти Архимеда: он был убит в 212 году до н. э. при взятии Сиракуз
римлянами по время второй Пунической войны Рима с Карфагеном. Визан-
Византийский писатель конца XII века н. э. Цеци, автор «Хилиад (тысяч) исто-
историй», сообщает, что Архимеду п момент смерти было около 75 .пет; тем самым
определяется приблизительная дата его рождения — 287 год до н. у. Отцом
Архимеда был астроном Фидий (упоминаемый им в «Псаммите»).
Архимед жил в эпоху, когда греческая культура и язык получили миро-
мировое значение в связи с завоеваниями Александра Македонского и с образо-
образованием эллинистических государств. Эпоха эллинизма занимает три века
мировой истории: ее началом принято считать основание Александрии C32 г.
до и. а.) и концом — завоевание Римом Египта, последнего остававшегося
свободным эллинистического государства C0 г. до н. ».). Литература и искус-
искусство этого времени, конечно, не могли сравниться с классическими образ-
образцами эпохи демократической Греции V—IV веков до н. э., но в области точ-
точных наук эллинистические ученые добились очень многого: III лек до п. э.
бил, пожалуй, апогеем научного творчества Древней Греции л ряде спе-
специальных областей. В математике и течение этого времени от Евклида, автора
«Начал», до Аполлония Пергского, автора «Конических сечений», были
созданы настоящие шедевры, остающиеся до нашего времени классическими
образцами математического творчества.
Главным центром научной деятельности в рассматриваемый период
была Александрия с ее громадной библиотекой и музеем. В области точных
наук (математики и естествознания) в III веке до н. э., а также в области
филологии во II веке до н. э. александрийские ученые сделали очень много,
и с александрийскими математиками Архимед поддерживал тесные связи. Из
них в псфвую очередь надо назвать астронома Конона Самосского, известно-
известного главным образом по анекдоту с волосами Вереники *). Этот «галантный
*) Кг;гдя в 246 году до н. э. египетский властитель Птоломей III Эвергет отправился в далекий
поход на Антиохию и начал третью Сирийскую войну, его супруга Вероника, молись аа благо-
благополучное окончание похода, принесла в жертву богам свои волосы. Через пекоторос время после
окончания похода окапалось, что ее волос в храме нет: тогда гасиш'пгый придворный астроном
Копии заявил, что эти волосы были помещены богами на небе в качестпе uonoru сооисз^ии «Волос
Вероники».
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
астроном» был в действительности очень крупным ученым, оказавшим
большое влияние пи научное развитие Архимеда. Архимед мог познаколтнться
с Кононом или непосредственно и Сицилии, где Конон одно время произво-
производил астрономические наблюдения, или в Александрии во время своего пре-
пребывания там. Конон давал Архимеду темы для научных работ, как, напри-
например, задачу о спиралях, о чем говорит и «Математическом собрании» Папп
Александрийский (книга IV, 21); «эту теорему предложил (ngouteive) Ко-
Конон, самосский геометр, а доказал ее Архимед». Как мы знаем из собствен-
собственных слов Архимеда, последний посылал Копону для критики свои мате-
математические работы, а с учеником его Досифеем поддерживал отношении
и после смерти Koiroiia, которую относят it тридцатым годам III века
до н. о.
Другим александрийцем, с которым Архимед поддерживал связи, был
Эратосфен Кирсиский B85—205 гг. до н. э.). В 245 г. до н. э. Эратосфеи был
приглашен в Александрию уиомяпутым уже Птоломеем III Эвергетом в каче-
качестве воспитателя наследника престола Птоломея IV Филопатора. Эратосфеи
был весьма разносторонним ученым: он занимался арифметикой («решето
Эратосфепа» для нахождения простых чисел известно каждому школьнику),
геометрией (об его решении делийской задачи мы еще будем говорить) и астро-
астрономией (он составил описание, звездного неба — «Катастеризмы»); он про-
произвел первое измерение дуги земного меридиапа, положив тем начало мате-
математической географии, занимался хронологией и заведовал Александрий-
Александрийской библиотекой. За разносторонность враги называли его о р-^та (бета —
вторая букиа греческой азбуки) — «во всем второй». К Эратосфепу Архимед
обратился со своим замечательным «Эфодом», излагающим те методы, при
помощи которых Архимеду удалось сделать свои выдающиеся открытия;
наконец, Эратосфену же была послана «Задача о быках».
Родина Архимеда, Сиракузы, и течение всего TII века до п. э. находи-
находилась между двумя, и даже тремя, враждующими пародами, боровшимися
за обладание богатой и плодородной Сицилией, а именно греками, карфаге-
карфагенянами и римлянами. Когда Архимеду бг,тло около десяти лет, в Сицилии
знаменитый эпирский царь Пирр, стремившийся основать новую монархию
на западе греческого мира в Италии и Сицилии, вел войну с римлянами и кар-
карфагенянами. Война Пирра оказалась безрезультатной; в борьбе с ним выдви-
выдвинулся Гиерон (возможно, бывший родственником Архимеда), в 270 г. до н. э.
сделавшийся правителем Сиракуз. Первая половика его царствовапия не
была мирной: ему сначала пришлось отбиваться от мамертинцев -италийских
наемников,— захвативших Мессину; затем л эту борьбу вмешались, с одной
стороны, римляне, с другой — карфагеняне, и разразилась первая: Пуниче-
Пуническая война B04—241 гг. до н. э.), в результате которой вся Сицилия, за
исключением области Сиракуз, стала римской «провинцией». Во время этой
войны Гиерон первоначально действовал в союао с карфагенянами, по по-
время вышел из войны, так что Сиракузы остались «свободными». С 241 г.
до н. г>. начинается мирный период царствовании Гиерона, старавшегося
поддерживать хорошие отношения со всеми сторонами; тем не менее он дея-
деятельно готовился к отражению возможных покушений на свободу Сиракуз
и усиливал обороноспособность родного города, привлекши к этой работе,
как говорит Плутарх, и Архимеда. В 227 г. до п. э. Гиерон вместе с сопра-
соправителем Гелоном (своим сыном) оказали помощь Родосу после постигшего
его землетрясения; интересно отметить, что в числе подарков были «пять-
«пятьдесят трехлоктевых катапульт» (Полибий, История, книга V, 88).
ТТонольно приходит в голову, что эти катапульты представляли особую цен-
ценность потому, что были созданиями Архимеда.
йг:тупительнл.п статья и. н. веселовского
Вероятно, и течение этого мирного промежутка Архимеду удалось побы-
побывать в Александрии и познакомиться тал) с Ковопом и Эратосфсном. Во время
сноего пребывания и Египте, как говорит историк Диодор (нторая полонила
I века до н. э.), Архимед изобретает кохлею, или архимедов винт, служа-
служащий для поднятия наверх воды. Знакомство с Копоном, вероятно, послу-
послужило толчком к развитию огромных математических способностей Архимеда.
"¦¦U, Ш'ШГ''
¦'¦ -..'¦': ¦¦ ¦¦¦ al», '
' .<¦¦'-¦-•"¦>-> u.... ^«^. ^ ....
Архпмсд. Домииико Фсти (XVII л.). Картинная
галерея. Дрезден.
Первые ei-o пропзводоиия были посвящены механике; после же смерти Коно-
па Архимед пишет ряд видающихся математических произведений. Инте-
Интересно отметить, что в 240 г. до н. о. Архимеду бьио уже около сорока семи
лет, так что дошедшие до пас его математические цроизиедешш написаны
им уже по дтеньшеи мере к пятидесятилетнем возрасте. Первое из дошедших
до нас сочинений Архимеда «Квадратура параболы» можно предположи-
предположительно отнести к 235 г. до н. э.; Архимед умер п 212 г. до и. э. Таким обра-
лом, расцвет математической деятельности Архимеда обнимает какие-нибудь
20—25 лет. Этот период был прерван н.ччашкойся в 218 г. до н. я. второй
Пунической войной между Римом и Карфагеном. Сиракузы были вовлечены
а эту войну, и в 212 г. до н. :). Архимед, руководивший обороной Сиракуа,
погиб от меча римского солдата.
Каким рисовался образ Архимеда следующим поколениям? Полибий,
«писывавший осаду Сиракуз всего через какие-нибудь 50—60 лет носле
ВОТУПИТНЛЫХАЯ СТАТЬЯ И. Н. ЪКСЕЛОВСКОГО
смерти Архимеда, в дошедшем до нас и приведенном ниже (см. стр. 44)
тексте говорит только об инженерной деятельности Архимеда, по соответ-
соответствующая часть истории Полибии дошла до нас только в извлечениях.
Римский историк Тит Ливии, использовавший Полибия и своей истории
Рима, называет Архимеда unicus spectator cocli siderumque — «не имею-
имеющий себе равных наблюдатель неба и звезд».
Глапным образом как об астрономе пишет об Архимеде и Цицерон;
однако последний знал Архимеда и как математика, так как сумел найти
могилу Архимеда ло помещенному ка ней изображению гаара и цилиндра —
в память одного из математических достижений Архимеда, которое послед-
последний считал самым большим своим открытием.
Диодор, историк середины I века до н. э., говоря об изобретении архи-
архимедова винта пишет: «По не только поэтому нужно удишштьсн таланту Архи-
Архимеда. Мы обялапьг ему еще многими другими более замечательными произ-
произведениями, известными всему миру. Мы опишем их с тщательностью и в под-
подробностях, когда дойдем до описания эпохи Архимеда» (Историческая библио-
библиотека, книга V, 37). К сожалению, часть истории Диодора, описывавшая
опоху Архимеда, до нас не дошла.
В конце того же века знаменитый архитектор Витрувий говорит об Архи-
Архимеде как о разностороннем ученом. .Во введении к первой книге «Архитек-
«Архитектуры» он пишет об идеальном архитекторе: «Но такие гении очень редки;
мало людей, вроде Аристарха Самосского, Филолая, Архита Тарентского,
Аполлонии Пергского, Эратосфена Киренского, Архимеда и Скопи на
Сиракузского, которые сумели с помощью расчетои и знании тайн природы
сделать большие открытия в механике и гномонигее и оставили потомству
об атом ученые труды». Интересны лица, с которыми Витрувий сопоставляет
Архимеда: это Аристарх Самосский — математик, физии и астроном, созда-
создатель первой гелиоцентрической системы мира; затем пифагореец Филолай —
философ, математик и тоже автор системы мира, согласно которой в сере-
середине мира находился центральный огонь; Архит Тарентский — друг Плато-
па, известен как математик, механик и замечательный полководец; Аполло-
Аполлоний Пергский — автор ряда замечательных математических произведений
но арифметике и геометрии («Конические сечения»), и, по-видимому, творец
астрономической теории эпициклов; об Эратосфене мы уже говорили; все»
зто люди больших и, главное, разносторонних интересов и способностей.
Во второй половине первого века нашей ары Силий Италик — ученый,
поэт эпохи Флавиев, автор исторического зпоса о второй Пунической войне-
ценит Архимеда как человека «поднявшегося своим гением далеко за пре-
пределы человеческого», «знавшего нее тайны природы», которому ияыестпо,.
«является ли Земля неподвижной, или прикрепленной к оси вращении;
по какой причине разлитое цо земному шару море остйвтеи прикованным
к поверхности Земли; в чем заключается причина волнения его вод и различ-
различных фаз Луны; какому закону следуют явления прилива и отлива». «Можно*
верить, продолжает поэт, что Архимед исчислил все земные песчинки» и что-
оп мог «руками одной слабой гкепщины спустить на воду корабль и поднять-
вверх по наклону нагроможденные на нем скалы» (De ЬсНо punico sccundo,
книга ХГУ).
Все эти отзывы рисуют Архимеда как всестороппего ученого — астро-
пома, естествоиспытателя, механика, они мало говорят об Архимеде как:
о математике, но ото шголне попятно: математика не была предметом, зна-
знакомство с которым было распространенным среди широкой публики. Мы при-
привели зти отзывы в противовес очень распространенной характеристике Архи-
Архимеда, данной Плутархом, который в противоположность этим авторам
1 f :
vt, ,"-.*•„. :'?
. *• «*^: • ¦ ж
3iii;
Афинская школа. Рафаялг. (XVI в.). Фреска. Патикан. Рим. Архимед л прапо.м гшжтюм углу склонился
с циркулем над абаком,
-10 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСКЛОПСКОГО
рисует Архимеда преимущественно как математика. Причина этого заклю-
заключается совсем не в том, что Плутарх был математиком, или iro крайней мере
любил математику. Причина этого заключается в том, что все вы шеприведен-
ные авторы писали ещо под очень сильным влиянием эллинистического образа
мышлении, в то время как деятельность Плутарха относится уже к совер-
совершенно другой зпохе. Плутарх жал в начале II века пашей эры в эпоху,
когда консервативные настроения, зародившиеся ещо во времена Августа,
достигли своего полного развития. Б эту зноху классической реставрации
забывается и реализм эллинистической литературы, и разносторонность
научной деятельности эллинистических ученых. Т5 качестве идеалов выста-
выставляются поэты, ораторы и философы классической эпохи Афинского госу-
.дарства, начинается возрождение философии Аристотеля и Платопа. В обла-
области науки разнимаются лишь медицина и математика, прячем последняя
не как самостоятельная наука, а скорее как служанка астрономии, или,
верное, астрологии; при этом, комично, много зпачил и культ математики,
' имевший место у Платона и пифагорейцев, возрождение философии которых
как раз приходится на первые дна пека нашей эры. Истинный ученый
рисуется как человек не от мира сего, погруженный в созерцание идей выш-
пего мира, к которому нрипадлежат и математические) образы. Все это сле-
.дует иметь в виду, читая характеристику Архимеда, данную Плутархом
в биографии римского полководца Марцелла.
«Архимед имел лозиыгаенную душу и глубокий ум, и, обладая громад-
громадными богатствами геометрических теорий, он не хотел оставить пи одного
сочинения относительно построения тех машин, которые доставили ему
славу знания, не только доступного человеку, но почти божественного...
По всей геометрии нельзя найти более трудных и глубокомысленных задач,
которые были бы решены так просто и ясно, как те, которыми занимался
Архпдсод. Одни приписывают эту ясность его высоким дарованиям, другие
же — тому напряжешюму труду, при помощи которого ему удавалось дать
своим открытиям такое выражение, что они становятся доступными без
труда. Если читателг. сам не находит доказательства, то при изучении архи-
архимедовых сочинении! у него создается впечатление, что он и сам смог бы без
¦трудя найти решение,— таким легким и быстрым путем Архимед приводит
к тому, что он хотел доказать. Поэтому не кажется пепероятным, что он, как
рассказывают, будучи околдован геометрией, забывал о пище и пренебре-
пренебрегал заботами о своем теле. Часто его насильно заставляли принимать ванну
и натираться мазями, а оп чертил па золе геометрические фигуры и на споем
намазанном маслом теле проводил пальцем линии,— настолько он был
охвачен оги'ми занятиями и действительно одухотворен музами. И хотя
у него было много прекрасных открытий, он, говорят, просил своих род-
родственников и друзей начертить на его могиле только цилиндр и содержащийся
п нем шар и указать соотношение между объемами этих тел. Таков был
Архимед, который благодаря своим глубоким познаниям в механике смог,
насколько это от ного зависело, сохранить от поражения и себя самого
¦и спой город».
Отношение Архимеда к механике Плутарх рисует следующим образом:
«Архимед не придавал большого значения всем этим (римским) маши-
машинам, которые, ио «ущестпу, не могли идти в сравнение с его собственными,
и не потому, что он как-пибудь особенно ценил свои изобретения; он сам
рассматривал их лишь как простые геометрические игрушки, которыми
он занимался в свободное время и то большей частью но настоянию царя
Гиерона, который постоянно старался направить ого занятия от чисто интел-
интеллектуальных предметов к материальным вещам и сделать его рассуждения
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
в некоторой стенени доступными чувствам и ощутимыдш для среднего чело-
человека при помощи применения их к общежитейским занятиям».
Стоит отметить наконец, также следующее свидетельство Панна (Биб-
(Библиотека, книга VIII, 3).
«Причину же и количественные характеристики (rivXcyov) всего этого
{то есть механических и р и б о р о в) позпал сиракузянип
Архимед, как утверждают некоторые. Лнлоть до наших времен только он
один пользовалси для всяких целей разнообразием и своих природных
дарований и замысла, как говорит Гемин в книге «О порядке математических
наук». Аитиохиец Карп говорит где-то, что сиракузяпин Архимед сочинил
только одну книгу по .механике, а именно касающуюся построения небес-
небесного глобуса, считая все остальное недостойным описания».
Опираясь па мнение Плутарха, иногда рисуют Архимеда как чистого
математика, ввившегося за презираемую им технику только в тот момент,
когда его родному городу стала грозить смертельная опасность. Такого рода
«цепка основана на однобокой характеристике Архимеда; если придержи-
натьси фактов, то Архимед и начал свою научную деятельность как меха-
механик, и закончил ее как механик же, и в математических его произведениях
механика явлпется могучим средством для получения математических
результатов, да и сами оги результаты не являются бесплодно висящими
в воздухе, а применяются для обоснованна механических теорий.
II
Так как первые работы Архимеда были посвящены механике, то необхо-
необходимо коротко остановиться на истории развития античной механики, тем
более, что в настоящее время нет еще специальных работ, посвященных
этому вопросу механики.
Название «механика» произошло от греческого «\iv\yavixy) (подразуме-
(подразумевается xiyyii)» — механическое искусство. Самое слово н.т]%а\'г( — машина —
первоначально обозначало подъемную машину, употреблявшуюся и театрах;
отсюда произошло известное выражение Deus ex machine — бог, спускаю-
спускающийся на театральной машине для разрешения запутанного хода действия
трагедии. Таким образом, «механическое искусство» родилось на сцене, но
это не должно нас удивлять: в обществе, основанном на рабском труде, не
было и не могло быть никаких экономических стимулов для развития маши-
машиностроения. Что же касается специально театра, то нужно отметить, что
в то же самое время, о котором идет речь (V век до н. э.), театр дал толчок
к развитию еще одной математической науки, а именно геометрической опти-
оптики, или лучше сказать — перспективы, появлепие которой было вызвано
нуждами сценических декораторов.
Греки различали два вида движений — естественные и искусственные.
Первые совершались сами собой без «сякого постороннего вмешательстиа;
к ним греки относили падение тяжелых и поднятие легких тел, а татке
круговые движения небесных светил. Что касается вторых, то они для своего
осуществления непременно требовали некоторого двигателя. То, что мы
теперь понимаем под термином «сила», в обоих этих видах движений носило
различные имена. В естественных движениях пашей силе соответствовала
ролл (от pizteiv — тот же корень и смысл, что в нашем «ринуться», или
лучше, «рыпаться»), что мы в дальнейшем, следуя Галилею, переводим тер-
термином «момент» (этот смысл понятие momentum до известной степени сохра-
сохранило в английской математической терминологии и в настоящее время).
Эта рблт], вероятно, считалась присущим телам стремлением, неотделимым
\2 ВСТУПИТЕЛЬНАЯ СТАГЬЯ и. II. ВЕСЕЛОЕСКОГО
от материи, хотя Аристотель сделал попытку и л случае естественного дви-
движения искать причину его вне тела, d так называемом свойственном каждому
роду тел «месте», к которому эти тела должны стремиться; так «местом»
тяжелых тел была Земля, а «местом» легких тел — огни — находящаяся
над воздухом огненная сфера. Что же касается искусственного или насиль-
насильственного движения, то причину его древние греки искали уже определенна
вне движущегося тела: причина эта называлась ouvequg. Количественное
определение oOvccuig мт.т находим у Аристотеля: он определяет ее как вели-
величину, пропорциональную весу движущегося тела и скорости его движения
(вернее — пройденному пути, разделенному па время). Понимаемая в таком
смысле бпл>а[Л? в точности соответствует нашему понятию «мощности»,
и действительно, па латинском языке термин 6uvau.ig передавался как poteiitia,
откуда произошло французское puissance — мощность. Было бы неправиль-
неправильным толковать формулу Аристотеля в том смысле, как это делает Мах, кото-
который и ньютоновском определении силы как произведения массы па ускоре-
ускорение, смело заменяет слово «ускорение» словом «скорость» и утверждает, что,
по Аристотелю, сила равнялась произведению массы на скорость. Прежде
всего, у Аристотеля отсутствует термин «равнялась»; затем наше понятие
«массы» оставалось грекам неизвестным (его в механике заменяла чиста
геометрическая ц?уевос; величина); что же касается веса, то все указывает
на то, что греки не считали его постоянным; вес тела, по представлению-
даже средневековых механиков, мог увеличиваться при помещении тела
на более длинное плечо рычага, затем при увеличении скорости движения
(знаменитое vires acquirit eundo — приобретает силу от движения — вполне
естественный выв од из наблюдения, что удержать падающее тело гораздо труд-
лсе, чем поддерживать покоящееся) и т. д. Это определение силы вполне
отвечало уровню технического развития общества, в котором в качестве
двигателей употреблялись животные и люди: если хочешь свезти вдвое бо-
более тяжелый груз, то запряги вдвое больше лошадей, если хочешь втрое
увеличить скорость движения, возьми втрое больше живых двигателей.
Такое понятие о «силе» еще до сих пор живет в нашем термине «лошади-
«лошадиная сила».
Очень трудпо ответить на вопрос, знал ли Аристотель принцип возмож-
возможных перемещений. Некоторые исследователи, в частности академик
А. П. Крылов, решают этот вопрос утвердительно; лично я не мог найти
ничего похожего ни и произведениях самого Аристотеля, ни в вышедших
из ого школы «Механических задачах» — первом дошедшем до нас произве-
произведении, посвященном механике. Следует, однако, заметить, что этот принцип
совершенно естественно получается из аристотелевского определения fiovajxic:,
если только считать коэффициент пропорциональности одинаковым у срав-
сравниваемых мощностей; равенство «сил» будет требовать и равенства произве-
произведешь грузов на скорости. В этом убеждает нас сама формулировка так назы-
называемого «золотого правила» механики: «что выигрывается в силе, то теряется
в скорости». Правда, эту формулировку мы в первый раз встречаем только
в «Механике» Геропа (I век н. э.), но Герон, несомненно, воспроизводит более
раннюю литературу. Во всяком случае нужно отметить, что греки приме-
применяли принцип возможных перемещений лишь к машинам, которые можно
снести к рычагу; закона равновесия сил на наклонной плоскости они так
я не смогли открыть, и он был впервые установлен только в XIII веке н. а.
Аристотелево определенно «силы» как мощности страдало очень боль-
большим недостатком: из него вытекало, что если сила равна нулю, то и ско-
скорость должна обратиться в нуль, ест устранить двигатель, то прекратится
и движение, а если движение существует, то всегда должна существовать
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОБСКОГО 13
и вызывающая это движение сила. Такое воззрение годилось для объясне-
объяснения движения попозок, везомых лошадьми, ни никак не могло удержаться
с развитием греческой артиллерии. Когда в 409 г. до п. э. карфагеняне начали
завоевательные походы в Сицилии, то наемный характер их армий требовал
быстрых военных действий и развития осадной техники. В борьбе с карфа-
карфагенянами л Сиракузах, родине Архимеда, возникла военная тирании Дио-
Дионисия Старшего (IV век до и. э.), который произвел «мобилизацию промыш-
промышленности» для военных целей. Результатом этой мобилизации было изобрете-
изобретение метательных орудий (катапульт и др.), усовершенствование осадных
машин и кораблестроения. Из западной Греции новые открытия перекину-
перекинулись и в восточную, которая в IV пеке до н. э. тоже от гражданских ополче-
ополчений перешла к наемным армиям; Филипп и Александр Македонские имели
в своих «штабах» большое количество «военных инженеров», л военная тех-
техника играла уже большую роль в последующих войнах эллинистических
государств; чтобы убедиться в атом, достаточно прочитать относящиеся к рас-
рассматриваемому периоду части истории Диодора Сицилийского. Быстрота тем-
темпов развития военной техники в течение IV века до н. э. характеризуется сле-
следующим фактом: еще в V веке до п. э. вплоть до самого его конца господ-
господствующим типом греческого судпа была так называемая триера, имеющая
три ряда весел, но уже около 300 г. до н. э. в морских флотах эллинисти-
эллинистических государств употребляются декеры-корабли с десятью рядами весел
и появляются еще более крупные суда. Возможно, что именно развитие
военной техники вызвало в области математики интерес к делийской задаче
и способствовало развитию теории конических сечений, в области же меха-
механики оно припело к возникновению теории механического подобия, к по-
появлению большого количества литературы по военной механике и, наконец,
к круттшиию аристотелевой теории силы, которая, по существу, была уста-
реннюй уже в самый момент своего возншшонендн; если полег стрелы еще
можно было объяснять тем, что ее движет возмущенный спуском тетивы воз-
воздух (так называемая теория антиперистазиса), то искать ы воздухе причину
движения тяжелого камня, выброшенного из катапульты, было уже совер-
совершенно невозможно.
Каково же было новое определение силы? Ввиду почти полного исчез-
нопепин эллинистической литературы приходится отыскивать это новое
определение в сочинениях более поздних авторов, главным образом коммен-
комментаторов Аристотеля. Как упомянуто Галилеем, один из таких комментато-
комментаторов, Александр Афродизскин (около 200 г. н. э.) сообщает, что знаменитый
астроном древности Гиппарх (писавший и в области механики) объяснял дви-
движение брошенного тела тем, что двигатель сообщает брошенному телу неко-
некоторую «силу», которая поддерживает движение, постепенно расходуясь; ког-
когда эта сила полностью иссякнет, движение прекращается. Вряд ли можно
считать, что Гиппарх действительно является автором такого определения
силы; по всей вероятности, он, для которого механика ire была основ-
основной специальностью, просто воспроизводит обьтчное в его эпоху опреде-
определение силы (Галилей приводит это определение в своем юношеском неза-
незаконченном произведении «De motu»). Это эллинистическое определение си-
силы встречается также и в комментариях Симиликия и Иоанна Филопона к
Аристотелю (VI век и. э.); через посредство этих комментаторов (Симгошкий
был переведен во второй половине XIII века Вильгельмом из Мербеке —
переводчиком Архимеда) эллинистическое определенно силы становится
известным и западноевропейским механикам позднего средневековья; под
именем impetus это определение силы встречается у Альберта Саксонского,
Николая Кузанского и Леонардо да Винчи. Понимаемая в таком смысле
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И- Н. НЕСЕЛОВСКОГО
«сипа» полностью отвечает современному понятию о живой силе; еще Декарт
измерял силу (если пользоваться современной терминологией) той работой,,
которую надо сообщить движимому те;иу, чтобы поднять его па определен-
определенную высоту. Можно думать, что укреплению этого определили» па enponeii-
скойпочве способствовало развитие артиллерии, также как создание гречес-
греческой артиллерии было причиной его появления.
Весьма вероятно, что Архимед пользовался общепринятым в его время
определением силы при построении своих военных машин; однако в чисто
теоретических его произведениях это определение силы не встречается. По-
видимому, это объясняется тем, что вопросы динамики в то время математи-
математической трактовке еще не поддавались, и Архимед вполне правильно сосредо-
сосредоточил свое внимание на вопросах, касающихся статического равновесия.
Одним из раппих произведений Архимеда было какое-то (не дошедшее
до нас) сочинение но механике, точное название которого неизвестно, то ли
это neqi t,v\Gyv (о равноплечих рычагах), то ли просто ил]%а\чха. Этим сочи-
сочинением пе мог быть дошедший до нас трактат «Оравновесии плоских фигур»,
так как он не соответствует тем ссылкам, которые содержатся в трудах
Геропа, Панпа и самого Архимеда, и не содержит самого главного — опре-
определения центра тяжести, которое Архимед, очевидно, считал в то время уже-
пполпе известным. Составить себе представление об этом раннем сочинении
Архимеда нозиоляют фрагменты, сохранившиеся у Ппппа, л «Механике»
Геропа, а также у самого Архимеда.
Стержневым понятием всей статики Архимеда является понятие о цен-
центре тяжести, которое по исем данным самим Архимедолт и было установлено.
Действительно, пи Аристотель, ни «Механические проблемы», которые при-
приписываются третьему преемнику Аристотеля в управлении Лицеем Стратону
Лампсакскому, ничего о центре тяжести не знают, в то время как уже около-
250 г. до н. э. если не раньше, Архимед свободно оперирует этим понятием*).
Доархнмедовское происхождение понятия о центре тяжести отстаивает
С. Я. Лурье л своем сочинении «Архимед» (стр. 71), опираясь на следую-
следующий отрывок из «Механики» Герона.
«Стоик Поеидошш дал центру тяжести, или момента, физическое объяс-
объяснение, сказавши, что центр тяжести, или момента, есть такая точка, что если
за последнюю подвесить данный груз, то он будет в ней разделен па две рав-
равные части. Поэтому Архимед л его последователи в механике более подробно
рассмотрели это положение и установили разницу между точкой подвеса
и цептром тяжести».
Так как Архимед упоминается здесь после Посидония, то получается
впечатление, что он и жил после Посидония, и исправил введенное Посидо-
нием неправильное определение центра тяжести. По следует, однако, иметь
в виду, что «Механика» Герона дошла до нас в арабском переводе сирийца
Косты ибн-Лука из Баалбека л что у нас нет никакой гарантии, что в под-
подлиннике действительно стояло кто (равные), а не iaoppojtouvta (уравновеши-
(уравновешивающиеся). За последнее говорит упоминаемое в тексте «подвешивание за
точку»; термин «равновесие относительно точки» мы у Архимеда встречаем,
но «деление точкой тела на дне рапные части», да еще при «подвешивании»
несколько нас удивляет; приходится помогать делу тем, что центр тяжести
рассматривать как точку пересечения линий или плоскостей, делящих на
две равные части данную плоскую фигуру или тело.
•) В евнзи с этим стоит отметить, что в своих рашшх механических произведениях («Книга
ouojj») А[ишмед пошлин о центре тяжести еще lie имел, чем и «.(л-нешиитен некоторые его «аппПки
и расчетах.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 15
С. Я. Лурье замечает, что указанное понимание центра тяжести повто-
повторяется и в других местах «Механики» Герона; так, на основании упомянутого
неправильного определении паходится центр тяжести треугольника (кни-
(книга II, 35), затем деление тела па две уравпоиепшпающттеся части плоскостью,
проведенной через точку опоры, встречается при изучении подъема цилиндра
по наклонной плоскости (книга 1, 23) и при определении дейстиия рычага
на тело, опирающееся на землю (книга II, 9). Основываясь ла этих местах,
а также на том, что Посидоний в тексте Герона упоминается раньше Архи-
Архимеда, С. Я. Лурье, следуя английскому историку математики Хису, пред-
предположил, что актором вышеупомянутой: теории является пе хорошо всем
известный сирийский стоик 1 леца до н. э. Посидоний Родосский, учитель
Цицерона, а совсем почти неизвестный стоик Посидоний Александрийский,
живший несколько ранее Архимеда; этому самому Посидоштго и нужно при-
приписать честь введения в науку понятии о центре тяжести, причем сначала
это понятие было получено из неправильного предположении, что линия,
или плоскость, делящая тело на две равные части, должна обязательно
пройти через центр тяжести.
При более тщательном изучении дела выясняются следующие обстоя-
обстоятельства. Второй и третий тексты, упомянутые С. Я. Лурье, а именно, тек-
CTi.r, относящиеся к рычагу и наклонной плоскости, дол жни быть просто
устранены из рассмотрения на том основании, что они пе содержат никакого
упоминания о центре тяжести (и примере с подъемом цилиндра но наклонной
плоскости говорится только о «центре круга», и случае же с рычагом вообще
никакой центр не упоминается). Что же касается первого текста, приводи-
приводимого С. Я. Лурье, а именно относящегося к центру тяжести треугольника,
то детальное рассмотрение его является для теории С. Я. Лурье роковым.
Этот текст представляет собой часть довольно большого отрывка, касаю-
касающегося определения центров тяжести некоторых плоских фигур*). Л самом
начале автор действительно говорит, что треугольник ABC, положенный иа
медиану АГ), «не будет иметь момента пи п какую сторону, так как
треугольники AJ3D и ADC равны» (подчеркнуто мной, И. /?.), но все даль-
дальнейшее изложение, касающееся определении центров тяжести четырех-
четырехугольника и пятиугольника, совершенно не основывается на упомянутом
ложном принципе; там, наоборот, везде подразумевается равенстно не пло-
площадей, а моментол. Все изложение может быть сделано сояершенно правиль-
правильным, если и подчеркнутой фразе опять вместо слон «раины» читать «равпо-
весягци». Можно, конечно, думать, что слона «ранцы» к рассматриваемом
тексте являются подлинными, но что ГГосидониЛ Родосский, который вряд ли
шел далее определения центров тяжести самых простых фигур (параллело-
(параллелограммов, треугольников, кругов), предпочел дать, если не совсем правиль-
правильное, то по всяком случае более короткое и наглядное объяснение; для
периода упадка механики в конце эллинистической эпохи это по псяком
случае вполне подходит. Пралда, в рассматриваемой книге Поендошш
упоминается раньше Архимеда, по порядок упоминания авторов в тексте
сочинения не всегда совпадает с хронологическим порядком их опублико-
опубликования: Герон мог начать с популярного произведения Посидоння, а потом
перейти уже к более серьезному и трудному тексту Архимеда. Таким обра-
образом, предшественника Архимеда, стоика Посидония Александрийского,
как антора понятия о центре тяжести можно целиком вычеркнуть из исто-
истории механики.
*) Этот отрывак помещен в нашем издании среди «Механических фрагментов» Архимеда (см.
стр. 7а—7Ь).
16 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛ ОБСКОГО
Безусловно верным в тексте Герона является то, что понятие о центре
тяжести как о точке подвеса он считает предшествующим всякому иному
пониманию центра тяжести, но и определение центра тнжести как точки
подвеса тоже принадлежит Архимеду. У Паппа (книга VIII, 5) архимедово
определение центра тяжести читается так:
«Центром тяжести каждого тела является некоторая расположенная
внутри него точка — такая, что если за нее мысленно подвесить груз, то
•он остается в покос и сохраняет первоначальное положение».
?*. Приблизительно такое же определение центра тяжести как точки под-
подвеса мы встречаем у Евтокия и Симпликия (см. «Механические фрагменты»,
стр. 68, 72): варианты заключаются лишь в том, что подвешивание иногда
заменяется подппранием, как можно видеть из упомянутого текста Папла
и параллельного ему текста из «Механики» Герона (книга I, 24), определенно
восходящих к одному источнику. Что касается этого источника, то Папп
называет два имени — Герона и Архимеда; поскольку в тексте Герона
имеются некоторые неясности, а у Паппа все изложено правильно, то с ве-
вероятностью, близкой к достоверности, можно утверждать, что :>тмм основным
источником как для Панна, так и для Герона является Архимед.
Понятий о центре тяжести сложилось у Архимеда па основании чисто
практических исследований распределения давления груза между поддер-
поддерживающими его опорами. Это можно видеть, с одной стороны, из выше-
вышеупомянутого текста Паппа — Герока, с другой — из того обстоятельства,
что, как мы знаем из арабских источников, Архимед написал «Книгу опор»,
отрывки из которой содержатся в вышеприведенной «Механике» Герона.
Правда, если судить по этим отрывкам, он не оказался особенно счастливым
в получешшх результатах; его теория расчета многооноргтой балки («Меха-
(«Механика», Герона, книга I, 26) совершенно неверпа, так как из приведенных
там рассуждений вытекает, что в случае балки, лежащей на трех опорах,
средняя опора будет всегда нести нолопнну воса всей балки, независимо от
своего положения; томно так же нельзя согласиться с архимедовским расче-
расчетом консольпой балки (там же, 27—28). Удивляться этому не приходится;
в распоряжении Архимеда ice бмло никаких приборов для измерения давле-
давлений на опоры. В связи с этим можно отметить, что Леонард» да Винчи тоже
ошибался при определешш давлений на опоры и подставки, хотя натяжения
ворсвок определялись им совершенно правильно (конечно, в статически опре-
определимых случаях).
Работы Архимеда в области строительной механики не были едшесткен-
ными плодами его технических занятий; Архимеду пршшсынается целый ряд
механических изобретений. Правда, подробный список их, составленный
ого соотечественником историком Диодором Сицилийским, к сожалению,
до нас не дошел, так что нам приходится собирать у античных писателей
сохранившиеся отрывки этого списка.
На мерном месте среди этих изобретений следует поставить архимедов
винт или кохлею (улитку). Вот тексты, касающиеся этого прибора.
Об употреблении'его в Египте говорит историк Диодор (книга I, 34):
«Нил после разливов наносит на тюля новью количества ила, и обитатели
легко могут орошать нее поле при помощи изобретенной Архимедом Сира-
кузским машины, которая по причине своей формы, носит название улитки».
Об употреблении его п Испании тот же Днодор сообщает (книга V, 37):
«Горнорабочие встречаются иногда с подземными реками, быстрое тече-
течение которых они уменьшают, отлодя их в паклонные рвы, и неутолимая
жажда золота заставляет их доводить до конца спои предприятия. Самое
удивительное заключается в том, что они могут целиком вывести всю поду
ВСТУПИТЕЛЬНАЯ СТАТЬЯ Ы. Н. ВЕСЕЛОВСКОГО • 17
при помощи египетских винтов, которые изобрел Архимед Смракузский во
время своего пребывания в Египте. Они таким образом постепенно подымают
воду вллоть до отверстия рудника и после осугаепня подземных галерей
спокойно в mix работают. Эта машина так искусно устроена, что с ее помощью
можно поднять громадные массы воды и даже легко вынести целую реку из
земных глубин на поверхность».
Об этом же говорит писатель TI лека пашей эры Ателей в своих «Дейп-
лософистах» (книга V):
«Хотя бы отстойная вода (к трюме корабля) была бы л очень
глубокой, ее отсасывал один недолей при помощи изобретенного Архиме-
Архимедом бесконечного пинта».
Некоторые авторы оспаривают авторстно Архимеда и этом изобретении
на том основании, что пи географ Страбон, упоминающий об этой машине
в своем описании Египта, ил Витрувий, ни механик Филон не называют
при ее описании имени Архимеда; однако в атом случае можно поверить
Диодору, по-видимому, специально занимавшемуся изобретениями своего
великого земляка.
Иначе обстоит дело с изобретением Архимедом влита. Его изобретение
приписывает Архимеду тот же Атеней («Демппософцсты», книга X), который,
рассказывая известный анекдот о том, как Архимед либо вытащил на сушу
корабль, либо паоборот спустил его на воду, говорит:
«Когда люди много трудились лад тем, чтобы спустить этот корабль
на воду, знаменитый механик Архимед сделал это один с помощью неболь-
небольшого числа людей. Действительно, он добился успеха при помощи выдуман-
выдуманного им винта, так кап именно ему мы обязаны этим изобретением».
О том же говорит византийский автор XII пека, известный комментатор
Гомера, Евстафий, еиископ Фосснлоникийский:
«Архимед считается первылт изобретателем випта (c'Ait;), причем эта
машина доставила ому большую славу» (Комментарии к Илиаде, III).
Приведенные свидетельства не могут считаться доказательными по сле-
следующим причинам:
1°. Рассказ Атенея является иторой версией известного рассказа Плу-
Плутарха, с той только разницей, что у Плутарха в качестве машины упоми-
упоминается полиспаст, что более вероятно. Мм имеем еще и третью версию у Сим-
лликия (VI век н. э.) в комментарии к «Физике» Аристотеля, где знаменитое
«дай точку опоры, и я приведу в движение Землю» евнзкшается с изобрете-
изобретением «харпстиона» (нечто ироде десятичного рычага или весов) — прибора,
который под названием «карастуна» был предметом исследований арабских
и средневековых механиков, а у французского историка науки Дюэма изо-
изобретение «харистиолга» приписывается сыну известного астронома Птолемея.
По-видимому, и Атеней, л Симпликий пазыпали прибор Архимеда послед-
последним слоном механической науки их времени.
2°. Свидетельство Евстафия сомнительно и в том отношении, что гре-
греческое слово iKi^ употреблмлось для обозначения и винтовой линии, и спи-
спирали (о которой Архимед действительно писал), так что смешение в этом
случае вполне всронтпо.
III
Греческая геометрия в то нремя, когда к ее изучению приступил Архи-
Архимед, была уже вполне сложившейся дисциплиной. Она уже имела свою кано-
каноническую книгу — дошедшие до нас «Начала» Евклида, завершившие собой
целую эпоху, в течение которой вырабатывалась стройная система греческой
2 Архимед
18 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ЛЕОЕЛОВСКОГО
геометрии. Можно отметить следующие три характерные черти грече-
греческой геометрии: это, во-первых, геометрические построения при помощи
циркуля, во-вторых, воззрение на геометрические фигуры и тела как на
некоторые величины и, наконец, в-третьих, строгие логические доказатель-
доказательства в изложении геометрии.
Геометрические построения при помощи циркуля, по всей видимости,
были введены в ионийской геометрической школе, из представителей кото-
которой нам известны Фалес и Эноиид Хиосский. Ионийская школа была тесно-
связапа с вавилонской наукой, откуда были заимствованы и космологи-
космологические представления милстцев, и астрономические предсказания затмений,
и знамспитая теорема Фалеса о вписанном в круг угле, опирающемся на диа-
диаметр, и, по-видимому, даже само употребление циркуля дли геометрических
построений. Результаты работ этой школы сохранились в нерпой полошше
книги 1 «Начал» Евклида и в большей части теорем книги Ш; характер-
характерными для нее являются исследование вписанных в круг прямолинейных
фигур*), понимание равенства фигур в нашем современном смысле как сов-
совпадающих при наложении и, наконец, отсутствие метрических элементов
(одно и то же слово яедкредеих упохроблялог.ь^лли обозначения и всей окруж-
окружности, и какой-нибудь ее части — дуги).
Метрические понятия разрабатывались во второй греческой школе,
которая восходит к Пифагору. Основным понятием пифагорейской мате
матики было число, которое мыслилось материально как собрание единиц—
мопад. Из этих монад те, которые обладали положением, представляли маши:
точки, тс же монады, которые были лишены положения, представляли наши
арифметические единицы. Геометрия пифагорейцев была своего рода отде-
отделом арифметики, учением о специальных группировках единиц в виде квад-
квадратов, прямоугольников, линий, многоугольников, кубов, параллелепипе-
параллелепипедов и т. д. Понятие равенства фигур и тел в этой школе совпадало с натгтам.
понятием о равновеликости. Наиболее характерными чертами пифагорей-
пифагорейской геометрии являются преобразования равноволикнх фигур (квадратура,,
«приложение (ладароХг) площадей», то есть построение на данной прямой
прямоугольника, равновеликого заданной площади, и т. п.) и своеобразный
математический атомизм, тесно связанный с идеей целойисленнос.ти отноше-
отношений между геометрическими величинами. Первоисточник пифагорейской
математики мы можем искать и Египте с его модулярной теорией архитек-
архитектуры, где размеры всех деталей здания определялись через отношения
к некоторой длине, взятой за единицу,— модулю. 1?сли египетские жроцы
могли сказать историку Геродоту (Г век до п. з.), что площадь грани Хеопсо-
вой пиралтиды равняется квадрату, построенному на высоте лирамиды, то
они могли сказать то же самое и Пифагору во время пребывания последнего
в Египте**), а это уже представляет первый пример употребления средней
пропорциональной.
Если первый дне характерные черты греческой геометрии имеют пегре-
пегреческое происхождение, то третья — введение логических доказательств —
является специфически греческой; по существу, именно оно сделало геометрию
настоящей наукой, а не только собранием практических правил. Если вави-
вавилонские и индусские математики дали очень точные приближенные значе-
значения для кпадратпого корна из двух, то только греки могли доказать, что
отношение длины диагонали квадрата к стороне последнего не может быть.
*) Характерно, что диагональ квадрата или прямоугольника Квклнд тазыьяет диаметром.
."*) У нас нет серьезных оснований для сомнений и пребывании Пифагора в .Египте (см. ком-
комментарии к третьему тому русского издания «Начал» Евклида, М.. 1У50, стр. 297—299).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 19
выражено точно ири помощи отношения двух целых чисел; таким образом,
родилось понятие о несоизмеримых отношениях.
Открытие иррациональности квадратного корня из двух имело очень
важное значение в истории греческой математики. Оно нанесло такой удар
пифагорейском философии, от которого последняя уже но могла оправиться.
Оказалась неверной ее исходная идея — математический атомизм,— и пифа-
пифагорейская школа со пторой половины V века начинает быстро вырогкдатьси,
обращаясь л ту математическую мистику, которая характерна для пифа-
пифагорейцев эпохи Платона, много воспринявшего от идеалистической фило-
философии пифагореизма. После крушения пифагореизма греческая математика
получает определенный уклон в сторону геометрии, ибо если нельзя совер-
шеппо точно вычислить J/ 2, то можно всегда построить и его, и все другие
квадратные иррациональности; таким образом, ионийские методы снова
выступают на первый план; но второй книге «Начал» Евклида обыкновен-
обыкновенные алгебраические преобразования трактуются чисто геометрически,
создается столь характерная для греков и хорошо заметная также и у Архи-
Архимеда геометрическая алгебра.
Объединителем ионийской и пифагорейской геометрии выступил в конце
V века до н. э. Гиппократ Хиосский, алтор первого учебника геометрии типа
«Начал» Елклида. Символом такого объединения является впервые поста-
поставленная Гиппократом задача о квадратуре круга — построении квадрата,
равновеликого данному кругу: чисто пифагорейское представление о квад-
квадратуре соединяется с употребительной у ионийцев фигурой круга (следы
употребления круга в пифагорейской геометрии нам совершенно неизвестны).
Поставленная Гиппократом задача о квадратуре круга была одним из пред-
предметов геометрических исследований Архимода; последний и сочинении
«О спиралях» дал способ построения прямой, длина которой равна длине
окружности некоторого круга, а в «Измерении круга» вычислил (конечно,
приближенно) отношение между длинами окружности круга и его диаметра.
После крушения идеи целочисленное™ отношений между элементами
геометрических фигур греческая геометрия конца V и начала IV веков до
н. э. занялась исследованием квадратичных иррациснальностей, правильных
многоугольников (в частности, пятиугольника и слязашюго с ним понятия
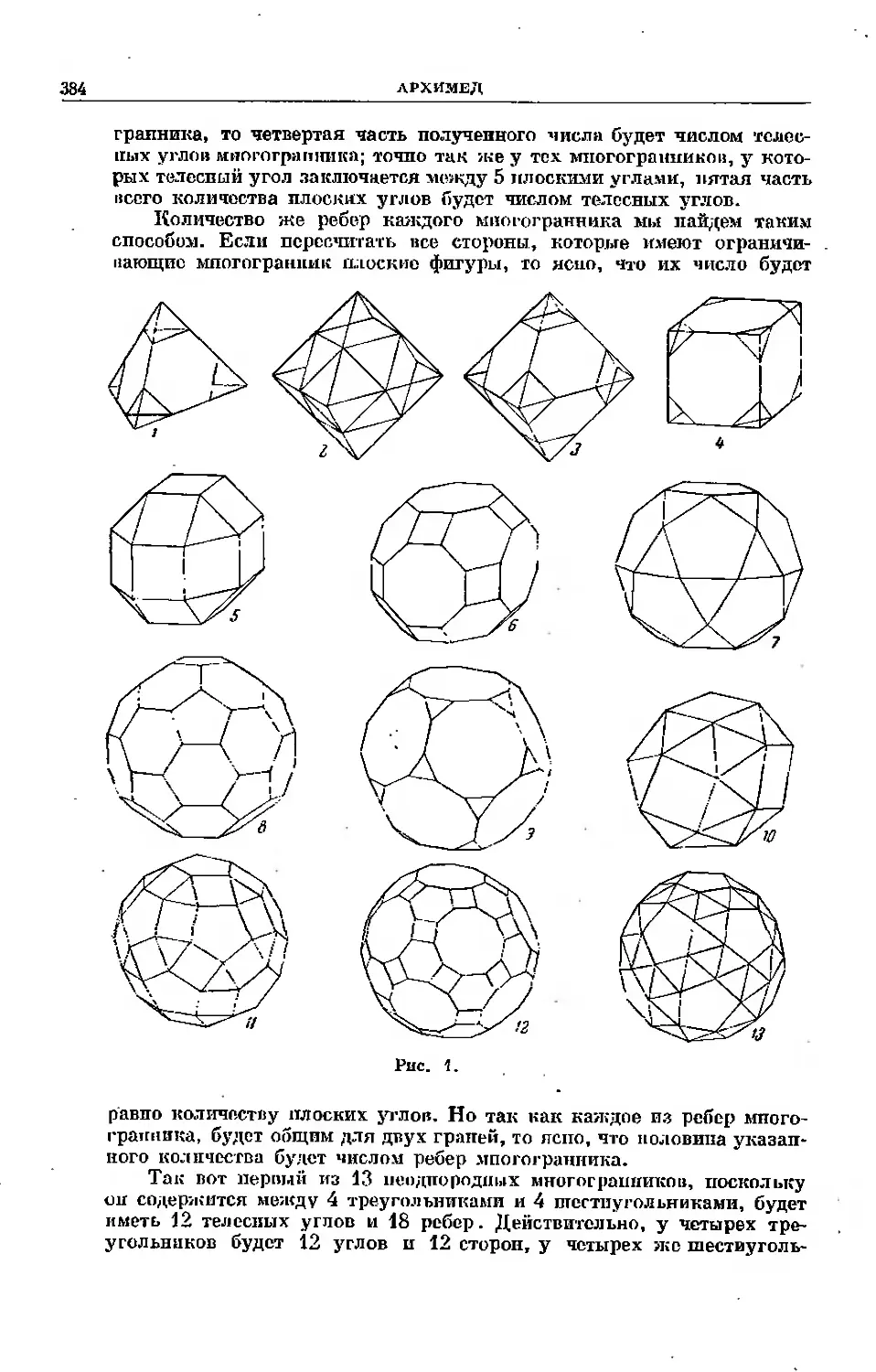
о золотом сечении) и, наконец, пяти правильных многогранников. Этот
утаи развития греческой математики тоже отразился в творчестве Архимеда,
который занимался обобщением теории правильных многогранников (три-
(тринадцать архимедовых полуправильных миогограипиков); «ода же можно
отнести материал «Стомахил», в котором идет речь о слежении фигур из раз-
различных заданных элементов и о разделении площади на части, находящиеся
с пей в рациональных отношениях. Нужно, однако, иметь в виду, что то, что
для Пифагором цен представляло предмет серьезных исследований, у Архимеда
разрабатывалось и связи с математической игрой типа наших головоломок.
Математический атомизм Пифагора был также отправной точкой иссле-
исследований великого материалиста древности Демокрита, который высоко ста-
пил самого Пифагора. Однако материалистическая философия Демокрита
была, диаметрально противоположной пифагорейскому идеализму. Если
у Пифагора основой было «число», применение которого к физическим явле-
явлениям приводило к математическому атсмизму, то отправной течкой всей
философии Демокрита были реальные физические атомы — «неделимые»,
из которых составляются все тела природы, в том числе и математические
тела и фигуры. Даже в математике Демокрит пошел дальше Пифагора; он
рискнул определить объем пирамиды и конуса при помощи разбиения на
весьма малые элементы — «неделимые». Архимед хорошо знал великого
20 ШТЯГИТКЛЬилЯ СТАТЬЯ И. II. ifECUJIOBCKOrO
атомиста и с похвалой уномипает его л «Эфоде»; однако атомистические ме-
методы он считал пригодными лишь для ilpeдвapитeльнг.Ix исследований, после
чего полученные геометрические нрсдложэния должны были доказываться
при погяощи строго логических методов; в математике учителем Архимеда
бил по Демокрит, а Евдокс-
Евдокс Кпидский (около 410—356 гг. до п. :.».) является одним из вели-
величайших математиков всех времен и народов. Трудно переоценить заслуги
этого математика, результаты работ которого мы имеем в V, VI, второй
половило- XI и в ХМ книгах «Начал» Евклида. В книге V «Начал» излагается
евдоксона теория отношении для несоизмеримых величин, полное значение
которой было понято в широких математических кругах лишь в XIX веке
после создания Дслекиндом теории иррациональных чисел. Евдокс достроил
перпую кинематическую модель нланетных движений (гомоцентрические сфе-
сферы Евдокса), положил начало сферической геометрии. Он же, по-видимому,
дал тс методы определении сравнительных величин и расстояний Солнца,
Лупы и Земли, которыми впоследствии воспользовался «Коперник антично-
античного мира» Аристарх Самосский (III век до и. а.). В геометрии Евдокс создал
метод исчерпывания, который для Архимеда был единственным строго науч-
научным методом определения площадей и объемов криволинейных фигур и тел.
Поскольку епдоксов метод исчерпывания по всегда правильно пони-
понимается, не будет лишним более детально рассмотреть его сущность. Теория
Епдокса доиыа до пас в книгах XI (вторая половина) и XII «Начал», где
методом Епдокса доказываются следующие теоремы:
1) Площади двух кругов относятся, пак квадраты диаметров.
2) Объемы двух треугольных пирамид с равными высотами относятся,
как площади оснований.
3) Конус равен третьей части цилиндра с теми же основапиом и высотой.
4) Объэмы двух равновысоких конусов или цилиндров относятся, как
площади их оснований.
Г>) Объемы нодооных конусов или цилиндров относятся, как кубы их
диаметров.
Для нашзй цели достаточно будет проанализировать доказательство
одной из этих теореад, хотя бы первой из вышеупомянутых, поскольку метод
доказательства псех их является, но существу, одним п тем жа. Этот анализ
полезно будет провести, сопоставляя рассуждения Епдокса с современным
доказательством.
Мы сначала определяем площадь круга как предэл площадей вписанных
и описанных многоугольников при неограниченной удвоении их сторон;
Квдокс ограничивается лишь вписанными многоугольниками я опирается
при доказательстве па следующие два пр&дложвпим: 1а. Если от некоторой
величины отнять болыпэ половины, от остатка тоже отнять больше поло-
половины и так делать постоянно, то можно получить остаток, меньший любой
заданной величины. 2°. Площадь треугольника, вписанного в сегмент, больше
половины площади этого сегмента. Еодокс доказывает, что разность между
площадью круга и площадью вписанного в этот круг многоугольника при
неограниченном удпозник числа сторон последнего может быть сделана мень-
меньше любой ладанной величины..
Мы доказываем, что площади подобных вписанных многоугольников
относятся, как квадраты диалютров; Евдокс дзлает то же самое.
После этого мы говорим, что если дне переменные величины находятся
лес время в одинаковых отношениях, то в тех же самых отношениях будут
находиться и их пределы, так что, посколы^у площади двух подобных
«писанных миогоугольпиков относятся, как квадраты диаметров описанных
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 21
около них кругоп, то, следовательно, площади этих кругом тоже будут отно-
относиться, как квадраты их диаметров. При этом паше исходное положение
о неременных и их пределах долгое время принималось почти за аксиому.
Евдокс же доказывает положение, равносильное паишму.
Доказательство Евдокса может Сыть изложено следующим образом.
Пусть мы имеем две последовательности величин
blt b.,, hs, ..., bn, ...,
соответственные члены которых связаны соотношением an~kbn, где к —
некоторое постоянное число.
При увеличении п члены первой последовательности неограниченно
приближаются к некоторой величине Sa, а члены второй последователь-
последовательности точно так }itc приближаются к величипе $ь, оставаясь псе время меньше
своих соответственных пределов. Требуется доказать, что эти пределы
Sa и Sh будут тоже связаны соотношением
Sa-h.-Sb.
Допустим, что это неверно, по одна на этих величин, например Sn,
будет меньше, чем к-&\, и раппа Т:
Увеличивая п, мы всегда можем добиться, чтобы разность Sb—Ь.п сде-
в
ого числа —
k
^ в
лалась меньше люоого заданного числа —:
k
Отсюда
kbn>kSb-e.
Так как число е может бт.тть выбрано сколь угодно малым, то мы всегда
можем сделать, чтобы
кЪп>Т.
Но ап~к1>п; следовательно,
что невозможно, ибо величина ап приближается к своему пределу, оставаясь
всегда меньше его. Таким образом, мы показали, что
Представив основное равенство
an = kbn
в виде
мы можем аналогично показать, что
Sb>k'Sa,
22
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСГСЛОВСКОГО
ИЛИ
Оба эти неравенства показывают то, что требовалось доказать:
Рис. 1.
У Архимеда ми можем проследить дальнейшую эволюцию метода
"Еидокса.
Во второй (чисто математической) части «Квадратуры параболы» Архи-
мод, совершенно так же как и Евдокс, пользуется последовательностью вели-
величин, приближающихся к предельной величине снизу — площадь параболы
постепенно «исчерпывается» вписываемыми и рассматриваемый сегмент тре-
треугольниками. Но уже в лтеханяческой части доказательства (первой) Архп-
мед заключает исследуемую площадь между двумя суммами трапеций,
из которых одна больше, а другая меньше ее. В трактате «О шаро и цилиндре»
Архимед показывает, что отпонгепие ука-
указанных двух сумм может быть сделано
сколь угодно близким к единице. В сле-
следующих за этим произведениях «О спира-
спиралях» и «О коноидах и сфероидах» доказа-
доказательство приобретает другой пид: Архимед
показывает, что разность рассматриваемых
двух сумм может быть сделана сколь
угодно малой. Так как имеппо эта форма
метода исчерпывания применяется и в
«Измерении круга», то мы получаем осно-
основание думать, что «Измерение круга» напи-
написано не лонжо диух последних упомяну-
упомянутых ароизввдвпий (в трактате «О спиралях» Архимед дает геометриче-
геометрическое построение прямой, длина которой равняется длине окружности),
и во всяком случае пе раньше двух книг «О шаре и цилиндре».
К Евдоксу же, или но псяком случае к его школе, следует отнести и соз-
создание совершенно новой отрасли геометрии, а именно теории кривых вто-
' рого порядка, пли, если пользоваться термином греческой математики,
конических сечений.
Причины, иызвапшие к жи:ши этот повый отдел математики, можно
видеть в следующем.
Одним из наиболее лажных вопросов геометрии V века было определе-
определение, или, лучше сказать, сравнение между собой различных площадей. Вся-
Всякий многоугольник можно разбить на треугольники, площадь каждого тре-
угольпика равна площади прямоугольника со сторонами, рапными основа-
основанию и половине высоты. Чтобы представить площадь многоугольника в виде
одной фигуры, надо уметь складывать друг с другом площади различных
прямоугольников, а для этого нужно уметь строить их па одном основании,
после чего суммирование площадей приводится к простому суммированию
пмсот. Операция «прииеденля площадей к одному основанию» называлась
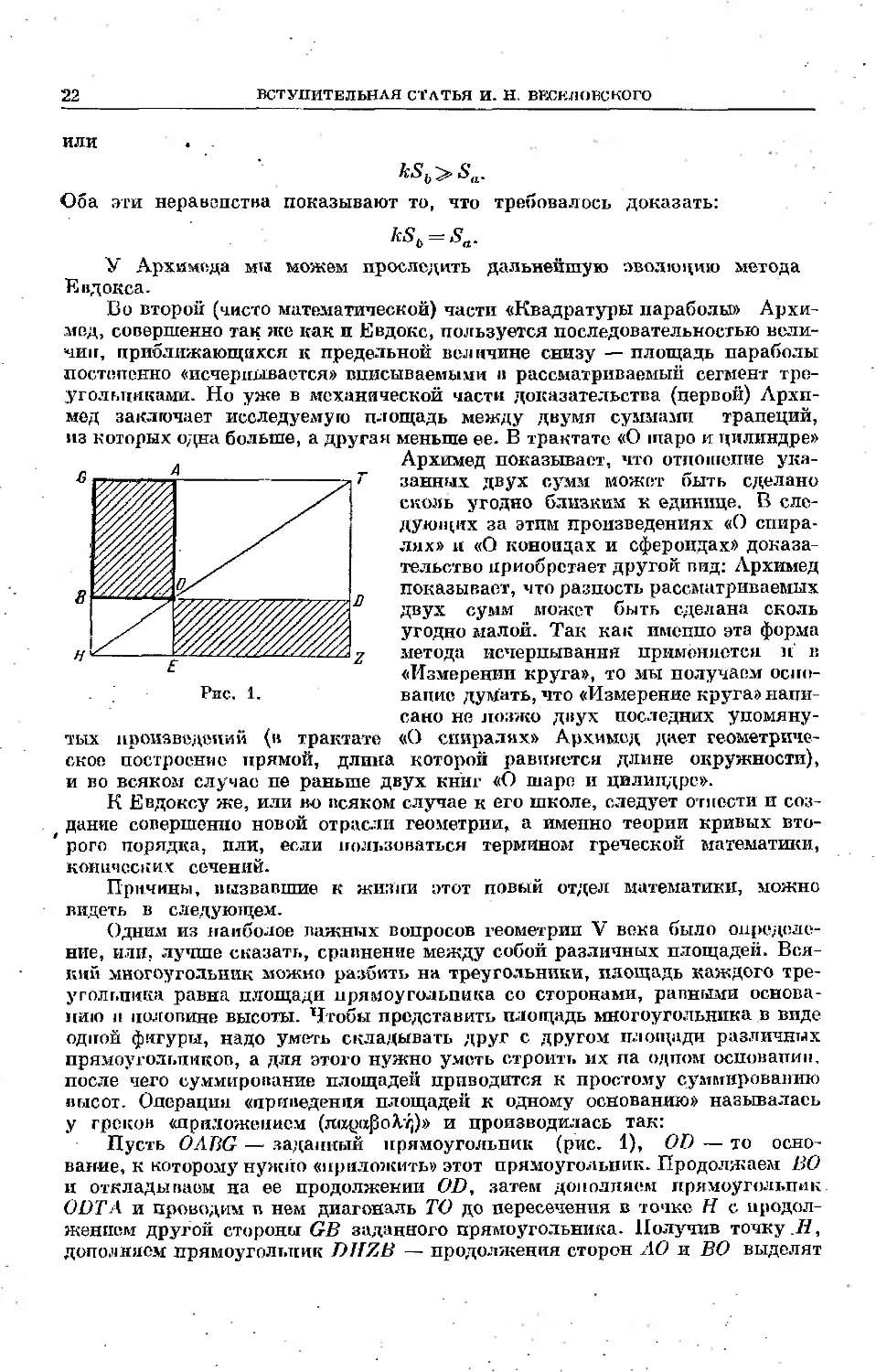
у грекмн «приложением (тохунфоА./;)» и производилась так:
Пусть OABG — заданный прямоугольник (рис. 1), OD — то осно-
основание, к которому нужно «приложить» этот прямоугольник. Продолжаем ВО
и откладынаом на ее продолжении OD, затем дополняем прямоугольник
ODTA и проводим v. нем диагональ ТО до пересечения с точке Н с продол-
продолжением другой стороны GB заданного прямоугольника. Получив точку.Л,
дополняем прямоугольник DJIZB — продолжения сторон АО и ВО выделят
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. П. ВЕСЕЛОВСКОГО 23
в ном прямоугольник ODEZ, который и будет искомым; он построен па осно-
иапии OD и имеют площадь, равную площади заданного прямоугольника
OABG. Алгебраически, нахождение второй стороны ОЕ, как нетрудно видеть,
сводится к нахождению четвертой пропорциональной для линий О А, ОВ и 01):
При ттомощи «яаоар"о>/г» любой многоугольник может быть прообразован
в прямоугольник. Дальнейший шаг на этом пути заключался в преобразова-
преобразовании полученного многоуголышка в квадрат. Эта операция выполнялась при
помощи нахождения третьой, или, как мы тенорь гово-
говорим, средней пропорциональной, равносильной реше-
решению уравнения
. xa — ab,
где а и Ь — стороны заданного прямоугольника, а
х — сторона равного ему квадрата. При помощи
упомянутых пропорциональных можно было построить
квадрат, площадь которого равна площади любого
многоугольника, так что оставалось лишь сравнивать
между собой различные квадраты. Для этого строился
ряд квадратов, площади которых относились бы как
числа натурального ряда. Если некоторый квадрат мы
пршшмаем за единицу (рис. 2), то квадрат, равный двум,
получался на диагонали {/2 этого квадрата. Чтобы
построить квадрат, равный трем, нужно найти гипотенузу
прямоугольного треугольника, катеты которого равняются стороне = 1 и диа-
диагонали = |/ 2 первого квадрата. Продолжая таким образом, можно получить
сколько угодно квадратов, образующих натуральный рид чисел. Существо-
Существование такой операции доказано для древних египтян, употреблявших два
локти в 20 и в 28 дюймон (чтобы удвоить данный кпадрат, или вообще данную
площадь, надо размеры его, измеренные в двадцатидюймовых локтях, пере-
перестроить и двадцатмвосьмпдюймовыс: отношение 28: 20=14 : 10=1,4^у 2);
ее знали вавилоняне, помещавшие в своих строительных справочниках
довольно точное значение у 2; ее применяли индусы первого тысячелетия
до н. а., которым приходилось, сохраняя форму жертвенника, увеличивать
«го ллощадь от 2 до 7 раз.
Когда эта теория была построена, встал вопрос о распространении ее
на многогранники и в первую очередь на параллелепипеды. Первым шагом
на этом пути было построение натурального ряда кубов и в первую очередь
построение куба, равного удвоенному дан irony кубу. Необходимость реше-
решения атой. задачи вызывалась еще тем, что в самом конце V века возникла
метательная артиллерия и для увеличешш дальности полета выбрасываемых
стрел и камней требовалось пропорциональное увеличение объема упругих
тяжей, приводивших в движение катапульту.
У/гсе Гиппократ Хиосский показал, что задача удвоения (или вообще
укеличгтгия в произвольное число раз) куба может быть лшдолнша при
помощи нахождения двух средних пропорциональных х, у между задан-
заданными величинами а м Ь, отношение -?- которых представляло то, в котором
следовало увеличить объем заданного куба:
и: х~х: у~у:Ь.
24
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И- Н. ВКСЕЛОВСКОГи
Рис. 3.
Эта задача могла быть решена при помощи пересечения каких-нибудь
двух из трех следующих кривых:
Перпме две представляют параболы с взаимно перпендикулярными
осями, а третья — равностороннюю гиперболу. Такова, конечно, точка
зрения современного нал математика, владеющего п полной мерс алгебраи-
алгебраическим знакоиоложением; для нас уравнение является гораздо более удоб-
удобным к употреблению, чем изображаемая им кривая: для греков же, по имев-
имевших такого символического аппарата, любивших конкретность и нагляд-
наглядность, наоборот, кривая липия
была более удобным орудием для
математических и сел едований.
Греки пользовались двумя
способами получения новы х кри-
кривых. Во-шфвых, кривая могла
быть образована движением
некоторой точки; первым при-
примером таких «геликоидальных»,
как их называли греки, кривых
была квадратриса софиста Гип-
пия Элидского (V век до п. э.)>
придуманная им, но всей види-
видимости, для деления угла на про
пзвольпое число частей. Во-вто-
Во-вторых, кривую можно было полу-
получить, рассекая какую-нибудь из-
известную кривую поверхность: это были так называемые «выгнутые» (коцтймп)
кривые. Мы внаем, что Квдокс решил задачу об удиоении куба именно при помо
щи таких ш\тйХа1 удаццш. Решение его до нас по дошло, но его брат и ученик
Мепехм решал задачу при помощи пересечения двух парабол или гиперболы
о параболой, и в «Конических сечетшях» Аполлонии (книга I, определение 4
и ел.) под именем каця.б'кт \Qa\iuai понимаются именно конические сечения.
Таким образом, именно Еидокс указал один из способов, которым могли
быть получены соответствующие кривые; они ншучались при помощи сече-
сечении различных конусов, образующие которых при вершине составляли пря-
прямой, тупой или острый угол.
Известный историк математики Цейтов очень убедительно рисует кар-
картину получения парабол м у2—2рх как «сечения прямоугольного конуса»;
под этим именем знает параболу Архимед; опо употреблялось вплоть до
Аполлония, который первый ввел современное привычное нам название.
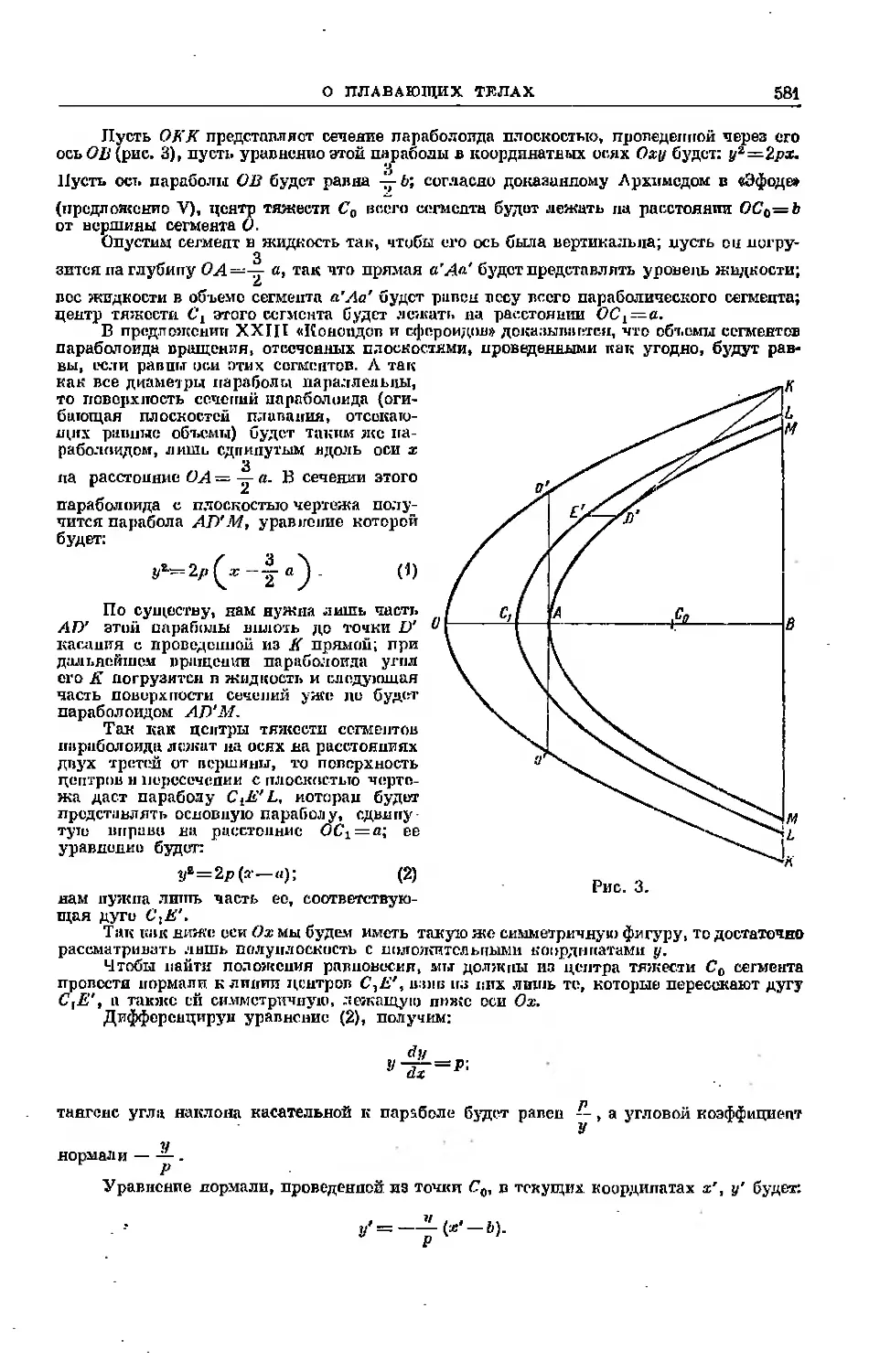
Возьмем конус OEF (рис. 3) с прямым углом при вершипе О, пересе-
пересечем его плоскостью, проходящей через точку А и перпендикулярной к обра-
образующей ()Е\ эта плоскость в сечении с поверхностью конуса дает параболу
Л/АР, ось симметрии которой будет прямая AKL — сечение проведенной
плоскости с другой, проведенной чорез ось конуса перпендикулярно к пер-
первой секущей плоскости. Следуя современной терминологии, будем назы-
называть абсциссами а; расстояния АК, AL, измеряемые но этой оси,
а перпендикулярные к ней прямые, вроде LM,— ордината м и у *).
*) Последнее слово представляет переделку латинского ordiuatim applicaluc, что » свою очередь
является переводом греческого хахсуилмах, ХЕха\цё\чл^— проведенные правильным, упорядоченным
образом; так назымалнсь прямые, недотеидйкулприые к оси параболы, проведенные до пересечении
с кривей, или вообще половины хорд, соответствующих какому-нибудь диаметру.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 25
Через какую-нибудь точку L оси параболы проводим плоскость, нер-
пепдикулярную к оси конуса; она в пересечении с конической поверхно-
поверхностью даст окружность CMD, и мы по известному слойстну окружности можем
написать:
у* = LM* = CL ¦?/).)
Но для гипотенуаы CL равнобедренного прямоугольного треугольника ACL
имеем ¦ ¦ ¦.
CL = ЛЬу'2]"
точно так же, если через иерипшу Л перпендикулярно к оси конуса про-
провести АЛ, то
LD - АВ-= АКУЪ.
где точка А* представляет пересечение оси AKL параболы с осью ОК конуса.
Таким образом, если положить АК~р, то получим
г/ - А /,|/2 - AKV 2 =- Чрх,
где x=AL — абсцисса точки М параболы.
Правильность этой реконструкции Цейтена подтверждается древней
терминологией: у Архимеда параметр р=АК параболы называется JJixQi
той a|ovog — прямой, проведенной до оси, т. е. до оси того конуса, сечение
которого образует нашу параболу.
Самоназвание «парабола»связано с операцией «приложения» (яаосфо?а|'):
площадь квадрата у2, будучи «приложена» к прямой 2р как к основанию,
дает высотой абсциссу х. Остальные две кривые связаны с так называемыми
«приложениями с недостатком или с избытком»; возможно, однако, что сна-
сначала были исследованы геометрические свойства тех крииых, которые полу-
получаются в сечениях тупоугольного и остроугольного конуса, а потом уже
соностанлень! с указанными типами «приложений».
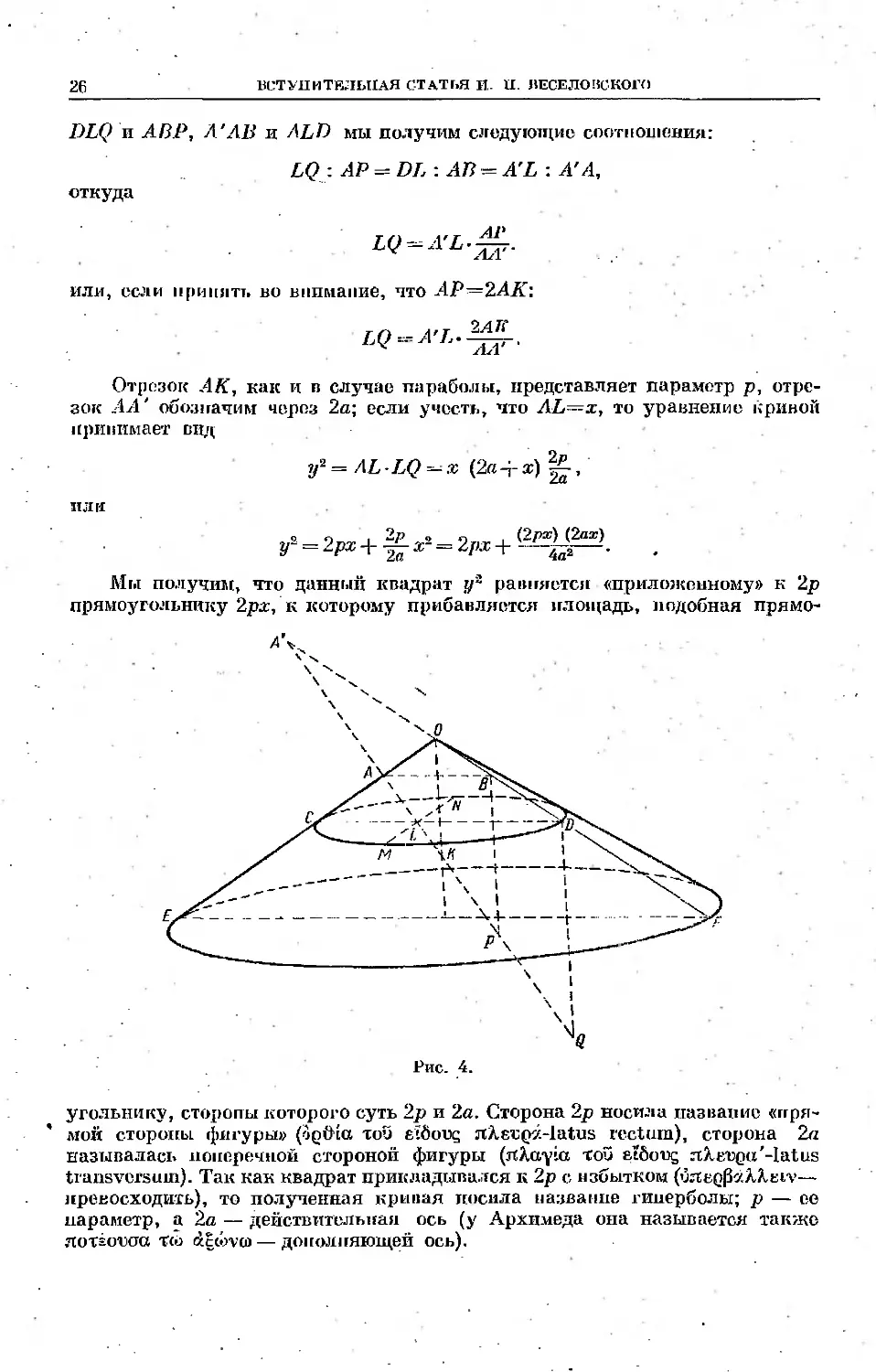
Пусть OEF (рис. 4) будет осевое сечение конуса с тупым углом при ж;р-
шине О, а прямая ОК — его ось. Через какую-нибудь точку А проведем
плоскость, перпендикулярную к образующей ОЕ; ата плоскость в сечении
с поверхностью конуса образует кривую AMIS'.
Продолжии другую образующую OF конуса до пересечения в точке А'
с прямой AQ — липшш пересечении проведенной секущей плоскости с осе-
осевым сечением OEF конуса; прямая AQ, очевидно, будет осью симметрии
нашей кривой. Возьмем на этой оси какую-нибудь точку L на расстоянии
AL — x от верщипы п попытаемся найти снизь между абсциссой х и соответ-
соответствующей ей ординатой y-LM нашей кривой. Через точку L перпендику-
перпендикулярно к оси конуса проведем плоскость, которая в сечении с поверхностью
конуса образует круг с диаметром CD. Тогда
Так как СА перпендикулярна к AQ, а CD перпендикулярна к DQ, про-
проведенной параллельно оси конуса, то все четыре точки С, A, D, Q будут
лежать на окружности, построенной на CQ кад па диаметре; тогда по свой-
свойству секущих и круге, проведенных через одну точку, будем иметь
. CL -
Если К — точка пересечения. AQ с осью конуса, прямая АВ парал-
параллельна CD, а ПР параллельна оси конуса, то из подобия треугольников
26
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. XI. НЕСЕЛОВСКОГО
DLQ и АВР, Л'ЛЬ* и ALD мы получим следующие соотношения:
LQ : АР = DL : АП = ,4'Z : Л'Л,
откуда
или, если принять во внимание, что АР=
,,т 2АТС
АР
'ЛЛ"
Отрозок АК, как и п случае параболы, представляет параметр р, отре-
отрезок АА' обозначим через 2а; если учесть, что AL=x, то уравнение кривой
принимает вид
или
Мм получим, что данный квадрат у'г равняется «прило;коыыому» к Чр
прямоугольнику 2рл,'к которому прибавляется площадь, подобная прямо-
Рис. 4.
угольнику, сторопи которого суть 2р и 2а. Сторона 2р ностеш название «яря-
мой стороны фш-уры» {ogOfa тоО eifioix; nXe^Qa-latus rectum), сторона 2я
ыазыпалась поперечной стороной фигуры (rtXa-yia той etfio^g nXeuQu'-Iatus
transversum). Так как квадрат прикдадыпцлея к 2р с избытком (иякфякХыу—
превосходить), то полученная криная тгосила название гиперболы; р — се
параметр, а 2а — действительная ось (у Архимеда она называется также
яотаояхта № accovo) — дополняющей ось).
ВСТУПИТЕЛЬНАЯ (УГЛТ1.Я И. II. ИКСК.П0КСКОГО
27
Уравнение гиперболы Архимед употребляет в виде
У2 _ р
ж Bй-}"ж) а '
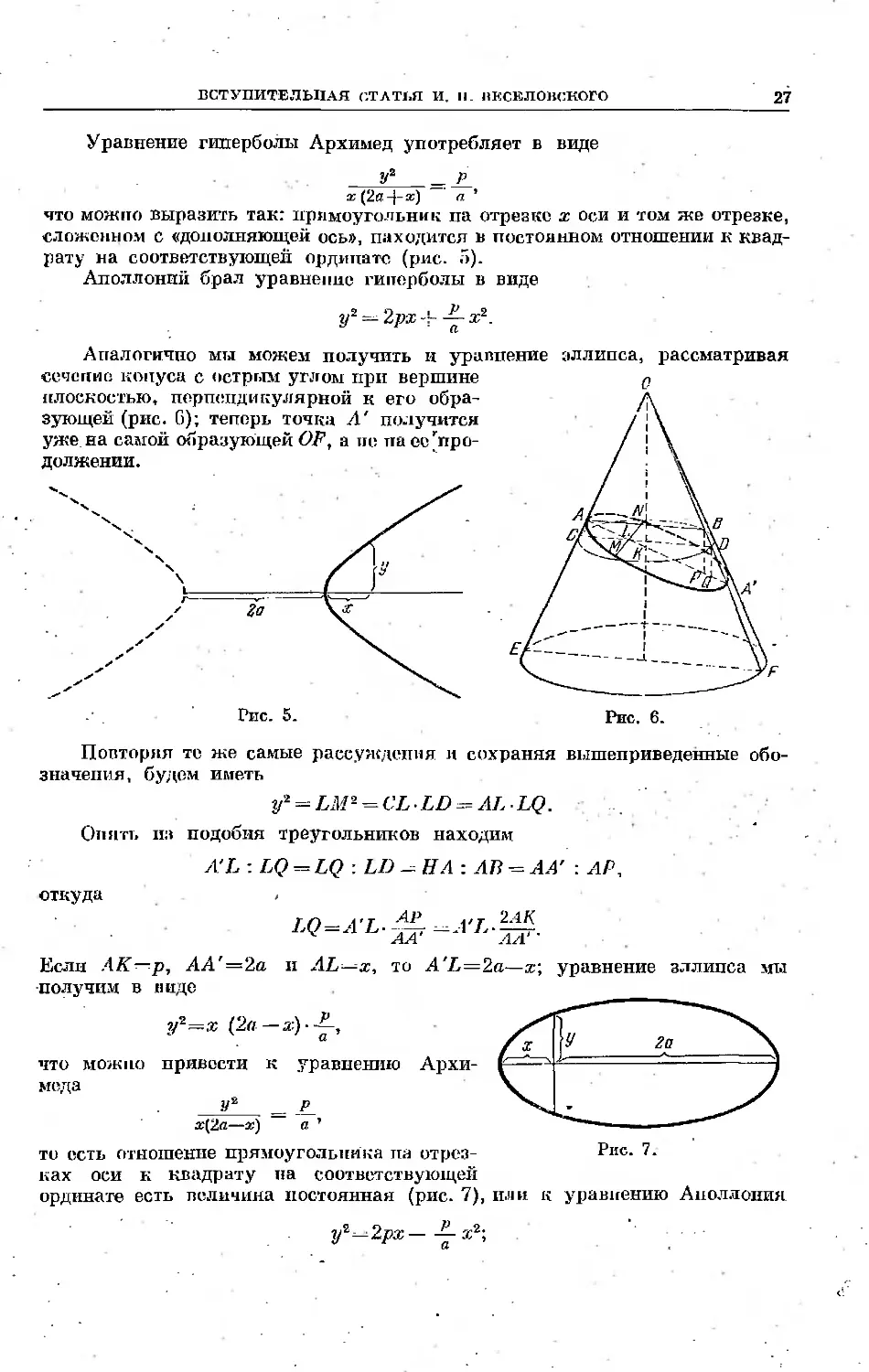
что можно выразить так: прямоугольник па отрезке х оси и том же отрезке,
сложенном с «дополняющей ось», находится в постоянном отношении к квад-
квадрату на соответствующей ординате (рис. я).
Аполлонии брал уравнение гиперболы в виде
Аналогично мы можем получить и уравнение эллипса, рассматривая
сечепио конуса с острим углом при вершине
плоскостью, перпендикулярной к его обра-
образующей (рис. G); теперь точка А' получится
уже на самой образующей OF, а пи па ее'про-
ее'продолжении.
А'
Рис. 5.
Рис. 6.
Повторил те же самые рассуждения и сохраняя вышеприведенные обо-
обозначения, будем иметь
Опять пи подобия треугольников находим
Л'Ь : LQ = LQ : LD _= НА : ЛВ = АА' : АР,
откуда
АР
2ЛК
Если АК—р, АА'=2а и AL^x, то A'L=2a—х; уравнение эллипса мта
получим в виде
что можно привести к уравнению Архи-
Архимода
у2 = р_
х[2а—х) а '
Рис- 7-
то исть отношение прямоугольника па отрез-
ках оси к квадрату па соответствующей
ординате есть величина постоянная (рис. 7), или к уравнению Аполлония
28 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. КНСБЛОВСКОГО
так как теперь при «приложении» у2 к прямой 2р «недостает* (ГлМты) пло-
площади, подобной прямоугольнику со сторонами 2а, 2р, то полученная кривая
носит название «эллипса». Прямая 2а является большой осью этого эллипса.
Если положить х—а, то получится выражение для малой оси алпипса. Если
через Ъ обозначить ее половину, то мы будем иметь
Ьй=2ра— ра=ра,
откуда получается известное выражение для параметра эллипса:
Классическими книгами но теории конических сечений во времен;!
Архимеда были «Начала теории конических сечений», составленные Евкли-
Евклидом, а также другая книга, принадлежащая геометру Аристею. На ту или
другую из атих книг ссылается Архимед везде, где оп без доказательства
приводит теоремы, полученные своими предшественниками. Обе :>тм книги
до нас но дошли, но о содержавшемся в них материале мы можем составить
себе представление, читая перпые четыре книги «Конических сечении Апол-
дошш», и которых он резюмирует труды предшествующих ему авторов.
Во ксякон случае Архимеду были известны следующие свойства копи-
ческих сечений:
1°. Середины хорд, параллельных какому-нибудь направлению, лежат
на одной прямой — диаметре, сопряженном этому направлению. Диаметр
и общем случае ire будет перпендикулярным к сопряженным с ним хордам,
но в косоугольных координатах с началом в точке пересечения диаметра
с кривой и осями, направленными соответственно по диаметру и касатель-
касательной к кривой л точке — начале координат, уравнение кривой будет иметь,
тот же вид, только соответствующий этому направлению параметр р будет
иметь другую неличину.
Если учесть, что Архимед знал, что касательная к коническому сече-
сечению, проведенная в конце диаметра, будет параллельна хордам, сопряжен-
сопряженным с этим диаметром, то можно сказать, что Архимеду были изнестны урав-
уравнения всех трех кривых второго порядка, отнесенных к косоугольным осям
координат, а именно диаметру я касательной в его кершине.
2°. Все диаметры параболы параллельны. Но Архимед рассматривает
гиперболу как состоящую только из одной ветви; центр гиперболы и свой-
свойства сопряженных диаметров были открыты только Аполлонием.
3°. Свойства касательных к коническим сечениям, а именно, что каса-
касательная к параболе пересекает ось в точке, расстояние которой от перпшны
иапабшш равно абсциссе точки касания и что для эллипса ато расстояние
будет больше, а для гиперболы — меньше соответствующей абсциссы. Затем
он знал, что поднормаль к параболе имеет постоилмую величину.
4°. Если из какой-нибудь точки провести касательные к любому кони-
коническому сечению, а из другой точки внутри или вне кривой провести парал-
параллельные зтим касательным две секущие, то произведении отрезков этих секу-
секущих относятся, как квадраты параллельных им касательных.
i)°- Существование асимптот у гиперболы, а также, что площадь прямо-
прямоугольника на прямых, проведенных из какой-нибудь точки гиперболы парал-
параллельно ее асимптотам до пересечения с последними, является величиной
постоянной (наше уравнение ху—const). Точно так же Архимед знал, что
отрезки касательной к гиперболе между точкой касагшя и асимптотами равны,
как можно видеть из найденного Евтокием доказательства Архимеда одной
леммы из второй книги «О шаре и цилиндре».
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 29
Новым период деятельности Архимеда начался, вероятно, после 240 г.
до п. э., когда с наступлением мира Архимед получил возможность побынать
я Александрии и запязать дружеские отношения с Эратосфепом и Конопом
(Архимеду в это время било уже около пятидесяти лет). За это время (при-
(приблизительно тридцатые годы III века до н. э.) Архимед создал ряд произве-
произведений, доставивших ему бессмертную славу. Первым из :mix произведений
является «Квадратура параболы», написанная вскоре после смерти Конона
м открывающая ряд «посланий» Архимеда к ученику и другу Конона мате-
математику Досифсю, с которым Архимед, как видно из вступлений к посланиям,
'поддерживал переписку. Эта «досифееиская» группа сочинений Архимеда
состоит из «Квадратуры параболы», первом и второй книг сочинения «О шаре
и цилиндре», составлявших первоначально два совершенно самостоятельных
произведения *), затем книги «О спиралях» и, наконец, сочиголшя «О конои-
коноидах п сфероидах». Порядок появления этих произведений легко устаналли-
иается на основе тех сведений, которые дают нам введения к этим посланиям.
•Самым ранним произведениелт в этой группе является «Квадратура пара-
оолы», представляющая, как можно пидсть иэ вступления, первое послание
к Досифею, написанное после получения известия о смерти Конона. Б ,чтом
послании Архимед использует открытый им механический метод определе-
определения площадей и объемов геометрических фигур и тел, разнообразные при-
приложения которого он описывает позднее в своем «Эфодо». Из вступления
к «Эфоду» видно, что нахождение площади параболического сегмента было
лервой задачей, решенной Архимедом при помощи механического .метода.
За «Квадратурой параболы» идет первая книга сочинения «О шаре и цилин-
цилиндре»; во вступлении к этой книге Архимед упоминает о посланном уже ранее
сочинении «Квадратура параболы». Задачи, исследуемые во второй книге
сочинепия «О шаре и цилиндре», как видно иэ предисловия, были поста-
поставлены Архимедом еще до смерти Конона, равно как и те, которые были разо-
разобраны в перкой книге; в этом сочинении «О шаре и цилиндре» Архимед обе-
обещает «как можно скорее» прислать предложения, касающиеся спиралей
л коноидов. Как мм знаем из «Эфода», теоремы, касающиеся объема шара
л его частей, а также коноидов и сфероидов, были первоначально найдены
.механическим методом; однако в отличие от того, что было сделано в «Квад-
«Квадратуре параболы», Архимед теперь дает только окончательный строго мате-
дгатический пывод установленных теорем. После сочинения «О шаре и цилин-
цилиндре» была написана работа «О спиралях», тема которой бшш дана Архимеду
¦еще Кононом. Во вступлении Архимед говорит, что после смерти Конона
уже «прошло много лет», однако тот факт, что Архимед работал над темой,
пачатой им еще до смерти Конона, не позволяет понимать это «много» иначе
как 5—10 лет. В том же самом предисловии Архимед говорит о «Коноидах
и сфероидах» как о еще не посланной книге. Содержащиеся в этой работе
предложения доставили Архимеду при доказательстве много труда, так что
эта книга, которая по первоначальному плану должна была идти перед кни-
книгой «О спиралях», оказалась самым последним произведением рассматривае-
рассматриваемой группы: математические доказательства теорем, содержащихся и сочи
метши «О коноидах и сфероидах» Архимед нашел только после того, как им
уже была решена поставленная задача относительно спиралей.
•) Предложении иериий книги llaira цитирует просто кап «О шаре и цилишше», го: называя
книгу «первой».
'¦V
30 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
Бое предложения, доказываемые в посланиях к Досифею, представляют-
собой целостную группу. Как таковую их рассматрмпзл и сам Архимед (см.
вступление к книге «О спиралях»), причем объединяющим звеном для Архи-
Архимеда было то, что соответствующие задачи были поставлены им еще до смерти
Конотга и, по псей вероятности, обсуждались в переписке с последним,
а может быть, и той или другом мере и были поставлены Кононом Архимеду.
Вот ;>то единство всей группы и не позволяет растягивать на слитком боль-
большой промежуток времени работу, прошводеипую Архимедом при решении
этих задач.
В отношении следующих произведений Архимеда мы находимся к не-
несколько более трудном положении, так как далеко не все из них дают доста-
достаточно материала, позволяющего нам совершенно точно определить их хро-
хронологическую последовательность. Среди этих произведений можно выде-
выделить «механическую» группу, состоящую из трех произведений: двух книг
«О равновесии плоских фигур», послания к Эратосфену о механических тео-
теоремах (так называемый «Эфод») и, наконец, двух книг «О плавающих телах».
Что касается произведения «Равновесие плоских фигур», то, следуя за
Гейбергом, большинство исследователей (Хис, у нас С. Я. Лурье) считают
его самым ранним из дошедших до пас сочинений Архимеда и разбивают его
на два самостоятельных произведении: первую книгу, содержащую общие
теоремы о нахождении центра тяжести, и вторую книгу, касающуюся нахо-
нахождения центра тяжести сегмента параболы, причем эта последняя поме-
помещается после «Квадратуры параболы». Вряд ли можпо согласиться с таким
разделением на две части рассматриасмого произведения. Во-первых, «Рав-
иопссис плоских фигур» но структуре очень похоже на сочинение «О плаваю-
плавающих телах», которое тоже разбито па две книги, первая из них посвящена
общим теоремам, а пторая — одному частному вопросу, а имепно условиям
равновесия плавающего сегмента параболоида. Во-вторых, первую книгу
«Равновесия» трудно рассматривать как самостоя тельное произведение, спе-
специально посвященное вопросу о нахождении центра тяжести: в ней нет даже
определения понятия о центре тяжести, не рассматринается положение центра
тяжести круга, неправильного четырехугольника и вообще многоугольника;
по сущестиу, даются лишь положения центров тяжести тех фигур (прямо-
(прямоугольник, треугольник, трапеция), которые нужны для доказательства теорем
второй книги; затем основную теорему — о равновесии рычага — Архимед
доказывает три рааа: для соизмеримых и несоизмеримых прямоугольников
в первой книге и для криволинейных площадей, могущих быть приведен-
приведенными к прямоугольникам (киндрнруемых) в предложении I второй книги.
Наконец, формально-математический характер самого произведения
не позволяет считать его первым наброском теории центра тяжести; есте-
естественнее всего считать основной целью этого произведения определение
пептра тяжести сегмента параболы, а первую книгу рассматривать как
своего рода введение. Само собой разумеется, что если рассматривать обе
книги как единое произведение, то они должны быть написаны после «Кнад-
ратуры параболы». По можно думать, что они паписаны и после «Коноидов
и сфероидов»: действительно, и последнем сочинении Архимед сформулировал
новые определения подобия кривых лторого порядка и как раз этими опре-
определениями он пользуется при доказательстве теорем второй книги (подроб-
(подробности см. в комментарии к рассматриваемому сочинению); кроме того, при
доказательстве предложения V второй книги «Равновесия плоских фигур»
Архимед пользуется предложением XXXI «Коноидов».
Точно так же после «Коноидов» наимсагг и «Эфод». Это вытекает из сле-
следующих соображений:
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II.' ВЕСЕЛОВСКОГО ' 31
1°. Во вступлении к «Эфоду» Архимед, говоря о посылаемых в этом
сочинении новых теоремах, указывает, что они отличаются от найденных
мм ранее теорем, в которых объемы коноидов, сфероидов и их частей срав-
сравнивались с объемами конусов и цилиндров.
2е. Последней леммой 11 «Эфода» является предложение, доказанное
в сочинении «О коноидах».
3°. В первом предложении «Эфода» содержится ссылка на сочинение
«О равновесии» и ряд лемм текстуально повторяют тгредложения первой
клити «Равновесия плоских фигур»; таким образом, получается, что «Эфод»
написан после «Равновесия плоских фигур».
Трактат «О плавающих телах» написан после «Коноидов», в тексте
которых находятся предложения XX Ш и XXIV, являющиеся основными
при выводе условий равновесия плавающего сегмента параболоид*1- Далее,
во второй книге «О плавающих телах» цитируется сочинение «О равнове-
равновесии», в связи с определением центра тяжести сегмента параболоида; это.
позволяет думать, что «О равновесии плоских фигур» — первая часть более
общего сочинения «О равновесии» — была уже паписаиа. Затем механи-
механический способ определения центра тяжести сегмента параболоида дается
в предложении V «Эфода»; таким образом, вполне естественно предполо-
предположить, что трактат «О плавающих телах» написан после «Эфода». То обстоя-
обстоятельство, что вторая книга трактата «О плавающих телах» пмеет вид пезакон-
ченпого сочинения, позволяет думать, что мы имеем дело с самым послед-
последним произведением Архимеда.
Два оставшихся произведения Архимеда «Измерение круга» и «Псам-
«Псаммит» своим характером резко выделяются из ряда остальных произведений
Архимеда; в них па первое место выступает вычислительная сторона мате-
математики. Достоверно лишь то, что «Псаммит» написан после «Намерения
круга», поскольку в последнем сочинении имеется ссылка на первое. Что»
касается «Измерения круга», то нужно отметить следующее:
1°. Одна из основных том «Измерения круга» — определение длины
окружности — тесно связана с предложением XVШ книги «О спиралях»;
мы уже говорили выше, что форма, в которой применяют метод Евдокса,
является одинаковой в обеих рассматриваемых книгах.
2е. Во втором предложении «Эфода» упоминается о том, что площадь
круга равна площади треугольника, основание которого равно окружности,
а высота — радиусу (первое предложение «Измерения круга»); отсюда видно,
что Архимед во время написании «Эфода» во всяком случае уже работал над
этим вопросом.
3°. При доказательстве предложения XIII «Эфода» Архимед стоял на
пороге открытия центра тяжести полукруга, который он обязательно полу-
получил бы, если бы знал числовую величину площади полукруга. То обстоя-
обстоятельство, что в предложении XIV он избрал обходный путь для доказатель-
доказательства теоремы об отношении площади полукруга к квадрату па диаметре при
помощи введения вспомогательной параболы, позволяет думать, что число-
числовая величина отношения окружности к диаметру была еще ему неизвестна,,
и :зто свидетельствует о том, что «Эфод» был написан до «Измерения круга».
Так как «Псаммит» посвящен умершему в 216 г. Гелону, сыну и сопра-
соправителю царя Гисрона, то он должен был быть написанным до этого года.
Общий хронологический порядок сочинений примерно таков:
V'. Квадратура параболы.
2е1. О шаре и цилиндре.
3°. О спиралях.
4°. О коноидах и сфероидах.
32 НОТУНИТЕЛЬНАН СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
5°. О равновесии плоских фигур.
6°. Эфод.
7°. О пл акающих телах.
8'- Намерение круга.
9°. Псаммит *).
Первые четыре произведения относятся к периоду, когда Архимед
переходил от механики к математике, стараясь добиться наибольшей воз-
возможной строгости доказательств, даже задерживая ради этой доли опубли-
опубликование уже полученных результатов, как это имело место с «Коноидами».
Следующие три произведения относятся к hoboaij- периоду деятельности
Архимеда, когда он выступил н роли создателя математической физики,
прилагая строгие математические теории к объяснению физических явле-
явлений. Эту сторону деятельности Архимода тем более важно отметить, что,
по мнению Плутарха, Архимед был ученым, готовым забыть ради матема
тики и практическую деятельность, и материальный мир, и прозу окру-
окружающей жизни. На самом деле вышедший из технической среды Архимед
снова в нее вернулся, причем он сделал ото не только под нлиииисм грозив-
грозившей родному городу опасности.
Таким образом, в маучиой деятельности Архимеда мы можем различить
следующие периоды:
1°. Период инженерной деятельности — введение понятия о центре
тяжести и его определение в случае простейших фигур и 'тел.
2'. Период посланий к Досифою — разработка методов определения
площадей и объемов математических фигур и тел.
3°'. Период запястий математической физикой — установление матема-
математической теории рычага, центров тяжести и равновесия плавающих тел.
4°. К последнему периоду относятся арифметико-астрономические
работы, которыми в дальнейшем нам еще придется заняться более детально;
irmca же перейдем к описанию других сочинений Архимеда, дошедших до
пас и отрывках или в отдельных цитатах позднейших писателей.
ТТа перпом месте мы должны постанить опубликованную и 1773 г. изве-
известным немецкий писателем Лессиигом «Задачу о бы пах», принадлежность
которой Архимеду некоторыми исследователями оспаривается. Если она
действительно принадлежит Архимеду (таково мнение и автора этих строк),
то ее можно отнести к четвертому периоду деятельности Архимеда.
Затем по упоминаниям в «Математическом собрании» Паппа нам изве-
известно сочинение «О полуправильных многогранниках». Вероятно, в некото-
некоторой спязи с этим произведением находится «Стомахий», от которого до пас
дошло дна отрывка: один в арабском переводе, а другой, открытый Гейбер-
гом в Константинопольском палимпсесте имеете с «Эфодом».
* Наконец, к «Метрике* Герона сохранилось несколько отрывков сочи-
сочинений Архимода, посвященных измерению площадей и объемов правильных
и неправильных тел, которые тоже можно отнести к последнему периоду
деятельности Архимеда. К их числу принадлежат сочинения «О призмах
и цилиндрах» и «О йен ран ильных поверхностях и телах».
К разряду астрономических работ Архимеда относятся «Катоптрика»,
«О величине года» и, наконец, «Об изготовлении небесной сферы».
Кроме того, в том же «Псаммите» Архимед упоминает еще об арифме-
арифметическом сочинении «ПосланникЗевксиппуалее^ао/сйг—«Оначалах», в кото-
котором излагались основы придуманной Архимедом системы счислении.
*) Два последних проивиедспип могли быть пшшеаны и ранге {после 3" и 4°).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ЕЕСЕЛОВСКОГО 33
Арабские источники относят к Архимеду еще следующие произведения:
1) О круге, 2) О семиугольнике в круги, 3) О взаимно касающихся кругах,
4) О параллельных прямых, 5) О треугольниках, 6) О свойствах прямоуголь-
прямоугольных треугольников, 7) Данные.
Из этих книг пам и какой-то степени известно содержание «Книги о семи-
семиугольнике» но публикации немецкого исследователя Карла Шоя в 1927 г.
[22J. Рассмотрение этой книги показывает, что она в целом не при надлежит
Архимеду, но содержит ряд извлечений из сочинений Архимеда в перера-
переработанном виде. Оригинал зтой книги был написан большим знатоком Архи-
Архимеда, харранским астрономом и математиком Сабитом ибн Курра (он же
написал «Книгу лемм», впервые изданную в 1E59 г. Фостером в латинском
переводе); возможно, что материал последней в какой-то мери заимствован
из сочинении «О круге», доказательств из которого приводятся аль-Бируни
в «Книге нахождения хорд в круге»*).
Нам остается теперь дать общую характеристику математических дости-
достижений Архимеда. Говорят, "что Архимед был гений, далеко опередивший свое
время. Конечно, гениальность Архимеда оспаривать не приходится, но
пуяшо еще подчеркнуть, что вся математическая деятельность Архимеда
представляет нелосредстнеппоц продолжение и развитие тех идей, которые
были заложены его предшественниками. Основная идея всей математической
деятельности Архимеда второго периода заключалась в определении пло-
площадей и объемов различных тел и фигур. Определение площадей много-
многоугольников удалось свести к определению площадей квадратов: оставалась
лишь площадь круга, которую сквадрировать не сумели. В области стерео-
стереометрии еще пифагорейцами была поставлена задача об объемах параллеле-
параллелепипедов и призм; сведение их к кубам повлекло за собой постановку делий-
делийской задачи. Исследования Евдокса показали, что определение объемов
пирамид, а следовательно и многогранников вообще, может быть сведено
к кубатурам, а нахождение объема конуса — к объему цилиндра, во времена
Евклида еще ничего пи бшю известно ни об объеме, пи о поверхности шара.
Архимед показал, что определение поверхностей конуса, цилиндра **) и шара
может быть сведено к нахождению площади круга, что определение объе-
объемов шара и его частей, а также объемов эллипсоида, гиперболоида и пара-
параболоида вращения, тоже сводится к определению объема конуса, а следо-
следовательно в конечном счете к определению объема цилиндра. Таким образом,
элементарными фигурами для Архимеда оказались квадрат и круг и куб
и цилиндр. Дальнейшей задачей исследования стало выражение площади
круга в виде некоторого прямоугольника, для чего понадобилось опреде-
определить длину окружности круга. Соответствующая задача была поставлена
и решена Архимедом в трактате «О спиралях» (предложение XVIII, дающее
построение прямой, равной длине данной окружности) и в «Изме-
«Измерении круга», где та же задача решалась вычисление м. Для цилин-
цилиндров соответствующая задача, по всей вероятности, была разрешена Архи-
Архимедом в не доптодгпем до нас сочинении «О призмах и цилиндрах». Таким
образом, были заложены основы измерения поверхностей и об-ьемол; в не
дошедшем до нас сочинении «О неправильных поверхностях и телах» (упо-
минитом в «Метрике» Геропа) Архимед дал практические способы и для
самого общего случая. • ¦ ¦ • ¦•
*) Перевод отрывка ив Блруии, а также «Книги о кругах», выполненный Б. А. Розеифольдом
помещен в этом излаяли.
*•) Обратите внимание на своеобразную формулировку в первой книги «О шаре и цилиндре»
предложений, в которых Архимед дает боковые щшерхиости цилиндра и конуса.
3 Архимед
34
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ЛЕСЕЛОВОКОГО
Нельзя сказать, что математические исследования п духе Архимеда
полностью оборвались с его смертью, исследований неизвестного автора
о сферических спиралях (Пали, книга IV, 35) определенно находится л круге
идей Архимеда. Ра иным образом доказанная Архимедом теорема, что из
всех шаровых сегментов с одинаковой выпуклой поверхностью наибольшим
является полушарие, нашла свое продолжение в аналогичной задаче дли
полукруга (Папп, книга V, 11—18) и, наконец, и исследованиях Зенодора
об изолеримстрических фигурах и телах.
Только в области математической физики Архимед стоит совершенно
одиноко: ни до пего, ни| после идея возможности представить математи-
чески процессы щшроды не приходила в голову
ни одному греческому ученому; это сделали вави-
вавилонские астрономы, приблизительно в то же вре-
время, что и Архимед.
Новым в исследованиях Архимеда был также
своеобразный метод, применявшийся им для ис-
следонания и предварительного решения задач,
а именно метод механического интегрирования,
изложенный им п «Квадратуре параболы» и в
«Эфоде».
Для того чтобы яснее показать в современ-
современном обозначении основную идею механического
метода Архимеда, применим его к решению сле-
следующей простой задачи.
Пусть требуется найти площадь, заключен-
заключенную между осью абсцисс, дугой параболы, за-
заданной уравнением
и ординатой ее, соответствующей абсциссе ОА=1
(рис. 8).
Представим себе раипоплечий рычаг .AOG'
Рис. 8. длины 21 с точкой опоры в О; па одной из его
половин расположим илтересующую нас площадь
ОАВ п разобьем ее на ряд весьма тонких полосок ширины Ах. Пусть KL
будет одна из этих полосок, соответствующая абсциссе ОК=х\ тогда
ордината y~KL будет ах2 и вся площадь полоски
&S = ax*.Ax.
Если мы сдвинем ее на конец рычага А, то момент отой полоски относи-
относительно точки О будет
I ¦ AS = I ¦ ах2 Ах.
Постараемся теперь уравновесить этот момент при помощи подвешива-
подвешивания полоски MN-Ах к левой стороне рычага па таком же расстоянии ОМ=х
от точки О. Величину соответствующей ординаты MN определим, сравни-
сравнивая моменты относительно О обеих полосок. Таким образом, будем иметь
х - AfN ¦Az =
откуда
alx.
ВСТУПИТКЛЬНЛП СТАТЬЯ IT. Н. ВЕСЕЛОЕСКОГО 35
Поступая так с каждой полоской, мы получим на левом плече ричага
ряд полосок, непрерывно распределенных по длине GO. Так как ординаты
полосок па леном плече рычага будут пропорциональны расстояниям х,
то концы их расположатся по прямой линии ONT; величина последней
ординаты GT будет al2.
После того как распределение полосок по левому плечу OG рычага будет
закончено, мы получим, что вся интересующая нас площадь ОАВ, сосре-
сосредоточенная на конце А, будет уравновешена треугольником ОСТ, прикреп-
прикрепленным к стороне OG. Площадь этого треугольника равна
расстояние от вершины О его центра тяжести будет
Следовательно, сравнивая момепт этого треугольника с моментом от во
сительпо О искомой площади S, сосредоточенной в А, мы будем иметь
2 1
откуда находим величину S:
Но соответствующая абсциссе ОА=1 ордината будет аР=АВ; таким
образом:
то есть искомая площадь равна одной трети площади прямоугольника,
построенного на абсциссе О А и конечной ординате АВ.
Мы видим, что успех вывода получается в результате понижения сте-
степени рассматриваемой кривой — пахождепие площади, ограниченной
криной 2-й стенспи и двумя прямолинейными отрезками, сводится к опре-
определению центра тяжести площади, ограниченной кривой первой
степени, то есть прямой.
Этот механический метод, конечно, являлся индивидуальным достоя-
достоянием Архимеда, несомненно пришедшего к нему в результате своих предше-
предшествующих занятии в области механики.
В этой связи уместно остановиться на вопросе об отношении Архимеда
к двум своим великим иредшестисниикам Демокриту и Евдоксу. Их обоих
Архимед упоминает в своих сочинениях; во введении к «Эфоду» Архимед
говорит о Демокрите как о первом авторе, нашедшем теорему об объеме
пирамиды и конуса, а в первой книге «О шаре и цилиндре» оп, гопоря о той
же самой теореме, упоминает только Евдокса. На основании этих фактов
проф. С. Я. Лурье выставил гипотезу о том, что после сочинения первой
книги «О шаре и цилиндре» Архимед «впервые познакомился с работами
Демокрита», на которые ои «несомненно с жадностью набросился», оказав-
оказавшись «у истоков того атомистического интегрирования, которое ему с тру-
трудом и по частям приходилось реставрировать из отдельных намеков и прие-
приемов в трудах по механике, написанных его предшественниками», и в кото-
которых он нашел «как раз то, что он искал и чего не хватало ему в математике».
(С. Я. Лурье, «Архимед», стр. 138—139).
36 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВС1ЮГО
С- Я. Лурье можно сделать следующие два возражения:
Во-первых, он забыиает, что своеобразный механический способ инте-
интегрирования был в полной мере использован Архимедом уже при написании
«Квадратуры параболы» и при доказательстве предложений первой книги
сочинения «О шаре и цилиндре», когда, как признает сам С. Я. Лурье,
Архимед «не знал еще трудов Демокрита».
Во-пторых, можно заключить, что Архимед был знаком с атомистиче-
атомистической математикой даже при написании перкой книги «О шаре и цилиндре».
Во втором предложении первой книги «О шаре и цилиндре» Архимед
доказывает, что д.;1я двух данных неравных величии можно всегда найти две
такие неравные прямые, чтобы отношение большей прямой к меньшей было
меньше отношения большей величины к меньшей. Даваемое Архимедом
доказательство носит очень искусственный характер: если две заданные
величины суть А и В (А>В), то искомое отношение мы просто получили
бы, взяв отношение
f . Л—В\ ' . f ... . А—В\
( Л J- у.В пли Л:[^В-\ — j .
Однако доказательство Архимеда, избегающее деления разности А~В
становится вполне целесообразным, если он учитывал возможность, что две
бесконечно близкие друг к другу величины А и В разнятся па одно неде-
неделимое.
При доказательстве предложения IX этой книги Архимеду нужно пока-
8ать, что вылуклая поверхность конуса между двумя образующими будет
больше площади треугольника, заключенного между теми же образующими.
Для этого он опирается на положение, что в трехгранной пирамиде одна
боковая грань всегда будет меньше суммы двух других граней. Соответ-
Соответствующее положение может быть очень легко усмотрено из следующего
рассуждения: так как одна сторона треугольника всегда меньше суммы двух
других, то же самое будет иметь место для каждого из тех треугольников,
на которые можно будет разбить пирамиду плоскостями, параллельными
основанию. Таким образом, или Архимед совершенно не думал о доказатель-
доказательстве вспомогательной теоремы, считая ее очевидпой, или же он употребил
изложенное доказательство по той простой причине, что другого доказатель-
доказательства пет и не может быть, так как указанная вспомогательная теорема
в общем случае является неверной (см. комментарий к этому
месту, стр. 45 J — 453); изложенного же доказательства Архимед не хотел поме-
помещать, не считая его (и совершенно правильно) вполне строгим ввиду его
атомистичности *).
Таким образом, то, что Архимед умолчал о Демокрите к книге «О шаре
и цилиндре» и упомянул о нем в «Эфоде», проще всего объясняется тем, что,
давая описание предварительного метода получепия решения,
Архимед счел возможным упомянуть и о Демокрите; что же касается стро-
строгих математических доказательств, то для Архимеда образцом был не Демо-
Демокрит, по Ендокс.
Но и но отношению к Евдоксу Архимед сохранил свою индивидуальт
ность. В то время как в чистом методе Евдокса к предельному значению
приближались только с одной стороны, «исчерпывая» определяемую вели-
величину, Архимед при доказательстве большинства теорем, связанных с опре-
определением площади фигуры, подлежащую определению величину заключает
•) Нужно, впрочем, отмстить, что в разобранном Архимедом частном, случае теорема будет впол-
вполне правильной.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВИСКЛОВСКОГО
.между дпумя фигурами — вписаппой и описанной,— разность площадей
которых может быть сделана меньше любой наперед заданной величины;
затем оп определяет величину, которая заключается между площадями
вписанной и описанной фигур, и доказывает, что эта величина и предста-
представляет определяемую площадь. По существу, он делает то же, что и мы при
введении понятия об интеграле. Таким образом, Архимедом были вычислены
интегралы, равносильные нашим , sin x dx при определении поверхности
шара и \ x2dxn \ (ax"-\-hx)dx при определении поверхности, описанной спи-
спиральной линией, и объема сегментов параболоида, гиперболоида и эллипсоида
вращения.
Можно, кроме «предвосхищения» интегрального исчисления, как иыра-
жается Хис, пайти у Архимеда известное предвосхищение и основных поня-
понятий дифференциального исчисления,— того, что мы назвали бы теперь опре-
определением отношения беско-
бесконечно малых величин. С
8той точки зрения инте-
интересно предложение XVIII
книги «О спиралях», в
котором длина окружпо-
сти сравнивается с дли-
длиной подкасателыюй к спи-
спирали. Пусть точка О пред-
представляет полюс спирали,
радиус-вектор которой за
время первого оборота
сделался равным г=ОЛ, а
прямая AD является каса-
касательной в точке А кспира-
ли. Пусть CD и АС пред-
представляют перемещения описывающей спираль точки по радиусу и 'перпен-
'перпендикулярно к нему (рис. 9). ГТронодим ОВ перпендикулярно к СМ ипродол*-
жаом касательную AD до пересечения и В с этой прямой; тогда длина ОБ
будет представлять длину окружности радиуса /¦. Доказательство сводится к
установлению пропорции
*>ис- <J-
Треугольник ACD по существу представляет не что иное, как диффет
реициалышн треугольник Барроу — Ньютона, и не исключена позмож-;
ность, что идея этого треугольника появилась у Исаака Барроу именно
в результате изучения сочинений Архимода, которые были изданы Барроу
в 1675 г. с переделанпыми доказательствами. Во всяком случае изучение
Архимеда математиками XVII века было необходимой подготовительной
работой к появлению классического анализа бесконечно малых/
Еще с большим правом мы можем видеть н Архимеде основателя мате-
математической физики: как творения его колоссального инженерного таланта
в сочетании с математической подготопкон появляются работы третьего
«механического» периода деятельности Архимеда, когда он определил поло1
жение центроп тяжести сегмента параболы («О равновесии плоских фигур»),
а также конуса и сегментов параболоида, гиперболоида и аллипсоида вращения
(«Эфод»); знание положения центра тяжести сегмента параболоида позво-
позволило ему математически определить положения равновесия плавающего
38 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. НЕСЕЛОЛСКОГО1
в жидкости сегмента параболоида («О плавающих телах»). Инженерная
интуиция Архимеда была настолько велика, что, как показывает детальный
разбор его выводов (см. комментарий к предложениям II—X второй книги
«О плавающих телах»), и основе его исследований, по существу, лежат те
самые теоремы, которые были установлены только во второй половине
XIX века проф. Московского университета А. Ю. Давыдовым и француз-
французским математиком Дюпеном. Основным отличием метода Архимеда от сов-
современного является то, что Архимед определяет устойчивые положепия
равпинесня не при помощи формального критерия метацентра, а непосред-
непосредственно исследуя ноисдение плавающего тела при его отклонениях от поло-
положения рановесия. При таком чисто физическом методе исследования у Архи-
Архимеда, естественно, получаются только положения, соответствующие устой-
устойчивому равновесию.
Эта «физичноегь» мышления совершенно исключает представление об
Архимеде как о гениальном математике-формалисте. В «Псаммите», есть
одно место, на которое коммептаторы-ыатематпкп не всегда обращают вни-
внимание. Архимед пытается определить видимый диаметр Солнца. Он хорошо
знает, что «получить точное значение этого угла — дело нелегкое, потому
что ни глаз, ни руки, ни приборы, с помощью которых производится
отсчет, не являются достаточно надежными для точности результата».
Искомую величину он находит не из умозрительных соображений, а чисто
экспериментальным способом, вводя даже поправку на ширину зрачка.
Найдеппая им величина углового диаметра Солнца оставалась непревзой-
непревзойденной вплоть до XVII века (результат Архимеда 32Э55',5 — верхняя гра-
граница и 32С27' — нижняя граница; Коперник считал 31е 48'; истинные зна-
значения 31°28' в апогее и 32С37' и перигее. Таким образом, верхняя граница,
полученная Архимедом, не хуже величины, найденной Коперником).
К последнему периоду творчества Архимеда мы отнесли «Измерение
круга» и «Псаммит». Специфически поным моментом в этом периоде является
то, что Архимед от геометрических построений определяемых величин пере-
переходит к вычислению их; это подводит нас к рассмотрению еще недостаточно
изученного вопроса о греческой арифметике, или, лучше сказать, логис-
логистике — искусству вычислений*), так как под арифметикой у греков пони-
понималось то, что мы теперь назвали теорией чисел.
Однако Архимед не только использовал достижения современной ему
науки относительно способов вычисления; он был и в этой области актив-
активным создателем новых научных цслпостей. Так как греческая система счис-
счисления не позволяла удобно изображать большие числа, Архимед в не дошед-
дошедшем до нас сочинении яео'[ aQXoiv — «О началах» — заложил основание
новой системы счисления, усовершенствованной им в дошедшем до нас
«Псаммите», где он дал систему счисления, пригодную для изображения дей-
действительно астрономических чисел, могущих выразить количество песчи-
песчинок, содержащееся в объеме вселенной. «Астрономическая направленность»
«Псаммита» позволяет нам дать ответ па вопрос о том, какие причины заста-
заставили Архимеда под конец его жизни, примерно в двадцатых годах 111 века
до н. э., заинтересоваться вычислительной математикой и создать системы
счисления, приспособленные к обозначениям очень больших чисел. О том,
*) О способах иычислений у греков см. Приложение I.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 39
что эти причины заключались не только в индивидуальных интересах Архи-
Архимеда как ученого, говорит тот факт, что Архимед не был единственным мате-
математиком той эпохи, интересовавшимся способом ааписи очень больших чисел.
В дошедшем до нас отрывке второй книги «Математической библиотеки»
Паппа имеется пересказ одного из арифметических сочинений младшего
современника Архимеда и, вероятно, его соперника Аполлония Пергского,
автора известных «Конических сечений». Это сочинение, называвшееся,
вероятно, Q/cut?kiov (средство для ускорения родов), говорило о способах
умножения больших чисел и о ноной системе счисления, позволявшей запи-
записывать эти большие числа. Как мы знаем из комментария Евтокия к «Изме-
«Измерению круга», Аполлоний дал более точное значение отношения окруж-
окружности к диаметру, чем то, которое приводится в «Измерении круга»; иоз-
можно, что полемика между Архимедом и Аполлонием повела к появлению
«Задачи о быках».
Эти «вычислительные» тенденции в греческой математике еще более
усиливаются в последующем ее развитии. Творении Архимеда и Аполлония
являются своего рода венцом гречцркой геометрии, но вместе с тем они озна-
меповали и ее завершение; после Аполлония развитие греческой геометрии
как-то сразу обрывается: «род» великих математиков пс иссякает, но они
начинают запинаться совершенно другими вопросами. Эратосфен является
творцом математической географии, Гиипарх кладет начало сферической
тригопомотрии и вычислительной астрономии. После Гипларха математику
приблизительно на две тысячи лет «берет под опеку» астрономия, причем
это имеет место не только у греков, но и у индусов, и у арабов, и у средне-
средневековых математиков, вплоть до времен Коперника, Кеплера и Ньютона.
Создается впечатление, что греческая математика испытала какие-то мощ-
мощные влияния нового фактора, который коренным образом изменил весь
дальнейший процесс ее развития. Таким фактором, как показали исследо-
исследования первой половины двадцатого пека, была вавилонская планетная
астропошш, которая качала развиваться примерно с VI века до н. э. Этот
век в истории науки явился такой же переломной эпохой, какой в дальней-
дальнейшем ее развитии был, например, XVII век. Именно в этом веке произошла
ликвидация старого религиозного миропопимания. В Греции он был озна-
ознаменован рождением светской науки — материалистической и рационали-
рационалистической философии ионийской школы и основанной на строгих логических
доказательствах математики. На востоке тот же самый процесс шел иначе.
Точпо так же были сданы в архив все старые легенды о божественном сотво-
сотворении мира. Религия сосредоточилась всецело в области морали и ушла
из области естествознания. Боги перестали быть творцами и деспотическими
правителями мира; переселившись на псбо и разместившись по различным
планетам, они стали лишь подчиненными и толкователями какой-то высшей
силы — фатума, предначертания которой можно открыть по движениям
планет; их движения стали рисоваться настолько закономерными, что их
уже можно зарапес предсказать и нредвычислить. Начиная с VI века до н. э.,
вавилоняне нродвычисляют побисные явления и к 111—II векам до н. э.
достигают таких успехов, что оказываются в состоянии предсказывать нас-
наступление затмений, противостояний и соединений планет. Вавилонские
астрономы Набуриаилу и Кидинну определяют длину года, продолжитель-
продолжительность различных видов месяца и периоды планетных обращений. Восточная
философия в лицо стоицизма с его пестрой смесью материалистических пред-
представлений с фатализмом и астрологией начинает господствовать в греческом
мире; обоснованием зтой философии считалась не зпающая никаких богов
вавилонская вычислительная астрономия. Крушение эллинистических
40 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОНСКОГО
государств под железной пятой римских завоевателей еще более усиливает
и тяжелое настроение среди порабощенных народов, и надежды на лучшее
будущее, время наступления которого можно будет определить, если суметь
надлежащим образом прочесть веления фатума, выраженные в закономер-
закономерных движениях планет не только в течение настоящего, но — самое важ-
важное — в течение будущего времени.
Но для того чтобы предсказывать" движения планет, нужно уметь их
предвычислять, а для этого уже недостаточно было «домашней логистики»,
дававшей правила счета в пределах только первой тысячи; необходимо было
познакомиться с той математикой, которой пользовались вавилонские
астрономы, а эта математика оперировала с числами, гораздо большими тех,
которые могло предстаиить себе воображение среднего грека. Перед наукой
поэтому встала задача разработки новых методов вычислений. Работы Архи-
Архимеда и Аполлония являются первыми шагами в этом направлении, когда
из вавилонской системы счислений берется лишь осповной принцип пози-
позиционности. В дальнейшем следование вавилонским способам иычислепий
становится псе более и более рабским и закапчивается принятием целиком
вавилонских способов вычислений для всех астрономических расчетов.
Вскоре после смерти Архимеда, в самом пачале II века, антор так называе-
называемой XIV книги «Начал» Евклида алексапдриец Гипсикл и своем «Анафо-
piMte» пользуется введенным вавилонским астрономом Кидипну способом
представления постепенного изменения скорости движения планет при
помощи арифметической прогрессии — нечто аналогичное введенному Гали-
Галилеем равноускоренному и равнозамедденному движениям. Немного позже
великий греческий астроном Гиппарх пользуется вавилонскими данными
относительно продолжительности года и месяца. От грекон вавилонская
астрономия и математика переходят и к римлянам. Как широко было рас-
распространено у пнх знание астрономии, показывают, например, следующие
факты. Накануне решительного сражения при Пидне во время Персеевой
войны Сульпиций Галл предсказал наступление лунного затмения. В I веке
до и. э. друг Цицерона Нигидцй Фигул, астролог и математик, уже вполне
усвоил методы вавилонской вычислительной астрономии; немного позже
пояпдеяие ватшлонской астрологии в Риме отличено у Горация:
Tu ne quaesieris, scirenetas, quern mihi quem tibi
Fincrn di dederint, Leiiconoe, nee Babylonios:
Temptaris nurneros...*)
В эпоху Птолемея вавилонские тестидесятеричные дроби являются
уже основным средством астропомических гычислепий. Как показывают
схолии к Евклиду, византийским математикам XI—XII веков п. э. эти
дроби были очепь хорошо известны, а в Западной Европе гаестидесятерич-
пые дроби под названием minutiae physicaies, в противоположность обык-.
повенны.м дробям (minutiae vulgares), были в употреблении вплоть до XVII ве-
века, и в настоящее время еще живут в наших минутах и секундах.
VI
Когда Тит Ливии называл Архимеда «единственным в своем роде наб-
наблюдателем неба и звезд», то он, возможно, повторял высказывания об Архи-
Архимеде ближайших к нему поколений, в первую очередь, вероятно, Полибия,
изложению которого Ливии следует, рассказывая события второй Пуни-
•) Не сирашипяЛ ты, ведать грешно, какой мне и тсОи Левконоп, пошлют боги конец, и вавилон-
Ч(ла пь не ьытьй. (Сды, книга I, 11).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ЕЕСЕЛОЕСКОГО 41
ческой войны. Для Полибия, бывшего прежде всего государственным дея-
деятелем, тонко понимавшим взаимную связь политических событий, а не уче-
ученым, Архимед, конечно, был важен в первую очередь как защитник Сира-
Сиракуз; общую характеристику Архимеда Полибий дал, вероятно, в соответ-
соответствии с теми представлениями о нем, которые сложились к кругах широкой
публики, помнившей только последние работы Архимеда перед самой осадой
Сиракуз. Если это верно, то Архимед занялся астрономией уже на склоне
лет; чтобы правильно оценить значимость полученных им результатов в обла-
области астрономии лучше всего сравнить их с результатами измерения расстоя-
расстояния Солнца и Луны от Земли, которые были получены его непосредственным
предшественником, а именно упоминаемым им в «Псаммите» Аристархом
Самосским.
Согласно исследованиям Аристарха, диаметр Солнца —7 диаметрам
Земли.
1 7
Диаметр Лупы = ^ диаметра Солнца = ^ диаметра Земли.
•Расстояние Луны от Земли=30 диаметрам Луны^Ю-^- диаметрам
Земли.
Расстояние Солнца от Землп=~210 диаметрам Земли.
Интересно сравнить результаты исследований Аристарха с работой
Архимеда. Прежде всего, Аристарх считал Землю за точку, иными словами,
считал, что наблюдатель находится в центре Земли, а Архимед учитывал,
что наблюдатель находится па поверхности Земли, и поэтому приводил
наблюдения к центру. Затем Аристарх давал только относительные размеры
мира, Архимед ввел величину земного радиуса и, таким образом, получил
и абсолютные размеры мира. С другой стороны, Аристарх искал верхнюю
И нижнюю границы измеряемых величин (у него, например, отношение диа-
1 1
метра Солнца к диаметру Земли заключается между пределами б-^-и 7-g-),
в то время как Архимед брал одну только верхнюю границу. Расстояние
от центра Земли до центра Солнца у него составляет 5000 диаметров Земли
и диаметр Солнца в 30 раз больше диаметра Земли; что касается Луны, то
он просто принимает ее диаметр равным диаметру Земли; так как угол, вод
которым виден диаметр Луны с поверхности Земли равен 30', то расстояние
от Земли до Луны будет равно диаметру Лупы, деленному на sin 30', то
есть 120 диаметрам Луны (в четыре рала больше, чем у Аристарха), или,
так как Архимед считает диаметры Земли и Луны равными — 120 диамет-
диаметрам Земли.
Астрономические сочинения Архимеда не ограничиваются «Псаммитом»,
им было написано сочинение, посвященное построению пебеспой сферы;
инжеятерпые устремления были настолько сильны в Архимеде, что они про-
проявились даже и области чистой астрономии. Историю этой сферы лучше всего
рассказать, цитируя известные нам источники.
На первом месте надо поставить диалог Цицерона «О государстве»;
описываемые в нем события происходят во второй половине II века до н. э.
Упоминаемый в нем Сульпиций Галл был очень образованным римлянином.
В первой книге «О государстве» мы читаем (книга I, 14):
«Л вспоминаю, как К. Сульпиций Галл, как вы хорошо знаете, одип
из самых ученых людей пашей страны, находился однажды в гостях у М. Мар-
целла, бывшего недавно консулом вместе с пим, и разговор зашел о чудесном
явлении, в точности похожем на случившееся недавно. Галл заставил при-
привести ту зпамецитую сферу, единственную добычу, которой предок
42 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
Марцелла захотел украсить свой дом после взятия Сиракуз, города полного
всяких сокровищ и диковинок. Я часто слышал разговоры об этой сфере,
¦считавшейся шедевром Архимеда, и признаюсь, что с первого взгляда она
мне не показалась чем-то особенно выдающимся. Марцслл пожертвовал
в храм Доблести другую архимедову сферу, которая была гораздо более
известна и имела более представительный вид. Но когда Галл начал с не-
необыкновенным знанием дела объяснять устройство этого прекрасного про-
произведения, я не мог не подумать, что в этом сицилийце был гений, равняться
с которым человеческая природа не казалась способной. Галл рассказывал
нам, что изобретения таких сплошных сфер относятся к глубокой древпости,
что первый образец такой сферы был построен Фалесом Милетским, что
в дальпойшем учепик Платона Ёвдокс Книдский изобразил на ее поверх-
поверхности различные созвездия, прикренлепные к небесному своду, и что много
лет спустя не бывший астрономом, но имевший известный поэтический
талант Лрат описал в стихах все небо по Евдоксу. Оп прибавил, что для
возможности представления движений Солнца, Луны и пяти звезд, которые
мы называем блуждающими, пришлось отказаться от употребления сплош-
сплошной сферы, па которой было бы невозможно их воспроизвести, и придумать
другую совершенно отличного вида; и что в изобретении Архимеда чудес-
чудесным было искусство, с которым on мог объединить в одной системе и вос-
воспроизвести при помощи одного вращения все очень отличающиеся друг от
друга движения и различные периоды обращения различных светил. Когда
Галл приводил сферу в движение, то при каждом обороте можно было видеть,
как Луна появлялась вслед за Солнцем на земном горизонте, подобно тому
как она появляется каждый день на небе; далее можно было видеть, как
Солнце исчезнет так же, как и па пебе, и затем понемногу Луна погружается
в земную тень в тот самый момент, когда Солпце с противоположной
стороны...».
На этом интересном месте к сожалению обрывается дошедший до нас
текст Цицерона.
Сфсфа Архимеда, пожертвованная Марцеллом в храм Доблести, по-види-
по-видимому, для многих римлян была основным пособием для изучения астроно-
астрономии. Следы знакомства с этой сферой можно установить в течение долгого
времени после эпохи Цицерона.
Во второй половине II века н. э. мы встречаемся с несколько загадоч-
пым свидетельством неистового карфагенского пресвитера Тертуллиана:
«Обрати нпммапие на изумительное чудо Архимеда; я говорю об этой
гидравлической машине, где столько колес, столько различных деталей,
столько сочленений, столько выходов для голоса, и целые армии флейт соста-
составляют одну неразличимую массу».
Обыкновенно это понимают в смысле изобретенного Архимедом гидра-
гидравлического органа. Однако такому толкованию препятствуют следующие
соображения:
1е. Архимед не является изобретателем гидравлического органа; все
историки древности признают в этом вопросе приоритет александрийца
Ктесибия.
2°. Вряд ли можно допустить, чтобы гидравлические органы III века
до н. э. могли уцелеть в конце II века п. э.
3е. Собрание «колос» не подходит к гидравлическому органу.
С другой стороны, мы знаем, что сфера Архимеда приводилась п движе-
движение «скрытым внутри воздухом» (spiritus inclusus), согласно описанию поэта
Клавдиапа (V век п. э.). Так как от такого врага науки, каким был Тертул-
лиан, нельзя ожидать очень большой точности, то можно думать, что «изу-
ВСТУПИТЕЛЬНАЯ СТАТЬЯ IT. Н. ВЕСЕЛОВСКОГО 43
митслытым чудом» Архимеда была именно сохранявшаяся в храме Доблести
астрономичсс кая сфера.
4epe:i каких-нибудь сто лет в эпоху Джжлетиапа об архимедовой сфере
говорит Лактанций (De mortibus persecutorum, книга 111, 5):
«Я вас спрашиваю, ведь мог же сицилиец Архимед воспроизвести образ
и подобие мира в выпуклой округлости меди, где он так разместил и поста-
поставил Солнце и Луну, что они как-будто совершали каждодневно неравные
движения и воспроизводили небесные вращения; он мог не только показать
восход и заход Солнца, рост и убывание Луны, по сделать так, чтобы при
вращении этой сферической поверхности можно было видеть различные тече-
течения планет; так неужели же Г»ог пе мог воспроизвести и сотворить патураль-
пые пещи, подобие которых мог сделать человек споим искусством и хит-
хитростью».
В конце IV века, когда при Грациапе и Феодосии I христианство одер-
одержало окончательную победу над язычеством, о сфере Архимеда вспоминает
один из последних языческих писателей Макробий в комментарии ко «Сну
Сципиона», книга II, 3):
«Так же и Архимед считал, что он определил число стадий, на которое
от поверхности Земли удалена Луна, а от Луны — Меркурий, от Мерку-
Меркурия — Венера, от Венеры — Солнце, от Солнца — Марс, от Марса —
Юпитер и от Юпитера — Сатурн; пси же расстояние от Сатурна до самого
звездоносного неба он думал измерить только рассуждением».
Для определения расстояния Солнца от Земли Архимед, как мы знаем,
прибег к измерению при помощи опыта. Задача действительного определе-
определения расстояний между различными планетами была в его время совершеппо
непосильной; их можно было определить только предположительно, исходи
из периодов их обращений. Для «звездоносного неба» у него не было даже
и этих числовых даппых, поэтому ему, конечно, пришлось ограничиться
лишь рассуждением. Единственной целью, для достижения которой
такие вычисления были необходимы, яиляется только построение небес-
небесной сферы.
Еще раз мы встречаемся с этой сферой в произведениях последнего
талантливого римского поэта Кландиапа (начало V века п. э.), который
посвятил ей одну из своих эпиграмм:
«Неба устав, законы богов, гармонию мира —
Все Сиракуяский старик мудро на Землю привес.
Воздух, скрытый внутри, различные движет светила
Точно по дапиьш путям, сделав творепьо живым.
Ложиый бижит зодиак, назначепкьш ход выполняй,
Лик поддельный Jlyiiu hhubi. каждый месяц идет.
Смелым искусством гордясь, сбой мир приводя во вращеньо,
Звездами вышних небес правит умом человек».
Вскоре после написания этого гордого стихотворения в 410 г. готы
захватили Рим; в последовавшем грабеже языческих храмов, вероятно,
погибла и небесная сфера Архимеда.
VII
В самом конце своей жизни Архимеду снова пришлось вернуться
к тому, чем он занимался в начале своей творческой деятельности: ему
пришлось применить свои инженерные и механические познания для обо-
обороны родного города. Во время второй Пупической войны Сиракузы
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. НКСЕЛОВСКОГО
оказались вовлеченными в борьбу Карфагена с Римом и римский пол-
полководец Марцслл осадил Сиракузы, душой обороны которых стал семи-
семидесятипятилетний Архимед. Дальнейшее течепие событий лучше всего из-
изложить языком подлинных источников, каковыми в данном случае япля-
ются Полибий, Тит Ливии и Плутарх.
Наиболее ранний источник — «История» Полибий, написанная при-
примерно через 50—60 лет после разрушения Сиракуз. В книге VTII его «Исто-
«Истории», дошедшей до нас во фрагментах, мы читаем следующее:
«Когда Епикид и Гиппократ *) завладели Сиракузами, то сами прериали
дружбу с римлянами и прочих граждан припудили к тому же. Римляне,
раньше еще уведомленные о насильственной, смерти сиракузского тирана
Гисропима **), выбрали в проконсулы Лппия Клавдия, дали в его распоря-
распоряжение сухопутное войско, а начальство над флотом возложили на Марка
Клавдия ***). Начальники расположились станом невдалеке от города и реши-
решили, что сухопутное войско поведет приступ против города со стороны Гек-
сапил, а флот—против Ахрадинм •***) у портика, именуемого Скитским,
где стена тянется вдоль моря. Приготовивши шалаши *****), метательные
орудия и все прочес, нужное для осади, римляне надеялись при многочис-
многочисленности рабочих рук покончить с приготовлениями в течепие пяти дней
и но дать неприятелю подготовиться. Но при этом они не приняли и расчет
искусства Архимеда, не догадались, что иногда дарование одного человека
способно сделать больше, чем огромное множество рук. Теперь они убеди-
убедились в этом по опыту. Город был достаточно крепок уже тем, что окружаю-
окружающая его стена покоилась на высотах и поднимающемся перед городом
утесе; к ним трудно было подойти, sa исключением немногих определенных
пунктов, даже и тогда, если бы осаждаемые не оказывали никакого со-
сопротивления.
Кроме того, упомянутый Архимед заготовил впутри города, а равно
и против нападающих с моря такие средства обороны, что защитникам не
было необходимости утруждать себя непредусмотренными работами на
случай неожиданных способов нападения; у них заранее готово было все
к отражепию врага в любом случае.
Итак, Апний сделал попытку приблизиться с шалашами и лестницами
к той части стены, которая с востока упирается в Гсксанмлы, а Марк сшестью-
десятью пятипалубными судами направился против Ахрадины. Находив-
Находившиеся на каждом судне люди вооружены были лукямн, пращами и легкими
дротиками, чтобы прогонять врага, нападающего с зубцов стен. Вместе
с тем римляпе сняли у восьми пятипалубиых судов весла, у одних с правой
стороны, у других с левой, открытыми стенками связали суда попарно
и, действуя веслами только с наружных боков, стали подвозить к городской
степе так называемые самбуки. Устройство этого осадного орудия следую-
следующее: делается лестница « четыре фута ширины и такой длины, чтобы она
при устапоике достигала верхнего края стены, с обеих сторон en ограждают
и закрывают высокими перилами, лотом кладут ее наискось вдоль сопри-
соприкасающихся столок спязанных между собою судов, так что лестница высту-
выступает далеко за корабельные носы. На вершинах мачт укрепляют блоки
с канатами. Когда нужно действовать, канат привязывают к верхнему
•) Вожди демократической антиримской партии п Снракутах.
•*) Пятнадцатилетнего внука Гиерона, последнего отпрыска его династии.
: •*•) Марцелла.
••¦•) Часть города Сиракуз.
*¦*•¦) Так навивались поднижи ыс крытые галереи, подвозимые или подносимые к стенам для
прикрытии осаждавших.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВБСЕЛОВСКОГО /»5
краю лестницы, и люди, стоящие па корме, тянут его на блоке, а другие,
находящиеся на передней части корабля, следят за правильным подъемом
лестницы и подпирают ее шестами. Наконец, при помощи гребцов, разме-
размещенных по обоим наружным бортам, римляне подходят с кораблями к суше
и стараются только что описанное сооружение приладить к стене. На «ер-
шине лестницы паходится доска, с трех сторон огороженная плетнем; на ной
стоят четыре человека, которые и ведут борьбу с неприятелем, находя-
находящимся на зубцах стены и противодействующим установке самбуки. Как
только лестница установлена так, что эти четыре ноипа возвышаются над
стеной, боковые стенки плетня снимаются, и воины тотчас с двух сторон
взбираются на зубцы или башки: прочие товарищи их следуют за
ними по самбуке, надежно прикрепленной канатами к обоим кораблям.
Сооружение это не без основания получило такое название: когда ма-
машина поднята, то корабль в соединении с лестницей напоминает по виду
самбуку *).
Итак, по изготовлении самбуки римлянп решились подойти к башням.
Однако Архимед соорудил машины, приспособив их к метанию снарядов
на любое расстояние. Так, если неприятель подплывал издали, то Архимед
поражал его из дальнобойных каыпеметальниц тяжелыми снарядами или
стрелами и повергал в трудное и беспомощное положение. Когда же снаряды
пачинали летать иолерх неприятеля, то Архимед употреблял в дело мень-
меньшие машины, каждый раз сообразуясь с расстоянием, и наводил на римлян
такой ужас, что они никак пе решались идти на приступ или приблизиться
к городу па судах. Наконец, Марк, раздосадованный неудачами, вынужден
был сделать попытку тайком тючьто подойти к городу тта кораблях. Когда
римляне подошли к берегу на расстояние выстрела, Архимед употребил
другое средство, направленное против воипол, сражавшихся с судо»> именно:
он велел сделать в степе приблизительно на высоте человеческого роста
множество отверстий, с паружнои сторош.т имевших в ширину пальца четы-
четыре; у отверстий изнутри стены он поставил стрелков и маленькие скорпи-
скорпионы**), через отверстия обстреливал корабельных воинов и тем отнимал
у них всякую возможность сделать что-нибудь. Таким образом, далеко
или близко находился неприятель, Архимед не только разрушал «се его
планы, по и производил в его рядах большие опустошения. Как только
римляне покушались поднять самбуки, Архимед приводил машины в бое-
боевое состояние по всей стене. Все время они оставались невидимы, но лишь
только требовалось употребление их в дело, машины изнутри выдвигались
за зубчатые укрепления. Некоторые машины метали намни весом не менее
десяти талантов***), другие выбрасывали груды свинца. Каждый раз, как
только самбуки приближались, жерла архимедовых машин отклонялись
вместе с подставкой вправо или влево, смотри по надобности, и при помощи
освобождаемого блока сбрасывали камни на неприятельское сооружение.
Вследствие этого не только ломалась машина римлян, но и корабль, и нахо-
диншиеся на нем солдаты подвергались большой опасности.
Некоторые машины отражали нападение неприятеля, защищенного
и прикрытого плетнем от стрел, выпускаемых через отверстия в стене;
в таком случае бросаемые камни соответствующей тяжести прогоняли напа-
нападающих римлян с передних частей корабля. Кроме того, с машины спуска-
спускалась прикрепленная к цепи железная лапа; управлявший жерлом машины
•) Самбукой назывался музыкальный инструмент.
•*) Стреломсты небольшого калибра.
•••) Около 250 кг. ¦ ¦ .
4C ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ПЕСЕЛОВСКОГО
захватывал п каком-нибудь месте этой лапой нос корабля и потом опускал
вниз находящийся внутри города копец машины. Когда нос судна был таким,
образом поднят и судно поставлено отвесно на корму, то плечо рычага за-
закреплялось неподвижно, а лапа вместе с цепью отделялись от машины осво-
освобождающего приспособления. Бследстнме этого некоторые суда ложились,
на бок, другие совсем опрокидывались, большинство же от падения носом
с значительной высоты в море погружались м наполнялись водой, внося
большой беспорядок и ужас среди экипажа. Изобретательность Архимеда
приводила Марка в отчаяние; с прискорбием он видел, как осажденные глу-
глумятся над его усилиями и какие опи причиняют ему потери. Однако, под-
подшучивая над своим положением, Марцелл говорил, что Архимед уго-
угощает его корабли морской водой, а его самбуки как бы с позором про-
прогоняются с поаойки палочными ударами. Так окончилась осада Сира-
Сиракуз с моря.
Аппий с сухопутным войском очутился в столь же трудном положении,
и потому совсем отказался от приступа. Действительно, паходясь еще на
далеком расстоянии от города, римляне сильно терпели от камнеметальниц
и катапульт, из которых были обстрелилаемы; ибо сиракузпне имели в за-
запасе множество превосходных и метких метательных орудий. Оно и понятно,,
так как Гиероп дал па них средства, а Архимед изобрел и мастерски построил
машины.
Итак, когда римляне приближались к городу, то одни были
непрерывно обстреливаемы чорез отверстия в стене, о которых было сказано
выше, терпели урон и не могли продолжать наступление, другие же, рас-
считывалшие пробиться вперед силой и огражденные плетенками, гибли
под ударами камней и бревен, падавших сверху. Много бед римлянам
сиракузянс иричипяли и теми лапами у машин, о которых я говорил раньше;
лапы поднимали воинов в полном вооружении и кидали их оземь. Наконец,
Аппий с товарищами возвратился па стоянку, устроил совещание с трибу-
трибунами, на котором и было принято единогласное решение испытать всевоз-
всевозможные другие средства, во только отказаться от надежды взять Сиракузы
приступом; согласно принятому решению, они так и действовали. Ршшяне
оставались под стопами города в течение восьми месяцев, и пе было такой
уловки или отважного дела, перед которым они остановились бм, но на при-
приступ идти они уже ни разу не осмеливались.
Такова чудесная сила одного челонека, одного дарования, умело напра-
направленного на какое-либо дело. Вот и теперь: располагая столь значительными
силами сухопутными и морскими, римляне могли бы быстро овладеть горо-
городом, если бы кто-либо изъял из среды сиракузян одного старца. Но так как
этот один был среди сиракузяп, то римляне не дерзали нападать на город
или по крайней мере употреблять те способы нападения, отразить кото-
которые Архимед был и силах».
Приведенный текст Полмбия интересен в следующем отношении. Иногда
приходится слышать, что Архимеда, бывшего, по существу, замечательным
математиком и склонным, по свидетельству Плутарха, лишь к теоретиче-
теоретическим паукам, только опасность, грозящая родному городу, заставила изяться
за практическую деятельность по его обороне. Внимательное чтение приве-
приведенного отрывка Полибия показывает, что оборона Сиракуз Архимедом
не была и не могла быть импровизацией; наоборот, Архимед готовился
к ней очепь давно и но заданию и па средства царя Гиерона построил ряд
военных машин. В связи с этим очень интересно то, что Архимед имел ряд
метательных орудий, действовавших на различные расстояния; это уже пред-
предполагает известный математический расчет. Какого рода этот расчет был,.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
мы можем составить себе представление на ословапии сохранившейся поен-
поенной литературы. Считалось, что длина полега выброшенного ядра прямо
пропорциональна объему того упругого тяжа, который приводил в движение
детали машины, сообщающие скорость ядру. Между прочим, этот расчет
совершенно правилен, так как можно очень просто показать, что при посто-
япстве угла возвышения орудия дальность полета ядра будет прямо про-
пропорциональна его начальной живой силе, последняя же получается из
потенциальной энергии закрученного тяжа, которая при однпаковой сте-
степени напряженного состояпия прямо пропорциональна объему тяжа. Таким
образом, на основе некоторого числа опытов вполне возможно конструиро-
конструировать камнеметы и стреломсты, действующие на заданном расстоянии; Архи-
Архимед, очевидно, это хорошо знал. То обстоятельство, что зта теория была
известна около 240 года до н. э., доказывается упоминанием о ней в письме
Эратосфепа к царю Итоломею Эвергету, касающемся задачи об удвое-
удвоении куба.
То, что Архимед не был кабинетным ученым, убедительно доказы-
доказывается той необычайной его изобретательностью в организации оборопных
мероприятий, которая так ярко изображена в приведенном ниже рассказе
Поли бия.
Полибий был одним из источников для описания истории второй Пуни-
Пунической войны у Тита Линия A век до н. э.). Мы находим в книге XXIV его
римской истории:
«После этого началась осада Сиракуз и с суши — от Гексапил —
и с моря — от Лхрадинт.т, степы которой омываются морем. При этом рим-
римляне, взявшие Леонтины с первого же натиска под действием только ужаса,
были вполпе уверены, что в каком-нибудь месте они прорвутся в обширный
и разбросанный но большому пространству город, и придвинули к стенам
всю наличность осадных машин. И начатое с такой силой предприятие
увенчалось бы успехом, если бы в то время не было одного человека.
Этим человеком был Архимед, единственный в своем роде созерцатель неба
и светил, но еще более удивительный изобретатель и конструктор военных
машин и сооружений, при помощи которых он с очень небольшим усилием*)
мог делать тщетными все попытки врагов, даже если эти попытки стоили
колоссальных усилий. Стена города проходила по неровной и холмистой
местности; многие части ее были очень высокими и трудно доступными, но
в некоторых местах она была низкой и пологие стены делали возможным
восхождение. Поэтому Архимед поставил па стене в качестве защиты раз-
различного рода метательные оружия, сообразуя их с природой местности.
На стену же Ахрадины, которая, как сказано было выше, омывалась морем,
Марцелл вел наступление с шестнадцатью нентерами**). Находившиеся же
па других судах лучники, пращники и легковооруженные велиты***), мета-
метательные орудия которых очень трудно отражать для неопытных воинов,
не позволяли никому безнаказанно оставаться на степах. Так как для мета-
метательных орудий требуется некоторое расстояние, то эти корабли стояли
вдали от стен. Другие пенторы были соединены попарно бок к боку, причем
внутренние весла были сняты и оба корабля как один приводились в движе-
движение лишь внешними веслами; на них стояли многоэтажные бапши и другие
приспособления для разрушения стен. Против всего зтого морского поору-
жепия Архимед расположил по стенам метательные орудии различной
•) Parvo jnomento — выралгение, ваимствованнсе из механики.
••) Шнтера — судно с пятью рядами весел.
••*) Велиты — род войска у римлян.
48 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ПЕСЕЛОВСКОГО
величины. В далекие корабли он мотал громадного веса камни, а близкие
осыпал! более легкими, а вследствие этого и в большем количестве, метатель-
метательными снарядами. Наконец, для того чтобы сиракузские воины безнаказашго
могли обстреливать неприятеля, он проделал в стене снизу до перку отвер-
отверстии шириной почти в фут, из которых они, оставаясь скрытыми, могли
поражать врага стрелами и среднего калибра скорпионами*). Пите жо кораб-
корабли, которые подходили ближе, чтобы выйти из поражаемой орудиями обла-
области, он при помощи выступающего за стену рычага, набрасывал прикреплен-
прикрепленную крепкой цепью железную лапу: когда последняя захватывала нос
корабля, то при помощи опускающегося до земли тяжелого спипцоиого
противовеса нос корабля подымался и последний становился на корму;
затем после внезапного освобождения корабль, как бы сброшенный со стены,
к громадному ужасу матросов так ударялся о морскую поверхность, что
набирал воды даже п том случае, когда падал в прямом положении. Таким
образом, был отражен приступ с моря и всю надежду римляне возлагали
на нападепие всеми силами с суши. Но и эта часть стен была вооружена раз-
личпого рода метательными орудиями, которые в течение долгого времени
изготовлялись аа глот Гиерона единственным в своем роде искусством
Архимеда. Последнему помогала также п природа местности, так как скала,
на которой находились фундаменты степ, большой частью была настолько
крутой, что врагу тяжелый урон причиняли снаряды не только выбро-
выброшенные из орудия, по даже двигавшиеся только под действием собствен-
собственного веса.
По той жо самой причине подъем был очень труден вследствие крутизны
и движение было очень опасным. Таким образом, после обсуждении, видя
тщетность всякого рода попыток, римляне постановили прекратить штурм
и только при помощи блокады с суши и с моря отрезать осажденных от
подвоза провианта».
Наконец, третью версию истории Сиракузской осады мы читаем у Плу-
Плутарха, автора начала II века н. :»., в его жизнеописании Марцолла. :
«Марцелл производил нападения и с суши, и с моря. Аппий водил в сра-
сражение сухопутные войска, Марцелл командовал шестьюдесятью пентерами,
наполненными всякого рода оружием и стрелами. Он приказал связать между
собой восемь больших кораблей, поставил на них осадную машину и под-
подплывал с нею к стенам, надеясь на успех ввиду обширности и тщательности
своих приготовлений и славы своего имени. Но все это было пустяками для
Архимеда и архимедовых машин. Последний до сих пор еще не создал ничего,
заслуживающего внимания. Большая часть того, что он сделал, было еде--
лано мимоходом,— оп занимался математикой как бы для забавы. Первым
польстил самолюбию царь Гиерон. Он убедил Архимеда, вместо занятий
отвлеченными предметами, заняться хотя бы отчасти предметами реальными
и, соединив свои теоретические построения с практикой, сделать их понят-
понятнее и яснее для обыкновенных людей. Механике — науке, любимой многими
и пользующейся широким распространением,— положили начало Евдокс
и Архит. Они желали сделать геометрию интереснее, менее сухой, и нагляд-
наглядными примерами, с помощью механики, решали задачи, которые не легко
получались путем логических доказательств и чертежей. Так, например,
они решили посредством механики задачу о двух средних иропорциональ-
пых линиях, задачу, на которую необходимо ссылаться в математике во
многих случаях, и решили ее при помощи «месографа» **), проводя кривые ** *)
*) См. примечание на стр. 45.
••> Привор для черчения средних пропорциональных (от }i?<jr\— средняя).
••*¦) В подлиннике «ttjuwxaiv, к разряду которых относились конические сечения. ' <¦•¦.'
ВСТУПИТКЛЫ1АЯ СТАТЬЯ И. Н. НЕСЕЛОНСКОГО 49
и делая сечения тол. Платон был недоволен. Он укорял их к том, что они
уничтожают математику и лишают ее достоинстп, переходи от предметов
умопостигаемых, отвлеченных, к реальным, и снопа сводят ов к занятию
реальными предметами, требующему продолжительной и трудной работы
ремесленника *). Тогда механика отделилась от чистой математики. Фило-
Философы долгое время не интерссопались ею, пока она не сделалась одной из
наук, находящих себе применение на войне. Архимед, между прочим, писал
однажды сноему родственнику и другу, царю Гиерону, что данной силой
(ovvd(Xtii) можно иодпять данную тяжость fljayog). В юношески смелом
доверии к силе своего доказательства он сказал, говорят, что, если бы у него
била другая земля, ом перешел бы на пее и сдвинул с места нашу. Удивлен-
Удивленный Гиерон стал просить его доказать свои слова и привести в движение
какое-либо большое тело малой силой. Архимед приказал посадить на цар-
царскую грузовую триеру, с громадным трудом с помощью многих рук выта-
щештую па берег, большой экипаж, положить на нее обыкновенный груз,
и, усевшись на некотором расстоянии, без всяких усилий, спокойно двигая
рукой конец полиспаста, стал тянуть к себе триеру так тихо и ровно, как
будто она плыли по морю. Пораженный этим, царь оценил нажность меха-
механики и упросил Архимеда построить для него машипи, которые служили
бы и для наступления и для обороны от какой угодно осады. Царю но приш-
пришлось употреблять их — почти вся его жизнь протекла п мире и спокой-
спокойствии; по теперь машины эти пригодились енракузцам, а вместе с машинами
и их изобретатель. Когда римляне осадили город с двух сторон, сиракузцы
испугались. От страха каждый молчал, потому что не надеялся оказать
сопротивление такой грозной силе. Но когда Архимед привел в действие свои
машины, то в неприятельскую пехоту попеслись пущенные им различного
рода стрелы и камни невероятной величины, которые летели с таким шумом
и силой, что ничто не могло выдержать их удара; опрокидывая всех задетых
ими, они приводили и смятение ряды воинов. Со стороны моря он разместил
на стенах другие машины., которые опускали сразу на корабли громадные
бревна в виде лапы, захватывали их, подымали силой противовеса, затем
выпускали их и погружали а волны. Другие корабли он зацеплял за нос
железными лапами или носами наподобие журавлиных и, поставив на корму,
топил. (Некоторые корабли он притягивал к земле при помощи тянувших
в рапные стороны веревок; там, повертевшись немного, они разбивались
о скалы, находившиеся под городской стопой, и большая часть экипажа
погибала. Часто можпо было видеть поднятый в воздух корабль, который
к ужасу окружающих вертелся с большой быстротой; когда его экипаж был
разбросан в разные стороны, как камни из пращи, то корабль разбивался
о стону, или, после освобождении от крюка, падал в море. Машина, кото-
которую Map цел л поставил на восьми кораблях, связанных вместе, называлась
самбукой, по сходству ее с музыкальным инструментом того же имени.
Она находилась на довольно далеком расстоянии от стен, когда Архимед
бросил на нее камень r десять талантов, а за ним другой и третий, которые
ударив машину со страшным шумом и силой, разбили ее связи и так расша-
расшатали корабли, что они отделились друг от д^уга. Марцслл, не янаи что
делать, поспешно отступил с флотом и приказал также отойти и пехоте.
*'] Знаменитое место, повторяющееся и л ;|ругщс сочинениях Плутарха, ин которого в середине
XIX века воапиклц легенда, что греческие математики, в частности Платон, запрещали пользоваться
каким бы то ии было инструментами, кроме цирнуля и линейки. В атом отношении верно лишь то,
чгги в «Няяапах» Евклида мм дуъ'1'их построении. Как Ма увидим ниже. Архимед совершенно
спокойно ттозьэопался так набиваемыми veineu; (иетаыкапи) для решении задач, приводившихся
к кубическим ураныснинн.
4 Архимед
50 ВСТУПИТЕЛЬНА!! СТАТЬЯ II. II. ПВСЕЛОВСКОГГ)
IT a военном совете было решено па следующий день до наступлении
утра, если удастся подойти поближе к стенам, чтобы дальнобошшш ланиты
Архимеда бросали стрелы поверх их голов, а тс, которые оп мог бы употре-
употребить на близком расстоянии оказались бы бесполезными, так как удар на
таком малом расстоянии не мог бы получить большой силы. Но Лрхимед
уже заранее приготовил для этом цели машины, который могли действовать
на всех расстояниях, и короткие стрелы, вылетавшие друг за другом почти
непрерывно*). Оп проделал в стенах отверстия па небольшом расстоянии
друг от друга и поставил в них среднего калибра скорпионы, которых враги
. не могли наметить и которые часто поражали всех приближающихся. Когда
римляне подошли вплотную к стенам и уже думали, что находятся в безо-
безопасности, то на них посыпался дождь стрел и на их головы полетели отвесно
падающие камни, так что не было ни одного места п стене, откуда бы в них
не стреляли. Они решили отступить, но едва они удалились ла некоторое
расстояние, как Архимед обрушил на отступающих такое количество стрел,
что истребил большое количество воинов и разбил много кораблей, в то время
как сами они не могли причинить крагу никакого урона, так как Архимед
большую часть своих машин расставил в укрытии за стенами;- поражаемые
отовсюду римляне, не видч, откуда наносятся удары, казалось, сражались
с богами. Между тем Марцелл, иабавясь от опаспости, шутил над своими
техниками, говоря, что они дерутся с математиком Бриареем **), который,
как бы играя, погружает их корабли и море и с позором прогоняет их, а, бро-
бросая разом столько стрел, оставляет далеко позади мифических сторуких
нсликанов. Псе остальные сиракузяпс были только телом для архимедовых
машин — один он был душой, которая псе двигала и всех направляла.
Все другие средства защиты были оставлены; город и для защиты, и для
нападения пользовался только машинами Архимеда. Наконец, видя, что
римляне так напуганы, что при одном виде спускавшейся со стены перовки
или бревна обращались в бегство, крича, что это какая-нибудь новая маши-
машина, которую Архимед хочет па них направить, Марцелл прекратил всякие
нападения и превратил осаду в блокаду».
После этого следует та характеристика Архимеда, которая была при-
приведена нами в самом начале статьи. Нетрудно видеть, что рассказ Плутарха,
восходящий в конечном счете к Полибию, представляет не совсем грамотную
амплификацию простого рассказа Нолнбия. Восемь попарно связанных судов
Полибия с четырьмя самбуками превратились в одну колоссальную самбуку,
носимую всеми восемью судами, связанными имеете. В рассказе появились
поднятые в воздух корабли, приводимые «о вращение и разбрасывающие
экипаж в стороны, как будто из пращи; ничего подобного у Полибия пет
и сам по себе этот факт невероятен. Еще хуже та ретушировка, которой
Плутарх подвергает Архимеда. В его рассказе есть определенное противо-
противоречие. В начале оп говорит, что «последний до сих пор еще не создал ничего,
заслуживающего внимания»; можно подумать, что только опасность, грозив-
грозившая родному городу, заставила Архимеда заняться механикой. В дальней-
дальнейшем жо, говоря о первой встрече Архимеда с Гиероном, он употребляет вы-
выражение: «в юношески смелом доверии (vEaviED^ojxevog ***)) к силе своего
доказательства»; иными слонами, можпо думать, что Архимед занимался
механикой с самого юношества. Мы видели, что Архимед действительно
*) Такие прототиин пулемета, Илп, лучше сказать, стуеломета, действительно были мзлестпы
в яллишнггической воеттй технике (полнбилы).
**) Мифический сторукяй гшаит.
»••) (jT vectvieuonrai поступать или говорить, как юноша.
НСТУПИТЕЛЬИАЯ СТАТЬЯ И. Н. ВЕСЕЛОНСИОГО
обратился к чистой математике сравнительно поздно; первой его специаль-
специальностью была именно механика. Дли «сякого беспристрастного читателя,
поппакомшипегося с рассказами Нолибим м Тита Ливия, совершенно ясно,
что Архимед был том, что мы сейчас назвали бм главным военным инжене-
инженером царя Гиерона, и его работа по подготовке носшшх машин била выпол-
выполнена во всяком случае до 216 года до н. :». — года смерти Гиерона, т. е. по
крайней морс за четыре года до осады Сиракуз Map цел л ом.
При установлении порядка, в котором были написаны сочинения Архи-
Архимеда, мы видели, что после «Досифеевских» сочинений Архимед снова воз-
возвращается к механике, пишет трактат «О раипоиесии», определяет положение
Смерть Архимеда. Мозаика, вероятно, из школы Рафаэля.
Городская галерея во Фрапкфурте-на-Майпе.
центров тяжести различных тел и, наконец, закладыпает основы гидро-
гидростатики. Внимательное чтение рассказа Лолибия позволяет сделать, как
кажется, довольно вероятное предположение о причинах такого возвращения
Архимеда к механике. Полибий говорит о машине, которая, захватывая нос
корабля, ставила его на корму и приподымала. Дли того чтобы рассчитать
такую машину, нужно, кроме знания законов рычага, иметь совершенно
ясное представление о потере веса, которую испытывает погруженное в воду
тело, иными словами, знать известный закон Архимеда, изложенный л пер-
первой книге ого трактата «О плавании». В связи с этим позволительно сделать
предположение, что причиной, заставившей Архимеда лернуться к механике,
были именно военные заказы царя Гиерона. Если этот царь, как мы знаем
из истории Полибия (книга V, 88) и Диодора (книга XXVI, 8), помог Родосу
после землетрясения 227 г. до и. э. также и поенными машинами *), то в это
время Архимед ужо должен был работать у Гиеропа; таким образом,
*) «Гшрсш и Гелон . . . даровали им евпеолу от пошлин дли идущих к ним судов рг;дян и пнть-
деент трехлоктешлх катапульт» (Полибий, V, 88).
4*
52 НСТУЛИТКЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОВСКОГО
двадцатые годы И иека до п. э. будут наиболее вероятным временем,
к которому мы должны отнести механические произведения Архимед» второ-
второго периода.
У Плутарха лее мы находим и наиболее полное описание обстоятельств
смерги Архимеда, погибшего во время грабежа римлянами взятых Сиракуз.
«Всого более жалел Марцелл о смерти Архимеда. Последний находился
дома, рассматривая какую-то геометрическую фигуру; так как он погрузился
в это исследование всем своим умом и всеми чувствами, то не заметил шума,
производимого бегавшими туда и сюда римлянами, и не знал, что город
уже был в их власти. Вдруг перед ним явился солдат с приказом следовать
за ним к Марцелл у. Архимед отказался идти, пока не найдет доказатель-
доказательства сноой задачи. Раздраженный римдялин вытаскивает меч и убиваег его.
Другие говорят, что какой-ro солдат пошел на него с мечом чтобы убить,
а Архимед настоятельно стал просить его подождать немного, пока он
закончит задачу, но солдат, которому было мало дела до его доказательства,
пронзил его мечом. Третьи говорят, что Архимед сам пошел к Марцеллу,
неси в ящике математические инструменты — солнечные квадранты, небес-
небесные глобусы и угломеры для измерения видимой величины Солнца, но поиав-
шиеся ему по дороге солдаты подумали, что он несет в ящике золото, и убили
его, чтобы овладеть этим золотом. Во нсяком случае, все историки признают,
что Марцелл был очень опечален смертью Архимеда, сторонился убшищ,
как святотатца и, приказавши отыскать родственников Архимеда, милостиво
с ними обошелся».
У Тита Ливия (книга XXV7, 31) говорится только, что Архимед был убит
не знавшим его солдатом, в то время, как он занимался геометрическими
исследованиями, от которых его не мог отвлечь шум, происходящий во взя-
взятом городе.
VIII
Так погиб Архимед, один из величайших математиков всех времен
я пародов. Нам остается проследить за дальнейшей судьбой его математи-
математического наследства.
Мы уже говорили, что эпоха Архимеда и его младшего современника
Аполлония была временем наивысшего расцвета классической греческой
геометрической школы; со II пека до н. э. характер греческой математики
резко изменяется, на первый план выдвигаются вычислительные методы,
и греческая математика становится, если можно так выразиться, «служан-
«служанкой астрономии». Мы видели, что это течение проявилось уже в коице науч-
научной деятельности Архииода, который отдал ему дань в «Псаммите»; после
него эта сторона математического развития настолько усиливается, что
Архимеда как математика просто забывают. Цицерон, открывший заново
могилу Архимеда но время спой службы п Сицилии, знает Архимода как
инженера и «открывателя числовых соотношений»; Тит Линий, как мы
видели, считает Архимеда только астрономом и конструктором военных
машип. Однако сочинения Архимеда продолжали жить; и I веко. н. э. их
знает Герон Александрийский, м конце III века Архимедом много занимается
Папп Александрийский; но ул«е в VJ веко строитель Св. Софии Исидор
Милетский и его ученик и комментатор Архимеда Ентокий Аскалонскик
знают только трактаты «О равновесии плоских фигур», «О таре и цилип-
дро» и л очень фрагментарном виде «Измерение крута». Б IX. веке в эпоху
расцвета при Македонской династии Констаптинопольского университета
Архимеда начинают знать гораздо больше; к этому времени относятся две
l.-*3>'::-: ' ' "',V'>^'*^fr "'-¦*¦• !:'"' • '?'¦'-:"':-. ''*
14№»^*в»«йий^< ¦ ;\ /
JLE..»*^ .i^. Jr»it» .JVu ^. .. i_ , ¦"• . . **.
Страница из найденного ГепПергом в иерусалимском монастыре Константп-
иопапьского палимпсеста (X п.).
54 ВСТУПИТЕЛЬНАЯ СТАТЬИ ГГ. Н. ВКСЕЛОВСКОГО
основные рукописи сочинений Архимеда; утраченная рукопись, принадле-
принадлежавшая в XV веке Георгию Валле, и недавно A907 г.) найденный констан-
константинопольский палимпсест, который являются основой всех современных
изданий токстои Архимеда.
Несколько более посчастливилось Архимеду у арабон. Здесь на норном
месте следует и оста нить харранца Сабита ибп Курра (836—901 гг.), пере-
переводчика сочинения Архимед» «О шаре и цилиндре» и «Геометрии» Евклида.
По-видимому, он был единственным арабским математиком, от которого оста-
лись специально механические произведения; его особенно интересовал
вопрос об определении условий равновесия неравноплечего рычага с учетом
веса последнего, необходимый для прапильной конструкции десятичных
весов. Ог Сабита до нас дошли две архимедовские антологии; одна из них
«Книга ледш» н средневековом латинском переподе (Liber assumptorum)
была известна очень даппо (впервые издана Фостером в Miscellanea — Лон-
Лондон, 1659), другая же «О семиугольнике» найдена очень недавио и и составе
собрания сочинений Архимеда публикуется нами впервые. Кроме того,
Сабит самостоятельно нанимался и другими темами из работ Архимеда:
ему принадлежит «Книга о правильном четырнадцатиграннике», иредста-
нляюгцом одно из полуправильных архимедовых тел.
Около 1000 г. н. э. знаменитый каирский астроном иби аль-Хайтам,
«Оптика» которого была настольной книгой всех западноевропейских астро-
астрономов вплоть до Кеплера, тоже занимался архимедовскими темами, вполне
владея интеграционными методами Архимеда. Он определяет объем сегмента
параболоида вращения, причем делает это другим способом, чем Архимед,
и независимо от него, так как «Коноиды и сфероиды» оставались неиявест-
пьши арабским математикам. Он также решает задачу об определении объела
параболического веретена — так называлось тело, полученное от вращения
параболы вокруг хорды, перпендикулярной к се оси — и правильно опре-
определяет его объем как -.-= объема цилиндра, описанного около веретена.
Кроле того, он занимался теорией правильного семиугольника, давши его
построение при помощи конических сечешш, отличное от того, которое мы
находим в трактате ибн Курры.
В Западную Европу сочинения Архимеда попали только после кон-
константинопольского погрома 1204 г., когда, вероятно, и был перевезен в Евро-
Европу манускрипт, находившийся позже у Георгия Баллы. Первый перевод
сочинений Архимеда на латинский язык был сделан францисканцем Биль-
гельмом из Мербеке, другом Фомы Акшшского. Этот перевод, законченный
в 1209 г., был найден Розе в Ватикане только в 1884 г. Этот перевод настолько
буквален, что передаются даже греческие члены F, т„ to), так что может
служить независимым источником для установления текста Архимеда, но
в сущэстве дела учопгай францисканец вряд ли разбирался. Дли нас пере-
перевод этот важен тем, что до самого недавнего времени: мы лишь из него знали
трактат «О плавающих телах» Архимеда; только открытие константинополь-
константинопольского палимпсеста Гейбергом познакомило нас примерно более чем с двумя
третями греческого текста. Часть перевода Мербеке была напечатала Лукой
Гауриком в Ленсции в 1503 г. (первое печатное издание сочинений Архи-
Архимеда); однако ато издание осталось настолько незамеченным, что знаменитый
Тарталья смело присвоил его себе и опубликовал в 1543 и 1565 гг. как «пере-
«перевод с греческого».
О пол о 1450 г. был выполнен второй латинский перевод Архимеда Яко-
Яковом Кремопским. В 1468 г. его переписал знаменитый Региомоптан и привез
в Нюренборг для опубликования. Однако ранняя смерть Региоионтапа не
щи-.¦"¦¦¦..:;¦¦ _¦,:.._ ¦¦:.¦..:;;:¦:; ¦^¦¦¦¦:;-фщг^Ж--;?*^. :'&::?---$;-<:::%^?~'ШШ
•*'¦¦''%'''''*¦ П А ^4 I4 JS. ~* ^^~Gt *%? (*} КЛ f+'%i&-А:~''с''~ ^'~'': *'-¦'«-'-" г^"''"" *^^^Ш
i^^:'-'Q V АБ;" EXTANT Ш'ЫШЩ^Ш
¦:--:J*Ze".--'.'¦ ¦ ¦ : " ¦¦^ ¦>-¦¦¦/•• •^••-.'- /.''"As
ШёШ
lif^^eS^ -¦ »2Ц|^И
Титульный лист сочинений Архимода издания Рино (Париж, 1^5).
56 ВСТУПИТЕЛЬНА!! СТАТЬЯ И. Н. ИЕСЕЛОВСКОГО
позволила ему выполнить свое намерение, так что первое издание греческого
текста Архимеда было выпущено только в 1544 гг. в Базеле на основе
рукописей, происходящих от текста Георгия Баллы). После итого рабо-
работы Архимеда входят в обиход ученого мира. Б 1558 г. выходит п Вене-
ции перевод Комманднно (второе издание с добавлением трактата «О пла-
плавающих телах» вышло в Болонье в 1565 г.), который уже иполне понимал
Архимеда.
К 1548 г. относится переработка сочинений Архимеда фра Мавролико
из Мессины. Последний >ie только вполне понимал Архимеда, но даже
иглользонал его методы для получения новых результатов. К трактату
«О равпхтесии» Маиролико добавил книгу о равновесии пространственных
тел, в которой были определены центры тяжести шара и ого частей, паралле-
параллелепипеда, призмы, октаэдра с параллельными гранями, пирамиды и сег-
сегмента параболоида. Это первое самостоятельное применение метода инте-
интеграции Архимеда, к сожалению, было напечатано только в 1E85 г. Поэтому
первым появивлгммея в печати самостоятельным исследованием при помощи
методов Архимеда было Do Centre gravitatis solidorum («Книга о центре
тяжести тел» Коммапдино (Болонья, 1505)), в котором даются положения
центров тяжести призмы, цилипдра, конуса, шарового сегмента (иным
способом, чем у Мавролико), усеченной пирамиды и конуса (вместо с их
объемами), правильных многогранников и сегмента параболоида вращения.
Начиная с этого времени, появляется целый ряд сочинений, поскящепный
вопросу о нахождении центра тяжести. В числе их нужно назвать одно из
первых научных произведений Галилеи, опубликованное им только it виде
приложения к Discorsi e dimostrazioni matcmatiche, иоскященное определе-
определению центра тяжести пирамиды (в дошедших до нас сочинениях Архимеда
этот центр не определен). Затем идет не предстанляющео ничего нового по
сравнению с Коммандино «Begbinselcn der Wceghkonst* («Основания
статики») Стевина (Лейден, 1586), «In duos Archimedi aequiponderaiitiurn
libros paraphrasis» («Передожение двух архимедовых кнвг о равновесии»
Гвидо Убальди (Псзаро, 1588), Т)е cenlro gravitatis libri tres» («Три книги
о центре тяжести») Луки Валорно A604), «Theoremata de Centro Gravitatis
Holidorum» («Теоремы о центре тяжести тел») Жана Шарля делли Файль
(Антверпен, 1632) и, наконец, венчающие весь ряд таких произведений
четыре тома «De Centro Gravitatis» («О центре тяжести») венского иезуита
Гульдена (Вена, 1С35—1641). Из этих произведений наибольший интерес
представляет сочинение Луки Валерио. В нем даются положения пентров
тяжестей тетраэдра, октаэдра, трапеции, усеченной трехгранной иырампды,
причем определение производится при помощи алгебраических формул, так
что Валерио является своего рода предшественником предельпого перехода;
данный им способ определения объема тара перешел в наши школьные
учебники геометрии. Поело определения объемов сферических сегментов
и усечетшх пирамид даются положении центра тижести полушара и сфе-
сферическою сегмента (пак мы теперь знаем, они были найдены Архимедом,
но решения его стали нам известными только после открытия «Офода»),
Затем рассматриваются параболоид и гиперболоид вращения (так же и усе-
усеченные), сферические пояса и, наконец, центры, тяжести сегментов сфероида
и гиперболического коноида. Небольшая книжка делля Файля интероспа
тем, что и ней впервые определяются центры тяжести круговых сектора
и сегмента.
В XVII веке на пер кое место выступают общие интеграционные методы
Архимеда, а также его гидростатические работы; в этом смысле Архи-
Архимеда можно было бы назвать ведущим математиком XVI1 века. Галилей,
Фронгиспис к оксфордским изданиям классических математических
произведений (Евклид, Архимеди др.). Перевод надписи: «Арлстппп,
сократический философ, будучи ныбришеи после кораблекрушения па
бсрог Родоса и увидев начерчеиньге геометрические фтп'урьт, как пере-
передают, сказал громко своим спутникам: «Будем надеяться на лучшее,
ибо я вижу следы людей». Лмтрукий, Об архитектуре, предисловие?
к fi-й кшпи».
:5« вступительная статья и. н. веселовского
довольно пренебрежительно относившийся к Аристотелю, не называет Архи-
Архимеда иначе как «divinissirao ArcMmcdc». Занятия Галилея бесконечно малы-
малыми пеличиггами, о которых мы узнаем из его писем и упоминаний в первом
диалоге «Босед и доказательств...», были продолжены его учениками: Тор-
ричоллп, первым определившим длину дуги параболы, и Кавальери в его
«Геометрия неделимых» (Болонья, 1G35). Крупным архимедистом был уже
упомянутый пыше Стевпн. Отдал дань Архимеду и молодой Гюйгенс, про-
продолживший работы Архимеда по исследованию равнолесия плавающих тел
(этой теме была посвящена одна из оставшихся не напечатанными юноше-
юношеских работ Гюйгенса) и определению длины окружности. Мы встречаемся
с бесконечно малыми у Кеплера, не стремившегося к строгости опубликован-
опубликованных произведений Архшмеда, в его «Stereometria doliorum». В этом отпо-
шешш интересно отметить, что хотя «Эфод» был найден только в 190G г.,
но описанный в нем метод квадратур Архимеда был, по существу, угадан
и Гюйгенсом, и другими архимедистами. Архимедова строгость, например,
характерное заключение определяемой криволинейной площади или тела
между двумя прямолинейными фигурами — вписанной и описанной —
была оценена значительно позже, чуть ли не Эйлером, или даже только
с начала XIX века, когда встал вопрос о строгом обосновании основных
теорем интегрального исчисления.
Б связи с этим истает интересный «опрос, почему греческая математика,
так далеко продвинувшаяся вперед и лице Архимода, не дошла до открытия
анализа бесконечно малых. Иногда зто объясняют статичностью, уравнове-
уравновешенностью классического идеала, исключающей всякую возможность изме-
изменении, которая является характерной особенностью современного исчисле-
исчисления бесконечно малых. Дело, однако, объясняется не особенностями грече-
греческого национального характера, но особенностями греческой математической
мысли эпохи Архимеда и ему предшествующего времепи.
Как мы видели выше, осповпой идеей иопийской школы была идея гео-
геометрического построении, исключающая всякие метрические элементы.
С другой стороны, основной идеей пифагорейской математики была идея
ч и с л а; с точки зрения пифагорейской школы геометрия была учением
о фигурах — об известных формах распределения единиц в пространстве.
Понятие о {i?ysOog — геометрической величине, представляющей часть
континуума,— носило тоже вполне определенный количественный характер
и исключало идею об изменении: числа и фигуры могли быть больше или
моныне одна другой, но не могли увеличиваться или уменьшаться. Идея
изменения у греков была связана с совершенно другой категорией — кате-
категорией качества: два человека не могли быть более д в у м я, чем два яблока,
но л гобой предмет мог быть более или менее красным, теплым, тяжелым
и т. д. Таким образом, идея изменения лежала вне области математики
и попала в последнюю очень отдаленным обходтгым нутом. В эпоху позднего
европейского средневековья в XIV веке у англичанина Суиссста в его «Cal-
«Calculator» и несколько позднее у француза Николая Орема появилась идея
графического изображения изменения качеств — появились произведения,
носившие заглавия «De latitudinibus formarum, De intension» et remissione
i'ormaruin» («Об увеличении и уменьшении качеств»), в которых ралиомер-
пое движение изображалось прямоугольником — ширина (latiludo) формы
оставалась неизменной (uniformis), откуда, между прочим, и произошло
позднейшее латинское название равномерного движения — motus unii'or-
mis; равномерно-переменное изменение изображалось в виде треугольника
или трапеции и называлось uniformiter — dilformis и т. д. Копечпо, из такой
чисто словесной классификации различных типов изменения, которую мы
Г у АРХИМЕД А ДУ
"'-¦ ¦;?¦ '¦ двЪ книги, ¦'¦ ;л:;: \
'¦'••;о шар* й цилиндр*, vv
•: . ;" ИЗМ1>РЕН1Е КРуГА ¦-\у\/\:
, ¦::: А и леммы.":- .-'릦'•.''.-•;
ПЕРЕВОД!» СЪ ГГЕ^ЯСКАГО
ТЯП0ГРА4Ш ДЕПАРТАМЕНТА НАРОДИАГО
Титульный лист первого перевода сочинений Лрхимода
на русский язык (СПб., 182.41.
fj() ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
находим в сочинениях Орсма (из них не «се еще опубликованы или даже
огшсапы), вряд ли могло получиться что-нибудь серьезное, но самый шаг —
объединение качественного изменения с геометрической интерпретацией —
был очень важным: идея изменения иыражалась в геометрической интерпре-
интерпретации*). Конечно, в настоящий момент мы не можем "оказать, каким образом
из идей Суиссета и Орема возникли (или даже могли возникнуть) современ-
современные нам понятия переменной величины, но дальнейшее развитие математики
второй половины XVII века пошло именно по линии развития понятия
о норемспной величине; если Архимеда можно считать родоначальником
интегрального исчисления, то открытие дифференциального исчисления
Лейбницем к Ньютоном дало такие простые и сильные методы, что способы
прямого интегрмропания Архимеда оказались выброшенными за борт,
и Архимед оказался и ряду почитаемых, но не читаемых классиков мате-
математической науки, которыми занимаются лишь филологи, но не математики.
Вслед за базельским изданием последовало издание учителя Людовика XIII
француза 1'ипо (Rivaltus), дающее лишь греческий текст предложений, за
которым следует латинский иереиод доказательств с произвольными изме-
изменениями (Париж, 1615). Третьим но счету было оксфордское издание Торел-
ли A792), за которым последовало издание датского филолога Гейберга
в трех томах A880—1881); второе издание гейберговского текста вместе
с шшопайденным «Эфодом» и другими сочинениями Архимеда появилось
в 1910—1913 гг.; с этого последнего издания и сделан предлагаемый перевод.
*) Оспошиан лдсп предшествующего изложения заимствована мной иу доклада В. П.
на семинаре но истории математики прн МГУ, которому п приношу спою благодарность.
АРХИМЕЛ
СОЧИНЕНИЯ
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
Наиболее ранние произведения Архимеда были посвящены механике. Они по дошли
до иас, но некоторое представление о них (правда, далеко не полное) можно составить
но цитатам из сочинений Архимеда у более поздних авторов. ¦*
К числу таких ннторон относится:
1°. Герои Александрийский, эпоху жизни которого в настоящее время относят
к I веку нашей эры. От него мы имеем «Механику», которая дошла до нас ю арабском пере-
переводе Косты ибн .Луки ал-Ьа'лпякки (т. е. из Паа.чьбска); она была найдена в конце
XIX века и впервые опубликована в тейбнерокском издании Геропа {т. I, Лейпциг.
1900 г.) в арабском подлиннике и немецком переводе. Не лее места и атом тексте понятны
и верны, и мы не всегда можем точно установить авторов имешщихся ошибок. Может
быть, некоторые из атих ошибок сделаны самим Архимедом, но еще более вероятно, что
они принадлежат Героиу или Косте ибн Луке.
'ir. Шип Александрийский (III век я. э.), автор «Математической библиотеки»,
последняя (восьмая) книга которой посвящена механике.
К этим двум авторам нужно добавить Симшшкия, византийского комментатора
Аристотеля (VI век н. э.) и его близкого современника Ектокия Аскалолского, оставив-
оставившего важные комментарии к сочинениям Архимеда; эти комментарии принято помещать
в полных изданиях сочинений Архимеда.
Сам Архимед в трактате «О плавании» упоминает свое механическое сочинение
«О равновесии (\aoQQonvxA). Ото, очевидно, трактат «О равновесии плоских фигур», но
ряд ссылок (касающихся центров тяжести круга, цилиндра, призмы, конуса, параболоида
вращения) «с может относиться к этому сочинению. Возможно, что оно дошло до иас
в неполном виде и, что, кроме книг о равновесии плоских фигур, были и книги, посвя-
посвященные равновесию телесных фигур; однако можно утверждать, что дошедшее до пас
сочинение «О равновесии плоских фигур» ле могло быть первым сочинением Архимеда
но механике. Вторая книга итого сочинения совершенно определенно должна быть напи-
написана поспе «Кнадратуры параболы». Поатому некоторые авторы считают, что первая книга
«О равновесии плоских фигур» представляла самостоятельное сочинение, предшествовав-
предшествовавшее «Квадратуре параболы». Но даже и и этом случае оно не могло быть первым сочи-
сочинением Архимеда по механике. Действительно, в нем нет определения центра тяжести,
которое, очевидно, предполагается изпестным; затем, самые доказательства часто (центр
тяжести прямоугольника и треугольника) ведутся искусственным способом от против-
противного, так что они скорее обращены к любящим строгость математикам, чем к механикам-
практикам; первоначальный способ нахождения центров тяжести прямоугольника и тре-
треугольника, конечно, был совершенно отличным и может быть заключался в разложении
площади на ряд «неделимых» прямых (см. отрывок из «Механики» Гсрона, II, 35—41).
Ба существование более ранпего сочинения но механике Архимеда указывают
и ссылки, имеющиеся ю «Квадратуре параболы». Этим сочинением, посвященным опре-
определению центра тяжести простейших фигур, могло быть упоминаемое Панпом сочинение
«О рычагах» (Пео) ?/и\»1У • собственно «О равноплечих рычагах»). Возможно, что в нем
и давилось то определение центра тяжести, которое мы находим у ТТапиа {VIII, 5) и Геро-
на («Механика», 1, 24): оба последних текста настолько близки друг к другу. *1ТО в выс"
шей степени вероятно, что они восходят к одному и тому же: источнику, которым и явля-
являлось упомянутое сочинение Архимеда. Вероятно, к нему же относится и упоминание
АРХИМЕД
Qpg («О центрах тяжести») у Симпликия, так что иг:т надобности принимать
гипотезу об особом сочинении под указанным заглавием.
Наконец, п арабской «Механике» Геропа имеются ссылки на «Книгу опор» Архи-
Архимеда («Механика», I, 25, 26~28, 30—31). В указанном тексте имеется доиоиыю значи-
значительное: количество ошибок и несообразностей, и если уж приписывать их в какой-то
доле Архимеду, то мы должны признать «Книгу опор» самым радним его сочинением.
Сопоставив все скааанное, можно высказать следующее предположение.
Самым рашшм произведением Архимеда была вышеупомянутая «Книга опор».
Изучение вопросов распределения давлений и устойчивости равновесия привело Архи-
Архимеда к кнедению понятия о центре тяжости, причем соответствующая теория (вероятно,
с точкп зрения практической механики) была развита в книге «О рычагах». Наконец,
математическое излолсснис теории центра тяжести было дало им в сочинении «О равно-
равновесии», которое было значительно больше дошедших до нас днух книг «О равновесии
плоских фигур».
Распределение механических фрагментов в настоящем илдашш произведено сле-
следующим образом.
Па первом месте помещен, большой отрывок из «Механики» Геропа, соответствую-
соответствующий архимедовой «Книге опор». Изложение в нем еще детское. Вес млогооиорной балки
для каждого пролета считается распределенным поровну между ограничивающими ятот
пролет опорами. В случао консольной балки считается, что опора под консолью выдер-
яшиаст нагрузку, соответствующую удвоенной длине выступающей части плюс половина
длины оставшейся части; вес этой части, таким образом, считается распределенным по-
поровну между опорой под консолью и оставшейся опорой как и в случае простой много-
онорпой балки. То.пько в случае сосредоточенных нагрузок давления на оноры нахо-
находятся правильно. Ото показывает, что во время написания «Книги опор» Архимед (если
нмшеупоыянутые ошибки принадлежат ему, а не Гсролу) еще ле знал, что «ее тела можно
считать сосредоточенным в его центре тяжести.
Рассмотрение давлений па опоры естественно привело Архимеда к одпоопорной
балке или рычагу; следующие фрагменты относятся к предполагаемой книге «О равно-
равноплечих рычагах». Здесь на первом месте стоят две цитаты из Паппа, касающиеся архи-
архимедова доказательства закона рычага; доказательство, имеющееся у Геропа, отнести
к Архимеду можно только условно. Далее помещен отрывок из комментария Евтокия,
иажный для уяснения понятия о момоптс (о/эя*]). Затем идут два текста из Геропа и Паппа,
касающиеся ппроделения цоптра тяжести, относительно которых можно сказать с уверен-
уверенностью, что их источник восходит к Архимеду; места и них, восходящие к Архимеду,
отмечены курсивом. Оба последних текста важны н том отношении, что oira раскрывают
самый процесс возникновения понятия о центре тяжести из рассмотрения давлений на
опоры. После них дан небольшой фрагмент из Симпликия.
Затем идут две цитаты из «Квадратуры параболы» и большой отрывок из Герона,
касающийся определения центра тяжести треугольника и многоугольников и показы-
показывающий .начальные стадии развития способов его нахождения; какая-то часть его может
восходить к Архимеду.
Наконец, последними идут цитаты из «Эфода» и «О плавающих телах», проливаю-
проливающие некоторый свет на то, что содержалось п не дошедших до пас кпигах сочинения
«О равновесии».
КНИГА О11ОР
I. ГЕРОИ, МКХАТШГСА, КН. 1, 25—28, 30—31*)
B5) Нам совершенно необходимо разъяснить кое-что о давлении,
передаче и переносе с количественной стороны в той мерс, как это нужно
для нпедстши. Архимод применял в этой части (механики) искус-
искусств», доведенное им до совершенства в книге, озаглавленной «Книга
опор». Мы разъясним то из нее, в чем мы нуждаемся для других вопро-
вопросов; воспользуемся из лее тем, что отпосится к количественной стороне
в той мере, п которой это нужно для изучающих.
Постановка (задачи) здесь такова: если имеется несколько
колонн, im которых находятся поппрочные балки или стона, причем
положения на краях одинаковы или различны, то есть балка или стона
*) См. [31J, стр. 71—85.
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
65
Н
В
D
Рис. 1.
могут выступать за один из концов или за оба конца, а расстояпия
между колоннами могут быть равны или пе равны, то мы хотим узнать,
сколько веса приходится на каждую колонну.
Пример этого: люди несут длинное брскпо, равномерное го весу,
(летав) на ранпых расстояниях по длине бревна, причем выступает
один из концов или оба конца; мы хотим узнать, сколько веса прихо-
приходится на каждого человека; это требуется (узнать) и при обоих
(выступающих концах) и при одном.
B6) Пусть на колоннах находится груз АВ равномерный по тол-
толщине и однородный {рис. 1}. Если он находится на двух колон-
колоннах АС и BD, то на каждую из них приходится половина веса АВ.
Пусть имеется еще одна колонна EF, делящая расстояние АВ
как угодно, и мы хотим узнать, сколько
веса приходится на каждую из колонн АС,
EF и BD. Представим себе, что груз АВ
разделен it точке Е вертикальной линией
но колонне {EF), тогда нам ясно, что
со стороны АЕ на каждую из колонн АС
и EF приходится половина ее веса, а со
стороны ЕВ на каждую из колонн EF и
ВТ) приходится половина ее веса, так как
пет никакой разницы it том, как распреде-
распределяется (вес) на колонны, находится ли
на них целая или разделенная (тя-
(тяжесть), поскольку как целая, так и разде-
разделенная все равно находится на колоннах. Следовательно, па колон-
колонну EF приходится половина веса ЕВ, и половина веса АЕ, то есть поло-
lunra всего веса АВ, па колонну АС приходится половина веса АЕ, а на
колонну BD половина веса ЕВ. Поэтому если мы разделим половину
АВ в отношении расстояпия АЕ к расстоянию ЕВ, то вес части,
пропорциональной (расстоянию) АЕ, придется па АС, а вес (части),
пропорциональной расстоянию ЕВ, — на BD.
Если мы поставим еще одну колонну HG, то нам ясно, что на АС
придется половина (веса) АЕ, на BD — половина (веса) НВ,
на EF — половина АН, а на НС — половина BE. Половина АЕ, поло-
половина НВ, половина АН и половина ЕВ вместе (равны) АВ, то есть
тому, что находится на всех колоннах.
Если колонн еще больше, мы узнаем, сколько веса получает каждая
из лих, с помощью того ?ке способа.
B7) Если так, то предположим, (что имеются) две одинаково
расположенные опоры АВ и CD {рис. 2} и пусть на них находится
тело АС, равномерное по размерам и весу. Мы уже говорили, что на
каждую из опор АВ и CD приходится ноловипа веса АС. Перенесем
теперь опору CD, приблизив ее к АВ, пусть ее положение — EF.
Мы хотим узнать, сколько веса теперь приходится на долю АВ и EF.
Заметим, что расстояние АЕ или равно расстоянию ЕС, или меньше
его, или больше его. Пусть сначала {АЕ) равно {ЕС). Тогда нам
ясно, что вес АЕ уравновешивается несом ЕС. Поэтому, если мы
уберем опору АВ, груз АС останется в том 5ке состоянии (равнове-
(равновесия), поэтому нам ясно, что на опору АВ не придется никакого веса
и весь пес АС придется (только) на одну (опору) EF.
Если расстояние СЕ больше расстояния ЕА, груз АС опустится
со стороны С.
о Архимед
АРХИМЕД
Если же расстояние СЕ меньше ЕА, пусть СЕ равна ЕН {рис. 3}.
Тогда СИ находится в равновесии на одной (колонне) RF. Поме-
Поместим (в точке Н) колонну HG и представим себе, что груз разделен
в точке Н. Тогда (вес) СН придется (только) па одну EF, а на
каждую из опор АВ и HG — по половине (веса) АИ. Поэтому, если
мы уберем опору HG, к точке // будет приложена вся сила, (которая
г
Рис. 2.
G Г
Рис. 3.
приходилась) на эту опору, если тело (груза) соединено. Поэтому
на (опору) А В t придется половина веса НА, а на (опору) EF —
все остальное, то есть СН и половина АН, Если мы представим себе,
что (груз) АС разделен пополам в точке К, то КЕ — половина АН.
Поэтому если опора, которая сначала была под Е, теперь будет под
точкой К, на пес придется весь вес АС, и чем больше удалится опора
от точки, делящей груз пополам, тем
большая часть веса придется па (опору)
АВ, остальной же «ее (придется) на
другую опору.
B8) Если так, то предположим, что
две опоры АВ и EF расположены, как
указано в предыдущем случае, и пусть
груз ЕС избыточный. Разделим груз АС
пополам в точке К. Мы доказали, что
на опору АВ (приходится) вес КЕ, а на
опору EF — остальная часть веса АС.
Предположим теперь, что под точкой С
(помещена) опора CD {рис. 4}. Уже
доказано, что (п этом случае) на опору АВ придется половина
веса АЕ, на опору DC — половина веса ЕС, а на опору EF — половина
(всего) веса АС. Перед тем, как мы поставили опору CD, мы
показали, сколько веса приходится па каждую из (опор) АВ и EF.
Поэтому пам ясно, что после того, как под грузом помещена опора (CD),
на опору АВ придется веса больше, чем раньше, на половину ЕН,
то есть на половину ЕС, а (опора) EF получит веса меньше, чем
она получала сначала, на величину ЕС. В силу сказанного на (опо-
(опору) DC придется вес половины ЕС, так как после того, как под груз
была помещена добавочная онора, па опору EF приходится меньше
(веса) па величину, равную ЕС, а на опору АВ приходится больше
веса на половину ЕС. Поэтому на (опору) CD придется остальная
половина веса ЕС. Та же величина получится и по другому способу.
Поэтому нам ясно, что если груз находится па опорах, которые
поддерживают его, и к этим опорам добавлена еще одна опора, то на
одни из первоначальных опор будет приходиться больше веса, чем
Рис. 4.
МЕХАНИЧКСКИЕ ФРАГМКНТЫ
67
D
Рис. 5.
до добавления (опоры), а на другие опоры — мепьше веса, чем до
добавления. Так, если были опоры АВ, EF и CD и на АВ приходилась
половина веса АЕ, то как мы видели, после того как (опора) CD убра-
убрана, па АВ приходится половина веса АК. Нам пени, что (часть гру-
груза) ЕС повиснет и станет действовать, как рычаг. Поэтому она снимет
часть тяжести, (приходящейся) на АВ, а на EF
придется (тяжести) больше, чем на ней было /-I ~л ^Г- \р
сначала, и груз АВ останется на своем месте.
C0) Предположим, что на опорах АВ и
CD {рис. 5} находится тело EF, однородное
по весу и равномерное по толщине, и пусть
оно выступает со стороны обеих опор. Мы
хотим узпать, сколько веса приходится на
каждую из опор. Так как мы доказали, что
если груз AF находится на (опорах) CD и АВ,
то CD получает больше веса, чем ЛВ, на удвоенную величину CF, a
если (груз) СЕ находится на (опорах) CD и АВ, то АВ получает
больше веса, чем CD, на удвоенную величину АЕ, нам ясно, что
на CD приходится настолько больше веса, чем на АВ, па сколько
удвоенная вел ичина CF превышает удвоенную величину АЕ. Если CF
и АЕ равны, то на каждую из (опор) CD и АВ приходится одина-
одинаковый вес; чем больше одно расстояние по сравнению с другим, тем
больше веса придется на соответствующую опору.
Из сказанного нами следует, что если на колоннах или опорах
находятся поперечные балки или степа, равномерные по толщине
и однородные по весу, и расстояния между опорами различны, мы
можем узнать, па какую из опор приходится больший вес и каков избы-
избыток веса. Если на опорах находятся поперечные балки или нечто подоб-
подобное, это уяснится для нас благодаря тому же самому способу. Точно
так же если люди несут дерево или камень на руках или на веревках,
причем некоторые из них находятся посередине, а некоторые — на
? F концах, и груз выступает с одной сто-
Аг— 1 i 1* роны или с обеих сторон, для нас ясно,
сколько веса приходится на каждого.'
C1) Пусть другой груз АВ, такжо
равномерный (по толщине) и однород-
однородный но весу, находится на одинаковых
опорах АС и BD {рис. 6}. Тогда нам
ясно, что каждая из опор получит
половину веса АВ. Подвесим к АВ в
точке Е груз. Если точка Е делит АВ
пополам, нам ясно, что па каждую из
олор приходится половила веса АВ и
половина веса груза, подвешенного или положенного в точке Е.
Если же точки Е пе делит {АВ) пополам, то разделим вес груза
в отношении BE к АЕ, тогда часть веса, пропорциональная ЕВ, при-
приходится на (опору) АС, а часть веса, пропорциональная ЕА, на
(опору) BD^tl, кроме того, каждая из опор получает половину
(веса)$АВ. Если мы подвес*™ другой груз в точке F и разделим
его вес в "отношении AF к FB, то на (опору) DB придется часть
веса, пропорциональная AF, а на (опору) АС— часть веса, пропор-
пропорциональная FB и, кроме того, на каждую из опор придется поло-
половина (веса)' АВ. О том, (чему равно) отношение FB к АС, уже
5*
6
6
Гис. С.
АРХИМЕД
сказано, сказано и о том, какие веса приходятся на опоры до подве-
подвешивания грузов в Е и F, следовательно, сказано о полной нагрузке,
которая приходится па опоры АС и BD. Тем же способом мы узнаем,
сколько иеса приходится на каждую из них и при подвешивании дру
гих грузов.
О РЫЧАГАХ
П. ТТА1Ш, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА, КН. VU1, 24*)
«В книге «О рычагах» Архимеда, а также в «Механике» Фило-
Филона**) и Геропа доказано, что большие круги пересиливают меньшие,
если вращение происходит около одного и того же центра».
III. ГЕРОИ, МЕХАНИКА, КН. II, П. 7***)
Представим себе два круга с одним и тем же центром Л {рис. 7},
пусть линии ВС и DE — их диаметры. Пусть оба круга могут вра-
вращаться около точки А, являющейся их центром, и
установлены перпендикулярно горизонту. Если мы
подвесим в точках В и С равные грузи F иН, то нам
ясно, что круги не наклонятся пи в одну сторону,
так как веса /' и // равны, расстояния ВА и АС
также равны, так что ВС — коромысло весов,
которое может вращаться около точки подвеса Л
Если же перенести груз, находящийся в С, и
подвесить его в Е, то груз F опустится впиз и
наклонит оба круга. Если мы добавим [в точку Е]
груз G, то он уравновесит груз F, если груз G
относится к грузу F как расстояние ВА к рас-
расстоянию АЕ. Поэтому мы можем рассматривать
1'ис. 7. линию BE как весы, которые могут вращаться
около точки подвеса А. Это доказал Архимед п своой книге о ранповесни
(книга первая, предложения VI и VII). Отсюда ясно, что можно сдвинуть
большую величину малой силой.
IV. ПАПП, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА, КН. VIII, 1 !••••)
; «Т? той же самой теории*****) относится задача: как двинуть данный
груз заданной силой******); это механическое изобретение Архимеда,
о котором он, как передают, сказал «дай мне где стать, и н сдвину Землю».
V. ЕВТОКИЙ, КОММЕНТАРИИ К ТРАКТАТУ
«О РАВНОВЕСИИ ПЛОСКИХ ФИГУР»*******)
«Момент (pCTTTfj)... является общеродовым понятием для тяжести
и легкости, как говорит Аристотель и, следуя ему,— Птолемей. Тимей
же у Платона утверждает, что всякий момент рождается лишь от тяже-
*) См [821. стр. 1068. 19 и ел.
**) Финок Византийский (II век до к. э.), автор большого курса «Механики» (из которого до
пли йтагмеиты ивух книг).
кас дошли фрагменты двух книг).
***) См. [811. стр. 111—43
*) См. [321. стр. 1060.
• •"> i.;m. |iZ|. стр. iuou.
*««**) Подразумевается теория дюдиитип тяжелых тел.
ф*»***),В подлиннике 6'Н'<хц«. что соответствует нашей «мощности»
¦«»•****) См. [15], 1-е издание, т. Ш, стр. 306.
(см. вступительную статью).
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ 69
сти, а легкость он считает лишением*). Любители ггаук могут
прочитать об этих мнениях и составленной Птолемеем книге о момен-
моментах, в физических, сочинениях Аристотеля, и платоповом «Тимее»
и в комментариях к ним. Л рассматриваемой книге Архимед называет
центром момента (/Mvzpov vrj; owtj;) плоской
фигуры точку, при подвешивании за которую
фигура остается параллельной горизонту; цен-
центром момента или тяжести двух или более пло-
плоских фигур он называет точку подвеса рычага,
остающегося параллельным горизонту, если
прикрепить к его концам упомянутые фигуры.
Пусть, например, дан треугольник ABC {рис. 8}
и в середине его точка D, обладающая тем
свойством, что при подвешивании за нее тре-
треугольник остается параллельным горизонту. 1>ис- 8-
В таком случае ясно, что части его А, В и С
уравновешивают друг друга и ни одна из них не будет иметь боль-
большего момента ((i-L.Xov psnei) к горизонту. Точно так же, если дан
рычаг АВ и к нему подмешены такие величщш А и В, что при подве-
подвешивании за С части А и В рычага уравновешивают друг друга, то он
останется параллельным горизонту и точка С будет центром подвеса
для величин А и В».
': VI. ГЕРОИ, МЕХАНИКА, КН. I, J, 2Л**) ':
Никто не отрицает, что о наклонении и отклонении в действитель-
действительности говорят только о телах. Если же мы говорим о плоских или телес-
телесных геометрических фигурах, что некоторая точка является их цен-
центром поворота и центром тяжести, то это достаточно разъяснено Архи-
Архимедом. Это будет понятно после того, что мы сообщим. Посидоиий***)
из школы стоиков дал физическое определение центра наклона и тяже-
тяжести: он сказал, что центр тяжести или наклона это такая точка, что
если подвесить и пей груз, он разделится на две равные части. Архимед
и его последователи в искусстве механики уточнили эти слова и уста-
установили разницу между точкой подвеса и центром наклона. Точка под-
подвеса — это такая точка тела или другого предмета, что если подвесить
его в этой точке, все его части будут находиться в равновесии, а не
будут качаться и наклоняться; равновесие же наступает тогда, когда
один предмет уравновешивает другой, как это имеет место в случае
весов, колеблющихся в плоскости горизонта дли в параллельной ей
плоскости. Архимед сказал, что грузи не наклоняются {если они под-
подвешены) на некоторой линии или в некоторой точке. Ото бывает па
линии, когда груз (подвешен) в двух точках этой линии, причем эта
линия не наклонена и плоскость, проведенная через эту линию перпен-
перпендикулярно горизонту, остается перпендикулярной (горизонту), как
бы ни перемещалась линия; тогда груз, (подвешенный) па линии,
не наклоняется. Когда мы говорим, что груз наклоняется, мы имеем
в виду его падение вниз, т. е. движение к земле. Раиповесие в точке
бынаст, когда груз подвешен н ней и при всяком движении части тела
•) отбодок — технический термин аристотелевской физики; в данном случае педраоуме-
вается лишение тяжести.
**) См. [31]. стр. 63—71. ¦ • ....
*"*) См. ъступиуельную статью, главу II. ..• .. ... .. ¦ . .: .-.
70 АРХИМЕД
движутся одинаково по отношению друг к другу. Груз уравновешивает
другой груз, если они подвешены в двух точках линии, разделенной
(точкой опоры) пополам, или в точке, делящей ее (в другом отпо-
. шении), причем линия становится параллельной горизонту, если
величины грузов относятся друг к другу обратно расстояниям точек,
в которых они подвешены, (от точки опоры). То, что подвешенные
таким образом грузы будут находиться в равновесии по отношению
к наклону, доказал Архимед в своих книгах о равновесии фигур, поль-
.- зуясъ при этом рычагами.
Точка подвеса и опоры — одно и то же, так как и точка подноса
и опоры оказывают одно и то же силовое действие: опора, к которой
подвешен груз, несет его; только опор может быть много и даже беско-
бесконечно много.
Что же касается центра наклона, то это единственная точка
в каждом теле, в которой сходятся перпендикуляры (к горизонту),
проведенные из точек подвеса*). У некоторых тел центры наклона
бывают тше их самих, как это имеет место в случае сводов и запястий.
То, что линии подвеса сходятся в одной общей точке, нам будет ясно,
если мы представим себе плоскость, перпендикулярную горизонту,
рассекающую тело на уравновешивающие друг друга части**). Тогда нам
ясно, что эта плоскость делит тело пополам, поэтому она проходит
через тело. Если мы представим себе другую плоскость, делящую тело
так оке, как зта плоскость, она также пройдет через тело. Эти две
плоскости пересекутся по линии и если бы эта линия пересечения не
прошла через точку подвеса, оказалось бы, что тела и уравновешивают
и не уравновешивают друг друга.
Примспим эти выводы к опорам. Представим себе тело, опираю-
опирающееся на лилию в плоскости***). Пусть части тела находятся в равно-
равновесии (относительно) этой линии. Если продолжить эту линию, она
пройдет внутри тела. Если бы она находилась вне тела, то ппе тела
находилась бы и плоскость, но мы видели, что это невозможно. Следо-
нате.иьно, линия пройдет лнутри тела и разделит его на части, уравно-
уравновешивающие друг друга. Если мы представим себе в качестве точки
равновесия другую точку, отличную от этой, окажется, как в первом
случае, что линия, проходящая через эту точку, пройдет внутри тела,
поэтому эти дне линии различны. Если провести через них две пло-
плоскости, они не (обязательно) пересекутся, так как через две линии
можно провести две непересекающиеся плоскости****). Получится то же
самое, что в первом случае, поэтому это невозможно. Таким образом,
мы узнаем, что эти плоскости пересекаются и линии встречаются',
поэтому эти линии находятся в одной плоскости. Если продолжить
эту плоскость до поверхности тела, то точки пересечения образуют
линию. Тогда имеется третья точка, попадающая вне атой линии.
Представим себе, что ота точка — также точка равновесия, то есть
*) Имеется в виду обычный enoci б определения центра тяжести путем подвешивания тела в
различных точках и нахождения точки пересечения вертикалей, проходящих через точки поивеса.
•*) Дальнейший текст Гсрона следует читать вместе с приведенным ниже текстом Паппа.
Курсивом отмечены места совпадающие в обоих текстах. 8ти места с наибольшей вероятностью
можно считать текстом садаого Архимеда. Отметим, что текст Пашш лучше текста Героиа, у кото-
которого встречаются несообразности и неясности.
***) Необходимость вставки отого слона иидпа из текста Паппн (п. 7).
*"¦••) По-видимому, мысль автора такопа: если имеются две точки равновесия, ие гаходящиеся
на одиой вертнкллн. через них можно провести дпе вертикали, а через них — дпе непсрссрквгтие
друг друга плоскости. Так как каждая такая плоскость должна делить тело на две урапнопртиьат
щие друг друга части; в таном случае получилось бы. что одна и та же часть тела находилась бы
одновременно и равновесии с двумя частями тела, одна из которых превосходит другую на часть
тела, находящуюся между двуми параллельными плоскостями.
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ 71
что тело {подвешенное) в этой точке, находится в равновесии*).
Проведем через эту точку линию {равновесия) внутрь тела. В силу
сказанного нами если провести эту линию., она встретит две линии
{подвеса), через которые проведена плоскость, и притом только
в точке их пересечения, так как если линия встречает две пересекающиеся
линии, а сама находится в другой плоскости, она встречает их в их
точке пересечения, ибо если бы она встречала их пе в их точке перс-
сечения, то необходимо часть этой линии находилась бы в одной пло-
плоскости, а остальная часть — в другой плоскости. Следовательно, все
линии подвеса встречаются в одной точке', эта точка и называется
центром наклона и тяжести.
VII. ПАПП, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА, КН. VIIT, 5-Й**)
E)... Мы говорим, что центром тяжести некоторого тела является
некоторая расположенная внутри него точка, обладающая тем свой-
свойством, что если за нее мысленно подвесить тяжелое тело, то оно остает-
остается в покое и сохраняет первоначальное поло-
положение. Эта точка, существующая пе только в А
геометрически правильных телах, но и в телах
неправильной формы, может быть найдена при
помощи следующих рассуждений.
Вообразим некоторую вертикальную пло-
плоскость ABCD {рис. 9j, направленную к центру с
мира, куда, по-пидимому, имеют стремление
{Ьохгр?) все тела, обладающие весом; пусть пря- Рис" 9'
мая АВ параллельна той плоскости, на кото-
которой мы паходимся***). Если какое-нибудь обладающее весом тело поло-
положить на прямую АВ так, чтобы оно полностью рассекалось продолже-
продолжением упомянутой плоскости, то оно может иногда занять такое положе-
положение, что будет оставаться в покое, ие вращаясь и не падая вниз.
Если это случилось и мы мысленно продолжим плоскость A BCD, то
она рассечет лежащее тело па две части, обладающие одинаковыми
моментами и взаимно уравновешивающиеся, если тело как бы под-
подпереть этой плоскостью****). Если затем переставить груз так, чтобы
он касался прямой АВ другой своей частью, то можно при поворачива-
поворачивании дать ему такое положение, что он, будучи отпущен, останется
в покое и не упадет. Если снова вообразить плоскость ABCD продолжен-
продолженной, то она разделит груз на две взаимно уравновешивающиеся
части и пересечется с первой плоскостью, делившей тот же груз
па две взаимно уравновешивающиеся части; если бы эти плоскости не
пересеклись, то те же самые части были бы и уравновешивающимися
и не уравновешивающимися, что нелепо.
G) После этих предпосылок вообразим прямую АВ, перпендику-
перпендикулярную к горизонтальной плоскости {рис. 10} и, следолательно,
направленную к центру мира; затем аналогичным образом положим
груз на точку А так, чтобы он, пользуясь прямой АВ в качестве
*) Иысяь автора тякоиа: ои нашел две точки подвеса, провел черев них две линии подвеса,
которые оказались в некоторой плоскости, образующей в сечении с поверхностью тела прикую,
на которой находятся обе первые точки подвеса. Он берет третью точку подвеса, не находящуюся на
этой кривой, и локазыпает. что линип подвеса, проходящая через эту точку, проходит через точку
(пересечения иврпых двух линий подвеса.
*•) С.н. [32J, стр. 1030 и ел.
**¦) То есть горизонтальной. . ¦ . • ¦
•***) То есть плоскостью ABCD ' ...-...¦:'..
72
АРХИМЕД
Л
Рис. 10.
подставки, когда-нибудь остался в покое па точке А, как он оставался
неподвижным на проведенной через нее плоскости. Если теперь, сохра-
сохраняя тело неподвижным, продолжить прямую АВ, то некоторая ее
часть будет находиться внутри рассматриваемого тела. Вообразим,
что последнее стало в некотором положении неподвижным; тогда
снова наложим его на указанную прямую другой частью так, чтобы
оно опять стало неподвижным; я утверждаю, что тогда продолженная
прямая АВ встретится с первоначально заключавшимся внутри тела
А отрезком- Действительно, если бы она пс встретилась, то
оказалось бы возможным, что некоторые плоскости, проведен-
проведенные через каждую из этих прямых, не пересекаются друг с
другим внутри тела, причем каждая из них разделяет груз на
части, которые одновременно являются и уравновешивающими-
уравновешивающимися и не уравновешивающимися, что нелепо; следовательно,
упомянутые прямые встретятся внутри тела. Точно так же
если в других положениях помещать груз на точку А так,
чтобы он оставался в покое, то снова продолженная АВ обя-
обязательно встретится с заключающимися внутри тела отрез-
отрезками первоначальных прямых. Из этого ясно, что такие вооб-
воображаемые прямые будут пересекать друг друга в одной и той же
точке; эта точка и называется центром тяжести. Яспо, что если
груз мысленно подвесить за центр тя?кести, то он не перевернется,
но будет сохранять любое приданное ему в начале положение, так
как все плоскости, проведенные через эту точку, будут разделять
груз на взаимно уравновешивающиеся части, у которых не будет
никакой причины для лерскерачивания.
(8) Пот в этом и заключается сущность теории центра тяжести;
доказываемые ею элементарные свойства последнего ты можешь узнать,
познакомившись с книгами Архимеда «О равновесии» и с «Механи-
«Механикой» Герона; в дальнейшем же мы изложим лишь то, что не является
известным большинству.
VIII. СИМПЛИКИЙ. КСМЕПТАРИИ К КНИГЕ АРИСТОТЕЛЯ «О НЕБЕ»
«Теория центра тяжести, относительно которой много и хорошо
написали Архимед и многие другие, имсот своей целью определить
центр данной тяжести, то есть некоторую точку на теле, при подве-
подвешивании за которую верепкой тело остается в том же положении без
изменения наклона».
IX. АРХИМЕД, КВАДРАТУРА ПАРАБОЛЫ, 6*)
«Действительно, каждое из подвешенных тел, укреплеппое в ка-
какой-нибудь точе{о, остается неподвижным к таком положении, когда
точка подвеса и центр тяжести подвешенного тела находятся на одном
перпендикуляре; это тоже доказано».
X. ГЕРОН, МЕХАНИКА, КН. II, 35-41**)
C5) Нам необходимо доказать кое-что... о более важных вещах,
которые разъясняли Архимед и другие.
*) См. стр. 81 этого издания.
•*) См. [32J, стр. 189—199.
МЕХАНИЧЕСКИЕ ФРАГМКНТЫ
73
Прежде всего сообщим, как определяем центр тяжести треуголь-
треугольника, равномерного по толщипе и однородного по весу. Пусть данный
треугольник — треугольник ABC {рис. 11}. Разделим линию ВС
пополам в точке D и соединим точки А и D. Если опереть треугольник
на линию AD, он не наклонится ни в ту, ни в другую сторону, так как
треугольники ABD и ADC равны*). Точно так же, если мы разделим
линию АС в точке Е и соединим точки В ц Е vl если опереть треуголь-
треугольник на линию BE, он также не наклонится ни в ту, ни в другую сто-
сторону. Так как треугольник, будучи оперт на каждую из линий AD
и BE, находится в равновесии
своих частей и не наклоняется ни
в ту, ни в другую сторону, общая
точка, в которой эти две линии
пересекаются, является центром
тяжести, это — точка F. Необхо-
Необходимо представлять себе точку F в
середине толщины треугольни-
треугольника ABC. Поэтому нам яспо, что
если мы соединим точки А и D,
разделим линию AD в точке F
на такие две части, (одна) из которых AF — удвоенная (другой) FD,
то точка F будет центром тяжести. Действительно, если мы соеди-
соединим точки D и Е, линия АВ будет параллельна линии DE, так как
линии АС и ВС разделены в точках D и Е (пополам); таким обра-
образом, отношение АС к СЕ равно отношению АВ к ED, но липия
АС — удвоенная литая СЕ, откуда следует,
что линия АВ — удвоенпая ED. Но линия АВ
относится к ED как линия AF к DF, сле-
следовательно, AF — удвоенная FD, в силу
того, что фигуры ABF и DFE обладают
равными углами.
C6) Мы хотим определить то же самое
для четырехугольника. Пусть данный че-
_ тырехугольник — четырехугольник ABCD
В {рис. 12}. Соединим точки В и D и разде-
разделим BD пополам и точке Е, соединим также
(точки) А и Е, Е и С и разделим линии АЕ
и ЕС в точках F и Н таким образом, что-
чтобы AF была удвоенной FE, а СН — удноепной НЕ. Тогда центр (тя-
(тяжести) треугольника ABD — точка F, а центр треугольника BDC —
— точка //. Мы получим то же самое, если будем представлять себе
весь вес треугольника ABD (сосредоточенным) в точке F, а весь
вес треугольника BCD — н точке //. Тогда лилия FH становится веса-
весами, па концах которых находятся зти величины. Поэтому если мы
разделим липию FH в точке G таким образом, что СН относится к FG
как вес F, то есть вес треугольника ABD, к весу Н, т. е. весу треуголь-
треугольника BDC, то точка G, в которой оба веса уравновешиваются, являет-
является центром (тяжести) этого четырехугольника.
C7) Мы хотим определить то же самое для пятиугольника ABCDE
{рис. 13}. Соединим BE и определим центр тяжести треугольника
*) Под ранними трвугольниками ядесь имеются в виду равновеликие треугольник-! (кон-
(конгруэнтные треугольники назывались «равными и подобными треугольниками»). В подлиннике могло
также стоить «рашюисенщиео.
Рис. 12.
74
АРХИМЕД
ABE, пусть это будет точка F; пусть центр тяжести четырехугольника
BCDE будет в точке И. Соединим точки ? и Н и разделим линию FII
па две части таким образом, чтобы часть HG относилась к GF, как
вес треугольника ABE к весу четырехугольника BCDE. Поэтому
точка G — центр тяжести фигуры ABCDE.
Такой же способ мы будем применять и для всех многоугольников.
C8). Если дан треугольник ABC, равномерный по толщине и несу,
и под точками А, В и С находятся одинаково расположенные опоры
{рис. 14}, то мы хотим определить, ка-
какую величину веса треугольника ABC
Рис. 14.
несет каждая мз этих опор. Разделим линию ВС пополам в точке D,
соединим точки А и D и разделим линию AD на дно части в точ-
точке Е таким образом, что часть АЕ — удвоенная ED. Тогда точ-
точка Е — центр тяжести всего треугольника. Нам нужно распределить
этот вес по опорам. Если мы пред-
представим себе линию AD а равно-
равновесии подвешенной в точке Е, то
вес и D будет удвоенным весом
в А, так как линия АЕ — удвоеп-
ная линия ED. Если мы предста-
представим себе, что вес в D распреде-
распределен по точкам В и С таким
¦¦л образом, чтобы линия ВС находи-
находилась в равновесии, то на каждую
из точек В и С придется половина
веса в D, так как линии BD и DC
равны. Но вес в D был удвоенным весом в А. Следовательно, иеса во
всех трех точках А, В и С равны и, значит, опоры будут нести
равные нагрузки.
C9) Пусть дан треугольник ABC, также равномерный по весу
и толщине и находящийся на одинаково расположенных опорах
{рис. 15}, и пусть в точке Е, расположенной где угодно, положен
или подвешен груз. Мы хотим определить, какую долю веса, (поме-
(помещенного) в Е, несет каждая из опор. Соединим (точки) А и Е и про-
продолжим АЕ до D. Разделим нес в Е на две части таким образом, чтобы
треугольник находился в раиновесни, будучи оперт на линии AD.
Тогда отЕюшенае веса и D к весу и А равно отношению линии АЕ к ли-
линии ED. Далее разделим вес в D так, чтобы (линия) ВС находилась
в равновесии, будучи поднешена (в />). Тогда отношение веса в С
Рис. 15.
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
75
Рис. 16.
к весу в В равпо отношению линии BD к линии CD. Вес в D найден,
следовательно, найдены и веса в В и С; вес в А также найден. Следо-
Следовательно, найдены веса во (всех трех) опорах.
D0) Если дан треугольник ABC и подвешены известные грузы
в точках А, В и С {рис. 16}, то мы хотим определить внутри тре-
треугольника такую точку, что если подлесить треугольник в этой точке,
он будет находиться в равнове-
равновесии. Разделим линию АВ в точ-
точке D таким образом, что линия BD
относится к AD как вес \\ A vl ве-
весу в В. Тогда точка D будет
общим центром тяжести обоих
грузов. Соединим точки D и С ли-
линией DC и разделим ее в точке Е
таким образом, что отношение ли- в*
нии СЕ к линии ED равпо отно-
отношению веса в D к весу в С. Тогда
точка Е будет общим центром
тяжести всех трех грузов. Следовательно, она и будет точкой подвеса.
D1) Мы хотим определить то же самое и для многоугольников.
Пусть фигура ABCDE — многоугольник {рис. 17}. Подвесим и точ-
точках А, В, С, D и Е известные грузы. Разделим линию АВ в точке F
таким образом, что отношение линии BF к FA равно отношению веса
в А к весу в В. Тогда точка F — (об-
(общий) цептр (тяжести) двух грузов, нахо-
ДЯТЕ1ИХСЯ на АВ. Разделим также ли-
пню DE в точке Н таким образом, что
отношение линии DH к линии НЕ ракпо
отношению веса в Е к весу и D. Тогда
точка Н — общий центр тяжести точек Е
и D. Соедипим FH и разделим FH в точ-
точке G таким образом, что отношение об-
щего (веса) в А и В к общему (весу)
и D и Е равно отношению HG к GF.
Тогда точка G — общий центр тяжести
точек А, В, D и Е. Соединим точки С и
G линией CG и разделим ее б точке К
таким образом, что линия СК отно-
относится к KG как (общий) вес в А, В, D и Е к весу в С. Тогда,
следовательно, точка К будет общим центром тяжести всех грузов.
XI. АРХИМЕД, КВАДРАТУРА ПАРАБОЛЫ, 6
в
Разделим липию ВС в Е так, что-
чтобы СЕ была вдвое больше ЕВ, прове-
проведем КЕ параллельно DB, и разделим
ее в G пополам {рис. 18}; тогда точ-
точка G будет центром тяжести треуголь-
треугольника BDC; зто действительно доказа-
доказано в «Механике»*).
*) Архимед не гоиорит: «докавано в книге «О равновесии»: следовательно, в момент
написания трактата «Квадратура параболы» книга «О равновесии» еще не существовала.
76 АРХИМЕД
XII- АРХИМЕД, О ПЛАВАНИИ, RII. Ц, 2*)
«Действительно к «Началах механики» доказано, что если отпять
какую-нибудь величину, не имеющую одного и того же центра тяжести
с целой величиной, то центр тяжести остатка будет находиться на
прямой, соединяющей центры тяжести целой и отнимаемой величин,
если продолжить ее в ту сторону, н которой находится центр тяжести
целой величины»**).
О РАВНОВЕСИИ
ХШ- АРХИМЕД, ЭФОД, ЛЕММЫ***)
7. Центром тяжести круга является точка, которая одновременно
является и геометрическим центром круга.
8. Центр тяжести всякого цилиндра находится на середине его оси.
9. Центр тяжести всякой призмы находится на середине ее оси.
10. Центр тяжести всякого конуса находится на ого оси и точке,
делящей последнюю так, чтобы отрезок, прилегающий к иершиие, был
втрое больше остатка.
XIV. АРХИМЕД, ЭФОД, 1****)
«Разделим прямую ТК (медиану треугольника ЛТЪ) в точке X
так, чтобы ГК была втрое больше КХ; тогда точка X будет центром
тязкести треугольника AZF; это действительно доказано в книге
«О ракповесии» (?vto?? taoppomxoic)».
XV. АРХИМЕД, О ПЛАВАНИИ, КН. II, 2*****)
«Действительно, в книге «О равновесии» доказано, что у вся-
всякого сегмента прямоугольного коноида (-параболоида вращения)
центр тяжести будет находиться на оси к точке, разделяющей послед-
последнюю так, чтобы отрезок, прилегающий к вершине, был идпое
больше остатка».
*) См. стр. 336 этого издания.
**) Ом. предложение VIII иериой книги «О равновесии плоских фигур». Однако употреблен-
ими в рассматриваемой книге способ докяэятельстла от противного, а также употребленные Архи-
Архимедом при цитировании выражения позволяют думать, что в данном случае Архимед имел в виду
более ранне?, сочинение, тем более, что он несколькими строками выше, говори о центре тяжести
сегмента параболоида вращения, цитирует трактат «О равновесии» (см. ниже, фрагм. XV).
•**) Г.м. стр. 299 этого издании.
****) См. стр. 301 втого издания.
¦*•**) См. стр. 336 этого издания.
КВАДРАТУРА ПАРАБОЛЫ
Архимед Досифею желает благоденствия!
Узпаиши о смерти Конона, делавшего вес для пас из дружбы,
и о том, что ты был близок к Конону и сведущ в геометрии, мы очень
опечалились о покойном и как о друге и как о выдающемся матема-
математике. Поэтому мы решили написать тебе, подобно тому как обычно
писали Конону, и послать некоторые геометрические теоремы, оставав-
остававшиеся ранее неизвестными, а теперь полученные нами; они были
сначала обнаружены нами при помощи механических методов, а затем
доказаны также и геометрически.
Некоторые из занимавшихся ранее геометрией пытались доказать,
что возможно найти площадь, ограниченную прямыми линиями и рап-
рапную заданному кругу или его сегменту; затем они пробовали пре-
превратить в квадрат площадь, заключающуюся между прямой и сече-
сечением целого конуса*), пользуясь при этом не вполне дозволенными
предположениями, вследствие чего болыпипстио >татематиков и не
признало за ними решения этой задачи. Что же касается сегмента,
ограниченного прямой и параболой, то, насколько пам изкестпо,
никто из предшествующих математиков не пытался его квадрирокать,
нами же эта квадратура в настоящее время найдена. Действительно,
можно доказать, что всякий сегмент, заключенный между прямой
и параболой, составляет четыре трети треугольника, имеющего с сег-
сегментом одно и то же основание и рапные высоты. При этом доказатель-
доказательстве принимается следующее предположение.
Если имеются две неравные площади, то, постоянно прибавляя
к самому себе избыток, на который большая площадь превосходит
меньшую, можно получить площадь, которая была бы больше любой
заданной ограниченной площади. Этой леммой пользовались также
и -дшвшие ранее геометры.
При помощи именно этой леммы опи доказали, что круги находят-
находятся друг к другу к двойном отношении их диаметров, шары — друг
к Другу в тройном отношении их диаметров, и также что всякая пира-
пирамида составляет третью часть призмы, имеющей с пирамидой одпо
*) 1Год несколько странным выражением «сечение целого конуса» (следовало бы скавать
«остроугольного конуса»), но всей нидимости, подразумеваете!! эллипс.
78
АРХИМЕД
и то же основание и одинаковую высоту. Доказательство того, что
всякий конус составляет третью часть цилиндра, имеющего с конусом
одно и то же основание и одинаковую высоту, опи изложили, приняв
некоторое предположение, подобное упомянутой лемме. При этом
каждая из упомянутых теорем считается ничуть но менее правильной,
чем другие, доказываемые без помощи упомянутой леммы; поэтому
совершенно достаточно, чтобы такую же степень достоверности имели
и теоремы, излагаемые нами теперь. При доказательстве мы сначала
показываем, как эта теорема была обнаружена нами при помощи меха-
механики, а затем уже, как она доказывается
геометрически. Предварительно излагаются
основные свойства конических сечений, не-
необходимые для доказательства. Будь здоров!
I
Если АВГ {рис. 1} — парабола, прямая
Рис. 1. БД параллельна диаметру или сама является
диаметром*), а прямая А Г параллельна каса-
касательной к параболе в точке В, то АЛ будет равна ДГ; и если АД рае-
на ДГ, то прямая А Г и касательная к параболе в В будут параллельны»
II
Если АВГ {рис. 2} — парабола, прямая ВД параллельна диаметру
или сама является диаметром, прямая ЛАГ параллельна касательной
к параболе в точке В и ЕГ — касатель-
касательная к параболе в точке Г, то прямые.
ВА и BE будут равны.
III
Если АВГ {рис. 3} — парабола,
прямая ВЛ параллельна диаметру или:
сама является диаметром, и параллельно касательной к парабо-
параболе в точке В проведены какие-нибудь прямые АА и EZ, то отношение
линий В А в BZ будет равно отношению квадратов па АД к EZ.
Все эти теоремы доказаны в «Началах теории конических сече-
;ний» [1].
") Под диаметром здесь и ниже подразумевается ось параболы
КВАДРАТУРА ПАРАБОЛЫ
79
IV
Пусть АВГ {рис. 4.} будет сеемент, заключающийся 'между прямой
и параболой, пусть прямая БД проведена из середины АГ параллелъ-
'¦ но диаметру или сами является диаметром, и соединяющая прямая ВГ
продолжена. Если параллельно БД провести
какую-нибудь другую прямую Z0 так, что-
чтобы она пересекала прямую, проходящую черея
R
точки В и Г, то ZB будет иметь к ©Н то же самое отношение, что
ДА к AZ,
Действительно, через точку II проведем прямую КП параллельно
АГ; тогда отношение линий ВД и ВК будет таким же, как отношение
квадратов на ДГ и КН;
"вк
вг
BI
Е0
гд
\А
Аи
зто доказано (п предложении III). Следовательно, отношение линий
ВГ и В1 будет равно отношению квадратов па ВГ и на Вв.
вга
Вв2
так как AZ равна КН; значит, линии ВГ, ВО и BI будут составлять
пропорцию*). Таким образом, БГ к В0 имеет то же самое отноше-
отношение, что Г0 к 01;
Г0 ••)
01
значит, как ГД относится к AZ, так и BZ будет относиться к 0Н***).
ez
вн
Но ДГ равна ДА; тогда ясно, что ДА будет иметь к AZ то же самое
отношение, что Z0 к 6Н.
Z©
V
Пусть АВГ {рис. 5} будет сегмент, заключающийся между пря-
прямой и параболой, из точки А параллельно диаметру проведена пря-
прямая ZA, а из точки Г — касательная TZ к параболе в точке Г. Если
в треугольнике ZAT параллельно AZ провести какую-нибудь прямую,
«) Так как ВГ : BI - ВД : ПК = ДГ2 : КП* = (ДГ : AZJ — (ВГ : ВвJ, -п.. асгаи,
ВГ-ве!- ВГ2-В1, т. е. Вв2=ВГ-В1 и ВГ:Вв=Вв:В1.
••) Имеем ВГ : ВЬ— F16 : BI; отсюда
ВГ : № — (ВГ i B0) : (В© ± BI) = Гв : в1. . .
••*) В самом дгас, ¦• -'
ГЛ : AZ=Br: Вв — Гв : в! = вХ : вН.
80
АРХИМЕД
то эта прямая разделится параболой в том же самом отношении,
а каком ЛГ разделится проведенной, прямой, причем отрезок прямой
А Г, прилежащий к А, будет соот-
соответствовать ближайшему к А отрез-
отрезку проведенной прямой.
Проведем параллельно AZ ка-
какую-нибудь прямую ДЕ, и пусть
сначала ДЕ разделит АГ пополам.
Тогда, так как АВГ есть парабола,
прямая ВД проведена параллельно
диаметру, а прямые АЛ и ДГ рав-
равны, то АГ будет параллельна каса-
касательной к параболе в точке В (пред-
(предложение I).
Далее, так как ДЕ параллельна
диаметру и из точки Г проведена
касательная ГЕ к параболе в точке
Г, а прямая ДГ параллельна каса-
касательной к параболе к точке В, то ЕВ
будет равна ВД (предложение II);
таким образом, АД к ДГ имеет то
же самое отиошение, что ДВ к BE.
ад _ дв
вг — be
Теперь, если проведенная пря-
прямая сечет А Г пополам, то теорема
уже доказана; в противном случае проведем параллельно AZ какую-
нибудь другую прямую КЛ; следует доказать, что АК будет иметь к КГ
то же самое отношение, что Кв к 0Л.
АК _ ке
кг ~ ел
Действительно, так как BE равна ВД, то и IA"будет равна KI; значит,
ЛК относится к КТ, как АГ к ДА.
ЛК АГ
KI ДА
Но KI так же относится к Кв, как ДА к ЛК.
KI ДА
Кв АК . • .; • ---
что доказано в предыдущем*); таким образом, Кв к 0Л и АК к КГ име-
имеют одно и то же отношение**)
Кв АК
ел * кг
Итак, предложение доказано [2].
•) Согласно иредпожению IV. имеем:
К1:10 = ЛЛ:КД :
¦ Отсюда, «переворачивая»,
(KI - 16) : KI = (А А - KD) : АА, т. с. Кв : KI - АК . Л Д.
* *) Действительно, ия продыдущией пропорции, имим:
-Отсюда
<КЛ - Кв) : Кв-^ (АГ - АК) : ЛК, т. с. Лв : Кв = КГ : ЛК-
КВАДРАТУРА ПАРАБОЛЫ
81
Рис. 6.
VI
Вообразим, [как ато делается в теоретических исследованиях]*),
что лежащая перед нами [видимая] плоскость перпендикулярна
к горизонту, [затем] представим, что та ее часть, которая от липни
АВ {рис. 6} простирается л сторону Д, будет нижней, простирающая-
простирающаяся же в противоположную сторону — верхней; пусть ВДГ будет
прямоугольный треугольник с иря- ., р к р
мым углом при В, сторона ВГ кото-
которого равна половине равноплечего
рычага; [предполагается, конечно,
что АВ равна В Г]; подвесим рас-
сматрипаемый треугольник п точках
В и Г, а с другой стороны рычага, в
точке А, подвесим некоторую пло-
площадь Z, и пусть площадь, подве-
подвешенная в точке А, уравновешивает
треугольник ВДГ в том положении, какое оп теперь имеет. Я утверж-
утверждаю, что площадь Z будет третьей частью треугольника ВДГ.
Действительно, так как рычаг предполагается уравновешенным,
то мы можем считать, что линия АГ параллельна горизонту, а прямые
в плоскости, перпендикулярной к горизонту, проведенные под прямым
углом к ЛВ, будут тоже перпендикулярны к горизонту. Разделим
линию ВГ в точко Е так, чтобы ГЕ была вдвоо больше ЕВ: параллельно
ДВ проведем прямую КЕ и разделим ее пополам в точке 0; тогда, как
доказапо в «Механике»**), точка 0 будет центром тяжести треуголь-
треугольника ВДГ. Если теперь у треугольника ВДГ уничтожить подвесы в В
и Г и подвесить его в точке Е, то треугольник останется в том же самом
положении, какое оп имел перед этим; действительно, доказано так-
также и то, что каждое тело, подвешенное в какой угодно точке, будет
оставаться неподвижным в таком положении, когда точка подвеса
и центр тяжести подвешенного тела находится на одном перпендикуля-
перпендикуляре. Так как положение треугольника ВГД относительно рычага остает-
остается тем же самым, то оп будет продолжать уравповешивать площадь Z.
Если же подвешенная в точке А площадь Z и подвешенный в точке Е
треугольник ВДГ находятся в равновесии, то ясно, что они будут
обратно пропорциональны длинам (соответствующих плеч), и получится,
что, как АВ относится к BE, так и треугольник ВДГ будет относиться
к площади Z: но АВ втрое больше BE; значит, и треугольник ВДГ
будет втрое больше площади Z.
Очевидно также, что и обратно, если треугольник ВДГ будет
втрое больше площади Z, то равновесие сохранится.
VII
Пусть будет опять равноплечий рычаг АГ {рис. 7} с серединой
в точке В; подвесим его за точку В. Пусть ГДП — тупоугольный тре-
треугольник с основанием АН и высотой, равной половине рычага; под-
подвесим треугольник А ГН в точках В и Г, vf пусть подвешенная в точке А
*) оте tOTiv гп iv ts. flEfiigia—неясное место, которое Гейберг считает хюздиейшей вставкой
и поятому ставит d киадратных скобках.
**) Ото может быть вообще каким-нибудь сочиненном по механике; но Солее вероятно, что это
одно иг ранних сочинений самого Архимеда, например, Пео.' '
6 Архимед
82
АРХИМЕД
площадь Z будет уравновешивать треугольник ГАН в занимаемом
им положении. Докажем точно так же, что площадь Z будет третьей
частью треугольника ГДН.
Действительно, лодпесим в точке Л еще некоторую площадь (Л),
являющуюся третьей частью треугольника ВГП; тогда треугольник
„кг ВДГ уравновесится с площадью Z+Л.
Теперь, так как треугольник ВГН урав-
уравновешивается с Л, а треугольник ВГД
с площадью Z вместе с А, и площадь
Z+Л является третьей частью треугольни-
треугольника ВГД, то ясно, что треугольник ГДН
будет также втрое больше площади Z.
VIII
Рис. 7.
Пусть будет равноплечий рычаг АВГ
{рис. 8} с серединой В, подвешенный
за точку В; пусть ГДЕ будет прямо-
прямоугольный треугольник с прямым углом
при Е, подвешенный к рычагу в точках Г и Е; подвесим в точке А
некоторую площадь Z, и пусть она уравновешивает треугольник ГДЕ
в занимаемом положении; пусть отношение АВ к BE будет равно
отношению треугольника ГДЕ я , „ г
к некоторой площади К.
Я утверждаю, что площадь
Z будет меньше треугольника
ГДЕ, но больше плогцади К.
Действительно, возьмем
центр тяжести треугольника Рис. 8.
ДЕГ — пусть он будет в точке
0 — и параллельно ДЕ проведем прямую 611. Так как треугольник
ГДЕ уравновешивает площадь Z, то площадь ГДЕ имеет к Z то же самое
отношение, что АВ к ВН: так что Z будет меньше площади ГДЕ.
Поскольку же треугольник ГДЕ относится к Z, как ВА к ВН, а к
„ „ „ площади К — как ВА к BE,
то ясно, что треугольник ГДЕ
имеет к К большее отноше-
отношение, чем к Z, таким образом,
Z будет больше К.
К
IX
Пусть А.Г {рис. 9} бу-
будет опять равноплечий рычаг
Рис. 9. с серединой В, а ГДК —
тупоугольный треугольник
с основанием ДК. и высотой ЕГ; подвесим его к рычагу в точках
Г и Е, а в точке А подвесим площадь Z, и пусть она уравнове-
уравновешивает треугольник ДГК в занимаемом положении; пусть отношение
АВ к BE будет равно отношению треугольника ГДК к некоторой пло-
площади А. Я утверждаю, что площадь Z будет больше Л, по меньше
треугольника ДГК.
Доказывается это точно так же, как предыдущее. .
КВАДРАТУРА ПАРАБОЛЫ
X
Пусть АВГ {рис. 10} будет опять равноплечий рычаг с середи-
серединой В, а ВДНК — трапеция с прямыми углами при В и Н и со сторо-
стороной КД, стремящейся к точ-
точке Г*), пусть отношение АВ
к ВН будет равно отношению
трапеции ВДКН
площади Л.
В точках В и Н подвесим к
рычагу трапецию ВДНК, а в
точке А — площадь Z, и пусть
она уравновешивает трапецию
ВДКН в занимаемом ею поло-
И утверждаю, что
к некоторой
площадь Z будет меньше А.
Разделим прямую АГ в точке Е так, чтобы ЕЙ имела к BE такое
же отношение, как удвоенная АВ и KII к удвоенной КН и ВД.
ЕН 2&В+КП
BE " 2К1Н-БЛ
Затем проведенную через Е параллельно ВД прямую EN разделим
в точке 0. пополам; тогда, как доказано в Механике**), точка 0 будет
центром тяжести трапеции ВДКН. Если теперь подвесить трапецию
в Е, a is точках В и Н освободить, то на основании того же, что и в пре-
предыдущем, она будет оставаться в покое в том же самом положении
и уравновесит площадь Z. Так как теперь подвешенная в Е трапеции
ВДНК уравновешивает подвешенную в А площадь Z, то отношение
АВ к BE будет равно отношению трапеции ВДНК к площади Z; так
как ЛВ имеет к BE большее отношение, чем к ВН, то ;шачит и трапеция
ВД1ТК будет иметь к Z большее отношение, чем к Л; таким образом Z
будет мептлпе А.
XI
Пусть АГ {рис. 11} будет равноплечий рычаг с серединой В,
а КДТР — трапеция, у которой стороны КД, ТР стремятся к точке Г,
а ДР и КТ перпендикулярны к В Г, причем
д ft и г сторона ДР попадает в точку В. Пусть отпо^
| шение АВ к ВП будет равно отношению
трапеции ДКТР к некоторой площади А.
Подвесим к рычагу трапецию ДКТР к
точках В, Н, а площадь Z — п точке А, и
пусть Z уравновешивает трапецию ДКРТ в
занимаемом его положении. Тогда подобно
предыдущему докажем, что площадь Z будет
И. меньше А.
*) В тексте употребляется техническое выражение греческой математики—vEuowa— ер
щаяся, склоняющаяся; так называлась прямая, продолжение которой проходило через заданную-
точку. [Ом. комментарии к работе «О спиралях», стр. 519.1
**) В сохранившихся сопинснипх Архимеда соответствующее доказательство имеется п XV пред-
предложении первой книги трактата «О равновесии плоских фигур». ¦ ' '
¦ ¦ ' 6я*
84
АРХИМЕД
f> К I И
г
А
Г и
XII
Пусть АГ {рис. 12} будет опять равноплечий рычаг с серединой В,
а ЛЕКН — трапеция с прямыми углами при точках Е, II и со сторо-
сторонами КА и ЕН, стремящимися к точке Г. Пусть отпошение АВ к ВН
будет равно отношению трапеции ЛКЕГ1 к некоторой площади М;
пусть также отношение АВ к BE будет равно отношению трапеции
ДКЕН к некоторой площади Л. Под-
Подвесим к рычагу трапецию ЛК.ТСН в
точках Е, Н, а площадь Z — в точ-
точке А, и пусть Z уравновешивает
трапецию в занимаемом его положе-
положении. Я утверждаю, что площадь Z
будет больше А, но меньше М.
Действительно, я нзял центр тя-
тяжести трапеции ЛКЕН, и пусть он
будет в (on паходитси подобно пре-
дыдущему); затем я провожу пря-
прямую Ш параллельно ЛЕ. Теперь если подвесить трапецию к рычагу
в точке I, а в точках Е и Н освободить, то она останется в покое в том
же самом положении, и на основании того же, что и выше, будет по-
ирежнему уравновешиваться площадью Z. Но так как трапеция, под-
подвешенная в точке I, уравновешивает площадь Z, подвешенную в точ-
точке А, то трапеции будет иметь к шющади Z то же самое-отношение, что
АВ к BI. Теперь ясно, что
трапеция ЛКЕН имеет к Л Л US— Ч_ г
большее отпошение, чем к Е,
а к М меньшее, чем к Z; та- j—
ним образом, площадь Z бу- 1_
дет больше Л, но меньше М.
Рис. 12.
М
Т
Рис. 13.
хш
Пусть АГ {рис 13} бу-
будет опять равноплечий рычаг
с серединой В, а КДТР —
трапеция, у которой стороны
КА, ТР стремятся к точке Г,
а стороны AT, KP перпенди-
перпендикулярны к В Г. Подносим ее к рычагу в точках Ей ТС, а в точке А
подвесим площадь Z, и пусть она уравновешивает трапецию АКТР
в занимаемом его положении. Пусть отношение АВ к BE будет равно
отношению трапеции АКТР к некоторой шющади Л, и пусть отно-
отношение АВ к ВН будет равно отношению этой же самой трапеции
к некоторой площади М. Тогда подобно предыдущему докажем,
что площадь Z будет больше Л, но меньше М.
XIV
Пусть В6Г {рис. 14} будет сегмент, заключенный между прямой
и параболой. Пусть спачала прямая В Г будет перпендикулярна
к диаметру параболы; и.ч точки В параллельно диаметру проведем пря-
прямую ВА, а из точки Г ироведем касательную ГА к параболе в Г; тогда
¦ КВАДРАТУРА ПАРАБОЛЫ
85
треугольник В ГА будет прямоугольным. Разделим прямую В Г па
какое-нибудь количество равных отрезков BE, EZ, ZH, HI, IF и из
точек делепмя параллельно диаметру параболы проведем прямые
Е2, ZT, НГ, 13, затем из точек пересечения этих прямых с парабо-
параболой проведем к Г соединительные прямые и продолжим их. Я утвер~
экдию, что треугольник ВАГ будет меньше утроенных трапеций КЕ,
AZ, АШ, N1 вместе с треуголь-
треугольником Е1Г, но больше утроенных
трипещй ЪФ, 110, III с тре-
уеолънитм ЮГ.
Действительно, пропедем
прямую АВГ, отложим АВ,
равную В Г и вообразим рапно-
плечий рычаг АГ с серединою В;
подиесим его за В; подвесим
также к рычагу треугольник
ВАГ в точках В и Г, а с другой
стороны рычага, н точке А под-
подвесим площади Р, X, У, Q, Q
и пусть площадь I' урашюве-
щивает трапецию АЕ в занимае-
занимаемом ею положении, площадь X
уравновешивает трапецию Z2,
площадь Y — трапецию ТН,
площадь Q — трапецию TI и,
наконец, площадь ? — треуголь-
треугольник SIT; тогда и псе площади справа уравновесят все площади слева,
так что треугольник ВАГ окажется втрое больше площади Р+Х+ЧЦ-
+ Q+A (предложение VI). Так как ВГ0 есть сегмент, заклгочеппый
между прямой и параболой, из топки В параллельно диаметру прове-
проведена прямая ВА, а из точки Г — касательная ГА к параболе в Г,
и также проведена некоторая прямая 2Е, параллельная диаметру, то
ВГ будет иметь к BE то же самое отношение, что 2Е к ЕФ (предло-
(предложение V); также и прямая ВА будет иметь к BE то же отношение,
что трапеция ДЕ к КЕ*). Подобным же образом докажем, что прямая
АВ относится к BZ, как трапеция 2Z к AZ, что она же относится к ВН,
как трапеция ТН к МН и, наконец, к BI — как трапеция П к N1.
Теперь, так как имеется трапеция АЕ с прямыми углами при точках В,
Е и со стремящимися к точке Г сторонами, уравновешенная в занима-
занимаемом сю положении площадью Р, подвешепной к рычагу в точке А,
и так как отношение ВА к BE равно отношению трапеции ДЕ к трапе-
трапеции КЕ, то значит, как было доказано (предложение X), площадь КЕ
будет больше площади V.
Далее, имеется трапеция Z2 с прямыми углами при точках Z, Е
и со стремящейся к Г стороной 2Т, уравновешенная в занимаемом ею
положении площадью X, подвешенной к рычагу л точке А, и отношение
АВ к BE равно отношению трапеции Z2 к ZCP**), а отношение АВ к BZ
*) В самом деле, ВА —ИГ; кроме того:
ЕФ: Е2 = ВК: Вд = (ЕФ + ВК): (ЕЕ + ВД) — трап. КЕ : трап. ДЕ.
•*) Действительно,
АВ : BE = EZ : ЕФ = трап. Z2 : трап. ЪФ.
АРХИМЕД
ргишо отпопгению трапеции ZS к AZ*); тогда, как тоже было доказа-
доказано (предложошш XII), площадь X будет меньше трапеции AZ, но
больше ZO.
На том же основании и площадь Y будет меньше трапеции МН,
но больше 0Н, площадь О будет меньше трапеции N01 И, но больше
Ш, и так же площадь Д будет меньше треугольника Е1Г, но больше
треугольника ПО (предложение VIII). Теперь, так как трапеция КЕ
больше площади Р, трапеция AZ больше X, трапеция МЫ бслыио х?,
трапеции N1 больше Q и треугольник 01Г болыпе ?, то ясно, что все
первые упомянутые площади будут больше площади Р (вместе с) X,
W, fl(u) ?. Но площадь Р (вместе с) X, V, Q (и) ^ составляет третью
часть треугольника ВДГ; значит, ясно, что треугольник В ГА 65'дет
меньше взятых вместе утроенных трапеции КЕ, AZ, МН, N1 и тре-
треугольника Е1Г. Далее, так как трапеция '/.Ф меньше площади X, тра-
трапеции 011 меньше XY, трапеция Ш меньше Q и треугольник ЮГ
меньше А, то ясно, что все упомянутые выше площади (вместе взятые)
будут меньше площади Д (вместе с) Q, W (и) X; теперь ясно, что
треугольник ВАГ будет больше взятых вместе утроенных трапеций
Z<t>, 6H, Ш и треугольника 1Г0**), но меньше взятых вместе утроен-
утроенных (площадей) поименованных ранее.
XV
Пусть опять ©à [рис. 15} будет сегмент, заключенный между
прямой и параболой, но только теперь прямая В Г уже не будет пер-
перпендикулярна к диаметру параболы. Тогда ВГ необходимо образует
тупой угол или с параллельной диаметру прямой, проведенной в сто-
сторону сегмента из точки В, или с прямой, проведенной таким же обра-
образом из точки Г. Пусть тупой угол образуется с прямой, проведенной
из В. Из точки В проведем прямую БД, параллельную диаметру, а из
точки Г — касательную ГЛ к параболе в Г, прямую В Г разделим на
какое-нибудь количество равных отрезков BE, EZ, ZH, III, 1Г, из
точек Е, Z, Н, I параллельно диаметру пропедем прямые Е2, ZT, II Г,
13 и из точек пересечения атих прямых с параболой проведем к Г сое-
соединительные прямые и продолжим их.
И утверждаю, что треугольник ВАГ будет меньше утроенных тра-
трапеций ВФ, AZ, МИ, N1 вместе с треугольником Г1Е, но больше ijmpo-
еппых трапеций 7Д), 110, ТП вместе с треугольником Г01.
Продолжим ВД в обратную сторону. Проведя перпендикуляр
ГК, я откладываю АК> равную ГК. Теперь опять вообразим равно-
равноплечий рычаг ЛГ с серединой К и подвесим его за К; к одной полошше
рычага подиесим треугольник ГКА в точках ГК в tow положении,
какое он теперь занимает, а с другой стороны рычага в точке А нодвс-
" сим площади Р, X, W, Q, Д, и пусть площадь Р уравновешивает тра-
яецию АЕ в занимаемом поло>кении,площадь X уравновешивает тра-
трапецию Z2, площадь *F — трапецию ТП, площадь Q — трапецию Г1 и,
наконец, площадь ? — треугольник Г13; тогда все площади справа
*) Аналогично
АВ: BZ = ZT: 2© = Е2: EA~(ZT + EZ): (Z© + ЕА> = трап. Z2 : трап. ZA.
**) Дейетвителько, трсугслышк ВГД. равный утроенной сумме площадей p+X+V-l-O-1-Д, будет
более чем втрое Оольчге суммы этих плгацядей, без первой 1», я иначит, и подавно более чем втрое
больше суммы траисций Z<t>, 6H, 1Г1 и треугольника 1Г0-
КВАДРАТУРА ПАРАБОЛЫ
87-
уравновесят все площади слева, так что треугольник ДВГ окажется
втрое больше площади Р (вместе с) X, Y, ?2 (и) А (предложение VII).
После этого подобно предыдущему*) докажем, что трапеция ВФ будет
больше площади Р, трапеция 6Е будет больше площади X, а трапеция
р
л
V
S2
А |
В
Л
и
/ /л.
/и.
^—7
л
/
/м
/
/
/
¦
/ /
/
f
.-¦¦'
Гнс. 15.
ZO меньше ее; трапеция МН будет больше площади ХР, a IT0 меньше
ее; затем трапеция N1 будет больше площади Q, а Ш меньше ее;
и, наконец, треугольпик Е1Г будет больше площади А, а треугольпик
ПО меньше ее; теперь ато ясно.
XVI
Пусть опять В0Г (рис. 1С} будет сегмепт, заключенный между
прямой и параболой: черезз точку В происдем прямую ВД, параллель-
параллельную диаметру параболы, а через Г — касательную к параболе в Г.
Пусть площадь Z будет третьей частью треугольника ВДГ.
Я утверждаю, что сегмент ВвГ будет равен площади Z.
Действительно, если он не равен, то будет или больше, или же
меньше. Пусть сначала оп будет, если возможно, болыпо; тогда избыток,
на который сегмент В6Г превосходит площадь Z, будучи складываем
сам с собой, когда-нибудь станет больше треугольника ВГЛ. Следова-
Следовательно, можпо взять некоторую меньшую зтого избытка площадь, кото-
которая была бы какой-то частью треугольника ВДГ. Пусть треугольник
ВГЕ будет меньше упомянутого избытка, и одновременно является
некоторой частью треугольника ВДГ; тогда прямая BE будет такой же
*) Т. е. кал в предложении XIV, е той лишь разницей, что вместо предложений VIII, X. XII
придется использовать предложения IX, XI. XIII.
88
АРХИМЕД
частью от БД. Разделим ВА на части, равные BE и пусть точки делений
будут Н, I, К; из точек И, I, К проведем к Г соединительные прямые;
они, конечно, пересекут параболу, так как прямая ГЛялляется касатель-
касательной к ней в точке Г. Через точки пересечения отих прямых с параболой
проведем параллельно диаметру прямые МФ, NP, Ев, ПО; они будут
параллельны и прямой БД. Теперь, так как треугольник 13ГЕ меньше
избытка, на которых"! сегмент ВвГ преносходцт площадь Z, то ясно,
что площадь Z и треугольник ВГЕ, вместе взятые, будут меньше сег-
сегмента. Но треугольник ВГЕ ранен
трапециям ME, ФА, 6Р, ©О, через
которые проходит парабола, взя-
взятым вместе с треугольником Г02;
действительно, трапеция ME яв-
является общей, трапеция МЛ равна
трапеции ФЛ, трапеция AS равна
61', трапеция Х5 равна О© и тре-
треугольник ГХП рапеп треугольнику
Г02; следовательно, площадь Z
будет меньше вместе изятых тра-
трапеций МЛ, ЕР, П© и треугольни-
треугольника НОГ *).
Но треугольник ВДГ втрое
больше площади Z; тогда треуголь-
треугольник ВДГ будет меньше утроенных
трапеций МЛ, SP, ©П и треуголь-
треугольника ПОГ, а это невозможно,
так как доказано (предложения XIV
и XIII), что он будет более чем
втрое больше. Итак, сегмент В©Г
не будет больше площади Z.
Теперь я утверждай», что он
не будет и меньше. Действительно,
пусть он будет, если возможно, меньше. Значит, и в данном случае
избыток, па который площадь Z превосходит сегмент ВвГ, будучи
прибавляем сам к себе, когда-нибудь превзойдет и треугольник ВДГ.
Но можно взять пекоторую меньшую этого избытка площадь, которая
была бы какой-то частью треугольника ВДГ. Пусть треугольник ВГЕ
будет меньше этого избытка и одновременно некоторой частью тре-
треугольника ВДГ, все остальное сделаем так же, как раньше. Теперь,
так как треугольник ВГЕ мопыпе избытка, на который площадь Z
препосходцт сегмент ВвГ, то вместе взятые треугольник BE Г и сег-
сегмент В0Г будут меньше площади Z. Но площадь Z мепьше вместе
взятых четырехугольников ЕМ, ON, WE, ЦТ и треугольника ГП2,
так как треугольник ВДГ, втрое больший площади Z, одновременно
меньше утроенных упомянутых площадей, имеете взятых, как ото
доказано л предыдущем (предложения XIV, XV); значит, треуголь-
треугольник ВГЕ вместе с сегментом ©à будут меньше четырехугольников
ЕМ, ON, E4f, ПТ и треугольника ГП2. Таким образом, по отнятии
Рис. 16.
*) ME + №» + ЗЧГ -|- ПТ I- П2Г > сеем. В©Г,
ми+фл+ер+ ©о+гог=кгв,
откуда ¦ вычитая,
мл+ер+пе + пог > вег - вге > z.
КВАДРАТУРА ПАРАБОЛЫ
89
общего сегмента треугольник БЕГ оказался бы меньше оставшихся
площадей; зто же невозможно, так как доказано, что треугольник BE Г
равен вместе взятым трапециям ЕМ, ФЛ, ©Р, GO и треугольнику
ГО2, которые больше оставшихся площадей. Значит, сегмент Б6Г не
будет меньше площади Z [3]. Но также доказано, что он не будет
и больше; значит, этот сегмент ранен площади Z |4].
XVII
После того как это доказано, ясно,
что всякий сегмент, заключенный между прямой и параболой,
составляет четыре трети треугольника, имеющего с сегментом то же
самое основание и равную высоту.
Действительно, пусть будет сегмент, заключенный между прямой
и параболой, пусть его вершина*) будет в точке В {рис. 17}. Впишем
в него треугольник В0Г, имеющий с
сегментом то же основание и равную
высоту. Так как точка в есть вер-
инша сегмента, то прямая, проведен-
проведенная из Э параллельно диаметру,
разделит ВГ пополам и ВГ будет
параллельна касательной к пара-
параболе в точке 0 (предложение I).
Проведем Е0 параллельно диаметру;
затем из В также параллельно диа-
диаметру проведем прямую ВА, а из
Г — касательную ГД к параболе в
Г. Так как К0 параллельна диамет-
диаметру, ГД — касательная к параболе в
Г, а ЕГ параллельна касательной к
параболе в 0, то треугольник ВДГ
будет в четыре раза больше треу-
треугольника В6Г**). Но так как тре-
треугольник ВДГ втрое больше сегмен-
сегмента ВвГ (предложение XVI) и вчет-
вчетверо больше треугольника ВвГ, то
ясно, что сегмент ©à будет состав-
составлять четыре трети треугольника В ©Г.
Рис. 17.
Для сегментов заключеппых между прямой и какой-нибудь кри-
кривой линией***), я называю основанием эту прямую, высотой — паи-
больший перпендикуляр, который можно опустить из точки кривой на
основание сегмента, а вершиной — ту точку, из которой проводится
па ибол ы п ий иерпендикуля р.
*) Интересно "отметить, что Архимед уже л этом месте пользуется термином «вершина пара-
параболического сегмента», определение которого будет дано ниже (перед приближением XVlIi). Это
вначит. что остальная часть трактата (предложения ХЛ 111—XXIV) иирпсиачалмю составляла осо-
особое сочинение.
**) Действительно, К© —вК «предложение 1Г>,и значит, В& = 4 Ев. так как ВЕ = ЕГ.
***) xa\jino'!jx? YOorwxaC. В трактате «О шаре и цилиндре» (кн. I аксиома 1) Архимед употре-
употребляет втот термин дли <. Хшвначения кривой линии. Стоит отметить, что в некоторых местах «Кони-
«Конических сечений» Аполлония, а также, иерчятио, и в тексте Еидпкса (см. астуцительную статью,
гл. 111) под бтлм термином понимались наши криные второго порядка.
90
АРХИМЕД
Рис. 18.
XVIII
Если в сегменте, заключенном между прямой и параболой, провести
из середины основания прямую, параллельную диаметру, то вершиной
сегмента будет та точка, в которой
прямая, проведенная параллельно диа-
диаметру, пересекает параболу.
Пусть АВГ {рис. 18} будет сег-
сегмент, заключенный между прямой и
параболой; из середины АГ проведем
прямую ДВ параллельно диаметру. Так
как в параболе прямая ВД проведена
параллельно диаметру, а прямые АД
и А Г раины, то ясно, что прямая ЛГ
и касательная к параболе п точке В будут параллельны (предложе-
(предложение 1). После этого ясно, что из нерпендикулярон, опущенных на АГ
с параболы, наибольшим будет проведешшй из В; таким образом,
точка В будет вершиной сегмента.
. . / XIX * ¦-- -"-.:..'
В сегменте, заключенном между прямой и параболой, линия, про-
проведенная из середины основания {параллельно диаметру), будет
составлять четыре трети прямой, про-
проведенной {таким же образом) из середины
половина основания.
Пусть АВГ {рис. 19} будет сегмент,
заключенный между прямой и параболой;
из середины прямой АГ параллельно
диаметру проведем прямую БД, а из
середины АД — прямую EZ, а также
проведем прямую Z6 параллельно АГ.
Теперь, так как в параболе прямая БД
Е
й
Рис. 19.
^vucpj], itui tian и параоолез прямая i3ii
проведена параллельно диаметру, а прямые АД, Z6 параллельны
касательной к параболе в В, то отношение липий ВД и ВВ будет
равно отношению квадратов иа АЛ и Z6 (предложение Ш>;' зна-
значит, лилия ВД будет в четыре раза
Л /; -$ больше В0*). Теперь ясно, что ли-
линия ВД будет составлять четыре тре-
трети от EZ**).
XX
А Г Если в сегмент, заключенный ме-
Рис. 20. жду прямой и параболой, вписать
треугольник, имеющий с сегментом
одно и то оке основание и равную высоту, то вписанный треугольник
будет больше половины сегмента.
Пусть АВГ {рис. 20} будет упомянутый сегмент; впишем в него
треугольник АВГ, имеющий с сегментом то ?ке самое основание и рав-
равную высоту. Так как этот треугольник имеет с сегментом то же самое
*) Так как ZO является половиной АД.
**) Так как 6Д =ЗВе и 6& = EZ.
КВАДРАТУРА ПАРАБОЛЫ 91
основание и ту же высоту, то точка В необходимо будет вершиной
сегмента; значит, АГ будет параллельна касательной к параболе
в точке В. Через В параллельно АГ проведем прямую ЛЕ, а из точек
А и Г параллельно диаметру проводом прямые АД и ГЕ; они по-
попадут вне сегмента. Теперь, так как треугольник АВГ составляет
половину параллелограмма АЛЕ Г, то ясно, что он будет больше
половины сегмента.
Следствие
После доказанного ясно, что в данный сегмент можно вписать
такой многоугольник, чтобы остающиеся (по краям) сегменты были
меньше всякой наперед заданной площади; действительно, если отни-
отнимать все время больше половит.!, то на основании доказанного ясно,
что, постоянно уменьшая остающиеся но краям сегмеиты, мы можем
сделать их меньше всякой наперед заданной площади*).
XXI
Если в сегмент, заключенный между прямой и параболой, вписать
треугольник, имеющий с сегментом то же самое основание и ту же
высоту, а в оставшиеся сегменты вписать другие треугольники, имею-
имеющие те же самые основания и высоты, что и у этих сегментов, то
треугольник, вписанный в весь сегмент, будет в восемь раз больше
каждого из треугольников, вписанных е сегменты, оставшиеся (по
краям).
Пусть ЛВГ {рис- 21), будет сегмент такой, как сказано выше; пря-
прямую АГ разделим пополам в точке Л и параллельно диаметру проведем
прямую ВД; тогда точка В будет вер-
вершиной сегмента (предложение XV111).
Значит, треугольник ЛВГ имеет с сег-
сегментом то же самое основание и ту же
высоту. Затем разделим прямую АД попо-
пополам в точке Е и проведем прямую EZ,
параллельную диаметру параболы и пере-
секающую А В в точке 0; тогда точка Z
будет вершиной сегмента AZB. Таким
образом, треугольник AZB имеет то же с"
самое основание и ту же высоту, что и
сегмент [AZBJ. Требуется доказать, что треугольник АВГ будет в
восемь раз больше треугольника AZB.
Прямая ВД составляет четыре трети от EZ (предложение XIX)
и вдпое больше Ев; значит, Е0 будет вдвое больше 0Z**). Таким
образом, треугольник АЕВ вдвое больше треугольника ZBA, так как
треугольник ЛЕ0 вдвое больше A0Z***), а треугольник 0ВЕ вдвое
*) На основании леммы Квдскса («Начала» Етошлда, X, I).
12 ¦
¦ ••) Д^йстиитслыю, Ев = —BA = -y-EZ; значит, j : ¦•¦-- -: -
6Z= -^-EZ и E6=20Z.
***) Треугольники АЕв и AZ6 имеют одну и ту те першину А и лежащие на одной прямей
осисшания Яв и E0=2Z0. Точно также трсугилышки 2ЬЭ и вВЕ имеют общую вершину В и не-
нежащие на одной щ>нмсй оснопатвд Ев и Z0. .. ¦ . . . . ....
92
АРХИМЕД
больше Z6B. Таким образом, треугольник АБГ будет л восемь раз
больше треугольника AZB*). Подобным же образом проведем доказа-
доказательство и относительно треугольника, вписанного в сегмент ВНГ.
XXII
Если имеется сегмент, заключенный между прямой и параболой,
и взято любое количество площадей, составляющих непрерывную
{пропорцию) в о??гношении четырех к одному, причем наибольшая из
этих площадей равна треугольнику, имеющему с сегментом то же
самое основание и ту же высоту, то все эти площади, вместе взятые,
будут меньше сегмента.
Пусть АД BE Г {рис. 22} будет сегмент, заключенный между пря-
прямой и параболой, и взято несколько площадей Z, Н, в, I, составляю-
составляющих непрерывную пропорцию, в которой
каждая предыдущая площадь в четыре
раза больше последующей; лусть наиболь-
наибольшая из них Z равна треугольнику, имею-
имеющему с сегментом одно и то же основание
и равную пысоту.
Л утверждаю, что согмопт будет
больше площадей Z, II, 0, I (вместе
взятых).
Пусть В будет вершина всего сегмен-
сегмента, а Д и Е — першины сегментов, остаю-
остающихся (по краям). Так как треуголь-
треугольник АВГ в восемь раа больше каждого
из треугольников АД В и BE Г, то ясно,
что он будет в четыре раза больше их
обоих вместе. И если треугольник АВГ
равен площади Z, то вследствие этого
треугольники АД В и BE Г вместе будут
раипы площади II. Точно так же дока-
докажем, что треугольники, вписываемые в остающиеся но краям сегменты,
имеющие с ними те же самые основания и высоты, будут все вместе
равны площади 0, а треугольники, вписываемые в сегменты, получаю-
получающиеся после этого, будут равны площади i; значит, все эти взятые
площади будут вместе рашш некоторому многоугольнику, вписанному
в сегмент. После этого ясно, что они будут меньше этого сегмента.
XXIII
Если взять несколько величин, образующих непрерывную пропор-
пропорцию в отношении четырех к одному, то все эти величины вместе, сло-
сложенные с третьей частью наименьшей, составят четыре трети наи-
наибольшей {рис. 23j**).
Рис. 22.
*) Вели треугольник AZB есть половина АЕП, а АЕВ—иолотша АБА и, наконец, ABA—по-
ABA—половина АВГ, то следовательно:
4-ААВГ.
*) в рукописях эти величины изображены отревками пряных.
КВАДРАТУРА ПАРАБОЛЫ
г
н
СП
Рис. 23.
Пусть будет нзято в непрерывной пропорции несколько величин
А, В, Г, Д, Е, из которых каждая в четыре раза больше последующей,
и пусть Л будет наибольшей; затем пусть Z будет третью от В, Н —
третью от Г, 6 — третью от Л и I — третью от Е. Так как Z — треть В,
а В — четвертая часть А,
то обе величины В и Z
вместе составят третью
часть А. На том жо ос-
новапии Н и Г вместе
составят треть В, за-
затем, 0 vi А вместе соста-
составят треть Г и, наконец,
I и Е вместе составят
троть Д; тогда вместе
взятые В, Г, А, Е, Z,
Н, 6, I составят третью
часть от вмпсте взятых
А, В, Г, Д. Но величи-
величины Z, Н, 0 составляют третью часть от В, Г, Д; значит, оставшиеся
величины В, Г, А, Е, I будут третьей частью остатка Л. После этого
ясно, что величины А, В, Г, А, Е, взятые вместе с I — третьей частью
от Е,— составят четыре трети от А.
xxrv
Всякий сегмент, заключенный между прямой и параболой, состав-
составляет четыре трети треугольника, имеющего с нам одно и то же осно-
основание и равную высоту.
Пусть АД BE Г {рис. 24} будет сегмент, заключенный между пря-
прямой и параболой, а АВГ — треугольник, имеющий с сегментом одно
и то же основание и равную
высоту; пусть площадь К со-
составляет четыре трети тре-
треугольника АВГ. Требуется
доказать, что эта площадь
равна сегменту ААВЕГ.
Действительно, если она
не равна, то будет или боль-
больше, или меньше. Пусть сна-
сначала сегмент АД BE Г будет,
если возможно, больше пло-
площади К.
Итак, я вписал треуголь-
треугольники АД В, BE Г, как было
сказано выше, и оставшиеся
по краям сегменты вписал
другие треугольники, имею-
24. щИе с ЭТими сегментами те же
самые основания и высоты, и
затем в получающиеся после этого сегменты постоянно вписыиаю но
два треугольника, имеющие с этими cej-лгонтами те же самые основа-
основания и высоты; тогда остающиеся сегменты сделаются когда-нибудь
меньше того избытка, на который сегмент А ДВЕ Г превосходит
К
Л
I
94 АРХИМЕД
площадь К, так что вписанный многоугольник будет больше площади К,
а это невозможно. Действительно, плюются площади, образующие
непрерывную пропорцию и отношении четырех к одному, а именно
первая — треугольник АВГ, в четыре раза больший обоих треуголь-
треугольников АД Л vi БЕГ вместе взятых, затем эти самые треугольники,
которые в четыре раза больше треугольников, вписываемых в следую-
следующие сегменты, и так все премя далее; ясно, что все эти площади вместо
будут меньше, чем четыре трети от наибольшей площади {АВГ), тогда
как К составляет четыре трети от наибольшей площади.
Значит, сегмент АД BE Г не будет больше площади К.
Пусть теперь, если возможно, он будет меньше.
Возьмем площадь Z, равную треугольнику АВГ, затем пло-
площадь Н, равную четверти Z, далее — в, равную четлерти И, и будем
так брать постоянно в непрерывной пропорции до тех пор, пока по-
последняя площадь не окажется меньше того избытка, на который пло-
площадь К превосходит сегмент; дусть эта меньшая площадь будет I;
тогда площади Z, Н, в, 1 вместе с третью от I составят четыре трети
от Z (предложение XXIII).
Но и К также составляет четыре трети от Z; значит, К будет равпа
площадям Z, Н, в, I, взятым вместе о третьей частью от h Так как
площадь К превосходит площади Z, II, в, 1 на величину, меньшую 1,
а сегмент (АДВЕГ) —на величину, большую I, то ясно, что пло-
площади Z, IT, в, I будут больше сегмента. Это же невозможно, так как
доказано, что если влито любое количество площадей, образующих
непрерывную пропорцию в отношении четырех к одному, причем
наибольшая равна вписанному в сегмент треугольнику, то все эти
площади . вместе будут меньше сегмента (предложение XXII); зна-
значит, сегмент АДВЕГ не меньше площади К. По доказано также, что
он не будет и больше; значит, он будет ранен площади К. Но площадь К
составляет четыре трети треугольника АВГ; значит, сегмент АДВЕГ
равен четырем третям треугольника АВГ [5].
О ШАРЕ И ЦИЛИНДРЕ [1]
КНИГА I
Архимед Досифею желает радоваться!
Я уже послал тебе запись паших открытий имеете с доказатель-
доказательством, что всякий еегмепт, заключенный между прямой и параболой,
составляет четыре трети треугольника, имеющего с сегментом одно и то
же основание и одинаковую тшеоту; позднее, когда нам пришли на
ум другие стоящие внимания теоремы, мы потрудились над их доказа-
доказательствами. Теоремы эти таковы:
во-первых, поверхность есякого шара в четыре раза больше его
большого круга;
затем, поверхность всякого шарового сегмента равна кругу, радиус
которого равен прямой, проведенной из вершины сегмента к окружности
круга, составляющего основание сегмента;
кроме того, для всякого шара цилиндр, имеющий основанием боль-
большой круг этого шара, а высотой — прямую, равную диаметру шара,
и сил*) будет в полтора раза больше этого шара, и поверхность его
тоже в полтора раза больше поверхности этого шара.
Конечно, эти свойства были и раньше по самой природе присущи
упомянутым фигурам, но они все же оставались неизвестными тем,
кто до нас занимался геометрией, и никому из них не пришло на ум,
что все эти фигуры являются соизмеримыми друг с другом; поэтому
я не поколебался бг.т сравнить эти теоремы с теми, которые были откры-
открыты другими геометрами, и в частности с наиболее выдающимися теоре-
теоремами, которые были установлены для тол Епдоксом, а именно, что вся-
всякая пирамида составляет третью часть призмы, имеющей с пирамидой
одно и то jkc основание и одинаковую высоту, и что всякий конус со-
составляет третью часть цилиндра, имеющего с конусом одно и то же осно-
основание и одинаковую высоту; действительно, хотя эти свойства по самой
природо всегда были присущими указанным телам, новее же оказалось,
что они остались неизвестными многим жившим до Евдокса знамени-
знаменитым геометрам и ни одному из них не пришли на ум. Теперь же их
могут усмотреть все, имеющие к тому силы. Било бы очень хорошо,
* То есть объем его.
96 АРХИМЕД
если бы они были обпародовапм еще при жизни Конона; он был, как
мы считаем, наиболее способным продумать их и дать о них подходя-
подходящий отзыи. Полагая, что было бы очень хорошо передать их сведущим
в математике людям, мы посылаем тебе запись их доказательств;
теперь их могут рассмотреть все занимающиеся математикой. Будь
здоров!
Прежде всего излагаются аксиомы и необходимые для доказатель-
стна их допущения.
Аксиомы [2]
1. На плоскости существуют некоторые ограниченные кривые*)
линии, которые или целиком находятся по одну сторону от прямых,
соединяющих их концы, или ничего не имеют по другую их сторону.
2. Тогда выпуклой в одну и ту же сторону я называю такую
линию, для которой прямые, соединяющие две произвольные ее точки,
будут или все находиться по одну сторону этой линии, или же неко-
некоторые по одну ее сторону, другие же па самой линии, но никакая такая
прямая не. будет находиться по другую ее сторону.
3. Подобным же образом существуют некоторые ограниченные
поверхности,, которые не лежат сами на плоскости, по имеют на
плоскости свои границы, причем эти поверхности будут или целиком-
находиться по одну сторону от плесжети, содержащей их границы,
или ничего не будут иметь по другую сторону от нее.
4. Выпуклыми в одну и ту же сторону я называю такие поверх-
поверхности, для которых прямые, соединяющие две произвольные их точки,
будут или все находиться по одну сторону этой поверхности, или же
некоторые по одну сторону, другие же на самой поверхности, но ника-
никакая из них не будет находиться с другой ее стороны.
5. Телесным сектором я называю фигуру, ограниченную поверхно-
поверхностью конуса, отсеченного шаром с центром е вершине конуса, и той
частью поверхности шара, которая лежит, внутри конуса.
С. Телесным ромбом я называю фигуру, состоящую из двух конусов,
имеющих одно основание, вершины, расположенные по разные стороны
от плоскости основания, а оси — на одной прямой.
Д о п у щ с п и я
Я принимаю следующее:
1. Из всех линий, имеющих одни и те же концы, прямая будет
наименьшей.
2. Две другие линии, расположенные на плоскости и имеющие те
же самые концы, будут всегда неравными, если обе они выпуклы в одну
и ту же сторону, и одна из них или целиком объемлется другой линией
и соединяющей их концы прямой, или же часть ее объемлется. другой,
часть же является общей обеим линиям; при этом меньшей будет объем-
лемая линия.
3. Подобным же образом из поверхностей, имеющих общую грани-
границу, расположенную на плоскости, наименьшей будет плоскость.
*) Как видим us дальнейшего текста, иол словом крииые (хицл-ОЯси) Архимед понимает здесь
вообще любые лшпш, отличающиеся от прямой.
О ШАРЕ И ЦИЛИНДРЕ 97
4. Две другие поверхности, имеющие общую границу, расположен-
расположенную на плоскости, будут всегда неравными, если обе они выпуклы в одну
и ту же сторону и одна из них или целиком объемлется другой поверх-
поверхностью и плоскостью, содержащей их общую границу, или же часть ее
объемлется другой, часть же является общей обеим поверхностям;
при этом меньшей будет объемлемая поверхнсстъ.
5. Далее, большая ия двух неравных линий, поверхностей или тел
превосходит меньшую на такую величину, которая, будучи складываема
сама с собой, может превзойти любую заданную величину из тех, кото-
которые могут друг с другом находиться в определенном отношении [3].
При наличии этих допущений ясно, что если мы впишем в круг
многоугольник, то периметр вписаппого многоугольника будет меньше
окружности круга, так как каждая из сторон
этого многоугольника будет меньше отсекае-
мой ею дуги окружности.
Если около круга описать многоугольник,
то периметр описанного многоугольника будет
больше периметра круга.
Опишем около круга многоугольник, как
предполагается {рис. 1}. Я утверждаю, что
периметр описанного многоугольника будет
больше периметра круга.
Действительно, прямые Б А, ЛЛ, имеете
взятые, будут больше дуги ВЛ вследствие того,
что они объемлют эту дугу, имеющую с ними те же самые концы; по-
подобным же образом вместе взятые прямые ДГ и ГВ будут больше дуги
ЛВ, а вместе взятые ЛК и Кб больше дуги Л©, вместе взятые ZH,
Пв больше Z6 и, наконец, вместе взятые ЛЕ, EZ больше AZ; следо-
следовательно, весь периметр рассматриваемого многоугольника будет
больше окружности круга.
II
Если даны две неравные величины, то можно найти две неравные
прямые таким образом, чтобы большая прямая имела к меньшей отно-
отношение меньшее, чем отношение большей величины к меньшей.
Пусть будут две неравные неличины АВ и А, и пусть большей бу-
будет АВ (рис. 2}. Я утверждаю, что можно найти две неравные прямые,
которые удовлетворяли бы высказанному требованию.
Пользуясь построением второго предложении первой книги
Евклида, отложим Г5Г, равную Д, и возьмем некоторую прямую ZH;
тогда, складывая ГА с самой собой, мы когда-нибудь превзойдем Д.
Возьмем ее нужное число раз кратпой; пусть полученная линия бу-
будет АВ. Определим теперь НЕ так, чтобы ZH была больше НЕ во столь-
столько же раз, во сколько А6 больше АГ; значит, как ©А к ЛГ, так
и ZH к НЕ,
вА ZH
АГ ~НВ
и обратно — как ЕП (относится) к HZ, так и АГ к А6.
вн аг
hz ле
1 Архимед
98
АРХИМЕД
А6
в
8
Поскольку же А0 больше Д. к.чи, что то же, больше ГВ, то, значит,
ГА имеет к Л© отношение меньшое, чем ГА к ГВ.
.ГА
По как ГА (относится) к Ав, так и EII к IIZ; значит, ЕН к HZ
имеет отношение меньшее, чем ГА к ГВ; тогда, «присоединяя»*), най-
найдем, что EZ к ZTI будет иметь отношение меньшее, чем АВ
к В Г. ТТр В Г ранпа А; значит, EZ имеет к ZIT отпошеппе
меньшее, чем АВ к Д.
Итак, найдены две перанпые прямме, удовлетворяющие
НУ- поставленному условию, [т. с, что большая имеет к мень-
меньшей отношение, меньшее того, которое большая иеличина
имеет к меньшей] [4J.
III
Если даны две неравные величины и круг, то можно впи-
вписать в круг многоугольник и описать около него другой та-
таким образом, чтобы сторона описанного многоугольника
имела к стороне вписанного многоугольника отношение
меньшее, чем отношение большей величины- к меньшей.
Пусть обе заданные величины будут А, В (рис. 3}, за-
заданный же круг расположен выше. Я утверждаю, что
можно выполнить задание.
Рис. 2. Найдем две ирядтые в и КА, из которых большей пусть
будет (г), таким образом, чтобы 0 находилась к КА is отно-
отношении меньшем, чем большая величина (А) к меньшей (В); из
• точки А под прямым углом к АК
проведем AM, а из К проведем КМ
так, чтобы КМ равнялась 6; [это ведь
возможно].
Затем в круге проведем под пря-
прямым углом два диаметра ГЕ и AZ. Те-
Теперь, раздели» угол ДНГ пополам,
половину его еще раз пополам и про-
продолжая такое деление нее ирсмя, мы
придем к некоторому углу, меньшему,
чем удвоенный угол АК М- Пусть таким
углом будет Nil Г.
Соединим точки N, Г; тогда NT
будет стороной равносторонпего мно-
многоугольника с четным числом сторон
[действительно, поскольку угол N11Г
целое число раз измеряот прямой угол
ДНГ, то и дуга NT целое число раз
измеряет четверть окружности ГА, а
значит целое число раз измеряет и всю
окружность. Таким образом, NT, оче- Нис- •*•
видно, является стороной раиностороннего многоугольника]. Разделим
П
*) Это значит составляя щдшзиидную дфонирцию со сложением:
КН + HZ АГ + ГВ
HZ ^ ГВ
О ШЛНГС И ЦИЛИНДРЕ
угол THN пополам прямой На, проводом из точки В касательную OS П
к кругу и продолжим линии HJN1I и НГО; тогда ПО будет стороной
описанного около круга равностороннего многоугольника; [очевидно,
что этот многоугольник будет подобен вписанному многоугольпику со
сторопой NF]. Теперь, поскольку угол NHF меньше удвоенного угла
ЛКМ и равен удвоенному углу ТОГ, то угол ТНГ будет меньше угла
ЛКМ. Углы же при Л и Т прямые; значит, МК будет иметь к ЛК отно-
отношение, большее, чем ГН к НТ. ¦
МК ГН
лк нт
Но ГН равна Ни,; значит, отношение HS к НТ,
к N.F, будет меньше, чем отношение МК к ЛК.
а также ПО
НТ
МК А
КЛ И
КЛ
Далос, МК находится к КЛ и отношении меньшем, чем А к В,
и ПО есть сторона описанного многоугольника, a NT — вписанного,
что и требовалось найти.
IV.
Далее, если, имеются две неравные величины и сектор, то молено
описать вокруг сектора многоугольник и вписать в него другой так,
чтобы сторона описанного многоугольника находилась к стороне вписан-
вписанного в отношении, меньшем того, кото-
которое большая величина имеет к меньшей.
Пусть будут опять две неравные
величины Е и Z {рис. 4}, и пусть боль-
большая из них Е; пусть будет некоторый
круг АВГ, имеющий центр и А, и при
точке А .построен сектор АДВ; требует-
требуется около сектора AUA описать и в пего
вписать многоугольник, имеющий рав-
равными все стороны, за исключением сто-
сторон ВД, АЛ**), так, чтобы выполнить
задание.
Пайдедх две неравные прямые Н и
6К (пусть большая будет Н) такие,
чтобы Н имела к ВК отношение мень-
меньшее, чем большая величина к меньшой
Н . Е
вк z
Рис.
[это ведь возможно]; и точно так же, проведя из © под прямым углом
к К© прямую 0Л, построим КЛ, равную II [это возможно, поскольку
Н больше 6К]. Разделяя угол ЛАВ пополам, половину его опять попо-
пополам и продолжая так псе время, мы придем к некоторому углу,
*) С нашей точки з|хшш, ато равносильно утверждению, что если а О, то sec a,> sec p.
*•) Предполагается, что боковые радиусы сектора входят в иеримстр обоих многоугольников
как ?1шсиш1ого, так и описанного. .-.. ¦• ¦• ¦- ;.
7*
dOO
АРХИМВД
с
f •
r.
ЕО
АН
который будет меньше удвоенного угла КЛ©. Пусть таким углом будет
АЛМ: тогда AM будет стороной многоугольника, вписанного н круг.
Если рассечем угол АДМ прямой AN пополам и из N проведем каса-
тельную к кругу прямую NEO, то ата прямая будет стороной описаи-
. ного около того же круга многоугольника, подобного вышеупомянутому;
тогда совершенно так же, как и раньше, покажем, что 30 будет нахо-
находиться к AM в отношении меньшем, чем отношение величины Е к Z.
с ;:
Дом круг и две неравные величины; описать около круга многоуголь-
многоугольник и вписать в него другой так, чтобы описанный имел к вписанному*)
отношение меньшее того, которое большая величина имеет к меньшей.
Пусть будут круг А {рис. 5} и две неравные величины Е, Z, из
которых большая Е; требуется вписать и круг многоугольник и описать
около него другой так, чтобы выполнялось поставленное задание.
Я беру две неравные прямые Г, Д, из которых большей пусть бу-
будет Г, таким образом, чтобы Г имела к Д отношение меньшее, чем
Е к Z:
г
Г"
если взять для Г и А среднюю пропорциональную Н,
то Г будет больше Н.
Опишем около круга многоугольпик и впишем в него другой так,
чтобы сторона описанного многоугольника имела к стороне вписанного
; отношение меньшее, чем Г к Н, [как мы уже выучились]; тогда ква-
!драт**) первого отношения будет меньше квадрата второго. Но квад-
квадрат отношения сторон равен отношению
{площадей) многоугольников, [так как по-
слодние подобны], квадрат же отношения Г
к IT равен отношению Г к А.
Таким образом, описанный многоуголь-
^ ' ник имеет к вписанвому отношение мень-
меньшее, чем Г к Д; значит, и подавно, описан-
описанный многоугольник имеет к вписанному
отношение меньшее, чем Ё к Z.
Рис. 5.
VT
Подобным же образом докажем, что,
если даны две неравные величины и сек-
сектор, то можно описать около сектора мно-
. ,. . . гоугольник и вписать в него другой, подобный
первому, так, чтобы отношение описанного многоугольника ко вписан-
вписанному было меньше того, которое большая величина имеет к меньшей.
Точно так же ясно, что если даны круг, сектор и некоторая пло-
площадь, то можно, вписывая в круг или в сектор равносторонние много-
*) Мы сказали бы: «чтобы площадь огоййнйого вмела к площади вписанного».
=¦ ¦ **) В подлиннике бшЯлаюе : ktfyog—двойное отношение:: у греков сложение отношений было
фаииосилыю их умножению. ¦ ¦ : •¦ ¦
•I
О ШАРЕ И ЦИЛИНДРЕ
В
угольники и продолжая делать то же самое с получающимися по
краям сегментами, дойти до такого сегмента круга или сектора, кото-
который был бы меньше заданной площади: это доказано в «Началах»*).
. Требуется доказать, что если даны круг, сектор и некоторая пло-
площадь, то можно около круга или сектора описать многоугольник та-
таким образом, чтобы оставшиеся по краям части**) описанной фигуры
были меньше заданной площади; достаточно будет доказать ато для
круга и провести то же рассуждение и для сектора.
Пусть будут даны круг А {рис. 6} и некоторая площадь В. Около
этого крута можно описать многоугольник так, чтобы его части, оста-
остающиеся между многоугольником и окружпостью,
взятые вместе, были меньше площади В; ибо если
имеются две неравные величины, из которых боль-
большая равна вместе взятым кругу и заданной пло-
площади, а меньшая одному только кругу, то опи-
опишем около круга многоугольник и впишем в него
другой так, чтобы описанный имел ко вписанному
отношение меньшее, чем упомянутая большая
величина к меньшей. Тогда этот описанный мно-
многоугольник и будет тем, остающиеся части кото-
которого будут меньше заданной площади В.
Действительно, если описанный многоуголь-
многоугольник имеет ко вписанному отношение меньшее того,
в котором вместе язятые круг и площадь В на-
находится к этому же кругу, и круг больше впи- Рис. 6.
санного многоугольника, то описанный много-
многоугольник и подавно будет иметь к кругу отношение меньшее, чем
имеете взятые круг и площадь В имеют к этому ?ке кругу; тогда
после «выделения»***) части описанного многоугольника будут иметь
к кругу отношение меньшее, чем площадь В к кругу; значит, части
описанного многоугольника будут меньше площади В.
Или таким образом, поскольку описанный многоугольник имеет
к кругу отношение меньшее, чем вместе взятие круг и площадь В
к кругу, то вследствие этого описанный многоугольник будет меньше
указанных величин, вместе взятых; таким образом, и все его части
(лежащие вне круга) будут меньше площади В.
То же самое и относительно сектора.
VII ;
Если в равнобедренный конус****) вписать пирамиду, имеющую
основанием равносторонний многоугольник, то поверхность этой пира-
пирамиды за вычетом основания равна треугольнику, имеющему основание
равным периметру основании пирамиды, а высотой — перпендикуляр,
опущенный из вершины пирамиды на одну из сторон основания.
*) Евклид, XII, 2.
**) Вуквально: отрезки. ., .
•••) Это значит—составления производной пропорции с иычиташгем: ' '
опис. мц-к—А (Л + В) -А
А < А
•***) То есть конус, имеющий в осеиом сечешга равнобедренный треугольник, иными словами,
обыкновенный прямой круговой конус.
.102
АРХИМЕД
Рис. 7.
Пусть будет рапнобедрепный конус, основание которого есть
круг АВГ {рис. 7] и в него «писала пирамида, имеющая основанием
равносторонний многоугольник АВГ: я утверждаю, что поверхность
ее за вычетом основания равна вышеназванному треугольнику.
Так ьак конус янлиется равнобедренным и в ic овании пирамиды
лежит равносторонний многоугольник, то высоты ограничив io.i.iix
пирамиду треугольников будут ралны меж-
между собой. Основаниями этих треугольников
являются АВ, ВГ, ГА, (общая) высота же
упомянутая; таким образом, зти треуголь-
треугольники вместе, [то есть поверхность пирамиды
за вычетом треугольника АВГ], будут рав-
равны треугольнику, имеющему основание, рав-
равное вместе взятым АЛ, В Г, ГА, высотой
же — упомянутую прямую.
[Более ясно другое доказательство*).
Пусть будет равнобедренный конус,
осполанием которого является круг АВГ
{рис. 8}, першиной же точка Д: пусть в этот
конус вписана пирамида, имеющая основа-
основанием равносторонний треугольник АВГ,
и проведены линии АА, ДГ, ДВ; я утверждаю, что треугольники АДВ,
АДГ, ВДГ равны треугольнику, основание Е
которого равно периметру треугольника
АВ Г, а опущенный нз верптипы на это осно-
основание перпендикуляр равен перпендикуляру,
опущенному из Д на сторону В Г.
Проведем перпендикуляры ДК, ДА, ДМ;
они, конечно, равны между собой. Возьмем
треугольник EZH, имеющий основание EZ
равным периметру треугольника АВГ и
«тлеоту Н(ь) ранной ДА. Так как прямоуголь-
прямоугольник на ВГ, АЛ вдвое больше треугольни-
треугольника АВГ, прямоугольник между АВ, ДК
вдвое больше треугольника АВД и прямо-
прямоугольник между АГ, ДМ вдоое больше тре-
треугольника АДГ, то, значит, прямоугольник
между периметром треугольника ЛВГ, то
есть между EZ, и АЛ, или Нв, будет вдвое
больше треугольников АДВ, ВДГ, АДГ,
вместе взятых. Также и прямоугольник Рис. 8.
между EZ.HB вдвое больше треугольника
EZII; значит, треугольник EZH будет равен треугольникам АДВ, ВАГ
и АДГ, вместе взятым].
VIII
Если около равнобедренного конуса описана пирамида, то поверх-
поверхность пирамиды за вычетом основания равна треугольнику, имеющему
основанием прямую, равную периметру основания {пирамиды), а высо-
высотой — сторону конуса.
'*)' Из' этих слон и»дно, что ШЕкепомсщеннОе докаяатсльство не принадлежит Архимеду.
О ШЛРЕ И ЦИЛИНДРЕ
103
Пусть будет конус, основание которого есть круг АВГ, и около
конуса описана пирамида {рис. 9), так что ее основание, то есть много-
многоугольник AEZ, будет описано около круга АВГ. ^
Я утверждаю, что поверхность этой пирамиды за
вычетом основания равна вышеупомянутому тис-
угольнику-
Действителыто, так как [ось конуса перпен-
перпендикулярна к основанию, т. е. к кругу АВГ, и]
прямые, соединяющие центр этого круга с точ-
точками касания, перпендикулярны к касатель-
¦ пым, то прямые, соединяющие вершину конуса
с точками касания, будут перпендикулярны к ДЕ,
EZ, ZA. Таким образом, вышеупомянутые перпен-
перпендикуляра НА, IIB, ИГ равны между собой, ибо
они являются сторонами конуса. Возьмем тре-
треугольник вКЛ, имеющий сторону вК равной
периметру треугольника AEZ, а перпендику-
перпендикуляр ЛМ равным НА. Так как прямоугольник
между АЕ, АН ндное больше треугольника ЕАН,
прямоугольник между AZ, НВ вдвое больше
треугольника AZH и прямоугольник между EZ,
ГИ вдвое больше треугольника EHZ, то, значит,
прямоугольник между ©К и АТТ, или МЛ, вдвое
больше треугольыикои ЕЛИ, '/ЛИ, EHZ тшесте
взятых. Такгке и прямоугольник между 6К,
ЛМ вдвое болынц треугольника ЛК6; вследст-
вследствие этого поверхность пирамиды за вычетом основании Аудет равна
треугольнику, имеющему основанием прямую,
равную периметру
конуса.
AEZ, а высотой сторону
IX
Если прямая линия пересекает круг, явля-
являющийся основанием некоторого равнобедренного
конуса, и от. ее концов проведены прямые линии
к вершине, конуса, то треугольник, заключенный
между этой секущей и прямыми, соединяющими
ее концы с вершиной, будет меньше поверхности
конуса между этими соединяющими с вершиной
прямыми.
Пусть круг АВГ {рис. 10} будет основа-
основанием равнобедренного конуса, а точка Л — его
вершиной; гфонедем в круге какуто-штбудь пря-
прямую АГ и соединим точки Л, Г с веришной
прямыми АЛ, ДГ. Я утверждаю, что треуголь-
треугольник АДГ будет меньше конической поверхности, заключенной между
АД, А Г.
Разделим дугу ЛВГ пополам в точке В и проведем соединяющие
прямые АВ, ГВ, АВ; тогда треугольники АВД, В ГА вместе будут
больше треугольника АДГ. Пусть 0 будет величина, на которую выше-
вышеупомянутые треугольники превышают треугольник АДГ; тогда 0 будет
или меньше (суммы) сегментов АВ, ВГ, или же нет.
Рис. 10.
104 АРХИМЕД
Пусть сначала © будет не меньше их {суммы).
Так как имеются две поверхности — коническая между АД, АВ
вместе с сегментом ЛЕВ и треугольник АЛВ — и обе опи имеют одну
и ту же границу — периметр треугольника АДВ, то объемлющая
поверхность будет больше объемлсмой: значит, коническая поверхность
между АД, АВ вместе с сегментом АЕВ будет больше треугольника
АБА. Точно так же (коническая поверхность) между ВД, ДГ вместо
с сегментом FZB больше треугольника ВАГ; тогда вся коническая
поверхность вместе с площадью 0 будет больше обоих упомянутых
треугольников. Но упомнпутые треугольники равны треугольнику
АДГ вместе с площадью в. Отнимем общую площадь 0; тогда остав-
оставшаяся коническая поверхность между АД, АГ будет больше треуголь-
треугольника АДГ.
Пусть теперь 0 будет меньше (суммы) сегмептоп АВ, ВГ.
Разделяя пополам дуги АВ, ВГ, а затем пополам их половинки,
. мы придем к сегментам (в сумме), меньшим площади 0*). Пусть это
будут сегменты (S4e + S'eb + ?bz + Szv < ©)> ограниченные прямыми
АЕ, ЕВ, BZ, 7.Г.
Проведем ДЕ и AZ. Тогда по той гке причине поверхность конуса
между АД, ДЕ вместе с сегментом па АЕ будет больше треугольника
АДЕ, а поверхность между ЕА, ДВ вместе с сегментом на ЕВ больше
треугольника ЕДВ; значит, поверхность (конуса) между АД, ДВ
вместе с сегментами на АЕ, ЕВ будет больше треугольников АДЕ,
ЕВА. Поскольку же, согласно доказанному, треугольники АЕД, ДЕВ
больше треугольника АВД, то значит, и подавно поверхность конуса
между АД, ДВ вместе с сегментами на АЕ, ЕВ будет больше треуголь-
треугольника АДВ. На том же основании и поверхность конуса между ВД, ДГ
вместе с сегментами на BZ, ZT больше треугольника ВДГ; значит,
вся поверхность между АД, ДГ вместе с упомянутыми сегментами будет
больше треугольников ABA и АВГ. Но эти треугольники равны тре-
треугольнику АДГ и площади 0, причем упомянутые сегменты (в сумме)
меньше площади Э; значит, остающаяся поверхность конуса между
АД, ДГ будет больше треугольника АДГ [5, С].
X
Если к кругу, являющемуся основанием конуса, мы проведем каса-
касательные, лежащие в одной плоскости с кругом и пересекающиеся между
собой, а затем полученные точки касания и пересечения касательных
соединим прямыми с вершиной конуса, то треугольники, заключаю-
заключающиеся между касательными и прямыми, соединяющими с вершиной
конуса, будут больше отсекаемой ими части конической поверхности.
Пусть будет конус, основанием которого является круг АВГ
{рис. 11}, а вершиной — точка Е; к кругу АВГ проведем касатель-
касательные АД и ГД, расположенные в той же самой плоскости, и вершину
конуса Е соединим с точками А, Д, Г прямыми ЕА, ЕД, ЕГ. Я утвер-
утверждаю, что треугольники АДЕ, ЛЕГ**) будут больше конической поверх-
поверхности, находящейся между прямыми АЕ, ГЕ и дугой АВГ.
• На осноцакии предложения Vf.
•* То есть сумма втих треугольников.
О ШАРЕ И ЦИЛИНДРЕ
105
Разделим дугу ЛВГ в точке В пополам и проведем к кругу
касательную HBZ, параллельную АГ; точки Н, Z соединим с Е пря-
прямыми НЕ, ZE. И так как прямые ДН, AZ, взятые вместе, боль-
¦ ше HZ, то добавим к обеим НА, ZT, тогда АД и АГ вместе будут боль-
больше АН, HZ, ZF,
Рис. 11.
АД + ДГ > АН 4-HZ
Так как АЕ, ЁВ, ЕГ суть образующие*) конуса, то они равны между
собой, поскольку конус равнобедренный; точно так же они перпенди-
перпендикулярны**); [прямоугольники асе между вы-
высотами и основаниями вдвое больше соответствую-
соответствующих треугольников;] следовательно, треугольни-
треугольники АЕД, ДЕГ будут больше треугольников
. АНЕ, IIEZ, ZEI\ [ибо АН, НГ, ZV меньше ГА,
.-. ДА, высоты же у тех и других равны.] [ГГсно,
, что прямая, соединяющая вершину прямого кс-
нуса с точкой касания на основании, будет перпен-
. I дикулярна к касательной.]***)
Пусть треугольники: АЕЛ и ДЕГ превышают
треугольники AEII, HEZ, ZET на площадь в.
Тогда площадь в будет ил и меньше отреэкоп АН ВК А
и В7ГЛ (между касательными и окружностью
¦ круга), или же не меньше их.
Пусть сначала опа будет пе меньше. Так как
¦¦/-. имеются две составленные поверхности, а именно
поверхность пирамиды с основанием — трапецией
¦ ¦ HATZ и вершиной Е и коническая поверхность
между АЕ, ЕГ вместе с сегментом АВГ, и обе они
имеют одну и ту же границу — периметр треугольника ЛЕГ, то ясно,
что поверхность пирамиды за вычетом треугольника АЕГ будет больше
конической поверхности вместе с сегментом АВГ. Отнимем общий сег-
сегмент ЛВГ; тогда оставшиеся треугольники АНЕ, HEZ, ZET вместе с
отрезками по краям ЛПВК, BZTA будут больше конической поверх-
поверхности между прямыми АЕ, ЕГ. Но площадь © не менее отрезков
АНВК, BZTA; значит, и подавно треугольники АНЕ, HEZ, ZET
вместе с в будут больше конической поверхности между ЛЕ, Е Г.
Но треугольники АНЕ, HEZ, TEZ вместе с в равны треугольни-
треугольникам АЕД, ДЕГ; значит, треугольники АЕД, ДЕГ больше упомянутой
конической поверхности.
Пусть теперь 0 будет меньше этих отрезков по краям.
Тогда, точно так же описыпая все время около сегментов много-
многоугольники, разделяя пополам остающиеся по краям дуги и проводя
касательпые, мы придем к некоторым отрезкам, которые будут меньше
площади В. Пусть полученные такие отрезки будут АМК, KNB,
ВЕЛ, ЛОГ, которые вместе меньше площади 6.
Соединим полученные точки с Е. Тогда опять ясно, что треуголь-
треугольники АНЕ, HEZ, ZET, взятые вместе, больше треугольников АЕМ,
MEN, NEB, SEO, ОЕГ, (ибо основания у первых больше, а высоты оди-
одинаковы]. Кроме того, пирамида, имеющая основанием многоугольник
*) Вукиально: сторсиы (е)
**) К карательным АН, HZ. Zr.
***) Отмеченная Гсйбергом двойная интерполяция.
¦:¦ •¦¦:<
10G
АРХИМЕД
AMNSOF, а вершиной Е, точно так же будет, если вычесть тре-
треугольник АЕГ, иметь поверхность большую, чем коническая поверх
пость между АБ, ЕГ, взятая имеете с сегментом АВГ. Отнимем общий
сегмент АБГ; тогда оставшиеся треугольники АЕМ, MEN, NEH,
SEO, ОЕГ вместе с отрезками по краям АМК, KNB, ВЗЛ, ЛОГ будут
болыпо конической поверхности между АЕ, ЕГ. Но площадь 6 больше
упоминутых отрезков по краям; треугольники же АЕН, HEZ, ZET,
как показано, больше треугольников А ЕМ, MEN, NEH, SEO, ОЕГ;
значит, и поданно треугольники АЕН, HEZ, ZET вместе с площадью 6,
то есть треугольники АДЕ, АЕГ, будут больше конической поверхно-
поверхности между прямыми АЕ, ЕГ [6].
XI
Если па поверхности прямого цилиндра имеются две прямые, то
поверхность цилиндра между этими прямыми больше параллелограмма,
заключающегося между находящимися на. поверхности цилиндра пря-
прямыми и другими, соединяющими их концы.
Пусть будет прямой цилипдр, основание которого круг АВ,
а противоположное — круг ГД*) {рис. 12}; проведем соединяющие
прямые АГ и ВА; я утверждаю, что цилиндриче-
цилиндрическая поверхность, отсеченная прямыми АГ, ВД,
больше параллелограмма АГВД.
Разделим каждую из дуг АВ, ГД пополам в
точках К, Z и проведем соединяющие прямые АЕ,
ЕВ, TZ, ZA. Так как АЕ и ЕВ вместе больше АВ,
и построенные на них параллелограммы равновы-
соки, то параллелограммы, основания которых АЕ
и ЕВ, а высота та же, что и у цилиндра, вместе
взятие, будут больпте параллелограмма АВГД. На
сколько же они будут больше? Пусть они больше
на площадь Н, Тогда площадь Н будет или мень-
меньше плоских сегментов АЕ, ЕВ, TZ, ZA, или же
не меньше.
Пусть сначала она будет не меньше. Так как
отсеченная прямыми АГ, ВД цилиндрическая по-
поверхность вместе с (сегментами **)} АЕВ, TZA
имеет границей плоскость параллелограмма
АГВД, и так как поверхность, составленная из параллелограммов
с остюпаниими АЕ, ЕВ и высотой той же, что у цилиндра, и [плоских
фигур] ЛЕВ, V'/Л, имеет границей (ту же самую) плоскость парал-
параллелограмма АВДГ, и перпая поверхность объемлет вторую, причем
обе они выпуклые в одну сторону, то отсеченная прямыми АГ, ВД
цилиндрическая поверхность имеете с плоскими сегментами АЕВ, TZA
будет больше поверхности, составленной из параллелограммов с осно-
основаниями АЕ, ЕВ и с той же высотой, что у цилиндра, и из треуголь-
треугольников АЕВ, Г/Л.
Отнимем общие треугольники АЕВ, TZA; тогда оставшаяся цилин-
цилиндрическая поверхность, отсеченная прямыми АГ, ВД, вместе с плоскими
сегментами АЕ, ЕВ, TZ, ZA будет больше поверхности, составленной
Рис. 12.
*) dvpaais ftiv i ЛИ кукЯик. «mevaviiov 6i ГД—терминология «Начал» Квклица. Мы сказали
бы просто- с основаниями ЛВ и ГД-
**) Сегмент АЕВ—сегмент, стирающийся на хорду АВ и содещиащий точку Е. .
О ШАРЕ И ЦИЛИНДРЕ
из параллелограммов с основаниями АЕ, ЕВ и с той же нысотой, что
у цилиндра.
Но параллелограммы с основаниями АЕ, ЕВ и с высотой той же,
что у цилиндра, равны параллелограмму АГВД вместе с площадью II;
значит, оставшаяся цилиндрическая поверхность, отсеченная прямыми
АГ, ВД, будет больше параллелограмма АГВД.
Пусть теперь площадь Н будет меньше плоских сегментов АЕ, ЕВ,
FZ, ZA.
Разделим пополам каждую из дуг АЕ, ЕВ, FZ, 7Л в точках в, К,
А, Ми проведем соединяющие прямые А0, 6Е, ЕК, KB, ГА, AZ, ZM,
МЛ; [таким образом, от плоских сегментов АЕ, ЕВ, FZ, ZA отнимутся
треугольники АвЕ, ЕКВ, FAZ, ZMA, не меньшие их полонии]. Если
мы будем действовать так все время, то получатся некоторые сегменты,
которые будут меньше площади II. Пусть они получепи и будут АЭ,
вЕ, ЕК, KB, ГА, AZ, ZM, МЛ. Тогда подобным же образом докажем,
что параллелограммы, основания которых суть Ав, GE, ЕК, KB,
а высота —та ?ке, что и у цилиндра, будут больше параллелограммов,
основания которых суть АЕ, ЕВ, а высота — та же, что и у цилиндра.
И так как цилиндрическая поверхность, отсекаемая прямыми АГ, ВД,
вместе с плоскими сегментами АЕВ, Г7Л, имеет границей плоскость
параллелограмма АГВД, а поверхность, составленная из параллело-
параллелограммов, основания которых суть Л€), 6Е, ЕК, KB, а высота — та же,
что и у цилиндра, и из прямолинейных фигур ЛЭЕКВ, FAZMA (тоже
имеет границей плоскость параллелограмма ЛГВЛ, то отсекаемая пря-
прямыми АГ, ВД цилиндрическая поверхность имеете с плоскими сегмен-
сегментами АЕВ, TZA будет больше поверхности, составленной из параллело-
параллелограммов, основания которых суть Ав, вЕ, ЕК, KB, а нысота — та же,
что и у цилиндра, и из прямолинейных фигур ЛвЕКВ, FAZMA)*).
Отнимем общие прямолинейные фигуры АвЕКВ, FAZMA; тогда оста-
остаток — отсекаемая прямыми АГ, ВЛ цилиндрическая поверхность вместе
с плоскими сегментами АВ, вЕ, ЕК, KB, ГЛ, AZ, ZM, МД будет боль-
больше поверхности, составленной из параллелограммов, основания кото-
которых суть А©, 6Е, ЕК, KB, ГЛ, AZ, ZM, МЛ, а высота — та же, что
и у цилиндра.
Параллелограммы же, основания которых суть А0, 0Е, ЕК, KB,
а высота — та же, что и у цилиндра, больше параллелограммов, осно-
основания которых суть АЕ, ЕВ, а высота та же, что и у цилиндра; значит,
и цилиндрическая поверхность, отсекаемая прямыми АГ, ВД, вместе
с плоскими сегментами Ав, BE, EK, KB, FA, AZ, ZM, MA, будет боль-
больше параллелограммов, основания которых суть АЕ, ЕВ, а высота —
та же, что и у цилиндра.
Но параллелограммы, основания которых суть АЕ, ЕВ, а высо-
высота — та же, что и у цилиндра, равны параллелограмму АГАВ и пло-
площади Н; значит, и цилиндрическая поверхность, отсекаемая прямы-
прямыми АГ, ВД, вместе с плоскими сегментами Ав, вЕ, ЕК, KB, ГА,
AZ, ZM, МД будет больше параллелограмма АГВД и площади Н
вместе взятых.
После же отнятия сегментов Ав, вЕ, ЕК, KB, ГА, AZ, ZM, МД,
меньших площади Н, оставшаяся цилиндрическая поверхность, отсе-
отсекаемая прямыми АГ, ВД, будет больше параллелограмма АГВД.
*) ООорианный конец фразы восстанавливается Гейбергомсогласио сделанному и XIII веке
латинскому переводу Вильгельма иа Мербеке. ¦ ¦ . ¦ -.
АРХИМЕД
XII
Если па поверхности какого-нибудь прямого цилиндра имеются две
прямые и от конца этих прямых к кругам, являющимся основаниями
цилиндра, проведены некоторые касательные, находящиеся в плоскости
оснований и {попарно) пересекающиеся, то параллелограммы, заклю-
заключенные между касательными и сторонами цилиндра, будут больше
поверхности цилиндра между обеими прямыми, находящимися на
поверхности цилиндра.
Пусть круг АВГ {рис. 13} является основанием некоторого
прямого цилиндра, и пусть на поверхности последнего имеются две
прямые, кокни которых суть А и Г; из то-
точек А и Г проведем касательные к кругу,
лежащие в его плоскости, и пусть они
пересекутся в Н. Сообразим также, что и
на другом основании цилиндра из концов
тех же самых прямых на его поверхности
проведены прямые, касательные к соответ-
соответствующему кругу. Требуется доказать, что
параллелограммы, заключающиеся между
касательными и сторонами цилиндра,
будут больше поверхности цилиндра, со-
соответствующей дуге АВГ.
Проведем касательную EZ и из точек
Е, Z параллельно оси цилиндра проведем
прямые до [поверхности] другого основа-
основании; тогда параллелограммы, заключаю-
заключающиеся между АН, ИГ и сторонами ци-
цилиндра, будут больше параллелограм-
параллелограммов, заключающихся между АЕ, EZ, ZT и боками цилиндра, [ибо EH, HZ
более EZ, и после прибавления ЛЕ, ZT общих, НА, IIГ взятые вме-
вместе будут больше АЕ, EZ, ZF вместе взятых]. Тогда пусть площадь
К будет то, на сколько первые параллелограммы больше вторых. Поло-
Половина площади К будет или больше вместе взятых фигур, заключенных
между прямыми АЕ, EZ, ZT и дугами АД, АВ, В©, ЭГ, или нет.
Пусть сначала она будет больше. Поверхность, составленная из
параллелограммов на АЕ, EZ, ZF, трапеции AEZT и (трапеции),
противолежащей ей на другом основании цилиндра, имеет границей
периметр параллелограмма на АГ. Но тот жп самый периметр будет
границей и поверхности, составленной из поверхности цилиндра,
соответствующей дуге АВГ, сегмента АВГ и (сегмента), протипо-
лежащего ему; таким образом, обе упомянутые поверхности оказывают-
оказываются имеющими одну и ту же границу, которая расположена на плоско-
плоскости, обе они являются выпуклыми в одну сторону и одна из них объем-
лет другую и имеет с ней некоторую общую часть; значит, объемлемая
поверхность будет меньше. Тогда после отнятия общих сегмента АВГ
и противолежащего ему поверхность цилиндра, соответствующая дуге
АВГ, будет меньше поверхности, составленной из параллелограммов
на АЕ, EZ, ZT, фигур АЕВ, BZT и им противолежащих. Но поверхно-
поверхности упомянутых параллелограммов вместе с упомянутыми фигурами
меньше поверхности, составленной из параллелограммов на АН, НГ,
(ибо они были бы равны только после прибавления площади К, боль-
большей упомянутых фигур]; после этого ясно, что параллелограммы,
Гис. 13.
О ШАРЕ И ЦИЛИНДРЕ
109
заключающиеся между ATI, ГН и боками цилиндра, будут больше
поверхности цилиндра, соответствующей дуге АВГ.
Если же половина площади К. лс больше упомянутых фигур, то
к сегменту проводятся касательные до тех пор, пока остающиеся по
краям фигуры не сделаются меньше половины К, и все остальное
докажется совершенно так гке, как и раньше.
После доказанного ясно, ч-ю если в равнобедренный конус вписать
пирамиду, то поверхность пирамиды за вычетом основания будет
мепыие конической поверхности, [так как каждый из треугольников,
ограничивающих пирамиду, будет меньше конической поверхности,
заключенной между сторонами троуголытика; значит, и вся поверх-
поверхность пирамиды за вычетом основания будет меньше поверхности
конуса, тоже за пычетом основания], и что если около равнобедренного
конуса описать пирамиду, то поверхность пирамиды за вычетом осно-
основания будет больше поверхности конуса за вычетом основания.
Из доказанного также ясно, что если л прямой цилиндр вписать
призму, то поверхность призмы, составленная из параллелограммов,
меньше поверхности цилиндра за вычетом обоих оснований, [так как
каждый параллелограмм призмы меньше соответствующей ему части
цилиндрической поверхности], и что если около прямого цилиндра
описать призму, то составленная из параллелограммов поверхность
призмы больше поверхности цилиндра за вычетом обоих оснопаний.
XIII
Поверхность всякого прямого цилиндра за вычетам оснований равна
кругу, радиус которого является средней пропорциональной между сто-
стороной цилиндра и диаметром его основания.
Пусть круг А {рис. 14} будет осно- л. , к
ванием некоторого прямого цилиндра; пусть I
прямая ГД равна диаметру круга A, a EZ рав- Г
на стороне цилиндра; пусть Н будет средней
пропорциональной между ГД, EZ, и круг
В имеет радиус, равный Н; требуется дока-
доказать, что круг В равен поверхности цилин-
цилиндра за вычетом оснопаний.
Действительно, если on не равен, то будет
или больше, или меиытто. Пусть сначала он
будет, если возможно, меньше. Тогда име-
имеются две неравные величины, а именно
поверхность цилиндра и круг В, и мы
можем в круг В вписать равносторонний
многоугольник и околю пего описать другой
так, чтобы опмсапш.щ имел ко вписанному
отношение, моньнтио того, которое; поверх-
поверхность цилиндра имеет к кругу В. Пред-
Представим себе, что первый многоугольник вписан, а нтором описан; около
круга А опишем прямолинейную фигуру, подобную той, которая опи-
описана около В, и на этой прямолинейной фигуре построим призму; опа,
конечно, тоже будет описанной около цилиндра. Пусть периметр пря-
прямолинейной фигуры, онисаттттой около круга А, будет равен КД, пусть
прямая AZ равна КД, а ГТ составляет половину ГД; тогда треугольник
КДТ будет равен прямолинейной фигуре, описанной около круга А,
Рис. 14.
iiO АРХИМЕД
[тан как он имеет основание, рапное ее периметру, а высоту, равную
радиусу круга А], параллелограмм жо ЕЛ район (боковой) поверх-
поверхности при:шы, описанной около цилиндра, [так как он заключается
между стороной цилиндра и прямой, равной периметру основания
призмы]. Отложим прямую ЕР, равную EZ; тогда треугольник ZPA
будет ранен параллелограмму ЕЛ, а, следовательно и (боковой)
поверхности призмы. II так как описанные около кругов А и В прямо-
прямолинейные фигуры подобны, то [эти фигуры] будут иметь то ?ке самое
отношение, что и квадраты на радиусах; значит, треугольникКТД будет
относиться к прямолинейной фигуре, описанной около круга В, как
квадрат на ТЛ к квадрату на Н, [ибо ТД и Н равны радиусам соответ-
соответствующих кругов]. Но отношение квадрата на ТЛ к квадрату на Н
равно отношению линий ТД и PZ.
ТАЗ _ ТА
Н2 ~ PZ
[ибо Н, будучи средней пропорциональной для ГД и EZ, будет также
сродней пропорциональной и для ТД и PZ. Это по следующей причине:
так как ДТ равна ТГ, а РЕ рапна EZ, то ГД вдвое больше ТЛ, a PZ
вдлое больше РЕ; значит, как ЛГ (отпоситсн) к ДТ, так будет и PZ
к ZE. Следовательно, произведение ГД и EZ равно произведению ТД
и PZ. Но произведение ГД и EZ равно квадрату Н; значит, и произве-
произведение ТЛ, PZ равно квадрату Н. Следовательно, как ТД к Н, так будет
и Н к PZ; значит, как ТД к PZ, так и квадрат ТД к квадрату Н, ибо
если имеются три прямые в непрерывной пропорции, то первая будет
относиться к третьей, как фигура, построенияи на первой, относится
к фигуре, подобной и подобно построенной на второй прямой*)]; отно-
отношение же линий ТД и PZ равно отношению (площадей) треугольни-
треугольников КТЛ и PAZ, [ибо КД и AZ равны]; следовательно, треугольник
К.ТЛ будет относиться к прямолинейной фигуре, описанной около кру-
i га В, как треугольник ТКД к треугольнику PZA. Значит, треугольник
ZAP будет равен прямолипейпой фигуре, описанной около круга В;
; таким образом, (боковая) ттоверхностьнризмы, описанной около цилин-
цилиндра А, будет равна прямолинейной фигуре, описанной около круга В.
И поскольку прямолинейная фигура, описанная около круга В, к фигу-
фигуре, вписанной в этот же круг, имеет отношение, меньшее того, которое
поверхность цилиндра А имеет к кругу В, то и (боковая) поверх-
поверхность призмы, описанной около цилиндра, к прямолинейной фигуре,
вписанной в круг В, будет иметь отношение; меньшее, чем (боковая.)
поверхность цилиндра к кругу В; и после перестановки (бокопая
поверхность призмы к боковой поверхности цилиндра будет иметь отно-
отношение мепыиоо, чем вписанная в круг В фигура к кругу В), а это
невозможно, [ибо доказано, что поверхность призмы, описанной около
цилиндра, больше поверхности цилиндра, а игшеапнан в круг В фигура
меньше круга В]. Таким образом, круг В не будет меньше (боковой)
поверхности цилиндра.
Пусть теперь, если возможно, он будет больше. Тогда опять вообра-
вообразим прямолинейную фигуру, вписанную в круг В, и другую, описан-
описанную около пего таким образом, чтобы описанная имела ко вписанной
отношение .меньшее, чем круг В к поверхности цилиндра; в круг А
впишем многоугольник, подобный вписанному в круг В, и на много-
•) Из цроцорции о : Ь=1> : с следует о : с == а 2 : ьа.
о ш л ре и цилиндр*:
угольнике, вписанном в этот круг (А), построим призму. Пусть опять
прямая КД будет равна периметру прямолинейной фигуры, вписанной
в круг Л, и 7Л рапиа КД. Тогда треугольник КТД будет больше прямо
линейной фигуры, «писанной в круг Л, [так как основанием он имеет
оо периметр, а высота его больше, перпендикуляра, опущенного из
центра на одну из сторон многоугольнина], а параллелограмм ЕЛ равен
составленной из параллелограммов поверхности призмы, [так как он
заключается между стороной цилиндра и прямой, равной периметру
прямолинейной фигуры, являющейся основанием призмы]; таким обра-
образом, и треугольник PAZ будет ранен поверхности призмы. Но так как
прямолинейные фигуры, лписаппые п круги А и В, подобны, то они
относятся друг к другу, как квадраты радиусоп соответствующих кру-
кругов. Но и треугольники КТД, ZPA находятся друг с другом в двойном
отношении *) радиусов этих кругов; следовательно, прямолинейная
фигура, вписанная в круг А, будет иметь к прямолинейной фигуре,
вписаппой и Г?, то же самое отношение, что треугольник КТД к тре-
треугольнику AZP.
Но прямолинейная фигура, иписанная в круг А, меньше треуголь-
треугольника КТД; следовательно, и фигура, вписатшая в круг Г5, будет меньше
треугольника ZPA, а следовательно, меньше и {боковой) поверхности
призмы, вписанной в цилиндр, а это невозможно, [так как прямолиней-
прямолинейная фигура, описанная около круга. Б, имеет ко вписанной фигуре
меньшее отношение, чем круг В к (боковой) поверхности цилиндра,
и после лерестапопки (описанная около круга В фигура имеет к кру-
кругу В меньшее отношение, чем вписанная фигура к боковой поиерхно-
сти цилиндра). Но фигура, описаппая около круга Г5, больше круга В;
значит, вписанная в круг Б-фигура больше (боковой) поверхности
цилиндра, а следовательно, и (боковой) поверхности призмы].
Итак, круг Г5 будет не больше поверхности цилиндра. Доказано же, что
он и не меньше; значит, он будет ей равен [7].
XIV
Поверхность всякого равнобедренного конуса за вычетом основания
равна кругу, радиус которого есть средняя пропорциональная между
стороной конуса и радиусом круга, являющегося
основанием конуса.
Пусть будет равнобедренный конус, оспоиа-
ние которого круг А {рис. 15}; пусть радиус
этого круга будет Г, а сторона конуса Д; пусть
Е будет средней пропорциональной между Г и Д,
0
и круг Г5 имеет радиус, равный Е; я утверждаю, /¦ |
что круг В ранен поверхности конуса за вычетом К
основания.
&
В
Действительно, если он но равен ей, то бу-
дет или больше, или мзныие. с'
Пусть сначала он будет меньше. Тогда имеются
две неравные величины — поверхность конуса и круг В, причем большей
является поверхность конуса; значит, можно вписать в круг В равносто-
равносторонний мпогоуголыгак и описать около него другой, подобный вписанно-
вписанному, так, чтобы описанный имел ко вписанному отношение меньшее того,
*) То есть как киадрати радиусов.
112 АРХИМЕД
которое поверхность конуса имеет к кругу В. Теперь вообразим, что
около круга Л описан многоугольник, подобный описанному около
круга В, и па многоугольнике, описанном около круга А, построена
пирамида, имеющая ту же вершину, что и конус. Так как многоуголь-
многоугольники, описанные около кругов Л и В, подобны, то они имеют друг
к другу отношение, равное двойному отношению их радиусов, то есть
двойному отношению Г и Е, или {отношению) линий Г и Д. Но
отношение линий Г и Д равно отношепию многоугольника, описанного
около круга Л, к (боковой) поверхности пирамиды, описанной око-
около конуса, [ибо Г рапна перпендикуляру, опущенному из центра на
одну из сторон многоугольника, а Д равна стороне конуса; периметр же
упомянутого многоугольника будет общей высотой двух прямоуголь-
прямоугольников, половины которых соответственно равны многоугольнику, опи-
описанному около круга А и боковой поверхности пирамиды, описанной
около конуса}*). Значит, прямолинейная фигура, описанная около
круга А, к прямолинейной фигуре около круга В имеет то же самоо
отношение, что и к (боковой) поверхности пирамиды, описанной
около конуса; таким образом, (боковая) поверхность нирамиды рав-
равна многоугольнику, онисаппому около круга В. Теперь так как много-
многоугольник, описанный около круга 11, ко вписанному многоугольнику
имеет меньшее отношение, чем поверхность конуса к кругу В, то и
(боковая) поверхность описанной около конуса пирамиды будет
к многоугольпику, пписанному в круг В, иметь меньшее отношение,
чем (боковая) понерхность конуса к кругу В, а это невозможно,
(ибо доказано, что поверхность пирамиды больше поверхности конуса,
тогда как многоугольник, вписанный п круг В, меньше круга BJ. Итак,
круг В не будет меньше (боковой) поверхности конуса.
Теперь я утверждаю, что он не будет и больше. Действительно,
пусть, если возможно, он будет больше. Тогда опять вообразим много-
многоугольник, пписанный в круг В, и другой, описанный около пего, так,
чтобы описанный имел ко пписанному отношение меньшее того, которое
круг В имеет к (боковой) поверхности конуса, вообразим много-
многоугольник, вписанный в круг А и подобный пписанному в круг В, и по-
построим на нем пирамиду, имеющую ту же вершину, что и копус. Теперь
так как вписанные в круги А и В многоугольники подобны, то они
будут находиться друг к другу в двойном отношении их радиусов;
значит, отношение одного многоугольника к другому будет равняться
отношению линий Г и Д. Но Г имеет к Д большее отношение, чем то,
которое многоугольпик, вписанный вокруг А, имеет к (боковой) поверх-
поверхности пирамиды, вписанной и конус, [ибо радиус крута А к стороне
конуса имеет большее отношение, чем перпендикуляр, опущенный из
центра на одну из сторон многоугольника, имеет к перпендикуляру,
опущеннодгу на зту сторону иа вершины конуса]; значит, многоуголь-
многоугольник, вписанный в круг А, к многоугольпику, вписанному в В, будет
иметь большее отношение, чем к (боковой) поверхности пирамиды;
так что (боковая) поверхность пирамиды будет больше многоуголь-
многоугольника, вписанного в круг В. Но многоугольник, описанный около кру-
круга В, имеет ко вписанному моныпее отношение, чем круг В к (боковой)
поверхности конуса; значит и подавно описанный около круга В мттого-
*)В тексте просто xolvto fii 5фое ¦»! пео.:ц.?тро5 то» тАтгуЛл'ои nQiq та Т]ц,1<гт) хп>\ eHp
как вто темное место наверняка не принадлежит Архимеду, то я счел себя в праве дать более рас-
распространенный и имеющий смысл персиод. ¦ ¦ - *'
О ШЛСК II ЦИЛИНДРЕ
угольник будет к (боковой) поверхности пирамиды, вписанной и конус,
иметь меньшее отношение, чем круг В к (боколой) поверхности
конуса, а это невозможно, [так как описанный многоугольник больше
круга В, (боковая) же поверхность пирамиды в конусо меньше {боко-
{боковой) поверхности конуса}. Значит, круг В не будет больше поверх-
поверхности конуса.
Но уже докапано, что он не будет и меньше; значит, он ей равен.
XV
Поверхность*) всякого равнобедренного конуса имеет к основанию
такое же отношение, пак сторона конуса к радиусу его основания.
Пусть будет равнобедренный конус, основание
которого — круг А {рис. 16}; пусть прямая В
равна радиусу круга А, а Г равна стороне конуса;
требуется доказать, что поверхность конуса имеет
к кругу А такое же отношение, как Г к В.
Вояьмем К — среднюю пропорциональную
между В и Г — и построим круг Д, имеющий
радиус, равный Е; значит, круг Д будетравен( боко-
боковой) поверхности конуса; [г»то доказало и преды-
предыдущем].
Доказано также, что круг А имеет к кругу
А отношение, равное отношению линий Г и В,
[ибо каждое из этих отношений равно двойному Pjl«'-
отношению Е и В, так как круги будут относиться
друг к другу, как квадраты на диаметрах или на радиусах, а диаметры
относятся, каких половины, или радиусы; последние же равны В и Е].
Теперь ясно, что (боковая) поверхность конуса имеет к кругу А
отношение, равное отношению линий Г и В.
XVI
Если рассечь равнобедренный конус плоскостью, параллельной
основанию, то поверхность конуса между обеими параллельными плос-
плоскостями будет равна кругу, радиус которого является средней пропор-
пропорциональной для стороны конуса между параллельными плоскостями и
прямой, равной вместе взятым радиусам обоих кругов, лежащих
е параллельных плоскостях.
Пусть будет конус, у которого треугольник осевого сечения есть
АВГ {рис. 17}; рассечем его параллельной основанию плоскостью:
пусть она образует сечение ДЕ; осью конуса пусть будет ВН; построим
круг, радиус которого является средней пропорциональной между АЛ
и вместе взятыми AZ и НА; пусть это будет круг 0; я утверждаю, что
круг 0 будет ранен поверхности конуса, заключенной между АЕ и AT.
Действительно, построим круги А и К так, чго радиус круга К
квадрирует прямоугольник между ВД, AZ, а радиус круга А кпадрирует
прямоугольник между ВА, АН; тогда круг Л будет ранен (боковой)
поверхности конуса ЛВГ, а круг К — (боковой) поверхности кону-
конуса ЛЕВ. Так как (прямоугольник) между ВЛ, АН равен (прямо-
(прямоугольнику) между ВА, AZ (вместе с прнмоуголытиком) между АД
*) Подразумевается боковая поверхность.
Архимед
114
АРХИМЕД
и вместе взятыми AZ и АН,
ВА- А П = ВЛ - &Z 4- АД WZ + ЛИ)
вследствие параллельности AZ и АИ*), а прямоугольник между АВ, АН
квадрируется радиусом круга Л, прямоугольник
между БД, AZ квадрируется радиусом круга К а
(прямоугольник) между ДА и вместе взятыми AZ,
АН квадрируется радиусом круга в, то, значит,
квадрат на радиусе круга Л равен вместе взятым
квадратам па радиусах кругов К и в; таким обра-
аом, и круг Л будет равен вместе взятым кругам К,
В. Но круг Л равен (боковой) поверхности конуса
ВАГ, а круг К — (боковой) поверхности конуса
ДВЕ; значит, остаток—поверхность конуса между
параллельными плоскостями ДЕ, АГ — будет
равен кругу 0.
[Пусть имеется параллелограмм ВАН
[рис. 18}, и пусть ВН будет его диаметр. Рассе-
Рассечем сторону ВА в какой-пибудь точке Д и че-
через Д проведем А6 параллельно АН, а через Z
лроиедум КЛ параллельно ВА; я утверждаю, что
(прямоугольник) между ВА, АН равен вместе
взятым (прямоугольнику) между БД, А7, (и прямоугольнику) между
АД и вместе взятым AZ, АН.
Действительно, так как (прямоугольник) между В А, АН пред-
представляет весь параллелограмм ВН, (прямоугольник) между ВЛ,
AZ—параллелограмм BZ и прямоугольник
между ДА и вместе взятыми AZ,AH — гно-
гномон M.N5 (ибо (прялмоугольник) между
ДА, АН представляет параллелограмм КН
вследствие равенства «дополнений»**) Кб и л
ДА,: а (прямоугольник) между АА, AZ —
параллелограмм ДА), то, следовательно,
весь параллелограмм ВН, то есть (прямо- '
угольник) между В А, АН, равен прямо-
прямоугольнику между ПА, AZ вместе с гномо-
гномоном MNS, который в свою очередь равеп прямоугольнику между ДА
и вместе взятыми АН, AZJ***).
Рис. 17.
И
и
Рис. 18.
Л е м м ы
1. Конусы, имеющие равные высоты, относятся друг к другу, как
основания; имеющие же равные основания относятся, как высоты
(Начала, XII, 11, 14).
2. Если цилиндр рассечен плоскостью, параллельной основаниям,
то один из получившихся цилиндров относится к другому, как одна us
соответствующих осей к другой (Начала, XII, 13).
*) Имеем B.VAH — Вд-ДН-i- ДА-АН и АН : AZ - АВ : Вд, откуда АН-ВД = АВ- AZ, т. с.
ЕЛ- АН — AB-AZ-f АД-АН = ВД-Дг-|- АД (.4Z }- АН).
*•) пацап^ощш. — термин «Начал» Евклида A.4Я).
***) Эта теорема, вспомогательная к пркцлож^нию XVI, являстсн позднейшей вставкой. Евто-
ьий имел рукопись Архимеда бея этой теоремы, так как он дает специальное пояснение к предложс-
пю XVI.
О ШАГЕ И ЦИЛИНДРЕ
115
3. Конусы,-, имеющие с цилиндрами одни и, те же основания {и рав-
равные высоты), имеют друг к другу то же самое отношение, что и цилин-
цилиндры (Следует из предложения 10 книги XII «Начал»).
4. У равных конусов основания обратно пропорциональны высотам;,
и конусы, у которых основания обратно пропорциональны еысота.а,_
будут равны (Начала, XII, 15).
5. И конусы, диаметры оснований которых относятся, как оси,
[то есть как высоты], будут друг к другу в тройном*) отношении
диаметров (Начала, XII, 12).
Все это доказано предшествующими писателями.
кд
XVI1
Если даны два равнобедренных конуса и поверхность одного конуса
равна основанию другого, а перпендикуляр, опущенный из ijcumpa основа-
основания первого конуса на сторону, ранен еысоте (второго конуса), то оба
конуса будут равны.
Пусть будут дна равнобедренных коиуса АВГ, AEZ {рис. J9},
и пусть основание конуса АВГ равно поверхности конуса AEZ, высо-
высота же АН равна перпендикуляру Кб, опущенному из центра 6 основа-
основания на одну иа сторон конуса, например ДЕ;
и утверждаю, что оба конуса будут равны.
Так лак основание (конуса) АВГ равно по-
поверхности (конуса) AEZ, [равные же величины
к одному и тому же имеют одно и то же отноше-
отношение], то, значит, как основание ВАГ к осиога-
|гию AEZ, так будет и поверхность AEZ к оснона-
нию AI'IZ. Но поверхность конуса относите» к
своему основанию, как А в к вК, [ибо доказано, что
поверхность всякого равнобедренного конуса имоот
к основанию то же самое отношение, как сторона
конуса к радиусу основания, то j есть как ДЕ к
Ев. Но как ЕД к вА, так будет и Ев к 0К,
Ев . » :
= W
ибо соответствующие треугольники] имеют] равные
углы].
Затем 6К равна АН; значит, основание ВАГ бу- Рис. 19.
дет к оспонапию AEZ, как высота AEZ к высоте АВГ.
Таким образом, у конусов АВГ, AEZ основания обратно про-
пропорциональны высотам; значит, конус ВЛГ равен конусу AEZ.
XVIII
Всякий ромб, составленный из двух равнобедренных конусов, равен
конусу, имеющему основание, равное (боковой) поверхности одного из
конусов, составляющих ромб, а высоту, равную перпендикуляру, опущен-
опущенному иа вершины второго конуса на сторону первого конуса.
Пусть будет составленный из двух равнобедренных конусов
[рис. 20J роыб АВГД, основание которого есть описанный па диаметре В Г
*) То есть в возведенном в третью степень.
S*
llfi
АРХИМЕД
N0
ДЕ~
круг, итлсота ;кс АЛ; возьмем также некоторый другой (конус) ТТ6К,
имеющий основание, равное (боковой) поверхности конуса АНГ,
высоту же, равную перпендикуляру, опущенному из точки Д на АВ
или на ее продолжение; пусть этот перпендикуляр будет AZ, пысота же
конуса 0HK будет ЭА; тогда 6А равна AZ; я утверждаю, что этот конус
.будет равен вышеназванному ромбу.
Построим другой копус MN5, имеющий осиовапие, равное осно-
основанию конуса АВГ, а высоту, равную АД; пусть эта высота будет МО.
Так как N0 равпа АД, то значит — как N0 к ДЕ, так и АД к ДЕ.
АД
Но как АД к ДЕ, так и ромб АВГД к конусу ВГД,
АД ромб АВГД
ЛК
N0
ЛЕ
конус ВГД
а как N0 к ДЕ, так и конус MN3 к конусу ВГД,
конус MNS
конус ВГД
[ибо основания их раины]; :шачит, как конус MN3 к конусу ВГД, так
и ромб АВГД к конусу ВГД;
КОНУС MN?
«он у с ВГД
ромб АВГД
конус ВГД
следовательно, if опус MNE равен ромбу АВГД. Но так как поверх-
поверхность конуса АВГ раина основанию конуса H6R, то, аначит, как
поверхность конуса ЛИГ к ого основанию, так и основание конуса Н6К
к основанию конуса MNE, [ибо основание конуса АВГ равно осно-
основанию конуса MNSJ. 1То как поверхность ко-
конуса АВГ к его основанию, так будет и АВ к
BE, или АД к ZA [вследствие подобии треуголь-
треугольников]; значит, как основание IIВК к основа-
основанию MNS, так и АД к AZ.
Но АД равна N0 [но предположению], а
AZ равна 6А; значит, как основание конуса
НЭК к основанию конуса MNE, так и вы-
высота N0 к ©Л. Значит, у конусов Н0К, MNE
оснонапия обратно пропорциональны высотам;
следовательно, :>ти копусм равны. Но дока-
лани, что конус MNE равняется ромбу АВГД;
значит, и конус Н6К равен ромбу АВГД.
XIX
•N
Если равнобедренный конус рассечен пло-
плоскостью, параллельной основанию, затем на
полученном круге построен копус, имеющий
вершиной центр основания, и образовавшийся
ромб отнят от всего конуса, то Окаймление
будет равно конусу, имеющему основание, равное поверхности конуса.
заключенной между параллельными плоскостями, а высоту, равную
перпендикуляру, опущенному из центра основания на одну из сторон
конуса.
Пусть будет равнобедренный конус АВГ {рис 21}; рассечем
его плоскостью, параллельной основанию; пусть полученное сечение
1Чтс. 20.
О ШАРЕ И ЦИЛИНДР*:
117
Л/
'.Г
будет АЕ, а центр осповании Z; на круге с. диаметром ДЕ построим
конус, имеющий вершину Z, тогда ромб BAZE будет составлен из двух
равнобедренных конусов. Возьмем еще некоторый конус К6А, осно
вание которого равно поверхности (конуса АВГ, заключенной)
между АЕ, АГ, а высота раина перпендикуляру ZH, опущенному и а
точки Z на АВ. Я утверждаю, что если
ромб BAEZ вообразить отпитым от кону-
конуса АВГ, то окаймление будет равно ко-
иусу 0КЛ.
Построим два конуса ММЕ, OIIP тя-
кне, чтобы основание конуса MNE было
раки о поверхности конуса АГ5Г, а пмсота
равнялась ZH, [тогда «следствие этого
конус MNS будет равен конусу АВГ;
действительно, если имеются два равнобед-
равнобедренных конуса, у которых поверхность
одного конуса равна основанию другого
и перпендикуляр, опущенный из центра
основания первого конуса та сторону
его, равен высоте второго, то оба конуса
будут ралны], и чтобы основание конуса
ОПР было равно поверхности конуса
ДВЕ, а высота равнялась ZH; [тогда ко-
конус ОПР будет равен ромбу BAEZ. как
уже было доказано выше]. Так как по-
поверхность конуса АВГ складывается из
поверхности конуса ДВЕ и той, которая
заключается между АЕ и АГ, и поверх-
поверхность конуса АВГ равна осноканию ко-
конуса MN3, поверхность конуса ДВЕ равна основанию конуса ОПР, а по-
поверхность между ДЕ, АГ равна основанию конуса ©КА, то. значит,
основание конуса MNS равно (вместе взятым) основаниям конусов
ВКА и ОПР. И все конусы имеют одинаковую высоту; значит, ко-
конус MN3 равен конусам 0KA и ОПР. По конус MNS равен кону-
конусу АВГ, конус же ОПР — ромбу BAEZ; значит, остающийся конус
6КА будет равен окаймлению.
XX
Если в составленном из равнобедренных конусов ромбе рассечь один
конус плоскостью, параллельной основанию, и на полученном круге
построишь конус, имеющий ту же вершину, что и другой конус, затем
полученный таким образом ромб отнять от всего ромба, то окаймление
будет равно конусу, имеющему основание, равное поверхности, заключен-
заключенной, между параллельными плоскостями, а высоту, равную перпенди-
перпендикуляру, опущенному из вершины второго конуса на сторону первого
конуса.
Пусть будет ромб АВГД, составленный из раппобедранных копусои
{рис. 22}; один из этих конусов рассечем плоскостью, параллельной
(«снованию, и пусть полученное сечение будет EZ; на круге, описанном
на диаметре EZ, построим конус, имеющий вершину в А; пусть полу-
полученный ромб будет EBAZ. Вообразим, что он отнят от целого ромба,
и построим конус 0KA, имеющий основание, равное поверхности между
Рис. 21.
118
АРХИМЕД
п
о
АГ и EZ, а высоту, равную перпендикуляру, опущенному ил точки Д
па прямую ВА или ее продолжение; я утверждаю, что конус 0КЛ будет
равен вышеупомянутому окаймлению.
Построим два конуса MN3 и ОПР; пусть основание конуса MNE
будет равно поверхности конуса АВГ, высота же равна АН; [тогда,
согласно доказанному выше,
конус MNE будет ранен ром-
ромбу ABTAJ; у конуса же 0111'
основание пусть будет равно
поверхности конуса EBZ, а вы-
высота равна АИ; [тогда точно так
же конус ОПР будет равняться
ромбу EBAZj. Но подобно (вы-
(выше доказанному) поперхноет!.
конуса АВГ складывается ж\
•V поверхности конуса EBZ и той,
которая заключена между EZ.
АГ; поверхность конуса АВГ
равна основанию конуса MN5,
поверхность к опуса EBZ равна
основанию конуса ОПР, и но
р , 29 верхность между EZ и АГ равни
"с" "' оспованиго конуса GKA; значит.
основание конусе MNE равно
(вместе взятым) основаниям конусов ОПР и 6КЛ. Й все эти конусы
имеют одинаковую высоту; значит, коиус MNE равен конусам 6КЛ,
ОПР. Но конус MNS равен ромбу АВГД, конус же ОПР равен ром-
ромбу EBAZ; значит, остающийся конус
0КЛ будет равен остающемуся окай-
окаймлению.
XXI
Если е круг вписан многоугольник
с. четным числом равных сторон и в
нем проведены Упрямые, соединяющие
стороны многоугольника, и все парал-
параллельные какой-нибудь одной из стяги-
стягивающих две стороны этого многоуголь-
многоугольника, то ecu соединяющие '> {взятие
еместе) будут иметь к диаметру круга
то же отношение, какое прямая, стя-
стягивающая число сторон, на единицу
меньшее половины всего их числа, име-
имеет к одной стороне, многоугольника.
Пусть будет круг АВГА и в него вписан многоугольник
AEZBH0rMNAAK {рис. 23}; проведем соединяющие прямые ЕК,
ZA, ВА, HN, ОМ; ясно, что они будут параллельны прямой, стяги-
стягивающей две (смежные) стороны многоугольника; я утверждаю, что
все упомянутые прямые (взятые вместе) будут к диаметру круга иметь
то же отношение, что ГЕ к ЕЛ.
Проведем соединяющие прямые ZK, ЛВ, ИД, 0N; тогда ZK будет
параллельна ЕА, ВЛ параллельна ZK, затем АН параллельна ВЛ
6N же АН и ГМ параллельна GN. .
О ШАРЕ И ЦИЛИНДРЕ Ц9
[Поскольку имеются две параллели ЕА, KZ и проведены две пере-
пересекающие ЕК, АО, то], значит, как ЕВ к ЗА, так и КЕ к ВО.
ЕВ ^ КЕ
ЗА " "SO"
Но как КЕ к 50, так и Z1I к ПО,
Ka_ Zn
НО = ХЮ
как /ite Z1I к ПО, так и АП к TIP,
•ли _ л_п_
НО ~ ПР
я как ЛП к ПР, так и В2 к 21\
АП В?
ПР~ -F
и далее, как В2 к 2Р, так и А2 к ST,
"Sp" = Tr
как же AS u 2T, так и НГ к ГТ,
Д2 НГ
¦ затем как НГ к ГТ, так и NT к ГФ,
Тф
как же NT к ГФ, так и 6Х к ХФ,
НГ _ Nr
"ГТ ГФ
Nf _ вХ_
ГФ " "ХФ
и наконец, как вХ к ХФ, так и MX к ХГ.
~хф~ ~ хг
[И как псе (предыдущие) ко всем (последующим), так и один
(из предыдущих) к одному (своему последующему)]; значит, как
ЕЕ к ЕЛ, так и ЕК, ZA, BA, HN, 6M (вместе взятые) к диаметру АГ
ES KS + SK 4- Zn 4- ГГЛ + BZ 4- ZA -|- НГ 4- ГЫ 4- 6Х + ХМ __ ЕК + ZА 4- ВД 4- HN 4- 6М
Но как ЕВ к ЕА, так и ГЕ к ЕА; значит, как ГЕ к ЕА, так и все
ЕК, ZA, ВД, HN, ОМ к диаметру АГ [8].
ГЕ ЕК 1- ZA + ВД Ч- HN4- вМ
ЕЛ ~ АГ" " • '
XXII
Если в круговой сегмент вписан многоугольник, имеющий кроме
основания четное число равных сторон, и проведены прямые, параллель-
параллельные основанию сегмента, соединяющие стороны многоугольника, то все
проведенные прямые и половина основания будут иметь к высоте сегмен-
сегмента то оке отношение, какое прямая, соединяющая (конец) диаметр{н)
круга со стороной многоугольника, имеет к этой стороне много-
многоугольника.
В «руге АВГА (рис. 24} проведем какую-нибудь прямую АГ
и па АГ построим вписанный л сегмент АВГ мпогоугольник, имеющий
кроме основания АГ четное число равных сторон; проведем ZH, Ев,
120
АРХИМЕД
которые будут параллельны основанию сегмента; я утверждаю, что
ZH, Ев, АН будут к BS, как AZ к ZB.
ZH + Ев -!- АЕ _ AZ
ВВ ZB
Опять, так же (как и нише), проведем соединяющие прямые
ЯЕ, А©; они, конечно, будут нараллельтш BZ; тогда, вследствие того
А
&
Рис. 25.
же, кап KZ к KB, так и HR кКЛ, и ЕМ к МА, и М0 к MN, и ЕЛ
к SN
KZ
KB
НК
ЕМ
Мб
MN
ЕА
КЛ МЛ " MN SN .
[и как все ко всем, так и один к одному]; значит, как ZH, ЕВ, АЕ
к ВВ, так и ZK к КВ.
УДЦ-Кв+АЗ
ZK
BS
AZ
zb
ZK
К»"
Но как ZK к KB, так и AZ к ZB,
ZH
значит, как AZ к /13, так и ZH, Ев, АЕ к SB [8J.
_ zh ;-вв+АВ
НВ
ХХШ
Пусть АВГА будет большой круг шара [рис. 25}, и в него ини-
сан равносторонний многоугольник, и пусть число сторон его являет-
является кратным четырех*); пусть АГ, ДВ будут (два взаимно перпендику-
перпендикулярных) диаметра. Тогда если круг АВГА, вмещающий этот много-
многоугольник, будет вращаться около неподвижного диаметра АГ, то-
ясно, что окружность этого круга будет перемещаться по поверхности
шара, вершины же многоугольника, кроме тех, которые находятся
в точках А, Г, будут двигаться по окружности кругоп, описанных на
*) В подлиннике jietqeioOoj rati «тсавод-пусть будет измеряться четверной. Как замечает ком-
комментатор Архимеда, Евтокнй, требование. чтоСы число сторон вписанного многоугольника было
кратным четырех, раиноенльно требованию, чтоОы вес стороны многоугольника двигались только-
по коническим поверхностям; если бы число сторон многоугольника было кратным только двух, т<ь
две средние стороны оииимиали Оы цилиндрическую поверхность, для которой не выведены теоремы
равносильные предложениям XVII-XX.
О ШАРЯ И ЛИЛИНДРИ
поверхности сферы и перпендикулярных к кругу АВГД; диаметрами
этих кругов будут служить параллельные ВЛ прямые, соединяющие
лсртины многоугольника. Стороны многоугольника будут двигаться
по некоторым конусам, а имспло XL и AN по поиорхности конуса,
основанием которого является круг на диаметре ZN, а вершина нахо-
находится в точки А; затем ZII, MN будут двигаться но некоторой иони-
ионической поверхности, имеющей оснолатшем круг па диаметре МП, а вер-
шитгой — топку пересечения продолжений ZTI и MN друг с другом
и с АГ; стороны ВН, МД будут двигаться по конической поверхности,
основанием которой является круг на диаметре БД, перпендикуляр]или
к кругу АВГД, а вершиной — точка, в которой продолжения ВИ и ДМ
пересекаются между собой и с ГА. Точно так же и в другом полукруге
стороны будут двигаться но коническим поверхностям, тоже подобным
иышеуказанным. Таким образом, получится некоторая вяисанная
в шар и ограпнчонная упомяпутыми коническими поверхностями фигу-
фигура, поверхность которой будет меньше поверхности шара.
Если рассечь шар проходящей через ВД п перпендикулярной
кругу АВГД плоскостью, то поверхность каждого полушария и новерх-
пость вписанной в пего фигуры будут иметь общую границу, лежащую
на одной плоскости; действительно, границей обеих поверхностей
является окружность круга, построенного па диаметре ВД и перпенди-
перпендикулярного к кругу АВГД; обе эти поверхности будут выпуклыми
в одну сторону, причем одна из них объемлется другой поверхностью
и плоскостью, заключающей их общую границу. Подобным же обра-
образом, и поверхность заключенной «о втором полушарии фигуры будет
меньше поверхности полушария. Таким образом, вся поверхность
фигуры, заключенной в шаре, будет меньше поверхности шар» [9].
XXIV
Поверхность фигура*), вписанной в шар, равняется кругу, радиус
которого квадрирует прямоугольник между стороной фигуры и прямой,
Рис. 2fi.
равной всем вместе взятым линиям, соединяющим вершины много-
многоугольника и параллельным прямой, стягивающей две его стороны
{рис. 26}.
Пусть АВГД будет большой круг шара, и пусть в лого вписан
равносторонний многоугольник, число сторон которого есть крат-
пос четырех; на этом вписанном многоугольнике вообразим фигуру,
») О которой шла речь в XXIII.
122 АРХИМЕД
вписанную в шар, и проведем соединяющие прямые EZ, Ив, ГД,
КЛ, MN, параллельные прямой, стягивающей дне стороны много-
многоугольника; построим круг 5, радиус которого квадрировал бы прямо-
прямоугольник между АЕ и прямой, равной вместе взятым EZ, НЭ, ГД,
КЛ, MN; я утверждаю, что этот круг будет равен поверхности фигуры,
шшеанной п шар.
Построим круги О, П, Р, 2, Т, Г; пусть радиус О квадрирует
прямоугольник между ЕА м половиной EZ, радиус П квадрирует
прямоугольник между ЕА иполопиной вместе взятых EZ, 118, радиус Р
квадрирует прямоугольник между ЕА и половиной вместе взятых
Н6 и ГД, радиус 2 кпадрирует прямоугольник между ЕА и полови-
половиной вместе пзятых ГД, КЛ, радиус Т кпадрирует прямоугольник между
АЕ и половиной вместо взятых КЛ, MN, радиус Г квадрирует прямо-
прямоугольник между АЕ и половиной MN.
Тогда вследствие этого круг О будет равняться поверхности конуса
AEZ, круг II — поверхности конуса, заключающейся между EZ, II6.
круг Р — между 110, ГД, круг 2 — между ДГ, КЛ, затем крух- Т
будет равен конической поверхности между КЛ, MN, и круг Г равен
поверхности конуса MBN; значит, все эти круги вместе взятые будут
рални поверхности вписанной фигуры. Затем ясно, что радиусы кру-
кругов О, И, Р, 2, Т, Г квадрируют прямоугольник между АЕ и дваж-
дважды взятыми половинами EZ, Н0, ГД, КЛ, MN, или просто на EZ, II0.
ГД, КЛ, MN; значит, вместе взятые квадраты на радиусах кругов
О, II, Р, 2, Т, Г будут равняться прямоугольнику между АЕ и все-
всеми EZ, Нв, ГД, КЛ, MN.
Но также и радиус круга Н квадрирует прямоугольник между АЕ
я составленной из всех EZ, НВ, ГД, КЛ, MN прямой; значит, радиус
круга S квадрирует все вместе взятые квадраты на радиусах кругов
О. П, Р, 2, Т, Г, следовательно, круг Е будет равен всем кругам
О; П, Р, 2, Т, Г.
Но, как показано, круги О, II, Р, 2, Т, Т взятые вместо равны
нонерхности вышеупомянутой фигуры; таким образом, круг Н будет
равек поверхности рассматриваемой фигуры [0].
XXV
Поверхность вписанной в шар фигуры, ограниченной коническими
поверхностями, меньше учетверенного большого круга шара {рис. 27}.
Пусть АВГД будет большим кругом шара, и пусть в него будет
вписан равносторонний Ги равноугольный]*) многоугольник, число
сторон которого есть кратное четырех; вообразим (построенную) на
нем фигуру, ограниченную коническими поверхностями; я утверждаю,
что поверхность вписанной фигуры будет меньше учетверенного боль-
большого круга тара.
Проведем El, BM, стягивающие две стороны многоугольника,
и параллельные им ZK, ДВ, НА; построим круг 1* так, чтобы его ради-
радиус квадрировал прямоугольник на ЕА и на прямой, равной всем вместе
взятым El, KZ, ПЛ, НА, (-Ш.
рад. Г)г^Е
Тогда, согласно доказанному выше, :ггот круг будет равен поверхности
.*) В подлиннике "ajQrix&yavbv—четноуголыдай.
О ШАРБ И ЦИЛИНДРЕ
123
упомянутой фигуры. Но поскольку доказано, что пряма и, рапная всем
El, KZ, ВД, НА, ЭМ, относится к диаметру АГ круга, как ГЕ к ЕА,
& + ZK -:- ВД + НА + вМ
АГ
ГЕ
то, значит, прямоугольник па прямой, равной всем упомянутым
вместе взятым, и на ЕА, или квадрат па радиусе круга Р, будет равен
прямоугольнику между АГ и ГЕ.
Но прямоугольник между АГ, ГЕ меньше квадрата на А Г, зна-
значит, и квадрат на радиусе Р меньше квадрата на АГ; [значит, радиус
круга Р будет меньше АГ; таким образом, диаметр круга Р меньше
удвоенного диаметра круга АВГД; следовательно, два диаметра круга
АВГД больше диаметра круга Р, и учетперснш.тй квадрат на диа
метре круга АВГД, то есть А Г, болыпе квадрата па диаметре
круга Р. Но как учетверенный квад-
квадрат АГ к квадрату на диаметре круга
Р, так будут и четыре круга ЛЛГЛ к
кругу Р; значит, четыре круга АГ5ГЛ
•больше круга PJ; значит, круг Р мень-
меньше учетверенного большого круга. Но
круг Р, по доказанному, равен по-
поверхности вышеупомянутой фигуры;
значит, поверхность этой фигуры бу-
будет меньше учетверенного большого
круга шара [0].
XXVJ
Вписанная в шар фигура, ограничен-
ограниченная коническими поверхностями, равна
конусу, имеющему основанием круг, рав-
равный поверхности фигуры, вписанной е
шар, а высотой прямую, равную перпен-
перпендикуляру, опущенному ия центра шара
на одну из сторон многоугольника.
Пусть будет шар, в нем большой
круг АВГД {рис. 28) и все остальное, рис 27.
как выше; пусть будет прямой конус Р,
имеющий оспоиапием поверхность вписанной в шар фигуры, а высоту,
равную перпендикуляру, опущенному из центра шара на одну из сторон
многоугольника; требуется доказать, что конус Р равен вписанной
в шар фигуре.
На кругах, диаметры которых ZN, HM, t)A, IK, построим конусы,
имеющие вершипу в центре шара; получится телесный ромб, состав-
составленный из копуса, основание которого есть построенный на диаметре
ZN круг, вершина же — точка А, и из конуса, основанием которого
является тот же самый круг, «ершиной же точка X; он будет равен
конусу, имеющему основанием поверхность конуса NAZ, высоту те,
равную опущенному из X на AZ перпепдикуляру. Далее, окаймление
ромба, ограничепноеповерхностыо конуса, заключающейся между парал-
параллельными плоскостями, проведенными чорез ZN, HM, и двумя кони-
коническими поверхностями ZNX, IIMX, будет равно конусу, имеющему
основание, равное поверхности конуса между параллельными плоско-
плоскостями через МП, ZN, а высоту, равную перпендикуляру, опущенному
124
АРХИМЕД
из X ни ZH, как это ул;е било доказано. Затем окаймление конуса.,
ограниченное конической поверхностью между параллельными пло-
плоскостями через НМ, БД, поверхностью конуса МНХ и кругом
на диаметре БД, будет равно конусу, имеющему оснонапие, равное
поверхности конуса между плоскостями через НМ, БД, а высоту,
равную опущенному лз X на ВИ перпендикуляру. Подобным же обра-
образом ir л другом полушарии ромб ХКГ1 и окай-
окаймления конусов будут раппы таким же и в та-
таком же числе конусам, как и те, которые были
рассмотрены лише. Теперь ясно, что и вся впи-
вписанная в шар фигура будет равна всем упомяну-
упомянутым конусам. Но конусы эти равны кол/усу Р,
так как конус Р имеет высоту, равную высоте;
каждого из упомянутых конусов, основание
же, ранное всем их основаниям. Итак, ясно, что
вписанная в шар фигура будет равна построен-
построенному конусу [9].
XXVII
Вписанная в шар фигура, ограниченная
коническими поверхностями, будет меньше
учетверенного конуса, имеющего основанием
большой круг шара, а высоту, рамную радиусу
Рис. 28. шара.
Пусть будет конус I* {рис. 29}, равный
вписанной а шар фигуре, имеющий основа-
основание, ранное поверхности вписанной фигуры, а высоту, равную лер-
пендикуляру, опущенному из центра шара на одну из сторон ипи-
иписанного мн огоугольника;
пусть еще будет копус S,
имеющий основание, рав-
равное кругу АВГД, а высо-
высоту, равную радиусу круга
АИ ГА.
Теперь, так как ко-
копус I* имеет основание,
равное поверхности впи-
вписанной в шар фигуры, а
высоту, равную перпенди-
перпендикуляру, опущенному из X
на AZ, и, по доказанному,
поверхность вписанной
фигуры меньше учетверен-
учетверенного большого круга в
шаре, то, значит, основа-
основание конуса Р будет
меньше учетверенного
оспования конуса S. Также и высота конуса Р меньше высоты ко-
конуса Е; поскольку же конус Р имеет основании, меньшее учетверен-
учетверенного основания конуса S, и высоту, меньшую высоты последнего, то
ясно, что и сам копус Р будет меньше учетверенного конуса Н. Но
конус Р равен вписанной фигуре; значит, вписанная фигура меньше
учетверенного конуса Н [0].
Рис. 2У.
О ШАРЕ 11 ЦИЛИНДРЕ
12Г)
XXVIII
Пусть АВГД {рис. 30] будет большим кругом шара; опишем
около круга АВГД ратшосторонний и равноугольный многоугольник,
и пусть число сторон его будет кратным четырех; затем вокруг много-
многоугольника, описашюго около круга, опишем еще один охватывающий
его круг с тем же центром, что и у круга АВГД. Затем плоскость EZ1K-),
в которой находятся многоугольник и круг, будем вращать около
неподвижной (оси) ЕН; тогда ясно, что окрулшость кругл АБГЛ
будет перемещаться по поверхности шара, а окружность круга EZHC-)
пойдет но поверхности другого шара, имеющего тот же центр, что
и меньший шар, точки касания сторон многоугольники опишут па
поверхности меньшего шара круги,
(плоскости которых) перпепдикулярнтд
(плоскости) круга АВГД, углы же
многоугольника, кроме тех, которые
при точках Е, Н, пойдут по окружно-
окружностям кругов, начерченных на поисрхно-
•стн большого шара и перпендикуляр-
перпендикулярных кругу EZH0, а стороны много-
многоугольника будут двигаться по кониче-
коническим поверхностям совершенно так же,
как и it предшествующем; таким обра
зом, фигура, ограниченная количо
-скими поверхностями, будет описана
около меньшего шара и впнсипа в боль-
больший. А что поверхность описанной фи-
фигуры больше поверхности шара, дока-
жетсн так. Пусть КД будет диамет-
диаметром некоторого круга на меньшем шаре, причем К и Д суть точки,
в которых (дне) стороны описанного многоугольника касаются кру-
круга АВГД. Рассечем шар плоскостью, проходящей через КД (и) пер-
перпендикулярной к плоскости круга АВГЛ; тогда той же плоскостью рас-
рассечется и поверхность описанной около шара фигуры. Яспо также, что
(обе поверхности отсеченных частой — и шара, и фигуры —) будут
иметь одни и те же границы, лежащие на плоскости, так как границей
обеих поверхностей будет окружность круга, построенного на диаметре
КД и перпендикулярного к к нугу АВГЛ; затем обо поверхности будут
выпуклыми в одну и ту тс сторону, и одна из них объемлется другой
поверхностью и плоскостью, имеющей те же границы; объемлемая
поверхность сегмента шара будет меньше поверхности описанной около
него фигуры. Подобным же образом и поверхность другого сегменты
шара будет меньше поверхности «писанной около него фигуры; следо-
следовательно, ясно, что и вся поверхность шара будет меньше поверхности
описанной около него фигуры [10].
XXIX
Поверхность фигуры, описанной около шара, равна кругу, радиус
которого квадрирует прямоугольник между одной стороной много-
многоугольника и прямой, равной всем вместе взятым, прямым, соединяющим
углы многоугольника и параллельным какой-нибудь прямой, стягиваю-
стягивающей две стороны многоугольника.
Рис. 30.
126
ЛРХИМКД
Действительно, фигура, описаннаи около меньшего шара, будет-
одновременно вписанной в больший; но доказано, что поверхность-
вписанной в шар фигуры, ограниченной коническими поверхностями,
равна кругу, радиус которого квадрирует прямоугольник между
одной стороной многоугольника и прямой, равпой всем соединяющим
углы многоугольника прямым, параллельным какой-нибудь стягиваю-
стягивающей две стороны многоугольника прямой; так что ясно и высказанное
выше.
XXX
Поверхность описанной около шара фигуры больше учетверенного-
большого круга в шаре.
Пусть будут шар, круг и все остальное так же, как и раньше,
и пусть круг Л будет равен поверхности заданной фигуры, описанной
около меньшего шара (рис. 31).
Рис. 31.
Так как и круг EZHB вписан равносторонний многоугольник
с четным числом углов, {-на все (вместе взятые) прямые, соединяющие-
стороны многоугольника, являясь параллельными Z6, будут иметь.
к Z© то же отношение, как <9К к KZ; значит, прямоугольник между
одной стороной мпогоугольника и прямой, равной всем (лрямтлм),
соединяющим стороны многоугольника, будет равен прямоугольнику
между Z0 и GK; поэтому радиус круга Л будет кпадрировать прямо-
прямоугольник между Z6 и 6К; значит, радиус круга Л будет больше 6К.
Но 6К равна диаметру^круга АВГД, [ибо она в два раза больше ХМ —
радиуса круга АВГД1.1 Теперь ясно, что круг Л, или поверхность фигу-
фигуры, описанной около меньшего шара, будет больше учетверенного-
большого круга в этом шаре [101.
XXXI
Фигура, описанная около меньшего шара, равна конусу, имеющем!/'
основанием круг, равный поверхности фигуры, а высоту, равную радиусу
шара.
Действительно, описанная около меньшего шара фигура будет
одновременно вписанной в больший тар; вписанная же фигура, огра-
О ШАРЕ И ЦИЛИНДРЕ
127
виченная коническими поверхностями, будет, согласно доказанному,
равна конусу, имеющему основанием круг, равный поверхности фигуры,
а высоту, равную перпендикуляру, опущенному из центра шара на
одну из сторон многоугольника; этот же перпендикуляр равен радиусу
меньшего шара; теперь предложенное ясно.
С я е д с т в и е
Из этого ясно, что описанная около меньшего шара фигура
более учетверенного конуса, имеющего основанием большой
круг {меньшего} шара, а высоту, равную радиусу (того же} шара.
Действительно, так как отой фигуре равен конус, имеющий осно-
основание, равное ее поверхности, высоту же, равную [перпендикуляру,
опущенному из центра шара на одну из стороп многоугольника, то
есть] радиусу меньшего шара, и так как поверхность фигуры, описанной
около того же шара, больше учетверенного большого круга в таре, то,
значит, описанная около шара фигура будет более; учетверенного кону-
конуса, имеющего основанием большой круг, а высотой радиус шара, так
как конус, равный фигуре, будет более учетверенного упомянутого
конуса, [так как при равных высотах он имеет более чем в четыре раза
большее основание].
XXXII ,
Если в шар вписана фигура и около него описана другая такая же,,
построенная, как и раньше, на. подобных многоугольниках, то поверх-
поверхность описанной фигуры к поверхности вписанной будет иметь (отпошс-
шение, равное) двойному отношению стороны многоугольника, опи-
описанного около большого круга, к стороне вписанного в тот же круг
многоугольника, сама же [описанная\ фигура будет иметь ко вписанной
тройное отношение*) тех же прямых.
Пусть АВГА будет (больший) кругом шара {рис 32}; в пишем в не-
него ринпосторонний многоугольник с числом сторон, кратным четырех.
и опишем другой, подобный вписанному,, так, чтобы стороны опи-
описанного многоугольника касались круга в серединах дуг, отсекаемых
сторонами вписанного многоугольника; пусть в круге, охватывающем
описаши.ш многоугольник, EH, ZB будут взаимно перпендикулярные
диаметры, одинаково расположенные с диаметрами АГ, ВД; вообразим
*) ТоГесть возведенное в третью степень.
128 АРХИМЕД
прямые, соедтгяющие противоположные углы многоугольника и парал-
параллельные друг другу и прямой ZBA0. При вращении периметров много-
многоугольников но дугам окружностей около неподвижного диаметра ЕН
получатся две фигуры — одна вписанная в шар и другая— около него
описанная. Требуется доказать, что поверхность описанной фигуры
имеет к поверхности вписанной отношение, равное двойному отноше-
отношению ЕЛ к АК, сама же описанная фигура имеет ко вписанной отноше-
отношение, рапное тройному тому же самому.
Пусть круг М будет ранен поверхности фигуры, описанной около
шара, а круг N равен поверхности вписанной; тогда радиус круга М
будет квадряровцть прямоугольник .между ЕЛ и прямой, рапной псем
(прямым), соединяющим углы описанного многоугольника, радиус
же круга N будет квадрировать прямоугольник между АК и прямой,
равной всем (прямым), соединяющим углы вписанного многоугольни-
многоугольника. И так как упомянутые многоугольники подобны, то будут подобна
и прямоугольники, построенные на упомянутых линиях, [то есть со-
соединяющих углы или стороны многоугольников, так что они будут
иметь друг к другу то же отношение, как квадраты сторон многоуголь-
многоугольников. Но отношение прямоугольников между упомянутыми линиями
будет одинаконо с двойным отпопкшисм радиусов кругов М, N; таким
образом, диажггры кругов М, N будут находиться в том же отношении,
что и стороны многоугольников, круги же имеют друг гг другу отно-
отношение, равное двойному отношению диаметров, сами ни; круги равны
поверхностям описанной и вписанной фигур]; отсюда ясно, что поверх-
поверхность фигуры, описанной около шара, к поверхности фигуры, вписан-
вписанной в шар, имеет отношение, равное двойному отношению ЕЛ к АК.
Возьмем еще два конуса О, Я; пусть конус S имеет псиованиии
круг S, ранный кругу М, а конус О — круг О. равный кругу N:
пусть высота конуса S будет равна радиусу шара, а высота О равна
перцендикуляру, опущенному из центра шара на АК; тогда, [как ужо
было доказано,] конус 3 будет равен фигуре, описанной около гаара.
а конус О — вписанной. Но так как оба многоугольника подобны, то
ЕЛ ллгеет к ЛК такое же отношение, как радиус шара к опущенному
из центра шара на АК перпендикуляру; значит, высота конуса Н имеет
к высоте конуса О такое же отношение, как ЕЛ к АК. Также и диаметр
круга М относится к диаметру круга N, кап ЕЛ к АК; значит, диаме-
диаметры оснований конусов S и О имеют с высотами одинаковое отношение;
[значит, конусы от» подобны]; поэтому конус Е к конусу О будет
иметь отношение, равное тройному отношению диаметра круга Л1
к диаметру круга N. Теперь ясно, что описаннни фигура ко вписанной
имеет отношение, равное тронному отношению ЕЛ к АК.
XXXIII
Поверхность всякого шара равна его учетверенному большому кругу.
Пусть будет какой-нибудь шар, и пусть Л — его учетверенный боль-
большой круг; я утверждаю, что круг А равен поверхности тара {рис. 331.
Действительно, если он не равен, то будет или больше, или меньше.
Пусть сначала поверхность шара будет больше круга А. Тогда имеются
две неравный величины — поверхность шара и круг А; значит, можно
взять две неравные прямые так, чтобы отношение большей к меньшей
было меньше того, в каком поверхность шара находится к кругу (А).
Возьмем такие прямые В и Г, и пусть Л будет средней пропорциональ-
О ШАРЕ И ЦИЛИНДРЕ
129
пой между В и Г. Вообразим, что шар рассечен по кругу KZI1© пло-
плоскостью, проходящей через центр; пообразим также пписанный в этот
круг и описанный около него многоугольпики такие, чтобы описанный
был подобен вписанному и чтобы сторопа описаппого имела к стороне
вписанпого отношение, меньшее того, которое Б имеет к Д; [значит,
двойное отношение сторон будет меньше двойного отношения прямых.
Но двойное отношение В к Д будет равно отношению В к Г, и днойпое
отношение стороны описанного многоугольника к стороне шшсашгого
будет отношением поверхности описан- в
ной фигуры к поверхности вписанной |; "
значит, поверхность фигуры, описанной
около шара, к поворхпости вписанной
фигуры имеет меньшее отношение, чем
поверхность шара к кругу А, а это не-
невозможно; действительно, поверхность
описанной фигуры больше поверхности
пгара, поверхность же вписанной фигу-
фигуры меньше круга А, [так как доказа-
доказано, что поверхность вписанной фигуры
меньше учетнеренного большого круга
и шаре, круг же А равен учетверен-
учетверенному большому кругу]. Значит, поверх-
поверхность шара не будет больше круга А.
Теперь я утверждаю, что опа не
будет и меньше. Действительно, пусть
опа будет меньше, если это возможно;
таким же образом найдем прямые В и
Г так, чтобы В имела it Г отношение,
меньшее того, в котором круг А пахо-
дится к поверхности шара, и среднюю
пропорциональную между В и Г нря-
мую А; затем снова впишем и опишем
два многоугольника таких, чтобы сто-
сторона описанного имела (к стороне тши-
санного) отношение, меньшее В к Д,
[что будет и после удвоения*) обоих
отпошоний]; таким образом, поверхность описанной фигуры к по-
поверхности вписанной будет иметь отношение меньшее, [чем В к Г.
Но В имеет к Г отношение меньшее], чем круг А к поверхности шара,
а это ненозможно; действительно, поиерхпость описанной фигуры боль-
больше круга А, а поверхность вписанной меньше поверхности шара.
Таким образом, поверхность шара не будет и меньше круга А.
Доказано иге, что она и не больше; значит, поверхность тара равна
кругу А, то есть учетверенному большому кругу.
XXXIV
Всякий шар в четыре рана больше конуса, имеющего основание,
равное большому кругу шара, а высоту, равную радиусу шара.
Пусть будет некоторый шар и в нем большой круг ЛВГД {рис. 34}.
Теперь если шар не будет (ровно) и четыре раза больше упомянутого
Рис :\я.
¦} То есть иозведения в квадрат.
9 Архимед
130
АРХИМЕД
конуса, то пусть, если возможно, он будет более чем в четыре раза
больше. Пусть будет конус 2, имеющий основание, п четыре раза боль-
большее круга ЛВГД, высоту же, ранную радиусу шара; тогда шар будет
больше конуса S. Итак, имеются две неравные величины — шар
и конус; значит, можно взять две неравные прямые так, чтобы большак
имела к меньшей отношение, меньшее того, в каком тар находится
к конусу Н. Пусть это будут К и И. Возьмем Т п 0 так, чтобы К. от I,
I от 8 и 6 от II разнились бы на одно и то же;
к __[=i_e=e -н
вообразим также, что, как и раньше, в круг ЛВГД вписан многоуголь-
многоугольник с числом сторон, кратным четырем, и около него описан другой,
подобный «писанному, и пусть сто-
сторона описанного многоугольника
имеет к стороне вписанного отноше-
отношение, меньшее того, к котором К бу-
будет к I. Пусть А Г, ВД будут пваим-
по перпендикулярные диаметры.
ГСсш теперь около неподвижного
диаметра ЛГ будем вращать пло-
плоскость, в которой находятся оба мно-
многоугольника, то получатся дне фи-
фигуры, из которых одна будет описа-
описана, другая ?ко вписана в шар, при-
причем отношение описанной фигуры к
вписанной будит равняться тройному
отношению стороны многоугольники,
описанного около круга ЛВГД к сто-
стороне вписанного в него. По сторона к стороне имеет отношение, мень-
меньшее чем К к I; значит, описанная фигура имеет к вписанной отноше-
отношение, меньшее тройного отношения К к I. По отношение К к Н
больше; тройного отношения К к I;
к кз
Ьто ясно из сделанных предположении] 111]. Значит, и подавно они
санная фигура имеет к вписан ной отношение, меньшее того, которое1 К
имеет к И.
Но К имеет к Н отношение меньшее, чем шар к конусу Е: (зна-
(значит, оиисанная_фигура имеет к вписанной отношение меньшее, чем
шар к конусу 'а), и после перестановки (описанная фигура к мару
имеет отношение меньшее, чем вписанная к конусу Е); это же невоз-
невозможно, так как описанная фигура больше шара, вписанная же меньше
конуса Е [вследствие того, что конус 5 в четыре раза больше конуса,
имеющего основание, равное кругу АВГД, а высоту, равную радиусу
шара, вписанная же фигура меньше четырежды взятого упомянутого
конуса]. Таким образом, тар во будет более чем в четыре раза больше
упомянутого конуса.
Пусть теперь, если возможно, он будет менее четырежды взятого
упомянутого конуса: иными словами, шар будет меньше конуса Е.
Возьмем прямые К и Н так, чтобы К была большо II и имела к пей отно-
отношение меньшее того, в каком конус S паходится к шару, затем постро-
построим такие же прямые Э и I, как и раньше. Нообразим многоугольник,
Рис. 34.
О ШАРЕ И ЦИЛИНДРЕ
К К:
впмсаниый в круг АВГД, и другой, описанный около него, такие, что-
чтобы сторона описанного многоугольника имела к стороне вписанного
отношение меньшее, чем К к I, и все остальное устроим так же, как и
раныпз. Таким образом, отношение описанной телесной фигуры ко впи-
вписанной будет ршшяться тройному отношению стороны многоуголышка,
описанного около круга АВГД, к стороне «писанного. Но сторона
к стороне имеет отношение меньшое, чем К к I; значит, описанная
фигура к вписанной будет иметь отношение, меньшее тройного отно-
отношения К к I.
Но К к Н имеет отношение, большее тронного отношения К к \;
я
значит, описанная фигура будет иметь к «писанной, отношение мень-
меньшее, чем К к Н. Но К к Н имеет отношение меньшее, чем конус Е
к шару: (значит, описанная фигура нмеот к вписанной отпошенне
меньшее, чем конус Е к шару); это же невозможно, ибо вписанная
фигура меньше шара, описанная же больше конуса Е. Значит, шар не
будет меньше четырежды взятого конуса, имеющего основание, ранное
кругу ЛВГА, а высоту, равную радиусу сферы. Но доказано, что он
не будет и больше; значит, шар будет равняться упомянутому конусу,
четырежды взятому.
1С л е д с т в и ej- Из доказанного ясно, что всякий цилиндр,
имеющий основанием большой круг ишра, а высоту, равную его диаметру,
будет в полтора раза больше шара, и что поверхность его вместе с осно-
основаниями будет в полтора раза больше поверхности шара.
Действительно, вышеупомянутый цилиндр в шесть раз больше
конуса, имеющего то же самое основание и высоту, равную радиусу
шара, а шар, по доказанному, будет в четыре раза больше того же
конуса; отсюда ясно, что цилиндр будет в полтора раза больше шара.
Затем доиерхность цилиндра за вычетом основания, по доказанному,
раина кругу, радиус которого является средней пропорциональной
между стороной цилиндра, и диаметром его основания, сторона же
упомянутого обнимающего сферу цилиндра раина диаметру основания
[так что, очевидно, их средняя пропорциональная будет тоже равна
диаметру основания]. Далее, круг, имеющий радиусом диаметр осно-
лания, будет в четыре раза больше этого основания, то есть боль-
большого круга шара. Таким образом, поверхность цилиндра за вычетом
оснований будет в четыре раза больше упомянутого круга, а значит,
вся поверхность цилиндра вместе с основаниями — в шесть раз больше
большого круга. Поверхность же шара в четыре раза больше большого
круга; значит, вся поверхность цилиндра в полтора раза больше поверх-
поверхности шара.
XXXV
Поверхность фигуры, вписанной в сферический сегмент, равна
кругу, радиус которого квадрирует прямоугольник, построенный на
одной стороне многоугольника, вписанного в соответствующий сегмент
большого круга, и прямой, равной всем прямым, параллельным основанию
сегмента, вместе с половиной этого основания.
Пусть будет шар и в пем сегмент, оснонанием которого является
построенный на АН круг {рис. 35}. [Ннишем в шар, как было
сказано раньше, фигуру, ограниченную коническими поверхностями);
9*'
132
АРХИМЕД
пусть также будут большой круг АП6 и мпогоугольпик ArEOZAIT
с четным числом (равных) сторон за исключением стороны АН;
;. возьмем круг Л, радиус которого квадрирует прямоугольник между
стороной АГ и прямой, равной всем EZ, ГД, взятым вместе с половиной
основания, то есть АК;
и* = ЛГ(ЕИ-| ГД+АЮ . Л
требуется доказать, что
этот круг равняется по-
поверхности вписанной фи-
фигуры.
Возьмем круг М, ра-
радиус которого квадрирует
прямоугольник между сто-
стороной EG и половиной EZ;
(рад.
Рис. 35.
круг М будет тогда равен поверхности конуса, основанием которого
является круг, построенный на EZ, а вершиной точка 0. Возьмем и дру-
другой круг N, радиус которого квадрирует прямоугольник между ЕГ
и половиной вместе взятых EZ, ГД;
он будет равен поверхности конуса между проведенными через EZ, ГД
параллельными плоскостями. Так же возьмем еще круг S, радиус кото-
рого квадрирует прямоугольник между АГ и половиной вместе взя-
тых ГД, АН;
он будет равеп конической поверхности между параллельными плоско-
плоскостями через АН, ГД.
Теперь все круги вместе будут раппы полной поверхности фигуры
и квадраты на их радиусах равны прямоугольнику между одной сторо-
ной А Г и прямой, равной EZ, ГД, взятым вместе с ЛК — половиной
основания.
. ЕJ
АГ
Ио также и радиус круга Л квадрирует ту же самую площадь;
значит, круг А будет равен всем кругам М, N, Н (вместе взятым),
а следовательно, и поверхности впиейнной фигуры.
XXXVI
Рассечем шар плоскостью, не проходящей через центр; пусть AEZ
{рис. ЗС} будет его большой круг, пересекающий под прямым углом
сокупгую плоскость; в сегмент АВГ впишем равносторонний много-
многоугольник с четным числом сторон за исключением основания ЛВ.
Если, подобно предыдущему, будем вращать фигуру около неподвиж-
неподвижной (оси) TZ, то углы Д, Е, А, В будут двигаться по кругам с диамет-
диаметрами ДЕ и АВ, стороны же многоугольника — по коническим:цоверх-
О ШАРЕ И ЦИЛИНДРЕ
133
яостям; таким образом, получится ограниченная коническими поверх-
поверхностями телесная фигура, имеющая основанием круг на диаметре АВ
и вершину в Г. Подобно предыдущему, эта фигура будет иметь но-
нсрхноеть, меньшую поверхности охватывающего
сегмента; действительно, и фигура, и сегмент име-
имеют одну и ту же лежащую в плоскости границу,
а именно окружность круга, построенного па диа-
диаметре АВ; кроме того, обе поверхности являются л]
ныпуклыми в одну и ту же сторону и одна из них
объемлстся другой.
XXXVII
Рис. 30.
Поверхность вписанной в сферический сегмент
фигуры меньше круга, радиус которого равен пря-
прямой, проведенной из вершины сегмента, до окружности круга,
являющегося основанием сегмента.
Пусть будет гаар и в нем большой круг ABEZ (рис. 37]; возьмем
сферический сегмент, основанием которого служит описанный на
диаметре ЛВ круг; [впишем затем в шар
упомянутую фигуру, а в сегмент круга—
многоугольник], и также все остальное,
причем ©Л будет диаметром шара; затем по-
после проведения АЕ и ©А построим круг М,
радиус которого будет равен А6. Требует-
Требуется доказать, что круг М будет больше по-
поверхности {«писанной) фигуры.
Дейстпитольно, было доказано, что
поверхность фигуры равна кругу, радиус
которого квадрирует прямоугольник меж-
между ЕЭ и вместе взятыми EZ, ГД,КА, и так-
также было доказало, что прямоугольник меж-
между Ев и имеете взятыми EZ. ГД, КА
равен прямоугольнику между ЕЛ и Кб*);
.: (прямоугольник) же между ЕЛ и Кб меньше (квадрата) па. АО,
БЛ-Кв<Л0а
[то есть (прямоугольника) между Л 6 и Кб]**).
Теперь видно, что радиус круга, равного поверхности (вписан-
(вписанной) фигуры, будет меньше радиуса круга М; следовательно, ясно, что
".' . круг М больше поверхности (вписанпой) фигуры. •;
XXXVIII
Вписанная в сегмент {меньший полушария) фигура, ограничен-
ограниченная коническими поверхностями, взятая вместе с конусом, имеющим
основание одно и то же с фигурой, а вершину в центре шара, будет равна
конусу, имеющему основание, равное поверхности фигуры, а высоту,
*) Согласно предложению XXII.
Действительно,
А02~К0-Лв > Кв- ЕЛ-
АРХИМЕД
Piic. 38.
равную перпендикуляру, опущенному из центра шара на одну из сто-
сторон многоугольника (образующего вращением фигуру).
Пусть будет шар и в нем большой круг с центром Е и сегмент АВГ,
меньший полукруга {рис- 38.}. Подобно предыдущему, в сегмент
АВГ виишем многоугольник с четным числом (равных) сторон за
исключением АГ; пусть при вращении
шара около неподвижной (прямой) ВЛ
получится ограниченная коническими
поверхностями фигура; па круге с диамет-
диаметром АГ построим конус, имеющий ворши-
ну в центре (шара), и возьмем конус К,
имеющий осионание, равное поверхности
фигуры, а высотой перпендикуляр, опущен-
опущенный из центра Е па одну из сторон много-
многоугольника. Требуется доказать, что конус
К будет равен ограниченной (кониче-
(коническими поверхностями) фигуре, взятой
вместе с конусом АЕГ.
На кругах с диаметрами ©Н, AZ по-
построим конус'л, имеющие вершину в точ-
точке Е; тогда телесный ромб ПВЭЕ будет
ранен конусу, основание которого равно
поверхности конуса HB0, а высота равна
перпендикуляру, опущенному изЕ на HTS, окаймление же, ограниченное
(конической) поверхностью между параллельными плоскостями, (iipo-
веденными) чероз TI0, ZA и конусами ZEA, HE0, будет равно конусу,
основание которого ракао (конической) иоиерхности между парал-
параллельными плоскостями через Ив, ZA, а высота рапна перпендикуляру,
опущенному из Е на ZH. Далее, окаймление, ограниченное (кониче-
(конической) поверхностью между параллельными плоскостями через ZA,
АГ и конусами АЕГ, ZEA, будет равно конусу, основание кото-
которого равно (конической) поверхности между параллельными плоско-
плоскостями чероз 2А, АГ, а высота — перпендикуляру, опущенному
из Е на ZA.
Теперь (все) пышеназванные копусм будут ранни рассматривае-
рассматриваемой («писанной телесной) фигуре имеете с конусом ЛЕГ. Дейстни-
телыю, они имеют высоту, равную перпендикуляру, опущенному из Е
на одну из сторон многоугольника, а основания, равные (вместе)
поверхности фигуры AZHBeAT; также и конус К имеет ту нее высо-
высоту и основание, равное поверхности ток иге фигуры; значит, этот конус
будет равен всем упомянутым конусам. Ио было доказано, что упомя-
упомянутые конусы равны рассматриваемой фигуре вместе с конусом АЕГ;
и значит, конус К равен рассматриваемой фигуре имеете с кону-
конусом АЕГ.
С л <! д с т в и е
Из этого ясно, что конус, имеющий основанием круг, ради-
радиус которого равен прямой, нроведепной из першинга сегмента
к окружности круга, являющегося оспонаниом сегмента, а высоту,
ранную радиусу тара, будет больше упомянутой вписанной фигуры,
взятой вместе с конусом (АЕГ). Действительно, упомянутый конус
больше конуса, рапного рассматриваемой фигуре, взятой вместе
с конусом, имеющим то же основание, что и сегмент, а вершину в цент-
О ШАРЕ И ЦИЛИНДРК
135
ре гаара, иными словами, больше конуса, имеющего основапис равным
поиерхности фигуры, а В1.гсоту, равную перпендикуляру, опущенному
из центра па одну из сторон многоугольника; в самом деле [как уже
было доказано], основа пир. первого конуса больше основания второго,
и его высота больше высоты второго.
XXXIX
Пусть будет шар и в нем большой круг АВГ {рис. 39}; пусть
прямая АВ отсечет сегмент, меньший полукруга; пусть центр будет в Д;
из центра Д до А, В проведем соеди-
соединяющие прямые АД, ДВ и около полу-
чигшгегося сектора опишем многоуголь-
многоугольник (с четным числом равных сторон),
а около лого круг; тогда последний
будет иметь тот же центр, что и круг
АВГ. Если вращающийся около непо-
движпой прямой ЕК многоугольник
вернется п исходное положепио, то опи-
описанный круг будет перемещаться по
поверхности шара, углы многоуголь-
многоугольника опишут окружности с параллель-
параллельными АВ диаметрами, соединяющими
углы многоугольника, а точки каса-
касания сторон многоугольника с меньшим
кругом опишут окружности на меньшем
шаре, диаметрами которых будут пря-
прямые, нараллельпые АВ, соединяющие
эти точки касания и, наконец, стороны многоугольника будут пере-
перемещаться по коническим поверхностям. Так Судет образована огра-
ограниченная коническими поиорх л остями описанная фигура, основанием
которой будет построенный на ZJ.1 круг. Поверхность упомянутой фигуры
будет больше поверхности меньшего сегмента, основанием которого
является построенный на АВ круг.
Действительно, проведем касательные AM и BN; они будут дви-
двигаться по конической поиерхности, и фигура, образованная много-
многоугольником AM0EANB, будет иметь понсрхность большую, чем сфе-
сферический сегмент, основанием которого является построенный на
диаметро АВ круг; [действительно, они имеют одну и ту же лежащую
в одной плоскости границу, а именно круг па диаметре АВ, и сегмент
объемдется фигурой]. Но коническая поверхность, образованная ZM,
HN, будет больше понсрхности, образоианной MA, NB; действитель-
действительно, ZM будвт больше МА [ибо она стягивает прямой угол], и NH
больше NB, а если так, первая поверхность будот больше второй,
Гкак это прилито в постулатах]. После этого ясно, что поверхность
¦описанной фигуры будет больше поверхности сегмента в меньшем
шаре.
Следствие
Кроме того, ясно, что поверхность фигуры, описанной около
сектора, равна кругу, радиус которого квадрирует прямоугольник
между одной стороной многоугольника и всеми прямыми, соеди-
соединяющими углы многоугольника, взятыми вместе с половиной
136
АРХИМЕД
рад.
основания упомянутого многоугольника, [так как описанная около
сегмента фигура является одновременно вписанной в сегмент большо-
большого шара]; [все это ясно из вышеизложенного].
XL
Поверхность описанной около сектора фигуры больше круга, радиус
которого равен прямой, проведенной из вершины сегмента к окружно-
окружности круга, являющегося его основанием.
Пусть будет шар с большим кругом АБГД и центром Е; опишем
около сектора многоугольник AKZ и около последнего круг; пусть будет
образована фигура, как и раньше {рис. 40]. Пусть N будет круг,
радиус которого квадрирует прямоуголь-
прямоугольник между одной стороной многоуголь-
многоугольника и всеми соединяющими прямыми,
взятыми вместе с половиной КЛ. Flo упо-
упомянутая площадь равняется прямоуголь-
прямоугольнику между M6hZII; [последняя является
высотой сегмента большего тара]; зна-
значит, радиус круга N кладрирует прямо-
прямоугольник между МО и IIZ.
По HZ больше, чем Д S, [которая
является высотой меньшего сегмента. Дей-
Действительно, если мы проведем соединяю-
соединяющую KZ, то она будет параллельной ДА.
И AI3 параллельна КЛ, a ZE общая; зна-
значит, треугольник ZKH подобен треуголь-
треугольнику ДЛЗ. Далее, ZK более АД; значит,
и ZH больше Да], Мб же равна диаметру Рис. 40.
ГА; {действительно, проведем соединяю-
соединяющую прямую ЕО; поскольку МО равна OZ, a 0E равна EZ, то, зна-
значит, ЕО будет параллельна Мвп, следовательно, М.& в два раза боль-
больше ЕО. Но и ГД в два раза больше ЕО; значит, Мб равна ГД]. в
прямоугольник между ГД и ДЕ равен квадрату на АД.
Таким образом, поверхность фигуры KZA будет больше кругл,
радиус которого равняется прямой (АД), проведешюй из вершины сег
мента к окружности круга, являющегося его основанием, а именно,
построенного на диаметре АВ; действительно, круг N равняется поверх-
поверхности фигуры, описанной около сектора.
Следствие 1
Описанная около сектора фигура, взятая вместе с конусом,
основанием которого служит круг, построенный на диаметре
КЛ, а вершиной — центр шара, оказывается равной конусу, основа-
основание которого равно поверхности фигуры, а высота — перпенди-
перпендикуляру, опущенному из центра на сторону многоугольника, [который,
конечно, равен радиусу шара, так как описанная около сектора фигура
будет и вписанной п сегмент большего шара, имеющего тот же самый
центр; сказанное ясно из предыдущего).
О ШАРЕ И ЦИЛИНДРЕ
13?
г..:
Следствие 2
Из этого же ясно, что описанная фигур», взятая вместе
с конусом, будет больше конуса, имеющего основанием круг,
радиус которого ранен прямой, проведенной от вершины сегмента
меньшего шара к окружности круга, являющегося его основанием,
а высота равна радиусу (меньшего шара), так как конус, ранный
фигуре, взятой вместе с конусом, будет иметь основание, большее выше-
вышесказанного круга, высоту же, равную радиусу меньшего шара.
XLI
Пусть будут опять тар и в нем большой круг, сегмент А Б Г, мерь-
ший полукруга, и центр А {рис 41); впишем в сектор АВГ много-
многоугольник с четным числом (равных) сторон и опишем около него
другой, ему подобный, так, чтобы
стороны одного были параллельны
сторонам другого, затем около опи-
описанного многоугольника опишем
круг, и пусть подобно предыдущему
при вращении обоих кругов (вместе
с многоугольниками) около непо- *'
движноё прямой НВ образуются
фигуры, ограниченные коническими
поверхностями. Требуется доказать,
что поверхность описанной фигуры
имеет к поверхности вписанной
отношение, равное двойному отно-
отношению стороны описанного мно-
многоугольника к стороне вписанного,
отношение же самих фигур, взятых
вместе" с соответствующими конуса-
конусами, будет равно тройному тому же
отношению.
Действительно, пусть будет круг
М, радиус которого квадрирует
прямоугольник между одной сто-
роной олисапного многоугольника
и всеми прямыми, соединяющими
его углы, вместе с половиной EZ;
круг М будет равен поверхности
описанной фигуры. Затем возьмем
другой круг N, радиус которого
квадрирует прямоугольник между одной стороной вписанного многоу-
многоугольника и всеми прямыми, соединяющими его углы, вместе с половиной
АГ; и он будет равен поверхности вписанной фигуры. Но упомянутые
площади относятся между собой, как (квадраты) на сторонах ЕК и АЛ
[и, следовательно, как многоугольник к многоугольнику, так будет
и круг М к кругу N]; теперь ясно, что поверхность онисапной фигуры
к поверхности вписанной имеет отношение, равное двойному отноше-
отношению ЕК к АЛ, [тому же самому, что и у многоугольников].
Пусть будет еще конус Е, имеющий основание, равное кругу М,
а высоту, равную радиусу меньшего шара; этот конус равен описанной
Рис. 41.
.'#:'¦'
ш
АРХИМЕД
фигуре вместе с конусом, основанием которого является круг на EZ,
а вершина в Д. Пусть будет другой конус О, имеющий оснонание, равное
N, а нмеоту, равпую перпендикуляру, опущенному из А па АЛ; он
равен вписанной фигуре вместо с конусом, основанием которого являет-
является крух'иа диаметре АГ, вершиной же центр Д; обо всем этой было напи-
написано раньше. Теперь [поскольку]*) ЕК относится к радиусу меньшего
шара, как АЛ к перпендикуляру, опущенному из центра [Л] на АЛ;
доказано же, что как ЕК к АЛ, так будет и радиус круга М к радиусу
круга N [к один диаметр к другому]; тогда получится, что как диаметр
круга, являющегося основанием конуса 3, к диаметру круга, являю-
являющегося основанием конуса О, такинысота конуса 2 к высоте конуса О;
[следовательно, конусы подобны]. Значит конус 2 к конусу О имеет
отношение, равное тройному отношению одного диаметра к другому.
Теперь ясно, что описанная фигура вместе с конусом ко «писанной
фигуре с конусом же имеет отпошение, равное тройному отношению
ЕК к АЛ.
ХЫ1
Поверхность всякого сферического сегмента, меньшего полушария,
равна кругу, радиус которого равен прямой, проведенной из вершины
сегмента до окружности круга, являющегося основанием сегмента.
Пусть будет шар, в нем большой круг АВГ {рис. 42} и сегмент,
меньший полушария, основанием которого является построенный на
Рис. 42.
АГ круг, перпендикулярный к кругу АВГ; возьмем круг Z, радиус
которого равен АВ; требуется доказать, что поверхность сегмента
АВГ ратша кругу Z.
Депстиительно, если они не равны, то пусть эта поверхность будет
больше круга Z.
Возьмем центр Л и продолжим прямые, соединяющие Д с А и Г.
Затем, имея две перанпые пеличины — поверхность сегмента и круг Z —
впишем в сектор АВГ равностороншт многоугольник с четным числом
сторон и опишем другой, ему подобным, так, чтобы описанный
многоугольник имел ко вписанному отношение меньшее, чем отношение
поверхности сферического сегмента к кругу Z. После вращения круга,
как и раньше, получатся две ограниченные коническими поверхностя-
поверхностями фигуры, из которых одна будет описанной, а другая вписанной,
*) Как видно us комментария Ектслшя, слова •плстишкт» (taei) и тексте Архимед», которым
ли расиолягал, нв было.
О ШАРЕ И ЦИЛИНДР И
139
и поверхность описанной фигуры будет относиться к поверхности
вписанной, как описанный многоугольник ко вписаппому, так как
каждое из :>тих отношений равняется двойному отношению стороны
описанного многоугольника к стороне нписаилого. Но, (согласно
предположению), описанный многоугольник имеет ко вписанному
¦отношение мспыпее, чем поверхность упомянутого сегмента к кругу Z,
и поверхность описанной фигуры больше поверхности сегмента; сле-
следовательно, поверхность вписанной фигуры больше круга Z, а это
невозможно, так как доказано, что упомяпутая поверхность фигуры
меньше круга такой величины.
Пусть теперь круг (Z) будет больше поверхности (сегмента);
тогда опишем н впитаем подобные многоугольники, и пусть описанный
будет ко вписанпому иметь отношение меньшее того, которое круг (Z)
имеет к поверхности сегмента*). (Так как многоугольники отно-
относятся, как поверхности соответствующих фигур, то поверхность опи-
описанной фигуры к поверхности вписанной будет иметь отношение, мень-
меньшее отношения круга Z к поверхности сегмента, и следовательно,
после перестановки — отпошепие поверхности описанной фигуры к кру-
кругу Z будет меньше отношении поверхности вписанной фигуры к поверх-
поверхности сегмента; но так как поверхность вписанной фигуры меньше
поверхности сегмента, то и поверхность описанной фигуры должна
быть меньше круга Z, а это невозможно). Итак, поверхность сег-
сегмента не будет меньше**) круга Z. Доказано же, что и не больше***),
значит, обе эти поверхности раины.
XU11
Далее, если сферический сегмент больше полушария, то его поверх-
поверхность точно так же будет равна кругу, радиус которого равен прямой,
проведенной из вершины сегмента к окружности круга, являющегося
его основанием.
Пусть будет шар и в нем большой круг (АВГ) {рис. 43};
вообразим шар рассеченным плоскость»), перпендикулярной к той,
Рис. АХ
которая проходит через АТС; пусть сегмент АВД будет меньше полуша-
полушария и диаметр В Г перпендикулярен к АЛ; точки В и Г соединим: с А
*) I! этом месте текст предстагагает лакуну, которая заполняется примерно так. как показано
в угловатых стойках.
**) В текста оптибпчнп «бопъгае».
***) В тексте ошибочно «меньше».
140
¦ •АРХИМЕД
прямыми ВА и АГ. Пусть Е будет круг, радиус которого ранен АВ,
a Z — круг, радиус которого ранен АГ, и Н — круг, радиус которого
равен В Г; следовательно, круг И будет равен кругам Е, Z*). Но круг
II равен всей поверхности шара, [так как он в четыре раза боль-
больше круга, построенного на диаметре ВГ], а круг Е равен поверхности
сегмента ЛВД, [это ведь доказано для сегмента, меньшего полушарил];
¦ значит, остающийся круг Z будет равен поверхности сегмента АГД,
который уже больше полушария. . д ¦
XLIV ' ¦"'
¦• Всякий сферический сектор равен конусу, имеющему основание,
равное поверхности сферического сегмента, соответствующего атому
сектору, а высоту, равную радиусу шара.
Пусть будет шар и в нем большой круг АВД (рис. 44} с центром Г;
пусть еще будет конус, имеющий основанием круг, равный поверх-
поверхности (сегмента), соответствующей
дуге АВД, и высоту, равную ВГ;
требуется доказать, что сектор АВГД
будет равен упомянутому конусу.
Если это не так, то пусть сектор
будет больше конуса; пусть упомя-
упомянутый конус будет 6; тогда, имея
две неравные величиям — сектор и
конус,— найдем дне линии Д, Е, и
пусть Д будет больше Е и имеет к
Е отношение меньшее, чем сектор к
конусу.
Возьмем еще две прямые Z, Н та-
такие, чтобы Д от Z, Z от Н и Н от Е
. отличались на ранные {отрезки);
A-Z=Z-H=H-E
затем около плоского сектора кру-
круга опишем равносторонний много-
многоугольник с четным числом сторон и
впишем в него ему подобный так, | '
чтобы сторона описанного имела к стороне вписанного отношение
меньшее того, которое Д имеет к Z; затем, подобно предыдущему, вра-
вращая круг, образуем две фигуры, ограниченные коническими поверх-
поверхностями; тогда описанная фигура, взятая вместе с конусом, имеющим
вершину в Г, будет иметь ко вписанной фигуро'с соответствующим кону-
конусом отношение, равное тройному отношению стороны описанного мно-
многоугольника к стороне вписанного. Но сторона описанного много-
многоугольника (к стороне «писанного) имеет отношение меньшее, чем
Д к Z; значит, упомянутые телесные фмгурм (описанная ко вписан-
вписанной с их конусами) будут иметь отношение меньшее, чем тройное
д отношение Д к Z. Но Д к Е имеет отношение, большее тройного отно-
отношения Д к Z**); значит, телесная фигура, онисаштая около сектора,
будет иметь ко вписанной отношение меньшее того, какое прямая Л
л г и к
Рис. .44.
* ) Действительно, Н = П ¦ ВГг -= я (А В2 I • А Г2) — Е -|- Z.
••) См. комментарий [Ji] is аналогичному месту и предложении XXXIV.
О ШАРЕ И ЦИЛИНДРЕ 141
имеет к Е. А (согласно предположению) Д к Е имеет отношение
. . меньшее, чем телесный сектор (ЛВГД) к конусу ©; значит, телесный
сектор (АВГД) к конусу в будет иметь отношение большие, чей!
описанная около сектора фигура ко вписанной. II после перестановки:
. (сектор АВГА к описанной фигуре вместе с конусом будет иметь отно-
отношение большее, чем отношение конуса © ко вписанной фигуре вместе
с ее конусом); но описанная телесная фигура (вместе с ее конусом)
больше сектора (ЛВГД)*), и, значит, нлисаыная в сектор фигура (с ее
конусом) будет больше конуса В, а это невозможно; действительно,
выше было доказано, что она меньше такого конуса, [именно имеющего
основанием круг, радиус которого равен прямой, соединяющей верши-
вершину сегмента с (какой-нибудь точкой) окружности круга, являюще-
являющегося основанием сегмента, а высотой — радиус шара; таким же кону-
конусом будет упомянутый конус 6, ибо основанием он имеет круг, ранный
• поверхности сегмента, то есть упомянутому кругу, а пысота его равна
. радиусу шара]. Итак, телесный сектор не будет больше конуса 6.
Тогда пусть конус в будет больше телеспого сектора (АВГД).
Опять точно так же пусть Д, будучи более Е, имеет к ней отношение,
меньшее того, которое конус F) имеет к сектору (АВГЛ); затем
точно так же возьмем прямые Z и Н так. чтобы их разности были оди-
одинаковы,
z=^z-h=h--e '¦*
и пусть сторона многоугольника с четным числом (равных) сторон,
описанного около плоского сектора, имеет к стороне такого же вписан-
вписанного отношение, меньшее того, которое Д имеет к Е, [и образуем вокруг
телеспого сектора соответствующие телесные фигуры]. Теперь точно
так же докажем, что описанная около сектора телеспая фигура имеет ко
вписанной отношение, меньшее того, которое прямая Д имеет к Е
и конус в имеет к сектору (АВГД); [таким образом, этот сектор
имеет к конусу (в) меньшее отношение, чем вписанная в сектор**)
телеспая (фигура) к описанной]. Но- сектор больше вписанной
я него' фигуры; значит, и конус 0 больше описанной фигуры, а это
невозможно; [действительно, доказано, что такой конус меньше этой
фигуры, описанной около сектора]; значит, рассматриваемый сектор
будет р&веи конусу в.
. . '" КНИГА II
Архимед желает радости Досифею
Ты уже просил меня написать доказательства для тех проблем,
формулировки которых я посылал к Конону; при изложении большей
части их приходится пользоваться теоремами, доказательства которых
я уже послал тебе, а именно:
A) что поверхность всякого шара в четыре раза больше его боль-
большого круга,
B) что поверхность всякого сферического сегмента равняется
кругу, радиус, которого равен прямой, проведенной из вершины сегмента
к окружности основания,
*) В тексте написано ошибпчно «гц^цаток» (сегмента).
•*) В теисте опить ошибочно написано «в сегмент».
142
АРХИМЕД
ГАЗ
1182
ГА2
C) что для всякого шара цилиндр, имеющий основанием большой
круг шара и высоту, ранную диаметру шара, и сам будет по величине
в полтора раза больше шара и его поверхность в полтора раза больше
поверхности шара, и
D) что всякий телесный сектор равен конусу, имеющему основа-
основанием круг, равный поверхности сферического сегмента, находящегося
в этом секторе*), а высоту, равную радиусу соответствующего шара.
В этой, кияге я посылаю тебе аацись доказательств тех теорем
и задач, которые получаются из вышеупомянутых теорем; что же касает-
касается тех, решение которых находится при помощи других исследований,
а именно относительно спиралей и коноидов, то я постараюсь послать
их тебе возможно скорее.
Первая из вышеупомянутых проблем была такая. Для заданного
шара найти плоскую фигуру, равную поверхности итого шара. Ее
рептепие непосредственно получается из ныгаеупомянутых теорем:
действительно, учетверенный большой круг шара будет плоской фигу-
фигурой и равен поверхности тара.
I
Вторая задача была такова: для заданного конуса или цилиндра-
найти шар, разный этому конусу или цилиндру.
Пусть Л будет данный копус или цилиндр, а В — шар, равный
этому А {рис. 45.}. Вшьмем цилиндр FZA, в полтора раза больший
конуса, или цилиндра А, и другой
цилиндр, в полтора раза больший ша-
шара Л; основанием итого цилиндра будет
круг на диаметре Ш-), а ось КЛ равна
диаметру шара В; тогда цилиндр Е будет
равен цилиндру К. [У равных цилинд-
цилиндров основания обратнопропорциональны
высотам]; значит, круг Е относится к
кругу К, или (квадрат) на ГД к (квад-
(квадрату) на Н0, как прямая КЛ к J5Z.
ISZ
Но КЛ равна 1Г6, [ибо у цилиндра, и
полтора рака большего шара, ось равна
диаметру шара, а круг К является
большим кругом raapaj; значит, как
(кнадрат) на ГД к (квадрату) па Н0.
таи будет и Н0 к EZ.
не
Рис. 45.
Пусть квадрат иа И В будет равен прямоугольнику между ГД и ММ;
тогда как ГД к MN, так и квадрат на ГД к квадрату на НВ, или Htf
*) Речь идет, конечно, о сегменте шарн, опирающемся на ту же часть поверхности шара, что
сектор.
О ШЛРЕ И ЦИЛИНДРЕ
к EZ, посад же перестановки — как ГА к НВ, так и НВ к MN,
и MN к EZ.
Гл Нв JMN
Нв MN EZ
Но оби прямые ГД и EZ даны; значит, Нв и MN будут двумя средними
пропорциональными для двух данных прямых; :тачит, будут данными
и обе IIЭ, МЛ'.
Синтез же задачи производится так: пусть данный конус или
цилиндр будет А; требуется найти шар, который бтлл бы ранен конусу
или цилиндру А.
Для конуса или цилиндра Л построим в полтора раза больший ци-
цилиндр, основанием которого будет круг на диамстро ГД, а осью — пря-
прямая EZ, и возьмем между ГД и KZ две средний пропорциональные 116,
MN, так чтобы было —как ГД к НВ, так и НВ к MN и MN к EZ.
гл не mn
Нв MN EZ
и вообразим цилиндр, основанием которого Пыл бы круг на диаметре
HG, а ось КЛ равнялась диаметру НВ; тогда я утверждаю, что>
цилиндр Е будет равен цилиндру К.
Действительно, поскольку ГД будет к Нв, как MN к EZ,
ГА MN
НИ '" EZ
и поело перестановки, ГД к MN, пак НВ к EZ.
ГЛ II©
MN EZ
а Ив раина КЛ, [следовательно, как ГД к ММ, то есть как квадрат
па ГЛ к квадрату на Нв, так будет vi круг Е к кругу KJ, то, иначит,
как круг Е к кругу К, так будет л КЛ к EZ, [следовательно, у цилин-
цилиндров Е и К основания обратно пропорциональны высотам]; значит,
цилиндр Е равен цилиндру К. Но цилиндр К в полтора раза больше
шара, диаметр которого 116; значит, и шар, диаметр которого равен
116, то есть шар В, будет равен данному конусу или цилиндру А [1].
11
Всякий сферический сегмент равен конусу, имеющему то же осно-
основание, что и сегмент, а высотой прямую, которая к высоте сегмента
имеет такое же отношение, как вместе взятые радиус шара и высота
дополнительного сегмента к высоте дополнительного сегмента.
Пусть будет шар и и нем большой круг, диаметр которого АГ
(рис. 46); рассечем шар плоскостью, проходящей через BZ и перпенди-
перпендикулярной к АГ; пусть центр шара будет В. Сделаем, чтобы отношение!
вместе взятых ВА, АЕ к ЛЕ равнялось отношению некоторой прямой
ДЕ и ГЕ,
вЛ + А К АН
АЕ ~ Г V.
кром<_> того, сделаем, чтобы отношение вместе взятых в Г, ГЕ к ГЕ
равнялось отношению некоторой прямой КЕ к ЕА;
вг + ге _ _ке
ГЕ " ЕА"
144
АРХИМЕД
затем на круге с диаметром BZ построим два конуса, имеющих верши
нами точки К, Д; я утверждаю, что конус BAZ равен сферическому
сегменту при Г, а конус BKZ — сегменту при точке А.
Проведем прямые Вв, 6Z и нообразим конус, имеющий основанием
круг ни диаметре BZ и вершину в точке 6; пусть еще будет конус М,
имеющий основанием круг, равный поверхности сферического сегмен-
сегмента BTZ, то есть круг с радиусом 13Г, а высоту, рапную радиусу шара;
Рис. 46.
тогда конус М будет равен телесному сектору BP6Z, как доказано
в 1 книге. Поскольку же как ЛЕ к Е Г, так и вместе взптыс 6А, АЕ к АЕ,
ДК _ В А + АЕ
КГ АИ
то, «выделяя»
дБ - ЕГ @А + АЕ) - АЕ
ГЕ
АЕ
получим, что как ГА к ГЕ, так л 6А к АЕ, то есть как Г0 к АЕ,
ГД _ «А _ Г^
~гв" ~ "ае" "~"ais
а после перестановки — как А Г к ГВ, так ГЕ к ЕЛ;
АГ ^ ГЕ
ге ел
и, «присоединяя»,
дг -;- ге г Е + ra
вГ = " АЕ
как 6Д к 6Г, так и ГА к АЕ, то есть как Е5падрат на ГВ к квадрату
на BE;
8А ^ ГА ГА-ГВ JjB^
,вГ ~ ЛЕ 'ЕЛГЕ~ ВЕ2
значит, как А© к Гв, так и квадрат на ГИ относится к квадрату на BE.
_дв __ГВ^
Гв~ ВЕ2 ¦ ' -.-..... —
#«*•»¦*#, mi/fa/tm-i** ^fJU-, *->#ki «H*
:;:.-M
Ж
Фотокопия страницы греческой рукописи, содержащей отрывок сочипения
Архимеда «О гааре и цилиндре».
Архимед
14В АРХИМЕД
Но ГВ равна радиусу круга М, a BE — радиусу круга на диаметре
BZ; значит, как Д© к ©Г, так будет и крут М к кругу на диаметре
BZ. И ©Г равна оси копуса М; значит, как А© к оси конуса М, так
и круг М к кругу на диаметре BZ; следовательно, конус, имеющий осно-
основанием круг М, а высотой радиус шара, ранен телесному ромбу BAZ©,
[как доказывается и леммах 1 книги. Или же таким образом: поскольку
как Д© к висоте конуса М, так и круг М к кругу на диаметре BZ,
то, значит, конус М равен котгусу, основанием которого является круг
на диаметре BZ, а высотой А©, ибо у них основания обратпо пропор-
пропорциональны высотам. Но конус, имеющий основанием круг па диаметро
BZ, а высотой Д0, будет равен телесному ромбу BAZBJ. По конус М
равен телесному сектору BFZ©; значит, телесный сектор BTZ0 будет
равен телесному ромбу BAZ©. Если отнять общий им конус, основанием
которого янляется круг на диаметре BZ, а высотой ЕВ, то оставшийся
конус BAZ будет равен сферическому сегменту BZT.
Точно так же докажем, что копус BKZ равен сферическому сег-
сегменту BAZ. Дейстпительно, так как вместе взятые ©Г, ГЕ относятся
к ГЕ, как КЕ к КА.
•ГЕ КЕ
ГЕ
вг
гк
КА
ТО,
КЕ
]
как
вг
ЕЛ
значит, после
-ЕА
ЕЛ
К Л к АЕ, так
«выделения»
и ©Г к ГЕ.
ЛЕ ГЕ
Но вГ равна ©А; значит, после перестановки как КА к А©, так
и АЕ к ЕГ;
КА_ АК
Ав ЕГ
отсюда же, «присоединяя»,
JK Л ±_А®_ АЕ + ЕГ
Ав ЕГ
как К© к ©А, так и АГ к ГЕ, то есть как (кпадрат) на ВА к (квад-
(квадрату) на BE.
КО _ ЛГ
«Л ~ ГЕ
Построим еще круг N, имеющий радиус, равный АВ; он будет,
следовательно, равен поверхности сегмента BAZ. Затем вообразим
копус IV, имеющий высоту, равную радиусу шара; он будет рапеп
телесному сектору B©ZA, как это доказано в первой книге. Поскольку
же доказано, что как К© к ©А, так и (квадрат) на ЛВ к (квадрату)
на BE, то есть как (квадрат) на радиусе круга N к квадрату на радиусе
круга с диаметром BZ, или же как круг N к кругу на диаметре BZ,
и так как А© равна высоте конуса N, то, значит, как К© к высоте
копуса N, так и круг N к кругу на диаметре BZ; значит, конус N,
или же сектор B©ZA, будет равен телу B©ZK. Добавим общий конус,
основанием которого является круг на диа.адетре BZ, а высота Ев; тог-
тогда иесь сферический сегмент ABZ будет равен конусу BZK, что и тре-
боналось доказать.
О ШАРЕ И ЦИЛИНДРЕ
147
Следствие
Отсюда ясно, что и иообще сферический сегмент к конусу, имею-
имеющему то же самое основание, что и сегмент, и равную высоту, отно-
относится, как вместе «зятые радиус шара и высота дополнительного'
сегмента относятся к высоте дополнительного сегмента; таким образом,,
как ДЕ к ЕГ, так и конус AZB, или сегмент BFZ, к коиусу BFZ.
При тех же самых предположениях докажем, что конус KBZ рав-
равняется сферическому сегменту BAZ. Пусть будет конус JN, имеющий
основание, равное поверхности шара, а иысотой — радиус шара; этот
В
Рис. 47.
конус равен шару, [ибо как доказано, шар и четыре раза больше кону-
конуса, имеющего основанием большой круг тара, а высотой его радиус.
Но и конус N будет в четыре раза больше этого конуса, так как и его
основание, и поверхность шара в четыре раза больше соответственно
основания второго конуса, и большого круга в шаре]. Поскольку же
вместе пзятые С-)А, АЕ будут к ЛЕ, как А К к ЕГ,
ел -|- ае
АБ
АЕ
ЕГ
8А
АЕ
ЬТ
ГА
НА
то, «выделяя»
_ АЕ-ЕГ
~~ ЕГ
и переставляя, получим, что как 0Г к ГА, так и АЕ к ЕГ.
ЛЕ
;~кг~~
Затем, так как КЕ кЕА относится, как вместе взятые вГ, ГЕ к ГЕ,
вГ + ГЕ
ГЕ
то, «выделяя»
КИ - ЕЛ
АИ
ЕГ
и переставляя, получим, что КА к в Г, то есть к ВА, будет, как АК
к ЕГ,
КА
вЛ
КА
вЛ
- АЕ
~ ЕГ
то есть как ©Г к ГА.
ег
= ' ГЛ
. После этого, «присоединяя», получим,
КА + А0 _ вГ + ГА
ел " -" лг
148 АРХИМЕД
поскольку же Л© равна ©Г, то как К© к вГ, так и вД к ДГ,
ке
©г
КД
дв
КД
ед
дг
и вся КД будет
АО
ДГ
то есть как К©
ке
к
к
Д©,
©Л;
де
значит, прямоугольник между ДК и ©А равен прямоугольнику между
Дв к 0К.
ДК-0А =Дв-6К
Далее, так как К© относится к ©Г, как ©Д к ГД,
ке _ ел
ег ~ дг
или поело перестановки: (Кб к ©Д, как В Г к ГД), и доказано, что
как ©Г к ГД, так и АЕ к ЕГ,
8Г _ АЕ
~гд 1г~.
то, значит, как К© к ©Д, так и АЕ к ЕГ.
_ке_ _^а.е_
ед '~ ег
Следовательно, как (квадрат), на КД к (прямоугольнику) между
К© и ©Л, тик и квадрат на АГ к прямоугольнику между АЕ, ЕГ*).
КА2 ЛГ2
КД-Л6 АК ЕГ
Но (прямоугольник) между К© м ВД, согласно доказанному,
равен прямоугольнику между КД и АВ; значит, как квадрат на КД
к прямоугольнику между КА, А©, то есть как КД к А©, так и квадрат
на АГ к прямоугольнику между АЕ, ЕГ, то есть к квадрату па ЕВ8.
КД
Afcf ЕВ2
Но АГ равна радиусу круга N; значит, как (квадрат) па радиусе
круга IS7 к (квадрату) на BE, то есть как круг N к кругу на диаметре
BZ, так и КД к А©, то есть КД к высоте конуса N: значит, конус N,
то есть шар, будет ранен телесному ромбу JiAZK. [Или же так: посколь-
поскольку круг N относится к кругу на диаметре BZ, как ДК к высоте конуса N,
то, значит, конус N будет равняться конусу, основанием которого
яиляется круг на диаметре BZ, а высота ДК, так как у обоих основания
обратно пропорциональны высотам. Но последний конус ранен телос-
*) Уто равенство микст быть получено так. Из иротцщпп КН:вд~~АК: КГ получаем сна-
чнла «присоединением»
(Кв -}- ЯД) : вД = (АК -f КГ): ПК
Яо8иолнм лбе членя it HRa;tpBT;
КД2 : Д0* = АГ2 : ГЕ2. ( I )
Первоначальную npouoiiiuuo К»:«Л—АЕ:ЕГ мы можем нредлтинпть к нид«
(Ке-вД) : вД« = (АЕ-ЕГ) : ЕГ2- .. <2)
Теперь на сравнения оОсих пропорций A) и B) получаем
: (К0-«Д) «= АГ2 : (АЕ- ЕГ) .
О ЩЛРЕ U ЦИЛИНДРЕ
149
ному ромбу BKZA; следовательно, конус N, то есть шар, будет равен
телесному ромбу BZKA]. Из конусов, составляющих последний, конус
BAZ будит, согласно доказанному, равняться сферическому сегменту
BFZ; значит, остающийся конус BKZ будет равен сферическому сег-
сегменту BAZ.
III
Третья задача была такова: данный шар рассечь плоскостью так,
чтобы поверхности получившихся сегментов находились бы друг к другу
в отношении, равном заданному.
Пусть это уже сделано; пусть большой круг шара будет ААВЕ, а
его диаметр АВ. Проведем плоскость, перпендикулярную к АВ, и пусть
ГА
ГВ
Рис. 48.
эта плоскость образует в круге АДВЕ сечение ДЕ; проведем соединяю-
соединяющие прямые АД и ВД.
Так как отношение поверхности сегмента ДАЕ к поверхности сег-
сегмента ДВЕ (является данным), и круг, радиус которого равен АЛ, равен
поверхности сегмента ДАЕ, а круг, радиус которого равен АВ, рапен
поверхности сегмента ДВЕ и упомянутые круги будут друг к другу, как
квадрат па АА к квадрату па ЛВ, то есть как ЛГ к ГВ, то, значит,
будет данным и отношение АГ к ГВ; следовательно, будет данной
и точка Г. Далее, АВ перпендикулярна к ДЕ; значит, будет дана поло-
положением и проходящая через АЕ плоскость.
Синтез задачи проианодится так. Пусть будет шар, у которого
большой круг ЛВДЕ и диаметр АВ; и пусть заданное отношение будет
тем, которое прямая Z имеет к Н. Разделим АВ в точке Г так, чтобы
отношение АГ к ГВ равнялось отношению Z к Н;
через полученную точку Г рассечем шар плоскостью, перпендикуляр-
перпендикулярной прямой АВ; пусть общее сечение будет ДЕ; проведем соединяющие
прямые АД и ДВ и построим два круга К, Э такие, чтобы круг в имел
радиус, равный ЛД, а круг К — радиус, равный ДВ; тогда круг в будет
равен иомерхпости сегмента ДАЕ, а круг К — поверхности сегмента
ABE, как уже доказано в первой книге. И так как угол ЛАВ — прямой
и ГД — перпендикуляр, то будет, что как АГ к ГВ, то есть как Z к Н,
150
АРХИМЕД
так и квадрат па АА к квадрату на ДВ, то есть квадрат на радиусе
круга Э к кнадрату на радиусе круга К, то есть как круг в к кругу К,
и, наконец, как поверхность сферического сегмента ААЕ к поверхно-
поверхности сегмента ДВЕ.
IV
Разделить данный шар так, чтобы его сегменты имели друг к дру-
другу отношение, равное заданному.
Пусть данный шар будет АВГД (рис. 49}; требуется рассечь его
плоскостью так, чтобы: сферические сегменты имели друг к другу отно-
отношение, равное заданному.
Рассечем его плоскостью через AT; тогда отношение сферического
сегмента ЛДГ к сферическому сегменту АВГ будет заданным. Рассечем
также шар через центр (плоскостью, перпендикулярной к АГ>;
Рис. 49.
пусть сечепием будет большой круг АВГД с центром К и диаметром ДВ;
затем сделаем так, чтобы вместе взятые КД, ДХ имели к ДХ такое же
отношение, как некоторая прямая РХ к ХВ,
ЕД+ДЗС
хв
а вместе взятые KB, BX имели к ВХ такое же отношение, как некоторая
другая прямая АХ к ХД,
и иронедем соединяющие прямые АЛ, ЛГ, АР, РГ; тогда конус АЛГ
будет ранен сферическому сегменту АДГ, а конус АРГ— сегменту
АВГ; значит, будет заданным и отношение конуса АЛГ к конусу АРГ
[2]. Но как один конус относится к другому, так будет относиться
и ЛХ к ХР, [поскольку конусы имеют одпо и то же основание — круг
на диаметре АГ]; следовательно, отношение ЛХ к ХР является данным.
<1). Па основании предыдущего, согласно построению, имеем,
что АД будет к КА, как KB к ВР и ДХ к ХВ.
ЛА
БД
KB
А\
B). И так как РВ будет к ВК, как КД к ЛА, то после «присо-
«присоединения» РК будет к KB, или к КД, как КЛ к АД;
РВ+ВК КД+ЛЛ
РК
КЛ
'АЛ
KB ~ ЛА КЛ АЛ \
зпачит, вся РА будет ко всей КА, как КА к ЛД,
РК+КЛ _ТА_
КА+ДЛ ~ КЛ
КЛ
ЛА
О ШАРЕ И ДИЛИНДРЕ 151
и, следовательно, (прямоугольник) между РЛ, ЛД равен квадрату
на ЛК. Значит, как РЛ к ЛД, так будет и (квадрат) на КЛ к (квад-
(квадрату) на ЛД.
гл _ кла
ЛД ~~ ЛЛ*
лл _ дт
дк xiT
C). И поскольку ЛА будет к ДК, как ДХ к ХВ,
то после «обращения» и "«присоединения» будет, как КЛ к ЛД, так
и БД к ДХ,
КА+АЛ ВХ + ХД КЛ _ J3A
ЛД ' ~ ДХ ~ ~ЛД ДХ
[и, значит, как киадрат на КЛ к квадрату на ЛД, так будет и квадрат
на БД к квадрату на ДХ.
D). Далее, поскольку ЛХ будет к ДХ, как вместе взятые KB,
ВХ к ВХ, то после «выделения» — как ЛА к ДХ, так и KB к ВХ].
лх—хд лд кв
ДХ " ДХ ИХ
E). Теперь отложил» прямую BZ, равную KB; ясно, что (ее
конец Z) упадет далее Р, [и получится, что как ЛД к ДХ, так будет
и ZB к ВХ; таким образом, как ДЛ к ЛХ, так и BZ к ZX].
F). Поскольку же отношение ДЛ к ЛХ является данным, то,
значит, будет данным и отношение РЛ к ЛХ. Теперь, так как отношение
РЛ к ЛХ составлено из отношений РЛ к ЛД и ДЛ к ЛХ,
и РЛ будет к ЛД, как квадрат ка ДВ к квадрату па ДХ,
ГЛ _ ЛВ2
а ДЛ к ЛХ, как BZ к ZX,
ДЛ _ PZ
то, значит, отношение РЛ к ЛХ составится из отношения квадрата на
ДВ к квадрату на ДХ и отношения BZ к ZX.
гл _ рдг яг
G). Сделаем теперь, чтобы отношение РЛ к ЛХ равнялось отно-
шепию BZ к некоторой прямой Z8.
Но отношение РЛ к ЛХ дано; значит, будет дано и отношение ZB к ZG,
Дана также и прямая BZ, ибо она равна радиусу; значит, будет дан-
данной и Ze. Следовательно, отношение BZ к Z6 составляется из отноше-
отношения квадрата на ВД к квадрату на ДХ и отпошения BZ к ZX.
ни _вда BZ
Но отношение В7 к Z© сложится из отношений BZ к ZX и ZX к Z0;
152
АРХИМКД
[отбрасываем общее отношение BZ к ZX]; тогда останется, что (квад-
(квадрат) па ВД, то есть заданная величина, так относится к квадрату
(на) ДХ, как XZ к ZB, то есть тоже к заданной величине.
ад
По прямая ZA дана; следовательно, заданцую прямую AZ требуется
разделить в точке X так, чтобы отношении XZ к заданной прямой
[ZBJ равнялось отношению ладанной площади [кладрата на ВД]
к (квадратур на ДХ. Выраженная в таком общем ниде задача требу-
требует диоризма*), но при наличии условий, присущих рассматриваемой
задаче, [а именно, когда ДВ вдвое больше BZ и Z0 меньше ZB, как
следует из произведенного анализа], диоршм не требуется. Итак, дело
сводится к такой задаче:
Даны две прямые ВД, BZ, причем ВД вдвое больше BZ, а па прямой
BZ дана точка t); требуется рассечь ДВ в некоторой точке X так,
чтобы (квадрат) па ВД относился бы к (квадрату) на ДХ., как
отрезок XZ к Z0; анализ и синтез этой задачи будут даны в конце.
Синтез же основной задачи произведотсн так:
Пусть заданное отношение представляется отношением большей
прямой П к меньшей 2; пусть дан некоторый шар, рассеченный через
Рис. 50.
центр плоскостью, причем в сечении получается круг АВГД с диаметром
ВД и центром К. {рис. 50}. Отложим равную К-В прямую BZ и рас-
рассечем BZ в точке 6 так, чтобы 6Z относилась к 6В, как П к 2, затем
рассечем ВД и точке X так, чтобы XZ относилась к 0Z, как (квадрат)
на ВД к (квадрату) на ДХ,
и проведем через X перпендикулярную к ВД плоскость. Я утверждаю,
что эта плоскость так рассечет тар, что больший сегмент будет отно-
относиться к меньшему, как прямая II к S.
Действительно, сделаем, чтобы вместе взятые прямые KB, BX от-
относились к ВХ так же, как ЛХ к ДХ,
ЛУ
BY
а вместе ваятые прямые КД, ДХ относились к ХД, как РХ к ХВ,
K&+&Y _ РХ
ХД
ХВ
*) См. комментарий ?2], стр. 483 и ел.
О ШАРЕ И ЦИЛИНДРЕ 153
И проведем соединяющие прямые АЛ, Л Г, АР, РГ; тогда, как мы дока-
доказали в анализе, согласно построению, (прямоугольник) между
РА, АД будет равен (квадрату) на АК,
и как КЛ к АЛ, так будет и БД к ДХ;
кл _ кд^
лл лх
таким образом,'как (квадрат) па КЛ к (квадрату) на ЛД, так будет
И (киадрат), на БД к (квадрату) на ДХ.
Но так как (прямоугольник) между РЛ и АД равен (квадрату) на
ЛК [и отношение РЛ к АД равно отношению (квадрата) на ЛК к
(квадрату) на АЛ], то получится, что РА относится кЛД,как (квадрат)
на БД к (квадрату) на ДХ или как XZ к Z6.
—
лд
Далее, поскольку вместе взятые KB, ВХ относятся к БХ, как АХ к ХД,
и KB равна BZ, то, значит, ZX будет к ХВ, как АХ к ХД*).
кн+кх _ zx_ лх^
их "" хи = хд
После «переворачивания»**), как XZ к ZB, так и ХЛ к ЛЛ;
XZ _ ХД
¦/.а ~лд
РА
лд
ЛЛ
таким образом, как ЛД к АХ, так и BZ к ZX. Затем, поскольку РА
к АД, как XZ к Z0,
и ДЛ к АХ, кик BZ к ZX,
то по равенству в «перемешанной» пропорции***) будет, что как РЛ
к АХ, так и BZ к Z6;
ГА _ ВЯ
ЛХ ~ /-и
и, следовательно, как АХ к ХР, тик и Z0 к 6В.
лх ze лх _ z&
гл-лх" bz- ze ' xv ~"нй
Но как Z@ к 6В, так и П к 2;
и значит, как ЛХ к ХР. то есть как коттус АГЛ к конусу АР Г или сфе-
сферический сегмепт АДГ к сферичес/ишу сегменту АВГ, так и прямая
П к S.
*) ZX^ZBfBX, ЛХ=Лй-гЛХ.
а с
* *) Операция *исуси<.Ч!&чиъакия (avtxvxQetyttvxt)» состоит в той, что us пропорцлк -г=ъ~
о и
образуется —=—- Здесь -^ ~ ^А_ .
***) См. «Начала», V. 21.
154
АРХИМЕД
V
Построить сферический сегмент, подобный одному и равный дру-
другому, из заданных сферических сегментов.
Пусть АВГ и EZII будут два заданных сферических сегмента;
пусть у сегмента АВГ основанием будет круг на диаметре АВ, а верши-
вершиной точка Г, и у сегмента EZH основанием будет круг на диаметре EZ,
а вершиной точка II. Требуется найти сферический сегмент, который был
бы равен сегменту АВГ и подобен сегменту EZH {рис. 51}.
/ й
Рис. 51.
Пусть он найден и будет 0КЛ; пусть его основанием будет круг
на диаметре 0К, а вершиной точка Л. В соответствующих шарах возь-
возьмем (большие) круги ANBT, 6НКЛ, EOZH; пусть их диаметры
TN, ЛЕ, НО будут перпендикулнрпм к основаниям соответствующих
сегментов, а центры находятся в точках П, Р, 2. Сделаем, чтобы
отношение вместе взятых прямых IIN, NT к NT равнялось отпошению
некоторой прямой XT к ТГ;
ШЧ-УТ
отношение же вместе взятых РЗ, НГ к ЕГ равнялось отношению
некоторой прямой ЧТ к ГА
РЕ+ЕГ _ Ч'Т
~ Т
и отношение вместе взятых SO, ОФ к ОФ равнялось отношению некото-
некоторой прямой ИФ к ФН,
204-ОФ
ФН
и вообразим конусы, основаниями которых будут круги на диаметрах
АВ, 6К, EZ, а вершинами точки X, V, Q; тогда кгнус АВХ будет равен
сферическому сегменту АВГ, конус ^вК ранен гегмелту GKA и конз*с
EQZ — сегменту EIIZ; все это уже было доказано.
Так как сферический согмепт ЛИГ равен сегменту 6КЛ, то, значит,
и кмгус ЛХВ бз7дет ранен конусу Ч!6К; 1у равных же конусов основа-
основания обратно пропорциональны высотам]; значит, круг на диаметре АВ
О ШАРЕ И ЦИЛИНДРЕ 155
будет к кругу на диаметре ©К, как прямая ЧТ к XT. Но первый круг
относится ко второму, как (квадрат) на АВ к (квадрату) на ©К;
значит, как (квадрат) на ЛВ к (квадрату) на (Ж, так будет и ЧТ
к XT.
¦5кг
Тт~
И так как сегмент EZH подобен сегменту 6КЛ, то, значит, и конус
EZQ будет подобен конусу Ч'©К [это еще будет доказано]*); следова-
следовательно, как QCD к EZ, таи будет и \РГ к ©К.
Цъ ч'г
"Ей = «к
Но отношение ОФ к EZ дано; следовательно, будет дано и отношение ЧТ
к 0К. Пусть это отношение будет таким же, как отношение XT к не-
некоторой прямой А;
1'Т XT
«к д~
так как XT дана, то, значит, будет дала и Д. И поскольку ЧТ к XT,
или (квадрат) на АВ к (квадрату) на 0К, относятся, как прямые
6К и Д,
то положим (квадрат) на 6К равным (прямоугольнику) между ЛВ
и некоторой прямой 1;
АВ-1
тогда получится, что как (квадрат) на АВ к (квадрату) на 0К,
так будет и АВ к I.
АВ
~ 1
Но доказано, что отношение (квадратов) на АВ и на 0К равно отно-
отношению 0К и Д, и после перестановки отношение АВ к ©К будет равно
отношению I к Д.
АВ I
ек " д
Но как АВ к ©К, так будет ©К к I
ав ек
«к" i
[вследствие равенства (квадрата) на 0К (прямоугольнику) между
АВ и IJ; значит, как АБ к ©К, так н вК к I и I к Д.
Ав_ек_ j_
ек i '"¦ д
Следовательно, ©К и I будут двумя средними пропорциональными
в непрерывной пропорции между двумя заданными прямыми АВ и Д.
Л синтез этой задачи произподитси так. Пусть АВГ будет тот
сегмент, которому искомый должен быть равен, a EZH — тот, кото-
которому он должеп быть подобен; пусть большие круги соответствующих
шаров б^гут ABFN, EHZO, их диаметры TN, НО и центры П, X.
*) Для нас и, вероятно, длп Архимеда это яллнетсп очештдньтм, но Евтокий дает этому поло-
положению подробное доказательство. Это объясняется тем, что греки не имели осщего понятии о подобии
фигур и определяли его для каждого типа фигур самостоятельно; таи, услоиисм подобия сегментов
было равенство соответствующих им центральных углов, а условием подобия конусов — равенство
отношений высит к диаметрам оешшаний.
156 АРХИМЕД
Сде-таем, чтобы отношение вместе взятых прямых ITN, NT к NT равня-
равнялось отношению некоторой примой XT к ТГ,
IIN-I NT XT
NT ~ ТГ
а отношение вместо кзятых 20, ОФ к ОФ равнялось отношению неко-
некоторой примой ОФ к ФН;
ОФ " Фн
тогда конус ХАВ будет равен сферическому сегменту АГВ, а (конус)
ZQE — (сегменту) EHZ. Сделаем, чтобы отношение ОФ к EZ равня-
равнялось отношению ХТ к некоторой прямой Л,
ыф _ хт
EZ i
и между дпумя заданными прям ими АВ, Д возьмем две средние пропор-
пропорциональные ©К, I так, чтобы как АВ к ©К, так и Кб к I и I к А;
АВ_КЯ I
вк i "" д
на 6К построим круговой сегмент ©КЛ, подобный круговому сег-
сегменту EZH, затем дополним круг; пусть его диаметр будет A3. После
этого вообразим шар с большим кругом A0SK и центром Р, и через ©К
проведем перпендикулярную AS плоскость; тогда сферический сег-
сегмент, расположенный со стороны Л, будет подобен сферическому
сегменту EHZ вследствие того, что подобии и соответствующие кру-
круговые сегменты.
Теперь я утлерждаю, что этот сегмент будет также равен сфери-
сферическому сегменту АВГ. Сделаем, чтобы отношение вместе взятых
РЗ, ЕГ к ЕТ равнялось отношению некоторой прямой ЧТ к ГА;
PE+ST _ WT
вт —' ел
тогда конус Ч1Г0К будет равен сферическому сегменту вКЛ. И так
как конус Ч'©К подобен конусу ZOE, то значит, как ОФ к EZ, то есть
как ХТ к Д, так и ЧГГ к 0К;
_яф _хт _vr
EZ Д " ВК
а после перестановки и «обращения» получится, что как *РГ к ХТ,
так и вК к А.
чт ^«к
хт ^ ~д"
И. так как АВ, Кв, I, А составляют (непрерывную) пропорцию, то
отношение (квадратов) на АВ и ©К равно отношению ©К к А.
Но как ©К к Л, так и ЧТ к ХТ;
"д" = "хт" .
и, значит, как (квадрат) на АВ к (квадрату) на К©, то есть как
круг на диаметре AJ3 к кр5*гу на диаметре ©К, так будет и прямая
к ХТ;
АВ2 ЧТ
О ШАРЕ И ЦИЛИНДРЕ
157
следовательно, конус ХЛВ будет равен конусу Y0K, так что и сфери-
сферический сегмент АВГ будет равен сферическому сегменту ВКЛ. Итак,
построен сегмент ВКЛ, ранний данному сегменту АГВ и подобный
другому данному сегменту EZIT.
VI
Для двух данных сегментов, принадлежащих одному или различ-
различным шарам, построить сферический сегмент, подобный одному из дан-
данных и имеющий поверхность, равную поверхности другого сегмента.
Пусть на дугах АВГ и AEZ будут даны дпа сферических сегмента
{рис. 52), пусть дуге АВГ соответствует тот, которому должен быть
Рис. Г>2.
ЛР
PN
NP
РА
подобен искомый, а дуге AEZ — тот, поверхности которого должна
равняться поверхность искомого.
Пусть требуемое будет выполнено и сферический сегмент КЛМ
подобен сегмэнту АВГ и имеет поверхность, ранную поверхности сег-
сегмента AEZ. Представим себе центры :jtiix шаров и мропедем через них
плоскости, перпендикулярные к основаниям сегментов, и пусть н сече-
сечениях с шарами получатся большие круги KAMN, ВАГ6, EZHA, а в се-
сечениях с основаниями сегментов — прямые КМ, ЛГ, AZ; пусть AN,
В6, ЕН будут диаметры шаров, перпендикулярные к КМ, ЛГ, AZ,
и проведены прямые ЛМ, ВГ, EZ.
Так как поверхность сферического сегмента КЛМ равна поверх-
поверхности сегмента AEZ, то, значит, круг с радиусом Л М будет равен кругу
с радиусом EZ, [ибо ноперхпости упомянутых сегментов, как было
доказано, равны кругам, радиусы котортлх представляют прямые, про-
педепные от вершин сегментов к окружностям оснований], так что
прямая МЛ будет равна EZ. Поскольку же сегмент КЛМ подобен сег-
сегменту АН Г, то ЛР будет к PN, как ВП к Пв,
кп
NP+РЛ
ив
тогда после «обращения»
еп
пв
и «присоединения»
вп+пв
ип
158 архимкд
NA будет к ЛР, как 6В к ВП.
ил _ ев
Но как РА к ЛМ, так будет и ВП к ГВ,
рл вп
лм - гв
[ибо соответствующие треугольники подобны]; значит, как NA к ЛМ,
или к EZ, так и вВ к В Г.
NA NA 6В
ЛМ ~* KZ '" ВГ
После перестановки {NA к В0, как EZ к ВГ};
_na _ш_
ве "" вг
отношение же EZ к ВГ дано, ибо даны обе прямые, следовательно,
будет дано и отношение AN к Вв. И прямая Вв дана; значит, дана
и AN; таким образом, будет дан и соответствующий шар.
А синтез производится так. Пусть данные два сферических
сегмента будут ЛВГ, ДЕ7,, причем искомый должен быть подобен сег-
сегменту АВГ и иметь поверхность, равную поверхности сегмента AEZ.
Выполним те же еншхе построении, что а при анализе, и сделаем, чтобы
отношение ВГ к EZ равнялось отношению В0 к некоторой прямой AN;
вг_ ве
EZ~ AN
на диаметре AN построим круг и вообразим шар с большим кругом
AKNM; прямую NA разделим п точке Р так, чтобы NP была к РА,
как 0П к ПВ,
NP _ _0П_
РА~ ПВ
поверхность шара рассечем плоскостью, проведенной через Р
и перпендикулярной к AN, и проведем соединяющую прямую ЛМ; тог-
тогда круговые сегменты, построенные па прямых КМ, А1\ будут подобны,
так что будут подобны и соответствующие сферические сегменты.
И поскольку 6В будет к ВП, как NA к ЛР
_©В _ NA
НЕТ ЛР^
(ибо так получается после «выделения»*)), и как ПВ к ВГ, так и РА
к ЛМ,
ПВ _±±
ВГ ~ ЛМ
то, значит, 0В будет к NA, как ВГ к ЛМ.
ей вг
NA AM
Но также было, что как 6В к AN, так и ВГ к EZ;
ев вг
AN EZ
значит, EZ равна AM, так что и круг с радиусом EZ бз7дет равен кругу»
радиус которого равен ЛМ. Но круг, имеющий радиусом EZ, равен
*) В дейстпитрлыгасти после «присоединения»
(WU-H1B) : ви=(ЛГ+ГА): АР.
О ШАРЕ И ЦИЛИНДРЕ
159
поверхности сегмента AEZ, а круг, радиус которого равен ЛМ, ранен
поверхности сегмента КЛМ (это было доказано в первой книге); зна-
значит, и поверхность сегмента КЛМ будет равна поверхности сфериче-
сферического сегмента AEZ, и сегмент КЛМ подобен сегменту ЛВГ.
V [
От данного шара отсечь плоскостью сегмент так, чтобы этот сег-
сегмент имел заданное отношение к конусу, имеющему с сегментом одно
и то же основание и равную высоту.
Пусть дан шар с большим кругом АВГД {рис. 53}; пусть ВД будет
его диаметр. Плоскостью, проходящей через ЛГ, требуется рассечь
зтот шар так, чтобы сферический
сегмент ЛВГ имел заданное отно-
отношение к конусу АВГ.
Пусть псе это сделано; пусть
центр шара будет н точке Е, и пусть
отношение вместе взятых ЕД, AZ
к AZ будет равно отношению неко-
некоторой прямой HZ к ZB;
EA+UZ HZ
ZB
тогда конус АГН будет равен сегмен-
сегменту АШ\ Значит, дапо и отношение Рис. 53.
конуса ЛНГ к конусу АВГ, а следо-
следовательно, и отношение прямой HZ к ZB. Но HZ относится к ZB, как
имеете нзнтые ЕД. AZ к AZ; зпачит, будет данным и отношение вместе
взятых ЕД, AZ к AZ, Га также и отношение ЕД к AZ; следовательно,
будет дана и AZ], а также и АГ. И так как пместе пзятые ЕД, AZ имеют
к AZ отношение большее, чем вместе
взятые ЕД, ДВ к ДВ,
Eu+uZ ЕД1ДВ
¦ >
&Z ^ ДП
и вместе взятые ЕД, ДВ равны утро-
утроенной ЕД, а ВД ранпа удвоенной ЕД,
то, значит, вместе взятые ЕД, AZ
имеют к AZ отношение большее, чем
три it двум. И отношение вместе взя-
взятых ЕД, AZ к AZ ранпо заданному;
значит, при выполнении синтеза
заданное, отношение должно быть
больше, чем три к двум.
Синтез проблемы произво-
производится так. Пусть будет дан шар
с большим кругом АВГД, диаметром
ВД и центром К {рис. 54], и пусть заданное отношение, равное
отношению прямых 0К к КЛ, будет больше, чем три к двум. Но-
отношение трех к двум представляет отношение вместе взятых пря-
прямых ЕД, ДВ к ДВ;
ЕА4-АВ
160
АРХИМЕД
значит, 6К будет иметь к КЛ отношение, большее того, которое вместе
взятые ЕД, ДВ имеют к АВ;
вК ^ ЕЛ+ДВ
кл
L
лк
лк
дв
значит, после «выделения»*) 6Л будет иметь к ЛК большее отношение,
чем ЕА к АВ.
K&+AZ
&Z" '
ДВ
Сделаем, чтобы отношение 6Л к ЛК равнялось отношению ЕА к неко-
некоторой прямой AZ;
= ~\z
через полученную точку Z перпендикулярно к. J3A проведем прямую
AZr, u через эту прямую ЛГ перпендикулярно к ВЛ проведем плос-
плоскость. Я утверждаю, что сферический сегмент АВГ имеет к конусу
АВГ то же отношение, что GK к КЛ.
Действительно, сделаем, чтобм отношение вместе взятых ЕД, AZ
к AZ равнялось отпошению некоторой прямой HZ к ZB;
HZ . -
~ZB~
тогда конус ГАН будет равен сферическому сегменту АВГ. И так как
6К относится к КЛ, как вместе взятые ЕА, AZ к AZ, или как HZkZB,
то есть как конус АН Г к конусу АПГ, и конус АН Г равен сферическо-
сферическому сегменту АВГ, то, значит, как сегмент ЛВГ к конусу ЛВГ, так
будет и ВК к КЛ.
VIII
Дели шар рассечен плоскостью, не проходящей через центр, то боль-
больший сегмент имеет- к меньшему отношение, которое будет .меньше
двойного, но больше полуторного отношения поверхности большего
сегмента к поверхности меньшего [3].
Пусть будет шар и в нем большой круг АВГЛ с диаметром ВД
{рис. 55]; рассечем его плоскостью, проходящей через АГ и перпен-
перпендикулярной к кругу АВГА; пусть больший сегмент шара будет АВГ.
Рис. 55.
Я утверждаю, что сегмент АВГ имеет к АД Г отношение, меньшее двой-
двойного, но большое полуторного отношения поверхности большего сег-
сегмента к поверхности меньшего сегмента.
•> <ек-кл>: лк > Ел: ли.
О ШАРЕ И ЦИЛИНДРЕ 161
Действительно, пронедем соединяющие прямые I3A и АД; пусть
центр шара будет Е; сделаем, чтобы отношение вместе взятых ЕД, AZ
к AZ равнялось отношению некоторой прямой ©Z к ZB,
Ea+az ez
az ~ zb
а отношение вместе взятых ЕВ, BZ к BZ равнялось отношению некото-
некоторой прямой HZ к ZA,
KB+BZ HZ
BZ ZA
и вообразим конусы, имеющие основанием круг на диаметре АГ, а вер-
вершины в точках G и Н; тогда конус AGF будет равен сферическому сег-
сегменту АВГ, а конус АГН — сегменту АДГ, и поверхность сегмента
АВГ к поверхности сегмента АДГ будет относиться, как (квадрат) на
В А к (квадрату) па АД; это уже было написано выше. [Требуется
доказать, что больший сферический сегмент имеет к меньшему отно-
отношение, меньшее двойного отношения поверхности большего сегмента
к поверхности меньшего сегмента.] Я утверждаю, что отношение кону-
конуса А6Г к конусу АН Г, или прямой Z© к прямой ZH, будет меньше
двойного отношения (квадрата) на В А к (квадрату) на АД, то
есть отношения прямой BZ к прямой ZA.
Так как отношение вместе взятых ЕЛ, AZ к AZ равно отношению
0Z к ZB,
KA-4-AZ 8Z
AZ 7М
[и отношение вместе взятых ЕВ, BZ к BZ равно отношению ZH к ZA],
то BZ будет к ZA, как 0В к BE,
BZ 855 6Z—BZ ©В
ел be
ибо BE равна ДЕ; [все это уже было доказано раньше].
Далее, поскольку отношение вместе взятых ЕВ, BZ к BZ равно
отношению IIZ к ZA,
EB+BZ _ НZ
BZ Za~
то пусть прямая ВК будет равна BE (ясно, что 6В будет больше BE,
так как BZ больше ZA); тогда получится, что как KZ к ZB, так и
IIZ к ZA.
KZ _ 'HZ
"zl~ ~~ ~гд~
Но как ZB к ZA, так, согласно доказанному, будет и 6В к BE,
ZB _ вВ
?л ш
и BE равна КБ; значит, как ©Г5 к ВК, так и KZ к ZH.
0В_ _ K/L
ВК ZII
И так кап 6Z имеет к ZK отношение меньшее, чем GB к ВК,
«z _, ев
Yk~" "вкГ
а как GB к ВК, так по доказанному и KZ к ZH, то, значит, GZ имеет
к ZK отношение меньшее, чем KZ к ZII;
fr)Z _KZ_ ' .' '....-•. .:..:.
гк" * 7м ' ..:;¦¦.'¦¦
11 Лрхиысд
162
АРХИМЕД
значит (прямоугольник) между 0Z, ZH меньше (квадрата) на ZK.
: ZK*
Следовательно, (прямоугольник) между 0Z, ZII к (квадрату) па
ZH, [то есть Z0 к ZII], имеет отношение меньшее того, какое (квадрат)
на KZ имеет к {квадрату} на ZII.
HZ-ZH
[Но (квадрат) на KZ к (квадрату) на ZH имеет (отношение,
равное) двойному отношению KZ к ZH]; значит, 6Z имеет к ZIT отно-
отношение, меньшее двойного отношения KZ к ZH.
[По KZ к Z1I (будет, как BZ к ZA; значит, 6Z к ZTI) имеет отноше-
отношение, меньшее двойного отношения BZ к ZA], а это мы и искали.
И так как BE равна ЕД, то (прямоугольник) между BZ, ZA
меньше (прямоугольника) между BE, ЕД*),
BZZA < BE-ЕЛ
значит, ZB имеет к BE отношение меньшее, чем ЕД к А7,, или 6В к BZ;
хв „
be
ZB2
ЕД вВ
дг ~~ bz
значит, (квадрат) на ZB будет меньше (прямоугольника) между
ВВ, BE или (прямоугольника) между 0В, ВК.
Пусть (прямоугольник) между 6В, ВК будет ранен (квадрату)
на некоторой прямой BN;
WII - ПК -JJN*
тогда как 6В к ВК, так будет и (квадрат) на OJN к (кпадрату)
на NK**)'.
ав _er*L
Яо (квадрат) на 6Z к (квадрату) на ZK имеет больше? отношение,
чем (квадрат) на BN к (квадрату) на NK,
Zli
кк*"
[и, значит, (квадрат) па ©Z к (квадрату) на ZK. шшкт отношение
большее, чем ©В к ВК, или GB к BE, или же KZ к ZH]; .чпачит, 6Z
имеет к ZH отношение, большее полуторного отношения KZ к ZII;
и
I ZH /
|:>то (будет доказано) под конец] [4]. Но отношение BZ к ZH равно
отношению конуса АВГ к конусу АИ Г, или сегмента АВГ к сегменту
АДГ, отношение же KZ к ZTI равно отношению BZ к ZA, или (квад-
(квадрата) на ВА к (квадрату) на ЛД, или поверхности сегмента АВГ
к нешерхности сегмента АДГ. Итак, больший сегмент имеет к меньшему
отношение, меньшее двойного, но большее полуторного отношения
поверхности большего сегмента к поверхности меньшего.
*) Геометрическиято равносильно тому, что при рлипых периметрах шшщвдь киадрата' Судет
дольше площади соответстиующего прямоугольника.
••> BN : ВК=вВ : BN—@B+BN) : (BN+ 11К)=6М : .VK-
О ШАРЕ И ЦИЛИНДРЕ
¦ ¦ Иным способом
Пусть будет шар с большим кругом АВГЛ, диаметром АГ и цент-
центром Е; рассечем его проходящей через БД плоскостью, перпендикуляр-
перпендикулярной к АГ {рис- 56]. Й утверждаю, что больший сегмент ДАВ к мень-
меньшему В ГА имеет отноше-
отношение, меньшее двойного, но
большее полуторного от-
отношения поверхности сег-
сегмента АВД к поверхно-
поверхности сегмента ВГД.
Проводим соединяю-
соединяющие прямые АВ и В Г;
тогда отношение одной
поверхности к другой бу-
будет таким же, как отноше-
отношение круга с радиусом АВ
к кругу с радиусом В Г, или отношение примой А6 к О Г. Положим,
что каждая из прямых AZ и ГН будет равна радиусу круга. Тогда отно-
птеттие сегмента ВЛД к сегменту ВГД составляется из того отношения,
которое сегмент ВАЛ имеет к коггусу с основанием, равпьш кругу на
диаметре ВД и с вершиной и точке А, затем из того, которое этот конус
имеет к конусу с тем же основанием и с вершиной и точке Г и, наконец,
из того, которое только что упомянутый конус имеет к сегменту ВГД.
сегмент ВАЛ сегмент ВАЛ минус ВЛД кпнуг ВГД
Рис. 56.
e-егмеит ВГД
сегмент ВГД
конус ВАЛ конус В ГА
Но отношение сегмента ВАЛ к конусу ВАЛ есть отношение Нв к ВГ,
сегмент ВАЛ Нв
конус ВАЛ "= "Sf"
отношение конуса ВАД к конусу ВГД ость отношение Л в к в Г, •
кину с ВАЛ
АО
©Г
кии ус ВГД
и отношение конуса ВГЛ к сегменту ВГД есть отношение АВ к 6Z,
конус ВГД
сегмент НГЛ"
Ав
отношение же, составленное из (отношений) Нв к вГ и Ав к вГ,
будет отношением (прямоугольника) между Нв, в А к (квадрату)
на 6 Г,
НИ Afi
. ©Г »Г"
отношение же (прямоугольника) между IT0, ОА к (квадрату) на
вГ, составленное с отношением Ав к 0Z, будет отношением (прямо-
(прямоугольника) между Нв, 6Л, (умноженного) на 0А, к (квадрату)
па в Г, (умноженному) на 9Z,
не-ел лв
ег* ez «r« • ez
а (прямоугольник) между ПВ, 0А, (умноженный) на вЛ, пред-
представляет (квадрат) на вА, (умноженный) на 0П. Таким образом,
(нужно доказать, что) квадрат на 6А, (умноженный) на 011, имеет
164 АРХИМЕД
к (квадрату) на 6Г, (умноженному) па ©Z, отношение, меньшее
двойного отношения А© к ©Г,
[ибо двойное отношение А© к ВГ есть отношение (квадрата) на А©
к (квадрату) на ©Г]. Следовательно, (квадрат) на А©, (умножен-
(умноженный) на ©Н, к (квадрату) на ©Г, (умноженному) на ©Z, (дол-
(должен) иметь отношение, меньшее, чем (квадрат) на А0, (умно-
(умноженный) на ©II, к (квадрату) на ©Г, (умноженному) на 0Н.
вга-ez
-
Итак, (нужно доказать), что (квадрат) на ©Г, (умноженный)
на Z©, больше (квадрата) на ©Г, (умноженного) на ©II,
иди что ©Z больше 0Н; (последнее же очевидно).
Теперь я утверждаю, что больший сегмент имеет к меньшему отно-
отношение, большее полуторного отношения поверхностей.
По доказанному, отношение сегментов равно отношению (квад-
(квадрата) на Л0, (умноженного) на ©Н, к (квадрату) на Г0,
(умноженному) на ©Z, а полуторное отношение поверхностей равно
отношению куба на АВ к кубу на ВГ; итак, и утверждаю, что (квад-
(квадрат) па А©, (умноженпый) па ©II, к (квадрату) на Г©, (умно-
(умноженному) на ©Z, имеет отношение болыпео, чем [куб па АВ к кубу
на ВГ, или чем] куб ла А© к кубу на ©В *), или чем отношение,
составленное из отношения (квадрата) на А© к (квадрату) на В©,
и отношения А© к ©В.
Но отношение (квадратов) па А© к ©В, взятое с отношением
А© к ©В, равно отношению (квадрата) на А© к (прямоугольнику)
между Г© и 0В**);
А6" Ав АвД
ева" ев"~ re ев
отношение же (квадрата) на А© к (прямоугольнику) между В©,
©Г равно отношению (квадрата) на А©, умноженного на ©Н,
к (прямоугольнику) между 150, ©Г, (умноженному) па ©Н;
А62 Ав2-«К'
ввег вв-ег-wii
я утверждаю, следовательно, что (квадрат) па А©, (умноженный)
на ©Н, имеет к (квадрату) на Г©, (умноженному) на 0Z, отно-
отношение большее, чем [(квадрат) па А© к (прямоугольнику) между
В©, ©Г или] чем (квадрат) пц А©, (умноженный) на ©Н, к (пря-
(прямоугольнику) между В0, ©Г, (умноженному) на ©Н.
Авз-йн AR2-BH
е-вг-ен
Значит, нужно доказать, что (квадрат) на ©Г, умноженный ла
©Z, будет меньше (прямоугольника) между В©, ©Г, (умножен-
(умноженного) на II©,
r«2.ez < вв-вг- не
а это то же самое, что доказать, что (квадрат) на Г© имеет к (прямо-
*) Это следует и» подобия треугольников А11Г и АВ©.
**) Так как вВ«=А8.8Г.
О ШАРЕ И ЦИЛИНДРЕ 165
угольнику) между Вв, в Г отношение меньшее, чем IIв к 0Z
Г62 ^ НО
во-ег ^ «z
[иными словами, нужно доказать, что 110 имеет к 0Z отношение
большее, чем Г в к ©В].
Из Е перпендикулярно к ЕГ проведем прямую ЕК и из точки
В опустим на нее перпспдикуляр ВА. Нам остается доказать, что 110
имеет к 0Z отношение большее, чем Г6 к ЭВ.
не . _ги
Но 0Z равна имеете взятым Л0 и КЕ; значит, нужно доказать, что Нв
к вместе взятым 6А и КЕ имеет отношение, большее, чем Г0 к 6В;
АИ+КК -* вВ
если из 6Н отнять Г0, а из КЕ прямую ЕЛ, равную В©, то остается
доказать, что полученные остатки ГП и вместе взятые АВ и КЛ имеют
друг к другу отношение большее, чем ГЭ к 6В, или ©В к 6А, или же
ЛЕ к ЬА,
ГН _ _ГИ_ _ t-'B _ ЛЕ
л«+кл'* нв ~ на ~" и а
или после перестановки, что (ГН, или) КЕ имеет к ЕЛ отношение
большее, чем вместе взятые КЛ, ©А к ©А,
J9L > кл+на
ЕЛ оА
или же, поело выделения, что КЛ имеет к ЛЕ отношение большее, чем
КЛ к ©А. (Следовательно, остается доказать, что) ЛЕ меньше ©А;
(это же очевидно) [4J.
IX
Из всех сферических сегментов, ограниченных равными поверхностя-
поверхностями, наибольшим будет полушарие.
Пусть будет шар с большим кругом АВГЛ и диаметром ЛГ, и дру-
другой шар с большим кругом EZH0 и диаметром EII. Рассечем один шар
плоскостью через центр, а другой — не через центр- пусть секущие пло-
плоскости будут перпендикулярны к диаметрам АГ, ЕН и дадут сечения
по линиям АВ и Z0; тогда соответствующий дуге ZE0 сферический сег-
сегмент будет полушарием, [из сегментов же, соответствующих дуге
ВАЛ (рассматриваемый может быть) па одном чертеже меньше полу-
полушария, а па другом, обозначенном звездочкой, больше полушария],
пусть поверхности упомянутых сегментов будут равны. Я утверждаю,
что полушарие, соответстпующое дуге ZE0, Судет больше сегмента,
соответствующего дуге ВАА {рис. 57;.
Так как поверхности упомянутых сегментов раины, то ясно, что ВА
равна прямой EZ, [ибо доказано, что поверхность всякого сегмента равна
кругу, радиус которого равняется прямой, проведанной из вершины'
сегмента к окружности круга, составляющего основание сегмента.
Поскольку на чертеже со звездочкой дуга ВАЛ болыпеполуокружности],
то ясно, что квадрат на ВА будет меньше удвоенного квадрата на АК,
166
АРХИМКД
но больше удвоенного квадрата на радиусе *). Пусть (квадрат) на ВА
будет вдвое больше квадрата на АР;
ГВ
ГК •'•" АК
пусть прямая ГЗ равна радиусу круга АВЛ, и отношение ГЗ к ГК
равняется отношепию некоторой прямой МА к АК,
МА
и пусть на круге с диаметром ВД будет построен конус, имеющий вер-
вершину в точке М; тогда этот конус будет равен сферическому сегменту,
соответствующему дуге ВАЛ. Пусть также EN будет равна ЕА, я на
Рис. 57.
круге с диаметром BZ построен конус, имеющий перпшну в точке N;
тогда а этот конус будет равен полушарию, соответствующему дуге
6KZ. Но прямоугольлмк между АР, РГ более прямоугольника между
АК, КГ,
АР-РГ>АК-КГ
ибо его меньшая сторона больше меньшей стороны другого прямоуголь-
прямоугольника**), и (квадрат) на АР равен прямоугольнику между АК., ГЗ;
АР2=АК-ГЕ
действительно, он составляет половику (квадрата) на АВ ***).
*) Обозначим радиус круга через г, тогда ВА*=ЛК- АГ=2г- ак. Если г<АК<2г, то
2гИ<ВА2< 2 А К*.
Ксли бы дуга ВАД была меньше окружности, то АК<г
2г2 > ВА« > 2АК2-
Отсюда иидио. что в первоначальном тексте Архимед брал только один чертеж, именно тот, который
позднейший комментатор обозначал звездочкой.
*•) Если дуга АВ равна четиерти окружности, то АР равна радиусу г, и АР-РГ—2/2. Если
АВ больше четиерти окружности, то АР^-r и, согласпо рапсе сказанному, меньше АК; следова-
следовательно, меньшими сторонами в обоих ирлмоугольпикях будут Рг и КГ- причем ГГ5КГ- Так как
АРН-РГ^АК+КГ, и из двух прямоугольников с равными периметрами больше будет тот, который
О люкс подходит к квадрату, то
АР>РГ>АК-КГ.
Ксли же дуга АВ меньтпе четверти окружности, то АР-^r и АК<ТК: следовательно, меньшими сто-
сторонами в обоих прямоугольниках будут лр и АК. Так как теперь АР будет больше АК (из ранен-
ства 2AP»-=BAV2AK2). го опять АР-РГ>ЛК-КГ.
•••) Имеем ЛИС=АК-АГ=АК-2ГН.
О ШАРЕ И ЦИЛИНДРЕ . 167
Теперь вместе взятые (левые части) будут больше вместе взятых
(правых);
АР-РГ-1- АРг>АК-КГ-|-АКГЗ
[значит, (прямоугольник) между ГА, АР больше (прямоугольника)
между ЕК, К А]. По (прямоугольник) между SK, КА равняется
(прямоугольнику) между МК, КГ *),
ЗК-КА = МККГ
[так что (прямоугольник) между ГА, АР будет больше (прямоуголь-
(прямоугольника) между МК, КГ]; таким образом, ГА будет иметь к КГ отноше-
отношение большее, чем МК к АР.
га мк
кг * ар
Но отношение АГ к ГК равно отношению (квадрата) на АВ к (квад-
(квадрату) на ВК**);
АГ
теперь ясно, что половина (квадрата) на АВ, равная квадрату на АР,
будет иметь к (квадрату) на ВК отношение большее, чем МК к уд-
удвоенной АР, которая ранни AN***);
ЛР2 . МК
значит, круг па диаметре Z6 к кругу иа диаметре ВД будет иметь отно-
inmiHc большее, чем МК к AN. Таким образом, конус, имеющий основа-
основанием круг на диаметре ZB, а вершиной точку N, будет больше конуса,
имеющего основанием круг на диаметре ВД, а вершиной точку М;
теперь ясно, что полушарие, соответствующее дуге EZ0, будет больше
сегмента, соответствующего дуге ВАЛ.
гн ма ег+гк мл+лк
*) Из пропорции yrsr=-7-f— получаем «ирисосдашеттем» —фгг—= гг;— • откуда
2К-АК=МК-КГ.
**) Таи как АВ»=ЛК-Лг и ВК'=ЛК-КГ. :
•*) Из ряивисти 2ЛР'=ВА2 и ВЛ — EZ (условие равенства поверхностей сегментов) имеем:
2APS=BA!=EZ'=2AES, отсюда ЛГ=ЛЕ и AN=2AP, так Как 1Ш ривна ЕЛ — радиусу круга
ЕгвН
1
О КОНОИДАХ И СФЕРОИДАХ
Архимед Досифею оюелает благоденствия!
В этой книге я посылаю тебе запись доказательств остальных пред-
предложений, етце не имеющихся у тебя в посланном ранее, а также некото-
некоторых других, найденных мпото позднее, к рассмотрению которых я уже
часто приступал, но должен был отступить, так как видел некоторые
трудности в их исследовании; но этой причине я но издал и свет эти
предложения одновременно с другими. Потом уже, занявшись ими более
тщательно, я разрешил те трудности, которые задерживали меня ранее.
Это были оставшиеся от прежних теоремы, касавшиеся прямоугольного
коноида *); к ним я добавил теперь найденные позже теоремы относи-
относительно тупоугольного коноида **) и сфероидальных фигур, из которых
одни я называю удлипеппыми, другие же сплющенными***).
Предложения, касавшиеся прямоугольного коноида, были таковы:
Если какое-нибудь сечение прямоугольного конуса ****), вращаясь
около неподвижного своего диаметра *****), норлстся в исходное поло-
положение, то фигуру, описанную при этом сечением прямоугольного ко-
конуса, мы будем называть прямоугольным коноидом, диаметр, оста-
остававшийся неподвижным—его осью, а точку, в которой ось коноида
доходит до его поверхности,—вершипой коноида.
Если какая-нибудь плоскость касается прямоугольного коноида,
то всякая другая плоскость, проведенная параллельно касательной,
отсечет от коноида некоторый сегмент; основанием отсеченного сегмента
мм будем называть часть секущей плоскости, ограниченную линией пере-
пересечения с коноидом, вершиной — ту точку, в которой первая плоскость
касается коноида, а осью — заключенную в сегменте часть прямой,
пронедеппой через вершину этого сегмента параллельно оси коноида.
Для рассмотрения было предложено доказать следующее.
Если от прямоугольного коноида отсечь сегмент плоскостью, пер-
перпендикулярной к его оси, то отсеченный сегмент будет в полтора раза
больше конуса, имеющего с этим сегментом те же самые основание и ось.
*) То есть параболоида вращения.
**) Гилероолонд иращения (диучолмй). вернее, одна его полость.
***) Эллипсоиды иращения иокруг большой и малой осей.
****) Парабола.
*****) Ось параболы.
О КОНОИДАХ И СФЕРОИДАХ 169
Также если от прямоугольного коноида отсочь два сегмолта прове-
проведенными произвольно плоскостями, то отсеченные сегменты будут иметь
друг к другу отношение, равное двойному *) отношению их осей.
Относительно же тупоугольного коноида мы предлагаем следующее.
Если в плоскости имеются сечение тупоугольного копуса**),
его диаметр***) и ближайшие к сечению тупоугольного копуса пря-
прямые****), и если около удерживаемого неподвижным диаметра вращать
ту плоскость, в которой .находятся упомянутые линии, то после ее воз-
возвращения в исходное наложение ближайшие к сечению тупоугольного
конуса прямые, очевидно, опишут раннобедренный конус, вершиной
которого будет точка пересечения ближайших прямых, а осью — оста-
остававшийся неподпижпым диаметр. Фигуру, описанную сечением тупо-
тупоугольного конуса, будем назылать тупоугольным коноидом-, нелодвиж-
ный диаметр — его есью, а точку, в которой эта ось доходит до поверх-
поверхности коноида,— его вершиной. Конус, описанный ближайшими к
сечению тупоугольного копуса прямыми, мы назонем объемлющим
коноид *****I а прямую, заключенную между вершинами коноида и
объемлющего коноид копуса, назонем дополняющей ось******).
Если какая-нибудь плоскость касается тупоугольного коноида
и другая плоскость, проведенная параллельно касательной, отсечет
некоторый сегмент коноида, то основанием, отсеченного сегмента мы
будем называть часть секущей плоскости, ограниченную линией пере-
сечепия с коноидом, вершиной — ту точку, в которой касательная
плоскость касается коноида, а осью — заключенную ч сегменте часть
прямой, проведенной через вершины сегмента и конуса, объемлющего
коноид, часть же этой прямой между упомянутыми вершинами будем
называть дополняющей ссъ.
Бес прямоугольные коноиды будут подобными друг дру-
Гу **2**22^. из тупоугольных же коноидои будем называть подобными
те, у которых подобны конусы, объемлющие коноид ********).
Для рассмотрения и доказательства предлагается следующее:
Если от тупоугольного ксноида отсечь сегмент плоскостью, перпен-
перпендикулярной к его оси, то отсеченный сегмент к кспусу с теми же осно-
основанием и осью, что и у сегмента, будет находиться в том же отношении,
какоо вместе взятые ось этого сегмента и утроенная прямая, дополняю-
дополняющая ось, имеют к оси сегмента и удвоенной прямой, дополняющей ось.
Также если от тупоугольного коноида отсечь сегмент плоскостью
не перпендикулярной к оси, то отсеченный сегмент к фигуре, имеющей
с сегментом то же основание и ту же ось (эта фигура будет коническим
сегментом), будет находиться в том же отношении, какое вместе взятые
ось этого сегмента и утроенная прямая, дополняющая ось, имеют ко вме-
вместе взятым оси сегмента и удвоенной прямой, дополняющей ось.
Относительно же сфероидальных фигур мы предлагаем следующее.
Если сечение остроугольного конуса (эллипс), пращаясь около
удерживаемо 1-о неподвижным наибольшего диаметра, вернется в исход-
исходное положение, то описанную фигуру назовем удлиненным сфероидом.
*) То есть возведенному во вторую степень.
**) Гипербола; ведшее, одна ее истоь.
***) Ось гиперболы.
****) Асимптоты гиперболы. Этот термин (буквально: несовпадающие) был введен уже
после Архимеда Аполлонием Пергским.
*•*••) Асимптотический кпнус.
••*«**) Яго Вуцет дейстпитслышп полуось гиперболы.
••*•**•) Все пацаболы подобии. См. Аполлоний. Конические сечения, книга "VI, II.
****) Согласно Евклиду («Начала», книга XI, определение 24), подобными конусами
навываготся те, у которых пропорциональны оси и диаметры оснований.
J70 АРХИМЕД
Если же эллипс вращается около удерживаемого неподвижным
наименьшего диаметра (малой оси), то фигуру, описанную после
возвращения п исходное положение, назовем сплющенным сфероидом.
Осью каждого из сфероидов назовем удерживаемый неподвижным диа-
диаметр (ось эллипса), вершиной — точку, в которой ось доходит до
поверхности сфероида, центром — середину оси и диаметром — про-
проведенную через центр перпендикулярно к оси прямую.
Если параллельные плоскости касаются какого-нибудь из сферои-
сфероидов, не пересекая его, и параллельно касательным плоскостям проведена
другая плоскость, рассекающая сфероид, то основанием обоих образован-
образованных таким образом сегментов назовем часть секущей плоскости, содер-
содержащуюся внутри кривой сечения со сфероидом, их вершинами — точки,
в которых параллельные плоскости касаются сфероида, и осями — за-
заключенные внутри сегмептоп части прямой, соединяющей их вершины.
Л что касательные плоскости имеют с поверхностью сфероида лишь одну
общую точку, и что соединяющая точки касания прямая лроходит через
центр сфероида, это мы еще докажем.
Подобными мы назовем такие сфероиды, оси которых находятся
в том же отпошепии, что и диаметры. Сегменты же сфероидов и коноидов
мы назовем подобными, если они отсекаются от подобных фигур, имеют
подобные основания, а оси их, которые или перпендикулярны к пло-
плоскостям оснований, или образуют равные углы с соответствующими диа-
диаметрами оснований, находятся в том же отношении, что и соответствую-
соответствующие оси диаметры оснований.
Относительно сфероидов предлагается рассмотреть и доказать сле-
следующее. Если рассечь какой-нибудь сфероид плоскостью, проходящей
через центр и перпендикулярной к его оси, то каждый из получающихся
сегментов будет в два раза больше конуса с теми же основанием и осью,
что и у сегмента. Если же секущая плоскость перпендикулярна к оси,
но не проходит через цет?тр, то наибольший из полученных сегментов
будет относиться к конусу с теми же оспонапием и осью, как вместе взя-
тыо половина оси сфероида и ось меньшего сегмента относятся к оси мень-
меньшего сегмента, а меньший сегмент будет относиться к конусу с теми же
основанием и осью, что и у сегмента, как вместе взятые молонина оси
сфероида и ось большего сегмента относятся к оси большего сегмента.
Если какой-нибудь из сфероидов рассечен плоскостью, проходящей
через центр, но не пернендикулярпой к оси, то каждый из получившихся
сеглгептои будет в два раза больше фигуры с теми же основанием и осью,
что и у сегмента (это будет конический сегмент).
Если же сфероид рассечен плоскостью, не проходящей через центр
и не перпендикулярной к оси, то наибольший из полученных сегментов
будет относиться к фигуре с теми же основанием и осью, что и сегмент,
как вместе взятые половина прямой, соединяющей вершины сегментов,
и ось меньшего сегмента относятся к оси меньшего сегмента, а меньший
сегмент к фигуре с теми же основанием и осью будет относиться, как
вместе взятые полоиина соединяющей вершины обоих сегментов пря-
прямой и ось большего сегмента относятся к оси большего сегмента. (Полу-
(Получаемая фигура и в атик случаях будет коническим сегментом.)
Бели упомянутые предложения доказаны, то при их помощи можно
пайти и много других теорем и задач, как, например:
подобные сфероиды и сегменты сфероидов и коноидов находятся
друг с другом в тройном *) отношении их осей;
•) То есть воеведенном о третью степень.
О КОНОИДАХ И СФЕРОИДАХ 171
у ранпых сфероидов квадраты диаметров обратно пропорциональ-
пропорциональны осям, и если у двух сфероидон квадраты диаметров обратно пропор-
пропорциональны осям, то эти сфероиды равны;
а также задачи, как, например:
от данного сфероида или коноида отсечь сегмент плоскостью, прове-
проведенной параллельно заданной, так, чтобы отсеченный сегмент был равен
данному конусу, цилиндру или шару*).
Предварительно я налишу все необходимые для доказательств
теоремы и указания, а затем перейду и к объяснению предложений.
Будь счастлив!
Определения
Если рассечь когтус плоскостью, встречающейся со всеми его сто-
сторонами (образующими), то сечение будет или кругом, или эллипсом.
Если сеченио — круг, то ясно, что часть, отнятая с той стороны, где
находится вершина конуса, будет и сама конусом. Если же в сечении
получается эллипс, то часть, отпятую от конуса с той стороны, где па-
. ходится вершина конуса, будем называть коническим сегментом.
Основанием сегмента будем называть часть плоскости, ограниченную
эллипсом, вершиной — ту точку, которая будет и вершиной конуса,
а осью — прямую, соединяющую вершину конуса с центром эллипса.
И если цилиндр рассечь двумя параллельными плоскостями, лстре-
чающими все стороны (образующие) цилиндра, то сечения будут или
кругами, или же равными и подобпыми аллипсами. Если сечения будут
кругами, то ясно, что отсеченная параллельными плоскостями часть
цилиндра тоже будет цилиндром. Если же сечения будут эллипсами, то
часть цшищдра между параллельными плоскостями назопем цилиндри-
цилиндрическим сегментом. Основаниями сегмента пазовем части плоскостей,
ограниченные эллипсами, а осью — прямую, соединяющую центры
эллипсов; эта ось будет находиться па одной прямой с осью цилиндра.
(Л е м м а.) Если имеется любое число величин, одинаково превы-
превышающих одна другую {составляющих арифметическую прогрессию),
причем разность равна наименьшей из этих величин {первому члену),
а также одинаковое количество других величин, каждая из которых
равна наибольшей из первых величин, то все величины, равные наиболь-
наибольшей, взятые вместе, будут меньше удвоенных всех величин, одинаково пре-
превышающих одна другую, но больше удвоенных этих величин, оставшихся
после исключения наибольшей.
Доказательство этого очевидно**).
I
Если имеется любое количество некоторых величин и равное количе-
количество других величин, причем одинаково расположенные (величины обоих
- рядов) имеют попарно одно и то же отношение, и если первые величины
все, или только некоторые из них, находятся в каких-нибудь отношениях
*) Архимодопы доказательства этих теорем и задач или ыс сохранились, или, может быть, даже
не были опубликованы.
*•) В нашем обозначении
2[а+2а+.. . +(п-1)а}<п.па<2{а+2а+ . . .
или
п(п—
172
АРХИМЕД
А
В
с третьими величинами, а соответствующие величины второго ряда
находятся в тех оке самых отношениях с величинами четвертого ряда,
то все первые величины ко всем соответствующим им величинам (треть-
(третьего ряда) будут иметь то же самое отношение, как все величины второго
ряда ко всем соответствующим им величинам (четвертого ряда) [1].
Пусть имеются некоторые величины: А, В, Г, А, Е, Z и равное коли-
количество других величин Н, 0, I, К, Л, М, имеющих с ними попарно одно
и то же отношение, и пусть А имеет к В то же самое отношение, как Нк0,
m
а В к Г (то же самое), как в к I
и точно так же и все остальные;
д_
Е
Е
Z ~
к
25.
Л
Л
il
пусть также величины А, В, Г, Д, Е, Z находятся в'каких-нибудь отно-
отношениях с (третьими) величинами N, Е, О, ГТ, Р, I, а величины IT, в,
I, К, Л, М паходятся в тех же самых отношениях с соответствующими
леличинами (четвертого ряда) Т, Г, Ф, X, V, Й, и пусть то отношение,
которое А имеет к N, будет тем же самым, которое Н имеет к Т,
А
"IT
Е
11^
Т
а отношение, которое В имеет к S, будет тем же самим, которое
имеет к Г;
г
и точно так же и все остальные {рис. 1}. Требуется доказать, что все
А, В, Г, А, Е, Z вместе взятые ко всем N, S, О, П, Р, 2 будут иметь то же
h
А В Г А Е Z И в I К Л М N 3 О П Р L Т Г Ф X V Я
Рис. 1.
самое отношение, как все вместе взятые Н, в, I, К, Л, М ко леем Т,
Г, Ф, X, Т, О.
Поскольку N имеет к Л то же самое отношение, как Т к Н,
А ~ Ы
а А к В то же отношение, как Н к в,
А Н
"в =-в-
О КОНОИДАХ И СФЕРОИДАХ 173
и В к Е то же, как О к Г,
Т= г"
то N будет иметь к S то же самое отношение, как Т к Г;
вследствие того же, как S к О, так будет и ГкФ
о ~ ф
и точно так жо и все остальные.
о ф
п~ ~~х~
п__ х_
р ^
Тогда все А, В, Г, Д, Е, Z имеют к А то же самое отношение, как все
Н, 6, I, К, Л, М к Н,
А Н
а А имеет к N то же отпштение, как Н к Т,
A- JL
N ~ Т
и N ко всем N, S, О, 11. Р. 2 имеет то же самое отношение, как Т ко
всем Т, Г, Ф, X, Y, U;
N Т
N + S4-O -г И-г V ¦+¦ Z ~ Т + Г-1- Ф+ X + ЧГ+ Q
теперь ясно, что нее А, Л, Г, Л, Е, Z ко всем N, Е, О, П, Р, 2 будут иметь
то же самое отношение, как лее 17, ©,1, К, Л, М ко леем Т, Т, ф, X,
А.±_5± r + A+E-[-Z НЧ-e+I+K + A + M ¦
il-J-Ё i-O + il + P-i-2 T + r-J-ii-'-X + 'P'+H
Так же ясно, что если из величин А, В, Г, Д, Е, Z выбрать А, В, Г,
*А, Е, имеющие отношения к N, Е, О, И, Р, причем Z не будот иметь отно-
отношения ни к одной леличипе, а из величии TI, Э, 1, К, Л, М, выбрать
Н, 0, I, К, Л, имеющие соответственно те же самые отношения к Т,
Т, Ф, X, х?, причем М не будет иметь отношении пи к одной неличине,
то точпо так же вес А, В, Г, Д, Е, Z ко всем N, Е, О, П, Р будут
иметь то жо самое отношение, как вес И, в, I, К, Л, М ко всем Т, Т,
Ф, X, Y.
А + В -Ь Г + Л Ч- Е -I- Z _ H + Q--I4-K +
N + E-t
II
¦
Если имеется некоторое количество равных друг другу линий и к каж-
каждой из них с избытком в виде квадрата прикладывается некоторая пло-
площадь, причем стороны этпих избыточных {квадратов) будут одинаково
превышать одна другую и разность {двух последовательных сторон)
174
АРХИМЕД
будет равняться наименьшей из них*), и если имеются другие пло-
площади, количество которых равняется количеству первых, а величина
каждой равняется наибольшей из первых, то эти площади ню сеем (взя-
(взятым вместе первым) будут иметь отношение, меньшее того, которое
(прямая), равная вместе взятым стороне наибольшего избыточного
(квадрата) и одной из (первоначально данных) равных друг другу
прямых, имеет к (прямой), равной вместе взятым третьей части сто-
стороны наибольшего избыточного (квадрата,) и половине одной из рав-
равных друг другу прямых, а если (из первых площадей) исключить наи-
наибольшую, то к оставшимся эти (вторые) площади будут иметь отно-
отношение, большее упомянутого**).
Пусть имеется некоторое количество равных друг другу прямых,
на которых гтоит А {рис. 2}, п к каждой из них с избытком и ииде
А
I
Л
Л
Л D
1
и
1
н
\
Л
/
в
Л
к
1
в
Л
к.
1
в
к
1
в
Рис. 2.
квадрата прикладывается площадь, пусть стороны В, Г, Д, Е, Z, Н
этих избытков одинаково превышагот одна другую, и пусть разность их
равна наименьшей; пусть наибольшая будет В, а наименьшая — Н;
пусть также имеются и другие площади, на каждой из которых стоят
0, Т, К, Л, причем количество этих площадей равняется количеству
первых, а величина каждой равняется наибольшей, (а именно) той,
которая приложена к линии A I В; пусть прямая в вместе с I будет рав-
равна А, а К вместе с Л равна В, и каждая из линий О имеете с I будет вдвое
больше I, а каждая из К вместе с Л втрое бол пню К. Требуется доказать,
что псе площади, которые обозначены (буквами) в, I, К, Л. ко псем
*) Архимед пользуется терминологией так назыиаемого «приложения площадей». «Приложить
яаданную площадь S к некоторой прямой о», значит на отрезке а построить лрнмоугольпик, пло-
площадь которого jkiuiki S; лдегая сторона втого прямоугольника х определится на урикиспнн
ax~S.
«Приложение с мвиытиом в вида квадрата». с нашей точки s[«iniii. рашгогилыт рмпгиию княярат-
пого уравнения
ах x* — S.
**) Лрхпмсд отринт площади
UX+.V*. п-2х\ BлJ, ..., л-пл'г(пхK
и утверждает, что
„ п {«¦ nx-'r(<uK1 „ ше-'г«
(n.v-r.vz)i-("-2x ! 4jc*)-i-. . -| -(в-лх !-п2.т2) ' w a
' ~ ' 2
п {а-пх)+(пхJ\
c-v-i •
|
и— 1)*—(n— I
itx|a
"nxa
О КОНОИДАХ И СФКРОИДЛХ 175
другим площадям АТС, ЛГ, ЛД, АЕ, AZ, АН будут иметь отношение,
меньшее того, которое прямая 0+1+К+Л имеет к прямой Ц-К, а
к площадям, оставшимся после исключения наибольшей АВ, будут
иметь отношение, большее упомянутого.
Пусть имеются некоторые площади, обозначенные (буквой) А,
одинаково превышающие одна другую, причем разность равняется наи-
наименьшей (из этих площадей), [ибо и лрикладынаемые площади и мх
ширины одипакоио превышают одна другую]*), а также другие пло-
площади, обозначенные G, I, количество которых равняется количеству
первых, а величина каждой равняется наибольшей; тогда лее площади
0,1, взятые вместе, будут меньше удвоенных всех площадей А, но боль-
больше удвоенных всех таких площадей, оставшихся после исключения наи-
наибольшей **)- Эти площади, обозначенное 1, меньше всех илощадей А,
но больше всех их за исключением наибольшей***). Далее, имеются
некоторые линии 13, Г, Л, Е, Z, Н, одииаконо превышающие одна дру-
другую, причем разность равна наименьшей (из иих), и другие линии,
обозначенные К, Л, по количеству равные этим, а по величине равные
каждая наибольшей (из них); тогда квадраты на всех прямых, рав-
ni.rx друг другу и наибольшей, будут менее утроенных квадратов на
прямых, одинаково превышающих одна другую, но более утростшх
квадратов па этих прямых, если исключить квадрат на наибольшей; ато
доказано в уже изданной книге о спиралях****). Таким образом, все
площади, обозначенные К, будут меньше всех нлощадей В, Г, Д, Е,
Z, Н, но больше илощадей Г, Д, Е, Z, Н*****); так что псе площади,
обозначенные I, К, будут меньше всех площадей, обозначенных АВ,
АГ, АЛ, АЕ, AZ, АН, но больше площадей ЛГ, АД, АЕ, AZ, АН******).
Теперь ясно, что все площади 0, I, К, Л ко всем площадям АВ, АГ,
АД, АЕ, AZ, АН имеют отношение, мспьптее того, которое прямая 6Л
имеет к ТК, ко всем же таким площадям, кроме АВ, имеют отношение,
большее упомянутого [1].
*) Гейбсрг устраннет фразу, постапленную в скобках, на основании языковых данных. Под
«прикладываемой площадью» (ла<гсф?.т1ца)следует подразумевать приложенную к прямой А площадь
прямоугольника, обозначенного буквой А.
**) На основании лемми, стонщей перед первым предложением, мы можем написать:
2 { Ах + А.2х+ ... + Ап*} >п (А-тмс) > 2 {АЖ+А.2.Т+ . . . у A (n-I).v} ,
где -г, как и вмше, обозначает сторону наименьшего ттз избыточных квадратов, а A=e + J шио,
как иьтше.
***) Мы имеем 1+2+.. .+«==¦"foj* и 1-; 2+.. .-Ни—))—"("~<) ¦ Архимед хочет ска-
n(n+l) n та (п— I)
зать, что — ., >п->———- .
*•••) В предложении X. В наших обозначениях ото равносильно неравенствам
3 {л=' + B.тJ+. . .+(иа:)г> >
*•»**) R наших обозначениях
так как площадь к——тг— ¦
******) Так как прямая I равна половине прямой А, то площадь 1=—-— . Полученные
ctji.7 и наших обозначениях запишутсн таи:
(axfx2)-(«.2a:-i-4x2)+... i {a(TL-l)x i (n-
176
АРХКМКД
АК2
AZa
Ill
< 1 >. Если прямые, проведенные из одной и той же точки, каса-
касаются какого-нибудь конического сечения, и внутри конического сечения
проведены другие прямые, параллельные касательным и пересекающие
друг друга, то прямоугольники между их *) отрезками находятся между
собой в том же отношении, как и квадраты на касательных, причем
прямоугольник между отрезками каждой прямой соответствует квадра-
квадрату на, касательной, параллельной этой прямой.
Это доказано в «Началах теории конических сечений» [2J.
< 2>. Если от одной и тойже,параболы каким-либо образом отсечь
два сегмента, имеющих одинаковые диаметры, то будут рампы и сами
эти сегменты, и вписанные е них треугольники, имеющие те же основа-
основания и высоты, что и соответствующие
сегменты: диаметром же сегмента я
называю прямую, делящую пополам
все прямые, проведенные параллель-
параллельно основанию этого сегмента.
Пусть будет парабола АВГ и
от псе отсечены два сегмента АЛЕ
и &ВГ; пусть AZ будет диаметр
сегмента АДЕ, а ВН — диаметр сег-
сегмента 0ВГ, и пусть AZ и ВИ будут
равны. Требуется доказать, что бу-
будут равны и сегменты АДЕ, 0ВГ и
вписанные в них упомянутым обра-
образом треугольники {рис. 3}.
Пусть сначала прямая в Г, от-
отсекающая один из сегментов, будет
перпендикулярна к диаметру (о с и)
параболы. Возьмем щмшую, на которой квадрируются абсциссы пара-
боли, вдвое большую (расстояния от вершины параболы) до оси
(производящего конуса); пусть ята прямая будет N. Из точки А
опустим пернондикуляр АК на AZ. Так как AZ является диаметром
сегмента, то прямая ЛЕ делится в точке Z пополам, и AZ будет парал-
параллельна диаметру параболы; значит, опа разделит пополам нее прямые,
проведенные параллельно АЕ. Пусть отношение кладрата на AZ к
квадрату на АК будет равно отношению некоторой примой М к N.
Л
N
Тогда прямые, проведенные параллельно АЕ от кривой до AZ**),
квадрируются, если на прямой, равной М, построить прямоугольник,
ширина которого будет рапна прилежащему к точке Л отрезку, отсекае-
отсекаемому ими от прямой AZ (это доказывается в теории конических сече-
сечений) ***), поэтому AZ, кнадрируясь, будет равняться прямоугольнику
между М и AZ.
-M-AZ
Но и вН, квадрируясь, равняется прямоугольнику между N и ВН,
-N-BH
Рис. 3.
*) Прямых, проведенных внутри конического сечения.
**) О™ будут ординаты точек параболы в системе координат. оСраяуемой диаметром пара-
параболы it касательной в се начале.
***) Речь нлет об ураинении параболы в косоугольных координатах: уг=2р'х, где параметр 2р'
и есть наша прямая N.
О КОНОИДАХ И СФЕРОИДАХ
177
так как (Н)Н перпендикулярна к диаметру; значит, поскольку мы пред-
предположили AZ и ВН равными, квадрат на AZ к квадрату на ©IT будет
иметь отношение, как у М к N.
м
вн*
Но кнадрат на AZ имеет к квадрату па АК то же отпошение, что Мк N;
значит, 6Н и ЛК равпы.
ен = ак
. Также равны и ВТГ с AZ; значит, прямоугольник между 0Н и ВП будет
равен прямоугольнику между АК и AZ.
«H-im—лк>дг
Таким образом, треугольник ©НВ будет равен треугольнику AAZ;
значит, будут равны и удвоенные треугольники <Г6В и АЕА). Но
сегмент АДЕ составляет четыре трети треугольника АДЕ, а сегмент
©ВГ — четыре трети треугольника ©ВГ. Таким образом, ясно, что будут
равны и сегменты и ¦вписанные в них треугольники*).
Если ни одна из прямых, отсекающих сегмепты, не будет перпен-
перпендикулярна диаметру параболы, то отложим на диаметре параболы пря-
прямую, равную диаметру одного сегмента, и через конец отложенной
прямой проведем перпендикуляр к
диаметру; таким образом, получится
сегмент, который будет равеп каж-
каждому из данных сегмептов. Теперь
предложенное становится очевид-
очевидным.
IV
Всякая площадь, ограниченная
эллипсом., имеет к кругу с диаметром,
равным большему диаметру эллипса,
то же самое отношение, что мень-
меньший диаметр эллипса к большему
или к диаметру круга.
Пусть будет (рис. 4} эллипс
АВГД с наибольшим диаметром АГ
и наименьшим ВД; пусть още будет
круг с диаметром АГ. Требуется
доказать, что ограниченная эллипсом
площадь имеет к кругу то же самое
отношение, что ВД к ГА или к EZ.
Пусть отношение ВД к EZ равняется
• отношению некоторого круга, обо-
обозначенного W, к кругу AETZ. Я ут-
• верждаю, что круг W будет рален
зшшпеу.
Если круг W не ранен площади,
ограниченной эллипсом, то пусть
сначала он, если возможно, будет больше. Тогда можно лписать в круг
¦ Y многоугольник с четным числом сторон, который был бы больше пло-
площади АВГД. Представим, что он вписан; впишем также и в круг AETZ
Рис. 4.
*) См. «Киадратура параболы», предложения XVII и XXIV..
12 Архимед
178
АРХИМЕД
прямолинейную фигуру, подобггую вписанной в круг Y; череа ее вер-
вершины проведем прямые, перпендикулярные к диаметру АГ и соединим
прямыми точки пересечения этих перпендикуляров с эллипсом; полу-
получится некоторая вписанная и эллипс прямолинейная фигура, которая
будет относиться к прямолинейной фигуре, вписанной в круг AETZ,
как ВА к EZ.
Действительно, так как перпендикуляры 0Е и КЛ разделяются
в точках М и В в одном и том же отношении, то ясно, что трапеция ЛЕ
будет иметь к трапеции 6М то же отношение, что 0Е к 6И. Но тон же
причине и каждая из оста.;1ышх трапеций в круге к соотиетствующей
трапеции в эллипсе будет иметь то же отношение, что ЕВ к Вв. Точпо
так же и прилежащие к точкам А и Г треугольники в круге будут иметь
то же отношение к таким же треугольникам в эллипсе; но тогда и вся
прямолинейная фигура, вписанная it круг AETZ, ко всей прямолиней-
прямолинейной фигуре, вписанной н эллипс, будет иметь то яге отношение, что EZ
к ВА. Эта фигура будет находиться в том же самом отношении и к впи-
вписанной в круг Ч1", так как и оба круга находятся в том же самом отноше-
отношении; значит, прямолинейная фигура, вписанная в круг Чг, будет равна
прямолинейной фигуре, вписанной т» эллипс; а это невозможно, так как
эта фигура больше всей площади, ограниченной эллипсом.
Тогда пусть, если это возможпо, круг Y будет меньше :>ллштса.
Опять можно вписать в эллипс многоугольник с четным числом сторон,
который был бы больше круга Т. Впишем его, проведем через его вер-
вершины прямые, перпендикулнршле к АГ, и продолжим их до окружности
круга; опять получится вписанная в круг АЕ прямолинейная фигура,
которая будет ко вписанной в иллинс иметь отношение, как EZ к ВА.
Вписавши подобную ей фигуру в круг W,
мы докажем, что эта вписанная в круг Т
фигура будет равна вписанной в эллипс,
а это невозможно*); значит, круг W не
будет и меньше площади, ограниченной
эллипсом. Таким образом, не по, что
упомянутая площадь эллипса имеет к кру-
кругу AETZ то же отношение, что ВД к EZ.
Л сякая площадь, ограниченная эллип-
эллипсом, ко всякому кругу имеет такое оке
отношение, как прямоугольник между
главными диаметрами эллипса к квадрату
на диаметре круга |рис- 5}.
Пусть будет некоторая площадь X,
ограниченная эллипсом, диаметры которо-
которого суть АГ и ВА, причем большим диа-
диаметром будет А Г; пусть, кроме того, будет
круг W с диаметром EZ. Требуется доказать,
что площадь X к кругу Ч1" имеет то же отношение, что прямоугольник
между АГ и ВА к квадрату на EZ.
На диаметре АГ опишем круг. Тогда площадь X к кругу на диамет-
диаметре АГ имеет то же отношепие, как прямоугольник между АГ и ВА к ква-
*) Тан как тогда вписанная в круг W фигура оказалась бы больше круга W.
О КОНОИДАХ И СФЕРОИДА*
179
драту на А Г, так как уже доказано, что они относятся, как ВД к АГ.
Далее, круге диаметром АГ к кругу с диаметром EZ имеет то же отно-
отношение, что квадрат на АГ к квадрату
на EZ. Отсюда ясно, что площадь X от-
относится к кругу "*?, так же, как прямо-
прямоугольник между А Г и ВЛ к квадрату
на EZ.
VI
Площади, ограниченные эллипсами, на-
находятся друг к другу в таком же отноше-
отношении, как прямоугольники между диамет-
диаметрами эллипсов [рис. 6}.
Пусть А и В будут площади, огра-
ограниченные двумя эллипсами, пусть ГД
будет прямоугольник, построенный на
диаметрах эллипса, ограничивающего пло-
площадь A, a EZ — прямоугольник на диа-
диаметрах другого эллипса. Требуется дока-
доказать, что площадь А так относится к В,
как ГД к EZ.
Возьмем какой-нибудь круг XF; пусть
КЛ будет квадрат на его диаметре. Нло- **ис- *•¦
щадь А относится к кругу Чг, как ГД кКА,
круг же XF к площади В относится, как КА к EZ; таким образом,
ясно,что площадь А имеет к В то же самое отношение, что ГД к EZ.
Следствие
Отсюда обнаруживается, что площади, ограниченные подобными
эллипсами, имеют друг к другу то же отношение, что и квадраты на
соответственных диаметрах эллипсов.
VII
Если дан эллипс с прямой, восставленной из его центра перпендику-
перпендикулярно к плоскости, в которой этот эллипс находится, то можно найти
конус, имеющий вершиной конец восстановленной прямой, причем задан-
заданный эллипс будет находиться на поверхности этого конуса {рис. 7).
Пусть дан некоторый аллиис и из его центра восстановлена прямая,
перпендикулярная к плоскости, в которой этот эллипс находится.
Через восставленную прямую и наименьший диаметр эллипса про-
проведем плоскость; пусть п этой плоскости АВ будет наименьший диа-
диаметр, а Д — центр эллипса, далее, ГД будет восстанленная из центра
перпендикулярная прямая и Г — ее конец; заданный же эллипс пред-
представим описанным на диаметре АВ it плоскости, перпендикулярной
Е{ ГД. Требуется найти конус, имеющий «ершиной точку Г, на поверх-
поверхности которого будет находиться заданный эллипс.
Продолжим прямые, проведенные из Г к А, В и из А проведем AZ
так, чтобы прямоугольник между ЛЕ и EZ относился к квадрату на ЕГ,
Е{ак квадрат половины наибольшего диаметра относится к квадрату на
ЛГ; это возможно потому, что рассматрипаемое отношение будет больше
12*
180
АРХИМЕД
'-¦-r.Y—\н
отношения прямоугольника между АА и ДВ к квадрату на ДГ.
AE.EZ АД-АР
ЕГ2~ ДГ2
Через AZ проведем плоскость, перпендикулярную к той, в которой
находятся АГ и AZ; в этой плоскости онипкш круг на диаметре AZ и пос-
построим на этом круге конус, имеющий
вершиной точку Г. Докажем, что за-
заданный эллипс будет находиться па
поверхности этого конуса.
Если он не будет находиться на
поверхности зтого конуса, то необхо-
необходимо, чтобы на эллипсе существовала
некоторая точка, которая не была бы
на поверхности рассматриваемого ко-
конуса. Представим, что на эллипсе
лзята некоторая точка В, которая но
находится на поверхности атого ко-
конуса. Через точку Э проведем 6К
перпендикулярно к АВ; протюденная
прямая будет перпендикулярна и
к плоскости, в которой находится АГ
и FZ. Продолжим проведенную из Г к К прямую; пусть она встретит AZ
в точке А. Через А перпендикулярно к Z А в круге, описанном на AZ,
проведем прямую AM; точку М, находящуюся на окружности круга AZ,
вообразим приподнятой (над плоскостью чертежа). Кроме того, через А
и Е параллельно АВ проведем SO и ПР. Так как прямоугольник
между ЕА и EZ к квадрату на ЕГ имеет то же самое отношение, что
квадрат на половине наибольшего диаметра (аА) к квадрату на ДГ,
Рис. Т.
BA-EZ
ЕГа
а кпадрат па ЕГ к прямоугольнику между ЕП и ЕР имеет то же отно-
отношение, что квадрат на АГ к прямоугольнику между АД и АВ,
ДГ2
ЕГа _.
ЕП-ЕР~ АД-ДЬ
то прямоугольник между ЛЕ и EZ будет иметь к прямоугольнику между
ПЕ, ЕР то же отношение, что квадрат па половипе наибольшего диа-
диаметра {аА) к прямоугольнику между АД и ДВ.
ПЕ-ЕР^АД-ДВ
Но как прямоугольник между АТС и EZ к (прямоугольнику) между
ПЕ и ЕР, так и прямоугольник между АЛ и AZ отпосится к (прямоуголь-
(прямоугольнику) между ?Л, АО, ¦-„«
АЕ' EZ АА * AZ
ПЕ-ЕР~ ВЛ-ЛО ':
а как квадрат на половине наибольшего диаметра к (прямоугольнику)
между АД и ДВ, так и квадрат на ЭК относится к (прямоугольнику)
между АК и KB,
ДА"
А&-&В
AK-KR
Jr :r/.
-'=• V r V •¦ Y "';."¦>..- "'¦¦'¦;-"'¦' .-:.v." ;.
**«•
Фотокопия страницы rpewcKoii рукописи, сол^ржащей отрывок сочинения.
Архимеда «О коноидах и сфероидах».
L82 АРХИМЕД
значит, прямоугольник между АЛ и AZ к прямоугольнику между ЕЛ
и ЛО имеет то же отношение, что и квадрат па 0К к (прямоугольнику)
между АК и КВ.
лл-ля ек2
ЗАЛО АККВ
Но (прямоугольник) между НЛ и ЛО имеет к квадрату на ГЛ то же
отношение, что прямоугольник между АК и KB к квадрату на КГ,
алло_ -лк-кв
гл2 кга
значит, (прямоугольник) между АЛ и AZ будет относиться к квад-
квадрату на ГЛ как квадрат на 0К к квадрату на КГ.
AA-AZ
глв -^
Но прямоугольник между АЛ, AZ равен квадрату па ЛМ,
АЛ-ЛХ=ЛЫ8
так кап ЛМ проведена перпендикулярно к диаметру в полукруге на AZ;
значит, квадрат* на ЛМ имеет к квадрату на ЛГ то же отношение, что
квадрат па 6К к квадрату на КГ;
лма _ ека
лга кг2
таким образом, точки Г, В, М будут находиться на одной прямой. Но
ГЫ лежит на поворхпости конуса; значит, ясно, что и точка 0 будет
находиться на поверхности конуса. Ио было предположено, что она по
находится; значит, на эллипсе не будет ни одной точки, которая не нахо-
находилась бы па поверхности вышеупомянутого конуса. Таким образом,
и весь эллипс будет находиться на поверхности этого конуса [31.
VIII
Если дан эллипс и прямая, восставленная из его центра, не перпен-
перпендикулярная к плоскости эллипса, но лежащая в плоскости, проведенной
через другой диаметр эллипса перпендикулярно к той плоскости, в ко-
которой находится эллипс, то можно найти конус, имеющий вершиной
конец восставленной прямой, прицель заданный эллипс будет находиться
на его поверхности [рис. 8j [4J.
Пусть ВА будет диаметр эллипса, Л — его центр, а ДГ — восстав-
леппая, как сказано, из центра прямая; сам эллипс вообразим себе
расположенным на диаметре АВ и плоскости, пернепдикулярной к той,
в которой находятся АВ и ГА. Требуется найти конус, с вершиной
в точке Г, на поверхности которого будет находиться заданный эллипс.
Так пак ГА не перпендикулярпа к плоскости эллипса, то прямые АГ
и ВГ пе будут равными. Пусть прямая ЕГ будет равна ГВ, а N равпа
нолопине второго диаметра, сопряженного с АВ. Через А параллельно ЕВ
проведем прямую ZH; на ЕВ восставим плоскость, перпендикулярную
к той, к которой находятся АГ и ГВ, и в этой плоскости на диаметре ЕВ
опишем круг, если квадрат иа N будет равняться прямоугольнику между
ZA и АН, или же, если он не будет равняться, то эллипс — так чтобы
квадрат на другом диаметре относился к квадрату на ЕВ, так же как
квадрат на N к прямоугольнику между ZA и АН. Затем возьмем
конус, имеющий нершину а точке Г, на поверхности которого будут
О КОНОИДАХ И СФЕРОИДАХ
183
находиться описанные на диаметре ЕВ круг млн эллипс; это возможно,
так как прямая, проведенная из Г к середине ЕВ, перпендикулярна
к плоскости, проведенной через ЕВ;
па этой же поверхности будет нахо-
находиться и эллипс, описанный на диа-
диаметре АВ.
Действительно, если бы он там
не находился, то на эллипсе име-
имелась бы точка, которая лс будет на
поверхности конуса. Вообразим, что
взята некоторая точка в, не находя-
находящаяся па поверхности конуса; из 0
на ЛВ опустим перпендикуляр GK и
соединяющую ГК продолжим; пусть ,,
она встретится с ЕВ в Л, а через Л
и плоскости, перпендикулярной*)
к проходящей через ЕВ, пронедем
некоторую прямую ЛМ, перпенди-
перпендикулярную к ЕВ; точку М на поверх-
поверхности конуса представим себе припод-
приподнятой (над плоскостью чертежа).
Через Л проведем также параллель-
параллельную ЛВ прямую IIP; тогда как квад- Рис. 8.
рат на N к прямоугольнику между
ZA и АТТ, так и квадрат на Л М относится к прямоугольнику между
ЕЛ и ЛВ,
=
гд-дн. ел-лв
и как (прямоугольник) между ZA и АН к (прямоугольнику) между
АА и АВ, так и прямоугольник между ЕЛ, ЛВ к (прямоугольнику)
между ПЛ, ЛР;
ZA-AH ЕЛ ¦ ЛВ
АД-ДВ "" ПЛ-ЛР
тогда получится, что квадрат на N относится к (прямоугольнику)
между АА и АВ, как квадратна ЛМ к (прямоугольнику) между ПЛ
и ЛР.
ЛД'ДВ ДЛ-ЛР .
Но мы имеем также, что квадрат па N к прямоугольнику между АД
иАВ относится, как квадратна 6Кк прямоугольнику между ЛК и KB,
_Ni_=_eK2 _
АД-ДВ АК-КН
так как в одном и том же эллипсе проведени два перпендикуляра (N
и 6К) к диаметру АВ; значит, отношение квадрата наЛМ к прямоуголь-
прямоугольнику между ПЛ, ЛР будет таким же, как отношение квадрата на 6К
к прямоугольнику между АК и КВ.
ЛМ*
ПЛЛР"
вк*
ЛК КК
Но прямоугольник между ПЛ и ЛР относится к квадрату на ГЛ, как
*) К прямым Л Г и ГВ.
184 " • ' ' архимед
прямоугольник между АК и KB к квадрату на КГ;
пл-лр лк-кв
гла кг!
.чначит, квадрат на ЛМ имеет к кпадрату на Л Г то же отношение, что
и кнадрат на 0К к квадрату на КГ;
лм2 ек2
отсюда следует, что точки Г, в, М расположены на одной прямой- Но
ГМ находится на поверхности конуса; отсюда ясно, что и точка 6 будет
находиться на поверхности конуса; мы же предположили, что она там
не находится; таким образом, обнаруживается правильность утверж-
утверждения, подлежащего доказательстлу.
' ' IX .. га
Если дай эллипс и прямая, восставленная ив его центра, не перпен-
перпендикулярная {к плоскости эллипса), но лежащая в плоскости, проведен-
проведенной через некоторый диаметр эллипса перпендикулярно к той плоскости,
в которой находится эллипс, то
можно найти цилиндр, имеющий
ось па продолжении восставленной
ч линии, причем заданный эллипс
\ будет находиться на поверхности
этого цилиндра (рис. 9}.
Пусть В А будет некоторым
диаметром эллипса, Д — его цент-
центром, а ГД — восставленной, как
сказано, из центра прямой; сам
эллипс вообразим себо расположен-
Рис. 9. пмм на диаметре АВ в плоскости,
перпендикулярной к той, в которой
находятся АВ и ГА. Требуется пайти цилиндр, имеющий ось на пря-
прямой ГА, на поверхности которого будет находиться заданный эллипс.
Из точек А и В параллельно ГД проведем прямые AZ и ВН; взятый
диамотр эллипса будет или равен расстоянию можду пряьпами AZ, BII.
или больше его, или же меньше.
Пусть он, во-первых, будет равен ZH, а ZH перпендикулярна к ГД.
Восставим па ZH плоскость, перпендикулярную к ГД; в этой плоскости
пусть будет круг на диаметре ZH и пусть на атом круге будет цилиндр,
имеющий осью ГА; на поверхности этого цилипдра и будет находиться
заданный эллипс.
Действительно, если бы он там не находился, то на эллипсе будет1
некоторая точка, которая не была бы на поверхности цилиндра. Пред-
Представим себе, что взята такая не находящаяся на поверхности цилиндра
точка эллипса 6; опустим из 0 на прямую АВ перпендикуляр 0К;
он будет перпендикулярен и к плоскости, в которой находятся АВ
и ГД. Через К параллельно ГА проведем КА и из А восставим к ZH пер-
перпендикуляр AM в описанном на ZH круге; точку М представим себе
приподнятой (над плоскостью чертежа) па окружности полукруга
на диаметре ZH; тогда одно и то же отношение будут иметь квадрат на
перпендикуляре ©К к прямоугольнику между АК и KB и (квадрат)
О КОНОИДАХ И СФЕРОИДАХ 185.
на ZF к прямоугольнику между АД и ЛВ, .
нк2 zr2
АК-КВ~АД-ДВ
)'' так как ZH равна другому диаметру (эллипса согласно предположе-
предположению) *). Но прямоугольник между ZA и ЛН относится к прямоуголь-
прямоугольнику между АК и КБ, как квадрат на ZT к квадрату на АД**);
ZA-ЛН Zr2
AK.-K.li
АД3
значит, прнмоугольпик между ZA, АН будет равен квадрату на ©К.
H = 6K4 . .
Но он также рапеп и квадрату на AM***); значит, перпендикуляры
©К и МЛ раины. Далее, прямые ЛК и М© параллельны****), так что
будут параллельны и ДГ и М©. Следовательно, прямая в М будет нахо-
находиться на поверхности цилиндра, так как она проведена параллельно
оси цилиндра из точки, лежащей на его поверхности; после этого ясно,
что и точка © будет находиться на поверхности цилиндра. Было же
предположено, что она там не находится; таким образом, обнаружипает-
ся истинность предложения, которое требовалось доказать.
Если другой диаметр эллипса равен расстоянию между прямыми,
провиденными через концы первого диаметра параллельно прямой, вос-
восставленной {из центра эллипса), то ясно, что цилиндр, объемлющий
этот эллипс, будет прямым (круговым).
Пусть теперь второй диаметр эллипса будет больше ZH (расстоя-
(расстояния между параллельными ГА прямыми, проведенными через концы
м
<Н
диаметра эллипса А и В); пусть прямая ITZ будет равна этому второму
диаметру {рис. 10). Восстании на FIZ плоскость, перпендикулярную
к той, в которой находятся прямые АВ и ГА; возьмем в этой плоскости
круг с диаметром ITZ, и пусть на этом круге будет цилиндр с осью ДР.
Тогда при помощи тех же самых рассуждений докажем, что заданный
эллипс будет находиться на поверхности этого цилиндра.
Пусть, наконец, второй диаметр будет меньше ZIT {рис. 11). Пусть
квадрат на ГЗ представляет избыток квадрата на ZF (половине ZH)
*) Точка Д является центром эллипса, a Zr=jj-ZH перпендикулярным к АВ диаметром..
-) Иа пропорции |? = АН=_|Г_. , . ;. ;>
***) По известному свойству круга.
***•) Это следует из равенства перпендикуляров МЛ. вк, восставленных к плоскости чертежа..
186 АРХИМЕД
над киадратом на половине второго диаметра. Восставим из точки
Е перпендикулярно к плоскости, в которой находятся АВ и ГА, пря-
прямую, раипуго половине атого диаметра; пусть это будет прямая SN;
точку N представим приподнятой (над плоскостью чертежа); пря-
прямая ГМ будет равна FZ*). В плоскости, в которой находятся прямые
. ZH и FN, сшитом круг на диаметре ZH; он пройдет через точку N.
Па этом круге пусть будет цилиндр с осью ГА; на поверхности этого
цилиндра и будет паходиться заданный эллипс.
Дейстпительно, если бы он там не находился, то на нем была бы
некоторая точка, не лежащая на поверхности цилиндра. Возьмем на
зллипсе такую точку в; перпендикулярно к прямой АВ проведем 6К;
затем пусть из К параллельно ГА пройдет КЛ, а из Л и полукруге с диа-
mctpomZH проведемпрямуюЛМперлспдикулярнок ZH. Представим, что
точка М находитсм па окружности полукруга, описанного на ZI.T; из точки
М на продолжение прямой КЛ опустим перпендикуляр МО; оп будет
перпендикулярен и к плоскости, в которой находятся АВ и ГА, так как
КЛ перпендикулярна к ZII. Тогда (квадрат) на МО относится к (кна-
драту) на МЛ, как квадрат EN к квадрату на NT**)
МО2 SNS
МЛ2 КГ2
Но квадрат на МЛ так относится к прямоугольнику между АК и KB,
как квадрат на 1"N к квадрату на АД,
ыл" гк3
так как квадрат на МЛ равен прямоугольнику между ZA и ЛН, а квад-
квадрат на FN равен квадрату на fZ***); значит, квадрат на МО будет отно-
относиться к прямоугольнику между АК и KB, как квадратна SN к ква-
квадрату на АА.
МО* SN2
АККВ АД2
Но квадрат на Кб относится к прямоугольнику между АК и KB, как
кпадрат на SN к квадрату на АД,
Кб' EN2
АК-КВ
так как SN рапна половине другого диаметра оллипса; отсюда ясно, что
перпендикуляры МО и KB равны; следовательно, КО и ЭМ будут
параллельны. Так как Мб параллельна оси цилиндра и точка М нахо-
находится на поверхности последнего, то и Мб необходимо будет находиться
па поверхности цилиндра; отсюда ясно, что на поверхности последнего
будет паходиться и точка 6. Этого же, (согдасно предположению),
не было; отсюда ясно, что аллинс необходимо должен лежать на поверх-
поверхности цилиндра [3].
*) Так как NS будет половика второго диаметра и
rE*=zr!~Naa.
**) Из подобия треугольников TEN и ЛОМ с параллельными сторонами.
.») Кроме ^ЛН Г|
О КОНОИДАХ И СФЕРОИДАХ ¦ 187
X
Более ранними математиками*) было доказано, что нсякий конус
имеет к другому конусу отношение, равное составленному из отноше-
отношений оснований и высот; таким же образом можно доказать, что всякий
конический сегмент к другому коническому сегменту имеет отношение,
равное составленному из отношений омгонанпй и высот.
Далее, что всякий цилиндрический сегмент в три рази больше кони-
конического сегмента с теми же основанием и высотой, может быть доказано
тем же способом, как и то, что всякий цилиндр в три раза больше конуса
•с теми же основанием и высотой, что и у цилиндра.
XI
A) Если прямоугольный коноид рассечь плоскостью, проходящей
через ось, или параллельной оси, то сечение будет параболой, и притом
тождественной с той, которая охватывает упомянутое тело; ее диа-
диаметр будет общей линией пересечения двух плоскостей, из которых одна
является секущей фигуру, а другая проводится через есь перпендикуляр-
перпендикулярно к секущей плсскости.
Если же рассечь его плоскостью, перпендикулярной к оси, то сече-
сечение будет кругом, имеющим центр на ecu.
B) Если тупоугольный коноид рассечь плоспсстью, проходящей
через ось, или параллельно оси, или через вершину конуса, объемлющего
коноид, то сечение будет гиперболой; при этом если секущая плоскость
проходит через ось, то эта гипербола будет тождественна с той, кото-
которая охватывает фигуру, если же сечение происходит параллельно оси,
то только ей подобна, если же плоскость сечения проходит через вершину
конуса, объемлющего коноид, то сечение не будет даже ей {то есть упо-
упомянутой гиперболе) подобно; диаметром гиперболы будет общая линия
пересечения плоскости, секущей фигуру, с плоскостью, проведенной через
есь перпендикулярно к секущей.
Если же рассечь его плескоетъю, перпендикулярной к ecu, то сечение
будет кругом, имеющим центр на оси.
C) Если какой-нибудь из сфероидов рассечь плоскостью, прохо-
ходящей через ось или параллельной оси, то сечение будет эллипсом,
причем если плоскость сечения проходит через ось, то тождественным
с охватывающим фигуру, если же она параллельна оси, то только ему
подобным; диаметром эллипса будет общая линия пересечения плоско-
плоскости, секущей фигуру, с плосксстью, проведенной через ось перпендикуляр-
перпендикулярно к сжущей.
Если же рассечь его плоскостью, перпендикулярной к оси; то сече-
сечение будет кругом, имеющим центр на оси.
D) Если какое-нибудь из упомянутых тел рассечь плоскостью,
проходящей через есъ, то перпендикуляры, опущенные на секущую пло-
ксетъ из точек, лежащих на поверхнести тела, но не на линии селения,
упадут внутри ачения тела.
Доказательства всех этих предложений очевидны [5].
*) Под этими «Солсс ранними математиками» подразумевается Евдокс. труды которого дошли
до нас ? книге XII еиклидоиых «Начал».
188
АРХИМЕД
XII
Если прямоугольный коноид рассечь плоскостью, не проходящей через
ось, а также не параллельной и не перпендикулярной к оси, то в сечении
получится эллипс, большим диаметром которого будет заключенный
внутри коноида отрезок линии пересечения плоскости, секущей фигуру,
с плосксспью, проходящей через ось и перпендикулярной к ней, а меньший
диаметр будет равен расстоянию между двумя проведенными через концы
большого диаметра прямыми, параллельными ecu.
Пусть прямоугольный коноид будет расссчсп плоскостью, как
указано (рис. 12}; пусть АВГ будет сечение коноида другой плоскостью,
перпендикулярной к секущей и проходящей
через ось, а прямая ГЛ — пересечением этой
же плоскости с плоскостью, секущей фигуру;
пусть прямая ВД будет осью коноида и диа-
диаметром параболы. Требуется доказать, что
сечение коноида плоскостью, проходящей
через АГ, будет эллипсом, больший диаметр
которого равен АГ, а меньший равен ЛА,
если прямая ГЛ проведена параллельно ВД, а
АЛ перпендикулярна к ГЛ.
Вообразим, что нзята какая-нибудь точ-
точка К сечения и иа К опустим на ГА перпен-
перпендикуляр Кб; тогда К0 будет также перпен-
перпендикуляром к плоскости, в которой находится
парабола ЛГВ, так как и секущая плоскость
будет перпендикулярна к той те самой пло-
плоскости. Через 0 под прямым углом к ВД проведем EZ, и через прямые
EZ и Кб проведем плоскость; последняя будет перпендикулярна к ВД;
тогда коноид будет рассечен плоскостью, перпендикулярной к оси; так
что полученное сечепие будет кругом с центром в Д; значит, К© будет
киадрнровать прямоугольник на Z0 и ©Е,
Рис. 12.
[ибо на EZ построен полукруг и перпендикуляр Кб будет средней про-
пропорциональной для отрезков Ев, 6Z]. Параллельно АГ проведем ка-
касательную MNk параболе (пусть точкой касания будет N), а параллель-
параллельно EZ проведем прямую ВТ. Прямоугольник на А© и в Г будет отно-
относиться к прямоугольнику между Ев, ©Z, как квадрат на NT к квадрату
на ВТ,
ле-ег
NT2
как уже было доказано (предложение III, 1). Но NT равна ТМ, так-
как ВР равна ВМ; значит, и прямоугольник между. Л0 и в Г имеет
к квадрату на К0 то иге отношение, что квадрат на Т М к квадрату па ТВ;
кеа
значит, квадрат на перпендикуляре вК к прямоугольнику между Ав,
в Г будет иметь то же отношение, что квадрат на ВТ к квадрату на ТМ.
де-ег
О КОНОИДАХ И СФЕРОИДАХ
189
Так как треугольники ГАА и Т MB подобпьт, то квадрат на перпенди-
перпендикуляре 6К. к прямоугольнику между Ав и в Г будет иметь то же отно-
отношение, что квадрат на АЛ к квадрату па АГ.
№? _ АЛ»
Ав-вГ АГ2 . .
Подобным же образом докажем, что квадраты на других перпендику-
перпендикулярах, опущенных па прямую АГ с (линии) сечения, будут к пря-
прямоугольникам между (соответствующими) отрезками АГ иметь то же
отношение, что квадрат ЛЛ к квадрату АГ; таким образом, ясно, что
сечение будет эллипсом, наибольшим диаметром которого будет АГ,
а наименьший будет ранеп АЛ.
..;. XIII
Если тупоугольный коноид рассечь плоскостью, которая встречала
бы есг стороны конуса, объемлющего коноид, и не была бы перпендикуляр-
перпендикулярна к ecu, то евчение будет эллипсом, наибольшим диаметром которого
является заключенный вну-
внутри коноида олгрезок ли-
линии пересечения плоскости,
секущей коноид, с плоско-
плоскостью, к ней перпендикуляр-
перпендикулярной, проведенной через ось.
Рассечем тупоуголь-
тупоугольный коноид плоскостью,
как указано (рис. 13}.
Пусть гипербола АВГ пред-
представляет сечение коноида
другой плоскостью, про-
проходящей через ось, и перпендикулярной к первой секущей плоско-
плоскости,- пусть прямая АГ будет сечением плоскости, секущей фигуру,
а ВЛ — осью коноида и диаметром гиперболы. Вообразим какую-ни-
какую-нибудь точку К, взятую на линии сечения и опустим из К иа АГ перпенди-
перпендикуляр Кб; последний будет также перпендикуляром к плоскости, в ко-
которой лежит гипербола АВГ. Через в перпендикулярно к ВА проведем
EZ, а через прямые EZ и К© проведем плоскость, пересекающую
коноид; таким образом, последний будет рассечен плоскостью, перпен-
перпендикулярной к оси, так, что в сечении получится круг с центром в Д;
следопатолыто, перпендикуляр па Кв будет квадрироиать прямоуголь-
прямоугольник истцу Ев, 0Z;
теперь проведем параллельно АГ касательную MN к гиперболе в топ-
топке N и прямую ВТ, параллельную EZ; тогда прямоугольник между Кб
и &Z будет относиться к прямоугольнику между Ав, вГ, как квадрат на
ВТ к квадрату на TN;
Рис. ГЛ.
Хе-ег
таким образом, квадрат на перпендикуляре Кб относится к прямоуголь-
прямоугольнику между Ав и ©Г, как (квадрат) на ВТ к квадрату на TN.
Ав-вГ"
Подобным же образом докажем, что квадраты других перпендикуляров,
!90 ¦ ¦ ¦ архимед
опущенных с линии сечения на АГ, к прямоугольникам между отрез-
отрезками, образуемыми этими перпендикулярами на АГ, будут относиться,
как квадраты на БТ и па TN. При этом ВТ будет меньше TN, так как
и МТ меньше TN, (a MT больше ВТ), поскольку МБ меньше, чем
ВР; последнее же нвляется характерным свойством гиперболи. Таким
образом, ясно, что сечение будет представлять эллипс с наибольшим
диаметром АГ [6].
XIV
Если удлиненный сфероид рассечь плоскостью, не перпендикулярной
к оси, то в сечении получится эллипс, наибольшим диаметром которого
будет заключенный внутри сфероида отрезок общей линии пересечения
плоскости секущей фигуры с плоскостью, перпендикулярной к ней и про-
проходящей через ось.
Если сечение производится плоскостью, проходящей через ось
или параллельной оси, то предложенное очевидно. 1'ассечем сфероид,
какой-нибудь другой плоскостью; если, кроме того, рассечь его пло-
плоскостью, проходящей через ось и перпендикулярной к секущей, то
в еечепии со сфероидом получится
эллипс АВГА, а в сечении с секу-
секущей плоскостью — прямая ГА.
Пусть ВЛ будет осью сфероида и
диаметром эллипса, точка X —цен-
—центром и ПР — наименьшим диамет-
диаметром {рис. 14}. Проведем ВТ, пер-
перпендикулярную к ВД, и касатель-
касательную HN к эллипсу в точке N,
параллельную А Г; через X парал-
параллельно ЛГ проведем также МЛ.
Подобно предыдущему докажем, что квадраты на перпендикулярах,,
опущенных из точек кривой сечепия на АГ, находятся с прямоуголь-
прямоугольниками между отрезками АГ п том же самом отношении что квадрат на
ВТ к квадрату па TN.
_ ВТ2
Ав "ВТ ~~ TN*
Что полученное сечение будет эллипсом и АГ его диаметром, очевидно,
а что ЛГ будет наибольшим диаметром, требуется доказать.
Прямоугольник между ПХ, ХР имеет к (прямоугольнику) между
MX, ХЛ то же отношение, что (квадрат) на ВТ к (кпадрату) на NT,
ПХ-ХР ВТ»
МХ-ХЛ
так как ПР и МЛ проведены параллельно касательным. Но прямоуголь-
прямоугольник между ПХ, ХР будет меньше (прямоугольника) между MX, ХЛ,
так как ХП меньше ХЛ; значит, и квадрат на ВТ будет меньше квадрата
иа TN; таким образом, и квадраты на перпендикулярах, опущенных па
АГ из (точек) кривой сечении, будут меньше прямоугольников между
отрезками ЛГ.
вк*<Аввг
Теперь ясно, что диаметр ЛГ будет наибольшим*).
*) Действительно, если точка в будет совпадать с серединой ЛГ. то мы имеем: вК* <
<(~2~) » то есть ^ полудиаметр, соответствующий АГ. — будет больше исрпсвдшсуяпрногс-
ему полудиамстра 6К.
О КОНОИДАХ И СФЕРОИДАХ
Если сплющенный эллипсоид рассечь плоскостью, то все получится
так же, но отрезок внутри сфероида будет наименьшим диаметром.
Из этого ясно, что во всех атих толах сечения параллельными друг
другу плоскостями будут подобными, так как квадраты перпендикуля-
перпендикуляров (опущенных из точек линии сечешш) будут иметь одинаковые
отношения к прямоугольникам между (соответствующими) отрезками.
XV
A) Л прямоугольном коноиде прямые, проведенные параллельно оси
из любой точки на поверхности коноида, будучи продолжены в сторону
выпуклости коноида, пройдут вне последнего, продолженные же в про-
противоположную сторону— попадут внутрь последнего.
Дсйстпительно, если пронести плоскость через ось и ту точку, через
которую проводится прямая, параллельная оси, то в сечении получится
парабола, диаметр которой будет и осью коноида; для параболы же пря-
прямая, проведенная параллельно диаметру через всякую точку кривой,
со стороны выпуклости попадает вне параболы, с противоположной ?ке
стороны—внутри последней; таким образом, предложенное очевидно.
B) В тупоугольном коноиде прямые, проведенные из любой точки
на его поверхности параллельно какой-нибудь линии, проведенной в ко-
коноиде через вершину объемлющего коноид конуса, будучи продолжены
в сторону выпуклости коноида, пройдут вне последнего, продолженные
же в противоположную сторону попадут внутрь его.
Действительно, осли провести плоскость через прямую, проведен-
проведенную в коноиде через вершину объемлющего коноид конуса, и через ту
точку, из которой проводится рассматриваемая прямая, то в сечении
получится гипербола, диаметром которой будет прямая, проведенная
в коноиде через вершину объемлющего конуса*). Для гиперболы же
прямая, проведенная через всякую точку кривой, идущая параллельно
с прямой, проведенной указанным способом, и продолженная п сторону
выпуклости кривой, пройдет «не ее, продолженная же в противополож-
противоположную сторону попадет внутрь.
C) Если плоскость касается коноида, не пересекая его, то она
касается только в одной точке, причем, плоскость, проведенная через
ось и точку касания, перпендикулярна, к касательной плестсти.
Действительно, пусть, если возможно, она будет касаться конопда
в нескольких точках. Если ми возьмем какие-нибудь две точки, в кото-
которых ота плоскость касается коноида, и через каждую из них проведем
прямую, параллельную оси, то плоскость, проведенная через эти пря-
прямые, будучи продолжена, или пройдет через ось, или же Судет ей парал-
параллельна; таким образом, в сечении получится какое-нибудь коническое
сечение, и взятые точки окажутся на некотором коническом сечешш,
так как они лежат и на поверхности коноида и на секущей плоскости.
Тогда прямая, соединяющая взятие две точки, будет внутри конического
сечения, а следовательно, окажется и внутри поверхности коноида. По
эта прямая находится па касательной плоскости, так как па последней
лежат обе выбранные точки; значит, некоторая часть касательной пло-
плоскости окажется внутри коноида; это же невозможно, так как предполо-
предположено, что эта плоскость не пересекает коноида. Таким образом, рассмат-
рассматриваемая плоскость будет касаться коноида только в одной точке.
*) См. комментарий |7J.
192 АРХИМЕД
Л что плоскость, проведенная через точку касания и ось, будет
перпендикулярна к касательной плоскости, то это очевидно, если каса-
касание происходит л ьсршине коноида. Действительно, если через ось
коноида провести две плоскости, то в сечениях получатся конические
сечения, имеющие своим диаметром ось, и лежащие на касателыюй пло-
плоскости прямые будут касаться этих конических сечений в конце диа-
диаметра. Прямые же, касающиеся конических сечений п конце диа-
диаметра, образуют с последним прямые углы; таким образом, в касатель-
касательной плоскости будут две прямые, перпендикулярные к оси. Значит,
касательная плоскость будет перпенди-
перпендикулярна к оси, а поэтому и к всякой
проходящей через ось плоскости.
Пусть теперь плоскость будет ка-
касаться копоида не в вершине послед-
последнего. Проведем плоскость через точку
касания и ось; и сечении с коноидом
получится коническое сечение АВГ
{рис. 15). Пусть ВД будет осью (ко-
(коноида) и диаметром (сечения), сече-
сечением касательной плоскости будет пря-
прямая же E0Z, касающаяся конического
сечония в точке в. Из в опустим на ВД
перпендикуляр 0К и проведем через К
плоскость, перпендикулярную к оси; она
образует п сечении круг с центром К.
Сечение этой (последней пл оскости) и ка-
касательной плоскости будет касателыюй к кругу прямой; значит,
последняя образует с 6К прямые углы; отсюда же следует, что она
будет перпендикулярна и к плоскости, в которой находится К0 и ВД.
Таким образом, ясно, что к этой же самой плоскости будет перпенди-
перпендикулярна и касательная плоскость, так как расположенная в ней пря-
прямая*) будет перпендикулярна к этой же самой плоскости.
XVI
A) Если какой-нибудь из сфероидальных фигур касается плоскость,
не пересекающая этой фигуры, то она будет касаться только в одной
точке, и плоскость, проведенная через точку касания и ось, будет пер-
перпендикулярна к касательной плоскости.
Действительно, пусть она будет касаться в нескольких точках.
Тогда, если мы возьмем точки, в которых эта плоскость касается сферо-
сфероида, и через каждую из ипх провидим параллельную оси прямую, и через
эти прямые проведем плоскость, то ее сечение с коноидом будет эллип-
эллипсом, и эти точки окажутся на коническом сечении. Теперь прямая,
соединяющая эти точки, будет внутри конического сечения, а следова-
следовательно, окажется внутри и поверхности сфероида. Но эта прямая нахо-
находится па касателыюй плоскости, так как на ней же лежат и взятые точки;
значит, какая-то часть касательной илоскости будет внутри сфероида.
Но это не имеет места, ибо, согласно предположенному, она не пересе-
пересекает сфероида. Таким образом, ясно, что она будет касаться только
в одной точке. А что проведенная через точку касания и через ось лло-
*) Речь идет о проведенной через в касательной к кругу.
О КОНОИДАХ И СФЕРОИДАХ 193
сгсость будет перпендикулярна к касательной плоскости, мы докажем
подобно тому, как и для коноидов.
B) Если какую-нибудь иг коноидалъных или сфероидальных фигур
рассечь проходящей через ось плоскостью и провести прямую, касаю-
касающуюся полученного сечения, и на карательной восставить плоскость,
перпендикулярную к секущей, то она будет касаться фигуры в той же
самой точке, в которой проведенная прямая касается конического сечения.
Действительно, она пе коснется поверхности этой фигуры л какой-
нибудь другой точке; иначе перпендикуляр, опущенпый из этой точки
на секущую плоскость, попал бы кии конического сечопия, так как он
попадет на касательную плоскость, поскольку упомянутые плоскости
будут перпендикулярны друг к другу; это же невозможно, ибо дока-
доказано, что он упадет внутрь сечения *).
C) Если какой-нибудь из сфероидальных фигур касаются дне парал-
параллельные 'плоскости, то прямая, соединяющая точки касания, пройдет,
через центр сфероида.
Действительно, это очевидно, если обе плоскости перпендикулярны
к оси; пусть же они не будут перпендикулярны. Тогда плоскость, про-
проведенная через ось и точку касания одной пло-
плоскости, будет перпендикулярна к касательной
плоскости, а следовательно, и к плоскости, ей
параллельной. Значит, необходимо, чтобы пло-
плоскость, проходящая через ось и каждую точку
касания, была одной и той же. В противном слу-
случае будут дво плоскости, перпендикулярные к
одной и той же плоскости, и проведенные через
одну и ту же прямую, по являющуюся пер-
перпендикулярной к этой плоскости, ибо ми пред- ис*
пологкили, что ось не будет перпендикулярной
к параллельным плоскостям; значит, ось и обо точки касания будут
находиться а одной и той же плоскости, и сфероид будет рассечен пло-
плоскостью, проходящей через ось (рис. 10}. В таком случае сечение будет
эллипсом, сечении же касательных плоскостей будут параллельными
прямыми, касающимися эллипса в точках касания плоскостей; если же
две параллельные прямые касаются эллипса, то центр эллипса и точки
касания будут находиться на одной прямой.
XVII
Если к какой-нибудь из сфероидальных фигур провести две парал-
параллельные касательные плоскости и. кроме того, через центр сфероида про-
провести плоскость, параллельную касательным, то прямые, проведенные
через точки полученной линии сечения параллельно прямой, соединяющей,
точки касания, попадут вне сфероида {рис. 17}.
Предположим все сказанное уяге существующим и возьмем на полу-
полученной линии сечония какую-нибудь точку, затем через взятую точку
и прямую, соединяющую точки касания, проведем плоскость; тогда
последняя рассечет как сфероид, так и обе параллельные плоскости.
*) Так как ятот перпендикуляр лежит в касательной плоскости, то он должен обязательно
попасть на прямую, касательную к коническому сечеиию; все >кс точки касательной, кроме точки
касании, будут находиться вне конического сечения. Доказательство, что указанный перпендикуляр
попадет внутрь конического сечения, дано (или, вернее, подразумевается) и последней части пред-
предложения XI.
13 Архимед ' ¦
194
АРХИМЕД
И
Рис. 17.
Пусть ссчоаио сфероида будет [эллипс] АГ5ГД, сечения касательных пло-
плоскостей — прямые EZ, 6H, взятая точка Л, прямая, соединяющая точки
касания, пусть будет БД (последняя, конечно, пройдет через центр),
сечение же плоскости, параллельной касательным плоскостям, бу-
дст ГЛ", 'эта прямая также пройдет через-
центр, поскольку через центр проходит и
соответствующая плоскость. Теперь так
как АВГД будет или кругом или эллипсом,
и ее касаются две прямые EZ, Ив, а через
¦л центр проведена параллельная им ЛГ, то
ясно, что проведенные через А Г, парал-
параллельно ВД прямые будут касательными к
сечению и попадут пне сфероида [8].
Если же параллельная касательным
плоскость тге будет проведена через центр,
как, например, КА, то ясно, что из проводи-
проводимых через точки сочения (параллельно ВД)
прямых те, которые будут со стороны меньшего сегмента, попадут пне
сфероида, те же, которме с противоположной стороны — внутрь его.
XVI11
Всякая сфероидальная фигура, рассекаемая плоскостью через
центр, и сама рассекается этой плоскостью пополам, и ее поверхность.
Действительно, рассечем сфероид через центр плоскостью; тогда
он будет рассечен или через ось, или же перпендикулярно к ней, или же
не нерппттдикулярно к оси. Если сфероид сечется через ось, или
же перпендикулярно к оси, то ясно, что и сам «и u его поверхность
разделятся пополам, так как одна его
совпадать с другой, а также и ио-
верхпость одной его части с поверх-
поверхностью другой.
Так пусть теперь сфероид будет
рассечен плоскостью, не проходящей
через ось и не перпендикулярной
к осп. Если мы рассечем сфероид
плоскостью, перпендикулярной к
секущей и проходящей через ось, то
сечением самой фигуры пусть будет
эллипс АВГД, его диаметр и ось
сфероида — прямая ВД и центр — в,
сечением же плоскости, рассекшей
сфероид через центр, пусть будет
прямая АГ (рис. 18}. Возьмем еще какой-нибудь другой сфероид,
равный атому и подобный; пусть при сечении его плоскостью через ось
получится эллипс EZITN, его диаметр и ось сфероида пусть будет EI1,
а центр К {рис. 19); проведем через К прямую ZN, образующую угол К,
равный углу в, и пусть на ZN будет восставлена плоскость, перпен-
перпендикулярная к той, в которой находится сечение EZHN; тогда полу-
получатся два равных и подобных друг другу эллипса АВГЛ и EZHN;
они совпадут друг с другом, если совместит!. EII с ВД, a ZN с А Г. Тогда
и плоскость, проходящая через NZ, совпадет с плоскостью через АГ,
так как обе они проходят через одну и ту же прямую и перпендику-
будет,
очевидно,
Е
и
Рис. 19.
О КОНОИДАХ И СФЕРОИДАХ
195
лярны к одной и той же плоскости. Тогда и сегмент, отсеченный по
>NZ от сфероида и находящийся с той стороны, где Е, совпадет с другим
сегментом, отсеченным поАГ от другого сфероида и находя мнимся с той
стороны, где В; совпадут также и оставшиеся сегменты и поверхности
одних сегментов с поверхностями других. Затем если мы поместим ЕН на
Г$А так, чтобы точка Е легла на А, а Н — на В, прямая же между точ-
точками N, Z—на прямую ме?кдУ точками А, Г, то ясно, что друг с дру-
другом совпадут и оба эллипса и что Z попадет в Г, а N в А. Точно так же
и проходящая через NZ плоскость совпадет с плоскостью, проходящей
через АГ, и из отсеченных плоскостью но ЛГ сегментов тот, который
находится со стороны Н, совпадет с тем из отсеченных плоскостью но
АГ сегментов, который будет со стороны В, а тот, который находится
со стороны Е, совпадет с тем, что со стороны Л. Но так как один и тот
же сегмент совпадает с каждым из двух сегментов, то ясно, что оба
эти сегмента будут раины; поэтому же будут равны и поверхности
(сегментов).
XIX
Если дан сегмент какого-нибудь ин коноидов, отсеченный перпендику-
перпендикулярной к оси плоскостью, или же сегмент какого-нибудь из сфероидов,
не больший половины этого сфероида и точно так же отсеченный, то
можно вписать в него телесную д ;
фигуру и описать около него дру-
другую, состоящую из имеющих рав-
равную высоту цилиндров, и притом
так, чтобы, описанная фигура была
больше вписанной на величину,
меньшую любой, наперед заданной
телесной величины.
Пусть дан сегмент, как, на-
например, АВГ, сечение его прове-
проведенной через ось плоскостью бу-
будет ЛВГА, сечение же отсекшей
его плоскости пусть будет прямая
АГ, а ось сегмента и диаметр сече-
сечения ВА {рис. 20}. Поскольку секу-
секущая плоскость предполагается
перпендикулярной к оси, то ссче-
нио будет кругом с диаметром ГА.
Пусть на этом круге будет ци-
цилиндр, имеющий осью ВА; тогда
его поверхность пройдет вне сег-
сегмента, поскольку последний является сегментом коноида или сфероида,
не большим половины сфероида. Если этот цилиндр мы будем постоян-
постоянно делить пополам перпендикулярной к оси плоскостью, то когда-нибудь
получится остаток, меньший заданной телесной величины; пусть таким
его остатком будет цилиндр, имеющий оснопаниеш круг на диаметре АГ,
а осью ЕА, я меньший заданной телесной величины. Раздолий ВА в Р,
О, 1.1, Е на равные ЕД части, черен точки деления параллельно АГ
проведем к коническому сечению прямые, н на этих проведенных пря-
прямых восставим перпендикулярные к ВД плоскости; в течениях получат-
получатся круги, имеющие центры па ВД. На каждом из этих кругов построим
13*
/
i
Г
в р
/Л 0
' Л
С1
{
\
л
\
А
1
Г
Рис. 20.
J96
АРХИМЕД
два цилиндра, оба с осью, рапной ЕА, один в ту сторону от круга, где
находится А, другой жо в ту, где находится В; таким образом в сегменте
получится некоторая вписанная телесная фигура, составленная из
цилиндров, построенных в ту сторону, где находится А, и другая оли-
саннаи, составленная из цилиндров, построенных в ту сторону, где
находится В. Остается лишь доказать, что описанная фигура превосхо-
превосходит вписанную на величипу, меньшую любой заданной телесной вели-
величины. Каждый из цилиндров во вписанном фигуре будет равен цилиндру,
построенному на том же круге в ту сторону, где находится В, как,
например, цилиндр &Н равен &L, цилиндр КЛ равен КМ и точно так
же и остальные, причем все вместе взятые такие цилиндры одной фигуры
будут равны всем цилиндрам другой. Теперь ясно, что описанная фигу-
фигура будет больше лписаппой на цилиндр, имеющий основанием круг па
диаметре АГ и ось ЕА; этот же цилиндр меньше заданной телесной вели-
величины.
XX
Если дан сегмент какого-нибудь из коноидов, отсеченный плоскостью,
не перпендикулярной к оси, или же сегмент какого-нибудь из сфероидов,
не больший, половины этого сфероида и точно так же отсеченный, то
можно вписать в него телесную фигуру и описать около него другую,
составленную из цилиндриче-
цилиндрических сегментов, имеющих рав-
равную высоту, и притом так,
чтобы описанная фигура была
больше вписанной на величину,
меньшую любой наперед задан-
заданной телесной величины.
Пусть будет дан такой сег-
сегмент, как сказано; рассечем его
другой плоскостью через ось,
перпендикулярной к отсекшей
заданный сегмент плоскости;
пусть сечение данной фигуры
будет коническое сечение АВГ
{рис. 21}, сечение же отсекшей
сегмент плоскости пусть будет
прямая ГА. Теперь, поскольку
отсекшая сегмент плоскость
предполагается не перпендику-
перпендикулярной к оси, то сечение будет
эллипсом с диаметром ЛГ. Пусть
будет параллельная ЛГ касательная ФГ к коническому сечению, и
пусть она касается п В; восставим наФГ плоскость, параллельную той,
которая проходит через АГ; и эта плоскость будет в В касаться нашей
фигуры. И если сегиепт принадлежит прямоугольному коноиду, то из
В параллолыш оси проведем ВА, если же тупоугольному,то прямую,
проведенную к В от вершины объемлющего коноид конуса, продолжим
в виде ВД, если же сегмент принадлежит сфероиду, то пусть ВА будет
отсеченной частью прямой, проведенной (из центра) до В; ясно, что ВД
разделит АГ пополам, так что В будет вершиной сегмента, прямая же
ВД — его осью. Получится некоторый эллипс на диаметре АГ и линия
ВА, восстаплонная из центра в плоскости, перпендикулярной к той,
Рис, 21.
О КОНОИДАХ И СФЕРОИДАХ
в которой паходится эллипс, и проходящей через другой диаметр {эл-
{эллиптической грани). Теперь можно найти цилиндр, имеющий ось ВА,
на поверхности которого будет паходиться эллипс, построенный на диа-
диаметре АГ (предложение IX); поиерхпость этого цилиндра окажется вне
сегмента, поскольку последний принадлежит коноиду или сфероиду
и (в последнем случае) не больше лолошшы сфероида. Получится неко-
некоторый цилиндрический сегмент, имеющий основаниями эллипсы на
диаметре АГ и осью прямую ВА; если этот сегмент мы будем делить
пополам плоскостями, параллельными той, что проходит через АГ.
то (в конце концов) получится остаток, меньший наперед заданной
телесной величины. Пусть сегмент, имеющий основанием эллипс на
диаметре АГ, а осью ЕА, будет меньше наперед заданной телесной
величины. Разделим АВ на части, равны»; ДЕ, через точки деления па-
параллельно АГ проведем до конического сечения прямые и на этих
проведенных прямых восставим плоскости, параллельные той, которая
проходит через АГ; эти плоскости рассекут поверхность сегмента и об-
образуют эллипсы, подобные тому, который ла диаметре АГ, вследствие
параллельности соответствующих плоскостей. На каждом таком эллпи-
се построим два цилиндрических сегмента, имеющих ось, равную ДЕ,
одип в ту сторону от эллипса, где находится А, другой же — в ту, где
находится В; тогда получатся две некоторые телесные фигуры, одна впи-
вписанная в сегмент, другая же описанпая около него, составленные из
цилиндрических сегментов, имеющих равную высоту. Остается дока-
доказать, что описанная фигура превосходит вписапную на величину, мень-
меньшую наперед заданной телесной величины. Подобно предыдущему дока-
докажем, что описанная фигура превышает вписанную па сегмент, имеющий
ослопалисм эллипс на диаметре АГ и ось ЕД; последний же меньше на-
наперед заданной телесной величины. . .
XXI
Изложил псе это, перейдем к доказательству теорем, предложен-
предложенных относительно рассматриваемых фигур.
Всякий сегмент прямоугольного коноида, отсеченный плоскостью,
перпендикулярной к оси, будет в полтора раза больше конуса, имеющего
те же самые основания и ось, что и сегмент.
Пусть будет сегмент прямоугольного коноида, отсеченный пло-
плоскостью, перпендикулярной к оси; рассечем его через ось другой пло-
плоскостью, и пусть в сечении с поверхностью получится парабола АВГ,
в сечении же с плоскостью, отсекшей сегмент, прямая ГА, ось сегмента
будет ВА; пусть также будет копус, имеющий с сегментом тс же
самые основание и ось, вершина которого В. Требуется доказать, что
сегмент коноида будет в полтора рааа больше этого конуса.
Построим конус W (рис. 22], который был бы в полтора рааа боль-
больше конуса, остюпаписм которого является круг на диаметре АГ,
а осью—прямая ВД; пусть также будет цилиндр, имеющий основанием
круг на диаметре АГ и ось ВД; тогда конус Т будет половиной цилиндра,
1поскольку конус Т в полтора раза больше упомянутого выше копуса].
Я утверждаю, что сегмент коноида будет равен конусу Чг.
Действительно, если он ему не равен, то будет или больше или
меньше. Пусть сначала, если возможно, он будет больше. Впишем
в сегмент телесную фигуру {рис. 23] и опишем около него другую,
198
АРХИМЕД
Рис, 22.
составленную из цилиндров, имеющих одинаковую высоту, таким обра-
образом, чтобы описанная фигура превосходила вписанную на величину,
мепыпую той, на которую сегмент коноида больше конуса 4f, и пусть
из цилиндров, составляющих описанную фигуру, наибольший
будет иметь основанием круг
на диаметре АГ и ось ЕД,
наименьший же будет иметь
основанием круг на диамет-
диаметре 2Т и ось Ш, а из ди-
липдров, которые составляют
«писанную фигуру, наиболь-
наибольшим будет имеющий основа-
основанием круг на диаметре КА, а
осью ДК, наименьшим же —
имеющий основанием круг
на диаметре ST и осью в1;
плоскости всех этих цилинд-
цилиндров продолжим до поверхно-
поверхности цилиндра, имеющего ос-
новапием круг на диаметре
АГ и осью БД; тогда весь
цилиндр будет разделен на
цилиндры, количество кото-
которых ралпо их количеству в
описанной фигуре, и которые
по величине равны наиболь-
наибольшему ii:j этих цилиндров. И
так как описанная около сег-
сегмента фигура превосходит
вписанную на величину,
меньшую той, на которую
сегмент больше конуса, то
ясно, что и описанная в сег-
мент фигура будет больше ко-
конуса !f. Первый цилиндр из
содержащихся в целом ци-
цилиндре, а именно, имеющий
осью ДЬ, с первым цилиндром во вписанной фигуре, имеющим осью ДЕ,
находится и том же самом отношении, какое квадрат на ДА имеет к
квадрату на КЕ; это же отношение равно тому, которое ВД имеет к BE *),
ААа _ ВА
КЕ& В И
и тому, которое ДА имеет к ЕЕ.
ВД _ ДА
BE ЕЕ
Точно так же докажем, что второй цилиндр из содержащихся в целом
циливдро, а именно имеющий ось EZ, со вторым цилиндром во вписан-
вписанной фигуре с той же осью EZ будет находиться в том же отношении,
что ПЕ, или АД. it ZO, и что каждый из остальных цилиндров, содср-
*) На основании основцого свойства параболы, выражаемого па современном математиче-
математическом языке урапнешюм j/-=2jpx, абсциссами ж булут BE. Вд, а соответствующими ординатами
V будут i^lv, ла.
О КОНОИДАХ И СФЕРОИДАХ 199
жащихся л целом цилиндре и имеющих оси, равные ДЕ, с соотпетствую-
щим цилиндром во вписанной фигуре с той же самой осью будет находить-
находиться в таком же отношении, как половина диаметра его основании к отрез-
отрезку этого самого диаметра между прямыми АВ и ВД. Таким образом,
псе цилиндры, находящиеся в цилиндре, основание которого есть круг
на диаметре ЛГ, а ось — прямая Д1, со всеми цилиндрами во вписан-
вписанной фигуре будут находиться в том же самом отношении, которое вс(!
взятые вместе прямые — радиусы кругов, являющихся оснолалиями
упомянутых цилиндров, имеют ко имеете взятым всем прямым —
отрезкам этих радиусов, содержащихся между ЛВ и ВЛ.
Но нее иеркме упомянутые прямые будут более чем вдвое больше
вторьтх упомянутых прямых без АД*); таким образом, и все цилиндры,
заключающиеся в цилиндре с осью Д1, будут более чем вдвое больше
вписанной фигуры; значит, и подавно целый цилиндр, ось которого АВ,
будет более чем вдвое больше вписанной фигуры.
Но этот цилиндр был вдвое больше конуса W; значит, вписанная
фигура меньше конуса Ч?, а это невозможно, ибо доказано, что она боль-
больше. Таким образом, коноид не будет больше конуса Ч1".
Точно так же он не будет и меньше. Действительно, снова впишем
и опишем рассматриваемые две фигуры так, чтобы они различались
между собой на величину, меньшую той, на которую конус W больше
коноида, и устроим все остальное совершенно так же, как и прежде.
Теперь, поскольку вписанная фигура будет меньше сегмента и вписанная
отличается от описанной на пеличину, меньшую той, па которую сег-
сегмент мспыпе конуса Чг, то ясно, что описанная фигура будет меньше копу-
са Ч1". Тогда точно так же первый из цилиндров в целом цилиндре, именно
имеющий ось ДЕ, к первому из цилиндров в описанной фигуре с том же
¦самой осью ЕА, будет иметь то же самое отношение, что квадрат на АД
к себе самому; второй же из цилиндров целого цилиндра, имеющий ось
EZ, ко второму цилиндру в описанной фигуре с осью EZ будет иметь
то же самое отношение, что квадрат на ДА к квадрату на КЕ.
Это же отношение будет тождественно с тем, которое имеют ВД
к BE и ДА к ЕЕ, ¦ • ..-
АД2 ВД ДА
КЕ2 BE ИЗ
и каждый из остальных цилиндров в целом цилиндре, имеющих оси
рапными-ДЕ, к соответствующему цилиндру и описанной фигуре с той
же самой осью будет иметь такое же отношение, как половина диаметра
его основания к своему отрезку между прямыми АВ и ВД; таким обра-
образом, вес цилиндры в целом цилиндре, ось которого есть пряма» ВД,
ко всем цилиндрам в описанной фигуре будут иметь то же самое отно-
отношение, что все первые прямые ко всем вторым лрямым.
шилипдр АЛГД п-АД
¦<ш. ФигГ'ангд ~ ад-; ее ; oz ; ...
tf. раз
*) Следует отметить небольшой недосмотр Архимеда. Если считать, что прямая ВД разделена
¦<ta n частей, раяных ЕЛ, то в написанную пропорцию входит всего та—1 цилиндров и соответственно
прямых АД, а также ЕЕ, ZO и т. д. Пусть прямая АД будет равна пх, тогда эт — 1 прямых ЕЕ, ZO
и т. д. дадут в сумме:
х+2х+... -Hn-I)*—|n*<n-l),
что будет pOBiro «двое меныне (п—1)АД ^(n—i)nx. Таким образом, все цилиндры, заключающиеся
в цилиндре с осью Д1, ромно пдвое больше вписанной фигуры; более чем вдвое больше будет только
sccii- цилиндр АВГ, состоящий из п цилиндрических сегментов.
200
АРХИМЕД
Но все прямые, являющиеся радиусами кругов — оснований этих
цилиндров, будут меньше «сох удвоенных прямых, составляющих их
отрезки, вместе с АЛ.
Теперь ясно, что все цилиндры в целом цилиндре будут меньше
удвоенных всех цилиндров в описанной фигуре; значит, цилиндр, имею-
имеющий основанием круг на диаметре АГ и ось БД, будет меньше удвоен-
удвоенной описанной фигуры. Но это не так: он будет более чем вдвое боль-
большим, ибо он вдвое больше конуса Ч\ в то время как описанная фигура,
согласно доказанному, дшнь-
ше конуса *?". Значит, сегмент
коноида не будет и меньше
конуса ЛГ. Но доказало, что-
он и не больше; значит, ов
будет в полтора рава больше
конуса, имеющего с сегмен-
сегментом те же самые основание и
ось [9].
XXII
Рис. 24.
И если сегмент прямо-
прямоугольного коноида будет от-
отсекаться плоскостью, не пер-
перпендикулярной к оси, он точ-
точно так же будет в полтора
раза больше сегмента конуса,
имеющего то же самое основа-
основание и ту же ось, что и cet-
мент коноида.
Пусть будет сегмент пря-
прямоугольного коноида, отсе-
отсеченный указанным образом;
рассечем его плоскостью, про-
проходящей через ось и перпен-
перпендикулярной к плоскости, от-
отсекшей сегмент; пусть сечение
фигуры будет парабола АВГ,
а сечение плоскости, отсек-
отсекшей сегмент, — прямая А Г;
пусть ФТ* будет касательная
к параболе в В, параллельная
АГ; параллельно оси прове-
проведем БД; последняя разделит
АГ пополам; затем на ФТ восставим плоскость, параллельную той,
которая проходит через АГ; ота плоскость будет касаться коноида
в (точке) Б, причем точка В будет вершиной сегмента, а БД его осью
{рис. 24 и 25).
Теперь поскольку проходящая через АГ плоскость рассекла коно-
коноид, не будучи перпендикулярной к его оси, то и сечении получится
эллипс, паибольший диаметр которого будет АГ. Тогда, имея эллипс па
диаметре ГА и линию ВД, которая проведепа из центра эллипса в пло-
плоскости, восстаилеппой через диаметр перпендикулярно к той, в которой
находится сам эллипс, мы можем найти цилиндр, имеющий ось на одной.
Рис. 25.
О КОНОИДАХ И СФЕРОИДАХ 20*
прямой с ВД, на поверхности которого будет находиться этот эллине
(предложение IX); также можно найти и конус, имеющий вершиной
точку В, на поверхности которого будет находиться рассматриваемый
эллипс {прсдл<укепие VIII); таким образом, получится некоторый
цилиндрический сегмент, имеющий основанием эллипс на диаметре ЛГ
и осью —прямую ВД, и вместе с ним конический сегмент, имеющий те же
самые ось и основание, что и сегменты цилиндра и коноида. Требуется
доказать, что сегмент коноида будет в полтора раза больше этого кони-
конического сегмента.
Пусть будет копус \F, в полтора раза больший этого конического-
сегмента; тогда цилиндрический сегмепт, имеющий те и*е основание
и ось, что и рассматриваемый сегметтт, будет в два рана больше конуса W,
ибо последний в полтора раза больше конического сегмента, имеющего
те же основание и ось, что и рассматриваемый сегмент, упомянутый же
: конический сегмент будет третьей частью цилиндрического сегмента,
имеющего то же основание и ту же ось, что и конический сегмент. Необ-
Необходимо, чтобы сегмент коноида равнялся конусу Чг-
Действительно, если он не равен, то будет или больше, или меньше.
Пусть сначала он, если возможно, будет больше. Тогда впишем в сег-
сегмент телесную фигуру и опишем около него другую, составленную из
цилиндрических сегментов, имеющих равные высоты, так, чтобы
описанная фигура превосходила вписанную на величину меньшую той,
на которую сегмепт коноида больше конуса W; и плоскости сечений
продолжим до поверхности цилиндрического сегмента, имеющего те
же основание и ось, что и сегмепт коноида. Опять первый сегмент
п целом цилиндрическом сегменте, имеющий ось ДЕ, будет к первому
сегменту вписанной фигуры с осью ДЕ иметь то же самое отношение,
что квадрат па АД к квадрату на КЕ; ибо сегменты с одинаковой высотой
имеют друг к другу то же самое отношение, что и основания, осно-
основания же их, являясь подобными эллипсами, имеют то же самое отно-
отношение, что соответственные их диаметры п квадратах, и АА, КЕ будут
половинами соответственных диаметров. Но какое отношение имеют АА
к КЕ в квадратах, такое и*е отношение будет иметь и ВЛ к BE линейно,
АЛ» _ ВД
КВ2 ~ BE
так как ВД параллельна диаметру, а АД и КЕ параллельны касатель-
касательной в В; какое же отношение ВД имеет к BE, то же самое имеет и АД
к ЕЗ.
ВД ^ЛД
BE ~ ЕЕ
Таким образом, первый сегмент в целом цилиндрическом сегменте
к псрпому сегмепту вписаппой фигуры будет иметь то же самое отноше-
отношение, что АД к ЕЕ; и каждый из остальных сегментов в целом цилинд-
• рическом сегменте с высотой, равной ДЕ, к соответствующему сегменту
во вписанной фигуре с той же осью будет иметь такое же отношение,
как половина диаметра его основания к заключающемуся между АВ
и ВД ее отрезку. Таким образом, подобно предыдущему докажем, что
вписанная фигура больше конуса W, а цилиндрический сегмент с теми
же основанием и осью, что и у сегмента коноида, более чем в два раза
больше вписанной фигуры; таким образом, он будет более чем в два
раза больше и конуса \F. Это же не так, но он только в два раза больше
его. Значит, сегмент коноида не будет больше конуса ?. При помощи
202
АРХИМЕД
таких же рассуждений докажем, что он и не меньше; таким обра:юм,
ясно, что он будет ему равен. Итак, сегмент коноида в полтора раза боль-
больше конического сегмента, имеющего то же самое основание и ту же ось,
что и рассматриваемый сегмент.
XX Ш
Если от прямоугольного коноида отсечь два сегмента — один пло-
плоскостью, перпендикулярной к оси, другой же — не перпендикулярной,
так, чтобы оси обоих сегментов были равны, то будут- раты и сами
сегменты.
Отсечем от прямоугольного коноида два сегмента, как было ска-
сказано; рассечем такэтес коноид плоскостью через ось [и другой плоско-
плоскостью, перпелдикулирной к оси]; пусть сечение коноида будет пара-
парабола АВГ с диаметром
ВД, ссчепия же обеих
упомянутых плоско-
плоскостей —прямые AZ, ЕГ,
причем ЕГ будет сече-
сечением плоскости, перпен-
перпендикулярной к оси, я
ZA — не перпендику-
перпендикулярной; пусть равные
ДРУГ другу оси этих
согментон будут Вв,
КЛ, а вершины В, Л.
Требуется доказать, что
сегмент коноида с вер-
шиной В будет равен
сегменту коноида с вер-
вершимой Л {рис. 2E}.
Действительно, так
как от одной и той же
параболы отсечены дпа
сегмента AAZ и ЕВ Г, и
их диаметры КЛ и Вв равны, то и треугольник ЛЛК будет равен E0B;
ибо уи*е доказано (предложение ТП), что треугольник AAZ ранен
треугольнику ЕВГ. Опустим перпендикуляр АХ на продолжение КЛ.
Поскольку Вв и КА равны, то будут равпы и Ев, АХ*).
Пусть в сегмент с вершиной В будет вписан конус, имеющий с этим
сегментом то же самое основание и ту же ось, в сегмент же с вершиной А
пусть будет шшеап конический сегмент, имеющий то же самое основа-
основание, что сегмент коноида, и ту же ось; изЛ опустим яа AZ перпендикуляр
AN; он будет высотой конического сегмента с мерши ной Л. Конический
сегмент с вершиной А и конус с вершиной В имеют друг к другу отно-
отношение, составленное из отношений оснований и высот; значит, опи будут
иметь отношении, составленное из того, которое площадь, ограни-
ограниченная иллинсом с диаметром AZ, имеет к кругу на диаметре ЕГ,
и из того, которое NA имеет к В0.
Рис. 20.
гтшг. г.егм. AZA
конус ГВК
шишпе AZ NA
" "круг ЕГ ' В6
•) Из равенства площадей треугольников ИвВ и АКЛ следует Вв.Ев=КЛ.ЛХ.
О КОНОИДАХ И СФЕРОИДАХ 203
Площадь жо, ограниченная эллипсом, к рассматриваемому кругу
имеет то же самое отношение, что прямоугольник между обоими диа-
.. метрами к квадрату на ЕГ,
¦шкгапс AZ AZ ¦ IIZ
~jqvyr ЕГ "" БГ2
Ги конический сегмент с вершиной Л имеет к конусу с вершиной
В отношение, составленное из того, которое КА имеет к ЕВ, и того,
которое NA имеет к В0,
кон, сегм. AZA_ КЛ КА
•конус ГВЕ ~~ Е© ' BG
ибо КА является половиной диаметра основания конического сегмента
с вершиной Л, а Ев — полониirofi диаметра основания конуса, в то
иремя как AN, Вв являются их высотами. Но AN имеет к Б0 то же
самое отношение, что и к КЛ, так как Вв равна КА; также и AN имеет
к КА отиошепие, как ХА к AKJ*).
AN XA
К Л ~ ЛК
Теперь конический сегмент имеет к конусу отношение, составленное
из того, которое АК имеет к АХ {ибо АХ равно Ев), и ия того, кото-
которое AN имеет к Вв**).
«кон. ссгм. AZA _ АК AN
"конус ГВЕ АХ ' Вв
Но одно из упомянутых отношений, а именно АК к АХ, будет тем же
самым, что и отношение ЛК к AN,
АК _ АК
ЛХ AN
значит, конический сегмент имеет к конусу отношение, как ЛК к AN
и AN к Вв.
тт. ссгм. AZA = AK AN
конус ГВЕ ""AN" Be
Но Вв равна КА; ясно, что конический сегмент с вершиной А будет
равен конусу с вершиной В. Теперь очевидно, что рассматриваемые сег-
сегменты будут рашпд, ибо один из них будет в полтора раза больше кону-
конуса, а другой — конического сегмента, равного упомянутому конусу.
XXIV i
Если от- прямоугольного коноида отсечь два сегмента произвольно
проведенными плоскостями, то сегменты будут иметь друг к другу
такое же отношение, как и квадраты на их осях.
Отсечем от прямоугольного коноида как-нибудь два сегмента,
и пусть ось одного из них равна будет К, а другого — А; требуется
доказать, что эти сегменты будут иметь друг к другу то же самое отно-
отношение, что квадраты на К и А {рис. 27].
Рассечем коноид плоскостью чероз ось сегмента, и пусть сечение бу-
будет парабола ЛВГ с осью БД: отложим ВА рашгой К и проводом через Д
*) Гсйберг не считает стоящее в квадратных скобках место подлинным, так как оно не вяжется
с общим ходом докаяательстиа.
**) Согласно предложению XII, диаметры шшипса AZ будут А'/, и ZIJ, половинами которых
будут АК и АХ. Радиус круга в основании конуса будет Е©—АХ; таким образом, отношение нло-
лцадей эллипса и круга будет:
:ДК- АХ АК
Е©2 " АХ "
204
АРХИМЕД
плоскость, перпендикулярную к оси; тогда сегмент коноида, имеющий.
основанием круг на диаметре АГ и осью БД, будет равен сегменту, имею-
имеющему ось, равную К. Теперь если
К раьна Л, то очевидно, что и атк
сегменты будут равны друг другу,
ибо каждый из них равен одному
и тому же; равны также и квадра-
квадраты на К, Л, так что сегменты бу-
будут иметь такое же отношение, как
квадраты на их осях. Если же Л
не равна К, то пусть Л будет раи-
раина Вв; проведем через в пло-
плоскость, перпендикулярную к оси;
тогда сегмент, имеющий основа-
основанием круг на диаметре EZ, a
осью Вв, будет равен сегменту,
имеющему ось, равную А. Теперь
ыгишедт в них конусы, имеющие
основаниями круги на диамит-
( ? pax АГ, EZ и вершиной точку В;
тогда копус, имеющий ось ВД, к
Рис. 27. конусу, имеющему ось Вв, будет
иметь отношение, составленное из
того, которое квадрат на АД имеет к квадрату на вЕ, и того, которое
ДВ имеет к В в линейно.
конус ВД АД2 ДВ
"конуг. Вв '' вва" В©
Какое же отношение ДА имеет к вЕ в квадратах, такое же отношение
будет иметь ВД к Вв линейно,
ДА2 БД
значит, копус, имеющий ось ВД,к конусу с осью Вв имеет отношение,
составленное из того, которое ЛВ имеет к вВ, и нз того, которое ДВ
имеет к Вв; а это будет тождественно с тем, которое квадрат на ДВ
имеет к квадрату на <ЭВ. Но отношение конуса, имеющего ось ВД,
к конусу, имеющему ось 6В, будот тем же самым, какое сегмеят коно-
коноида с осью ДВ имеет к сегменту с осью вВ [ибо каждый л полтора раза
больше соответствующего конуса]. И сегменту с осью ВД будот равен
сегмент коноида, имеющий ось, равную К, сегменту же с осью 6В равен
сегмент коноида, имеющий ось, равную Л, и ВД равна К, а 0В равна Л;,
после этого ясно, что сегмент коноида, имеющий ось, равную К, будет
с сегмептом коноида, имеющим ось, ранную Л, находиться в том же самом
отношении, что квадрат на К к квадрату на Л.
XXV
Всякий сегмент тупоугольного коноида, отсеченный плоскостью,
перпендикулярной к его оси, к конусу, имеющему с сегментом одно и то>
Же основание и равную высоту, имеет такое же отношение, какое прямая,
равная вместе взятым оси сегмента и утроенной дополняющей ось*),
*) Действительной полуоси гиперболы.
О КОНОИДАХ И СФВРОИДЛХ
205
1
и
Q
и
Q
м
Т>
N
Ф
имеет к прямой, равной вместе взятым оси сегмента и удвоенной допол-
дополняющей ось {рис. 28].
Пусть будет некоторый сегмент тупоугольного коноида, отсеченный
плоскостью, перпендикулярной к оси; рассечем его другой плоскостью,
проходящей через ось;
пусть сечение самого
коноида будет гипербо-
гипербола АВГ, а отсекшей сег-
сегмент плоскости — пря-
прямая АГ; пусть ось сег-
сегмента будет ВД, а до-
дополняющая ось В©, и
пусть прямой Вв будут
равны Z0 и ZII. Тре-
Требуется донизать, что
этот сегмент к конусу,
имеющему с сегментом
те же самые основание
и высоту, будет иметь
отношение, как НА к ZA.
Пусть будет ци-
цилиндр, имеющий с сег-
мсптом то же самое
основание и ту же ось;
пусть его стороны бу-
будут ФА, Г Г; пусть так-
также будет некоторый ко-
конус !F, который к ко-
конусу, имеющему с сег-
сегментом то же основание
и ось ВД, имеет то гко
отношение, что НА к
AZ; я говорю, что этот
сегмент копоида будет
равен копу су Ч?.
Действительно, если
он не ранен, то будет
или больше, или мень-
меньше. Пусть сначала он,
если возможно, будет больше. Втшпвш в этот сегмент телесную фигуру
к опишем около пего другую, составленную из цилиндров равной высо-
высоты, так, чтобы описанная фигура превосходила «писанную на велп-
чипу, меньшую той, на которую сегмент коноида больше конуса У;
затем плоскости всех этих цилиндров доведем до боковой поверхности
цилиндра, имеющею основанием круг на диаметре А Г и осью ВА;
тогда целый цилиндр будет разделен на цилиндры, по количеству
равные цилиндрам в описанной фигуре, а по величине равные наиболь-
наибольшему из этих цилиндров. И так как описанная фигура превышает впи-
вписанную па величину, меньшую того, чем сегмент коноида превышает
конус *Р, и оштсаппая фигура больше сегмента, то ясно, что и впи-
вписанная фигура больше конуса 'F. Пусть ВР будет третьей частью ВД;
Рис. 28.
Bv= ^ ВА
206 АРХИМКД
тогда НД будет утроенной 6Р *).
в1>
И так как цилиндр, имеющий основанием круг на диаметре АГ и ось.
ВД, к KOirycy с тем же самым основанием и той же осью имеет то же
отношение, что НД к 8Р **),'
цилиндр ВА _ НА
c ВА. ~ &V
и упомянутый конус к конусу Y относится, как ZA к НД,
конуг. ИД ZA
конус W НД
то в переставлоякой пропорции трех величин ***) упомянутый цилиндр
к конусу 1Г будет иметь такое же отношение, как ZA к 01'.
цилиндр ВА Zu_
конус V ёр"
Отложим линии, обозначенные В, количество которых равнялось бы
количеству отрезков прямой ВЛ, а величина каждой была бы равпа ZJB;
к каждой из них приложим площадь с избытком в виде квадрата,
и пусть наибольшая площадь будет равна прямоугольнику между ZA,
АВ, а наименьшая — прямоугольнику между ZI, IB, причем стороны,
избытков одинаково превышают одна другую, [ибо ранные им отрезки,
находящиеся на прямой, тоже одинаково превышают один другого];
пусть сторона наибольшего избытка N равна прямой ВД, а наименьшего-
равна BI****), пусть также будут и другие площади, обозначенные Q,
количество которых равно количеству первых, а величина каждой равна,
наибольшей из них — прямоугольнику между ZA и ЛВ. Тогда цилиндр,
имеющий основанием круг на диаметре АГ и ось ЛЕ, с цилиндром,,
имеющим основанием круг на диаметре КЛ и ось ДЕ, будет находиться
в том же отношении, какое имеют квадраты на ДА и КЕ,
цилиндр ЛГЕ _ АА8
цнлищц» КАД ~ ~
но это отношение будет тем же самым, которое прямоугольник между 7Л.
и ВД имеет к прямоугольнику между ZE и БЕ,
АА2 _ ZA-AB
"КЕ2" "ZE-BE
так как это имеет место для всякой гиперболы*****), [ибо удвоенная,
«дополняющей», то есть прямой, проведенной из центра, являете}! ш>-
*) Так как НВ—зев и ВД--ЗВР.
**) То есть 3. так кап IIA==3©P.
***) См. «Начала» Еьклнда, книга V, предложение J8.
****) Таким образом, крайняя праваи площадь будет раина
EN-I K==-ZB.BA + BA2=ZA-AB,
следующая за ней илеио
S3H-Me-—ZB.BEt-BE«=sJUSO?B,
и крайняя лепая
—ZB.BI+BIS=ZI-I».
*****) Если череа л: и у будем обозначать айсциссу и ордшгату гиперболн, отиесешюйг
к действительной пои к касательной и вершине, а черев 2а обозначим длину действительной осп,
то архимедова «ургшнение» гиперболы мы запасали бы так:
У?
j( ,) .2.+s)
Т> натпм «-лучае j/,-=АД, ;/ч=КЕ. Sj=BA, лч--Ш1, 2a=ZB, отиуда и следует написанная*
Архимедом пропорция:
.ДА"
О КОНОИДАХ И СФЕРОИДАХ 207"
перечной стороной фигуры]*). Теперь лрнмоуголышк между 7Л и БД
равен площади EN**), прямоугольник между ZE и BE равен площа-
площади НМ, ибо S равна ZB, Мраила BE и N равна БД; значит, цилиндр,
имеющий основанием круг на диаметре ЛГ и ось ДЕ, с цилиндром,
имеющим основанием круг па диаметре КЛ и ось ДЕ, будет находиться
в таком же отношении, как площадь Q с площадью ЕМ.
Подобным же образом докажем, что и каждый из остальных цилинд-
цилиндров в целом цилиндре, имеющий ось, равную ДЕ, с цилиндром во вии-
салпой фигуре с той ж« самой осью будет находиться в таком же отно-
отношении, какое площадь Q имеет к соответствующей из площадей, при-
приложенных к Н с избытком в виде квадрата. Таким образом, имеются
некоторые величины, а именно цилиндры в целом цилиндре, каждый не-
некоторых имеет ось, равную ДЕ, и другие величины—площади Q- и рав-
равном с ними количестле, которые попарно имеют одно и то же с Q отноше-
отношение, так как и цилиндры равны друг другу, и площади тоже равны
друг другу, и некоторые нз этих цилиндров находятся в определенных
отношениях с другими цилиндрами, а именно с теми, что во вписан-
вписанной фигуре, последний же цилиндр не имеет отношения пи к чему***),
а также и некоторые из площадей Q находятся в тех же самых отноше-
отношениях с другими соответствующими им площадями, приложенными
к Е с избытком в виде квадрата, последняя же площадь не имеет отно-
отношения ни к чему; после этого ясно, что все цилиндры в целом цилиндре
ко псом цилиндрам во вписанной фигуре будут иметь то же самое отно-
отношение, что все площади Q ко всем приложенным площадям за исклю-
исключенном наибольшей. По доказано (предложение II), что нее площади
Q ко всем приложенным площадям за исключенном наибольшей будут
иметь отношение большее того, которое имеет (прямая) N вмести
с S к (прямой), ранной вместе взятым половине Е и третьей части N;
таким образом, и вось цилиндр ко вписанной фигуре будет иметь боль-
большее отношение, чем ZA к 6Р****); но, согласно доказанному, последнее
отношение имеет целый цилиндр к конусу Ч1; значит, целый цилиндр
ко вписанной фигуре имеет отношение большее, чем к конусу Ч?. Таким
образом, конус Убудет больше вписанной фигуры; это же невозможно,
так как доказано, что вписанная фигура больше конуса Ч*. Значит,
сегмент коноида не будет больше конуса W.
Но он также не будет и меньше. Действительно, пусть он, если воз-
возможно, будет меньше. Снова впишем в сегмент телесную фигуру и опи-
шем около него другую, составленную из цилиндров, имеющих равную
высоту, таким образом, чтобы описанная фигура превосходила вписан-
вписанную на величину меньшую той, на которую конус больше сегмента;
и нее остальное, сделаем таким же. Теперь поскольку вписанная фигура
меньше сегмента, а описанная превосходит вписанную на величину,.
*) '« y&Q CuAoMTics t»g лотеоиоав. rouxtcra. тйе. ек той x&vrcov, nfanyia ёах: too e!6ox?S
дополнение интерполятора с те рмщшлсл-ией эпохи Аполлонии. Если мм перепишем ураиневие
гиперболы в виде
где h- ueinmipUH постоянная, то 2п Судит горизонтальной, то есть поперечной, стороной прлмс
угольника 2а+х, к котор и «прикладывается е избытком в виде ишщшта» площадь hyS..
**) То есть сумме плпгцадей с буквами N и Е.
***) Так лак число цилиндров во кписанппй фигуре на один меньше числа дилинлрои в целом
цилиндре.
• **•) мы имеем N^-Вл, E~ZB, N + H—Z.A,
208 АРХИМЕД
меньшую той, на которую конус W меньше сегмента, то ясно, что и опи-
описанная фигура будет меньше конуса W. Тогда опить первый цилиндр
в целом цилипдре, имеющий ось ДЕ, с первым цилиндром в описанной
фигуре, толю имеющим ось ДЕ, будет находиться в том же отношении,
как площадь ?1 с BN, [ибо они равны друг другу], и каждый из осталь-
остальных цилиндров и целом цилиндре, имеющих оси, равные ДЕ, с соответ-
соответствующим цилиндром в описанной фигуре, имеющим ту же самую ось,
будет находиться в таком гке самом отношении, как площадь Q с соот-
соответствующей ей площадью, приложенной к S вместе с избытком, вслед-
вследствие того, что каждый из описанных цилиндров, кроме наибольшего,
будет равен каждому соответствующему из вписанных, считая и наи-
наибольший. После этого и целый цилиндр к описанной фигуре будет иметь
то же самое отношение, что и нее площади Q к соответствующим им пло-
площадям, приложенным вместе с избытками. И опять уже было доказано,
что все площади Q ко всем другим имеют меньшее отношение, чем то,
в котором прямая S (вместе) с N находится к прямой, равной вместе
взятым половине S и третьей части N; таким образом, и весь цилиндр
к описанной фигуре будет иметь отношение меньшее, чем Г/А к 6Р.
Но как ZA к ЭР, так будет и весь цилиндр к конусу У; значит, тот же
•самый цилиндр к описанной фигуре имеет отпопгепис меньшее, чем
к Ч/. Таким образом, описанная фигура будет больше конуса 4f, а ото
нйвонможно, так как доказано, что описанная фигура меньше конуса W.
Значит, сегмент коноида не будет и меньше конуса V. Поскольку же
он не будет ни больше, ни меньше, то предложенное доказано [10].
XXVI
И также, если сегмент тупоугольного коноида отсекается плоско-
плоскостью, па перпендикулярной к оси, то он к коническому сегменту с теми
же самыми основанием и осью, что и у сегмента коноида, будет иметь
такое же отношение, какое прямая, равная вместе взятым оси сегмента
и утроенной дополняющей ось, имеет к прямой, равной вместе взятым
пси сегмента и удвоенной дополняющей ось (рис. 29}.
Действительно, пусть будет отсеченный, как сказано, сегмент
тупоугольного кон >ида; рассечем эту фигуру другой плоскостью,
проходящей через ось и перпендикулярной к плоскости, отсекшей сег-
сегмент; пусть сечение фигуры будет гипербола АВГ, сечение же отсекшей
согминт плоскости — прямая ГА, вершина же конуса, объемлющего
коноид, пусть будет точка 0; проведем через В параллельно АГ касатель-
касательную ФТк коническому сечению, и пусть она будет касаться его в точке
В, затем продолжим прямую, соединяющую © с В; тогда последняя раз-
разделит АГ пополам, и вершиной сегмента будет точка В, осью его ВД
и дополняющий ось — В6; пусть прямой ВО будут равны 6Z и ZH.
Восставим на ФГ некоторую плоскость, параллельную той, которая
проходит через АГ; она будет касаться коноида в В. И так как коноид
рассекла плоскость через А Г, ire являющаяся перпендикулярной коси,
то сечение будет эллипсом с наибольшим диаметром ГА. Итак, имеется
аллипс па диаметре АГ и линия ВД, проведенная из центра к плоскости,
которая восставлена через диаметр перпендикулярно к той, в которой
находится этот эллипс; тогда можно найти цилиндр, имеющий ось
на одной примой с ВД, на поверхности которого окажется рассматри-
рассматриваемый эллипс на диаметре АГ. Если им построим его, то получится
некоторый цилиндрический сегмент, имеющий то же самое основание
О КОНОИДАХ И СФЕРОИДАХ
209
и ту же ось, что и сегмент коноида; другим основанием итого цилиндри-
цилиндрического сегмента будет плоскость, проходящая через ФГ. Затем можно
также пайти конус с вершиной в точке В, на поверхности которого
окажется рассматриваемый эллипс на диаметре АГ. Если мы построим
Я
Й
п
Q
-
м
¦=
/г
И
г
(
N
/
/ ,
У >?
Г&-
И/ /р Y
¦^ /
/в
/
/
\/
YV
/
/
/
V
71
Рис. 20.
его, то получится некоторый конический сегмент, ммеющи к те же самые
основание и пег. с сегментами коноида и цилиндра. Трибуотся доказать,
что сегмент коноида к упомянутому коническому сегменту имеет то же
самое отношение, что НА к AZ.
Пусть то отношение, которое ПА имеет к AZ, будет иметь конус Ч;
к коническому сегменту. Если сегмент коноида не равен конусу У,
то пусть, если это возможно, он будет больше. Тогда и сегмент коноида
впишем телесную фигуру и опишем около него другую, составленную
из цилиндрических сегментов, имеющих одинаковую высоту, так,
чтобы описанная фигура превосходила вписанную на величину, мень-
меньшую той, на которую сегменг коноида больше конуса Ч1'. Теперь, так
Архимед
210 • ''¦ АРХИМЕД
как описанная фигура, будучи больше сегмента, превышает вписан-
вписанную фигуру на величину меньшую той, на которую сегмент коноида
превышает конус Ч1", то ясно, что вписанная фигура будет больше конуса
V. Продолжим плоскости всех «писанных в сегмент цилиндрических
сегментов до поверхности цилиндрического сегмента, имеющего те же
самые основание и ось, что и сегмент коноида, и пусть ВР будет третьей
частью ВД; и все остальное устроим точно так же-, как и раньше. Тогда
опять первый цилиндрический сегмент в целом сегменте цилиндра,
а именно имеющий ось ДЕ, к первому цилиндрическому сегменту во
вписанной фигуре, тоже имеющему ось ДЕ, будет иметь такое же отно-
отношение, как квадрат на АД к квадрату КЕ, так как сегменты цилиндра,
имеющие равные высоты, относятся друг к другу, как основания, осно-
основания же их вследствие подобия эллипсов будут иметь друг к другу то
же самое отношение, что квадраты на соответствующих диамотрах их.
Но отношение квадрата на АД к квадрату на КЕ будет тем же самым,
какое прямоугольник между ZA, ДВ имеет к прямоугольнику между
ZE, ЕВ.
АД* ZA-AB
кка ZE-EB
так как ZA проведена через в — точку пересечения асимптот, а ЛА
и КЕ параллельны касательной в В. Но прямоугольник между ZA,
ДВ равен площади ?2, а прямоугольник между ZE, ЕВ — площади Н
(вместе с) М; тогда первый сегмент в целом цилиндрическом сегменте,
имеющий осью ДЕ, к первому сегменту во вписанной фигуре с той же
осью ДЕ будет иметь то же самое отношение, что площадь Q к пло-
площади Н (вместе с) М. И каждый лз других сегментов в целом цилиндри-
цилиндрическом сегменте, имеющих ось, равную АЕ, к соответствующему ему
сегменту во вписанной фигуре с осью, равной ДЕ, будет иметь то же •
самое отношение, что площадь Q к соответственной площади, лрило-
жешшй к 3 с избытком в виде квадрата. Таким образом, снова имеются
некоторые величины, а именно сегменты в целом цилиндрическом сег-
сегменте, и другие величины — площади И в равном с цилиндрическими
сегментами количестве, которые попарно имеют одинаковое отношение
с первыми, и сегменты цилиндра находятся в определенных отношениях
с другими сегментами во вписанной фигуре за исключением последнего,
который не имеет себе соответствующего, а также площади L1, находя-
щиеся в таких же отношениях соответственно с другими площадями,
приложенными к Е с избытком в виде квадрата, причем последняя пло-
площадь но имеет себе соответствующей; таким образом, ясно, что «се пер-
первые цилиндрические сегменты ко всем вторым цилиндрическим сег-
сегментам будут иметь то же самое отношение, что все площади Q ко всем
. приложенный площадям за исключением наибольшей. Но все площади
• Q ко псем приложенным площадям за исключением паибольшей имеют
. большее отношение, чем прямая S (вместе с) N к прямой, равной вме-
вместе взятым половине S и третьей части N. Таким образом, весь цилинд-
цилиндрический сегмент ко вписанной фигуре имеет большее отношение,
чем ? (вместе с) N к прямой, равной вместе взятым половине S и
третьей части N, а следовательно, большее и того отношения, какое
ZA имеет к 01*. Значит, весь цилиндрический сегмент ко вписанной фи-
фигуре имеет большее отношение, чем к конусу У, что невозможно, тан
как доказано, что вписанная фигура больше конуса "У. Итак, сегмент
коноида но будет больше конуса Т.
О КОНОИДАХ И СФЕРОИДАХ
Если бы сегмент коноида был меньше конуса Т, то, вписавши п сег-
сегмент телесную фигуру и описавши около него другую, составленную из
цилиндрических согментоп, имеющих равную высоту, так, чтобы' опи-
описанная фигура превосходила вписанную на величину меньшую той,
на которую конус *F болыпо рассматриваемого сегмента, опять подоб-
подобным же образом докажем, что описанная фигура будет меньше конуса W
и что цилиндрический сегмент, имеющий те же самые основание и ось,
что и сегмент коноида, бу-
будет иметь к описанной фи- p
гуре отношение меньшее,
чем к конусу W, что не-
возможпо. Таким образом,
сегмент коноида но будет
и меньше конуса Ч1". Итак,
предложенное является до-
доказанным.
М
I
/
/V
f/
/
V
'\
X \
II
\
\
\
t, 71
№
/
XXVII
Если какую-нибудь
сфероидальную фигуру рас-
рассечь плоскостью, проходя-
проходящей через центр и перпен-
перпендикулярной к оси, то по-
половина сфероида будет
вдвое больше конуса, имею-
имеющего то же самое основание
и ту же ось, что и сегмент
{рис. 30}.
Пусть будет сферои-
сфероидальная фигура, рассечен-
рассеченная плоскостью, перпен-
перпендикулярной к оси и про-
проходящей через центр 0;
если мы рассечем ее другой
плоскостью, проходящей
через ось, то сечением фи-
фигуры будет эллипс АВГЛ,
его диаметрам и осью сфе-
сфероида будет прямая ВД,
а их центром — точка 0;
при этом безразлично, бу-
будет ли ВД наибольшим
диаметром эллипса или жо наименьшим; пусть сечение плоскости,
рассекшей фигуру, будет прямая ГА; тогда последняя пройдет через
центр и будет перпендикулярна к ВД, так как плоскость предпола-
предполагается проходящей через центр и перпендикулярной к оси. Требуется
доказать, что половина сфероида, имеющая основанием круг на диа-
диаметре АГ, а вершиной точку В, будет вдвое больше конуса, имеющего
с сегментом то же самое оснонанис и ту же самую ось.
Пусть некоторый конус aF будет вдлое больше конуса, имеющего
с сегментом то же самое основание и ту же самую ось ©В. Я говорю,
что половина сфероида будет равна конусу Y. .. ..
14»
S
г
/
/
/
/
г
/
/
Т
/
/
/
/
•
Рис. 30.
212
АРХИМЕД
Действительно, если половина сфероида но равна конусу V, то
пусть ока, во-первых, будет, если возможно, больше. Тогда и сегмент,
равный половине сфероида, впишем телесную фигуру и опишем около
пего другую, состошцую из цилиндров, имеющих равную высоту, так.
Фотокопия страницы греческой рукописи, содержащей отрыпок сочи-
сочинения Архимеда «О коноидах и сфероидах».
чтобы описанная фигура превышала вписанную на величину, моньтую
той, иа которую половина сфоропда превосходит конус Ф. Теперь,
поскольку описанная фигура, будучи больше половины сфвроида, пре-
посходпт вшгеаьную фигуру на величину, миныпую той, на которую
половина сфероида больше конуса W, то ясно, что и фигура, вписанная
в этот сегмент, равный половине сфероида, будет больше конуса W
Пусть будет цилиндр, имеющий «снованием круг на диаметре АГ
О КОНОИДАХ И СФЕРОИДАХ 213
и ось В0. Поскольку этот цилиндр втрое больше конуса с теми же осно-
основанием и осью, что и у сегмента, а конус Чг вдвое больше того же
конуса, то ясно, что цилиндр будет в полтора раза больше конуса 1У.
Плоскости всех цилиндров, из которых складывается вписанная фигура,
продолжим до поверхности цилиндра, имеющего то же самое основание,
что и сегмент, и ту же самую ось; тогда весь цилиндр окажется разде-
разделенным на цилиндры, количество которых будет рашю количеству
цилиндров в описанной фигуре, а всличипа раипа наибольшему из
этих цилиндров. Отложим теперь линии, об означенные Е, количество
которых равно количеству отрезков прямой В©, а неличина каждой
равна В©; на каждой из этих линий построим квадрат. От последнего из
этих квадратов отнимем гномон *), имеющий сторону, раллую В1; этот
гномон будет равен прямоугольнику между BJ и1А**). От пред-
предшествующего квадрата отнимем гномон, ширина которого равняется
удвоеппой ВТ; он будет ранен прямоугольнику между ВХ и ХД. Затем
от каждого следующего квадрата будем отнимать гнемон, ширина
которого па одни отрезок <В1) будет больше ширины предшествующего
отнятого гномона; каждый из этих гномонов будет равен прямоуголь-
прямоугольнику, построенному на двух отрезках прямой БД, один из которых
равен ширине соответствующего гномона. Таким образом, остаток от
второго квадрата будет квадрат, имеющий сторону, равную BE. Теперь
первый цилиндр из составляющих целый цилшгдр, а имепно имеющий
ось 6Е, с первьш цилиндром во ннисаппои фигуре с той же самой осью
0Е будет находиться в таком же отношении, какое кнадрнт па А в имеет
к квадрату на КЕ или какое прямоугольник между В© л вД имеет
к прямоугольнику между BE и ЕД ***);
А62 ВВ-6А
КЕ2 ~ ВЕ-ЕД
таким образом, первый цилиндр к соответствующему ему другому
цилипдру имеет то же отношение, как первый квадрат к гномону, отни-
отнимаемому от второго квадрата. Точно так же и каждый из остальных
цилиндров, имеющих ось, равную BE, с соответствующим цилиндром
во вписанной фигуре с той же самой осью находится в таком же отно-
отношении, какое квадрат, стоящий на месте, соответствующем рассматри-
рассматриваемому цилиндру, имеет к гномону, отнятому от следующего за ним
квадрата. Таким образом, имеются некоторые величины, а именно
цилиндры, составляющие целый цилиндр, и другие, а именно пост
роенные на прямых Е, Н-кнадраты, количество которых равно
количеству цилиндров и которые находятся попарно в тех же самых
отношениях, и эти цилиндры имеют отношение к другим величинам,
а именно к цилиндрам во вписанной фигуре, причем последний цилиндр
ни к чему не имеет отношения, и квадраты находятся в таких же отно-
отношениях к соответствующим другим величинам, а именно отнимаемым
от квадратов гномонам, причем последний квадрат ни к чему не имеет
отношения: таким образом, все цилиндры в целом цилиндре ко всем
*) Так кааыпается остаток в виде буквы Г, получившийся после отнятии из данного квадрата
другого квадрата. Сторотюй гномона называется разность сторон обоих ккадратив — уменьшаемого
и вычитаемого.
**) Действительно, этот гномон рапен равнести квадратов
Не*—(В©— BI)Z—2Вв-В1-В1!--В1BВв—В1)^ВЫл.
***) По иэиестиому свойстиу отрезков диаметра эллипса, частным случаем которого пвляетси
теорема элементарной геометрии о произведении отрезков диаметра круга или гипотенузы прямо-
прямоугольного треугольника.
. 214 АРХИМКД
другим рассматриваемым цилиндрам будут иметь такое же самое отно-
отношение, как все квадраты ко всем отнимаемым от них гномонам; значит,
цилиндр, имеющий с сегментом то же самое основание и ту же ось, будет
к вписанной фигуре иметь такое же отношение, как все квадраты ко
всем отнимаемым от них гномонам. Но все эти квадраты будут более
чем и полтора раза больше всех отнимаемых от них гномонон; действи-
действительно, имеются некоторые отложенные линии ЕР, S2, ЕТ, В Г, ЕФ,
одинаково превышающие одна другую, причем наименьшая из них равна
их разности; имеются также и другие линии, а именно обозначенные
двумя буквами 2Н7 количество которых равно количеству первых,
а величина каждой из которых раина наибольшей из первых; тогда
квадраты всех величии, каждая из которых равна наибольшей, будут
менее чем в три раза больше всех квадратов величин, одинаково пре-
превышающих одна другую, по более чем в три раза больше всех этих квад-
квадратов за исключением наибольшего*); это доказано в уже изданной
книге «О спиралях», (предложение X, следствие). Поскольку же все
первые квадраты будут мэньгае утроеппых отнимаемых от них вторых
квадратов, то ясно, что они будут более чем в полтора разабольше остат-
остатков; значит, они будут более чем в полтора раза больше гномонов. Таким
образом, и цилиндр, имеющий с сегментом то же самое основание
и ту же ось, будет более чем в полтора раза больше вписанной фигуры,
что невозможно, так как он в полтора раза больше конуса \Р, а вписан-
вписанная фигура, как доказано, больше конуса У. Значит, половина сфероида
не будет больше конуса Чг.
Но она также и не меньше. Действительно, пусть она, если воз-
возможно, будет меньше. Тогда снова виишом в половину сфероида телес-
телесную фигуру и опишем около нее другую, составленную из цилиндров,
имеющих одинаковую высоту, так, чтобы описанная фигура превосхо-
превосходила списанную на величину, меньшую той, на которую конус Чг более
половины сфероида, и все остальное сделаем совершенно так яге, как
и прежде. Теперь, поскольку вписанная фигура меньше сегмента, то
ясно, что описанная фигура будет меньше конуса ЧЛ Тогда опять пер-
первый цилиндр п целом цилиндре, имеющий ось ©Е, к пир пому цилиндру
в описанной фигуре с той же осью 6Е, будет находиться в том же отпо-
; - - шении, какое первый квадрат имеет к себе самому, второй же цилиндр
в целом цилиндре, имеющий ось ЕП, со вторым цилиндром в описанной
фигуре с той же осью ЕП будет находиться в том же самом отношении,
¦ какое второй квадрат имеет к отнимаемому от пего гномону; и каждый
из остальных цилиндров в целом цилиндре, имеющих ось, равную 6Е,
с соответствующим цилиндром в описанной фигуре с той же самой
осью будет находиться в том же самом отношении, какое занимающий то
¦¦¦¦ же место квадрат имеет к отнимаемому от него гномону; значит, и все
цилиндры в целом цилиндре ко псом цилиндрам в описанной фигуре
будут иметь то же самое отношение, как все квадраты к (величине),
равной вместе взятым первому квадрату и отнимаемым от всех осталь-
'*"'¦ ных гномонам. И все квадраты будут менее полтора раза взятой (ве-
(величины), равной первому квадрату вместе со всеми отнимаемыми от
остальных гномонами, так как опи будут более чем втрое больше квад-
квадратов па одинаково превышающих одна другую (прямых) за исшноче-
*) Иными словами, ¦ ,-
*• 14-14---.-Кп-1)*<~<14-24--..+»¦*. ....
О КОНОИДАХ И СФЕРОИДАХ
нием квадрата па наибольшей; значит, цилиндр, имеющий то же осно-
основание, что сегмент, и ту же ось, будет менее чем в полтора раза больше
описанной фигуры, что невозможно, так как он в полтора раза больше
конуса W. Значит, пололииа сфероида не будет меньше конуса *?.
Поскольку же она не будет ни больше, ни меньше, то значит, она будет
ей раина [11].
XXVIII
И если сфероид будет рассечен проходящей через центр плоскостью,
не перпендикулярной к оси, то томно так же половина сфероида будет
вдвое больше конического сегмента, имеющего те же самые основание
и ось, что и сегмент коноида {рис. 31}.
Действительно, рассечем (так) сфероидальную фигуру; если, кро-
кроме того, рассечь ее другой плоскостью, проходящей через ось и пер-
перпендикулярной к (первой) секущей плоскости, то сечением фигуры
Рис. 31.
будет эллипс АВГД с центром 0, а сечением плоскости, рассекшей фигу
РУ. будет прямая АГ; последняя будет проходить через 0, поскольку
рассматриваемая плоскость предполагается проведенной через центр.
Таким образом, получится некоторый эллипс на диаметре АГ, ибо отсе-
отсекающая плоскость предполагается проведенной не под прямым углом
к оси. Проведем параллельно АГ прямые КЛ, MN, касающиеси оллипса
в В и Л, затем на КЛ и MN восставим плоскости, параллельные той,
которая на АГ; эти плоскости будут касаться сфероида и точках В и А,
соединяющая ВД пройдет через в, и точки В, Д будут вершинами полу-
получившихся сегмоптип, а ВО, 6Д — их осями. Теперь можно найти ци-
цилиндр, имеющий ось BG, па поверхности которого будет находиться
рассматриваемый эллипс па диаметре АГ; после же его построения полу-
получится некоторый цилиндрический сегмент, имеющий одни и те.же осно-
основание и ось с полусфероидом; далее можно также найти и конус с вер-
вершиной в точке В, па поверхности которого, будет находиться: рассмат-
рассматриваемый эллипс на диаметре ЛГ. После его построения получится
некоторый конический сегмопт, имеющий те же основание и ось, что
¦и сегмент сфероида. Я утверждаю, что половина сфероида будет вдвое
больше итого конуса. : . ,, ,_
216 АРХИМЕД
Пусть будет конус Чг в два раза больший упомянутого конического
сегмента. Ec.iiи половина сфероида не ракпа конусу Чг, то пусть сначала
она, если возможно, будет больше; тогда я вписываю в полошшу сфе-
сфероида некоторую телесную фигуру и описынаю другую, составленную
из цилиндрических сегментов равной высоты, так, чтобы описанная
фигура была больше вписанной на величину меньшую той, на которую
половила сфероида больше конуса W. Теперь подобно предыдущему
докажем, что кписанпая в половину сфероида фигура будет больше кону-
конуса Чг и что цилиндрический сегмент, имеющий те же основание и ось,
что и сегмент сфероида, будет в полтора раза больше конуса *?, но
более чем в полтора раза больше фигуры, вписанной в половину сфе-
сфероида, что невозможно. Значит, половина сфероида не будет больше
конуса W.
Если бы половина сфероида была меньше конуса W, то впишем
в половину сфероида некоторую телесную фигуру и опишем около нее
другую, составленную мз цилиндрических сегментов одинаковой высоты,
так, чтобы О1гисанная фигура была Польше вписанпой на величину,
меньшую той, на которую конус W больше половины сфероида. Затем
опять подобно предыдущел1у докажем, что описанная фигура будет
меньше котгуса *Р' и что цилиндрический сегмент, имеющий те же самые
основание и ось, что и сегмент сфероида, будет п полтора раза больше
описанной фигуры, что невозможно. Таким образом, половина сфероида
пе будет и меньше конуса W. Поскольку же она не больше и не меньше,
то должна быть равна. Теперь становится явным то, что требовалось
доказать [11].
XXIX
Если любую сфероидальную фигуру рассечь плоскостью, перпенди-
перпендикулярной к оси, но не проходящей через центр, то меньший сегмент к ко-
конусу с теми же основанием и осью, чти и у сегмента, будет иметь то же-
самое отношение, чтпо вместе взятые половина оси сфероида и ось боль-
большего сегмента к оси большего сегмента {рис. 32}.
Пусть будет какой-нибудь сегмент сфероидальной фигуры, отсе
ченний плоскостью, перпендикулярной к оси, но не проходящей через
центр; если рассечь его другой плоскостью, проходящей через ось,
то сечение фигуры будет эллипс АПГ, диаметр сечения и ось сфероида
BZ, центр 0, сечение же плоскости, отсекающей сегмент, будет прямая
АГ; последняя образует с BZ прямые углы, так как рассматриваемая
плоскость предположена перпендикулярной к оси; пусть отсеченный
сегмент, вершина которого в точке В, будет меньше половины сфе-роида
и пусть ZII равна Вв. Требуется доказать, что сегмент с вершиной
в точке В к конусу, имеющему с сегментом то же самое оспопапие и ту
же ось, будет иметь то же самое отношение, что ДП к AZ.
Пусть будот цилиндр, имеющий то же самое оспование и ту же ось,
что и меньший сегмент; пусть также будет конус W, который к конусу,
имеющему то же основание (и ту же ось, что и сегмент), имеет то же
отношение, что ЛН к AZ; я говорю, что конус W будет ранен сегменту,
имеющему вершиной точку В.
Действительно, если он не равен, то пусть сначала, если возможно,
будет меньше. Тогда я вписываю в сегмент телесную фигуру и описы-
описываю около него другую, составленную из имеющих равную высоту
цилиндров, таким образом, чтобы описанная фигура превосходила впи-
С) КОНОИДАХ И СФЕРОИДАХ
217
санную на величину меньшую той, на какую сегмепт сфероида меньше
конуса Чг. Так как описанная фигура, будучи больше сегмонта, превос-
превосходит вписанную на величину меньшую той, на которую сегмент более
z
/
//
Л"
\N
х М
е \
л
в
J
N
и г
0
0
и
0
\
\
\
\
\
Рис. 32.
конуса, то ясно, что вписанная фигура больше конуса У. Пусть ВР
будет третьей частью ВА.
RF = -g-BA
Так как ВН втрое больше В0,
пи — зве
а ВЛ птроо больше ВР,
нд-знр
то ясно, что ДН будет втрое больше 0Р;
ди = зер
тогда цилиндр, имеющий то же самое оснонание, что и сегмент, и ось ВД,
имеет к конусу с теми же оснопанисм и осью такое же отношение, как
ДН к ЭР.
цилиплр ВЛ _ ЛН
кину с ЛВГ ~~ 6Р
Упомянутый же конус имеет к конусу V то же самое отношение, что
AZ к АИ.
ЛИГЛ7.
конус ЧГ ~ "Д11
218 АРХИМЕД
Теперь, в переставленной пропорции цилиндр, имеющий с сегментом
те же самые основание и ось, к конусу У будет иметь то же отношение,
- :. .. ЧТО AZ К 6Р. "... :
пилиндр ИД UZ
копус"*1' W
Теперь отложим линии, обозначенные EN, количество которых равно
количеству отрезков па прямой ВД, а величина каждой равна ZA;
пусть также каждая из линий ЕО равна будет ВД; тогда каждая из N0
будет вдвое больше ©Д. Приложим к каждой из них некоторую пло-
площадь, имеющую шириной ВД, так, чтобы каждая из фигур с диаметром
была квадратом. Затем от первого квадрата отнимем гномон, имеющий
ширину, равную BE, от второго — гномон с шириной, равной I3X,
и таким же образом от каждой следующей площади будем отнимать гно-
гномон, имеющий ширину, на единицу меньше ширины предшествующего
ему отнимаемого гномона; тогда гномон, отнимаемый от первой площади,
будет ранен прямоугольнику между BE, EZ *), и остающаяся площадь,
приложенная к N0 с избытком в виде квадрата, будет иметь сторону
избытка равной ДЕ; отнимаемый от второй площади гномон равен пря-
прямоугольнику между ZX, ХВ, я остающаяся площадь, приложенная к N0
с избытком в виде квадрата, {будет иметь сторону избытка равной 2ДЕ)
и нее остальные будут иметь подобно этим. Плоскио грани всех цилин-
дрон, из которых составляется вписанная в сегмент фигура, продол-
продолжим до поверхности цилиндра, имеющего те же самые основание и ось,
что и сегмепт; тогда весь цилиндр окажется разделенным ыа цилиндры,
количество которых будет равпо количеству цилиндров в описанной
фигуре, а величина равна наибольшему из них. Теперь первый цилиндр
в целом цилиндре, имеющий ось ДЕ, к первому цилиндру во вписанной
фигуре с той же осью ДЕ будет иметь то же самое отношение, что квад-
квадрат на ДГ к квадрату на КЕ.
цилиндр ABA _ ДГ2
цилиндр ККД~ ке2
Это отношение будет таким же, которое прямоугольник между ВД
и AZ имеет к прямоугольнику между BE и EZ. i
ДГа ВД- AZ
KEi-Btl-EZ
Итак, один цилиттдр имеет к другому то же самое отношение, что первая
площадь к отнимаемому от псе гномону. Точно так же и каждый из
остальных цилиндров к целом цилиндре, имеющих ось, равную ДЕ,
к соответствующему ему цилиндру во вписанной фигуре с той же самой
осью будет иметь то же отношение, что занимающая одинаковое с ним
место площадь к отнимаемому от нее гномону. Теперь плюются некото-
некоторые величины, а именно цилиндры во всем цилиндре, и другие величи-
величины, приложенные к HN площади, имеющие ширину, равную ВД,
: в одинаковом количестве с упомянутыми цилиндрами и находящиеся
попарно в том же самом отношении, и первые цилиндры находится в от-
отношениях с другими цилиндрами, а именно теми, которые во вписан-
вписанной фигуре, причем последний цилиндр первого ряда не имеет себе
соответствующего, а также площади, (относящиеся) к другим шгоща-
*) Действительно, если учесть, что 2Д—ВЛ-{-2Аб, то рассматриваемый пгомон будет ранен
29)ил B19 4ЕЛ)ЕЛ-= В \«+2Лв- ВД—2Д©-ЕД—Е&' = Вд!—ЕД*+2дв-ВЕ=ВЕШД->-ВД}+
)ВЕЕ
О КОНОИДАХ И СФЕРОИДАХ 219
дям, а имсптто к отнимаемым от них (гномонам), причем соответствую-
соответствующие будут в тех jkc самых отношениях, последняя же площадь не имеет
¦ себе соответствующей; теперь ясно, что все первые цилиндры ко всем
вторым будут иметь то же самое отношение, что все упомянутые пло-
площади ко всем гномонам; значит, цилиндр, имеющий с сегментом то же
самое основание и ту же ось, ко вписапной и сегмент фигуре будет иметь
то же самое отношение, что псе площади ко всем гномонам. И так как
имеются некоторые отложенные равные линии JNO, и к каждой при-
приложена некоторая площадь с избытком в виде квадрата, причем стороны
избытков одинаково превышают одна другую, причем разность равна
наименьшей стороне, а также имеются и другие площади, приложенные
к EN, имеющие ширину, равную БД, в количестве, одинаковом с первы-
первыми, а по величине равные каждая наибольшей из них, то ясно, что нее
площади, каждая из которых раппа наибольшей, ко всем другим пло-
площадям будут иметь отношение меньше того, которое EN имеет к прямой,
равной вместе взятым половине N0 и третьей части ЕО (предложение
III). Таким образом, ясно, что эти же самые площади ко всем гномонам
будут иметь отношение больше того, которое имеет SN к прямой, рав-
равной имеете взятым половине N0 и двум третям ЕО; аначит, цилиндр,
имеющий с сегментом то же самое основание и ту же ось, ко вписапной
в сегмент фигуре имеет большее отпошение, чем NE к прямой, равной
вместе взятым половине N0 и двум третям SO. Но EN равна AZ,
половина N0 равна Д6, а дне трети SO равны ДР; значит, весь цилиндр
ко вписанной в сегмент фигуре имеет большее отношение, чем AZ
к 0Р. Но отношение AZk ©P, как доказано, равно тому, которое тот же
самый цилиндр имеет к конусу W; значит, цилиндр имеет ко вписанной
фигуре большое отношение, чем к конусу W, что невозможно, ибо дока-
доказано, что вписанная фигура будет больше конуса V. Таким образом,
сегмент сфероида не будет больше конуса W.
Но пусть, если возможно, он будет меньше его. Тогда оннть впи-
впишем в сегмент некоторую телесную фигуру и опишем около него
другую, состанленную из цилиндров равной высоты, так, чтобы опи-
описанная фигура превосходила вписанную на величину меньшую той, на
которую конус V будет больше сегмепта, и все остальное мы устроим
совершенно так же, как и раньше. Теперь, поскольку вписанная фигура
меньше сегмента, а описанная превышает ее на величину мепыпую той,
на какую конус ^? больше сегмепта, то ясно, что и описанная: фигура
будет меньше конуса "У. Затем опять первый цилиндр в целом цилиндре,
имеющий ось ДЕ, к первому цилиндру в описанной фигуре с той же
самой осью будет иметь то же самое отношепие, что последняя площадь
из приложенных к SN и имеющих ширину, равную БД, к себе самой,
так как оба рассматриваемых цилиндра равны; второй же цилиндр в це-
целом цилиндре, имеющий ось, равную ДЕ, к соответствующему ему
цилиндру в описанной фигуре имеет то зке самое отношение, что первая
из приложенных к SN площадей с шириной, равной ВЛ, к отнимаемому
от нее гномопу, и каждый из остальных цилиндров в целом цилиндре,
имеющих ось, равную ДЕ, к соответствующему ему цилиндру в описан-
описанной фигуре имеет то же самое отношепие, что занимающая то же место
площадь среди приложенных к SN к отнимаемому от нее гномопу, при-
причем первым считается последний *). Теперь все цилиндры в целом ци-
цилиндре ко всем цилиндрам в описанной фигуре будут иметь то же, самое
*) Имеггио тот, от которого ничего не отнимается, вес же остальные следуют 8а ним в своем
порядке, который на нашем чертеже будет 4. 1, 2, 3.
220
АРХИМЕД
отношение, что все площади, приложенные к SN, к площади, рашюй
вместе взятым занимающей последнее мгето площади и всем гномонам,
отнимаемый от других, на основании тех же соображений, что и выше.
Поскольку доказано, что все, площади, приложенные к HN, ко всем
площадям, приложенным к N0 с избытком в виде квадрата за исключе-
исключением наибольшей, имеют'отношение большее того, которое SN имеет
к прямой, равной вместе взятым половине N0 и третьей части НО *),
то ясно, что вти же самые площади к остаткам, которые вместо равны
площади, занимающей последнее место, и всем гномонам, отнимаемым
от остальных, будут иметь отпошение меньшее того, которое SN имеет
к прямой, равной имеете взятым половипе iNO и двум третям ВО. Теперь
ясно, что цилиндр, имеющий то же оспопаттис, что и сегмент, и ту же
ось, будэт к описанной фигуре иметь отношение меньшее того, капог
ZA имеет к ВР. Отношение же AZ к 6Р равно отношению упомянутого
цилиндра к конусу W; лначыт, итог цилиндр к описанной фигуре имеет
отиошение меньшее, чем к конусу Ч'', что невозможно, так как, согласно
доказанному, описанная фигура меньше конуса V. Значит, сегмент
сфероида не будет меньше этого конуса. Поскольку же он не будет
ни больше ни мспьше, то, значит, он будет ранен последнему.
XXX
И такэк?. если сфероид рассечь плоскостью, не перпендикулярной к оси
и не проходящей через центр, то меньший его сегмент к коническому сег-
сегменту с тем же основанием и той окр. осью будет иметь то же самое
отношение, что прямая, равная
вместе взятым половине прямой,
соединяющей вершины полнивших-
полнившихся сегментов, и оси большего сег
мента, имеет к оси большего
сегмента {рис. 33}.
Рассечем какую-нибудь сфе-
сфероидальную фигуру, как сказано;
если рассечь ее другой плоскостью,
проходящей через ось и перпенди-
перпендикулярной к секущей плоскости, то
сечение фигуры будет эллипс АВГ,
а плоскости, секущей фигуру, пря-
прямая ГА; параллельно АГ пропедем
111? и 2Т, касающиеся конического
сечения в В и Z, и восставим на них
плоскости, параллельные той, ко-
которая проходит через АГ; они будут
также касаться сфероида в В и Z,
и вершинами получипщихся сег-
сегментов будут точки В, Z. Теперь
• » прииодем прямую, соединяющую
Рис. 33. вершины сегментов; пусть она
будет BZ; она пройдет через центр;
пусть центром сфероида и аллипса будет <д. Так как фигура предпола-
предполагается рассеченной плоскостью, пе перпендикулярной к оси, то сечение
*) Предложение II.
О КОНОИДАХ И СФЕРОИДАХ 221
будет эллипсом с диаметром ГА. Возьмем теперь цилиндр, имеющий
ось на одной прямой с ВД, на поверхности которого будет находиться
эллипс, что на диаметре АГ, а также конус, имеющий вершину в точке
В, на поверхности которого будет тот же лллипс с диаметром АГ; тогда
получится некоторой цилиндрический сегмент, имеющий то же самое
основание и ту же ось, что и сегмент сфероида, а также конический сег-
сегмент с теми же основанием и осью. Требуется доказать, что сегмент
сфероида с вершиной В к коническому сегменту с теми же основанием
и осью имеет то же отношение, что ATI к AZ; пусть ZH равна 6Z.
Возьмем некоторый колус Y, имеющий к коническому сегменту
с теми же основанием и осью, что и у сегмента сфероида, то же самое
отношение, что АН к AZ. Если теперь сегмент сфероида по рапен иону-
су W, то пусть сначала, если возможно, он будет больше. Тогда я пписываю
в сегмент сфероида телесную фигуру и описылаю около него другую,
составленную из цилиндрических сегментов одинаковой высоты, так,
чтобы описанная фигура превышала «писанную на величину меньшую
той, на какую сегмент сфероида больше конуса Т. Тогда подобно преды-
предыдущему докажем, что вписанная фигура больше конуса W, а цилинд-
цилиндрический сегмент, имеющий те же основание и ось, что и сегмент
сфероида, ко вписанной фигуре имеет отношение большее, чем к кону-
конусу 4f, что невозможно. Итак, сегмент сфероида не больше конуса XF.
Но пусть он, если возможно, будет меньше. Тогда опять впишем
в сегмент телесную фигуру и опишем около него другую, составленную
из цилиндрических сегментов ралпий величины, так, чтобы описанная
фигура превышала лписанпую на величину меньшую топ, на какую
конус ~? больше сегмента.
Опять на основании таких же рассуждений докажем, что описанная
фигура меньше конуса х? и что цилиндрический сегмент с теми же осно-
основанием и осью, что и у сегмента сфероида, будет к описанной фигуре
иметь меньшее отношение, чем к конусу 4f, что невозможно. Значит,
сегмент сфероида по будет также и меньше конуса. Теперь становится
явным то, что требовалось доказать.
XXXI
Если любую сфероидальную фигуру рассечь плоскостью, перпендику-
перпендикулярной к оси и не проходящей через центр, то больший сегмент к кону-
конусу, имеющему с ним то же самое основание и ту -же ось, имеет такое
же отношение, как прямая, равная вместе взятым половине оси сферо-
сфероида и целой оси меньшего сегмента, к оси меньшего сегмента (рис. 34}.
Рассечем какой-нибудь сфероид, как сказано; если рассечь его дру-
другой плоскостью, проходящей через ось и перпендикулярной к секущей
плоскости, то сечением фигуры будет эллипс ЛВГ, диаметр которого
и ось фигуры будет ВД, а сечением секущей плоскости будет прямая ГА;
она, конечно, перпендикулярна к ВД. Пусть большим из оегмеитоп будет
тот, у которого вершина В, а центр сфероида — точка в. Приложим пря-
прямую ДП, равную Лв, и BZ, равную ей же; требуется доказать, что сег-
сегмент сфероида с вершиной В к конусу с тем же самым основанием, что
и у сегмента, и той же осью будет иметь такое же отношение, как ETI к ЕД.
Рассечем сфероид плоскостью, проходящей через центр и перпен-
перпендикулярной к оси, и пусть на полученном круге будет конус, имеющий
вершиной точку Д; тогда весь сфероид будет вдвое больше сегмента,
имеющего оышпанпем круг на диаметре КЛ, а вершиной точку Д,
222
АРХИМЕД
упомянутый же сегмент в два раза больше конуса, имеющего то же
основание, что и сегмент, и ту же ось {это доказано) *); значит, целый
сфероид будет в четыре ра»а больше упомянутого конуса. Этот же конус
с конусом, имеющим основанием круг на диаметре А Г, а вершину
/г
в точке Д, находится в отношении, составленном из того, которое прямая
©Д имеет к ЕД, и того, которое квадрат на К© имеет к квадрату на ЕА;
но отношение, которое квадрат на К© имеет к квадрату па ЕА,
будет тем же самым, которое прямоугольник между В© и ©А имеет
к прямоугольнику между BE и ЕД.
ке2 _ ве- ва
ЕА а ~~ bEE'V
Пусть теперь отношение 0Д к ЕД будет раппо отношению некото-
некоторой прямой ЕД к ©Д;
вд _ г,\
ед ~ уд
тоща прямоугольник между ЕД и В© к прямоугольнику между Вв
и ВД будет иметь такое же отношение, как А© к ДЕ.
ШТё& = "дё
Отношение же, составленное из того, которое прямоугольник между ЕД,
©В имеет к прямоугольнику между В©, ©Д, и из того, к*то;ни> прямо-
прямоугольник между В©, ©Д имеет к (прямоугольнику) можду BE, ЕД,
будет тем же самым, которое прямоугольник между ЕД, В© имеет
к прямоугольнику между BE, ЕД;
ЕД-вВ Вв-вД ЕД-РС-)
ве-ед веГёд ^ ш?7ед -. •
тогда конус, имеющий основанием круг на диаметре КА, а вершиной
точку Д, с конусом, имеющим основанием круг на диаметре А Г, а вер-
шштсн точку Д, будет находиться в таком же отношении, как прямо-
прямоугольник между ЕД, В© с прямоугольником между BE, ЕД.
КЛЛ
ЛГД
ЕЛ ¦ В0
bli-ЁД
•) В предложении XXVII.
О КОНОИДАХ И СФЕРОИДАХ 223
^ Конус же, имеющий основанием кругла диаметре АГ, а вершиной точку
Д, к сегменту сфероида с теми же основанием и осью имеет такое же
отношение, как прямоугольник между БЕ, КД к прямоугольнику между
ZE, ЕД.
кпнуе АГД BE • ЕД
сегмент АГД ZE ¦ ЕЛ
[то ость как БЕ к EZ, ибо сегмент, меньший половины сфероида, к ко-
пусу с теми же основанием и осью, что и у сегмента, имеет, согласно
доказанному, такое же отношение, как прямая, рашшя вместе взятым
половине оси сфероида и оси большего сегмента, к оси большего сег-
сегмента; это же отношение будет го, какое ZE имеет к BEJ, значит, конус,
содержащийся в половине сфероида, к сегменту сфероида, меньшему его
половины, имеет то же самое отношение, что прямоугольник между ЕД»
Б В к прямоугольнику между ZE, ЕД.
конус КЛА __ ЕД- Вв
сегмент АГД ZE -Ед
Поскольку целый сфероид к конусу, содержащемуся в половине сфе-
сфероида, имеет такое же отношение, как прямоугольник между 7Л1, ЁД
к прямоугольнику между Вв, ЕД,
_сфероид Ztf-SA
конус КЛД ~ В« -йд
[ибо первый прямоугольник вчетверо больше второго], копус же, что
в полоиипе сфероида, к сегменту, меньшему половины сфероида, имеет
то же самое отношение что прямоугольник между Е Д, В6 к (прямоуголь-
(прямоугольнику) между ZE, ЕД,
Гкгнус КАЛ ЕА ¦ Вв
сегмент ЛГД ~ ZE ЁД
то и целый сфероид к своему мепыпему сегменту имеет то же отноше-
отношение, что прямоугольник между ZH, ЕЛ к прямоугольнику между ZE, ЕД;
сфероид ZH-'ЕД
сегмент АГД " ZB. ЕД
итак, больший сегмент сфероида имеет к меньшему то же отношение,
что избыток, на какой прямоугольник между ZII, ЁД превышает
прямоугольник между ZE, ЕЛ, имеет к прямоугольнику между ZE, ЕД.
см-иснт АГВ ZP-SA - ZE-KA
Ссгшсит АГД 7К-ЕЛ
Но прнмоуголышк между ZH, SA превосходит прямоугольник между
ZE, ЕД на вместе взятые прямоугольники между ЁД, ЕН и ZE, НЕ*),
ЯП* ЕД — ZE ¦ ЕД ^=* ЕД ¦ И!XI ¦*¦[- Z. )?¦ Е.1?
значит, больший сегмент сфероида имеет к меньшему то же самое отно-
отношение, которое (величина), ранная обоим прямоугольникам между
ЕД, ЕН, и ZE, ЕЕ, имеет к прямоугольнику между ZE, ЕД. Но мень-
меньший сегмент сфероида к конусу, имеющему с ним те же основание
и ось, относится, как прямоугольник между ZE, EA к прямоугольнику
между BE, ЕД,
сегмент АГД _ ZIC- ЕД
АГД~ "" ВКЛЁД
[ибо последнее отношение то же, что и у ZE к BE], конус же, что
*) Действительно, ZH-BA-ZE-EA-^ZB- ЕД+ЕН-ЕД- ZK-EA+ZE-EE—ЕН-ЕД | ZE-EE.
224 АРХИМЕД
в меньшем сегменте, к конусу, что в большем сегменте, имеет то же
самое отношение, что прямоугольник между BE, ЕД к киадрату на BE,
конус ЛГА _ BE- ЕЛ
конус АГВ ~ иЕ2
ибо эти конусы находятся в отношении их высот, так как они имеют одно
и то же оскоьание; таким образом, больший сегмент сфероида но впи-
саппому в него конусу относится, как (величина), равная вместе взя-
взятым прямоугольникам между ЗД, ЕН, и ZE, НЕ к квадрату на BE.
сегмент ЛГВ ЕА•ЕН+ZE-ВВ
конус ЛГВ BV?
Это же отношение будет тем, которое прямая ЕН имеет к ЕД,
сегмент АГВ _ ЕН
конус АГВ ~ ЕД
ибо прямоугольник между SA, ЕН к прямоугольнику между ЕД, ЕА
имеет такое лее отпошение, как ЕН к ЕД, а прямоугольник на ЕЕ,
ZE к прямоугольнику между ZE, 6E имеет такое же отношение, как
ЕН к ЕД;
ав-яв_.Ен
ZE-вЕ К&
действительно, SE имеет к 6Е то же самое отношение, что ЕН к ЕЛ
SF. .ЕН
ек ~ ед
вследствие того, что ЕД, 6Д, ДЕ составляют пропорцию, и вД рав-
равна НД *). Теперь (величина), равная вместе взятым прямоуголь-
прямоугольникам между ЕД, ЕН и ZE, SE к (величине), равной вместе взятым
прямоугольникам между ЗЛ, ЕД, и ZE, 6Е, будет иметь то ню отноше-
отношение, что ЕН к ЕД. Затем квадрат на ЕВ равен обоим прямоугольникам
между ЕД, ЕД и ZE, ©E,
ЕН8 = ЕЛ-Кй-| ZE-8E
так как квадрат на Вв равен иримоугольняку между ЕД, ЕЛ **),
Вв* = ЕД¦ЕЛ
а избыток, на который квадрат па BE превышает квадрат на Вв, равен
прямоугольнику между ZE, BE, так как ВВ и BZ равны ***).
BE8- Be2=ZE.«K
Теперь ясно, что больший сегмент сфероида с конусом, имеющим
те же основание и ось, находится п том же отношении, как ЕЙ с ЕД.
, XXXII
И также, если сфероид рассекается плоскостью, не перпендикулярной,
к оси и не проходящей через центр, то бблыиий его сегмент к коническому
сегменту с теми же основанием и осью будет иметь такое же отношение,
какое прямая, равная вместе вяятым половине {прямой), соединяющей
. .. з\ ел зд—до ел 30 гвл
•) Мм имеем "Tg" — Тр" • ИЛИ «л—'Kp~"\v~ ' т" е" ТП?" ~ ТР""' ипи» вследствие равенства
„„ Е» НЛ л Ев|вВ НЛ4-ЛЕ НЕ ПЕ
вл и ПЛ: с.„- — -г^-- Отсюда «присоединением» —{--— =—=^ или ¦-_^=.-_ .
**) Так кпк В«=вД и ©л!=ЕЛ-ЕД, согласно пропорции, определяющей точку Z.
•*•> Действительно, »Е«—Вв*—(BE-fBtt)tW3—Вв>—EZ-Ktt.
О КОНОИДАХ И СФЕРОИДАХ
п
т
де
ЕД
вершины полученных сегментов, и оси меньшего сегмента, имеет к оси
меньшего сегмента {рис. 35}.
Рассечем сфероид плоскостью, как сказано выше; если рассечь его
другой плоскостью, проходящей через ось и перпендикулярной к се-
секущей плоскости, то сечение
фигуры будет эллипс ЛВГД,
а плоскости, секущей фигуру,
— прямая ГА; параллельно
ЛГ проводом ПР и ЕТ — ка-
сательные к эллипсу в Б, Д—
и восставим на них плоскости,
параллельные той, которая
проходит через ЛГ; охи пло-
плоскости будут касаться сферо-
сфероида п В, Д, и точки В, Д бу-
будут вершинами получивших-
получившихся сегментов. Проведем ВД,
соединяющую вершины полу-
получившихся сегментов; послед-
последняя пройдет через центр.
Пуста, центр будет в, сегмент
же, больший половины сфе-
сфероида, — тот, вершина которого В; приложим прямую ЛИ, равную Дв,
и BZ, равную ой же. Требуется доказать, что больший сегмент сфероида
к коническому сегменту с теми же основанием и осью имеет то же самое
отношение, что ЕН к ЕД.
Рассечем сфероид через центр плоскостью, параллельной той, кото-
которая проходит черна А Г, и впитом в половину сфероида конический
сегмент, имеющий вершиной точку Д; пусть отношение Дв к ЕД будет
равно тому, которое некоторая прямая ЁД имеет к 6Д.
ЗД : .
Г"ёд~ . ,-.-•:- > ¦ ..
Тогда подобно предыдущему докажем, что конический сегмент, впи-
вписанный в половину сфероида, к коническому сегменту, вписанному
п меньший сегмент сфероида, будет иметь то же самое отношение, что
прямоугольник между ЕД, Вв к (прямоугольнику) между BE, ЕД,
Рис.
кон. еегм. КАД
НА-ИВ
:ве-'ед
кон. еегм. АГД"
¦ и конический сегмент, вштсаппым и меньший ссгметтт сфероида, к тому
сегменту, в который оп вписан, будет иметь то же самое отношение,
что прямоугольник между БЕ, ЕД к прямоугольнику между ZE, ЕД;
ной, еггм. АГЛ _ ЕЕ• Ед
еегм. сфер. АГД ~ ZE- ЕД
теперь конический сегмент, вписанный в половину сфероида, будет
относиться к меньшему сегменту сфероида, как прямоугольник между
ЕД, Вв к прямоугольнику между ZE, ЕД.
кор. сегм. КАЛ __ ЕЛ ¦ В0
сени. сф..р. ЛГД ~ ZE- ЕД
Теперь целый сфероид к коническому сегменту, вписанному в по-
половину сфероида, будет иметь то же самое отношение, что нримоуголь-
15 Архимед . •
226 АРХИМЕД
ник между ZH, 5Д к прямоугольнику между В0, SA,
сфероид АПГД _ ZH-SA
кон. сегм. КЛД "" В0- ЕД
ибо каждый предыдущий в четыре раза больше своего последующего;
упомянутый же конический сегмент к меньшему сегменту сфероида
будет иметь то же самое отношение, что прямоугольник между ЕД,
Вв к прямоугольнику между ZE, ЕД;
коп. сегм. КЛД ЕД • ВЭ
сегм. сфер. АГД ZE-ЕД
тогда целый сфероид к своему меньшему сегменту будет иметь то же са-
самое отношение, что прямоугольник между ZII, SA к прямоугольнику
между ZE. ЕД,
сфвроид ZH-ЕЛ
сегм. сфер. АГД ZE-ЕД
а больший сегмент будет иметь к меньшему то же самое отношение, что
избыток, па который прямоугольник между ZH, ЕД превышает прямо-
прямоугольник менаду ZE, ДЕ, имеет к ZE, ЕД.
сегмент А ВГ _ |ZH- БД — ZE- НА
сегмент АДГ ~ Zifi- кд
Меньший же сегмент ко вписанному в него коническому сегменту имеет
то же самое отношение, что прямоугольник между ZE, ЕД к прямоуголь-
прямоугольнику между BE, ЕД,
сегмент АДГ __ ZE-EA
копГсёгм. АДГ ~~ ЙЕ.ЕА
[ибо доказано, что он будет иметь то же отношение, что ZE к BE]; кони-
конический же сегмент, вписатшый в меньший сегмент сфероида, к кониче-
коническому сегменту, вписанному в больший сегмент сфероида, будет иметь
такое же отношение, как прямоугольник между BE, ЕЛ к квадрату
па БЕ;
КОн. сегм. АГД _ ВЕ-ЕА
кон. сегм. АГВ ~ ВЕг
действительно, упомянутые конические сегменты имеют отношение
своих высот, так как основание у них одно и то же, а их высоты имеют
то же отношение, что ДЕ к ЕВ; теперь больший сегмент сфероида ко
вписанному иного коническому сегменту будет иметь то же отношение,
что избыток, на который прямоугольник между HZ, SA превышает
прямоугольник между ZE, ЕД, имеет к квадрату па BE.
сегмент АГВ _ HZ-SA — ZT5-KU
иен. сегм. АГВ Ю?
Это же отпошспйе, как мы докажем подобно предыдущему, будет тем
же самым, которое ЕН имеет к ЕД.
С) СПИРАЛЯХ
Архимед приветствует Досифея
В тех книгах, которые были посланы через Гераклида, ты имеешь
запись большей части тех ранее посланных Конону теорем, доказатель-
доказательства которых ты все время просил меня дать; в этой же книге я посы-
посылаю тебе запись некоторой части из оставшихся. Не удивляйся, что
я публикую их доказательства только после долговременной задержка;
ото произошло вследствие того, что я хотел сначала показать их людям,
занимающимся математикой и пожелавшим в них разобраться; ведь
сколько геометрических теорем, которые в начале казались плохо обос-
обоснованными, с течением времени получили окончательную разработку;
Конон скончался, так и не имев достаточно времени для того, чтобы
в них разобраться; а он мог бы сделать их совершенно ясными, нашел бы
доказательства и всех этих теорем, прибавил бы к ним и многие другие
и далеко продвинул бы вперед геометрию; мы ведь хорошо знаем
присущую ему незаурядную способность понимания математики и не-
необычайное трудолюбие. Теперь же, хотя много лет уже прошло после
смерти Конопа, мы еще не слышали, чтобы кто-нибудь продвинул вперед
решение хотя бы одной из поставленных задач.
Все эти задачи я хочу представить тебе одну за другой, поскольку
вышло так, что после тех задач, которые не были мною решены,
я прибавил еще две задачи для того, чтобы тех, которые утверждают,
что они все открыли, и не приводят никаких доказательств открытого,
можно было бы уличить и заставить согласиться с тем, что они открыли
невозможное. Поэтому мы сочли необходимым сообщить тебе и пере-
перечислить все эти задачи, упомянувши и те, доказательства которых уже
отосланы тебе, и те, которые отправляются в этой клиге.
Первая из этих задач была такова: для заданного тара найти пло-
плоскую фигуру, равную поверхности этого шара. Она первая и была
решена в изданной книге о шаре; действительно, после того как было
доказано, что поверхность всякого шара в четыре раза больше боль-
большого круга отого шара, стало ясно, что можно найти плоскую фигуру, рав-
равную поверхности этого шара. («О шаре и цилиндре», книга 1, XXXIII.)
Вторая задача: для данного конуса или цилиндра найти шар, равный
этому конусу или цилиндру. (Там же, кн. 11,1.) Третья: данный шар рас-
рассечь плоскостью так, чтобы его сегменты имели друг к другу заданное
15*
228 архимед
отношэние. (Там же, кн. II, IV.) Четвертая: данный.шар рассечь
плоскостью так, чтобы его сегменты имели поверхности, находящиеся
в заданном отношении друг к другу. (Там же, кн. JJ, III.} Пятая:
заданный сегмент шара сделать подобным другому данному сфериче-
сферическому сегменту. (Там же, кп. II, V.) Шестая: для двух заданных сег-
мзнтов одного и того же или же разных шаров найти некоторый сфери-
сферический сегмент, который был бы подобен одному из этих сегментов
и имзл бы поверхность, равную поверхности другого сегмента. (Там же,
кн. 11, VI.) Седьмая: от заданного шара отсечь плоскостью такой сег-
мэнт, чтобы к конусу с тзм же основанием, что у итого сегмента, и с рав-
равной высотой он имел заданное отношение, большее чем три к двум.
(Там же, кн. II, VII.)
Решения всех вышеупомянутых задач доставил тебе Гераклид,
а то, что было помещено после, было неверным. Ото были следующие
предложения: если какой-нибудь шар рассечен плоскостью на
неравный части, то больший сегмзнт будет иметь к меньшему двойное
отношзние большзй поверхности к меньшей. Что это неверно, вполне
ясно из того, что уже послано к тебе, ибо там находится следующее:
если какой-нибудь шар рассечь плоскостью, перпендикулярной к ка-
какому-нибудь диаметру этого шара, то. поверхность большего сегмента
'¦"¦¦ к поверхности меньшего будет иметь то ?ке самое отношение, что боль-
• ншй отрезок диаметра к меньшему, и что больший сегмент шара имеет
:- и мэныпзму отношении, которое меньше двойного, но больше полутор-
; ного отношения большей поверхности к меньшей. (Там же, кн. II,
VI11.) Неверной была и помещенная последней задача, а именно, что
': если рассечь диаметр какого-нибудь шара так, чтобы квадрат па боль-
большем отрезке был ранен утроенному квадрату на меньшем отрезке,
и через полученную точку перпендикулярно к диаметру провести рассе-
! мающую шар плоскость, то фигура такого же вида, какой является
'¦¦" большой сегмент этого шара, будет наибольший из всех других шаровых
¦ ¦ сегмзнтов, имеющих одинаковую поверхность. Что лто неверно, ясно
¦ ¦ из уже отосланных теорем, так как доказано, что полушарие является
наибольшим из всех сферических сегментов, ограниченных рапными
: поверхностями. (Там же, кн. II, IX.)
Ilocie этого были следующие предложения, касающиеся конуса.
Если парабола при неподвижном диаметре сделает полный оборот
•, ' вокруг диаметра как оси, то фигуру, описанную параболой, назовем
коноидом; если какая-нибудь плоскость касается коноидальной фигуры
и другая плоскость, проведенная параллельно касающейся, отсекает
некоторый сегмент коноида, то отсекающую плоскость назовем осно-
основанием отсеченного сегмента, а его вершиной — ту точку, в которой
другая плоскость касается коноида. Тогда, если упомянутую фигуру
рассэчь плоскостью, перпендикулярной к оси, то яспо, что сечение будет
кругом, и надлежит доказать, что отсеченный сегмент будет п полтора
раза больше конуса, имеющего то гке самое основание, что и сегмент,
•; и одинаковую высоту. («О коноидах и сфероидах», XXI.) Затем, если
от коноида отсочь два сегмента проведенными как-нибудь плоскостями,
то ясно, что полученные сечения будут эллипсами, если только секу-
¦"¦ ; щие плоскости не перпендикулярны к оси вращения, и надлежит дока-
доказать, что эти сегменты имеют друг к другу то же самое отношение, какое
• ' в квадратах имеют друг к другу прямые, проведенные параллельно оси
из вершин сегментов до секущих плоскостей. («Оконоидах и сфероидах»,
'- - XXIV.) Доказательств этих предложений я пока тебе не посылаю.
¦ •/¦
О СПИРАЛЯХ 229
После них были следующие предложения относительно спирали
{они в некотором роде представляют совершенно отличный класс задач,
не имеющий ничего общего с перечисленными выше), доказательства
их мы для тебя и написали в этой книге. Эти предложения такопы:
Если какая-нибудь лрямая и плоскости, равномерно вращаясь
вокруг одного своего конца, удерживаемого неподвижным, вернется
опять п исходное положение, и одновременно по вращающейся при-
примой равномерно движется некоторая точка, выходя из неподвижного
конца, то эта точка на упомянутой плоскости опишет спираль. Я утвер-
утверждаю, что площадь, заключенная между этой спиралью и прямой,
вернувшейся в исходное положение, будет третьей частью круга, опи-
описанного из неподвижной точки, как из центра, радиусом, равным
части прямой, пройденной движущимся точкой в течение одного оборота
этой прямой. (Предложение XXIV.)
И если какая-нибудь прямая касается спирали в самой крайней ее
точке, а другая лрямая, перпендикулярная к вращающейся и вернув-
вернувшейся в исходное положение прямой, проведена из неподвижного ее
конца до пересечения с касательной, то я утверждаю, что эта нроисден-
ная (до касательной) прямая будет равна окружности упомянутого
круга. (Предложение XV11I.)
И если вращающаяся прямая с движущейся по ней точкой сделает
несколько оборотов и вернется опять в исходное положение, то я ут-
утверждаю, что по отношению к площади, прибавившейся прп списыва-
списывании второго оборота спирали, площадь, прибавившаяся при третьем
обороте, будет вдвое больше, прибавившаяся при четвертом — втрое,
при пятом — вчетверо больше, и во всех последующих оборотах при-
прибавившиеся площади будут всегда больше площади, прибавившемся
при втором обороте, в число ран соответственно ряду последовательных
чисел, а площадь, описанная при первом обороте, будет шестой
частью площади, прибавившейся при втором обороте. (Предложение
XXVII.)
И если па части спирали, описанной в течение одного оборота,
ваять двв точки, соединить их прямыми с неподвижным концом вращаю-
вращающейся прямой линии, из неподвижной точки, как из центра, описать
два круга радиусами, равными этим соединяющим с неподвижным кон-
концом прямым, и меньшую из этих соединяющих продолжить, to я утвер-
утверждаю, что площадь, ограниченная дугой большего круга, находящейся
между упомянутыми прямыми с той же стороны, что и спираль, затем
самой спиралью и продолженном соединяющей прямой, будет иметь
такое же отношение к площади, ограниченной дугой меньшего круга,
той же самой частью спирали и соединяющей их концы прямой, какое
радиус меньшего круга вместе с двумя третями разности радиусов
большего и меньшего кругов имеют к радиусу меньшего круга вместе
с одной третью упомянутой разности. (Предложение XXV1J.1.)
В :>той книге я даю доказательства ятих и некоторых других пред-
предложений относительно спирали; при этом, как делается и и других гео-
• метрических сочинениях, предварительно излагаются нужные для их
доказательства предложения. При этом из лемм, находящихся в ранее?
изданных книгах, я и здесь пользуюсь следующей:
Если имеются две неравные прямые или площади, то, прибавляя
к себе самой разность, на которую большая превосходит меньшую, мож7
но превзойти всякую наперед заданную величину из тех, которые могут
иметь друг к другу отношение. ' ' ' -,-«.> '
?30 АРХИМЕД
I
Если некоторая точка равномерно *) движется по какой-нибудь
линии и на последней бер'утся две линии, то взятые линии будут иметь
друг к другу то же самое отношение, что и времена, в течение которых
точка прошла эти линии.
Пусть некоторая точка равномерно движется по линии ЛВ {рис. 1},
и на ной взяты две липии ГД, АЕ; пусть ZII будет время, в течение
которого она прошла ГД, а Н0 — время, п течение которого она про-
прошла ДЕ. Требуется доказать, что ли-
А ГАЕ" ния ^ имеет к ДЕ то же самое отно-
—*—¦—• шение, что и время ZII к Н6.
л '/. и в к Действительно, составим линии АД,
'—'—'—' ' '-*' * ДВ из линий ГД, ДЕ, складывая каж-
рЙС 1 дую из них произвольное число раз
саму с собой, лишь бы АД оказалась
больше ДВ; ватем пусть время ZH
' уложится в некотором времени ЛН столько же раз, сколько линия ГД
укладывается в АД, а время ©Н уложится во времени КН столько же
раз, сколько линия ДЕ укладывается в ДВ. Так как предполагается,
что точка равномерно движется по линии АВ, то ясно, что каждую
линию, равную ГД, она проходит в то же самое время, что и самое ГД;
отсюда следует, что и составленную линию АД она пройдет в такое же
время, каким будет составленное время ЛН, поскольку линия ГД в
линии АД и время ZH во времени ЛН содержатся одинаковое число
раз. Вследствие того же самого и линию БД точка пройдет в такое
же время, каким будет и время КН. Так как линия АД более ВД, то
ясно, что линию ДА точка пройдет в большее время, чем линию ВД, так
; что и время ЛН будет больше, чем время KIJ- Точно так же докажется,
что если составить какие-нибудь времена из времен ZH, H0, складывая
каждое из них произвольное число раз само с собой, так, чтобы одно
из полученных времен было больше другого, то и из линий, получен-
полученных сложением такое же число раз ГД и ЛЕ, будет больше та, которая
соответствует большему времени. Теперь ясно, что линия ГЛ будет
иметь к ДЕ то же самое отношение, что и время ZIT к времени 110 [1].
И
Если каждая из двух точек равломерно движется по некоторой линии
не одной и той же {для обеих точек) и на каждой из smux линий берутся
по две линии, из которых первые проходятся обеими точками в одинако-
одинаковое время, и точно так оке и вторые, то взятые липии будут иметь друг
к другу одно и то же отношение.
Пусть некоторая точка равномерно движется по линии АВ, а дру-
гая — но КЛ {рис. 2}; возьмем на АВ две линии ГД, ДЕ, а па КЛ —
липии ZH, II0; пусть точка, движущаяся по линии АВ, проходит
линию ГД во время, равное тому, в какое другая точка, движущаяся до
КЛ, проходит ZH, и точно так же пусть первая точка проходит линию
•) В подлиннике 1Сотах«'>е o,!>ti tavxip—буквально «равпоскоро сама с собой». У греков «ско-
«скорости» как самостоятельного понятия еще не было; скорость по существу была только качеством.
Различались более или менее скорые движения; термин «равноскорый» употреблялся при срав-
тгении скоростей двух тел; вот почему Лрхяпед еикцналько добавляет «равноокоро с а ж я
с в о б о й».
О СПИРАЛЯХ 231
А
Л
Г
Z
м
л
/1
N
И
в
3
И
к
АЕ во время, равное тому, в какое вторая точка проходит 110. Требуется
доказать, что ГД будет иметь к АЕ то же самое отношение, что 2Н
к Н0.
Пусть MN будет время, в течение которого первая точка проходит
линию ГА; тогда вторая точка в то же самое время пройдет ZH.
Далее, пусть NS будет время, в течение которого первая точка про-
проходит линию АЕ; тогда вторая точка в то же время пройдет В0;
и. одно и то же отношение будут иметь линия ГД к АЕ и время MN
к N В, а также линия ZH к Н0 и время MN
к NH. Теперь ясно, что ГД будет иметь к ДЕ то
же самое отношение, что ZII к Н6.
III
Для любого количества заданных кругов
можно найти прямую, которая была бы больше Рис. 2.
¦вместе взятых окружностей этих кругов.
Действительно, если около каждого круга описать многоугольник,
то ясно, что прямая, составленная из всех утих периметров, будет боль-
больше всех (вместе взятых) окружностей кругов.
IV
Если даны две неравные линии, а именно прямая и окружность круга,
то можно найти прямую, которая была бы меньше большей из задан-
заданных линий, но больше меньшей.
Действительно, если разность, на которую большая линия превос-
превосходит меньшую, повторить слагаемой такое число раз, чтобы результат
оказался больше данной прямой, и последнюю разделить на такое же
число равных частей, то одна такая часть будет меньше этой разности.
Теперь, если окружность будет больше прямой, то ясно, что после добав-
добавления одной такой части к прямой последняя будет больше, чем мень-
меньшая из заданных линий, но меньше, чем большая; если же окружпость
будет меньше, то после добавления одной та-
, ? , кой части к окружности последгшя будет
больше, чем меньшая из заданных линий, но
меньше, чем большая; действительно, прибав-
прибавляемая часть будет меньше разности.
Если дан круг и касающаяся круга пря-
прямая, то можно из центра круга провести к
р „ касательной прямую так, чтобы (отрезок)
прямой между касательной и окружностью
круга имел к радиусу меньшее отношение,
чем дуга круга между точкой касания и проведенной прямой к любой
заданной окружности *).
Пусть будет дан круг АВГ {рис. 3} и центр его К, и пусть AZ ка-
касается круга в В; пусть также будет дапа и какая-нибудь окружпость
*) Греческий язык не знает разницы между всей окружностью в какой-нибудь ее часть
(дугой): л та и другая обозначаются одним словом лсолфёю
232
архймкд
62
круга; можно взять некоторую прямую, которая была бы больше задан-
заданной окружности, и пусть прямая Е будет больше этой заданной окруж-
окружности. Из центра К параллельно AZ пропедем ЛН и отложим прямую
116, равную Е, так, чтобы она «стремилась» к В. Прямую, соединяющую
центр К с 0, продолжим; тогда 0Z будет иметь к ©К то же самое отпо
шенис, что В© к 011.
ве
Значит, ZB к 0К имеет меньшее отношение, чем дуга В© к заданной
окружности, потому что прямая В© меньше дуги В0, а ©Н больше
заданной окружности. Итак Z0 имеет к радиусу меньшее отношение,
чем дуга В© к заданной окружности [2].
ТВ
©К
н
н
BN
VI
Если дан круг и в круге линия, меньшая диаметра, то между цент-
центром круга и его окружностью можно вставить прямую, которая так
пересекла бы заданную в круге линию, чтобы часть вставленной прямой
между окружностью и прямой, данной в круге,
г" ' имела заданное отношение к (линии), соеди-
И< —— ияющей находящиеся на окружности концы
обеих прямых — вставленной и данной е круге,
если только заданное отношение будет меньше
того, которое половина прямой, данной в
круге, имеет к перпендикуляру, опущенному на
нее из центра.
Пусть будет дан круг АВГ с центром К
{рис. 4}; пусть в нем дана линия ГА, меньшая
рис 4. диаметра, и задано отношение Z к II, меньшее
того, которое Г0 имеет к К©, где К© — пер-
перпендикуляр, (опущенный па АГ). Проиедем
параллельно АГ из центра прямую K.N и перпендикулярно к КГ
прямую ГЛ; тогда треугольники ГВК и ГКЛ будут подобны.
Теперь как Г0 к 0К, так будет и КГ к ГЛ;
кг
гл
значит, Z будет иметь к IT отношение меньшее, чем КГ к ГЛ.
ГЛ . . /ч
Тогда отношение Z к Н равняется тому, которое КГ имеет к некоторой
прямой, большей, чем ГЛ. Пусть эта прямая будет BN;
"вТГ
поместим BN между окружностью и прямой (KN) так, чтобы (она про-
проходила) через Г (действительно, так провести секущую можно).
Поскольку otra больше ГЛ, то попадет вне ее. Так как KB имеет к BN
то же самое отношение, что Z к II,
А.
и
то, значит, и ЁВ будет иметь к ВГ то же самое отношение, что Z к И [3].
О СПИРАЛЯХ
233.
¦Е
VII
Если при тех же самых данных продолжить прямую в круге, то
между центром и продолженной прямой можно так вставить прямую,
чтобы ее часть между окр1жностыо и продолженной прямой имела
заданное отношение к соединяющей {находящиеся на окружности) концы
вставленной и продолженной прямых, если
только заданное отношение будет, больше
того, которое половила прямой, заданной в
круге, имеет, к перпендикуляру, опущенному
па лее из центра.
Пусть лри тех же самых данных ли-
линия (АГ) в круге будет продолжена {рис. 5);
пусть заданное отношение Z к Н будет боль-
больше того, которое Г0 имеет к ©К, оно будет
больше и того, которое КГ имеет к ГЛ*).
Тогда отношение Z к И равняется тому,
которое КГ имеет к некоторой прямой, мень-
меньшей, чем ГЛ. Пусть ата прямая будет «стремящаяся» к Г прямая IN
(действительно, так провести секущую можно);
Z _ КГ
Н ~ IN
поскольку она меньше ГЛ, то попадет ипутрь ГЛ. Так как КГ (или KI)
имеет к IN то же самое отношение, что Z к Н, то и EI будет иметь
к IГ то ян; самое отношение, что Z к II [4].
Рис. 5.
BI
1Г
и
VIII
Z
н
_кг_
rs
Если дан круг и в круге линия, меньшая диаметра, а также другая,
которая касаегтгя круга в конце прямой, заданной в круге, то между
центром круга и данной (в круге) прямой можно вставить некоторую
прямую так, чтобы ее часть между окружностью круга и прямой, дан-
данной в круге, имела заданное отношение к
отсеченной ею части касательной, если
только заданное отношение будет меньше
того, которое половина прямой, заданной
в круге, имеет к перпендикуляру, опущен-
опущенному на нее из центра круга.
Пусть данный круг б у дот АВГЛ
{рис. 0} и в круге дана прямая ГА, мепь-
шан диаметра; пусть прямая ЕЛ касается
этого круга в точке Г; и (заданное) отно-
отношение Z к И будет меньше того, которое
ГВ имеет к ЭК; тогда оно будет меньше
и того, которое ГК имеет к ГЛ,
- г« _ гк^ Рис. 6.
«к ¦¦' г л
если провести КЛпараллельно 6Г. Пусть КГ имеет к Г Е тоже отно-
отношение, что Z к Ы;
7. ¦ ... ....
*) Как и в предыдущем предложении, ГЛ предполагается перпендикулярной к КГ.
АРХИМЕД
тогда ЕГ будет больше ГЛ. Происдсм окружность круга через точки К,
Л, S. Так как ЕГ более ГЛ и прямые КГ, ЕЛ взаимно перпендикуляр-
перпендикулярны, то можно вставить еще одную прямую Ш, «стремящуюся» к К
и равную МГ. Тогда прямоугольник между SI и 1Л имеет к прямоуголь-
прямоугольнику между КЕ и 1Л то же отношение, что EI к КЕ;
SI-IA _ EI
КЕ- JA~ КИ
а прямоугольник между KI, IN к прямоугольнику между KI, ГЛ— то
же отношение, что IN к ГЛ,
KT-IN _ TN .
KI-ГЛ ~ГЛ"
так что IN будет к ГЛ, как ,Е1 к КЕ *);
IN SI
ГЛ — КЕ"
и-, значит, ГМ будет к ГЛ, как ЕГ к ГК,
_ГМ___ЕГ_
ГЛ ~~ КГ
или ЕГ к KB, как SI к КЕ**);
ВГ SI
KB "" КЕ
и остатки 1Г иЪЕ будут иметь то же самое отношение, что ЗГк ГК***),
ir вг
BE ГК
или Н к Z. Итак, к касательной проведена прямая KN и часть ее BE
между касательной и данной прямой (ЛГ)
имеет к отрезку AГ) касательной то же
самое отнош ние, что Z к II.
IX
Если при тех же самых данных продол-
продолжить прямую, данную в круге, то между
центром круга и продолженной прямой мож-
можно вставить другую прямую так, чтобы ее
часть между окружностью и продолженной
прямой имела заданное отношение к отсечен-
отсеченной части касательной от точки касания,
если только заданное отношение будет больше того, которое половина
прямой, данной в круге, имеет к перпендикуляру, опущенному на нее из
центра.
Пусть дан круг АВГД (рис. 7} и в этом круге проведепа прямая
ГА, меньшая диаметра; пусть Е Г касается круга в точке Г и (заданное)
отношение Z к Н будет больше того, которое Г0 имеет к ©К;
Рис. 7.
rz
н
ге
ек
тогда оно будет больше и того, которое КГ имеет к ГЛ.
*) Так как KIIN=3I-IA как произведении отрезков секущих, проведенных через точку I.
и KI : КЕ=А1 : Л г вследствие параллельности КЛ и ЕГ.
**) По построению ГМ—IN.
ЕГ-SI jr_ - ¦¦
' BE '
О СПИРАЛЯХ
235
Пусть КГ имеет к ГВ то же отношение, что Z к Н;
кг z
гз "~ н
тогда (ГН) будет меньше ГЛ.
Опять проведем круг через точки S, К, Л. Так как ЗГ меньше ГЛ
и прямме КМ, ЕГ взаимно перпендикулярны, то можно встанить пря-
прямую Ш, «стремящуюся» к К и равную ГМ. Так как прямоугольник
между El, IA имеет к прямоугольнику между Л1, КЕ то же отношение,
что EI к КЕ,
El-IA 5T
Л1 ¦ КЕ "" KB"
и прямоугольник между EI, 1Л равен прямоугольнику менаду KI, Ш,
ЕГ-ГЛ = КГ-П\Г
а прямоугольник между Л1, КЕ равен прямоугольнику между К1, ГЛ
А1-КЕ = К1-ГА
вследствие того, чтоКЕ относится к IK, какЛГ кЛ1, то, значит, как EI
к КЕ, так будет и прямоугольник между KI и IN к прямоугольнику
между КГ и ГЛ, то есть как N1 к ГЛ или ГМ к ГЛ.
KI-1N _ N1 ГМ
HI
_NI
KI-ГЛ ~ ГЛ ~ ГА
Но и ГМ так относится к ГЛ, как ЕГ к КГ или к KB;
ГМ
ГЛ
EI
ЕР
КГ
ЕГ
КЪ
значит, как EI к КЕ, так будет БГ к KB;
_ЕГ_
KB
и остаток 1Г будет к остатку BE, как ЕГ к ГК.
гг
ЕГ
гк
Но отношение 2Г к ГК равно тому, которое Нимеет к Z; значит, к про-
продолженной прямой (АГ> приставлена прямая КЕ, и ее часть BE меж-
между продолжепттой прямой и окружностью имеет
к отсеченной части ГТ касательной то же самок
отношение, что Z к II.
в
к
г
л
л
м
Е
г
г
и
0
.
Рис. 8.
Если отложено любое количество последо-
последовательных линий, одинаково возвышающихся
одна над другой *), причем соответствующая
разность равняется наименьшей (из этих ли-
линий), и такое же количество других линий,
равных каждая наибольшей (из первых), то
квадраты на прямых, равных наибольшей, взя-
взятые вместе с квадратом на этой наибольшей и прямоугольником,
построенным на наименьшей (линии) и (линии), равной всем, одина-
одинаково возвышающимся одна над другой, вместе взятым, будут втрое
больше всех вместе взятых квадратов на одинаково возвышающихся
одна над другой прямых.
Пусть отложено любое количество последовательных линий, одина-
одинаково возвышающихся одна над другой {рис. 8} А, В, Г, А, Е, Z, Н, 0,
•) Мы сказали бы просто «составляющих арифметическую прогрессию».
236 ¦' АРХИМЕД
и пусть © равна соответствующей разности; к В прибавим 1, равную в,
к Г же К, равную Н, к Д же Л, рапную Z, к Е же М, равную Е, к Z же N,
равную А, к Н же Е, рапную Г, к в же О, равную В; тогда все полу-
полученные линии будут раины друг другу и наибольшей.
Требуется доказать, что квадраты иа псех :кгих прямых, то есть А
и пновь получившихся, взятые вместе с кпадратом на Л и прямоуголь-
прямоугольником, построенным ла Э и на прямой, раиной всем А, В, Г, А, Е, Z,
Н, 0, имеете взятым, будут птрое больше всех квадратом на А, 13, Г, А,
Е, Z, Н, 0, ваятых вместе.
K)H(A + AL(EiM)H<Z + WH(H-! ЕJ + @ + ОJ + AS+¦
Г + Д + E-i-Z |-Н4-в)(А8-НВ* + 1>9 + Л* + К* I Z2-fH2 + ©2j
Действительно, квадрат на прямой BI равен вместе взятым квадратам
па I, В с двумя прямоугольниками между В, I;
(В 4-1J = 12 -f-BM 2IM
квадрат на К Г равен вместе пзятым квадратам на К, Г и двум прямо-
прямоугольникам между К, Г;
Г2+2Г-К -• - ^ .-.-.•-¦.. ....
подобным же образом и квадраты на всех других линиях, ранных А,
будут равны квадратам соответствующих отрезком вместе с диумя пря-
прямоугольниками между этими отрезками.
-|- 2Д-Л : .. .
== оа -\-1J -и 20 • О
Теперь квадраты па А, В, Г, A, Z, Е, И, 0 вместе с квадратами на I.
К, Л, М, JN, 3, О и с добавленным квадратол! па А будут идное больгпе
взятых вместе квадратов на А, В, Г, А, Е, Z, II, 6-
А2 .; ца + Г* + г\з -!- Еа + z* -j- lia + е« + in + К« -< Л* i- M2 +- N^ + S« -) О* + А» =
=2 (А2 I-- В2 f I-з .(- да [- Е2 + 7Л+ ИЗ + 02)
Нам остается доказать, что удвоенные прямоугольники между отрез-
отрезками каждой .'пенни, равной А, с добавлением прямоугольника на ©
и прямой, равной всем А, В, Г, А, Е, Z, II, 0, вместе взятым, будут
равны квадратам па Л, В, Г, А, Е, Z, Н, 0.
2 (B-I+I-K-f-A.A I E-M + Z-NH Н-Н + в-О) : «(А ! В + Г-!-А \ К ! Я
Так как дна прямоугольника между В, I равны двум прямоугольникам
между В, 6),
2B-I-- 2В-в
дпа же прямоугольника между К, Г равны прямоугольнику между 0
и учетверенной Г, ибо К вдвое более 0,
2Г-К--4Г-В
дна прямоугольника на А, Л равны прямоугольнику между (-) и уше-
ушестеренной А, ибо А птрое больше 0,
2Л-Л-0Д-в
и точно так же все остальные удвоенные прямоугольники на соответ-
О СПИРАЛЯХ 237
ствующих отрезках будут ралпи прямоугольникам между в и линиями
(Е, Z, К, в), взятыми в кратности последовательных четных чисел,
2Е-Л=8Е-е - ... ¦, .... ' . . ¦¦ ; .. :
2z-N=ioz-e <.. ¦¦ ; ¦ .:: ¦...-, -. ;• "¦ ¦¦ ¦
2н-з = 12н-е
2в-о= не-е ¦ ' ' "¦ "¦'
то все оки, взятые имеете с добавлением прямоугольника между 0 м пря-
прямой, раиной вместо взятым всем Л. В, Г, Д, Е, Z, Н, в, будут равны
¦•• прямоугольнику между 0 и прямой, ралной вместе взятым А, утроен-
утроенной 13, упятеренной Г и всем следующим линиям в кратностях после-
последовательных нечетных чисел.
2 (В-1 + Г-К + Д-Л + E-M + Z-N-f П-В-в.О)-| 0(А-| В + Г Н Д + Е -|- Z -Ь Н -| »).=
=МЭ(А + ЗВ + 6Г + 7ДН-0ЕЧ- 11Z + 13II+ 156)
Но квадраты на А, В, Г, Д, Е, Z, Н, В будут тоже равны прямоуголь-
прямоугольнику между теми же самыми линиями. Действительно, квадрат на А
равен прямоугольнику между 0 и прямой, равной вместе взятым А
и всем остальным линиям, каждая из которых равна А,
А* = в[А-КИ + 1) + (Г+К)-| <Д + Л) + <Е + М)-I (Z-; N) I Ш -|- Е) + (в + О)]
ибо в измеряет А такое же число раз, как сама Л измерит" .('вместе
взятые) все равные ей прямые вместе с А *); таким образом, квадрат на
А будет равен прямоугольнику между 6 и прямой, равной А вместе с
удвоенными В, Г, Д," Е, Z, Н, 0, ' . . ..=. .!''
А2 -= в [А + 2 (В + Г f Д -f Е + Z ~ II +¦ в)] . ^
ибо псе рапные Л прямые, за исключением лишь самой А, будут вдвое
больше всех вместе взятых В, Г, Д, Е, Z, Н, 0. Точно так же й квадрат
на В будет равен прямоугольнику ме?кду 0 и прямой, ранной В «месте
с удвоенными Г, Д, Е, Z, II, 0;
В2 =.- в [В + 2 (Г + Л + Е + Z + II -j вI
далее, квадрат на Г будет равен прямоугольнику между 0 и прямой,
равной Г вместе с удвоенными Д, Е, Z, Н, 0;
г2=егг-| 2 (д-f е-;-Z + п-I-в)] " ' '"
и точно так же квадраты па других будут равны прямоугольникам
между © и прямыми, равными рассматриваемой прямой вместе с удвоен-
удвоенными оставшимися. . ¦?."
Д2 = 0 [д-|_ 2 (Е + Z-i-11-fe)] ¦••; f ,.
в [Z + 2 (II + 0)]
в [II Н- 2в] ' • ' .'
в.е
Теперь ясно, что квадраты на всех этих прямых будут раины прямо-
прямоугольнику между 0 и прямой, равной вместе взятым Л, утроенной В,
упятеренной Г н всем следующим и кратпостях последовательных не-
нечетных чисел.
Следствие
Из утого ясно, что все квадраты на прямых, равных наибольшей,
взятые вместе, будут меньше утроенных квадратов на всех одинаково
возвышающихся одна над другой прямых, поскольку они будут втрое
*) В нашей случае А=8© и имеется семь прямых, равных А, а именно B+I и т.'д.' ¦ •¦ >¦
238
АРХИМЕД
больше, (чем квадраты на всех одипаково возвышающихся прямых),
только после добавления некоторой величины, но они будут больше
вместе взятых утроенных квадратов на всех таких прямых, кроме наи-
наибольшей, так как добавленная величина
меньше утроенного квадрата на наибольшей*). И, следовательно, если
построить подобные фигуры на всех таких прямых, как на одинаково
возвышающихся одна над другой, так и па прямых, равных наиболь-
наибольшей, то построенные на прямых, равных наибольшей, вместе взятые,
будут меньше вместе взятых утроенных фигур на прямых, одинаково
возвышающихся одна над другой, по будут больше вместе взятых ут-
утроенных всех таких фигур, за исключением лишь построенной на наи-
наибольшей прямой, ибо подобные фигуры имеют те же отношения, что
и квадраты соответственных сторон [5].
XI
Если отложено любое количество последовательных линий, одина-
одинаково возвышающихся одна над другой, а затем будут отложены и другие
линии, количество которых на единицу меньше количества линий,
одинаково возвышающихся одна над другой, и величина каждой равна
наибольшей {из первых), то все вместе взятые квадраты на линиях,
равных наибольшей, к квадратам на одипаково возвышающихся одна над
другой линиях, кроме наименьшей, будут иметь отношение меньшее,
чем квадрат на наибольшей к {пло-
{площади), равной вместе взятым прямо-
прямоугольнику, {построенному) на наи-
наибольшей и наименьшей линиях, и
третьей части квадрата на разно-
разности между наибольшей и наименьшей
линиями, а к квадратам на одина-
одинаково возвышающихся одна над другой,
линиях, кроме квадрата на наиболь-
наибольшей, они будут иметь отношение,
большее указанного.
Пусть отложено любое количе-
количество последовательных линий, одина-
одинаково возвышающихся одна над дру-
другой, гдеЛВ больше ГД.ГД больше EZ,
EZ больше 116, 110 больше IK, IK больше ЛМ и ЛМ больше N5
{рис. 9); прибавим к ГА прямую ГО, равную взятой один раз разности
(между двумя последовательными прямыми), к EZ прямую ЕП, равную
удвоенной разности, к II6 прямую HP, равную утроенной разности,
и таким же образом ко всем остальным; тогда получатся линии, которые
будут равны между собой и каждая из пих равна наибольшей. Требует-
Требуется доказать, что вместе взятые квадраты па всех таких получившихся
линиях ко всем квадратам на одинаково возвышающихся одна над
другой линиях, кроме лишь квадрата на N5, будут иметь отношение
Ф
Г-
х-
Е
V
И
и
1
а-
Л-
q
в
Z в
Рис. 9.
К М
*) Результат, выраженный в следствии, в ссшременной формулировке может быть записав так:
3 (of + о| + ... + al-0 <
3 («?
где a. =»ai.
... + „I),
о спиралях 239
меньшее, чем квадрат па АВ к (площади), равной вместе взятым пря-
прямоугольнику между АВ, NE и третьей части квадрата на NT,
од»4-znz4-6р24-кг:24-ытм-Ег2 , ав2
AB.NS+ i,
3
а к квадратам на тех же самых линиях, кроме квадрата на АВ, они будут
иметь отношение, большее указанного.
ОД» + Zna + 8Р2 4- KS2 4- МТД + ГЕ2 АВ2
ГД* 4 EZ2 4- И©2 + 1К> 4- AM» 4- NE2 >
От каждой из линий, одинаково возвышающихся одна над другой, отде-
отделим часть, равную разности [6]; тогда отношение квадрата на АВ ко
вместе взятым прямоугольнику между АВ, ФВ и третьей части квадрата
на АФ будет равно тому, которое квадрат на ОА имеет к прямоуголь-
прямоугольнику между ОА, АХ и третьей часта квадрата па ХО, а также тому,
которое квадрат на IIZ имеет к прямоугольнику между HZ, ^PZ и
третьей части квадрата на ?П, а также тем, которые квадраты на
других линиях имеют к подобно образованным площадям;
ав« ода nzs р©а
-|' А<1>2 ОЛ-ХА + -|-ХО2 nZ-WZ-^-^VU^ FO ¦ Qfi + "|" й
ТМ2 ГЕ2
тогда все квадраты на ОА, IIZ, P0, SK, ТМ, ГН ко всем прямоуголь-
прямоугольникам между NS и прямой, равной всем упомянутым линиям, а такжо
третьим частям квадратов на ОХ, ГРГ, Рй, S^b, ТЦ, TN будут иметь
то же самое отношение, что квадратна АВ ко вместе взятым прямоуголь-
прямоугольнику между АВ, ФВ и третьей части квадрата на ФА *).
NE (ОД + HZ +P0 + гК + ТМ + ГЕ> + -^-@X2 + ПЧ™ + ?№-\- 2/^2 +тЦа + Г№) АВФВ + -|- ФА*
Если теперь показать, что прямоугольник между NS и прямой, рав-
равной всем вместе взятым ОА, ITZ, P0, 2К, ТМ, ГЗ, и третьей части
квадратов на ОХ, ПЧ', Р Й, 2^, ТЦ, TN будет меньше квадратов на
АВ, ГА, EZ, Нв, IK, ЛМ, но больше квадратов на ГА, EZ, Н0, 1К,
AM, N3, то предложение будет доказано.
Примоугольник на N3 и прямой, равной всем вместе взятым ОД,
HZ, Рв, 2К, ТМ, YE, и третьи части квадратов на OX, EW, P Q,
2%, ТЦ, TN будут вместе равны квадратам на ХА, YZ, QK, ^К,
CjM, N3 вместе с прямоугольником между NH и прямой, равной всем
вместе взятым OX, IW, PQ, 2^Ь, ТЦ, TN, и с третьей частью квадра-
квадратов на OX, IW, VQ, 2$Ь, Tq; TN; а квадраты иа АВ, ГА, EZ, IIв.
IK, AM, (вместе взятые), равны (вместе взятым) квадратам на ВФ,
ХД, WZ, Q0, ^К, GT^I, квадратам па АФ, ГХ, ЕУ, HQ, 1^>, АЦ и пря-
прямоугольнику между ВФ и удвоенной прямой, равной вместе взятьш АФ,
ГХ, EZ, HQ, I^fc, АЦ.
АВ8 + ГД2 -|- EZ2 + Н02 + IK3 4- AM2 = (ВФ8 -|- ХД2
4- (АФ2 4- ГХ2 4- EW2 4- HQ2 4- ffcz + Л(^2) + 2ВФ (АФ 4- ГХ + EZ 4- HG
•) См. Комментарий. Предполагается, что Ф11=Хд=Iг2=ав=
2-50 " АРХИМЕД
Теперь для обоих этих (выражении) будут общими квадраты на пря-
прямых, равных N3, а прямоугольник между NH и прямой, равной ОХ,
ГГУ, Ш\ /5fc2, QT. TN, меньше прямоугольника на ВФ и удвоенной пря-
прямой, равной АФ, ГХ, К?, IIQ, 1%>, Aq, так как только что упомяну-
упомянутые линии равны ГО, ЕП, РП, 12, ЛТ, TN
АФ -|- ГХ + EV -I HQ + lv?u + ЛС| = ГО + ЕП -Ь РН -f 12 + ЛТ -Ь TN
и больше остатков (после вычитаний ОХ—ГО, 1V?—ЕП, DP—PH,
^12 q
АФ+ГХ-f EV+1IQ ¦ Г^Ъ + Л^ > ГХ-I
а квадраты на ЛФ, ГХ, ЕЧГ, Н Q, IJfc,, AQ, (вместе взятые), больше
третьей части киадратов на ОХ, 1\ЧТ, Р Q, Б^>, TCj, TN, (вместе взя-
взятых),
АФ2 + ГХ2 + EW2 + Hfis | I^fc8 -|- ЛЦг ,> -j-(OX2 + nV2 + Mi2 + ?^Ь2 -I- C2
как доказано выше (следствие к предложению X); значит, упомянутые
*" '' (первыми) площади будут меньше (вместе ваятых) квадратов на АВ,
гд, ez, не, 1К, лм."
ns (од -I- nz + ре -1 2к + ты + rs) + -*- (ох* + пчг2+га2 -ь ?
Остается доказать, что они будут больше квадратов па ГА, EZ, HB, IK,
ЛМ, N3. Опять квадраты на ГЛ, EZ, Нв, IK, AM, N5 равняются
(вместе взятым) квадратам на.ХГ, ЕЧ1", HQ, 1$Ъ, ЛЦ, квадратам на ХД,
WZ, ?20, /%~К, q M, JNS и прямоугольнику между NS и прямой,
равной удвоенным всем (вместе взятым) ГХ, ЕЧГ, Ни, I)Jfc, Aq.
+ Нв2 + IK2 + AM2 + NE2 = ГХа + ЕЧГ2 + Hfi2 + I$52+ Aq2 + XД2 + W7? + И02 +^ K2 +
+ K22 + 2NS <ГХ+ Ef + HQ -f 1U -l лЦ)
И квадраты на ХД, YZ, Q6, ^К, MQ, NS будут общими (для обоих
выражений), а прямоугольник между NS и прямой, равной всем ОХ,
ПЧ'", Р Q, 21^Ь, Tq, TN, больит прямоугольника между N3 и удвоен-
удвоенной прямой, равной всем ГХ, EV, И Q, l^b, Aq. И, наконец, квадраты
' на ХО, гРП, QP, %2, qT, X"N будут более чем нтрое больше квадратов
на ГХ, ЕЧГ, IIQ, 1^>, Л^; ибо было доказано и это. Итак, упомянутые
площади, взятые вместе, будут больше квадратом на ГД, EZ, 110, 1К,
AM, NS.
•-• - - Следствие
И поэтому, если мьт построим подобные фигуры па всех прямых,
и на одинаково возвышающихся одна над другой, и на ранных нанболь-
шей из них, то все фигуры, построенные на прямых, ранных наиболь-
наибольшей, ко всем фигурам на нрямих, одинаково возвышающихся одпа над
другой, кроме лишь фигуры па наименьшей, будут иметь отношение,
меньшее того, которое квадрат на наибольшей примой имеет к (площади.),
равной вместе взятым прямоугольнику между наибольшей м наимень-
наименьшей линиями и третьей части квадрата на разности между наибольшей
и наименьшей; ко всем'лее (построенным) па них фигурам, за исклю-
исключением фигуры, построенной на наибольшей, они будут иметь отноше-
отношение, большое того же самого; действительно, подобные фигуры будут
иметь то же самое отношение, что и квадраты (па соответствующих
линиях). ¦¦
о спиралях 241
Определин и я
1. Если на плоскости проведена прямая линия, которая, сохраняя
один свой конец неподвижным и вращаясь с одинаковой скоростью,
любое число раз воркетси в исходное положение, и если одновременно
с вращением этой линии какая-нибудь точка будет с: лостояштой скоро-
скоростью перемещаться по этой примой, начиная движение мл неподвиж-
неподвижного копца, то эта точка опишет на плоскости спираль.
2. Конец прямой, остающийся при ее вращении неподвижным, назо-
назовем началом стирали.
3- Положенно лишни, от которого рассматриваемая прямая начала
вращаться, назовем началом вращения.
4. Прямую *), которую в течение первого оборота пройдет точка,
движущаяся по прямой, назовем первой прямой, а ту, которую та же
точка пройдет в течение второго оборота, пазопем второй прямой;
подобным жо образом пазовсм и все остальные одипакоными именами
с соответствующими оборотами.
5. Площадь иге, заключенную между спиралью, описанной при
первом обороте, и той прямой, которая является первой, будем назы-
называть первой площадью, заключенную между спиралью, описанной при
втором обороте, п второй прямой, мы назовем второй, и псе последую-
последующие будем называть так же.
6. И если из точки, являющейся началом спирали, провести какую-
нибудь прямую линию, то все, что находится с той стороны прямой,
в которую происходит вращение, мьт будем называть передним, что же
находится с другой стороны — задним**).
7. Круг, описанный из той точки, которая является началом спи-
спирали, как из центра, радиусом, равным первой прнмой, будем назы-
называть першод, описали ьш из того же центра вдвое больший радиусом,
будем называть вторым, и таким же образом будем называть нее за ним
следующие.
XII
Если к спирали, описанной в течение одного какого-нибудь оборота,
провести из начала спирали несколько прямых, образующих друг с другом
равные углы, то эти прямые будут превы-
превышать друг друга на равные величины.
Пусть будот некоторая спираль и про-
проведенные к ней прямые АВ, АГ, АД, АЕ,
AZ {рис. 10}, образующие друг с другом
одинаковые углы. Требуется доказать, что
одинаково АГ превышает АВ, АД превыша-
превышает ЛГ, и подобно этому все остальные. Рис. 10.
Действительно, в то лее самое время, в *
которое вращающаяся прямая из положении АВ доходит до положении
АГ, и движущаяся по прямой точка пройдет то расстояние, на кото-
которое ГА превышает АВ, в то же время, в которое прямая перейдет из
АГ в ЛД, точка пройдет расстояние, на которое АЛ превышает АГ. Но
вращающаяся прямая проходит в одинаковое время и.ч АВ н АГ и и»
ЛГ в АЛ, так как соответствующие углы раины; значит, и одинаковое;
*) Собственно говоря, «отреаок». Греки мыслили прлмую линию всегда ограничится.
* *) В тексте лооауо'щчча (ведущие) и 4даде\'а (следующие).
Архимед.
242
лихиМИД
время и движущаяся по прямой точка пройдет как то расстояние,
на которое ГЛ превышает АВ, так и то, на которое АА превышает АГ.
Значит, одинаково прямая АГ превышает АВ и А А превышает АГ;
точно так же и все остальные.
ХШ
Если какая-нибудь прямая касается спирали, то она касается
ее только в одной точке.
Пусть будет спираль с точками А, В, Г, Д, {рис. 11}; пусть нача-
началом спирали будет точка А, началом же вращении—прямая АД,
и пусть какая-нибудь прямая ZE каса-
касается спирали. Я говорю, что она касает-
касается последней только в одной точке.
Пусть, если возможно, она будет
касаться спирали в двух точках Г, Н;
соединим Л с Г и А с II и угол, заклю-
заключающийся между АГ, AIT, разделим
пополам; пусть 0 будет точка, в кото-
которой прямая, делящая пополам данный
угол, встречается со спиралью. Тогда
прямая АН на такую же величину
будит превышать АЭ, как А0 — прямую АГ, поскольку рассматри-
рассматриваемые прямые образуют друг с другом равные углы; таким образом,
ATI и АГ, вместе взятые, будут вдвоо больше А6.
Но в треугольнике обе стороны будут более чем вдвое больше лри-
мой [А0], делящей пополам угол между ними [7]; ясно, что та точка,
в которой Ав встречается с прямой ГН, будет находиться между А и
0; значит, EZ пересекает спираль, таи как одна из точек на прямой Г0Н
будет внутри спирали. Предположено же, что опа является касательной;
значит, RZ касается спирали только в одной точке.
XIV
Если к спирали, описанной в течение, первого оборота, провести дав
прямые из точки, являющейся началом спирали, и продолжить их до
окружности первого круга, то проведенные к спирали прялгые будут иметь
между собой то же самое отношение, что и дуги крупа, заключающиеся
между концом спирали и концами продолженных
прямых на окружности, если брать дугу от
конца спирали до передней стороны (прялюй).
Пусть спираль, описанная в течение первого
оборота, будет АВГА0 {рис. 12}, пусть точка А
будет началом спирали, а прямая 0Л — началом ,
вращения; пусть круг 6KII будет нервмм, пусть
из точки Л идут к спирали прямые АЕ и АЛ и
доходят до окружности первого круга в точках
Z, И. Требуется доказать, что АЕ будет иметь
к АА то же самое отношение, что дута 6KZ
к дуге ВКН. Рис j2
Действительно, если вращать линию А<?>,
то ясно, что точка О будет равномерно пере-
перемещаться по окружности круга 0К11, и точка А при своем
дпнжшиш пойдет по литии ЛВ: когда точка 0, двигаясь по окруж-
о спиралях 243
ности круга, пройдет дугу ©KZ, то А пройдет прямую АЕ, и также,
когда точка А пройдет прямую АА, то 0 пройдет дугу 0KTI,
причем каждая будет двигаться равномерно; отсюда ясно, что АЕ
к АА будет иметь то же самое отношение, что дуга 0KZ к дуге 6KH,
[как было доказано выше в первых предложениях] (см. предложение II).
Подобным же образом докажем, что то же самое будет иметь место
и тогда, когда одна и я проведенных прямых попадет в конец спирали.
XV
Если к спирали, описанной в течение второго оборота,'провеспш пря-
прямые из начала спирали, то эти прямые будут иметь друг к другу то же
самое отношение, что и вышеупомянутые дуги, если взять их вместе
с целой окружностью рассматриваемого круга.
Пусть будет спираль АВГЛ6 {рис. 13}, причем дуга АВГА6 опи-
описана в течение первого оборота, а дуга ЭЛЕМ в течение второго,
«пусть к ней идут прямые АЕ и АЛ. Требуется Л
доказать, что АЛ имеет к ЛЕ то же самое отноше-
отношение, что дуга 0KZ вместе с целой окружпостью
круга к дуге ©КБ, (тоже взятой вместе) с целой
окружностью того же круга.
Действительно, в одно и то же время точ ка
А, двигаясь по прямой, пройдет линию АЛ, и
точка 6, двигаясь по окружности круга, пройдет
всю окружность итого круга и еще дугу 0KZ,
и точно так же точка А пройдет прямую АЕ, Рис. 13.
а точка В — всю окружность круга в еще дугу
6КН, причем каждая будет днигаться равномерно. Теперь ясно, что
линия ЛЛ к АЕ будет иметь то же самое отношение, что дуга 0KZ
вместо с целой окружностью круга к дуге (-ЖТ1 тоже с целой окруж-
окружностью круга.
Таким же образом докажем, что если к описанной в течение третьего
оборота спирали провести прямые, то они будут иметь друг к другу то
же самое отнопгопие, что упомянутые дуги вместе с дпажды взятой ок-
окружпостью целого круга. Точно так же можно показать, что прямые,
проведенные к другим спиралям, будут иметь друг к другу то же самое
отношение, что вышеупомянутые дуги, если брать каждую с окружностью
целого круга, взятою столько раз, сколько раз без одного будет
совершено обращений, даже если одна из проведенных прямых попадет
к конечную точку спирали.
XVI
Если прямая линия касается спирали, описанной в течение, первого
оборота, и точка касания, соединена прямой линией с. точкой, которая
является началом спирали, та углы, образованные касательной с соеди-
соединяющей, будут не равны, причем угол с передней стороны будет тупим,
а с задней стороны — острым.
Пусть ЛВГД0 (рис. 14] будет спираль, описанная в течение пер-
первого оборота, пусть точка Л будет началом спирали, прямая А0 —
началол1 вращения, а (-ЖТТ —первым кругом, и пусть некоторая пря-
прямая EAZ касается спирали в точке А; от А к Л проведем соединяющую
прямую АА. Требуется доказать, что AZ образует с АА тупой угол.
244
ЛРХНМЕД
PI
"ар
Из центра А радиусом АД опишем круг ATN; дуга этого круга
с передней стороны (прямой АД) необходимо попадет внутрь спирали,
а с задней стороны—пне ее, так как прямая, проведенная из А к спирали,
в передней стороне будет больше АЛ, а про-
исдеппая л задней — меньше. Что угол, за-
ключепшлй между прямыми АД и Д7, не будет
острый!, очевидно, поскольку он больше угла
нолукруга*), а что оп не будет прямым,
следует доказать так.
Пусть, если возможно, он будет прямым;
тогда прямая EAZ будет касаться круга ATN.
Б таком случае возможно из точки А так под-
подставить прямую к касательной, чтобы пря-
прямая, заключающаяся между касательной и
дугой круга, имела к радиусу этого круга
отношение меньшее того, которое дуга, заклю-
заключенная между точкой касания и нодстаклеп-
пой прямой, имеет к некоторой данной дуге
(предложение V). Пусть и одета пленная прямая будет AI: она пересечет
спираль в точке А. а окружность круга ANT а Р; и пусть прямая Р1
имеет к АР отношение меньшее того, которое дуга АР имеет к дуге A NT;
¦ ^р
значит, вся прямая 1А будит иметь к АР отношение меньшее того, кото-
которое дуга PANT имеет к дуге ANT, или того, которое дуга 2HKG имеет
к дуге НК6.
14.
. РД J- ANT
ГНК
ant пке
Но отношение дуги 2ГТК0 к дуге НК© будет тем же самым, какое
прямая АА имеет к АА: .
шее
АЛ
АД
AI
(это докапано (в предложении XIV)), значит, А1 будет иметь к АР
отношение меньшее?, чем АА к АА,
. АА
¦ АД
а. :)то невозможно, ибо РА раипа АА. Значит, угол, заключенный
мажду АА, AZ, не будят прямым. Доказано также, что он и не острый;
значит, он будет тупым, а остающийся (АДЕ) острым.
Подобным же обраиом докажем, что то же самое будет иметь место
и осли. касательная будет касаться спирали в ее конечной точке [8J.
XV ГТ
И то ж? самое бу<)ет иметь место, если прямая, касается спирали,
описанной в течение второго оборота.
Действительно, пусть прямая EZ {рис. 15} будет касаться в А спи-
спирали, описанной в течение второго оборота, и пусть все остальное будет
*) На криволинейный угол АДР. Ср. Еиклвд, III. 16.
О СПИД'АЛЯХ
245
сделано так же, как л раньше. Тогда точно так же окружность круга
PNA с передний стороны попадет внутрь спирали, с задней же — вне ее;
угол AAZ не будет прямым, а обязательно тупым. Пусть он,
*# Vs* а
« -:-/•-.-*¦¦
e*».*/-/*
"I/
f . л
_-\_cJj
'.:¦ ."".5
" "¦¦.'.?
::i'S
.¦..:-
Фотокопия страницы греческой рукописи, содержащей отрывок
сочинения Архимеда «О спиралях».
если возможно, будет прямым; тогда EZ будет касаться круга PNA
в точке Д. Опять проведем к касательном прямую AI, и пусть опа пересе-
пересечет спираль в X, а окружность круга PNA — в Р, и пусть РТ имеет
к РА отношение меньшее того, которое дуга АР имеет ко всей окружно-
окружности круга APN вместе с дугой ATNT (было доказано, что это возможно
246
АРХИМЕД
Рис. 15.
(предложение V)); и значит, вся 1А к АР будет иметь меньшее отноше-
отношение, чем дуга PANT вместо со всей окружностью круга к дуге ANT
тоже вместо со всей окружностью круга. Но отношение дуги PANT
вместе со всей окружностью круга ANTP к дуге ANT со всей окруж-
окружностью круга ANTP будет тем же самым, какое дуга 2ITK.6 со всей
окружностью кузуга в?НК имеет к дуге
НК6 со всей окружностью круга ©SHK,
отношение же упомянутых последними
дуг будет тем же самим, какое прямая
ХА имеет к прямой АЛ (это доказало
{« предложении XJ.1»; значит, 1А к АР
будет иметь меньшее отпошение, чем
АХ к АД, а это невозможно, [ибо РА
равна АА, a IA больше АХ]. Теперь
ясно, что угол, заключенный между AAZ,
будет тупым, а остающийся (АДЕ)—
острым.
То же самое будет иметь место и
(итом случае), когда касательнам будет
касаться спирали в ее конечной точке.
Подобным же образом докажем,
что если какая нибудь прямая будет
касаться спирали, описанной в течение какого угодно оборота,
пусть даже в конечной ее точке, то эта касательная образует неравные
углы с прямой, соединяющей точку касания с началом спирали, при-
причем с передней стороны этот угол будет тупым, а с задней стороны —
острым.
XVIII
Если прямая линия касается спирали, описанной в течение первого
оборота, в конечной ее точке и если из точки, являющейся началом спи-
спирали, проведена некоторая прямая перпендикулярно к началу вращения,
то проведенная прямая ветре-
тится с касательной и прямая,
заключенная между касатель-
касательной и началом спирали, будет
г-
равна окружности первого круга.
Пусть будет спи раль АБГД6
{рис. 16}, пусть точка А будет
началом спирали, линия 6А —
началом вращения, круг 0HK — Ркс. 16.
первым кругом; пусть некоторая
прямая 6Z касается спирали в точке в и из А проведена прямая AZ
перпендикулярно к ВА; тогда она обязательно встретится с 0Z, так
как Z0, вА заключают острый угол. Пусть она встретится с ней в
точке Z. Требуется доказать, что прямая ZA будет равна окружности
круга ОКБ.
Если нет, то она будет или больше, или меньше. Пусть сначала она,
если возможно, будет больше. Тогда я беру некоторую прямую АА,
it оторая меньше прямой ZA, но больше окружности круга ВПК. Теперь
имеются некоторый круг ВПК, » этом круге линия ©И, меньшая*) его
*) Архимед вабыл указать, что точка н представляет пересечение с кругом вНК каса-
касательной 6Z к спирали.
о спиралях
247
диаметра, м отношение вА к АЛ, которое будет больше того, которое
половина IT В имеет к перпендикуляру, опущенному на нее из А, так
как оно больше отношения 0А к AZ*). Тогда можно из А так под-
подставить прямую AN к продолжению (Нв), чтобы ее часть NP между
окружностью и продолжением (Н0) имела к ©Р то же самое отноше-
отношение, что 6Л к АЛ (предложение \'П);
_вА
АЛ"
тогда JN Р будет иметь к РА такое же отношение, как прямая ОР к АЛ.
РА
вр
АЛ
Но вР имеет к ЛЛ меньшее отпошепие, чем дуга 0Р к окружности
круга вНК,
лл * "окр. епк
так как прямая 0Р меньше дуги ©Р, а прямая АЛ больше окружности
круга ©НК; значит, и NP будет иметь к РА отношение меньшее, чем
у дуги 0Р с окружностью круга ©НК,
-<¦
РА окр. вНК
и вся NA будет иметь к АР отношение меньшее того, которое дуга 6Р
:. вместе со всей окружностью этого круга имеют к окружности круга
6НК.
А'Р i РА
РА
, ер 1 г,кр. вн к
окр. «ПК
Но отношение дуги ©Р имеете со всей окружностью круга ©НК к этой
окружности круга 6IIK будет тем же самым, какое ХА**) имеет к А©
(это доказано (в предло-
предложении XV}); значит, NA v-
имеот к АР меньшее отно-
отношение, чем ХА к Л0,
NA.^. ХА_ •
АР Ав
а это невозможно, так как
NA больше АХ, а АР рав-
равна 0А. Итак ZA не будет
больше окружности круга
вНК.
Тогда пусть, если вой
можно, ZA будет меньше
окружности круга 0HK {рис. 17}. Я опять взял некоторую прямую
АЛ, которая теперь будет больше AZ, но меньше окружности круга
6IIK, и провожу из точки 0^параллельпо AZ прямую 0М. Тогда
опять имеются круг вНК, в нем линия ©И, меньшая диаметра, другая
@М), касающаяся круга в точке 0, и отношение А0 к АЛ меньшее
того, которое половина И© имеет к перпендикуляру, опущенному на
*) Отношение половины Ив кперпендикулиру, опущенному из А на Нв, равняется тангенсу
угла AZ6, или отношению Лв:А2.
**) Архимед опять пабыл укапать, что точна X предстандяст пересечение вставленной прямой AN
со спиралью.
Рис. 17.
248 АРХИМЕД
пес из А, поскольку оно меньше, отношения 6А к AZ. Тогда можно
из А провести к касательной такую прямую АП, чтобы се часть PN
между ладанной в круге прямой (ВН) и окружностью имела к отсечен-
отсеченной части 6П касательной такое же отношение, как у 0А к АЛ {предло-
{предложение VHI);
PN 6A
вП АЛ
эта прямая АП пересекает круг в Р, а спираль в X. Поело перестановки
NP будет иметь к РА то же самое отношение, что 611 к АЛ.
np _ ел
РА ~ АЛ"
Но 0П имеет к АЛ большее отношение, чем дуг» 0Р к окружности
круга вНК,
_еп_. Eр
АЛ ^ икр. ©ПК
так как прямая ЭП больше дуги 01'* ), а АЛ меньше окружности круга
0IIK; значит, вП имеет к (АЛ, или NP к) АР большее отношение, чем
дуга вР к окружности круга 6ИК,
en = _np_ ,> ep
АЛ ~ АР '** окр.
так что и РА будет иметь к AN большее отношение, чем окружность
круга вНК к дуге вКР **).
PA .. окр. 6HK
AN екр
Но отношение окружности круга 0HK к дуге 0KP будет тем же
самьш, какое прямая 0А имеет к АХ; (это доказало (в предложении
XIX»; значит, РА имеет к AN большее отношение, чем 6Л к АХ,
ра ^ ел
AN > АХ
а это невозможно. Итак ZA не будет ни больше, ни меньше окружности
круга ЭНК; следовательно, равна ей [9].
*) Ото показывает, что Архимеду было известно предложение, равносильное нашему, что тан-
тангенс дуги больше этой дуги.
**) Это неравенство иоя^чаетеп на исходного
NP ^ дуга вУ
РА "*<Ж|>. вНК"
при помощи «обращения»
ар ^ окр, енк
Ш ^~ дуга вР
и «переворачивания.)
ар окр, енк
АР—PN окр. вик-дуга вР '
Мы получили бы его, вычти обе части основного неравенства не единицы
. NP дуга 6Р
РА - окр. вНК" '
откуда
NA дуга
АР окр. вНК "
О СПИРАЛЯХ
249
XIX
Если прямая касается спирали, описанной в течение второго оборота,
в конечной ее точке, и если из начала спирали проведена какая-нибудь
прямая перпендикулярно к началу вращения, то она встретится с ка-
касательной, и прямая между касательной и началом спирали будет, вдвое
больше окружности второго круга.
Пусть А13Г6 {рис. 18} будет спираль, описанная в течение пер-
первого оборота, а 6ЕТ — в течение второго, пусть 6КН будет первый
Рис. 18.
круг, a TMN — второй; пусть также будет некоторая прямая TZ.
касающаяся спирали п Т, и ZA [гроведена под прямым углом к ТА;
она встретится с TZ, так как доказано, что угол ATZ острый. Требуется
доказать, что прямая ZA будет вдвое больше окружности круга TMN.
Действительно, если она не вдвое больше, то будет или более чем
вдвое больше, или же менее чем вдлое больше. Пусть сначала она будет,
если возможно, более чем вдвое больше; возьмем некоторую прямую АА,
которая была бы менее, чем прямая ZА, и более ч&м вдвое больше окруж-
окружности круга TMN.
ZA > ЛА > 2 окр. TMN
Теперь имеется некоторый круг TMN и в этом круге данная
линия TN, меньшая диаметра, и (отношение) ТА к АА большее того,
которое половина TN имеет к перпендикуляру, опущенному на нее из А;
тогда можно из А приставить к продолжению TN прямую AS так,
чтобы ее часть Р2 между окружностью и продолженной прямой имела
к ТР то же самое отношение, что ТА к АЛ (предложение VII);
ТР
ТА
АЛ
пусть AS
ТА
ТР
АЛ
пересекает круг в Р, а (иторой оборот) спирали — в X;
и после перестановки Р2 будет иметь к ТА то же самое отношение,
что ТР к АЛ.
_ тр
~~ АЛ
Но ТР имеет к АЛ отношение меньшее, чем дуга ТР к удвоенной
окружности_круга TMN, , .
ТР ¦'• :¦¦
'- г 1.ьр. tmn • •¦...••..
250 АРХИМКД
так как прямая ТР меньше Дуги ТР, а прямая АЛ больше, чем удвоен-
удвоенная окружность круга TMN; значит, Р2 имеет к АР меньшее отноше-
отношение, чем дуга ТР к удвосппой окружности круга TMN;
тр
АР - 2 окр. TMN
тогда вся 2А к ЛР будет иметь меньшее отношение, чем дуга ТР вме-
вместе с дважды пзнтоп окружностью круга TMN к дважды взятой окруж-
окружности круга TMN.
2Р + РА ,, TV + 2 окГ). TMN
ЛР v 2 окр. TMN
Но отношение обеих упомянутых дуг будвт том ;ко самым, какое
ХА имеет к AT (это доказано (в предложении XV); значит, AS будет
иметь к ЛР отношение, меньшее чем ХА к ТА, что невозможно. Итак,
прямая ZA не будет более, чем удвоенная окружность круга TMN.
Подобно же этому докажем, что она не будет и менее, чем удпоенная
{окружность). Таким образом, ясно, что она будет ровно вдвое больше.
Тем л;с самым способом можно доказать, что если какая-нибудь
прямая касается спирали, описанной при каком-нибудь обороте в ко-
конечной ее точке, и прямая, проведенная из начала спирали перпен-
перпендикулярно к началу иращения, пстречается с касательной, то (получен-
(полученная при пересечении прямая) будет раина окружности круга, взятой
в кратности, соответствующей (порядковому) числу оборотов.
XX
Если прямая линия касается спирали, описанной в течение первого
оборота, не в конечной ее точке, и точка касания соединена с началом спи-
спирали, затем из начала спирали, как из центра, описан круг радиусом,
равным этой соединяющей прямой, и из начала спирали проведена неко-
некоторая прямая перпендикулярно к {прямой), соединяющей точку каса-
касания с началом спирали, то проведенная прямая встретится с касатель-
касательной и прямая между местом встречи и началом спирали будет равна
Риг. 19,
дуге описанного круга между тачкой касания и сечением описанного круга
с началом вращения, если брать дуги от точки на начале вращения
к передней стороне.
Пусть ЛВГА {рис. 19} будет спираль, описаллая в течение первого
оборота, и пусть некоторая прямая EZ касается ее в точке А; соединим А
прямой АА с началом спирали, и из центра А радиусом АА опишем круг
о спиралях 251
AMN; пусть он лересечет начало вращения в К; проведем также ZA.
перпендикулярную к АА. То, что она встретится (с AZ), очевидно; а то,
что прямая ZA равна дуге KMNA, требуется доказать.
Если она не равна, то будет или больше или меньше. Пусть сна-
сначала она будет, если возможно, больше. Возьмем некоторую прямую
ЛА, которая была бы меньше прямой ZA, но больше дуги KMNA.
ЖА > ЛА > дуга KMNA
Опять имеется круг KMN, в нем линия AS, меньшая диаметра, и от-
отношение А А к АЛ большее того, которое полони па AN имеет к перпен-
перпендикуляру, опущенному на пес из А; в таком случае можно из А приста-
приставить к продолжению NA прямую АЕ так, чтобы ЕР имела к ДР то же
самое отношение, что ДА к АЛ;
ИР __ ДА
АР "" АЛ
((в предложении VII) доказано, что зто возможно). Тогда ЕР будет
иметь к АР то же самое отношение, что ДР к АЛ.
ер _ ар_
АР АЛ
Но ДР имеет к АЛ меньшее отношение, чел! дуга ДР к дуге КМ А,
ар ^ др
АА кмл
так как прямая ДР меньше дуги АР, а АЛ больше дуги КМЛ; таким
образом, прямая ЕР имеет к РА отношение меньшее, чем дуга АР
к дуге КМД,
ЕР ^ АР
ул кмд
так что и АЕ имеет к АР меньшее отпоитсиш;, чем дуга КМР к дуге КМД.
ЕР + РА ^КМА+АР
AV " кмд
Но отношение дуги КМР к дуге КМД будет тем же самым, какое пря-
прямая ХА имеет к АД;
КМР __ ХА
значит, ЕА имеет к АР отношение меньшее, чем АХ к ДА,
JA_ ^АХ_ . '
АР ЛА
что невозможно. Итак, ZA будет не больше дуги КМД. Подобно пре-
предыдущему покажем, что она будет и не меньше; следовательно, она
равна (дуге КМД).
Тем же самым образом можно доказать, что, если прямая касается
спирали, описанной в течение второго оборота, не в конечной ее точке
и если лее остальное будет сделано совершенно так же, то прямая меж-
между местом встречи с касательной и началом спирали будет равна всей
уже вычерченной окружности круга и еще дуге между упомянутыми
точками, отсчитываемой совершенно так же. И если какая-нибудь пря-
прямая касается спирали, описанной в течение какого-нибудь оборота не
252 ¦ АРХИМЕД
в конечной ее точке и все остальное будет сделано совершенно так же,
то прямая между упомянутыми точками будет раина окружности опи-
описанного круга, виятой л кратности па единицу меньше сделанного
числа оборотов, и еще (дуге) между упомянутыми точками, взятой
тем же самим обрааом*).
XXI
Пели взять площадь, заключенную между спиралью, описанной
при первом обороте, и первой прямой**) на начале вращения, то можно
описать около нее плоскую фигуру и вписать другую такую же, состоя-
состоящую из подобных секторов так, чтобы описанная фигура была больше
вписанной на. величину, меньшую любой заданной площади.
Пусть АВГА {рис. 20} будет спираль, описанная при первом обо-
обороте, пусть точка в будет началом спирали, прямая 0А — началом вра-
вращения, ZHIA — первым кругом, а АН и
ZI— его взаимно перпендикулярными диа-
диаметрами. Если мы будем все время делить
пополам прямой угод и заключающий его
сектор, то когда-нибудь оставшаяся часть сек-
сектора будет меньше заданной; пусть получив-
получившийся сектор А6К будет меньше наперед
заданной площади. Разделим все четыре пря-
прямых угла па части, равные углу, заключен-
заключенному между А6 и GK, и прямые, образу-
образующие эти углы, продолжим до спирали. Пусть
точка пересечения прямой 0К со спиралью
будет А; из центра в оциппш круг радиусом. 6А;
тогда часта» его окружности, находящаяся с передней стороны, попадет
внутрь спирали, ас задней стороны — вне ее. Теперь опишем дугу [ОМ]
до встречи с 0Л [в точке OJ, а также до следующей за ОК прямой @М).
доходящей до спирали. Пусть точка пересечения ©М со спиралью
будет ]N; из центра © радиусом 0N опишем, круг так, чтобы дуга этого-
круга встретилась с 0К и со следующей за 6Л1 прямой @Р), дохо-
доходящей до спирали. Точно так же через все остальные точки, в которых
прямые, образующие равные углы, пересекают спираль, опишем из
центра 0 круги так, чтобы дуга каждого из них встретилась с предыду-
предыдущей и с последующей прямыми; тогда около взятой площади будет
описана некоторая фигура, состоящая из подобных секторов, и другая
такая вписана. Докажем, что описанная фигура будет больше вписан-
вписанной па величину, меньшую наперед заданной площади.
Действительно, сектор 0ЛО равен 0MA, сектор 8ГШ равен 0NP,.
а 0Х? равен 0XT, и каждый из остальных секторов вписанной фигуры
равен имеющему с ним общую сторону сектору описаппой фигуры.
Таким обрааом, ясно, что всо секторы (описанной фигуры) равны
(соответствующим секторам вписанной); значит, фигура, вписанная
в эту площадь, раина описанной около нее, за исключением лить
сектора 0AK, так как из всех секторов описанной фигуры не будет взят
только он один. Теперь ясно, что описанная фигура будет больше впи-
вписанной на сектор АКв, который меньше наперед заданной (площади).
*) То есть от начала иращения к передней стороне.
**) См. определение 4.
о спиралях 253
С л е д с т в и е
Из этого ясно, что около упомянутой площади можно описать, как
сказано, фигуру так, чтобы описанная фигура была больше этой пло-
площади на величину, меньшую всякой наперед заданной площади, а затем
и вписать фигуру так, чтобы рассматриваемая площадь была больше
вписанной фигуры на величину, меньшую всякой наперед заданной
площади.
¦ XXII
Если взять площадь, заключенную между спиралью, описанной при
втором обороте, и той прямой, которая является второй прямой на,
начале вращения, то можно описать около нее плоскую фигуру, соста-
составленную из подобных секторов, и вписать другую так, чтобы, описанная
фигура была больше вписанной па {величину),
меньшую всякой наперед заданной площади.
Пусть АВГДЕ {рис. 21} будет спираль,
ошшакиая при втором обороте; пусть точка
© будет л а чал ом спирали, прямая А© — на-
началом вращения, а ЕА — пторой из прямых,
находящихся на начале вращения; пусть круг
AZTT будет вторым кругом, а АГН, Z1 — его
взаимно перпендикулярными диаметрами.
Тогда опять, разделяя пополам прямой угол
и сектор, заключающий этот прямой угол, мы
когда-нибудь придем к остатку, меньшему па-
перед заданной (величины), и пусть получен-
полученный сектор ©КА будет меньше наперед задан-
заданной площади. Теперь если разделим прямые углы на части, равные углу
K0A, и псе остальное сделаем точно так же, как и раньше, то описан-
описанная фигура будет больше вписанной на величину меньшую, чем сектор
A0K; действительно, она будет больше па тот избыток, которым сектор
0ЛК превосходит сектор 0EP.
С л е д с т в и с
Теперь ясно, что можно (сделать так), чтобы описанная фигура
Яыла больше взятой площади на (величину), меньшую всякой наперед
заданной площади, я также чтобы взятая площадь была больше лштсан
ной фигуры на (величину), меньшую всякой наперед заданной площади.
Тем же самым способом выясняется, что если взять площадь, заклю-
заключенную между спиралью, описанной в течение какого угодно оборота,
и соответствующей ей по порядку прямой из тех, которые находятся на
начальном положении вращения, то можно описать около нее упомяну-
упомянутую плоскую фигуру так, чтобы описанная фигура била больше взятой
площади на (величину), меныпую всякой наперед заданной площади,
и затем вписать такую же фигуру так, чтобы взятая площадь была
больше вписанной фигуры на (нечичину), меныпую всякой наперед
• заданной площади.
XXIII :
Если взять площадь, заключенную между {дугой) спирали, мень-
меньшей описанной в течение одного оборота и не имеющей конца в начале
спирали, и прямыми, проведенными из обоих концов этой {дуги) спирали
25-4 АРХИМЕД
{к началу спирали), то можно описать около этой площади плоскую фи-
фигуру, состоящую из подобных секторов, и вписать е нее другую такую
же, так, чтобы описанная фигура превосходила вписаппую на (величину),
меньшую всякой наперед заданной площади.
Пусть будет спираль ЛВГДЕ {рис. 22}, концы которой суть А, Е;
пусть начало спирали будет 0; проведем соединяющие прямые АВ и
©Е. 3атеы из центра в опишем круг радиусом 6 А;
пусть «и встретится с вЕ в точке Z. Постоянно
разделяя пополам угол при 0 и соответствующий
сектор 6AZ, мы когда-нибудь получим остаток,
меньший наперед заданной (площади). Пусть
сектор ®АК будет меньше наперед заданной
площади. Тогда подобно предыдущему опишем
круги, проходящие через те точки, и которых
спираль пересекают прямые, образующие при ©
рапные углы, так, чтобы каждая дуга встречала
предшествующую и следующую за ней прямую;
|>||С- —• тогда получится некоторая плоская фигура,
состоящая из подобных секторов, описанная
около площади, заключенной между спиралью ЛВГЛЕ и прямыми Л0,
6Е, и другая такая же вписанная, причем описанная фигура будет
превосходить вписанную на (величипу), меньшую заданной площади,
так как сектор 0AK будет меньше этой последней *).
Следствие
Из этого ясно, что около упомянутой площади можно описать, как
указано, плоскую фигуру так, чтобы описанная фигура была больше этой
площади на (величину), меньшую всякой наперед заданной площади,
и затем вписать так, чтобы упомянутая площадь была больше вписап-
ной фигуры на величину, меньшую нсякой наперед заданной площади.
XXIV
Площадь, ааключенная между спиралью, описанной в течение пер-
первого оборота и первой из прямых, находящихся на начале вращения,
будет третьей частью первого круга.
Пусть будет спираль АВГАЕ0 {рис- 23}, описанная в течение пер-
первого оборота, пусть точка 0 будет началом спирали, а ©А — первая
прямая из тех, которые находятся на начале вращения; круг AKZHI
будет первым кругом, а круг q — его третьей частью. Требуется дока-
доказать, что вышеупомянутая площадь равна кругу <j.
Действительно, если это не так, то она будет или больше, или же
меньше. Пусть сначала она, если возможпо, будет меньше. Тогда около
площади, заключенной между спиралью АВГАЕ0 и прямой ©А, можно
описать плоскую фигуру, составленную из подобных секторов, так,
чтобы опмсаннаи фигура была больше этой площади на величину, мень-
меньшую того избытка, на который круг q превышает упомянутую пло-
площадь. Опишем ее, и пусть из секторов, составляющих упомянутую
фигуру, наибольшим будет 0AK, а наименьшим 6Е0; ясно, что опи-
*) Иабмток илищади оиисжшой фигуры над вписанной ране» изОытку шющади ссктоуа вАК
над площадью сектора ДЕ«, что меньше площадн сектора ©ЛК.
О СПИРАЛЯХ
255.
Рис ТА.
\
санная фигура будет меньше круга q. Теперь продолжим прямые, обра-
образующие при 0 равные углы, вплоть до встречи их с окружностью кру-
круга; получатся некоторые лилии, а именно проведенные из © до спирали,
одинаково возвышающиеся одна над другой, из которых наибольшей
будет 0А, а наименьшей вЕ, и
наименьшая будет равна разно-
разности (между двумя последова-
последовательными прямыми); кроме того,
имеются и некоторые другие
линии, а именно доходящие из в
до окружности круга, причем
по количеству они будут равны
первым, по величине же каждая
из них будет равна наибольшей
из первых; далее, на всех этих
прямых, как на тех, которые
одипаково возвышаются одна
наД Другой, так и на тех, кото-
которые равны друг Другу и наибольшей ил первых, построены подобные
секторы; значит, секторы, построенные на прямых, ранных на-
наибольшей, будут менее взятых имеете утроенных секторов, построен-
построенных на прямых, одинаково возвышающихся одна над другой; зто
доказано (следствие предложении X). Ш>
секторы на прямых, равных друг другу и
наибольшей, раины кругу AZHJ, секторы же
па прямых, одинаково возвышающихся одна
над другой, равны описанной фигуре; значит,
круг AZIIl будет менее утроенной описан-
описанной фигуры. Но он и три раза больше круги.
q; значит круг q будет жшьпго описанной
фигуры. Но он не меньше, а больше; значит,
площадь, ограниченная спиралью АВГАЕ©
и прямой А07 будет не меньше площади q.
Но она также будет и не больше. Дейст-
Действительно, пусть она будет, если нозможно,
больше. Тогда опять можно в площадь, за-
заключенную между спиралью АВГДЕ0
{рис. 24} и прямой АЭ, вписать фигуру так,
чтобы упомянутая площадь была больше
вписанной фигуры на (величину), меньшую
той, на которую упомянутая площадь более
круга q. Впишем ко, и пусть из составляющих
вписанную фигуру секторов наибольшим
будит 0PH, наименьшим же О BE; тогда ясно, что вписанная
фигура будет больше круга <}. Теперь продолжим прямые, образующие
при €> равные углы, пока они не попадут на окружность круга. Тогда
опять получатся некоторые линии, одинаково возвышающиеся одна
над другой, именно доходящие из точки 0 до спирали, из которых наи-
наибольшей будет в А, наименьшей же BE, причем наименьшая равна раз
ности (двух последовательных линий), имеются также и другие линии,
именно доходящие из 0 до окрулшости круга AZHI, причем по количе-
количеству они будут равны первым, по величине же каждая из них будет рав-
равна наибольшей из первых; и на всех отих прямых, как на тех, которые
2А.
АРХИМЕД
равны друг другу и наибольшей, так и па тох, которые одинаково воз-
возвышаются одна над другой, построены подобный секторы; значит, сек-
секторы, построенные па прямых, равных наибольшей, будут более чем
в три раза больше тех секторов, которые построены на прямых, одина-
одинаково возвышающихся одна над другой, если исключить сектор на наи-
наибольшей: это доказано (следствие предложения X). Но секторы, пост-
построенные на прямых, ранных наибольшей, ратщы кругу AZH1, секторы
ж<: па лрямых, одинаково возвышающихся одна над другой, кроме нал-
большего, равны вписанной фигуре; значит, круг AZHI будет более
чем в три раза больше вписанной фигуры. Но он в три раза больше круга
<j; значит, круг q будет больше вписанной фигуры. По он не больше,
а меньше; значит, площадь, ограниченная спиралью АВГДЕФ и пря-
прямой Ав, не будет и больше круга q. Итак, круг q будет равен [пло-
[площади, заключенной между спиралью и прямой A0J [10].
XXV
Площадь, заключенная .между спиралью, описанной в течение
второго оборота, и второй из прямых, находящихся на начале враще-
вращения, имеет ко второму кругу то же отношение, что 7 к 12; это не что
иное, как отношение, которое амехте взя-
взятые прямоугольники между радиусами пер-
первого и второго кругов и третья часть квад-
квадрата на разности (между радиусами) второго
и первого кругов имеют к квадрату на
радиусе второго круга.
Пусть будет спираль АВГДЕ {рис. 25},
описанная в течение второго оборота, пусть
точка 6 будет началом спирали, прямая
вК — норной 1тз прямых па начале враще-
вращения, а АЕ — второй из прямых на начало
вращения; пусть круг AZHI будет вторым
и АН, 1Z будут его взаимно перпендикуляр-
HiiiMii диаметрами. Требуется доказать, что
площадь, ограниченная спиралью АВГДЕ
и прямой АЕ, имеет к кругу AZHI такое
же отпогаепие, как 7 к 12.
Пусть будет некоторый круг q, и пусть
квадрат на радиусе круга q равен прямо-
прямоугольнику между А®, ©К вместе с третьей
частью квадрата на АЕ: тогда круг q будет
относиться к AZTI1, так 7 к 12, так как взятое в квадрате отношение
ого радиуса к радиусу круга AZHI будет именно таковым*).
Докажем теперь, что круг q будет ранен площади, заключенной
между спиралью АВГДЕ и прямой АЕ.
В самом деле, если это не так, то он будет или больше, или мень-
меньше. Пусть сначала он будет, если возможно, больше. Тогда можно
около рассматриваемой площади описать плоскую фигуру, составлен-
Рис. 25.
*) Дейстиительно. так как Лв=20Е, то
__
__
7
12 -
О СПИРАЛЯХ.
257
ную из подобных секторов, так, чтобы описанная фигура была больше
рассматриваемой площади на (величину), меньшую той, на которую
круг q больше этой площади.
Опишем ее, и пусть из секторов, составляющих описанную фигу-
фигуру, наибольшим будет 0AK, наименьшим же в()Д; ясно, что описан-
описанная фигура будет меньше круга q. Продолжим прямые, образующие
при в равные углы, пока они не попадут па окружность второго круга.
Теперь имеются некоторые линии, одинаково возвышающиеся одна
над другой, а иметю проведенные из 0 к спирали, из которых наиболь-
наибольшей будет ВА, наименьшей же 0Е; также будут и другие лилии,
а именно доходящие из 0 до окружности кру-
круга AZHI, причем количество их па одну ли-
линию меньше количества нериых, и по величине
они раины друг другу и наибольшей (из пер-
пых); затем и на тех, которые равны наиболь-
наибольшей, и на тех, которые одинаковн возвы-
возвышаются одна над другой, построены подобные
«екторы, только на наименьшей FЕ) сектор
не построен; значит, секторы па прямых,
равных наибольшей, к секторам, построенным
на прямых, одинаково возвышающихся одна
над другой, кроме лишь наименьшей, будут
иметь меньшее отношение, чем квадрат на
наибольшей ВА ко лместе взятым прямо-
прямоугольнику между АВ, 0Е и третьей части
квадрата на ЕА; ято доказано (в следствии
предложения XI). Но секторам, постро-
построенным на прямых, равных друг другу и
наибольшей, ранен круг AZHI, секторам же,
построенным на прямых, одинаково позны-
шающихся одна над другой, кроме лишь
сектора на наименьшей, будет равна описанная фигура; значит, круг
(AZHI) к описанной фигуре будет иметь меньшее отношение, чем
квадрат на А© к имеете взятым прямоугольнику между А©, ©Е и
третьей части квадрата ла АЕ.
Но отношение квадрата на А0 ко вместе взятым прямоугольнику
между А0 и BE с третьей частью квадрата на АЕ будет тем гке самым,
какое круг AZHI имеет к кругу q; значит, круг AZHI к описанной
фигуре будет иметь меньшее отношение, чем к кругу q; значит, круг q
будет меньше описанной фигуры. По он тте меньше, а больше; значит,
круг <j не будет больше площади, заключенной между спиралью
АВГДЕ и прямой АЕ.
Но он также и не меньше. Действительно, пусть он будет, если
возможно, меньше. Тогда опять можно в площадь, заключипнуго меж-
между спиралью и прямой АЕ, «писать плоскую фигуру, состанлеппую
из подобных секторов, так, чтобы площадь заключенная между спи-
спиралью АВГАЕ и прямой АЕ, была больше вписанной фигуры на (ве-
(величину) меньшую той, на которую та гке самая площадь больше
круга q.
Впишем ее, и пусть из составляющих вписанную фигуру секторов
наибольшим будет ВКР {рис. 2С}, а наименьшим 0ЕО; ясно, что впи-
вписанная фигура будет больше круга q. Продолжим прямые, образующие
при В ранные угли, пока они не попадут па окружность круга. Опять
17 Архимед
Рис. 26.
258 Архимед
у нас имеются некоторые линии, одинакопо возвышающиеся одна над
другой, а именно доходящие из в до спирали, наибольшей из которых
является 6Л, наименьшей же 6Е; имеются также и другие линии,
а именно доходящие из 0 до окружности круга, причем количество их
будет на одну меньше количества первых, л о величине же они будут
равны друг другу и наибольшей из первых; и на одинаково возвышаю-
возвышающихся одна над другой и па ранных наибольшей построены подобные
секторы; значит, секторы па прямых, равных наибольшей, к секторам,
построенным на одинаково возвышающихся одна на другой, кроме
¦ лишь сектора на наибольшей, будут иметь большее отношение, чем
квадрат на 8А ко вместе взятым прямоугольнику между А0 и <г)Е
с третьей частью квадрата на ЕЛ- Но всем секторам, построенным на
прямых, одинаково возвышающихся одна над другой, кроме лишь
наибольшей, равна вписанная и рассматриваемую ллощадь фигура,
а другим {секторам} — круг (AZH1); значит, круг AZHL ко впи-
вписанной фигуре будет иметь отношение большее, ч«м квадрат на ВА
ко вместо взятым прямоугольнику между 6А и 0Е с третьей часты»
квадрата на АЕ, то есть большее чем круг AZHI к кругу q.
Значит, круг q будет больше вписанной фигуры, что невозможно,
так как он был меньше ее. Значит, круг q не будет и меньше площади,
ограниченной спиралью АВГАЕ и прямой АЕ; таким образом, on
будет ей ранен.
Следствие
Таким же образом докажем, что площадь, заключенная между
(дугой) спирали, описанной в течение какого-нибудь оборота, и пря-
прямой, порядок которой соответствует (порядковому) числу того же
оборота, к кругу, порядок которого соответствует (порядковому)
числу того же оборота, будет иметь такое же отношение, какое вместе
взятые прямоугольник между радиусом круга того же самого порядка
и радиусом круга, порядок которого на единицу меньше числа оборо-
оборотов, и третья часть квадрата на разности между большим и меньшим
радиусами упомянутых кругов имеют к квадрату па радиусе большего
круга из упомянутых.
XXVI
Площадь, заключенная ,кежд>/ дугой спирали, меньшей описанной
в течение одного оборота и не имеющей конца в начале спирали, и пря-
прямыми, проведенными из обоих концов этой {дуги} к началу спирали,
имеет к сектору, радиус которого равен большей прямой, соединяющей
конец этой дуги с началом спирали, а дуга заключается между обеими
упомянутыми прямыми с той лее стороны, где и спираль, такое же
отношение, какое вместе взятые прямоугольник между обеими пря-
прямыми, проведенными из концов дуги к началу спирали, и третья часть
квадрата па разности между большей и меньшей из этих прямых имеют
к квадрату на большей прямой из соединяющих концы дуги с началом
спирали.
Пусть будет (дуга) спирали АВГДЕ {рис. 27} меньшая той,
которая описывается в течение одного оборота, пусть ее концами будут
А, Е, началом же спирали —- точка 0; из точки в, как из центра, опи-
опишем круг радиусом 0А, и пусть 0Е встречается с его окружностью
О СПИРАЛЯХ 259
в Z. Требуется доказать, что площадь, заключенная между спиралью
АВГДЕ и прямыми АВ, ©Е, имеет такое жо отношение к сектору AGZ,
какое вместе пзятыо прямоугольник между А0, 6Е и третья часть квад-
квадрата на EZ имеют к квадрату на 0А.
Пусть будет круг q, имеющий радиус, квадрнрующий (вместе
взятые) прямоугольник между Ав и ©Е и третью часть квадрата
ла EZ, и угол при центре, равный углу при 6; тогда сектор qX к сек-
- тору ©AZ будет иметь такое же отпошенме, какое прямоугольник меж-
между Ав, 6Е и третья часть квадрата на EZ имеют к квадрату на 0А;
Ав-ЙИ | 4" EZ2
сектор qx |__3
сектор BAZ в.Д2
ведь именно таково взятое в квадрате отношение их радиусов. Дока-
Докажем, что сектор Xq будет равен площади, заключенной между спи-
спиралью АВГЛЕ и прямыми А0,
©Е. Действительно, если не
так, то он будет или больше,
или меньше. Пусть сначала он
будет, если возможно, больше;
тогда около упомянутой пло-
площади можно описать плоскую
фигуру, составленную из по-
подобных секторов так, чтобы
описанная фигура была больше
упомянутой площади па вели-
величину, меньшую тон, на которую „ ,„
сектор qX превосходит упомя-
упомянутую площадь. Опишем ее, и
пусть иа секторол, составляющих описанную фигуру, наибольшим
будет ©АК, иаимопынидг же ©ОД; ясно, что описанная фигура будет
меньше сектора Xq. Продолжим прямые, образующие при (м) равные
углы, до тех пор, пока они не попадут на окружность сектора 0AZ.
Теперь имеются некоторые прямые, одинаково возвышающиеся одна
над другой, а именно доходящие из в до спирали, наибольшей из кото-
которых является 6А, а наименьшей 0Е; имеются также и другие прямые
по количеству на одну мепыпе количества первых, а по величине раи-
пые друг другу и наибольшей FА), а именно прямые, доходящие
от 0 до дуги сектора A©Z, кроме прямой 0Z; на всех этих прямых,
как на равных друг другу и наибольшей, так и на одинаково позвы-
шающихся одна над другой, построены подобные секторы, только на
0Е сектор не построен; тогда секторы на прямых, равных друг другу
и наибольшей, к секторам на прямых, одинаково возвышающихся одна
над другой, кроме лишь сектора на наименьшей, будут иметь меньшее
отношение, чем квадрат на ©А ко вместе взятым прямоугольнику
между АВ, 0Е и третьей части квадрата на EZ. Но секторам, построен-
построенным на прямых, равных друг другу и наибольшей, равен сектор 0AZ,
секторам жо па прямых, одинаково возвышающихся одна над другой,
равна описанная фигура; таким образом, сектор 6AZ к описанной фигу-
фигуре имеет отношение меньшие, чем кнадрат на ВА ко вместе взятым (пря-
(прямоугольнику) между ВА, ©Е и третьей части квадрата на ZE. Но
отношение квадрата на 0А к упомянутым будет тем же самым, какое
сектор 6AZ имеет к сектору Xq; таким образом, сектор Xq будет
17*
260
АРХИМЕД
Рис. 28.
меньше описанной фигуры. Но он не меньше, а больше; значит, сектор Хс|
будет не больше площади, заключающейся между спиралью АТС ГДЕ
и прямыми Л6, 6Е.
Но он не будет также и меньше. Действительно, пусть он будет
меньше, и пусть все остальноо будет сделано совершенно так же. Тогда
опять можно вписать в эту площадь плоскую фигуру, состоящую из
подобпых секторов, так, чтобы упомяпутая площадь была больше впи-
вписанной фигуры на (величину) меньшую той, на которую эта же самая
площадь превосходит сектор Xq.
Впишем ее, и пусть из секто-
секторов, составляющих вписанную
фигуру, наибольшим будет 6ВГ
f рис. 28}, наименьшим же 06Е;
ясно, что вписанная фигура
будет больше сектора Xq. Те-
Теперь опять имеются некоторые
линии, одинаково возвышаю-
возвышающиеся одна над другой,— имен-
именно, доходящие от 0 до спира-
спирали, из которых наибольшей бу-
будет 0Л, а наименьшей 6Е;
имеются также и другие ли-
линии _ именно доходящие из 0 до окружности сектора 0AZ, кроме
лишь 6А, по количеству на одну меньше одинаково возвышающихся
одна над'другой, по величине же ранпые друг другу и наибольшей
(из них)- па каждой из них построены подобные секторы, лишь на
нчийольшей из одинаково возвышающихся одна над другой сектор не
построен- тогда секторы да прямых, рапных друг другу и наиболь-
наибольшей к секторам на одинаково возпышающихся одна над другой, кроме
лишь сектора на наибольшей, будут иметь большее отношение, чем
квадрат на 0А к (прямоугольнику) между 0А, 6Е, и третьей части
1-вадрата на части EZ, так что и сектор 6AZ имеет ко вписанной фи-
rvpe большое отношение, чем к сектору Xq; таким образом, сек-
сектою Х-» будет больше вписанной фигуры. Но он не больше, а мень-
меньше- значит сектор Xq не будет и меньше площади, заключенной
между спиралью АВГДБ и прямыми А©,
<6Е; значит, оп будет ей равен.
XXVII
Из площадей, заключенных между спира-
спиралями и прямыми на начале вращении, третья
будет вдвое больше второй, четвертая втрое
¦больше ее, пятая вчетверо, и всегда каждая
следующая будет больше второй площади в
кратности, соответствующей последователь-
последовательным числам, а первая площадь будет ше-
шестой частью второй.
Пусть предложенная спираль будет
Рис. 29.
же
Г
прямая
N -
О СПИРАЛЯХ 2М
четвертая, S — пятая. Требуется доказать, что площадь К будет -^
частью следующей, площадь М — вдвое больше Л, а N — втрое боль-
больше Л, и каждая следующая больше Л в кратности, соответствующей
последовательным числам.
Что К является -тг частью от Л, доказывается так. Поскольку дока-
доказано, что площадь К (вместе с) Л имеет ко второму кругу такое же
отношение, как 7 к 12, а второй круг к первому — как 12 к 3 (зто ведь
очевидно), и первый круг относится к площади К, как 3 к 1, то, значит,
площадь К будет ~g от Л *). Далее доказало, что площадь К (с) Л
и М относится к третьему кругу, как вместе ввятые прямоугольник
между в Г, вВ и третья часть квадрата на ГВ относятся к квадрату
на Г0.
к|Л+м гв.ев+^-гв2
площ. 3-ги круга pgS
Но третий круг относится ко второму, как квадрат на Г6 к квадрату
на 0В,
площ. 3-го круга _ ГОа
илищ. 2-го круга 0В^
а второй круг к площади К (с) Л — как квадрат на i50 ко вместе
взятым прямоугольнику между ВЭ, вЛ и третьей части квадрата
на ЛВ;
илощ. 2-го круга B©s
К"гЛ
значит, площадь К (с) Л (и) М относится к К (с) Л, как прямо-
прямоугольник между Г0, 6В и третья часть квадрата па ГВ к прямоуголь-
прямоугольнику между ВЭ и 6А с третьей частью квадрата на АВ.
к+а+м
Вв.вЛ+4-АВ»
о
Оба же последних относятся друг к другу, как 19 к 7 **), так что пло-
площадь К (с) Л (и) М относится к площади Л (с) К, как 19 к 7;
тогда одна М относится к К (с) Д, как 12 к 7. А К (с) Л относится
к Л, как 7 к 6; теперь ясно, что М будет вдвое больше Л.
Докажем теперь, что следующие площади имеют (к Л) отноше-
отношения соответственно последовательным числам.
*) Действительно, площадь К + Л, ограниченней спщ>ялъю и второй прямой, относится
ко второму кругу, как 7 к 12 (предложение XXV) второй круг вчетверо больше иерього. таи как
вВ2«А, и плищадь К равна 1/3 первого itpyFa (предложение ХХ1\). Таким образом, площадь К
111 7 i (i
равна -д- • — -= гтт второго круга, а площадь Л равна тт;— rs = т~а второго круга, и следовательно,
площадь К составляет одну шестую площади Л.
3.2 + 1
. "•) Положим 6А=ЛВ=ВГ=1; тогда отношение, стоящее еправа, будет т- =—- ;
2,1+i
262 АРХИМКД
Площадь К (с) Л, М, N (и) Е имеет к кругу с радиусом 0Е
такое же отношение, как вместе взятие прямоугольник между Ев,
вД и третьи часть квадрата на ДЕ к квадрату на 0Е.
K+A4-M+W+B = Ев"еЛ ЛЕ
Круг ©Е вв« "
Круг с радиусом вЕ относится к кругу с радиусом (Ь)Д, как квад-
квадрат на 0Е к квадрату на 0Д,
круг вЕ 0Еа
круг ед
круг же с радиусом Л в относится к площади К (с) Л, М (и) N, как
квадрат на вД ко вместе взятым (прямоугольнику) между 0Д
и 0Г и третьей части квадрата на ДГ;
круг е& _ e.js
К+Л+АН-N 0двг+
и, значит, площадь К (с) Л, М, N (и) 2 относится к К с Л, М
и N, как вместо взятые (прямоугольник) между вЕ, €)Д и третья
часть кнадрата на ЛЕ относятся к (прямоугольнику) мшкду Дв, 6Г
и третьей части квадрата на ДГ;
К+А-1-MJN+B
и после «выделения» площадь S отпосится к К (с) Л, М и N, как избы-
ток прямоугольника ЕВ, 0Д с третьей частью квадрата на ЕД
над прямоугольником между Д0, 6Г, (взятым) с третьей частью
квадрата на ГД, относится к прямоугольнику между Д0 и 0Г с третьей
частью квадрата на ДГ.
. (ОЕ ¦ 0Л+ -у ДЕ2) - (Дв- ©Г+ -j ДГ2)
К-|Л I-M+W
деегч- ,,-дг2
о
Но избыток вместе пзятых (первых) над вместе взятыми (вторыми)
будет таким же, как разность прямоугольников между Е6-6Д и меж-
между Дв и вГ, разность же ;>та будет прямоугольник между Д0, ГЕ;
- (дв-вг+ -^ дг2)-«к¦ ьь-де-вг-лв (вв-вг)-лв-vе
ииачпт, Е относится к площади К (с) Л, М и N, как (прямоуголь-
(прямоугольник) между вД, ГЕ ко имеете взятым прямоугольнику между ДО,
в Г и третьей части квадрата на ГД.
з де-гЕ
дв.№+|
При поилупщ тех же самых (рассуждений) докажем, что N относит-
относится к площади К (с) Л (и) М, как (прямоугольник) между ©Г
и ВД ко вместе взятым (прямоугольнику) между Г8, ©В и третьей
части квадрата на ГВ;
n ег-вл
к+л+м^
О СПИРАЛЯХ 263
значит, N относится к площади К (с) Л, М и N, как (прямоуголь-
(прямоугольник) между 6Г, ВЛ ко вместе взятым прямоугольникам между 0Г,
БД и 0Г, 0JB вместе с третьей частью квадрата на ГВ,
«г- нл
[и обратно]; последние жо равны прямоугольнику между Д0. 6Г
и третьей части квадрата на ГД.
«г - вд+ег • ев;- !г гк2=дв • «г | -i- гд2
Теперь так как площадь Н относится к К (с) А, М и N, как прямо-
прямоугольник на 6Д, ГЕ ко вместе взятым (прямоугольнику) между ДЭ,
0Г и третьей части квадрата на ГД, а К (с) Л, М и N относятся к N,
как вместе взятью (прямоугольник) между Д0, ©Г и третья часть
квадрата на ГА относятся к прямоугольнику между ВГ, ДВ *), то,
значит, В будет относиться к N, как (прямоугольник) между 0Д,
ГЕ к (прямоугольнику) между в Г, ЛВ.
JL ел-г и
Т1о (прямоуголытик) между 6Д, ГЕ имеет к {прямоугольнику)
между 0Г, АВ то же отношение, что вД к вГ, так как ГЕ равна
ВА; теперь ясно, что и Н будет иметь к N то же отношение, что 6Д
к 0Г.
Е ©Л
ег
Подобным же образом докажем, что N относится к М, как вГ
к 0В,
jv ет^
м "вв
а М относится к А, как Вв к Л0,
прямые же [Е0], Д0, Гв, В0, А0 относятся как последовательные
(целые) числа.
XXVIII
Если на спирали, описанной в течение какого угодно оборота,
взять две точки, не являющиеся ее концами, взятые точки соединить
пряными с началом спирали и из начала спирали, как из центра, описать
круги радиусами, равными расстояниям от взятых точек до начала
спирали, т.о площадь, ограниченная больший дугой окружности .между
этими прямыми, (частью) спирали между теми же прямыми и про-
продолжением (м,еньшей) прямой, будет относиться к площади, ограни-
ограниченной меньшей дугой, той же самой (частью) спирали и прямой, сое-
соединяющей их концы, как радщ;с меньшего круга с двумя третями раз-
разнести между радиксами большего и меньшего кругов отнссится к радиу-
радиусу меньшего круга с одной третью той оке самой разности.
*) Сюда, но существу, в должно относиться выражение ей обратно», поставленное и квад.
х. сносках.
264
АРХИМЕД
Пусть будет спираль АТЗГД {рис. 30}, описанная в течение одного
оборота; возьмем на ней две точки Л и Г так, что точка в будет нача-
началом спирали *); соединим А и Г с © и из центра 0 опишем круги радиу-
радиусами вА, вГ. Требуется доказать, что площадь Е относится к П, как
Ав с двумя третями НА относится ко имеете взятым Ав и одной тре-
трети ПА.
В А«+ 8 НА
П
Согласно доказанному (в предложении XXVI), площадь-N {вместе
с) П относится к сектору НГ0, как (прямоугольник) между Н6,
Ав с третьей частью квадрата на АН относятся к квадрату на Нв;
N[11
нге
не-
АП8
не*
з
значит, одна площадь S относится к N + П, как (прямоугольник)
между ©А, АН с двумя третями квадрата на НА относится ко вместе
взятым (прямоугольнику) между Ав, 0Н и
третьей части квадрата на НА**).
, еЛ-Л]Ы--|-ПАа
4- НА*
NJ-H
И так как площадь N, П относится к секто-
сектору N,n, E, как вместе взятые (прямоугольник)
между 0А, ©II и третья часть квадрата на НА
относятся к квадрату на 0Н,
N-t-n »--—¦-¦-
.N+11-.-E
Рис. 30.
а сектор N,n, S относится к сектору N как (квадрат) на 6Н к
(квадрату) на 6Л,
N+TT + E
fc>A«
то площадь N,II относится к N так же, как вместе взятые (прямоуголь-
(прямоугольник) между 6А и 611 и третья часть (квадрата) на НА относите»
к (квадрату) на 6А;
N-I П
значит, N, П относится к П, как вместе взятке (прямоугольник)
между П0, 0А и третья часть квадрата на НА относятся ко вместе
взятым (прямоугольнику) .между ПА и 0А и третьей части квадра-
*) JleWmpOw ёя' a'vToig6ao ca|i8SxToiA, Г,
**) Имеем
*Ш2.- ( Ив - А& -;- j АИЗ\ -= Нв • АН - *¦ АН? = НЛ2 + А© • АН - ^ АН2 »¦= Ав - АН +1 А Н*.
О СПИРАЛЯХ.
2С5-
та на НА *).
п
S
п
5
п
HA-0A+-i-HA2
Так как площадь Е относится к N,11, как «месте взятые «пря-
«прямоугольник» между ©Л; АН и дне трети квадрата на НА относят-
относятся ко вместе взятым (прямоугольнику) между II©, ©А и третьей части
квадрата на ПА, а илощадь г\,П относится к II так гкс, как вместе
взятые (прямоу голыш it) можду НВ, ВА и третья часть квадрата на НА
относятся ко вместе взятым (прямоугольнику) между НА, А©
и третьей части квадрата на НА, то S будет относиться к 11, как вме-
ст© взятые (прямоугольник) между ©А, АН и две трети квадрата
па НА относятся ко вместе взятым (прямоугольнику) на ©А, АН
и одной трети (квадрата) на НА.
©А.АН+-|-
вА-АН|- y АН»
Но вместе взятые (прямоугольник) между ЭЛ, АН и две трети (квад-
(квадрата) на. НА относятся ко вместе взятым (прямоугольнику) между
©А, АН с одной третью (квадрата) на НА, как вместе взятые ©А
и дне трети НА относятся ко имеете взятым ©А и одной трети НА;
теперь ясно, что площадь Е к площади П имеет то же самое отношение,
что вместе взятые ©А и дне трети НА ко вместе взятым ©А и одной,
трети НА.
0А+ -|- НА
6А+
1
ПА
*) Если
N + 1Г
IX
©А
¦ен + 1
АИ2
^ АН»-At»*
5
ИЗМЕРЕНИЯ КРУГА
1
Всякий круг равен прямоугольному треугольнику, причем радиус
круга равен одной ин прилегающих к прямому углу сторон, а периметр —
основанию треугольника.
Пусть круг АВГД {рис. 1} относится к треугольнику Е, как
высказано в предложении; я утверждаю, что он будет ему равен.
Риг. 1.
Действительно, пусть, если нозможно, круг будет болыгте; впишем
и него-квадрат АГ, будем (постоянно) делить дуги пополам, (и прово-
проводить прямые BZ, ZA, AM, МД и т. д.), и пусть (когда-нибудь) полу-
получатся сегменты меньшие той разницы, на которую круг больше тре-
треугольника; тогда полученная прямолинейнан фигура будет также
больше треугольника. Возьмем центр (круга) N и (проведем) перпен-
перпендикуляр N3; тогда ]\5 будет меньше соответствующей стороны тре-
треугольника (Е). Также и периметр прямолинейной фигуры меньше
оставшейся стороны, поскольку оп меньше периметра круга; значит,
получоппая прямолинейная фигура будет меньше треугольника Е,
<а это нелепо.
ИЗМЕРЕНИЕ КРУГЛ
267
Пусть теперь круг, если возможно, будет меньше треугольника Е;
опишем около пего квадрат, разделим пополам его стороны и через
получегаше точки (делений) проведем касательные; тогда угол ОАР
будет прямым. Следовательно, ОР будет больше МР, так как PJVI рав-
равна РА; и значит, треугольник РОП будет больше половины фигуры
OZAM. Возьмем такие сегмептм, подобные 1IZA, чтобы они были (вместе)
меньше избытка, на который треугольпик Е больше круга ЛВГД;
тогда и описанная прямоугольная фигура будет менее Е, а ото пелепо;
действительно, она больше, так как NA раина (вертикальному) кате
ту этого треугольника, а периметр ее больше основания треугольника.
Значит, круг будет ранен треугольнику Е.
II
Круг к квадрату на диаметре относится *), как И в 14 [рис. 2}.
Пусть будет круг с диаметром АВ; опишем около него квадрат Г1Т,
и пусть ДЕ равна удвоенной ГД, a EZ — седьмой части ГА. Теперь,
так как АГЕ имеет к А ГД
отношение как 21 к 7, и Г - л- z
АГД имеет к AEZ отноше-
отношение, как 7 к 1, то ATZ будет
к АГА, как 22 к 7.
Но кпадрат ГП в че-
четыре раза больше тре-
треугольника АГД, треуголь-
треугольник же AFAZ равен кру-
кругу АВ, [так как катет А Г
равен радиусу, а основание, как будет доказано, чуть-чуть больше трех
диаметров и одной седьмой]; значит, круг к квадрату на ГН относится
как 11 к 14 [1J.
III
Периметр всякого круга равен утроенному диаметру с избытком,
который, меньше седьмой части диаметра, но больше десяти семьдесят
первых [2].
Пусть будет круг с диаметром АГ и центром Е (рис 3], затем каса-
касательная TAZ и угол ZE Г—третья часть прямого угла; тогда EZ отно-
относится к ZT, как 306 к 153, а ЕГ к TZ относится, как 265 к 153. ^
Разделим угол ZET пополам прямой ЕЙ; тогда как ZE к ЕГ,
тик будет и ZII к НГ,
Рнс. 2.
КГ ~~ ПГ
[будем также «переставлять» и «присоединять»];
ZH+НГ
ГЕ НГ
тогда как имеете взятие ZE, ЕГ к ZI\ так и ЕГ к ГП;
ZE+КГ _ _ЕГ_
таким образом, ГЕ и ГН имеет отношение большие, чем 571 к 153.
*) Такая формулировка (бее указании на приближенный характер отношения) подтверждает,
что до нас дошел испорченный текст Архимеда.
268
АРХИМЕД
EH2
Значит, в квадратах ЕН имеет к НГ отношение, как 349450 к 23409,
НГ» 23 408"
следовательно, в первых степенях имеет отношение как 591 -g- к 153.
ЕН _ ~8~
НГ ~ 1&3
Опять делим пополам угол ПЕГ прямой ЕС-);^тогда пактом же
7.
Рис. 3.
основании Е Г будет иметь к Гв большее отношение, чем 1162 -тг к 153;
Гв "*¦ to»"
значит, @Е имеет к в Г большее отношение, чем 1172 -г- к 153.
о
вв. 1|721Г
Делим пополам еще угол 0ЕГ прямой ЕК; тогда ЕГ имеет к ГК
большее отношение, чем 2334 ¦?- к 153.
sr^
ГК 163
Значит РЖ имеет к ГК большее отношение, чем 2339 -г к 153.
ЕК
ГК ' 15»
Делим гаде пополам угол КЕГ прямой ЛЕ; тогда ЕГ имеет к Л Г
[а первой степени] отношение большее, чем 4673у к 153.
ЕГ-..
лг ' 1 b:t
Теперь, так как угол ZET, будучи третьей частью прямого, раз-
разделен пополам четыре раза, то угол ЛЕГ будет ти прямого. Отложим
от Е в другую сторону равный ому угол ГЕМ; тогда угол Л ЕМ равен ^
прямого; и, значит, прямая ЛМ будет стороной описанного около круга
ИЗМЕРЕНИИ КРУГА 269
. многоугольника, имеющего 9(> сторон. Теперь, так как КГ, во доказан-
доказанному, имеет к ГЛ отношение большее, чем 4073у к 153, и АГ вдвое
иолынс ГЕ, a AM ндвое больше ГЛ, то значит, АГ к периметру 90-уголь-
ника имеет большее отношение, чем 4673— к 14С88.
t
И (ати 14 688) будут втрое больше, (чем 4673 ~}, причем остаются
(i(i7 ij-, которые несколько меньше седьмой части 4673 -} , тал что (пери-
(периметр) многоугольника, описанного около круга, будет более диаметра
в три раза с дробью, которая меньше седьмой его части; значит,
периметр круга будет и лодавпо меньше, чем (диаметр, взятый)
три раза с добавлением седьмой части.
Пусть будет круг с диаметром ЛГ {рис. 4} и угол ВАГ составляет
третью часть прим ого; тогда ЛВ имеет
к В Г отношение меньшее, чем ЩГ>1 к 780.
АВ I3S1
ИГ - 7КО
[а ЛГ к ГВ, как 1560 к 780].
Разделим пополам угол ВАГ примой
All. Теперь так как угол ВА11 равен г
НПЗ, а также и НАГ, то и угол НТВ
ранен ИЛ Г. Дпл«е примой угол АН Г
является общим; значит, и третий угол
И'ЛГ ранен третьему углу АГТГ. Тогда треугольник АИ Г будет равно-
равноугольным с треугольником TUZ; следовательно, отношение АИ к IIГ
равно отношениям ГН к IJZ и Л Г к TZ.
ли _ гп _аг
и г hz~ rz
Ho как АГ к TZ, так и вместе взятые ГА, АВ к В Г,
Гй ВГ
и. значит, как вместе взятые ВА, АГ к В Г, так и АН к НГ.
ВА+АГ АН
ВГ " НГ
Вследстиие этого АН будет иметь к ИГ меньшее отношение, чем
2911 к 780, а АГ к ГН меньшее отношение, чем .40134 у+у к *^°-
Делим пополам угол ГАН прямой Ав; тогда вследствие того же
А© будет иметь к в Г меньшее отношение, чем 5924 ^--1 -^ к 780, или
4
1823 к 240, так как каждый (иоследуюлдай) составляет ^ (предыдуще-
(предыдущего); таким образом, АГ будет иметь к Г0 отношение меньшее, чем
*838я- к 240. (Делим) еще. пополам угол ВАГ прииой КА; 1тогда}
АК имеет к КГ меньшее отношение, чем 1007 к 6E,
Л К 1007
КХ 88
271) ЛРХИМКД
11
Tin; как каждый (последующий) составляет ^ (предыдущего); зна-
\
чит, ЛГ к КГ (имеет меньшие отношение), чем 1009-тг к 66. (Делим)
еще пополам угол К. А Г прямой Л А; тогда ЛЛ имеет к АГ меньшее отно-
1 1
шеппс, чем 201(i-jr к ОС, а Л Г к ГЛ— меньшее, чем 2017 -^ к 66.
Значит, обратно {отнолгенш ГА к ЛГ больше, чем 66 к 2017-,-.
По ГЛ есть сторона многоугольника с 9(> сторонами; поэтому!*) пери-
периметр рассматриваемого многоугольника имеет к диаметру большее отно-
А А
тонне, чем 0330 к 2017 —, что больше 2017 -j- бо-тее чем в три раза с де-
десятью 71-ми долями; следовательно, периметр 96-угольника, «писанного
и круг, более чем и три и =j раза больше диаметра, так что окружность
будет и подавно больше, чем и три и =т раза.
Итак, периметр круга Судет более чем в три раза больше диаметр»
с избытком меньшим седьмой части, но больлиш ^ [3J.
ФРАГМЕНТЫ, ОТНОСЯЩИЕСЯ К «ИЗМЕРЕНИЮ КРУГА»
1.Диофант |20] (ипд. Тлшюри, II, стр. 22, 16).
«Архимед понизал, что 30 равносторонних треугольников равны 13 квадратам».
Если черта а обозначим пторипу треуго.;пшш»-а и сотпетсинмшо къадрата, то их
площади будут соответственно раины а*±-т-и я2. Израиснстла 30-«s—-f—=13-n2
-- 2fi
находим У 3=-r= .
15
2. Гороп, Метрика, по. 1, 37.
«Архимедсш в «Намерении кругя» доказано, что всякий сектор будет половиной
прямоугольника, заключешиош между дугою сектора И радиусом того круга, к которому
принадлежи г сокторл.
3. Г крон, Метрика, ни. I, 2В.
«Тот же самий Архимед и книге «О призмах (яе(>1 nAiv difiiav) и цшишдрах» пока-
показывает, что периметр всякого круга имеет к диаметру большее отношение, чем 211 87&
с it) S
(Ы.аюое) к C7441 {\\.Ху\ш), но меньшее, чем 1У7 888 (М, ^солт)) к 62 351 (Mr ptv«)».
, ' Гсйберг замечает, что вривцдсноые числа, по-видимому, лгпорчшил:, так как
Таким обра;юм, оба предложенных отношения будут больше, чей л=3,14159. Гейберг
f к 211S75 „ .,.,,¦.
предлагает вместо М, t,v|ia читать М, ^vjmft— C7 Wk\ тогда "yf^i" ~ ^
t« t» 195 888 ... . ,
пместо же М, ?<олт) читать М, ешяг) —195 888; тогда-р2заГ~=' "'"
П. Таииерн (см. Гсйберг [1-5,11, стр. 542) предлагает исправить так: вместо М, ешое
ка 10 i6
читать М, аюор=211 872, а вместо М, L,v>nr\ читать М, ешлр—liM 882-
*) Тгкег в фигурных скобках рставлеи иа «Математической библиотеки» Паппа, книга VII.
49, стр. B«S.
•*) Точнее 3,i4f*53.">...
•¦») Точнее 3,1734...
ИЗМЕРЕНИЕ КРУГА
271
О НЕПРАВИЛЬНЫХ ПОВЕРХНОСТЯХ II ТЕЛАХ
ГЕРОН, МЕТРИКА, КН. I, 39:
«Теперь, «аи я полагаю, необходимо сказать и относительно неправильных поверх-
востой, каким образом падо их измерять. 1С ели нонерхгюсть является плоской, ограни-
ограничивающая я№ ev- .чш\ив пенранилылой, то нужно па vrioii линии паять несколько смежных
точен т:п;, чтобы последовательно соединяющие их прямые лишл но слишком отклоня-
отклонялись от линии, ограничивающей фигуру, и поело этого измерить фигуру инк многоуголь-
многоугольник, иодразделмя гга треугольники. К ел и и«е новс:рхгшс".ть не будет плоский, кик, напри-
например, у статуи или чего-нибудь подобного, то нужно ваять возможно болси тонкий папирус
или полотно и обтянуть им но чпг-тям поверхность, пони последняя не будет им кругом
охвачена, а затем, расправив шшкруг. или полотно на плоскости, измерять, как сказало
выше, ограниченную непраинлыцш линией площадь и тиким образом, найти величину
поверхности. Если будут какие-нибудь другие поверхности пли фигуры на поверхностях,
то их нужно измерить согласно пышесказанпому».
ТАМ ЖЕ, КН. II, ВВЕДЕНИЕ.
«После измерения прямолинейных и не прямолинейных поверхностей мы должны
в норндке очереди перейти к тслим, поверхности которых мы уже измерили и предыдущей
книге, а именно к телам, ограниченным плоскостями, сферическим, затем коническим
и цилиндрическим и, iraitoiruii, пепралильным; так кик соответствующие методы предста-
илнкпт.я удтштсльними, то их открытие некоторые, следун yciiiiioiiiTiimciicE традиции,
относит к Архимеду. Принадлежат ли они Архимеду или кому-нибудь другому- псе ратшо
необходимо будет описать и их».
ТАМ /KB, UH. II, 20.
«После того как мы измерили геометрически правильные тела, мы считаем не леж-
шш при описании методов тшерелли сказать кое-что и относительно ncnpiiiiM.:ibHijx тел,
ироде похожих на дрелесиие корни или ки.мпи; некоторые рассказывают, что необходимый
для этого способ был изобретен Архимедом. Если подлежащее измерению тело нвлнется
удобонерпносимым, то нужно будет, сделан прямоуголыгый сосуд, могущий вместить
это тело, наполнить его водой и опустить в нее неправильное тело; тогда ясно, что неко-
некоторое колнчнетко поды пыльетсн, тик что, какой был объем у опущенного и ипду тела,
столько поды педостияет и этом вместилище после того, как тело будет па «его вынуто.
Если мы измерим сдслнвшпсся пустым иристрапстно, то и найдем объем опущенного тела.
Можно тит;ж(! ипмерить его и ипаче; если обленитг. неправильное тело воском пли глиной
так, чтобы оно после нокрытия сделалось вполне прнмоугольным; зитем после ого и.чме-
решш нужно спить глину, сделать из пп\ прямоугольный параллелепипед, измерить ого
и отнять от получишгого в перлом измерении; тогда остаток покажет об'ьем тела. Мето-
Методом пблеплппания должно ш>,:>(..юпатьси таюке и ггои изыерепии тез, которые нельзя
Переноси1!!.».
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР, ИЛИ О ЦЕНТРАХ
ТЯЖЕСТИ ПЛОСКИХ ФИГУР
КНИГА ПЕРВАЯ
Сделаем следующие допущения:
1. Равные тяжести на. равных длинах уравновешиваются, на нерав-
неравных же длинах не уравновешиваются, но перевешивают тяжести на
большей длине.
2. Если при равновесии тяжестей па каких-нибудь длинах к одной
ия тяжестей будет что-нибудь прибавлено, то они не будут уравнове-
уравновешиваться, но перевесит та тяжесть, к которой было прибавлено.
'Л. Точно так же если от одной из тяжестей будет отнято что-
нибудь, то они не будут уравновешиваться, по перевесит та тяжесть,
¦от ко/порой не было отнято.
4. При совмещении друг с другом равных и подобных *) плоских
фигур совместятся друг с другом и их центры тяжести.
5. У неравных же, но подобных фигур центры тяжести будут по-
подобно же расположена. Под подобным расположенном точек в подобных
фигурах мы подразумеваем такое, в котором прямые, проиедетшые из
этих точек к вершипам равных углов, образуют равные углы с соот-
ветстненными сторонами.
6. Если величины уравновешиваются на каких-нибудь длинах, то
на тех же самых длинах будут уравновешиваться и равные им.
7. Но всякой фигуре, периметр которой везде выпукл в одну и ту же
¦сторону, центр тяжести должен находиться внутри фигуры.
При :>тих .предположениях:
Г
Тяжести, уравновешивающиеся па равных длинах, будут т-аже
равны.
Действительно, если бы они били неравными, то после отлитии
от большей избытка они не уравновесятся, поскольку что-то отнято
от одной из двух уратагопгашшающихеи тяжестей. Таким обрааом, урав-
поветиигпощиссн на равных длинах тяжести будут тоже ракньт.
*) То есть конгруэнтных, так как геометрическое равенство греки понимали в смысле
¦равновеликое т и.
Г) РАВНОВЕСИИ ПЛОСКИХ ФИГУР
273
Рис.. 1.
11
Неравные гпяжгсти на равных длинах не уравновешиваются, по
перевешивает большая.
Дейстиителг.но, после отнятия избытка они будут ураиновептивать-
ся, поскольку рапные тяжести на равных длинах урапнопспшнаются.
Тогда после прибавления отнятого перевесит большая, поскольку
было что-то прибавлено к одной из уравновешивающихся тяжестей.
III
Неравные тяжести будут уравновешиваться на неравных длинах,
причем большая тяжесть на меньшей длине.
Пусть А, В будут неравные тяжести, и пусть А будет большая,
причем они уравноневгииаютсн на длинах ЛГ, ГВ {рис. 1}. Требуется
доказать, что АГ будет мень-
меньше ГВ.
Действительно, пусть она
не будет .мепыне. Тогда после
отнятия избытка, па который А
превышает В, перевесит И, ио-
сколысу что-то было отнято от одной из уравновешивающихся тяжестей.
Но она не перевесит; действительно, если ГА равна ГВ, то они ураинсь
весятся {как равные тяжести на равных длинах], если же ГА больше
ГВ, то перевесит А, так как равные тяжести на норы иных длипах не
уравпопешниаютсн, по перевешивает тяжесть па большей длине. На
основании зтого А Г будет меньше ГВ.
Тан же ясно, что уратювешмиающиеся на неравных длинах тяже-
тяжести по рапиы, причем большая тяжесть будет на меньшей длине.
IV
Если две равные величины не имеют одного и того же центра тяже-
тяжести, то для величины, составленной из обеих этих величин, центром
тяжести будет середина прямой, соединяющей центры тяжести этих
величин.
Пусть точка Л будет центром тяжести для (величины) Л, а точ-
точка В — для (величины) В, и пусть соединяющая ЛИ разделяется
пополам в Г {рис. 2}; я утверждаю,
что для величины, составленной из
обеих отих величин, центром тяже-
тяжести будет Г.
Действительно, если это не так,
то пусть центром тяжести {для ве-
величины, составленной из А, В|, бу-
рИС- 2. Дет> если возможно, Л, [ибо раныпе
было показано, что он находится
на ABJ *). Тогда если точка Д бу-
будет центром тяжести величины, составленной из А, В, то при за-
закреплении А получится равповесие; нначит, иеличины Л, В будут
идиому из предшествующих сочинений Архинедк, которое
") Возможно, что комментатор, которому ирииаплсжпт вМ|>пжсгшр. влключешню и кпадрат-
пые скпПки. отемлпет читателя к идиому из предшествующих сочинений Аихимсшн кто.™ сшв
было ему доступно.
18 Архимед
274
АРХИМЕД
уравновешиваться на длинах АД, АВ; ото же невозможно, [ибо рав-
ныо тяжести па неравных длинах пс уравновешиваются]. Поело этого
ясно, что Г будет центром тяжести величины, составленной из А, 13.
Л
г
Рис. 3.
Если центры тяжести трех величии лежат на одной прямой, при-
причем эти величины имеют одинаковую тяжесть, и прямые, лежащие меж-
между центрами, равны, то для величины, составленной из всех этих вели-
величин, центром тяжести будет точ-
точка, которая является, центром тя-
тяжести для средней {величины).
Пусть будут три величины А,
В, Г, а их центры тяжести — точ-
точки А, В, Г, лежащие на одной
прямой; пусть также {величины
А, В, Г) равны, и А Г, ГВ — рав-
равные прямые {рис. 3}; я утверж-
утверждаю, что для величины, составленной из всех этих величин, центром
тяжести будет точка Г.
Действительно, так как величины Л, В имеют одинаковую
тяжесть, то центром их тяжести будет точка Г, поскольку АГ, ГВ рав-
равны. Jlo и для величины Г центром тяжести будет точка Г; тогда ясно,
что и для величины, составленной из всех, центром тяжести будет точ-
точка, которая является центром тяжести для средней.
Следствие 1
Из этого ясно, что если имеется любое нечетное количество вели-
величин, центры тяжести которых лежат на одной прямой, причем вели-
величины, одинаково отстоящие от середины, имеют рапные тяжести, и
прямые, заключающиеся между их центрами, равны, то для величины,
составленной иа всех этих величин, центром тяжести будет точка,
которая является центром тяжести ^__^
для средней из них. ' ' ' '
Следствие 2
Также если эти величины будут
Рис. А.
в четном кол ичестио, причем их
центры тяжести лежат на одной пря-
прямой, л как средние величины, так и, одинаково от них отстоящие
имеют равную тяжесть, а прямые между центрами равны, то для
величины, составленной из всех этих неличин, центром тяжести
будет середина прямой, соединяющей центры тяжести этих величин,
как нарисовано ниже (рис. 4}.
VI
Соизмеримые величины уравновешиваются на длинах, которые
будут обратно пропорциональны тяжестям.
Пусть А, В будут соизмеримые величины, центры которых А, В;
возьмем некоторую длину ЕД, причем пусть как А к В, так будет а
О 1'ЛВНОВЕСИИ ПЛОСКИХ ФИГУР
275
длина ДТ к длине ГЕ {рис. 5}; требуется доказать, что для величины,
составленпой из обеих величин Л, В, центром тяжести будет Г,
Действительно, поскольку А отпосится к В, как ДГ к ГЕ,
А &г
В " ГЕ
и Л соизмерима с В, то, значит, ГД соизмерима с ГЕ, то есть прямая
соизмерима с прямой, так что у ЕС, ГА есть общая мера. Пусть она
будет N; отложим ДН, ДК, равные каждая ЕГ, и ЕЛ, ранную Л Г.
Тогда поскольку ДН равна ГЕ, то и
ДГ раина ЕН, так что и ЛЕ равна ЕН.
Значит, ЛИ вдвое больше ДГ, а НК
вдвое больше ГЕ, так что .\ измерит и
каждую из ЛН, НК, поскольку она изме-
измеряет их половины. 11 поскольку как А к
В, так и ДГ к ГЕ,
г
А
ДГ
ГЕ
Л
Е
All
N
КН
ЛН
!тзг
как же ДГ к ГЕ, так и ЛН к ПК
К Г Н
ЛН
НК
Рис. 5.
(так как каждая из вторых вдвое больше соответствующей из лерпых
прямых), то, значит, как А и Б, тал и ЛИ х НК.
ЛИ
нк
Пусть А будет во столько раз больше Z, во сколько ЛИ больше N;
тогда кап ЛН к N, так и А к Z.
А
z
Но также будет, что как КП к ЛН, так и 13 к А;
в
А
КН
N
тогда «по равенству» как КП к N, так и В к Z;
в
значит, КН от N и В от Z будут равнократными. Доказано жй, что и А
есть кратное Z, так что Z будет общей мерой для А, В. Теперь если
мы разделим прямую ЛН на части, раиные N, величину же А на части,
равные Z, то равновеликие К отрезки в ЛИ будут в равном количе-
количестве с частями в А, равными Z. Таким образом, если па каждый из
содержащихся и ЛИ отрезков наложить величину, ранную Z, так,
чтобы она имела центр тяжести в середине отрезка, то все эти величи-
величины вместо будут ршшы Л и для составленной из всех их величины
центром тяжести будет Е, так как все они будут в четном числе и в
одинакоиом количестве с каждой стороны от Е вследствие того, чтоЛЕ
• равна ЕН,
Подобным же образом докажем, что если на каждый из содержа-
содержащихся в КН отрезков наложить величину, равную Z, так, чтобы она
имела центр тяжести в середине отрезка, то все оти величины вместе
будут равны В, и для составленной из всех их величины центром тяже-
тяжести будет Д; тогда величина А будет наложена в Е, величина же В и Д.
18*
276
АРХИМЕД
Таким образом, получатся равные друг другу величины, расположен-
пыо по прямой, центры тяжести которых равно удалены друг от друга,
причем в четном числе; следовательно, ясно, что для составленной из
всех их нелпчшш центром тяжести будет точка, делящая пополам пря-
прямую, на которой находятся центры промежуточных величин. Посколь-
Поскольку жо ЛЕ раьиа ГА, а ЕГ равна АК, то, значит, л вся Л Г будет parnia
Г К; так что для составленной из всох величины центром тяжести будет
точка Г. Итак, сели А приложить в Е, а В в А, то они будут находиться
и равповесия но отношению к Г.
. VII
И далее, если величины будут несоизмеримыми, то они точно так же
уравновесятся па длинах, которые обратно пропорциональны этим
¦величинам.
Пусть ЛВ, Г будут несоизмеримые величины, а ДЕ, EZ — длины,
и пусть АВ имеет к Г то же самое отношение, что длина ЕД к длине EZ
{рис. В}; я утверждаю, что для
А Е Z величины, составленной из обоих
1 ' ' АВГ, центром тяжести будет Е.
Действительно, если АВ, поме-
помещенная в Z, не уравновесится с Г,
помещенной в Д, то ЛВ или будет
больше, чем нужно для равно-
равновесия с Г, или нот.
Пусть она будет больше; от-
отнимем от ЛВ меньше того избыт-
Рис. С. ка, на который АВ является боль-
больше, чем пужно для равновесия
с Г, так, чтобы остаток А был
соизмерим с Г. Поскольку теперь величины А, Г соизмеримы и Л
имеет к Г отношение меньшее, чем ЛЕ к EZ, то А и Г не уравновесятся
на длинах ДЕ, EZ, если А поместить в Z, а Г в Д. Таким же образом
докажем и и том случае, когда Г будет больше того, что нужно для
равновесия с АВ *).
VIII
Если от какой-нибудь величины отнимем некоторую се часть,
не имеющую того жг самого центра тяжести, что и целая, то для
остающийся величины центр тяжести получится, если линию, соеди-
соединяющую центры тяжести целой величины и отнимаемой, продолжим
в ту сторону, где находится центр целой величины, и на продолжении
соединяющей упомянутые центры отложим отрезок так, чтобы к рас-
расстоянию между центрами он имел то же самое отношение, какое тя-
тяжесть отнимаемой величины имеет к тяжести остающейся.
*) Доказательство должно быть пополнено так. Гели мм от ЛВ отнимем "В так. что А. являясь
оиамеримой с Г. нее же будет перемешивать последнюю, то отношение Л к Г должно быть больше
'отношения КА к RZ u саном меле, при равновесии относительно точки Е мы имели бы равенство
Г
кд
КЛ
А + В
В —i—r^—
же А иерсБстниаст, то
; полученное противоречие и докаиыиает теорему
Л ЕД Л ЕД
- - > ¦??=-; но в действительности — < __ , так
1 Ft?t I tu?t
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
277
Г 'А в
II
Рис. 7.
Пусть центр тяжести некоторой неличины АВ будет Г; от АВ
отнимем {величину) АД, центр тяжести которой пусть будет Е; затем
на продолжении соединяющей ЕГ отложим FZ, имеющую к ГЕ то же
самое отношение, как величина АД
имеет к ДН {рис. 7}; требуется до-
доказать, что у иеличипы АН центром
тяжести будет точка Z.
Действительно, пусть это не так,
по, если возможно, пусть им будет
точна 0. Тогда, так как у величины
АД центром тяжести является Е,
5' ДН же — точка 0, то для величины, составленной из обеих, центр
тяжести будет на Е0, разделенной так, чтобы ее отрезки были обратно
пропорциональны отим величинам; тогда точна Г не будет сечением, соот-
соответствующим упомянутому. Значит, Г не будет центром величины, со-
стаиленной из АД, ДН, то есть АВ. Но она им является, ибо так было
предположено; значит, 0 не будет центром тяжести величины ДН.
IX
У всякою параллелограмма центр тяжести находится на пря-
прямой, соединяющей середины противоположных сторон параллелограмма.
Пусть будет параллелограмм ЛВГД и EZ — прямая, соединяющая
середины АВ, ГД {рис. 8}; я говорю, что у параллелограмма АВГД
центр тяжести будет на EZ.
Действительно, пусть это не так, по, если возможно, пусть он
будет и 6; проведем 01 параллельно АВ.
Будем все время делить KB пополам до тех пор, лона не нолучит-
сп отрезок {КК>, меньший 10; разделим каждую из АЕ, ЕВ на рав-
равные ЕК части и из точен деления
проведем прямые, параллельные
EZ; тогда весь параллел ограмм раз-
разделится на параллелограммы, рав-
равные и подобнее KZ. Теперь, если
равные и подобные K.Z параллело-
параллелограммы наложить друг па друга, то
соннадут друг с другом и их центры
тяжести. Таким образом, получатся
некоторые величины, а именно равные К Z параллелограммы, ив четном
количестве, причем их центры тижести расположены на прямой, и как
средние пеличипы, так и все находящиеся по обе стороны от стед-
них равны, и прямые между центрами равны; значит, у величины,
состанлешюй из всех этих, центр тяжести йудет па прямой, ссединя-
шщеи центры тяжести диух средних площадей. Но он побудет там, ибо
0 находится вис средних параллелограммов. Теперь ясно, что центр
тяжести параллелограмма ЛВГД будет на прямой EZ.
X
У всякого параллелограмма центром тяжести будет точка, в ко-
которой встречаются диаметры, {то есть диагонали).
Пусть будет параллелограмм АВГА и в пем прямые—EZ, де-
лящаи пополам АВ и ГД, и К.А, делящая АГ и ВД {рис. 9}; тогда
Е К
Ргс. 8.
278
АРХИМЕД
у параллелограмма ЛВГД цонтр тяжести будет па EZ, ибо это доказа-
доказано. Но по той же причине он будет и на К.Л; значит, точка 0 и есть
центр тяжести; но в 0 встречаются диаметры параллелограмма, так
что предложенное доказало.
Иначе
То же самое можно доказать и иначе.
Пусть будет параллелограмм ЛВГД, и пусть его диаметр будет ДВ
{рис. 10}. Значит, треугольники АВД, ВДГ раины и подобны друг
Другу, так что при наложении треугольников друг на друга совпадут
и их цептры тяжести. Пусть у треугольника АВД центром тяжести
А
1
I
i
Рис. 9.
Рис. 10.
будот точка Е; разделим ДВ в 0 пополам, продолжим и отложим Z6,
равную BE. Тогда если наложить треугольник ЛВД на треугольник
ВДГ и поместить сторопу АВ на ДГ, а ЛД на ВГ, то и прямая 0Е
ляжет на Z0 и точка Е понадет па Z. Но она также должна попасть
и па центр тяжести треугольника ВДГ. Теперь, так как у треугольника
АВЛ центром тяжести является точка Е, у ДВГ же — Z, то ясло, что
у величины, составленной из обоих этих треугольников, центром тяже-
тяжести будет середипа прямой EZ, какой и является точка 0.
XI
Если будут два подобных друг другу треугольника и в них взяты
точки, подобно расположенные по отношению к треугольникам, причем
одна точка будет центром тяжпсти того треугольника, в котором она
находится, то и другая точка будет центром тяжести того треуголь-
треугольника, в котором она находится. [Под подойпым расположением точек
по отношопию к подобным фигурам aim подразумеваем такое, в котором
прямые, проведенные из этих то-
точек к ранным углам, образуют рав-
равные углы с соответствующими
Пусть будут два треугольника
АВГ, AEZ, и пусть как А Г к AZ,
так и АВ к ДЕ, и ВГ к EZ;
АГ
АВ
ДЕ
I'llC. 11.
пусть в упомянутых треугольниках
будут подобно расположенные
Гио отпотешпо к треугольникам АВГ, AEZJ точки 0, N, и пусть 0
будет центром тяжести треугольника АВГ {рис. 11}; я утверждаю, что
N будет центром тяжести треугольника AEZ.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
279
Действительно, куоть ото по так, ко, если возможно, пусть цент-
центром тяжести треугольника AEZ будет 11; проведем соединяющие пря-
прямые ©А, 6В, 0Г, AN, EN, ZN, ДН, Ell, ZH. Теперь, поскольку тре-
треугольник ART подобен треугольнику АЕ'Л и центрами тяжести являют-
являются точки В, Н, у подобных же фигур подобно расположены и центры
тяжести, [так что образуются равные углы с соответственными сторо-
пами каждой с каждыми], то, значит, угол ПАЕ будет равен углу вАВ.
Но угол 0А13 равен углу EAN [вследствие того, что точки 0, N подоб-
подобно расположены]; значит, и угол EAN будет равен углу ЕДП, больший
меньшему; это жо невозможно. Значит, точка IV не может нр. быть цент-
центром тяжести треугольника ДЕ7; значит, она им является.
XII
Если будут два подобных треугольника и у одного треугольника
центр тяжести находится на прямой, которая проведена от какого-
нибудь угла к середине основания, то и у другого треугольника центр
тяжести будет на подобно прове-
проведенной линии. &
Пусть будут два треугольника
АВГ, AEZ, и пусть как АГ к AZ, /(-
так- и АВ к ДЕ, и ВГ к ЪЕ\
дг
АВ
ЛЕ
ВГ
вн
ВА
ЕЛ
АН
ДМ
ВН
ве
ав
A U
разделив АГ пополам в Н, про-
проведем ВН, и пусть центр тяжести 0 .
треугольника АВГ Судет на НИ
{рис. 12}; я утверждаю, что и у Гж. 12
треугольника AZ центр тяжести бу-
будет на и од об но проведенной прямой.
Разделим Д7 пополам и М, соединим Е с М и сделаем, чтобы как
ВН к В0, так и ME к EN,
и проведем соединяющие прямые А0, 0Г, ДМ, NZ. Поскольку поло-
половина ГА есть АН, половина же AZ есть ДМ, то, значит, как В А к ЕД,
так и АН к ДМ;
л к
""лаГ
и при равных углах стороны пропорциональны; значит, угол АН В
раьон углу ДМЕ, и кап АН к ДМ, так и ВII к ЕМ;
вн
" "ем
но также как ВН к В0, так и ME к EN,
и значит, «по равенству» как АВ к ДЕ, так Вй к EN,
ве
EN
Но при равных углах стороны пропорциональны; если же так, то угол
1?А6 будет равен углу EAN, так что и остающийся угол 0АГ будет
280
АРХИМЕД
ГА
AM
равсп углу NAZ. На том же основании и угол ВГ0 будет равен EZN,
и угол 0Г11 район KZM. Доказано же, что и угол AB0 равен ДЕ№;
так что и остающийся угол 6ВГ будет равсп NEZ. На основании вс«?го
•лтого точки 0, N будут подобно расположенными, [обраауи равные
углм с соответственными сторонами]. Тенерь, поскольку точки в, N
подобно расположены и в является центром тяжести треугольника АВГ,
то, значит, и N будет центром тяжести AEZ.
ХШ
У есякого треугольника центр тяжести будет иа прямой, которая
проведена из угла к середине основания.
Пусть будот треугольник АВГ и в нем прямая АД, проведенная
к середине оспопания 13Г {рис. 13}; требуется доказать, что центр тя-
тяжести АВГ будет па АА.
Действительно, пусть это не так, по, если возможно, он будет в 0;
лроиедем через него 61 параллельно В Г. Постоянно деля ДГ пополам,
придем когда-нибудь к отрезку»
который будет меньше ©I; раз-
разделим каждую из ЬД, ДГ на
равные ому части, происдом через
точки деления прямые, парал-
параллельные АД, и соединим EZ, ПК,
AM; они будут, копечпо, парал-
параллельны ВГ. Теперь у парал-
параллелограмма MN цгнтр тяже-
тяжести будет на ТХ, у К5 же на ТГГ
у ZO же на ТД; значит, у величи-
величины, составленной из всех их,
центр тяжести будет на прямой
2А. Пусть он будет в Р; соединим PG (прямой), продолжим ее и парал-
параллельно АД проведем ГФ. [Треугольник] АДГко всем вместе треугольни-
треугольникам, построенным па AM, MR, KZ, Zr и подобным АА Г, имеет такое яке
отношение, какое ГА имеет к AM, нследствис того, что прямые AM, MK,
ZI\ KZ ранни. Поскольку же и треугольник ЛАВ ко всем вместе подоб-
подобным треугольникам, построенным на АЛ, ЛН, НЕ, ЕВ, имеет то же
самое отношение, что ВЛ к АЛ, то, значит, треугольник АВГ ко «сем
упомянутым треугольникам имеет то же отношение, какое. ГА имеет
к AM. Но ГА имеет к AM большее отношение, чолг ФР к Pfc
Рис. 13.
так как отноше1ше ГА к AM будет тем же самым, что у Гксей] ФР к 1'П
[воледстшш подобия соответстиующих треугольников]; и, йпачит,
треугольник АВГ ко всем упомянутым имеет большее отногиепие, чем
ФР к Р&; и таким образом, «выделяя» *) — параллелограммы MN,
К2, ZO к треугольникам, осталшимся (r окаймлсшш), будут иметь
большее отношение, чем Ф0 к 0Р. Сделаем тенерь так, чтобы прямые
Х6 и 6Р были между собой в отношении этих параллелограммов к
оставшимся треугольникам. Тогда, поскольку имеется некоторая вели-
*) Треугольник АВГ без Окаймления будет иметь и треугольникам окаймления большее'
отношение, чем ФР—^в к 6I1.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 28t
чина АВГ, центром тяжести которой является 9, и от нее отнимается
всличппа, составлеппая из параллелограммов MN, KE, причем цент-
центром тяжести отнимаемой величины будет точка Г, то, значит, у остаю-
остающейся величины, составленной из окаймликчцмх треугольник он, центр
тяжести получится, если на продолжении прямой Рв отложить отре-
отрезок, имеющий к 0Р то же отношение, какое имеет отнятия неличина
к остатку. Значит, точка X будпт центром тяжести величины, составлен-
составленной ия окаймления; ято же невозможно, так как если провести через X
прямую, параллшшиую АД, то рее треугольники будут и плоскости
за ней, [то есть по одну сторону]. После итого предложенное становится
. очевидным.
То же самое иначе
Пусть будет треугольник АВГ; проведем прямую АД к середине
В Г (рис. 14}; я утверждаю, что на АА находится центр тяжести тре-
треугольника АВГ.
Действительно, пусть это не так; если возможно, пусть он будет
в 0; соединим А и 0, 0 и В, © и Г, затем проведем ЕА, ZE к серединам
ВА, ЛГ, далее параллельно А0 проведем ЕК,
ZA и соединим К и Л, Л и Д, Д и К, А и
0, М и N.
'Гак как треугольник АВГ подобен тре-
треугольнику Д7Г ислодствио того, что ВА па-
параллельна ZA, и центром тяжести треуголь-
треугольника АВГ является то^ка 6, то, впачлт, у
треугольника ZAT центром тяжести булот
точка А, так как точки В, А подобно распо-
расположены в каждом из этих трсуголы-пшон,
[поскольку они образуют равные углы с
соотиетствепными сторонами; ото педьисно].
11а той же «сноиашш и у ЕВД центром
тяжести будет точка К; таким образом, у величины, составленной из
обоих этих треугольникои ЕВД, '/ЛГ, центр тяжести пуде? на сере-
середине лрнмой КЛ, [так как треугольники ЕВД, ТАГ раины]. И сере-
серединой КЛ будет К; поскольку как BE к ЕА, так и ЕК. к ©К,
ВР. J1K
иа — ёк"
как же PZ к ZA, так и ГА к Л0;
_rz_ гл
za ~"л«
если же так, то ВГ будет параллельна КЛ. Мы соединили Д и 0; зна-
значит, как ВД к А Г, так и KN к NA;
_вл
дг
таким образом, у величины, составленной из обоих упомянутых тре-
треугольников (ЕВД и ZAT), центром будет N. У параллелограмма же
AEAZ центром тяжести будет точка М; таким образом, у ьеличипи,
соста пленной из «сох их, центр тяжести 65'дот на прямой MN. hoy АВГ
центром тяжести будет точка 0; значит, MN, будучи продолжена, npoir-
дст чороз точку 0, ото же невозможно. Значит, центр тяжести треуголь-
треугольника АВГ не может не быть на прямой АД; значит, он будет на пей.
282 АРХИМЕД
XIV
У всякого треугольника центром тяжести будет точка, в которой
встречаются прямые, проведенные из углов к серединам сторон.
Пусть будет треугольник А13Г ipuc. 15}; проведем АД к середине
В Г и BE к середине АГ; тогда центр тяжести треугольника АВГ будет
па каждой из АД, BE, ибо ото доказано. Таким образом, точка в {их
пересечении) будет центром тяжести.
XV
У всякой трапеции, имеющей две стороны, параллельные друг дру-
другу, центр тяжести будет на прямой, соединяющей середины парал-
параллельных, разделенной таким образом, чтобы отрезок ее, кончающийся
й -
Рис. 15. Рис. 1С.
в середине меньшей из параллельных, имел бы к остающемуся отрезку
то отношение, которое имеет прямая, равная удвоенной большей сторо-
стороне, взятой вместе с меньшей, к прямой, равной удвоенной меньшей вме-
вместе с большей из параллельных.
Пусть будет трапеция АВГД, имеющая параллельными АД, ВГ,
и пусть EZ соединяет середины ЛД, В Г {рис. 1C}. Тогда очевидно, что
центр (тяжсрли) трапеции будет на EZ. Дййсттггелыю, если продол-
продолжить ГД11, ZKH, 13AE1, то ясно, что они придут в одну л ту же точку,
и центр тяжести треугольника ИВ Г будет па 11Z, и точно так же центр
тяжести треугольника АИД будет на HZ; значит, и у остающейся тра-
асции АВГД центр тяжести будет на EZ. Соединяющую НА раздоим
на три равные части в точках К, 0, через них параллельнп ВГ проведем
A0M, NKT u соединим Л и Z, В и Е, О и 3; тогда у треугольника
ДВГ центр тяжести будет на 0М, так как ВВ является третьей частью
от ВД [и Мв проведена через точку в параллельно основанию].
По центр тяжести треугольника ДВГ будет также и на AZ; таким обра-
aoiK, Н будет центром тяжести уломянутого треугольника. На том же
основании и точка О будет центром тяжести треугольника АВД; значит,
у неличипи, составленной из обоих треугольников АВД. ВАГ, которой
и является трапеция, центр тяжести будет на ирнмой OS. Но также
на EZ будет и центр тяжести упомянутой трапеции; таким образом,
центром тяжести трапеции ABVA будет точка II. Тогда треугольник
ВДГ должен относиться к АВД, как ОП к ПН.
тр-и ВАГ ОП_
тр-n АВД ~ ПЗ . ¦ '
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 283
Но как треугольник ВД Г к треугольнику АВД, так будет и ВТ к АД,
тр-в ВАГ ВТ
тр-И АВД ~ Аи.
оп рп
US ** ШГ
как же. ОП к IIS, так и РП к 112,
рп
и, значит, как 13Г к АД, так и РП к 112,
АД " 112
так что и как дне ВГ имеете с АД к двум АД вместе с ВГ, так и две РП
вместе с Л 2 к диум 112 вместе с РП *).
2ВГ4-АА 21'Щ П2
2АД+ВГ^ 2111 * IIP
Но дне РП вместо с П2 будут вместе взятыми ZP, РП, то есть ПЕ,
две же Г1? имеете с РП будут имеете ьзвтыми РХ, 211, то есть HZ;
значит, предложенное доказано.
КНИГА ВТОРАЯ
1
Если две площади, ограниченные {каждая) прямой и параболой
и могущие быть «приложенными» к заданной прямой, не имеют одного
и того же центра тяжести, то для величины, составленной из них
обеих, центр тяжести будет па прямой, соединяющей их центры тяже-
тяжести, причем вышеупомянутую прямую on раяделит таким образом,
что ее отрезки будут обратно пропорциональны этим площадям.
Пусть АВ, ГД {рис. 17; будут упомянутые площади, пуст], их
центры тяжести буяут и точках Е, Z, и лусть Z0 шгеет к BE такое аде
отношение, как АВ к ГД.
Z6 _ ул. Л В
"ей" ~ ил г,\
Требуется доказать, что для яеличипы, составленной из обеих площа-
площадей АВ, ГД, цептр тяжести будет и точке 0.
Пусть каждая из Zll, ZK pauna EG, EA же пусть будет равна ZB,
то есть НЕ; тогда А© будет равна К0;
*) Гассматрниасмвн пропорция мьжет быть устаноилсиа таким образом:
_ВГ_ = ^1^ ЙВГ 2РН
А& Ш2 'АД П? '
отсюда, «прнсоедшшя», находим.
2БГ 1-АД _ 2PII !-П2
АД
Аналогично
I ВГ
ВГ PIT
Теперь us пропорций
2ВГ г Аи _ 2РП-»-т: ^АЛ_ US ВГ _ I'll
АД ~ J12 ' ВГ "" I'LL ' 2АД+ВГ 2[Ji. |-ЛР
шл зэллючасл) «во pauwjorjiys, чго
2ВГ+АД _ 2РП+П1:
' 2П1-+РЛ "
284
АРХИМКД
и далее, как ЛН к ЫК, так и АВ к ГД,
АН _ пл. АВ ¦ Z&
_
НК ИЛ. ГД ,_ »Е
ибо члены первого отношения вдвое больше соответствующих членов
второго.
HK=2HZ=2E»
Приложим теперь к ЛН площадь ЛВ по обе стороны от ЛН так, чтобы
площадь MN равнялась ЛВ; тогда точка Е будет центром тяжести
и|шлижим типирь к i\n. плшцадь лп но out,' t/гиронм от jvn так, чтоим
площадь MN равнялась ЛВ; тогда точка Е будет центром тяжести
(прямоугольника) MN. Теперь дололшш (прямоугольник) КЗ; тогда
MN будет относиться к N3, как .
ЛИ к ПК.
ял-MN
пл. N3 '
АН
HJC
Flo также и АВ паходится с ГД в
отношении ЛН к НК,
ил. А В _ ^Л1Г
пп. ГД Ilk"
и, значит, как АВ к ГД, так и MN
к NE, или
ЦП. А В п.п. MN
ПП. ГД "" ПЛ. NS
«перестановкой» (площади АВ и MN
относятся, как площади ГА и NS);
1 Г
II ,*
я
7.
\
¦
ft
К
и
¦л. АН _ пл. ГД
ил. MN~" пл. Л
Гис. 17.
но АВ равпа MN; значит, ГД равна N3, и центром тяжести последней
будет точка Z. И так как Л0 раина 6К, а вся ЛК делит пополам проти-
противоположные стороны, то для всей площади ИМ центром тяжести будет
точка 0. Но площадь МП равпа составленной из обеих MN, N3; зна-
значит, точка 0 будет цептром тяжести площади, составленной из обеих
АВ, ГД Ш.
II
Если в сегмент, ограниченный прямой и параболой, вписать тре-
треугольник, имеющий с сегментом то же самое основание и равпую высо-
высоту, затем Р оставшиеся сегменты ипмсать треугольники, имеющие с эти-
этими сегментами то we самые основания п равные высоты, и постоянно
вписмиать тем ?кс самым образом треугольники и остающиеся сегменты,
то получится фигура, которую будем пазывать виисанпой в сегмент
«определенным образом». Тогда ясно, что во вписанной таким образом
фигуре прямые, соединяющие ближайшие к вершине углы и следующие
за ними, Судугп параллельны основанию сегмента, разделятся пополам
диаметром сегмента и сами разделят этот диаметр е отношениях
ряда последовательных нечетных чисел, если за единицу принять отрезок
у веришна сегмента. Все это должно быть доказано в надлежащем
месте \2\.
Если в сегмент, ограпичсипый примой и параболой, вписывается
«определенным образом» прямолинейная фигура, то центр тяжести
вписанной фигуры будет на диаметре сегмента.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
285
Пусть АВГ {рис. 18} будет такой сегмент, как сказано; тшшем в него
«определенным образом» прямолинейную фигуру АЕ2НВ01К.Г; тре-
бустсн доказать, что центр тяжести этой прямолинейной фигуры будет
на БД.
В
Рис. 18.
Действительно, так как у трапеции АЕКГ центр тяжести будет
па ЛД, у трапеции EZIK центр на МЛ, у трапеции ZII6I центр на MN
и, наконец, у треугольника 1IB0 центр тяжести на BN, то ясно, что
и у всей прямолинейной фигуры центр тяжести будет па ВД.
III
Если в каждый из двух подобных сегментов, ограниченных прямой
и параболой, вписать «определенным образом» прямолинейную фигуру,
так, чтобы вписанные прямолинейные фигуры имели равное количество
сторон, то центры тя-
тяжести этих прямоли-
прямолинейных фигур одинаково
разделят диаметры
этих сегментов.
Пусть будут два
сегмента АВГ, ЕОП
{рис. 19); впишем в ггих
«определенным образом»
прям ол и иейпые фигуры,
и пусть они имеют рав-
поо друг другу количе-
количество веек сторон. Пусть
диаметры этих сегмен-
сегментов будут ВД, ОР;
нроводсм соединяющие
прямые ЕК, ZT, IIG
и >-Т, ГФ, Х'У. Так
как ВД и РО пронедеп-
иыми параллельными
разделятся в отношениях ряда последовательных нечетных чисел и ко-
количества их отрезков одииакоиы, то ясно, что отрезки этих диаметров
будут к таких же отношениях и параллельные прямые будут иметь
такие же отнопмшин. И у трапеций АЕК.Г и Е2ТП цептры тяжести
будут подобно расположены на прямых ЛА, QP, поскольку АГ с ЕК
имеют то же самое отношение, что п SII с ST. Затем у трапеций EZ1K,
2ГфТ центры тяжести иодобпо разделят AM, Q^> и У трапеций ZII0I,
Рис. 19.
286
АРХИМЕД
ГХ?Ф центры тяжести подобно разделят MN, q^b. Также и у треуголь-
треугольников 11130, XO\F центры тяжести будут подобно расположены на BN,
Oq. Значит, трапеции и треугольники имеют (по площади) одно и то же
отношение. Теперь ясно, что у всей прямолинейной фигуры, вписанной
в согмепт А13Г, центр тяжести разделит ВД подобно тому, как центр
тяжести фигуры, вписанной в сегмент ЕО11, разделит ОР. Это и тре-
требовалось доказать 13}.
IV
Во всяком сегменте, ограниченном прямой и параболой, центр тя-
тяжести будет на диаметре сегмента.
Пусть АВГ {рис. 20J будет такой сегмент, как сказано, и пусть его
диаметром будет ВД. Требуется доказать, что у упомяпутого сегмента
центр тяжести будит на ВЛ.
Действительно, если это не так, то пусть он будет (в точке) Е;
проведем через него EZ параллельно ВД. Затем виишем в сегмент
треугольник АВГ, имеющий (с сег-
сегментом) то же самое основание и
рапную высоту; и пусть треуголь-
треугольник АВГ к площади К имеет то же
самое отношение, что TZ к AZ.
пд. АВГ Г2 '
им. К ¦" AZ
м
и.
Л Z
Рак. 20.
Затем впишем в сегмент «опреде-
«определенным образом» прямолинейную
фигуру так, чтобы остающиеся но
краям сегменты были мспьше К,
Тогда у вписанпой прямолинейной
фигуры центр тяжести будет на ВД.
Пусть ол будет 0; проведем соеди-
соединяющую лрнмуюВЕ, продолжим ее
и параллельно ВА проведем ГА. Яс-
Ясно, что вписанная в сегмент прямо-
прямолинейная фигура к остающимся сегментам имеет отношение большее, чем
треугольник АВГ к К *). lio как треугольник АВГ к К, так и TZ
к 7Л. Значит, и впвдаплая прямолинейная фигура к остающимся по
краям сегментам имеет большее отпошенис, чем TZ к ZA, то есть как
ЛЕ к Е0. Пусть теперь МК к Ев имеет то же самое отношение, что пря-
прямолинейная фигура к сегментам. Тогда, поскольку Е есть центр тяжести
всего сегмента, а 6 — вписанной в него прямолинейной фигуры, то
ясно, что центр тяжести остатка, то есть величины, составленной из
остающихся по краям сегментов, получится, если продолжить 6Е
и отложить пекоторуш прямую, которая имела бы к GE то же отноше-
отношение, что вписанная прямолинейная фигура к остающимся но краям
сегментам. Таким образом, центр тяжести величины, составленной из
остающихся по краям сегментов, был бы в точке М; это же нелепо.
Действительно, если провести через М прямую параллельно 13Д, то
все остающиеся, по краям сегменты будут лежать по одну ее сторону.
Теперь ясно, что центр тяжести (параболического сегмента) будет на ВД.
•) Мсйствитглмю, вта фигура Больше треугольника ЛВГ, а площадь К в свою очередь больше
остающихся серицитов.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
287
&
1'ис. 21.
V
Если в сегмент, ограниченный прямой и параболой, вписать wnpe-
деленным образом» прямолинейную фигуру, то центр тяжсапи всего
сегмента будет ближе к вершине сегмента, чель центр епшанной пря-
прямолинейной фигуры.
Пусть АВГ {рис. 21} будет сегмент такой, как скапано, а ЛВ —
его диаметр. Сперва впишем и него «определенным образом» треуголь-
треугольник ЛВГ и разделим БД в Е так, чтобы ЕЕ была и диа раза больше ЕД.
Тогда точка Е будет центром тяже-
тяжести треугольника АВГ. Каждую из
АВ, 13 Г рааделим в точках Z, Н по-
пополам и через Z и Н пара л лслыто БД
проведем ZK, ЛИ. Тогда центр тя-
тяжести сегмепта АКБ будет на ZK,
центр же тяжести сегмента В ГА—
на НЛ. Пусть эти центры тяжести
будут 0,1; проведем соединяющую
прямую 01. И так как 0ZHI —
параллелограмм и ZN равна NH,
то, значит, и Х0 будет равна XI.
Таким образом, центр тяжести величины, составленной из обоих сог-
мсптои ЛКВ, 13ЛГ, будет на середине 61, то ость в точке X, [ибо оба
сегмента раины] *). Поскольку же у треугольника АВГ центр тяжести
есть точка Е, у величины же, составленной из обоих сегментов АКБ,
ВЛГ, центр есть точка X, то ясно, что центр тяжести псего сегмента АВГ
будет па ХЕ, то сечь между точками X, Е.
Таким образом, центр тяжести всего сегмента будет ближе к вер-
вершине, чем центр тяжести треугольника, вписанного в него «определен
пым образом».
После ;)того ипишем в сегмент «определенным образом» пятиуголь-
пятиугольную прямолинейную фигуру ЛКВЛГ {рис. 22]. И пусть для всего сег-
Aieirra диаметром будет НА, для
каждого же из (боковых) сегментов
диаметрами будут KZ, All. И так
как и сегмент АКБ вписывается
«определенным образом» прямоли-
прямолинейная фигура, то центр тяжести
всего сегмента будет ближе к верши-
вершине, чем центр тяжести прям олипой-
iioii фигуры. Пусть теперь центром
тяжести сегмента <АКВ) будет 0,
а центром тяжести треугольника—
I; далее, пусть центром тяжести
сегмента ВЛГ будет М, а центром тяжести треугольника — К. Тогда
у величины, составленной из обоих сегментов АКБ, ВЛГ, центром тяже
сти будет X, у величины же, соотавленпой из обоих треугольников АКБ,
ВЛГ, центром тяжести будет Т. Далее, так как у треугольника АВГ
й
Рис. 22.
•) Сигмпгг Л К (I pmieii четырем трптнм треугольника АКТ! или восьми третям треугольника
BKZ; точно так жп сегмент ИЛ г pniwn восьми трет-пм треугольника НЛН. По треугольники BKZ
и ИЛИ равнннеликч. кик имеющие равные, иараллелышс и одинаково отстоящие от иолпикы В
основания к ? и ЛИ.
28R
АРХИМКД
центром тяжести будет Е, у поличном же, составленной из обоих сег-
мептоп АКВ, ВАГ, цептром будет X, то ясно, что цептр тяжести всего
сегмента А13Г будот па прямой ХЕ. если рассечь ее так, чтобм отноше-
отношение треугольника АВР к вместо взятым сегментам АКВ, ВАГ было
таким же, как отношение кончающегося в точке X отрезка этой прямой
к .меньшему ее отрезку. У пятиугольника же АКВАГ цептр тяжести
будет па прямой ЕТ, если рассечь ее так, чтобы отношение треугольни-
треугольника А13Г к импсте изнтым треугольникам АКВ, ВАГ было таким же,
как отношение кончающегося в Т ее отрезка к остатку. Теперь, так как
треугольник АВГ имеет к треугольникам КАВ, А13Г отношение боль-
большее, чем к соответствующим сегментам, то ясно, что у сегмента АВГ
центр тяжести будет ближе к вершине, чем у упомянутой вписаппой
прямолинейной фигуры. И то же самое рассуждение будет и относитель-
относительно всех лримолннейпых фигур, вписываемых в сегменты «определен-
«определенным образом».
VI
Если дан сегмент, ограниченный прямой и параболой, то возможно
«определенным образом» вписать в него прямолинейную фигуру так,
чтобы, прямая между центрами тяжести сегмепта и вписанной прямо-
прямолинейной фигуры была меньше любой наперед заданной прямой.
Пусть будет дан сегмент АВГ {рис. 23} такой, как сказано, цент-
центром тяжести которого будет 0; впишем в пего «определенным образом»
треугольник АВГ. Пусть наперед задан-
заданная прямая будет Z, и пусть отношение
треугольника АВГ к некоторой площади
X будет такое ;кс, как у В© я Z.
пл. апг вв
ил. X ~2~
Л
Рис.. 2Л.
Впишем «определенным образом» в сегмент
АВГ яряАЮЛипсйнуго фигуру АКВАГ так,
чтобы остающиеся но краям сегменты
вместе были меньше X. Пусть у вписан-
вписанной прямолинейной фигуры центром тиже-
сти будет Е. И говорю, что &Е будет
меньше Z.
Действительно, если не так, то она
будет или равна, или больше. Так как
прямолинейная фигура АКВАГ имеет к
остающимся по краям сегментам отношение
большее, чем треугольник АВГ к площади
X, то ость ВВ к Z, а также и Вв имеет к Z отпошение не меньшее, чем квЕ,
вследствие того, что 0Е не меньше Z, то, значит, и подавно прямоли-
прямолинейная фигура АКВАГ будет иметь к остающимся по краям сегмептам
отношение большее, чем Вв к 015. Таким образом, если мы сделаем,
чтобы прямолинейная фигура АКВАГ к остающимся по краям сегмен-
сегментам относилась, как некоторая прямая к BE, [так как центр тяжести
сегмента АВГ будот в, то продолжим Ев и отложим некоторую пря-
дгую, которая имела бы к К0 то же отношение, что и прямолинейная
фигура АК13АГ к остающимся и» кранм сегментам], то :>та прямая будет
больше вВ. Пусть теперь 116 будет к ОЕ, (как АКВАГ к остающимся
сегментам). Тогда II будет центром тяжести величины, составленной
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
289
КЬ
кл "
на остающихся по краям сегментов,- это же невозможно. Действытель-
по, если через Н провести прямую параллельно ЛГ, то эти сегменты
будут по одну сторону от нее. Теперь ясно, что BE будет меньше Z.
Это и требовалось доказать.
VII
У двух подобных сегментов, ограниченных прямой и параболой,
центры тяжести делят диаметры в том же самом отношении.
Пусть ЛВГ, EZ11 {рис. 24} будут два сегмента такие, как сказано,
диаметры которых суть ВД, ZW, и пусть у сегмента АВГ центром тяже-
тяжести будет точка К, у BZH же—Л.
Требуется доказать, что точки К, Л
делят диаметры в одном и том же
отношении.
Действительно, если это но так,
то пусть как KB к К А, так и ZM
к Мб;
ZM
мё
впишем и сг.гмопт EZII «определен-
«определенным образом» прямолинейную фигу-
фигуру так, чтобы расстояние между цент-
центрами тяжести сегмента и вписанной
прямолинейной фигуры было мень-
меньше ЛМ, и пусть у вписанной прямо-
прямолинейной фигуры центром тяжести
будет точка S; впишем также в
сегмент АВГ прямолинейную фигу-
фигуру, подобную «писанной в EZH; 1ято значит: подобную вписанной
«определенным образом»]; у нее центр тяжести будет ближе к верпнше,
чем у сегмента *); это we невозможно (предложении V>. Теперь ясно,
что ВК имеет к КЛ то ?кс самое отношение, что ZA к Л6,
• . VIII
У всякого сегмента, ограниченного прямой и параболой, центр тя-
тяжести делит диаметр сегмента так, что прилежащий к вершине
сегмента отрезок е полтора раза
больше отрезка у основания.
Пусть ЛВГ {рис. 25} будет
сегмент такой, как сказано; пусть
его диаметр будет БД, центр же
тяжести — точна 6. Требуется
доказать, что В0 будет » полто-
полтора раза больше ЭД.
Впишем «определенным обра-
образом» в сегмент АВГ треугольник
АВГ, центр тяжести которого
Рис. 24.
Гис. 25.
пусть будет Е; разделим пополам каждую из А13, ВГ и проведем
•) Действительно, осям S ость центр тпияияи многоугольника EZH. лежащий иьшип М, то
цептр тяжести подобного многоугольника АВг должен лежать выше точки К, делящей НА и том же
саном отношении, в какой М долит Z©; точка же К является иеитрок тяжести сегмента АЬГ.
19 Архимед
290 АРХИМЕД
KZ, НЛ (параллельно 13Д); они будут диаметрами сегментов АКБ,
ВЛГ. Теперь пусть у сегмента АКБ центром тяжести будет М, у ВЛГ
же — N; проведем соединяющие прямые Z1I, MN, КЛ; тогда у вели-
чипм, составленной из обоих сегментов, центром тяжести будет X.
И поскольку как В в к 0А, так и КМ к MZ,
вы км
«Д " MZ
то после присоединения и перестановки: как ВД к KZ, так и АН к М/.
вг±^ ^®_ ¦ - ¦ ¦ " ¦ ¦ "
KZ MZ
Но ВД в четыре раза больше KZ; (;ш> доказывается в конце, где знак
KB [Л]); значит, и ДО в четыре риза больше MZ, так что и остаток 13В
в четыре раза больше остатка КМ, то есть SX; и, значит, нместг и.чя-
тые остатки В2, XG «трое больше 2LX.
Пусть В2 «трое больше 22; значит, и Хв будет втрое больше
ЗХ. И поскольку ВД в четыре раза больше В2 (ибо и это доказывает-
доказывается), В2 ?ке втроо больше Ё?, то, значит, ЗВ будет третьей частью
ВД *). По и КА будет третьей частью АН, так как центр тяжести тре-
треугольники АВТ будет и Е; значит, и остаток ЗЕ будет третьей частью
ВД. И. так как для всего сегмента центром тяжести является точка в,
для величины же, составленной из обоих сегментом АКБ, НАГ, центром
тяжести будет X, для треугольника же АН Г — точка Е, то получится,
что как треугольник АВГ к остающимся сегментам, так и Х0 к 0Е.
Но треугольник АВГ втрое больше обоих сегмептов, [так как весь
сегмент составляет четыре трети треугольника АВГ]; значит, и Хв
втрое больше вЕ. По было доказано, что ХЭ втрое больше ХЕ; зна-
значит, ЕЕ будет и нить раз больше Ев,
то есть АЕ в пять раз болыпо Ев (ибо АЕ и НЕ равны).
Таким образом, Ав будет в тесть раз больше НЕ.
Но ВД втроо больше ДЕ; значит, Вв будет в полтора раза больше ЭД,
что и требовалось доказать [5].
IX
Если четыре линии будут пропорциональны в непрерывной про-
пропорции и. отношение наименыи-ей к разности между наибольшей, {то
есть первой), и наименьшей, {то есть четвертой), будет равно отно-
шению некоторой взятой линии к трем пятым раяности между наи-
наибольшей из пропорциональных и третьей, отношение же, в котором
1 4
*> Действительно. ВД=4В2, ВЗ = BS + ХЕ = BE ~ ^ BE = e- BE, откупа
..',,_ . BS : Вд--=! В?:4В? =pi.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 291
вместе взятые удвоенная наибольшая us пропорциональных, учетверен-
учетверенная вторая, ушестеренная третья и утроенная четвертая находятся
к вместе взятым упятеренной наибольшей, удесятеренной второй,
удесятеренной третьей и упятеренной четвертой, будет равно отно-
отношению другой взятой линии к разности между наибольшей из про-
порииональных и третьей, то обе взятые линии имеете составят две
пятых от наибольшей [EJ-
Пусть будут четыре, кропорционнльныо линии АВ, ВГ, ВД, BE
{рис. 2(i), и пусть линия ZH имеет то жв отношение к трпм
пятым АД, что BE к ЕА,
ZH _ BE
JTTa k A ... ;
отношение же линии Н6 к АД пусть будет равно отноше-
отношению удвоенной АВ, учетнерешюй В Г, ушестеренной ВД и
утроешюй BE, (вместе взятых), к упптерешлой АВ, уде-
удесятеренной ГВ, удесятеренной ВЛ и упятеренной НЕ.
НВ 2АВ-ИВГ4-0БД+ЗВЕ
АЛ " ЯАВ-МОГВ+ГОВД |-6ВЕ • Л'
Трсбустсн доказать, что Z0 составляет две пятых от АВ. z
Так как АН, В Г, ВЛ, BE пропорциональны, е
ЛВ ВГ ВЛ
ВГ " ПА "" ПК '. ¦ i. ¦
то I) том же самом отношении будут и АГ, ГА, АН) *). _
И вместе изитыс ЛВ, ВГ и 13Д, а также удвоенная от вместе взятых АВ,
ВГ к удвоенной ВД имеет то же самое отношение, что АД к ЛЕ, а также
и вместе ниятыс ДВ, ВГ к ЕВ, и пср пркдыдущие ко ясем последую-
последующим **).
2 (ЛЯ+ВГ) _ АД . А ВЦ-ВТ _ ДВ-^ВГ • .У. ¦
Значит, АД к ДЕ имеет то же самое отношение, что удвоенная А В с, ут-
утроенной ВГ и ВЛ к раипой удвоенной ВЛ и BE.
2АВ-1-ЗВГ1 ВД_ АД • л. '
~ 2ВД+ВЕ ДЕ ...
И отношение, в каком удвоенная АВ с учетверенной ВГ, учетверенной
13Д и удвоенной BE находится к удвоенной ДВ имеете с ЕВ, это отно-
отношение ДА будет иметь к меньшой чем ДЕ (прямой); пусть она имеет
его к ДО.
2АВ!<ВГ+4ВД+2ВК АЛ ,,„.„,,,. " • '- " .
2ВД+ВЕ Ш <A0'AbJ
-) И:, ОС„Ои„,,й пропорц». -в?— "Иг" - "=!¦ «"«.•••™»и™» АВ ~ ВГ ВГ "" ВД ВЛ " ВВ
У
АГ _ ГД _ ДЕ ЛГ ВГ
нмучаяи -jjjr - вд - ьк и
= "Р5Г ¦ Поскольку
ВГ + ВД
ВД BE
19*
292 АРХИМЕД
чл: ~\ И то же отношение будут иметь попарно взятые члены этой пропорции
я.5:.:г. к первым.
АД+АО _ BВД ¦'-ВК) Н2ЛВ-У4ВГ-МВА+2ВЕ)
АЛ — ~2А 11+4 ВГ+4ВД+2ВЁ
Теперь ОЛ будет иметь к АД то же отношение, что удвоенная АВ с учет-
верейной ВГ, ушестеренной ВД и утроенной БЕ к (линии), составлен-
составленной из удвоенной от имеете взятых АВ, BE м учетиеронной от имеете
изятых ГВ, ВД.
ОА _ JA В | 4ВГ-1-6ВЛ+ЗВЕ
АД " 2 (AB-i-BE)+* (ВГ+ВД) . .
Но и АД имеет к НВ то же отношение, что и упятеренная от вместе
взятых А13, BE с удесятеренной от вместе взятых ГВ, ВД к составлен-
составленной из удвоенной АВ, учетверенной ГВ, утроенной ЕВ и ушестерен-
ушестеренной ВД.
АД 6(ЛИ|-ВЕ)-Н0(ГВ+ВД)
Нв " 2АВ+4ГВ-КШВ+6ВД
Так как отпошевия поставлены несогласно, то есть в перемешанной
пропорции, то «по равенству» О А будет иметь к Нв то же отношение,
что упятеренная от вместе влитых АВ, BE с удесятеренными ГВ, ВД
к составленной из удвоенной от вместе взятых ЛВ, BE м учетверенной
от вместе изятых ГВ, ВД.
ОА 5<АВ+РКН-10(ГВ|ВД)
Нв " 2 {ЛВ-: HK)+>i (ГВ+ВД)
Но составленная из упятеренной от вместе ыннтых АВ, BE с удесяте-
удесятеренной от вместе взятых ГВ, ВД к составленной из удвоенной от вместе
взятых' Ali, BE и учетверенной от вместе взятых ГВ, ВД имеет то же
¦ отношении, как пять к двум. И, значит, АО относится к Нв, как пять
' ; к двум.
АО Ь
не" *
Далее, так как ОД имеет к ЛА то же отношение, что ЕВ с удвоен-
удвоенной ВД к составленной из удиоошюй от вместе взятых Л13, BE с учет-
"" ' воренной от вместе взятых 1'В, ВД,
ОД КВ+2ВА
и Jtau Л.Д к Д15, тан и составленная на удвоенной АВ, утроенной ГВ
и ВД относится к ЕВ с удвоенной ВЛ,
ад _ :;лв|-Г!гв-!-ва
д! ~ ЕВ-1-2ИД : ;
то при несогласно поставленных отношениях, то есть в перемешанной
пропорции, будет «по равенству», что кик ОД к АЕ, так и удвоенная ЛВ
с утроенной ВГ и с ВД к составленной из удвоенных от имеете взятых
АВ, BE и учетверенных ГВ, ВД.
од ' 2ац| авг+пд ¦ "'' ¦'¦
:
Таким образом, как ОЕ к ЕД, таи будет и ГВ с утроенной ВА и удвоен-
удвоенной ЕВ к удвоенной от имеете взятых АВ, BE и учетверенной от вместе
взятых ГВ, ВД,
ОЕ _ | ДК ОД _ 2(АВ+ВВ)+4(ГВ+ВА)-BАВ+ЗГВНВДI ГВ+ЭВД+2ЕВ . ¦ ^
ёл ' | лр — ~г1ав+вец-4 (гв+вд) J' 2(AB+nE)^-'i(rв^Eд) .: '
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 293
Но как ДЕ к ЕВ, так после «присоединения» будет и АГ к ГВ *),
ЛЕ АГ
ЕВ ~ ГВ
а также и утроенная ГД к утроенной ДВ и удвоенная ДЕ к удвоен-
удвоенной ЕВ,
АГ ГД ДК ЛГД 2ЛЕ
гь ~ вд ев ад и зев
а, следовательно, и составленная из ЛГ, утроенной ГА и удвоенной ДЕ
к составленной из ГВ, утроенной ЛВ и удвоенной ЕВ. ......
АГ _ АГ+ЗГА1-2АЕ ЛЕ •
ГВ ""* ГВ+ЗйВ"| 2KB "" ЕВ
- - Теперь опить при несогласно постаилеппых отношениях, то есть в иере-
. . "¦ мстявной пропорции, «во равспстяу» ЕО будет иметь л ЕВ то же отпо-
шенио, что АГ с утроенной ГД и удвоенной ДЕ к удвоенной от име-
имеете взятых АВ, BE с учетверенной от вместе взятых ГВ, ВД.
ЕО АГ|-ЗГА+2АЕ
ЕВ~2(АВ|ВК)+4(ГВ+ВД) • -•
: Теперь вся ОВ и BE имеет то же отношение, что утроеппая АВ с ушесте-
ушестеренной ГВ и утроенной 13Д к удиоенпоч от вместе пзятых АВ, BE
с учетверенной от вместе взятых ГВ, ВД.
ОВ _ г OElTSB _ 2АВЧ-(АГ+ГВ)+ЗГР-К-1ГД+ЗВД)|ВД-К2ДЕ+2ВЕI _ ЗАВ+ВГВ 1-1ВД
BE L BE ~~ 2(AB+JJE>-!-4 (ГВ+ВД) J = 2 (АВ t-UlS)+i (ГВ 1-ВЛ)
И поскольку ЕЛ, ДГ, ГА находятся в том же отношении,
Ей _ ^Г_ __ ЕВ+ВД = ДВ+ВГ
йГ ~ ГА ~ ДВ^-В1' "Г.Н-!-ВЛ
что и каждая < сумма двух вместе взятых) ЕВ и ВД.ДВ и В Г, ГВ a
ВА**), то получится, что как ЕД к ДА, так и вместо взятие ЕВ, ВД
относятся к вместе ваятым ДВ, ВГ с вместе взятыми ГВ, ВА.
кл _ г лп т ев+вл
ДА - I ДГ+ГА J ~~ (ДВ+ВГ)+(ГВ+ВА)
И значит, после «присоедипения» будет как АЕ к АД, так и вместе
взятые ЕВ, ВА с вместе взятыми АВ, В Г и вместе взятыми ГВ, ВД
¦ (а ото будут вместе изятте ЕВ, ВЛ с удвоенной от вместе взятглх ДВ,
В Г) ко вместе ваятым ВД, В А с удвоенной В Г.
АЕ _ г АА+ДЕ _ (ЕВ-!-ВА)+(АВ+ВГ)+(ГВ4-ВА)| _ (ЕВ+ВАН-2 (ДВЧ-ВГ)
АЛ I ЛД (ДВ-:.ВГ)-НГИ+ВА) I " (Вй+ВД)+2ВГ
То же самое отношение будут иметь и удвоопные, то есть как ЕА к АД,
так и удвоенная от вместе пзятых ЕВ, ВА с учстверенпой от вместе взя-
взятых ГВ, ВД к удвосшюй от вместе взятых АВ, ВД с учетвереппой ГВ.
ЕЛ 2(ЕВ1ВЛ)+4(ГВ-!-К&)
ЛЛ ~ 2 (ЛВ+Вй)+4ГВ
*) Собстиопю roDOpH, после «выделения»,так k;ikii;i исходной пропорции ~— — -цгг получаем
сГ DJlt
АВ - ВГ ВД - BE АГ ДЕ
— т. е.
Ж5 ВЁ ' ГВ ~"МВ "
• м мы ,™,<.г.» АВ_ГВ ДЬ ЛГ_П1_ДЕ (>ггк,ча ЛВ l-Br..rB-f-ВД АВ ¦{- BE
*) Мы имеем -—-.jj-^—H—____. отсюда ^^ = —^ вв—
АВ + ВГ ГД+ ВД, ЛВ+ВЕ
... наконец, ГА = йГ - = Ей •
294 ' АРХИМЕД
Таким образом, как ЕА к трем пятым АД, так и составленная из
удвоенной от имеете взятых АВ, BE и учетверенной от вместе взятых
ГВ, ВА относится к трем пятым составленной из удвоенной от вме-
вместе нзятых АВ, ВА и учетверенной ГВ. . г.
КА _ 2 (А В •¦ ВЕ1-И (ГН- ВД) : ."¦¦ "¦¦
4- Аи -?-{2(АВ-|-ВД)-г4ГЫ ¦ ,. .
Но как ЕЛ к трем пятым АД, так будет и ЕВ к ZH. .:. ¦
ЕА _ ЕВ ¦ -- ..- - ¦ ¦: ¦-.
— лд zu
И, значит, как ЕВ к ZH, так а удвоенная от вместе взятых АВ, BE
с учетверенной от вместо взятых АВ, В Г относится к трем пятым состав-
составленной из удвоенной от вместе взятых АВ, ВД с учетвереппой ГВ.
КВ^ 2 (AB-I-BEH-4 <ДВ 1-ВГ)
ZH 4- {2 (АВ+ВД)-!-4 ГВ} "'
'О
Но также было доказано, что как OJH к ЕВ, так и утроенная от вместе
взятых АВ, ВД с yjnecTepeiinoii ГВ относится к удвоенной от вместе
взятых АВ. BE с учетверенной от вместе взятых ГВ. ВД.
ОВ 3 (АВ »-Вй)+ВГВ
ЕВ "" 2 (АВТВЕ) г4 1ГВ-1-ВЛ)
И, значит, «по равенству» как ОВ к ZH, так н составленная из утроец-
пол от вместе вдятых АВ, ВД с ушестеренной ГВ относится к трем
питым составленной из удвоенной от вместе взятых АВ, ВД с учетве-
учетверенной ГВ. . , . .
ои з (лв-^вд)+бгв ' /
-i {2 <АВ+ВЛН-4ГВ>
Но составленная из утроенной от вместе взятых АВ, ВД с ушестерен-
ушестеренной V4 к составленной из удвоенной от вместе взятых АВ, ДВ с учет-
учетверенной ГВ имеет отношение, как три к двум,
а (АВ + ВАН-6ГВ _ _3_
| 4ГВ ~ 2
к трем пятым же ее имеет отношение, как пять к двум. Также доказано,
что и АО имеет к И в отношение, как пять к двум. Значит, и вся ВА
ко всей ZB имеет отношение, как пять к двум.
Если же так, то Z0 составляет две пятых от АВ. Это и требова
лось доказать.
X " '
У всяком усеченного сегмента параболы, центр тяжести находится
на прямой, являющейся диаметром сегмента, и расположен следующим
образом: если разделить эту прямую па пять равных частей, то он
лежит па средней части так. что отрезок ее, ближайший к меньшему
основанию {сегмента), имеет к оставшемуся отрезку такое же отно-
отношение, как прямоугольный параллелепипед, имеющий основанием квадрат
на большем, из оснований сегмента, а высотой прямую, равную вместе
взятым удвоенному меньшему из оснований и большему, к параллелепи-
параллелепипеду, имеющему основанием квадрат на меньшем из оснований сегмента,
высотой же прямую, равную вместе взятым удвоенному большему из
оснований и меньшему.
О РАВНОНИСИИ ПЛОСКИХ ФИГУР 295
Пусть в параболе будут две (параллельные) прямые АГ, ДЕ.
Пусть диаметром сегмента АВГ будет 13Z {рис. 27}. Тогда ясно, что Z1I
будет также диаметром усеченного сегмента АДЕГ, [так как АГ, ДЕ
параллельны касательной в 13 к сечению]. Пусть при разделении
прямой HZ на пять равных частей средней частью будет 0К. Пусть
01 имеет к IK то же отноше-
отношение, что it параллелепипед, ~ SOT
имеющий основанием квад-
квадрат на AZ, высоту же, рав-
равную вместе кзнтым удвоен-
удвоенной ДН и AZ, к параллеле-
параллелепипеду, имеющему основани-
основанием квадрат на ДН, высоту
же, равпую имеете взятым
удвоенной AZ и ДН.
Ы_ AZaBAH+AZ)
ГК "' А]
Требуется доказать,'что у сегмента АДЕГ центр тяжести есть I.
Пусть MN будет равна" ZB, a NO равна 1113; воиьмем для MN, NO .
среднюю пропорциональную NE и четьертую пропорциональную TN.
И пусть как ТМ к TN, та*к будот и Z0 к некоторой прямой, начинаю-
начинающейся от I, куда бы ни попала другая ее точка (ибо безразлично, будет ли
она между Z, Н или жо между НВ); пусть ото будет IP.
тм _ zw
TN " ~1Р
И так как прямая ZB лвлнотся диаметром сегмента параболы, то она
будет или главной осью параболы ялтг параллельной этой оси, прямые
же AZ, Д11 будут проведенными к ней ординатами *), ибо они пара.я л о ль-
льны касательной в В к параболе. Если же ато так, то будет: как квадрат
на Л2 к квадрату на ДН, так и ZB к ВН линейно, то есть, как MN
линейно к N0, так и квадраты на MN и №,
AZ* ZH MN МК
*
лн* "¦ вн - no ив* •. ..
и, значит, как квадраты tia AZ и ДН, так и квадраты на MN к NS;
так что и линейно они будут в том н;с самом отношении.
AZ MN
ЛН ¦ N3
И, значит, как куб на AZ к кубу на ДИ, так и куб на MN к кубу па NE.
AZ* _ MJ4^ ¦ " "
.mis ~~кв?
Но как куб на AZ к кубу на ЛН, так будет и сегмент АВГ к сегмен-
сегменту ДВЕ; \..
AZ3 г AZ»-AZ _ ZB-AZ -1 _ сегмент ВАГ " . •- ".'
Там» "I диа-лн ~ ВЦ-аи ]~ссгмсит две
как же куб на MN к кубу на NE, так и MN к NT.
MN» r MN M№ MN MN» MN ЛТМ MN NS ¦¦ MN
N» _ г MN_ MN^ MN MN» _ MN _ЛПв_ __ MN NS -¦ _
NS» ' ' I NS ' MSB "" N2 ' MM-NO "" NS~' NO "~ NZ TK J" TN~
*) iBiavi^ividC KCicxVfisvai — «iipunc^ciiiiMe улорддочецным оСрааомь, откуда наш терния
¦чордтштав.
296 АРХИМЕД
Таким образом, «выделяя», получим
сегмент ВАГ—согисит ДВЕ MN—NT
ДВЕ КТ
как сегмент АДГЕ к сегмепту ДВЕ, так и МТ к NT, то есть три пятых
HZ к IP *).
И так как параллелепипед, имеющий основанием квадрат на AZ,
высотой же прямую, составлсипую из удвоенной ДИ и AZ, относится
к куОу па AZ, как удвоенная ДН с AZ к ZA, и так же, как удвоенная
N5 с NM к NM,
AZ»C&IM-AZ) 5AH±AZ_fo АИ KS , NM | _ 2N2J-NM
AZ» AZ I" AZ + "MM" ¦"" ИМ J = NM
и как куб на AZ к кубу па ДН, так и MN к NT,
^lNS» J~ nt
как же куб на ДН к параллелепипеду, имеющему основанием квадрат
на АН, высотой же прямую, составленную из удвоенной AZ с АН, так
и ДН к составленной из удвоенной AZ и ДН, и как TN к составленной
из удвоенной ON и TN,
„ АХ
¦ „ N2
" TN
1
МО
' N2
.MN
N2
—
1
WO
та
¦ -H
, TN
2N0-TN
H) 2AZ+UH ~j
_ i
2 КО КЗ +1
то получились четыре величины, а именно: параллелепипед, имеющий
основанием квадрат на AZ, высотой же прямую, составленную из удво-
удвоенной ДН и AZ, затем куб на AZ, куб на ДП ii параллелепипед, имею-
имеющий основанном квадрат на ДП, высотой же прямую, составленную
из удвоенной AZ и ДН. Утя величины, взятые попарно, образуют про-
пропорцию с четырьмя следующими величинами: с составленной из удвоен-
удвоенной NS и NM, затем с MN* затем еще с NT и, наконец, с составленной
из удвоенной N0 и NT. Значит, «но равенству» получится, что паралле-
параллелепипед, имеющий основанием квадрат на AZ, высотой же — прямую,
составленную из удвоенной ДН и AZ, относится к параллелепипеду,
имеющему основанием квадрат на ДП, высотой же — прямую, состав-
составленную из удвоенной AZ и ДН, как прямая, составленная из удвоенной
NS и MN, к прямой, составленной из удвоенной N0 и NT.
AZ*BAI1 | А У.) = 2KS-I-MJV
All* <2AZ | ДЫ) 2X6": КТ
Но как первое упомянутое тело ко второму, так и 61 к IK.
AZa BДН I AZ) «I
ДН2 BAZ"+AH) IK
И, значит, как 61 к IK, так и одна составленная прямая к другой.
в! 2N5-I NM
IK ~" 2K0+NT"
Таким образом, «присоединяя»,
Ш+IK BNS+NM) {-f2KO I NT)
• IK ' 2N0 i.NT
и пзягшщ пять раз предыдущие,
:>6К _ IONS h-SNM MONO ' ЬМТ
IK "~ 2JMO I NT
лолучим, что как ZII к IK, так и упятеренная от вместе взятых MN,
-) По условию
ifT 76 S
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 297
NT и удесятеренная от имеете взятых NS, КО к удвоенной ON и NT.
ZH _ 5 (MN4-NT)+IO PCS-S-NO)
IK — 2ON-,-N'i' ¦¦ .
И как ZH к ZK, являющейся (по построению) двумя пятыми первой,
так будут упятеренная от вместе взятых MN, NT и удесятеренная от
вместе ввятых 314, N0 к удвоенной от вместе взятых MN, NT и учет-
учетверенной от вместе взятых EN, NO.
ZH _ 5 (MN * КТ) ' IQ (NS I КО)
ZK "" 2 (AlN-r-NT)+* WE : NO)
Следовательно, будет, что ZH к ZI, как и упятеренная от вместе взятых
MN, NT и удесятеренная от вместе вяятых EN, NO к составленной из
удвоенной MN, учетверенной NE, ушостерспной ON и утроенной NT.
FZH _ 7.II 5<MN-?-NT)-l 101X5-1 X-Qi
ZI ZK-K1 ~ 2ЫХ+4М5—GON-: 3NT"
Так как имеются в непрерывной пропорции 4 прямые MN, NH, ON, NT
MN _ _NS _ ON ¦ - ¦ ¦ •
NS" ~~' ON XT
и как NT к ТМ, так будет и некоторая взятая прямая PI к трем пятым
от ZH, то есть от МО;
NT i Pt i PI PI
как же составленная из удвоенной NM, учетверенной КЕ, ушестерен-
ушестеренной КО и утроенной КТ к составленной из упятеренной от вместо вая-
тых MN, NT и удесятеренной от вместе взятых ЕЛГ, N0, так и некото-
некоторая другая прямая IZ к ZH, то есть к МО,
2MN-S-4NB-I ОКО ! «NT IZ IZ
Ь (M24+NT)-M0 (SN i NO) ZH MO
то, согласпо предыдущему предложению, получится, что (PI+ IZ)
составляют дне интих от MN, то есть от ZB. Таким образом, у сегмента
АВГ центром тяжести будет точка Р (предложение \'111>. Пусть у сег-
сегмента Д13К центром тяжести Судет точка X. Значит, у сегмента АДЕГ
центр тяжести будет на продолжении прямой ХР, причем это продол-
продолжение будет так относиться к названной прямой, как верхний сегмент
к оставшемуся усеченному сегменту. Это же и будет точка 1. Действв>
тельно, так как 13Р составляет три пятых от ZB, a BX —. три питых от
НВ, то, значит, три пятых от остатка HZ будет ХР.
xv = Гвр - вх ~ -|-{ZB - нвI = 4- iiz
Теперь, поскольку как усеченный сегмент ААЕГ к сегменту ДВЕ, так
и МТ к NT, как же МТ к TN, так и три пятых 1JZ, то есть ХР, к PI,
то, значит, как усеченный сегмент АДЕГ к сегменту ДВЕ, так и ХР
к Р1. И у всего сегмента центром тяжести является точка Р, у сегмента
же ДВЕ центр тяжести X. Теперь ясно, что у усеченного сегмента АДЕГ
центром тяжести будет точка I [7].
V
ПОСЛАНИИ К ЭРАТООФКНУ.
О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
Архимед Эршпосфсну желает благоденствовать!
И ужо послал тебе запись предложений найденных мной теорем,
предоставив тебе найти их доказательства, о которых я до сих пор ничего
еще не говорил. Предложении теорем были таковы.
Первой теоремы: если в прямую призму с основаниями в виде парал-
параллелограммов *) вписать цилиндр, имеющий основания на противолежа-
противолежащих параллелограммах, а стороны на остальных плоских {гранях) приз-
призмы, и провести плоскость через центр круга, лежащего в основании
цилиндра, и одну их сторон квадрата в противолежащем основании,
то проведенная плоскость отсечет от цилиндра сегмент, заключаю-
заключающийся между двумя плоскостями и поверхностью цилиндра (одной из
этих плоскостей является сама проведенная, другой — основание
цилиндра, а поверхность будет та, которая заключается между упомя-
упомянутыми плоскостями), то отсеченный от цилиндра сегмент будет ше-
шестой частью целой призмы.
Предложение второй теоремы было таким: если в куб вписать ци-
цилиндр с основаниями на противолежащих параллелограммах и с поверх-
поверхностью, касающейся четырех остальных плоских (граней), и затем в тот
же самый куб вписать другой цилиндр с основаниями на других паралле-
параллелограммах и с поверхностью, касающейся четырех остальных плоских
(граней), то фигура, заключенная между поверхностями этих цилинд-
цилиндров, то есть находящаяся внутри обоих цилиндров, составляет две
трети всего куба.
Так вот, эти теоремы получились отличными от найденных ранее;
дейстинтельпо, в прежних теоремах копоидальпые и сфероидальные
тела, а также их сегменты лил сравнивали по величине с конусами
и цилиндрами, и ни одно из этих тел не оказалось равным телесной
фигуре, ограниченной плоскостями; из рассматриваемых же тел, огра-
ограниченных двумя плоскостями и цилиндрическими поверхностями,
каждое оказывается равным одной из телесных фигур, ограниченных
плоскостями.
*) Прямоугольников, в дапноК случае просто квадратов.
V
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 299
В этой книге я посылаю тебе запись доказательства двух этих
теорем.
Знал, что ты являешься, как я говорю, ученым человеком и но
праву запимасть выдающееся моею в философии, а также при случае
можешь оценить и математическую теорию, я счел нужным написать
тебе и в этой же самой книге изложить некоторый особый метод, при
помощи которого ты получишь возможность при помощи механики
находить некоторые математические теоремы. И уверен, что атот метод
будет тебе ничуть не менее полезен и дли доказательства самих теорем.
Действительно, кое-что из того, что ранее было мною усмотрело ирм
помощи механики, позднее было также доказано и геометрически, так
как рассмотрение при помощи этого метода еще не является доказа-
доказательством; однако получить при помощи этого метода некоторое пред-
предварительное представление of) исследуемом, а затем найти и само
доказательство, горавдо удобнее, чем производить изыскания ничего
но зная. Поэтому и относительно тех теорем о конусе и пирамиде, для
которых Евдопс первый нашел доказательство, а именно, что всякий
конус составляет третью часть цилиндра, а пирамида — третью часть
призмы с тем же самым основанием и равной высотой, немалую долю
ласлуги я уделю и Демокриту, который первый высказал это положение
относительно упомянутых фигур, хотя и бон доказательства. И нам
допелось найти публикуемые тслерь теоремы тем же самым методом,
как и предыдущие; поэтому я и решил написать об отом методе и обнаро-
обнародовать его, с одной стороны, для того, чтобы не оставались пустым зву-
звуком прежние мои упоминании о нем, а с другой, поскольку я убежден,
что он может принести математике немалую пользу; я предполагаю, что
некоторые современные нам или будущие математики смогут при помо-
помощи указанного метода найти и другие теоремы, которые нам еще не
приходили в голову.
Первым мы опишем то, что нервым и было нами обпаружено при
помощи механики, а имешю, что всякий сегмент параболы составляет
четыре трети треугольника с тем же основанием и равной высотой, а за-
затем и каждую из теорем, шшучештых памп при помощи этого метода;
в конце же книги мм напишем геометрические доказательства тех тео-
теорем, предложения которых мы ранее послали тебе.
Леммы
1. Если от одной величины отнять другую, причем центром тяже-
тяжести и первоначальной величины и отнимаемой является одна и та же
точка, то эта оке точка будет* центром тяжести и остатка.
2. Если от одной величины отнять другую, причем центры тяжести
первоначальной величины и отнимаемой не находятся в одной и той же
точке, то центр тяжести величины, получающейся о остатке, будет
находиться на прямой, соединяющей центры тяжести первоначальной
и отнимаемой величин, если продолжить ее и нанести на ней отрезок,
имеющий к расстоянию между указанными центрами то же самое
отношение, какое вес отнимаемой величины имеет к весу остающейся.
<«О равновесии», кн. Т, предложение V111.)
3. Если центры тяжести любого количества величин находятся на
одной прямой, то иа этой же прямой будет находиться и центр тяже-
тяжести величины, составленной из всех этих величин.
4. Центром тяжести всякой прямой будет ее середина.
300
АРХИМЕД
5. Центром тяжести всякого треугольника будет точка, в которой
пересекают друг друга прямые, проведенные из вершин треугольника
к серединам его сторон («О равновесии», кн. i, предложение XIV.)
6. Центром тяжести всякого параллелограмма будет точка, в ко-
которой сходятся его диаметры. («О равновесии», кн. 1, предложение Х.>
7. Центром тяжести круга будет его центр.
8. Центром тямести всякого цилиндра будет середина его оси.
9. Центром тяжести всякой призмы будет середина ее оси.
10. Центром тяжести всякого конуса будет точка, разделяющая
его ось так, что прилегающий к вершине отрезок будет втрое больше
остатка.
11. Также будем пользоваться и следующей теоремой. («О коноидах
и гферпнлах», предложение J.)
Если имеется любое количество величин в равном числе с другими
величинами, причем одинаково расположенные величины, взятые попар-
попарно, находятся в одном и том же отношении, затем, если первые величины
все или частью будут находиться в каких-нибудь отношениях к треть-
третьими,, а соответственные им вторые величины в таких же отношениях
к четвертым, то взятые вместе все первые величины, ко всем третьим
будут иметь то же самое отношение, что все вторые ко всем четвер-
четвертым [1].
I V : ¦':-,
Пусть А13Г будет сегмент, заключающийся между прямой АГ
и параболой АВГ; разделим АГ пополам к Л, параллельно диаметру
проведем ABE я соединяющие прямые АВ и В Г {рис. 1}.
Рис, I
Я утверждаю, что сегмент АВГ составляет четыре трети тре-
треугольника ЛВГ *). ^ ¦
*) Си. коимонтзриа к «Квадратуре параболы*, стр. 65D.
ПОСЛАНИЕ К ЭРАТОСФЕНУ, О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 301
Из точек А и Г проведем AZ, параллельную ДВЕ, и TZ, касатель-
касательную л параболе; продолжим ГВдоК и отложим Кб, равную ГК. Вообра-
Вообразим равноплечий рычаг Г0 с сорединий К и какую-нибудь прямую МЗ,
параллельную КД.
Так как ГВА — парабола, ТЪ — касательная к ней и ГД — ордина-
ордината, то ЕВ равна ВД (это доканывается в началах теории конических
сечений); вследствие этого, а также иследствие того, что ZA и ME
параллельны ЕД, прямая MIS будет равна ]\*Е, a ZK равпн КЛ. И по-
поскольку ГЛ относится к AS, как MS к ЕО,
ГА _ MS
as so
[это доказывается в лемме) *), л 11Л к AS, как ГК к KN,
гл _ гк
AS KN
и ГК pairna К0, то, значит, ВК будет к KN, как М2 к НО.
«к _ мв
KN SO
И так как точка N есть центр тяжести прямой Ми, ибо MN раина NE,
то, следовательно, если взять прямую TII, равную ЕО и имеющую
центр тяжести в в, так, чтобы Тв равнялась вII, то прямая ТвИ
уравновесит MS, остающуюся в своем положении, вследствие того,
что отрезки BN обратно пропорциональны весам TII и ME, то есть
С-Ж к KN будет, как МЗ к НТ.
ВК _ МЗ
КК ~ I1T
Таким образом, точка К будет центром тяжести величины, составленной
из обоих весов <ТН и ME). Аналогично и все промеден.ные, парал-
параллельно ЕД прямые в треугольнике ZAP будут в сноих положениях урая-
ноыешиваться со своими отрезками, отсеченными параболой, если пере-
перенести последние в 6 так, чтобы К была центром тяжести величин™,
оостаилошюй ия каждой пары таких прямых. И так как треугольник
FZA составляется из всех таких прямых, находящихся в треугольни-
треугольнике TZA, а сегмент АВГ составляется из вевх подобных ЕО прямых,
взятых внутри параболы, то, значит, треугольник /АГ, останаясь в сво-
своем положении, будет относительно точки К уравпоиопинать параболи-
параболический сигмепт, помещенный центром тяжести в © так, чтобы К была
центром тнжисти величины, составленной ин ппх обеих. Раэдилим теперь
ГК и точке X так, чтобы ГК была итров больше КХ; тогда точна X
будет центром тяжести треугольника AZP (это докапано в сочинении
«О равновесии»). Тогда поскольку треугольник ZA1\ оставаясь в споем
положении, уравпошшшвает относительно К сегмент ВАГ, помещен-
помещенный центром тяжести в В, и центр тяжести треугольника AZT будет в X,
то, значит, треугольник AZT к сегменту АВГ, помещенному центром
и в, будет относиться, как вК к ХК.
Ио 6К втрое больше КХ: значит, и треугольник AZT будет втрое
больше сегмента АВГ. Но треугольник ZAr в четыре раза Оолыио тре-
треугольника АВГ, так как ZK равна КА, а АД равна ЛГ; значит, cei--
мент АВГ составляет четыре трети треугольника АВГ; [это теперь
ясно] **).
•) В лейст1!итс.-1ытасти эти доказано п предложении V «Квадратуры параболы».
•*) Последние слова Гсйбсрг удаляет, пап не вяжущиссп'г. начальными словами следующего
параграфа.
302
¦АРХИМЕД
И
II
Хотя это всем вышеприведенным рассуждением и не доказано,
но всежо оно производит впечатление, что окончательный выл од правл
леи; поэтому мы, видя недоказанность выведенного, но подозревай его
правильность, предложим найденное нами и опубликованное ранее
геометрическое доказательство *).
При помощи того же метода можно найти, что всякий шар будет
в четыре раза больше конуса с основанием, равным большому кругу ша-
шара, и с высотой, равной радиусу шара, а также, что всякий цилиндр
с основанием, равный большому кругу шара, и высотой, равной диаметру
шара, будет в полтора раза
¦V » больше, шара. Это усматривает-
усматривается так [рис. 2j.
Пусть будет шар с большим
кругом А В ГА и взаимно пер-
перпендикулярными диаметрами
А Г, НА; возьмем и шаре круг
на диаметре ВД, перпендику-
перпендикулярный к кругу АИГД; на этом
перпендикулярном круге по-
построим конус с вершиной в точ-
// / ке А; затем, продолжив (боко-
(боковую) поверхность этого конуса,
рассечем его проходящей че-
через Г плоскостью, параллель-
параллельной основанию; в сечении полу-
получится перпендикулярный к АГ
круг с диаметром EZ- На этом
«руге построим цилиндр, имею-
имеющий ось, равную АГ; пусть ЕЛ,
Z11 будут боковыми сторонами
цилиндра. Затем продолжим ГА,
отложим А0, равную ей, н пообразим равноплечий рычаг Г0 с середи-
: ной А. Параллельно ВД проведем какую-нибудь прямую MN; пусть
она пересечет круг АВГА r точках S, О. диаметр АГ в 2, прямую
АЕ в II, a AZ в>.
На прямой MN восставим перпендикулярную к АГ плоскость:
последняя в сечении с циллндром образует круг с диаметром MN, и се-
' : . чеиии с шаром АВ.ГД -•¦- круг с диаметром НО и с конусом AEZ —
круг с диаметром ПР.
И так как (прямоугольник) между ГА. А2 равен (прямоуголь
пику) между М2, 211,
ГА-АХ = М?-2И ¦ ¦
(ибо А1* равна 2М, а А2 равна П2), а (прямоугольник) между ГА.
AS равен (квадрату) на A3, или вместе нзятмм (квадратам) на ЕЕ
и 211;
га as = as2 = вг> + хп4
м
Рис. 2.
*) В сохранившемся тексте «Эфида* итого доказательства нет; исроигоо, иерсиисчик просто
ве счел нужным ишторять доказательство, которое уже Сило им воспроизведено при списывании
«Кпадритурм параболы».
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 303
то, значит, (прямоугольник) на MJS, 211 будет равен квадратам на
32 и 211.
Поскольку же ГА относится к AS, как MS к 2Г1,
~аТ = ~ш"
и ГА равна Ав, то, значит, 0А будет и А2, как MS к SJI или как
(квадрат) па MS к (прямоугольнику) между MS, 2П.
ал м? _ ms8
А2 ~ 2П ~М2 2П
Согласно же доказанному, (прямоугольник) между М2, 2П ра-
ранен (квадратам) па Е2 и 211; зпачит, АВ будет к А2, как (кнадрат)
на MS к (кнадратам) на S2 а 211, («месте взятым).
По (квадрат) на MS к (кнадратам) па 3S и S11 будит, как
(квадрат) на MN к (квадратам) на 30 и ПР.
аи* ¦;.- хп2 но2 + пр*
Как ;ке (кнадрат) на MN к (квадратам) на 30 и IIP, так и круг
в цилипдрс с диаметром MN будет относиться ко имеете изятым обоим
кругам, и тому, что в конусо с диаметром Г1Р, и тому, что и шаре с диа-
диаметром ЕО;
¦ мге* ^ круг па mn
SO8 Н- IIP2 ~ "РУГ 11а -ПР -I- КРУГ на 2О
зпачит, как ВА к А2, так и круг н цилиндре будет относиться к кругам
в таре и в конусе.
вл круг на MN
Ajf ~ круг «а Ш* Н- круг на ЕО
Теперь, поскольку fc)A относится к А2, как (указанные круги, то)
круг и цилшпдрс, оставаясь в своем положении, будет относительно
точки А находиться и равновесии с обоими кругами на диаметрах 30.
ПР, вели перенести их в 0 и расположить так. чтобы центр тяжести
каждого из них находился в точке 0. Теперь, если в параллелограм-
параллелограмме AZ провести параллельно EZ какую-нибудь другую прямую и на
проведенной прямой восстановить плоскость, перпендикулярную
к А Г, томы подобным же образом докажем, что круг, полученный п.ци-
п.цилиндре, оставаясь в том жи положении, будет относительно точки А
находиться в равновесии с обоими кругами, получившимися, в шаре
и в конусе, если последние перенести на рычаг и поместить и 0 так,
• '¦ чтобы центр тяжести каждого из них оказался в в. Если теперь, беря
такие круги, заполнить ими как цилиндр, так и шар с конусом, то
цилиндр, оставаясь и том же положении, будет относительно точки А
находиться и раиноиесии со вместе нзятыми шаром и конусом, если
перенести их на рычаг в В и поместить так, чтобы центр тяжести каждо-
каждого из них оказался в Ь. Теперь, так как упомянутые тела будут нахо-
находиться в равповесии относительно точки А, причем цилипдр остается
расположенный вокруг центра тяжести К, а шар и конус, как сказано,
перенесены и расположены вокруг центра тяжести 0, то получится, что
0А к АК будет относиться так же, как цилиндр к шару с конусом.
НА цилиндр
АК ~ шар + конус ¦ V
304 АРХИМЕД
Но ©Л вдвое больше ЛК; значит, и цилиндр будет вдвое больше вместе
взятых шара и копуса.
Цилмлдр же втрое больше конуса; значит, три конуса будут равны
двум таким же конусам и двум шарам. Отнимем два общих конуса;
ни&чит, одшт конус, имеющий в осевом сечепигг треугольник AEZ, равен
двум упомянутым шарам.
Но конус, имеющий в осевом сечении треугольник AKZ, будет ра-
равен восьми копусам с осевым сечением — треугольником АВД, так как
EZ вдвое больше ВД. Зяачит, восемь упомянутых конусов будут раины
двум шарам; следовательно, шар с большим кругом АВГД будет ч четы-
четыре раза больше конуса, у которого вершина есть точка А, а основание —
круг на диаметре ВД, лорпендикулярньш к АГ.
В параллелограмме AZ через точки В, Д параллельно АГ проведем
прямые ФВХ, WAQ и вообразил! цилиндр, у которого основания будут
круг» на диаметрах Ф?, XQ, а ось АГ. Теперь так как цилиндр с осс-
иым сечением — параллелограммом ФЙ вдвое) больше цилиндра с осе-
осевым сечекиелх — параллелограммом ФА, последний же итрое больше
конуса с осевым сечением — треугольником АВД, как доказывается
в «Началах» [Евклид, кн. XII, лредложеиие 10J, то, гшнчит, цилиндр
с осевым сечением — параллелограммом Фй будет в шесть раз больше
конуса с осевым сечением — треугольником ABA. Но доказано, что
шар с большим кругом АВГД в четыре раза больше атого самого конуса;
значит, рассматриваемый цилиндр будет и полтора раза больше шара,
что и требовалось доказать.
Когда все это было установлено, то у меня появилась мысль, что
поверхность всякого шара будет в четыре раза больше большого круга
в этом шаре, так как всякий шар и четыре раза больше конуса, имею-
имеющего основанием большой круг, а высоту, ранную радиусу шара.
Я предположил это потому, что, с одной сторопы, всякий круг равен
треугольнику, имеющему основанием окружность круга, а высоту, рав-
равную радиусу круга *), а с другой, всякий шар ранен конусу, имеющему
основанием поверхность птара, а высоту, равную радиусу шара [2|.
III
При помощи того же метода обнаруживается, что цилиндр, и.нею-
щий. основания, разное наибольшему кругу сфероида **), а выеотпу, равную
оси сфероида, будет в полтора раза больше этого сфероида; если же это
усмотрено, то ясно, что, если любой сфероид рассечь плоскостью, про-
. ходящей ч/прея центр и перпендикулярной к оси, то полученная половина
сфероида будет вдвое больше копуса с теми же основанием и осью, что
, и. у отсеченной части.
Действительно, пусть будет некоторый сфероид {рис. 'Л)\ рассечем
его проходящей ч«!ре» ось плоскостью; на поверхности сфероида пору-
поручится эллипс А В ГЛ, у которого диаметры пусть будут АГ, ВД, а центр К.
В сфероиде возьмем перпендикулярный к АГ круг на диаметре ВД
и вообразим конус, имеющий основанием упомянутый круг, а верши-
вершиной — точку А, затем, продолжив поверхность этого конуса, рассечем
его параллельной основанию плоскостью, проходящей через Г; тогда
в сечении получится перпендикулярный к А Г круг на диаметре EZ.
*) Это — первое предложение в «Измерении круга» (стр. 26
*•) Так Архимед иазнияет эллипсоид вращении.
ПОСЛАНИЕ К ОРАТОСФКНУ. О ЙЯКХАНИЧЕСКИХ ТЕОРЕМАХ
305
Пусть также Судет цилиндр, имеющий осповалием тот же самый круг
на диаметре EZ, а осью — прямую АГ; продолжив ГА, отложим равную
ей прямую А0 и вообразим равноплечий рычаг с серединой в А; в па-
параллелограмме AZ параллельно EZ проведем какую-нибудь прямую
MN и на отой прямой MN восставим плоскость, перпендикулярную
н
А
Ф
А
Z
у
К 1
? *•¦
I'm;. 3.
к Л Г. Эта последняя образует в цилиндре сечепио-круг с диаметром
MN, в сфероиде сечепис-круг с диаметром ЕО и и конусе сечепис-круг
с диаметром ПР.
И поскольку ГА относится к А2, как ЕАкАПили как М2к2П,
ГА ЕЛ _ MZ
"AS "" ЛИ 2Ш ~
м ГА равна АО, то, значит, как в А к А2, так и М2 к SII.
В Л _>1?
Л? =~2Й" ;-
Но как М2 к 211, так будет и (квадрат) на М2 к (прямоугольнику)
люгкду М2 и 211,
"sfF = Mi~iEn
а (прямоугольнику) между Mi' и 2П будут рапны (квадраты) на
и 2Еа 13 J.
Действительно, как (прямоугольник) между А2, 2Г относится
к (квадрату) на 2?, так будет и (прямоугольник) между АК, КГ,
то есть (киадрат) на АК, к (квадрату) па KB, (так как оба отношения
будут равны отношению большой полуоси эллипса к параметру] ¦);
АК КГ
KB2
А К*
KB*
*) *v Xi> Tins лЛат'«е -iQos t^v «gSiav e--<m>—Оукиально «в отношении поперечной (гориеон-
талмюй) к ирпмой» -термины, аанметповянныи ии «Конических евчений» Аполлония (книга I. пред-
предложение 21). Бели напиши» урамгсине эллипса и иидс
ч* -= 2 — ж г xz или у* = 2»>ж —— х.
а «Я а
то iiacnuiiTpiiDaeitioc отношение будет ряино отцошпнню откладываемой горизонтально большой
полуоси « и перпендикулярному ей иарамстру р = —эллипса. Поставленную is киидрнтных скоГ>-
ках фраау Гейбсрг считает ноамггейшей иетивьоЛ «следствие уиотребпекин припадлежащих Апол-
Аполлонию терминов.
20 Архимед
306 АРХИМЕД
как же (квадрат) на ЛК к {квадрату) на KB, так будет и (квадрат) на
А? к (квадрату) на SI1.
АКа . AS2 f=AS1Sr j
Тогда после перестановки получится, что как (квадрат) на Ail
к (прямоугольнику) между AS, ЕГ, так будет и (нвадрат) на ITS
к (квадрату) на SS.
Но как (квадрат) »на AS к (прямоугольнику) между AS, 2Г, так
будет и (квадрат) па 211 к (прямоугольнику) между 2Г1, ПМ;
значит, (прямоугольник) между МП, П2 будет равен (квадратуV
на 32.
МП 112 = 32*
Прибавим общий (квадрат) иа FIS; значит, (прямоугольник) меж-
между MS, L1I будет раьеи имеете взятым (квадратам) на 11S и
на SB. - ¦
МП •
Ы2 -гп = П22 -j- 2S*
Следовательно, <Ь)Л будет итпоентъеи к Л2, jrait (квадраг) на >1Z
ко вмег.те взятым (квадратам) иа 1121 if S3. •
ел
¦ Но как (квадрат) ua MS ко вместе взятым квадратам па STI и 2Е,
так и круг в цшпшдре с диаметром MN будет относиться к обоим
кругам с диаметрами ДР я ОН;
круг MX
. таким образом, но отношению к точке А круг с диаметром MN, остава-
оставаясь и cuoii.vf положении, будет ураинешепшватьен с обоими кругами ип
диаметрах НО, ПГ, если их перенести на рычаг в в так, чтобы контр
тяжести каждого круга был в точке в.
(Но у круга с диаметром MN, остающегося в своем положении,
• центр тяжести будет в S), у обоих же кругон с диаметрами НО, ПР
после их перенесения центр тяжести будет в 6; и, значит, как 0А
к AS, так будет и круг с диаметром МЛ* к обоим кругам с диаметра-
ян 30, ПР.*
8А круг MN
\2 ' круг ZO + К1»уг ш'
Теперь, еслпТв^иаридлеяогряыно AZ параллельно EZ провести какую-
нибудь другую прямую и на проведенной прямой восставить плоскость,
перпендикулярную к АГ, то подобным же образом можно будет дока-
доказать, что но отношению к точке А круг, получившийся и цилиндр*?.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 307
оставаясь и своем положении, будет уравновешивать оба круга, иолу-
¦шыиисся в сфероиде и в конусе, если перенести их на рычаг в 0 так,
чтобы центр тяжести каждого из них был л G. Кечи такими кругами
заполнить как цилиндр, так и сфороид с конусом, то но отношению it точ-
точке А цилиндр, оставаясь 11 своем положении, будет находиться в равно-
равновесии со сфероидом и конусом, если перенести их на рычаг в В и. поме-
поместить таи, чтобы центр тнжецти каждого ив них был в толко (-). Но у ци-
цилиндра центром тяжести будет точка К, у вместе ваятьгх же сфероида
и конуса центром тяжести будет, как уже сказано, точка 0; тогда полу-
читсн, что как в А к АК, так и цилиндр будет ко вместе взятым сфероиду
и конусу. Но Л0 вдвое болыпо АК.; значит, и цилиндр будет вдвое
больше, сфероида и конуса, имеете iuihtmx: значит, один цилиндр будет
равен двум конусам и двум сфероидам. Но один цилиндр равен трем
таким конусам; значит, три конуса будут равны двум конусам и днум
сфероидам.
Отнимем общие два конуса; значит, остающийся конус с осевым
сечением — треугольником AEZ — будит равен двум сфероидам; но
тот лее самый единственный конус равен ъисыш конусам с осевым сече-
сечением — треугольником ABA; значит, восемь упомянутых конусов
будут раины двум сфероидам и, следовательно, четыре конуса равны
одному сфероиду; значит, сфороид будет в четыре раза больше конуса,
у которого вершиной является точка А, а основанием — перпендикуляр-
перпендикулярный к АГ круг на диаметре ВД, и половина сфероида будет вдвое боль-
больше упомянутого конуса.
Теперь I» параллелограмме AZ черен точки В, А проведем прямые
ФХ, WQ, тшраллельпые АГ, и вообразим цилиндр, у которого основа-
основаниями будут круги на диаметре ФУ, XQ, а осью — прямая АГ. Этот
цилиндр с осевым сечением — параллелограммом Ф?2 — вдиое больше
цилиндра с осевым сечоиием — параллелограммом ФА, так как у них
основания равны и одна ось вдвое больше другой, сам же цилиндр
с осиным сечением — параллелограммом ФА — втрое больше конуса
с вершиной л точке А и с основанием — перпендикулярным к АГ кру-
кругом на диаметре ВА; значит, цшпшдр с осевым ,,.
сеченном — параллелограммом Ф?2 — будет в
шесть риз больше упомянутого конуса. Но дока-
доказано, что сфероид в четыре раза болыио этого
самого конуса; значит, цилиндр будет в пол- /
тора раза больше сфероида. //
Я А /
i
IV =
А что всякий сегмент прямоугольного ко-
коноида, отсеченный плоскостью, перпендикуляр-
перпендикулярной к оси, будет в полтора раза больше ко-
конуса, имеющего с сегментом те же самые осно-
основания и высоту, при помощи toi'o же метода
можно обнаружить так: л М
Пусть будет прямоугольный коноид Рис. 4.
{рис. 4}; рассечем его проходящей через ось
плоскостью, и пусть в сечении с поверхностью его получится
парабола АВГ; рассечем его также другой плоскостью, перпен-
перпендикулярной к оси, и пусть В Г будет общим еечением обеих этих пло-
плоскостей. Пусть ось сегмента будот АА; продолжим АА в сторону в,
20»
SOS ' '¦ АРХИМЕД
отложим рашую ей нрялгую А& и вообразим равноплечий рычаг Д0
с серединой А. Пусть основанием сегмента будет перпендикулярный
к АЛ круг на днаягстре ВГ; вообразим конус, имеющий основанием круг
с диаметром ИГ, а вершиной точку А. Пусть будет также цилиндр,
имеющий основаниям круг с диаметром ВГ, и ось АД; в полученом
параллелограмме проведем какую-нибудь параллельную В Г прямую МН
и im этой прямой ЛШ восстании перпендикулярную к АА плоскость;
она в енчопии с цилиндром образует круг, диаметр которого MN,
в сечешш же с прямоугольным коноидом — круг, диаметр которого SO.
И так как ВАГ — парабола, АД — ее диаметр и Е2, ВД будут
проведенными ординатами, то как ДА к AS, так будут относиться
и (квадраты) на ВА и BS.
. ВД*
Но ДА равна А6; алачит, ©А относится к А2, как {квадрат) л а
к (квадрату) на SH. ¦
6а
Но как (квадрат) на М2 к (квадрату) на 22, так и находящийся
is цилиндре круг с диаметром MN будет относиться к кругу с диамет-
диаметром НО в сегменте прямоугольного коноида,
круг MN
круг SO
значит, вЛ i: AS будет, как круг с диаметром MN к кругу с диамет-
диаметром БО.
А? ""_ круг SO
Следовательно, находящийся в цилиндре круг с диаметром MN, оста-
оставаясь в своем положении, будет относительно точки А уравновешивать
круг с диаметром ЭО, перенесенный на рычаг 0 и помещенный так,
(чтобы его центром тяжести была точка) в. И (у круга с диаметром)
MN центром тяжести будет 2, у круга же с диаметром SO после его
перенесения центром тяжести будет 0, и в обратной пропорционально-
пропорциональности ВА к AS имеет то же самое отношение, что круг с диаметром МN
к кругу с диаметром 3().
ВА _ круг MN
А2 ~ 'круг 3d
Тенерь если в параллелограмме ЕГ параллельно ВГ провести какую-
нибудь другую прямую л яа зтой проиеденпой прямой иосставить нер-
дйБдикулярную к Ав плоскость, то можно будет подобным же образом
доказать, что полученный в дилтшдро круг, оставаясь в своем положе-
положении, будет относительно точки А уравловешивать полученный в сегмен-
сегменте прямоугольного коноида круг, переносенпый на рычаг в 0 так, чтобы
его центром тяжести была, точка в. Если такгш образом заполнить
:••=;• в цилиндр, и сегмент прямоугольного коноида, то остающийся в своем
; положенжг цилнндр будет отлоентсльло хоткн А уравновешивать сег-
сегмент прямоугольного коноида, перенесенный в 0 па рычаг и помещен-
помещенный так, чтобы его центр тяжести бшг и О. Поскольку же упомянутые
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
309
AS
уравновешиваются относительно точки А и если разделить
АД в точке К пополам, получоннан точка К будет центром тяжести
цилиндра, а у перенесенного сегмента центром тяжести будет 0, то
и оОратноп пропорциональности вА будет иметь к АК то же самое
отношение, что цилиндр к сегменту. Но в Л вдвое больтп АК; значит,
и цилиндр вдвое больше сегмента.
Ыо этот яге сошли цшгвнлр втрое больиге конуса, тлеющего осдовани-
ем круг с диаметром В Г, а неркпшои точку А; теперь ясно, что сегмент
¦ будет в полтора рапа бдльшс отого самого конуса.
V
А что у сегмента прямоугольном) коноида, отсеченного плоскостью,
перпендикулярной к оси, центр тяжести будет на оси сегмента в точ-
точке, делящей ее таким образом, чтобы прилегающая к вершине ее часть
была вдвое более остающегося отрезка,
этим методом усматривается так:
Пусть будет сегмент прямоуголь-
прямоугольного коноида, отсеченный перпенди-
перпендикулярной к оси плоскостью (рис. 5}.
Рассечем его другой плоскостью, про-
ходящей через ось, и пусть в сечении я
ее с поверхностью получится парабола
АВГ; пусть В Г будет общим сечепием
этой секущей плоскости с той, кото-
которая первоначально отсекла сегмент.
Пусть осью ейгмента и дшшотром па-
параболы А13Г будет прямая АД; (про-
(продол жни ДА, отложим равную ей пря-
прямую Ав и) вообразим равноплечий
рычаг Л в с серединой А. Пусть также
в'сегмент будет вписан конус с боковыми сторонами В А и АГ. 13 па-
параболе проведем какую-нибудь прямую ЕС), параллельную В Г, и пусть
она пересечет параболу и точках Е, О. стороны же конуса в точ-
точках Д, Р.
Так как в параболе опущены на диаметр перпендикуляры Е2, ВД,
то ДА будит к A2I, как (квадрат) па ВД к (квадрату) на EZ.
вд»
Но как Л А к А?, так будет и ВД к Ii2;
Рис. 5.
АЛ ВА
П2
а как ВД к US, так будет и (квадрат) ВД к (прямоугольнику) между
ИД, П2;
ВД ВД*
П2 ~ ВД. П?
следовательно, получится, что (квадрат) иа ВД к (квадрату) на S2
будет, кал (квадрат) иа ВД к (прямоугольнику) на ВЛ, II2.
вд8 вд*
310 АРХИМЕД
Значит, (квадрат) на 32 б\»дет равен (прямоугольнику) между
НД-П2;
поэтому 13Д, 23, 2П составляют (непрерывную) пропорцию,
вд _ хв
2S 211*
ы вследствие этого ВД к П2 будет, пак (квадрат) па Е2 к (квадрату)
на 211.
ВА _ BS*
П2 vnis
По как 13Д к 112, так будет и ДА к AS, то есть 6Л к AS,
^а _ j>a_
А?~ AX
и, значит, как в А к А2, так и (квадрат) на 8S к (квадрату) на 2П-
вд ^а _ j>a
IIS А?~ AX
иа
Теперь восставим на SO перпендикулярную к АД плоскость; она
и сегменте прямоугольного коноида образует круг с диаметром ВО,
в конусе же — круг с диаметром ПР. И поскольку 6А к AS, как
(квадрат) иа ES к (квадрату) на SIT, а как (квадрат) па SS к
(квадрату) н« 2111, тик будет и круг с диаметром НО к кругу с диа-
диаметром ПР,
круг ВО
ПР
то, значит, ВА будет к AS, как круг с диаметром ЕО к кругу с диа-
диаметром ПР.
6А __ круг ВО
~ JIP
Значит, круг с диаметром ЕО, остаиаясь и своем положении, уравнове-
уравновесит отпосительпо точки А круг с диаметром ПР, исрепссошый иа ры-
рычаг в в так, чтобы центром его тяжести была точка в. Теперь так как
у остающегося в своем положении круга с диаметром ЕО центром тя-
тяжести является 2, у перенесенного же круга с диамстроы ПР центром
тяжести будет, как сказано, точка © и в обратной пропорциональности
GA к AS имеет то же отношение, что круг с диаметром ЕС) к кругу с
диаметром ПР, то, значит, эти круги будут но отношению к точке А
уравновешиваться.
Теперь если в параболе параллельно ВГ провести какую-нибудь
другую прямую и на проведенной прямой косстаиить плоскость, пер-
перпендикулярную к ЛД, то подобным же образом можно будет доказать,
что подученный в сегменте прямоугольного коноида круг, оставаясь
в своем положении, уравновесит относительно точки А полученный в ко-
nyei! круг, перенесенный па рычаг в 6 и помещенный так, чтобы «го
центром тяжести была точка В. Если теперь тнкнмк кругами запол-
заполнить и сегмепт, и конус, то все круги в сегменте, оставаясь в своих поло-
положениях, будут относительно точки А уравновешиваться со «семи круга-
кругами в конусе, перенесенными на рычаг в в и помещенными так, чтобы
ПОСЛАНИЕ К ЭРАТОСФВНУ, О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
311
АГ-
"АЕ
».г
ЛЕ
их центром тяжести была точка в; тогда п сегмент прямоугольного
коноида, оставаясь в своем положении, будет уравновешивать относи-
относительно точки Л конус, перенесенный па рычаг в в и помещенный так,
чтобы его центром тяжести была точка Й. Далек, так как у обеих воли-
чин *), рассматриваемых как одна, центром тяжести является А,
а у конуса после перенесения центром тяжести будет В, то, значит, у ос-
оставшейся величин и **) центр тяжести будет на прямой AG>, если продол-
продолжить ее за А и отложить на пой такую прямую АК, чтобы А6 имела
к пой то же отношение, что сегмент к конусу. Но сегмент в полтора
раза больше конуса; значит, и 6Л будет в полтора раза больше ЛК,
и центром тяжести (сегмента) прямоугольпого коноида будет точка К,
разделяющая прямую АЛ так, чтобы часть ое при вершине сегмента
была вдвое больше остающегося отррзка.
" .- VI
Центр тяжести всякого полушария находится на прямой, являю-
являющейся его осью, если рассечь ее так, чтобы прилезающий к поверхности
полушария отрезок ее имел &
. к остающемуся отрезку то
же отношение, что пять к ,у М
трем.
Пусть будет шар {рис. С5};
pacci!4(>M его плоскостью,
проходнщой череа центр, в
пусть « сечении с поверхно-
поверхностью получится круг АВГД.
Пусть АГ, ВЛ будут вза- .
имно перпендикулярные диа-
диаметры круга; восставим на . Vnt- "•
ВД плоскость, пориендику-
лнрную к АГ. Пусть, далее, будет конус, имеющий основанием круг на
диаметре ВД, и вершину в точке А, и пусть БА, АД будут боковые
стороны конуса. Продолжим ГА, отложим А0, равную ГА, и вообра-
вообразим, что прямая вГ будит равноплечим рычагом с серединой в А.
В полукруге ВАЛ проведем какум-пибудь параллельную ВД прямую
ЕО, и пусть она нересичет окружность полукруга в точках 2, О,
боковые стороны конуса в точках II, Р, а прямую АГ в Е. Восставим
на НО плоскость, перпендикулярную АК; пустъ она в полушарии
образует круг с диаметром SO, а в конусе круг с диаметром ПР.
Поскольку мы имеем, что ЛГ к АЕ будет, как (квадрат) па SA
к (квадрату) на АЕ. •¦ ••
SA*
акв '
я (квадрат) на ЗА равен вместе взятым (квадратам) на АЕ и ЕЕ,
-= АТ5* I- ЕЕВ
а АЕ равна ЕП, то, значит, АГ будет к АЕ, как вместе взятые (квадра-
(квадраты) на ЗЕ и ЕП к (квадрату) на ЕП.
SB* -- EUg
¦~ кпа - ___
*) То есть и сегмента, и конуса. ¦ .
**) То есть евгисита.
Ш АРХИМЕД
Но как (квадрат) на SR вместе с (квадратом) на ЕП будут к (квадра-
(квадрату) па ЕП, так и круг па диаметре 30 вместе с кругом на диаметре ПР
будут относиться к кругу на диаметре TIP. И ГА равна Ав; значит,
как вА к АЕ, так и круг на диаметре SO вместе с кругом на диаметро
ПР будут к кругу на диаметре ПР.
WA круг SO -V круг ПР
АВ ~" кругШ»
Значит, оба круга с диаметрами ЕО, ПР, оставаясь в своих положениях*
уравновесят относительно точки А круг с диаметром ПР, перенесен-
перенесенный в в так, чтобы ого центром тяжести была точка в. Теперь, так-
как у обоих остающихся л своих положениях кругов с диаметрами 30,
ПР центром тяжести является Е, у перенесенного же круга с диа-
диаметром IIP центром тяжести будет 0, то как КА к А В, так и круг
с диаметром ПР относится к кругам с диаметрами НО, ПР.
ВА_ _ КРУГ ПР
Ав ~~ круг SO -г круг Ш»
Подобным же образом если мы в полуокружности *) проведем какую-
нибудь другую прямую, параллельную ВНД, и на проведенной прямой
носсташта перпендикулярную к АГ плоскость, то оба круга, получен-
полученные в полушарии и в копусе, оставаясь в своих положениях, будут
относительно точки А ураыконешииать получившийся в конусе круг,
перенесенный на рычаг и помещенный при в. Теперь если такими кру-
кругами заполнить и полушарие, и конус, то все круги в полушарии « в ко-
конусе, оставаясь в сиоих положениях, уравновесят относительно точки
А иге круги в конусе, перенесенные ка рычаг в в и помещенные так,
чтобы центром их тяжести была точка в; таким образом, полушарие
и конус, оставаясь в своих положениях, уравновесят относительно'
точки А копус, перенесенный на рычаг в (-) и помещенный так, чтобы
его центром тяжести был» точка 0... **).
(Пусть цилиндр MN, иодлошсииый в t), рален конусу АВД; рассечем его пло-
плоскостью^ перпендикулярной к ог,и, так, чтобы цшшядр 1А уравновешивал относительно-
точки Л конус АВД; тогда остающаяся чвдть цилиндра И будет уравновешивать
полушарие.
Возьмем теперь яа прямой АН такую точку Ф, чтобы АФ была втрое больше ФИ,.
тогда Ф будет центром тяжести колуса А В А. Затем лозъмем такую точку X, чтобы All
относилась к АХ, как 8 к 5. Так как цилиндр М ура и fioti сшивает конус АВД относи-
относительно точки А, то, значит, ни.шгтдр М 65'дет к конусу АВД, как ФА к вА или как 3 к 8.
Но конус АВД равен всему цилиндру MN; эяачнт, цилиндр MN будет относиться к своей
части М, как 8 к 3; значит, остающаяся часть X будет относиться ко всему цилиндру,
как 5 к 8, или конус А ВА будет относиться к цилиндрической части N, как 8 к а или как
АН к АХ>.
И так как шар в четыре раза больше конуса, основанием которого-
является круг на диаметре ВД, а осью прямая ЛН, то...
{..-полушарие будет относиться к конусу, как 2 к 1, то есть кап Ав к АН. Янатит, «но-
равенству» получится, что полушарие будет к цилиндру Л", как Ли к АХ. IJo цилиндр»
N с центром тяжести в относительно точки А уравновешивает полушарие; значит, цен-
центром тяжести полушария будет точка X, рассекающая ось так, чтобы не часть, прилегаю-
прилегающая к поверхности цолушара, относилась к оставшемуся отрезку, как 5 к 3>.
*) В подлиннике ошибочно «в есчыши п|шмо>1олыюго конуса*, то есть в параболе.
"*) Остальная часть предложения, за исключением одной фразы, утрачена. В .угловых скобках
дается реконструкция, понещешган i> издании Гсйберга.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
313
VII
При помощи того же метода можно обнаружить, что всякий сфери-
сферический сегмент относится к конусу с теми же самыми основанием
и осью, что вместе взятие радиус шара и высота оставшегося сегмента
к высоте оставшегося сегмента *).
(Пусть будет шар с большим кругом АВГД и взаимно перпендикулярными диа-
диаметрами А Г, ТГ {рис-. 7J; ракссчем с!гд перпендикулярном к А Г плоскостью, которая
образует сегмент, имеющий ослопа ниш круг на диаметре С А, и пусть ВД пересекает
прямую АГ в точке Н: иа полученном круге построим конус с ворпшного А. Затем
па круге, «писанном па диаметре ТУ, построим конус с тон же вершиной А; по-
поверхность зтого конуса, будучи продолжена, пересечет гтлоскоси., п]>оведегтнук>-
через В/\, и обринуот в сечении
круг с диаметром EZ; в этой те
самой шоскостп из центра TI ра-
радиусом, равным прямой А Г, оии-
шем круг с диаметром КЛ и ла
этом круге построим цилиндр с
осью АН, примоугцлыюо оссазое
течение которого будит ФЛ. За-
Затеи, продолжив в обв сторошл
прямую ЛГ, отложим ГЙ, рав-
равную радиусу шара, и А в, рашгую
АГ; вообразим, что Г© будит
ралноплечим рычагом с середи-
серединой А.
Теперь в параллелограмме
ФЛ параллельно БД проведем
прямую MN, и ла этой ирялшй)
MN восставим пло-
плоскость, перпендикуляр-
перпендикулярную к А Г; она и сечении
с цилиндром образует
круг с диаметром MN,
в сечении же со сфоричо-
ским сегментом—круг с диаметром SO, в конусе же, у которого основа-
основание—круг на диаметре EZ, a uej)innua в точке Л, она образует круг с
диаметром ПР. .Чатем подобно предыдущему докажем, что круг с диамет-
диаметром MN, оставаясь и споем положении, относительно точки А уравнове-
уравновесит оба круги с диаметрами SO, ПР, осли их перенести на рычаг в 0 так,
чтобы центром тяжести каждого из них была точка 0; то же самои мож-
можно будет доказать и по отношению ко всем таким кругам. Теперь, если
такими кругами заполнить и цилиндр, и конус, и сферический сегмент,
¦. . то цилиндр, оставаясь в своем положении, уравновесит (относительно
точки А) вместе взятые б опус и сферический сегмент, перенесенные па
рычаг и помещенные и в. Рассечем АН и точках Ч?, X так, чтобы АХ
была равна XTI, а НТ была третьей частью АН; тогда центром тяжести
цилиндра будет точна X, ибо oiia является серединой оси АН. Теперь,
так как упомянутые тела * *) относительно точки А находятся в равнове-
равновесии, то цилиндр будет относиться ко вместе взятым конусу с диаметром
основания EZ и сферическому сегменту ВАА, как вА к АХ. И так как
НА втрое больше H\f, то (прямоугольник) меяаду ГП, IIУ будет
*) Дальше в подлиннике испорченное место, Боестанашшадеыое со образцу предложения и.
••) В подлиннике характерное выражение ЧИт
.314 АРХИМЕД
третьей частью (прямоугольника) между АН, IT Г.
ГН-Н1У = — АН-ИГ "*
Но (прямоугольник) между АН, НГ равен {кввдр&ту} на НВ;
АН-НГ=НВв
тогда (прямоугольник) между ГН, HV будет третьей частью (квадрата)
па НИ •).
ГН-ШГ-- — ВН2 ' '
(If о киадрат ил АН равен утроенному лрямоугопьпику между АН, ИЧ* или утроен-
утроенному прямоупмп.пику между tAX, AT.
так кап АН к ЛХ будет, как ЛЧГ к ТН, или как дни к единице.
11 тик как вЛ рапыа КII и ЛН равна НЕ, то квадрат на в А будет относиться
К третьей части кподратп на ЛН, как цилиндр с основанием - - кругом па диаметре КЛ—
к конусу AKZ: .
в А2 цтгаиндр КЛ
_1_ „ . 2 конус AEZ "
Но квадрат ни НА относится к третьей части квадрата па АН, как квадрат на вА к нрямо-
угопмшку лкякду АХ -АV:
¦у АН* ЛХ'АЧ"
поэтому как кпадрт ил вЛ к прямоугольнику между АХ, AV, так будет и цилиндр
к ю>нусу>.
Докапано жо, что как вА к ЛХ, так будет и цилиндр с основанием—
кругом на КА—к шаровому сегменту АВЛ и конусу.
НЛ цплипдр ФЛ
АX ~ сегмент АВД+конус AEZ
<И вЛ равна А Г, "или ЛЧ' v. ЧТ):
:шачнт, как квадрат на НА. ко вместе
((мятым прямоугольпикам между AT, АХ и YT, АХ, так будет отиоентьен и цилиндр
к иегмепту АПД вместе с конусом AEZ
НА «А2 Ь\- 0А2 цилинлр ФА
__^_
АХ"=ЩТаХ" fAY-; УГ) АХ ~ AY• AX--I-ТГ • АХ~~ сегмент АВД~ конус AEZ "
удся относиться к сег
ццдиылр ФА _ в
Отсюда следует, что 1^илиндр будся относиться к сегменту, как квадрат па вА к прямо-
прямоугольнику между Ч'Г, ЛХ:
сегмент АЬД ~~ Ч/Г • АХ '
Но цилиндр к конусу ЛПЛ относится, как квадрат ira вА к третьей части квадра-
квадрата на ВН:
* цилиндр ФА 6Аа
^^
о
*) Дальше в подлиннике: iioiop'rtiuioc место, которой может быть приблизительно восстанов-
восстановлено на оспонакии достаточно большого количества сохранившихся отрывочных спои, ,
ПОСЛАНИЕ К ЭГАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 315
а» квадрат на ©Л к третьей части квадрата кл Ш? будет, как квадрат па «А к прямо
угольнику между ГЛ, НТ*):
НА» НА"
-Значит, сегмент АНД будет относиться к кинусу АВЛ, как прямоугольник между ЧТ,
АХ к прямоугольнику между ГИ, IIW. Поскольку ж« АИ пдвос больше ЛХ и 'раина
вмпехе; изятмм ЛМ' и VII, то есть трем VII, а ЧФ раина 441 с IIГ, то есть трети ЛИ и НГ,
то иримоуголышк шйкду ЧТ, АХ будет раиел имеете впиты» прямауголт.никям- между
i АН, 4"?Н и НГ, -^-YH:
¦О 2. 2»
чтлх-=^-ah-^-vh ! нг--'1''1'
или прямоугольнику между XFH м ( — А Г ИГ j, то ггть прямоугольнику между
и НЯ:
-| AH-j ~НГ--| НгЛ -= Vll [^ ЛГ j-Hf \=TII HQ.
Таким обраиом получается, что сегмент ADA Судет относиться к кояусу ЛБД, как НИ
к ИГ>**).
v\n
Подобным же образом можно обнаружить, что всякий сезмент сфе-
сфероида, отсеченный плоскостью, перпендикулярной (к оси), будет отно-
относиться к конусу, имеющему с сегментом те же самые основания и ось,
как вместе взятые полуось сфероида и ось противолежащего сегмента
относятся к оси противолежащегосн екгмеита ***).
IX
У всякою сферического сегшнтп центр тяжести находится на
той же прямой, которая будет и осью сегмента, если разделить ее.
так, чтобы часть ее при вершине сегмента имела к остатку то же
самое отношение, какое вместе, взятые ось этого сегмента и учетверен-
учетверенная ось противолежащего сегме-нти- имеют ко вместе взятым оси это-
этого сегмента и удвоенной оса противолежагцего сегжюпа.
(Луеть Судет шар {рис. 8J; отсечем от него некоторой плоскостью сегмент; пусть iipn
течении шара другой плоскостью, проходяще» через центр и перпендикулярной к
nepiiuii, получается и сечении с попоржпостг.и» шара круг ЛИГА),
в сечении жо ****) с плоскостью, отсекшей сегмент,— прямая ВЛ;
пусть также лрямаи ГА будет диаметром, нврнечщнкулярным к пря-
прямой 13Д, и пересечет ее и точке Н; таким образом, у того сегмента, вер-
вершина которого находится в точке Л, осью Судет прямая АН, у цротнпо-
лежащего же сегмента осью будет НГ. Разделим прямую АН в точке X
*) Так как ВН»=АН.ГН-8Ч»'Н.ГП.
**) Нужно иметь и ыаду, что прямая ГО но построению равна радиусу шара или - Л Г- Далее
мм имеем:
сегмент ABA Уг-АХ _ УП-ИВ
_
конус АВЛ ГННЧ' "' rflllV^rH
***) Доказательство этого предложения см. в Комментарии {41.
****) Начяяо утрачэно; формулировка предложение ьоесгаияилипаетеп по типу предложении л..
310
АХ
хн
АРХИМЕД
так, чтобы А.Х. относилась к ХН, как АН вместе с учетиерепной НГ
к АП вместе с удвоенной НГ.
АИ-Н 4НГ
' АИ + 2ПГ
Я утверждаю, что у того сегмента, вершина которого в точке А, цент-
центром тяжести будет X.
сто взятых . . . догме .... вершина которого . - . точка . . ..
НА. . . име точку Н. Отношение центр . . .X.
Если . . . рассечь игур . . . очк вот в ...
сто взят . . .*) и продолжим АГ, отложим равную ей прямую Ав и
ранную радиусу тара прямую ГЕ; затем вообразим равноплечий рычаг
Z
N М
АГ
Рис. S.
Гв с серединою А. В плоскости, отсекающей сегмент, опишем круг с
центром Н и радиусом, равным АН, и на этом круге построим конус,
имеющий: вершипу в точке А; пусть боковые стороны конуса будут АЕ
и AZ. Параллельно EZ проведем какую-нибудь прямую КЛ; пусть она
встретится с окружностью сегмента н точках К, Л, с боковыми сторо-
сторонами конуса AEZ в точках Р, О, а с прямой АГ в точке П. Теперь,
поскольку ЛГ относится к ЛП, как (киадрат) на КА к (квадрату) на
АП,
КА2
и (квадрат) на К А равен вместе взятым (квадратам) на АП и ПК,
АЦг+ШСя
(кпадрат) же па АП равен (квадрату) на ПО,
КЛ2=АЦг+ШСя
ибо (квадрат) на АН равен (квадрату) на ЕН, то, значит, как ГА
к АП, так будут вместе взятые (квадрат) на КП и (квадрат) на ПО
к (киадрату) на ОН.
га _ кпг-)- по*
АП 0д2
•) Относительно этих пяти с половиной строк, которым соотестст иует 11 строк первоначаль-
первоначальной рукописи, Гейберг делает примечание: «Восполнить мги строки не могу, trait как не вишу, чегу
не хв»"гает для подгитоики докааахсльства».
ПОСЛАНИЕ К. ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 31?
Но кап вместе взятые (квадраты) на К11 и на ПО к (квадрату) на ПО,
так будут и вместе взятые круги па диаметрах КЛ и ОР тс кругу на
диаметре ОР.
И ГА равна А0; значит, как 6Л к АП, так будут и круги на диа-
диаметрах КЛ и ОР к кругу на диаметре О Р.
8А круг КА 4- "РУГ ОР
АП ~ ' круг OF
Теперь, так как имеете изятые круги на диаметрах КЛ, ОР относятся
к кругу па диаметре ОР, как А6 к ПА, то переставим круг на диаметре
ОР и поместим его на рычаг в 0 таи, чтобы его центром тяжести была
точка 0; значит, как ©Л к АП, так м круги па диаметрах КА и ОР,
оставаясь в своих положениях, будут относиться к кругу на диаметре
ОР, перенесенному на рычаг в 0 и помещенному так, чтобы «го центром
тяжести была точка 0; значит, крута в сегмеито БАЛ л в иолу ее AEZ
будут уравновешивать относительно точки А круг а конусе AEZ.
Подобным же образом и все круги в сегменте ВАЛ и в конусе AEZ,
вместе взягые, оставаясь в своих положениях, будут уравновешивать
относительно точки А псе круги в конусе AEZ, перенесенные на рычаг
в 0 и помещенные так, чтобы у них центром тяжести была точка в;
таким образом, сферический сегмент ABA вместе с конусом A1SZ,
оставаясь и своих положениях, будут уравновешивать относительно
точки Л конус EAZ, перспесеппый на рычаг и Й и помещенный так,
чтобы его центром тяжести была точка в. Пусть теперь конусу, имею-
имеющему основанием круг па диаметре EZ и вершиной — точку А, будет
равен цилиндр MN. Рассечем АН в точке Ф таи, чтобы АН была в че-
четыре раза больше ФП; тогда точка Ф будет центром тяжести конуса EAZ
(ибо ато уже било написано раньше), (лемма 10). Затем перпендикуляр-
перпендикулярной (к оси АО) плоскостью рассечем цилиндр MN так, (чтобы цилиндр
М) уравновешивался с конусом EAZ. Теперь так как вместе взятые
конус EAZ и: сегмент ABA, оставаясь н своих положениях, уравновеши-
уравновешиваются с копусом EAZ, перенесенным на рычаг в 0 и помещенным так,
чтобы его центром тяжести была точка 0, и так как цилиндр MN
равен конусу EAZ, каждый из цилиндров М и N расположен при 0
и цилиндр MN уравновешивается со имеете взятыми сегментом и копу-
сом, то цилиндр N будет относительно точки А уравпоиешивать сфери-
сферический сегмент. И (поскольку] сферический сегмент ВАЛ относится
к конусу, основанием которого является круг на диаметре ВД, a jjcjj-
Ш1шом — точка А, как SH к НГ,
«егмент_ВАД _ SH
кякус НАЛ ~ НГ
ибо это написано раньше (предложение VII). Но как конус ВАЛ к ко-
конусу EAZ, так и круг на диаметре ВА к кругу на диаметре EZ,
iwiiyo ВАЛ _ круг ВА
конус EAZ " круг EZ
а как один круг к другому, таи и будет и (квадрат) на BII к (квадрату)
на НЕ,
ВД _ ВНД
круг EZ "" HES
и (квадрат) на ВН равен (прямоугольнику) между ГН, ПА;
ВНа=ГН-НА
318 АРХИМЕД
а квадрат на НЕ равен квадрату на ПА; и, наконец, (прямоугольник)-
.между ГН и НА к (квадрату) на НА относится, как Ш к НА;
г» ил гн
НА* НА
значит, как копус ВАЛ к конусу EAZ, так будет и ГП к НА. Но выше
было доказано, что конус ВАА к сегменту ВАЛ относится, как ГИ к НЕ;
конус ВАЛ _ ГН
сегмент ВАА ПН
значит, «по равенству» — как сегмент ВАЛ к конусу EAZ, так будет
и ЗН к НА. И поскольку АХ относится к ХН, как НА имеете с учет-
jiepeiuroii НГ к АН с удвоенной НГ,
АХ НА + 4 ИГ
ХН ~~ АН + 2HF
то и «обратно» — как ИХ к ХА, так ы удвоенная ГН вместе с НА будет
к учетверенной ГН вместе с НА.
нх агн + на
ХА " 4ГП •- НА
Отсюда «присоединением» получится, что НА будет к ЛХ, как ушесте-
ушестеренная ГН вместе с удвоенпой НА будут к НА «мосте с учетверенной II Г.
НА 6ГН + 2НА -¦¦', ¦¦ ¦-
АХ ' 11А+4НГ
И четвертой частью ушестеренной ГН вместо с удвоенной МЛ
будет НЕ;
6ГН-1- 2НА
1 -"=•
для учетиеренноп жо НГ имеете с НА четвертой частью будет ГФ
*"Г t- НА .
~ 4
(это действительно очевидно) *); значит, как НА к АХ, так будет
к 2Н к ГФ;
КА 21
ЛХ ' Г
таким обрклом, ЗН будет к ПА, как ГФ к ХА.
гн гф
НА " ХА
Но было доказано, что как SII к НА, так и сегмент с иершшюй в точ-
точке А и с основанном — крутом на диаметре ВД — относится к конусу
с нершипой в точке А и основанием — кругом на диаметре EZ.
Значит, как согмеит ВАЛ к конусу EAZ, так будет и ГФ. к ХЛ.
И так как цилиндр М но отношению к А ураниоюеншнаот коиус EAZ,
и у цилиндра ( М) центром тяжести будет в, у конуса же EAZ центродг
тяжести будет Ф, то, значит, получится', что коиус J5AZ будет относить
ся к цилиндру М, пак (->Л к АФ, то есть как ГА к АФ. И конус EAZ
*) П самом дели;
ПОСЛАНИИ К ЭРАТОСФВНУ. О МКХАНИЧЕСКИХ ТЕОРЕМАХ 31»
равен цилиндру MN; значит, после «выделения» *) цилиндр MN будет-
к цилиндру ;\\ как А Г к ГФ.
цилиндр MN_ Л1"
ЦПЛ1ШД]! N ~ 1*1»
Но цилиндр MJN ранен конусу EAZ; значит, конус KAZ будет к цилинд-
цилиндру N, как ГА к ГФ, то есть как ©Л к ГФ.
кпиус BAZ _ ГА __ НА
цилиндр -\ ГФ ГФ
Но было доказало, чти сегмент 13АД относится к конусу EAZ, лак ГФ
к ХА;
«сгмиНТВАА _ _ГФ
КОНУС BAZ ~" ХА
значит, «по равенству» будит, что как сегмент АВД к цилиндру N, так
и 0А к АХ.
сегмннтАВА_ вА
ЦИ.11ШДР N АХ
И было доказано, что сегмент ВАД но отношению к Л ураиновешилавт
цилиндр N, а у цилиндра N центром тяжести янляется точка В; нначит,
• •: у сегмента ВАД центром тяжести будет точка X.
X
Подобно :>тому можно обнаружить, что у всякого сегмента сферои-
сфероида центр тяжести находится на той же прямой, которая будет а осью
сегмента, если разделить ее так, чтобы часть ее при вершине сегмента
имела к остатку то же самое отношение, какое вмеаЛе взятые ось это-
этого сегмента и учетверенная ось противолежащего сегмента имеют ко-
вместе взятым оси этого сегмента и удвоенной оси противолежащего
сегмента [5J.
XI
При помощи того же метода можно обнаружить, что всякий сег-
сегмент тупоугольного коноида **) имеет к конусу с теми же самыми осно-
основанием и высотой такое же отношение, как вместе взятая ось сегмента
и утроенная «добавленная к оси» ***) ко вместе,взятым оси сегмента коно-
коноида и удвоенной «добавленной к оси», и что центр тяжести (сег,ментп.а\
тупоугольного коноида {получится), если рассечь ось так, чтобы от-
отрезок при вершине имел к остатку то же самое: отношение, какое утро-
утроенная ось вместе с увосъмеренной «добавленной к оси» имеют к оси того же
самого коноида вместе с учетверенной этой самой «добавленной к пей».
я) Правильней Яыло снаеать «нереиоричииая» (*имттоёчяп'т1); деСстлитслыш, операции «выде-
ленше» состоит в том, что иа ироиорими и:Ь = с: d получаетсн пропорция (п—)j) r b=(r.-d) : <1,
операции иге «персворачивашшо при под нт к пропорции (а—Ь) : «—(с -d) : с. К нашем случае
цилиндр MN __ ГА цилиндр MN — цилиндр М _ АГ - АФ ГФ
ЦП.ЧШ.Ц11 М ЛФ ' ' " ЦИЛИНДР MN "' А Г ~ АГ '
OTKyJlil <'ОбраЛ11!ИШ!М» ' ¦ t
цилиндр MN АГ
цилиндр N ~ ГФ
"*) Так Архимед низииапт то, что мы назвали бы одной полостью двуполого гиперболоида ира-
ткпип.
•**) Так Архимед называет действительную полуось пшсрСшш.
320
АРХИМЕД
Л'
Рис.
И ид многих других . . . обнаруживаемых . . . мы опустим - . . ,
так как рассматриваемый метод достаточно разъяснен всем вышесказан-
вышесказанным*) [В|.
XII
При помощи того же самого .метода можно обнаружить, что если
н прямую призму г. квадратными основаниями вписать цилиндр, у ко-
которого основания расположены па. противоположных квадратах, а по-
поверхность касается остальных четырех [параллелограммов] граней,
и провести плоскость через центр круга,
являющегося основанием цилиндра, и одну
из сторон противолежащего квадрата, то
фигура, отсеченная проведенной плоско-
плоскостью, составляет шестую часть всей приз-
призмы. Покапавши, (как это делается при
помощи механического метода), мы в даль-
дальнейшем дадим геометрическое доказатель-
доказательство.
Вообразим прямую призму с квадрат-
квадратными основаниями и и этой призме впи-
вписанный, как сказано, цилиндр; пусть
параллелограмм АВ будет сечением содер-
содержащей цилиндр «ризмы плоскостью, пер-
перпендикулярной к той, которая отсекла цилиндрический сегмепт, а общим
сечением плоскости, отсекшей от цилиндра сегмент, и той плоскости,
которая была проведена через ось перпендикулярно отсекшей от цилин-
цилиндра сегмент, пусть будет нрямая КГ {рис. 9}; пусть, далее, осью цилиндра
и чризмм будет прммая ГД, и пусть прямая EZ рассекает ее под пря-
прямым углом и пополам; проведем через ЕЯ плоскость, перпендикуляр-
перпендикулярную к ГД; она я сечении с призмой образует р
квадрат, в сечении же с цилиндром — круг
{рис.. J0}. Пусть сечением призмы будет
квадрат MN, а сечением цилиндра — круг
ЕОГ1Р, и пусть этот круг касается сторон
указанного киадрата в точках 3, О, 11, Р;
пусть общим сечением плоскости, отсекшей *
от цилиндра сегмент, и плоскости, проведен-
проведенной через EZ перпендикулярно к оси цилин-
цилиндра, будет прямая КЛ; прямая П(-)Н пересечет
ее пополам **).
В полукруге ОПР под прямым углом к ы о
ПХ проведем некоторую прямую 2JT и вое- Рис. 10.
ставленную на 2Т перпендикулярно к НП
плоскость продолжим в обе стороны от плоскости, в которой находится
кругЗОПР; в ссчешш с полуцилиндром, основанном которого является
V
\
Л
*) Конечную фризу можно дополнять так: «и из многих других <теорем>, обнаруживаемых
<8тпи же методом, остзльпыо мы опустим (<od> nr.Ul.tor'foMiv <ие> повьисн)...».
licicne слова «опустим» и подлиннике идет непонятнее е.чоно 6i]... те>; с сомнительными бук-
буквами и и с».
••) Оба рис. 9 и 10 представляют своего рола вертикальную и гориаонтя^ъну'О проекции рас-
рассматриваемой геометрической фигуры. Однако ш: нужно забывать, что по существу мела обе они
поляютси диутя взаимно перпендикулярными сечениями, проведенными черев пептр приамы.
ПОСЛАНИК К 01'АТОСФ1'Л1У. О Д1КХАШ1Ч.КСК11Х 'ГВДРЕМАХ 821
полукруг ОПР, а высотой — осьиризмы, она образует па рал л ел о грамм,
у которого одна сторона раина 2Т, а другая будет образующий цилинд-
цилиндра; в течении же с ссгмукгом, отсеченным от цилиидра, oua образует
параллелограмм, у которого одна сторона раина ZT, а другая 1ST;
таким образом, прямая NT должна быть так проведена и параллело-
параллелограмме ДБ {рис. 9}, чтобы она, будучи параллельна 1Ю, отсекла пря-
прямую EI, равную 11Х. Так кап ЕГ является параллелограмм ом, прямая
N1 параллельна 0Г и через них проведены лрлмып Е0 и ITS, то полу-
получится, что как Е(У к 01, так и UT к 1'N, то есть В?2 к Л\.
ею _ тпг_ _ ш_
ы ~ гк " ггч"
По пак BQ к Г.\, так и получившийся в иол у цилиндре параллелограмм
будет относиться к параллелограмму, нолучшиаему&и « отсеченном
от цилиндра гегмомте, ит> у обоих параллелограммов будет одна и та же
сторона 2?Т. Далее, Е0 раниа 011, а 16 раина Х6 *); и так как П0
равна 0Е, то, значит, как 03 к 0Х, так и получившийся в нолупилппд-
ро параллелограмм относится к тому, который получился в отсеченном
от цилиндра сегменте.
Пообрагшм, что нолучишлийся в сигмепте параллелограмм перенесен
и помнили в 5 так, чтобы ого щштром тяжести была точка Н; затем
нообразим раиноилечий рычаг П2 с серединой в 0; тогда параллело-
параллелограмм в полуцилиндра, останаясь в своем положении, будет по отноше-
отношению к точке 0 уравпонешиваться с параллелограммом, получившимся
и цпзшндрическом евгмепте, перенесенным ла рычаг и Е и иомощенпым
так, чтобм его центром тяжести была точна Е. И так как у получивше-
получившегося в подуцплиндре параллелограмма центром тяжести является X,
а у получиигпогпся и отсеченном сегменте и керелееннного параллело-
параллелограмма центром тяжести яллется Н, и BE будет к 0Х так же, как
параллелограмм, имеющий, как мы сказали, цпнтром тяжести точку X,
будет относиться к параллелограмму, имеющему, как мы сказали,
щштром тнжести точку 3, то, значит, по отношению к точке 0 паралле-
параллелограмм с центром тяжести X будет ураиповешиваться с параллелограм-
параллелограммом, у которого центр тяжести в S. Подобным же образом докажем, что
если в полукруге ОПР иол прямым углем к ПН кровести какую-нибудь
другую прямую, ни 'приведенной прямой тихетанмть перпендикулярную
к 1.10 плоскость и продолжить ее в обе г.торгаш от той плоскости, в кото-
которой находится круг ЕОПР, то получившийся в полуцилиндре паралле-
параллелограмм, остаиняпъ и сшюм положении, будет относительно точки 0
уравновешивать параллелограмм, получившийся в отсичеппом от цилин-
цилиндра сегменте, перенесенный на рычаг л S и помещенным так, чтобы его
центром тяжести бшга точка Е. Значит, и все иоиучившиеся в полу-
полуцилиндре параллелограммы, оставаясь и своих положениях, будут
относительно точки 0 ураинопсшииать все параллелограммы, получив-
ншеся и отсеченном от цилиндра екгмепте, перенесенные ч помещенные
на рычаге в точке S; таким образом, и полуцилиндр, оставаясь в своем
положении, будет относительно точки в уравиоиипвиать отсеченным
сегмент, перенесенный на рычаг в S и помещенный таи, чтобы его цент-
центром тяжести была точка 3.
*) Пти pnnericTjsii и следующие яа ними лушиы Архимеду, когда он переходит от рис. S и рис. 10.
па котором II будут постись пни рнссундонил как и отом, гак и в следующим предложениях.
2,1
322
АРХИМЕД
X:
; \
i /
7. Z1
II.
XIII
Пусть опять будет перпендикулярный к оси параллелограмм*)
MN и круг SO <ПР) {рис. 11}; проведем соединяющие прямые 0М,
0Н, восставим на них плоскости, перпендикулярные к той, в которой
находится полукруг 0111', и упомянутые плоскости продолжим в обе
стороны; получится некоторая призма,
имеющая основание такое же, каким яиля-
отся трсуголыппсбЛШ**), а высоту, равную
оси цилиндра, и ата призма будет четвертой
частью «сей призмы, содержащей цилиндр.
Теперь и полукруге ОДР и is квадрате MN
проиедсм какие-нибудь прямые КЛ, ТГ,
одинаково отстоящие от прямой 11?; они
пересекут окружность полукруга 011Р в
точках К., Т, диаметр ОР — в точках 2,Z
и прямые 0Н, ЭМ — в точках Ф, X; затем
па прямых КЛ, ТГ восставим плоскости,
норпендикулярные к ОР, и продолжим их
и обе стороны от той плоскости, в которой
находится (круг SOUP; тогда каждая из
них и) полуцилиндре с основанием — полукругом01J.P— и с той же са-
самой высотой, что и у цилиндра, образует сечением параллелограмм, одна
сторона которого раина К?, а другая равна оси цилиндра; и призме
011М они точно также образуют параллелограмм, одна сторопа которо-
которого равна АХ, а другая равна оси; точно таи же в том жо самом полу-
полуцилиндре получится некоторый (другой) параллелограмм, у которого
одна сторона равна TZ, а другая раина оси цилиндра, а в призмо —
параллелограмм, у которого одна сторона раина прямой ТФ, а другая
рагша оси цилиндра... ***).
<Так как центры тяжести параллелограммов, расположенных ла прямых 2К,
ZT, находятся в серединах прямых 2К, ZT, то центром тяжести обоих этих параллело-
параллелограммов, пзятмх вместе, будет точка А', в которой прямая, соединяющая центры тяжести
этих нараллслограммои, пересечет 0П. На. том л;е основании центром тнжести обоих
иараллелограммоп, расположенных на прямых ХЛ, ТФ, будет точка В', в которой ири-
маи, соединЯ1ощ;1Л сгредишл прямых ХЛ, ГФ, ысресечет прямую ЕВ. По параллелограм-
параллелограммы на прямых ?К, ZT так относятся к нараллелог]>»ммам па ХЛ, ГФ, как прямая ?К.
к ЛХ, или как прямая 2К. к ХР. Но SK отпоетттся к XV, как кладрат на К2 к прямо-
прямоугольнику между 2К. и 2Р, и квадрат ил 2К. p:nicir прямоугольнику между 21'-SO;
значит, К2 будет к SP, как прямоугольник между 2Р, 20 к примоуголышку между
SK, 2Р, то ес*ь как 20 к 2К
^К _ 2К2 21>-20_ 2()
2Р ~~ 2Р-2К ^ 2Р-2К" 2R '
Дп'дсп, 2О равняется SP вместе л удвоенной 2в, или ЛХ вместе с удвоетгок Х2
аначит, 2O будет к 2K, как пмрстс пзятие АХ с j^uoiuinoii XX, относятся к 2К, или,
взмв половипм, как XS с ннлолтюй АХ будет к ноаовине 2К.
у v | "-^
20 АХ+2Х2 /-А^ г
v ы ' v a v it
*) Счсаовало бы сказать «киадрат».
• •) Нужно иметь п липу, что треугольник ©МН расчюлижси л пред и ем сечс-нии призмы, м гле-
допателыю, нь мошет быть ее оспоиапиим.
••¦) Конец предложения утцачец." и переносе: дастся реконструкции I'efiCepra; в шплштиых Чер-
Чертежах Оукв А' и Л' не имеется.
ПОСЛАНИЕ К ЭРЛТООФЕНУ. О МКХЛНИЧКСГШХ ТКОГЕМАХ
323
Но половина ЛХ имеете с XI* раина И'в, половина же 2К есть А'в; значит, параллело-
параллелограммы jin SK и ZT к параллелограммам ли ХА я ГФ будут относиться, кик В'йк А'в.
Таким образом, лыпюуиомяпутмо парпллгаограммы будут относительно точки в уравно-
уравновешивать друг друга. То же самое буди* справедливо л отцокительпо псех других постропп-
лых таким же образом инраллодограммоп; апатит, полуцилиндр ОПР и лризма J16M,
заиолниппыс TciiiiiMii параллелограммами, будут урпшкшеттшиать друг друга относительно
точки в. Но относительно точки в полуцилиндр ОПР, оставаясь п своем иоложопии,
ураиповегпииасгг отсеченный ог цилиндра сегмент, помещенный на рычаго так, чтобы
его ц«нтр тяжести был п точке 3 (предложении XII). Дплве, S0 jiaBiia П0; зяачит,
отпеченный от цилпплра сегмелт, ломсщсиныи и ТТ, будет относительно точки 0 ураино-
вешилать 1гризму J[0M. По Центр тяжести упомянутой приамы будет на прямой E0,
если рассечь ос так, чтобы ос часть при 0 была вдвое пильню остающегося отрезка. Зна-
Значит, отсочкнпмй от цилиндра сегмент таге отцоситсн к призме НвЫ, как дыг трети Е0
к ПЭ, или как 2 к 3. Но при™» НвМ состаилжл1 четвертую часть всей призмы; значит,
цилиндрический шгмепг будет panwr ее шоктой части [7].
XIV
Пусть будет прямая призма с квадратными основаниями, и пусть
одно из ее оснований будот квадрат АВГА {рис. 12}. Umimosi в ату приз-
призму цилиндр, к пуст!, оснонашюи цилиндра будот круг EZT16, "касаю-
"касающийся сторон квадрата ЛВГД в точках Е, Z, II, 6. Через центр этого
круга и ту на сторон квадрата, которая
находится л противолежащей А13ГА л.чо-
скостн и соответствует ГА, проведем пло-
плоскость; ота плоскость от целой призмы
отсечет другую призму, которая будет чпт-
вертой частью целой приз.чы; эта самая
(отсеченная) призма будет заключаться
между тремя параллелограммами и двумя
протило.южалпшп друг другу треуголь-
треугольниками. В шшукруго EZH опишем парабо-
параболу, и пусть... {ее диаметром, заключен-
заключенным)... в сечении, будет Ж. В парал-
параллелограмме ATI пара;кчсш>но KZ проведем
некоторую прямую MN; она пересечет
окружность полукруга и точке 3, а па-
параболу— и Л. И (прямоугольник) между MN и NA ранен (квадрату)
на NZ
mn • гсл = NZ*
(ото действительно очевидно *)). Вследствие атого получится, что MN
будет относиться к МЛ, пак (квадрат) на KII к (квадрату) на Л2**).
II
Ш
Рис. 12.
UN
кп2
На прямой MN иосстаиим плоскость, перпендикулярную к ЕН; зта
•) Дсйгтпителык», если поить Z и кнчестиг. начала коирдинат, и.-шрапнть ось х но ZK. а ось у
по Zr, то уравнения т1раПолк ZAII Судат иметь пил
Тан !<ик парабола должна проходить через точку н, дли которой ж—ZK и u = Iik Судтт соответ-
соответственно раины радиусу круга В., то уравнение параболы ZAH Судет
уЪ =- Их,
Архимед пишет ei4> n вило
**) Ни имеем;
MW
MN»
21*
324 лрхимкд
плоскость и сочетал с призмой, отсеченной от целой иризаш, образует
прямоугольный треугольник, у которого одна из сторон, прилегающих
к прямому углу, будет MN, а другая, лежащая в плоскости, проходящей
через ГА, и проведенная из N перпендикулярно к ГД, будет раина оси
цилиндра; гипотенуза же этого треугольника будет находиться в самой
секущей плоскости. (Восставленная на Л1\ лерпендикулярная к ЕН
плоскость) в сечении с сегментом, отсечелпым от цилиндра плоскостью,
проведенною через ЕН и противолежащую ГД сторону кьадрата (верх-
пего основания призмы), образует прямоугольный треугольник, у ко-
которого одна из сторон, прилегающих к прямому углу, будет М5, а дру-
другая — ироипдаппая на ловирхлостн цилиндра из точки Е, лерленди-
кулирнаи к плоскости. KN прямая, гипотенуза же: (в секущей пло-
плоскости). Теперь поскольку (прямоугольник) между MN и МЛ
равен (квадрату) на ME
{это действительно очивндло *)), точно так же получается, чтг> (MN)
будет к (МЛ, как квадрат на MN) к (квадрату на ME).
ык мм*
МЛ MSa
Но как квадрат на ( MN к (квадрату) па ) М5, так будет и получивший-
получившийся и лриамо треугольник ла MN к получившемуся в отсеченном
поверхностью цилиндра сегменте треугольнику на MB; значит, как
MN к МЛ. так будет и один треугольник к другому.
UN УОН* _ Гг к »я МЛ*
МЛ щ=г 1>к на МЛ
Если в параллелограмме, описанном (около параболы, параллельно)
KZ пронести какую-нлбудь другую прямую и на проведенной прямой
(восставить перпендикулярную) к ЕН плоскость, то подобным же
образом докажем, что получившийся в принме треугольник будет отно-
относиться к (треугольнику) н сегменте... (отсеченном)... от цилиндра,
как прямая, проведенная и параллелограмме АН параллельно К.7.,
будет отпоситься к своему отрезку между параболой EliZ u диаметром
КН. Теперь, если заполнить параллелограмм АН прямыми, проведен-
проведенными параллельно K.Z, а заключенный между параболой и диаметром
сегмент заполнить заключенными в этом сегменте отрезками...**),
(прямым)... проведепным в параллелограмм» АН параллельно KZ.
и получится, что все треугольники в призме будут относиться ко всем
треугольникам, заключенным в отсеченном сегменте цилиндра, как
все крямы» в параллелограмме АИ ко всем прямым, заключенным меж-
между параболой и прямой ЕН. Но из треугольников в призме составляется
эта самая призма, из треугольников в (отсеченном от цилиндра) сег-
сегменте составляется (отот сегмент), из параллельных KZ прямых в па-
параллелограмме АН составляется, параллелограмм АН, из... (отрезков)
... между параболой и прямой ЕН составляется (сегмент) [параболыJ.
Значит, призма будет относиться к сегменту цилипдра, как параллело-
грамм АИ к сегменту EZTI. заключенному между параболой и прямой E1I.
*) Дейсгвитсяьпо:
М:=2 — HM-ME = (MN — МК) ( MN-г МК)= MNa-NZi<= HJH-MS- Кд= MX- MA.
•*) В подлиннике лакуна в 17 строк.
ПОСЛАНИЕ К аГАТОСФЕНУ. О МЕХАНИЧЕСКИХ 'ГЕОТЕМАХ
325
Но параллелограмм ДН в полтора раза больше сегмента, заключен-
заключенного между параболой и прямой ЕН (это докавыиается в ранее изданных
сочинениях *)); значит, и призма Судет в полтора раза больше сегмента,
отсв4С11пого от цилиндра; вначит, каких чантон будет дне в сегменте
цилиндра, таких жи будит n irjm:i.\m три. Каких жй частой ц этой принме
три, тиких в цилой призме, заключающей ци-ииндр, будет 12, нследстиые
того, что первая призма составляет 1/4 второй. Значит, каких частей
в цилиндрическом сегменте две,.таких в целой призме Судет 12; таким
образом, отсеченшлй от цилиндра сегмент составляет шестую часть
призмы [8].
XV
Пусть будет прямая призма с квадратными основаниями, одним
из которых является квадрат АВГД; ппишем в ату призму цилиндр,
основапием которого пусть будет круг EZII; этот круг (касаотся) сто-
сторон квадрата в точках Е, /, И, 0. Пусть его центр (будет К: через)
диаметр ЕЯ (и одну из сторон) ...{противолежа.- ^
щего квадрата)...(проводем плоскость), нта пло-
плоскость от целой при.чмы отвпчот некоторую пры.чму,
а от цилиндра — цилиндрический сегмент. (Я ут-
утверждаю, что) этот сегмент, отсеченный от цилин-
цилиндра проведенной плоскостью, будет, как мы дока-
докажем, гиестой частью целой призмы.
Прежде «сего докажем, что ъ отсеченный от ц
цилиндра сегмент можпо вписать телесную фи-
фигуру, составленную пи призм, имеющих равны»
иысоты и подобные треугольные основания, и
другую такую же описать так, чтобы описанная
фигура была больше миисанной на нолишшу, мень-
меньшую всякой заданной величины... **)
Е
(В полукруге EZII {рис. 13} Яудем вес время делить попо-
пополам доамитр ЕЙ и чорел точки деления параллельно КZ прово- '¦Jlt:- '¦*¦
дить прямые, псфе.гекающис окружность полукруга; через
точки то, в которых :>Tii прямые пересекают окружность, будем проводить парал-
параллельные КII прямые и продолжать их " обе стороны до встречи в днумя (Злижайшими
napa.ii.ic.TT.ubiMu К'А прямыми; лят^м гт них и других паралло.п.пых щлшых будем пос-
гтао.'11Ш> Ш10ск«111ти, ггерпе^;икулягрныс- к плоскости полукруга; тогда :'ти плоскости как
внутри цилиндрического сегмента, так и вне ого пбрануют призмы о равными высотами
и г. основаниями — прямоугольными треугольниками, расположенными на прямых,
параллельных К 7,, Деление прямой iuH пополам будем продолжать до тех пор, пока дои
прилегающие к К 7, приемы не окажутг-н меммме яаданлоп величины; тпгдц состаплетшя
из призм и описи пная околи пплинлрнчгс!!!!!-!) сегмента телесная фигура будет такую же
вплетшую превосходить ijii зкяичиму, мспмпуг» илдашкш. Деиспште.и.но, описаннан
фигура будет отличаться «т вписанной на две иршшы, прилегающие- к KZ, так как нг-ом
осталын>гм нрттимам описанной фигуры будет соотиотг/гливать г-тотп.ко жи равных им призм
впнеасгппй фигуры.
Затеях, есш в том же полукруге, пциса-п, нириболу EZH {рис. 14 \ и через точки
пересечения с прямыми, параллельными ZK, провести прямые, параллельные ЕН, про-
продолжая их в обе стороны, как было екплвно раш.нк1, то начучится составлпппня и;$ нара.ч-
.¦ifjMirpiiMMon фигурса, ошпннван около параболи'нгского сегмента, и другая такая жп,
вписанная в него, из которых нервнн будет превосходи-п. иторую на два параллелограмма,
к
N
/
/
*) См. предложение XXIV лКпадрг1турьт иа];або.чые.
*А\ ^ -
D подлиннике пропуск четирпх столОпов или пгшйливитепьно 80 строк, <>т которых сохра-
сохранились лить ипслелнмс гловн. Дальнейшая реконструкция даетгл Геибеггом применительно к пред-
предложениям XIX, ХХ\' трактата «О коноидах и сферсидвх»: и текст Гейберга внесены некоторые
11СП[К1К.С1Т1Ш.
326
АРХИМЕД
2
прилегающие к ZK; при лч>м каждч-чу из таких параллелограммов будет соответствовать
приема нытеупомимутмх телесных фигур.
T(!iicpi»i если отсеченный от цшшпдра сегмент пс будет рапеы шестой части цолой
ириздш, то on будет пли больше, "или метши». Пусть сначала он, если возможно, будет
Chiji мни; тогда отсеченная наклоштой плоскостью призма будет пенсе чем в полтора раза
больше цилиндрического сегмента.
Инишсм в последним телесную фигуру и опишем около пего другую так, как это
было yica;t:i<io выше, и пусть онпсашшм фигура будет превосходить вписанную па вели-
чичу, меньшую \ia:iкогти между сегментом, и дпумн. тоетнми приемы; тогда, поскольку
oiiiicaiiiiau около сегмента фигура будет больше этого
И сегмента, впиедшмя фигура будет больше двух третей
л)>и;)М1,т. Теперь мм уже доказали (предложение XIV),
что все прямые в параллелограмме ДН (рис 12) отно-
относятся ко исем прямьпы в параболическом сегменте EZI1,
как все треугольники и 1гри:ше, отсеченной иаклонпоЙ
плоскостью, ко всем треугольникам л сегменте, отсе-
отсеченном от цилмпдра. Построим ыа атих треугольниках,
ж лик на основаниях, прммьт, высоты которых Судут
/ равны отрезкам, на которые разделена прямил ГСП;
д тогда каждой приамс, из кочормх соегйп^яшеп отсс-
чинпаи наклонной плоскостью призма, за ггеключегшем
лини, диух причитающих к ZK, будит соответстловать
приема, w.i которых сосхан.'шется вписанная в цллил
лрич(><:[;ни сегмент телесиан фигура. По как упомя-
упомянутые прямые л па]>:1:1лелог[)имме АН к прямым is
и!|раболич1.'Ском сегменте EZH, так будут и и.чраллело-
грнммы, па которые разделен парнллелограмм ДН,
относиться к параллелограммам, вписанным в кониче-
,\ | ^bJy? gkoo геченне; значит, каждому параллелограмму, на
' которые ра:!де-Т1яетсп параллелограмм ЛИ, за исключе-
Рис. 14. пнем лишь двух, прилежащих к */К, будет соответ-
<:.тв(>ват[> параллелограмм л фигуре, вписылиой и
параболический сегмент. Таким обрачом (лемма 11), отсеченная наклонной плоско-
с-хтыо призма буд(!Т относиты-н к телесной фигуре, шшсашюм в цилиндрический сегмент,
как neci. ппрал^с.гограмм АН к фигуре, шшеяшюй в параболический сегмент, И так как
(ухесченная наклонной плоскостью U(wi:imu икимис вэятм'О полтора ра;»а т\ипи«дрическо1О
сегмента, последний же превосходит пнисанную в iwro Tc:iecnyio фигуру на величину,
меньшую :!.чда1нмш, то eni> меньшую, чем разность между цилиндрическим сегментом
и дпумя третями описанной' наклонной призмы,)
то значит отсеченная наклонной плоскостью приема будет меньше
в полтора раза изятого тела, шгисапиого п цилиндрический сегмент-
Нг> уже докатят), чти иризма, отсеченная иаклоппой плоскостью, от-
носится к телу, вписанному к цилиндрический сегмент, как параллело-
параллелограмм ДН ко всем паралле..и«раммам, вписанным в сегмент, заключен-
заключенный между параболой и прямой ЁН; значит, параллелограмм ДН
будет менее чем и полтора раза больше всех параллелограммов, впи-
вписанных в сегмент, заключенный между параболой и прямой E1I; это же
невозможно, так как в другом мосте *) доказано, что параллелограмм
ДН будет в полтора раза боньше cei-мспта, заключающегося между пара-
параболой и прямой ЕН. Значит,
(цилиндрический сегмент не будет больше... шестой части целой призмы.
Пусть теперь оя, если ьоаможио, будет меньше; тогда отсеченная наклопнон пло-
плоскостью приема будет более чем в полтора раза больше цидиидричм-гсого сегмента. Впи-
Впишем I» еегмепт а опишем около него такие же телесные фигуры, как и выше, так, чтобы
oiinciuiiiitfi фигура прешм'.ходила «писанную на пеличипу мсиьшую той, ил которую две
трети приемы, отсечетюй наклонной плоскостью, превосходят "упомянутый, цилиндри-
цилиндрический сегмелт; тогда, поскольку виисншюя темесгсияг фигура меньше цилиндрического
сегмията, тч> Y1 «пкканиля телеспая фигура будет меньше, чем дв« трети продмы, отсечен-
отсеченной наклонной плоскоетмо.
*> См.
параГюлы», XXl%' (с:тр. Р.1).
ПОСЛАНИИ И ОРЛТОСФЕНУ. О МЕХАНИЧЕСКИХ ТНП'НМАХ 327
Затеи, вписан б сегмент, ааклотчшший лмакду параболой EZIT и прямой ЕЙ, и опи-
описав околи него параллелогргишы так иге, как это допили и w.imc, мы подобно тому,
как и выше, докажем, что отдельные приамы в ттризмв отсеченной наклонной плоскостью,
¦будут относиться к отдельным призм.чм тиесыой фигуры, описанной около цилиндри-
цилиндрического сигмепта, кук отдельные ннриллилограымы, содержащиеся и н.-фгш.кяограмме
ДЛ, к отдрлг.пыя параллелограммам а фигуре, оиясатюм около сегмента, .-шш^очелнси'О
между иц|>»бсы11>й E'ZH и>
прямой (КН>, и что нее пршмы и отсеченной наклонной плоскостью
призме ко doom призмам в фигуре, описанном около цилиндрического
сегмента, будут иметь то же самое отношение, какое все параллелог-
параллелограммы б параллелограмме АН имеют ко «сем параллелограммам в
фигуре, описанной около сегмента, ваключешюго между параболой
и прямой ЕН; иными словами, призма, отсеченная наклонной плос-
плоскостью, будет HMOTii такое же отношение к описанной около цилин-
цилиндрического сегмента фигуре, какое параллелограмм АН имеет к фигу-
фигуре, описанной около сегмента, заключенного между параболой и
прямой ЕН; но отсеченная наклонной плоскостью нриэма более чем
и полтора раза больше телесном фигуры, описапной
<около цилипдрнчрс,К1>10 сегмент»: .чпачмт, и параллелограмм ДН будет более чем в пол-
полтора pane больше фигуры, опппмпшй около сегмента, заключенного между параболой
и прибит ЕН. Уто же невозможно, так кок в другом месте докншиш, что сараллсло-
jyMuuiu AJJ в полтора pu;ia больше шгмшгга, aajuiiovonnorv ыозкду ия]>;нш.чои EZJT я лря-
ыой ЕН. Следовательно, цилиндрический сгишонт гю будет испыП1! шкетом чисти веси
приемы. Поскольку же доказано, что он не будет и больше се, то значит, <т будет равен
шестой -части этпй призмы, что и требовалось доказать) [9J.
•) Kuiien енччвсиия утрлчщ. Он должен Снл содержать ыехгшическое и геометрическое дикя-
зательстно второй ирсдложеписй AiiXhmo;iom теоремы, н именно, что тело, в.'шлючснное между дпумя
цилиндрами с взаимно перпендикулярными осями, инисмнньтми н куб так, чодбы их оснопання
лежали на противоположных гранях, а боковые поверхности кяеались остальных четырех граней
ttyCa, Сучат иавггяться дсум грегнм ятпго куба. Попытка рекчистр^цгга оОоях этик докааательегв
iuiiicjiui в иоммеятарии [10].
О ПЛАВАЮЩИХ ТЕЛАХ
КНИГА ПЕРВАЯ
Предположим, что жидкость имеет такую прирежу, что ив ее ча-
частиц, расположенных па одинаковом уровне и прилежащих друг к дру-
другу, менее сдавленные выталкиваются более сдавленными, и что каж-
каждая из ее частиц сдавливается жидкостью, находящейся пад ней по отве-
отвесу, если только жидкость но заключена л каком-нибудь сосуде и не
сдавливается еще чем-нибудь другим.
Рис. 1.
Если поверхность, рассекаемая любой плоскостью* проходящей че.ре&
одну и ту же точку, всегда дает в сечении окружность круга с центром
в той самой точке, через которую проводятся
секущие плоскости, то ото поверхность будет
шаровой.
Действительно, пусть будет некоторая поверх-
поверхность, которая при сечении плоскостью, проходя-
проходящей через точку К {рис. 1}, всегда образует окруж-
окружность круга с центром в этой самой точке К. Если
эта поверхность не будет поверхностью шара, то но
будут равными все лишш, которые идут от центра
к поверхности. Пусть А, В, Г, Д будут точки на
поверхности, причем л плои АК и ВК не ранцы;
проведем через КА, KB плоскость, и пусть она образует в сечении с
поверхностью пинию ЛАВГ; эта линия будет, конечно, круговой с цент-
центром « точке К, так как рассматриваемая поверхность предполагалась
обладающей таким свойством *). Значит, линия КА, KB ire будут нерав-
неравными; поэтому необходимо, чтобы эта поверхность была шаровой.
П
Поверхность всякой жидкости, установившейся неподвижно, будет
иметь форму шара, центр которого совпадает с центром Земли.
*) Именно, что иессечешш ее плоскостями, приходящими черса точку К, нылягствп круговыми..
О ПЛАВАЮЩИХ ТКЛАХ
829-
Вообразил! некоторую жидкость, которая устапоштлась неподвиж-
неподвижно; рассечем ое поверхность через центр Земли плоскостью; пусть центр
Земли будет К {рнс. 2), а линия сечения поверхности АВГА. Я утер-
ждаю, что линия АВГД будет окруяшостью круга с центром л К.
Действительно, если это не так, то прямые, выходящие из К. к линии..
АВГД, не будут раины друг другу. В таком случае нозьмем некоторую'
прямую, которая была бы больше одних и меньше других из линий,
выходящих из К к липни АТЗГД, и из центра К опишем круг радиусом,
ранным птой линии; тогда тшерхность этого круга пойдет так, что-
часть ее расположится вин линии
АНГЛ, часть же внутри, так как
радиус ее будет больше некото-
некоторых из пиний, выходящих от К к
линии АВГД, и меньше других.
Пусть окружность описанного
круга будет ZH11; проиедсм из В
в К прямую и построим прямые
Рис.. 2.
ZK, КЕЛ, образующие равные
угли <АК13 и ВКЛ), затем из
центра К опишем некоторую дугу
НОП, которая находилась бы на плоскости (чертежа.) и в жидкости;,
тогда расположенные по дуге ?011 частицы жтщког.ти будут находиться
на одном уронне и прилегать друг к другу- Те из них, которые нахо-
находятся иа дуге SO, будут сдавливаться жидкостью, расположенной до-
уроппя ZB, и те, которые находятся иа дуге ОН,— жидкостью до уроп-
ня BE; следовательно, частицы жидкости, расположенные на дугах
SO и Oil, будут сдавливаться неодинаково: таким образом, лте нее сдан-
линиемгас будут вытиснены более сдаиливае.мыдш; олсдоинтелыю,
жидкость не останется неподвижной. Мы же предположили, что она
установилась так, что остается неподвижной; значит, необходимо, чтобы
линия А13ГА была окружностью круга с центром и К. Подобным же
образом докажем, что если как-нибудь иначе рассечь поверхность жидко-
жидкости плоскостью, проходящей через центр Земли, то евчгаше будет
окружностью круга и центр ео будет тот же, что и щштр Земли. Теперь
ясно, что поверхность установившейся неподшшшо жидкости имеет
форму шара с тем же центром, что и у Земли, ибо она такоиа, что при
рассочении ее плоскостями, проходящими через одну и ту же точку,
в сечении получаются окружности с центрами в той самой точке, через
которую проходят секущие плоскости.
TII
Геле*), равнотяжелые с жидкостью, будучи опущены в эту
жидкость, погружаются так, что никакая их часть и? выступает
над поверхностью жидкости, и ие будут двигаться вниз.
Опустим в жидкость какое-нибудь тс;ю из равнотяжелтлх с птой
жидкостью, и пусть, если возможно, некоторая часть его будет высту-
выступать над поверхностью жидкости; пусть жидкость установится а таком.
*) У Архимеда иитсрееппе итлрамипие: tojv oteq?u)V jiEVfifrEav xa ujoflnQeovrra— Оуишшыю:
«ie из объемных величин, которые ^ивнотняселы...» Архимед, но существу, .имел дело с геометриче-
геометрическими телами, и его cteuRu цруеоеа представляют пространственную аналогию eniire№
(плоских иеличин), о которых шла речь в книгах «О рааиояесии штпеких фигур»-
АРХИМЕД
положении, что будет оставаться неподвижной. Вообразим некоторую
плоскость, проведенную через центр Земли, через жидкость и через
это тело; пусть ее сечение с поверхностью жидкости будет дуга АВГД
{рис.. 3}, а с рассматриваемым телом — фигура EZB11, центр же Земли
пусть будет К. Тогда часть ВГН0 тела будет в жидкости, часть же
BKZF — вне ее. Вообразим, что тело охвачено плраммдообраэной фигу-
фигурой, имеющей в основании на поверхности воды параллелограмм *),
а вершиной — цоптр «Земли. Пусть КА
и К М будут сечения граней пирамиды
с той плоскостью, в которой находится
дуга АВГД. Около центра К опишем
еще одну шаровую поверхность так,
чтобы она проходила впутри жидкости
и ниже тела EZHO, и рассечем ее пло-
плоскостью; латсм возьмем другую пира-
пирамиду, ранную и подобную той, кото-
которая охватывает погруженное тело, и
смежную с ней; пусть КМ и KN будут
сечепия се граней; в жидкости шюбра-
пекоторьгй объем Р2ТГ, охвачен-
р
ный жидкостью, равный и подобный части ВНвГ первого тела, по-
погруженной и жидкость. Тогда частицы жидкости в периой пирамиде,
расположенные под той частью поверхности, где находится дуга НО,
а также соответствующие частицы в другой пирамиде, где находится
дуга 110, будут лежать на одном уровне и в непрерывной связи друг
с другом. Однако они не испытывают одинакового давлении; действитель-
действительно, те частицы, которые расположены ш» ЕО, сдавливаются телом (J11EZ
и той жидкостью, которая находится между поверхностями НО, AM
и гранями первой пирамиды, те же, которые расположены по 110,
сдавливаются жидкостью, находящейся между поверхностями ПО,
МЛ" и грашшя вгорой пиргшядм. Тогда давление на жидкость, находя-
находящуюся между MN, 011, будет меньше, так как (объем) Р2ТГ будет
мсныпе тела Е/.Н8 (ибо этому (объему) раина только часть НВГв, и
она предполагается одинаковой ло величине и рыннотнжелой (с жидко-
жидкостью)**), а остальные части в обеих пирамидах одинаковы). Теперь
ясно, что часть жидкости, соответствующая дуги 011, будет вытолкну-
вытолкнута тон частью, которая соответствует дуге ОН, и жидкость никак tie бу-
будит неподвижной. Было же предположено, что она неподвижна; значит,
никакая часть тела не будет выступать над поверхностью жидкости.
Погрузившись же, тело не будет двигаться вниз, так как все части
жидкости, находящиеся на одном уронне, будут давить одинаково вслед-
вследствие того, что тело является рав нетяжел мм с жидкостью II].
IV
Тело, более легкое, чем жидкость, будучи опущено в эту жидкость,
не погружается целиком, но некоторая часть его остается над поверх-
поверхностью жидкости.
Пусть будет тело более легкое, чем жидкость, и пусть он«, будучи
опущено в жидкость, погрузится целиком, «ели возможно, так что
*) То есть прямоугольник.
**) Фраза d скобках, по-видимому, ирсдставнисх позднейшую вставку; во ценном сл>чче слоиа
«одинаковой по величине» совершении излишни.
О ИЛЛНЛЮЩИХ ТЕЛАХ
331
над поверхностью жидкости не будет никакой его части, и жидкость
устаиоиится неподвижно. Вообразим некоторую ллоскость, прове-
проведенную черен центр Земли, жидкость и погруженное тело; пусть по-
поверхность жидкости рассечется отой плоскостью по дуге А13Г {рис. 4},
погруженное тело даст л сечении фигуру, обозначенную через Z, а
центр Земли пусть будет К; вообра.шм, как и выти, некоторую пир ами-
амиду, охватывающую тело Z, имеющую иершипу и точке К; пусть прове-
проведенной через ART плоскостью ое грани будут пересекаться jjo лилиям
АК, KR; возьмем также другую пирамиду, равную и подобную этой,
si пусть ее грани тон же самой плоскостью
пересекаются по линиям KB, КГ; затем и
•жидкости, ниже погружоппого тела опи-
опишем другую шаровую поверхность с цепт-
ром в К, и пусть она пересекается выше-
вышеупомянутой плоскостью но дуге НОП;
вообразим еще во пторой пирамиде ныде-
лсними объем жидкости II, равпый телу Z;
тогда частицы жидкости в первой иира-
миде, расположенные под поверхностью,
соотнетстпующен дуге НО, а также во
второй пирамиде под поверхностью, соотиетстиугощей дуге ОН, будут
находиться на «дном уровне и прилегать друг к другу. По они не
исимтмкгшт одинакоиого данленин, так как в jicpuoii пирамиде они
сдавливаются телом Z и окружающей его жидкостью, занимающей
в .чтой пирамиде место А, В, О, 2, а но пторой пирамиде они сдавливают-
сдавливаются окружающей жидкостью, занимающей в пирадшде место П, О, 13, Г;
нес же тела (Z будет меньше веса) II, поскольку тело Z, будучи ран-
пым Ы по величине, предполагается более легким, чем жидкость;
веса же окружающий объемы Z, II жидкости будут в каждой из кмрамнд
одинаковыми; значит, частицы жидкости, расположенные по пешерх-
ности, соотлетстиумщей дуге ОП, будут испытывать болыпео давление;
следовательно, менео сданлииаемые >гастш(ы ш.1теснятся и жидкость
по будет оставаться неподвижной. Hci она предполагалась таковой;
значит, тело не погрузится целиком, но
некоторая его часть будет находиться
над поверхностью жидкости.
Тело, более легкое., чем жидкость,
будучи опущено в эту жидкость, погру-
погружается, настолько, чтобы объем жидко-
жидкости, соответствующий погруженной
{части тела), имел вес, равный веху
всего тела.
Пусть будет сделало то же, что и
раш.ити, и пусть жидкость будет не-
неподвижной; пусть тел1) EZH© (рис. 5) будет более легким, чом
жидкость. Теперь, поскольку жидкость осотастс/г неподвижной, частицы
«е, расположенные пк одном урошю, будут ислытивать пдикалоное
;[авлешш; следопателыи), жидш>ст1| под иошрхшютями, сг>тлетст»ующи-
ми дугам SO и ПО, будит сдаилинаться одинаконо, так что одинакова
будет и тяжесть, (которой они придавливаются. По вое жидкости
332
АРХИМИД
в нерпой шгрялщцс, за исключением объема В110Г, будет ранен несу
(жидкости со второй нирамидо), за исключением части жидкости
Р2ТТ; теперь ясно, что вес тела EZHB будет равен весу жидкости
I'2'ГГ. После атогп очевидно, что объем жидкости, соответстьуяшщй
погруженной части опущенного тела, имеет вес, равный весу всего тела..
VI
Тела более легкие, чем жидкость, опущенные в эту жидкость на-
насильственно, будут выталкиваться вверх с. силой, равной тому весу,
на который жидкость, имеющая равный объем с телом, будет гпямхлее
этого тела.
Пусть будет некоторое тело А {рис. 0} более легкое, чем жидкость;,
пусть В будет нес тела Л, а И + Г — вес жидкости в объеме, равпоы Л.
Требуется доказать, что насильно по-
погруженное в жидкость тело Л будет1
выталкиваться вверх с силой, равной]
весу Г.
Возьмем
имеютцее нес,
составленное
1'ис. 6.
какое-нибудь тело Д,
равный Г; тогда тело,,
нз абъединенных вместо
обоих тел А, Л, будет легче жидкости,
(в том же объеме), так как вес тела, со-
составленного из обоих, будет В -[- Г, вес
же жидкости в равном объеме будет
больше, чем В -|- Г, так как В + Г
представляет вес (жидкости) в объеме,
рапном А. Теперь тело, состаилсшюе и*
обоих тол А, Д, будучи опущено в жидкость, погрузится настолько,
чтобы жидкость и объеме, равном погруженной части, имела вес, рав-
равный несу всего теля, как »то доказано ш,шге. Пусть дуга АВГД пред-
представляет поверхность некоторой жидкости. Теперь, поскольку коли-
количество жидкости в объеме, равном телу А, имеет вес одикаконый с
весами обоих тел А, Д, то ясно, что погруженная часть этого тела,
будет иметь объем, равный А, остальная же часть его, именно Д, будет
находиться над поверхностью жидкости; действительно, если ом это-
тело погрузилось иначе, то получилось бы (противоречие) с тем, что-
было доказано (раньше). Теперь ясно, что (с какой силой) тело А
вмтнлкннастсн кверху, (с такой же пилой оно будет нридашишаться)
книзу находящимся над ним телом Д, поскольку ни то, ни другое не
пересиливают друг друга. Но Д давит вниз с тяжестью, равной весу
Г, так как было предположено, что вес тела Д ранен Г; теперь то, что.
требовалось доказать, будет очевидпо.
\П1
Тела, более тяжелые, чем жидкость, опущенные в эту жидкость*
будут погружаться, пока не дойдут до самого низа, и в жидкости ста-
станут*) легче на величину веса жидкости н объеме, равном объему погру-
погруженного тела.
*) Характерное инраяодис «станут легче teaaovviai кои^отеря)», показывающее, что грекга
вес олпога ц того же тела не считали постоянным; они «вес» понимали как «давление».
О ПЛАВАЮЩИХ ТЕЛАХ
333
Что тело будет погружаться, попа щ> дойдет до самого дна, оченид-
iio, так как находящиеся под ним частицы жидкости будут испытывать
большое давление, чем другие, располо?кснньте на одной с ним уровне,
так пак тело предполагается более тяжелым, чем жидкость; а что оно,
как сказано, (в жидкости) станет легче, это следувт доказать.
Пусть Судет некоторое тело А {рис. 7} более тяжелое, чем жидкость;
пусть вес тела А Судет Б -|- Г, вес же жидкости в объоме, ранном А,
будет В. Требуется доказать, что тело А,
находясь в жидкости, будет иметь вес,
раин ы ii Г.
Возьмем некоторое тело Д, (более
легкое, чем жидкость в ого объеме: пусть)
вес тела Д будот рнкии несу Л, нос же
жидкости, имеющей одинаковый с Д объолт,
пусть будет равел весу В -|- Г. Если мы
сложим оба наши тела А и Д в одно, то
составленное тело будет рав нетяжелым с • р"с- 7-
жидкостью; действительно, вес обоих этих
тел ранен вместе взятым весам В -|- Г л 13, вес же жидкости, имеющей
объем, равный обоим телам, равен тем ж» самый иесам. Значит, если
эти тела опустить в жидкость, то они будут и равновесии с жидкостью
и не будут двигаться пи нппрх, пи нниз; вследствие этого тело А пойдет
вниз с такой же силой, с какой тело Д будет увлекаться вверх; тело
же А, поскольку оно легче жидкости, будет двигаться вверх с силой,
раиной весу Г, так как докапано, что более легкие, чем жидкость, тела,
будучи насильно погружены в :>ту жидкость, движутся ниорх с силой,
равной тому весу, на который жидкость, имеющая объем, равный атому
телу, будет тяжелее последнего. Но жидкость, имеющая равный объем
с телом Д, будет тяжелее тнла Д на нес Г;
теперь ясио, что тело А будет двигаться
выла (с силой, равной весу V).
Предположим, что все тела, движу-
движущиеся*) (и жидкости вверх), будут поды-
подыматься но отвесной линии, проведенной
через их центр тяжести.
VJ.Il
Если какое-нибудь тела, более легкое,
чем жидкость, и имеющее форму сегмента
шара, будет опущено в жидкость таким
образом, чтобы основание сегмента не ка-
касалось жидкости, то это тело установит-
установится в прямом положении, так что ось сег-
сегмента будет расположена по отвесу; и
если кто-нибудь принудит тело стать так, чтобы основание сегмента
касалось жидкости, то оно не останется в наклонном положении, но.
будучи отпущено, снова станет прямо.
Представим, что в жидкость онущипо такое тело, как скапано;
вообразим плоскость, проведенную через ось сегмента и центр Земли,
и пусть АВГД {рис. 8} будет сечение атой продолженной плоскости
"> Надо помнить, что и i-реческой механике идея дпижптшн Пыла неразрывно связана с идеей
силы; поэтому ближе к смыслу было бы снизить «иыталкииаемые в жидкости Bt
334 АРХИМЕД
с поверхностью жидкости, а дуга EZH6 — с опущенным в жидкость,
толом; пусть ос г» сегмента будет 0Z; тогда центр шара будет на OZ.
(Предположим) сначала, что сегмент больше полушария; пусть
центр (его) будет К, и пусть толо, если возможно, будет паклонено-
само но себе или под чьим-нибудь воздействием. Требуется доказать,
что оно пе «станется в покое, но лернстся в прямое положение, так что
Z и в будут находиться на otugciioh лини,!.
Действительно, поскольку тело предполагается наклоненным, то
7j и в по будут находиться на отиесном лшпш. Через К и А проведем
прямую КЛ (Л мы предполагаем цсптром Земли); на прямой КЛ будет
лежать ось находящейся п жидкости части тела, отпекаемой поверх-
поверхностью жидкости, ибо если поверхности двух щаров пересекают друг
друга, тосечешге будет кругом, перпендикулярным к прямой, соединяю-
соединяющей центры атих шаров. Центр тяжести фигуры, находящейся и иоде
и отсеченной дугой BiNl1, находится на КЛ; пусть :>то будет Р. Центр
же тяжести всего сегмента, соответствующего дуге 6HZE, паходится
на Z©, пусть он будет Е. Тогда доптр тяжести (оставшейся фигуры,
находящийся вне) поверхности «оды, найдется па продолжении РЕ,
если отложить некоторый отрезок ?Е, который имеет к ЕР то ни*
отношение, что вес части сегмента, соответствующей дуге 13ХГ, к весу
той его части, которая будет вис жидкости; ото уже доказано («О равно-
равновесии плоских фигур», км. I, предложение VIII). Пусть центр упомя-
упомянутой фигуры будет 22. Теперь, так как вес той части тела, которая на-
находится иле жидкости, будет стремиться вниз но прямой Л2, вес же
той части, которая и жидкости (будит стремиться) вверх но прямой
РК, то ясно, что тело не останется в iroKoe, no что части его, прилежа-
прилежащие к Е, пойдут впил, прилежащие же к 11 — вверх и что так двигать-
двигаться они будут все время, пока Z0 не станет отвесной. Когда же Z6 ста-
станет отвесной, то центры тяжести обеих частей, как той, что в жидкости,
так и Toi'i, что вис се, будут па одной и той же отвеспой линии (они будут
на ZO); тогда веса будут взаимно давить друг па друга но одной и той
же отвесной линии, один вниз, а другой вверх. Таким образом, тело-
будет оставаться неподвижным, ибо ни
один не сможет вытолкнуть другой.
То же самое получится, если фигура
будет полушарием ими меньше полуша-
полушария Г21.
IX
И так эхе если какое-нибудь телоТ
более легкое, чем жидкость, будет опу-
опущено в эту жидкость так, чтобы все его
основание было целиком в жидкости, mo-
тело установится в прямом положении
так, что его ось расположится по отвесной линии.
Вообразим, что и жидкость опущено тело такое, как сказано;
вообразим также плоскость, проведенную через ось сегшепта и через
центр Нпмли; пусть сечение поверхности жидкости будет окружпость
АВГЛ {рис. У), а тела — дуга EZH и прямая ЕЯ; пусть ось сегмепта
будот ZB, и пусть, если возможно, Z0 не будет отвесной; требуется
доказать, что тело не останется в покое, по вернется в прямое положение.
Центр шара будет на Z6 (предположим сначала опять, что тело
будет больше полушария); пусть он будет К. Через К и центр Земли Л
О ПЛАВАЮЩИХ ТЕЛАХ
335.
ггроиедем прямую КЛ; тогда часть тела, находящаяся вне жидкости
м отсекаемая, лоиерэгностью жидкости, будет иметь свою ось (на прямой,
проходящей) через К, и на оенгшании того же, что и иыше, ее центр-
тяжести будет на Л'К; пусть он будет в 1\ Центр тяжести иесго сегмента
будет на ZO между К. и Z; пусть он будет Т. Значит, центр тяжести
остальной части сегмента, находящейся в «оде, найдется на лродолже-
нии прямой ТР, если нанести на ней некоторый отрезок, которым имел
бы к ТР то ;ко самое отношение, что вес. части сегмента, находящейся
шю жидкости, к весу той части, которая в жидкости; пусть центр упо-
упомянутой фигуры будет О, а отвесная ллния, проведенная через О,
будет ОЛ; теперь, вес части сегмента, которая иле жидкости, пойдет
вниз ло прямой РА, и той части, что н жидкости,— пнерх гго прямой ОЛ.
Следовательно, тело не останется в покое, но те его части, которые при-
прилегают к II, пойдут вниз, тс же, что к Р^ — вверх, и так будет впе время,
пока 9Z не сделается отвесной *).
КНИГА ВТОРАЯ
I
Если какое-нибудь тело, более легкое, чем жидкость, опустить а эту
жидкость, то оно по тяжести будет находиться е том оке отношении
с жидкостью**), какое погруженный объем имеет,
ко всему объему.
Опустим в жидкость какое-ниоудь тол о ФА
{рис. iO), янляющвеся более легким, чем эта
жидкость; пусть п о груженная часть его будет Л,
находящаяся »ко пне жили ости—Ф. Требуется
доказать, что ФА по тяжести будет относиться
к равному объему жидкости, как Л к ФА.
Мозьмем какую-нибудь жидкую массу N1,
имеющую с ФА равный объем, и пусть объем Ф
будет pancn N, a А ранен I, и далее, пусть вес
массы ФА будет П, вое массы XI будет РО, а вое I
будет Р; значит, ФА шюст к NT то же самое отно-
отношение, что В к РО. Но так как тело ФА опу- Рис. 10.
щепо н жидкость, будучи легче отой жидкости,
то ясно, что (жидкость) в объеме погруженной части имеет равный
вое с массой ФА, как это доказано (в предложении V книги I); значит,
*) Разбор олучяпп, когда сегмент рапен полушарию или меньше его, отсутствует; и тексте-
веревшш Вильгельма из Мсрбско в конце помещены, чертежи, иллюстрирующие оба эти случая:
Значение букв: ©7. — ось сегмента (в — точка со пересечения с основвнисм), Т — центр
тяжести сегмента, О и ]• • центры тяжести погруженной и иаходпшяйсн кие жидкости его чпотейг
ОЛ и РА — вертикали, соединяющие центр Л Земли с центрами тяжести О и Р обеих частей согмеита.
•*) У греков термины «тяжелый» и «легкий» понимались тлюкс н п смысле большего в мень-
меньшего удельного nwia.
АРХИМЕД
вес И будет равен Р, так как 13 ость бос всего те.иа ФЛ, а Р — вес жидко-
жидкости I, объем которой был сделан равным объему погружишюй чаг/ги А;
значит, вес тела ФА будет относиться к иосу Л'1, как Р к РО. Но от-
отношение 1* к РО будет раино отношениям I к IN и А к ФЛ; значит,
предложенное доказано.
II
Прямой сегмент прямоугольного коноида *), ось которого не более
полуторной прямой «до оси»**), опущенный в жидкость так, чтобы, его
основание не касалось жидкости, при всяком отношении по тяжести
к жидкости, будучи, поставлен наклонно, не остается наклонным,
по возвращается в прямое положение. Прямым же положением сегмента
я называю такое, когда отсекшая его плоскость оказывается параллель-
параллельной поверхности воды.
Пусть будет сегмент прямоугольного коноида таком, как сказано
«ыше; л оставим его в наклонное положение. Требуется доказать, что
он не останется в по-
покое, но возвратится в
прямое положение.
Рассечем его пло-
плоскостью, проходящей
через ось и перпендику-
перпендикулярной к (плоскости,
совпадающей с поверх-
поверхностью) жидкости; пусть
сеченном сегмента бу-
будит парабола АПОЛ
(рис. И), осью сегмента
и диаметром параболы
будет прямая N0, сече-
сечением же поверхности
жидкости лрямая 12.
Таи как сегмент не
стоит прямо, то АЛ не
будет параллельна 12,
так что N0 не образует прямого угла с 12. Проиедем теперь па-
параллельную (поверхности жидкости) касательную KQ к параболе
п точке II, и ии П параллельно N0 лроведем ПФ; тогда НФ разделит
12 пополам, как это доказало в теории конических сечений. Раз-
Разделим ПФ так, чтобы П13 была вдвое больше ВФ, a NO разделим в Р
так, чтобы ОР была вдвое больше PN; тогда Р будет центром тяжести
большого телесного сегмента, а В — центром тяжести телесного сег-
мопта IJTOX; действительно, в (книгах) «О равновесии»***) доказано,
что центр тяжести сегмепта прямоугольного коноида находится па оси,
разделенной так, чтобы прилегающий к вершине отрезок оси бы.ч вдвое
больше оставшейся части. Далее, если отнять телесный сегмент 1П02
от всего тела, то центр тяжести остатка будет па прямой ВГ; действи-
*) То ость cej'MCiiTa параболоида иращенпя, отсеченного плоскостью, перпендикулярной
к оси.
*•) Ого параметр р п уравнении j/*=2px к дальнейшем переводится слоном «параметр».
***) Вероятно, и продолжении трактата «О раиковссии илоски* фигур». J3 сохраитшпгхся сочи-
сочинениях Архимеда это доказательство имеется и «Уфоде» (предложение V).
О ПЛАВАЮЩИХ ТЕЛАХ
337
тсльно, и «Началах механики»*) доказано, что осп и от данной иеличи-
иы отпять какую-нибудь часть, тге имеющую общего центра тяжести
с долой величиной, то центр тяжести остатка будит на прямой, соеди-
соединяющей центры тяжести целой величины и отнимаемой части, если
продолжить ату прямую в ту сторону, где находится центр тяжести
долой пеличмны. Поэтому продолжим 13Р до Г, и пусть Г будет центром
тяжести остающейся неличины. Теперь, так как N0 в полтора рала боль-
больше ОР и по более полуторного параметра, то ясно, что РО не будпт более
параметра; значит, 171* образует с Ki2 неравные углы [3J, причем угол
Р1Ш будет острым; значит, инриемдииуляр, опущенный .из Р на 1IQ,
упадет между точками II и Q. Пусть он пойдет по Р0; значит, Р6 будет
перпендикулярна к плоскости, (параллельной той), и которой находит-
находится 21, то ость поверхности жидкости. Пронодем из точек 13, Г прямые,
параллельные РВ; находящаяся вин жидкости часть сегмента пойдет
mum по прожданному и.ч Г перпендикуляру, так как предполагается,
что каждая тяжесть движется вниз но перпендикуляру, проведенному
через во центр; часть же, находящаяся л жидкости, будучи более легком,
чем эта жидкость, пойдет вверх по перпендикуляру, проведенному
через V>. И так пак об» (эти массы) данят друг на друга не но одной
и той же отвесной линии, то фигура ни останется неподвижной; но часть,
прилежащая к Л, пойдет вверх, а прилежащая к Л — вниз, и так будет
нее время, пока сегмент пе станет прямо 14].
III
Прямой ceSMEian прямоугольного коноида, ось которого не более
полуторного параметра, при всяком отношении по тяжести к жидко-
яти. отрценный в жид-
кость так, чтобы его к Я а
основание целиком на-
находилось в жидкости,
будучи поставлен на-
наклонно, не останется
наклонным, но встанет
так, что ось его пой-
дет по отвесней линии.
Опустим такой,
пак сказано, сегмент и
жидкость, и пусть осно-
основание его будет в яхнд-
кости{рис. 12};рассечем А
его через ось плоско-
плоскостью, перпендикуляр-
перпендикулярно^ к понопхппеги жид-
жидкости; пусть сечением сегмента Судет парабола АПОЛ, осып сегмента и
диаметром параболы — прямая 11Ф, сочепием же поверхности жидко-
жидкости линия 12. Теперь, так как сегмент лежит наклонно, то ось его
отвесной по будет; значит, 11Ф не образует равных углов с 12. (Парал-
(Параллельно 12) проведем в точке О {.касатольпую KQ) it параболе АПОЛ;
пусть центром тяжести тола ЛПОЛ будет Р, а центром тяжести тела
ПЮ2 — точка В; соединяющую прямую 13Р продолжим, и пусть Г
Рис. 12.
•) 'Jilv ioie 2roi);tini; icw niixxviwnv—элементарный куре механики, может
ияплс!иищий Архимеду. См. «О раыюрсиии плоских фигур», is». I, "VIII.
быть, и не
22 Архимед
338
АРХИМЕД
будет центром тяжести тела 1БЛА. Теперь совершенно так же дока-
жом, что угол между РО, ОК будет острым, так что лерпепдикуляр,
опущенный из Р па KQ, упадет между К и О; пусть он будет Р6.
Если через Г и В проведем прямые, параллельные Рв, то часть сег-
мзнта, заключенная и жидкости, пойдет ннерх но прямой, проведенной
через Г, находящаяся же вне жидкости — вниз по прямой, прове-
проведенной через В, и тело А ПОЛ не останется в жидкости и приданном
ему положении, но прилежащая к А часть будет двигаться шзерх, а
прилежащая к Л — вниз, пока линия ПФ не сделается отвесной [5J, ffij.
IV
Если прямой сегмент прямоугольного коноида будет легче жидкости
и ось его более полуторного параметра, а по весу к равному объему жид-
кости он имеет отношение не меньшее, чем квадрат {па отрезке),
равном разности между осью и полуторным параметро.и к квадрату
на оси, то, будучи опущен в жидкость так, чтобы его основание не кала-
лось жидкости, и поставлен наклонно, сегмент не остается наклонным г
по возвращается в прямое положение.
Пусть будет сегмент прямоугольного коноида такой, как сказано,
и пусть он, будучи опущен в жидкость, если возможно, станет не прямо,
но наклонно; если рассечь
его через ось плоскостью,
перпендикулярной к по-
поверхности жидкости, то
сечеписм сегмента будет
парабола А1ЮА {рис. 13},
осью сегмепта и диаметром
параболы —прямая NO и,
наконец, сечением поверх-
поверхности жидкости IE. Кслм
сегмент не стоит прямо, то
N0 не образует е 12 рав-
равных углов. Проведем
KQ — касательную к па-
параболе в точке 11, парал-
параллельную 12; аатсм из Л
параллельно ОХ проведем
ПФ и найдем центры тяжести; у тела А ПОЛ центром пусть будет Р,
а у погруженной в воду части центром будет В; проведем соединяющую
прямую ВР н продолжим до Г, и пусть Г будет центром тяжести
части, находящейся над жидкостью. И так как NO в полтора рааа
больше РО и более полуторного нарамстра, то ясно, что РО будет
больше параметра. Пусть РМ равпа параметру, и ОМ вдное больше 1Ш.
Так как N0 в полтора рапа больше РО, а 110 в полтора раза боль-
больше ОМ, то, значит, остаток N11 будет и полтора раза больше остатка РМ,
значит, ось сегмента будет на отрезок НО больше полуторного парамет-
параметра РМ.
И так как предполагалось, что по тяжести сегмент имеет к жидкости
отношение не меньшее того, которое квадрат на разпости между осью
и полуторным параметром имеет к квадрату па оси, то ясно, что пи
тяжести сегмент имеет к жидкости отношение но меньшее того, которое
кпадрат на НО имеет к квадрату на N0. Отношение по тяжести сеимгеи-
О ПЛАВАЮЩИХ ТЕЛАХ 339
та к жидкости равно отношению цпгруженнон части ко исиму сегменту,
как уже доказано <в продложепкн 1), а отошеиио погруженной части
ко нсому сегменту равно тому, которое имепт ккадрат па Цф к квадрату
на N0; действительно, в книге «О коноидах» доказано, что если от пря-
прямоугольного коноида отсечь два сегмента произвольно проведенными
плоскостями, то нти сегменты будут иметь друг к другу то же самое
отношение, что и квадраты их осей («О коноидах», предложение XXIV).
Такидг образом, киадрат на 11Ф if квадрату ла ДО имеет огншшлис
не меньшее, чем квадрат на НО к кнадрату на ХО; поэтому 1ТФ не мене*!
НО, и ВП не менее МО*); значит, если из М провести перпендикуляр
М0 и N0, то он упадет между В и П. И так как ГТФ параллельна
диаметру, МО перпендикулярна диаметру и РМ раина параметру, то
прямая, соединяющая Р с 0, будучи продолжена, образует прямые углы
с касательно!! в П**); значит, она образует прямые углы и с J2, и с со*-
ответсткующей 12 поиерхиостыо жидкости. Если через В и Г провести
прямые, параллельные Рв, то у поверхности жидкости получатся пря-
прямые углы и заключенная и жидкости часть сегмента коноида пойдет
вверх по прямой, проведенной чс>ре:1 Б параллельно Рв, находящаяся же
вне жидкости часть пойдет вниз но проиедоппой через Г параллели
к РВ, и так будет все время, пока сегмент коноида не станет прямо [7J.
Если прямой сегмент прямоугольного коноида легче жидкости и ось
его более полуторного параметра, а по весу он имеет к жидкости отно-
отношение Tie большее, чем разность между квадратом оси и кеадратпм раз-
разности между осью и полуторным параметром имеет к квадрату оси,
то будучи, опущен в жидкость так, чтобы его основание было целиком
погружено в воду, и поставлен наклонил, он не останется наклонным,
но встанет так, что его ось будет, направлена па отвесу.
Опустим такой, как сказано, сегмент и жидкость, и пусть ого осно-
основание будет цел иком в жидкости {рис. 14); есл и рассечь его через ось пло-
плоскостью, перпендикулярной к поверхности жидкости, то и сечении по-
получится парабола Л ПОЛ, осью сегмента и диаметром параболы будет
прямая N0 и сеченном поверхности жидкости прямая 12. И так как ось
сегмента не будет отвесной, то N0 не образует с 12 равных углов. Про-
Проведем К?2 — касательную к параболе А110Л в точке П, параллельную 12,
а через II прямую НФ, параллельную МО, и возьмем центры тяжести;
пусть у сегмента AI10A центром будет Р, а у части его, находящийся
пне жидкости,— В; соединяющую прямую ВР продолжим до Г; пусть Г
будет центром тяжести части, погруженной п жидкость. Возьмем РМ
равной параметру и сделаем так, чтобы ОМ была вдвое больше ИМ,
и пусть все остальное будет сделано так же, как и выше. Теперь,
поскольку предполагается, что сегмент »о тяжести имеет к жидкости отно-
отношение не большее, чемразностьквадратонна N0 н 011 имеет к квадрату
на N0, а отношение по тяжести сегмента к ранному объему жидкости
раино отношению погруженной части тела ко всему этому телу (как
доказано в первой теореме), то, значит, погруженная часть сегмента
ко всему сегменту имеет отношение, не большее указанного; значит,
*) Действительно, для цедтра тяжести В сегмента Ш02 имеем Bn=-jj- ФП nM0 = j ОН.
¦*) Действительно, РМ есть субнормаль, а ем — ордината точки касания II.
АРХИМЕД
весь сегмент к части, находящейся вне жидкости, имеет отношение не
большее, чем квадрат на N0 к квадрату на ПО.
Но весь сегмент к своей части, находящейся впо жидкости, отно-
относится как квадрат N0 к квадрату ПФ; значит, квадрат на N0 к квадра-
Л'
Рис. 14.
ту на ПФ имеет отношение не большее, чем квадрат на N0 к квадрату
на 110.
КО'
ПФ2
но*
Следовательно, ПФ будет не менее 011 и 1ГО не менее МО. Значит, отвес-
отвесная линия, проведенная из М к РО, пересечет ВЦ между 11 и В; пусть
она пересечет ое в в. И так как к параболе прямая ПФ параллельна РО,
а МЭ перпендикулярна к диаметру, н, наконец, PiVl раина параметру,
•го ясно, что проведанная прямая Рв образует прямые углы с K11Q,
а апачит, и с 12. Следовательно, Рв перпендикулярна к поверхности
жидкости, и прямые, проведенные через точки В и Г параллельно Рв,
будут перпендикулярны к поверхности жидкости; значит, пасть тела,
находящаяся вне жидкости, пойдет кшюу в жидкость но перпендикуля-
перпендикуляру, проведенному через М, находящаяся же и жадности часть пойдет
вверх но перпендикуляру, проведенному через Г, и сегмент АПОА
не останется в покое, но будет двигаться: и жидкости, пока N0 по сде-
сделается отвесной [8J.
VI
Если прямой сегмент прямоунолъного коноида легче жидкости
и имеет ось, отношение которой к параметру более чем три к двум,
по менее чем пятнадцать к четырем, то, будучи опущен в жидкость так,
чтобы его основание касалось жидкости, сегмент не останется наклонен-
наклоненным так, чтобы его основание имело одну общую точку с жидкостью [У].
Пусть будет сегмент такой, как сказано: пусть он, буду41* опущен
» жидкость, установится, как показано {рис. 15}, так, что его основа-
основание будет касаться жидкости в одпой точке. Если рассечь его через ось
плоскостью, перпендикулярной к поверхности жидкости, то сечением
сегмента будет парабола АНОА, сечением поверхности жидкости —
О ПЛАВАЮЩИХ ТИЛАХ
341
прямая А2, а осью сегмента и диаметром (параболы) — прямая N0.
Разделим последнюю в точке Ф тик, чтобы ОФ (шла пдное больше ФИ,
а в точке Q так, чтобы N0 отпосилась кФО, как пятнадцать к четырем;
затем проведем ОК. перпендикулярно к N0. Тогда отношение N0
Рлс. I.V
кФЕ2 будет больше отношении Г\О к параметру. Пусть ФВ раппа пара-
параметру; параллельно А2 проиедем прямую ПТ, касательную к параболе
Л ПОЛ в точке II, а также прямую 111, параллельную N0. Пусть снача-
сначала прямая 1JT пересечет прямую KQ. Так как и сегменте АПОЛ, за-
заключенном между прямой и нараболой, прямая КН параллельна АА,
прямая Ш параллельна диаметру и пересекается с КУ и, наконец.
Л2 параллельна касательной a JI, то необходимо, чтобы отношение 1JI
к ПП было pairno или больше отношения NQ к ?20; ято уже было
доказало в леммах [10]. Прямая НУ в полтора раза больше QO, и
следоиателыю, 1П или роино в полтора раза, пли же более чем в пол-
полтора раза больше IIII; поэтому 1111 или равна, или же меньше уд-
удвоенной HI*).
Пусть 110 в дпа раза больше HI; тогда в будет центром тяжести
заключенной в жидкости части сегмента; пропедем 0Ф и up одолжим;
пусть Г будет центром тяжести части, выступающей из жидкости.
Из В перпендикулярно N0 проиедем Ш\ Так как Ш параллельна диа-
диаметру КО, а 13Р ему нерлипдикулирпа, и ФВ раина параметру, то ясно,
что продолженная Ф1* образует рапные углы с касательной в точке П
к параболу АПОЛ, а следовательно, и с AS, и с поверхностью жидко-
жидкости. Если мы через 0 и Г. проведем прямые, параллельные ФР, то они
тоже будут перпендикулярны к поверхности жидкости; заключенная
пнутри жидкости часть сегмента АПОЛ будет итти вверх по отнесной
прямой, проходящий через Н, а чисть, находящаяся вне жидкости, будет
опускаться иниз по отвесной прямой, проходящей через Г. Таким обра-
образом, тело повернется и его основание но будет касаться жидкости в одной
точке.
*) Двйсгпптслмю, Ш : ПП=-(ПН HII) : ПН—l+jplj-З^, откуда HJ : Till Js ^.
342
АРХИМЯД
т
Если Ш не пересечет прямой KQ, как изображено на второй
фигуро {рис. 16), то ясио, что точка в — центр тяжести погруженной
части — будет лежать между
II и I; все же остальное бу-
будет доказано так же [101.
VU
Если прямой сегмент пря
моуголъпого коноида легче
жидкости и имеет ось, боль-
большую полуторного параметра,
по меньшую параметра, уве-
увеличенного в отношении пят-
пятнадцати к четырем, то, буду-
будучи опущен в жидкость так,
чтобы все основание его цели-
целиком находилось в жидкости,
сегмент никогда не станет
так, чтобы его основание
касалось*) поверхности жид-
жидкости, но установится так,
что все основание его полно-
полностью будет находитыя в жид-
жидкости и ни в одной точке не
коснется ее поверхности.
Пусть будет такой, как сказано, сегмент; пусть он, будучи опущен,
как сказано, в жидкость, установится так, чтобм его основание каса-
касалось поверхности жидкости. Требуется доказать, что он не останет-
останется в покое, но наклонится так, что его основание пив одной точке не
коснется поверхности
жидкости.
Если рассечь его
плоскостью, лерпепди-
куляркой к поверхности
жидкости, то сечением
«го будет парабола
Л ЛОЛ {рис. i7}, сече-
НИОМ JIOBCpXiloCTII ЖИД-
ЖИДКОСТИ — прямая ?А, а
осью сегмента и диамет-
диаметром параболм — пряма»
11Ф. ()i i я ть раздел им 11Ф
к точке V так, чтобы PI I
ы.тла вдиое больше РФ,
а в точив Q так, чтобы /1
ФИ л мел а к PQ отно-
отношение пятнадцати к че-
четырем; проведем перпендикуляр RK.: тогда VQ будет меньше пара-
параметра. Отложим РН, равную параметру, и проведем ТО — ка-
касательную к параболе » О, параллельную ZA, а затем NO, па-
Ф
Гис 17.
•) Касалось, т. е. ннело общую точку.
О ПЛАВАЮЩИХ ТЕЛАХ
343
раллельную ПФ. Пусть сначала N0 пересечет Kfl в точке I. Тогда
подобно предыдущему докажем, чт» КО будет или в полтора раза или
более чем в полтора раза больше
01; (в последнем случае) 01
будет меньше удвоенной IN.
Пусть ОВ Судет вдвое больше
13N, и все остальное сделаем
так же, как и раньше; подобно
(предыдущему) докажем, что Р(-)
образует прямые углы с ТО и
•с поверхностью жидкости, а
прямые, проведенные через В и
Г параллельно Р6, будут пер-
перпендикулярны поверхности жид-
жидкости. Теперь находящаяся вне
жидкости часть сегмента пойдет
иниз в жидкость но перпендику-
перпендикуляру, проведенному через В, а
часть, находящаяся в жидкости,
пойдет вверх по перпендикуляру
через Г; яспо, что тело накло-
наклонится так, что его основание ни
будет пи в одпой точке касаться
поверхности жидкости, потому
что часть, (касавшаяся поверх- ^ис- 18-
ноети жидкости) в одпой точке
(Л), опустится (вниз) со стороны Л. Также ясно, что то же самое
можно будет доказать и в том случае, когда ON не будет пересекать
пК {рис. 18} [11].
VIII
Если прямой сегмент прямоугольного коноида с осью, большей полу-
полуторного параметра, но меньшей этого параметра, увеличенного в от-
л ношении пятнадцати к чет.ырем,
" имеет по тяжести к жидкости
отношение меньшее, чем квадрат
разности оси и полуторного пара-
параметра к квадрату оси, то, будучи
опущен в жидкость так, чтобы его
основание не касалось жидкости,
сегмент ме возвратится в отвесное
положение, а останется в наклон-
наклонном, положении, причем его ось
образу т с поверхностью жидкости
угол, равный тому, который бу-
будет указан.
Пусть будет сегмент такой,
г к . как сказано; пусть БЛ {рис. 19}
ри g раина его оси, ВКндиоебольше КЛ,
ис" " аКР равна параметру; пусть также
'1В в полтора раза больше ВР, аТД в полтора раза больше К.Р; пусть от-
отношение, которое сегмент «о тяжести имеет к жидкости, pauuo тому,
лрхимед
которое квадрат на Ф+Х имеет к кпадрату на ДВ, м пусть Ф будет
вдпое больше, чем X. Ясно, что Ф-S-X имеет ц ЛЪ отношение, мень-
ureis того, которой ТВ имеет к ВД, так как ТВ есть разность, па ко-
которую ось больше полуторпого наралгетра *); значит, Ф+Х. меньше ВТ,
так что и Ф будет меньше ВДЭ. Пусть Ф равна PTF; першшдикулярш»
БД проведем VE, кладрат па которой равняется половин» прямо-
прямоугольника между КР п BY, и проведем соединяющую прямую ВК.
¦Требуется доказать, что у и ом я нуты и сегмпнт, опущенный, как сказано,
к жидкость, установится в наклонном положении так, что его ост» обра-
образует с никерхностыо жидкости угол, равный ЕВЧ1'**).
Олустим в жидкость некоторый сегмопт, и пусть его основание
не будет касаться поверхности жидкости; при атом, если возможно, пусть
ось образует с поиерхиостыо жидкости угол, пе равнмй В, по сначала
больший. Если рассечь сегмент через ось плоскостью, перпендикулярной
к жжорхности жидкости, то evo сечением будет парабола АПОА, сече-
сечением поверхности жидкости — пр»м>ш 22, а осью [сегмента! и диа-
мстром (параболы) — прямая NO. Параллельно HS проведем каса-
касательную ПГ к параболе АЛОА в точно П, затем приведем ИМ парал-
параллельно N0 и III тфлепдикулирно TSO, п пусть OQ раина ВР, a "РК.
painra Q0, п. Ш\ перпендикулярна к оси. Поскольку предполагается,
что осьсо.гмента образует с поверхиостью жидкости угод болышш, чем В,
то ясно, что в треугольнике ШГ угол aipn Г будет больше В; тогда
кнадрат на Ш к квадрату на 1Г будет иметь отношенио большее, чем
квадрат на E*F к квадрату иа УВ. Но квадрат на III к квадрату па IT
имеет то же отношение, что КР к ТТ; отношение же киадрата па R^V
к кпадрату на ЧГВ рапно отношению иолопкпи К.Р и ЧГВ; значит, КР
к VI будет иметь большее отношение, чем половина КР к YB
значит, Г1 будет моньигс удиоениой ЧЛВ. По 1 Г вдвое более 01; значит,
Of меньше V15,
окта
и IQ будет полыни
У t ) i , ( > г~ ' )
•) a MEi|rav ¦>) iiuio>.iok о «Joiiv -tecs цеуда toe ccgovos - букиалыю, «на кото])*» ось более чем
в 3/з p:i:i:i больше ларлыстра (прямой до иси)>.
**) В наших обозначениях: Bi=-=0N=-;,-6, BK-'<. КР —р, отношение а плотностей тела-
и жидкости будет:
Далее, ТВ= -1 кр= -§" (Ь ~ p)> ф+х <- вт иф < &—J' = BP- Полагаем © = !>*¦ и 47K*=-i- "•
= -i-Kl'-H'I', где 1№=Ш>—i>v=b— р—Ф. Если обозначим угол MBU' черса В, то
**») Имеем О» = Ь, «Q~p и, слсДоьателыю, ОЙ—Ь—р—ВР. Кепи угол ПГ1> В, то
iH в II нриисдем нормаль, то начинающаяся в I субнормаль будет раина пярамктру f>-KI'
ш«-ке-п,
О ПЛАВАЮЩИХ ТК.71ЛХ 34Г)
Но VP равна Ф; значит, Ш больше Ф. И так кап, согласно пред-
предположению, сегмент но тяжести имеет к жидкости отношение, как квад-
квадрат на Ф-|-Х к кпадрату на ГЗД, и отношение но тяжести сегмента к жид-
жидкости равно отношению погруженной части но всему сегменту, а отно-
отношение погруженном чаети ко вашу пигменту будет тем же, что у (киадра-
та> на I f М к (квадрату) на ON, то, .чпачит, квадрат па Ф | X к квадрату
на ВЛ будет иметь то же самое отношение, что квадрат па МП к квадра-
квадрату па ON; значит, Ф+Х будет равняться ТТМ. Но ПН, согласно дока-
докапанному, больше Ф; значит, ясно, что ИМ будет мент.ше ПН, ваятой
полтора раза, а 1111 болт; чем вдвое больше ИМ*).
Пусть TTZ вдвое больше ZM; тогда в будет центром тяжести всего
тела, a Z — центром тяжести его части, погруженной в жидкость;
центр тяжести остающейся части будет на продолжении соединяющей
прямой ZC-). Пусть это про-
• долженме дондет до Г; поел е
этого так же, как и ран ыпе,
докажем, что 0Н будет пер-
перпендикуляром к поверх-
поверхности жидкости и находя-
;" щийсн внутри жидкости
сегмент пойдет из жидкости
; вверх но проведенному че-
рол Z перпендикуляру к по-
поверхности жидкости, а на-
находящаяся впе жидкости
часть пойдет вниз, в жпд-
¦' ¦•' кость,' по перпендикуля-
перпендикуляру, проведенному червя Г;
таким образом, при уно-.. ;.,._:
мянутом угл© паклона сег- 1>ш'- 'м-
мент не останется в покос. ¦ ¦•-
Но он также не .вврнетси в отвесное положение. Ото ясно из сле-
следующего; из проведенных черен Z и Г пнршящикуляров тот, который
проходит через '/, упадет с той стороны от TZ**), где находится А,
а проведенный через Г — с той стороны, где Л, поэтому ясно, что,
согласно вышесказанному, центр Z пойдет вверх, а Г онли, так что-
прилегающей к А часть всего тела пойдет вниз.
Это было иажио для доказательства.
Пусть топерь при тех же предположениях ось сегмента образует
с новерхпостыо жидкости угол меньший, чем В {рис. 20}; тогда.
откуда
'¦¦¦¦ : и* и "
Мм имеем
KI' .. Е\У2 _1_ КР-ВУ 1 КР
П > 4MiS ~ 2 игВ" ~ 2 Ч'Я
и, слсдоиатслыи), Г1<2ЧГВ. Так как ьершина О параболы делит оуполал еубтангенс Г1, то OI^.VB-
п. иледоиатслыю, . ..¦ ...
ID = ОН - 01 = (Ь - р) - 01 > ВР - ЧГВ = ЧГР.
Отношение ii плитиостеЕ тела и жидкости будет
_ (Ф | X)Z _ ИМ»
лда ~ ON* '
Так как вд ^- ON, го П М = Ф -I- X. так как 1С = ПН > Ф и X =* Ф, то ИМ < -jj- НИ и ПН >2НИ.
Это TTQKCtiiunacT, что 7. — центр тп)»ссти погруженной части сегмента находится между II и Н.
**) Так и под.-11Ш1шке. Мы сказали бы «м- вн».
АРХИМЕД
квадрат на Ш к квадрату на 1Г будет иметь меньшее отпошепие, чем
квадрат на ЕУ к квадрату на ^FB, и, значит, КР имеет и XI меньшее
отношение, чем полоиина КР к VB. Тогда 1Г будет более чем вдвое
больше Ч/Ъ, и, значит, Ш меньше, чем WP. Тогда и ПН будет мень-
меньше Ф. Но МП равна Ф-|-Х; ясно, что ПМ более полуторной 1111, а ПН
меньше удвоенной ПМ. Пусть П7 будет идпое бильше ZM. Тогда цент-
ром тяжести всего сегмента будет 0, а части, находящейся в жидкости,
—Z; если провести соединяющую прямую Z0 м продолжить, то центр
тяжести части, находящейся вне жидкости, будет на продолжении.
Пусть он будет Г; проведем через Z и Г перпендикуляры к поверхности
жидкости, параллельные Н0; тогда ясно, что весь сегмент не останется
ненодкижным, но наклонится так, что ось его образует с поверхностью
жидкости угол, больший того, который она образует теперь.
Поскольку сегмепт пе установится пц при большем, ни при мень-
меньшем чем В угле наклона оси с жидкостью, то ясно, что он установится
только при угле, ранном В; и таком случае 10 будет равна ЧГВ, ill
равна ЧФ и Ф раина 1111; значит, МИ будот в полтора раза больше ПН,
а ПН в два раза больше IIМ. Следовательно, II будет центром тяжести
части, находящейся в жидкости; таким обрааом, последняя пойдот
вверх по тому же самому перпендикуляру, по какому пойдет вниз
часть, находящаяся вне жидкости, значит, сегмент останется неподвиж-
неподвижным, так как обе части будут толкать друг друга в противоположные
¦стороны [12J.
*
IX
Если прямой сегмент прямоугольного коноида с осью, большей полу-
полуторного параметра, но меньшей этого последнего, увеличенного в отно-
отношении пятнадцати к четырем^ имеет по тяжести в жидкости отноше-
отношение большее, чем разность
квадрата оси и квадрата
излишка оси над полутор-
полуторным параметром к квадра-
квадрату ecu, то on, будучи опу-
опущен в жидкость так чтобы
его основание целиком нахо-
находилось в жидкости, и по-
поставлен наклонно, не вста-
встанет отвесно, но останется
в наклонном положении,
причем ось его с поверхно-
поверхностью жидкости составит
угол, равный тому же, что
и выше.
Пусть будет сегмепт та -
кой, как сказано; отложим
ДВ (рис. 21} равной оси сегмента, и пусть ВК будет идиос больше КД, аКР
равна параметру, иТВ м полтора рала больше ВР; пусть также отноше-
отношение, которое по тяжести сегмепт имеет к жидкости, будет том, какое раз-
разность квадрата на ВД и квадрата па Ф+Х имеет к квадрату на ВД,
причем Ф вдвое больше X. Теперь ясно, что разность, на которую квад-
квадрат на ВД превышает квадрат па ВТ, имеет к кнлдрмту па ИД меньшее
отношение, чем то, какое разность, на которую квадрат ВД ирскмигает
I.
О ПЛАВАЮЩИХ ТГСЛЛХ 347
квадрат па Ф+Х, имеет к кнадрату на БД, так как ВТ есть разность,
на которую ось больше полуторного параметра. Значит, квадрат на ВД
больше квадрата на Ф+Х на (величину), большую той, на кото-
которую кнадрат па ВА больше квадрата на UT, так что Ф+Х будет мепь-
шс ВТ и, следовательно, Ф-меньше В Р.
Пусть теперь InF раина Ф; перпендикулярно ВД пропсдсм ЧГЕ,
квадрирующую половину {прямоугольника] между КР и ЧГВ. Я гово-
говорю, что сегмент, опущенный в жидкость так, чтобы его основание было
. целиком в жидкости, установится так, что ось его с поверхностью жидко-
жидкости составит угол, ранный Б.
Опустим сегмент в жидкость, лак сказано, и пусть ось его не состав-
составляет с поверхностью жидкости угол, равный В, по сначала состанит
угол больший, чем В.
Если рассечь ого плоскостью, перпендикулярной к поверхности
-жидкости, то сеченном сегмента будет парабола ЛПОЛ, сечением по-
поверхности жидкости — прямая TI, а осью [сечения] и диаметром пара-
параболы — лримая КО; разделим последнюю u Q, в так же, как и рань-
раньше; параллельно Т1 проведем ГII касательную к параболе в 11, а так-
также ИМ параллельпо N0 и 112 перпендикулярно к оси. Так как ось
сегмента составляет л поверхностью жидкости угол, больший угла при
В, то и угол 2ГП будет больше угла В; значит, квадрат на П2 к квад-
квадрату Ла 2 Г будет иметь большее отношение, чем кнадрат на Ч'Е к квад-
квадрату на Ч'В.
Значит, КР будот иметь к 2Г отношение большее, чем полови-
половина КР к ^В;
КР
значит, 2 Г меньше удвоенной ?В, а 20 меньше VB, и, следовательно,
2?2 будот больше PW и ПН больше Ф. И так как сегмент по тяжести
относится к жидкости, как излишек квадрата на ВД над киадратом
на Ф+Х относится к кнадрату на ВД, а отношение сегмепта по тяжести
к жидкости равно отношению погруженной части ко всему сегменту,
то ясно, что погруженная его часть ко всему сегменту будет иметь то жи
¦отношение, какое излишек киадрата на ВД пад кнадратом на Ф+Х
имеет к кнадрату на ВД; тогда и весь сегмент к своей части, находящей-
находящейся вне жидкости, будет иметь то же отношение, какое квадрат на ВД
имеет it квадрату па Ф+Х. Отношение же всего сегмепта к части,
находящейся инс жидкости, равно отношению квадрата на N0 к квадрат
ту на Ш'1;
ид* ко*
*
г им
значит, МП равна Ф+Х. По доказано, что ГШ более Ф; значит, МП
будет менее X; следовательно, ЛИ будет больше удвоенной ИМ.
Пусть IIZ будет вдвое более ZM; продолжим соединяющую Z6 до Г;
тогда центр тяжести всего сегмента будет 0, части, находящейся bhi>
жидкости, —Z, а части, находящейся внутри ее, на в Г; пусть он будет
в Г. Подобно предыдущему докажем, что 0Н будот перпендикулярна
к (поверхности жидкости и что прямые, мроведенпые через Z и Г па-
раллельпо 6IT), будут тоже перпендикулярны к поверхности жидко-
жидкости. Значит, находящаяся вне жидкости часть сегмента пойдет иниз
по перпендикуляру, проведенному через Z, а находящаяся внутри будет
348
уМ'ХИМЕД
подыматься по иориендикуляру, проведенному через Г; следовательно,.
liiiiMi сегмент не лнккст оставаться неподвижным и наклонном положе-
Ш1И. Но он также и пе покоряется так, чтобы ось его стала перпенди-
перпендикулярной к ironcpxiiocTH жидкости, так как тогда прилегающие к Л
части пойдут вниз, прилегающие же к Л — иисрх па основании таких
жо рассуждений, как и в преды-
предыдущей.
Коли же ось образует с по-
поверхностью жидкости угол мень-
меньший, чем при В, то подобно преды-
предыдущему докажем, что сегмент не-
останется неподвижным, но будет
наклоняться до тех нор, пока ось
его не образует с поверхностью
жидкости угол, равный В [131.
X
Если, прямой сегмент прямо-
прямоугольного коноида легче жидкости
и имеет ось, превышающую пара-
параметр « отношении большем, чем
пятнадцать к четырем, то, будучи
опущен в жидкость так, чтобы ос-
основание его не Касалось жидкости,
он иногда установится прямо A),
иногда же наклонно; иногда его
основание будет, только в одной
точке касаться поверхности жид-
жидкости, причем ото может быть
при двух углах наклона C, 5),
иногда он станет так, что его
основание будет смачиваться на
большей площади {4), иногда же
так, что его основание пи в одной
точке не будет касаться поверх-
поверхности жидкости BS\); при какихже
отношениях по тяжести к жидкости будет иметь место каждый из
этих случаев, выяснится в дальнейшем [14].
Пусть будет сегмент такой, как сказано; если рассечь его плоско-
плоскостью, перпендикулярной к поверхности жидкости, то сечением его
ноиерхдостл будет парабола Л ПОЛ jpuc. 22}; пусть осью сегмента
и диаметром параболы будет БД; разделим ПЛ в К так, чтобы ВК была
«двое больше КА, а в Т таи, чтобы ДВ откосилась к КТ как пятнад-
пятнадцать к четырем. Ясно, что КТ больше параметра. Пусть КГ равна нара-
ыетру л Р? будет половиной ВР; тогда и 2В буд«т в полтора раза
больше ВР. Соединивши А, В и восстании перпендикуляр ТЕ, нроледсм
EZ параллельно ВД; затем, разделил АВ пополам в I-), параллельно ВД
проведем 611 и лозыгом параболы АЕ1 па диаметре EZ и АВД иа диа-
диаметре 0П так, чтобы сегменты АЫ, АЙЛ были подобны сегменту ABA;
тогда парабола АЕ1 пройдет через К а перпендикуляр, восставлен-
восставленный и V к ВД, пересечет параболу AEI. Пусть он пересечет ее в точках
Г, Г; через Г и Г параллельно ЬД проведем ТХ, FN; пусть они пере-
О ПЛАВАЮЩИХ TJWIAX 349
секут параболу АвД и точках S, Ф; проведем также касателт.ные JV?
и ОЦ к параболе Л ПОЛ в точках О, II. Таким образом, данм три знклю-
чеппых между прямом и 1гараболами сегмента Л11ОЛ, АЕ1, АвД,
примшо и тгодобн1ло друг другу, но не рапные; их оспования лежат
на одной и toi'i жк примой, и из точки N проведены прямые NE, ЗЧГ,
N0; значит, О Г имеет к ГЕ отношение, елстаипопноо из тех, которые
1Л имеет к ЛЛ, и ЛЛ к Д1*).
ОГ IA АД
~ГЗ " ЛА Д1
Но ЛТ относится к ЛА, пак дна к пяти, ибо ТВ будет к ИД, как дна
к пяти; такжо и Е13 к 13Л и Д/ к ЛЛ, а Л1 и ЛА являются удвоенными
прямыми AZ и ДА; затем ЛЛ относится к Д1, кии пять к одному, и от-
отношение, составленное из тех, которые имеют два к пяти и пять к одно-
одному, будет тем тс, что отпошепие двух к одному; значит, О Г будет вдвое
больше Га. На том же осноианин ПТ будет вдвоо больше ГФ. П«-
скольку н;е Д2 в полтора риза больше Ki\ то ясно, что В2 предстан-
ляет разность оси и полуторного параметра [15J.
{1) Теперь, если согмепт по тяжести имеет к жидкости то же отно-
отношение, что киадрат па 132 к квадрату на МЛ, или жо большое этого
отношения, то он, будучи опущен и жидкость так, чтобы его основапие
но касалось жидкости, станет прямо, ибо ранее (предложение IV) было
доказано, что если сегмент имеет ось, большую полуторного параметра,
и если по тяжести он имеет ц жидкости отношение не меньшее того,
которое квадрат разности между осью и полуторным параметром имеет
к ккадрату па оси, ю он, будучи опущен в жидкость так, как сказано,
установится в примой положении.
B) Если же сегмент но тяжести имеет к жидкости отношение мень-
меньшее того, которое кнадрат па 2Ii имеет к ккпдрнту на НЛ, но большее
того, которое квадрат па OS имеет к квадрату па ВД, то он, будучи
опущен в жидкость и наклонен так, чтобы его основание не касалось
жидкости, установится наклонно так, что его основание не будет ни
в одной точке касаться поворхпостн жидкости и его ось образует
с поверхностью жидкости угол, больший чем Cj {рис. 22).
•) Провспсм гбщуот касательную Лги ко иссм трем параболам л точке А; ето яевможпп, так
как если All- Hw, то n ZK— Ии и IiO = em, где течки т. t>, с, w пре^стивляют иероежченип втой
кас;ггсльн< Я с прямыми 1Ш. ZK, КО ч ДВ. Мм внаем («Квадратура иарабо.'и.!», V), что пенная
ияра.гле:1Ы1;1)! «ги грнмпп, ириисцешшн мпжду сгиоьгшисм иираГишическсг» сегмента и кисятслмюП,
и книце tifiii плннп рассекается параболой на итреак», которые п^ииорцчоиа.чьныотрезнам осшшашш;
.MIIUMil CJ!Ub«XMI\t
«О : ON —AN: NA.
сГ: TN = AN: N1,
СЕ : ?N =- AK : ХД.
Состанляп проивводные пропорции со сложением, мы можем шшшг.чть:
СО : (СО + ON) = АХ : (AN + NA).
сГ : (сГ + TN) -^ AN : (AN ¦(¦ KJ),
ca : (cS -I- SN) — AN : (AN" ¦(¦ КД),
•откуда ¦ .:
CO — -Л?<г?>' .г _ AN¦ cX _ AN-cN
AA * At ' АД *
теперь
or
= <Г - CO »- AN- <:N {~ - ~гг) ¦
I AI AA I
ГЗ =- c3 - cV = AN- CN (—. ^r-\,
\ АЛ Л1 /
и наконец.
ОГ _ АЛ - AT . AI - AA ]_Л_ Л а
Г2 """ЛЛ-Л1 = АД-АТ~*ЛЛ~:~1й"
350
ЛРХИМКД
C) Если же сегмент по тяжести имеет к жидкости то же отношение,
что квадрат ла ЕО к квадрату па ВА, то of, будучи опущен в жидкость
и наклонен, таи, чтобы его основание по касалось жидкости, установит-
установится наклонно так, что ого основание только в одной точке (Л) коснется
поверхности жидкости, и его ось образует с поверхностью жидкости
угол, равный Cj.
D) Если же сегмент по тяжести имеет к жидкости отношение мень-
меньшее того, которое квадрат на НО имеет к квадрату на ВД, но больше»»
того, которое квадрат на ПФ имеет к квадрату на ВД, то он, будучи опу-
опущен it жидкость и поставлен наклоппо так, чтобы его основание не каса-
касалось жидкости, установится наклонно так, что основание его рассе-
рассечется жидкостью на большом протяжении.
E) Если же сегмент по тяжести имеет к жидкости то же самое
отношение, что квадрат на ПФ к квадрату на ВД, то он, будучи опущен
в жидкость и поставлен паклонно так, чтобы его основание не касалось
жидкости, установится наклонно так, что его основание только в одной
точке будет касаться поверхности жидкости и его ось образует с послед-
последней угол, равпый ? (рис. 22).
@) Еслц же сегмент по тяжести имеет к жидкости отношение мень-
меньшее того, которое квадрат на ПФ имеет к квадрату на ВД, то он, будучи
опущен в жидкость и поставлен наклонно так, чтобы его основание
не касалось жидкости, установится наклонно так, что его ось образует
с поверхностью жидкости угол, мень-
/1 ший ?, а основание его ни « одной
точке не коснется поверхности жид-
жидкости.
Все это будет доказано после-
последовательно.
{Случай 2)
Пусть сначала сегмент имеет по
тяжести к жидкости отношение боль-
большее того, которое квадрат на SO име-
имеет к квадрату лаВД, но меньшее того,
которое квадрат разности между оськ>
и полуторным параметром имеет к
квадрату на ВД; предположим, что
вышеприведенная фигура построена
(рис. 23}, л пусть отношение сегмента
к жидкости по тяжести будет равш*
отношению квадрата иа некоторой
прямой V к квадрату на ВД; тогда Чг
будет больше, чем ЕО {рис. 22}, но
меньше разности между осью и полуторным параметром. Между парабо-
параболами Л ПОЛ и ЛЕД вставим некоторую прямую К0, равную V, и пусть она
оставшуюся параболу пересечет в fo, а прямую Ра в точке 13'; докажем,
что 0%> будет вдвое больше. /JbN, совершенно так же, как было дока-
доказано, что Оо*) пдпое больше аЕ; затем из точки 0 проведем касатель-
касательную 0<} к параболе АИОЛ и прямую ОТ, перпендикулярную к ВД,
и соединим А с N; тогда прямые AN и XN будут равны друг другу,
Рис. 23.
•> Черте»; подлинника для ясности несколько изменен; в подлиннике О стоит июеето нашего
и имеете и тем U Дальнейшем изложении сотщаласт с М.
О ПЛАВАЮЩИХ ТЕЛАХ
351
так как проведенные н подобных сегментах АГЮЛ и ЛЕД примыо Л IN
и АХ, образующие одинаковые углы г оспованиями, будут иметь-
то же отношение, что и ЛЛ к АЛ,
AN _ АД
АХ АЛ
и па основании второй из построенных фигур {риг-. 23) AN будет
раина X.N и параллельна (касательной) 6Ц *).
Требуется доказать, что сегмопт, опущеппый в жидкость так, что
его основание не будет ни в одпой точке касаться жидкости, устана-
нится наклонно в этом полпженди, и его ось образует с поверхностью-
жидкости острый угол, больший угла Cj. Пусть сегмент будет опущен
и станет так, что его основание- в одной точке иоспется поверхности--
жидкости; если рассечь его через ось
плоскостью, перпендикулярной к по-
верхпооти жидкости, то сечением сег-
сегмента будет парабол а АГЮЛ {рис. 2Л},
поверхности жидкости — прямая
ОЛ, а осью (сегмента) и диаметром
(параболы) будет БД. Рассечем 13Д в
точках К и Р, как сказано вшш**),
затем параллельно АО проведем пря-
прямую ТГГ, касающуюся параболы в
точке П, далие проведем Пв парал-
параллельно НА и 112 перпендикулярно
к ВЛ. Так как сегмент по тяжести
имеет к жидкости то же отношение,
что квадрат па lF к квадрату па ВЛ,
отношение же и о тяжести сегмента
- к жидкости равно отношению погру-
погруженной части ко всему сегменту, и
отношение погруженной части ко все-
¦ му телу равно отношению квадрата
на 611 к кладнату на ДВ, то, значит, \F !
будет равна 611. Значит, и NB (рис. 23) будет равна вП; следовательно,
сегменты ЛИХ [рис. 23} и Л11О {рис. 24} будут друг другу раины.
Л так как и равных и иодобпых сегментах А1ЮЛ {рис. 24] и АМХ.Л
[рис. 23} от кшщмн оснований проведены прямые ОА, АХ, и отсечен-
нгле части образуют с диаметрами равпыо углы (ца основании третьей
из построенных фигур), то углы при Ц и Г будут равны. Значит, CjB
и ГВ тоже будут paBHiii; следовательно, раины и 2Р с ТР, и HZ с ©В',
¦~ и Z6 с B'N. Так как 6В' меньше удвоенной B'N***), то ясно, что 11Z
будет меньше удвоенной Z0. Пусть 1IQ будет равна удвоенной ?28;
пронедя соединяющую прямую KQ, продолжим со до Е; точка К будет
центром тяжести всего сегмента, Q — центром тяжести части, находя-
находящейся в жидкости; тогда центр тяжести част», которая ннс жидкости,,
найдется на линии КЕ; пусть он будет Е. Но K.Z перпендикулярна-
к поверхности жидкости, а значит, будут порпшдпкулярами и прямые,
цроведстше через Е и Q параллельно K.Z. Слсдолательно, сегмент
*) Если AN—NX, то лрпмая Кб Судет диаметром параболы АПОА, сопряженным хпрлс-
АХ it, янпчнт, хорда АХ параллельна касательной ($Cj в иертине диаметра.
**> То есть чтобы К была центром тяжести сегмента, а КР — параметром.
***) Действительно, ©5^>=2^?>N {Рис 23}.
Риг,. 24.
352
ЛРХИМКД
не останется в покое, но станет так, что его основание ни л одной точке
не коснется жидкости, ибо в настоящем положении оно касается жидко-
жидкости только и одной точке. Ясно, что сегмент установится так, что ось
его образует с ионерхностып жидкости угол больший, чем С}. _
(С л уча й 3)
Пусть сегмент имеет по тяжести к жидкости такое отношение, как
квадрат па SO к квадрату на ВД {рис. 25), и опущен в жидкость в на-
наклонном положении. Если рассечь ого черев ось плоскостью, перпенди-
перпендикулярной к поверхности жидкости, то сечением тела будет парабола
А1ЮЛ {рис. 26}, соченной поверхности жидкости — прямая ОТ, а осью
сегмента и диаметром парабол и — прямая ИЛ; разделим ИЛ так же,
как л раньше, параллельно ТО проведем касательную JIN и параболе
л I
л
II N
Рис. 26.
в точке П, :ттем параллельно ВЛ проиедем 110, а перпендикулярно
к ВД проведем К2. Трвбустси доказать, что сегмент не останется на-
наклонным в таком положении, но Судет наклоняться до тех пор, пока его
оспонааис па коснется жидкости и одной точке.
Пусть будет перед нами (фигура) {рис. 25} и сделано то же, что
и на предшествующей, фигуре; проведем ТО перпендикулярно к ВД
и соединяющую A3 продолжим до X; тогда АЕ будет равпа ЕХ;
прошлом также О^, лараллельпую АХ. И так как предполагается, что
сегмент имеет но тяжести к жидкости то же отношение, что квадрат
па ЕО к квадрату па ВД, то такое отношение будет «меть и погружен-
погруженная часть ко всему телу, то есть квадрат на ПО к квадрату па ВД, а зна-
значит, 116 {рис. 26} будет равняться ЕО {рис. 25}. И так как у согментоп
IBO и ЛВХ диаметры раины, то будут ранпы и сегменты. Далее, так
как и равных и подобных сегментах А1ЮЛ и АОХЛ {рис. 25 и 26} про-
м прямые АХ и 10, отсекающие ранные сегменты, исходя одна
О ПЛАВАЮЩИХ ТКЛЛХ
353
из конца основания, другая же пе из конца, то ясно, что меньший
острый угол с диаметром всего сегмента состаиит та прямая, которая
проведена из конца основания. И так как угол Ц будет меньше угла N,
то значит, и RT {рмс. 25} будет больше, чем Б2 {рис. 2E}, а ТР {рис. 25}
меньше, чем P2I {рис. 26}; поэтому и Ост меньше, чем П$Ъ, (и оЗ)
больше, уем foO. И так как Оо вдвое больше <хЗ, то ясно, что и П^Ь
будет больше удвоенной 5^>8. Пусть ПН будет'вднос больше Н0; кро-
ведем соединяющую ПК и продолжим до ?3. Тогда центром тяжести
всего сегмента будет К, части, находящейся в жидкости — II, а внеш-
внешней — некоторая точка на KQ; пусть она будет Q. После этого совер-
совершенно так же докажем, что К$?> будет порпендикулярпа к поверхности
жидкости так же, как и прямые, про-
проведенные через Н и Q параллельно
К^Ь. Ясно, что сегмент не остапется
неподвижным, по будет наклоняться
до тех пор, пока его основание не
коснется в одной точке поверхности
жидкости, как это показано па треть-
третьей фигуре (рис. 27), относящейся к
рассматриваемой третьей теореме; и
и таком положении сегмент устано-
установится неподвижным.
Действительно, в рашшх сегмен-
сегментах А1ЮЛ {рис. 27} и АОХЛ
{рис. 25} от концов оспований про-
ведешл прямые АХ, АО, отсекающие
одинаковые части; совершенно так
же, как и раньше, докажем, что
сегмент ЛГТХ равен АПО; следова-
следовательно, АО и АХ образуют раиные
острые углы с диаметрами сегмен-
сегментов, так как углы: при _\ и С\ равны.
/IN
Рис. 27.
у р ] р
Пусть прямая IVffb будет идиое больше у^>6; если: провести соединяю-
соединяющую прямую ^К и продолжить до Й, то центром тяжести всего сегмен-
сегмента будет К, той его части, которая в жидкости,—$>, а цептр тягкести
внешней части (будет лежать) пи линии Kft; пусть он будет Q. Далее,
К$й перпендикулярна к поисрхаостя ?кицкости. Теперь часть, находя-
находящаяся в жидкости, будет подниматься, а находящаяся ви« жидкости —
опускаться по одной и той же прямой; таким образом, сегмент остается
нсподиижннм и основание его касается жидкой поверхности в одной
точке, а ось сегмента с поверхностью жидкости образует угол, ранный
лшшеук аза иному.
(Случай 6> [16]
Далее, пусть сегмент по тяжести имеет к жидкости отношение
меньшее того, которое квадрат на Л в имеет к квадрату ла 13Д {рис. 28};
пусть опо будет равно отношению квадрата на гР (к квадрату на БД);
тогда V будет меньше '0N. Между сегментами ЛМД и А1ЮЛ вставим
прямую Ш, нарал;гсльнук] БД и равнук» Чг; пусть она пересечет про-
промежуточную параболу в Г, а прямую ЕР — в Ц. Тогда, так же как
было доказано, что ГО вдвое больше ТЕ {рис. 22}, докажем, что ПГ
вдвое больше П.
23 Архимед
354
Л1'ХИМЕД
Проводом IIQ, касательную к АНОА и точке П, затем ПЕ — пер-
перпендикулярную к БА, и соединяющую 1Л (продолжим) до X;
пряма» АХ будет равна IX п АХ параллельна 1X42. Требуется дока-
доказать, что данный сегмент, будучи опущен в жидкость и наклонен так,
чтобы его осношшне не касалось
жидкости, установится в наклон-
наклонном положении так, что его ось с
поверхностью жидкости образует
угол, (меньший угла при Ф {рис.
28}, и основание его ни в одной
точке не коснется поверхности
жидкости.
Опустим его в жидкость и
установим так, чтобы его основа-
основание) в одной точке коснулось по-
поверхности жидкости; если рассечь
сегмент через ось плоскостью,
перпендикулярной к поверхности
жидкости, то сече и ней поверхно-
поверхности сегмента будет парабола A1IBA
{рис. 29}, сечением поверхности
жидкости — прямая AZ, а осью
(сегмента) и диаметром парабо-
параболы — ВЛ; разделим ВЛ и точках
К и Р подобно предыдущему, за-
том проведем параллельно AZ каса-
касательную III к параболе в Ы, про-
проведем Нв параллельно ВА и ИХ
перпендикулярно ВЛ. Так как
сегмент имеет к жидкости такое же отношение по тяжести, какое
квадрат на 4F к квадрату на ВД, и отношение по тяжести сегмента
Рис. 2!).
к жидкости рапно отношению кладрата на IIв к квадрату на ВЛ по
той же причине, что и выше, то яспо, что IK-) будет равна Ч1"; поэтому
будут равны и сегменты AIIZ и АПХ {рис. 28]. И так как в равных
О ПЛАВАЮЩИХ ТЕЛАХ
355
и подобных сегментах АПОЛ, ЛИйЛ из концов оснований проведены
прямыо ЛХ, AZ, отсекающие равные части, то ясно, что они образуют
равные углы с диаметрами сегментов. Поэтому в треугольниках HI2,
HQE углы при I и Й равны; следовательно, будут равны и прямые
SB и ЕВ, а значит, будут равны и 1'Р с ЕР, а также и 11$ъ с ГШ
и $Ъ0 с НТ*). И так как If Г иди ос больше П, то ясно, что Н$& меньше
удвоенной$Ьв. Пусть ИГ будет вдвое больше ТО; продолжим соеди-
соединяющую ГКТ; центром тяжести всего сегмента будет К, части находя-
находящейся в жидкости — Г, а той, что пне жидкости, (точка) па линии КТ;
пусть она Судет Т. Тогда
совершенно так же, как в
предыдущей теореме, обна-
обнаружится, что сегмент не
останется неподвижным, по
наклонится так, что его
основание не будет ни в од-
одной точке касаться поверх-
поверхности жидкости.
Теперь докажем, что
он установится так, что
его ось с поверхностью
жидкости образует угол,
меньший угла Ф. Дейст-
Действительно, пусть, если воз-
возможно, он установится так,
что будет составлять угол,
не меньший: угла Ф; сде-
сделаем все остальное {рис. 30}
так же, как и на тре-
третьей фигуре. Тогда совершенно таи же докажем, что 611 будет рав-
равна W, а, следовательно, и ТП {рис. 28}. Так как угол Л не меньше Ф,
то, значит, ГВ не будет более 2В, а ГР не менее 2Р, н Н ^ не менее
0Ц**). Итак как IIIв полтора рааа больше ПГ {рис. 28), 11Г же мень-
меньше 6Cj, к Н0 {рис. 30} равна Ш, а 11$Ъ не меньше вЦ, то $Ь Н будет
больше IIГ; япачит, Н^- будет больше удвоенной $?>в. Пусть НГ
будет «двое больше Г6; продолжим соединяющую ГК; тогда подобно
предыдущему обнаружится, что сегмент не остапется неподвижным,
но наклонится так, что его ось с поверхностью (жидкости будет состав-
влятг. угол, меньший Ф),
(Случай 5)
Подобно этому докажем, что если сегмент имеет по тяжести к жидко-
жидкости то же самое отношение, что квадрат на N0 {рис. 28} к квадрату иа
ВД, то он, будучи онущей в жидкость так, чтобы его основание не каса-
касалось поверхности жидкости, установится так, что его основание только
в одной точко коснется поиерхности жидкости, и ось его с поверхностью
жидкости составит угол, ранний углу лри Ф.
Рис. 30.
берутся на рис. 29, а тр-к PZR и линии ЕВ, ЕР,
*) Тр-к НИ и .-пиши ZB.IP. И^),
ПН и HI — на рис. 28.
•») Линии П«, Г1-1, П^Ь берутси иа jinc. 30, a I». 2V ч вС| на рис. 28.
23»
356
АРХИМЕД
(Случай Л) [17]
Пусть будет опять сегмент, имеющий к жидкости отношение по
тяжести большее того, которое квадрат на ZH {рис. 31} имеет к (квад-
(квадрату) па ВД, но меньшее того, которое квадрат на 30 имеет к (квадра-
^ ту) на ВД; пусть отношение но тя-
»Л жести, котороесогмент имеет к жид-
жидкости, будет равно тому, которое
квадрат на Т имеет к (квадрату)
на ВД; ясно, что 47 будет больше
ZH, но меньше НО. Вставим между
сегментами АЕД, АПОЛ прямую,
равную V и параллельную ВЛ,
а именно Ф1, пересекающую проме-
промежуточную параболу в Г; опять дока-
докажем, что ФТ будет вдвое больше
XI, подобно тому как ОГвдвое боль-
больше ЕГ {рис. 22}. Через Ф прово-
дем Фй — касательную к парабо-
параболе АПОЛ в Ф; подобно преды-
предыдущему докажем, что А1 равна XI
и АХ параллельна ФЙ. Требуется
доказать, что рассматриваемый сег-
. Рис. 31. ' мент, опущенный в жидкость так,
чтобы основание его не касалось
поверхности жидкости, и поставленный наклонно, наклонится так,
что erf» основание рассечется жидкостью во многих точках.
Опустим его в жидкость, как
сказано. И пусть сначала он
станет наклонясь, так, что его
основание пи в одной точке
пе коснется поверхности жид-
жидкости; если рассечь его через
ось плоскостью, перпендикуляр-
перпендикулярной к поверхности жидкости,
то на ловерхлости сегмента по-
получится сечение АВГ {рис. '.Щ, а*
на поверхности жидкости EZ,
а осью [сечения] и диаметром
|сегмента] будет ВД; разделим
ВД в К и Р подобно тому, как
выше, и параллельно EZ прове-
проведем НА касательную к параболе
АВГ в II, затем проведем Н0
параллельно ВД и 112 перпен-
перпендикулярно к ВД. Так как сег-
сегмент относится но тяжести кжнд-
кости, как квадрат на XV к квадрату на ВД, то ясно, что Т будет равна Н©
(это докажется совершенно так же, как и раньше), так что 110 будет
ранна ФТ {рис. 31} и, значит, сегменты АФХ, EBZ будут равны друг
другу. Поскольку же в равпых и подобных сегментах АПОА, АВГ
проведены прямые АХ, EZ, отсекающие равные сегменты, и одна про-
проведена из конца основания, другая же не из конца, то прямая, прове-
О ПЛАВАЮЩИХ ТЕЛАХ
357
денная из конца основапия, образует меньший острый угол с диаметром
сегмента. И так как в треугольнике HAS угол Л больше угла Я в тре-
треугольнике ФТ?2, то ясно, что В2 будет мепьше ВТ, a ZP больше РТ,
л Hffi> больше ФН; значит, $Ь0_ будет меньше, чем III; и так как ФГ
вдвое больше TI, то ясно, что
будет более чем вдвое больше'
Пусть НА' будет вдвое боль-
больше А'6; тогда из всего этого
ясно *), что сегмент но останется в
покос, но будет наклониться до тех
пор, пока его основание не кос-
коснется в одной точке поверхности
жидкости.
Пусть оно коснулось ее в одной
точке, как это изображено на треть-
третьей фигуре {рис. 33}, и пусть псе ос- .
стальное будет устроепо как и рань-
раньше; тогда опят), докажем, что вН
будет равпа Ф1, и что сегменты
АФХ и ABZ равны друг другу. И
поскольку в ранных и подобных
сегментах Л ПОЛ {рис. 31}, АВГ
проведены прямые АХ, AZ, отни-
отнимающие равные сегменты, то они образуют равные углы с диаметрами
сегментов; значит, у (треугольников) ЛН2,Ф'Ш углы при Л и ?2 равны,
и прямая BE равна ВТ, а IP равна РТ, Effi> раина ФН и $Ъ0 равна Ш;
поскольку же Ф Г вдвое бол ьтпе П, то ясно, что 11% будет более чем вдвое
больше $ЬЙ. Пусть HP будет вдвое больше РВ; из этого опять ясно,
что сегмент не останется в покое, по будет наклоняться в сторону А.
И так как было предположено, что сеглшпт касается ?кмдиосш только
и одной точке, то ясно, что основание будет охвачено водой на большем
П р ОТИ/КСНИИ И 81.
•) Точка А'— центр глгнеегх погруженной частя — будег лежать правее вертикали Йу^й-
. центр тяжести т выступающей части будет, наоборот, левее к^-
0" ^
ПСАММИТ
I
Некоторые люди полагают, государь Гелон, что число песка но
величине бесконечно; я говорю не только о песке, который имеется
в окрестностях Сиракуз и остальной Сицилии, но и о том, который
имеется но всох странах, как населенных, так и не населенных. Есть,
однако, и такие, которые не считают его бесконечным, но тем не менее
думают, что не сущестиуст такого имеющего название числа, которое
было бы больше его количества.
Для держащихся такого мнения ясно, что если вообразить состав-
лонную из песка массу такой величины, какой стала бы масса Земли
после заполнения всех имеющихся па ней морей и впадин вплоть до
высотг.1, раиной высочайшим горам, то и подавно нельзя определить
имеющее название число, которое было бы больше такого количества
лоска. Что касается меня, то я постараюсь показать тебе при помощи
геометрических доказательств, которые ты можешь понять, что среди
чисел, котормо получили от нас название и опубликованы в иашгеаппок
к Зевкошшу книге *), некоторое превосходят не только число песчинок
в объеме, равном заполненной, как мы сказали, Земле, но даже в объеме,
рапном миру. Как ты знаешь, большинство астрономов **) называют
миром тар, центр которого совпадает с центром Земли, а радиус равен
прямой, заключающейся между центрами Со;гнца и Земли; ато ты узнал
из написанных астрономами доказательств. Но Аристарх Самосский [1J
выпустил в свет книгу о-некоторых гипотезах, из которых следует,
что мир гораздо больше, чем понимают обычно. Действительно, он
предполагает, что понодиижные ялезды и Солнце находятся в покое,
а Земля обращается вокруг Солнца по окружности круга, расположен-
расположенной посредине между Солнцем и неподвижными звездами***), а сфера
неподвижных звезд имеет тот же центр, что и у Солнца, и так велика,
что круг, по которому, как он: предположил, обращается Земля, так же
относится к расстоянию неподвижных звезд, как центр сферы: к ее
поверхности. Но хорошо известно, что это невозможно; так как центр
*) Не дошедшее до нас сочинение Архимеда. Зевксипп — неизвестное лицо.
*•) В подлиннике астрологов.
*•*) У Архимеда сказано более кярхшшо ev niorj> тф Сеч»ц> — «посредине бегоний
и круглом ицподриме или цирке, где происходили конские состязания.
псаммит 359
сферы lie имеет никакой ветчины, то нельзя предполагать, чтобы он
ими л какое-нибудь отношение к поверхности сферы. 1.1 а до поэтому ду-
думать, что Аристарх подразумевав следующее: поскольку ми пред-
предполагаем, что Земля является как бы центром мира, то Земля к тому,
что мы назвали миром, будет иметь то же отношение, какое сфера, по
которой, как думает Аристарх, обращается Земля, имеет к сфере
неподнижних звезд; иа таких предпосылок он объясняет наблюдающиеся
явления и, по-видимому, считает, что величина сферы, но которой оп
заставляет двигаться Немлю, и будет равна тому, что мы называем ми-
миром. Так вот мы утверждаем, что если бы аз песка был составлен
шар такой же пелнчины, какую, по предположению Аристарха, имеет
сфера неподвижных знсзд, то и в таком случае можно было бы указать
никоторые из чисел, получишиих название в вышеупомянутом сочине-
сочинении, которые превзошли бы число песка, заполняющего объем, равный
названной сфере. Сделаем следующие предположения: во-первых,
окружность Земли составляет приблизительно 300 мириад стадий [2];
но in.: больше, хотя, как ты знаешь, некоторые*) пытались доказать,
что она составляет приблизительно ЯО мириад стадий. Я же иду дальше
и, полагая, что величина Земли приблизительно в десять раз больше той,
которую принимал it предшестпоианптио, считаю, что се окружность
составляет примерно 300 мириад стадий, но не больше; затем, что диа-
диаметр Земли больше диаметра Луны, а диаметр Солнца Польше диаметра
Земли, принимая то же, что и большинство предшествующих астроно-
астрономов; далее, что диаметр Солнца приблизительно в тридцать раз больше
диаметра Луны, но не больше, хотя из предшествующих астрономов
Ендокс считал его только в девять раз больше, Фидии же, мой отец,—
в двенадцать раз больше, а Аристарх пытался доказать, что диаметр
Солнца более чем в восемнадцать раз, но менее чем и двадцать раз боль-
больше диаметра Луны; н ж и иду дальше «того и, чтобы мое предложение
было бесспорно доказанным, принимаю, что диаметр Солнца нриблизи-
тильно в тридцать раз больше диаметра Лупы, по не больше; [3] кроме
этого, я считаю, что диаметр Солнца больше стороны (правильного)
тысяче угольника, вписанного и большой круг сферы мира. Такое нред-
пнложение я делаю, ибо Аристарх нашел, что (диаметр) видимого
(диска) Солнца составляет приблизительно семьсот двадцатую часть
круга зодиака; в моих исследованиях я также пытался способом, изло-
изложенным ниже, при помощи инструментов найти угол, н кото^шй может
вместиться Солнце, если взять леригину и глазу [4]. Получить точное
значение этого угла — дело нелегкое, потому что ни глаз, ни руки,
ни приборы, при помощи которых производится отсчет, пе обеспечтшают
достаточной точности; однако теперь па этом долго задерживаться не
время, так как это разъяснялось и .много раз в других местах; мне жо
для доказательства предложенного достаточно найти угол, не больший
того, имеющего вершину и .глазу угла, в который вмещается Солнце,
и затем другой угол, не меньший имеющего вершину в глазу угла,
в который нмещается Солнце. Поместив длинную линейку на отвесную
подставку, расположенную в месте, откуда и предполагал наблюдать
восходящее Солнце, обточив па токарном станке небольшой цилиндр
и поставив его отпоено на линейку, я сейчас же посте восхода направ-
направляя линешу иа Солнце, когда оно находится близ горизонта н на пего
еще можно прямо смотреть, и помещал глаз у конца линейки; при этом
•> Пи-кидимолу, Диксарк Мессспский, один из учеников Аристотеля, нгишмаишиКсн опре-
определением высоты гор а ьооПщо величины поверхности Земли.
ЗСО АРХИМЕД
помещенный между Солнцем и глазом цилиндр затенял Солпцо. Отодви-
Отодвигая цилиндр от глаза, я устанавливал ого в положении, когда Солнце
начинало чуть-чуть появляться с обеих сторон цилиндра. Ткнеръ, если
бы смотрящий глаз бил как бы точкой, и из места на конце линейки,
где помещался i лаз, были проведены касательные к цилиндру, то угол,
заключенный между проведенным» прямыми, был бы меньше имеющего
вершину в глазу угла, в который может вместиться Солнце, так как кое-
что от Солнца усматривалось по обе стороны цилиндра; поскольку
же глаз нельзя считать смотрящим как бы из одной точки, но из
некоторой площади, то я взял круглую площадку, по величине не
меньшую зрачка, и поместил ее на конец упомянутой липешш в то
место, где находился глаз: если провести прямые, касательные и к этой
1глощад[{о, и к цилиндру, то заключенный между ними угон будет
меньше имеющего вершину в глазу угла, в который может быть вмещено
Солпце. Площадочка же с величиной, не меньшей зрачка, отыскивается
следующий образом: берутся дна тонких цилиндра одинаковой толщи-
толщины, из которых один белый, а другой пет, н помещаются перед глазом
так, чтобы белый был на пекотором расстоянии от него, не белый же
помещался возможно ближе к глазу, и даже касался бы лица. Если
взятые цилиндры уже зрачка, то ближайший цилиндр будет охватывать-
охватываться лучами зрения, и белый цилиндр будет за ним видеп целиком, если
оба они намного уже прачки; если же они не намного уже зрачка., то
с обеих сторон ближайшего к глазу цилиндра будут видны какие-то
части белого; если взять цилиндры подходящей толщины, чтобы один
из них заслонял другой, но не большую площадь, то площадочка, шири-
ширина которой равнялась бы толщине производящих такое действие
цилиндров, несомненно била бы не меньше зрачка. Угол, не меньший
имеющего вершину в глазу угла, в который вмещалось бы Солнце,
находился следующим образом: если на линейке отодвинуть от глаза
цилиндр настолько, чтобы он целиком заслонял Солпце, и от конца
линейки, где помещался глаз, провести прямые, касательные к цилин-
цилиндру, то угол, заключенный между цроведшшыми прямыми, будет пе
меньше имеющего вершину в глазу угла, в который могло бы вместиться
Солнце [5]. Если найденными таким способом углами измерить прямой
угол, то оказалось, что при делении прямого угла на 164 части угол с
вершиной в точке *) меньше одной такой доли, при делении я^е прямого
угла на 200 частой мопыпии (из наблюденных углов) будет больше
одной такой доли; из этого ясно, что имеющий вершину в глазу угол,
в который мояаю было бы вместить Солнце, будет меньше одной 104-й
доли прямого угла, но больше одной 200-й его доли [61. Если верить
этому, то .можно показать, что диаметр Солпца будет больше стороны
тыснчеугольника, вписанного в большой круг мировой (сферы). Во-
Вообразим плоскость, проведенную через центр Солнца, центр Земли
и глаз, когда Солнце стоит невысоко над горизонтом; пусть продолже-
продолжение атой плоскости пересечет мировую сферу по кругу АВГ (рис. 1);
Землю — по ДЕ55, а Солнце — по кругу 211; пусть цоптр Земли будет
в В, Солнца — в К, а глаз в Д; проведем из точки Д касающиеся круга
211 прямые ДА и ДЗ (пусть они касаются и точках N м Т), а из
центра в — касательные вМ и 00 (пусть они касаются в X и Р)т
и пусть прямые ВМ и 60 иоресскают круг АВГ в точках А и В. Прямая
6К будет более ДК, так как Солнце предполагается находящимся над
*) 6V orivp (or ortfya — делаю укол, точку); вдесь, возможно, текст испорчон. Пи-видимому,
етит угол соответствовал полученному без поправки на величину зрачка.
ПСАММИТ
361
о
Рис. 1.
горизонтом; таким образом, угол, заключенный между ДА и ДЗ,
будет больше угла, заключенного между ©М и ВО. Угол же, заключен-
заключенный между ДЛ и ДЗ, будет больше одной двухсотой доли прямого
угла, по меньше доли, которая получится при делении прямого угла
на 1(И части, ибо он ранен имеющему вершину в глазу углу, и который
вмещается Солнце; таким образом, угол, заключенный между 6М
и ©О, будет меньше одной доли прямого угла, получающейся при
делении последнего на 1G4
части, а прямая ЛВ будет
меньше отрезка, стяги-
стягивающего дугу окружности
круга Л13Г, разделенной
на G56 частей •). Но пери-
периметр упомянутого много-
многоугольника имеет к радиу-
радиусу круга АВГ отношение
меньшее чем 44 к 7, так
как у всякого многоуголь-
многоугольника, иписашшго в круг,
периметр имеет к радиусу
меньшее отношение, чем
44 к 7; как ты зпаешь,
нами было доказано, что
окружность всякого круга
больпте утроенного диаметра па величину, меньшую одной седьмой
части, а периметр вписанного многоугольника меньше окружности.
Тогда НА будет иметь к GK отношение меньшее, чем 11 к 1148**);
таким образом 1JA будет меньше сотой доли ВК. Но прямая 13А равна
диаметру круга 211, так как ее полонии и ФА равна КР; действитель-
действительно, из концов ранних прямых ©К и ЙА опускаются перпендикуляры
в одной и том же углу; ясно, что диаметр круга 211 Судет меньше сотой
доли ©К. Далее диаметр Ев Г лгепыпе диаметра круга 2Н, так как
круг AEZ меньше круга 211 17]; значит, оба (радиуса) в Г и К.2
вместе будут меньше сотой доли ©К; таким образом 0К имеет к Г2
меньшее отношение, чем 100 к 09. И тан как ОК. не меньше 6Р, а 2Г
меньше ДТ, то, значит, 6Р будет иметь к ДТ отношение меньшее, чем
100 к 99. Так как у прямоугольных треугольником 0KP и ДКТ сторо-
стороны КР и КТ равны, а ЙР и ДТ не равны, и (-)Р больше, -го угол, заклю-
заключенный между ДТ, ДК к углу, заключенному между 0Р, 6К, имеет
большее отношение, чем (Ж к ЛК, по меньшее чем GP к AT; действи-
действительно, если у двух прямоугольных треугольникои будут рапиыпо одной
из сторон, прилегающих к прямому углу, две же другие не равны, то
больший из углов при неравных сторонах имеет к меньшему углу
отношение большее того, которое большая сторона из стягивающих пря-
прямой угол имеет к меньшей, но меньптсс того, которое большая пз при-
прилегающих к прямому углу линий имеет к меньшей 18]. Таким образом,
угол, заключепный между ДА и ДЕ, имеет т: углу, заключенному между
GO и вМ, отношение меньшее, чем ВРкДТ, которое меньше, чем 100 к 99;
так что угол, ваключенный между АЛ, ДЕ, к углу, заключенному между
0М и GO, имеет меньшее отношепие, чем 100 к 99. И так как угол,
*) Имеем 656=4-164.
**) Отношение ВА к вк будет меньше
от -у , то сеть менее -у
.362 . АРХИМЕД
заключенный между ДА и Д5, больше одной двухсотой доли прямого
угла, то и угол, заключенный между в М и 00, будет больше, чем 99 до-
долин прямого угла, разделенного на 20000частей; таким образом, он бу-
будет больше одной доли, получающийся при делении лрнмого угла на 203
чисти *). Значит, 13А будет больше (хорды), сгагииающей один отрезок
окружности круга ЛВГ, разделенной па 812 частей **). По ЛВ раина
диаметру Солнца; значит ясно, что диаметр Солнца будет больше
стороны тысячеуголышка [9].
II
После этих предпосылок можно доказать, что диаметр мира будет
меньше диаметра Земли, увеличенного и десять тысяч раз, или что
диаметр мира будет меньше, чем мириад раз взятые сто мириад {100 х
X 10 000-10 000 - 101*') стадий. Действительно, поскольку пред-
предполагается, что диаметр Солнца не более чем в тридцать раз больше
диаметра Луны, а диаметр Земли больше диаметра Луны, то ясно,
что диаметр Солнца будет меньше взятого тридцать раз диаметра Земли.
.Далее, так как было доказано, что диаметр Солнца больше стороны
тысячеугольннка, вписанного и большой круг мировой (сферы), то
ясно, что периметр упомянутого тыснчеугольника будет меньше взя-
взятого тысячу раз диаметра Солнца. Но диаметр Солнца меньше, чем
тридцать раа взятый, диаметр Земли, так что периметр этого тътсяче-
уголышка будет меньше, чем тридцать тысяч раз взятый диаметр Зем-
Земли. Теперь, так как периметр тьтсячеугомьника меньше трех мириад
раз взятого диаметра Земли, но более чем в три раза больше диаметра
мира (ибо доказано, что диаметр мелкого круга меньше третьей части
периметра всякого многоугольника, вписанного в круг, если только
этот многоугольник равносторонний и имеет большее число углов,
чем у шестиугольника), то в диаметр мира будет меньше мириады раз
bsktoco даамйтра Земли. Итак, доказано, что диаметр мира меньше
мириады раз взятого диаметра Земли. А что диаметр мира будет мень-
шо чем мириады раз взятые сто мириад стадий, ясно из следующего;
так как предположено, что периметр Земли не более трехсот мириад
стадий, и периметр Земли более чем в три раза больше ее диаметра
(так как у всякого круга окружность более чем в три раза больше диа-
диаметра), то ясно, что диаметр Земли будет меньше чем 100 мириад ста-
стадий. Теперь, так как диаметр мира меньше мириады ра.ч взятого диа-
диаметра Земли, то ясно, что диаметр мира будет меньше чем мириад раз
нзятые 100 мириад стадий.
Такие предположения я сделал относительно величин и расстоя-
расстояний (в мире), относительно же песка предполагаю следующее: если
взять количество его (в объеме), не большем макового зернышка, то
в шаг число песчинок будет не больше десяти тысяч, а диаметр мако-
макового зернышка не меньше сороковой части дюйма. Эти предположения
я делаю из следующего наблюдения: я положи.:! па гладкой линейке
маковые зернышки но прямой так, чтобы они касались друг друга и
нашел, что 25 маковых зернышек занимают длину, большую дюйма.
Желая возможно бесспорпее доказать выставленное положение, я беру
диаметр макового зернышка еще меньше, а именно ранным сороковой
части дюйма, но не мспынс-
*) Лсйсткнтсльпо, 99>20 000-—?¦
•*) 812=4-203.
ПСАММИТ 363
III
Бот каковы мои ире,и1оложонпя; кроме того, я думаю, что было
бы полезным наложить здесь правила наименования чисел, чтобы
другие (читатели), которые не имели в руках книги, написанной мной
Зсвксиппу*), не затруднились тем, что в настоящий книге об этих чис-
числах ничего не сказано **). Так вот дня чисел до десятков тысяч (мириад)
остаются обычно употребляемые нами названия, после же десятков
тысяч, как мы полагаем, достаточно считать мириадами вплоть до
.мириады мириад. Упомянутые до сих нор числа вплоть до мириады
мириад назовем первыми, а мириаду мириад нериых чисел пазовем
рдшгицей вторых чисел, далее буцоя считать единицы вторых чнеел
и из таких единиц составим десятки, сотни, тысячи и мириады вплоть
до мириады мириад. Затем мириаду мириад вторых чисел назовем еди-
единицей третьих чисел; после этого будем считать единицы третьих
чисел, а за единицами десятки, сотни, тысячи п мирим дм пилота до
мнриади мириад. Таким же образом, мириаду мириад третьих чисел
назовем единицей четвертых чисел, а мириаду мириад четвертых
чисел назоисм единицей пятых чисел. Продолжая так постоянно, мы
дадим названия числам вплоть до мириады мириад мириадо-мириад-
ных чисел. Вполне достаточно зпать числа только до атих пор, но мож-
можно идти и далее. Действительно, пусть упомянутые до сих пор числа
называются числами первого периода, а последнее число первого перио-
периода назовем единицей первых чисел второго периода. Далее мириадз'
мириад первых чисел второго периода паяипом единицей вторых чисел
второго периода. Точно так же последнюю единицу этих чисел пазовем
единицей третьих чисел второго периода; если постоянно продолжать
таням образом, то числа второго периода получат имена вплоть до ми-
мириады мириад мириадо-мириадяых чисел. Далее, последнее число
пторого периода назовем единицей первых чисел третьего периода
и будем тан продолжат!, вплоть до мириады мириад мириадо-мириал-
ных чисел мириадо-мириадпого периода. После установления
таких пазнаиий возьмем числа в непрерывной пропорции, начи-
начиная от единицы, причем следующей за единицей будет десятка;
восемь первых та них чисел имеете с единицей будут принадлежать
к тан называемым первым числам, другие следующие за ними восемь —
к так называемым вторам числам, и остальные будут называться ана-
аналогично упомянутым и соответствии с расстоянием октады рассматри-
рассматриваемых чисел от первой октады. Таким образом, восьмое число первой
октады этих чисел будет тысячей мириад, а перное число второй октады,
поскольку оно и десять ран больше предшествующего, будет мириадой
мириад; оно является единицей нторых чисел. Восьмое число второй
октады будет тысяча мириад пторых чисел. Далее иервои число третьей
«ктады, поскольку оно и десять раз больше предшествующего, будет
мириадой мириад вторы * чисел; оно является единицей третьих чисел.
Ясно, что так можно получить октады любого порядка I10J.
Полезно также знать и нижеследующее. Если некоторые из чисел,
составляющих нспрерыипую пропорцию, начиная от единицы, пере-
перемножаются с другими из той же самой пропорции, то полученное число
будет принадлежать к той же самой пропорции, отстоя от большего
*.) См. сноску на стр. 35R.
.) С. су р
e; относится к «тем иа других <читателеи>», а не к числам, как иногда переводят.
304 АРХИМЕД
из перемножаемых чисел настолько, насколько меньшее из перемно-
перемножаемых чисел в пропорции отстоит от единицы* причем расстояние
произведении от единицы будет па единицу меньше числа, получаю-
получающегося от сложения расстояний от единицы взаимно перемножаемых
чисел. Действительно, пусть будут некоторые числа в непрерывной
пропорции, начинай от единицы: А, 13, Г, Д, Е, Z, H, G, I, К, Л, пусть
единицей будет Л; помножим Д па 0, и пусть в результате получит-
получится Ф. Возьмем в непрерывной пропорции А, которое отстопт от 0
пастолъко же, насколько А отстоит от единицы; требуется доказать,
чтоФ будет равно Л. Действительно, так как и непрерышшй пропорции
чисел А от Л и Л от 0 отстоят одинаково, то Д будет иметь к А то же-
самое отношение, что А к в. Но А будет Д раз кратным А; значит,
и Л будет Д раз кратным в; таким образом, Л будет равна Ф. Теперь
ясно, что полученный результат будет принадлежать к той же непре-
непрерывной пропорции л будет настолько же отстоять от большего из (чи-
(чисел), перемножаемых между собой, пасколько меньшее отстопт or
единицы. Ясно также, что его расстояние от единицы будет на единицу
меньше числа, равного сумме расстояний чисел Д и 0 от единицы;
действительно, ряд А, В, Г, Д, Е, Z, II, 0 дает столько чисел, насколь-
насколько ('i отстоит от единицы, а ряд I, К, А содержит на одно число меньше-
тез чисел, на которые Д отстоит от единицы, их будет реявво столько,.
если присчитаем числа от А до 0*).
; iv
Теперь, устаповив такие отчасти предположения, а отчасти доказа-
доказательства, перейдем к доказательству основного предложения. Так как
предположено, что диаметр макового зернышка не мепыпе сороковой.
части дюйма, то ясно, что шар, имеющий диаметр в один дюйм,
может вместить пе больше шести мириад и четырех тысяч (то есть 64 000)
маковых зернышек, так как имеппо в упомянутое число раз этот шар
будет больше тара, имеющего диаметром одну сороковую часть дюй-
дюйма; ибо доказано, что шары находятся друг к другу в тройпом отногае-
П1ш их диаметров. Поскольку предположено, что число песчинок в объе-
объеме, соответствующем величине макового зернышка, не будет больше-
чем десять тысяч, то ясно, что если шар дюймового диаметра
наполнить песком, то число последнего пе будет больше мириады pas
взятых шести мириад и четырех тысяч. Это число представляет шесть
единиц вторых чисел и четыре тысячи мириад первых чисел: значит,
опо будет мсвыпе чем 10 едишщ вторых чисел. Шар, имеющий дкамотр
в 100 дюймов, будет больше шара дюймового диаметра в 100 мириад
раз, ибо шары имеют друг к другу тройное отношение своих диаметров.
Таким образом, если сделать из песка шар такой величины, чтобы
диаметр его равнялся 100 дюймам, то ясно, что число находящихся
в нем песчинок будет мепьше того, которое получилось бы от умножения
десяти единиц вторых чисел на 100 мириад. Поскольку десять едишщ
вторых чисел являются десятым числом от единицы в непрерывной
*) Надо иметь в ъиду, что. ведн счет, греки всегда учитывали и то число, от которого счет
начинялся; например 2 но гречески било иторым числом от 1,4 — вторым числом от 3 и т. д. В про-
прогрессии
I, 10, 102, JC3, 10\ 105. 1С6, I07, 1С8, 10е, 10и>
число 10' было шестым, а 10* — пятым числом от единицы; их произведение 10'** было десятым
числом от единицы (Ю = 6|э—1).
ПСАММИТ 36.1
пропорции с десятикратным возрастанием членов, а сто мириад явля-
являются седьмым числом после единицы в той же самой пропорции, то
ясно, что иолучепное число в той же самой непрерывной пропорции
будет шестнадцатым членом, если считать от единицы {так как доказано,
что оно отстоит от единицы па число, которое будет на единицу меньше
вместе нзнтых расстояний от единицы взаимно перемножаемых чисел).
Иа этих шестнадцати чисел восемь первых, считая и единицу, ирииад-
ложат к названным памп первым числам, следующие за ними восемь
относятся ко вторым, причем последнее число из пих будет тысячей
мириад вторых чисел. Теперь ясно, что количество песчинок в (объеме),
равном по величине шару с диаметром в 100 дюймов, будет меньше,
чем тысяча мириад вторых чисел. Далее, шар, имеющий диаметр в
мириаду дюймов, будет в 100 мириад раз больше шара, имеющего
диаметр в 100 дюймов. Если теперь сделать из песка шар такой вели-
величины, чтобы его диаметр равнялся мириаде дюймов, то ясно, что число
песка будет меньше того, которое получается от умножения тысячи
мириад (единиц) вторых чисел на сто мириад. Поскольку же тысяча
мириад вторых чисел является шестнадцатым числом в пропорции от
единицы, а 100 мириад будут седьмым от единицы в той же самой про-
пропорции, то ясно, что получившееся число будет двадцать вторым в той
же самой пропорции, считая от единицы. Иа этих двадцати двух (чисел)
восемь первых от единицы принадлежат к назнапным нами первым
числам, восемь следующих за ними будут так называемыми вторыми,
а остальные шесть — третьими, причем последнее иа пих будет десятью
мириадами единиц третьих чисел. Теперь ясно, что количество песчи-
песчинок в (объеме), равном по величине шару, имеющему диаметр вдеенть
тысяч дюймои, меньше чем 10 мириад (единиц) третьих чисел. И тав*
как шар, имеющий диаметр в одну стадию, меньше шара, имеющего
диаметр в десять тысяч дюймов*), то ясно, что количество лесчинок
в шире, имеющем диаметр в одну стадию, будет меньше чем 10 мириад
третьих чисол. Далее шар, имеющий диаметр в 100 стадий, будет в сто
мириад раз больше шаря, имеющего диаметр н одну стадию. Следова-
Следовательно, если сделать из песка шар такой величины, чтобы его диаметр
равнялся 100 стадиям, то ясно, что число песчинок в нем будет меньше
того, которое получается от умножепин десяти мириад (единиц) треть-
третьих чисел на 100 мириад. И так как десять мириад (единиц) третьих
чисел будет двадцать вторым числом в пропорции от единицы, а 100
мириад — седьмым от единицы в той же самой пропорции, то ясно, что
получающееся число будет двадцать восьмым от единицы в той же самой
пропорции. Из этих двадцати восьми чисел носемь первых от единицы
будут так называемыми первыми, восемь следующих за ними будут
вторыми, еще носемь следующих третьими, остальные же четыре будут
принадлежать к так называемым четвертым, причем последнее из них
будет тысячей единиц четвертых чисел. Теперь я ело, что количество
песчинок в объеме, равном по величине шару, имеющему диаметр
в 100 стадий, будет меньше чем тысяча единиц четвертых, чисел. Далее,
шар, имеющий диаметр в десять тысяч стадий, будет в 100 мириад раз
больше шара, имеющего диаметр в 100 стадий. Поэтому, если сделать
из песка шар с диаметром и десять тысяч стадий, то ясно, что количе-
количество песчинок в нем будет меньше чисча, получающегося при умножении
тысячи сдиницчетвертыхчисел на ЮОмириад. И так как тысяча единиц
*) По Гершгу (Defiiiitlones, 131) стадия содержит 9в00 дюймов.
зва архимкд
четвертых чисел будет двадцать восьмым числом я пропорции от
единицы, а сто мириад — седьмым от единицы в той же пропорции, то
ясно, что получающееся число <1033) будет тридцать четвертым от еди-
единицы в той же пропорции. Из этих тридцати читырех чисел восемь пер-
1U.IX, считая и единицу, будут так называемыми первыми, восемь сле-
следующих за ними — вторыми, иоссмь следующих за иими — третьими,
еще восемь следующих — четнертымн, а дна остальных будут принад-
принадлежать к так начинаемым: .пятым, причем последнее из них будет иред-
станлять десять единиц пятых чисел. Теперь ясно, что количество пес-
песчинок в объеме, равном но величина шару, имеющему диаметр в мириаду
стадии, будит меньше чем 10 единиц пятых чисел. Далее шар, имеющий
диаметр л 100 мириад стадий, будет в сто мириад рал больше шара,
имеющего диаметр в мириаду стадий. Таким образом, если сделать иа
лоска шар диаметром 100 мириад стадий, то ясно, что число песка в нем
будет мепьше того, котороо получается при умножении десяти единиц
пятых чисел на 100 мириад. И так как десять единиц пнтых чисел будут
тридцать четвертым числом п пропорции от едипнцы, а 100 мириад —
седьмым от единицы в той жо самой пропорции, то ясно, что получаю-
получающееся число будет сороковым от единицы r тон же пропорции. Из этих
сорока чисел восемь первых, считая и единицу, будут так называемыми
первыми, восемь следующих за ними — вторыми, восемь эа этими —
третьими, восемь после третьих — четвертыми, а восемь после них —
гак называемыми питыми, причем последпее из них будет тысячей
мириад (единиц) пятых чисел. Теперь яспо, что количество песчинок
и объеме, равном по величине шару, имеющему диаметр и 100 мириад
стадий, будет меньше чем тысяча мириад (единиц) пятых чисел. Шар же,
имеющий диаметром десять тысяч мириад стадий, будет в 100 мириад раз
больше шара, имеющего диаметром 100 мириад стадий. Поэтому если
сделать ив песка шар диаметром десять тысяч мириад стадий, то ясно,
что количество песка будет меньше числа, получающегося при умноже-
умножении тысячи мириад (единиц) пятых чисел на 100 мириад. Но так как
тысяча мириад {единиц) пятых чисел будет в пропорции сороковым
от единицы, а 100 мириад — седьмым от единицы в той же самой про-
пропорции, то ясно, что получающееся число будет сорок шестым от едини-
единицы. Из этих сорока шести чисел восемь первых, считая и единицу,
будут так называемыми первыми, восемь за ними — вторыми, восемь
за этими — третьими, восемь за третьими — четвертыми, ьосемь за
четвертыми — пятыми, остальные же шесть принадлежат к так назы-
называемым шестым, причем последнее число из них будет 10 миряад единиц
шестых чисел. Поэтому ясно, что количество песчинок в (объеме),
равпом по величине шару, имеющему диаметром десять тысяч мириад
стадий, будет меньше чем 10 мириад (едипиц) шестых чисел. Шар же,
имеющий диаметром десять тысн ч раз 100 мириад стадий, будет в 100 ми-
мириад раз больше пиара, имеющего диаметр к десять тысяч мириад
стадий. Теиерь, если сделать из песка шар диаметром десять тысяч
раз 100 мириад стадий, то ясно, что количество песка и нем будет мень-
меньше, чем число, получающееся при умножении 10 мириад единиц шестых
чисел на 100 мириад. Но так как десять мириад (единиц) шестых чисел
будут в пропорции сорок шестым числом от единицы, а 100 мириад —
в той же самой пропорции седьмым от единицы, то ясно, что получаю-
получающееся число будет и той же пропорции пятьдесят вторим от единицы.
Из утих пятидесяти двух чисел сорок восемь, считан и единицу, будут
так называемыми первыми, вторыми, третьими, четвертыми, пятыми
ПСАММИТ 387
и шестыми, остальные зкс четыре относятся к седьмым, причем последнее
из них будет тысячей едишщ седьмых чисел. После .ггого ясно, что коли-
количества песчинок б (объеме), но величине равном шару, имеющему диа-
диаметр в десять тысяч раз по 100 мириад стадий, будет меньше, чем тысяча
единиц седьмых чисел. Так как доказано, что диаметр мира мепыле,.
чем десять тысяч раз по 100 мириад стадий, то ясно, что количество пес-
песка в (объеме), ранном но величине миру, будет меньше, чем 1000единиц
седьмых чисел. Теперь доказано, что количество носка в (объеме),
равном но неличное тому, что большинство астрономов называют миром,,
меньше чем 1000 единиц седьмых чисел; а что количество песка » (объе-
(объеме), равном по величине такому шару, каким, по предположению Ари-
Аристарха, лнлиетси сфера неподвижных зиевд, будет меньше 1000 мириад
(единиц) восьмых чисел, еще нужно доказать. Если предположить,
что Земля к тому, что мы называем, миром, имеет то же отношение, что>
атот мир к сфере неподвижных зисзд, пак полагает Аристарх, то то же
отношение будут иметь друг к другу и диаметры зтмх сфер. Но, как
доказано, диамотр мира мепыне, чом взятый десять тысяч раз кратным'
диаметр Земли; следовательно, ясно, что диаметр сферы неподвижных
звезд будет меньше чпм десять тысяч рай взятий диаметр мира. Посколь-
Поскольку же шары, имеют друг к другу тронное отношение диаметрон, то ясно,
что сфера исподнижпых звезд, согласно предположению Аристарха,
будет меньше, чем десять тысяч раз взятая мириада мириад наших
миров. Доказано же, что количество песчинок в (объеме), равном но-
величине миру, будет меньше 1000 единиц седьмых чисел; следовательно,,
ясно, что, если сделать ил песка шар такой величины, какой, по прпд-
ипложслию Аристарха, янляетси сфера пеподвиишых звезд, то соответ-
соответствующее число песчинок будет меньше того числа, которое полу-
получается ири умножении тысячи единиц седьмых чисел на десять тысяч
раз взятую мириаду мириад. И так как 1000 единиц седьмых чисел
будет в пропорции пятьдесят иторым числом от единицы, а десять тысяч,
раз мириада мириад — тринадцатым от единицы и той же пропорции,,
то ясно, что получающееся число будет шестьдесят четвертым числом'
от единицы в той же самок пропорции; ото число будет восьмым в ряду
восьмых чисел, то есть тысячей мириад (единиц) восьмых чисел. После-
зтого нспо, что количество песчинок в (объеме), рапном по величине
сфере неподвижных звезд, как се мыслит Аристарх, будет меньше, чем
тысяча мириад (одиниц) восьмых чисел. Все пто, государь Гелоп,
я предполагаю, покажется не очень вероятным большинству людей
и всем не освоившимся с математикой; для тех же, которые нослриннли
ее и усиоили касающееся расстояний и неличин Земли, Солнца, Луны
и всего мира, пто будет поело данного мной доказательства вполне-
достоиерпым; поэтому я полагал, что и для тебя не будет недостойным-
поразмыслить об этом 111].
КАТОПТРИКА
1. ТЕОН, КОММЕНТАРИЙ К «ПТОЛЕМЕЮ» 1, ст. 10
«И падающий из него (глаза) на воздух лучи подвергаются пре-
преломлению и делают угол зрения большим, как и доказывает Архимед
в «О катоптрике», говоря, что помещенные в воду пред-
предметы кажутся большими и тем больше, чем
ниже они уходя т».
•>. ОЛИМПИОДОР, КОММЕНТАРИЙ К МЕТЕОРОЛОГИИ АРИСТОТЕЛЯ
(сг. 211, 18 Basse (И, ст. 94 изд. Meier)
«Иначе это же самое, а именно, что луч зрения преломляется,
доказывает Архимед на примере брошенного в сосуд перстня».
3. ПСЕВДО-ЕВКЛИД, КАТОПТРИКА, post 6 (ст. 28в, 17)
«Если поместить что-нибудь в сосуд и удалить глаз настолько,
чтобы этот предмет не был виден, то после вливания воды помещенный
лредмет может быть снова увиден с того же самого расстояния».
СХОЛИЯ К КАТОПТРИКЕ ПСЕВДО-ЕВКЛИДА, Л6 7 (ст. 348, 17)
«Архимед же говорит так {рис. 1}: угол F или будет равен Е,
или же меньше, или боэтыпе. Пусть сначала F
будет больше К; значит, Е будет меньше. Предпо-
Предположим теперь, что глаа будет в Л и луч снова от
глаза отразится к наблюдаемому предмету В; зна-
значит, угол К будет больше, чем F. Но он был и
меньше, что нелепо».
В-глаз ^U 4- АПУЛЕЙ, Апология. 16
«Кроме того, что я сказал им (то есть филосо-
рис 1 фам), необходимо и такое рассуждение, почему в
ллоских зеркалах предметы и изображения пред-
представляются одинаковыми, и выпуклых и сферических уменьшен-
уменьшенными, в погнутых же, наоборот, увеличенными; но какой при-
причине правая меняется местом с лсиой, когда в одном и том же зеркале
КАТОПТРИКА
369
изображение то уходит вглубь, то выходит наружу; почему вогнутые
здркала, помещенные против Сшшца зажигают подложенный трут,
отчего происходит то, что радуги в облаках являются различными,
а два солнца одинаково подобными, и миогоо другое в том же роде,
о чем в огро.мном томе рассуждает сиракузянин Архимед».
5. ПСЕВДО-ПСЕЛЛ, Synopsis mathematica, ст. 73, над. Xylander'a
При отсутствии (irtooia) диоптры можно и иначе воспользоваться
тем методом, как когда-то Архимед. Когда некоторые спросили отно-
относительно высоты находящейся перед ними пирамиды, он искусно при-
прикрепил отвесный шест у солнечной тени от пирамиды, так чтобы обе
тени как шеста, так и пирамиды, бы;ги па одной плоскости; получив
таким обра.чом два подобных треугольника, он выпел отсюда следующее
заключение: отношение лежащей на плоек нети тени шеста к самому
шесту будет тем же самым, что тени пирамиды на той же плоскости
к самой пирамиде. После этого, измерив тень пирамиды, он объявил
нопрощающим высоту пирамиды.
24 Архимед
ОБ УСТРОЙСТВЕ НЕБЕСНОЙ СФЕРЫ
ПАТТИ, V1TT, 3, сг. 1026, О
«Карп Аптиохийсинн где-то говорит, что сиракузянин Архимед
состниил только одно механическое сочинение, а именно, об устройстве
небесного глобуса, по найдя из других предметов ничего достойного
сочинения».
ИРОК Л,' КОММЕНТАРИЙ К ЕВКЛИДУ, ст. 41. 16
«Устройстио небесной сферы, воспроизводящей круговращения
небесных тел, книгу о котором сочинил также и Архимед».
МАКРОГЛШ, COTI СЦИПИОНА, II, 3
«Также и Архимед считал, что оп определил число стадий, ка ко-
которое от поверхности Земли удалена Луна, а от Лупы — Меркурий,
от Меркурии — Венера, от Венеры — Солнце, от Солнца — Марс,
от Марса — Юпитер, от Юпитера — Сатурн; все же расстояние от Са
турна до самого звездоносного неба он, как думал, измерил только
рассуждением. Однако это архимедово измерение отвергнуто платони-
платониками, как не сохраняющее двойных и тройных интериалов».
ИППОЛИТ, О11ГОПЕРЖЕНИЕ ВСЕХ ЕРЕСЕП, изд. Dusiclter, ст. 6C, 52
«Расстояние от поверхности Земли до лунной орбиты сам... Ари-
Аристарх оценивает jj своем сочинении в... стадии, Архимед же ы554 мириа-
ди и 4130 единиц, от лунной до солнечной орбиты стадий 502E мириад
и 20E5 единиц, от нее до орбиты Вещфы стадий 2027 мириад и 20E5 еди-
единиц, от пес до орбиты Меркурия стадий 5081 мириада и 7165 единиц,
от пее до орбиты Марса стадий 4054 мириады и 1108 единиц, от ней до
орбиты Юпитера стадий 2027 мириад 50E5 единиц, от пее до орбиты
Сатурна стадий 4037 мириад 20fio единиц, от нее же до зодиака и самой
последней окружности стадий 2008 мириад 4005 единиц. Таковы пере-
переданные Архимедом расстояния орбит друг от друга и глубины сфер;
периметр же зодиака он принимает стадий: 4 вторых числа 473fl мириа-
мириада; таким образом, получается, что расстояние от центра Земли до
ОБ УСТРОПС'ГВК НЕБЕСНОЙ СФЕРЫ 371
самой крайней поверхности будет тестой частью упомянутого числа*),
расстояние же от поиерхяоети Земли, на которой лил живем, до зодиака
поручится, если шестую часть упомянутого числа уменьшить на четыре
мириады стадий, которые представляют расстояние от центра Земли
до ее поверхности. От орбиты Сатурна до Земли, как он говорит, будет
вторых чисел одна единица 2160 мириад 4454 единицы, от Меркурия
(EriXptov) до Земли 5208 мириад 8259 единиц, от Воперы до Земли
5081 мириада 51E0 единиц... так lot расстояния и глубипы сфер Архимед
дает такими. Изложенные Архимедом числа п пронодимыо другими
отношения касательно расстояний, если они не будут находиться
в сояиучных отношениях, то есть и так называемых платоновских
диойных и тройных, то оказываясь вне созвучий, они по могут сох-
рапить гармоничного строения вселенной..., а что остальные данные
Архимедом числа относительно расстояний планет не находится в со-
созвучных отношениях, легко установить, если подумать, как и в каких
отношениях они находятся друг к другу.
¦ ¦ О ВЕЛИЧИНЕ ГОДА
ГШШАРХ У ПТОЛЕМЕЯ, АЛЬМАГЕСТ, Ш, \
Из этих наблюдений ясно, что различия продолжительности
разных годои сиисршсшю ничтожны; что же касается солнцестояний,
то я упорен, что и я и Архимед и и наблюдениях и в вычислениях ошиб-
ошиблись но более чем на четвертую часть дня.
*) Числи л принимается равный 3.
E)
ЗАДАЧА,
[КОТОРУЮ АРХИМЕД НЛ1ПЕЛ П ЭПИГРАММАХ И ПОСЛАЛ
НЛ РАЗРЕШЕНИЕ ЗАНИМАЮЩИМСЯ ПОДОБНЫМИ ВОПРОСАМИ
АЛЕКСАНДРИЙСКИМ УЧЕНЫМ В ПОСЛАНИИ
К ЭРЛТОСФЕНУ КМРЕНСКОМУ
Сколько у Солпца быков, пайди для меня, чужестранец.
(Tiit их, подумав, считай, мудрости если по чужд).
Как па полях Тринакрийской Сицилии остроиа тучных
Их в четырех стадах много когда-то паслось.
5 Цветом стада различались: блистало одно млечно-бслым,
Темной морской волны стада другого был цист.
Рыжим трстие было, последнее пестрым. И в каждом
Стаде была самцов множеством тяжкая мощь,
Все же храня соразмерность такую: представь, чужестранец.
Белых: число быков в точности быяо равно
10 Темных бы кон половине и трети и полностью рыжим;
Темных число битков четверти было равно
Пестрых с нрмбаиленпой пятой и также полностью рыжим;
Построй жо шерсти быкои так созерцай чис.:ю:
1Г) Части шестой и седьмой от стада быков серебристых
Также и рыжим всем ты их число поравняй.
В тох же стадах коров было столько: число белошерстых
В точности было равно темного стада всего
Части четвертой и третьей, коль сложить ты обе их вместе;
'10 Темных число жо коров части четвертой опять
Пестрого стада равнялось, коль пятую долю добавишь
И туда же быков в общее стадо причтешь.
То же, чья пестрая шерсть, равночисленным множеством были
Рыжего стада частям пятой и с нею тестой.
25 Рыжих коров же считалось количество равным полтрсти
Белого стада всого с частиго взятой седьмой.
Сколько у Солпца быков, чужестранец, коль точно ты скажешь.
Паи раздельпо назвав тучных быков число,
Так же раздельно коров, сколько каждого цвета их было,
30 Но назовет хоть никто в числах иевеждой тебя,
Все ж к мудрецам причислен пе будешь. Учти же, пожалуй,
Свойства такие еще Солнца быков числа.
ЗАДАЧА, КОТОРУЮ АРХИМЕД НАШЕМ В ЭПИГРАММАХ 373
Если быков среброшерстых ты с томными вместе смешаешь
Так, чтобы тесно они стали бы в ширь и в длину
35 Мерою равной, тогда на обширных полях Сицилийских
Плотным квадратом они л.чшцадг, большую ааймут.
Если же рыжих и нсстрых в одно смешаешь ты стадо,
Лесенкой станут они, счет с единицы начав,
Так что фигуру опи треугольную нам образуют;
40 Цвета иного быков нам нет нужды добаьлять.
Если ты ото найдешь, чужестранец, умом пораскинув,
И сможешь точно назиать каждого стада число,
То уходи, возгордившись победой, и будет считаться
Что в от ой мудрости ты все до конца превзошел.
Текст задачи о быкпх был шюрлтле опубликован Лсссипгом п Beilriigo zur Ueschiclile
und Litturatur (Braunschweig, 1773, стр. 421 и ел.). Нет никаких оснований сомне-
сомневаться о принадлежности птой эпиграммы Архимеду, так как и но стилю, и по содер-
содержанию она подходит к арифметический эпиграммам той нпохи и, кроме того, с именем
Архимеда упоминается в древней схолии к платоновскому Хармлду. Из математиков
ей занимались Несссльманн (Algebra dcr Gricchcn, стр. 81 и ел.), Поль Танлери (Mtjmoi-
res dc ia Societe de Sciences de fiordeuux, 1880, III, стр. ЗС9 и ел.) и Хиос (Heath, Dio-
phantus of Alexandria, стр. 142).
Пусть X, У, Z, T обозначают соответственно числа белых, черных, рыжих и пестрых
быков, и. х, у, z, t — числа корол такого же цвета. Тогда между этими неизвестными
мы имеем следующую систему урцлпшшй:
(стр. 10-11) X=^-\1-}y-\Z, A)
(стр. 12-13) у = (!.-• ±ЛГ-|2, Ш
(стр. 14- 16) j\-^A..|"l)x:-Z. {.'!)
(стр. 17- 19) х=^.\-^(у-\-у), {Л)
(rap. 20-22) t,
(стр. 23-24) t = (±+±J(Z\ z), F)
(стр. 25-20) z = ? 1 -| A ^ {X-| ¦ x). G)
¦ К этим уравнениям прибавляются еще такие условия:
(стр. 33—36) А'+У=](вадратпому числу,
(стр. 37—39) Z~T= треугольному числу.
Мы имеем семь уравнений с восемью неизвестными, причем полученные решения
должпы удовлетворить двум условиям: суммы двух полученных пар должны давить квад-
квадратное (.иримоугилмюо) число и треугольное.
Начнем решение с первых трех уравнений, которые можно представить и следую-
следующем виде:
Исключая из иерлих двух уравнений У, найдем:
3?4 л рхиме д
Регааи это уравнение вместе с третьим, находим:
1580
Найди Т, последовательной подстановкой определяем У и X:
.178 T-1&Z
Так как 891 =3*-11, а 297 = 3'-11 и 1)9=3*-11 и коэффициенты при Z являются
несократимыми дробями, а вес неизвестные должны быть числами целыми, то наимень-
наименьшими значениями А', У, Z, Т, удовлетворяющими этим уравнениям, будут:
Л'=222С, У=1602, 2=891, Г=1580
или, вообще:
X=2226п =2-3- 7 • 53п,
Будем подставлять найденные значения в уравнения 4—7, которые можпо пере-
переписать так:
D) *=^B.3».8вя-Н<).
E) У=~B*.5-Ш-\-1),
(С) <=^C»-11»-|-я),
G) ^=|| B-3.7.53»-и^).
Последовательная иодсталолка у, I, z n уравнение D) приведет лас к уравнению
41557а;=7 206 360й
«¦ли. если разложить на множители, помп», что 4657 есть простое; число:
4657ж=23-3-5.7-23-373л.
Отсюда получаем, что длн целости * необходимо, чтобы
п.=4657/»', *=7 20G ЗбОге',
где п' -¦¦ проичшо.'н.ное целое чпьло.
Подставляя пайдеппмс зплчешкг в уравнении A)—G), находим:
X=2 • 3 • 7 • 53-4657«' -= 10 306 482я',
У =, 2-З2-89-4657м':= 7 460514ге',
Z = 3* ¦ 11. • 4657/1/ = 4149 387л',
Г=22-5-79-4657и'=7358060ге\
х-=2:|-^-5-7-23-373я' = 7 206360»',
у= 2- З2-17 - 15991га' = 4 8УЗ 246л',
z=3й-13- 46489и' ^ 5 439 2-13п',
Если положит!, п' =1, то мм полупим гсшмепмпис числа, удоплстворяющие первым
семи уравлепинм. Быть в состоянии, лнйти- эти числа, значит но Архимеду яе заслужи-
заслуживать названия «невежды в числах».
П гепберговском издании Архимеда после текста изложенной эпиграммы прове-
проведена древняя схолия:
«При помощи :>того стихотворения Архимед очень песо выразил поставленную за-
задачу: его слова надо понимать так, что всего должно быть четыре стада быков, а именно.
ЗАДАЧА. КОТОРУЮ АРХИМЕД НАШЕЛ В ЭПИГРАММАХ 375
первое белошерстых быков и Tsopoa, общее количество которых составляет двойных,
мириад 14 простых 582 и единиц 73В0 (т. о. 1 Л05 827 360), другое темных быков и корон,
общее количество которых будет У диошшх мириад 8830 простых и 800 единиц
( = 988 300 800), еще одно пестрых быкои и коров, общее количество которых будет
8 длойиых мириад 0991 простых и 400 единиц (8С9 910 400); последнее »ие стадо рыжих
имеет общие количество 7 двойных мириад, 6708 простых и 8000 единиц (т. е. 767 088 000);
таким образом, общее количество во всех чотырсх стадах составляет 40 двойных мириад
U112 простых и E560 единиц D 031. 126 560). И стадо белошерстых имеет быков — 8 двой-
двойных мириад 2931 простых и 8560 единиц (829 318 560), и корив 5 двойных мириад 7650
простых и 8800 единиц E76 508 800), темное стадо имеет быков 5 двойных мириад 9684
простых и 1120 единиц EУ6 841 120) и коров 3 дпонных мириады 9145 простых и 9680
<!Д[1пиц C!I 459 680), стадо пестрых имеет быкин 5 двойных мирицд 8864 простых в 4800
единиц E88 644 800) и коров 2 двойных мириады 8126 простых и 5600 единиц
B81 265 600), стадо же ртдоих имеет быкои 3 двойных мириады З1.!)л простых и 900 еди-
единиц C31 950 Н(Ю) и коров 4 двойных мириады 3513 простых и 7040 единтгц D35 137 040).
И количество белых быков рашю половине и третьей части количеств» темных быков
и, кроме того, лесму стаду рыжих, количество темных равно четвертой и пятой чисти
пестрых быков и всему количеству рышнх, количество пестрых быков рнвпо шестой
а седьмой части белых и стп,е всему количеству рыжих; днлес, количество белых Киров
равно третьей п татпертой частям itcoro стада темных, количество темных коров равно чет-
четвертой ы пятой частям всего стада пестрых, количество н»е пестрых рашю иятий и шестой
частям всего стада рыжих. Затем количество рыжих коров было ранни шестой и седьмой
частим всего стада белых. И стадо белых и темных быкои вместе образует квадратное
число, стадо же рыжих и пестрых быкои вместе образует треугольник, как и следует для
каждого цвета из предположенных пропорций».
Относительно этой схолии следует сделать дна замечания. По-порвых, употребляю-
употребляющаяся в ней система нумерации принадлежит -Аполлонию: она соответствует делению па
классы по четыре разряда (лмеето наших трех): единицы, мириады (десятки тысяч), двой-
двойные, тройные и т. д. мириады. Но-вторых: гпшдоппые решения являются совершенно пра-
правильными, если ограничиться первыми семью уравненными: пни получаются из наших
формул, если irpJTiWTf, п' — 80. Дало, однако, обстоит ьоиершепно плачи, если лжг попро-
попробуем проверить остальные требования- Сумма белых и. черных быков будет:
X 'гУ = 2.3-7.53-4657-80 f 2-За-80-4657-80-
=2-3-4В57-80G-53-?-3-К9)=2-3-4б57-80-2-11-2Я,
что никоим образом нк равняется квадратному числу. Точно тай же и сумма стад рыжих
я пестрых быков
Z~r=34-11-4657-80 | 22-5-79-4657-80=
= 4(i57-80C*-ll f 28-5-79)-=4657-80-7-353=24-Г>-7..453-4057
не может быть приведена к виду ~—' треугольного числа.
Нужно добавить, что строки 33—36 в подлшшиио читаются так:
/ 1*1 Г
qoi finv глв1 |xi|aiato я
¦' '
S, '-OTuvT 5p.nj-:c't>v
Ш i -
etg p«©os ei€ eu>"S те, xi о ад
nXtvOou (вар. nMfiuvG) &invivnit]g яебю.
Слова iOo^KTQoi 6--S fteOoS eis e^Qig мояспо иопимать, что n iviyouny и л ширину
ч п с. л ;i быков были одинаковыми, или же, что д л и я i* были одинаковыми. Так
как вместо .T^lvOoi; (-ii:ihti.i, четыреугольлика) можно читатт, и nXifiov* (-множества, коли-
количества), то более вероитныы будет толкование, что киадратичм доляспи быть число
быков; однако это место мощно понимать и п смысле квадрцтлости занимаемой и л о-
щ а д и; тогда число быков дачнлто состоять и;» двух множителей, лишь приблизительно
равных одни другому.
Таким образом, мы ыожем различить задачи: во-нервых, считать, чго сумма X-j-K
должна быть только прямоугольный чис-нш: тогда поручается так называемая задача
Пурма, рептенная им в Zeitschiil't f. Maihemsillk und Physik (llislorisch, Litteral. Ablei-
Lung), т. XXV A880), стр. 15С и ел.; во-вторых, что указанная сумма должета быть дей-
действительно полним квадратом. В дальнейшем изложении я следую тексту немецкого
перевода хисовскоги издания Архимеда.
37G АРХИМЕД
Потребуем, чтобы сумма Z-\-T равнялась треуголт.пому числу пида '' ^д ¦ :
C* -11 -|- 22 • 5- 79) • 4657«.'=Ч.ЩА1.
Сумма, стоящая в скобках, равна 2471 = 7-353, такпм образом:
Так как g может быть или четным, или нечетным числом типа 2s, или 2я—1, то-
напте уравнение принимает вид
* Bs± I)- 7-353-4Ш7П'.
Представил! п' в виде произведения двух мпожитеяей, из которых один и содержатся
без остатка в s, другой же г> в 2.<±1; тогда мы будем иметь следующие 1С пар совместных
уравнений:
(I) — B) s := и 2s ±1=7- 353- 4657»,
C) — D) s=--7u 2s ± 1 — 353- 4657»,
E) — F) j?=353и 2* ± 1 = 7 - 4657»,
G) — (8) *=4657м 2я ± i ^=7-35:^,
(9)—A0) « = 7 ¦ 353« 2s ± i = 4657»,
(II) -A2) s=7-4C57a 2s ± 1 ~353i>,
A3) —A4) *=35S-4657« 2r±1=7»,
A5) — AE) *=7-353-4657a 2s±l=v.
Если решить каждую n.j этих сопместнгах пар и сравнить наименьшие полученные
результаты, то окажете», что самый малспький из этих результатов будет соответствовать
уравнениям
s=7м, 2а— 1 =- 353- 4657v,
что дает вам
м^= 117 423, v=l, и'^к»=
Сооткстстлующие этому п' решения булут:
V= 876035 935 422,
Z= 487 23346!) 701,
Г= 864 005479380,
x= 846192 410280,
y— 574 579 B25 058,
r= 638 688 708 099,
t= 412838 131860.
Сумма чисел Х+У будет при этом:
X J-Y = 2- 3- G • 53 ; -3 • 8!)) • 4657 • 117423=
=28-З.Ц-29.4657-3!«-4349,=
= B* • 3* - 4349) • A1 - 29 - 4637) ^
= 1409 076-1485 583,
что представляет число, близкое к квадратному.
Ксли же мы потребуем, чтобы сумма X-f-Y была бы точным квадратом, то нам при-
придется удовлетворить уравнению
ели
2 • 3 • G • 53 -|- 3 • 89) 4657л'=рг,
ЗАДАЧА, КОТОРУЮ АРХИМЕД НАШЕЛ В ЭПИГРАММАХ 377
что удовлетворяется, если мы положим;
л' = 3-11-29-4657»^--4 456749|г,
где | — любое целое число.
Соответствующие решения будут:
А'=2-32-711-29-53-46572-|г=4С 200808 287 018|*.
Y=2-33-11 -29-89-4С57»-|2=33249 638 308986 ?3.
362863,
х=23-32-5-7-Ц.23-29-373-4657.?"=32 116 937 72364О|«,
»/ = 2.3з.Ц.17-2915ШI.4657-?»=21807 9С9217 254|г,
г=33- И-13-29-4СШ9-4б57-|г= 24 241 207098 537|«,
*=<2з.За-5-711а-29-7б1-4657-4г=15Ш127 2
Теперь величина ?'- должоа ещо удовлетворить уравнению
ЕЛИ
2 " -
Если умножить обе части на 8 и положить:
то ми получаем уравнение Пелля
<г—1=2.3-7. И-29-353и*
или
Бели бы иропести решение этого уравнения дальше, то для числя А' белых бы кон
получилось бы значение порядка
для общего числа быков
7766-10я165".
Для того, чтобы зашгеатъ все восемь чисел, понадобился бы том п 660 страниц,
если считат!., что на каждой странице умещается 2500 цнфр. Пот, что .чначило для Архи-
Архимеда «будет считаться, что п отой мудрости ты вес до конца црепзошел». Архимед сделал
хлпдиокроиный вы:юп своему протипг1ику (Эратосфону или. Анол-юнию), uucianun ому
задачу, которая, как он знал, финичоеки не может быть разрешена.
СТОМАХИЙ
I
1. Посксмеьку так называемый Стомахий может служить предметом
разнообразных теорий относительно перестановок составляющих его
фигур, то и счел необходимым сначала изложить ... {об отдельных
его частях) ..., на которые он разделяется, о том, чему каждая из них
может быть уподоблена, затем о том, какие углы, взятые но два...
(дают в сумме два прямых), причем это сказано для того, чтобы можно
было знать условия взаимного прикладывания получающихся из них
фигур, а именно, когда получающиеся в этих фигурах стороны будут
точно расположены по одной прямой, и когда они,
представляя незначительные отклонения, все же могут
обмануть зрение; все это имеет прямое отношение к
технике складывания, так как не допжпо отбрасывать
составленные фигуры, если при самом небольшом
отклонении (от двух прямых углов, они) могут обма-
путь зрение.
2. Может теперь случиться, что из них немалое
количество фигур ... (может быть сложсно(?)) ... вслед-
вследствие того, что ... (возмо)жно переставить в другое
место равной и равноугольной фигуры... и внять
Дру( гую)...*). Иногда бывает, что две фигуры смеете рав-
равны и подобны одной фигуре, или же две фигуры вместе
равны и подобны имеете взятым двум (другим) фигурам, и при помощи
перестановки можпо получить большее количество фигур. Предвари-
Предварительно мы изложим некоторую теорему, относящуюся сюда.
'Л. Пусть будет прямоугольный параллелограмм ZF {рис. 1};
(разделим пополам) EZ в К. и проведем из Г и В прямые ГК, BE. (Про-
иедом также) FZ, продолжим ГК, BZ, и пусть они встретятся в Д)
...ГН. Поскольку ЕК раина K.Z, то иГК.то есть BZ, будет (равна) ZA.
Таким образом, PZ будет больше Z& и, следовательно, угол ZAF будет
больше угла ZTA. Но углы НВЛ, ZFB равны, так как каждый из них
есть половина прямого; следовательно, и угол ГНВ будет больше
Рис. -I.
Ест
*) Приводим ото темное место к подлиннике:
|liV o5v 65 Ct'JTUJV uuK okiytiiV OX"n^TtiW.-,O-.,Cia-TrJ,.-<ftto>V<0t>T0V
«JOB
СТОМАХИЙ
379
Рис. 2.
НГВ, поскольку угол ГПВ равем двум внутренним л ротявол ежащим
углам НВД и IIА В *), так что ГВ Судет больше ВН. Значит, если мы
разделам ГН пополам в X, то угол ГХВ будет тупым; дейст-
действительно, так лак ГХ равна ХН, а ХВ — общая, то (в треу-
треугольниках ГХВ и НХВ) по две стороны равны,
а основание ГВ больше ВН, значит, и одип угол
будет больше другого. Следонатольно, угол ГХВ будет
тупым, а смежный— острым. Но 5441л ГВП есть по-
половина прямого (ибо это предположено относительно
параллелограмма), угол же ВХН острый...
4 *•)
5. Разделим ГЛ {рис. 2} пополам в Е, и через Е
проведем EZ параллельно ВГ; тогда TZ, ZA будут
квадратами. Проведем диаметры ГД, В13, ЕД и ран- г
делим ГН, ЕЛ пополам и в и X, затем проведем сое-
соединяющие прямые В©, XZ и через К... параллель-
параллельно ВЛ проведем К..., ...3. Следовательно, па основании предыду-
предыдущей теоремы в треугольнике ВГв угол при в будет тупой, остающийся
же острый ...ясно же..
11
Книга Архимеда о делении ф и г ур ы
Стсмахия на четырнадцать связанных
с пей фигур, находящихся с ней
в (рациональных) отношениях
Нарисуем параллелограмм***), и пусть он будет ABGD {рис. 3};
разделим BG пополам, в Ё, восставим EZ перпендикулярно к BG,
л ров едем диагонали AG, BZ и ZG, разделим такте BE пополам в Н
и восставим НТ перпендикулярно к НЕ; затем приложим к точке Н
лпленку, направим ее на точку А и проведем ПК, ра.чделаи AL пополам
и М и проведем ИМ', тогда прямоугольник АЕ
будет разделен на семь частей. После этого
разделим CD пополам в N, а также ZG в С,
проведем ЕС, приложим, линейку к точкам В
и С и проведем СО, проведем еще CN; тогда и
прямоугольник ZG будет раздел он па семь ча-
'! стей, но иным способом, чем первый прямо-
прямоугольник, а вес], квадрат будет разделен па
четырнадцать частей.
Докажем теперь, vto каждая из четыр-
четырнадцати частей находится со всем квадратом
» рациональном отношении.
Так как ZG является диагопалью прямо-
прямоугольника ZG, то треугольник DZG будет
половиной этого прямоугольника и, следова-
следовательно, 1/4 квадрата. По треугольник GNC есть 1/а от треугольника
DZG, потому что если продолжить ЕС, то она пройдет через точку D, и
тогда треугольник GDC будет нпловиной треугольника DZG и равен
вместе взятым треугольникам С NC nDNC; елсдоиатслыто, треуголь-
Рис. 3.
*) И У1 «л НГ/ меньше угла НДВ, а пвд равен НГВ.
**) Конец з и весь 4 црочеегь невозможно.
•••) То есть квадрат.
380 АРХИМЕД
ник GNC будет 1/1В квадрата:
тр-к «Л'С = ~ ЛЦСР.
Если мы, кроме этого, учтем, что линия ОС направлена в точку В,
как она в дейстцителышсти и начерчена, н линия Л'С будет параллель-
параллельна стороне BG квадрата, а следовательно, и треугольника ОВС,
то, таким образом, мы будем иметь пропорцию
BG : Л'С ~= СО : NO.
Но BG в четыре рааа больше NC, значит, и GO будет в четыре раза
больше N0; поэтому GN будет в три раза больше N0, и треугольник
67VC равен трем треугольникам ONC. Но так как мы показали, что
треугольник GNC составляет х/1в квадрата, то треугольник ONC
будот ^g квадрата:
тр-к QNG = ~ ABCD.
4 О
Далее, так как треугольник GDZ есть-^- киац,рата и поэтому треуголь-
ник GNC будет т^ егп, а треугольник NCO его/„ , то для четырехуголь-
четырехугольника DOCZ остается -п- площади квадрата
Затем, согласно предположению, линия NC проходит через точку
F, и CF является параллельной к GE; поэтому мы имеем пропорцию
EG : CF=EQ: CQ^CQ: lfQ.
И так как F.Q равна 2CQ и GQ равпа 2 FQ*), то троуголышк ?()G
будет вдвое больше каждого из треугольников GCQ и Л'/^. Но ясно,
что треугольник EGZ равшг двум треугольникам EFG, так как ZE
равна двум FE. И так как треугольюш EGZ составляет -г хшадрата, то
треугольник EFG будет -л- последнего. Но треугольник EFG втрое
о
больше каждого из треугольников EFQ и GCQ; зпачит, каждый из
этих треугольников будет ^ квадрата AG.
тр-к EFQ=-^j-ABCD; три GCD = -У-ABGD.
И треугольник EGQ вдвое больше каждого из треугольников EFQ
и GCQ; зпачит, он будет ^квадрата-
гр-к EGQ = ~? ABGD.
Далее, так как ZF равпа EF, то треугольник ZFG равол
троугольшису EFG; если мы теперь отнимем треугольник GCQ, раи-
nijii трсу2ч)лт.иийу EFQ, то останется четырехугольпик FQCZ, равный
треугольнику EGQ; следовательно, четырехугольник FQCZ будет
1 ¦ ¦ ¦
-ф квадрата AG:
*) Так как EG=2CF.
СТОМАХИЙ 381
Теперь мы разделили прямоугольник ZG на 7 частей и переходим
к делению другого прямоугольника.
Так как BZ и ЕС являются двумя параллельными диагоналями,
и ZF равна EF, то треугольник ZLF ранен EFQ; поэтому треугольник
ZLF есть уj квадрата АС:
тр-к ILF= ^ ABGD.
Поскольку ВН равна НЕ, то треугольник BEZ будет в четыре раяа
больше треугольника ВНТ, так как каждый из пих будет прямо-
прямоугольным. Но тик как BEZ есть -у квадрата ABGD, то треугольник
ВНТ будет тц последнего.
тр-и ННТ--ПГ ABGD
Далее, согласно нашему предположению, линия НК проходит через
точку А, следовательно, мы имеем пропорцию:
лв -. ыт=вк ¦ кт.
Но АВ равна 1НТ\ значит, и ВК равна 2КТ и, следовательно, ВТ
равна ЗКТ; таким образом, треугольник ВНТ будет втрое больше
треугольника КИТ. Но так как треугольник ВНТ есть -у.- всего квад-
квадрата, то треугольник КИТ будет js последнего:
тр-к' КИТ—- -fs ABGD.
Далее, треугольник ВКН ндное больше треугольника КИТ и, следо-
следовательно, равен -у квадрата.
трчГ ПКН — -'- ABCD
Затем, так как BL равна 2ZL и AL раина 2LF*), то треугольник
yliJL будет 1»Д1юе больше треугольника ALZ и треугольник X/^Z
вдвое больше треугольника ZLF. Но так кик трертольпип ZLF
составляет ^твсего квадрата, то треугольник ALZбудет ^последнего,
тр-к ALZ— -~- ABGD
и значит, треугольник ABL будет ->г его. По треугольник ARM
равен треугольнику BML; значкт, каждый из атих трсугольни-
кон будетр квадрата.
тр-к А ПМ = тп-1» KML = -— ЛПСП.
' 12
ТСщв остается пятиугольник LFEIIT, равный полоиине шестой части
*) В подобных треугольниках ABL и Z1.F сторона AB^
382 АРХИМЕД
вместе с нолошшой восьмой части всего квадрата *).
-l-(-L + -L) ЛИС/.).
Таким образом, мы разделили и (прямоугольник) АЕ на 7 частей;
тем самым и вся фигура ABGD разделена па 14 частей, находящихся
с ней в (рациональных) отношениях; а это и есть то, что мы хотели.
СТОМАХИЙ АРХИМЕДА
Рассматриваемое сочинение имеет своей целью дать математическую теорию игры
вроде современных головоломок, п которой состап.'шлись из данных кусочков геометри-
геометрические фигуры заданного вида, причем составление должно было быть или совершенно
точным, или же допусти)осе, и некоторое приближение.
ПредлагаемЕ.ш текст состоит из дпух отрывков. Начальный греческий текст явй-
ден Гейбергом в апимепитим Константинопольским палимпсесте, открывшем нам «Эфод»
в греческий текст трактата «О плавающих телах»; ол .найден в достаточно испорчеплом
состоянии и в некоторой степени исправлен по консультации Гейбсрга с датским матема-
математиком П. Хегардом A*. Ileegsm)). Вторая часть сохранилась п арабском переводе в руко-
рукописях берлинской библиотеки и бодлеяиской библиотеки в Оксфорде. По берлинским
рукописям этот отрииои был издан Генрихом Зутером п 1.899 г. (AbhantHungen z. Ce-
schichte dur Mathematik, 1X.4U1 и ел. A89!))); данный Зутсром немецкий перевод и поме-
помещен л издании Гейберга с небольшими изменениями.
О Стомахии Л|>химеда (латппскйй термин lorailus) гопорят латинские г]»амматики
ио:»д1К!Й ;шохи Марий Викторин и Лтилш! Фортушщнан (Koil, (Irammalici Jatini т. VI,
стр. 100 и ел. и 271 и ел.)-
Перт.ш пишет: «Как тот архимедовский Joculus, составленный из четырнадцати
пластинок слониной кости квадратных, или треугольных, и в том и в другом случае раз-
различно оформленных, подобных как бы строительным деталям; в нем при ограниченном
И определенном количестве пластинок вследствие многообразного их вида можно иаобра-
аить то корабль, то меч, то деревцо или какие-нибудь другие фигуры».
Лтилпп Фортунациап пишет: «Архимедовский loculus, имсюбппт \Л пластивок из
слоновой кости с раипообраяными углами, заключенных в киадрытную форму, и, когди
мы перекладываем, изображающргй то шлем, то кинжал, то колонну, то корабль, и иро-
и.шодищий Пссчисленшле фигуры; в нашем детстве этот locultis принес много пользы
для укрепления памяти».
Соответствующая игра была распространенной в Позднюю эпоху римской импе-
империи {IV—VI века и. а.).
*) Нетрудно показать, что зтот пятиугольник состапляе» -^ uccro киадр:1та, что Лрхкшсд
записывает ио египетскому образцу:
1 7 1 4-|-3_1 -II-
О МНОГОГРАННИКАХ
11Л1Ш, МАТЕМАТИЧЕСКАЯ БИШШОГГКЛ V, 34 Ifnllsdi, т. 1, стр. ЗЛ2
*
«Таковыми являются не только указанные божествешиейншм
Платоном пят), тол, а именно — тетраэдр, гексаэдр, октаэдр и доде-
додекаэдр, пятои же икосаадр, но и пайдевныо Архимедом тринадцать
числом [рис. 1}, заключающиеся между равносторонними, раныоуголь-
пымк, но не подобными друг другу многоугольниками.
Перным из них является октаэдр, заключенный между 4 тре-
треугольниками и 4 шестиугольниками.
За ним следуют три четьцжаддатиграппика, из которых первый
заключается между 8 треугольниками и A квадратами, второй — между
6 квадратный и 8 шестиугольниками, третий же; между 8 треугольни-
треугольниками и 6 восьмиугольниками.
После них идут дна диадцатитеетиграипика, ш которых первый
заключается между 8 треугольниками и 18 квадратами, второй же-
между 12 квадратами, 8 шестиугольниками и C восьмиугольниками.
После них будут три тридцатидвухграншша, из которых первый
заключается между 2,0 треугольниками и. 12 пятиугольниками, нторой —
между 12 пятиугольниками и 20 шестиугольниками, третий же — меж-
между 20 треугольниками и 12 десятиугольниками.
После них идет один трпдцатиносьмигранник, заключающийся
между .42 треугольниками и (> квадратами.
За ним следуют дин шеотидесятидвугранпика, из которых первый
заключается между 20 треугольниками, !Ю кнадратами и 12 пятиуголь-
пятиугольниками, второй же — '30 пнадратамд, 20 шестиугольниками и 12 деся-
десятиугольниками.
После них идет последний девлностодвухгранник, заключающийся
ме;кду 80 треугольниками и 12 пятиугольниками.
Сколько же углов и ребер имеет каждая ид дтпх J3 млогогранныл
фигур, можно усмотреть следующим образом: у тех многогранников,
у которых телеспие углы заключаются только между тремя плоскими
углами, если пересчитать все плоские углы, которые содержат все
грани многогранника, то ясно, что число телесных углов будет равно
третьей части полученного числа, у тох же многогранников, у которых
телесные углы заключаются только между четырьмя плоскими, то,
«ели пересчитать все плоские угли, которые имеют все грапи много-
384
АРХИМЕД
грапника, то четвертая часть полученного числа будет числом телес-
телесных углов многогранника; точно так же у тех многогранников, у кото-
которых телесный угол заключается между 5 плоскими углами, пятая часть
неего количества плоских углов будет числом телесных углов.
Количество же ребер каждого многогранника мы найдем таким
способом. Если пересчитать все стороны, которые имеют ограничи-
нающие мпогограниик плоские фигуры, то ясно, что их число будет
Рис. 1.
равно количеству плоских углов. Но так как каждое из ребер мпого-
грашшка, будет общим для двух граней, то ясно, что половина указап-
иого количества будет числом ребер мпогограттака.
Так пот перпмй из 13 неоднородных многогранников, поскольку
он содержится между 4 треугольниками и 4 шестиугольниками, будет
иметь 12 телесных углов ы 18 ребер. Действительно, у четырех тре-
треугольников будет 12 углов и 12 сторон, у четырех же шествуголь-
О МНОГОГРАННИКАХ 385
никоя 24 угла и 24 сторопы; так как общео число получается равным
36, то число телесных углов пеобходимо будет третьей частью выше-
упомлпутого числа, поскольку каждый, из его телесных углом заклю-
заключается между 3 плоскими углами, кил и честно же ребер будет полови-
половиной этого числа; то есть ЗУ, так что ребер будет 18.
Из четырнадцатиграшшков первый заключается между 8 тре-
треугольниками и 6 квадратами, так что он имеет 12 телесных углов, ибо
каждый «го угол заключается между четырьмя плоскими углами; ребер
же оп будет иметь 24. Второй из четырпадцатиграшшков, поскольку он
:«аклгочается между 6 киадратами и 8 шестиугольниками, будет иметь
2\ телесных угла, ибо каждый из его углов заключается между 3 плос-
плоскими углами; ребер же он имеет 36... (третий же из четырнадцнтигран-
пикои, заключающийся между 8 треугольниками и 6 восьмиугольни-
восьмиугольниками, будет иметь 24 угла и 36 ребер)...
Из дпадцатнтссти грани икон периый, поскольку on содержится
между 8 треугольниками и 18 квадратами, будет иметь 24 т.„к спых угла
и 48 ребер. Второй же из двадцатишестиграшшков, поскольку он со-
содержится, между 12 киадратами, 8 шестиугольниками и 6 восьмиуголь-
восьмиугольниками, будет иметь 48 углов и 72 ребра.
Иа тридцатидиугранпиков первый, поскольку он содержится
между 20 треугольниками и 12 пятиугольниками, будет иметь 30
телесных углоп и 60 ребер. Второй же из тридцатидвугранникок,
поскольку он содержится между 12 пятиугольниками и 20 шести-
шестиугольниками, будит иметь 60 телесных углоп и 90 ребер. Третий же ии
тридцатидвугранников, поскольку он содержится между 20 тре-
треугольниками и 12 десятиугольниками, будет иметь 60 телесных углов
и 90 ребер.
Тридцативосьмигратшк, содержащийся между 32 треугольни-
треугольниками и шестью квадратами, будет иметь 24 телесных угла и
60 ребер.
Из шестидесятпдвуграшшков первый, поскольку он заключается
между 20 треугольниками, 30 квадратами и 12 пятиугольниками, будет
иметь 60 телесных углоп м 120 рвбер. Остающийся шестидесятидиу-
гранник, поскольку он заключается между 30 квадратами, 20 шести-
угольпиками и 12 десятиугольниками, будет иметь 120 телесных углов
и 180 ребер.
Допяностодвугранник же, заключающийся между 80 треугольни-
треугольниками и 12 пятиугольниками, будет иметь60 телесных углов и 150 ребер».
ВАТИКАНСКИЕ СХОЛИИ К 11АППУ (ITuRsch, т. Ш)
A) «Октаэдр имеет 4 треугольника., 4 шестиугольника, 18 ребер,
12 телесных углои; каждый из телесных углов заключается между
3 плоскими углами, на которых два шестиугольника и пднн трнуголь
пик, так что до 4 прямых ио. хватает одного и днух третей прямого
угла. Он получается из нерпой пирамиды, если разделить се ребра на
три равные части и через точки деления провести плоскости и выбросить
углы.
B) {Первый) четырнадцатиграшшк заключается между 8 тре-
треугольниками и 6 квадратами; он имоит 24 рнбра и 12 телесных углов,
каждый из которых содержится можду 4 плоскими углами, из которых
два принадлежат квадрату, два же треугольнику, таи что до 4 прямых
не достает одного и двух третей прямого угла. Он получается из куба,
25 Архимед
да. архимвд
если разделить ребра ого пополам и череи тички деления, пронести
плоскости, отбросан нее 8 углов.
C) (Второй) четырпадцатигранннк заключается между (> квадра-
квадратами и 8 шестиугольниками, имкет 36 ребер и 24 телесных угла, каж-
каждый ии которых заключается между 'Л плоскими углами, из которых дна
принадлежат шестиугольнику и один квадрату. Он получается и»
октаадра, если разделить па три части каждое из его ребер, нровютн
чоро;* точки д|>Л1!11Ия плоскости и отбросить (> углов.
D) Третий (из четырнадцати!ранпиков}, поскольку он заклю-
заключается между 8 треугольниками и C иоеьмнугольниками, будет иметь
24 телесных угла, каждый из которых содержится между 3 плоскими
углами, иа которых два принадлежат восьмиугольнику и один тре-
треугольнику; ребер гке он имеет 36. Он получается из куба, если каждое
и» его puftnp разделить так, чтобы получилось три отрезка, из которых
средний и квадрик; будот вдвое больше каждого из крайних (то ость
если а средний, а Ь крайний, то а —¦ Ь\'2).
E) ^Первый) дпадцатишестигранник получается из четьтрнадцатп-
грашшка, заключающегося между 8 треугольниками и (} квадратами,
если разделить каждое иа его ребгр титлам, черсм точки дольний
пронести плоскости и ...»
ГЕГОН, Dcfinilioncs, 104 ctji. 6в и ел.
«Архимед же говорит, что он всего шшк'.ч тринадцать тел, могущих
быть вписанными и шар, добавив к вывЕоупошшутым пяти (правильным
многогранникам) еще восемь. Из них чггырнилцатиграшшк был иа-
иестен и Платону; был же он двоякого рода — один составленный из
8 треугольников и E квадратов, то есть из земли и воздуха, какой знали
и некоторые из древних, другой же — из восьми квадратов и f? тре-
треугольников, что кажется более трудным».
В герокош-кчх слонах пш-ржатся дно ошибки: Архимед открыл не 8, a l.j miioio-
гранникоп, которые вес могут быть пи и сыпными в им\\\; ат отиоелтельно второго
четырнйдц;гп1Г])ашн]кц oir ;i»(!T нси'^лп.коилс спо.нчшя, как movkuo индоть из приведен-
приведенного rmiml'. yiioMiniiiiini! о и(!Ш1<: и ио:|дух(! объясняется тем, что IItiutou считал атомы,
аомли имеющими форму куба, атомы же ш>:!дука—форму октаэдры, состоящего h;j
п]]:шилы1ЫХ тргуголi.iiiiков.
- (9
ТРАКТАТ АБУ-Л-Х АСА! IA САНИТЛ ИБН КУРРЫ
О ПОСТРОЕНИИ ОПИСАННОЙ ОКОЛО ГИЛ1»А ТЕЛЕСНОЙ ФИГУРЫ
С ЧЕТЫРНАДЦАТЬЮ (. )С I.! (ШЛ Н И Я М L1
Мы хоти.м объяснить, как построить отнимающую данный ша|>:
фигуру с четырнадцатью рашшгторопиимп и ранноуголышмн осно-
основаниями, f&t
Эта фигура пс принадлежит к чтму многогранников с подобными
гранями; наоборот, носом ь идее граней япляются треугольниками п
шесть — четырехугольниками, lipinn'.ai птрнш1 оклады наются со imv
рыми согласно одинаковому распо-
расположению, и сторона полученного ^ j
тела является no,:FOBiiiiou диаметра
шара.
Пу»:гь {рис. IJ круг ЛВС йудот
наибольшим кругом и» всех кругов
данного шара, п котором мы хотим
построить многогранник; пусть/) бу-
будет его центром. Есаы та желаем по-
построить в данном круге телесную фи-
фигуру с четырнадцатью пещшанилми,
как мы описали выше, то строим
сначала в круге ABC рниносторонппн
и равноугольный шестиугольник
AEFBCG. И;» центра/) к углам шести-
шестиугольника нроподим линии DA, D.K.
J)F, ПН, DC, DG. Тогда треугольники, на которые разделяется этим»
линиями шестиугольная фигура, будут рннносторонними треугол1х-
ииками. Па треугольниках ADE, FDB, CDG строим из рапносторон-
них. треугольников пирамиды, которые насыпаются тнтраэдрами *)-
Пусть ил nupiirnniii будут в точках Н, J, А"; проиндем соединительные
прямые ИЗ, JK, КН. Затем на треугольниках EDF, ВВС, DGA
J'hc. 1.
*) Ьукиялыю «фигурами огня», тлк как » илнтшюипнсй фчлиссфии а гемм огня считались
¦¦.¦яяющими фс1|1му iijiaFiuibH'.го тетраэдра; правильный октаидр. цув и ирлшшьтшЛ ииосиздр но яняпс»-
'¦.[иным гтцич1иг;1М нпамвя.чись на срсцисясклвпм Имщ-цкс «фигурой ноадуха». «фигурой зсяили» и ефип--
,1-i.i йоды», а праииЛ1.ный додсниндр нааыналси «фигуцнй нибй». так как, согласно Платону, ату форму
никл весь ш:р и долим.
ZS*
388 АРХИМЕД
с другой стороны площади круга построим другие тетраэдры совершен-
совершенно так же, как мы строили вышеупомянутые. Затем между точками на
их исршинах проведем соединительные прямые.
Теперь я утверждаю: Мы построили в данном шаре фигуру с четыр-
четырнадцатью равносторонними и равноугольными основаниями, из кото-
которых восемь являются равносторонними треугольниками, а шесть остаю-
остающихся — равносторонними и прямоугольными четырехугольниками.
И каждая из их сторон раина каждой из сторон упомянутых треуголь-
треугольников, их взаимное соедъшшкю следует совершенно особому располо-
расположению, причем ребро полученного тела является половиной диаметра
шара.
Доказательство этому таково: из точки II, являющейся вершиной
тетраэдра ADEH, опускаем перпендикуляр на плоскость его основа
имя ADE; пусть этот перпендикуляр будет HL. Из точки L проводим
к точкам A,E,F,D линии AL, LE, LFt LD. Так как линия HL перпен-
перпендикулярна к плоскости ADE, то она будет перпендикулярна ко всем
линиям, которые можно через ее конец провести в упомянутой пло-
плоскости. Следовательно она будет также перпендикулярна к обоим
линиям AL и LD. Тогда оба квадрата, построенные па обеих линиях
UL и AL, будут вместо равны квадрату, построенному на АН,
а оба квадрата, получающиеся ла обеих линиях III, и LD, будут вместе
раины квадрату, построенному яа DI1.
Ли? |- Li;*-, ел*
Но квадрат линии АН равен квадрату линии DH, так как треугольник
A.HD раиносторонеп, ибо он является одной из граней тетраядра.
Следовательно, оба квадрата обеих линий HL a AL будут вместе равны
обоим квадратам па обеих лилиях UL и LD.
¦HL* I ЛЬ* = НЬ*+Ы)*
Если мы вычтем общий ква;фат линии UL, то останется, что квадрат
лшши AL раиеп квадрату линии IJ). В таком случае обе линии AL,
LD в обоих треугольниках ALE, LDE раипы;
м. = ld
точно так же к этих треугольниках будут раины обй линии АЕ a ED.
•гак как сторона шестиугольника является половиной диаметра. Затем
сторона LE будет и обоих треугольниках общей. Следовательно, оба
эти треугольника будут равны; и каждый из углов этих треугольников
будет так же равен ему соответствующему. Таким образом, линия LE
делит угол AED пополам. Но угол ЛЕО равен двум третям прямого,
так как треугольник ЛЕО равносторонний. В таком случае угол LED
будет третью прямого угля, а угол DEF — двумя третями прямого
угла, так как треугольник EDF равносторонний; следовательно, сово-
совокупность LEF этих углов составит прямой угол. Тогда квадраты,
• построенные на обеих линиях LE, EF, будут вместе равны квадрату,
построенному иа LF.
ТРАКТАТ АБУ-Л-ХАСАНА САЬНТЛ ИЕН KYFPI.1 38Й-
Прибавим общий квадрат, построенный на 11L. Тогда квадраты,
построоппые на линиях LE, EF, HL, будут вместе равны квадратам
на линиях LF и LI1.
I.KS | EF* + HLa - LF
Что касается обоих квадратов на линиях LE и #L, то они будут
равны квадрату, построенному на ЕН',
так как HL перпендикулярна ко hcwi прямым, проведенным ии точки L
на плоскости ADE, которая сонпндает с плоскостью круга ABC.
И точно таи мо, если провести соединительную линию HF, то оба
квадрата, построенные на обеих линиях ///,, LF, будут имеете равны
квадрату, ног/гроенпому на линии HF.
Следовательно, оба квадрата, построипчъш на обеих линиях ЕН,
EF, равны квадрату, построенному па линии FII.
п* + kf2 ¦ /-и3
Следовательно, угол FE1T будет прямым. Подобным же способом
установим, что yro.it EFJ тоже будот прямым. Далее фигура IIEFJ
будет четырехсторонником, у которого дно. стороны Eff, FJ перпен-
перпендикулярны к стороне EF. И эта фигура расположена а одной пло-
плоскости. И так как мы имеем три линии ЕН, FJ, EF, одна из которых
нвлмвтея стороной (правильного) шестиугольника и круге ABC,
а остальные две линии раины диум сторонам итого шестиугольника,
то три стороны плоской фигуры EIIJF раины, л два вышеупомянутых
угла являются прямыми. И таким образом выясняется, что эта фигура
представляет равносторонний прямоугольный четырехугольник.
И точно так же выяснено, что каждый пл днух четырехуголышко»,
соответствующих упомянутому четырехугольнику, и именно оба четы-
четырехугольника BJKC и GKHA, будут прямоугольными и раиносторил-
ними, и что лежащие с другой стороны три четырехугольника, оспоиа-
пиями которых являются линии АЕ, FB, CG, будут также прямо-
прямоугольными и раиносторонними. И стороны всех этих шести четырех-
четырехугольников раины, так как они равны сторонам шестиугольника и круп;
ABC. Точно так же стороны иыходящих. и:« этих четырихуголыгикои-
шеетч треугольников, котор.7.тл1И ямлмнутся треугольники АЕН, FJB,
С KG и им соответствующие с другой стороны, имеющие основаниями
лилии RF, ВС и GA, будут тоже равны друг другу и сторонам шести-
шестиугольника в круге ABC. Следовательно, они будут равны сторонам
шести нышеупомяпутых квадратом. Что же касается треугольники
ITJK, то каждая ии его сторон будет одпонремеипо одной из сторон:
четырехугольников EffJF, BJKC, GKHA, каждая из которых раин»
стороне шестиугольника. Следовательно, нее они равпы друг другу.
Точно так же обстоит и с треугольником, лежащим с другой стороны
и соответствующим треугольнику HJК. Таким образом, оба эти три
угольника ралносторонни и оба равны остальным шести треугольни-
треугольникам, о которых мы уже упоминали.
Теперь все яти фигуры заключают тело с четырнадцатью основа-
основаниями, построенное нами согласно описанному. И его основания имеют
одинаковое расположение, та it как каждый из треугольников окружен
по сторонам тремя четырехугольниками, а каждый из четырехуголь-
390 АРХИМЕД
пиков окружен пи сторонам, четырьмя треугольниками. И каждый
из углов этого тола заключается между двумя углами четырехуголь-
четырехугольника и двумя углами заключенного между лшш трвуголышка. И то же
самое одинаковым обра:юм имеет место у исех его угли п. Таким обра-
образом, вес то углы тоже будут равны.
Что касается того, что упомянутый нами заданный шар обпимает
построенную телесную фигуру, то это ясно потому, что круг ABC
проходит через принадлежащие углам телесной фигуры точки А, Е, F,
В, С, С. И линии, проведенные из центра этого шара к остальным
углам при точках /f, /, А", а и мои но линии DTI, DJ, DK и им соответ-
сткующис с другой стороны, будут раины друг другу и также равны
колонии» диаметра шара, так как они являются сторонами перво-
первоначально построенных нами тетраэдров. Таким образом, поверхность
тара проходит через всо углы этой, построенной нами телесной фигуры,
и сторона упомянутой телесной фигуры с четырнадцатью основаниями
раина полонии? диаметра шара.— Да будет хнала Гюгу, плактитслю
мира*).
¦) Текст опубликован и (.>u<-ll<:ri п. Sludten z. (ieselilclite d. Mathematik, Abtti. B. Studien,
Л1. П. стр. 185—198.
КНИГА ЛЕММ АРХИМЕДА*)
]J ПЕРЕВОДЕ ТКБИТЛ БКН КОРЫ [1] С РАЗЪЯСНЕНИЯМИ
УЧЕНОГО ЛЛЬМОХТЛСШЛПИЛЬГАСАНЛ ГАЛИ БКП АХМАДА
11 АСУ ЭНСКОГО [2]
Ученый Альмоххаесо увернет, что эта ил ига итнисится к Архиме-
Архимеду*, в ней находится ряд Красиных предложений, хотя л малочислен-
малочисленных, по и высшей степени полезных, касающихся начал геометрии,
ноли коленных и изящных; занимающиеся геометрией ученые причин
еляют эту книгу к тем промежуточным сочинениям, которые надлежит
читать между кинтмй En ил иди и Альмагестом; действительно, некото-
некоторые места предложении последней книги нуждаются для своего разъяс-
разъяснения » других предложениях. И сам Архимед указал на такие пред-
предложения и ссылался на них в других своих произведеняях, говоря,
напримвр, «как мы показали и предложениях о прямоугольниках**)
и еще «как мы доказали л нашем изложении, рассуждая о треугольни-
треугольниках», накинец, «как мы докапали п предложениях о четырехугольни-
четырехугольниках»; п пятом предложении он принодит и высшей степени оригиналь-
оригинальное доказательство.
Затем Абусахлъ Альиухи [3J панисал книгу под заглавием «О по-
порядке предложений в книге лемм Архимеда», и дал более общее п луч-
лучшее докизатнльстио итого предложении, а также разобрал все те «дока-
«доказательства», который ^пимент от присоединения отношения [4]. Когда
я узнал «б этом, то к более темным местам этой книги я добавил объяс-
объяснения или примечания на полях, .чатем вес им указанное подкрепил
предложениями, как мне показалось нужным, и взя.:г из предлогкепий
Абусахля дна, необходимых для объяснения пятого предложения [5J,
опустив остальные ряди краткости и вследствие того, что они не
являются необходимыми.
I
Если два круга ЛЕВ и CED взаимно касаются в точке Е {рис. 1}
« их диаметры ЛВ, CD параллельны и если соединить дне точки В, D
сточкой касания Е (прямыми) DE и BE, то линия BDE будет прямой.
*) Книга пе[|еьрдеиа г латинского С сохранением латинизирсишшых иясч арабских
•*) 1-м. сноску и rfiffijUTonwniiio II.
АРХИМЕД
Пусть оба дсптра будут G, F; проведем соединяющую линию GF
и продолжим до Е; затем прошлом DH параллельно GF. Так как H.F
равна GD и GD будет раин ой EG, то от ран-
ранных прямых FB,FE останутся GF, или DH,
пНВ, который будут друг друту раины, в так-
также будут раиигл углы НОВ a HBD. И так как
углы EGD, EFB прямые, а углы EGD, DHB
ракпы, то останутся два угла GED^ GDE,
которые будут равпы друг другу и диум
углам 1IDB, HBD; следовательно, угол EDG
будет равен углу DBF. И угол GDB возь-
возьмем общим; значит, оба угла GDB, FBI)
(которне равны двум прямым) равпы двум
Рис. 1. углам GDB, GDE. Следопателыю, и отм
углы будут также ранни диум прямым;
значит, линия EDB будет прямой; я это и есть то, чего мы хотели ffi].
\\
Пусть СНА {рис. 2} будет полукруг, которого касаются пря-
прямые- DC, DB и {прямая} BE перпендикулярна АС; если соединить А
и D, то BF будет равна FE.
Доказательство. Соединим -1 с В, продолжим ее по пря-
прямой и проведем CD до пересечения с ней и
G; затем соединим С с В. И так как угол
СВА есть угол и полукруге, то оп будет пря-
прямым; остающийся угол CBG чоянс будет пря-
прямым u DBEC будет ирямоугодышм паралле-
параллелограммом. Слсдоиатсльно, в прямоугольном
треугол i.niiKe GBC из В проводится перпенди-
перпендикуляр BD к оспошпгию и прямые BD и DC
раины, так как они являются касательными
к кругу; значит, CD будет раннятьея DG,
как мы это показали н составленных нами
предложениях о прямоугольных*). И так
как в треугольнике GAC линия BE прове-
проведена параллельно основанию к из D — сере-
середины оспоиания — проведена линия DA, пср«с<Мхатощая параллель
в F, то BF будет равна FE. А это н «ть то. чего мьг хотели Г7|.
Ш
Пусть С А (рис. 3} будет сегмент круга и В какая-нибудь на
нем точка; если BD перпендикулярна к А С и отрезок DE равен DA,
а дуга BF равна дуге В А, то соединяющая CF будет равна СЕ.
Доказательство. Проведем соединяющие л ноли АВ. BF,
FE, ЕВ. Так как дуга ВА раина дуге BF, то и прямая АВ будет равна
BF. И так как AD равна ED и оба угла при D прямые, a DB — общая,
то, значит, АВ patma BE, а «следствие того, что BF и BE расшы, будут
равдше и оба угла BFE, ВЕР. И так как четырехугольник CFBA вписан
*) Вероятно, пропущепо слово «огреугольииках».
КНИГА ЛЕММ АРХИМЕДА
ЗЯЗ
Рис. 3.
¦в круг, то угол CFB с противолежащим ому углом CABt или с углом
BE А, будут раины /шум прямым. По угол СКВ имеете с углом BE A
раним двум прямым: значит, оба угля СРВ и СЕН будут равны.
И (после вычитания BFE и BEF) оста-
остаются равные углы CFE, СЕР; значит,
СЕ будет раина СР. А зто и ость то,
чего мм хотели [8].
IV
Пусть ABC {рис. 4} будет полу-
полукруг; построим па диаметре АС два
полукруга АО и DC и восставим пер-
перпендикуляр DH; получающаяся фигура,
которую Архимед называет «арбело-
ном» *) (это будет площадь, ограниченная дугой большого полукруга
и двумя окружностями малых кругов) будет равна кругу, диаметром
которого является перпендикуляр /)Я [f)J.
Доказател i. с т в о. Так как линия DB будет средней про-
пропорциональной между обеими линиями DA, /)С, то прямоугольник
на AD u DC будет равш квадрату им
DB. Возьмем (циажды) прямоугольник
на AD и DC имеете с квадратами на AD
и па DC; получится удвоенный прямо-
прямоугольник ми AD,DC г-двумя квадратами
на AD и на DC, то есть кнадрат на АС,
равный удвоепному квадрату на DB
вместе с двумя квадратами на AD, DC.
Отношение кругон таково же, как отно-
отношение квадратов (их диаметров); сле-
следовательно, круг с диаметром АС будит
ранен удвоенному кругу с. диаметром DB вместе с диумя кругами на
диаметрах AD и. DC и. полукруг АС будет ранен кругу с диаметром DB
и двум полукругам AD, DC. Отнимем два общих полукруга A/), DC;
останется фигура, заключенная между полукругами AC, AD, DC (зто
и есть фигура, которую Архимед паивал «нрбелон») и ранний кругу,
диаметр кпторого DH. А это и есть то. чего мы хотели.
]'нс.
Если дан полукруг АВ {рис. 5.}, ни его диаметре, где-нибудь взята
точка С, пи диаметре построены два полукруга АС и СВ, из С восста-
восставлен перпендикуляр CD к АВ и с обеих сторон {от него) построены
два круга, касающиеся как этого перпендикуляра, так и обоих полу-
полукругов, то эти два круга будут равны.
Д о к а з а т е л ь с т и о. Пусть один ил атих кругов касается f)C
в К, полукруга АВ a F к полукруга АС я С; проведем диаметр НЕ;
он будет параллелен диаметру АВ, вследствие того, что углы HECS
АСЕ прямые. Проведем соединяющие линии/7/ и ПА; тогда линия АР
будет прямой, как сказано в предложении Т. Пусть АР и СЕ встретятся
в D так, как они выходят под углами А, С, которые (в сумме) меньше
двух прямых. Проведем также соединяющие линии РЕ и ЕВ; линия
— скребок,
394
АРХИМЕД
FEB тоже будет прямой, как ми сказали (предложение 1), и перпен-
дикулярноы. к AD, так как угол AFB прямой, как угол и полукруге АВ.
Ироиедем соединяющие прямые IIG и GC; тогда ПС будет тоже пря-
прямой [10J. Проведем соединяющие прямые EG и GA; тогда ЕА будет
прямой; продолжим ее до / и
соединим И с /, прямая ВТ то-
тоже будет перпендикулярной к
At; приведем соединяющую
прямую D1. И так как AD и
АВ суть две прямые и из D про-
проведена DC. перпендикулярная
к АВ, л ни В проведена BF.
перпендикулярная к DA, и ати
пер неидмкулнры пересекаются
друг с другом в Е, а АЕ, про-
продолженная до J, перпендику-
перпендикулярна к ВТ, то BID будет пря-
прямой, как мы показали в пред-
предложениях, написанных в коммлпт&рии к трактату о прямоугольных
треугольниках И1]. И так как углы AGC, А1И прямые, то BD и CG
будут параллельными и отношение AD к DH. раплоо отношению АС
к НЕ*), будет раин о отношению АВ к ВС;
Рис. 5.
АР
ПН
ПК
J
ш:
прямоугольник можду АС, СВ, следовательно, будет равен прямо-
прямоугольнику между АВ, НЕ. И точно так же для круга LMN докажем,
что прямоугольник между АС, СВ будет ранен прямоугольнику между
АВ и диаметром этого круга; отсюда докажем, что диаметры кругов
EFG, LMN раины; значит, яти два круга будут равны. А это и есть
то, что мы хотели.
VI
Если дан полукруг ABC {рис. 6} и на его диаметр*' взята точка Z),
причем AD в полтора раза больше DC, затем па AD и DC описаны
два полукруга и между тремя
{указанными) полукругами по-
построен касающийся каждого из
пах круг EF, в котором проведен
диаметр EF, параллельный
диаметру АС, то требуется
найти, отношение диаметра АС
к диаметру EF.
Пропадем дне соединяющие
линии АЕ и ЕВ, а также две
линии CF и FB; тогда СВ и АВ А
будут прямыми, как сказано и
цирком предложении. Затем на- Ш;' '"
чертим дко линии FGA, Elf С —
можно покапать, что они тоже будут прямыми; точно так же {будут
прямыми) и обе линии DE и DF; проведем соединяющие прямыеDI,
И.) подобия греуголышиов ЛОС a Him.
КНИГА JJEMM Л1'.\1Ш14ДА 395
DL, а также ЕМ и FN и продолжим последние до О и Р. И так как и
треугольнике AED прямая AG перпендикулярна к ED, a. DI перпенди-
перпендикулярна к АЕ, и обе эти прямые н.чанмпо пересекаются вМ, то, значит,
#М6> тонн* будет перпендикуляром, как иго мы показали и написанном
памп рассуждении о спойствах треугольники, с доказать!ьстном чего
мы уже встретились в предыдущем предложении; точна так же и FP
будет перпендикуляром к С А. И так как два угла у L л у ? прямые,
то DL будет параллельна АВ, и также Z>/ параллельна 67?; значит,
отношение Л/> и DC будет таким же, пак отношение AM к /7W и
как отношение /16* к 0/\
.-¦и» am _ао
и отношение CD к DA будет таким же, как CN к NE, или как СР
к РО.
<:i) cn а'
Но AD и полтора рапа больше DC; значит, АО будет и полтора раза
больше ОР и ОР и полтора раза больше СР. Значит, три линии АО,
ОР и PC бу,чуг пропорциональны, я каких единиц будет* в СР четыре,
таких в ОР будет шесть, в АО денять и в С А де пятнадцать. И так как
РО раина EF, то отношений АС к EF будет таким же, как отношение
девятнадцати к шести.
Таким образом, мы нашли требуемое отношение. Точно так же,
если бы отношение AD к DC было каким угодно, например четырех
к трем, или пяти к четырем, или каким-нибудь другим, то рассужде-
рассуждения были бы такими же. Это и есть то, чего мы хотели. [12].
VII
Если оком) квадрата один круг описан, а другой вписан в него,
то описанный круг будет вдвое больше вписанного.
Действительно, пусть АВ {рис. 7}, будет круг, обнимающий
кнндрнт АВ, a CD — иписашшй и него; пусть диаметр кнадрата
будет АВ, он же будет диаметром описанного круга; прове-
проведем CD —диаметр --писанного круга — па-
параллельно (стороне) АЕ, которая будет
ему рак на. И гак как квадрат л а АЛ «двое
больше кнадрата на АЕ, или CD, и отно-
отношение кнадратон на диаметрах равно отно-
отношению одного круги к другому, то, сле-
следовательно, круг АИ будет вдиос больше
круга СП. Это и есть то, чет мы хо-
хотели.
VIII
Если в круге как-нибудь проведена линия Рис. 7.
АВ {рис. 8}, продолжена по прямой, па ней
отложена ВС, равная полудиаметру кру<>а, полученная точка С сое-
соединена с центром D круга и соединяющая прямая продолжена до Е,
то дуга АЕ будет втрое больше дуги HF Г13].
Дейстнитслым, нронедем EG параллельно АВ и проведем сое-
соединяющие прямые Dli, DC. 'Гак как дна угла DUG и DGE равны, то
396
АРХИМЕД
I'ur,. 8.
II
угол GDC будет вдвое больше угла DEG. И так как угол BDC равен
углу BCD, а угол CEG равен углу АСЕ, то угол GDC будет вдво»
больше угла CDB, и весь угол BDG
втрое больше угла BDC, и дуга BG, рав-
равная дуп» АЕ, будет «трое больше дуги
BF. А это и есть, то, чего мы хотели.
IX
Если в круге две прямые линии АИ,
CD {рис. 9} пересекают друг друга nod
прямым углом (по не в центре), то две
дуги AD, С В будут ранены двум дугам
AC, DB.
Проведем параллельно АВ диаметр
#/', который рассечет CD пополам в С;
тогда дуга ЕС будет ранна ED. Так как дуги EDF и ECF являются одно-
: временно полуокружностями, и дуга ЕП равна дуге ЕЛ вместо с дугой
AD, то дуга CF с двумя дугами ЕЛ, AD будет равна полуокружности.
Затем дуга ЕЛ равна дуге HF; значит, дуга
СВ с дугой AD будет раина полуокружности.
И остаются две дуги ЕС'! ЕЛ, то есть ду-
дуга АС вместе с дугой DB, тоже ранние полу-
полуокружности. А ото п (>сть то, чего мы хо-
хотели.
X
Если будет круг. ЛВС {рис. 10}, каса-
касательная к нему DA, секущая его DB и е.щс
касательная DC, то после того как будут
проведены СЕ, параллельно DB, соединяющая Рис. 9.
ЕЛ, пересекающая DB в F, и опущен из F
перпендикуляр FG на СЕ, последний рассечет СЕ пополам в точке G.
Соединим А и С. Так как DA — касательная, а АС — секущая
к кругу, то угол D Л С равен углу, попадающему в противоположный
сегмент АС, то есть углу А ЕС.
Последний же ранен углу AFD
вследствие того, что СЕ и BD па-
параллельны; значит, и углы DAC.
AFD будут равны. И в диух тре-
треугольниках DAF, AHD равны два
угла AFD, HAD и угол D общий;
вследствие этого *) прямоугольник
между FD, DH будет ранен квад-
• рату па DA, или квадрату на ПС.
FD 1I1 — Л.Л2 = Г>Сг р.,-
И так как отношение FD к DC то же, что у CD к DH,
УР
SB-
IjH
*) Иа подобия треуголышкои АЛ7> и AIID имеем FD ¦. AD—AD: 1)ц.
КНИГА ЛЕММ АРХИМЕДА
и угол D общий, то треугольники DFC, DCH будут подобными и угол
OFC рапным DCH, который и свою очередь равен углу DAH. А атот
последний равсп углу AFD; следовательно, два угла AFJ), CFD раины
и угол DFC равсп углу FCE. Но DFA равен углу АЕС\ следовательно,
в треугольнике FRC дна угла ири С и Е равны, два угли при G пря-
пряные и сторона GF общая; вследствие этого CG Судет равна GE. Зна-
Значит, СЕ распекается п G пополам. А ято и есть, то, чего мы хотели.
XI
Если в круге две линии АВ, CD {рис. 11} взаимно пересекаются
под прямыми углами в точки И, которая не является центром, то все
квадраты на АЕ, BE, EC, ED равны квадрату на диаметре.
Проведем диаметр AF и соединяющие прямые AC, AD, CF, DB.
И так как угол AED прямой, то он ранен углу ACF. Угол ADC ра-
равен углу AFC, вследствие того, что они стоят па дуге АС, и в двух
треугольниках ADE, AFC остальные углы CAF
и DAE равны; одновременно будут раины две
дуги CF, DB, а значит, равны и их хорды. Дна
квадрата па DE, ЕВ равняются квадрату на
BD или CF,
два квадрата на АЕ, ЕС рання ютсн квадрату на
СА,
ЕС*^САЪ
и два квадрата на CF. СА равняются квадрату
па FA,
Рть. 11.
или па диаметре. Значит, ш-л- квадраты на АЕ, ЕВ, СЕ, ED будут
равны квадрату па диаметре.
\ яд" + ск2 -ь ео* = лил
А это и есть то, чего мы хотели.
XII
Если к полу крупу на диаметре АН {рис. i'A] из точки С проведены,
касательные в точках D, Е, также соединяющие прямые ЕЛ, DB, вяа-
umiio пересекающиеся в F, затем соединяющая прямая CF продолжена до
С, то СО будет перпендикулярна к АВ.
Проведем соединяющие прямые 1)Л, ЕВ. Так как угол BDA пря-
прямой, то и треугольнике DAB остальные два угла DAB, DHA будут
раины одному прямому. Но так как угол АЕВ -пики примой, то они
будут и ему раины. Восьмом общин угол FBE; оба угла DAB, ABE
будут равны вмести шштым FBE, FEB или углу DFK — пнвшнему
и (троуголышке) FHE. И так кик CD кас.агтея круга, a DB его пере-
пересекает, то угол CD В раиляется углу DAB п равным образом угол CEF
равняется углу ЕЙ А; значит, диа угла CEF, CDF вместе будут раины
углу DFE. Из пашего трактата о четырехугольных фигурах стано-
нится ясно, что если между двумн ранными линиями, встрнчающимися
и некоторой точке (как обе наши линии CD и СЕ), провести две взаимно
398
ЛРХИМКД
пересекающиеся липни (как наши DF и EF), так что содержащийся
между ними угол (наш угол /') будет равен двум имеете иаятым углам,
которые получаются в точках и^алмлого пересечения обеих пар линии
(это будут дна угла при D и Е), то линия, выходящая из точки встречи
н и точку пересечения (наша лилия CF),
будет равна любой из встречающихся ли-
липни (то ость CD или СЕ) *); иследстлие
:>того CF будет paima CD; значит, угол CFD
ранен углу CDF или углу DAG. Но угол
CFD имеете с углом DFG ранен двум
прямым; лначит, угол BAG с углом DFG
ранен дпум прямым, и и четырехугольнике
ЛDFG остаются дна угла ADF, AGF, рав-
равные «место двум прямым. Но угол ADH
прямой; значит, будет прямым и угол A.GC,
и GC будет перпендикулярной к АВ. А
зто и есть то, чего мы хотели.
XIII
Если в круге две линии АВ, CD
Рис. 12. {рис.13! взаимно пересекаются, причем АВ,
но не CD будет диаметром круга, то по
проведении ш обеих точек А. В двух перпендикуляров АЕ, BF к пря-
прямой CD, на последней будут отсечены, равные {отрезки) CF, DE.
Проведем соединяющую прямую ЕВ и из / —центра круга — пер-
перпендикуляр 1G к CD и продолжим его до Н на прямой ЕВ. Так пак
IG есть перпендикуляр, опущенный из центра на линию CD, то он
разделит се пополам n G. п так как IG, AE суть дна перпендикуляра
к тон жо прямой CD, то они будут параллельны. fl
Поскол ьку же В[ равна 1Л. то и ВН будет равна
НЕ; и вследствие отого ранетгетна, а также по-
потому, что BF параллельна HG, нрямая/'С будет
paitiia GE, и па днух рашшх прямых GC, GD
(по вычитании равных), останутся равпые пря-
прямые FC, ED. A rm> и ость то, чего мы хотели.
XIV
Если будет полукруг АН [рис. 14}, от его
диаметра АВ отсечены равные прямые ЛС, HD
а ни линиях AC, CD, ОН построены полукруги,
причем центром, двух полукру.юе па АН и CD будет точка. Е, то по
проведении к АН перпендикуляра EF, продолженного до точки G, кру.'
на диаметре FG будет равен площади фигуры, заключающейся между
большим полукругом, находящимися, внутри его двумя полукругами
и средним полукругом, который будет вне большого полукруга. И это
есть фигура, которую .Архимед называет «салинонъ [141.
будег
суши
бить вн
) Бопелли и споем издании дикашшает »тп следующим образом. Продолжим ПС. и пусть СИ
КНИГА ЛКММ АРХИМЕДА
•:до
Так как DC разделена пополам is Е и к пей прибавлена С А, то дин
квадрата ни А)<1, С А ндвос больше двух кнадратов па DE, ЕА
¦ЪА--{-СА*=2 (ПК- i-K/l3)
(Евклид «Начала», II, 10). Но FG равна DA;
FC = [EG + EF — ЕЛ + ED\ ^.. Л I)
значит, дна квадрата на FG, АС лдвио большо двух кпадратои.
a&DE, НА.
УС- j АС" = 2 (DEi ¦•-¦ 1?ЛЪ
И так как Л В ндиое больше АЕ, и 6YJ
идноо больше A'i>,
то два квадрата на АВ, DC и четыре
раза большо днух кнадратов на DE,EA
или бдпоо больше Д1$ух кнадратов на
GF, АС.
АН" + DC2"= •'. {ПК- - К Ah -1 («К*-г ЛСг)
Вследствие птого дна круга с диамет-
диаметрами АН, DC пдное больше тех, диа-
диаметры которых суть GF, АС, и половины кругов с диаметрами АВ
и CD раним двум кругам с диаметрам» OF и АС. По круг с диаме-
диаметром АС ранни двум полукругам АС, Ш). Значит, есчи отнять от них
дна общих полукруга АС, ВО, то останется фигура, ограниченная
четырьмя полукругами АВ, CD, DB, AC (которая и является той,
которую Архимед называет «салинон»), равиая кругу, диаметр кото-
которого FG. А это и есть то, чего мы хотели.
XV
Если дай гиицкруг АВ {рис. 15} и « нем АС хорда пятиугольника,
причем, половиной дуги АС будет AD, и проведены аядиияющая пря-
прямая CD, продолженная вплоть до Е, нашем соединяющая прямая DB,
пересекающая С А в F и опущен из F
перпендикуляр FG па АВ, то линия EG
будет равна полудиаметру крут [15J.
Пролсдсм соединяющую прямую
СВ; пусть // будет центр круга, при-
ш!Д1:м HD, DG, и АР. Так как угол
ABC, осноиннием которого является
сторона пятиугплшика, равен двум
пятым прямого угла, то каждый n:i
двух углов CBD, DBA будет пяток
¦частью прямого. И угол DIIA вдвое больше угла DBH; значит, угол
DHА будет двумн пятыми прямого угла. Так как в двух треугольниках
CBF, GHF дна угла при В равны, углы О и С прямые и сторона FB
общая, то ВС ршша BG. И тик как в днух треугольниках CBD, GHD
две стороны СИ п /3G ранпы и так же раины два угла при В, а сторона
BD общая, то дна угла BCD и BCD раины. И каждый из них есть шпеть
пятых прямого *) и равен втняшгему углу DAE вписанного в круг четы-
•) Утл ЬСА примой, а угол ACD=AllD=l/b части примого.
400
АРХИМЕД
рехугольника В ADC *), значит, остается угол DAB, равный углу OGA,
и DA будет равна DG. Итак как уголDHG ранен диум пятым частям
прямого, а угол DGII — ник'.ти питым, то в остатке получается угол
IIDG — дво пятых прямого, и DC будет равна GIF. Так как угол ADE,
явлшощннея 1ШСШШ1М для вписанного и круг четырехугольника ADCB,
будет равен углу СВА, то он будет составлять две пятых прямого угла
и равен углу GDH. И так как в двух треугольниках EDA, HDG
будут дна равных угла EDA, IIDG, а также дна угла DGII, DAE и две
стороны DA, DG, то ЕА будет раьпа HG. Возьмем AG общей; тогда EG
будет раина АН. А это и есть то, чего мы хотели.
[\ отсюда ясно, что линия DE равна полудиаметру круга; так
как угол DAE равии углу DGII, то линия DH поэтому равна линии
DE. И и утверждаю, что ЕС разделяется в D в криштм и среднем
отпопшиии, причем большим отрезком является DE; и. так как ED
есть хорда шестиугольника, a DC — десятиугольника, то это уже
доказано в книге «Начал» (Евклид, кн. XIII, предложение 9). А »то
и есть то, чего мы хотели.
*) Дсйстнитсльио. угол DAB образует iK0° как с углом BCD (no свойств? випсииного четы-
четырехугольника), так и с углом DAK (uo сиойствг смежных углов).
КНИГА АРХИМЕДА О ПОСТРОЕНИИ КРУГА,
РАЗДЕЛЕШГОГО ТГА СЕМЬ РАВНЫХ ЧАСТЕЙ
Перевод Абу-л-Хагана Сабита vf>n Нурры ал-Харрани [1]
Исправление а редакция бедного Мутафы Сиддики [2],
да помилует его Аллах]
Ко имя Аллаха милостивого, милосердного]
Сочинение состоит из одной книги и восемнадцати предложений.
Я гсиюрго поело хналы Аллаху и молттш за пророка-избранника, за его семей-
семейство и за его друзей. Желая пероимсать ату книгу, я смог достать то.чыт дефектный
экземпляр, испорченный n.i-:ia невежества того, кто его переиистлиал, и недостаточного
попимнния им (предмета). (' большим трудом мне удалось исслелшшть и ироанализи-
роиать задачи этой книги и принести предложения этой тспигн п порядок при помощи
легких и близких но jiiu'iirmrin разъяснений. К ним я лобшш.'г никоторые дпкаяатпль-
втиа позднейших <учепых> |3]. Да поможет Аллах этому споим епдийстпипм!
Предложения
Т*)
Проведем {линию) АВ и отметим на ней две точки С и D {рис. 1}
таким образом, что квадрат CD равен квадратам АС и ИВ. Тогда
5
Гис. 1.
я утверждаю, что квадрат АВ равен удвоенной плоскости из АВ на
СВ [4].
*) Номера предложений написаны л рукописи кн полях.
¦J(> Архимед
402 АРХИНКД
Так как киадраты АС и DB раины квадрату CD,
то, если мы прибавим к обоим сторонам квадрат CD и удвоенную пло-
плоскость и;{ АС па CD, получится, что три квадрата AC, CD n DB
и удвоенная плоскость из АС на CD ратшы удвоенному квадрату CD
и удвоенной, плоскости из АС па CD.
АС* | CD* :- И1>а |. 2.4С- CD - 2CD* -|- *Л
Но удиоошм.ш кнадрат CD и удвоенная плоскость из АС на CD раним
удвоенной плоскости из AD на DC.
a-:- 2АС- ГО *- 1АГ>- DH.
Поэтому три liisaApara AC, CD и DB и удвоенная плоскость из АС
на CD раним удноеиной плоскости из AD па DC. Так как кнадрат AD
рикен is над pa гам Л6' и CD it удноенной плоскости \\.\ АС на 67J,
-« Ai;z I- С?«й-I- 2AC-CD
то кпндрпты .-1/J) и DB раины удвоенном плоскости w.\ AD на DC.
Прибапим к обеим сторонам удиоеилую плоскость w.i DB на ^1Л>. Тнгца
квадраты AD и Z)B и удиоонпая плоскость из AD иа DB, то ость киад-
рат АВ, равны удвоенным плоскостям и:» AD па Z)C и n;s Af) па /^Л",
то есть удвоенной шюскости из AD на СВ.
ЛИ2 ^2ЛЯ-СВ
Это и есть то, чвго мы хотели.
11
[Д р у I- и м с и о с о б о м {рис. 2]. Так как квадрат АВ ранги
трем квадратам AC, CD и DB и трем уднпгниым плис копям \\л ЛС
п& CD, из АС на ЯЯ и и:> CD па Z)
fjD ! ЛС1- l)lt ¦¦ (П. Щ))
и квадрат CD pa ном квадратам АС ч DH,
то квадрат АН ранен удинешшму киадрату ttJ н трг.м уд«« м
плоскостям из АС на Ci>, «н .4С на Z)j5 и из Г/> на /J/У. Так как
УДНО01ШЙЯ плоскость из АВ па CD раина удиоеппому К1»адрату CD и
удвоенным нлоскостим из АС на Г/) и ii:j DB на С?>.
2AHCD = 2ГС*-1 2 (.4t-CO + Wt-CC)
то квадрат /1/? ракон удвосниыи плоскостям из АВ на С7>« ия ,4Сиа
КНИГА О ПОСТРОЕНИИ KlWTA, РЛЗДКЛКННОГО НА СЕМЬ РАВНЫХ ЧАСТЕЙ 4]Й8
Но удвоенная плоскость ни АВ па CD равна удноеппым плоско-
плоскостям из С В ни CD и мя АС на СО, а удоогашыа плоскости на АС па CD
и из АС па DH равпы. уднооппон плоскости из АС па СИ. Позтому
квадрат АВ ранни удвоенным плоскостям n:i СИ па CD и из АС на СВ,
то есть удвоенной плоскости \\л AD на СИ.
Ла - 2 iCIt-CD + AC-O!) -= 2AD-CH
А это и есть то, чего мы хотели. |
III
В каждом прямоугольном треугольнике удвоенная плоскость из
одного катета и гипотенузы как одной линии на другой катет, и гипо-
гипотенузу как одну линию равна квадрату периметра как одной линии.
Пусть треугольник — ABC я
{рис. Щ, а npH.Mo.ii угол — В.
Продолжим АС п се направле-
направлении о обе стороны и отложим
AD, рннную АВ, и СЕ, рапную i
ВС. Тогда очевидно, что DC € ~ " ".•
ратша АВ и АС, АЕ равна PjIC- 3-
у] С и СВ, a DE рншта периме-
периметру треугольника. Так как квадрат АС ранен сумме квидратои АВ и
ВС, то есть АО и СЕ,
W* =- ЛИ2 -| ПС* -" 4D* ^ С*.*
то удноютная плоскость из DC на АЕ равна квадрату DE (лредл. I).
А ЭТО И (!Г.ТЬ ТО, ЧСГО МЫ ХОТ13ЛИ.
Я ruiiopi»: другим oiiocofioM, лрмп.-и-сжащим Лбу Лли ал-Хуйуби l&j.
Так как плоскость иа DC на АЕ р.шил кикдрцгу Л6' и трем плоскостям из АС ¦
на СЕ, и.1 >JC па /ID к «з /Ш ни СЕ,
D -|-АП-СК
л !;иад|Ш1 -1С pnniMi кл,чд))атим D.\ м
-
т(| удмшчшая шкммеослъ из DC на ЛА' равна трем квадратам DA, АС, СВ » трем
удшошидм плоскостям ил АС на CJT, из >)t' n;i AD и на /ID на СЕ, ' в nfte это
ймегсе равяо квадрату Dti.
2DCAE - DA* + ACS + С?2-|- 2ЛС-СК Ч- 24С-AD -\- 2AD-CE =- WBa
П<кш1му удвоенная плоскость п:< П6' на АЕ ]>сШна кпадрнту /J/i.
2/Jf • ЛЕ = ПЕ*
А :гтч и ость то, чего мы хотели [6].
IV
В каждом прямоугольном- треугольнике, если опустить us ем пря-
прямого угла высоту на его гипотенузу, то кваОрпт периметра (треуголь-
(треугольника) как одной линии равен удвоенной плоскости иа гипотенузы на
периметр и эту высоту как иа одну линию. . - ,.;..-.-
404
АРХИМЕД
Пусть а треугольника ЛВС {рис. 4), прямой угол — В, а
опущенная высота — ИВ. Продолжим АС в ее направлении в обе
стороны. Отложим ЕА, равную АИ, СС, рапную СВ, и GH, равную J?/).
12
15
25
Рис. 4.
20
?
-н
Тогда я утверждаю, что квадрат EG равен удвоенпой плоскости из АС
на ЕЯ.
Действительно, так как HG или BD относится к CG или СВ, как
, или ИВ, к Л С,
НО
ВС
CG
ся
SA
то, «присоединяя», получим, что ПС относится к CG, как ЕС ч АС,
ЕС
~АС
переставляя, получим, что СП относится к ЕС, как CG к АС,
L
~АС
и, (снова) « присоединяя», получим, что ЕП относится к ЕС, как AGnAC.
ЕС"'
АС
2ЕН
Поэтому плоскость ид ЕП на АС равна плоскости из ЕС на AG « удвоен-
удвоенная плоскость из ЕН па АС равна удвоенной плоскости ия ЕС на АС.
Но удвоенная плоскость ия ЕС на AG равна квадрату ЕС. (предл. (II).
АС = 2ЕС • AG ¦-= ii'G*
Поэтому квадрат i?Cf ранен удвоенной плоскости из АС на /?//. Л »то
и есть то, 4ei%o мы хотели [7].
Д р у г и м с н о с u б о м. Ксриемсн к тому я;с треугольнику
и его высоте и продолжим ВС в ее направлении в обе стороны {рис.5;.
Отложим CG, равную
А АС, БЕ, равную АВ, и
ЕН, равную BD. Тогда я
утверждаю, что квадрат
EG равен удвоенной пло-
плоскости из GC на СП.
В Действительно, так
25 "^ как плоскость из BE, или
АИ, па ВС равна плоско-
плоскости из ЕН, или BD, иа С(\
или АС, то удвоенная
плоскость из KB на #Г равна удвоенной плоскости из ЕН па CG.
12
20
Рис. 5.
КИИГА О ПОСТРОЕНИИ КРУГЛ. РАЗДЕЛЕННОГО НА CJSML РАВН1ДХ ЧАСТЕЙ 405
Но кмадриты ЕВ и ВС раины квадрату CG
НЕ* |- НСЯ = CG*
и квадрат ЕС равен удвоенной плоскости ив ЕВ на ВС и квадратам ЕВ
и ВС.
?С8= 2ЕЧ- ПС + ЕВ* -|- ВС2
Поэтому квадрат ЕС равен удвосппой плоскости из ЕЛ па CG и квад-
квадрату CG.
КС*=* 2KB-СС -г CG*
ГТрибаним к обоим сторонам кнадрат CG. Тогда квадраты ЕС и СО
равны удвоенной плоскости из ЕН па CG и удвоенному кнадриту CG.
Поэтому кнадрат EG puucu удвоенной плоскости из GC па СЕ и кпадра-
там GC и СЕ, то есть ранен удвоенному квадрату GC и удвоенным
плоскостям из GC на ЕЙ и из GC па СЕ,
КС2 = 2СС ¦ СЕ -f¦ GC2 + CiSz ~ !HGC* + GC ¦ EH + GC ¦ CE)
а это равно удвоенной плоскости из GC на СИ и удвоенному квадрату
G61, то есть удвосппой плоскости GC на GIJ. Поэтому квадрат EG равен
удвосппой плоскости ив GC на GH.
А это и есть то, чйто мы хотели.
[Я говорю: другим способом, принадлежащим Абу ил-Хубуби. Квад-
Квадрат СЕ равен трем квадратам ЕВ, ВС и GC вместе с удносшшми илоскосияыи
из СС на СЕ и из НС на В/С,
GE*=EB2+BC2+GC2+2(.GC- CE+1IC ¦ BE)
а удвоенная плоскость GC на GH равна удвоенному квадрату GC и удвоенной
плоскости n.i СС на СИ.
GC ¦ GU=i2GCi+2GC- CH
Но кнадрат СС ринетт киадрцтпм BE к ВС, удвоенная плоскость ия СС на СД
равна удпоршгым плоскостям ил СС на ЕП и из 6Y; па CVi, о удпоонна» ило-
CKOCTi. из СС на Ь77 раяна удш.-енной плоскости ил KB на ВС. Поэтому удвоенная
плоскость из СС па СЛ равна трем квадратам Eli, ВС и GC и удвоенным пло-
плоскостям из GC на С? и иа ВС на Z#?.
2GC СН=ЕИй + BCZ+GC2+ 2 (GC. СЕ+ВС. BE)
Поэтому кпадрат СЕ рнпшг удлоеиной плоскости из СС ни GH.
А это и есть то, чего мы хотели.
Другим способом,
Квадрат СЕ ривин квадратам СС и СЕ и удвоенной
Другим способам, принадлежащим Абу Абдаллаху анг-Шашги [8].
падратам СС и СЕ и удвоенной плоскости из СС иа СЕ.
Но квадрат СЕ равен квадратам СО и BIS, то есть кпадрату ПС, и удвоенной
плоскости иа СВ иа BE.
. be
Поэтому кпадрат GE ранен удвоенному квадрату СС и удвоенным плоскостям ия
ОС на СЕ и из СЛ на #Я.
GBz=2GC8+2(GC-r;E+CB.fiE) • :
По удвоенный квадрат СС и удвоенная плоскость на СС на СЕ равны удвоенной
илоскисти из СС на СЕ,
2GC*'t- 2GC ¦ CK=2GC ¦ СЕ
406 ЛГХИМЕД
удвоенная плоскость и» СП а& BE рал на удвоенной плоскости из СС на Eli,
2CDBE=2GC-EH
а удвоенные плоскости на ОС на GE и из СС на ЕП — это удвоенная плоскость
ии СО на СП. Следовательно, квадрат СЕ раьеп удвоенной плоскости из СС на 677.
CE'^ZGV-GII
Л ото и есть то, чего мы хотели.)
VI
В каждом прямоугольном треугольнике с разнижи катетами квад-
квадрат периметра как одной линии вместе с квадратом разности между
катетами равен, квадрату гипотенузы, и одно-
одного из катетов как одной линии вместе с квад-
квадратом гипотенузы и другого катета как од-
одной линии.
Пусть к треугольнике ЛЯС {рис. 6} пря-
прямой угол — В. Отложим на ВС линию BD,
равную АВ. Тогда я утверждаю, что квадрат
периметра как одной .пинии имеете с квадратом
''»"¦¦ И- ОС район квадрату АВ и АС как одной линии
имеете с квадратом ЛС и ВС как одной линии.
Действительно, квадраты ВС п BD раины квадрату СО и удвоен-
удвоенной плоскости из ВС на BD.
НС' + 1Н>*— CD8 -f 2IIC-BD
Но 1Ш равна Л# и квадрат АС ранен квадрату CD и удвоенной пло-
плоскости из ЛВ па ВС. . :
AC'i = cD'1 ¦¦¦ гли-нс
Прибавим к обеим сторонам киадрат Ah и удвоенную плоскость из АВ
па АС. Тогда квадраты АВ и АС я удвоенная плоскость из АВ па АС,
то есть квадрат АВ вместе с АС как одной линии, раппгл квадратам
АВ й CD и удиошшой плоскости ш АВ на АС имеете с СВ как одной
линии.
АВ* -!- АС' + 2АП-АС -- САИ + ЛС)* —.Аи* | СС2 -f 2.ДН МС + СВ)
Прибаиим еще раз к обеим сторонам квадрат AC n ВС как одлой линии.
Тогда кпадрат АС и ВС как одной линии вместе с кнадратом .4/? и АС
как одной линии равпи квадратам АВ и 67), кмадрату ЛС и .ВС как
одной липки и удвоенной плоскости из АВ ни AC jr Z?C как па одной
линии. Но квадрат АВ, квадрат АС и ВС как одной линии и удиоонная
" плоскость из ЛВ на АС и #С как па одной линии ралпы квадрату пери-
периметра троуголышка. Следовательно, квадрат АС и ВС как одной
jJUHiiit имеете с Кондратом АВ и -46' как одной линии рапси квадрату
nepmierjia треугольника как одной линии «месте с ккадратим CD. А это
и «сть то, что мы хотолн [9].
' •• VII
Д р у г и м с н о с о б о м. Пусть в треугольнике ABC {рис. 7}
прямой угол — В. Продолжим АС и ее папранлешш в обе стороны.
Отложим АН, равлуго АВ, СС, равную СВ, и СН, равную избытку ВС
над АН. Тогда ЕС равна АН и AC, AG раина АС и ВС, а вся /?6г равна
КНИГА О ПОСТРОЕНИИ КРУГЛ. .РАЗДЕЛЕННОГО НА CBMI. РАВНЫХ ЧАСТЕЙ 407
периметру треугольника и я утверждаю, что квадраты EG и GH раины
кпадратам ЕС и АС.
Действительно, так как киадрат АС равен квадратам АВ и ВС,
то осп. киадратам: СП и CG, а квадраты СН и CG равны квадрату СП
J)
яо
Г, 5 н 15 С 2Ь А К ?
Гнс. 7.
и удвоенной плоскости из 67/ на CG, то квадрат АС р.-пн?ц кнадрату G1I
и удвоенной плоскости из СИ на CG.
ЛСг = ЛВ3 ¦! ВС2 -- СН* + СС2 = С7Нг + 2СН- CG
Н» <7// равна АЕ, поэтому квадрат АС ранен кнадрату СП и удвоенной
плоскости из Л?' на CG.
Прибапим к обеим сторонам удвоенную плоскость из ЕА на АС. Тогда
квадрат АС и удпошшан плоскость ип ЕА па АС равны квадрату СП
и удноеппой плоскости го ЕА да AG.
в fi-^IT8 | 2ЛК. ЛС
Прибаним еще раз к обеим сторонам квадрат ЕА. Тогда квадрат ЕС
равен киадратам ЕА и СП и удвоенной плоскости из ЕА на ЛС
Затем прибавим еще раз к обеим сторонам киадрат АС. Тогда киад-
paTiji ЕС и AG ранпы трем киадратам ЕА, АС и 67/ и удвосшюй пло-
плоскости из #.Л на AG.
Но кнадрпт ЕС район киадратам ЕА и AG и удвоенной плоскости из
?\4 на Л С.
¦ АС
Поэтому квадраты EG и G// раины квадратам Л'С и AG.
Это и ость то, чего мы хотела.
|Я говорю: д р у г и 11 с н о с о б о м, лушпадлежащим Лбу Али ал-Хубу-
би. Кипдрити ЕС и ЛС, ]>»ппы клодратпм ЕА и СС, удвоенному квадрату АС
и удвоенным плоскостям из НА на АС и из СС на /1С.
А-С* I JO*=ffi4B+C1C'-i-2JlC*+2 (^.-l ¦ ЛС\-СG. АС)
Квадраты EG и Си раины четырем квадрата» ЕА, AC, CO n Gil и трем удвоен-
удвоенным плоскостям из ЕА на СС, из НА пц ЛС и из АС па С61.
KOB+GM*-BAB+AC"+CG4CHB+2{BA.CC | БД./1С ;-Л«.СС)
Но удьоегшая плоскость из К^1 на СС, то есть из СИ на СС, равна удвоенному
кнадрату 67/ и удпошшой плоскости на СП па СИ.
• СН
408 АРХИМЕД
Поэтому, если мы щтбиким к обеим сторонам квадрат fifi, получитек, что квад-
квадрат Off и удвоенная плоскость из ЕЛ на СО равны квадратам СИ и CG, то есть
квадратам ЕА и CG, а квадраты ЕЛ и CG равны квадрату АС.
Поэтому квадраты EG и GH равны квадратам ЕА и CG, удвоенному квадрату
-<4С и удпоепным илоскостям из ЕА на АС и из /1С на CG.
. СС)
Следовательно, квадраты ?'6' и GH равны квадратам ЕС и /1С.
А это и есть то, чего мы хотели.
Другим способом, црипадлежащим Абу Абдаллаху аш-Шаияи.
Квадрат ЕС равен квадратам ЕА и АС и удиоошюй плоскости из ЕА на АС,
ВСв=Л.Ба |ЛСЙ|-2ЛВ. АС
а квадрат ЛС равен квадратам ЛС и СС и удвоенной плоскости из АС на CG.
АОг=ЛСв 1 CCZ г2 AC .CG
Но квадраты ЕЛ и CG равны квадрату АС, поэтому квадрати ЕС и AG равны
утроенному квадрату J-1G' и удвоеннымплоскомям из ЕА на АС и из CG на АС.
с-мс ¦ со
Так как удвоепш.ш квадрат АС, удвоенный плоскости из ЕА на ЛС и из CG на АС
и удлоеопая илоскость ив ЕА uu C6' рашмл клидриту EG,
• ЛС 1-ГG¦ 2
то если мы произведем сложение it отбросим общее, останется: квадраты У?С и АС
и удвоенная плоскость из ЕА па CG равны квадратам EG и ЛС.
Приблштм к обеим сторонам квадраг СП. Представим себе, что липни ЕА и CG
состанляют одну линию, разделенную пополам, и к пен нрисоединеаа TIG. Тогда
квадраг всей (липни, состоящей из) ЕА и CG смеете с квадратом HG равен
удвошшьш квадратам ЕА и CG.
{ЕА
Поэтому удвоенная плоскость из ЕА на СС а квадрат СП равны квадратам ЕА
и СО, то есть квадрату ЛС.
2ЕА. CG-i-GH &~-ЕАг+СС2=АСг
Если отбросить это, останется: квадраты EG и GU равпы квадратам ЕС и AG.
А это и есть то, чего мы хотели.]
VIII
Проведем {линию) АВ и отметим па ней две точки С и D {рис. 8}
таким образом, чтобы плоскость из CD на АВ была равна плоскости
Рис. 8.
из АС па BD. Тогда я утверждаю, что удвоенная плоскость из АВ на
CD равна плоскости из AD па СВ.
Действительно, так как плоскость из АС на DB равна плоскости
из CD на АВ,
AC-DB^CD-AB ' . '¦
КНИГА О ПОСТРОЕНИИ КРУГЛ, РАЗДЕЛЕННОГО НА СЕМЬ РАННЫХ ЧАСТКП 409
. то удпоепная плоскость из АС на DB ранна трем плоскостям из АС
па CD, из ВС на CD и из АС на DB. Поэтому удвоенная плоскость
ни АВ на CD равна трем указанным плоскостям.
2CD-AH — 2АС- «В = AC CD -j- ЛС- CD + АС ¦ DB
Но плоскости из АС на G/) и из АС на ?)/? равны плоскости ин ЛС
на 67?,
AC-CD i-Au-DH = ACCH
поэтому удповниая плоскость из АВ на С'/) раина плоскостям из АС
на Си и из ВС т\ CD. Но плоскости из АС на 67* и из ВС на 67) равны
плоскости из Л/J на СВ,
2ABCD^AC-CB+IICCD=AD.CH
поэтому удвоенная плоскость из АВ на CD равна плоскости из AD
на С/?. А это и есть то, чего мы хотели [10].
гх
Пусть ABC — треугольник с прямым углом В {рис. 9}. В него
вписан круг DEG. Проведем {линию) DE и продолжим ее и {линию) ВС
в их направлениях, пока они не встретятся в точке И. Тогда я утвер-
утверждаю, что ВII равна AD.
Доказательство этого. Соединим А и П. Тогда AD равна АЕ.
Продолжим DE до встречи с АН. Поэтому плоскость из HD на
НЕ вмести с квадритои АЕ равна кнадрату АН [11]. Но квадрат АН
раисп квадратам АВ и ВН. А
Поэтому плоскость из HD па
НЕ вместо с квадратом АЕ
ранца квадратам АВ и ВН.
Но плоскость из HD на НЕ
равна квадрату HG.
'к г-г. Нс2
Поэтому квадраты АН и ВН
равны квадратам АЕ и IIG. *
Отнимем от обеих сторон квадрат ВН, останется: квадрат А В райе»
удвоенной плоскости из ИВ на BG и квадратам ВС и АЕ.
= 1ИП. UG + HGS + АЕ2
Отнимем от обеих сторон квадрат АЕ, останется: удвоенная плоскость
из АЕ на ЕВ и квадрат ЕВ раины удвоенной плоскости из ИВ на BG
и киадрату BG.
ПАЕ- КЬ Н К«в= 2IID-UG + «6*
Но KB равна BG, поэтому удвоенная плоскость из АЕ на ЕВ равна
АРХИМЕД
удвоенной плоскости из НВ ua BG.
КЙ = 2I Н 1H
Так как ЕВ равна ВС, то АЕ, то есть AD, равна В//. Л это и есть то,
чего mi>[ хотели.
X
Сохраним тот же чертеж. Ми утверждаем, что СИ относится
к ИВ, как DC к ЕВ.
Доказательство этого. Восстание и точно С перпендикуляр CF
{к ВС), продолжим IID в ее
направлении и будем продол-
продолжать эти дне линии, пока они
не встретятся it F {рис. 10).
Так как CF и АН параллельны,
треугольник FCD подобен тро-
угольнику ADE и АЕ отно-
относится к CF, как AD к CD.
АЕ AD
Поэтому, переставляя, полу-
получим, что АЕ относится к AD,
как СР к CD. Но АШ раина AD,
поэтому CF~ равна CD. Так как bic, 10.
(треугольник ВЕН подобен
треугольнику FCU), то СИ относится к ИВ, как б'/1, то есть CD,
к Ш?.
СИ
CF
CD
Л это и есть то, чего мы хотели.
XI
Сохраним тот же чертеж {рис. 11}. Мы утверждаем, что пло-
плоскость ил AD на DC равна площади треугольника {ABC).
Доказательство этого. Так
как < в силу X предложения) И С
относится к ///?, как CG к СВ,
плоскость из НС на ВО равна
Плоскости мл И В на CG.
HCDG- llli-CG
Так как (в силу VIII придло-
ассния) плоскость из НС па ВС
раина удвоеппой плоскости ин
AD па DC
НС- НС •= < 2UC-CH = Zlill. CG > = 2AD-VC
и НВ paima AE, a BG равна
BE и вся АВ равна IIG. то
плоскость м,ч АВ на ВС равна
удвоенной плоскости из AD на Z)C. Но {плоскость из) АВ па
раина удвоенной площади треугольника. Поэтому плоскость из AD на
DC равна площадл треугольника. Л это и есть то, чего мы хотели [12].
КНИГА О ПОСТРОЕНИИ КРУГЛ. РАЗДЕЛЁННОГО НА СКМГ, РАВНЫХ ЧАСТЕЙ 411
XII
Друг и м с и о с .и б о м. Представим себе прямоугольный тре-
треугольник ABC с прямым углом И {рис. 12}. В него вписан круг DEG.
Тогда я утверждаю, что плоскость ua AD на DC равна площади
треугольника.
Действительно, .«миля AD раина АЕ, a CD ранпл CG. Поэтому
квадрат АС равен квадратам АЕ и CG и удвоенной плоскости
из AD на DC. д
AV* = Ail" Ч- CG2 + 2AD ¦ НС
Но квадрат АС равен квадратам АВ и ВС,
АСа"ЛВа+ВСя
поэтому квадраты АВ и ВС раины квадра-
квадратам АЕ и CG и удвоенной плоскости из AD
на DC. Евли мы отнимем от обеих сторон
квадраты АЕ и CG, остапется: кнадраты ?'#
и BG и удвоенные плоскости из ЕВ я я АЕ и
иа CG на Gfl раины удлоетшой плоскости из
AD на Z)?\
?Н*+ UG2 4- 2 (ЕВ.АЕ + CG-GJi) == 2AD. DC
По квадрат ЕВ ранен киадрату BG и квадрат НС вместе с плоско-
плоскостью кп CG ua 67? раной плоскости из СВ ва Z?G.
ИО* Ч- CG ¦ Gti ™ С В ¦ UG
Поэтому удноеппые плоскости из ЕВ па _4# и на СВ па ,/?(? раины
удвоенной плоскости из AD ua DC.
1KB-ЛИ -=- 2C2J. !SG = 2A1). DC
. Но ЕВ равна BG, поэтому удвоенные плоскости из GB на ЛЕ и ил ЕВ
на СВ равны удвоенной плоскости из AD па DC.
2GII- ЛИ -|- ZED ¦ СИ -• 2АД. DC
Так как удноонлая плоскость из АЕ па ВС равна удвоенным плоско-
. стям из GB па АЕ ы из CG >ш ИВ, то есть (удиоенной плоскости из
GB на АЕ и) удвоенной шшскости из AD на
•iAHDC = 2 (G«-AE -- CG-AK) ~- 2 (С«-ЛЙ -I- .ID-DC)
то, если мы сложим каждую сторону с (чютлетствушщеи ей из двух
Apyi'nx сторон и отнимем общую удиоенную плоскость из GH па АЕ,
то останется: удвоенные плоскости из АЕ на С В а. из ЕЙ на СВ равны
учетверенной плоскости мз AD na DC.
2 {АЕ- НС -!- ВП' ПС) = <2(AD-DC¦[ 2СС-ЛК}> = i-U)- DC
Поэтому удвоенная плоскость из AD un DC раипа плоскостям из АЕ
на СВ и ил ЕВ на ZJC, го есть равна шюскости mi АВ на ВС.
DC = AU'DC
Но плоскость из АВ па С/? равна двум площадям треугольника. Сле-
донатнлыю, плоскость из AD ua DC раьна площади треугольника.
Л ато и ость то, чего мы хотели.
412
АРХИМЕД
XIII
Другим способом. Построим линии DH и EF, каждая
из которых равна CD {рис. 13!. Тогда BF равна СВ. Так как квадрат
АС равен квадратам АО и D1T и удвиоиной плоскости из AD на
DH, а также квадратам АВ и BF, то квадраты Л/) и DII и удвоенная
плоскость из AD на Z?# равны квадратам АВ А
и ZJF. Но квадраты AD и Z)// и удвоепная
плоскость из AD на DH равны квадрату АН и
учетверенной плоскости via Л1> на DH. Поэто-
Поэтому квадраты АВ и BF равны квадрату AU и
учетверенной плоскости из AD ua DH.
АС1 — -АОй-
J- 2ЛО. D/I
- ОН = ДВ*
iAD
Но квадрат .Д// и учетверенпая плоскость из
AD на DII рмвим квадрату AF я удвоенной
плоскости из АВ и BF.
АН в + iAD ¦ DH = <AB* + BF2>= AF3 H- 2ЛВ • BF
G
Рис. 13.
Поэтому если мы отнимем равные квадраты АН
и AF, останется: учетверенная <плоскость из) AD яа DIJf равна
удвоенной плоскости из А В на BF.
Если мы возьмем полопины отого, {получим, что удвоенная плоскость
из AD на DII рани» плоскости мн АВ па BF, то есть удвоенной пло-
Л1ади треугольника. Поэтому если) мм еще раз поступим так же, {мы
получим шютцадь треугольника). А ато и есть то, чего мы хотели.
XIV
Пусть треугольник ABC — прямоугольный треугольник с прямьСм
углом В, и пусть AD равна АВ, а ЕС равна ВС {рис. 14}. Тогда я утвер-
утверждаю, что [удвоенная] плоскость из ED па периметр треугольника
равна учетверенной площади треугольника.
Рис. 14.
Продолжим АС к ее папраплешш к обе стороны и отложим AG,
равную АВ, СН, равную СВ, и HF, равную ED. Тогда вся GH равна
периметру треугольника, а линии GA и CF, имеете взятые, равны АС.
Так как удиоеимаи плоскость на АС иа GH вместе с плоскостью из HF
на GH равна квадрату GII, а квадрат GII равен трем кладратам GA,
АС и СН и трем удвоенным плоскостям иа GA на АС, из GA на СИ
и из АС на СН, то удвоенная плоскость из АС на GH вместе с пло-
плоскостью из HF на GH раина трем квадратам GA, АС и СН и трем
КНИГА О ПОСТРОЕНИИ КРУГА, РАЗДЕЛКННОГО НА СЕМЬ РАВНЫХ ЧАСТЕЙ 413
удвоенным плоскостям на GA на АС, из GA па СН и из АС на СИ.
2АС СП + HF-GH = СЛа-|- АСа\- СНа-\- 2 (GAAC + GA-CH + АС-СП)
Но плоскость из АС на GH раина кпадрату АС и плоскостям из GA
на АС и из СИ на АС,
AC-GH = ACs + fiAAC + СНАС
а квадрат И С равен квадратам GA и СН.
иса^елач-слг
Поэтому удвоенная плоскость из АС на Gff равна трем квадратам СИ,
АС и СП и удиоенным плоскостям из GA ни Л С и из СН на .АС
2ЛС СН = САг + АС2 + СИ* -1- 2 «3.4 -ЛС -.- СН- АС)
Если мы от обеих сторон (одного из предыдущих равенств) отнимем
общую удвоенную плоскость из АС на GH-, останется: плоскость из HF
на GIT равна удноенной плоскости из GA па СН, то есть удвоенной
плоскости из АВ па НС.
И f • tin = 2GA. СП = 2Л13.ВС
Но плоскость из АВ на ВС равна двум площадям треугольника. Сле-
Следовательно, плоскость ия HF на GII, то есть плоскость из ED ка
перимнтр треугольника, равна учетисфиниой площади треугольника.
А это и есть то, чего мм хотели ИЗ].
XV
Пусть ACDВ — полукруг с центром G, в нем хорда А С {рис. 1.5).
Раздсшм дугу ВС пополам в D. Соединим В и D и отложим АЕ, рав-
равную АС. Тогда я утверждаю, что плос-
плоскость ия GB на BE равна квадрату DB.
Соединим D л C,D и A. D и С, D
и Е. Так как дуги CD и DB раины,
углы CAD и DAH рапнм. Тик как АС
раина АЕ, a AD — общая (сторона
днух ранных треугольников), то DE
равна СО, то есть DB, и угол DEB ра-
район углу DBE, то есть BDG. Поэтому " ? s
ЕВ относится к BD, как DB к BG. Рис. 15.
ЯП ~ BG
Поэтому плоскость из GR па BE равна квадрату DB. А это и ость то,
чего мы хотели [14].
XVI
Сохраним предыдущий чертеж. Мы утверждаем, что плоскость
из пемудиамстра на АС вместе с квадратом DB равна удвоенному
квадрату полудиаштра.
(Дейстнытелыго}, удвлоиимн кпадраг GB, го есть плоскость на
АВ па GB, ранен плоскости аи GB на АЕ имеете с плоскостью из GB
на BE,
-_>G/;a= AP-GB тСП-AK-i- GH- UK
то есть из 67? на АС (или из пол\диаметра на АС) вместе с плоскостью
ил GB на ЕВ.
АРХИМЕД
Но в силу предыдущего (предложения) шюскость из GB па BE
раина квадрату DB. Поэтому удвоенный квадрат GB равен плоскости
из нолудиамотра на АС вместе с квадратом DB. Л это и теть то, чего
мы хотели.
XVII
Представим себе квадрат ABCD [рис. 16}. Продолжим сторону
АВ в ее направлении до Е и проведем диагональ ВС. Поместим один
конец линейки в точке D, а другой
ее конец — на линии ЕА так,
чтобы он рассек ЕА в такой точ-
точке G, а АС в такой точке II и ВС
в такой точке F, что треуголь-
треугольник С А Н равен треугольнику CFD.
Проведем через точку F линию
KFL, параллельную АС. Тогда я
утверждаю, что плоскость из АВ
на К В равна квадрату GA, пло-
скоетъ из GK на АК равна квад-
ИС- '" рату KB и каждая из линий ВК и
GA длиннее линии АК.
Дейстнитслыю, так как плоскость из CD на FL раина плоскости
и» GA на АН,
Fb~CA-AU
то линия CD, или АВ, относится к GA, как АИ к FL.
ли
Так как каждый на треугольников GAH и GKF подобен треугольнику
FLD, то АН относится к FL,-как GA к LD или КВ.
CD
CD
с. л
АИ
14. '
ли
ал
FI.
ал
lilt
Поэтому Aft oTiior-итеи к GA, лай С А к КВ.
С.А
КИ
Точно таи же, FL, или .-IA", относите» и А"/\ или КН. как 1А>, или К И,
ч GK.
(Ж
Поэтому плоскость из АВ на KB раина квадрату СЛ, плоскость ил
GK на ЛК равна квадрату KB а каждая и:» линий GA и KB длиннее
линии ЛИГ. Л е>то и есть то, чшч> мы: хотели [15).
XV Ш ' .
Мы хотим построить круг, разделенный ни семь равных частей.
Пронедсмг линию АВ с иянсстнмни концами {рис. 17} и при поиощи ирв-
дыдущего построения отметим на .neii такш; дне точки С и./.), что пло-
плоскость из AI) на CD равна квадрату DH, плоскость пл СВ на DB раина
квадрату АС,
АО-CD ^
f".
.*'/*¦ *"*<*.*" *¦ t „' '» •>'t ¦.¦«¦*.. *л *,'я*','.-*<|
*¦-¦ ' ¦¦ '.¦-•"-'*
rt>OTOKoi!iiii страницы арабской рукописи, ro;y ж
начало Книги о построении круга, разделенного нн
сеть раиных чистин
416
ЛРХИМКД
и каждая из линий АС и DB цдаиее CD. Построим из трех линий АС,
CD и DB треугольник CED так, что сторона СЕ равна лшшн АС, а сто-
роиа ТУЕ равна линии DB, н соединим А сEt яЕ сВ. Опишем около тре-
треугольника ЛЕВ круг AEBUG и про-
продолжим линии ЕС и J?Z) в их напра-
направлениях до окружности; пусть они
пересекут ,ее в точках О и //. Сое-
Соединим В с G и проведем и.» С ли-
линию CF до пересечения (линий Z?G и
ЕЙ). Так как стороны АС и CJ? тре-
треугольника АСЕ рпшш, то угол ЕАС
равен углу А ЕС и дуга AG рав-
равна дуге Z?Z?. Так как плоскость из
AD на CD^ равна квадрату DB, то
есть DE,
Рис. 17.
то треугольник AED подобен тре-
треугольнику CEI) и угол D./1Z? равен
углу CED, а дуга G// ранца дуге
?Z?. Таким образом, три дуги ЕВ,
AG м GH равны друг другу. Поэтому GB параллельна ЛЯ и угол САЕ,
то есть CED, рацеи углу DBF. Поэтому угол СЕТ) равен углу DBF.
Так как угол CDE равен углу FZ^Zf и линия ED равна линии Z>#, то
CD равна Z?^', а СЕ раина/7? и чет яро точки В, Е, С mF лежат на одном
круге. Так как плоскость из СИ на DB раина квадрату АС, или ЕС, и
линия С В раина FE, а ?Ш равна DE, то плоскость из fZ? на ED равна
киадрату Z??
УК'
и треугольник /'Zi'C подобен треугольнику CZfD. Поэтому угол DCE
равен углу EFC. Но угол DCE равен двум углам САЕ, лоатому угол
CFE ранен двум углам САЕ. Но угол CFD равен углу DBE. Поэтому
угол DBE равен двум углам САЕ и дуга АЕ равна двум дугам ЕВ.
Так как угол DEB pa пои углу DBE, то дуга НВ также paima удвоенной
дуге ЕВ. Поэтому если разделить каждую из дуг АЕ и fill пополам,
то половины будут равны дугк ЕВ. Следовательно, круг АЕВНС раз-
разделен па семь равных частей. А это и есть то, чего мы хотели 116].
Хввла единому Аллаху и молитва за пророка, после которого ужо не было про-
рокоп. Исправление и редактиропаиие этого памочатслышго сочинения .чанончепо испра-
исправляющим пером бедного хаджи Мустафы Сиддики ибтт Оалиха, да благословит его все-
всевышний Аллах и да помилует его и всех мусульман, в воскресенье седьмого (числа месяца)
джуыада ал-ула тысяча сто пятьдесят Третьего года (хиджры) [17].
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ
. В ПЕРЕДАЧЕ- АЛ-БИРУНИ
1. ТЕОРЕМА О ЛОМАНОЙ ЛИНИИ, ВПИСАННОЙ В КРУГ
¦ ' УТВЕРЖДЕНИЕ
Если вписанная в дугу круга прямап линия сломана на- две неравные
части и я опущу на нее иа середины этой дуги перпендикуляр, то она
разделится им пополам [1].
Рис. I.
При .м с р. Па .гкшаыую -чннию А НС {рис. 1 j п.ч середины D дуги
ABC опущен перпендикуляр /Ж. Я утверждаю, что ломаная линия ABC
разделена пополам, то ость АЕ рампа
сумме ЕВ и ВС.
ЛОКАЗАТЕЛЬСТИО ЭТОГО ИЗ «КШ1ГИ
KPVTOU» АРХИМЕДА И КИШИ «НАЧАЛА
ГЕОМЕТРИИ» C.RPliMA Ч>И1КЖС)ГО
Он говорил: итлоним дугу ОН,
равную дуге DB {рис. 2}, соединим
DH и /?/>', Jiof-троил! EG, раипую EH.
ii (Юодиним DG и DA. Тогда » силу
тип), что перпендикуляр DE общий,
линии DG п DB ранны. Так как ду-
дуга DB [)iiiniu дуге UU. \\ остшяпален дуга НА раина дуге ВС, дна
угла Hi)Л и DАН раины углу DHA, то ость yiviy DGB. По угол DGH
[.'lit:. 2.
27
АРХИМЕД
pauon углам GAD w GDA, поэтому угли GDA и ПО А равны. Так кап DG
рак на DH, a DA—общая, основания AG и АН равны. Но АС равна ЛИ,
поэтому AG равна ВС. Так кап GE раина ЕВ, то GA вместо с ЕС
равна ЕЙ вместе ft СВ. [Л это и есть то, что ми хотели доказать}.
АРХИМЕД в «КНИГЕ КРУГОВ»
С другой стороны, достоверно, что Архимед и «Книге кругов» и
Серен в «Началах геометрии» доказывали это и не тик, как мы расска
лывали.
Он продолжал АИ а ос направлении {рис. 3}, строил EG, ранную
ЕЛ, и соединял DA, DC, DG и OB. 'Гак как хорды AD и DC равны,
та 1H и DC равны и боковые стороны {равнобедренного треугольника)
Alt и DC раины, ffo-этому. так как DG и DC равны, ухшлОЛН, ОСИ
к DC И равны, поскольку дуга DA
ранпа дуге НС. Добавим общую
лугу ЛЫС', тогда дуга DAHC ран
иа дуге DCHA. Но угол DBC опи-
опирается на лугу DAHC, а углы
DAB и ADH ¦ на дугу DC А.
Лоэтому угол DBC ря1шл углам
DAB и ADB и внешнему углу
DBG треугольника ADB, равному
углам D А В и ЛОВ, не смежным с
ним. Поэтому углы О ВС и О ВС
равны. Но (шло доказано, что
углы DGB и TJCB раины. 11о»тому
оставшиеся углы СОВ и GDB таы-
/'1"" 3- жк равны. Но DG pauna DC,
OB общая, поэтому осноианяя
СИ и ВС ратп.г. Нпотому линии СИ и BE (имеете) равны линии GE,
то есть ЕЛ. [А &т«> п есть то, что мы хотели доказать].
АРХИМЕД И НЕКОТОРЫЕ ГРЕКИ
Архимоду I? «Книге кругов» и Серову принадлежит и третье док»
зательство. Оно же находится и среди задач, принадлежащих грекам,
по-видимому, Аполлонию, которые перевел Юхаана ибн Юсуф.
Он говорил: [продолжим АВ в ее направлении (рис. 3} и отложим
НО, ракную ЕЛ, а пронодем соеднипющпе DC, DB n DG-. Так как/
хорда круга DC образует сегмент DBC, меньший полукруга, и не но:!
можно, чтобы ятот сегмент был больше полукруга, так как дуга AD рав
на дуге DCt а от круга нельзя отделить дпе равные дуги, каждая из ко-
которых болктпе полукруга, если они но имеют общей части, то угол DBC,
ииисашндй п сегмент,— тупом. Так как AD — хорда в круге 1раг,ная
хорде DCI, то сегмент./>СД больше полукруга. Поэтому «писанный угол
DBA — острый, и чнтанпипи;» угол DBC — тупой. Поятому углм DGH
и DCB равны, линии ОС и DG раины и их отношение к общей линии DB
одно и то ясс. Поэтому треугольники DBG м DBC таковы, что угол С
•|дпого из mix равен углу G другого, а их стороны, примыкающие к дру
сим углам, проиорцконамьиы. Так как каждый из углов 1УВС и 2)li(J
польше прямого, то остальные углы {этих треугольников) равны и эти
треугольники подобны. Они также равны [hBG раина ВС. Поэтому ВС
вместе с BE равны ЕА. А это и есть то, что мы хотели доказать].
ТВОРИМЫ ЛРХИМКДА. СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-БИРУНИ
2. ТЕОРЕМЫ АРХИМЕДА О ТРЕУГОЛЬНИКЕ
ДОКАНАТЕЛЬСТВО ДЕЙСТВИЙ АРХИМЕДА ДЛЯ ОПРЕДЕЛЕНИЯ (МЕСТА
ПАДЕгШЯ) ВЫСОТЫ ТРЕУГОЛЬНИКА С ИЗВЕСТНЫМИ СТОРОНАМИ
Архимед сказал: отнимем квадрат одной из двух сторон {треуголь-
{треугольника) от квадрата, другой, разделим остаток на. основание и прибавим
частное к основанию и возьмем, половину суммы; получится более длин-
ный ии двух отрезков основания, на которые оно делится высотой, то
есть «.местом падения камня»; если же мы вычт?м частное из основа-
основании, и возьмем половину остатка, пом/читс.ч поме короткий на апшх
отрезков [2].
(Докаиательстно.) Пусть (дан) треугольник ADB {рис. 4J и его
иыгсота DE. Опишем около него круг и отложим на нем (дугу) DC, ран-
ранную DA, иронедем соединяющую ВС, построим па АЕ квадрат AG,
я на BE — квадрат EF, отложим ЕМ, рапную ЕВ, нронедом МО парал-
параллельно EGwFKL параллельно А В и дополним плоскую фигуру AJ'.
I[литому, так какDB ранни и квадрате />/i к НЕ. и. /J.I p;imi» n кнадрате
DE п В А и кнадрат DE ofiiiuiii в обоих
квадратах, то если мы вычтем квадрат
HI) aw квадрата DA, получится то же.
что и при иычнтапии квадрата BE ил
квадрата НА. Этот остаток янляетси
гномоном QZN'. 'Гак как .чипни FK, КХ
II ХМ рашш и линии 7<7\ КО и МЛ
также раины, то рашш и плоские фи-
фигуры FO, КО и ML. Поэтому плоская
фигура FH раина гномону QZN. Но FP,
го есть AM, равна ВС, так как линии
AM и ME рашш линиям ЕЙ и ВС*).
Следовательно, плоская фигура FII
ость произнеденш-» па ЛИ пи ВС. Поэто-
Поэтому если мы разделим ее, на основание, ''"'"¦ '-
н частном получится ВС. Ксли мы
прибавим к атому осин ни и не, то и сумме будет ломаная линия А ВС, а
ос половина АЕ есть оолее длинная часть основания; если же мы
нычтем ее из основания, то остгпютсп MB, vv половила BJi более
коротка» часть осмгонаняп до «места падетшл камня».-
ДЕЙСТВИИ Л1'ХИМ]?ДЛ ДЛЯ <ОиЬ>]СДКЛЕ1ШЯ)
ПЛОЩАДИ ТРЕУГОЛЬНИКА ПО ИЗБЫТКАМ
Архимед сказал: если умножить шмовипу суммы трех сторон тре-
треугольника на ее избыток над одной uj них, {умножить) произведение
на ее избыток над второй и {умножить) произведение на избыток
над третьей и извлечь корень ия произведения, получится площадь
треугольника [3J.
+ ЛН
4) тик как, но теореме <¦ ломянмй линии (стр. 416). АК^ХВ+ВС. то AM** AK—1
420 АРХИМЕД.
Д о к а з а т с л ь с т в г). (Возьмем) треугольник ЛВС {рис. 5},
ошшгом около него круг, опустим -л.ч середины дуги АВС—точкв
I.) — перпендикуляр 1)Е на ЛБ, опишем из центра А расстоянием
AG дугу GUI1*, тогда Л/> раина ь квадрате DG и СЛ, а квадрат DF,
. (удвоенное) произведение DF на FA и квадрат-РЛ,. (имеете взятые),
ранцы квадратам DG м СЛ, равной/М. Поэтому если мы отнимем
раппьге квадраты AF и ЛС, останется: квадрат /.^ и (удвоенное) лро-
и.чмедшшс DF на /'Л равны квадрату J)G. Точно так же Л# (ппши
я квадрат» />/5 и /?Л, поэтому квадраты i)/ и FA и удьосшюе про-
произведение JD.F на AM ранны квадрату
BE, квадратам ЕН и ЯА и удвоенному
произведению ЕН на НА. Но ЯЛ раина
Л/\ поэтому если мы отбросим оба
равных квадрата, останется: ниад,ра?
DF и удиоеииов произведение DF на
FА равны квадратам DE и ЕН и
удвоенному произведению ЕП на Д^1;
»то равно также квадрату DC. Тре-
Треугольник OGA подобен треугольнику
i)blli, так нпк угол DCG, равный углу
DA.G, ранен углу ТУВЕ, так как «ни опираются на одну дугу.
Поэтому DE относится к ЕВ, как DG к GA; но DG относится
к GA, как квадрат DG к произпедепию DG ни G.4 и как произведе-
произведение DG на СЛ к квадрату GА, а также как квадрат DE к проня-
педепию /Ж на ?/? и как произведении i>E па ?/^ к кнадрату ?Д.
Исли огнять »т пропорциональных величин пропорциональные вели-
величины, находящиеся в том же отношении, отношение остатков будет
тем же самым. Поэтому отнимем киадрат DE от квадрата Z)C,
остаток ранен кнадрату ЕН и удпоеппому произведению ЕН на ЯЛ,
то есть нроиапедению ЕП на сум.му ЕН и (удиоепной НА, то есть
произведению /Ш па сумму ?Л и) НА, пзптую один раз. Отнимем про-
ияведенне Х>.Л' на ?*# от »рои,чведения /^Д1 яа й?У1; нстагок есть площадь
треугольника Л#С, что вытекает из равенства треугольника Л/)С
сумме треугольников ABCnBDM [4J. Пусть (Ж рашш AY^; если мы выч-
вычтем квадрат GK, то есть ЕВ, из квадрата СЛ, то остаток равен произве-
произведению СК на К А, но разность пропорциональных величин*), то есть
произведение Eft на сумму ЕА и Ли, относится к площади треуголь-
треугольника ABC, как зта л.чои*ад!> к иропяисдепвю СК на .ЙГЛ. Но АЕ — по-
лоиипа (суммы) сторон АВиВС,яЛС—половина стороны ЛС, поа-
тому ЕА и ЛС вместе дают половину суммы сторон треугольника (ABC),
if, следовательно, ЕЙ — избыток (суммы) ЕА и АС, или половины
суммы сторон (треугольника ЛВС), над суммой НА и AG, ami AC,—
это один избыток. В силу равенства GK a Eli сумма АЕ и GK ранни
стороне ЛИ; следаватсл&ио, ЛК — избыток суммы ЕА я AG ниц ЕВ
и НА, или .-1#, это -— второй избыток. Так как ЕВ и ВС равпы АЕ,
то ЕВ, ВС п АС равны половине суммы сторои (треугольника AJiC),
поэтому наиыток ;»того над ВС — это ЕИ и АС. По KG paisiia ЕВ и GC
раина AG, поэтому КС — избыток полусуммы сторон над ВС, это —
третий нлбыток. Ксли умножим плоскую фигуру из ЕН на ЕА и AG,
то еегь oflj.ta пя диух крайних членов (пропорции), иа плоскую фигуру
из СК на КЛ, то есть на другой крайний член, получится квадрат сред-
лг;).кц.лк.к'ш:
ТЕОРЕМЫ АРХИМЕДА. СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-БИРУНИ
421
него члена, или площади треугольника {ЛВС). Таким образом, если
мы умножим ЕЦ', то есть первый избыток, па ЕЛ (цмосте с> АО, то
есть на половину суммы стороп {треугольника ЛВС), умионшм АК,
¦или нторой избыток, на СК, то есть третий избыток, а затем умножим
одно иа зтйх произведений на другое, ими если мы умножим ЕА {име-
{имеете с) АО, или иолошшу суммы сторон на КЛ, произведение — па ЕН,
а {полученное) лрош-шоденис — на СК, получится квадрат площади
треугольника. Счедовательно.еспи мы навлечем корень ия ятого, полу-
получится искомое [5].
КНИГА О КАСАЮЩИХСЯ КРУГАХ
АРХИМЕДА,
УБИТОГО В ДВЕСТИ ДВЕНАДЦАТОМ ГОДУ ДО ГОЖДЕСТЛЛ
Во имя Аллаха милости ноги, милосердного!
I*)
Архимед ска»ал: если даны несколько кругов, последовательно
касающихся друг друга, причем их центры находятся на одной (прямой)
линии, и из точки, отмеченной на продолжении этой линии, в ее напра-
направлении проведена касательно;! к :>тим кругам, то круги **) находится
в непрерывной пропорции, а если эти круги находятся е непрерывной
пропорции, то при продолжении касательной к двум последовательным
кругам из них она будет касаться остальных кругов.
Пример итого. Предположим, что круги, последовательно ка-
касающиеся друг Друга, крути с центрами А. В и С. и пусть центры Л,
Рис. 1.
в и С находятся на прямой линии АС {рис. 1}. Предположим, что кру-
круги касаются друг Друга в точках I) и Е. Отмстим на линии АС точку О
и проведем mi нее линию, касающуюся кругов в точках И, F и К.
Тогда я утверждаю, что круг {А) относится к кругу Д. как круг Я
к кругу С.
*) Номера предложений « хайдарабадском игшашш отсутствуют.
•} То есть площади кругов.
КНИГА О КАСАЮЩИХСЯ КРУГАХ 423
Д о к а а а т с л ь с т » о этого. Из точек касания черен центры
проведем диаметры (это будут линии К ЛЬ, FBM и IICN) и соединим
<точки) L к D, D н F, М и К и Е и Я. Так как линии ЛХ, FM и HN
¦ ¦ проводспы ия точек касания, череи центры, то все они перпендикулярны
касатильной. Следовательно, они параллельны. Поэтому угол LAD
равен углу DBF "и равиобедреипыи треугольники LAD и DBF (подоб-
(подобии). Следовательно, угол ADL рамен yrxy.BDF. Поэтому, так как линия
АВ прямая, линия LF также прямая. Точно так же доказывается, что
линия МП прямая. В силу того, что и прямоугольных треугольниках
LKF и MFIT углы ALF и ВМП раины, их остальные углы, то octi. KFL
и FIIM также равны. Следовательно, линия LF параяле:1ыга лirnim
Mff. В силу того, что треугольники KLF и МРИ подобны, отношение
LK к. KF равно отношению MF kFJI, или, переставляя, отношение LK
ч MF рапно атпотетшю KF к FH. Но отношение KL к FM равно отно-
отношению К А к FB, то есть ранио отношению KG к GF.
К.1, = КО
FM = GF
Следовательно, отношение {К(т) к GF ралио отношению KF к КН.
Kg kf
GF = Jilt
В силу того, что отношение всей KG ко исей GF равно отношению вычи-
вычитаемой KF ц вычитаемой ЕЙ, отношении остатка FG к остатку GH рашто
итношсшоо KG к GF.
to _ ко
gh ~ gi~
Но отпоишнш! KGuFG равно отношении) КЛ kF/J, то есть равно отно-
отношению KL к FM, '¦¦¦ ¦
KG KL
PC " FM
а отношение FG )j GH равно («ношению FB л НС, то есть ранно отно-
отношению FM к IIN.
l-G _ FM
СП HN'
Следовательно, отношеат1 KL it FM равно отношению FM к /УЛ.
7'М' ~ ИЛ
Поэтому отношение кнадрата KL к квадрату /'М равно отношению клал-
рата FM к квадрату //$
Но круги относятся друг к другу, как квадраты их диаметров, поэтому
круг А относится к кругу И, кап круг В к кругу С. А это и есть то,
что мы хотели докапать.
Пусть эти круги находятся и непрерывном пропорции и мы пред-
предположим, что линии GH касается двух кругов С п. В а точках // и F.
Тогда я утперждаю, что если мы продолжим линию Gil it се напра-
направлении, она будет касаться оставшегося круга.
Д о к а я а т е л ь с т в о этого. Проведем через точку А линию
нараллельпо лилии FM, это будет диамотр K.AL. Соединим {точки)
F и К и дополним оставшуюся часть чертежа так же, как в предыдуп^ем
424 АРХИМЕД
предложении. Тогда нам ясно, что линия LD — в одном напри клешш
с линией DF, а линия LF параллельна лшши МП. Поэтому треугольник
KLF подобии треугольнику FMH. Так как круги находятся в непрерыв
ной пропорции, отношение KL к FM равно отношению FM к Н N.
к и __?*?,
рм '' на
Но отношение KL &FM7 то есть отнотетше ЛЬ к FB, ратаю отношению
LD к DF, то есть равно (отношению) LD к ME,
KL __ I.D _ U> ¦ - -,j.. ¦
fM ' /)/»' мь1 ¦;''..
а отношение FM к HN, то «сть отношение ВЫ к С//^, ранно отношению
А/? it ЙЯ, то есть равно отпошению OF к ?7/.
Но отношение LD к ЕМ был» ранпо отношению АГЛ к FM и, следо-
naTCJrbHo, oTHOJiieiiiie KL к fM равно отношению LD к A/fi и равно отно-
отношению ?>/" к ?V/, то есть равно отношению неси LP ко всей А/Я.
Д?, ___ 1.D _ DF _ 1.P
FM " «А1 ~ ЯН МП
Так как отношение LK к А'Л/ равно отпошсиию LF к МП, то заключен-
заключенные между шшм угли раины и треугольники KLF и FMH подобны.
Поэтому угол LKF рйтж углу MFH и, так как угол MFH прямой, угол
LKF также прямой и линия KL параллельна линииFM. Следовательно,
угол KFM тоже прямой. Но, так как угол BFH также бил прямым, ли-
линия (IF — в одном направлении с линией FK и, следовательно, касается
круга А.
Точно так же доказывается, что если кругов больше, эта линия
касается всех их.
II.
(Дока нате льет в о итого предложения друг и м с и о-
с « б о м>- Предположим, что круги такие же, как раньше. Соединим L
к К, KwD,{D и F), F « Е, Е и Н, Н и N и проведем из точки О линию,
Рис. 2.
касающуюся обоих кругов А и В; это будет линия DM {рис. 2]. Поэто-
Поэтому липия DM перпендикулярна к линии LG. В силу того, что обе линии
КМ и MD касаются круга А, л иппнКМ раина лншш AID. Точно так же
ллкия FM раина лшши MD. Поэтому псе три липни KM, MD u FM
раины а круг, описанный из центра М расстоянием МК, является
кругом KDF, проходящим через точки К, D, F. Поэтому угол KDF
прямой. Но угол LKD также прямой и ливни LK и FD параллельны.
КНИГА О КАСАЮЩИХСЯ КРУГАХ 425
Точно так же доказывается, что линии DF и EII тоже параллельны.
В силу того, что линия СИ К касается круга Л в точке К, а линия KD
образует с ней угол FK {D}, ранний углу KLD, треугольники LKD
и KDF — прямоугольные п оставшийся угол KDL равен оставшемуся
углу KFD. Понтому треугольники LKD и KDF подобны. Но треуголь-
треугольник LKD подобен треугольнику DFK, а треугольник KDF подобен
треугольнику РКН Следовательпо, треугольники LKD, KDF,(DFE),
FEH и EI1N подобны. Поэтому отношение LK к KD раино отношению
KD к F7), ранио отношению DF к FE и равно отношению FE к ЕЙ.
LK _ H.D _ D_F_ _ I'E
КО ~ FD "" УЕ "* ЬИ
Поэтому, если мы отбросим средние члены, получится: отношение LK
к DF раиио отношению DF к EII. Но отношение LK к DF раьно отно-
отношению LD к DE,
LK LD
DF DK
а отпошенис DF к Е!1 равно отношении» DE к EN.
DF DK
Следовательно, отношение LO к DE равно отношению DE к EN.
LD DE
DE = UN
Следовательно, отношение квадрата LD к квадрату DE раино отноше-
отношению квадрата /)Е к квадрату EN.
UK _ DK*
Db». ~" UN*
Поэтому круг А относится к кругу В, как круг В к кругу С. А это и
есть то, чти мм хотели доказать.
Пусть теперь эти круги находится в пепрсрышюй пропорции и пусть
линия GH касается кругов В и С в точках // и F. Тогда я утпорждаю,
что если мы продолжим линию GHF и ое напраплинии, то она будет
касаться круга А.
Доказате л ь с т в о этого. Соединим (точки) Л7 и If, H и
В, Е vlF, F и D и происдом чкроа точку D линию параллельно линии
FE, это будет лlumu. DК. Соедшшм (точки) F и Л', К \\L. В силу того,
что киник KD Hapa:i«emiwa линчи FE, угол KDL pawcu углу FED.
Угол EFD прямой, он ранен углу FDK, так как линии DK и FE парал-.
лелыты. Угол DKL прямой, так как он вписан и полукруг LKD. Сле-
ловатсльпо, yro.;i FDK равен, углу DKL. Следипятельно, линия LK
параллкльнн линии DF. В силу тогю, что эти треугольники {FEII и
EHN) подобны, как было докапано раиыно, отпошиние NM к НЕ
ранпо отношению НЕ к EF u раино отношению EF к FD. Следонательно,
отношение N11 к EF раино двойному отношению NH к НЕ.
KF "\ НЕ )
Но отпишеиие N1/ к EF равно отнонишню EF к DK, a NH относится
к НЕ, как EF к FD. Следовательно, отиошиипе EF к DK раино двой-
двойному отношению EF к FD.
DK ~\ FD )
426 архимкд
Поэтому отношепие EF к FD равно отношению FD к DK.
ЕИ _ VD
FD ~ DK
Но между этими линиями заклшчнны равные углы, поэтому треуголь-
треугольник KDF подобен треугольнику DFE и угол DKF равен углу FDE.
Но раньше (установлено, что) угол 1IFE равеп углу FDE, поэтому угол
HFE равен углу FKD.В силу того, что угли KFD, FDK (и FKD) равны
двум прямым, а угол ATZV рамен утпу /)FE, углы KFD, D^/i1 (и //.FA")
также равим двум прямым. Поэтому липия KF находится па продолжении
линии СИ. Точно так же, если угол FKD равен углу DLK, то линия
GK касается круга А и силу того, что сказапо и третьей книге сочинения
Евклида, озаглавленного «Начала» [1].
У нас получилось также доказательств того, что если дна круга
касаются друг друга ипешпим обраиом и между ними имеется общая
«касательная» линия, именно линия FK, то касательная является сред-
средней в нспркрьсииой пропорции между диаметрами кругом, так как в силу
подобия треугольников LD относится к KF, как KF к DE.
Ш
Если даны два касающихся круга, центры которых находятся па
некоторой прямой линии, и из точки, взятой на продолжении этой линии,
проведена прямая, касающаяся обоих кругов, то круги относятся друг
к другу, как квадраты касательных.
11 р и м е р этого. Предположим, что два круга — круги с цент-
центрами А н В, и пусть центры А и В находятся на некоторой прямой
линии {рис. 3). Продолжим ли-
нию АВ, отметим па круге В точ-
точку Е и проведем линию, истречаю-
щую линию АВ н {D) и касаю-
касающуюся круга В н Е и круга А в G.
Тогда я утверждаю, что отношение
круга А к кругу В раыго отноше-
отношению кнадрата касательной GD к
квадрату касательной ЕВ.
Л. Доказательство это-
этого. Соединим (точки) Е и В. В силу
того, что оба угла AGD и ИН1) прямые, линия GA параллельна линии
ЕВ. Поэтому отношение GA к ЕВ, то есть отношение диаметра круга А
а диаметру круга В, равно отношению касате.чыюй CD к касательной
ED. Поэтому отношепие квадрата диаметра круга А к квадрату диа-
диаметра круга В, то есть отношение круга А к кругу В, равно отношению
квадрата касательной GD к квадрату касательной DE. А это и есть то,
что мы хотели докапать.
Если даны круги, последовательно касающиеся друг друга, причем
их центры находятся па одной {прялюй) линии, а сами они нахо-
находятся в непрерывной пропорции, и из их центров проведены карательные
к ним по порядку, то круги относятся друг к другу, как квадраты
касательных.
A1 р и мер этого.) Предположим, что касающиеся круги.—круги
с центрами А, В, С и D, и пусть центры А, В, С и D находятся на од-
КНИГА О КАСАЮЩИХСЯ КРУГАХ 427
ной линии (рис. 4); пусть круги находятся в непрерывной пропорция.
Проведем из (тонок 11, С и D) на линии Л (D) касательные к кругам
А, В и. С по порядку; ото будут линии BF, С К и Oh. Тогда я утверждаю.
Fur. •'..
что круг А относится к кругу В, как квадрат л и кии HF к кладрату ли-
линии СК, а пру В относится к кругу С, как квадрат линии (УК к квад-
квадрату лш[ни DL.
Доказательств того. В силу того, что круги находятся
и непрерывной пропорции, отношение диаметра ME к (диаметру) EG
раино отношению EG к GH. Ксли мы намвшш (диаметры ЕС и 6'// их
половинами), то получится, что ME относится к ?В, как EG к 6С.
¦У/А КО
или, присоединяя, Af# отпмсится к й?. как Л'61 к СС.
MJ< КС
ни " со
Но лилия Bf — средний и непрерывной пропорции между МБ и BE.
Mfl-BE
;i линия ЛГ6' — сродная и непрерывной пропорции между ЕС и CG.
Следовательно, BF относится к BE, как КС к CG или, переставляя, BF
относится к ЛГС, как #Л к 6Y,'*).
кс" ~ "со
Но Efi относится it GC, как ME к КС. Следовательно, BF относится
к ЛГ6\ как диаметр ME к (диаметру) /"G.
me
~ ~eg~
Поэтому отношение квадрата ME к квадрату ЕС, то есть отношении
круга Л к кругу В. рашю отношению квадрата BF к киадрату КС.
А это и есть то, что мы хотели доказать.
his' ~" l/f ПК ~^ НЕ I '
EG EC НС _( КС VI
' кс ' са ~ \ cg i ' ¦ '
CG ~ НС СО \ CG
BF _ КС BF _ BE
HE CG ' КС CG '
АРХИМЕД
У пас получилось отсюда доказательство того, что лкпип РВ, Л'С
и LD, находящиеся в непрерывной пропорции, параллельны. Доказать
это легко, мы приблизимся к этому, если соединил! точки касания с цепт-
рами, тогда у нас получатся прямоугольные треугольники, подобные
и по форме и по положению.
MG
И утверждаю, что то же самое будет, если провести касательные
не из центров, а из концов диаметров, как изображено на этом чертеже
{рис. 5}.
Д о и а » атсл ь с т » о этого. 13 силу того, что диаметр ME отно-
относится к (диаметру) EG, кап ЕС к 67/, «присоединяя», получим, чти
отношение МО к СЕ рав-
равно отношению ЕН к ПС.
ЕН
Но линия GF — средняя в
непрерыиной пропорции
между лишшми MG и GE,
а линия KII— средняя
и шшрермнной пропорции
можду линиями ЕН и HG.
Рис. 5.
Поэтому отношение FG к КН равно отношению EG к GH.
FG
EG
GH
то есть отношению ME к EG*). Поэтому отношение квадрата ME
к квадрату EG, то ость отношение круга А к кругу В, равно отношению
квадрата кнеатшi.noii FG к квадрату касательной КН.
Так же, как раньше, доказывается, что эти касательные, находя-
находящиеся в непрерывной пропорции, параллельны, сколько бы их ни было.
i
VI
Если даны кру,:и, касающиеся внутренним образом в одной точке
и находящиеся в непрерывной пропорции и из концов их диаметров про-
проведены, касательные к ним по порядку, то круги относится друг к другу,
как квадраты касательных.
II р и м i; р :>то1A. Предположим, что эти круги — круги с диамет-
диаметрами Л/У, АС и AD, и пусть они находятся и непрерывной пропорции
и касаются друг друга в точке А {рис. 6}. Проведем из точек С и D
касательные к кругам (с; диаметрами АВ и АС), это будут линии СЕ
\Klt)
КН*
MGCE , GE
l-HHG " ( HG
)Ч
ME .г
HO )
КНИГА О КАПАЮЩИХСЯ КРУГАХ
42Й
и DC. Тогда я утверждаю, что круг АНИ относится к кругу AGC, как
квадрат касательной ЕС к квадрату касательной GJ).
Д о к а з а т е .;i ь с т в о этого. В силу того, что DA относится
к АС, как С А к АВ, «выделяя», перестаиляя (и рассуждал), как раньше,
получим, что GD относится к ЕС, как С Л
к АВ. Следовательно, отношение квадрата GD
.к .квадрату ЕС равно отношению квадрата С А
к квадрату АВ, то есть отпошепшо круга CGA
к кругу ВЕЛ. Л зто и есть то, что мы хотели
докапать.
VII
Вообще, если даны круги, касающиеся ли-
линий, образующие вместе с линиями, проведен-
проведенными через и.г центры, равные у;:лы, то круги
относятся друг к другу, как {квадраты) коса- 1'ис. в.
тельных.
II р и м с р этого. Предположим, что два круга — круги с центра-
центрами А и В, проведем через эти центры линии АС и BD, нроиедем каса-
касательную СЕ к кругу Л и касательную DG к кругу В, и пусть угол АСЕ
ранен углу HDG {рис. 7}. Тогда я утверждаю, что круг А относится
к кругу В, как квадрат каемтолыюй СЕ к квадрату касательной DC
Риг. 7.
Д о к а а а т о л i. с т в о этого. В силу того, что прямоугольные
треугольники АЕС и ZJGZ) подобны, отношение ЕС к GZ) раино отно-
1П0МИЮ /?Л « GJS. Поэтому инадрат ЕС относится к квадрату GD, как
квадрат .пиния АЕ к квадрату линии GB, то есть как (квадрат) диа-
мптра круга А к (квадрату) диаметра круга В, то есть как круг А
к кругу В. А зто и t'.CTb то, что мы хотели докапать. ...
V11I
Пели даны два. касающихся круга и ия концов .шнии, проходящей
через их центры и точку касания, проведены два линии, пересекающиеся
между собой и касающиеся крумж, то отношение крупов друг к другу равно
двойному отношению {квадратов) линий, пересекающихся между собой
и касающихся кругов [2]. . . ... , =
. П р и м с р этого. Предположим, что два круга — круги t: цент-
центрами А и В, касающиеся и т»чк« С {рис. 8}. Провидим и линию,, про-
проходящую чореа их центры, зто будет .чинил DC К. Проведем ия точек D
я Н две пересекающиеся линии, касакициеся кругов в точках G. и П.
430
ЛРХИМЕД
Тогда я утверждаю, что отношение круга -1 к кругу В раино двойном>
отношению (квадрата) касательной ОН к (квадрату) касательной EG.
Доказательст » о этого. В силу того, что отношение круга
Л к кругу В рапно диойному отношению диаметра DC к диаметру СЕ.
а отношение диаметра DC к диаметру СЕ равно отношению плоскости
из ED на DC к плоскости из DE на ЕС [3], отношение круга А к кругу В
раин» двойному отношению плоскости ия ED на DC к плоскости ия /JA"
на ЕС, то есть равно (диойному) от
ношению кладрата касательной DH
к квадрату касательной EG. А это
н м'ть то, что мы хотели доказать.
[X
Если дан круг, и из одного из кон-
цое его диаметра проведена касатель
ная к нему, а из другого конца
Рис. 8. этого диаметра проведена секущая,
встречающаяся г каеаткАЬпай. ли>
плоскость ия ськущей но «• часть, находящуюся внутри круга, равна
квадрату диаметра.
(Л р и мер этого). Предположим, что этот круг — круг с диа-
диаметром АВ {рис. 9}. Проведем ил точки -4 касательную к нему (ато будет
лилия АС) и соединим HDC. Тоща
я утиерждаю, чти плоскость ir:i C11
яа ВО равна киадрату АВ.
Доканатсль с. т а о этого.
Соединим (точки) А и D. В силу
того, что прямоугольный треуголь-
треугольник СВА подобен прямоугольному
треугольнику ADB, отношение СИ
к ВА равпо отшшшнпю В А к ВО.
Поэтому плоскость из СВ на BD
равна квадрату АВ. А это и есть
то, что мы хотели доказать. ри<. ()
Дока з а т е л ь с т в о этого
предложения д р у г и м слое о-
о ом. В силу того, что квадрат СВ, то есть плоскость и» СВ на СИ
имеете с плоскостью п:\ С Я на BD. рат»«" квадрату С А вместо г кпв-
дратом АВ,
а плоскость из ВС на CD равна квадрату СИ, оставшаяся площадь из
С# на #0 равна оставшемуся квадрату АИ. А это и есть то, что мы хо
тел и доказать.
Д о к а з а т е л ь с т » о этого предложения еще одним способом-
В силу того, что плоскость из 67) на BD раина квадрату AD, то если
мы прибавим общий киадрат DB, получится: кпадраты AD и DB. то
есть квадрат АВ, равны плоскости из CD па DB вместе с киадратом DB,
то есть плоскости из СВ на DB. А это и pcti. то, что мы хотели доказать.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
431
Точно так же, если провести какую угодно линию, как EGB {рис. 10},
плоскость из всой липии на ее часть, находящуюся внутри круга, равна
квадрату его диаметра,и плоскости,
заключенные между каждой линией -' г •'¦
н ее частью, находящейся внутри
круга, равны.
XI
Если линия касается круга « кон-
конце его диаметра и из точки, взятой
на ней, проведена другая линия, каса-
касающаяся этого круга, то плоскость
аз одной из частей касательной на
другую равна пмккости ия всей линии,
проходящей через центр, на ее. часть от центра круга до его окружности,
а плоскость из всей касательной нп ее. часть между точкой встречи и точ-
точкой касания равна плоскости из линии, проходящей через центр, па ее
•теть между точкой встречи- и центром круга.
Прим в р итого. Предположим, что этот круг — круг с центром .Л
и диаметром ВС {рис. 11}. Прпнндвм и» точки И касательную к ному.
Рис. ю.
Рис. 11.
это будет линия BU. Возьмем на линии BD произвольную точку (пусть
это будет точка D) и проведем из нее другую липию. касающуюся круга
в точке Л, ито будет линия DEC. Она пересечет линию, проходящую
через центр, и точке G. Тогда я уч-понждаю, что плоскость DE на EG
раина плоскости n;i GB на НА и что плоскость из DG на GE рашга
плоскости из BG на GA.
Доказатольст и о зтш-о. Соединим (точки) А и. Е. Тогда
r силу того, что п треугольниках. DBG и GEA прямой угол DBG одгюго
из них равен прямому углу другого треуголышка, а угол DGB общий,
эти треугольники подобны. Поэтому отношение GB к BD, то есть к DE.
panuo отношению GE к ЕА, то есть к НА. Поэтому плоскость из GH
на ВЛ ранпа плоскости из DE na EG.
Я утверждаю, что плоскость ил DG и» GE равна плоскости
из BG на GA.
Доказательство итого. И силу того, что треугольники
DBG и GAE подобны, отношение ?>G к GB рнвяо отношению АС к GE.
Поэтому плоскость из DG на GE раина плоскости из BG на GA. Л ято
и есть то, что мы хотели докапать.
' АРХИМЕД
XII.
Если касательная, проведенная из конца диаметра, капается не
в точке В, а в точке С, как линия CD {рис. 12}, то плоскость из DE на
EG равна плоскости из АС на CG, а плоскость из EG на CD равна пло-
скости из АС ни CG.
Доказательство зтого. В силу того, что треугольники
GEA и GCO подобны, отношение GE к ЕА, (то есть к АС), раино
Рис. 12.
{отношению) GC к CD, го есть к El). Поэтому плоскость ия GE на ED
равна плоскости из АС на CG.
Я утверждаю, что плоскость из ЕС на СЬ равна плоскости
lutAG на GC.
Доказательство этого. В силу того, что треугольники
(GEA и GCD) подобны, отношение EG к GA раино отношению CG
к GD . Поэтому плоскость из KG на GD рявнд плоскости и:» GA на GC.
Это и есть то, что мы хотели доказать.
УU
Д оказат е л ь с т в о этого нредложоиин д п у г и м с и о с о-
б о м. Опишем около прямоугольного треугольника AGE круг GF(А)
{рис. 13}. Тогда линия AG — его Д1гамртр. ГТроксдем линию FCH.
\\ силу того, что лишж/7? разделена
пополам в точке С и на дие |раулич-
ные части в точке D, плоскость из FJ.)
ira DH пысстр с квадратом CD рпким
квадрату СП.
Ш ':-CD2=CH-
Но плоскость iv&FD ка DH раина
. плоскости из GD нн DE, а квадрат CD
рапой киадрату ED. Поэтому пло-
плоскость н.} GD на /)Л' вместе с кмадра-
том ED, п* есть плоскость из GK на
EJ), ранна кладрату СИ.
Но квадрат СН равен плоскости из АС на CG. 1[оутому плоскость из
А С на CG раина плоскости из GE на Е1>. Л это и есть то, что мы хотели
доказать.
Точно так же, к силу того, что плоскость из IID на DF, то есть пло-
плоскость из ED на GD, меньше квадрата ПС, то ость плоскости из АС на
КНИГА О КАСАЮЩИХСЯ КРУГАХ
433
СС, на квадрат CD, а квадрат DG больше киадрята СС па квадрат CD,
плоскость мз ED на DG имеете с квадратом CD, то есть плоскость из
EG на DG, равна плоскости из АС па CG вместе с квадратом GC,
то ость плоскости из АС на GC. А это и есть то, что мы хотели доказать.
XIV
Если дани два круга, касающихся друг, друга внутренним образом,
и проведена линия, касающаяся их обоих, образующая прямой угол
с. линией, проходящей через точку касания и центра, а из точки,
взятой на линии, проходящей че-
через центры, проведены две другие
касательные к этим кругам, пере-
пересекающие первую касательную, то
отношение большего круга к мень-
меньшему равно двойному отношению
плоскости, заключенной между
частями касательной к болыиему
кругу, к плоскости, заключенной
между частями, касательной к мень-
меньшему кругу.
II р и м с р итого. Предполо-
Предположим, что круг с центром А каса-
касается круга с центром В инутрсиннм
образом л точки С {рис. 14}. ТТрп-
недсм через точку киса пня и центры линию CDEG, так что диаметр кру-
круги Л —линия CD, а диакотр круга В — линия СМ. Пропадем из точки G
линии GHF и GKL, касающиеся атнх кругов в точках // и К. Тогда
я утверждаю, что отношении круга А к кругу В рашш двойному
отношению плоскости лз GH на HF к плоскости из GK на KL.
Доказательство :>того. И силу того, что линии С А от-
относится к СВ, как плоскость ш GC па С А к плоскости из СС па СВ,
то, как доказано в предыдущем предложении <Х.1>, плоскость из GC
на С А равна плоскости из GH на HF,
ca-t:A=cnni-
а плоскость из СС на СВ раина плоскости ил GK на KL,
GC-CO=GK-Kl.
отношение С А к СВ раипо отношению плоскости из GII на JTF к пло-
плоскости из GK на KL.
Рис.
са
си
он
GK-KL
Но С А относится к СИ, как удноошшя С А к удвоенной СВ, то есть как
диаметр CD к диаметру СИ.
СА. СП
си ~ се
Поэтому диаметр CD относится к диаметру СЕ, как плоскость из GH
на IIF к плоскости GK на. /</..
со сп-ну
CJi ~ CK.-KL
Но отношение кпадрата диаметра CJ9 к квадрату диаметра СЕ равно
дпойному отношению CD к С/?, а ккадрптм диаметров кругов относятся
28 Лрхимед
¦434
АРХИМЕД
Рис. 15.
друг к другу, как сами крути. Поэтому отношение круга А к кругу В
равно двойному отношению диаметра CD к диаметру СЕ, то есть paitiio
дпошкшу отношению плоскости из GII на ///' к плоскости GK на KL.
Л это п есть то, что мы хотели доказать.
XV
Если даны два непересекающихся круга с центрами на некоторой
(примой) линии и из их центров проведены пересекающиеся линии,
касающиеся этих- кругов, то плоскость, заключенная между частями одной
ия касательных, равна плоскости,,
заключенной между частями другой
касательной.
II р и м с р втого. Предположим,
что дна непересекающихся круга-
круги с центрами и точках А и В
линии АВ {рис. 15}. Пронедем и»
центров А и В линии АС и BD, каса-
касающиеся кругов те точках /) и С и
пересекающиеся в точки Е. Тогда я
утпорждаю, что плоскость из АЕ на
ЕС равна плоскости BE na ED.
Д и к инатсльств о этого. Соединим (точки) Г) и А, С и В.
К силу того, что прямоугольные треугольники ADE и ВСЕ подобны,
отношение АЕ к ED равно отношению BE к ЕС. Поатому плоскость и»
АЕ на КС равна плоскости из BE на
ED. Л это и есть то, что мы хотели
доказать.
XVI
Доказательство итого
предложения другим с и о с о-
С) о м- В силу того, что оба угла
ADB и АСИ — прямые, а треуголь-
треугольники ADB и АС В находятся на одной
линии АВ,треугольники ADBylACB
ШМ1ПЩ11.Г и полукруг. Проведем через
них полукруг АОСВ {рис. 10|. В силу того, что лилии АЕС и BED
пересекаются в круге it точно Е, плоскость из АЕ на КС раина плоско-
плоскости из BE на El). А :»то и есть то, что мы хотели доказать.
XVII
Если даны две касательные к одному кругу и ии точки, взятой но
продолжении линии, проходящей через точки касания, в ее направлении,
проведена касательная к кругу, пересекающая одну из касательных
и оканчивающаяся па другой, то отношение всей проведенной линии к ее
части, находящейся вне касательных, равно отношению большей из ча-
частей между касательными, на которые она делится точкой касания,
к меньшей.
{Пример ;>того.) Предположим, что дне лишпт А В*) и АС
касаются круга BC[G] в точках И и С {рис. 17, 18, 19]. Соединим
Глс. 16.
*) На рис. I 7 лшшн НИ.
К1ШГЛ О КАСАЮЩИХСЯ КРУГАХ
435
(точки) В и С и продолжим линию ВС в ее направлении. Возьмем па
ее продолжении точку Л и пропадем и я точил D еще одну касательную
1'нс. 17.
и
к кругу; ят0 будет линия DEGH, пусть она касается [круга] » точ-
точке С. Тогда я утверждаю, что ПО относится к DE, как HG к GE.
Д о к а з а т е л ь с т и о этого. Ли-
пин ИВ и А С должны быть обязательно
либо параллельны, либо но параллельны.
Предположим, что они параллельны
{рис. 17}. Тогда угол BIID (треуголь-
(треугольника ВIID) равен углу СЕТ) треуголь-
треугольника CED. Поэтому отношение IID к
DE равно отношению FIB к ЕС. Но
линия HG раина линии ПВ, так как
атл линии — касательные к кругу,
нринедешшс нл одной точки JI, и точно
так ж« липни KG panna линии ЕС.
Поэтому IID относится к- Т)Е, как IIG
к GE.
]Ссли же они ш! 1гараллельны, то
они .встрпчаютсн в точке {рис. 18 и 19}.
Мпшшдрм и.ч точки Е линию, параллель-
параллельную линии ЛВ, это будет линия EF. В
силу того, что линии А В и АС — каса-
касательные к кругу, они раины. Поэтому
угол АСЕ ранен углу ABC. Но угол
JiFC равен углу ABC и силу параллельности линий. Поэтому угол EFC
ранен углу ECF. Поэтому линия EF равна линии ЕС. Точно так же,
в силу того, что IID относится к 1)Е, пак ИВ к EF, то ость к ЕС, ли-
iiiut IIВ равпа лишш НС и линия ЕС равна линии КС, то I1D отно-
относится к DE, как HG к GE. А это и есть то, что мы хотели доказать.
XV111
Если дана касательная к кругу, проведенная в конце диаметра,
и из точки, взятой на продолжении диаметра в его направлении, про-
проведена другая касательная к кругу, встречающая перпендикуляр к диамет-
диаметру и перпендикуляр, опущенный на нее us точки касания, являющейся-
концом диаметра, то отношение всей проведенной линии к ее части между:
Рис. 19.
436
АРХИМЕД
DLi
EG
DA
AC
DE
KG
Eli
DG
EC
взятой точкой {на продолжении диаметра) и точкой касания равно от-
отношению ее части между точкой касания и перпендикуляром к чалти
этой линии между точкой касания и точкой падения перпендикуляра,
опущетшео на нее.
II р и м о р »того. Предположим, что атот круг - - круг с центром
Л я пусть его диаметр - линия CF {рис. 20}. Носставим перпендикуляр
к диаметру, касающийся круга,
это будет линия С.Е. Продолжим
линию CF и позьмем на се про-
продолжении точку, ;по будет точка
)). Происдсм из точки /) ли-
И ншо, касающуюся круги в точке
G, это будет линия DE. Опустим
из точки С нерпепдикуляр па
линию DE, это будет ли пил СП.
1'ис-.. 20. Тогда и утвсрасдию, что ED от-
относится к DG, как EG к ОН.
Доказательство этого. Соединим (точки) А (и) G.
Тогда в силу того, что угол AGO прямой и угол CUD также, пря-
прямой, СИ параллельна линии AG и прямоугольный треугольник DEC
подобен прямоугольному треугольнику DAG. Поэтому отношение DE
к ЕС, то ость отношение DE к EG, рапно отношению DA к AG, то
есть л АС.
ДА
Но DA относится к АС, как DG к GIL
DC
"GH
Поэтому DE относится к EG, как GD к GII,
DG
'-GB
или, переставляя, ED относится к DG, как EG к GH.
UG
~сн
Это и ость то, что мы хотели доказать.
Выделил, мы докажем, что EG относится к GD, как ЕН к HG.
ЕН
на
XIX
При том же положении.
я утверждаю, что EG отно-
относится к Gh как AF, проведен-
проведенная из центра*), kFD.
Д о к а з а т е л lctiio
отого. Соединим (точки) Е и
A, G и /'"{рис. 21}. Тогда в силу того, что лилии СЕ раина линии
линия С А равиа линии A G, и у треугольников {АСЕ и AGE) одно и то же
Рис. 21
•) Греческое 'ей niv xevtooe-таи греки обозиачяли радиус. Этот термшг, а также *расстоя-
иис!> (гцеч. Лкхсгтчц») па стр. ',24 и ссылки им то, что Лрхимсл Сыл уПмт в 212 г. «ди Рождестиа»
па cti> '<22 показывают, что оригинал книги Сыд написан по-гречески.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
437
s
Рис. 22.
па
Ъв
основание, угол САЕ равен углу СЛЕ. Поэтому угол CAG- - удвоенный
угол САЕ. Но угол CAG — удвоенный угол CFG, так как один из них
центральный угол, а другой «писанный угол, и они опираются па одну
и ту же дугу. Позтому угол САЕ район углу CFG и линия ЕА
параллельна липни GF. Поэтому
EG относится к GD, как AF к
FO. Л ато и есть то, что мы хо-
хотели доказать.
XX
Если дана касательная {к
Kpysy), проведенная в конце диа-
диаметра, но не в точке С, а в дру-
другом конце диаметра, как па этом чертеже линия FK {рис. 22}, то я
утверждаю, что HG относится к ПО, пак GK к КО.
Д о к а з а г е л ь с т в о этого. В силу того, что прямоугольный
треугольник СП О подобен прямоугольному треугольнику FKO, отно-
отношение СИ к. НО панно отношению KF к JKI), то есть равно отношению
С К. к КО. Л ото и есть то, что мы хотели доказать.
XXI
Если диаметр круга продолжен в еио направлении и из точки, взятой
на его продолжении, проведена касательная к кругу, а из точки касания
опущен перпендикуляр на диаметр, то вся линия, проведенная через
центр, относится к ее части, находящейся вне круга, как большая из
частей, па которые диаметр де-
делится перпендикуляром, к мень-
меньшей части.
(Пример атого.) Пред-
Предположим, что тот круг—круг
с центром А, и пусть «го диамет-
диаметром будет ВС {рис. 23). Продол-
Продолжим его в его напранлении и
23. отметим на его продолжении
точку О. Ыронсдсм h:i ней ли-
линию, касающуюся круга и точке В. Опустим из точки В перпендику-
перпендикуляр на линию ВС, это будет EG. Тогда я утворихдаю, что ВО относится
к DG, как BG к GC.
Д о к а з а т о л I, с т к о этого. Соединим (точки) Е и Ht Е и С.
Тогда и силу того, что треугольники ВТ) К и КТ)С подобны, ВО относит-
относится к ОЕ, как DE к ОС, и ВО относится к ОЕ, как BE к ЕС.
IiE ПК
Поэтому отношение ВО к ОС раино двойному отношению ВО к ОЕ
и, следовательно, равно диойиому отношению BE к ЕС.
(В силу того, что треугольники BGE и EGC подобны, BG отно-
относится к СЕ, как GK к GC, a BE относится к ЕС, как GE к GC). Позтому
отношен но НС к GC ротто {двойному отношению GE к GC, или) д ионному
отношению ВС к СЕ.
на
Go \ ом )
438
АРХИМЕД
DC
Следовательно, BD относится к DC, как BG к СС.
иг,
А это и ость то, что мм хотели доказать.
Д о к и з а т о л ьство этого предложения Друг и м с и о-
с о С о м. (Продолжии линию DF до точки //.) Проведем от линии ВС
дне линии ВН и CF, образующие вместе с пен прямой угол и за-
капчнканнщшеи ни линии HD {рис. 24} [4]. Тогда липни ВН, QK
Рис. 2Л.
и CF параллельны. 13 силу того,что BD относится к DC, как ВП
к CF,nmi как НЕ к EF,
UD _ НЕ
DC ~ Ы>
а НЕ относится к EF, как ВО к G6\
НЕ _ flfl
Л1/'- '" Gt.1
то Ш) otiiochtch к DC, как />'G к CY*.
ад вс
Ято и есть то, что мы хотели доказать.
ХХ11
Если с сегменте круга сломана {прямая) линии {на две части),
стягивающие две неравные дуги, и из точки, делящей сегмент пополам,
опущен перпендикуляр на большую из частей ломаной линии, то он раз-
разделит ломаную линию пополам Ь>].
(П р и м е р этого.) Предположим, что сегмент круга имеет
основание АВ {рис. 25}, и сломаем в нем линию АСВ в точки С. Пусть
линия АС больше линии СВ. Разделим дугу АВ сегмента пополам
в точке J) и опустим из нее
перпендикуляр на линию АС,
ото будет t)E. Тогда я утвер
ж даю, что линия АС (В) разде-
разделится II точке Е пополам,то есть,
что линия АЕ рашт линиям ЕС
и С В («место.)
Д о к и я я т а л ьство ито-
итого. Отложим на большей ду re DA
дугу, равную меньшей дуге DC, это будет дуга Dlf. Соединим (точки)
Л и //, // и 1/, А и D. Отложим на большей линии АЕ линию, равную
(меньшей) лшши ЕС; это будет линия EG. Соединим (точки) D и G.
В силу того, что перпендикуляр DE является общей линией (треуголь-
(треугольников CDE a Ct)ti), DC раина DC, а также DJI, поэтому эти три линии
panm,i. В силу того, что дуга АН птиоситсм к дуге AIID, как угол ADH
И
Рис. 25.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
к углу ACD и. отношение дуги НО к дуге AHD равно отношению угла
HAD к углу ACD , то дуги ЛИ и //У) вместе, относятся к дуги AHD,
как углыНА1> и ADH к углу ЛС7Л Но дуги AtfnHD равны дуге AIID;
поэтому углы НОЛ W.HAD равны углу Л CD, то есть углу DCR. 1.1 о угол
ОО'Л' равен углам G^IJO и GDA. Следовательно, углы HI)А и //ЛЬ*
рашпл углам С:/Ш и GDA. Но угол /Л17) ранен углу GAD, поэтому
оставшийся утая ПОА равен оставшемуся GDA. И силу того, что ли-
линии DG и DII раины, линия DA общая (линии) треугольников ADG
и ADH, а два угла {HAD и GAD) равны, основание АС равно основа-
основанию АН. Но линия АП ранпа линии СВ, а линия СЕ равна лпшии ЕС;
следовательно, вся „ипшя АИ равна линиям ЕС и СВ. А это и исть го,
что мы хотели докапать.
XX ГЦ
Д о и я з а т е л ь с т « о итого предложения другим с п о-
с о Г> о м. Начертим тот же чертеж, что и раньше. Дополним круг
A.GBD [рис. 2E л 27} и продолжим линию АС и ое направлении. Пред-
Предположим, что линия EII раина
линии ЕЛ и соединим {точки) С
и J), D н //, Н и J), Л и D.
В силу того, что дуга AD равна
дуге DCB, хорда .41) раина хор-
хорде DB, а линия />// равна ли-
линии AD. Пой том у линия Off
раина линии DB. T3 силу того,
что угол DAC равен углу DBC,
-гак как они опираются на одну
и ту же дугу, а угол DHK ра-
равен углу DAE, то угод DHE
р;шеи углу DBC. Точно таи же,
в силу того, что дуга DAGB
равна леей дуге DCHCA, угол
DCB оиирнется ни дугу О ЛОВ,
а углы DAC и А ОС вместе опи-
опираются на дугу ОС ВС Л, так
как I) АС опирается на дугу DC,
а угол ADC — на дугу СВСЛ,
то мы получаем, что угли DAC -
и ADC (вместе) равны углу
DCH. По угол ОСИ \ianen углам
DAC n ADC {имеет}. Лмвтому
угол ЛСЯ ранен углу DCB.
Но было доказано, что угол
ОНС равен углу ВВС. Поэтому
оставшийся угол HDC (в тре-
треугольнике HDC) ранен остав-
оставшемуся углу В1)С{ в треуголь-
треугольнике BDC) и, в силу того, что
линия DH равна линии DB, ли-
линия DC — общая (линия треугольников БОС и if DC) и два угла (отих
треугольников) равны, то линия СИ равна СВ. J [оптому линия ЕС
а СИ (имеете) равны лилиям ЕС л ?// (пмостс), то естч, линии ЛЯ.
А ато и ость то, что мы хотели доказать.
Рис. 2С.
I'm:. 27.
АРХИМВД
XXIV
Д о к а з а т о л ь с т в о этого лродложвния е щ с о д л и м
с и о с о б о м. Сохраним тот жо чертеж. Мы утиерждаем, что и силу
того, что дуга DC И меньше полукруга, угол, вписанный н нес, имешю
угол DC В, ту ной. Точно так иге, в силу tovo, что луга ОНА больше полу-
полукруга, угол, вписанный в иео, имешш угол DC Л острый. Поэтому угол
DC И тупой. Таким образом, углы DC В л DCII тупые. Так как угол
DHC ранен углу DBC, линия DH раина линии DII, а линия DC —
обща» (линия) треугольников DCH и DCB, то угол 11 одного на этих
трсуго.:1.1>шшои paiu.'ii углу В другого из них. Поэтому стороны, загопо-
чяюпиюдка других угла, пропорциональны, а остаишиеся дни угла DCII
и DC/is каждый из которых больиш прямого, раины. (Но так как линия
Dli pnniia линии D1I', а линия DC — общая линия этих треугольников,
»ти треугольники равны.) Поэтому линия СИ раипа линии С В и вся
линия ?11, то есть линия АЕ, painia лшшям ЕС и СВ (имеете). Это
и есть то, что мы хотели дпказать.
«Книга о касающихся кругах» Архкмода окончена.
Хнала Аллаху единому, и ыолитиа ла его пророка Ыухадпгсда н вго
семейство!
E)
%
:>'¦'
и
КВАДРАТУРА ПАГА1ЮЛМ
Точное па.чнание рассматриваемого сочипгсмия ним неизвестно: имеющиеся и руко-
рукописях ;ыгл;шне «rtsTQaY&)VLO|v>e лооофоАлДО не может принадлежать Архимеду, так
как последний называл параболу «сечением прямоугольного конуса».
Как видно из ввелонии Архимеда, это сочиненно ипляется самым перпим его посла-
посланием к Доспфою, написанным вскоре поело получения и:шестня о смерти Кмноиа, т. с.
но лея к ом случаи шх:ле240 г. до и. э. Из ввод >ния к «Эфоду» следу|уг,что определение пло-
площади параболического сегмент» было нерпой, задачей, ралрппегшоы Архимедом с пи-
иощмо его метода механического пнтогпироваипя.
Ушимшаемап во введении лпмма а настоянию время носит ншпишие лксиомм Архи-
Архимеда, хотя сам Архимед укншвнет, что аналогичным приложением пользовались
и жишпио до него геометры. Тиковыми ннляютгя Нвдокс, дпишиндоказатольг/пш теорем
о гыощнди круга (Евклид, Начала, XII, 2) и iiTuocHTO.ni.но tioi,eMou ниримиды (Евилид,
XII, 7) и Konyi:a (^ыилнд, XII, 10), a :ui ним Квклид, которому принадлежитдокааатвдь-
стпо теоремы, касающейся объомц uiiipa (Киилид, XII, 18).
В архимедонских формулировках упомянутых пр(.-д.;юж<!1гвй в «Клидратуре пара-
Яо.пы» с-чещуст отм1!Тигь ынша «двойное» и «тройное» отношение. Когда Архимед, еле-
лун споим ирслшсстисмшисам, пишет, что круги иахпдитси и двойном, а шары и тройном
отношении их днамстроп, то это значит, что речь идит об этом отношении, «o:iподенном
во вторую или cooTiicTi-.Tufiiiio третью степень.
[11 Архимед даст 6i!3 всяких докпзнтелмяв три осноннме тспрсмы теории параболы,
4-<u.iiiUfci. ||-ч <t[Tii4u:ia теории конических i-.cyiiiinii» Евклида или Лрмстия. Оба эти сочи-
сочинения до пас подошли, но изложенный и них материал пошел в сохринпишиося до нтггоя-
гц1!п» врелпмш «Кннические сочения.» Auojijioi;1!R Пергского BС5—170 гг. до п. э.), ылад-
шси'о мшремешшка Архимеда. Чтобы познакомить читателя с тем, как доказывались
эти теоремы в эпоху Архимеда, Приводим доказательств, соотиитстаушпртх тгорсм вместе
с некоторыми д])угнмн, к ним 0ТП0СИЩ1ШНСЦ, из ncpnoii книги уномннутого сочинения
Аполлония.
XI. Если конус сечется плоскостью, проходящей через ось,
и так-ме другой, плоскостью, пересекающей основание конуса тю пря-
прямой, перпендикулярной, к осшняшию треугольника, получаемого е осевом
сечении, если, кроме того, диаметр конического сечения будет парал-
параллелен одной из сторон треугольника в осевом сечении, то веяния пря-
прямая, проведенная от коническою сечения параллельно линии пересе-
пересечения секущей плоскости с основанием конуса, вплоть до диаметра
конического сечения, будет квадрироаить прямоугольник, заключенный
между отсекаемым е.ю отрезком диаметра, считан, от вершины кони-
ческоао сечения, а некоторой другой прямой, которая к отрезку
образующей, конуса между его вершиной и вершипей конического
сечения имеет такое же отношение, как ктдрпт на основании треу-
i.io.<ibuuna, получающегося в аееаом сечения, к прямоугольнику ме,*сду
двумя осталеными сторонами треугольника. Такие коническое сечение
мы будем называть параболой.
Пусть будет конус (рис. 1),исршина которого точка А, а основание—
круг БГ; рассечем его плоскостью, проходящей через ось, и пусть
и сечении получится треугольник АЬГ; рассечем конус также и другой
КОММЕНТАРИИ
плоскостью, пересекающей -.уто основание по прямой ЛЕ, перпендику-
перпендикулярной к ВГ, и пусть эта плоскость образует на поверхности конуса
сечение — крипую AEZ; пусть диаметр Z11 итого оечепия будет парал-
параллелен одной и;» сторон треугольника осиного сечепик, а именно АГ;.
иа точки Z перпендикулярно к ирнмой ZH про-
проведем ZO и сделаем, чтобы как квадрат на В Г
к прямоугольнику между ВА и А Г. так была
и ZW к ZA;
возьмем на сечении какую-нибудь яроизиоль-
ную точку К и черо» К проведем КА парал-
жмыш ДЕ. Н утверждаю, что квадрат па КА
будет ранен прямоугольнику между 6Z и УЛ.
Действительно, через А проведем MJN
параллельно ВГ; тогда и КЛ будет иараллель-
на ДЕ; следоиатслыго, проходящая через КЛ,
MN плоскость будет параллельна плоскости
через В Г, АЕ, то есть основанию конуса. Зна-
Значит, плоскость, нроисденная через КЛ, ЬШ,
даст круг с диаметром MN. Но КЛ будет мер-
пелдикуллрпа к MN, поскольку ДЕ цериендякулярла ВГ; следователь-
ио, иримоугольяик между МА и AN будет раъсн квадрату на КЛ.
МЛ-Л№=КЛ2
И поскольку как к кадрит на ИГ (относится) к прямоугольнику между
В А, Л Г, так и в'Л к 'АЛ,
в г" ftz_
влаг~'гл
и квадрат на ВГ к прямоугольнику между 13Л, АГ имеет отношешю,
составляющееся из отношений В Г к ГЛ и ВГ к В А:
ВГ"
ВА-ЛГ"
ВГ
ГА
_
вл
то, значит, отношении WZ к ZA сог/ган^яется и» отношений ВГ к ГА
и ВГ к ВЛ.
в?.
ГА
ИГ
НА
Но как BV к ГА, так и MN к NA, то есть МЛ к AZ,
_вг
ГА~
иг
мх
NA
мл
Л2
как же В Г к ВЛ, так и
к ZA.
М» _ ЛМ_ N А
МЛ '~'Ш " /.X"
Значит, отношение
к AZ и NA к 7Л.
MN к МА, то есть AM к MZ. и остаток МЛ.
0Z к ZA складглвастся из отношений МЛ
ez
za"
МА
AZ
ZA
Но отношение, составленное из МЛ к AZ м NA к ZA, будет отноше-
нием прямоугольника между МЛ и AN к прямоугольпику лгежду AZ
КВАДРАТУРА ПАРАБОЛЫ
445
и ZA. .Значит, кик 0Z к ZA, так и прямоугольник между МЛ и AN к пря-
прямоугольнику мкжду AZ и '/А. Но как 6Z к ZA, так будет к прямоуголь-
прямоугольник между BZ и ZA к прямоугольнику между А'Л и ZA, если взять
AZ и качистис общей высоты.
ZA " AZ-ZA
Значит, как прямоугольник между МЛ и AN к прямоугольнику
между AZ и '/>А, так и прямоугольник между BZ и ZA к прямоугольнику
между AZ и ZA.
МЛ-AN WZ-ZA
Л2-2А "" AZ-ZA
Следовательно, прямоугольник между МЛ и AN будет равен пря-
прямоугольнику между BZ a ZA.
Но прямоугольник между МЛ и AN равен киадрату па КЛ; значит,
и квадрат на КЛ будет равен прямоугольнику между 0Z и ZA.
Подобное евченис мы будем называть параболой, прямую же BZ,
на которой киадрируются проведенные к диамвтру ординаты, будем
назынать «прямой стороной» (dgoiu tiXevqz — latus
rectum)*).
XX. Если в параболе провести к диаметру от
кривой две ординаты, то отсеченные ими на диаметре
отрезки, считая от вершины, относятся, как квад-
квадраты на ;>тих ординатах.
Пусть будет парабола с диаметром А13; нозьмем
па пен некоторые точки Г, Л и из :>тих точек прове-
проведем к АН ординаты ГЕ, AZ. Я утверждаю, что как
квадрат на AZ к квадрату на ГК, так будет u ZA
к АЕ (рис. 2).
7?
7А
ЛИ
Рис. 2.
Дейстнитсльпо, пусть прямая, па которой кпадрируются ординаты
(параметр), будвт АИ; тогда квадрат на А'/, будпт paoeu прямоуголь-
прямоугольнику между ZA к АН,
ГБ
а киадрат на ГЕ равен прямоугольнику мсгкду ЕА л АН.
Следовательно, как квадрат на AZ н квадрату па ГК, так будет w тгрп-
моугольтгик между ZA и АН к прямоугольнику можду ЕА и АН.
¦1Z2 Z.A-AII
1TJS " I-.A ¦ АН
Но пак (грнмоугольиик между ZA и All к прямоугольнику между
ЕА и АН, так и ZA к АЕ; и, слодоватилмн», пак квадрат AZ к квад-
квадрату на ГК, так и ZA к АЕ.
*} ->го наш
2-р п
параболы
44В КОММЕНТАРИИ
XXX П Г. Если на параболе езятъ какую-нибудь точку и провести
через нее ординату к диаметру, и если затем отсекаемый ею на диаметре
отрсшк, считая от вершины, приставить ни.
продолжении диаметра к вершине (в противо-
противоположную сторону), то прямая, соединяющая
полученную таким образом точку со взятой {на
параболе), будет касаться конического сечения.
.Пусть будет парабола а диаметром АВ; про-
ведем ординату ГД, отложим АЕ раиной ЕД и
соединим А а Г. Я утверждаю, что АГ при про-
продолжении окажется вне конического сечения
(рис. 'А).
Действительно, пусть она, если возможно*
Рис. 3. попадет внутрь как прямая FZ; проведем орди-
ординату 11В. Квадрат на ВН имеет к квадрату на ГД
большее отношение, чем .киадрат на ZR к квадрату на ГД,
га*
но как квадрат на ZB к квадрату на ГД, так будет и квадрат на ВЛ
к квадрату на ЛД,
/,Н* 15 Л*
ГД2 " АЛ*
а как квадрат на НВ к квадрату па ГД, так и BE к ДЕ;
ив* ви
значит, BE имеет к ЕД большее отношение, чем киадрат на ВА к квадрату
на АД.
BE .. В А а
ЕЛ ** АД*
Но как BE л ЕД, так будет и учетлерпгнкгн прямоугольник между
и ЕА к учетверенному прямоугольнику между АЕ и ЕД;
*ВВ- К А
и, значит, учетверенный прямоугольник между BE и ЕЛ к учетверенному
прямоугольпику между ЛК и КЛ имеет бо;и»шее отношение, чем квад-
квадрат на ВЛ к киадрату на АД.
•ibe-j:a
4 Л Е- ЕД ' АД*
,> ¦
Следовательно, после перестановки, учетверенный прямоугольник
между BE и ЕА и квадрату иа АВ имеет большое отношение, чем учет-
и прямоугольник между АЕ и ЕД к квадрату на АД;
4ВЕ-ЙА . 4АЕ-КА
АВ* АД2
ото же невозможно; действительно, вследствие равепства АЕ и ЕД
учетверенный прямоугольник между ЛК и ЕД, будет равен квадрату на
АД,
КВАДРАТУРА ПАРАБОЛЫ
447
учетверенный же прямоугольник между НЕ и Е А будет меньше квадрата
на В А,
*вк-еа
так как точка К не будет делить АН пополам*).
Следовательно, прямая А Г пн попадет пнутрь конического сече-
сечения; значит, она будет его касаться.
ХЫ1. Цели прямая, касательная к параболе, встречается с диамет-
диаметром и из точки касания проведена к диаметру ордината, если яатем us
какой-нибудь точки, взятой па коническом сечении, проведены к диаметру
две прямые, из которых одна парал-
параллельна касательной, а другая — про-
проведенной из точки касания ординате,
то образованный этими прямыми тре-
треугольник будет равен параллелограмму,
заключающемуся, между ординатой, про-
проведенной из точки касания, и отрезком
{диаметра) между параллельной ей
прямой и вершиной конического сечения.
Пусть будет парабола с диаметром
ЛК; прстедем к данному коническому
сечению касательную АГ, опустим
ординату в Г, затем из какой-нибудь
произиолыюй точки (Д) проведем АЪ,
через А проведем прямую АЕ парал-
параллельно Л Г, а через Г прямую ГН
параллельно TJZ, наконец, черин В прямую LVII параллельно в Г.
II утверждаю, чтотроугольник AEZ будет ранен параллелограмму IIZ.
Действительно, так как АГ касается конического сечении и ГЙ
проведена ординатой, то АВ будет равна Вв;
РИГ.
значит, А0 вдвое больше 813. Следовательно, треугольник АН Г будот
ранен параллелограмму В Г. If поскольку, как квадрат на ГН к квад-
квадрату на AZ, так и ВН к BZ,
а в
нследотвяо осноииого сиойства данного конического сечения, а как
квадрат на ГО к кнадрату па AZ, так относится треугольник А Г©
к треугольнику I5AZ, как же (-Ш к BZ, так относится параллелограмм
110 к параллелограмму T1Z; следовательно, кап треугольник АГН
к треугольнику ЕД/, так и параллелограмм НИ к параллелограмму ZH.
Значит, после перестановки, как треугольник АвГ к параллело-
параллелограмму В Г, так и треугольник EAZ к параллелограмму IIZ.
Но треугольник АГ0 ранен параллелограмму Ив; значит, и тре-
треугольник EAZ будет ранен параллелограмму I1Z
XIЛ'Г. Если прямая, касающаяся параболы, встречается с диамет-
диаметром, то прям ая проведенная через точку касания параллельно диаметру
в сторону этого конического сечения, разделит, пополам все прямые,
проведенные внутри параболы параллельно касательной.
*) Доказательство, очевидно, оснолино на том, что при а 4-l)=corist щюиаведение аЬ будот шесть,
максимум при а~Ь.
448
КОММЕНТАРИИ
Пусть будет парабола с диаметром АВД, и пусть АГ касается сече-
сечения; через Г параллельно АЛ проведем (?)Г, нозыш!.ч на сечении какую-
нибудь лроизколькую точку А
и проведем A NZE пара;хлольно
АГ. Я утверждаю, что AN бу-
будет раина NZ (рис. 5).
Проведем ординаты Вв,
KZTI, АД. 'Гак как на основа-
основании доказанного в сорок вто-
второй тсороме треугольник ЕЛД
будет равен параллелограмму
ИМ, а треугольник EZH —
параллелограмму ВК, то, зна-
значит, остающийся параллело-
параллелограмм НМ будет равен остаю-
остающемуся четшреху гол ьнику
AZHA. Отнимем общий пятиугольник MAI1ZX; тогда остаток — тре-
треугольник KZX будет равен треугольнику АМХ. Но KZ параллельна
ЛМ; значит, ZN будет равна AN.
Рис. 5.
Интересно отмстить различие терминологии у Архимеда и Аполлония.
;ний 1 попинает диаметр п нашем смысле этого слова как геометрическое место се-
родик хорд, парал.'нип.цых данному иаправлепиго; у Лрхи-
меда же диаметр соотвптстпует ii;nireii оси ивриболы —
.диаметру, перпендикулярному к разделяемым им пополам
хордам.
* 12) Хи:«; ука:и.тает, что до1>а:<ыииомое предложение
])аи1[огл|Л1.по с, сов]HМС|11ЮЙ точки зрения прсобразовапшо
уралнопия иараиолм к другим координатным осям (рис. 6).
Если первоначалмго ось абсцисс х шла по DA и начало
координат бм.'ю л точке В, то уравнение параболы имело
вид
откуда
Мели положим АД = а и лозьмем новые координатные оси х и у С началом в
точке Л, как покаянно па чертеже, то
ЛК-.^а-, К0-2/, ВД^~-
Док;|;[;нш:>п и предложении V лронордия
Кв:вА = ЛК:КГ
представится так:
у : |B«—х) "^~ jf j ¦= х: Bо—ас).
¦и окончательно:
у {2а—jc) — л {2а —ас) ху.
У —
а-Bя—аг)
что и прсдставянся уравнение параболы, отнесенной к координатным осям Аху и про-
а, — \.
КНЛДРАТУРА ПАРАБОЛЫ
44W
|3| Идея механического доказательства Архимеда ваключается в следующем. Возъ-
.мом ращюплпчин рычаг ГА7, в точкой опоры в А и плечом А Г, равным основанию 2и
яараболического сегмента. Пусть КЛ — у будет ордината, соотпетствующал абсциссе
АК = #. Бели мы разобьем всю площадь параболического сегмента на бесконечно тон-
тонкие прямоугольники с основаниями Ах к высотами, равными ординатам параболы, то
площадь прямоугольной полоски, соотистстоую-
щий ординате КЛ-у, будет:
Лу
л
Bа — х)
у ¦ Дж = 5 ^—-
2/>
Перенесем эту полоску в точку Г; ее момент отно-
относительно Л будет:
у-Л.я:-2а-=-?в-Bв — х) г-Дг.
Если мы хотим уравновесить этот момент
полоской, помещенной на .телом плече рычага
на тнгеом же расстоянии АМ-* от точки опоры
А, то необходимая длина у' —MN полоски
Дудит:
Нетрудно иидсть, что эта длина соответствует* прямой КЛ предыдущего чертежа.
licmi взять все такие полоски, то их концы расположатся ио прямой ZE, а сами
они заполнят площадь треугольника AZE с основанием AZ = 2a и высотой АЕ= — -.
Так как этот треугольник, расположенный по всей длипе левого илоча рычага ураииове-
щивасг параболический сегмент, помещенный на конце правого плеча рычаг», ти, обо-
лпачив 5тР=1Уа и <Усе,,м—iS1», мы имеем:
или
от1{уда
2а*
чт» и требовалось я
[4] Оч«1гь важно отмстить изменение, внесенное Архимедом в доказательство но
сравнении) с первым предложением «Эфода». Подобно тому, как мы теперь при опреде-
определении шющадп криполинейпий трапеции :тк;л(.>ч»см ео между двумя суммами площадей
примо.чгшешшх трапеций, из которих одна больше, а другая меньше определяемой пло-
площади, так и Архимед строит даа рнда трапеций, {рис. 15, ктр. 87;-, из которых трапеции
ВФ, AZ, МК, N1 пместо с троугольпиком Г1Е больше параболического сегмелти В0Г, я
трапеции ФХ, вН, Ш и треугольник ПО меньше его. Отличие заключаете;! лишь в том,
что мы определяем площадь тфнполшгейной трапеции как общий предел, к которому
стремятся обо указанный суммы при неограниченном увеличении числа равных отре.чкол,
па которые делится основание трапеции, а Архимед, дополт.ствуетгя интуитиииым. шшк-
тием площади параболического сегмента. В связи С ятшя нужно отметит:, одно обстоя-
обстоятельство: ппредложениях XIV и XV па рапные отрезки делится пг.лопанис ОГ сегмента
it в предложении XVI — сторона БД треугольника ПА Г. Можно, конечно, доказать,
что из равенства отрезков ВГ следует равенство отреякои ВД и наоборот, iro пидить в этом
ошибку Архимеда нельзя, так как п предложении XVI равенство отрезкой БД играет
существенную роль в доказательстве, тогда как и предложениях XLV и XV равенство
отрезков ВГ упоминается только при построении и яе имеет никакого значения для дока-
доказательства теоремы.
29 лрхимед
450 КОММЕНТАРИИ
15] Предложение XVIII—XXIV представляют собой, по существу, работу отдель-
отдельную, присоединенную к наложению механического метода определения площади пара-
параболического сегмента. Часть, содерм<ащаи предложения XVIII—XXIV, Паникина в не-
несколько iiiioii стиле, чем предшествующа» часть трактата: снимала даются определения,
и текст каждой теоремы содержит формулировку ире.члшкешш, :м .которой следует дока-
доказательство.
Данное Архимедом в птих предложениях .-цжаштелмяшо сводится, но существу,
к суммнрошшнп) геометрической ирогреессиш:
, я . a it , a 4
Архимед, живший в опоху, когда для бесконечных процессов математикой не было
еще выработано специального алгоритма, вынужден был каждый раз yauono uociipouauo-
дить то, что у нас охватывается общей теорией пределов. В предложении X X111 он дока-
доказывает, что сумма конечного числа таком бесконечно убывающей геометрический ирогрес-
4
сии отличаетен пт - я на величину, равную одном трети последнего члена взятой суммы.
О
О ШЛРЕ И ЦИЛИНДРЕ
]1ЕРВАЯ КНИГА
[1] Расематрипаомоо сичинашс принадлежит к я игл у наиболее читавшихся ироии-
ьедишй Архимеда; поэтому в сохранившихся до нашего времеяи списках с.опершеггн!»
исчезли особенности дорийского диалекта Архимеда, пчииь заметнме в ого «Книдратуро
параболы». Кромо того, текг.т того сочипешш испешреп пеганками лоздпгшпих ком-
монтаторов, которые мы помешаем в квадратных скобках.
Оно состоит ил двух совершенно пьзавигимых друг от друга сочинений, па иото-
рт.тх поидиеГшше иядвтнли сделали «перную» и «вторую» книги: это видно Jia тог», что
IJaiur, цитируя первую книгу «JJhipa п цилиндра», ничего не говорит о том, что цитируй-
мм» место принадлежит нерпой книге. II даже л .чтой «первой Kuuif:», имеются две отдель-
пые части. Первая из них обнимает предложения I— XVI и поишщсни определению
боковой поверхности конуса и цилиндра, втирая же (тзредмо/пепии XV П—JCLlV) ммгот
целью онрододоние jiobujixhocth и объеме шара.
|2| Архимед n«i4Miia(!T сино изложение с шчаи-ормх «акпгом». По гущсстпу, таип-
11ы.мп можно нанвать лишь 1-о и 3-е положения, оста.чм1Г.тг жо носят характер о«ред«-
.11!|]цй; в латпнеком нирсподо Гшбпргк oiffl *»к и назыьаются DtjliiiilioiiLS. UacTouuiiiMir
аксиомами, г, MiiriK-ii точки прения, ллдяются лит, тс, которые: УУрхши-д назьшаст допу-
допущениям к (JrflflPuVOJlBVK).
\'А\ Допущении 5 предгтавлист тгзвсйтлую акси<шу Архимеда; аналогичное поло-
;к("шн: 6 мл о ужо 171с:!И1Н> Евдоксо-vi, но в формулировке Архимеда есть отличие. Он гово-
говорит о pii:inocTii двух величин, котирня будучи складываема сама с собой может лрсипойти
-•iiufiyK) заданную «еличипу, а у Евдокса ату роль играет меш.шия из ераиливаимых иели-
чин. Иамеиоиие формуанретки у Архимеда ДсГмжте.рхснс nfiwiciiRuT тем, что Ajixiimoji,
лотсл исключить случай, когда разность величин продстнвляш1 леденимую (сточки зре-
зрении .математической! атомизма). ¦
[¦!] С нашей точки зрения. :>то нредложеине может нолизатькя
а дока:1атслТ|СТ11о, которой д«ет Архимед, неоправданно слоя>лым. Это
можно были бм вамспить примерно елслут'-пшм:
Пусть имеются ^ве лс;|)тшг.т вышчинм, кото]>ые мм, следуя примеру Архимеда,
и;шГфи;шли Сил Л tin Л; пусть А13">Л. Поаьмем pa:niocTi> АН—Т)~&- Гпзделнм Д пополам
и образуем две величины D-,- ~ и IX тогда отношение ( D-\- ~ \. D будет
эадашгого отнотепия АН: D, 'гго и требеналоеь доказать.
Но С точки :ipiMi«ic Лрхимсяи, такое доказательство ни пшше.тс.н «раномерш-тм. Дока-
:шкисмпя теоргита нужна Архимеду для доказательства третьего лредложентш — воз-
возможности nor:T]!oeiii!Ji диух ммогоуго.мышкон — одного описанного, а другого вииеан-
лпго и круг,— так, чтобы отношение стороны иннсаиног» .многоугольника и г-оотнетствуш-
тцей eaojiwic вписаппого (отноиепис .мпведемо большее единицы) Гшло лгеш-шн любого
.'шдашюго отполтения большего единицы. Так ка7! раяность сторон описанного и вписан-
вписанного М||[)гоугп.||[|циков яваиотся величиной босконечпО малой, ii значит, и прямые АН
и 7J (о-пгоптении котормх лзобрнмвет аадапгюс, большее единицы, отношение) могут отли-
отличаться друг от друга гга очень малую политику, то с точки зрении античной матсмнтики
могло быть сделано гледукипое 1го.ч/ш>кеште: что будет, если обе прямые ЛИ и D отли-
отличаются друг от друга на одну неделимую, математический атом, из которых состав-
составляются прямые'-} При таяой постановке вопроси приведенное выше докиаателыггпо,
осп'пвнгшос па возможности деления атого 11еделим(»го, отпадает пимо собой.
Интересно, что Архимед построил свое доказат(?.чг.ство так, что подобное поараже-
мио сделать у>ко нельии.
|31 13 оппнйо доказательства теоремы лежит слодующес иоложилис: «треугольники
ЛВ.А, ]11'Л будут больше треугольника АЛ Г».
452
КОММЕНТАРИИ
Доказательство этого положения доставило очень много затруднений колгментато-
рам Архимеда, начиная от Ектокпя, Упомянутое положение можно доказать таким
образом *).
Пусть круг с центром О представляет основание рассматриваемого конуса; порпен-
дикулирнок плоскости чертежа и» точки О восставлена высота ОД = h конуса. Пусть АГ
в представляет какую-нибудь хорду, а В — середина дуги
АВ Г. Требуется днкашнть, что сумма площадей граней АВД
и В ГА больше грани АГД.
Рассмотрим сначала случаи А Г>АВ (рис. 1). Тогда пер-
перпендикуляр ОН, опущенный из центра круга на хорду АГ,
будет меньше перпендикуляра (УЛ, оиущенпого из О на АВ.
Точки Z и Н будут основаниями перпендикуляров, опущен-
опущенных из вершины Д конуса на ЛВ и АГ. Мы имеем:
ил.
^-грЛВу ОД2—OZ2 ,
u.i. ЛДГ^-i- АГ
Имеем
ил. aba
Так как
то
АГ<ЛВ~ВГ=2ЛВ,
ил. АДГ<пл. АБД |-пл. ВДГ.
Пусть теперь АГ < АВ (рпс. 2). Проведем диаметр
ВОЕ. Так как хорды АЕ = ЕГ будут каждая меньше А Г,
то, согласно предыдущему,
пл. АДГ<11Л. AAE-f-пл. ЕДГ.
Для доказательства теоремы лам остается сравнить площади граней АВД и АЕА. Так
как площадь треугольника ОАВ равна площади треугольника ОЛЕ, то
OZAB = OK-ЛЕ,
где ОК представляет перпендикуляр, опущенный из О на хорду А К, откуда
АЕ
А В
Площадь грани АВД будет:
а грани АЕД:
^-^- АВ
Квадраты удвоенных площадей АВД и ЛЕЛ будут:
Bпл. ABA)*=AB1-OAs-!-AB3-OZa=AtJ!!-OA2-| AR2-OK«,
Bпл. АЕДJ=АЕ2-ОД2Ч-ЛЕ2ОКг.
Так как ЛЕ<АГ<АВ, то ид. АЕА<пл. АВД, и, следовательно,
ил. АДГ<пл. АВД—пл. ВГД.
*) Идея пинссприиедсппого доказательства сообщена мне проф. М. Я. Выгодским, которому
и приношу на аю благодари оегь.
О ШАРЕ И ЦИЛИНДРЕ
453
Затруднения комментаторов объясняются тем, что лемма, принимаемая Архимедом
без доказательства, а общем глучас по является спраисдамиой. Действительно, предста-
представим себе трехгранную пирамиду (рис. 3), вершина которой совпадает с вершиной прямого
угла равнобедренного прямоугольного треугольника с горизонтальной гипотсиулой,
являющегося большей гранью Соколом поверхности этой пирамиды (пусть катеты этого
треугольпика ранцы с), я остальные дне грани лродстнвляют лежащие в вертикальны}:
плоскостях, пршшугилмшо треугольники, общий иятет Ь которых является высотий пирн-
миды, и два остальных представляют проекции а катетов с ни гориаонтальлую плоскость
основания; в таком случае
Сумма площадей обеих вертикальных гранен нашей пирамиды равпн будет:
аЬ,
а п.чпщадь паклопгюй грили
1
Кглн взять высоту Ь так, чтобы удовлетворялось нераиепство
а
2"'
ти
то есть площадь большей паклоияой грани будет более суммы площадей двух остальных.
Интересно отмстить, что методами итомистической математики рассматриваемая
лемма «докалывается» очень просто. Сечениями, парал-
параллельными основанию, разбиваем боковую поверхность
нишей пирамиды на ряд бесконечно тонких треугольни-
треугольников, в каждом ii:i которых одна сторона будет меныш
суммы дпух других. Ес:ш мы составим все нернпенстпа
подобного рода и просуммируем их, то получится, что
одна из баковых rpauiui пирамиды будет миньте суммы
площадей двух остальных граней, что и требовалось
докатить.
[Ь] Основная идеядоказательстла Архимеда обоих
предложений проста до гениилмюстн, но изящество ее
пметулаот лишь, если инбавить доказательство от нп.шш-
¦111 \- лшгсматических подробностей.
\\ девптом предлпжепии Архимеду требуется до-
доказать, что боковая поверхность конуса будет больше
боковой поверхности вписанной в него пирамиды. До-
Достаточно провести доказательство липгь для кониче-
конического секторн, соотпетстпуютего одной гршго пирамиды, как Архимед ото и Д1шаег.
Лес доказательство основывает»! па том, что, вписывая в сегмент круга много-
уголышки, мал;IIel сделать отрезечки М1в.кду периметром этих многоугольников и дугой
1>к))ужности меньшими любой заданной величины.Л (предло/кснис, VI). Пусть такой много-
уголг.штк Tiiinciiu, и пусть па нем построена иирамида, одной гранью кт'прой служит тот
самый треугольник, площадь 5тр которого должна Сыть меньше отрезка конической
нопирхности мс/кду крайними сторонами этого треугольника. Каотдня грань пирамиды
отделит от конуса некоторый конический сегмент. Пусть аадашти величина Д йудет
лепьши 1>азкости между Соковой поверхностью <Ь'Шф лпрцмндЫ, nuiicaiiuoii в^конический
сегмент, за исключением, конечно, треугольной грани в нлшцндью &'тр, и этой, последней:
Рис. Я.
Яхроме того, мы можем написать, что отреаок коиичиской поверхяо<?ги Sllon вместе
с суммой отрезочкоп между окружностью и иернмптром вписанного многоугольника будет
больше упомянутой боковой поверхности ниримиды; при этом вместо еуммы площадей-
отрезочков круга мы можем взять большую ее величину А:
454 КОММЕНТАРИИ
Вычтем почленно из обоих членов верхнего неравенства соответствующие члены
нижнего; после очевидны* сокращения получаем:
что и требовалось доказан..
Доказательство десятого цред.'кккенин осиоимнцстся на том, что сумма гглощндей
отрспочкоп меа**ду окружностью и нериметродг описанного около jree многоугольника
может бмтг, сделана меньше любой* задаппой величины Л.
Требуется докапать, что площадь двух треугольников, обр.чтитгашшх двумя обра--
дующими конуса и проведенными 1» концах этих образующих касательными, буд,1!т больше
коотпетстиушщего отрюка конуса. Описываем около основания конуса иоследоватслт.ны(;
многоугольники, строим па них лирамидтл так, чтобы удовлетворялись перавеиста
—Утр ¦ - Sna\t i> Л,
(-r;.iiадыва>г почленно полученные неранепстнп, получаем:
2Sn, > SlVlU,
что и требовалось диказпть.
Соб(![)Ш(чтмо :)ii;i.noni4no дока^ыиаютси н и])е;(.'ик|;ош1Я XI и XII ;\лн р
171 J'accMiVrpiiuacMoe предложение каг<и.-к:я (шредслелия боковой повирхногти
цилиндра — injpjiiiiii ii;i»ccthi.th нам пример м hctojjhh греческом мптомптаки, когда пло-
площадь, p:ir.no.no;i;ei!iia>j на крннои нонерхности, срилитишшси с некотором плоской фигу-
фигурой. Если данную Лрхшы.-дом теорему ныри.ипъ и сопремшшой формулировке, то для
Gii 11(>и(!р\1нм:ти цгиги »д|)П мы будем иметь формулу
что вполне соответствует современной
S
riviH :sij Л' считать {>адиус осш>в:шия цилиндра, а за 11 — его иысоту.
Лрхнмед siwei, что лежащий л осповашш данного циттлдра круг радиуса И мозкио
заключить между дпумя описанным и вписанным многоугольниками, отношение площа-
площадей которых может быть сделано меньше любого взятого отношения, большего единицы.
Площадь описанного многоугольника он определяет как произведение пололшш его
периметра L на радиус кругл ./>':
\
^инке—~ 'Л-
С другой стороны, испо, что боковая поверхность S oiiiicaiinoii около цилиндра
призмы, построенной на этом я;е самом описанном многоугольнике, будет раина
где И общая пмсота цилиндра и призмы. Отлошешш двух этих площадей будет равно
Ерли мм хотим представить no.iyuejrno(; отношение л виде ычюшелия площадей
двух подобии^ фигур, то рассматриваемое линем мне отношение И : 2/1 мы дол жим будем
:шмсмнт1. тношением днух квадратов; таким образом, солертенло ecrecjueiiiLO ноялляетсн
дюдоСнын первому многоугольник, оиксиыньш около круга, радиус Q которого янляется
средней пропорциональной между* И и 211, или, что то же, между 2R ч II:
q*=R-2H=21U1.
Млощадг. многоугольника, ojnicujiiioro около :>того круга, будет paisna 6oi*:oiii>if
шшерхнести л|>и:<мы, оиш-апной около цилиндра.
Еслл 'H'pis» А нболлачнм. ируг, состиилягощий основа кие рпсемнтригаемого цилип/уж,
а через И ¦¦ ¦ круг, описанный, радиусом у. то им бур,им имел-и следующие шесть
? ^ic—'^|!а многоугольника и круге Л:
*' S'—"ва миогоуголышка is круге В;
О ЩАР13 И ЦИЛИНДРЕ 455
. S — боковая поверхность цилиндра,
В — илощадЕ> круга В.
К этим жчшчгпшм прибавляются- еще две боотмодс поверхности «?опис я «Уи|ШС д»уд-
прими, описанной и вппепшюй около цилиндра (^0Ш1с>*'впис^; 1Ш аТ!1Х келичинах Архи-
Архимед и сгроит свои, основанное на методе исчеривпия докпннтсльство.
Требуитея докатить, что S = В.
Предположим «начала, что ¦?>?. Строим около круги В такие дли многоугольники —
ншк-аннын н шшсиппмй, чтобы имилп мести иормпснстио
*• другой стирпны,
6'л
ЧА
v"
"•пне
*¦• ыпис
"с лис
<
Л'
" '
"опис
"uihm:
так как 5сш:с>^", a^B1nic<H- Тнким обриаом, мы приптлнк иротпкорочию.апг.тплляющому
пин отбросить сделанную гипотезу.
Предположим теперь, что S<li. Тогда опята строим thihii- многоугольники, чтобы
имело м(!сто неравенство
" шик1
Тпк кик Л'Ош1С>^1 то для оироиержешш упоминутого неравенства нам остается лишь
Д1)кц;;;1ть, что $JJUC будет всегда меньше «V.
Бписыиасм и круг Л и оши-ынпем окило т!ГО м-иогоупмьиикп, подобные построен-
построенным для круга И; тогда
..л ?н
с'
" ЦПИС
°оиис
Пусггь /. иудея- иоримстр м1Ю|-оуго-Ы1Н1{а, вписанлого в круг- А, а Н ¦¦ • радиус
последнего; мы имшм:
бокоппя поверхность призмы, кпшчшшш it цилшгдр Л, будет:
it
Так как отношение — : U paisno отиишеишо соотпетстпепяых многоугольников,
пгшеаыных и описанных D круги Л if И-
_•¦!.•_ Л'А„.„ к
шик1.
' пине
то
о" с-" 2W и — <[ 9iJ
пнис ипис «->впис &п
..1
..II
' клис
то есть Л'Вп,1С будит МСШ.ШО .Ymii: — поверхности вписанной в цилиндр приз»ш, а следо-
вателт.ыо, и подавно меньше S —- йокоиой поверхности цилиндри. Полученное противо-
противоречие уст))аняет и :игу гипотезу, так что у нас остается липп. одна лозмошиость S=Ji.
,4iti5oiii.iTno, что Архимед но о продол и от но верх кость цилиндра как произведение
окружности (снования па сторону цилиндра; по-пиднмешу. «Измерение круга» еще не
бы.К) наппсяин.
[8| Оба прсдложсШ'Ш XXI -XXIF, по сутцмяяу, {шинисильита получению суммы
рлли трпгоиоистричееких функции.
450
КОММЕНТАРИИ
Пусть 2л будет число сторон правильного многоугольника, вписанного в круг или
в согыект. Тогда предложение XXI будет равносильно следующему равенству:
sin
2п . , . (я—
\-... - -sin -
1
г
2re '
а предложение XXII — такому равенству:
2 { sin —j-sin 1- ... +sin -
l~costf
если через 0 обозначить угол, соответствующий половине дуги того cernwrra, л который
виисьтластся правильный млогоуголышк с 2п сторонами.
19] Группа предложений XXIII—XXVII определяет
нижнюю граяпцу дли величины поверхности и объема
шара — :>то будет поверхность и объем тела вращепи»,
образованного виисанным в большой круг тара правиль-
пим многоугольником с 4п сторонами.
Поверхность ракгммтрввисмого тела вращинии пред-
представится как сумма поверхностей усеченных конусов,
основаниями которых являются круги, описанные Hpir
вращении вершинами правильного многоугольника.
Пусть К.А предстппляег одну из сторон правил мило
многоуголыиша (рис. 4), описавшую коническую повер-
поверхность КАК,А1, а АВ представляет такую же сторону пра-
иильпого мпогоуголышка, прилегающую к оси вращении
А А,. Обозначим радиус шара через g, угол А ОК. через а
и угол КОЛ через Аи (этот угол мы, конечно, стали бы
Тогда боковая поверхность AS усеченного конуса КК,ЛЛ,.
Рис.. \.
считав
будет:
бесконечно малым)
&S = я (КМ -[-
=я{е sin а | о sin (а+Да){ рАа.
Искомая поверхность S будет равна сумме AS:
S= 2 AS—я V! 2Q sin a
предложению XXI, мы имеем:
. 2q sin a
AB
QAa
откуда
Таким образом,
Лес"
то есть
причем обе указанные величины'различаются ыа бесконечно малую величину -^-Дая.
В обозначениях интегрального исчисления процесс, применяемый. Архимедом, может
был. совершенно точно выражеп формулой
я те
S = л У 2е sin ae da=2яоа J sin a ria —¦ 4яе*.
6 о .
Что касается объема рассматриваемого тела вращения, то оя получится как сумма
объемов тел, происшедших от вращения треугольников типа ОКЛ; каждый из таких
объемов будет равниться одной трети произведения поверхности, описанной стороной
КЛ, на длину перпендикуляра ОН, опущенного из О на К.Л- Так как длина этого перпен-
перпендикуляра будет одной и той же для всех треугольников типа ОКЛ, то рассматриваемый
О ШАРЕ И ЦИЛИНДРЕ 457
об ьем будет равен
Он бз#д"т мельпгс объема вонуся, имеющего основяяием учетверенлый большой круг
шара, а высотой — радиус последнего, но разница между ними, равная -^-nQ'&a2, будот
о
величиной бесконечно малой.
[10| В предложениях XX.VITT—XXXI Архимед строит верхний предел для поверх-
поверхности и объема шара. Он рассматривает тело, полученное и результате иращеннн пра-
иш1ыюго многоугольника, описанного около большого круга заданного шара. Тнк как
этот многоугольник можно считать вписанным в никоторый другой круг радиуса Я, ti>
к Т1!лу, полученному от его вращения, можпо приложить те же самые выводи, что и ранее;
единственная разница будет заключиться в том, что длина перпендикуляра, опущенного
из центра шар» па сторону описанного многоугольника, будет ранпяться радиусу г внут-
внутреннего шаря, а длина хорды А,В, соединяющей конечную точку /1, диаметра с другим
концом В прилегающей к последнему стороны АВ, будет раина диаметру 2г внутреннего
шара.
Если Я — радиус лпешнего тара, то сторона описанного мпогоугольпика будет
ЯДп. Формула для »S" -- поверхности описанной фигуры — примет вид
где
У 2П sin а- 7?Да=2Л Ъг,
и окончательно
так пак К>г.
Что касается объема V, то он будот равен
то есть бо.и.шс объюш конуса, имеющего в качество основания учетвороппый большой
круг внутренней, сферы, а высотой — радиус г последней.
[111 В подробностях лывода имеется очень иптереецня деталь, на которой стоит
остаиоБитьсп.
Архимед задастся двумя прямыми К и Н, отношение которых меньше отношения
тара к конусу. Требуется построить дна многоугольника, кубы сторон которых имели бы
отношение меньшее К : Н. Можно были йы получить стороны этих многоугольников,
напиши дно средние пропорциональный между К и Н:
К :Л = Л:М=М:Н:
тогда
Л ) "' Л ' М " Н ~~ Н '
так что отпошение прямых К it Л можно било бы взять в качестпе отношений сторон иско-
искомых многоугольников. Дне средние пропорциональные, в геометрической пропорции Архи-
Архимед заменяет длумя средними пропорции пал ьдыми л арифметической пропорции:
¦ к—i = i—е=е-и, • ¦ ¦
считая, очевидно, общеизвестным, что
Кз К
J 3 И '
Для последнего- неравенства Ёвтокин в слоем комментарии дает следующее докаэа-
тельстпо: • . . .
КОММЕНТАРИИ
«Пусть даны две неравные линии АВ и ГК (рис. 5). Отнявши от
АВ линяю ВЛ, равную ГК, разделим остаток АЛ на три равные части
в точках Е и Z и ни тем положим KB 11 и ZB- -0,
тогда W и II удовлетворяют поставленному уело- Л
впю •).
I;
)
Итак, 9 утверждаю, что отношение АВ : ГК /
будет больше куба отнотения АВ : 11. ^
Пусть отношение АВ к Н будет равно отно-
отношении) Н к некоторой линии Л:
АН Ь
Так как линия А В превышает Н па ту же самую
свою часть, па которую II, в свою очередь, пр«-
11Ы1ПЯОТ Л,
//
в.
м
аи-п
Л К
Рис. 5.
А в и
и всякая часть линии АВ будет больше той же части линии II, то,
следовательно, разность между ЛБ и 11 больше разности между Н и А:
А В- II > Н-Л
Но разность между АВ и 11 равна разности между Н и в;
лн-п-н- »
следовательно, И превышаете 0 иа «сличину, большую разности 11—А;
и- »> к-л
поэтолту Л будет больше 0.
Затем сделаем так, чтобы отношение Н : А равнялось отношению А
к некоторой прямой М;
Н:Л=гЛ:М
тогда М и подавно будет больше ГК Теперь так как четыре длины АН,
Н, А, М находятся в шшреныннок пролорции,
то отнонгепие AL5 : М будет равно кубу отношения АВ : Ц. Следова-
Следовательно, отношение АВ : ГК больше куба отношения АВ : Н».
С пашей точки :ijicmwT, утверждение Архимеда раипосшп.ио следувшюму.
Даны две прямые Кт-- а а Н=Ь, причем а—b—Л. а построены еще дне прямые:
Так как
;<г
поскольку вторая дробь < 1_ ибо
то I3 > К*Н
4 1
2ЬЛ-[-7Д2=а2-|;-,тД2,
«5 о
и. < И
*1 У Ептокин л В coofDCTCTEyrjTapxiiMKMORoii линия К. прямая ГК—архимедовой II. a KB*
и ZB=6 соптиетс-ruyior архимедовым uytmi.iM I и Й.
О ШЛРЕ И ЦИЛИНДРЕ 459
¦Ото керащчгство аналогично неравенству для квадратного корня
? " + 2 b>Y ah ,
Tii есть средняя нрмфметическан двух чисел болте их среднем геометрической.
: ЛТОРАЯ КНИГА
Вторая книги «О himjio и iim.'liiii;i/>o» штакомит нас с .методами, при помощи, которых
греки .-шмспнлн нашу современную школьную алгебру. I'euieiiHt; задачи распадалось на
лис части аналитическую п синтетическую. В аналитической части задача предпола-
предполагается решенной и отыскивается соотношение между заданными ш-личпнамн w искомыми;
к r.obpoMcinim.u обозначении это было Ом равносильно составлению ураынснмн, содержн-
жего неизпестную, и определению ноианестпон из атого уранпиния. Мы считаем геомет-
геометрическую задачу рипгиимий, если нам удалось ее снести к алгебраическому уравнению
тин или л!>угий степени, решение которого нроиинидитг.и но нннеедпым формул<>м. У гре-
тш аналитическое исслидоиаиие задачи считилос-!. законченным, если ets уда-чош, свести
к некоторой стандартной геометрической задаче, решение которой было общеизвестным.
Собранием таких стандартных янднч были евклидовсктге «Ua1.ii», уиплиншощие, когда
ту или другую геометрическую ве-тчину jii>;kiio считать далиой, то есть можно оиродо-
лнть ия основании:к1Д1Ш11ы\- условии. JToc-iu того как аналитическая часть решения была
:ыкончены, начинало! синтез, раыюенльпмн is некотором смыск; naiiieii цроверке реше-
решении путем подстановки найденного корни н иериопачалыюе уравнение г:.:ш построении;
цепь рассуждений црослежила.тась обрат)тым ходом — от пайденшлх рсигепий гречоский
амтематик посходил к даииым и таким об]ниом докаямппл нранилыюсть напдонного реше-'
1ШЯ. Пнщому исследованию уравнения у гренои соответствовал диоризм — опредстеяие
yc.inmiiii, при которых рассматриваемая задача могла иметь решение.
[1] В качестве иллюстрации иьппескапанного разберем ход рассуждений Архимеда
при решении задачи, разобранной п первом предложении: требуется построить шар, объем
которого был бы равен оадлшю.чу конусу или цилиндру.
Так как объем цилиндра, ouiu:aiinoro около шара, u iio-'iTojia рала больше обч.еми
:>rnrf) nmfia, то решение аадачи сводится к c,:ie,4yi<iin,eii: нужно иси-троить цилиндр, объем
[;<)TOj)oro был бы в цшггора раза бо.и.пге заданною конуса или цмлпндрп (:ito легко можег
иыть достигнуто лргт помощи соотпетствуимцего увеличения in;rcorn,i коиупа или цилиндр;!
при сохранении неизменным осшшапия), а затем построить нтпрой цилиндр с клндрят-
ш.гм осиным сечением, риииинелмкпн первому цилиндру. Диамт-р основания лирного
цилиндра Л и "высота 1Г шииютс.я, таким обратим, .чадлгтцым!:; ищется равная диамотру
]!Ы('ота Z пторого цилиндра, описанного около шара. С нашей тоЧ];и зрешги, решенш.'
сводился к кубич(>скому ураллепшо
Will
Так как у греков геометрические задачи, свя.чннные г игшлечешием квадратного
Kiifjua n:s пронянвяеияп диух прязгкх, дошались при иолощп нахождения сдодиен пропор-
цп опальной между итимя прямыми, м золоти, сплошные с извлечением кубического корпя,
<.пц,«! со времен Гиппократа Хиосскогп B-я половина V века до н. з.) прмтюднлжм, к нахо-
нахождению двух средних пропорциональных, то Архимед снодмт решение рассматриваемой
задачи тоже к нахождению двух кредмих пропорциональлмх между заданными диамет-
jiom А основания и пысотои Н цилиндра, согласно соотношению
Д8: Д2Ц —Д*Ц : Д||* = ДНа : Н8,
H.IH после и:шлечения кубического корня
Первая предп-яя пропорцийпадьпая |^'Д2И и будет искомой прямой Z, рнляой диаметру
к i ooTiiej'("niD!iio высоте mckomoi-o цилиндра, описашюго око:го шарн.
Евтокпй в своем комментарии к Архимеду приводит п ниенгей степени интересный
mtiscT, ьчи:!1[О!дийсп ис.ториии так называемой Цслийской проб-пемы (ацдачи ofi удвоении
nyoa), it которой Архимед сводит рассматриваемую задачу:
«Цришшсдн iiiiit.iiiK задачи ж найдя, 'что ее решение снодитси к определении) двух
пропорпиоиял ышх, образующих iiciipcpijiiinyio нринорцию с. дпумя заданными
460
КОММЕНТАРИИ
прямыми, он (Архимед) говорит просто «пайдем», но описания самого способа построения
их ми у него не находим и должны обратиться к сочинениям многих знаменитых людей,
а» пинавшихся этой ладачей. Нз них мы оставляем в стороне решение Евдокса К индского,
так как последний во впедении говорит, что задача решенн им при помощи «кривых»
(кпцлУКт) линий, я а доказательстве он этими «кривыми» линиями совсем не пользуется;
кроме того, найдя обыкновенную Fit]oT)uivT) — буквально: разделенная, то есть состоя-
состоящая из четырех членов пропорция') пропорцию, он пользуется сю пак непрерывной, а тиках
втлдумка недопустима ire только дли Евдокса, по и для лвц, очень мало занимавшихся
геометрией. Итак, д:гя пыясш.чшя хода лыслой шнестпмх .мужей опишем в отдельности
предложенпые лаждым и.ч пих способм решения этой задачи.
Р с ш с f и с П л а т о я а
Дапы dee прямые; найти две средние пропорциональные, обра-
образующие с ними непрерывную пропорцию.
Пусть прямые АВ, В Г (рис. 6а), для которых требуется найти две
средние пропорциональные, будут перпендикулярны друг к другу.
Продолжим эти прямые до А и Е и построим прямой угол ZH6 (рис. 66),
Рис. Ка.
Рис. 66.
пусть по одной его стороне ZH двигается линейка КА в некотором жело-
желобе, преданном и ZH так, чтобы линейка оставалась все время парал-
параллельной ИВ. Этого можно добиться, если взять другую линейку вМ.
составляющую одно целое с 1Ш и параллельную ZH. Если мы яа перед-
передних поверхностях линеек ZH, 6М прорежем желоба секмронидного
сечения *) м в эти желоба поместим шпеньки, составляющие с линей-
кой К А одно це.:юо, то при движении КА будет все время оставаться
параллельной 116. Устроивши все это, поместим одну из сторон углат
например НО, так, чтобы она проходила через точку Г, затем передви-
передвинем весь угол и линейку КА так, чтобы точка Н попала на прямую BE,
но сторона Нв все время проходила бю через Г; после этого сделаем
так, чтобы липейкаКА точкой К касалась прямой ВД, а остальной своей
частью проходила череа А. Тогда век будет, как па девон чертеже:
прямой угол M0H займет положение ГЕД, а линейка ZH расположится
по прямой ДА. Как только удастся этого добиться, задача будет решена;
действительно, так как мри точках Д и Е находятся прямые углы, то
мы будем иметь, что ГВ относится к BE, как BE к ВД и ДВ к ВА.
гв
BE
BE
вд
дв_
вд
•) Мы сказали бы: п виде «ласточкина хвоста».
О ШАРЕ И ЦИЛИНДРЕ
161
Р о «с о и. II в Г с р v 11 а («М с с h а 111 с а.» и «М с 1 о р о i с а»)
Пусть даны две прямые АВ, В Г, для которых требуется найти
две средние пропорциональные. Расположим мх таи, чтобы они обра-
образовали при В прямой угол и дополним параллелограмм ВД; проведем
прямые АГ, ВД; они, очевидно, рав- .
ны между собой и пересекаются
пополам; построенный на одной из
пих круг пройдет и чирез копцы дру-
другой, так как рассматриваемый нарал-
лелограмм будет прямоугольным.
Продолжим ДГ, ДА и вообразим ли-
липе и ку ZBI-I, которая вращалась бы
окон о некого)! ого неподвижного гвоз-
дя Б. Будем двигать ату л клейку
так, чтобы она нересекла ДЫ и AZ
в точках, находящихся на равних
расстояниях EZ и ЕН от точки Е. Предстаиим, что ото уже сделано,
и линейка находится в положении ZBH, причем, как сказано, прямые
EZ и EI1 сделались равными. Из точки Е опустим на ГД перпендикуляр
Ев, который, очевидно, разделит ГД пополам.
Таи как ГД разделилась в точке 6 пополам и к ней добавился
отрезок TZ, то прямоугольник между AZ и ZF вместе с квадратом на
Г0 равен кнадрату па 6Z.
Рис. 7.
Прибаиим к обоим членам квадрат на Е0, тогда прямоугольник
между AZ и ZF вместе с квадратик на Г0 и квадратом на ©Е равен
квадрату па Z0 вместе с квадратом на f-)E.
Но квадрат на Z0 вместе с квадратом па 0Е равен квадрату на Г15,
Е2=ГЕ4
квадрат на Z0 вместе с квадратом на 0Е равен квадрату на EZ.
Значит, 1фнмоугольник между AZ и ZF вместе с квадратом на ГЕ
равен киадрату на EZ. Тпчио так же докажем, что прямоугольник
между АН и НА вместе с киадратом па АЕ равен квадрату па ЕН.
Затом АЕ равна ЕГ и НЕ равпа EZ; значит, прямоугольник между AZ
и ZT ранен прямоугольнику между ДП и ПА.
=-AHHA
Если жо прямоугольник между крайними равен прямоугольнику между
средпими, то четыре прямых составляют пропорцию; значит, ZA так
относится к ДП, как All к ZT.
дн zr
7.А
Но 2Д относится к ДН, как ZT к ГВ и как 13А к АН,
= "аТГ
КОММЕНТАРИИ
так как в треугольнике ZATI проведены ГВ и ЛИ параллельно ДК
и AZ. .Члачпт, ВЛ к АН, как ЛИ я ТТ., или ГА к ГВ.
вл
лн
л_м_
"гх
rz
гв'
Таким образом, All и I'Z будут средними пропорциональным if
для ЛВ и ВГ, что и требовалось найти.
Р « hi е н и с Ф и л о л а \1 и ;i u н т и некого
A к и ига «И о I о р о i с а»)
Пусть линии, к которым требуется найти дно средние пропорцио-
пропорциональные, будут ЛВ и ВГ (рис. 8). Расположим их так, чтобы они ofijia-
н р и В прямой угол; затем, проведя прямую Л Г, опишем полу-
полуокружность ЛВКГ и проведем АД
перпендикулярно к В А и TZ пер-
лендикулярпо к ВГ. К точке В при-
приложим движущуюся лшпейку, кото-
которая пересекла бы АД п TZ, и будем
крашать ее около В до тех нор, пока
расстояние ВД по станет равным
расстоянию EZ, то есть расстоя-
расстоянию между точками пересечения
линейки с окружпостыо круга и
прямой TZ. Представим, что ли-
линейка занимает положение ABtiZ,
причем, как уже сказано, ЛВ раина
EZ. Я утверждаю, чти ЛЛ и СТ. будут средними пропорциональными
дли АВ н В Г.
Деистинтелмю, представим себе ДА и ZI" лродолжеппыми до пере-
сечения в точке (-). Ясно, что вследствие параллельности ВА и ZH
угол при точке В. будет прямым, м окружность АЕГ при своем продол-
продолжении пройдет и через точку в. Теперь, поскольку'АВ равна EZ и,
следовательно, прямоугольник между ЕД и ДВ равен прямоугольнику
между BZ и 7,4,
Рис. 8.
но прямоугольник между ЕА, ДВ равен прямоугольнику между НЛ.
ДА,
ЕД-АВ—ИД-ДЛ
ибо 1саждып ма :rnix прямоугольников равен квадрату на касательной
к окружности, нроисдешшй и;$ точки А. Точно так же. нрямоугильпш;
между В/ и /К равпп лрялюуголышку между BZ и ZT.
ltZ-ZV.—HZ-2l'
так как- каждый из этих прямоугольников точно так же будет раиси
квадрату на касательной из точки Z; отсюда следует, что прямоугольник
между ОД и ЛЛ равен прямоугольнику между 0Z и ZT
и, значит, Д0 относится к OZ, как TZ к ДА
Л0 _ Г%_
W/. "•' АЛ
и как ВД относится к WZ, так и ВГ к TZ и ДА к АВ,
ВЛ . ВГ _ ДА
«2 ~ TZ ~ АВ
О ШАРЕ И ЦИЛИНДРЕ
• так как и треугольгшко A(-)Z прямые В Г и 13Л пропсдопы параллельно
AG и (-JZ. .'Зпачит, 13Г относится к FZ, как VA к ДЛ и как ДА к АВ.
J'Z ДЛ АИ
что и трсбопаяось докапать.
Должно :шмотит1,, что :>то построении почти гон ершен л о тождественно с: .построе-
.построением Героин. Действительно, прямоугольник Вв будет тем же самым прямоугольником,
который борется и и построении Героин; то же можно скакать и о продолженных кгоро-
иах вЛ и НГ II днижущейсл около В линейке. От геромшекоги рассматриваемое построе-
построестанет ргшньш EZ. Таким обрааом, оба гшстроегпш дают один и тот же ркаультнт,
но филоиопстюе построение; якпяотся боа се удобным для практики;дш'|ст1шт<шыю, гораидо-
прощп добнт1,гя pniiuiiCTiin АН и EZ (дли чс:го достаточно разделить линейку Л7. на нико-
никоторое 4UCI0 llpiIJIOVKillUIIX ДРУГ К другу равных UTpCUKOD), ЧОЯ J4-TilililB.4HBHTb Iipil ПОМОЩИ
циркуля*) раш'.иггнн .пиши КД и K.Z.
Р о hi с н и о А п о л л о н и я
Пусть прямы:!', для которых, трейуетгн нилти дио средние пропор-
цнопальиш;, будут ВЛ и А Г, образующие при точке А пряном угол.-
Из центра В радиусом АГ опишем дугу K0A.
Затем им центра I1 радиусом АВ шишгем дугу
MQN; пусть ома пересечет К6Л в точке в;
проведем соединнющис прямые 0А, (-JJ3 и
©Г; тогда В Г будет прямоугольпикемт м (т)Л
ого ;<лаг<1Е1«.иью. Разделим WA помолами точ-
точке Е и опишим u:i ццитра S икружиость,
пересекающую продолжения прямых АВ
и. А Г а точках Д, Е таким образом,, чтобы Д
и Е были па одпогт прямой с (h); итого можно
добиться, если около точки в двигать иинсй-
ку, шфог.рлсаищую. АД и АЕ, до тех пор,
пока лрямыц, ироиедеыиыс из точки 2 до Д
и Е, не будут равны друг другу.
Добившись итого, мы получим искодюо решение, так кап олисам-
ное построение тождественно с данными Гсронол и <1>илином, так что
и п эт«1м глучпо мг»к1то будет применить тп же самое доказательство.
Р с- ш е л л i>. Д и о iv ,:i
а в
к и п г с «О к а у с т if к а х»
Пронвдим it круге дна взаимно перпендикулярных диаметра
Л13 и ГД, по обе стороны от точки 13 отложим дне равпые дуги ЕН
и BZ, через точку Z проведим Z1I параллельно АН и соединим точки Д
и В прямой. Я утверждаю, что Z1I и ПД будут двумя средними пропор-
пропорциональными длн ГII к II В.
Пршшдим через Е прямую ГСК, параллельную АВ; тогда ЕК
раина ZIT к КГ равна НД; это будот очевидным, если соединить А
прямыми с Е и Z; и самом деле, углы ГАЕ, ZAA равны, и при точках К
и Н буД5Т прямые углы; тогда вследствие равенства АЕ iiAZ все стороны
*) Интересно отмстить греческий термин для пиркулп xaQxivoj- рак. По-ьидидкшу. первые:
цирпули были с изогнутыми ножками наподобие нашгго кронцирнулп.
КОММЕНТАРИИ
я углы одного треугольника будут рампы соотиетстпующим сторонам
и углам другого, а значит, будут равны и остатки ГК и ИД. Теперь,
так как ДК относится к КЕ, как АН к Н0
и ДК к КЕ, как КК к КГ л
дк
кк
КК
нг
lie
кг
(ибо ЕК будет средней пропорциональной
для ДК, КГ), то, значит, ДК относится к
КЕ, как ЕК к КГ в как ДН к Кв. ''
Ml
' кг не
Далее, АК равна ГИ, КЕ равна ZH,
КГ равна 11Д; значит, ГН отиоситси к IIZ,
как ZH к ПД и как ДП к Н0.
!ZH
ДН
не
Рис. 10.
Если с каждой стороны В взять рапные дуги MB, 13N, через N провести
N 3 параллельно АВ и соединить Д и М прямой, то совершенно так
же М? и 2Д будут средними пропорциональными между ГЗ и ЕО.
Если ми подобным образом между В и Д проведем достаточно большое
число непрерывно расположенных лараллельных прямых, затем отло-
отложим от В к Г дуги, соответственно ранные отсекаемым этими прямыми
от точки В дугам, и полученные концы соединим с А прямыми вроде
АЕ и А М, то эти прямые пересекут соответствующие им между В и А
параллели н некоторых точках (и нашем примере в 0 и О); если соеди-
соединить эти точки по линейке прямыми, то мы получим некоторую начер-
начерченную в круге линию, обладающую тем свойством, что если через любую
ее точку пронести прямую, параллель-
параллельную ЛВ, до пересечения с окружностью,
то ата проведенная прямая и отсекае-
отсекаемый ею па диаметре ко направлению
к А отрезок будут средними пропорцио-
пропорциональными для другого отрезка диаметра
но направлению к Г и той части прове-
проведенной прямой, которая заключена меж-
между диаметром ГА и построенной в круге
линией.
После этой предварительной под-
подготовки возьмем дне прямые, для ко-
которых требуется отыскать дне средние
пропорциональные; пусть это будут А и
В. Возьмем круг с,цтеумя взаимпо перпен-
перпендикулярными диаметрами и начертим в
нем при помощи последовательных точек упомянутую кривую A0Z.
Сделаем, чтобы отношение ГП к НК было равно отношению А к В.
¦затем продолжим соединяющую прямую ГК до пересечения с построен-
построенной линией; пусть точка пересечения будет 0. Через 0 проведем AM
параллельно EZ; тогда, согласно вышеизложенному, МА и АД будут
средними пропорциональными для ГА и А0.
А
в
м
Рис.11.
ГЛ
лм
лд
ЛА
О ШАРЕ И ЦИЛИНДР*!
465
гл _ rii
"Ав ПК
Затем, поскольку ГА относится к Лв, как ГН к ПК
Г1!
ПК
и ГП к ПК, как Л к В,
I'D Jl
ик~ в"
то если мы между Аи В вставим прямые N и а так, чтобы все эти прямые
били соотнстствонно пропорциональны ГА, AM, АД, АО,
_А N 2_ В_
ГЛ ""¦ AM ~" АЛ ЛР
то N, S и будут средними пропорциональными для А и 13, что и тре-
бона.чось отыскать.
Решение П а п н а во «Введении м механик у»
<к п и г а VIII, 2й>
ТТапп поставил задачу: определить куб, который находился бы
в данном отношении к другому кубу. Данный им способ доказатель-
доказательства применим и к рассматринаемой пами задаче, так как нполне
очевидно, что, решив его задачу, мы одновременно найдем решение
и предложенной нам; ибо если для двух данных прямых будет
найдена вторая из нужных нам средних пропорциональных, то сей-
сейчас я;с будет ияинстма и третья. Сям он дословно говорит следую-
следующие: опишем полукруг АВГ, из центра Д опустим перпендикуляр .АВ
и около точки А будем двигать линейку так, чтобы один ее конец лежал
неподвнжпо на закрепленном в точ-
точке А гиоздике, а другой переме-
перемещался между точками В и Г, дви-
двигаясь вокруг гвоздя А как центра.
Сделавши это, поставим ссб(> цолыо
отыскать два куба, находящиеся
между собой в заданном отношении.
Пусть это отношение будет равнять-
равняться отношению прямых 13А и ДЕ;
проведя соединяющую прямую ГЕ,
продолжим ее до точки Z. Ьудем за-
затем двигать между В и Г линейку, по-
пока часть ео между прямыми ZE, ЕВ
не сделается равной части, заклю-
заключенной между прямой BE и окруж-
окружностью ВК Г. Ксли дкигнть соответст-
соответственно линейку, то этого мы легко до-
достигнем после нескольких попыток.
Пусть ято будет сделано, и линейка займет положение АК, так что
отрезки Ив и 6К будут равными. Я утверждаю, что куб на ВД будет
иметь к кубу на Д0 отношение, равное заданному, то есть отноше-
отношению ВД к ДЕ.
Вообразим, что паша окружность описана полностью; соединяю-
соединяющую л и шло КД иродолжим до точки А, после чего [гроведем АН. Нос-
Архимед
/7
1 / м
"\
N
\
F.
-
\
Л
\
в \
Л
Рис. 12.
4E6 КОММЕНТАРИИ
педния будет параллельна ВД, так как Кв равно Н0, и КД равно ДЛ.
Проведем ЛЛ и Л Г. Так как угол АЛГ прямой (как вписанный и полу-
полукруге) и ЛМперпендикулярна к АГ, то квадрат на AM к квадрату иа
AM относится, как ГМк МЛ и как квадрат на AM к квадрату на МП.
AM2 _ I'M _ AM8
AM* МЛ МН*
Прибавим *) к обеим частим последнего равенства отношение А М
к МП. Тогда отнопшние, составленное и.ч ГМ к МЛ и AM к МП, то
есть отношение ГМ к МН, будет тем же самым, что и отношение, сос-
составленное из (отпошошш) квадрата иа ЛМ к квадрату па М1{ и (отно-
(отношения) AM к МН. Но отношение, составленное из (отношения) квад-
квадрата на AM к квадрату на МН и (отношения) AM к МН, будет равно
отношению куба иа AM к кубу на МН.
ГМ
ММ
m
AM
Mil
МП*
Но
гл
ДЕ
и AM
АД
™ де
ГМ ото»
относится
к МН, кик АЛ к Дв;
следовательно, отношение ВА к ДЕ **), то есть заданное, будет равно
отноитшпо куба на ВЛ к кубу на Дв.
Должлп обратить внимание на то, что это построение совпадает
с предложенным Дпоклом, отличаясь от него только тем, что Диокл
при помощи ряда последовательных точек описывает некоторую распо-
расположенную между А и В кривую линию, на которой с ее пересечении
с продолжением ГЕ берется точка II, а в рассматриваемом построении Н
находится нрн помощи линейки АК, движущейся около Л. А что точка
П будет одной и той же, найдем ли мы ее при помощи линейки, как в
данном построении, или же но способу Диокла, и этом мы можем убе-
убедиться следующим образом. Продолжив МИ до N, проведем прямую
К.\. Поскольку Кв равна GH и HN параллельна в13, то и К 3 будет
раина ЕМ. Линия ЗВ будет общим перпендикуляром, так как KN
делится пополам прямой, проведенной через центр, и они встречаются
под прямим углом. Таким образом, в треугольниках КвЕ и E0N
одно основание равно другому, а вследствие этого и дуга KB раина
В.\. Отсюда вытекает, что точка И находится на кривой Диокла, и рас-
рассуждения остаются теми же самыми. Действительно, Диокл сказал, что
ГМ относится к MN, как MN к МА и как AM к МП.
US '" МА " МН
По NM равно МА, так как диаметр пересекает NA под прямым
углом; значит, ГМ относится 1; МА как AM к МА и как AM к МН.
гм лм am
МЛ .VIA МН
•) Нужно плминть. что иа языке греческой математики прибавить отношение — значит
на пего иомно.инть.
**) Вд—АЛ--ГД как радиусы.
О ШАРЕ И ЦИЛИНДРЕ
Таким образом, для ГМи МН средними пропорциональными будут
ЛМ я МЛ. Но ГМ к МП, как ГД к ДЕ
I'M _ГД
&ш "" лк"
и ГМ относится к МЛ как AM в МН и как ГА к Д6.
гм am _ гд
мл мн ~~ да
Следовательно, для длух прямых ГД и ДК второй пропорциональной
будет та самая Дв, которую пашол и ГГанн.
Р в пт е н и с Свор а
Пусть даны две неравные прямые АВ, В Г; требуется найти для
АВ, ВГ две средние пропорциональные в непрерывной пропорции.
Пронодем из В прямую ДВЕ мод прямим, углом к АВ, аатом опишом
лол у круг ДАЕ с центрам В и радиусом ВА: пряную, соединяющую
точки Е л Г, продолжим до Z и че-
через Д кроведем некоторую прямую л
так, чтобы Ив равнялась вК (это
дейстинтельно всегда можно сде-
сделать). Затем из точек Ы и К опу-
опустим па АЕ перпендикуляры НА и
K.NM. Итак, поскольку мы имеем,
что К в относится к вН, как MB
к ВЛ, 4 в —м
_
им
"ВЛ
S
Рис. 13.
и К в равна 61 [, то, значит, и MB
равна ВЛ, а следоиателыю, и оста-
то if МИ равен АД, и вен ДМ рав-
равна ЛЕ. Отсюда следует, что МД относится к Л А, как ЛЕ к ЕМ.
МА
ДА
лл"
дм
ДМ
Но МД относится к ДА, как КМ к НА, а АЕ относится к Е М, как КМ
к ПЛ; • ¦ ¦
км
НА
__
км
ватой?., так как AM относится к МК, кик КМ к А1К, то значит, ДМ
относится к ME, как квадрат на ДМ к квадрату па МК, или как квад-
квадрат на ДВ к квадрату на Вв, или как квадрат на АВ к квадрату на В0,
А31Д Л1|? Л В»
так как ДВ равна ВА.
Затем, поскольку МА относится к АН, как ЛЕ к ЙВ, МД к ЛВ,
как КМ к ВВ, и ЛЕ к ЕВ, как НА к ГВ, то, значит, КМ относитсн
к вВ, как НА к ГВ,
"вв " гв
км
НА
м после перестановки КМ относится к НА, как вВ к ГВ.
ев
30»
468
КОММЕНТАРИИ
Но КМ относится к НЛ, как МД к ДЛ и как ДМ к ME,
ки
НА
дм
ME
АВ8
ОВВ
i •
м\ _ ам
~ ЛЛ ~ ME
затем, пак мы видели выше, ДМ относится к ME, как квадрат на АВ
к квадрату на вВ,
_ два
и, значит, квадрат на АВ к квадрату па 0В относится, как К М к ИЛ.
Г КМ 1 _ В»
— I НА 1 ВГ
Возьмем среднюю пропорциональную 3 между ЭВ и ВГ; так как
. квадрат на АВ относится к квадрату на 6В, как 0В к ВГ, квадрат на
АВ к квадрату на В© имеет отношение, равное двойному отношению
АВ к В6,
ABB
ев
ВГ
ев
и отношение 6В к ВГ равно двойному отпоиюпию 0 В к 3,
ел он
'-Е~"~В-
то, гшачит, АВ относится к вВ. как Вв к 3.
Но ВВ относится к 3, как S к В Г,
Е ¦ •¦ ¦
АБ
и, следовательно, ЛВ относится к В0, как 0В к 3 к как 3 к ВГ.
- .Ё5_- _5_
" s ~ вг
Это построение будет, очевидно,
тем же самым, которое описали Папп
и Диоде.».
Решение М с и е х м а
Пусть будут две прямые А, Е. и
требуется для Л, Е найти две средние
пропорциональные.
Пусть это сделано, и соответствую-
соответствующие прямые будут В, Г; А относится
к В, как В к Г и как Г к Е.
После этого отложим где-нибудь *)
прямую ЛН, ограниченную а точке Д,
затем к Л приложим линию AZ, равную Г, проведем под прямым
углом. 6Z и отложим Z0, равную В. Поскольку три прямые А, В, Г
'составляют пропорцию, то прямоугольник между А и Г равен
квадрату на В.
Таким образом, прямоугольник между А и Г, то есть на AZ, будет
равен квадрату ма В, или квадрату на Z0; следовательно, точйа 0
•) Xii|>iiKrcpiirie uhipnviciumc:
Qecei—отложи» положением; то есть бее этого допол-
дополнении хеюфш милеет шшпмтч.гп it u смысле нашего «иойьмеы» прямую, определенную только но лели-
чянс. но не ээдаипуго нилжм
О ШАРЕ И ЦИЛИНЛРК
будет лежать на проходящей через Д параболе*). Проведем параллели
GK и ДК. Поскольку дам прямоугольник между В, Г (он равен пря-
прямоугольнику между А, Е **), то будет известен и прямоугольник между
Кб, 0Z. Следовательно, точка О будет находиться па гиперболе, пос-
построенной на асимптотах КД и AZ***). Таким образом, точна Э дана,
а следовательно, будет дана и точка Z.
Построение производится таи. Пусть данные прямые будут А
и Е; отложим ограни чеппуго и точке А прямую ДН и через точку Д про-
проводом параболу с осью ДН и параметром А; пусть проведенные под пря-
прямым угломкДН лишш будут квадрироиать****) площади, построенные
на А и имеющие своей шириной отсекаемые ими отрезки на оси ДН,
начиная от точки Д. Построим эту параболу; пусть она будет Д0, а
ДК будет перпендикуляр118 r ДН. Затем па асимптотах КД и AZ пост-
построим гиперболу так, чтобы проведенные (xaTceyouivcu) от нее параллельно
¦ КД и AZ прямые образовали площадь, равную прямоугольнику между
А, Е*****). Эта гипербол а Пересе чет пара бол у; пусть точка лир есечелия
будет 0. Проведем перпендикуляры 6К и GZ. Так кап квадрат на Z6
равен прямоугольнику между А и AZ,
то А относится к Z0, как 0Z к ZA.
A 0Z
ze ~ гд
Далее, поскольку прямоугольник между Л и Е равен прямоугольнику
между 0Z, ZA,
то получится, что как А относится к Z6, так и ZA к Е.
Но А относится к Z0, как Z6 к ZA, и как ZA к Е.
А
Zfc>
Л
Ш
ЯЛ
~ к
Z0
Но а
Zi
""я
¦) Ecuiii положим Д/.=л-, BZ-^ij и A—2ji. то урлишяин: этой параболы (Зудет:
*•) Эт<1Т результат мшкио легко получить следующим спосс^ом. Возимом пропорцию
А : И=В : Г=Г : Е.
Мм имеем:
отсюда
В-Г-А-Е.
••*) Если положим А—о. И=Ь. то уравнение этой гиперболы будет:
i
*•••) frtvexiT-ffcoaav. Ото значит, что линия ©Z n квадрате должна равняться площади прямо-
прямоугольника г. шириной АИ—х и длиной А=2». Это лырншеиие равносильно нашему уравнению парг-
..^.7) Иы снизали бы: прппавсиение се координат лг=ж и Z6^y равнялось бы А-Е или ab. что
равносильно уранисшки гиперболы: ху=аЪ. . .¦ ¦
470
КОММЕНТАРИИ
Положим В равным 6Z, Г равным AZ; тогда -'А относится к В как
и к Г и как Г к К.
A _В Г
в ~ г JT
Таким образом, А, В, Г, Е составляют непрерывную пропорцию, что
и требовалось сделать.
И ним с п о с о б о м
Пусть две заданные прямые АВ, ВГ будут перпендикулярны друг
к другу. Пусть для них средние вропорпиопалыше будут ДВ и BE,
так что ГВ относится к ВД, как 13Д и BE и как BE к В А.
Г В = ВД _ J3K
ВЛ BE
Проведем перпендикуляры AZ и EZ. Так как ГВ отиоентси [к ВД
пак ДВ к BE,
г в лв
ВД '¦ НЕ
то, значит, прямоугольник между ГВ м BE, то есть прямоугольник
мож.чу одной из заданпых линий и BE, будет равен кнадрату на ВД,
или квадрату на EZ.
ГВ-ВЕ -BA2^
Так как прямоугольник можду заданной линией и BE равен квад-
квадрату на EZ, то точка Z находится на параболе, построенной на оси
BE. Патем, так как АВ относится к BE,
как BE к ВД,
АВ BE
UK ВД
то примоуголышк между АВ и ВЛ. то
есть другой заданной линией и ВД, бу- А
дет равен кнадрату на ЕВ или на AZ;
значит, Z находится на параболе с осью ВД.
Но опа находится и па другой нараболе с 1>ис- 15-
осью BE, значит, топка Z известпа. Затем,
так как ZA и ZE перпендикулярны, то будут известны и точ-
точки Д с Е.
Построение производится так: пусть две заданные прямые АВ
и ВГ будут взаимно перпендикулярны; продолжим их из точки В до
бесконечности. На оси БЕ построим параболу так, чтобы се опущопиые
на RE ординаты квадриронадись ла ВГ *). Затем на оси ДВ строим
параболу так, чтобы ее ординаты киадрнровались па АВ **). Обе эти
параболы пересекут друг друга; пусть точка их пересечения будет Z.
Проведем из Z иерлендикулярм ZA и ZE. Так как в одной параболе
*) Ото поражение равносильно формуле 7.Е' — BE-В Г. или уравнению х'~ЪГ-у.
•*) Строим ll;ip;iRo:iy ЙЛ'-^ДВ-ВД пли у: = ЛВ-.т.
О ШАРЕ И ЦИЛИНДРЕ
471
?5_
проведена ордината ZE, то есть АВ, то, значит, прямоугольник между
ГВ и BE равип квадрату па ВД
к = ид*
и поэтому ГВ отпосится к ВД как ДВ к BE. Но ДВ относится к БЕ,
как ГВ к ВД и, следовательно, ГВ относится к БД, как ВД к BE
и как ЕВ к 13А,
_ ва кв .
"~вё~ ~~па~
что и требоиалось получить.
Строится же парабола при помощи «диабета» изобретенного
ггапиш учителем милетским механиком Исидором и описанного им
в составленном им комментарии к работе Герона «О построении
сводов».
Решение Ар хита
и з л о ш с ни и Евдвиа
Г
Пусть {рис. 1С) заданные, две прямые будут АД и Г; требуется для
АЛ и Г найти две средние пропорциональные.
На большей из них АД опишем круг АВД2 и вставим в него пря-
иуго АН, ранную Г; пусть опа, будучи продолжена, пересечет в точке П
касательную к кругу, прове-
проведенную из точки Л. Проведем
BEZ, параллельную ИДО, и ио-
обраннм на полукруге ЛВД
прямой полуцилиндр, а на АД
перпендикулярный к ЛВД по-
полукруг, расположенный на
прямоугольники осевого соче-
ния полуцилиндра. Этот полу-
полукруг при своем вращении от Д
к В около ноподиижною кон-
конца Л диаметра будет перпг.е-
кать цилиндрическую повс:рх-
ность и, таким образом, лычер-
тит иа пей некоторую линию.
Треугольник АИД будем вра-
вращать около неподвижной пря-
прямой АД в сторону, противопо-
противоположную движению полукруга;
тогда этот треугольник образу-
образует коническую поверхность с
образующей АН, которая при
прящонаи первейчот начерчен-
начерченную па цилиндре кривую в пс-
которой точке; одновременно В опишет на конической поверхности
полукруг. Пусть и пересечении вышеупомянутых линий движущийся
полукруг занимает положении Д'КА, вращающийся треугольник
находится в положении ДАЛ, притом точкой упомянутого пересечения
будет К; далии, пусть В .VIZ будет описанной точкой Pi полукруг,
a BZ — общая линии «го пересечения с кругом ВДХА. Проводом пороз К
перпендикуляр к плоскости полукруга ИДА; конец :>того порнинднну-
ляра попадет на окружность круга ЛВД, так как цилиндр будет прямым.
Рис. 1.6.
472 КОММЕНТАРИИ
Пусть ятот перпендикуляр будет KI, пусть далее соединяющая прямая
А1 пересечет BZ в точке в, а образующая конуса АЛ пересечет полу-
полукруг BMZ н точке М. Провидом прямые КД', ML Мб. Так как каж-
каждый из полукругов A'KAhBMZ перпендикулярен к расположенной под
ними плоскости, то значит, и общее сечепие Мб будет перпендикулярно
к плоскости круга ВАЛ; следовательно, Мб будет перпендикулярна
и к KZ.
Таким образом, прямоугольник между 0В и 6Z, или прямоуголь-
прямоугольник между в А и ©1. равоп квадрату на Мб;
следовательно, треугольник AMI будет подобен каждому из треуголь-
треугольников MT0 и MAG. Далее, угол IMA прямой; прямым будет также
и угол Д'КА; зиачит, КД' и ЛИ будут параллельны, н получится про-
пропорция: Д'Л относится к АК, как КА к Al u как 1Л к AMJ
Л'А КА ТА
АК LAI хАМ
вследствие подобия треугольников. Таким образом, четыре прямые
Д'Л, АК, Al, AM составляют непрерывную пропорцию. Затем AM
раина Г, так как она равпа АВ; значит, для заданных прямых АД
и Г найдены две средние пропорциональные АК. и Al.
Решение Эратосфена.
Царю Птоломею Эратосфш желает радости!
Рассказывают, что один из древних трагиков вывел на сцену Миноса,
заботящегося о построении могилы для Главка. Когда он узнал, что
эта могила будет иметь во всех направлениях но сто футов, то сказал:
1$пял слишком малый объем ты гроба царского;
Двойной пусть Судет он; так, красоты лс трогая,
Удвой скорее гроба каждоо члешмше.
Ясно, что он ошибся, так как после удвоения сторон, площадь уве-
увеличивается в четыре раза, а объем в восемь раз. Поэтому гсоыетры
и разыскивали, каким образом, удноить данный объем, сохраняя его
в той же самой форме. Эта задача и получила паз панно удвоения куба,
так как они, предполагая некоторый куб данным, старались его удво-
удвоить. В течение долгого времени эта задача затрудняла всех математиков;
первый Гиппократ Хиосский нашел, ^п-о если для двух данных линий,
из которых большая равна удвоенной меньшей, найти две средние
пропорциональные, составляющие с ними непрерывную пропорцию, то
тем самым будет достигнуто и удвоепие куба, так что его трудная зада-
задача .превратилась в другую не, легче.
Немного времени спустя некоторые делшщы, пытаясь, согласно обе-
обету, удвоить жертвенник, пришли, как рассказывают, к тем же самым
трудностям и в послании к геометрам, работавшим у Платонв в Акаде-
Академии просили дать им решение. Те трудолюбиво принялись за это дело
и стали искать, каким образом для двух данных прямых найти дье
средние пропорциональные: говорят, что Архит Тарентский получил
решение при помощи полуцилиндров, а Квдокс при помощи так
называемых выгнутых (хаилиАсдо) линий*). Однако вышло, что
*) Под втим названием подразумевались кривые, получаемые сечением кривых поверхно
стей, upocrelUunmt из которых являются конические сс-чечин.
О ШАРЕ И ЦИЛИНДРЕ
47»
Рис. 17а.
А К
KB
АЕ
ZB
они доказали лишь возможность такого построения, выполнить же
его па самом деле и дать практический способ не смогли, если но счи-
считать короткого способа Мемсхма, да и то затруднительного. Нами же
придуман легкий способ решения при помощи инструментов; пользу-
пользуясь им, дли двух данных прямых ми можем найти, но только две, но
и сколько угодно средних лропорциопальных. После этого мы сможем
лообще любой заданный ограпи-
чеппык параллелограммами объем
превращать в куб. одну форму
преобразовывать в другую, делать
подобной и увеличивать, сохра-
сохраняя подобие, и жертвенники и
храмы. Также меры жидкостей и
сыпучих тел (как, например, ме-
дтш и метрет) мы сможем про-
нращать в куб и по стороне послед-
него измерять вместимость раз-
различных сосудов. Это .изобретение
будет полезно и для желающих
увеличить размеры катапульт и камнеметов, так как для увеличения
длины броска цумшо пропорционально увеличить все — и ширину, и ве-
величину, и отверстия, и втулки, и вставляемые тяжи, а этого нельзя сде-
сделать "без пахождепия средпих пропорциональных. Доказательство
способа, а" также устрой-
устройство упомянутого инстру-
инструмента, я описал тебе шике.
Пусть ЛЕ и ДО
(рис. 17а) будут дне за-
заданные неранние прямые,
для которых требуется
паити дно средине пропор-
пропорциональные в непрерыв-
непрерывной пропорции. Восстания
перпендикуляр Л К к не-
некоторой прямой Ев, по-
построим на Ев три поелс-
донателмшх одинаковых прямоугольника AZ, ZT, 10 и проведем их
диаметры AZ, ЛН, 10; последние будут параллельны.
Затем, сохраняя па месте средпий прямоугольник Z.I., надвинем па
него AZ и задвинем иод него 10, как это изображопо на рис. 176,
и будем переднигать их, пока точки А, В, Г, Д не окажутся на одной
прямой. Проведем через точки А, В, Г, Д прямую; пусть она пересечет-
пересечется it точке К с продолжением Е0. Тогда АК относится к KB, как
ЕК к KZ,
ЕК
KZ
нсподетиис параллелизма прямых ЛИ к ZB u ЛК относится к KB,
как ZK к КН,
АК
KB
ZK
КII
кследстние параллелизма прямых А'/, Ш1. Следовательно, АК отпч-
474 КОММЕНТАРИИ
сится it KB, или ЕК к KZ, как KZ к КН.
а к _ тек kz
KB ~ KZ КН
Затем, так как RK. относится к КГ, кап ZK к КН,
вк zk
кг ~~ кы
вследствие параллелизма 13Z и ГН, и НК относится к КГ, как ПК к КН,
вк нк
кг к«
вследствие параллелизма ВП и Гв, то, значит, ВК относится к КГ
как ZK к КН и как ПК к KG.
НК '/.К НК
КГ КН " Кв
Но ZK относится к КП, как ЕК к KZ, л, значит, ЕК относится
к KZ, кап ZK к КН или ПК к Кв.
I«K ZK НК
К7. КН К©
Но ЕК относится к KZ, как А К к BZ,
КК АЕ
KZ B2
ZK к КП, как BZ к ГН, и НК к КО как ГН к Лв
zk _ Jbz_ пк _ га .
кп ~~ ги ' W ~ лв
и, значит, АЕ относится к BZ, как F5Z к ГП и как ГП к Дв.
А К KZ ГП
BZ ~~ ГН ДО
Таким образом, для АЕ и Д© найдены две средние пропорциональ-
пропорциональны» BZ и ГН.
Теперь геометрически задача является решенной. Для нахождения
двух средних пропорциональных на практике при помощи инструмен-
инструментов устроим из дерева или из слоновой кости, или же из меди, нластиы-
ку, которая складывалась бы из трех тончайших одинаковых табличек;
средпяя из этих табличек закреплена неподвижно, а две крайние могут
двигаться в желобках. Размеры и пропорции этих табличек могут быть
какими угодно, так как доказательство производится дли всех размеров
совершенно одинаково; для получения возможно большей точности
при нахождении линий нужно постараться устроить так, чтобы все
таблички при сближении оставались параллельными, не образовывали
между собой промежутков к равномерно налегали друг на друга.
На даре, щншесенпом по обету, ииструмепт сделан из мс:ди и укре-
укреплен свинцом иод самой капителью колонны, под ним же помещены
краткое доказательство, фигура и надпись-
Я. сообщу тебе и это для того, чтобы у тебя было и то, что находится
на принесенном по обету даре. Из обеих фигур па колонне нарисована
только вторая.
«Для двух данных прямых найти две средние пропорциональные
в непрерывной пропорции. Пусть будут даны прямые ЛЕ и Лб. Я свожу
вместе таблички на инструменте, пока точки А, В, Г, Д не окажутся
па одной лрямой; вообразим, что они при этом расноло;катсн, как на
фигуре. В таком случае как АК к KB, так в параллелях AE-,13Z будет
О ШАРК И ЦИЛИНДР К
475
и ЕК к KZ, а в параллелях AZ, ВП так будет м ZK к КН. Значит, как
КК к KZ, так и KZ к K1I. Но как будут друг к другу последние, так
будут и АЕ к В'/ » BZ к ГТ1. Подобным же образом докажем, что
как ZB к ГН, так и ГН к ДВ; следовательно, АЕ, BZ, ГН, А в состав-
составляют пропорцию. Таким образом, дли двух данных линий найдены две
средние пропорциональные. Если же данные линии пе будут равны
АЕ к А0, то, сделанши их пропорциональными АЕ и Л6, найдем две
средние для последних и перенесем на первые, вьпголнпк таким обра-
образом задание. Если гкс требуется найти большее число средних пропор-
пропорциональных, то в приборе число табличок нужно bhhtj. на одну больше,
чем число отыскиваемых средних; доказателт.стио останется том же
самым».
Если из малого куба дииГмсоы .ч.члп.шглястгп. устроить,
: ДРУГ> или данпый объем те форме другой нрипвстИ)
Чтоб хорошо удалось тебе это, вздумал ли погреб
Ти измерят!., или ров, или широкую пасть
Глуби колодца, ионьми на смежных концами пластинках
Средние -чипми дне, сжатые между таблиц.
Иг. приГнч'аГг дли тог» ты к тяжелым цилиндрам Лрхитй,
Конуса ты но секи, корни Мснсхма триад;
Также но надо держать с богоравным Еи.-кжсом сонета,
Иигпутых .пиний его форшл не надо чертить.
С :>тимн' us ты тмб.<1ич1:;ши тменчи средних построишь,
Двигаясь смо:го вперед, с- меньшей ия данных начав.
Счастлив ты, Птолошш, ты с сыном отец лечпо юный.
Леек, что приятно веш-да и дли царей, и для муз,
Сам ты его одарил, л конце; же, а Зс!ВС, царь яибсышй,
Пусть ил тиоей он руки скипетр высокий ыоашнт.
Пусть же евгршитен всо :ito, и кажлпн смотрящий пусть скагкит:
«Это Кипени сын выдумал Прат(х:фсш.
Р «meк не Никомеда в книге
— «О к о п х о и д альп ы. х л и н и н х»
Затом устройство прибора, служащего для той же самой цели,
описывает Никомид в составленном им сочинении о конхоидах. Этим
он, по-видимому, необычайно гордится и
очень осмеивает изобретение Эрнтосфопа
как и иемоханичоскоо. и вместе с тем
лишенное геожу-филоского смысла. Мы
присоединяем к ужо написанному ы ого,
чтобы по пропустить никого ии лапнмав-
шихся этой задачей, а также м для срав-
сравнения его изобретешш с зратосфеноиым.
Сущность его теории такоиа.
Представим себо две взаимно ntsp-
нсидикулнрыыо линейки. Л В и ГД, сое-
соединенные между собой так, чтобы они со-
стапляли одну ионорхность; пусть на ли-
линейке АБ будет бороздка с секиропидшлм
сечением, в которой может перемещаться
пензугака, а на линейке ГЛ на линии,
делящей пополам ее ширину, в приле-
гающеп к А части будет цилиндр, состав-
составляющий одно целое с линейкой л лишь немного возвышающийся над
ее поверхностью; затем пусть будет друган ливойка EZ, имеющая
«76
КОММЕНТАРИИ
па небольшом расстоянии от конца Z прорез Ив, могущий охватить
цилиндр Д; в точке Е этой линейки пусть будет круглое отверстие,
в котором может поместиться ось, составляющая одно целое с полауш-
кой, движущейся в сскировидной бороздке, которая находится ни
линейке АВ. Липсйку EZ насаживают прорезом НО па цилиндр Д,
а отверстием Е на соединенную с ползуншой ось. Если взять конец К
линейки и двигать его по направлению от А к В и обратно, то точка Е
будит псе время перемещаться но линейке АВ, а прорез IIВ будет дви-
двигаться около цилиндра Д; во время движении средняя линия линейки
KZ будет постоянно щкисадлть через оси цилиндра А, а отрезок ЕК
линейки — сохранять свою ве-
величину. Если в точке К поме-
поместить что-нибудь пишущее, то>
на поверхности пачертится не-
некоторая линия AMN, которую
Никомед пазыиает первой кон-
хоидальпой линией; длина от-
отрезка ЕК называется радиусом
конхоиды, а точка Д — ее по-
полюсом.
Пикодтод доказывает, что. одним из свойств этой линии является
то, что она до малости близко может подойти к линейке АВ, так что
если между этой линией и линейкой АВ провести какую-нибудь прямую,
то она всегда будет пересекать конхоиду. Первое легче*уяснить на
другом чертеже. Пусть АВ (рис. IS) будет линейка, Г — полюс, ЛК —
радиус конхоиды, и ZE11 — конхоидальная- линия; проведем из Г
две прямые Гв и TZ, отрезки KG
и AZ которых будут, конечно, рав-
равными. Я утперждаю, что перпенди-
перпендикуляр Z М будет меньше перпен-
перпендикуляра 6N.
Действительно, так как угол
МЛ Г больше угла NKl\ то допол-
дополнение МАГ нериого угла до двух
прямых будет меньше такого же
дополнения NK6 второго угла.
А так как углы при М и N пря-
прямые, то угол при Z будет больше
угла при ©. Если построить угол
MZ Н, равный углу при 6), то KB,
или AZ, будет иметь к НМ то же
самое отношение, что 2Z к ZM. Значит, ZA будет иметь к 0Л1 отно-
отношение, меньшее чем к ZM, а поэтому (i)N будет болылс ZM.
Второе спнйетко заключается ъ том, что всякая прима», проведен-
проведенная между АВ и кривой, обязательно пересечет кривую. Это можно
выяснить так.
Проведенпая прямая будет или параллельна АВ, или нет. Пусть
сначала она будет параллельна, как, например, ZII6 (рис. 20). Пусть
отношение ЛИ к ИГ равняется отношению ДЕ к некоторой прямой К.
Рис. 20.
нг к
Радиусом К опишем из центра Г окружность; пусть она пересечет
Z1I в точке Z: проводом соединяющую прямую TZ. Тогда ДН относится
О ШАРЕ И ЦИЛИНДРЕ
477
к Н1\ как ZA к ZF.
нг
нг
2л
2Г
Но ДН относится к 11Г, или ДЕ к К, как ДЕ к TZ.
_йЕ_
К
дЕ
Следовательно, ДЕ равно AZ; значит, точка Z лежит на кривой.
Пусть теперь проведенная прямая но будет параллельна АВ, по
пойдет, например, как M11JN. Через 11 пронедем примут Z1I, парал-
параллельную ЛВ; тогда ZH пересечется с кривой, а М>1 и подаипо.
Все это кмтвкаот как следствие из снойстн прибора., а нужное для
дальнейшего мы докажем так.
Пусть заданы угол А и находящаяся вне его точна Г; требуется
провести прямую Г11 так, чтобы отреяок ее КМ равнялся данной прямой.
Из точки Г опустим на ЛВ перпендикуляр Г0 и продолжим его
(рис. 21); пусть Дв будет равна данной прямо». Из полюса Г опишем
па линейке ЛВ первую конхоидаль-
ную линию EAZ с заданным радиу-
радиусом Д9; согласно доказанному, она ..
пересечет АН. Пусть точка пересе-
пересечении будет И; приведши прямую ГН,
тогда КН и будет равна заданной
прямой ДВ.
Доказавши это, возьмем две взаимно перпендикулярные прямые
ГЛ и ЛА. (рис. 22), для которых требуется найти две средние пропорци-
пропорциональные ь непрерывной пропорции. Дополним прямоугольник АВГЛ.
и разделим каждую из АВ и ВГ в точках Л и К пополам; сооднттющую
прямую ДЛ продолжим, и пусть она с продолжением ГВ пересечется
в точке II; затем перпендикулярно к ВГ проведем EZ и сделаем Т7,
равной ЛА, проведем соединяющую прямую ZTT и параллельную ей
линию ГН. Нол у чинши угол КГ6, припедем Z(-)K из заданной точки Z
так, чтобы 6К равнялась АД пли TZ (что это нозможпо, ясно из свойств
конхоиды). Теперь соединяющую прямую КА продолжим, и пусть она
в точке М пересечет продолжение АВ. Я утверяадаю, что ГЛ к КГ, как
КГ к МА и как МЛ к АЛ.
ГЛ
кг
кг
МА_
"АЛ
Так как В Г разделена и Е пополам и к ней прибавлена КГ, то,
значит, прямоугольник между ВК и КГ вместе с квадратом на ГЕ
равен квадрату на ЕК.
вк ¦ кг -!- riis = Ека
КОММЕНТАРИИ.
ПрнЙцинм к обеим частям квадрат на EZ; тигли прямоугольник
меж,у «к н Ы имеете с квадратами на ГЕ и EZ, риннммн квадрату на
Г/, оудот район квадратам на КЕ и EZ, равным квадрату ла KZ."
ПК-КГ ! ГК* E/.*-=KE*-h KZ^KZ2
Уатедг, ггоскольку МА относится к AU, или МЛ кЛК, как Г$Г к ГК,
МЛ Д1Д иг
А И " "ЛК~ ' "ГК~
то, значит, МЛ относится к АВ, как В Г к ГК.
МА ВТ
ли ¦" гк
Теперь АЛ будет поломшпж АВ, а ГП удвоенной ВГ (таи как Л Г
и дна раза больше ДВ); тогда МЛ относится к АД, как НГ к ГК
МА НГ
АД - ГК
Но IT Г относится к ГК, как ZO к 6К,
нг z®
iic.-ilvh:tiuip нарплдыьносхя HZ и Гв; коатому, «присоединяя», <имеом>
МА и АЛ имеете относятся и ДА, как Z6 и вК имостс к Кв,
МЛ -- ЛЛ Z<-) j вК
ДА " КЙ~~
то о«ть МД относится к ДА, как ZK к Кв.
МЛ ZK
ДА" Кв
Но, по предположению, ЛЛ равна TZ, равна ВК; значит, и МА
ракия ZK, и квадрат на МД равен квадрату на ZK. Тепорь квачрат на
МЛ равен прямоугольнику между. В М и МЛ пмосто с квад])атом па ДА
МЛ*—ЬМ-МА | ЛЛ*
и но доказанному, кладрат на ZK район прямоугольнику между ВК
и h.1 имеете с ква^ютом на VZ.
zks- Пк-кг-т-rz*
Затем, согласно иредположепмю, АД равна TZ; значит, и прямо-
прямоугольник между ВМ и МА равен прямоугольнику между ВК и КГ.
НМ-МА = ПК-КГ
'liiким гйрязом, MB относится к ВК, как К.Г.к AM,
мв кг
ВК AM
по ТШ относится к ВК, как Т'А к ГК,
ВМ ГЛ
ВК ГК
и, значит, ГЛ к ГК относится, как ГК к AM.
гл _ гк
ГК. AM
И также ГА к ГК относится, как МА к АЛ,
ГЛ МА
ГК = ЛА - ¦ . ¦
О ШАРЕ М ЦИЛИНДРЕ 479
следовательно, Л Г относится к ГК, как ГК к AM, как AM к ЛЛ.
Л Г_ _ ГК AM
ГК ' "" Л Ы АЛ
1?а этом кончается текст Ёвтокия, касающийся на дачи о нахождении двух средних
иропорцпонялмтых, к которой сводится задача об удвоении куйн. Остистей скакать не-
несколько слип об истории зтон задачи.
Уже древние сткитяио злалтг, i;uicu.u образом ыежгю утончить вдвое площадь
iuOuii фигуры, не леи л» со формы. Дли :>тоц цели шит имели два локти — один и 28 дюй-
мон, п другой п 21). Так как отношение этих локтей 28:20 = 4,4 дюжно
принять равным У2 —1,414, то для двукратного увелплшщн площади какой-нибудь
фигуры нужно, измерив все длины ее в двадцатвдюимовых локтях, построит!, ко, откла-
откладывая порученные ранмеры и дьадцатииосьмидюнмовых локтях, что слодитеш к увели-
чемдою лтшеивдх размеров б у 2 рил. Отпшь точные эынчещш у Z помещены л иавылои-
скых строительных справочниках и и иддвйских книгах. Нн греческой почло это привело
к открытию иррншшналт.шкти "|/2, что бтлло сделан» лркб.тпнителмго около 500 г, до п.
иррццишшяшокте& летело в Аштюютики к шшсш> шгшиглошш ндотрмчшдагаг,
!маи1ш<!грки ьсо сиотвегетъующие оиерацип легко мигли быть иытюлншш при помощи
простейших инструментов — циркули и линейки, при переходе же к (^термометрическим
задачам греческие математики сраиу столкнулись с необходимостью имкть дела с кублми
и кубичными корннми. Зпднчм об удвоении куби, требующая ретпепия пристейтнггго урав-
б
р р
апипн тротыгй степени, бьтлн, конечно, первой, которую им пришлось разрешать. 11и]шым
матешатином, имя которого связано с ятои задачей, был Гишюкрат Хиосским (вторая
нг>лолии!1 V liiiKfi до п. я.), шжазаштшй, что эта лудача можст быть npni!t>;i(riia к нахожде-
дпух средпгтх ирглюрцггошитьпых. Толаком к атому открытию для 1'яплогфята, ве-
вероятно, были мулыкалышо нссл(?доваЕтия пттфмгиреш^еи V иска до и- а., гшии-машиихсл
ион рогом о делении (iciLOUiiurc) музыкадыюго интервала — октплы - па дно и на три
рлицью части. При этих и:н.к-кациях: было устаноллоно, что музыкальный ицт1;риал можот
быть разбит на два ели нн три раьных интервала, выролшющихся целояиг^емшьши отло-
шеггиямтт, только в тех счучяях, когда делимый интервал характсрэтяуотсн отнаттнгшк^м
двух киадратных или кубических чисел. С конца V иска до и. о. л снизи с ивобрптелвдм
r-i- «г
P-, — _. г - __ ,.
артиллерии — стрелAметоп тт тгамгнфштов, оинмуицых на примннвдти упругих тяжей,
появился отце: «дин стимул дли шшыток уеншнниго рютгшип делийской пндычи — рпботы
пи yconcpiuoiicTuiiiiaiiino мигательных машин. Мы знаем, чти для увсличения идлос даль-
дальности полоти снаряда и параболическом движении нужно и;ишс увеличить (ло
скую иниргию, а так как потенциальная энергия упругого тела пропорциональна
ооъиму, то для укапанной цели трибовалост» удвоение о бьем л тяжа. По nccif ш?|ншт-
1ЮСТИ. не случайно, чти нирт.тй давший теоретической решение этой яадачи Лрхнт TajK:iiT-
cKirif (нирпая но юница IV иика до н. о.) был ьыдашиц1мск полководцем. Дальнинтпне;
р1ЧТ№лпя были jnuij Ei^ioncuoi в Мснсхмом (около 350 г. ло п- ».)f
оби па ocHOMUfiiiH теории кшгпческих сочиций. Что каса(У1Ся ^цгподлмого ?птокп(ш репги-
нил Платона, то око пни всякого гомгголия яшяетгл нодложпим*), Эратосфеи ни но vmv-
денгтн к иослаипю к царю Мтоломсш. гти в поспнтнтсдиыюй нндниси (стпхотнориая ее
часть) не упомипаот имени Платона б числе рстшшншх задачу, хотя говорит о послании
дсинГшон к Платону, Слодукицнм но примени решонием делийской задачи было прс?дло-
ж<ншои Нритосфоним, сояршештком Архимеда. Бес остальные уполшпаимып Еито-
vm ршшпшя ирипадложат ужо к послоархимедовской йнохе. Их можно разделить на
ff группы; Лполло;1шг, Ипкоиода и. Даокла, К группе Аполлония (лиглдщего соирсисд-
пика Архимеда) относятся pfiiirenitfi Филола Византийского (аитора норлого чогтимпо
дошедшего до пас курка мгхагшки, жппттюго около 100 г. до я. э.) и Гсроиа
рлиского, нннютного компилятора, врсмл жилш! которого определилось очснг> раилич-
110 — между II веком до и после нашей ары**). Никомсд и Дыикя относятся, но ucwi
лоронтпсшти, к порнок половине П пека до н. :>. (до Гиттпарха), япллнсь но всяком случаи
пами классического тторкода гр<»чеси(ш гсомст]1ии. Ршиснис Ликоыеда осмишан'о пл
нрилюпинии конхоиды, кривой, развившейся на основе прпмкпепия тук называемых
«вставою> или «стремлений» (vk'XTBiS, i не И па Li onus); что касается Диокла, то сто рмис-
*) Ван-дср-Вардсн в «ПроЛущдмощсЙпн науке» (стр. 225 русского перевода) уПсдитсльно доии-
зал. что ото решение, ргишо кем л истории о посольстве долийцев к Платону, взяты \т диалога Эрато-
«U l
••) Нейг.|бауот1 показал (см. «Пробужлающяксн наукао, стр. 1172), что on it сыр ас мое Гпроттом
злтмяппе имело место б 62 году ы. в, Токст Ептокии днит еще опип локнл^тглы гцо иокциеР даты
живим Герияа. Тли кя« распространение в Рллн* дорийской ярхитситууъз со (й
Апо мопорпм Пантеона) относите» ко времени Траппы, то автор «О построении спадов*
жил около 100 г. я
480
КОММЕНТАРИИ
яис основано иа применении гак насылаемой циссоиды — кривой третьего порядка, урав-
уравнение которой легко может быть получено, если положим:
ОА = х, АС^у, 1Ю = а.
Действительно, согласно принципу построения
кривой:
АН АН AD
АЛ AD
что после подстановки даст:
АС
х-\-а
а" —
или, после очевидных упрощений:
у/о»-а? = (а—*)*,
Кривая состоит из двух симметричных ветвей, которые в точках Л/ и Л' иы.ходят
:ш пределы окружности и стремятся к асимптоте, нрохидящей через Е перпендикулярно
к оси Ох. Иа том №с принципе основывается решение писателя монца 111 в. и. а. Паппа
Александрийского, автора «Математической библиотеки», и Спора, о котором мы ничего
не знаем.
|2J С современной точки зрения, решение этой задачи может быть выпо;л1спо сле-
следующим образом.
Пусть сикущаи плоскость убудет АГ: объем сегмента ЛАГ, согласно доказанному
в предложении И, будет jiauen объему конуса, основание которого составляет круг на диа-
диаметре ЛГ, а высота АХ так отно-
относится к пмсоте АХ рассматривае-
рассматриваемого сегмента, как сумма радиуса
KB— .U шара с высотой ВХ сег-
сегмента, дополнительного к сегменту
ЛВГ, относится к высоте ВХ этого
второго cerMCina, Аналогично,
объем сегмента АСГ будет равен
об-ьему конуса AFT с тем же осно-
основанием л с высотой -РХ, отношение
которой к ПХ будет ран по (КД-Н
+ ЛХ) : АХ. Положим ДХ=-з,
XB=i/, ЛХ = и, XP—v, радиус
шара обозначим через И, и пусть
заданное отношение объемов сег-
сегЛГ АВГ б )
Рис. 24.
д н
ментов ЛАГ и АВГ будет )г, тогда
летворяет уравнению
k = u : в=АХ : ХР, у=.'Ш- х и неизвестное х удов-
удовчто после очевидных уприщсиин приведет нас к уравнению третьей степени относительно х:
Сущность метода, который применяет Архимед, заключается в следующем. Он пред-
предполагает задачу решенной, иными слонами, наВдсгтпой дочку X диаметра ВД, черев кото-
которую проводится искомая секущая плоскость; с нашей точки кропил, это равносильно
введению днух неизвестных хну, связанных уралнепием
х+у—211. A)
Затем он вводит вспомогательные неизвестные АХ —а и ХГ—v, определяемые
уравнениями
B)
О ПТЛРН И ЦИЛИНДРЕ
и снязапяыс соотношением
2L-*.
Вместо наших четырех поизвсстпых величин Архимед имеет три неизвестных
точки X, Л, Р. Мы определили бы из уравнении B) а C) пеизаестные иней подста-
пили их и уравнение D); Архимед при ггомоши соотнетпешш B) и C) исключает точки Л
и Р и старается выразить отношение и : г; черен величины, определяемые только положе-
положением точки X. Заботя несколько вперед, *".т должны сказать, чти вместо отношения
и : ?/ = & Архимед борет отношение
к-1-ti к-\-1
причем ото отношоние он ирс^^стаюиит в таком виде:
|/-| v _ РА __ РА АЛ _ u-\-v и—х
гг ЛХ ЛД ЛХ гг —а; и " к' >
После этот мы проследим ын иупктам весь ход решопия Архимедом задачи.
<!•> Архггнод преобразует уравнения B) гг C) к более удобному виду. В его обозна-
чр.гшях уравнение B) будм-:
: ¦ • • • ¦ . " КАЧ ДХ РХ ¦ " :
Д.
откуда «выделением»:
или, так как КД—KB:
Аналоигчпо иа уравнения C)
получается
ДК " ХВ
Таким обрпяом, соединяя обе нолучекние пропорции вместе, будем иметь:
ДЛ _ KB _ ДХ
или в наших обозначениях:
ДХ
КД РХ-ХП
ЛХ~ ХВ
кв дх
ЬР " ХН
KB-I-BX
ВХ
KB ЛД
ВХ ДХ
л л дх
хв '
РБ
— ВХ
ЛХ
ХА
1
ДК "
и — х
л
ВР
И
v—y
хв
X
B> Поело этого Архимед определим ГЛ : ЛА, стоящее периым множителем в равен-
равенстве D'). Для этого пропорцию
_ВР___КЛ_
ВК ~~ ДЛ
он песледопатслыю преобразует присоединением:
РВ-^-ВК КЛ4-&А
вк
РК
КД
рк+кл
КД-^-ЛЛ
РЛ
ДЛ
к л
ЛД '
кл
ЛД ' .
К л
КЛ ЛД
Архимед
482 КОММЕНТАРИИ
и так как КЛ есть средняя пропорциональный между РЛ и ЛД, то
РЛ _ КЛ8
Ли ~ *
ДА
КД
ЛЛ
К,\-!-ДЛ
ЛД
к л
хд
ВХ
хд
ВХ + ХА
ДХ
вд
C) Теперь Архимед определяет отношение КЛ: ЛЛ. Из основного равенства
пункта <1>
Кй ВХ
оы получает «обращением»
и «присоединением»
ЛД ДХ
Илию этого отношение РЛ : ЛД выражено только через величины, занисящпе от точки Хг
РЛ _ ВД8
ЛЛ ~~ ЛХ* '
или и буквениых обозначениях:
цЦ-р'_ 4Д»
и—х ~ w2
<4> Этот пункт Гейберг считает позднейшей вставкой, основываясь па том, что
в комментарии Ептокия рассматриваемое место не содержится. Оц посаящен определе-
определению второго множителя ДЛ : ЛХ в соотношении D'). Из основного соотношения, опре-
определяющего ЛХ
ЛХ KB-f ВХ
(а)
имеем «иыдслшшпм»
Хл
лх-
дх
хв
хл
ЛЛ
1
KB
ВХ '
KB
ДХ ИХ "
Отсюда ира помощи следующего нреобрлдоиания, ли отмеченного в тексте Архи-
Архимеда, мы можем последоиателыю получить иа (а):
ДХ ВХ
лд-тдх Kii-t-ux *
дх _ вх
~~К5С~ кв-вх '
что после привлечения неходпой пропорции принимает пид
ЛЛ _ KB
ЛХ ~~ KB f ВХ '
или в буквенных обеюпачегшях
и-х П
и И -у '
<Г>> Откладмнасм XZ — fi+y, или BZ — ВК —Л; конец Z полученного отрезка ляжет
вправо от точки Р. Дсисхвитслыш, в конце пункта U> мы имели раиенстпо
Р» _ КА
В К ~~ ЛД '
О ШЛРЕ И ЦИЛИНДРЕ 483
откуда
лд
BZ=BK=BP-
КД
так как
АЛ ЛХ
то D7' > ВР-
КД X
Основная пропорция
ЛД:ДХ-КИ:(КП-| ИХ)
теперь перепишется в виде
AA:AX = 13Z:ZX.
<6> После этого мы читаем у Архимеда: «Поскольку we отношение ДА к ЛХ является
данным, то, значит, будет данным и отношение РЛ к ЛХ». Так как отношение ДА к ЛХ
BZ Н
рипнястсн ——=——;— то, строго говоря, его нельзя считать «данным»; оно будит «дан-
ним» только п том случае, когда положение; точки X стинвт уже и.шостным, а :>то будет
1'Л
только после подстановка в наше уравнение D'), где отношение —^ действительно ока-
ЛХ
к -1-1
зыкаете}! равным заданной величине —-— . Результат птоп подстановки Архимед полу-
чает в виде
РЛ РЛ ЛЛ _ ВД» I.1Z
ЛХ ~ ЛД ' ЛХ ~ ЛХ* * ZX ; ( '
п прапой части этого «уравнении» точки В, Л, Z, являются известными и сдипстиенньш
«шн1ннс!ст1п.1м.) будет лишь положение точки X.
С нашин точки аршшя, иолучишюс равенство равносильно уроикепию
или
<7> После этого Архимпд приступает к «решению» полученного урапнсиия». Он
«полннчает иго сгонегп.», ииодя вспомогательнуи) «>чку 0, определяемую из пропорции
PA:AX = HZ:Z0
и переписывает основную пропорцию (Ь) в виде
T1Z ZX ВЛа BZ
ZX ZC-) ДХ2 '/X '
BZ
что после сокрищепин на - прииодитсл к виду
BAa:AX2=XZ:Ze.
Задацпуш прямуто AZ требуется разделить в точке X тик, чтобы пади и паи площадь (ВД2)
так относилась к квадрату первого отремка ДХ. кик игороГг огрсзл< XZ к заданной
длине Z3. Решение этой задачи Архимед обещал дать и конце сочинения, но им и до-
дошедшим до нас тексте Архимеда, пи в том, к.ггорьш читали ближайшие к Архимеду
комментаторы Дсгогсл и Диогшсодор, п конце книги никакого решения поставленной
яадичн не находится. Это решение было нгшдеио бплес поздним комментатором
Ар.\имс,1П Евтокпим.
Б KtixiMuiirajjHU J-!btokiiii к этому ке;ту гопорнтсм следующее.
Архимед обещал дать решение этой задачи в конце, по обещанное
нельзя было пайти ни в одном из списков. Поэтому, как мы мыяснили,
и Дионисодор не мог отыскать обещанного; но будучи в состоянии
справиться с недостающей леммо», on u решении этой задачи пошел
. совершенно другим путем, который мы ниже и оиишгм. Точпо так же
и Диокл в своей книге «О каустиках» высказал мнение, что Архимед.
31*
484
КОММЕНТАРИИ
лить обещал решение, но своего обещания не сдержал; поэтому caw
Диокл попытался восполнить недостающее; его решение мы тоже при-
приведем и дальнейшем. По он, так же как и Диописодор, решил задачу
при помощи способа, не имеющего ничего общего с потерянным дока-
доказательством. Между тем я, не;боясь продолжительных поисков, в одной
старой кпиго нашел запись некоторых теорем; хотя эта запись пред-
отаиляла большие неясности и ошибки, а также различного рода
неправильности в чертежах, однако она была очень похожи на иекпмоо,
тем более, что она сохраняла излюбленное Архимедом дорийское наре-
наречие и, кролю того, была написана со свойственной дреипости термино-
терминологией (так, парабола называлась «сечением прямоугольного конуса»,
а гипербола — «сечением тупоугольного конуса»); поэтому у меня
возникло подозрение, что эти тео--
ремы как раз представляют то са-
самое, что Архимед обещался напи-
написать в копце.
Так вот мы старательно за-
занялись разбором записанного
текста, который лам показался
очень трудным ислодкччшо упомяну-
упомянутого множества ошибок, и понем-
понемножку выясняя его смысл, записали
его более современным и ясным
Рис. 25.
языком. Сначала дадим полностью
запись первой теоремы, чтобы выяснить самым общим способом то, что
Архимед говорит о границах возможности решения задачи; отсюда
вытекут более специальные приложения, касающиеся условий, содер-
содержащихся в сделаппом им анализе этой задачи.
Дани прямые А13 и АГ и площадь Д; требуется найти на АВ такую
точку Е, чтобы отношение АЕ к АГ равнялось бы отношению площа-
площади А к ЕВ2 {рис. 2Л}.
Анализ"
Пусть это будет сделано; построим АГ перпендикулярно к АВ
и соединяющую прямую ГЕ продолжим до Z. Затем чщигл Г проведем
прямую ГН, параллельную АВ, а через В прямую ZBTI, параллельную
АГ и пересекающую обе линии ГЕ и Г1?. Дополним прямоугольник
II в л через Е проведем прямую КЕД, параллельную каждой из прямых
Гв, HZ; пусть затем площадь А будет раина прямоугольнику .между
ГН и ИМ.
ГН-1Ш; Д
Итак, поскольку ЕА относится к А Г, как Д к квадрату на ЕВ,
иа _ л
АГ ЕВ*
и как ЕА к А Г, так и ГН к HZ,
ЕА ГН
АГ 117.
•и ГН к I1Z, как квадрат па ГН к прямоугольнику между ГН, HZ,
ГН ГН* • ' ... .. .
IV/.
'rir-nz
О 1J ГА РЕ И ЦИЛИНДРЕ
то, значит, как квадрат па ГН к прямоугольнику между ГН, IIZ, так
и площадь Д к квадрату на ЕВ, то есть к квадрату ua KZ.
* А А
ГН
Затки, после перестановки — как квадрат на ГП к площади Д,
• то есть к прямоугольнику между ГП, Н М, так и прямоугольник между
ГН, HZ к квадрату на ZK.
Но как квадрат на Ш к прямоугольнику между ГП, ИМ, так
и П.1 к II М; и значит, как ГН к II М, так и прямоугольник между ГН,
IIZ к квадрату на ZK.
гн nr.nz
нм
Но как ГН к НМ, так и прямоугольник между ГН, HZ к прямоуголь-
прямоугольнику между МН, HZ,
гн гн itz
НМ МII. 117,
если взять HZ в качестве общей высоты.
Значит, пак прямоугольник между ГИ, 11Z, к прямоугольнику
между МП, HZ, так и прямоугольник между Ш, 11Z к квадрату на ZK
гн-irz гн wz
Таким образом, прямоугольник между МП, 1.1 Z ранен квадрату на ZK.
МиПЙ = ЙК2
Итак, если мы на оси ZH построим проходящую через точку Н пара-
параболу так, чтобы «с ординаты квадрировались па НМ,
ZK*=II3I-llZ
то она пройдет через К и будет нполпе определена по своему положе-
положению, тан' как НМивлиетои заданной по величине (она вместе с заданной
линией ГН заключает заданную площадь Д).
мп*нг — д ¦
Таким образом, точна К лежит на заданной своим положением
иараболе; пусть эта парабола цостроена, как сказано, и будет ПК.
Далее, так как площадь 6Л равна ГВ, то есть прямоугольник
между 6К, КЛ равен прямоугольнику между А.В, 1311,
вк-кл —лв-вн
и если мы через точку В проведем гиперболу с, асимптотами ©Г и ГН,
ек • кл — ху = а в- вн
то она пройдет черрн точку К [на основании теоремы, обратной 8-й тео-
теореме*) книги II «Конических сечений» Аполлония], и будет определена
по своему положению, так как каждая из прямых <ЭГ, ГН, а также
точка 13 будут заданы своим положением.
Пусть эта гипербола, согласно сказанному, построена и будет КВ.
Таким образом, точка К находится на заданной по сноему положению
*) И дейстпнтелыгооти иго можно вмиести из 12-й.теоремы той же книга.
¦486
КОММЕНТАРИИ
гиперболе. Но опа находится также м на заданной но еноему положе-
положению параболе; значит, точка К будет заданной. Опустим из пес перпен-
перпендикуляр К.Е па заданную своим положением прямую АВ; значит, будет
дана и Е.
Исследование (йюо(о|ход)
Так как ЕЛ относится к заданной прямой А Г, как заданная пло-
А к квадрату па Eli, 3 э
J2A = Д
А Г" ив»
то, значит, в двух параллелепипедах с основаниями, соответственно квад-
квадратом на ЕВ и площадью А, и соответственно высотами ЕА и АГ,
основания оПратно пропорциональны высотам: значит, оба параллеле-
параллелепипеда будут раины; значит, квадрат па ЕВ, умноженный на ЕА, равен
веданной площади А, помноженной на АГ.
Iilia-EA = Д.ЛГ
Но квадрат па BE, умноженный на ЕА, будет наибольшим мз всех
построенных подобным образом на 13А произведений, сели только, как
будет доказано впоследствии, BE будет вдвое больше ЕА. Таким обра-
образом, произведение ладатюй площади и заданной линии не должно быть
больше квадрата на BE, умноженного на ЕА.
Синтез задачи производится так.
Пусть заданная нря.мая будет АВ и некоторая другая данная АГ
и данная площадь А. Требуется разделить АВ так, чтобы отношение
одного ее отрезка к заданной прямой А Г равнялось отношению данной
площади А и квадрата на оставшемся отрезке {рис. 20}.
Иозьмсм АЕ — третью часть АО. Тогда параллелепипед на А и АГ
будет или больше параллелепипеда на квадрате BE с высотой ЕА,
или равен этому параллелепипеду, или же меньше. Если он будет
больше, то, согласно доказанному в анализе, построение будет иеиоз-
можпым. Если он будет равен, то точка Е удовлетворяет условиям зада-
задачи: действительно, при равенстве объемои параллелепипедов основания
будут обратпо пропорциональны
высотам, так что как ЕА к А Г,
так и А к квадрату ни BE.
Если же шющадь А, умножен-
умноженная на АГ, будет мепьше квадрата
на BE, умноженного на ЕА, то
построение производится так.
Построим АГ перпендикуляр-
перпендикулярно к АВ и через Г проведем пря-
муго TZ, параллельную АВ, а через
Впрямую BZ, параллельную АГ,
и пусть она с продолжением ГЕ пересечется в точке Н. Дополним пря-
прямоугольник Z6 и через Е проведем прямую КЕА, параллельную ZH.
Так как площадь А, умноженная на АГ, мепьше квадрата на BE.
умноженного на ЕА,
Д.АГ<ВЕ*-ЕА
то как ЕЛ к Л Г, так будет и А к некоторой площади, меньшей квадрата
на BE или квадрата на ПК.
Рис. 26.
О ШАРК И ЦИЛИНДРЕ 487
Тогда пусть отношение ЕА к ЛГ будет равно отношению площади Л
к квалрату на II М, и пусть площадь А равна прямоугольнику между
TZ, ZN.
Теперь поскольку ЕАк А Г относится, как площадь Д, то ость пря-
прямоугольник между YZ и ZN, к киадрату па НМ
КА T'Z ZN
и кап ЕА к ЛГ, так FZ относится к ZH,
¦ЕА _Г7.
а г ~ ziT
как же Г/?к7П,так и квадрат на FZ к прямоугольнику между FZ, ZH,
и как прямоугольник между FZ, ZN к квадрату па НМ.
_У7, 1Z^ = TZ-ZN
zh ~Tzzh iIMe
Затем после перестановки — как квадратна ^кпрямоутольпику между
TZ, ZN, так и прямоугольник между FZ, ZII к квадрату на ИМ.
Но кик квадрат на Г'А а прямоугольнику между FZ и ZN, так же
и FZ к ZN.TaKjKC будет, если взятьZ1I общей высотой, и прямоуголь-
прямоугольник между TZ и ZH к прямоугольнику между NZ и ZH,
_TZ T7.-7AI
ZN"~ KZ-7.il
и значит, как прямоугольник между FZ и ZII к прямоугольнику между
KZ и ZH, так и ирямоуголлоик меладу FZ и ZH к киадрату на ИМ;
l'Z.ZH FZ-ZH
"WZZH ~ нл*
елсдоватолыш, квадрат на ИМ будет ранен прямоугольнику между
HZ и ZN.
HM.S = HZ.ZN
Таким образом, если на оси ZII построить проходящую через Z
параболу таи, чтобы се ординаты квадрировались на ZK, то она прой-
пройдет через точку М. Построим ее, ы пусть Она будет MEZ.
Затем, поскольку площадь 0Л раина AZ, то есть прямоугольник
между GK и КЛ равен прямоугольнику между АВ и BZ,
то если через точку В провести лшерболу с асимптотами &Г и FZ, oua
пройдет через К
вк.кл —ли ~ AB-nz
[па основании теоремы, обратной 8-й A2-й) теореме книги II «Кони-
«Конических сечений»Аполлония]. Построим ее; пусть ато будет кривая ВК,
пересекающая параболу и точно S. Из S на АВ опустим перпендику-
перпендикуляр ЗОП и проведем через Н прямую Р S2, параллельную АВ.
Теперь, тан как В5К есть гипербола, в Г, FZ — ее асимптоты, и пря-
прямив Р2, ?П проведены параллельпо АВ и BZ, то прямоугольник
между Р В и ВП будет ралси прямоугольнику между ЛВ и BZ,
PS.SII —АП-НВ
и значит, прямоугольник РО будет ранен OZ. Поэтому, если соединить
точку Гс 2 прямой, то последняя пройдет через О. Проведем ее; пусть
КОММЕНТАРИИ
она будет Г02. Теперь, поскольку О А относится к ЛГ, как ОВ к BS,
то есть как TZ к Z?,
ОА ОЛ J-JJ
АГ На ~~ Z2
как же VZ к Z2, так относится, если взять ZN общей нысотой, и пря-
прямоугольник между TZ, ZN к прямоугольнику между 2Z, ZN,
TZ rZ ZN
ZZ 22-ZN
то значит, как ОА к ЛГ, так и прямоугольник между TZ, ZN к прямо-
прямоугольнику между 2Z, ZN.
ОА ГУ. XN
АГ ~ XZ-ZM
Но прямоугольник между TZ, ZN равен площади А, а прямоуголь-
прямоугольник между 2Z и ZN равен квадрату па 2JE или квадрату на ВО
?И ¦ км -- ?Sa = во* .. . .:¦:
но свойствам параболы. Значит, как ОА к АГ, так будет и площадь А
К квадрату на 130.
ОА Л
ЕА
АГ
Таким обрнзом, точка О, удовлетворяющая условиям задачи, найдена.
Доказательство л с м мы д и о р и з м а
Л что при BE, вдвое большем ЕА, квадрат па BE, умноженный на
ЕА, будет наибольшим из всех построенных подобным образом на 13А
произведении, до кажется так {рис. 27}: „
Пусть опять, как :>то било в анализе,
данная прямая А Г будет перпендикулярна к АВ;
продолжим соединяющую прямую ГЕ, и пусть
она в точке Z пересечет прямую, проведенную
через В параллельно А Г. Через точки Г, Z па-
параллельно АВ проведем прямыв 0Z и ГН, про-
продолжил* ГЛ до (-> и черси Е параллельно ей
проводам прямую КЕЛ- Пусть отношение БА gi \ /
к Л Г будет равно отношению прямоугольника л IV'/' XW
между ГН, Н М к квадрату на ЕВ;
ш-ни
тогда квадратна BE, умноженный па Е А, будет
ршюн прямоугольнику .между ГП, НМ, умно-
ясешюму па ЛГ,
•КАг=(ГП-НМ)ЛГ
так Kaic у двух рапных параллелепипедоп ocirona-
ния обратно пропорциональны высотам. Я ут-
утверждаю, что прямоугольник между ГН, IIМ, Рис. 27.
умноженный па А Г, будет наибольшим из всех
объемов, построенных подобный образом на АВ. Проведем через точку
II параболу о осью ZH так, чтобы се ординаты квадрировались на Н М-
\
к
к
А
А
V /
у
1
О ШАРЕ И ЦИЛИНДРЕ 48»
Она, согласно доказанному ио время анализа, пройдет через К
и пересечется с, параллельным диаметру параболы продолжением 0Г
[па основании 27-й *) теоремы книги 1 «Конических сечешш» Алоллония].
Продолжим ее, и пусть она пересечется и точки i\. Затем через точку В
проведем гиперболу с асимптотами КГ и ГП; она тоже пилидет через
точку К, как это было доказано во ирсмя анализа. Пусть эта гипербо-
гипербола будет ВК.
Продолжив ZH, отложим ранную ей прямую II В, проведем соеди-
соединяющую прямую ЕК и продолжим до О. |11а основании 34-й C3-й)
теоремы книги I «Конических сечений» Аполлония] прямая SK будет
касательной к параболе. Так, как согласно предположению, BE в два
.: ; раза больше ЕА, то есть ZK в два раза больше Кв, л треугольник ОвК
подобен треугольнику EZK, то и ЕК будет и два раза больше КО.
гк = 2ко
Затем SK в дна раза больше КП вследствие того, что SZ в два
раза больше SH и ПИ параллельна KZJ;
ак = 2кп -.'.''.- ' ..
значит, ОК равна К П. Таким образом, прямая ОКН, имеющая с гитгер-
болой общую точку К и заключенная между асимптотами, делится и точ-
точке К пополам; это значит, что она будет касаться гиперболы [па основа-
\\ шш теоремы, обратной 3-й теореме книги II «Конических сечений»
: Аполлонии]. Пол той sue точке К эта прямая касается и параболы; зна-
| чит, и парабола коснотся гиперболы в точке К.
• . Представим теперь, что гипербола продолжен» до Р; лозьмем па АН
' ; " какую-нибудь тичку Е, затем через ? лродедем прямую Т2Г, иарал-
•'¦) лсльную ГВ; пусть она пересечется с гиперболой в точке Т; чорез Т
\ параллельно ГН проведем ФТХ. Теперь, поскольку по свойству асим-
асимптот гиперболы площадь ФГ будет раина ГЕ, то иоеле отнятия об-
¦ той площади Г2 площадь Ф2 будет равна ПН, и поэтому примам,
соединяющая.точки Г и X, пройдет и через 2**): пусть ото будет
прямая FSX.
Если гР есть точка пересечения цараболы с примой ФТХ и по
свойстлу параболы квадрат иа Ч'Х ранен прямоугольнику между ХН
и ИМ,
WX2-HM«XII
то квадрат ни ТХ будет меньше прямоугольника между ХН и НМ.
Пусть лиадрат па ТХ раийи прямоугольнику между ХН и II Q.
тхя = хн-ио
Так как 2А к АГ относится, как ГН к НХ,
_2А_ ГН . . 1
АГ ~ НХ '
•л пак ПТ к ПХ, так, если взять IIQ общей высотой, и прямоугольник
между ГН, IIП относится к прямоугольнику между ХН и HQ, или
к равному ему квадрату на XT, то есть к киадрату па BS,
ГН ГН-НЯ nr.frfl ГA-Н»
ВХ XH-IIU
•) 2Й-Й.
*) Из равенства ФА-А2=2Г-BS следует «X : ВХ~Y1 : ГГ, то сеть треугольники- ГГ?
П подобны; следовательно, гхх Судет ирнмаи. ¦ ¦• ¦
КОММЕНТАРИИ
то, значит, квадрат па В2, умпожешшй на ZA, будет район прямо-
прямоугольнику между ГН и Н Q, умложсиному на ГА.
BX'-SA (П1П?У-ГА
Но прямоугольник между ГИ, II ?2, умноженный на ГА, меньше
прямоугольника между ГН, НМ, умноженного на ГА.
<ГН- НО) ГА < (ГН-НМ) ГА
Значит, квадрат на H2J, умноженный на SA, будет меньше квадра-
квадрата на BE, умноженного па ЕА.
BS*-EA <MES-HA
Подобным же образом докажем это и для всех точек, взятых меж-
между Е и В.
Теперь возьмем любую точку 2 между Е и А {рис. 28}. Я
утверждаю, что точпо тик же квадрат на НЕ, умноженный на ЕА,
будет больше кнадрата на В2, умноженного ла 2А. Действитель-
по, произведи то же самые построения,
проводом через 2 параллельную КЛ пря-
прямую Т2Д, и пусть опа пересечется с ги-
гиперболой в точке Т (она с ней действительно
пересечется вследствие своей параллельности
асимптоте); аатем проир;№ннии через Т па-
параллельно АВ прямая ФТХ пусть пересе-
пересечется с продолжением HZ и точке X. Далее,
тик как ito сиоиству гиперболы прямоугольиик
ФА равен АН, то пряма», соединяющая точ-
точки Г мХ, пройдет и через 2. Проведем ее,
и пусть она будет Г?Х. < Точка Т есть пересе-
пересечение прямой ФХ с параболой IIKN. > Затем
поскольку по сиоиству параболы квадрат на
ГХ равен прямоугольнику между XII и ИМ,
ГХ
ТХ-
то, значит, квадрат на ТХ будет меньше пря-
прямоугольника менаду ХН и НМ.
Рис. 28.
Пусть квадрат на ТХ равпяется прямо-
прямоугольнику между ХН и HZ.
ТХ2= XH-HZ
Так как 2А относится к АГ, как ГП к IIX, и так же, если взять
• HZ общей высотой, относится прямоугольник между ГН и IIZ к прямо-
прямоугольнику между XII и HZ, то есть к квадрату на ТХ или к квадрату
на В2,
ЕЛ ГН ni-IiZ ГН-IIZ ГН-JIZ
а г
их
Tn-jtz_
"xii- iiz
BS2
то значит, киадрат па В2, умноженный на 2А, будет равен прямо-
прямоугольнику между ГН, HZ, умноженпому на ГА.
Но прямоугольник между ИГ, НМ больше прямоугольника между
ГН и IIZ; значит, квадрат па BE, умноженный на ЕА, будет больше
квадрата на В2, умноженного па 2А.
KA >В2*-2А
О ШАРЕ И ЦИЛИНДРЕ
491
Подобным же образом докажем и для всех точек, взятых между Е
и А. Но то ?кс самое доказано и для всех точек между Е и В; значит,
квадрат па. ПК, умпожошгьшна ЕЛ, будет больше исех подобных же пост-
построенных па ВАпараллслешшедои, если 13Е будет и дна раза больше ЕА.
Ш этом кончайте* приводядшй Квтокиом текст. 1-Тсть пчетл, серьезные г.оащюжо-
ния п пользу того, что он дейстпитрлыю принадлежит Архимеду. Что можно ска :<iti,
о нремспн его возникновении? I [[.-которая искусственность .постановки задачи — деление
пропорционально заданным отрезку и площади — долпег очень сомнительной возмож-
возможность самостонтелышго появления этой .чндачи, тогда как связь ее с дилемшш шара в дан-
данном отношении у Архимеда вполне удовлотвнрнтельво ибъиеняет причину \\р. появления.
Еслп додача онридюшшп объема итлра была впервые разрешена только Архимедом, то
рассматриваемый теист не мог полникнуть ранее :>lioxii Архимеда. С другой стороны,
упоминаемая Евтокисм устар«шг.ть терминологии (оиределтшг: нараболы как сечиние
прямоугольного конуса) покачивает, что этот тпкет записан еще до Лполлошгшюп р|;фо[1МЫ
терминологии — ппсдс|шн современных нм.-шаний: эллипса, гиперПоли, ннраинлы, так
что и много ihuikr ;шохи Архимеда ятот теист
нояшшнуть по мог. Если принять вп ннимание
еще yuuMiinaiiMbiii Eltокном дорийгкип диалект
и то обгтоятелыяво, что поело 212 г. до н. э.—
крушения Сиракуз — оспивппг» представителя
доршша в эллинистический пкриод — трудно
ожидать каких-нибудь научных подвигов на
почне Великой Греции п Сицилии, а также
и то, что этай задачей, запима.чен Архимед, то
и|1()|Ц1! и естественнее псего действительно от-
ксегн этот твксг к Лрхгпкщу. Едиистпсинос
пийражеипе, которое можно Сыло бы сделать,
;|аклюпагощеесп п том, что ни в одном списке «О
шаре и цилиндре» раеиматрешаемое решение не
пстречастся, доказывает лишь то, что Архимед
но какой-то причине не поместил его в отосланное
Досифшо послание, и больше ничего.
Затем нужно, копочни, принять во внима-
внимание и необычайное изящество самого решения;
для этого представим задачу в современном
обозначении (рис. 29).
Трсбувтся прямую АВ = а разделить так,
чтобы отношение мерного со отрезка AM к задан- Рис. 29.
ной прямой ЛС = Ь равнялось отношению .чаднп-
ной гтлощади А —ар к квадрату нторшо отрезка MB. Полояшм МП— х; тогда постав-
поставленное т]11!бование приведет к уравнению
а —ж _ а-р
или
(«—х) х'^
Нетрудно лпдеть, что иолучкппоо урапнсиие рлпкосилыш системе спидутщих двух
ур»виШ1Ш'| с дпумя леизьестнымл:
— уравнение гиперболы с асимптотами СО и CG — и
- ¦¦ ураппепис параболы о осью Оу. Мта iimisum примерно тпжп сауки;, что бмлti иродложеао
Молохмим дая рашспия делийской лй.чйчн; тем самым upoJiuuairrvn локотормй (Ж(;т па общий
ход рассуждений Архимеда при рпшяпш зтой лпдичи. Н особенности красиво получаете»
ш;сл1>доваиц(| иоаможностя решения (диоризм) (рис. 30).
Не меняя общности иадачи, мы можим с.читагь постояшшми АВ - а, КС — Ь
и менять лишь величину площади А = ар; этозпачит, что при ри.чличних данных мы можем
пользовитт.ся олнпи и тнй же гиперболой (u x)y—ah; чт« jko катится параболы, то по
мере уве.нч(!нин Д будит упеличипптыш и р, иными гловами, наши rrnpa(i(i;ia х*-—ру будет
нее более и б плес отходит!, плечзо ин напрпп-лои.иш к прямой АС. Для возможности реше-
492
КОММЕНТАРИИ
дня задачи необходимо, чтобы рассматриваемые гипербола и парабола пересекались
Если р сравнительно невелико, то пересечение буд*л иметь место, причем, как нетрудно-
видеть, мы будем получать д в с течки ш'ресечг-пим, из которых одна N дана ил чер-
чертеже, а другая получится там, где иарабола подойдет
достаточно близко к асимптоте гиперболы. На чертеже
изображена гипербола J3NKP на три параболы. Одна и»
них (/) дает дпе точки пересечения К и Р, вторая (///)
леггсит целиком пне гиперболы, не имея с последней
никаких общих точок, наконец, для третьей (/7) дпе точки
ш?рт!чеи11>1 елниаются в одну и гипербола с иариболой.
имеют общую касательную и точке К. Этот предельный слу-
случай и является наиболее паленым дли исследования, так как
диет граничу между областью лозможных решений (параболы
типа /) и лепозможпых (параболы типа ИI). Архимед пока-
покалывает, что ото буде1 тогда, когда перпендикуляр КЕ
разделит прямую АН ь отпошепми 1 : 2. Он проводит общую
касательную ОКПЕ. Так как ОП является карательной к
гиперболе, то точки касания К. будет серединой заключенного
между асимптотами отрезка этой касательной. Далее, так
как прнмая OS будет касательной к параболе, то расстоя-
расстояние UE точки S* иоресечения касательной с осью параболю
от се вершимы должно равняться абсциссе HZ точки писа-
писания. Отсюда легко получается:
Рис. 30. чтп и дает нам нужное предельное условие возможности
решения.
Разобран постановку задачи в самом общем яйле, Евтокстй переходит к выяснению
особенностей ее поетанонкн и том чистиом случае, который требуется при решении задачи
о делении шара. On пишет:
Чтобы ближе подойти к самому способу выражений Архимеда,
представим себе, как па чертеже в основном тексте {рис. 31}, диаметр
шара ДВ, радиус BZ и заданную пря-
прямую Z6. Мы дошли до того, гово-
говорит он, что «данную прямую AZ нуж-
нужно разделить в точке X так, чтобы
отношение XZ к -ладанной прямой Z
(Z6) равнялось отношению задан-
заданной (площади) к квадрату на ДХ.
Выраженная ь таком общем виде
задача требует диоризма». Дей-
стпителыю, если заданная площадь,
помноженная па заданную прямую,
будет больше квадрата па ДВ,
(помноженного) на BZ, то задача, как доказано, нсвозможпа; если
же она раина, то условиям задачи удовлетворяет точка В и полученное
решение не имеет никакого зпачения для поставленной Архимедом
в самом начале цели, так как шар ня в каком отношении делиться
не будет.
Значит, понимаемая в общем видо задача требовала дпормзма.
«Но при тех условиях, которые присуши рассматриваемой задаче», то
есть чтобы ДВ была в два раза больше ZK и BZ была больше ZB, «дио-
ризм не нужен». Действительно, заданные площадь — квадрат на ДВ
и прямая Z0 дают в произведении величину, меньшую квадрата на ДВ,
(умноженного) л a BZ, так как BZ большо 6Z, а при этом условии,
31.
О ШАРЕ И ЦИЛИНДРЕ
493
как ми доказали, возможно решение задачи и известен самый способ
се решения.
После этого Евтошш приводит решения оспоиной задачи о делении шара, данное
Диописодорои и Диоклом:
«Как мы уже сказали, Дипнисодор, пе находя нигде обещанного
Архимедом окончания и не чувствуя себя и состоянии восетаиоиить не-
недостающее, пошел иным путем и дал неплохой способ решения леей зада-
задачи; поэтому и мы полагали необходимым присоединить К уже написан-
написанному и его решение, исправив его по мерс возможности, так кап оно
вследствие людской небрежности в большей части изложения предста-
представляло большие неясности иа-нн значительного количества ошибок
и списках, бывших в нашем распоряжении.
Решение Д и о н и с о д о р а
Рассечь плоскостью данный шар так, чтобы его сегменты находились
6 заданном отношении.
Пусть будет шар с диаметром АВ и отношение, рашюе тому, в ко-
котором ГД находится к ДЕ. Требуется плоскостью, перпендикулярной
к АР, рассечь iiiap так, чтобы его сег-
сегмент с вершипой А имел к сегменту с
вершиной В то же самое отношение,
что ГЛ к ДЕ {рис. 32}.
Продолжим В А до точки Z, и пусть
AZ будет равна половине АВ. Пусть
затем отцошонио ГЕ к ЕД будет равно
' отпошению ZA к Ail;
ГЕ ZA
ЕД — ЛН -
пусть АН Судет перпендикулярна АВ.
Возьмем для ZA и АН среднюю про-
пропорциональную АЭ;
К
Рыс. 32.
конечно, Л0 будет больше НА. Через точку Z проведем параболу
с осью ZT5 и параметром АН; она пройдет черен 0, таи как прямоуголь-
прямоугольник между ZA к АН ранен квадрату на Ав. Пусть эта парабола будет
2("Ж. Через В параллельно А0 пронедем прямую ПК, и пусть она
пересечет параболу и К. Через точку II пронедем гиперболу с асимлто-
тами ZB и ВК; она пересечет параболу между точками в и К. Пусть
точка пересечения будет А. Из А опустим на АВ перпендикуляр AM
и затем через точки Н иА параллельно АВ пронедем прямые П.\ и A3.
Таи как НА — гипербола, АВ и ВК — се асимптоты и АН, IIN
сш>тнетствсш1О лараллслыш MA u ЛЕ, то прямоугольник между АН,
flM равен прямоугольнику между МЛ, A3
согласно 8-й {12-й) теореме книги J1 «Конических сечений» Лполло-
иик. По HN pauun ЛЕ, а Л? равна МБ; следовательно, прямоуголь-
прямоугольник между ЛМ и MB равен прямоугольнику между НА и АВ.
494 КОММЕНТАРИИ
Так как прямоугольник между крайними равен примоугольлику
между средними, то четыре упомянутые прямые составят пропорцию:
таким образом, AM к НА, как АВ к ВМ;
AM А В
НА " ВМ
значит, квадрат иа ЛМ относится к квадрату па IIА, как квадрат
ыа АВ к квадрату па ВМ.
АВЯ
ИМ* ВЫ*
Далее, так как по свойству параболы квадрат на ЛМ равен прямо-
прямоугольнику между ZM и ЛИ,
AM*"-ZM-AH
то, ииэчш, ZM относится к МЛ, как МЛ к АН.
7.М ЫА
МЛ " ' АН
Таким образом, как первая к третьей, так будут относиться и киад-
киадрат на первой к квадрату па второй, и квадрат ыа второй к квадрату на
третьей («Начала», кн. V); значит, ZM относится к ЛИ, как киадрат
на Л М к квадрату иа НА.
Но по доказанному квадрат на ЛМ к квадрату на АН относится, как
квадрат на АВ к квадрату иа ВМ,
ЛМг AR8
и, значит, квадрат на ЛВ относится к квадрату на ВМ, как ZM к АИ.
аи* _ _км
ВМ»"" АН
Отношение квадрата па Л В к квадрату на В М будет ракно отпоите-
нию к ругой с радиусами АВ, ВМ; значит, отношение кругов будет ранио
отношению ZM к АН.
прут А Н _ ZM
круг ИМ АН
Следовательно, конус, имеющий основанием круг с радиусом АВ,
а высоту ЛИ, будет равен конусу, имеющему основанием круг с ради-
радиусом ВМ, а нысоту ZM, так как если у двух конусов основания обрат-
обратно пропорциональны высотам, то эти конусы равны. Но конус,
имеющий основанием круг с радиусом Л13 и высоту ZA, и конусу, име-
имеющему то же основание и высоту АИ, будет относиться, как ZA к АН,
или кап ГЕ к ЕЛ, так как конусы с одинаковыми основаниями относят-
относятся, как полеты. Таким образом, конус, имеющий основанием круг
с радиусом АВ и высоту ZA, к конусу, имеющему основанием круг
с радиусом ВМ и нысоту ZM, будет относиться, как ГЕ к ЕД. Но конус,
имеющий основанием круг радиуса АВ и высоту AZ, равен шару (на
диаметре АВ), конус же, имеющий оснонаиисм круг радиуса ВМ
и высоту ZM, равен сферическому сегменту с uepuiuiioii В и высотой
ВМ, как зто будет доказано дальше. Таким образом, шар иа диаметре
О ШАРЕ И ЦИЛИНДРЕ 495
АВ к конусу с иысотой ZM относится, как ГЕ к ЕА.
шар (АН) ГВ
конус |ZM) ~ Ей
Отсюда «выделением»
тар - конус (Hm'-ZH) _ ГВ - ВД
конус (ВМ2- ZM; ВД
Значит, плоскость, проведенная черев ЛМ, перпендикулярная
к АВ, рассечет шар в заданном отношении,
(ceiiieur ua AM): (сегмент ни ЕМ) ~= ГЛ : ЛЕ
что и требовалось сделать.
Л что конус, имеющий основапием круг радиуса ВМ.'а высоту ZM,
равен сферическому сегменту с иершшюй В и высотой 13 М, можно
доказать так:
Сделаем, чтобы ZM. относилась к МЛ, как ОМ к MB,
ЯМ _ОМ_
МЛ ~" MB
тогда конус, имеющий то же основание, что и сегмент, и высоту ОМ,
будет равен сегменту*).
Далее, так как ZM к МА, как ОМ к MB, и после перестановки
ZM к МО, как ЛМ к MB,
7,М AM
Л1О " MB
по AM к MB относится, ник квадрат па ИМ к квадрату на MR или
как круг с радиусом ИМ к кругу с радиусом MB,
AM _ AM-BIB _ ПМа _ КРУГ (ПМ)
мв " 31l!a MB8 *4>yr (MB)
то значит, круг с радиусом ПМ к кругу с радиусом MB относится,
как MZ и МО.
Таким образом, конус, имеющий основанием круг радиуса MB,
а высоту ZM, будет ранен конусу, плюющему основанием круг
радиуса II М, а высоту МО," так как у обоих основания обратно пропор-
пропорциональны высотам. Отсюда же следует, что рассматриваемый конус
с радиусом MB и высотой MZ будет равен и сегменту с высотой ВМ.
Рсшонио Диокла и кпяге «О каустиках»
ОС этой же задаче пишет и Диокл и книге «О каустиках», начи-
начиная со следующего проднглонии.
«В Кинги «О шаре и цилиндре» Архимед показал, что всякий сфери-
сферический сегмент равен конусу, имеющему то ?кс осноииние, что и сег-
сегмент, и высотой прямую, имеющую к опущенному ив вершины согмйи-
та на основание перпендикуляру отношение, равное тому, которое
вместе лиитыс радиус mafia и высота противолежащего сегмента имеют
к высоте противолежащего сегмента. Таким обрааом, если шар А13Г
*) Действительно, ил основании предложения IT книги второй «О шипе и цилиндрср сегмент
ВМ будет равен конусу с тем ии> основанием и с высотой 11, определяющейся формулой
! АП
496
КОММЕНТАРИИ
с диаметром АВ и центром Е рассекаются какой-нибудь плоскостью
по кругу с диаметром ГА {рис. 33}, и, если мы сделаем, чтобы отношение
ЕА вместо с ZA is ZA равнялось бы отношению 11Z к ZB,
ЕЛ -i- ZA
ZA
112
а ЕВ вместе с BZ относились бы к ZB, как 6Z в ZA,
ЕВ + BZ
6Z
ZA
ZA
в А
AZ
_пв
то, согласно доказанному, сферический сегмент ГД будет равен конусу,
основ апнем которого является построенный на диаметре ГД круг, а высо-
высотой ZH, сегмент же ГАД ра-
f ^— -ч^ вей конусу с тем же самым
основанием и с высотой 6Z.
Затем, предложивши рассечь
данный шар этой плоскостью
так, чтобы получившиеся
сферические сегменты, нахо-
находились друг к другу в задан-
заданном отпотетт, и произведи
описанное построение, Архи-
Архимед говорит, что будет также
дано отношение конуса, осно-
основанием которого является
круг на диаметре ГД, н вы-
высотой Z0, к конусу с тем же самым основанием и с высотой ZIL Л так
как построенные на равных основаниях конусы отвеятся между собой,
как высоты, то будет данным и отношение 0Z к ZH.
Далее, так как 6Z относится к ZA, как ЕВ вместе с BZ к ZB,
ЕВ-Н HZ
ZB
то, «выделяя», GA относится к AZ, как КГ} к ZB.
_ ев
По той же самой, причине НВ относится к ZJ3, как ЕВ к ZA.
ЕВ
~ АИ
После этого дело приводится к такой задаче:
Задав положением прямую АВ и две данные (конечные ее) точки
Л, В и величиной некоторую прямую ЕВ*), рассечь АВ в точке Z ?пак,
чтобы после добавления двух прямых GA и В11 отношение 6Z к ZH
было данным, и кроме того, чтобы 0А к А/ было, как ЕВ в ZB u ИВ
к BZ, как ЕВ к ZA;
AZ
34.
ZB
НВ
BZ
ЕВ
ZA
это будет доказано далее. Архимед же, разобрав псе это подробнее, свел
дело к другой задаче, которая в кшггв «О таре и цилиндра» ие peiucna.
*) так как Днокл несколько обоБщадх задачу, то эта прнмая ЕВ может и не быть равной
рядиусу шара.
О ШАРЕ И ЦИЛИНДРЕ
497
.Заданы положением прямая АВ и две данные точки А, В и {величи-
{величиной некоторая прямая и) отношение, в котором, находятся прялгыеТ и А;
требуется рассечь пря^иую АВ в
точке Е и приложить ZA, 11В
так, чтоб hi была: пак Г к А, так
и YAi к ЕН, как ZA к АЕ, ток
и данная прямая к BE, как НВ
к BE, так и та же данная, пря-
прямая к ЕА {рис. ЗЛ}.
(А нами з). Пусть зто
сделано. Иернгащинуяярпо АВ
проведем ВАК и Л13 М, постро-
построим АК и ВМ, равные каждая
заданной прямой, и соединяю-
соединяющие прямые КЕ и МК продол-
продолжим до Л и 0. .Чатем соединим
К и М и пропадем через Л пря-
прямую АХ, параллельную Л В, а
через точку Е прямую SEOII,
параллельную NK. Теперь, по-
поскольку, согласно предположе-
предположению, ZA к АЕ, как MB к BE,
ZA_
AF,
~ ВЁ
Рис. ЗА.
и, вследствие подобия треугольников, MB к БЕ, как ©А к АЕ,
мп _ ел
W ~ ае
то, значит, ZA к ЛЕ, как В А к АЕ,
ZA 0А
АЕ АЕ
иткуда ZA равна вА.
za - ел
ГIо той же самой причине LSII равна ВА.
вн = вл
Далее, так как 0А вместе с АЕ относится к MB вместе с BE, как
К Л вместе с АЕ к ЛВ вместе с BE
8А +АЕ _ КА -|- АЕ
MB + НЕ ¦" АВ + МЕ
(ибо каждое ни этих отношений равно отношению ЛЕ к ЕВ), то, зна-
значит, прямоугольник между в А имеете с АЕ и АВ имеете с BE равен
прямоугольнику М1чкду К А н-месте с. АЕ м MB вместе с БЕ.
(«Л + А.Е) (AR + ЕЕ) — (КЛ + АЕ) (ИВ -¦- BE)
Построим АГ и ВБ, [Kinrjue каждая КА. Теперь так как ©А вместе
с ЛЕ paBirw/Е,ЛВ вмвето с ЛЕраниы EH, RA имеете о АЕ раним РЕ,
¦ MB имеете с BE равны Si.O, и доказано, что прямоугольник-между 0А
вместе с, АЕ к ЛВ вместе с BE равен прямоугольнику между КА вместо
с АЕ и MB имеете с BE, то, следовательно, прямоугольник между ZE
и КН ривип прямоугольнику между РЕ и Е2; коатому если точка Р
будет между Л и Z, то точка X попадет за Н и обратно.
498 КОММЕНТАРИИ
Теперь, поскольку Г к Д, mm ZE к ЕН
г _ /к
"л" ~"~ШГ
и ZK к ЕН, или прямоугольник между ZE, ЕЙ к кнадрату на EH,
ZK ЯК- К If
ЕН ЕН2
¦го, следовательно, Г к Д будет, как прямоугольник между /К, 151
к квадрату на Elf.
I' _ /Е- КН
Но, согласно доказанному, прямоуголыгак между ZK. ЕН равен пря-
прямоугольнику между РЕ, Е2;
/.К- К\\ |«К-Е2
значит, Г к Д, кик прямоугольник между РЕ и В2 к квадрату на КН.
EII2
Отлсниим ЕО, равную ЙЕ, и соединяющую прямую НО продолжим
и обе стороны; пусть во'/.сгаьлепные из 2 и Р иорисидмкуляры пере-
пересекутся с :>гой прямой в точках Т и Г. Теперь, кап как ТГ проходит
через заданную точку Л, образуя с заданной но положению прямой
ATJ угол К130, равный половине прямого, то ТГ будет дана но положе-
положению. Затем прямые 25Т, РГ, проведешше vi3 заданных по положению
точек 2, Р, пересекают ее и точках Т, Т; значит, ТТ будет задана
и «ю ислнчинс п по положению. Далее, поскольку ьеледсткис подобия
треугольников КОВ, 2TJS ирпмая ТИ относится к ВО, как 2Н к ИМ,
" ВО ~ ПК
то, «иншчюдпняя», ТО к О|{ относятся, как 2Е к KB,
ТО ЕЕ
ОП ЕВ
Яо ВО к ОГ относится, как НЕ к КР;
ВО BE
ОГ К*
значит, «no pfiiiiiicTijy» ТО относится к ОГ, как 2Е к ЕР.
ТО 2Е
ОГ ЕР
Но ТО относите»! к ОТ. как прямоугольник меязду ТО, ОТ к квадрату
на ОГ
•го то-or
и 2R к КР, как прямоугольник между 2Е и ЕР к квадрату па ЕР;
?Е _ 2К-ЯР
ЕР ~ ЕР2
:шачит, прямоугольник между ТО и ОТ к квадрату на ОГ относится,
как прямоугольник мгжду 2К и ЕР к квадрату па ЕР;
торг si:- rp
после же пер^станоикм прямоугольник между ТО и ОГ относится
О 1ПАРЕ И ЦИЛИНДРЕ /j()t|
I? прямоугольнику между 2Е и ЕР, как" кнадрат на ОТ' к кцадрату
на ИР. "
ТОРГ _ ОГ*
ЕЕ-ЕР " В1.«
Г1о киндрат н« ОГ равкн двум квадратам на КР, таи пак и киадрятнаОИ
равон: диум кпадратам на BE; влачит, прямоугольник между 'ГО и ОГ
равен двум прямоугольникам между 2Ж и ISP.
TOO1-2BR Kl'>
Но, пак докапано, HpHuoyi олышк между 2Е и Е1' отиос.итгн
it кпадрату на 1511, как Г i; Л; яначнт, и прямоугольник между ТО и ОГ
к квадрату на КН относится, как 2Г к Д. Далее;, квадрат на EII равен
квадрату на SO, так как каждая па EJ.I ч SO равна АВ вместе с НЕ;
япачит, прямоугольник между 'ГО, ОГ относится к кладряту ни SO.
как 2Г к Д, "
ТО-ПГ _ 2Г
и поскольку отношение 2 Г : Д дано, то, значит, будет дано и отношение-
прямоугольника между ТО, ОГ и кнадрату и» SO. Таким образом,
если мы сделаем, чтобы отношение 2Г : Л*) раипялосМ) отиозпинию ТГ
к некоторой другой прямом Ф и опишем на ТГ иллиис так, чтобы
под углом ЕО13 (то есть полошше прямого) ординаты нвад-
p ни iipnMoii Ф с недостатком, нодо^ним прямоугольнику
ТГФ**), то .чтот иллипс. пройдйтчерез S coiviacu» тооромо, обратной
20-й B1-й) теореме книги I. «Конических сечепнй» Аполлония. Пусть
нтот oiiiiciiiciiinii :).1.чшгс. йудет I'ST; тогди ш*.помни точка 2 будет
находиться па -о/ипикч*. заданном ciiohm лоли/К^нием.
Далее, так как ЛК Пудот диагональю прямоугольника 14'М, то
црямоу]олышкмежду NE, 311 равеп нрямоуголышку между ЛВ, ИМ.
Поэтому если через точку В проведем гиперболу с асимптотами
ОК и КМ, то ока пройдет чорез S; тан как положении точки В,
обеих прямых АН, JBM, а дначит, и асимптот вК, КМ, являются извест-
известными, то :>та riiuop6(jjia будет ладана споим положением. Пусть эта
построенная гипербола будет SB. Таким обрааом, точка S находится
на заданной споим положением гиперболе и уже находилась на эпдап-
пом своим положением у.ч.чннсе; следовательно, точка 3 дана. Так как
на нее опущен перпендикуляр НЕ, то, значит, будет дана и точка Е.
Ннтем так как МП к И 1С относится, пак ZA к АЕ,
ян у. а
к к л к
и АЕ дана, то будет дана и AZ, По той же причине будет дана a II1J.
С и и т v. з же нронзиоднтси так:
Пусть по том жо самим- чертеже будет даня поджокнпкш разделению*
прямая A1J, .чатом другая заданная прямая ЛК и заданное отношение
*) ]< подлиннике ошибочно А : 2Г.
**) По <:oH|jeMennoti терминологии атч Судет эллипс с ;uibmct|iijm ТГ и дарамстгом Ф, ор
ii.Ti-ы SO кс1Т1)|1()Г1) но ncp!iviuiiii<-yjiHi)]ibi к диаметру нллнпса 'ГГ. а иОрллуют с ним угол и
It «бинплчмшнх rr.nnci-'i чертеж:', уряшгпнис итого -.мтлигтеа будет;
Фбудет параметром. ctdi'i'iicnsTnyioiiliiM направлению пекущих под углом в 4 Л" к Яжиичру
через 1/ oCoaimч!ш ио.чудипметр. егшрнжпнпый с напрашплшем дннмгтрв ТГ, tv
Ф " 1/»ТГ~ = ~ТТ~ '
32*
500 коммкнтлкии
Г : Д. Перпендикулярно к АВ проведем ВМ, равную АК, затем соеди-
соединяющую прямую КМ, построим АР и В2, равные каждая К.А, и из
точек Р и Е восставим перпендикуляры РГ и 2Т. При точке В
построим угол АВО, равный половине прямого, и пусть ВО, продол-
продолженная в обе стороны, пересечет прямые 2Т, РГ в точках Т яТ.
Затем сделаем, чтобы как 2Г к Л, так и ТГ относилась к Ф *),
•»г тг
и опишем на ТГ эллипс так, чтобы проведенные под углом, равным
половине прямого, ординаты ккадрироиались на прямой Ф с недостат-
недостатком, подобным прямоугольнику между ТГ и Ф. Затем ироиодем через
точку В лостроотшую на асимптотах АК, КМ гиперболу КЕ, пересеиа-.
ющую эллипс к точке 3, из ? опустим на АВ перпендикуляр НЕ
к продолжим его до П. Далее через Е проведем A3N параллельно АВ;
продолжим прямые КА, MB до точек 0, А, продолжим также соединя-
соединяющую ME, и пусть она пересечется с КК и точке в.
Теперь, поскольку ВЗ есть гипербола, а 0К. КМ — ее асимпто-
асимптоты, то на основании 8-й {12-й} теоремы книги 11 «Конических сече-
ггай» Аполлония прямоугольник между N3. ЗП равен прямоуголь-
прямоугольнику между АВ. ВМ,
.\тг-гп —аи-вм
поэтому КЕЛ Судет п]>ямой лиштей.
Построим AZ, равную 0А, и ВИ, ранную АВ; так как А к удвоен-
удвоенной Г относится, как Ф к ТГ гг как- квадрат па 30 к прямоугольнику
между ТО, 0Г
_Д Ф_ 50а
2Г " ТГ " ТО-ОГ
согласно 20-й B1-й) теореме 1 книги «Конических сечений» Аполло-
нин. то, значит, удвоенная Г относится к Д, как прямоугольник между
ТО. ОГ к квадрату па 30. Далор. так как ТВ относится к ВО, как SB
к RE
ТВ
во
то
о в
ко
ОI
го
ЕВ
" BE
и <«г рисоединя я »- - ГО
= ~Ш~
я«> ВО к ОГ, как НЕ
BE
' ЕР
к О В
к ЕР
то. значит. «ш> рапеистпу»
. как ? К
ТО и ОГ.
к ЕВ.
кнк 2Е к ЕР.
ОГ ' ЕР
Таким образом, прямоугольник между ТО, ОГ к квадрату па ОГ
относится, как прямоугольник между SE, ЕР к квадрату на ЕР,
ТОРГ ZE-EP
' ОГЙ " ЕР2
Ио1и, после перестановки, прямоугольник между ТО, ОГ относится
к прямоугольнику между 2Е и ЕР, как квадрат иа ОГ к квадрату на
ЕР. Но квадрат на ОГ равен двум квадратам на ЕР, так как и киадрат
*) Та же ошибка в подлиннике, что в ныше.
О ШАРЕ И ЦИЛИНДРЫ 501
аа ВО равен диум квадратам на BE, ибо BE равна НЮ вследствие того,
что каждый ии углов при точках В и О равен половине прямого. Тогда
прямоугольник между ОТ. ОТ равен двум прямоугольникам между
SE, ЕР.
Поскольку же доказано, что удвоенная Г относится к Л, как нрн-
моугольник между ТО, ОТ к квадрату на ВО
2Г _ ТО-ОТ
то, значит, если нзить половины нре;шдущих, Г относится к Л, как
прямоугольник между НЕ, ЕР к квадрату па ЕО и как прямоуголь-
прямоугольник между ГЁ, ES к квадрату па ЕН,
2В-ВР 2E-PJ5
SO2 ЕЫа
так как SO равна ЕП, вследствие того, чти каждая иа этих прямых ран-
ранца Л В вместе с BE.
Теперь поскольку ВЛ вместе с АЕ к MB имеете с BE относится
как К А имеете с АЕ к АВ имеете с- В К
KA -1- АК
мв + ве" лв + ве"
. (так как каждое из рассматриваемых отношение ранни отношению АЕ
к ЕВ), то значит, прямоугольник между ВА имеете с АЕ н АВ вместе
с BE ранен прямоугольнику между КА вместе с АЕ и MB вместе с BE.
1«А +¦ АК).(ЛВ ~ В К) — {КА • ЛЕ) (JIH j BE)
Но 6А-| ЛЕ равны ZE, ЛВ ;• BE равны EH, КА+АЕ равны РЕ, MB -j- BE
рашш Е2; значит, прямоугольник между ZE, P1H равен прямоуголь-
прямоугольнику между РЕ, КЕ.
ZE-EH = PE-E?
Но Г относится к 4, как прямоугольник -между РК, ЕЯ к кпадрату на
ЕП; значит, Г относится к Л, как прямоугольник между ZE, EH к
квадрату на ЕН и как ZE к ЕН.
Г MS-EII ZE
Л Ш12 ЕН
Зятем гак как MB к BE относится, ккк О А к АЕ
мв ел
be ~ ае'
и 6А равна ZA, то, значит, МБ относится к BE. как ZA к АЕ.
МН ZA
ВЫ АЕ
По той же самой причине К А к ЛЕ относится, как ИВ к БЕ.
ка нв
АЕ BE
. . . Таким образом, если даны (величиной и положением) прямая АВ
и (только величиной) другая нрямая АК и отношиние Г : Д, то вот на
АВ взята точка Е и прибавлены прямые ZA, НВ так, что ZK и ЕБ
• : находятся в задаппом отношении; натод, если данная прямая АК равна
502
КОММЕНТАРИИ
MB, то Ы.М к BE относится, как ZA к АЕ,
MB ZA »
~НВ ~ А В
и КА к ЛЕ относится, как НВ к BE,
к л ив
~лЁГ ~~йк~
что и трсбоналось сделать.
Поело того как это доказано, мы можем заданный шар делить в дан-
данном отношении так: пусть АВ{рис. 35} будет диаметр данного шара, Е
его центр, и отпошепие, в котором должны находиться между собой
сфсри>юскио сегменты, пусть будет рапно Г к Д.
А "'
НА
" AZ
ftB
НА
AZ
1IZ
7.А
В К
«Z
Рис. 35.
Берем на АВ точку Z и прикладываем прямые НА, ВВ так, что-
чтобы Г относилась к Д, как HZ к Z0,
а НА относились к AZ, как ЕВ к I3Z,
ИИ
"~ яг
и вВ к ВЯ, как ЕА к AZ;
ЕЛ
" ТтГ
(и заданная прямая будет равна радиусу шара ЕВ или ЕА); доказано,
что пси это выполнить иозлшжно. Чориз точку Z перпендикулярно к АВ
проводим прямую KZA и рассечем шар проиеденной через КЛ плоско-
плоскостью, перпендикулярной к ЛВ. JI утверждаю, что полученные сфери-
сферические сегменты будут относиться друг к другу, как Г к Д.
Дейстиитсльни, так как НА относится к AZ, как ЕВ к BZ,
__ЕВ_
HZ
то, значит, «присоединяяо, получаем, что HZ относится к ZA, как ЕВ
вместе с BZ к BZ;
ЕВ + BZ
слрдоиательпо, конус, имеющий основанием круг с диаметром КЛ
и имсоту ZH, будет равен сферическому сегменту с тем же основанием
и с высотой ZA. Затем, так как вВ отпосится к BZ, как ЕЛ к AZ,
AZ
то, «присоединяя», получаем: 6Z к BZ, как ЕЛ вместе с AZ к AZ;
_ ЕА -;- А35
еяедоватольио, конус, имеющий леповаииом круг с диаметром КЛ
О ШАРЕ И ЦИЛИНДРЕ 503
ч высоту Z0, будет равен сферическому сегменту с тем же основанием
и с нысотом BZ. Так как упомянутые конусы, находящиеся ita одном
оспожшпи, относятся между собой, кац высоты, то есть как HZ к Z0,
или как Г к А, то, значит, ати сферические сегменты будут находиться
между собой и заданном отношении, что и требовалось сделать.
|:i| При чтении этого предложении необходимо иметь л "иду, что иод «двойным
¦отпошчшем» Архимед подразумевает отношение, иозледпппоо но нторуго стс!11(!пь, а «полу-
«полуторным* отношением он называет отношение, возледеппоо л степень 3/2; таким образом,
данное предложение можно п некотором смысле рассматривать как периос появление
.дробного аджа.чателя стоиепн.
Днлио стоит отметить, что рассматриваемое предложение иредстоиляиг единствен-
единственный пример, когда наложение докизательстна А;)химсда может быть очень упрощено,
пи выходя из области операций, дшитленнт.гх и цеетичной математике.
Первая чисть предложения сивершенш) естестиеиио доказывается так (рис. 55 па
«тр. ffiO).
Мусггь HZ и Л2 продставляют высоты ернипивасмых сопясшов, причем fiZ>AZ;
отношение поверхностей обоих сегментов будет рално о'хпотииию этих высот, дейстии-
тольнн:
АЛ* ^ ZA-BA — ~ZA "
Пусть ЬЪ и HZ представляют высоты тех копусов, объемы которых равны объемам соот-
иетстпукици х сегментов:
ez=BzEA:'AZ ,
AZ
а-до КВ^^КА 11рпдстан.л1К!т радиус шара. Огиошспии объсмоп обоих сегментов равно отно-
высот этих копуш»:
Так как ЕЛ-.= ЕВ и EZ>AZ, то второй множитель будет мсшыпо единицы,
откуда сроку получается:
ez ^/-rz
ZH ^ ZA
и первая часть теоремы доказана: отношение объемов обоих согаемтов меньше возведен-
возведенного н кладрат отношения их iiouepx нос/гей.
В н:1ло/1сени[| Архимидц истрсчаютс.н все (ктюнпые моменты вмппшрпиодоитио доиа-
нате.'1ьгтиа, по они натупгснаиы припходящнмч иторостелншьпии :>;ie.MLMiTaMu; л частиости,
Архимед вводит точку'К, чтобы, было KB | I}/.= KB-|-B/ = KZ.
Сначала он «я неходиого равенства
\ I А ГГ
A)
ешрвделяег отношение
шли, так как EB=BF
Второй исходное
BZ/ZA:
BZ
ZA
ZB
©Z
EA-j-AZ
©В
I5R
равепстло
HZ
ZA
EA+AZ
AZ
«Z—ZR
ИД
BZ
" ZA •
ER-T-BZ
13Z
вн
.КЛ
«В
KB
B)
504 KOMMEHTAVHH
IIZ __
гд~
BZ
Z.A ""'
KZ
KZ
ZII "
сразу iwy дает:
пли после перестановки:
При атом Архимед устанавливав, что вН>В? -факт совершенно ненужный
для доказательства первой части теоремы — на пропорции B), тик как nZ>ZA.
Определяя 1УТЫОШ1ШИ0 BZ/ZA ия B) и D), находим:
шГ="гн ' <5>
Так как
ев pz _ ев-fBZ _ ez
ВК "" /A ~BK-|-ZA~" Eb+ZA
и
ez _ ez _
то, поскольку UZ > Д?, он на основании E) пишет:
^<i^JS^ (б>
ZK ^ »к ZH ' l '
li правой части, отпешшше KZ/7j]1, согласно D), представляет отношение поверх-
поверхностей ofionx сегментов, тогда как oZ/ZH будет отиишшшо их объемнв.
Дальнейшие операции уже плолне понитлы. Ми неравенства (Г>) ми имеем:
©Z-ZH < KZ2
ZH ^ HZ».'
что н доказипает первую часть предложения.
Rent бы оба наши сегмента были подсбгты, то их объемн относились бы как^кубы,
а поверхности - ¦ к»к киадрагм сходствопннх сторон; следоиатил ыю, отношение объомои
равнялись бы возведенному в степень */•, или, как сказали бм греки, полуторному отно-
отношению их иолерхпосте». И лаш(>м случае, когда оба сегмента не подобны, отношение
объема большего сегмента к объему меньшего будет больше полуторпого отношения соот-
встстнующих поверх постей.
Так как объемы относится, как высоты конусии 0Z/ZU, а иоаерхяости — как
иысоты сегменто» WLj'/.S, н ti:i основных формул A) м C)
EA-i AZ
ZII ~ ZA* ' ЕЛ 4-BZ '
то после возиедения и квадрат обеих частей этого рапииства мы получили бы:
HZ(E.-\+AZ)»
ez ~\2 / ijz
zii ) =L za
и для цыказатсаьстка нашей теоремы нам. иршшшет» бы толика убедиться, что последний
миыжмт(\11>> больше единицы.
Мы имеем:
I iZ- ZA2 | liZ- BA'-j-ZHZ • ZA ¦ К-A
"AZ (EAH-iJZM" ~AZ-BZ* |-AZ¦ ЕД2 -2BZ-ZA¦ БД '
Разность числителя и знаменателя этой дроби можно представить в виде
(BZ AZ)-EA2-|-BZ-ZA(/A HZ) = (BZ--ZA) (EV — RZ-ZA).
О ШЛРК И. ЦИЛИНДРЕ
51>Г>
Тик кик BZ>ZA, то первый множитель положителен; что касается второго множи-
множителя, то мы без труда докажем, что ЕЛа> BZ-ZA. Действительно, соединим ла рис. 36
центр Е круга с вершшкш Л периенднкуляра AZ. Мм
имеем: ,
ЕАа>Л2в,
или
Таким образам,
«Z
zrr
HZ
7л
)
«Z / HZ V'/г
Z11 > V ZA ) '
Рис. 3E.
что и донизывает выставленное положение.
Докалатол^стпо Архимеда начинается как рая с установления фякта, что ЕА* =
=ВЕ.ЕА> BZ-ZA. Отсюда оп получает:
ZB _ Ей
или на оепоиапни следствии из нашего уравнения B), тнк тык ВК —БД:
Отсюда он получает:
или, так как 13Е^=ВК:
где BN есть средняя пропорциональная между вВ и ВК:
ИВ _ BN
BN ~ ВК '
. Отсюда
вВ BN»
ВК.
BN
От1юшени«! т-р- мы мижем вычислить так:
ВК
и елсдовательпо,
Далее, так как
и ez>zK, то
bn ©в —eB-i-BN_reN
^К""" BN ~NB + BK~.NK"'
©В 0N3
ПК
6N_
6N
WK
NKS "
6Z+ZN
KZ-I-ZN
<'zT
6Na
NK8 ^ ZKa
откуда
©7.2
0В
ZKS ' BK
на основании цашего равенства E).
ZH
Б06
КОММЕНТАРИИ
И» неравенства
Лрхпмсд заключает, что
ez» ^ kz
—
ум
без всяких дополнительных пояснений. Так как отношение BZ/ZH равно отношению
KZ BZ
объемов сегментов, а ¦утт = 1уТ (см* Равепство D)) — отношению их поверхностей, то
/. JI АД
теорема доказана.
14 ] К сожалению Архимед не поясняет, каким образом он получает нужное ему
неравенство с полуторной степенью
6Z г КУ, N»/»
zn >^. zifj "
Доказательство, которое даст комментатор Архимеда Евгокнй, таково:
Вообразим {рис. 37} раздельно расположенные прямые АВ, Г, А
такие, что отношение квадрата на АВ к квадрату иа Г больше отноше-
отношения Г к Д. А
ав8 -.JL 1г
Я утверждаю, что отношение АВ к Д будет боль-
больше возведенного в полуторную степень отноше-
отношения Г к Л.
Возьмем для Г, Д среднюю пропорциональную Е *).
Тогда, так как отношение квадрата ла АВ к кнад-
рату на Г больше отношения Г к Д
г
А К*
I
.L I i
Рис. 37.
и отношение кпадратов на ЛВ и Г ранно двойному отношению АИ к Г,
а отношение Гн А равно двойному отношению Г к Е, то, значит, отно-
отношение АВ к Г больше отношения Г к Е.
Сделаем теперь, чтобы Е к Г относилось, как Г к BZ'
в
г
BZ
BZ
г
Так как четыре приыыс BZ,F, E, Д составляют непрерывную про-
пропорцию.
г
в
в
д
то отношение BZ к Д равно трижды взятому множителем отношению BZ
к Г, или Г к Е.
Г \а
Г Е
•) Так что -jT = -?¦
г* Д
*) Из итого |iani:»CTRa вытекает, что Aft>BZ.
О ШЛРК И ЦИЛИНДРЕ 507
Но отношение Г к Д равно дважды нзитому множителем отношению
Г к 15.
г
/ г у
Д ' \ Е /
Следовательно, отношение 13Z к Д равно отношению Г к Д, взято-
взятому множителем полтора раза.
bz i г у/~
д ~ * д '
Таким fi6pa»0A(, итпшщмшц ATJ к Д будет больше отношении Г к Д,
влитого множителем полтора раза.
Мы иидим, что ппедеыие дробной степени для отношений произошло у греков в и;шс-
CTiioii степени 6сссо.чцйтолыю бдигодцря тому, что греки рассматривали умножение отно-
отношений инк их слижемие.
Помещенное и конце этого иредлолхснии доказательство «иным способом» прид ли
может принадлежать Архимеду. Ни гопори уме о том, что оно, кик гонорнт Хмзс, ые
ииляетея ни более ясным, ни более коротким, чем иродыдущее, метод доказагельстпа,
состоящий л преобразовании искомого отношения и сведения его ;> уже доказанному
ели очепидиому, соиершенио «е и дуло Архимед»-
E| Л атом предложении ми видим перлый пример так называемой изопериметри-
чеекой ладичи. Ho:i;iiiee мы имеем ц(>лое исследование ftO6 игкшеринетрических фигурах»,
принадлежащее александрийскому математику Зенодору и освещенное ч пятой книге
«Математического собрания» Паппа Александрийского.
О КОНОИДАХ И СФЕРОИДАХ
Это проскшсдопие, первое и лштежггичаская литературе, касающееся ловорхпостей
второго норидка, согласи» первоначальному плану, изложенному во введении к трак-
трактату «О спиралях», должно было Ныть четпертмм в ряду нослашш, обращенных
к Доснфею, ни и действительности оно оказалось пятым.
Основной задачей рассматриваемого нроияж'Дшшя нпл истей, определение объемов
сегментов параболоида, гиперболоида и эллипсоида вращении. Йта задача была решена
Архимедом при помощи механического способа, как налагается л «Эфоде» (предложе-
(предложение Ш, IV, VIII, XI). В сочииеипи «О коноидах и сфероидах» ррется строгое ыатема-
тическос обоснование ршнепия поставленной задачи, для чего доказывается двадцать
вводных предложений.
11] Предложения I и II носят арифметический характер, продолжая исследования,
начатые it предложениях X м XI трактата «О спиралях».
[2| Предложение III содержит вспомогательные теореми ия теории конических
сечений..Первой является теорема, доказанная и «Началах теории конических сечений».
Доказательство этого предложения «одержите»
в «Конических сечениях» Аполлония (киша П1,
предложение 17), но было Сы очень сложно иос-
ироигшодить всю цепь рассуждепий по Аиол-
лоиию, привлекая все необходимые предвари-
тельиые теоремы; ыоагому мы дадим доказатель-
доказательство в современной фирме, польяунсь методами
аналитической геометрии. Это тем более необхо-
необходимо, что в труде Хипеа это предложение обхо-
обходится молчанием, а и переводе Чиалиниы «Ко-
гкшдов* при докал.чтельстис ;>того предложения
допущена грубая ошибка. Рассматриваемая тео-
теорема у Аполлония формулируется тан: «Если
две нрнмые, касательные к коническому сечению,
или к окружности круга, пстречаются в одной
точке, и из*двух произпо;] ьлых точек, взятых па
коническом сечении, проведены прямые, парал-
параллельные этим касательным, пересекающие друг
друга и коническое сечение, то произведения
отрелков каждой ил этих прямых будут относиться, как кпадраты соответствующих
касательных».
Если в.шть начало координат и щ-рппгие конического ссчепня и ось абсцисс совпа-
совпадающей с ocbjo последнего, то уравнение любого конического сеченпя может быть пред-
стаилено в форме
у •=2рх -~ ¦ Аа:*,
Рис. 1.
где fc>0 дли гиперболы, А==О ;yi« uupa»o:iu и fc<0 дли эллипса.
Пусть из некоторой точки А с координатами хг, yt проведешл касательные АВ, АГ
к колипескому сеченшо (рис. 1).
Пусть а будет угол, который образует с осью Ох одна га этих касательных, напри-
например АВ, a q — расстоянии от А до точки касания В. Координаты точки В могут быть
предстаплеиы г» пиде
*=a:j-)-Q cos а,
О КОНОИДАХ И СФКРОИДАХ 509
Мы можом найти координаты х и у, решив пти уравнения совместно с уравнением кри-
кривой \?^=2+к*
(?/t+Qsin a)a
Для п мы получим посте нреобрапонншш квадратное уравнение
(sin»a--Acosao)o«-!-2lff]sinn—Л-(г, \-[t) i:osa} Q-Hv?—2pxt--kxl) — 0.
Так как всякая прямая пересекается с коническим сочипием и двух точках, который
¦в случае касания сливаются в одну, то рнссматрипаемое урапиояие должно иметь ратшт.т<;
корни. Для этого .необходимо, чтобы
{?/, sin га•¦- к (Xl ;¦ />) cos «}*= (sin2 a — Л cos2 a) (i/f — Zp^—kxj).
Если разделим обо части последнего равенства на cos* а, то для определения tga ггплучится
кнадраглоп .уравнении: это значит, что па любой точки плоскости можно пролести к кони-
коническому сечению, иообще говори, две касательные. 1\гли точка А иыбрака так, что длн
tga получаются действительные корни, то соответствующие касательные будут ЛВ и АГ.
Таи как а случае квдииия для расстояния ц ицлучаютои равные корпи, то для квад-
квадратов А1В и ИГ мы будем иметь выражение
. У?—2 М
где л лцдмшгатело вместо а нугкпо подстапнть соответственно значения углов, образуемых
*-, осьго Ох каждой ил прямых ЛИ и Л Г.
Возьмем теперь искоторуш точку Л с координатами х.,, у2, лежащую по другую сто-
сторону кривой. Из :>той точки параллельно ЛЬ и АГ проледсм прямые ЕХ и ©II. Коорди-
Координаты точек, находящихся на иигкдой и.ч :ithx прямых, могут быть представлены анало-
аналогия и ьши выражениями
V~lfo-\ rsina.
Для г — расстояния ДЕ и AZ, иди соответственно Л В и ЛП, от точки А до кривой, мы
будем иМ(ЯЬ аналогичное уравнение
a2 a— A- c<jsa re) г* -\ ¦ 2 {у„ sin а—/с (л3 -|- р) cos а} г -\- (j/4— 2//х2 ¦¦ fcz'i) — 0.
Но ieuej)b корни rj, г» этого уравнении должны иметь разные :щаки, так как АН и AZ,
и соответстьешю Лв тт АН. имеют различные направления; следовательно, прои:ш(!дение
абсолютных пеличип г,, г., будет равняться
Г1>г" sin» о- A ci>se a '
Пусть а, представляет угол с осью Ох прямой АВ, а а2 ¦ прямой А Г; и iaK(»i случае:
si ц2 гаа - ¦ /c cos» a2 ' ' " ' sin2 re» - /• cos2 ft.,
Мы имеем:
АВ* АГ* yf—2рх, — kxl
ЛЕ-AZ "Т'Д«-АТ1~ i/SS*i '
что и доказывает высказанную теорему. Длн. того чтобы прапаи чисть била полоздитсль-
ной, достаточно iibjitji точки А и А но рияпые стороны от римшатрниасмого конического
¦оечеппя, кик и сделано нн рис. 1.
Вторая часть предложения Ш требует преобразования ураписшш нарабо.Ы к косо-
косоугольным осям координат, началом котормх служит точка А (рис. 2), ось Ох совпадает
«прямой АК, а ось Оц — с параллельной JH-) касатольион, приведенной п точке Д. Выска-
Высказанное Архимедом вспомогатилънос предложение может бить сформулировано так:
Если 7Ева = Л'-В1Т, где Л' = 2/> ¦ параметр параболы, соответствующий прямо-
прямоугольной системе координат, в которой ось х предстапляет ось параболы ВН, а ось у - ¦
касательную к параболе в ее вергаггне, то AZa—-Д/.AZ, где <V" и М связаны соотношением
N: M = AK*: A2*.
510
КОММЕНТАРИИ
Пусть новая, система координат представляется совокупностью припоях ДК — диа-
диаметра параболы — и ТДТ-! — касательной к ней в точке А. Пусть АЕ представляет
хорду, liHpn.'iJHMiMiyfo :ггой касательной, делящуюся в точке Z попонам; диаметр АК, как
известии, будит иа'-раллелси оси Г>>1 параболы.
Пусть Ш1 и \Н'х будут абсциссы, гчютпетстыующш! кргшгшм точкам Л и Е хорды
АЕ; тогда по осшшному снойству параболм мм ишшм:
или, так как ИР,: A1L-OJ»,: 011, НИ : Ш', = ОП*: (M'f.
Тогда, прнмышн операцию «нерсиорачминли»», получаем:
ИП -D1', _ ОПа OPf
1Ш " ОН1 "'
или
Ж : Ш-^ШР : (О11-:-ОР,)-@П
,. откуда после сокращения на nPL:
0112=1Ш-(()П—OVL).
Это punciLcriio можно переписать
так:
(Ш1 -И())г--ВП{AШ -МО)
.= m ia-|- 1ш. вр,—2вп- во
Рис. 2.
или
Помножим обе части и:) Л72 — квадрат параметра параболы, соответствующего
оси В И; тогда
. 1Ю'= (ЛГ-IUГ) (Л' • ПР,) = ЛИ3- КР?,
или
Ураииснис jiapaGo.nu, огнесннггоВ к нг.им AR u ЛТ, будет
откуди для точки А:
Мы имеем:
Далее, так как AZ —ZE, то
ЛК = Е1»! -'г 5Д = Л11 • ЕД,
откуда АП—EPt=22A; поэтому
AZ* : АК * = А '/* : (ЕД^.: д \\. Ц pj.
Но ЕД* = Л*-ВЕ и АП-EPi—Л'-ВО, как было доказано шлпе; значит,
AZ2 : Л К2 ¦= А/,й : Л- (BE | - НО),
где BS представляет аебцнесу точки Л касания. Так кап у параболы подкасательиал ST"
раина удвоенной абсциссе, то ВЕ+ВО—TO=AZ, и мы имеем:
О КОНОИДАХ И СФЕРОИДАХ 511
Сравнивал это с новым уравнению! параболы, полугары инримстр М:
„ .. AZ*
131 Задачи, ностап.чечшые в предложениях VII---1X, могут быть формулированы
двояко. Во-нерцьтх, если ыа рис-. 7 текста (стр. \7Ч) рассматривать эллипс АлВ как основа-
основание, a ГА пак высоту колуси, который, конечно, будет, с наше» точки зрипия, аллнп-
тпч(х:кш1, то дело идет об определении круговых сечений заданного эллиптического
ноII.уса. Во-вторых, можно рассматрипать Aali как аплиитическое сечение некоторого
кругоного конуса с вершиной Г, осномаиие которого требуется найти. Исп говорит за
то, что Лрхимод рассматривал постапленпую аадачу именно с последней точки зрении.
В предложении VII Архимед ставит такуш задачу:
Дай эллипс с малой осью -АД и большой у& а равнобедренный треугольник ЛВГ
(рис. 3); черем точку Л трсбуетгя Tait пронести прямую AZ, псрссенающую в ГС и У,
uj)OAOJi»KciitTii ииеоты ГД и боковой стороны Г И дшптго треугольника, чтобы имело»
место рпвенслио
(ЛЕ¦ KZ) : КГ»=--Лу* •¦ ЛГ2.
ApxHMivi считяст эту задачу возможной потому, что
AE-EZ АЛ-АВ
'Ттоби nouiiTi. :iuii<ieiiHc этот условия, обратим ннима-
нИ11 на то, что и j.ii.iniii-,c АВ
АА.дв<Л-у*.
а и круге AftZ
где. Во 11Сф1тс;идикушнjina к AZ и, следовательно, нарал-
лелмш Ду- Таким образом,
AEEZ АА-ДИ
ЕЙ» > Д^в '
Поскольку рис -1
иииучеипеп! ними рннппстно будет :жт!ивал1Ч1тпо арлимед<шу, еили тшыи АД — ДИ < Ду„
то есть если АЛ яи.чнктся мппьшпй глпшшй гтолуосып эллипса АуВ.
Решении поставленной задачи ApxniJCfl не дяст, но оно может быть получено сле-
следующим образом.
Пусть па рис. 3 угол ГАВ —я. Мы будем :iiihti> iio.io/кч'нис секущей п.их'.кости AEZ,
сгли буд(!Т известен угол BAZ-=(p, или отрс:«ж Л.К. Псчкшсгтцая точка К определится
нз уралношш
AE-EZ Лу*
ЕГ2
И я треугольника А К Г имеем по теореме синусов:
ЕГ _ sin(a--<p)
АЕ = eosa '
а и:! треугольника ГЕ'/:
ЕГ sin (<х--(@
EZ ~~ cos a
Иодстаилнн эти значения в нпше урашнмше, получаем:
Bin (rt 4- ф) sin (a--- ф) _ А Г"
cos" а ~'Лу*
¦512
КОММЕНТАРИИ
откуда
(sin n cos (p-|-siri q> r.os a) (din a cos q>—sin cp cos a)—~v~ c°s2 a,
sin2 rt cos2<p —sin2<p cos3 a=-:—s- cos-.a,
ЛГ*
sin2 «¦¦ siu*a sin*«p—cos2™ shi"zcp= -¦ -^ cos2 u,
sin2 u—sin' q> = -т-i" •¦<>si!«,
at окончательны
Имеем:
ел едователь но.
si»2 cp — ь!Л2 a гг—j- cosB о.
ГД
АЛ
_ ГА /А-у* —АЛ»
Тек как ГА > ГД и Лу > АД, тп задача допускает решение.
После этмго Архимед доказывает, что исе точки йллипса лежаттна поверхности
конуса с основанием A6Z и вершиной Г (этот конус, естественно, уя«с яе будет прямим).
Произисди описанием1 R тексте построение, Архимед начинает с исходной пропорции:
ЛЁ-EZ Да2
ЕГ2
ll;i подобия треугольника!) ГАВ и ГПР получаем:
ЕГ8 ГЛ2
АД-ДВ '
откуда
A)
B)
(АЕ ¦ EZ) : (ПЕ ¦ ЕР) = Ля2: {АД ¦ А В) -
Д<-1лес, ия подобия треугольников АНЕ, ASA, и ЛОЖ, EPZ имеем:
АЕ:ЕП==АЛ:Л?,
KZ : КР- AZ : АО,
откуда
(Л Е ¦ RZ) : (ПЕ ¦ КР) = (А А ¦ AZ): (S Л - Л<)).
Заметим но ciioiicTiiy arpestnoa мои^цу параллельными секущими ал.чииса
Л«2: (АД-ДВ) = ORS: (ЛК- KB). ¦ C)
Теперь, с|):шиипая пропорции A) и C), мы мон«ем написать:
(ЛЛ-AZ): (ЗЛ-Л0)=6Ка : (ЛК-КВ). D)
Да.кч-, ii:i подобии, треугольников ЛВГ и НОГ инеем:
(EA-AO):l'A2^(AK-KR):rK2, . . E)
что дает нам «do равемстиу»:
(ЛЛ-лг):ГЛа-=вК2:ГК2.
О КОНОИДАХ И СФКРОИДАХ
513
Бели в точке Л параллельно 0К проведем перпендикуляр ЛМ до пересечения
с поверхностью я о и у с а, то по свойству круга получаем;
и наше равенство принимает вид,
Зто озиача«т, что треугольники ГКВ и ГЛм подобны ияпч!о luiiimi ГвМ есть прк-
кая. Так пак точки Г и М лежат па поверхности конуса, то, значит, и принадлежащая
эллипсу приизполыпш точна 0 тоже буд(!т лежать на
цшкгркиости конуса Г Л/.
[4| При построении фигуры дли доказательства
предложения VIII (см. рис. 8 т стр. №;'>) нужно от-
отметить следующий момент.
Если имеет место равенство N*<=ZA -Д1Т, то точ-
точки Z, Н н конец отрезка, изображающего примут N,
будут находиться на окружности, построенной яа
диаметре ZH; тогда построенная ла KB подобная кри-
лая тоже будет окружностью.
Бели же N4 ио равно Zd-AII, то сочепис конуса
илоскостыо, проведенном через ZII перпендикулярно к
с плоскости чертежа, будет прсудставдять :>ллипс; по-
поэтому на RB и строится аплкпе, иодоб|тый упомяну-
упомянутому. Дальнейшее доказательство проходит ыюлле
аналогично предыдущему.
|5] Дпказптольстпо перлон) утнериедснин, а имен-
именно что сечение параболоида цращилия плоскостью,
параллельной оси, будся- такой же параболой, как и
образующая параболоид, можно пронести таи.
Путь ОГ представляет oi-.i. параболоид», АиВ —
парабола, иолучепинн в ссчеитш параболоида пло-
плоскостью, проходящей через ось. Раеесчем параболоид
плоскостью, иар'ляяси.ио» оса ОГ и перниидику.мир-
перниидику.мирной к илоскости чертежа. Пусть прямая ДГС предста-
представляет след этой плоскости на плоскости чертежа
(рис. Л,а). Тогда, осли смотреть сверху, сечение пара-
параболоида пзобр(шится линией вДН (рис. 4, б); тре-
требуется доказать, что ато будет парабола, совпадающая
С пераоилтальпой ЛОВ.
Согласно оспопиому свойству параболы, киадра-
Tbi ординат возрастают пропорционально абсциссам;
если обозначим коэффициент пропорциональности че-
через 2р, то будем иметь:
ЛГ»-2р-0Г,
или нообще:
л,
Нам предгтоит пайтгг соотношение между квадра- i-
том ординаты WK к соответствующей абс!\иссуи ЛЕ.
Если через точку Е провести плоскость., перпендикулярную к оси ОГ, то мы в сече-
сечении с параболоидом получим картину, изображенную на рис. 4, в. Uo свойству прямых
в окружности мы будем имоть:
Но АЕ =
Далее,
таким образом,
33 Лрхямсд
Г—КГ; сиедонатсльпо,
*=(ЛГ—ЕГ) (ЛГ+ЕГ)=АР>_ЕГ=.
514
КОММЕНТАРИИ
или вообще
г='2.рх.
Мы получили уравнение, совпадающее с первоначальным. -
Второе утверждении о том, что сечение гиперболоида вращения плоскостью, парал-
параллельной оси, представляет гиперболу, подобную данной, мы доказали бы таким мак образом.
Пусть ОГ представляет ось гиперболоида, К • центр его, то есть лиршину асимп-
асимптотического конуса, ЛОВ — основную гиперболу. Плоскость, лараллельлаи оси, пере-
пересекает плоскость чертежа (рис. 5, й) по прямой ЛАЕ и дает л сечения с гиперболоидом
линию ДвЛ (рис. Б, б); требуется докапать, что вто будет гипербола, подобная первой.
ТСкли ОК. — действительную полуось гиперболы — обозначим через и, параметр
гиперболы обозначим через /» и положим ОГ=я, АГ — у, то гипербола (см. всту-
вступительную статью) может быть представлсла следую-
следующим уравнением:
уа—— - (Iiii-j х) х.
п
F. Совершенно так же, как в случае параболы,
можем написать:
Г
©Е2=Л Е • ЕВ = АГ*- ЕГ2,
или
—?- Bо+ОГ) ОГ— ? Bа [-OZ) OZ =
= i {2« (ОГ — OZ) Ч ОГ*—OZS}
=?. (ОГ - OZ) \2а+ ОГ Ч-OZ}=•?¦ ZT {2а-}- 2OZ+ZT}.
Но a+OZ=OiA-bO1A=AU — действительной полуоси
I,-р попой гиперболы ДКВ; если мы обозначим эту полу-
ось через alt то уравнение кривой сечения будет:
Глс. 5.
// или, если положить — = —:
в, а ai
это будет уравнение птппрболы, параметр pt и действительная полуось а^ которой уве-
увеличены в одном и том же отношении а : о,; ипыми словами, мы получили уравнение
гиперболы, подобной димнои.
Аналогично этому можно доказать соответствующее предложение и для удлинен-
пого аллипсонда, если взять уравнение основного эллипса в виде
где р — параметр, я 2а соответствует большой оси эллипса, вокруг которой происходит
вращение. Для сплющенного эллипсоида нужно лишь в ураиш-нии произвести следую-
следующую замену: вместо у взпть Ъ—х, а вместо х влить a—у, и помнить, что р = — , где Ь —
малая полуось эллипса. Если положить р'^=---, то уравнение эллипса будет:
О КОНОИДАХ М СФЕРОИДАХ
515
Несколько сложней обстоит дело п том случае, когда сечение гиперболоида прово-
проводится череп центр •— першипу асимптотического копуш К. Пусть КОГ иредставотнет ось
гипербол иид.ч, кривая ЛОВ — сечение; гиперболоида плоскостью чортсока; пусть
сскущан плоскость проходит перпендикулярно к плоскости чертежа, образуя
в пересечении с последней прямую КДЁ; точка
Д будет представлять вершину кривой сече-
сечении, расположенной в плоскости, перпендикуляр-
перпендикулярной в плоскости чертежа; требуется доказать, что ¦
ото будет гипербола, но и» :>тот раз уже не являю- "'
щаяся подобной основной гиперболе ОЛВ-
Так как АВ ыредатавлялуг диаметр кругового
сечения, периендикул ирного к ое-и, то ордината у
кривой сечения будет расположена п плоскости
этого круга. Мы имеем:
у*=АЕ ¦ К В.
Проведем череп точку Е диаметр, сопряжен- .,
ный с прямой КЕ; иуг.ть это буд1>т ММ; тогда WE —
= NK. Воз|/Мсм прямую ДЕ в качеств оси абсцисс,
а и качестве оси ординат гю:»г.мем параллель-
параллельную MN касательную ЛТ|; пусть :>та касательная
пересекается в тпчке Т с другой касательной ОТ,
проведенной в нертинс; О оснотюй гшкфболы.
Тогда, пользуясь первой Теоремой предложения
Ш, можем написать:
АЕ-ЕВ ME-NE
ОТ2
откуда
ДТ*
ОТ3
а — - • MF"
Рис. 6.
По ME представляет ордипату гиперболы по отггопгеииго к косоугольпым осям ДЕ
и АТь уравнение гиперболы в этой системе координат будет:
где л.,=КД, ж, = ДЕ, j/i = ЕМ, а р, -- параметр, соответствующий дааметтто КЕ Т»к
Kai; oci, х криаом сечения соппадает с ЛЕ, а ось у перпевдикулярна к плоскости чертежи,
то мы можем положить xl^x и писать: ' ft
Это будет ypaBiiciiTie гиперболы.
Чтобы дока;(;хт1., что эта гипербола не будет подобна основной, будем рассуждать так
ироиедсм 4tiji(!.4 точку Д плоскость, мпрадлельмуго оси f)J' и иерпевдику-ифную
к плоскости чертежа; мы зияем, что и сечении получится гипербола, подобная оснонной-
нам остается только доказать, что ота гипербола не будет подобна рпегмятригаемой
Возьмем и качестве начала 1гоо[щипатточку К. Так как ДЕ=я:1 — КЕ—КД—ж- КЛ
где КД есть дейстпите^ьная иолуом, а, нашей гиперболы, то ураплеиие гиперболы будет:
или, если вместо у будем писать у-,:
Ашиогвчло, если для тшхербилта сслпипя Л&Х позынпм « т:ачпг,тт?с пачаяа коорди-
координат точку Л — основание» перпендикуляра КЛ к прямым КГ и AZ, то со уравнение пред-
станитсн н виде * "
33*
КОММКНТАРИИ
„ч-.и- Если бы эти гиперболы были подобии, то мы вмели бы:
¦¦': <Ш Ж-^JL
ЛТа* КД о "
Возьмем две точки Е и 7, лежащие ла прямой, перпендикулярной к оси: для точки Б
будет yf=AE-KR, а для точки Z будет у§ =AZ-ZB. Мы видим, что у|>«/|. Далее,
для точки Е
г?—КА2 = КЕ«— К Д*=КГ*—АД* • ЕГ*— КАг,
а для точки Z
*|_ ЛЛВ= Л Z=—АЛ8=КГ4— АД2-
Таким образом, . >
*J—R4s>a;l—ЛЛ«.
Отсюда следует:
х\—ЛД*
иными словами, гицерболи обоих, сечений подобными не инимются.
[(>] Мы видела выше, что подкасательиая параболы равна удвоенной абсциссе
точки касания. Можно показать, чю для гиперболы нодк&сатсльнан будет меньше
удиое.-шой абсциссы, а дтя эллипса—Co;n>ii[e.
[7J П дакачигельспи; второй теоремы XV-ro иредяожепал ииеетс*г rteкоторый ие-
досмогр. Если кику1о-ии!>удь точку А на шшерхности коноида и вершину О асимптоти-
асимптотического конуса соединить прямой, то через эту примую можно привести сколько угодно
плоскостей, которые, соглаг.ао второму утиирждешио предложении XI, будут пересекать
коноид по гиперболам. Среди этих сечений йущгт выделиться диа: сеченае плоскостью,
проведенной черс» Прямую ОА и ось коноида, и сечение плоскостью, проведенной черея
ОА перпендикулярно к первой из упомянутик плоскостей.: обе эти плоскости рассматри-
рассматриваются в комментарии |41. Только для сечения второй плоскостью прямая ОА будет
осью получившейся гиперболы; в случае же сечения через ОА и ось прнмаы ОА будет
лишь одним и;» диаметров гиперболы, осью ;«с ее будет ось когговда. Аналогично этому
дли всех остпньных сечении плоскостями, проведенными через АО, эта прямая будет
лишь одним из диаметров гиперболы, получившейся ь сечении.
[8J Под АГ Архимед нпдрачумеиаег не только примую АГ, но и кривую—сечение
эллипсоида плоскостью, проходящей, чорея АГ и перпендикулярной к плоскости чер-
чертежа. То же самое спрапедлнио и относительно КА.
[9J Положим РЛ — z, В.\ — nz п радиус АД — Ала. Если в качестве оси ж взять ВД,
то уравнение парабоми АВГ будет y*=№nzx и соответстиукмции айсциссе ВЕ =
= (и—1)а радиус КЕ определится равенством KK*=**»t (и -1)га, так что объем самого
нижнего вписанного дилиидра будет
а всей вписанпой фигуры
17в„„с=л/B» {1+2-1 ¦. - • +(n~-l)}zi=3tk*n? (и
Объем nrcii опяпашюй фигуры будет:
Т'опис = nlfri {14-2-1- -. - 4-и} -3=
Мы имеем:
Гвпис < як*п*г>{2 < Гонце-
ОСт.ем конуса Т, равный полокпп^ объема цилиндра АВГД, будет
Y=i\k*n42nz/2=я АД2ВА/2;
он заключен между VBn;1c и V'ohhc» отличающимися друг от друга на величину, кото-
которую можно сделать сколь угодно малой.
[10] Пусть ЛЕ = 2, ВА = иг и вВ—в. Ордината КЕ опредсяяотсн согласно архи-
мсдону «ураииению» гииерболы равенством
самого нижнего вписанного цилиндра будет:
О КОНОИДАХ И СФЕРОИДАХ 517
a всей списанной фигуры, состоящей из (в—1) цилиндров:
Уапио=щ
Выражение » скобках можем переписать так:
йамепип (и -1) Fia n, мы увеличим ото иыражснис; таким образом,
я-АЛ** [rPi „ . z\ , /,J , 1
Объем описанной фигуры (« цилиндров) будет:
Заменив (л-|~4) пи п, мы уменьшим эти пыраженио
М/, , Л J
тС2а+тJ+-3
Таким образом,
Г1 Л . »\, 1 1 ^.,
Так как г может быть сделано очень малым, то отбросим г/3 и фигурных скобках.
Поскольку я = В0, вг=ВД ы BZ = 2U©, то средний член мощно переписать так:
— я-АДа-ВД , а это и будет интересующий нас объем конуса Т.
[И| Полагаем eE=z u B0=«z=a. Согласно «уравнению» эллипса радиус КЕ
самого нижнего ииисашюго цилиндра определяется раиенстьом
я-0Гг
а его объем я-КЕ2г=-—|—z(a2 — zs). Объем isceii ьписанной фигуры, состоящи! из
(п—1) цилипдроЕ, будит:
Выражение, стоящее и скобках, кап нетрудно ьидстг», будет равно тт-п3— -к ^- • От-
бросив вычитаемое, мы можем написать:
Чтобы получить описанную фигуру, надо приСанить ко вписанной только один нижпий
цилиндр с радиусом a=-nz, иными мамами, и скобках вместо («— 1) (nz)* взять п(пг)я.
Тогда
—1)
== -в, (в - у" [ » (*—1L -^
Выражение и скобках будет равно "Т в*+2"~"в"* Опросив два последние члена, мы
уменьшаем ныражение; таким образом,
2 я-еРчУ 2
'оиис^-jr ^j =-т П-В! Я-В6.
Заклгочагощаяся между VBunD и И.ишс величина, равная двум третям объема цилиндра
АГНМ, как раз и дает интересующий нас объем конуса W.
О СПИРАЛЯХ
Моего, которое трактат «О спиралях» занимает « ряду произведений Архимеда,
легко устанавливается на основании посланий к Дисифею, помещенных в этом трактате
и в сочинении «О шаре и цилиндре». Сочинение «О спиралях» написано л о с л е обеих
книг «О шаре и цилиндре», но до трактата «О коноидах и сфероидах», хотя по первона-
первоначальному плапу оно должно было следовать аа «Коиогдами».
Тема трактата «О спиралях» была предложена Архимеду Коноыом Самосским
(П а п II, Математическое собранно, кн. IV, 30). Есть оспопання полагать, что основной
гадачей Архимеда было определение длины окружности. Действительно, llann (там же,
кн. IV, йЛ), рассуждай пи одной задаче, связанной с решением вопросов, поставленных
в предложенных VI11 и IX книги «О спиралях», цитат: «Этой задачей пользуется Архимед
дли того, чтобы доказать, что окружность круга ранца некоторой примой». Действи-
Действительно, и предложениях XVII[—XX Архимед дает способ, при помощи которого можно
построить прямую, равную но длине гшдашгой окружности или любой ее части.
Трактат «О спиралях» интересен тем, что он представляет одно из немногих сочи-
нешти греческой математики (но пс единственное), где широко используется идея движе-
движения; :1дось Архимед в известном смысле предвосхищает идеи современного дифферен-
дифференциального исчислении, генезис которого, как известно, бил тесно свшап с задачей, про-
проведении касательной к заданной припой. 1) рассматриваемом сочинении Архимед решает
задачу о проведении касательной к Архимедовой спирали — кривой, которую он опре-
определяет как происшедшую в результате некоторого движения точки на плоскости. В »той
связи уместно будет указать, что греки разделяли кривые на дла класса:
1 . хаилОДса — кривые, получающиеся в результате сечения плоскостью некоторой
поверхности; классическим примером таких кривых являются конические сечении, для
которых, как будто, и был впервые установлен термин хацлОХоа.
2°. i\iy.ti?,ibb\s—кривые;, образуемые движением. Первым примером таи ой кри-
кривой яилнетсн кпадратриса Гипппл Элидекого, которую Динострат, быпгаий в этой области
предшественником Архимеда, применил для определения длины окружности. Вторым
примером является Архимедова спираль, которую можно определить как траекторию
точки, участвующей л двух дппжеиних, нриможшешюм и равномерном (относительном)
но прямой, равномерно пранииощенея но к руг одного и;» своих концов (переносном).
[11 Предложения I и II поент чисто механический характер. Они интересны тем,
'что но употребляющейся и них терминологии можно восстановить гсторшо возникнове-
возникновении понятия о равномерном дпшкепии.
Первоначальной ступенью бмло устпповлинис понятия iffum^S — равноскортай:
так пн:1[Л1ш.'1нс.ь д п а дниженип, в которых в одпо и то же времл проходились одмшко-
иыо расстояния, причем характер движении не играл большого значения: с точки зрения
греческих механиков, 'юоха'/.к-Л былп бы, например, продолжающиеся одинаковое вркми
движения двух свободно падающих тел.
На второй ступени понятие «рапноскррости» применилось уже к одному дви-
движению. Движение"наяьтпалось iooToyfjS а. :>хК ?га«тш — равпоскорым себе самому, сели
были ршшоскормми отдельные части, па которые можно было бы подразделить соответ-
соответствующее днк»кс!ше. «Равпоскорое себе са\юму» движение ул(с совпадает с пашим равно-
равномерным движением, если определять его как такое, в котором в одинаковые промежутки
времени проходятся одинаковые расстояния. В рапломерпом дкижепии пройденный путь
подрастает пропорционально проссшт, Архимеду приходилось доказывать ато,
чти он я пополняет v лредлО'Ксннн I по всем нранплам определении пропорциональности,
которые были « свое время даны Евдоксом Кцидским и дошли до нас п книге V «Начал»
Евклида (определение Г>).
[2] Предложения V—IX интересны л том отрошении, что они показывают, каким
математическим аппаратом ечиг^.чи возможным пользоваться без всяких объяснений
Архимед и современные ему математики. Эти предложения требуют построений при
О СПИРАЛЯХ
510
помощи так насыпаемых «стремлений» (vboCkic;), или, как иногда говорят, «вставок»,
далеко не псе ил которых могут быть произведены при помощи циркуля и линейки.
В предложении V речь идет о проведении такой секущей, чтобы ее отргсюк Z0
между касательной и окружностью был миньте любой заданной длины (рис. й). Если
поломим, что радиус. ВК окруишосты равня-
равняется 1, а угол BK0, соотиетстиующын дуге
В в, равен а, то это предложение в современ-
современной формулировке равносильно следующему.
г, six а—1
Предел отношения при а, стре-
стремящемся к нулю, равен пулю.
Для решении поставленной задачи Архи-
Архимед палашей некоторой длиной Ё, которая
может быть взята скол i. угодно малой, и стро-
строит равную :>Toii длине прямую Нв так, чтобы
она имела свои концы па окружности и на пря-
прямой КТТ, пршшденной чоре.! центр К парал-
параллельно рассматриваемой касательной ESZ, и
при этом «стремилась» к точке касании В.
Это построение может быть выполнено при
помощи циркуля и линейки. Дейетпительно,
если мы положим радиус окружности равимм Л, заданную дднпу 6Н —rf, обозначим
искомую хорду Б в через х и опустим перпеддикуллр КА на секущую Ш1, проведенную
« точку касания И, то будем иметь:
ВКа = ВЛ-ВН,
или
Рис. 1.
откуда искомая длина а: определится как корень квадратного уравнении а:2-] их— 2Я*=0:
- ныраженне, которое может быть построено при помощи циркуля и липейки. Вместо
соотнитстлующего построения Архимед говорит просто: «отложим рапную Е прямую JI8
так, чтобм она стремилась к В», считан соответствующее построение общеизвестным;
оно, дейктиителыю, легко может быть выполнена, если дпигпть линейку с нанесенной,
на «ей длиной вИ = «/так, чтобы точки Ни 11 ыкровлицались по прямой и окруж/гдеги,
а продолжение линейки проходило бм чере:1 точку И.
[Л\ В предложении VI стелится следующая задача (рис. 2). Если в круге радиуса R
нроведена хорда АГ заданной длины 2rf, то тробуптся так пронести сежущую ВК, чтобы
отношение НЕ : В Г —А; было, заданный и
меньшим отношении
Архимед определяет примут BN так,
чтобы /с=:КГ: BN, и помещает ее таи, что-
чтобы концы ее ско.чьиили по окружности и
примой KN, параллельной ЛГ, причем сама
прямая постоянно проходила бы чероа .ча-
.чади иную точку Г. Эта надача, очень близ-
близкая по типу к предыдущей, уя.-с по может
быть решена при помощи циркули и ли-
нинтси. Дейстлитсльпо, если опустим п<:р-
попдикуллр ГД яа параллельный АГ
диаметр ZII и положим BN = D, КД = а,
ГД^=Л и NK=s, то для определения х будем иметь урапыешн (по теореме об отрезках
секущей)
BNTN = ZN-IIN или D
которое может быть приведено к виду
Гис. 2.
—а)*={х\ Н) (ж-
520
КОММЕНТАРИИ
что дает там уравнение 4-й степени, корни которого не могут бить построелы при помощи
циркуля и линейки. Если положить у=х*—IIs, то искомая величина х могла выбыть
получена как абсцисса точки пересечения нпраболы
и гиперболы
Архимед п в этом случае говорит просто: «Поместим BN между окружностью и прямой
KN так, чтобы она проходила через Г».
IM Предложение VII решает такую задачу (рис. 3):
К продолжению л&цпщюй прямой АГ пронести такую секущую КЕ, чтобы ее отре-
отрезок IE имел к П заданное отношение к, большее того, которое Г0 имеет к 6К ими,
если провести ГА перпендикулярно к ГК, того,
которое ГК имеет к ГЛ.
Архимед определяет длину IN из соотно-
соотношения: /с— Д: IN, где Л по-прежнему радиус
круга, и затем помещает полученную длину IN
между окружностью и прямой К Л тик, чтобы
продолжение ее нрихи^ило через цадасшум точ-
точку Г — задача, ехидная с юй, которая разби-
разбирается в предложении V.
Если положим КН = В, Ш=1>, КЛ = а,
ГД=Ь, KN=:r, то для определения х бу-
будем иметь уравнение BN-IIN=^rN-IN или
рис з (П-\-х) (x-lt)-D Yb*-\-(x—«)B. тождественное
" *' с тем, которое мы имели в предыдущем пред-
предложении.
Если положить Tti^y, то для определения х и у мы будем иметь два уравнения:
• {%—**)*>
Первое уравнение будет уравнением гиперболы, второе же — уравлепием пара-
параболы; таким образом, рассматриваемая задача тоже могла бы быть решена при помощи
конических сечений.
При помощи подобных же кривых может быть получено и решение veOciS, ыа
котором ociioubinaioTiMi предложения VIII и IX. Дело идет о задаче такого рода:
В заданном круге проведены, две азаимио перпендикулярные прямые КМ ы AS:
Рис. Л.
требуется из точка К провести пряную KN тек, чтобы отрезок ее IN между прямой
A3 и окружностью имел заданную величину (рис. 4).
Осипшие ооответстиующей зидачи дано в «Математической библиотеке» Паппа
Александрийского (к". IV, 52—54).
52. «Я помещаю решение той задачи ни «стремления», которой воспользовался
Архимед п книге «О спиралях», дабы у тейп по било затруднений при чтении упомянутой
книги. Мы воспользуемся следующими геометрическими местами, которые полезны и для
многих других телесных *) задач.
Пусть дана положением прямая ЛВ (рис. 5), и пусть из заданной точки Г к ней про-
иедена мекоторан прямая ГД и затем церпеидикулярно к ЛВ восставлена ДЕ; пусть отпо-
*) Так Папп назыиает аэдачи на построение, решаемые при помощи конических сечений.
О СПИРАЛЯХ
521
шепие ГД к ДЕ будет заданным; и утверждаю, что точка Е будс:т лежать па гипербиле.
Проводом чирен Г прямую УХ, параллельную лерлелдикуляру Л К; лпнчит, точка Z будет
заданной. Затем приводим ЕН параллельно AD и пусть отношение ГД к ДЕ будет тем
же самым, что у VL к ZH или ZK.:
ГД : ДЕ =rZ : Z0 = TZ : ZK;
тогда будет в ада mi oil a каждая па точек в, К. Так как ГД2 к ДЕ2 отяоеится, как PZ*
к Z6a:
то будет данным и отношение их остатков 7Д2, то есть ЕН2 к КН. И В:
ГА2 ГД«—VZ"ЙД2 Eli»
—Z0)
КН-
Точки К и 0 даяы; :ina>iur, E будет находиться па гиперболе, проходящей че-
через Э и Е.
53. Пусть прямая ЛВ дана велттчшюй и положением и ЛГ перпендикулярна к пей;
пусть АГ-ГВ буд(!т равно произведению оаданной прямой @1 на 1'Л; » утвирждаю, что-
точка Д будет лежать ua некоторой иадапной своим иилижсыисм икраболи (рис. 6).
.Разделим ЛН пополам в Е и проведем под примым углом EZ; ljycTL ЕВ2 будот равец
прямоугольнику на вндашюй прямей {&) и EZ; следовательно, Точка Z Судет данной.
Рис. 6.
Параллельно АН проведем ЛП; тогда квадрат ЕГ, или ДН, будет равен нрлмоуголышку
на даппой прямой <©) и '/ГГ. Точка Z дапа; значит, точка Д находится па параболе, про-
проходящей терез A, Z, П и имеющей ось EZ.
54. Поело атих предварительных замечаний анилин задачи, предложенной вначале,
производится г.:л!дуищим способом. Дан положением круг ЛВГ (рис. 7) и и пем тоже
положением дапы прямая ВГ и некоторая точка А на окружности; между примой ВГ
и дугой ВЕГ вставить прямую, равлуто заданной (Нв> и «стремшпуюси» к (А).
Предположим, что задача решен»; отложена ЕД, равная JHW; Ш'рппндикупяряо
к ВГ проведем Ли, рапдуш АЛ. Тик как к маднннеш положением щишон ВГ из заданной
точки Л проведена АД ц ии точки Д восставлен равный ей перпендикуляр AZ, то, значит,
точна Z буд1!т находиться на гиперболе. Далее, так как НД-ДГ ]1авио ЛД-ЛГС или гД-ДВ
и ирнман ДЕ дана, то, значит, ВЛ-ДГ будет ралпо прямоугольнику ип ладинпой прямой
ДЕ и AZ; следовательно, точка Z будет и на пищйоле; значит, точка Z дина *). Птой зада-
задачей пользуется Архимед дли того, чтобы доказать, что окружнчгть iqiyia равна никоторой
прямой. Однако некоторые ебинплшт tjro в том, что он не сипсим правильно воспользо-
воспользовался «телесной» аяднчей,... и доказывают, что прямую, puuuyui пкрунсностл, можно
било См найти и нри помощи «плоских» (то есть решаемых при помощи цирку:ш и липий-
г;и) паднч, 1м:ли воспользоваться упомянутыми тенремами относительно спиралей».
К тнксту Паипа остается сделать очепь немного примечаний. Что упомянутая
в п. 52 криваи ©Е будот гиперболой, мы можем убедитьси следующим образом.
Положим, что заданное отношение ГД:ДЕ —/с, YZ—h; тогда K.Z=UZ = -r-.
ГД® Flla
Пусть 7А—Х и ЕД = {/;1 получоппую в конце формулу -г-г-у = "*
' ЛЬ" hH'HW
*) Рпссмятривосмый текст. помсшсппыИ но 2-м томе изданного Гульчем ппппопсиого «СоОра-
ii». пе (ii>iJi гплкогтыо рпзоСраи иадятелсм. Гульч тшаннл «тот тенст инвесшому исмеииому мате-
математику Впльперу (аьтор •'грории двтгркинаитопо). и тот бг^гстро нашел решение, которое было поме-
помещено в приложениях к последнему C-му) тому нвдашш Панна.
522
КОММЕНТАРИИ
мы можем в наших обозначениях переписать так:
. h
-
что легко приводится к таду
X*
ж-
¦В задаче Архимеда ft=.l; тогда исследуемое уравнение принимает вид
Искомая кривая будет гиперболой с центром в Z л действительной полуосью ZB=~ ;
мнимая полуось будет h.
Задача п. 53 решается еще проще (рис. 6). Положим «заданную прямую» равной
^ ^^ р\ пусть, кроме того, ZH =ги НД—у.
р у, р
Мы имеем:
Ar-rR=/)-rA
или
Далее, ЕВЗ ^р. ji z, или АЕ2=р. Е Z.
Имс;см paiieiiCTua
AE2-i/!!=p.(EZ—г),
игГкоторых после иочлешюго вычи-
¦ишнм получаем:
—' илиестиоо уравнение параболы с
вершиной п точке 7. и осью ZE.
Чтп касается основной задачи
п. 54, то Киллер переделал вытпе-
' припеденпый чертеж следующим об-
1>ис. 8. разом (рис. 8).
Дан круг и п нем прямая ВГ =
— 2а; черк! заданную точку А требу-
требуется провести прямую ЛЕ так, чтобм отреаок ЕД равгшлен яадашюй прямой Нв—р.
Опустим из А на IJJ' периепдикулир АО=Л и положим отрезок ОГ — Ь. Ес:.чи О принять
за начало координат, то, если положить ОА=| и 2Д = ДА-—tj, будем иметь:
АД2—ОА2+ОЛ»,
то есть точка Z лежит на гиперболе
веришна KOTOjtoii пахидитсл в точке Н па расстолпии ОН —ОА = А.
Затем
или
мы получили уран цепне параболы, на которой находитсн точка Z.
Если начала координат пчять и точке О' — середине прямой ИГ — и положить
¦О'Д"=а:, то уравнение иараболм перепишется в виде
(а-\-х)(а — х)^=ру,
О СПКРАЛЯХ Г,23
ИЛИ
Это будет парабола, проходящая через концы заданной прямой В Г и имеющая всршипу
в точке К, лежащей на расстоянии
то буде р, рдщая р
точке К, лежащей на расстоянии
С/К-* .
Р
Если рассматривать только одну ветвь гиперболы, я именно проходящую черел точ-
точку Н, то поставленм.чп задача будет иметь дна решении, соответствующие дьум точкам
пересечения п.чятой no/niir гиперболы к упомянутой параболой.
Упреки Архимеду, что последний «не; совсем правильно писнользовался «телесной»
(то есть решаемой при иомощи конических сечений) задачей», представляют интерес только
в том отношении, что позволяют думать, что изложенной у ГЬппа решение действительно
принадлежит Архимеду.
[Б] В отом предложении Архимед подходит к формуле, определяющей сумму
квадратов чисел натурального ряда, или, n 6o.iee общем случае, сумму квадратов чисил,
составляющих арифметическую прогрессию, пазность которой равна ее парному члену.
Ес;.чи через а-, обоаначим общий член этий прогрессии, а через в число наятых чло-
bdb, то устапаилкцаютоо Лрхилн>д(>м соотношение п солремеппнй формулировке могчет
-быть выршкепо так:
(п-5-1)в»=2 2. а\ (-( 2 „|-в1 V „.),
откуда для г.умми квадратов получпется фпрмула
з v «?=(«•;- i)eb-s-ei 2 в|.
Интчфесгго отмстить, что правило суммцропании квадратов чисел натурального ряда было
известно сопремешшиам Архимеда*)! пи и л ош: ним математинам эиохи Селевкидоп (см. текст
Луврского муж-я АО (M&'t, ony5.'iiiic<iiiaiiiu>iii Ыейгебиуаром в 1-м томе «Malhemalische
KoilscbrifLtexU:». И своей книге «Архимед» С. Я. Лурье дал красивый геометрический
вывод соответствующей формулы).
Слодстпие из предложении X устанавливает следующие основные неравенства,
необходимые Архимеду п дпльпейшем ияложонии:
3 (*?+*!+... fl~i) < »< < 3 ("Г+й2+. • • +О.
где числа й„ а»,..., ап составляют арифметическую прогрессию, разность которой рав-
равняется ее наименьшему члену.
[61 В текста Гейберга доказательство рассматриваемого предложения содержит
лишнее, по существу, условие: предложите, справедливое для всякой арифметической
прогрессии, доказывается и предположении, что ее разпостг. рлтшп ciuiiMeiibUieMy члену;
так построен и чертпк, ('инровождаюншй ато доказательг/nio. Чтобы выяснить, и какой
степени можно считать зто условие принадлежащим Архимеду, разберем детальнее ход
доказательств.
В современной форме предложение XI мы выразили бы так:
Дана арифметический прогрессия
«1. "а. аз «n-i. "п.
ли, гл. ат,, нэ, jj%, лм, из.
Обозначим через d абсолютную величину разности прогрессии. Архимед строит
})ЯД ПрЛМЫ.К
ОД= ОГЧ-ГД=й-|-ов=в1,
=--ХЬ| IK =
КОММЕНТАРИИ
Прямая NT=rS— JNS=6t?=ral— «„ или я iiameii формулировке а^-ап. Есл»
предположить, что d — ап, то выражение в,—ап^а„— (п—l)d. Так как Архимед поль-
пользуется бо.чее общим выражением, то ясно, что он пе предполагал равенства между наи-
наименьшим числом и разностью.
Требуется доказать справедливость неравенств
(n-i)nj а* (»-1)Д?
Архимед говорит: «От каждой из линий, одинакото возвышающихся одна над
другой, отделим часть, равную разности» — это будут прямые ФВ=ХД = Ч'^=Йв^
=S?'K. = CjM = NS, рапные наименьшему члену. Если в тексте Гсйбсрга вместо слов»
«разности» (та wtegox?) читать «наименьшей» (гаг^а/юта). то мы получим более общее
хкфпжсипе теоремы, нглмпочккщви предположение о равенстве an^d; в тшшигй таепеав
иеринтаи, что в первоначальном тексте Архимода именно так И было.
Архимед начинает с очевидного равенства
iz? jn-Daj
( 7
Для того чтобы убедиться в справедливости теоремы, нужно доказать, что
где
Имеем:
=(« -1) «i+ [<*Ч- ¦ ¦ • + (и— IJ <*21 т в ("
Сравпиьаси составные части всех этих, выражений:
(и—1) а&=(« -1) й?, »(в — 1) а&,
п (п—1) <ton > (и—1J dan >{«—1) (и—2) tffln,
... -у (п—IJ d* >^j^ (n— l)
(на осповании следствии из предложения X), откуда и вытекает справедливость искомых
[7] «13 треугольнике обе стороны будут более чем вдеое Солъше прямой, делящей
пополам угол между ними», так как сулма обеих сторон больше удвоенной медианы,
а медиана больше биссектрисы; действительно, нетрудно доказать, что последняя иро-
ходит между медиане»! и писотой.
[8] К предложении XVI ричь идет о касательной к спирали, mibnni слогами, рас-
рассматриваются задачи, аналогичные тем; из которых развилось солремпшое дифферся-
циильное исчисление. ГТ])ежде всего Архимед устанавливает, что угол касательной к спи-
спирали с радиусом-вектором точки касании будет тупым, если провести касательную в сто-
сторону возрастания радиуса-вектора.
Пусть (рис. 9) прима л ДТ будет касательной к спирали ДА. Требуется показать,
что прямая АД, соединяющая напало А спирали с тичкой Д касания, образует с Д1 тупой
угол. Через точку А проводим окружность радиусом АД=(> с центром в А; так как со-
стсфоны поарас-тапия радиуса вектора спираль лежит вне этой окружности, то угол AI
не может быть острим, так как он больше «угла полуокругкпости». Лод «углом полу-
полуокружности» греческие математики понимали криволинейный зтгол> виртина которого
лежала на окружности, а сторонами били диаметр п дуга окружности. Этот угол отли-
отличается от прямого и прямолинейного угла AAI на криполиньймый угол IAP между касц-
тсльпой и дугой АР. Эти криволинейные углы ивляютсн «нсархимедопыми» величинами^
то есть такими, к которым неприложима аксиома Архимеда (повторяя любую малую вели-
о спиралях 525
чину слагаемым нроизполыю большое число раз, можло получить лсличипу, превышаю-
превышающую любуй» заданную); поэтому из того, что угол АД1 большо угла полуокружности,
еще не следует, что об будет обязательно тупым, и Архимед доказывает, что од не ыижет
бить прямым.
Действительно, если бы он был прямым, то касательная Д1 к спирнли была бы одно-
одновременно касательной и к кругу ВАГ. В таком случае на основании предложения V можно
Рис. !>.
провести такую секущую AZ, чтобы ее отрезок PZ был бесконечно малым по отношению
к дуге АР (мы сказали бы бесконечно малым второго порядка, если считать дугу ДР бес-
бесконечно малой первого порядка). В действительности же душ ДР и прямая 1'А меньшая,
чем ZP, являются бесконечно малыми одного порядка, т»к как их отношение, равное
отношению скоростей движения но окружности и по лращакццейся прямой, будет конеч-
конечной величиной.. Таким образом, гипотеза, что угол АЛ1 прямой, исключается.
В связи с этим интересно рапобрать ход мыслей Архимода при доказательстве пред-
предложении V.
Для того чтобы убедиться в том, что отрезок PZ является бесконечно малым по отпо-
шегттао к дуге ЛР, нужно показать, что отпошепне ZP : ДР может быть сделанным меньше
любого заданного числи.
Через цитр Л проводим прянгую АГН параллельно касательной Д1 и продолжаем
хорду ДР до пересечения с этой прямой в точке Н. Тогда
ZP ZP АР
""' др М'" РЙ '
Но ЛР есть постоянная величина, равная радиусу окружности, длина же РН может быть
сделала сколь угодно большой; таким образам, отношение ZP : ДР может быть сделано
меньше ксякои наперед заданной по личины.
[9] Предложения XVIII — XX являются центральными во всей книге, так как они
решают задачу о построении прямой, равной длине заданной окружности. Тик как длина
окружности пропорциональна радиусу этой последней (что, конечно, было хорошо известно
Архимеду), то пени, что задача определения длины любой окружности будет решена,
с:<:ли только удастся онредолшч, длину одной какой-нибудь окружности. Эту задачу как
рая и решает предложение XVIII, которое гласит: длина окружности в ПК первого круга
рал па отрезку ZA, который касатслышл 0Z к спирали, проведенная и точке в —конце
«первой» прямой, — отс-иаог от прямой АЛ, шфнепдикудярлой к «первой прямой» ЛЭ
(рис. 10).
Чтобы понять ocnoniryio идею доказательства этой теоремы, обратим нлимание на
криполишгйпыи треугольник, o6pa;iniiiiiiiH.iu дугой спирали ВХ,, дугой первого кру-
круга ЮР, и отрезком радиуса-ипктора Р,Х,; так как отрезок Р,Х, и дуга Ы\ проходятся
и одинаковое прими (условие рай номерпостя состатщых дттжепии — прямолинейного
по Art и пр;ицс![шя по вР,), то их отношение будет рлшштьср! dtiiohiciiiiio пути А0, прой-
пройденного точкой но рндиусу-псктору п тсчея|ип одного оборота, ко всей длине окружности
КНв, описанной точной в нп нрсын ndpuoro оборота. Если время прохождения дуги вР(
и прямой PtX[ ми будем бсс)груд(;.ч;,но уменьшать, то в пределе получим прямоугольный
треугольпик, гипотепуаа которого нойдот по касательной ©N,, один иа катетоп пойдет
и» iiepiiciiJtirFty.'uipy к в А, а другой станет параллельным 8А; так как этот предельный
треугольник будет подобен треугольнику A0Z, то мы
А в Х1Р1 Лв
оир. КПв "~ 6Pi ~~ AZ
526
КОММЕНТАРИИ
откуда
о и р у ясность КII в = AZ.
Нот в адм аокяючается. основная идея доказать!ъства Архимеда; рассмотрим его-
детальнее.
Пели двигаться по ширили в сторону вращении и заменить криволинейный тре-
треугольник JipiiMOJiiuiciiinjM, то получит»! треугольник t)JJiN|; посмотрим, как будет
изменяться отлошеши; его стороп iS|Pi: Р,©. В исходном положении, когда треугольник
был бесконечно малым, ато отношение равнялось отношению полетилы длины хор-
хорды Н0 к длине перпендикуляра, опущенного ид точки А на ату хорду; по мерс удале-
удаления Pt от в отношение ИД*! : Pj©, как нетрудно видеть, будет увеличиваться; нот почему
Л,
Рис. 10.
п формулировке вспомогательного предложения VII говорится: отношение N[P, к ©Р,
должно бить больше тога, которое нолошша заданной в круги иримон 011 имеет к пер-
перпендикуляру, опущенному на нее и» центра.
Если двигаться п сторону, обратную вращении!, то отрезок K|Pj обратятся п NBP2,
отренск в!Ч| перейдет в 0N.», а дуга 9Р, аамеиитси хордой Р2в, которая станет теперь
гипотенузой. При движении, от в к 11 отношение Р.ЛМ2 *. КЗв будет уменьшаться; пачаль-
ная его пелнчина в точке 0 равнялась тангенсу угла 0ZA, то есть тому же самому
отношению, что и выше; нот почему в предложении. V11I гоооритпп, что отношение P2N«
к N,0 или к отрезку касательной 0Z должно быть меньше отношения половины хорды
©Н к перпендикуляру, опущенному па нео из центра.
Таким образом, хотя окончательное доказателыупю Архимеда статично (оио изло-
изложено в обычной форме приведения: к абсурду), идея переменности составляет подоплеку
всех его рассуждении.
Окончательная форма докадатедмггни Архимеда, такают. 1) Пусть длина окруж-
окружности (обозначим ее через С) меньше примой AZ; возьмем прямую АА,, которая меньше
AZ, но больше С; тогда отношение А0 : АЛ, будет больше предельно»!, так что можно
провести такую прямую AN1!, чтобы имела место пропорции
ИЛИ
NtP,: А0=0Г, : AAL < «Р. : С.
. Затем, вспомипан, что A0=APlt «присоединением» получаем:
А0 ^ С
AN,: А© < (С+0?!): С—А Х± : Ав (предложение XV),
О СПИРАЛЯХ
527
что приводит к нелепому ЛТ1ВОДУ ANj^AX,.
2) JTycrr. длина окружности С больше AZ. Поэьмсм прямую АЛ.,, которая больше AZ,
но меньше С; тогда отношении Лв : АЛ» будет меньше придельного; следовательно, на
основании предложении V111 можно провеет такую прямую ЛГ1 (]шс. 17. стр. 247),.
чтобы имела место пропорции:
Рв.\в: ЛРг=П0 : ЛЛ2 > 6РЙ : С.
Тогда, «переворачивая», получаем:
APS- Ра\8 . - ВКР, АХ«
А1'
АО
откуда ANa<|AXji, что нелепо. W
Таким образом, длин» окружности С должна Сыть pnium AZ.
110] П своих комментариях к переводу трактата «О спиралях» немецкий исследо-
литсль Члалина предлагает следующую реконструкцию Гпио»иг.н идей Архимеда при»
открытии теоремы, рассматриваемой в И] едложенни XXIV.
Предположим (рис. 11), что ш> оси абсцисс мы отклгадмппем угол w поворота радиуса-
вектора сэткрмлн, « по оси ординат — соответствующие величины радиуса-вектора г.
Тан как длина г пропорциональна углу ф пово-
поворота, то iiauuciiMocTi, между г и q; вырагкаеггея г
примой линией О Г. Пусть ОА—2л лредстаплиет
уго.ч, соответг.тпующий первому полному обороту,
а АГ=О1 — так называемую «первую прямую»— В
радгтуе-поктор, соотвстстпуплцмй иначипию <j; =2я.
Разобьем ОА-— 2it ни п равных частей Лф и на
соответствующих радиусах »-|,гя,..., г„ построим
примоуго.1ышки, как показано ни чертпке. ]Сгли
мы будем вргпцмть вск> эту фигуру нокруг ()А
как оси, то прямоугольник ОАПГ образует ци-
цилиндр, ii треугольник ОА]'--конус. Обьеы зтого
конуса состаиляет одну треть объема всего ци- q
липдра, равного OA-ji-Ar2i=2n-n-of. Каждый
из прямоугольничков при пращешш образует
цилиндрик, объем которого рапияетсл пгг-Дф. Ути
цилиндрнЕчи соответствуют прупшым ceitTopaAf,
из которых составляются вписанная и опнеан-
нап около спирали фигуры. Площадь каждого из зтих евкторол"рииниется —¦ >-2-Дср и,
следовательно, п 2я раз меньше соотистствуютего цилиндрика. Таким образом, пло-
площадь i'j, ограниченная спиралью п течение; первого оборота, будет равна сумме
г
r<
г,
rf
г
^/
Г'
¦?
Рис. 11.
в этом и заключайте» идея, лежащая в основании рассматриваемого предложения.
ИЗМЕРЕНИЕ КРУГА
В дошедшем до лас виде это сочинение состоит из трех теорем, пероая из которых
определяет площадь круга как произведение полунериметра на радиус, третья дает отно-
отношение между длиной окружности и диаметром, .наконец, вторая, которую следовало бы
•поместить после третьей, даст .величину площади круга и вндс ее отношения к квадрату
диаметра. Именно в таком виде око существовало в VI веке и. а., как «окадиваст еохра-
luiiiimiucH комментарий Ептокия, по не может быть сомнений л том, что нервопачалыю
»то сочинение имело значительно большие размеры. На это указыиают сохранившиеся
цитаты у Диофанта и Герона*), наконец, тот фант, что IIaim цитирует псе иеряоо предло-
предложение, то есть половину имеющейся у пас книги, для того «чтобы не обращаться и сочи-
сочинению Архимеда из-за одной оюй теоремы». За то Ясс самое говорят и чисто внутренние
характеристики рассматриваемого сочинения: в new отсутствует доказательство такой
¦важной тсореми, как постаикство отношения длины, окружнштта к диаметру; шжоиец,
•второе предложение помещено неудачно: оно оггределкшю должно стоять после третьего.
Относительно времени написания «Измерении круга» можно с полной достоверпо-
<;тыо утверждать только то, что оно было написано до «ilсаммита». Ясна свизь итого про-
н.тодешия с трактатом «О спиралях», предложение XVIII которого даст геометрическое
построение длины окружности некоторого радиуса; об :>т«й связи говорил и биограф Архи-
Архимеда Гераклмд. В комментарии Ептокия к «Измерению круга» мы читаем:
«Эта камаи книга, как говорит Геракдпд в «Жиаисоиисашт Архимеда», необхо-
необходима для житейской лраитяки, так как она ыокавыпаст, что окру/кшх'ть втрое больше
диаметра, причем получающийся избыток будет меньше седьмой части диаметра, но более
десяти семьдесят первых чается его. Это, говорит он, дано лишь приблизительно; при
помощи же некоторых спиралей Архимед дашел прямую, которая совершенно точно рав-
равняется окружности зада иного круга».
С трактатом а спиралях «Измерение круга» имеет то общее, что форма применения
метода истощении яв:шстс» одинаковой с вгло.нт.эоъашшй ti последних, посланиях к Дпса-
-фею, а именно еО спиралях» и «О коноидах». Это позволяет утверждать, что «Измерение
круги» по всяком случае написано поело «Шара, к цилиндра», в котором метод ие.тслцекия
имеет более раннюю форму. Наконец, «Измерение лруга» ренко отличается от
чисто геометрических сочинений Архимеда споим вычислительным характером; рапным
¦образом в пользу более позднего написания «Измерения круга» говорит его снизь с «UcaM-
митом» и занятиями Архимеда астрономией, которые, по ьрей пидвмости, относятся
К иолднейнн'му периоду деятельности Архимеда (Титу Ливию, оиисъшающему смерть
Архимеда, последний известен только кик астроном). Сохранившиеся у Герона фрагменты
книг «О ««правильных поверхностях и телах* и «О призмах и. цюиидрах» позволяют
думать, что мотрлческяо иссл едопалии Архимеда ле ограничивались одним то-чкко «Изме-
«Измерением круга».
[1] Перное и второе предложения «Измерения круга» касаготси аадячи о квадратуре
круга, iiirreuecoTtamnL'H в течение долгого времени математиков лсех ирелгея и народов.
Возможны два пида постановки этой задачи.
Во-первых, можно отыскивать кпадрат, пяощйдь которого равняется площади дан-
данного круга; так ставилась смугветствующая задача и. в египетской матемглики, где цдо-
щад!. круга считалась репной квадрату, стороны которого рл и пились s/ft диаметра круга.
Ro-вторых, можно было определять длину окружности круга яадннмого радиуса
и затем уже определить нлоиладь круга, исходя из длины его окружности; так ставилась
задача в навилолскои математике, где отношение длины окружности к диаметру — наше
число л — принималось рнштым 3.
О греческой .математике задача о квадратуре круга встала по пторой половине
V века до п. э., notafe того как удалось дяя веяной прямолинейном фигуры найти квадрат,
•) Си. стр, 270 книг*.
ИЗМЕРЕНИЕ КРУГА 529
ИЛОЩОДЬ КОТОрИГО раПИЯ.ТаСЬ ПЛОЩАДИ ЭТОЙ фигуры. СлС'ДУИНЦИЫ 1Ш1Г0М, (.'CTCCTHCHUO,
or.r.riii постановка задачи о нахождении кмндрмта, площадь которого ржшялась бы пли-
щадгс :!пдл]|ного крута. Этой :ia;(;i'icii шннмилмгь Анаксагор, Лмтифом и Гип.нокрит Хиос-
Хиосский. О репттоняя Анаксагора ним ничего не пшшгтыо, но решении Антифона и Гиппократа
оснащены и тексте, приведенном и;шистпым коммилтатором Аристотеля Симилпкпем
и его lioMWiiTHpiiMx к «Фи.чики». Этот ti:i«:t ныссп о-чсии. нинемш! значение для всей исто-
|)ии греческой матсмитишг; так кап он не потея еще и арсенал сошяских нг.торикои мате-
математики, то ми нришдом «го ядесь как пиобяодммып докуымкт для оевмпепия дипрхнме-
Лоисгнш истории: ни дичи о кнадратури круга *).
«11:i многих, отысиимакшич решении аадачи t) кпадратури прут (она заключалась
и tow, чтобы построить кнадрат, pajmuii данному кругу), и Лптифоп, и Гиппократ счи-
Tii.'iii, что utiuriu реншпло, но оба одинаково ошибались. При :>том, как мм упндим ниже,
ошибка .Антифона не подлежит геометрическому разбору, так как он пи исходи.'! и а прин-
н,|||нш геолстритт, ошибку же. Гиппократа следует ри.'шбрать геометрически, поскольку
он остаиалг'п несший принципам геомитрли. Нсщь нужно раабирить только то рассужде-
рассуждения, и которых соблюдаются (imm'iipH-iiriiiiiibH' ирмпцктгы научного ыс<тодм и леи же upu-
иодят к пенорным иаключемипм; рассуждшиш sue, уничтожающие и отбрйшвающие
it сторону :)TiT принципы, ритору не подлежат.
Лнт;тфо«, начертил круг, иши'пл и него ггсиоторуш площадь, огр.-щиче/шую много-
угольной фигурой n:i чт-.'ia тех, которис мыумс"! ннисынать, ii;ui[i[:m(-[i niurciiiiirwii киад-
рат. Затем он делил пополам каждую сторону ккадрата и от г.егчшшм нронодмл иод щммыыи
yr.iann линии к окружности, которые, конечно, дышл и пополам соответетнукдцие с:ст-
м(Ч1чы кругл. Потом полученные точки псрсссчсшш с окружностью он соединял прямыми
г, концами линий, составляющих киадрат, таи что iior.ho проведения :>тмх прямых получа-
получались чотыри треуголт.никм, и ис:и шшюшнй» фигура обращалась ч тюг.ьыиуголышк.
С.:и:луя тому жо методу, он патин делил пополам каждую ии сторон иосьыиуголышка,
от i-fJLH'iinif к окружности иронолил под uj)flM[.iMii углами липни и точки, л которых иропс-
Д1Ч1Г1ЫС Л1.'ри(!1тд11куляры доходили до окружности, соединял ирлмммн с концами ра;ь
деленных crnpoir, обращая таким оорлигш лиисанпую ФИГУ1>У л пгестпнднитиугшп.пик-
Затем, следуя тсм жп immlim рассуждениям, он снопа Д1г.:кт.гг гтороиы шшеалного шестиад-
¦(атгтугольиика, иронодил (о^днииющпп прямые и таким обратим снопа удппинал число
гтороп iiiMirairuoro Miioi'oyi-o.'ii.iiiiKij. Tin; on дг.гтл псе ujxrMt! до тех noj>, пока не истощи-
истощилась пел площадь, заключенная нмз'трлт круга; он предполагал, что п результате в itpyr
будет пттсаЕТ ггекоторый многоупи ик, стороггы которого, лследстши; их малосит, сов-
совпадут с окружностью круги. Для вс-нкого <ко Miioroy]-().!i.никл мк[ можем1 построить ра«-
Mi.ii'i ему киадрат, как мы ;щаем u:i «Начал». Такипт обра:кш, ii])(.-j;uo,:Fiiru>i, что i юл угон-
угоним ii мткн'оугольиик [Piinoii lipyry, n nni'Tpomiriin 1,-иадр<1Т, paiiiii.iii :>тому многоугольнику,
мы том самым сможем: построить и ккадраг, paiinr.iji заданному кругу.
Ото :)а>>Л1очсл^с, очевидно, нротилоречич1 геометрическим нриш^шам, но, однако,
Александр **) irn прав, когда говорит, что ото происходит потому, что геометр предпола-
предполагает, что круг касается, прямой и олнои точке, п Антифон :>то отисргает, ведь геометр ш;
irpixmi предиопагагт лто, а дока:!мнает u noci.Moii книге ***). «Тучик; было бы скапать, что
п гчомптрии имеете.» окнокное ucuicimpniw, утнерждашшое о ненопмоноюгтн совпадения
нрншон <¦¦ 0|.])уЖ11»сть1(),'нбс> ипешняи прямая пмиет с кругом только одну общую точку,
а инутренняя только дне. но ни Hibi(№, и касание имеет миуго только и одной to'WC. Таким
образом, рассекая иге вртея площадь, аагиночающукк^я между ирнмеш и окру ясностью
круга, он шгкогди не истенцит :>ту площадь и но достигнет окружности круга, хотя Пи
деление площади продолжалось до бесконечнос-ти. Если бы ом мог достичь постамсчмгоп
цели, то был бы уничтожен геочетрическии принцип, утпкржлающнн, что нро^транстнен-
iif>ie шми'лгрп.! янляютск .'irJifflUMK до бесконечности. Эндсм ****) так и гоцорит, что имтгно
р.)тот принцип и отпорI'iie'rcii Антифоном **«**}.
Однако квадрнтури круга при помощи сигжмггпп, по мнению Ллек:санД[1а, заслужи-
заслуживает и Г1гометричес:г;ого разбора. Иод 1%падрату]х>1'1 при помощи сегментов он подразуме-
*) Тсксг пится но кггиге: С. Л. Drctsciiiici <1 к г. l>ie Geometric unri die C'rcomclci' vnr
fJfiS. lAiifitftc. 1K7Q. CTfj. LDC» —121 -
**) Александр Лфродиаский — iisneCTiii.iii воммлщлтоп Ллистнтслн {ucpjiiiR шицлшпл jll ш:-
к.1 п. п.).
***) В Ц9йAтв1пшы1псто в третьей книге («1Тачдла». тп, 10).
*••*) Ученик Лрист1ТЯЛ1т. автор «Истории геометрии».
• ••*•) ц смн8и г. цсш^имсм Лтгтифонп (и-чиестпый софист пторой иолопмны V пека до н. э.) juiitp-
рехнш xjciioMniiTh. идею Лпаксягора. то>т<о яяиишнпшггося кипдрнтурой В[)угк. о тпк пн^'паеммх i»-
мойочерпх. Анякснгор нродпиднгнл. что нпждям сколь угодно малая часть данного тела ни сшюй
сущности тождественFra с отим телом; таи, любая чисть мяса все равно истгштсн мясом, ksik Вымяля
яти 'меть пи была. Эта идеп. сопсршоггис пепрпшшьпин с точки яроник физики, янлнотся uuojjiit
[ifiiiiiiijl'iiFiifOli мчтемнтически — оиоль угодно милак часть окружности явс-тавм Вупрг окружиог.илп.
а не upFiMoti линией, и не точкой. Весьма пилмпжио иолтиму что я жгп теории гомойолггр аародилясь
имегшг) на ьгатематичеекой почье в противовес атомистам, точку цренин ноторых рнлдглнл и Апгифии.
отрицншпий возмодавтеть бссконичного делении тел. ...
>•'' Архингл
53и
КОММЕНТАРИИ
вист изобретенную Гипиократом Хитч-.ким квадратуру при помощи луночек, так как
«улочка есть некоторый сегмент круга. Доказательство этой квадратуры заключается
В следующем.
Пусть, говорит он, на примет АИ описан полукруг АВГ (рис. 1);
разделим ЛВ пополам в Д и из Л под сгрямым углом к АВ проведем ДГ,
а из полученной точки Г — соединяющую прямую ГА; последняя будет
стороной квадрата, вписанного в тот круг,
половиной которого нплметен АВГ. Затем
на Л Г опишем полукруг АЕГ. Так как
квадрат на АВ равняется квадрату на АГ
пм1мгтс с квадратом на ГВ —другой стороне
квадрата, вписанного в полукруг {ибо АВ
будет гипотенузой прямоугольного треу-
треугольника), и отношение кпадрцтом «а диа-
диаметрах [»шно отношению описанных на
них кругов и полукругов (как доказано
н XII книги «Начал»), то полукруг АГВ будет вдвое больше полукруга
АЕГ. Но полукруг ЛГВ вдвое больше и квадранта АГД; значит, этот
квадрант тоже будет равен полукругу ЛЕГ. Отпимем общий сегмент,
заключающийся между стиролом квадрата и дугой АГ; тогда остаю-
остающаяся луночка АЕГ будет раина треугольнику ЛГА, а последний
некоторому квадрату. Докапавши таким образом возможность квад-
квадратуры луночки, он на основании вышеизложенного пытается следую
щим образом получить и квадратуру круга.
Пусть дана некоторая прямая А В и на пей описан полукруг (рис.2);
возьмем прямую ГА, вдвое большую АВ, построим на ней полукруг
и вшшшм и иого стороны ГЕ, J*]Z и 7Л правильного шестиугольника. На
ятих сторонах опишем полукруги РПК, K0Z и ZKA; тогда каждый из
полукругов, построенных
на сторонах шестиуголь-
шестиугольника, будет равен полу-
полукругу ла ЛВ, тан как Л В
равна стороне шестиуголь-
шестиугольника (действительно, диа-
диаметр вдвое больше радиуса,
а стороны шестиугольника
равны радиусам, и ГА
вдвое больше ЛВ). Таким
образом, все четыре, полу-
полукруга равны между собой и ьсе четыре, нзятмс имеете, и четыре раза
больше полукруга ЛВ. Но полукруг на ГА тежо в четыре раза болынг
полукруга па АВ, ибо ГД вдвое больше ЛВ, и, елсдопательно, квадрат
па ГА будет и четыре раза больше кнадрата на АВ, а как квадратм ни
диаметрах, так относятся друг к другу и описанные на них круги и по-
полукруги. Итак, квадрат на ГА в четыре раза больше кнадрата на АВ.
и полукруг на ГД будет ранок четырем полукругами полукругу на А В
и трем полукругам на сторонах шестиугольника. От полукруга на ГА
и полукругов на сторонах нЕестиугольника отнимем общие сегменты,
заключающиеся между сторонами шестиугольника и дугами полукруга
ГА; тогда остающиеся луночки ГНЕ, E6Z, ZKA вместе с полукругом
АВ будут равны трапеции TEZA; если от этой трапеции отнять разни-
разницу, то есть площадь, равную трем луночкам (таи как доказано, что лу-
луночка равняется некоторой прямолинейной фигуре), то и остатке полу-
Рис. 2.
д;',|
чится площадь, равнан полукругу на АВ; полученную в результате
прямолинейную фигуру удваиваем и, удвоив, квадрнруом, то есть
строим ранный cii квадрат; атот кнадрнтбудет равен кругу, построешю-
му на диаметре АН, и, таким образом, ккадрнтурн круга окажется
выполненной.
Хотя изложенный способ и остроумен, но тем но менее полученное
заключение яиляетсл ложным, поскольку II качостие общего положения
¦ принято такое, которое но является в общем, случае доказанным. Дей-
Действительно, доказан» возможность квадрированпя не всякой луночки,
но только той, которая построена на стороне вписанного в круг квадра-
квадрата, а паши луночки достроены на сторонах вписанного и круг правиль-
правильного шестиугольника; поэтому доказательство возможности квадрату-
квадратуры круга при лом ищи луночек непригодно ипр пидержинает испытания,
т«к пак оно содержит ложное заключение. Действительно, оно пред-
предполагает, что нахождение квадратуры -чулочки на стороне квадрата
дает возможность ныполнения и квадратуры круга, как будто на такие
лупочки можно было бы разложить всякий круг, и затем, взяв равный
луночке киадрат столько раз, ни сколько луночек разлагается круг,
полагают, что квадрат, равный всем этим луночкам, имеете взятым,
будет ранен и кругу. При :ггом дплае.тси ошибочное предположение
о возможности различения «а луночки любого круга, И дейстнитмь-
кости жз лип состаилепии из луночек круга между линиями луночек
всегда остается некоторая площадь, ограниченная с обеих сторон кри-
кривыми линиями, которая но является ни луночкой, пл квадрируемой
площадью, так что тч будет кпадрнрушьшм и любом «руг, и усилии
получить подобным образом, квадратуру не могут уиенчаться уцлехцм.
И каждому, иоста[ИШ1.Ш!лгу задачу о вьшолнегпга квадратуры круга прл
помскци луночек, нет ыадойпости разделять круг на луночки; если бы
:лч> дажо и было возможно, то и тогда непьян было бы при помощи
луночеи (жвадрировать круг, ибо не доказана позмсленость 7свадрату-
ри неккой луночки. И не разделяя круг на луночки, можно было бы
orfi скнадрировать, если бы оказалось нозможным найти кнадратуру
луночек, построенных на стороне вписанного в круг правильного
шестиугольника, а не только на стороне киадрата. В этом именно
и заключается причина ложности заключения: после нахождения квад-
квадратуры лупочки только на сторонетенядрата доказательство ведется так,
как будто стали кнцлрируеммми иго какие угодно луночки, шг которые
можно разделить круг.
Как говорит Александр, нокитормг полагают, что t?c.-in Г>ы и области
чисел удалось найти такое число, которое было С>ы и киадратньш
и циклическим, то и » области прострапственньтх величин можно был«
бм выполнить квадратуру круга. Как он говорит, каадратиьгм числом
является равноравпоо (ошакс-; ino;) число, н цикличестлгми нязнали
¦inivia, составленный из ряда последовательных нечетных чисел, на
пример, единицы, трех, пяти,-семи, дивят». Если наптн кнадритноечисло,
которое одновременно било бы и циклическим, как, например. Ж>
(оно является квадратным, так кик получается от умножения 0 ил
самого себя, п циклическим, так как образуется и результате сложения
нечетных чисел 1, Я, 5, 7, 9, 11), то, по их мнению, станет пайдештон и
' квадратура круги. Однако доказательство ;>того, как гопорит Александр,
получается не на оснопаиии геометрических принципов, а на основа-
основании арифметических, ибо то, что такое-то число является квадратным,
» такое ¦-- циклическим, относится к области арифметических принципов:
:vi*
532 КОММЕНТАРИИ
К :iTMii слонам Александра следует добавить, что первоначально
арифметики начинали циклическими не те числа, которые получались
и результате сложения последовательных нечетных чисел, а те, квад-
квадраты которых оканчивались на тц яке самые числа. С этой точки ярения
¦ циклическим числом будет 2Г>, так как пятью пить равно 2Ъ, a 3(i, но не
четыре, довить или шестнадцать, хотя последние и получаются в резуль-
результате сложения последовательных нечетных чисел; такие числа будут
только квадратными, таи как квадратные числа возникают путем иосле-
дгшахслмшго прибавления почетных чисел. И может быть перимй,
шшдмшн такое понятие, сказал не то, что циклическими называются
пси числа, возникшие в результате последовательного прибавления
нечетных чисел, а только то, что при таком последовательном прибав-
прибавлении нечетных могут получиться и циклические, но что это бывает не
нсегда; действительно, циклическим числом будет 125, кактюлучинтееся
ид умножения о на 25, латим 216, как 0X30, хотя ити числа и не почу-
¦lnu>mr н результате сложении носледоиатйльиых нечетных чисел, «ели,
конечно, ил считать, что ати числа яьляютсм не циклическими, но сфе-
ричоскими, получинншмися циклически из плоских циклических чисел.
Нужно, однако, отметить и то, что псякий, нашедший число, нвляв-
щр.еси одновременно и циклическим, и сферическим, никоим образом не
имел, мрака думать, что он том самым а в области пространственных
келичин отыскал квадратуру круга, хотя возможно, что человеку,
обнаружиинтму среди чисел такое, которое одновременно является
к циклическим, и квадратным, ирингло в голову поискать квадратуру
круга и в области пространственных величин.
Наш наставник Аммонии*) говорил, что, по-видимому, нот тткакой
необходимости и том, чтобы результаты, обнаруженные но отношению
к числам, были справедливы и по отношению к геометрическим величи-
величинам. Прямая и окружность являются совершенно разнородными, и нет
ничего удивительного, по его стонам, в том, что не удается пайти пря-
молиноипой фигуры, ранной кругу, как :>то и обнаруживается я отпо-
ciri'ivir.no углов; ведь ни для угла полукруга**), пи для его дополне-
дополнения до прямого угла (так называемого рогооиризного угла) нельзя
найти иикакпго прямолинейного угла, который Г»ыл бы им равен. Воз-
Возможно, говори.:! он, что именно вследствие итого до сих нор и не уда-
удалось найти ту теорему, которую искали такие, знаменитые люди и даже
сам Лрхимэд. Яжеотиочал пясти пни ку, что если квадрнруется луночка,
iu>cT[»miniati па стороне квадрата (ибо :jtо получается вне всяких сомне-
intii), и луночка, состамленияя из дуг, им:н;т одинаковую природу
с кругом, то что же можзт препятствовать тому, чтобы и сам круг тоже
оказался киадрируеымм. Ведь если считать, что наличие рогов уничто-
уничтожает подобие луночки кругу, то тем более не может быть никакая луноч-
луночка одного рода с прямолинейной фигурой; а имютс к тем луночка па
стороне киадрата вполне определенно квадрируетси. тогда пак пи угол
полукруга, ни рогообразный угол м.ккду прямой и окружностью, не
только но являются одного рода с примолшшиггсгми углами, но ire мо-
могут быть сравниваемы даже между собой. ;
Я не думаю, что все выннч-ка.чашгое было бы достаточным для того,
чтоПы отказаться от поисков квадратуры круга. К комментариях
*) Аммоний, сии Термин, ллсксапдрпеи, fir.iiiuutii учеником афинского iirnr.~i:<T<iiiiiioi Hpoit.iu
(автора изиестпмх комментярмсн к «Началам» iinftnujia). в 480 г. и. о. и учивший иоялпое в Алккслп-
дрии.
**) Так наныпаотсн кртюлиисйшлй угол wi:»icjiy диамг-трим и Дугпй «кругвиости и конке Отип>
кругл
js «Катогоршшв Ями.чих*) гокорит, что Аристотель может быть и не,
нашел квадратуры круга, погшфагорейцм ее нашли; на его слонам, ато
можно ьидеть на до канате льсти а пифагорейца Секста, иоспришшшего
метод по наследству с самого начала школы. Позднее, говорит он, квад-
квадратуру круга осуществили Архимед при помощи спиралiiiiой линии,
Нчкомод**) при помощи так лалынашой i; кадр атрием, Аполлонии при
помощи некоторой кривом, которую он пазы нал «сестрой улитки»
и которая ТОЖДССТНСШ1Н нииомедонои, затем Карп при помощи некото-
некоторой кривой, которую он называет возникшей из двойного движения;
многие другие, говорит оп, получали разными способами решении этой
задачи, но ни один из них по получи.:! построений, отличных от моха-
НИЧССКИХ.
Каи » уже сказал, Александр па основании пил еженных соображе-
соображений, полагает, что он обнаружил ложность заключении, при ломощи
которого Гиппократ, найдя квадратуру луночки, построенной только
на стороне квадрата, применяет ев так, как будто она была бы докаяапа
и д.чл луночки ла стороне шестиугольника. Однако Ендрм в «Истории
геометрии» гопорит, что Гшпгпкрат докалил ншшожность квадратуры
не только л у ночница сторож» к на драта, но, если можно так им раниться,
и иообще. Впдь у всякой лупочки шп'Шиия дуга млн раина полуокруж-
полуокружности, или больше ее, или меньше, и если Гиппократ квадрирует и лу-
луночку с дугой, равном полуокружности, и луночки с дугами большими
и меньшими полуокружности, то, по-видимому, задачу можно считать
решенной и вообще- Поэтому и и:«Л(]Жу дословно все то, что говорит
Евд::м, добаилин .ними, небольшие гго»снопня со ссылками на «Начала»
Евклида, необходимые вследствие конспективного стили Ендсма,
который по дранному обычаю сокращенно излагал доказательства.
Нот что он говорит во второй книге «Истории геометрии»***).
«.Квадратуры луночек, считавшихся ранее замечательными фигура-
фигурами вследствие своего родства с кругом, были описаны впервые Гиппокра-
Гиппократом- ы, по-видимому, были изложены, (толпе удовлетворительно**'**);
поэтому мы, касаясь отого предмета, будем излагать более подробно.
Начавши эти. исследования, Гиппократ, установил в качестве пер-
первого положения, необходимого для обпаювпния доказательства, следую-
следующее: подобные сегменты кругов имеют друг к другу такое же отношение,
как квадраты их оснований. Это он доказал после того, как было уста-
установлено, что круги имеют между собой то же отношение, что и квад-
квадраты диаметров. Но иторой раз ято было докааапо Евклидом в двенад-
двенадцатой книг.} «Начал», где предложение было формулировано так: круги
относятся друг к другу, как киадраты на диаметрах. Действительно,
подобнее сегменты имеют друг к другу такое же отношение, unit и соот-
иетстпукнцие круги, ибо подобными сегментами нвлшотся такие, какие
составляют одну и ту же часть круга; так, например, полукруг подобен
полукругу, и третья часть круга —третьей части. Поэтому подобные
*) Яыгишх сирийский !ге< плагошш IV пенл п. а., лнннмапшмйся пифагорейской математикой
ц написавший биографию Лнфагпра.
**) Ягтпших ошибается." :шш> читать Дмюптрвт.
•••) Подлинный niKCTl'Inдойн моняю выделить из обшпго триста Пныттлшшп вследствие! ocoflcu-
ностей математического лОоапачечгип оиохи Аристотеля. Сп ирсмки Мькдида гломятрические пВрявы
стали обозиачатьсп, как и в инстипщее щгкмя: оточки А. прямая Л Не. но в апох-у Аристотеля писали
«точка, на которой Л Vn:T!.A) щшмпн. на которой ЛВо. Эта филологическая работа пперпые Была
выполнена французским ииприкгм матемптики Нолем Толнери; в втом издании мы пользуемся
нопейшрй fjoKoncTpyuuuctt О. Епкпсра. Текст Еилсиш «ыдслеи куренном, ио очоСспиостн матема-
математического пбозггнчснин у Квдема и переводе опущены.
**••) ках*. TQ'inu ё'ВД Bfl
534 КОММЕНТАРИИ
сегменты, вмещают и раины*; углы: у полукругов эти углы являются
прямыми, у. сегментов, больших полукруга, соответствующие углы
меньше.мряадого, причем на столько, на сколько рассматриваемый сег-
сегмент больше полукруга, у сегментов же меньших полукруга, больше
прямого на столько, на сколько сегмент меньше полукруга.
После того как это было доказано, Гиппократ начал с того, чти
показал, каким образом можно квадрировать луночку, у которой наруж-
наружной дугой является полуокружность; это он сделал, описав полукруг
около прямоугольного равнобедренного треугольника и построив на
основании круговой сегмент, подобный тем, которые отсекаются боковыми
сторонами. Это положение Евклид «зял в качестве 33-й теоремы третьей
книги, формулирован его так; «па данной примой построить круговой
сегмент, вмещающий угол, равный данному прямолинейному углу;
если на основании построить такой сегмент, чтобы он вмещал угол,
равный том углам, которые находятся в сегментах, отсекаемых боко-
боковыми сторонами, то этот сегмент будет подобен боковым, ибо подобные
сегмаитьг Квклид определил » тринадцатой книге*) как такие, которые
вмещают равные углы.
Так как сегмент, построенный на основании, равен обоим сегмен-
сегментам на других сторонах (ибо, согласно доказанному в предпоследней
теореме первой книги «Начал» Евклида, в прямоугольных треугольны
ках квадрат гипотенузы равен вместо взятым квадратам на сторонах,
заключающих примой угол, а отношение квадратов на основаниях
равно отношению подобных круговых сегментов),
и в качестве общей части добавлена гшщадъ тре-
треугольника, находящаяся над построенным на осно
вании сегментам, то получиешаяся луночка будет
равна взятому треугольнику; теперь луночку,
которая, согласно доказанному, равна треуголь
нику, уже можно стадрировать; действительно,
в одиннадцатой теореме второй книги «Начал»
Евклида показано, как строите» квадрат, равный
данной ирямоугольной фигуре. Таким образом.
Гиппократ л?.гпо нашел квадратуру луночки в пред-
предположении, что внешняя дуга последней есть по-
полуокружность.
И след за этим он предполагает, что внешняя
¦ Рис.. :\. дуга луночки, больше полуокружности, и строит
трапецию, у которой три стороны равны между
гобой, а квадрат наибольшего из параллельных оснований втрое
больше квадрата каждой из остальных (рис. 3); затея около этой тра
¦ пеции он описывает круг и строит па большей стороне сегмент, пи
¦ добный тем, которые отсекаются от круга тремя равными сторонами**)
То, что около этой трапеции можтт описать круг, ты докажешь так.
Разделив пополам углы трапеции на основании У-го предложения пер-
первой книги «Начал» и проводя диагонали (BE и ЕД), тьг найдешь, что,
¦ так как ВА раина АГ, а сторон* AR общая и углы равны, то... и т. д.***).
А что упомянутый сегмент больше полукруга, станет ясно, если
провести в трапеции диаметр (ВГ); так как он стягивает две сто
*> В действительности в третьей.
"*) ll:i рис. :i йтот c.ltmi-jit. oupainemmft выпуклостью кперху, опущен.
•*•) Точка Е пресечения биссектрис будет центром круга, так как AJS—КГ по построении'
и треугольники АНЕ и АГЕ равны, откуда КМ— КГ=ЛЕ — ЕД.
7
ИЗМГСРВНИЕ КРУГА
53ft
рони трапеции, то его квадрат необходимо будет более удвоенного квад-
квадрата стороны, оставшейся ни трех равных. Действительно, так как ВЛ
более АГ, то соединяющие их равные стороны ЛГ и 13А при продол-
продолжении встретятся в Z, ибо если ВА к ДГ равны и параллельны,и пря-
шт, сое^аияющис концы двух равных и параллельных прямых,
тоже ракнгл и параллельны, то А Г должна была бы быть раиной ВД.
что пенозможио. Если же ВА и Л Г встречаются u Z, то углы ZAI"
и ГАВ раинi.i двум прямым на оспинами и 1;.»-го предложения первой
книги Евклида. Угол ГАВ больше угла TAZ (как внешний угол тре-
треугольника по отношению к ннутршшему на осноиэшш 32-го предложе-
предложении первой кпиги); значит, квадрат на ВГ будет больше удвоенного
квадрата каждой из сторон ВА л А Г, а следовательно, и ГД. Значит,
квадрат наибольшей стороны трапеции необходимо должен, быть мень-
меньше вместе взятых- квадратов диаметра (ВГ) и той. стороны ип остав-
оставшихся, которая вместе с диаметром стягивает вышеупомянутую
наибольшую сторону, ибо вместе взятые квадраты на В Г и па ГА более
чем втрое больше квадрата на ГД, а кпадрат на ИД только ьтроо боль-
больше последнего. Следовательно, угол, опирающийся на большую сторону
трапеции, будет острым, и сегмент, в котором он находится, будет
больше полукруга; дуга же этого сяглжнта является внешней окруж
ностью луночки.
Квадратуру этой луночки Е-идемч насколько я могу судить, обошел;
«на, вероятно, была следующей:
Луношса вмзетс с сегмунтом, ипстроеяпым на большей стороне
трапеции, будит ришм трапеции вместо, с трелт сегментами, отсекае-
отсекаемыми тремя прямыми, рмиными ГД, ¦
и сегмент, построенный на большей
стороке трапеции, равен трем сег-
сегментам круга, отсекаемым тремя: рав-
равными сторонами, так как квадрат
большей стороны трапеции предпола-
предполагается: равным имосте взятым киад-
ратам трех этих сторон, и подобны»
сегменты относятся друг к другу
как кнадраты па основаниях; если
же от пакных отгшть пороипу, то
будут равны и остатки, м, следила-
тельно, луночка будет раина трапе-
трапеции. Кще короче ты найдешь :»то так.
Сегмент на большей стороне трапоции раьен трем сегментам, описанным
на рапных, сторонах, так как квадрат на перьой втрое больше квадрата
на каждой из последних; если к ним добавить площадь, заключающую-
заключающуюся мзжду тремя, ранными сторонами и дугой большого сегмента, то полу-
получится луночка, которая будет равна трапеции- Если мы сквадрируем
эту последнюю, так как мы ведь умеем киадрировать всякую прямо-
прямолинейную фигуру, то тем самым получится и квадратура луночки,
внешняя дуга которой больше полуокружности.
В том случае, когда эта дуга меньше полуокружности, Гиппократ
для построения такой луночки сделал следующее (рис. 4). Пусть будет
круг с диаметром АВ и центром К и линия ГД делит ВК пополам
и, под прямым углом; между ней и окружностью вставим EZ так, чтобы
0}ьа стремилась к В, и квадрат на EZ был в полтора раза больше квадрата
на радиусе. Прямую EfT проведем параллельно АВ и соединим К с Е и Z.
Рис. 4.
536 КОММЕНТАРИИ
Пусть последняя соединяющая при своем продолжении на Z встретится
в пипке 11 с прямой ЕН и опять соединим J.5 с Z и И. Тогда ясно, что
прямая Yi'/j при своем продолжении, пройдет через В, ибо EZ предпола-
предполагается «стремящейся» к В, и ВН будет равна ЕК. Возможно, что кто-
нибудь смог бы доказать это и покороче;, я же доказываю ото па оснопа-
нии предыдущего так.
Согласно предположению, АГ неросекает ВК помолам и нод иря-
MiiiM углом; :шачнт, на АГ будет находиться центр круга, которня мы
(шишом около трапеции (KK.BII) (иа основании ел оделчшя из первой
ToopeMiii третьей книги «Начал» Евклида). Так как Е11 параллельна KB
и их пересекла пряма» ГД, то последняя образует внутренние углы,
раннмц вмзетс двум ирнлшм (ня основании предложении 2!)-го первой
книги); но углы при Г прямые; значит, будут прямыми и углы
при Д. Про\о;\ищАН через цент]) прямая ГЛ, пересекающая под
прямым углом ЕН, разделит и ос пополам ли основании третьего пред-
предложения третьей книги «Начал». Теперь, так как АН равна ДЕ, сторона
AZ общая и углы при Д прямым, то и основание ZTT будет равно основа-
основанию ZE. Также и BZ равна ZK., вследствие того, что 13 Г равна ГК, a VL
общая и углы при Г прямы:»; теперь, так как дно стороны HZ, ZB раины
соответственно двум сторонам ZE, KZ и вертикалын.ю углы (при Z)
ранни, то основании Ш? будет равно основанию Klv.
Теперь около треугольника EZ1I опишем окружность, согмвпты.
которой па EZ и ZH будут подобны сегментам на ER, KB, Ш1. Если
все это так, то я упшрждаю, что около трапеции ЕКВН можно описать
круг. Действительно, около треугольника KEJI можно описать круг,
ибо в плтом нр(!длон4е1ги|| четверток книги «Начал» показывается, как
описмиаотсм круг око.ю данного треугольника. Тшшрь, если я докажу,
что прямая, соедишпощан центр этого круга с точкой К, равна линин,
соединяющей атот центр с точкой В, то описываемый кругонои сегмент,
очевидно, пройдет и чоро» ЕКН, и через J3, и полученный сегмент круга
обнимет трапецию и такой же сегмент будет, заключать и треуголь-
треугольник EZII. Пусть цинтр этого круга Л — и проиедем соединяющие пря-
прямые ЛК, ЛИ, ЛК, Л13; так как треугольник ЕЛИ равнобедренный (ибо
равны прямые, проведенные из центра), то будут раины и углы
ЛНЕ и ЛЕН при основании .вследствие 5-го предложения первой книги
Евклида. Также и угол ВНЕ равен углу КЕН, так как по доказанному
ВН равна КЕ: значит, и щ>сь угол НИЛ будет ран«п всему углуКЕЛ.
Но КГ? равна [ill; следовательно, к ос ко на и не КЛ равно ЛИ; значит,
ЛН (>>!<^угр<11>н» рлдпусу Л К.; таким пот образом и описывается сегмвпт *).
Если все ото так. то получившаяся луночка, внешняя дуга которой
ЕКВН, будет равна прямолинейной фигуре, составленной из трех
треугольников ZBIT, 7.RK, ZKE. Действительно, находящиеся внутри
луночки сегменты, отрезаемые от прямолинейной фигуры (EKLUTZ)
прямыми KZ и Z1I, равны отрезаемым прямыми ЕК, К И, НИ сегментам,
находящимся вне рассматриваемой прямолинейной фигуры, так как
каждый внутренний сегмент в полтора раза больше внешнего, ибо.
согласно предположению, квадрат на EZ в полтора раза больше радиу-
радиуса, то есть прямых ЕК, KB, ВН, поскольку доказано, что последний
*) Пимилпкпй aa5i.i.i пешлзить, что иослюсииые на V.7. и ЕК сегменты будут подобны др>-|%
Другу.
Угол К/К лдгше больше угла ZBK. Если И есть икитр круга KZH. то к треугольнике MKZ
угол MZE«=OO°—ЕГ5К; следовательно, центральный угол EMZ вдиос Сольпт угля ZKK. который
опирпстси па дугу кк круга игисанного около трапеции ЕКЬН; ито и доказывает подобие сегмен-
сегмента Е/, круга E/.JI и сегмента ЕК круга ЕКМ1.
ИЗМЕРЕНИЕ КРУГА 537
прямая ПИ тоже ранни КК. Если же кьадрат па каждой из EZ, EII
в полтора рана (юльше каждой n;i упомянутых трех прямых, и отношение
киадратов на мримых раин» отиошеишо соответствующих ссгментон, то,
сугедонатсльно, два внутренних сегмента будут равны трем внешним.
Так кик эта луночка составляется из трех внешних сегментов и части
прямолинейной фигуры, лежащей вне двух внутренних сааментов,
а прямолинейная фиеура с этими двумя сегментами равна луночке без
трех внешних сегментов, и два первых сегмента равны трем последним,
то луночка будет равна упомянутой прямолинейной фигуре.
А что эта луночка имеет внешнюю дугу, меньшую полуокружности,
он доказывает, опираясь на то, что угол (ЕК11), находящийся во
внешнем сегменте, будет тупим,, так как в 3-м гтредлоншшш третьей
книги «Начал» Евклида доказало, что угол в сегменте, ысмъпшм полу-
полукруга, будет болыие прямого. А что угол (ЕКЕ1) тупой, он доказывает
тан: поскольку квадрат на прямой EZ в полтора раза больше квадрата
на радиусе и квадрат на прямой KB более чем вдвое болыие квадрата на
прямой BZ (ибо, как я локажу, угол при Z будет больше (прямого) и ПК
раина К.К), то ясш>, что КК больше 13Z, и НЕ ь первой стошпни более
удвоенной BZ. Таким образом, квадрат на КК будет, следовательно, более
чем вдвое болыие KZ велндствип подобия треугольников ВЕК и BKZ.
Действительно, как ЕВ к 1Ж, так будет и ЕК к ZK, и кпндрат на ЕК
бол ос чрм вдвое бо.:гыпс киадратя ни KZ *). Но квадрат на прямой EZ
в полтора раза больше квадрата на ЕК; следовательно, квадрат, на EZ
будет больше вместе елятых квадратов на ЕК и KZ**), как ото имеет
место, например, д-чя чисел В, \, 2.
Если бы кпадрат на КК был ровно н;цию больше квадрата на
KZ и ивадрат на ZE в полтора раза больше кнадрата на ЕК, то квад-
квадрат па EZ равнялся бы вместе взятым квадратам на ЕК и KZ. Посзсоль-
ку же ккндрят ка КК. бо.:юе ^гем »д»ос болтнпе квадрата па KZ. то кнад-
рат па EZ будет больше вмнето взятых квадратов на ЕК и KZ. Следо-
Следовательно, угол при К будет тупым и, значит., сегмент, в котором on
находится, будет меньше полукруга***).
Таким образом Гиппократ нашел квадратуру для всякой луночки,
будет, ли ее внешняя дуга равна, больше или меньше полуокружности,
а но только для построенной u<i стороне киадрата как иоисствовал
Александр.
*) HK2-'IJB-KZ.:i'KZ2.
*•) 13Za .-ЕКв-':-КЯ*.
***) Ввиду того, ччо «иолпкыгияе Cumu.thkhr скорее затемпнют дело, полезно иалотить сущ-
сущность всего доканптгльстпа отделыго.
Гиппократ хочет шжяяа-и.. что угол ЕКН йудпт тупым; рпн зтнго uy>i«uo y6rrniTi.cn. что инвд-
раг стороны KZ, лежащей нузотнп него, будет больше суммы квадратои диух ^иугнк сигрпн ЕК и
К'/.. МЫ 1!!М[!!Ш:
KZ2- | KJC«;
остивтеи док»аить, что - Г.Кг..-К/.а. В т|)су|'о.1ь;пиа: IIK.Z угол HZK Судет тупой, потому что смеж-
смежный с ним угол ЕХК it 'гргуголышш: EZK шглпе.тся острым, поскольку сш меньше угла KKZ: сдедо-
иатслыю.
KB
откуда
и. слсдоьатслыш
КОММЕНТАРИИ
Вместе с тем следующим образом он сквадрироеал сраау и круг,
и луночку (рис. 5). Пусть около центра К описаны два круга и во второй
степени диаметр внешнего будет в шесть раз больше диаметра внутрен-
внутреннего; вписав во внутренний круг шестиугольник ABFAEZ, продолжим
соединяющие центр (с, вершинами шестиугольника) прямые КА, KB,
КГ до окружности внешнего круга и соединим прямыми II и в, 0 и I,
II и 1; очевидно, что Ив и 01 будут также сторонами шестиугольника,
шгисаипого ц больший круг. На прямой HI опишем сегмент, подобный
тому, который отсекается прямой 116. Так как во второй степени
прямая III необходимо будет в три раза больше прямой 011 — стороны
шестиугольника (ибо примни, стягивающая
дне стороны шестиугольника и вместе с
третьем стороной заключающая примой
угол — тот, который содержится, и полукру-
полукруге —, будет по второй стонепи равняться
диаметру, а диаметр но второй степени в
четыре раза больше раиной радиусу стороны
шестиугольника, так как прямые вдвое
большие линейно будут вчетверо большими
во второй стеиепи) и. эта сторона 611 во
второй степени й шесть раз больше прямой
А В, то ясно, что описанный на НI сегмент ока-
г жется равным вместе взятым сегментам, от
Рис. о. нимаемым от внешнего круга прямыми Ив и
01, с добавлением тех, которые отнимают-
отнимаются всеми сторонами шестиугольника от внутреннего круга, ибо подоб-
подобные круговые сегменты относятся друг к другу, как квадраты ни
основаниях, так как подобпые круги относятся между собой, как квад-
квадраты на диаметрах; таким образом, «с:ш HI во второй степени втрое
больше II в н ПВло второй степени равна 01, и каждой из этих прямых
во второй степени равны вместе взятые все шесть сторон внутреннего
шестиугольника, ибо, согласно предположению, диаметр внешнего
круга во второй степени и шесть раз больше диаметра внутреннего,
л отношение диаметров равно отношению радиусов, а радиус равен
стороне шестиугольника, как гласит следствие из предпоследней теоре-
теоремы четвертой книги «Начал» Еиклмда, и, наконец, отношение сегментов
рацио отношению квадратов на основаниях. Таким образом* луночка
II61 от отмеченного теми же буквами треугольника будет разниться
на те сегменты, которые отнимаются от внутреннего круга сторонами
упомянутого шестиугольника. Действительно, сегмент на III равнял-
равнялся сегментам, построенным на Нв и в! вместе с теми сегментами.,
которые отнимаются сторонами шестиугольника; значит, сегменты Нв
и в! будут меньше сегмента III на площадь сегментов, отнимаемых
шестиугольником. Если к обоим частям в качестве общей прибавить
часть треугольника, находящуюся выше сегмента HI, то получится,
что из нее и сегмента на III составится треугольник, а из нее же и сег-
сегментов Н6> и в! составится луночка. Значит, луночка будет меньше
треугольника TTG) на площадь отнимаемых шестиугольником сегмен-
сегментов. Значит, луночка и отнимаемые шестиугольником сегменты будут
равны, треугольнику. И после добавления общего шестиугольника упомяну-
упомянутый треугольник вместе с шестиугольником будут равны этой назван-
названной луночке вместе с внутренним кругом, ибо треугольник равнялся
луночке вместе с отнимаемым шестиугольником сегментами внутреннего
ИЗМ1СРКНИЕ КРУГА
круга. Таким образом, гели чшмомсно сквадрироватъ упомянутые прямо-
прямолинейные фигуры, то можно, значит, спвадрироешпь и круг вмесюл-
с луночкой.
Так йот нужно поминать, что достижения Гишшкрата Хиосского
знает лучше Евдом, который бил ближе к нему но времени, (чем
Александр), и яиляется уишижш Аристотеля. Что ;ке касается
киадратуры круга при помощи сегментов, которую Аристотель отвергает
как ниш Сочную, или >к« кнадратуры при помощи лупочик, как он
говорит не вполне ясно, то Александр вполне нраиильно оспаривает
ее, если только она та же самая, что и при помощи луночек».
Мы привели полностью весь текст Симплшшя, поскольку он характеризует поло-
положение греческой геометрии и в V вг-кп до п. ;>., и л V веке и. э., и iffloxy ей упадка. Что
касается исел^допшиш Гиппократа, то пель.чя яе лризнать ил очень остроумными, хоти,
как показывает тс;кст Нпдема, Гиппократ допустил сшибку, считая, что квадратура круга
м«и«;г считаться найденной, если изтшетиы способы квадратуры трех луночек, внешние
дуги которых рапиы, больше или меньше полуокружности. Эти мпемше, по-видимому,
ранде-чил и Епдем (снова №тг tqosxov E'6<)gav»noo'f)'t}i)vaL) и с еще большей стшшныо вероят-
вероятности сам Симплшшй, по в оиоху Аристотеля ошибочность пшшифатпвспон кпадратуры
была уже общепризнанной, что, кигк^ию, хороню было известно и Александру Лфродия-
«кому. Однако принадлежащую лое.чидпиму критику Гиппократ;! иелъил квн.шфицнре)-
и«т[> иначе!, ч?!М как ociionaiiiiyxi на грубой ошибке: стоит только сравнить наши рисун-
рисунки - it 3, а также обратить влпмаште на роль шестиугольника и самой последний кпадра-
туре Гиппократа, чт(и1ы сказать, чги Ллелсапдр псе перепутал. Заштшя глупость отяо-
ситегп.ми квадратных и циклических 4ik:i:.:i ирицндлия;ит, конечно, неонкфагирейцам
начала пашей ври, замечание Бидима, что Гиппократ «нериьгй» описал их, никазьшает
нсно, что, вопреки Ямвлнху, первые иифагоршцы квадратурой круга но запималис!..
Точно так жи верх комизма иредстаиляет весь разговор Лммимия с Симпликксм.
Что задача о квадратуре круга не [-.питалась решенном, покаиьтваст то, что новое
еи решение дал Динострат. брат Мшноеын и учелпк Кпдокса Киидского, испо.чьяуи кри-
кривую, которую незадолго до него изобрел есфист Гшшии Элидскшг, но всей видимости,
для раздел они и угла ва три части. Эта криван — пернаи u j'pe4ec,K0fl математике, полу-
ченпия как траектория некоторого движения, носит имя квадратрисы Дшюстрата. При-
Приводим касающийся отой кривой текст «Математического собралпя» Паппа (книга IV,
30- 34), япляющийсн нашим иегрионгтичником для рассматривисмой теории.
«30. Для осущоствлешш киадратуры круга Дииоктрат, Никомед
и другие более поздние математики пользуются некоторой привой,
получившей имя от этого ер основного своистш; п ^
она называется квадратригом и имеет следую- '
iti.ee происхождение.
Нозг»ме.м квадрат ЛВГД (рис. ()) и uoicjiyr A
как центра ошшк-м дугу окружности НЕД;
пусть щшмам АН диия«!Тсн так, что точка
В описывяет окружность ШЛА, а точка А
остается ниподпижной; однонремйнно другай
прямая 13Г, оставаясь всегда параллельной АД,
щфеиещаетел Tais, что не кот-ц 13 псе время
двниа!т<:я но ВЛ, причем » одно и то же время
прими» А13, нращаясь равномерно, проходит
у1ол ВАЛ (иными слонами, точка В — дугу
ВЕЛ), а прямая В Г, тоже двигаясь раииомпр-
но, нрпходнт расстояние БА (то есть точка В — прямую ВА). Тогда
получится., что л концо движения обе прямые А В и ВГ олнуиремевио
сокиадут с ЛД. При атом движении прямые ВГ н ВЛ будут перипскать
друг друга в точке, коаора;! все времн перемещается вместе с ними и опи-
описывает никоторую, заключающуюся между прямыми ЛВ, АД и дугой
ВЕЛ, линию BZH, которая будет выпуклой в одну сторону; эта линия
оказывается очень полезной для нахождения квадрата, рапного данному
540
КОММЕНТАРИИ
кругу. Ошшииоо сиойгтно мой кришш заключается в следующем:
если пронести какую-нибудь прямую AZE, то вся дуга ВЕЛ будет так
же относиться к дуге ЕЛ, как прямая АВ к Z0; ото вытекает из самого
способа получения рассматриваемой кривой.
31. Однако эта липни не удовлетворяет Спора,— по моему мнению,
правильно — но следующим причиним. Во-первых, эта линия уже
предполагает осущестклеинон ту самую цнль, для достижения которой
является предназначенном. Действительно, кап можпо заставить дви-
двигаться из В две точки тик, чтобы в равное время точка, движущаяся но
прямой, пришла бы и А, а точка, движущаяся по окружности — в Д,
если не знать сначала отношения прямой АВ к дуге ВЕД; ведь именно
. в атом отношении должны необходимо находиться скорости обоих этих
движении. liaTiwi «ели мы дли одновременного сонертепин. указанных
диижшнш пользуемся клкпми-то неопределенными скорпстшш, то
требуемый результат .может быть достигнут только случайно; а это разве
не бессмысленно? Далее невозможно определить ту точиу кршюй, кото-
которая необхо/тми для ьыпешнчнш квадратуры круг», а именно точку ее
нерп-имения <¦¦ прямой АЛ. Игр вышеупомянутое можно представить себе
ла прилагаемом чертеже; ьчнд.а прямые ЛИ и 13Г будут при своем
дппжешш приближаться к конечному положению, то они совпадут
с прямой ЛД и никоим образом не дадут точки взаимного пересечения;
они перестанут пересекаться еще до достижения совпадения с АД,
а ведь ато пересечение должно быть концом рассматриваемой линии,
то есть точкой, где она встречается с прямой АД. Можно, конечно,
сказать, что наша линия продолжается до примой АЛ, как мы предпола-
предполагаем это относительно прямых линий, но ато не будет следовать из
основных предположении; да и тогда точку Н можно будет взять, уже
зная предварительно отношение длин дуги и прямой. Если же это
отношение не дино, то нн следует, доверия авторитету изобретших се,
пользоваться итон линией, скорее относящейся к механике, чем к гео-
геометрии. Покажем предварительно, как при помощи этой линии решает-
решается иос-таклсипая задача.
Пусть дан киадрат АНГЛ и описанная около центра Г дуга окруж-
окружности В]?Д (рис. 7); если образована, как сказано иынн», кнащштрнса
BUG, то можно показать, что дуга ЛЕН так относится к прямой. В Г,
как ЪГ к прямой. Гв. Действительно, если это не так, то упомянутое
отношение будет paimo отноничшн) ВГ или к большей чем Гв прямой,
ила же R меньшей.
круга
541
Пусть сначала, если ло:;можно, вто отношение будит равно отно-
отношению 13Г к большей, чем ГЫ, прямил ГК. Около центра Г опишем
АУ1'У ZHK, пересекающую кпндритрису и точке Л, опустим перпенди-
перпендикуляр МЛ, it соединяющую I'll продолжим до Е (рис. 8). Теперь, так как
дуга ДЕН так относится к jipujuuii В Г, как В Г, или ГД, к ГК, а отноше-
отношение ГД к ГК. ришю отношению луг НКЛ и Z.I.IK (так кик отношение
дииметроп крутой .равно отношению соответствующих дуг), то ясно,
что дуга ZI1K будет равна прямой БГ. И таи как вследствие основ-
основною епойотии кривой отношение дуг ВЕД л ЕЛ равно отношению пря-
прямых НГ и МЛ, то, значит, отношение дугп ZHK к дуге ПК равно отно-
отношению примы.* В Г л МЛ. Но докапано, что дуга Z1I.K раина прмой ВГ;
апачит, и дуга ПК будет раина прямой 11Л,
что полепи. Следонателыш, отношение дуги
ВЕД и прямой ВГ не будет равно отиопш-
нию ВГ к прямой, бош.пшн чнм 1'fc).
152. Я утлерждаю тенп|л., что оло по бу-
будет punno и отношению В Г к прямая, мень-
меньшой чем ГМ. Действительно, пусть вто отип-
теине будет, если вонможно, равно отпо-
inemtio Sil1 к некотором примой КГ; около
центра Г опишем дугу '/МК, перпоидику-
/шпно к ГД нроподем КМ, пересекающую
кмадратрису в 11 и соидиляющую ГЦ hjio-
долгим до Е (рис. 9). Тогда, подобно и ми-
дыдущвму, докажем, что дуга /МК будит
равна прямой В Г, и отпошети1- дуги 11КД
к ИЛ, или дуг Z.V1K к МК равно отношению прлмых ВГ и ПК.
M:i итого ясно, что дуга МК будет раина нрллтм КII, что нелепо.
Значит, отнитепне дуги ВКД к npnuoii В Г по будет равно отношению
ВГ к прямо», M[>fjj,jucij чем V&. Т1о доказано, что оно не может быть
равно и отношению В.Г и прямой, большей, чем ГН: счодоиитолыго, око
будет равно отшмпенито ВГ к самой прямой Гв.
Точно так juc ясно, что пели мы тюньмом тргтыо п]1опг)рцииналь-
муюдля прямых ЙГи ГВ, то полученная прямая будит раина дут В БД,
н уч|упи;рет1ам — окружности нешо круга. Если то. ннидена прямая,
равная окружности круга, то ясно, что легко построить и квадрат,
ранный атому самому кругу; как Лрхимед доказал, прямоугольник
М1!»{ду npjiMuii. piuiiioii периметру круга, и радиусом будит пдпое больше
этого круга».
i (
mtrujuxiia тлпгисмаи Нипшм лалыняшая история л-яадратрнгы: пчмичкпо,
чти мм им«ш Н1!1фк[л>шмуи1 ."шиит 1>а;шития, котораи от Дииострата чсрги Ктслида педпт
if Лрхммгдо. Ирсдостппля!»! слово самому Маппу.
«33. Таконн нроиг.хождеиле нышпупомянутоП кривой, которая, как
. мы сказали, более относится к ыехапиш1; геометрически постанлсишую
аадачу можно решить ('..педуюкцнм 1)Пра;я)м при iiomiimui «гоометрияеглсих
мест па нонорхноетн»*).
Пусть будет дан положением киадрант АВГ круга. Лролсдсм (ия
центра) какую-нибудь прямую ВД и опустим на В Г перпендикуляр EZ,
которой'! имел б]л: заданноо отношение к ду'<ъ- ЛГ (р:ш:. 10); я. утво|)ждню,
что точкя К будет «алндиться ла пужлон ним линии.
*) Нал этим именем иипсстим приипяттсжитпс Клклпду дне ндш'н.
КОММЕНТАРИИ
Представим себе, что на дуге ДГ построена поверхность прямого
цилиндра и на пой кадаиа положением описанная винтовая линии
ГН0; пусть также дана сторона 6Л цилиндра. В точках В, Е восставим
(ранные 6Д) перпендикуляры К1 и ВЛ к плоскости круга, а.через (-)
проведем параллельную ВД прямую ВЛ. Поскольку но свойству винто-
винтовой линии отношение прямой KI к дуге ДГ является дашшм, и отноше
нис EZ к А.Г тоже дано, то будет известно и отношение EZ к Е1." Пря-
Прямые EZ и EI задапы положением; значит, задана положением и соеди-
соединяющая ZJ. Она же лерпондику-
лирла к ИГ; следовательно, прямая Zi
II точка I будут находиться в плоско-
плоскости, секущей цилиндр, (проведенной
черо:» прямую ВГ), и на некоторой
линейчатой *) поверхности (так как-
прямая вЛ, перемещаясь по винтовой
линии в1ТГ и прямой АВ, тоже задан-
заданной положением, всегда остается парял-
аг лелыюи плоскости нижнего основания
цилиндра); следовательно, точка I. a
также и К тоже находятся на рассма-
рассматриваемом геометрнческом месте. Таким
образом, можно подучить общее реше
пие'задачи; если же отионншш; прямой KZ к дуге ДГ будет равно отно-
отношению В А к дуге АДГ, то получается вышеупомянутая квядратриса.
fr. 34. Поставленную задачу можно подобным же образом рошап.
и при помощи вннтолий .пинии (спирали)**), построенной па плоскости.
Пусть отношение прямой HZ к дуге ДГ будет одинаково с отношс
нием прямой ЛИ к дуге АДГ; пусть за то время, в течение которою
прямая АВ, «ращаясь «округ точки Л, пгпгсыиает дугу АЛ Г, некоторая
движущаяся по йен и выходящая из А
точка доходит ди I? в тот момент, когда
АВ занимает положение ВГ; эта точка. |,
гшиншт спираль ЛИВ (рис. 11). Таким
чбрааом, отношение ;*АВ к 131 f будет
равно, отношению дуги АД Г к ГД и по-
после перестановки отношение прямой: АВ
к дуге АДГ равно отношению ПН
к дуге ГД.
Но в том же отношении будет и
KZ к А Г; следовательно, ВИ будет
равна ZE. Восстании к плоскости перпендикуляр КН, рашшн ВИ;
следовательно, точка К будет на нонкрхности цилиндроида, построен-
построенного на спирали (ЛИВ). Но она также находится и на некоторой
конической поверхности (действительно, соединяющая ВК будет на
конической поверхности, образующей половину прямого угла с, плое
костью ЛИГ и проходящей через ладанную точку В); следовательно,
точка К находится на рассматриваемом геометрическом месте. Через К
проиодим прямую ЛК1 параллельно ВД и опускаем па плоскость нерш'-и
дикулярм ВЛ и El; следовательно, ЛК! будет находиться ва
U
*) В тсксто «шпбично
**) Hy>KIIO KHCTIj II НИЛу. ЧТО ||Л Г|ЮЧ|!ГК11 И
обоэпнчпются нлпчм словом гАг?
. И HIIIITilli;i>l
(II.J
ИЗМИРЕЩ1Е КРУГЛ 543
идальшш *) ионерхности (так как прямая ЛК1 перемещается и ло задав-
там лоложением прямой НА и также ло заданной положением кривой
линии, на которой находится К); следовательно, на той же поверхно-
поверхности окпжотся и точка I. Но она будет также находиться и па некоторой
плосногли (дейстнителыш, ZE раина El, так как оиа рнниа 13Н, и /1,
будучи перпендикулярна к ИГ, тюки задана положением); следователь-
следовательно, и точка 1 будит на рассматриваемой кривой, а значит, и Е. И ясш>,
что если угол АВ Г прямой, то получается вышеупомянутая къадратрисн».
К этому тиксту необходимо fделить несколько замечаний. И глаж; 3;i рассматри-
рассматривается линия, представляющая н игтоетлом смысле обобщение клэдратрисы (последняя
получается и частном случаи, к игла отношение прямой EZ к дуге ГД будет равно отно-
отношению прямой ЛИ к дуге ЛАГ); рассматршшгмие геометрическое место, описываемое
точкой I, продетаhjthct лшшо пересечения некоторой неподвижной, иронедсчпюй черев
прямую И Г, плоскости- с. линейчатой поверх iloi:t>>jo, образуемой дьнжечшем прямой,
скольнящей пи перпендикуляру ИЛ и mnrnmoii лишш Г8и остающейся все примя парал-
параллельной плоскости квадранта ЛВГ. Точка Е будет проекцией на плоскость А13Г точки I;
при движении последней точка Е опишет на плоскости квадранта ЛИГ некоторую линию,
которая и представляет обобщении кладратрисы. После/шин получается, иг.] и проходя-
проходящая 'чириз Л Г п.'юскшггь инклолока под углом и АЬ" к плоскости ЛВГ и шаг иимтолон
линии ГЬ в четыре jia.ia больмю радиуса ГЛВ.
В главе 34 рассматрынаоген другое иостропнис кпидратрисы, которая получается
пик проекция на плоскость ЛВГ лишти пересечения плоскости, лроксделной под углом
в 4"|° к плоскости ЛИГ, и линейчатом поверхности, пилучиишеися в рсяультато движения
прямой линии, uapa.uiivihnoii ЛВГ и скользящий но шГриендвкуляру ВЛ и Kpunoii дпоя-
кой кришоны, получагаюй и результате ггересечемия конической полерхности с осью ВЛ
к с образующими, иаклопеппыми под углом ^й" к плоскости ЛЕИ, и цилиндрической
ноперхности с образующими, парй.1ЛЕ>лмм>тмп ПЛ, построенной на Архимедовой спирал»,
прохолищой через точки AHR.
Кому принадлежит это остроумной обобщение киадратрисы? Папн упомгнает
о «гег>митрических местах на ironopxfiocTB», но пазыипн автора, но ил книги VTI «Мате-
«Математического собрания» (VJI, 3) мы уянием, что :>тим ттмечши ианыпил^о. дш; книги, irpn-
надленсашппе Евклиду, к которому, нерешию, и следует отнести построение, описантк-
н главе 'Л'Л; в тыком случае окапалось бы, что в ишуху Ньклида биптокйн лишш была уже
пяиестной. Ппстроснис главы .У| уже предполагает что-то вроди Лрхмк'допоя сштрали,
однако построение еоответстнугшдей. линии и довольно существенных чертях отличается
от Архимедова способа; если и это построении относится к доархимедоппкому периоду,
тогда reiioaiTC идей Архимеда, приведший его к решению задачи о квадратуре круга
При ПОМОЩИ (ТГИрпЛИ, CTailOliJSTCH СОНОриНПЛО KLffM-Vl.
Нам оста(!тся теперь пзнесить иси доводы pro п i-ontra OTnociiTcJM.fio иринаддиж-
ности Евклиду ofiuux построении, описанных п главах !!3 и 34. Сммым сгрмлпым доводом
является упоминании «геометрич(!ских мест на поверх ногти л (умолчмпие llaDiia of) Евкли-
Евклиде может объясняться тем, чти принадлежность Евклиду :miro сочинении Пыла (ifimeiriur
стной, так что Папп мог ограничиться упоминанием Евклида лишь в 011щ['М перечне
i-о'гшгеrrnii, согтиплялптих курс, высшей гиомитрии у греков); правда, термин лге-имитри-
ческих мест па ионгрхшктн» мог со временем сделаться назвали см геометрической дис-
дисциплины, вроде цитируемых Архимедом «конических сечений». Дале(! надо отметить
тесную ciniai. обоих построений с ивадрлтрисой; однако [1аличш;'Арх.]1мелоиой спирили
ко нтореш построении скорее п)Пйрит и пользу «Ипкомеда и других более полднях
математиков», упоминаемых Пцпппм п качало цитируемого отрывка (глалк 30). Таким
odpasoii, прЕпад.'н'Жиопч, ofioirx построений Кпклплу нельзя i-чнтать абсолютно доказан-
доказанной, хотя она и яилнетгя штлие пояможной.
Гели бы «l-'l:iMepenui! T>pyi-a» дошло ли нас полностью, то мы, вероятно, читали бы
н нем основную тгорому, утиорждакицуи», что дли ни окружнисти проиортщопальла диа-
диаметру (в «Началях» Евклида доказывается то.'м.ко, чти площади кругов относятся, как
ква драты диаметр0") ¦
В качестве восполнения mavti недостатки дагм отрывок из «Мат[;.матичесшIЧ) соб-
собрании» [liiiuiii (книга V, И---1.Ч), содержащий доканатсльство упстяпутом
«11... Окружности кругом относятся друг к другу, как диаметры.
Пусть будут два круга АН, ГЛ с диаметрами АН, ГЛ. Я утнерждаю,
*> Линейчатой.
комм интл ми и
что отношение окружмосты круга АВ л окружиостл круга ГД одина-
одинаково с отношением прямых АВ и ГД (рис. 12).
Так как круг ЛВ относится к кругу ГД,- как квадрат АВ к киндра-
ту ГЛ, и учетверенный круг АН равен прямоугольнику, построенному
на прямой АВ и окружности «нютиотстиуюмичч) круга, а учетверенный
круг ГД ранок прямоугольнику,
построенному на прямом ГД и
окружности круга ГА (это уже
доказано выше), то, елсдователь-
но, прямоугольник между АВ и
окружностью круга АВ относит-
относится к прямоугольнику между ГД
и' окружностью круга ГД, как
квадрат на А В к квадрату на ГД.
Рис. 12. После перестановки прямоуголь-
прямоугольник между ЛВ я окружностью АВ
к квадрату на ЛИ относится т«к же, как прямоугольник между ГЛ
и окружностью ГА к квадрату на ГЛ: следовательно, отношении окруж-
окружности круга ЛВк прямой ЛВ равно отношению окружности ГД к при-
примой ГД, и после перестановки окружность АВ относится к окружности
ГД так же, как Л В к ['А.
12. Это можно доказать и не нрилшням тиоримм, что прямоуголь-
прямоугольник между диаметром круга и его окружностью вчетиоро больше этого
круга. Действительно, у вписанных it круги или описанных около них
подобных многоугольников периметры относятся друг к другу, как
радиусы, так что и окружности круги» относите» друг к другу, как
диаметры.
Пусть будет опить круг ЛВГ г.шчпром Л и рлдиусом Д13; проводом
из Д какую-нибудь прямую ЛИ; тогда периметр круга ЛВГ к /iyi-е BZE
относится, как круг АЬГ и
сектору ВДЕ (риг. 1.3). •
Теперь, пели дуга I3ZE со-
соизмерима с периметром А13Г
круга, то, разделив периметр
АИГ круга па представляющие н\
общую .меру дуги, и сойди и и к
точки деления с центром Д пря-
прямыми, мы. получим совпадаю-
HHIO друг с другом секторы,
число которых будет puimo чи- l4i(. ,.,
слу общих мор в окружности,
и, счедонятольно, отношение
периметра АВГ круга к дуге BZE будет равно отношению .круга АВГ
к сектору ВДЕ. Если же окружность и не будет соизмеримой с ду-
roit В/Е, то все равно отношение круга ЛВГ к сектору ИЛЕ будет
р;ишо отиоиншию и«римотра АВГ к дуге HZK.
Пусть, если возможно, отношение круга АН Г к.сектору ВДВ будет
рапно отношению периметра АВГ к дуге liZ, которая сначала пусть
будет меньше душ -BE; возьмем какую-нибудь другую дугу ВН, кото-
ран била бы больше BZ, но .менее J3ZE, и однолромиптобыла соизмери-
соизмеримой с, периметром ЛВГ. как это делается в леммах сферики, и соединим
А с И. Тогда на основании итлпсияложвппого круг АН Г будет относить-
относиться к сектору 15АП, как периметр ЛВГ круга к дуге HZII. Не» периметр
ИЗМЕРЕНИЕ КРУГА 545
АВГ круга к дуге BZ11 имеет меньшее отношение, чем к дуге BZ, то
есть чем отношение круга АН Г к сектору БЛЕ; тогда круг АВГ
к сектору ВДН будет иметь меньшее отношение, чем к сектору ВДЕ, что
invioiio; следовательно, отношение круга АВГ к сектору ВДЁ не Судет
рашшться отпошопшо ого периметра АВГ к дуге BZ-, которая была бы
меныне дуги BZE.
Но я утверждаю, что оно не будет рапно отношению периметра АВГ
к дуге, большей чем BZK. Пусть, сечи иозможно, оно будет рашю отно-
икшню к дуго ВЕГ; точно так жо иозьмим какую-нибудь дугу BE0.
Которая была бы больше, дуги BZE, но меньше, чем ВЕГ, и одновремен-
одновременно была соизмеримой с периметром АВГ круга, и соединим Д с В. Теперь,
так пак снова отношение круга АВГ к сектору ВД0 pauiio отношении)
периметра ВАГ круга к дуге ВЕВ, а периметр АВГ к дуге BE0 имеет
большее отношение, чем к дуге ВЕГ, то есть чем отношение круга АВГ
к сектору ВДЕ, то, конечно, круг АВГ к сектору ВД0 будет иметь
большее отношение, чем к ссиггору JME, что нелепа; значит, ото-
шеиие круга АВГ к сектору ВДЕ не будет равно отношению его пери-
периметра АВГ к дуге, большей чем BZE.
Но уже доказано, что отто не
равно отношению и к меньшей чем
13ZE дуге; значит, круг ЛИГ отно-
относится к сектору ВДЕ, как его пери-
периметр АВГ к дуге BZE.
13. Подобные сегменты кругов
относятся друг к другу, как квад-
квадраты мх оснований, а их дуги отно-
относятся, как основания. р11С jg
Пусть АВГ и ДЕХ будут подоб-
подобные сегменты кругом. Я утверждай),
что сегмент АВГ относится к AEZ, как кладрат АГ к квадрату AZ,
дуга же АВГ относится к дуге AEZ, кик прямая АГ к AZ {рис. 15).
Дополним оба круга, козьмем их центры 11, в и соединим А с II,
11 с Г и Д с 0, 0 с Z. Теперь, так как сегменты АВГ и ДЕЯ подобны, то
угол при II ранен углу при 0, треугольник АН Г подобен A0Z и дуга
АВГ подобна AEZ. Следовательно, круг АВГ относится к сектору
АНГВ, как периметр круга АВГ к дуге АВГ, или как четыре прямых
угла к углу при II. Так же и круг AEZ к сектору A0ZE относится, как
. периметр круга AEZ к дуге AEZ, или как четыре прямых угла к углу
при (-). Но угол в равен углу II; значит, круг АВГ относится к секто-
сектору ЛНГВ, пак круг AEZ к сектору ДН/Е, и после моростамойки круг
АВГ относится к AEZ, как сектор АН Г И к сектору 40ZK. Но отно-
отношение одного круга к другому ранни отношению квадрата на АН
к киадриту нн Д0, то есть отношению треугольника АН Г к треуголь-
треугольнику A0Z; следонатолыш, отношение сектора АНГВ к сектору Д0/Е
равно отношению треугольника АН Г к треугольнику A0Z. Тогда
остающийся сегмент АВГ относится к сегменту AEZ, как треуголь-
треугольник А1.1.Г к треугольнику ABZ, то ость инк киадрат на АГ к квад-
квадрату иа AZ.
Теперь я утнерждаш. что дуга АВГ относится к дуге AEZ, как
АГ и AZ.
Действительно, после тох же самых построений получится, что
оттшнпше окружности круга АВГ к окружности круга AEZ paiuio
отношению дуги АВГ к AEZ. Но как окружности кругов друг к другу.
35 Архимед
KOMMEHT Л РИ И
так относятся и радиусы АН к Лв, или АГ к AZ; следовательно, дуга
АВГ относится к дуге AEZ, как АГ к А7,».
Возможно также, что в «Измерении круги» заключал им» предложения относительно
арошюиа и калинона, приводимые в «Кгшге лемм» и у Панна (кн. IV, 14—20).
|21 Задача о киадратуре круга была решена Архимедом дна рана: и первый: раз
он решил со геометрически при помощи Архимедовой спирали (см. трактат «О спиралях»,
предложение XVIII), о чем мы ужи говорили выше; теперь нам остается разобрать второе
ело решении, приведшей к определению числового значения отношения окружности к диа-
диаметру; ито решение ш составляет третье предложение рассматриваемой книги.
Ото предложение распадается на две части: в нерпой Архимед .гртз помощи онисан-
ш.1Х многоугольников находит нижний предел отношения окружности к диаметру, во
uTopoii при помощи вниеншшх многоугольников он ищет верхний предел того зке отно-
отношении.
В обопх случанх его исходная точка одни и та же: он рассматривает прямоугольный
треугольник, и котором один острый угол равняется 30" (рис. 3 текста); и этом треуголь-
треугольнике отношение большего катета ЕГ к меньшему FZ будет равняться \[Ъ. Для иедичины
YW Архимед дает следующие значении.:
265<v-5 1351
153 ^ ' ^ 780 •
Вопрос о том, каклм образом Архимед нашел эти значении, долгое время занимал
всех историков математики. Дошедший до нас комментарий Евтокия не даст никакого
ответа на интересующий нас вопрос: Евтокий просто ссылается на труды Птолемея, Тсопа
и Герона об и;ш.'кГченин квадратных корней, а сам только проверяет результаты Архимеда
ficnocpc,4CTBWHiLiM yMiKMKCiiF№M 11о.:!уче1шмх чисел.
В пастоящее время мы иаходимси в лучшем положении, чем Гейбсрг в эпоху выхода
п С1»ст 3-го тьма первого индания сочинений Арх1шеда A8S1), так как теперь* нандепа
считиишаяся в то лрсияи потерянной «А1етрика» 1'ерона. Вот n'i'<j говорится там об извле-
извлечении квадратного корня из 720 (кн. I, 8).
«Так как 720 не имеет рационального корня, то корень из пего
ми найдем с ничтожношмой разницей так: поскольку ближаштиш
к 720 кнндрат будет 729, имеющий корнем 27, то разделим 720 на 27;
получается 2E и две трети; прибавь 27; получится 52 и две трети. От
этого (иозьми) лолошшу; получится 20-| -^ | ¦— . Значит, корень из
720 оудет приблизительно 20 f-^- + -^-. Действительно, 20 , -т-\--т,
помноженное само на себя, днет 720^:, так что рн:шнца Судет состав-
составлять 36-ю долю единицы. Если бы мы захотели сделать разницу еще
меньшей 3C-й части, то вместо 729 возьмем только что найденное число
720 —. и, нродолаи то яге самое, найдем разницу, которая окажется
cJU
значительно меньше ^».
Исследования последних лет показывают, что атот метод, который можно иллюстри-
иллюстрировать формулой
где Ао — приближенное значение (Лд — имеет патшлоишюс происхождение. Винплоняяо
применяли его для нахождении приближенного значения }/ 2, а также для нахождения
гипотенузы по заданным катетам а и 6, из которых один а значительно больше другого.
Формула, которой они пользовались, была такова
у а* И,з = о,.|-?_;
она легко получается из предыдущей, если положить Ао ранним а
ИЗМЕРЕНИЕ КРУГА §47
Теперь мы мажем паюередствиггпо обратиться к самому сочинению Архимеда.
Каким образом были лолучепм приближенные значепвя у 3:
153 ^ * ^ 780 '
Само произведение Архимеда ие даст ответа на этот вопрос; попробуем отыстить ua
него сами. Разложим на ллюжнтшш знаменатели ооиих приближенных значений:
153 = 3.3-17 = 3.51,
780^22.3-5.13=3-5-52.
Если помножить на 5 числитель и знаменатель первой дроби, то мы будем иметь:
Выбор чисел 15 и ГJ=2-2С не случаен; депепштиимго,
13*^225, 26* = 076=3-22Г>-| 1=.'М5Ч-1-
Архимед подобрал два числа, обладающих тем свойством, что утроенный квад-
квадрат одного ия них только на единицу отличаете» от киидрата другого числа, так что
дробь j-з могла бы быть взята в качестве приближенного значения у 3. Между прочим,
пориык ия.приведенных нами фрагментов к «Шмерешпо крутя» (стр. 270) прямо указывает,
что ато приближенное значинпе j/з было .Архимеду bjucctho. Носло этого дело стано- •
вится ясным: для того чтобы получить йолее точное значение у', Архимед полагает:
о_26»-1
6 TV"
следоиителт.ьш,
Стоящий и числителе корень легко изллскастси но иаинлоискому принилу:
Есчи умножить :тамсца?Ы1ь ла 15, то мы лолучисм одлоиа архшиедоиых
иых значений УЗ. Нетрудно нидоть, что полупенное по иавилолскому иранилу нрибли-
jKeimoe значение корня бущя всегда ипачишем с избытком. Архимед это, конечно, знал.
Чтобы получить нужное ему втнрои приближение с недоститколг, он второй рил приме-
применяет тот н«: прием — дмшт iio^'ifiojiutiMOC иыражонне на уже найденный корень, иными
словами, иольяуетсл средним гармимичискнм. Мы имеем:
Так пак нужно по-чучить приближение с недостатком, то можно улсличить вычитав-
мую дробь, для чего уменьшаем зламспатель, замелив ^ единицей. Таким образом, най-
найденный с недостатком корепь будет:
Ук;|:{<ишую операцию можно вообще имранить формулой
>а± -
2« ± 1 "
д-м привило имеется в арабской математике.
За*-
548 КОММЕНТАРИИ
Xitsc. указывает иа арабского мителптгкл X века,- ил,-Кар.\-и; авгор этих строк пстре-
тил его имеете с героновским и руководство марокканского математика ХШ века ион
Т
Таким
образом:
vV-1
у ¦> —
1325
> 15-51"
265
Поели этого niinniiaui-ен г.иистншыи процесс вычисления птпошщшп окружности
К диаметру. Архимед :шм1;пяст окружность периметром оншчишого многоугольника, при-
приближая ого к окружности ири помощи последовательного удвоении числа сторон. Так как
у Архимеда в числителе отношения стоит диаметр (собственно говоря, радиус EZ), то
при злмене окружног.ти описанным многоугольником получается величина, мшг.шая — .
Архимед ншпет (дли ясности мы заменяем неравенствами его приближенные ранен-
еггнп) (])мс. 3 текста):
Ш_ Ж |ЕГ 2В5
7Т " 1Г>3 ' rz > 153 '
Разделив пополам угол '?КГ, мы по свойству бисссктрисга
ZE:Er = Z[I:Hr.
Отсюда
ZE--KT Zr
ЕГ "" Г И '
или
ZE-I ЕГ ЕГ .
zr ~гн ;
ГЙ" *"" УЛГ1 TZ -^ 153 ^ 158 ~" i 53 '
Далее,
ЕН2 _ ЕГ2+ГН* ^ 5718+1538 ^_ 349 450
откуда
ЁН
ИГ ' 153
иричсм корень, стоящий в числителе, надо извлечь с недостатком.
П далыюишом Архимеду приходитси извлечь три корня с недостатком и четыре
с избытком, причем подкоренное пыражсцие получается и результате сложения дпух
квадратом.
Иерпьтм таким корнем, иотирмн ему пршплосг. извлекать с недостатком, был корень
п.* суммы 571М-153*=349 450. Так как число 349 450 стоит и тексте Архимеда, то испо,
что Лрхимод изллскал корень именно в этой форме.
Каким-нибудь способом (налрпмвр, и:« таблицы квадратов чисел от 1 до 100, анало-
аналогичной вапилонской, давав|исй кпадра-гы чисел от I до 00) Архимед мог ггайти первое при-
приближение для корня, а именно 590, пользуясь тем, что 59*—3481. Пторое приближение
он тогда мог бы найти но вавилонскому правилу
Так как 7 х8-.—= 59-я-, то алименатеяь можно положить рапным 5!) ,у ; таким иб-
разом, приближенное яначепяе кории, которое по правилу должно быть избыточным
(ввиду .чамины знаменатели эт», конечно, нужно ироперить), получилось бы и ниде
^349450=591 у.
Так как Архимеду нужно приближение с недостатком, то он поступает по изложен-
изложенному нами тлше нрапилу; только теперт. ому приходится увеличить ла едилипу
ИЗМКРЕНИВ КРУГА 549
аиымспатель дроби „ , поскольку она не и ы ч и т а о т с. я, но прибавляет к я;
мы HMGt'Ai:
У 349 450 > 591 -i.
о
Собственно говоря, когда мы вместо 59 вяили 59 — , мы ужи получили приближен-
приближенное значение с недостатком, как можно проверить непосредственным возведением в квад-
1 1
рат числа 591 -=-; однако число 501 -г- выгодно еще: н и том отношении, что дальнейшие
.'itiTii поыучнмтся более простыми г, ноп.моркой в знаменателе, чем с семеркой.
Разделив мце. раз пополам угол ГЕН прямой 156), Архимед получает:
откуда
И
Мы имс.пи
откуда
Ев 1
вг
(ЦК- ИГ): КГ^НГ:
EII
ИГ
ЕГ
Гв "
/ ЕГа-
ег
ЕГ НЕ-^-ЕГ
«Г HI' "
1
" 153 * ГН -"¦
591 I-+S71 Г
153
А/ ( ЦК1
-Гв* \ \
:вГ,
571. '
153'
IB2J
J53 '
НГ
Зимстнм, что в :>том Место Лрхимед, по нроизнеди промежуточных вычислений,
о пишет: «значит, GE имеет к НГ большее отношен
Здесь Архимеду приходится лгачислить выражение
просто пишет: «значит, GE имеет к НГ большее отношение, чем 1172 -д- к 153*.
о
Так как он де дает окончательною чтелоного значения подкоренного пы|>ажглип,
как ато ол сделил п нредцдуще-и случае, то не будем этого дс.чать и мы, а прими применим
вавилонскую формулу для пычисления гипотенузы, помня, что 153*— 23 40!).
' 2-11E2-^-
1G15-.--
Пмиплпив доление. найдем, что частное рлшю 1С у-. Отбросив дройпую часть
4
(так кии приближение получаете» с недостатком), мы получим, что искомый корень
будет
550 КОММЕНТАРИИ
Дальше; Архимед делит пополам угол ©ЕГ прямой ЕК. Аналогично предыдущему
о» получнот:
«Е:ЕГ^ВК:КГ,
(НЕ |-ЕГ):ЕГ=-вГ:ГК,
ГК " »Г '* 153 153 *
Архимеду приходится вычислять выражение
2-2334-=-
4
Выполнив деление во втором слагаемом, найдем в частном 5 т- , что после от-
/i668 y
брасывамия дроби можно принять за 5; таким образом,
у. 2334 у )"-! 153* =w 2334 -1 \ 5=233SI -^ .
: У
прямой ЕА даст п»м:
Топерь отношение ЕК : КГ будет больше 2339 —: 15.3. Новое деление угля КЁГ пополам
КЕ:ЕГ = КЛ:АГ,
(КЕ гт'):К1'=ЕГ:ЛГ,
откуда
«г = j«, jl ^^!!i, 2334 4674
Л Г КГ 'КГ > 153 '" 153 153 '
Найдено отношение радиуса ЕГ к прямой ГЛ, яллнтолн:йся полонипой стороны
правильного 96-уголышка. Отношение диаметра к периметру описанного правильного
Уб будет больше дроби
4E73-| |
153-96 ~ 14688
Таким образом,
л > 1468S
14 688
4673-~- 4673-^
i 1
так как 067 —7 = 4672 — .
Во второй части предложения, где Архимед шцет число, меньшее п ( точнее говоря,
большее— ),сму при и:тл(;чении корпя придется брать приближенные значения с из-
битком.
И.1МЕРКНИЕ КРУГА 551
При прон:шодстпс пмчиелоиий (рис. 4. текста) Архимед начинает г, изучения пниеаи-
лого в шяукруг треугольника АИГ, у которого гипотенуза ЛГ ншястся децшетрон,
а угол ГЛВ но-прежпему равен 30°. Мы имеем:
АН
ВГ
АГ
.".3
V лн8-
1351
780
НГ»
ГН
Проведя АН — биссектрису угла ВАГ, из подобия треугольников ЛГИ u FIIZ получим:
АН ^ ГН ^ АГ
иг ": н/ ~ rz "
По свойствам биссектрисы получаем:
АГ _ АТЗ _ АЦ -! АГ_ АН -j- АГ
Л В
Гак как -ртг*
_ 1351
rz
ЛГ
BZ TZ-I-ZB "
2 IRK)
1 ^ 780 ' Т0
АН Л В ,
НГ ВГ '
Л Г
ГН "
ГВ
„2911
- 780 "
Таким обраном, Архпмоду приходится пайтн нпиилшмеепко с изПыгком у^2911а-г 7802,
сделаем это и 1Ш; нодкороииое члеш буД1Т '.) 082 321. В качестве первого приближении
мы можем взять 3000; тогда
Так пак нам иуиию щтбянжоиио с шЯытном, то чпеяитояь посменной дроби мы
можем увеличить до 1500, что даст нам стошцео у Архимеда число ;i013 -"- -«- "I" 7" •
3013 :- 1 -I-JL
Таким обриаом, отношение -^гт < =п^ .
Дальши Архимед опять делттт ГАИ пополам прямой Ав. Тогда анилогичыо
Ав .ЛГ+АИ ^ 30t3-'-4+T , 2911 4
" ГН ^ 780 Ь
©Г " ГН ^ 780 ' 780 780
Числится*, и знаменатель утой дроби можно сокрятигь на 13,- после сокрагцектгя
будем имить:
1 4
Лв , tVK>~^^--/l 1823
¦ <. -
©Г ^ 00 "" 240 '
Теперь
АГ _ У АН* ;-(-)Г* V/i823*+240a
ГН "" Гй ^ 240
Соответствующий корень можно опять панти по вавилонской формуле для вычис-
вычислении глнотонуаы:
Деление 28 800 на 182.4 дает и чнетпол 15 и в естатие 145R; таким образом, искомый
король будет 1838 j^^. ffocvn-днюю /(fioCr, Лрхидюд полагай рапной -^-; дайстпитоиыю,
1455- 145 — 1600,
1823-182=1641,
552 КОММЕНТАРИИ
т. с. прибяплспдо к чиклтттслю и вычитание из знаменателя их десятых долей дает прибли-
приблизительно одинаковые числа, и особенности если несколько уменьшит:, знаменатель, что
:е даот лриб.'1иж1.-лш? с избытком.
Таким образом,
... 9
АГ №38-fi"
Разделим угол вАГ jioiiojulu прямой АК. Аналогично предыдущему будем иметь:
ЛК Ав+ЛГ _ 1823
•• " 'JJSII • -">/fl "
КГ ©Г - 24» "" 2Ф " 24»
Имеем:
9
Й~ _ 36В1.11-9 _ 402Ж) 1007
И-240 11-240 "" 11-240 = 66
об]1й:юм,
ЛК ^ 1007
17- < ¦
КГ ^ 66
АГ _ Yak2—гкз
гк ~ ^' чч
Имеем:
-i,
следовательно,
АГ
ГК. ^ 66 ¦
Повои ди:к!ЯИО пополам угла КАГ прямой ЛА даьт:
ЛЛ ЛК+АГ
7
7\г гк "^ 66 "• вб ~ 66
"•
АГ _ /AATZTAT /( М1В
ГЛ " ГА < С6
Имеем
201В— V-I-Wi2 =2O1«4--|-
У b 2-2016-i-
ь
4
о
АГ
ГЛ ^ 66 '
Так как ГА является стороной 96-уголышка, вписанного в круг, то отношение диа-
диаметра, круга к периметру рассматриваемого uuncaиного миогоугмлышка будет мелыис
ОТНОШСШ1Л
АГ
ИЗМЕРЕНИЕ КРУГА 55Я
откуда для отношения окружности к диаметру будем иметь:
^ 6336
я> г-
20" т
Изложенную реконструкцию Архимедова процесса ияплпчмшя квадратных корней
приходится рпосматривать лишь ishk гипотезу, но эта гшюте.ш заслужилаот внимания
хотя 6м ло той причине, что ола пе постулирует никаких специальных алгорифмом, вроде-
нопрермпамх дробей и т. д., существование которых у грекоп само но себе «щк
нуждается в доказательстве-; по существу, и :>том процессе нримениется одна лишь фор-
формула 1'ероиа, то ость как раз та," которую уиомипнст и Еытотеий в своем комментарии.
Чтобы объяснить появление числа Зщ у Архимеда, Гу.м.ч поступает так:
„ '^Т ., 1137
^О т— — О-
2017| 8069'
4 4
Уполпчим на 1 3[гам(.чга'Г('.гь 80G9. Тогда после сежратешш на 3:
1137 _ 379
8070 ~~ 2Й90 "
1 1
Величина последнего отггошони» ло?кит л«:?кду — и -=-
i О
7 -^ 2090 " 8 '
У Паппа в книге VII «Математического i-oopamiii» докпаывастси теорема:
ас а «-1-е с
> >ф>
На оснопапкп атой теоремы
37» ^ 379-|1
2GM -' 2690--8 ^ 8 '
или
379 ^380 10 \
ИМО " 2638 "" 71 " 8 '
Таким образом, отношение окружности к диалн'Тру бу;и!т более чем 3=т, по менее чем 3-=- .
Полученные Арх-ивдадом псяичины, выраженные в десятичных дробях, будут;
3 4---= 3.14286,
3~ =3 3,14084.
Они д;нот для п три верных знака.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
Трактат «О ралновегин плоских фигур» состоит из двух книг: л первой дастся мате-
млтпчесюш цьшод иакопа равновесия рычага (предложения VI и VII) и определяются
центры тяжести параллелограмма (предложения ГХ и X), треугольника (предложения
XI -XIV) и тр;тс;ции (предложение XV); вторая книги посвящена определению центров
тяжести параболического сегмента (предложения II—VIII) и параболической трапеции
(предложении IX и X). Относительно места итого трактата в ряду сочинений. Архимеда
¦сушестнует большое разнообразие мнении: рид авторов {например, среди зарубежных
историков Хине, и среди советских — С. Я. Лурье) — относит ia-о к самому началу дея-
деятельности Архимеда и разбивают ия две самостоятельные части, считая, что вторая ккига
приставляет совсфцшпно сямостонтелыгое сочинение. К связи с этим Хизс устаиаилипист
¦следующий порядок написании Сочинении Архимедом:
1:\ О равновесии плоских фигур, книга I.
2е. Квадратура иараио.'|Ы.
3°. О рилмошжмн ii;hki;hx фигур, киша П.
¦Второй вопрос, сия.'Шпнмй с трактатом «О равпоиееии плоских фигур», заключается
в следующем: имеем ли мы весь текст этого трактата, или же дшпедшрв до пас произве-
произведение представляв только часть более полного сочинения Архимеда ло этому лопросу?
Дело п том, что в трактате Архимеда «О плавающих телах» пместсл ссылка на «icroQQonucfo,
что шюппе соотпетствует заглавию рассматриваемого трактата jteQl (sitijt^fitev iaoQQOJtiuv
или nefr. iooono.-tiuv). Однако саман ссылка касается определения центра тяжести сегмента
параболоида, которого и трактате; «О равлопоенн плоских фиг5'р», ношено, ие имия'Ся.
1? спя:!!! с :>тим можно думать, чти, кроме трактата о равновесии плоских фигур, Архимед
в качестне cCTtscTBomioro П1ЮДО.11Ж|!1ШЯ iianm::i.;i трактат и о р;)пнош:гни пространственных
-фигур; it ото сочинение могли вомаи определении центров тиздести цилиндра и конуса,
цитируемые п «Офоде», может бить, iipu:iMi>i и пирамиды, а затом сегментов тара, эллип-
эллипсоида," параболоида и гиперболоида вращения; механические способы доказатс;1ьства
<5OOTDvT<:Tnyioinnx теорем по.мещепы и том же самом «Эфодс».
Г>.1ижайшсе рассмотрение трактата «О равновесии плоских фигур» исключает воа-
моттють отнесения era к числу самих ранпах ироизаедшшй Лрхжмсди. Исая бы мы
допустили такую шыможмость, га л:ш пришлось бм раздюить указанное; сочинение на
два совершенно с.имостоято.чышх произведения. Против такого разделении можно выста-
выставить рад существенных возражений. Прежде всего мы, конечно, должны до какой-то сте-
степени считаться с традицией, рпссиатримазищсй обе эти книги как две части одного и того
же произведении. Затем нужно иметь п виду, что еоверптенло такую же структуру имеет
¦состоящее и» двух книг сочинение: Архимеда «О нлаттющих телах», перная книга которого
посвящена общим вопросам, а кторая рассматривает только одну задачу: услоляя равно-
равновесия плавающего сегмента параболоида вращения; между тем до сих лор спи: пи один
историк не предлагал риядюить трактат «О плавающих телах» па два соворчгешю само-
самостоятельных сочинения. Далее, трактат «О равновесии шюских фщ-ур», даже л состапе
перпой его книги, пикпк но может быть отнесен к числу ранних сочинений Архимеда.
Д.-1И лпй цели достаточно срвв1тить механические тсоргмы «Квад]1атури параболы» с соот-
ветстнугощими местами первой книги трактата «О раншшесии». В перном сочинении очень
заметна конкретная, заимгтпоиаипая из практики осноиа; гопоритсн о ]1ычагах (Е.иусб),
о иодвеигенЕсых грузлх, само равновесие иродполигаегсяг иракгичесш-г осуществгшия,
то есть усгойчИБЫм. Ничего подобного ис встречается во иторим, казалось бы специально
поеилщеппом механике, сочинении: и нем отсутствует какое-либо упоминание о рыча-
рычагах ¦ - их место занимают простые геометрические л шиш, и само равновесие стаповится
каким-то неопределенным, отвлеченно математическим; мы но можем сказать, будет ли
•оно устойчивым, нсустоЁпипим или же безразличным. Затем нужно отметить какой-то
г-кециалЕлю-математичсский чисто формальный способ доказательства теорем: они боль-
большей частью доказываются от противцого, причем форма доказательства одинакова как
и нерпой, так и но второй книгах. Стоит хотя бы сравнить дока.:атг;лет»о
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 555
XIII первой книгп и теоремы IV второй книги, оба основанные па аксиоме о том, что центр
тижести выпуклой фигуры ire может находиться вне en контура, чтобы иочупстнонать
•справедливость сделанного замечания. Идея второго доказательства теоремы Xlll imp-
bovl книги, по существу, одинакова с доказательством теоремы V второй киши. Мате-
Материал пертюй книги (центр тяжести прямоугольники, треугольника и трапеции), по сущв-
чмпу, нодготонлнет нес необходимое для доийзательктиа теорем лторой книги (центр
тнжкли параболического сегмепта и параболической трапеции). Следует отмстить также
логическую связь между предложениями ucpuoii и шорой книг; таи,
постулат 5 первой книги необходим для доказательства предложения III второй
книги
постулат 7 » » » дли доказательства, предложений IV и V'l
второй книги
предложение IV » » » для доказательства предложений V л VIII
втирой книги
предложение VIII» » » для доказательства предложении IV, VI и
X второй книги
предложение XIII» » » для доказательства предложения II вто-
второй книги
предложение XIV» » » для докалитсяьства предложений IIJ, V и
VIII второй книги
.предложение XV » » » д.чя доказагшп.стпи предложений II и III
второй книги
Особо нужно отметить предложения VI и VII первой книги и предложение Т юго-
рой книги. По сущистпу, они продстапляют математическое дежазатольс/хио закона раимо-
исснл рычага, постепенно обобщаемое для различных тппоп фигур. В пред-чожшши \;1 ,ча-
•когг рашюиесия рычага дикааыыйетсн дли соизмеримых примоуголышкои, о иредл(йкс!нин
VII он нбобщаетси па случай ш^ои.ттернмьтх нрнмоугшыпгаоп, наконец, в Hjie'VfoJKe-
ции 1 uTopoii книги он рашростр.пшетсн на случаи криволинейных фигур, но только квад-
рируемглх, то есть тпкнх, которые могут быть принршцрны в нрллоуголт.штки. Общего
доказате.гьс.ти.ч ;iiir«oiiii рплполесий рычага мы у Архимеда не находим, хотя, конечно,
Архимед был шюлш* уверен в его пригшлыюстн и нсоднокритцо поЛ1>:юи?и]Ся им, например,
и предложениях «Эфода».
Точно так же не выдерживает критики аргумипт, касающийся того, что » ряде нро-
и;тг!дег1ИЙ Архимеда имеются ссылки на первую книгу «О раышжесик плоских фигур*.
Для этого стоит только более внимательно рассмотреть форму :>тих ссылок. Ссылка л пред-
предложении VI «Квадратуры параболы» касается центра тижисти треугольника; нм гопори
уже о тон, что в вохра шшшии:я тексте «О ралнопнсии» нет самого суи^естиеткн-и —
ле доказано, что расстояние центра тяжести треугольника от сгиопаиия ранпо
трети иысотн,— самая форма ссылки - - Ьгдкмтал iv xo?g u.r\%a\'iy.o\? — докл.-з.чно п меха-
механике — иошшмппет, что п данлом песте подразудювастся другоо сочинение;; иначе стоило
бы ;v toiS tcrooio.-tixois. В том же самом предлогкелии доказательство оииратг.н на то,
что при рамшииснн цсптр тяжести и тоткп подвеса должны лржать на одпом перпендику-
перпендикуляре, причем соотве!тг,тнуго1ц;ш ссылки гоиропождастся слогами «это тоже уже доказано».
В трактате «О [lainioueCHii» ничого индоОиого нет; оченпдио, д&:ю идет о йолос раннем про-
игжедении Архимеда. Ссылка на такое бплее рагшек нромгшедение имеется и в самом
трактате «О равновесии». В предложении IV nojiuoii mnira гонори'пмг о том, что уже
было доказано (jiQofiifteiv.TaO. что центр тяжести двух масс, лежащих на одетой прямой,
тоже лонсит па этой прямой. Ссылки типа oEfieiy.tai evtoiS "iaopiomHoLc; имеются только
о «Эфодс* (предложогше I — центр тяжести треугольники) и и трактате «О плавающих
телах» (предложение II — центр тяжести сегмента нараболоидн). Таким образом,
можно только утверждать, что трактат «О равновесии» ланисан до «Эфодл» и до трактата
«О плпплтощпх телах».
За то, что трактат «О рапнопесоти плоских фигур» не был первым механическим про-
иаведогпсем Лрхшица, голорнг а f-ама форма (;го нпложенля. Трактат представляет строго
логически построенное нроциисдинии, из которого лытриилена яся [;oni{pt!Timn физический
основа; не дается определения центра тяжести (оно, очемидш), ужи нредиолагается ияве-
стиым), к формулиропке закона равновесия рычага говорится только о равновесии на
«длпгтх». Особенно показателей тот факт, что в рассматриваемом произыедепии уже пред-
предполагается и:шестн!.1м, что центр тижести треугольника делит медиану в отношении
1:2*); это положение, которым Архимед иользуетсн при определении кпадрятури
параболы, необходимо должно было стоить в проигшеденнп, касагопсемся оир(!де-1ег[ия
*) Архимед исиольаует его при нахождении центра тяжести прямолинейной трянецпи
<кн. I. нред.|. 15).
556
КОММЕНТАРИИ
Рис. 1.
центра THStftiCTii вообще. Таким образом, лп.т приходим к выводу, что цель и характер-
трактата «О равновесии» таковы: Лрхпмед хотел, во-первых, математизировать меха-
механические теории определении цситрп тяжести, изложенные им в более риппнх со-
сочинениях, и, во-втормх, применить их к нахождению центра тяжести параболического-
сегмента как целого, так л усеченного; открытии сногоб квадратуры параболического
с(,тмш!т.г1, он, естественно, считал споим долгом определить и положение центра тяжести
такого сегмента.
Если считать, что первая книга содержала липц. необходимый подготовительный
материал дли второй, то можно легко объяснить отсутствие в пей одной теоремы, которая
обязательно должна была бы в ней быть, если бм ата книга представляла самостоятель-
самостоятельное сочинение ли тему о нахождении центров тяжести плоских фигур. Л говорю о центре
тппессти круга (соотиетствующее предложение находится в чпеле лемм *Эфода»).- Было бы
очень легко .построить соответствующее доказательство тстш «кс истодами, котормс приме-
применяются в первой книге. В самом деле, придиоложнм,
что центр тяжести круга (рис. 1) не совпадает с его
геометрическим центром О, а находится в некоторой
точке С. В рассматриваемый круг вписываем квадрат,
две стороны которого параллельны отрезку ОС; центр
тяжести квадрата совпадает с центром О круга; значит,
центр тяжести ft оставшейся части будет лежать на
продолжении отрсика ОС в такой точке, дли которой
отношение расстоянии ОС и СП равннлпсь бы обратно-
обратному отношению площади квадрата к шшщидпм четы-
четырех остпшиихеи сегментов. Екли получении я точка D
будет заключаться одутри круга, то" раащвнявищ по-
нолам дуги получепных сегментов, впишем в круг вось-
восьмиугольник, центр тяжести которого будет опять сов-
совпадать с центром О круга, л то время нак центр ти-
жести оставшихся сегментов будет находиться в не-
некоторой точке К, которая будет лежать на продолже-
продолжении отрезка ОС и на большем расстоянии от центра О
круга, чем точка D. Так как суммарна» площадь сег-
сегментов, получающихся при последовательном удвоении
числа сторон вписываемых многоугольников, может быть сделана меньше любой задап-
noii величины» то центр тяжести этой площади в конце концов может бить удалей за
пределы окружности, если только центр тяжести круга не будет совпадать с его гео-
геометрическим центром.
Но если обе книги трактата «О равновесии.* представляют чимтт одного и того же
сочинения, то время его нанисиция .может быть установлено следующим образом. Мм уме
говорили, что трактат «О равновесии» ланисан до «Офода», — что дает нам terminus an It
qiieni; с другой стороны, terminus post quern опрсдсаясхси тем, что в предположениях
V" 11 и V1I1 второй книги Архимед полт.ауетгя определением подобия криволинейных фигур,
которое дано в трактате «О коноидах и сфероидах». За это же говорит то обстоятельств!,
что при докаяательстпе предложения V пторой книги «О ратшопссии» Архимед опирается
па предложение I [1 того же трактата «О коноидах» (о равенстве площадей двух параболи-
чисиих сегментов, имеющих одну и ту же ось, но раншле основания). Таким образом,,
место, занимаемое рассматриваемым сочинением и ряду произведений Архимеда, опре-
определяется совершенно точно; трактат «О равновесии» написан в промежутке между трак-
трактатом «О коноидах* и «Эфодом». В свяли с этим стоит отметить, что формулиропки лемм
«Эфода» B, 3, 5, <>) почти дослоыпо повторяют формулиропки соответствующих предло-
предложений V11I, V, ХШ—XIV, X первой книги «О рашювесин плоских фигур».
Коли рассматривать обе книги трактата «О равновесии плоских фигур» как попытку
дать строго логическое обоснование системе механических теорем, то естественно выдви-
выдвинуть иопрос, в какой мере была достигнута Архимедом поставленная им себе цеди.. Это
тем более ппжко, что и споен «Истории механики» Мах пмстунпл с критикой построения
Архимеда, укашыая, что, опираясь только на постулаты, ныдшшутые Архимедом, никоим
образом нельзя безупречно логически доказать ocuoiuioii ^акон равновесия рычага, содер-
жаншйся в предложениях VI—VII иервон книги «О равновесии». Основное его возраже-
возражение сводилось к тому, что постулат Архимеда о том, что рашшс грузы уравновешиваются
на раипмх плечах еще ги: определяет формы зависимости момента силы от длины ее плеча;
мы с ранним пряном .можем определять момент как произведение силы на квадрат или
iiyo ее плеча, тогда как основной закон рапиопссия рычага TjiefiycT только линейной зави-
зависимости момента от дли ми плела.
.Конечно, и общей логической схеме построения Архимеда, с пашей точкя лрения,
не хватает самого главного -• - определенияцептра тяжести: это отсутствие мы можем
объяснить тем, что соответствующее определение считалось уже общеизвестным, а между
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
557
тем это определение, исходящее из того фпктц, что тело, подпертое! в центре тяжести,
находится в безразличном равновесии как бы ого ли прящять вокруг центра тяжести, уже
необходимо предполагает линейную зависимость иеличини момента от длины плеча;
при более сложных зависимостях понятие центра тижюти тернст смысл. При наличии
этого определения ырхнмедопскан теория рычага становится логически вполне строгой.
Исрпмо три постулата (памньтс грузы на равных плечах уравновешиваются; яа не-
неравных перетягивает груз на большом плече; от прибавлении (или отлитии) иикого-
кибудь груза к системе грузов, уже лаходищихся п равновесии, последнее лирушмется)
необходимы длн дока.щтел сстви первых трех предложений первой книги *).
В четвертом постулате мы у«ке встречаемся с ноинтиом центра тягкости: если опре-
определять его как точку опоры при безналичном положении ран пошлин, то можно докизнть,
что щчггр тяжести двух тол, рассматриваемых как од(го, находится на прямой, соединяю-
соединяющий центры тяжести этих тел. Это положение било сформулиролило Архимедом в третий!
лемме «Эфода»; ни основании его Архимед донизывает четвертую я ингуш теоремы первой
книги «О раиновос-ии» (относительно центра тяжести двух и трех ранных грузов, находя-
находящихся на одпон ирлмоГг).
Четпертый л пятый иостулнты, касающиеся положения центин. тяжести подобных
и конгруэнтных фигур, употрсблиются Архимедом при доказательстве предложелий IX,
X и XI шгриои книги и предложения 111 второй книги.
Особенный интерес представляет шестой постулат. Он читается так.
«Если т«ла (величины — (лв^гФы.С) находится в равновесии, то будут находиться
it равновесии л им равные».
Бели не полимать этот постулат как простую таитологшо, то придется си.чзать
следующее:
Действие груза, приложенного ч данной точке, определяется только его /хличиной,
т. е.\ совершенно tie зависит от его формы или ориентации.
Понимаемый так шестой постулит погшолнет заменить несколько масс одной, поме-
помещенной В центре их тяжести; и этом смысле он и употроблнется Архимедом при доказа-
талг.стпо предложений VI и VII нерпой
книги и предложения I втором книги. Та- о
ким образом, :>тот постулат как раз л лред-
• ставляет собой то положение, за «пропуск» М
которого Архимеда упршенл Мах.
Теперь доказательство :штсолн рыча-
рычага приобретает вполне строгую логиче-
логическую форму. Идет его легче всего выи- f
снить, если прииссти это доказательство в
Toii форме, которая была ему да!га Гали-
Галилеем (см. второй диалог «М ох пничеекпх рас-
рассуждений и доказательств») (рис. 2).
Пусть в точке О подвешено за середи-
середину коромысло A1N, имеющее длину 2@+6).
К этому коромыслу при помощи бесконечного множества вертикальных ниревочек при-
прикреплена одггородЕШя балка KL такой же длины 2(а-\-Ь). Вся система будет, оченидно,
и рил повесив, которое не нарушится, если мы ря-зрежем балку по липии СС — на два
отрезка: КС -длины 2« и CL — длины lib. После итого обрезаем нее леровки, кроме
д«у\. АЛ н ЛП, находящихся в серединах отрелкоа KL и CL: от итог» ривнокесиетоже
т; нлруинпчмг. Таким образом, нелкчиыц КС—.2а ни нлеч!! АО = Ь будет урпттопешнвать
ъе.'шчину CL—2b >ю плече ОВ=а\ иными словами, при равшшпе.ии приложенный п А и В
грузы будут обратно пропорциональны соотш'тг.тв.у.кицим плечам.
Нояможкость нолорцчипаштя чистой балки вокруг осей АЛ и ПИ боа нарушения
рапггонегия эквивалентна требуемому Махом закону пропорциональности моментов лер-
aoii. i-.Ti4ifiitn длиггы пл(!чи и исключает нсяккй другой закон, например, квадратичной
за» пси мости, так что доказательство Архимеда, вопреки Маху, является вполне строгим.
Пос'-'шдцттй, седьмой постулат (центр тижисти выпуклой фигуры лежит инутри г,ч;
контура) необходим Архимеду длл доказательствапридложииий IX н XIT1 iiepuoii книги
и предложений IV и VT второй книги.
Для двух книг «О рапнопссни плоских фитур» мы имеем подробный комментярин,
cocTau.:i(!iiiiT.rii Kbtokugm Лскалонекнм, учкником знлмелитого строителя св. Софии в Кон-
гтаитипоноло Исидора Милетского (VI век я. Ь.). Из итого комментария мы берем наи-
наиболее интересные места, относящиеся ко второй книге (комментарии к первой книги боль-
большого интереса не представляют).
с
в
жшшшж
с
—2а »;¦ ,
Рис.. 2.
•) 3} перемоле пришлось несколько отклониться от поллиннииа. У Архимеда у,
p (л; T'j gioo;... — iro имлют естестиеннпо стремлоиии наклониться в сторону груза...». Ср. во
легуингсльпой статье о смысли слов ieittiv рвпч
558
КОММЕНТАРИИ
fl | Евтоюш в споем комментарии питает:
«Ои (Архимед) п формулировки первой тооромы говорит:
„Предположим площади ЛВ, ГЛ, ограпичешгыс примой и параболой п могущие-
быть мриложешгыми к заданной прямой1'. 11а основании доказанного здесь этого устацо-
Т1ИТ!. и(!во:змо5Кгю. По в книге «О шаре w цилиндре» on сказал, что им Выло доказано, что-
т.чкпн фигура составляет четыре трети треугольника, имеющего то же самое основание-
и ранную пысоту; так кик четыре троти треугольника являются прямолинейной плоской
фигурой, то мм можем равную им площадь приложить к зидпипой прямой; следовательно,
ясно, чти мы здмсем сделать то же самое и для упомянутых фигур».
Из этого отрывка следует, что в эпоху Евтокия сочинение «О квадратуре параболы»-
но было изпостио. Лид «приложением» площади к примой подразумевается построение
па этой примой равновеликого данной площади прямоугольника.
[2] Ёвтокий пишет:
«Все .')то должно быть доказано в надлежащем месте». Поскольку лысказаняое-
утверждение не вполне; иегго, то необходимо несколько поговорит!, об этим, приводя
отрыиок из «Конических сечений» Аиоллоитгя (рис. 3).
«Пусть будит фигура, ограниченная параболой АВГ в прямой ЛГ;
пусть диаметр этеш фш-урнбудет ВД. Ясно, что вершиной сегмента будет
точка В; ибо, иертипами линий Аполлоний . называет лежащие
па этих линиях концы днамстрок. Если мы проведем АВ, ВГ, то
получится треугольник АН Г, имеющий с сегментом то же самое основа-
основание и рапную высоту, а именно опущенный из В па АГ перпендику-
перпендикуляр; ибо ВД не всегда будет осью.
Если ли, взяв вершины Е, '/. сегментов АВ, ВГ, прождем через,
них Ев, ZK параллельпо ВА, то они будут диаметрами сегментов АВ,
ВГ. Дейстиителыю, относительно параболы доказано,что все пряли^е,
проио.'юшше параллельно диаметру, будут и сами диаметрами этого
конического сечения. Итак, Е, Z будут вершинами сегментов, и прове-
проведенные через Е, Z касательные параллельны АВ, ВГ. Значит, и EAZ
будет параллельна ЛАГ, так как Et), ZK будут параллельны и раины,
яиляись диаметрами ранных сегментов, и налагаются друг па друга,
как это доказано в шестой книге «Коническихсечений» (Аполлоний, VI,
19). И так как КНв параллельна ВД, то 13Н : НА=-Д0 : 6A. Но ИВ =
— АН, ибо ЕП делит ее пополам, будучи диаметром, сопряженным
с касательной. Значит, и Д0=вЛ. На том же оспонашш и ДК КГ.
По вся АД равна ДГ. Значит, и Дв=ДК и на основании этого EA=AZ.
Таким образом, он правильно i-оворит, что соединяющая вершины сег-
сегментов будет параллельна основанию главного сегмента и разделится
пополам диаметром этого сегмента.
Теперь прокедем соединяющие линии ЛЕ, ЕВ, BZ, ZT, разделим
их пополам в точках М, N, Е, О. через М, JN, Е, О параллельно ВД
проведем ПМР2, Т\,ГФ, XEYZ, QOQ^ и проведем A.IJ, ПЕ,
1LT, ТВ, ВХ, XZ, ZQ, ?>Г. а также Т,ЛХ и П,В,Г,Д,К,2«.
Из ньнпе;1ока:шш1ого ясно, что ТХ, EZ и HQ будут параллельны АГ
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
559'
и что Т,А=,АХ, EA=AZ, .П,А — ,Д ?2. Теперь я утверждаю, что они
делят ВД па отрезки, относящиеся, как ряд нокледовательних нечет-
нечетных чисел, то есть если Т$,А—1, то ,АЛ—3, А#Л- 5 и ,ДД 7. Действи-
Действительно, поскольку АН --1Ш и Е(-)' параллельна БД, то и Ав—0Д.
Значит, АД ндкое больше АВ, а также а ЕА: ЛДя=4ЕЛа. Но АЛ* : ЕЛа=
— ВД : 13Л, согласно доказанному (Аполлоний, I, 20 — наше уравне-
уравнение у*—2рх)\ значит, ЛЛ^ЗЛ13, то есть если Л13=1, то ЛД=3. На
том же основании если АВ- -4, то ЛА=12. И так как EN=NB,
E,Z=-,ZA и вФ=ФД, то КА ьдвое больше Л Z, то есть, ТА,.
иЕЛа^4Т,Л8; значит, Л В -413,А, так что Л, Л -3,АВ. Таким обра-
образом, если АВ=4, то 13,А=-1, ,АЛ=3, АД--12. Далее, поскольку
АМ=МЕ, АР=РП и А2--56, то будут раины и Л2, Z6, 0Ф, ФД.
Значит, если ЛД-=4, то 2Д^ГТ,Д --3, и АЛ2=Н6, а ГТ,Д2-=9. II если
ДВ—IB, то ВУД=9; и, значит, остаток ,АА -7. Теперь, поскольку
доказано, что если ВД---1Н, то И,А—1, ,АА—3, ,ДЛ -7 и остаток
Л,Д--5; ипачит, ВА рассекается параллельными на отрезки в отно-
отношениях ряда нослодоиательных нечетных чисел, если за единицу при-
принять отрезок при нерпшне сегмента».
[3] Евтокий пишет:
«Подобные сегменты сечений ifonyc.il Аполлоний в книге шестой «Конических сече-
сечений» определил кил тпнис, а которых при проведении в каждом одинакового числа пря-
прямых, иираллельных ос:нолаишо, эти параллели, а ташке и осиоиания йудут находиться
между собой в тех же снмых отношениях, что и отсекаемые ими на диаметре отрезки, счи-
считая от вершины, равно кик и сами :>ти отрезки. Там же доказано, что н все параболы
будут подобны друг другу».
9то определение расходится с общепринятым теперь определением подобия; так,
л гиыеле Аполлония подобными будут два треугольника, а которых основания будут
нронорцнежальлы лыкотим, хогя бы углы а этих треугольниках и не были соответстиепно-
ранними.
В атом определении шггересны следы атомняма: подобиями фигурами називаются
фигуры, могущие быть ра:ы омом игами ла подобные элемента, хотя бы'иосле^чштс и были
бесконечно малыми, как это имют место для двух иараГюлн'кчжих гсч-мсптон!
Иомеща(!М еоотпетстиующие места из книги шестой «Конических сечений» Аполло-
Аполлония (но переводу Vw Eerke, сделанному с латинского переводя Гяллся пятой, nieeroii.
и седьмой книг, «Конических геченийл, дапиупиих до наг только я ирабском нггреводе).
«О it р с д с л и и if с 7. Подобными сегментами мы называем
такие, у которых оснонапия оопа.чуют одинаковые углы с диаметром,,
а также такие, в которых
при згротюдении одинако-
¦ iioro числа линии, па рал-
лелмтг.тх iKujoisnifnro, раз-
разделяющих соответстиую-
щио диаметры па части,
находящиеся в одинако-
одинаковых отношениях, будут
одииако иьтми oTnoidi'i i и я
основании и прогкндеиных
jiapii.:uioJiew к отсекаемым
ими от диаметра отрезкам,
считая от першипы.
П р с д л о н< о ir и с 11.
Нее параболы являются :" ¦ ¦
подобпыми друг другу.
Пусть ЛН и ГД будут дне параболы с осями ЛК, ГО; я утиерждаю,.
что оти конические сечения будут подобны друг другу.
й
т/
560
КОММЕНТАРИИ
Пусть All, ГХ будут параметрами этих сечений; сделаем так, что-
чтобы некоторая прямая ЛК так относилась к прямой ЛИ, как прямая
ГО и ГХ. Затмг разделим прямую АК в каких-нибудь точках Z, в;
разделим также прямую ГО в тех же самых отношениях и точках М, S
и щфпендмкулнрпи к осям ЛК, ГО восставим прямые ZE, ОН, КБ
и МЛ, N2, ДО. Далее, поскольку прямая КБ будет средней пропор-
пропорциональной между ПА, АК, так же, как
прямая ЛО будет средней пропорциональ-
пропорциональном между прям ими ГХ, ГО, то прямая
KB будет" к КЛ, как ДО к ОГ*).
Далее, так как прямая Б| вдпое боль-
больше ВК, а прямая Ау вдвое больше
прямой ДО, то прямая Щ будет от-
относится к АК, как прямая Ду к ГО.
Равпым образом, так как прямая ПА
будет к ЛК, как прямая ГХ к ГО, а
прямая АК. будет к А в, как прямая
ГО к ГЗ, то «по равенству» прямая
ПА будет к Л6, как ГХ к ГЗ. Из атош
оченидпо, согласно только что доказан-
доказанному, получится, что прямая Р11 будет
относиться к А(Ь), как ЛТ к Г S и на
оыгомапии тех же самых рассуждений
прямая Е1 будет к AZ, как тЛ к ГМ.
Таким образом, отношения перпендикуля-
перпендикуляров В|, HP, EI к отсекаемым ими па
оси прямым АК, А0, AZ будут соответственно теми же самыми,
что отношения перпендикуляром Д\', XT, Лт к отсекаемым ими пря-
прямим ГО, 2Г, ГМ. По отрезки, отсеченные па одной оси, пропорцио-
пропорциональны отреякам другой оси; следовательно, 'коническое сечение АВ
будет подобно ссчепию ГА, что и требовалось доказать».
I'i] Комментарий Ептогнш:
«Ото (/оказывается в конце, где ниш; N15***). Вслед за этим
докажем упомянутое мы {рис. 5}.
Пусть будет парабола АВГ, диаметр которой ИД. Проведем орди-
ординату АД, соединим А и В, разделим ЛВ к Z пополам, и через Z парал-
лельно'ВД проведем EZ; она будет диаметром сегмента А13. Затем из Е,
Z параллельно ординате проведем EII, Z6. Поскольку AZ равпа BZ,
то АИ вдвое больше ZH, и ДВ вдвое больше И6, и АД ндпое- болынс ZB,
то ость Е11. Таким образом, квадрат АД будет в четыре раза больше
инадрата ЕН, а вследствие этот ДВ будет линейно в четыре раза боль-
больше Ш1 (Аполлоний, 1, 20). Так как ВД вдвое больше В6, то и ВВ
Рис. 5.
*) Д
Тога»
КВ2^11Л ¦ ЛК, ДО*=ГХ ¦ ГО.
ПД : ДП^ГХ : ГО.
¦ КС II*-АК ПА АКАК2
Д(.J " ГХ. ГО ~ГХ' ГО ~ТО*
откуда
KB: ДО—КЛ : ГО.
**) Соответствующего мостя и подлиннике ис имеется.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР 561
вдвое больше ВН. Но ОН равна ИВ и 6Н равна EZ, так как EHZ0 —
параллелограмм. Значит, 1311 равна EZ и 13Д л четыре раза боль-
больше ZE».
С нашей точки лроппя, ато прост» следует ия уравнения параболы уг—2рг: если
АД =- j/[ вдвое больше ЕН -у.,, то отношение zL= П&и a:*- Till будет
[5f Самым интересным в атом доказательстве шшяется следующее: оно по существу
мило сияла ею с семью предыдущими теоремами, которые даже ишшготся недостаточными
для строгогц его доказательства. Дейстимтслыю, все рассуждения и предложении VIII
опираюгец иа следующие доа положения:
1) нее диаметры параболы параллельны друг Другу,
2) центры тяжести всех параболических сегментов делят в одинаковом отношении
их диаметры.
Первое положение нигде не доказываете», ко поскольку оно молчаливо подразу-
подразумевается при доказательстве предложения V, можно думать, что Архимед считал его
общеизвестным.
Что же касаотг,я второго пункта, то у Архимеда ои дока.чип только для п о д о б-
нн х сегментов (предложение VII), каковыми сегменты АКВ и АВГ (в нашем смыкле)
ПС ЯВЛЯЮТСЯ.
Точного огтределеявя подобия параболических сегментов Архимед но дает, считая,
по-видимому, достаточным определение, приведенное им вн инпдении к трактату «О коно-
коноидах» и по существу совпадающейс цитиропанпым Витокием определением Аполлония.
Г) современном обоаначншш доказательство предложения VIII можно провести
тап (рис. 25 текста):
Так как площадь параболического сегмопта АВГ составляет -^-площади троуголь-
О
ника АВГ, то примем последггюш яа 3; тогда ллошадь сегмента АВГ будет раина 4, а сумма
нлнщадей сегмептоп АКВ и ВАГ составит 1. Если примем ПА им ось ординат, то пенопиая
формула для определения ординаты центра тяжести напишется в пишем случае так:
4-Д©=3-АЕ+1-Дг,
где в, Е, 5 пролстапляшт центры тяжести сегмента АВГ, треугольника АВГ и площади,
состаилинной из обоих сегмеитон Л К. Л и ВАГ. Мы имеем:
ДЕ = ^-ВД; AS=AX-.-MZ = -i-
Пусть X представляет отношение ординаты Д0 к ИД и соответствепно MZ к KZ. Так
как K.Z — -- ВД, то мы получим:
де>=?„-вл, mz^xkz=x~вл.
Иодетавив эти нс-еичины в оеншшую фоуагулу, иолучим:
4?„-вд=з-4 вл -м-;' 1 ва-!-^-
Сократив яа ВД и определив -из полученного уравнения X, иайдем:
иными словами, В0 = -:- ед.
Г0| Рассматриваемое предяожентге играет роль леммы к следующему за ним пред-
предложению X, в котором речь идет об определении центра тяжкети усеченного параболиче-
параболического сегмента, рассматриваемой] как разность двух cgi-mimitob.
П пропедении доказательства ппрахтст иообык но лепное искусстпо Архимеда п опе-
оперировании пропорциями. Для нас, нзбн.юпацпых попремснным алгебраическим зиако-
поло/тичгаем, .что искусство уже ипялстси и<;дост>пным.
[7| Чтобы исио предстаиить себе ход мыслей Архимеда при доказательстве этой
теоремы, пожалуй, лучше исего буди1 начать ои ра.чбор с самого конца.
36 Архимед
562
КОММЕНТАРИИ
Архимед рассматривает усечепный сегмент ЛАЕ Г как разность двух параболиче-
параболических сымситпц АВГ и ДВЕ. Пусть X будет центром тяжести сегмента ВЕД, Р — центром
тяжести АВГ и, наконец, I — центром тяжести рассматриваемого сымепта ЛДЕГ.
В таком случаи, поскольку Р есть точка приложения равнодействующей кесов обоих ссг~
мситов ДВЕ и ААЕ1', мы можем
XI»: П — ссгм. ЛАЕГ :№гм. ДВЕ.
Теперь
хр=вр—1зх=|- мт,—~пи=¦-
|
- вп)=-|nz,
так кпк, соглавпо предложению VIII, расстояние центра тяжести параболического сег-
mciit:i от ворипшы состаиляст 3/5 его т.тсоты.
Далее,
сеем. ААЕГ=согм. АВГ—ссгм. ДВЕ.
Таким образом, ми можем написать пропорцию
-Г 1IZ : Р1 = (сегм. АВГ—сигм. ЛБЕ): ссгм. АНЕ.
с)
Площадь параболического сегмента раина 2/3 лроазведелия основания ш высоту; таким-
о6рп:зо.м,
сегм. АВГ : сегм. ABE=(AZ-BZ): (АН СМ).
Но но основному cuoiicTny параболы
BZ: BH —
Та ним образом,
согк. АВГ : сегм. ABE =
Получоцнос огЕЮШсние Архиисд, если можно так выразиться, линеаризует, то есть,
заменяет отношением первых, стопглшй двух длин. TlpiiMCEieiinuvi вп прием ишшется
o6i,i»rniJM в гречослой математике и осуществляется путом виедслшя средних пропорцио-
пропорциональных. Он fii-per:
MN^BZ; КО--mi,
затем
2 В = MX MN_ N5 _/ MN
Ы1 NO ~~~кё, ' SO 4.~N3
если NS является сродной прогторщшналмшй между MX и NO:
Таким образом.
•JiiJ ' me ¦
Нпсдмгпе четвертой пропорциональной NT по раимктву
ZB : ВИ—MN : NO = NH : XT
О РАВНОВКСИИ ПЛОСКИХ ФИГУР 503
дает сам желаемый результат:
ZB3/» ZB ZR1/a MN MN MiV WB MN
Вна/» ^lilf" Blll/e ~ NO ' MS ' " N3 ' NT "" KT '
Теноръ, иозвращаясь к исходному равенству
-2- HZ: Р1 = (ссгм. АВГ—сегм. ABE): сегм. ДВЕ,
замепнем площади пропорциональными им величинами:
4- HZ : PI=^(ZBS/*—BII8") : BH"/s,
и переписываем равенство в виде
5 ц MM —NT
NT
откуда
IP 3 NT
J12 G MX-NT "
Затем из предложения VIII мы зцаом, что
A)
Так как нам желательно ппйти no.-io/ivcinsn цинтра тяжости / на отроякс IIZ=OM
= MN—NO, то иаходим отношение ZJJ: 11Z:
¦ 11Z" ~ b OM"~ 5" МЛ" - - NO "
IZ
Тпиерь простым иьпнтаиш-м мы можем пайти куя{1кк; нам отношение --ру:
11А
( '
IZ ZP IP ^l f 2.W.V 3NT 1
HZ ""HZ HZ "'¦> \ AIN —NO IviN — NTJ" (>
Нслнчпцьт, входящие n пртлую члетп рпнеигти» C), состашпиот нспрсривную про-
пропорцию
MN: X5: — ХЕ : SO — NO : NT.
Обозначим отношение КЗ: MN 4<;pc:i |; тогда
fe "'MX ~ UZ ~ AZ» '
так что
„_ДН
s~ AZ '
: i
то ег.ть ? ргишо отнотонию ординат nnj:a6i)jiLi и точках II и Z.
После этнго яы мо;кем написать:
NS = |-MN, N()^?a-MN, ЛТТ=|*-МК- D)
Если мы подставим эти значемшн и формулу C), то после сокрищоннн на MN будем
имоть: . :
VL \ Г_2 3?_»_\
HZ"" 5" ti-|» 1-E»J
Вьтрижспие, етоящео в скобках, мы преобразуем так:
23^ 2A
3G*
564 КОММЕНТАРИИ
Если мы теперь помножим числитель и ,ш;шеиитслт. этой дроби па MN и вослол].»
чуемся формулами D), то лолучим имеющее»! у Архимеда выражение
IZ _^2MN4-4N3 I-6XO+3NT
HZ " MN-|-2X5+2Nl>-|-XT * {)
Дальнейшим ход рассуждеяий Архимеда может быть восстановлен иочти с полной
достоверностью.
Простой взгляд на формулу E) показывает, что
IZ 2
HZ > 5 '
о
Отложим ZK = -.;- HZ и вычтем из длины IZ:
i>
I f2MN+4NB4-6i\O-l-3?fT ,,-j _ l 2NO + XT
i MN b2NE-j-2NO-[-»\T "J" 5 MN-{-2NS-t-2KO4-NT "
7M 2NO '-NT
'MN |-2N3-|-2NO + NT '
Так как ZH = 58K, то легко получазтен, что
T_ZII MN+2NB
W 5 \vlN-b2NB-|-2NO-l NT'
откуда
Ш_ MN+2N3
Теперь Архимеду нужно от вспомогательных линий MN, N3, N0 и NT перейти
к первоначальным линиям параболического сегмента. Он пишет:
¦ _1В_ MN-b2N3 MN NT
IK
Ив равенств D) видно, что
AZ
MN
ХН
.MN
MM
xo
" NT
1
NT
i
s
AZ8
All
AH5"
Таким образом,
-Ш— А^±МП AZS АН
IK ~~ AZ ' ЛИ* ' 2AZ4-AH '
или
IB _AZ2 (AZ !-2AH) ...
IK "ДН2 BAZ , ДН)" K '.
Мы изложила вероятный ход миелем Архимеда при получении вм формулы {%).
Что касается приводимого им в предложении X доказательства, то оно развивается так.
Архимед начинает с формулы A). Затем он от формулы ((i) идет обратным путем к фор-
формуле E). Посае этого ол," складывая формулы A) и E), при помощи вспомогательного
предложения IX доказывает, что
TZ , PZ _ 2 MN
TTz"'• 'нТ~"ь Hz"'
откуда получается, что точка Р будет центром тяжести параболического сегмента АВГ,
после чого ои заканчивает доказательство тем, с чего начали мы.
ПОСЛАНИЕ К ЭРАТОСФЕНУ
О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
Полное заглаипс рассматриваемого сочинения такоио: tkqi t«v ji^Xftviwuv iiroprj.uct
tov jtois 'VQazooftivtyv щоЬо$ (или ссрьбюу). Слово ?фо6оС обозначает «приступ, доступ,
ьход»,*г(р;йш\' — деньги или »iinuci.i, дающиеся на дорогу; очень часто переводят его сло-
словом «метод» (буквально спутник). (Сокращенно принято обозначать это сочинение словом
«Эфод»., или «Яфодик» (scpofiuwv), которое тоню встречается в других постах к качестве
названия атой книги.
Интерпола история открытия этого сочинения. Приват-доцент Петербургского уни-
университета Пападопуло Ксрнмслс указал ни имеющуюся в Константинополе рукопись
духовного содержания па пергаменте, на котором ран со был написал другой текст (так
иа.-нлшемый палимпсест). Отдельные места итого текста математического содержания при-
привлекли внимание известного датского фп.юлога Гойберга, кото1)Ый побыиал n Констан-
Константинополе и 1800 и 1908 гг. и прочил большую часть этой рукописи, восстанет ленную им
при помощи фотографического снимка и личного осмотра. Оказалось, что рукопись,
кроме ужи известных рниса сочинский Архимеда, содержала апачительиуш часть трак-
трактата «О плавающих телах», известного pnucu только ллатвискаы нерелоде, а также «Эфод»,
который ранее был известен лишь u;i упоминаний п слопаре Сииды
и цитат и Гсропоиой «Метрике», которая л сана была открыта
и опубликована twim<o n 1Я03 г. Первое издание aioio тгп{ктн было
сделано Гойбергом (см. 118]); с итого n:uiairEiH был, между прочим,
«¦-делан русский шф^ид |^<>]. Дальмийтаи чтение позволило Гсй-
бергу разобрать еще некоторую часть текста; в этом виде ом и был
помещен во птором томе второго издания сочинений Архимеда,
с которого и делается предлагаемый перевод.
Время написания «Эфода» может быть определено из сле-
следующих соображений. «Эфод» шшмг.ан после обеих книг «О шаре
и цилиндре», так как с ssum оцртдечгетг.я центр тяжести сфиричееко-
го сегмента, объем которого дается но второй книге упомянутого
сочинении. Далее л «Эфоде» приводится .:imi_\i;i ii:i трактата «О коно-
кдах». Затем Архимед уки^ывает, что дье последние теоремы «Яфода»
отличаются от более ранних, л которых сегменты ко пои дои и сфе-
сфероидов сравнивались с конусами и цилиндрами, тогда как здесь
рассматршшемме тела, ограниченные кривыми поверх частями,
сравниваются с телами, ограниченными плоскостями; это noKti-'iM-
вацт, что «Эфод» опубликован после «Коноидов». Далее, уномшшипя
о трактате «О равновесии» показывают, что последний к моменту
написания «Эфода» уже был опубликован.
[1] Из помещенных и лача.чо «Эфода» лемм наиболее инте-
интересной является 10-я, говорящая о центре тнжекттг конуса. Можно
кысказать следующее пруцпологкепие относительно пути, которым
шел Архимед при определении центра тяжести конуса.
Архимед рилбнвал копуп плоскостями, параллельными основанию, па очень тонкие
диски риЕшон ПМСОТЫ, объемы которых били пропорциональны квадратам расстояния
до вершины. Так как ординаты параболы тоше пропорциональны квадратам соответствую-
соответствующих абсцисс, то нахождение центра тяжести конуса можно свести к нахождению центра
тяжести сегмента параболы у = о.х~, заключенного между осью абсцисс и конечной
ординатой (рис. 1).
П «Квадратуре параболы» было доказано, что площадь параболического сегмента/
2 j
О МВД равна — площади прямоугольяика ОАВА. В таком случае, если принять площадь
Рис. 1.
566
КОММЕНТАРИИ
ОА13Д за 6, то площадь сегмента ОМВД будет равна <i, а площадь сегмента О МП равна. I.
Цсеггр тяжести сегмента ОМВ лежит ни его оси ММ', делящей пополам отрепки П13 и О А.
Мы uoncuM рассматривать сегмент ОАВМ как разность между треугольником ОАВ и сег-
сегментом ОМВ. Если дли симметрии удвоить все ;пчг ijiniypr.i и отсчитмппть расстояния х
центров тижости от О (нес они будут инслп уджхшия лежать на оси ОА), то мы можем
написать следующее равенство:
илот. ОШ'-ховг=2 илощ. ОМВ-хомв-|-ипо1Ц. ОМВГ-а:омвг.
Бели положить ОА = 1,то отсюда получим:
откуда искомое расстояние OK=a: будет:
Таким образом, центр тяжести конуса будет лежать на пси ого па расстоянии трех
четвертей от вершили.
Зитем трибует разъяснений л е м м а 11-й, доказательство которой Архимед дал
» трактате «О коноидах». Понимать эту лемму надо следующим образом.
Пусть ним даны два ряда пропорциональных величия «1( а», ая,...\ bL, b», Ья,... таких,
что
Отпогаепие каждой соотпотпглсшюй пары этих всличтг бз'дет одним и тем же; обо-
обозначим его через а : Ь.
Возьмем загим ряд третьих величин, каждая ия которых будпт стоять в некотором
отпотении i; величинам ш;риого ]>ида, причем отношеаин »ти, иообщс говоря, могут быть
неодинаковыми:
ci=^i«i» ce=ЯзЛг, cs=Я3а3, ...
Пусть будет еще дан ряд четвертых величин, которые будут стоять в таких же отяо-
шопиях к соответствующим ьеличшгам второго ряда:
Лемма заключается в том, что сумма некоторого числа величин первого ряда к сумме
некоторого (вообще говори, ицого) чист величин третьего ряда будет иметь то же самое
отношение, что сумма соответственных шашчнн
второго ряда к сумме соотпстстхсииых ate вели-
величин четвертого ряда:
To обстоятельство, что Архимед пользуется
положением, полное доказательство которого
дастся только в книге *О коноидах и сфероидах»
(предложение} 1), позволяет думатт., что «Эфод»
нииисап после упомянутого сочинения. Однако
все содержание «Эфодя» характерно для более
jiajineii стадии деять-лыюсти Архимгда, когда он
в широкой степени пользовался механическим
методом доказательства. Таким оСразом, дли нпс
«Эфод» Архимеда имеет громадное значение л том
отношении, что noauo.JtiLT наиишуть в мастер-
мастерскую его гения, познакомиться с теми путими
его творческой работы, следы которых были
потом заглажены ирп опубликовании закопче/ь
jeux проиппедении.
[2] Лродложепия II u 1JI касаются онр|'Д1меиия объема шара и сфероида (так
Архимед низмшнуг эллипсоид ирлщеиии).
Пусть т|№буится определить объем тара АВГД диаметра БД. Проводим АВ и АД
и сгроымкопусЛЕЯ и цилиндр HZEA (рис. IL), оси которых енпнадают с диаметром АГ.
ПОСЛАНИЕ К ОРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 567
Продолжаем последний влопо, откладываем Aft —АГ и проводим ссчшдоо MN, uapucii-
дикуляркоо к диамотру АГ; это сочепни выделит и конусе круг с диаметром ПН, в шаре
круг с лиаяетром ОН и, наконец, в цилиндре круг с диаметром MN. Проведя все такие
¦сечении, мы разобьем рассматриваемые тела на ряд дисков бесконечно малой толщины;
попытаемся перетащить диски, образующий шар, на конец Н плеча Aft рычага Г6, имею-
имеющего точку одбры в Л, и посмотрим, как можно будет их уравиопосить. Для этого соста-
составим отношение Л? : Аи. 1?го можно будит приставить в таком виде:
А?_ AS _ AS-MS
А0 ~ MS ~~ MS2 '
¦Но:
Л2.М2=АЗ-ЛГ
Таким образом,
Л2
Ав"" М2*
А2
Л0 ""
Теперь, выражая уеяоиия равновесия рычага, будем иметь:
Л S ¦ М N2 = А0 • (lit12 -!- О?«).
Так кпк круги относятся, кик квадраты радиусов, то это отношение можно было би
шсрелисать а вице
[(круг MX)¦ AS = (круг UP+круг 0S).A6.
Дли получоггия атого равеистпа в современном обозначении надо было бы просто
помпожи-п. обе части на число п.
Полученный результат можно истолковать так, что круг MN цилипдра па плече
А2!, то ость и своим положьиии, уравновишиьаот круг ПН конуса и круг OS шара, пере-
несенный на конец илечп АН. Если мм сдолаом это для псех кругов, составляющих паши
тела, то найдем, что цилиндр EZHA, оставаясь и своем полонянин, урапиовишипивт riftp
л копус, ucpvaecontihio «а плечо А&. Так кок ценгр тяаыхтя цшшндра находится на серо-
дино его оси, то мы имеем:
(шар)-Ав i (конус) А6 —(цилиндр)-—^-.
Но циликдр EZIIA будет и три раза больше копуса AEZ; значит,
— -1 \ копус AEZ—-^-конуса AHZ.
Далкс, копус AEZ Судет в восемь раз больше конуса АВД; впачит, шар на диаметре
ВД будот только в четыре раза больше этого конуса. Так как конус АИД п шепть раа
меяьше обиимгиощего шар цилш1Д])а ФХ I'W, то отсюда заключаем, что этот последний.
•цилиндр будет в — раза больше обнимаемого им шара.
13] Доказательство Архимед нроподит следующим ui>pu:iOM. Он берет обобщенную
теорему степени точки для эллипса:
А2-2Г АК-КГ ЛК»
КВ«" ~ КБ" '
которая следует из часто встречающегося у Архимеда урапгтелид эллипса:
х B-7 —ж) _ а_
где о — Оолг.тиаа полуось, а р= параметр оллннса.
Таи как АК : KU — AS : 21II, то мы получаем:
2S*
568
КОММЕНТАРИИ
Далее из пропорции А? : ?Г—= ATI : ПЕ — 2 IF : ПМ получается
А2-2Г 211 JIM •
Сравшшая обе. полученные пропорции, лаходмм:
или
что и требовалось доказать.
Теперь мы люжсм шписать равепство
ИЛИ
AS ¦ S М2 — Л 0 ¦ A12
А2:-Ю»=А6.A1Г*+и5а),
и вен остальное доказательство пойдет аналогично придложипию II для шара.
[4] I) предложении VIII Архимид опредслиет объ1:и сегмента сфероида, то гать
:м;тпсочда вращения. Так как Архим1.'д не докапмласт эюй теоремы, то покажем, как
можио было бы осуществить это доказательств».
В сечении сфероида ми нмбс»1 оллнис (рис. 3), большая ось которого А Г -- 2а.,
а малая 1"Г^2?>. Охкладьишим АН=2Ь ч дополпж^м ирямоу1ч>льинк А в) Tait, чтг»См
АФ^АН — 2^. Зятем строим далпаелгчлй рычаг с. плечах А© -- АГ = 1а и откллдыипги
TQ— a. Rco остальшли буипы на рис. 3 имеют те жо самые .тачеиш:, что в »л
рис. 7 (стр. 313).
Аналогично предложит™ III мы дюгисм установить равенство
А 2 ¦ МЛ'2=АГ • A1 Ps+OS2),
откуда получается, что цилиндр ФЛ и твоем иолоиссшш уравпояешниает конус АЕ/
я ссч'Мемт АНД, иереиссснимс к точку 0:
цп.т. ФА-----At» (ион. AKZ-_ сегм- АНД).
Затем яаходим oriioiiicutie цилнидра ФА и «опусу EZ:
Имеем:
цил. ФА : кон. AEZ=AI1- : 4 HZ2.
АН=26=АГ--- , f IZ = А И -~
с а
ПОСЛАНИЕ К ЭРАТОСФЕИУ. О МВХЛНИЧЕСКИХ ТЕОРЕМАХ
56»
Таким образом, для отношения упомянутых цилиндра и копуга мы получаем то же
самоо выражение, что и в предыдущем предложении VII:
цил. ФЛ
А0»
А©2
кон. АЕ'/Г 1/яЛН2 "" АХ-AT '
Так как в условиях данной теоремы справедливо равенство предложения VII
щцт. ФА _ А«
__
коп. AEZ + cei-м. АВД~ АХ ~АТ-АХ+ТГ-АХ '
то будет иметь место и равенство
цид- ФА _ А в3
сегм. лид~ТГ-АХ " '•••"¦
Остается пиита othoijiciiitc цшптлдра ФЛ к конусу ЛВА. Мы имеем:
A)
B)
икл. ФЛ
АН2
коп. АНД
1/„АН-НГ~
так как из уравнения эллипса, если положить АТ1=а:, 13Н=-у, мы будем иметь:
образом,
пил. ФЛ
Л в»
кон'ЛИД '/зЛН-ИГ КЧ'-НГ '
Окончание доказательства проводите»
.чца.чопгшо докаяательстлу предложения VII.
[о| Предложении X касается определения
центра тяжести сегмента сфероида, то есть
:j.:ijiиисоида «ращении. Архимед точно также
но диет доказательства сформулированной тео-
теоремы; оно, дойт.тнител ьно, и ян нужно, так
как псе доказательство лижет бытг, пронедено
точно таи же, как и для предложения IX.
13 чертеже должны быть сделаны следующие
изменения. Пряма» А Г будет бачыпой осью 2о
эллипса, заменнющего круг А В ГА; прямые
АИ и AZ проводится чнро.ч концы малой оси '
2Ь упомянутого пллипса. Это отразится толь-
только на формуле, определяющей отношение
объемои конусов ЛБА п AEZ, а именно мы
будем иметь:*
КII :ЛП —Ь:а,
ВН'=ГН-АЕ—з- ("о уравнению эллипса).
Отсюда видно, что окончательная форму-
формула, оирсделнюгпни отношении объемов конусов
АИД и AEZ, остается той и«е саыоГг, а следо-
следовательно, останется тем же самым и иесь конец
доказательства.
[{>| Иродлонсиния II—XJ мы можем
рассматривать как исходную стадию работы
Архимеда над «Шаром и цилиндром» и «Коноидами и сфероидами». В дальнейшем он
освободился от чисто механических доказательств и дал строгие геометрические доказа-
доказательства, опубликованные им в указанных произведения*. Сначала он сделал это только
для шири и его частей: нахождение строгих докилательсти для теорем, касающихся копип-
дон и сфероидов, оказалось более трудным; они были получены только после окончания
работы над трактатом «О синралях». Остальная часть книги должна была быть носияпцчга
раабору дпух новых теорем, формулировка которых была дана в начали. Из этих теорем
570
КОММИНТЛРИИ
почти полностью сохранилось доказательство первой, которому посвящены предложения
XII—XV. Теорема эта заключается п следукицем.
В призму «писан цилиндр, основаниями которого служат круги, вписанные в верх-
верхнее и нижнее основания приамы.. Черен центр нижнего основания и одну ин сторон верхнего
основания проведена плоскость. Требуется доказать, что отсекаемый ею сегмент цилиндра
¦составляет одну шестую часть обч-ема призмы (риг,. Л).
Пусть секущая плоскость будит 0'1">Г'М". Пудом рассекать полуцилиндр имеете
с сегментом плоскостями, параллельными грани М'M"N'N" призмы. 13 сечештях с ци-
линдром получатся прямоугольники 2' 2'" T'V", имеющие высоту, рапную высоте
призмы; ь селениях жо с сегментом будут получаться прямоугольники 2'2"Т'Т",
имеюгцие г, перпимп одинаковые осчюпаштя 2'Т', по меньшую высоту 2'2" = TN.
Из подобия треугольников ГХГ п ГУВ легко заключаем, что
откуда
ГИ : rv=rN: ЧгП=ил. S'S'T'T* : ил. Z'T
TN ¦ п.1. 2' Т' SWT"'= TV- нл. Z'S" Т' Т*.
Это значит — прямоугольник сечения полуцилиндра в своем положении уравпопе-
сит прямоугольник сечения сегмента, помещенный на ипеча Г1? — половине стороны
ири:шг,1. Суммируя вес аналогичные равенства, получим, что полуцилиндр в своем поло-
положении уравновесит сегмент на плече, равном иол о» и но стороны приемы. Из этого следует,
что если См нам был известен объем полуцилиндр;!, то есть в конечном счете площадь
полукруга, и расстояние центра тнжести полукруга от ого основания, то задача была би
решо.ча. Остается решшъ вопрос, где находится центр
тяжести полукруга.
Ег-ли чсре:1 g обогишчим' радиус полукруга, а через
// — высоту нричмы, то полученный Архимедом резуль-
результат выразится таи:
так как расстояние центра тягкести полукруга от осиова-
4 о
нпд будет ;f-. Отсюда получается
о
1'нг. 5.
т. е. одной шестой объема приемы, сторона основания
которой ринна 2р_.
Таким выглядело би решение, если считать известным положение центра тяжести
полукруга. Но этого Архимед как раз не мог предполагать изпостммм; полому ему приш-
пришлось сделать попытку определения статического момента полуцилиндра относительно
его прямоугольного осноиашш, т. с. ироизисдсния объема иолуцилипдра на расстояние
центра тяжести от основаiiiiи.
|7| В предложении ХШ Архимед, выражаясь современным языком, определяет
статический момент полуцилиндра относительно плоскости его основания. Пусть па рис. 5
квадрат M.V изображает среднее сечение призмы, а ОПР — нужный нам полукруг п сече-
сечении полуцилиндра с диаметром OF в гсачегтие основания. Речь идет оо определении суммы
произведений ординат 2!К на расстоянии центров тмжес-ш этих ординат от точки 2.
В наших обозначениях искомая сумма будет:
Проподсм диагональ Нбн отложим BZ=S0. Так лак Z0=2P=AX, то
Выражение, стоящее в правой частя, нредстап-тяст сумму произведений отрезков
АХ на расстояния 2Х+ --— их тцттрои тягкестсй от осп ОР, т. с. шятмй отписителыю
тон же овн статический момент треугольника ИМ1Т, или, что то ;кс, статический момент
призмы на осиошшпи П9М с той жо высотой, что и полуцилиндр. Последний статиче-
статической момент ми знаем; он будет ранен произведению объема треугольной призмы, т. е.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХЛНИЧКСКИХ ТЕОРЕМАХ
571
Одной четверти объема всей призмы, па расстояние центра тяжести треугольника НбМ
от вершины, то есть -^-28. Если положим по-прежнему сторону основания приамырав-
о
ной 2q, to искомый статический момент полуцилиндра будет:
Приравнивая полученную величину произведению V'cernrGi получаем уже известную
«аи формулу
|4
Так как Архимед зпал величину площади полукруга, то рассматрилаемая я а дача
позволила бы ему определить положение центра тяжести полукруга. Возможно, что он
и патолкнулад ца :>ту задачу п своих исследованиях относительно цецтпои тяжести
плоских фигур. Однако тообстоятельстпо, что он попробоиал дать еще другое решение
рассмотрииампш ладит и, в котором он сводит ео к определению площади параболиче-
параболического сегмента, гопорнт за то, что но нримя гдадйлля «Офода» ому ни Был лзаестед
момент нлощндгг полукруга.
[8J Б предложении XIV Архимед, оставии в покои полуцилиндр, сравнивает
объемы сегмента цилиндра с треугольной приямнй, отсеченной от всей призмы той s*c
плоскостью, и плоскости сечения проводит нгрнецдику-
Лярио к оси ОР, так что теперь в сечениях обеих фигур » // г-
получаются прямоугольные треугольники, высоты кото-
которых будут рнкшл высоте IJ 1:ри:шы. Треугольники,
¦состаплягонше отсеченную приему, псе одинаковы, со-
составляющие цилиндрический сегмент имеют основания
рллпмми еоответстнуинцим ординатам MS полукруга
(рис. С). Таким обра;юм, отношение искомых объемов
Судет: в
V...
-S
мв»
i И М-ME
J" MN« =
ПК«-МК*
XI (НК-МК)О-ПЧ-МК)
г.
к
J
Рис. С.
Для .чппеарилацпи последнего отпошепия пропедем паряболу через точки Е, Z, Н
¦с осью Z0; тогда но сиобстпу параболы:
MKS; ШС-'= IZ : ZK -= A.N: MN.
Мы имеем таким об раним:
V,.P
vUIU,aHU~^->K* mn y—^J us ¦
Но псе ординаты МЛ панолпят площадь параболического сегмелтц EZH, вне же
MN ¦ - нлон(..1дь прямоугольника ГА13Ц. В «Киадрлтурп нпряоолыв было доказано (пред-
ло/Коино XXIV), что тг.мщцпдь иарибо.сическоп) сегмента EZH состаплнит две триги пло-
площади прямоугольника ГДЕЫ; таким ибрапом,
V -V 2
г СОГМ ¦ У 71
3
откуда
—= •> ' отссч.
[9] Рассмотреншм! доказательстио легло п основу строгого митематического доказа-
доказательства по методу исчермышшия, которое Архимед дал. в предложении XV. Вспомога-
Вспомогательной для него является упомянутая иышо лемма 11.
Во:п,?.гм| кнадратноиссчснис АВГД риссмятрипасмсш прилмы и ипитем я одну его ио-
яовииу полукруг 11ZE, в п другую—параболу Ыв?(|шс. 7). Разделим нримую НИ инпо-
лам, молоиншл ПК и КЕ еще раз пополам, затем еще риз пополам и т. д. до тех нор.
внка 'изучающиеся полоски по станут меньше некоторой заданной наперед по.чичицы
(ее Mo;itno iiuojia-ib скнль угодно мал'пй). Затем заключим полукруг и параболу между
572
КОММЕНТАРИИ
вписанной и описанной фигурами, разность между которыми, а именно два прилегаю1-
щих и KB и K.Z прямоугольника, может быть сделана меньше любой заданной величины.
На прямоугольниках, вписанных и описанпьтх около полукруга, построим треугольные
призмы, две ил которых, построенные на KZ и ЕЕ, изображены на чертеже. Долоеки,
яа которые разделен прямоугольник ГДЕН, ыпляются основаниями треугольных призм
тина ЕЛ", KZ', которые в спвокуи-
Zr лости составит трсугольнук! призму,
оСъси которой равен четверти объе-
объема всей нри;шы.
11уеть МН — ордината полукру-
полукруга, а МЛ—соответстнующая ей орди-
ордината параболы. Примни М5Ч, равная
половине стороны квадрата, будет
одновременно радиусом полукруга и
осью параболы. Выше мы видели., что
M22:MN«=MA:M14.
Это значит, что объемы призм,
построенных па прямоугольниках
типа МЗ-МЕ, будут пропорцио-
пропорциональны площадям прямоугольников
им МЛ-ME. Пусть ве.чичшш ря-
ряда а,, а2, аа,.„ будут представлять
объемы призм тина Ei', величины
ряда р\, р2» [*»»•••—площади прямо-
прямоугольников типа ЛЕ; далее в качестве
величин ряда Yit Ys» \'з>--- возьмем
объемы при;ж типа EN', из которых
составляется большая призма, объем
которой рапниетйя четперти прямо-
прямоугольной призмы, а в качестве ве-
величин ряда йц <\>, б3.... возьмем
прямоугольники типа AM, дающие
т! сумме прямоугольник Л ВНЕ, две
трети площвди которого раины пло-
площади параболического согмента
ГСШ1К. Наша надача состоит п том,
чтобы показать, что объем цилиндри-
цилиндрического сегмента будет тоже равнять-
равняться двум третям треугольной призмы,
построенной на АН.
Положим, что это ле имеет места: тогда мы всегда можем построить таких два впи-
вписанных и оптеашшх около цилиндрического сегмента тела, составленных из треуголь-
треугольных призм, чтобы разность между ними была меньше разности между объемами сегмент»
н приемы.
Предположим сначала, что объем сегмептв будет больше дпух третей объема призмы.
Так как рй:нгость между объемами вписашпого и описанного тел больше разности между
объемами сегмента и вписанного в него теля, то объем вписанного тела будет тоже больше
дпух третей объема приемы. Соглгияю лемме 11 ряд а — сумма при:<м, составлвгощнх
вписанное в сегмент тело, будет тик относиться к ряду у — объему призмы па ДН, как
рнд Р — сумма вписанных в параболическим сегмент прнмоугольииков ко всему ирямо-
yro.'ii.iimty АН — рнду 6. Ио это равенство ненопможно, так как первое отношение
более дпух третей, в то время как второо меньше двух третей. Значит, объем цилиндри-
цилиндрического сегмента не будет больше двух третей объема призмы.
Пусть теперь он будет мепкгое двух третей объема призмы. Тогда объем тела, огисан-
пого около цилиндрического сегмента, может быть сделан меньше двух третей объема
приемы; следовательно, и площйдт. описанной около параболического сегмента фигуры
будет меньше двух третей площади прямоугольника АН, что невозможно, так как две
трети последней площади ужо рашил площади параболического сегмента.
[10! Утраченный конец книги должегг был содержать механическое и геометриче-
геометрическое докалательстпа следующей теоремы:
Если куб «писан в цилиндр, основаниями которого служат дка круга, вписанные
в противоположные грани куба, и затем другой, такой же цилиндр с основаниями на двух
других гранях, то заключающееся между поверхностями обоих цилиндров тело, т. е.
общий им обоим о57-е.ч, равняется Осум третям перкоаачплъко&о куба.
Рис. 7.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
573
¦ Механическое доказательство этой теоремы реконструировано Цсйтепом *).
Для понимания доказательства следует обритять внимание ни форму тела, объем
которого подложит определению (рис. 8). К го сочен ия плоскостями, параллельными осно-
основаниям одного из цилиндров, будут представлять окружности, а сечения плоскостями,
параллельными осям цилимдрои, будут представлять квадраты, стороны которых при
передвижении от Л до центра К подрастают от иулп до величины, равной оси каждого
Рис. 8.
цилиндра. Дальнейшее дпкаяатклыгпо иедетсн дли сечения фигуры плоскостью, ирохо'
дящен через ее центр тяжести, кап :>то обнчпо делается у Архимеда. К этой плоскости
относятсн и все буквы п дальнейших обозначениях (рнс. Н).
Пусть будет куб ФЧ'ХГ, в который, вписан цилиндр с осью БД й боковыми сторо-
сторонами ФХ п ТГ. Пусть и тот же самый куб будет пиисни другой цилиндр, ось которого
перпендикулярна к плоскости ФЧ'ХГ; эта плоскость, проходящая через ось ЛД ncpuuri»
цилиндрн, образует и сечении го вторым цилиндром круг ЛВГД, касающийся в точках Л,
В, Г, Д сторон кпндр&та <D4.'X.V; прямые Л Г и ВД будут взаимно перие]]йикуляряымв
диаметрами рассматриваемою круга. Сочцннан Л с J) л Л it продо.члпгм их до пероссче1-
ния с прямой TV в гичках R и Z; тогда KJ' = J'Z=.AI\ Дополним прямоугольник RZC-M-
Загем вообралим, что иа А лропедены четыре прямые к порпшпам приходящего через ВА
и перииыдикулнрлого к АГ ииадратц; если продолжить их до поресечеиия с плоскостью,
проходящей черог( EZ и перпендикулярной к АГ, то получится пирамида, вершила кото-
которой А, а оснонипио— порпиндниу.тпршлй. к А Г квадрат ко гторопой KZ; дополним эту
пирамиду тяк, чтобм 1голучилас|/ш5адратная ири»ма с теми и«: оснопатшем и высотой,
что и у пирамиды ("а риг". 8 эти пирамид;! и прп.-жа ire изображены).
Йослп итого нроиедом л прямоугольники h'L какую-нибудь прямую MN, парал-
параллельную К'/,, и 1пд атой iipinuoii лосставим iukickoctl, Шфпспдпку.тярную к АГ. В пере-
пересечении с интересующим нас телом, яаклютгашыи инутри обоих цплипярол, oini образует
квадрат со сторонпй 'HI, n пересечении же с призмой и иирамндпн соогпетственпо квад-
квадраты со сторонами MN и SF (они «а рис. 8 тоже ие изображены). Продолжим ГА до Й,
отложим АН, jiamiyio А Г, гг предстаиим себе р!тпопле1шй рычаг Ы i t: серединой А.
Теперь, так как АО*=Л1'-АГ и А1<=М2, AS=^E2, то мы можем написать:
далее АО2 = О22 J-SE2; значит,
— M2-SE;
02*-r-S2*= MS-23.
Затем мы жмеем пропорции:
MS : 23.-
ПА : А2 = ГА : А2= NfS : 2S,
(MS-2E)- (MS2): (О1'В+2Е«)=
S: @ПЧ-5Гй).
•) Blbllctliecn Mathcmatlca, VII. 3i6 и д. AЯ07).
574
КОММЕНТАРИИ
и MN
еисм
Таким образом,
НА : AS = (MN2): (ОПВ f SP2).
НА: AS —(киадр. па MN): (кладр. на ОП-| квадр. па ЕР).
Это значит, что квадрат на MN, оставаясь в своем положении, будет относительно-
точки Л ураиовешилать квадраты со сторонами ОП и ЕР, переиеселныо и Помещенные
спошщ центрами тяжести в точку И:
ЛН-(квадр. на ОП+квадр. иа ЗР) = А2 (квадр. па MN).
Так как из квадратов па 011 состоит интересующее «ас тело, я из квадратов на ЕР
N построенные нами пирамида и приима, у которых «ысотой янлмится АГ, а осноьа-
I — квадрат со'стороной MN, то просуммировав лее аналогичные равенства, получим:
АН-(тело -[-пирамида А13Х)^=ЛК-(призма ЕВ).
Таким образом, призма Ев, оставаясь в слоем положении, будет уравнгшетнилать.
относительно точки Л упомянутые пирамиду и находящееся внутри обоих цнлиндроп тело,
если их uvpvttwrn и поместить центрами тяжести и точку И. Так лак центр тяжм-.ти нрн-.яш
находится и точки К, и ЛН=2АК, то упомянутая призма Судет вд.оз больше пирамиды
вместо с находящимся ьиутри обоих ци.пшдрст! телом:
призма =¦ 2 (чело¦+-пирамида).
Но пирамида ривиа одной трети призмы с теми жо основанием и иысотой; отсюда
следует, что находисцееся внутри обоих цилиндров тело, будучи взито дважды, равно,
одной трети приемы шла просто будет равно одной шестой призмы fc.fc>. Но приума L»
в четыре рила больше кубп ?Х; пничит, тело,
иаходяшееся внутри иошфхностегй обоих ци-
цилиндров, будет равно двум третям куба Ч'Х,
что и требовалось доказать.
.Мы привели механическое доказатель-
доказательство рассматриваемой теоремы приблизитель-
приблизительно в тех же формах, в каких оно было бы,
вероятно, дано Архимедом (конечно, за ис-
исключенном а.~] rofi pa li'i ее к ого зн аи опол онсеиня
н нростраистпмашого hl-jitcjico — Архимед удо-
но.чьст»Aиалси бы сечением по средней пло-
плоскости, той, на которой у нас рассталлены
букны, пак ато показано га рис. 9). Чтобы
пронести геометрическое! доказательство рас-
смитрппаемпЁ. теоремы, иужии диаметр АГ
разделить па достаточно большое число рав-
равных частей и через полученные точки деле-
деления пронести плоскости, ш-рниндикуляриые-
к А Г. Эти плоскости л сеченинх с кубом ФГ,
а также с рассматриваемым т&кш образуют
кпяцраты. Затем вписываем в рассматривае-
рассматриваемое' тело и описыппем около него телесные
фигуры, состоящие из элементарных приам и отличающиеся друг от друга менее чем иа
любую заданную величину; :>тн нри:шм Пудут иметь квядратные исновании, а высотами
у них будут служить отрезки диаметра А"Г. Таким обриаом, получится картина, подоб-
подобная изображенной на рис. 7, стой только p!t:iHitu.cii: что теперь вместо треугольных призм
будут киалрлт е. Каждой элементарной призме вписанной или omieaimoii фигуры будет
в кубе соотне-тгпюпать ялеммттнрпаи прппма, асиавште которой буцат painitt voitoutm
грани куба; таи как отношении объемов двух таких элементарных лрияи с одной и то" же
высот»» буд|;т раин» отношении] квадраток сторон оснований, то мы можем посиольяо-
вап.1и той же самой вспомогательной параболой что и в предложении XV, и провести
докадегсльство тем же самым способом. Это доказательство, реконструированное п стиле
Архимеда, имело бы приблизительно такой ппд:
«Пусть будет куб Ф^Х Г и в него ниисан цилиндр, ось которого ЕЛ и цококыс сто-
роны фх и Vf. Пусть в этот же куб шшеап ци.|ипд|>. ось которого будет иерпспдику
Рис. 0.
некоторое тело, которое в сечении с плоскостями, параллельным^ а»ЧгХТ". Судет давать
Круги, в сечении же с, плоскостями, перпендикулярными к АГ, будет даиать квадраты.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
575
Я утверждаю, что ото заклгочетшое между поверхностями обоих цилиндров тело будет
составлять дне трети куба.
Прежде nct>ro докажем, что п ато заключающееся между поперхпостями двух упо-
упомянутых ци.пшдрои тело можно вписать тилеспуш фигуру и около исто описить другую
такую ми, причем обе они составляются! из ириям, имркяцих рашплс нмеоты и подобные
квадратные основания, и построены таи, что-
чтобы описанная фигура превосходила «писан-
«писанную, па величину, меньшую пенкой наперед
заднн:юй величины.
Пудсм в круге ЛБГА постоянно долить
пополам диаметр ЛГ и через точки деления
проводин, параллельные ВЛ лримыс, пересе-
пересекающие окружность круга АШ'Д; антсм че-
pi>:i точки пересечении ашх прямых с. окруж-
окружностью круга будеы проводить прямые, ннрпл-
jjt-л r.ijbic А Г, и иродо.чжать их в «fit; стороны,
вика нии по встретятся г, дпумн Слижлщиимн
прямыми, r!iip;i.'i;ie:ii.Hi.).\iii БД; далее и точках
деления диаметра AJ1 будем икч-танлять нер-
п>-'||дИ1,-у.'!]|[]Ы uuepx u imn;j от плоскости круга
А1!ГД и на каждом на этих нертпдикуляроь
откладывать прямые, р;шиые находящимся в
круге отре.чкам примой, параллелмкн! RA,
лроходшцей черел осноиаиис этого ш.-рнендн-
нуляра.Лнтеы па ипходяцихсл и и.югкшгга
к]>уга ЛИГА взапшю перпендикулярных пря-
прямых будем строит!, плоскости, нерпендику-
ллрпыв к ii.'iorkdctii круги ЛВГД, а череа
еопцм иосстап.'к'нпых ni'prieii.'uib'y.'iiipoii булсм
нролодить плоскости, mijKi.iMu.'ii.ubic> плоскости круга Л13ГЛ, п})(>до.-1>1>:1п их п обе
сторошл до пересечения с дпу.чи плоскостями, ирохпдтцими черел со^едптю, парал-
ВД В d
V
/^"^
i
\
\
\
\
л
м sj
/
N
Г
Pile. 10.
?
р ду , рдц р д, р
ВД, прямые. В со эти плоскости кик инутри odetix цилпндрнчепгих лоиерх-
постей, так и лне пх обрнпуют призмы, имеющие одинаковые высоты и и качестве основа-
оснований кппдргпъг, расположенные на прямых, пара.члельпых прямой ВД. Будем продолжать
дглиелис прямой ЛГ попилим до т<;х нор, пока дне прилегающие к ИЛ призмы не окажутся
меньше заданной величины; тогда соспнысчшля n:i лрилм телес-
телесная фигура, ош'.салная около тола, ограниченного поверхно-
поверхностями обоих 1(г!.'1иплро13) будет превосходить талую >ис вппсаи-
пую на лсличнпу, меньшую заданной: действительно, первая
Судет от.-цтчатьги от in'ojioii на леличпиу двух прилежат их к 13Д
нрм:!м, так к;п< леем (хггнлмшм лриампм ouvciDinoii фигуры
будот соосн(!тствопать такое же количество ранных призм
оипсанши! фмгу!<ы. rj
Siitl-m вплетем в полукруг ЛВГ параболу .А13Г и через
T04KFf ее иересечепии с пмямммн, параллельными ВК, проведем
прямые, пара.чле.чьные Л Г, продолжая ах указанным ранее'
сирином.
После этого получатся две фигуры, из которых одна опи-
описана около сегмента параболы, о дру)ал впшана и него; oficoiiti
составлены ип пароллыюгргишоп, причем первая из них прево-
превосходит вторую на дпа прплокишкх к V.K параллелограмма,
причем все атм иарнлле.'ки juimmij будут ncmnpjio гоотпетстио-
иать упомянутым ранее, призмам внж'ашюн и сгшглшюё телсо-
пых фигур.
Теперь, если заключенное между диуми кклщгдричесчгнмп
поиерхиогтлмп тело не будет рппио диум третям куба, то оно-
Судет ii.ru болиии, пли меш.пк1. Пусть сикчила ояо будит, если
iiu:tM0>Ki{0, больше.; тогда куб ФЧ'Х Г будет менее чем полтора pa::a v.nvio!- тело, аиклго-
чениое момеду обоими цилиндрами
F
/
Г
\|
\
А
\
Рис. ii.
куГ, ФТХГ < ~ те.пд.
Впитпем в тело, как сказано, телесную фигуру и оштггм другую, и притом так,
чтоЯы oiiKcnciiinn фнгурл превосходила бы ппнепиную на леличнпу, м(!цыную разности
между этим телом и диуыя третями куба; тогда ^писанная фигура будет больше дпух
576 КОММЕНТАРИИ
третей куба:
2
вписанная фпгура> т- куба Ф'Р'ХГ.
о
Каждой квадратной призме, вписанной в тело, половина стороны основания кото-
которой M2i будет соответствопать образующая куб квадрат паи призма, иол опила стороны
¦осиопаиия которой MN, a имсота одинакова с пернои; при этом первая призма будет отно-
относиться ко второй, как кналрат МЗ к квадрату MX. Пусть при мая MN пересечет вписан-
вписанную а полукруг параболу в точке Л; было доказано (предложение XIV), что MN* будет
к МЗа, кап МЛГ к соответствующей ординате параболы МЛ:
Но как MN к МЛ, тан будет построенный па MN параллелограмм к построенному
на МЛ и имеющему высоту, одинаковую с той, которую имеет первый параллелограмм,
а так же и с той, которую имеют кпидратлыс приемы, из которых составляются вписан-
иые и заключенное между обоими цилиндрами tiki о и описанные около него телесные
фигуры. Теперь мы имеем диа рида пропорциональны:* величин, а именно вписанные
в цилиндрическое тело квадратные прдоми ME2 и вписанные в параболу параллелограм-
параллелограммы МЛ, причем каждом л в величии первого ряда соответствует имеющая ту же высоту
квадратная призма, из которых составляется куб, а соответствующей величине второго
ряда — находящийся с ней в том же самом отношении параллелограмм A1N, m которых
cocTiiu.quiiTCii содержащий параболу прямоугольник ЛЕ. Значит, как все параллелограм-
параллелограммы, из которых складывается параллелограмм ЛЕ, ко всем соответствующим параллело-
параллелограммам, Аромс двух, из которых складывается вписанная в параболу прямолинейная
фигура, так будут и псе квадратные призмы, ии которых складмвпется куб «ЬЧ^ХГ, ко
всем гоотлотствующпм прнамам, кроме двух, ид которых состаплиетси телесная фигура,
ышеакиая п заключенное мсисду двумя цилиндрами тело:
ларапл. ЛЕ : V иаралл. МЛ=куб ФТХГ : ^] призм. MS2.
И так кап состоящая из прилм МЕа телесная фкгура, вписанная в заключенное
между обоими цилиндрами тело, будет больше чем две трети Kj'oa, то состоящая из парал-
лелогрнммов МЛ фигура, пипешшаи в параболу, будет Больше чем две трети параллело-
параллелограмм;* ЛЕ:
•4 1 2
2j паралл. МЛ>-ГГ параля, АЕ;
а это же невозможно, поскольку » другом месте было доказано, что сегмент, заключаю-
заключающийся между параболой и прямой АГ, состав.чяет дье трети параллелограмма ЛК. Зда-
чит, заключенное между обоими цилиндрами тело не будет больше двух третей куба ФЧ'ХГ.
Пусть теперь оно, если возможно, будет меньше; значит, куб ФТХГ будет более
чем и полтора раза больше тела:
куб ФТХГ>4тс-та.
Тогда, опить описав и вписав вышеупомянутые телесные фигуры так, чтобы они раз-
НТТЛИС1. между co6oii на величину, меньшую тон, па которую две трети куба превышают
заключенное между обоими цилиндрами тело, мы точно так №е докажем, что все призмы,
заключающиеся в кубе, будут так относиться ко всем при:шам, сод(.'ржаи(нмси в описаи-
пой около тела фигуре, как псе параллелограммы, содержащиеся в параллелограмме АЕ,
ко всем параллелограммам фигуры, описашюи около сегмента, заключенного между пара-
параболой и прямой А Г:
^ призм MX : V призм MS*=V паралл. MN : Уттра/.л. AM,
то есть куб будет относиться к фигуре, описанной около заключенного между обоими
цилиндрами тела, как параллелограмм АЕ к фигуре, описанном около сегмента, заклю-
заключенного между параболой и прямой А Г:
*
куб ФЧ'ХГ: ^] призм М52^нира:1л. ЛЕ : V иарала. МЛ.
ПОСЛАНИЕ К ЭРАТОСФБНУ. О МКХЛШГЧЕСКИХ ТЕОРЕМАХ 577
Но куб ФЧ'ХГ будет более чем в полтора раза болг.те телесной фигуры, описалнон
около ааключепного мииеду обоими цилиндрами тела:
куб Ф?ХГ>-^- опис. фигуры;
значит, и параллелограмм ЛЕ будет более чем в голтора ра.ча больше фигуры, описанной
около сегмента, заключенного между параболой и прямой АГ:
3
чарами. А? > -^ опис. плшцпди;
это ;ко иолоаможио, так как доказано, что пмраллслограмм АЕ л полтора раза больше
сегмента, заключен кого между параболой и прямой А Г. Зцнчит, тело, заключенное меж-
между обоими цилиндрами, не будет и меньше дпух третей куба. Значит, если оно не может
быть ни бо-и.шо, ни меньше двух третей куба ФЧОСГ, то оно должно быть им равно; это
а трсбопалоеь доказать».
37 дрхимся
- О ПЛАВАЮЩИХ ТЕЛАХ
р отяосится к числу поздних сочиаепий Архимода. Оно uaimcano oupe-
делегто поздиео трактата «О равновесии плоских фигур», так кап в нем встречаются
ссылки на этот трактат. Оно написано позднее «Коноидом», па одно из предложений кото-
которых оно опирается, п, вероятно, позднее «Эфода», в котором содержится теорема о поло-
положении центра тяжести сегмента napa6o:ioii;ia. To обстоятельство, что конец второй книги
не получил окончательной отделки, позволяет думать, что мы имеем дело с последним
проиадедепием Архимеда.
Любопытна история того, как это произведение дошло до лас. Очень долго оно»
было известным только п латинском переиоде Вильгельма из Мербеке A215—1282), кото-
который сделал несколько переводов с греческого для своего друга, шшес-люго схоласт»
Фоми Аквмнского. Вильгельмом был сделан перевод всех сочинений Архимеда; руко-
рукопись эгого перевода была обиарумюпа в I88'i г. Лдлевтижш Розе в Батики некой библио-
библиотеке. Если верить словам Рожера Бзкоиа, ицписапшеги про него: «Hie VVillidmus Flemin-
gus, qui iiiliilrtovit digmirn neque in scicnliis пецие in linguis (этот флимипдец Вильгельм,
не .чнашими ничего достойного им в иауках, ни а языках)», то Вильгельм из Мербеке вряд
ли хорошо ионим».! Архимеда (хотя относительно знания Вильгельмом языков Вокоп
определенно не прав). Греческий текст был открыт только в 1905 г. Гсйбсргом в Кои-
стактштполычеом палимпсесте, сохранившем для нас примерно около трех четвертей
текста Архимеда; утраченный текст воспсшистся но переводу Мербеке.
Сочинение «О плавающих течах» состоит из двух книг; в первой свободпая поверх-
поверхность воды считается сферической, а во второй— плоской.
Первая книга состоит из девяти предложении. Два первых устанавливают, что сво-
свободная поверхность ооци, огсружа/ощей Землю, ял.тпется сферической, причем центр
сферы совпадает с центром Земли. Хотя сферичность Земли и вообще мира была признана
еще греческими философами эпохи Платона и Аристотеля, тем не менее против результата
Архимеда, по-видимому, восстал даже его друг Эратосфеи Кирепский, основатель мате-
математической географии. В первой книге «Географии» Страбоп иишет: «Ри:>ве не смешно
теперь видеть, кап математик Эратосфсп отказывается прислать установленпый Архиме-
Архимедом II сочинении ^О плавающих в жидкости телах" принцип, что поверхность пгякой покоя-
покоящейся жидкости принимает форму мара, центр которого совпадает с центром Земли,
а подь это принцип, который теперь принимается всяким мало-мальски знающим мате-
математику» (Географии, книга I, гл. 111, 11).
Первое предложение 2-й книги формулирует принцип ареометра, а остальные
девять рассматривают уклонил рапнокесни плавающего в жидкости сегмента параСо-
лоида. Тракгоика вопроса. Архимедом явлпетси чисто физической. Архимед устанавливает
иоложоние равновесия тем, что определяет, будет ли тело, отклоненное от этого положе-
положения, возвращаться в него или ист; таким образом, определенные положелия будут соот-
соответствовать только устойчивому рапиош:сию. Первые четыре предложения (II—V) ка-
касаются вертикальных положений равновесии, следующие четыре {VI—IX) — ия клял них
соложений, когда основамио сегмента целиком находится или внутри, или вне Жидкости;
последнее предложение дает общий разбор вопроса о возможности положении раыюлесия,
когда поверхность жидкости также пересекает плоскость основания плавающего сег-
сегмента. Изучение последнего предложении показывает, что Архимед тлел лутом, лишь
в чистиостих отличающимся от того метода, который бил установлен во второй Половит?
XIX века (теоремы Дюпена — Давыдова); однако нельзя согласиться с мнением одного из
перепндчиков Архимеда, пмспио II. Фср-Экке, что «:>ти предложения удивительным образом
выражают всю ту теорию метацентра, которая должна была освободить всю теорию ко-
кораблестроительства от прежнего эмпириями»; наоборот, А рхимся чисто физически проперял
условии устойчивости равновесия, не обращаясь ни к какому теоретическому критерию.
Б новейшее время приходится слышать мнение, что иырабогапная Архимедом тео-
теория по имела никакого практического применения и что было бы лучше, если бы Архимед
\
О ПЛАВАЮЩИХ ТЕЛАХ 57а
разработал условия равновесия бесконечно длинного параболического цилиндра, иными
слонами, решил бы то, что теперь насыпается lj.jockou задачи") гидромеханики. По суще-
сгпу, Архимед и решал такую задачу, поскольку для тела вращения все плоские сечения
чере.-i вертикальную ось равнозначны, так что достаточно рассмотреть условии равнове-
сия для колебаний тела в плоскости какого-нибудь одного из этих сечений.
Это обстоятельство заставляет критически отнестись к старому, сохранившемуся
у Витруяия рассказу о том, кап бил огкрыт закон Архимеда. 13 тексте Витруния
(«Архитектура», книга IX, гл. 3) говорится:
«Во время своего царствования в Сиракузах Гиерон, после благополучного окон-
чашш всех своих мероприятий, дал обет пожертвовать в какой-то храм золотой венок
бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное
но в«су количество зилота. В назначенный день мастер принес спою работу царю, который
нашел ее отличыО выполненной; после взвешивания венок окапался соответствующим
выданному весу ио-'юта, ни при испытании последнего на пробирном камне оказалось, что
мастер часть золота заменил серебром. Царь был ичеиь раздражен stum обманом, но не
будучи в состоянии уличить мастера ь едшшниоп им хрансо, попросил Архимеда приду-
придумать дли итого способ. Однажды, когда целиком занятый :>тим делом Архимед садился
в ванну, oir заметил случайно, что ио мере погружения его тела в поду последили перели-
Ba.'iacii через край- Это наблюдение сразу позволило ему налти нужную идею, и радость
настолько наполнили иго душу, что он сралу выскочил пи ванны и, бегая голым т> дому,
кричал, что он нашел то, что искал, говоря по-гречески: ..Эврика! Эврика!"»
Если обдумать атот рассказ более и лимитен ь и о, то становится ясным, что к откры-
открытию закона Архимеда он никакого отношения не имеет. Чтобы уличить недобросовестного
ювелир», Архимеду было необходимо определить объем немца и сравнить его нес с весами
сооть-етстпушщмх объемов серебра и золота; как ясно из всего рассказа, объем венца был
определен по киЯччсстау иытисксииий води.
Канона бы ни была первоначальная причина зарождения закона Архимеда, нрядли
можно думать, что единственным его практическим приложением было уличение недобро-
недобросовестных мастеров. Полибий пиш(!т, что при обороие Сврнкул Лрхнмгд при помогли
хрюков И рычагин нриподымя.-i rf опрокиднвпл корабли римлян: для того чтобы построить
вужный для этого механизм, необходимо провзвьсти его расчет, последний мсп невозмо-
невозможен без »нинии закона Архнмсдц.
[1] «Погрузившись же, тело не будет двигаться (о'<ТQrp&tal) вниз, так пак все
части жидкости, находящиеся па одном уроене (тя l? 'iot)i3 netfiEva), будут давить одина-
одинаково вследствие того, что тело является раанотяжелым с жидкостью»,— ото место иногда
толковали и том смысле, что равнотяжслое с жидкостью тело будет л равновесии только
у поверхности жидкими, а не в любом положении л ну три жидкости, и соответственно упре-
упрекали Архимеда п ошибке. Такого род:) толкование появляется необходимым; дальиейшие
слова ой один-ановости давления, то есть об отсутствии побудительной силы для движе-
движения, шжазыпают, что мысль Архимеда заключалась в том, что движение вниз считалось
невозможным именно ве-ледстнио отсутствия причины для движения.
[2] Установленные- уже в XIX пеке теоретические положения, необходимые для
решения поставленной задачи, таковы:
Если тело легче жидкости, то плоская фигура, отсекаемая в теле продолжением
¦урошш жидкости, носит название плоскости плавания: так как doc жидкогти и оЕп.кме
погруженной части равняется весу псего тела я вес тела постоянен, то объем чясти тела,
отсекыомон плоскостью плавания, тоже будет постоянным, как бы ни наклонялось пла-
плавающее в жидкости тол о. Огибающая всех илоглсостей плана мня называется noetpxno-
стыо сечении: это будет геометрическое место центров тяжести плоскостей плавания.
Геометрической место центров тяжести рапных объемов, расположенных под раз-
различными плос7;оетями нлалапия, намывается поверхностью центров; касательная плос-
плоскость к поверхности центров параллельна плоскости плавания, которой соответствует
точка касания; нормаль к плоскости плавания будет однонремснио нормалью» к EOBipx-
иости центров. Так как перпендикуляр, опущенный на плоскость илаиниия из центра
тяжести, будет нанраплен но вертикали, то 'разыскание положений равновесия плаваю-
плавающего тела сводится к проводепию ил центра тяжести нормалей п поверхности центров;
каждой такой нормали будет соответстволать определенное положение равновесия.
Условия устойчивости определенного положения равновесия формулируются так.
Проведем чирез ццрмпль к поверхности центров илогаость, которая рассечет эту поверх-
поверхность центрон по некоторой кривой; направления нормалей к поверхности центров будут
совпадать с нормалями к кривой еечения. Таи как сферический сегмент, расг.митрииагмый
Архимедом, имеет ось симметрии (плоскость плавании будет окружностью), то центры
кривизны всех таких линий сечения будут одинаковыми; бесконечно близкие к основная
(вертикальной) нормали линии действии давлений поды, совпадающие с направлениями
нормалей к поверхности центров, будут пересекаться в одном и том же центре кривизны;
этот центр кривицпы можно пршштг» за своего рода точку подвеса для .плавающего'
37*
580
Комментарии
в жидкости тела; эта точка насыпается метацентром. Чтобы устойчивость равновесия
была обеспечена, центр тяжести плавающего тела должен быть оияее метацентра; если
целтр тяжести находится нише метацентра, то равиол1;сис будет неустойчивым.
Когда сферический сигзгонт плавает выпуклостью книзу, поверх постг. центров будет,
очевидно, шаропой поверхностью с центром, гоппаднюшим с центром сферического сег-
сегмента; радиус же равняете» расстоянию ОА от центра сферической поверхности сегмента
ДО центра тяжести А погруженной части. В нашем случае метацентр будет и точке О,
центр тяжести Г сегмента будет находиться ниже О: сюсдонательио, положение равнове-
равновесия будет устойчивым.
Когда сегмент будет плавать выпуклостью кнкрху, то центр тяжести Г всего сег-
сегмента будет лежать ш.тше ого геометрического центра О. Пусть А Судет центр тяжести
находящейся вне воды части сегмента, расстояние ()А будет постоянным; мы считаем его
известным, когда отношение плотностей плавающего тела и жидкости будет видано.
Рис. 1.
Рис. 2.
Также можно считать известным объем погруженной части и положение ее центра тяже-
тяжести В. При отклонениях сегмента от положения равновесии центр тяжести А будет пере-
перемещаться но окружности радиуса OA^g, который можно считать известным, а центр тя-
жести В — по кривой Вр% которая, как легко доказать, тоже будет окружностью; поверх-
поверхность центров будет поверхностью вращения, образованной этой кривой вокруг оси АС.
Пусть Г — центр тялессти всего сегмента; если отлглиспио весок свободной и погру-
погруженной частей равно ¦/. (это шюлме определенная величина, папиешцая от соотношения
плотностей т«.та и жидкости), то отношение расстояний аГ и рТ будет постоянным:
аГ:рг=-АГ:ГВ=1:к.
Таким обрааом, кривая Bf> может быть получена из окружности Ла подобным пре-
образопаннем, причем центром подобия служит точк.ч Г, а коэффициент подобия отрица-
отрицателей и равен — х, так как аир" лежат по разные стороны от Г. Кривая вр будет
окружностью, цшгтр М которой лежит на прямой АС так, что центр подобия Г оказы-
оказываете» между М н О. Если расстояние ОГ —6, то МГ=хб. Таким образом, метацентр М
лежит выше центра тяжести Г н равновесие; будет устойчиным.
Мы видим* что кривая цептроп (сечопие поверхности центром) состоит из двух дуг
окружностей, соотпетствующих положениям плапанпя сегмента, когда плоская его часть
находится целиком в жидкости или вне жидкости. Отметим, что Архимед умел па ходить
объемы сферических сегмептоп («О паре и цилиндре», кп. II, предложение П) и положе-
положение центров их тяжести («Эфод», предложение IX); следовательно, в обоих этих случаях
он мог при любом соотношении плотностей плавающего тела и жидкости провести псе
вычисления до контра. В Том случае;, когда поверхность жидкости пересекала плоское
оглюпанис сегмента, уже нет осношший думать, что Архимед и теперь мог определить
объем и положение центра тяжести погруженной части тела; екни бы и в этих случаях
«и построили соответствующие .кривые центров, то получили, бы еще два положения
равновесия, но последнее было Вы неустойчивым.
[31 Для понимании" текста предложений второй книги пужио злать некоторые свой-
свойства касательных к параболе, а Именно:
Если парабола отнесена к системе координат, где начало соцпадаст с кершипой,
ось абсцисс идет но оси параболы, а ось ординат по касательной к параболе в вершине,
так что уратшецие параболы будет у2=2/>зг, то для касатс:н>пой, проведенной и любой
точке параболы, субтангенс будет равняться удвоенной абсциссе точки касания, а суС-
иормиль имеет лостоянпую величину, равную параметру р.
14) Идея архимедова доказательства предложения П заключается в том, что
•если ОР < р, то нормаль и точке касания 11 пересечет, ось ON между Р и N, так что
угол Р1Ш будет острым (рис. 11, сгр. 33E).
О ПЛАВАЮЩИХ ТЕЛАХ
581
Пусть ОКК прсдстапляст сечение параболоида плоскостью, проледеппой через его
ось Ой (рис. 3), пусть уравнение этой параболы в координатных осях Оху будет: уг=2рх.
Пусть ост. параболы ОВ будет равна -^-Ь; согласно доквааншшу Архимедом в «Эфоде»
(предложение V), центр тяжести Со всего сегмента будет лежать па расстоянии ОС0=Ь
от вершины сегмента О.
Опустим сегмент в жидкость так, чтобы его ось была вертикальна; пусть он пигру-
о
зитея па глубину OA—-J а, так что прямая а'Ал' будет представлять уровень жидкости;
вес жидкости в объеме сегмента а'Ла' будет равен несу всего параболического сегмента;
центр тяжести Ct этого сегмента будет лежать на расстоянии ОС1=а.
В предложении XXIII «Коноидов и сфероидов» дока.-швгштси, что объемы сегментов
параболоида пращештя, отссчешшх плоскостями, проведенными кап угодно, будут рав-
вы, если рапш.г оси этих сегментов. Л так
как все диаметры параболы параллельны,
то поверхность сечений параболоида (оги-
(огибающая плоскостей плавания, отсекаю-
отсекающих риншдо объемы) будет таким же па-
раболсшдом, лишь едпинутым лдоль оси х
па расстонние О А ¦= -^- а. В сечении этого ,
параболоида с плоскостью чертежа полу-
получится парабола AD'M, уравнение которой
будет:
¦§¦<.)-
По существу, нам нужна лишь часть
АТУ этой цараГшлы шинпь до точки D'
касании с проведенной из К прямой; при
дальнейшем ирлщсшп! параболоида угпл
его К погрузитсн п жидкость и слпдукицая
часть поверхности сачеикй уже ле будет
параболоидом AD'M.
Так как центры тяжести сегментов
параболоида л;»кат на осях на расстояниях
двух третей от першиым, то поверхность
центров и пересечении с плоскостью ч(;рте-
жа даст параболу C^E'L, иоторац будет
представлять основную параПолу, сдвину-
сдвинутую Biipuiiii ja« расстоиние 06^ = 0; ее
уравиеяие будет:
B)
ее, соответствую-
Рис. 3.
нам нужна лить часть
щая дуге С.Е'.
Так кик ниже оси Ох мы будем иметь такую же симметричную фигуру, то достаточно
рассматривать лишь полуплоскость с иололтотсльпымы координатами jy.
Чтобы найш положения равновесия, ач.г должны из центра тяжести Со сегмента
провести нормали к линии центров С,/:', и.шк и.; них лишь те, которые пересекают дугу
CfE', а также ей симметричную, лежащую ниже оси Ох.
Дифференцируй уравнение B), получим:
* dx p>
тангенс угл« наклона касательной к параболе будет равен —, а угловой коэффициент
V
нормали ——.
Уравнение яормали, проведенной из точки Со, в текущих, координатах х', у' будет:
582
КОММЕНТАРИИ
Решая это уравнение совместно с уравнением B), находим координаты точек пере-
пересечения нормали с параболой 6',?''. Так как в точке пересечения у=у\ *=*', то мы
будем иметь:
:8~" Р>
Первая пара решений соответствует положению равновесия ири вертикальной оси
ОВ, пторап пара (пли, лучше сказать, две пары) решений будет соответствовать положе-
положению равновесия, когда ось ОБ сегмента отклонится от вертикали и ту или другую стороиу
на некоторый угол а. Нужио помнить, что
птирая пара peineuiui может иметь место,
только если проведении я на Со нормаль
пересечет параболу C,fi' между С, и К'.
Одно из необходимых условий суще-
существовали» положении равновесия, соответ-
соответствующего второй ппрс решений, будет
заключаться d том, что подкоренное выра-
выражение для у.2 должно бы-ib положительным
(если оно рашю нулю, то нерван и втора»
пара решения сшшадают):
или
—р>а.
В предложении II мы имеем ON=
3 3
=:OJB=.-^- Ъ пе превышает — -р, иными
словами, Ъ<^р. Это показывает, что в
рассматриваемом случае возможно лишь
положение равновесия, в котором ось
г-егм сита керт и кал ъла.
Будет ли ато равновесие устойчи-
устойчивым? Вместо чисто физического доказа-
доказательства Архимеда мы могли бы восиоль-
зоиатьем понятием метацентра, определись
радиус крнпипиьт линии центров или основт
пой параболы j/2=2pz в ее вершине, кото-
Рис 4 рый, лак известно, рапен параметру р.
Если от точки С, отложим отрезок C,Af—p,,
то расстояние ОМ метацентра будет равно
а+р, так как fc</>, то ири любом значении а отрезок ОМ будет больше отрезка O6'0=fc,
иными словами, метацентр будет лежать мине центра тяжести Сл сегмента.
[5| В предложении [11 Архимед рассматривает случай, когда сегмент плавает, имен
основании целиком погруженным л жидкость. Объемы сегментов параболоида вращении
относятсн, как квадраты их осей («Коноиды и сфероиды», XXIV). Если сшюстаиить это
а" ОА*
с первым предложением рассматриваемой второй книги, то отношепие ту , равное т-^
(рис. 3), даст нам отношепие плотностей плавающего тела и жидкости.
Пусть сегмент опущен основанием КК и жидкость так, чтобы ось его ОВ была вср-
тикалъна, и уровень жидкости пойдет по примой Ь'Ь' (рис. 4). Объем сегмента Ъ'Ь'КК будет
paDen объему сегмента Оа'а'; если, мы обозначим отношение 7в=^2 и примем объем
v
всего сегмента ОКК за единицу, то
объем сегм. Оо'о'=объсм сегм. Ь'Ь'КК—к2,
а объем сегм. Ь'ОЬ' = 1—А-3.
Рассмотрим сегмент ОЬ'Ь', находящийся над поверхностью поды. Для оси OBt
мы имеем:
OBJ _ l~ftB
OB*
О ПЛАВАЮЩИХ ТКЛАХ 583
откуда
и, наконец,
г
Огибающая последовательных положений поверхности плавания будет параболой
°, уравнение которой
D)
2
Центр тяжести сегмента ОЬ'Ь' лажодится на оси ODV на расстоянии 0С3-=^ -g-O.Bi=
= ¦j/fci—as; при качании оегмеятв около вертикального положения равновесия ои будет
персмош,атьси по параболе Л'С3А\ уршшснио котнрий будет:
y*=--2p{z— /feCT^s). E)
Теперь мы можем заняться построением липни, но которой будет перемещаться
центр тяжести сегмента Ь'ККЬ'. Абсцисса ОС» отого центра можст быть найдена из соот-
соотношении
ношении
A—
откуда
з ¦- ¦
Аналогично ¦ .;„ .
0 = Ь— /Ьа—а«=6 A— |А1^Л«).
Отсюда видно, что отношение
~ Л* '
го есть обратному отшшелшо объемов соответствующих сегментов, как исследовало
и;кид<чт[,.
Чтобы получить пужную нам ветвь ЕгСй лиаии цеят^юв, перестроим параболу
NC3N около центра подобия Со так, чтобы расстоншш СОСВ увеличились в отношении
<1—/ia) : A2; d реау.чьтато получится ироходни^я через точку С2 парабола, иарамстр
которой увеличится в том же самом отношении, то есть будет равен:
1 — *а
Уравнедие этой параболы, сыт пачало координат взять в точке 6'„, будет
то есть
F)
Урапнепие "нормали к этой параболе, проведенной из начала координат С„, полу-
получится, как а раньше:
584 КОММЕНТАРИИ
Так как в точке пересечения нормали с параболой (С) у — у' и х—х', то получаем два
решения:
1) If=0,
Первое; отвечает вертикальному положению оси ОВ, а второе — возможному на-
наклонному положепшо. Соответствующая ордината ;/ определится после подстановки х
в уравнение F);
G)
Условия действительности значения у требуют, чтобы
P<.b(i — Yl—А-*),
или
16] Так как Архимед рассматрилпет только те положения равновесия, л которых
оспопаптте сегмента находится целиком в воде или шге ее, то нам понадобятся лишь части
С1Е1 и C2.fe'2 парабол центров, котормо определятся так:
Поскольку в обоих случаях плавании в лаклоилом положении конец оегшиапин
сегмента в пределе должен лежать на поверх intern воды, то из Л' иужпо построить каса-
касательные к параболам ЛИ и ВЛР и из топки касании параллельно оси Ох провести прямые
до пересечения с параболами центров, имеющими вершины соответственно в С, и С2; точ-
точки ?t и Еъ и будут концами нужных нам дуг.
Если исршииа О сегмента погружена н иоду (рис. 3), то мы найдем крайнюю точ-
точку /?, линии центров, если построим касательную KD' к параболе AD'Al а Д1ровсдем ТУЕ'
параллельно Ох.
Уравнение параболы AD'M будет
координаты точки К, лежащей яа параболе уя—2рх,
Искомое уравнение касательной будет:
f (у)
решая оба уравнении совместно и полагай, как и нише, х=х% у—у\ будем ииоть:
Для искпк«еиик х умножаем кторск: уравнение на 2 и ив резумьтотд кычитаем
аервос:
у-—2у V5pl>=2pa
откуда
Так как из точки К можно привести к парабол» две касательные — вправо
и влево от К, а нам нужна только левад, то борем для у меньший корень:
у — Узр ( УЪ — У а).
Максимальное значение квадрата ординаты, соответствующей положению равно
весия, будет:
О ПЛАВАЮЩИХ ТЕЛАХ 585
для точки пересечения нормали из Со с линией центров С El. мы имели z=fc—•/». Подста-
Подставив ото аиачоинс в уравнение B), получим:
у*=2р{Ь- а—р).
Разность этих величая должна быть положительна:
Vtaa*—У2=Р {36-| За—6 УпЬ—2Ь+2а-\-2р},
то есть
Ь-\-5а-\~2р—В /^>0,
или
вЬ — 5« ¦ Ь=Ь{УаЬ—а) (б- /об) = 5 /a (/?- [/"о) — у'
Таким образом, оелгг принять по внимание условие; C), то дли возможности плава-
ыин сегмента в наклонном положении мы должны иметь:
4 С1-у у)Eкт' (8)
¦ Случай, когда сегмент плавает с целиком погруженным оеггопасшем, можно нри-
вести к предыдущему, если иместо 013 = -^-а па риг.. 3 взять 013^=-^- а' (рис. 4); тогда
анапогичлос уелсшие позможиости илаиать в пак.чошгом положении паптгатстся так:
где
Мы уста попили следующие иозможяын положения ралиопсспя:
1) два соотлетствующих иертикалындау no.'iожению рнвновесия оси ОН,
2) дна нак.'Ш[Шых положении с Bepmntioii О сегмента а жидкости,
3) диа наклонных положения с вершиной О ште жидкости.
Кроме зтого, имеются еще два положения, когда один из углов сегмента KtK лахо-
дился вне жидкости; они соответствуют линиям, соединяющим точки Ji'i и Ег- Эти поло-
положения Лрхпмод сопершеппо не рассматривал.
Дли иыясисппя условии устойчивости найденных положений равновесия нужно
определить радиусы крилиаиы линии центров и соответствующих точках. Н точках Ct
и 6'2 главная нормаль социалист с осью параболы центров и равна ее иараметру; следова-
I l(i
телыю, расстояние метацентра от линии центров будет р в точке С, и р' = р 8 в точке С2.
Таи кап при устойчи-пом рапнопег-ии центр тяжести Со должен лежать ниже мета-
метацентра, то мы будем иметь:
В поло/копии С\ высота метацентра равна р, высота центра тяжести Си будет
С,С0=-6—о. Услоние устойчипости требует:
Ь—
то есть
Если
то это равенство будет иметь место независимо ог а, то есть и от плотности плавающего
тела. В этом состоит предложение II второй книги.
В положении С2 параметр р' будет:
586. КОММЕНТАРИИ
расстояние С„Сг цептра тяжести сегмента (см. стр. 583):
Условия устойчивое:™ требуют, чтобы
или
, Если
то равновесие будет устоГштвым шяависимо от илоткостя плавающего тела А2; в этом
состоят предложение III иторой книги.
[7| Пол се общие случаи устойчииого ралиопссия требуют рассмотрения плотности
плавающего тела, иными словами, глубины л его погружения. Условие устойчивости
пишем н виде
4*><ф-1|а. A0)
i . Преобразуем его так, чтобы выделить глубину в:
: . • 3 3 ....
2
Разделим обе часги'яа'й и возведем в квадрат, помня, что гг"**—плотности пла-
вшащего тела:
-. Таким образом, вертикальное положение равновесия останется устойчивым, если
плотность плавающего тела d будет равна или больше отношения, стоящего в левой части
неравелства:
(ЬУ
В OToirf состоит предложение IV Архимеда.
|8| Когда согмент плавает в вертикальном положении основанием кверху, условием
устойчивости будет:
3 , 3
где ^—Ь у1-4'=т-^6*—а?=-^-а' представляет, как мы видели выше, высоту части
Zt ? Z*
сегмента, находящейся вые ншдкости; объем погру;кеипои части будет, как мы видели,
равным объему сегмента параболоида с высотой-^- («—а').
Написанное выше равенство мы можем преобразовать так:
О .ПЛАВАЮЩИХ ТЕЛАХ 587
C "\2
-„-6 ) , получим:
В левой части стоит илотпость d ллапающего тела по отношению к ишдкости; в пра-
3 3 3
вон — b будет ось сегмента, а — Ь—— р представляет разность между осью и полу-
dt d* Z,
торным параметром.
Мы получаем результат, сформулированный в предложении V.
Положение равнокссия сегмента параболоида, обращенного вершиной вверх и с вер-
вертикально направленной нгмо, будет устойчивым, если плоти ость плавающего тела будет
не бол г.[по отношении разности квадратов оси сегмента и избытка оси над полуторным
параметром к" кпадрату оси сегмента.
Доказательство V предложения у Архимеда строится совершенно аналогично дока-
доказательству IV; нндо только учесть, что прямая IKD раина -\уу Ья— а*.
Определим область устойчивости равновесия сегмента параболоида при вертикаль-
вертикальном положении осп.
Если ось пе более полуторного параметра, то равновесие будет устойчивым в вер-
вертикальном положении, будет ли основание сегмента ноликом вне или внутри жидкости.
Если ось более полуторного параметра, то положение устойчивого равновесия зави-
зависит и от шютппсти плавающего тола. Если принять плотность жидкости за единицу, то
плотность тела будег меняться от 0 до 1. Обозначим отношение ( —т-? j через е. Тогда,
если плотность сегмента будст большее, то устойчивым будет вертикал ъное положешие
•осноиаиисм вверх; если же плотность Судет- меньше 1—е, то устойчивым будст положение
равновесия основанием вниз. Можно 'иоставить вопрос: при каких соотношениях Ь и р
вообще- исфтикнлмюе положение сегмента будет устойчиво?
Если е——, to при d>e устойчивое равновесие будет а положении основанием
вверх, а при й<е—основанием выи»; при d=e возможны оба положения рашювесия.
Если е «С-^-, то вся область изменения d разделяется па три части: первый интервал
будст от 0 до е, второй от е до 1—е и третий от 1—е до 1. В первом интервале устойчи-
устойчивым будем положение основанием иниз, во втором возможны оба положения, равновесия,
в третьем будет устойчивым положение основанием вверх.
Кепи е >• — , то интервалы будут от 0 до I—е, от 1—е до е и от е до 1, прнлем сред-
среднему интервалу не будут соответствовать никакие возможные положения равновесия
с вертикальной осью.
[9| В предложениях VI—IX Архимед определяет положения равновесия, когда
ось сегмента расположена паклсш/ro. Накажем, что если равновесие пагшогкно, то оио
всеггда будпт устойчив им.
Для !>той цели нам нужно определить высоту метацентра, иными слонами, радиус
кривизны сечении поверхности центров; как мы видели, ата линия будет параболой,
одинаковой с параболой, полученной ь сечении параболоида вращения.
Если уравнение этой параболы
Уг = 2рх,
то, как мы знаем из математики, радиус кривизны с л точке, ордината которой равна у,
'будет
„
Рассмотрим положение равновесия, соответствующее случаю, когда основание сег-
сегмента будет целиком находиться вне поверхности жидкости (рис. 5).
Пусть APOL представляет сечение параболоида плоскостью чертежа, точка О будет
тершиной параболы, ON — осью ее, точка if, лежащая на расстоянии ОЙ=—- ON, будет
588
КОММЕНТАРИИ
центром тяжести всего параболического сегмента. Пусть AS представляет сечение поверх-
поверхности плана пня, JCZ — параллельная ей касательная к парабол и в Р; тогда FP лредста-
2
вит oiM. погруженного в жидкость сегмента, а точка В, лежащая па расстомнин ВР =-5- PF,
о
будет центром тшкости сегмента ASOP. Точка В — центр тяжести погруженной части —
принадлежит поверхности цпнтрои, сечение которой будет параболой, одинаковой с пара-
параболой АРОТ.. Прямая Ш{ должна быть пер-
пендпкулярпа к касательной СП л В к атой
параболе, параллельной сечению поверх-
поверхности плавания AS\ этого требуют условия
равновесия. Равновесие будет устойчивым,
если расстояние BU будет мслыпе высоты,
метацентра или радиуса кривизны парабол»
APOL, одинаковой с лтшией центров.
Мы имеем:
По Л1), как субнормаль, рнпна парамет-
параметру Pi й BD—.PE представляет ординату у-
точки Л касания прямой СИ и линии цент-
центров. Таким образом,
а высота мстацелтра
Так как множитель -—' g больше единицы, то q > Wf, то есть устойчивость равяо-
весия обеспечена.
И» чертсяса видно, что
или в наших обозначениях
Ь>р-\-а.
что даст гоометричкогси уже выведенное нами условие возможности равновесии ирю
наклонном положении осы
К _ V -
6 — Я>/>. " ~^—-к =_ 2
Обратимся к случаю, когда сегмент
плавает, имея основании це:шком ногру-
жсиным в жидкость (рис. 6). Пусть при
обозначениях предыдущего чертежа та же
В предстапляст центр тяжести части сег-
сегмента ЛОРА, находящейся над поверхно-
поверхностью AS жидкости, расстояние PB——PF.
Точка Л, лежащая па расстоянии ОН = 6,
будет центром тяжести всего сегмепта, а
точка С прсдстанл пет центр тяжести по-
погруженной части; опя лежит на линии
(параболе) цилгроя ДЛЯ этой последней.
В положении равиорссяи точки В, 1! и С
должны лежать на перпендикуляре к ли-
линии плашшия AS n нараллелг.нмм ей каса-
касательным KZ и С/1. Рассуждении, аналогич-
аналогичные предыдущим, убеждают нас, что ЛЕ
есть параметр р параболы APOL, a UD —па-
—параметр р' параболы центров (дейстпителыю,
1W: ПР.—ПС: ИВ=от ношен иго объемов сегментов APS wAT.S). Так лак CD представляет
ординату точки касании С прямой CU с линией центров погруженной части, то ЛС=
Рис. 6.
О ПЛАВАЮЩИХ ТЕЛАХ
589
р'а, что, очевидно, будет меньше радиуса кривизны q' линии центров и точке С:
г
[101 Предложении VI и VII посвящеяы определению наибольшей леличггш.1 Ь,
.при которой согмеит может шшнать так, чтобы его основание но пересекалось
поверхностью жидкости. При уста-
установлении этого предала Архимед
пользуется леммой, доказательство
которой не сохранилось в дошедшем
до пас теисте. Эта лемма заключает-
заключается в следующем.
Пусть через кикуго-нибуд!. точ-
точку параболы В проведена секущая
П& и параллельная цй касатель-
касательная ЕЗ, через точку касапття R про-
проведена прямая EZ, параллельная
оси, и в какой-нибудь точив Г оси
восставлен перпендикуляр ГД; тогда
отношение EZ: ЁД будит больше
или ран но отношению А Г : ГО, где
А есть основание перпендикуляра,
¦опущенного из точки В на ось
(рис. 7).
Приподим доказательство этой теоремы, данное Хизсом. Из точки касания Е опус-
опускаем перпендикуляр ЕМ на ось О А; тогда по свойству касательных к параболе будем
иммь:
МО = ОН,
гдо S есть точка пересечения касателытой ЕЕ <"• осью.
Нам нужно доказать перавенство
EZ:ЕД >АГ:ГО
¦ - EZ.1'0 >АГ-ЕЛ,
"¦>. -г-
EZ-ГО — АГ-ЕД>0.
Рис. 7.
или
то есть
Имеем;
Таким образом,
АГ-ОА—ОГ,
ЕД=01'~0М.
EZ.Or—АГ-ЕД = Ег-ОГ—ОА-ОГ — ОМ-ОГ+ОГа+ОА-ОМ=
= ОГа—ОГ @А-1-0М—EZJ+OA-OM.
Но ОА+ОМ=ЕОЧ-ОА=ЕЛ, а ЗА—EZ=SA- se = A»; следопательно,
EZ-ОГ—АГ-ЕД = ОГа—ОГ-А0+ОА-ОМ.
Затем из подобия треугольников EMS и BAG имеем:
А0:АВ=МЗ:ЕМ.
или ' -'. -
Ав:АВ=20М:ЕМ."
Но 0М=к, ЕМ = у; если уравнение параболы будет у*=2рх, то АВг=2р-0А,
•а ЕМ"=2р-0М. Возведем обе части нашей пропорции в квадрат:
•откуда после сокращений:
А0«:АВ«=4ОМ»:ЕМ*,
Ав2 : 2/i.OA =4OMa Яр ОМ,
А0*=4ОЛ-ОМ.
590
КОММЕНТАРИИ
Теперь
или
Ег.ОГ-АГ.ЕА=ОГ*-ОГ-Ле+^-,
EZ ¦ ОГ - АГ ¦ ЕД = (^ОГ -
wo будет или больше нуля при ОГ Ф —, или же рапш.тм нулю, если ОГ^*— .
Па основании атой теоремы Архимед паходит предельную величину отношения
Ь : р, соотпитстиующую плаванию сегмента, когда поверхность жидкости проходит через-
край оинопаиия.
Пусп. APOL (рис. 8) — сечвлио сегмента плоскостью чертежа, AS — поверхность
жидкости, ON — оси параболы. Проведем касательную ПР, нараллельпую АН, и IP,
параллельную ON; точка / разделит AS пополам. Пусть У будет центр тяжести
всего сегмента; при рыпиопесии перпендикуляр 1?В к касательной должен пройти
через U — центр тяжести погруженной части. Так как HZ есть ордината точки каса-
касания, то FZ представляет параметр р. Имеем.
OF^b, Pfl^a.
По доказанной лемме мы имеем
РН
14
NZ
ZO
Берем предела ими случай равенства и пе-
репнсывасы в наших обозяачешшх
(и
3
откуда
и. окончательно
Рис. 8.
„_!*.
Искомое предельпое соотпошепис можпо получитт, другим путем. Выясняя возмож-
пости плапаиия сегмента в положении, когда поиерхиость жидкости не пересекает осно-
основания сегмента, мы вывели неравенство (8) (стр. 585):
Р>-о 1-1/-Г
Определим максимальную возможную величину правой части; для этого нам придет-
придется искать максимум выражения A—z)[5z—1). Дифференцируя, находим
5A—г)— Eг—1) = 0,
6 - Q
откуда г ~ J74. При этом зпачении z наше произведение будет равно ~. Таким образом,-
4 2
прапал часть нашего неравенства при всякой плотности жидкости будет больше — b=-^ by
и ми получаем:
ваи
Р>-Тг{ -тгЪ ) =
.:•..!
О ПЛАВАЮЩИХ ТЕЛАХ 591
5 9 й "
Так пак JVF=-j= OJN, то A'Z=-? ON, &ZO=-= ON, шгыми словами, отношение
Л'2 : Z0=3 : 2.
Поскольку РП : Pl^IVZ: ZO = 3 : 2, а расстояние РТ центра тяжести Т погружен-
погруженном части удрллстворяе* пропорции РТ : /V—3 : 2, то РТ-^РН, иными словами, центр
тяжести Т будет или совпадать с Н (случай рашшпесия), или лежать между И u P,
то есть сегмент будет пеплывать так, что его основание будет над пмшгрхностыо воды.
То же самое будет иметь место, когда FZ-^p будет больше —ON, иными словами,
15
когда ON меньше -тгр\ » этом заключается теорема, сформулированная в предло-
предложении VI.
Может случиться, что перпендикуляр ZH ( ЙК. на рис. 1С, г.тр. 542) перепечет пара-
параболу правее точки касании П, a ix:i. IF погруженной части—ь точке Н, лежащее правее П
(птормй чаг/гный случай, отмеченный Архиме-
Архимедом). Тогда перпендикуляр DP пересечет продол-
продолжение III в точке Р, лежащей ищ|> правое Л,
и очевидно, что цептр тяжести й погруженной
части, находящийся левее Р па расстоянии
ТП —-т" 1П, будет и подавно левее нормали ФР,
так что течка А подымется над поверх иостыо
жидкости. Hi) существу, а-л> ритшосильно тиму,
что при малых плотностях плавающего тела
паклонпос положение равновесия, при котором
угол А лежит па полерхностп жидкости или
шике ее, является невояможиим.
[11] njiL\iJfOJKi;iine V11 доказывается conep- pjfc g
шенно лкалогичпо; второй упомянутый Архи-
Архимедом мучай равпосилеп тому, что при плот-
плотности плакаштпго тела, приближающееся к единице, невозможно положение рапновс-
сии, когда ъерхиий. конец основания сегмента будит находиться на пешеркиости воды
или выше се.
Не представит большого труда найти предельный угол, при котором тело будет
плавать, каснясг, поверхности жидкости лишь одпой точкой основания; для этого тре-
требуется определит!, угол наклона оси сегмента к поверхности жидкости при Ела-
в алии.
3
Пусть (рис. 9) О ЕВ будет парабола сечепия сегмента г. осью ОЛ—-^-h точка С пред-
представляет цептр тяжести сегмента (ОС=Ь), расстояние СМ равно параметру р, а кривая
3
LDL" представляет параболу плавании; отрезок ??) = ОЛ^=—о, а точка F — центр
тяжести сегмента ВЕЛ ( FD=^— J ; через точку F проходит парабола центров. В поло-
положении равновесия CF должна бить яорыалью к параболе центров, а параллельная ей пря-
прямая DN — нормалью к параболе плавания (ЬВ — сечение поверхности жидкости).
Прямую LK — абсциссу точки латания — обозначим через х. Так как 1(JV = CM — пара-
параметру р, то, обоуиачап угол KDJ4 черел Ц>, можно
t -KN - Р
По так м<с
. • --. {п _ KD = у
Отсюда
=
Но GK=-.2LK, a
LK^ON—KA'—OL = OC\-FD—KlV—OL=b-\-?-—p—|п=»Ь—р—а.
... ¦ Z A r ¦ ¦¦¦'"
592 КОММЕНТАРИИ
Таким: образом, окончательно
Эта формула даст величину угла наклона оси, при котором сегмент будет плавать
с основанием, находящимся впе Поверхности жидкости. Она одинаково применима и к слу-
случаю, когда сегмент плавает, будучи погружен, основанием в жидкость; только в атом слу-
случае нмд а нужно подразумевать дно трем оси сегмента, находящегося над поверхностью
жидкости.
Прсдольпап величина угла наклони оси к поверхности Жидкости upir плавании сет-
мепта, когда основание его кнеабтся поверхности жидкости только в одной точке, опре-
определится очень просто. Мы имеем:
Но мы видели выше (стр. 584), что наибольшая асличипа ординаты у> соответ-
соответствующая плаванию в указанном полоиссыии, рннма
Следовательно,
=
[12] В предложениях VIII и IX Архимед определяет аеличипу тангепса угла пла-
плавания.
Для возможности плавания в наклонном положении необходимо неравенство
ft—а>/>, или а<6—jb.
Плотность d плавающего тела по отношению к жидкости равяа ^-, но
d< >- _cw
или, поскольку ось cei-мепта ON=-=-b:
ом» ¦
Необходимое построение на оси Архимед ироиаводит отдельно. Отрезок IiD--=OIV
представляет ось сегмента, К — центр его тижести, КР — параметр р, отрезок TD=
'Л 3
=-^ р *); тогда отрезок BT=OJV—^-р представит линию, столщую в числителе пра-
.. ^
вой части неравенства для й. Так как плотность тела относительно жидкости d опреде-
определяется формулой
(ф-!-Х)а (уФ )
OJV* ОХ*
и ВТ—^г ИР, то отсюда следует, чго Ф<НР. Архимед полагает Ф равной отрезку
это будся наше а.
п о
*) Это нетрудно получить из елодующшс соображений. Ксли J.t'i'=- UP = -j {BD—KD—
3 OV 4 3
= -^K>.\ j KP)=OiV—-|K"P, TO rt>=HD—ЬГ. естественно. Судет равняться ^ А'Р. Точку Т
проще получить, исходя us точки D, пра помощи вычитания полуторного параметра КР.
О ПЛАВАЮЩИХ ТЕЛАХ 593
Архимед сгрншт угол ф по формуле
№* BP—PW ~ (Ь—р)—а *
После этого Архимеду остается лишь доказать, что лри таком угле наклона равно*
весис будет иметь место и что оно будет устойчивым. Он достигает обоих целей, доказы-
доказывая, что равновесие не может иметь места ни при больших, аи при меньших .'шнченпях
угла наклона. Его доказательство сводится к тому, что центр тнгкести Z погруженной
части не может лс?кать ни прайсе, ни левее перпендикуляра ГН, опущенного из центра
тяжести Г на касательную ИГ, параллельную поверхьости жидкости S2.
|13] Придяожснно IX является аналогичным приплонселшш V и VII; в нем также
фигурирует предельная вачнчина плотности
C \*
GW--?- p \
с тон только разницей, что теперь плотность плавающего тела должна .быть не меньше,
а бо.'и.шс этой тшличины:
В соотвегстнии с этим произойдут некоторые изменении в формулировке теоремы.
'Гак как теперь плотность плавающего тепа иредполстгается равной
С40"
то иен», что Ф нр(!д<!Т!1вляет, кап н выпгс, тщяму а, сиотпетствующую диум третям оси
сегмента, вьгстуиа[1)Щ(;го над поверхностью жидкости. Если вечгги рассу}ВДения примсии-
Tiuii.iio к этому сегдтонту, то псе докааатильство будет раэвив«ты;я нналогичио докаэатель*
стну предложении VIII.
114] Обширное и р и д л о ж с п и е X рассматривает положения равновесия при
4
параметре р, меньшем — ос-ir кегмонта,— значении, при котором еще возможно илава-
ние с. оснопмннсм, касающимся иоверхпости жидкости в одной точке. В атом случаи
в записимости от плотности плавншщего тела иоздншшм следующие лысеть положении
равиоиссия, обо:шичшшых в пашам пср>:подс Архимеда цифрами:
A) Ось сеглентн стоит перш нал ыш.
B) Ось сигмеита паплоина; осиоиаггш; пне поверхности жидкости.
C) То же; основание ние поверхности жидкости, касается последний и одной точке.
D) То же, оспоьанис jiaeceitaCTCH поверхностен) жидкости.
E) То же; иснопапис вне жидкости к касается поверхности иоследкой п одной точке:
(В) То ми»; осяовапис целиком пне жидкости.
[15] Для понимания дальнейшего na>iiiio представить себе физический смысл- обо-
значений рис. 22 текста (стр. 348). Точка К 1|р(?детавляет центр тяжести сегмента АОВЛ
/^
(ЫК=2КД); прямая КТ, равная ^ БД, предстап.тиот паиболыпую величину параметра р.
полсвкии. ВД —15, ДК=5 и КТ=4, то ТВ будет piuiini С; иными словами,
2 <>
ВТ——-ВА. Точк!1 S получается при помощи пос^тении В2 —-^- В1'; отрсяок 2Д=-
3 3
= ВД—132=-п- (])К—BF) = tj-KP или полуторному параметру р. Таким образом, В2!
представляет величину -^ (L -р), входящую в выражение , ..—r-j—'— ', если отношение
D0"
38 Архиисд
D0"
594 • КОММЕНТАРИИ
плотностей сегмента и жацкости болите этого ъианенпя, то возможно плавание сегмен-
сегмента п вертикальном положении (случай 1). Параболы Л ЙА и AJSI представляют нскоторув;-
аналогию с современными параболами и лапания (сеченый) и центров; однако не нужно
выбывать, что точка А предполагается лежащий на поверхности жидкости и проведенныг
через псе прямые ЛЛ, АХ и другие предотаиляют основания сегментов, ou7.(;mj.i которых,
будучи ианолиены жидкостью, могут уравновесить нес плннакицего сегмента при ра:>-
ллчимх целнчинах отношении плотностей сегмента и жидкости.
Так как параметр р — К.Р меньпте КТ, то прожданная черен Р горизонталь пере-
пересечет параболу центров в дпух точках Г и Г; проведенные через itux иертитсали опредв-
ЛЯК1Т в пересечении с параболой шшвиним точки Н w Ф, а с параболой Л ПОЛ точки О
и II. Прямые АХ и ЛФ (последняя на рис. 22 ни приведен:)) определят1 соответствующие
сечения сегмента поверхностью жидкости; точки С.) и II будут иерпшнами погружен пых
сегментов АОХ и ПАФ, а проведенные п них касательные OQ и IIV определят ооот-
ветстиующие раишшесшо углы наклона (случаи 3 и 5),
Идея определения положепнц равновесии сегмента очешь проста: отношение (/
плотностей cgtmoiitii и жидкости Архимед выражает в види квадрата отношения некоторой
примой У к оси corMoHia ВЛ н определенную таким образом прямую вставляет между
параболами ЛПОЛ и ЛОЛ. ГСслн Чг будет болыни ИБ, то, согласно теореме IV, сегмет
будет илавап. и ииртикалыюм полшкокни (случай 1); если Т равняется ОГ или ПФ, то
сегмент будет плавать, пмин одну точку (Л) на поверхности жидиости (случаи 3 и 5).
Остальные три случая будут соопютмъоват!. таким пиачепиям Y: . .•¦ ..
мучай 2: В2>Ч'>ОГ,
случай 4: ОГ>У>ПФ,
случай Ч: ПФ > ?.
Доказательство во всох случаях проиаподится обычным для Архимеда методом — исг-н-
дованисм де11ствия приложенных к сегменту кил.
flfj] Текст Архчмода для последних трех случае* не явяяетгл впаипе кохргом»
шимсн. Прежде всего ато отражается па порядке изложения; после 3-го случая разби-
ривтеп не 4-й, а 6-й; кроме того, не вес обстоит в порядке и иа чертежах. Тик па рис. 28
точна Г, а с ней и вся нрямия MX, должны быть передвинуты так, чтоби Г попала в шь
ресичение примой ЗР с параболой центров. Равным образом примая N0 должпа
быть с.двип5та влево так, чтобы она иротнла черси точку пересечения прямой Е1* с па-
параболой центров; тогда она будет соотшлствовать прямой 11Ф рис. 22 и рассматрива-
рассматриваемая прямая Ш окая<ется ;итеи ПФ. В таком случае угол Ф рис. 2fi соответствует
углу 'V рис. 22.
Доказательство Архимеда сводится к тому, что теперь угол Q оси сегмента с поверх-
цостью жидкости будет .меньше предельного угла V рис, 22S.
Рис. 28 относится и к изложению случаи 5, где встречается та же прямая 6N, соот-
ветстлующая ПФ рис. 22-.
{17] Последним {)аибираетс>1 случай Л, тоответствующий такому положению пла-
плавающего тела, при котором основание сегмента разрешается поверхностью лсидкостн. Дл»
того чтобы ;>то имело место, необходимо, чтобы плотность плаиакпцего тела была болыш.'
отпотснин (ФП : ВД)*, ио миш.ше Ч(;м @5 : 13ЛJ, если пользоваться обозначениями
рис. 22 текста. В таком случае между параболами АвД и ABA придется вставлять пря-
прямую, меньшую OS, но большую чем ПФ. Доказательство Архимеда сводится к тому,
что сигмой? не «пмкит находиться в равновесии ци тогда, когда его основание находится
вне жидкости (рис. Л2 текста), ии когда его основание голым и одной точке тсасаетсн
поверхности жидкости (рис. 33), яо должен наклониться еще более так, что угол его оси
в горизонтом будет меньше предельного угла q рис. 22.
A8] В зависимости от плотности плавающего тела Архимед устанавливает две
области, в которых возможно плавании тела с оснояаш-шм, находящимся ине жкдкости.
Физически объяснить появление этих областей можно таким образом.
Начнем со случая, когда плотность тела, шит, лучше сказать, наша величина <я,
или -тр a — длина оси вегмепти погруженной части тела, будет ралпа пулю; тогда тело
будет просто лежать на поверхности жидкости, причем ось его будет образовывать
«"горизонтом-угол Ц:, тангенс которого мы получим, положи» п—О в общей формуле
Если мы будем увеличивать плотность тела, или величину а, то тело начнет погру-
погружаться в жидггость и одновременно увеличила™, угол наклона своей оси с горизонтом.'.
В первую очередь увеличение объема погруженной пасти пойдет за счет погружения cisr-
иеита ц приближении поверхности гкндкостя к нижнему углу основания; ото будет при-
О ПЛАВАЮЩИХ ТЕЛАХ 595
исходить до тех пор пока угол Ф, определяемый по лышспривсденной формул!1, не сде-
сделается равным минималытому углу <prajn. который удоплетнориет формуле
Vp
- ~ "
дометим, что этот угол тоже попристает к утонченном а. Дальнейшей ул сличите плот-
плотности тела повлечет за собой увеличение; здтоплсшии оснопания и увеличение угла ц.
Затопление осповаиия лс будет продолжаться беспредельно, по uoc.-ir достижении иското-
p(iii максимальпой величины будет уменьшаться иследстиио унеличешш yr.ua наклона
оси до тех пор, пока нижний угол оснолания не покажете» нн поверхности жидкости;
¦ после итого увеличении обч.ема погруженной части будет происходит!, исключительно на
«•ют увеличении угла наклона оси - - мы получим иторую ибласть нл.'шнпия тела с осно-
основанием вяе поиерхпосги жидкости. Эти будит продолжиться до тех пор, пока л не сделает-
сделается рашшм /;¦¦-/<; и :>тот момент тело станет отнеси о; при дальнейшем уж-.шчепин а тело>
будет просто погружаться п жидкость, причем ось остается псе и рем я вертикальной.
Когда а ершшнетен с Ь, то ест|. плотность теля сделается равной плотности жидкости,
то плоскость основания оин'гь совпадет с, шшермюстью жидкости.
После предложения X б переводи ilqrfiiiKe стоит: «Arehimcilis dts iiiKi(I(?T)t.ibuN in
humiclo liber sccundus explicit» — «Кончайте)! шорни шгига Архимеда о тел их, пла ною-
ноющих в жидкости». Также па этом кончается греческий текст Константинопольского'
палимпсеста.
Мы ожидали бы, что после предложения X последует аналогичный раз(п;р поло-
положений раштолесия при плакании сегмента с полностью погруженным осипиннш'м, как ото
сделано и предложшшях III, V, VIT, IX сохрашшшегоси текста. Это ойстоительстло,
а также и необычный характсф иилояп'ния предложении X, но сущкетпу объсдиши(Ш1е|-с)
минимум пять самост(.)ктелы[ых теорем1, но^поляет думать, что рассматриваемое прг>-
и;шедеи11е Архимеда не было им закончено и, лгожст быть, япляетсн самым последним
его сочинением. Оно представляет ныстую точку .пиши разиитпя, которая началечгь
п «Коноидах и сфероидах» и продолжалась в «Эфоде». 11 трактате «О плаианшщх темах»
Архимед далеко обогнал еиою :яюлу. Об этом свидетельствую полное отсутсизип л еохрк-
пиишеиси античной литературе сведении об этом сочинении Архимед», если не считать
короткого упоминания во лведсиии и восьмой книге «Математического собгаиия» Наина
Алскснтгдрийглчого, где атохппик Карп Аптиохийскнй говорит о иен как о «математиче-
«математической игрушке». Не лучше обстояло дело и йо время напныстпего разиитил культуры исла-
ислама, как можно нидс'п. h:i шхрнцишнегося арабского игиюжппш трактата Лрхнмсдп,
которое1 мы приводим ниже.
К II н г а Л р х и м е д а о т я ж ести и л с г к о с т и ::
Некоторые тела и жидкости тяжелее других. О теле говорят, что
оно тяжел он (другого) тела, или о жидкости говорят, что она тяжелее
другой жидкости, или же о теле говорят, что оно тяжелее жидкости,
«ели, когда берут их количества одтшаионого объема, а латем извелшиакхг,
то одно окаяынается тян;о.;1со другого (то ость вес одного больше леса
другого). Ксли их net; одинакои, то не говорят, что одно из них тяжелее
другого. То, о чем говорят, что оно тяжелее,— большее iro весу.
Мы полагаем, что природа жидкости такова,, что се смежные час-
частицы гладкие; поэтому то, что давит больше, нытеспяот то, что давит
меньше. .На всякую частицу жгдкости дннпт то, что находится верти-
вертикально над пей, если только жидкость не заперта к чем-нибудь, чти
заставляет ее частицы дапить на другие предметы. Всякая стоятая
жидкость не движется и се форил — форма тара.
Если пскоторое тело рашю по весу никоторой жидкости и бро-
бросить тело » эту жидкость, то оно погрузите и в пои только до тех пор,
пока его поверхность по сравняется с поверхностью жидкости. Если
же некоторое тело легче некоторой жидкости и бросить тело и эту жид-
жидкость, то оно не погрузится и нее целиком и часть его выступит над
поверхностью жидкости.
38»
596 КОММЕНТАРИИ
Если некоторое, тело легче некоторой жидкости и бросить его в эту
жидкость, так что погрузится только часть его, и если «зять некоторое
количество жидкости, рашше по объему той части (тела), которая погру-
погружена в нее, то оказыиаетсл, что вес итого количества жидкости равен
весу этого -тела.
Если некоторое тело легче л-жоторой жидкости и утопить его в этой
жидкости, то оно будет подниматься с силой, раиной силе избытка веса
количества жидкости, ранного по объему этому телу, над весом этого
тела.
Если некоторое тело тяжелее некоторой жидкости и бросить его
п эту жидкость, то его лес в жидкости равен избытку веса тела над
весом количества жидкости, равного ио объему этому телу.
Если тело легче жидкости и имеет форму сегмента шарм и бросить
тело в эту жидкость, то оно всплывет, причем его осношпше не сопри-
соприкоснется с жидкостью и тело будет стоять прямо, так что ось сегмента
круга будет кортикальной, а если ее наклонить, то после соприкоснове-
соприкосновения основания (сегмента тара) с жидкостью ось не останется наклон-
пой, а напротив, возвратится к прямому положению.
Если некоторое тело легче некоторой жидкости и бросить тело
в ату жидкость, то лес этого тела будет относиться к весу количества
жидкости, равного jto объему этому телу, как лес части этого тела,
погруженной в жидкость, к весу всего этого тела.
Ннига Архимеда окончепа*).
Манускрипт дает изложение первой книги «О плавающих толах» вместе с первым
предложением второй книги. Весь конец последней, относящийся к сегменту параболоида
вр:нцэиия, выпущен; удиилятьсн этому ие приходится, поскольку «Коноиды» остались
арабам шмгавеспгции.
В Западной ГСврэпс трактат «О плавающих телах» пошшлся в XIII леке в переводе
Вияьгелша и» Мернеке, использованием: также п изданиях Луки Гаврика и Тартальп.
П опрос, о том, насколько они понимали это произведении, лучше оставить открытым.
Иаарпае ато иотшапаа «ш варсчяеи во второй натопит* XVI пока, у Фядариго Колда/ш-
дяпо {150D —1575) п ого латинском издании Архимеда, где он сделал попытку восстано-
восстановить места, недостающее в нерэвоцв МерЗеке; как стало видно в дальнейшем, реставра-
реставрации Коммапднпо оказалась правильной. Ионное понимание мы встречаем у Христиана
Гюагчиса, одно из юпошвеких иропзпедоииИ которого, увидевшее свет ччхн.ко и копце
XIX века п национальном издании его сочинений, было пос.пищепо определению jio.io-
жеггш! рапнинесия плавающего паралл(!лоштш:да. Продолжателями Гкптгспса в XVIII ве-
веке оказались автортл теории корабля Буге к Эйлер, а и XIX — Дюпен во Франции и иро-
фосиор Московского университета А. Ю. Давидов, давшее полпоч гсоритяческое рете-
пие расодатрипаимого попросп. Мы уже имели возможность видеть, насколько близко
окгпалцеь современная теории к методике Архимеда при определении плавания сегмента
параболоида
Было бы, одяало, иенравилг.ным доводить модорлиайцдда до тктого отождествле-
отождествления обеих методик — Архимеда и современной. Осиоштоо раилкчае между математикой
Архимеда и соирсыецпой здклгочается п «ом, что мы стремимся получить наиболее общее
рушение нопрос:;]. иг* ski* и роизведения Архимеда представляют решении частных задач.
Правда, эти рмпения настолько гопиимт, что Архимеда мозкло .тгазвать родоначальни-
родоначальником классической математики XVII и XVIII веков, но тон пе менее попгаток со^данжя
общих теоу)Ий мы у Архимеда лочти по замечаем. Так п трактате «О плавающих телах»
обе задачи на раниопссис сегментов шнра и парайолоида решаются conepmcmiu незави-
независимыми друг от Ллуга методами. В иредло»И(!ни1т II второй книги Архимед близко под-
подходит it попитию метацентра (но сущестпу, ему осталось сделать только предельный
переход), по примененный им физический метод определения устойчивости полностью
исключает мысль о возможности его применения. Одна из парабол Архимеда очень
близка к современной поверхности сечении; однако по:!можиость использования Лрхи-
*) Книга Лр5;имея;1 о тиисссги и легкости (Мякала ли Аршимилис Фи-л-сикп ва-л-хнс|"фа)
перевСЕСГгя с рукописи 2E7/4 (листы 22 об.—23) Парижской 1 Талионалытой библиотеки. Микрофильм
этой рукописи бил прислан r-люй И. Мейер-Щагал. Псрсоод проиаиедсн В. А. Розснфельдим при
КОнсульгации М. А. Саяьс.
О ПЛАВАЮЩИХ ТВЛАХ 597
мидом настоящей поверхности сечений является исключенной хоти бы ио той причине,
что Архимед не был в состоянии построить ее полностью (в случаях плавания с полу-
полузатопленным основанием), а для греческой математики существующими считались только-
то обралы, которые так или иначе мш-лл быть построены.
Вышесказанное яплястся сираведлшп.ш пе только для рассматриваемого произве-
произведения. В посланиях к Досифею Архимед занимался задачами, которые п настоящее время
решаются при помощи интегрального исчисления, ио тем lie менее общего нонятия об
иптеграло у пего не было; определение площадей сегмента параболы и объема парабо-
параболоида иращешш, с пашей точки прения, могут быть сведены к иычшлению одного и того
то интеграла, но Архимед -решает их t:on<rpiaeim» памтненмымя яруг от друга дгетода-ни.
Архимеду два раза пришлось решать задачу на максимум л минимум — л предложениях
IV и IX второй кпиги«Ошаре и цилиндре» и в предложении VI второй книги «О плава-
плавающих телах*, но примененные им методы в сохраненном Евтокием текст решения и при
нахождении продельпой величины отиошсппп параметра пнраболы сечения сегмента к его
оси («О плаваюших телах», 11,6) не имеют друг с другом ничего общего. И трактате «О етга-
dh.muk» Архимед определяет касатсльпую методом, который, по существу, одинаков
с робервалевским методом сложении скоростей, по только у Гоберволл метод мог Сыть
применен ко многим кривым, а у Архимеда только к специально построенной кривой.
Однако псо :ito показывает только, чти Архимид, несмотря на всю ежом гениальность,
псе «ко был греческим математиком, а разница ме;клу греческой и co«pt!Meinioii математи-
математикой ма/кчт быть охарактеразоваиа следующим вамечанясм. На жалобы ца]1И Птолемея
по поведу трудности геометрии Евклид отпечал, что в геометрии царской дороги не суще-
существует. После открытки анализа бесконечно малых Лейбниц писал:
*Мы открылп ту царскую дорогу, на отг.утктпие которой жаловался Птолемей».
ПСАММИТ
Слово «псаммит» (\\-,ащх:ХГ\5 or г|;«и}м>е — лесок) не имеет на русском языке себе адэ
киатттого; передать его словом «песочник» :шачило бы просто выдумать новое слово.
Поэтому обычно принято переводить его по содержанию книги «Исчисление песчинок».
Рассматриваемое сочинение является одним пз самых поздних и ряду известных
нам сочинений Архимеда. Оно ннписапо после «Измерении круга», но до смерти Гслопа
B1В г. д» п. э.) — сына и соправителя сирикуаского царя Гиерона.
Особенностями итого сочинения, н оста пиши его споем целью определить число нес-
чинок в объеме шара, являютс» астрономическое содорткапие и арифметический харак-
характер — еоидапис нумерации для очень больших чисел. Обо эти отличительные черты тесно
сви.ишм между собой. Передача па Запад достижений вавилонской ш.тпн'лит^и.ной
астрономии, находившейся и III пеке до л. о. в апогее своего развития, поставила .иолрос
о способах икойраженин больших чисел, для чего существующая греческая нумерация
была абсолютно но приспособлена. Способу изображения таких чисел посвящепо ire дошед-
дошедшее до пас послание к Зевксшшу, о котором упоминается в тексте «Псаммита». Около
того «sts иреиггаи другой большой математик Аполлоний Пергский написал «Быстроечст»
(QxuioKtov — точнее «средство для быстрого разрешении от бремени»), в котором ой
n:i.[<ira.i новую систему счисления больших чисел и правила действий с ними; возможно,
что результатом полемики Архимеди с Ано.июнием или, как думают некоторые, с Эрато-
сфипом было появление «Задачи о быках», принадлежность которой Архимеду очень
вероятна.
В тесной свя;ш с астрономией лежит еще одна особенность этого произведении —
употребление отношений между углами к прямыми линиями; вместе с дошедшим до пас
сочинением Аристарха «О иеличинах и расстояниях Солпца и Луны» рассматриваемая
книга Архимеда мвлжггог своего ptw« предтечей греческой тригонометрии, пад которой
в дальнейшем работал ряд астрономов, начинай с Гшшарха.
[1] Упоминаемый здесь Аристарх Самосскни, творец первой гелиоцентрической
системы мира — «Коперник античного мира» — был знаменитым греческим астрономом
иериш половины III пека до и. и. До нас дошло только одно сочиненно Аристарха
«О величин о и расстояниях Солнца и Луни», в котором имеются данные о сравнитель-
сравнительных величинах диаметров и расстояний Со.-нща и Луны. В :>том сочинении Аристарх
еще стоит на почве геоцентрической теории строения, солнечной системы. Указание
Архимеда на то, что, по миопию Аристарха, орбити Земли относится к сфере неподвиж-
неподвижных звезд, как центр к окружности, пернее всего было бы понимать и том смысле, что
Аристарх считал мир бесконечным; Архимед несколько извращает его мвд;ль, ло всей
нероптног/ги стой целью, чтобы сделать теорию Аристарха доступной для математических
исчислении, хотя и с очень большими, но все же конечными числами.
12) Так как величина греческой стадии составляет около ISO метро», то 3 000 000
стадий будут равняться примерно 450 тысячам километров, что примерно и десять раз
больше истинной длины ценного лклатора, составляющей только 40 228 км.
[3] В дейсгвнтельности диаметр Солнца в 109 раз больше диаметра Земли и в 436 раз
больше диаметра Лупы.
[4] Сторона правильного тысячеугольпика соответствует центральному углу
л 0,36°, то есть раина 2l'fi". Истинная пеличииа видимого диаметра Со:нща колеблется
мегкду 31'28" (в апогее) и 32'37" (в перигее). Аристарх считал видимый диаметр Солнца
равным 'Ли'.
[5J Мы имеем здесь очень редкий в сохранившейся литературе греков пример акспс-
римента.иышт определения физической величины, сопровождающегося поправкой на
неточность наблюдения (Архимед принимает п расчет пеличипу зрачка).
Как следует из комментируемого текста, а также из сохранившихся фрагментов
«Катоптрики», Архимед рассматривал процесс зрении как совершающийся при помощи
лыхол.Я1цих ил глаза и как бы ощупываклцих наблюдаемый предмет лучей зрения. Теория
ПСАММИТ'.:
590
¦Н'о опытл но различному юл копалась комментаторами; следующее описание, по-види-
по-видимому, будут наиболее соответствующим действительности.
Архимед наблюдает Солнце вблизи горизонта, когда на пего, можно смотреть гла1-
нами. Он- Серег горизонтальную линейку, обращал последнюю и восходящему Солнцу^
На ату пластинку он помещает круглмй цилиндр (слоио ьлфь? - • примой — в тексте —
иаэпоипст думать, что :>тот лнлвпдр стамнясл игртякалнпа, хотя некоторый комментаторы,
Данная Ршю рекоттструкция прибора Архимеда для определения
диаметра Солнца.
¦мирпмер пторой л:щ<п'гми, Архимеда фрянцуи Рлбо, полагают, что цилипдр был положен
па лииеику горизонтально); затем", поместив гляа у конца, ликейкя, оп нередпгггаег
цилиндр до тех пор, пока последний не закроит диск Солнца (но мнению Рлпо, Солнце
->акрнпас!тся пе Соковой поверхностью, по круглым основанием цилиндра); в этом поло-
Цшшндр
Рис. i.
Зрачок
ГРис, 2.
иссини ori измеряет угол между прямыми, идущими от глнла к цилиндру и касающимисп
ого боковых с.Т(>ро1г*(рпг.. 1); полученная mmнчмпа дает верхний предел зпачшия угла,
IIOJC КОТорЫМ: Ш!,ШМ!) СиЛППв.
Архимед :in;i(!T, что найденная величина угла Судет Польше истинной вследствие
того, что иа самом деле крайние ирнтелыгые лучи выходили ке из одггой м той же точки
глина, ио из дпух различных точек, находипшихся по краям гориаоптад i,noro дипмотра
фачка; можно было бы полупить более точное; значение угла штдныисти Солнца, если
у-'нч:тг., что на снмои деля вершина угла щ яппяетси не точкой, iu> некоторым диском,
дшшстр которого ривияется горизонтальному диаметру зрачка, как это hokueiuho па рис. 2;
если иставить атот диск па место, занимаемое глазом, и найти угол р между крайними
лучами, соединиющимк кран цилиндра л зрачка, то этот угол р даст нижний предел дли
угла пидн мости Солнца.
Таким оСразом, дело сводится к тому, чтоСы определит!, диаметр прачка. Для этой
цепи Архимед делает сшедуюшее: считая, что если лучи пыходит на г.иазя лпра.ч.имьБЫМ
пучком, то ширина пучка лучей будет равна горипоитальпому диаметру зрачка; он устраи-
устраивает так, чтобы параллельность зрительных лучей была обеспечена. Для этой цели он
йерст два тонких цилиндра одинакового диаметра (рис. 3); шли последний рапен диа-
диаметру зрачка, то зрит<!.чыше лучи идут параллельным пучком и аадшш цилиндр й
¦600
КОММ1ШТАРМИ
полностью заслонен передним (рис. 3 вверху); если те диаметр цилиндров меньше диа-
диаметра зрачка, то лучи от нричка пойдут сходящимся пучком и яадпий. цилиндр будет или
полностью видел (рис. 3 лиияу), или лишь отчасти заслонен передним (рис. 3 н середипе).
Таким обраиом, задача состоит в том, чтобы найти два одинаковых цилиндра такой тол-
толщины, чтобы задний j гол и остью заслонялся меред-
пим, если иоследтшй приставлен к самому глазу.
Наименьшая толщина цилиндром, вызывающая
такое явление, и даст размеры горизонтального
диаметра зрачка.
|f.i] В результате поставленных опытов Архи
мед нашел следующие значения углов:
верхний предел и — -т^- rf=32'55".5.
QZZH
{-Зрачок
Рис. 3.
\
нижние предел р—-пт,;г d=2T.
Испитая величина видимого диаметра Солнца
колеблется между 31 '28" и 32'37", то есть в сред-
среднем 32'; таким образом, верхний предел, полученный
Архимедом, достаточно близко подходит к истинно-
истинному. Коперник считал ьндимгай диаметр Соллца ран
пым 31'48*.
[7| Диаметр Земли мшгыш.! диаметра Солнца. Такого мнения держались большин-
большинство астрономов ;>нохи^Архимеда. Мы находим его у Аристарха Самосского; вероятно,
ато обстоятельство и было причиной принятия последним гелиоцентрической теории.
По-видимому, впервые стал держаться итого мне-
мнения знаменитый математик Евдокс Кпидскнй
(середина IV пока до н. а.). Такое представле-
ние ицлучилось ии наблюдспий над затмениями;
диаметр намттой тени на расстоянии орбиты Зем-
Земли mciil.uic диаметра Земли, что может получить-
ел лишь я том случае, м-ли диаыегтр Со:шца бгсп.-
ше дипоштра Зсшли. Если известны отношении
расстояний Луны и Солнца от центра Земли, ън-
димые диаметры Солнца и Лупы и видимый диа-
диаметр зомиой тени ни расстоянии орбиты Луны
(он может бить устаноилоы ло времени продол-
продолжительности луппого натмелия), то могут быть
определены и отпошшшя истиппых величин
диамегров Солш;а, Земли, Луны гг земиой тени
на расстопппи лунной орбиты.
[8] Архимед рассматривает прямоугольные треугольники 0KP и ДКТ, у которых
катеты КР и КТ одинаковы, а гипотенуза 6К больше, чем AT, u следовательно, из остаю-
остающихся катотоп вР болмпс, чс;м ЛТ. Он хочет иокаяятт., что отношеггае угла КДТ (поло
вина измеренного угла видимости Солнца) к углу КОР (половина угли лидвмости Солнца
ял центра Земли) будет .чаключатьсямежду отношениями вК г АК и (-)J* : AT
вК Z ТЛК ^ №
Рис. 4.
ДК
ГСкли перепипгем :>то соотношенпе в виде
ДТ
_АК_ Z КвР ДТ
0К ' Z ТДК. " вР
АК (Ж
К вР
AT HV
КТ ' КР" ^ 1- ТАК ^ КТ • KJ'
(отрсякя КТ и КР равны, как радиусы), то неравенство будет равносильно следующему:
sinKBP _ Z КвР ^ igKBP
sin ТДК
^ gJ_
ТАК > lg ТАК '
Для нас лти неравенства являются простым игаражештм фяктл, что угол растет быстрее
своег<1 с.имуга, но медленное своего тангенса.
ПСАММИТ
601
Дли Архимеда эти неривенстиа вытекали из следующей теоремы.
Если, у двух прямоугольных треугольников имеются одинаковые «горизонтальные»
катеты и неравные «вертикальные», то больший из у&лои, прилежащих к перченым кате-
катетом, имеет к меньшему отношение, большее соотношения соответствующих гипоте-
гипотенуз, но меньшее отношения соответствующих кат-етос.
Оту теорему Архимед сообщает бея доказательства, считпя последнее, очевидно,
общеизвестным. Приводим доказательство этой тсорстгга, помещенное в сочинениях Архи-
Архимеда, изданных в 1С 15 г. учителем Людовика ХШ французом
Давидом Рипо в tiro издании трудоп Архимеда.
«Пусть будут треугольники ADC и НОС с прямым углом
при /), построенные на одном и том же катете DC, и имеющие
неравные катеты AD и B.D, причем AD > ВО; в таком случаи
я гшютонуза АС будет больше гипотенузы ВС.
Архимед утперждает, что больший угол ВВС будет иметь
к меньшему углу Л отношение, которое больше отношения
АС: СВ, но М1ШЫП0 отношения AD:BD.
Параллельно AD лроподнм прямую СС; откладываем
СЕ=ВС и этим радиусом и» цшггра С описынаем дугу UKF.
Затем точки В и Е соединяем прямой ВНС, пересекающем ли-
линию СО п точке С, лижцщей вне окруишог.ти BRF. Далее из
точки // проводим прямую ВП, ппраллельную АС, и из центра В
радиусом ИН описываем дугу JIIK. Так как сторона BIT бо-iсо
П1), то эта окружность пройдет лне треугольника BDTI, но рас-
ссчег треугольник ВНС, тли как лежащая протип тупого угла
1ШС сторона ПС будит более ВП.
Л треугольниках АКТ) и CEG рипиы углы при ?,', также рис. 5.
угол Л равен ACG, как пнутрмшип накрест лежащие, н ечкдо-
нателыю, равны и остальные: :шачит, стороны атих трсуго.п.никол пропорциональны
после i
откуда
нереста нопки
«присоединением»
BE+EG
EG
BE
ЕА
BE
EG
АЕ+ЕС
ЕС
GE
~ ЕС '
АЕ
ЕС '
BG
EG
АС
' ЕС
Но отношение BG к EG будет равно отпошеншо треугольников BGC и ECU-; следова-
следовательно, так jko будет относиться сторона АС к стороне ЕС или к рапной ей стороне ВС:
АС : UC-^
BCG : Тр-к F.CG.
По гектор ВСЕ содержит треугольник ВСЕ, так кнк ирнмаи ВТС пересекает круг; следо-
следовательно, сектор ВСЕ к треугольнику ECQ имеет большее отношение, чиж треугольник
ИКС к тому же треугольнику КСС
сект. ПСЕ тр-ь- ВСЕ
"тр-к ЕСС > тр-к ECG '
Но сектор BCf\ к сектору RFC имеет отпогаепие болинео, чем к треугольнику EGC
сект. ПСЕ сект. ВСЕ
сект. EFC
тр-к ECG
Следовательно, отношение сектора ВЕС к сектору ECF будет бшыие, чем отношение тре-
уголыгакоп ИКС и ECG
Отсюда «присоединением»
сект.
сект. HCF
сект. ВСЕ тр-к ВЕС
сект. ECF тр-п ЕСС
. ECF .. тр-к BEC+ip-к ЕСС
^ тр-к ЕСС
¦60S КОММЕНТАРИИ
то есть весь сектор BCF к сектору ЕС If имеет большее отношение, чем треугольник BCG
к треугольнику EGG ' -.
сект. BCF тр-к ЛСС ' • " ¦¦
сект. ECF > тр-к ECU '
и это значит, что отношение углов UCF и F.CF будет больше отпотений линий НС к ЕС
или АС к 7i?', как показано выше
угол BCF -.АС ¦ ¦
; -. угол UCF >~ВС~"
По угол UCF равен углу DJIC, а угол UCF ранен углу /1; следоиатсчыш, угол DBC
к углу iMC имеет большее отшшпяше, vijm больш.чл гипотенуза АС к меньшей ?47.
Вторая Шишкина предложения усчаиавапии^гси клкдутощим образом. Трсуголь-
пик ИКС имеет к треугольнику ШШ отношение большее, чем сектор ГШК к тому жи
треугольнику
; ; тр-к ВНС сект.
'¦ . тр-к В^// ' тр-к
Но втот сектор к евкгору KJH имеет мииыпее отношение, чем к тр|.1у1юльйику Ш)И
сект. ВПК
: сект' BJTI' < тр-к ЙШ *
Следоштшыю, троугольпик НПС к треугольнику ПРИ ммсот fiiwii>uiw dthdiiiohuo,' чии
епктор /ША' к епктору ШН
тр-к В/fC сект. }ШК
¦гр-к i//W > сект. 'liJH '
И поело «присоединения»
тр-к ДДС-1-тр-к ДЛЯ .. сект. Ш1К-\-сект. HJJI
тр-л J3DH * сект. i<J7/
получается, что лось треугольник Ш)С к синей части 1ЮЛ, ти есть J)C к ii/У, или Л/)
к 7Ш (пслодстбио подобия треугольников AJJC и BDU, обусловлитого параллельно-
параллельностью /W^ оснопанию /1С), будит иметь большое отиотипис, чем сектор JlfK к сектору ./////
или угол />Л/7 к углу 7J/1C
¦гр-к ЫЮ _ 1Ю __?li> -. сект. J1!K
Тр-к unW~ dh~~ вЪ~> Лш*
как и било предложено
^ HD '
«[0] Рассуждения, пзложонпыо в лопце этой главы, позволяют лам составить
торос представление об астрологических работах Архпмода. Непосредственный иредше-
cTiiRiiiiRK Архимеда Аристарх Самоссктг при определении расстояний Сшшца и Луны
от Земли считал иос.и-днюю Tirritoii, Архимед же, иьтражи>к:.ь современным языком, про-
проводит свои наблюдения к центру Земли, виымы слешами, имеет понятно о том, что ми
теперь называем параллаксом. Обычно считают, что лледенис и астрономические расчеты
параллакс;» было сделано инаменитим астрономом Гиннархим Л]|11б:шзителыто чире»
лятьдесит лет после смерти Архимеда».
{101 Архимедом нумерация чисел такопа:
Бее числа от 1 до 1С8, кроме иоследнего, мааыаатотся первыми •), число же 10" нанм-
иастс.п единицей вторых чисел; числа от 10в до 10s'2, кроме последнего, иазыпаются ста-
старыми**), число же 10s — единицей третьих чисел, числа от 10й до К)*'1', кроме
последнего, называются третьими, число же 10s'3— единицей четвертых чисел и
т.д.; числа от ц)8"*108-1) Д[> Ю8'10 , щюмс последнего, называются мириадо-лшриад-
ными.
•) Или числами первой октадк. поскольку числа 1, 10, 102, 1С3. 10*, 10ь. 10*. t О7'
первую «окгаду» в бесконечной непрерывной пропорции
I : 1С : Юг: 10s : 10* : 10s : 10е : 107 : 10" ...
*•) Или числами itTupoti октады {1С8. 10в. 101и, .... 1015).
ПСАММИТ ¦ ¦ ¦ ¦ Г>(),4
Все имшеукшшшые числа составляют и совокупности первый период. По такой же
«;хеме строите» первые, вторые и т. д. чныта.»/ад/;огн периода, только и качестве: исходной
единицы для второго периода берется число yl=108"i0li; все числа от А до АЛО9, кроме
последнею, на;швйштся первыми числами второго периода, число ике Л-К)" - - единицей
лторых чисел этого периода, числа от Л-Юк до АЛО6'", кроме последнего, называются
чторыми числами старого периода, чнею ж» ^4.10"**— единицей третьих чисел этого
пириода и т. д.; числа от A-iOs'^lOH~Xi до /1а, кроме последнего, пазылаютсн мириадо-
мираавными числами второго периода, число же А" бер!!тся п качестве основной еднницм
для построении чисел третьего периода от Ая до А', причем А' берется едппипеи длл
чисел четвертого периода и т. д. и т. д.
Архимед доподит :ito построение до мириадо-мириадного периода, единицей ко-
горого служит число Л1СЯ~', и заканчивает [свою классификацию числом AiS>*~
= 108'108<")*'=е108'101Л. Пирочем, для решения той конкретной надачя, которую ста-
нит ccfie А])химед в рассматриваемом сочинении, ему пи тробуптея ниходит!! даже за
пределы первого периода, поскольку он устанавливает, чго чигло нмстшюк, яаисмшикшшх
сферу поподнижегых нвеуд, заведомо не превосходит тысячи мириад единиц восьмых
чисел первого периода, то есть числа 'IOa-lOll-lOs=l(lli3.
111] Во всем расчете Архимеда поражает ниобтлчайная (мы сказали бы излишняя)
осторAжиость л ojinpiipoTiaiiim с большими числами, гюка'.илнпкицам, что псии/.юиапие ими
еще было новинкой для громадного большинства. То, что Ci.hu> необходимом и зпоху
Архимеда, в настоищж нремя скорее яв.чяется помехой при чтении; поэтому не будет
липшим- представить псе расчеты Архимеда п более лаглиднпй, ирииьптш для нас форме.
Число песчинок в объеме макового :)орнмн1ка = 10 000 песчинок. Один дюйм содержит
'и) макопых церпышск; следовательно,
Шар диаметром а один дюйм будет содержать 40:чх1')')()()---(Й-107
песчинок или меньше чем 10е песчинок
Шар диаметром в 100 дюймов будет содержатыть более A00):М0"
—1016 песчинок
Шар диаметром в 10 000 дюймов будет содержать меньше A00K-101ь
— 10sl песчинок
Стадия равна UBOO дюймон; следовательно, шар диаметром в одау ста-
цию будет содержать менее —10al песчинок
Диамет]1 Земли содержит не более миллиона A0я) стадий; «лодопатель-
fo, число песчинок в объеме Земли будет не более 106*а-1021 —10;в песчинок
Диаметр мира В 10 000 рая больше диаметра Земли; следовательно, чис-
число песчшток л объеме; мира будет 104-3-10зв —10м песчинок
Диаметр сферы леподыижных :ннк!д я 10 000 раз больше диаметра мира;
следовательно, число песчинок н сфере неподвижных звезд будет
10*-»-10 й _1003 песчинок
Полученное число, равное Ю7'817, ко нумерации Архимеда будет
рапно 107-107-s, то есть тысяче мириад единиц иосьмых чисел A.07*8).
КНИГА ЛЕММ
(Книга лемм» сохранилась только в виде арабский обработки и латинского перевода
этой обработки. Несомлспио принадлежат Архимеду предложения IV и VI вместе со-
вспомогательным предложепием I, относящиеся к фигуре, названной Архимедом «арбс-
jioii», а ташке предложении VIII, дающею способ трисекции угла, в предложение XIV,
определяющее! площадь фигуры, названной Архимедом «салипон».
Сочинение был» издано впервые С. Фостером п ебориикс «Смесь» (Miscellanea),
пышедшем в .Лондоне в lfisa г. в латинском переводе с арабского. В 1661 г. этот перевод
был переиздан Иореллл. Текст, пздшшый Борелли, был переиздай б классическом издании
готипепий Архимеда, опубликованном Гсйбергом.
Три арабские рукописи атого сочшншин, с. которых производился перевод Фостерп,
хранятся в библиотеке Медичи во Флоренции.
[1] TcfiirroM бен Корой (Thebit ben Кога) латинский переводчик называет Абу-л-Ха-
сана Сабита ибн Курру ал-Харранп (836—901) — одного из крупнейших учепых сред-
средневекового Востока. Сабит ибн Курра был уроженцем месопотамского города Харрана.
выходцем из сомьи лпездрпоклоппикоп — сабпеп, потомков вавилонских жрецов. Сабит
ибн Курря был ые то.чько астрономом, пак его предки, но и математиком и механиком.
Сабит ибн Курра работал главным об]>азом в Багдаде, ему принадлежит перевод и коммен-
комментарии к «Альмагесту» Птолемея, перевод «Конических сечелим» Аполлония, коммептарпи
к «Началам» Евклида, механическим трактат о ртачажимх рссах и большое число тракта-
трактатов но геометрии, арифметике, теории отношений, тригонометрии и астрономии, я тикнее
переподы .многих научпых сочинений с греческого и сирийского па арабский. Три книга
«Конических сечении» Аполлонии и три сочинении Архимеда сохранились до нашего
времени только is переводах или обработке Сабита ибн. Курры.
[2J Ученым Альмохтассо Лбильгасапом Гали беи Ахмадом Насуэнским (doctor
Almoclitasso Abilhasan Ilali ben Ahmiid Nasiiensis — латинский переводчик называет
Абу-л-Хасана 'Алй иби Ахмада аи-Иасавй (умер около 1030 г.), уроженца Пасы в Хора-
сапе (около ныпешпего Ашхабада Туркменской ССГ). Слово AlmocMasso — трапскрип-
ция арабского слова ал-мухтас — «выдающийся» (слова doctor Almochtasso соответст-
соответствуют арабским словам, означающим «выдающийся ученый»). Ап-Ыасави работал п Р«?с
и Исфахане при дпоре буидских су.чтаноп, а затем п Галпс при дпоре Махмуда Гу^иеви
Ан-Ыасаии - - автор нескольких математических трактатов, наиболее крупным из кото-
которых квляется арифметический трактат, где излагаете» ряд математических приемов
индийского и китайского происхождения. ¦
|3] Абусах.чем Алькухи (AbusaM Alkuhi) латинский иереподчик называет Абу
Cax.ia ал-Кухп, уроженца Табаристана, работавшего в Пагдаде около BS8 г. Ал-Кухи был
йAлыиим знатоком греческой математики.
Таким образом, историю «Книги лемм» можно представить так. Сабит ибн Курра
перевел ряд лемм, принадлежавших Архимеду; черол сто лет ал-Кухи систематизировал
их, еще через нитьдесят air-Насави комментировал их, а следующий за ним автор руко-
рукописи (если под ним скрывается не сам ан-Ыасави) сократил их. Такая длинная история
объясняет то, что в целом рукопись не стоит на достаточной митсмитической высоте, не
нее теоремм интересны, а про пторое предложение приходится сказать, что его можно
и должно было доказать лучше.
[4] Словами «присоединение отношения» здесь переведены латинские слова сот-
pcisitid proportionis. Неясно, идет ли здесь речь о так называемом «присоедппепии» отно-
отношений (componendo—ouv-Oevti), равносильном образованию из пропорция а: Ъ=с : d
производной (а \-Ь) : u=(c-|-d) : d или о «сложении* отношений, равносильном нашему
умножению их.
Г51 По-видимому, ил книги ал-Кухи кзяты предложения I л IV.
КНИГА ЛЕММ
605
16] Пак правильно заметил ал-Писави, иредложеяггп остается верным и в том слу-
случае, когда оба круги имеют внешние касание; именно и тнкий форме они и употребляется
в предложении VI (стр. 39»).
[7] При доказательство предполагаете.!!, чм обе касательные DD и DC являются
перпендикулярными друг к другу, о чем не говорится пи слова в формуляровке предло-
предложения. Эта ошибка ученых-арабоп была обнаружена
ужо Фостером; Торелли показал, что предложение
остается веригам и я том случае, когда .касятелышо 1Ш
и DC не будут взаимно перпендикулярными.
Доказательство в ;>том случае пойдет так:
Пусть мы имеем полукруг ЛВС с центром О,
к которому протшдипы касательные 1Ю и CD. Фигу-
Фигура OBDC будет тан назынаемтлм дельтоидом; BD—DC,
как касательные, проведенные к кругу иа одной точки,
ОН=ОС, кик радиусы, и углм О/Ш-ОСЛ, как прямые.
Отсюда легко заключаем, что прямик OD — ось симмет-
симметрии: дельтоида йудот перпендикулярна к ВС. Вследствие
того, что угол ABC будет прямым, как угол .в нолукру-
ге, заключаем, что прямая ABG будет параллельна OD,
из равенства же прямых АО и ОС убеждаемся в равен-
равенстве прямых CD и (ID. Значит, точка i) явлиется серп-
дипой примой СС\ тогда, если опустить перпендикуляр
BE на АС и пропости /Ш, из подобия треугольников
ABE и AGC заключаем, что itF-^FK, т. к. GD = DC.
В примечании Гсйбврг приводит доказательство
«.H-IIacami в предположении, что BV перпендикулярна
к fCD; так как BD — DC, то угол DC В рилцц углу
ВВС; но углы ЛВС и DUG г.оетаиатот в суммп прямой
угол, так !7{fi как и углы ЛСВ и СОВ; следовательно,
угол DUG рапииется CGB, n.'in BD — DG—ЛС.
Книга. Архимеда «О ирямоуголг.иых треуголь-
треугольниках», ссылка на т(ото!>ут дана в тексте докаяатсчь-
ства этого предложения, упоминается, только у мрабеш.
[81 Это предложении исиольнуетси в «Альмагосте» Птолемея (книга 1, 10).
J9] Это предложение, раипо лак и оба последующих, без сомиения посходят
к Архимеду. ЫазВ'1нн1> «арбстои» произошло от греческого слона, обозначающего
скребок для лмделкн кожи, па который, лоходит
рассматрииаомаи фигуу>а.
[10] «Ироседем соединяющие линии НС и СС;
токда НС будет тоже прямой».—Ото следовало бы
из иредлюгеспип I, если бы иоследнее было дока.члио
и для случая вистииго касаияя wpyi'on. Соотиегстиу-
ющео доказательство мелкно провести так:
Пусть AGC к ИСК будут два круга, внешне
касающихся друг Друга в точке G; пусть АС и НЕ
будут взаимно параллсльпыо диаметры :>гнх кругов.
Требуется доказать, что лимш AGE ii CGII, соеди-
соединяющие точку касания G с концами обоих диа-
iroipon AC и У?//, будут прямыми.
Пусть К и Q будут циитрами обоих кругоп;
создиияющля их прямая пройдет таре» точку КИС1Ш11Я
С. Вследствие нйра^шельности НЕ и АС замечаем,
что угол IIKG равен углу AQC, откуда следует,
что равнобедренные треугольники JiKG и GQC подобны и угол FIGK район углу QGC.
Но угол ИСК состншшог два прямых е углом IrtGQ, поскольку KCQ есть ирямая
линия; гледопятелыю, будет рлпна двум прямым и сумма углов 1JCQ и QGC, то есть
линии JJCC тоже будет примой.
Аналогично докажем и то, что линия AGF. будет прямой.
[11] «Как мы, показали е предложениях, написанных е комментарии к трактату
о прямоугольных треуеолъникая» — Доказательство ап-Насави основывается на том, что
высоты в треуголт.штко пересекаются и одной точке.
Дейстпитодмю, пусть BID (рис. 3) пе Судет прямой; протюдем тогда прямую черпз h
и D, которая пересечет AT n точке т, но соппидающсй с /; тогда угол АтЬ будет прямой,
так как AI будет т*сотой дли третьей стороны HD треугольника. По угол AIB тонсу
будет прямым, пак (жирамщпнея иа диаметр; следопателыю, угол Amli ривен AFB, что
Рис.
606
КОММЕНТАРИИ
[12] Ji «Математическом собрании» ]lamia (кн. IV, Vi—20) имеются гаце теоремы,
касающиеся арбслопа.
14. «Л некоторых книгах прмнодмтсн дрениес предложение такого рода:
Возьмем три клгающиегя друг друга полуокружности АВГ, АДЕ, EZr
и в заключающуюся ме.исду их окружностями фигуру, которую называют
арбелои, впишем насколько к/п/гов,
касающихся друг друга и основных
полукругов; пусть центры этих кру-
кругов будут Н, в, К, А (рик. 4). Тре-
Требуется показать, что опущенный и.,
центра II на AV перпендикуляр бу-
будет равен диаметру круга, описан-
описанного около Н, далек, что перпенди-
перпендикуляр, опущенный из в, будет вдвое
больгис диаметра круга около в,
а перпендикуляр из К. втрое больна-
соответствующего диаметра, и вооб-
вообще последовательные перпендикуляры
Рис. 3.
будут кратными- соответствующих
диаметров в прогрессии натурального ряда чисел, причем вписывание круеоь
может продолжаются до бесконечности.
Пусть АВГ и AAR будут полукруги {рис. 5), опишем касательные к из
окружностям круги, с центрами Z, 11, в, а также, следующие га ними
вплоть до точки А. Теперь то, что опущенный wi Z на АГ перпендикуляр
будет равен радиусу круга 'А, является очевидным; еще я утверждаю, что
Рис. 4.
Рис, 5.
перпендикуляр, опущенный мл A, будет втрое больше. раОиуса круга И,
опущенный из 0—в пять раз больше {радиуса круга в) и все следующие,
перпендикуляры будут больше соответегпвующиг. радиусов в кратносгпя:г
п оследова тел иных печегп пых чисел».
Хотн Пиии не назыгшст имени Архимеда, чел- же гиггорств» последнего ииляитсн
очень псроитным; ла это указывают:
1) получивший от Архимеда слое название фигура арйиюн,
2) ссылка я докааатс-льетт: на предложение I «Книги лемм», снизанное с несо-
несомненно щшнадлежа1дими Архимиду теоремами Л—в, а, наконец,
3) «начни достойное Архимода изящество основной доказынсЦ-vroti теоремы (гл. 1^)-
Одмгша и в этом случаи к Архимеду можно относить самое Гшлммее лить осиопнуи»
идею доказательства, его подробности в данном тексте наверняка принадлежат Пяпну
и;;и другим комментаторам.
[13] В этой теореме мы встречаемся с третьей из .чнямвдитшх ладач древности,
л именно разделением угла на три части. Вояпишювение зтой задачи было, конечно,
связано с. ггостросиис.м пршиин.ных многоугольников; д;л1 ее решения, по исей видимости,
Гн.тл» придумано .чпамепитым софистом Гишшсм Элидским (пторая половина V пека jn>
КНИГА ЛЕММ
607
п. ¦».) та самая ивпдраприод, которой ми шиимилисл. » комментарии к «Кчадратурог.руга».
Ришыше уадачи при бомощи киадритрисы яилмегся очевидным.
Пусть в круги ЛОВ требуется разделить па три части угол ЛОМ (рис. С). Проведем
киадратрису ВКЛЕГ, черен точку К ее пересечения со стороной ОМ угла проводим ДЕ
параллельно ОА, нолучшпмй отрезок ОД дс'.ты на трг рышши части A'/., ZJ-I, ПО, череа
тични деления Z, 11 параллельно О Л нролодн-м ZI9, II1 и точки Л, Е пересечении этих
iijdimlix к кппдрнтрпссш соединяем с вершиной О угли
мрнмылш OAN и Otll; тогда заданный угол ЛОМ раа-
дслится па три раипмс чисти M0N, N011 и ПОЛ.
Подобно тому, как мм это сделали относительно
удвоения куба и кладратуры круга, щшиодлм осиошюй
текст, касающийся истории трисекции угаа и древности
(Па±ш, кн. IV, 3(i—44).
36. «Когда дрешшс геометры захотели данный
прямолинейный угол ра.чделпть па три равные чисти,
то им пстрстшilcl :шт[>у;ик'пия последующий причине.
Мы гонорим, что геометрические: проблемы раздел нюген
на три ннда: один из них насыпаются плоскими, другие
телесными, третьи я»: линейными. Те нидичи, который
могут Сыть раэршшшм при помощи ир»\шх линии и
окружностей круга, влолне законно можно вагщатт,
илосюши, так как линии, при помощи которых
отыскивается решение таких падая, имеют сиое иро-
0
I'iic. (i.
исхояедшие на плоскости. Ти Hte аадичи, решение которых требует применения одного
или нескольким конических сечении, называются телесными, так как для их построения
необходимо пользоваться поиерхностями тел, а именно коническими. После них остяетси
третий нид .чпдйч, так иааыиасмих линейных; дли построения (u ;jtom случае), кроме упо-
упомянутых, берутся и другие кривые, имеющие очень равнообразное и даысо очень 1«;кус-
сгвсиаоч происхождение, получаясь от сечений мепсс нравильных ловерхнестещ и в ре-
лультате сложных дпижслий. Такими яплиются линии, изучаемые и так иипышемых
«геометрических местах па поверхности*, а также другие более сложные, чем упомянутые,
и о большом количестве;, лаидениыо Демитрием Ал<!1«синдрипскилг и «Линейных построе-
построениях» (iv Toifi vt>«H.ni>«"S :яютяоЕа1) и (|>илоиом Тиипским при соединении (fg enijihny.^c)
илектои'дальиых и других разнообразных поверхностей, сСладатсишо многими удини-
тс;1Ы1Ы.ми ос;пот110.1ми характершггикнми. Некоторые вз этих крипых удостоились больших
исследований со стороны новейших геометров: одной из них яилямсл линия, гагмшшши
Меиелаем «имрйдоксильнои». К итиму jne роду принадлежат и другие крилые — спирали
и ниптовыи липни, киадратрисы, конхоиды и цкесочды. Невидимому, у геометров счи-
считается не малой ошибкой, если кто-нибудь и» них плоскую задачу решает при ломоши
конических сечений, или еще более сложных линий, юи шюСще при помощи неснойстиен-
иых классу данной задачи и|)Илых, кик, пасримс1]), задача о параболе п книге V «Коничес-
«Конических сечений» Аполлония *) пли то, что делает Архимед ь книге.' «О спиралях* для доккна-
пжльстпп иредложепнои им теоремы, что окружность опксаиного при первом обращении
круги ралпа прямой, нропедепной из начала спирали до касательной *•), где он посполь-
зовался «стремлениями» н уадпче, решаемой при помощи кошпесмих сечений и кругов.
При наличии такого сущеотпенного различия и классах задач первые геометры и не
смогли данную аадачу относительно угла, нилшишушсм но природе телесной, решить при
Н0.Ч0ЩЙ плоских ностроегшй; так как они еще «с были янакомы о коническими сечениями,
те) но этой причине и затруднялись; поздним ;ке при помощи конических сичшгий оказа-
оказалось «о:|Можным разделить угол па три ранный чисти при использовании описанного 1гижс
«с.тром лен ни».
Дан прямоугольный параллелограмм АВГД и продол тон а
сторона В Г; требуется пронести прямую АЕ так, чтобы отрвиок EZ был
равсп заданному {рис. 7[.
Пусть это уже сделано; проведем ДН и HZ параллельно EZ и ЕД.
Теперь, так как EZ дана, то будет данной и равная ей АН. Затем дана
•> И цинге V Лпол.ттсшш ничего пелобпого не шпямсн. Мсжог Смть, следует читать «шфш;й
ншпф». гдг и ирсплпжении Ь2 геворитен о построении париОолы на плоскости. Ikibskhkiio также, чти
Лисллгшй нпк и ниже Архимед, порицается еспершешю незаслуженно.
**) Ото пгеллгжеши XVIII книги «О спиралях». Для лонязатрльстоа этого предложения тре-
требуется испгльзлв!1Т1. пргдложения "VH и VIII. которые лейитиитсльно получаются при помощи
«стремлгнгй». причем едко иэ них (предлежгние VIII) трсВуст примсапннн иоетроснин, оншшмлрнтного
iinxciiiW'iiHK) перссечонмп гппербильг и параСплы. Приведенпыб Я'лми & примечаниях к соитЕетствую-
щсину кевту йнйлрз иикаамивпт. что без примгшчшн i<(:HirarcitiTX сечопий решение вядачи невовможно.
Персптпо мысль Поппа выключалась е том, чго если задача решается при помощи конических сечений,
то нет смысла ппяьясвяться «стрвмлрпинми». ¦ • ....
608
КОММЕНТАРИИ
\
н
точка Д; следовательно, И будет находиться на окружности заданного
своим положением круга. Далее дана {величина) прямоугольника
между ВГ и ГА; поскольку он равей
прямоугольнику исяеду BZ и ЕД, то
будет данным и прямоугольник меж-
между BZ и ЕЛ, иди прямоугольник меж-
между BZ и ZH; следовательно, точка Н
находится на гиперболе. Но она на-
находится также и на кадаттй. поло-
положением о к ружности; с л ед овате л ьяо,
будет данной и точка Н.
37. После этого синтез задачи
производится следующим образом.
Пусть заданный параллелограмм бу-
будет АВГА, а задай пая по величин*!
прямая — М {рис. 8}. Пусть АК будет раьпа М; через точку А прове-
проведем гиперболу ДИв с асимптотами АВ, В Г (это мы разберем позд-
позднее), а через точку
К — окружпость круга ,^_^___^^^___ Г
K.II с центром А, перс- й* ' ^^
секающую гиперболу н
Н; затем, проведя HZ
параллельно А Г, про-
проведем соединяющую
прямую ZA. И утверж-
утверждаю, что EZ будет рав- '
на М.
Действительно, про-
проведем соединяющую пря-
прямую ИД и НА парал-
параллельно К Л; следователь-
следовательно, прямоугольник меж-
между Z1I и НА или прямоугольник между BZ и ZJI будет равен прямо-
прямоугольнику между ГД и ДА или между ВГ и ГЛ. Значит, как ZB к ВГ
или как ГД к АЁ, так будет относиться и ГД к ZH;
_zb_ гд гд
"ВГ = ДЕ '~" 7.Н
следовательно, ЕА будпг раина ZH; значит, AZ1IE — параллелограмм;
значит, EZ раииа ALI или
? z\.K, или М.
3S. После того как это
доказано, заданный прямо-
прямолинейный угол делится на
три части следующим обра-
образом.
Пусть заданный угол
АВГ будет первоначально
рис 9 острым {рис. 9}; из некото-
некоторой точки опустим перпенди-
перпендикуляр А Г и, дополнив парал-
параллелограмм TZ, продолжим сторону ZA но направлению к Е. Затем,
имея прямоугольный параллелограмм TZ, проведем между ЕА и АГ
стремящуюся к В прямую ЕД, которая была бы равна удвоенной АВ
М
Vac. 8.
КНИГА ЛЕММ
609
(что это возможно, показано выше). Я утверждаю, что угол ЕВГ
яндяетои третьей частью заданного угла А В Г.
Деистнитолыш, разделим ЕД пополам в Н и соединим А и Н;
тогда три прямив ДП, НА и НЕ будут равными*); ялачит, ДЕ ндпос
больше ЛИ. По ДЕ также вдиоо больше и АВ; значит, ВА равна АН
и угол АВД равен углу АНД. Но угол АНД вдвое больше угла ЛЕД,
или ЛВГ: следонатольно, угол АВД вдвое больше угла ДВГ. Если
теперь разделить лоцол&м угол ЛВД, то угол АВ Г будет разделен на
три ранные части.
39. Если бы заданный угол был прямым {рис. 10), то, отло-
отложив какую-нибудь прямую В Г, построим на ней равносторонний
В
Рис. 10.
Рис. 11.
треугольник ВДГ; разделив затем угол ДВГ пополам, получим раз-
разделенный на три части угол АВГ. *
40. Пусть теперь заданный угол АВГ будет тупим {рис. 11}; про-
недом ВД лертгевдикулярио к В Г; затем отделим ДВХ — третью часть
угла ЛВГ и ЕВД —третью часть острого угла ЛВД (это уже показано
нами выше); тогда угол EBZ
будет третьей частью угла Л В Г.
Если при каждом из сторон АВ
и В Г построим но углу, ранно-
ранному EBZ, то и разделил задан-
заданный угол на три равные части.
4J. Теперь займемся реше-
решением оставленной нами ранее
задачи. Пусть даны положеии-
. см дно прямые АВ л В Г и ка-
какая-нибудь точка Д; требуется
провести черен Д гиперболу с
асимптотами ЛВ, ВГ {рис. 12}.
Пусть :>то сделано к про-
проведена гипербола ЕДЯ; из точ-
точки 4 проводом к пей касатель-
нун» АДГ, диаметр НВД и пря-
прямую AG, параллельную В Г.
Так как IIД и Л в дины положе-
положением, то будот данной и точка в.
Затем, так как АВ и В Г являются асимптотами гиперболы, а Л Г —
ласательнпн, то АД будот равна Л Г, и кнадрат на каждой из них будет
*) Если \Н—НЕ и угол EAi Tip»MOii, то Н Судет центром круга иа диаметре АВ, окруж-
окружность которого проходит нерсв А.
Зй Лрхпмпд
Гпс. 12.
610 КОММЕНТАРИИ
равен четвертой части фигуры, построенной на ДН *), (это доказывает-
доказывается в предложении 3 книга II Аполлония «Конические сечения»). Так
как ГА рашш ДА, то и В6 будет равна 6А. Но Вв дана; следователь-
следовательно, будет данной и 0А. Затем дана точка 0; следовательно, будет дан-
данной и Л; значит, будет дана положением и прямая ДГ. Далее, АГ дана
и по величине, так что будет данным и квадрат на АГ. Но последний
равен построенной на НА фигуре; значит, будет данной и эта фигура.
Затем дана НД (она будет идноо больше прямой ВД, заданной но вели-
величине, так как дана каждая из точек В и Л); следовательно, будет дап-
ной и прямая сторона (Jalus rectum — параметр) кривой. Таким обра-
образом, получилась такая задача; заданы величиной и положением две
прямые — ИД и параметр; требуется построить на диаметре ИД гипер-
гиперболу, у которой прямой, на которой квадрируются ординаты •*) была бы
другая заданная прямая, и соответствующие ПД ординаты были бы
параллельны заданной положением примой АГ. Все это разрешено
в первой книге «Конических сечений» «предложение 53).
А2. Синтез задачи производится так. Пусть АВ, ВГ будут задан-
заданные положением прямые, а А — заданная точка. Проводим Дв парал-
параллельно ВГи 0А, ртшую В©, затем соединяющую АД продолжаем к Г,
а соединяющую 13Д продолжаем (назад) и откладываем ВЯ равной
ВД; пусть квадрат на А Г будет равен прямоугольнику па НА и неко-
некоторой другой прямой К; затем на диаметре ПД и параметре К строим
гиперболу EAZ так, чтобы проведенные к НА ординаты были парал-
параллельны АГ; тогда АГ будет касательной к построенному коническому
сечению. Затем АД равна ДГ (так как Вв равна GA), и ясно, что квад-
квадрат каждой из прямых АД и ДГ будет равен чотперти построенной на
НД фигуры; следовательно, АВ, 13Г будут асимптотами гиперболы
EAZ; таким образом, построена прохо-
проходящая через точку Д гипербола, име-
имеющая заданные прямые асимптотами.
43. Если не пользоваться «стремле-
«стремлениями», то третью часть заданной дуги
можно будет получить и иначе, при
помощи следующего «телесного» гео-
геометрического места.
Пусть положением задана прохо-
проходящая через точки А и Г прямая; через
заданные точки А и Г проведем ломаную АВГ так, чтобы угол АГВ
был пдвое больше угла ГАВ; тогда точка 13 будет на гиперболе (рис. 13}.
Проведем перпендикуляр ВД и отложим ДЕ равной ДГ; тогда
соединяющая BE будет равна АЕ. Отложим EZ равной ДЕ; тогда
TZ будет втрое больше ГА. Пусть АГ будет втрое больше Ш; тогда
точка Н будет заданной, и остающаяся прямая AZ трог больше
ПД. И так как разность квадратов на BE и EZ есть квадрат на ВД
и этой же самой разности будет равен прямоугольник между ДА и AZ,
- EZ2 = АК2 - ЕЛ2 = (ЛЕ + ЕД) (ЛЕ _ ЕХ)
*\ Произведению Mi на паршютр ft.
**) Эта прямая, иа которой къалрируюгеп орднпатм, соответствует нашему параметру.
КНИГА ЛЕММ
611
то, значит, прямоугольник между ДА и AZ, то есть трижды взятый
прямоугольник между АД и АН, будет равен квадрату на БД;
следовательно, точна 13 будет на гиперболе, действительная ось
которой АН, а параметр втрое больше АИ*). Далее ясно, что
точка Г при вершине Н конического сечения отсекает прямую ГН,
равную половине действительной оси АН гиперболы.
Синтез задачи очеииден; требуется прямую А Г разделить так,
чтобы АН была бы вдвое больше ГН и на оси АН построить проходящую
через точку Н гиперболу, параметр которой был бы итрое больше АН,
и затем показать, что эта гипербола действительно производит задан-
заданное отношение углои при Г и А, равное двум. Легко видеть, что пачор-
ченная таким образом гипербола отсекает третью часть заданной дуги
окружности, крайними точками которой яиляттен Л и Г.
44. Некоторые анализ задачи о делении па три части заданного
угла или дуги излагают другим способом, тоже не пользуясь «стремле-
HUUMH». Пусть рассуждение будет касаться дуга, поскольку пет никакой
разинцы, двлить ли дугу или угол. Пусть это будет сделано, и от
заданной дуги АВГ отсечеоа третья часть ВГ [рис. 14}. Проведем
соединяющие А с В, В с Г и Г с А; тогда угол АГВ вдвое больше угла
ВАГ. Разделим угод АГВ пополам прямой ГД и опустим перпенди-
перпендикуляры BZ и ДЕ; тогда АД будит раина ДГ, а значит, и АЕ рипна ЕГ;
следовательно, точка Е дана. Теперь, так как отпошеппе АГк ГВ равно
отношению АД к ДВ или АЕ к EZ,
АГ
гв
ГА
АЕ
АЛ
*ЛВ
АЕ
то, значит, после перестановки ГА так относится к АЕ, как ГВ к EZ.
гв
EZ
Но ГА вдвое больше АЕ; значит, и В Г будет вдвое больше EZ; следо-
следовательно, кпадрат на ВГ, или киадраты на EZ a ZT, (имеете взятые),
будут в четыре раза больше квадрата на EZ.
') Бели положить вд-
=у и &Н=х, то уравнение гиперболы будет:
ЗАИ „
г,2 = 2р*-ь|?1
АН
39*
КОММЕНТАРИИ
AZ
ZK
Теперь, поскольку являются заданными топки Е и Г, проведен
перпендикуляр BZ м задано отношение квадрата на EZ, к сумме квад-
квадратов на 13Z и ZT\ то точка В будет, следовательно, находиться на
гиперболе. По она находится также и па заданной положением окруж-
окружности; следовательно, точка В дапа. Сиптоз
задачи является очевидным.
45. Деление на три части заданного угла
или дуги является, как мы покакали, «телес-
«телесной» задачей; деление же заданного угла или
дуги в данном отпошепим будет уже «линей-
«линейной» задачей. Это доказано нонешними гео-
геометрами; мы опишем два способа ее решения.
Пусть Л0 (рис. 15) будет дугой круга
К.Л0; требуется разделить ее и заданном
отношении.
Проведем к центру прямые ЛБ, В в и
иосст&ним 13К — перпендикуляр к 130; за-
затем чороз К проведем квадратрису КАДГи
опущенный перпендикуляр АЕ разделим в Z
так, чтобы отношение AZ к ZE рашшлось заданному отношению,
в котором мы хотим разделить данный угол; далее проводим 7Л парал-
параллельно В Г, соединяющую прямую ВД(М) и опускаем перпендикуляр
ЛИ. Так как вследствие основного свойства квадратрисы АЕ так отно-
относится к ДН, или ZE, как угол АВГ к
ДВГ, то после в им деления» получится;
что AZ так относится к ZE, как угол
ЛВД к углу ДВГ,
_ Z ABA
~ L ЛВГ
то есть заданное о'шошепис равняется
оттгошепшо углов АВД и ДВГ или дуг
AM и М0.
46. Мпачс дуга АГ*} округкмостл АПГ
(рис. 10) может быть разделена так. Точно
так же проводим к центру прямые ЛВ и
В Г и описываем из В спираль BZAT, на-
начальным положением вращения когорой
является прямая ГВ; пусть заданное отно-
отношение р»Ш|,чотск oTimiiiiiiiuio ДЕ к J5B. Через точку Е около центра В
описываем дугу окружности EZ, пересекающую спираль в Z; соеди-
соединяющую BZ продолжаем до Н; тогда но свойству спирали ДВ будет
относиться к BZ или к BE, как дуга АН Г к Г11
Рис.
BE
АНГ
ГИ
и после «выделения»— пак ДЕ к ЕВ, таи и дуга АН к НГ.
ЛЕ'_ АН
*) Сольшан полуокруишости.
КНИГА ЛВММ ' E13
Но отношение ДЕ к Е13 равному данному; следовательно, и отношение
дуги АН кНГ равно данному; следовательно, дуга разделена в задан-
заданном отношении».
Переходя к Архимеду, нужно отмитнть, что он, ио всей видимости, как и в квадра-
квадратуре, круга, тоже дал два решения поставленной задачи: в самом общем случае падение
на любое число равных частей может быть выполнено При помощи Архимедовой
спирали, в частном же случае делении угла на три части он дал решении, изложенной
в предложении VII «Книги лемм»; :>ту красивую теорему известный историк математики
Морнц Кантор с ио.чным правом счптаот принадлежащей Архимеду.
(М1 Уто предложение без всякого сомнения tojko восходит к Архимеду. Значение
слова «саииион* в точности неизвестно. М. Кантор производит его от ao?vos (морское)
волнение, качка, толкуя его как «волнообразную липиш», Хн;ю считает, что :щ№ь скрыто
испорченной латинское слово saliiium ¦¦- силогша; издатель Архимеда Гойберг сближает
его со словом ckAlvov — сельдерей, па лист которого эта фигура будто Оы похожа.
[15J Ото предложение, касающееся пятиугольника, продставлкет сстсстоепншй
переход к следующей, тоже восходлщой it Сабиту ибн Kypj)O «Книге о семиугольнике*.
,,. ¦ г
КНИГА О ПОСТРОЕНИИ КРУГА, РАЗДЕЛЕННОГО НА СЕМЬ
РАВНЫХ ЧАСТЕЙ
«Книга о построении круга, разделенного на семь равных частей», посвященная
построению правильного семиугольника, сохранилась только в виде арабской обработки,
принадлежащей тому же Сабиту ибп Курре, которому принадлежит обработка «Книги
JlfeMM*
Изложение этого сочинения было опубликовало в кшц-с Карла Шоя A2**1 стп 74.
84) и в статье И. Тролфкс [44], стр. 636—651).
Единственная сохранившаяся рукопись «Книги» храпится в Каире в Египетской
Иапттопалытп библиотеке (ДЬ 7805/1о, лл. 105—110). Микрофильм этой рукописи был
любезно прислан переводчику директором Национальной библиотеки Фуадом Сайидом
и передан «о время XXV М спаду народи ого конгресса востоковедов в Москве каирский
профессором Амином4 ал-Холи. Перевод рукописи осуществлен Б. Л. Розепфельдом.
[1] См. комментарий к «Книге, лемм».
[2] Переписчик и редактор рукописи Мустафа Сиддикй лил в XVIII веке (п копцо
рукописи укапано, что она переписана в 1740 г.).
{31 Предисловие написано Сидцпкп t;>ro очевидно из слов «желая переписать эту
книгу»; Сабит пбн Курра сказал бы: «желая перевести эту книгу»). Добаплсннме Сиддикй
доказательства некоторых теорем Архимеда принадлежат средневековым комментаторам
Архимеда, жившим л X—XI веках. Нее добавления Сиддикй к тексту, который он счи-
считает восстановленным текстом Архимеда, начинаются слонами «я говорю».
14] Выражение «плоскость из А на В» (здесь: сатх а фи б) означает прямоугольник,
построенный па отрезках А и IS, то есть равносильно выражению «прямоугольник между
А и В» в переводах сочинений Архимеда, сохранившихся на греческом' языке. Однако
адесь предлог фи между обозначениями отрепков — тот >пс, что между сомножителями
при умножении чисел.
[51 Абу'Алй ал-Хасап ибн Харис ал-Хубубй — уроженец Хорезма, автор изве-
известного математического трактата о разделе насдедстп. Доказательства ал-Хубуби неко-
некоторых теорем Архимеда сохранились к «Трактате об определении хорд в круге» ал-Биру-
пи. В рукописи вместо «ХубуСГю паписано «Джуйубп» {эти имена отличаются только
диакритическими точками).
[й] Г[р<щлоя<ецяе Ш можно представить и следующей алгебраической форме:
если аи b - - катеты прямоугольного треугольника, с — его гипотенуза, a. p — полупе-
полупериметр, то
|7] Предложение LV в алгебраической форме, может бить выражено так: если k
высота, опущенная на гипотенузу то.го же треугольника, то
=2с Bр-\ А).
Предложение V — др>1Ч)е доказательство предложе!гая IV.
18] Абу'Лбдаллах Мухаммад иби Ахмад aw-Шашги— египетский математик, автор
пеенолг.ких геометрических трактатов. Доказательства аш-Шанни некоторых теорем
Архимеда такгке сохранились в «Трактате об определении хорд в круге» ал-Бируни.
[9J Предложение VI может быть выражено в виде
Предложение VII — другое доказательство предложения VI.
КНИГА О ПОСТРОКНИИ КРУГА, РАЗДЕЛЕННОГО НА СЕМЬ РАВПЫХ ЧАСТЕЙ 015
110] Предложение VIII может быть выражено следующим образом: если
x-\-y-\-z— 2s и 2sy—xz.
[it] Ото утпорждоние вытекает из обобщенной теор&мы Пифагора для треуголь-
треугольника АНИ: высота итого треугольника, опущенная из вершины А на продолжение сто-
стороны ЕП, пересекает эту прямую в середине отрезка ЛЕ, и в силу обобщенном теоремы
Пифагора /UJ*=AR*-\-EU*+2EH- ^ , откуда следует, что А1Р=АЕ*-\ HD-HK.
[121 Предложения IX иХ явлшотси, по существу, подготовительными к выводу
«формулы Геропа» для прямоугольного треугольника. Есаи мы положим hC—-a и уШ=^Ь,
то л силу предложения IX AD=p—a, a n силу предложения X ЬС?=р—ft. Поэтому пред-
предложение XI ралпоснльБО указанному частному случаю «формулы Гсрона» в виде
S=[p-a) (р-Ь),
где S — площадь треугольника.
Предложении XLI и XIII—другие доказательства предложения XI.
|13] Предложение* XIV дает второй р.ид «формулы Герона» для прямоугольного
треугольника:
S=p(p—c).
Если перемножить формулы предложений XI и XIV, то мы получим «формулу
Герона»
,?2==р (р—а) (р- Ь) (р—с),
которая, таким образом, доказана для прямоугольного треугольника.
П передаче ал-Пируни «отгранилось докн^итсльстпо общего с-лучая «формулы
Герона», которую! а.ч-Бирупз' так;кс прниисыпнег Архимеду (см. «Теоремы Архимеда,
сохранившиеся в передаче ал-Бируни», стр. 41!)—20
настоящего издании).
[14] Это предложение представляет большой
интерес; ово по сущ(!ству равносильно известной
тригонометрической формуле
I-У
Рис. 1.
¦ — cos a
которую обычно считали известной только дли эпо-
эпохи Птолемея A1 век н. :>.)•
[1п] Предложение XVII п нашей формулиров-
формулировке сводится к следующему. Возьмем квадрат AHCD
(рис. 1) сп стороной а, проледем диагональ DC и
прямую DF.F так, чтобы площадь треугольника С1УГ
ралпяласт, площади треугольника AF.F\ мы имеем здесь пример построений типа
veicrei.9, которые по лремена Архимеда принадлежали к числу унотреблнемых элсмеп-
тарных 1шстрос!пи.й. Через точку Г пересечения проведенной прямой OF с диагопа.чыо ВС
проводим прямую KL параллельно АС и обозначим череп у и z отрезки, на который эта
прямая рассекает противоположные стороны кладрата:
у^АК, z=BK. : . .
Ксли через х обозначим отрезок AF:
та ллл упомянутых отрезков будут иметь место отношения:
A) ABKB^AF* или «2=г2,
B) FK-ЛК^КВ* или (x-\-y)y~z*,
к которым присоединяется еще очевидное уравнение
C) »+*=*.
Продложеннс XVII н заключается в устптюляептг первых двух отпошений.
КОММЛШТЛР1Ш
Из равенства треугольников AFE и СОТ согласно построению заключаем:
х-АЕ=ау
или
а : х—АЕ : у.
И» подобия треугольников AI'E, DLT и FKT заключаем:
AEiTL^AF-.LD
или
АЕ : у=х : г,
откуда
а : х = х '. z,
что равносильно равенству (-1).
Далее,
ила
что доказывает рнпепктпо B).
Если исключить из уравнений A), B) и C) неизвестные jh:, то для определения аг
мы придем к уравнению третьей степени:
[16] Предложение XVIII посвящмю непосредственному построению ссмиуголышца.
Здесь (рис. 17 текста) берется некоторая пряман Alt — хорда будущего круга, "л который
будет вписан семиугольник. Эта прямая, которая предполагается известной, делится
в точках С и D так, чтобы
, CBDD=ACK
Если положить АС=х, CD=y, DE = z, то эти равенства равносильны следующим:
то есть уравнениям B) л A) предшествующего предяожепгия. 'Лятьч строится треуголь-
треугольник CRD, в котором СЕ —С А и DE=DJ3; полученная точка Е будет третьей вершиной
треугольника ABE, около которого мы олисыиаем круг: прямая BE будет стороной семи-
семиугольника, внисйниого в этот круг.
Продолжаем ЕС и ED до пересечения с окружностью в точках G и II, проводим
НС?, пересекающую НЕ в точке F, и соединяем CFl
Вследствие равпобедреппости треугольника АСЕ легко убеждаемся в том, что.
дуга AG равна дуге ЕВ. Затем по построению ADCD—BD*, или Elf, то есть
AD:DE = DE:CD,
а это значит, что треугольники AED и CED, имеющие общий угол при Е, будут подобны;
отсюда следует равенство углою СЕП и СЛЕ и таким образом дуга I1G окалмвается рав-
равной дугам AG л EU.
Затем m параллачышети ЛЕ и TIG следует равенство углов ARC и ABG, а так
как угол CED=CEA, то мы заключаем о равспство углов CEF и СИР. Поело этого из
равнобедренности треугольника BED мы заключаем, что фигура BECF представляет
равнобедренную трапецию, около которой может быть описана окружность. Из равен-
равенства треугольников ЕВС и EBF следует, что
DF=EC=CA=x, BD=EI),
DP=--CD^=y,
FE=CD+DB=y+z.
Из соотношепил СВ-ПВ=ЕСг=АС2 следует, мо
Cli:EC—EC:BD,
что в нашем случае могнет бмп, лергаисано так:
КНИГА О ПОСТРОЕНИИ КРУГА, РАЗДЕЛЕННОГО НА CKSIL РАВНЫХ ЧАСТЕЙ 617
а ото равносияг.мо тому.что треугольники ECDw ECF с. общим углом при К будут иодобны:
или
Затем угол 1И7Е=углу RFJJ = углу F-FC (из подобия треугольников EDC и f'-FC),
а это значит, что угол EFC иди IHIIC = углу KCD, или удвоенному углу САЕ\ гтаммн сло-
слонами, дуга .?/1 будет вдиоо больше дуги ЛИ; разделив дугу ЕЛ пополам, .ми получим
еще дни дуги, раышс. ЕЛ. Затем ия равеистлц углов DKB и /J^A" заключаем, что дуга ЙЛ*
будет тоже равпа дуго АЕ, или удвоенной дуге .#.?. Таким образом, разделив /Ш попо-
пополам, мы получаем еще дне дуги, рапные. ПК, и значит, весь круг разделился па семь рав-
пмх частей.
Обе последние теоремы доказываются совершенно самостоятельно и неуаиисимо
ох иред1лдущих лрщпожений, t которыми их роднит лишь то обстоятельство, ч-ю на
продскнкевпях одной сторивы CD откладываются дпедругип стороны СЛ=СЕ a DU—DE.
Наличие этой чисто внешней связи показывает, что перед нами но подлинное сочинение
Архимеда, а сочинение того же. мша, что «Книга лемм», которая посходит к тому тки
Сабиту ион Курре. Однако и том, что в основе обоих сборников лежат иодлшшьте работы
Архимед», вряд /иг возможно сомневаться.
И7] Дата переписки рукописи — 31 июля 1740 г.
И книге Шол [22] помещен еще (стр. 85 и ел.) трактат о семиугольнике ибн ал-Хай-
сама (Альхазсп), рукопись которого хранится в библиотеке India Office в Лондоне-
(Н 734/21).
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ
В ПЕРЕДАЧЕ АЛ-БИГУПИ
Формулировки трех геометрических теорем Архимеда, принадлежащие глиому
Архимеду, и принадлежащие) ему доказательства одной из этих теорем сохранились в гео-
геометрическом трактате средневекового среднеазиатского ученого Абу-р-Рийхана Ахмада
ебя ДГухаммада ал-Бгёрупй (973—1048) «Трактат об определении хорд в тфуге при помощи
свойств впитанной в него ломаной линии» (Рисяла фй истрггхрадж ал-аптар фн-д-даира би
хаваем ал-хатг ал-мупхапй ал-ваки' фйха). Этот трактат сохранился до нашего времспи
и виде четырех рукописей: и Еаигснпурс (Восточная публичпая библиотека, № 2468/42),
Лейдене (Уципорентетская библиотека. Cod. or. 513/5), Каире (Египетская Националь-
Национальная библиотека, № 7805/11) и Стамбуле (Пиблиотека Мурада Моллы, № 1396/14); бап-
иипурская рукопись йыла издана Осмапийским университетом в Хайдерабаде в 1948 г.
(стр. 1—108), немецкий перевод лейденской рукописи был издан Г. Зутером в 1911 г.
[21] (стр. 11—78).
Приводятся переводы отрывков из трактата ал-Бируни, посвященных теоремам Архи-
Архимеда. Переводы выполнены С. А. Крлспопой иод редакцией Б. А. Розенфельда; перевод™
осущестад сны с хамдерабадского издания банкиыурской рукописи; пробелы в этой руко-
рукописи цосполпены по изданию Зутер.ч лейденской рукопися. Эти дополнения приведены
в кладратных скобках.
[1] Формулировка этой теоремы приведена на стр.4—5 хайдерабадского издания
и на стр. 12 перевода Зутера. Доказательства Архимеда приведены па стр. 7—8, 18—1У
и 20—21 хпйдорабидского издания и па стр. 13—15 переиода Зутера. Кроме трех доказа-
доказательств этой теоремы, принадлежащих самому Архимеду, в банкццурской рукописи при-
nejieirn еще 18 доказательств, а в лейденской — еще 20 доказательств этой теоремы, при-
принадлежащие различным ученым средневекового Востока — Ибп ал-Хамсаму, ал-ХубуСи,
аш-Шашш, ал-Джурдисанм, ас-Спджизи, Азархуру Джашиису, учлтвлю ал-Бируни Ибп
Ираку и самому ал-Кируни. Эта и;с теорема под тта:ш;шш;м «предпосылка Архимеда»
приведена в тригонометрической книге сочинении а.-1-Бирупи «Канон Мас'уда' по астро-
si.imeii и звездам» (ал-Кануп ал-Мас'уди фи-л-хайа na-н-пуджум, стр. 273).
Теорема состоит в том, что если ломаная ЛИС вписана в дугу ARC и из середины
лтой дуги опущен перпендикуляр на большее звено ломаной, то основание этого перпен-
перпендикуляра делит ломаную пополам. И в банкипурской и в лейднтской рукописях указано,
что доказательства Архимеда взяты из его кпиги, которую ал-Бпруии называет «Книгой
кругов» (Китаб ад-даваир), и что третт.с. из этих доказательств uej>eBen с греческого на
арабской Юхапнл ибн Юсуф (Иоанн, сын Иосифа), иавег.тпый также иод именем ал-Касс
(праппглавный священпик). В бапкипурской рукописи указано также, что эти доказа-
доказательства были воспроизводетнд в к>.шго «Начала геометрии» александрийского матема-
математика IV века Серена Фивского. Очевидно, что «Кппга кругов» — сокращенное название
«Книги о касающихся кругах». В обработке «Книги о касающихся кругах», перевод кото-
которой приводится па стр. 421—439 этого издания, указанные доказательства, изложены
•л предложениях XXIV—XXVI в несколько другой редакция; чертежи в трактате
ал-linpyim являются зеркальными отражениями соответствующих чертежей «Книги о
касающихся кругах».
f2j Эта теорема приведена в хайдсра(>адстсом издяпии па стр. 58—59, в лейдепской
рукописи ота теорема отсутствует. Ал-Блрупи ие указывает ил аитора доказательства, пи
в каком сочинении Архимеда доказана :>та теорема.
Теорема состоит в том, что если основание, треугольника а (рис. 1 и 2), а его
остальные стороны b в с, а прямоугольные проекции сторон Ь и с на оетюпапио или его
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-БИРУНИ 619
продолжение — Ь' и с', и если ?>>е, то
эта теорема равносильна «обобщенной теореме Пифагора», которую можно записать фор-
формулами Ь«=а2+с=—2ас' (в< у\ Р=а*+с*+2ас' ( JJ> у j, cs=as-|-b2—2яЬ', до- .
казапиой Евклидом б предложениях 12 и 13 книга II «Начал».
[3] Эта теорема состоит п том, что площадь S произвольного треугольника со сто-
сторонами а, Ь, с и полупс!римс;тром р равна
S= Yp (р-а) (р~Ь) (р-с).
Эту теорему обычно называют «теоремой Герона», так как европейцы впервые позна-
познакомились с ней ил сочинений Гсропа. В хаидерабадском издании эта теорема приведена
а
Рис,
Г
г 1
1.
о
Рис. 2.
3
!?,
па стр. 61—64, в переводе Зутвра — на игр. 39—40- В банкипурской рукописи автор
доказатььства пе указатт, в лейденской рукописи доказательство приписывается аш-
IIIалии. Ал-Г>ырупи не укияыласт, в каком сочипенпи Архимеда доказана эта теорема.
О 1фнна;(Ж!Ж[гости этой теоремы Архимеду свидетельствует и хорасапскии математик
Абу-л-Вафа ал-Пуаджапи (9-'iO—908), который также приводит дна доказательства этой
теоремы (см. письмо Шоя к Троифке от ]К септября 1925 г. на оспошпгии ипалипа араб-
арабской рукописи TJiurston 111 Оксфордской университетской библиотеки.
В «Книге о семиугольнике», как мы видели, доказан частный случай этой теоремы
для прямоугольного треугольника (с:тр. 400).
Общео до!;азатсльстло форми Героыа содержится п Героновгаг «Метрике» (пни-
га I, Щ. Несмотря на то, что доказатььстно носит общий характер, чертеж в книге
Герона воспроизводит прямоугольный треугольник; таким образом, весьма возможно,
что нршюдииоо Героттом доказательство восходит непосредственно к Архимеду; поэтому
воспроизводим относящийся сюда теист Геропа.
«Дашл три стороны треугольника; найти его площадь.
Это возможно сделать, проведя одну высоту, и, найдя со величину,
определить шющадь треугольника, но пусть будот нужно определить
площадь помимо пахозкдепия высоты.
Пусть будет дан треугольник ABC и пусть каждая из АВ, ВС, С А
будет данной; найти его площадь.
Впишем » треугольник круг DEF, центром которого пусть будет Я;
соединим Л и И, В и Н, С п И, D и И, Е и II, F л //. Тогда ВС-ЕН
будет вдвое больше, треугольника ВИС, CA-FII вдиое больше треуголь-
треугольника АСИ, {АН-DJl ыдпое больше треугольника АВН); значит, про-
произведение периметра треугольника ABC на ЕН, то есть на радиус кру-
круга DEF, будет вдвое больше треугольника ABC. Продолжим С В и от-
отложим ВО ранной AD; значит, CBG будет полопиной периметра тре-
уголыпшп ABC, вследствие того, что AD равна At<\ DB же равна BE
и FC равна СЕ\ значит, CG-EH будет равно треугольнику ЛВС. Но
620
КОММЕНТАРИИ
СО-ЕЙ будет квадратным корнем из квадрата СС, помноженного на
квадрат ЕН:
CCEU — VcC2-EUa;
значит, площадь треугольника ABC, помноженная на самое себя, будет
равна квадрату GC, помноженному да квадрат ЕП.
Проводом HL пернсидикулярпо к CJf и BIj перпендикулярно к СВ и
соединим Си L. Поскольку каждый из углов, СИЛ и CBL будет прямым,
то четырехугольник CHBFj
будет вписанным в круг; зна-
значит, углы СИВ и CLB будут ¦
вместе равны двум прямым.
Но такжо и углы СНВ и AHD
будут рм1ни>г диум прямым
вследствие того, что приле-
прилежащие к Н углы разделены
пополам нряммми АН, ВТ1,
СП, и углы CUB, A/W вме-
вместе будут равны АНС, ЛИВ,
н вес они в сумме равны
четырем нряммм; значит,
угол AHD будет равен углу
CLB; также и прямой угол
AD1I ранен прямому углу
CBIj\ значит, треугольник
АН О будет подобен треуголь-
треугольнику CBL. Значит, как ВС
к BL, так и AD к DII, то
есть BG к ЕЙ: Рис. з.
ВС: BL = AD : ОН = BG : ЕН, • —"
и обратно *), пак СВ к ВС, так и BL к Elf, то есть ВК к КЕ:
CB:BG-=BL: ЕВ = ВК : КБ
вследствие того, что BL параллельна ЕН; затем, «присоединяя», —
как CG к BG, так и BE к ЕК:
(СВ -)¦ ВС) : BG = (ВК -^ КЕ) : КЕ,
СС : ВО = БЕ : ЛК,
таким образом, как квадрат на CG к прямоугольнику между CG и GBr
так и BE-ЕС к СЕ-ЕК, то есть к EJJ2:
CG* : (CG ¦ GB) = (BE ¦ ЕС) : (СЕ ¦ ЕК),
: (CG- GC)=(
: ЕЯ2
так как « прямоугольном треугольнике из вершимы прямого угла оиу-
щен на основание перпендикуляр ЕН; таким образом, CG2, помножен-
помноженный на EI1*, откуда квадратный корень давал площадь треугольника
ABC, будет равсп прямоугольнику CG-GB, помноженному на СЕ ЕВ:
CG* ¦ EH2 = (VG ¦ GB) ¦ (СЕ ¦ ЕВ).
И каждая из CG, GB, BE, СЕ является данной; действительно, CG
есть половина периметра треугольника ABC, BG есть избыток, на
который половина периметра превосходит СВ, a BE есть избыток, на
*) Читай «переставляя».
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ В ПЕРЕДЛЧК АЛ-ЕИРУИИ «21
который половина периметра превосходит АВ, так как ЕС равна CF,
a BG равна Ар', поскольку она же равна и AD:
КС — CF, BG = AF.
Значит, будет данной и площадь треугольника ABC.
[4] Теорема о том, что площадь треугольника ACU равна сумдш площади тре-
треугольника ABC и нроизпеденик Dft-ЕВ, также доказываемая и трактате ал-Иирунп,
я в. шется следствиом теоремы Архимеда о ломаной линии: если AR—HB—BC и FM-=BE,
то треугольник AMD ранен треугольнику IIDC, так шкАМ—ВС, L>M=DU и AD=DC
к треугольник АПС равповелик пятиугольнику AMDHC, состоящему ил трпугольпикоп
ABC и TSDM, а площадь треутолмгика BDM jionna нроналсдопмю Dli-iiB.
DG DE VG3 DGGA DK» DK-EB
[.,] Ыу имеем ^«з^;- отсюда = = -
DG-GA — DR-EU
DG-GA—DE.EB GA*~ ЕВ*
DC*-nE-* ал. ЛВС
¦¦ V У-U (EA+AG) {АК ¦ СК).
Если через р ойозпачим нолулсримстр треугольника ABC, то
ЕН -¦¦¦¦ КЛ -.- АО = -у (АВ -I- ВС) + AG- 2AG ~ Р - АС,
АК ¦= AG - GK - 4^ - ЕВ = 4г - <лв ~ J> ~ *;А + ^ ~ АВ ~ r' ~
¦ЕА + АС =-|-UB + «СИ--|-АС = Р.
СК - 4? + А"И = 4? Н- Ail - АК ¦¦= А« -1 4г - 4-
_АЛ ЛС ВС (АВ4ВС + ЛС) „, р^
" 2 ¦ 1" ~ г ~ 2
Таким образом,
ил. AIJC = Vy (р - At) {р - АВ) № - ВС).
КНИГА О КАСАЮЩИХСЯ КРУГАХ
«Книга о касающихся кругах», так же кап «Книга лемм» и «Книга о построении
круга, разделенного па семь равных частей», сохранилась только о виде арабской обра-
обработки, принадлежащей, по-видимому, тому же Сабиту нбн Курре, которому принадле-
принадлежали обработки этих сочинений. Ёдинствшная сохранившаяся рукопись этого сочинения,
озаглавленная «Китаб фй-д-даваир ал-мутамасса», хранится в Банкипурской Восточной
публичной библиотеке (ЛЬ 24G8/28). Эта рукопись опубликована Османийским универ-
университетом п Хайдерабадс (part 2). Перевод, осуществлен С. А. Розенфельдом с хайдера-
бадского издания.
Вместе с «Клигой о касающихся кругах» в хайдерайадском издании опубликована
рукопись Jss 24С8/29 той зке библиотеки (part 1), озаглавленная «Книга о началах
геометрии Архимеда, переведенная с: греческого на арабский язык Лбу-л-Хасапом'Али
ибн Яхьей, клиентом повелителя правоверных, Сабитом вбн Куррой, умершим в дпести
восемьдесят восьмом году хцджры». Эта книга содержит доказательства 19 геометрических
предложений, а из которых относятся к свойствам круга, а остальные 14 — к свойствам
треугольников (и.ч них 4 относятся к свойствам равностороннего треугольника и 4 —
к свойствам ратюбедрспного треугольника). Элементарный характер этих предложений'
(например, предложение VII о равенстве вмпот равностороннего троуголЫшка) пе даст
возможности включить эту кпигу в собрание сочинений Архимеда.
111 ЗДесь имеется в виду предложение 32 книги III «Начал» Евклида. В арабском
тексте «Начала» названы словом «ал-устуксат», означающим «стихии, элементы», ивляю-
щимся транскрипцией греческого названия «Начал» (SxX)
Предложение 32 читается так: «Если некоторая прямая касается круга и от точки
касания тшутри круга ироведена некоторая секущая круг прямая, то углы, которые эта
прямая образует с касательном (F.KDi/i его дополнение до 180°), будут равны углам в на-
накрест лежащих сегментах крута».
[2] Здесь в арабском тексте пропущено слово «квадратов»; аналогичный пропуск
произведем и ири формулировке примера, а и доказательстве вместо слов «двойному
отпотшянш» написано «отлоишиню». Систематический характер этих пропусков указы-
указывает на ошибку одного и» переписчиков этого сочинения. Нужно отметить, что в класси-
классической математике грекоп четвертые степени линий не употреблялись, как не могущие
быть построенными геометрически; таким образом, эта и теорема XI, в которой встре-
встречается двойное отпоншинс площадей, не могут восходить к Архимеду.
{31 См. примечание 14 j к «Кпиге о построении круга, разделенного на семь рав-
пых частей». Здесь слово «цлоскость» передано пе словом сатх, а равнозначным словом
мусаттах. Разнобой в терминологии объясняется, вероятно, лкусами переписчиков трак-
трактата, которые, как видно ил нродисловия переписчика к «Кивго о ностроепин круга»»
дово-чьно свободно обращались с текстами переписываемых ими сочинений.
\А 1 Рис. 24 отсутствует в рукописи, по д.тя пего оставлено пустое место.
151 Это предложение Архимеда играло очень важную роль в развитии тригономет-
тригонометрии на средневековом Востоке. В тригонометрической клиге своего «Канона Мас'5гда
по астрономии и звездам» с^еднеазиатстий! ученый Абу-р-Райхан ал-Г>ир5'ни основывает
па нем дока:1ател м-тиа мпогих тсюреи трыгонометршг, называя его «предпосылкой Архв-
меда». В своем «Трактате об определении хорд в круге» ал-Бируни приводит три дока-
доказательства этого предложения, данные Архимедом в «Книге о касающихся кругах» (кото-
(которую ал-Бнруии называет «Книгой кругов»), а таюко приводит многочисленные доказа-
доказательства ятого предложения, принадлежащие средневековым комментаторам Архимеда
(см. «Теоремы Архимеда, сохрашгошиесм в передаче ал-Пирунн»).
ПРИЛОЖЕНИЯ
о
СПОСОБЫ ЗАПИСИ ЧИСЕЛ И ВЫЧИСЛЕНИЙ
' ' В ДРЕВНЕГРЕЧЕСКОЙ МАТЕМАТИКЕ
У грекоп йнли п употреблении дпа способа обозначении чисел: алфавитный и при
помощи так пиакгаигммх гиродиаиовских :пшков.
В следующий таблиц» даны числовые значения отдельных букв греческого алфавита
вместе с греческими и семитическими (еврейскими) названиями этих букл.
ЧИСЛОВЫЕ ЗНАЧЕНИЯ ПУКП ГРЕЧЕСКОГО АЛФАВИТА
Число
1
г
3
4
5
6
7
8
9
10
20
30
40
50
60
70
80
90
100
200
300
4A0
500
600
700
800 "
900
Буква
гтечсско-
го алфа-
алфавита
IX
В
1
е
6
С
¦п
0
1
?v
V
6
0
я
q
о
я
•t
CD
т
1b
т
Греческое наввание
букпы
альфа
бета
гамма
дельта
эпсилон ¦
вну (дигамма)
дяета
эта (Н) . .
чета
лота
каппа
лаыбда
ми
пи
«си
«микрон
Ш1
копии
ро
С11ГМН
тау
фи
хи
ПСИ
омега
сампи*)
Ссшйтическос и.чзпание букви
алоф (бык)
бет (дом)
шмель (верблюд)
далет (дверь)
хс: (hi;)
вау (столб, на котором стояла
палатка)
зайи
хет (плетет.)
Tt:T
иод (рука)
каф
ламсд (острый стержень, кото-
которым подгоняли бт>т«(ш)
мим (иода)
лун (рыба)
самек
айп (глаз)
не (рот) ¦ . .
коф (зцтылок)
рсш (голова)
шин (зуб)
тау (крест)
i -
•) Этот внак не входил в алфавит и употреПляятвя только для обозначения
чикла 900. Ок представляет елинпис пиух букв: сигмы (дорийское назвЕЕие «евн»)
и пи, откуда произошло и плавание.
Порядок цифр следует семитическому алфавиту, кончавшемуся на букве «тау»,
за идинственпым исключением: между буквами «ие» и «коф» у семитои стояла еще «цадс» —
40 Архннбд
626 ПРИЛОЖЕНИЯ
твердое tli; вес букли, стоящие после т—300, являются специфически греческими. Более1
того, указанный алфавит инляетси восточпо-греческим (ионийским); западный (халкид-
ский алфавит), or которого произошла современная латинская азбука, имел некоторые
оглнчни. Это показывает, что упомянутый способ изображения чисел при помощи буки
мог возникнуть только в восточной Греции (Ионии.) и представляет специально греческое
изобретение. Если бы греки заимствовали ого с востока вместе с азбукой, то ом обяза-
обязательно понтимся би и в !шиадмых алфавитах и, в частности, вместе с латинским алфавитом
и у римлян. Что касается времени создания рассматриваемого обозначения чисел, то
наличие дигаммы (позднее она была заменена буквой S — знаком для сигмы я конце
слова) и коипы (С), исчезнувших очень рано, покалывает, что возникновение алфавитной
системы обозначения чисел относится к самим начальным стадиям развития греческой
культуры. Документально эта система заевндетвдьстпована лишь для середигод с V лежа,
но мы не очень ошибемся, если отпеоом ее поииикггопение к VI или даже: VII лекам до
п. э. В течение классического периода эта система употреблялась преимущественно
я посточной Греции; с конца IV века она распространилась по всему греческому миру
и был» перепита и семитическими пародами.
При помощи указанных знаков можно било писать вес числя от 1 до 999. Для обо-
зпачешш тысяч (от одной до депяти) перед буквой стапился слева внизу значок; так
число 1851 грскн записали бы так:
,UG>VU.]
Для обозначения десятков тысяч употреблялся знак М (начальная буква
слова U.0Q101 — мириада, то есть декить тыеич), причем соответствующее число десят-
коя писалось вверху:
ха
М|р" =210062.
Дроби с числителем единица обозначались цифрой знаменателя с штрихом справа
вверху:
*' = Й>
если числитель пс равнялся единице, то его значение писалось над знаменателем или
слепа от пего. Половила обозначалась специальным знаком Z, очень похожим
на египетское обозначение половины. Точно так же египетским можно иаяпать способ
представления дробной части числа в виде суммы нескольких дробей с числитслими, рав-
равными единице. Для того чтобы выделить в тексте числа от обыкновенных бук», пад ними
сверху ставилась черта. Вот примеры, заимствованные из Архимедова «Измерения круга»:
гл
M,dv 349450,
^ 591 у-,
4673-1,
...... 3013 1-|-^=3013 -| ,
1838 -^ ,
- , 10
ит 71-
Другой способ обозначения чисел при помощи геродиаповеких *) знаков заключался
в следующем.
Единицы обозначались черточкой I, пятерки буквой П или Г {начальной буквой
слова (jtivxe — шт.), десятки буквой Д (ЛЕКА. — десять), сотни — Н (НЕК.ЛТОЛ1 —
сто), тысячи X (x'Jiioi), десятки тысяч — М (iiuqioi — мириада). При помощи «умноже-
«умножения» пятерки на десятки, сотпи и т. д. получались знаки для 50, 500, 5000, 50 000:
Р = 50 , P=5D0 , Р=5000 , Г=50Ш
*) По имени описавшего его грамматика TI века п. ь. Герояиана, сыпа енамсиитого Аполло-
Аполлония Дисколз, котирый ЛвлЯоткЯ ТБирдОМ греческого синтаксисах.
ЗАПИСЬ ЧИСЕЛ И ВЫЧИСЛЕНИЙ В ДРЕВНЕГРЕЧКСКОЙ МАТЕМАТИКЕ 627
Вычисления производились при помощи абака — счетных досок, вроде наших сче-
счетов, па котором единицы различных разрядов обозначались жетонами — псефами (\|nj<poi)-.
Самос ранней упоминание о счетных жетонах встречается в «Афинской лолитии» Аристо-
Аристотеля при объяснении процедуры выборов и подсчета голосов. Греческий абак (само иаз-
впиис ср(х| обозначает «доска») дошел до пас в виде так называемой евламияекой доски,
относящейся примерно к 111—II векам до и. э.,
рисунок которой помещен ниже. Помещении»
сбоку знаки соответствуют изображениям по
геродиаповой системе следующим числам:
Т —талант F000 драхм).
F-5C0D , Х~Ш , F-SDO , Н-ЯЮ ,
Р -50
- 1
А - 1
Г -5
Т-
г -1
ХГН1"йГ Н СТХ
Саламннскан доска.
Нижние, не разделенные пополам полоски
соответствуют драхме и се долим. Очень инги-
роспо, что основпаи часть доели представляет
полосы, разделенные пополам. Для десятичной
системы счисления подобное разделение является
немного странным, по оно унорпо повторяется и
на римском абаке, и на китайском суанпапп, по-
показывая, что когда-то это деление имело пмысл.
Мьт можем объяг.пить это, егли предположим,
что прототип спламнпской доски был выработан
в стране, гдо каждый разряд числа требнвал для
своего обозначения двух знаков; такпй страной
была как риз Ьаьилоиин с ее шютидесятсричиои
системой счисления, где каждый разряд состоая
из десятков и единиц. Лторым признаком вави-
вавилонского происхождения салампнекой доски яв-
является обозначение на вей таланта — специфиче-
специфически навил опекой единицы веса, равной 60 минам
или GHOO драхм, так как греки, когда они перепи-
перепили вавилонскую монетную систему замелили де-
деление мины на 00 шекелей более подходящим для
их системы счисления делением на 100 драхм.
Мы обладаем более чем скудными сведениями о том, какими способами греки про-
производили арифметические вычисления. Конечно, сложение и вычитание пастолько просты,
что дс требуют вообще никаких комиелтарисл. Относительно умпоткюгил мы имеем при-
примеры, приведенные Евтокием в его комментарии к «Измеревпю круга» Архимеда.
Греки пользовались тем зке способом умножения, что ими, « той только разницей, что
мы начинаем умножение с: низших раиридов множителя и множимого, а греки начинали
с высших. Интересно, что совершенно так же, кап греки, поступали средневековые
абацистм эпохи Герберта (X—XI иска) и швялопские вычислители, начиная с третьего
тысячелетия до н. э. Это сходство дает прапо предположить, что вообще греческие способы
арифметических вычислений мало отличались от методов, изложеввых в самом раннем,
принадлежащем Герберту трактате об абаке;, тем более, что последний паперляка пред-
представляет собой лишь переработку античных методой арифметических вычислений.
Об античных способах деления мы имеем гораздо более скудные сведения. П гре-
греческих источниках мы не имiu-м ни одного примера производила деления.
Зато относительно методики извлечения кпадратпого корня у Архимеда мы теперь
знаем гора идо больше, чем исследопатили, трудмишиеси пятьдесят лот тому на.чад. Откры-
Открытая в иачале XX вика «Метрика» Герона Александрийского вмс-сто г. влппл онскими мате-
математическими текстами дала нам твердое основавис для восстановления методики извле-
извлечения кладрггтиого корня Архимедом.
Способ извлечения квадратного корня, изложенный п «Метрит;» Герина и в вапилон-
СБ11Х математических текстах, состоял в том, что если известно какое-нибудь приближен-
приближенное значение /10 квадратного корня и;) некоторого числа /1, то более точное его значепио
можно найти по следующей формуле:
40*
628 ПРИЛОЖЕНИЯ
Числа Ао и -г- представляют собой два приближенных значения квадратного кор-
ня, из которых одно является значением с недостатком, а другое — с избытком. Так как
истинный кореш, заключается между ними, то вполне естественно, что арифметическое
среднее обоях этих ниачепий даст более точную величину искомого квадратного корни.
Положим Аи-^х и -j- =у; тогда
"о
А=ху,
и искомый кадратиый король представляет геометрическое среднее для х и у
Мы можем приближенно представить его в виде арифметического среднего
ТСелибымыхотслииолучитыю вапи.ншекпму способу следующее значение: квадрат-
квадратного корня, то должны были бы разделить Л иа иолучеппое приближенное значение
I'T- xy
откуда
2xV ' 2 \ х "Г у )
Мы получаем третье «средиео», употреблявшееся в греческой, математике, а именно
среднее гармоническое. Таким обраяом, все три греческих «средних» оказываются свя-
связанными ыемкду собой в операции извлечения квадратного корня: если среднее геометриче-
геометрическое У ху дает точную величину квадратного корня из произведения ху, то среднее ариф-
метическое — (х-\-у) дает, как нетрудно видеть, приближение с избытком, а среднее гар-
гармоническое — приближение с недостатком. Как показывает кпига X «Начал» Евклида,
первичное аиачемше цгот) — медиаль — относилось именно к среднему геометрическому,
называвшемуся просто «средним» баз немцах прилагательных; таким образом, вполне
естественно предположить, что и два других «средних» возникли первоначально в связи
е операцией имлечения киалратного корни. То обстоятельство, что все г»ти три средних
петрсчаютеэт в совместной комбипацяи уже у Архита Тарентского, позволяет предполо-
предположить, что указанный способ изплечеття кладрат!гого корпя был уже известен грекам
еще и :шо\-у Платона в IV веке до u. :i. Каким образом при его иомгащт Архимед мог
вычислить встречающиеся в «Измерении круга» квадратные корни, показано нами о ком-
комментарии к названному сочинению (стр. 547 и ел.).
. ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ»
В комментарии ко пторой книге «О пл.чпающих телах» мы указали на незакончен-
незаконченность отого произведения Архимеда. .В связи с утим не может не представить интереса
вопрос, что могло бы стоять в ненаписанной части книги.
В конце предложения X Архимед рассматривает вопрос о положении равновесия
сегмента параболоида, когда параметр р меньше т-т оси сегмента. В зависимости от
плотности плавающего тела Архимед устанавливает две области, в которых возможно
плавание сегмента с: основанием, находящимся
вне жидкости, а именно когда плотность тела Л- I) 1 ' f
будет или близка к нулю, или же почти равна
плотности жидкости. В качество меры плотно-
плотности мы можем япять величину оси погружен-
погруженной части сегмента, которую мы обозначали
через — а. Определенно предельных значении а
нал можем произвести по методу Архимеда.
Пусть па приложенном рисунке ABL бу-
будет парабола, получающейся п сечении тела
плоскостью, проходящей через ось, парабо-
парабола AUCI представляет параболу центров, а
парабол» AVQD соответствует пашей параболе
плавания. Центр тяжести" сегмента будет в
точке Л' (А'/)= -у ПК); отрезок КН равен па-
параметру р параболы ABL, a ID г.остаилиет
две питых AL.
Ч играя И проведем параллельную AL
прямую до пересечения в С и U с параболой
AI; отрезки Си и UJi будут ординатами, соответствующими плаванию с нижним углом
основания ни поверхности жидкости, a OQ и PV дадут пarm -^-a—длины оси погружен-
погруженных частей сегмента, соответствующих искомым предельным положениям. Значения
отношений плотности тела к жидкости для этих пшюжоний мы получим, во;н«!дя в квад-
OQ PV
рат отношения -^j а -тг= ¦
Возьмем начало коордииат в точке В, пусть ось абсцисс пойдет по Л2), а ось орди-
герпендикулнрно к ЛП влело. Урапневие параболы AbL будет:
нат лерпендикулнрно
Уравнение- параболы ACI бу,чет:
—впх
Наконец, урнвнише последней плраболы AQ1) будет:
<J30 ПРИЛОЖЕНИЯ
2
Расстояние BR—x будет равно — BD—р. Подставляя ато выражение в уравнение
параболы АС1, получаем:
/ 2 \2 3 AD2 ( Ь \
\У~~Ь ) ~~ 5 BD vlf> P)'
что может быть приведено к виду
откуда получаются корпи:
2
Таким образом,
У Архимеда, тангенсы соотвитстиушщих предельных углол наклона будут:
К=~2Л?»
*" V * 4 BD
К 4 ?f?»
Переходим к определению предельных величшт OQ и PV погруженных осей. Дли
этого нам пужпо найти рамюпть абсцисс парабол AB.L и AQD, соответствующих опре-
определенным ординатам yt и //.>.
Уравнения этих ua]>a6o:i будут: "• — •
, AD*
Умножим первое урависпис ла два и вичтем из иего второе, помпп, что ординаты у
в обоих уравнениях одинаковы, но абсциссы различны. Ксля обо;шачим абсциссу пара-
параболы AQD через г3, а абсциссу параболы AJ.iL через а^, то будем иметь:
Остюда опрйделитси нужный нам отрезок &—х2—хх
. BD Г./ 1 ...4.2 1 , RD BD
Если вместо ;/ встаитсм найденную величину
но после очевидных упрощений получим:
ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ» 631
Таким образом мы приходим к следующему выводу:
Iй. Если плотность тела по отношению к жидкости меняется в пределах от 0 до
/0,52—0,60 ду;—0,48 1/ i—? jPjy J , то тело плавает с осиоиацием, находящимся пад
жидкостью.
2°. Если плотность тела лежит в пределах
•@,52-0,60 JL_o.«e |/i- f {f))Z до
то голо будет плавать с полузатопленным основапвдо.
3е. Если нлогпость тела иеппетея в пределах
от @,52-0,60 ^--±-{),тл/\-~-§Л лоЛ---^--^
то тело будет плавать и наклонном положении, имея основание пад поверхностью
жидкости.
4°. Если плотность тела меняется в пределах от \ 1 --jr-.jv- J до 1, то тело будет
шшцать, имея ось вертикальной.
Для случаи плавании сегмента г. погруженным ословяштем надо вместо погружен-
погруженной части рассматрттать часть сегмента, находящуюся ипе поиезрхыости жидкости и заме-
заменить относительную плотность тела, ве дополнением до едгшмцы. В таком случае мы полу-
получили бы предложении, аналогичные 3, 5, 7 и 9 сохрапилшейся части второй книги. Нет
никакого соыпепин, что Архимед был и состопиии сделать это; мм же ограничимся лишь
формулировкой окончательных реаультатоп.
1". Если ПЛОТПОСТ1. т(ша изменяется от 1 до
I -@,52-0,60 ^-0,^/^
то сегмент нланает и наклонном положении, имел основание полностью под поверхно-
поверхностью жидкости.
2°. Если плотность тела мепяетси и пределах
о, .1-
до 1 -
то сегмент плавает с полузатопленным основанием.
3°. Если плотность тела меняется в пределах
от
1 _ Л),52-0,в07^ J-0,48
то сегмент плавает в пяклонпом иояогкенип с оспопацпем, находящимся Oo-inocn,io под
поперхиостыо жадности.
4". Накопоц, если плотность тела моияетси и пределах от 1— ( 1—2 liD ) д0
ну-1я, то сегмент плавает с иортикальиой осью, имея основание hii;i:c ноперхпости
жидкости.
Соотиетстнующио угли наклона могут быть определены по той жо формуле
если только вместо а Срать величину оси сегмента, находящейся вне поверхности жидкости
632 ПРИЛОЖЕНИЯ
Окончательные результаты исследования Архимеда могут быть сформулированы так:
1°. Если ось сегмента не превышает чг- параметра р, то сегмент может плевать
с вертикальной осью, имея основание безразлично над ллн под поверхностью жидкости.
Плапапис сегмепта в наклонном положепип невозможно.
!? 15
2°. Если длина оси сегмента заключается в пределах от ~у р до -т р, то плавание
в наготоппом положвпип становится возможным, но осионнпио сегмента должно
быть или на;), или под поверхностью жидкости. Предельными значениями плотности
являются
Г 3 р
{*¦' 2 ВП ' И *~
\i ТТЛ)) ¦
4
гт Р '? Р 4
При ttt^=-s- эти пределы равны пулю и единице; если -?t^*=tf » т0 мы получаем
UL} «5 BJJ 10
з р у_ з / з р у 16
ио и сем промежутке от -if=~k П° ~i7T\ — Тг первый предел будет пиже второго. Таким
образом, мы замечаем следующие три области изменения плотности тела.
а) Если плотность тела заключается п пределах от нуля до ( 1—-^ j?-= ) , то воз-
возможно или плавание тела л вертикальном положении с погруженным основанием, или же
в наклонном положении с основанием вне жидкости.
б) Если плотность тела заключается в пределах от Г1~~-Г/?Ь) до ^ V*~^BD- '
то возможно плопанпе только п вертикальном положении, причем основание может без-
безразлично находиться иад и под поверхностью жидкости.
и) Если плотность тела заключается в пределах от 1 — f 1 —~ -~j- j до 1, то воз-
возможно плавание тела или к кортикальном положении ¦: осноиашшм лис жидкости, или
п пакленном лоложспии с еншоланнем внутри жидкости.
3°. Тецерь рассмотрим случай, когда отношение ¦—- будет больше -.^-. В таком
ыучае возможно солпадсние обоих предельных величин плотности; »то будет, вели
2 ВТ)) -1 l^1 2 BD
или
1-А-Е— l/I
2 BD~ V 2 '
Отсюда
во~ л ^
l
что можпо положить naunmi примерно — .
Ь 15 3»
Таким образом, если длина оси сегмента изменяется в пределах от 7"^~^ТР
и приблизительно до f>p, то мы будем иметь по-прежнему три области: г
а) При небольших плотностях н.-шпание возможно в лортикапьном положении
основанием вниз или п наклонном положении основанием виерх, причем последнее может
быть или целиком вис поверхности жидкости, или отчасти.
6} При плотностях тела, несколько отличающихся в ту или другую сторону от поло-
половины, пояможпо плавание только в вертикальном положении.
и) При плотностях, приближающихся к единице, возможно плавание в вертикаль-
пом положении оснопапием вверх или ь наклонном положении основанием шшз, причем
последнее или целиком, или отчисти находится ниже поверхности жидкости.
Если BD более 5у>, то средиия область пропадает соксем, а две крайние начинают
отчасги налагаться одна па другую.
БИБЛИОГРАФИЯ
БИБЛИОГРАФИЯ
Издание трудов Архимеда основывается на следующих рукописях:
1. Кодекс Георгия Балл ьт. Сам кодаке утерял, но его содержание может
быть восегаиоилгаю на основании следующих рукописных копий:
¦a) Codex Laurcnt-ianus (XV п.) во Флоренции,
b) Codex Marcianus (XV в.),
c) Codes Parisiuus 2360 (XVI п.),
d) Codex Parisinus 2361 A544 r.)
2. К о п с т а л т и п о п о я ь с к м ii палимпсест (X п.). найденный и шфуса-
.шыском монастыре и прочтенный Гейбергом в 1906—1908 годах.
3. Л в т и п с. к и й перевод сочинений А р х и м е д и Вильгельма
из Мербоке (XII век), сделанный настолько буквально, что па его основании
мозлпо восстановить греческий оригинал. Хранится в Ватиканской библиотеке. ¦
I. П е ч а т п ы с и а дани л сочинений Л р х и At e д а
4. Archimedis орста, quac; qtiidem ex.sUmt Oiruiia (с комментарием 1?итокин), Basileae,
Joh. llurvagius, 1544.
5. Archiriodisopera noimiillaaFod.CoinmaiidJnormjM'rinlatminri converse, Vencliis, 1523.
ti. Archimedis dc iis quao vebuitlur in aqua libri duo a Fed. Cimimandiuo nnililuti ct illust-
rati, Conoiiiiie, 1565.
7. ArchimediH opera qnai; exstant, novis demonstrationibus illustrala per Dav. HivalLum.
Taris. 1615.
8. Lemmata Arcbijtiodia apud Graecos et Jiiitino» joiujii-ldr.m desidiii'ala о votuslo codice
ЛТ. S. araliic» a Job. Gravio traducla et mine jn'muim cum arabum scholiis publicata...
a Sartiucle Forstcr, Londini, 1C57.
9. Aifiniraudi Archirncdis Syracusani monumenta oinnia matliomalira quao exstant ex
Lraditiono D. Fr, Maurolici, Panormi, 1685.
10. Archimedis opera, Apollonii Pergaei Coniconini libri IV..., r,ondon, 1675 (Banowius).
11. I.essing G. E., Reitrage zur Geschichte und I.lteraLur, BrauiiHchweig, 1773 (nopiioo
издание задачи о биках, стр. 421 м ел.).
12. Archinjedis quao supisrsuat oinnia cum Kutocii AscaloiiiLnc coimncntariis «x versionc
Jos. ТогеШ, Osonii, 1792.
13. P e у га г d P., Ocuvres crArchiinf'dc, traduitfs lilleralc-Kicnf. avoc. tin coinin(>iilaire,
Paris, 1807.
M. Archiincdos voxi SyrakiiH Vorhandcne VVm-Ье, aus deni «riccbibchcn ijbcrscfzt... vim
Xizzc, Straleund, 1824.
15. Archimedis opera omnia cum commentariis Entocii, ed J. L. Ileibuig, T—III. J.eipzio-,
Teubnur, 1880—1881, 2-е над., 1 A910), II AУ1.3).
Hi. II e a L h T. L., The works of Archimedes edited in modern notation will» introductory
chapters nambsidge, 1897. (Немецкий перкпол с лополнгаптнми Fr. К. I i о т'я,
Berlin, 1914.)
СЗО БИБЛИОГРАФИЯ
17. SutCT ТТ., Fin Friignicnt mis Ardiimndis Sloniachion. Abhandlungcn sur Geschichte-
der Mathematik, IX, 491 с ил. A899).
18. H e i b e r g J. L., Eme neue Sdirift des Archimedes. Hermes, XLII, 235—297 A907).
19. Ver E о с к с P., Lcs oouvres completes il'Archimede tradnilcs du grec en irancais,
Paris—BruxcIJes, 1921.
20. Ciwal i n a A., Archimedes Ubersetzungcn mit Kommentar. Oshvald's Klassiker
der exalcten Wiss«ijschaften. 5 выпусков, Leipzig, 1922—1925.
21. Snler H., Das Buch dcr Auffindung tier Sehnen im Kreisc von al-J3iruni. Bibliotheca
Mathomatica, 3 Folge, XI, 12—26 A910/11).
22. S с h о у С, Die trigonometrisclicn Lehren des pcrsischtui Astronomcn... al-Birani,
Hannover, 1927 (перевод «Книги о семиугольнике», ст. 77—84).
II. Русские переводы трудов Архимеда
23. II е т р у ш о is с к и й, Архимеда дио книги о шаре и цилиндре, измерение круга
и леммы, Спб., 182?
24. II е т р у ш с и с к я и, Архимеда «Псаммит», Сиб., 1824.
25. Тракта* Архимеда «Об измерении, круга». Перев. 13 а щ о в к о-З ахарчепко-
(в его переводе «Начал» Евклида), Киев, 1880.
26. Гей борг И., Ноное сочинение Архимеда. Послание Архимеда к Эратосфену
о некоторых теоремах механики, Инд. Mathesis, Одесса, 1909.
27. Архимед, Г ю й г с п с, Ламберт, Л е ж а н д р. Четыре сочипепил
о квадратуре круга, Malheris, Одесса, 1911. (Переиздаыы 1934, 1936.)
28. «Псаммит» Архимеда, Лкрев. Г. Ы. Попова, Птгр., 1922 (Переиздан 1932.)
29. Начала гидростатики (Архимед, Стеиин, Галилей, Паскаль). Пере». А. П. Долго-
в а, 1!K2, 2-е над., 1933. (Персвсдсяа первая книга «О плавающих телах» ж первое
предложение ма uroj>oii.)
Ш. Сочинения греческих авторов, содержащие
упоминании о математических трудах Архимеда
30. Герои A si о к г, & и д р и й с к и й, Метрика, Пего Alexandrinus Opera, Lipsiac,
Ш,2—252, 1903.
31. Его же «Механика», ucpen. с арабского, L. Nix. Opera, Lipsiae, IV, 2—252, 1900,
32. П а и п Александрийский, Математическое собрание, Иад. Гульча.
Керлин, I—III, 1876—1878.
IV. Общие работы и биографии Архимеда
33. Heiberg J. L., Quaeslionos Archimedean, Tlauniae, 1879.
34. II u I t к ch F., (Статья «Archimedes» в Real-Encyclopadie der ldassiselieii Altertums-
wissenschuften, Pauly-Wissowa, II, 507—539.
35. H e a t h Т. Г... Arcbimedes, London, 1920.
36. Czwalin a A., Archimedes, Leipzig—Tenbner, 1925 (ешь русский перевод, ГТТИ,
1!K'i).
37. К 1 i с hj Fr.— Wolff G., Archimedes, Berlin, 1927.
3S. DijksLorhnis К. Т., Archimedes, Grouingon, 1938; «Enclitics», XV—XVII,
XX, 1938—1944. Англ. перевод: Copenhagen, 1G56.
39. Л у р ь с С. Н., Архимед, Изд. Акад. паук, 1945 (имеется дополненный румынскиir
перевод).
40. К а г а и В. Ф., Архимед, Гостсгхиздаг, 1949.
f\\. R ее к л о и с к и и И. П., Архимед, Учпедгиз, 1957.
библиография 637
V. Исследования о G отдвлыплх работах А р х и ы о д а
А. М а т <: м а т и к а
42. Wieleitno т, Das Fortloben der Arehimuiiischcn InfiniLesiinal Methodon bis sum
Beginn des 17 JahrbundRrts. Quellen untl Studicn гиг GescMchtc der MnLliemalik, I,
201—220 A931).
43. M n 1 I e r C, Wie land Archimedes die von Him gcgcbcncn Niiiierungswcrto dcr \/~3,
Quellen und Stndicn, II, 281—285 A932).
44. Tropfke I., Die Sifiboueckaliharidhmg den Archimedes, Osiris, I, 636—651 A936).
¦45. Баш.мак о в а И. Г., Дифференциальные методы и работах Архимеда, Историко-
ыатематичыжио исследования, VI A953).
В. М с i а и и к а
•46. М а с h К., Die МесиялПс in ibrer liiitwicliliing, Leipzig, 1—17 (НИМ).
47. D ii h с m P., Les origines de la Stutiquc, I, Paris, 1—12, C1—98 A905).
48. Stein W., Uct Bcgyiff d«s Sch-weTpunlites bei Archiiuotles, Qxidlcn v. Studien, I,
221—224 A930).
4d. R e i m a nn Dora, Historische Studien fiber Ы. Madh's Darstellmig di^r EnLwick-
lung des Hcbelsatzes, Quellen u. Studien. Ill, 554—592 A936).
СОДЕРЖАНИЕ
НРЕДИСЛОНИЕ ПЕРЕВОДЧИКА ... . . S
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. П. Песемлского Ь
АРХИМЕД. СОЧИНЕНИЯ
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ GS
КВАДРАТУРА ПАРАБОЛЫ 77
О ШАРК И ЦИЛИНДРЕ 85
О КОНОИДАХ II СФЕРОИДАХ IBS
О СПИРАЛЯХ . . . 227
ИЗМЕРЕНИЕ КРУГА 266
О РАВНОНИСИИ ПЛОСКИХ ФИГУР, ИЛИ О ЦЕНТРАХ ТЯЖЕСТИ
ПЛОСКИХ ФИГУР S72
послание к ардтосФЕНУ. о икхамических теоремах . . гок
О ПЛАВАЮЩИХ ТЕЛАХ . . . 32S
ПСАММИТ Зй8.
КАТОПТРИКА 36&
ОВ УСТРОЙСТВЕ НЕБЕСНОЙ СФКРЫ 370
ЗАДАЧА, КОТОРУЮ АРХИМЕД НАИГВЛ К ОПИГРАМЛГАХ И СОСЛАЛ
НА РАЗРЕШЕНИЕ ЗАНИМАЮЩИМСЯ ПОДОБНЫМИ ВОПРО-
ВОПРОСАМИ АЛЕКСАНДРИЙСКИМ УЧЕНЫМ В ПОСЛАНИИ К ЭРА-
ТОСФЕНУ КИРЕНСКОМУ 372.
СТОМЛХИЙ 378
О МНОГОГРАННИКАХ 383.
ТРАКТАТ ЛБУ-Л-ХАСАНА САБИТА ИВЫ КУРРМ О ПОСТРОЕНИИ
ОШГСАННОИ ОКОЛО ШАРА TJGЛЕСНОЙ ФИГУРЫ С ЧЕТЫР-
ЧЕТЫРНАДЦАТЬЮ ОСНОВАНИЯМИ 387-
КНИГА ЛЕММ АРХИМЕДА В ПЕРЕВОДЕ ТЕЛИТ Л ВЕНКОРЫ С РАЗЪ-
«СНЕНИНМИ УЧЕНОГО ЛЛЬМОХТАССО АБИЛЬГАСАНА ГАЛИ
КВН АХМАДА ПАСУОНСКОГО 39t
КНИГА АРХИМЕДА О КОСТРОКНИИ КРУГА. РАЗДЕЛЕННОГО НА
СЕМЬ РАВНЫХ ЧАСТЕЙ. ПЕРИИОД АБУ-Л-ХАСАПА САВИ-
ТА ИБН КУРРЫ АЛ-ХАРРЛПИ 401
ТИОРЕМЫ АРХИМЕДА, СОХРАНЯВШИЕСЯ В ПЕРЕДАЧЕ АЛ-ЕИРУШ1 41С
КНИГА О КАСАЮЩИХСЯ КРУГАХ АРХИМЕДА, УБИТОГО В ДВЕСТИ
ДВЕНАДЦАТОМ ГОДУ ДО РОЖДЕСТВА 422.
КОММЕНТАРИИ
КВАДРАТУРА ПАРАБОЛЫ 44»
О ШАРЕ И ЦИЛИНДРВ 451
О КОНОИДАХ И СФКРОИДАХ 50&
СОДЕРЖАНИИ 639
II СПИРАЛЯХ 5t8
ИЗМЕРКНИЕ КРУГА - ... э28
О РАВПОВИСИИ ПЛОСКИХ ФИГУР 55<
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАЛ1Р1КСКИХ ТЕОРКМАХ . . Ь6Г.
О ПЛАВАЮЩИХ ТЕЛАХ 678
ПСАММИТ &»S
КНИГА ЛЕММ 604
КНИГА О ПОСТРОЕНИИ КРУГА. РАЗДКЛПШЛШ'О НА СЕМЬ РАП-
РАПНЫХ ЧАСТКЙ 614
ТЕОИЗМЫ АРХИМЕДА, СОХРАНИ НШИКСЯ И ПКРЕДАЧЕ AJJ-DH-
РУН1Т 618
КНИГА О КАСАЮЩИХСП КРУГАХ 622
ПРИЛОЖЕНИЯ
СПОСОБЫ ЗАПИСИ ЧИСЕЛ И ВЫЧИСЛЕНИЙ В ДРЕВНЕГРЕЧЕСКОЙ
МАТЕМАТИКИ 62Ь
ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАНАЮЩМХ ТКЛАХ» С26
БИБЛИОГРАФИЯ 635
АРХИМЕД. СОЧИНЕНИЯ
М., Физматгия, 1962 г., 610 стр. с илл.
Редактор Л. 10. Чернышева
Оформление художника В. Л. Селютинскаго
Художественный }«дактор И. Я. Румянцев.
Техн. редакторы Л. П. Колесникова и JI. Я.
Корректоры В. В. Кцэке-цова и О. А. С«гал.
* * *
Сдано и набор 3/Ш 1SC3 1\ Ыодписаио к печа-
печати 13/X 1962 г. ВУиигa JOXlOSl/ie. Фив. исч. л. 40.
Условн. печ. л. 54.8- Уч.-изд. л. 50. Тираж 4000 акз.
Псиа книга 2 р. ТО к. Заказ 200.
* * »
Государстпян ш>с иадате льсгво
фИ8ико-матсмитич<!С1;о Й дитерату ры.
Москва, В-71, Ленинский проспект, 15.
* * •
Московский типография Л1 fi Мосгорсовнархозя.
Мокква, Грс\-прудиый пер., S.