СОЧИНЕНИЯ
ПЕРЕВОД АРАБСКИХ ТЕКСТОВ
Б. А. РОЗЕНШЕЛЬДА
ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1 9.6.2

Архимед. Один из античных бюстов.

О ПЛАВАЮЩИХ ТЕЛАХ
КНИГА ПЕРВАЯ
Предположим, что жидкость имеет такую природу, что ив ее
частиц, расположенных па одинаковом уровне и прилежащих друг к
другу, менее сдавленные выталкиваются более сдавленными, и что
каждая из ее частиц сдавливается жидкостью, находящейся над ней по
отвесу, если только жидкость но заключена л каком-нибудь сосуде и не
сдавливается еще чем-нибудь другим.
I
Если поверхность, рассекаемая любой плоскостью* проходящей через
одну и ту же точку, всегда дает в сечении окружность круга с центром
0в той самой точке, через которую проводятся
секущие плоскости, то эта поверхность будет
шаровой.
Действительно, пусть будет некоторая
поверхность, которая при сечении плоскостью,
проходящей через точку К {рис. 1}, всегда образует
окружность круга с центром в этой самой точке К. Если
эта поверхность не будет поверхностью шара, то но
будут равными все лишш, которые идут от центра
1,,1С- *• к поверхности. Пусть А, В, Г, Д будут точки на
поверхности, причем лишш АК и ВК не раины;
проведем через КА, KB плоскость, и пусть она образует в сечении с
поверхностью пинию ЛАВГ; эта а иная будет, конечно, круговой с
центром в точке К, так как рассматриваемая поверхность предполагалась
обладающей таким свойством *). Значит, линия КА, KB не будут
неравными; поэтому необходимо, чтобы эта поверхность была шаровой.
II
Поверхность всякой жидкости, установившейся неподвижно, будет
иметь форму шара, центр которого совпадает с центром Земли.
*) Именно, что иессечешш ее плоскостями, приходящими черся точку К, шляются круговыми-

О ПЛАВАЮЩИХ ТИПАХ Д29"
Вообразил! некотирую жидкостт,, которая установилась
неподвижно; рассечем ое поверхность через центр Земли плоскостью; пусть центр
Земли будет К. {рнс. 2), а линия сечения поверхности АВГА. Я утвер-
исдаю, что линия АВГА Судет окружпостью круга о центром и К.
Действительно, если это не так, то прямые, выходящие из К. к линии.
АВГА, не будут раины друг другу. В таком случае низшем некоторую'
прямую, которая была бы больше одних и меньше других из линий,
выходящих из К к липни АВГД, и из центра К опишем круг радиусом,
рапным птой линии; тогда тшерхность этого круга пойдет так, что-
■часть ее расположится вне линии
АН ГА, часть же внутри, так как А.
радиус ее будет больше
некоторых из пиний, выходящих от К к
линии АВГА, и меньше других.
Пусть окружность описанного
круга будет ZH1I; проведем из В
в К прямую и построим прямые 7-
ZK, КЕЛ, образующие равные
угли <АКВ и ВКЛ), затем из Рис- 2"
центра К опишем некоторую дугу
НОП, которая находилась бы на плоскости (чертежа) и в жидкости;,
тогда распологкенные по дуге ЕОП частицы жидкости будут находиться
на одном уронне и прилегать друг к другу■ Те из них, которые
находятся на дуге SO, будут сдавливаться жидкостью, расположенной до-
уровня ZB, а те, которые находятся на дуге ОН,— жидкостью до
уровня BE; следовательно, частицы жидкости, расположенные на дугах
SO и Oil, будут сдавливаться неодинаково: таким ибразом, менее сдан-
линаемгос будут вытеснены более сдавливаемыми; оледопатсльно,
жидкость не останется неподвижной. Мы же предположили, что она.
установилась так, что остается неподвижной; значит, необходимо, чтобы
линия АВГА была окружностью круга с центром и К. Подобным же
образом докажем, что если как-нибудь иначе рассечь поверхность
жидкости плоскостью, проходящей через центр Земли, то сечение будет
окружностью круга и центр ео будет тот же, что и центр Земли. Теперь
ясно, что поверхность установившейся неподвижно жидкости имеет
форму шара с тем же центром, что и у Земли, ибо она такова, что при
рассечении ее плоскостями, проходящими через одну и ту же точку,
в сечении получаются окружности с центрами в той самой точке, через
которую проходят секущие плоскости.
TII
Геле*), равнотмжелые. с жидкостью, будучи опущены в эту
жидкость, погружаются так, что никакая их часть не выступает
над поверхностью жидкости, и не будут двигаться вниз.
Опустим в жидкость какое-нибудь тело из равнотяжелтлх с птой
жидкостью, и пусть, если возможно, некоторая часть его будет
выступать над поверхностью жидкости; пусть жидкость установится в таком.
*) У Архимеда интересное выражение: twv птЕоеш\> u-EVefrEav xa «Joflraceov-rra— буквально:
«ie ия объемных величин, которые равнотняселы...» Архимед, но существу, имел дело с геометриче-
, , > » ,
скнмн телами, и его cteueu jis-yeoea представляют пространственную аналогию елгяеВи цеуефеа
(плоских величин), о которых гала речь в книгах «О равновесии плоских фигур0-

:nn
АРХИМЕД
положении, что будет оставаться неподвижной. Вообразим некоторую
плоскость, проведенную через центр Земли, через жидкость и через
это тело; пусть ее сечение с поверхностью жидкости Судет дуга АВГД
{рис.. 3}, а с рассматриваемым телом — фигура EZB11, центр же Земли
пусть будет К. Тогда часть ВГН0 тела будет в жидкости, часть же
BKZF — вне ее. Вообразим, что тело охвачено плрамидообраэной
фигурой, имеющей в основании на поверхности воды параллелограмм *),
а вершиной — цоптр «Земли. Пусть КА
и К М будут сечения граней пирамиды
с той плоскостью, в которой находится
дуга АВГД. Около центра К опишем
еще одну шаровую поверхность так,
чтобы она проходила впутри жидкости
и ниже тела EZTTO, и рассечем ее
плоскостью; патом возьмем другую
пирамиду, рапную и подобную той,
которая охватывает погруженное тело, и
смежную с ней; пусть КМ и XN будут
сечения се граней; в жидкости
вообразим некоторый объем PZTT,
охваченный жидкостью, равный и подобный части ВНвГ первого тела,
погруженной и жидкость. Тогда частицы жидкости в первой пирамиде,
расположенные под той частью поверхности, где находится дуга НО,
а также соответствующие частицы в другой пирамиде, где находится
дуга 110, будут лежать на одном уровне и в непрерывной связи друг
с другом. Однако они не нснытынают одинакового давления;
действительно, те частицы, которые расположены ш» ЕО, сдавливаются телом 011EZ
и тон жидкостью, которая находится между поверхностями НО, AM
и гранями первой пирамиды, те же, которые расположены по 110,
сдавливаются жидкостью, находящейся между поверхностями 110,
МЛ" и гранима вгорои пирамядм. Тогда давление на жидкость,
находящуюся между MN, 011, будет меньше, так как (объем) Р2ТГ будет
меньше тела Е/.Н8 (ибо этому (объему) раина только часть НВГв, и
она предполагается одинаковой ло величине и рмннотнжелой (с
жидкостью)**), а остальные части в обеих пирамидах одинаковы). Теперь
ясно, что часть жидкости, соответствующая дуге 011, будет
вытолкнута тон частью, которая соответствует дуге ОН, и жидкость никак ие
будет неподвижной. Было же предположено, что она неподвижна; значит,
никакая часть тела не будет выступать над поверхностью жидкости.
Погрузившись же, тело не будет двигаться вниз, так как все части
жидкости, находящиеся на одном уровне, будут давить одинаково
вследствие того, что тело является pan нетяжелым с жидкостью AJ.
IV
Тело, более легкое, чем жидкость, будучи опущено в згпу жидкость,
не погружается целиком, но некоторая часть его остается над
поверхностью жидкости.
Пусть будет тело более легкое, чем жидкость, и пусть оно, будучи
опущено в жидкость, погрузится целиком, если возможно, так что
*) То есть прямоугольник.
**) Фраза d скобках, по-видимому, ирсдставлисх позднейшую пстаику; во всяком случче слоиа
«одинаковой по иеличиис» совершении излишни.

О ГШЛНЛЮЩИХ ТЕЛАХ
331
над поверхностью жидкости пе будет никакой его части, и жидкость
устапоиится неподвижно. Вообразим некоторую плоскость,
проведенную черен центр Земли, жидкость и погруженное тело; пусть
поверхность жидкости рассечется отой плоскостью по дуге АВГ {рис. 4},
логружетше тело даст л сечении фигуру, обозначенную через Z, а
центр Земли пусть будет К; вообра.шм, как и выше, некоторую
пирамиду, охватывающую тело Z, имеющую перкшпу и точке К; пусть
проведенной через ART плоскостью ое грани будут пересекаться по лилиям
АК, KR; возьмем также другую пирамиду, равную и подобную этой,
si пусть ее грани тон же самой плоскостью
пересекаются по линиям К13, КГ; затем н
•жидкости, ниже погру?коппого тела
опишем другую шаровую поверхность с
центром в К, и пусть она пересекается
вышеупомянутой плоскостью но дуге ЕОП;
вообразим еще во пторой пирамиде
наделенный объем жидкости II, равпый телу Z;
тогда частицы жидкости в первой нира-
миде, расположенные под поверхностью,
соответствующей дуге НО, а также во
второй пирамиде под поверхностью, соотиетствующей дуге ОН, будут
находиться на «дном уровне и прилегать друг к другу. По они не
исимтмкакл одинакоиого данленин, так как в леркой пирамиде они
сдавливаются телом Z и окружающий его жидкостью, занимающей
л :>той пирамиде место А, В, О, 2, а но второй пирамиде опи
сдавливаются окружающей жидкостью, занимающей в пирамиде место П, О, 13, Г;
нес же тела (Z будет меньше веса) II, поскольку тело Z, будучи ран-
пым Ы по величине, предполагается более легким, чем жидкость;
веса же окружающей объемы Z, II жидкости будут в каждой из кирамнд
одинаковыми; значит, частицы жидкости, расположенные по поиерх-
ности, соответствующей дуге ОП, будут испытывать большее давление;
следовательно, менео сдавливаемые частицы вытеснятсл и жидкость
по будет оставаться неподвижной. На она предполагалась таковой;
значит, тело не погрузится целиком, но
некоторая его часть будет находиться
над поверхностью жидкости.
Тело, более легкое., чем жидкость,
будучи опущено в эту жидкость,
погружается настолько, чтобы объем
жидкости, соответствующий погруженной
{части тела), имел вес, равный весу
всего тела.
Пусть будет сделано то же, что и
ралг.ше, и пусть жидкость будет
неподвижной; пусть тело EZH© (рис. 5) будет более легким, чем
жидкость. Теперь, поскольку жидкость осотастся неподвижной, частицы
ее, расположенные пк одном уровне, будут испытывать одияалоное
давление; следовательно, жидкость л од поверхностями, сотлететвующи-
ми дугам SO и ПО, будет сдаилинаться одинаконо, так что одинакова
будет и тяжесть, которой они придавливаются. По вес жидкости

332
АРХИМИД
в нерпой шфялщцс, за исключением объема В110Г, будет ранен весу
(жидкости со второй нирамидо), за исключением части жидкости
Р2ТТ; теперь ясно, что вес тела EZHB будет равен весу жидкости
l'2'ГГ. После этого очевидно, что объем жидкости, соответствующий
погруженной части опущенного тела, имеет вес, равный весу всего тела..
VI
Тела более легкие, чем жидкость, опущенные в эту жидкость
насильственно, будут выталкиваться вверх с силой, равной тому весу,
на который жидкость, имеющая равный объем с телом, будет тяжелее
этого тела.
Пусть будет некоторое тело А {рис. 0} более легкое, чем жидкость;,
пусть В будет нес тела Л, а 13 + Г — вес жидкости в объеме, равпоы Л.
Требуется доказать, что насильно
погруженное в жидкость тело Л будет1
выталкиваться вверх с силой, равной]
весу Г.
Возьмем какое-нибудь тело Д,
имеютцее нес, равный Г; тогда тело,,
составленное из объединенных вместе
обоих тел А, Л, будет легче жидкости,
(в том же объеме), так как вес тела,
составленного из обоих, будет В -|- Г, вес
же жидкости в равном объеме будет
больше, чем В -|- Г, так как В + Г
представляет вес (жидкости) в объеме,
рапном А. Теперь тело, состаилсппос и*
обоих тол А, Д, будучи опущено в жидкость, погрузится настолько,
чтобы жидкость н объеме, равном погруженной части, имела вес,
равный несу всего теля, как »то доказано ш,шге. Пусть дуга АВГД
представляет поверхность некоторой жидкости. Теперь, поскольку
количество жидкости в объеме, равном телу А, имеет вес одикиконый с
весами обоих тел А, А, то ясно, что погруженная часть этого тела,
будет иметь объем, равный А, остальная же часть его, именно Д, будет
находиться над поверхностью жидкости; действительно, если бм это-
тело погрузилось иначе, то получилось бы (противоречие) с тем, что-
было доказано (раньше). Теперь ясно, что (с какой силой) тело А
вмталкшшетен кверху, (с такой же силой оно будет нридаяливаться)
книзу находящимся над ним телом Д, поскольку ни то, ни другое не
пересиливают друг друга. Но Д давит вниз с тяжестью, равной весу
Г, так как было предположено, что вес тела Д ранен Г; теперь то, что.
требовалось доказать, будет очевидпо.
VII
Тела, более тяжелые, чем жидкость, опущенные в эту жидкх>стъг
будут погружаться, пока не дойдут до самого низа, и в жидкости
станут*) легче на величину веса жидкости н объеме, равном объему
погруженного тела.
*) Характерное инраяодис «станут легче {vaaiimiai у.ощохе'оя)», показывающее, что грекга
вес одного ц того же тела не считали постоянным; они «вес» понимали как «давление».
«Л/.
А' ( 1 ^

О ПЛАВАЮЩИХ ТЕЛАХ
333
Что тело будет погружаться, попа не дойдет до самого дна, оченид-
по, так как находящиеся под ним частицы жидкости будут испытывать
большое давление, чем другие, расположенные на одной с ним уровне,
так пак тело предполагается более тяжелым, чем жидкость; а что оно,
как сказано, (в жидкости) станет легче, это следувт доказать.
Пусть Судет некоторое) тело А {рис. 7} более тяжелое, чем жидкость;
пусть вес тола А будет Б -|- Г, вес же жидкости в объеме, равном А,
будет В. Требуется доказать, что тело А,
находясь в жидкости, будет иметь вес,
равный Г.
Возьмем некоторое тело Д, (более
легкое, чем жидкость в его объеме: пусть)
вес тела Д будет ранен несу Л, нос же
жидкости, имеющей одинаковый с Д объем,
пусть будет равен весу В -|- Г. Если мы
сложим оба наши тела А и Д в одно, то
составленное тело будет рав нетяжелым с
жидкостью; действительно, вес обоих этих
тел ранен вместе взятым весам В -|- Г и В, вес же жидкости, имеющей
объем, равный обоим телам, равен тем же самый весам. Значит, если
эти тела опустить в жидкость, то они будут в равновесии с жидкостью
и не будут двигаться пи вверх, пи вниз; вследствие этого тело А пойдет
вниз с такой же силой, с какой тело Д будет увлекаться вверх; тело
же А, поскольку оно легче жидкости, будет двигаться вверх с силой,
раиной весу Г, так как докапано, что более легкие, чем жидкость, тела,
будучи насильно погружены в ату жидкость, движутся ниерх с силой,
равной тому весу, на который жидкость, имеющая объем, равный атому
телу, будет тяжелее последнего. Но жидкость, имеющая равный объем
с телом Д, будет тяжелее тела Д на вес Г;
К теперь ясио, что тело А будет двигаться
выла (с силой, равной весу V).
Предположим, что все тела,
движущиеся*) (и жидкости вверх), будут
подыматься по отвесной линии, проведенной
через их центр тяжести.
VJ.Il
Если какое-нибудь тела, более легкое,
чем жидкость, и имеющее форму сегмента
шара, будет опущено в жидкость таким
Л образом, чтобы основание сегмента не ка-
рис 8 салось жидкости, то это тело
установится е прямом положении, так что ось
сегмента будет расположена по отнесу; и
если кто-нибудь принудит тело стать так, чтобы основание сегмента
касалось жидкости, то оно не останется в наклонном положении, но.
будучи отпущено, снова станет прямо.
Представим, что в жидкость опущено такое тело, как скапано;
вообразим плоскость, проведенную через ось сегмента и центр Земли,
и пусть АВГД {рис. 8} будет сечение атой продолженной плоскости
"> Надо помнить, что и п>еческой механике идея дшиксиин Гшля неразрывно связана с идеей
силы; поэтому ближе к смыслу было бы снизить «иыталкниаемые в жидкости вьерх».
,1
в
Г
J

334
АРХИМЕД
с поверхностью жидкости, а дуга EZH6 — с опущенным в жидкость,
толом; пусть ось сегмента будет 0Z; тогда центр шара будет на OZ.
(Предположим) сначала, что сегмент больше полушария; пусть
центр (его) будет К, и пусть тело, если возможно, будет паклонсно-
само по себе или под чьим-нибудь воздействием. Требуется доказать,
что оно пе «станется в покое, но лернстея в прямое положение, так что
Z и в будут находиться на отвесной лини,!.
Действительно, поскольку тело предполагается наклоненным, то
Ъ и в по будут находиться на отвесной линии. Через К и А проведем
прямую КЛ (Л мы предполагаем цептром Земли); на прямой КЛ будет
лежать ось находящейся в жидкости части тела, отсекаемой
поверхностью жидкости, ибо если поверхности двух щарои пересекают друг
друга, тосечешге будет кругом, перпендикулярным к прямой,
соединяющей центры атих шаров. Центр тяжести фигуры, находящейся и иоде
и отсеченной дугой BN Г, находится на КЛ; пусть :>то будет Р. Центр
же тяжести всего сегмента, соответствующего дуге 6HZE, паходится
на Z6, пусть оп будет Е. Тогда центр тяжести (оставшейся фигуры,
находящейся вне) поверхности воды, найдется па продолжении РЕ,
если отложить некоторый отрезок £Е, который имеет к ЕР то же-
отношение, что вес части сегмента, соответствующей дуге 13ХГ, к весу
тон его части, которая будет вис жидкости; ото уже доказано («О
равновесии плоских фигур», кн. I, предложение VIII). Пусть центр
упомянутой фигуры будет 22. Теперь, так как вес той части тела, которая
находится иле жидкости, будет стремиться вниз но прямой AS, вес же
той части, которая и жидкости (будет стремиться) вверх и о прямой
РК, то ясно, что тело не останется в некое, но что части его, прилежа-
щи с к Е, пойдут вниз, прилежащие же к 11 — вверх и что так
двигаться они будут все время, пока Z0 не станет отвесной. Когда же Z6
станет отвесной, то центры тяжести обеих частей, как той, что в жидкости,
так и той, что вис се, будут па одной и той же отвеспой линии (они будут
на ZO); тогда веса будут взаимно давить друг па друга но одной и той
же отвеспой линии, один вниз, а другой вверх. Таким образом, тело
будет оставаться неподвижным, ибо ни
один не сможет вытолкнуть другой.
То же самое получится, если фигура
будет полушарием или меньше
полушария Г2|.
IX
И так же если какое-нибудь телоТ
более легкое, чем жидкость, будет
опущено в эту жидкость так, чтобы все его
основание было целиком в жидкости, то
тело установится в прямом- положении
так, что его ось расположится по отвесной линии.
Вообразим, что и жидкость опущено тело такое, как сказано;
вообразим также плоскость, проведенную через ось сегмепта и через
центр Нпмли; пусть сечение поверхности жидкости будет окружпость
АВГА {рис. Щ, а тела — дуга EZH и прямая ЕЯ; пусть ось сегмента
будет ZB, и пусть, если возможно, Z0 не будет отвесной; требуется
доказать, что тело не останется в покое, по вернется в прямое положение.
Центр шара будет на Z6 (предположим сначала опять, что тело
будет больше полушария); пусть он будет К. Через К и центр Земли А

О ПЛАВАЮЩИХ ТЕЛАХ
335.
проведем прямую КЛ; тогда часть тела, находящаяся вне жидкости
и отсекаемая, ловерэгностъю жидкости, будет иметь свою ось (на прямой,
проходящей) через К, и на оенгшании того же, что и выше, се центр-
тяжести будет на _\К; пусть он будет в Р. Центр тяжести леего сегмента
будет на ZO между К. и Z; пусть он будет Т. Значит, центр тяжести
остальной части сегмента, находящейся в «оде, найдется на
продолжении прямой ТР, если нанести на ней некоторый отрезок, который имел
бы к ТР то же самое отношение, что пес части сегмента, находящейся
шю жидкости, к весу той части, которая в жидкости; пусть центр
упомянутой фигуры будет О, а отвесная ллния, проведенная через О,
будет ОЛ; теперь, вес части сегмента, которая вне жидкости, пойдет
вниз ло прямой РЛ, а той части, что н жидкости,— пнерх по прямой ОЛ.
Следовательно, тело не останется в покое, но те его части, которые
прилегают к II, пойдут вниз, тс же, что к Р^ — вверх, и так будет все время,
пока 9Z пе сделается отвесной *).
КНИГА ВТОРАЯ
I
Если какое-нибудь тело, более легкое, чем жидкость, опустить в эту
жидкость, то оно по тяжести будет находиться в том оке отношении
с жидкостью**), какое погруженный объем имеет,
ко всему объему. Л
Опустим в жидкость какое-ниоудь тол о ФА
{рис. 10}, янляющееся более легким, чем эта
жидкость; пусть погруженная часть его будет Л,
находящаяся же пне жидкости — Ф. Требуется
доказать, что ФА по тяжести будет относиться
к равному объему жидкости, как Л к ФА.
Иозьмем какую-нибудь жидкую массу N1,
имеющую с ФА раипьш объем, и пусть объем Ф
будет ранен N, а А равен I, и далее, пусть вес
массы ФА будет П, вое массы XI будет РО, а вес I
будет Р; значит, ФА шюст к NT то же самое
отношение, что В к РО. Но так как тело ФА опу- Рис. «).
щепо н жидкость, будучи легче отой жидкости,
то ясно, что (жидкость) в объеме погруженной части имеет равный
вес с массой ФА, как это доказано (в предложении V книги I); значит,
*) Разбор случаев, когда сегмент рапеи полушарию или меньше его, отсутствует; и тексте-
веревшш Вильгельма из Мсрбске в конце помещены, чертежи, иллюстрирующие оба »ти случая:
Значение букв: ©7. — ось сегмента (в — точка со пересечения с основанием), Т — центр
тяжести сегмента, О и ]• • центры тяжести погруженной и находящейся кие жидкости его частей,.
ОЛ и РЛ — вертикали, соединяющие центр Л Земли с центрами тяжести о и Р обеих частей сегмента.
•*) У греков термины «тяжелый» и «легкий» понимались также н п смысле большего в
меньшего /дельного ni'ca.

зз«
АРХИМЕД
вес \i будет равен Р, так как 13 ость бос всего тела ФЛ, а Р — вес
жидкости I, объем которой был сделан равным объему погруженной части А;
значит, вес тел» ФА будет относиться к весу Л'1, как Р к РО. Но
отношение 1* к РО будет равно отношениям I к IN и А к ФЛ; значит,
предложенное доказано.
II
Прямой сегмент прямоугольного коноида *), ось которого не более
полуторной прямой «до оси»**), опущенный в жидкость так, чтобы его
основание не касалось жидкости, при всяком отношении по тяжести
к жидкости, будучи, поставлен наклонно, не остается наклонным,
по возвращается в прямое положение. Прямым же положением сегмента
я называю такое, когда отсекшая его плоскость оказывается
параллельной поверхности воды.
Пусть будет сегмент прямоугольного коноида таком, как сказано
выше; л оставим его в наклонное положение. Требуется доказать, что
он не останется в
покое, но возвратится в
прямое положение.
Рассечем его
плоскостью, проходящей
через ось и
перпендикулярной к (плоскости,
совпадающей с
поверхностью} жидкости; пусть
сеченном сегмента
будет парабола АПОЛ
(рис. И), осью сегмента
и диаметром параболы
будет прямая N0,
сечением же поверхности
жидкости прямая 12.
Так как сегмент не
стоит прямо, то АЛ не
будет параллельна 12,
так что N0 не образует прямого угла с 12. Проведем теперь
параллельную (поверхности жидкости) касательную KQ к параболе
п точке II, и ии П параллельно N0 лроведем ПФ; тогда НФ разделит
1Z пополам, как это доказало в теории конических сечений.
Разделим ПФ так, чтобы П13 была вдвое больше ВФ, a NO разделим в Р
так, чтобы ОР была вдвое больше PN; тогда Р будет центром тяжести
большого телесного сегмента, а В — центром тяжести телесного
сегмента 1П0Х; действительно, в (книгах) «О равновесии»***) доказано,
что центр тяжести сегмепта прямоугольного коноида находится па оси,
разделенной так, чтобы прилегающий к вершине отрезок оси бы.ч вдвое
больше оставшейся части. Далее, если отпять телесный сегмент 1П02
от всего тела, то центр тяжести остатка будет па прямой ВГ; действи-
*) То ость сешеиха параболоида вращения, отсеченного плоскостью, перпендикулярной
к оси
-■*) Ого параметр р п уравнении у'=2рх. к дальнейшем переводится слоном «параметр».
***) Вероятно, и продолжении трактата «О равновесии и.-гоекмх фигур». J3 сохраитшпгхся
сочинениях Архимеда ато доказательство имеется и «Уфодее (предложение V).

О ПЛАВАЮЩИХ ТЕЛАХ
337
тсльно, л «Началах механики»*) доказано, что осп и от данной величи-
иы отпять какую-нибудь часть, не имеющую общего центра тяжести
с целой величиной, то центр тяжести остатка будит на прямой,
соединяющей центры тяжести целой величины и отнимаемой части, если
продолжить ату прямую в ту сторону, где находится центр тяжести
целой пел и чины. Поэтому продолжим 13 Р до Г, и пусть Г будет центром
тяжести остающейся неличины. Теперь, так как N0 в полтора рала
больше ОР и но более полуторного параметра, то ясно, что РО не будет более
параметра; значит, 171* образует с K.S2 неравные углы [3J, причем угол
Р1Ш будет острим; значит, перпендикуляр, опущенный .из Р на 1IQ,
упадет между точками П и Q. Пусть он пойдет по Р0; значит, Р6 будет
перпендикулярна к плоскости, (параллельной той), и которой
находится 21, то ость поверхности жидкости. Пронодем из точек 13, Г прямые,
параллельные) РВ; находящаяся вне жидкости часть сегмента пойдет
mum по про поденному из Г перпендикуляру, так как предполагается,
что каждая тяжесть движется вниз но перпендикуляру, проведенному
через ее нонтр; часть же, находящаяся л жидкости, будучи болое легкой,
чем эта жидкость, пойдет вверх по перпендикуляру, проведенному
через Р. И так пак «бе. (эти массы) данят друг на друга не но одной
и ток же отвесной линия, то фигура ни останется неподвижной; но часть,
прилежащая к Л, пойдет внорх, а прилежащая к Л — вниз, и так будет
псе нрелтя, пока сегмент пе станет прямо 14].
III
Прямой сегмент прямоугольного коноида, ось которого не более
полуторного параметра, при всяком отношении по тяжести к жидко-
<сти. опущенный, в жид-
во
Л
кость так, чпгооы его
основание целиком
находилось в жидкости,
будучи поставлен
наклонно, не останется
наклонным, но встанет
■ так, что ось его
пойдет по отвесной линии.
Опустим такой,
пак сказано, сегмент и
жидкость, и пусть
основание его будет в яхнд-
кости{рис. 12};рассечем д*
его через ось
плоскостью, иериепдикуляр-
]H)ii к понорхнпети
жидкости; пусть сечением сегмента будет парабола А ПОЛ, осью сегмента и
диаметром лярабалк — прямя» 11Ф, сечением же поверхности
жидкости, линия 12. Теперь, так как сегмент лежит наклонно, то ось его
отвесной но будет; значит, ПФ пе образует равных углов с 12.
(Параллельно 12) проведем в точке О (касательную КО) к параболе А ПОЛ;
пусть центром тяжести тола ЛПОЛ будет Р, а центром тяжести тели
ПЮ2 — точка В; соединяющую прямую 13Р продолжим, и пусть Г
•) 'Jilv ioi£ 2roi);tini; icw uTjy.-xviKmv—элементарный куре механики, может быть, и не
принадлежащий Архимеду. См. «О ряыюрииии плоских фигур», is». I, "VIII.
22 Архимед
Рис. 12.

338
АРХИМЕД
будет центром тяжести тела 1БЛА. Теперь совершенно так же дока-
жом, что угол между РО, ОК будет острым, так что иерпепдикуляр,
опущенный из Р па KQ, упадет между К и О; пусть он будет Р6.
Если через Г и В проведем прямые, параллельные Рв, то часть сег-
мзнта, заключенная и жидкости, пойдет вверх но прямой, проведенной
через Г, находящаяся же вне жидкости — вниз по прямой,
проведенной через В, и тело А ПОЛ не останется в жидкости в приданном
ему положении, но прилежащая к А часть будет двигаться шзерх, а
прилежащая к Л — вниз, пока линия ПФ не сделается отвесной [5J, \(\\.
IV
Если прямой сегмент прямоугольного коноида будет легче жидкости
и ось его более полуторного параметра, а по весу к равному объему
жидкости on имеет отношение не меньшее, чем квадрат {на отрезке),
равном разности между осью и полуторным параметром к квадрату
па оси, то, будучи опущен в жидкость так, чтобы его основание не
касалось жидкости, и поставлен, наклонно, сегмент, не остается наклонным\
но возвращается в прямое положение.
Пусть будет сегмент прямоугольного коноида такой, как сказано,
и пусть он, будучи опущен в жидкость, если возможно, станет не прямо,
но наклонно; если рассечь
л его через ось плоскостью,
перпендикулярной к
поверхности жидкости, то
сечением сегмента будет
парабола АПОА {рис. 13},
осью сегмента и диаметром
параболы —прямая NO и,
наконец, сечением
поверхности жидкости 12. Кат
сегмент не стоит прямо, то
N0 не образует с 12
равных углов. Проведем
KQ — касательную к
параболе в точке 11,
параллельную 12; аатсм из П
параллельно ОХ проведем
ПФ и найдем центры тяжести; у тела АПОА центром пусть будет Р,
а у погруженной в воду части центром будет В; проведем соединяющую
прямую ВР н продолжим до Г, и пусть Г будет центром тяжести
части, находящейся над жидкостью. И так как NO в полтора раза
больше РО и более полуторного нараметра, то ясно, что РО будет
больше параметра. Пусть РМ равпа параметру, и ОМ вдвое больше ИМ.
Так как N0 в полтора рапа больше РО, а 110 в полтора раза
больше ОМ, то, значит, остаток NLI будет и полтора раза больше остатка РМ,
значит, ось сегмента будет на отрезок НО больше полуторного
параметра РМ.
И так как предполагалось, что по тяжести сегмент имеет к жидкости
отношение не меньшее того, которое квадрат на разпости между осью
и полуторным параметром имеет к квадрату на оси, то ясно, что пи
тяжести сегмент имеет к жидкости отношение но меньшее того, которое
квадрат на НО имеет к квадрату на N0. Отношение по тяжести сегмеи-

О ПЛАВАЮЩИХ ТЕЛАХ
339
та к жидкости равно отношению цпгруженной части ко исиму сегменту,
как уже доказано <и ггродложешш 1), а отпотейте погруженной часта
ко всему сегменту равно тому, которое имеет кнадрат па ПФ к квадрату
на N0; действительно, в книге «О коноидах» доказано, что если от
прямоугольного коноида отсечь два сегмента произвольно проведенными
плоскостями, то нти сегменты будут иметь друг к другу то же самое
отношение, что и квадраты их осей («О коноидах», предложение XXIV).
Такилг образом, кнадрат на 11Ф if квадрату ла ДО имеет отношение
не меньшее, чем квадрат на НО к киадрату на ХО; поэтому 1ТФ не мене*!
НО, и ВП не менее МО*); значит, если из М провести перпендикуляр
М0 и N0, то он упадет между В и П. И так как ГТФ параллельна
диаметру, МО пернепдикулярпа диаметру и РМ раина параметру, то
прямая, соединяющая Р с 0, будучи продолжена, образует прямые углы
с «асательной в П**); значит, она образует прямые углы и с J2, и с со*-
ответсткующей 12 понерхпостыо жидкости. Если через В и Г провести
прямые, параллельные Рв, то у поверхности жидкости получатся пря-
мыс углы и заключенная и жидкости часть сегмента коноида пойдет
вверх по прямой, проведенной черед Б параллельно Рв, находящаяся же
вне жидкости часть пойдет вниз по проведоппой через Г параллели
к РВ, и так будет все время, пока сегмент коноида не станет прямо [7J.
V
Если прямой сегмент прямоугольного коноида легче жидкости и ось
его более полуторного параметра, а по весу он имеет к жидкости
отношение не большее, чем разность между квадратом оси и квадратом
разности между осью и полуторным параметром имеет к квадрату оси,
то будучи опущен в жидкость так, чтобы его основание было целиком
погружено в воду, и поставлен наклонно, он не останется наклонным,
по встанет так, что его ось будет направлена по отвесу.
Опустим такой, как сказано, сегмент и жидкость, и пусть ого
основание будет цел ином в жидкости {рис. 14); есл и рассечь его через ось
плоскостью, перпендикулярной к поверхности жидкости, то в сечении
получится парабола Л ПОЛ, осью сегмента и диаметром параболы будет
прямая N0 и сечепнем поверхности жидкости прямая 12. И так как ось
сегмента не будет отвесной, то N0 не образует с 12 равных углов.
Проведем К£2 — касательную к параболе АПОЛ в точке П, параллельную 12,
а через II прямую ПФ, параллельную МО, и возьмем центры тяжести;
пусть у сегмента АПОЛ центром будет Р, а у части его, находящейся
вне жидкости,— В; соединяющую прямую ВР продолжим до Г; пусть Г
будет центром тяжести части, погруженной и жидкость. Возьмем РМ
равной параметру и сделаем так, чтобы ОМ была вдвое больше ИМ,
и пусть все остальное будет сделано так же, как и выше. Теперь,
поскольку предполагается, что сегмент по тяжести имеет к жидкости
отношение не большее, чемразностьквадратонна N0 н 011 имеет к квадрату
на N0, а отношение по тяжести сегмента к равному объему жидкости
равно отношению погруженной части тела ко всему этому телу (как
доказано в первой теореме), то, значит, погруженная часть сегмента
ко всему сегменту имеет отношение, не большее указанного; значит.
*) Действительно, для цедтра тяжести В сегмента Ш02 имеем ВП=-5- ФП и МО
**) Действительно, РМ есть субнормаль, а ОМ — ордината точки касания II
= тон.
'LS

.МО архимгсд
весь сегмент к части, находящейся вне жидкости, имеет отношение не
большее, чем квадрат на N0 к квадрату на ПО.
Но весь сегмент к своей части, находящейся впо жидкости,
относится как квадрат N0 к квадрату ПФ; значит, квадрат на N0 к
квадрату на Г1Ф имеет отношение не большее, чем квадрат на N0 к квадрату
на 110.
КО8 ,. МО*
ПФ2 *"" НО2
Следовательно, 11Ф будет не менее 011 и 1IB не менее МО. Значит,
отвесная линия, проведенная из М к РО, пересечет ВЦ между 11 и В; пусть
она пересечет ее в в. И так как л параболе прямая ПФ параллельна РО,
а МО перпендикулярна к диаметру, и, наконец, PiVl раина параметру,
то ясно, что проведанная прямая Р0 образует нрнмые утлы с K11Q,
а апачит, и с 12. Следовательно, Рв перпендикулярна к поверхности
жидкости, и прямые, проведенные через точки В и Г параллельно Р6,
будут перпендикулярны к поверхности жидкости; значит, часть тела,
находящаяся вне жидкости, пойдет кпиау в жидкость но нерноидикуля-
ру, проведенному через В, находящаяся же в жидкости часть пойдет
вверх но перпендикуляру, проведенному через Г, и сегмент АПОА
не останется в покое, но будет двигаться в жидкости, пока N0 по
сделается отвесной [8J.
VI
Если прямой сегмент прямоугольного коноида легче жидкости
и имеет ось, отношение которой к параметру более чем три к двум,
по менее чем пятнадцать к четырем, то, будучи опущен в жидкость так,
чтобы его основание касалось жидкости, сегмент не останется
наклоненным так, чтобы его основание имело одну общую точку с жидкостью [У].
Пусть будет сегмент такой, как сказано: пусть он, будучи опущен
и жидкость, установится, как показано {рис. 15}, так, что его
основание будет касаться жидкости в одпой точке. Если рассечь его через ось
плоскостью, перпендикулярной к поверхности жидкости, то сечением
сегмента будет парабола АПОА, сечением поверхности жидкости —

О ПЛАВАЮЩИХ ТИЛАХ 341
прямая А2, а осью сегмента и диаметром (параболы) — прямая N0.
Разделим последнюю в точке Ф так, чтобы ОФ била иди ос больше ФИ,
• а в точно Q так, чтобы N0 относилась кФ&, как пятнадцать к четырем;
затем проведем QK перпендикулярно к N0. Тогда отношение N0
Рис. 1.V
кФЕ2 будет больше отношения SO к параметру. ПустьФВ равна
параметру; параллельно А2 проиедем прямую ПТ, касательную к параболе
Л ПОЛ в точке IJ, а также прямую 111, параллельную N0. Пусть
сначала прямая IJT пересечет прямую KQ. Так как и сегменте АПОЛ,
заключенном между прямой и параболой, прямая КН параллельна АЛ,
прямая Ш параллельна диаметру и пересекается с КУ и, наконец.
Л2 параллельна касательной и П, то необходимо, чтобы отношение 1JI
к ПП было ракло или больше отношения Nii к DO; ято уже было
доказало в леммах [10]. Прямая £2N в полтора раза больше QO, и
елсдоиателыю, 1П или ропно в полтора раза, или же более чем в
полтора раза больше IIII; поэтому 1111 или равна, или же меньше
удвоенной HI*).
Пусть 110 н два раза больше HI; тогда в будет центром тяжести
заключенной в жидкости части сегмента; проведем 0Ф и продолжим;
пусть Г будет центром тяжести части, выступающей из жидкости.
Из В перпендикулярно N0 проиедем ВР. Так как Ш параллельна
диаметру КО, a UP ему перпепдикулярпа, и ФВ равна параметру, то ясно,
что продолженная ФР обрадует рапные углы с касательной в точке П
к параболе АПОЛ, а следовательно, и с AS, и с поверхностью
жидкости. Если мы через 0 и Г. проведем прямые, параллельные ФР, то они
тоже будут перпендикулярны к поверхности жидкости; заключенная
внутри жидкости часть сегмента АПОЛ будет иттм вверх по отнесной
прямой, проходящий через 0, а чисть, находящаяся вне жидкости, будет
опускаться иниз по отвесной прямой, проходящей через Г. Таким
образом, тело повернется и его основание но будет касаться жидкости в одной
точке.
*) Двйстептслмю, Ш:ПН —(ПК I- III) : ПН-1+— - 3 т,. отку; a HJ : IIU £г g.

АРХИМЯД
Рис. 16.
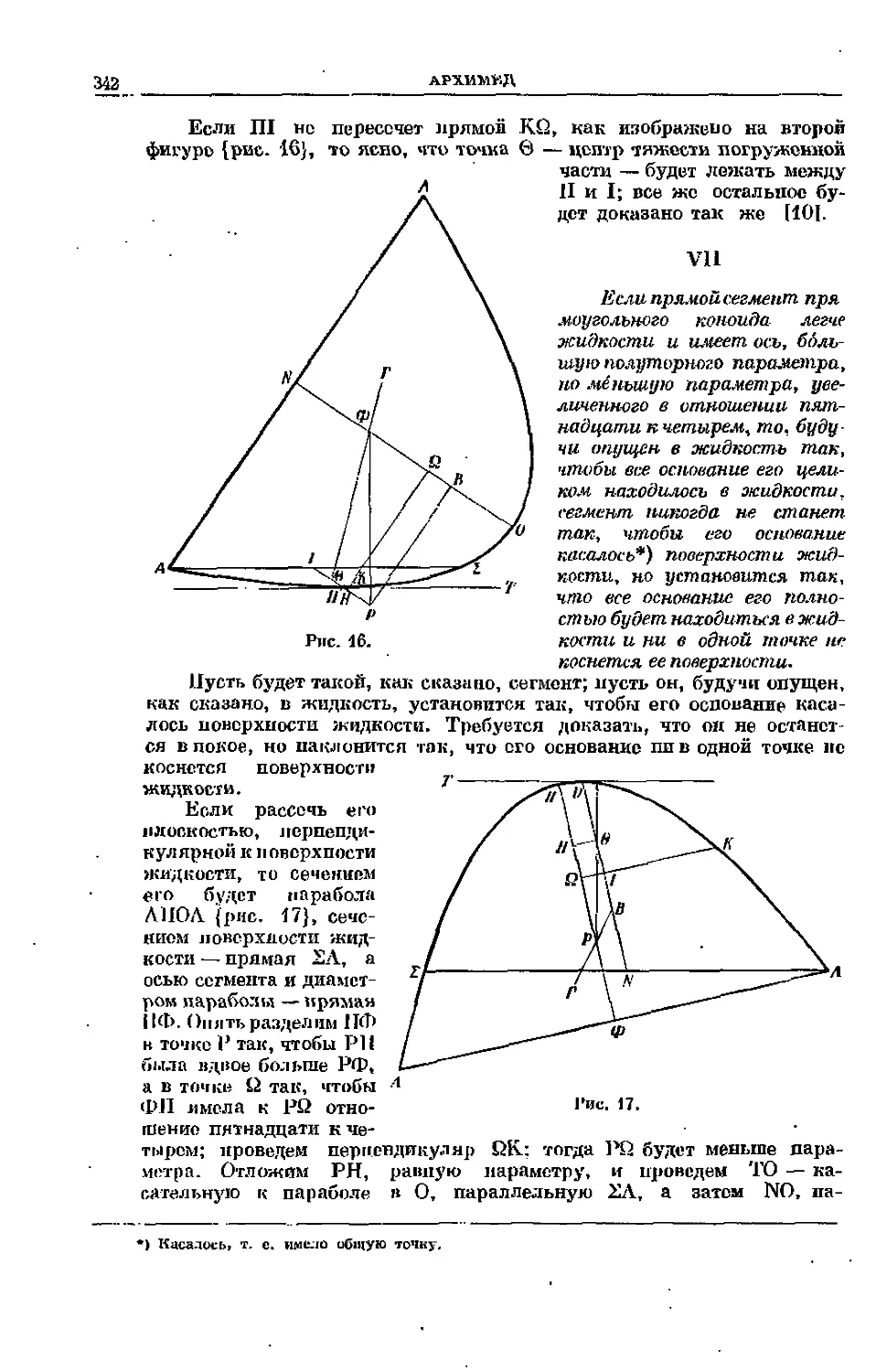
Если Ш не пересечет прямой KQ, как изображено на второй
фигуре {рис. 16), то ясно, что точка в — центр тяжести погруженной
части — будет лежать между
II и I; все же остальное
будет доказано так же [101.
VU
Если прямой сегмепт пря
моуголъного коноида легче
жидкости и имеет ось,
большую полуторного параметра,
по .меньшую параметра,
увеличенного в отношении
пятнадцати к четырем, то.
будучи опущен в жидкость так,
чтобы все основание его
целиком находилось в жидкости,
сегмент никогда не станет
так, чтобы его основание
касалось*) поверхности
жидкости, но установится так,
что все основание его
полностью будет находиться в
жидкости и ни в одной точке на
коснется ее поверхности.
Пусть будет такой, как сказано, сегмент; пусть он, будучи опущен,
как сказано, в жидкость, установится так, чтобм его основание
касалось поверхности жидкости. Требуется доказать, что он не
останется в покое, но наклонится так, что его основание пив одной точке не
коснется поверхности
жидкости.
Если рассечь его
плоскостью, лерпепди-
кулярной к поверхности
жидкости, то сечением
«го будет парабола
Л J ЮЛ {рис. 17},
сечением ловерхиости
жидкости — прямая £Л, а
осью сегмента и
диаметром параболм — прямая
11Ф. ()i i я ть раздел им 11Ф
к точке V так, чтобы PI I
была вдное больше РФ,
а в точки И так, чтобы л
ФИ имела к PQ
отношение пятнадцати к
четырем; проведем перпендикуляр
метра. Отложим РН, равную
сательную к параболе » О,
Гис. 17.
QK.: тогда PQ будет меньше дара-
нараметру, и проведем ТО —
непараллельную 2А,
а затем NO, па-
*) Касалось, т. е. имело общую точку.

О ПЛАВАЮЩИХ ТЕЛАХ
343
в/
Н/С/
^хО
(р /
раллельную ПФ. Пусть сначала N0 пересечет КС1 в точке I. Тогда
подобно предыдущему докажем, что ISO будет или в полтора раза или
более чем в полтора раза больше /
01; (в последнем случае) 01
будет меньше удвоенной IN.
Пусть ОВ Судет вдвое больше
13 N, и все остальное сделаем
так же, как и раньше; подобно
(предыдущему) докажем, что Р(-)
образует прямые углы с ТО и
•с поверхностью жидкости, а
прямые, проведенные через В и
Г параллельно Р6, будут
перпендикулярны поверхности
жидкости. Теперь находящаяся вне
жидкости часть сегмента пойдет
«низ в жидкость по
перпендикуляру, проведенному через ТЗ, а
часть, находящаяся в жидкости,
пойдет вверх по перпендикуляру
через Г; яспо, что тело
наклонится так, что его основание ни
будет пи в одпой точке касаться
поверхности жидкости, потому
что часть, (касавшаяся
поверхности жидкости) в одпой точке
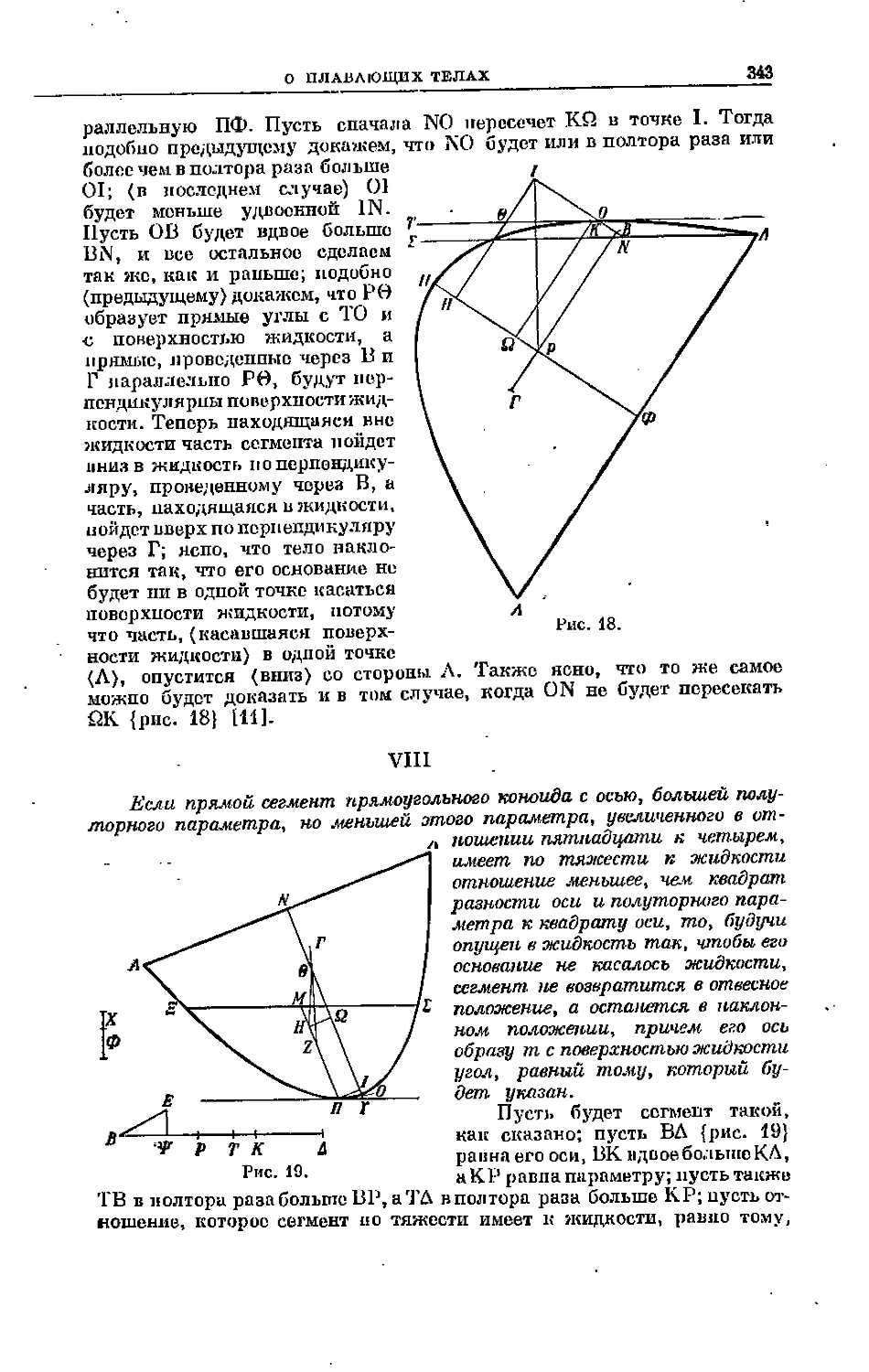
(Л), опустится (вниз) со стороны Л. Также ясно, что то же самое
можно будет доказать и в том случае, когда ON не будет пересекать
QK {рис. 18} [11].
Рис. 18.
VIII
Если прямой сегмент прямоугольного коноида с осью, большей
полуторного параметра, но меньшей этого параметра, увеличенного в от-
л ношении пятнадцати к четырем,
" имеет по тяжести к жидкости
отношение меньшее, чем квадрат
разности оси и полуторного
параметра к квадрату оси, то, будучи
опущен в жидкость так, чтобы, его
основание не касалось жидкости,
сегмент не возвратится в отвесное
положение, а останется в
наклонном положении, причем его ось
образу т с поверхностью жидкости
угол, равный тому, который
будет указан.
Пусть будет сегмент такой,
как сказано; пусть БЛ {рис. 19}
раина его оси, 13К идаоебольшеКЛ,
аКР равна параметру; пусть также
'1В в полтора разабольптеВР, аТЛ в полтора раза больше К.Р; пусть
отношение, которое сегмент но тяжести имеет к жидкости, равно тому,

Ш
АРХИМЕД
которое квадрат на Ф+Х имеет к квадрату на ДВ, м пусть Ф будет
вдвое больше, чем X. Ясно, что Ф-S-X имеет ц ЛЬ отношение, мень-
ureis того, которое ТВ имеет к ВД, так как TJ3 есть разность, на
которую ось больше полуторпого параметра *); значит, Ф+Х меньше ВТ,
так что и Ф будет меньше ВР. Пусть Ф равна PW; перпендикулярно
БД проведем VE, квадрат на которой равняется половин» примо-
уголышка между КР и BY, и проведем соединяющую прямую ВК.
Требуется доказать, что у и ом я нуты и сегмент, опущенный, как сказано,
к жидкость, установится в наклонном положении, так, что его ост»
образует с пмкерхностью жидкости угол, равный EBW**).
Опустим в ?кидкост.г, некоторый сегмопт, и пусть его основание
не будет касаться поверхности жидкости; при атом, если возможно, пусть
ось образует с поверхностью жидкости угол, пе равный В, по сначала
больший. Если рассечь сегмент через ось плоскостью, перпендикулярной
к поверхности жидкости, то evo сечением будет парабола АПОА,
сечением поверхности жидкости — пр»м>ш 22, а осью [сегмента! и
диаметром (параболы) — прямая NO. Параллельно HS проведем
касательную ПГ к параболе АПОА в точке П, затеи проведем ПМ
параллельно N0 и III перпендикулярно TSO, п пусть ОЙ равна ВР, a PR
равна Q0, и Ш1 перпендикулярна к оси. Поскольку предполагается,
что осисегмента«бракует с поверхностью жидкости, угод больший, чем В,
то ясно, что в треугольнике ШГ угол ири Y будет больше В; тогда
квадрат на" Ш к квадрату на 1Г будет иметь отношение большее, чем
квадрат на E*F к квадрату па УВ- Но квадрат па III к квадрату па IT
имеет то же отношение, что КР к П; отношение же квадрата па EV
к квадрату на ЧГВ равно отношению половины К.Р и ЧГВ; значит, КР
к VI будет иметь большее отношение, чем половина КР к YB;
значит, П будет меньше удвоенной V/B. По 1 Г вдвое более 01; значит,
01 меньше VB,
окта
и IQ будет больше ЧФ***).
*) a MEifcrov ■>) iiuio>.iok о rc£oi>v trxs tieysi too ccgovos - букмалыго, «на кото])ую ось оолсе чем
в з/s ;>:i:i,'i больше параметра (прямой ло оси)».
**) В наших обозначениях: Bi*=0N=-;,-6, ВК-'<, КР —р, отношение а плотностей тела-
и жидкости будет:
D ь)- D >•)
9 9 1
Далее, ТВ= — ВР= -^ (Ь - р), Ф+Х < ВТ иФ < fc—jj = BP. Полагаем Ф = 1>ЧГ и Ч7К*=— и- ВЧ'=
= ■~KV№, где V4'=lSV—l>'V=b—p—<l>. Если обозначим угол KBU' через В, то
**») Имеем Ot» = b, «Q—р и, следовательно, ОЙ—Ь—р—ВР. Кепи угол ПП> В, то
lj-2 '>_\ll-B2 •
Kcih в II нринедем нормаль, то начинающаяся в I субнормаль будет р.'иша параметру р —КР.
ВЯЛИС1ТШ ш»-ке-п.

О ПЛАВАЮЩИХ TK-'IAX 34Г)
Но ЧФ равна Ф; значит, Ш больше Ф. И так кап, согласно
предположению, сегмент но тяжести имеет к жидкости отношение, как
квадрат на Ф-|-Х к кпадрату на НА, и отношение но тяжести сегмента к
жидкости равно о-тпошению погруженной части но всему сегменту, а
отношение погруженной части ко всему сегменту будет тем же, что у (квадра-
та> на ГШ к (квадрату) на ON, то, .чпачит, квадрат па Ф-| X к квадрату
на ВЛ Судет иметь то же самое отношение, что квадрат па МП к
квадрату па ON; значит, Ф+Х будет равняться ТТМ. Но ПН, согласно
доказанному, больше Ф; значит, ясно, что ИМ будет мент.ше ПН, взятой
полтора раза, а 1111 болт; чем вдвое больше ИМ*).
Пусть TTZ вдвое больше ZM; тогда в будет центром тяжести всего
тела, a Z — центром тяжести его части, погруженной в жидкость;
центр тяжести остающейся, части будет на продолжении соединяющей
прямой ZC-). Пусть это
продолжение дойдет до Г; поел е ^М
этого так же, как и ран ыне, g*
докажем, что 0Н будет
перпендикуляром к
поверхности жидкости и
находящийся внутри жидкости
сегмент пойдет из жидкости
вверх но проведенному че-
рол Z перпендикуляру к
поверхности жидкости, а
находящаяся впе жидкости
часть пойдет вниз, в
жидкость, по
перпендикуляру, проведенному через Г;
таким обралом, при уно-..
мянутом угле паклона
сегмент не останется в покос. ■ ■■-
Но он также не .вернется в отвесное положение. Ото ясно из
следующего; из проведенных черен Z и Г перпендикуляров тот, который
проходит через '/, упадет с той стороны от TZ**), где находится А,
а проведенный через Г — с той стороны, где Л, поэтому ясно, что,
согласно вышесказанному, центр Z пойдет вверх, а Г вниз, так что
прилегающая к А часть всего тела пойдет вниз.
Это было важно для доказательства.
Пусть теперь при тех же предположениях ось сегмента образует
с новерхпостыо жидкости угол меньший, чем В {рис. 20}; тогда
Рис. 20.
Ш» _ КР
и* п "
KB EV* 1 KP-BV
f.j '" \jrjj-i 2 UrBa
i КР
2 Ч'Я
откуда
Мм имеем
и, елсдоиатслыю, Г1<2ЧГВ. Так как ьершина О параболы делит пополам еубтангенс П, то 01<ЧГВ.
п. следовательно, . ..■ ...
1П = ОН - 01 = (Ь - р) - 01 > ВР - Ч/В = ЧУР.
;Отношеннс d плотностей тела и жидкости будет
i _ № I X)Z _ ИМ»
ON* '
: Ф -I- X. так как IB = ПН > Ф и X =* Ф, то ИМ < -|- 1Ш и ПН >2НИ.
Зто пежагшпает, что 7. — центр тяжести погруженной части сегмента находится между II и Н..
**) Так и П0Д71ШИШКЁ. Мы сказали бы «от вн».
Так как ИЛ -- ON, то ПМ:

:ме
АРХИМЕД
квадрат на Ш к квадрату на 1Г будет иметь меньшее отпошепие, чем
квадрат на ЕУ к квадрату на ЧРВ, и, значит, КР имеет к XI меньшее
отношение, чем половина КР к YB. Тогда 1Г будет более чем вдвое
больше VB, и, значит, Ш меньше, чем WP. Тогда и ПН будет
меньше Ф. Но МП равна Ф-|-Х; ясно, что ПМ более полуторной 1111, а ПН
меньше удвоенной ИМ. Пусть П7 будет вдвое больше ZM. Тогда
центром тяжести всего сегмента будет 0, а части, находящейся в жидкости,
—Z; если провести соединяющую прямую Z0 м продолжить, то центр
тяжести части, находящейся вне жидкости, будет на продолжении.
Пусть он будет Г; проведем через Z и Г перпендикуляры к поверхности
жидкости, параллельные Н0; тогда ясно, что весь сегмент пе останется
неподкнжным, но наклонится так, что ось его образует с поверхностью
жидкости угол, больший того, который она образует теперь.
Поскольку сегмепт пе установится пи при большем, ни при
меньшем чем В угле наклона оси с жидкостью, то ясно, что он установится
только при угле, рапном В; и таком случае 10 будет равна ЧГВ, Ш
равна Ч'Р и Ф равна 1111; значит, МП будет в полтора раза больше ПН,
а ПН в два раза больше ПМ. Следовательно, 11 будет центром тяжести
части, находящейся в жидкости; таким обрааом, последняя пойдот
вверх но тому же самому перпендикуляру, по какому пойдет вниз
часть, находящаяся вне жидкости, значит, сегмент останется
неподвижным, так как обе части будут толкать друг друга в противоположные
■стороны [12J.
IX
Если прямой сегмент прямоугольного коноида с осью, большей
полуторного параметра, но меньшей этого последнего, увеличенного в
отношении пятнадцати к четырем^ имеет по тяжести к жидкости
отношение большее, чем разность
квадрата оси и квадрата
излишка оси над
полуторным параметром к
квадрату оси, то on, будучи
опущен в жидкость так чтобы
его основание целиком
находилось в жидкости, и
поставлен наклонно, не
встанет отвесно, но останется
в наклонном положении,
причем ось его с
поверхностью жидкости составит
угол, равный тому же, что
и выше.
Пусть будет сегмепт та -
кой, как сказано; отложим
ДВ (рис. 21} равной оси сегмента, и пусть ВК будет вдиос больше КД, аКР
равна параметру, иТВ в полтора рала больше ВР; пусть также
отношение, которое по тяжести сегмепт имеет к жидкости, будет том, какое
разность квадрата на ВД и квадрата па Ф+Х имеет к квадрату на ВД,
причем Ф вдвое больше X. Теперь ясно, что разность, на которую
квадрат на ВД превышает квадрат па ВТ, имеет к кнлдрмту па ВД меньшее
отношение, чем то, какое разность, на которую квадрат ВД превышает
1'ис. 21.

О ПЛАВАЮЩИХ ТГСЛЛХ 347
кнадрат па Ф+Х, имеет к кнадрату на БД, так как ВТ есть разность,
на которую ось больше полуторного параметра. Значит, квадрат на ВД
больше квадрата на Ф+Х на (величину), большую той, на
которую кнадрат па ВА больше квадрата на ВТ, так что Ф+Х будет мепь-
шс ВТ и, следовательно, Ф. меньше В Р.
Пусть теперь InF раина Ф; перпендикулярно ВЛ проыедем ЧГЕ,
квадрирующую полошшу {прямоугольника] между КР и ЧГВ. Я
говорю, что сегмент, опущенный в жидкость так, чтобы его основание было
целиком к жидкости, установится так, что ось его с поверхностью
жидкости составит угол, рапным Б.
Опустим сегмент в жидкость, лак сказано, и пусть ось его не
составляет с поверхностью жидкости угол, равный В, по сначала состанит
угол больший, чем В.
Если рассечь ого плоскостью, перпендикулярной к поверхности
-жидкости, то сечением сегмента будет парабола ЛПОЛ, сечением
поверхности жидкости — прямая TI, а осью [сечения] и диаметром
параболы — прямая КО; разделим последнюю и Q, в так же, как и
раньше; параллельно Т1 проведем ГII касательную к параболе в 11, а
также ИМ параллельпо N0 и 112 перпендикулярно к оси. Так как ось
сегмепта состаиляет с. поверхностью жидкости угол, больший угла при
В, то и угол 2ГП будет больше угла В; значит, квадрат на П2 к
квадрату Ла 2 Г будет иметь большее отношение, чем кнадрат на Ч'Е к
квадрату на 4*15.
Значит, КР будет иметь к 2 Г отношение большее, чем
половина КР к «FB;
КР
яг что
значит, 2 Г меньше удвоенной ¥В, а 20 меньше Ч'В, л, следовательно,
2£2 будет больше PW и ПН больше Ф. И так как сегмент но тяжести
относится к жидкости, как излишек квадрата па ВД над квадратом
на Ф+Х относится к квадрату на ВД, а отношение сегмепта по тяжести
к жидкости равно отношению погруженной части ко всему сегменту,
то ясно, что погруженная его часть ко всему сегменту будет иметь то же
отношение, какое излишек квадрата на ВД пад кнадратом на Ф+Х
имеет к квадрату на ВД; тогда и весь сегмент к своей части,
находящейся вне жидкости, будет иметь то же отношение, какое квадрат на БД
имеет it квадрату па Ф+Х. Отношение же всего сегмепта к части,
находящейся пне жидкости, равно отношению квадрата на N0 к квадрат
ту на Ш'1;
ВД* _ Гч'Оа
<Ф I Х)а ИМ*
значит, МП равна Ф+Х. По доказано, что ГШ более Ф; значит, МП
будет менее X; следовательно, ЛII будет больше удвоенной ИМ.
Пусть IIZ будет вдвое более ZM; продолжим соединяющую Z6 до Г;
тогда центр тяжести всего сегмента будет 0, части, находящейся bhi>
жидкости. —Z, а части, находящейся внутри ее, на в Г; пусть он будет
в Г. Подобно предыдущему докажем, что ОН будет периендикулярни
к (поверхности жидкости и что прямые, нроведенпые через Z и Г
параллельпо 6IT), будут тоже перпендикулярны к поверхности
жидкости. Значит, находящаяся вне жидкости часть сегмента пойдет иниз
но перпендикуляру, проведенному через Z, а находящаяся внутри будет

348 уМ'химед
подыматься по перпендикуляру, проведенному через Г; следовательно,,
весь сегмент не может оставаться неподвижным и наклонном
положении. Но он также и не повернется так, чтобы ось его стала
перпендикулярной к поверхности жидкости, так как тогда прилегающие к Л
части дойдут вниз, прилегающие же к Л — вверх на основании таких
жо рассуждений, как и а
предыдущей.
Коли же ось образует с
поверхностью жидкости угол
меньший, чем при В, то подобно
предыдущему докажем, что сегмент не
останется неподвижным, но будет
наклоняться до тех пор, пока ось
его не образует с поверхностью
жидкости угол, равный В [131.
X
Если, прямой сегмент
прямоугольного коноида легче жидкости
и имеет ось, превышающую
параметр в отношении большем, чем
пятнадцать к четырем, то, будучи
опущен в жидкость так, чтобы
основание его не касалось жидкости,
он иногда установится прямо A),
иногда же наклонно; иногда его
основание будет только в одной
точке касаться поверхности
жидкости, причем ото может быть
при двух углах наклона C, 5),
иногда он станет так, что его
основание будет смачиваться на
большей площади D), иногда
так, что его основание ни в одной
точке не будет касаться
поверхности и жидкост и {2 fi); при каких же
отношениях по тяжести к жидкости будет иметь место каждый ил
этих случаев, выяснипи-м. в дальнейшем [141.
Пусть будет сегмент такой, как сказано; если рассечь его
плоскостью, перпендикулярной к поверхности жидкости, то сечением его
ноиерхлостл будет парабола Л ПОЛ jpuc. 22}; пусть осью сегмента
и диаметром параболы будет ВД; разделим ПЛ в К так, чтобы ВК била
«двое больше КД, а в Т так, чтобы ДВ откосилась к КТ как
пятнадцать к четырем. Ясно, что КТ больше параметра. Пусть КГ равна irapa-
ыетру л Р£ будет половиной ВР; тогда и 2В будет в полтора раза
больше ВР. Соединивши А, В и восстании перпендикуляр ТЕ, нроведем
EZ параллельно ВД; затем, разделил ЛВ пополам в 6, параллельно ВД
проведем 611 и возьмем параболы ЛЕ1 на диаметре EZ и А6Д на
диаметре б!1 так, чтобы сегменты АЫ, АЙЛ были подобны сегменту ABA;
тогда парабола АЕ1 пройдет через К и перпендикуляр,
восставленный и Р к ВД, пересечет параболу AEI. Пусть он пересечет ее в точках
Г, Г; через Г и Г параллельно ВД проведем XX, TN; пусть они пере-

О ПЛАВАЮЩИХ TJWIAX
349
секут параболу АвД и точках S, Ф; проведем татке касательные TW
и ОЦ к параболе А ПОЛ в точкнх О, II. Таким образом, даны три
заключенных между прямом и параболами сегмента Л110Л, AEI, АвД,
прямые и подобнее друг другу, но не рапные; их оспования лежат
на одной и toi'i же ицнмой, и из точки N проведены прямые NE, ЗЧГ,
N0; значит, О Г имеет к ГЗ отношение, составленное из тех, которые
1Л имеет к ЛЛ, и ЛЛ к Д1*).
ОГ 1Л АД
ГЗ ~ ЛА AI
Но ЛТ относится к ЛА, как дна к нити, ибо ТВ будет к ИД, как дна
к пяти; такжо и Е13 к 13Л и А'А к ЛЛ, а Л1 и ЛА нвляютон удвоенными
прямыми AZ и ДА; затем ЛЛ относится к AI, кии пять к одному, и
отношение, составленное из тех, которые имеют два к пяти и пять к
одному, будет тем тс, что отпоигепие двух к одному; значит, О Г будет вдвое
больше Га. На том же. осиоианин ПТ будет вдвоо больше, ГФ. Нн-
скольку н;е Д2 в полтора раза больше К1\ то ясно, что В2 предстак-
ляет разность оси и полуторного параметра [15J.
{1) Теперь, если согмепт по тяжести имеет к жидкости то жо
отношение, что кнадрат па 132 к квадрату на МЛ, или жо большое этого
отношения, то он, будучи опущен и жидкость так, чтобы его осповапие
не касалось жидкости, станет прямо, ибо ранее (предложение IV) было
доказано, что если сегмент имеет ось, большую полуторного параметра,
и если но тяжести он имеет ц жидкости отношение не меньшее того,
которое квадрат разности между осью и полуторным параметром имеет
к квадрату па оси, ю он, будучи опущен в жидкость так, как сказано,
установится в примой положении.
B) Если же сегмент но тяжести имеет к жидкости отношение
меньшее того, которое кнадрат па 2IJ имеет к кнадрату на НЛ, но большее
того, которое квадрат па 02 имеет к квадрату па БД, то он, будучи
опущен в жидкость и наклонен так, чтобы его основание не касалось
жидкости, установится наклонно так, что его основание не будет ни
в одной точке касаться поверхности жидкости и его ось образует
с поверхностью жидкости угол, больший чем Cj {рис. 22).
*) Проведем гбщуот касательную Лги ко иссм трем параболам л точке А; вто rosmojkiio, так
как если ЛИ- Bw, то I! ZK— Ии и lift = Win, где тс-чки т, t>, с, w представляют пересечения втой
квелтельн! й с прямыми 1Ш. ZK, КО и АВ. Ми внаем («Квадратура иарнбекш», V), что пенная
параллельна)! «ги прямая, ирииецешшн между основанием параболического сегмента и писательной,
и книце tifiii плннп рассекается параболой на отрезки, которые пропорциональны отрезкам основании;
.HIILIMH CJIObUMll,
«О : ON —AN: NA.
cT: TN = AN: N1,
СЕ : £N =- AK : ХД.
Состанляп производные пропорции со сложением- мы можем нлпиоать:
СО : (CO + ON) = АХ : (AN + NA).
сГ : (сГ + TN) — AN : (AN |- K1),
сЕ : (cS -J- EN) ^ AN : (AN I NA).
•откуда
„ AN-cN „ AN-cX _ AN-cN
AA Л.( АД
теперь
ОГ = < Г - CO »- AN- i.N (~ - -~) .
\ AI AA /
ГЗ —сЗ-еГ= AN-cN/-^ ^-\,
\ AA Al /
и наконец.
ОГ =AA - AT.AI - AA 1A_ . Лй_ " " "'"'
гз "aaai " ад-аТ~*ал : la. ' ". ■ . =

350 лгхимид
C) Если же сегмент но тяжести имеет к жидкости то же отношение,
что квадрат ла ЕО к квадрату па ВД, то of, будучи опущен в жидкость
и наклонен таи, чтобы его основание по касалось жидкости,
установится наклонно так, что ого основание только в одной точке (Л) коснется
поверхности жидкости, и его ось образует с поверхностью жидкости
угол, равный Cj.
D) Если же сегмент по тяжести имеет к жидкости отношение
меньшее того, которое квадрат на НО имеет к квадрату на ВД, но больше»»
того, которое квадрат на ПФ имеет к квадрату на ВД, то он, будучи
опущен it жидкость и поставлен наклоппо так, чтобы его основание не
касалось жидкости, установится наклонно так, что основание его
рассечется жидкостью на большом протяжении.
E) Если же согмент по тяжести имеет к жидкости то же самое
отношение, что квадрат на ПФ к квадрату на ВД, то он, будучи опущен
в жидкость и поставлен паклонно так, чтобы его основание не касалось
жидкости, установится наклонно так, что его основание только в одной
точке будет касаться поверхности жидкости и его ось образует с
последней угол, равпый ¥ (рис. 22).
@) Если же сегмент по тяжести имеет к жидкости отношение
меньшее того, которое квадрат на ПФ имеет к квадрату на ВД, то он, будучи
опущен в жидкость и поставлен наклонно так, чтобы его основание
не касалось жидкости, установится наклонно так, что его ось образует
с поверхностью жидкости угол, мень-
J ,\ ший ^, а основание его ни а одной
точке не коснется поверхности
жидкости.
Все это будет доказано
последовательно.
(Случай 2)
Пусть сначала сегмент имеет по
тяжести к жидкости отношение
большее того, которое квадрат на SO
имеет к квадрату лаВД, но меньшее того,
которое квадрат разности между оськ>
и полуторным параметром имеет к
квадрату на ВД; предположим, что
вышеприведенная фигура построена
(рис. 23}, и пусть отношение сегмента
к жидкости по тяжести будет равно-
отношению квадрата на некоторой
Рис. 23. прямой V к квадрату на ВД; тогда Чг
будет больше, чем ЕО {рис. 22}, но
меньше разности между осью и полуторным параметром. Между
параболами Л ПОЛ и ЛЕД вставим некоторую прямую N6, равную У, и пусть она
оставшуюся параболу пересечет в fo, а прямую Fa в точке В'; докажем,
что 0%> будет вдвое больше /JbN, совершенно так же, как было
доказано, что Оо*) «двое больше оЕ; затем из точки 0 проведем
касательную ЬЩ к параболе АПОЛ и прямую ОТ, перпендикулярную к ВД,
и соединим А с N; тогда прямые AN и XN будут равны друг другу,
•) Черте»; подлинника для ясности несколько изменен; в подлиннике О стоит июеето нашего
Н и имеете и тем U Дальнейшем изложении сотщалает с М.

О ПЛАВАЮЩИХ ТЕЛАХ 351
так как проведенные н подобных сегментах АГЮЛ и ЛЕД прямые Л IN
и АХ, образующие одинаковые углы г оспованиями, будут иметь-
то же отношение, что и АЛ к АЛ,
AN _ АД
АХ АЛ
и па основании второй из построенных фигур {риг-. 23) AN будет
раина X.N и параллельна (касательной) 6Ц *).
Требуется доказать, что сегмент, опущеппый в жидкость так, что
его основание не будет ни в одпой точке касаться жидкости,
установится наклонно в этом положении, и его ось образует с поверхностью-
жидкости острый угол, больший угла Cj. Пусть сегмент будет опущен
и станет так, что его оспованио в одной точке иоспется поверхности--
жидкости; если рассечь его через ось
плоскостью, перпендикулярной к
поверхности жидкости, то сечением
сегмента будет парабол а АГЮЛ {рис. 2Л},
поверхности жидкости — прямая
ОЛ, а осью (сегмента) и диаметром
(параболы) будет БД. Рассечем ВД в
точках К и I', как сказано выше**),
затем параллельно АО проколом
прямую ТГГ, касающуюся параболы в
точно П, далее проведем ПН
параллельно НА и 112 перпендикулярно
к ВЛ. Так как сегмент по тяжести
имеет к жидкости то же отношение,
что кпадрат па lF к квадрату па ВЛ,
отношение же и о тяжести сегмента
к жидкости равно отношению
погруженной части ко всему сегменту, и
отношение погруженной части ко все-
• му телу равно отношению квадрата
на 611 к кладрату на ДВ, то, значит, \F !
будет равна 611. Значит, и NB (рис. 23) будет равна вП; следовательно,
сегменты А ИХ [рис. 23} и Л110 {рис. 24} будут друг другу равны.
Л так как и равных и нодобпых сегментах А110Л {рис. 24} и АМХЛ
{рис. 23} от кгнщш! оснований проведены прямые ОА, АХ, и
отсеченное части образуют с диаметрами равные углы (ца основании третьей
из построенных фигур), то углы при Ц и Г будут равны. Значит, CjB
и ГВ тоже будут равны; следовательно, раины и 2Р с ТР, и HZ с ©В',
- и ZH с B'N. Так как НВ' меньше удвоенной B'N***), то ясно, что 11Z
будет меньше удвоенной Z6. Пусть ГЮ будет равна удвоенной £2Н;
проведя соединяющую прямую KQ, продолжим се до Е; точка К будет
центром тяжести всего сегмента, Q — центром тяжести части,
находящейся в жидкости; тогда центр тяжести части, которая пне жидкости,,
найдется на линии КЕ; пусть он будет Е. Но K.Z перпендикулярна-
к поверхности жидкости, а значит, будут перпендикулярами и прямые,
цроводотше через Е и Q параллельно K.Z. Следолательно, сегмент
*) Если AN—NX, то лрпмая Кб Судет диаметром параболы АПОА, сопряженным хпрлс-
АХ и, апачнт, хорда АХ параллельна касательной eCj в иерлтине диаметра.
**> То есть чтобы К была центром тяжести сегмента, а КР — параметром.
***) Действительно, ©^>=2^>N {рис. 23}.
// /'
Риг,. 24.

352
ЛРХИМКД
не останется в покос, по станет так, что его основание ни и одной точке
не коснется жидкости, ибо в настоящем положении оно касается
жидкости только и одной точке. Ясно, что сегмент установится так, что ось
его образует с нонерхностыо жидкости угол больший, чем С}. _
(С л уча й 3)
Пусть сегмент имеет по тяжести к жидкости таков отношение, как
квадрат па 30 к квадрату на ВД {рис. 25}, и опущен в жидкость в
наклонном положении. Если рассечь ого черев ось плоскостью,
перпендикулярной к поверхности жидкости, то сечением тела будет парабола
А1ЮЛ {рис. 26}, сечением поверхности жидкости — прямая ОТ, а осью
сегмента и диаметром парабол и — прямая ИЛ; разделим ИЛ так же,
как л раньше, параллельно Ю яроведом касательную JIN и параболе
Рис. 25 Рис. 26.
в точке П, иатсм параллельно ИЛ пронедем 110, а перпендикулярно
к ВА проведем К2. Требуется доказать, что сегмент не останется
наклонным в таком положении, но будет наклоняться до тех пор, пока его
ocuoiiamtc na коснется жидкости и одной точке.
Пусть будет перед нами (фигура) {рис. 25} и сделано то же, что
и на предшествующей фигуре; проведем ТО перпендикулярно к ВД
и соединяющую ЛЗ продолжим до X; тогда A3 будет равпа ЕХ;
прополем также- О^, параллельную АХ. И так как предполагается, что
сегмент имеет но тяжести к жидкости то же отношение, что квадрат
па ЕЮ к квадрату па ВД, то такое отношение будет иметь и
погруженная часть ко всему телу, то есть квадрат на ПО к квадрату па ИД, а
значит, 116 \ рис. 26} будет равняться ЕО {рис. 25}. И так как у сегментов
IBO и ЛВХ диаметры раины, то будут раины и сегменты. Далее, так
как I» равных и подобных сегментах А1ЮА и АОХА {рис. 25 и 26}
проведены прямые АХ. и 10, отсекающие рапные сегменты, исходя одна

О ПЛАВАЮЩИХ ТКЛАХ
353
из конца основания, другая, же не из конца, то ясно, что меньший
острый угол с диаметром всего сегмента состаиит та прямая, которая
проведена из конца основания. И так как угол Ц будет меньше угла N,
то значит, и RT {рмс. 25} будет больше, чем Б2 {рис. 2E}, а ТР {рис. 25}
меньше, чем Р2 {рис. 26}; поэтому и Ост меньше, чем П$Ъ, (и оЗ)
больше, уем ")fc&. И гак как Оа вдвое вольта <гЕ, то ясно, что и П^Ь
будет больше удвоенной 5^>в. Пусть ПН будет'вдвое больше НО;
проведем соединяющую ПК и продолжим до £3. "Тогда центром тяжести
всего сегмента будет К, части, находящейся в жидкости — II, а
внешней — некоторая точка на Кй; пусть она будет Q. После этого
совершенно так же докажем, что К$Ъ будет перпендикулярна и поверхности
жидкости так же, как и прямые,
проведенные через Н и Q параллельно
К^Ъ. Ясно, что сегмент не остапется
неподвижным, по будет наклоняться
до тех пор, кока его основание пе
коснется в одной точке поверхности
жидкости, как это показано па
третьей фигуре (рис. 27>, относящейся к
рассматриваемой третьей теореме; и
и таком положения сегмент
установится неподвижным.
Действительно, в ранних
сегментах А1ЮЛ {рис. 27} и АОХЛ
{рис. 25} от концов оспований про-
ведешл прямые АХ, АО, отсекающие
одинаковые части; совершенно так
же, как и раньше, докажем, что
сегмент ЛПХ равен А ПО;
следовательно, АО и АХ образуют раиные
острые углы с диаметрами
сегментов, так как угли при _\ и С\ равны.
Пусть прямая IVfo будет вдвое больше у^>6; если провести
соединяющую прямую ffiiK и продолжить до Й, то центром тяжести всего
сегмента будет К, той его части, которая в жидкости,—$>, а цептр тяжести
внешней части (будет лежать) па линии Kft; пусть он будет Q. Далее,
К$й перпендикулярна к поверхности жидкости. Теперь часть,
находящаяся в жидкости, будет подниматься", а находящаяся вне жидкости —
опускаться по одной и той же прямой; таким образом, сегмент остается
неподвижным и основание его касается жидкое поверхности в одной
точке, а ось сегмента с поверхностью жидкости образует угол, раьный
нынюул аза иному.
ИМ
Рис. 27.
(Случай 6> [Щ
Далее, пусть сегмент но тяжести имеет к жидкости отношение
меньшее того, которое квадрат на Л" в имеет к квадрату на 13Д {рис. 28};
пусть опо будет равно отношению квадрата на х¥ (к квадрату на БД);
тогда V будет меньше '0N. Между сегментами АМД и AIIOA вставим
прямую Ш, параллельную БД и равную Чг; пусть она пересечет
промежуточную параболу в Г, а прямую !ЕР — в Ц. Тогда, так же как
было доказано, что ГО вдвое больше ТБ {рис. 22}, докажем, что ПГ
вдвое болыпе П.
23 Архимед

354
AI'XH'MEA
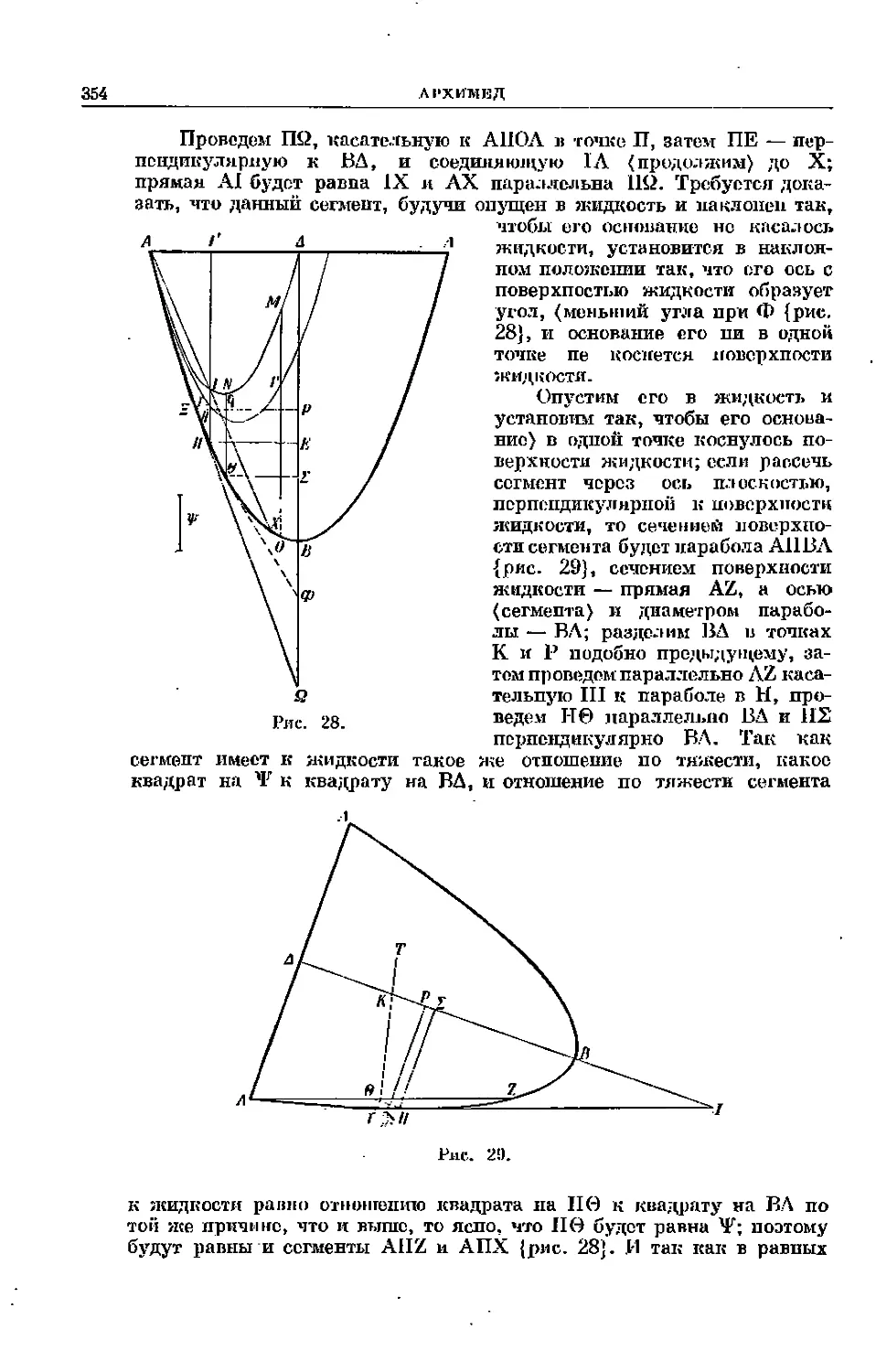
Проводом ПЙ, касательную к АНОЛ и точке П, затем ПЕ —
перпендикулярную к ВА, и соединяющую 1Л (продолжим) до X;
пряма» АХ будет равна XX и АХ параллельна НО. Требуется
доказать, что данный сегмент, будучи опущен в жидкость и наклонен так,
чтобы его осношшне не касалось
жидкости, установится в
наклонном положении так, что его ось с
поверхностью жидкости образует
угол, (меньший угла при Ф {рис.
28}, и основание его ни в одной
точке пе коснется поверхности
жидкости.
Опустим его в жидкость и
установим так, чтобы его
основание) в одной точке коснулось
поверхности жидкости; если рассечь
сегмент через ось плоскостью,
перпендикулярной к поверхности
жидкости, то сеченной
поверхности сегмента будет парабола А11ВА
{рис. 29}, сечением поверхности
жидкости — прямая AZ, а осью
(сегмента) и диаметром
параболы — ВЛ; разделим ВЛ и точках
К и Р подобно предыдущему,
затем проведем параллельно AZ
касательную III к параболе в Ы,
проведем Ив параллельно ВА и XIX
перпендикулярно ВЛ. Так как
сегмент имеет к жидкости такое же отношение по тяжести, какое
квадрат на 4F к квадрату на ВД, и отношение по тяжести сегмента
г>//
Рис. 2!).
к жидкости ранно отношению квадрата на 116 к квадрату на ВА по
той же причине, что и выше, то яспо, что IK-) будет равна Ч*"; поэтому
будут равны и сегменты AXIZ и АПХ {рис. 28]. И так как в равных

О ПЛАВАЮЩИХ ТЕЛАХ
355
и подобных сегментах АПОЛ, AW/Л из концов оснований проведены
прямыо ЛХ, AZ, отсекающие равные части, то ясно, что они образуют
равные утлы с диаметрами сегментов. Поэтому в треугольниках HIS,
1ШЕ углы при I н Й равны; следовательно, будут равны и прямые
SB и ЕВ, а значит, будут равны и 1'Р с ЕР, а также и П$ь с ПН
и $Ъ0 с НТ*). И так как ПГ иди ос больше П, то ясно, что Н^й меньше
удвоенной $Ьв. Пусть IIГ будет вдвое больше ТО; продолжим
соединяющую ГКТ; центром тяжести иесго сегмента будет К, части
находящейся в жидкости — Г, а той, что пне жидкости, (точка) па линии КТ;
пусть она Судет Т. Тогда
совершенно так же, как в
предыдущей теореме,
обнаружится, что сегмент не
останется неподвижным, по
наклонится так, что его
основание не будет ни н
одной точке каеатьсп
поверхности жидкости.
Теперь докажем, что
он установится так, что
его ось с поверхностью
жидкости образует угол,
меньший угла Ф.
Действительно, пусть, если
возможно, он установится так,
что будет составлять угол,
не меньший угла Ф;
сделаем все остальное {рис. 30}
так же, как и на
третьей фигуре. Тогда совершенно таи же докажем, что вII будет
равна W, а, следовательно, и ТП {рис. 28}. Так как угол Л не меньше Ф,
то, значит, ГВ пе будет более 2В, а ГР не менее 2Р, н Н ^ не менее
©Cj**). Итак как IIIв полтора раяа больше ПГ {рис. 28), ПГ же
меньше 6Ц, к Н0 {рис. 30} равна П1, а П$Ъ не меньше вЦ, то $Ь Н будет
больше II Г; япачит, Н^- будет больше удвоенной $£>в. Пусть НГ
будет вдвое больше Г6; продолжим соединяющую ГК; тогда подобно
предыдущему обнаружится, что сег-мспт не остапется неподвижным,
но наклонится так, что его ось с поверхностью (жидкости будет состав-
влять угол, меньший Ф),
Рис. 30.
(Случаи 5)
Подобно этому докажем, что если сегмент имеет по тяжести к
жидкости то же самое отношение, что квадрат на N0 {рис. 28} к квадрату на
ВД, то он, будучи опущен в жидкость так, чтобы его основание не
касалось поверхности жидкости, установится так, что его основание только
в одной точке коснется поиерхности жидкости, и ось его с поверхностью
жидкости составит угол, ранний углу лри Ф.
*) Тр-к НИ и .-пиши XB,IIJ. П^), ^е берутся на рис. 29, а tjj-k PZR и линии ЕВ, ЕР,
ПН и HI — на рис. 28.
•») Линии П«, ГН, П^Ь берутся, на fine. 30, a IB. 2V ч вС| на рис. 28.
23*

356
АРХИМЕД
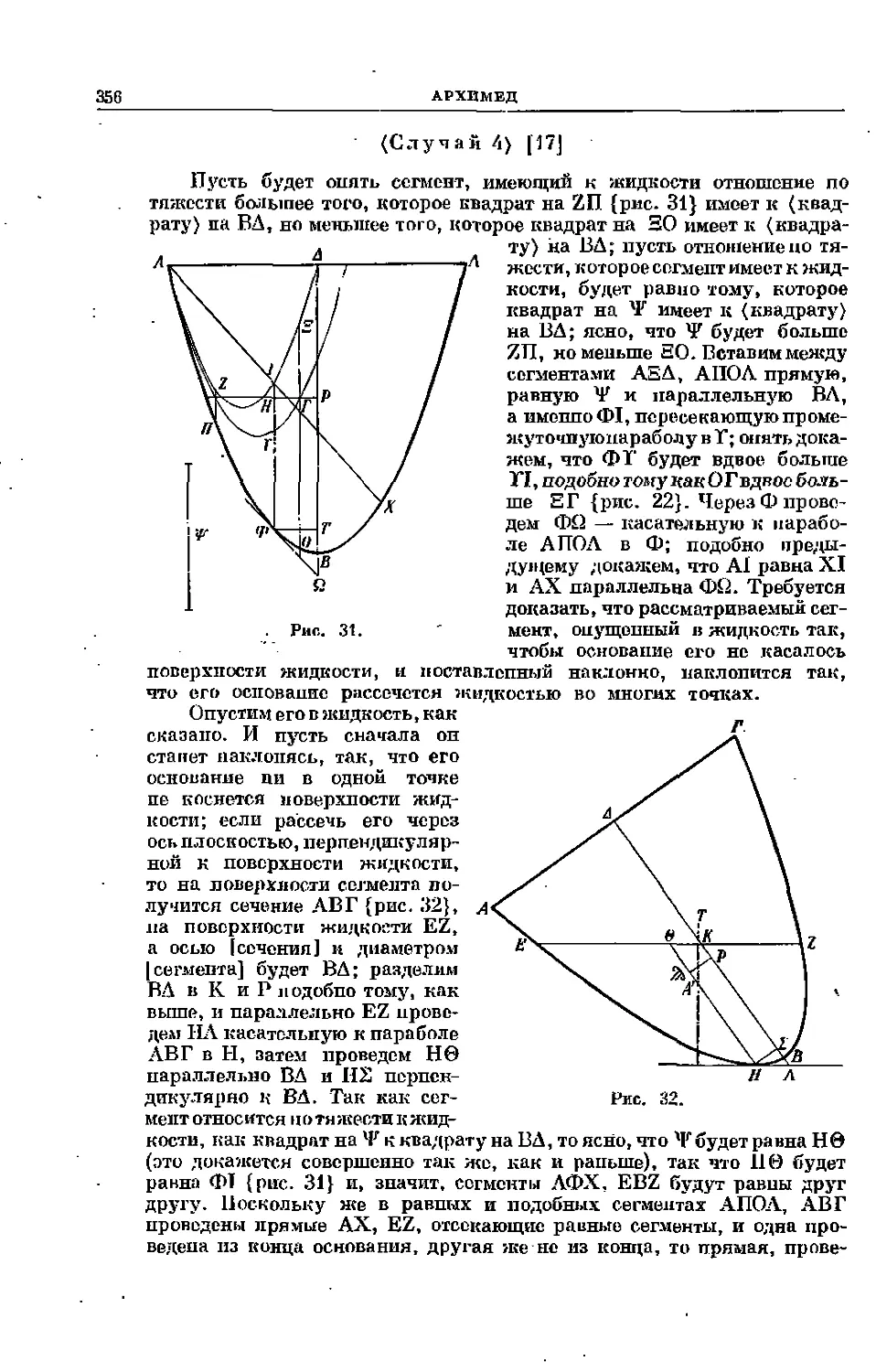
(Случай 4) [17]
Пусть будет опять сегмент, имеющий к жидкости отношение по
тяжести большее того, которое квадрат на ZH {рис. 31} имеет к
(квадрату) па ВД, но меньшее того, которое квадрат на 30 имеет к
(квадрату) на ВД; пусть отношение но
тяжести, котороесегмент имеет к
жидкости, будет равно тому, которое
квадрат на Т имеет к (квадрату)
на ВД; ясно, что Ч? будет больше
ZTI, но меньше ЕО. Вставим между
сегментами АЕД, АПОЛ прямую,
равную Y и параллельную ВЛ,
а имеппо Ф1, пересекающую
промежуточную параболу и Г; опить
докажем, что ФТ будет вдвое больше
XI, подобно тому как ОГвдвое
больше ЕГ {рис. 22}. Через Ф
проведем Фй — касательную к
параболе АПОЛ в Ф; подобно
предыдущему докажем, что А1 равна XI
Я и АХ параллельна ФЙ. Требуется
доказать, что рассматриваемый сег-
Рис 31. мент, опущенный в жидкость так,
чтобы основание его не касалось
поверхности жидкости, и поставленный наклонно, наклонится так,
что его основание рассечется жидкостью во многих точках.
Опустим его в жидкость, как
сказано. И пусть сначала он
станет наклонясь, так, что его
основание пи в одной точке
не коснется поверхности
жидкости; если рассечь его через
ось плоскостью,
перпендикулярной к поверхности жидкости,
то на поведал ости сегмента
получится сечение АВГ {рис. 32}, а
па поверхности жидкости EZ,
а осью [сечения] и диаметром
|сегмента] будет ВД; разделим
ВД в К и Р подобно тому, как
выше, и параллельно EZ
проведем НА касательную к параболе
АВГ в Н, затем проведем Н0
параллельно ВД и Н2 перпен- // л
дикулярно к ВД. Так как сег- Рис. 32.
мент относится нотнжести к
жадности, как квадрат на XV к квадрату на ВД, то ясно, что Т будет равна Н©
(это докажется совершенно так же, как и раньше), так что 110 будет
равна ФТ {рис. 31} и, значит, сегменты АФХ, EBZ будут равны друг
другу. Поскольку же в равпых и подобных сегментах АПОА, АВГ
проведены прямые АХ, EZ, отсекающие равные сегменты, и одна
проведена из конца основания, другая же не из конца, то прямая, прове-

О ПЛАВАЮЩИХ ТЕЛАХ
357
денная из конца основапия, образует меньший острый угол с диаметром
сегмента. И так как в треугольнике HAS угол Л больше угла Q в
треугольнике ФТ£2, то ясно, что В2 будет меньше ВТ, a ХР больше РТ,
л Н$> больше ФН,- значит, $Ь0 будет хюиыие. чем III; и так как ФГ
вдвое больше TI, то ясно, что Н$э
будет более чем вдвое больше^) в.
Пусть НА' будет вдвое
больше А'6; тогда из всего этого
ясно *), что сегмент но останется в
покос, но будет наклониться до тех
пор, пока его основание не
коснется в одной точке поверхности
жидкости.
Пусть оно коснулось ее в одной
точке, как это изображено на треть-
си фигуре {рис. 33}, и пусть все
остальное будет устроепо как и
раньше; тогда опять докажем, что вН
будет равпа Ф1, и что сегменты
АФХ и ABZ равны друг другу. И
поскольку в равных и подобных
сегментах Л ПОЛ {рис. 31}, АВГ
проведены прямые АХ, AZ,
отнимающие равпые сегменты, то они образуют равные углы с диаметрами
сегментов; значит, у (треугольников) ЛН2,Ф'Ш углы при Л и £2 равны,
и прямая BE равна ВТ, a IP равна РТ, Ecft> раина ФН и $ЫЭ равна Ш;
поскольку же Ф Г вдвое больше П, то ясно, что 11% будет более чем вдвое
больше /^H. Пусть HP будет вдвое больше РВ; из этого опять ясно,
что сегмент не останется в покое, по будет наклоняться в сторону А.
И так как было предположено, что сеглшпт касается жидкости только
в одной точке, то ясно, что основание будет охвачено водой на большем
п р отнжении И 81.
*) Точка А' — центр тпжвми погруженной части — будег лехмчъ правее вертикали Й%).
а центр тяжести Т выступающей части будет, наоборот, левее к^-

О ПЛАВАЮЩИХ ТЕЛАХ
Лрсизведемие относится к числу поздних сочинений Архимеда. Оно ииппсапо оире-
делегсно поздно!) трактата «О равновесии плоских фигур», так кап в нем встречаются
ссылки на этот трактнт. Оно написано позднее «Коноидов», па одно из предложений
которых оно опирается, п, вероятно, позднее «Эфода», в котором содержится, теорема о
положении центра тяжести сегмента napa6o:ioii;ia. To обстоятельство, что конец второй книги
не получил окончательной отделки, позволяет думать, что мы имеем дело с последним
произведением Архимеда.
Любопытна история того, как это произведение дошло до лас. Очень долго оно
было известным только в латинском переиоде Вильгельма из Мербеке A215—1282),
который сделал несколько переводов с греческого для своего друга, известного схоласт»
Фомы Аннинского. Вильгельмом был сделан перевод всех сочинений Архимеда;
рукопись этого перевода была обиаружоиа в I88'i г. Валентином Розе в Батики некой
библиотеке. Если верить словам Рожера Взкона, написавшего про него: «Hie Willielmus Flemin-
gus, qui uiliilfiovit digmim neque in scion Li is nei]iie in Unguis (этот фламандец Вильгельм,
не .чнашими ничего достойного пи в науках, пи в языках)», то Вильгельм из Мербеке вряд
ли хорошо понимал Архимеда (хотя относительно знания Вильгельмом языков Вокоп
определенно но прав). Греческий текст был открыт только в -1905 г. Гсйбсргом в
Константинопольском иалимцсссто, сохранившем для нас примерло около трех четвертей
текста Архимеда; утраченный текст воснолнистси по переводу Мербеке.
Сочинение «О плавающих течах» состоит из двух книг; в первой свободпая
поверхность воды считается сферической, а во второй— плоской.
Первая книга состоит из девити предложений. Два первых устанавливают, что
свободная поверхность вони, окружающей Землю, является сферической, причем центр
сферы совпадает с центром Земли. Хотя сферичность Земли и вообще мира была признана
еще греческими философами эпохи Платона и Аристотеля, тем не менее против результата
Архимеда, по-видимому, восстал даже его друг Эратосфеи Кирспскнй, основатель
математической географии. В первой книге «Географии» Страбоп пишет: «Разве не смешно
теперь видеть, кап математик Эратосфеи отказывается иризяать установленный
Архимедом^ и сочинении ^О плапаюличх в жидкости телах" принцип, что поверхность всякой
покоящейся жидкости принимает форму мара, центр которого совпадает с центром Земли,
а ведь это принцип, который теперь принимается всяким мало-мальски знающим
математику» (Географии, книга I, гл. 111, 11).
Первое предложение 2-й книги формулирует принцип ареометра, а остальные
девять рассматривают условия равновесии нлагаюшего в жидкости сегмента
параболоида. Трактовка вопроса Архимедом является чисто физической. Архимед устанавливает
положение равновесия тем, что определяет, будет ли тело, отклоненное от этого
положения, возвращаться в него или ист; таким образом, определенные положения будут
соответствовать только устойчивому равновесию. Первые четыре предложения (И—V)
касаются вертикальных положений равновесия, следующие четыре (VI—IX) — наклпппзлх
соложений, когда основамио сегмента целиком находится или внутри, или вне жидкости;
последнее предложение дает общий разбор вопроса о возможности положении равновесия,
когда поверхность жидкости также пересекает плоскость основания плавающего
сегмента. Изучение последнего предложении показывает, что Архимед шел путем, лишь
в чнетиостнх отличающимся от того метода, который бил установлен во второй ноловияе
XIX века (теоремы Дюпена — Давыдова); однако нельзя согласиться с мнением одного из
переводчиков Архимеда, Именно II. Фер-Экке, что «:>ти предложения удивительным образом
выражают всю ту теорию метацентра, которая должна была освободить всю теорию
кораблестроительства от прежнего эмпиризма»; наоборот, А рхимед чисто физически проверял
условии устойчивости равновесия, не обращаясь ни к какому теоретическому критерию.
Б новейшее время приходится слыотать мнение, что иырябтаття Архимедом
теория по имела никакого практического применения и что было бы лучше, если бы Архимед

О ПЛАВАЮЩИХ ТЕЛАХ
57S
разработал условия равновесия бесконечно длинного параболического цилиндра, иными
слешами, решил бы то, что теперь начинается плоской задачи") гидромеханики. По суще-
сгпу, Архимед и решал такую задачу, поскольку для тела вращения все плоские сочинил
через вертикальную ось равнозначны, так что достаточно рассмотреть условии
равновесия для колебаний тела в плоскости какого-нибудь одного из этих сечений.
Это обстоятельство заставляет критически отнестись к старому, сохранившемуся
у Витруаия рассказу о том, кап бил открыт закон Архимеда. В тексте Витруния
(«Архитектура», книга IX, гл. 3) говорится:
«Во время своего царствовании в Сиракузах Гиерон, после благополучного окон-
чапин всех своих мероприятий, дал обет пожертвовать н какой-то храм золотой венок
бессмертным богам. Он условился с мастером а большой иене за работу и дал ему нужное
но вису количество вшила. В назначенный день мастер принес спою работу царю, который
нашел ее отлично выполненной; после взвешивания венок оказался соответствующим
выданному несу золота, но при испытании последнего на пробирном камне оказалось, что
мастер часть золота заменил серебром. Царь был ичень раздражен этим обманом, но не
будучи в состоянии уличить мастера ь сделанной им храме, попросил Архимеда
придумать дли итого способ. Однажды, когда целиком занятый этим делом Архимед садился
в ванну, он заметил случайно, что но мере погружения его тела в поду последили
переливалась через край. Ото наблюдение сразу позволило ему найти нужную идею, и радость
настолько наполнили его душу, что он сразу выскочил из ванны и, бегая голым по дому,
кричал, что он нашел то, что искал, говоря по-гречески: „Эврика! Эврика!"»
Если обдумать атот рассказ более внимательно, то становится ясным, что к
открытию закона Архимеда он никакого отношения не имеет. Чтобы уличить недобросовестного
ювелир», Архимеду было необходимо определить объем венца и сравнить его нес с весами
соответствующих объемов серебри и золота; как ясно из всего рассказа, объем венца был
определен по киЯиче.егау иытссксилиш води.
Какова бы ни была первоначальная причина зарождения закона Архимеда, нрядли
можно думать, что единственным его практическим приложением было уличение
недобросовестных мастеров. Полибий пишет, что при обороне Сиракуз Архимед при помогли
крюков и рычагнв приподыми.-! и опрокидывал корабли римлян: для того чтобы построить
нужный для этого механизм, необходимо произвести его расчет, последний мсп
невозможен без знании закона Архимеда.
[1] «Погрузившись же, тело не будет двигаться (о<СОфсетаi) вниз, так пак все
части жидкости, находящиеся па одном уроене (та =£ 'ioois Keifieva), будут давить
одинаково вследствие того, что тело является раанотяжелым с жидкостью»,— ото место иногда
толковали и том смысле, что равиотяжслое с жидкостью тело будет в равновесии только
у поверхности жидкости, а не в любом положении пнутри жидкости, и соответственно
упрекали Архимеда и ошибке. Такого рода толкование не является необходимым; дальнейшие
слова об один-ановости давления, то есть об отсутствии побудительной силы для
движения, шжазыпают, что мысль Архимеда заключалась и том, что движение вниз считалось
невозможным именно вследствие отсутствия причины для движения.
|2] Установленные уже в XIX пеке теоретические положения, необходимые для
решения поставленной задачи, таковы:
Если тело легче жидкости, то плоская фигура, отсекаемая в теле продолжением
■уровни жидкости, носит название плоскости плавания: так как вес жидкости в объеие
погруженной части равняется весу всего тела я вес тела постоянен, то объем части тела,
отсекаемой плоскостью плавания, тоже будет постоянным, как бы ни наклонялось
плавающее п жидкости тело. Огибающая всех плоскостей плавания называется
поверхностью сечении: это будет геометрическое место центров тяжести плоскостей плавания.
Геометрическое место центров тяжести рапных объемов, расположенных под
различными плоскостями плавания, называется поверхностью центров; касательная
плоскость к поверхности центров параллельна плоскости плавания, которой соответствует
точка касания; нормаль к плоскости плавания будет одновременно нормалью и к rjoBipx-
иости центров. Так как перпендикуляр, опущенный на плоскость плавания из центра
тяжести, будет направлен но вертикали, то разыскание положений равновесия
плавающего тела сводится к проведению из центра тяжести нормалей п поверхности центров;
каждой такой нормали будет соответствовать определенное, положение равновесия.
Условия устойчивости определенного положения равновесия формулируются так.
Проведем чгрса пирмпль. к поверхности центров плогаоеть, которая раесьчгт эту
поверхность центров по некоторой кривой; направления нормалей к поверхности центров будут
совпадать с нормалями к кривой сечения. Таи как сферический сегмент, рассматриваемый
Архимедом, имеет ось симметрии (плоскость плавании будет окружностью), то центры
кривизны всех таких линий сечения будут одинаковыми; бесконечно близкие к основной
(вертикальной) нормали линии действия давлений воды, совпадающие с направлениями
нормалей к поверхности центров, будут пересекаться в одном и том же центре кривизны;
этот центр кривизны можно пршштг» за своего рода точку подвеса для плавающего'
37*

580 Комментарии
в жидкости тела; эта точка называется метацентром. Чтобы устойчивость равновесия
была обеспечена, центр тяжести плавающего тела должен быть ниже метацентра; если
целтр тяжести находится выше метацентра, то равновесие будет неустойчивым.
Когда сферический енгмонт плавает выпуклостью книзу, поверх постг. центров будет,
очевидно, шаровой поверхностью с центром, совпадающим с центром сферического
сегмента; радиус же равняется расстоянию ОА от центра сферической поверхности сегмента
ДО центра тяжести А нагруженной части. В пашем случае метацентр будет в точке О,
центр тяжести Г сегмента будет находиться ниже О: следовательно, положение
равновесия будет устойчивым.
Когда сегмент будет плавать выпуклостью кверху, то центр тяжести Г всего
сегмента будет лежать выше его геометрического центра О. Пусть А Судет центр тяжести
находящейся вне воды части сегмента, расстояние ОА будет постоянным; мы считаем его
известным, когда отношение плотностей плавающего тела и жидкости будет видано.
Рис. 1. 1>ис. 2.
Также можно считать известным объем погруженной части и положение ее центра
тяжести В. При отклонениях сегмента от положения равновесии центр тяжести А будет
перемещаться но окружности радиуса OA^g, который можно считать известным, а центр
тяжести В — по кривой Вр\ которая, как легко доказать, тоже будет окружностью;
поверхность центров будет поверхностью вращения, образованной этой кривой вокруг осп А В.
Пусть Г — центр тяжести всего сегмента; если отношение весок свободной и
погруженной частей равно и (:>то вполне определенная величина, аапиешцая от соотношения
плотностей тела и жидкости), то отношение расстояний аГ и РГ будет постоянным:
аГ:рг=-АГ:ГВ=1:к.
Таким образом, кривая Bf> может быть получена из окружности Л<х подобным
преобразованием, причем центром- подобия служит точка Г, а коэффициент подобия
отрицателен и равен — х, так как аир" лежат по разные стороны от Г. Кривая вр будет
окружностью, центр М которой лежит на прямой АС так, что цептр подобия Г
оказываете» между М н О. Если расстояние ОГ —6, то МГ=хб. Таким образом, метацентр М
лежит выше центра тяжести Г и равновесие будет устойчивым.
Мы пнднм, что припая цептроп (сечопие поверхгюстц центром) cotyrour из двух дуг
окружностей, соответствующих положениям плавания сегмента, когда плоская его часть
находится целиком в жидкости или вне жидкости. Отметим, что Архимед умел па ходить
объемы сферических сегментов («О паре и цилиндре», кп. II, предложение П) и
положение центров их тяжести («Эфод», предложение IX); следовательно, в обоих этих случаях
он мог при любом соотношения плотностей плавающего тела и жидкости провести псе
вычисления до контра. В Том случае, когда поверхность жидкости пересекала плоское
основание сегмента, уже нет оснований думать, что Архимед и теперь мог определить
объем н положение центра тяжести погруженной части тела; сели бы и в этих случаях
мы построили соответствующие кривые центров, то получили бы еще два положения
равновесия, но последнее было Вы неустойчивым.
[31 Для понимании текста предложений второй книги пуя;ио знать некоторые
свойства касательных к параболе, а Именно:
Если парабола отнесена к системе координат, где начало совпадает с л ершиной,
ось абсцисс идет по оси параболы, а ось ординат по касательной к параболе в вершине,
так что уравнение параболы будет у2=2рх, то для касательной, проведенной в любой
точке параболы, субтангенс будет раиняться удвоенной абсциссе топки касания, а
субнормаль имеет постоянную величину, равную параметру р.
14) Идея архимедова доказательства предложения II заключается п том, что
«ели ОР < р, то нормаль п точке касания 11 пересечет ось ON мслзду Р и N, так что
угол Р1Ш будет острым (рис. 11, сгр. 336).

О ПЛАВАЮЩИХ ТЕЛАХ
581
Пусть ОКК предстапляст сечение параболоида плоскостью, проледеппой через его
ось Ой (рис. 3), пусть уравнение этой параболы в координатных осях Оху будет: уг=2рх.
Пусть ост. параболы ОВ будет равна -^-Ь; согласно доквааншшу Архимедом в «Эфоде»
(иредложенио V), центр тяжести С0 всего сегмента будит лежать па расстоянии ОС0=Ь
от вершины сегмента О.
Опустим сегмент в жидкость так, чтобы, его ось была вертикальна; пусть он пигру-
3
зитея па глубину 0,4—-— а, так что прямая а'Ал' будет представлять уровень жидкости;
пес жидкости в объеме сегмента а'Ла' будет рапен несу всего параболического сегмента;
центр тяжести Ct этого сегмента будет лежать па расстоянии ОС1=а.
В предложении XXIII «Коноидов и сфероидов» докааынаетсн, что объемы сегментов
параболоида «ращения, отссчешшх плоскостями, проведенными кап угодно, будут рав-
вы, если раины оси отмх сегментов. Л так
как все диаметры параболы параллельны, ^тК
то поверхность селений параболоида
(огибающая плоскостей плавания,
отсекающих риншдо объемы) Судет таким же
параболоидом, лишь едпипутым вдоль оси х
па расстоиние О А = -^-«. В сечении этого
параболоида с плоскостью чертежа
получится парабола AD'M, уравнение которой
будет:
i/2— 2р(х-^аЛ
С)
По существу, нам нужна лишь часть
АТУ этпы параболы вплоть до точки D' О
касания с проведенной из К прямой; при
дальнейшем вращении параболоида угил
его К погрузитен п жидкость и следующая
часть поверхности сечений уже по будет
параболоидом AD'M.
Так как центры тяжести сегментов
параболоида лежат на осях на расстояниях
двух третей от вершины, то поверхность
центров н пересечении с плоскостью
чертежа даст параболу CtE'L, иоторан будет
представлять основную параболу, сдвину-
туте вправо на расстоиние ОС\ = а; ее
уравнение будет:
«■=?,(*_.): B) рис3
нам нужна лишь часть ее,
соответствующая дуге С.Е'.
Так кик ниже оси Ох мы будем иметь такую же симметричную фигуру, то достаточно
рассматривать лишь полуплоскость с шмюжнтелмшмы координатами у.
Чтобы найга положения равновесии, ш,г должны из центра тяжести С0 сегмента
провести нормали к линии центров С,/:', ваш: u;s них лишь те, которые пересекают дугу
С,Е', а также ей симметричную, лежащую ниже оси Ох.
Дифференцируя, уравнение B), получим:
их
— V.
тангенс угла наклона касательной к параболе будет равен —, а угловой коэффициент
Ч
нормали ——.
Уравнение нормали, проведенной из точки С0, в текущих, координатах х', у' будет:

582
КОММЕНТАРИИ
Решая это уравнение совместно с уравнением B), находим координаты точек
пересечения нормали с параболой 6',£''. Так как в точке пересечения j/=j/', *=*', то мы
будем иметь:
I Я71 = «, I У-t-
-Ъ—р,
--± \f2p(b-a~p).
Первая пара решений соответствует положению равновесия ири вертикальной оси
ОВ, пторан пара (или, лучше сказать, две пары) решений будет соответствовать
положению равновесия, когда ось ОВ сегмента отклонится от вертикали в ту или другую сторону
на некоторый угол о. Нужно помнить, что
пторая пара решений может иметь место,
только если проведенная на С0 нормаль
пересечет параболу C,/i' между С, и К'.
Одно из необходимых условий
существовании положении равновесия,
соответствующего второй паре решений, будет
заключиться в том, что подкоренное
выражение для j/o должно быть положительным
(если оно равно нулю, то первая и вторан
пара решения сшшадают):
Ь~а>р, Щ
или
Ь—р>в.
В предложении II мы имеем ON=
3 3
=:OJB=.-^- Ъ пе превышает —-р, иными
словами, Ь^р. Это показывает, что в
рассматриваемом случае возможно лишь
положение равновесия, в котором ось
сегм сита isivpr и кал ът\.
Будет ли зто раввовесис
устойчивым? Вместо чисто физического
доказательства Архимеда мы могли бы восиоль-
зоиатьси понятием метацентра, определить
радиус крншмнм линии центров или основт
ной параболы j/2=2pz в ее вершине,
которое 4 рый, лак известно, равен параметру р.
Если от точки С, отложим отрезок C,Af—p,,
то расстояние ОМ метацентра будет равно
а+р, так как fc</>, то ири любом значении а отрезок ОМ будет больше отрезка O6'0=fc,
иными словами, метацентр будет лежать пншп центра тяжести Сл сегмента.
[5| В предложении [11 Архимед рассматривает случай, когда сегмент плавает, имен
основанию целиком погруженным л жидкость. Объемы сегментов параболоида вращении
относятси, как квадраты их осей («Коноиды и сфероиды», XXIV). Если соностанить зто
ла ОА»
с первым предложением рассматриваемой второй книги, то отношепие ту . равное т-^
(рис. 3), даст нам отношепие плотностей плавающего тела и жидкости.
Пусть сегмент опушен основанием КК и жидкость так, чтобы ось его ОВ была вср-
тикалъна, и уровень жидкости пойдет по примой Ь'Ь' (рис. 4). Объем сегмента Ъ'Ь'КК будет
равел объему сегмента Оа'а'\ если мы обозначим отпошепис т^=Л2 и примем объем
всего сегмента ОКК за единицу, то
объем сегм. Оо'о'=объсм сегм. WRR—h*,
а объем сегм. Ь'ОЬ' = 1—А-3.
Рассмотрим сегмент ОЬ'Ь', находящийся над поверхностью воды. Для оси ОВ^
мы имеем:
OBj _ 1—ft2

О ПЛАВАЮЩИХ ТКЛАХ 583
откуда
и, цаконец,
ощ^.ос^&у
0Bt=~ У&—<Р.
Огибающая последовательных положений поверхности плавания будет параболой
РВ^Р, уравнение которой
.;, . •• |- ' j,*=2p (ш~| /5==^ . D)
2
Центр тяжести сегмента ОЬ'Ъ' лаходится на оси ОВ1 на расстоянии ОС^— -o-O.Bi.=
= j/"fc*—о2; при качании оегмеята около вертикального положения равновесия ои будет
перемещаться по параболе Л'С3А', ураииение которий будет:
у^-2р{х~\г1К^). E)
Теперь мы можем заняться построением линии, но которой будет перемещаться
центр тяжести сегмента Ь'ККЬ'. Абсцисса ОС., отого центра может быть найдена из
соотношении
A—А»)ОСи+А»-ОСв=1-ОС0,
откуда
s
Ь-A-/^) l^giZ^i ,,l-(l-A-«J
ос2 -о р
Wa=bi-li-k*-b~-bs.ii-iv(i-yi=*).
Аналогично .;„ .
С3С0 = Ь— \fb*—a*=b (l— |Al_**).
Отсюда видно, что отношение
Срб'а 1— А» ' :.:..-■'
С3С0 ~ Л* '
го есть обратному отяошшшо объемов соответствующих сегментов, как исследовало
ожидать.
Чтобы получить нужную нам ветвь ЕгС± липни центров, иерсстроим параболу
NC^N около центра подобия Са так, чтобы расстоянии С„С2 увеличились в отношении
<1—Ла) : A2; D реаультато получится проходящая через точку С2 парабола, параметр
которой увеличится в том же самом отношении, то есть будет равен:
1 —А»
■ ft-*-*!--
Уравнение этой параболы, если пачало координат взять в точке С„, будет
j/2=2p, (С0С2—ж),
то есть
'^^ТГ^ (l_/i_*«) (!-*•)-*} .
F)
Урапнепие "нормали к этой параболе, проведенной из начала координат С„,
получится, как и раньше:
«• = 1 *' ■ ■-"•■■ •
» . Р /с*

S84
КОММЕНТАРИИ
Так как в точке пересечения нормали с параболой (С) у — у' и х—х', то получаем два
решения:
1) У=0,
_. 1-А« , .
^) *=/—йВ— ■
Первое отвечает вертикальному положению оси С*В, а второе — возможному
наклонному положепшо. Соответствующая ордината у определится после подстановки х
в уравнение F);
G).
Условия действительности значения у требуют, чтобы
Р<Ъ{\ — УТ=Щ,
или
Р < С0С3.
16] Так как Архимед рассматривает только те положения равновесия, л которых
основание сегмента находится целиком в воде или вне ее, то нам понадобятся лишь части
CtEr и C2.fe'2 парабол центров, которые определятся так:
Поскольку в обоих случаях плавании в наклонном положении конец оспоиаяии
сегмента в пределе должен лежать на поверхности воды, то из Л' иужпо построить
касательные к параболам ЛМ и 12ЛР и из топки касания параллельно оси Ох провести прямые
до пересечения с параболами центров, имеющими вершины соответственно в С, и С2;
точки Bi и Ей н будут концами нужных нам дуг.
Если и ерш и на О сегмента погружена к иоду (рис. 3), то мы найдем крайнюю
точку /?i липни центров, если построим касательную KD' к параболе AD'Al а проведем ТУЕ'
параллельно Ох.
Уравнение параболы AD'M будет
y*=2pQ;—~а^ ,
координаты точки К, лежащей на параболе у3—2рх,
а:=~Ь, у=У'АрЬ.
Искомое уравнение касательной будет:
»--V55=f(*'-10;
решая оба уравнении совместно и полагай, как и нише, х=х', у—у', будем имоть:
Уг — У У'&рЬ = р ( х- ■ — bj
Для исключения х умножаем второе уравнение на 2 и ив результата кычитаем
аервос:
у-—2у \fipb='ipa~3,pb,
откуда
ylt s= угрЬ ± У'дрь-. {ъра - ЪрЬ)—Yty (угь ± Уа).
Так как из точки К можно провести к парабол» две касательные — вправо
и влево от К, а нам нужна только левая, то берем для у меньший корень:
У = У*р{/Ъ-Уа).
адрата ординаты, coi
Уык^Зр(Ь-\-а-2УаЬ);
Максимальное значение квадрата ординаты, соответствующей положению равно
весия, будет:

О ПЛАВАЮЩИХ ТЕЛАХ 585
для точки пересечения нормали из С0 с линией центров С El. мы имели z= fc—-n.
Подставив ото значение в уравнение B), получим:
lj*=2p{b—a—p).
Разность этих величая должна быть положительна:
Ухаяя.—у2=р {36-1- За—6 /«6—2Ь+2а-\-2р],
то есть
Ь-\ 5a-j 2p—6 /оЬ>0,
или
2/>>б/вЬ—5« -6=й(Ув6—о) (Ь —угвб)=5Уо(/Ь- [/"о) —■^ft(^rb—"Кв) =
= (/6- V«)E/a-V^}=6(l - |/|)E ]/|--0 ■
Таким образом, если принять по пнимание условие; C), то дли возможности
плавания сегмента в наклонном положении мы должны иметь:
<-«>*>К1-/т)E/т-0-
(8)
Случай, когда сегмент плавает с целиком погруженным основанием, можпо
принести к предыдущему, если вместо ОВ = ^—а па рис. 3 взять 01}^=-^ «' (рис. 4); тогда
аналогичное условие возможности плавать в пак.чоипом положении напитается так:
'-•>'>4(-/т)(»Ут-0-
(9)
где
e' = fcj/l—*s.
Мы установили следующие возможные положения рнпнопсеття:
1) два соответствующих вертикальному положению равновесия оси ОБ,
2) дна наклонных положении с вершиной О сегмента в жидкости,
3) дна наклонных положения с вершиной О вне жидкости.
Кроме этого, имеются еще два положении, когда один из углов сегмента KtK
находился вне жидкости; они соответствуют линиям, соединяющим точки Ji'i и Ег- Эти
положения Архимед совершенно не рассматривал.
Дли выяснения условий устойчивости найденных положений равновесия нужно
определить радпусы кривизны линии центров в соответствующих точках. 1) точках Ct
и 6'2 главная нормаль совпадает с осью параболы центров и равна ее параметру; следова-
1—А?
телыю, расстояние метацентра от линии центров будет р в точке С, и р' = р 8 в точке С2.
Так кап при устойчивом равновесии центр тяжести С0 должен лежать ниже
метацентра, то мы будем иметь:
В положении С\ высота метацентра равна р, высота центра тяжести С0 будет
С,С0=-6—о. Условие устойчивости требует:
Ъ—а<р,
то есть
3 ^ 3 , 3
Yb<Tp+Ta.
Если
3 , . 3
ТЬ<ТР-
то это равенство будет иметь место независимо ог а, то есть и от плотности плавающего
тела. В этом состоит предложение II второй книги.
В положении С2 параметр р' будет:
1 **

586.
КОММЕНТАРИИ
расстояние С„Сг цептра тяжести сегмента (см. стр. 583):
Условия устойчивости требуют, чтобы
Если
-~Ь<у/.+-|*^1-*'-
3 3
то равновесие будет устойчивым независимо от плотности плавающего тела А2; в этом
состоит предложение III кторой книги.
[7| Пол се общие случаи устойчииого равновесия требуют рассмотрения плотности
плавающего тела, иными словами, глубины а его погружения. Условие устойчивости
пишем и виде
4»<|-м4-. . (Ю)
i . Преобразуем его так, чтобы выделить глубину в:
: . ■ . 3 3
—т—<0-
2
о2
Разделим обе части'иа'й и возведем в квадрат, помня, что т^""—плотлости
плавающего тела:
(FT""'
-. Таким образок, вертикальное положение равновесия останется устойчивым, если
плотность плавающего тела d будет раина или больше отношения, стошцето в левой чисти
неравенства:
d>{±zMl
В OToirf состоит предложение IV Архимеда.
[8] Когда сегмент плавает в вертикальном положении основанием кверху, условием
устойчивости будет:
^ъ<'±Р±1ъуь=ё, («О
где ^—Ь V^l— к3=-^\ГТ?—аг=— а' представляет, как мы видели выше, высоту части
сегмента, находящейся вне жидкости; объем погруженной части будет, как мы видели,
равным объему сегмента параболоида с высотой-^- (а—а').
Написанное выше равенство мы можем преобразовать так:
G
(*-*ОЧ40Ч*0"

О .ПЛАВАЮЩИХ ТЕЛАХ 587
C "\2
--6 1, получим:
.GO'-d'-IO'
В левой части стоит плотность d плавающего тела по отношению к жидкости; в пра-
3 3 3
вон — Ь будет ось ctu-мелта, а — Ь—— р представляет разность между осью и
полуторным параметром.
Мы получаем результат, сформулированный л предложении V.
Положение равновесия сегмента параболоид», обращенного вершиной вверх и с
вертикально направленной немо, будет устойчивым, если плоти осп, плавающего тела будет
не бол г.[по отношении разности квадратов оси сегмента и избытка оси над полуторным
параметром к" квадрату оси сегмента.
Доказательство V предложения у Архимеда строится совершенно аналогично
доказательству IV; надо только учесть, что прямая ПФ равна-j-l'fc*—и*.
Определим область устойчивости равновесия сегмента параболоида при
вертикальном положении осп.
Если ось пе более полуторного параметра, то рапповские будет устойчивым в
вертикальном положении, будет ли основание сегмента целиком вне или внутри жидкости.
Если ось более полуторного параметра, то положение устойчивого равновесия
зависит и от плотности плавающего тола. Если принять плотность жидкости за единицу, то
/' Ь— р\»
плотность тела будет меняться от 0 до 1. Обозначим отношение I —■— \ через е. Тогда,
если плотность сегмента будет большее, то устойчивым будет вертикальное положение
•основанием вверх; если же плотность будет меньше 1—е, то устойчивым будет положение
равновесия основанием вниз. Можно'поставить вопрос: при каких соотношениях о и р
вообще вертикальное положение сегмента будет устойчиво?
• i
Если е——, то при d>e устойчивое равновесие будет в положении основанием
вверх, а при й<е—основанием выи»; при d=c возможны оба положения равновесия.
1
Если е<^— , то вся область изменения d разделяется па три части: первый интервал
будет от 0 до <?, второй от е до 1—е и третий от 1—е до 1. В первом интервале
устойчивым будем положение основанием вниз, во втором возможны оба положения, равновесия,
в третьем будет устойчивым положение основанием вверх.
1
Если е >• — , то интервалы будут от 0 до 1—е, от 1—е до е и от е до 1, причем
среднему интервалу не будут соответствовать никакие возможные положения равновесия
с вертикальной осью.
[9| В предложениях VI—IX Архимед определяет положения равновесия, когда
ось сегмента расположена паклигггго. Покажем, что если равновесие возможно, то оно
всеггда будет устойчивым.
Для атой цели нам нужно определить высоту метацентра, иными словами, радиус
кривизны сечении поверхности центров; как мы видели, эта линия будет параболой,
одинаковой с параболой, полученной в сечении параболоида вращения.
Если уравнение этой параболы
у2 = 2рх,
то, как мы знаем из математики, радиус кривизны с в точке, ордината которой равна у,
-будет
„ (fa-H/aK/a
Рассмотрим положение равновесия, соответствующее случаю, когда основание
сегмента будет целиком находиться пне поверхности жидкости (рис. 5).
Пусть APOL представляет сечение параболоида плоскостью чертежа, точка О будет
шершиной параболы, ON — осью ее, точка В, лежащая на расстоянии Ofc=— ON, будет

588
КОММЕНТАРИИ
центром тяжести всего параболического сегмента. Пусть AS представляет сечение
поверхности плана пня, JCZ — параллельная ей касательная к парабол и в Р; тогда FP
представит ось погруженного в жидкость сегмента, а точка В, лежащая па расстомнни ВР =-5- PF>
о
будет центром тигкести сегмента ASOP. Точка В — центр тяжести погруженной части —
принадлежит поверхности центров, сечение которой будет параболой, одинаковой с
параболой АРОТ.. Прямая ВВ должна быть пер-
L пендикулярна к касательной СП л В к этой
параболе, параллельной сечению
поверхности плавания AS; этого требуют условия
равновесия. Равновесие будет устойчивым,
если расстояние ВВ будет мслыпе высоты,
метацентра или радиуса кривизны параболы
APOL, одинаковой с линией центров.
Мы имеем:
По BD, как субнормаль, равна
параметру Pi a BD—PE представляет ординату у-
точки В касания прямой СИ и линии
центров. Таким образом,
bb^Vu^Tp^
а высота мстацелтра
„г_г_„2
Так как множитель - -— больше единицы, то q > BR, то есть устойчивость равдо-
весия обеспечена.
И» чертежа видно, что
или в наших обозначениях
OB>IW-^DE=RD+BP,
Ь>р-\-а,
нами условие возможности равновесии up»
что дает геометрически уже выведенное
наклонном положении осы
Ь—а>р.
Обратимся к случаю, когда сегмент
плавает, имея основание целиком
погруженным в жидкости (рис. ti). Пусть при
обозначениях предыдущего чертежа та же
В предстапляст центр тяжести части
сегмента ПОРА, находящейся над
поверхностью AS жидкости, расстояние PB——PF.
Точка Л, лежащая па расстоянии ОН = 6,
будет центром тяжести всего сегмепта, а
точка С предстаплпет центр тяжести
погруженной части; опа лежит на линии
(параболе) центров ДЛЯ этой последней.
В положении равновесия точки В, 1! и С
должны лежать на перпендикуляре к
линии плапаиия AS и параллельным ей
касательным KZ и С/1. Рассуждении,
аналогичные предыдущим, убеждают нас, что НЕ
есть параметр р параболы APOL, a UD
—параметр р' параболы центров (действительно,
BD: BE —ВС: /f£?=отношению объемов сегментов ЛМ wAT.S). Так как CD представляет
ординату точки касании С прямой CU с линией центров погруженной части, то ДС=

О ПЛАВАЮЩИХ ТЕЛАХ 589
=yPj/B+p'a1 что, очевидно, будет меньше радиуса кривизны q' линии центров в точке С:
[101 Предложении VI и VII посвящены определению наибольшей лсличины Ь,
при которой согмент может п.чинать так, чтобы его основание не пересекалось
поверхностью жидкости. При
установлении этого предела Архимед
пользуется леммой, доказательство
которой не сохранилось в дошедшем
до пас теисте. Эта лемма
заключается в следующем.
Пусть через какую-нибудь
точку параболы В проведена секущая
В0 и параллельная цй
касательная ЕЗ, через точку касания R
проведена прямая EZ, параллельная
оси, и в какой-нибудь точив Г оси
восставлен перпендикуляр ГД; тогда — _
отношение EZ: ЕА будет больше л
или ран но отношению А Г : ГО, где
А есть основание перпендикуляра,
-опущенного из точки В на ось
(рис. 7).
Приподим доказательство этой теоремы, данное Хизсом. Из точки касания Е
опускаем перпендикуляр ЕМ на ось ОЛ; тогда по свойству касательных к параболе будем
иметь:
МО = ОЕ,
гдо Е есть точка лересечевия касательпой ЕЕ с осью.
Нам нужно доказать перавенство
EZ:ЕД >ЛГ:ГО
или
■ - EZ.VO >АГ-ЕЛ,
то есть ""• ■шЯ"
EZ-ГО —АГ-ЕА>0.
Имеем;
Таким образом,
EZ-ОГ
АГ-ОА-
ЕД=С)Г-
-ОГ,
• ОМ.
-АГ-ЕД = Ег-ОГ—ОА-ОГ — ОМ-ОГ+ОГа+ОА-ОМ=
= ОГа—ОГ (ОА-^ОМ—EZJ+OA-OM.
Но ОА-г-ОМ=ЕО-|-ОА=ЕЛ, а ЗА—EZ=SA- 30 = Л0; следопательио,
EZ-ОГ—АГ-ЕД = 0Га—ОГ-А0+ОА-ОМ.
Затем из подобия треугольников EMS и BAG имеем:
А0:АВ—МЗ:ЕМ.
или ■'. -
Ав:АВ=20М:ЕМ."
Но OM=z, ЕМ = у; если уравнение параболы будет у*=2рх, то АВ8=2р-ОА,
•а ЕМ"=2р-ОМ. Возведем обе части нашей пропорции в квадрат:
А0«:АВ«=4ОМ»:ЕМ*,
Ав2 : 2/i. ОЛ =40Ма Яр ОМ,
•откуда после сокращении:
А02=4ОЛ-ОМ.

590
КОММЕНТАРИЙ
Теперь
■■■'•■■ -*'*Vt-i.
Л ДО
EZ-ОГ—А1'.ЕД=ОГ2—ОГ-Л0+^-
EZOr
-АГ.ЕА = @Г-4®у.
ио будет или больше нуля при ОГ Ф —, или же равным нулю, если ОГ=^= — .
Па основании атой теоремы Архимед паходит предельную величину отношения
Ь '. р, соответствующую плаванию сегмента, когда поверхность жидкости проходит через-
край основания.
Пусп. APOL (рис. 8) — ссчвлие сегмента плоскость»! чертежа, AS — поверхность
жидкости, ON — оси параболы. Проведем касательную IIP, параллельпую АН, и IP,
параллельную ON; точка / разделит AS' пополам. Пусть F будет центр тяжести
всего сегмента; при равновесии перпендикуляр PU к касательной должен пройти
через U—центр тяжести погруженной части. Так как IIZ есть ордината точки
касания, то FZ представляет параметр р. Имеем.
'-■ ОР^Ь, РП^а.
По доказанной лемме мы имеем
РН ^ NZ
14 > ZO '
Берем предельный случай равенства и
переписываем в наших обозначениях
откуда
^a:a = ^+pj:(b~p),
• 3(b-/»)=2^~-l-Jp)
м ?■-
и. окончательно
Рис. 8.
2 ,
Р=ть.
Искомое предельпое соотпошепис можно получить другим путем. В мясняя
возможности плавания сегмента в положении, когда поверхность жидкости не пересекает
основания сегмента, мы вывели неравенство (8) (стр. 585):
'>1(-/*)(»/И-
Определим максимальную возможную величину правой части; для этого нам
придется искать максимум выражения A—z)Ez—1). Дифференцируя, находим
5A—г)_ Eг—1) = 0,
6 8
откуда г~тту При этом зпачении z паше произведение будет равно ~. Таким образом,-
4 2
правая часть нашего неравенства при всякой плотности жидкости будет больше— *=-£■ *»
Ю о
и мм получаем:
р>хь-
или

О ПЛАВАЮЩИХ ТЕЛАХ
•591
Так пак MF-
15 'V'
то
A'Z=-^r ОЛ', а 20=
1а
6
:15
ОЛ', шгыми словами, отношение
Л'2 : Z0=3 : 2.
Поскольку РП : PI^IVZ : ZO = 3 : 2, а расстояние РТ центра тяжести Т
погруженном части удоллстворяет пропорции РТ : PJ—'S: 2,то РТ^РН, иными словами, центр
тяжести 7" будет или совпадать с Н (случай рашшпесия), или лежать между Н и Р,
то есть сегмент будет всплывать так, что его основание будет над поверхностью воды.
То же самое будет иметь место, когда FZ^p Судет больше -^tW, иными словами,
15
когда OJV меньше
15 „•
в этом заключается теорема, сформулированная в
предложении VI.
Может случиться, что перпендикуляр ZH ( ЙК. на рис. 1С, г.тр. 542) пересечет
параболу правде точки касании П, а ось IF погруженной части—ъ точке Н, лежащее правее П
(пторпй частный случай, отмеченный
Архимедом). Тогда перпендикуляр DP пересечет
продолжение III в точке I1, лежащей ищп «ранее Л,
и очевидно, что цептр тяжести й погруженной
части, находящийся' левее Р па расстоянии
2
ТП —-т- 1П, будет и подавно левее нормали ФР,
так что течка А подымется над поверх иостыо
жидкости. По существу, ато равносильно тиму,
что при малых плотностях плавающего тела
паклонпос положение равновесия, при котором
угол А лежит па поверхности жидкости или
ниже ее, является невозможным.
[11] Предложенш; VII доказывается совер- pjfc g
шенно аналогично; второй упомянутый
Архимедом мучай рпвпосилеп тому, что при
плотности плавающего тела, приближающейся к единице, невозможно положение
равновесии, когда ъерхиий. конец основания сегмента будет находиться на поверхности, воды
или выше се.
Не представит большого труда найти предельный угол, при котором тело будет
плавать, касаясь поверхности жидкости лишь одпой точкой основания; для этого
требуется определит!, угол наклона оси сегмента к поверхности жидкости при
плавании.
Пусть (рис. 9) ОЕВ будет парабола сечепия сегмента
3
:. оеыо ОЛ—-.,- Ь, точка С

представляет центр тяжести сегмента (ОС=Ь), расстояние СМ равно параметру р, а кривая
LDL" представляет параболу плавании; отрезок ED--
?OL^— а, а точка
центр
тяжести сегмента BEII ( FD=^— ); через точку F проходит парабола центров. В
положении равновесия CF должна быть нормалью к параболе центров, а параллельная ей
прямая LW — нормалью к параболе плавания (ЬВ — сечение поверхности жидкости).
Прямую LK — абсциссу точки латания — обозначим через х. Так как 1(JV = CM —
параметру р, то, обоуиачап угол KDM череп ф, можно написать:
. KN р
у
Но так же
*6Ф=-7Т
KD
Отсюда
Но GK=-.2LK, a
tg=cp
VK СК
Р
СК
LK^ON—KN—OL = OC \-FD—A'iV—OL= b-j-^-—p — 4 " — b~P~a>

592
КОММЕНТАРИИ
Таким: образом, окончательно
Эта формула дает леличину угла наклона оси, нри котором сегмент будет плавать
с основанием, находящимся впе Поверхности жидкости. Она одинаково применима и к
случаю, когда сегмент плавает, будучи погружен. ос1говаиием в жидкость; только в атом
случае под а нужно подразумевать две трети оси сегмента, находящегося над поверхностью
жидкости.
Предельная величина угла наклона оси к поверхности жидкости нри плавании сет-
ментп, когда основание его кнеабтея поверхности жидкости только в одной точке,
определится очень просто. Мы имеем:
Но мы видели выше (стр. 584), что наибольшая аеличина ординаты у,
соответствующая плаванию в указанном положении, рннма
Следовательно,
Ч Фсшч = .,,,? Г?=Г •
[12] В предложениях VIII и IX Архимед определяет асличипу тангенса угла
плавания.
Для возможности плавания в наклонном положении: необходимо неравенство
ft—а>/>, или а<6—p.
Плотность d плавающего тела по отношению к жидкости равяа ^ • но
d<
jb-p)* \2Ь-^Т>)
* "...cw
з
или, поскольку ось сегмепта ОЛ*=-^-Ь:
Необходимое построение на оси Архимед производит отдельно. Отрезок IiD--=OIV
представляет ось сегмента, К — центр его тижести, КР — параметр р, отрезок Т.Р=-
'Л 3
=-5- р *); тогда отрезок iJ:7'=OAr—jr-p представит линию, стоящую в числителе пра-
вой части неравенства для й. Так как плотность тела относительно жидкости d опреде-
ляетси формулой
и ВТ—^г ВР, то отсюда следует, что Ф<7?/>. Архимед полагает Ф равной отрезку Р*&\
это будет наше а.
3 3
*) Это нетрудно получить из елодующшс соображений. Ксли Лт=— ИР = -х IBD—ICD—Kl')=
2t 2t
3 OV Ч Ч
= -^@:\ j KP)=ON— -| КР, то TD=HD—ЬТ, естественно, Судет равняться ^ КР. Точку Г
проще получить, исходя из точки D, при помощи вычитания полуторного параметра КР.

О ПЛАВАЮЩИХ ТЕЛАХ
593.
Затем Архимед строшт угол ф по формуле
Ь V #ijr« £Ч« i)P —PV
1
{Ъ~р)-а '
После этого Архимеду остается лишь доказать, что лри таком угле наклона равно-
весис будет иметь место и что оно будет устойчивым. Он достигает обеих целей,
доказывая, что равновесие не может иметь места ни при больших, нгс при меньших .'шаченпях
угла наклона. Его доказательство сводится к тому, что центр тнжести Z погруженной
части не может лежать ни припое, ни левее перпендикуляра ГН, опущенного из центра
тяжести Г на касательную ИГ, параллельную поверхьости жидкости S2.
|13] Придложсыно IX является аналогичным предложениям. V и VII; в нем также
фигурирует предельная вачнчинп плотности
OA7i
3 V
(«»-40
ON* '
с тон только разницей, что теперь плотность плавающего тела должна .быть не меньше,
а больше этой величины:
ON' — (OJV—~p^j
*> oN% •
В соответствии с этим произойдут некоторые изменении в формулировке теоремы.
'Гак как теперь плотность плавающего тепа иредполагаетен равной
~" С40" '
cw*
то иен», что Ф представляет, кап и выпгс, длину а, соответствующую двум третям оси
сегмента, выступающего над поверхностью жидкости. Если вести рассуяздения
применительно и этому сегменту, то псе доказательство будет развиваться аналогично
доказательству предложении VIII.
Ц4 J Обширное предложение X рассматривает положения равновесия при
4
параметре р, меньшем j= оси сегмента,— значении, при котором еще возможно илава-
ч^. ' •• • i 1"
ние с. осношшиси, касающимся иоверхпости жидкости я одной точке. В этом случаи
в зависимости от плотности плавающего тела возможна следующие 1несть положении
равновесия, обозначенных в пашам переводе Архимеда цифрами:
A) Ось сеглситн стоит вертикально.
B) Ось сегмента наклонна; основание пне поверхности жидкости.
C) То же; основание ние поверхности жидкости, касается последней в одной точке.
D) То же, оспованис рассекается поверхностью жидкости.
E) То же; основание вне жидкости к касается поверхности иоследней п одной точке:
(В) То Ж1>; основание целиком пне жидкости.
[15] Для понимания дальнейшего важно представить себе физический смысл обо-
значений рис. 22 текста (стр. 348). Точка К представляет центр тяжести сегмента АОВЛ
(ЫК=2КД); прямая КТ, равная ^ БД, представляет наибольшую величину параметра р.
Если положить ВА — 15, ЛК=5 и КТ=4, то ТВ будет равна С; иными словами,
ВТ—-V-BA- Точки £ получается при помощи построения В2 —-|г- П1'; стрелок 2Д=-
5 ~
3 3
= ВД—В2= — (])К—BF) = -^-KP или полуторному параметру р. Таким образом, В£
з [4 <*-/•> У —.
представляет величину -у (I -р), входящую в выражение , ..—r-j—— ; если отношение
D0'
38 Архинед

594 • КОММЕНТАРИИ
плотностей сегмента и жч^остп больше этого значения, то возможно плавание
сегмента п вертикальном положении (случай 1). Параболы Л ЙА и AJSI представляют нскоторуш
аналогию с современаыми параболами и лапания (сечений) и центров; однако не нужно
забывать, что точна А предполагается лежащей на поверхности жидкости И проведенньи-
через псе прямые ЛЛ, АХ и другие представляют основания сегментов, об?,емм которых,
будучи заполнены жидкостью, могут уравновесить нес плаиающего сегмента при ра:>-
Л|1чпых величинах отношений плотностей сегмента и жидкости.
Так как параметр р — КР меньше К'Г, то проведенная черен Р горизонталь
пересечет параболу центров в двух точках Г и Г; проведенные через itux вертикали
определяют в пересечении с параболой плавании точки Н it Ф, а с параболой А ПОЛ точки О
и II. Прямые АХ и ЛФ (последняя на рис. 22 но проведена) определят соответствующие
сечения сегмента поверхностью жидкости; точки С.) и II будут вершинами погруженных
сегментов АОХ и ПАФ, а проведенные п них касательные ОС н UV определят соот-
ветстиующие равновесию углы наклона (случая 3 и 5).
Идея определения положепий равновесии сегмента очень проста: отношение (/
плотностей сегмента и жидкости Архимед выражает в виде квадрата отношения некоторой
нркмой У к оси сегмента ВЛ н определенную таким образом прямую вставляет между
параболами ЛПОЛ и ЛОЛ. ГСслн 1г" будет больше НБ, то, согласно теореме IV, сегметп
будет плавать и вертикальном положении (случай 1); если Т равняется ОГ или ПФ, то
сегмент будет плавать, имен одну точку (Л) на поверхности жидкости (случаи 3 и 5).
Остальные три случая будут соответствовать таким значениям Y: . .>
мучай 2: В2>Ч'>ОГ,
случай 4: ОГ > V > ПФ,
случай Ч: ПФ>¥.
Доказательство во всох случаях производится обычным для Архимеда методом — неси-
дованисм действия приложенных к сегменту сил.
1И>] Текст Лрхимода для последних трех случае* не явяястш вполне похрапи»
шимсн. Прежде всего ато отражается па порядке изложения; после 3-го случая
разбирается не 4-й, а С-й; кроме того, не вес обстоит в порядке и па чертежах. Тик па рис. 28
точка Г, а с ней и вся прямая MX, должны быть передвинуты так, чтоби Г попала в ш*-
ресичение примой Е\> с параболой центров. Равным образом щшмая N0 должпа
быть сдвинута влево так, чтобы она иротнла через точку пересечения прямой ЕР с
параболой цонтроп; тогда она будет соответствовать прямой ИФ рис. 22 и
рассматриваемая прямая Ш окажется левей ПФ. В таком случае угол Ф рис. 28 соответствует
углу V рис. 22.
Доказательство Архимеда сводится к тому, что теперь угол Q оси сегмента с
поверхностью жидкости будет меньше предельного угла V рис, 22.
Рис. 28 относится и к изложению случаи 5, где встречается та же прямая 6N,
соответствующая ПФ рис. 22.
{17] Последним разбирается случай Л, соответствующий такому положению
плавающего тела, при котором основание сегмента разрешается поверхностью жидкости. Дли
того чтоби ;ito имело место, необходимо, чтобы плотность плавающего тела была болыш.'
отпоптсиия (ФП : ВД)*2, но меньше чем @=-: 13ЛJ, если пользоваться обозначениями
рис. 22 текста. И таком случае между параболами АвД и ABA придется-вставлять
прямую, меньшую OS, но большую чем ИФ. Доказательство Архимеда сводится к тому,
что сегмент tic может находиться в равновесии ни тогда, когда его основание находится
вне жидкости (рас. 32 текста), пи когда его основание только в одной точке касается
поверхности жидкости (рис. 33), но должен наклониться еще более так, что угол его оси
с горизонтом будет меньше предельного угла q рис. 22.
A8] В зависимости от плотности плавающего тела Архимед устанавливает две
области, в которых возможно плавание тела с основанием, находящимся вне жидкости.
Физически объяснить появление зтих областей можно таким образом.
Начнем со случая, когда плотность тела, или, лучше сказать, наша величина а,
3 ..
или -т,- а — длина осп сегмента иогружепнон части тела, будет равна пулю; тогда тело
будет просто лежать на поверхности жидкости, причем ось его будет образовывать
с горизонтом'угол (J-, тангенс которого мы получим, положив а—О в общей формуле
Если мы будем увеличивать плотность тела, или величину а, то тело начнет
погружаться в жи;р;ость и одновременно увеличивать угол наклепа своей оси с горизонтом.'.
В первую очередь увеличение объема погруженной пасти пойдет за счет погружения
сегмента и приближении поверхности жидкости к нижнему углу основании; ото будет про-

О ПЛАВАЮЩИХ ТЕЛАХ
.185
исходить до тех пор пока угол Ф, определяемый но лышспривсденпой формул!1, но
сделается равным минимяльпому углу q>rajn, который удовлетворяет формуле
наметим, что этот угол тоже возрастает к увеличением а. Дальнейшее увеличение
плотности тела повлечет за собой увеличение; затоплении осиоиания а увеличите угла q-.
Затопление основания не будет продолжиться, беспредельно, по после достижении некото-
|ш максимальной величины будет уменьшаться вследствие унеличинш угла наклона
оси до тех пор, пока нижний угол оснолания не покажете» нн поверхности жидкости;
■ после итого увеличение об'1.1'ма погружен ной части будет происходить исключительно но
счет увеличения угла наклона оси ■ -мм получим иторую область плавания тела с
основанием вне поверхности жидкости. Это будет продолжиться до тех пор, нокн а не
сделается равным h-—p\ в :>тот момент тело станет отнеси о; при дальнейшем увеличении а тело'
будет просто погружаться п жидкость, прячем ось остается псе и рем и вертикальной.
Когда а сравняется с Ь, то есть плотность теля сделается равной плотности жидкости,
то плоскость основания опить совпадет с поверхностью жидкости.
После предложения X в переводе Мербоке стоит: «Arehimcilis do iri»i<I<?TitibiiH in
humido liber sccundus explicit»— «Кончается вторая книга Архимеда о тел их, пла
ноющих п жидкости». Также па этом кончается греческий текст Константинопольского-
палимпсеста.
Мы ожидали бы, что после предложения X последует аналогичный разбнр
положений равновесия при плавании сегмента с полностью погруженным основанием, как ото
сделано п предложениях III, V, VIT, IX сохранившегося текста. Это обстонтельстло,
а также и необычный характер изложения предложении X, по существу объединяющего
минимум нить самостоятельных теорем, позволяет думать, что рассматриваемое прг>-
изведенпе Архимеда не было им закончено и, может быть, является самым последним
его сочинением. Оно представляет высшую точку -пиши развития, которая началечеь
п «Коноидах и сфероидах» и продолжалась в «Эфоде». 11 трактате «О плаиающпх телах»
Архимед далеко обогнал свою цпоху. Об этом свидетельствует полное отсутствие и
сохранившейся античной литературе сведении об этом сочинении Архимеда, если не считать
короткого упоминания во введении и восьмой книге «Математического собрания» Наина
Алексаггдрийского, где механик Карп Лптиохийскнй говорит о иен как о
«математической игрушке». По лучше обстояло дело и йо время наивысшего развития культуры
ислама, как можно видеть h:i сохранившегося арабского изложении трактата Архимеда,
которое мы приводим ниже.
К II и г п Л р х и м е д и о т я ж е с т и и л с г к о с т и
Некоторые тела и жидкости тяжелее других. О теле говорят, что
оно тяжелой (другого) тела, или о жидкости говорят, что она тяжелее
другой жидкости, или же о теле говорят, что опо тяжелее жидкости,
если, когда берут их количества одинакового объема, а латем навешивают,
то одно оканынается тяжелее другого (то ость вес одного больше леса
другого). Ксли их пес одинаков, то не говорят, что одно из них тяжелее
другого. То, о чем говорят, что оно тяжелее,— большее по весу.
Мы полагаем, что природа жидкости такова,, что се смежные
частицы гладкие; поэтому то, что давит больше, вытесняет то, что давит
меньше, fla всякую частицу жидкости дннпт то, что находится
вертикально над пей, если только жидкость не заперта к чем-нибудь, чти
заставляет ее частицы давить на другие предметы. Всякая стоптал
жидкость не движется и се форна — форма тара.
Если пскоторое тело рашю по весу некоторой жидкости и
бросить тело и эту жидкость, то оно погрузите и в нее только до тех пор,
пока его поверхность по сравняется с поверхностью жидкости. Нсли
же некоторое тело легче некоторой жидкости и бросить тело в эту
жидкость, то опо не погрузится в нее целиком и часть его выступит над
поверхностью жидкости.
38*

596
КОММЕНТАРИИ
Если некоторое тело легче некоторой жидкости и бросить его в эту
жидкость, так что погрузится только часть его, и если «зять некоторое
количество жидкости, рашше по объему той части (тела), которая
погружена в нее, то оказывается, что вес итого количества жидкости равен
весу этого тела.
Если некоторое тело легче шжоторой жидкости и утопить его в этой
жидкости, то оно будет подниматься с силой, раиной силе избытка веса
количества жидкости, рапного по объему этому телу, над весом этого
тела.
Если некоторое тело тяжелее некоторой жидкости и бросить его
п эту жидкость, то его лес в жидкости равен избытку веса тела над
весом количества жидкости, равного по объему этому телу.
Если тело легче жидкости и имеет форму сегмента шарм и бросить
тело в эту жидкость, то оно всплывет, причем его осноиашш ас
соприкоснется с жидкостью и тело будет стоять прямо, так что ось сегмента
круга будет вертикальной, а если ее наклонить, то после
соприкосновения основания (сегмента тара) с жидкостью ось не останется наклон-
пой, а напротив, возвратится к прямому положению.
Если некоторое тело легче некоторой жидкости и бросить тело
в эту жидкость, то лес этого тела будет относиться к весу количества
жидкости, равного но объему этому телу, как лес части этого тела,
погруженной в жидкость, к весу всего этого тела.
Ннига Архимеда окончепа*).
Манускрипт дает изложение первой книги «О плавающих телах» вместе с первым
предложением второй книги. Весь конец последней, относящийся к сегменту параболоида
вр:нцэиия, выпущен; удиилятьси этому ие приходится, поскольку «Коноиды» остались
арабам иеизвеспгции.
В Западной ГСврэпс трактат «О плавающих телах» пошшлся в XIII леке в переводе
Вильгельма I» Мероеке, использованием также п изданиях Луки Гаврика и Тартальп.
Вопрос, о том, насколько опи понимали это произведении, лучше оетанить открытым.
Иаарпае ато иотшяпаа «ш встречаем во второй по.-гоиигге XVI пика, у Фодериго Колда/ш-
дяпо {150Э —1575) п ого латинском издании Архимеда, где он сделал попытку
восстановить места, недостающее в переводе МерЗске; как стало видно в дальнейшем,
реставрации Коммапднпо оказалась правильной. Ионное понимание мы встречаем у Христиана
Гмяпмса, одно из юношеских ироязпвдечшй. которого, уиадгашгее «вот rtxif.rw и конце
XIX века п национальном издании его сочинений, было посшищеио определению
наложении рапноиссия плавающего параллелепипеда. Продолжателями Гюйгспса в XVIII
веке оказались авторы теории корабля Буге к Эйлер, а и XIX — Дюпон во Франции и
профессор Московского университета А. Ю. Давидов, давшее полпоч гсоритяческое рете-
пие рассматриваемого вопроса. Мы уже имели возможность видеть, насколько близко
оказалась современная теории к методике Архимеда при определении плавания сегмента
параболоида
Было бы, однако, неправильным доводить модернизацию до нюллого
отождествления обеих методик — Архимеда и современной. Основное различие между математикой
Архимеда и современной" заключается в том, что мы стремимся получить наиболее общее
решение вопроса, псе же нроялаедсния Архимеда представляют решении частных задач.
Правда, эти решения настолько гепиалмш, что Архимеда можно назвать
родоначальником классической математики XVII и XVIII веков, но том пе менее попыток создания
общих теорий мы у Архимеда почти не замечаем. Так п трактате «О плавающих телах»
обе задачи на равновесие сегментов шара и параболоида решаются совершении
независимыми друг от Друга методами. В предложении II второй книги Архимед близко
подходит те попитию метацентра (но существу, ему осталось сделать только предельный
переход), по примененный им физический метод определения устойчивости полностью
исключает мысль о возможности его применения. Одна из парабол Архимеда очень
близка к современной поверхности сечений; однако возможность использования Архи-
*) Книга Архимеда о тияеесги и легкости (Макала ли Аршимитдас Фи-л-сикп ва-л-*н() фа)
перевСЕСГгя с рукописи 2E7/4 (листы 22 об.—23) Парижской Напионалытой библиотеки. Микрофильм
этой рукописи был прислан r-люй И. Мейер-Шагял. Псрсапд произведен В. А. Роаснфельдим при
консультации ДГ. А. Саяьс.

О ПЛАВАЮЩИХ ТВЛАХ
597
мидом настоящей поверхности сечений является исключенной хоти бы ио той причине,
что Архимед не был в состоянии построить ее полностью (в случаях плавания с полу-
аптоплеппым основанием), а для греческой математики существующими считались только-
то обралы, которые так или иначе могли быть построены.
Вышесказанное яплястся справедлииым пе только для рассматриваемого
произведения, в посланиях к Досифею Архимед занимался задачами, которые в настоящее время
решаются прет помощи интегрального исчисления, ио тем lie менее общего понятия об
иптеграло у пего не было; определение площадей сегмента параболы и объема
параболоида л ращения, с пашей точки прения, могут быть сведены к вычислению одного и того
зие интеграла, но Архимед решает их совйршенл» пвиятешлымя друг от друга методами.
Архимеду два раза пришлось решать задачу на максимум л минимум — л предложениях
IV и IX второй кпиги«Ошаре и цилиндре» и в предложении VI второй книги «О
плавающих телах*, но примененные им методы в сохраненном Квтокием тсксти решения и при
яахождепии предельпой величины отношении параметра параболы сечения сегмента к его
оси («О плаваюших телах», 11,6) не имеют друг с другом ничего общего. И трактате «О спи-
рнлих» Архимед определяет касатсльпую методом, который, по существу, одинаков
с роберналевским методом сложении скоростей, по только у Гобервалл метод мог быть
применен ко многим кривым, а у Архимеда только к специально построенной кривой.
Однако псо :ito показывает только, что Архимед, несмотря на всю слою гениальность,
псе «ко был греческим математиком, а разница ме;клу греческой и сопркмепной
математикой может быть охарактеризована следующим замечанием. На жалобы цари Птолемея
по поводу трудности геометрии Евклид отличал, что в геометрии царской дороги не
существует. После открытки анализа бесконечно малых Лейбниц писал:
*Мы открыли ту царскую дорогу, на отг.утстпие которой жаловался Птолемей».

ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ»
В комментарии ко второй книго «О плавающих телах» ми указали на
незаконченность отого произведения Архимеда. .В связи с этим не может не представить интереса
вопрос, что могло бы стоять в ненаписанной части книги.
В конце предложения X Архимед рассматривает вопрос о положении равновесия
А
сегмента параболоида, когда параметр р меньше т-т оси сегмента. В зависимости от
плотности плавающего тела Архимед устанавливает две области, в кото])Ых возможно
плавание сегмента с: основанием, находящимся
вне жидкости, а именно когда плотность тела д
будет или близка к нулю, или же почти ралпа
плотности жидкости. В качество меры
плотности мы можем лэнть величину оси
погруженной части сегмента, которую мы обозначали
через — а. Определенно предельных значении а
мм можем произвести по методу Архимеда.
Пусть па приложенном рисунке ABL
будет парабола, получающейся и сечении тела
плоскостью, проходящей через ось,
парабола AUCI представляет параболу центров, а
парабол» AVQD соответствует пашей параболе
плавания. Центр тяжести" сегмента будет в
I
точке Л' (KD— -л- ПК); итрозок КП равен па-
раметру р параболы ABL, a ID ('.оставляет
две пятых AL.
Черен И проведем параллельную AL
прямую до пересечения в С и U с параболой
AI; отрезки Си и UJi будут ординатами, соответствующими плаванию с нижним углом
основания ни поверхности жидкости, a OQ и PV дадут пап и -^- о—длины оси погружен-
пых частей сегмента, соответствующих искомым предельным положениям. Значения
отношении плотности тела к жидкости для этих пшюжоний мы получим, воаведя в квад-
OQ PV
рат отпошсипя угу", и -^р -
Возьмем начало координат в точке В, пусть ось абсцисс пойдет по ]SD, а ось
ординат перпендикулярно к ПТУ влево. Уравнение параболы ABL будет:
У
Уравнение параболы АС1 будет:
( xj~t АиУ
ADS
3 Am /■
5 JSD
Наконец, уравнение последней параболы AQ1) будет:
__ 1 АР2 ( 1
/
вп\
f 1 ^\2
2 ВО
С* 4*0

<J30 ПРИЛОЖЕНИЯ
2
Расстояние Bii—x будет равно — ЛО—р- Подставляя ато выражение в уравнение
параболы ACI, получаем:
( 2 лп\- 3 ЛТ>* ( 4 ип N
что может сыть приведено к виду
откуда получаются корпи:
"--тЧ^/^т&У
Таким образом,
У Архимеда, тангенсы соответствующих предельных углов наклона будут:
_р 5^ _р 1
VR 2AD f iAl^^
1 т К * 4 ДО
СЛ 2 AD
1 К 4 Я£>
Переходим к определению предельных величин OQ ы PF погруженных осей. Дли
этого нам нужно найти рамюсть абсцисс парабол АВЬ и AQD, соответствующих
определенным ординатам yt и //.>.
Уравнения этих iiapaoo.i будут: "• — •
Уипожим первое уравнение ла два и вычтем из него второе, помпя, что ординаты у
в обоих уравнениях одинаковы, но абсциссы различны. Если обозначим абсциссу
параболы AQD через г3, а абсциссу параболы AJ.iL через хи то будем иметь:
Л1У*
l\y~i;AD) -у*^ш1х-~х,)—г
Остюда определнтсн нужный нам отрезок &—х2—хх
. BD Г,./ 1 ...4.2 1 ,BD BD < . ... „„ Л£«1 , Ш)
Если вместо ;/ вставим найденную величину
это после очевидных упрощений получим:

ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ»
631
Таким образом мы приходим к следующему выводу:
Iй. Если плотность тела по отношению к жидкости меняется в пределах от 0 до
/0,52—0,60-ijj-—0,48 1/ i—-т-JiiT ) > 'f0 тело плавает с основанием, находящимся пад
ЖИДКОСТЬЮ.
2°. Если плотность тела лежит в пределах
от @,52-0,60^-0,48 j/i- $ {дУ ДО («Ш-ОДЮ^-^в /l-ЭД'.
то голо будет плавать с полузатопленным основанием.
3е. Если нлогпость тела мсппется в пределах
■ от (о,52-0,60^0,48/^^)алоA.-|йОг'
т<1 тело будет плавать и наклонном положении, имея основание пад поверхностью
жидкости.
4°. Если плотность тела меняется в пределах от I 1 --jr-/>: ) до 1, то тело будет
'^ Z ISsJ J
шшцать, имея ось вертикальной.
Для случаи плавания сегмента г. погруженным основанием надо вместо
погруженной части рассматривать часть сегмента, находящуюся ипс поиерхыости жидкости и
заменить относительную плотность тела, ве дополнением до единицы. В таком случае мы
получили бы предложении, аналогичные 3, 5, 7 и 9 сохранившейся части второй книги. Нет
никакого сомшщин, что Архимед был и состопини сделать это; мм же ограничимся лишь
формулировкой окончательных реаультатоп.
1". Если плотнеет!, т(ша изменяется от 1 до
1 ..-@,52-0,60 £-.й/,8у^£)\
то сегмент плавает и наклонном положении, имен основание полностью под
поверхностью жидкости.
2°. Если плотность тела меняется п пределах
от .1...@)ГЙ-.О,60^-0,48 /l-^/^У
до 1 -((,,52-0,60^-;-0,48 /l-.^)\
то сегмент плавает с полузатопленным основанием.
3°. Если плотность тела меняется в пределах
„ 1-@,Г>2-0,60^ !-0,48 /l457&)S
«•-f-lro)"-
то сегмент плавает в пиклонпом положении с основанием, находящимся полпостыо под
поперхиостыо жадности.
4". Накопоц, если плотность тела моияетси и пределах от 1— ( 1—v" Туп ) д0
ну-т, то сегмент плавает с вертикальной осью, имея основание ниже поверхности
жидкости.
Соответствующие угли наклона могут быть определены по той жо формуле
если только вместо а брать величину оси сегмента, находящейся вне поверхности жидкости^

632
ПРИЛОЖЕНИЯ
N 2
Окончательные результаты исследования Архимеда могут быть сформулированы так:
3
1°. Если ось сегмента не превышает -^- параметра р, то сегмент может плавать
с вертикальной осью, имея основание безразлично над или под поверхностью жидкости.
Плапанис сегмепта в наклонном положении невозможно.
I? 15
2°. Если длина оси сегмента заключается в пределах от -!;- р до -г р, то плавание
в натотоппом положении становится возможным, но основание сегмента должно
быть или над, или под поверхностью жидкости. Продельными значениями плотности
являются
гт Р 2 р 4
При yyri="T эти пР°ДелЬ1 равны пулю и единице; если -Sr)f=TF • т0 мы получаем
•к. 2 BDJ ~ 23 * ^Х 2JWJ~25'
р 2 л 4
во всем промежутке от ~-=-о-До у37>~Т? ПСРВЫИ предел будет пиже второго. Таким
образом, мы замечаем следующие три области изменения плотности тела.
C р N
1 :у -77^, )
можно или плавание тела в вертикальном положении с погруженным основанием, или же
в наклонном положении с основанием вне жидкости.
б) Если плотность тела заключается в пределах от М — — -?= J до 1—( 1—Т"вп- '
то возможно плавание только в вертикальном положении, причем основание может бег-
различно находиться иад и под поверхностью жидкости.
в) Если плотность тела заключается в пределах от 1 — [1 —~ -бт. ) До ^ > то
возможно плавание тела или в вертикальном положении с основанием вис жидкости, или
в пакленном положении с основанием внутри жидкости.
3°. Тецерь рассмотрим случай, когда отношение ■—- будет больше -.,.■. В таком
случае возможно совпадение обеих предельных величин плотности; вто будет, если
V. 2 DDJ У 2 BDJ '
2 BD V 2
Отсюда
1
что можпо нопожить равным примерно — .
"* 15 3*
Таким обра:.юм, если длина оси сегмента изменяется в пределах от -j р — 3-^-р
и приблизительно до Ьр, то мы будем иметь по-прежнему три области: f
а) При небольших плотностях плавание возможно в вертикальном положении
основанием вниз или в наклонном положении основанием вверх, причем последнее может
быть или целиком вне поверхности жидкости, или отчасти.
6} При плотностях тела, несколько отличающихся в ту или другую сторону от
половины, пояможно ллапание только в вертикальном ло-тожении.
в) При плотностях, приближающихся к единице, возможно плавание в вертикаль-
пом положении оснопапием вверх или в наклонном положении основанием вниз, причем
последнее или целиком, или отчисти находится ниже поверхности жидкости.
Если BD более 5у>, то средняя область пропадает совсем, а две крайние начинают
отчасги налагаться одна на другую.
или